code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# +
# Some common packages used throughout the notebook
# %load_ext autoreload
# %autoreload 2
# Import the NumPy module
import numpy as np
# Convient for outputting dictionaries
import json
import matplotlib.pyplot as plt
# %matplotlib inline
# +
from skimage import data, color, exposure
from satsense import SatelliteImage
from satsense.generators import CellGenerator
# Supported image formats include RGB, Quickbird and Worldview
from satsense import RGB, QUICKBIRD, WORLDVIEW2
# URI to the image
image = SatelliteImage.load_from_file('/home/bweel/Documents/projects/dynaslum/data/satelite/056239125010_01/056239125010_01_P001_MUL/08NOV02054348-M2AS_R1C1-056239125010_01_P001.TIF',
QUICKBIRD)
print(image.shape)
# +
fig, ax1 = plt.subplots(1, 1, figsize=(18, 8), sharex=True, sharey=True)
generator = CellGenerator(image, (25, 25), length=(10, 20))
cell = generator.get(61)
ax1.axis('off')
ax1.imshow(cell.gray_ubyte, cmap=plt.cm.gray)
ax1.set_title('Input image')
ax1.set_adjustable('box-forced')
# +
from satsense.features import Pantex
w = [(25, 25), (50, 50), (100, 100)]
print(w)
pantex = Pantex(windows=w)
p = pantex(cell)
print(p.shape)
print(p)
# +
from sats
fig, ax1 = plt.subplots(1, 1, figsize=(18, 8), sharex=True, sharey=True)
ax1.axis('off')
ax1.imshow(cell.gray_ubyte, cmap=plt.cm.gray)
ax1.set_title('Input image')
ax1.set_adjustable('box-forced')
|
notebooks/demo_notebooks/GLCM - Pantex.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import tensorflow as tf
from sklearn.utils import shuffle
import re
import time
import collections
import os
def build_dataset(words, n_words, atleast=1):
count = [['PAD', 0], ['GO', 1], ['EOS', 2], ['UNK', 3]]
counter = collections.Counter(words).most_common(n_words)
counter = [i for i in counter if i[1] >= atleast]
count.extend(counter)
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
index = dictionary.get(word, 0)
if index == 0:
unk_count += 1
data.append(index)
count[0][1] = unk_count
reversed_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reversed_dictionary
with open('english-train', 'r') as fopen:
text_from = fopen.read().lower().split('\n')[:-1]
with open('vietnam-train', 'r') as fopen:
text_to = fopen.read().lower().split('\n')[:-1]
print('len from: %d, len to: %d'%(len(text_from), len(text_to)))
concat_from = ' '.join(text_from).split()
vocabulary_size_from = len(list(set(concat_from)))
data_from, count_from, dictionary_from, rev_dictionary_from = build_dataset(concat_from, vocabulary_size_from)
print('vocab from size: %d'%(vocabulary_size_from))
print('Most common words', count_from[4:10])
print('Sample data', data_from[:10], [rev_dictionary_from[i] for i in data_from[:10]])
concat_to = ' '.join(text_to).split()
vocabulary_size_to = len(list(set(concat_to)))
data_to, count_to, dictionary_to, rev_dictionary_to = build_dataset(concat_to, vocabulary_size_to)
print('vocab to size: %d'%(vocabulary_size_to))
print('Most common words', count_to[4:10])
print('Sample data', data_to[:10], [rev_dictionary_to[i] for i in data_to[:10]])
GO = dictionary_from['GO']
PAD = dictionary_from['PAD']
EOS = dictionary_from['EOS']
UNK = dictionary_from['UNK']
for i in range(len(text_to)):
text_to[i] += ' EOS'
class Chatbot:
def __init__(self, size_layer, num_layers, embedded_size,
from_dict_size, to_dict_size, learning_rate, batch_size):
def cells(reuse=False):
return tf.nn.rnn_cell.LSTMCell(size_layer,initializer=tf.orthogonal_initializer(),
reuse=reuse)
self.X = tf.placeholder(tf.int32, [None, None])
self.Y = tf.placeholder(tf.int32, [None, None])
self.X_seq_len = tf.placeholder(tf.int32, [None])
self.Y_seq_len = tf.placeholder(tf.int32, [None])
batch_size = tf.shape(self.X)[0]
encoder_embeddings = tf.Variable(tf.random_uniform([from_dict_size, embedded_size], -1, 1))
decoder_embeddings = tf.Variable(tf.random_uniform([to_dict_size, embedded_size], -1, 1))
encoder_embedded = tf.nn.embedding_lookup(encoder_embeddings, self.X)
main = tf.strided_slice(self.X, [0, 0], [batch_size, -1], [1, 1])
decoder_input = tf.concat([tf.fill([batch_size, 1], GO), main], 1)
decoder_embedded = tf.nn.embedding_lookup(encoder_embeddings, decoder_input)
attention_mechanism = tf.contrib.seq2seq.BahdanauAttention(num_units = size_layer,
memory = encoder_embedded)
rnn_cells = tf.contrib.seq2seq.AttentionWrapper(cell = tf.nn.rnn_cell.MultiRNNCell([cells() for _ in range(num_layers)]),
attention_mechanism = attention_mechanism,
attention_layer_size = size_layer)
_, last_state = tf.nn.dynamic_rnn(rnn_cells, encoder_embedded,
dtype = tf.float32)
last_state = tuple(last_state[0][-1] for _ in range(num_layers))
with tf.variable_scope("decoder"):
rnn_cells_dec = tf.nn.rnn_cell.MultiRNNCell([cells() for _ in range(num_layers)])
outputs, _ = tf.nn.dynamic_rnn(rnn_cells_dec, decoder_embedded,
initial_state = last_state,
dtype = tf.float32)
self.logits = tf.layers.dense(outputs,to_dict_size)
masks = tf.sequence_mask(self.Y_seq_len, tf.reduce_max(self.Y_seq_len), dtype=tf.float32)
self.cost = tf.contrib.seq2seq.sequence_loss(logits = self.logits,
targets = self.Y,
weights = masks)
self.optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(self.cost)
y_t = tf.argmax(self.logits,axis=2)
y_t = tf.cast(y_t, tf.int32)
self.prediction = tf.boolean_mask(y_t, masks)
mask_label = tf.boolean_mask(self.Y, masks)
correct_pred = tf.equal(self.prediction, mask_label)
correct_index = tf.cast(correct_pred, tf.float32)
self.accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
size_layer = 128
num_layers = 2
embedded_size = 128
learning_rate = 0.001
batch_size = 16
epoch = 20
tf.reset_default_graph()
sess = tf.InteractiveSession()
model = Chatbot(size_layer, num_layers, embedded_size, len(dictionary_from),
len(dictionary_to), learning_rate,batch_size)
sess.run(tf.global_variables_initializer())
def str_idx(corpus, dic):
X = []
for i in corpus:
ints = []
for k in i.split():
ints.append(dic.get(k,UNK))
X.append(ints)
return X
X = str_idx(text_from, dictionary_from)
Y = str_idx(text_to, dictionary_to)
# +
maxlen_question = max([len(x) for x in X]) * 2
maxlen_answer = max([len(y) for y in Y]) * 2
maxlen_question, maxlen_answer
# -
def pad_sentence_batch(sentence_batch, pad_int, maxlen):
padded_seqs = []
seq_lens = []
max_sentence_len = maxlen
for sentence in sentence_batch:
padded_seqs.append(sentence + [pad_int] * (max_sentence_len - len(sentence)))
seq_lens.append(maxlen)
return padded_seqs, seq_lens
for i in range(epoch):
total_loss, total_accuracy = 0, 0
X, Y = shuffle(X, Y)
for k in range(0, len(text_to), batch_size):
index = min(k + batch_size, len(text_to))
batch_x, seq_x = pad_sentence_batch(X[k: index], PAD, maxlen_answer)
batch_y, seq_y = pad_sentence_batch(Y[k: index], PAD, maxlen_answer)
predicted, accuracy, loss, _ = sess.run([tf.argmax(model.logits,2),
model.accuracy, model.cost, model.optimizer],
feed_dict={model.X:batch_x,
model.Y:batch_y,
model.X_seq_len:seq_x,
model.Y_seq_len:seq_y})
total_loss += loss
total_accuracy += accuracy
total_loss /= (len(text_to) / batch_size)
total_accuracy /= (len(text_to) / batch_size)
print('epoch: %d, avg loss: %f, avg accuracy: %f'%(i+1, total_loss, total_accuracy))
for i in range(len(batch_x)):
print('row %d'%(i+1))
print('QUESTION:',' '.join([rev_dictionary_from[n] for n in batch_x[i] if n not in [0,1,2,3]]))
print('REAL ANSWER:',' '.join([rev_dictionary_to[n] for n in batch_y[i] if n not in[0,1,2,3]]))
print('PREDICTED ANSWER:',' '.join([rev_dictionary_to[n] for n in predicted[i] if n not in[0,1,2,3]]),'\n')
|
neural-machine-translation/17.lstm-seq2seq-bahdanau.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Plotting with Seaborn
# + [markdown] slideshow={"slide_type": "slide"}
# ## What is seaborn
#
# * Seaborn is a statistical plotting library
# * Has build-in default styles
# * Designed to work nicely with pandas dataframes
# + [markdown] slideshow={"slide_type": "slide"}
# ## Installation
#
# If seaborn is not installed on your system, you need to install seaborn first with either:
# ```
# conda install seaborn
# ```
# or
# ```
# pip install seaborn
# ```
# + [markdown] slideshow={"slide_type": "slide"}
# ## Documentation
#
# Seaborn documentation available at [http://seaborn.pydata.org/examples/index.html](http://seaborn.pydata.org/examples/index.html)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Imports
#
# First we import seaborn and numpy
# + slideshow={"slide_type": "fragment"}
import seaborn as sns
import numpy as np
# %matplotlib inline
# + [markdown] slideshow={"slide_type": "slide"}
# ## Data
# Seaborn comes with built-in data sets!
# + slideshow={"slide_type": "fragment"}
tips = sns.load_dataset('tips')
tips.head()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Plot types
#
# In this lecture we will learn how to build following plots using seaborn:
#
# * distribution plots
# * categorical plots
# * matrix plots
# * regression plots
# + [markdown] slideshow={"slide_type": "slide"}
# ## Distribution Plots
#
# Let's discuss some plots that allow us to visualize the distribution of a data set. These plots are:
#
# * distplot
# * jointplot
# * pairplot
# * rugplot
# * kdeplot
# + [markdown] slideshow={"slide_type": "slide"}
# ## distplot
#
# The `distplot()` shows the distribution of a univariate (one variable) set of observations. It it is mixture of matplotlib `hist` function (with automatic
# calculation of a good default bin size) with the seaborn `kdeplot` function (`kdeplot` plots a kernel density estimate, which is an estimation of the probability density function of a random variable that produced the data sample).
# + slideshow={"slide_type": "fragment"}
sns.distplot(tips['total_bill'])
# Safe to ignore warnings
# + [markdown] slideshow={"slide_type": "slide"}
# To remove the kde layer and just have the histogram use:
# + slideshow={"slide_type": "fragment"}
sns.distplot(tips['total_bill'],kde=False,bins=30)
# + [markdown] slideshow={"slide_type": "slide"}
# ## jointplot
#
# `jointplot()` allows you to basically match up two distplots for bivariate data. With your choice of what **kind** parameter to compare with:
# * `scatter`
# * `reg`
# * `resid`
# * `kde`
# * `hex`
# + slideshow={"slide_type": "slide"}
sns.jointplot(x='total_bill',y='tip',data=tips,kind='scatter')
# + slideshow={"slide_type": "slide"}
sns.jointplot(x='total_bill',y='tip',data=tips,kind='hex')
# + slideshow={"slide_type": "slide"}
sns.jointplot(x='total_bill',y='tip',data=tips,kind='reg')
# + [markdown] slideshow={"slide_type": "slide"}
# ## pairplot
#
# pairplot will plot pairwise relationships across an entire dataframe (for the numerical columns) and supports a color hue argument (for categorical columns).
# + slideshow={"slide_type": "slide"}
sns.pairplot(tips)
# + [markdown] slideshow={"slide_type": "slide"}
# `pairplot` function has `hue` argument that expects categorical attribute, so that each category is displayed in a different color, with colors palette defined by `palette` argument.
# + slideshow={"slide_type": "slide"}
sns.pairplot(tips, hue='sex', palette='coolwarm')
# -
sns.pairplot(tips, hue='day', palette='coolwarm')
# + [markdown] slideshow={"slide_type": "slide"}
# # Categorical Data Plots
#
# Now let's discuss using seaborn to plot categorical data! There are a few main plot types for this:
#
# * boxplot
# * barplot
# * countplot
#
# Let's go through examples of each!
# + slideshow={"slide_type": "slide"}
tips = sns.load_dataset('tips')
tips.head()
# + [markdown] slideshow={"slide_type": "slide"}
# ## barplot and countplot
#
# These very similar plots allow you to get aggregate data off a categorical feature in your data.
# + [markdown] slideshow={"slide_type": "slide"}
# A bar plot represents an estimate of central tendency for a numeric variable with the height of each rectangle and provides some indication of the uncertainty around that estimate using *error bars*. Bar plots include 0 in the quantitative axis range, and they are a good choice when 0 is a meaningful value for the quantitative variable, and you want to make comparisons against it.
#
# See [this](https://stackoverflow.com/questions/29481134/how-are-the-error-bands-in-seaborn-tsplot-calculated) discussion on StackOverflow to get a better insight into what error bars are.
# + slideshow={"slide_type": "slide"}
sns.barplot(x='sex', y='total_bill', data=tips)
# + [markdown] slideshow={"slide_type": "slide"}
# You can change the estimator object to your own function, that converts a vector to a scalar:
# + slideshow={"slide_type": "slide"}
sns.barplot(x='sex', y='total_bill', data=tips, estimator=np.std)
# + [markdown] slideshow={"slide_type": "slide"}
# ### countplot
#
# This is essentially the same as barplot except the estimator is explicitly counting the number of occurrences. Which is why we only pass the x value:
# -
sns.countplot(x='sex',data=tips)
# + [markdown] slideshow={"slide_type": "slide"}
# `sns.barplot(x='sex', y='total_bill', data=tips, estimator=np.count_nonzero)` will produce similar results, but without considering zero vaules for `y`.
# + slideshow={"slide_type": "fragment"}
sns.barplot(x='sex', y='total_bill', data=tips, estimator=np.count_nonzero, ci=95)
# + [markdown] slideshow={"slide_type": "slide"}
# ## boxplot
#
# boxplots and violinplots are used to shown the distribution of categorical data. A box plot (or box-and-whisker plot) shows the distribution of quantitative data in a way that facilitates comparisons between variables or across levels of a categorical variable. The box shows the quartiles of the dataset while the whiskers extend to show the rest of the distribution, except for points that are determined to be “outliers” using a method that is a function of the inter-quartile range.
# + slideshow={"slide_type": "fragment"}
sns.boxplot(x="day", y="total_bill", data=tips,palette='rainbow')
# -
sns.boxenplot(x="day", y="total_bill", data=tips,palette='rainbow')
# + slideshow={"slide_type": "slide"}
# Can do entire dataframe with orient='h'
sns.boxplot(data=tips,palette='rainbow',orient='h')
# + slideshow={"slide_type": "slide"}
sns.boxplot(x="day", y="total_bill", hue="smoker",data=tips, palette="coolwarm")
# + [markdown] slideshow={"slide_type": "slide"}
# # Matrix Plots
#
# Matrix plots allow you to plot data as color-encoded matrices and can also be used to indicate clusters within the data (later in the machine learning section we will learn how to formally cluster data).
#
# Let's begin by exploring seaborn's heatmap and clustermap:
# + slideshow={"slide_type": "slide"}
flights = sns.load_dataset('flights')
tips = sns.load_dataset('tips')
# + slideshow={"slide_type": "slide"}
tips.head()
# + slideshow={"slide_type": "slide"}
flights.head()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Heatmap
#
# In order for a heatmap to work properly, your data should already be in a matrix form, the sns.heatmap function basically just colors it in for you. For example:
# + slideshow={"slide_type": "slide"}
# Matrix form for correlation data
tips.corr()
# -
sns.heatmap(tips.corr(),cmap='coolwarm')
# + slideshow={"slide_type": "slide"}
sns.heatmap(tips.corr(),cmap='coolwarm',annot=True)
# + [markdown] slideshow={"slide_type": "slide"}
# Or for the flights data:
# + slideshow={"slide_type": "slide"}
flights.pivot_table(values='passengers',index='month',columns='year')
# + slideshow={"slide_type": "slide"}
pvflights = flights.pivot_table(values='passengers',index='month',columns='year')
sns.heatmap(pvflights)
# + slideshow={"slide_type": "slide"}
sns.heatmap(pvflights,cmap='coolwarm',linecolor='white',linewidths=1)
# + [markdown] slideshow={"slide_type": "slide"}
# # Regression Plots
#
# Seaborn has many built-in capabilities for regression plots, however we won't really discuss regression until the machine learning section of the course, so we will only cover the **lmplot()** function for now.
#
# **lmplot** allows you to display linear models, but it also conveniently allows you to split up those plots based off of features, as well as coloring the hue based off of features.
#
# Let's explore how this works:
# + slideshow={"slide_type": "slide"}
tips.head()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Regression plots
# + [markdown] slideshow={"slide_type": "slide"}
# There are two main functions in seaborn that are used to visualize a linear relationship as determined through regression: [`regplot()`](https://seaborn.pydata.org/generated/seaborn.regplot.html#seaborn.regplot) and [`lmplot()`](https://seaborn.pydata.org/generated/seaborn.lmplot.html#seaborn.lmplot).
#
# Both function are closely related, and share much of their core functionality.
#
# Very nice introduction to regression plots can be found [here](https://seaborn.pydata.org/tutorial/regression.html#regression-tutorial).
# + [markdown] slideshow={"slide_type": "slide"}
# Both [`regplot()`](https://seaborn.pydata.org/generated/seaborn.regplot.html#seaborn.regplot) and [`lmplot()`](https://seaborn.pydata.org/generated/seaborn.lmplot.html#seaborn.lmplot) draw a scatterplot of two variables, `x` and `y`, and then fit the regression model `y ~ x` and plot the resulting regression line and a 95% confidence interval for that regression:
# + slideshow={"slide_type": "slide"}
sns.regplot(x='total_bill',y='tip',data=tips)
# + slideshow={"slide_type": "slide"}
sns.lmplot(x='total_bill',y='tip',data=tips)
# + [markdown] slideshow={"slide_type": "slide"}
# The main difference between `regplot()` and `lmplot()` is that `regplot()` accepts the `x` and `y` variables in a variety of formats including simple numpy arrays, pandas Series objects, or as references to variables in a pandas DataFrame object passed to data. In contrast, lmplot() has data as a required parameter and the x and y variables must be specified as strings.
# + slideshow={"slide_type": "slide"}
sns.regplot(x=tips['total_bill'],y=tips['tip'])
# + [markdown] slideshow={"slide_type": "slide"}
# Other than this input flexibility, `regplot()` possesses a subset of `lmplot()`’s features, so we will demonstrate them using the latter.
# + [markdown] slideshow={"slide_type": "slide"}
# ### Conditioning regression plots on other variables
#
# `lmplot()` provides an easy interface to show a linear regression plots that allow exploring interactions with up to three additional categorical variables.
# + [markdown] slideshow={"slide_type": "slide"}
# `hue` parameter allows to add a third dimensions representing a categorical value and presenting it using colors or markers
# + slideshow={"slide_type": "fragment"}
sns.lmplot(x='total_bill',y='tip',data=tips,hue='sex', markers=['o', '+'])
# + [markdown] slideshow={"slide_type": "slide"}
# ### Using a Grid
#
# We can add oen or two additional variables through columns and rows with the use of a grid. Just indicate this with the col or row arguments:
# + slideshow={"slide_type": "fragment"}
sns.lmplot(x='total_bill',y='tip',data=tips,col='sex')
# + slideshow={"slide_type": "slide"}
sns.lmplot(x="total_bill", y="tip", row="smoker", col="time",data=tips, size=4)
# + slideshow={"slide_type": "slide"}
sns.lmplot(x='total_bill',y='tip',data=tips,col='day',row='smoker',hue='sex',palette='coolwarm')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Aspect and Size
#
# Seaborn figures can have their size and aspect ratio adjusted with the **size** and **aspect** parameters:
# + slideshow={"slide_type": "slide"}
sns.lmplot(x='total_bill',y='tip',data=tips,col='day',row='smoker',hue='sex',
palette='coolwarm', aspect=1.5,size=8)
# -
|
plotting with seaborn/.ipynb_checkpoints/1_seaborn_plots-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Nirzu97/pyprobml/blob/multi-gpu-training-torch/notebooks/multi_gpu_training_torch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="UeG2yP57tJBX"
# #Train a CNN on multiple GPUs using data parallelism.
#
# Based on sec 12.5 of http://d2l.ai/chapter_computational-performance/multiple-gpus.html.
#
# Note: in colab, we only have access to 1 GPU, so the code below just simulates the effects of multiple GPUs, so it will not run faster. You may not see a speedup eveen on a machine which really does have multiple GPUs, because the model and data are too small. But the example should still illustrate the key ideas.
# + id="9_2hHiscs-cH"
import numpy as np
import matplotlib.pyplot as plt
import math
from IPython import display
import torch
import torchvision
from torch import nn
from torch.nn import functional as F
from torch.utils import data
from torchvision import transforms
import random
import os
import time
np.random.seed(seed=1)
torch.manual_seed(1)
# !mkdir figures # for saving plots
# + [markdown] id="ngd9TmIVuAN6"
# # Model
#
# We use a slightly modified version of the LeNet CNN.
# + id="EgrwcqORtJdL"
# Initialize model parameters
scale = 0.01
torch.random.manual_seed(0)
W1 = torch.randn(size=(20, 1, 3, 3)) * scale
b1 = torch.zeros(20)
W2 = torch.randn(size=(50, 20, 5, 5)) * scale
b2 = torch.zeros(50)
W3 = torch.randn(size=(800, 128)) * scale
b3 = torch.zeros(128)
W4 = torch.randn(size=(128, 10)) * scale
b4 = torch.zeros(10)
params = [W1, b1, W2, b2, W3, b3, W4, b4]
# Define the model
def lenet(X, params):
h1_conv = F.conv2d(input=X, weight=params[0], bias=params[1])
h1_activation = F.relu(h1_conv)
h1 = F.avg_pool2d(input=h1_activation, kernel_size=(2, 2), stride=(2, 2))
h2_conv = F.conv2d(input=h1, weight=params[2], bias=params[3])
h2_activation = F.relu(h2_conv)
h2 = F.avg_pool2d(input=h2_activation, kernel_size=(2, 2), stride=(2, 2))
h2 = h2.reshape(h2.shape[0], -1)
h3_linear = torch.mm(h2, params[4]) + params[5]
h3 = F.relu(h3_linear)
y_hat = torch.mm(h3, params[6]) + params[7]
return y_hat
# Cross-entropy loss function
loss = nn.CrossEntropyLoss(reduction='none')
# + [markdown] id="vkQPS6zAuP6t"
# # Copying parameters across devices
# + id="h8U6mWcduCuy"
def get_params(params, device):
new_params = [p.clone().to(device) for p in params]
for p in new_params:
p.requires_grad_()
return new_params
# + colab={"base_uri": "https://localhost:8080/"} id="jIYjX1lRuc2K" outputId="f712afcb-67d0-4c4b-8a5d-26055e6bacf6"
# Copy the params to GPU0
gpu0 = torch.device('cuda:0')
new_params = get_params(params, gpu0)
print('b1 weight:', new_params[1])
print('b1 grad:', new_params[1].grad)
# + colab={"base_uri": "https://localhost:8080/"} id="82NV4DDtvCxa" outputId="36f3197c-d967-4b5a-e475-0dc10d129069"
# Copy the params to GPU1
gpu1 = torch.device('cuda:0') # torch.device('cuda:1')
new_params = get_params(params, gpu1)
print('b1 weight:', new_params[1])
print('b1 grad:', new_params[1].grad)
# + [markdown] id="OMvps-jrvQmD"
# All-reduce will copy data (eg gradients) from all devices to device 0, add them, and then broadcast the result back to each device.
# + id="Kkd7DqszuuCY"
def allreduce(data):
for i in range(1, len(data)):
data[0][:] += data[i].to(data[0].device)
for i in range(1, len(data)):
data[i] = data[0].to(data[i].device)
def try_gpu(i=0):
"""Return gpu(i) if exists, otherwise return cpu()."""
if torch.cuda.device_count() >= i + 1:
return torch.device(f'cuda:{i}')
return torch.device('cpu')
# + colab={"base_uri": "https://localhost:8080/"} id="sYkATwb0vhbP" outputId="b32101ce-7e1b-491e-bcbd-2eb10a14cfcc"
data_ = [torch.ones((1, 2), device=try_gpu(i)) * (i + 1) for i in range(2)]
print('before allreduce:\n', data_[0], '\n', data_[1])
allreduce(data_)
print('after allreduce:\n', data_[0], '\n', data_[1])
# + [markdown] id="JPF2qz7Xvn0p"
# # Distribute data across GPUs
# + colab={"base_uri": "https://localhost:8080/"} id="0St4qm0RvhmV" outputId="a706001b-e363-4b22-ebb0-eec50a41342a"
data_ = torch.arange(20).reshape(4, 5)
#devices = [torch.device('cuda:0'), torch.device('cuda:1')]
devices = [torch.device('cuda:0'), torch.device('cuda:0')]
split = nn.parallel.scatter(data_, devices)
print('input :', data_)
print('load into', devices)
print('output:', split)
# + [markdown] id="D9Oo0Htvv4vK"
# Split data and labels.
# + id="nrQymW40vqQQ"
def split_batch(X, y, devices):
"""Split `X` and `y` into multiple devices."""
assert X.shape[0] == y.shape[0]
return (nn.parallel.scatter(X, devices), nn.parallel.scatter(y, devices))
# + [markdown] id="Gp-2SIaUv_Hh"
# # Training on Fashion MNIST
# + id="ilYJZjkq6C9D"
def load_data_fashion_mnist(batch_size, resize=None):
"""Download the Fashion-MNIST dataset and then load it into memory."""
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="../data",
train=True,
transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data",
train=False,
transform=trans,
download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=4),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=4))
# + id="tA_QeZH5rp1o"
class Animator:
"""For plotting data in animation."""
def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
figsize=(3.5, 2.5)):
# Incrementally plot multiple lines
if legend is None:
legend = []
display.set_matplotlib_formats('svg')
self.fig, self.axes = plt.subplots(nrows, ncols, figsize=figsize)
if nrows * ncols == 1:
self.axes = [self.axes,]
# Use a lambda function to capture arguments
self.config_axes = lambda: set_axes(self.axes[
0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
self.X, self.Y, self.fmts = None, None, fmts
def add(self, x, y):
# Add multiple data points into the figure
if not hasattr(y, "__len__"):
y = [y]
n = len(y)
if not hasattr(x, "__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i, (a, b) in enumerate(zip(x, y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x, y, fmt in zip(self.X, self.Y, self.fmts):
self.axes[0].plot(x, y, fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
class Timer:
"""Record multiple running times."""
def __init__(self):
self.times = []
self.start()
def start(self):
"""Start the timer."""
self.tik = time.time()
def stop(self):
"""Stop the timer and record the time in a list."""
self.times.append(time.time() - self.tik)
return self.times[-1]
def avg(self):
"""Return the average time."""
return sum(self.times) / len(self.times)
def sum(self):
"""Return the sum of time."""
return sum(self.times)
def cumsum(self):
"""Return the accumulated time."""
return np.array(self.times).cumsum().tolist()
class Accumulator:
"""For accumulating sums over `n` variables."""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
# + id="FqnIuSGwxG0L"
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""Set the axes for matplotlib."""
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
if legend:
axes.legend(legend)
axes.grid()
# + id="vBqC89zOr_Si"
def accuracy(y_hat, y):
"""Compute the number of correct predictions."""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = torch.argmax(y_hat, axis=1)
cmp_ = y_hat.type(y.dtype) == y
return float(cmp_.type(y.dtype).sum())
def evaluate_accuracy_gpu(net, data_iter, device=None):
"""Compute the accuracy for a model on a dataset using a GPU."""
if isinstance(net, torch.nn.Module):
net.eval() # Set the model to evaluation mode
if not device:
device = next(iter(net.parameters())).device
# No. of correct predictions, no. of predictions
metric = Accumulator(2)
for X, y in data_iter:
X = X.to(device)
y = y.to(device)
metric.add(accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
# + [markdown] id="prMQdt8MO8nf"
# ## Train function
# + id="21qD8zr0wYCk"
def sgd(params, lr, batch_size):
"""Minibatch stochastic gradient descent."""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
# + id="PCAo71EDv6FL"
def train_batch(X, y, device_params, devices, lr):
X_shards, y_shards = split_batch(X, y, devices)
# Loss is calculated separately on each GPU
losses = [
loss(lenet(X_shard, device_W),
y_shard).sum() for X_shard, y_shard, device_W in zip(
X_shards, y_shards, device_params)]
for l in losses: # Back Propagation is performed separately on each GPU
l.backward()
# Sum all gradients from each GPU and broadcast them to all GPUs
with torch.no_grad():
for i in range(len(device_params[0])):
allreduce([device_params[c][i].grad for c in range(len(devices))])
# The model parameters are updated separately on each GPU
ndata = X.shape[0] # gradient is summed over the full minibatch
for param in device_params:
sgd(param, lr, ndata)
# + id="APWm5BzdwQHi"
def train(num_gpus, batch_size, lr):
train_iter, test_iter = load_data_fashion_mnist(batch_size)
devices = [try_gpu(i) for i in range(num_gpus)]
# Copy model parameters to num_gpus GPUs
device_params = [get_params(params, d) for d in devices]
# num_epochs, times, acces = 10, [], []
num_epochs = 5
animator = Animator('epoch', 'test acc', xlim=[1, num_epochs])
timer = Timer()
for epoch in range(num_epochs):
timer.start()
for X, y in train_iter:
# Perform multi-GPU training for a single minibatch
train_batch(X, y, device_params, devices, lr)
torch.cuda.synchronize()
timer.stop()
# Verify the model on GPU 0
animator.add(epoch + 1, (evaluate_accuracy_gpu(
lambda x: lenet(x, device_params[0]), test_iter, devices[0]),))
print(f'test acc: {animator.Y[0][-1]:.2f}, {timer.avg():.1f} sec/epoch '
f'on {str(devices)}')
# + [markdown] id="jG99sNIE9gAd"
# # Learning curve
# + colab={"base_uri": "https://localhost:8080/", "height": 278, "referenced_widgets": ["17e83459288e43ac8088417a3c17f50a", "<KEY>", "92fc1300abd14924bda55c2fc27a6be2", "0c9f83a074944cc79701e4c1bea4ffe3", "<KEY>", "0e4af2f1365741eba162ece21129c00c", "8891ef07661e4a7db1dfc92086ec1339", "7559a4d3c9084537864ac91a175d165d", "<KEY>", "0e865b83d2aa4c9eb8a9e4e964c98503", "<KEY>", "620994e0f5264d259888a0479e26d6d4", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "ff6951b41e414229a3f65ed1a0697a05", "<KEY>", "6f4017f38ebd4b11877284d2b11e5fb9", "c08eb93637b24f39923d803c0c9ed624", "<KEY>", "<KEY>", "2a9f917e9f4f438f95c17ba1893403d7", "<KEY>", "<KEY>", "827b4683f7ac41f487f2a72d47ebdf6e", "<KEY>", "ed4af550200b4614ad6c30d15c6eb93e", "ba5fede5fc5540778c338aea4fcbba9f", "2e645cb8ab054f8fa284dda1cc3f0a64", "ff1622d3a8974431951644ef80f20a8f", "ebc04a5733c742a987213bd7d6d88a7c"]} id="ysVlYgDQwhQ7" outputId="71a0fe79-5454-4244-8b4f-fabb468d53e5"
train(num_gpus=1, batch_size=256, lr=0.2)
|
notebooks-d2l/multi_gpu_training_torch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jonkrohn/ML-foundations/blob/master/notebooks/regression-in-pytorch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="oIX4xnrwiFZX"
# # Regression in PyTorch
# + [markdown] id="XZJhl8MciFZY"
# In this notebook, we use the PyTorch **automatic differentiation** library to fit a straight line to data points. Thus, here we use calculus to solve the same regression problem that we used the Moore-Penrose Pseudoinverse to solve in the [*Linear Algebra II* notebook](https://github.com/jonkrohn/ML-foundations/blob/master/notebooks/2-linear-algebra-ii.ipynb).
# + id="SdljCv4y09g-"
import torch
import matplotlib.pyplot as plt
# + id="RHG-NNVF09g_" outputId="441fd4cc-1d12-4e4d-a2ab-669bd9654ba0" colab={"base_uri": "https://localhost:8080/"}
x = torch.tensor([0, 1, 2, 3, 4, 5, 6, 7.]) # E.g.: Dosage of drug for treating Alzheimer's disease
x
# + [markdown] id="kbPWO45yiFZi"
# The $y$ values were created using the equation of a line $y = mx + b$. This way, we know what the model parameters to be learned are, say, $m = -0.5$ and $b = 2$. Random, normally-distributed noise has been added to simulate sampling error:
# + id="R6Z0z32d09hA"
# y = -0.5*x + 2 + torch.normal(mean=torch.zeros(8), std=0.2)
# + [markdown] id="jW-52Td409hA"
# For reproducibility of this demo, here's a fixed example of $y$ values obtained by running the commented-out line above:
# + id="mntwNZyB09hA" outputId="993dc960-863a-4e86-e0ee-b5285d636814" colab={"base_uri": "https://localhost:8080/"}
y = torch.tensor([1.86, 1.31, .62, .33, .09, -.67, -1.23, -1.37]) # E.g.: Patient's "forgetfulness score"
y
# + id="poVitT8409hA" outputId="8f51a69f-66af-445d-b269-f4022a6c7c8a" colab={"base_uri": "https://localhost:8080/", "height": 295}
fig, ax = plt.subplots()
plt.title("Clinical Trial")
plt.xlabel("Drug dosage (mL)")
plt.ylabel("Forgetfulness")
_ = ax.scatter(x, y)
# + [markdown] id="6hl2KtAM09hB"
# Initialize the slope parameter $m$ with a "random" value of 0.9...
# + [markdown] id="hvAa4nXz09hB"
# (**N.B.**: In this simple demo, we could guess approximately-correct parameter values to start with. Or, we could use an algebraic (e.g., Moore-Penrose pseudoinverse) or statistical (e.g., ordinary-least-squares regression) to solve for the parameters quickly. This tiny machine learning demo with two parameters and eight data points scales, however, to millions of parameters and millions of data points. The other approaches -- guessing, algebra, statistics -- do not come close to scaling in this way.)
# + id="IXY3nd3r09hB" outputId="e5608780-f2e0-490e-dd8c-add6eab20f9a" colab={"base_uri": "https://localhost:8080/"}
m = torch.tensor([0.9]).requires_grad_()
m
# + [markdown] id="loz5ja6Z09hB"
# ...and do the same for the $y$-intercept parameter $b$:
# + id="ofqXHEGL09hB" outputId="41020643-2e32-42d5-8e56-99cbaca94b6c" colab={"base_uri": "https://localhost:8080/"}
b = torch.tensor([0.1]).requires_grad_()
b
# + id="BJ1-Rioe09hC"
def regression(my_x, my_m, my_b):
return my_m*my_x + my_b
# + id="UbCaQY1R09hC"
def regression_plot(my_x, my_y, my_m, my_b):
fig, ax = plt.subplots()
ax.scatter(my_x, my_y)
x_min, x_max = ax.get_xlim()
y_min = regression(x_min, my_m, my_b).detach().item()
y_max = regression(x_max, my_m, my_b).detach().item()
ax.set_xlim([x_min, x_max])
_ = ax.plot([x_min, x_max], [y_min, y_max])
# + id="9auSbE4A09hC" outputId="39491dcd-d064-4dd4-c705-aa9745adf2c1" colab={"base_uri": "https://localhost:8080/", "height": 266}
regression_plot(x, y, m, b)
# + [markdown] id="tALo3vf_09hC"
# **Return to slides here if following *Calculus I* class.**
# + [markdown] id="Ws53tPJF09hC"
# ### Machine Learning
# In four easy steps :)
# + [markdown] id="3egph_ZU09hC"
# **Step 1**: Forward pass
# + id="901_nf3f09hC" outputId="bae3e29c-85e2-41ec-8dbf-e1de3401b208" colab={"base_uri": "https://localhost:8080/"}
yhat = regression(x, m, b)
yhat
# + [markdown] id="AAV5AN8Y09hD"
# **Step 2**: Compare $\hat{y}$ with true $y$ to calculate cost $C$
# + [markdown] id="VIUzVfyIiFZ4"
# There is a PyTorch `MSELoss` method, but let's define it outselves to see how it works. MSE cost is defined by: $$C = \frac{1}{n} \sum_{i=1}^n (\hat{y_i}-y_i)^2 $$
# + id="sRAbg8lQ09hD"
def mse(my_yhat, my_y):
sigma = torch.sum((my_yhat - my_y)**2)
return sigma/len(my_y)
# + id="V6I7Cmi409hD" outputId="c17956a3-4d2b-4dfc-cb41-c2c35aa4d8c8" colab={"base_uri": "https://localhost:8080/"}
C = mse(yhat, y)
C
# + [markdown] id="avZjfPNQ09hD"
# **Step 3**: Use autodiff to calculate gradient of $C$ w.r.t. parameters
# + id="GmouXexF09hE"
C.backward()
# + id="cOYw5LOV09hE" outputId="c168314c-e1d1-4a30-eb12-c4cb2ad20e05" colab={"base_uri": "https://localhost:8080/"}
m.grad
# + id="vyvLxxYy09hE" outputId="f0e03874-1b5f-4a8c-9231-1177536d891d" colab={"base_uri": "https://localhost:8080/"}
b.grad
# + [markdown] id="iWn_fH0t09hE"
# **Step 4**: Gradient descent
# + id="-H18htep09hE"
optimizer = torch.optim.SGD([m, b], lr=0.01)
# + id="l6Ca-YTp09hE"
optimizer.step()
# + [markdown] id="bfMF3B2709hE"
# Confirm parameters have been adjusted sensibly:
# + id="GOr74kGm09hF" outputId="5a198564-d43f-45ad-c8fe-e6c5629bf4dc" colab={"base_uri": "https://localhost:8080/"}
m
# + id="Ht7U_2_G09hF" outputId="dc44855c-1d4d-48c3-cf26-29d32385e0e1" colab={"base_uri": "https://localhost:8080/"}
b
# + id="qQIUjHPY09hF" outputId="45fe08d1-1f03-42c6-9d49-8e10309e1795" colab={"base_uri": "https://localhost:8080/", "height": 265}
regression_plot(x, y, m, b)
# + [markdown] id="mwo0UsoA09hF"
# We can repeat steps 1 and 2 to confirm cost has decreased:
# + id="76e1mVu209hF" outputId="428741db-dc8f-45c8-f640-d276dd03b285" colab={"base_uri": "https://localhost:8080/"}
C = mse(regression(x, m, b), y)
C
# + [markdown] id="r6dAqwRw09hF"
# Put the 4 steps in a loop to iteratively minimize cost toward zero:
# + id="wejSZX2q09hF" outputId="05546d2f-07e1-4c47-804e-f603aa65e949" colab={"base_uri": "https://localhost:8080/"}
epochs = 1000
for epoch in range(epochs):
optimizer.zero_grad() # Reset gradients to zero; else they accumulate
yhat = regression(x, m, b) # Step 1
C = mse(yhat, y) # Step 2
C.backward() # Step 3
optimizer.step() # Step 4
print('Epoch {}, cost {}, m grad {}, b grad {}'.format(epoch, '%.3g' % C.item(), '%.3g' % m.grad.item(), '%.3g' % b.grad.item()))
# + id="fJeq0EFA09hG" outputId="cb5d5429-040b-4cc7-97aa-94c8f32def4d" colab={"base_uri": "https://localhost:8080/", "height": 265}
regression_plot(x, y, m, b)
# + id="S3B8PB5g09hG" outputId="aad1a876-75fb-4108-a5e2-f2780df48027" colab={"base_uri": "https://localhost:8080/"}
m.item()
# + id="yYaCN83C09hG" outputId="0e6e4fcf-85cb-4baf-d281-e95fc89c8e47" colab={"base_uri": "https://localhost:8080/"}
b.item()
# + [markdown] id="GfoFI9-x09hG"
# **N.B.**: The model doesn't perfectly approximate the slope (-0.5) and $y$-intercept (2.0) used to simulate the outcomes $y$ at the top of this notebook. This reflects the imperfectness of the sample of eight data points due to adding random noise during the simulation step. In the real world, the best solution would be to sample additional data points: The more data we sample, the more accurate our estimates of the true underlying parameters will be.
|
notebooks/regression-in-pytorch.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.7.0
# language: julia
# name: julia-1.7
# ---
# # Orthogonal Polynomials
#
# Fourier series proved very powerful for approximating periodic functions.
# If periodicity is lost, however, uniform convergence is lost. In this chapter
# we introduce alternative bases, _orthogonal polynomials (OPs)_ built on polynomials that are applicable in
# the non-periodic setting. That is we consider expansions of the form
# $$
# f(x) = \sum_{k=0}^∞ c_k p_k(x) ≈ \sum_{k=0}^{n-1} c_k^n p_k(x)
# $$
# where $p_k(x)$ are special families of polynomials, $c_k$ are expansion coefficients and
# $c_k^n$ are approximate coefficients.
#
# Why not use monomials as in Taylor series? Hidden in the previous lecture was that we could effectively
# compute Taylor coefficients by evaluating on the unit circle in the complex plane, _only_ if the radius of convergence
# was 1. Many functions are smooth on say $[-1,1]$ but have non-convergent Taylor series, e.g.:
# $$
# {1 \over 25x^2 + 1}
# $$
# While orthogonal polynomials span the same space as monomials, and therefore we can in theory write an
# approximation in monomials, orthogonal polynomials are _much_ more stable.
#
#
#
# In addition to numerics, OPs play a very important role in many mathematical areas
# including functional analysis, integrable systems, singular integral equations,
# complex analysis, and random matrix theory.
#
# 1. General properties of OPs: we define orthogonal polynomials, three-term recurrences and Jacobi operators
# 2. Classical OPs: we define Chebyshev, Legendre, Jacobi, Laguerre, and Hermite.
# 3. Gaussian quadrature: we see that OPs can be used to construct effective numerical methods for singular integrals
# 4. Recurrence relationships and Sturm–Liouville equations: we see that classical OPs have many simple recurrences that
# are of importance in computation, which also show they are eigenfunctions of simple differential operators.
#
#
# ## 1. General properties of orthogonal polynomials
#
# **Definition (graded polynomial basis)**
# A set of polynomials $\{p_0(x), p_1(x), … \}$ is _graded_ if $p_n$ is
# precisely degree $n$: i.e.,
# $$
# p_n(x) = k_n x^n + k_n^{(n-1)} x^{n-1} + ⋯ + k_n^{(1)} x + k_n^{(0)}
# $$
# for $k_n ≠ 0$.
#
# Note that if $p_n$ are graded then $\{p_0(x), …, p_n(x) \}$
# are a basis of all polynomials of degree $n$.
#
#
# **Definition (orthogonal polynomials)**
# Given an (integrable) _weight_ $w(x) > 0$ for $x ∈ (a,b)$,
# which defines a continuous inner product
# $$
# ⟨f,g⟩ = ∫_a^b f(x) g(x) w(x) {\rm d} x
# $$
# a graded polynomial basis $\{p_0(x), p_1(x), … \}$
# are _orthogonal polynomials (OPs)_ if
# $$
# ⟨p_n,p_m⟩ = 0
# $$
# whenever $n ≠ m$.
#
#
# Note in the above
# $$
# h_n := ⟨p_n,p_n⟩ = \|p_n\|^2 = ∫_a^b p_n(x)^2 w(x) {\rm d} x > 0.
# $$
#
# **Definition (orthonormal polynomials)**
# A set of orthogonal polynomials $\{q_0(x), q_1(x), … \}$
# are orthonormal if $\|q_n\| = 1$.
#
# **Definition (monic orthogonal polynomials)**
# A set of orthogonal polynomials $\{q_0(x), q_1(x), … \}$
# are orthonormal if $k_n = 1$.
#
#
# **Proposition (expansion)**
# If $r(x)$ is a degree $n$ polynomial, $\{p_n\}$ are orthogonal
# and $\{q_n\}$ are orthonormal then
# $$
# \begin{align*}
# r(x) &= ∑_{k=0}^n {⟨p_k,r⟩ \over \|p_k\|^2} p_k(x) \\
# & = ∑_{k=0}^n ⟨q_k,r⟩ q_k(x)
# \end{align*}
# $$
#
# **Proof**
# Because $\{p_0,…,p_n \}$ are a basis of polynomials we can
# write
# $$
# r(x) = ∑_{k=0}^n r_k p_k(x)
# $$
# for constants $r_k ∈ ℝ$.
# By linearity we have
# $$
# ⟨p_m,r⟩ = ∑_{k=0}^n r_k ⟨p_m,p_k⟩= r_m ⟨p_m,p_m⟩
# $$
# ∎
#
# **Corollary (zero inner product)**
# If a degree $n$ polynomial $r$ satisfies
# $$
# 0 = ⟨p_0,r⟩ = … = ⟨p_n,r⟩
# $$
# then $r = 0$.
#
#
# OPs are uniquely defined (up to a constant) by the
# property that they are orthogonal to all lower degree polynomials.
#
# **Proposition (orthogonal to lower degree)**
# A polynomial $p$ of precisely degree $n$ satisfies
# $$
# ⟨p,r⟩ = 0
# $$
# for all degree $m < n$ polynomials $r$ if and only if
# $p = c q_n$. Therefore an orthogonal polynomial is uniquely
# defined by $k_n$.
#
# **Proof**
# As $\{p_0,…,p_n\}$ are a basis of all polynomials of degree $n$,
# we can write
# $$
# r(x) = ∑_{k=0}^m a_k p_k(x)
# $$
# Thus by linearity of inner products we have
# $$
# ⟨cp_n,∑_{k=0}^m a_k p_k⟩ = ∑_{k=0}^m ca_k ⟨p_n, p_k⟩ = 0.
# $$
#
# Now for
# $$
# p(x) = c x^n + O(x^{n-1})
# $$
# consider $p(x) - c p_n(x)$ which is of degree $n-1$. It satisfies
# for $k ≤ n-1$
# $$
# ⟨p_k, p - c p_n⟩ = ⟨p_k, p⟩ - c ⟨p_k, p_n⟩ = 0.
# $$
# Thus it is zero, i.e., $p(x) = c p_n(x)$.
#
# ∎
#
# A consequence of this is that orthonormal polynomials are always a
# constant multiple of orthogonal polynomials.
#
#
# ### 3-term recurrence
#
# The most _fundamental_ property of orthogonal polynomials is their three-term
# recurrence.
#
# **Theorem (3-term recurrence, 2nd form)**
# If $\{p_n\}$ are OPs then there exist real constants
# $a_n, b_n ≠0,c_{n-1} ≠0$
# such that
# $$
# \begin{align*}
# x p_0(x) &= a_0 p_0(x) + b_0 p_1(x) \\
# x p_n(x) &= c_{n-1} p_{n-1}(x) + a_n p_n(x) + b_n p_{n+1}(x)
# \end{align*}
# $$
# **Proof**
# The $n=0$ case is immediate since $\{p_0,p_1\}$ are a basis of degree 1 polynomials.
# The $n >0$ case follows from
# $$
# ⟨x p_n, p_k⟩ = ⟨ p_n, xp_k⟩ = 0
# $$
# for $k < n-1$ as $x p_k$ is of degree $k+1 < n$.
#
# Note that
# $$
# b_n = {⟨p_{n+1}, x p_n⟩ \over \|p_{n+1} \|^2} ≠ 0
# $$
# since $x p_n = k_n x^{n+1} + O(x^n)$ is precisely degree
# $n$. Further,
# $$
# c_{n-1} = {⟨p_{n-1}, x p_n⟩ \over \|p_{n-1}\|^2 } =
# {⟨p_n, x p_{n-1}⟩ \over \|p_{n-1}\|^2 } = b_{n-1}{\|p_n\|^2 \over \|p_{n-1}\|^2 } ≠ 0.
# $$
#
#
#
# ∎
#
#
#
#
# Clearly if $p_n$ is monic then so is $x p_n$ which leads to the following:
#
# **Corollary (monic 3-term recurrence)** If
# $\{p_n\}$ are monic then $b_n = 1$.
#
#
# **Example** What are the monic OPs $p_0(x),…,p_3(x)$ with respect to $w(x) = 1$ on $[0,1]$?
# We can construct these using Gram–Schmidt, but exploiting the 3-term recurrence to reduce the computational cost.
# We have $p_0(x) = q_0(x) = 1$, which we see is orthogonal:
# $$
# \|p_0\|^2 = ⟨p_0,p_0⟩ = ∫_0^1 {\rm d x} = 1.
# $$
# We know from the 3-term recurrence that
# $$
# x p_0(x) = a_0 p_0(x) + p_1(x)
# $$
# where
# $$
# a_0 = {⟨p_0,x p_0⟩ \over \|p_0\|^2} = ∫_0^1 x {\rm d} x = 1/2.
# $$
# Thus
# $$
# \begin{align*}
# p_1(x) = x p_0(x) - a_0 p_0(x) = x-1/2 \\
# \|p_1\|^2 = ∫_0^1 (x^2 - x + 1/4) {\rm d} x = 1/12
# \end{align*}
# $$
# From
# $$
# x p_1(x) = c_0 p_0(x) + a_1 p_1(x) + p_2(x)
# $$
# we have
# $$
# \begin{align*}
# c_0 &= {⟨p_0,x p_1⟩ \over \|p_0\|^2} = ∫_0^1 (x^2 - x/2) {\rm d} x = 1/12 \\
# a_1 &= {⟨p_1,x p_1⟩ \over \|p_1\|^2} = 12 ∫_0^1 (x^3 - x^2 + x/4) {\rm d} x = 1/2 \\
# p_2(x) &= x p_1(x) - c_0 - a_1 p_1(x) = x^2 - x + 1/6 \\
# \|p_2\|^2 &= \int_0^1 (x^4 - 2x^3 + 4x^2/3 - x/3 + 1/36) {\rm d} x = {1 \over 180}
# \end{align*}
# $$
# Finally, from
# $$
# x p_2(x) = c_1 p_1(x) + a_2 p_2(x) + p_3(x)
# $$
# we have
# $$
# \begin{align*}
# c_1 &= {⟨p_1,x p_2⟩ \over \|p_1\|^2} = 12 ∫_0^1 (x^4 - 3x^3/2 +2x^2/3 -x/12) {\rm d} x = 1/15 \\
# a_2 &= {⟨p_2,x p_2⟩ \over \|p_2\|^2} = 180 ∫_0^1 (x^5 - 2x^4 +4x^3/3 - x^2/3 + x/36) {\rm d} x = 1/2 \\
# p_3(x) &= x p_2(x) - c_1 p_1(x)- a_2 p_2(x) = x^3 - x^2 + x/6 - x/15 + 1/30 -x^2/2 + x/2 - 1/12 \\
# &= x^3 - 3x^2/2 + 3x/5 -1/20
# \end{align*}
# $$
#
#
# ### Jacobi matrix
#
#
# The three-term recurrence can also be interpreted as a matrix known
# as the Jacobi matrix:
#
# **Corollary (Jacobi matrix)**
# For
# $$
# P(x) := [p_0(x) | p_1(x) | ⋯]
# $$
# then we have
# $$
# x P(x) = P(x) \underbrace{\begin{bmatrix} a_0 & c_0 \\
# b_0 & a_1 & c_1\\
# & b_1 & a_2 & ⋱ \\
# && ⋱ & ⋱
# \end{bmatrix}}_X
# $$
# More generally, for any polynomial $a(x)$ we have
# $$
# a(x) P(x) = P(x) a(X).
# $$
#
# For the special cases of orthonormal and monic polynomials we have extra structure:
#
# **Corollary (orthonormal 3-term recurrence)** If
# $\{q_n\}$ are orthonormal then its recurrence coefficients satisfy $c_n = b_n$.
# That is, the Jacobi matrix is symmetric:
# $$
# X = \begin{bmatrix} a_0 & b_0 \\
# b_0 & a_1 & b_1\\
# & b_1 & a_2 & ⋱ \\
# && ⋱ & ⋱
# \end{bmatrix}
# $$
#
# **Proof**
# $$
# b_n = ⟨x q_n, q_{n+1}⟩ = ⟨q_n, x q_{n+1}⟩ = c_{n-1}.
# $$
# ∎
#
#
#
# **Remark** Typically the Jacobi matrix is the transpose $J := X^⊤$.
# If the basis are orthonormal then $X$ is symmetric and they are the same.
#
# **Remark (advanced)** If you are worried about multiplication of infinite matrices/vectors
# note it is well-defined by the standard definition because it is banded.
# It can also be defined in terms of functional analysis where one considers these
# as linear operators (functions of functions) between vector spaces.
#
# **Remark (advanced)** Every integrable weight generates a family of
# orthonormal polynomials, which in turn generates a symmetric Jacobi matrix.
# There is a "Spectral Theorem for Jacobi matrices" that says one can go the
# other way: every tridiagonal symmetric matrix with bounded entries is a Jacobi
# matrix for some integrable weight with compact support. This is an example of what
# [<NAME>](https://en.wikipedia.org/wiki/Barry_Simon) calls a ``Gem of spectral theory'',
# that is.
#
#
# **Example (uniform weight Jacobi matrix)** Consider the
# monic orthogonal polynomials $p_0(x),p_1(x),…,p_3(x)$ for $w(x) = 1$ on $[0,1]$ constructed above.
# We can write the 3-term recurrence coefficients we have computed above as the Jacobi matrix:
# $$
# x [p_0(x)| p_1(x)| ⋯] = [p_0(x)| p_1(x)| ⋯] \underbrace{\begin{bmatrix} 1/2 & 1/12 \\
# 1 & 1/2 & 1/15 \\
# & 1 & 1/2 & ⋱ \\
# & & ⋱ & ⋱ \end{bmatrix}}_X
# $$
# We can compute the orthonormal polynomials, using
# $$
# \|p_3\|^2 = \int_0^1 (x^6 - 3x^5 + 69x^4/20 -19x^3/10 + 51x^2/100 - 3x/50 + 1/400) {\rm d}x = {1 \over 2800}
# $$
# as:
# $$
# \begin{align*}
# q_0(x) &= p_0(x) \\
# q_1(x) &= \sqrt{12} p_1(x)= \sqrt{3} (2 x - 1) \\
# q_2(x) &= \sqrt{180} p_2(x) = \sqrt{5} (6x^2 - 6x + 1) \\
# q_3(x) &= \sqrt{2800} p_3(x) = \sqrt{7} (20x^3-30x^2 + 12x - 1)
# \end{align*}
# $$
# which have the Jacobi matrix
# $$
# x [q_0(x)| q_1(x)| ⋯] = x [p_0(x)| p_1(x)| ⋯] \underbrace{\begin{bmatrix} 1 \\ & 2\sqrt{3} \\ && 6 \sqrt{5} \\ &&& 20 \sqrt{7}
# \end{bmatrix}}_D = [q_0(x)| q_1(x)| ⋯] D^{-1} X D =
# \begin{bmatrix} 1/2 & 1/\sqrt{12} \\
# 1/\sqrt{12} & 1/2 & 1/\sqrt{15} \\
# & 1/\sqrt{15} & 1/2 & ⋱ \\
# & ⋱ & ⋱ \end{bmatrix}
# $$
# which is indeed symmetric. The problem sheet explores a more elegant way of doing this.
#
#
# **Example (expansion)** Consider expanding a low degree polynomial like $f(x) = x^2$ in $p_n(x)$. We have
# $$
# ⟨p_0, f⟩ = ∫_0^1 x^2 {\rm d} x = 1/3
# ⟨p_1, f⟩ = ∫_0^1 x^2 (x - 1/2) {\rm d} x = 1/12
# ⟨p_2, f⟩ = ∫_0^1 x^2 (x^2 - x + 1/6) {\rm d} x = 1/180
# $$
# Thus we have:
# $$
# f(x) = {p_0(x) \over 3} + p_1(x) + p_2(x) = [p_0(x) | p_1(x) | p_2(x) | ⋯] \begin{bmatrix} 1/3 \\ 1 \\ 1 \\ 0 \\ ⋮ \end{bmatrix}
# $$
# We multiply (using that $b_2 = 1$ for monic OPs) to deduce:
# $$
# x f(x) = x[p_0(x) | p_1(x) | p_2(x) | ⋯] \begin{bmatrix} 1/3 \\ 1 \\ 1 \\ 0 \\ ⋮ \end{bmatrix}
# = [p_0(x) | p_1(x) | p_2(x) | ⋯] X \begin{bmatrix} 1/3 \\ 1 \\ 1 \\ 0 \\ ⋮ \end{bmatrix}
# = [p_0(x) | p_1(x) | p_2(x) | ⋯] \begin{bmatrix} 1/4 \\ 9/10 \\ 3/2 \\ 1 \\ 0 \\ ⋮ \end{bmatrix}
# = {p_0(x) \over 4} + {9 p_1(x) \over 10} + {3 p_2(x) \over 2} + p_3(x)
# $$
#
#
#
#
# ## 2. Classical orthogonal polynomials
#
# Classical orthogonal polynomials are special families of orthogonal polynomials with a number
# of beautiful properties, for example
# 1. Their derivatives are also OPs
# 2. They are eigenfunctions of simple differential operators
#
# As stated above orthogonal polynomials are uniquely defined by the weight
# $w(x)$ and the constant $k_n$. We consider:
#
# 1. Chebyshev polynomials (1st kind) $T_n(x)$: $w(x) = 1/\sqrt{1-x^2}$ on $[-1,1]$.
# 2. Chebyshev polynomials (2nd kind) $U_n(x)$: $\sqrt{1-x^2}$ on $[-1,1]$.
# 2. Legendre polynomials $P_n(x)$: $w(x) = 1$ on $[-1,1]$.
# 3. Hermite polynomials $H_n(x): $w(x) = \exp(-x^2)$ on $(-∞,∞)$.
#
# Other important families discussed are
#
# 1. Ultrapsherical polynomials
# 2. Jacobi polynomials
# 3. Laguerre polynomials
#
#
# ### Chebyshev
#
# **Definition (Chebyshev polynomials, 1st kind)** $T_n(x)$ are orthogonal with respect to $1/sqrt{1-x^2}$
# and satisfy:
# $$
# T_0(x) = 1, T_n(x) = 2^{n-1} x^n + O(x^{n-1})
# $$
#
#
# **Definition (Chebyshev polynomials, 2nd kind)** $T_n(x)$ are orthogonal with respect to $1/sqrt{1-x^2}$.
# $$
# U_n(x) = 2^n x^n + O(x^{n-1})
# $$
#
#
# **Theorem (Chebyshev T are cos)**
# $$
# T_n(x) = \cos n \acos x
# $$
# In other words
# $$
# T_n(cos(θ)) = \cos n θ.
# $$
#
#
# **Proof**
#
# We need to show that $p_n(x) := \cos n \acos x$ are
# 1. graded polynomials
# 2. orthogonal w.r.t. $1/\sqrt{1-x^2}$ on $[-1,1]$, and
# 3. have the right normalisation constant $k_n = 2^{n-1}$ for $n = 2,…$.
#
# Property (2) follows under a change of variables:
# $$
# \int_{-1}^1 {p_n(x) p_m(x) \over \sqrt{1-x^2}} {\rm d} x =
# \int_{-π}^π {cos(nθ) cos(mθ) \over \sqrt{1-cos^2 θ}} \sin θ {\rm d} θ =
# \int_{-π}^π cos(nθ) cos(mθ) {\rm d} x = 0
# $$
# if $n ≠ m$.
#
# To see that they are graded we use the fact that
# $$
# x p_n(x) = \cos θ \cos n θ = {\cos(n-1)θ + cos(n+1)θ \over 2} = {p_{n-1}(x) + p_{n+1}(x) \over 2}
# $$
# In other words $p_{n+1}(x) = 2x p_n(x) - p_{n-1}(x)$.
# Since each time we multiply by $2x$ and $p_0(x) = 1$ we have
# $$
# p_n(x) = (2x)^n + O(x^{n-1})
# $$
# which completes the proof.
#
# ∎
#
# Buried in the proof is the 3-term recurrence:
#
# **Corollary**
# $$
# \begin{align*}
# x T_0(x) = T_1(x) \\
# x T_n(x) = {T_{n-1}(x) + T_{n+1}(x) \over 2}
# \end{align*}
# $$
#
# In the problem sheet you will show the following:
#
# **Theorem (Chebyshev U are sin)**
# For $x = \cos θ$,
# $$
# U_n(x) = {\sin(n+1) θ \over \sin θ}
# $$
# which satisfy:
# $$
# \begin{align*}
# x U_0(x) &= U_1(x)/2 \\
# x U_n(x) &= {U_{n-1}(x) \over 2} + {U_{n+1}(x) \over 2}.
# \end{align*}
# $$
#
# ### Legendre
#
# **Definition (Pochammer symbol)** The Pochammer symbol is
# $$
# \begin{align*}
# (a)_0 &= 1 \\
# (a)_n &= a (a+1) (a+2) ⋯ (a+n-1).
# $$
#
# **Definition (Legendre)** Legendre polynomials
# $P_n(x)$ are orthogonal polynomials with respect to $w(x) = 1$ on $[-1,1]$, with
# $$
# k_n = {2^n (1/2)_n \over n!}
# $$
#
# The reason for this complicated normalisation constant is both historical and
# that it leads to simpler formulae for recurrence relationships.
#
#
# Classical orthogonal polynomials have _Rodriguez formulae_, defining orthogonal
# polynomials as high order derivatives of simple functions. In this case we have:
#
# **Theorem (Legendre Rodriguez)**
# $$
# P_n(x) = {1 \over (-2)^n n!}{{\rm d}^n \over {\rm d} x^n} (1-x^2)^n
# $$
#
# **Proof**
# We need to verify:
# 1. graded polynomials
# 2. orthogonal to all lower degree polynomials on $[-1,1]$, and
# 3. have the right normalisation constant $k_n = {2^n (1/2)_n \over n!}$.
#
# (1) follows since its a degree $n$ polynomial (the $n$-th derivative of a degree $2n$ polynomial).
# (2) follows by integration by parts. Note that $(1-x^2)^n$ and its first $n-1$ derivatives vanish at ±1$.
# If $r_m$ is a degree $m < n$ polynomial we have:
# $$
# ∫_{-1}^1 {{\rm d}^n \over {\rm d} x^n} (1-x^2)^n r_m(x) {\rm d}x
# = -∫_{-1}^1 {{\rm d}^{n-1} \over {\rm d} x^{n-1}} (1-x^2)^n r_m'(x) {\rm d}x =
# ⋯ = (-1)^n ∫_{-1}^1 (1-x^2) r_m^{(n)}(x) {\rm d}x = 0.
# $$
# (3) follows since:
# $$
# {{\rm d}^n \over {\rm d} x^n}[(-1)^n x^{2n} + O(x^{2n-1})] =
# (-1)^n 2n {{\rm d}^{n-1} \over {\rm d} x^{n-1}} x^{2n-1}+ O(x^{2n-1})] =
# (-1)^n 2n (2n-1) {{\rm d}^{n-2} \over {\rm d} x^{n-2}} x^{2n-2}+ O(x^{2n-2})] = ⋯ =
# (-1)^n 2n (2n-1) ⋯ (n+1) x^n + O(x^{n-1})
# $$
# which satisfies:
# $$
# (1/2)(1/2+1) ⋯ (n-1/2) = {1 \over 2^n} (1+2) ⋯ (2n-1)
# $$
#
# ∎
#
# **Theorem (Legendre 3-term recurrence)**
#
#
#
#
#
#
# ## 3. Gaussian quadrature
#
# Consider integration
# $$
# \int_a^b f(x) w(x) {\rm d}x.
# $$
# For periodic integration we approximated (using the Trapezium rule) an integral by a sum.
# We can think of it as a weighted sum:
# $$
# {1 \over 2π} \int_0^{2π} f(θ) {\rm d} θ ≈ ∑_{j=0}^{n-1} w_j f(θ_j)
# $$
# where $w_j = 1/n$. Replacing an integral by a weighted sum is a known as a _quadrature_ rule.
# This quadrature rule had several important properties:
# 1. It was _exact_ for integrating trigonometric polynomials with 2n-1 coefficients
# $$
# p(θ) = \sum_{k=1-n}^{n-1} p̂_k \exp({\rm i}k θ)
# $$
# as seen by the formula
# $$
# ∑_{j=0}^{n-1} w_j f(θ_j) = p̂_0^n = … + p̂_{n-1} + p̂_0 + p̂_n + ⋯ = p̂_0 = {1 \over 2π} \int_0^{2π} p(θ) {\rm d} θ
# $$
# 2. It exactly recovered the coefficients ($p̂_k^n = p̂_k$) for expansions of trigonometric polynomials with $n$ coeffiicents:
# $$
# p(θ) = \sum_{k=-⌈(n-1)/2⌉}^{⌊(n-1)/2⌋} p̂_k \exp({\rm i}k θ)
# $$
# 3. It converged fast for smooth, periodic functions $f$.
#
# In this section we consider other quadrature rules
# $$
# \int_a^b f(x) w(x) {\rm d}x ≈ \sum_{j=1}^n w_j f(x_j)
# $$
# We want to choose $w_j$ and $x_j$ so that the following properties are satisfied:
# 1. It is _exact_ for integrating polynomials up to degree $2n-1$:
# $$
# p(θ) = \sum_{k=0}^{2n-1} c_k q_k(x)
# $$
# 2. It exactly recovers the coefficients for expansions:
# $$
# p(θ) = \sum_{k=0}^{n-1} c_k q_k(x)
# $$
# 3. It converges fast for smooth functions $f$.
# We will focus on properties (1) and (2) as property (3) is more involved.
#
# The key to property (1) is to use _roots (zeros) of $q_n(x)$_.
#
# **Lemma** $q_n(x)$ has exactly $n$ distinct roots.
#
# **Proof**
#
# Suppose $x_1, …,x_j$ are the roots where $q_n(x)$ changes sign, that is,
# $$
# q_n(x) = c_j (x-x_j) + O((x-x_j)^2)
# $$
# for $c_j ≠ 0$. Then
# $$
# q_n(x) (x-x_1) ⋯(x-x_j)
# $$
# does not change sign.
# In other words:
# $$
# ⟨q_n,(x-x_1) ⋯(x-x_j) ⟩ = \int_a^b q_n(x) (x-x_1) ⋯(x-x_j) {\rm d} x ≠ 0.
# $$
# This is only possible if $j = n$.
#
# ∎
#
#
#
# **Lemma (zeros)** The zeros $x_1, …,x_n$ of $q_n(x)$ are the eigenvalues of the truncated Jacobi matrix
# $$
# X_n := \begin{bmatrix} a_0 & b_0 \\
# b_0 & ⋱ & ⋱ \\
# & ⋱ & a_{n-2} & b_{n-2} \\
# && b_{n-2} & a_{n-1} \end{bmatrix} ∈ ℝ^{n × n}.
# $$
# More precisely,
# $$
# X_n Q_n = Q_n \begin{bmatrix} x_1 \\ & ⋱ \\ && x_n \end{bmatrix}
# $$
# for the orthogonal matrix
# $$
# Q_n = \begin{bmatrix}
# p_0(x_1) & ⋯ & p_0(x_n) \\
# ⋮ & ⋯ & ⋮ \\
# p_{n-1}(x_1) & ⋯ & p_{n-1}(x_n)
# \end{bmatrix}
# $$
#
# **Proof**
#
# We construct the eigenvector (noting $b_{n-1} p_n(x_j) = 0$):
# $$
# X_n \begin{bmatrix} p_0(x_j) \\ ⋮ \\ p_{n-1}(x_j) \end{bmatrix} =
# \begin{bmatrix} a_0 p_0(x_j) + b_0 p_1(x_j) \\
# b_0 p_0(x_j) + a_1 p_1(x_j) + b_1 p_2(x_j) \\
# ⋮ \\
# b_{n-3} p_{n-3}(x_j) + a_{n-2} p_{n-2}(x_j) + b_{n-2} p_{n-1}(x_j) \\
# b_{n-2} p_{n-2}(x_j) + a_{n-1} p_{n-1}(x_j) + b_{n-1} p_n(x_j)
# \end{bmatrix} = x_j \begin{bmatrix} p_0(x_j) \\
# p_1(x_j) \\
# ⋮ \\
# p_n(x_j)
# \end{bmatrix}
# $$
#
# ∎
|
notebooks/OrthogonalPolynomials.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Plotting massive data sets
#
# This notebook plots about half a million LIDAR points around Toronto from the KITTI data set. ([Source](http://www.cvlibs.net/datasets/kitti/raw_data.php)) The data is meant to be played over time. With pydeck, we can render these points and interact with them.
# ### Cleaning the data
#
# First we need to import the data. Each row of data represents one x/y/z coordinate for a point in space at a point in time, with each frame representing about 115,000 points.
#
# We also need to scale the points to plot closely on a map. These point coordinates are not given in latitude and longitude, so as a workaround we'll plot them very close to (0, 0) on the earth.
#
# In future versions of pydeck other viewports, like a flat plane, will be supported out-of-the-box. For now, we'll make do with scaling the points.
# +
import pandas as pd
all_lidar = pd.concat([
pd.read_csv('https://raw.githubusercontent.com/ajduberstein/kitti_subset/master/kitti_1.csv'),
pd.read_csv('https://raw.githubusercontent.com/ajduberstein/kitti_subset/master/kitti_2.csv'),
pd.read_csv('https://raw.githubusercontent.com/ajduberstein/kitti_subset/master/kitti_3.csv'),
pd.read_csv('https://raw.githubusercontent.com/ajduberstein/kitti_subset/master/kitti_4.csv'),
])
# Filter to one frame of data
lidar = all_lidar[all_lidar['source'] == 136]
lidar.loc[: , ['x', 'y']] = lidar[['x', 'y']] / 10000
# -
# ### Plotting the data
#
# We'll define a single `PointCloudLayer` and plot it.
#
# Pydeck by default expects the input of `get_position` to be a string name indicating a single position value. For convenience, you can pass in a string indicating the X/Y/Z coordinate, here `get_position='[x, y, z]'`. You also have access to a small expression parser--in our `get_position` function here, we increase the size of the z coordinate times 10.
#
# Using `pydeck.data_utils.compute_view`, we'll zoom to the approximate center of the data.
# +
import pydeck as pdk
point_cloud = pdk.Layer(
'PointCloudLayer',
lidar[['x', 'y', 'z']],
get_position=['x', 'y', 'z * 10'],
get_normal=[0, 0, 1],
get_color=[255, 0, 100, 200],
pickable=True,
auto_highlight=True,
point_size=1)
view_state = pdk.data_utils.compute_view(lidar[['x', 'y']], 0.9)
view_state.max_pitch = 360
view_state.pitch = 80
view_state.bearing = 120
r = pdk.Deck(
point_cloud,
initial_view_state=view_state,
map_provider=None,
)
r.show()
# +
import time
from collections import deque
# Choose a handful of frames to loop through
frame_buffer = deque([42, 56, 81, 95])
print('Press the stop icon to exit')
while True:
current_frame = frame_buffer[0]
lidar = all_lidar[all_lidar['source'] == current_frame]
r.layers[0].get_position = '@@=[x / 10000, y / 10000, z * 10]'
r.layers[0].data = lidar.to_dict(orient='records')
frame_buffer.rotate()
r.update()
time.sleep(0.5)
|
bindings/pydeck/examples/04 - Plotting massive data sets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
##fizz buzz; for nums 1 to 100 print:
## num if not mult 3 or 5
##fizz if mullt 3 not mult 5
##buzz if not mult 3 by mult 5
##fizzbuzz if mult 3 and the 5 .... this is already the code!
# -
for n in range(100):
if n%3 !=0 and n%5 != 0:
print(n)
if n %3 ==0 and n%5 != 0:
print('fizz')
if n %3!=0 and n%5 == 0:
print('buzz')
if n %3 ==0 and n%5 == 0:
print('fizzbuzz')
|
Note_books/Explore_Models/Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 66. Plus One
# #### Content
# <p>Given a <strong>non-empty</strong> array of decimal digits representing a non-negative integer, increment one to the integer.</p>
#
# <p>The digits are stored such that the most significant digit is at the head of the list, and each element in the array contains a single digit.</p>
#
# <p>You may assume the integer does not contain any leading zero, except the number 0 itself.</p>
#
# <p> </p>
# <p><strong>Example 1:</strong></p>
#
# <pre>
# <strong>Input:</strong> digits = [1,2,3]
# <strong>Output:</strong> [1,2,4]
# <strong>Explanation:</strong> The array represents the integer 123.
# </pre>
#
# <p><strong>Example 2:</strong></p>
#
# <pre>
# <strong>Input:</strong> digits = [4,3,2,1]
# <strong>Output:</strong> [4,3,2,2]
# <strong>Explanation:</strong> The array represents the integer 4321.
# </pre>
#
# <p><strong>Example 3:</strong></p>
#
# <pre>
# <strong>Input:</strong> digits = [0]
# <strong>Output:</strong> [1]
# </pre>
#
# <p> </p>
# <p><strong>Constraints:</strong></p>
#
# <ul>
# <li><code>1 <= digits.length <= 100</code></li>
# <li><code>0 <= digits[i] <= 9</code></li>
# </ul>
#
# #### Difficulty: Easy, AC rate: 42.0%
#
# #### Question Tags:
# - Array
# - Math
#
# #### Links:
# 🎁 [Question Detail](https://leetcode.com/problems/plus-one/description/) | 🎉 [Question Solution](https://leetcode.com/problems/plus-one/solution/) | 💬 [Question Discussion](https://leetcode.com/problems/plus-one/discuss/?orderBy=most_votes)
#
# #### Hints:
#
# #### Sample Test Case
# [1,2,3]
# ---
# What's your idea?
#
# 简单的加法法则,注意进位即可
#
# ---
# + isSolutionCode=true
from typing import List
class Solution:
def plusOne(self, digits: List[int]) -> List[int]:
idx = len(digits) - 1
carry = 1
while carry and idx >= 0:
digits[idx] += carry
carry = digits[idx] // 10
digits[idx] %= 10
idx -= 1
return digits if carry == 0 else [carry] + digits
# -
s = Solution()
print(s.plusOne([1,2,3]))
print(s.plusOne([4,3,2,1]))
print(s.plusOne([0]))
print(s.plusOne([9,9]))
print(s.plusOne([9,8]))
import sys, os; sys.path.append(os.path.abspath('..'))
from submitter import submit
submit(66)
|
51-100/66.plus-one.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pytorchNLP
# language: python
# name: pytorchnlp
# ---
import nltk
from nltk.tokenize import sent_tokenize, word_tokenize
from nltk.corpus import stopwords
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# +
emma = nltk.corpus.gutenberg.sents('austen-emma.txt')
emma_sentences = []
emma_word_set = []
for sentence in emma:
emma_sentences.append([word.lower() for word in sentence if word.isalpha()])
for word in sentence:
if word.isalpha():
emma_word_set.append(word.lower())
emma_word_set = set(emma_word_set)
# +
def TermFreq(document, word):
doc_length = len(document)
occurances = len([w for w in document if w == word])
return occurances / doc_length
TF(emma_sentences[5], 'ago')
# +
def build_DF_dict():
output = {}
for word in emma_word_set:
output[word] = 0
for doc in emma_sentences:
if word in doc:
output[word] += 1
return output
df_dict = build_DF_dict()
df_dict['ago']
# +
def InverseDocumentFrequency(word):
N = len(emma_sentences)
try:
df = df_dict[word] + 1
except:
df = 1
return np.log(N/df)
InverseDocumentFrequency('ago')
# +
def TFIDF(doc, word):
tf = TF(doc, word)
idf = InverseDocumentFrequency(word)
return tf*idf
print('ago - ' + str(TFIDF(emma_sentences[5],'ago')))
print('indistinct - ' + str(TFIDF(emma_sentences[5],'indistinct')))
# +
def loadGlove(path):
file = open(path,'r')
model = {}
for l in file:
line = l.split()
word = line[0]
value = np.array([float(val) for val in line[1:]])
model[word] = value
return model
glove = loadGlove('glove.6B.50d.txt')
# +
embeddings = []
for word in emma_sentences[5]:
embeddings.append(glove[word])
mean_embedding = np.mean(embeddings, axis = 0).reshape(1, -1)
print(mean_embedding)
# +
embeddings = []
for word in emma_sentences[5]:
tfidf = TFIDF(emma_sentences[5], word)
embeddings.append(glove[word]* tfidf)
tfidf_weighted_embedding = np.mean(embeddings, axis = 0).reshape(1, -1)
print(tfidf_weighted_embedding)
# -
cosine_similarity(mean_embedding, tfidf_weighted_embedding)
|
Chapter03/TF-IDF.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="PH5LgcD_eYZH" colab_type="code" colab={}
import pandas as pd
import requests
from bs4 import BeautifulSoup
import re
import random
import time
import sys
# + id="E1YMH8Ezf5cy" colab_type="code" outputId="e0186afd-a366-426c-ee65-6a1a1a109241" colab={"base_uri": "https://localhost:8080/", "height": 1000}
URL ="https://www.drugs.com/medical_conditions.html"
r=requests.get(URL)
soup = BeautifulSoup(r.content, 'html5lib')
print(soup.prettify())
# + id="qboT0NLTgWtx" colab_type="code" outputId="a5332213-e11d-4ba0-ccc7-1c9b1882a672" colab={"base_uri": "https://localhost:8080/", "height": 454}
alpha_list=[]
ul = soup.find("ul",{"class":"ddc-paging"})
#print(ul)
for li in ul.findAll("li"):
alpha_list.append(li.a['href'])
alpha_list
# + id="Y2DuqGZjhrbC" colab_type="code" outputId="874896d7-2083-4f4a-d9a5-8d40a5e3831a" colab={"base_uri": "https://localhost:8080/", "height": 1000}
dlist=[]
for alphabet in alpha_list:
url='https://www.drugs.com/'+alphabet
#print(url)
r2=requests.get(url)
soup2=BeautifulSoup(r2.content,'html5lib')
ul2=soup2.find("ul",{"class":"ddc-list-column-2"})
#print(ul2)
for li2 in ul2.findAll("li"):
#print(li2)
x='https://www.drugs.com'+li2.a['href']
print(x)
dlist.append(x)
# + colab_type="code" outputId="07fbaccd-4ed7-4588-81a9-16b8d628dad4" id="7dkUIuYr4ZhQ" colab={"base_uri": "https://localhost:8080/", "height": 1000}
druglist={}
names=[]
Drugs=[]
stime=time.time()
for disease in dlist:
drugs=[]
url3=disease
r3=requests.get(url3)
soup3=BeautifulSoup(r3.content,'html5lib')
name = soup3.find("h1").text.replace("Medications for","")
tr = soup3.findAll("tr",{"class":"condition-table__summary condition-table__summary--generic"})
for drug in tr:
t= drug.find("td",{"class":"condition-table__drug-name valign-middle"})
if(t.a.text==''):
data="NO DRUGS AVAILABLE."
else:
data=t.a.text
drugs.append(data)
name = soup3.find("h1").text.replace("Medications for","")
names.append(name)
Drugs.append(drugs)
dtime=time.time()
print(name,":",drugs,"---->",dtime-stime)
druglist={
"Disease":names,
"Drugs":Drugs
}
# + id="Z6Wqo4604nHf" colab_type="code" colab={}
df = pd.DataFrame.from_dict(druglist)
df.to_csv('drugs2disease.csv')
# + id="LDYR1hGdT34Z" colab_type="code" colab={}
df = df.replace('\n',' ', regex=True)
# + id="MLvOhHbbUn8R" colab_type="code" outputId="bca5044e-4692-4d62-8934-7548e7728c17" colab={"base_uri": "https://localhost:8080/", "height": 402}
df
# + id="MlMgUir2c6Uf" colab_type="code" colab={}
import pandas as pd
import numpy as np
# + id="cw-7RigneIWG" colab_type="code" colab={}
xd = pd.DataFrame.from_dict(Drugs)
xd.to_csv('drugs.csv')
# + id="NFnEFunwdJNd" colab_type="code" outputId="3d8d63ea-0fca-4ec7-b871-44804da43b75" colab={"base_uri": "https://localhost:8080/", "height": 162}
x = druglist.rstrip("\n")
|
DrugsScrap.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 911 Calls Capstone Project
# For this capstone project we will be analyzing some 911 call data from [Kaggle](https://www.kaggle.com/mchirico/montcoalert). The data contains the following fields:
#
# * lat : String variable, Latitude
# * lng: String variable, Longitude
# * desc: String variable, Description of the Emergency Call
# * zip: String variable, Zipcode
# * title: String variable, Title
# * timeStamp: String variable, YYYY-MM-DD HH:MM:SS
# * twp: String variable, Township
# * addr: String variable, Address
# * e: String variable, Dummy variable (always 1)
#
# Just go along with this notebook and try to complete the instructions or answer the questions in bold using your Python and Data Science skills!
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('911.csv')
df.head()
df.info()
# ** What are the top 5 zipcodes for 911 calls? **
df['zip'].value_counts().head(5)
# ** What are the top 5 townships (twp) for 911 calls? **
df['twp'].value_counts().head(5)
# ** Take a look at the 'title' column, how many unique title codes are there? **
df['title'].nunique()
# ## Creating new features
# ** In the titles column there are "Reasons/Departments" specified before the title code. These are EMS, Fire, and Traffic. Use .apply() with a custom lambda expression to create a new column called "Reason" that contains this string value.**
#
# **For example, if the title column value is EMS: BACK PAINS/INJURY , the Reason column value would be EMS. **
df['Reason'] = df['title'].apply(lambda x: x.split(':')[0])
# ** What is the most common Reason for a 911 call based off of this new column? **
df['Reason'].value_counts()
# ** Now use seaborn to create a countplot of 911 calls by Reason. **
sns.countplot(x='Reason', data=df)
# ** Now let us begin to focus on time information. What is the data type of the objects in the timeStamp column? **
type(df['timeStamp'][0])
df['timeStamp'] = pd.to_datetime(df['timeStamp'])
type(df['timeStamp'][0])
df['timeStamp'].iloc[0]
# **You can use Jupyter's tab method to explore the various attributes you can call. Now that the timestamp column are actually DateTime objects, use .apply() to create 3 new columns called Hour, Month, and Day of Week. You will create these columns based off of the timeStamp column, reference the solutions if you get stuck on this step.**
df['Hour']= df['timeStamp'].apply(lambda h: h.time().hour)
df['Month'] = df['timeStamp'].apply(lambda h: h.date().month)
df['Day'] = df['timeStamp'].apply(lambda h: h.dayofweek)
dmap = {0:'Mon',1:'Tue',2:'Wed',3:'Thu',4:'Fri',5:'Sat',6:'Sun'}
df['Day'] = df['Day'].map(dmap)
# ** Now use seaborn to create a countplot of the Day of Week column with the hue based off of the Reason column. **
sns.countplot(x='Day', data=df, hue='Reason', palette='viridis')
plt.legend(loc='center left', bbox_to_anchor=(1.0, 0.9))
# **Now do the same for Month:**
sns.countplot(x='Month', data=df, hue='Reason', palette='viridis')
plt.legend(loc='center left', bbox_to_anchor=(1.0, 0.9))
# ** Now create a gropuby object called byMonth, where you group the DataFrame by the month column and use the count() method for aggregation. Use the head() method on this returned DataFrame. **
byMonth = df.groupby('Month').count()
byMonth.head()
byMonth['lng'].plot(grid='ticks')
# ** Now see if you can use seaborn's lmplot() to create a linear fit on the number of calls per month. Keep in mind you may need to reset the index to a column. **
sns.lmplot(x='Month', y='twp', data=byMonth.reset_index())
# **Create a new column called 'Date' that contains the date from the timeStamp column. You'll need to use apply along with the .date() method. **
df['Date'] = df['timeStamp'].apply(lambda d: d.date())
df['Date'].head()
# ** Now groupby this Date column with the count() aggregate and create a plot of counts of 911 calls.**
byDate = df.groupby('Date').count()
byDate['lat'].plot()
plt.tight_layout()
# ** Now recreate this plot but create 3 separate plots with each plot representing a Reason for the 911 call**
df[df['Reason'] == 'EMS'].groupby('Date').count()['lat'].plot()
plt.title('EMS')
plt.tight_layout()
df[df['Reason'] == 'Fire'].groupby('Date').count()['lat'].plot()
plt.title('Fire')
plt.tight_layout()
df[df['Reason'] == 'Traffic'].groupby('Date').count()['lat'].plot()
plt.title('Traffic')
plt.tight_layout()
# ** Now let's move on to creating heatmaps with seaborn and our data. We'll first need to restructure the dataframe so that the columns become the Hours and the Index becomes the Day of the Week. There are lots of ways to do this, but I would recommend trying to combine groupby with an [unstack](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.unstack.html) method. Reference the solutions if you get stuck on this!**
df.groupby(by=['Day','Hour']).count()
df.groupby(by=['Day','Hour']).count()['Reason']
dayHour = df.groupby(by=['Day','Hour']).count()['Reason'].unstack()
# ** Now create a HeatMap using this new DataFrame. **
plt.figure(figsize=(12,6))
sns.heatmap(dayHour, cmap='viridis')
plt.figure(figsize=(12,6))
sns.clustermap(dayHour, cmap='viridis')
dayMonth = df.groupby(by=['Day','Month']).count()['Reason'].unstack()
dayMonth.head()
plt.figure(figsize=(12,6))
sns.heatmap(dayMonth, cmap='viridis')
plt.figure(figsize=(12,6))
sns.clustermap(dayMonth, cmap='viridis')
|
6.Calls Capstone project/911 Calls Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="1bwt4pT9zPNB"
# # **Integer Programming Method for Edge Data Distribution (EDD) problem**
# + id="yz3S6US745Ly" colab={"base_uri": "https://localhost:8080/"} outputId="ab8048a2-1d1e-4ebb-cf99-f342f29b6e7f"
# Install required libraries of python-pulp.
# !pip install pulp
# + id="BvlHYzlbDvVV" colab={"base_uri": "https://localhost:8080/"} outputId="4a45e14d-6ce0-40a6-a2ed-9d2b30ca0fee"
# Pick the test case to evaluate EDD.
print("Enter 1 for small input testcase OR 2 for large input test case")
n = int(input())
fileName = ""
if (n == 1):
fileName = "/content/input.txt"
elif (n == 2):
fileName = "/content/large_input.txt"
# + id="X6y56ZaH48M_"
inputFile = open(fileName, "r")
V, E, R = [int(x) for x in inputFile.readline().split()] # V, E, R - vertex, edges and destination edge servers.
dLimit, gamma = [int(x) for x in inputFile.readline().split()]
G = {(i, j): 0 for i in range(V+1) for j in range(V+1)}
dest_edge_servers = []
edges = []
Gamma = {(i, j): 0 for i in range(V+1) for j in range(V+1)} # To keep track of the cost with any edge.
CETC = 100 # Cloud to Edge Server Transmission Cost
for i in range(E):
(u, v, w) = [int(x) for x in inputFile.readline().split()]
edges.append((u, v))
Gamma[u, v] = w
Gamma[v, u] = w
for i in range(R):
v = [int(x) for x in inputFile.readline().split()]
dest_edge_servers.append(v[0])
inputFile.close()
DLimit = dLimit
for (x, y) in edges:
G[x, y] = 1
G[y, x] = 1
for x in range(1, V+1):
G[0, x] = 1
Gamma[0, x] = CETC
# + id="imbl2hwr8r6c"
# Import pulp and create a minimize optimization problem.
import pulp as plp
opt_model = plp.LpProblem("IP_Problem", plp.LpMinimize)
# + id="8e8xay0z80b7"
# H[v] to denote if edge server 'v' is visited or not in EDD.
H = {(i): plp.LpVariable(cat=plp.LpBinary, name="H_{0}".format(i)) for i in range(V+1)}
# T[u, v] to denote if edge (u, v) is used or not.
T = {(i, j): plp.LpVariable(cat=plp.LpBinary, name="T_{0}_{1}".format(i, j)) for i in range(V+1) for j in range(V+1)}
NT = {(i, j): plp.LpVariable(cat=plp.LpInteger, name="NT_{0}_{1}".format(i, j)) for i in range(V+1) for j in range(V+1)}
PT = {(i, j): plp.LpVariable(cat=plp.LpInteger, name="PT_{0}_{1}".format(i, j)) for i in range(V+1) for j in range(V+1)}
# D[v] to denote the depth of edge server 'v' in EDD IP.
D = {(i): plp.LpVariable(cat=plp.LpInteger, name="D_{0}".format(i)) for i in range(V+1)}
# + id="scJxCdLu_bpe" colab={"base_uri": "https://localhost:8080/"} outputId="30d46d17-154f-41a1-c310-6b97a78659fa"
if (DLimit == CETC): # Base condition when D_limit = CETC.
print("Optimal Solution")
print("Optimal Cost = " + str(R*CETC))
else:
# Optimization problem statement.
opt_model += plp.lpSum(Gamma[i, j] * T[i, j] for i in range(V+1) for j in range(V+1))
# Constraint H[j] == 1 for j in destination edge servers.
for j in dest_edge_servers:
opt_model += H[j] == 1
# Constraint on Depth D[j].
opt_model += D[0] == 0
for j in range(1, V+1):
opt_model += D[j] <= DLimit
opt_model += D[j] >= D[0] + CETC
# Constraint on summation of T(i, j) == H[j].
for j in range(1, V+1):
opt_model += plp.lpSum([T[i, j] for i in range(V+1)]) == H[j]
# Constraint on T[i, j] == 0, edge (i, j) is not present in G.
for i in range(V+1):
for j in range(V+1):
if (G[i, j] != 1):
opt_model += T[i, j] == 0
# Constraint on NT to be -INF or 1 depending on T[i, j] = 0 Or 1 respectively.
for i in range(V+1):
for j in range(V+1):
opt_model += NT[i, j] == (T[i, j] - 1)*V*100 + 1
# Constraint on PT to be +INF or 1 depending on T[i, j] = 0 Or 1 respectively.
for i in range(V+1):
for j in range(V+1):
opt_model += PT[i, j] == (-1)*(T[i, j] - 1)*V*100 + 1
# Constraint on T[c, v] >= 1, i.e., atleast one edge there must be from the cloud.
opt_model += plp.lpSum([T[0, i] for i in range(1, V+1)]) >= 1
# Constraint on consecutive edges depth.
for i in range(V+1):
for j in range(V+1):
if(G[i, j] == 1):
opt_model += D[j] - D[i] - (Gamma[i, j] * NT[i, j]) >= 0
opt_model += D[j] - D[i] - (Gamma[i, j] * PT[i, j]) <= 0
# Constraint on T[c, v] = 1, if D[v] = 1. Obvious.
for i in range(1, V+1):
opt_model += T[0, i] >= (-1)*(D[i] - CETC + 1) + 2
# Constraint for having H[i] = 1, if any 'j' is visited from 'i' such that T[i, j] = 1.
for i in range(1, V+1):
for j in range(1, V+1):
opt_model += T[i, j] + T[i, j] <= H[i] + H[j]
status = opt_model.solve()
print(plp.LpStatus[status] + " Solution")
print("Optimal Cost = " + str(plp.value(opt_model.objective)))
print("")
for i in range(V+1):
for j in range(V+1):
if (plp.value(T[i, j]) == 1):
print(T[i, j] , plp.value(T[i, j]))
print("")
for i in range(V+1):
print(D[i] , plp.value(D[i]))
|
Code Sem 8/Integer Programming 2/BTP_IP_Phase2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/gagan3012/project-code-py/blob/master/model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="lsTTbIxoSXTc" outputId="bcdb7549-f96e-48c1-c75b-1122426f7211"
lines = ['https://github.com/Garvit244/Leetcode',
'https://github.com/shichao-an/leetcode-python',
'https://github.com/algorhythms/LeetCode',
'https://github.com/wuduhren/leetcode-python',
'https://github.com/csujedihy/lc-all-solutions',
'https://github.com/vJechsmayr/PythonAlgorithms',
'https://github.com/HuberTRoy/leetCode',
'https://github.com/qiyuangong/leetcode',
'https://github.com/MTrajK/coding-problems',
'https://github.com/JushuangQiao/Python-LeetCode',
'https://github.com/Jack-Lee-Hiter/AlgorithmsByPython',
'https://github.com/sapanz/Hackerrank-Problem-Solving-Python-Solutions',
'https://github.com/arsho/Hackerrank_Python_Domain_Solutions',
'https://github.com/swapnanildutta/Hackerrank-Codes',
'https://github.com/markopuza/Competitive-programming-in-Python',
'https://github.com/deepaksood619/Python-Competitive-Programming',
'https://github.com/ndb796/Python-Competitive-Programming-Team-Notes',
'https://github.com/harshitbansal373/python',
'https://github.com/yashagrawal300/python-programs',
'https://github.com/bmegha98/Python-Practice',
'https://github.com/geekcomputers/Python',
'https://github.com/smilejay/python',
'https://github.com/yuzhoujr/leetcode',
'https://github.com/franklingu/leetcode-solutions',
'https://github.com/kumailn/Algorithms']
len(lines)
# + id="8ArghELG6QZ5"
from subprocess import call
import math
import os
import csv
csv_columns = ['text']
for line in lines:
call(['git', 'clone', line.strip(), f'resources/{line.strip().split("/")[-1]}'])
json_data = []
total_files = []
count = 0
for line in lines:
for currentpath, folders, files in os.walk(f'resources/{line.strip().split("/")[-1]}'):
for file in files:
if file[-3:] == '.py':
print(file)
count += 1
total_files.append(os.path.join(currentpath, file))
print('files: ', len(total_files))
for file in total_files:
with open(file, "r") as f:
try:
t = f.readlines()
except UnicodeDecodeError:
print('DecoderError: ', file)
summary = ''.join(t)
summary = str(summary).strip()
bos_token = '<|title|>'
eos_token = '<|endoftext|>'
data = bos_token + summary + eos_token
json_data.append({'text': data})
# + id="JHdBhEpR6cfD"
with open("data.csv", 'w') as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=csv_columns)
writer.writeheader()
for data in json_data:
writer.writerow(data)
# + id="tH8MJYkm8Ldt"
import pandas as pd
df = pd.read_csv('/content/data.csv')
# + id="oeTMr6_W-o4x" colab={"base_uri": "https://localhost:8080/", "height": 203} outputId="3a623365-7b5c-4fb0-975d-2a8e5bf3a801"
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="EAmmNuZOUqeY" outputId="e87655e1-5dc6-4aa4-b3d5-bb8beb95ca8a"
from sklearn.model_selection import train_test_split
train, eval = train_test_split(df, train_size=.9, random_state=2020)
print(len(train))
print(len(eval))
train = train['text'].tolist()
eval = eval['text'].tolist()
with open('train_tmp.txt', 'w') as file_handle:
file_handle.write(str(train))
with open('eval_tmp.txt', 'w') as file_handle:
file_handle.write(str(eval))
# + id="8JxD4TxQ-qCt"
# !git clone https://github.com/huggingface/transformers
# !pip install transformers
# !pip install datasets
# !pip install wandb
# + id="-ojIGLxZU1eK"
import os
os.chdir("/content/transformers/examples/")
os.chdir("./language-modeling")
# !pip install -r requirements.txt
# + colab={"base_uri": "https://localhost:8080/", "height": 105} id="9Z51w4XLXjh-" outputId="5ba7017c-1f7a-4feb-df0a-73f84bacf84d"
import wandb
wandb.login()
# + colab={"base_uri": "https://localhost:8080/"} id="yIpfn72NV9Md" outputId="c7e068df-bdac-4094-d8a7-ae5ac494c6b4"
# %env WANDB_PROJECT=project-code-py
# !python run_clm.py \
# --model_type gpt2 \
# --model_name_or_path gpt2 \
# --train_file "/content/train_tmp.txt" \
# --do_train \
# --validation_file "/content/eval_tmp.txt" \
# --do_eval \
# --per_device_train_batch_size 1 \
# --per_device_eval_batch_size 1 \
# --save_steps -1 \
# --num_train_epochs 5 \
# --fp16 \
# --output_dir="/content/model" \
# --report_to wandb
# + id="NXsM18Oe-1hf"
|
notebooks/model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# To follow this tutorial, you need to install the [geemap] and [xarray_leaflet](https://github.com/davidbrochart/xarray_leaflet/tree/master/xarray_leaflet) Python packages. Use the following conda commmands to create a conda env and install packages:
#
# - `conda create -n gee python`
# - `conda activate gee`
# - `conda install mamba -c conda-forge`
# - `mamba install geemap xarray_leaflet -c conda-forge`
# Import libraries
import os
import geemap
# Specify input raster datasets
out_dir = os.path.join(os.path.expanduser('~'), 'Downloads')
landsat = os.path.join(out_dir, 'landsat.tif')
dem = os.path.join(out_dir, 'dem.tif')
# Download samples raster datasets
#
# More datasets can be downloaded from https://viewer.nationalmap.gov/basic/
if not os.path.exists(landsat):
landsat_url = 'https://drive.google.com/file/d/1EV38RjNxdwEozjc9m0FcO3LFgAoAX1Uw/view?usp=sharing'
geemap.download_from_gdrive(landsat_url, 'landsat.tif', out_dir, unzip=False)
if not os.path.exists(dem):
dem_url = 'https://drive.google.com/file/d/1vRkAWQYsLWCi6vcTMk8vLxoXMFbdMFn8/view?usp=sharing'
geemap.download_from_gdrive(dem_url, 'dem.tif', out_dir, unzip=False)
# Create an interactive map
Map = geemap.Map()
# Add local raster datasets to the map
#
# More colormap can be found at https://matplotlib.org/3.1.0/tutorials/colors/colormaps.html
Map.add_raster(dem, colormap='terrain', layer_name='DEM')
Map.add_raster(landsat, bands=[5, 4, 3], layer_name='Landsat')
# Display the map
Map
|
examples/notebooks/25_load_rasters.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] heading_collapsed=true
# # PA003: Churn Predict
# -
# # 0.0 Import
# +
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import inflection
import math
import pickle
import inflection
from IPython.core.display import HTML
from scipy.stats import shapiro, chi2_contingency
from sklearn import preprocessing as pp
from scikitplot.metrics import plot_cumulative_gain, plot_lift_curve
# from boruta import BorutaPy
from BorutaShap import BorutaShap
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score, GridSearchCV
from sklearn.metrics import confusion_matrix, f1_score, recall_score, precision_score, accuracy_score, classification_report
from catboost import CatBoostClassifier, metrics, Pool
from xgboost import XGBClassifier
from imblearn.combine import SMOTETomek
# from sklearn.preprocessing import StandardScaler, MinMaxScaler , RobustScaler
import warnings
warnings.filterwarnings("ignore")
# -
# ## 0.1.Helper function
def my_settings():
# %matplotlib inline
# plotly settings
plt.style.use( 'ggplot' )
plt.rcParams['figure.figsize'] = [25, 12]
plt.rcParams['font.size'] = 8
# notebook settings
display(HTML('<style>.container{width:100% !important;}</style>'))
np.set_printoptions(suppress=True)
pd.set_option('display.float_format', '{:.3f}'.format)
# seaborn settings
sns.set(rc={'figure.figsize':(25,12)})
sns.set_theme(style = 'darkgrid', font_scale = 1)
my_settings()
# +
def numerical_descriptive_statistical(num_attributes):
"""
Shows the main values for descriptive statistics in numerical variables.
Args:
data ([float64 and int64]): Insert all numerical attributes in the dataset
Returns:
[dataframe]: A dataframe with mean, median, std deviation, skewness, kurtosis, min, max and range
"""
# Central Tendency - Mean, Median
ct1 = pd.DataFrame(num_attributes.apply(np.mean)).T
ct2 = pd.DataFrame(num_attributes.apply(np.median)).T
# Dispersion - std, min, max, range, skew, kurtosis, Shapiro-Wilk Test
d1 = pd.DataFrame(num_attributes.apply(np.std)).T
d2 = pd.DataFrame(num_attributes.apply(min)).T
d3 = pd.DataFrame(num_attributes.apply(max)).T
d4 = pd.DataFrame(num_attributes.apply(lambda x: x.max() - x.min())).T
d5 = pd.DataFrame(num_attributes.apply(lambda x: x.skew())).T
d6 = pd.DataFrame(num_attributes.apply(lambda x: x.kurtosis())).T
d7 = pd.DataFrame(num_attributes.apply(lambda x: 'not normal' if shapiro(x.sample(5000))[1] < 0.05 else 'normal')).T
# concatenate
m = pd.concat([d2, d3, d4, ct1, ct2, d1, d5, d6, d7]).T.reset_index()
m.columns = ['attributes', 'min', 'max', 'range', 'mean', 'median', 'std', 'skew', 'kurtosis', 'shapiro']
return m
def categorical_descriptive_statstical(data , col):
"""
Shows the the absolute and percent values in categorical variables.
Args:
data ([object]): Insert all categorical attributes in the dataset
Returns:
[dataframe]: A dataframe with absolute and percent values
"""
return pd.DataFrame({'absolute' : data[col].value_counts() , 'percent %': data[col].value_counts(normalize = True) * 100})
# +
def correlation_matrix(data , method):
"""Generates a correlation matrix of numerical variables
Args:correlation_matrix
data ([DataFrame]): [The dataframe of the EDA]
method ([string]): [The method used, it can be ‘pearson’, ‘kendall’ or ‘spearman’]
Returns:
[Image]: [The correlation matrix plot made with seaborn]
"""
# correlation
num_attributes = data.select_dtypes( include = ['int64' , 'float64'])
correlation = num_attributes.corr( method = method)
# correlation.append('exited')
# df_corr = data[correlation].reset_index(drop=True)
# df_corr['exited'] = df_corr['exited'].astype('int')
# mask
mask = np.zeros_like(correlation)
mask = np.triu(np.ones_like(correlation , dtype = np.bool))
# plot - mask = mask ,
ax = sns.heatmap(correlation , fmt = '.2f' , vmin = -1 , vmax = 1, annot = True, cmap = 'YlGnBu' , square = True)
return ax
# +
def without_hue(plot, feature):
total = len(feature)
for p in plot.patches:
percentage = '{:.1f}%'.format(100 * p.get_height()/total)
x = p.get_x() + p.get_width() / 2 - 0.05
y = p.get_y() + p.get_height()
plot.annotate(percentage, (x, y), size = 12)
def plot_cat_overview(df, cat_attributes, target):
cat_attributes.remove(target)
plots_lin = math.ceil(len(cat_attributes)/2)
fig, axs = plt.subplots(plots_lin,2, figsize=(25, 10), facecolor='w', edgecolor='k')
fig.subplots_adjust(hspace = .5, wspace=.20)
axs = axs.ravel()
for c in range(len(cat_attributes)):
ax1 = sns.countplot(ax=axs[c], x=cat_attributes[c],hue=target, data=df)
without_hue(ax1,df1.exited)
# -
def sum_of_na (data):
return pd.DataFrame({'Sum of NA' : data.isna().sum(), '% NA': data.isna().sum()/data.shape[0]})
def lift_score(y, y_pred, **kwargs):
df = pd.DataFrame()
df['true'] = y
df['pred'] = y_pred
df.sort_values('pred', ascending=False, inplace=True)
N = len(df)
churn_total = df['true'].sum() / N
n = int(np.ceil(.1 * N))
data_here = df.iloc[:n, :]
churn_here = data_here['true'].sum() / n
lift = churn_here / churn_total
return lift
def knapsack(W, wt, val):
n = len(val)
K = [[0 for x in range(W + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
K[i][w] = 0
elif wt[i-1] <= w:
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
max_val = K[n][W]
keep = [False] * n
res = max_val
w = W
for i in range(n, 0, -1):
if res <= 0: break
if res == K[i - 1][w]: continue
else:
keep[i - 1] = True
res = res - val[i - 1]
w = w - wt[i - 1]
del K
return max_val, keep
# ## 0.2. Loading Data
df_raw = pd.read_csv(r'~/repositorio/churn_predict/data/raw/churn.csv')
df_raw.head()
# # 1.0. Data Description
#
# - **RowNumber** : O número da coluna.
# - **CustomerID** : Identificador único do cliente.
# - **Surname** : Sobrenome do cliente.
# - **CreditScore** : A pontuação de Crédito do cliente para o mercado de consumo.
# - **Geography** : O país onde o cliente reside.
# - **Gender** : O gênero do cliente.
# - **Age** : A idade do cliente.
# - **Tenure** : Número de anos que o cliente permaneceu ativo.
# - **Balance** : Valor monetário que o cliente tem em sua conta bancária.
# - **NumOfProducts** : O número de produtos comprado pelo cliente no banco.
# - **HasCrCard** : Indica se o cliente possui ou não cartão de crédito.
# - **IsActiveMember** : Indica se o cliente fez pelo menos uma movimentação na conta bancário dentro de 12 meses.
# - **EstimateSalary** : Estimativa do salário mensal do cliente.
# - **Exited** : Indica se o cliente está ou não em Churn.
df1 = df_raw.copy()
df1.columns
df1.duplicated('CustomerId').sum()
df1.info()
# ## 1.1 Rename Columns
# +
old_columns=list(df1.columns)
snakecase = lambda x : inflection.underscore(x)
new_columns = map(snakecase , old_columns)
# rename columns
df1.columns = new_columns
# -
# ## 1.2. Data Dimensions
print('Numbers of rows: {}'.format(df1.shape[0]))
print('Numbers of cols: {}'.format(df1.shape[1]))
# ## 1.3. Data Types
df1.head()
df1.dtypes
# ### 1.3.1. Change Data Types
df1.exited = df1.exited.astype('bool')
df1.has_cr_card = df1.has_cr_card.astype('bool')
df1.is_active_member= df1.is_active_member.astype('bool')
# ### 1.3.2. Check unique values
df1.nunique()
# ### 1.3.3. Remove Variables
cols_drop = ['row_number', 'surname', 'customer_id']
df1 = df1.drop(cols_drop , axis = 1)
# ## 1.4. Check NA
df1.isna().sum()
# ## 1.5. Data Descriptive
num_attributes = df1.select_dtypes(include=['int64', 'float64'])
cat_attributes = df1.select_dtypes(exclude=['int64', 'float64'])
# ### 1.5.1. Numerical Attributes
#
m = numerical_descriptive_statistical(num_attributes)
m
# ### 1.5.2. Categorical Attributes
#
cat_attributes.columns
x = df1[['geography' , 'exited']].groupby('geography').count().reset_index()
x
plot_cat_overview(cat_attributes, list(cat_attributes.columns), 'exited')
categorical_descriptive_statstical(cat_attributes , 'geography')
categorical_descriptive_statstical(cat_attributes , 'gender')
categorical_descriptive_statstical(cat_attributes , 'has_cr_card')
categorical_descriptive_statstical(cat_attributes , 'is_active_member')
categorical_descriptive_statstical(cat_attributes , 'exited')
# ### 1.5.3. Multivariate Analysis
#
#
correlation_matrix(df1 , 'spearman')
# ### 1.5.4. Outliers Numerical Attributes
#
num_cols = num_attributes.columns.tolist()
i = 1
for col in df1[num_cols]:
plt.subplot(2,3,i)
ax = sns.boxplot( data = df1 , x = col)
i += 1
# **Important informations:**
#
# - There are outliers in **credit_score, num_of_products and age**
# - The **churn ratio is 20.37%**
# - **70.6%** of the members **has credit card**
# - More than **50% of the clients** are **from France**
# # 2.0. Feature Engineering
#
df2 = df1.copy()
df2.head()
# ## 2.1. Balance_age
# +
# balance_per_age
balance_age = df2[['balance', 'age']].groupby('age').mean().reset_index()
balance_age.columns = ['age' , 'balance_age']
# merge
df2 = pd.merge(df2, balance_age, on = 'age' , how = 'left')
# -
# ## 2.2. Balance_country
#
# +
balance_country = df2.loc[:, ['geography', 'balance']].groupby('geography').mean().reset_index()
balance_country.columns = ['geography', 'balance_per_country']
# merge
df2 = pd.merge(df2, balance_country, on = 'geography', how = 'left')
# -
# ## 2.3. Balance_tenure
#
# +
balance_tenure = df2.loc[:, ['tenure', 'balance']].groupby('tenure').mean().reset_index()
balance_tenure.columns = ['tenure', 'LTV']
# merge
df2 = pd.merge(df2, balance_tenure, on = 'tenure', how = 'left')
# -
# ## 2.3. Salary_gender
#
# +
estimated_salary_gender = df2.loc[:, ['gender', 'estimated_salary']].groupby('gender').mean().reset_index()
estimated_salary_gender.columns = ['gender', 'estimated_salary_per_gender']
# merge
df2 = pd.merge(df2, estimated_salary_gender, on = 'gender', how = 'left')
# -
correlation_matrix(df2, 'pearson')
# # 3.0. Data Filtering
#
df3 = df2.copy()
# # 4.0. Exploratoria Data Analysis (EDA)
#
df4 = df3.copy()
# # 5.0. Data Preparation
#
df5 = df4.copy()
df5.columns
df5.head()
# +
df5.exited = df1.exited.astype('int64')
df5.has_cr_card = df1.has_cr_card.astype('int64')
df5.is_active_member= df1.is_active_member.astype('int64')
# -
# ## 5.1. Rescaling
# +
mms = pp.MinMaxScaler()
rbs = pp.RobustScaler()
#Balance
df5['balance'] = rbs.fit_transform(df5[['balance']].values)
#EstimatedSalary
df5['estimated_salary'] = rbs.fit_transform(df5[['estimated_salary']].values)
#LTV
df5['LTV'] = rbs.fit_transform(df5[['LTV']].values)
# -
# ## 5.2. Encoding
# +
#gender - label encoding
gender_dict = { 'Male':0 , 'Female':1 }
df5['gender'] = df5['gender'].map( gender_dict )
# #Geography - One Hot Encoding
# # one hot encoding encoding
df5 = pd.get_dummies(df5, prefix=['country'], columns=['geography'])
# df5 = pd.get_dummies(df5, prefix=['gender'], columns=['gender'])
# questions_encoding = {'False': 0,'True': 1}
# df5['is_active_member'] = df5['is_active_member'].map(questions_encoding )
# df5['has_cr_card'] = df5['has_cr_card'].map(questions_encoding)
# df5['exited'] = df5['exited'].map(questions_encoding)
# -
# ## 5.3. Balanicing Data Set
# +
x = df5.drop('exited', axis = 1)
y = df5.exited
x_train, x_test,y_train, y_test = train_test_split(x , y , test_size=0.33 , random_state = 42, stratify = y)
# +
# balance dataset
up_sampler = SMOTETomek(random_state=42 , n_jobs = -1)
x_train_res , y_train_res = up_sampler.fit_resample(x_train , y_train)
# +
fig , axes = plt.subplots(1,2, figsize = (25,5))
fig.suptitle('Comparation before x After Smote Tomek')
axes[0].set_title('Before Up sample')
ax1 = sns.countplot(ax = axes[0] , x=y_train)
axes[1].set_title('After Up sample')
ax1 = sns.countplot(ax = axes[1] , x=y_train_res)
# -
# # 6.0. Feature Selection
#
df6 = df5.copy()
# +
# no model selected default is Random Forest, we will use a CatBoostClassifier. If classification is True it is a Classification problem.
#cat_boruta = CatBoostClassifier(random_state=42)
# rf = RandomForestClassifier(n_jobs=-1 )
# Feature_Selector_rf = BorutaShap(model = rf,
# importance_measure='shap',
# classification=True)
# Feature_Selector_rf.fit(X=x_train_res, y=y_train_res, n_trials=100, verbose=True, train_or_test = 'train', random_state=42)
# +
model = XGBClassifier(n_jobs=-1 )
Feature_Selector_rf = BorutaShap(model = model,
importance_measure='shap',
classification=True)
Feature_Selector_rf.fit(X=x_train_res, y=y_train_res, n_trials=100, verbose=True, train_or_test = 'train', random_state=42)
# -
# Returns Boxplot of features
Feature_Selector_rf.plot(X_size=12, figsize=(12,8),
y_scale='log', which_features='all')
# + [markdown] heading_collapsed=true
# # 7.0. Machine Learning Modelling
#
# + hidden=true
df7 = df6.copy()
# + hidden=true
# + [markdown] heading_collapsed=true
# # 8.0. Performance Metrics
#
# + hidden=true
df8 = df7.copy()
# + hidden=true
# -
# # 9.0. Deploy to Production
#
df9 = df8.copy()
|
notebooks/.ipynb_checkpoints/v3.0_model_churn-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import load_model
from tkinter import *
import tkinter as tk
import win32gui
from PIL import ImageGrab, Image
# +
model = load_model('mnist-2-1.h5')
def predict_digit(img):
#resize image to 56x28 pixels
img = img.resize((56,28))
#convert rgb to grayscale
img = img.convert('L')
img = np.array(img)
# print('Image to be predicted...')
# plt.imshow(img, cmap = 'gray')
# plt.show()
#reshaping to support our model input and normalizing
img = img.reshape(1,28,56,1).astype(float)
img = img/255.0
#predicting the class
# the model predicts in batches, since we are just inferencing on one image threfore we just take the first array of
# ouptut in our variable 'res'.
res = model.predict([img])[0]
indices = res.argsort()[-2:][::-1]
res = [(indices[0], res[indices[0]]), (indices[1], res[indices[1]])]
return res[0], res[1]
class App(tk.Tk):
def __init__(self):
tk.Tk.__init__(self)
self.x = self.y = 0
# Creating elements
self.title('Handwritten Digit Recognition')
self.canvas = tk.Canvas(self, width=500, height=400, bg = 'black', cursor="cross")
self.label1 = tk.Label(self, text="Draw..", font=("Helvetica", 48))
self.label2 = tk.Label(self, text="Draw..", font=("Helvetica", 48))
self.classify_btn = tk.Button(self, text = "Recognise", command = self.classify_handwriting)
self.button_clear = tk.Button(self, text = "Clear", command = self.clear_all)
# Grid structure
self.canvas.grid(row=0, column=0, pady=0, sticky=W, rowspan = 2)
self.label1.grid(row=0, column=1,pady=0, padx=0)
self.label2.grid(row = 1, column = 1, pady = 0, padx = 0)
self.classify_btn.grid(row=2, column=1, pady=2, padx=2)
self.button_clear.grid(row=2, column=0, pady=2)
self.canvas.bind("<B1-Motion>", self.draw_lines) # event handler for mouse events
def clear_all(self):
self.canvas.delete("all")
def classify_handwriting(self):
# code to convert drawing on canvas to an image
HWND = self.canvas.winfo_id() # get the handle of the canvas
rect = win32gui.GetWindowRect(HWND) # get the coordinate of the canvas
a,b,c,d = rect
rect=(a+4, b+4, c-4, d-4) # padding to the image
im = ImageGrab.grab(rect)
# predict what the image is...
class_1, class_2 = predict_digit(im)
digit_1, acc_1 = class_1 #it holds the larger variable class_1
digit_2, acc_2 = class_2
self.label1.configure(text = str(digit_1)+ ',' + str(int(acc_1 * 100)) + '%\n')
if acc_2 > 0.1:
self.label2.configure(text = str(digit_2)+ ',' + str(int(acc_2 * 100)) + '%\n')
else:
self.label2.configure(text = '!')
def draw_lines(self, event):
# draw on the canvas
self.x = event.x
self.y = event.y
r= 9 # control the width of strokes
self.canvas.create_oval(self.x+r, self.y+r, self.x - r, self.y - r, fill='white',outline = 'white')
app = App()
mainloop()
# -
|
MNIST-2/App.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import gc
import os
import cv2
import sys
import json
import time
import timm
import torch
import random
import sklearn.metrics
from PIL import Image
from pathlib import Path
from functools import partial
from contextlib import contextmanager
import numpy as np
import scipy as sp
import pandas as pd
import torch.nn as nn
from torch.optim import Adam, SGD, AdamW
from torch.optim.lr_scheduler import CosineAnnealingLR
from torch.utils.data import DataLoader, Dataset
from albumentations import Compose, Normalize, Resize
from albumentations.pytorch import ToTensorV2
os.environ["CUDA_VISIBLE_DEVICES"]="2"
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
# -
# !nvidia-smi
# +
train_metadata = pd.read_csv("../../../resources/DF20-Mini/DanishFungi2020-Mini_train_metadata_DEV.csv")
print(len(train_metadata))
test_metadata = pd.read_csv("../../../resources/DF20-Mini/DanishFungi2020-Mini_test_metadata_DEV.csv")
print(len(test_metadata))
# +
train_metadata['image_path'] = train_metadata.apply(lambda x: '/local/nahouby/Datasets/DF20/' + x['image_path'].split('/SvampeAtlas-14.12.2020/')[-1], axis=1)
test_metadata['image_path'] = test_metadata.apply(lambda x: '/local/nahouby/Datasets/DF20/' + x['image_path'].split('/SvampeAtlas-14.12.2020/')[-1], axis=1)
train_metadata['image_path'] = train_metadata.apply(lambda x: x['image_path'].split('.')[0] + '.JPG', axis=1)
test_metadata['image_path'] = test_metadata.apply(lambda x: x['image_path'].split('.')[0] + '.JPG', axis=1)
train_metadata.head()
# +
@contextmanager
def timer(name):
t0 = time.time()
LOGGER.info(f'[{name}] start')
yield
LOGGER.info(f'[{name}] done in {time.time() - t0:.0f} s.')
def init_logger(log_file='train.log'):
from logging import getLogger, DEBUG, FileHandler, Formatter, StreamHandler
log_format = '%(asctime)s %(levelname)s %(message)s'
stream_handler = StreamHandler()
stream_handler.setLevel(DEBUG)
stream_handler.setFormatter(Formatter(log_format))
file_handler = FileHandler(log_file)
file_handler.setFormatter(Formatter(log_format))
logger = getLogger('Herbarium')
logger.setLevel(DEBUG)
logger.addHandler(stream_handler)
logger.addHandler(file_handler)
return logger
LOG_FILE = '../../logs/DF20M-ViTxCNN/EfficientNet-B3-224.log'
LOGGER = init_logger(LOG_FILE)
def seed_torch(seed=777):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
SEED = 777
seed_torch(SEED)
# -
class TrainDataset(Dataset):
def __init__(self, df, transform=None):
self.df = df
self.transform = transform
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
file_path = self.df['image_path'].values[idx]
label = self.df['class_id'].values[idx]
image = cv2.imread(file_path)
try:
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
except:
print(file_path)
if self.transform:
augmented = self.transform(image=image)
image = augmented['image']
return image, label
# +
HEIGHT = 224
WIDTH = 224
from albumentations import RandomCrop, HorizontalFlip, VerticalFlip, RandomBrightnessContrast, CenterCrop, PadIfNeeded, RandomResizedCrop
def get_transforms(*, data):
assert data in ('train', 'valid')
if data == 'train':
return Compose([
RandomResizedCrop(WIDTH, HEIGHT, scale=(0.8, 1.0)),
HorizontalFlip(p=0.5),
VerticalFlip(p=0.5),
RandomBrightnessContrast(p=0.2),
Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
),
ToTensorV2(),
])
elif data == 'valid':
return Compose([
Resize(WIDTH, HEIGHT),
Normalize(
mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
),
ToTensorV2(),
])
# +
N_CLASSES = len(train_metadata['class_id'].unique())
train_dataset = TrainDataset(train_metadata, transform=get_transforms(data='train'))
valid_dataset = TrainDataset(test_metadata, transform=get_transforms(data='valid'))
# +
# Adjust BATCH_SIZE and ACCUMULATION_STEPS to values that if multiplied results in 64 !!!!!1
BATCH_SIZE = 32
ACCUMULATION_STEPS = 2
EPOCHS = 100
WORKERS = 8
train_loader = DataLoader(train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=WORKERS)
valid_loader = DataLoader(valid_dataset, batch_size=BATCH_SIZE, shuffle=False, num_workers=WORKERS)
# +
from efficientnet_pytorch import EfficientNet
model = EfficientNet.from_pretrained('efficientnet-b3')
model._fc = nn.Linear(model._fc.in_features, N_CLASSES)
# +
from torch.optim.lr_scheduler import ReduceLROnPlateau
from sklearn.metrics import f1_score, accuracy_score, top_k_accuracy_score
import tqdm
with timer('Train model'):
accumulation_steps = ACCUMULATION_STEPS
n_epochs = EPOCHS
lr = 0.01
model.to(device)
optimizer = SGD(model.parameters(), lr=lr, momentum=0.9)
scheduler = ReduceLROnPlateau(optimizer, 'min', factor=0.9, patience=1, verbose=True, eps=1e-6)
criterion = nn.CrossEntropyLoss()
best_score = 0.
best_loss = np.inf
for epoch in range(n_epochs):
start_time = time.time()
model.train()
avg_loss = 0.
optimizer.zero_grad()
for i, (images, labels) in tqdm.tqdm(enumerate(train_loader)):
images = images.to(device)
labels = labels.to(device)
y_preds = model(images)
loss = criterion(y_preds, labels)
# Scale the loss to the mean of the accumulated batch size
loss = loss / accumulation_steps
loss.backward()
if (i - 1) % accumulation_steps == 0:
optimizer.step()
optimizer.zero_grad()
avg_loss += loss.item() / len(train_loader)
model.eval()
avg_val_loss = 0.
preds = np.zeros((len(valid_dataset)))
preds_raw = []
for i, (images, labels) in enumerate(valid_loader):
images = images.to(device)
labels = labels.to(device)
with torch.no_grad():
y_preds = model(images)
preds[i * BATCH_SIZE: (i+1) * BATCH_SIZE] = y_preds.argmax(1).to('cpu').numpy()
preds_raw.extend(y_preds.to('cpu').numpy())
loss = criterion(y_preds, labels)
avg_val_loss += loss.item() / len(valid_loader)
scheduler.step(avg_val_loss)
score = f1_score(test_metadata['class_id'], preds, average='macro')
accuracy = accuracy_score(test_metadata['class_id'], preds)
recall_3 = top_k_accuracy_score(test_metadata['class_id'], preds_raw, k=3)
elapsed = time.time() - start_time
LOGGER.debug(f' Epoch {epoch+1} - avg_train_loss: {avg_loss:.4f} avg_val_loss: {avg_val_loss:.4f} F1: {score:.6f} Accuracy: {accuracy:.6f} Recall@3: {recall_3:.6f} time: {elapsed:.0f}s')
if accuracy>best_score:
best_score = accuracy
LOGGER.debug(f' Epoch {epoch+1} - Save Best Accuracy: {best_score:.6f} Model')
torch.save(model.state_dict(), f'../../../checkpoints/DF20M-EfficientNet-B3-224_best_accuracy.pth')
if avg_val_loss<best_loss:
best_loss = avg_val_loss
LOGGER.debug(f' Epoch {epoch+1} - Save Best Loss: {best_loss:.4f} Model')
torch.save(model.state_dict(), f'../../../checkpoints/DF20M-EfficientNet-B3-224_best_loss.pth')
# -
torch.save(model.state_dict(), f'../../../checkpoints/DF20M-EfficientNet-B3-224-100E.pth')
|
experiments/DF20-Mini-ViTxCNN/EfficientNet-B3-224.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (learn-env)
# language: python
# name: learn-env
# ---
# # VAR Model - Predicting Housing Price
#
# This notebook demonstrates how I developed the VAR model for housing price prediction and made a price forecast for 12 months. Please read my data cleaning notebook for data cleaning, descriptive statistics, and EDA.
#
# Contents of this notebook:
# 1. Granger Causality Test and Dickey-Fuller Test
#
# 2. Modeling (Grid Search)
#
# 3. Model Validation
#
# 3. Forecasting
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.stattools import grangercausalitytests, adfuller
from statsmodels.tsa.api import VAR
import statsmodels.api as sm
from matplotlib.pylab import rcParams
import itertools
import warnings
warnings.filterwarnings('ignore')
# -
# First, I read a housing market dataset. USPS's population inflow data has alredy been merged to this dataset. For detailed data cleaning process and EDA, please read my data cleaning notebook.
df = pd.read_csv('Data/df_realtor.csv')
print('Realtor housing price data covers from', df.yearmonth.min(), 'to' , df.yearmonth.max())
print('The data includes', df.zips.nunique(), 'zipcodes.' )
# For the time series analysis, I change the date to the datetime format and set date and zip code in indexes.
# +
# change zips to 5 digit strings
df['zipcode'] = '000' + df.zips.astype('str')
df['zipcode'] = df.zipcode.str[-5:]
# change 'date' to the datatime
df['date']=pd.to_datetime(df.yearmonth, format='%Y%m')
# Set multiindex with date and zip code
df = df.set_index(['zipcode', 'date']).sort_index()
# -
# I double-check that this data frame incldues only zip codes in Washington DC metropolitan area.
# +
# Zip codes included in Washington DC metropolitan area
WashingtonDC = df[df['czname']=='Washington DC']
WashingtonDC.index.get_level_values(0).unique()
# -
# Drop unecessary columns. The model use three time series; listings price, number of listings, and population net inflow.
# +
DC = WashingtonDC[['median_listing_price', 'active_listing_count', 'netinflow']].dropna()
DC
# -
# Before start analysis, I split my data set into train and test set. I use the 2021-09 as a cutoff month. As a consequence, train set has 44 observation and test set has 4 observations.
# +
# use 2021-09 as the cutoff point
train_data = DC.iloc[DC.index.get_level_values('date') < '2021-09']
test_data = DC.iloc[DC.index.get_level_values('date') >= '2021-09']
# -
print('Number of observation in train set for each zip code:', len(train_data.index.unique(level='date')))
print('Number of observation in test set for each zip code:', len(test_data.index.unique(level='date')))
# # 1. Granger Causality Test and Dickey Fuller Test
# ### Granger’s Causality Test
# First, I run the Granger causality test for three time series in my model. I check the causality between all possible combinations of three time series. If the P-Values are smaller than 0.05, I drop the corresponding zip code from my sample.
# Below, I created a function for granger causality test.
#
# +
maxlag=12
test = 'ssr_chi2test'
def grangers_causation_matrix(data, variables, test='ssr_chi2test', verbose=False):
"""This function returns p-values of Granger causality test of all combinations of the time series.
The rows are the response variable, columns are predictors
data : pandas dataframe containing the time series variables
variables : list containing names of the time series variables
"""
df = pd.DataFrame(np.zeros((len(variables), len(variables))), columns=variables, index=variables)
for c in df.columns:
for r in df.index:
test_result = grangercausalitytests(data[[r, c]], maxlag=maxlag, verbose=False)
p_values = [round(test_result[i+1][0][test][1],4) for i in range(maxlag)]
if verbose: print(f'Y = {r}, X = {c}, P Values = {p_values}')
min_p_value = np.min(p_values)
df.loc[r, c] = min_p_value
df.columns = [var + '_x' for var in variables]
df.index = [var + '_y' for var in variables]
return df
# -
# I run the granger causality check for all zip codes and drop the zip codes which failed the test.
# +
# To store zip codes which failed the test
drop_list=[]
# list of zip codes
zips=train_data.index.get_level_values(0).unique()
for x in zips:
# Check granger causality and store in the data frame
g = pd.DataFrame(grangers_causation_matrix(train_data.loc[(x, ),], variables = train_data.columns))
# Check each p-value in the stored table. If one of the p-values are greater than 0.05, add the zip code in drop list.
if max(g.iloc[1,0], g.iloc[2,0], g.iloc[0,1], g.iloc[2,1], g.iloc[0,2], g.iloc[1,2]) > 0.1:
drop_list.append(x)
print(f'The following {len(drop_list)} zip codes failed the Granger Causality test:', drop_list)
# -
# I drop the above zip codes.
train_df = train_data.drop(drop_list)
test_df = test_data.drop(drop_list)
all_df = DC.drop(drop_list)
# ### Dickey-Fuller Test
# I performed the Dickey-Fuller test for stationarity check of a time series.
# Below, I conducted the ADFuller test three times. The first test was with an original time series (i.e., no differencing, no moving average). And if a zip code fails this first test, I take a difference of a time series and redo the Dickey-Fuller test. If failed again, I take the second difference and try the ADFuller test. And any zip codes which failed the test with a second difference were dropped from this analysis.
#
# To run the test throughout all zip codes in my sample, first, I run the test and store the result in the data frame. And then, I evaluate the p-value and filter the zip code that failed the test. Zip codes that passed the first test are stored in 'diff0' list. Zip codes which need a second test with difference terms, I stored in 'diff1'.
# +
# For each time series I tun the Dickey-Fuller test and report the p-values
# to store the results
dtest = pd.DataFrame()
df_p = []
df_l = []
df_m = []
Zipcode = []
zips = train_df.index.unique(level='zipcode')
for x in zips:
p_val_1 = adfuller(train_df.loc[(x, ),]['median_listing_price'])[1] # extract p-value
p_val_2 = adfuller(train_df.loc[(x, ),]['active_listing_count'])[1]
p_val_3 = adfuller(train_df.loc[(x, ),]['netinflow'])[1]
df_p.append(p_val_1)
df_l.append(p_val_2)
df_m.append(p_val_3)
Zipcode.append(x)
dtest['Zipcode'] = Zipcode
dtest['Dickey_Fuller_p'] = df_p
dtest['Dickey_Fuller_l'] = df_l
dtest['Dickey_Fuller_m'] = df_m
dtest.head()
# -
# The cell below filters out the zip codes by p-value. If it's smaller than 0.05, the zipcode is stored in 'diff0'. If it's larger than 0.05, the zipcode is sotred in 'diff1'.
# +
# Create a new column of maximum value of three Dickey_fuller p-values. Use this column to decide which zipcode need to take a difference.
dtest['max_p'] = dtest[['Dickey_Fuller_p','Dickey_Fuller_l','Dickey_Fuller_m']].max(axis=1)
#List of zipcode which pass Dickey-Fuller test without taking difference
diff0 = list(dtest[dtest.max_p <=0.05].Zipcode)
# List a zipcode which failed Dickey-Fuller test, thus need to take difference
diff1 = list(dtest[dtest.max_p > 0.05].Zipcode)
print( f'{ len(diff0)} zipcodes passed DF test in original scale.')
print( f'{ len(diff1)} zipcodes failed, so I take a difference and try again.')
# -
# I take a difference and redo Dickey-fuller test.
# +
# for each series check Dickey-Fuller test and report the p-values
# to store the test results
dtest1 = pd.DataFrame()
df_p = []
df_l = []
df_m = []
Zipcode = []
# now I do test only for the counties which failed the earlier test
zips = diff1
for x in zips:
p_val_1 = adfuller(train_df.diff().dropna().loc[(x, ),]['median_listing_price'])[1] # extract p-value
p_val_2 = adfuller(train_df.diff().dropna().loc[(x, ),]['active_listing_count'])[1]
p_val_3 = adfuller(train_df.diff().dropna().loc[(x, ),]['netinflow'])[1]
df_p.append(p_val_1)
df_l.append(p_val_2)
df_m.append(p_val_3)
Zipcode.append(x)
dtest1['Zipcode'] = Zipcode
dtest1['Dickey_Fuller_p'] = df_p
dtest1['Dickey_Fuller_l'] = df_l
dtest1['Dickey_Fuller_m'] = df_m
dtest1.head()
# -
# In below, I filter the zip codes which failed the second DF test.
# +
# Create a new column of maximum value of three Dickey_fuller p-values. Use this column to decide which zipcode need to take a difference.
dtest1['max_p'] = dtest1[['Dickey_Fuller_p','Dickey_Fuller_l','Dickey_Fuller_m']].max(axis=1)
#List of zipcode which pass Dickey-Fuller test without taking difference
diff1_1 = list(dtest1[dtest1.max_p <=0.05].Zipcode)
# List a zipcode which failed Dickey-Fuller test, thus need to take difference
diff2 = list(dtest1[dtest1.max_p > 0.05].Zipcode)
print( f'{ len(diff1_1)} zipcodes passed DF test after taking a first difference.')
print( f'{ len(diff2)} zipcodes failed, so I take a second difference and try again.')
# +
# for each series check Dickey-Fuller test and report the p-values
dtest2 = pd.DataFrame()
df_p = []
df_l = []
df_m = []
Zipcode = []
zips = diff2
for x in zips:
p_val_1 = adfuller(train_df.diff().diff().dropna().loc[(x, ),]['median_listing_price'])[1] # extract p-value
p_val_2 = adfuller(train_df.diff().diff().dropna().loc[(x, ),]['active_listing_count'])[1]
p_val_3 = adfuller(train_df.diff().diff().dropna().loc[(x, ),]['netinflow'])[1]
df_p.append(p_val_1)
df_l.append(p_val_2)
df_m.append(p_val_3)
Zipcode.append(x)
dtest2['Zipcode'] = Zipcode
dtest2['Dickey_Fuller_p'] = df_p
dtest2['Dickey_Fuller_l'] = df_l
dtest2['Dickey_Fuller_m'] = df_m
dtest2.head()
# +
# Create a new column of maximum value of three Dickey_fuller p-values. Use this column to decide which zipcode need to take a difference.
dtest2['max_p'] = dtest2[['Dickey_Fuller_p','Dickey_Fuller_l','Dickey_Fuller_m']].max(axis=1)
#List of zipcode which pass Dickey-Fuller test without taking difference
diff2_1 = list(dtest2[dtest2.max_p <=0.05].Zipcode)
# List a zipcode which failed Dickey-Fuller test, thus need to take difference
diff3 = list(dtest2[dtest2.max_p > 0.05].Zipcode)
print( f'{ len(diff2_1)} zipcodes passed DF test in original scale.')
print( f'{ len(diff3)} zipcodes failed and will be dropped from the sample.')
# -
# In below, I drop the zipcodes which failed stationary test after taking 2nd order difference.
# drop from train, test, and alldateset.
train = train_df.drop(diff3)
test = test_df.drop(diff3)
alldata = all_df.drop(diff3)
# +
print(f'After Granger’s Causality and Dickey Fuller test, my sample includes {alldata.index.unique(level="zipcode").nunique()} zipcodes.' )
print(f'Converage periods are {alldata.index.unique(level="date").min()} to {alldata.index.unique(level="date").max()}.')
# -
# # 2. Modeling
# ### Rationality of using VAR (multivariate AR) model
# I chose VAR model for my housing price prediction. It includes three time series; (1)housing price times series (my main focus), (2) number of active listings in an area, and (3) population net inflow in an area. In a competitive market, housing price in each zip code is set by demand and supply in a market. In this model, the number of active listings is a supply variable, and net population inflow captures the size of the demand in an area. As I show in my EDA notebook, these three time series are closely related.
# ### Pre-processing to train the model individually for each zip code.
# I train a model for each zip code individually. To streamline the modeling process, I create a list of a data frame. Each data frame is for one zip code. In this way, I can use for loop to run grid search, model validation, and forecasting for all zip codes at once.
# I separate a list of a data frame by how many times I took the difference of a time series. Zip codes that passed the DF test without differencing, I stored in (diff0). Zip codes that took the first difference are in (diff1), and zip codes that took two times are in (diff2). This grouping helps me later when I roll back the differenced time series.
# +
# Define a list of data frames which took 1st difference.
# Original scale
train_orig1 = []
test_orig1 = []
test_orig1_1 = []
all_orig1 = []
# Differenced data
train_diff1 = []
test_diff1 = []
all_diff1 = []
# Store data in the lists
for x in diff1_1:
train_orig1.append(pd.DataFrame(train.loc[(x, ),]))
test_orig1.append(pd.DataFrame(test.loc[(x, ),]))
test_orig1_1.append(pd.DataFrame(test.loc[(x, ),])[1:])
all_orig1.append(pd.DataFrame(alldata.loc[(x, ),]))
train_diff1.append(pd.DataFrame(train.loc[(x, ),].diff().dropna()))
test_diff1.append(pd.DataFrame(test.loc[(x, ),].diff().dropna()))
all_diff1.append(pd.DataFrame(alldata.loc[(x, ),].diff().dropna()))
# +
# Define a list of data frames which takes 2nd difference.
# Original scale
train_orig2 = []
test_orig2 = []
test_orig2_1 = []
all_orig2 = []
# Differenced data
train_diff2 = []
test_diff2 = []
all_diff2 = []
# Store data in the lists
for x in diff2_1:
train_orig2.append(pd.DataFrame(train.loc[(x, ),]))
test_orig2.append(pd.DataFrame(test.loc[(x, ),]))
test_orig2_1.append(pd.DataFrame(test.loc[(x, ),])[2:])
all_orig2.append(pd.DataFrame(alldata.loc[(x, ),]))
train_diff2.append(pd.DataFrame(train.loc[(x, ),].diff().diff().dropna()))
test_diff2.append(pd.DataFrame(test.loc[(x, ),].diff().diff().dropna()))
all_diff2.append(pd.DataFrame(alldata.loc[(x, ),].diff().diff().dropna()))
# +
# List of data frame with no differencing
train_diff0 = []
test_diff0 = []
all_diff0 = []
# Store data in the lists
for x in diff0:
train_diff0.append(pd.DataFrame(train.loc[(x, ),]))
test_diff0.append(pd.DataFrame(test.loc[(x, ),]))
all_diff0.append(pd.DataFrame(alldata.loc[(x, ),]))
# -
# rename the dat frame
diff2 = diff2_1
diff1 = diff1_1
# ### Grid search for the order (P) of VAR model
# I run a grid search for each zip code to find the VAR model's best order using train data. For the model selection, I use AIC scores. Because the number of observations in my train dataset is very small for each zip code, I limit my search up to 4 lags.
def grid(data):
order = []
for i in [1,2,3,4]:
model = VAR(data)
results = model.fit(i)
order.append(results.aic)
order
min_value = min(order)
order = order.index(min_value)+1
return order
# In below, I run grid search function with training data for all zip codes. First, I run for zip codes in diff0 (data without differencing).
# +
# Run grid search for zip codes in diff0 and store the order in order0
order0 = []
for df, name in zip(train_diff0, diff0):
order = grid(df)
order0.append([name, order])
order0 = pd.DataFrame(order0, columns = ['name','order'])
order0
# -
# The table above report the order with the lowest AIC for each zip code in diff0 list.
#
# I do the same grid search for counties in diff1 list.
# +
# Grid search for zip codes in diff1 and store the order of the model in order0
order1 = []
# Use train_diff1 data (one time differenced train data)
for df, name in zip(train_diff1, diff1):
order = grid(df)
order1.append([name, order])
order1 = pd.DataFrame(order1, columns = ['name','order'])
order1.head()
# -
# Finally, I run the grid search for counties in diff2 list.
# +
# Grid search for zip codes in diff2 and store the order of the model in order0
order2 = []
# use train_diff2 data (two times differenced data)
for df, name in zip(train_diff2, diff2):
order = grid(df)
order2.append([name, order])
order2 = pd.DataFrame(order2, columns = ['name','order'])
order2.head()
# -
# The best orders with the lowest AIC for each zip code is now stored in a data frame named order0, order1, order2.
#
#
# ### Model Validation with test time series
#
# Next, I train the model with selected order from above, and check the model's prediction accuracy using the test time series. For the accuracy score, I use Root Mean Squared Error (RMSE).
#
# In the cell below, I define a function which fits training data on the tuned model and get the prediction for the test period.
# +
# Fit training data on the model with selected order.
# Make prediction for the test period.
def fitpredict(train, test, zip_df, order_df): # training data (train_diff0-2), list of zipcodes(diff_df0-2), VAR order(order0-2)
# To store the prediction
prediction = []
for train_df, name in zip(train, zip_df):
# 1. Fit the training data into the model
model = VAR(train_df)
# get the number of order from the grid serach results
order = order_df.loc[order_df.name==name, 'order']
x = int(order)
model_fitted = model.fit(x)
# prediction period
month = pd.date_range('2021-09-01','2021-12-01', freq='MS')
# 2. Predict using the train data
# get the lag order of the fitted model to adjust the length of dataset
lag_order = model_fitted.k_ar
# input data for prediction
forecast_input = train_df.values[-lag_order:]
# Prediction for the test period (this case 2021-09-01 to 2021-12-01)
i = zip_df.index(name)
fc = model_fitted.forecast(y=forecast_input, steps=4) # steps = the test period #steps=len(test[i])
df_forecast = pd.DataFrame(fc, columns = ['median_listing_price','active_listing_count', 'netinflow'], index=month) #index=test[i].index
prediction.append(df_forecast)
return prediction
# -
# in below, I apply the fitpredict function for all zipcode.
# +
# Input the zipcodes, train data, and VAR order into fitprediction dunction.
# 0, 1, 2 indicates number of difference of time series, and zipcodes are stored by the number of difference.
predict0 = fitpredict(train_diff0, test_diff0, diff0, order0)
predict1 = fitpredict(train_diff1, test_diff1, diff1, order1)
predict2 = fitpredict(train_diff2, test_diff2, diff2, order2)
# -
# ### Rolling back differenced time series.
# Before evaluating the predicted values, I need to bring the differenced data back up to its original scale. In the following cels, I create a function to roll back the differenced data. For counties in diff1, I differenced the data one time, so the prediction is one time difference. To roll back to the original scale, I sum up all differences and add it back to the last observed data of the training set. The below is the function to roll back for the differenced data.
#
# The function below rolls back the first order differencing to the original scale.
# +
# This function roll back the first order differencing to get the original scale
def invert_diff1(df_train, df_forecast):
"""Revert back the first differencing to get the forecast to original scale."""
df_fc = df_forecast.copy()
columns = df_train.columns
for col in columns:
# create cumusum for forcasting (differenced data)
df_fc[str(col)+'_cumsum'] = df_fc[str(col)].cumsum()
# add a column of the last observed data from the training. Here, this training data should be stored in the original scale.
df_fc[str(col)+'_last'] = df_train[col].iloc[-1]
# add the acumulative change to the last observed data in original scale.
df_fc[str(col)+'_o'] = df_fc[str(col)+'_last'] + df_fc[str(col)+'_cumsum']
df_fc_o = df_fc[['median_listing_price_o', 'active_listing_count_o', 'netinflow_o']]
# rename the columns of df_fc_o to match with the original
df_fc_o.rename(columns={'median_listing_price_o':'median_listing_price', 'active_listing_count_o':'active_listing_count',
'netinflow_o': 'netinflow'}, inplace=True)
return df_fc_o
# -
# I apply the roll-back function defined above to one-time differenced time series.
# +
predict1_rolled = []
for df_train, df_pre, name in zip(train_orig1, predict1, diff1):
# apply invert difference function.
df_fc = invert_diff1(df_train, df_pre)
predict1_rolled.append(df_fc)
# -
# The next function rolls back the second order differencing to get the original scale.
# +
# This function roll back the second order differencing to get the original scale
def invert_diff2(df_train, df_forecast):
"""Revert back the second order differencing to get the forecast to original scale."""
df_fc = df_forecast.copy()
columns = df_train.columns
for col in columns:
# create cumulative sum of forcasting (= accumulative 2nd order change)
df_fc[str(col)+'_cumsum2d'] = df_fc[str(col)].cumsum()
# add a column of the last observed data from the training. Here, this training data should be stored in the original scale.
df_fc[str(col)+'_last'] = df_train[col].iloc[-1]
# add a column of the second last observed data from the training.
df_fc[str(col)+'_2last'] = df_train[col].iloc[-2]
# change of the second last observed and the last observed
df_fc[str(col)+'_change'] = df_fc[str(col)+'_last'] - df_fc[str(col)+'_2last']
# add the acumulative 2nd change + the last observed change + the last observed original data
df_fc[str(col)+'_o'] = df_fc[str(col)+'_last'] + df_fc[str(col)+'_change']+ df_fc[str(col)+'_cumsum2d']
df_fc_o = df_fc[['median_listing_price_o', 'active_listing_count_o', 'netinflow_o']]
# rename the columns of df_fc_o to match with the original
df_fc_o.rename(columns={'median_listing_price_o':'median_listing_price', 'active_listing_count_o':'active_listing_count',
'netinflow_o': 'netinflow'}, inplace=True)
return df_fc_o
# +
predict2_rolled = []
for df_train, df_pre, name in zip(train_orig2, predict2, diff2):
# apply invert difference function.
df_fc = invert_diff2(df_train, df_pre)
predict2_rolled.append(df_fc)
# -
# To calculate RMSE, I adjust the data frame for the first or second differenced time series. Because I took the difference after the train test split, the test data for these time series are fewer than the prediction. So I drop the corresponding rows from the prediction data.
#
# +
predict1_rolled_1 = []
for df, name in zip(predict1_rolled, diff1):
df1 = df[1:]
predict1_rolled_1.append(df1)
predict2_rolled_1 = []
for df, name in zip(predict2_rolled, diff2):
df2 = df[2:]
predict2_rolled_1.append(df2)
# -
# Using the rolled back prediction, I calculate RMSE.
# #### RMSE Function
def rmse(test, predict, zip_df):
# To store RMSE for each variables.
summary_rmse = pd.DataFrame()
RMSE1=[]
RMSE2=[]
RMSE3=[]
Zipcode=[]
for df, name in zip(predict, zip_df):
predict1 = df['median_listing_price']
predict2 = df['active_listing_count']
predict3 = df['netinflow']
i = zip_df.index(name)
test1 = test[i]['median_listing_price']
test2 = test[i]['active_listing_count']
test3 = test[i]['netinflow']
rmse1 = np.sqrt(mean_squared_error(test1, predict1))
rmse2 = np.sqrt(mean_squared_error(test2, predict2))
rmse3 = np.sqrt(mean_squared_error(test3, predict3))
Zipcode.append(name)
RMSE1.append(rmse1)
RMSE2.append(rmse2)
RMSE3.append(rmse3)
summary_rmse['Zipcode'] = Zipcode
summary_rmse['RMSE_price'] = RMSE1
summary_rmse['RMSE_listing'] = RMSE2
summary_rmse['RMSE_inflow'] = RMSE3
return summary_rmse
# I apply RMSE function for each zip code. RMSE for all zip codes are stored in one table as below.
# Calcuate RMSE by using rmse function
rmse_df0 = rmse(test_diff0, predict0, diff0)
rmse_df1 = rmse(test_orig1_1, predict1_rolled_1, diff1) #test_orig1,
rmse_df2 = rmse(test_orig2_1, predict2_rolled_1, diff2)
# Create one large dataframe wchich store the all RMSE
rmse_df = rmse_df0.append(rmse_df1).append(rmse_df2)
rmse_df
# #### Comparison with Naive model's RMSE
# To evaluate VAR model, I compare with RMSE of naive model. Naive model for the time series is shifting the time series by one period. So, the next week's revenue change is equal to today's revenue change. In below, I calcuate RMSE of naive model for all zip codes.
# +
# Calculate a prediction by naive model
def rmse_naive(data, zip_df):
# to store RMSE for all zipcodes
rmse_df = pd.DataFrame()
rmse_naive = []
Zipcode = []
for df, name in zip(data, zip_df):
# Get housing price
price = df['median_listing_price']
# Naive model prediction
naive = price.shift(1)
# Calculate RMSE
rmse = np.sqrt(mean_squared_error(price[1:], naive.dropna()))
# store
rmse_naive.append(rmse)
Zipcode.append(name)
# store results in data frame
rmse_df['RMSE_naive'] = rmse_naive
rmse_df['Zipcode'] = Zipcode
return rmse_df
# -
# Using the anove function, I calculate the naive model RMSE for all zip codes.
# Calcuate naive model RMSE
rmse_naive0 = rmse_naive(all_diff0, diff0)
rmse_naive1 = rmse_naive(all_diff1, diff1) #test_orig1,
rmse_naive2 = rmse_naive(all_diff2, diff2)
# Create one large dataframe wchich store the all RMSE
rmse_naive_df = rmse_naive0.append(rmse_naive1).append(rmse_naive2)
rmse_naive_df.head()
# Comparison
# Merge to VAR's rmse table
rmse_df_1 = rmse_df.merge(rmse_naive_df, on='Zipcode', how='left')
# Compare
rmse_df_1.describe()
# RMSE of housing price by VAR model widely varies across zipcodes (from 3641 to 545165). Median RMSE is 32300. Given the majority of housing pice are around 600,000, this prediction is not bad. My model's prediction will be off the real value by 6%.
#
# Comparison with narive model RMSE shows that mean, median, min, max values of RMSE for the VA model is significantly lower than naive model's RMSE. So, my VAR model improved the prediction accuracy.
#
#
# # 4 Forecasting
#
# I forecast the housing price for 2022 for all zip codes. First, I fit the model into an entire sample. Using that model, I make an out-of-sample prediction.
#
# In the function below, I fit the model on the complete dataset and get a forecast for 2022 for zip code. The following function is almost identical to the earlier fitprediction function with minor changes.
# +
def forecast(data, zip_df, order_df): # complete dataset (all_diff0-2), list of zipcodes(diff_df0-2), VAR order(order0-2)
"""
Input: complete train data, list of county ids, and exogenous data.
Output: predictions
"""
# To store 12 months forecast
forecast12 = []
for df, zipcode in zip(data, zip_df):
# 1. Fit the model on the complete dataset
model = VAR(df)
# get the number of order from the grid serach results
order = order_df.loc[order_df.name==zipcode, 'order']
x = int(order)
model_fitted = model.fit(x)
# 2. Get forecast for the next 12 month
# get the lag order of the fitted model
lag_order = model_fitted.k_ar
# input data for forecasting
forecast_input = df.values[-lag_order:]
# forecasting months
month = pd.date_range('2022-01-01','2022-12-01', freq='MS')
# Get forecast for 2022-01-01 to 2022-12-01)
fc = model_fitted.forecast(y=forecast_input, steps=12) # steps = the test period
df_forecast = pd.DataFrame(fc, columns = ['median_listing_price','active_listing_count', 'netinflow'], index=month) #, index=month
forecast12.append(df_forecast)
return forecast12
# -
# Apply the function and get prediction.
# +
# Input the zipcodes, train data, and VAR order into fitprediction dunction.
# 0, 1, 2 indicates number of difference of time series, and zipcodes are stored by the number of difference.
forecast0 = forecast(all_diff0, diff0, order0)
forecast1 = forecast(all_diff1, diff1, order1)
forecast2 = forecast(all_diff2, diff2, order2)
# -
# #### Rolling back differenced time series.
# Using invert_diff function created earlier, I roll back the differenced time series (diff1 and diff2) to its original scale.
# First, I apply the invert_diff1 function to roll back the first order differencing to get the original scale
# +
forecast1_rolled = []
for df_train, df_pre, name in zip(train_orig1, forecast1, diff1):
# apply invert difference function.
df_fc = invert_diff1(df_train, df_pre)
forecast1_rolled.append(df_fc)
# -
# Next, I apply the invert_diff2 function to roll back the second order differencing to get the original scale
forecast2_rolled = []
for df_train, df_pre, name in zip(train_orig2, forecast2, diff2):
# apply invert difference function.
df_fc = invert_diff2(df_train, df_pre)
forecast2_rolled.append(df_fc)
# ### Store forecast in one data frame
#
# Forecasted values are stored in a separate data by number of differencing. In the cell below, I create a one large data frame which sored forecasted value in one data frame.
# +
# Store forecasted values in list of data frame format.
forecast0_df = []
for df_pre, name in zip(forecast0, diff0):
df_pre['zipcode']=name
forecast0_df.append(df_pre)
forecast1_df = []
for df_pre, name in zip(forecast1_rolled, diff1):
df_pre['zipcode']=name
forecast1_df.append(df_pre)
forecast2_df = []
for df_pre, name in zip(forecast2_rolled, diff2):
df_pre['zipcode']=name
forecast2_df.append(df_pre)
# merge a list of DataFrames into a single DataFrame
fc_0 = pd.concat(forecast0_df)
fc_1 = pd.concat(forecast1_df)
fc_2 = pd.concat(forecast2_df)
# append fc_0, fc_1, fc_2
fc = fc_0.append(fc_1).append(fc_2)
# merge forecast dataframe and observed data
DC1 = DC.reset_index()
fc1 = fc.reset_index()
fc1.rename(columns={'index':'date'}, inplace=True )
dcforecast = DC1.merge(fc1, on = ['date','zipcode'], how='outer')
# forecast and observed price are currently in the different column. Now append forecast to the historic time series
dcforecast.median_listing_price_x.fillna(dcforecast.median_listing_price_y, inplace=True)
dcforecast.netinflow_x.fillna(dcforecast.netinflow_y, inplace=True)
dcforecast.active_listing_count_x.fillna(dcforecast.active_listing_count_y, inplace=True)
# Drop forecast columns and rename columns.
dcforecast.drop(['median_listing_price_y', 'active_listing_count_y', 'netinflow_y'], axis=1, inplace=True)
dcforecast.rename(columns={'median_listing_price_x': 'median_listing_price',
'active_listing_count_x':'active_listing_count', 'netinflow_x':'netinflow' }, inplace=True)
# -
# Finally, I calculate yearly changes of the forecast and save it in the csvfile.
# +
# Calcualte the yearly changes
dcforecast['change_price'] = dcforecast.groupby(['zipcode'])['median_listing_price'].pct_change(12)
dcforecast['change_listing'] = dcforecast.groupby(['zipcode'])['active_listing_count'].pct_change(12)
dcforecast['change_inflow'] = dcforecast.groupby(['zipcode'])['netinflow'].pct_change(12)
# # save in csv
fc.to_csv('Data/dcforecast12.csv', index=False)
DC.to_csv('Data/dchistoric.csv', index=False)
dcforecast.to_csv('Data/dcfull.csv', index=False)
# +
# Calcualte the yearly changes
# Set Multiinde x with daye and zip code
df_final = dcforecast.set_index(['zipcode', 'date']).sort_index()
# create a data frame which shifted by 12 month.
df_shifted = df_final.shift(12).head(20)
# merge shifted data and original data
df_shifted.reset_index(inplace=True)
df_final.reset_index(inplace=True)
df_save = df_final.merge(df_shifted, on=['zipcode', 'date'], how='left')
# calculate the year on year changes.
df_save['price_change'] = df_save.median_listing_price_x - df_save.median_listing_price_y
df_save['listing_change'] = df_save.active_listing_count_x - df_save.active_listing_count_y
df_save['inflow_change'] = df_save.netinflow_x - df_save.netinflow_y
# Drop unnecessary columns
drop=['median_listing_price_y', 'active_listing_count_y', 'netinflow_y', ]
df_save.drop(drop, axis=1, inplace=True)
df_save.rename(columns={'median_listing_price_x':'median_listing_price', 'active_listing_count_x':'active_listing_count',
'netinflow_x':'netinflow'}, inplace=True)
# -
df_save.to_csv('Data/housepricefc.csv')
|
Model1_VAR_HousingPrice.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Final Thoughts
#
# This brings us to the conlusion of the fundamentals of deep learning. This chapter is dedicated towards summarising what we have done and what the future challenges are at the time of writing.
#
# There are 3 fundamental layers in Deep Learning.
# 1. Dense Layers
# 2. Convolutional Layers
# 3. Recurrent Neural Nets (Rather LSTMs)
#
# An area that we have not covered in this course was combining all 3 different types. One such example would be caption generation where an image is 'read in' via CNN and this is put in through a LSTM to generate the relevant text. Another similar application is visual question answering where you have an image and you may ask questions about the image (eg. Is <NAME> sitting next to <NAME>?). In this case the inputs are an image (processed via a CNN) and the question processed via word embeddings and a LSTM. The main take away is that you should start thinking of Deep Learning problems as putting together Lego blocks, choosing the correct layer for the relevant input.
# 
# *Visual Question Answering [demo](https://github.com/anantzoid/VQA-Keras-Visual-Question-Answering)*
#
# Some of the DL methods that are variants of the above networks and are worth mentioning but are beyond the scope of fundamentals are:
# - [Attention Neural Nets](https://arxiv.org/abs/1409.0473):
#
# These are the current choice of NN when it comes to Translation. It allows the network to pay attention to which part of the text is being translated, while it simultaneously translates the text. Previously the whole sentence was read in before translation started.
# - [Fast R-CNN](https://arxiv.org/abs/1504.08083)
#
# Region based CNNs. These allow you to segment relevant objects from images/ videos and can be quite useful for tracking/ general creepiness.
# - [WaveNet](https://deepmind.com/blog/wavenet-generative-model-raw-audio/)
#
# Recently released by Google allows you to synthesise text to speech. The algorithm has been gettting faster and more human like in speech synthesis.
# - [Cycle GAN](https://github.com/junyanz/CycleGAN)
#
# The most famous example was of converting a horse to an image of a Zebra and vice versa (https://www.youtube.com/watch?v=9reHvktowLY). GANs will have quite alot of artistic applications in the future.
#
# Even if you do not understand the mathematics behind these algorithms most authors release the code. Then it is simply a matter of using it as you would any other software module.
#
# ## Exciting Future Prospects
# Reinforcement Learning is perhaps by far the most interesting area in DL. We have taught robots how to walk using RL but yet to teach them how to fold clothes. This may be done via a different method of Deep Learning called behavioural cloning where you learn by imitating humans.
# 
# *Distributional Bellman [Demo](https://flyyufelix.github.io/2017/10/24/distributional-bellman.html)*
#
# Considering how new GANs are there is quite a lot of interesting research in this area. Most of it has concentrated around how to train them as they are extremely difficult to train. However, cycle GAN, [pix2pix](https://affinelayer.com/pixsrv/) GANs are extensions of the original paper that came up with very interesting applications.
#
# Deep Learning still requires quite a large amount of examples for it to learn. Humans on the other hand only require a few examples to extrapolate from previous experience to understand what a given object is. [One shot learning](https://sorenbouma.github.io/blog/oneshot/) aims to use fewer examples to train Neural Networks.
#
# DL remains largely as black box devices. This may be good enough for most applications, however it also makes them susceptible. There were papers written recently on pixel level attacks on NNs which caused the image to be classified incorrectly which can have dangerous implications in robotics (eg. self driving cars). Understanding/ visualising Deep Learning remains an active area of research.
# 
# *From: [Attacking Machine Learning with Adversarial Examples](https://blog.openai.com/adversarial-example-research/)*
#
# ## Future Direction of DeepSchool.io
# The next few months will be heavily involved on making a course in Reinforcement Learning. I will also be converting the current content into PyTorch, unless Keras creates a PyTorch backend.
#
#
# ## Good Reads
# 1. [Software 2.0 by <NAME> - Director of AI, tesla](https://medium.com/@karpathy/software-2-0-a64152b37c35)
#
# ## People to Follow
# 1. <NAME> https://twitter.com/AndrewYNg
# 2. <NAME> https://twitter.com/karpathy
# 2. <NAME> (Keras Author) https://twitter.com/fchollet
# 3. Hardmaru https://twitter.com/hardmaru
# 4. <NAME> https://twitter.com/goodfellow_ian
# 3. <NAME> (RL researcher) https://twitter.com/awjuliani
#
|
DL-Keras_Tensorflow/Lesson 22 - Final Thoughts.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: default:Python
# language: python
# name: conda-env-default-py
# ---
# + [markdown] tags=[]
# # Hurricane Damage Image Classification
#
# This uses a newly created data set of hurricane damage photos to train and classify 5 common disaster response categories:
# - electricUtility
# - downTrees
# - fire
# - flood
# - structural damage
#
#
# It uses PyTorch (pytorch.org) and the DenseNet 161 dataset to fine-tune train the custom model on sagemaker studio lab (https://studiolab.sagemaker.aws) for our disaster recovery objective.
#
# ## Steps in this notebook
# In this notebook, we will go through a few steps, they are:
# 1. install packages
# 2. extrct disaster images
# 3. load the DenseNet-161
# 5. train(fine-tune) a model
# 6. test a model
# 7. show predictions graphs and confusion metrix
# 8. save the model
#
# ## Real-time predictions
# Once the model is saved to a tgz file, it is uploaded to an S3 buckert where an EC2 instance with a basic API used to get realtime predictions
#
# **This notebook is based on the AWS computervision examples for sagemaker studio** (https://github.com/aws/studio-lab-examples)
# + [markdown] tags=[]
# ## 1. Install packages
# -
# Here we'll install python packages for later use
#
# - **torch**: [PyTorch](https://pytorch.org/) is a Python package that provides two high-level features: (1) Tensor computation (like NumPy) with strong GPU acceleration (2) Deep neural networks built on a tape-based autograd system
#
# - **torchvision**: The torchvision package consists of popular datasets, model architectures, and common image transformations for computer vision.
#
# - **matplotlib**: Matplotlib is a plotting library for the Python programming language and its numerical mathematics extension NumPy.
# + tags=[]
# %pip install torch
# %pip install torchvision
# %pip install matplotlib
# %pip install sklearn
# #%pip install sagemaker
# -
import torch
import torchvision
# Use is_available() to determine if your system supports CUDA.
if torch.cuda.is_available():
device = "cuda:0"
else:
device = "cpu"
device
# + [markdown] tags=[]
# ## 2. Prepare dataset
#
# Next, you will need to download a Kaggle dataset manually from their [dataset download page](https://www.kaggle.com/pratik2901/multiclass-weather-dataset). Once you've done that, create a new folder here called "dataset", and upload those files into that directory.
#
# Please make sure your files looks like this once you are done.
# ```
# -- root
# -- notebook
# -- dataset
# -- cloudy
# -- rainy
# -- shine
# -- sunrise
# ```
# + tags=[]
# !unzip -o "training_dataset.tar"
# -
# ### 2.1 Reading Image Data
def GetImagesFromFolder(PATH, Class_Folder, ext):
"""
This module can be used to import image data.
It also takes care of resizing the images to 240x240 Pixels.
So that the images can be used for DenseNet-161 model fine-tuning.
"""
images = [Image.open(file).convert('RGB').resize((240,240),resample=Image.LANCZOS) for e in ext for file in glob.glob(PATH+Class_Folder+'/*.' + e)]
print(f"Found {len(images)} in folder {Class_Folder}")
np.random.shuffle(images)
return images,np.array([Class_Folder for i in range(len(images))])
# +
"""
Read the image from given path.
1. use LabelEncoder from sklearn to encode the folder names and the class number.
2. for each folder, add image and labels to ALL_IMAGES and ALL_LABEL.
"""
import os
import datetime
import glob
from PIL import Image
import numpy as np
from sklearn.preprocessing import LabelEncoder
DATA_PATH = './dataset/'
FOLDERS = os.listdir(DATA_PATH)
print(FOLDERS)
### if you found the folder contains other subfolder than the image classes,
### remove them before calling the label encoder
if os.path.exists("./dataset/.ipynb_checkpoints/"):
os.rmdir("./dataset/.ipynb_checkpoints/")
ALL_IMAGES,ALL_LABELS = [],[]
images_population ={}
ext = ['jpg','jpeg']
for Class_Folder in FOLDERS:
IMAGES,LABELS = GetImagesFromFolder(DATA_PATH,Class_Folder,ext)
images_population[Class_Folder] = LABELS.shape[0]
ALL_IMAGES.extend(IMAGES)
ALL_LABELS.extend(LABELS)
le = LabelEncoder().fit(FOLDERS)
print(le)
le_name_mapping = dict(zip(le.classes_, le.transform(le.classes_)))
print(le_name_mapping)
# -
#
# ### 2.2 Splitting Dataset to differernt splits for Training, Tesing & Validation:
from sklearn.model_selection import train_test_split
TRAIN_IMAGES, X_val_test, TRAIN_LABELS, y_val_test = train_test_split(ALL_IMAGES, ALL_LABELS, test_size=0.20, random_state=42,stratify=ALL_LABELS)
VAL_IMAGES, TEST_IMAGES, VAL_LABELS, TEST_LABELS = train_test_split(X_val_test, y_val_test, test_size=0.50, random_state=42,stratify=y_val_test)
# ### 2.3 Create Dataset class:
# +
from torch.utils.data import DataLoader,Dataset
class WeatherDataset(Dataset):
def __init__(self, ImageData, Target, transform=None):
self.ImageData = ImageData
self.Target = torch.LongTensor(le.transform(Target))
self.transform = transform
def __getitem__(self, index):
x = self.ImageData[index]
y = self.Target[index]
if self.transform:
x = Image.fromarray(np.uint8(np.array(self.ImageData[index]))) # Memory Efficient way
x = self.transform(x)
return x, y
def __len__(self):
return len(self.ImageData)
# + [markdown] tags=[]
# ## 3. Dataset Normalization
# This is a utility function to find out MEAN & STD for Normalizing Training Data
# +
from torchvision import transforms
def get_mean_std(loader):
# VAR[X] = E[X**2] - E[X]**2
channels_sum, channels_squared_sum, num_batches = 0,0,0
for data,_ in loader:
channels_sum +=torch.mean(data,dim=[0,2,3])
channels_squared_sum += torch.mean(data**2, dim=[0,2,3])
num_batches += 1
mean = channels_sum/num_batches
std = (channels_squared_sum/num_batches - mean**2)**0.5
return mean,std
batch_size = 14
transform = transforms.Compose([transforms.Resize((230,230)),transforms.ToTensor()])
dataset = WeatherDataset(TRAIN_IMAGES, TRAIN_LABELS, transform=transform)
loader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, num_workers=4)
mean,std = get_mean_std(loader)
print(f"Data loader has:\n*\tmean= {mean.tolist()}\n*\tstd= {std.tolist()}")
# +
transform = {'train':transforms.Compose([transforms.ColorJitter(),
transforms.RandomRotation(30),
transforms.Resize((240,240)),
transforms.RandomResizedCrop(230),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(mean=mean,std=std),#transforms.RandomErasing()
]),
'val':transforms.Compose([transforms.Resize((230,230)),
transforms.ToTensor()]),
'test':transforms.Compose([transforms.Resize((230,230)),
transforms.ToTensor()])}
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
batch_size = {'train':8, 'val':8,'test':8}
##{'downTrees': 0, 'electricUtility': 1, 'fire': 2, 'flood': 3, 'structural': 4}
## Confirm this with the cell output above
dataset_classes = ['downTrees', 'electricUtility', 'fire', 'flood', 'structural']
image_datasets = {'train': WeatherDataset(TRAIN_IMAGES, TRAIN_LABELS, transform=transform['train']),
'val': WeatherDataset(VAL_IMAGES, VAL_LABELS, transform=transform['val']),
'test': WeatherDataset(TEST_IMAGES, TEST_LABELS, transform=transform['test'])
}
dataset_sizes = {x: len(image_datasets[x]) for x in ['train', 'val','test']}
dataloaders = {indx: torch.utils.data.DataLoader(image_datasets[indx], batch_size=batch_size[indx], num_workers=4, pin_memory=True, shuffle=True)
for indx in batch_size.keys()}
print("Size for Dataset:\n\t* Train: %d\n\t* Valid: %d\n\t* Test: %d"%(dataset_sizes['train'],dataset_sizes['val'],dataset_sizes['test']))
# -
# ## 4. Load the DenseNet-161
import gc
def train_model(model, criterion, optimizer, model_checkpoint=0, early_stop = 10, num_epochs=5):
start_time = datetime.datetime.now().replace(microsecond=0)
model = model.to(device)
# number of epochs to train the model
valid_loss_min = np.Inf # track change in validation loss
early_stop_cnt = 0
last_epoch_loss = np.Inf
globaliter = 0
final_loss = np.Inf
for epoch in range(1, num_epochs+1):
globaliter+=1
# keep track of training and validation loss
train_loss = 0.0
valid_loss = 0.0
###################
# train the model #
###################
model.train()
train_corrects = 0
for data, target in dataloaders['train']:
data, target = data.to(device), target.to(device)
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
_, preds = torch.max(output, 1)
# calculate the batch loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update training loss
train_loss += loss.item()*data.size(0)
train_corrects += torch.sum(preds == target.data)
train_loss = train_loss/len(dataloaders['train'].dataset)
train_acc = (train_corrects.double()*100)/len(dataloaders['train'].dataset)
######################
# validate the model #
######################
model.eval()
val_corrects = 0
for data, target in dataloaders['val']:
data, target = data.to(device), target.to(device)
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
_, preds = torch.max(output, 1)
# calculate the batch loss
loss = criterion(output, target)
# update average validation loss
valid_loss += loss.item()*data.size(0)
val_corrects += torch.sum(preds == target.data)
# calculate average losses
valid_loss = valid_loss/len(dataloaders['val'].dataset)
valid_acc = (val_corrects.double()*100)/len(dataloaders['val'].dataset)
# print training/validation statistics
print('Epoch: {} \tTraining Loss: {:.6f} \tValidation Loss: {:.6f}'.format(epoch, train_loss, valid_loss))
print('\t\tTraining Acc: {:.3f} \t\tValidation Acc: {:.3f}'.format(train_acc, valid_acc))
# save model if validation loss has decreased
if valid_loss <= valid_loss_min:
print('\t\tValidation loss decreased ({:.6f} --> {:.6f}).'.format(valid_loss_min,valid_loss))
if model_checkpoint != 0:
torch.save(model.state_dict(), '/kaggle/working/model.pt'.format(train_acc, valid_acc))
print('Model Saved: /kaggle/working/model.pt'.format(train_acc, valid_acc))
valid_loss_min = valid_loss
elif valid_loss == np.nan:
print("Model Loss: NAN")
if (last_epoch_loss < valid_loss) and last_epoch_loss != np.Inf:
early_stop_cnt +=1
if early_stop_cnt == early_stop:
print('-'*50+"\nEarly Stopping Hit\n"+'-'*50)
break
else:
print('-'*50+f"\n\t\tEarly Stopping Step: {early_stop_cnt}/{early_stop}\n"+'-'*50)
else:
early_stop_cnt = 0
last_epoch_loss = valid_loss
print(f"Training Completed with best model having loss of {round(valid_loss_min,6)}")
del data,target
gc.collect()
end_time = datetime.datetime.now().replace(microsecond=0)
print(f'Time Taken: {end_time-start_time}')
return model
# +
from torchvision import models
import torch.nn as nn
#import torch.nn.functional as F
##This is the total number of classes and predictions
n_classes = 5
epochs = 10
n_classes = len(dataset_classes)
print(n_classes)
model_ft = models.densenet161(pretrained=True)
# Using Model as Feature Extractor
for param in model_ft.parameters():
param.requires_grad = False
num_ftrs = model_ft.classifier.in_features
model_ft.classifier = nn.Linear(num_ftrs, n_classes)
model_ft = model_ft.to(device)
# -
# ## 5. Fine-tune the pre-trained model on the labelled weather data
#
# Setup the hyperparameters, for example learning rate, momentum, decay and optimization function.
# +
import torch.optim as optim
# Cross Entropy Loss
criterion = nn.CrossEntropyLoss()
# SGD Optimizer
lr = 0.01
momentum = 0.5
decay = 0.01
optimizer_ft = optim.SGD(model_ft.parameters(), lr=lr, momentum = momentum, weight_decay = decay)
# -
print('Training of Model:')
model_ft = train_model(model_ft, criterion, optimizer_ft,model_checkpoint=0,num_epochs=epochs)
# ## 6. Test the model
# Visualize the predict label and the truth label
# +
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import itertools
def visualize_model(model, num_images=6):
was_training = model.training
model.eval()
images_so_far = 0
fig = plt.figure(figsize = (num_images,num_images))
with torch.no_grad():
for i, (inputs, labels) in enumerate(dataloaders['test']):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images//2, 2, images_so_far)
ax.axis('off')
ax.set_title(f'Predicted: {dataset_classes[preds[j]]} | Actual: {dataset_classes[labels[j]]}')
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
model.train(mode=was_training)
return
model.train(mode=was_training)
if device.type == 'cuda':
inputs = inputs.cpu()
labels = labels.cpu()
gc.collect()
# +
def imshow(img):
# Convert from tensor image
plt.imshow(np.transpose(img, (1,2,0)))
visualize_model(model_ft, num_images=50)
# -
# ## 7. Show predictions graphs and confusion metrix
# - [Confusion matrix](https://en.wikipedia.org/wiki/Confusion_matrix): In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as an error matrix, is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one.
# +
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
size = len(classes)*2
plt.figure(figsize = (size,size))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title,fontsize=20)
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes,fontsize=12)
plt.yticks(tick_marks, classes,fontsize=12)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label',fontsize=16)
plt.xlabel('Predicted label',fontsize=16)
def model_verification(loader,batch_size,model,n_classes=5):
classes = list(le.inverse_transform([i for i in range(n_classes)]))
prediction_list,label_list = [],[]
with torch.no_grad():
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
predicted = outputs.argmax(dim=1).detach()
prediction_list.extend(predicted.tolist())
label_list.extend(labels.tolist())
cm = confusion_matrix(prediction_list,label_list)
plot_confusion_matrix(cm, classes)
if device.type == 'cuda':
inputs = inputs.cpu()
labels = labels.cpu()
gc.collect()
# -
# + tags=[]
model_verification(dataloaders['val'],batch_size['val'],model_ft,n_classes=5)
# -
torch.save(model_ft, 'disaster_model_output.pth')
# +
#model_import2 = torch.load('model_weights.pth')
# -
|
hurricane_recovery_5classes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.6 64-bit (''univai'': conda)'
# language: python
# name: python37664bitunivaicondac2ef9ed280934475b3c4ee15c34f14c7
# ---
# # COVID-19 India Matplotlib Overview
# > Tracking coronavirus total cases, deaths and new cases in India
#
# - author: <NAME>
# - image: images/covid-overview.png
# - permalink: /covid-overview-linde-matplotlib-exp/
# - hide: false
# - badges: false
# +
#hide
## Import essential packages below
import pandas as pd
import numpy as np
import requests
import json
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import matplotlib as mpl
import seaborn as sns
from IPython.core.display import display,HTML
# %matplotlib inline
# +
#hide
# This is a helper dictionary we will use later to map between state abbrevations and names
url = 'https://raw.githubusercontent.com/hargun3045/dashboards/master/abb_dict.json'
r = requests.get(url)
abb_dict = r.json()
# +
#hide
#This helper function will be handy later to select only the columns which are days
#valid_i is a valid_index because sometimes raw data from api can have last column empty
def get_dates(df):
dt_cols = df.columns[~df.columns.isin(['stateABB','states'])]
valid_i = -1
for i in range(-1,-len(dt_cols),-1):
if not df[dt_cols[i]].fillna(0).eq(0).all():
valid_i = i
break
return valid_i, dt_cols
# +
#hide
# This giant function takes raw data from api and wrangles it into a nice dataframe for further processing
def get_frame(name):
# pdb.set_trace()
url = f'http://api.covid19india.org/states_daily_csv/{name}.csv'
df = pd.read_csv(url)
df.set_index('date',inplace = True)
df = df.T
df = df.iloc[:-1,:]
df.fillna(0,inplace=True)
df = df[df.columns].astype(int)
df = df.rename_axis('stateABB').reset_index()
df['states'] = df['stateABB'].map(abb_dict)
df = df[[df.columns[-1]] + list(df.columns[:-1])]
df =df.iloc[1:,:]
df = df[df.states.notna()]
df.sort_values(by = [df.columns[-1]], ascending = False, inplace = True)
df.drop(['stateABB'],axis = 1)
df = df.groupby('states').sum().cumsum(axis=1)
df.reset_index(inplace = True)
return df
# -
#hide
# We use above helper fucnction to get us timeseries dataframe for confirmed cases and deceased cases
dft_cases = get_frame('confirmed')
dft_deaths = get_frame('deceased')
#hide
# helper function get_dates used to find valid columns and index
#We also define two important column entries, today and yesterday
valid_i, dt_cols = get_dates(dft_cases)
dt_today = dt_cols[valid_i]
dt_yday = dt_cols[valid_i -1]
#hide
# Using groupby on timeseries dataframe to get latest cases, and past-cases (pcases)
#Here past cases are a day earlier, but this can be changed
dfc_cases = dft_cases.groupby('states')[dt_today].sum()
dfc_deaths = dft_deaths.groupby('states')[dt_today].sum()
dfp_cases = dft_cases.groupby('states')[dt_yday].sum()
dfp_deaths = dft_deaths.groupby('states')[dt_yday].sum()
#hide
# Here we build a nice table that gives us a view across states
#TIP: Do a df_table.head() to see what's happening
df_table = (pd.DataFrame(dict(Cases = dfc_cases, Deaths = dfc_deaths, PCases = dfp_cases, PDeaths = dfp_deaths))
.sort_values(by = ['Cases','Deaths'], ascending = [False, False])
.reset_index())
for c in 'Cases, Deaths'.split(', '):
df_table[f'{c} (+)'] = (df_table[c] - df_table[f'P{c}']).clip(0)
#Clip ça veut dire, les chiffres negatif sont interdit
df_table['Fatality Rate'] = (100* df_table['Deaths']/ df_table['Cases']).round(2)
#hide
#Building the summary tab
# Here we build a summary dictionary, with key data from the table
#Tip: print the dictionary
metrics = [df_table.columns[index] for index in [1,2,5,6]]
s_mah = df_table[df_table.states == 'Maharashtra'][metrics].sum().add_prefix('MH ').astype(int)
s_del = df_table[df_table.states =='Delhi'][metrics].sum().add_prefix('DEL ').astype(int)
s_guj = df_table[df_table.states == 'Gujarat'][metrics].sum().add_prefix('GUJ ').astype(int)
summary = {'updated': pd.to_datetime(dt_today).date(), 'since': pd.to_datetime(dt_yday).date()}
summary = {**summary, **df_table[metrics].sum().astype(int), **s_mah, **s_del, **s_guj}
#hide
#Data on new cases
#Making new dataframe of cases per day (Note, dataframe from helper function gave the cumulative each day)
dft_ct_new_cases = dft_cases.groupby('states')[dt_cols].sum().diff(axis=1).fillna(0).astype(int)
dft_ct_new_cases.sort_values(by = [dft_ct_new_cases.columns[-1]], ascending = False,inplace = True)
# +
#hide_input
# A basic HTML layout to display India summary
overview = '''
<!-- ####### YAY,HTML!! #########-->
<h1 style="color: #5e9ca0; text-align: center;">India</h1>
<p style="text-align: center;">Last update: <strong>{update}</strong></p>
<p style="text-align: center;">Confirmed cases:</p>
<p style="text-align: center;font-size:24px;">{cases} (<span style="color: #ff0000;">+{new}</span>)</p>
<p style="text-align: center;">Confirmed deaths:</p>
<p style="text-align: center;font-size:24px;">{deaths} (<span style="color: #ff0000;">+{dnew}</span>)</p>
'''
update = summary['updated'].strftime('%B %d %Y')
cases = summary['Cases']
new = summary['Cases (+)']
deaths = summary['Deaths']
dnew = summary['Deaths (+)']
html = HTML(overview.format(update=update, cases=cases,new=new,deaths=deaths,dnew=dnew))
display(html)
# +
#hide_input
#3 BIG THINGS ARE HAPPENING HERE
#1: Gridspec, check out documentation. It's the best way to arrange multiple plots
#2: Each plot is a timeseries of the number of cases each day
#3 We're writing things in the plot using ax.text. For example, In this case to mention the state
# But you can write anything. check ax.text
df = dft_ct_new_cases
df.loc['Total'] = df.sum()
n = 10
ax = []
fig = plt.figure(figsize = (16,32))
gs = fig.add_gridspec(n+2, 3)
# gs = fig.add_gridspec(2, 3)
ax1 = fig.add_subplot(gs[0, :])
ef = df.loc['Total'].reset_index()
ef['date'] = ef['date'].astype('datetime64[ns]')
ax1.bar(ef.date,ef.Total ,color = 'r',alpha=0.5)
ax1.xaxis.set_major_locator(mdates.WeekdayLocator())
ax1.xaxis.set_major_formatter(mdates.DateFormatter('%b %d'))
ax1.text(0.02, 0.5,'Daily case count', transform = ax1.transAxes, fontsize=25);
ax2 = fig.add_subplot(gs[1,0])
ef = df.loc['Maharashtra'].reset_index()
ef['date'] = ef['date'].astype('datetime64[ns]')
ax2.bar(ef.date, ef.Maharashtra,color = 'r',alpha=0.5)
ax2.xaxis.set_major_locator(mdates.WeekdayLocator())
ax2.xaxis.set_major_formatter(mdates.DateFormatter('%b %d'))
maxyval = ef.Maharashtra.max()
ax2.set_ylim([0,maxyval])
ax2.text(0.05, 0.5,'Maharashtra', transform = ax2.transAxes, fontsize=20);
ax3 = fig.add_subplot(gs[1,1])
ef = df.loc['Gujarat'].reset_index()
ef['date'] = ef['date'].astype('datetime64[ns]')
ax3.bar(ef.date, ef.Gujarat,color = 'r',alpha=0.5)
ax3.xaxis.set_major_locator(mdates.WeekdayLocator())
ax3.xaxis.set_major_formatter(mdates.DateFormatter('%b %d'))
ax3.set_ylim([0,maxyval])
ax3.text(0.05, 0.5,'Gujarat', transform = ax3.transAxes, fontsize=20);
ax4 = fig.add_subplot(gs[1,2])
ef = df.loc['Delhi'].reset_index()
ef['date'] = ef['date'].astype('datetime64[ns]')
ax4.bar(ef.date, ef.Delhi,color = 'r',alpha=0.5)
ax4.xaxis.set_major_locator(mdates.WeekdayLocator())
ax4.xaxis.set_major_formatter(mdates.DateFormatter('%b %d'))
ax4.set_ylim([0,maxyval])
ax4.text(0.05, 0.5,'Delhi', transform = ax4.transAxes, fontsize=20);
for i in range(n):
ax.append(fig.add_subplot(gs[i+2,:]))
ef = df.iloc[i+3].reset_index()
ef['date'] = ef['date'].astype('datetime64[ns]')
ax[i].bar(ef.date,ef.iloc[:,-1],color = 'r',alpha=0.5)
ax[i].text(0.02,0.5,f'{ef.columns.values[-1]}',transform = ax[i].transAxes, fontsize = 20);
ax[i].xaxis.set_major_locator(mdates.WeekdayLocator())
ax[i].xaxis.set_major_formatter(mdates.DateFormatter('%b %d'))
ax[i].set_ylim([0,200])
sns.despine();
# -
#hide_input
#Finally, not everything can be represented by graph, so a simple print of the dataframe
# for a raw numbers view of the table
print(df_table.head(20).to_string(index=False))
|
_notebooks/2020-03-21-DashboardV1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Contact angle solver Young-Dubré
# ### Loading in some libraries
import numpy as np # mathematics and matrices in Python
from pyswarm import pso # particle swarm optimisation
# ### Defining classes and functions
# +
class Solvent:
def __init__(self, g_LW, g_plus, g_minus, angle):
self.g_LW = g_LW
self.g_plus = g_plus
self.g_minus = g_minus
self.angle = angle
def surface_tension(self):
return self.g_LW + 2.*np.sqrt(self.g_plus*self.g_minus)
def young_dubre(solvent, gamma_surf):
gs1, gs2, gs3 = gamma_surf
return 2.*(np.sqrt(gs1*solvent.g_LW)+np.sqrt(gs2*solvent.g_minus)+np.sqrt(gs3*solvent.g_plus))- \
(1.+np.cos(np.deg2rad(solvent.angle)))*solvent.surface_tension()
class Three_solvent_system:
def __init__(self, s1, s2, s3):
self.s1 = s1
self.s2 = s2
self.s3 = s3
def objective(self, gamma_surf):
SSE = sum([
young_dubre(self.s1, gamma_surf)**2,
young_dubre(self.s2, gamma_surf)**2,
young_dubre(self.s3, gamma_surf)**2
])
return SSE
# -
# ### Solver settings
lb = [0.0, 0.0, 0.0] # lower bounds of surface props.
ub = [1000.0, 1000.0, 1000.0] # upper bounds of surface props.
# ### Contact angle set 1
# +
water = Solvent(21.8, # gamma_LW
25.5, # gamma_plus
25.5, # gamma_minus
31.7) # contact angle
glycerol = Solvent(34.0, 3.92, 57.4, 40.0)
diiodomethane = Solvent(50.8, 0.01, 0.0, 48.9)
# -
system = Three_solvent_system(water, glycerol, diiodomethane)
pso(system.objective, lb, ub)
# ### Contact angle set 2
# +
water = Solvent(21.8, 25.5, 25.5, 44.2) # contact angle
ethyleneGlycol = Solvent(29.0, 3.0, 30.1, 84.7)
diiodomethane = Solvent(50.8, 0.01, 0.0, 65.0)
# -
system = Three_solvent_system(water, ethyleneGlycol, diiodomethane)
pso(system.objective, lb, ub)
# Hierboven kan je zien dat hij convergeert naar je MATLAB systeem maar aan de waarde van je doelfunctie `558.91` zie je dat de <NAME> vergelijking niet echt goed voldaan is
|
young-dupre.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/ShahkarHassan/SMART-CROWD-ANALYZER/blob/master/Age_and_Gender_Prediction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="af0B5bzjmUXP" colab_type="text"
# #### Mounting Drive
# + id="QmCZexMtmc9l" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="2c1859fe-c11f-4e78-cb2e-d862a26c974d"
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] id="YIaY5SI2mmz-" colab_type="text"
# #### Data Preprocessing
# + id="IQNPu55rmq88" colab_type="code" colab={}
fldr="drive/My Drive/Face_data_based_ml/UTKFace"
# + id="qaxkAByxo4Bh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 180} outputId="128f7f0c-865e-462c-f781-d50f59b09242"
import os
files=os.listdir(fldr)
# + id="yKUxDh4ypHYP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="b54f4717-7af1-4f8e-e491-cc1a04855d7a"
import cv2
ages=[]
genders=[]
images=[]
for fle in files:
age=int(fle.split('_')[0])
gender=int(fle.split('_')[1])
total=fldr+'/'+fle
print(total)
image=cv2.imread(total)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image= cv2.resize(image,(48,48))
images.append(image)
# + id="2t9s0wFV0Rt8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 231} outputId="5cb19b79-8b4a-4452-9f4a-d5eb7c47363f"
for fle in files:
age=int(fle.split('_')[0])
gender=int(fle.split('_')[1])
ages.append(age)
genders.append(gender)
# + id="_ssUXRvTtdBq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 180} outputId="1ee5ff51-6d3f-4822-c75e-4cd9526bb9ba"
from google.colab.patches import cv2_imshow
cv2_imshow(images[24])
# + id="wi2sJZBr04yY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="620d1cf9-602e-47b9-ff26-473ddd8a4e16"
print(ages[24])
print(genders[24])
# + id="jQyKZxGp8KUJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 65} outputId="4f21ac89-8eeb-48f6-c1d7-c74982ba39db"
cv2_imshow(images[53])
# + id="bNAJPpEG8MiZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="2c2040c7-fb83-4895-9e22-d91810bf4528"
print(ages[53])
print(genders[53])
# + id="wcVToBvvzYSy" colab_type="code" colab={}
import numpy as np
images_f=np.array(images)
genders_f=np.array(genders)
ages_f=np.array(ages)
# + id="Zl76gFvMzoVh" colab_type="code" colab={}
np.save(fldr+'image.npy',images_f)
np.save(fldr+'gender.npy',genders_f)
np.save(fldr+'age.npy',ages_f)
# + [markdown] id="R_A3LwGS0-1r" colab_type="text"
# Male = 0
# Female= 1
# + id="Yk6SSk2I1Guq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="2a89aa9a-814b-4db3-e9cc-21e2ce5930a2"
values, counts = np.unique(genders_f, return_counts=True)
print(counts)
# + id="s55Necnf3BGx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 336} outputId="4a8cce05-c785-4807-8680-4df28bbac8af"
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
gender = ['Male', 'Female']
values=[4372,5047]
ax.bar(gender,values)
plt.show()
# + id="m39_Ut8F4XsN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 153} outputId="3d46a961-1320-4935-8920-d401995d4bb7"
values, counts = np.unique(ages_f, return_counts=True)
print(counts)
# + id="-qfptlwh4qPp" colab_type="code" colab={}
val=values.tolist()
cnt=counts.tolist()
# + id="fdD8XIB-5H40" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="46e75445-b286-477a-e910-65b99fdd1eca"
plt.plot(counts)
plt.xlabel('ages')
plt.ylabel('distribution')
plt.show()
# + id="vojKD91Z56qj" colab_type="code" colab={}
labels=[]
i=0
while i<len(ages):
label=[]
label.append([ages[i]])
label.append([genders[i]])
labels.append(label)
i+=1
# + id="JgKxJJIT7kap" colab_type="code" colab={}
images_f_2=images_f/255
# + id="guje-Pjx727F" colab_type="code" colab={}
labels_f=np.array(labels)
# + id="5-Ouhd9P78UI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="529a5052-ecce-4348-d406-10d3b7945dba"
images_f_2.shape
# + id="eNuuuNi-8BkW" colab_type="code" colab={}
import tensorflow as tf
from sklearn.model_selection import train_test_split
# + id="_hmmID2C8Ss5" colab_type="code" colab={}
X_train, X_test, Y_train, Y_test= train_test_split(images_f_2, labels_f,test_size=0.25)
# + id="DqTM5WSy8cK4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 255} outputId="12bf465d-1e41-4c03-d635-22310658cb37"
Y_train[0:5]
# + id="IeIqY-7F8oWB" colab_type="code" colab={}
Y_train_2=[Y_train[:,1],Y_train[:,0]]
Y_test_2=[Y_test[:,1],Y_test[:,0]]
# + id="42UhBOkE9CVV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="f3c7d1f7-5709-4242-d90e-21668d1d5d2f"
Y_train_2[0][0:5]
# + id="iO5BZ53v9XRI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="2ad106f5-baa0-4646-d856-30417d882ad5"
Y_train_2[1][0:5]
# + [markdown] id="m-jnZOef9caT" colab_type="text"
# ### Model
# + id="s8-iyoLN9Z8p" colab_type="code" colab={}
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Flatten,BatchNormalization
from tensorflow.keras.layers import Dense, MaxPooling2D,Conv2D
from tensorflow.keras.layers import Input,Activation,Add
from tensorflow.keras.models import Model
from tensorflow.keras.regularizers import l2
from tensorflow.keras.optimizers import Adam
import tensorflow as tf
def Convolution(input_tensor,filters):
x = Conv2D(filters=filters,kernel_size=(3, 3),padding = 'same',strides=(1, 1),kernel_regularizer=l2(0.001))(input_tensor)
x = Dropout(0.1)(x)
x= Activation('relu')(x)
return x
def model(input_shape):
inputs = Input((input_shape))
conv_1= Convolution(inputs,32)
maxp_1 = MaxPooling2D(pool_size = (2,2)) (conv_1)
conv_2 = Convolution(maxp_1,64)
maxp_2 = MaxPooling2D(pool_size = (2, 2)) (conv_2)
conv_3 = Convolution(maxp_2,128)
maxp_3 = MaxPooling2D(pool_size = (2, 2)) (conv_3)
conv_4 = Convolution(maxp_3,256)
maxp_4 = MaxPooling2D(pool_size = (2, 2)) (conv_4)
flatten= Flatten() (maxp_4)
dense_1= Dense(64,activation='relu')(flatten)
dense_2= Dense(64,activation='relu')(flatten)
drop_1=Dropout(0.2)(dense_1)
drop_2=Dropout(0.2)(dense_2)
output_1= Dense(1,activation="sigmoid",name='sex_out')(drop_1)
output_2= Dense(1,activation="relu",name='age_out')(drop_2)
model = Model(inputs=[inputs], outputs=[output_1,output_2])
model.compile(loss=["binary_crossentropy","mae"], optimizer="Adam",
metrics=["accuracy"])
return model
# + id="9Ia-ldz8-oT3" colab_type="code" colab={}
Model=model((48,48,3))
# + id="hslItvTK-74B" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 989} outputId="bc8e831a-e899-47a0-d6b6-bb599902f39e"
Model.summary()
# + [markdown] id="p6qugq2n_ArD" colab_type="text"
# #### Training
# + id="h9CACTIq_DVp" colab_type="code" colab={}
from tensorflow.keras.callbacks import ModelCheckpoint
import tensorflow as tf
# + id="YmPivfSj_K0l" colab_type="code" colab={}
fle_s='Age_sex_detection.h5'
checkpointer = ModelCheckpoint(fle_s, monitor='val_loss',verbose=1,save_best_only=True,save_weights_only=False, mode='auto',save_freq='epoch')
Early_stop=tf.keras.callbacks.EarlyStopping(patience=75, monitor='val_loss',restore_best_weights=True),
callback_list=[checkpointer,Early_stop]
# + id="-BHmKYgL_R4p" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="c70ceab4-ffa4-4620-8be6-0e105dd5caee"
History=Model.fit(X_train,Y_train_2,batch_size=64,validation_data=(X_test,Y_test_2),epochs=500,callbacks=[callback_list])
# + [markdown] id="4GTxXMmZMoIG" colab_type="text"
# ### Evaluation
# + id="039DUHa3HqrK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 139} outputId="06865cb7-e9a3-4f36-f8e1-4b291edcb3cc"
Model.evaluate(X_test,Y_test_2)
# + id="YuvpiE1wMHh1" colab_type="code" colab={}
pred=Model.predict(X_test)
# + id="MxGHD2z3MSVg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 136} outputId="6fc49b3a-9a65-4cde-aa07-74a7b26f1ba1"
pred[1]
# + id="h1JH3UesNbWl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 366} outputId="0857b6e5-7c66-415f-a2aa-9a5ad99ab620"
plt.plot(History.history['loss'])
plt.plot(History.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.subplots_adjust(top=1.00, bottom=0.0, left=0.0, right=0.95, hspace=0.25,
wspace=0.35)
# + [markdown] id="vLLBBZ85N2hX" colab_type="text"
# ### For Gender
# + id="jtHjuedANlXJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 366} outputId="b51f9738-24ef-472e-907e-8d7def35d9a9"
plt.plot(History.history['sex_out_accuracy'])
plt.plot(History.history['val_sex_out_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.subplots_adjust(top=1.00, bottom=0.0, left=0.0, right=0.95, hspace=0.25,
wspace=0.35)
# + [markdown] id="fw_q7kswNSHB" colab_type="text"
# ### For age
# + id="-pEsL-KEMsJ2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="797727c8-fd85-4c5b-99e1-834127f92eb5"
fig, ax = plt.subplots()
ax.scatter(Y_test_2[1], pred[1])
ax.plot([Y_test_2[1].min(),Y_test_2[1].max()], [Y_test_2[1].min(), Y_test_2[1].max()], 'k--', lw=4)
ax.set_xlabel('Actual Age')
ax.set_ylabel('Predicted Age')
plt.show()
# + [markdown] id="UkP6tH4INWVu" colab_type="text"
# #### For Gender
# + id="cNqvx_y5NNsD" colab_type="code" colab={}
i=0
Pred_l=[]
while(i<len(pred[0])):
Pred_l.append(int(np.round(pred[0][i])))
i+=1
# + id="_V3vuxZsPCTW" colab_type="code" colab={}
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
# + id="xDIumUnTO8L8" colab_type="code" colab={}
report=classification_report(Y_test_2[0], Pred_l)
# + id="jZEel7nVPfSM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 170} outputId="417c40c3-0634-443a-8e0b-d4589f8d74d2"
print(report)
# + id="UD15IsW0QDIL" colab_type="code" colab={}
results = confusion_matrix(Y_test_2[0], Pred_l)
# + id="nTihY-5eQJPa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="055628c1-4014-4680-8516-6aff13a432dd"
import seaborn as sns
sns.heatmap(results, annot=True)
# + id="x-w4R3GTQcLr" colab_type="code" colab={}
def test_image(ind,images_f,images_f_2,Model):
cv2_imshow(images_f[ind])
image_test=images_f_2[ind]
pred_1=Model.predict(np.array([image_test]))
#print(pred_1)
sex_f=['Male','Female']
age=int(np.round(pred_1[1][0]))
sex=int(np.round(pred_1[0][0]))
print("Predicted Age: "+ str(age))
print("Predicted Sex: "+ sex_f[sex])
# + id="I53sQfZPRJlj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 99} outputId="55c7f6ab-3515-4d73-d13f-dc4f0b991a83"
test_image(57,images_f,images_f_2,Model)
# + id="fO8yiT2iR1Q6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 99} outputId="2beaaaa1-be5e-4a93-a95a-264f2fa6586d"
test_image(137,images_f,images_f_2,Model)
# + id="rfDMx_vbSDAC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 99} outputId="318948d5-5c66-476f-d4fa-8683b9e6bcef"
test_image(502,images_f,images_f_2,Model)
# + id="P4XV-ZlJSKeK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 99} outputId="7d9c8b1c-7175-4576-8055-d218664737f7"
test_image(24,images_f,images_f_2,Model)
# + id="BKGe42ik-9j6" colab_type="code" colab={}
# + [markdown] id="IoVsWIpj--Wg" colab_type="text"
# # **TESTING OUR OWN PICTURE**
#
#
#
# + id="iNIkKw5z_JXh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 969} outputId="f54c0ff1-6655-4648-a8fc-cd2ce88524f2"
model2 = tf.keras.models.load_model(
'/content/drive/My Drive/FYP/Age_sex_detection.h5'
# `custom_objects` tells keras how to load a `hub.KerasLayer`
)
model2.summary()
# + id="0LFrv3SMAaMf" colab_type="code" colab={}
q=[]
import numpy as np
images_f=np.array(q)
images_f_2=images_f/255
# + id="CUth1aREAa2x" colab_type="code" colab={}
import cv2
image= cv2.imread('/content/sample_data/111.jpeg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image= cv2.resize(image,(48,48))
q.append(image)
images_f=np.array(q)
images_f_2=images_f/255
# + id="Ps9YqF4d_RfV" colab_type="code" colab={}
def testage(ind,images_f,images_f_2,Model):
cv2_imshow(images_f[ind])
image_test=images_f_2[ind]
pred_1=Model.predict(np.array([image_test]))
#print(pred_1)
sex_f=['Male','Female']
age=int(np.round(pred_1[1][0]))
sex=int(np.round(pred_1[0][0]))
print("Predicted Age: "+ str(age))
print("Predicted Sex: "+ sex_f[sex])
# + id="IUGTAAXT_UL4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 99} outputId="ff340c87-a1bf-4384-e778-a0c42e1d3ed8"
testage(0,images_f,images_f_2,model2)
|
Age_and_Gender_Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Principal Component Analysis Tutorial
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
# ## Step 1: Get the Data
# For this exercise we will create a 3D toy data. This is arbitrary data so we can guess in advance how our results will look. To make things easier in the following sections we will convert the data into a toy dataframe.
# +
x = np.random.randint(low = -10, high = 10, size=100)
y = np.random.normal(-2*x + 3, size=100)
z = np.random.normal(x**2, size=100)
df= pd.DataFrame({'X': x, 'Y': y, 'Z': z})
#round for simplicity
df = df.round()
df.head()
# +
#plot our data
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, zdir='z', c= 'red')
plt.savefig('plots/toy_pca_3d.png')
plt.show()
# -
# ## Step 2: Subtract the Mean
# For PCA to work we need to have dataset with a mean of zero. We can subtract the average across each dimension easily with the code below
#confirm we are getting the means for the feature space
means = df.mean(axis=0)
means
df_mean = df - df.mean(axis=0)
df_mean.head()
# ## Step 3: Calculate the Covariance Matrix
# The non diagonal terms are the covariance of one dimension with another, for example X and Y are negatively correlated.
df_cov = df_mean.cov()
df_cov.head()
# ## Step 4: Calculate Eigenvectors and Eigenvalues of Covariance Matrix
# We compute the eigenvectors v and eigenvalues w with numpy's linear algebra package: [numpy.linalg.eig](https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.eig.html). The eigenvectors are normalized such that the column v[:, i] is the eigenvector corresponding to the eigenvalue w[i]. The computed eigenvalues are not necessarily ordered, this will be relevant in the next step.
eigenval, eigenvect = np.linalg.eig(df_cov)
print(eigenval)
print(eigenvect)
# ## Step 5: Choosing Components and New Feature Vector
# Now that we have eigenvectors and eigenvalues we can begin the dimensionality reduction. As it turns out, the eigenvector with the highest eigenvalue is the principle component of the dataset. In fact the eigenvector with the largest eigenvalue represents the most signficant relationship between the data dimensions.
#get the sorted indeces of eigenvalues
eigval_sort_idx = np.argsort(eigenval)
eigval_sort_idx
feature_vector = eigenvect[:, eigval_sort_idx[1:]]
feature_vector
# ## Step 6: Deriving the New Dataset
# In the last part we take the transpose of the vector and multiply it on the left of the original dataset, transposed.
#take note of feature vector shape
feature_vector.shape
# evaluate shape of data
df_mean.shape
# The transposed feature vector is the row feature vector where the eigenvectors are now in the rows such that the most significant eigenvectors are at the top.
#
# The row data adjust is the mean adjusted data transposed, where the each row holds a separate dimension.
# +
row_feature_vector = feature_vector.T
row_data_adjust = df_mean.T
df_reduced = np.matmul(row_feature_vector, row_data_adjust)
df_reduced.shape
# -
final_data = pd.DataFrame(df_reduced.T, columns=['vect_1','vect_2'])
final_data.head()
plt.scatter(final_data['vect_1'], final_data['vect_2'])
plt.xlabel("1st Vector")
plt.ylabel("2nd Vector")
plt.title("Reduced Data")
plt.savefig('plots/reduced_data.png')
plt.show()
# ## Step -1: Getting the Old Data Back
row_data_adjust = np.matmul(row_feature_vector.T, df_reduced)
row_data_adjust.shape
row_data_adjust_df = pd.DataFrame(row_data_adjust.T, columns=['X', 'Y', 'Z'])
row_data_adjust_df.head()
original_data = row_data_adjust_df + means
original_data =original_data.round()
original_data.head()
|
pca_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Open CamHD database on Pangeo (ooi.pangeo.io)
import pandas as pd
dbcamhd = pd.read_json('dbcamhd.json', orient="records", lines=True)
dbcamhd.tail(3)
print("Total files: %i" % len(dbcamhd))
print("Total frames: %i" % dbcamhd.frame_count.sum())
|
open_database.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="wJcYs_ERTnnI"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="HMUDt0CiUJk9"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="77z2OchJTk0l"
# # Convert Your Existing Code to TensorFlow 2.0
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/beta/guide/migration_guide">
# <img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
# View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/guide/migration_guide.ipynb">
# <img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
# Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/guide/migration_guide.ipynb">
# <img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
# View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/r2/guide/migration_guide.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="meUTrR4I6m1C"
# Important: This doc for users of low level TensorFlow APIs. If you are using the high level APIs (`tf.keras`) there may be little or no action you need to take to make your code fully TensorFlow 2.0 compatible. Check your [optimizer's default learning rate](#keras_optimizer_lr).
# + [markdown] colab_type="text" id="C0V10enS1_WU"
# It is still possible to run 1.X code, unmodified (except for contrib), in TensorFlow 2.0:
#
# ```
# import tensorflow.compat.v1 as tf
# tf.disable_v2_behavior()
# ```
#
# However, this does not let you take advantage of many of the improvements made in TensorFlow 2.0. This guide will help you upgrade your code, making it simpler, more performant, and easier to maintain.
# + [markdown] colab_type="text" id="GUp_x0bOgaac"
# ## Automatic conversion script
#
# The first step, before attempting to implement the changes described in this doc, is to try running the [upgrade script](./upgrade.md).
#
# This will do an initial pass at upgrading your code to TensorFlow 2.0. But it can't make your code idiomatic to 2.0. Your code may still make use of `tf.compat.v1` endpoints to access placeholders, sessions, collections, and other 1.x-style functionality.
# + [markdown] colab_type="text" id="0w5LiSYsy1mh"
# ## Top-level behavioral changes
#
# If your code works in TensorFlow 2.0 using `tf.compat.v1.disable_v2_behavior()`, there are still global behavioral changes you may need to address. The major changes are:
# + [markdown] colab_type="text" id="1y-W0Mz_zB6Y"
# * *Eager execution, `v1.enable_eager_execution()`* : Any code that implicitly uses a `tf.Graph` will fail. Be sure to wrap this code in a `with tf.Graph().as_default()` context.
#
# * *Resource variables, `v1.enable_resource_variables()`*: Some code may depends on non-deterministic behaviors enabled by TF reference variables.
# Resource variables are locked while being written to, and so provide more intuitive consistency guarantees.
#
# * This may change behavior in edge cases.
# * This may create extra copies and can have higher memory usage.
# * This can be disabled by passing `use_resource=False` to the `tf.Variable` constructor.
#
# * *Tensor shapes, `v1.enable_v2_tensorshape()`*: TF 2.0 simplifies the behavior of tensor shapes. Instead of `t.shape[0].value` you can say `t.shape[0]`. These changes should be small, and it makes sense to fix them right away. See [TensorShape](#tensorshape) for examples.
#
# * *Control flow, `v1.enable_control_flow_v2()`*: The TF 2.0 control flow implementation has been simplified, and so produces different graph representations. Please [file bugs](https://github.com/tensorflow/tensorflow/issues) for any issues.
# + [markdown] colab_type="text" id="_Ni9zLLvwcOR"
# ## Make the code 2.0-native
#
#
# This guide will walk through several examples of converting TensorFlow 1.x code to TensorFlow 2.0. These changes will let your code take advantage of performance optimizations and simplified API calls.
#
# In each case, the pattern is:
# + [markdown] colab_type="text" id="uP0O8Pc45LNs"
# ### 1. Replace `v1.Session.run` calls
#
# Every `v1.Session.run` call should be replaced by a Python function.
#
# * The `feed_dict` and `v1.placeholder`s become function arguments.
# * The `fetches` become the function's return value.
# * During conversion eager execution allows easy debugging with standard Python tools like `pdb`.
#
# After that add a `tf.function` decorator to make it run efficiently in graph. See the [Autograph Guide](autograph.ipynb) for more on how this works.
#
# Note that:
#
# * Unlike `v1.Session.run` a `tf.function` has a fixed return signature, and always returns all outputs. If this causes performance problems, create two separate functions.
#
# * There is no need for a `tf.control_dependencies` or similar operations: A `tf.function` behaves as if it were run in the order written. `tf.Variable` assignments and `tf.assert`s, for example, are executed automatically.
#
# + [markdown] colab_type="text" id="jlBOqROL5NmN"
# ### 2. Use Python objects to track variables and losses
#
# All name-based variable tracking is strongly discouraged in TF 2.0. Use Python objects to to track variables.
#
# Use `tf.Variable` instead of `v1.get_variable`.
#
# Every `v1.variable_scope` should be converted to a Python object. Typically this will be one of:
#
# * `tf.keras.layers.Layer`
# * `tf.keras.Model`
# * `tf.Module`
#
# If you need to aggregate lists of variables (like `tf.Graph.get_collection(tf.GraphKeys.VARIABLES)`), use the `.variables` and `.trainable_variables` attributes of the `Layer` and `Model` objects.
#
# These `Layer` and `Model` classes implement several other properties that remove the need for global collections. Their `.losses` property can be a replacement for using the `tf.GraphKeys.LOSSES` collection.
#
# See the [keras guides](keras.ipynb) for details.
#
# Warning: Many `tf.compat.v1` symbols use the global collections implicitly.
#
# + [markdown] colab_type="text" id="rGFhBzoF5FIq"
# ### 3. Upgrade your training loops
#
# Use the highest level API that works for your use case. Prefer `tf.keras.Model.fit` over building your own training loops.
#
# These high level functions manage a lot of the low-level details that might be easy to miss if you write your own training loop. For example, they automatically collect the regularization losses, and set the `training=True` argument when calling the model.
#
# + [markdown] colab_type="text" id="oaY37_6L4la5"
#
# ### 4. Upgrade your data input pipelines
#
# Use `tf.data` datasets for data input. These objects are efficient, expressive, and integrate well with tensorflow.
#
# They can be passed directly to the `tf.keras.Model.fit` method.
#
# ```
# model.fit(dataset, epochs=5)
# ```
#
# They can be iterated over directly standard Python:
#
# ```
# for example_batch, label_batch in dataset:
# break
# ```
#
# + [markdown] colab_type="text" id="_Mwsd0SK4oIs"
# #### 5. Migrate off `compat.v1` symbols
#
# The `tf.compat.v1` module contains the complete TensorFlow 1.x API, with its original semantics.
#
# The [TF2 upgrade script](upgrade.ipynb) will convert symbols to their 2.0 equivalents if such a conversion is safe, i.e., if it can determine that the behavior of the 2.0 version is exactly equivalent (for instance, it will rename `v1.arg_max` to `tf.argmax`, since those are the same function).
#
# After the upgrade script is done with a piece of code, it is likely there are many mentions of `compat.v1`. It is worth going through the code and converting these manually to the 2.0 equivalent (it should be mentioned in the log if there is one).
# + [markdown] colab_type="text" id="X_ilfTGJ4Yml"
# ## Converting models
#
# ### Setup
# + colab={} colab_type="code" id="bad2N-Z115W1"
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version 2.x # Colab only.
except Exception:
pass
import tensorflow as tf
import tensorflow_datasets as tfds
# + [markdown] colab_type="text" id="FB99sqHX2Q5m"
# ### Low-level variables & operator execution
#
# Examples of low-level API use include:
#
# * using variable scopes to control reuse
# * creating variables with `v1.get_variable`.
# * accessing collections explicitly
# * accessing collections implicitly with methods like :
#
# * `v1.global_variables`
# * `v1.losses.get_regularization_loss`
#
# * using `v1.placeholder` to set up graph inputs
# * executing graphs with `Session.run`
# * initializing variables manually
#
# + [markdown] colab_type="text" id="e582IjyF2eje"
# #### Before converting
#
# Here is what these patterns may look like in code using TensorFlow 1.x.
#
# ```python
# in_a = tf.placeholder(dtype=tf.float32, shape=(2))
# in_b = tf.placeholder(dtype=tf.float32, shape=(2))
#
# def forward(x):
# with tf.variable_scope("matmul", reuse=tf.AUTO_REUSE):
# W = tf.get_variable("W", initializer=tf.ones(shape=(2,2)),
# regularizer=tf.contrib.layers.l2_regularizer(0.04))
# b = tf.get_variable("b", initializer=tf.zeros(shape=(2)))
# return W * x + b
#
# out_a = forward(in_a)
# out_b = forward(in_b)
#
# reg_loss = tf.losses.get_regularization_loss(scope="matmul")
#
# with tf.Session() as sess:
# sess.run(tf.global_variables_initializer())
# outs = sess.run([out_a, out_b, reg_loss],
# feed_dict={in_a: [1, 0], in_b: [0, 1]})
#
# ```
# + [markdown] colab_type="text" id="QARwz4Xd2lc2"
# #### After converting
# + [markdown] colab_type="text" id="x0AVzBFRBPcU"
# In the converted code:
#
# * The variables are local Python objects.
# * The `forward` function still defines the calculation.
# * The `Session.run` call is replaced with a call to `forward`
# * The optional `tf.function` decorator can be added for performance.
# * The regularizations are calculated manually, without referring to any global collection.
# * **No sessions or placeholders.**
# + colab={} colab_type="code" id="lXEZoLMP2cWJ"
W = tf.Variable(tf.ones(shape=(2,2)), name="W")
b = tf.Variable(tf.zeros(shape=(2)), name="b")
@tf.function
def forward(x):
return W * x + b
out_a = forward([1,0])
print(out_a)
# + colab={} colab_type="code" id="YmE96A_1jZTg"
out_b = forward([0,1])
regularizer = tf.keras.regularizers.l2(0.04)
reg_loss = regularizer(W)
# + [markdown] colab_type="text" id="ycDxY9nL268-"
# ### Models based on `tf.layers`
# + [markdown] colab_type="text" id="K-bIk7wL48U7"
# The `v1.layers` module is used to contain layer-functions that relied on `v1.variable_scope` to define and reuse variables.
# + [markdown] colab_type="text" id="8I_qKpT73KyM"
# #### Before converting
# ```python
# def model(x, training, scope='model'):
# with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# x = tf.layers.conv2d(x, 32, 3, activation=tf.nn.relu,
# kernel_regularizer=tf.contrib.layers.l2_regularizer(0.04))
# x = tf.layers.max_pooling2d(x, (2, 2), 1)
# x = tf.layers.flatten(x)
# x = tf.layers.dropout(x, 0.1, training=training)
# x = tf.layers.dense(x, 64, activation=tf.nn.relu)
# x = tf.layers.batch_normalization(x, training=training)
# x = tf.layers.dense(x, 10, activation=tf.nn.softmax)
# return x
#
# train_out = model(train_data, training=True)
# test_out = model(test_data, training=False)
# ```
# + [markdown] colab_type="text" id="b8_Ii7CQ3fK-"
# #### After converting
# + [markdown] colab_type="text" id="BsAseSMfB9XN"
# * The simple stack of layers fits neatly into `tf.keras.Sequential`. (For more complex models see [custom layers and models](keras/custom_layers_and_models.ipynb), and [the functional API](keras/functional.ipynb).)
# * The model tracks the variables, and regularization losses.
# * The conversion was one-to-one because there is a direct mapping from `v1.layers` to `tf.keras.layers`.
#
# Most arguments stayed the same. But notice the differences:
#
# * The `training` argument is passed to each layer by the model when it runs.
# * The first argument to the original `model` function (the input `x`) is gone. This is because object layers separate building the model from calling the model.
#
#
# Also note that:
#
# * If you were using regularizers of initializers from `tf.contrib`, these have more argument changes than others.
# * The code no longer writes to collections, so functions like `v1.losses.get_regularization_loss` will no longer return these values, potentially breaking your training loops.
# + colab={} colab_type="code" id="DLAPORrN3lct"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.04),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
train_data = tf.ones(shape=(1, 28, 28, 1))
test_data = tf.ones(shape=(1, 28, 28, 1))
# + colab={} colab_type="code" id="6nWh6IXvkMKv"
train_out = model(train_data, training=True)
print(train_out)
# + colab={} colab_type="code" id="YnAdIDLlj3go"
test_out = model(test_data, training=False)
print(test_out)
# + colab={} colab_type="code" id="sAgqwCJBMx_x"
# Here are all the trainable variables.
len(model.trainable_variables)
# + colab={} colab_type="code" id="uX6knaYMNM8p"
# Here is the regularization loss.
model.losses
# + [markdown] colab_type="text" id="9moqw5E_4Cwl"
# ### Mixed variables & `v1.layers`
#
# + [markdown] colab_type="text" id="80DEsImmq6VX"
# Existing code often mixes lower-level TF 1.x variables and operations with higher-level `v1.layers`.
# + [markdown] colab_type="text" id="oZe9L6RR4OcP"
# #### Before converting
# ```python
# def model(x, training, scope='model'):
# with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# W = tf.get_variable(
# "W", dtype=tf.float32,
# initializer=tf.ones(shape=x.shape),
# regularizer=tf.contrib.layers.l2_regularizer(0.04),
# trainable=True)
# if training:
# x = x + W
# else:
# x = x + W * 0.5
# x = tf.layers.conv2d(x, 32, 3, activation=tf.nn.relu)
# x = tf.layers.max_pooling2d(x, (2, 2), 1)
# x = tf.layers.flatten(x)
# return x
#
# train_out = model(train_data, training=True)
# test_out = model(test_data, training=False)
# ```
# + [markdown] colab_type="text" id="y6ORX7cD4TkD"
# #### After converting
# + [markdown] colab_type="text" id="2BaRwog5CBpz"
# To convert this code, follow the pattern of mapping layers to layers as in the previous example.
#
# A `v1.variable_scope` is effectively a layer of its own. So rewrite it as a `tf.keras.layers.Layer`. See [the guide](keras/custom_layers_and_models.ipynb) for details.
#
# The general pattern is:
#
# * Collect layer parameters in `__init__`.
# * Build the variables in `build`.
# * Execute the calculations in `call`, and return the result.
#
# The `v1.variable_scope` is essentially a layer of its own. So rewrite it as a `tf.keras.layers.Layer`. See [the guide](keras/custom_layers_and_models.ipynb) for details.
# + colab={} colab_type="code" id="YcCAjNuP4NVh"
# Create a custom layer for part of the model
class CustomLayer(tf.keras.layers.Layer):
def __init__(self, *args, **kwargs):
super(CustomLayer, self).__init__(*args, **kwargs)
def build(self, input_shape):
self.w = self.add_weight(
shape=input_shape[1:],
dtype=tf.float32,
initializer=tf.keras.initializers.ones(),
regularizer=tf.keras.regularizers.l2(0.02),
trainable=True)
# Call method will sometimes get used in graph mode,
# training will get turned into a tensor
@tf.function
def call(self, inputs, training=None):
if training:
return inputs + self.w
else:
return inputs + self.w * 0.5
# + colab={} colab_type="code" id="dR_QO6_wBgMm"
custom_layer = CustomLayer()
print(custom_layer([1]).numpy())
print(custom_layer([1], training=True).numpy())
# + colab={} colab_type="code" id="VzqaIf4E42oY"
train_data = tf.ones(shape=(1, 28, 28, 1))
test_data = tf.ones(shape=(1, 28, 28, 1))
# Build the model including the custom layer
model = tf.keras.Sequential([
CustomLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
])
train_out = model(train_data, training=True)
test_out = model(test_data, training=False)
# + [markdown] colab_type="text" id="dS5ed_jjOkvh"
# Some things to note:
#
# * Subclassed Keras models & layers need to run in both v1 graphs (no automatic control dependencies) and in eager mode
# * Wrap the `call()` in a `tf.function()` to get autograph and automatic control dependencies
#
# * Don't forget to accept a `training` argument to `call`.
# * Sometimes it is a `tf.Tensor`
# * Sometimes it is a Python boolean.
#
# * Create model variables in constructor or `Model.build` using `self.add_weight()`.
# * In `Model.build` you have access to the input shape, so can create weights with matching shape.
# * Using `tf.keras.layers.Layer.add_weight` allows Keras to track variables and regularization losses.
#
# * Don't keep `tf.Tensors` in your objects.
# * They might get created either in a `tf.function` or in the eager context, and these tensors behave differently.
# * Use `tf.Variable`s for state, they are always usable from both contexts
# * `tf.Tensors` are only for intermediate values.
# + [markdown] colab_type="text" id="ulaB1ymO4pw5"
# ### A note on Slim & contrib.layers
#
# A large amount of older TensorFlow 1.x code uses the [Slim](https://ai.googleblog.com/2016/08/tf-slim-high-level-library-to-define.html) library, which was packaged with TensorFlow 1.x as `tf.contrib.layers`. As a `contrib` module, this is no longer available in TensorFlow 2.0, even in `tf.compat.v1`. Converting code using Slim to TF 2.0 is more involved than converting repositories that use `v1.layers`. In fact, it may make sense to convert your Slim code to `v1.layers` first, then convert to Keras.
#
# * Remove `arg_scopes`, all args need to be explicit
# * If you use them, split `normalizer_fn` and `activation_fn` into their own layers
# * Separable conv layers map to one or more different Keras layers (depthwise, pointwise, and separable Keras layers)
# * Slim and `v1.layers` have different arg names & default values
# * Some args have different scales
# * If you use Slim pre-trained models, try out `tf.keras.applications` or [TFHub](https://tensorflow.orb/hub)
#
# Some `tf.contrib` layers might not have been moved to core TensorFlow but have instead been moved to the [TF add-ons package](https://github.com/tensorflow/addons).
#
# + [markdown] colab_type="text" id="1w72KrXm4yZR"
# ## Training
# + [markdown] colab_type="text" id="56PQxTgy2bpI"
# There are many ways to feed data to a `tf.keras` model. They will accept Python generators and Numpy arrays as input.
#
# The recommended way to feed data to a model is to use the `tf.data` package, which contains a collection of high performance classes for manipulating data.
#
# If you are still using `tf.queue`, these are now only supported as data-structures, not as input pipelines.
# + [markdown] colab_type="text" id="m6htasZ7iBB4"
# ### Using Datasets
# + [markdown] colab_type="text" id="loTPH2Pz4_Oj"
# The [TensorFlow Datasets](https://tensorflow.org/datasets) package (`tfds`) contains utilities for loading predefined datasets as `tf.data.Dataset` objects.
#
# For this example, load the MNISTdataset, using `tfds`:
# + colab={} colab_type="code" id="BMgxaLH74_s-"
datasets, info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
# + [markdown] colab_type="text" id="hPJhEuvj5VfR"
# Then prepare the data for training:
#
# * Re-scale each image.
# * Shuffle the order of the examples.
# * Collect batches of images and labels.
#
# + colab={} colab_type="code" id="StBRHtJM2S7o"
BUFFER_SIZE = 10 # Use a much larger value for real code.
BATCH_SIZE = 64
NUM_EPOCHS = 5
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
# + [markdown] colab_type="text" id="SKq14zKKFAdv"
# To keep the example short, trim the dataset to only return 5 batches:
# + colab={} colab_type="code" id="_J-o4YjG2mkM"
train_data = mnist_train.map(scale).shuffle(BUFFER_SIZE).batch(BATCH_SIZE).take(5)
test_data = mnist_test.map(scale).batch(BATCH_SIZE).take(5)
STEPS_PER_EPOCH = 5
train_data = train_data.take(STEPS_PER_EPOCH)
test_data = test_data.take(STEPS_PER_EPOCH)
# + colab={} colab_type="code" id="XEqdkH54VM6c"
image_batch, label_batch = next(iter(train_data))
# + [markdown] colab_type="text" id="mSev7vZC5GJB"
# ### Use Keras training loops
#
# If you don't need low level control of your training process, using Keras's built-in `fit`, `evaluate`, and `predict` methods is recommended. These methods provide a uniform interface to train the model regardless of the implementation (sequential, functional, or sub-classed).
#
# The advantages of these methods include:
#
# * They accept Numpy arrays, Python generators and, `tf.data.Datasets`
# * They apply regularization, and activation losses automatically.
# * They support `tf.distribute` [for multi-device training](distribute_strategy.ipynb).
# * They support arbitrary callables as losses and metrics.
# * They support callbacks like `tf.keras.callbacks.TensorBoard`, and custom callbacks.
# * They are performant, automatically using TensorFlow graphs.
#
# Here is an example of training a model using a `Dataset`. (For details on how this works see [tutorials](../tutorials).)
# + colab={} colab_type="code" id="uzHFCzd45Rae"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
# Model is the full model w/o custom layers
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_data, epochs=NUM_EPOCHS)
loss, acc = model.evaluate(test_data)
print("Loss {}, Accuracy {}".format(loss, acc))
# + [markdown] colab_type="text" id="akpeOb09YBhq"
# ### Write your own loop
#
# If the Keras model's training step works for you, but you need more control outside that step, consider using the `tf.keras.Model.train_on_batch` method, in your own data-iteration loop.
#
# Remember: Many things can be implemented as a `tf.keras.callbacks.Callback`.
#
# This method has many of the advantages of the methods mentioned in the previous section, but gives the user control of the outer loop.
#
# You can also use `tf.keras.Model.test_on_batch` or `tf.keras.Model.evaluate` to check performance during training.
#
# Note: `train_on_batch` and `test_on_batch`, by default return the loss and metrics for the single batch. If you pass `reset_metrics=False` they return accumulated metrics and you must remember to appropriately reset the metric accumulators. Also remember that some metrics like `AUC` require `reset_metrics=False` to be calculated correctly.
#
# To continue training the above model:
#
# + colab={} colab_type="code" id="eXr4CyJMtJJ6"
# Model is the full model w/o custom layers
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
metrics_names = model.metrics_names
for epoch in range(NUM_EPOCHS):
#Reset the metric accumulators
model.reset_metrics()
for image_batch, label_batch in train_data:
result = model.train_on_batch(image_batch, label_batch)
print("train: ",
"{}: {:.3f}".format(metrics_names[0], result[0]),
"{}: {:.3f}".format(metrics_names[1], result[1]))
for image_batch, label_batch in test_data:
result = model.test_on_batch(image_batch, label_batch,
# return accumulated metrics
reset_metrics=False)
print("\neval: ",
"{}: {:.3f}".format(metrics_names[0], result[0]),
"{}: {:.3f}".format(metrics_names[1], result[1]))
# + [markdown] colab_type="text" id="LQTaHTuK5S5A"
# <a name="custom_loop"></a>
#
# ### Customize the training step
#
# If you need more flexibility and control, you can have it by implementing your own training loop. There are three steps:
#
# 1. Iterate over a Python generator or `tf.data.Dataset` to get batches of examples.
# 2. Use `tf.GradientTape` to collect gradients.
# 3. Use one of the `tf.keras.optimizers` to apply weight updates to the model's variables.
#
# Remember:
#
# * Always include a `training` argument on the `call` method of subclassed layers and models.
# * Make sure to call the model with the `training` argument set correctly.
# * Depending on usage, model variables may not exist until the model is run on a batch of data.
# * You need to manually handle things like regularization losses for the model.
#
# Note the simplifications relative to v1:
#
# * There is no need to run variable initializers. Variables are initialized on creation.
# * There is no need to add manual control dependencies. Even in `tf.function` operations act as in eager mode.
# + colab={} colab_type="code" id="gQooejfYlQeF"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
optimizer = tf.keras.optimizers.Adam(0.001)
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
@tf.function
def train_step(inputs, labels):
with tf.GradientTape() as tape:
predictions = model(inputs, training=True)
regularization_loss = tf.math.add_n(model.losses)
pred_loss = loss_fn(labels, predictions)
total_loss = pred_loss + regularization_loss
gradients = tape.gradient(total_loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
for epoch in range(NUM_EPOCHS):
for inputs, labels in train_data:
train_step(inputs, labels)
print("Finished epoch", epoch)
# + [markdown] colab_type="text" id="kS7WW5Z75ve3"
# ### New-style metrics and losses
#
# In TensorFlow 2.0, metrics and losses are objects. These work both eagerly and in `tf.function`s.
#
# A loss object is callable, and expects the (y_pred, y_true) as arguments:
#
#
#
# + colab={} colab_type="code" id="C5_TVrBlbBcy"
cce = tf.losses.CategoricalCrossentropy(from_logits=True)
cce([[1, 0]], [[-1.0,3.0]]).numpy()
# + [markdown] colab_type="text" id="JFDc1v0XbAyB"
# A metric object has the following methods:
#
# * `Metric.update_state()` — add new observations
# * `Metric.result()` —get the current result of the metric, given the observed values
# * `Metric.reset_states()` — clear all observations.
#
# The object itself is callable. Calling updates the state with new observations, as with `update_state`, and returns the new result of the metric.
#
# You don't have to manually initialize a metric's variables, and because TensorFlow 2.0 has automatic control dependencies, you don't need to worry about those either.
#
# The code below uses a metric to keep track of the mean loss observed within a custom training loop.
# + colab={} colab_type="code" id="HAbA0fKW58CH"
# Create the metrics
loss_metric = tf.keras.metrics.Mean(name='train_loss')
accuracy_metric = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')
@tf.function
def train_step(inputs, labels):
with tf.GradientTape() as tape:
predictions = model(inputs, training=True)
regularization_loss = tf.math.add_n(model.losses)
pred_loss = loss_fn(labels, predictions)
total_loss = pred_loss + regularization_loss
gradients = tape.gradient(total_loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
# Update the metrics
loss_metric.update_state(total_loss)
accuracy_metric.update_state(labels, predictions)
for epoch in range(NUM_EPOCHS):
# Reset the metrics
loss_metric.reset_states()
accuracy_metric.reset_states()
for inputs, labels in train_data:
train_step(inputs, labels)
# Get the metric results
mean_loss = loss_metric.result()
mean_accuracy = accuracy_metric.result()
print('Epoch: ', epoch)
print(' loss: {:.3f}'.format(mean_loss))
print(' accuracy: {:.3f}'.format(mean_accuracy))
# + [markdown] colab_type="text" id="Hf718XCgDAGJ"
# ### Keras optimizers
# + [markdown] colab_type="text" id="A6El-NxAQ8aF"
# The optimizers in `v1.train`, like `v1.train.AdamOptimizer` and `v1.train.GradientDescentOptimizer`, have equivalents in `tf.keras.optimizers`.
# + [markdown] colab_type="text" id="qgP89WdSDQx-"
# #### Convert `v1.train` to `keras.optimizers`
#
# Here are things to keep in mind when converting your optimizers:
#
# * Upgrading your optimizers [may make old checkpoints incompatible](#checkpoints).
# * All epsilons now default to `1e-7` instead of `1e-8` (which is negligible in most use cases).
# * `v1.train.GradientDescentOptimizer` can be directly replaced by `tf.keras.optimizers.SGD`.
# * `v1.train.MomentumOptimizer` can be directly replaced by the `SGD` optimizer using the momentum argument: `tf.keras.optimizers.SGD(..., momentum=...)`.
# * `v1.train.AdamOptimizer` can be converted to use `tf.keras.optimizers.Adam`. The `beta1` and `beta2` arguments have been renamed to `beta_1` and `beta_2`.
# * `v1.train.RMSPropOptimizer` can be converted to `tf.keras.optimizers.RMSprop`. The `decay` argument has been renamed to `rho`.
# * `v1.train.AdadeltaOptimizer` can be converted directly to `tf.keras.optimizers.Adadelta`.
# * `tf.train.AdagradOptimizer` can be converted directly to `tf.keras.optimizers.Adagrad`.
# * `tf.train.FtrlOptimizer` can be converted directly to `tf.keras.optimizers.Ftrl`. The `accum_name` and `linear_name` arguments have been removed.
# * The `tf.contrib.AdamaxOptimizer` and `tf.contrib.NadamOptimizer`, can be converted directly to `tf.keras.optimizers.Adamax` and `tf.keras.optimizers.Nadam`. The `beta1`, and `beta2` arguments have been renamed to `beta_1` and `beta_2`.
#
#
#
# + [markdown] colab_type="text" id="Ef60-wJ2bR3l"
#
# #### New defaults for some `tf.keras.optimizers`
# <a id="keras_optimizer_lr"></a>
#
# Warning: If you see a change in convergence behavior for your models, check the default learning rates.
#
# There are no changes for `optimizers.SGD`, `optimizers.Adam`, or `optimizers.RMSprop`.
#
# The following default learning rates have changed:
#
# * `optimizers.Adagrad` from 0.01 to 0.001
# * `optimizers.Adadelta` from 1.0 to 0.001
# * `optimizers.Adamax` from 0.002 to 0.001
# * `optimizers.Nadam` from 0.002 to 0.001
# + [markdown] colab_type="text" id="5Cf1ks48Q3uc"
# ### TensorBoard
# + [markdown] colab_type="text" id="0tx7FyM_RHwJ"
# TensorFlow 2.0 includes significant changes to the `tf.summary` API used to write summary data for visualization in TensorBoard. For a general introduction to the new tf.summary, there are [several tutorials available](https://www.tensorflow.org/tensorboard/r2/get_started) that use the TF 2.0 API. This includes a [TensorBoard TF2.0 Migration Guide](https://www.tensorflow.org/tensorboard/r2/migrate)
# + [markdown] colab_type="text" id="JmMLBKs66DeA"
# ## Saving & Loading
#
# + [markdown] colab_type="text" id="5_QKn3Kl6TUu"
# <a id="checkpoints"></a>
# ### Checkpoint compatibility
#
# TensorFlow 2.0 uses [object-based checkpoints](checkpoints.ipynb).
#
# Old-style name-based checkpoints can still be loaded, if you're careful.
# The code conversion process may result in variable name changes, but there are workarounds.
#
# The simplest approach it to line up the names of the new model with the names in the checkpoint:
#
# * Variables still all have a `name` argument you can set.
# * Keras models also take a `name` argument as which they set as the prefix for their variables.
# * The `v1.name_scope` function can be used to set variable name prefixes. This is very different from `tf.variable_scope`. It only affects names, and doesn't track variables & reuse.
#
# If that does not work for your use-case, try the `v1.train.init_from_checkpoint` function. It takes an `assignment_map` argument, which specifies the mapping from old names to new names.
#
# Note: Unlike object based checkpoints, which can [defer loading](checkpoints.ipynb#loading_mechanics), name-based checkpoints require that all variables be built when the function is called. Some models defer building variables until you call `build` or run the model on a batch of data.
#
# The [TensorFlow Estimator repository](https://github.com/tensorflow/estimator/blob/master/tensorflow_estimator/python/estimator/tools/checkpoint_converter.py) includes a [conversion tool](#checkpoint_converter) to upgrade the checkpoints for premade estimators from TensorFlow 1.X to 2.0. It may serve as an example of how to build a tool fr a similar use-case.
# + [markdown] colab_type="text" id="_ONjobDD6Uur"
# ### Saved models compatibility
#
# There are no significant compatibility concerns for saved models.
#
# * TensorFlow 1.x saved_models work in TensorFlow 2.0.
# * TensorFlow 2.0 saved_models even load work in TensorFlow 1.x if all the ops are supported.
# + [markdown] colab_type="text" id="ewl9P3oZ6ZtR"
# ## Estimators
# + [markdown] colab_type="text" id="YprVP9g3l6eG"
# ### Training with Estimators
#
# Estimators are supported in TensorFlow 2.0.
#
# When you use estimators, you can use `input_fn()`, `tf.estimator.TrainSpec`, and `tf.estimator.EvalSpec` from TensorFlow 1.x.
#
# Here is an example using `input_fn` with train and evaluate specs.
# + [markdown] colab_type="text" id="N5kZeJsF8lS2"
# #### Creating the input_fn and train/eval specs
# + colab={} colab_type="code" id="AOlXGO4J6jDh"
# Define the estimator's input_fn
def input_fn():
datasets, info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
BUFFER_SIZE = 10000
BATCH_SIZE = 64
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label[..., tf.newaxis]
train_data = mnist_train.map(scale).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
return train_data.repeat()
# Define train & eval specs
train_spec = tf.estimator.TrainSpec(input_fn=input_fn,
max_steps=STEPS_PER_EPOCH * NUM_EPOCHS)
eval_spec = tf.estimator.EvalSpec(input_fn=input_fn,
steps=STEPS_PER_EPOCH)
# + [markdown] colab_type="text" id="_o6J48Nj9H5c"
# ### Using a Keras model definition
# + [markdown] colab_type="text" id="IXCQdhGq9SbB"
# There are some differences in how to construct your estimators in TensorFlow 2.0.
#
# We recommend that you define your model using Keras, then use the `tf.keras.estimator.model_to_estimator` utility to turn your model into an estimator. The code below shows how to use this utility when creating and training an estimator.
# + colab={} colab_type="code" id="aelsClm3Cq4I"
def make_model():
return tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
# + colab={} colab_type="code" id="HJb6f8dtl6rr"
model = make_model()
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
estimator = tf.keras.estimator.model_to_estimator(
keras_model = model
)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# + [markdown] colab_type="text" id="-ptTxL1q6flL"
# ### Using a custom `model_fn`
#
# If you have an existing custom estimator `model_fn` that you need to maintain, you can convert your `model_fn` to use a Keras model.
#
# However, for compatibility reasons, a custom `model_fn` will still run in 1.x-style graph mode. This means there is no eager execution and no automatic control dependencies.
# + [markdown] colab_type="text" id="Avgqf8IKfd51"
# <a name="minimal_changes"></a>
#
# #### Custom model_fn with minimal changes
# To make your custom `model_fn` work in TF 2.0, if you prefer minimal changes to the existing code, `tf.compat.v1` symbols such as `optimizers` and `metrics` can be used.
#
# Using a Keras models in a custom `model_fn` is similar to using it in a custom training loop:
#
# * Set the `training` phase appropriately, based on the `mode` argument.
# * Explicitly pass the model's `trainable_variables` to the optimizer.
#
# But there are important differences, relative to a [custom loop](#custom_loop):
#
# * Instead of using `Model.losses`, extract the losses using `Model.get_losses_for`.
# * Extract the model's updates using `Model.get_updates_for`.
#
# Note: "Updates" are changes that need to be applied to a model after each batch. For example, the moving averages of the mean and variance in a `layers.BatchNormalization` layer.
#
# The following code creates an estimator from a custom `model_fn`, illustrating all of these concerns.
# + colab={} colab_type="code" id="iY16eZKW606-"
def my_model_fn(features, labels, mode):
model = make_model()
optimizer = tf.compat.v1.train.AdamOptimizer()
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
training = (mode == tf.estimator.ModeKeys.TRAIN)
predictions = model(features, training=training)
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)
reg_losses = model.get_losses_for(None) + model.get_losses_for(features)
total_loss = loss_fn(labels, predictions) + tf.math.add_n(reg_losses)
accuracy = tf.compat.v1.metrics.accuracy(labels=labels,
predictions=tf.math.argmax(predictions, axis=1),
name='acc_op')
update_ops = model.get_updates_for(None) + model.get_updates_for(features)
minimize_op = optimizer.minimize(
total_loss,
var_list=model.trainable_variables,
global_step=tf.compat.v1.train.get_or_create_global_step())
train_op = tf.group(minimize_op, update_ops)
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=total_loss,
train_op=train_op, eval_metric_ops={'accuracy': accuracy})
# Create the Estimator & Train
estimator = tf.estimator.Estimator(model_fn=my_model_fn)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# + [markdown] colab_type="text" id="XVxHmU2ccfAG"
# #### Custom `model_fn` with TF 2.0 symbols
# If you want to get rid of all TF 1.x symbols and upgrade your custom `model_fn` to native TF 2.0, you need to update the optimizer and metrics to `tf.keras.optimizers` and `tf.keras.metrics`.
#
# In the custom `model_fn`, besides the above [changes](#minimal_changes), more upgrades need to be made:
#
# * Use [`tf.keras.optimizers`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers) instead of `v1.train.Optimizer`.
# * Explicitly pass the model's `trainable_variables` to the `tf.keras.optimizers`.
# * To compute the `train_op/minimize_op`,
# * Use `Optimizer.get_updates()` if the loss is scalar loss `Tensor`(not a callable). The first element in the returned list is the desired `train_op/minimize_op`.
# * If the loss is a callable (such as a function), use `Optimizer.minimize()` to get the `train_op/minimize_op`.
# * Use [`tf.keras.metrics`](https://www.tensorflow.org/api_docs/python/tf/keras/metrics) instead of `tf.compat.v1.metrics` for evaluation.
#
# For the above example of `my_model_fn`, the migrated code with 2.0 symbols is shown as:
# + colab={} colab_type="code" id="uf8J3nloeze2"
def my_model_fn(features, labels, mode):
model = make_model()
training = (mode == tf.estimator.ModeKeys.TRAIN)
loss_obj = tf.keras.losses.SparseCategoricalCrossentropy()
predictions = model(features, training=training)
# Get both the unconditional losses (the None part)
# and the input-conditional losses (the features part).
reg_losses = model.get_losses_for(None) + model.get_losses_for(features)
total_loss = loss_obj(labels, predictions) + tf.math.add_n(reg_losses)
# Upgrade to tf.keras.metrics.
accuracy_obj = tf.keras.metrics.Accuracy(name='acc_obj')
accuracy = accuracy_obj.update_state(
y_true=labels, y_pred=tf.math.argmax(predictions, axis=1))
train_op = None
if training:
# Upgrade to tf.keras.optimizers.
optimizer = tf.keras.optimizers.Adam()
# Manually assign tf.compat.v1.global_step variable to optimizer.iterations
# to make tf.compat.v1.train.global_step increased correctly.
# This assignment is a must for any `tf.train.SessionRunHook` specified in
# estimator, as SessionRunHooks rely on global step.
optimizer.iterations = tf.compat.v1.train.get_or_create_global_step()
# Get both the unconditional updates (the None part)
# and the input-conditional updates (the features part).
update_ops = model.get_updates_for(None) + model.get_updates_for(features)
# Compute the minimize_op.
minimize_op = optimizer.get_updates(
total_loss,
model.trainable_variables)[0]
train_op = tf.group(minimize_op, *update_ops)
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=total_loss,
train_op=train_op,
eval_metric_ops={'Accuracy': accuracy_obj})
# Create the Estimator & Train.
estimator = tf.estimator.Estimator(model_fn=my_model_fn)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# + [markdown] colab_type="text" id="g1l6VnOTodfA"
# ### Premade Estimators
#
# [Premade Estimators](https://www.tensorflow.org/guide/premade_estimators) in the family of `tf.estimator.DNN*`, `tf.estimator.Linear*` and `tf.estimator.DNNLinearCombined*` are still supported in the TensorFlow 2.0 API, however, some arguments have changed:
#
# 1. `input_layer_partitioner`: Removed in 2.0.
# 2. `loss_reduction`: Updated to `tf.keras.losses.Reduction` instead of `tf.compat.v1.losses.Reduction`. Its default value is also changed to `tf.keras.losses.Reduction.SUM_OVER_BATCH_SIZE` from `tf.compat.v1.losses.Reduction.SUM`.
# 3. `optimizer`, `dnn_optimizer` and `linear_optimizer`: this arg has been updated to `tf.keras.optimizers` instead of the `tf.compat.v1.train.Optimizer`.
#
# To migrate the above changes:
# 1. No migration is needed for `input_layer_partitioner` since [`Distribution Strategy`](https://www.tensorflow.org/guide/distribute_strategy) will handle it automatically in TF 2.0.
# 2. For `loss_reduction`, check [`tf.keras.losses.Reduction`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/losses/Reduction) for the supported options.
# 3. For `optimizer` args, if you do not pass in an `optimizer`, `dnn_optimizer` or `linear_optimizer` arg, or if you specify the `optimizer` arg as a `string` in your code, you don't need to change anything. `tf.keras.optimizers` is used by default. Otherwise, you need to update it from `tf.compat.v1.train.Optimizer` to its corresponding [`tf.keras.optimizers`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers)
#
#
# + [markdown] colab_type="text" id="v0Kljg-AHyqv"
# #### Checkpoint Converter
# <a id="checkpoint_converter"></a>
#
# The migration to `keras.optimizers` will break checkpoints saved using TF 1.x, as `tf.keras.optimizers` generates a different set of variables to be saved in checkpoints. To make old checkpoint reusable after your migration to TF 2.0, try the [checkpoint converter tool](https://github.com/tensorflow/estimator/blob/master/tensorflow_estimator/python/estimator/tools/checkpoint_converter.py).
# + colab={} colab_type="code" id="h9FiYN9mIPli"
# ! curl -O https://raw.githubusercontent.com/tensorflow/estimator/master/tensorflow_estimator/python/estimator/tools/checkpoint_converter.py
# + [markdown] colab_type="text" id="DMc6zDJaJwNw"
# The tool has builtin help:
# + colab={} colab_type="code" id="9JNZFX3rJLXv"
# ! python checkpoint_converter.py -h
# + [markdown] colab_type="text" id="dt8ct9XCFqls"
# <a id="tensorshape"></a>
#
# ## TensorShape
#
# This class was simplified to hold `int`s, instead of `tf.compat.v1.Dimension` objects. So there is no need to call `.value()` to get an `int`.
#
# Individual `tf.compat.v1.Dimension` objects are still accessible from `tf.TensorShape.dims`.
# + [markdown] colab_type="text" id="x36cWcmM8Eu1"
#
#
# The following demonstrate the differences between TensorFlow 1.x and TensorFlow 2.0.
# + colab={} colab_type="code" id="PbpD-kHOZR4A"
# Create a shape and choose an index
i = 0
shape = tf.TensorShape([16, None, 256])
shape
# + [markdown] colab_type="text" id="kDFck03neNy0"
# If you had this in TF 1.x:
#
# ```python
# value = shape[i].value
# ```
#
# Then do this in TF 2.0:
#
# + colab={} colab_type="code" id="KuR73QGEeNdH"
value = shape[i]
value
# + [markdown] colab_type="text" id="bPWPNKRiZmkd"
# If you had this in TF 1.x:
#
# ```python
# for dim in shape:
# value = dim.value
# print(value)
# ```
#
# Then do this in TF 2.0:
# + colab={} colab_type="code" id="y6s0vuuprJfc"
for value in shape:
print(value)
# + [markdown] colab_type="text" id="YpRgngu3Zw-A"
# If you had this in TF 1.x (Or used any other dimension method):
#
# ```python
# dim = shape[i]
# dim.assert_is_compatible_with(other_dim)
# ```
#
# Then do this in TF 2.0:
# + colab={} colab_type="code" id="LpViGEcUZDGX"
other_dim = 16
Dimension = tf.compat.v1.Dimension
if shape.rank is None:
dim = Dimension(None)
else:
dim = shape.dims[i]
dim.is_compatible_with(other_dim) # or any other dimension method
# + colab={} colab_type="code" id="GaiGe36dOdZ_"
shape = tf.TensorShape(None)
if shape:
dim = shape.dims[i]
dim.is_compatible_with(other_dim) # or any other dimension method
# + [markdown] colab_type="text" id="3kLLY0I3PI-l"
# The boolean value of a `tf.TensorShape` is `True` if the rank is known, `False` otherwise.
# + colab={} colab_type="code" id="-Ow1ndKpOnJd"
print(bool(tf.TensorShape([]))) # Scalar
print(bool(tf.TensorShape([0]))) # 0-length vector
print(bool(tf.TensorShape([1]))) # 1-length vector
print(bool(tf.TensorShape([None]))) # Unknown-length vector
print(bool(tf.TensorShape([1, 10, 100]))) # 3D tensor
print(bool(tf.TensorShape([None, None, None]))) # 3D tensor with no known dimensions
print()
print(bool(tf.TensorShape(None))) # A tensor with unknown rank.
# + [markdown] colab_type="text" id="8u63n5S7Y9IX"
# ## Other Changes
#
# * Remove `tf.colocate_with`: TensorFlow's device placement algorithms have improved significantly. This should no longer be necessary. If removing it causes a performance degredation [please file a bug](https://github.com/tensorflow/tensorflow/issues).
# + [markdown] colab_type="text" id="vKX6AdTAQhB-"
# ## Conclusions
#
# The overall process is:
#
# 1. Run the upgrade script.
# 2. Remove contrib symbols.
# 3. Switch your models to an object oriented style (Keras).
# 4. Use `tf.keras` or `tf.estimator` training and evaluation loops where you can.
# 5. Otherwise, use custom loops, but be sure to avoid sessions & collections.
#
#
# It takes a little work to convert code to idiomatic TensorFlow 2.0, but every change results in:
#
# * Fewer lines of code.
# * Increased clarity and simplicity.
# * Easier debugging.
#
#
|
site/en/r2/guide/migration_guide.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercícios com Inteiros
#
# ## Exercício 1
# Dada uma seqüência de números inteiros não-nulos, seguida por $0$, imprimir seus quadrados.
# +
def main():
n = int(input('Digite um número inteiro, 0 para canelar: '))
soma = 0
while n != 0:
soma += n
n = int(input('Digite um número inteiro, 0 para canelar: '))
print(f'Soma: {soma}')
main()
# -
# ## Exercício 2
# Dado um número inteiro positivo $n$, calcular a soma dos $n$ primeiros números inteiros positivos.
# +
def main():
soma = 0
n = int(input('Digite um numero para calcular a soma dos n primeiros numeros inteiros: '))
for i in range(1, n + 1):
soma += i
print(f'a soma dos numeros de 0 ate {n} eh: {soma}')
main()
# -
# ## Exercício 3
# Dado um número inteiro positivo $n$, imprimir os $n$ primeiros naturais ímpares.
#
# Exemplo: Para $n = 4$ a saída deverá ser $1, 3, 5, 7$.
# + pycharm={"name": "#%%\n"}
def main():
n = int(input('Digite a quantidade de numeros impares que serao impressos: '))
for i in range(0, n):
print(i*2 + 1)
main()
# -
# ## Exercício 4
# Dados um inteiro $x$ e um inteiro não-negativo $n$, calcular $x^n$.
# +
# O jeito que provavelmente vão pedir para fazer
def main():
x = int(input('Digite um valor de x: '))
n = int(input('Digite um valor de n: '))
prod = 1
for i in range(n):
prod *= x
main()
# +
# Outro jeito ex.4
def main():
x = int(input('Digite um valor de x: '))
n = int(input('Digite um valor de n: '))
print(f'{x} elevado a {n} é iguala {x**n}') # o operador ** significa "elevado"
main()
# -
# ## Exercício 5
# Uma loja de discos anota diariamente durante o mês de março a quantidade de discos vendidos. Determinar em que dia desse mês ocorreu a maior venda e qual foi a quantidade de discos vendida nesse dia
#
# +
def main():
maior = 0
for i in range(1,32):
discos_vendidos = int(input(f'Digite a quantidade de discos vendidos no dia {i} de março: '))
if discos_vendidos > maior:
maior = discos_vendidos
dia_maior = i
print(f'A maior venda ocorreu no dia {dia_maior} e foi de {maior} discos vendidos')
main()
# -
# ## Exercício 6
# Dados o número $n$ de alunos de uma turma de *Introdução aos Autômatos a Pilha (MAC 414)* e suas notas da primeira prova, determinar a maior e a menor nota obtidas por essa turma (Nota máxima = $100$ e nota mínima = $0$).
# +
def main():
n = int(input('Digite o número de alunos: '))
menor, maior = 0, 0
for i in range(1, n+1):
nota = int(input(f'Insira a nota do {i}º aluno (0 - 100): '))
if nota > maior:
maior = nota
if nota < menor:
menor = nota
print(f'A maior nota foi {maior} e a menor nota foi {menor}')
main()
# -
# ## Exercício 7
# Dados $n$ e uma seqüência de $n$ números inteiros, determinar a soma dos números pares.
# +
def main():
n = int(input('n: '))
soma = 0
for i in range(1, n +1):
x = i * 2
soma += x
print(soma)
main()
# -
# ## Exercício 8
# Dado um inteiro não-negativo $n$, determinar $n!$
# +
# solução sem recursividade
def main()
n = int(input('Digite um numero: '))
fact = 1
for i in range (1,n+1):
fact *= i
print(f'O fatorial de {n} eh {fact}')
main()
# -
# ## Exercício 9
# Dados $n$ e dois números inteiros positivos $i$ e $j$ diferentes de $0$, imprimir em ordem crescente os $n$ primeiros naturais que são múltiplos de $i$ ou de $j$ e ou de ambos.
#
# Exemplo: Para $n = 6$ , $i = 2$ e $j = 3$ a saída deverá ser : $0, 2, 3, 4, 6, 8$.
# +
def main():
n = int(input('n: '))
i = int(input('i: '))
j = int(input('j: '))
mult = 0
cont = 0
while cont < n:
if mult%i == 0 or mult%j == 0:
print(mult, end=' ')
cont += 1
mult += 1
main()
# -
# ## Exercício 10
# Dizemos que um número natural é triangular se ele é produto de três números naturais consecutivos.
#
# Exemplo: $120$ é triangular, pois $4*5*6 = 120$.
#
# Dado um inteiro não-negativo $n$, verificar se $n$ é triangular.
# +
def main():
n = int(input('n: '))
num = 0
flag = False
while n >= num * (num+1) * (num+2):
if num * (num+1) * (num+2) == n:
flag = True
break
num += 1
if flag:
print(f'O número {n} é triangular! {n} = {num}*{num+1}*{num+2}')
else:
print(f'O número {n} não é traingular.')
main()
# -
# ## Exercício 11
# Dado um inteiro positivo $n$, verificar se $n$ é primo.
# +
def main():
n = int(input('n: '))
soma = 0
if n == 2:
print(f'{n} é um número primo')
elif n == 1 or n % 2 == 0:
print(f'{n} não é um número primo!')
else:
for cand in range(1, n+1):
if n % cand == 0:
soma += 1
if soma > 2:
print(f'{n} não é um número primo!')
else:
print(f'{n} é um número primo')
main()
# -
# ## Exercício 12
# Dados dois números inteiros positivos, determinar o máximo divisor comum entre eles usando o algoritmo de *Euclides*.
#
# Exemplo:
#
# 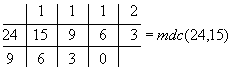
# +
def main():
n = int(input('n: '))
m = int(input('m: '))
# algoritmo de Euclides
anterior = n
atual = m
resto = anterior % atual
while resto != 0:
anterior = atual
atual = resto
resto = anterior % atual
print(f'MDC({n},{m}) = {atual}')
main()
# -
# ## Exercício 13
# *(MAT 89)* Dizemos que um inteiro positivo $n$ é perfeito se for igual à soma de seus divisores positivos diferentes de $n$.
#
# Exemplo: $6$ é perfeito, pois $1+2+3 = 6$.
# Dado um inteiro positivo $n$, verificar se $n$ é perfeito.
# +
def main():
n = int(input('n: '))
soma = 0
for divisor in range(1,n):
if n % divisor == 0:
soma += divisor
if n == soma:
print(f'O número {n} é perfeito!')
else:
print(f'O número {n} não é perfeito.')
main()
# -
# ## Exercício 14
# Um matemático italiano da idade média conseguiu modelar o ritmo de crescimento da população de coelhos através de uma sequência de números naturais que passou a ser conhecida como **sequência de Fibonacci**. O $n$-ésimo número da sequência de Fibonacci $F_{n}$ é dado pela seguinte fórmula de recorrência:
#
# <center><img src='https://www.ime.usp.br/~macmulti/figuras/Image115.gif'></center>
#
# Faça um programa que, dado $n$, calcula $F_{n}$.
# +
def main():
n = int(input('n: '))
f_ant = 0
f_atual = 1
for i in range(1, n):
f_prox = f_ant + f_atual
f_ant = f_atual
f_atual = f_prox
print(f'F({n}) = {f_atual}')
main()
# -
# ## Exercício 15
# Dizemos que um número $i$ é congruente módulo $m$ a $j$ se $i$ % $m = j$ % $m$.
#
# Exemplo: $35$ é congruente módulo $4$ a $39$, pois $35$ % $4 = 3 = 39$ % $4$.
#
# Dados inteiros positivos $n$, $j$ e $m$, imprimir os $n$ primeiros naturais congruentes a $j$ módulo $m$.
# +
def main():
n = int(input('n: '))
j = int(input('j: '))
m = int(input('m: '))
i = 0
while n != 0:
if i % m == j % m:
print(i)
n = n - 1
i += 1
main()
# -
# ## Exercício 16
# Dado um número natural na base binária, transformá-lo para a base decimal.
#
# Exemplo: Dado $10010$ a saída será $18$, pois $1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 18$.
# +
def main():
num = input('Digite um número em binário: ')
soma = 0
for i in range (len(num)):
x = int(num[-1-i]) * 2**i
soma += x
print(soma)
main()
# -
# ## Exercício 17
# Dado um número natural na base decimal, transformá-lo para a base binária.
#
# Exemplo: Dado $18$ a saída deverá ser $10010$.
# +
def main():
num = int(input('Digite um número em decimal: '))
while num >= 1:
if num > 1:
num = num // 2
else:
num = 0
print(num % 2, end= '')
main()
# -
# ## Exercício 18
# Dados três números naturais, verificar se eles formam os lados de um triângulo retângulo.
# +
def main():
a = int(input('Lado a: '))
b = int(input('Lado b: '))
c = int(input('Lado c: '))
if a > b and a > c:
hip = a
cat_1 = b
cat_2 = c
elif b > a and b > c:
hip = b
cat_1 = c
cat_2 = a
elif c > a and c > b:
hip = c
cat_1 = a
cat_2 = b
if hip**2 == cat_1**2 + cat_2**2:
print('É um triângulo retângulo!')
else:
print('Não é um triângulo retângulo :c')
main()
# -
# ## Exercício 19
# Dados três números, imprimi-los em ordem crescente.
#
# +
def main():
a = int(input('a: '))
b = int(input('b: '))
c = int(input('c: '))
maior = 0
medio = 0
menor = 0
if a > b and a > c:
maior = a
if b > c:
medio = b
menor = c
else:
medio = c
menor = b
elif b > a and b > c:
maior = b
if a > c:
medio = a
menor = c
else:
medio = c
menor = a
elif c > a and c > b:
maior = c
if a > b:
medio = a
menor = b
else:
medio = b
menor = a
print(f'{menor} < {medio} < {maior}')
main()
# -
# ## Exercício 20
# *(FIS 88)* Qualquer número natural de quatro algarismos pode ser dividido em duas dezenas formadas pelos seus dois primeiros e dois últimos dígitos.
#
# Exemplos:
# * $1297: 12$ e $97.$
# * $5314: 53$ e $14.$
#
# Escreva um programa que imprime todos os milhares ($4$ algarismos) cuja raiz quadrada seja a soma das dezenas formadas pela divisão acima.
#
# Exemplo: raiz de $9801 = 99 = 98 + 01$.
# Portanto $9801$ é um dos números a ser impresso.
# +
def main():
from math import sqrt
for i in range(1000, 10000):
num = str(i)
esq = int(num[:2])
dire = int(num[2:])
if sqrt(i) == esq + dire:
print(i)
main()
# -
# ## Exercício 21
# *(POLI 87)* Dados $n$ e uma seqüência de $n$ números inteiros, determinar quantos segmentos de números iguais consecutivos compõem essa seqüência.
#
# Exemplo: A seguinte seqüência é formada por $5$ segmentos de números iguais: $5, 2, 2, 3, 4, 4, 4, 4, 1, 1$
# +
def main():
n = int(input('n: '))
anterior = int(input('1º: '))
cont = 1
for i in range(2, n+1):
atual = int(input(f'{i}º: '))
if atual != anterior:
cont += 1
anterior = atual
print(f'Segmentos de números iguais: {cont}')
main()
# -
# ## Exercício 22
# *(POLI 89)* Dados $n$ e uma sequência de $n$ números inteiros, determinar o comprimento de um segmento crescente de comprimento máximo.
#
# Exemplos:
#
# Na sequência: $5, 10, 3, 2, 4, 7, 9, 8, 5$ o comprimento do segmento crescente máximo é $4$.
#
# Na sequência $10, 8, 7, 5, 2$ o comprimento de um segmento crescente máximo é $1$.
# +
def main():
n = int(input('n: '))
anterior = int(input('1º: '))
tam = 1
tam_max = 1
for i in range(1, n):
num = int(input(f'{i+1}º: '))
if num > anterior:
tam += 1
if tam_max < tam:
tam_max = tam
else:
tam = 1
anterior = num
print(f'Comprimento do segmento crescente: {tam_max}')
main()
# -
# ## Exercício 23
# Dizemos que um número natural $n$ é palíndromo se
#
# * $1º$ algarismo de $n$ é igual ao seu último algarismo,
# * $2º$ algarismo de $n$ é igual ao penúltimo algarismo, e assim sucessivamente.
#
# Exemplos:
#
# $567765$ e $32423$ são palíndromos.
#
# $567675$ não é palíndromo.
#
# Dado um número natural $n \geq 10$ , verificar se $n$ é palíndrome.
#
# +
def main():
n = input('n: ') # string
cont = 0
for i in range(len(n)):
if n[i] == n[-(i+1)]:
cont += 1
if cont == len(n):
print(f'{n} é palíndromo.')
else:
print(f'{n} não é palíndromo.')
main()
# -
# ## Exercício 24
# São dados dois números inteiros positivos $p$ e $q$, sendo que o número de dígitos de $p$ é menor ou igual ao número de dígitos de $q$. Verificar se $p$ é um subnúmero de $q$.
#
# Exemplos:
#
# * $p = 23$, $q = 57238$, $p$ é subnúmero de $q$.
# * $p = 23$, $q = 258347$, $p$ não é subnúmero de $q$.
#
# +
def main():
p = input('p: ')
q = input('q: ')
achou = False
for i in range(len(q) - len(p) + 1):
if p == q[i:len(p)+i]:
achou = True
print('oi')
if achou:
print(f'{p} é subnúmero de {q}')
else:
print(f'{p} não é subnúmero de {q}')
main()
|
Macmulti/exercicios_com_inteiros.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using the Jupyter Graffiti API
#
# Jupyter Graffiti has a simple Python API you can use to control Graffiti from Python code. You can play back (and cancel playback) any Graffiti movies using the API.
#
# You can also execute some global activities on all Graffiti in a Notebook using the API.
# ### Accessing the API
# Whenever a Graffiti is selected (either click inside the code containing a Graffiti, or edit a markdown cell containing a Graffiti and click inside the Graffiti-ized text), the Graffiti Editor Panel will show a button labeled `Create Sample API Calls`. Click this button to add a cell below the cell containing the Graffiti you selected, with sample API calls shown in the cell (commented out). The Graffiti ID you need to call the API is shown.
# For instance, clicking the `Create Sample API Calls` button can create a cell something like this:
# +
# Graffiti Id: rilpp9b_3ipign7
# --------------------------------------
import jupytergraffiti
# jupytergraffiti.api.play_recording('rilpp9b_3ipign7')
# jupytergraffiti.api.play_recording_with_prompt('rilpp9b_3ipign7', ' Click **here** to learn more.')
# jupytergraffiti.api.stop_playback()
# jupytergraffiti.api.remove_unused_takes('rilpp9b_3ipign7')
# jupytergraffiti.api.remove_all_unused_takes()
# -
# In the data above, the Graffiti ID is `rilpp9b_3ipign7`. You can see that ID being used in several sample calls to the API. The table below lists all the API calls that are currently available to you.
#
# You call any API function by first `import jupytergraffiti` to bring in the API object, then use:
#
# `jupytergraffiti.api.<function>` to call the API.
#
# Note: if you are not using the Python kernel, the API will not work as it is written currently only in Python. If demand for it arises we would accept ports to other kernels (the API is relatively simple as it just calls exposed functions in the Javascript extension).
# ### API Reference Table
# #### API Calls Controlling Graffiti Movie Playback
#
# | API Call | Description |
# | -: |:--: |
# |`play_recording(<key>)`| Start playing the given Graffiti's movie (if it has one) from the beginning.|
# |`play_recording_with_prompt(<key>, <prompt>)`| Start playing the given Graffiti's movie (if it has one) from the beginning, but first show a prompt in the Graffiti Playback panel. A user click on that panel starts movie play. You may want to use this if you trigger a hint movie but don't want to make watching it obligatory.|
# |`stop_playback()`| If a Graffiti is currently playing, cancel playback.|
# #### API Calls Managing Graffiti More Broadly
#
# | API Call | Description |
# | -: |:--: |
# |`remove_unused_takes(<key>)`| Remove any movie takes except the active take from the Graffiti data directory. This can save you a small amount of space especially if you've made many takes.|
# |`remove_all_unused_takes()`| Remove any movie takes except the active take from all Graffitis. This can save you a reasonable amount of space especially if you've made many takes over all movies.|
# |`remove_all_graffiti()`| Remove all Graffiti from this Notebook. You will be prompted to confirm. After this call is done, be sure to save the Notebook and reload.|
# |`disable_graffiti()`| Remove all Graffiti from this Notebook and deactivate Graffiti as if you'd never activated it. You will be prompted to confirm. After this call is done, be sure to save the Notebook and reload.|
# |`transfer_graffiti()`| If you make a copy of a Notebook with Graffiti in it, make this API call to move all Graffiti to the new notebook and assign a new Graffiti ID to this notebook. Do this to prevent the two notebooks from overwriting each other's Graffiti.|
# |`package_graffiti()`|This call will create a tarball of the current notebook and its `jupytergraffiti_data` directory for transport. You can use this call but we recommend using `nbzip` instead, which ships with the Docker installation or is available on the Binder demo page.|
#
|
user_manual/Graffiti API.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="6kyrAlHMGFWa" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="a4645279-332a-4d3d-e908-43d6b2f82c5e"
import tensorflow as tf
import keras_preprocessing
from keras_preprocessing import image
from keras_preprocessing.image import ImageDataGenerator
import shutil
TRAINING_DIR = "Training"
training_datagen = ImageDataGenerator(rescale = 1./255,
width_shift_range=0.2,
height_shift_range=0.2)
VALIDATION_DIR = "Validation"
validation_datagen = ImageDataGenerator(rescale = 1./255)
train_generator = training_datagen.flow_from_directory(
TRAINING_DIR,
target_size=(224,224),
class_mode='categorical',
batch_size = 32
)
validation_generator = validation_datagen.flow_from_directory(
VALIDATION_DIR,
target_size=(224,224),
class_mode='categorical',
batch_size= 4
)
# + id="gKO1W3suMc2J" colab={"base_uri": "https://localhost:8080/", "height": 490} outputId="44524191-21dc-4151-c76e-5113d69411de"
from tensorflow.keras.optimizers import RMSprop, Adadelta
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(224, 224, 3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(3, activation='softmax')
])
model.summary()
model.compile(loss='categorical_crossentropy',
optimizer=tf.keras.optimizers.RMSprop(learning_rate=0.001),
metrics=['acc'])
# + id="qlWbmjrjO6fB" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="1624f6d6-e8b8-45b3-a89f-75869ce0ad39"
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if(logs.get('val_loss')<=0.08 and logs.get('loss')<=0.08):
print('\nReached ^98%')
self.model.stop_training = True
callbacks = myCallback()
history = model.fit(
train_generator,
steps_per_epoch = 24,
epochs = 100,
validation_data = validation_generator,
validation_steps = 24,
callbacks=[callbacks]
)
model.save('COVIDcnn.h5')
# + id="BZ5uF_aaPgg0" colab={"base_uri": "https://localhost:8080/", "height": 581} outputId="bb682c0f-fc6c-4305-e587-bc9533db6d36"
# %matplotlib inline
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'g', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.savefig('/content/drive/My Drive/covidieeedataset/accCNN2.png')
plt.figure()
plt.show()
plt.plot(epochs, loss, 'r', label='Training loss')
plt.plot(epochs, val_loss, 'orange', label='Validation loss')
plt.title('Training and validation loss')
plt.legend(loc=0)
plt.savefig('/content/drive/My Drive/covidieeedataset/lossCNN2.png')
plt.figure()
plt.show()
# + id="iUuOIqIbRT37" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="d819dab4-7d28-49e0-f938-ec06eab549f1"
import tensorflow as tf
model = tf.keras.models.load_model('/content/drive/My Drive/covidieeedataset/CNN32.h5')
# + id="U6-n8mONgI5g"
import numpy as np
import keras
from keras.preprocessing import image
import os
prediction = []
x = []
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/COVID')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/COVID/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/NORMAL')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/NORMAL/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/VIRAL')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/VIRAL/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
# + id="-M_IMtLdXqmC" colab={"base_uri": "https://localhost:8080/", "height": 254} outputId="1951c0c1-cd91-45be-d69a-ad6827922351"
import numpy
from sklearn import metrics
y_act = validation_generator.classes
labels = [0, 1, 2]
print(metrics.confusion_matrix(y_act, np.array(prediction), labels=labels))
# Printing the precision and recall, among other metrics
print(metrics.classification_report(y_act, np.array(prediction), labels=labels))
# + id="pxN2gXzGTQM6" colab={"base_uri": "https://localhost:8080/", "height": 265} outputId="f4e5490a-df25-483b-8224-cb451350441a"
import seaborn as sn
import pandas as pd
import matplotlib.pyplot as plt
lbl = [0, 1, 2]
df_cm = pd.DataFrame(metrics.confusion_matrix(y_act, np.array(prediction), labels=lbl),
['COVID-19', 'Normal', 'Viral pneumonia'],
['COVID-19', 'Normal', 'Viral pneumonia'])
sn.heatmap(df_cm, annot=True, annot_kws={"size": 12}, cbar=False, cbar_kws={"orientation": "horizontal"})
plt.yticks(rotation=0)
plt.savefig('/content/drive/My Drive/covidieeedataset/confusionmatrixCNN.png', bbox_inches='tight',dpi=100)
plt.show()
# + id="astpU7OQXkVi"
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/COVID')
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/COVID/'+paths[20], target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x_train = np.vstack([x]) / 255
# + id="GZZare8FYNZC"
model = tf.keras.models.load_model('/content/drive/My Drive/covidieeedataset/covidCNNmodel.h5')
# + id="JFuIwf3umTkJ"
import matplotlib.pyplot as plt
def visualize_conv_layer(layer_name):
layer_output=model.get_layer(layer_name).output
intermediate_model=tf.keras.models.Model(inputs=model.input,outputs=layer_output)
intermediate_prediction=intermediate_model.predict(x_train)
row_size=4
col_size=8
img_index=0
print(np.shape(intermediate_prediction))
fig,ax=plt.subplots(row_size,col_size,figsize=(10,8))
for row in range(0,row_size):
for col in range(0,col_size):
ax[row][col].imshow(intermediate_prediction[0, :, :, img_index], cmap='gist_heat')
img_index=img_index+1
plt.savefig('/content/drive/My Drive/covidieeedataset/infernoMapCNN.png')
# + id="dpJ2TvfuXRnT" colab={"base_uri": "https://localhost:8080/", "height": 469} outputId="8d56253a-4095-4d13-ea23-23b2144d9bba"
visualize_conv_layer('conv2d_17')
# + id="UYT5-2pJYoc3" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="026a0e96-e125-438f-8b81-0b931b663426"
import numpy as np
train_images = [206, 280, 280]
validation_images = [25, 35, 35]
test_images= [25, 35, 35]
plt.bar(range(len(train_images)),train_images, 0.5, color='#d62728')
plt.bar(range(len(validation_images)),validation_images, 0.5, bottom=train_images)
plt.bar(range(len(test_images)),test_images, 0.5, bottom=np.array(train_images)+np.array(validation_images))
plt.xlabel('Classes')
plt.ylabel('Number of Images')
plt.title('Distribution of the dataset')
plt.xticks(np.arange(3), ('Covid-19', 'Viral Pneumonia', 'Normal'))
plt.yticks(np.arange(0, 360, 25))
plt.legend(('Train', 'Validation', 'Test'))
plt.savefig('/content/drive/My Drive/covidieeedataset/dataset.png')
plt.show()
# + id="5rIBDYIS9HIT"
import tensorflow as tf
model = tf.keras.models.load_model('/content/drive/My Drive/covidieeedataset/covidCNNmodel.h5')
# + id="V8zZJRnNF0Do" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="7fde0343-0b9d-432c-9a98-a44bb04a9b47"
import numpy as np
from keras.preprocessing import image
import os
prediction = []
x = []
#paths = ['/content/drive/My Drive/COVID/VIRAL/Viral Pneumonia (102).jpg', '/content/drive/My Drive/COVID/NORMAL/NORMAL (102).jpg', '/content/drive/My Drive/COVID/images/Validation/covid/extubation-13.jpg']
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/COVID')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/COVID/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/NORMAL')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/NORMAL/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
paths = os.listdir('/content/drive/My Drive/covidieeedataset/Testing/VIRAL')
for i in range(len(paths)):
img = image.load_img('/content/drive/My Drive/covidieeedataset/Testing/VIRAL/'+paths[i], target_size=(224, 224))
#print(type(img))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x]) / 255
#print(type(images))
classes = model.predict(images, batch_size=256)
prediction.append(list(classes[0]).index(max(classes[0])))
# + id="Qtrqcdf6F1x7"
import numpy
from sklearn import metrics
y_act = validation_generator.classes
labels = [0, 1, 2]
print(metrics.confusion_matrix(y_act, np.array(prediction), labels=labels))
# Printing the precision and recall, among other metrics
print(metrics.classification_report(y_act, np.array(prediction), labels=labels))
# + id="Ocgj4sRJF3oj" colab={"base_uri": "https://localhost:8080/", "height": 265} outputId="9b86154e-b557-4eea-8515-5ba9b29dd771"
import seaborn as sn
import pandas as pd
import matplotlib.pyplot as plt
lbl = [0, 1, 2]
#plt.figure(figsize=[8, 5])
df_cm = pd.DataFrame(metrics.confusion_matrix(y_act, np.array(prediction), labels=lbl),
['COVID-19', 'Normal', 'Viral pneumonia'],
['COVID-19', 'Normal', 'Viral pneumonia'])
sn.heatmap(df_cm, annot=True, annot_kws={"size": 12}, cbar=False, cbar_kws={"orientation": "horizontal"})
plt.yticks(rotation=0)
plt.savefig('/content/drive/My Drive/covidieeedataset/confusionmatrixCNN.png', bbox_inches='tight',dpi=100)
plt.show()
|
COVIDcnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from zipfile import ZipFile
import pandas as pd
import numpy as np
import subprocess
import os
def fetchdata():
cli_command = "kaggle competitions download -c cat-in-the-dat -w"
subprocess.run(cli_command, shell=True) # Get data from kaggle
zip_files = [files for files in os.listdir() if files.endswith('.zip')]
# Unzip files if not already unzipped
unzipped_filenames = [files.replace('.zip','') for files in zip_files]
if not all(x in os.listdir() for x in unzipped_filenames):
for file in zip_files:
with ZipFile(file, 'r') as zip:
zip.extractall()
fetchdata()
data = pd.read_csv('train.csv')
print(data.head())
print(data.info())
print(data.describe())
# %matplotlib inline
import matplotlib.pyplot as plt
data.hist(bins=50, figsize=(20,15))
plt.show()
categorical_data = strat_train_set.drop('target', axis=1)
categorical_data_labels = strat_train_set['target'].copy()
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
tree_reg = DecisionTreeRegressor()
tree_reg.fit(categorical_data, categorical_data_labels)
data_predictions = tree_reg.predict(categorical_data)
tree_mse = mean_squared_error(categorical_data_labels, data_predictions)
tree_rmse = np.sqrt(tree_mse)
print(tree_mse)
print('help')
'test'
|
.ipynb_checkpoints/Jupiter-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="8nIg0LFrEzP2" colab_type="code" colab={}
# Que 1
# + id="ZkQMh-GrE3a4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 50} outputId="6f5ca72b-0ac6-4928-ea81-3bcee9126efd"
altitude= int(input("Enter the altitude: "))
if altitude==1000:
print("Plane is safe to land")
elif altitude>1000 and altitude<5000:
print("Come down to 1000")
else:
print("Turn around and try later")
# + id="iIYeYxDDB1O5" colab_type="code" colab={}
#Que 2 :
# + id="ERSSbA3AGqRE" colab_type="code" colab={}
for num in range (1,201):
num=int(input("Enter any number between 1 to 200: "))
if num>1:
for i in range(2,num):
if (num%i)==0:
print("It is not a prime number")
break
else:
print("It is a prime number")
else:
print("It is not a prime number")
|
Assignment2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from aalpy.SULs import MdpSUL
from aalpy.learning_algs import run_stochastic_Lstar
from aalpy.oracles import RandomWalkEqOracle
from aalpy.utils import get_faulty_coffee_machine_MDP
# get faulty coffe machine found in Chapter 5 of Martin's Tappler PhD thesis
mdp = get_faulty_coffee_machine_MDP()
# get its input alphabet
input_alphabet = mdp.get_input_alphabet()
# wrap it in the SUL
sul = MdpSUL(mdp)
# +
# Define the eq. oracle
eq_oracle = RandomWalkEqOracle(input_alphabet, sul=sul, num_steps=1000, reset_prob=0.11,
reset_after_cex=True)
# start learning with verbose output
learned_mdp = run_stochastic_Lstar(input_alphabet, sul, eq_oracle, n_c=20, n_resample=200, strategy='classic', min_rounds=10,
max_rounds=50, print_level=3)
# -
# print the learned MDP
print(learned_mdp)
|
notebooks/MDP_Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Decision Trees
#
# - Simple Tree like structure, model makes a decision at every node
# - Useful in simple tasks
# - One of the most popular algorithm
# - Easy explainability, easy to show how a decision process works!
#
# ### Why decision trees are popular?
# - Easy to interpret and present
# - Well defined Logic, mimic human level thought
# - Random Forests, Ensembles of decision trees are more powerful classifiers
# - Feature values are preferred to be **categorical**. If the values are continuous then they are discretized prior to building the model.
#
# ## Build Decision Trees
#
# Two common algorithms -
#
# - CART (Classification and Regression Trees) → uses Gini Index(Classification) as metric.
# - ID3 (Iterative Dichotomiser 3) → uses Entropy function and Information gain as metrics
#
#
#
#
# ### Let's Construct the Decision Tree
# ### ID3 Implementation
# ### Part - I Data Preparation
import pandas as pd
data = pd.read_csv("titanic.csv")
data.head(n=5)
data.info()
# +
# We can drop those rows, or columns
# We can substitute some values, age --> mean or median age
# Sklearn Imputer
# +
columns_to_drop = ['PassengerId','Name','Ticket','Cabin','Embarked']
data_clean = data.drop(columns_to_drop,axis=1)
# -
data_clean.head(n=5)
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
data_clean["Sex"] = le.fit_transform(data_clean["Sex"])
data_clean.head()
data_clean.info()
avg_age = data_clean["Age"].mean()
print(avg_age)
data_clean = data_clean.fillna(avg_age)
data_clean.info()
data_clean.describe()
# ### Part II - Decison Tree
|
13. Decision Trees/Decision Trees.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from glob import glob
import numpy as np
stock_files = sorted(glob('/home/mayank/Downloads/technocolab_project/data/stock*.csv'))
stock_files
data = pd.concat((pd.read_csv(file).assign(filename = file)
for file in stock_files),ignore_index = True)
data
data.date = pd.to_datetime(data.date)
data.info()
sentimentalanalysis=pd.read_csv('analyzedJSON_data.csv')
sentimentalanalysis.head()
sentimentalanalysis.date = pd.to_datetime(sentimentalanalysis.date)
data.date = pd.to_datetime(data.date)
merged_data=pd.merge(data,sentimentalanalysis)
#merged_data = pd.merge(data, sentimentalanalysis, how='left', on='date')
# +
#merged_data.groupby(['date'], as_index=False).sum()
#merged_data.drop_duplicates(subset='date',keep='first',inplace=True)
# -
merged_data.info()
merged_data.head()
merged_data.shape
merged_data.drop(['Unnamed: 0','Unnamed: 0.1',"filename"],axis=1,inplace =True)
merged_data.head()
merged_data.isnull().sum()
merged_data.dropna(axis = 0,inplace =True)
merged_data.set_index("date", inplace = True)
import talib
# +
#merged_data['S_10'] = merged_data['close'].rolling(window=10).mean()
#merged_data['Corr'] = merged_data['close'].rolling(window=10).corr(merged_data['S_10'])
#merged_data['RSI'] = talib.RSI(np.array(merged_data['close']), timeperiod =10)
#merged_data['Open-Close'] = merged_data['open'] - merged_data['close'].shift(1)
#merged_data['Open-Open'] = merged_data['open'] - merged_data['open'].shift(1)
# -
#merged_data['target'] = np.where(merged_data['close'].shift(-1) > merged_data['close'],1,0)
merged_data['target'] = np.where(merged_data['close'].shift(-1) > merged_data['close'],1,0)
merged_data.drop(['Name','cont_len'], axis=1, inplace=True)
merged_data.info()
merged_data.dropna(axis = 0,inplace =True)
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.model_selection import train_test_split
#merged_data['target'] = merged_data.apply(lambda row: check_target(row), axis=1)
merged_data['cont_sent'] = merged_data['cont_sent'].replace({'Neutral': 0, 'Positive': 1, 'Negative': -1})
merged_data.dropna(axis=0,inplace=True)
# +
#from sklearn.preprocessing import MinMaxScaler
#scaler = StandardScaler()
#scaler.fit(merged_data)
#merged_data = scaler.transform(merged_data)
#scaler = MinMaxScaler()
# transform data
#scaled_data = scaler.fit_transform(merged_data)
# -
X = merged_data.drop('target', axis=1)
y = merged_data[['target']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40, random_state=1)
# +
#y_train[y_train==1].count()
# +
#y_train[y_train==0].count()
# -
model = LogisticRegression()
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
model_score = model.score(X_test, y_test)
print(model_score)
model.score(X_train, y_train)
# +
probability = model.predict_proba(X_test)
print(probability)
predicted = model.predict(X_test)
# -
print(metrics.confusion_matrix(y_test, predicted))
print(metrics.classification_report(y_test, predicted))
merged_data.groupby(["target"]).count()
# +
#from sklearn.model_selection import RepeatedStratifiedKFold
#from sklearn.model_selection import GridSearchCV
#model = LogisticRegression()
#solvers = ['newton-cg', 'lbfgs', 'liblinear']
#penalty = ['l2','l1']
#c_values = [100, 10, 1.0, 0.1, 0.01]
# define grid search
#grid = dict(solver=solvers,penalty=penalty,C=c_values)
#cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
#grid_search = GridSearchCV(estimator=model, param_grid=grid, n_jobs=-1, cv=cv, scoring='accuracy',error_score=0)
#grid_result = grid_search.fit(X_train, y_train)
# summarize results
#print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
#means = grid_result.cv_results_['mean_test_score']
#stds = grid_result.cv_results_['std_test_score']
#params = grid_result.cv_results_['params']
#for mean, stdev, param in zip(means, stds, params):
# print("%f (%f) with: %r" % (mean, stdev, param))
# -
|
LOGISTIC REGRESSION MODEL.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pyodbc as serv
# +
driver = '{ODBC Driver 17 for SQL Server}'
server = 'stay-safe.database.windows.net'
port = '1433'
database = 'staysafe'
username = 'owner'
password = '<PASSWORD>'
tc = 'yes'
pass
conn = serv.connect('DRIVER=' + driver + ';'
+ 'SERVER=' + server +';'
+ 'PORT=' + port + ';'
+ 'DATABASE=' + database + ';'
+ 'UID=' + username + ';'
+ 'PWD=' + password)
cursor = conn.cursor()
# +
cursor.execute('''CREATE TABLE animals(
id int,
breed varChar(80),
age int)''')
cursor.execute('''INSERT INTO animals(id, breed, age)
VALUES(0, 'Cat', 5)''') # can you see where i went wrong :D
cursor.execute('''INSERT INTO animals(id, breed, age)
VALUES(1, 'Dog', 10)''')
# +
cursor.execute('SELECT * FROM animals')
for row in cursor:
print(row)
# -
|
App-Side (Edward)/Database Handler (Py)/.ipynb_checkpoints/DatabaseConnection-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Quansight-Labs/uarray/blob/master/notebooks/2018.11.20%20PyData%20Presentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="bwt4avpVfWxa" colab_type="text"
# # ["A World Where Many Worlds Fit"](https://globalsocialtheory.org/topics/zapatismo/)
#
# + [markdown] id="Wr1-CwZc7O43" colab_type="text"
#
# [](https://javiersoriaj.wordpress.com/2013/06/09/postales-zapatistas-74-un-mundo-donde-quepan-muchos-mundos/)
#
#
#
# * Hardware becoming more hetergenous and parallel
# * Data increasing
#
#
#
# Need software to target many backends, that is pluggable and allows collaboration. Some existing work in Python land:
#
# * [`opt_einsum`](https://github.com/dgasmith/opt_einsum)
# * Extending NumPy dispatching: [NEP 18](http://www.numpy.org/neps/nep-0018-array-function-protocol.html)
# * [Tensor Comprehensions](https://facebookresearch.github.io/TensorComprehensions/introduction.html)
#
#
#
# Why? So that we can innovate at all levels of stack (hardware, compilation, algorithms, user interface) and share work!
#
#
#
# Like thin waist model of Internet Protocal. We working on the "thin waist" that supports common NumPy and SciPy algorithms and can target different hardware (GPU, CPU, FGPA) and software (NumPy, PyTorch, Tensorflow).
#
# * Very preliminary work
# * Lot's of fun problems would love collaboration!
# + [markdown] id="RvZtYO3Rhveb" colab_type="text"
# # Example
# + [markdown] id="vYCOHgg3xnrg" colab_type="text"
# Look at an example using numpy.multiply.outer. Recall that the outer method of ufuncs takes two arrays a, and b, and creates an array c, with shape a.shape + b.shape (tuple concatenation)
#
# so, for 1-d arrays if c = numpy.multiply.outer(a,b) we will get a 2-d array whose elements are:
#
# $c[i,j] = a[i] * b[j]$
# + id="TQMwmqcjxYDX" colab_type="code" outputId="9b1776b9-0b81-4cf9-8438-aaf127b20db3" colab={"base_uri": "https://localhost:8080/", "height": 104}
import numpy
numpy.multiply.outer(numpy.arange(5), numpy.arange(10))
# + id="pQkzP9Xq7O45" colab_type="code" colab={}
def outer_then_index(a, b):
return numpy.multiply.outer(a, b)[5]
# + [markdown] id="1jpQ2SDRxXU-" colab_type="text"
#
# + id="uNVhsuAbCXN_" colab_type="code" outputId="8868647a-acf6-461a-faf3-eaf6cd5f6002" colab={"base_uri": "https://localhost:8080/", "height": 35}
n = 10
outer_then_index(numpy.arange(n, dtype="float64"), numpy.arange(n, dtype="float64"))
# + [markdown] id="6v7xSc-HDMam" colab_type="text"
# ## Issues
# + [markdown] id="JOhF8ejxDZyH" colab_type="text"
#
# * Wasted work: $O(n^2)$ instead of $O(n)$
# * Execution tied to API: Requires NumPy-compatible array objects
# + [markdown] id="i-zlV7hPFJ0j" colab_type="text"
# ## Improved
# + id="HdEUoXNOFg95" colab_type="code" colab={}
def outer_then_index_optimized(a, b):
length_b = b.shape[0]
out = numpy.empty((length_b,))
for i in range(length_b):
out[i] = a[5] * b[i]
return out
# + id="ybtrCFkHL-Cb" colab_type="code" outputId="87f554dc-9d34-4133-fbb9-444ab7c73d8b" colab={"base_uri": "https://localhost:8080/", "height": 35}
outer_then_index_optimized(numpy.arange(n, dtype="float64"), numpy.arange(n, dtype="float64"))
# + [markdown] id="fc6r39BxrAtm" colab_type="text"
# I timed these two versions locally on my laptop and found that although at first the improved version is slower, it quickly becomes faster as $n$ increases, due to the differing time complexity:
# + [markdown] id="EcGmw-5OB_Kb" colab_type="text"
# [](https://github.com/Quansight-Labs/uarray/tree/master/benchmarks)
# + [markdown] id="4ouDifuqPSHd" colab_type="text"
# * No more waisted work (linear instead of quadratic)
# * Still requires NumPy-ish object, but only primitive operations
# + [markdown] id="Hemtj23gMFsu" colab_type="text"
# How to automate this translation?
# + [markdown] id="36rFDzsjNyjJ" colab_type="text"
# # Theory
# + [markdown] id="OPF9iZLuOmux" colab_type="text"
# In the 1980s <NAME> published ["A Mathematics of Arrays"](https://paperpile.com/app/p/5de098dd-606d-0124-a25d-db5309f99394) based on her work on [APL](https://en.wikipedia.org/wiki/APL_(programming_language).
#
# In it, arrays are defined by:
#
# * Shape (vector of integers)
# * Indexing (function from indices to value)
# + [markdown] id="0y0IeLB_RB01" colab_type="text"
# In `outer_then_index_optimized` above, we did the same, determining:
#
# * Shape of result, based on shapes of inputs
# * The value of each index of the result
# + [markdown] id="P5ia_IInVD_C" colab_type="text"
# We can use this to perform this translation by hand, then we will look into automating it.
# + [markdown] id="V2bgQWgagVOd" colab_type="text"
# ## Hand optimizing the example
# + [markdown] id="NqkElXgIZ4Js" colab_type="text"
# ### Definitions
# + [markdown] id="skBFC_h4VJmp" colab_type="text"
# I should start by presenting some notation we will use to the derivation that is from the above paper. Here are translations to roughly equivalent NumPy notation:
#
# * $\rho(x)$ = `x.shape`
# * $<x, y, z>$ = `numpy.array([x, y, z])`
# * $x \psi y$ = `y[x]` where `x` is a tuple of indices
# * $x \cdot_{\times} y$ = `numpy.multiply.outer(x, y)`
# * $x \downarrow y$ = `y[x:]`
# * $x ++ y$ = `numpy.concatenate([x, y])`
#
#
# And now we can define how outer product and partial indexing work in terms of these. We start by defining their shapes:
#
# $$
# \begin{array}{cc}
# \rho \left( x \psi y \right) \equiv (<0> \psi \rho(x) ) \downarrow \rho\left(y \right) & \texttt{(y[x]).shape == y.shape[x.shape[0]:]} \\
# \rho \left( x \cdot_{\times} y \right) \equiv \rho(x) ++ \rho(y) & \texttt{(np.multiply.outer(x,y)).shape == x.shape + y.shape}
# \end{array}
# $$
#
# And then how to index into them:
#
# $$
# \begin{array}{cc}
# z \psi (x \psi y) \equiv (x ++ z) \psi y & \texttt{y[x][z] == y[np.concatenate([x,z])]}\\
# (j++k) \psi (x \cdot_{\times} y) \equiv j \psi x \times k \psi y & \texttt{np.multiply.outer(x,y)[j+k] == x[j]*y[k] } \\
# \end{array}
# $$
# + [markdown] id="QBHoOhjeZ7LI" colab_type="text"
# ### Reducing
# + [markdown] id="zwjVnr-wcnqM" colab_type="text"
# #### Shape
# + [markdown] id="NynaN45Kghu9" colab_type="text"
# Assuming that both inputs are vectors and letting their lengthts be $c$ and $d$, we have:
#
#
# $$
# \rho\left(a\right) \equiv<c> \\
# \rho\left(b\right) \equiv<d> \\
# res \equiv <5> \psi \left(a \cdot_{\times} b\right)
# $$
#
#
# First let's figure out the shape of our result, simply by applying relevent equivalencies:
#
# $$
# \rho(res) \equiv \rho \left(<5> \psi \left(a \cdot_{\times} b\right) \right) \\
# \text{shape of partial index:} \\
# \equiv 1 \downarrow \rho \left(a \cdot_{\times} b\right)\\
# \text{shape of outer product:} \\
# \equiv 1 \downarrow \left(\rho a ++ \rho b\right)\\
# \text{shapes of inputs} \\
# \equiv 1 \downarrow \left(<c> ++ <d>\right)\\
# \text{concat vectors} \\
# \equiv 1 \downarrow <c d> \\
# \text{drop vectors} \\
# \equiv < d> \\
# $$
#
# The result shape is a vector with the length of $b$, which matches our code above.
#
# + [markdown] id="U4sOWiL97O4-" colab_type="text"
# #### Indexing
#
#
# + [markdown] id="4mbKwEnbcyPx" colab_type="text"
# Now we can index with the vector $<i>$ and see what the result is:
#
#
#
# $$
# <i> \psi res \equiv <i> \psi \left(<5> \psi \left(a \cdot_{\times} b\right) \right) \\
# \text{partial indexing} \\
# \equiv <5 \, i> \psi \left(a \cdot_{\times} b\right) \\
# \text{indexing outer product} \\
# \equiv \left(<5> \psi a \right) \times \left(<i> \psi b \right) \\
# $$
#
# This indexing expression matches the code we wrote above.
# + [markdown] id="7LEjXkoUeKdJ" colab_type="text"
# ## Automatically optimizing the example
# + [markdown] id="Hq3kEeMGiLnJ" colab_type="text"
# We have started building the [`uarray`](https://github.com/Quansight-Labs/uarray/tree/master/uarray#uarray) that includes a framework to register these types of definitions and reduce expressions:.
# + id="wM1jmAzG7Y2z" colab_type="code" outputId="5bda9f25-141b-4d55-dd8d-12937bd46e53" colab={"base_uri": "https://localhost:8080/", "height": 557}
# !pip install -U uarray==0.4
# + id="cb7WMHgP7O5A" colab_type="code" colab={}
from uarray import *
import numpy
# + [markdown] id="pWOObqjtilyH" colab_type="text"
# ### Inputs
#
#
# + [markdown] id="jLSdmk84iuxt" colab_type="text"
# Let's start by creating two arrays both with dimensionality of 1:
# + id="qIdIdKTl7O5C" colab_type="code" outputId="8fdd4eb8-b3e5-4871-aaf9-3b5d21ea62e7" colab={"base_uri": "https://localhost:8080/", "height": 139}
a = with_dims(unbound("a"), 1)
b = with_dims(unbound("b"), 1)
a
# + [markdown] id="3giioMfrirKO" colab_type="text"
# ### Result
# + [markdown] id="N9JIomHJi5lh" colab_type="text"
# Now we can build up our result given these two arrays
# + id="raJCnoqCiq6w" colab_type="code" outputId="7495f324-5672-414e-9285-0a0ea490b1b0" colab={"base_uri": "https://localhost:8080/", "height": 433}
res = Index(vector(5), OuterProduct(multiply, a, b))
res
# + [markdown] id="XchJ_HuPk3ej" colab_type="text"
# #### Verifying the Result
# + [markdown] id="zwEPWy5B7O5G" colab_type="text"
# Now we can call `replace` to do what we did above in an automated way.
#
#
# *We use the [MatchPy](https://github.com/HPAC/matchpy) library in Python to do this replacement, using pattern matching.*
# + id="GNX-pbgW7O5H" colab_type="code" outputId="e0db0aac-7c4c-443f-fc19-4fb2ed260d44" colab={"base_uri": "https://localhost:8080/", "height": 225}
replaced_res = replace(res)
replaced_res
# + [markdown] id="uYuLv0Pn7O5L" colab_type="text"
# However, this is still not totally intelligble.
#
# ##### Shape
#
# Let's make sure the shape is right. It should be equal to b's shape:
# + id="uApZFsSb7O5M" colab_type="code" colab={}
assert replace(Shape(replaced_res)) == replace(Shape(b))
# + [markdown] id="iN2F2rGkkHAk" colab_type="text"
# ##### Index
#
# Also, let's make sure indexing it gives the right result as well:
# + id="CNijG7H7jx7Z" colab_type="code" colab={}
i = with_dims(unbound("i"), 0)
expected_index = Scalar(Multiply(
Content(CallUnary(GetItem(a), Int(5))),
Content(CallUnary(GetItem(b), Content(i))),
))
assert replace(Index(vector_of(i), replaced_res)) == replace(expected_index)
# + [markdown] id="78qdF-GTlz23" colab_type="text"
# But how do we actually use these results?
# + [markdown] id="r7sd2xna7O5a" colab_type="text"
# # User Interface
# + [markdown] id="tCyExVSKm8ep" colab_type="text"
# We have started building some interface to build up these expressions and then to turn them into something we can execute.
# + [markdown] id="6eJm-3-j7O5b" colab_type="text"
# ## Using NumPy Syntax
#
#
# + [markdown] id="XYeu_JmgnCYi" colab_type="text"
# Starting with a NumPy-ish object that holds an expression tree inside to represent the array.
#
# Here is how we would build the same expression as above:
# + id="mG5S8IOi7O5d" colab_type="code" outputId="d868d40c-4986-4ff9-ef8c-913148593853" colab={"base_uri": "https://localhost:8080/", "height": 399}
numpy.multiply.outer(LazyNDArray(a), LazyNDArray(b))[10]
# + [markdown] id="kxGsll6xnRvE" colab_type="text"
# ## Compiling to NumPy code
# + [markdown] id="tzUdtih-nYUH" colab_type="text"
# We also provide an `optimize` decorator that:
#
# * Takes existing function that acceptst and returns NumPy arrays and returns a new function
# * Builds up array expression by using the `LazyNDArray`
# * Compiles that array expression to a Python AST for reduced code
# + id="ForMcp4m7O5f" colab_type="code" colab={}
outer_then_index_auto_optimized = optimize(1, 1)(outer_then_index)
# + [markdown] id="UdLbQrGn7O5j" colab_type="text"
# ## Produced Code
# + [markdown] id="riwUnlQYqfdv" colab_type="text"
# If we look at the code it generates, we see it matches semantically our optimized expression above, even though it's much uglier!
# + id="xBHmvkmuqenh" colab_type="code" outputId="2a978fa2-cacf-49e0-9ac4-71776ef29f0f" colab={"base_uri": "https://localhost:8080/", "height": 364}
print(outer_then_index_auto_optimized.__optimize_steps__['ast_as_source'])
# + [markdown] id="Co_giAQcrNGH" colab_type="text"
# # Steppping back
# + [markdown] id="l8q877HK8iYR" colab_type="text"
# ## Goals
#
# + [markdown] id="0-ArsHIuqtvS" colab_type="text"
# * Open and extensible interface
# * Focused on needs of community
# * Building structure to make it resiliant to change and long lasting
#
# + [markdown] id="TqCwlFwK8j9X" colab_type="text"
# ## Next steps
#
# + [markdown] id="mop4J8An8RHu" colab_type="text"
#
# * Expanding the NumPy / SciPi API coverage
# * Improving code generation
# * Add lower level backends
# * Adding type sypport for values
# * Make sure it is easy to target high level ops directly to backend
# * Making core system more sound
# * More declerative registrations
# * Verify semantics
# * Leverage SymPy
#
# + [markdown] id="ByIK53oP8l86" colab_type="text"
# ## Interesting Problems
# + [markdown] id="NyFn8J_Q8SOY" colab_type="text"
# * Algebraic pattern matching / symbolic computing
# * Category theoretic approaches
# * Friendly registration mechanisms
# * Low level optimizations
# * Compiler theory
#
#
# We need your help! Would love to chat about use cases as well.
#
# Thank you!
# + id="s_s4l7b5uaHc" colab_type="code" colab={}
|
notebooks/2018.11.20 PyData Presentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (myenv)
# language: python
# name: myenv
# ---
# + papermill={"duration": 1.879449, "end_time": "2022-01-17T20:07:54.339199", "exception": false, "start_time": "2022-01-17T20:07:52.459750", "status": "completed"} tags=[]
# %matplotlib inline
import pylab
import pandas as pd
import glob
from collections import defaultdict
# + papermill={"duration": 0.028004, "end_time": "2022-01-17T20:07:54.379793", "exception": false, "start_time": "2022-01-17T20:07:54.351789", "status": "completed"} tags=["parameters"]
sample_id='podar'
outdir = 'outputs.private'
# + papermill={"duration": 0.026414, "end_time": "2022-01-17T20:07:54.430506", "exception": false, "start_time": "2022-01-17T20:07:54.404092", "status": "completed"} tags=["injected-parameters"]
# Parameters
sample_id = "SRR12324253"
render = ""
outdir = "outputs.paper"
# + papermill={"duration": 0.032311, "end_time": "2022-01-17T20:07:54.484705", "exception": false, "start_time": "2022-01-17T20:07:54.452394", "status": "completed"} tags=[]
from IPython.display import Markdown as md
from IPython.display import display
md(f"# genome-grist gathergram for metagenome `{sample_id}`")
# + [markdown] papermill={"duration": 0.010672, "end_time": "2022-01-17T20:07:54.506226", "exception": false, "start_time": "2022-01-17T20:07:54.495554", "status": "completed"} tags=[]
# ## load gather CSV
# + papermill={"duration": 0.040646, "end_time": "2022-01-17T20:07:54.557243", "exception": false, "start_time": "2022-01-17T20:07:54.516597", "status": "completed"} tags=[]
# load gather CSV
gather_df = pd.read_csv(f'../../{outdir}/gather/{sample_id}.gather.csv')
# names!
print(f'reading from ../../{outdir}/gather/{sample_id}.genomes.info.csv')
names_df = pd.read_csv(f'../../{outdir}/gather/{sample_id}.genomes.info.csv')
# connect gather_df to all_df and left_df using 'genome_id'
def fix_name(x):
return "_".join(x.split('_')[:2]).split('.')[0]
gather_df['genome_id'] = gather_df['name'].apply(fix_name)
names_df['genome_id'] = names_df['ident'].apply(fix_name)
# + papermill={"duration": 0.038762, "end_time": "2022-01-17T20:07:54.607491", "exception": false, "start_time": "2022-01-17T20:07:54.568729", "status": "completed"} tags=[]
# CTB bug FIXME - should this ever happen??
# this ensures that only rows that share genome_id are in all the dataframes
in_gather = set(gather_df.genome_id)
names_df = names_df[names_df.genome_id.isin(in_gather)]
# reassign index now that we've maybe dropped rows
gather_df.index = range(len(gather_df))
names_df.index = range(len(names_df))
assert len(names_df) == len(gather_df), (names_df, gather_df)
# + papermill={"duration": 0.029838, "end_time": "2022-01-17T20:07:54.653850", "exception": false, "start_time": "2022-01-17T20:07:54.624012", "status": "completed"} tags=[]
# re-sort names_df to match gather_df order, using matching genome_id column
names_df.set_index("genome_id")
names_df.reindex(index=gather_df["genome_id"])
_ = names_df.reset_index()
# + papermill={"duration": 0.221376, "end_time": "2022-01-17T20:07:54.893787", "exception": false, "start_time": "2022-01-17T20:07:54.672411", "status": "completed"} tags=[]
pylab.figure(num=None, figsize=(8, 6))
pylab.plot(gather_df.index, gather_df["f_unique_to_query"]*100, '.')
pylab.title('fraction of hashes unique to query')
pylab.xlabel('gather rank order')
pylab.ylabel('f_unique_to_query, as %')
# + papermill={"duration": 0.279178, "end_time": "2022-01-17T20:07:55.185343", "exception": false, "start_time": "2022-01-17T20:07:54.906165", "status": "completed"} tags=[]
pylab.figure(num=None, figsize=(10, 10))
pylab.plot(gather_df.intersect_bp / 1e6, gather_df.iloc[::-1].index, 'gx', label='hashes classified to this species')
pylab.plot(gather_df.unique_intersect_bp / 1e6, gather_df.iloc[::-1].index, 'ro', label='hashes classified for this genome')
positions = list(gather_df.index)
labels = list(reversed(names_df.display_name))
pylab.yticks(positions, labels, fontsize='small')
pylab.xlabel('number (millions)')
pylab.legend(loc='lower right')
pylab.title(f'{sample_id}: gather hashes')
pylab.tight_layout()
|
gather/inputs/reports/report-gather-SRR12324253.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras import initializers
import keras.backend as K
import numpy as np
import pandas as pd
from tensorflow.keras.layers import *
from keras.regularizers import l2#正则化
# 12-0.2
# 13-2.4
# 18-12.14
import pandas as pd
import numpy as np
normal = np.loadtxt(r'E:\水泵代码调试\试验数据(包括压力脉动和振动)\2013.9.12-未发生缠绕前\2013-9.12振动\2013-9-12振动-1250rmin-mat\1250rnormalvibx.txt', delimiter=',')
chanrao = np.loadtxt(r'E:\水泵代码调试\试验数据(包括压力脉动和振动)\2013.9.17-发生缠绕后\振动\9-18上午振动1250rmin-mat\1250r_chanraovibx.txt', delimiter=',')
print(normal.shape,chanrao.shape,"***************************************************")
data_normal=normal[18:20] #提取前两行
data_chanrao=chanrao[18:20] #提取前两行
print(data_normal.shape,data_chanrao.shape)
print(data_normal,"\r\n",data_chanrao,"***************************************************")
data_normal=data_normal.reshape(1,-1)
data_chanrao=data_chanrao.reshape(1,-1)
print(data_normal.shape,data_chanrao.shape)
print(data_normal,"\r\n",data_chanrao,"***************************************************")
#水泵的两种故障类型信号normal正常,chanrao故障
data_normal=data_normal.reshape(-1, 512)#(65536,1)-(128, 515)
data_chanrao=data_chanrao.reshape(-1,512)
print(data_normal.shape,data_chanrao.shape)
# +
import numpy as np
def yuchuli(data,label):#(4:1)(51:13)
#打乱数据顺序
np.random.shuffle(data)
train = data[0:102,:]
test = data[102:128,:]
label_train = np.array([label for i in range(0,102)])
label_test =np.array([label for i in range(0,26)])
return train,test ,label_train ,label_test
def stackkk(a,b,c,d,e,f,g,h):
aa = np.vstack((a, e))
bb = np.vstack((b, f))
cc = np.hstack((c, g))
dd = np.hstack((d, h))
return aa,bb,cc,dd
x_tra0,x_tes0,y_tra0,y_tes0 = yuchuli(data_normal,0)
x_tra1,x_tes1,y_tra1,y_tes1 = yuchuli(data_chanrao,1)
tr1,te1,yr1,ye1=stackkk(x_tra0,x_tes0,y_tra0,y_tes0 ,x_tra1,x_tes1,y_tra1,y_tes1)
x_train=tr1
x_test=te1
y_train = yr1
y_test = ye1
#打乱数据
state = np.random.get_state()
np.random.shuffle(x_train)
np.random.set_state(state)
np.random.shuffle(y_train)
state = np.random.get_state()
np.random.shuffle(x_test)
np.random.set_state(state)
np.random.shuffle(y_test)
#对训练集和测试集标准化
def ZscoreNormalization(x):
"""Z-score normaliaztion"""
x = (x - np.mean(x)) / np.std(x)
return x
x_train=ZscoreNormalization(x_train)
x_test=ZscoreNormalization(x_test)
# print(x_test[0])
#转化为一维序列
x_train = x_train.reshape(-1,512,1)
x_test = x_test.reshape(-1,512,1)
print(x_train.shape,x_test.shape)
def to_one_hot(labels,dimension=2):
results = np.zeros((len(labels),dimension))
for i,label in enumerate(labels):
results[i,label] = 1
return results
one_hot_train_labels = to_one_hot(y_train)
one_hot_test_labels = to_one_hot(y_test)
# +
#定义挤压函数
def squash(vectors, axis=-1):
"""
对向量的非线性激活函数
## vectors: some vectors to be squashed, N-dim tensor
## axis: the axis to squash
:return: a Tensor with same shape as input vectors
"""
s_squared_norm = K.sum(K.square(vectors), axis, keepdims=True)
scale = s_squared_norm / (1 + s_squared_norm) / K.sqrt(s_squared_norm + K.epsilon())
return scale * vectors
class Length(layers.Layer):
"""
计算向量的长度。它用于计算与margin_loss中的y_true具有相同形状的张量
Compute the length of vectors. This is used to compute a Tensor that has the same shape with y_true in margin_loss
inputs: shape=[dim_1, ..., dim_{n-1}, dim_n]
output: shape=[dim_1, ..., dim_{n-1}]
"""
def call(self, inputs, **kwargs):
return K.sqrt(K.sum(K.square(inputs), -1))
def compute_output_shape(self, input_shape):
return input_shape[:-1]
def get_config(self):
config = super(Length, self).get_config()
return config
#定义预胶囊层
def PrimaryCap(inputs, dim_capsule, n_channels, kernel_size, strides, padding):
"""
进行普通二维卷积 `n_channels` 次, 然后将所有的胶囊重叠起来
:param inputs: 4D tensor, shape=[None, width, height, channels]
:param dim_capsule: the dim of the output vector of capsule
:param n_channels: the number of types of capsules
:return: output tensor, shape=[None, num_capsule, dim_capsule]
"""
output = layers.Conv2D(filters=dim_capsule*n_channels, kernel_size=kernel_size, strides=strides,
padding=padding,name='primarycap_conv2d')(inputs)
outputs = layers.Reshape(target_shape=[-1, dim_capsule], name='primarycap_reshape')(output)
return layers.Lambda(squash, name='primarycap_squash')(outputs)
class DenseCapsule(layers.Layer):
"""
胶囊层. 输入输出都为向量.
## num_capsule: 本层包含的胶囊数量
## dim_capsule: 输出的每一个胶囊向量的维度
## routings: routing 算法的迭代次数
"""
def __init__(self, num_capsule, dim_capsule, routings=3, kernel_initializer='glorot_uniform',**kwargs):
super(DenseCapsule, self).__init__(**kwargs)
self.num_capsule = num_capsule
self.dim_capsule = dim_capsule
self.routings = routings
self.kernel_initializer = kernel_initializer
def build(self, input_shape):
assert len(input_shape) >= 3, '输入的 Tensor 的形状[None, input_num_capsule, input_dim_capsule]'#(None,1152,8)
self.input_num_capsule = input_shape[1]
self.input_dim_capsule = input_shape[2]
#转换矩阵
self.W = self.add_weight(shape=[self.num_capsule, self.input_num_capsule,
self.dim_capsule, self.input_dim_capsule],
initializer=self.kernel_initializer,name='W')
self.built = True
def call(self, inputs, training=None):
# inputs.shape=[None, input_num_capsuie, input_dim_capsule]
# inputs_expand.shape=[None, 1, input_num_capsule, input_dim_capsule]
inputs_expand = K.expand_dims(inputs, 1)
# 运算优化:将inputs_expand重复num_capsule 次,用于快速和W相乘
# inputs_tiled.shape=[None, num_capsule, input_num_capsule, input_dim_capsule]
inputs_tiled = K.tile(inputs_expand, [1, self.num_capsule, 1, 1])
# 将inputs_tiled的batch中的每一条数据,计算inputs+W
# x.shape = [num_capsule, input_num_capsule, input_dim_capsule]
# W.shape = [num_capsule, input_num_capsule, dim_capsule, input_dim_capsule]
# 将x和W的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_dim_capsule] x [dim_capsule, input_dim_capsule]^T -> [dim_capsule].
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsutel
inputs_hat = K.map_fn(lambda x: K.batch_dot(x, self.W, [2, 3]),elems=inputs_tiled)
# Begin: Routing算法
# 将系数b初始化为0.
# b.shape = [None, self.num_capsule, self, input_num_capsule].
b = tf.zeros(shape=[K.shape(inputs_hat)[0], self.num_capsule, self.input_num_capsule])
assert self.routings > 0, 'The routings should be > 0.'
for i in range(self.routings):
# c.shape=[None, num_capsule, input_num_capsule]
C = tf.nn.softmax(b ,axis=1)
# c.shape = [None, num_capsule, input_num_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将c与inputs_hat的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_num_capsule] x [input_num_capsule, dim_capsule] -> [dim_capsule],
# outputs.shape= [None, num_capsule, dim_capsule]
outputs = squash(K. batch_dot(C, inputs_hat, [2, 2])) # [None, 10, 16]
if i < self.routings - 1:
# outputs.shape = [None, num_capsule, dim_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将outputs和inρuts_hat的前两个维度看作‘batch’ 维度,向量和矩阵相乘:
# [dim_capsule] x [imput_num_capsule, dim_capsule]^T -> [input_num_capsule]
# b.shape = [batch_size. num_capsule, input_nom_capsule]
# b += K.batch_dot(outputs, inputs_hat, [2, 3]) to this b += tf.matmul(self.W, x)
b += K.batch_dot(outputs, inputs_hat, [2, 3])
# End: Routing 算法
return outputs
def compute_output_shape(self, input_shape):
return tuple([None, self.num_capsule, self.dim_capsule])
def get_config(self):
config = {
'num_capsule': self.num_capsule,
'dim_capsule': self.dim_capsule,
'routings': self.routings
}
base_config = super(DenseCapsule, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
# +
from tensorflow import keras
from keras.regularizers import l2#正则化
x = layers.Input(shape=[512,1, 1])
#普通卷积层
conv1 = layers.Conv2D(filters=16, kernel_size=(2, 1),activation='relu',padding='valid',name='conv1')(x)
# Layer 3: 使用“squash”激活的Conv2D层, 然后重塑 [None, num_capsule, dim_vector]
primarycaps = PrimaryCap(conv1, dim_capsule=8, n_channels=12, kernel_size=(4, 1), strides=2, padding='valid')
# Layer 4: 数字胶囊层,动态路由算法在这里工作。
digitcaps = DenseCapsule(num_capsule=2, dim_capsule=16, routings=3, name='digit_caps')(primarycaps)
# Layer 5:这是一个辅助层,用它的长度代替每个胶囊。只是为了符合标签的形状。
out_caps = Length(name='out_caps')(digitcaps)
model = keras.Model(x, out_caps)
model.summary()
# +
#定义优化
model.compile(loss='categorical_crossentropy',
optimizer='adam',metrics=['accuracy'])
# -
import time
time_begin = time.time()
history = model.fit(x_train,one_hot_train_labels,
validation_split=0.1,
epochs=50,batch_size=10,
shuffle=True)
time_end = time.time()
time = time_end - time_begin
print('time:', time)
# +
import time
time_begin = time.time()
score = model.evaluate(x_test,one_hot_test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
time_end = time.time()
time = time_end - time_begin
print('time:', time)
# +
#绘制acc-loss曲线
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['val_loss'],color='g')
plt.plot(history.history['accuracy'],color='b')
plt.plot(history.history['val_accuracy'],color='k')
plt.title('model loss and acc')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'test_loss','train_acc', 'test_acc'], loc='center right')
# plt.legend(['train_loss','train_acc'], loc='upper left')
#plt.savefig('1.png')
plt.show()
# +
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['accuracy'],color='b')
plt.title('model loss and sccuracy ')
plt.ylabel('loss/sccuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'train_sccuracy'], loc='center right')
plt.show()
|
BCNcode/0_vibratioon_signal/1250/CN/CN_1250-021-512-x.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DBSM Altbestands-Analyse
import requests
from bs4 import BeautifulSoup as bs
import math
import concurrent.futures
# +
params = {}
base_url = 'https://services.dnb.de/sru/dnb.dea.archivalien'
params = {'recordSchema': 'MARC21-xml',
'operation': 'searchRetrieve',
'version': '1.1',
'accessToken': '8090beb04b8a8ce79c2da2c1ee6890b8'
}
#suchstring = 'JHR within "1450 1850"'
#suchstring = '''jhr within "* 1699" and jhr within "1600 *"'''
suchstring = 'sigRef="EB 96/182-B*"'
# -
def sru_import(suchlauf):
startrecord = suchlauf * 100 + 1
print(f'Suchlauf {suchlauf} ab record {startrecord}')
params.update({'maximumRecords':'100','startRecord': startrecord, 'query': suchstring})
sru_raw = requests.get(base_url, params=params)
xml_soup = bs(sru_raw.content, "lxml")
records = xml_soup.find_all('record', {'type': 'Bibliographic'})
with open(f'./data/{suchlauf}.xml', mode='w') as f:
f.write('''<?xml version="1.0" encoding="UTF-8"?>\n<collection xmlns="http://www.loc.gov/MARC21/slim">\n''')
for item in records:
f.write("%s\n" % item)
f.write('''</collection>''')
print(f'{suchlauf}.xml')
# Import der Datensätze als rdf
params.update({'maximumRecords':'10', 'query': suchstring})
sru_raw = requests.get(base_url, params=params)
sru_raw.url
sru_xml = bs(sru_raw.content, 'lxml')
ergebnisse = int(sru_xml.searchretrieveresponse.numberofrecords.string)
suchlaeufe = math.ceil(ergebnisse / 100)
f'{ergebnisse} Ergebnisse in {suchlaeufe} Suchläufen'
for suchlauf in range(suchlaeufe):
sru_import(suchlauf)
|
dea-testimport.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
from sklearn import preprocessing
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score,recall_score
from sklearn.metrics import f1_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
pd.options.mode.chained_assignment = None
# %matplotlib inline
# -
data_df = pd.read_csv(r"D:\Olympic Dataset\updated_data.csv",index_col=0)
len(data_df)
# In order to gain high accuracy in our prediction, we will encode variables.<br/>
# We want to predict if an individual can win an olympic medal.<br/>
data_df.head(5)
# First, we will encode the medals by:<br/>
# - Have medal = 1
# - Does not have medal = 0
#
df2 = data_df.replace({'Gold':1,'Silver':1,'Bronze':1,'No Medal':0})
df2.head(5)
# Next, we will encode the seasons by: <br/>
# - Summer = 1
# - Winter = 0
df2.replace({'Summer':1,'Winter':0},inplace=True)
df2.head(5)
# Now, we will encode the genders by: <br/>
# - Male = 1
# - Female = 0
df2.replace({'M':1,'F':0},inplace=True)
df2.head(5)
# ## Feature Selection
# The games column is essentially consisted of both the year and the season columns.<br/>
# Therefore, we will drop it.
new_df = df2.drop(columns=['Games'])
new_df.head(5)
print(len(new_df['Year'].unique()))
print(len(new_df['Age'].unique()))
print(len(new_df['Sport'].unique()))
print(len(new_df['Event'].unique()))
print(len(new_df['NOC'].unique()))
print(len(new_df['Team'].unique()))
# We will drop irrelevant columns:
new_df2 = new_df.drop(columns=['Name','NOC','Team','City','Event'])
new_df2.head(5)
# After all, the athlete's performance in every Olympic game and every sport it includes is measured by its own abilities.
new_df3 = new_df2.copy()
new_df3.head(5)
# Now, we will remove the discontinues sports and those with insufficient amount of data. <br/>
# We will remove sports with less than 1000 records.
new_df3.Sport.value_counts(sort=True,ascending=True)
updated_records = new_df3.Sport.value_counts().gt(1000)
updated_records
invalid_sports = ['Snowboarding','Freestyle Skiing','Synchronized Swimming','Baseball','Rhythmic Gymnastics','Taekwondo',
'Beach Volleyball','Triathlon','Softball','Curling','Rugby Sevens','Skeleton','Trampolining','Golf',
'Rugby','Tug-Of-War','Art Competitions','Lacrosse','Motorboating']
updated_df = new_df3.loc[~new_df3.Sport.isin(invalid_sports)]
updated_df.reset_index(drop=True)
sports = updated_df.Sport.unique()
sports
# Now, we will encode the sports by label encoder:
le = preprocessing.LabelEncoder()
updated_df.loc[:,['Sport']] = le.fit_transform(updated_df['Sport'])
# ## <br/>Binning numerical variables
# +
# Discretization using binning
#updated_df['Age'].value_counts()
#updated_df['Height'].value_counts().sort_index()
#updated_df['Weight'].value_counts().sort_index()
#updated_df['Year'].value_counts()
age_bins = [10, 16, 21, 26, 31, 36, 40]
age_labels=[0,1,2,3,4,5]
updated_df['Age'] = pd.cut(updated_df['Age'], age_bins, labels = age_labels)
height_bins = [125, 130, 140, 150, 160, 165, 170, 175, 180, 185, 190, 195, 200, 230]
height_labels=[0,1,2,3,4,5,6,7,8,9,10,11,12]
updated_df['Height'] = pd.cut(updated_df['Height'], height_bins, labels = height_labels)
weight_bins = [20, 40, 60, 75, 90, 100, 120, 150, 200, 220]
weight_labels=[0,1,2,3,4,5,6,7,8]
updated_df['Weight'] = pd.cut(updated_df['Weight'], weight_bins, labels = weight_labels)
# +
updated_df['Age'].value_counts().sort_index()
#updated_df['NaN']
#updated_df.isna().sum()
#updated_df.Age.unique()
# -
print(updated_df.Weight[updated_df['Age']=='NaN'])
updated_df.head(5)
print(updated_df.shape)
# <!-- But, we should ignore the discontinued sports! -->
# +
###################################### ML PHASE ######################################
# -
# At this point, after the whole process above, we are ready to start the ML phase.
#
# ## What are we trying to predict?
# We are attempting to forecast whether or not an individual can win an Olympic medal based on his personal statistics and skills.
# Essentially, our learning model is a supervised one.<br/>
# Our problem is a classification problem since we are trying to predict a certain categorical variable value.
#
# First, we will make use of a **logistic regression model**.
X = updated_df.drop(columns=['Medal'])
y = updated_df['Medal']
# Split into training and test sets & Scaling
scaler = StandardScaler()
scaler.fit(X.values)
scaled_features = scaler.fit_transform(X.values)
df_scaled = pd.DataFrame(scaled_features, columns=X.columns)
X1 = df_scaled
y1 = y
X_train, X_test, y_train, y_test = train_test_split(X1.values, y1, random_state=3, test_size=0.2)
print(X_train.shape, X_test.shape)
print(y_train.shape, y_test.shape)
# +
# set up the model, logistic regression model
lrm = LogisticRegression()
lrm.fit(X_train,y_train)
y_pred = lrm.predict(X_test)
# Measuring model performance
print('Accuracy Score:',lrm.score(X_test,y_test))
print('f1 score:',f1_score(y_test,y_pred,average='micro'))
print('Precision score:',precision_score(y_test,y_pred,average='micro'))
print('Recall score:',recall_score(y_test,y_pred,average='micro'))
# -
# Confusion Matrix
plt.figure(figsize=(5,5))
cm_lrm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm_lrm,annot=True,linewidth=0.5,fmt='.0f', cmap='coolwarm')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
# **We can see that the model above has not predicted even a single label as '1'**
# Next, we will use another algorithm, **decision tree!**
# +
dtc = DecisionTreeClassifier()
dtc.fit(X_train,y_train)
y_pred = dtc.predict(X_test)
print('Accuracy Score:',dtc.score(X_test,y_pred))
print('f1 score:',f1_score(y_test,y_pred,average='micro'))
print('Precision score:',precision_score(y_test,y_pred,average='micro'))
print('Recall score:',recall_score(y_test,y_pred,average='micro'))
# -
# Confusion Matrix
plt.figure(figsize=(5,5))
cm_dtc = confusion_matrix(y_test,y_pred)
sns.heatmap(cm_dtc,annot=True,linewidth=0.5,fmt='.0f', cmap='coolwarm')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
# Since the accuracy is 1, there might be an **overfitting** issue.<br/>
#
# We will handle it by using **Random Forest algorithm!**
# +
rfc = RandomForestClassifier(n_estimators=100)
rfc.fit(X_train,y_train)
y_pred = rfc.predict(X_test)
print('Accuracy Score:',rfc.score(X_test,y_test))
print('f1 score:',f1_score(y_test,y_pred,average='micro'))
print('Precision score:',precision_score(y_test,y_pred,average='micro'))
print('Recall score:',recall_score(y_test,y_pred,average='micro'))
# -
# Confusion Matrix
plt.figure(figsize=(5,5))
cm_rfc = confusion_matrix(y_test,y_pred)
sns.heatmap(cm_rfc,annot=True,linewidth=0.5,fmt='.0f', cmap='coolwarm')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
# Lastly, we will use **naive bayes**
# +
gnb = GaussianNB()
gnb.fit(X_train,y_train)
y_pred = gnb.predict(X_test)
print('Accuracy Score:',gnb.score(X_test,y_test))
print('f1 score:',f1_score(y_test,y_pred,average='micro'))
print('Precision score:',precision_score(y_test,y_pred,average='micro'))
print('Recall score:',recall_score(y_test,y_pred,average='micro'))
# -
# Confusion Matrix
plt.figure(figsize=(5,5))
cm_gnb = confusion_matrix(y_test,y_pred)
sns.heatmap(cm_gnb,annot=True,linewidth=0.5,fmt='.0f', cmap='coolwarm')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
# So, our best model was able to attain an 85% success rate!
# WOW Effect #2
# +
# Let us insert my own details and get the prediction result
# +
# Sex, Age, Height, Weight, Year, Season, Sport Medal
# Now, we have 37 different Sports encoded respectively from 0 to 36
#data = {'Sex':1, 'Age':1,'Height':1, 'Weight':1, 'Season':[0, 1], 'Sport':[i for i in range(0,37)]}
my_X = pd.DataFrame(0, index = [i for i in range(0,74)],
columns=['Sex', 'Age', 'Height', 'Weight', 'Year', 'Season', 'Sport'])
# Sex, Age
my_X.iloc[:,0:2] = 1
# Height, Weight
my_X.iloc[:,2] = 7
my_X.iloc[:,3] = 1
# Year
my_X.iloc[:,4] = 2020
# Seasons
my_X.iloc[0:37,5] = 0
my_X.iloc[37:74,5] = 1
# Sports
my_X.iloc[0:37,6] = list(range(0,37))
my_X.iloc[37:74,6] = list(range(0,37))
my_X
# +
# We will use our 2 best models - Random Forest & Gaussian Naive Bayes.
# Note that the Decision Tree model has an overfitting issue.
# Note that the Logistic Regression did not predict correctly even a single medalist
# -
# Random Forest
y_pred_rfc = rfc.predict(my_X)
result_df_rfc = pd.DataFrame(y_pred_rfc,columns=['Medal Prediction'])
sports_df1 = result_df_rfc[result_df_rfc['Medal Prediction']==1]
sports_df1.index
# Naive Bayes
y_pred_gnb = gnb.predict(my_X)
result_df_gnb = pd.DataFrame(y_pred_gnb,columns=['Medal Prediction'])
sports_df2 = result_df_gnb[result_df_gnb['Medal Prediction']==1]
sports_df2.index
# +
#print(my_X)
# -
# So, we can figure out after investigating our 2 top performencing models that:<br/>
# - The Random Forest Classifier predicted that I will get even not a single medal.
# - On the opposite side, the Gaussian Naive Bayes Model predicted that I have a potential to win an Olympic medal
# on 7 different sports! <br/><br/>
# We can conclude from
# that information that we can not predict for sure, but with pretty good stats we definitely can!
# Let us see which sports we are talking about:
predicted_indices = [0,1,2,3,4,5,6,37,38,39,40,41,42,43]
sports_X = my_X.loc[predicted_indices,:]
sports_X
sports_X['Sport'].unique()
le.inverse_transform(sports_X['Sport'].unique())
# Surprisingly, half of these sports, particularly basketball, are ones that I enjoy.<br/>
# Who knows, perhaps one day I'll win an Olympic medal...
|
ML & Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Copyright Netherlands eScience Center <br>
# ** Function : Analyze AMET from coordinated experiments** <br>
# ** Author : <NAME> ** <br>
# ** First Built : 2019.08.09 ** <br>
# ** Last Update : 2019.08.09 ** <br>
# Description : This notebook aims to analyze AMET taken as the residuals of TOA/surface flux fields from multiple coordinated experiments in Blue Action WP3. It contributes to the Deliverable 3.1. <br>
# Return Values : netCDF4 <br>
# Caveat : The fields used here are post-processed monthly mean fields. It includes AMET from:
# * EC Earth (DMI)
# * CMCC-CM (CMCC)
# * WACCM6 (WHOI)
# * NorESM (NERSC)
# * HadGEM (UoS)
# * EC Earth (NLeSC)
# %matplotlib inline
import numpy as np
import sys
#sys.path.append("/home/ESLT0068/NLeSC/Computation_Modeling/Bjerknes/Scripts/META")
import analyzer
import scipy as sp
import time as tttt
from netCDF4 import Dataset,num2date
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import cm
# constants
constant = {'g' : 9.80616, # gravititional acceleration [m / s2]
'R' : 6371009, # radius of the earth [m]
'cp': 1004.64, # heat capacity of air [J/(Kg*K)]
'Lv': 2264670, # Latent heat of vaporization [J/Kg]
'R_dry' : 286.9, # gas constant of dry air [J/(kg*K)]
'R_vap' : 461.5, # gas constant for water vapour [J/(kg*K)]
}
# |Model and Organization | Exp 1 | Exp 2 | Exp 3 | Exp 4 | time |
# |-----------------------|-------|-------|-------|-------|-----------|
# | EC Earth (NLeSC) | 10 | 10 | 1 | 1 | 1979-2015 |
# | EC Earth (DMI) | 20 | 20 | 20 | 20 | 1979-2015 (exp1&2) 1979-2013 (exp3&4) |
# | CMCC-CM (CMCC) | 10 | 10 | 0 | 0 | 1979-2014 |
# | WACCM6 (WHOI) | 30 | 30 | 30 | 30 | 1979-2014 (exp1&2) 1979-2012 (exp3&4) |
# | NorESM (NERSC) | 20 | 20 | 20 | 20 | 1979-2014 (exp1&2) 1979-2013 (exp3&4) |
# | HadGEM (UoS) | 10 | 10 | 5 | 5 | 1979-2014 (exp1&2) 1979-2013 (exp3&4) |
# | IAP-AGCM (IAP-NZC) | 15 | 15 | 15 | 15 | 1979-2015 (exp1&2) 1979-2013 (exp3&4) |
# | IPSL-CM (CNRS) | 30 | 30 | 20 | 20 | 1979-2014 |
# | MPIESM (MPI) | 10 | 10 | 10 | 10 | 1979-2013 |
################################ Input zone ######################################
# specify starting and ending time
# specify data path
datapath = '/home/ESLT0068/WorkFlow/Core_Database_BlueAction_WP3/AMET_netCDF'
# specify output path for figures
output_path = '/home/ESLT0068/NLeSC/Computation_Modeling/BlueAction/WP3/JointAnalysis_AMET/AMIP'
# how many models
models = 9
####################################################################################
# +
################################ Extract variables ######################################
# get path
# EC Earth (NLeSC)
datapath_NLeSC_exp1 = os.path.join(datapath, 'amet_ECEarth_NLeSC_exp1.nc')
datapath_NLeSC_exp2 = os.path.join(datapath, 'amet_ECEarth_NLeSC_exp2.nc')
datapath_NLeSC_exp3 = os.path.join(datapath, 'amet_ECEarth_NLeSC_exp3.nc')
datapath_NLeSC_exp4 = os.path.join(datapath, 'amet_ECEarth_NLeSC_exp4.nc')
# EC Earth (DMI)
datapath_DMI_exp1 = os.path.join(datapath, 'amet_ECEarth_DMI_exp1.nc')
datapath_DMI_exp2 = os.path.join(datapath, 'amet_ECEarth_DMI_exp2.nc')
datapath_DMI_exp3 = os.path.join(datapath, 'amet_ECEarth_DMI_exp3.nc')
datapath_DMI_exp4 = os.path.join(datapath, 'amet_ECEarth_DMI_exp4.nc')
# HadGEM (UoS)
datapath_UoS_exp1 = os.path.join(datapath, 'amet_HadGEM_UoS_exp1.nc')
datapath_UoS_exp2 = os.path.join(datapath, 'amet_HadGEM_UoS_exp2.nc')
datapath_UoS_exp3 = os.path.join(datapath, 'amet_HadGEM_UoS_exp3.nc')
datapath_UoS_exp4 = os.path.join(datapath, 'amet_HadGEM_UoS_exp4.nc')
# NorESM (NERSC)
datapath_NERSC_exp1 = os.path.join(datapath, 'amet_NorESM_NERSC_exp1.nc')
datapath_NERSC_exp2 = os.path.join(datapath, 'amet_NorESM_NERSC_exp2.nc')
datapath_NERSC_exp3 = os.path.join(datapath, 'amet_NorESM_NERSC_exp3.nc')
datapath_NERSC_exp4 = os.path.join(datapath, 'amet_NorESM_NERSC_exp4.nc')
# WACCM6 (WHOI)
datapath_WHOI_exp1 = os.path.join(datapath, 'amet_WACCM6_WHOI_exp1.nc')
datapath_WHOI_exp2 = os.path.join(datapath, 'amet_WACCM6_WHOI_exp2.nc')
datapath_WHOI_exp3 = os.path.join(datapath, 'amet_WACCM6_WHOI_exp3.nc')
datapath_WHOI_exp4 = os.path.join(datapath, 'amet_WACCM6_WHOI_exp4.nc')
# CMCC-CM (CMCC)
datapath_CMCC_exp1 = os.path.join(datapath, 'amet_CMCC-CM_CMCC_exp1.nc')
datapath_CMCC_exp2 = os.path.join(datapath, 'amet_CMCC-CM_CMCC_exp2.nc')
# IPSL-CM (CNRS)
datapath_CNRS_exp1 = os.path.join(datapath, 'amet_IPSL-CM_CNRS_exp1.nc')
datapath_CNRS_exp2 = os.path.join(datapath, 'amet_IPSL-CM_CNRS_exp2.nc')
datapath_CNRS_exp3 = os.path.join(datapath, 'amet_IPSL-CM_CNRS_exp3.nc')
datapath_CNRS_exp4 = os.path.join(datapath, 'amet_IPSL-CM_CNRS_exp4.nc')
# IAP-AGCM (IAP-NZC)
datapath_IAP_exp1 = os.path.join(datapath, 'amet_IAP-AGCM_IAP-NZC_exp1.nc')
datapath_IAP_exp2 = os.path.join(datapath, 'amet_IAP-AGCM_IAP-NZC_exp2.nc')
datapath_IAP_exp3 = os.path.join(datapath, 'amet_IAP-AGCM_IAP-NZC_exp3.nc')
datapath_IAP_exp4 = os.path.join(datapath, 'amet_IAP-AGCM_IAP-NZC_exp4.nc')
# MPIESM (MPI)
datapath_MPI_exp1 = os.path.join(datapath, 'amet_MPIESM_MPI_exp1.nc')
datapath_MPI_exp2 = os.path.join(datapath, 'amet_MPIESM_MPI_exp2.nc')
datapath_MPI_exp3 = os.path.join(datapath, 'amet_MPIESM_MPI_exp3.nc')
datapath_MPI_exp4 = os.path.join(datapath, 'amet_MPIESM_MPI_exp4.nc')
# get variable key
# EC Earth (DMI)
key_NLeSC_exp1 = Dataset(datapath_NLeSC_exp1)
key_NLeSC_exp2 = Dataset(datapath_NLeSC_exp2)
key_NLeSC_exp3 = Dataset(datapath_NLeSC_exp3)
key_NLeSC_exp4 = Dataset(datapath_NLeSC_exp4)
# EC Earth (DMI)
key_DMI_exp1 = Dataset(datapath_DMI_exp1)
key_DMI_exp2 = Dataset(datapath_DMI_exp2)
key_DMI_exp3 = Dataset(datapath_DMI_exp3)
key_DMI_exp4 = Dataset(datapath_DMI_exp4)
# HadGEM (UoS)
key_UoS_exp1 = Dataset(datapath_UoS_exp1)
key_UoS_exp2 = Dataset(datapath_UoS_exp2)
key_UoS_exp3 = Dataset(datapath_UoS_exp3)
key_UoS_exp4 = Dataset(datapath_UoS_exp4)
# NorESM (NERSC)
key_NERSC_exp1 = Dataset(datapath_NERSC_exp1)
key_NERSC_exp2 = Dataset(datapath_NERSC_exp2)
key_NERSC_exp3 = Dataset(datapath_NERSC_exp3)
key_NERSC_exp4 = Dataset(datapath_NERSC_exp4)
# WACCM6 (WHOI)
key_WHOI_exp1 = Dataset(datapath_WHOI_exp1)
key_WHOI_exp2 = Dataset(datapath_WHOI_exp2)
key_WHOI_exp3 = Dataset(datapath_WHOI_exp3)
key_WHOI_exp4 = Dataset(datapath_WHOI_exp4)
# CMCC-CM (CMCC)
key_CMCC_exp1 = Dataset(datapath_CMCC_exp1)
key_CMCC_exp2 = Dataset(datapath_CMCC_exp2)
# IPSL-CM (CNRS)
key_CNRS_exp1 = Dataset(datapath_CNRS_exp1)
key_CNRS_exp2 = Dataset(datapath_CNRS_exp2)
key_CNRS_exp3 = Dataset(datapath_CNRS_exp3)
key_CNRS_exp4 = Dataset(datapath_CNRS_exp4)
# IAP-AGCM (IAP-NZC)
key_IAP_exp1 = Dataset(datapath_IAP_exp1)
key_IAP_exp2 = Dataset(datapath_IAP_exp2)
key_IAP_exp3 = Dataset(datapath_IAP_exp3)
key_IAP_exp4 = Dataset(datapath_IAP_exp4)
# MPIESM (MPI)
key_MPI_exp1 = Dataset(datapath_MPI_exp1)
key_MPI_exp2 = Dataset(datapath_MPI_exp2)
key_MPI_exp3 = Dataset(datapath_MPI_exp3)
key_MPI_exp4 = Dataset(datapath_MPI_exp4)
# get amet
# dimension[ensemble, year, month, lat]
################################ AMET ######################################
# EC Earth (NLeSC)
AMET_NLeSC_exp1 = key_NLeSC_exp1.variables['amet'][:]
AMET_NLeSC_exp2 = key_NLeSC_exp2.variables['amet'][:]
AMET_NLeSC_exp3 = key_NLeSC_exp3.variables['amet'][:]
AMET_NLeSC_exp4 = key_NLeSC_exp4.variables['amet'][:]
# EC Earth (DMI)
AMET_DMI_exp1 = key_DMI_exp1.variables['amet'][:]
AMET_DMI_exp2 = key_DMI_exp2.variables['amet'][:]
AMET_DMI_exp3 = key_DMI_exp3.variables['amet'][:]
AMET_DMI_exp4 = key_DMI_exp4.variables['amet'][:]
# HadGEM (UoS)
AMET_UoS_exp1 = key_UoS_exp1.variables['amet'][:]
AMET_UoS_exp2 = key_UoS_exp2.variables['amet'][:]
AMET_UoS_exp3 = key_UoS_exp3.variables['amet'][:]
AMET_UoS_exp4 = key_UoS_exp4.variables['amet'][:]
# NorESM (NERSC)
AMET_NERSC_exp1 = key_NERSC_exp1.variables['amet'][:]
AMET_NERSC_exp2 = key_NERSC_exp2.variables['amet'][:]
AMET_NERSC_exp3 = key_NERSC_exp3.variables['amet'][:]
AMET_NERSC_exp4 = key_NERSC_exp4.variables['amet'][:]
# WACCM6 (WHOI)
AMET_WHOI_exp1 = key_WHOI_exp1.variables['amet'][:]
AMET_WHOI_exp2 = key_WHOI_exp2.variables['amet'][:]
AMET_WHOI_exp3 = key_WHOI_exp3.variables['amet'][:]
AMET_WHOI_exp4 = key_WHOI_exp4.variables['amet'][:]
# CMCC-CM (CMCC)
AMET_CMCC_exp1 = key_CMCC_exp1.variables['amet'][:]
AMET_CMCC_exp2 = key_CMCC_exp2.variables['amet'][:]
# IPSL-CM (CNRS)
AMET_CNRS_exp1 = key_CNRS_exp1.variables['amet'][:]
AMET_CNRS_exp2 = key_CNRS_exp2.variables['amet'][:]
AMET_CNRS_exp3 = key_CNRS_exp3.variables['amet'][:]
AMET_CNRS_exp4 = key_CNRS_exp4.variables['amet'][:]
# IAP-AGCM (IAP-NZC)
AMET_IAP_exp1 = key_IAP_exp1.variables['amet'][:]
AMET_IAP_exp2 = key_IAP_exp2.variables['amet'][:]
AMET_IAP_exp3 = key_IAP_exp3.variables['amet'][:]
AMET_IAP_exp4 = key_IAP_exp4.variables['amet'][:]
# MPIESM (MPI)
AMET_MPI_exp1 = key_MPI_exp1.variables['amet'][:]
AMET_MPI_exp2 = key_MPI_exp2.variables['amet'][:]
AMET_MPI_exp3 = key_MPI_exp3.variables['amet'][:]
AMET_MPI_exp4 = key_MPI_exp4.variables['amet'][:]
# EC Earth (NLeSC)
lat_NLeSC = key_NLeSC_exp1.variables['latitude'][:]
# EC Earth (DMI)
lat_DMI = key_DMI_exp1.variables['latitude'][:]
# HadGEM (UoS)
lat_UoS = key_UoS_exp1.variables['latitude'][:]
# NorESM (NERSC)
lat_NERSC = key_NERSC_exp1.variables['latitude'][:]
# WACCM6 (WHOI)
lat_WHOI = key_WHOI_exp1.variables['latitude'][:]
# CMCC-CM (CMCC)
lat_CMCC = key_CMCC_exp1.variables['latitude'][:]
# IPSL-CM (CNRS)
lat_CNRS = key_CNRS_exp1.variables['latitude'][:]
# IAP-AGCM (IAP-NZC)
lat_IAP = key_IAP_exp1.variables['latitude'][:]
# MPIESM (MPI)
lat_MPI = key_MPI_exp1.variables['latitude'][:]
# -
################################ Only for a first-check ######################################
#print(AMET_CMCC_exp1.shape)
#plt.plot(lat_NLeSC[:], np.mean(AMET_NLeSC_exp1[0,0,:,:],0))
plt.plot(lat_NLeSC[:], np.mean(np.mean(AMET_NLeSC_exp3[0,:,:,:],0),0))
print("*********** 60N ************")
print(lat_NLeSC[84])
print(lat_DMI[42])
print(lat_WHOI[32])
print(lat_NERSC[32])
print(lat_UoS[53])
print(lat_CMCC[32])
print(lat_CNRS[24])
print(lat_IAP[21])
print(lat_MPI[32])
print("*********** 20N ************")
print(lat_NLeSC[:200])
#print(lat_DMI[:100])
#print(lat_WHOI[:75])
#print(lat_NERSC[:75])
#print(lat_UoS[:127])
#print(lat_CMCC[:75])
#print(lat_CNRS[:56])
#print(lat_IAP[:50])
#print(lat_MPI[:75])
# +
################################ Annual mean at different lat ######################################
################################ only ensemble mean is used ######################################
####################### color map #######################
#### EC Earth (NLeSC) : 'dodgerblue' ####
#### EC Earth (DMI) : 'blue' ####
#### HadGEM (UoS) : 'red' ####
#### NorESM (NERSC) : 'green' ####
#### WACCM6 (WHOI) : 'cyan' ####
#### CMCC-CM (CMCC) : 'olive' ####
#### IPSL-CM (CNRS) : 'orange' ####
#### IAP-AGCM (IAP-NZC) : 'gray' ####
#### MPIESM (MPI) : 'orange' ####
####################### color map #######################
####################### linestyles ######################
#### exp 1 (control) : '--' ####
#### exp 2 (sic fixed) : '-' ####
#### exp 3 (PDO removed) : ':' ####
#### exp 4 (AMO removed) : '-.' ####
####################### color map #######################
# EC Earth (DMI)
ens, yy, mm, _ = AMET_DMI_exp1.shape
fig = plt.figure()
plt.hlines(0,np.amin(lat_DMI[:100]), np.amax(lat_DMI[:100]),'k')
# Exp1
# EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], np.mean(np.mean(np.mean(AMET_NLeSC_exp1[:,:,:,:200],0),0),0),
color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) Exp1')
# EC Earth (DMI)
plt.plot(lat_DMI[:100], np.mean(np.mean(np.mean(AMET_DMI_exp1[:,:,:,:100],0),0),0),
color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(lat_UoS[:127], np.mean(np.mean(np.mean(AMET_UoS_exp1[:,:,:,:127],0),0),0),
color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], np.mean(np.mean(np.mean(AMET_NERSC_exp1[:,:,:,:75],0),0),0),
color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], np.mean(np.mean(np.mean(AMET_WHOI_exp1[:,:,:,:75],0),0),0),
color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:75], np.mean(np.mean(np.mean(AMET_CMCC_exp1[:,:,:,:75],0),0),0),
# color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], np.mean(np.mean(np.mean(AMET_CNRS_exp1[:,:,:,:56],0),0),0),
color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], np.mean(np.mean(np.mean(AMET_IAP_exp1[:,:,:,:50],0),0),0),
color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
# MPIESM (MPI)
plt.plot(lat_MPI[:75], np.mean(np.mean(np.mean(AMET_MPI_exp1[:,:,:,:75],0),0),0),
color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp2
# EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], np.mean(np.mean(np.mean(AMET_NLeSC_exp2[:,:,:,:200],0),0),0),
color='dodgerblue', linestyle='-', linewidth=1, label='EC Earth (NLeSC) Exp2')
# EC Earth (DMI)
plt.plot(lat_DMI[:100], np.mean(np.mean(np.mean(AMET_DMI_exp2[:,:,:,:100],0),0),0),
color='blue', linestyle='-', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], np.mean(np.mean(np.mean(AMET_UoS_exp2[:,:,:,:127],0),0),0),
color='red', linestyle='-', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], np.mean(np.mean(np.mean(AMET_NERSC_exp2[:,:,:,:75],0),0),0),
color='green', linestyle='-', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], np.mean(np.mean(np.mean(AMET_WHOI_exp2[:,:,:,:75],0),0),0),
color='cyan', linestyle='-', linewidth=1)
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:75], np.mean(np.mean(np.mean(AMET_CMCC_exp2[:,:,:,:75],0),0),0),
# color='olive', linestyle='-', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], np.mean(np.mean(np.mean(AMET_CNRS_exp2[:,:,:,:56],0),0),0),
color='orange', linestyle='-', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], np.mean(np.mean(np.mean(AMET_IAP_exp2[:,:,:,:50],0),0),0),
color='gray', linestyle='-', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], np.mean(np.mean(np.mean(AMET_MPI_exp2[:,:,:,:75],0),0),0),
color='magenta', linestyle='-', linewidth=1)
# Exp3
# EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], np.mean(np.mean(AMET_NLeSC_exp3[0,:,:,:200],0),0),
color='dodgerblue', linestyle=':', linewidth=1, label='EC Earth (NLeSC) Exp3')
# EC Earth (DMI)
plt.plot(lat_DMI[:100], np.mean(np.mean(np.mean(AMET_DMI_exp3[:,:,:,:100],0),0),0),
color='blue', linestyle=':', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], np.mean(np.mean(np.mean(AMET_UoS_exp3[:,:,:,:127],0),0),0),
color='red', linestyle=':', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], np.mean(np.mean(np.mean(AMET_NERSC_exp3[:,:,:,:75],0),0),0),
color='green', linestyle=':', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], np.mean(np.mean(np.mean(AMET_WHOI_exp3[:,:,:,:75],0),0),0),
color='cyan', linestyle=':', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], np.mean(np.mean(np.mean(AMET_CNRS_exp3[:,:,:,:56],0),0),0),
color='orange', linestyle=':', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], np.mean(np.mean(np.mean(AMET_IAP_exp3[:,:,:,:50],0),0),0),
color='gray', linestyle=':', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], np.mean(np.mean(np.mean(AMET_MPI_exp3[:,:,:,:75],0),0),0),
color='magenta', linestyle=':', linewidth=1)
# Exp4
# EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], np.mean(np.mean(AMET_NLeSC_exp4[0,:,:,:200],0),0),
color='dodgerblue', linestyle='-.', linewidth=1, label='EC Earth (NLeSC) Exp4')
# EC Earth (DMI)
plt.plot(lat_DMI[:100], np.mean(np.mean(np.mean(AMET_DMI_exp4[:,:,:,:100],0),0),0),
color='blue', linestyle='-.', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], np.mean(np.mean(np.mean(AMET_UoS_exp4[:,:,:,:127],0),0),0),
color='red', linestyle='-.', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], np.mean(np.mean(np.mean(AMET_NERSC_exp4[:,:,:,:75],0),0),0),
color='green', linestyle='-.', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], np.mean(np.mean(np.mean(AMET_WHOI_exp4[:,:,:,:75],0),0),0),
color='cyan', linestyle='-.', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], np.mean(np.mean(np.mean(AMET_CNRS_exp4[:,:,:,:56],0),0),0),
color='orange', linestyle='-.', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], np.mean(np.mean(np.mean(AMET_IAP_exp4[:,:,:,:50],0),0),0),
color='gray', linestyle='-.', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], np.mean(np.mean(np.mean(AMET_MPI_exp4[:,:,:,:75],0),0),0),
color='magenta', linestyle='-.', linewidth=1)
plt.xlabel("Latitude",fontsize=9)
plt.ylabel("AMET (PW)",fontsize=9)
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.legend(frameon=False, loc=1, prop={'size': 7.5})
plt.show()
fig.savefig(os.path.join(output_path,'Annual_mean_ensAvg_AMIP.png'),dpi=200)
plt.close(fig)
# -
# peak of energy transport
print("EC Earth (NLeSC)")
print(np.amax(np.mean(np.mean(np.mean(AMET_NLeSC_exp1[:,:,:,:200],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_NLeSC_exp2[:,:,:,:200],0),0),0)))
print(np.amax(np.mean(np.mean(AMET_NLeSC_exp3[0,:,:,:200],0),0)))
print(np.amax(np.mean(np.mean(AMET_NLeSC_exp4[0,:,:,:200],0),0)))
print("EC Earth (DMI)")
print(np.amax(np.mean(np.mean(np.mean(AMET_DMI_exp1[:,:,:,:100],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_DMI_exp2[:,:,:,:100],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_DMI_exp3[:,:,:,:100],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_DMI_exp4[:,:,:,:100],0),0),0)))
print("HadGEM (UoS)")
print(np.amax(np.mean(np.mean(np.mean(AMET_UoS_exp1[:,:,:,:127],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_UoS_exp2[:,:,:,:127],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_UoS_exp3[:,:,:,:127],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_UoS_exp4[:,:,:,:127],0),0),0)))
print("NorESM (NERSC)")
print(np.amax(np.mean(np.mean(np.mean(AMET_NERSC_exp1[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_NERSC_exp2[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_NERSC_exp3[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_NERSC_exp4[:,:,:,:75],0),0),0)))
print("WACCM6 (WHOI)")
print(np.amax(np.mean(np.mean(np.mean(AMET_WHOI_exp1[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_WHOI_exp2[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_WHOI_exp3[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_WHOI_exp4[:,:,:,:75],0),0),0)))
print("CMCC-CM (CMCC)")
print(np.amax(np.mean(np.mean(np.mean(AMET_CMCC_exp1[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_CMCC_exp2[:,:,:,:75],0),0),0)))
print("IPSL-CM (CNRS)")
print(np.amax(np.mean(np.mean(np.mean(AMET_CNRS_exp1[:,:,:,:56],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_CNRS_exp2[:,:,:,:56],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_CNRS_exp3[:,:,:,:56],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_CNRS_exp4[:,:,:,:56],0),0),0)))
print("IAP-AGCM (IAP-NZC)")
print(np.amax(np.mean(np.mean(np.mean(AMET_IAP_exp1[:,:,:,:50],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_IAP_exp2[:,:,:,:50],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_IAP_exp3[:,:,:,:50],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_IAP_exp4[:,:,:,:50],0),0),0)))
print("MPIESM (MPI)")
print(np.amax(np.mean(np.mean(np.mean(AMET_MPI_exp1[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_MPI_exp2[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_MPI_exp3[:,:,:,:75],0),0),0)))
print(np.amax(np.mean(np.mean(np.mean(AMET_MPI_exp4[:,:,:,:75],0),0),0)))
# +
############################## Anomalies trend at different lat #################################
################################ only ensemble mean is used ######################################
####################### color map #######################
#### EC Earth (NLeSC) : 'dodgerblue' ####
#### EC Earth (DMI) : 'blue' ####
#### HadGEM (UoS) : 'red' ####
#### NorESM (NERSC) : 'green' ####
#### WACCM6 (WHOI) : 'cyan' ####
#### CMCC-CM (CMCC) : 'olive' ####
#### IPSL-CM (CNRS) : 'orange' ####
#### IAP-AGCM (IAP-NZC) : 'gray' ####
#### MPIESM (MPI) : 'orange' ####
####################### color map #######################
####################### linestyles ######################
#### exp 1 (control) : '--' ####
#### exp 2 (sic fixed) : '-' ####
#### exp 3 (PDO removed) : ':' ####
#### exp 4 (AMO removed) : '-.' ####
####################### color map #######################
# EC Earth (NLeSC)
ens_avg_NLeSC_exp1 = analyzer.statistics(np.mean(AMET_NLeSC_exp1[:,:,:,:],0))
ens_avg_NLeSC_exp1.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp1.trend(Dim_ens=False)
ens_avg_NLeSC_exp2 = analyzer.statistics(np.mean(AMET_NLeSC_exp2[:,:,:,:],0))
ens_avg_NLeSC_exp2.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp2.trend(Dim_ens=False)
ens_avg_NLeSC_exp3 = analyzer.statistics(AMET_NLeSC_exp3[0,:,:,:]) # only 1 member
ens_avg_NLeSC_exp3.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp3.trend(Dim_ens=False)
ens_avg_NLeSC_exp4 = analyzer.statistics(AMET_NLeSC_exp4[0,:,:,:])
ens_avg_NLeSC_exp4.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp4.trend(Dim_ens=False)
# EC Earth (DMI)
#ens_DMI_exp1 = analyzer.statistics(AMET_DMI_exp1[:,:,:,:])
#ens_DMI_exp1.anomaly()
#ens_DMI_exp1.lowpass()
ens_avg_DMI_exp1 = analyzer.statistics(np.mean(AMET_DMI_exp1[:,:,:,:],0))
ens_avg_DMI_exp1.anomaly(Dim_ens=False)
ens_avg_DMI_exp1.trend(Dim_ens=False)
ens_avg_DMI_exp2 = analyzer.statistics(np.mean(AMET_DMI_exp2[:,:,:,:],0))
ens_avg_DMI_exp2.anomaly(Dim_ens=False)
ens_avg_DMI_exp2.trend(Dim_ens=False)
ens_avg_DMI_exp3 = analyzer.statistics(np.mean(AMET_DMI_exp3[:,:,:,:],0))
ens_avg_DMI_exp3.anomaly(Dim_ens=False)
ens_avg_DMI_exp3.trend(Dim_ens=False)
ens_avg_DMI_exp4 = analyzer.statistics(np.mean(AMET_DMI_exp4[:,:,:,:],0))
ens_avg_DMI_exp4.anomaly(Dim_ens=False)
ens_avg_DMI_exp4.trend(Dim_ens=False)
# HadGEM (UoS)
#ens_DMI_exp1 = analyzer.statistics(AMET_DMI_exp1[:,:,:,:])
#ens_DMI_exp1.anomaly()
#ens_DMI_exp1.lowpass()
ens_avg_UoS_exp1 = analyzer.statistics(np.mean(AMET_UoS_exp1[:,:,:,:],0))
ens_avg_UoS_exp1.anomaly(Dim_ens=False)
ens_avg_UoS_exp1.trend(Dim_ens=False)
ens_avg_UoS_exp2 = analyzer.statistics(np.mean(AMET_UoS_exp2[:,:,:,:],0))
ens_avg_UoS_exp2.anomaly(Dim_ens=False)
ens_avg_UoS_exp2.trend(Dim_ens=False)
ens_avg_UoS_exp3 = analyzer.statistics(np.mean(AMET_UoS_exp3[:,:,:,:],0))
ens_avg_UoS_exp3.anomaly(Dim_ens=False)
ens_avg_UoS_exp3.trend(Dim_ens=False)
ens_avg_UoS_exp4 = analyzer.statistics(np.mean(AMET_UoS_exp4[:,:,:,:],0))
ens_avg_UoS_exp4.anomaly(Dim_ens=False)
ens_avg_UoS_exp4.trend(Dim_ens=False)
# NorESM (NERSC)
#ens_NERSC_exp1 = analyzer.statistics(AMET_NERSC_exp1[:,:,:,:])
#ens_NERSC_exp1.anomaly()
#ens_NERSC_exp1.lowpass()
ens_avg_NERSC_exp1 = analyzer.statistics(np.mean(AMET_NERSC_exp1[:,:,:,:],0))
ens_avg_NERSC_exp1.anomaly(Dim_ens=False)
ens_avg_NERSC_exp1.trend(Dim_ens=False)
ens_avg_NERSC_exp2 = analyzer.statistics(np.mean(AMET_NERSC_exp2[:,:,:,:],0))
ens_avg_NERSC_exp2.anomaly(Dim_ens=False)
ens_avg_NERSC_exp2.trend(Dim_ens=False)
ens_avg_NERSC_exp3 = analyzer.statistics(np.mean(AMET_NERSC_exp3[:,:,:,:],0))
ens_avg_NERSC_exp3.anomaly(Dim_ens=False)
ens_avg_NERSC_exp3.trend(Dim_ens=False)
ens_avg_NERSC_exp4 = analyzer.statistics(np.mean(AMET_NERSC_exp4[:,:,:,:],0))
ens_avg_NERSC_exp4.anomaly(Dim_ens=False)
ens_avg_NERSC_exp4.trend(Dim_ens=False)
# WACCM6 (WHOI)
ens_avg_WHOI_exp1 = analyzer.statistics(np.mean(AMET_WHOI_exp1[:,:,:,:],0))
ens_avg_WHOI_exp1.anomaly(Dim_ens=False)
ens_avg_WHOI_exp1.trend(Dim_ens=False)
ens_avg_WHOI_exp2 = analyzer.statistics(np.mean(AMET_WHOI_exp2[:,:,:,:],0))
ens_avg_WHOI_exp2.anomaly(Dim_ens=False)
ens_avg_WHOI_exp2.trend(Dim_ens=False)
ens_avg_WHOI_exp3 = analyzer.statistics(np.mean(AMET_WHOI_exp3[:,:,:,:],0))
ens_avg_WHOI_exp3.anomaly(Dim_ens=False)
ens_avg_WHOI_exp3.trend(Dim_ens=False)
ens_avg_WHOI_exp4 = analyzer.statistics(np.mean(AMET_WHOI_exp4[:,:,:,:],0))
ens_avg_WHOI_exp4.anomaly(Dim_ens=False)
ens_avg_WHOI_exp4.trend(Dim_ens=False)
# CMCC-CM (CMCC)
ens_avg_CMCC_exp1 = analyzer.statistics(np.mean(AMET_CMCC_exp1[:,:,:,:],0))
ens_avg_CMCC_exp1.anomaly(Dim_ens=False)
ens_avg_CMCC_exp1.trend(Dim_ens=False)
ens_avg_CMCC_exp2 = analyzer.statistics(np.mean(AMET_CMCC_exp2[:,:,:,:],0))
ens_avg_CMCC_exp2.anomaly(Dim_ens=False)
ens_avg_CMCC_exp2.trend(Dim_ens=False)
# IPSL-CM (CNRS)
ens_avg_CNRS_exp1 = analyzer.statistics(np.mean(AMET_CNRS_exp1[:,:,:,:],0))
ens_avg_CNRS_exp1.anomaly(Dim_ens=False)
ens_avg_CNRS_exp1.trend(Dim_ens=False)
ens_avg_CNRS_exp2 = analyzer.statistics(np.mean(AMET_CNRS_exp2[:,:,:,:],0))
ens_avg_CNRS_exp2.anomaly(Dim_ens=False)
ens_avg_CNRS_exp2.trend(Dim_ens=False)
ens_avg_CNRS_exp3 = analyzer.statistics(np.mean(AMET_CNRS_exp3[:,:,:,:],0))
ens_avg_CNRS_exp3.anomaly(Dim_ens=False)
ens_avg_CNRS_exp3.trend(Dim_ens=False)
ens_avg_CNRS_exp4 = analyzer.statistics(np.mean(AMET_CNRS_exp4[:,:,:,:],0))
ens_avg_CNRS_exp4.anomaly(Dim_ens=False)
ens_avg_CNRS_exp4.trend(Dim_ens=False)
# IAP-AGCM (IAP-NZC)
ens_avg_IAP_exp1 = analyzer.statistics(np.mean(AMET_IAP_exp1[:,:,:,:],0))
ens_avg_IAP_exp1.anomaly(Dim_ens=False)
ens_avg_IAP_exp1.trend(Dim_ens=False)
ens_avg_IAP_exp2 = analyzer.statistics(np.mean(AMET_IAP_exp2[:,:,:,:],0))
ens_avg_IAP_exp2.anomaly(Dim_ens=False)
ens_avg_IAP_exp2.trend(Dim_ens=False)
ens_avg_IAP_exp3 = analyzer.statistics(np.mean(AMET_IAP_exp3[:,:,:,:],0))
ens_avg_IAP_exp3.anomaly(Dim_ens=False)
ens_avg_IAP_exp3.trend(Dim_ens=False)
ens_avg_IAP_exp4 = analyzer.statistics(np.mean(AMET_IAP_exp4[:,:,:,:],0))
ens_avg_IAP_exp4.anomaly(Dim_ens=False)
ens_avg_IAP_exp4.trend(Dim_ens=False)
# MPIESM (MPI)
ens_avg_MPI_exp1 = analyzer.statistics(np.mean(AMET_MPI_exp1[:,:,:,:],0))
ens_avg_MPI_exp1.anomaly(Dim_ens=False)
ens_avg_MPI_exp1.trend(Dim_ens=False)
ens_avg_MPI_exp2 = analyzer.statistics(np.mean(AMET_MPI_exp2[:,:,:,:],0))
ens_avg_MPI_exp2.anomaly(Dim_ens=False)
ens_avg_MPI_exp2.trend(Dim_ens=False)
ens_avg_MPI_exp3 = analyzer.statistics(np.mean(AMET_MPI_exp3[:,:,:,:],0))
ens_avg_MPI_exp3.anomaly(Dim_ens=False)
ens_avg_MPI_exp3.trend(Dim_ens=False)
ens_avg_MPI_exp4 = analyzer.statistics(np.mean(AMET_MPI_exp4[:,:,:,:],0))
ens_avg_MPI_exp4.anomaly(Dim_ens=False)
ens_avg_MPI_exp4.trend(Dim_ens=False)
fig = plt.figure()
# Exp1
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], ens_avg_NLeSC_exp1._a[:200]*120, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) exp1')
#EC Earth (DMI)
plt.plot(lat_DMI[:100], ens_avg_DMI_exp1._a[:100]*120, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(lat_UoS[:127], ens_avg_UoS_exp1._a[:127]*120, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], ens_avg_NERSC_exp1._a[:75]*120, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], ens_avg_WHOI_exp1._a[:75]*120, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:75], ens_avg_CMCC_exp1._a[:75]*120, color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], ens_avg_CNRS_exp1._a[:56]*120, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], ens_avg_IAP_exp1._a[:50]*120, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
# MPIESM (MPI)
plt.plot(lat_MPI[:75], ens_avg_MPI_exp1._a[:75]*120, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp2
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], ens_avg_NLeSC_exp2._a[:200]*120, color='dodgerblue', linestyle='-',
linewidth=1, label='EC Earth (NLeSC) exp2')
#EC Earth (DMI)
plt.plot(lat_DMI[:100], ens_avg_DMI_exp2._a[:100]*120, color='blue', linestyle='-', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], ens_avg_UoS_exp2._a[:127]*120, color='red', linestyle='-', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], ens_avg_NERSC_exp2._a[:75]*120, color='green', linestyle='-', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], ens_avg_WHOI_exp2._a[:75]*120, color='cyan', linestyle='-', linewidth=1)
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:75], ens_avg_CMCC_exp2._a[:75]*120, color='olive', linestyle='-', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], ens_avg_CNRS_exp2._a[:56]*120, color='orange', linestyle='-', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], ens_avg_IAP_exp2._a[:50]*120, color='gray', linestyle='-', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], ens_avg_MPI_exp2._a[:75]*120, color='magenta', linestyle='-', linewidth=1)
# Exp3
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], ens_avg_NLeSC_exp3._a[:200]*120, color='dodgerblue', linestyle=':',
linewidth=1, label='EC Earth (NLeSC) exp3')
#EC Earth (DMI)
plt.plot(lat_DMI[:100], ens_avg_DMI_exp3._a[:100]*120, color='blue', linestyle=':', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], ens_avg_UoS_exp3._a[:127]*120, color='red', linestyle=':', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], ens_avg_NERSC_exp3._a[:75]*120, color='green', linestyle=':', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], ens_avg_WHOI_exp3._a[:75]*120, color='cyan', linestyle=':', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], ens_avg_CNRS_exp3._a[:56]*120, color='orange', linestyle=':', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], ens_avg_IAP_exp3._a[:50]*120, color='gray', linestyle=':', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], ens_avg_MPI_exp3._a[:75]*120, color='magenta', linestyle=':', linewidth=1)
# Exp4
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:200], ens_avg_NLeSC_exp4._a[:200]*120, color='dodgerblue', linestyle=':',
linewidth=1, label='EC Earth (NLeSC) exp4')
#EC Earth (DMI)
plt.plot(lat_DMI[:100], ens_avg_DMI_exp4._a[:100]*120, color='blue', linestyle='-.', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:127], ens_avg_UoS_exp4._a[:127]*120, color='red', linestyle='-.', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:75], ens_avg_NERSC_exp4._a[:75]*120, color='green', linestyle='-.', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:75], ens_avg_WHOI_exp4._a[:75]*120, color='cyan', linestyle='-.', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:56], ens_avg_CNRS_exp4._a[:56]*120, color='orange', linestyle='-.', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:50], ens_avg_IAP_exp4._a[:50]*120, color='gray', linestyle='-.', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:75], ens_avg_MPI_exp4._a[:75]*120, color='magenta', linestyle='-.', linewidth=1)
plt.xlabel("Latitude",fontsize=9)
plt.ylabel("AMET (PW/decade)",fontsize=9)
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.ylim(-0.12,0.04)
plt.legend(frameon=True, loc=3, prop={'size': 7})
plt.show()
fig.savefig(os.path.join(output_path,'Anomaly_trend_upto20N_ensAvg_AMIP.png'),dpi=200)
plt.close(fig)
fig2 = plt.figure()
# Exp1
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:], ens_avg_NLeSC_exp1._a[:]*120, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) exp1')
#EC Earth (DMI)
plt.plot(lat_DMI[:], ens_avg_DMI_exp1._a[:]*120, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(lat_UoS[:], ens_avg_UoS_exp1._a[:]*120, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(lat_NERSC[:], ens_avg_NERSC_exp1._a[:]*120, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:], ens_avg_WHOI_exp1._a[:]*120, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:], ens_avg_CMCC_exp1._a[:]*120, color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:], ens_avg_CNRS_exp1._a[:]*120, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:], ens_avg_IAP_exp1._a[:]*120, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
# MPIESM (MPI)
plt.plot(lat_MPI[:], ens_avg_MPI_exp1._a[:]*120, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp2
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:], ens_avg_NLeSC_exp2._a[:]*120, color='dodgerblue', linestyle='-', linewidth=1, label='EC Earth (NLeSC) exp2')
#EC Earth (DMI)
plt.plot(lat_DMI[:], ens_avg_DMI_exp2._a[:]*120, color='blue', linestyle='-', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:], ens_avg_UoS_exp2._a[:]*120, color='red', linestyle='-', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:], ens_avg_NERSC_exp2._a[:]*120, color='green', linestyle='-', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:], ens_avg_WHOI_exp2._a[:]*120, color='cyan', linestyle='-', linewidth=1)
# CMCC-CM (CMCC)
#plt.plot(lat_CMCC[:], ens_avg_CMCC_exp2._a[:]*120, color='olive', linestyle='-', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:], ens_avg_CNRS_exp2._a[:]*120, color='orange', linestyle='-', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:], ens_avg_IAP_exp2._a[:]*120, color='gray', linestyle='-', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:], ens_avg_MPI_exp2._a[:]*120, color='magenta', linestyle='-', linewidth=1)
# Exp3
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:], ens_avg_NLeSC_exp3._a[:]*120, color='dodgerblue', linestyle=':', linewidth=1, label='EC Earth (NLeSC) exp3')
#EC Earth (DMI)
plt.plot(lat_DMI[:], ens_avg_DMI_exp3._a[:]*120, color='blue', linestyle=':', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:], ens_avg_UoS_exp3._a[:]*120, color='red', linestyle=':', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:], ens_avg_NERSC_exp3._a[:]*120, color='green', linestyle=':', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:], ens_avg_WHOI_exp3._a[:]*120, color='cyan', linestyle=':', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:], ens_avg_CNRS_exp3._a[:]*120, color='orange', linestyle=':', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:], ens_avg_IAP_exp3._a[:]*120, color='gray', linestyle=':', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:], ens_avg_MPI_exp3._a[:]*120, color='magenta', linestyle=':', linewidth=1)
# Exp4
#EC Earth (NLeSC)
plt.plot(lat_NLeSC[:], ens_avg_NLeSC_exp4._a[:]*120, color='dodgerblue', linestyle='-.',
linewidth=1, label='EC Earth (NLeSC) exp4')
#EC Earth (DMI)
plt.plot(lat_DMI[:], ens_avg_DMI_exp4._a[:]*120, color='blue', linestyle='-.', linewidth=1)
# HadGEM (UoS)
plt.plot(lat_UoS[:], ens_avg_UoS_exp4._a[:]*120, color='red', linestyle='-.', linewidth=1)
# NorESM (NERSC)
plt.plot(lat_NERSC[:], ens_avg_NERSC_exp4._a[:]*120, color='green', linestyle='-.', linewidth=1)
# WACCM6 (WHOI)
plt.plot(lat_WHOI[:], ens_avg_WHOI_exp4._a[:]*120, color='cyan', linestyle='-.', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(lat_CNRS[:], ens_avg_CNRS_exp4._a[:]*120, color='orange', linestyle='-.', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(lat_IAP[:], ens_avg_IAP_exp4._a[:]*120, color='gray', linestyle='-.', linewidth=1)
# MPIESM (MPI)
plt.plot(lat_MPI[:], ens_avg_MPI_exp4._a[:]*120, color='magenta', linestyle=':', linewidth=1)
plt.xlabel("Latitude",fontsize=9)
plt.ylabel("AMET (PW/decade)",fontsize=9)
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.ylim(-0.18,0.06)
plt.legend(frameon=True, loc=4, prop={'size': 7})
plt.show()
fig2.savefig(os.path.join(output_path,'Anomaly_trend_global_ensAvg_AMIP.png'),dpi=200)
plt.close(fig2)
# -
# |Model and Organization | Exp 1 | Exp 2 | Exp 3 | Exp 4 | time |
# |-----------------------|-------|-------|-------|-------|-----------|
# | EC Earth (NLeSC) | 10 | 9 | 1 | 1 | 1979-2015 (exp1&2) 1979-2013 (exp3&4) |
# | EC Earth (DMI) | 20 | 20 | 20 | 20 | 1979-2015 (exp1&2) 1979-2013 (exp3&4) |
# | CMCC-CM (CMCC) | 10 | 10 | 0 | 0 | 1979-2014 |
# | WACCM6 (WHOI) | 30 | 30 | 30 | 30 | 1979-2014 (exp1&2) 1979-2012 (exp3&4) |
# | NorESM (NERSC) | 20 | 20 | 20 | 20 | 1979-2014 (exp1&2) 1979-2013 (exp3&4) |
# | HadGEM (UoS) | 10 | 10 | 5 | 5 | 1979-2014 (exp1&2) 1979-2013 (exp3&4) |
# | IAP-AGCM (IAP-NZC) | 15 | 15 | 15 | 15 | 1979-2015 (exp1&2) 1979-2013 (exp3&4) |
# | IPSL-CM (CNRS) | 30 | 30 | 20 | 20 | 1979-2014 |
# | MPIESM (MPI) | 10 | 10 | 5 | 5 | 1979-2013 |
# +
################################ Anomalies at certain sections ######################################
################################ only ensemble mean is used ######################################
####################### color map #######################
#### EC Earth (NLeSC) : 'dodgerblue' ####
#### EC Earth (DMI) : 'blue' ####
#### HadGEM (UoS) : 'red' ####
#### NorESM (NERSC) : 'green' ####
#### WACCM6 (WHOI) : 'cyan' ####
#### CMCC-CM (CMCC) : 'olive' ####
#### IPSL-CM (CNRS) : 'orange' ####
#### IAP-AGCM (IAP-NZC) : 'gray' ####
#### MPIESM (MPI) : 'orange' ####
####################### color map #######################
####################### linestyles ######################
#### exp 1 (control) : '--' ####
#### exp 2 (sic fixed) : '-' ####
#### exp 3 (PDO removed) : ':' ####
#### exp 4 (AMO removed) : '-.' ####
####################### color map #######################
# lat 60N
lat_NLeSC_60N = 84
lat_DMI_60N = 42
lat_WHOI_60N = 32
lat_NERSC_60N = 32
lat_UoS_60N = 57
lat_CMCC_60N = 32
lat_CNRS_60N = 24
lat_IAP_60N = 21
lat_MPI_60N = 32
# lowpass filter window
window=60 # month
# index
index_1979_2012 = np.arange(1,34*12+1,1)
index_1979_2013 = np.arange(1,35*12+1,1)
index_1979_2014 = np.arange(1,36*12+1,1)
index_1979_2015 = np.arange(1,37*12+1,1)
index_year = np.arange(1980,2020,5)
# EC Earth (NLeSC)
ens_avg_NLeSC_exp1 = analyzer.statistics(np.mean(AMET_NLeSC_exp1[:,:,:,lat_NLeSC_60N],0))
ens_avg_NLeSC_exp1.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp1.lowpass(Dim_ens=False)
ens_avg_NLeSC_exp2 = analyzer.statistics(np.mean(AMET_NLeSC_exp2[:,:,:,lat_NLeSC_60N],0))
ens_avg_NLeSC_exp2.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp2.lowpass(Dim_ens=False)
ens_avg_NLeSC_exp3 = analyzer.statistics(AMET_NLeSC_exp3[0,:,:,lat_NLeSC_60N])
ens_avg_NLeSC_exp3.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp3.lowpass(Dim_ens=False)
ens_avg_NLeSC_exp4 = analyzer.statistics(AMET_NLeSC_exp4[0,:,:,lat_NLeSC_60N])
ens_avg_NLeSC_exp4.anomaly(Dim_ens=False)
ens_avg_NLeSC_exp4.lowpass(Dim_ens=False)
# EC Earth (DMI)
ens_avg_DMI_exp1 = analyzer.statistics(np.mean(AMET_DMI_exp1[:,:,:,lat_DMI_60N],0))
ens_avg_DMI_exp1.anomaly(Dim_ens=False)
ens_avg_DMI_exp1.lowpass(Dim_ens=False)
ens_avg_DMI_exp2 = analyzer.statistics(np.mean(AMET_DMI_exp2[:,:,:,lat_DMI_60N],0))
ens_avg_DMI_exp2.anomaly(Dim_ens=False)
ens_avg_DMI_exp2.lowpass(Dim_ens=False)
ens_avg_DMI_exp3 = analyzer.statistics(np.mean(AMET_DMI_exp3[:,:,:,lat_DMI_60N],0))
ens_avg_DMI_exp3.anomaly(Dim_ens=False)
ens_avg_DMI_exp3.lowpass(Dim_ens=False)
ens_avg_DMI_exp4 = analyzer.statistics(np.mean(AMET_DMI_exp4[:,:,:,lat_DMI_60N],0))
ens_avg_DMI_exp4.anomaly(Dim_ens=False)
ens_avg_DMI_exp4.lowpass(Dim_ens=False)
# HadGEM (UoS)
ens_avg_UoS_exp1 = analyzer.statistics(np.mean(AMET_UoS_exp1[:,:,:,lat_UoS_60N],0))
ens_avg_UoS_exp1.anomaly(Dim_ens=False)
ens_avg_UoS_exp1.lowpass(Dim_ens=False)
ens_avg_UoS_exp2 = analyzer.statistics(np.mean(AMET_UoS_exp2[:,:,:,lat_UoS_60N],0))
ens_avg_UoS_exp2.anomaly(Dim_ens=False)
ens_avg_UoS_exp2.lowpass(Dim_ens=False)
ens_avg_UoS_exp3 = analyzer.statistics(np.mean(AMET_UoS_exp3[:,:,:,lat_UoS_60N],0))
ens_avg_UoS_exp3.anomaly(Dim_ens=False)
ens_avg_UoS_exp3.lowpass(Dim_ens=False)
ens_avg_UoS_exp4 = analyzer.statistics(np.mean(AMET_UoS_exp4[:,:,:,lat_UoS_60N],0))
ens_avg_UoS_exp4.anomaly(Dim_ens=False)
ens_avg_UoS_exp4.lowpass(Dim_ens=False)
# NorESM (NERSC)
ens_avg_NERSC_exp1 = analyzer.statistics(np.mean(AMET_NERSC_exp1[:,:,:,lat_NERSC_60N],0))
ens_avg_NERSC_exp1.anomaly(Dim_ens=False)
ens_avg_NERSC_exp1.lowpass(Dim_ens=False)
ens_avg_NERSC_exp2 = analyzer.statistics(np.mean(AMET_NERSC_exp2[:,:,:,lat_NERSC_60N],0))
ens_avg_NERSC_exp2.anomaly(Dim_ens=False)
ens_avg_NERSC_exp2.lowpass(Dim_ens=False)
ens_avg_NERSC_exp3 = analyzer.statistics(np.mean(AMET_NERSC_exp3[:,:,:,lat_NERSC_60N],0))
ens_avg_NERSC_exp3.anomaly(Dim_ens=False)
ens_avg_NERSC_exp3.lowpass(Dim_ens=False)
ens_avg_NERSC_exp4 = analyzer.statistics(np.mean(AMET_NERSC_exp4[:,:,:,lat_NERSC_60N],0))
ens_avg_NERSC_exp4.anomaly(Dim_ens=False)
ens_avg_NERSC_exp4.lowpass(Dim_ens=False)
# WACCM6 (WHOI)
ens_avg_WHOI_exp1 = analyzer.statistics(np.mean(AMET_WHOI_exp1[:,:,:,lat_WHOI_60N],0))
ens_avg_WHOI_exp1.anomaly(Dim_ens=False)
ens_avg_WHOI_exp1.lowpass(Dim_ens=False)
ens_avg_WHOI_exp2 = analyzer.statistics(np.mean(AMET_WHOI_exp2[:,:,:,lat_WHOI_60N],0))
ens_avg_WHOI_exp2.anomaly(Dim_ens=False)
ens_avg_WHOI_exp2.lowpass(Dim_ens=False)
ens_avg_WHOI_exp3 = analyzer.statistics(np.mean(AMET_WHOI_exp3[:,:,:,lat_WHOI_60N],0))
ens_avg_WHOI_exp3.anomaly(Dim_ens=False)
ens_avg_WHOI_exp3.lowpass(Dim_ens=False)
ens_avg_WHOI_exp4 = analyzer.statistics(np.mean(AMET_WHOI_exp4[:,:,:,lat_WHOI_60N],0))
ens_avg_WHOI_exp4.anomaly(Dim_ens=False)
ens_avg_WHOI_exp4.lowpass(Dim_ens=False)
# CMCC-CM (CMCC)
ens_avg_CMCC_exp1 = analyzer.statistics(np.mean(AMET_CMCC_exp1[:,:,:,lat_CMCC_60N],0))
ens_avg_CMCC_exp1.anomaly(Dim_ens=False)
ens_avg_CMCC_exp1.lowpass(Dim_ens=False)
ens_avg_CMCC_exp2 = analyzer.statistics(np.mean(AMET_CMCC_exp2[:,:,:,lat_CMCC_60N],0))
ens_avg_CMCC_exp2.anomaly(Dim_ens=False)
ens_avg_CMCC_exp2.lowpass(Dim_ens=False)
# IPSL-CM (CNRS)
ens_avg_CNRS_exp1 = analyzer.statistics(np.mean(AMET_CNRS_exp1[:,:,:,lat_CNRS_60N],0))
ens_avg_CNRS_exp1.anomaly(Dim_ens=False)
ens_avg_CNRS_exp1.lowpass(Dim_ens=False)
ens_avg_CNRS_exp2 = analyzer.statistics(np.mean(AMET_CNRS_exp2[:,:,:,lat_CNRS_60N],0))
ens_avg_CNRS_exp2.anomaly(Dim_ens=False)
ens_avg_CNRS_exp2.lowpass(Dim_ens=False)
ens_avg_CNRS_exp3 = analyzer.statistics(np.mean(AMET_CNRS_exp3[:,:,:,lat_CNRS_60N],0))
ens_avg_CNRS_exp3.anomaly(Dim_ens=False)
ens_avg_CNRS_exp3.lowpass(Dim_ens=False)
ens_avg_CNRS_exp4 = analyzer.statistics(np.mean(AMET_CNRS_exp4[:,:,:,lat_CNRS_60N],0))
ens_avg_CNRS_exp4.anomaly(Dim_ens=False)
ens_avg_CNRS_exp4.lowpass(Dim_ens=False)
# IAP-AGCM (IAP-NZC)
ens_avg_IAP_exp1 = analyzer.statistics(np.mean(AMET_IAP_exp1[:,:,:,lat_IAP_60N],0))
ens_avg_IAP_exp1.anomaly(Dim_ens=False)
ens_avg_IAP_exp1.lowpass(Dim_ens=False)
ens_avg_IAP_exp2 = analyzer.statistics(np.mean(AMET_IAP_exp2[:,:,:,lat_IAP_60N],0))
ens_avg_IAP_exp2.anomaly(Dim_ens=False)
ens_avg_IAP_exp2.lowpass(Dim_ens=False)
ens_avg_IAP_exp3 = analyzer.statistics(np.mean(AMET_IAP_exp3[:,:,:,lat_IAP_60N],0))
ens_avg_IAP_exp3.anomaly(Dim_ens=False)
ens_avg_IAP_exp3.lowpass(Dim_ens=False)
ens_avg_IAP_exp4 = analyzer.statistics(np.mean(AMET_IAP_exp4[:,:,:,lat_IAP_60N],0))
ens_avg_IAP_exp4.anomaly(Dim_ens=False)
ens_avg_IAP_exp4.lowpass(Dim_ens=False)
# MPIESM (MPI)
ens_avg_MPI_exp1 = analyzer.statistics(np.mean(AMET_MPI_exp1[:,:,:,lat_MPI_60N],0))
ens_avg_MPI_exp1.anomaly(Dim_ens=False)
ens_avg_MPI_exp1.lowpass(Dim_ens=False)
ens_avg_MPI_exp2 = analyzer.statistics(np.mean(AMET_MPI_exp2[:,:,:,lat_MPI_60N],0))
ens_avg_MPI_exp2.anomaly(Dim_ens=False)
ens_avg_MPI_exp2.lowpass(Dim_ens=False)
ens_avg_MPI_exp3 = analyzer.statistics(np.mean(AMET_MPI_exp3[:,:,:,lat_MPI_60N],0))
ens_avg_MPI_exp3.anomaly(Dim_ens=False)
ens_avg_MPI_exp3.lowpass(Dim_ens=False)
ens_avg_MPI_exp4 = analyzer.statistics(np.mean(AMET_MPI_exp4[:,:,:,lat_MPI_60N],0))
ens_avg_MPI_exp4.anomaly(Dim_ens=False)
ens_avg_MPI_exp4.lowpass(Dim_ens=False)
# interannual
fig = plt.figure(figsize=(8,4.5))
# Exp1
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp1._lowpass, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) Exp1')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp1._lowpass, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp1._lowpass, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp1._lowpass, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp1._lowpass, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp1._lowpass, color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp1._lowpass, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp1._lowpass, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp1._lowpass, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp2
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp2._lowpass, color='dodgerblue', linestyle='-', linewidth=1, label='EC Earth (NLeSC) Exp2')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp2._lowpass, color='blue', linestyle='-', linewidth=1)
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp2._lowpass, color='red', linestyle='-', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp2._lowpass, color='green', linestyle='-', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp2._lowpass, color='cyan', linestyle='-', linewidth=1)
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp2._lowpass, color='olive', linestyle='-', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp2._lowpass, color='orange', linestyle='-', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp2._lowpass, color='gray', linestyle='-', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp2._lowpass, color='magenta', linestyle='-', linewidth=1)
# Exp3
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp3._lowpass, color='dodgerblue', linestyle=':', linewidth=1, label='EC Earth (NLeSC) Exp3')
# EC Earth (DMI)
plt.plot(index_1979_2013[window-1:], ens_avg_DMI_exp3._lowpass, color='blue', linestyle=':', linewidth=1)
# HadGEM (UoS)
plt.plot(index_1979_2013[window-1:], ens_avg_UoS_exp3._lowpass, color='red', linestyle=':', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2013[window-1:], ens_avg_NERSC_exp3._lowpass, color='green', linestyle=':', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2012[window-1:], ens_avg_WHOI_exp3._lowpass, color='cyan', linestyle=':', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp3._lowpass, color='orange', linestyle=':', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2013[window-1:], ens_avg_IAP_exp3._lowpass, color='gray', linestyle=':', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp3._lowpass, color='magenta', linestyle=':', linewidth=1)
# Exp4
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp4._lowpass, color='dodgerblue', linestyle='-.', linewidth=1, label='EC Earth (NLeSC) Exp4')
# EC Earth (DMI)
plt.plot(index_1979_2013[window-1:], ens_avg_DMI_exp4._lowpass, color='blue', linestyle='-.', linewidth=1)
# HadGEM (UoS)
plt.plot(index_1979_2013[window-1:], ens_avg_UoS_exp4._lowpass, color='red', linestyle='-.', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2013[window-1:], ens_avg_NERSC_exp4._lowpass, color='green', linestyle='-.', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2012[window-1:], ens_avg_WHOI_exp4._lowpass, color='cyan', linestyle='-.', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp4._lowpass, color='orange', linestyle='-.', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2013[window-1:], ens_avg_IAP_exp4._lowpass, color='gray', linestyle='-.', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp4._lowpass, color='magenta', linestyle='-.', linewidth=1)
plt.xlabel("Time",fontsize=9)
plt.xticks(np.arange(13,yy*12+1,60), index_year,fontsize=8)
plt.xlim(-25,520)
plt.ylabel("AMET (PW)",fontsize=9)
plt.yticks(fontsize=8)
plt.ylim(-0.18,0.10)
plt.legend(frameon=False, loc=3, prop={'size': 7.5})
plt.show()
fig.savefig(os.path.join(output_path,'Anomaly_lowpass_{}_60N_ensAvg_AMIP_exp1234.png'.format(window)),dpi=200)
plt.close(fig)
# +
################################ Anomalies at certain sections ######################################
################################ only ensemble mean is used ######################################
################################ comparison between exp 1 and 2 ######################################
# EC Earth (DMI) interannual
fig = plt.figure(figsize=(8,4.5))
# Exp1
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp1._lowpass, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) Exp1')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp1._lowpass, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp1._lowpass, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp1._lowpass, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp1._lowpass, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp1._lowpass, color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp1._lowpass, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp1._lowpass, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp1._lowpass, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp2
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp2._lowpass, color='dodgerblue', linestyle='-', linewidth=1, label='EC Earth (NLeSC) Exp2')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp2._lowpass, color='blue', linestyle='-', linewidth=1)
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp2._lowpass, color='red', linestyle='-', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp2._lowpass, color='green', linestyle='-', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp2._lowpass, color='cyan', linestyle='-', linewidth=1)
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp2._lowpass, color='olive', linestyle='-', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp2._lowpass, color='orange', linestyle='-', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp2._lowpass, color='gray', linestyle='-', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp2._lowpass, color='magenta', linestyle='-', linewidth=1)
plt.xlabel("Time",fontsize=9)
plt.xticks(np.arange(13,yy*12+1,60), index_year,fontsize=8)
plt.xlim(-25,520)
plt.ylabel("AMET (PW)",fontsize=9)
plt.yticks(fontsize=8)
plt.ylim(-0.08,0.08)
plt.legend(frameon=False, loc=1, prop={'size': 7.5})
plt.show()
fig.savefig(os.path.join(output_path,'Anomaly_lowpass_{}_60N_ensAvg_AMIP_exp12.png'.format(window)),dpi=200)
plt.close(fig)
# +
################################ Anomalies at certain sections ######################################
################################ only ensemble mean is used ######################################
################################ comparison between exp 1 and 3 ######################################
# EC Earth (DMI) interannual
fig = plt.figure(figsize=(8,4.5))
# Exp1
# EC Earth (DNLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp1._lowpass, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) Exp1')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp1._lowpass, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI)')
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp1._lowpass, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp1._lowpass, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp1._lowpass, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp1._lowpass, color='olive', linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp1._lowpass, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp1._lowpass, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp1._lowpass, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp3
# EC Earth (DMI)
plt.plot(index_1979_2013[window-1:], ens_avg_DMI_exp3._lowpass, color='blue', linestyle=':', linewidth=1, label='EC Earth (DMI) Exp3')
# HadGEM (UoS)
plt.plot(index_1979_2013[window-1:], ens_avg_UoS_exp3._lowpass, color='red', linestyle=':', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2013[window-1:], ens_avg_NERSC_exp3._lowpass, color='green', linestyle=':', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2012[window-1:], ens_avg_WHOI_exp3._lowpass, color='cyan', linestyle=':', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp3._lowpass, color='orange', linestyle=':', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2013[window-1:], ens_avg_IAP_exp3._lowpass, color='gray', linestyle=':', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp3._lowpass, color='magenta', linestyle=':', linewidth=1)
plt.xlabel("Time",fontsize=9)
plt.xticks(np.arange(13,yy*12+1,60), index_year,fontsize=8)
plt.xlim(-25,520)
plt.ylabel("AMET (PW)",fontsize=9)
plt.yticks(fontsize=8)
plt.ylim(-0.08,0.08)
plt.legend(frameon=False, loc=3, prop={'size': 7.5})
plt.show()
fig.savefig(os.path.join(output_path,'Anomaly_lowpass_{}_60N_ensAvg_AMIP_exp13.png'.format(window)),dpi=200)
plt.close(fig)
# +
################################ Anomalies at certain sections ######################################
################################ only ensemble mean is used ######################################
################################ comparison between exp 1 and 4 ######################################
# EC Earth (DMI) interannual
fig = plt.figure(figsize=(8,4.5))
# Exp1
# EC Earth (NLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp1._lowpass, color='dodgerblue', linestyle='--', linewidth=1, label='EC Earth (NLeSC) Exp1')
# EC Earth (DMI)
plt.plot(index_1979_2015[window-1:], ens_avg_DMI_exp1._lowpass, color='blue', linestyle='--', linewidth=1, label='EC Earth (DMI) Exp1')
# HadGEM (UoS)
plt.plot(index_1979_2014[window-1:], ens_avg_UoS_exp1._lowpass, color='red', linestyle='--', linewidth=1, label='HadGEM (UoS)')
# NorESM (NERSC)
plt.plot(index_1979_2014[window-1:], ens_avg_NERSC_exp1._lowpass, color='green', linestyle='--', linewidth=1, label='NorESM (NERSC)')
# WACCM6 (WHOI)
plt.plot(index_1979_2014[window-1:], ens_avg_WHOI_exp1._lowpass, color='cyan', linestyle='--', linewidth=1, label='WACCM6 (WHOI)')
# CMCC-CM (CMCC)
#plt.plot(index_1979_2014[window-1:], ens_avg_CMCC_exp1._lowpass, color='olive, linestyle='--', linewidth=1, label='CMCC-CM (CMCC)')
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp1._lowpass, color='orange', linestyle='--', linewidth=1, label='IPSL-CM (CNRS)')
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2015[window-1:], ens_avg_IAP_exp1._lowpass, color='gray', linestyle='--', linewidth=1, label='IAP-AGCM (IAP-NZC)')
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp1._lowpass, color='magenta', linestyle='--', linewidth=1, label='MPIESM (MPI)')
# Exp4
# EC Earth (DNLeSC)
plt.plot(index_1979_2015[window-1:], ens_avg_NLeSC_exp4._lowpass, color='dodgerblue', linestyle='-.', linewidth=1, label='EC Earth (NLeSC) Exp4')
# EC Earth (DMI)
plt.plot(index_1979_2013[window-1:], ens_avg_DMI_exp4._lowpass, color='blue', linestyle='-.', linewidth=1)
# HadGEM (UoS)
plt.plot(index_1979_2013[window-1:], ens_avg_UoS_exp4._lowpass, color='red', linestyle='-.', linewidth=1)
# NorESM (NERSC)
plt.plot(index_1979_2013[window-1:], ens_avg_NERSC_exp4._lowpass, color='green', linestyle='-.', linewidth=1)
# WACCM6 (WHOI)
plt.plot(index_1979_2012[window-1:], ens_avg_WHOI_exp4._lowpass, color='cyan', linestyle='-.', linewidth=1)
# IPSL-CM (CNRS)
plt.plot(index_1979_2014[window-1:], ens_avg_CNRS_exp4._lowpass, color='orange', linestyle='-.', linewidth=1)
# IAP-AGCM (IAP-NZC)
plt.plot(index_1979_2013[window-1:], ens_avg_IAP_exp4._lowpass, color='gray', linestyle='-.', linewidth=1)
#MPIESM (MPI)
plt.plot(index_1979_2013[window-1:], ens_avg_MPI_exp4._lowpass, color='magenta', linestyle='-', linewidth=1)
plt.xlabel("Time",fontsize=9)
plt.xticks(np.arange(13,yy*12+1,60), index_year,fontsize=8)
plt.xlim(-25,520)
plt.ylabel("AMET (PW)",fontsize=9)
plt.yticks(fontsize=8)
plt.ylim(-0.08,0.08)
plt.legend(frameon=False, loc=3, prop={'size': 7})
plt.show()
fig.savefig(os.path.join(output_path,'Anomaly_lowpass_{}_60N_ensAvg_AMIP_exp14.png'.format(window)),dpi=200)
plt.close(fig)
# +
# peak of energy transport
print("EC Earth (NLeSC)")
print("std")
print(np.std(ens_avg_NLeSC_exp1._anomaly))
print(np.std(ens_avg_NLeSC_exp2._anomaly))
print(np.std(ens_avg_NLeSC_exp3._anomaly))
print(np.std(ens_avg_NLeSC_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_NLeSC_exp1._anomaly -
ens_avg_NLeSC_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_NLeSC_exp1._anomaly -
ens_avg_NLeSC_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_NLeSC_exp1._anomaly -
ens_avg_NLeSC_exp4._anomaly)))
print("EC Earth (DMI)")
print("std")
print(np.std(ens_avg_DMI_exp1._anomaly))
print(np.std(ens_avg_DMI_exp2._anomaly))
print(np.std(ens_avg_DMI_exp3._anomaly))
print(np.std(ens_avg_DMI_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_DMI_exp1._anomaly -
ens_avg_DMI_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_DMI_exp1._anomaly[:-24] -
ens_avg_DMI_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_DMI_exp1._anomaly[:-24] -
ens_avg_DMI_exp4._anomaly)))
print("HadGEM (UoS)")
print("std")
print(np.std(ens_avg_UoS_exp1._anomaly))
print(np.std(ens_avg_UoS_exp2._anomaly))
print(np.std(ens_avg_UoS_exp3._anomaly))
print(np.std(ens_avg_UoS_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_UoS_exp1._anomaly -
ens_avg_UoS_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_UoS_exp1._anomaly[:-12] -
ens_avg_UoS_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_UoS_exp1._anomaly[:-12] -
ens_avg_UoS_exp4._anomaly)))
print("NorESM (NERSC)")
print("std")
print(np.std(ens_avg_NERSC_exp1._anomaly))
print(np.std(ens_avg_NERSC_exp2._anomaly))
print(np.std(ens_avg_NERSC_exp3._anomaly))
print(np.std(ens_avg_NERSC_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_NERSC_exp1._anomaly -
ens_avg_NERSC_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_NERSC_exp1._anomaly[:-12] -
ens_avg_NERSC_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_NERSC_exp1._anomaly[:-12] -
ens_avg_NERSC_exp4._anomaly)))
print("WACCM6 (WHOI)")
print("std")
print(np.std(ens_avg_WHOI_exp1._anomaly))
print(np.std(ens_avg_WHOI_exp2._anomaly))
print(np.std(ens_avg_WHOI_exp3._anomaly))
print(np.std(ens_avg_WHOI_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_WHOI_exp1._anomaly -
ens_avg_WHOI_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_WHOI_exp1._anomaly[:-24] -
ens_avg_WHOI_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_WHOI_exp1._anomaly[:-24] -
ens_avg_WHOI_exp4._anomaly)))
print("CMCC-CM (CMCC)")
print("std")
print(np.std(ens_avg_CMCC_exp1._anomaly))
print(np.std(ens_avg_CMCC_exp2._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_CMCC_exp1._anomaly -
ens_avg_CMCC_exp2._anomaly)))
print("IPSL-CM (CNRS)")
print("std")
print(np.std(ens_avg_CNRS_exp1._anomaly))
print(np.std(ens_avg_CNRS_exp2._anomaly))
print(np.std(ens_avg_CNRS_exp3._anomaly))
print(np.std(ens_avg_CNRS_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_CNRS_exp1._anomaly -
ens_avg_CNRS_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_CNRS_exp1._anomaly -
ens_avg_CNRS_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_CNRS_exp1._anomaly -
ens_avg_CNRS_exp4._anomaly)))
print("IAP-AGCM (IAP-NZC)")
print("std")
print(np.std(ens_avg_IAP_exp1._anomaly))
print(np.std(ens_avg_IAP_exp2._anomaly))
print(np.std(ens_avg_IAP_exp3._anomaly))
print(np.std(ens_avg_IAP_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_IAP_exp1._anomaly -
ens_avg_IAP_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_IAP_exp1._anomaly[:-24] -
ens_avg_IAP_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_IAP_exp1._anomaly[:-24] -
ens_avg_IAP_exp4._anomaly)))
print("MPIESM (MPI)")
print("std")
print(np.std(ens_avg_MPI_exp1._anomaly))
print(np.std(ens_avg_MPI_exp2._anomaly))
print(np.std(ens_avg_MPI_exp3._anomaly))
print(np.std(ens_avg_MPI_exp4._anomaly))
print("diff")
print(np.mean(np.abs(ens_avg_MPI_exp1._anomaly -
ens_avg_MPI_exp2._anomaly)))
print(np.mean(np.abs(ens_avg_MPI_exp1._anomaly -
ens_avg_MPI_exp3._anomaly)))
print(np.mean(np.abs(ens_avg_MPI_exp1._anomaly -
ens_avg_MPI_exp4._anomaly)))
|
Analysis/AMET_analysis_series_report4D3.1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Demo Prophet Time Series Forecasting on Ray local
#
# <b>Suggestion: Make a copy of this notebook. This way you will retain the original, executed notebook outputs. Make edits in the copied notebook. </b>
#
# ### Description:
# This notebook goes along with the tutorial <a href="https://towardsdatascience.com/scaling-time-series-forecasting-with-ray-arima-and-prophet-e6c856e605ee">How to Train Faster Time Series Forecasting Using Ray, part 1 of 2<a>.
#
# This notebook demonstrates Time Series Forecasting Prophet algorithm on Ray. Example data is NYC yellow taxi from: https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page <br>
#
# Forecast goal: Given 6 months historical taxi trips data for NYC, your task is to predict #pickups at each location in NYC at monthly level for the next 2 months.
#
# ### Demo notes:
# Output shows timings using MEDIUM dataset <br>
# Both demo datasets are available in this github repo under data/ <br>
# SMALL dataset contains original, actual 260 items "clean_taxi_monthly.parquet" <br>
# MEDIUM dataset contains 2860 items with extra fakes "clean_taxi_monthly_fake_medium.parquet" <br>
# +
# install open-source Ray if you haven't already
# # !pip install "ray[default] installs the latest version; otherwise use a specific version
# # !pip install "ray[default]==1.9.0"
# install ARIMA library
# # !pip install pmdarima
# install Prophet library
# # !pip install kats
# install Anyscale to run Ray easily on a Cloud
# # !pip install anyscale
# +
###########
# Import libraries
###########
# Open-source libraries
import os # Python os functions
import logging #Python logging functions
import time # Python time functions
import warnings # Python warnings
warnings.filterwarnings('ignore')
import ray # Run distributed code
import numpy as np # Numerical processing
import pandas as pd # Dataframe (tabular data) processing
import matplotlib as mpl # Graph plotting
import matplotlib.pyplot as plt
# %matplotlib inline
import pickle
# Open-source ARIMA forecasting libraries
import pmdarima as pm
from pmdarima.model_selection import train_test_split
# Open-source Prophet forecasting libraries
# Note: using kats since it looks more actively maintained than original prophet
import kats
from kats.consts import TimeSeriesData
from kats.models.prophet import ProphetModel, ProphetParams
# !python --version
print(f"ray: {ray.__version__}")
print(f"numpy: {np.__version__}")
print(f"pandas: {pd.__version__}")
print(f"matplotlib: {mpl.__version__}")
AVAILABLE_LOCAL_CPU = os.cpu_count()
print(f"Found available CPU: {AVAILABLE_LOCAL_CPU}")
# -
# # Change how you want to run Ray below.
# <b>Depending on whether you want to run Ray Local or Ray in a Cloud:</b>
# <ul>
# <li><b>To run Ray Local, change below variables, then continue running cells in the notebook</b>: <br>
# RUN_RAY_LOCAL = True; RUN_RAY_ON_A_CLOUD = False</li>
# <li><b>To run Ray in a Cloud, change below variables, then continue running cells in the notebook</b>: <br>
# RUN_RAY_LOCAL = False; RUN_RAY_ON_A_CLOUD = True </li>
# </ul>
#
# +
###########
# CHANGE VARIABLES BELOW.
# To run Ray Local: RUN_RAY_LOCAL = True; RUN_RAY_ON_A_CLOUD = False
# To run Ray in a Cloud: RUN_RAY_LOCAL = False; RUN_RAY_ON_A_CLOUD = True
###########
RUN_RAY_LOCAL = True
RUN_RAY_ON_A_CLOUD = False
# +
###########
# Run Ray Local on your laptop for testing purposes
# Dashboard doc: https://docs.ray.io/en/master/ray-dashboard.html#ray-dashboard
###########
if RUN_RAY_LOCAL:
# num_cpus, num_gpus are optional parameters
# by default Ray will detect and use all available
NUM_CPU = AVAILABLE_LOCAL_CPU
print(f"You are running Ray Local with {NUM_CPU} CPUs")
# start up ray locally
if ray.is_initialized():
ray.shutdown()
ray.init()
else:
print("You are not running Ray Local")
# +
###########
# Run Ray in the Cloud using Anyscale
# View your cluster on console.anyscale.com
###########
if RUN_RAY_ON_A_CLOUD:
print("You are running Ray on a Cloud")
# # !pip install anyscale # install anyscale if you haven't already
import anyscale
# You can specify more pip installs, clone github, or copy code/data here in the runtime env.
# Everything in the runtime environment will override the cluster environment.
# https://docs.anyscale.com/user-guide/configure/dependency-management/anyscale-environments
my_env={ "working_dir": ".",
"pip": ["pmdarima", "kats"],
}
# start up ray in any cloud
if ray.is_initialized():
ray.shutdown()
ray.init(
"anyscale://christy-forecast5",
# runtime_env=my_env,
# optionally put pip installs in the cluster config instead of runtime_env
cluster_env="christy-forecast:4",
# Add extra quiet settings, since Prophet is noisy!
log_to_driver=False, # disable ray workers from logging the output.
configure_logging=True,
logging_level=logging.ERROR,
)
else:
print("You are not running Ray on a Cloud")
# -
# # Read 8 months clean NYC taxi data
#
# New York City Yellow Taxi ride volumes per location (8 months of historical data). <ul>
# <li>Original source: https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page</li>
# <li>Clean monthly source: https://github.com/christy/AnyscaleDemos/blob/main/forecasting_demos/data/clean_taxi_monthly_fake_medium.parquet?raw=true </li>
# </ul>
#
# Normally there is a data cleaning/prep step to convert raw data -> cleaned data. We'll dig into details of ETL later. <br>
# For now, let's just start with cleaned, aggregated monthly data for ARIMA and Prophet, since those algorithms are typically for strategic-level forecasting, not typically for detailed-level forecasting.
# + tags=[]
###########
# Read pandas dataframe
# If you cloned this notebook from github the data should be in your data/ folder
###########
# read 8 months of clean, aggregated monthly taxi data
# filename = "https://github.com/christy/AnyscaleDemos/blob/main/forecasting_demos/data/clean_taxi_monthly_fake_medium.parquet?raw=true"
# filename = "data/clean_taxi_monthly.parquet"
filename = "data/clean_taxi_monthly_fake_medium.parquet"
g_month = pd.read_parquet(filename)
# rename "time" column, since prophet expects that, arima doesn't care
g_month.reset_index(inplace=True)
g_month.rename(columns={"pickup_monthly": "time"}, inplace=True)
display(g_month.head())
# Train a model per item_id
item_list = list(g_month["pulocationid"].unique())
print(f"Number unique items = {len(item_list)}")
# -
# # Regular Python
# +
###########
# Assume below is already-existing regular Python code.
###########
# define file handler, not appending, to avoid growing logs
file_handler = logging.FileHandler('training.log', mode='w')
formatter = logging.Formatter('%(asctime)s : %(levelname)s : %(name)s : %(message)s')
file_handler.setFormatter(formatter)
# prophet logger - also need Class below to stop the noisy PyStan messages
prophet_logger = logging.getLogger('fbprophet')
prophet_logger.setLevel(logging.ERROR)
prophet_logger.addHandler(file_handler)
# This class is to suppress the Pystan noisy messages coming from Prophet
# Thanks to https://github.com/facebook/prophet/issues/223#issuecomment-326455744
class suppress_stdout_stderr(object):
'''
A context manager for doing a "deep suppression" of stdout and stderr in
Python, i.e. will suppress all print, even if the print originates in a
compiled C/Fortran sub-function.
This will not suppress raised exceptions, since exceptions are printed
to stderr just before a script exits, and after the context manager has
exited (at least, I think that is why it lets exceptions through).
'''
def __init__(self):
# Open a pair of null files
self.null_fds = [os.open(os.devnull, os.O_RDWR) for x in range(2)]
# Save the actual stdout (1) and stderr (2) file descriptors.
self.save_fds = [os.dup(1), os.dup(2)]
def __enter__(self):
# Assign the null pointers to stdout and stderr.
os.dup2(self.null_fds[0], 1)
os.dup2(self.null_fds[1], 2)
def __exit__(self, *_):
# Re-assign the real stdout/stderr back to (1) and (2)
os.dup2(self.save_fds[0], 1)
os.dup2(self.save_fds[1], 2)
# Close the null files
for fd in self.null_fds + self.save_fds:
os.close(fd)
###########
# Prophet train_model function, default train on 6 months, inference 2
###########
def train_model_PROPHET(
theDF: pd.DataFrame,
item_col: str,
item_value: str,
target_col: str,
train_size: int = 6,
) -> list:
"""This function trains a model using Prophet algorithm.
Args:
theDF (pd.DataFrame): Input data. It must have a "time" column.
theDF should not be indexed by "time".
item_col (str): Name of the column containing item_id or SKU.
item_value (str): Value of the item_id or SKU being forecasted.
target_col (str): Name of the column containing the actual value.
train_size (int, optional): Count of number of timestamps to use
for training. Defaults to 6.
Returns:
list: [
train (pd.DataFrame): Training data.
test (pd.DataFrame): Test data for evaluation.
model (pmdarima.arima.arima.ARIMA): ARIMA model for inference.
]
"""
# Set seed for reproducibility, use same seed in train AND inference
np.random.seed(415)
# split data into train/test
train, test = train_test_split(
theDF.loc[(theDF[item_col] == item_value), :], train_size=train_size
)
# convert pandas df to TimeSeriesData(df), with "time" column and any number of value columns.
train_ts = TimeSeriesData(train[["time", target_col]])
test_ts = TimeSeriesData(test[["time", target_col]])
# create a prophet model param instance
params = ProphetParams(
seasonality_mode="multiplicative"
)
# create a prophet model instance
model = ProphetModel(train_ts, params)
# fit model
with suppress_stdout_stderr(): #suppress pystan messages
model.fit()
# index train, test by time
train.set_index("time", inplace=True)
test.set_index("time", inplace=True)
return [train, test, model]
###########
# Prophet inference_model function
###########
def inference_model_PROPHET(
model: "kats.models.prophet.ProphetModel",
test: pd.DataFrame,
item_col: str,
target_col: str,
) -> pd.DataFrame:
"""This function inferences a model using Prophet algorithm. It uses
the actual values, if known, in the test evaluation dataframe
and concats them into the forecast output dataframe,
for easier evaluation later.
Args:
model (kats.models.prophet.ProphetModel): Prophet model.
test (pd.DataFrame): Test data for evaluation.
item_col (str): Name of the column containing item_id or SKU.
target_col (str): Name of the column containing the actual value.
Returns:
pd.DataFrame: forecast as pandas dataframe containing the forecast along
with actual values.
"""
# Set seed for reproducibility, use same seed in train AND inference
np.random.seed(415)
# Prophet inference on test data
forecast = model.predict(steps=test.shape[0], freq="MS")
# put both actual_value and predicted_value in forecast, for easier eval later
forecast.fcst = forecast.fcst.astype(np.int32)
forecast.fcst_lower = forecast.fcst_lower.astype(np.int32)
forecast.fcst_upper = forecast.fcst_upper.astype(np.int32)
forecast.columns = [
"time",
"fcst_prophet",
"fcst_prophet_lower",
"fcst_prophet_upper",
]
forecast = pd.concat(
[forecast, test.loc[:, target_col].reset_index(drop=True)], axis=1
)
forecast.set_index("time", inplace=True)
return forecast
# +
###########
# REGULAR PYTHON program flow to train and inference Prophet models
###########
# initialize objects
train = []
test = []
model = []
forecast = []
start = time.time()
# Train every model
train, test, model = map(
list,
zip(
*(
[
train_model_PROPHET(
g_month.copy(),
item_col="pulocationid",
item_value=v,
target_col="trip_quantity",
train_size=6,
)
for p, v in enumerate(item_list)
]
)
),
)
# Inference every model
forecast = [
inference_model_PROPHET(
model[p],
test[p],
item_col="pulocationid",
target_col="trip_quantity",
)
for p in range(len(item_list))
]
time_regular_python = time.time() - start
print(
f"Done! Prophet on Regular Python finished in {time_regular_python} seconds"
)
# +
###########
# inspect a few forecasts
###########
assert len(model) == len(item_list)
assert len(forecast) == len(item_list)
print(f"len(forecast): {len(forecast)}")
# plot first two forecasts
plt.figure(figsize=(8, 5))
for p, v in enumerate(item_list[0:2]):
display(forecast[p])
plt.plot(train[p]["trip_quantity"], label="Train")
plt.plot(test[p]["trip_quantity"], label="Test")
plt.plot(forecast[p]["fcst_prophet"], label="Forecast")
plt.legend(loc="best")
# -
# # Ray distributed Python
# +
# #%%timeit
###########
# Main Ray distributed program flow to train and inference Prophet models
###########
# Convert your previously-defined regular python functions to ray parallelized functions
train_model_PROPHET_remote = ray.remote(train_model_PROPHET).options(num_returns=3)
inference_model_PROPHET_remote = ray.remote(inference_model_PROPHET)
# initialize objects
train_obj_refs = []
test_obj_refs = []
model_obj_refs = []
forecast_obj_refs = []
# initialize data in ray object store on each cluster
input_data_ref = ray.put(g_month.copy())
start = time.time()
# Train every model
train_obj_refs, test_obj_refs, model_obj_refs = map(
list,
zip(
*(
[
train_model_PROPHET_remote.remote(
# g_month,
input_data_ref,
item_col="pulocationid",
item_value=v,
target_col="trip_quantity",
train_size=6,
)
for p, v in enumerate(item_list)
]
)
),
)
# Inference every model
forecast_obj_refs = [
inference_model_PROPHET_remote.remote(
model_obj_refs[p],
test_obj_refs[p],
item_col="pulocationid",
target_col="trip_quantity",
)
for p in range(len(item_list))
]
# ray.get() means block until all objectIDs requested are available
forecast_ray = ray.get(forecast_obj_refs)
time_ray_local = time.time() - start
print(
f"Done! Prophet on Ray Local finished in {time_ray_local} seconds"
)
# -
# # Verify forecasts
# +
# Run the Ray local code again to get the forecasts
###########
# Main Ray distributed program flow to train and inference Prophet models
###########
# Convert your previously-defined regular python functions to ray parallelized functions
train_model_PROPHET_remote = ray.remote(train_model_PROPHET).options(num_returns=3)
inference_model_PROPHET_remote = ray.remote(inference_model_PROPHET)
# initialize objects
train_obj_refs = []
test_obj_refs = []
model_obj_refs = []
forecast_obj_refs = []
# initialize data in ray object store on each cluster
input_data_ref = ray.put(g_month.copy())
start = time.time()
# Train every model
train_obj_refs, test_obj_refs, model_obj_refs = map(
list,
zip(
*(
[
train_model_PROPHET_remote.remote(
# g_month,
input_data_ref,
item_col="pulocationid",
item_value=v,
target_col="trip_quantity",
train_size=6,
)
for p, v in enumerate(item_list)
]
)
),
)
# Inference every model
forecast_obj_refs = [
inference_model_PROPHET_remote.remote(
model_obj_refs[p],
test_obj_refs[p],
item_col="pulocationid",
target_col="trip_quantity",
)
for p in range(len(item_list))
]
# ray.get() means block until all objectIDs requested are available
forecast_ray = ray.get(forecast_obj_refs)
time_ray_local = time.time() - start
print(
f"Done! Prophet on Ray Local finished in {time_ray_local} seconds"
)
# -
# Calculate speedup:
speedup = time_regular_python / time_ray_local
print(f"Speedup from running Ray parallel code on your laptop: {np.round(speedup, 1)}x"
f", or {(np.round(speedup, 0)-1) * 100}%")
# +
# Verify ray forecast is same as regular Python forecast
assert len(forecast_ray) == len(forecast)
assert len(forecast_ray[0]) == len(forecast[0])
assert forecast_ray[0].equals(forecast[0])
# +
###########
# inspect a few forecasts
###########
assert len(model) == len(item_list)
assert len(forecast) == len(item_list)
print(f"len(forecast): {len(forecast_ray)}")
# plot first two forecasts
train = ray.get(train_obj_refs)
test = ray.get(test_obj_refs)
plt.figure(figsize=(8, 5))
for p in range(len(item_list[0:2])):
display(forecast_ray[p])
plt.plot(train[p]["trip_quantity"], label="Train")
plt.plot(test[p]["trip_quantity"], label="Test")
plt.plot(forecast_ray[p]["fcst_prophet"], label="Forecast")
plt.legend(loc="best")
# -
# fancier plots
# plot first two forecasts
fig, axs = plt.subplots(2, 1, figsize=(8, 5), sharex=True)
for p, v in enumerate(item_list[0:2]):
print(f"Forecast for item {v}:")
display(forecast_ray[p])
ax = axs[p]
train[p].trip_quantity.plot(ax=ax, label="Train")
test[p].trip_quantity.plot(ax=ax, label="Test")
forecast_ray[p].fcst_prophet.plot(ax=ax, label="Forecast")
ax.legend(loc="best")
ax.set_title(f"item {v}")
# # Now run the same code as Ray Local, but this time run using Anyscale in any Cloud.
#
# <b>
# <ol>
# <li>Go back to top of notebook </li>
# <li>Change variables RUN_RAY_LOCAL = False; RUN_RAY_ON_A_CLOUD = True <br>
# ... And run the next 2 cells to propertly shutdown/start Ray </li>
# <li>Come back here to bottom of notebook <br>
# Run cell below.</li>
# </ul>
# </b>
# +
# %%timeit
###########
# Main Ray distributed program flow to train and inference Prophet models
###########
# Convert your previously-defined regular python functions to ray parallelized functions
train_model_PROPHET_remote = ray.remote(train_model_PROPHET).options(num_returns=3)
inference_model_PROPHET_remote = ray.remote(inference_model_PROPHET)
# initialize objects
train_obj_refs = []
test_obj_refs = []
model_obj_refs = []
forecast_obj_refs = []
# initialize data in ray object store on each cluster
input_data_ref = ray.put(g_month.copy())
start = time.time()
# Train every model
train_obj_refs, test_obj_refs, model_obj_refs = map(
list,
zip(
*(
[
train_model_PROPHET_remote.remote(
# g_month,
input_data_ref,
item_col="pulocationid",
item_value=v,
target_col="trip_quantity",
train_size=6,
)
for p, v in enumerate(item_list)
]
)
),
)
# Inference every model
forecast_obj_refs = [
inference_model_PROPHET_remote.remote(
model_obj_refs[p],
test_obj_refs[p],
item_col="pulocationid",
target_col="trip_quantity",
)
for p in range(len(item_list))
]
# ray.get() means block until all objectIDs requested are available
forecast_ray = ray.get(forecast_obj_refs)
time_ray_cloud = time.time() - start
print(
f"Done! Prophet on Ray in Cloud finished in {time_ray_cloud} seconds"
)
# -
time_ray_cloud = 96
# Calculate speedup running parallel Python Ray in a Cloud:
speedup = time_regular_python / time_ray_cloud
print(f"Speedup from running Ray parallel code in a Cloud: {np.round(speedup, 1)}x"
f", or {(np.round(speedup, 0)-1) * 100}%")
ray.shutdown()
|
forecasting_demos/nyctaxi_prophet_simple_MEDIUM_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Neural Nets t1
# In which I attempt some structure.
# %matplotlib widget
# #%matplotlib inline
# %load_ext autoreload
# %autoreload 2
# import Importing_Notebooks
import numpy as np
import matplotlib.pyplot as plt
import pickle
# A network built of components which:
# 1. accept an ordered set of reals (we'll use `numpy.array`, and call them vectors) at the input port and produce another at the output port - this is forward propagation. ${\displaystyle f\colon \mathbf {R} ^{n}\to \mathbf {R} ^{m}}$
# 1. accept an ordered set of reals at the output port, representing the gradient of the loss function at the output, and produce the gradient of the loss function at the input port - this is back propagation, aka backprop. ${\displaystyle b\colon \mathbf {R} ^{m}\to \mathbf {R} ^{n}}$
# 1. from the gradient of the loss function at the output, calculate the partial of the loss function w.r.t the internal parameters ${\displaystyle \frac{\partial E}{\partial w} }$
# 1. accept a scalar $\alpha$ to control the adjustment of internal parameters. _Or is this effected by scaling the loss gradient before passing??_
# 1. update internal parameters ${\displaystyle w \leftarrow w - \alpha \frac{\partial E}{\partial w} }$
#
class Layer:
def __init__(self):
pass
def __call__(self, x):
"""Computes response to input"""
raise NotImplementedError
def backprop(self, output_delE):
"""Uses output error gradient to adjust internal parameters, and returns gradient of error at input"""
raise NotImplementedError
# A network built of a cascade of layers:
class Network:
def __init__(self):
self.layers = []
self.alpha = 0.1 #FIXME
def extend(self, net):
self.layers.append(net)
def __call__(self, input):
v = input
for net in self.layers:
v = net(v)
return v
def learn(self, facts):
for (x, expected) in facts:
y = self(x)
e = y - expected
loss = e.dot(e)/2.0
agrad = e * self.alpha
for net in reversed(self.layers):
agrad = net.backprop(agrad)
return loss
# ## Useful Layers
# ### Identify
class IdentityLayer(Layer):
def __call__(self, x):
return x
def backprop(self, output_delE):
return output_delE
# ### Affine
# A layer that does an [affine transformation](https://mathworld.wolfram.com/AffineTransformation.html) aka affinity, which is the classic fully-connected layer with output offsets.
#
# $$ \mathbf{M} \mathbf{x} + \mathbf{b} = \mathbf{y} $$
# where
# $$
# \mathbf{x} = \sum_{j=1}^{n} x_j \mathbf{\hat{x}}_j \\
# \mathbf{b} = \sum_{i=1}^{m} b_i \mathbf{\hat{y}}_i \\
# \mathbf{y} = \sum_{i=1}^{m} y_i \mathbf{\hat{y}}_i
# $$
# and $\mathbf{M}$ can be written
# $$
# \begin{bmatrix}
# m_{1,1} & \dots & m_{1,n} \\
# \vdots & \ddots & \vdots \\
# m_{m,1} & \dots & m_{m,n}
# \end{bmatrix} \\
# $$
# #### Error gradient back-propagation
# $$
# \begin{align}
# \frac{\partial loss}{\partial\mathbf{x}}
# = \frac{\partial loss}{\partial\mathbf{y}} \frac{\partial\mathbf{y}}{\partial\mathbf{x}}
# = \mathbf{M}\frac{\partial loss}{\partial\mathbf{y}}
# \end{align}
# $$
# _SOLVE: Left-multiply or right-multiply?_
# #### Parameter adjustment
# $$
# \frac{\partial loss}{\partial\mathbf{M}}
# = \frac{\partial loss}{\partial\mathbf{y}} \frac{\partial\mathbf{y}}{\partial\mathbf{M}}
# = \frac{\partial loss}{\partial\mathbf{y}} \mathbf{x} \\
# \frac{\partial loss}{\partial\mathbf{b}}
# = \frac{\partial loss}{\partial\mathbf{y}} \frac{\partial\mathbf{y}}{\partial\mathbf{b}}
# = \frac{\partial loss}{\partial\mathbf{y}}
# $$
class AffinityLayer(Layer):
"""An affine transformation, which is the classic fully-connected layer with offsets"""
def __init__(self, n, m):
self.M = np.empty((m, n))
self.b = np.empty(m)
self.randomize()
def randomize(self):
self.M[:] = np.random.randn(*self.M.shape)
self.b[:] = np.random.randn(*self.b.shape)
def __call__(self, x):
self.input = x
self.output = self.M @ x + self.b
return self.output
def backprop(self, output_delE):
input_delE = self.M @ output_delE
self.M -= np.einsum('i,j', output_delE, self.input) # use np.outer?
self.b -= output_delE
return input_delE
# ### Map
# Maps a scalar function on the inputs, for e.g. activation layers.
class MapLayer(Layer):
"""Map a scalar function on the input taken element-wise"""
def __init__(self, fun, dfundx):
self.vfun = np.vectorize(fun)
self.vdfundx = np.vectorize(dfundx)
def __call__(self, x):
return self.vfun(x)
def backprop(self, output_delE):
input_delE = self.vdfundx(output_delE)
# ___
# ## Tests
# ### One identity layer
# See if the wheels turn:
net = Network()
net.extend(IdentityLayer())
all(net(np.arange(3)) == np.arange(3))
# It does not learn, as expected:
facts = [(np.arange(2*n, 2*n+2), np.arange(2*n+1, 2*n-1, -1)) for n in range(3)]
net.learn(facts)
net(np.arange(2,4))
# ### One map layer
net = Network()
net.extend(MapLayer(lambda x: x+1, lambda d: 1))
all(net(np.arange(3)) == np.arange(3)+1)
# It does not learn, as expected:
net.learn(facts), all(net(np.arange(5)) == np.arange(5)+1), net(np.arange(2,4))
# ### One affine layer
net = Network()
net.extend(AffinityLayer(2,2))
t = net.layers[0]
t.M, t.b
# Can it learn the identity transformation?
# from nnbench import NNBench
from matplotlib.widgets import Slider, Button, RadioButtons
class NNBench:
def __init__(self, net, ideal=lambda x:x):
self.net = net
self.ideal = ideal
def checkpoint_net(self):
self.net_checkpoint = pickle.dumps(self.net)
def rollback_net(self):
self.net = pickle.loads(self.net_checkpoint)
def training_data_gen(self, n):
"""Generate n instances of labelled training data"""
for i in range(n):
v = np.random.randn(2)
yield (v,self.ideal(v))
def plot_learning(self, n):
from matplotlib import pyplot as plt
# self.losses = losses = [self.net.learn(fact for fact in self.training_data_gen(n))]
self.losses = losses = [self.net.learn([fact]) for fact in self.training_data_gen(n)]
plt.yscale('log')
plt.plot(range(len(losses)),losses)
plt.show(block=0)
def knobs_plot_learning(self, n):
# from matplotlib import pyplot as plt
fig, ax = plt.subplots()
plt.subplots_adjust(left=0.25, bottom=0.25)
#t = np.arange(0.0, 1.0, 0.001)
a0 = 5
f0 = 3
#delta_f = 5.0
#s = a0 * np.sin(2 * np.pi * f0 * t)
losses = [self.net.learn([fact]) for fact in self.training_data_gen(n)]
l, = plt.plot(range(len(losses)), losses, lw=2)
ax.margins(x=0)
plt.yscale('log')
axcolor = 'lightgoldenrodyellow'
axfreq = plt.axes([0.25, 0.1, 0.65, 0.03], facecolor=axcolor)
axamp = plt.axes([0.25, 0.15, 0.65, 0.03], facecolor=axcolor)
sfreq = Slider(axfreq, '⍺', 0, 1, valinit=self.net.alpha)
samp = Slider(axamp, 'Num', 1, 1000, valinit=100, valstep=1)
big = max(losses)
ax.set_title(f"maxloss:{big}")
iax = plt.axes([0.025, 0.7, 0.15, 0.15])
def make_iax_image():
return np.concatenate([np.concatenate((l.M,np.array([l.b])),axis=0) for l in self.net.layers],axis=1)
def update_iax(img=[iax.imshow(make_iax_image())]):
img[0].remove()
img[0] = iax.imshow(make_iax_image())
def update(val,ax=ax,loc=[l]):
n = int(samp.val)
self.rollback_net()
self.net.alpha = sfreq.val
losses = [self.net.learn([fact]) for fact in self.training_data_gen(n)]
big = max(losses)
ax.set_title(f"max loss:{big}")
loc[0].remove()
loc[0], = ax.plot(range(len(losses)), losses, lw=2,color='xkcd:blue')
ax.set_xlim((0,len(losses)))
ax.set_ylim((min(losses),big))
update_iax()
fig.canvas.draw_idle()
sfreq.on_changed(update)
samp.on_changed(update)
resetax = plt.axes([0.8, 0.025, 0.1, 0.04])
button = Button(resetax, 'Reset', color=axcolor, hovercolor='0.975')
def reset(event):
sfreq.reset()
samp.reset()
button.on_clicked(reset)
rax = plt.axes([0.025, 0.5, 0.15, 0.15], facecolor=axcolor)
radio = RadioButtons(rax, ('red', 'blue', 'green'), active=0)
def colorfunc(label):
#l.set_color(label)
#fig.canvas.draw_idle()
pass
radio.on_clicked(colorfunc)
plt.show()
return 'gc protect:', update, reset, colorfunc,sfreq,samp, radio, button
bench = NNBench(net)
bench.checkpoint_net()
bench.plot_learning(100)
bench.ideal = lambda v: np.array([v[1], v[0]])
bench.knobs_plot_learning(100)
|
nbs/OLD/nnt1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Click the button below if you want to see the code behind the widgets. If you do click and want to go back to the 'no-code' view, scroll down until you find the 'hide code' button.
# +
"""
MIT License
Copyright (c) 2020 <NAME> - University of Kent
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
"""
import ipywidgets as widgets
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams
from IPython.display import display, HTML
javascript_functions = {False: "hide()", True: "show()"}
button_descriptions = {False: "Click to show code", True: "Click to hide code"}
def toggle_code(state):
"""
Toggles the JavaScript show()/hide() function on the div.input element.
"""
output_string = "<script>$(\"div.input\").{}</script>"
output_args = (javascript_functions[state],)
output = output_string.format(*output_args)
display(HTML(output))
def button_action(value):
"""
Calls the toggle_code function and updates the button description.
"""
state = value.new
toggle_code(state)
value.owner.description = button_descriptions[state]
def compound_interest_widget(xMin_init = 0, xMax_init = 1.1, yMin_init = 0, yMax_init = 3,
numTermsStr_init = '1', expFlag_init = False):
# Declare widgets for interactive input
xMin_slider = widgets.FloatSlider(min=0,
max=1.1,
description=r'Min $x$:',
value = xMin_init,
continuous_update =False)
xMax_slider = widgets.FloatSlider(min=0,
max=1.1,
description=r'Max $x$:',
value = xMax_init,
continuous_update =False)
yMin_slider = widgets.FloatSlider(min=0,
max=3,
description=r'Min $y$:',
value = yMin_init,
continuous_update =False)
yMax_slider = widgets.FloatSlider(min=0,
max=3,
description=r'Max $y$:',
value = yMax_init,
continuous_update =False)
numTermsStr_text = widgets.Text(value = numTermsStr_init,
placeholder='Enter numbers separated by commas',
description='N° terms:',
disabled=False)
expFlag_check = widgets.Checkbox(value = expFlag_init,
description='Include Exponential',
disabled=False,
indent=True)
# Link widgets as required
widgets.jslink((xMin_slider,'value'),(xMax_slider,'min'))
widgets.jslink((xMax_slider,'value'),(xMin_slider,'max'))
widgets.jslink((yMin_slider,'value'),(yMax_slider,'min'))
widgets.jslink((yMax_slider,'value'),(yMin_slider,'max'))
def compound_interest_plot(xMin, xMax, yMin, yMax, numTermsStr, expFlag):
numTermsList = numTermsStr.split(',')
if len(numTermsList) > 6:
numTermsList = numTermsList[0:6]
colors = ['b','r','g','m','c','y']
# Create figure, plot compounded functions
fig, ax = plt.subplots(figsize=(20,10))
mrkrSize = 2*rcParams['lines.markersize'] ** 2
for index, item in enumerate(numTermsList):
# Process entry if item is valid
if not item == '' :
numTerms = int(item)
step = 1/numTerms
rate = 1 + step
K,T = 1,0
ax.scatter(T, K, s=mrkrSize, c='b', alpha=0.6)
col = colors[index]
for n in range(numTerms):
if n == 0:
termLabel = r'N$^\circ$ terms: {:d}'.format(numTerms)
else:
termLabel = None
ax.scatter(T+step, K*rate, s=mrkrSize, c=col, alpha=0.6)
ax.plot([T,T+step], [K,K], col, linewidth=2, alpha=0.6, label=termLabel)
ax.plot([T+step,T+step], [0,K*rate], col+'--', linewidth=2, alpha=0.6)
T+=step
K*=rate
ax.plot([0,T],[K,K],col+'--',linewidth=1)
ax.annotate(r'Final value = ${:.4f}$'.format(K),[0,K],
xytext = [0.05,K+0.1], xycoords ='data', fontsize = 25,
clip_on = True)
# Plot the exponential if requested
if expFlag is True:
x = np.arange(0,1,1/500)
y = np.exp(x)
ax.plot(x, y,'k', linewidth=2, label=r'$\quad y = a^x$')
# Add legend and format axes to look nice
ax.legend(loc='lower center', frameon=False,prop={'size':20},ncol=6,
bbox_to_anchor=(0.5, -0.25))
ax.autoscale(enable=True, axis='both', tight=True)
ax.set_ylim(top = yMax, bottom = yMin)
ax.set_xlim(right = xMax, left = xMin)
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_visible(False)
ax.set_xlabel(r'$T$', fontdict = {'fontsize': 25},position=(1, 0))
ax.set_ylabel(r'$Assets$', fontdict = {'fontsize': 25},
position=(0, 1.05), rotation=0)
ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False)
ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False)
plt.tick_params(labelsize=20)
plt.tight_layout()
out = widgets.interactive_output(compound_interest_plot, {'xMin': xMin_slider,
'xMax': xMax_slider,
'yMin': yMin_slider,
'yMax': yMax_slider,
'numTermsStr': numTermsStr_text,
'expFlag' : expFlag_check})
output = widgets.VBox([out,
widgets.HBox([xMin_slider,
xMax_slider,
yMin_slider,
yMax_slider]),
widgets.HBox([numTermsStr_text,
expFlag_check])])
display(output)
# +
state = False
toggle_code(state)
button = widgets.ToggleButton(state, description = button_descriptions[state])
button.observe(button_action, "value")
display(button)
# -
# ### Deep(er) dive: Where does $e$ come from?
#
# As we discussed in the videos, the natural logarithm $y = \ln x$ and its inverse, the exponential function $y=e^x$ both rely on this 'special' number called $e$. Like $\pi$, $e$ is a mathematical constant that is irrational, i.e. it cannot be expressed as a ratio, and it's value is approximately 2.71828.
#
# The question we raised in the video was essentially as follows
# 1. All logarithms have this nice property that $\log(xy) = \log(x) + \log(y)$. You can pick any base you want and this property remains
# 2. Some bases make very practical sense, like base 10 (our number system is base 10) or base 2 (for computer/software engineering)
#
# Given points 1 and 2, why on earth would you pick this strange number as your preferred base? The notebook attempts to answer this while giving you an insight into the history of the concept.
#
# #### The problem of compounding interest in finance
#
# The number $e$ is named after genius Swiss mathematician <NAME> (1707-1783), who worked a lot with its theoretical properties (Euler in particular proved it was an irrational number). He is the one who popularised the notation $e$ for this constant, which means the guy obviously thought he was a big deal! Euler did not discover $e$, however, that credit should go to <NAME>, another giant swiss mathematician, who found out an expression for $e$ in 1683 (long before Euler). The route he used to find the value of $e$ was exactly the one we will use here, and had to do with finding the most profitable strategy for earning interest on a loan.
#
# Banking and finance massively expanded in post-renaissance Europe, as larger, more expensive and more risky enterprises were set off, such as the rise of manufacturing, financing shipping expeditions to open new trade routes, etc. But the maths behind finance (especially probability theory) wasn't yet understood, and lending still relied on rules of thumb.
#
# Bernoulli essentially started with this setting: suppose you invest in a business or a security that doubles your initial investment after a time $T$. Most examples of this thinking will use 1 year, but actually (a) that's not very realistic and (b) we don't really care how long $T$ is, only that it exists. Even if the annual interest rate is very low, eventually you will double your money!
#
# We can plot this below, and it produces a boring diagram. You give away your money, and after $T$ time has passed, you get your money back with 100% interest, so your wealth doubles at that point.
compound_interest_widget()
# Bernoulli then asked this crucial question: ***would it be a more profitable strategy to lend at the same rate for half the time***? In other words, you lend at the same rate, but ask for the loan to be repaid, with interest, at time $T/2$. You then re-lend all of what you received (capital plus interest) on the same terms, again for $T/2$. ***Are you better off?***
#
# The answer is yes, and it is easy to see why (diagram below). For every pound you lend initially, you receive £1.5 at the halfway point $T/2$. £1 of this is the repayment of the initial capital, 50p is the interest. Of course, because you lent the money for half the time, you only get half the interest. But crucially, when you re-lend the money again immediately at the same interest rate, you are now lending £1.50, not £1. So for the second half of the diagram, the same interest rate applies to a larger amount of capital! When you get paid back the second time, you receive £2.25: £1.50 of that is the initial capital you lent, 75p of interest.
compound_interest_widget(numTermsStr_init = '1,2')
# We can write this down as an equation. Let $A_1$ be the amount you get for each pound invested in a single loan $T$ (our first example). This is easy, you get £1 of capital and £1 of interest:
#
# $$A_1 = 1 + 1 = 2$$
#
# Let's do the same for when we lend twice over the period $T$, and call it $A_2$:
#
# $$A_2 \quad = \quad \left(1+\frac{1}{2}\right)\left(1+\frac{1}{2}\right) \quad = \quad \left(1+\frac{1}{2}\right)^2 \quad = \quad 2.25$$
#
# The first $1+1/2$ bracket tells us how much we have to re-invest when the first loan gets paid back (£1.50), the second bracket corresponds to the growth in value from the second loan.
#
# Bernoulli probably wasn't the first to figure out that you would benefit from getting some the interest paid early, but was the first to 'do the math'. The obvious question at this point is: ***can we improve on this result by making the loans even shorter and lending more often?***
compound_interest_widget(numTermsStr_init = '1,2,4')
# The diagram above shows what happens when you break $T$ down into four periods. At $T/4$, when the first round of lending is repaid, you only get 25p per pound of capital (you are only lending for 1/4 of the original period), but like before, getting paid some of the interest early so that you can increase the capital you are lending pays off in the long run.
#
# Using the same logic as before, the amount you get for breaking up $T$ into 4 successive rounds of lending can be written as:
#
# $$A_4 \quad = \quad \left(1+\frac{1}{4}\right)^4 \quad \approx \quad 2.4414$$
#
# In general, breaking the loan period down into $n$ rounds of lending, each returning $1/n$ of effective interest is given by the following formula:
#
# $$A_n \quad = \quad \left(1+\frac{1}{n}\right)^n$$
#
# You may have noticed, however, that while lending four times has increased the gain (so we are better off), it is less effective than the first time round. When we first split the lending period in two, we were 25p better off. Splitting into two again (so 4 loans) gained us 19.14p. So while this works, there is no 'magic money tree'.
#
# Bernoulli noticed this too, and so the ***real*** question that he answered was: what happens to the value of $A_n$ as you keep increasing $n$? Could you keep increasing your gains by lending for increasingly short periods of time, each earning smaller and smaller amounts?
compound_interest_widget(numTermsStr_init = '50',expFlag_init = True)
# As you can see for the example above, where you slice the initial time period $T$ into 50 successive loans, the step curve you get really looks like it is converging to the exponential function $e^x$. And the value of your capital after a unit amount of time $T$ is starting to look suspiciously close to the number I gave above. This is no surprise. Bernoulli showed that the value of $A_n$ when $n$ tends to infinity is actually $e$. More formally:
#
# $$\mathop\lim_{n \to \infty}A_n \quad = \quad \mathop\lim_{n \to \infty}\left(1+\frac{1}{n}\right)^n \quad = \quad e$$
#
# So to visualise this in our example, if you have a loan that pays £2 after $T$ time has elapsed for every pound you invest, the maximum gain you can get by compounding the interest continuously instead of paying it in one lump-sum at the end is £2.72.
#
# #### Wrapping up - A natural framework for growth
#
# This illustration shows that the exponential function is the natural way of tracking growth when two conditions are met:
# 1. The rate of growth is fixed over time. In our example this was the fixed rate of interest.
# 2. Growth happens continuously over time, and not in discrete jumps that happen at specific points in time. In our example this was the slicing of the loans into shorter and shorter periods of time, and in the limit, into a continuous process.
#
# As you an imagine, this has applications in a lot of places: even if a lot of biological or economic growth processes are actually discrete (like a cell dividing into two, or a firm being created), the individual units are so small, and there are so many of them that we can treat the overall process as continuous. The general form of the exponential in those cases is:
#
# $$A(t) = A_0 e^{rt}$$
#
# Where $A_0$ is the initial value of the quantity that is growing (or decaying if $r<0$), $r$ is the fixed rate of growth or decay (where 10% would be equal to 0.1) and $t$ is the amount of time elapsed. Our example of Mr Bernoulli's derivation simply had a combination of $r$ and $t$ that would be equal to one.
|
Where does e come from.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # plot MI decay for birdsong
import pandas as pd
from parallelspaper.config.paths import DATA_DIR, FIGURE_DIR
from parallelspaper.birdsong_datasets import BCOL_DICT
import numpy as np
from parallelspaper import information_theory as it
from parallelspaper import model_fitting as mf
from parallelspaper.utils import save_fig
from matplotlib import gridspec
import matplotlib.pyplot as plt
# %matplotlib inline
# ### load fit df and determine length to compute MI
starling_seq_df = pd.read_pickle(DATA_DIR / 'song_seq_df/starling.pickle')
CAVI_CATH_seq_df = pd.read_pickle(DATA_DIR / 'song_seq_df/CAVI_CATH.pickle')
BF_seq_df = pd.read_pickle(DATA_DIR / 'song_seq_df/BF.pickle')
seq_dfs = pd.concat([starling_seq_df, CAVI_CATH_seq_df, BF_seq_df])
fit_df = pd.read_pickle(DATA_DIR / 'MI_DF/birdsong/birdsong_fit_df_long.pickle')
song_d = {}
for species in np.unique(fit_df.species):
print(species)
species_fit_df = fit_df[fit_df.species == species]
species_fit_df.R2_concat.values
r2_100 = species_fit_df[species_fit_df.d == 100].R2_concat.values[0]
species_d = species_fit_df.d.values[(species_fit_df.R2_concat.values > r2_100 * .999)][-1]
song_d[species] = species_d
# #### get MI of the longest distance within 99.9% of $r^2$ of 100 syllables distance
n_jobs = 20; verbosity = 0
# +
MI_DF = pd.DataFrame(columns=['species', 'type', 'MI', 'MI_shuff', 'distances',
'MI_var', 'MI_shuff_var', 'results_power', 'results_exp', 'results_pow_exp'])
for species in np.unique(seq_dfs.species):
species_df = seq_dfs[seq_dfs.species ==
species].sort_values(by=['bird', 'rec_num'])
print(species)
# analysis by day
day_group = []
for bird in np.unique(species_df.bird.values):
bird_df = species_df[species_df.bird == bird]
for day in np.unique(bird_df.day.values):
day_df = bird_df[bird_df.day == day]
day_group.append(np.concatenate(day_df.syllables.values))
units = day_group
distances = np.arange(1, song_d[species])
(MI, var_MI), (MI_shuff, MI_shuff_var) = it.sequential_mutual_information(
units, distances, n_jobs=n_jobs, verbosity=verbosity)
sig = MI-MI_shuff
results_power, results_exp, results_pow_exp, best_fit_model = mf.fit_models(
distances, sig)
plt.loglog(distances, MI-MI_shuff)
plt.show()
MI_DF.loc[len(MI_DF)] = [species, 'session', MI, MI_shuff, distances,
var_MI, MI_shuff_var, results_power, results_exp, results_pow_exp]
# -
subset_MI_DF = MI_DF
subset_MI_DF['concat_results'] = subset_MI_DF.results_pow_exp
# ### plot main decay results for birdsong
# +
yoff=-.20
ncols = 4
zoom = 5
hr = [1, 0.5, 0.5, 0.5]
nrows = np.ceil(len(subset_MI_DF)/ncols).astype(int)
fig = plt.figure(figsize=(len(subset_MI_DF)*zoom,np.sum(hr)*zoom))
gs = gridspec.GridSpec(ncols=len(subset_MI_DF), nrows=4, height_ratios=hr)
for axi, (idx, row) in enumerate(subset_MI_DF.sort_values(by=['type', 'species']).iterrows()):
color = BCOL_DICT[row.species]
ax0 = plt.subplot(gs[0,axi])
ax = ax0
sig = np.array(row.MI-row.MI_shuff)
distances = row.distances
sig = sig
distances = distances
# get signal limits
sig_lims = np.log([np.min(sig[sig>0]), np.nanmax(sig)])
sig_lims = [sig_lims[0] - (sig_lims[1]-sig_lims[0])/10,
sig_lims[1] + (sig_lims[1]-sig_lims[0])/10]
if axi==0:
ax.set_ylabel('Mutual Information (bits)', labelpad=5, fontsize=18)
ax.yaxis.set_label_coords(yoff,0.5)
# model data
#row.concat_results.params.intercept = 0
distances_model = np.logspace(0,np.log10(distances[-1]), base=10, num=1000)
y_model = mf.get_y(mf.pow_exp_decay, row.concat_results, distances)
y_pow = mf.get_y(mf.powerlaw_decay, row.concat_results, distances_model)
y_exp = mf.get_y(mf.exp_decay, row.concat_results, distances_model)
y_pow_dat = mf.get_y(mf.powerlaw_decay, row.concat_results, distances)
y_exp_dat = mf.get_y(mf.exp_decay, row.concat_results, distances)
# plot real data
ax.scatter(distances, sig, alpha = 1, s=40, color=color)
ax.plot(distances_model, y_pow, ls='dotted', color= 'k', lw=5, alpha=0.5)
ax.plot(distances_model, y_exp-row.concat_results.params['intercept'].value, ls='dashed', color= 'k', lw=5, alpha=0.5)
# plot modelled data
ax.plot(distances, y_model, alpha = 0.5, lw=10, color=color)
# plot powerlaw component
ax1 = plt.subplot(gs[1,axi])
ax = ax1
ax.plot(distances_model, y_pow-row.concat_results.params['intercept'].value, alpha = 0.5, lw=10, color=color)
ax.scatter(distances, sig-y_exp_dat, alpha = 1, s=40, color=color)
# plot exponential component
ax2 = plt.subplot(gs[2,axi])
ax = ax2
ax.plot(distances_model, y_exp-row.concat_results.params['intercept'].value, alpha = 0.5, lw=10, color=color)
ax.scatter(distances, sig-y_pow_dat, alpha = 1, s=40, color=color)
# plot curvature
ax3 = plt.subplot(gs[3,axi])
ax = ax3
if axi==0:
ax.set_ylabel('Curvature', labelpad=5, fontsize=18)
ax.yaxis.set_label_coords(yoff,0.5)
ax.set_yticks([0.0])
ax.set_yticklabels(['0.0'])
else:
ax.set_yticks([0.0])
ax.set_yticklabels(['0.0'])
# curvature
distances = np.logspace(0,np.log10(song_d[row.species]), base=10, num=1000)
y_model = mf.get_y(mf.pow_exp_decay, row.concat_results, distances)
# get curvature of model_y
curvature_model = mf.curvature(np.log(y_model))
peaks = np.where((
(curvature_model[:-1] < curvature_model[1:])[1:] & (curvature_model[1:] < curvature_model[:-1])[:-1]
))
min_peak = peaks[0][0]
ax.plot(distances[5:-5], curvature_model[5:-5], alpha = 1, lw=5, color=color)
ax.set_ylim([-1e-4,1e-4])
peak_of_interest = int(min_peak)
ax.axvline(distances[peak_of_interest], lw=3,alpha=0.5, color=color, ls='dashed')
ax.set_xlabel('Distance (syllables)', labelpad=5, fontsize=18)
print(row.species, distances[peak_of_interest])
# axis labelling, etc
ax.tick_params(which='both', direction='in', labelsize=14, pad=10)
ax.tick_params(which='major', length=10, width =3)
ax.tick_params(which='minor', length=5, width =2)
ax.set_xscale( "log" , basex=10)
for axis in ['top','bottom','left','right']:
ax.spines[axis].set_linewidth(3)
ax.spines[axis].set_color('k')
ax.set_xlim([1,song_d[row.species]])
# set axis limits, etc
for ax in [ax1, ax2]:
if axi==0:
ax.set_ylabel('MI (bits)', labelpad=5, fontsize=18)
ax.yaxis.set_label_coords(yoff,0.5)
for ax in [ax0,ax1,ax2]:
ax.set_xlim([distances[0], distances[-1]])
ax.set_ylim(np.exp(sig_lims))
ax.tick_params(which='both', direction='in', labelsize=14, pad=10)
ax.tick_params(which='major', length=10, width =3)
ax.tick_params(which='minor', length=5, width =2)
ax.set_xscale( "log" , basex=10)
ax.set_yscale( "log" , basey=10)
ax.set_xticks([])
ax.set_ylim(np.exp(sig_lims))
for axis in ['top','bottom','left','right']:
ax.spines[axis].set_linewidth(3)
ax.spines[axis].set_color('k')
ax3.set_xticks([1,10,100])
ax3.set_xticklabels(['1','10','100'])
save_fig(FIGURE_DIR/'song_fig')
# -
# ### Dataset statistics
CAVICATH_stats_df = pd.read_pickle(DATA_DIR / 'stats_df/CAVICATH_stats_df.pickle')
Starling_stats_df = pd.read_pickle(DATA_DIR / 'stats_df/starling_stats_df.pickle')
BF_stats_df = pd.read_pickle(DATA_DIR / 'stats_df/BF_stats_df.pickle')
stats_df = pd.concat([CAVICATH_stats_df, Starling_stats_df, BF_stats_df])
stats_df
# ### Plot distribution
import seaborn as sns
from matplotlib.ticker import FixedLocator
fig, axs = plt.subplots(ncols=4, figsize=(20,2))
for i,l in enumerate(['CAVI', 'CATH', 'Starling', 'BF']):
ax = axs.flatten()[i]
wlp =stats_df[stats_df.species==l].recording_duration_syllable.values[0]
np.sum(np.array(wlp) == 1)/len(wlp)
ax.hist(wlp,bins=np.arange(100), density=True, color = BCOL_DICT[l])
ax.set_xlim([1,100])
# +
bw = 0.25
kwk = {"lw": 6, 'bw':bw}
d = 100
yoff=-.20
nrows = np.ceil(len(subset_MI_DF)/ncols).astype(int)
fig = plt.figure(figsize=(len(subset_MI_DF)*5,zoom/2.3))
gs = gridspec.GridSpec(ncols=len(subset_MI_DF), nrows=1)
bins = np.arange(-.5, 15, .85)
for li, (species,) in enumerate([['BF'],['CATH'], ['CAVI'], ['Starling']]):
ax = plt.subplot(gs[li])
wl = np.log2(np.array(stats_df[stats_df.species==species].recording_duration_syllable.values[0]))
sns.distplot((wl[wl<150]), color = BCOL_DICT[species], ax =ax, bins=bins,
kde_kws=kwk);
ax.axvline(np.median(wl), lw=3,alpha=0.5, color=BCOL_DICT[species], ls='dashed')
ax.set_xlabel('Bout length (syllables)', labelpad=5, fontsize=18)
ax.tick_params(axis='both', labelsize=14, pad=15)
for axis in ['top','bottom','left','right']:
ax.spines[axis].set_linewidth(3)
ax.spines[axis].set_color('k')
ax.grid(False)
ax.tick_params(which='both', direction='in', labelsize=14, pad=10)
ax.tick_params(which='major', length=10, width =3)
ax.tick_params(which='minor', length=5, width =2)
#ax.set_xscale( "log" , basex=10)
if li==0:
ax.set_ylabel('Prob. Density', labelpad=5, fontsize=18)
ax.yaxis.set_label_coords(yoff,0.5)
else:
ax.set_yticklabels([])
ax.set_xticks([np.log2(1),np.log2(10),np.log2(100)])
ax.set_xticklabels(['1','10','100'])
ax.set_xlim([np.log2(1),np.log2(song_d[species])])
ax.set_ylim([0,1])
minor_ticks = np.log2(np.array(list(np.arange(1,10)) + list(np.arange(10,100,10)) + list(np.arange(100,1000,100))))
minor_locator = FixedLocator(minor_ticks)
ax.xaxis.set_minor_locator(minor_locator)
save_fig(FIGURE_DIR/'bird_len_dist')
# -
|
notebooks/birdsong/10.0-birdsong-plot-MI-decay.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: dev
# language: python
# name: dev
# ---
# %matplotlib notebook
# Dependencies
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# Read data
housing_data = pd.read_csv("../Resources/housing_data.csv", header=None)
housing_data = housing_data.sample(frac=1).reset_index(drop=True)
# Create a bunch of samples, each with div items
div = 20
lim = len(housing_data) // div
samples = [housing_data.iloc[(i * div):(i * div + div), 13]
for i in range(0, lim)]
# +
# Calculate means
means = [s.mean() for s in samples]
# Calculate standard error on means
sem = [s.sem() for s in samples]
# +
# Plot sample means with error bars
fig, ax = plt.subplots()
ax.errorbar(np.arange(0, len(means)), means, yerr=sem, fmt="o", color="b",
alpha=0.5, label="Mean of House Prices")
ax.set_xlim(-0.5, len(means))
ax.set_xlabel("Sample Number")
ax.set_ylabel("Mean of Median House Prices")
plt.legend(loc="best", fontsize="small", fancybox=True)
plt.show()
# -
|
05-Matplotlib/3/Activities/06-Stu_Standard_Error/Solved/samples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # SimPEG DC&IP 3D Inversion
#
# <img align="right" width="300px" src="./images/inversion_dcip_thumbnail.png">
#
# This application provides an interface to the open-source [SimPEG](https://simpeg.xyz/) package for the inversion of direct-current (DC) and induced polarization (IP) data using a Laterally Constrained 1D approach.
#
# - Direct-current (potential) data inversion for the recovery of conductivity (S/m).
# - Apparent chargeability (V/V) data for the recovery of chargeability (SI).
#
# All inversion are performed on a 3D octree mesh.
#
# New user? Visit the [**Getting Started**](https://geoapps.readthedocs.io/en/latest/content/installation.html) page.
#
# [**Online Documentation**](https://geoapps.readthedocs.io/en/latest/content/applications/dcip_inversion.html)
#
# *Click on the cell below and press **Shift+Enter** to run the application*
# +
from geoapps.inversion.dcip_inversion_app import InversionApp
# Start the inversion widget
app = InversionApp()
app()
# -
# ## Plot convergence curve
#
# Display the misfit and regularization as a function of iterations by changing the path to inversion workspace (`*.geoh5`)
from geoapps.plotting import plot_convergence_curve
out = plot_convergence_curve(r"..\..\assets\EM1DInversion_.geoh5")
display(out)
# Need help? Contact us at <EMAIL>
|
geoapps/applications/Inversion_DCIP_app.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Decision Trees: Pre-prunning
from sklearn.datasets import make_moons
from sklearn.tree import DecisionTreeClassifier
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn import tree
import mglearn #this package will help us to paint margins
# I this notebook we are going to get acquainted with Decision Trees' algorithm application via **sklearn.tree**. Our goal will be to tune parameters of a model to decrease overfitting and to increase the accuracy on a test data.
# +
# Form the data
X,y = make_moons(n_samples=200,noise=0.3, random_state=42)
# +
# Picture the data
fig = plt.figure(figsize=(12,6))
mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
# +
# Use train_test_split to split initial data on the train and test subsets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# +
# Initialize a decion tree classifier and fit it on the train data
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train,y_train)
# -
# Let's plot the learned decision tree
plt.figure(figsize=(20,10))
tree.plot_tree(clf, filled=True);
# You may see that the maximum tree's depth is 8.
# +
# Picture the decison tree boundaries
fig = plt.figure(figsize=(12,6))
mglearn.plots.plot_2d_separator(clf, X, fill=True, alpha=.4)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y);
# -
print('Accuracy on the train:', round(accuracy_score(y_train, clf.predict(X_train)),2))
print('Accuracy on the test:', round(accuracy_score(y_test, clf.predict(X_test)),2))
# So, the figure above and accuracy on train and test subsets gives us a signal that the algorithm is overfited.
# **Task 1:** By tuning the depth of the dicision tree, find the optimal value that maximizes the accuracy on the test data.
# +
depth = []
acc_test = []
acc_train = []
fig = plt.figure(figsize=(12,5))
for i in ...:
clf = DecisionTreeClassifier(... random_state=42)
...
...
plt.plot(depth, acc_train, label='train')
plt.plot(depth, acc_test, label='test')
plt.xlabel('depth')
plt.ylabel('accuracy')
plt.legend()
plt.grid(True);
# -
# What the best value of the depth?
# **Task 1:** By tuning the depth of the dicision tree, find the optimal_depth that maximizes the accuracy on the test data.
# **Task 2:** By using the optimal_depth from the previous task, find the optimal value of the min_samples_leaf that maximizes the accuracy on the test data. (use random_state = 42)
clf = DecisionTreeClassifier(max_depth=4,.., random_state=42)
...
# What the best value of the parameters?
|
course_2/3_DT/DT_pre-pruning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 553} id="KOlOmwIysm1A" outputId="576662ab-e562-422e-9527-c7a3441b2ce7"
import pandas as pd
import copy
from sklearn.preprocessing import LabelEncoder
# https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/hasoc_2020_en_train_new_a.xlsx?raw=true
url_english_train = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/hasoc_2020_en_train_new_a.xlsx?raw=true'
url_german_train = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/hasoc_2020_de_train_new_a.xlsx?raw=true'
url_hindi_train = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/hasoc_2020_hi_train_a.xlsx?raw=true'
url_english_test = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/english_test_1509.csv?raw=true'
url_german_test = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/german_test_1509.csv?raw=true'
url_hindi_test = 'https://github.com/suman101112/hasoc-fire-2020/blob/main/2020/hindi_test_1509.csv?raw=true'
data_en = pd.read_excel(url_english_train)
data_en_test = pd.read_csv(url_english_test)
data_de = pd.read_excel(url_german_train)
data_de_test = pd.read_csv(url_german_test)
data_hi = pd.read_excel(url_hindi_train)
data_hi_test = pd.read_csv(url_hindi_test)
data_en['language'] = 0
data_en_test['language'] = 0
data_de['language'] = 1
data_de_test['language'] = 1
data_hi['language'] = 2
data_hi_test['language'] = 2
data = copy.deepcopy(data_en)
data = data.append(data_de, ignore_index=True)
data = data.append(data_hi, ignore_index=True)
data_test = copy.deepcopy(data_en_test)
data_test = data_test.append(data_de_test, ignore_index=True)
data_test = data_test.append(data_hi_test, ignore_index=True)
data = pd.concat([data, data_test])
labels = data[['task1', 'task2', 'language']]
le = LabelEncoder()
data['task1'] = le.fit_transform(labels['task1'])
le = LabelEncoder()
data['task2'] = le.fit_transform(labels['task2'])
data = data.drop(columns=['tweet_id','ID'])
data.head()
# + id="p9h98cbLwLbS" outputId="4cb6931c-2735-4a72-c657-7d3d8f734bc9" colab={"base_uri": "https://localhost:8080/", "height": 424}
data.to_csv('multilingual.csv')
|
Irirs_kedro/get-started/notebooks/multilingual_ext.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib notebook
import tensorwatch as tw
client = tw.WatcherClient()
stream = client.create_stream(expr='lambda v:(v.i, v.sum)')
text_vis = tw.Visualizer(stream)
text_vis.show()
line_plot = tw.Visualizer(stream, vis_type='line')
line_plot.show()
summary = tw.Visualizer(stream, vis_type='summary', cell=text_vis)
summary.show()
plotly_line = tw.Visualizer(stream, vis_type='plotly-line')
plotly_line.show()
|
notebooks/demo/simple_logging.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Computational Astrophysics
# ## Ordinary Differential Equations. 01
#
# ---
# ## <NAME>
#
# Observatorio Astronómico Nacional\
# Facultad de Ciencias\
# Universidad Nacional de Colombia
#
# ---
# ### About this notebook
#
# In this notebook we present some of the techniques to solve a system of Ordinary Differential Equations.
#
# `<NAME>. Numerical Methods for Physics. (1999). Chapter 3 `
#
# ---
# ## Ordinary Differential Equations
#
# A system of first-order ordinary differential equations (ODEs)
# is a relationship between an unknown (vectorial) function
# $y(x)$ and its derivative $y^\prime(x)$. The
# general system of first-order ODEs has the form
#
# \begin{equation}
# y^\prime (x) =f(x,y(x))\,.
# \end{equation}
#
# A solution to the differential equation is,
# obviously, any function $y(x)$ that satisfies it.
#
#
# There are two general classes of first-order ODE problems:
#
# 1. Initial value problems: $y(x_i)$ is given at some starting point $x_i$.
#
# 2. Two-point boundary value problems: $y$ is known at two ends (boundaries) of the domain and these **boundary conditions** must be satisfied simultaneously.
#
#
#
#
#
#
# ---
# ### Reduction to First-Order ODE
#
# Any ODE can be reduced to first-order form by introducing additional
# variables.
#
# #### Example
#
# \begin{equation}
# y''(x) + q(x) y'(x) = r(x)\,\,.
# \end{equation}
#
# Introducing a new function $z(x)$ this can be written as a system of first-order ODE,
#
# \begin{align}
# \text{(1)}\,\, y'(x) &= z(x)\\
# \text{(2)}\,\, z'(x) &= r(x) - q(x) z(x).
# \end{align}
#
# ---
# ## Explicit and Implicit Methods of Solution of ODE
#
# Broadly speaking, the methods for integrating ODEs are clasiffied into *explicit* and *implicit* methods.
#
# Explicit methods use differences of the system to construct and update of the solution using the current (and previous) values of the dependent variables. Some examples of explicit methods are Euler's and Runge-Kutta's methods.
#
# Implicit methods evaluate the right-hand side using the new value of the function that we are solving for.
# ---
# ## Errors and ODE
#
# All procedures to solve numerically an ODE consist of transforming
# a continuous differential equation into a discrete iteration procedure
# that starts from the initial conditions and returns the values of the
# dependent variable $y(x)$ at points $x_m = x_0 + m * h$, where $h$
# is the discretization step size assumed to be constant here).
#
# Two kinds of errors can arise in this procedure:
# 1. **Round-off error.** Due to limited float point accuracy. The global round-off is the sum of the local float point errors.
#
#
# 2. **Truncation error.**
#
#
# * Local: The error made in one step when we replace a continuous process
# (e.g. a derivative) with a discrete procedure (e.g., a forward difference).
#
# * Global: If the local truncation error is $\mathcal{O}(h^{n+1})$, then the global truncation error must be $\mathcal{O}(h^n)$, since the number of steps used in evaluating the derivatives to reach an arbitrary point $x_f$, having started at $x_0$, is $\frac{x_f - x_0}{h}$.
# ---
# ---
#
# ## Euler's Method
#
# We want to solve the ODE
#
# \begin{equation}
# y' = f(x,y)
# \end{equation}
#
# with the initial condition $y(x_0) = y_0$. We introduce
# a fixed stepsize $h$ and obtain an estimate of $y(x)$ at
# $x_1 = x_0 + h$ using Taylor's theorem,
#
# \begin{equation}
# \begin{aligned}
# y(x_1) &= y(x_0+h) = y(x_0) + y'(x_0) h + \mathcal{O}(h^2)\,,\\
# &= y(x_0) + h f(x_0,y(x_0)) + \mathcal{O}(h^2)\,.
# \end{aligned}
# \end{equation}
#
#
# By analogy, we obtain that the value $y_{n+1}$ of the function at the
# point $x_{n+1} = x_0 + (n+1) h$ is given by
#
# \begin{equation}
# y_{n+1} = y(x_{n+1}) = y_n + h f(x_n,y(x_n)) + \mathcal{O}(h^2)\,.
# \end{equation}
#
#
# This is called the **forward Euler Method**.
#
# ---
# Euler's method is extremely simple, but rather inaccurate and potentially unstable.
#
# The error scales $\propto h^2$ locally. However, if $L$ is
# the length of the domain, then $h = L / N$, where $N$ is the number of points
# used to cover it. Since we are taking $N$ integration steps, the global
# error is $\propto N h^2 = N L^2 / N^2 = L L/N \propto h$.
#
# Hence, forward Euler is a first-order accurate method globally.
#
# ### Stability
#
# Forward Euler is an **explicit** method. This means that
# $y_{n+1}$ is given explicitly in terms of known quantities
# $y_n$ and $f(x_n,y_n)$.
#
# Explicit methods are simple and efficient, but the drawback is that
# the step size must be small for stability.
#
#
# ### Example
#
# \begin{equation}
# \frac{dy}{dt} = -a y\,\,, \hspace{1cm}\text{with} \hspace{1cm}
# y(0) = 1\,,\,\, a > 0\,\,.
# \end{equation}
#
# The exact solution to this problem is $y = e^{-at}$,
# which is stable and smooth with $y(0) = 1$ and
# $y(\infty) = 0$.
#
# Applying forward Euler,
#
# \begin{equation}
# y_{n+1} = y_n - a\, h\, y_n = (1-ah) y_{n}
# \end{equation}
#
# \begin{equation}
# y_{n+1} = (1-ah)^2 y_{n-1} = \cdots = (1-ah)^{n+1} y_0\,\,.
# \end{equation}
#
# This implies that in order to prevent any potential amplification of
# errors, we must require that $|1-ah|<1$.
#
# In fact, there are 3 cases,
#
# | | | |
# |:-: | :-: | :--|
# | $0 < 1-ah < 1$ | : | $(1-ah)^{n+1}$ decays (good!) |
# |$-1 < 1-ah < 0$ | : | $(1-ah)^{n+1}$ oscillates (not so good!)|
# |$1-ah < -1$ | : | $(1-ah)^{n+1}$ oscillates and diverges (bad!)|
#
#
# This gives the stability criterion of $0< h < \frac{2}{a}$.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
def ODE(y):
a=2.
rhs = -a*y
return rhs
def FEuler(h, t0, q0):
'''
------------------------------------------
FEuler(h, t0, q0)
------------------------------------------
Forward Euler's method for solving a ODEs
system.
Arguments:
h: stepsize for the iteration
t0: independent parameter initial value
q0: numpy array with the initial values of
the functions in the ODEs system
------------------------------------------
'''
f = ODE(q0)
q1 = q0 + h*f
return q1
# Creation of the Grid
t_0 = 0.
t_f = 10.
n = 100
h = 0.2
#h = (t_f - t_0)/n
# Initial value
y_0 = 1.
# Variables setup
t = np.linspace(t_0, t_f, n)
y = np.zeros(n)
y[0] = y_0
# Main Loop
for i in range(1,n):
y[i] = FEuler(h, t[i-1], y[i-1])
# Plot
fig, ax = plt.subplots()
ax.plot(t, y, label=f'$h=$ {h:.1f}')
ax.set_title('Forward Euler Method')
ax.set_xlabel(r'$t$')
ax.set_ylabel(r'$y(t)$')
plt.legend()
plt.show()
# -
# Lets check the stability of the method.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
def ODE(y):
a=2.
rhs = -a*y
return rhs
def FEuler(h, t0, q0):
'''
------------------------------------------
FEuler(h, t0, q0)
------------------------------------------
Forward Euler's method for solving a ODEs
system.
Arguments:
h: stepsize for the iteration
t0: independent parameter initial value
q0: numpy array with the initial values of
the functions in the ODEs system
------------------------------------------
'''
f = ODE(q0)
q1 = q0 + h*f
return q1
# Initial Condition
y_0 = 1.
# Creation of the grid
t_0 = 0.
t_f = 10.
# Three stepsizes to compare
n1 = 100
h1 = (t_f - t_0)/n1
n2 = 15
h2 = (t_f - t_0)/n2
n3 = 10
h3 = (t_f - t_0)/n3
# Arrays to store the solution
t1 = np.linspace(t_0, t_f, n1)
y1 = np.zeros(n1)
y1[0] = y_0
t2 = np.linspace(t_0, t_f, n2)
y2 = np.zeros(n2)
y2[0] = y_0
t3 = np.linspace(t_0, t_f, n3)
y3 = np.zeros(n3)
y3[0] = y_0
for i in range(1,n1):
y1[i] = FEuler(h1, t1[i-1], y1[i-1])
for i in range(1,n2):
y2[i] = FEuler(h2, t2[i-1], y2[i-1])
for i in range(1,n3):
y3[i] = FEuler(h3, t3[i-1], y3[i-1])
fig, ax = plt.subplots()
ax.plot(t3, y3, color='crimson', label=f'$h_3=$ {h3:.1f}')
ax.plot(t2, y2, color='orange', label=f'$h_2=$ {h2:.1f}')
ax.plot(t1, y1, color='cornflowerblue', label=f'$h_1=$ {h1:.1f}')
ax.set_title('Forward Euler Method')
ax.set_xlabel(r'$t$')
ax.set_ylabel(r'$y(t)$')
plt.legend()
plt.show()
# -
# ---
# ## Predictor-Corrector Method
#
# Consider the modification
#
# \begin{equation}
# y_{n+1} = y_{n} + h\, \frac{f(x_n, y_n) + f(x_{n+1},y_{n+1})}{2}\,\,.
# \end{equation}
#
# This may be a better estimate as it is using the *average slope* of $y$.
#
# However, we don't know $y_{n+1}$ yet. We can get around this problem by using forward Euler to estimate $y_{n+1}$ and then use the above modification for a better estimate:
#
# \begin{equation}
# \begin{aligned}
# y_{n+1}^{(\mathrm{P})} &= y_n + h f(x_n,y_n)\,\,, & \text{(predictor)}\\
# y_{n+1} &= y_n + \frac{h}{2} \left[f(x_n,y_n) + f(x_{n+1}, y^{(\mathrm{P})}_{n+1}) \right]\,\,. & \text{(corrector)}
# \end{aligned}
# \end{equation}
#
# One can show that the error of the **predictor-corrector method**
# decreases locally with $h^3$, but globally with $h^2$. One says it is
# **second-order accurate** as opposed to the Euler method, which is
# first-order accurate.
# ---
# ---
#
# ## Runge-Kutta Methods
#
# The idea behind Runge-Kutta (RK) methods is to match the Taylor expansion
# of $y(x)$ at $x=x_n$ up to the highest possible order.
#
#
# ---
# ### RK2. Second Order RK Method
#
# For
#
# \begin{equation}
# \frac{dy}{dx} = f(x,y)\,\,,
# \end{equation}
#
# we have
#
# \begin{equation}
# y_{n+1} = y_n + a k_1 + b k_2\,\,,
# \end{equation}
#
# with
#
# \begin{align}
# k_1 &= h\,f(x_n,y_n)\,\,,\nonumber\\
# k_2 &= h\,f(x_n+\alpha h,y_n + \beta k_1)\,\,.
# \end{align}
#
# The four parameters $a,b,\alpha,\beta$ will be fixed so that the equation for $y_{n+1}$ agrees as well as possible with the Taylor series expansion
# of $y' = f(x,y)$:
#
# \begin{align}
# y_{n+1} &= y_n + h y_n' + \frac{h^2}{2} y_n'' + \mathcal{O}(h^3)\,\,,\nonumber\\
# &= y_n + h f(x_n,y_n) + \frac{h^2}{2} \frac{d}{dx} f(x_n,y_n) + \mathcal{O}(h^3)\,\,,\nonumber\\
# &= y_n + h f_n + h^2 \frac{1}{2}\left( \frac{\partial f_n}{\partial x} + \frac{\partial f_n}{\partial y} f_n \right) + \mathcal{O}(h^3)\,\,,
# \end{align}
# where $f_n = f(x_n,y_n)$.
#
# Now, we will consider our supposition
#
# \begin{equation}
# y_{n+1} = y_n + a h f_n + b h f(x_n + \alpha h, y_n + \beta h f_n)\,\,.
# \label{eq:rk2c}
# \end{equation}
#
# Expanding the last term in a Taylor series to first order in terms of $(x_n,y_n)$, we get
#
# \begin{equation}
# y_{n+1} = y_n + a h f_n + bh\left[ f_n + \frac{\partial f}{\partial x}(x_n,y_n) \alpha h +
# \frac{\partial f}{\partial y}(x_n,y_n) \beta h f_n \right]\,\,,
# \end{equation}
#
# and compare to read off the constants
#
# \begin{equation}
# a+b = 1\,\,,\hspace{2em} \alpha b = \frac{1}{2}\,\,\hspace{2em} \beta b = \frac{1}{2}\,\,.
# \end{equation}
#
#
# So there are only 3 equations for 4 unknowns and we can assign an arbitrary value to one of the unknowns. Typical choices are:
#
# \begin{equation}
# \alpha = \beta = \frac{1}{2}\,\,,\hspace{2em} a=0\,\,, \hspace{2em} b = 1\,\,.
# \end{equation}
#
# With this, we have for RK2:
#
# \begin{align}
# k_1 & = h f(x_n,y_n)\,\,,\\
# k_2 & = h f(x_n + \frac{1}{2}h, y_n + \frac{1}{2}k_1)\,\,,\\
# y_{n+1} & = y_n + k_2 + \mathcal{O}(h^3)\,\,.
# \end{align}
#
# This method is locally $\mathcal{O}(h^3)$, but globally
# only $\mathcal{O}(h^2)$.
#
# **Note:** Using $a=b=1/2$ and $\alpha=\beta=1$, we recover the predictor-corrector method!
#
# ---
#
# ### RK3
#
# \begin{align}
# k_1 &=h f(x_n,y_n)\,\,\nonumber\\
# k_2 &= h f(x_n + \frac{h}{2},y_n + \frac{1}{2} k_1)\,\,,\nonumber\\
# k_3 &= h f(x_n + h, y_n - k_1 + 2 k_2)\,\,,\nonumber\\
# y_{n+1} &= y_n + \frac{1}{6}(k_1 + 4 k_2 + k_3) + \mathcal{O}(h^4)\,\,.
# \end{align}
#
#
# ---
#
# ### RK4
#
# \begin{align}
# k_1 &=h f(x_n,y_n)\,\,,\\
# k_2 &=h f(x_n + \frac{h}{2},y_n + \frac{1}{2}k_1)\,\,,\nonumber\\
# k_3 &=h f(x_n + \frac{h}{2},y_n + \frac{1}{2}k_2)\,\,,\nonumber\\
# k_4 &=h f(x_n+h,y_n + k_3)\,\,,\nonumber\\
# y_{n+1} &= y_n + \frac{1}{6}(k_1 + 2 k_2 + 2 k_3 + k_4) + \mathcal{O}(h^5)\,\,.
# \end{align}
# ---
#
# ### Example
#
# Consider again the ODE
#
# \begin{equation}
# \frac{dy}{dt} = -a y\,\,, \hspace{1cm}\text{with} \hspace{1cm}
# y(0) = 1\,,\,\, a > 0
# \end{equation}
#
# with $y(0) = 1$.
# +
import numpy as np
import matplotlib.pyplot as plt
from RK4 import *
def ODE(x, y, a=1.):
rhs = -a*y
return rhs
# Initial Condition
y_0 = 1.
# Creation of the grid
t_0 = 0.
t_f = 20.
# Two stepsizes to compare
n1 = 100
h1 = (t_f - t_0)/n1
n2 = 15
h2 = (t_f - t_0)/n2
n3 = 10
h3 = (t_f - t_0)/n3
# Arrays to store the solution
t1 = np.linspace(t_0, t_f, n1)
y1 = np.zeros(n1)
y1[0] = y_0
t2 = np.linspace(t_0, t_f, n2)
y2 = np.zeros(n2)
y2[0] = y_0
t3 = np.linspace(t_0, t_f, n3)
y3 = np.zeros(n3)
y3[0] = y_0
for i in range(1,n1):
y1[i] = RK4(ODE, h1, 0, y1[i-1])
for i in range(1,n2):
y2[i] = RK4(ODE, h2, 0, y2[i-1])
for i in range(1,n3):
y3[i] = RK4(ODE, h3, 0, y3[i-1])
fig, ax = plt.subplots()
ax.plot(t1, y1, color='cornflowerblue', label=f'$h_1=$ {h1:.1f}')
ax.plot(t2, y2, color='orange', label=f'$h_2=$ {h2:.1f}')
ax.plot(t3, y3, color='crimson', label=f'$h_3=$ {h3:.1f}')
ax.set_title('RK4 Method')
ax.set_xlabel(r'$t$')
ax.set_ylabel(r'$y(t)$')
plt.legend()
plt.show()
# -
# ## Runge-Kutta Methods with Adaptive Step Size
#
# The RK methods above require choosing a fixed step
# size $h$ but, how should one choose this parameter?
#
# It would be better to choose an **error tolerance** and let $h$ be chosen
# automatically to satisfy this error tolerance.
#
# This implies that we need
#
# 1. A method for estimating the error.
# 2. A way to adjust the stepsize $h$, if the error is too large (or too small).
# ---
# ### Embedded RK Formulae
#
# Embedded RK formulae provide an error estimator. Now we will present the scheme for 3rd/4th order embedded RK (Bogaki and Shampine)
#
# \begin{equation}
# \begin{aligned}
# k_1 &= h f(x_n, y_n)\,\,,\\
# k_2 &= h f(x_n + \frac{1}{2} h, y_n + \frac{1}{2} k_1)\,\,,\\
# k_3 &= h f(x_n + \frac{3}{4} h, y_n + \frac{3}{4} k_2)\,\,,\\
# y_{n+1} &= y_n + \frac{2}{9} k_1 + \frac{1}{3} k_2 + \frac{4}{9} k_3 + \mathcal{O}(h^4)\,\,\\
# k_4 &= h f(x_n + h, y_{n+1})\,\,\\
# y^*_{n+1} &= y_n + \frac{7}{24} k_1 + \frac{1}{4}k_2 + \frac{1}{3}k_3 + \frac{1}{8} k_4 + \mathcal{O}(h^3)\,\,.
# \end{aligned}
# \end{equation}
#
# The error is
#
# \begin{equation}
# \delta y_{n+1} = y_{n+1} - y^*_{n+1}\,\,.
# \end{equation}
#
#
# In this scheme, $k_4$ of step $n$ is the same as $k_1$ of step $n+1$. Therefore, $k_1$ does not need to be recomputed on step $n+1$; simply
# save $k_4$ and re-use it on the next step.
# This trick is called **FSAL (First Same As Last)**.
#
#
# Given the error estimate $\delta y_{n+1} = y_{n+1} - y^*_{n+1}$
# we want that it says smaller than some tolerance, $|\delta y_{n+1}| \le
# \epsilon$ by adjusting $h$.
#
#
# Usually, one sets
#
# \begin{equation}
# \epsilon = \epsilon_a + |y_{n+1}|\epsilon_r
# \end{equation}
#
# where
#
# $\epsilon_a$ : absolute error tolerance.
#
# $\epsilon_r$ : relative error tolerance.
#
# ### Adjusting the Step Size $h$
#
# We define
#
# \begin{equation}
# \Delta = \frac{|\delta y_{n+1}|}{\epsilon}\,\,,
# \end{equation}
#
# and we want $\Delta \approx 1$.
#
# Note that for a $p$-th-order formula, $\Delta \sim \mathcal{O}(h^p)$.
# So if you took a step $h$ and got a value $\Delta$, then you change the step to $h_\text{desired}$,
#
# \begin{equation}
# h_\text{desired} = h \left|\frac{\Delta_\text{desired}}{\Delta} \right| ^\frac{1}{p}\,\,,
# \end{equation}
#
# to get the new $\Delta_\text{desired} = 1$.
#
# ---
#
# The algorithm to adjust $h$ can be written as follows:
# 1. Take step $h$, measure $\Delta$.
# 2. If $\Delta > 1$ (error too large), then
#
# - set $h_\text{new} = h \left| \frac{1}{\Delta} \right|^{\frac{1}{p}} S$, where $S$ is a fudge factor ($\sim$ $0.9$ or so).
#
# - **reject** the old step, redo with $h_\mathrm{new}$.
#
# 3. If $\Delta < 1$ (error too small), then
#
# - set $h_\text{new} = h \left| \frac{1}{\Delta} \right|^{\frac{1}{p}} S$.
#
# - **accept** old step, take next step with $h_\text{new}$.
#
#
|
10._ODE1/presentation/ODE01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
medicare = pd.read_csv("/netapp2/home/se197/data/CMS/Data/medicare.csv")
# +
train_set = medicare[medicare.Hospital != 'BWH'] # MGH
validation_set = medicare[medicare.Hospital == 'BWH'] # BWH and Neither
import numpy as np
fifty_perc_EHR_cont = np.percentile(medicare['Cal_MPEC_R0'],50)
train_set_high = train_set[train_set.Cal_MPEC_R0 >= fifty_perc_EHR_cont]
train_set_low= train_set[train_set.Cal_MPEC_R0 < fifty_perc_EHR_cont]
validation_set_high = validation_set[validation_set.Cal_MPEC_R0 >= fifty_perc_EHR_cont]
validation_set_low = validation_set[validation_set.Cal_MPEC_R0 < fifty_perc_EHR_cont]
# +
predictor_variable = [
'Co_CAD_R0', 'Co_Embolism_R0', 'Co_DVT_R0', 'Co_PE_R0', 'Co_AFib_R0',
'Co_Hypertension_R0', 'Co_Hyperlipidemia_R0', 'Co_Atherosclerosis_R0',
'Co_HF_R0', 'Co_HemoStroke_R0', 'Co_IscheStroke_R0', 'Co_OthStroke_R0',
'Co_TIA_R0', 'Co_COPD_R0', 'Co_Asthma_R0', 'Co_Pneumonia_R0', 'Co_Alcoholabuse_R0',
'Co_Drugabuse_R0', 'Co_Epilepsy_R0', 'Co_Cancer_R0', 'Co_MorbidObesity_R0',
'Co_Dementia_R0', 'Co_Depression_R0', 'Co_Bipolar_R0', 'Co_Psychosis_R0',
'Co_Personalitydisorder_R0', 'Co_Adjustmentdisorder_R0', 'Co_Anxiety_R0',
'Co_Generalizedanxiety_R0', 'Co_OldMI_R0', 'Co_AcuteMI_R0', 'Co_PUD_R0',
'Co_UpperGIbleed_R0', 'Co_LowerGIbleed_R0', 'Co_Urogenitalbleed_R0',
'Co_Othbleed_R0', 'Co_PVD_R0', 'Co_LiverDisease_R0', 'Co_MRI_R0',
'Co_ESRD_R0', 'Co_Obesity_R0', 'Co_Sepsis_R0', 'Co_Osteoarthritis_R0',
'Co_RA_R0', 'Co_NeuroPain_R0', 'Co_NeckPain_R0', 'Co_OthArthritis_R0',
'Co_Osteoporosis_R0', 'Co_Fibromyalgia_R0', 'Co_Migraine_R0', 'Co_Headache_R0',
'Co_OthPain_R0', 'Co_GeneralizedPain_R0', 'Co_PainDisorder_R0',
'Co_Falls_R0', 'Co_CoagulationDisorder_R0', 'Co_WhiteBloodCell_R0', 'Co_Parkinson_R0',
'Co_Anemia_R0', 'Co_UrinaryIncontinence_R0', 'Co_DecubitusUlcer_R0',
'Co_Oxygen_R0', 'Co_Mammography_R0', 'Co_PapTest_R0', 'Co_PSATest_R0',
'Co_Colonoscopy_R0', 'Co_FecalOccultTest_R0', 'Co_FluShot_R0', 'Co_PneumococcalVaccine_R0', 'Co_RenalDysfunction_R0', 'Co_Valvular_R0', 'Co_Hosp_Prior30Days_R0',
'Co_RX_Antibiotic_R0', 'Co_RX_Corticosteroid_R0', 'Co_RX_Aspirin_R0', 'Co_RX_Dipyridamole_R0',
'Co_RX_Clopidogrel_R0', 'Co_RX_Prasugrel_R0', 'Co_RX_Cilostazol_R0', 'Co_RX_Ticlopidine_R0',
'Co_RX_Ticagrelor_R0', 'Co_RX_OthAntiplatelet_R0', 'Co_RX_NSAIDs_R0',
'Co_RX_Opioid_R0', 'Co_RX_Antidepressant_R0', 'Co_RX_AAntipsychotic_R0', 'Co_RX_TAntipsychotic_R0',
'Co_RX_Anticonvulsant_R0', 'Co_RX_PPI_R0', 'Co_RX_H2Receptor_R0', 'Co_RX_OthGastro_R0',
'Co_RX_ACE_R0', 'Co_RX_ARB_R0', 'Co_RX_BBlocker_R0', 'Co_RX_CCB_R0', 'Co_RX_Thiazide_R0',
'Co_RX_Loop_R0', 'Co_RX_Potassium_R0', 'Co_RX_Nitrates_R0', 'Co_RX_Aliskiren_R0',
'Co_RX_OthAntihypertensive_R0', 'Co_RX_Antiarrhythmic_R0', 'Co_RX_OthAnticoagulant_R0',
'Co_RX_Insulin_R0', 'Co_RX_Noninsulin_R0', 'Co_RX_Digoxin_R0', 'Co_RX_Statin_R0',
'Co_RX_Lipid_R0', 'Co_RX_Lithium_R0', 'Co_RX_Benzo_R0', 'Co_RX_ZDrugs_R0',
'Co_RX_OthAnxiolytic_R0', 'Co_RX_Barbiturate_R0', 'Co_RX_Dementia_R0', 'Co_RX_Hormone_R0',
'Co_RX_Osteoporosis_R0', 'Co_N_Drugs_R0', 'Co_N_Hosp_R0', 'Co_Total_HospLOS_R0',
'Co_N_MDVisit_R0', 'Co_RX_AnyAspirin_R0', 'Co_RX_AspirinMono_R0', 'Co_RX_ClopidogrelMono_R0',
'Co_RX_AspirinClopidogrel_R0', 'Co_RX_DM_R0', 'Co_RX_Antipsychotic_R0'
]
co_train_gpop = train_set[predictor_variable]
co_train_high = train_set_high[predictor_variable]
co_train_low = train_set_low[predictor_variable]
co_validation_gpop = validation_set[predictor_variable]
co_validation_high = validation_set_high[predictor_variable]
co_validation_low = validation_set_low[predictor_variable]
len(predictor_variable)
# +
out_train_comp_gpop = train_set['Out_comp_cardiovascular_RC1']
out_train_comp_high = train_set_high['Out_comp_cardiovascular_RC1']
out_train_comp_low = train_set_low['Out_comp_cardiovascular_RC1']
out_validation_comp_gpop = validation_set['Out_comp_cardiovascular_RC1']
out_validation_comp_high = validation_set_high['Out_comp_cardiovascular_RC1']
out_validation_comp_low = validation_set_low['Out_comp_cardiovascular_RC1']
# -
def bart(X_train, y_train):
from bartpy.sklearnmodel import SklearnModel
from sklearn.model_selection import GridSearchCV
from bartpy.data import Data
from bartpy.sigma import Sigma
param_grid = [{
'n_trees': [10,30,50] #
}]
model = SklearnModel()
clf = GridSearchCV(estimator = model, param_grid = param_grid, n_jobs = 10, verbose = True)
best_clf = clf.fit(X_train, y_train.to_numpy())
print(best_clf)
return best_clf
def scores(X_train,y_train, best_clf):
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score
from sklearn.metrics import fbeta_score
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
import numpy as np
pred = np.round(best_clf.predict(X_train))
print(pred)
actual = y_train
print(accuracy_score(actual,pred))
print(f1_score(actual,pred))
print(fbeta_score(actual,pred, average = 'macro', beta = 2))
print(roc_auc_score(actual, best_clf.predict(X_train)))
print(log_loss(actual,best_clf.predict(X_train)))
def cross_val(X,y):
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_validate
from sklearn.metrics import log_loss
from sklearn.metrics import roc_auc_score
from sklearn.metrics import fbeta_score
import sklearn
import numpy as np
cv = KFold(n_splits=5, random_state=1, shuffle=True)
log_loss = []
auc = []
accuracy = []
f1 = []
f2 = []
for train_index, test_index in cv.split(X):
X_train, X_test, y_train, y_test = X.iloc[train_index], X.iloc[test_index], y.iloc[train_index], y.iloc[test_index]
model = bart(X_train, y_train)
prob = model.predict(X_test) # prob is a vector of probabilities
pred = np.round(model.predict(X_test)) # pred is the rounded predictions
log_loss.append(sklearn.metrics.log_loss(y_test, prob))
auc.append(sklearn.metrics.roc_auc_score(y_test, prob))
accuracy.append(sklearn.metrics.accuracy_score(y_test, pred))
f1.append(sklearn.metrics.f1_score(y_test, pred, average = 'macro'))
f2.append(fbeta_score(y_test,pred, average = 'macro', beta = 2))
print(np.mean(accuracy))
print(np.mean(f1))
print(np.mean(f2))
print(np.mean(auc))
print(np.mean(log_loss))
# +
import datetime
begin_time = datetime.datetime.now()
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 42)
co_train_gpop_sm,out_train_comp_gpop_sm = sm.fit_resample(co_train_gpop,out_train_comp_gpop)
best_clf = bart(co_train_gpop_sm,out_train_comp_gpop_sm)
cross_val(co_train_gpop_sm,out_train_comp_gpop_sm)
print()
scores(co_train_gpop, out_train_comp_gpop, best_clf)
print()
scores(co_validation_gpop,out_validation_comp_gpop, best_clf)
print(datetime.datetime.now() - begin_time)
# +
import datetime
begin_time = datetime.datetime.now()
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 42)
co_train_low_sm,out_train_comp_low_sm = sm.fit_resample(co_train_low,out_train_comp_low)
best_clf = bart(co_train_low_sm,out_train_comp_low_sm)
cross_val(co_train_low_sm,out_train_comp_low_sm)
print()
scores(co_train_low, out_train_comp_low, best_clf)
print()
scores(co_validation_low,out_validation_comp_low, best_clf)
print(datetime.datetime.now() - begin_time)
# +
import datetime
begin_time = datetime.datetime.now()
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 42)
co_train_high_sm,out_train_comp_high_sm = sm.fit_resample(co_train_high,out_train_comp_high)
best_clf = bart(co_train_high_sm,out_train_comp_high_sm)
cross_val(co_train_high_sm,out_train_comp_high_sm)
print()
scores(co_train_high, out_train_comp_high, best_clf)
print()
scores(co_validation_high,out_validation_comp_high, best_clf)
print(datetime.datetime.now() - begin_time)
# -
|
EHR_Only/BART/.ipynb_checkpoints/Comp_ND_SMOTE-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <address>
# © 2018 by Dr. <NAME><br>
# email: <a href="mailto:<EMAIL>"><EMAIL></a><br>
# Visit us at: <a href="https://www.pelagos-consulting.com">www.pelagos-consulting.com</a><br>
# </address>
# + tags=[]
|
FFTs_and_complex_numbers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Programming Exercise 5:
# # Regularized Linear Regression and Bias vs Variance
#
# ## Introduction
#
# In this exercise, you will implement regularized linear regression and use it to study models with different bias-variance properties. Before starting on the programming exercise, we strongly recommend watching the video lectures and completing the review questions for the associated topics.
#
# All the information you need for solving this assignment is in this notebook, and all the code you will be implementing will take place within this notebook. The assignment can be promptly submitted to the coursera grader directly from this notebook (code and instructions are included below).
#
# Before we begin with the exercises, we need to import all libraries required for this programming exercise. Throughout the course, we will be using [`numpy`](http://www.numpy.org/) for all arrays and matrix operations, [`matplotlib`](https://matplotlib.org/) for plotting, and [`scipy`](https://docs.scipy.org/doc/scipy/reference/) for scientific and numerical computation functions and tools. You can find instructions on how to install required libraries in the README file in the [github repository](https://github.com/dibgerge/ml-coursera-python-assignments).
# +
# used for manipulating directory paths
import os
# Scientific and vector computation for python
import numpy as np
# Plotting library
from matplotlib import pyplot
# Optimization module in scipy
from scipy import optimize
# will be used to load MATLAB mat datafile format
from scipy.io import loadmat
# library written for this exercise providing additional functions for assignment submission, and others
import utils
# define the submission/grader object for this exercise
grader = utils.Grader()
# tells matplotlib to embed plots within the notebook
# %matplotlib inline
# -
# ## Submission and Grading
#
#
# After completing each part of the assignment, be sure to submit your solutions to the grader. The following is a breakdown of how each part of this exercise is scored.
#
#
# | Section | Part | Submitted Function | Points |
# | :- |:- |:- | :-: |
# | 1 | [Regularized Linear Regression Cost Function](#section1) | [`linearRegCostFunction`](#linearRegCostFunction) | 25 |
# | 2 | [Regularized Linear Regression Gradient](#section2) | [`linearRegCostFunction`](#linearRegCostFunction) |25 |
# | 3 | [Learning Curve](#section3) | [`learningCurve`](#func2) | 20 |
# | 4 | [Polynomial Feature Mapping](#section4) | [`polyFeatures`](#polyFeatures) | 10 |
# | 5 | [Cross Validation Curve](#section5) | [`validationCurve`](#validationCurve) | 20 |
# | | Total Points | |100 |
#
#
# You are allowed to submit your solutions multiple times, and we will take only the highest score into consideration.
#
# <div class="alert alert-block alert-warning">
# At the end of each section in this notebook, we have a cell which contains code for submitting the solutions thus far to the grader. Execute the cell to see your score up to the current section. For all your work to be submitted properly, you must execute those cells at least once.
# </div>
# <a id="section1"></a>
# ## 1 Regularized Linear Regression
#
# In the first half of the exercise, you will implement regularized linear regression to predict the amount of water flowing out of a dam using the change of water level in a reservoir. In the next half, you will go through some diagnostics of debugging learning algorithms and examine the effects of bias v.s.
# variance.
#
# ### 1.1 Visualizing the dataset
#
# We will begin by visualizing the dataset containing historical records on the change in the water level, $x$, and the amount of water flowing out of the dam, $y$. This dataset is divided into three parts:
#
# - A **training** set that your model will learn on: `X`, `y`
# - A **cross validation** set for determining the regularization parameter: `Xval`, `yval`
# - A **test** set for evaluating performance. These are “unseen” examples which your model did not see during training: `Xtest`, `ytest`
#
# Run the next cell to plot the training data. In the following parts, you will implement linear regression and use that to fit a straight line to the data and plot learning curves. Following that, you will implement polynomial regression to find a better fit to the data.
# +
# Load from ex5data1.mat, where all variables will be store in a dictionary
data = loadmat(os.path.join('Data', 'ex5data1.mat'))
# Extract train, test, validation data from dictionary
# and also convert y's form 2-D matrix (MATLAB format) to a numpy vector
X, y = data['X'], data['y'][:, 0]
Xtest, ytest = data['Xtest'], data['ytest'][:, 0]
Xval, yval = data['Xval'], data['yval'][:, 0]
# m = Number of examples
m = y.size
# Plot training data
pyplot.plot(X, y, 'ro', ms=10, mec='k', mew=1)
pyplot.xlabel('Change in water level (x)')
pyplot.ylabel('Water flowing out of the dam (y)');
# -
# ### 1.2 Regularized linear regression cost function
#
# Recall that regularized linear regression has the following cost function:
#
# $$ J(\theta) = \frac{1}{2m} \left( \sum_{i=1}^m \left( h_\theta\left( x^{(i)} \right) - y^{(i)} \right)^2 \right) + \frac{\lambda}{2m} \left( \sum_{j=1}^n \theta_j^2 \right)$$
#
# where $\lambda$ is a regularization parameter which controls the degree of regularization (thus, help preventing overfitting). The regularization term puts a penalty on the overall cost J. As the magnitudes of the model parameters $\theta_j$ increase, the penalty increases as well. Note that you should not regularize
# the $\theta_0$ term.
#
# You should now complete the code in the function `linearRegCostFunction` in the next cell. Your task is to calculate the regularized linear regression cost function. If possible, try to vectorize your code and avoid writing loops.
# <a id="linearRegCostFunction"></a>
def linearRegCostFunction(X, y, theta, lambda_=0.0):
"""
Compute cost and gradient for regularized linear regression
with multiple variables. Computes the cost of using theta as
the parameter for linear regression to fit the data points in X and y.
Parameters
----------
X : array_like
The dataset. Matrix with shape (m x n + 1) where m is the
total number of examples, and n is the number of features
before adding the bias term.
y : array_like
The functions values at each datapoint. A vector of
shape (m, ).
theta : array_like
The parameters for linear regression. A vector of shape (n+1,).
lambda_ : float, optional
The regularization parameter.
Returns
-------
J : float
The computed cost function.
grad : array_like
The value of the cost function gradient w.r.t theta.
A vector of shape (n+1, ).
Instructions
------------
Compute the cost and gradient of regularized linear regression for
a particular choice of theta.
You should set J to the cost and grad to the gradient.
"""
# Initialize some useful values
m = y.size # number of training examples
# You need to return the following variables correctly
J = 0
grad = np.zeros(theta.shape)
# ====================== YOUR CODE HERE ======================
# ============================================================
return J, grad
# When you are finished, the next cell will run your cost function using `theta` initialized at `[1, 1]`. You should expect to see an output of 303.993.
# +
theta = np.array([1, 1])
J, _ = linearRegCostFunction(np.concatenate([np.ones((m, 1)), X], axis=1), y, theta, 1)
print('Cost at theta = [1, 1]:\t %f ' % J)
print('This value should be about 303.993192)\n' % J)
# -
# After completing a part of the exercise, you can submit your solutions for grading by first adding the function you modified to the submission object, and then sending your function to Coursera for grading.
#
# The submission script will prompt you for your login e-mail and submission token. You can obtain a submission token from the web page for the assignment. You are allowed to submit your solutions multiple times, and we will take only the highest score into consideration.
#
# *Execute the following cell to grade your solution to the first part of this exercise.*
grader[1] = linearRegCostFunction
grader.grade()
# <a id="section2"></a>
# ### 1.3 Regularized linear regression gradient
#
# Correspondingly, the partial derivative of the cost function for regularized linear regression is defined as:
#
# $$
# \begin{align}
# & \frac{\partial J(\theta)}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^m \left( h_\theta \left(x^{(i)} \right) - y^{(i)} \right) x_j^{(i)} & \qquad \text{for } j = 0 \\
# & \frac{\partial J(\theta)}{\partial \theta_j} = \left( \frac{1}{m} \sum_{i=1}^m \left( h_\theta \left( x^{(i)} \right) - y^{(i)} \right) x_j^{(i)} \right) + \frac{\lambda}{m} \theta_j & \qquad \text{for } j \ge 1
# \end{align}
# $$
#
# In the function [`linearRegCostFunction`](#linearRegCostFunction) above, add code to calculate the gradient, returning it in the variable `grad`. <font color='red'><b>Do not forget to re-execute the cell containing this function to update the function's definition.</b></font>
#
#
# When you are finished, use the next cell to run your gradient function using theta initialized at `[1, 1]`. You should expect to see a gradient of `[-15.30, 598.250]`.
# +
theta = np.array([1, 1])
J, grad = linearRegCostFunction(np.concatenate([np.ones((m, 1)), X], axis=1), y, theta, 1)
print('Gradient at theta = [1, 1]: [{:.6f}, {:.6f}] '.format(*grad))
print(' (this value should be about [-15.303016, 598.250744])\n')
# -
# *You should now submit your solutions.*
grader[2] = linearRegCostFunction
grader.grade()
# ### Fitting linear regression
#
# Once your cost function and gradient are working correctly, the next cell will run the code in `trainLinearReg` (found in the module `utils.py`) to compute the optimal values of $\theta$. This training function uses `scipy`'s optimization module to minimize the cost function.
#
# In this part, we set regularization parameter $\lambda$ to zero. Because our current implementation of linear regression is trying to fit a 2-dimensional $\theta$, regularization will not be incredibly helpful for a $\theta$ of such low dimension. In the later parts of the exercise, you will be using polynomial regression with regularization.
#
# Finally, the code in the next cell should also plot the best fit line, which should look like the figure below.
#
# 
#
# The best fit line tells us that the model is not a good fit to the data because the data has a non-linear pattern. While visualizing the best fit as shown is one possible way to debug your learning algorithm, it is not always easy to visualize the data and model. In the next section, you will implement a function to generate learning curves that can help you debug your learning algorithm even if it is not easy to visualize the
# data.
# +
# add a columns of ones for the y-intercept
X_aug = np.concatenate([np.ones((m, 1)), X], axis=1)
theta = utils.trainLinearReg(linearRegCostFunction, X_aug, y, lambda_=0)
# Plot fit over the data
pyplot.plot(X, y, 'ro', ms=10, mec='k', mew=1.5)
pyplot.xlabel('Change in water level (x)')
pyplot.ylabel('Water flowing out of the dam (y)')
pyplot.plot(X, np.dot(X_aug, theta), '--', lw=2);
# -
# <a id="section3"></a>
# ## 2 Bias-variance
#
# An important concept in machine learning is the bias-variance tradeoff. Models with high bias are not complex enough for the data and tend to underfit, while models with high variance overfit to the training data.
#
# In this part of the exercise, you will plot training and test errors on a learning curve to diagnose bias-variance problems.
#
# ### 2.1 Learning Curves
#
# You will now implement code to generate the learning curves that will be useful in debugging learning algorithms. Recall that a learning curve plots training and cross validation error as a function of training set size. Your job is to fill in the function `learningCurve` in the next cell, so that it returns a vector of errors for the training set and cross validation set.
#
# To plot the learning curve, we need a training and cross validation set error for different training set sizes. To obtain different training set sizes, you should use different subsets of the original training set `X`. Specifically, for a training set size of $i$, you should use the first $i$ examples (i.e., `X[:i, :]`
# and `y[:i]`).
#
# You can use the `trainLinearReg` function (by calling `utils.trainLinearReg(...)`) to find the $\theta$ parameters. Note that the `lambda_` is passed as a parameter to the `learningCurve` function.
# After learning the $\theta$ parameters, you should compute the error on the training and cross validation sets. Recall that the training error for a dataset is defined as
#
# $$ J_{\text{train}} = \frac{1}{2m} \left[ \sum_{i=1}^m \left(h_\theta \left( x^{(i)} \right) - y^{(i)} \right)^2 \right] $$
#
# In particular, note that the training error does not include the regularization term. One way to compute the training error is to use your existing cost function and set $\lambda$ to 0 only when using it to compute the training error and cross validation error. When you are computing the training set error, make sure you compute it on the training subset (i.e., `X[:n,:]` and `y[:n]`) instead of the entire training set. However, for the cross validation error, you should compute it over the entire cross validation set. You should store
# the computed errors in the vectors error train and error val.
#
# <a id="func2"></a>
def learningCurve(X, y, Xval, yval, lambda_=0):
"""
Generates the train and cross validation set errors needed to plot a learning curve
returns the train and cross validation set errors for a learning curve.
In this function, you will compute the train and test errors for
dataset sizes from 1 up to m. In practice, when working with larger
datasets, you might want to do this in larger intervals.
Parameters
----------
X : array_like
The training dataset. Matrix with shape (m x n + 1) where m is the
total number of examples, and n is the number of features
before adding the bias term.
y : array_like
The functions values at each training datapoint. A vector of
shape (m, ).
Xval : array_like
The validation dataset. Matrix with shape (m_val x n + 1) where m is the
total number of examples, and n is the number of features
before adding the bias term.
yval : array_like
The functions values at each validation datapoint. A vector of
shape (m_val, ).
lambda_ : float, optional
The regularization parameter.
Returns
-------
error_train : array_like
A vector of shape m. error_train[i] contains the training error for
i examples.
error_val : array_like
A vecotr of shape m. error_val[i] contains the validation error for
i training examples.
Instructions
------------
Fill in this function to return training errors in error_train and the
cross validation errors in error_val. i.e., error_train[i] and
error_val[i] should give you the errors obtained after training on i examples.
Notes
-----
- You should evaluate the training error on the first i training
examples (i.e., X[:i, :] and y[:i]).
For the cross-validation error, you should instead evaluate on
the _entire_ cross validation set (Xval and yval).
- If you are using your cost function (linearRegCostFunction) to compute
the training and cross validation error, you should call the function with
the lambda argument set to 0. Do note that you will still need to use
lambda when running the training to obtain the theta parameters.
Hint
----
You can loop over the examples with the following:
for i in range(1, m+1):
# Compute train/cross validation errors using training examples
# X[:i, :] and y[:i], storing the result in
# error_train[i-1] and error_val[i-1]
....
"""
# Number of training examples
m = y.size
# You need to return these values correctly
error_train = np.zeros(m)
error_val = np.zeros(m)
# ====================== YOUR CODE HERE ======================
# =============================================================
return error_train, error_val
# When you are finished implementing the function `learningCurve`, executing the next cell prints the learning curves and produce a plot similar to the figure below.
#
# 
#
# In the learning curve figure, you can observe that both the train error and cross validation error are high when the number of training examples is increased. This reflects a high bias problem in the model - the linear regression model is too simple and is unable to fit our dataset well. In the next section, you will implement polynomial regression to fit a better model for this dataset.
# +
X_aug = np.concatenate([np.ones((m, 1)), X], axis=1)
Xval_aug = np.concatenate([np.ones((yval.size, 1)), Xval], axis=1)
error_train, error_val = learningCurve(X_aug, y, Xval_aug, yval, lambda_=0)
pyplot.plot(np.arange(1, m+1), error_train, np.arange(1, m+1), error_val, lw=2)
pyplot.title('Learning curve for linear regression')
pyplot.legend(['Train', 'Cross Validation'])
pyplot.xlabel('Number of training examples')
pyplot.ylabel('Error')
pyplot.axis([0, 13, 0, 150])
print('# Training Examples\tTrain Error\tCross Validation Error')
for i in range(m):
print(' \t%d\t\t%f\t%f' % (i+1, error_train[i], error_val[i]))
# -
# *You should now submit your solutions.*
grader[3] = learningCurve
grader.grade()
# <a id="section4"></a>
#
# ## 3 Polynomial regression
#
# The problem with our linear model was that it was too simple for the data
# and resulted in underfitting (high bias). In this part of the exercise, you will address this problem by adding more features. For polynomial regression, our hypothesis has the form:
#
# $$
# \begin{align}
# h_\theta(x) &= \theta_0 + \theta_1 \times (\text{waterLevel}) + \theta_2 \times (\text{waterLevel})^2 + \cdots + \theta_p \times (\text{waterLevel})^p \\
# & = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_p x_p
# \end{align}
# $$
#
# Notice that by defining $x_1 = (\text{waterLevel})$, $x_2 = (\text{waterLevel})^2$ , $\cdots$, $x_p =
# (\text{waterLevel})^p$, we obtain a linear regression model where the features are the various powers of the original value (waterLevel).
#
# Now, you will add more features using the higher powers of the existing feature $x$ in the dataset. Your task in this part is to complete the code in the function `polyFeatures` in the next cell. The function should map the original training set $X$ of size $m \times 1$ into its higher powers. Specifically, when a training set $X$ of size $m \times 1$ is passed into the function, the function should return a $m \times p$ matrix `X_poly`, where column 1 holds the original values of X, column 2 holds the values of $X^2$, column 3 holds the values of $X^3$, and so on. Note that you don’t have to account for the zero-eth power in this function.
#
# <a id="polyFeatures"></a>
def polyFeatures(X, p):
"""
Maps X (1D vector) into the p-th power.
Parameters
----------
X : array_like
A data vector of size m, where m is the number of examples.
p : int
The polynomial power to map the features.
Returns
-------
X_poly : array_like
A matrix of shape (m x p) where p is the polynomial
power and m is the number of examples. That is:
X_poly[i, :] = [X[i], X[i]**2, X[i]**3 ... X[i]**p]
Instructions
------------
Given a vector X, return a matrix X_poly where the p-th column of
X contains the values of X to the p-th power.
"""
# You need to return the following variables correctly.
X_poly = np.zeros((X.shape[0], p))
# ====================== YOUR CODE HERE ======================
# ============================================================
return X_poly
# Now you have a function that will map features to a higher dimension. The next cell will apply it to the training set, the test set, and the cross validation set.
# +
p = 8
# Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p)
X_poly, mu, sigma = utils.featureNormalize(X_poly)
X_poly = np.concatenate([np.ones((m, 1)), X_poly], axis=1)
# Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p)
X_poly_test -= mu
X_poly_test /= sigma
X_poly_test = np.concatenate([np.ones((ytest.size, 1)), X_poly_test], axis=1)
# Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p)
X_poly_val -= mu
X_poly_val /= sigma
X_poly_val = np.concatenate([np.ones((yval.size, 1)), X_poly_val], axis=1)
print('Normalized Training Example 1:')
X_poly[0, :]
# -
# *You should now submit your solutions.*
grader[4] = polyFeatures
grader.grade()
# ## 3.1 Learning Polynomial Regression
#
# After you have completed the function `polyFeatures`, we will proceed to train polynomial regression using your linear regression cost function.
#
# Keep in mind that even though we have polynomial terms in our feature vector, we are still solving a linear regression optimization problem. The polynomial terms have simply turned into features that we can use for linear regression. We are using the same cost function and gradient that you wrote for the earlier part of this exercise.
#
# For this part of the exercise, you will be using a polynomial of degree 8. It turns out that if we run the training directly on the projected data, will not work well as the features would be badly scaled (e.g., an example with $x = 40$ will now have a feature $x_8 = 40^8 = 6.5 \times 10^{12}$). Therefore, you will
# need to use feature normalization.
#
# Before learning the parameters $\theta$ for the polynomial regression, we first call `featureNormalize` and normalize the features of the training set, storing the mu, sigma parameters separately. We have already implemented this function for you (in `utils.py` module) and it is the same function from the first exercise.
#
# After learning the parameters $\theta$, you should see two plots generated for polynomial regression with $\lambda = 0$, which should be similar to the ones here:
#
# <table>
# <tr>
# <td><img src="Figures/polynomial_regression.png"></td>
# <td><img src="Figures/polynomial_learning_curve.png"></td>
# </tr>
# </table>
#
# You should see that the polynomial fit is able to follow the datapoints very well, thus, obtaining a low training error. The figure on the right shows that the training error essentially stays zero for all numbers of training samples. However, the polynomial fit is very complex and even drops off at the extremes. This is an indicator that the polynomial regression model is overfitting the training data and will not generalize well.
#
# To better understand the problems with the unregularized ($\lambda = 0$) model, you can see that the learning curve shows the same effect where the training error is low, but the cross validation error is high. There is a gap between the training and cross validation errors, indicating a high variance problem.
# +
lambda_ = 0
theta = utils.trainLinearReg(linearRegCostFunction, X_poly, y,
lambda_=lambda_, maxiter=55)
# Plot training data and fit
pyplot.plot(X, y, 'ro', ms=10, mew=1.5, mec='k')
utils.plotFit(polyFeatures, np.min(X), np.max(X), mu, sigma, theta, p)
pyplot.xlabel('Change in water level (x)')
pyplot.ylabel('Water flowing out of the dam (y)')
pyplot.title('Polynomial Regression Fit (lambda = %f)' % lambda_)
pyplot.ylim([-20, 50])
pyplot.figure()
error_train, error_val = learningCurve(X_poly, y, X_poly_val, yval, lambda_)
pyplot.plot(np.arange(1, 1+m), error_train, np.arange(1, 1+m), error_val)
pyplot.title('Polynomial Regression Learning Curve (lambda = %f)' % lambda_)
pyplot.xlabel('Number of training examples')
pyplot.ylabel('Error')
pyplot.axis([0, 13, 0, 100])
pyplot.legend(['Train', 'Cross Validation'])
print('Polynomial Regression (lambda = %f)\n' % lambda_)
print('# Training Examples\tTrain Error\tCross Validation Error')
for i in range(m):
print(' \t%d\t\t%f\t%f' % (i+1, error_train[i], error_val[i]))
# -
# One way to combat the overfitting (high-variance) problem is to add regularization to the model. In the next section, you will get to try different $\lambda$ parameters to see how regularization can lead to a better model.
#
# ### 3.2 Optional (ungraded) exercise: Adjusting the regularization parameter
#
# In this section, you will get to observe how the regularization parameter affects the bias-variance of regularized polynomial regression. You should now modify the the lambda parameter and try $\lambda = 1, 100$. For each of these values, the script should generate a polynomial fit to the data and also a learning curve.
#
# For $\lambda = 1$, the generated plots should look like the the figure below. You should see a polynomial fit that follows the data trend well (left) and a learning curve (right) showing that both the cross validation and training error converge to a relatively low value. This shows the $\lambda = 1$ regularized polynomial regression model does not have the high-bias or high-variance problems. In effect, it achieves a good trade-off between bias and variance.
#
# <table>
# <tr>
# <td><img src="Figures/polynomial_regression_reg_1.png"></td>
# <td><img src="Figures/polynomial_learning_curve_reg_1.png"></td>
# </tr>
# </table>
#
# For $\lambda = 100$, you should see a polynomial fit (figure below) that does not follow the data well. In this case, there is too much regularization and the model is unable to fit the training data.
#
# 
#
# *You do not need to submit any solutions for this optional (ungraded) exercise.*
# <a id="section5"></a>
# ### 3.3 Selecting $\lambda$ using a cross validation set
#
# From the previous parts of the exercise, you observed that the value of $\lambda$ can significantly affect the results of regularized polynomial regression on the training and cross validation set. In particular, a model without regularization ($\lambda = 0$) fits the training set well, but does not generalize. Conversely, a model with too much regularization ($\lambda = 100$) does not fit the training set and testing set well. A good choice of $\lambda$ (e.g., $\lambda = 1$) can provide a good fit to the data.
#
# In this section, you will implement an automated method to select the $\lambda$ parameter. Concretely, you will use a cross validation set to evaluate how good each $\lambda$ value is. After selecting the best $\lambda$ value using the cross validation set, we can then evaluate the model on the test set to estimate
# how well the model will perform on actual unseen data.
#
# Your task is to complete the code in the function `validationCurve`. Specifically, you should should use the `utils.trainLinearReg` function to train the model using different values of $\lambda$ and compute the training error and cross validation error. You should try $\lambda$ in the following range: {0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10}.
# <a id="validationCurve"></a>
def validationCurve(X, y, Xval, yval):
"""
Generate the train and validation errors needed to plot a validation
curve that we can use to select lambda_.
Parameters
----------
X : array_like
The training dataset. Matrix with shape (m x n) where m is the
total number of training examples, and n is the number of features
including any polynomial features.
y : array_like
The functions values at each training datapoint. A vector of
shape (m, ).
Xval : array_like
The validation dataset. Matrix with shape (m_val x n) where m is the
total number of validation examples, and n is the number of features
including any polynomial features.
yval : array_like
The functions values at each validation datapoint. A vector of
shape (m_val, ).
Returns
-------
lambda_vec : list
The values of the regularization parameters which were used in
cross validation.
error_train : list
The training error computed at each value for the regularization
parameter.
error_val : list
The validation error computed at each value for the regularization
parameter.
Instructions
------------
Fill in this function to return training errors in `error_train` and
the validation errors in `error_val`. The vector `lambda_vec` contains
the different lambda parameters to use for each calculation of the
errors, i.e, `error_train[i]`, and `error_val[i]` should give you the
errors obtained after training with `lambda_ = lambda_vec[i]`.
Note
----
You can loop over lambda_vec with the following:
for i in range(len(lambda_vec))
lambda = lambda_vec[i]
# Compute train / val errors when training linear
# regression with regularization parameter lambda_
# You should store the result in error_train[i]
# and error_val[i]
....
"""
# Selected values of lambda (you should not change this)
lambda_vec = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
# You need to return these variables correctly.
error_train = np.zeros(len(lambda_vec))
error_val = np.zeros(len(lambda_vec))
# ====================== YOUR CODE HERE ======================
# ============================================================
return lambda_vec, error_train, error_val
# After you have completed the code, the next cell will run your function and plot a cross validation curve of error v.s. $\lambda$ that allows you select which $\lambda$ parameter to use. You should see a plot similar to the figure below.
#
# 
#
# In this figure, we can see that the best value of $\lambda$ is around 3. Due to randomness
# in the training and validation splits of the dataset, the cross validation error can sometimes be lower than the training error.
# +
lambda_vec, error_train, error_val = validationCurve(X_poly, y, X_poly_val, yval)
pyplot.plot(lambda_vec, error_train, '-o', lambda_vec, error_val, '-o', lw=2)
pyplot.legend(['Train', 'Cross Validation'])
pyplot.xlabel('lambda')
pyplot.ylabel('Error')
print('lambda\t\tTrain Error\tValidation Error')
for i in range(len(lambda_vec)):
print(' %f\t%f\t%f' % (lambda_vec[i], error_train[i], error_val[i]))
# -
# *You should now submit your solutions.*
grader[5] = validationCurve
grader.grade()
# ### 3.4 Optional (ungraded) exercise: Computing test set error
#
# In the previous part of the exercise, you implemented code to compute the cross validation error for various values of the regularization parameter $\lambda$. However, to get a better indication of the model’s performance in the real world, it is important to evaluate the “final” model on a test set that was not used in any part of training (that is, it was neither used to select the $\lambda$ parameters, nor to learn the model parameters $\theta$). For this optional (ungraded) exercise, you should compute the test error using the best value of $\lambda$ you found. In our cross validation, we obtained a test error of 3.8599 for $\lambda = 3$.
#
# *You do not need to submit any solutions for this optional (ungraded) exercise.*
# ### 3.5 Optional (ungraded) exercise: Plotting learning curves with randomly selected examples
#
# In practice, especially for small training sets, when you plot learning curves to debug your algorithms, it is often helpful to average across multiple sets of randomly selected examples to determine the training error and cross validation error.
#
# Concretely, to determine the training error and cross validation error for $i$ examples, you should first randomly select $i$ examples from the training set and $i$ examples from the cross validation set. You will then learn the parameters $\theta$ using the randomly chosen training set and evaluate the parameters $\theta$ on the randomly chosen training set and cross validation set. The above steps should then be repeated multiple times (say 50) and the averaged error should be used to determine the training error and cross validation error for $i$ examples.
#
# For this optional (ungraded) exercise, you should implement the above strategy for computing the learning curves. For reference, the figure below shows the learning curve we obtained for polynomial regression with $\lambda = 0.01$. Your figure may differ slightly due to the random selection of examples.
#
# 
#
# *You do not need to submit any solutions for this optional (ungraded) exercise.*
|
Program's_Contributed_By_Contributors/AI-Summer-Course/Assignments/ml-coursera-python-assignments-master/Exercise5/exercise5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hands On #4 - Balancing Cart Pole w/Q-learning
#
# ## Goal:
# * Introduce the CartPole Environment
# * More complex, Continuous
# * Implement Q-Learning for digitized CartPole
# * Later we will use function approx and remove the requirement for digitization
#
# ## Steps:
# 1. Get familiar with Cartpole environment
# * np.linspace() and np.digitize() for state space aggregation
# 2. Program Q Learning
# 3. Track & Plot Metrics to solve Cart Pole
# Reference :
# * Based on Udacity github https://github.com/udacity/deep-reinforcement-learning/tree/master/monte-carlo plus
# * My solution for the DQN https://github.com/xsankar/DQN_Navigation/blob/master/Navigation-v2.ipynb
# * Kaggle https://www.kaggle.com/sandovaledwin/q-learning-algorithm-for-solving-frozenlake-game/notebook
# * <NAME>abor's RL in Motion github https://github.com/philtabor/Reinforcement-Learning-In-Motion/tree/master/Unit-7-The-Cartpole
# ### 1. Install the required packages
#
# * No esoteric requirements
# * You can run them without docker
# * pip install -r requirements.txt
# * Requirements
# * python 3.6, pytorch, openAI gym, numpy, matplotlib
# * anaconda is easier but not needed
# * Miniconda works fine
# ### 2. Define imports
#
# python 3, numpy, matplotlib, torch, gym
# +
# General imports
import gym
import PIL # for in-line display of certain environments
import sys
import numpy as np
import random
from collections import namedtuple, deque, defaultdict
import matplotlib.pyplot as plt
# %matplotlib inline
# torch imports
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# -
# ### 2.1. Global Constants and other variables
# Constants Definitions
BUFFER_SIZE = int(1e5) # replay buffer size
BATCH_SIZE = 64 # minibatch size
GAMMA = 0.99 # discount factor
TAU = 1e-3 # for soft update of target parameters
LR = 5e-4 # learning rate
UPDATE_EVERY = 4 # how often to update the network
# Number of neurons in the layers of the Q Network
FC1_UNITS = 16
FC2_UNITS = 8
FC3_UNITS = 4
# Store models flag. Store during calibration runs and do not store during hyperparameter search
STORE_MODELS = False
# ### Work Area
# Work area to quickly test utility functions
import math
import time
from datetime import datetime, timedelta
'''
start_time = time.time()
time.sleep(10)
print('Elapsed : {}'.format(timedelta(seconds=time.time() - start_time)))
'''
print(math.radians(12))
print(math.radians(-12))
# ### 3.0 Create instance & Explore
import gym, PIL
env = gym.make('CartPole-v0')
env.reset()
# array = env.reset()
# ** render doesn't work reliably on a server. Uncomment when running ** locally **
# env.render()
# PIL.Image.fromarray(env.render(mode='rgb_array'))
# ### This what it will look like
# ### We don't need the render(). We run it on headless mode and inspect the results
# <img src="CartPole_Render.jpg">
# ### 3.1 Examine the State and Action Spaces
#
# * The state space is continuous, with an observation space of 4
# * {x,$\dot{x}$,$\theta$, theta_dot}
# * Cart Position, Cart Velocity, Pole Angle, Pole Velocity at tip
# * The angle, probably, is in radians
#
# The action space, on the contrary is simple viz. 0 = Left, 1 = Right
print(env.observation_space)
print(env.action_space)
act_space = [i for i in range(0,env.action_space.n)]
print(act_space)
# env.unwrapped.get_action_meanings() # AttributeError: 'FrozenLakeEnv' object has no attribute 'get_action_meanings'
print('[ 0 = Left, 1 = Right ]')
print(dir(env))
print(dir(env.unwrapped))
print('States = ',env.unwrapped.observation_space)
print('Actions = ',env.unwrapped.action_space)
num_states = env.observation_space.shape[0]
num_actions = env.action_space.n
# ### 4. Test the environment with Random Action
for i_episode in range(3):
state = env.reset()
tot_reward = 0
steps = 0
while True:
action = env.action_space.sample()
next_state, reward, done, info = env.step(action)
print('[',state,']','->', action,' : [',next_state,']', 'R=',reward)
# env.render()
tot_reward += reward
steps += 1
if done:
print('Episode {:d} finished after {:d} steps with a Total Reward = {:.0f}'.
format(i_episode+1,steps, tot_reward))
break
else:
state = next_state
# Pole angle +/-12 degrees, Cart Pos +/- 2.4 or 200 steps
# Cart Pos, Velocity, Pole Angle, Velocity
# 12 degrees = .2094 radians
# ## Q Learning
# ### Let us implement the Basic Q-Learning Algorithm
# <img src='../Qlearning_Alg.png'>
# ### Step 1 : Define policies
# ## $\epsilon$-Greedy
#
# <img src="../e_greedy.png" >
# +
def choose_e_greedy_action(env,Q,state,epsilon,nA):
action = np.random.choice(np.arange(nA), p=get_probs(Q[state], epsilon, nA)) if state in Q else env.action_space.sample()
return action
def get_probs(Q_s, epsilon, nA):
""" obtains the action probabilities corresponding to epsilon-greedy policy """
policy_s = np.ones(nA) * epsilon / nA
best_a = np.argmax(Q_s)
policy_s[best_a] = 1 - epsilon + (epsilon / nA)
return policy_s
# -
# ### We need to convert the continuous state space to discrete
# +
#discretize the spaces
poleThetaSpace = np.linspace(-0.20943951, 0.20943951, 10)
poleThetaVelSpace = np.linspace(-4, 4, 10)
cartPosSpace = np.linspace(-2.4, 2.4, 10)
cartVelSpace = np.linspace(-4, 4, 10)
def getState(observation):
cartX, cartXdot, cartTheta, cartThetadot = observation
cartX = int(np.digitize(cartX, cartPosSpace))
cartXdot = int(np.digitize(cartXdot, cartVelSpace))
cartTheta = int(np.digitize(cartTheta, poleThetaSpace))
cartThetadot = int(np.digitize(cartThetadot, poleThetaVelSpace))
return (cartX, cartXdot, cartTheta, cartThetadot)
# -
# uses global variavle env
def q_learning(n_episodes=2000, max_t=1000,
epsilon_start=1.0, epsilon_min=0.01, epsilon_decay=0.9995, # 0.995 gets to min by 1000 episodes
alpha=0.01, gamma=1.0):
"""Deep Q-Learning.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
epsilon_start (float): starting value of epsilon, for epsilon-greedy action selection
epsilon_end (float): minimum value of epsilon
epsilon_decay (float): multiplicative factor (per episode) for decreasing epsilon
alpha = step-size parameter
gamma = discount rate
"""
# initialize empty dictionary of arrays
Q = defaultdict(lambda: np.zeros(num_actions))
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
epsilon = epsilon_start # initialize epsilon
has_seen_13 = False
max_score = 0
# loop over episodes
for i_episode in range(1, n_episodes+1):
score = 0
max_steps = 0
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, n_episodes), end="")
sys.stdout.flush()
s_t = env.reset()
a_t = choose_e_greedy_action(env,Q,getState(s_t),epsilon,num_actions)
t = 0
while True:
s_t_d = getState(s_t)
# state, reward, done, info = env.step(action)
s_t_1, reward, done, prob = env.step(a_t)
# print(state,reward,done, prob)
s_t_1_d = getState(s_t_1) # Digitize state
a_t_1 = choose_e_greedy_action(env,Q,s_t_1_d,epsilon,num_actions)
best_a = np.argmax(Q[s_t_1_d])
Q[s_t_d][a_t] = Q[s_t_d][a_t] + alpha * (reward + gamma*(Q[s_t_1_d][best_a]) - Q[s_t_d][a_t])
a_t = a_t_1
s_t = s_t_1
score += reward
max_steps += 1
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
epsilon = max(epsilon*epsilon_decay, epsilon_min) # decrease epsilon
print('\rEpisode : {}\tAverage Score : {:5.2f}\tMax_steps : {}\teps : {:5.3f}\tMax.Score : {:5.3f}'.\
format(i_episode, np.mean(scores_window),max_steps,epsilon,max_score), end="")
if i_episode % 100 == 0:
print('\rEpisode : {}\tAverage Score : {:5.2f}\tMax_steps : {}\teps : {:5.3f}\tMax.Score : {:5.3f}'.\
format(i_episode, np.mean(scores_window),max_steps,epsilon,max_score))
if (np.mean(scores_window)>=195.0) and (not has_seen_13):
print('\nEnvironment solved in {:d} episodes!\tAverage Score: {:5.2f}'.\
format(i_episode-100, np.mean(scores_window)))
# torch.save(agent.qnetwork_local.state_dict(), 'checkpoint.pth')
has_seen_13 = True
if score > max_score:
max_score = score
return scores, Q
# obtain the estimated optimal policy and corresponding action-value function
start_time = time.time()
scores, QVal = q_learning(n_episodes=5000)
# env.close() # Close the environment
print('Elapsed : {}'.format(timedelta(seconds=time.time() - start_time)))
print(datetime.now())
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
print('Max Score {:2f} at {}'.format(np.max(scores), np.argmax(scores)))
print('Percentile [25,50,75] : {}'.format(np.percentile(scores,[25,50,75])))
print('Variance : {:.3f}'.format(np.var(scores)))
for k,v in QVal.items():
print('k={},v={}'.format(k,v))
# Construct the estimated optimal policy
QPolicy={}
for k,v in QVal.items():
QPolicy[k] = [0] * num_actions
QPolicy[k][np.argmax(QVal[k])] = 1
# ### Points to Ponder
# 1. Like our earlier lab we can decay $\epsilon$ in different ways
# 2. Even after 30,000 episodes it doesn't solve the environment.
# * There is opportunity for tweaking
# ## Test our policy
for i_episode in range(2):
state = env.reset()
tot_reward = 0
steps = 0
while True:
if getState(state) in QPolicy:
probs = QPolicy[getState(state)]
else:
print(".")
probs = [1.0/num_actions] * num_actions
action = np.random.choice(np.arange(num_actions), p=probs)
next_state, reward, done, info = env.step(action)
# print('[',state,']',' -> ', action,' = [',next_state,']', reward)
tot_reward += reward
steps += 1
if done:
print('Episode {:d} finished after {:d} steps with a Total Reward = {:.0f}'.
format(i_episode+1,steps, tot_reward))
break
else:
state = next_state
env.close()
# ## _That's all Folks !_
|
solutions/Q_Learning_01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # In this Notebook, We will Predict stock price of Apples using LSTM
# ## Import Neccessary Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# ### Read Dataset
Dataset = pd.read_csv('Datasets/apple_prices.csv')
Dataset
values = Dataset.values
print(values)
values.shape
# +
#values = values.reshape((len(values), 1))
#print(values)
#values.shape
# -
# ### Standardise and Normalize the data
from sklearn.preprocessing import StandardScaler
from math import sqrt
# train the standardization
scaler = StandardScaler()
scaler = scaler.fit(values)
print('Mean: %f, StandardDeviation: %f' % (scaler.mean_, sqrt(scaler.var_)))
# standardization the dataset and print the rows
normalized_dataset = scaler.transform(values)
for i in range(len(Dataset)):
print(normalized_dataset[i])
# inverse transform and print the rows
#inversed_dataset = scaler.inverse_transform(normalized_dataset)
#for i in range(len(Dataset)):
#print(inversed_dataset[i])
# ### Plot the Normalized the data
# lets take a look at our time series
Scaled_dataset = normalized_dataset
plt.plot(Scaled_dataset)
plt.xlabel('time period')
plt.ylabel('normalized series value')
# ### Define function for Window size for the data and return X and Y
def window_size_transforms(Series, Window_size):
X=[]
Y=[]
for item in range(0,len(Series)-Window_size):
X.append(Series[item:item+Window_size])
Y.append(Series[item+Window_size])
X = np.asarray(X)
X.shape = (np.shape(X)[0:2])
Y = np.asarray(Y)
Y.shape = (len(Y),1)
return X,Y
window_size = 5
X,Y =window_size_transforms(Scaled_dataset,window_size)
print(window_size_transforms(Scaled_dataset,window_size))
# ### Split the Dataset into Train and Test Dataset
# +
train_test_split = int(np.ceil(2*len(Y)/float(3))) # set the split point
# partition the training set
X_train = X[:train_test_split,:]
Y_train = Y[:train_test_split]
# keep the last chunk for testing
X_test = X[train_test_split:,:]
Y_test = Y[train_test_split:]
# NOTE: to use keras's RNN LSTM module our input must be reshaped to [samples, window size, stepsize]
X_train = np.asarray(np.reshape(X_train, (X_train.shape[0], window_size, 1)))
X_test = np.asarray(np.reshape(X_test, (X_test.shape[0], window_size, 1)))
# -
# ### Import Libraries for LSTM Neural Network
from keras.models import Sequential
from keras.layers import Dense,LSTM
import keras
# ### Define the Model
Classifier = Sequential()
Classifier.add(LSTM(5,input_shape = (window_size,1)))
Classifier.add(Dense(1))
# ### Define the Optimizer
optimizer = keras.optimizers.RMSprop()
# ### Compile and Fit the Model
Classifier.compile(optimizer=optimizer,loss='mean_squared_error')
Classifier.fit(X_train,Y_train,batch_size=50,epochs=1500)
# ### Predict the data
predict_X_train = Classifier.predict(X_train)
print(predict_X_train.shape)
predict_X_test =Classifier.predict(X_test)
print(predict_X_test.shape)
# ### Print the Trainig and Testing Error of the model
error_trainig = Classifier.evaluate(X_train,Y_train)
error_testing = Classifier.evaluate(X_test,Y_test)
print('Training Error = ' + str(error_trainig))
print('Testing Error = ' + str(error_testing))
# ### Plot the Orginal, Trainig and Testing Data
# +
# plot original series
plt.plot(normalized_dataset,color = 'k')
# plot training set prediction
split_pt = train_test_split + window_size
plt.plot(np.arange(window_size,split_pt,1),predict_X_train,color = 'b')
# plot testing set prediction
plt.plot(np.arange(split_pt,split_pt + len(predict_X_test),1),predict_X_test,color = 'r')
# pretty up graph
plt.xlabel('Day')
plt.ylabel('(normalized) Price of Apple stock')
plt.legend(['Original Series','Training Fit','Testing Fit'],loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
|
Apple_stock_prices.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Rizuuuhhh/CPEN-21A-ECE-2-2/blob/main/Operations_and_Expressions.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Pgh7Q0MX6ybR"
# #Operations and Expressions
# + [markdown] id="i2ayi3Z8sqpS"
# ##Boolean Operators
#
# + colab={"base_uri": "https://localhost:8080/"} id="DEuuECJvstzC" outputId="4f2f3334-2775-481d-b294-08cf12ddecd8"
a = 10
b = 9
c = 8
print (a>b)
c = print (a>b)
print(10>9)
print(10==9)
# + colab={"base_uri": "https://localhost:8080/"} id="wWfTbL9fuCKq" outputId="ce4b040d-b333-47ca-eab5-5acaccfad185"
print(bool("Hello"))
print(bool(15))
print(bool(True))
print(bool(False))
print(bool(1))
print(bool(0))
print(bool(None))
print(bool([]))
# + colab={"base_uri": "https://localhost:8080/"} id="mCiNOChgu3QO" outputId="642ee2c8-9f8f-4d95-828c-0056a407e9ea"
def myFunction(): return True
print(myFunction())
# + colab={"base_uri": "https://localhost:8080/"} id="cAk8j_0VvbGO" outputId="5e8d8ef3-df22-478a-e911-ed7f3991a704"
def myFunction(): return True
if myFunction():
print("True!")
else:
print("False")
# + colab={"base_uri": "https://localhost:8080/"} id="YWMVfyt9v-uM" outputId="47b036e4-da8c-4a30-f3dc-a0cf598fd5ad"
print(10>9)
a=6 #0000 0110
b=7 #0000 0111
print(a==b)
print(6==6)
print(a!=a)
# + [markdown] id="ZapX7V-9w6bT"
# ##Python Operators
# + colab={"base_uri": "https://localhost:8080/"} id="I0hRB2Vxw-Ep" outputId="bc21dc3f-8022-4d8d-96cb-dc9541ad9000"
print(10+5)
print(10-5)
print(10*5)
print(10/5)
print(10%5)
print(10//3)
print(10**2)
# + [markdown] id="F4zZkHm_ydKY"
# ## Bitwise Operators
# + colab={"base_uri": "https://localhost:8080/"} id="MtDwU60TyiVM" outputId="ad319954-a896-4d75-84e3-c106be2fb570"
a= 60 # 0011 1100
b= 13
print(a|b)
print(a^b)
print(~a)
print(a<<2)
print(a>>2) # 0000 1111
# + [markdown] id="wLHgKziI0zbi"
# ##Assignment Operators
# + [markdown] id="PsVT5i0-2ZaN"
# ##Logical Operators
# + colab={"base_uri": "https://localhost:8080/"} id="G5sEDRCt2dHS" outputId="7e981f2a-85b3-461d-c436-9b40774312d7"
a = 6
b = 5
a<b and a==a
print(a>b and a==a)
print(a<b or b==a)
# + [markdown] id="SVrw5Z0O4ZNo"
# ##Identity Operators
# + colab={"base_uri": "https://localhost:8080/"} id="C5MjxER-4c2c" outputId="90596a04-7821-411e-b408-c01a9479e545"
print(a is b)
a is not b
|
Operations_and_Expressions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Support Vector Regression (SVR)
# +
# %matplotlib inline
import matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# +
from sklearn import datasets ## imports datasets from scikit-learn
from sklearn.model_selection import train_test_split
from sklearn import model_selection
from sklearn.svm import SVR #for doing support vector regression
# -
data = datasets.load_boston() ## loads Boston dataset from datasets library
# define the data/predictors as the pre-set feature names
X = pd.DataFrame(data.data, columns=data.feature_names)
# Put the target (housing value -- MEDV) in another DataFrame
Y = pd.DataFrame(data.target, columns=["MEDV"])
#split the data
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = .25, random_state=25) #25% hold out for testing
model = SVR() #variable model stores scikit's SVR model
model.fit(X_train, y_train)
Y_pred = model.predict(X_test) #predicted Y values on the 25% hold out predictor data
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, Y_pred) #MSE
from sklearn.metrics import r2_score
r2_score(y_test, Y_pred)
|
section7/Lecture46.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import tensorflow as tf
import numpy as np
import pandas as pd
from matplotlib import pylab as plt
import os
# %matplotlib inline
# -
# ## 探索数据集
df_train = pd.read_csv('../data/train.csv')
df_test = pd.read_csv('../data/test.csv')
df_train.shape, df_test.shape
df_train.head(1)
df_test.head(1)
df_test.values.max()
df_train.iloc[:, 0].value_counts()
# +
example_imgs = df_test.iloc[:10].values.reshape(-1, 28, 28)
plt.rcParams['figure.figsize'] = (15, 6)
plt.rcParams['image.cmap'] = 'gray'
for index, img in enumerate(example_imgs):
plt.subplot(2, 5, index+1)
plt.imshow(img)
# -
# ## 划分数据集
# +
X_total = df_train.iloc[:, 1:].values.reshape(-1, 28, 28, 1)
Y_total = df_train.iloc[:, 0].values.reshape(-1, 1)
X_test = df_test.values.reshape(-1, 28, 28, 1)
X_total.shape, Y_total.shape, X_test.shape
# -
shuffle_indexs = np.random.permutation(X_total.shape[0])
X_total_shuffle = X_total[shuffle_indexs]
Y_total_shuffle = Y_total[shuffle_indexs]
# +
dev_size = 6000
X_dev = X_total_shuffle[:dev_size]
Y_dev = Y_total_shuffle[:dev_size]
X_train = X_total_shuffle[dev_size:]
Y_train = Y_total_shuffle[dev_size:]
# -
# ## 数据生成器
# #### 数据增强
def data_augmentation(X, Y=None):
if Y is None:
return X
else:
return X, Y
# #### 数据归一化
def normalize_data(X, Y=None):
if Y is None:
return X / 255
else:
return X / 255, Y
# #### mini batch 生成器
def batch_gen(X, Y, batch_size, repeat=1, num_parallels=4, augmentation=False):
m = X.shape[0]
steps_per_epoch = np.ceil(m / batch_size)
if Y is None:
dataset = tf.data.Dataset.from_tensor_slices(X)
else:
dataset = tf.data.Dataset.from_tensor_slices((X, Y))
if augmentation:
dataset = dataset.map(data_augmentation, num_parallels)
dataset = dataset.map(normalize_data, num_parallels)
dataset = dataset.batch(batch_size)
dataset = dataset.shuffle(buffer_size=10000)
dataset = dataset.repeat(repeat)
iterator = dataset.make_one_shot_iterator()
return iterator.get_next(), steps_per_epoch
# ## 构建神经网络
def build_placeholder():
with tf.name_scope('input_placeholder'):
X = tf.placeholder(dtype=tf.float32, shape=(None, 28, 28, 1), name='input_X')
Y = tf.placeholder(dtype=tf.int32, shape=(None, 1), name='lable_Y')
training = tf.placeholder(dtype=tf.bool, name='training')
return X, Y, training
def build_conv_layer(inputs, training, keep_prob, filters, kernel_size, strides, name):
with tf.name_scope('conv_layer_' + name):
Z = tf.layers.conv2d(inputs, filters=filters, kernel_size=kernel_size, strides=strides,
padding='same', use_bias=False,
kernel_initializer=tf.contrib.layers.xavier_initializer_conv2d())
Z_batch_norm = tf.layers.batch_normalization(inputs, training=training)
A = tf.nn.relu(Z_batch_norm)
A_dropout = tf.nn.dropout(A, keep_prob)
return A_dropout
def build_max_pool(inputs, pool_size, strides, name):
with tf.name_scope('max_pool_' + name):
pool = tf.layers.max_pooling2d(inputs, pool_size, strides, name='max_pool')
return pool
def build_flatten_layer(inputs):
with tf.name_scope('flatten_layer'):
flatten = tf.layers.flatten(inputs)
return flatten
def build_softmax_layer(inputs):
with tf.name_scope('softmax_layer'):
Z = tf.layers.dense(inputs, 10, kernel_initializer=tf.contrib.layers.xavier_initializer())
A = tf.nn.softmax(Z)
return Z, A
def build_cost(logits, labels):
with tf.name_scope('cost'):
labels_onehot = tf.one_hot(labels, 10, axis=-1)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=labels_onehot, logits=logits))
return cost
def build_accuracy(outputs, labels):
with tf.name_scope('accuracy'):
predicts = tf.argmax(outputs, axis=-1, output_type=tf.int32)
is_rights = tf.equal(predicts, tf.reshape(labels, (-1,)))
accuracy = tf.reduce_mean(tf.cast(is_rights, tf.float32))
return accuracy
def build_foreward(X, Y, training, keep_prob):
conv1 = build_conv_layer(X, training, keep_prob, 8, (3, 3), (1, 1), '1')
conv2 = build_conv_layer(conv1, training, keep_prob, 8, (3, 3), (1, 1), '2')
max_pool2 = build_max_pool(conv2, (2, 2), (2, 2), '2')
conv3 = build_conv_layer(max_pool2, training, keep_prob, 16, (3, 3), (1, 1), '3')
conv4 = build_conv_layer(conv3, training, keep_prob, 16, (3, 3), (1, 1), '4')
flatten = build_flatten_layer(conv3)
logits, outputs = build_softmax_layer(flatten)
return logits, outputs
CKPT_PATH = './model_save/model.ckpt'
COSTS_PATH = './model_save/costs_save.npy'
ACCS_PATH = './model_save/accs_save.npy'
STEPS_PATH = './model_save/step_save.npy'
# #### 训练
def train(lr, keep_prob, batch_size, epochs, print_step, metrics_step, resume=True):
tf.reset_default_graph()
X_pl, Y_pl, training_pl = build_placeholder()
logits_op, outputs_op = build_foreward(X_pl, Y_pl, training_pl, keep_prob)
cost_op = build_cost(logits_op, Y_pl)
accuracy_op = build_accuracy(outputs_op, Y_pl)
with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
optimizer_op = tf.train.AdamOptimizer(lr).minimize(cost_op)
train_next_op, train_steps_per_epoch = batch_gen(X_train, Y_train, batch_size, epochs, augmentation=True)
dev_next_op, _ = batch_gen(X_dev, Y_dev, batch_size, epochs)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
epoch = 1
step = 1
cost_list = []
acc_list = []
saver = tf.train.Saver()
if resume:
saver.restore(sess, CKPT_PATH)
cost_list = list(np.load(COSTS_PATH))
acc_list = list(np.load(ACCS_PATH))
step = np.load(STEPS_PATH)
epoch = int(np.ceil(step / train_steps_per_epoch)) + 1
try:
while True:
train_X_batch, train_Y_batch = sess.run(train_next_op)
_, cost, train_batch_accuracy = sess.run((optimizer_op, cost_op, accuracy_op), feed_dict={
X_pl: train_X_batch,
Y_pl: train_Y_batch,
training_pl: True
})
if step % print_step == 0:
print('epoch:{0} - step:{1} - cost:{2:.4f} - accuracy:%{3:.2f}'.format(
epoch, step, cost, train_batch_accuracy * 100))
if step % metrics_step == 0:
cost_list.append(cost)
acc_list.append(train_batch_accuracy)
step += 1
if step % train_steps_per_epoch == 0:
epoch += 1
except tf.errors.OutOfRangeError:
pass
saver.save(sess, CKPT_PATH)
np.save(COSTS_PATH, cost_list)
np.save(ACCS_PATH, acc_list)
np.save(STEPS_PATH, step - 1)
sess.close()
return cost_list, acc_list
# #### 参数
LR = 0.0001
KEEP_PROB = 1
BATCH_SIZE = 16
EPOCHS = 5
PRINT_STEP = 500
METRICS_STEP = 100
RESUME = False
costs, accs = train(lr=LR, keep_prob=KEEP_PROB, batch_size=BATCH_SIZE,
epochs=EPOCHS, print_step=PRINT_STEP, metrics_step=METRICS_STEP, resume=RESUME)
# #### 训练曲线
def plot(x, y, xlabel, ylabel, title):
plt.plot(x, y)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.title(title)
x_plot = list(range(1, (len(costs)) * PRINT_STEP, PRINT_STEP))
plot(x_plot, costs, 'steps', 'cost', 'steps - cost')
plot(x_plot, accs, 'steps', 'accuracy', 'steps - accuracy')
# #### 在验证集上评估训练结果
def evaluate(batch_size=16):
tf.reset_default_graph()
X_pl, Y_pl, training_pl = build_placeholder()
logits_op, outputs_op = build_foreward(X_pl, Y_pl, training_pl, 1)
accuracy_op = build_accuracy(outputs_op, Y_pl)
train_next_op, _ = batch_gen(X_train, Y_train, batch_size, 1)
dev_next_op, _ = batch_gen(X_dev, Y_dev, batch_size, 1)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
saver.restore(sess, CKPT_PATH)
train_acc_list = []
dev_acc_list = []
try:
while True:
train_X_batch, train_Y_batch = sess.run(train_next_op)
train_batch_accuracy = sess.run(accuracy_op, feed_dict={
X_pl: train_X_batch,
Y_pl: train_Y_batch,
training_pl: False
})
train_acc_list.append(train_batch_accuracy)
except tf.errors.OutOfRangeError:
pass
try:
while True:
dev_X_batch, dev_Y_batch = sess.run(dev_next_op)
dev_batch_accuracy = sess.run(accuracy_op, feed_dict={
X_pl: dev_X_batch,
Y_pl: dev_Y_batch,
training_pl: False
})
dev_acc_list.append(dev_batch_accuracy)
except tf.errors.OutOfRangeError:
pass
train_acc = np.mean(train_acc_list)
dev_acc = np.mean(dev_acc_list)
print('train_accuracy: %{:.2f}'.format(train_acc * 100))
print('dev_accuracy: %{:.2f}'.format(dev_acc * 100))
sess.close()
evaluate()
# #### 预测
def predict(X, batch_size=16):
tf.reset_default_graph()
X_pl, Y_pl, training_pl = build_placeholder()
_, outputs_op = build_foreward(X_pl, Y_pl, training_pl, 1)
next_op, _ = batch_gen(X, None, batch_size, 1)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
saver.restore(sess, CKPT_PATH)
output_list = []
try:
while True:
X_batch = sess.run(next_op)
output_batch = sess.run(outputs_op, feed_dict={
X_pl: X_batch,
training_pl: False
})
output_list.append(np.argmax(output_batch, axis=-1))
except tf.errors.OutOfRangeError:
pass
sess.close()
return np.concatenate(output_list, axis=0)
predictions = predict(X_test)
predictions.shape
# #### 预测结果写入csv文件
PREDICTIONS_PATH = './test.csv'
def save_predictions_to_csv(predictions, save_path):
df = pd.DataFrame({
'ImageId': np.arange(1, predictions.shape[0] + 1),
'Label': predictions,
})
df.to_csv(save_path, index=False)
return df
pre_df = save_predictions_to_csv(preditions, PREDICTIONS_PATH)
pre_df.head(3)
|
cnn_tensorflow/Digit_Recognizer_CNN_Tensorflow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# We will focus on integers and floating point numbers as an introduction.
# One of the biggest difference between Python 2 and Python 3 is their treatment on division on floating numbers. If you do 3/2 in Python 2, you will get 1.
3/2
2**4 # this means raising the power
# We now study how to assign labels to objects. There are several rules of creating object names. First, names cannot start with a number. Second, there can be no spaces in the names. Symbols are not allowed except underscores. And lastly, it's highly recommend that you use lowercase rather than uppercase.
a=10
a=a+2
a
# There are many built-in functions you can apply to numbers. We will study functions more in detail in the future. For now, we will just use some generic examples:
print(pow(3,2)) # power
print(abs(-47))
print(round(3.1415926,3)) # keep 3 digits
# Now let's learn another function called complex(). This function returns a complex number with the value real + imaginary times little i or converts a string or number to a complex number. If you are doing math or engineering that requires complex numbers (such as dynamics,control systems, or impedance of a circuit) this is a useful tool to have in Python. Notice that in Python, the little 'j' denotes the complex number the squared root of -1. If the imaginary part is omitted, it defaults to zero and the constructor serves as a numeric conversion like int and float. If both arguments are omitted, the function will returns 0j.
z1=complex(3,4)
print(type(z1)) # complex
print(z1)
z2=abs(z1) # absolute value
print(z2)
# We now study 'strings'. To start with, single quotes and double quotes can both be used to create strings. Double quotes can mask single quotes just like in R. The operator '\n' helps break up the line. The '\t' creates blank tabs (5 spaces). Note also that integers and numbers do not have the concepts of length while strings has.
print('This is the first line \nThis is the second line. Note that there are spaces \t Do you see it now?')
len('Hello World!') # note that you cannot do len(23) because integer has no concepts of length
# We now learn indexing. To index a string, Python requires bracket [] and the index always starts from position 0 from the left for default.
x='Hello World!'
print(x[0])
print(x[2])
print(x[-1])
print(x[:3]) # grab everything up to the third index, and 'up to' does not imply 'including'
print(x[:-2]) # grab everyhing up to the second to last letter on the RHS
# Strings are immutable. Once that string is created, the elements within it cannot be changed. However, you can concatecate strings using the plus sign. You can also use the asterisk to tell Python to 'repeat'.
y='<NAME> Peter'
print(x+'!! '+y)
letter='z'
print(letter*5)
# Now let's have a glimpse of some advanced concepts in Python, though we will delay most of the discussions in later lectures. The topic we want to have a mild introduction on is called 'Python method'. Strictly speaking, a **method** is a piece of code that is called by name that is associated with an object. For the most part, every object in Python has its own associated methods. For example, strings have associated methods that can help turn them into upper case, lower case, or proper case etc. In addition, since strings can also be split and counted, there are methods built to split the characters into different parts or to count the number of string characters. In a similar fashion, other types of objects have their own associated methods too. Here let's only focus on strings. For example, the associated methods include upper(), lower(), and split() etc.. In particular, the center() method allows you to place your string 'centered' between a provided string with a certain length. The expandtabs() will expand tab notations "\t" into spaces:
s='i am PeTeR'
print(s)
print(s.upper())
print(s.lower())
print(s.capitalize()) # proper case
print(x.count('o'))
print(x.find('o'))
'hello\thi'.expandtabs()
# Speaking of strings, it's inevitable to talk about a very important concept called 'classes', which is closely related to 'methods' since Python is an object-oriented-programming (OOP) language.
#
# To start with, we need to understand how OOP works. First, **Python objects** are Python’s abstraction for data. All data in a Python program are represented by objects or by relations between objects. Every object has an identity, a type and a value. Thus a string is an object. A number, say 45, is an object. You will see other types of more advanced objects in the future (say lists, dictionaries, sets, functions, modules etc.). An object’s type determines the operations that the object supports (e.g., does it have a length?) and also defines the possible values for objects of that type.
#
# Every object has a type, but the type can be user-defined. A **Python class** is essentially a mechanism Python gives us to create new user-defined types from Python codes. In this sense, a class and a type is extremely similar, except that people often use the class construct in a more general setting to create user-defined types. We will see more concepts like these in the lecture specifically dedicated to studying OOP.
#
# Not unlike the ambiguity between "class" and "type", A **Python instance** is synonymous to "object". Think of it this way: objects are instances of types. So,saying "42 is an instance of the type int" is equivalent to saying "42 is an int object". Many lazy programmers usually use "instance" and "object" interchangeably.
#
# In most respects, a method (associated with its object) is identical to a function except for two key differences. First, it is implicitly passed for the object for which it was called. Second, it is able to operate on data that is contained within the class. We often say that an object is an instance of a class - the class is the definition, the object is an instance of that data.
# We now study formats in Python. There are many ways to do this. The best way is to use the format method. This is the most Pythonic way of coding.
b=29
firstname='Peter'
lastname="Gao"
age=b # b is already defined as 28 previously
print("{0} {1} at the age of {2} was really cool.".format(firstname, lastname, age)) # Python starts counting from 0, not 1
print("{} {} at the age of {} was really cool.".format(firstname, lastname, age)) # the numbers are optional for format methods
print("{firstname} {lastname} at the age of {age} was really smart.".format(firstname="Robert", lastname="Frost", age=21))
print(firstname + ' was ' + str(age) + ' years old.') # the plus sign means concatenation
# Python can also handle more advanced number types. In mathematics and computing, hexadecimal (also base 16, or hex) is a positional numeral system with a 'radix', or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F (or alternatively a, b, c, d, e, f) to represent values ten to fifteen. Hexadecimal numerals are widely used by computer system designers and programmers. As each hexadecimal digit represents four binary digits (bits), it allows a more human-friendly representation of binary-coded values. One hexadecimal digit represents a nibble (4 bits), which is half of an octet or byte (8 bits). Each digit is referred to as a bit. In contrast, a binary number is a number expressed in the binary numeral system or base-2 numeral system which represents numeric values using two different symbols. Python can handle both types of data.
print(hex(246))
print(hex(512))
print(bin(128))
print(bin(12))
|
Lecture 01 Basic Data Types.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# First-class funtions
# +
def factorial(n):
'''return n!'''
return 1 if n < 2 else n * factorial(n-1)
factorial(10)
# -
factorial.__doc__
type(factorial)
help(factorial)
fact = factorial
fact
fact(5)
help(map)
map(factorial, range(11))
list(map(factorial, range(11)))
# Higher-order functions
fruits = ['strawberry', 'fig', 'apple', 'cherry', 'raspberry', 'banana']
sorted(fruits, key=len)
def reverse(word):
return word[::-1]
reverse('testing')
sorted(fruits, key=reverse)
list(map(reverse, fruits))
list(map(fact, range(6)))
list(fact(n) for n in range(6))
[fact(n) for n in range(6)]
list(map(factorial, filter(lambda n: n%2, range(6))))
[fact(n) for n in range(6) if n % 2]
from functools import reduce
from operator import add
reduce(add, range(100))
sum(range(100))
# ### Anonymous functions
# the _lamdba_ keyword create an anonymous function
sorted(fruits, key=lambda word: word[::-1])
[callable(obj) for obj in [str, abs, map, 23]]
# ### User defined callable types
# implement a \_\_call\_\_ instance method
# +
#bingocall.py
import random
class BingoCage:
def __init__(self, items):
# items, any iterable
self._items = list(items)
random.shuffle(self._items) #乱序
def pick(self):
try:
return self._items.pop()
except IndexError:
raise LookupError('pick form empty BingoCage')
def __call__(self): #callable, shortcut to bingo.pick()
return self.pick()
bingo = BingoCage(range(3))
bingo.pick()
# -
bingo()
callable(bingo)
# ### Function introsection
# \_\_call\_\_: the () opertator
# \_\_name\_\_: the function name
#
class C: pass
obj = C()
def func(): pass
sorted(set(dir(func))-set(dir(obj)))
#a sorted list of the attributes that exist in a function but not in an instance of a bare class
# ### Function parameters
# +
def tag(name, *content, cls=None, **attrs):
#*content: list
#**attrs: dict
"""Generate one or more HTML tags"""
if cls is not None:
attrs['class'] = cls
if attrs:
attr_str = ''.join(' %s="%s"' % (attr, value)
for attr, value in sorted(attrs.items()))
else:
attr_str = ''
if content:
return '\n'.join('<%s%s>%s</%s>' % (name, attr_str, c, name) for c in content)
else:
return '<%s%s />' % (name, attr_str)
tag('br')
# -
tag('p', 'hello')
print(tag('p', 'hello', 'world'))
tag('p', 'hello', id=33)
print(tag('p', 'hello', 'world', cls='sidebar', id=33))
tag(content='testing', name="img")
my_tag = {'name': 'img', 'title': 'Sunset Boulevard',
'src': 'sunset.jpg', 'cls': 'framed'}
tag(**my_tag)
# +
#function introspeftion
import bobo
@bobo.query('/')
def hello(person):
return 'hello %s' % person
#bobo -f hello_web.py
# +
#Function to shorten a string by clipping at a space near the desired length
def clip(text, max_len=80):
"""Return text clipped at the last space before or after max_len"""
end = None
if len(text) > max_len:
space_before = text.rfind(' ', 0, max_len)
if space_before >= 0:
end = space_before
else:
space_after = text.rfind(' ', max_len)
if space_after >= 0:
end = space_after
if end is None:
end = len(text)
return text[:end].rstrip()
#Extracting information about the function arguments
from clip import clip
clip.__defaults__
# -
clip.__code__
clip.__code__.co_varnames
clip.__code__.co_argcount
#Extracting the function signature using inspect module
from inspect import signature
sig = signature(clip)
sig
str(sig)
for name, param in sig.parameters.items():
print(param.kind, ':', name, '=', param.default)
sig = signature(tag)
my_tag = {'name':'img', 'title':'Sunset Boulevard', 'src':'sunset.jpg',
'cls':'framed'}
bound_args = sig.bind(**my_tag)
bound_args
for name, value in bound_args.arguments.items():
print(name, '=', value)
del my_tag['name']
bound_args = sig.bind(**my_tag)
# ### Packages for functional programming
# +
#
from functools import reduce
def fact1(n):
return reduce(lambda a, b: a*b, range(1, n+1))
# -
fact1(4)
help(reduce)
# +
from operator import mul
def fact2(n):
return reduce(mul, range(1, n+1))
# -
fact2(4)
# +
metro_data = [
('Tokyo', 'JP', 36.933, (35.689722, 139.691667)),
('Delhi NCR', 'IN', 21.935, (28.613889, 77.208889)),
('Mexico City', 'MX', 20.142, (19.433333, -99.133333)),
('New York-Newark', 'US', 20.104, (40.808611, -74.020386)),
('Sao Paulo', 'BR', 19.649, (-23.547778, -46.635833)),
]
from operator import itemgetter
for city in sorted(metro_data, key=itemgetter(1)):
print(city)
# -
cc_name = itemgetter(1, 0)
for city in metro_data:
print(cc_name(city))
from collections import namedtuple
LatLong = namedtuple('LatLong', 'lat long')
Metropolis = namedtuple('Metropolis', 'name cc pop coord')
metro_areas = [Metropolis(name, cc, pop, LatLong(lat, long))
for name, cc, pop, (lat, long) in metro_data]
metro_areas[0]
metro_areas[0].coord.lat
from operator import attrgetter
name_lat = attrgetter('name', 'coord.lat')
for city in sorted(metro_areas, key=attrgetter('coord.lat')):
print(name_lat(city))
|
notebook/fluent_ch5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from pynq.overlays.base import BaseOverlay
base = BaseOverlay("base.bit")
import time
#init display
from pynq.lib.arduino import Arduino_Displaycam
test = Arduino_Displaycam(base.ARDUINO)
test.init()
test.gpio()
test.pwm()
# +
from pynq.overlays.base import BaseOverlay
base = BaseOverlay("base.bit")
from pynq.lib.arduino import Arduino_SPOT
device = Arduino_SPOT(base.ARDUINO,Arduino_SPOT)
# -
device.clearWindow(1)
# +
from pynq.lib.arduino.spot_device import *
import asyncio
spot = SPOT(device)
spot.start()
# spot.device.setImageAddress()
# for i in range(0,1):
# spot.device.snapPic(100,0)
# #pickle
# spot.radar.savePicture(spot.device.drawAddr, "spottyThotty")
# print('pickled')
# #unpickle
# spot.radar.openPicture(spot.device.drawAddr, "spottyThotty")
# print('unpickled')
# #clear buffer
# for slot in spot.device.drawAddr:
# slot = bytes([0])
# print('cleared buffer')
# #draw
# spot.device.drawImage(100,0)
# print('redrawn')
# while(True):
# print(spot.device.readFromGPS())
# time.sleep(1)
import random
types = ['INTEREST', 'DANGER']
counter = 1
points = [Point('USER_{}'.format(i)) for i in range(0, 10)]
for i in points:
i.tag = 'Obstacle_{}'.format(counter)
i.createdBy = 'CB_{}'.format(counter)
i.distance = 'DISTANCE_{}'.format(counter)
i.type = types[random.randint(0, 1)]
i.currentLocation = (random.randint(-30, 30), random.randint(-30, 30))
counter += 1
spot.radar.addPoint(i)
# #init test points to draw
# point0 = Point('Brandon')
# point0.tag = 'Hot'
# point0.createdBy = '<NAME>'
# point0.distance = 69
# point0.type = 'DANGER'
# point0.currentLocation = (20,0)
# point1 = Point('Saurabh')
# point1.tag = 'Weird'
# point1.createdBy = '<NAME>'
# point1.type = 'INTEREST'
# point1.distance = 420
# point1.currentLocation = (-15,15)
# print(len(spot.radar.points))
# spot.radar.addPoint(point0)
# spot.radar.addPoint(point1)
# print(len(spot.radar.points))
spot.radar.userLocation = (0,0)
#loop testing
# while(True):
# spot.loop()
# time.sleep(0.5)
'''
Types of events:
TOP
BOTTOM
CW
CCW
ERROR
'''
@asyncio.coroutine
def buttonPress(num):
event = 'ERROR'
twistCount = 0
while True:
yield from base.buttons[num].wait_for_value_async(1)
if(num == 3): #01
twistCount = 1
while twistCount == 1: #01
if base.buttons[2].read() and base.buttons[3].read():
twistCount = 2
while twistCount == 2: #11
if base.buttons[2].read() and base.buttons[3].read() == 0:
twistCount = 3
while twistCount == 3: #10
if base.buttons[2].read() == 0 and base.buttons[3].read() == 0:
twistCount = 4
event = 'CCW'
yield from asyncio.sleep(0.1)
base.leds[num].off
elif(num == 2): #10
twistCount = 1
while twistCount == 1: #10
if base.buttons[2].read() and base.buttons[3].read():
twistCount = 2
while twistCount == 2: #11
if base.buttons[2].read() == 0 and base.buttons[3].read():
twistCount = 3
while twistCount == 3: #01
if base.buttons[2].read() == 0 and base.buttons[3].read() == 0:
twistCount = 4
event = 'CW'
while base.buttons[num].read() == 1:
base.leds[num].toggle()
yield from asyncio.sleep(0.1)
base.leds[num].off
elif(num == 1):
event = 'TOP'
while base.buttons[num].read():
base.leds[num].toggle()
yield from asyncio.sleep(0.1)
base.leds[num].off()
elif(num == 0):
event = 'BOTTOM'
while base.buttons[num].read():
base.leds[num].toggle()
yield from asyncio.sleep(0.1)
base.leds[num].off()
else:
event = 'ERROR'
spot.on_event(event)
tasks = [asyncio.ensure_future(buttonPress(i)) for i in range(4)]
# +
# '''
# self.write_TAG(100, 310)
# self.write_DISTANCE(100, 360)
# self.write_CB(100, 410)
# self.write_TYPE()
# '''
# device.clearAll()
# time.sleep(0.05)
# point = spot.radar.points[2]
# device.drawInfoState()
# if(point.type == 'DANGER'):
# device.write_CUSTOM(point.type, 200, 265, 0xf800) # Variable type
# else:
# device.write_CUSTOM(point.type, 200, 265, 0x07e8) # Variable type
# device.write_CUSTOM(point.tag, 190, 315, 0xffff) # Variable tag
# device.write_CUSTOM(str(point.distance) + ' meters', 270, 365, 0xffff) # Variable distance
# device.write_CUSTOM(point.createdBy, 300, 415, 0xffff) # Variable c/b
# +
@asyncio.coroutine
def txRead():
txc = 0
while True:
yield from asyncio.sleep(0.1)
while(device.hasMessages()):
val = device.readFromTX()
txc += 1
if(txc == 600):
txc = 0
break
# print(val);
tasks.append(asyncio.ensure_future(txRead()))
# +
@asyncio.coroutine
def loop():
while True:
yield from asyncio.sleep(0.3)
spot.loop()
tasks.append(asyncio.ensure_future(loop()))
# +
# @asyncio.coroutine
# def gpsSend():
# while True:
# yield from asyncio.sleep(3)
# gpsLoc = device.readFromGPS()
# if(gpsLoc[0] != None):
# gpsString = "g," + str(round(gpsLoc[0], 6)) + "," + str(round(gpsLoc[1], 6))
# print(gpsString)
# device.writeToTX(4, gpsString)
# tasks.append(asyncio.ensure_future(gpsSend()))
# +
# import psutil
# @asyncio.coroutine
# def print_cpu_usage():
# # Calculate the CPU utilisation by the amount of idle time
# # each CPU has had in three second intervals
# last_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
# while True:
# yield from asyncio.sleep(3)
# next_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
# usage = [(1-(c2-c1)/3) * 100 for c1,c2 in zip(last_idle, next_idle)]
# print("CPU Usage: {0:3.2f}%, {1:3.2f}%".format(*usage))
# last_idle = next_idle
# tasks.append(asyncio.ensure_future(print_cpu_usage()))
# -
if base.switches[0].read():
print("Please set switch 0 low before running")
else:
# spot.loop()
base.switches[0].wait_for_value(1)
|
Pynq_Neil_Copy_05.23/jupyter_notebooks/base/arduino/Testing/State Machine Test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="EpJAJBvziTTP"
# ### Post processing: ner-multi-fast
# + colab={"base_uri": "https://localhost:8080/"} id="-v1nfkf8OOaz" executionInfo={"status": "ok", "timestamp": 1617665263167, "user_tz": -120, "elapsed": 584, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="95edd094-733b-4538-ff0c-3122d27fd6e7"
# Import general modules for data processing
import pandas as pd
print("Succesfully imported necessary modules")
# + colab={"base_uri": "https://localhost:8080/"} id="pXbD87jnOOa2" executionInfo={"status": "ok", "timestamp": 1617665264419, "user_tz": -120, "elapsed": 1831, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="aa395968-7f1e-4477-efd3-77399747a893"
# Enable save and load to Google Drive
from google.colab import drive
drive.mount('/content/drive', force_remount=True)
# + id="cZ6lQULR1MN9"
# load corpus file
infile = '/content/drive/My Drive/e_rara_fulltexts/bernensia/corpus_bernensia_ger_LOC_ner-multi-fast-full-4.csv'
with open(infile, 'r') as f:
state = pd.read_csv(f, encoding="UTF-8", nrows=122)
# + colab={"base_uri": "https://localhost:8080/", "height": 739} id="ktAJ9_lfPBMu" executionInfo={"status": "ok", "timestamp": 1617665264427, "user_tz": -120, "elapsed": 1831, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="5693a124-69d9-479e-f169-34a9e2d1db7b"
state[100:122]
# + id="k-o3kVd6NLyd"
# load corpus file
infile = '/content/drive/My Drive/e_rara_fulltexts/bernensia/corpus_bernensia_ger_LOC_flair-ner-multi-fast-123.csv'
with open(infile, 'r') as f:
state1 = pd.read_csv(f, encoding="UTF-8", skiprows=[i for i in range(1,123)], nrows=8) # , skiprows=[i for i in range(1,51)]
# + id="7sOhui0vAg-P"
state1 = state1.rename(columns={"flair-ner-multi-fast": "ner-multi-fast"})
# + colab={"base_uri": "https://localhost:8080/", "height": 300} id="VYZaJcETG7wO" executionInfo={"status": "ok", "timestamp": 1617665264882, "user_tz": -120, "elapsed": 2279, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="01e8ef09-50ed-4780-ac84-f7c31b59fe7b"
state1
# + id="ejOMS1yytUjn"
# load corpus file
infile = '/content/drive/My Drive/e_rara_fulltexts/bernensia/corpus_bernensia_ger_LOC_flair-ner-multi-fast-130.csv'
with open(infile, 'r') as f:
state2 = pd.read_csv(f, encoding="UTF-8", skiprows=[i for i in range(1,131)]) # , skiprows=[i for i in range(1,51)]
# + id="SntcIWHbRhfN"
state2 = state2.rename(columns={"flair-ner-multi-fast": "ner-multi-fast"})
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="SxJjudirt7kE" executionInfo={"status": "ok", "timestamp": 1617665264884, "user_tz": -120, "elapsed": 2273, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="3571de9c-98af-42ac-894d-cf462dd8354f"
state2
# + id="H51bWsCG3_3_"
result = pd.concat([state, state1, state2], ignore_index=True, sort=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="qi_ziR2Y4Erj" executionInfo={"status": "ok", "timestamp": 1617665264884, "user_tz": -120, "elapsed": 2268, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="183b004d-a0de-42f1-bd64-0831b6bf20ba"
result[100:140]
# + [markdown] id="cuW-Z9aoCJVf"
# #### Aliging LOCs: flair
# + [markdown] id="WOyp0KM1hvmW"
# #### Clean brackets out: flair
# + id="ZbUkVj2zBwz4"
def remove_brackets(text):
brackets = ['[',']']
text_clean = [c for c in text if c not in brackets]
text_clean = ''.join(text_clean)
return text_clean
# + colab={"base_uri": "https://localhost:8080/"} id="Y7sD78IEB6IB" executionInfo={"status": "ok", "timestamp": 1617665264885, "user_tz": -120, "elapsed": 2265, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="db976b51-d104-467e-b147-acc69a67d196"
# remove brackets from LOCs
#result['ner-multi-fast_clean'] = ''
for i in result.index[123:133]:
clean_text = remove_brackets(result['ner-multi-fast'][i])
result['ner-multi-fast_clean'][i] = clean_text
# + colab={"base_uri": "https://localhost:8080/"} id="3Pk19xFcJoTg" executionInfo={"status": "ok", "timestamp": 1617665265849, "user_tz": -120, "elapsed": 3227, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="3f7d6383-4f12-47ac-e850-e396d4d3fa6c"
# Write to Google Drive
# %cd /content/drive/My\ Drive/e_rara_fulltexts/bernensia
outfile = "./corpus_bernensia_ger_LOC_ner-multi-fast-full-2.csv"
with open(outfile, "w") as f:
result.to_csv(f, index=False, columns=['e_rara_id', 'ner-multi-fast', 'ner-multi-fast_clean'])
# %cd /content/
print("Saved to Google Drive.")
# + colab={"base_uri": "https://localhost:8080/"} id="8GD4ZyoEU0FP" executionInfo={"status": "ok", "timestamp": 1617665265849, "user_tz": -120, "elapsed": 3225, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="f9c9b295-c6ee-4c51-91f4-1c94134f7a46"
test = remove_brackets(state['ner-multi-fast'][10])
print(test)
# + id="HB-lk2oy3WlL" colab={"base_uri": "https://localhost:8080/", "height": 190} executionInfo={"status": "error", "timestamp": 1617665266142, "user_tz": -120, "elapsed": 3517, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="7adbaf4c-7f93-484e-b632-e5a572eaf3e6"
# NOT IN USE
state = state.join(state50.set_index('e_rara_id'), on='e_rara_id')
# + [markdown] id="AHHQ5DM4h2bM"
# #### Read out compound entities: flair
#
# + id="PWywG4-SCuhs"
# load LOC file
infile = '/content/drive/My Drive/e_rara_fulltexts/bernensia/corpus_bernensia_ger_LOC_ner-multi-fast-full-2.csv'
with open(infile, 'r') as f:
state = pd.read_csv(f, encoding="UTF-8")
# + id="qRFxtAxVjQsp"
import re
def concat_loc(text):
pattern = r'[^a-zA-Z0-9,\x7f-\xff\s]'
text = re.sub(pattern, '', text)
text = re.sub(', BLOC,', '', text)
text = re.sub('SLOC,', '', text)
text = re.sub('ELOC,', '', text)
return text
# + id="RofhhbcXFaLX"
# concatenate LOCs
#result['ner-multi-fast_concat'] = ''
for i in result.index[123:133]:
concat = concat_loc(result['ner-multi-fast_clean'][i])
result['ner-multi-fast_concat'][i] = concat
# + id="-OY-bXG83C0S"
result[100:140]
# + id="CbUGecZBLGvK"
# Google Drive
# %cd /content/drive/My\ Drive/e_rara_fulltexts/bernensia
outfile = "./corpus_bernensia_ger_LOC_ner-multi-fast-full-5.csv"
with open(outfile, "w") as f:
result.to_csv(f, index=False)
# %cd /content/
print("Saved to file to Google Drive.")
# + [markdown] id="yDxcCHJBXvHP"
# ### Post processing: dbmdz-historic-ner-onb
# + colab={"base_uri": "https://localhost:8080/"} id="cske5V6_XvHQ" executionInfo={"status": "ok", "timestamp": 1619121201290, "user_tz": -120, "elapsed": 1058, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="e42c1ae7-f7ab-40bd-950a-0c2c0852d5bc"
# Import general modules for data processing
import pandas as pd
print("Succesfully imported necessary modules")
# + colab={"base_uri": "https://localhost:8080/"} id="K9OTEqTaXvHS" executionInfo={"status": "ok", "timestamp": 1619121242926, "user_tz": -120, "elapsed": 33521, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="c2c2f7ed-c299-4dcc-df3e-9c0fc6bb8842"
# Enable save and load to Google Drive
from google.colab import drive
drive.mount('/content/drive', force_remount=True)
# + id="btrj7wZ5XvHT" executionInfo={"status": "ok", "timestamp": 1619122176541, "user_tz": -120, "elapsed": 807, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}}
# load corpus file
infile = '/content/drive/My Drive/e_rara_fulltexts/bernensia/corpus_bernensia_ger_LOC_dbmdz-historic-ner-onb-I.csv'
with open(infile, 'r') as f:
state = pd.read_csv(f, encoding="UTF-8")
# + colab={"base_uri": "https://localhost:8080/", "height": 677} id="s_74GvlFXvHT" executionInfo={"status": "ok", "timestamp": 1619122179393, "user_tz": -120, "elapsed": 1156, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="fd940bc8-304a-4fc3-e6b2-ebaabf33bbb6"
state[50:70]
# + [markdown] id="2YWw8lXsXvHY"
# #### Aliging LOCs: flair
# + id="MO4Ppye8MlbK" executionInfo={"status": "ok", "timestamp": 1619122185134, "user_tz": -120, "elapsed": 875, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}}
result = state
# + [markdown] id="AbM9p9C6XvHY"
# #### Clean brackets out: flair
# + id="yx8-y0vuXvHY" executionInfo={"status": "ok", "timestamp": 1619122186880, "user_tz": -120, "elapsed": 943, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}}
def remove_brackets(text):
brackets = ['[',']']
text_clean = [c for c in text if c not in brackets]
text_clean = ''.join(text_clean)
return text_clean
# + colab={"base_uri": "https://localhost:8080/"} id="foSwFTmJXvHZ" executionInfo={"status": "ok", "timestamp": 1619122196169, "user_tz": -120, "elapsed": 1188, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="96323902-ef08-4b53-f12e-1738f55241de"
# remove brackets from LOCs
result['historic-ner-onb_clean'] = ''
for i in result.index[0:60]:
clean_text = remove_brackets(result['historic-ner-onb'][i])
result['historic-ner-onb_clean'][i] = clean_text
# + colab={"base_uri": "https://localhost:8080/", "height": 363} id="fpIRReVtQEHu" executionInfo={"status": "ok", "timestamp": 1619123025758, "user_tz": -120, "elapsed": 612, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="356ba7a5-28d9-42c8-c9f6-12d35b5c4f4c"
result[55:65]
# + [markdown] id="sUCtUZo_XvHb"
# #### Read out compound entities: flair
#
# + id="DYRTacVwXvHb" executionInfo={"status": "ok", "timestamp": 1619123035676, "user_tz": -120, "elapsed": 1078, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}}
import re
def concat_loc(text):
pattern = r'[^a-zA-Z0-9,\x7f-\xff\s]'
text = re.sub(pattern, '', text)
text = re.sub(', BLOC,', '', text)
text = re.sub('SLOC,', '', text)
text = re.sub('ELOC,', '', text)
return text
# + id="B0-EDHkVXvHc" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1619123088496, "user_tz": -120, "elapsed": 902, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="6db96b3f-50f0-4e33-b2ad-6819669b72d7"
# concatenate LOCs
result['historic-ner-onb_concat'] = ''
for i in result.index[0:60]:
concat = concat_loc(result['historic-ner-onb_clean'][i])
result['historic-ner-onb_concat'][i] = concat
# + colab={"base_uri": "https://localhost:8080/", "height": 363} id="n8RaE4eqQb5X" executionInfo={"status": "ok", "timestamp": 1619123222106, "user_tz": -120, "elapsed": 865, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgeucoVZdbDUDaaQBWBqFxRyP4yjPAl18LuuUrz=s64", "userId": "18347744419010233607"}} outputId="4893399a-de0f-4b4d-be1d-f34461944491"
result[55:65]
# + id="7Y64NP5ZXvHd"
# Google Drive
# %cd /content/drive/My\ Drive/e_rara_fulltexts/bernensia
outfile = "./corpus_bernensia_ger_LOC_dbmdz-historic-ner-onb-I-full.csv"
with open(outfile, "w") as f:
result.to_csv(f, index=False)
# %cd /content/
|
code/Flair_postprocessing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Методы анализа неоднородных данных
# ## Домашнее задание 5 (сдаваемое). Модели с фиксированными эффектами
# ## Deadline: 23.59 3 апреля
#
# Задание выполняется на базе данных hw5.dta. Краткое описание данных:
#
# * county - номер округа штата Северная Каролина
# * year - год
# * lncrime - натуральный логарифм числа преступлений на человека
# * lnpolice - натуральный логарифм числа полицейских на душу населения
# * lndensity - натуральный логарифм плотности населения
#
# ## Задание 1
#
# Рассмотрим парную регрессионную модель для оценивания взаимосвязи логарифма числа преступлений на человека (зависимая переменная) и логарифма числа полицейских на душу населения (предиктор). Так как данные панельные, оценить классическую "объединенную" модель на всей выборке некорректно. Можно воспользоваться уже знакомой Вам моделью с фиксированными эффектами (имеется в виду базовая модель с разными константами для пространственных единиц). Оценивать такую модель на практике мы пока с Вами не учились, но на данном этапе это и не нужно.
# * Ваша задача - получить FE-оценку (FE = fixed-effects) коэффициента при предикторе "логарим числа полицейских на душу населения" на основе взвевешенных оценок коэффициента при данном предикторе, полученных при оценивании регрессионной модели на отдельных подвыборках (в качестве подвыборки в данном случае выступает округ Северной Каролины)
# * Опишите, что выступает в качестве "веса" для оценок коэффициентов
# * Объясните алгоритм Ваших действий для получения нужной FE-оценки
import pandas as pd
import numpy as np
import statsmodels.formula.api as sm
# +
df = pd.read_stata('hw5.dta')
df.head()
# -
df['year'] = pd.Categorical(df.year)
df['county'] = pd.Categorical(df.county)
# __FE-estimate__ = weighted sum of coefficients estimated on subsample regressions, where __weights__ is a vector of "group variance" (variance of the predictor in a group) divided by the sum of all group variances.
# +
samples_coef = []
group_variance = []
# run regressions for counties separetely
for i in df['county'].unique():
# save estimated `lnpolice` coefficients
samples_coef.append(sm.ols(formula = 'lncrime ~ lnpolice',
data = df.loc[df['county'] == i]).fit().params[1]) # lnpolice coef
# save group variance
group_variance.append(np.var(np.array(df.loc[df['county'] == i, 'lnpolice'])))
# -
sum(samples_coef * (group_variance/sum(group_variance)))
# ##### Check the results on estimated FE model
FE_ols = sm.ols(formula = 'lncrime ~ lnpolice + C(county)', data = df).fit()
FE_ols.params[-1] # lnpolice coef
# ## Задание 2
#
# Проделайте то же самое упражнение, но уже для случая множественной регрессии. Добавьте в Вашу модель переменную "натуральный логарифм плотности населения" в качестве контрольной переменной.
#
# * Получите FE-оценку коэффициента при предикторе "натуральный логарифм числа преступлений на человека"
# * Объясните, что изменилось в алгоритме действия для получения нужной оценки в случае множественной регрессии
# To derive this estimate one can use the __Frisch–Waugh–Lovell (FWL) theorem__.
# Theorem (from Greene, 2012): "in the linear least squares regression of vector y on two sets of variables, X1 and
# X2, the subvector b2 is the set of coefficients obtained when the residuals from a regression of y on X1 alone are regressed on the set of residuals obtained when each column of X2 is regressed on X1."
#
#
# Imagine you're more a 'dirty pool' guy and detest fixed effects. Then the FWL-based algorithm of finging a `lnpolice` coefficient will be as follows:
# #### The algorithm FWL + FE-estimator (find `lnpolice` coef)
# +
# x_1 = lnpolice
# x_2 = lndensity
reg1 = sm.ols(formula = 'lncrime ~ lndensity', data=df).fit().resid # Qy
reg2 = sm.ols(formula = 'lnpolice ~ lndensity', data=df).fit().resid # QX
# assume that the intersept is a part of x_1, we would regress it only once
b = pd.DataFrame(np.column_stack((np.array(reg1), np.array(reg2))), columns=['res1','res2']) # data
fin = sm.ols('res1 ~ res2', data=b).fit()
fin.params # lnpolice coef
# -
# ##### Check it!
sm.ols(formula = 'lncrime ~ lnpolice + lndensity', data=df).fit().params
# However, we would prefer to account for the spacial heterogeneity. Let's add some fixed effects in a subtle way!
df['Qy'] = reg1
df['QX'] = reg2
# +
samples_coef_DVA = []
group_var_police = []
# run regressions for counties separetely
for i in df['county'].unique():
# save estimated `lnpolice` coefficients
final = sm.ols(formula = 'Qy ~ QX',
data = df.loc[df['county'] == i]).fit()
samples_coef_DVA.append(final.params[1]) # lnpolice coef
# save group variance
group_var_police.append(np.var(np.array(df.loc[df['county'] == i, 'QX'])))
#group_var_police.append(np.var(np.array(final.resid)))
# -
sum(np.array(samples_coef_DVA) * (np.array(group_var_police)/sum(np.array(group_var_police))))
# ##### Check the results on estimated FE model
FE_ols_DVA = sm.ols(formula = 'lncrime ~ lnpolice + lndensity + C(county)', data = df).fit()
FE_ols_DVA.params[-2] # lnpolice coef
# ## Задание 3 (самое важное)
#
# Сделайте выводы:
# * Какие пространственные единицы получают больший, а какие - меньший вес при получении FE-оценки? Критически оцените такую процедуру взвешивания.
# * На практике мы, как правило, получаем FE-оценки, запуская автоматический алгоритм. Тем не менее, каким образом исследователю может быть полезно знание о процедуре получения FE-оценки? Порассуждайте о том, какое смещение мы получаем в результате оценивания FE-модели вместо оценивания классической регрессионной модели на отдельных подвыборках.
#
# Делаем выводы:
#
# * Больший вес получают пространственные единицы с большей условной внутригрупповой вариацией по остаткам 'lnpolice'. Большая вариация несет больше информации, поэтому логично, что она должна сильнее влиять на итоговую оценку коэффициента -- вариацию в данных мы и хотим объяснить.
# * FE-estimator приведет к смещению в случае отсутсвия внутригрупповой вариации по показателю -- коэффициенты при таких группах обнулятся и не будут влиять на итоговый коэффициент при предикторе в FE-модели. То есть перед выбором в пользу и оценкой FE модели стоит посмотреть на внутрегрупповые вариации по показателю == посмотреть на особенность данных, построить графики с распределениями переменных
|
Multilevel reg. FWL and FE-estimator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example notebook
#
# > Time series classification with [tsai](). Papersweep will call this notebook and run it with multiple times with different parameters of the dataset and the architecture
# papermill parameters (this cell is tagged as 'parameters' in Jupyter)
install_deps = True
stable = True # True: latest version, False: stable version
# +
import sys
ISCOLAB = 'google.colab' in sys.modules
if ISCOLAB or install_deps:
if stable:
# !pip install tsai -q
else:
# !pip install git+https://github.com/timeseriesAI/tsai.git -q
import tsai
from tsai.all import *
print('tsai :', tsai.__version__)
print('fastai :', fastai.__version__)
print('fastcore :', fastcore.__version__)
print('torch :', torch.__version__)
# -
import wandb
from fastai.callback.wandb import *
wandb.init()
wandb.config.dsid = ifnone(wandb.config.get('dsid'), 'NATOPS')
X, y, splits = get_UCR_data(wandb.config.dsid, return_split=False)
tfms = [None, [Categorize()]]
dsets = TSDatasets(X, y, tfms=tfms, splits=splits, inplace=True)
dls = TSDataLoaders.from_dsets(dsets.train, dsets.valid, bs=[64, 128], batch_tfms=[TSStandardize()], num_workers=0)
wandb.config.arch = ifnone(wandb.config.get('arch'), 'InceptionTime')
k = {}
model = create_model(eval(wandb.config.arch), dls=dls, **k)
learn = Learner(dls, model, metrics=accuracy)
learn.fit_one_cycle(5, lr_max=1e-3, cbs=[WandbCallback()])
learn.recorder.plot_metrics()
|
_example_tsai.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Alignment and centrality
#
# #### In this notebook, we estimate alignment in conversations and quantify to which amount alignment is influenced by the centrality of the interlocutors.
# ---
# +
import pickle
import dill
import numpy as np
import pandas as pd
import pymc3 as pm
from collections import defaultdict, Counter
import utils
from talkpages import WikiCorpusReader, WikiCorpus
from alignment import Alignment
# %matplotlib inline
import matplotlib.pyplot as plt
# -
# > The conversations are taken from a selection of 10 topics from the Controversial TalkPages corpus.
TOPICS = ['religion',
'science',
'politics',
'history',
'people',
'philosophy',
'sports',
'linguistics',
'psychiatry',
'environment']
# > To count alignment, we use a selection of marker categories and tokens from the LIWC dictionaries. There is no overlap between any two categories due to some preprocessing (`marker selection.ipynb`).
# +
META_CATEGORIES = {'stylistic': [
'articles',
'negations',
'prepositions',
'numbers',
'pronouns'
],
'rhetoric': [
'tentative',
'certainty',
'discrepancy',
'inclusive',
'exclusive'
],
'discursive': [
'causation',
'insight',
'inhibition',
'communication',
'cognitive process',
'sensory process',
'motion'
],
'stance': [
'optimism',
'anger',
'anxiety',
'sadness'
]}
# Keep a list of category names for convenience.
CATEGORY_LIST = []
for cats in META_CATEGORIES.values():
CATEGORY_LIST.extend(cats)
# Load the filtered lists of markers.
with open('../../data/liwc/final.dict', 'rb') as f:
MARKER_DICT = pickle.load(f)
marker_list = []
for markers in MARKER_DICT.values():
marker_list.extend(markers)
MARKER_LIST = list(set(marker_list))
# -
# ----
# > We focus on `category-not-word` alignment to exclude cases of lexical repetition ([Doyle & Frank 2016](http://www.aclweb.org/anthology/P16-1050), pp. 531-532).
# +
MODE = 'category'
# MODE = 'cnw'
MAX_ITERS = 100000
N_SAMPLES = 4000
TRACE_SIZE = 1000
CAUCHY_ALPHA = -2
CAUCHY_BETA = 3
# -
for TOPIC in TOPICS:
print('{}\n{}'.format(TOPIC, '*'*15))
# Load category-not-word alignment counts (Doyle & Frank, 2016)
with open('./counts-{}/{}.dill'.format(MODE, TOPIC), 'rb') as f:
N_base_all, N_align_all, C_base_all, C_align_all, _, _, dyad2strength, _ = dill.load(f)
# Statistical modelling
for c, category in enumerate(CATEGORY_LIST):
print('{}, {}\n{}'.format(TOPIC, category, '*'*30))
# Data
N_base, N_align, C_base, C_align = [], [], [], []
tie_strengths = []
# collect the counts for this category of markers
for dyad in N_base_all:
if C_base_all[dyad][c] > N_base_all[dyad][c]:
continue
if C_align_all[dyad][c] > N_align_all[dyad][c]:
continue
try:
tie_strengths.append(dyad2strength[dyad])
except KeyError:
continue
N_base.append(N_base_all[dyad][c])
C_base.append(C_base_all[dyad][c])
N_align.append(N_align_all[dyad][c])
C_align.append(C_align_all[dyad][c])
if not any(N_base):
print('N_base: all zeros.')
if not any(N_align):
print('N_align: all zeros.')
if not any(C_align):
print('C_align: all zeros.')
if not any(C_base):
print('C_base: all zeros.')
if not (any(N_base) or any(N_align) or any(C_align) or any(C_base)):
continue
tie_strengths = utils.standardise(tie_strengths)
# A simple logistic model
with pm.Model() as model:
# Parameters
beta0 = pm.Cauchy('baseline intercept', alpha=CAUCHY_ALPHA, beta=CAUCHY_BETA)
alpha0 = pm.Normal('alignment intercept', mu=0, sd=0.25)
alpha1 = pm.Normal('coefficient tie-strength', mu=0, sd=1)
# Include a guessing coefficient for robust logistic regression
# (cfr. <NAME>, 2014, 'Doing Bayesian data analysis', pp. 635-636)
guess = pm.Beta('guessing coefficient', alpha=1, beta=9)
# Transformed parameters
mu_base = guess * 0.5 + (1-guess) * pm.math.invlogit(beta0)
mu_align = guess * 0.5 + (1-guess) * pm.math.invlogit(beta0+alpha0 + alpha1*tie_strengths)
# Model
base_count = pm.Binomial('C_base' , p=mu_base , observed=C_base, n=N_base)
align_count = pm.Binomial('C_align', p=mu_align, observed=C_align, n=N_align)
# Inference
with model:
print(model.check_test_point())
approx = pm.fit(n=MAX_ITERS, method='advi',
callbacks=[pm.callbacks.CheckParametersConvergence(diff='absolute')])
print('Sampling {} ...'.format(N_SAMPLES), end=' ')
full_trace = approx.sample(draws=N_SAMPLES)
print('Done.')
trace = full_trace[-TRACE_SIZE:]
trace_df = pm.trace_to_dataframe(trace)
trace_df.to_csv('./traces/{}/tiestrength/{}-{}.csv'.format(MODE, TOPIC, category))
print(pm.summary(trace))
pm.traceplot(trace, varnames=['baseline intercept',
'alignment intercept',
'coefficient tie-strength',
'guessing coefficient'])
plt.savefig('plots/traceplots/{}/tiestrength/{}-{}.pdf'.format(MODE, TOPIC, category))
pm.plot_posterior(trace)
plt.savefig('plots/posteriors/{}/tiestrength/{}-{}.pdf'.format(MODE, TOPIC, category))
# + active=""
# for TOPIC in TOPICS:
#
# print('{}\n{}'.format(TOPIC, '*'*15))
#
# # Load dataframes with precomputed marker counts
# csv_filename = './with_counts/{}_fullcounts.csv'.format(TOPIC)
# corpus = WikiCorpus(csv_filename)
#
# # Obtain dataframe of conversational turns
# turns = corpus.reply_pairs()
#
# # Generate network of TalkPages users
# # (bool) prune: prune to the largest connected component?
# users = corpus.get_users()
# net = corpus.social_network(prune=False)
#
# # Compute centrality for each user and include into the dataframe of reply pairs
# corpus.assign_tie_strength()
#
# # Initialise alignment tracker
# al = Alignment(corpus, MARKER_DICT)
#
# # Compute category-not-word alignment counts (Doyle & Frank, 2016)
# N_base_all, N_align_all, C_base_all, C_align_all, _, _, dyad2strength = al.counts(mode='category-not-word',
# all_info=True)
#
#
# # Statistical modelling
# for c, category in enumerate(CATEGORY_LIST):
#
# print('{}, {}\n{}'.format(TOPIC, category, '*'*30))
#
# # Data:
# # collect the counts for this category of markers
# N_base, N_align, C_base, C_align = [], [], [], []
# tie_strengths = []
#
# for dyad in N_base_all:
# N_base.append(N_base_all[dyad][c])
# C_base.append(C_base_all[dyad][c])
# N_align.append(N_align_all[dyad][c])
# C_align.append(C_align_all[dyad][c])
#
# tie_strengths.append(dyad2strength[dyad])
#
#
# # Transformed data
# N_base = utils.standardise(N_base)
# C_base = utils.standardise(C_base)
# N_align = utils.standardise(N_align)
# C_align = utils.standardise(C_align)
#
#
# # A simple logistic model.
# with pm.Model() as model:
# # Parameters
# beta0 = pm.Cauchy('baseline intercept', alpha=0, beta=2.5)
# alpha0 = pm.Normal('alignment intercept', mu=0, sd=0.25)
# alpha1 = pm.Normal('coefficient tie-strength', mu=0, sd=1)
#
# # Include a guessing coefficient for robust logistic regression
# # (cfr. <NAME>, 2014, 'Doing Bayesian data analysis', pp. 635-636)
# guess = pm.Beta(alpha=1, beta=9)
#
# # Transformed parameters
# mu_base = guess * 0.5 + (1-guess) * pm.math.invlogit(beta0)
# mu_align = guess * 0.5 + (1-guess) * pm.math.invlogit(beta0+alpha0 + alpha1*tie_strengths)
#
# # Model
# base_count = pm.Binomial('C_base' , p=mu_base , observed=C_base, n=N_base)
# align_count = pm.Binomial('C_align', p=mu_align, observed=C_align, n=N_align)
#
#
# # Inference
# with individual_model:
# start = pm.find_MAP()
# step = pm.NUTS(scaling=start)
#
# out_db = pm.backends.Text('./traces-tiestrength/{}-{}'.format(TOPIC, category))
#
# trace = pm.sample(draws=2000,
# random_seed=13,
# progressbar=True,
# tune=500,
# chains=4,
# trace=out_db)
#
#
|
src/LRAM - tie strength.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] colab_type="text" id="9yupXUk1DKOe"
# # MNIST from scratch
#
# This notebook walks through an example of training a TensorFlow model to do digit classification using the [MNIST data set](http://yann.lecun.com/exdb/mnist/). MNIST is a labeled set of images of handwritten digits.
#
# An example follows.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" id="sbUKaF8_uDI_" outputId="67a51332-3aea-4c29-8c3d-4752db08ccb3"
from __future__ import print_function
from IPython.display import Image
import base64
Image(data=base64.decodestring("iVBORw0KGgoAAAANSUhEUgAAAMYAAABFCAYAAAARv5krAAAYl0lEQVR4Ae3dV4wc1bYG4D3YYJucc8455yCSSIYrBAi4EjriAZHECyAk3rAID1gCIXGRgIvASIQr8UTmgDA5imByPpicTcYGY+yrbx+tOUWpu2e6u7qnZ7qXVFPVVbv2Xutfce+q7hlasmTJktSAXrnn8vR/3/xXmnnadg1aTfxL3/7rwfSPmT+kf/7vf098YRtK+FnaZaf/SS++OjNNathufF9caiT2v/xxqbTGki/SXyM1nODXv/r8+7Tb+r+lnxZNcEFHEG/e3LnpoINXSh/PWzxCy/F9eWjOnDlLrr/++jR16tQakgylqdOWTZOGFqX5C/5IjXNLjdt7/NTvv/+eTjnllLT//vunr776Kl100UVpueWWq8n10lOmpSmTU5o/f0Fa3DDH1ry9p0/++eefaZ999slYYPS0005LK664Yk2eJ02ekqZNnZx+XzA/LfprYgGxePHitOqqq6YZM2akyfPmzUvXXXddHceoic2EOckxDj300CzPggUL0g033NC3OKy00krDer3pppv6FgcBIjvGUkv9u5paZZVVhoHpl4Mvv/wyhfxDQ0NZ7H7EQbacPHny39Tejzj88ccfacqUKRmHEecYf0Nr8GGAQJ8gMHCMPlH0QMzmEBg4RnN4DVr3CQIDx+gTRQ/EbA6BgWM0h9egdZ8g8PeliD4RutfF/Ouvfz9OtZy8aNGiNH/+/GGWl1122XzseYuVNKtqsaI23Ghw0DYCA8doG8JqO+AUG2+8cVq4cGHaY4890vLLL5/WXXfdfI6jvPDCC3lJ8amnnkoezP3000/pl19+GThHtWpIPekYomTxFS7HnkqKjMsss0yGgFE4r62tSBFVJ02aNPyconi9V4/JwzHwT9ZNNtkkeZ6w5ZZbph133DH99ttv6ccff8zXX3nllcRRnHNfv2cNGMQWGRaOrWbUrjsGBRLAA6U4Lhoqw9h2223ztRBq6aWXzsbgvueffz4Lu9NOO2UnYTgrr7xy7tO9nOH111/Pbb744ov0ww8/jAvngAdFMvQDDjggG/0GG2yQX1GZNm1aziCCwzrrrJPl3muvvXKwePnll9M333wzHDCKWPbLMbuAkfISjnvvvXcW/emnn85lqCBqa4a65hiYR/Gk2RNGRlwm3n7ggQfmdrKD9sqJtdZaKxvCnDlz8n3Tp09PXmPYeuutc0SVNQjvnmuvvTa3efzxx9N33303PGZ5rF75DBvvqq233nrp22+/TWeddVbyikpgxCE4vQDhlQUBRfDw2esbs2fPTquvvnqviNN1PuIdJ4GErVx44YUZowsuuCB9+umn6eeff84BspmsWqljhPFDxjGGYx/lDkN33udajCoVlAjRzl4U8LjefRwnPjsXG8OJqKBd8NB1LTU5IHyCd7LJGOYXNoGjFqaGIKtrERDIDKtukfGMH/zRZa1A101+YBF44KfMYzO8VOYYjDWiukiGqc022yyXOUqdzTffPJ/z1ialeqNVxA9gi0wzlOJ5juJlR8JeddVV+ZrIKTq4ZvJp/8EHH+SU+txzz+W2SqmxVFZRplrH5DTRXmGFFdKuu+6azjjjjOzosl5g6D54CQCI4mGjhNQO5occckh2LvLTA6fqJOEnyhU6kNlkZmUuvrtNcFx77bUzhsZWXgoSsm6t4Dsa/tp2DErCmA04HAI4FLjaaqtlBhmnSKiNY4rDtHZFB6jFMMH0RVDH+nCPYxtDCFJnKkniRbDitWjTK3sykQUuMLPn3DZGX8SFnCG/fVyz5zCCBtIHTLshdzif8fERn8cKXxjCNOwCTu3Qf6yqhV4AQokiP489//zzM0DxnQYKwqAtIkko1kQzFFxvaNcJ6u3Pe+65J/cRRvDee+9lA2BInIyRff/997nNO++8k7t0vl2A6vHWynmyiPJ43WKLLbIijz/++LTddtvlTCdzwIWSg9yjxBJ0GN/DDz+c7zv77LOzbEceeWSekwVGgsOsWbNyNo0+qt7DfPvtt8/dmtvIGnPnzk3PPPPMsJ6rHrNef/BBeJA90RprrJEDcNhctMkXR/mnbccwuCjNGTbaaKMc8TBZprITxOdgOvbuKxqGz6LSJ598kseJ9Gi1CYmSv/76a3YyJZWMZJ6Ceskp8EMusihFEAyUmVaa8G2rxTNHIrd733///eH7YeaLNe5xrEzlWNF/HqQDf0Tm+GIbvYdD43MsKAIo/JDgE0G5aFfN8NaWYxiUshikqGYTTUSt0TCkjXsYNqJQQso+rgGa0vX58ccf56hQTtk+48F92rmvlnE1A0on2uKP0Yrw+Nxzzz0zn+ZhjKwRXq6vueaa2TmUiRQfS7SyNeMks9IV9vrvJOl/q622yo4Mfw5Pvm6TMclLdit6shh+YAMnq1E29tEsteUYBgMSgxa5MOAzJZcVXQs4bUR8XxhCHIwzMALCBuCcx5q0tF3u133l8XrRMchFiRYNyMxBKM/5IjZlWVzjULKwACISytIWFsi56aab5mvOKyEikmdAO/iHY+BDCRUZuoPD1e1akECyLseA7d13352DhdKak8Cmlt3U7TSl9p58FwejYK8ncAwKpDTnGDcARbWiAUjHiNEHsITSPlagpEZChcfrZzwSOfBOiQwXLuR3PjAhtwAD08iAMCO/a+5xPTIm3ALjwERf0V+c69QeT7ZujVdLDhgKBrANXAMreMESRkU7rdVPrXNtZ4xIpSLH1VdfnR3j4IMPzkbw2Wefpa+//jovo5188slZsZjArAcvFP3YY4+lSy+9NEdTdTTy0I5xHHfccfm1CH2LtuORKEqmkwVlVU+sBY+IdJRmE0zeeOONnEXuu+++7AhnnnlmWn/99XMJ5brtzTffzHMJx/o555xzkgdb0U8rRtAKrnTYqtG1Ml6teyxInHDCCdlGYByBmG2Z97ChVvFo2zEwbHCRTbqP7EDxPjN2pUBEe86AXAcsg+f10TYMSTvnRM1ulQe1wG/nHEXZZEJZUIYQ5cgWMsEgMgqclFdkdh+MbFFyuddnWMLNfTYkcuuXHlBkpFYNI3dS+mMMfCHHsZWadfUjmQVn8iLywscG21apMscQwR555JEM3KuvvpoZ5LHOmzgjAvBwzFt2/Oijj3Lm4Ayin/MU/eGHH+b2N998c/5MGSaZ44nw7OEd5Rx77LE5+1EehYXxkpes5li2K6+8Mhv8Lrvsko381ltvzcEBfvHQKh5auk9GPvHEE3NJAx+/eKL/HXbYIQcbK3nwN067xAk4s5VHdbvsx0nxrYQeKxJMZAfBA7GlRx99NC9EtCN7JY4RoPBeAHIAyrB3jpHYwqu1d02d7HpZcfqINo5dL7eJMXtxTzk2sgWFM/gcsnCakI2cFOk+523O+Qw7WaeYHYpYRp9xn4BkbPdWSfgJXYYM+ne+2xRj2sdx8EDu8rm4Ntp9pY4RSmb0CIPOAVNGoLA47yU4S2xen37ppZdy9CkLE/3lm8bJHzJbbiavt2Q9p7AkK7oyXAZOLk7gs9c4PJC0AOE8DDyrgJkaWgYQkSPYuAdpWySfteU8HhqKouYq+io6ZfGeZo7xpbT1+jt+jGULfprpq922ePHMBibwjWVq523KVrzBsIzTaMeu1DFi0HI0YyyYtAekY5MltbRyihFJiROBKIYTwMCTWJNubwdQFCXFapK9z96mtbjgs3thFKWnUgjBzNZIya5FOyUcPG36q4LwRgZ6Ix8HtBk3tirGGU0feAkslHfk5PzBh2cXSkvtWqWOOEaRGcoSHdXDMoYn1tK8yaON0ahbCWgFS/vxSnjn5F4ItLeiFAGAzCKc7MDA1OlIjc4pLFKE7FEyxb5ZPNTbtuiv2fvrtddfOFsYXcwj8d8qv/XGq3femLvvvnvOvrIYPPEjG+PDseDbDnXcMXiyiGiyyACOPvrovN95552zV3/++ef5zVveznlEo6CICvG5l/d4JSvHP+qoo7JjKDs4PkVSGPm9HSz9W5rlPEoCQYHjVFXyRGnBOcKA28VOP/qTBWX6YnS2IKB8qYL/enyGHPbKziOOOCLj6sGeslGW8L6Y4ANr2MY99fpsdL7jjmFwkSTSr6gDVCk+tmDQedcJ5LgdwaLPbu7xjJRRNlErSsiQhVHJlOEQoh182o1wRTnharwYs3itnWP9Rd/RD5mLW5yveh/YRhYMjItyBh/wjPat8tEVx6B00RKo5513XpIl7rzzzuwEourMmTOz95uIcyBfTSXYiy++mCOrSFS1klsFrNZ9eGPoJtmeyRx00EE5cpGbIi21XnbZZbkMee2117KMHIKMIVcotVb/vXoOz6I0+URoMlVFcBFE7L1+IjNYIo6v/fo+D3tC+FCR+FHuwNUCgfOtUlccI5hnJMoIBhN1sBICqMoNNaLP3pkiFGciIIBC4HaEbRWk0dyHb3Mp/EY0I6+NsytvyKxsKhpQr8ozGpm1IZ8IbV+PyllGuyh1YBXXOQEcy6R8M5eAHzuxxX3GRvbaCKJ4aRfXrjkG5jEbk00Prxi8SZTJKmc5/PDDc5v99tsvC+hBjWtqStmD0F4Ma1foMvDtfqZMUc3/lYjMSFFW3NS7JtyyoKzSiTocHoFJHMc+MlK7Mta7n9NbATJerbEYvQWIWCVitIyaXrV3nsG7H2Y2GVcbxyj6NX+waKEPmOvbfShwtjhQDDz5Ygt/uuoY+OPtnICDEMBTWsAQUu0NBBsDEgFEWOADAiDaVRERWsCq5i34IRN+TbTJgn8KwzOFuR4KDUXW7Kyik53Ep8w/+RkxWeO5S1EM5wVABguXMGp69dk1x87D0ObdL32GHI5tsDQGHtwbm/Hw4TpnKvNY5Ge0x113DEwT3tIsIdSnDIfxcxJAevCHfE9cXcmotHXfAw88kIFUdgFjLMn4HuZRuh9FExmjRCCnZxRqcPxz8ioUVk9eRhJkPAYHV8ZVFRkjjFSfAtw222yTy2OZ0iv15fHcQ4dKaMcwsBdEEL26RzaIh5+yK7LSBGPno8yOZX+vzRhfXzZ8cRrtyzzkzpr803XHwB8wTJYIRol+VY8zqMMBbP0f+cExE1qTdbU7x3jwwQdzVBYdesExKNiEWx2MfwoOAyCbJ9uRHZvUTcPmsENhGNE4HBKOHKNqZzQu3KNfX9H1nRABQZlbNkpt4SNo4DWIIesDj9qYnwki2giWqol3330348kZLPm7xvi1Pffcc7MzhA3gy/0oeIuxWtmPiWNgNCIFYwcCAa2FA1ikJZz1aeUVsBmge9TyoqGoIqKUFdEKCFXcU0/pHJizVMUnXBiBh6IicdTTzsEOnuZkDE/2rcJI4KMf/TF+0TucwDhkZ+DGL4/nGkPGV/AIC+2RvfP6ZPTI4gu5XNM/Um7RPzuIFyn1zW7wpQ9UHj+fbOHPmDlGCOGBGIeQQfwuq0jnISBQfOHft7JEHN94Q5xF6XLFFVfkyKIEGyuiGAo3r6BIx0imcM6k+6GHHspOEQbcDq+UTl4BwRu7PstUiPEJFsa9/PLL83nXg6d2xnUvoxS5L7744uGyh/wyRpRF9YwSHsHjE088kWWADQeRFThZkTgBstensZG5h4m56oEdcAp9CwTOVUlj6hgECcGBpA6XDazeiLKhVABQAhKB3cNxbEAL4KoEppm+gjf3OMafDf+UW7zeTL/ltqIiAxBMOIIxnLOHgbFsMGQ4InhE0nJfrXw2hnIRD3SFBKmYWDfqE49woFvOzZno3NxM0HDciMjBDsjEBgLTsJHYN+qjmWtj7hjBLKFFQgL7qRz14jHHHJPBcC2M3wRPVDT5ohzZRv0Z16O/sdozAKmdopUH5kftTrzJpl+lk29CcgpLw3BgpMbwwqF/S80pGJ6xO0WM+8Ybbxw2TuOEoTYakwyovB/JKdzDMVQOHvCRzXju890fL11aGhcMqqIxdwwCRkYQDZAaE7lWBhyosQEmQM439MgffDHm0Si8EcuBC0ezcQSZVKYktzFEW+3sfQ4natRvu9eMTS9F7IvHo+m/2fb6LNuCc0WsW+mzHq9j6hgE9YCHp5tkez2EAVjlMOmyUlU2Lis8ygVR0rykyoltPZCaOY9fr32Qp50X6xi7pWCGbsHBvwLgGIcddljGxvcsjOU1GseyiKjJQWydpiqNsBlei85BfhNxeJunVCl31x0jBOMAjJ9jRC3OEERDS7QMI0qQohIYgLSq7FJuMZbi9WZA7kRbvFAWx5Dyy449mjEDG/dyDPW4VSiy2iNvBcCSUdxyyy35OYHrqJUx843j8I/qQpA074BVVdR1x+AIHCIiIGewsqIuds41tSSlOxeOFHuOQ/E+2zPEuFYVKM32U3RMvGy44YbZMTg2B2+GOIXXJcjpR9lkUy/QyZ7GUU8zAD9RCiuR0oQYVv1IMAk7qFL+rjkGg7GZQPLufffdN69QKJtkCAKKjNGu1p7gMgWDYEDRpkpAmu0rnMLehie/RavcI49Sr1ZW0w6V91ac/IsxmdHPB0U5pQ+4+TExDudNUhPufnaKIn7N6m2k9h11jKLRqP+UQJb2eHh4uYjK0LW1D0MpCq0NR4g24RTR/0hCdvM6/m14FtljeTL4D/liedFeO7LYcyh7eMGDY8X16IM8Vp9kWjj2GwWG5IZb2FKVOHTMMTCvDKBgD2Z22223bNynnnpqVrZXBFxjQDZUFJiwIqKHN8qHO+64IxvN/fffn9vG/VWC0UpfeC5uZMEbg/ctM/8SzYOxZ599Nhs4ebSx0ECpcDFvMCdRggkesoQ+zaHU0N4EgAEnue2227JTON+LgaEVDFu5h+w2Wdl33GFkEUIQqYIqdYwwbJGO8q2xOydqUiTFWpJVPzsuUwhlzzFETxlGdFSCqaMB4XwvUzgKWU3AyW4uwFns4QMbilUyxbq8p/4cw3UEB8FDGQUDx/acqB8zRS2dw5qthe3VatPKucocg6JiYu3lP2nfawvekKVITzgJQLH24QTBtPZeE2D89957b27jwZ1IwIm8R2OMWHmJ+3pxTzaK8l+HyMrgTzrppMxqOIEsGoZvz0nsyWiliRMUl2G9aOk6POyLZVUvYtBpniL4wA1m9lVSW46BOQqKpTLK9FnUsxftvW4swssa4dkhCGFCMNfcp08lhM9KKc4h0obgsa8ShHb6Cv5DJnu8IwHB9TB852DkOlzIRV6kXbSVMfQj48BWdhE0TLr1Fe3zQR/+gRMK5yjuq4KjZccQ2SlYjexHmCnSkiLjtsesmlnpQ5naFo1A5GMAHoJxBI709ttv54ygntZWmWEcQMS9VQleRT9kNmfAG0P3HRPGbHnVudg4gEyJOAYiE0wikHAAcxHyxndO4KI/WHEK/Qzo7wjAXfaFNdurikaNtIERRTqmYIYdE2tGEs8hfJ8iFB/3xV67MCjG8NZbb6Unn3wyC+XfDxfnDxFp496qhK6qn5CDA5twK/fIRH5Gb0MMOhxCFgkKjOBoHqKEkmWvueaanG04iTHcP3CKQO0/e3ZhgceP2smqcKyKRuUYlEKhPDL+d5z1c4qVFTDnmBIZMwZ9DiKAzTmvCetPNFR7W7fXXt/KLddqTcyjr17bRybkEF5XiQhPHnMuDlF07MCB3I49l4EDxTrnfsFBJBxQbQSKeGoROqjdurWzIzoGJqRxS2KUf/rpp2flcRDRjRKVCdpFhCwz7rOVKE5z++235/7uuuuuXDq5P5yKEY0np8B3TKb9K1/vLTF0/7MiJtyRPYrq4fx+7R2e7vFDDzDyfx1goPwcUGMEYG/rFI3oGAYW0UUyimQIcRwGzbgpVsZAUTYE065xCtc5GUeSHTyg4kzKs/FKoSBljyhvTz6y2gseZAwlwgI+cNBGtpV9ZRj4BobjFY9O8g0bQcXWaRpxBE5hHuFnJ0XB6dOn56ge2QGDlK2dFSSG4b8kxVzEdSWGVxgYQLzrxJkIGgbTaUE73b9MZ/KNfIMOJpdcckndYZWmFAwv+wgydW/o8wsCK3xnz56dFzx8oxPGtk7QiI5h0FBaeGzRKYIpjDN2ig6lB9OiprmI60qNieIMIXvsQy7yotjH9eI+2hbPDY4bI8D+2JdnWTYY+iwDs78qaUTHEM0sI1pClAVMnqX9ImGQszB6DHoNOLzZNZlGRlEq9JNB9JOsRXvoxDGnsDTudwFUHTNmzMjDqEaU9xYvGgWiZnka0TEo16CeNyCM1SLtwmt5cNEoCOUa5xjQAIFWEGBP5rbKdTRr1qwcfGUMthXVTCt917pnRMdwE6ZiQm0JckADBMYCgWLwtXjTSeq/d5Y7ieag7wmDwMAxJowqB4JUicDAMapEc9DXhEFgcjxcM7vvR4on7bHS1q84WNkpUr/iEL+aOLRw4cIlQCmuIhUBmsjHlpQ9c7EmzjEsN1vd6DeCg8UVT+qRd7b6EQey8wMT+6El8RSu36xhIO8AgQYI9F94bADG4NIAgUDg/wHX+3lgThDIegAAAABJRU5ErkJggg==".encode('utf-8')), embed=True)
# + [markdown] colab_type="text" id="J0QZYD_HuDJF"
# We're going to be building a model that recognizes these digits as 5, 0, and 4.
#
# # Imports and input data
#
# We'll proceed in steps, beginning with importing and inspecting the MNIST data. This doesn't have anything to do with TensorFlow in particular -- we're just downloading the data archive.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 110, "status": "ok", "timestamp": 1446749124399, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="w5vKZqr6CDz9" outputId="794eac6d-a918-4888-e8cf-a8628474d7f1"
import os
from six.moves.urllib.request import urlretrieve
SOURCE_URL = 'http://yann.lecun.com/exdb/mnist/'
WORK_DIRECTORY = "/tmp/mnist-data"
def maybe_download(filename):
"""A helper to download the data files if not present."""
if not os.path.exists(WORK_DIRECTORY):
os.mkdir(WORK_DIRECTORY)
filepath = os.path.join(WORK_DIRECTORY, filename)
if not os.path.exists(filepath):
filepath, _ = urlretrieve(SOURCE_URL + filename, filepath)
statinfo = os.stat(filepath)
print('Succesfully downloaded', filename, statinfo.st_size, 'bytes.')
else:
print('Already downloaded', filename)
return filepath
train_data_filename = maybe_download('train-images-idx3-ubyte.gz')
train_labels_filename = maybe_download('train-labels-idx1-ubyte.gz')
test_data_filename = maybe_download('t10k-images-idx3-ubyte.gz')
test_labels_filename = maybe_download('t10k-labels-idx1-ubyte.gz')
# + [markdown] colab_type="text" id="gCtMhpIoC84F"
# ## Working with the images
#
# Now we have the files, but the format requires a bit of pre-processing before we can work with it. The data is gzipped, requiring us to decompress it. And, each of the images are grayscale-encoded with values from [0, 255]; we'll normalize these to [-0.5, 0.5].
#
# Let's try to unpack the data using the documented format:
#
# [offset] [type] [value] [description]
# 0000 32 bit integer 0x00000803(2051) magic number
# 0004 32 bit integer 60000 number of images
# 0008 32 bit integer 28 number of rows
# 0012 32 bit integer 28 number of columns
# 0016 unsigned byte ?? pixel
# 0017 unsigned byte ?? pixel
# ........
# xxxx unsigned byte ?? pixel
#
# Pixels are organized row-wise. Pixel values are 0 to 255. 0 means background (white), 255 means foreground (black).
#
# We'll start by reading the first image from the test data as a sanity check.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 57, "status": "ok", "timestamp": 1446749125010, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//<KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="P_3Fm5BpFMDF" outputId="c8e777e0-d891-4eb1-a178-9809f293cc28"
import gzip, binascii, struct, numpy
import matplotlib.pyplot as plt
with gzip.open(test_data_filename) as f:
# Print the header fields.
for field in ['magic number', 'image count', 'rows', 'columns']:
# struct.unpack reads the binary data provided by f.read.
# The format string '>i' decodes a big-endian integer, which
# is the encoding of the data.
print(field, struct.unpack('>i', f.read(4))[0])
# Read the first 28x28 set of pixel values.
# Each pixel is one byte, [0, 255], a uint8.
buf = f.read(28 * 28)
image = numpy.frombuffer(buf, dtype=numpy.uint8)
# Print the first few values of image.
print('First 10 pixels:', image[:10])
# + [markdown] colab_type="text" id="7NXKCQENNRQT"
# The first 10 pixels are all 0 values. Not very interesting, but also unsurprising. We'd expect most of the pixel values to be the background color, 0.
#
# We could print all 28 * 28 values, but what we really need to do to make sure we're reading our data properly is look at an image.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 887, "status": "ok", "timestamp": 1446749126640, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": <KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="F_5w-cOoNLaG" outputId="77dabc81-e3ee-4fcf-ac72-88038494fb6c"
# %matplotlib inline
# We'll show the image and its pixel value histogram side-by-side.
_, (ax1, ax2) = plt.subplots(1, 2)
# To interpret the values as a 28x28 image, we need to reshape
# the numpy array, which is one dimensional.
ax1.imshow(image.reshape(28, 28), cmap=plt.cm.Greys);
ax2.hist(image, bins=20, range=[0,255]);
# + [markdown] colab_type="text" id="weVoVR-nN0cN"
# The large number of 0 values correspond to the background of the image, another large mass of value 255 is black, and a mix of grayscale transition values in between.
#
# Both the image and histogram look sensible. But, it's good practice when training image models to normalize values to be centered around 0.
#
# We'll do that next. The normalization code is fairly short, and it may be tempting to assume we haven't made mistakes, but we'll double-check by looking at the rendered input and histogram again. Malformed inputs are a surprisingly common source of errors when developing new models.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 531, "status": "ok", "timestamp": 1446749126656, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="jc1xCZXHNKVp" outputId="bd45b3dd-438b-41db-ea8f-d202d4a09e63"
# Let's convert the uint8 image to 32 bit floats and rescale
# the values to be centered around 0, between [-0.5, 0.5].
#
# We again plot the image and histogram to check that we
# haven't mangled the data.
scaled = image.astype(numpy.float32)
scaled = (scaled - (255 / 2.0)) / 255
_, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(scaled.reshape(28, 28), cmap=plt.cm.Greys);
ax2.hist(scaled, bins=20, range=[-0.5, 0.5]);
# + [markdown] colab_type="text" id="PlqlwkX-O0Hd"
# Great -- we've retained the correct image data while properly rescaling to the range [-0.5, 0.5].
#
# ## Reading the labels
#
# Let's next unpack the test label data. The format here is similar: a magic number followed by a count followed by the labels as `uint8` values. In more detail:
#
# [offset] [type] [value] [description]
# 0000 32 bit integer 0x00000801(2049) magic number (MSB first)
# 0004 32 bit integer 10000 number of items
# 0008 unsigned byte ?? label
# 0009 unsigned byte ?? label
# ........
# xxxx unsigned byte ?? label
#
# As with the image data, let's read the first test set value to sanity check our input path. We'll expect a 7.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 90, "status": "ok", "timestamp": 1446749126903, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/<KEY>k/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="d8zv9yZzQOnV" outputId="ad203b2c-f095-4035-e0cd-7869c078da3d"
with gzip.open(test_labels_filename) as f:
# Print the header fields.
for field in ['magic number', 'label count']:
print(field, struct.unpack('>i', f.read(4))[0])
print('First label:', struct.unpack('B', f.read(1))[0])
# + [markdown] colab_type="text" id="zAGrQSXCQtIm"
# Indeed, the first label of the test set is 7.
#
# ## Forming the training, testing, and validation data sets
#
# Now that we understand how to read a single element, we can read a much larger set that we'll use for training, testing, and validation.
#
# ### Image data
#
# The code below is a generalization of our prototyping above that reads the entire test and training data set.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}]} colab_type="code" executionInfo={"elapsed": 734, "status": "ok", "timestamp": 1446749128718, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="ofFZ5oJeRMDA" outputId="ff2de90b-aed9-4ce5-db8c-9123496186b1"
IMAGE_SIZE = 28
PIXEL_DEPTH = 255
def extract_data(filename, num_images):
"""Extract the images into a 4D tensor [image index, y, x, channels].
For MNIST data, the number of channels is always 1.
Values are rescaled from [0, 255] down to [-0.5, 0.5].
"""
print('Extracting', filename)
with gzip.open(filename) as bytestream:
# Skip the magic number and dimensions; we know these values.
bytestream.read(16)
buf = bytestream.read(IMAGE_SIZE * IMAGE_SIZE * num_images)
data = numpy.frombuffer(buf, dtype=numpy.uint8).astype(numpy.float32)
data = (data - (PIXEL_DEPTH / 2.0)) / PIXEL_DEPTH
data = data.reshape(num_images, IMAGE_SIZE, IMAGE_SIZE, 1)
return data
train_data = extract_data(train_data_filename, 60000)
test_data = extract_data(test_data_filename, 10000)
# + [markdown] colab_type="text" id="0x4rwXxUR96O"
# A crucial difference here is how we `reshape` the array of pixel values. Instead of one image that's 28x28, we now have a set of 60,000 images, each one being 28x28. We also include a number of channels, which for grayscale images as we have here is 1.
#
# Let's make sure we've got the reshaping parameters right by inspecting the dimensions and the first two images. (Again, mangled input is a very common source of errors.)
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{}, {}]} colab_type="code" executionInfo={"elapsed": 400, "status": "ok", "timestamp": 1446749129657, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": <KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="0AwSo8mlSja_" outputId="11490c39-7c67-4fe5-982c-ca8278294d96"
print('Training data shape', train_data.shape)
_, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(train_data[0].reshape(28, 28), cmap=plt.cm.Greys);
ax2.imshow(train_data[1].reshape(28, 28), cmap=plt.cm.Greys);
# + [markdown] colab_type="text" id="cwBhQ3ouTQcW"
# Looks good. Now we know how to index our full set of training and test images.
# + [markdown] colab_type="text" id="PBCB9aYxRvBi"
# ### Label data
#
# Let's move on to loading the full set of labels. As is typical in classification problems, we'll convert our input labels into a [1-hot](https://en.wikipedia.org/wiki/One-hot) encoding over a length 10 vector corresponding to 10 digits. The vector [0, 1, 0, 0, 0, 0, 0, 0, 0, 0], for example, would correspond to the digit 1.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 191, "status": "ok", "timestamp": 1446749131421, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": <KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="9pK1j2WlRwY9" outputId="1ca31655-e14f-405a-b266-6a6c78827af5"
NUM_LABELS = 10
def extract_labels(filename, num_images):
"""Extract the labels into a 1-hot matrix [image index, label index]."""
print('Extracting', filename)
with gzip.open(filename) as bytestream:
# Skip the magic number and count; we know these values.
bytestream.read(8)
buf = bytestream.read(1 * num_images)
labels = numpy.frombuffer(buf, dtype=numpy.uint8)
# Convert to dense 1-hot representation.
return (numpy.arange(NUM_LABELS) == labels[:, None]).astype(numpy.float32)
train_labels = extract_labels(train_labels_filename, 60000)
test_labels = extract_labels(test_labels_filename, 10000)
# + [markdown] colab_type="text" id="hb3Vaq72UUxW"
# As with our image data, we'll double-check that our 1-hot encoding of the first few values matches our expectations.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 127, "status": "ok", "timestamp": 1446749132853, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//<KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="uEBID71nUVj1" outputId="3f318310-18dd-49ed-9943-47b4aae7ee69"
print('Training labels shape', train_labels.shape)
print('First label vector', train_labels[0])
print('Second label vector', train_labels[1])
# + [markdown] colab_type="text" id="5EwtEhxRUneF"
# The 1-hot encoding looks reasonable.
#
# ### Segmenting data into training, test, and validation
#
# The final step in preparing our data is to split it into three sets: training, test, and validation. This isn't the format of the original data set, so we'll take a small slice of the training data and treat that as our validation set.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 176, "status": "ok", "timestamp": 1446749134110, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": <KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="e7aBYBtIVxHE" outputId="bdeae1a8-daff-4743-e594-f1d2229c0f4e"
VALIDATION_SIZE = 5000
validation_data = train_data[:VALIDATION_SIZE, :, :, :]
validation_labels = train_labels[:VALIDATION_SIZE]
train_data = train_data[VALIDATION_SIZE:, :, :, :]
train_labels = train_labels[VALIDATION_SIZE:]
train_size = train_labels.shape[0]
print('Validation shape', validation_data.shape)
print('Train size', train_size)
# + [markdown] colab_type="text" id="1JFhEH8EVj4O"
# # Defining the model
#
# Now that we've prepared our data, we're ready to define our model.
#
# The comments describe the architecture, which fairly typical of models that process image data. The raw input passes through several [convolution](https://en.wikipedia.org/wiki/Convolutional_neural_network#Convolutional_layer) and [max pooling](https://en.wikipedia.org/wiki/Convolutional_neural_network#Pooling_layer) layers with [rectified linear](https://en.wikipedia.org/wiki/Convolutional_neural_network#ReLU_layer) activations before several fully connected layers and a [softmax](https://en.wikipedia.org/wiki/Convolutional_neural_network#Loss_layer) loss for predicting the output class. During training, we use [dropout](https://en.wikipedia.org/wiki/Convolutional_neural_network#Dropout_method).
#
# We'll separate our model definition into three steps:
#
# 1. Defining the variables that will hold the trainable weights.
# 1. Defining the basic model graph structure described above. And,
# 1. Stamping out several copies of the model graph for training, testing, and validation.
#
# We'll start with the variables.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 2081, "status": "ok", "timestamp": 1446749138298, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="Q1VfiAzjzuK8" outputId="f53a39c9-3a52-47ca-d7a3-9f9d84eccf63"
import tensorflow as tf
# We'll bundle groups of examples during training for efficiency.
# This defines the size of the batch.
BATCH_SIZE = 60
# We have only one channel in our grayscale images.
NUM_CHANNELS = 1
# The random seed that defines initialization.
SEED = 42
# This is where training samples and labels are fed to the graph.
# These placeholder nodes will be fed a batch of training data at each
# training step, which we'll write once we define the graph structure.
train_data_node = tf.placeholder(
tf.float32,
shape=(BATCH_SIZE, IMAGE_SIZE, IMAGE_SIZE, NUM_CHANNELS))
train_labels_node = tf.placeholder(tf.float32,
shape=(BATCH_SIZE, NUM_LABELS))
# For the validation and test data, we'll just hold the entire dataset in
# one constant node.
validation_data_node = tf.constant(validation_data)
test_data_node = tf.constant(test_data)
# The variables below hold all the trainable weights. For each, the
# parameter defines how the variables will be initialized.
conv1_weights = tf.Variable(
tf.truncated_normal([5, 5, NUM_CHANNELS, 32], # 5x5 filter, depth 32.
stddev=0.1,
seed=SEED))
conv1_biases = tf.Variable(tf.zeros([32]))
conv2_weights = tf.Variable(
tf.truncated_normal([5, 5, 32, 64],
stddev=0.1,
seed=SEED))
conv2_biases = tf.Variable(tf.constant(0.1, shape=[64]))
fc1_weights = tf.Variable( # fully connected, depth 512.
tf.truncated_normal([IMAGE_SIZE // 4 * IMAGE_SIZE // 4 * 64, 512],
stddev=0.1,
seed=SEED))
fc1_biases = tf.Variable(tf.constant(0.1, shape=[512]))
fc2_weights = tf.Variable(
tf.truncated_normal([512, NUM_LABELS],
stddev=0.1,
seed=SEED))
fc2_biases = tf.Variable(tf.constant(0.1, shape=[NUM_LABELS]))
print('Done')
# + [markdown] colab_type="text" id="QHB_u04Z4HO6"
# Now that we've defined the variables to be trained, we're ready to wire them together into a TensorFlow graph.
#
# We'll define a helper to do this, `model`, which will return copies of the graph suitable for training and testing. Note the `train` argument, which controls whether or not dropout is used in the hidden layer. (We want to use dropout only during training.)
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 772, "status": "ok", "timestamp": 1446749138306, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="V85_B9QF3uBp" outputId="457d3e49-73ad-4451-c196-421dd4681efc"
def model(data, train=False):
"""The Model definition."""
# 2D convolution, with 'SAME' padding (i.e. the output feature map has
# the same size as the input). Note that {strides} is a 4D array whose
# shape matches the data layout: [image index, y, x, depth].
conv = tf.nn.conv2d(data,
conv1_weights,
strides=[1, 1, 1, 1],
padding='SAME')
# Bias and rectified linear non-linearity.
relu = tf.nn.relu(tf.nn.bias_add(conv, conv1_biases))
# Max pooling. The kernel size spec ksize also follows the layout of
# the data. Here we have a pooling window of 2, and a stride of 2.
pool = tf.nn.max_pool(relu,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
conv = tf.nn.conv2d(pool,
conv2_weights,
strides=[1, 1, 1, 1],
padding='SAME')
relu = tf.nn.relu(tf.nn.bias_add(conv, conv2_biases))
pool = tf.nn.max_pool(relu,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
# Reshape the feature map cuboid into a 2D matrix to feed it to the
# fully connected layers.
pool_shape = pool.get_shape().as_list()
reshape = tf.reshape(
pool,
[pool_shape[0], pool_shape[1] * pool_shape[2] * pool_shape[3]])
# Fully connected layer. Note that the '+' operation automatically
# broadcasts the biases.
hidden = tf.nn.relu(tf.matmul(reshape, fc1_weights) + fc1_biases)
# Add a 50% dropout during training only. Dropout also scales
# activations such that no rescaling is needed at evaluation time.
if train:
hidden = tf.nn.dropout(hidden, 0.5, seed=SEED)
return tf.matmul(hidden, fc2_weights) + fc2_biases
print('Done')
# + [markdown] colab_type="text" id="7bvEtt8C4fLC"
# Having defined the basic structure of the graph, we're ready to stamp out multiple copies for training, testing, and validation.
#
# Here, we'll do some customizations depending on which graph we're constructing. `train_prediction` holds the training graph, for which we use cross-entropy loss and weight regularization. We'll adjust the learning rate during training -- that's handled by the `exponential_decay` operation, which is itself an argument to the `MomentumOptimizer` that performs the actual training.
#
# The vaildation and prediction graphs are much simpler the generate -- we need only create copies of the model with the validation and test inputs and a softmax classifier as the output.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 269, "status": "ok", "timestamp": 1446749139596, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="9pR1EBNT3sCv" outputId="570681b1-f33e-4618-b742-48e12aa58132"
# Training computation: logits + cross-entropy loss.
logits = model(train_data_node, True)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits, train_labels_node))
# L2 regularization for the fully connected parameters.
regularizers = (tf.nn.l2_loss(fc1_weights) + tf.nn.l2_loss(fc1_biases) +
tf.nn.l2_loss(fc2_weights) + tf.nn.l2_loss(fc2_biases))
# Add the regularization term to the loss.
loss += 5e-4 * regularizers
# Optimizer: set up a variable that's incremented once per batch and
# controls the learning rate decay.
batch = tf.Variable(0)
# Decay once per epoch, using an exponential schedule starting at 0.01.
learning_rate = tf.train.exponential_decay(
0.01, # Base learning rate.
batch * BATCH_SIZE, # Current index into the dataset.
train_size, # Decay step.
0.95, # Decay rate.
staircase=True)
# Use simple momentum for the optimization.
optimizer = tf.train.MomentumOptimizer(learning_rate,
0.9).minimize(loss,
global_step=batch)
# Predictions for the minibatch, validation set and test set.
train_prediction = tf.nn.softmax(logits)
# We'll compute them only once in a while by calling their {eval()} method.
validation_prediction = tf.nn.softmax(model(validation_data_node))
test_prediction = tf.nn.softmax(model(test_data_node))
print('Done')
# + [markdown] colab_type="text" id="4T21uZJq5UfH"
# # Training and visualizing results
#
# Now that we have the training, test, and validation graphs, we're ready to actually go through the training loop and periodically evaluate loss and error.
#
# All of these operations take place in the context of a session. In Python, we'd write something like:
#
# with tf.Session() as s:
# ...training / test / evaluation loop...
#
# But, here, we'll want to keep the session open so we can poke at values as we work out the details of training. The TensorFlow API includes a function for this, `InteractiveSession`.
#
# We'll start by creating a session and initializing the varibles we defined above.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="z6Kc5iql6qxV"
# Create a new interactive session that we'll use in
# subsequent code cells.
s = tf.InteractiveSession()
# Use our newly created session as the default for
# subsequent operations.
s.as_default()
# Initialize all the variables we defined above.
tf.initialize_all_variables().run()
# + [markdown] colab_type="text" id="hcG8H-Ka6_mw"
# Now we're ready to perform operations on the graph. Let's start with one round of training. We're going to organize our training steps into batches for efficiency; i.e., training using a small set of examples at each step rather than a single example.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 386, "status": "ok", "timestamp": 1446749389138, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="LYVxeEox71Pg" outputId="9184b5df-009a-4b1b-e312-5be94351351f"
BATCH_SIZE = 60
# Grab the first BATCH_SIZE examples and labels.
batch_data = train_data[:BATCH_SIZE, :, :, :]
batch_labels = train_labels[:BATCH_SIZE]
# This dictionary maps the batch data (as a numpy array) to the
# node in the graph it should be fed to.
feed_dict = {train_data_node: batch_data,
train_labels_node: batch_labels}
# Run the graph and fetch some of the nodes.
_, l, lr, predictions = s.run(
[optimizer, loss, learning_rate, train_prediction],
feed_dict=feed_dict)
print('Done')
# + [markdown] colab_type="text" id="7bL4-RNm_K-B"
# Let's take a look at the predictions. How did we do? Recall that the output will be probabilities over the possible classes, so let's look at those probabilities.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 160, "status": "ok", "timestamp": 1446749519023, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="2eNitV_4_ZUL" outputId="f1340dd1-255b-4523-bf62-7e3ebb361333"
print(predictions[0])
# + [markdown] colab_type="text" id="X5MgraJb_eQZ"
# As expected without training, the predictions are all noise. Let's write a scoring function that picks the class with the maximum probability and compares with the example's label. We'll start by converting the probability vectors returned by the softmax into predictions we can match against the labels.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 220, "status": "ok", "timestamp": 1446750411574, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="wMMlUf5rCKgT" outputId="2c10e96d-52b6-47b0-b6eb-969ad462d46b"
# The highest probability in the first entry.
print('First prediction', numpy.argmax(predictions[0]))
# But, predictions is actually a list of BATCH_SIZE probability vectors.
print(predictions.shape)
# So, we'll take the highest probability for each vector.
print('All predictions', numpy.argmax(predictions, 1))
# + [markdown] colab_type="text" id="8pMCIZ3_C2ni"
# Next, we can do the same thing for our labels -- using `argmax` to convert our 1-hot encoding into a digit class.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 232, "status": "ok", "timestamp": 1446750498351, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="kZWp4T0JDDUe" outputId="47b588cd-bc82-45c3-a5d0-8d84dc27a3be"
print('Batch labels', numpy.argmax(batch_labels, 1))
# + [markdown] colab_type="text" id="bi5Z6whtDiht"
# Now we can compare the predicted and label classes to compute the error rate and confusion matrix for this batch.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}, {"item_id": 2}]} colab_type="code" executionInfo={"elapsed": 330, "status": "ok", "timestamp": 1446751307304, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="U4hrLW4CDtQB" outputId="720494a3-cbf9-4687-9d94-e64a33fdd78f"
correct = numpy.sum(numpy.argmax(predictions, 1) == numpy.argmax(batch_labels, 1))
total = predictions.shape[0]
print(float(correct) / float(total))
confusions = numpy.zeros([10, 10], numpy.float32)
bundled = zip(numpy.argmax(predictions, 1), numpy.argmax(batch_labels, 1))
for predicted, actual in bundled:
confusions[predicted, actual] += 1
plt.grid(False)
plt.xticks(numpy.arange(NUM_LABELS))
plt.yticks(numpy.arange(NUM_LABELS))
plt.imshow(confusions, cmap=plt.cm.jet, interpolation='nearest');
# + [markdown] colab_type="text" id="iZmx_9DiDXQ3"
# Now let's wrap this up into our scoring function.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 178, "status": "ok", "timestamp": 1446751995007, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="DPJie7bPDaLa" outputId="a06c64ed-f95f-416f-a621-44cccdaba0f8"
def error_rate(predictions, labels):
"""Return the error rate and confusions."""
correct = numpy.sum(numpy.argmax(predictions, 1) == numpy.argmax(labels, 1))
total = predictions.shape[0]
error = 100.0 - (100 * float(correct) / float(total))
confusions = numpy.zeros([10, 10], numpy.float32)
bundled = zip(numpy.argmax(predictions, 1), numpy.argmax(labels, 1))
for predicted, actual in bundled:
confusions[predicted, actual] += 1
return error, confusions
print('Done')
# + [markdown] colab_type="text" id="sLv22cjeB5Rd"
# We'll need to train for some time to actually see useful predicted values. Let's define a loop that will go through our data. We'll print the loss and error periodically.
#
# Here, we want to iterate over the entire data set rather than just the first batch, so we'll need to slice the data to that end.
#
# (One pass through our training set will take some time on a CPU, so be patient if you are executing this notebook.)
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="4cgKJrS1_vej"
# Train over the first 1/4th of our training set.
steps = train_size // BATCH_SIZE
for step in range(steps):
# Compute the offset of the current minibatch in the data.
# Note that we could use better randomization across epochs.
offset = (step * BATCH_SIZE) % (train_size - BATCH_SIZE)
batch_data = train_data[offset:(offset + BATCH_SIZE), :, :, :]
batch_labels = train_labels[offset:(offset + BATCH_SIZE)]
# This dictionary maps the batch data (as a numpy array) to the
# node in the graph it should be fed to.
feed_dict = {train_data_node: batch_data,
train_labels_node: batch_labels}
# Run the graph and fetch some of the nodes.
_, l, lr, predictions = s.run(
[optimizer, loss, learning_rate, train_prediction],
feed_dict=feed_dict)
# Print out the loss periodically.
if step % 100 == 0:
error, _ = error_rate(predictions, batch_labels)
print('Step %d of %d' % (step, steps))
print('Mini-batch loss: %.5f Error: %.5f Learning rate: %.5f' % (l, error, lr))
print('Validation error: %.1f%%' % error_rate(
validation_prediction.eval(), validation_labels)[0])
# + [markdown] colab_type="text" id="J4LskgGXIDAm"
# The error seems to have gone down. Let's evaluate the results using the test set.
#
# To help identify rare mispredictions, we'll include the raw count of each (prediction, label) pair in the confusion matrix.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}, {"item_id": 2}]} colab_type="code" executionInfo={"elapsed": 436, "status": "ok", "timestamp": 1446752934104, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": "//lh6.googleusercontent.com/-wKJwK_OPl34/AAAAAAAAAAI/AAAAAAAAAlk/Rh3u6O2Z7ns/s50-c-k-no/photo.jpg", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="6Yh1jGFuIKc_" outputId="4e411de4-0fe2-451b-e4ca-8a4854f0db89"
test_error, confusions = error_rate(test_prediction.eval(), test_labels)
print('Test error: %.1f%%' % test_error)
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.grid(False)
plt.xticks(numpy.arange(NUM_LABELS))
plt.yticks(numpy.arange(NUM_LABELS))
plt.imshow(confusions, cmap=plt.cm.jet, interpolation='nearest');
for i, cas in enumerate(confusions):
for j, count in enumerate(cas):
if count > 0:
xoff = .07 * len(str(count))
plt.text(j-xoff, i+.2, int(count), fontsize=9, color='white')
# + [markdown] colab_type="text" id="yLnS4dGiMwI1"
# We can see here that we're mostly accurate, with some errors you might expect, e.g., '9' is often confused as '4'.
#
# Let's do another sanity check to make sure this matches roughly the distribution of our test set, e.g., it seems like we have fewer '5' values.
# + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}, "output_extras": [{"item_id": 1}]} colab_type="code" executionInfo={"elapsed": 352, "status": "ok", "timestamp": 1446753006584, "user": {"color": "#1FA15D", "displayName": "<NAME>", "isAnonymous": false, "isMe": true, "permissionId": "00327059602783983041", "photoUrl": <KEY>", "sessionId": "716a6ad5e180d821", "userId": "106975671469698476657"}, "user_tz": 480} id="x5KOv1AJMgzV" outputId="2acdf737-bab6-408f-8b3c-05fa66d04fe6"
plt.xticks(numpy.arange(NUM_LABELS))
plt.hist(numpy.argmax(test_labels, 1));
# + [markdown] colab_type="text" id="E6DzLSK5M1ju"
# Indeed, we appear to have fewer 5 labels in the test set. So, on the whole, it seems like our model is learning and our early results are sensible.
#
# But, we've only done one round of training. We can greatly improve accuracy by training for longer. To try this out, just re-execute the training cell above.
|
.ipynb_checkpoints/3_mnist_from_scratch-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
mylist = [1,2,3]
myset = set()
type(myset)
class Sample():
pass #no attributes
my_sample = Sample()
type(my_sample)
#every useful class has an __init__ method. self is the first parameter
class Dog():
def __init__(self, breed): #constructor
self.breed = breed
my_dog = Dog() #expecting a breed parameter.
my_dog = Dog(breed='Labrador')
type(my_dog)
my_dog.breed
# self keyword is a parameter that is hidden in most OOP languages, but in python, you have to explicitly define that. technically, "self" variable name can be replaced by any other, but use self only, as it makes more sense.
#
# self represents the instance of the object itself.
#
class Dog():
def __init__(self, mybreed): #constructor
#Attributes (characteristics of the object)
#We take in the argument
#Assign it to self.attribute_name
self.breed = mybreed #by convention, use parameter and attribute name as the same.
my_dog2 = Dog(mybreed = 'Huskie')
type(my_dog2)
my_dog2.breed
class Dog():
def __init__(self, breed, name, spots): #this method acts as constructor, and is predefined keyword.
self.breed = breed
self.name = name
self.spots = spots #bool
my_dog3 = Dog(breed='Lab', name='Wuf', spots=True) #there is no confirmation to make spots a boolean, due to flexibility of python
type(my_dog3)
my_dog3.spots
class Dog():
#class object attribute is the same for any instance of the class.
#no need for self keyword
species = 'mammal'
def __init__(self, breed, name, spots):
self.breed = breed
self.name = name
self.spots = spots
my_dog4 = Dog(breed = 'Lab', name='Tom', spots=True)
my_dog4.species #attributes are not callable..they are characterstics of the object
# methods are functions defined in a class, and take into consideration the class itself...through the use of self keyword
class Dog():
species = 'mammal'
def __init__(self, breed, name, spots):
self.breed = breed
self.name = name
self.spots = spots
#Operations/Actions taking the class into consideration ---> Methods
def bark(self):#this parameter connects this method to the actual object, and because it is defined inside the class, it will always has access to self
# print("WOOF! "+self.name)
print("Woof! My name is {}".format(self.name))
my_dog = Dog('Lab','Frankie',False)
my_dog.bark
my_dog.bark()
class Dog():
species = 'mammal'
def __init__(self, breed, name, spots):
self.breed = breed
self.name = name
self.spots = spots
def bark(self,number):
print("Woof! My name is {} and the number is {}".format(self.name,number))
my_dog5 = Dog('Lab','Terry',False)
my_dog5.bark(13)
class Circle():
pi = 3.1415
def __init__(self,radius=1):#A default value
self.radius = radius
# self.area = radius*radius*self.pi
self.area = radius*radius*Circle.pi #only if this is a class obj attribute, this is preferred, as it references to class object attribute
def get_circumference(self):
return 2*Circle.pi*self.radius
my_circle = Circle(4)
my_circle.pi
my_circle.radius
my_circle.get_circumference()
my_circle.area
# # Inheritance
class Animal():
def __init__(self):
print("Animal object created")
def who_am_i(self):
print("I am an animal object")
def eat(self):
print("Ok, I am eating")
my_animal = Animal() #note that __init__ is auto executed
class Dog(Animal): #Dog derieving from base class Animal
def __init__(self):
Animal.__init__(self)
print("Dog object created")
def bark(self):
print("Woof!")
def who_am_i(self):
print("I am a dog!")
def eat(self):
print("Ok, I am eating dog food")
my_dog = Dog()
my_dog.eat()
my_dog.who_am_i()
# methods belong to the object they act on. They are like and unlike functions at the same time
# # Polymorphism
class Dog():
def __init__(self,name):
self.name = name
def speak(self):
return self.name+" says woof!"
class Cat():
def __init__(self,name):
self.name = name
def speak(self):
return self.name+" says meow!"
niko = Dog("Niko")
felix = Cat("Felix")
print(niko.speak())
print(felix.speak())
for pet in [niko,felix]:
print(type(pet))
print(type(pet.speak()))
def pet_speak(pet):
print(pet.speak())
pet_speak(niko)
pet_speak(felix)
# Abstract classes are the ones, never meant to serve as a class, but only as a base class. Its instance is never meant to be created
class Animal():
def __init__(self,name):
self.name = name
def speak(self):
raise NotImplementedError("Subclass must implement this abstract method")
my_animal = Animal("Fred")
my_animal.speak() #this was never meant to be created..create a child class, and modify this function. All child classes therefore will show polymorphism
class Dog(Animal):
def speak(self):
return self.name+" says woof!"
class Cat(Animal):
def speak(self):
return self.name+" says meow!"
fido = Dog("Fido")
terra = Cat("Terra")
fido.speak()
terra.speak()
# # Special Methods
my_list = [1,2,3]
len(my_list)
class Sample():
pass
my_sample = Sample()
len(my_sample)
class Book:
def __init__(self,title,author,pages): #the first special method
self.title = title
self.author = author
self.pages = pages
b = Book("Famous Five","<NAME>", 128)
print(b) #what this did was just to convert b to its string version
str(b)
class Book:
def __init__(self,title,author,pages): #the first special method
self.title = title
self.author = author
self.pages = pages
def __str__(self):
return f"{self.title} by {self.author}"
b = Book("Famous Five","<NAME>", 128)
str(b)
class Book:
def __init__(self,title,author,pages): #the first special method
self.title = title
self.author = author
self.pages = pages
def __str__(self):
return f"{self.title} by {self.author}"
def __len__(self):
return self.pages
b = Book("Famous Five","<NAME>", 128)
len(b)
del b #erases the data related to this variable in the memory
class Book:
def __init__(self,title,author,pages): #the first special method
self.title = title
self.author = author
self.pages = pages
def __str__(self):#maybe called to give details related to the object
return f"{self.title} by {self.author}"
def __len__(self):
return self.pages
def __del__(self):
print("A book object deleted.")
b = Book("Famous Five","<NAME>", 128)
del b
|
OOP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py3-pythia]
# language: python
# name: conda-env-py3-pythia-py
# ---
# +
import os
import datetime
import json
import numpy as np
import pandas as pd
import pprint
from IPython.display import display, HTML
from pymongo import MongoClient
# +
# Connect to Mongo host & port
client = MongoClient(os.environ['MONGODB_NAME'], 27017)
# +
# Input the name of the database you'd like to connect to. Example 'sacred_demo' or 'pythia_experiment'
db_name = input()
# +
# Connect to db
db = client.get_database(db_name)
# +
# This is the date of the experiments you'd like to see. Right now it is set at any experiment run after this date
date = datetime.datetime(2016, 7, 28, 0, 0, 0, 0)
# +
# This mongo query displays the results and the arguments passed in to the model
cursor = db.default.runs.find({'start_time': {"$gt" : date}}, {'config': True, 'result': True, '_id': False})
count = 0
for doc in cursor:
count += 1
print("\n-----------------------------")
print("RUN NUMBER: " + str(count))
print("-----------------------------")
for key in doc['config'].keys():
if key == 'args':
result = {}
# Print data used for the experiment
args = doc['config']['args']
print("\nData: " + str(args[0]) + "\n")
# The way the config is set up, the first index is the data used and the remaining ones are the args
for d in args[1:len(args)]:
result.update(d)
df = pd.DataFrame(result).fillna(" ")
key_list = []
# I combine the dictionaries to make a nicer display for the pandas dataframe
for key in result.keys():
for key2 in (result[key].keys()):
key_list.append(key2)
args_df = df.reindex(key_list)
display(args_df)
else:
print("Running with a seed of: " + str(doc['config']['seed']) + "\n")
print("Results are:")
display(pd.DataFrame(doc['result']))
# +
# The same concept as earlier: display experiments after the specified date below
date_pythia = datetime.datetime(2016, 8, 16, 0, 0, 0, 0)
# +
# Enter the name of the db you would like to see
db_name = input()
# +
# Connect to db
db = client.get_database(db_name)
# +
# This is for the logic behind the visualization. If all elements within the lists are false,
# then the algorithm was not used
LDA_list = ['LDA_APPEND', 'LDA_COS', 'LDA_DIFFERENCE', 'LDA_PRODUCT', 'LDA_TOPICS']
BOW_list = ['BOW_APPEND', 'BOW_PRODUCT', 'BOW_COS', 'BOW_DIFFERENCE', 'BOW_TFIDF']
W2V_list = ['W2V_APPEND', 'W2V_DIFFERENCE', 'W2V_COS', 'W2V_PRODUCT']
W2V_associated_list = ['W2V_SIZE', 'W2V_WINDOW', 'W2V_WORKERS', 'W2V_MIN_COUNT', 'W2V_PRETRAINED']
CNN_list = ['CNN_APPEND', 'CNN_COS', 'CNN_PRODUCT', 'CNN_DIFFERENCE']
ST_list = ['ST_APPEND', 'ST_COS', 'ST_PRODUCT', 'ST_DIFFERENCE']
SVM_list = ['SVM']
WORDONEHOT_list = ['WORDONEHOT']
XGB_list = ['XGB']
LOG_REG_list = ['LOG_REG']
# +
cursor = db.default.runs.find({'start_time': {"$gt" : date_pythia}}, {'config': True, 'result': True, '_id': False})
count = 0
bool_listLDA = []
bool_listCNN = []
bool_listST = []
bool_listW2V = []
bool_listBOW = []
bool_listSVM = []
bool_listXGB = []
bool_listLOG_REG = []
bool_listWORDONEHOT = []
for doc in cursor:
count += 1
print("-------------------------")
print("RUN NUMBER: " + str(count))
print("-------------------------")
df = pd.DataFrame(doc['config'], index=['value']).T
for item in CNN_list:
bool_listCNN.append(df.get_value(item, 'value'))
if not any(bool_listCNN) == True:
df = df.drop(CNN_list)
if 'CNN_CHAR_VOCAB' in df.index:
df = df.drop(['CNN_CHAR_VOCAB'])
if 'CNN_VOCAB_TYPE' in df.index:
df = df.drop(['CNN_VOCAB_TYPE'])
for item in LDA_list:
bool_listLDA.append(df.get_value(item, 'value'))
if not any(bool_listLDA) == True:
df = df.drop(LDA_list)
for item in ST_list:
bool_listST.append(df.get_value(item, 'value'))
if not any(bool_listST) == True:
df = df.drop(ST_list)
for item in W2V_list:
bool_listW2V.append(df.get_value(item, 'value'))
if not any(bool_listW2V) == True:
df = df.drop(W2V_list)
for item in W2V_associated_list:
if item in df.index:
df = df.drop([item])
for item in BOW_list:
bool_listBOW.append(df.get_value(item, 'value'))
if not any(bool_listBOW) == True:
df = df.drop(BOW_list)
for item in SVM_list:
bool_listSVM.append(df.get_value(item, 'value'))
if not any(bool_listSVM) == True:
df = df.drop(['SVM', 'SVM_C', 'SVM_GAMMA', 'SVM_KERNEL'])
for item in XGB_list:
bool_listXGB.append(df.get_value(item, 'value'))
if not any(bool_listXGB) == True:
df = df.drop(['XGB', 'XGB_COLSAMPLEBYTREE', 'XGB_LEARNRATE', 'XGB_MAXDEPTH', 'XGB_MINCHILDWEIGHT'])
for item in LOG_REG_list:
bool_listLOG_REG.append(df.get_value(item, 'value'))
if not any(bool_listLOG_REG) == True:
df = df.drop(['LOG_REG', 'LOG_PENALTY', 'LOG_C', 'LOG_TOL'])
for item in WORDONEHOT_list:
bool_listWORDONEHOT.append(df.get_value(item, 'value'))
if not any(bool_listWORDONEHOT) == True:
df = df.drop(['WORDONEHOT', 'WORDONEHOT_VOCAB'])
display(df)
print("\nRESULTS ARE:\n")
display(pd.DataFrame(doc['result']))
# +
cursor = db.default.runs.find({ "experiment.name": "pythia_gridsearch"})
for doc in cursor:
print(doc)
# -
|
src/examples/get-results-from-sacred.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sqlite3
conn = sqlite3.connect('tutorial.csv')
c = conn.cursor()
def create_table():
c.execute('CREATE TABLE IF NOT EXISTS TEST(ID INT,NAME TEXT,PHONE TEXT)')
def data_entry():
c.execute("INSERT INTO TEST VALUES(01,'RAJU','01865052786')")
c.execute("INSERT INTO TEST VALUES(02,'YASMIN','01675519116')")
conn.commit()
def read_from_db():
c.execute('SELECT * FROM TEST')
for row in c.fetchall():
print(row)
create_table()
data_entry()
read_from_db()
c.close()
conn.close()
# +
import sqlite3
conn = sqlite3.connect('tutorial.csv')
c=conn.cursor()
def searchData():
c.execute("SELECT * FROM TEST WHERE NAME='RAJU'")
for row in c.fetchall():
print(row)
searchData()
c.close()
conn.close()
# +
import sqlite3
conn=sqlite3.connect('tutorial.csv')
c=conn.cursor()
def read_from_db():
c.execute("SELECT * FROM TEST")
for row in c.fetchall():
print(row)
def updateData():
c.execute("UPDATE TEST SET NAME = 'BASIS' WHERE NAME = 'Leads'")
conn.commit()
read_from_db()
updateData()
read_from_db()
c.close()
conn.close()
# +
import sqlite3
conn=sqlite3.connect('tutorial.csv')
c=conn.cursor()
def read_from_db():
c.execute("SELECT * FROM TEST")
for row in c.fetchall():
print(row)
def deleteData():
c.execute("DELETE FROM TEST WHERE NAME = 'BASIS'")
conn.commit()
read_from_db()
deleteData()
read_from_db()
c.close()
conn.close()
# +
import sqlite3 as lite
import sys
try:
con = lite.connect('test.db')
cur = con.cursor()
cur.executescript("""
DROP TABLE IF EXISTS Cars;
CREATE TABLE Cars(Id INT, Name TEXT, Price INT);
INSERT INTO Cars VALUES(1,'Audi',52642);
INSERT INTO Cars VALUES(2,'Mercedes',57127);
INSERT INTO Cars VALUES(3,'Skoda',9000);
INSERT INTO Cars VALUES(4,'Volvo',29000);
INSERT INTO Cars VALUES(5,'Bentley',350000);
INSERT INTO Cars VALUES(6,'Citroen',21000);
INSERT INTO Cars VALUES(7,'Hummer',41400);
INSERT INTO Cars VALUES(8,'Volkswagen',21600);
""")
con.commit()
except lite.Error, e:
if con:
con.rollback()
print "Error %s:" % e.args[0]
sys.exit(1)
finally:
if con:
con.close()
# -
|
pythonDatabase.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Train LSTM Network to Predict Occurrence of Next Event
# ### Load Libraries
# +
# Data manipulation libraries
import pandas as pd
import numpy as np
# Dask for lazy loading and computation of data
import dask.dataframe as dd
import time
from dask import delayed
import dask.array as da
#Word embedding
from gensim.models import Word2Vec
# Keras DeepLearning Framework
from keras.preprocessing.sequence import pad_sequences
from keras.models import Sequential
from keras.layers import Dense , Dropout, Embedding, LSTM
# -
# ### Load Data
# - log_file.csv is a transformed version of orignal event log data in xes format
# - Orignal dataset by:
# - <NAME>, B.F. (Boudewijn) (2017) BPI Challenge 2017. Eindhoven University of Technology. Dataset. https://doi.org/10.4121/uuid:5f3067df-f10b-45da-b98b-86ae4c7a310b
df = dd.read_csv("log_file.csv")
df.head()
# ### Group events
# - Group events part of same transaction
# - In absence of known final event in the sequence , added event type: 'End' after occurrence of last event.
event_grouped = df.groupby('Id')["event:concept:name"].apply(list)
event_grouped = event_grouped.map_partitions(lambda x: x + ["End"])
# ### Lazy loading of events for training Word2Vec Embedding
def gen_events(event_list):
for x in range(event_list.npartitions):
events = event_list.get_partition(x).compute()
events = events.tolist()
for x in events:
yield x
class generate_Sequence():
'''
Streaming class to generate grouped events in a lazy way to avoid issues of RAM
running out of Memory.
'''
def __init__(self, generator_function,event_list):
self.event_list = event_list
self.generator_function = generator_function
self.generator = self.generator_function(self.event_list)
def __iter__(self):
# reset the generator
self.generator = self.generator_function(self.event_list)
return self
def __next__(self):
result = next(self.generator)
if result is None:
raise StopIteration
else:
return result
iterate = generate_Sequence(gen_events,event_grouped)
w2vmodel = Word2Vec(iterate)
w2vmodel.save('w2v.model')
print('Size / Length of Each Word Vector: %s'%w2vmodel.vector_size)
print('Count of Distinct Events in the Journey of a Transaction: %s'%len(w2vmodel.wv.vocab))
# #### Extract Event Embedding Matrix to be used in training of LSTM Network
# +
embedding_matrix = np.zeros(shape = (len(w2vmodel.wv.vocab),w2vmodel.vector_size))
for i in range(len(w2vmodel.wv.vocab)):
embedding_matrix[i] = w2vmodel.wv[w2vmodel.wv.index2word[i]]
#print(embedding_matrix.shape)
embedding_matrix[0:2]
# -
# ### Data streaming pipeline for inputs to LSTM Network
# - Delayed Function
# - Delayed funciton output - X, y
# - Rechunk the dask array to size == Batch Size to be used for Training Model (512 in current
# scenario)
# - Generator Function to initiate above computation graph and feed data in batch size of 512
def input_feed(series):
X_temp , y_temp = [], []
for event in series:
for i in range(1, len(event)):
temp_x = event[0:i]
temp_x = [w2vmodel.wv.vocab.get(x).index for x in temp_x]
#print(temp_x)
X_temp.append(temp_x)
temp_y = w2vmodel.wv.vocab.get(event[i]).index
y_temp.append(temp_y)
X_events = pad_sequences(X_temp,maxlen= 50)
y_temp = da.array(y_temp)
y = da.from_array(y_temp,chunks = {0:512})
#print("Completed....")
return (X_events,y)
input_feed_dask = delayed(input_feed) # Delayed function does lazy computation on data
a = (input_feed_dask)(event_grouped) # delayed output
X_events = a[0]
y_events = a[1]
X_events, y_events
X_events_ar = da.from_delayed(X_events,dtype= float ,shape = (1202267, 50))
y_events = da.from_delayed(y_events,dtype = float, shape = (1202267,))
X_events_ar = X_events_ar.rechunk({0:512,1:-1})
y_events = y_events.rechunk({0:512})
chunkList = [(x,y) for x,y in zip(range(0,X_events_ar.shape[0]+X_events_ar.chunksize[0],
X_events_ar.chunksize[0]),
range(X_events_ar.chunksize[0],X_events_ar.shape[0]+X_events_ar.chunksize[0],
X_events_ar.chunksize[0]))]
len(chunkList)
# #### Generator function to stream batches to LSTM Network
def gen_inputs(x,y_array):
for chunks in chunkList:
X = x[chunks[0]:chunks[1]]
X = X.map_blocks(np.copy)
X = X.compute()
y = y_array[chunks[0]:chunks[1]]
y = y.map_blocks(np.copy)
y = y.compute()
y_transformed = np.zeros((len(y),27))
y_transformed[np.arange(len(y)),y] = 1
yield (X,y_transformed)
inp = gen_inputs(X_events_ar, y_events)
# ### LSTM Model Architecture
init = 'glorot_uniform'
model = Sequential()
model.add(Embedding(len(w2vmodel.wv.vocab),100,input_length= 50,
weights = [embedding_matrix], trainable = False))
model.add(LSTM(100,implementation =2 , kernel_initializer = init, return_sequences = False))
model.add(Dense(50,kernel_initializer = init, activation = 'relu'))
model.add(Dense(27,kernel_initializer = init, activation = 'softmax' , name ="output"))
print(model.summary())
model.compile(loss ='categorical_crossentropy',optimizer= 'rmsprop', metrics =['accuracy'])
est = model.fit_generator(inp, steps_per_epoch= np.ceil(1202267/512),verbose =1
,use_multiprocessing = True, workers = 6)
# ## Training Model by loading data in RAM
#
# - Training is faster as ther is no overhead on CPU side to compute Dask graph for every input batch
# - Drawback : with larger dataset RAM could run out of Memory
def input_feed(series):
X_temp , y_temp = [], []
for event in series:
for i in range(1, len(event)):
temp_x = event[0:i]
temp_x = [w2vmodel.wv.vocab.get(x).index for x in temp_x]
#print(temp_x)
X_temp.append(temp_x)
temp_y = w2vmodel.wv.vocab.get(event[i]).index
y_temp.append(temp_y)
X_events = pad_sequences(X_temp,maxlen= 50)
y_temp = np.array(y_temp)
#y = da.from_array(y_temp,chunks = {0:512})
#print("Completed....")
return (X_events,y_temp)
events = event_grouped.compute()
events.head()
X_events, y_events = input_feed(events)
X_events.shape, y_events.shape
y_transformed = np.zeros((len(y_events),27))
y_transformed[np.arange(len(y_events)),y_events] = 1
y_transformed.shape
init = 'glorot_uniform'
model = Sequential()
model.add(Embedding(len(w2vmodel.wv.vocab),100,input_length= 50,
weights = [embedding_matrix], trainable = False))
model.add(LSTM(100,implementation =2 , kernel_initializer = init, return_sequences = False))
model.add(Dense(50,kernel_initializer = init, activation = 'relu'))
model.add(Dense(27,kernel_initializer = init, activation = 'softmax' , name ="output"))
print(model.summary())
model.compile(loss ='categorical_crossentropy',optimizer= 'rmsprop', metrics =['accuracy'])
est = model.fit(X_events,y_transformed, batch_size= 512 , epochs= 20)
|
notebooks/train_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from gs_quant.session import GsSession
client_id = 'YOUR_CLIENT_ID'
client_secret = 'YOUR_CLIENT_SECRET'
GsSession.use(client_id=client_id, client_secret=client_secret)
# +
from gs_quant.data import Dataset
from datetime import date
weather_ds = Dataset('WEATHER')
data_frame = weather_ds.get_data(date(2016, 1, 1), date(2016, 1, 31), city=["Boston"], intervals=3)
print(data_frame)
|
GetData.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Mouse Peripheral Blood - merging annotated samples from MCA
# +
import scanpy as sc
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
from matplotlib import colors
import seaborn as sb
import glob
import rpy2.rinterface_lib.callbacks
import logging
from rpy2.robjects import pandas2ri
import anndata2ri
# +
# Ignore R warning messages
#Note: this can be commented out to get more verbose R output
rpy2.rinterface_lib.callbacks.logger.setLevel(logging.ERROR)
# Automatically convert rpy2 outputs to pandas dataframes
pandas2ri.activate()
anndata2ri.activate()
# %load_ext rpy2.ipython
plt.rcParams['figure.figsize']=(8,8) #rescale figures
sc.settings.verbosity = 3
#sc.set_figure_params(dpi=200, dpi_save=300)
sc.logging.print_versions()
results_file = './write/MCA_mou_PB_pp.h5ad'
# + language="R"
# # Load all the R libraries we will be using in the notebook
# library(scran)
# -
# ## Load
# Here we load the pre-processed datasets (which has been annotated), and the raw matrices (which won't be filtered on the gene level).
# ### Raw data
file_paths = '../../Munich/datasets/mouse/MCA_PB/'
adatas_raw = []
for i in glob.glob(file_paths+'*.txt.gz'):
print(i)
adatas_raw.append(sc.read(i, cache=True))
samples = ['PB_6', 'PB_3', 'PB_5', 'PB_2', 'PB_4', 'PB_1']
# Loop to annotate data
for i in range(len(adatas_raw)):
adata_tmp = adatas_raw[i]
adata_tmp = adata_tmp.transpose()
#Annotate data
adata_tmp.obs.index.rename('barcode', inplace=True)
adata_tmp.obs['batch'] = ['MCA_'+samples[i]]*adata_tmp.n_obs
adata_tmp.obs['study'] = ['MCA_PB']*adata_tmp.n_obs
adata_tmp.obs['chemistry'] = ['microwell-seq']*adata_tmp.n_obs
adata_tmp.obs['tissue'] = ['PB']*adata_tmp.n_obs
adata_tmp.obs['species'] = ['Mouse']*adata_tmp.n_obs
adata_tmp.obs['data_type'] = ['UMI']*adata_tmp.n_obs
adata_tmp.var.index.names = ['gene_symbol']
adata_tmp.var_names_make_unique()
adatas_raw[i] = adata_tmp
adatas_raw[0].obs.head()
# Concatenate to unique adata object
adata_raw = adatas_raw[0].concatenate(adatas_raw[1:], batch_key='sample_ID', index_unique=None)
adata_raw.obs.head()
adata_raw.obs.drop(columns=['sample_ID'], inplace=True)
adata_raw.obs.head()
adata_raw.shape
# ### Pre-processed data
file_paths = '../../PB_mouse/MCA/write/'
adatas_pp = []
for i in glob.glob(file_paths+'*.h5ad'):
print(i)
adatas_pp.append(sc.read(i, cache=True))
for i in range(len(adatas_pp)):
adata_tmp = adatas_pp[i]
adata_obs = adata_tmp.obs.reset_index()
adata_obs = adata_obs[['index', 'final_annotation', 'n_counts', 'n_genes', 'mt_frac']].rename(columns = {'index':'barcode'})
adata_obs.set_index('barcode', inplace = True)
adatas_pp[i].obs = adata_obs
# Concatenate to unique adata object
adata_pp = adatas_pp[0].concatenate(adatas_pp[1:], batch_key='sample_ID',
index_unique=None)
adata_pp.obs.drop(columns=['sample_ID'], inplace = True)
adata_pp.obs.head()
adata_raw.shape
adata_pp.shape
# Restrict to cells that passed QC and were annotated
adata_obs_raw = adata_raw.obs.reset_index()
adata_obs_pp = adata_pp.obs.reset_index()
adata_merged = adata_obs_raw.merge(adata_obs_pp, on='barcode', how='left')
adata_merged.set_index('barcode', inplace = True)
adata_raw.obs = adata_merged
adata_raw.obs.head()
adata_raw = adata_raw[~pd.isnull(adata_raw.obs['final_annotation'])]
adata_raw.shape
# ### Normalization
# +
# Exclude genes that are = 0 in all cells
#Filter genes:
print('Total number of genes: {:d}'.format(adata_raw.n_vars))
# Min 20 cells - filters out 0 count genes
sc.pp.filter_genes(adata_raw, min_cells=1)
print('Number of genes after cell filter: {:d}'.format(adata_raw.n_vars))
# -
#Perform a clustering for scran normalization in clusters
adata_pp = adata_raw.copy()
sc.pp.normalize_per_cell(adata_pp, counts_per_cell_after=1e6)
sc.pp.log1p(adata_pp)
sc.pp.pca(adata_pp, n_comps=15, svd_solver='arpack')
sc.pp.neighbors(adata_pp)
sc.tl.louvain(adata_pp, key_added='groups', resolution=0.5)
# Check if the minimum number of cells per cluster is < 21:in that case, sizes will be also passed as input to the normalization
adata_pp.obs['groups'].value_counts()
#Preprocess variables for scran normalization
input_groups = adata_pp.obs['groups']
data_mat = adata_raw.X.T
# + magic_args="-i data_mat -i input_groups -o size_factors" language="R"
#
# size_factors = computeSumFactors(data_mat, clusters=input_groups, min.mean=0.1)
# -
#Delete adata_pp
del adata_pp
# +
# Visualize the estimated size factors
adata_raw.obs['size_factors'] = size_factors
sc.pl.scatter(adata_raw, 'size_factors', 'n_counts')
sc.pl.scatter(adata_raw, 'size_factors', 'n_genes')
sb.distplot(size_factors, bins=50, kde=False)
plt.show()
# -
#Keep the count data in a counts layer
adata_raw.layers["counts"] = adata_raw.X.copy()
#Normalize adata
adata_raw.X /= adata_raw.obs['size_factors'].values[:,None]
sc.pp.log1p(adata_raw)
adata_raw.write(results_file)
|
notebooks/data_preprocessing/immune_cells/merging/MCA_PB_merging.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Import Libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
df = pd.read_csv('data.csv')
df.head()
df.describe()
df.info()
df = df.drop(['Unnamed: 32','id'],axis =1)
# ### Total percentage of data is missing
# +
missing_values_count = df.isnull().sum()
total_cells = np.product(df.shape)
total_missing = missing_values_count.sum()
percentage_missing = (total_missing/total_cells)*100
print(percentage_missing)
# -
# ### Label encoding from categorical featurtes
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(df['diagnosis'])
list(le.classes_)
df['diagnosis'] = le.transform(df['diagnosis'])
df
x = df.copy()
y = x.pop('diagnosis')
# +
for colname in x.select_dtypes('object'):
x[colname],_ = x[colname].factorize()
discrete_features = x.dtypes ==int
# +
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
# -
# ### show a few features with their Mutual Info scores
# +
from sklearn.feature_selection import mutual_info_regression
def make_mi_scores(x, y, discrete_features):
mi_scores = mutual_info_regression(x, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=x.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
mi_scores = make_mi_scores(x, y, discrete_features)
mi_scores[::1]
# +
def plot_mi_scores(scores):
scores = scores.sort_values(ascending=True)
width = np.arange(len(scores))
ticks = list(scores.index)
plt.barh(width, scores)
plt.yticks(width, ticks)
plt.title("Mutual Information Scores")
plt.figure(dpi=100, figsize=(8, 10))
plot_mi_scores(mi_scores)
# -
sns.lmplot(x='concavity_worst', y='compactness_worst',hue='diagnosis', data=df)
sns.lmplot(x='radius_worst', y='compactness_worst',hue='diagnosis', data=df)
# ### Apply linear Regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
regression_model = LinearRegression()
regression_model.fit(x,y)
y_predict = regression_model.predict(x)
rmse = mean_squared_error(y, y_predict)
r2 = r2_score(y, y_predict)
print('slope : ', regression_model.coef_)
print('Intercept : ', regression_model.intercept_)
print('RMSE : ', rmse)
print('R2 :', r2)
|
ML & DL Prediction Model/Breast Cancer Diagnosis/Breast cancer Prediction(Linear Regression).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="tsEBfvuJ2bqj"
# ## Finetuning a network
# + [markdown] id="KQnocSZEhNSu"
# Tasks
#
# (Note: In this task, if you are adapting the code based on the open-source projects, pls acknowledge the original source in your code files, and also clearly mention it in your report. Also you need to clearly highlight which parts are done by yourself)
# -
import argparse
from utils_ic import load_data, read_jason
from model_ic import NN_Classifier, validation, make_NN, save_checkpoint
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from torch import optim
'done'
# settable vars
data_dir = 'flowers'
archs = ['alexnet', 'densenet169'] # vgg11 alexnet densenet169
overwriteLossValues = True
# +
# misc functions
def train(
data_dir,
cat_names='cat_to_name.json',
arch='densenet169',
lr=0.001,
hidden_units=1024,
eps=1,
device='cuda',
save_dir=None,
freeze_feature_layers=False,
optim=None
):
cat_to_name = read_jason(cat_names)
trainloader, testloader, validloader, train_data = load_data(data_dir)
val_loss, model = make_NN(
n_hidden=[hidden_units],
n_epoch=eps,
labelsdict=cat_to_name,
lr=lr,
device=device,
model_name=arch,
trainloader=trainloader,
validloader=validloader,
train_data=train_data,
freeze_feature_layers=freeze_feature_layers,
optimizer_name=optim
)
if save_dir:
save_checkpoint(model, save_dir)
return val_loss
def saveLossValues(archs, results, path):
data = {arch: loss for arch, loss in zip(archs, results)}
lossdf = pd.DataFrame.from_dict(data)
lossdf.to_csv(path)
return lossdf
# -
# (1) Replace the used base model (densenet169) to another model (refer to https://pytorch.org/vision/0.8/models.html for more types of models). Pls compare the performance of these two models on the validation set.
# init results arr to store results
results = []
for i, arch in enumerate(archs):
print('training arch {}: {}'.format(i, arch))
save_dir = 'models/' + arch
# run training and save results
results.append(train(data_dir, arch=arch, save_dir=save_dir))
print('\n---------------------------\n')
print('all done')
if overwriteLossValues:
path = 'results/homework3p2q1.csv'
saveLossValues(archs, results, path)
# (2) Please try different training methods that use densenet169 as the base model (i.e., training the whole model from scratch, finetuning the model but only updating the top layers, finetuning the whole model), and compare their performance on the validation set. Please also draw the curves of training/validation losses over training steps for these methods, and give your analysis based on the observed curves.
# +
# get the saved loss values
lossdf = pd.read_csv('results/homework3p2q1.csv')
loss_values = lossdf[archs].T.values
# set the plot attributes before plotting the loss values
fig = plt.figure()
ax1 = fig.add_subplot()
ax1.set_ylabel('Loss')
ax1.set_xlabel('Epoch')
fig.set_figheight(5)
fig.set_figwidth(15)
plt.legend(archs)
# plot the loss values
t = np.arange(1, loss_values.shape[1] + 1, 1)
for result in loss_values:
plt.plot(t, result, '--o',label='line 1', linewidth=2)
plt.show()
# -
# (3) For the model based on densenet169, please also report its performance (when you use the training method of finetuning the model but only updating the top layers) on the testing set.
arch = 'densenet169'
print('training arch: {}'.format(arch))
save_dir = 'models/' + arch + '_frozen_hidden_layers'
loss_values = train(data_dir, arch=arch, save_dir=save_dir, freeze_feature_layers=True)
if overwriteLossValues:
path = 'results/homework3p2q3.csv'
saveLossValues([arch + '_frozen_hidden_layers'], [loss_values])
# +
arch = 'densenet169'
# get densenet169 results
lossdf = pd.read_csv('results/homework3p2q1.csv')
loss_values = lossdf[arch].values
loss_values = np.expand_dims(loss_values, axis=1) # add dimension to concat
# get dense169 with frozen feature extraction layers
lossdf2 = pd.read_csv('results/homework3p2q3.csv')
loss_values2 = lossdf2[arch + 'frozen_feature_layers'].values
loss_values2 = np.expand_dims(loss_values2, axis=1) # add dimension to concat
# concat both results
loss_values = np.concatenate((loss_values,loss_values2), axis=1).T
# set the plot attributes before plotting the loss values
fig = plt.figure()
ax1 = fig.add_subplot()
ax1.set_ylabel('Loss')
ax1.set_xlabel('Epoch')
fig.set_figheight(5)
fig.set_figwidth(15)
labels = [arch, arch + 'frozen_feature_layers']
plt.legend(labels)
# plot the loss values
t = np.arange(1, loss_values.shape[1] + 1, 1)
for result in loss_values:
plt.plot(t, result, '--o',label='line 1', linewidth=2)
plt.show()
# -
# (4) Please replace the base model to a new model which contains some convolutional layers. You need to write this new model by yourselves, and then report its performance on the validation set. Note, pls try different numbers of convolutional layers for your model, and compare their results, and give analysis for the results. You need to try at least 2 different numbers of conv layers.
#
# Extra tasks (not included in Homework 3):
# (5) Please try using two different learning rate scheduling schemes for densenet169, and compare the performance on the validation set.
# +
# specify model
arch = 'densenet169'
# set learning rates
learning_rates = [0.01, 10−3]
# init arr to store results
results = []
for i, lr in enumerate(learing_rates):
print('training lr {}: {}'.format(i, lr))
save_dir = 'models/' + arch + '_lr{}'.format(lr)
# run training to save results
results.append(train(data_dir, arch=arch, save_dir=save_dir, lr=lr))
print('\n---------------------------\n')
if overwriteLossValues:
path = 'results/homework3p2q5.csv'
saveLossValues([arch + '_lr{}'.format(lr) for lr in learning_rates], results)
# +
arch = 'densenet169'
# get densenet169 results
lossdf = pd.read_csv('results/homework3p2q1.csv')
loss_values = lossdf[arch].values
loss_values = np.expand_dims(loss_values, axis=1) # add dimension to concat
# get dense169 with different learning rates layers
lossdf2 = pd.read_csv('results/homework3p2q5.csv')
cols = [arch + '_lr{}'.format(lr) for lr in learning_rates]
loss_values2 = lossdf2[cols].values
# concat both results
loss_values = np.concatenate((loss_values,loss_values2), axis=1).T
# set the plot attributes before plotting the loss values
fig = plt.figure()
ax1 = fig.add_subplot()
ax1.set_ylabel('Loss')
ax1.set_xlabel('Epoch')
fig.set_figheight(5)
fig.set_figwidth(15)
labels = [arch] + []
plt.legend(labels)
# plot the loss values
t = np.arange(1, loss_values.shape[1] + 1, 1)
for result in loss_values:
plt.plot(t, result, '--o',label='line 1', linewidth=2)
plt.show()
# -
# (6) Please try using two different optimizers for densenet169, and compare the performance on the validation set.
optimizers = ['AdamW', 'SGD']
arch = 'densenet169'
for i, optim in enumerate(optimizers):
print('training optim {}: {}'.format(i, optim))
save_dir = 'models/' + arch + '_optim{}'.format(optim)
results.append(train(data_dir, arch=arch, save_dir=save_dir, optim=optim))
print('\n---------------------------\n')
if overwriteLossValues:
path = 'results/homework3p2q6.csv'
saveLossValues([arch + '_optim{}'.format(optim) for optim in optimizers], results)
# +
arch = 'densenet169'
# get densenet169 results
lossdf = pd.read_csv('results/homework3p2q1.csv')
loss_values = lossdf[arch].values
loss_values = np.expand_dims(loss_values, axis=1) # add dimension to concat
# get dense169 with different optimizers layers
lossdf2 = pd.read_csv('results/homework3p2q6.csv')
cols = [arch + '_optim{}'.format(optim) for optim in optimizers]
loss_values2 = lossdf2[cols].values
# concat both results
loss_values = np.concatenate((loss_values,loss_values2), axis=1).T
# set the plot attributes before plotting the loss values
fig = plt.figure()
ax1 = fig.add_subplot()
ax1.set_ylabel('Loss')
ax1.set_xlabel('Epoch')
fig.set_figheight(5)
fig.set_figwidth(15)
labels = [arch] + [arch + '_optim{}'.format(optim) for optim in optimizers]
plt.legend(labels)
# plot the loss values
t = np.arange(1, loss_values.shape[1] + 1, 1)
for result in loss_values:
plt.plot(t, result, '--o',label='line 1', linewidth=2)
plt.show()
# -
learning_rates = [0.1, 0.01]
[arch + '_lr{}'.format(lr) for lr in learning_rates] + [arch]
|
.ipynb_checkpoints/part2-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#https://www.youtube.com/watch?v=Z-5wNWgRJpk
import numpy as np
import pandas as pd
import pickle
from collections import Counter
from sklearn import svm,model_selection as cross_validation,neighbors
from sklearn.ensemble import VotingClassifier, RandomForestClassifier
def process_data_for_labels(ticker):
hm_days=7
df=pd.read_csv('sp500_joined_closes.csv', index_col=0)
tickers=df.columns.values.tolist()
df.fillna(0,inplace=True)
for i in range(1,hm_days+1):
df['{}_{}d'.format(ticker,i)]=(df[ticker].shift(-i) - df[ticker]) / df[ticker]
df.fillna(0,inplace=True)
return tickers,df
process_data_for_labels('XOM')
def buy_sell_hold(*args):
cols=[c for c in args]
# se o preço mudar mais de 2% no tempo predefinido antes
requirement=0.02
for col in cols:
if col>requirement:
return 1
if col<-requirement:
return -1
return 0
def extract_featuresets(ticker):
tickers, df=process_data_for_labels(ticker )
df['{}_target'.format(ticker)] = list(map(buy_sell_hold,
df['{}_1d'.format(ticker)],
df['{}_2d'.format(ticker)],
df['{}_3d'.format(ticker)],
df['{}_4d'.format(ticker)],
df['{}_5d'.format(ticker)],
df['{}_6d'.format(ticker)],
df['{}_7d'.format(ticker)]
))
vals=df['{}_target'.format(ticker)].values.tolist()
str_vals=[str(i) for i in vals]
print('Data spread:', Counter(str_vals))
df.fillna(0,inplace=True)
df=df.replace([np.inf, -np.inf], np.nan)
df.dropna(inplace=True)
df_vals=df[[ticker for ticker in tickers]].pct_change()
df_vals=df_vals.replace([np.inf,-np.inf],0)
df_vals.fillna(0,inplace=True)
x=df_vals.values
y=df['{}_target'.format(ticker)].values
return x,y,df
extract_featuresets('XOM')
def do_ml(ticker):
x,y,df=extract_featuresets(ticker)
x_train,x_test,y_train,y_test=cross_validation.train_test_split(x,y,test_size=0.25)
#clf=neighbors.KNeighborsClassifier()
clf=VotingClassifier([('lsvc',svm.LinearSVC()),
('knn',neighbors.KNeighborsClassifier()),
('rfor',RandomForestClassifier())])
clf.fit(x_train,y_train)
confidence=clf.score(x_test,y_test)
print('Accuracy', confidence)
predictions=clf.predict(x_test)
print('Predicited spread:',Counter(predictions))
return confidence
do_ml('BAC')
|
Jupyter/StockPrice/S&P500_ML.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Construction of pYPK0_TPI1_HIS3_ENO2
#
# [pYPKa_Z_TPI1](pYPKa_Z_TPI1.ipynb)
#
# [pYPKa_E_ENO2](pYPKa_E_ENO2.ipynb)
from pydna.all import *
p567,p577,p468,p467,p568,p578,p775,p778,p167,p166 = parse("yeast_pahtway_kit_standard_primers.txt")
# [Yeast Pathway Kit Standard Primers](ypk_std_primers.ipynb)
from Bio.Restriction import ZraI, AjiI, EcoRV
pYPK0 =read("pYPK0.gb")
promoter_clone = pYPKa_Z_TPI1 =read("pYPKa_Z_TPI1.gb")
gene_clone =read("pYPKa_A_ScHIS3.gb")
terminator_clone = pYPKa_E_ENO2 =read("pYPKa_E_ENO2.gb")
p =pcr( p167, p567, promoter_clone)
g =pcr( p468, p467, gene_clone)
t =pcr( p568, p166, terminator_clone)
pYPK0_E_Z, stuffer = pYPK0.cut((EcoRV, ZraI))
(pYPK0_E_Z, p, g, t)
asm =Assembly((pYPK0_E_Z, p, g, t), limit=31)
asm
candidate = asm.assemble_circular()[0]
candidate.figure()
result = candidate.synced(pYPK0)
result.write("pYPK0_TPI1_HIS3_ENO2.gb")
# ###[Download](pYPK0_TPI1_HIS3_ENO2.gb)
reloaded =read("pYPK0_TPI1_HIS3_ENO2.gb")
reloaded.cseguid()
|
notebooks/pYPK0_TPI1_HIS3_ENO2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Python: Essential Containers
#
# Let’s now delve further into the tools of the Python language. Python comes with a
# suite of built-in data containers. These are data types that are used to hold many
# other variables. Much like you might place books on a bookshelf, you can stick integers
# or floats or strings into these containers. Each container is represented by its own
# type and has its own unique properties that define it. Major containers that Python
# supports are list, tuple, set, frozenset, and dict.
#
# A data type is <em><strong>mutable</strong></em> if its value—also known as its state—is allowed to change after
# it has been created. On the other hand, a data type is <em><strong>immutable</strong></em> if its values are static
# and unchangeable once it is created.
#
# With immutable data you can create new variables
# based on existing values, but you cannot actually alter the original values. All of
# the data types we have dealt with so far—`int`, `float`, `bool`, and `str`—are immutable.
# ## Lists
# Lists in Python are mutable, one-dimensional, ordered containers whose elements may be any
# Python objects.
[6, 28]
[1e3, -2, "I am in a list."]
# Anything can go into a list, including other lists!
[[1.0, 0.0], [0.0, 1.0]]
# You can use the `+` operator on a list. You can also append to lists
# in-place using the `append()` or `extend()` method, which adds a single
# element to the end. `+=` works also.
[1, 1] + [2, 3, 5] + [8]
fib = [1, 1, 2, 3, 5, 8]
fib.append(13) # Try two arguments (13,3)
fib
fib.insert(3,100)
fib
fib.extend([21, 34, 55])
fib
fib += [89, 144]
fib
# List indexing is exactly the same as string indexing, but instead of returning strings it
# returns new lists. Here is how to pull every other element out of a list:
fib[::2]
# You can set or delete elements in a
# list. This is because lists are mutable, whereas strings are not,
fib[3] = "whoops" # Replace
fib
del fib[:6]
fib
fib[1::2] = [-1, -1, -1]
fib
# The same multiplication-by-an-integer trick for strings also applies to lists:
[1, 2, 3] * 6
# You can also create lists of characters directly from strings by using the `list()` conversion
# function:
list("F = dp/dt") # Including spaces, all spaces
# Another fascinating property is that a list will infinitely recurse if you add it to itself!
x = []
x.append(x)
x
x[0]
x[0][0]
# To explain how this is possible, we’ll need to explore of how Python manages memory.
# Python is <em><strong>reference counted</strong></em>, which means that variable names are actually references
# to the underlying values. The language then keeps an internal count of how
# many times a reference has been used and what its names are.
#
# Example:
x = 42 # Python starts by first creating the number 42 in memory.
# It sets the name x to refer to the point in memory where 42 lives.
y = x # It sees that y should point to the same place that x is pointing to
del x # x is deleted, but so it keeps both y and 42 around for later use.
# What about lists?
# - Lists are collections of names, not values.
# - The name a list gives to each of its elements is the integer index of that element.
# - The list itself also has a name.
# - This means that when a list itself has two or more variable names and any of them has an element changed, then all of the other variables also see the alteration.
#
# Example:
x = [3, 2, 1, "blast off!"]
y = x
y[1] = "TWO" # When y’s second element is changed to the string 'TWO', this change is reflected back onto x. This is because there is only one list in memory, even though there are two names for it (x and y).
print(x)
del x
print(y)
# ## Tuples
#
# Tuples are the immutable form of lists. They behave almost exactly the same as lists in every way, except that
#
# - you cannot change any of their values.
# - There are no `append()` or `extend()` methods,
# - and there are no in-place operators.
# - tuples are defined by commas (`,`)
# - tuples will be seen surrounded by parentheses. These parentheses serve only to group actions or make the code more readable, not to actually define the tuples.
a = 1, 2, 5, 3 # length-4 tuple
b = (42,) # length-1 tuple, defined by comma
c = (42) # not a tuple, just the number 42
d = () # length-0 tuple- no commas means no elements
type(d)
# You can concatenate tuples together in the same way as lists, but be careful about the
# order of operations. This is where the parentheses come in handy:
(1, 2) + (3, 4)
1, 2 + 3, 4 # it carries out 2 + 3 = 5, then makes a tuple.
# If you have a list that you wish to make immutable, use the function `type()`:
tuple(["e", 2.718])
# Note that even though tuples are immutable, they may have mutable elements. Suppose
# that we have a list embedded in a tuple. This list may be modified in-place even
# though the list may not be removed or replaced wholesale:
x = 1.0, [2, 4], 16
x[1].append(8)
x
# ## Sets
# Instances of the set type are equivalent to mathematical sets. Like their math counterparts,
# literal sets in Python are defined by comma-separated values between curly
# braces (`{}`). Sets are unordered containers of unique values. Duplicated elements are
# ignored.
# a literal set formed with elements of various types
{1.0, 10, "one hundred", (1, 0, 0,0)}
# a literal set of special values
{True, False, None, "", 0.0, 0}
# conversion from a list to a set
set([2.0, 4, "eight", (16,)])
# Repetition is ignored
{1.0, 1.0, "one hundred", (1, 0, 0,0)}
# 1 and 1.0 are considered repetition
{1.0, 1, "one hundred", (1, 0, 0,0)}
# The set of a string is actually the set of its characters. This is because strings
# are sequences,
set("<NAME>")
# To have a set that actually contains a single string, first put the string
# inside of another sequence:
set(["<NAME>"])
# Sets may be used to compute other sets or be compared against other sets.
s={1,2,3,6}
t={3,4,5}
s | t # Union
s & t # Intersection
s - t # Difference - elements in s but not in t
s ^ t # Symmetric difference - elements in s or t but not both
s < t # Strict subset - test if every element in s is in t but not every element in t is in s
s <= t # Subset - test if every element in s is in t.
hash([3])
# ## Dictionaries
#
# Dictionaries are hands down the most important data structure in Python. Everything
# in Python is a dictionary. A dictionary, or `dict`, is a mutable, unordered collection of unique key/value pairs.
#
# In a dictionary, keys are associated with values. This means that you can look up a
# value knowing only its key(s).
# The keys in a dictionary must
# e unique. However, many different keys with the same value are allowed.
#
# As with lists, you can store anything
# you need to as values. Keys, however, must be hashable (hence the name “hash
# table”).
#
# Like the sets, dictionaries are defined by
# outer curly brackets (`{}`) surrounding key/value pairs that are separated by commas
# (`,`).
# Each key/value pair is known as an item, and the key is separated from the value
# by a colon (`:`)
# +
# A dictionary on one line that stores info about Einstein
al = {"first": "Albert", "last": "Einstein", "birthday": [1879, 3, 14]}
# You can split up dicts onto many lines
constants = {
'pi': 3.14159,
"e": 2.718,
"h": 6.62606957e-34,
True: 1.0,
}
# A dict being formed from a list of (key, value) tuples
axes = dict([(1, "x"), (2, "y"), (3, "z")])
print(axes)
# -
# You pull a value out of a dictionary by indexing with the associated key.
constants['e']
axes[3]
al['birthday']
constants[False] = 0.0
print(constants)
del axes[3]
print(axes)
al['first'] = "You can call me Al"
print(al)
# Because dictionaries are mutable, they are not hashable themselves, and you cannot
# use a dictionary as a key in another dictionary. You may nest dictionaries as values,
# however.
d = {}
d['d'] = d
d['e'] = d
d
{} # define empty dict
set() # define empty set
# Tests for containment with the in operator function only on dictionary keys, not values:
"N_A" in constants
# Dictionaries have a lot of useful methods on them as well. For now, content yourself
# with the `update()` method. This incorporates another dictionary or list of tuples inplace
# into the current dict. The update process overwrites any overlapping keys:
axes.update({1: 'r', 2: 'phi', 3: 'theta'})
axes
# This is only enough to get started. Dictionaries are more important than any other
# data type and will come up over and over again. Their special place in the Python
# language will be seen in Chapter 5 and Chapter 6.
# ## Containers Wrap-up
#
# Containers Wrap-up
# Having reached the end of this chapter, you should now be familiar with the following
# concepts:
#
# - Mutability and immutability
# - Duck typing
# - Lists and tuples
# - Hash functions
# - Sets and dictionaries
|
lectures/ch03-containers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
# ___
# # Linear Regression with Python
#
# ** This is mostly just code for reference. Please watch the video lecture for more info behind all of this code.**
#
# Your neighbor is a real estate agent and wants some help predicting housing prices for regions in the USA. It would be great if you could somehow create a model for her that allows her to put in a few features of a house and returns back an estimate of what the house would sell for.
#
# She has asked you if you could help her out with your new data science skills. You say yes, and decide that Linear Regression might be a good path to solve this problem!
#
# Your neighbor then gives you some information about a bunch of houses in regions of the United States,it is all in the data set: USA_Housing.csv.
#
# The data contains the following columns:
#
# * 'Avg. Area Income': Avg. Income of residents of the city house is located in.
# * 'Avg. Area House Age': Avg Age of Houses in same city
# * 'Avg. Area Number of Rooms': Avg Number of Rooms for Houses in same city
# * 'Avg. Area Number of Bedrooms': Avg Number of Bedrooms for Houses in same city
# * 'Area Population': Population of city house is located in
# * 'Price': Price that the house sold at
# * 'Address': Address for the house
# **Let's get started!**
# ## Check out the data
# We've been able to get some data from your neighbor for housing prices as a csv set, let's get our environment ready with the libraries we'll need and then import the data!
# ### Import Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# ### Check out the Data
USAhousing = pd.read_csv('USA_Housing.csv')
USAhousing.head()
USAhousing.info()
USAhousing.describe()
USAhousing.columns
# # EDA
#
# Let's create some simple plots to check out the data!
sns.pairplot(USAhousing)
sns.distplot(USAhousing['Price'])
USAhousing.corr()
sns.heatmap(USAhousing.corr(), annot=True)
# ## Training a Linear Regression Model
#
# Let's now begin to train out regression model! We will need to first split up our data into an X array that contains the features to train on, and a y array with the target variable, in this case the Price column. We will toss out the Address column because it only has text info that the linear regression model can't use.
#
# ### X and y arrays
X = USAhousing[['Avg. Area Income', 'Avg. Area House Age', 'Avg. Area Number of Rooms',
'Avg. Area Number of Bedrooms', 'Area Population']]
y = USAhousing['Price']
# ## Train Test Split
#
# Now let's split the data into a training set and a testing set. We will train out model on the training set and then use the test set to evaluate the model.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=101)
# ## Creating and Training the Model
# %config IPCompleter.greedy=True
from sklearn.linear_model import LinearRegression
# instantiate an instance of the Linear Regression model
lm = LinearRegression()
lm.fit(X_train,y_train)
# ## Model Evaluation
#
# Let's evaluate the model by checking out it's coefficients and how we can interpret them.
# print the intercept
print(lm.intercept_)
lm.coef_
X.columns
X_train.columns
coeff_df = pd.DataFrame(lm.coef_,X.columns,columns=['Coefficient'])
coeff_df
# Interpreting the coefficients:
#
# - Holding all other features fixed, a 1 unit increase in **Avg. Area Income** is associated with an **increase of \$21.52 **.
# - Holding all other features fixed, a 1 unit increase in **Avg. Area House Age** is associated with an **increase of \$164883.28 **.
# - Holding all other features fixed, a 1 unit increase in **Avg. Area Number of Rooms** is associated with an **increase of \$122368.67 **.
# - Holding all other features fixed, a 1 unit increase in **Avg. Area Number of Bedrooms** is associated with an **increase of \$2233.80 **.
# - Holding all other features fixed, a 1 unit increase in **Area Population** is associated with an **increase of \$15.15 **.
#
# Does this make sense? Probably not because I made up this data. If you want real data to repeat this sort of analysis, check out the [boston dataset](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_boston.html):
#
#
# from sklearn.datasets import load_boston
# boston = load_boston()
# print(boston.DESCR)
# boston_df = boston.data
# ## Predictions from our Model
#
# Let's grab predictions off our test set and see how well it did!
predictions = lm.predict(X_test)
predictions
plt.scatter(y_test,predictions)
# **Residual Histogram**
# histogram plot of the residuals, the difference between the actual values and the predicted values
sns.distplot((y_test-predictions),bins=50);
# **If you get a <font color = red>_non-normal distribution_</font> it means that the chosen model (in this case, Linear Regression) wasn't a <font color = green>_good fit_</font> for this data**
# ## Regression Evaluation Metrics
#
#
# Here are three common evaluation metrics for regression problems:
#
# **Mean Absolute Error** (MAE) is the mean of the absolute value of the errors:
#
# $$\frac 1n\sum_{i=1}^n|y_i-\hat{y}_i|$$
#
# **Mean Squared Error** (MSE) is the mean of the squared errors:
#
# $$\frac 1n\sum_{i=1}^n(y_i-\hat{y}_i)^2$$
#
# **Root Mean Squared Error** (RMSE) is the square root of the mean of the squared errors:
#
# $$\sqrt{\frac 1n\sum_{i=1}^n(y_i-\hat{y}_i)^2}$$
#
# Comparing these metrics:
#
# - **MAE** is the easiest to understand, because it's the average error.
# - **MSE** is more popular than MAE, because MSE "punishes" larger errors, which tends to be useful in the real world.
# - **RMSE** is even more popular than MSE, because RMSE is interpretable in the "y" units.
#
# All of these are **loss functions**, because we want to minimize them.
from sklearn import metrics
print('MAE:', metrics.mean_absolute_error(y_test, predictions))
print('MSE:', metrics.mean_squared_error(y_test, predictions))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, predictions)))
# This was your first real Machine Learning Project! Congrats on helping your neighbor out! We'll let this end here for now, but go ahead and explore the Boston Dataset mentioned earlier if this particular data set was interesting to you!
#
#
# ## Great Job!
|
Section 15. Linear Regression/Linear Regression with Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # 1.0 Libraries For Preprocessing
# +
import time
start = time.time()
print("Importing libraries for the preprocessing")
# Library for Wrangling and loading
import pandas as pd
import numpy as np
# Libraries for Visualization
import seaborn as sns
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import plotly.express as px
# Libraries for Partitioning and Spark
from pyspark.sql import SparkSession
from pyspark.sql.types import *
import shutil
import hashlib
# Others
import warnings
import os
# Configuration
pd.set_option("display.max_columns",None)
pd.set_option("display.max_rows",None)
warnings.filterwarnings("ignore")
end = time.time()
print("Imported all libraries | Time Taken {}sec".format(str(end-start)))
# -
# # 2.0 Partitioning
# ## 2.1 Partitioning Parameter
N_PARTITION = 50 # Number of buckets
base_partitions_dir = "../data/external/Partition"
output_dir = "../data/external/output"
# ## 2.2 Collecting data columns
# LOADING PARAMETER
chunksize= 1e5
data_directory = r"..\Data\external\used_cars_data.csv"
# loading chunk of the data for the column list
def col_list(data_path, chunksize, progress=None):
print("Checking and loading file")
time.sleep(0.9)
for df_iter, chunk in enumerate(pd.read_csv(data_path, chunksize=chunksize, iterator=False)):
pass
col_list = list(chunk.columns)
return col_list
# ## 2.3 Function for Hashing id
# hashing the listing id to allow even partitioning across the dataset
def hash_(listing_id):
"""Creates an hashed column using the listing id for the vehicle"""
return int(hashlib.md5(str(listing_id).encode("utf-8")).hexdigest(), 16)
# ## 2.4 Creating dir for partition
def create_partition():
"""Creates an empty partition directory for the buckets"""
start = time.time()
print("Checking if the directory exists...")
time.sleep(0.9)
if os.path.exists(base_partitions_dir):
print("Directory found")
time.sleep(0.4)
print("Removing directory")
time.sleep(1)
shutil.rmtree(base_partitions_dir)
print("Removed the directory")
else:
print("No Such Directory found.")
# Delaying before creating the directories
time.sleep(2.5)
print("Creating empty folder list for partition")
time.sleep(0.9)
if not os.path.exists(base_partitions_dir):
# Creating partition directory
os.mkdir(base_partitions_dir)
# Making a new directory for the partitions
for i in range(N_PARTITION):
partition_path = os.path.join(
base_partitions_dir, "p{}".format(i)).replace("\\", "/")
# Printing the path
print('| {} | Partition left {} |'.format(partition_path,N_PARTITION-i))
if not os.path.exists(partition_path):
os.mkdir(partition_path)
else:
print("Path Already exist")
time.sleep(0.6)
end = time.time()
print("| Completed | Time Taken ------------------------- {}sec |".format(str(end-start)))
# Making the directory
dir = create_partition()
# ## 2.5 Creating blank partition
# +
chunksize= 1e5
data_directory = r"..\Data\external\used_cars_data.csv"
def create_blank_partition():
"""Creating a blank partition with the number of bucket"""
start = time.time()
data_list = col_list(data_directory, chunksize)
for i in range(N_PARTITION):
time.sleep(0.9)
file_base_dir = os.path.join(base_partitions_dir,"p{}".format(str(i)),"").replace("\\","/")
print(file_base_dir)
# Opening the file and writing it to the partition created
with open(file_base_dir+"vehicle_used_data.csv", "w") as f:
f.write(",".join(data_list))
end = time.time()
print("Time taken ------------------- | {}sec".format(str(end-start)))
return file_base_dir
dir_path = create_blank_partition()
# -
# ## 2.6 Partitioning by hashing
N_PARTITION = 50 # Number of buckets
# Partitioing and hashing the
def partition_by_hashing(df, progress=None):
# hashing the listing_id column into the number of partitions
df["hashed"] = df["listing_id"].apply(hash_) % N_PARTITION
for partitions, data in df.groupby("hashed"):
start = time.time()
print("Data partition: {}".format(str(partitions)))
# Removing hash columns from the dataset
data = data.drop("hashed", axis=1)
# Wrting the data to the partition
path_dir = os.path.join(base_partitions_dir,"p{}".format(partitions),"").replace("\\","/")
print("| writing data partition to {} |".format(path_dir))
# Writing the data to the path
with open(path_dir+"vehicle_used_data.csv", "a", encoding="utf-8") as f:
f.write("\n")
data.to_csv(f, header=False, index=False)
end = time.time()
print("Time taken {}sec".format(str(end-start)))
# ## 2.7 Writing data to each partition
chunksize = 1e5
for df_iter, data in enumerate(pd.read_csv(r"..\Data\external\used_cars_data.csv", iterator=True, chunksize=chunksize, encoding="latin1"),1):
print("Iter:",df_iter)
partition = partition_by_hashing(df=data)
print("\n")
#data = partition_by_hashing(df, name="listing_id", progress=None)
# # 3.0 Data Distribution with Spark
# ## 3.1 Data cleaning in parallel(configuration)
# # 4.0 Data Cleaning
# ## 4.1 Loading first Partition
# +
# LOADING FIRST PARTITION FILE
PARTITION = 0
TARGET = "price"
PARTITION_DIR = os.path.join("..\Data\external\Partition", "p{}".format(str(PARTITION)),"vehicle_used_data.csv").replace("\\","/")
used_data = pd.read_csv(PARTITION_DIR, header=0, delimiter=",")
used_data.head(2)
# -
data = used_data.copy()
def clean_data(data):
"""Removing some irrelevant columns in the dataframe"""
# Defining some columns to remove
cols = ["vin", 'description', "exterior_color", "wheel_system", "vehicle_damage_category", "trimId",
"theft_title", "sp_id", "main_picture_url", "longitude", "listing_id", "listing_color", "latitude",
"interior_color", "cabin", "major_options", "back_legroom", "bed", "bed_height", "bed_length",
"is_certified","owner_count","is_cpo", "is_oemcpo", "salvage", "wheelbase", "width","combine_fuel_economy",
"daysonmarket","dealer_zip","engine_cylinders","horsepower",
"franchise_dealer","front_legroom","fuel_tank_volume","height","length","franchise_make","savings_amount","transmission_display","trim_name","sp_name"
]
# Dropping the columns
data = data.drop(columns=cols)
# data = data.drop(cols, axis=1)
# listed date to pandas datetime
data["listed_date"] = pd.to_datetime(data["listed_date"])
# Transforming
data["transmission"] = data["transmission"].apply(lambda inf: str(inf).replace("A","Automatic").replace("M","Manual"))
data["Vehicle_power"] = data["power"].apply(lambda inf: str(inf).split("@")[0].strip().split(" ")[0])
data["Vehicle_torque"] = data["torque"].apply(lambda inf: str(inf).split("@")[0].strip().split(" ")[0])
data["max_seating"] = data["maximum_seating"].apply(lambda inf: str(inf).strip().split(" ")[0])
data["Listing_year"] = data["listed_date"].apply(lambda inf: inf.year)
data["engine_displacement"] = data["engine_displacement"].apply(lambda inf: inf/1000)
data["combined_MPG"] = (data["highway_fuel_economy"] + data["city_fuel_economy"])/2
# Replacing any "nan" with np.nan value ===> Null
data = data.replace({"nan":np.nan, "_": np.nan,"--":np.nan})
# Changing datatype
data["Vehicle_power"] = data['Vehicle_power'].astype(np.float).astype("Int32")
data["Vehicle_torque"] = data['Vehicle_torque'].astype(np.float).astype("Int32")
data["max_seating"] = data['max_seating'].astype(np.float).astype("Int32")
# data["isCab"] = pd.DataFrame(data["isCab"])
# data["isCab"] = data["isCab"].map({"False":False,"True":True})
# Dropping some more columns
data = data.drop(columns=["listed_date","maximum_seating","power",'torque'])
# Renaming some columns
data = data.rename(columns={"wheel_system_display":"Drivetrain",
"transmission":"Transmission",
"body_type":"body_style",
"city_fuel_economy":"city_MPG",
"engine_displacement":"engine_size",
"highway_fuel_economy":"highway_MPG",
"year": "Vehicle_year"})
return data
def clean_data(data):
"""C
"""
# Filtering the data
filtered_data = data[data["make_name"].value_counts() > 10000]
# Dropping some columns
filtered_data = filtered_data.drop(
["Unnamed: 0", "listed_date", "listed_year"], axis=1)
# Data Cleaning
filtered_data["fuel_tank_volume"] = filtered_data["fuel_tank_volume"].apply(
lambda volume: int(volume.strip().split(" ")[0]))
filtered_data["maximum_seating"] = filtered_data["maximum_seating"].apply(
lambda seating: int(seating.strip().split(" ")[0]))
filtered_data["transmission"] = filtered_data["transmission"].apply(
lambda trans: trans.replace("A", "Automatic").replace("M", "Manual"))
filtered_data["engine_displacement"] = filtered_data["engine_displacement"].apply(
lambda disp: disp/1000)
filtered_data["engine_cylinders"] = filtered_data["engine_cylinders"].apply(
lambda cyl: cyl.strip().split(" ")[0].strip())
filtered_data["mpg"] = (
filtered_data["city_fuel_economy"] + filtered_data["highway_fuel_economy"])/2
# Renaming some columns
filtered_data = filtered_data.rename(columns={"fuel_tank_volume": "Tank_Volume",
"engine_displacement": "engine_size",
"city_fuel_economy": "MPG city",
"highway_fuel_economy": "MPG highway",
"wheel_system": "Drivetrain"})
return filtered_data
new_data = clean_data(data)
new_data.head(2)
for feature in new_data.columns:
if new_data[feature].dtype == object:
print(feature, new_data[feature].nunique())
# ## Dealing with the missing values
def impute_missing_values(new_data, verbose: int):
"""Dealing with the missing values by imputation"""
# Performing input validation
if (verbose not in [0, 1]):
raise TypeError("Code ran into an Exception \
Because verbose is either a string or not 0 or 1")
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import KNeighborsRegressor
cat_fea = [
feature for feature in new_data.columns if new_data[feature].dtype == object]
num_missing_fea = [feature for feature in new_data.columns if new_data[feature].isnull(
).sum() > 0 and new_data[feature].dtype != object]
not_null_fea = [
feature for feature in new_data.columns if new_data[feature].isnull().sum() == 0]
# Label encoding the categorical feature
le = LabelEncoder()
print("Encoding the categorical feature")
for feature in cat_fea:
new_data[feature] = le.fit_transform(new_data[feature])
# imputing the missing features
estimator = RandomForestRegressor(random_state=42)
estimator_neighbour = KNeighborsRegressor(n_neighbors=5)
print("Imputing the missing values")
imputer = IterativeImputer(
estimator=estimator, max_iter=7, verbose=verbose, random_state=42
)
imputer.fit(new_data)
transformed = imputer.transform(new_data)
transformed_data = pd.DataFrame(transformed, columns=new_data.columns)
# Reverting the encoded cat features
print("Reverting encoded feature to original")
for feature in cat_fea:
transformed_data[feature] = le.inverse_transform(
transformed_data[feature])
return transformed_data
used_data.isnull().sum()
data.isnull().sum()
# +
# SPARK PARAMETER
# SPARK_HOME = r"C:\spark\spark" # The spark location
# LOG_DIR = r"C:\spark\tmp\spark-event" # Eventlogging location
import findspark
findspark.init()
# Spark configuration
import pyspark
conf = pyspark.SparkConf()
# Enabling logging
conf.set("spark.eventLog.enabled", False)
conf.set("spark.eventLog.dir", r"\tmp")
conf.set("spark.eventLog.compress",True)
# Enabling all cores usage
conf.set("spark.num.executor", 1)
conf.set("spark.executor.memory", "8g")
conf.set("spark.executor.cores",2)
# setting the appname for the spark ui
conf.setAppName("Data Cleaning")
# Set parent
conf.set("spark.master", "local[2]")
conf.getAll()
sc = pyspark.SparkContext(conf=conf)
sc
# -
sc.stop()
a = sc.parallelize(range(0,100), N_PARTITION).map(lambda x: clean_data(x))
# +
#using the main thing
# -
a.collect()
SELECT FROM table *
print(list(range(0,50)))
# Parallelizing the process
start = time.time()
sc.parallelize(list(range(0,100)),N_PARTITION).map(lambda x: clean_data(x)).collect()
sc.stop()
end = time.time()
used_data.head()
|
notebooks/preprocessing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 3. Train-Predict KNN
# Result:
# - Kaggle score:
#
# Reference:
# - http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier
# - http://scikit-learn.org/stable/modules/model_evaluation.html#model-evaluation
# ## Run name
# +
import time
import os
import pandas as pd
import gc
project_name = 'Google_LandMark_Rec'
step_name = 'Train-Predict_KNN'
time_str = time.strftime("%Y%m%d_%H%M%S", time.localtime())
run_name = project_name + '_' + step_name + '_' + time_str
print('run_name: ' + run_name)
# -
# ## 项目文件夹
# +
cwd = os.getcwd()
data1_folder = '/data1/kaggle/landmark-recognition-challenge/'
input_folder = os.path.join(data1_folder, 'input')
output_folder = os.path.join(cwd, 'output')
model_folder = os.path.join(cwd, 'model')
feature_folder = os.path.join(cwd, 'feature')
post_pca_feature_folder = os.path.join(cwd, 'post_pca_feature')
log_folder = os.path.join(cwd, 'log')
print('input_folder: \t' + input_folder)
print('output_folder: \t' + output_folder)
print('model_folder: \t' + model_folder)
print('feature_folder: \t' + feature_folder)
print('post_pca_feature_folder: \t' + post_pca_feature_folder)
print('log_folder: \t' + log_folder)
org_train_folder = os.path.join(input_folder, 'org_train')
org_test_folder = os.path.join(input_folder, 'org_test')
train_folder = os.path.join(input_folder, 'data_train')
test_folder = os.path.join(input_folder, 'data_test')
test_sub_folder = os.path.join(test_folder, 'test')
if not os.path.exists(post_pca_feature_folder):
os.mkdir(post_pca_feature_folder)
print('Create folder: %s' % post_pca_feature_folder)
# -
train_csv_file = os.path.join(input_folder, 'train.csv')
test_csv_file = os.path.join(input_folder, 'test.csv')
sample_submission_folder = os.path.join(input_folder, 'sample_submission.csv')
# ## 加载feature
# +
# %%time
import h5py
import numpy as np
from sklearn.utils import shuffle
np.random.seed(2018)
x_data = []
y_data = {}
x_test = []
image_size = 150
time_str = '20180311-151108'
cwd = os.getcwd()
# feature_cgg16 = os.path.join(cwd, 'feature', 'feature_VGG16_{}.h5'.format(20180219))
# feature_cgg19 = os.path.join(cwd, 'feature', 'feature_VGG19_{}.h5'.format(20180219))
# feature_resnet50 = os.path.join(cwd, 'feature', 'feature_ResNet50_{}.h5'.format(20180220))
# feature_xception = os.path.join(cwd, 'feature', 'feature_Xception_{}.h5'.format(20180221))
feature_inceptionV3 = os.path.join(cwd, 'post_pca_feature', 'post_pca_feature_InceptionV3_%s_%s.h5' % (image_size, time_str))
# feature_inceptionResNetV2 = os.path.join(cwd, 'feature', 'feature_InceptionResNetV2_%s.h5' % time_str)
# for filename in [feature_cgg16, feature_cgg19, feature_resnet50, feature_xception, feature_inception, feature_inceptionResNetV2]:
for filename in [feature_inceptionV3]:
with h5py.File(filename, 'r') as h:
x_data.append(np.array(h['train']))
y_data = np.array(h['train_labels'])
# x_val.append(np.array(h['val']))
# y_val = np.array(h['val_labels'])
x_test.append(np.array(h['test']))
# -
print(x_data[0].shape)
print(len(y_data))
print(x_test[0].shape)
# %%time
x_data = np.concatenate(x_data, axis=-1)
x_test = np.concatenate(x_test, axis=-1)
print(x_data.shape)
print(x_test.shape)
# +
# from sklearn.model_selection import train_test_split
# x_train, x_val, y_train, y_val = train_test_split(x_data, y_data, test_size=0.0025, random_state=5)
# print(x_train.shape)
# print(x_val.shape)
# print(y_train.shape)
# print(y_val.shape)
# -
# ## Train
set_y_data = list(set(y_data))
print(len(set_y_data))
# +
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_data, y_data, test_size=0.1, random_state=2017)
print(x_train.shape)
print(x_val.shape)
print(y_train.shape)
print(y_val.shape)
print(x_test.shape)
# -
set_y_train = list(set(y_train))
print(len(set_y_train))
# +
# %%time
from sklearn.neighbors import NearestNeighbors
clf = NearestNeighbors(
radius=2,
algorithm='brute',
leaf_size=10,
metric='cosine',
n_jobs=-1
)
clf.fit(x_train, y_train)
# -
# %%time
from sklearn.metrics import accuracy_score
y_train_pred = clf.kneighbors(x_train[:100], 20, True)
print(y_train_pred[0].shape)
print(y_train_pred[1].shape)
y_train_pred1 = [y_train[i] for i in y_train_pred[1][:, 0]]
# print(y_train_pred1.shape)
print(y_train_pred1[:10])
print(accuracy_score(y_train[:100], y_train_pred1))
# +
# %%time
from sklearn.metrics import accuracy_score
count = 100
# count = len(y_val)
y_val_nbs = clf.kneighbors(x_val[:count], 10, True)
print(y_val_nbs[0].shape)
print(y_val_nbs[1].shape)
# +
# %%time
y_val_pred = [y_train[i] for i in y_val_nbs[1][:, 0]]
# for i in range(count):
# print((y_val[i], y_val_pred1[i]), end=' ')
# if y_val[i] == y_val_pred1[i]:
# print('*')
# else:
# print(' ')
val_acc = accuracy_score(y_val[:count], y_val_pred)
print(val_acc)
# -
print(list(set(y_val_nbs[0][1])))
print(list(set(y_val_nbs[1][1])))
# %%time
y_test_nbs = clf.kneighbors(x_test, 1, True)
print(y_test_nbs[0].shape)
print(y_test_nbs[1].shape)
# %%time
y_test_pred = [y_train[i] for i in y_test_nbs[1][:, 0]]
print(len(y_test_pred))
print(y_test_pred[:10])
# ## Predict
sample_submission_csv = pd.read_csv(sample_submission_folder)
print('sample_submission_csv.shape is {0}.'.format(sample_submission_csv.shape))
display(sample_submission_csv.head(2))
# 这里证明os.listdir()得到的图片名称list不正确
files = os.listdir(os.path.join(input_folder, 'data_test', 'test'))
print(files[:10])
# 这里证明ImageDataGenerator()得到的图片名称list才是正确
from keras.preprocessing.image import ImageDataGenerator
gen = ImageDataGenerator()
image_size = (299, 299)
batch_size = 128
test_generator = gen.flow_from_directory(test_folder, image_size, shuffle=False, batch_size=batch_size)
print('test_generator')
print(len(test_generator.filenames))
print(test_generator.filenames[:10])
# +
# test_generator_filenames = np.array(test_generator.filenames)
# test_generator_filenames_file = os.path.join(output_folder, 'test_generator_filenames.npy')
# np.save(test_generator_filenames_file, test_generator_filenames)
# +
# %%time
test_dict = {}
for i, paire in enumerate(zip(test_generator.filenames, y_test_pred)):
image_name, label = paire[0], paire[1]
image_id = image_name[5:-4]
test_dict[image_id] = '%d %.4f' % (label, 1)
#确认图片的id是否能与ImageDataGenerator()对应上
for key in list(test_dict.keys())[:10]:
print('%s %s' % (key, test_dict[key]))
# -
# %%time
len_sample_submission_csv = len(sample_submission_csv)
print('len(len_sample_submission_csv)=%d' % len_sample_submission_csv)
count = 0
for i in range(len_sample_submission_csv):
image_id = sample_submission_csv.iloc[i, 0]
# landmarks = sample_submission_csv.iloc[i, 1]
if image_id in test_dict:
pred_landmarks = test_dict[image_id]
# print('%s %s' % (image_id, pred_landmarks))
sample_submission_csv.iloc[i, 1] = pred_landmarks
else:
# print(image_id)
# sample_submission_csv.iloc[i, 1] = '9633 1.0' # 属于9633的类最多,所以全都设置成这个类,可能会比设置成空得到的结果好
sample_submission_csv.iloc[i, 1] = '' # 设置成空
count += 1
if count % 10000 == 0:
print(int(count/10000), end=' ')
display(sample_submission_csv.head(2))
# +
run_name_acc = run_name + '_' + str(int(val_acc*10000)).zfill(4)
pred_file = os.path.join(output_folder, 'pred_' + run_name_acc + '.csv')
print(pred_file)
sample_submission_csv.to_csv(pred_file, index=None)
# -
print(run_name_acc)
print('Done !')
|
landmark-recognition-challenge/3. Train-Predict KNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: bigbang-env
# language: python
# name: bigbang-env
# ---
# # IETF Attendance using `ietfdata` library and the Datatracker
# We can produce similar graphs, more easily with more data and less code, using data stored in the IETF Datatracker and accessed using `ietfdata`.
from ietfdata.datatracker import *
from ietfdata.datatracker_ext import *
import pandas as pd
import matplotlib.pyplot as plt
import dataclasses
# +
datatracker = DataTracker()
meetings = datatracker.meetings(meeting_type = datatracker.meeting_type(MeetingTypeURI('/api/v1/name/meetingtypename/ietf/')))
full_ietf_meetings = list(meetings)
# -
ietf_meetings = []
for meeting in full_ietf_meetings:
meetingd = dataclasses.asdict(meeting)
meetingd['meeting_obj'] = meeting
meetingd['num'] = int(meeting.number)
ietf_meetings.append(meetingd)
meetings_df = pd.DataFrame.from_records(ietf_meetings)
# One way to get the registration count for a meeting is to download every individual's meeting registration and count them. (We don't have to do this regularly, because the datatracker actually provides counts and I've confirmed they are the same. Commented out below because the operation can be slow and isn't necessary, but feel to uncomment and try it out!)
dt = DataTrackerExt() # initialize, for all meeting registration downloads
# +
# ## this downloads every meeting registration for one particular meeting and counts them
#
# meeting110 = full_ietf_meetings[1]
# regs = dt.meeting_registrations(meeting=meeting110)
# registrations110 = list(regs)
# len(registrations110)
# -
# First, we can make a classic figure, looking at the attendance of all (numbered) IETF meetings, from the 1980s until today.
axes = meetings_df.plot(
x='date',
y='attendees',
kind='line',
legend=False,
title='Attendance at IETF Meetings')
axes.set_xlabel('')
plt.show()
# Do the recent virtual meetings especially stand out?
meetings_df['virtual'] = meetings_df.apply(lambda row: 'virtual' if row['city'] in ['Online', 'Virtual'] else 'inperson', axis=1)
df = meetings_df[meetings_df['date'] > datetime(2006,1,1,0,0)]
df.plot.scatter(x='date',
y='attendees',
c=df['virtual'].map({'virtual':'red', 'inperson':'blue'})
)
# Do the country or affiliation of participants differ for the recent virtual meetings? (Or on where the meeting is physically located?)
# This will construct a dataframe of every attendee's registration at every specified meeting. (Downloading this data takes a while!)
meeting_attendees_df = pd.DataFrame()
for meeting in ietf_meetings:
if meeting['num'] in [104,105,106,107,108,109]: # can filter here by the meetings to analyze
registrations = dt.meeting_registrations(meeting=meeting['meeting_obj'])
df = pd.DataFrame.from_records([dataclasses.asdict(x) for x in list(registrations)])
df['num'] = meeting['num']
meeting_attendees_df = meeting_attendees_df.append(df)
# Filter by those who actually attended the meeting (checked in, didn't just register).
meeting_attendees_df[meeting_attendees_df['attended'] == True]
grouped = meeting_attendees_df[meeting_attendees_df['attended'] == True].groupby(['num','country_code'])
country_ordering=grouped.size().unstack().sum(0).sort_values(ascending=False).index.values
reordered = grouped.size().unstack().reindex(columns=country_ordering)
virtual_nums = list(meetings_df[meetings_df['virtual']=='virtual']['num'])
fig, ax = plt.subplots(figsize=(7.5,5))
reordered.plot(
kind='bar',
stacked=True,
legend=False,
ax = ax
)
ahandles, labels = ax.get_legend_handles_labels()
ax.legend(reversed(ahandles[:10]), reversed(labels[:10]), bbox_to_anchor=(1, 0.9))
ax.set_xlabel('IETF Meeting')
plt.xticks(rotation=0)
[t.set_color('red') for t in ax.xaxis.get_ticklabels() if int(t.get_text()) in virtual_nums]
ax.set_ylabel('Attendance')
ax.set_title('IETF (Virtual) Meeting Attendance by Country')
plt.show()
fig.savefig('graphs/attendance-by-country-virtual.png',dpi=300, bbox_inches='tight')
# The virtual meetings have modestly higher attendance than recent meetings. The proportions by country are not obviously different in the virtual meetings, but there may be less variation of the proportion of attendance based on where the meeting is physically located. (That is, so far we don't see the big swings in US, Chinese, Japanese or German attendance, as we did when the meeting was physically located in the US, China, Japan or Europe.)
# ### Grouping by continent or region
# The UN Statistical Commission provides [list of countries including country codes and grouped into regions and subregions](https://unstats.un.org/unsd/methodology/m49/). (The included CSV is slightly modified from the UN version to correctly handle escaping commas in certain regional names.)
undf = pd.read_csv('unsd.csv')
undf
attended = meeting_attendees_df[meeting_attendees_df['attended'] == True]
attended_regions = attended.merge(undf, how='left', left_on='country_code', right_on='ISO-alpha2 Code')
# Map to North America and South America (to match IETF's practice and some common convention, even though the UN prefers Northern America and Latin America).
def preferred_region_names(series):
if series['Sub-region Name'] == 'Northern America':
return 'North America'
if series['Intermediate Region Name'] in ['Caribbean', 'Central America']:
return 'North America'
if series['Intermediate Region Name'] == 'South America':
return 'South America'
else:
return series['Region Name']
attended_regions['region'] = attended_regions.apply(preferred_region_names, axis=1)
grouped = attended_regions.groupby(['num','region'])
region_ordering=grouped.size().unstack().sum(0).sort_values(ascending=False).index.values
reordered = grouped.size().unstack().reindex(columns=region_ordering)
reordered
proportions = reordered.apply(lambda x: x*100/sum(x), axis=1)
proportions
reordered_meetings = reordered.merge(meetings_df, how='left', on='num')
def preferred_city_names(city):
if city in ['Virtual','Online']:
return 'Virtual'
if city == 'Montreal':
return 'Montréal'
return city
reordered_meetings['city'] = reordered_meetings['city'].transform(preferred_city_names)
combined_labels = reordered_meetings.apply(lambda x: str(x['num']) + '\n' + x['city'], axis=1)
fig2, ax2 = plt.subplots(figsize=(7.5,5))
reordered.plot(
kind='bar',
stacked=True,
legend=False,
ax = ax2
)
ahandles, labels = ax2.get_legend_handles_labels()
ax2.legend(reversed(ahandles[:10]), reversed(labels[:10]), bbox_to_anchor=(1, 0.9))
ax2.set_xlabel('IETF Meeting')
plt.xticks(rotation=0)
ax2.set_xticklabels(combined_labels)
ax2.set_ylabel('Attendance')
ax2.set_title('IETF Meeting Attendance by Region')
plt.show()
fig2.savefig('graphs/attendance-by-region.png',dpi=300, bbox_inches='tight')
fig2, ax2 = plt.subplots(figsize=(7.5,5))
proportions.plot(
kind='bar',
stacked=True,
legend=False,
ax = ax2
)
ahandles, labels = ax2.get_legend_handles_labels()
ax2.legend(reversed(ahandles[:10]), reversed(labels[:10]), bbox_to_anchor=(1, 0.9))
ax2.set_xlabel('IETF Meeting')
plt.xticks(rotation=0)
ax2.set_xticklabels(combined_labels)
ax2.set_ylabel('Attendance (%)')
ax2.set_ylim((0,100))
ax2.set_title('IETF Meeting Attendance by Region')
plt.show()
fig2.savefig('graphs/attendance-by-region-proportion.png',dpi=300, bbox_inches='tight')
# ### Affiliation
# We can also visualize the stated affiliations of the attendees, although the number of affiliations is much more diverse and messier than the country data.
aff_grouped = meeting_attendees_df.groupby(['num','affiliation'])
aff_grouped.size()
size_sorted = aff_grouped.size().sort_values(ascending=False).sort_index(level='num', sort_remaining=False)
size_sorted.reset_index().groupby('num').head()
aff_ordering=aff_grouped.size().unstack().sum(0).sort_values(ascending=False).index.values
aff_reordered = aff_grouped.size().unstack().reindex(columns=aff_ordering)
aff_ordering[1:50]
aff_reordered = aff_grouped.size().unstack().reindex(columns=aff_ordering[1:20])
fig, ax = plt.subplots(figsize=(15,5))
aff_reordered.plot(
kind='line',
legend=False,
ax = ax
)
ahandles, labels = ax.get_legend_handles_labels()
ax.legend(ahandles[:10], labels[:10], loc='upper left')
ax.set_xlabel('IETF Meeting Number')
ax.set_ylabel('Attendance')
ax.set_title('IETF Meeting Attendance by Affiliation')
plt.show()
# These attendance numbers by large companies are significant, but recall that the average meeting has over 1000 participants, so this excludes the vast majority of participants, and unaffiliated participants are always the largest single group (not shown in this graph).
#
# <div class="alert alert-info"><b>TODO</b>
# Some entity resolution to handle duplicates is necessary to make this chart actually useful (for both Cisco and Huawei, in particular, but it applies to many affiliations).</div>
fig.savefig('graphs/attendance-by-affiliation.png',dpi=300)
|
examples/attendance/IETF Attendance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
# %matplotlib inline
# -
def normalize(X):
n = X.shape[0]
mean = np.mean(X, axis=1).reshape((n, 1))
std = np.std(X, axis=1).reshape((n, 1))
X_new = (X - mean) / std**2
return X_new, mean, std
def sigmoid(Z):
return 1 / (1 + np.exp(-Z))
def plot_data(X, y):
ax = plt.gca()
ax.scatter(X[:,0], X[:,1], c=(y == 1), cmap=cm_bright)
def fwd_pass(X, params):
W = params["W"]
b = params["b"]
Z = np.dot(W, X) + b
A = sigmoid(Z)
cache = (W, b, Z, A)
return A, cache
def cost(A, Y):
m = Y.shape[1]
L = - Y * np.log(A) - (1 - Y) * np.log(1 - A)
J = np.sum(L) / m
return J
def bwd_pass(X, Y, cache):
n, m = X.shape
(W, b, Z, A) = cache
dZ = A - Y
dW = 1. / m * np.dot(X, dZ.T).reshape((1, n))
db = 1. / m * np.sum(dZ)
grads = {"dW" : dW, "db" : db, "dZ" : dZ}
return grads
def init_params(n, m):
W = np.random.randn(1, n) * 0.01
b = 0
params = {"W" : W, "b" : b}
return params
def update_params(params, grads, learning_rate):
W = params["W"]
b = params["b"]
dW = grads["dW"]
db = grads["db"]
params["W"] = W - learning_rate * dW
params["b"] = b - learning_rate * db
return params
def fit(X, Y, learning_rate = 0.01, num_iter = 30000, debug = False):
n, m = X.shape
params = init_params(n, m)
costs = []
for i in range(num_iter):
A, cache = fwd_pass(X, params)
curr_cost = cost(A, Y)
grads = bwd_pass(X, Y, cache)
params = update_params(params, grads, learning_rate)
if debug and i % 1000 == 0:
print("{}-th iteration: {}".format(i, curr_cost))
costs.append(curr_cost)
plt.plot(costs)
plt.ylabel("Cost")
plt.xlabel("Iteration, *1000")
plt.show()
return params
data_columns = ["exam1", "exam2"]
target_column = "submitted"
df = pd.read_csv("sats.csv")
X, Y = df[data_columns].values, df[target_column]
print('Training set: X={}, y={}'.format(X.shape, Y.shape))
plot_data(X, Y)
Y = Y.values.reshape((df.shape[0], 1))
# +
X, Y = X.T, Y.T
print(X)
print(Y)
print('X: {}'.format(X.shape))
print('y: {}'.format(Y.shape))
# -
X, mean, std = normalize(X)
X[:,:5]
Y.shape
mean
std
params = fit(X, Y, learning_rate = 0.1, num_iter = 200000, debug = True)
print(params)
|
LogRegr_Alt.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # read and transform google form data
# Google Form: https://goo.gl/forms/mahcMnQxzc2vZhoz2
# Google Sheets: https://docs.google.com/spreadsheets/d/1Xi5jk9rkfOewN16cOlH4aFuPKoXMzAj8d8Eawveglpc/edit#gid=22521621
#เรียนรู้ การดึงข้อมูลจาก Google Sheet จากการตอบแบบสอบถามของ google Form
from IPython.display import IFrame, YouTubeVideo, SVG, HTML
YouTubeVideo('mVXUZSyIq40', 400,300)
import pandas as pd
import numpy as np
print(f'pandas version: {pd.__version__}')
print(f'numpy version: {np.__version__}')
# +
# google form url: https://goo.gl/forms/mahcMnQxzc2vZhoz2
# google sheets generated by google form
# https://docs.google.com/spreadsheets/d/1Xi5jk9rkfOewN16cOlH4aFuPKoXMzAj8d8Eawveglpc/edit#gid=22521621
# note: replace 'edit#' with 'export?format=xlsx&'
url='https://docs.google.com/spreadsheets/d/1Xi5jk9rkfOewN16cOlH4aFuPKoXMzAj8d8Eawveglpc/export?format=xlsx&gid=22521621'
df = pd.read_excel(url)
df
# -
df.columns
new_colnames = ['timestamp', 'gender', 'age', 'product', 'price', 'service', 'overall']
df.columns = new_colnames
df
# ## recode gender
# +
d = {'Female': 'F',
'Male': 'M',
'Prefer not to say': 'X'}
df.gender.map(d, na_action='ignore')
# -
df.gender=df.gender.map(d, na_action='ignore')
df
# ## recode 'product', 'price', 'service', 'overall' columns
def label2val(s):
d = {'very dissatisfied': 1,
'dissatisfied': 2,
'neutral': 3,
'satisfied': 4,
'very satisfied': 5}
if s in d.keys():
v = d[s]
else:
v = np.nan
return v
label2val('satisfied')
df['product'].apply(label2val)
df[['product', 'price', 'service', 'overall']].applymap(label2val)
likert_cols = ['product', 'price', 'service', 'overall']
df[likert_cols]=df[likert_cols].applymap(label2val)
df
# ### read ALL sheets
url='https://docs.google.com/spreadsheets/d/1Xi5jk9rkfOewN16cOlH4aFuPKoXMzAj8d8Eawveglpc/export?format=xlsx'
dfs = pd.read_excel(url, sheet_name=None)
len(dfs)
dfs.keys()
dfs['resp'].head(10)
dfs['resp_mod']
dfs['lookup']
dfs['var_label']
# +
# dfs['resp'].to_csv('data/resp.csv', index=False)
# -
|
learn_jupyter/14_pandas transform google form data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # "Visualizing COVID-19"
# > "DataCamp Project: Visualizing COVID-19"
#
# - toc: true
# - branch: master
# - badges: true
# - comments: true
# - categories: [datacamp, projects, r]
# - hide: false
# + dc={"key": "4"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 1. From epidemic to pandemic
# <p><img style="float: left; margin:5px 20px 5px 1px; width:40%" src="https://www.nps.gov/aboutus/news/images/CDC-coronavirus-image-23311-for-web.jpg?maxwidth=650&autorotate=false"></p>
# <p>In December 2019, COVID-19 coronavirus was first identified in the Wuhan region of China. By March 11, 2020, the World Health Organization (WHO) categorized the COVID-19 outbreak as a pandemic. A lot has happened in the months in between with major outbreaks in Iran, South Korea, and Italy. </p>
# <p>We know that COVID-19 spreads through respiratory droplets, such as through coughing, sneezing, or speaking. But, how quickly did the virus spread across the globe? And, can we see any effect from country-wide policies, like shutdowns and quarantines? </p>
# <p>Fortunately, organizations around the world have been collecting data so that governments can monitor and learn from this pandemic. Notably, the Johns Hopkins University Center for Systems Science and Engineering created a <a href="https://github.com/RamiKrispin/coronavirus">publicly available data repository</a> to consolidate this data from sources like the WHO, the Centers for Disease Control and Prevention (CDC), and the Ministry of Health from multiple countries.</p>
# <p>In this notebook, you will visualize COVID-19 data from the first several weeks of the outbreak to see at what point this virus became a global pandemic.</p>
# <p><em>Please note that information and data regarding COVID-19 is frequently being updated. The data used in this project was pulled on March 17, 2020, and should not be considered to be the most up to date data available.</em></p>
# + dc={"key": "4"} tags=["sample_code"]
# Load the readr, ggplot2, and dplyr packages
library(readr)
library(ggplot2)
library(dplyr)
# Read datasets/confirmed_cases_worldwide.csv into confirmed_cases_worldwide
confirmed_cases_worldwide <- read_csv('datasets/confirmed_cases_worldwide.csv')
# See the result
confirmed_cases_worldwide
# + dc={"key": "12"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 2. Confirmed cases throughout the world
# <p>The table above shows the cumulative confirmed cases of COVID-19 worldwide by date. Just reading numbers in a table makes it hard to get a sense of the scale and growth of the outbreak. Let's draw a line plot to visualize the confirmed cases worldwide.</p>
# + dc={"key": "12"} tags=["sample_code"]
# Draw a line plot of cumulative cases vs. date
# Label the y-axis
ggplot(data=confirmed_cases_worldwide, aes(x=date, y=cum_cases)) + geom_line() + geom_point() + ylab("Cumulative confirmed cases")
# + dc={"key": "19"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 3. China compared to the rest of the world
# <p>The y-axis in that plot is pretty scary, with the total number of confirmed cases around the world approaching 200,000. Beyond that, some weird things are happening: there is an odd jump in mid February, then the rate of new cases slows down for a while, then speeds up again in March. We need to dig deeper to see what is happening.</p>
# <p>Early on in the outbreak, the COVID-19 cases were primarily centered in China. Let's plot confirmed COVID-19 cases in China and the rest of the world separately to see if it gives us any insight.</p>
# <p><em>We'll build on this plot in future tasks. One thing that will be important for the following tasks is that you add aesthetics within the line geometry of your ggplot, rather than making them global aesthetics.</em></p>
# + dc={"key": "19"} tags=["sample_code"]
# Read in datasets/confirmed_cases_china_vs_world.csv
confirmed_cases_china_vs_world <- read_csv('datasets/confirmed_cases_china_vs_world.csv')
# See the result
confirmed_cases_china_vs_world
# Draw a line plot of cumulative cases vs. date, grouped and colored by is_china
# Define aesthetics within the line geom
plt_cum_confirmed_cases_china_vs_world <- ggplot(data=confirmed_cases_china_vs_world) +
geom_line(aes(x=date, y=cum_cases, group=is_china, color=is_china)) +
ylab("Cumulative confirmed cases")
# See the plot
plt_cum_confirmed_cases_china_vs_world
# + dc={"key": "26"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 4. Let's annotate!
# <p>Wow! The two lines have very different shapes. In February, the majority of cases were in China. That changed in March when it really became a global outbreak: around March 14, the total number of cases outside China overtook the cases inside China. This was days after the WHO declared a pandemic.</p>
# <p>There were a couple of other landmark events that happened during the outbreak. For example, the huge jump in the China line on February 13, 2020 wasn't just a bad day regarding the outbreak; China changed the way it reported figures on that day (CT scans were accepted as evidence for COVID-19, rather than only lab tests).</p>
# <p>By annotating events like this, we can better interpret changes in the plot.</p>
# + dc={"key": "26"} tags=["sample_code"]
who_events <- tribble(
~ date, ~ event,
"2020-01-30", "Global health\nemergency declared",
"2020-03-11", "Pandemic\ndeclared",
"2020-02-13", "China reporting\nchange"
) %>%
mutate(date = as.Date(date))
# Using who_events, add vertical dashed lines with an xintercept at date
# and text at date, labeled by event, and at 100000 on the y-axis
plt_cum_confirmed_cases_china_vs_world +
geom_vline(data=who_events, linetype='dashed', aes(xintercept=date)) +
geom_text(data=who_events, y=1e+05, aes(x=date, label=event))
# + dc={"key": "33"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 5. Adding a trend line to China
# <p>When trying to assess how big future problems are going to be, we need a measure of how fast the number of cases is growing. A good starting point is to see if the cases are growing faster or slower than linearly.</p>
# <p>There is a clear surge of cases around February 13, 2020, with the reporting change in China. However, a couple of days after, the growth of cases in China slows down. How can we describe COVID-19's growth in China after February 15, 2020?</p>
# + dc={"key": "33"} tags=["sample_code"]
# Filter for China, from Feb 15
china_after_feb15 <- filter(confirmed_cases_china_vs_world, date >=
"2020-02-15" & is_china == 'China')
# Using china_after_feb15, draw a line plot cum_cases vs. date
# Add a smooth trend line using linear regression, no error bars
ggplot(data=china_after_feb15, aes(x=date, y=cum_cases)) +
geom_line() +
geom_smooth(method='lm', se=FALSE) +
ylab("Cumulative confirmed cases")
# + dc={"key": "40"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 6. And the rest of the world?
# <p>From the plot above, the growth rate in China is slower than linear. That's great news because it indicates China has at least somewhat contained the virus in late February and early March.</p>
# <p>How does the rest of the world compare to linear growth?</p>
# + dc={"key": "40"} tags=["sample_code"]
# Filter confirmed_cases_china_vs_world for not China
not_china <- filter(confirmed_cases_china_vs_world, is_china != 'China')
# Using not_china, draw a line plot cum_cases vs. date
# Add a smooth trend line using linear regression, no error bars
plt_not_china_trend_lin <- ggplot(data=not_china, aes(x=date, y=cum_cases)) +
geom_line() +
geom_smooth(method='lm', se=FALSE) +
ylab("Cumulative confirmed cases")
# See the result
plt_not_china_trend_lin
# + dc={"key": "47"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 7. Adding a logarithmic scale
# <p>From the plot above, we can see a straight line does not fit well at all, and the rest of the world is growing much faster than linearly. What if we added a logarithmic scale to the y-axis?</p>
# + dc={"key": "47"} tags=["sample_code"]
# Modify the plot to use a logarithmic scale on the y-axis
plt_not_china_trend_lin +
scale_y_log10(TRUE)
# + dc={"key": "56"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 8. Which countries outside of China have been hit hardest?
# <p>With the logarithmic scale, we get a much closer fit to the data. From a data science point of view, a good fit is great news. Unfortunately, from a public health point of view, that means that cases of COVID-19 in the rest of the world are growing at an exponential rate, which is terrible news.</p>
# <p>Not all countries are being affected by COVID-19 equally, and it would be helpful to know where in the world the problems are greatest. Let's find the countries outside of China with the most confirmed cases in our dataset.</p>
# + dc={"key": "56"} tags=["sample_code"]
# Run this to get the data for each country
confirmed_cases_by_country <- read_csv("datasets/confirmed_cases_by_country.csv")
glimpse(confirmed_cases_by_country)
# Group by country, summarize to calculate total cases, find the top 7
top_countries_by_total_cases <- confirmed_cases_by_country %>%
group_by(country) %>%
summarise(confirmed_cases_by_country = max(cum_cases)) %>%
top_n(7)
# See the result
top_countries_by_total_cases
# + dc={"key": "63"} deletable=false editable=false run_control={"frozen": true} tags=["context"]
# ## 9. Plotting hardest hit countries as of Mid-March 2020
# <p>Even though the outbreak was first identified in China, there is only one country from East Asia (South Korea) in the above table. Four of the listed countries (France, Germany, Italy, and Spain) are in Europe and share borders. To get more context, we can plot these countries' confirmed cases over time.</p>
# <p>Finally, congratulations on getting to the last step! If you would like to continue making visualizations or find the hardest hit countries as of today, you can do your own analyses with the latest data available <a href="https://github.com/RamiKrispin/coronavirus">here</a>. </p>
# + dc={"key": "63"} tags=["sample_code"]
# Run this to get the data for the top 7 countries
confirmed_cases_top7_outside_china = read_csv('datasets/confirmed_cases_top7_outside_china.csv')
#
glimpse(confirmed_cases_top7_outside_china)
# Using confirmed_cases_top7_outside_china, draw a line plot of
# cum_cases vs. date, grouped and colored by country
ggplot(data=confirmed_cases_top7_outside_china, aes(x=date, y=cum_cases)) + geom_line(aes(color=country, group=country)) + ylab("Cumulative confirmed cases")
|
_notebooks/2020-04-03-Visualizing-COVID-19.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Fourier Analysis
import matplotlib.pylab as plt
# %matplotlib inline
import numpy as np
from scipy.fftpack import fft, ifft, fftfreq
import pandas as pd
t = np.linspace(0,1,80)
x = 4*np.sin(2*np.pi*5*t)
plt.plot(t,x)
plt.xlabel('Time')
plt.ylabel('Value')
# ## Fast Fourier Transform
#
# The Fast Fourier Transform (FFT) is an efficient algorithm for calculating the Discrete Fourier Transform (DFT) and is the de facto standard to calculate a Fourier Transform. It is present in almost any scientific computing libraries and packages, in every programming language.
#
# Nowadays the Fourier transform is an indispensable mathematical tool used in almost every aspect of our daily lives. In the next section we will have a look at how we can use the FFT and other Stochastic Signal analysis techniques to classify time-series and signals.
#
#
x_freqdom = fft(x)
plt.plot(x_freqdom)
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
x_inv = ifft(x_freqdom)
plt.plot(t,x_inv)
print('Reconstruction error: ', sum((x-x_inv)**2))
# ### Example: Forecasting retail sales
# Let's see what how we can use the techniques before for forecasting.
df = pd.read_csv("./data/retail_sales.csv")
df.head()
df['sales'].plot()
# +
x = df['sales']
n = x.size # size of the series
t = np.arange(0, n)
p = np.polyfit(t,x,1)
x_notrend = x-p[0]*t
# -
plt.plot(x_notrend)
x_freqdom = fft(x_notrend)
plt.plot(x_freqdom[1:])
plt.xlabel("Frequency")
plt.ylabel("Amplitude")
x_freqdom
np.absolute(x_freqdom[0]) # Amplitude on frequency domain
np.angle(x_freqdom[0]) # Phase angle
fftfreq(x.size)
def fourierExtrapolation(x, n_predict, n_harm = 10):
n = x.size
t = np.arange(0, n)
p = np.polyfit(t, x, 1) # find linear trend in x
x_notrend = x - p[0] * t # detrended x
x_freqdom = fft(x_notrend) # detrended x in frequency domain
f = fftfreq(n) # frequencies
idxs = list(range(n))
# sort indexes by frequency, lower -> higher
idxs.sort(key = lambda i: np.absolute(f[i]))
t = np.arange(0, n + n_predict)
restored_sig = np.zeros(t.size)
for i in idxs[:1 + n_harm * 2]:
ampli = np.absolute(x_freqdom[i]) / n # amplitude
phase = np.angle(x_freqdom[i]) # phase
restored_sig += ampli * np.cos(2 * np.pi * f[i] * t + phase)
return restored_sig + p[0] * t
n_predict = 10
extrapolation = fourierExtrapolation(x, n_predict, n_harm=10)
plt.plot(np.arange(0, x.size), x, 'b', label = 'x')
plt.plot(np.arange(0, extrapolation.size), extrapolation, 'r', label = 'extrapolation')
plt.legend()
# # Your turn!
# Can you apply the same method to `SP500`?
|
05 Fourier Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Magic
# JupyterLibrary provides a few lightweight [IPython](https://ipython.readthedocs.io/en/stable/interactive/magics.html) [magics](https://jakevdp.github.io/PythonDataScienceHandbook/01.03-magic-commands.html) for its own testing purposes.
#
# If you like writing and executing Robot Framework Kernel, you might like a more full-featured experience:
#
# - [robotkernel](https://github.com/robots-from-jupyter/robotkernel)
# - [xeus-robot](https://github.com/jupyter-xeus/xeus-robot)
# %reload_ext JupyterLibrary
# The `%%robot` magic runs a cell of code as you would write in a `.robot` file. No funny stuff (by default).
# %%robot
*** Tasks ***
Log Something
Log Something
# The interactive help is pretty good.
# %%robot?
# Of note: you can specify extra arguments to `robot.run` with `-a`, the name of a local variable.
args = dict(include=["mytag:a"])
# +
# %%robot -a args
*** Tasks ***
Do thing A
[Tags] mytag:a
Log A
Do thing B
[Tags] mytag:b
Log B
Do thing AB
[Tags] mytag:a mytag:b
Log AB
# -
# ### Running JupyterLibrary
#
# The line below is a _Markdown Cell_... change it to a _Code Cell_ to run it
# # %%robot
# *** Settings ***
# Documentation A nice task suite
# Library JupyterLibrary
# Suite Setup Wait for New Jupyter Server to be Ready
# Test Teardown Reset JupyterLab and Close
# Suite Teardown Run Keyword and Ignore Error Terminate All Jupyter Servers
#
#
# *** Tasks ***
# A Notebook in JupyterLab
# Open JupyterLab
# Launch a new JupyterLab Document
# Add and Run JupyterLab Code Cell print("hello" + " world")
# Wait Until page Contains hello world
# Capture Page Screenshot ran-code.png
# ### With Widgets
#
# > There is some more stuff comming with `%%robot`, but for now, `ipywidgets.interact` can be used to quickly build UI around robot-generated artifacts
# +
from pathlib import Path
from IPython.display import display, Image
ipywidgets = None
try:
import ipywidgets
except:
pass
# -
if ipywidgets:
@ipywidgets.interact
def show_image(i=(0, 100)):
all_images = sorted(Path("_robot_magic_").rglob("*.png"), key=lambda p: p.stat().st_mtime)
if not all_images:
return
start = all_images[0].stat().st_mtime
i = min(len(all_images) - 1, i)
img = all_images[i]
delta = img.stat().st_mtime - start
display(f"[{round(delta)}s][{i} of {len(all_images)}] {img.name}", Image(img))
|
docs/MAGIC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # RCS XML
# +
# https://www.w3.org/TR/xml/
# +
# https://www.xmlfiles.com/examples/
# +
# https://www.w3schools.com/xml/dom_nodes.asp
# -
# ### Extensible Markup Language (XML) is a markup language that defines a set of rules for encoding documents in a format that is both human-readable and machine-readable.
# # Pluses
# * Can Desribe anything via Schemas very extensible (pun intended)(https://www.w3schools.com/xml/schema_intro.asp)
#
#
# # Minuses:
# * Verbose
# * Complex (structure hard to follow for more complicated xml files)
# # XML vs HTML
# #### HTML and XML common heritage with older markup language, SGML.
#
# https://www.w3.org/TR/WD-html40-970708/intro/sgmltut.html
#
# * Use HTML (and CSS) when you wish to target presentation in web browser.
# * Use XML when you wish to define custom markup for documents. XML will allow a document to be marked up for what content is rather than for how content should look. Content can then be decoupled from its presentation, allowing content to be independently translated to different media such as web or print automatically.
#
# * XML can make their own tags
# +
# HTML used to be valid XML, HTML5 is not fully compliant (not really important)
# XHTML seems to be pretty dead
# -
# # Many ways of working with XML in Python
#
# * https://stackabuse.com/reading-and-writing-xml-files-in-python/
# * untangle class based
# * xmltodict (my favorite)
# !pip install untangle
import untangle
with open('CustomersOrdersInNamespace.xml') as f:
xmlcontent = f.read()
len(xmlcontent)
print(xmlcontent)
type(xmlcontent)
data = untangle.parse('CustomersOrdersInNamespace.xml')
dir(data)
type(data)
data.Root # THis is where I start to dislike untangle
dir(data.Root)
data.Root.cdata
data.Customers
data.Root.Customers
type(data.Root.Customers)
dir(data.Root.Customers)
data.Root.Customers.Customer[1].ContactName
data.Root.Customers.Customer[2].FullAddress.Address.cdata
data.Root.Orders.Order[0].ShipInfo.ShipPostalCode.cdata
data.Root.
# +
# TODO see why untangle is not parsing !?
# -
# !pip install xmltodict
# Better idea convert XML to Python dictionary then to JSON
import xmltodict
import json
# ## xmltodict
#
# https://github.com/martinblech/xmltodict
mydict = xmltodict.parse(xmlcontent)
type(mydict)
# +
# https://docs.python.org/3/library/collections.html#collections.OrderedDict
# -
mydict.keys()
# We must now traverse the document tree (converted into dictionary)
mydict['Root']
mydict['Root']['Customers']
mydict['Root']['Customers']['Customer'][0]['ContactName']
myjson = json.dumps(mydict)
len(myjson),type(myjson)
with open("customers.json", "w") as write_file:
json.dump(mydict, write_file, indent=4)
# +
# import pandas as pd
# -
# +
# Exercise print out Customer's Name who ordered the heaviest package
# -
type(mydict['Root']['Orders']['Order'])
orders = sorted(mydict['Root']['Orders']['Order'], key = lambda el: float(el['ShipInfo']['Freight']))
heavyorder = orders[::-1][0]['CustomerID']
heavyorder
custlist = mydict['Root']['Customers']['Customer']
answer = [ el['ContactName'] for el in custlist if el['@CustomerID'] == heavyorder]
answer[0]
type(custlist)
custlist
# # XML databases were a thing but mostly died down
#
# Semi active - https://www.sedna.org/
# +
# Most everyone sane moved to JSON for submitting and receiving data
|
XML/RCS XML.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import keras
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
from PIL import Image, ImageOps
from keras.preprocessing import image
# +
img_path = "foto.jpg"
img = image.load_img(img_path, target_size=(28, 28))
x = image.img_to_array(img)
img_path = "foto.jpg"
img = image.load_img(img_path, target_size=(28, 28))
x2 = image.img_to_array(img)
# +
fototest = np.array([])
fototest = np.append(fototest, x)
# -
fototest
|
Cercalab0b.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
random_state=0)
# %matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c='White', marker='o', edgecolor='black', s=50)
plt.grid()
# # 分割式聚類
# # K-Means
from sklearn.cluster import KMeans
# +
km = KMeans(n_clusters=3,
init='random',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
# -
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
s=50, c='lightgreen', marker='s', edgecolors='black', label='cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
s=50, c='orange', marker='v', edgecolors='black', label='cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1],
s=50, c='lightblue', marker='o', edgecolors='black', label='cluster 3')
#質心
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolors='black', label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
# # K-means++ 演算法
# 老師說初始點選K-means++比較好
# #在選取初始質時,盡可能讓他們彼此遠離
from sklearn.cluster import KMeans
# +
km = KMeans(n_clusters=3,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
# -
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
s=50, c='lightgreen', marker='s', edgecolors='black', label='cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
s=50, c='orange', marker='v', edgecolors='black', label='cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1],
s=50, c='lightblue', marker='o', edgecolors='black', label='cluster 3')
#質心
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', edgecolors='black', label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
# # 轉折判斷法
# 群內誤差平和
# 聚類數目 k增加,失真就會減少
# “找出失真開始迅速增加的聚類數 k”
# +
print('Distortion: %.2f' % km.inertia_)
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
# -
# # 階層式聚類
# # Ward’s Method
from scipy.cluster.hierarchy import ward
from scipy.cluster.hierarchy import dendrogram
# 可以看出最好的 k,如果要把它分為三類,距離就擴增到20
linkage = ward(X)
dendrogram(linkage)
ax = plt.gca()
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
# # 密度式聚類
# # DBSCAN 演算法
# 密度大分成一群
# 成「半月型結構」的數據
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
# 聚類法的比較 2個
from sklearn.cluster import AgglomerativeClustering
# +
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))
#KMeans
km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
s=40, c='lightblue', marker='o', edgecolors='black', label='cluster 1')
ax1.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
s=40, c='red', marker='s', edgecolors='black', label='cluster 2')
ax1.set_title('K-means clustering')
#AgglomerativeClustering
ac = AgglomerativeClustering(linkage='ward',
affinity='euclidean',
n_clusters=2)
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac == 0, 0], X[y_ac == 0, 1],
s=40, c='lightblue', marker='o', edgecolors='black', label='cluster 1')
ax2.scatter(X[y_ac == 1, 0], X[y_ac == 1, 1],
s=40, c='red', marker='s', edgecolors='black', label='cluster 2')
ax2.set_title('Agglomerative clustering')
plt.legend
# -
from sklearn.cluster import DBSCAN
# +
db = DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db == 0, 0], X[y_db == 0, 1],
s=40, c='lightgreen', marker='o', edgecolors='black', label='cluster 1')
plt.scatter(X[y_db == 1, 0], X[y_db == 1, 1],
s=40, c='orange', marker='s', edgecolors='black', label='cluster 2')
plt.legend
# -
# # 聚類法的比較 3個
# +
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(13,3))
#KMeans
km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
s=40, c='lightblue', marker='o', edgecolors='black', label='cluster 1')
ax1.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
s=40, c='red', marker='s', edgecolors='black', label='cluster 2')
ax1.set_title('K-means clustering')
#AgglomerativeClustering
ac = AgglomerativeClustering(linkage='ward',
affinity='euclidean',
n_clusters=2)
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac == 0, 0], X[y_ac == 0, 1],
s=40, c='lightblue', marker='o', edgecolors='black', label='cluster 1')
ax2.scatter(X[y_ac == 1, 0], X[y_ac == 1, 1],
s=40, c='red', marker='s', edgecolors='black', label='cluster 2')
ax2.set_title('Agglomerative clustering')
#DBSCAN
db = DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db = db.fit_predict(X)
ax3.scatter(X[y_db == 0, 0], X[y_db == 0, 1],
s=40, c='lightblue', marker='o', edgecolors='black', label='cluster 1')
ax3.scatter(X[y_db == 1, 0], X[y_db == 1, 1],
s=40, c='red', marker='s', edgecolors='black', label='cluster 2')
ax3.set_title('DBSCAN clustering')
plt.legend
# -
|
K-means - using sklearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="wHmOCoJsfgOu" outputId="c093ae6b-445b-487e-e35b-a7c871b0b723"
from google.colab import drive
drive.mount('/content/drive')
# + id="zvO_AdL0fUsB"
import numpy as np
import matplotlib.pyplot as plt
import librosa
import soundfile as sf
import librosa.display
from glob import glob
import os
from tqdm import tqdm
# + id="dDMp4UtTfZjL"
def splitData(X, t, testFraction=0.2, randomize = False):
"""
Split the data randomly into training and test sets
Use numpy functions only
Inputs:
X: (np array of len Nsamples) input feature vectors
t: (np array of len Nsamples) targets; one hot vectors
testFraction: (float) Nsamples_test = testFraction * Nsamples
Outputs:
X_train: training set
X_test: test set
t_train: training labels
t_test: test labels
"""
if randomize is False:
tot_samples = np.random.RandomState(seed=42).permutation(len(X))
else:
tot_samples = np.random.permutation(len(X))
X_train = []
X_test = []
t_train = []
t_test = []
test_samples = max(1,int(len(X)*testFraction))
# print(tot_samples[:test_samples])
# print(tot_samples[test_samples:])
for i in range(test_samples):
X_test.append(X[tot_samples[i]])
t_test.append(t[tot_samples[i]])
for i in range(test_samples,len(X)):
X_train.append(X[tot_samples[i]])
t_train.append(t[tot_samples[i]])
return np.asarray(X_train), np.asarray(t_train), np.asarray(X_test), np.asarray(t_test)
def calc_spec(x):
n_fft = 1024
hop_length = 512
win_length = 1024
X = np.abs(librosa.stft(x, n_fft = n_fft, hop_length = hop_length, win_length = win_length, window='hann'))
X = librosa.power_to_db(X**2,ref=np.max)
return X
def audio2spec(x, norm=True, mfcc=True):
'''
Compute Mel-frequency cepstral coefficients (MFCCs)
Inputs:
x: np array of shape (Nsamples,)
Output:
X: (np array) spectrogram sequence
'''
X=[]
for sample in x:
if mfcc is False:
X.append(calc_spec(sample))
else:
X.append(librosa.feature.mfcc(S=calc_spec(sample), n_mfcc=20))
if norm is True:
X = (X-np.mean(X))/np.std(X)
return np.asarray(X)
# + colab={"base_uri": "https://localhost:8080/"} id="52f13dW7fa9-" outputId="15268827-3649-434e-947c-8b12b993c483"
# PARAMETER FOR STFT
SAMPLING_RATE=16000
DURATION=10
N_FFT = 1024
WIN_LENGTH = 1024
HOP_LENGTH = 512
# LOADING THE TRAINING SPECTROGRAMS
X = np.load('/content/drive/MyDrive/Sem 5/EE603/project/val_set/Final_Dataset/training_spectrogram.npy')
print(X.shape)
y = np.load('/content/drive/MyDrive/Sem 5/EE603/project/val_set/Final_Dataset/training_labels.npy')
print(y.shape)
# from sklearn.utils import shuffle
# X, y = shuffle(X, y)
# EXTRACTING THE MFCC FEATURES FROM THE SPECTROGRAM
def get_mfcc(X):
X_new = []
for i in range(len(X)):
mel_spectrogram = librosa.feature.melspectrogram(S=X[i], n_fft=N_FFT, hop_length=HOP_LENGTH)
mfcc = librosa.feature.mfcc(S=mel_spectrogram, sr=16000,n_mfcc=20)
mean = np.average(mfcc)
std = np.std(mfcc)
if(std == 0):
std = std + 1e-25
mfcc = (mfcc - mean)/std
X_new.append(mfcc)
return np.array(X_new)
X = get_mfcc(X)
# + id="v5QOyawffswZ"
# FUNCTIONS TO CONVERT STRING TO ONE-HOT-VECTORS
def one_hot_enc(cl_name):
if(cl_name == 'music'):
return 2
elif(cl_name == 'speech'):
return 1
else:
return 0
def string2ohv(y):
y_ohv = []
for i in y:
y_ohv.append(one_hot_enc(i))
return np.array(y_ohv)
# + colab={"base_uri": "https://localhost:8080/"} id="TxL48t-TffaJ" outputId="23f72858-9125-49d7-ae6f-6829388db32e"
X_train, y_train, X_test, y_test = splitData(X=X, t=y, testFraction=0.2, randomize=True)
print(X_train.shape)
print(X_test.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="4hUdeh-mfzfX" outputId="485c3065-2622-4096-a2cf-c8848b640153"
# RESHAPING THE DATA
def reshape(X, y):
# Reshape the data to make each entry in the spectrogram a training sample
X_new = []
y_new = []
for i in range(len(X)):
X_new.append(np.transpose(X[i]))
# print(X[i].shape[1])
y_new.append([y[i]]*X[i].shape[1])
# print(np.shape(y_new))
X_new = np.array(X_new)
y_new = np.array(y_new)
X_new = X_new.reshape((-1, X[0].shape[0]))
y_new = y_new.reshape((-1, 1))
print(X_new.shape)
print(y_new.shape)
return X_new, y_new
X_train, y_train = reshape(X_train, y_train)
X_test, y_test = reshape(X_test, y_test)
y_test = string2ohv(y_test)
y_train = string2ohv(y_train)
print(y_train.shape)
print(y_test.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="mlq1S3gGf1B3" outputId="0bf5efb7-3726-40ff-ae3c-e1b7bb80612a"
# PREPARING THE BAG OF FRAMES TO ESTABLISH TEMPORAL DEPENDENCE
def make_bags(X_prev):
X_new = []
X_new.append(X_prev[:7])
X_new.append(X_prev[:7])
X_new.append(X_prev[:7])
for i in tqdm(range(len(X_prev)-6)):
A = X_prev[i:i+7]
X_new.append(A)
X_new.append(X_prev[-7:])
X_new.append(X_prev[-7:])
X_new.append(X_prev[-7:])
X_new = np.array(X_new)
return X_new
X_test_reshaped = make_bags(X_test)
print(X_test_reshaped.shape)
X_train_reshaped = make_bags(X_train)
print(X_train_reshaped.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="SjfHTI00f2o2" outputId="75f86893-ec5e-476a-ac6d-99cd90818ff2"
X_train = np.reshape(X_train_reshaped, (np.shape(X_train_reshaped)[0],-1))
X_test = np.reshape(X_test_reshaped, (np.shape(X_test_reshaped)[0],-1))
print(np.shape(X_train), np.shape(X_test))
# + id="6gW-DBo_gL7J"
# for i, label in tqdm(enumerate(y_train)):
# if label[1] == 1:
# y_train[i] = 2
# elif label[0] == 1:
# y_train[i] = 1
# else:
# y_train[i] = 0
# for i, label in tqdm(enumerate(y_test)):
# if label[1] == 1:
# y_test[i] = 2
# elif label[0] == 1:
# y_test[i] = 1
# else:
# y_test[i] = 0
# + colab={"base_uri": "https://localhost:8080/"} id="ZRcM1vyFI-5J" outputId="ad7ce3b3-1d8c-4605-8a0f-ca15daa3fcc2"
# we'll use first 100 data items of every label, each as the templates
N = 100
templates = np.zeros((3, N, X_train[0].shape[0]))
counts = [0,0,0]
for i in tqdm(range(len(y_train))):
if counts == [N, N, N]:
break
if counts[y_train[i]] < 100:
templates[y_train[i], counts[y_train[i]]] = X_train[i]
counts[y_train[i]] += 1
print(np.shape(templates))
# + colab={"base_uri": "https://localhost:8080/"} id="SSdg8_c-KvgS" outputId="81fb4a52-cd52-49a1-9ad0-bc2629aa4b2f"
y_train_pred = np.zeros(len(X_train[:10**4]))
y_test_pred = np.zeros(len(X_test[:10**4]))
for i in tqdm(range(len(X_test[:10**4]))):
scores = [0,0,0]
for j in range(3):
for k in range(N):
scores[j] += np.linalg.norm(X_test[i]-templates[j][k])
y_test_pred[i] = np.argmin(scores)
for i in tqdm(range(len(X_train[:10**4]))):
scores = [0,0,0]
for j in range(3):
for k in range(N):
scores[j] += np.linalg.norm(X_train[i]-templates[j][k])
y_train_pred[i] = np.argmin(scores)
# + colab={"base_uri": "https://localhost:8080/"} id="LjvujFNFMyon" outputId="a61d206c-d82a-450d-b338-c792c9a066aa"
train_accuracy = np.mean(y_train_pred[:10**4].ravel() == np.asarray(y_train[:10**4]).ravel()) * 100
print('Train accuracy:', train_accuracy)
test_accuracy = np.mean(y_test_pred[:10**4].ravel() == np.asarray(y_test[:10**4]).ravel()) * 100
print('Test accuracy:', test_accuracy)
# + colab={"base_uri": "https://localhost:8080/"} id="XhsHkdZQh6cV" outputId="15c240b1-6aa0-4c71-f809-5a0cd8763059"
import sklearn
print(sklearn.metrics.f1_score(y_test_pred[:10**4], y_test[:10**4], average='macro'))
# + colab={"base_uri": "https://localhost:8080/"} id="oLpYyro6Nhkk" outputId="2056b683-e232-4bd7-908b-81143d849e7d"
from collections import Counter
print(Counter(y_train_pred[:10**4]), Counter(y_train[:10**4]))
print(Counter(y_test_pred[:10**4]), Counter(y_test[:10**4]))
|
FinalModelCodes/TemplateMatching_final.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import scipy.io as io
from tqdm import tqdm
gt_mat_path = 'data/SynthText/gt.mat'
im_root = 'data/SynthText/'
txt_root = 'data/SynthText/gt/'
if not os.path.exists(txt_root):
os.mkdir(txt_root)
print('reading data from {}'.format(gt_mat_path))
gt = io.loadmat(gt_mat_path)
print('Done.')
# -
gt['imnames'][0]
import subprocess
for i, imname in enumerate(tqdm(gt['imnames'][0])):
imname = imname[0]
img_id = os.path.basename(imname)
im_path = os.path.join(im_root, imname)
txt_path = os.path.join(txt_root, img_id.replace('jpg', 'txt'))
if len(gt['wordBB'][0,i].shape) == 2:
annots = gt['wordBB'][0,i].transpose(1, 0).reshape(-1, 8)
else:
annots = gt['wordBB'][0,i].transpose(2, 1, 0).reshape(-1, 8)
with open(txt_path, 'w') as f:
f.write(imname + '\n')
for annot in annots:
str_write = ','.join(annot.astype(str).tolist())
f.write(str_write + '\n')
txt_path = "data/SynthText/image_list.txt"
for i, imname in enumerate(tqdm(gt['imnames'][0])):
imname = imname[0]
img_id = os.path.basename(imname)
im_path = os.path.join(im_root, imname)
if i == 0:
with open(txt_path, 'w') as f:
f.write(img_id.replace(".jpg", ".txt") + '\n')
else:
with open(txt_path, 'a') as f:
f.write(img_id.replace(".jpg", ".txt") + '\n')
img_id.replace(".jpg", "")
# + active=""
#
|
0.Setup_synthtext.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Bootstrap and Jackknife comparison
#
# In this notebook we compare the bootstrap to the jackknife. Bootstrap resampling is superior to jackknifing, but the jackknife is deterministic, which may be helpful, and it can exactly remove biases of order 1/N from an estimator (the bootstrap removes biases of higher orders, too, but it does not remove the lowest order exactly).
from resample.jackknife import variance as j_var, resample as j_resample, bias as j_bias
from resample.bootstrap import resample as b_resample
import numpy as np
from scipy import stats
# +
rng = np.random.default_rng(1)
data = rng.normal(size=20)
# get mean and std deviation
def fn(d):
return np.mean(d), np.var(d, ddof=0) # we return the biased variance
# compute bias with the bootstrap
def b_bias(fn, sample):
theta = fn(sample)
b_rep = [fn(s) for s in b_resample(sample, random_state=rng)]
return np.mean(b_rep, axis=0) - theta
# compute variance with bootstrap
def b_var(fn, sample):
b_rep = [fn(s) for s in b_resample(sample, random_state=rng)]
return np.var(b_rep, axis=0)
# exact bias for biased standard deviation
# - we computed: s = 1/N * sum(x ** 2 - np.mean(x) ** 2)
# - correct is: N/(N-1) * s
# - bias is: (1 - N/(N-1)) * s = (N - 1 - N) / (N - 1) * s = - 1 / (N - 1) * s
print("theta ", np.round(fn(data), 3))
print("std.dev. (jackknife)", np.round(j_var(fn, data) ** 0.5, 3))
print("std.dev. (bootstrap)", np.round(b_var(fn, data) ** 0.5, 3))
print("bias (jackknife) ", np.round(j_bias(fn, data), 3))
print("bias (bootstrap) ", np.round(b_bias(fn, data), 3))
print("bias (exact) ", np.round((0, -1 / (len(data) - 1) * fn(data)[1]), 3))
# -
# The standard deviations for the estimates computed by bootstrap and jackknife differ by about 10 %. This difference shrinks for larger data sets.
#
# Both resampling methods find no bias for the mean, and a small bias for the (not bias-corrected) variance. The jackknife is getting closer, since the bias for sufficiently large N is dominated by the O(1/N) order that the jackknife removes exactly.
|
notebooks/jackknife_vs_bootstrap.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Scikit-Learn IRIS Model Using Flatbuffers Protocol (Experimental)
#
# * Wrap a scikit-learn python model using the Flatbuffers low level low-latency protocol.
# * Run locally on Docker to test
# * Deploy on seldon-core running on minikube
#
# ## Dependencies
#
# * [Helm](https://github.com/kubernetes/helm)
# * [Minikube](https://github.com/kubernetes/minikube)
# * [S2I](https://github.com/openshift/source-to-image)
#
#
# ```bash
# pip install sklearn
# pip install seldon-core
#
# ```
# ## Train locally
#
# +
import numpy as np
import os
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.externals import joblib
from sklearn import datasets
def main():
clf = LogisticRegression()
p = Pipeline([('clf', clf)])
print('Training model...')
p.fit(X, y)
print('Model trained!')
filename_p = 'IrisClassifier.sav'
print('Saving model in %s' % filename_p)
joblib.dump(p, filename_p)
print('Model saved!')
if __name__ == "__main__":
print('Loading iris data set...')
iris = datasets.load_iris()
X, y = iris.data, iris.target
print('Dataset loaded!')
main()
# -
# Wrap model using s2i
# ## Flatbuffers Protocol Test
# !s2i build . seldonio/seldon-core-s2i-python3:0.12 sklearn-iris:0.1
# !docker run --name "iris_predictor" -d --rm -p 5000:5000 sklearn-iris:0.1
# Send some random features that conform to the contract
# !seldon-core-tester contract.json 0.0.0.0 5000 -p --fbs
# !docker rm iris_predictor --force
|
examples/models/sklearn_iris_fbs/sklearn_iris.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:modnet-develop]
# language: python
# name: conda-env-modnet-develop-py
# ---
# # Prediction of experimental band gap
#
# This notebooks applies MODNet on the matbench experimental band gap data. It is a good example on how MODNet can be used for a composition only task.
# ## Dependencies
import numpy as np
from matminer.datasets import load_dataset
from modnet.models import MODNetModel
from modnet.preprocessing import MODData
import matplotlib.pyplot as plt
from pymatgen.core import Composition
# ## Dataset import:
# The matbench_expt_gap dataset contains measured band gaps for 4604 compositions of inorganic semiconductors from Zhuo et al., JPCL.
# +
from matminer.datasets import load_dataset
df = load_dataset("matbench_expt_gap")
df["composition"] = df["composition"].map(Composition) # maps composition to a pymatgen composition object
df.head()
# -
df.describe()
fig, ax = plt.subplots(facecolor="w")
ax.hist(df.where(df["gap expt"] == 0)["gap expt"], bins=1, density=False, label="Zero band gap")
ax.hist(df.where(df["gap expt"] > 0)["gap expt"], bins=11, density=False, label="Non-zero band gap")
ax.set_ylabel("Frequency")
ax.set_xlabel("Band gap (eV)")
ax.legend()
# ## MODData
# This instantiates the MODData
data = MODData(
materials=df["composition"], # you can provide composition objects to MODData
targets=df["gap expt"],
target_names=["gap_expt_eV"]
)
# Featurization of the moddata
# It will automatically apply composition only featurizers
data.featurize()
# ### train-test split
from sklearn.model_selection import train_test_split
split = train_test_split(range(100), test_size=0.1, random_state=1234)
train, test = data.split(split)
train.feature_selection(n=-1)
# if you want to use precomputed cross_nmi of the MP. This saves time :
# data.feature_selection(n=-1, use_precomputed_cross_nmi)
# ## MODNet model
model = MODNetModel([[['gap_expt_eV']]],
weights={'gap_expt_eV':1},
num_neurons = [[256], [128], [16], [16]],
n_feat = 150,
act = "elu"
)
# ### training
model.fit(train,
val_fraction = 0.1,
lr = 0.0002,
batch_size = 64,
loss = 'mae',
epochs = 100,
verbose = 1,
)
# ### Predicting
pred = model.predict(test)
pred.head()
mae_test = np.absolute(pred.values-test.df_targets.values).mean()
print(f'mae: {mae_test}')
|
example_notebooks/composition_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# default_exp utils.google_sheet
# -
# # utils.google_sheet
#
# > Utils handing google sheet operation
#
# - toc: True
|
notebooks/utils_google_sheet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # So easy, *voilà*!
#
# In this example notebook, we demonstrate how voila can render Jupyter notebooks with interactions requiring a roundtrip to the kernel.
# ## Jupyter Widgets
# +
import ipywidgets as widgets
slider = widgets.FloatSlider(description='x')
text = widgets.FloatText(disabled=True, description='$x^2$')
text.disabled
def compute(*ignore):
text.value = str(slider.value ** 2)
slider.observe(compute, 'value')
slider.value = 4
widgets.VBox([slider, text])
# -
# ## Basic outputs of code cells
# +
import pandas as pd
iris = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv')
iris
# -
|
notebooks/basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (enterprise dev)
# language: python
# name: enterprise_dev
# ---
# # Tutorial #2 Plotting Posteriors
import la_forge.core as co
import la_forge.diagnostics as dg
import matplotlib.pyplot as plt
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import numpy as np
coredir = '/Users/hazboun/software_development/la_forge/tests/data/cores/'
c0 = co.Core(corepath=coredir+'J1713+0747_plaw_dmx.core',
label='NG12.5yr Noise Run: Power Law Red Noise')
c1 = co.Core(corepath=coredir+'J1713+0747_fs_dmx.core',
label='NG12.5yr Noise Run: Free Spectral Red Noise')
dg.plot_chains(c0)
c1.set_burn(0)
dg.plot_chains(c1,
hist=False,
pars=c1.params[24:36],
ncols=4)
ecorr_pars = [p for p in c0.params if 'ecorr' in p]
dg.plot_chains([c0,c1],
plot_map=True,
ncols=4,
pars=ecorr_pars,
title_y=1.05,
legend_labels=['Power Law', 'Free Spectral'],
linewidth=2)
|
docs/_static/notebooks/tutorial2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Gaussian Process (GP) smoothing
#
# This example deals with the case when we want to **smooth** the observed data points $(x_i, y_i)$ of some 1-dimensional function $y=f(x)$, by finding the new values $(x_i, y'_i)$ such that the new data is more "smooth" (see more on the definition of smoothness through allocation of variance in the model description below) when moving along the $x$ axis.
#
# It is important to note that we are **not** dealing with the problem of interpolating the function $y=f(x)$ at the unknown values of $x$. Such problem would be called "regression" not "smoothing", and will be considered in other examples.
#
# If we assume the functional dependency between $x$ and $y$ is **linear** then, by making the independence and normality assumptions about the noise, we can infer a straight line that approximates the dependency between the variables, i.e. perform a linear regression. We can also fit more complex functional dependencies (like quadratic, cubic, etc), if we know the functional form of the dependency in advance.
#
# However, the **functional form** of $y=f(x)$ is **not always known in advance**, and it might be hard to choose which one to fit, given the data. For example, you wouldn't necessarily know which function to use, given the following observed data. Assume you haven't seen the formula that generated it:
# %pylab inline
figsize(12, 6);
# +
import numpy as np
import scipy.stats as stats
x = np.linspace(0, 50, 100)
y = (np.exp(1.0 + np.power(x, 0.5) - np.exp(x/15.0)) +
np.random.normal(scale=1.0, size=x.shape))
plot(x, y);
xlabel("x");
ylabel("y");
title("Observed Data");
# -
# ### Let's try a linear regression first
#
# As humans, we see that there is a non-linear dependency with some noise, and we would like to capture that dependency. If we perform a linear regression, we see that the "smoothed" data is less than satisfactory:
# +
plot(x, y);
xlabel("x");
ylabel("y");
lin = stats.linregress(x, y)
plot(x, lin.intercept + lin.slope * x);
title("Linear Smoothing");
# -
# ### Linear regression model recap
#
# The linear regression assumes there is a linear dependency between the input $x$ and output $y$, sprinkled with some noise around it so that for each observed data point we have:
#
# $$ y_i = a + b\, x_i + \epsilon_i $$
#
# where the observation errors at each data point satisfy:
#
# $$ \epsilon_i \sim N(0, \sigma^2) $$
#
# with the same $\sigma$, and the errors are independent:
#
# $$ cov(\epsilon_i, \epsilon_j) = 0 \: \text{ for } i \neq j $$
#
# The parameters of this model are $a$, $b$, and $\sigma$. It turns out that, under these assumptions, the maximum likelihood estimates of $a$ and $b$ don't depend on $\sigma$. Then $\sigma$ can be estimated separately, after finding the most likely values for $a$ and $b$.
# ### Gaussian Process smoothing model
#
# This model allows departure from the linear dependency by assuming that the dependency between $x$ and $y$ is a Brownian motion over the domain of $x$. This doesn't go as far as assuming a particular functional dependency between the variables. Instead, by **controlling the standard deviation of the unobserved Brownian motion** we can achieve different levels of smoothness of the recovered functional dependency at the original data points.
#
# The particular model we are going to discuss assumes that the observed data points are **evenly spaced** across the domain of $x$, and therefore can be indexed by $i=1,\dots,N$ without the loss of generality. The model is described as follows:
#
# \begin{equation}
# \begin{aligned}
# z_i & \sim \mathcal{N}(z_{i-1} + \mu, (1 - \alpha)\cdot\sigma^2) \: \text{ for } i=2,\dots,N \\
# z_1 & \sim ImproperFlat(-\infty,\infty) \\
# y_i & \sim \mathcal{N}(z_i, \alpha\cdot\sigma^2)
# \end{aligned}
# \end{equation}
#
# where $z$ is the hidden Brownian motion, $y$ is the observed data, and the total variance $\sigma^2$ of each ovservation is split between the hidden Brownian motion and the noise in proportions of $1 - \alpha$ and $\alpha$ respectively, with parameter $0 < \alpha < 1$ specifying the degree of smoothing.
#
# When we estimate the maximum likelihood values of the hidden process $z_i$ at each of the data points, $i=1,\dots,N$, these values provide an approximation of the functional dependency $y=f(x)$ as $\mathrm{E}\,[f(x_i)] = z_i$ at the original data points $x_i$ only. Therefore, again, the method is called smoothing and not regression.
# ### Let's describe the above GP-smoothing model in PyMC3
import pymc3 as pm
from theano import shared
from pymc3.distributions.timeseries import GaussianRandomWalk
from scipy import optimize
# Let's create a model with a shared parameter for specifying different levels of smoothing. We use very wide priors for the "mu" and "tau" parameters of the hidden Brownian motion, which you can adjust according to your application.
# +
LARGE_NUMBER = 1e5
model = pm.Model()
with model:
smoothing_param = shared(0.9)
mu = pm.Normal("mu", sigma=LARGE_NUMBER)
tau = pm.Exponential("tau", 1.0/LARGE_NUMBER)
z = GaussianRandomWalk("z",
mu=mu,
tau=tau / (1.0 - smoothing_param),
shape=y.shape)
obs = pm.Normal("obs",
mu=z,
tau=tau / smoothing_param,
observed=y)
# -
# Let's also make a helper function for inferring the most likely values of $z$:
def infer_z(smoothing):
with model:
smoothing_param.set_value(smoothing)
res = pm.find_MAP(vars=[z], fmin=optimize.fmin_l_bfgs_b)
return res['z']
# Please note that in this example, we are only looking at the MAP estimate of the unobserved variables. We are not really interested in inferring the posterior distributions. Instead, we have a control parameter $\alpha$ which lets us allocate the variance between the hidden Brownian motion and the noise. Other goals and/or different models may require sampling to obtain the posterior distributions, but for our goal a MAP estimate will suffice.
#
# ### Exploring different levels of smoothing
#
# Let's try to allocate 50% variance to the noise, and see if the result matches our expectations.
# +
smoothing = 0.5
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
# -
# It appears that the variance is split evenly between the noise and the hidden process, as expected.
#
# Let's try gradually increasing the smoothness parameter to see if we can obtain smoother data:
# +
smoothing = 0.9
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
# -
# ### Smoothing "to the limits"
#
# By increading the smoothing parameter, we can gradually make the inferred values of the hidden Brownian motion approach the average value of the data. This is because as we increase the smoothing parameter, we allow less and less of the variance to be allocated to the Brownian motion, so eventually it aproaches the process which almost doesn't change over the domain of $x$:
# +
fig, axes = subplots(2, 2)
for ax, smoothing in zip(axes.ravel(), [0.95, 0.99, 0.999, 0.9999]):
z_val = infer_z(smoothing)
ax.plot(x, y)
ax.plot(x, z_val)
ax.set_title('Smoothing={:05.4f}'.format(smoothing))
# -
# This example originally contributed by: <NAME>, http://github.com/akuz
|
docs/source/notebooks/GP-smoothing.ipynb
|