Add data for French Senior Team training
#22
by
LxYxvv
- opened
This view is limited to 50 files because it contains too many changes.
See the raw diff here.
- French_STS/download_script/download.py +88 -0
- French_STS/md/fr-Corrige-envoi-1-2023-2024.md +576 -0
- French_STS/md/fr-Corrige-envoi-5-2023-2024.md +396 -0
- French_STS/md/fr-Corrige-envoi-algebre-2023-2024.md +722 -0
- French_STS/md/fr-Corrige-envoi-arithmetique-2023-2024.md +232 -0
- French_STS/md/fr-Corrigé-Envoi-5-2019.md +180 -0
- French_STS/md/fr-corrige-envoi-1.md +228 -0
- French_STS/md/fr-corrige-envoi-2.md +65 -0
- French_STS/md/fr-corrige-envoi-4-2023-2024.md +309 -0
- French_STS/md/fr-corrige-envoi-5.md +424 -0
- French_STS/md/fr-corrigé-commenté-envoi-2.md +254 -0
- French_STS/md/fr-corrigé-commentaire-envoi-1.md +326 -0
- French_STS/md/fr-corrigé-commenté-envoi-3.md +393 -0
- French_STS/md/fr-corrigé-commenté-envoi-4.md +320 -0
- French_STS/md/fr-corrigé-commenté-envoi-5.md +391 -0
- French_STS/md/fr-corrigé-envoi-1.md +555 -0
- French_STS/md/fr-corrigé-envoi-2.md +865 -0
- French_STS/md/fr-corrigé-envoi-3.md +343 -0
- French_STS/md/fr-corrigé-envoi-4.md +279 -0
- French_STS/md/fr-corrigé-envoi-5.md +550 -0
- French_STS/md/fr-corrigé.md +274 -0
- French_STS/md/fr-ofm-2012-2013-envoi1-corrige.md +241 -0
- French_STS/md/fr-ofm-2012-2013-envoi2-corrige.md +142 -0
- French_STS/md/fr-ofm-2012-2013-envoi3-corrige.md +189 -0
- French_STS/md/fr-ofm-2012-2013-envoi4-corrige.md +353 -0
- French_STS/md/fr-ofm-2012-2013-envoi5-corrige.md +349 -0
- French_STS/md/fr-ofm-2012-2013-envoi6-corrige.md +207 -0
- French_STS/md/fr-ofm-2013-2014-envoi-1-solutions.md +302 -0
- French_STS/md/fr-ofm-2013-2014-envoi-2-solutions.md +96 -0
- French_STS/md/fr-ofm-2013-2014-envoi-3-solutions.md +407 -0
- French_STS/md/fr-ofm-2013-2014-envoi-4-solutions.md +133 -0
- French_STS/md/fr-ofm-2013-2014-envoi-5-solutions.md +222 -0
- French_STS/md/fr-ofm-2013-2014-envoi-6-solutions.md +343 -0
- French_STS/md/fr-ofm-2014-2015-envoi-1-solutions.md +133 -0
- French_STS/md/fr-ofm-2014-2015-envoi-2-solutions.md +135 -0
- French_STS/md/fr-ofm-2014-2015-envoi-3-solutions.md +231 -0
- French_STS/md/fr-ofm-2014-2015-envoi-4-solutions.md +315 -0
- French_STS/md/fr-ofm-2014-2015-envoi-5-solutions.md +266 -0
- French_STS/md/fr-ofm-2014-2015-envoi-6-solutions.md +245 -0
- French_STS/md/fr-ofm-2015-2016-envoi-1-solutions.md +164 -0
- French_STS/md/fr-ofm-2015-2016-envoi-2-solutions.md +99 -0
- French_STS/md/fr-ofm-2015-2016-envoi-3-solutions.md +313 -0
- French_STS/md/fr-ofm-2015-2016-envoi-4-solutions.md +135 -0
- French_STS/md/fr-ofm-2015-2016-envoi-5-solutions.md +256 -0
- French_STS/md/fr-ofm-2016-2017-envoi-1-solutions.md +206 -0
- French_STS/md/fr-ofm-2016-2017-envoi-2-solutions.md +400 -0
- French_STS/md/fr-ofm-2016-2017-envoi-3-solutions.md +210 -0
- French_STS/md/fr-ofm-2016-2017-envoi-4-solutions.md +294 -0
- French_STS/md/fr-ofm-2016-2017-envoi-5-solutions.md +226 -0
- French_STS/md/fr-pofm-2017-2018-envoi1-corrige.md +123 -0
French_STS/download_script/download.py
ADDED
|
@@ -0,0 +1,88 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
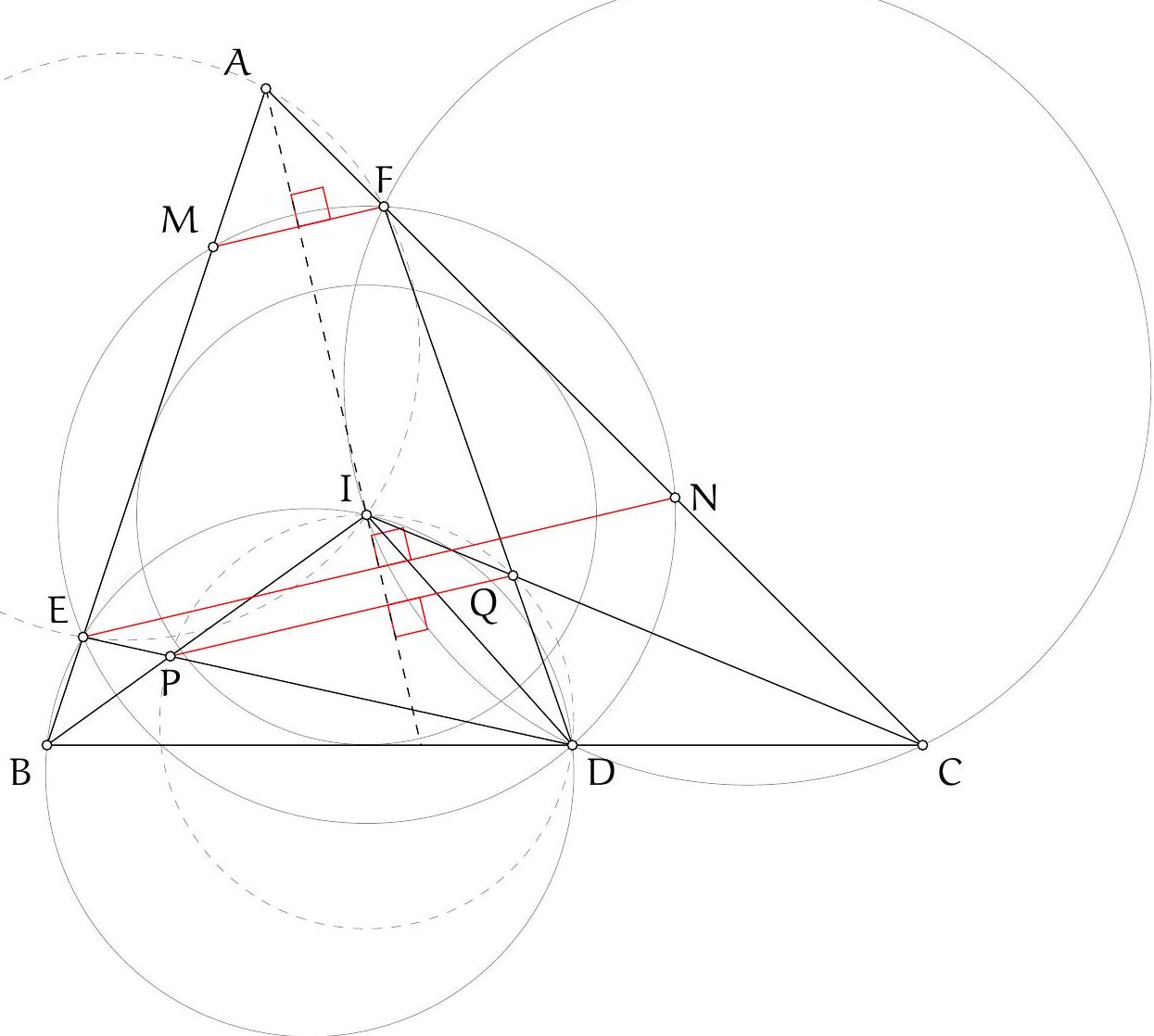
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# -----------------------------------------------------------------------------
|
| 2 |
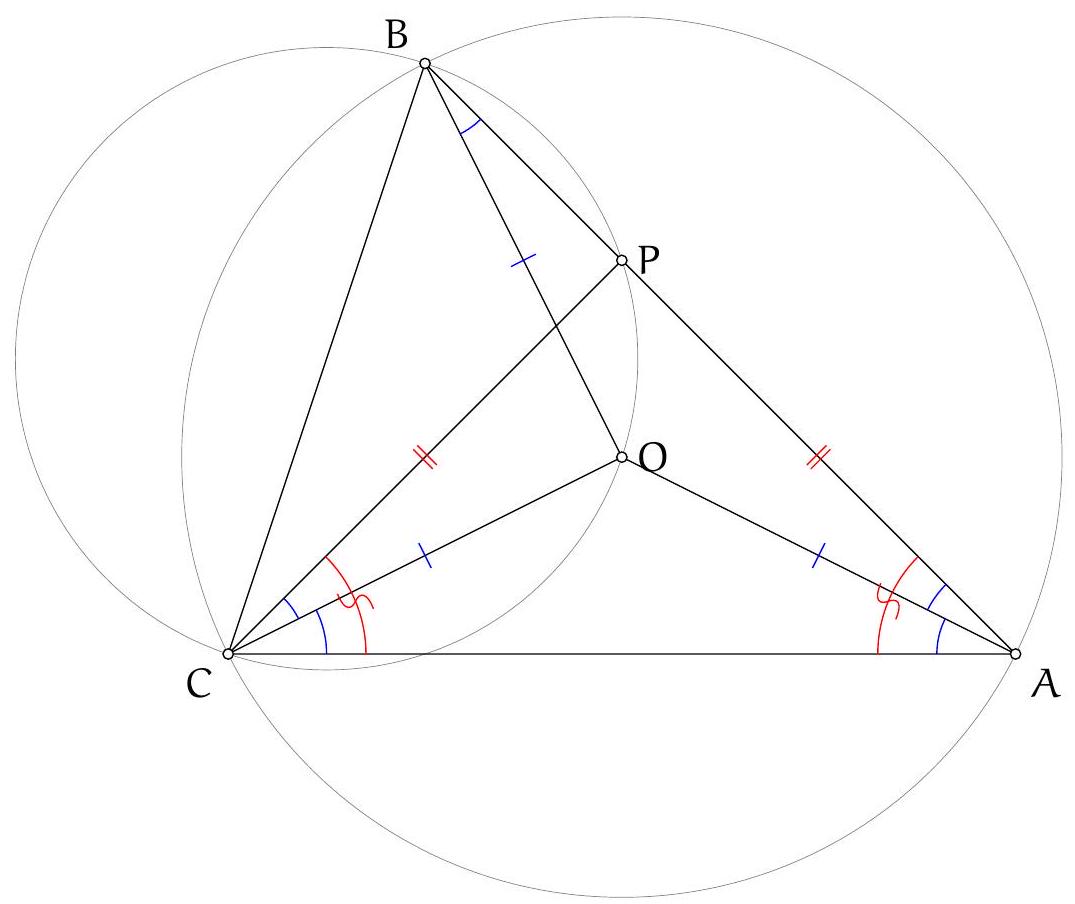
+
# Author: Jiawei Liu
|
| 3 |
+
# Date: 2024-11-21
|
| 4 |
+
# -----------------------------------------------------------------------------
|
| 5 |
+
'''
|
| 6 |
+
Download script for French TST Senior
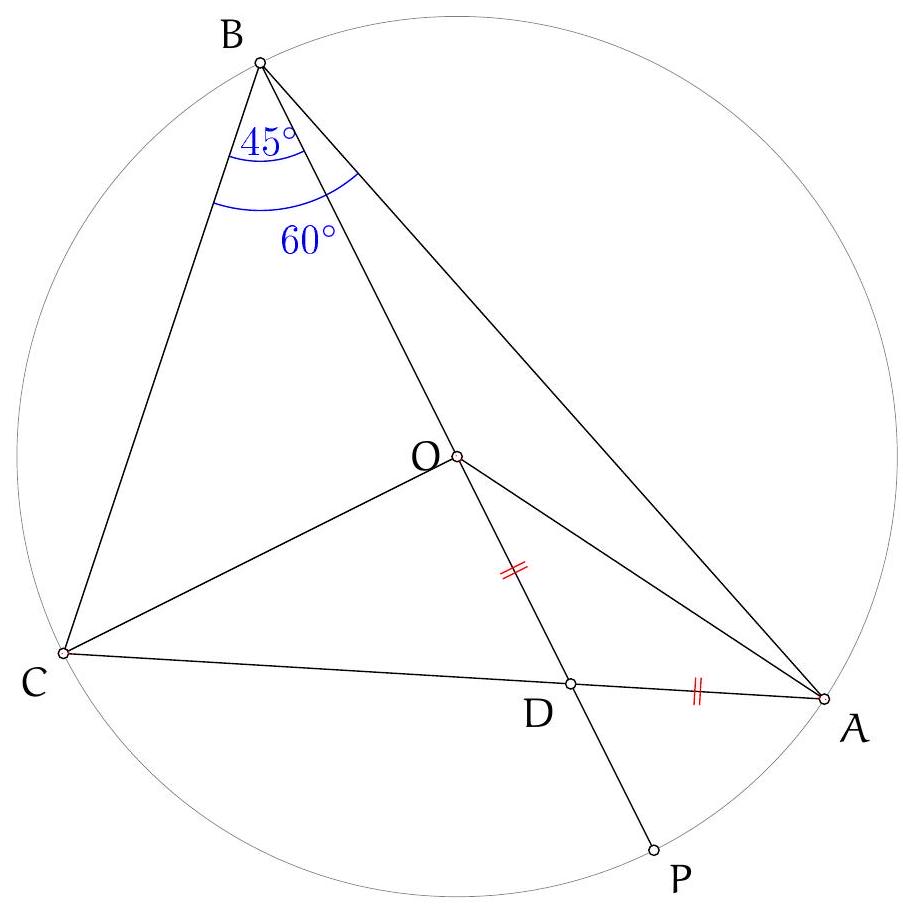
|
| 7 |
+
To run:
|
| 8 |
+
`python French_STS/download_script/download.py`
|
| 9 |
+
'''
|
| 10 |
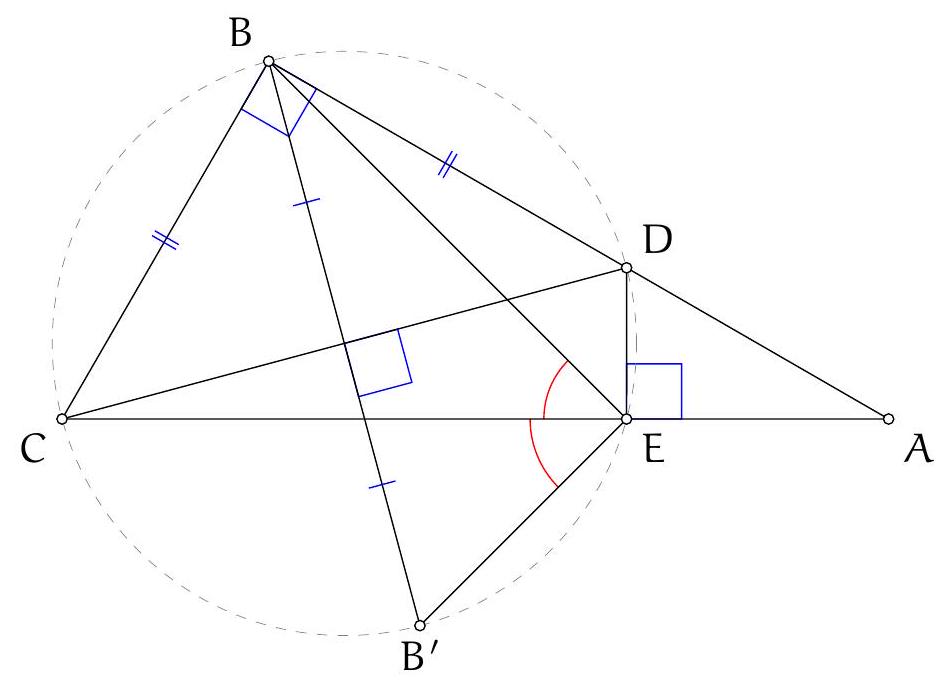
+
|
| 11 |
+
import requests
|
| 12 |
+
from bs4 import BeautifulSoup
|
| 13 |
+
from tqdm import tqdm
|
| 14 |
+
from pathlib import Path
|
| 15 |
+
from requests.adapters import HTTPAdapter
|
| 16 |
+
from urllib3.util.retry import Retry
|
| 17 |
+
from urllib.parse import urljoin, unquote
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
def build_session(
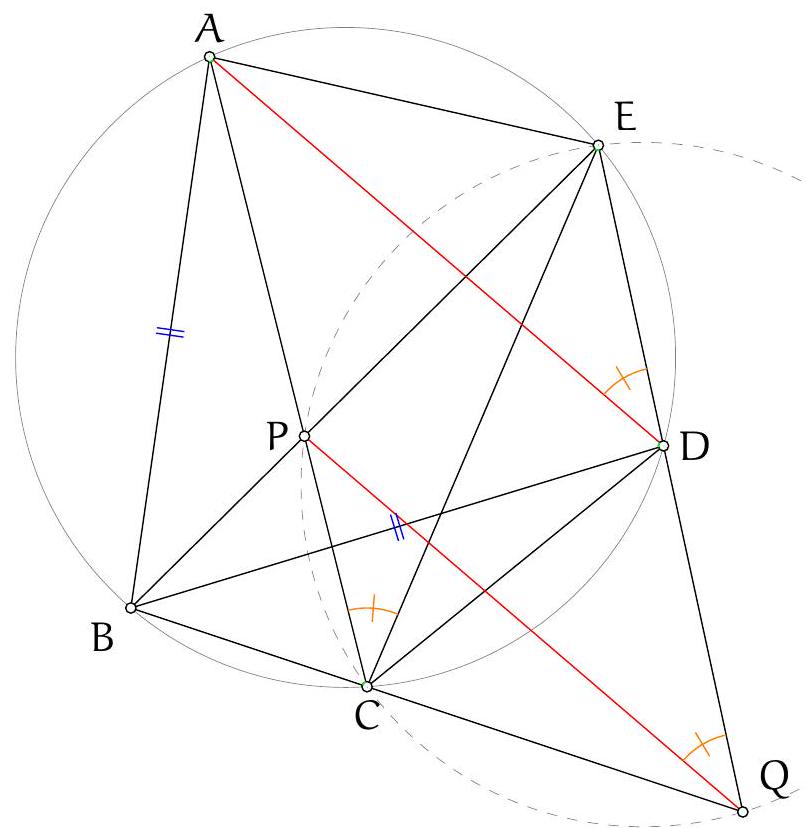
|
| 21 |
+
max_retries: int = 3,
|
| 22 |
+
backoff_factor: int = 2,
|
| 23 |
+
session: requests.Session = None
|
| 24 |
+
) -> requests.Session:
|
| 25 |
+
"""
|
| 26 |
+
Build a requests session with retries
|
| 27 |
+
|
| 28 |
+
Args:
|
| 29 |
+
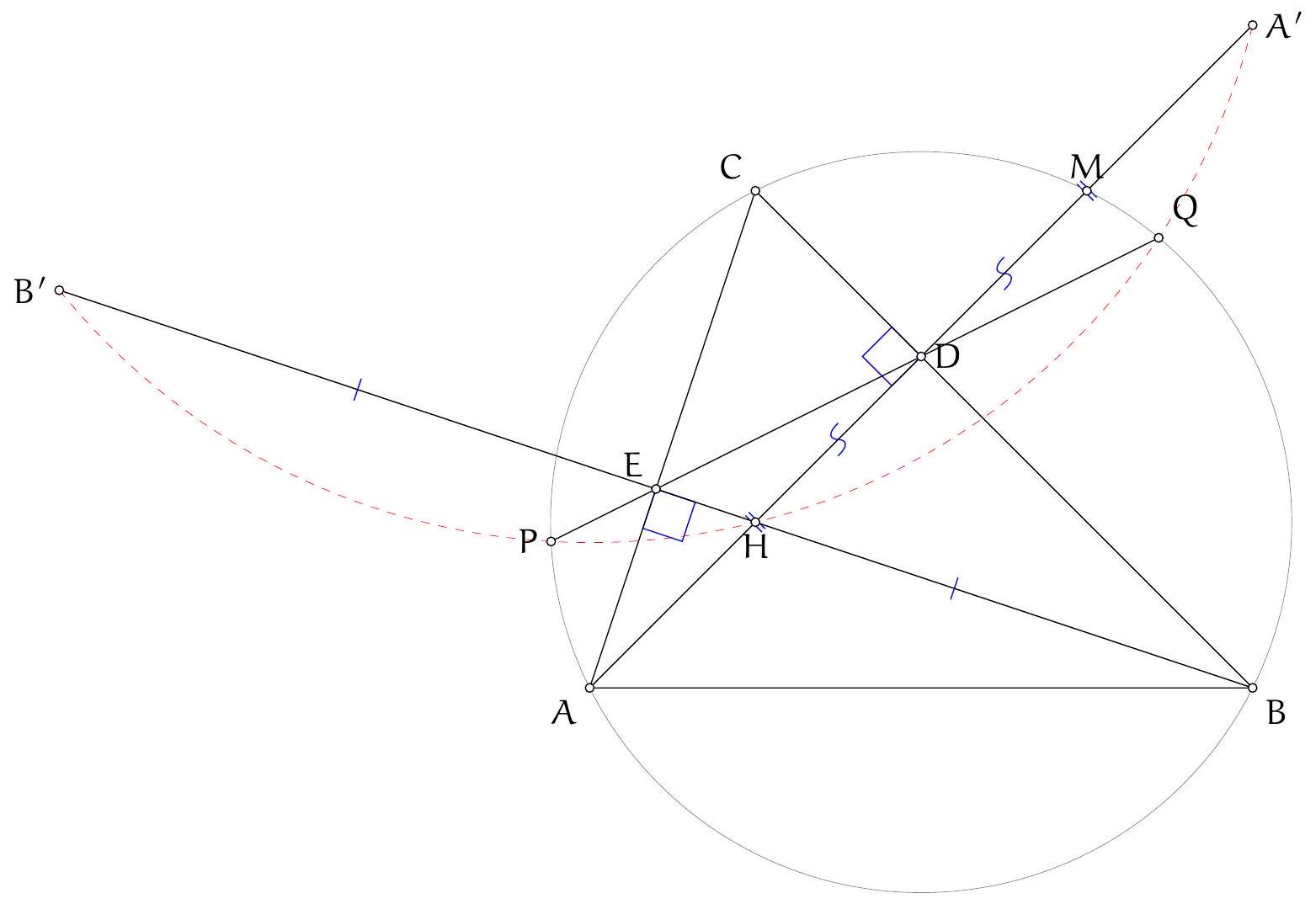
max_retries (int, optional): Number of retries. Defaults to 3.
|
| 30 |
+
backoff_factor (int, optional): Backoff factor. Defaults to 2.
|
| 31 |
+
session (requests.Session, optional): Session object. Defaults to None.
|
| 32 |
+
"""
|
| 33 |
+
session = session or requests.Session()
|
| 34 |
+
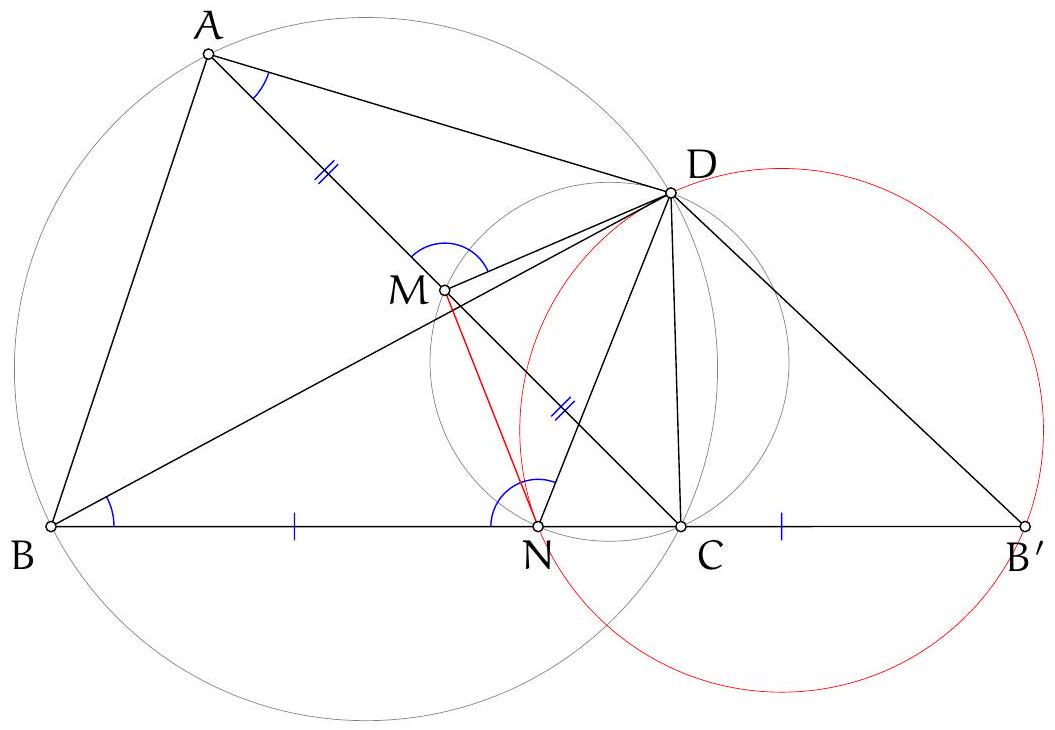
adapter = HTTPAdapter(max_retries=Retry(total=max_retries, backoff_factor=backoff_factor))
|
| 35 |
+
session.mount("http://", adapter)
|
| 36 |
+
session.mount("https://", adapter)
|
| 37 |
+
session.headers.update({
|
| 38 |
+
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/58.0.3029.110 Safari/537.3"
|
| 39 |
+
})
|
| 40 |
+
|
| 41 |
+
return session
|
| 42 |
+
|
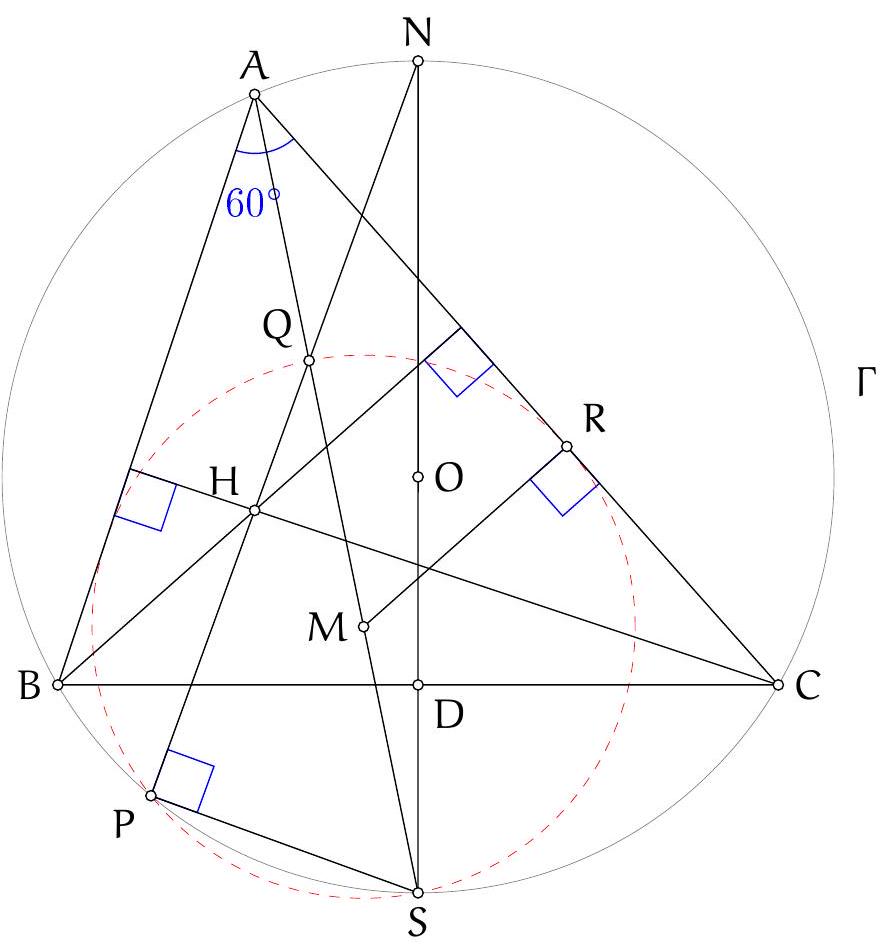
| 43 |
+
|
| 44 |
+
def main():
|
| 45 |
+
base_url = "https://maths-olympiques.fr/?page_id=71"
|
| 46 |
+
req_session = build_session()
|
| 47 |
+
|
| 48 |
+
output_dir = Path(__file__).parent.parent / "raw"
|
| 49 |
+
output_dir.mkdir(parents=True, exist_ok=True)
|
| 50 |
+
|
| 51 |
+
resp = req_session.get(base_url)
|
| 52 |
+
|
| 53 |
+
if resp.status_code != 200:
|
| 54 |
+
raise Exception(f"Failed to retrieve the page. Status code: {resp.status_code}")
|
| 55 |
+
|
| 56 |
+
soup = BeautifulSoup(resp.text, 'html.parser')
|
| 57 |
+
link_container = soup.find('table', {"id": 'tablepress-1'})
|
| 58 |
+
|
| 59 |
+
link_eles = link_container.find_all(
|
| 60 |
+
'a',
|
| 61 |
+
href=(
|
| 62 |
+
lambda t:
|
| 63 |
+
'.pdf' in t
|
| 64 |
+
and ('corrig' in t.lower() or 'solutions' in t.lower())
|
| 65 |
+
if t else False
|
| 66 |
+
)
|
| 67 |
+
)
|
| 68 |
+
|
| 69 |
+
for ele in tqdm(link_eles):
|
| 70 |
+
pdf_link = ele['href']
|
| 71 |
+
|
| 72 |
+
output_file = output_dir / f"fr-{unquote(Path(pdf_link).name)}"
|
| 73 |
+
|
| 74 |
+
# Check if the file already exists
|
| 75 |
+
if output_file.exists():
|
| 76 |
+
continue
|
| 77 |
+
|
| 78 |
+
pdf_resp = req_session.get(urljoin(base_url, pdf_link))
|
| 79 |
+
|
| 80 |
+
if pdf_resp.status_code != 200:
|
| 81 |
+
print(f"Failed to download {pdf_link}")
|
| 82 |
+
continue
|
| 83 |
+
|
| 84 |
+
output_file.write_bytes(pdf_resp.content)
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
if __name__ == "__main__":
|
| 88 |
+
main()
|
French_STS/md/fr-Corrige-envoi-1-2023-2024.md
ADDED
|
@@ -0,0 +1,576 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOI 1 : GÉOMÉTrIE <br> À RENVOYER AU PLUS TARD LE 5 DÉCEMBRE 2023
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2009 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
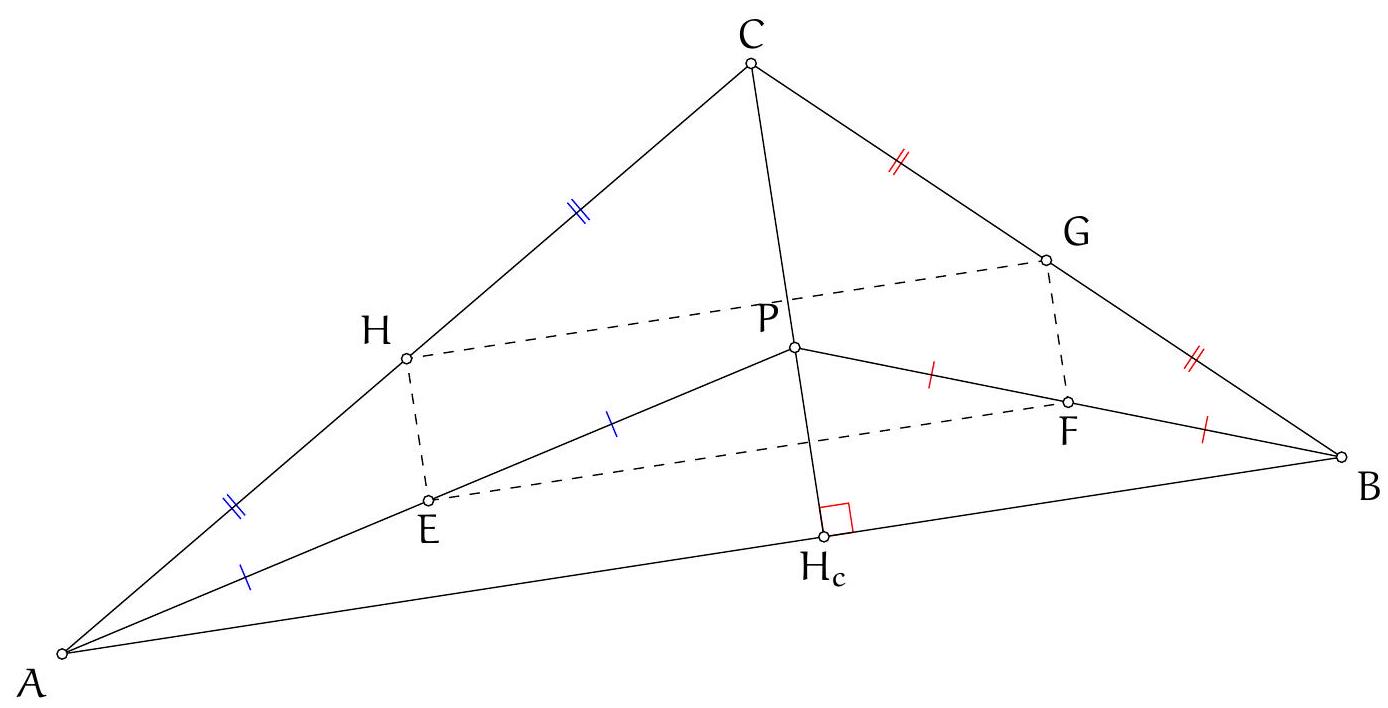
Exercice 1. Soient $A B C$ un triangle et $\mathrm{H}_{\mathrm{C}}$ le pied de la hauteur issue de C . Soit P un point sur le segment $\left[\mathrm{CH}_{C}\right]$ (autre que $C$ ), et soient $E, F, G, H$ les milieux respectifs de $[A P],[B P],[B C],[A C]$. Montrer que EFGH est un rectangle.
|
| 17 |
+
|
| 18 |
+
## Solution de l'exercice 1
|
| 19 |
+
|
| 20 |
+
|
| 21 |
+
|
| 22 |
+
Pour démontrer que EFGH est un rectangle, nous allons montrer que c'est un parallélogramme qui possède un angle droit.
|
| 23 |
+
|
| 24 |
+
Considérons le triangle $A C P$. Les points E et H sont les milieux respectifs des côtés $[A P]$ et $[A C]$. Par le théorème de la droite des milieux, (HE) // (PC).
|
| 25 |
+
Considérons le triangle BCP. Les points F et G sont les milieux respectifs des côtés [BP] et [BC]. Par le théorème de la droite des milieux, (FG) // (PC).
|
| 26 |
+
On a montré que les droites (FG) et ( HE ) sont toutes les deux parallèles à la droite (PC). Il s'ensuit que (FG) // (HE).
|
| 27 |
+
|
| 28 |
+
Considérons le triangle $A B P$. Les points $E$ et $F$ sont les milieux respectifs des côtés [AP] et [BP]. Par le théorème de la droite des milieux, ( $E F$ ) // ( $A B$ ).
|
| 29 |
+
Considérons le triangle $A B C$. Les points H et G sont les milieux respectifs des côtés [AC] et [BC]. Par le théorème de la droite des milieux, (HG) // (AB).
|
| 30 |
+
On a montré que les droites (EF) et (HG) sont toutes les deux parallèles à la droite ( $A B$ ). Il s'ensuit que (HG) // (EF).
|
| 31 |
+
|
| 32 |
+
Par conséquent, EFGH est un quadrilatère dont les côtés opposés sont parallèles deux à deux. Il s'ensuit que c'est un parallélogramme.
|
| 33 |
+
|
| 34 |
+
Par ailleurs, comme $\left(\mathrm{CH}_{c}\right) \perp(\mathrm{AB})$ et $(E F) / /(\mathrm{AB})$, on a $(E F) \perp\left(\mathrm{CH}_{c}\right)$.
|
| 35 |
+
De plus, $\left(\mathrm{CH}_{\mathrm{c}}\right) / /(\mathrm{EH})$. Il s'ensuit que $(\mathrm{EH}) \perp(\mathrm{EF})$.
|
| 36 |
+
Le parallélogramme EFGH possède donc un angle droit, ce qui démontrer que EFGH est un rectangle.
|
| 37 |
+
|
| 38 |
+
Remarque. Une autre façon de prouver que EFGH est un parallélogramme est d'utiliser que d'après le théorème de la droite des milieux, $(\mathrm{EH}) / /(\mathrm{CP}) / /(\mathrm{FG})$ et $\mathrm{EH}=\frac{1}{2} \mathrm{CP}=\mathrm{FG}$. Donc EFGH possède deux côtés opposés parallèles et de même longueur, c'est donc un parallélogramme.
|
| 39 |
+
|
| 40 |
+
Commentaire des correcteurs: L'exercice a été très bien réussi dans l'ensemble. Cependant pas mal d'élèves pourraient aller plus vite en utilisant les droites parallèles et perpendiculaires de la figure sans faire de chasse aux angles. Deplus, plusieurs élèves ont perdu des points car ils n'ont pas justifié pourquoi ils pouvaient appliquer le théorème de Thalès ou pourquoi le quadrilatère EFGH avait un angle droit...
|
| 41 |
+
|
| 42 |
+
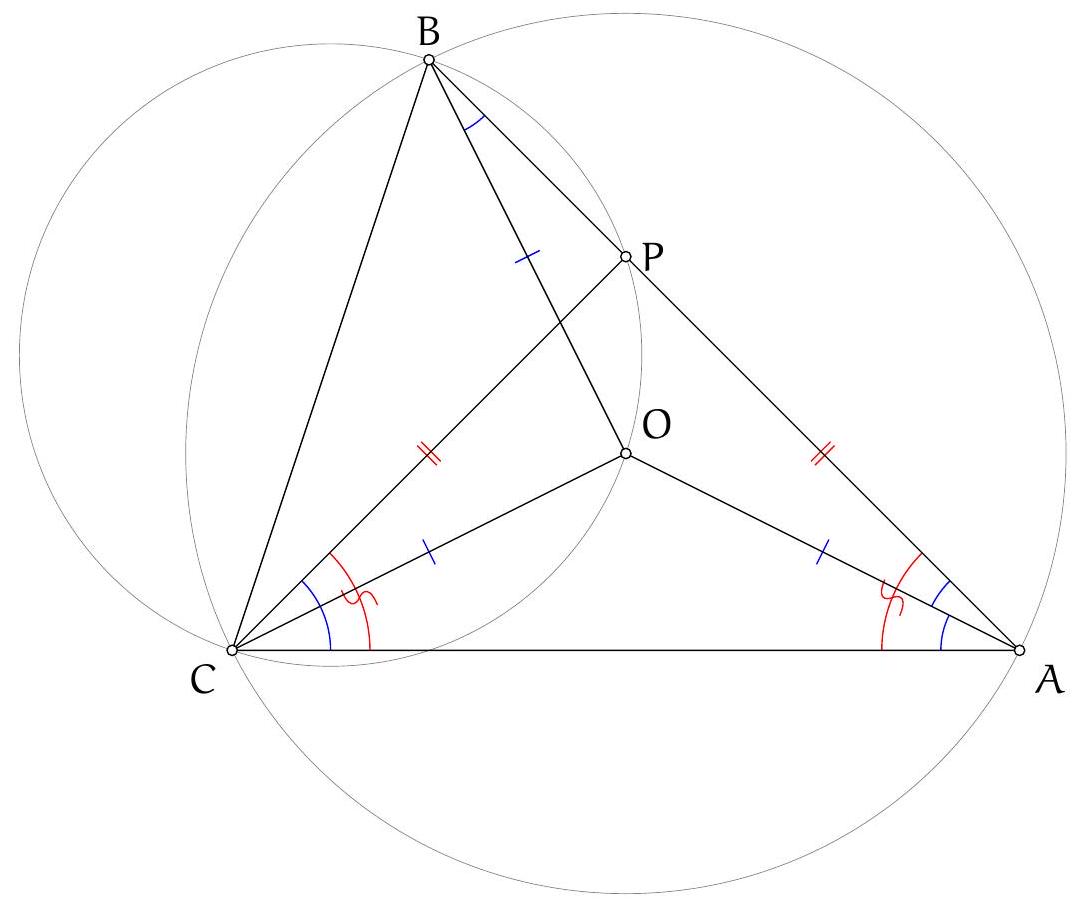
Exercice 2. Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
| 43 |
+
|
| 44 |
+
## Solution de l'exercice 2
|
| 45 |
+
|
| 46 |
+
|
| 47 |
+
|
| 48 |
+
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a:
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\begin{aligned}
|
| 52 |
+
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
|
| 53 |
+
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
|
| 54 |
+
& =\widehat{A C O}+\widehat{O B A}
|
| 55 |
+
\end{aligned}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{\mathrm{OAC}}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{\mathrm{CBA}}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
|
| 59 |
+
|
| 60 |
+
Commentaire des correcteurs : L'exercice a été très bien réussi et beaucoup abordé, certaines solutions sont particulièrement efficaces dans leurs chasses aux angles.
|
| 61 |
+
|
| 62 |
+
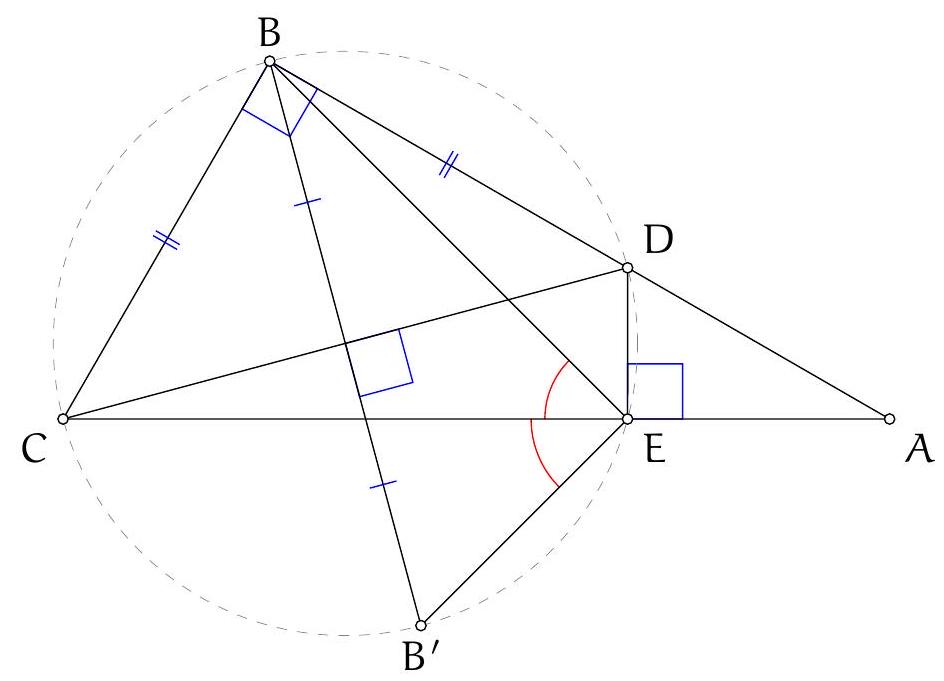
Exercice 3. Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de $B$ par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
| 63 |
+
|
| 64 |
+
## Solution de l'exercice 3
|
| 65 |
+
|
| 66 |
+
|
| 67 |
+
|
| 68 |
+
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}} \widehat{ } \mathrm{C}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $C, B, D, E, B^{\prime}$ sont cocycliques.
|
| 69 |
+
Alors on a :
|
| 70 |
+
|
| 71 |
+
$$
|
| 72 |
+
\begin{aligned}
|
| 73 |
+
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
|
| 74 |
+
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ}
|
| 75 |
+
\end{aligned}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
De plus:
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\begin{aligned}
|
| 82 |
+
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
|
| 83 |
+
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
|
| 84 |
+
\end{aligned}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
| 88 |
+
Solution alternative $n^{\circ} 1$
|
| 89 |
+
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\begin{aligned}
|
| 93 |
+
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
|
| 94 |
+
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
|
| 95 |
+
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
|
| 96 |
+
\end{aligned}
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
Commentaire des correcteurs : L'exercice est globalement très bien réussi. L'erreur la plus fréquente portait sur les conditions pour qu'un quadrilatère soit un carré.
|
| 100 |
+
|
| 101 |
+
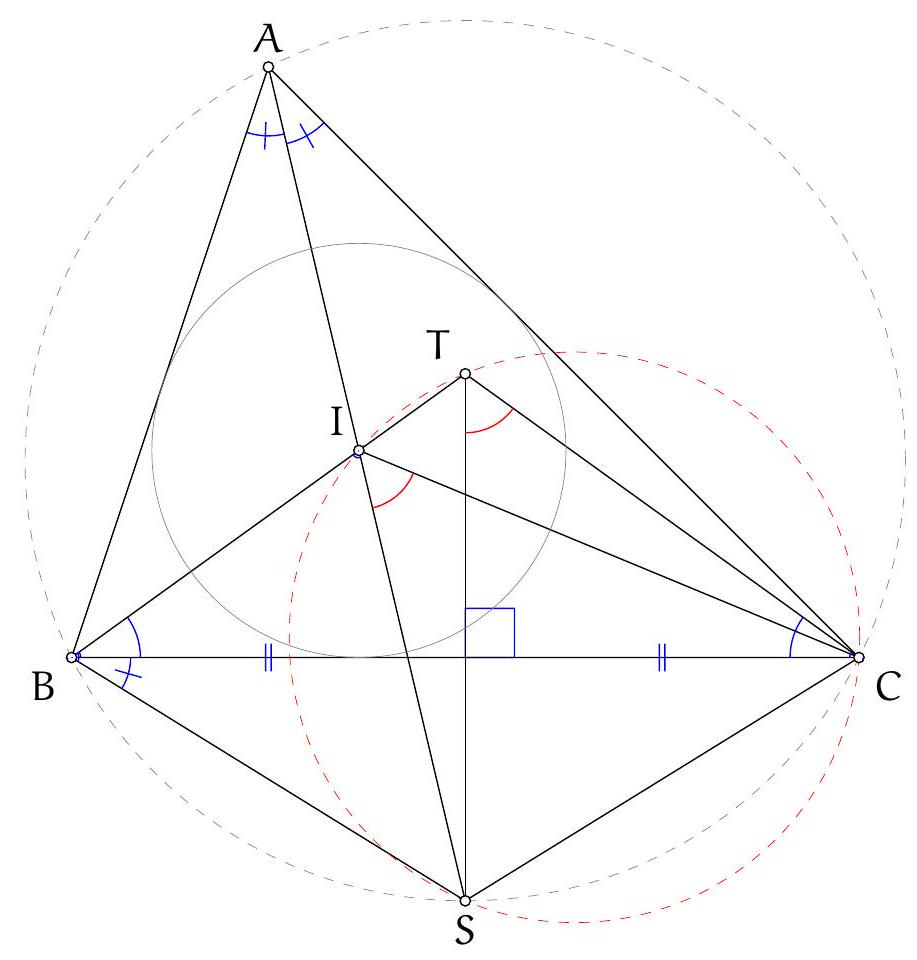
Exercice 4. Soient $A B C$ un triangle et I le centre de son cercle inscrit. La médiatrice de $[\mathrm{BC}]$ coupe ( $A \mathrm{I}$ ) en $S$ et (BI) et $T$. Montrer que $C, I, S$ et $T$ sont cocycliques.
|
| 102 |
+
|
| 103 |
+
## Solution de l'exercice 4
|
| 104 |
+
|
| 105 |
+
|
| 106 |
+
|
| 107 |
+
Pour montrer que $C, I, S$ et $T$ sont cocycliques, nous allons montrer que $\widehat{\text { SIC }}=\widehat{\text { STC }}$.
|
| 108 |
+
On rappelle que les bissectrices intérieures d'un triangle $A B C$ sont concourantes et que leur point d'intersection I est le centre du cercle inscrit dans le triangle. (AI) est donc la bissectrice de l'angle $\widehat{B A C}$.
|
| 109 |
+
|
| 110 |
+
Par conséquent, $S$ est défini comme le point d'intersection de la médiatrice de $[\mathrm{BC}]$ et de la bissectrice de l'angle $\widehat{B A C}$. Le théorème du Pôle Sud assure que $S$ appartient au cercle circonscrit au triangle $A B C$ et que $S$ est le centre du cercle antarctique du sommet $A$, ce qui assure que
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
\mathrm{SB}=\mathrm{SI}
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
On voit donc que triangle SBI est isocèle en S ce qui assure que $\widehat{\mathrm{SBI}}=\widehat{\mathrm{BIS}}$.
|
| 117 |
+
Par ailleurs les points $A, B, S$ et $C$ sont cocycliques. On a donc
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\widehat{S B C}=\widehat{S A C}=\frac{\widehat{B A C}}{2} .
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Calculons désormais la valeur de l'angle $\widehat{\text { SIC }}$. On a
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\begin{aligned}
|
| 127 |
+
\widehat{S I C} & =\widehat{\mathrm{BIC}}-\widehat{\mathrm{BIS}} \\
|
| 128 |
+
& =\widehat{\mathrm{BIC}}-\widehat{\mathrm{SBC}}-\widehat{\mathrm{CBI}} \\
|
| 129 |
+
& =\widehat{\mathrm{BIC}}-\frac{\widehat{\mathrm{BAC}}}{2}-\frac{\widehat{\mathrm{CBA}}}{2} .
|
| 130 |
+
\end{aligned}
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
Par ailleurs,
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\begin{aligned}
|
| 137 |
+
\widehat{\mathrm{BIC}} & =180^{\circ}-\widehat{\mathrm{CBI}}-\widehat{\mathrm{ICB}} \\
|
| 138 |
+
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}-\frac{\widehat{A C B}}{2} \\
|
| 139 |
+
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{A C B}}{2} \\
|
| 140 |
+
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{BAC}}}{2} \\
|
| 141 |
+
& =90^{\circ}+\frac{\widehat{\mathrm{BAC}}}{2} .
|
| 142 |
+
\end{aligned}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
Il s'ensuit que $\widehat{\text { SIC }}=90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}$.
|
| 146 |
+
Par ailleurs
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
\begin{aligned}
|
| 150 |
+
\widehat{\mathrm{STC}} & =90^{\circ}-\widehat{\mathrm{TCB}} \\
|
| 151 |
+
& =90-\widehat{\mathrm{CBI}} \quad \text { Le triangle } \mathrm{BCT} \text { est isocèle en } \mathrm{T} \\
|
| 152 |
+
& =90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2} .
|
| 153 |
+
\end{aligned}
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
On a donc montré que $\widehat{\text { SIC }}=\widehat{\text { STC }}$ ce qui assure que les points $C, I, S$ et $T$ sont cocycliques par la réciproque du théorème de l'angle inscrit.
|
| 157 |
+
Commentaire des correcteurs: L'exercice est très bien réussi. Beaucoup d'élèves ont procédé à une lourde chasse aux angles alors que le théorème du Pôle Sud simplifiait grandement la résolution du problème.
|
| 158 |
+
|
| 159 |
+
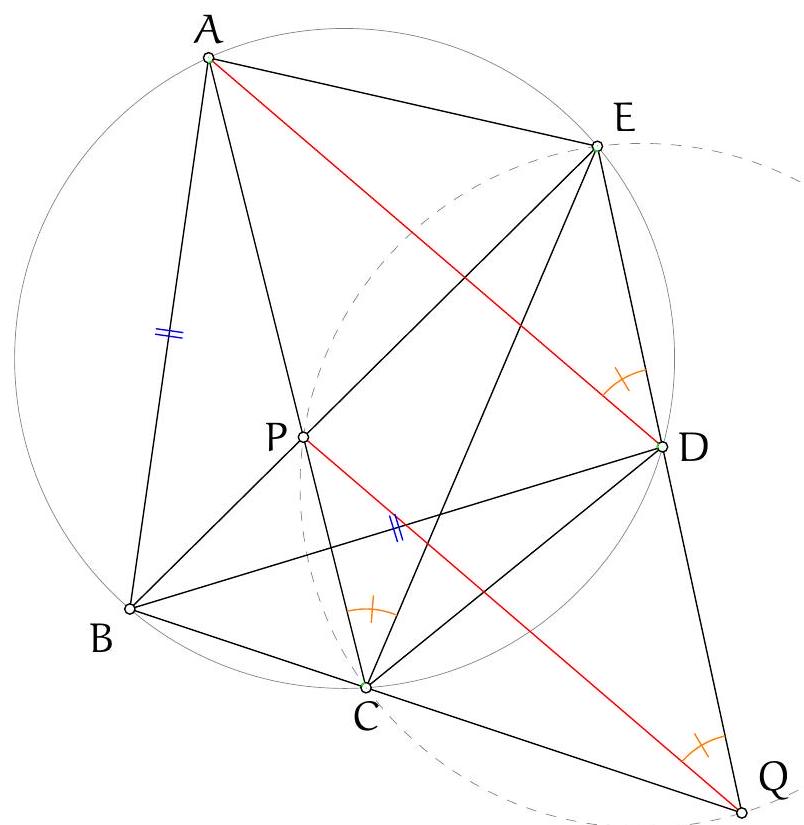
Exercice 5. Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
| 160 |
+
|
| 161 |
+
## Solution de l'exercice 5
|
| 162 |
+
|
| 163 |
+
|
| 164 |
+
|
| 165 |
+
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\begin{aligned}
|
| 169 |
+
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
|
| 170 |
+
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
|
| 171 |
+
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
|
| 172 |
+
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
|
| 173 |
+
& =180^{\circ}-\widehat{\mathrm{BED}} \\
|
| 174 |
+
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
|
| 175 |
+
\end{aligned}
|
| 176 |
+
$$
|
| 177 |
+
|
| 178 |
+
Ainsi on a montré que $\widehat{\mathrm{QCP}}+\widehat{\mathrm{PEQ}}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
|
| 179 |
+
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\begin{aligned}
|
| 183 |
+
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
|
| 184 |
+
& =\widehat{\mathrm{ECA}} \\
|
| 185 |
+
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
|
| 186 |
+
\end{aligned}
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
|
| 190 |
+
Commentaire des correcteurs : L'exercice a été bien traité par les personnes qui l'ont abordé. Quasiment tous les élèves ont pensé à traduire l'égalité de longueur en égalité d'angle, ce qui était le bon point de départ pour pouvoir ensuite faire une chasse aux angles. Ensuite, il fallait observer que le quadrilatère
|
| 191 |
+
|
| 192 |
+
EPCQ est cyclique pour continuer, ce qui en a bloqué certains. Certains qui n'ont pas vu cela ont réussi à s'en sortir avec une chasse aux angles plus lourde, d'autres ont réussi à appliquer le théorème de Thalès en introduisant un nouveau point.
|
| 193 |
+
|
| 194 |
+
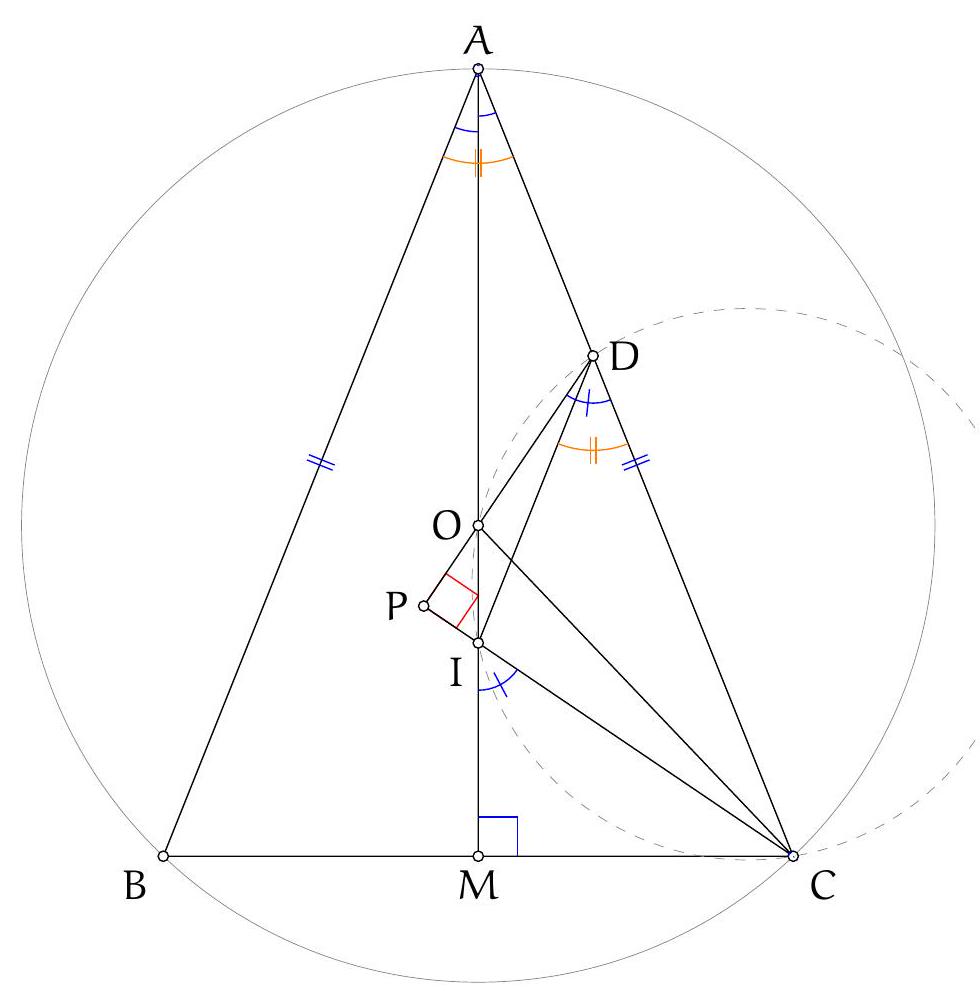
Exercice 6. Soient $A B C$ un triangle isocèle en $A$, $O$ le centre de son cercle circonscrit et $I$ le centre de son cercle inscrit. La parallèle à ( $A B$ ) passant par I coupe (AC) en D. Montrer que (CI) et (DO) sont perpendiculaires.
|
| 195 |
+
|
| 196 |
+
## Solution de l'exercice 6
|
| 197 |
+
|
| 198 |
+
|
| 199 |
+
|
| 200 |
+
Premièrement, comme $A B=A C, A, O$, I sont alignés et la droite $(A I)$ coupe $[B C]$ en son milieu $M$. On pose P l'intersection des droites (DO) et (CI).
|
| 201 |
+
|
| 202 |
+
Par chasse aux angles, on montre que I, O, D, $C$ sont cocycliques, en montrant que $\widehat{\mathrm{IOC}}=\widehat{\mathrm{IDC}}$. En effet :
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
\begin{aligned}
|
| 206 |
+
\widehat{\mathrm{IOC}} & =\widehat{\mathrm{MOC}} \\
|
| 207 |
+
& =\frac{1}{2} \widehat{\mathrm{BOC}} \text { car } O B=\mathrm{OC} \\
|
| 208 |
+
& =\widehat{\mathrm{BAC}} \text { par angle au centre } \\
|
| 209 |
+
& =\widehat{\mathrm{IDC}} \mathrm{car}(\mathrm{BA}) / /(\mathrm{ID})
|
| 210 |
+
\end{aligned}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Donc par réciproque du théorème de l'angle inscrit, $\mathrm{I}, \mathrm{O}, \mathrm{D}, \mathrm{C}$ sont cocycliques.
|
| 214 |
+
Montrons à présent que $\widehat{C P D}=90^{\circ}$. Pour cela, on va montrer que $\widehat{P D C}+\widehat{D C P}=90^{\circ}$ (puisque $\left.\widehat{\mathrm{CPD}}=180^{\circ}-\widehat{\mathrm{PDC}}-\widehat{\mathrm{DCP}}\right)$. On a :
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
\begin{aligned}
|
| 218 |
+
\widehat{\mathrm{PDC}}+\widehat{\mathrm{DCP}} & =\widehat{\mathrm{ODC}}+\widehat{\mathrm{DCI}} \\
|
| 219 |
+
& =\left(180^{\circ}-\widehat{\mathrm{CIO}}\right)+\widehat{\mathrm{ICB}} \text { par cocyclicité et bissectrice } \\
|
| 220 |
+
& =\widehat{\mathrm{CIM}}+\widehat{\mathrm{ICM}} \\
|
| 221 |
+
& =90^{\circ} \mathrm{car}(A \mathrm{II}) \perp(\mathrm{BC}) .
|
| 222 |
+
\end{aligned}
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Donc $\widehat{\mathrm{CPD}}=90^{\circ}$, ce qui prouve bien que les droites (CI) et (DO) sont perpendiculaires.
|
| 226 |
+
|
| 227 |
+
Commentaire des correcteurs : Exercice bien réussi dans l'ensemble. La plupart des copies rendues contenait une solution correcte.
|
| 228 |
+
|
| 229 |
+
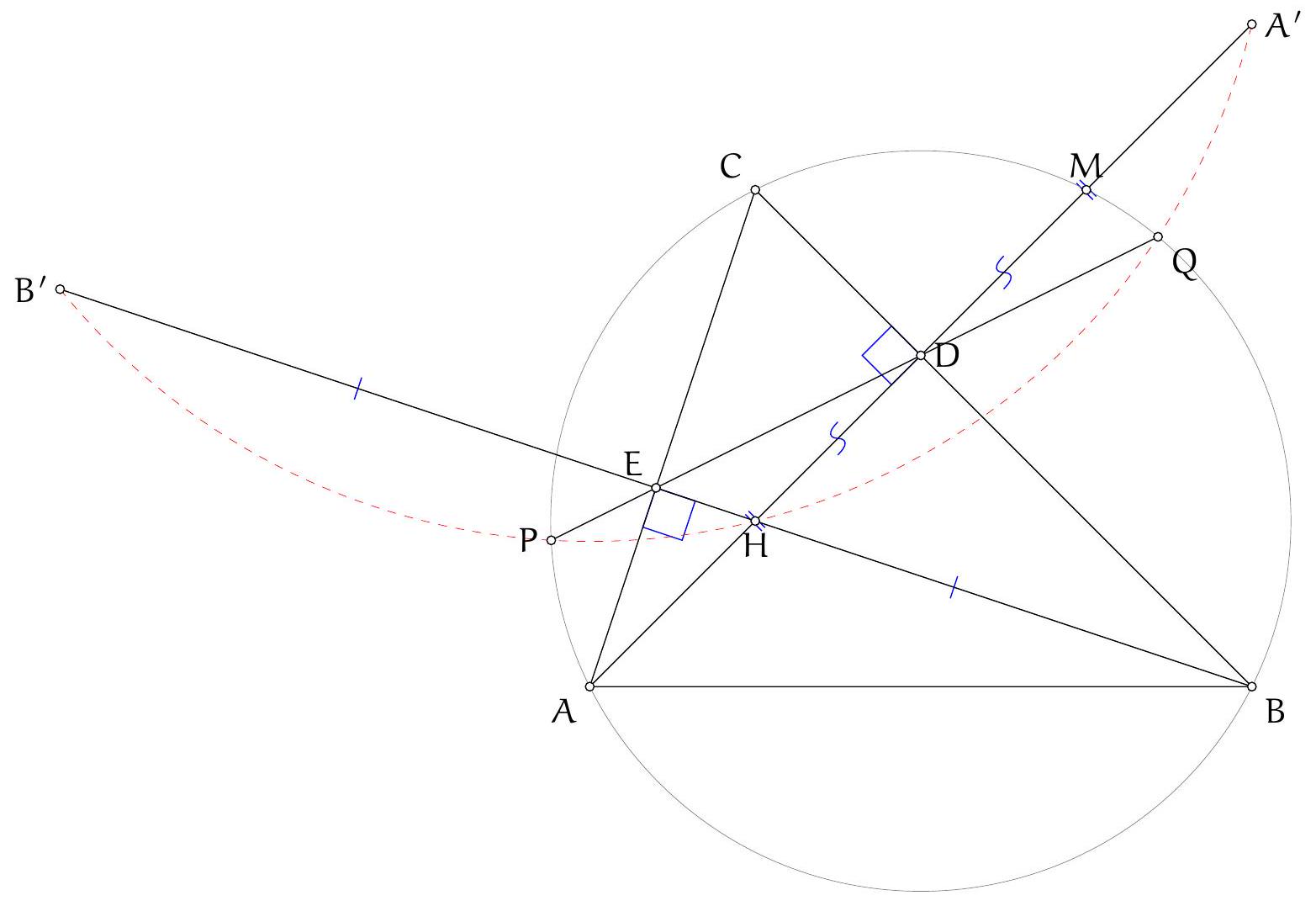
Exercice 7. Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à ( $B C$ ) et ( $A C$ ) respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|
| 230 |
+
|
| 231 |
+
## Solution de l'exercice 7
|
| 232 |
+
|
| 233 |
+
|
| 234 |
+
|
| 235 |
+
Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
|
| 236 |
+
|
| 237 |
+
Soit $M$ le symétrique de H par rapport à $(\mathrm{BC})$ : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
|
| 238 |
+
|
| 239 |
+
$$
|
| 240 |
+
\begin{aligned}
|
| 241 |
+
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
|
| 242 |
+
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
|
| 243 |
+
\end{aligned}
|
| 244 |
+
$$
|
| 245 |
+
|
| 246 |
+
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
|
| 247 |
+
Commentaire des correcteurs : L'exercice a été bien résolu. Cependant pas mal d'élèves pourraient aller plus vite en utilisant la puissance d'un point, plutôt que d'utiliser les triangles semblables associés à 4 points cocycliques et reprouver la puissance d'un point.
|
| 248 |
+
|
| 249 |
+
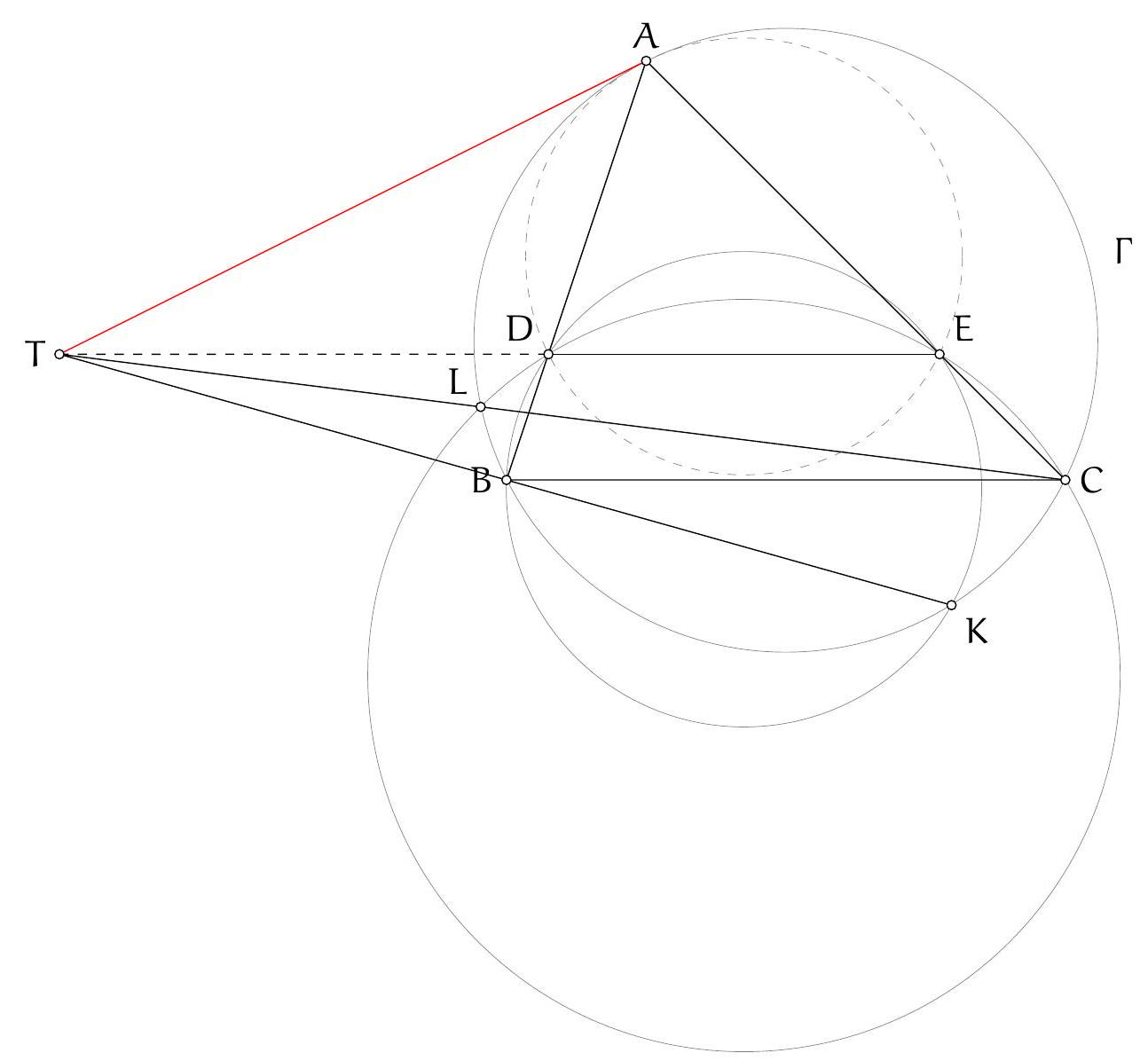
Exercice 8. Soient $A B C$ un triangle de cercle circonscrit $\Gamma, D$ un point sur $(A B)$ et $E$ un point sur ( $A C)$ tel que (DE) et ( $B C$ ) sont parallèles. Le cercle circonscrit à $A B C$ rencontre le cercle circonscrit à $B D E$ une seconde fois en $K$ et le cercle circonscrit à CDE une seconde fois en $L$. Soit $T$ le point d'intersection de (BK) et (CL). Montrer que (TA) est tangente au cercle $\Gamma$.
|
| 250 |
+
|
| 251 |
+
## Solution de l'exercice 8
|
| 252 |
+
|
| 253 |
+
|
| 254 |
+
|
| 255 |
+
On reconnait ici une situation classique :
|
| 256 |
+
|
| 257 |
+
- KBDE cyclique,
|
| 258 |
+
- KBLC cyclique,
|
| 259 |
+
- CLDE cyclique.
|
| 260 |
+
|
| 261 |
+
On sait que dans cette situation, les droites (KB), (CL), (ED) sont concourantes (il s'agit ici du fait que les axes radicaux de 3 cercles sont concourants). Or les droites (BK) et (CL) se coupent en $T$. Il suit que $\mathrm{T}, \mathrm{D}, \mathrm{E}$ sont alignés.
|
| 262 |
+
|
| 263 |
+
On sait alors, en exprimant la puissance de T par rapport aux trois cercles, que :
|
| 264 |
+
|
| 265 |
+
$$
|
| 266 |
+
\mathrm{TD} \times \mathrm{TE}=\mathrm{TL} \times \mathrm{TC}=\mathrm{TB} \times \mathrm{TK}
|
| 267 |
+
$$
|
| 268 |
+
|
| 269 |
+
Le fait de connaître le produit TD $\times$ TE incite à considérer un cercle passant par $\mathrm{D}, \mathrm{E}$, et comme on souhaite une propriété sur (TA), il est naturel d'introduire le cercle circonscrit à $A D E$.
|
| 270 |
+
|
| 271 |
+
Comme TD $\times$ TE $=T L \times T C, T$ a la même puissance par rapport aux cercles circonscrits à $A B C$ et $A D E$. Il est donc sur leur axe radical. Mais comme ( $D E$ ) est parallèles à ( BC ), les deux cercles sont tangents en $A$ d'axe radical la tangente commune à ces deux cercles en $A$. On peut le voir simplement par
|
| 272 |
+
angle tangentiel (en utilisant que $\widehat{A E D}=\widehat{A C B}$ ), autrement on peut le voir en considérant l'homothétie de centre $A$ envoyant $D$ sur $B$ : elle envoie $E$ sur $C$ donc elle envoie le cercle ( $A D E$ ) sur ( $A B C$ ), et donc ces cercles sont bien tangents.
|
| 273 |
+
|
| 274 |
+
On en déduit que $T$ est sur la tangente à $\Gamma$ passant par $A$, autrement dit que (TA) est tangente à $\Gamma$, comme voulu.
|
| 275 |
+
|
| 276 |
+
Commentaire des correcteurs : L'exercice n'a pas été beaucoup abordé, mais la totalité des élèves qui ont abordé l'exercice ont eu des très bonnes idées, y compris ceux qui n'ont pas abouti à une solution. Notamment, tous les élèves ont remarqué que les points $T, D, E$ sont alignés, ce qui était la première idée à avoir pour avancer dans l'exercice. Il fallait ensuite réussir à exploiter le parallélisme de (DE) et (BC), et là les élèves qui ont abouti utilisaient essentiellement deux approches différentes : soit justifier que les cercles circonscrits à $A D E$ et $A B C$ sont tangents en $A$ pour se ramener à montrer la tangence au cercle (ADE), soit par chasse aux angles en trouvant d'autres quadrilatères cycliques sur la figure.
|
| 277 |
+
|
| 278 |
+
Exercice 9. Soient $A B C$ un triangle non-isocèle et $I$ le centre de son cercle inscrit. Soit D un point sur $[B C]$ (autre que $B$ et $C$ ). Le cercle circonscrit à DIB coupe $(A B)$ une deuxième fois en $E \neq B$, et le cercle circonscrit à DIC coupe ( $A C$ ) une deuxième fois en $F \neq C$. Le cercle circonscrit à DEF rencontre ( $A B$ ) et ( $A C$ ) une deuxième fois en $M$ et $N$ respectivement. Les droites (IB) et ( $D E$ ) s'intersectent en $P$ et les droites (IC) et (DF) s'intersectent en Q. Montrer que les droites (EN), (FM) et (PQ) sont parallèles.
|
| 279 |
+
|
| 280 |
+
## Solution de l'exercice 9
|
| 281 |
+
|
| 282 |
+
|
| 283 |
+
|
| 284 |
+
Sur la figure, il semble que I est le centre du cercle (DEF), et que les droites (MF), (EN), (PQ) sont toutes perpendiculaires à $(A I)$ : c'est donc la stratégie qu'on va utiliser pour résoudre l'exercice.
|
| 285 |
+
|
| 286 |
+
- Lemme 1: Le point I est le centre du cercle circonscrit à DEF.
|
| 287 |
+
|
| 288 |
+
Preuve : Comme I est sur la bissectrice de $\widehat{\mathrm{DBE}}$ et sur le cercle circonscrit de DBE, c'est le pôle Sud (par rapport à B) dans ce triangle. Donc ID = IE. De même dans FCD, on obtient ID = IF. Donc $\mathrm{ID}=\mathrm{IE}=\mathrm{IF}: \mathrm{I}$ est bien le centre du cercle circonscrit de DEF.
|
| 289 |
+
|
| 290 |
+
- Lemme 2: Le quadrilatère PQID est cyclique.
|
| 291 |
+
|
| 292 |
+
Preuve : En effet, on a :
|
| 293 |
+
|
| 294 |
+
$$
|
| 295 |
+
\begin{aligned}
|
| 296 |
+
\widehat{\mathrm{QDP}} & =\widehat{\mathrm{QDI}}+\widehat{\mathrm{IDP}} \\
|
| 297 |
+
& =\widehat{\mathrm{FDI}}+\widehat{\mathrm{IDE}} \\
|
| 298 |
+
& =\widehat{\mathrm{FCI}}+\widehat{\mathrm{IBE}} \text { par angle inscrit } \\
|
| 299 |
+
& =\widehat{\mathrm{ICB}}+\widehat{\mathrm{CBI}} \text { par bissectrices } \\
|
| 300 |
+
& =180^{\circ}-\widehat{\mathrm{BIC}} \\
|
| 301 |
+
& =180^{\circ}-\widehat{\mathrm{PIQ}}
|
| 302 |
+
\end{aligned}
|
| 303 |
+
$$
|
| 304 |
+
|
| 305 |
+
Donc $\widehat{\mathrm{PIQ}}+\widehat{\mathrm{QPD}}=180^{\circ}$, d'où le fait que PIDQ est cyclique.
|
| 306 |
+
Lemme 3 : Les droites (PQ) et (AI) sont perpendiculaires.
|
| 307 |
+
Preuve : En effet $\widehat{\mathrm{QPI}}=\widehat{\mathrm{QDI}}=\widehat{\mathrm{FDI}}=\widehat{\mathrm{FCI}}=\frac{1}{2} \widehat{\mathrm{ACB}}$ par angle inscrit. De plus :
|
| 308 |
+
|
| 309 |
+
$$
|
| 310 |
+
\begin{aligned}
|
| 311 |
+
\widehat{\mathrm{AIB}} & =180^{\circ}-\widehat{\mathrm{IBA}}-\widehat{\mathrm{BAI}} \\
|
| 312 |
+
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{\mathrm{BAC}}}{2} \\
|
| 313 |
+
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{ACB}}}{2} \\
|
| 314 |
+
& =90^{\circ}+\frac{1}{2} \widehat{\mathrm{ABC}} .
|
| 315 |
+
\end{aligned}
|
| 316 |
+
$$
|
| 317 |
+
|
| 318 |
+
On en déduit que ( AI ) et (PQ) sont bien perpendiculaires.
|
| 319 |
+
|
| 320 |
+
- Lemme 4: La quadrilatère AEIF est cyclique.
|
| 321 |
+
|
| 322 |
+
Preuve : En effet BDIE et CFID sont cycliques, donc d'après le théorème de Miquel, AEIF l'est aussi.
|
| 323 |
+
|
| 324 |
+
- Lemme 5: Les droites (MF) et (EN) sont perpendiculaires à (AI).
|
| 325 |
+
|
| 326 |
+
Preuve : D'abord $\widehat{\mathrm{IEM}}=\widehat{\mathrm{IEA}}=180^{\circ}-\widehat{\mathrm{AFI}}=\widehat{\mathrm{IFN}}$ par angle inscrit. De plus $\mathrm{IE}=\mathrm{IM}=\mathrm{IF}=\mathrm{IN}$ (par le lemme 1), donc IEM et IFN sont deux triangles isocèles en I avec même angle de base : d'où IEM semblable à IFN. Mais comme IE = IF : ils sont même isométriques. On en déduit que $E M=F N$. Comme EMFN est cyclique, c'est un trapèze isocèle. On en déduit que (MF) et (EN) sont parallèles, toutes les deux perpendiculaires à (AI) (car I est le centre du cercle circonscrit et $A$ l'intersection des côtés, donc (AI) est axe de symétrie du trapèze isocèle).
|
| 327 |
+
|
| 328 |
+
- Finalement, (EN), (FM), (PQ) sont toutes les trois perpendiculaires à (AI), elle sont donc parallèles.
|
| 329 |
+
|
| 330 |
+
Commentaire des correcteurs : L'exercice n'a pas été beaucoup traité, mais la quasi totalité des élèves qui l'ont traité l'ont résolu. On notera qu'il y avait plusieurs configurations possibles dans la figure(ordre des points $E, M$ et $F, N$ sur les droites $(A B)$ et ( $A C)$. , bien qu'il ne soit pas demandé de traiter toutes les configurations. Attention à ne pas s'emmêler les pinceaux des les utilisations des théorèmes des angles inscrits, notamment dans le cas des angles supplémentaires.
|
| 331 |
+
|
| 332 |
+
## Exercices Seniors
|
| 333 |
+
|
| 334 |
+
Exercice 10. Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
| 335 |
+
Solution de l'exercice 10
|
| 336 |
+
|
| 337 |
+
|
| 338 |
+
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a :
|
| 339 |
+
|
| 340 |
+
$$
|
| 341 |
+
\begin{aligned}
|
| 342 |
+
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
|
| 343 |
+
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
|
| 344 |
+
& =\widehat{A C O}+\widehat{O B A} .
|
| 345 |
+
\end{aligned}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{O A C}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{C B A}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
|
| 349 |
+
|
| 350 |
+
Commentaire des correcteurs : L'exercice a éte globalement tres bien reussi !
|
| 351 |
+
|
| 352 |
+
Exercice 11. Soient $A B C$ un triangle, $O$ le centre de son cercle circonscrit. On suppose que $\widehat{C B A}=60^{\circ}$ et $\widehat{\mathrm{CBO}}=45^{\circ}$. Soit D le point d'intersection des droites $(\mathrm{AC})$ et $(B O)$. Montrer que $\mathrm{AD}=\mathrm{DO}$.
|
| 353 |
+
|
| 354 |
+
## Solution de l'exercice 11
|
| 355 |
+
|
| 356 |
+
|
| 357 |
+
|
| 358 |
+
Pour montrer que $A D=D O$ (c'est-à-dire que $A D O$ est isocèle en D ), nous allons montrer que $\widehat{\mathrm{DOA}}=\widehat{\mathrm{OAD}}$. Introduisons $P$ le point d'intersection (autre que $B$ ) de (BO) avec le cercle circonscrit de $A B C$.
|
| 359 |
+
|
| 360 |
+
D'une part, $\widehat{\mathrm{DOA}}=\widehat{\mathrm{POA}}=2 \widehat{\mathrm{PBA}}=2\left(60^{\circ}-45^{\circ}\right)=30^{\circ}$ d'après le théorème de l'angle au centre.
|
| 361 |
+
D'autre part, $\mathrm{OC}=\mathrm{OA}$ donc $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OAC}}=\widehat{\mathrm{ACO}}=\frac{180^{\circ}-\widehat{\mathrm{COA}}}{2}$. Or d'après le théorème de l'angle au centre, $\widehat{C O A}=2 \widehat{C B A}=120^{\circ}$. D'où $\widehat{O A D}=30^{\circ}$.
|
| 362 |
+
|
| 363 |
+
Finalement, $\widehat{D O A}=30^{\circ}=\widehat{\mathrm{OAD}}$, donc on a bien montré que $\mathrm{AD}=\mathrm{DO}$.
|
| 364 |
+
Commentaire des correcteurs: L'exercice à été vraiment très bien réussi par tous ceux qui l'ont abordé. Cependant, pour des exercices dont la solution tient sur quelques lignes, il vaut mieux bien justifier sa chasse aux angle, ce qui peut éviter des erreurs de calculs/ de recopiage. De plus, pas mal de copies auraient pu être raccourcies, les élèves faisant des détours conséquents dans leurs calculs.
|
| 365 |
+
|
| 366 |
+
Exercice 12. Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de B par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
| 367 |
+
|
| 368 |
+
## Solution de l'exercice 12
|
| 369 |
+
|
| 370 |
+
|
| 371 |
+
|
| 372 |
+
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}^{\prime} \mathrm{C}}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $\mathrm{C}, \mathrm{B}, \mathrm{D}, \mathrm{E}, \mathrm{B}^{\prime}$ sont cocycliques.
|
| 373 |
+
Alors on a :
|
| 374 |
+
|
| 375 |
+
$$
|
| 376 |
+
\begin{aligned}
|
| 377 |
+
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
|
| 378 |
+
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
|
| 379 |
+
\end{aligned}
|
| 380 |
+
$$
|
| 381 |
+
|
| 382 |
+
De plus:
|
| 383 |
+
|
| 384 |
+
$$
|
| 385 |
+
\begin{aligned}
|
| 386 |
+
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
|
| 387 |
+
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
|
| 388 |
+
\end{aligned}
|
| 389 |
+
$$
|
| 390 |
+
|
| 391 |
+
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
| 392 |
+
Solution alternative $n^{\circ} 1$
|
| 393 |
+
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
|
| 394 |
+
|
| 395 |
+
$$
|
| 396 |
+
\begin{aligned}
|
| 397 |
+
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
|
| 398 |
+
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
|
| 399 |
+
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
|
| 400 |
+
\end{aligned}
|
| 401 |
+
$$
|
| 402 |
+
|
| 403 |
+
Commentaire des correcteurs : L'exercice a été très bien réussi, certaines chasses aux angles auraient pu être évitées ou raccourcies en utilisant la cocyclicité des points ou le théorème du Pôle Sud.
|
| 404 |
+
|
| 405 |
+
Exercice 13. Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
| 406 |
+
|
| 407 |
+
## Solution de l'exercice 13
|
| 408 |
+
|
| 409 |
+
|
| 410 |
+
|
| 411 |
+
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
|
| 412 |
+
|
| 413 |
+
$$
|
| 414 |
+
\begin{aligned}
|
| 415 |
+
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
|
| 416 |
+
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
|
| 417 |
+
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
|
| 418 |
+
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
|
| 419 |
+
& =180^{\circ}-\widehat{\mathrm{BED}} \\
|
| 420 |
+
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
|
| 421 |
+
\end{aligned}
|
| 422 |
+
$$
|
| 423 |
+
|
| 424 |
+
Ainsi on a montré que $\widehat{Q C P}+\widehat{P E Q}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
|
| 425 |
+
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
|
| 426 |
+
|
| 427 |
+
$$
|
| 428 |
+
\begin{aligned}
|
| 429 |
+
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
|
| 430 |
+
& =\widehat{\mathrm{ECA}} \\
|
| 431 |
+
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
|
| 432 |
+
\end{aligned}
|
| 433 |
+
$$
|
| 434 |
+
|
| 435 |
+
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
|
| 436 |
+
Commentaire des correcteurs : L'exercice a été dans l'ensemble très bien traité. La plupart des solutions qui ont abouti consistaient à prouver EQCP cyclique et à conclure par chasse aux angles. D'autres ont trouvé des solutions avec des outils plus avancés, notamment certains ont utilisé des similitudes,
|
| 437 |
+
d'autres ont vu qu'on pouvait appliquer le théorème de Pascal dans l'hexagone dégénéré $A D E B B C$, d'autres encore ont utilisé des inversions. Il est cependant à noter qu'un bon nombre d'élèves font beaucoup de détours peu utiles dans leurs calculs, faisant parfois en 2 pages ce qui se prouve en 2 lignes : si avoir une solution qui fonctionne est évidemment un très bonne chose, il est encore mieux d'avoir une solution qui fonctionne et qui est efficace. Il n'était par exemple pas nécessaire ici d'introduire des points intermédiaires, tous les points utiles étaient définis dans l'énoncé. On notera aussi que si la grande majorité des copies rendent une figure, certains ne le font pas : rendre une figure propre est indispensable pour illustrer son raisonnement dans un problème de géométrie.
|
| 438 |
+
|
| 439 |
+
Exercice 14. Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à $(B C)$ et $(A C)$ respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|
| 440 |
+
|
| 441 |
+
## Solution de l'exercice 14
|
| 442 |
+
|
| 443 |
+
|
| 444 |
+
|
| 445 |
+
Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
|
| 446 |
+
|
| 447 |
+
Soit $M$ le symétrique de H par rapport à ( BC ) : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
|
| 448 |
+
|
| 449 |
+
$$
|
| 450 |
+
\begin{aligned}
|
| 451 |
+
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
|
| 452 |
+
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
|
| 453 |
+
\end{aligned}
|
| 454 |
+
$$
|
| 455 |
+
|
| 456 |
+
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
|
| 457 |
+
Commentaire des correcteurs : L'exercice a été globalement bien réussi par ceux qui l'ont essayé. Le fait que les symétriques de H sont sur le cercle circonscrit à $A B C$ est un lemme souvent utile, qu'il est bon d'avoir en tête, et qu'il n'y a pas besoin de reprouver à chaque fois qu'on en a besoin (dire "il est connu que" est suffisant).
|
| 458 |
+
|
| 459 |
+
Exercice 15. Soit $A B C D$ un quadrilatère convexe cyclique, $M$ le milieu de $[A C]$. Le cercle circonscrit à $C D M$ rencontre $(B C)$ une deuxième fois en $N$ (autre que $C$ ). Soit $B^{\prime}$ le symétrique de $B$ par rapport à $N$. Montrer que (MN) est tangente au cercle circonscrit de $B^{\prime} D N$.
|
| 460 |
+
|
| 461 |
+
## Solution de l'exercice 15
|
| 462 |
+
|
| 463 |
+
|
| 464 |
+
|
| 465 |
+
Sur la figure, on repère des triangles semblables. En effet, on a par angle inscrit :
|
| 466 |
+
|
| 467 |
+
$$
|
| 468 |
+
\widehat{M A D}=\widehat{C A D}=\widehat{C B D}=\widehat{N B D}
|
| 469 |
+
$$
|
| 470 |
+
|
| 471 |
+
Toujours par angle inscrit, on a :
|
| 472 |
+
|
| 473 |
+
$$
|
| 474 |
+
\widehat{\mathrm{DMA}}=180^{\circ}-\widehat{\mathrm{CMD}}=180^{\circ}-\widehat{\mathrm{CND}}=\widehat{\mathrm{DNB}}
|
| 475 |
+
$$
|
| 476 |
+
|
| 477 |
+
On en déduit que les triangles $A M D$ et BND sont semblables. Mais alors $A D C$ et $\mathrm{BDB}^{\prime}$ sont semblables. En effet on a $\widehat{B^{\prime} B D}=\widehat{C B D}$, et $\frac{B B^{\prime}}{A C}=\frac{2 B N}{2 A M}=\frac{B N}{A M}=\frac{B D}{A D}$, et donc ADC est semblable à $\mathrm{BDB}^{\prime}$. Il suit que :
|
| 478 |
+
|
| 479 |
+
$$
|
| 480 |
+
\begin{aligned}
|
| 481 |
+
\widehat{M N D} & =\widehat{M C D} \text { par angle inscrit } \\
|
| 482 |
+
& =\widehat{A C D} \\
|
| 483 |
+
& =\widehat{\mathrm{BB}^{\prime} \mathrm{D}} \text { car } \mathrm{ADC} \sim \mathrm{BDB}^{\prime} \\
|
| 484 |
+
& =\widehat{\mathrm{DB}^{\prime} \mathrm{D}}
|
| 485 |
+
\end{aligned}
|
| 486 |
+
$$
|
| 487 |
+
|
| 488 |
+
Donc par réciproque de l'angle tangentiel, (MN) est tangente au cercle circonscrit à $\mathrm{B}^{\prime} \mathrm{DN}$, ce qu'on voulait montrer.
|
| 489 |
+
Commentaire des correcteurs: L'exercice pouvait se résoudre avec des outils élémentaires (repérer des triangles sembables grâce aux égalités d'angles, déduire d'autres paires de triangles semblables, récupérer l'égalité d'angles voulue), mais pouvait également être raconté en adoptant le point de vue des similitudes, qui donne plusieurs raccourcis dans les étapes précédemment citées. Cette deuxième approche a été celle choisie par la plupart des élèves ayant répondu au problème, et a rencontré beaucoup de succès dans les résultats obtenus, mais un peu moins de succès dans la consistance de la démarche : introduire la similitude de centre D est superflu si on a déjà montré par chasse aux angles que $\triangle \mathrm{DAM} \sim$ $\triangle \mathrm{DBN}$.
|
| 490 |
+
|
| 491 |
+
Exercice 16. Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$ et soit $\Gamma$ son cercle circonscrit. Soient H l'orthocentre de $A B C$ et $S$ le milieu de l'arc $\widehat{B C}$ ne contenant pas $A$. Soit $P$ le point de $\Gamma$ tel que $\widehat{S P H}=90^{\circ}$. Montrer qu'il existe un cercle passant par $P, S$ et qui est tangent à ( $A B$ ) et ( $A C$ ).
|
| 492 |
+
|
| 493 |
+
## Solution de l'exercice 16
|
| 494 |
+
|
| 495 |
+
|
| 496 |
+
|
| 497 |
+
D'après le théorème du pôle Sud, $S$ est le point de concours de la bissectrice de $\widehat{B A C}$ et de la médiatrice de $[B C]$. Soit $O$ le centre de $\Gamma$ et $N$ le pôle Nord. Comme $[S N]$ est un diamètre de $\Gamma$, la condition $\widehat{S P H}=90^{\circ}$ se réécrit $P, H, N$ alignés. Introduisons alors $Q$ le point d'intersection de (AS) et (PN).
|
| 498 |
+
|
| 499 |
+
Remarquons que comme $\widehat{S P Q}=90^{\circ}, \mathrm{P}, \mathrm{S}$ se situent sur le cercle de diamètre [QS], c'est donc un candidat pour être le cercle recherché. On aimerait montrer qu'il est tangent à ( $A B$ ) et à ( $A C$ ). Posons $M$ le milieu de $[Q S]$ et $R$ le projeté orthogonal de $M$ sur $[A C]$. Le but est de montrer que $R$ est sur le cercle de diamètre $[Q S]$, de sorte à avoir la tangence avec (AC) (et pour des raisons de symétrie on aura la tangence avec (AB)).
|
| 500 |
+
|
| 501 |
+
Soit D le milieu de $[B C]$. On sait que (HD) et $(A O)$ se coupent sur $\Gamma$, et que $(A H) / /(O M)$ (les deux sont perpendiculaires à ( $B C$ ), donc par droite des milieux $A H=2 O D$. Or par angle au centre, $\widehat{S O C}=60^{\circ}$ donc SOC est équilatéral $(\mathrm{OS}=\mathrm{OC})$, et donc $2 \mathrm{OD}=\mathrm{OS}=\mathrm{OC}=\mathrm{ON}$. De plus, comme $(A H) / /(N S)$, d'après le théorème de Thalès, $\frac{A Q}{S Q}=\frac{A H}{N S}=\frac{1}{2}$ donc $Q S=2 A Q$.
|
| 502 |
+
En particulier $M Q=M S=\frac{Q S}{2}=A Q$. Or $\widehat{M A R}=30^{\circ}$ donc $M R=\frac{1}{2} A M=M Q$ (en effet $\sin \left(30^{\circ}\right)=\frac{1}{2}$ ), donc R est bien sur le cercle de diamètre [QS], donc ce dernier est tangent à (AC) (en R).
|
| 503 |
+
Donc il existe bien un cercle passant par $P, S$ et qui est tangent à $(A B)$ et $(A C)$ : le cercle de diamètre [QS].
|
| 504 |
+
Commentaire des correcteurs : L'exercice était très bien réussi par ceux qui l'ont rendu, la connaissance de la droite d'Euler ou l'utilisation astucieuse du théroème du pole sud pouvait raccoucir certaines
|
| 505 |
+
preuves.
|
| 506 |
+
|
| 507 |
+
Exercice 17. Soient $A B C$ un triangle et $O$ le centre de son cercle circonscrit. Soit d la parallèle à (BC) passant par $O$. Soit $A^{\prime}$ le symétrique de $A$ par rapport à ( $B C$ ). La parallèle à ( $A^{\prime} B$ ) passant par $C$ coupe d en $C_{1}$, et les droites $\left(A^{\prime} C\right)$ et $\left(B C_{1}\right)$ s'intersectent en $C_{2}$. La parallèle à ( $A^{\prime} C$ ) passant par $B$ coupe $d$ en $B_{1}$, et les droites $\left(A^{\prime} B\right)$ et $\left(C B_{1}\right)$ s'intersectent en $B_{2}$. Montrer que les points $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques.
|
| 508 |
+
|
| 509 |
+
## Solution de l'exercice 17
|
| 510 |
+
|
| 511 |
+
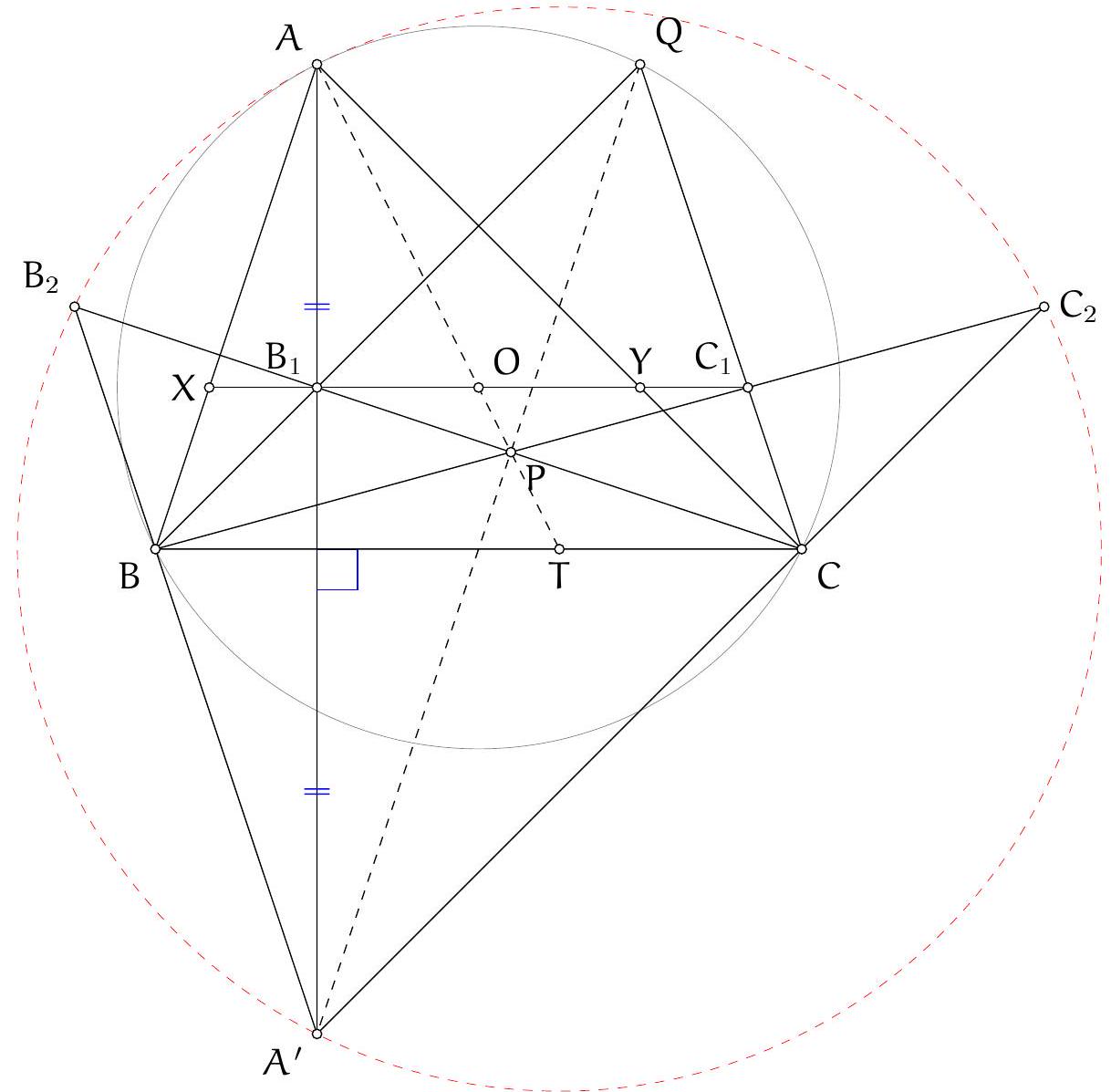
|
| 512 |
+
|
| 513 |
+
On pose $P$ le point d'intersection des droites $\left(C B_{1}\right)$ et $\left(B C_{1}\right)$, et $Q$ le point d'intersection de $\left(B B_{1}\right)$ et $\left(C C_{1}\right)$. On pose également Tl'intersection de $(A O)$ et ( $\left.B C\right)$. On peut alors remarquer plusieurs propriétés sur la figure, qu'on va montrer.
|
| 514 |
+
|
| 515 |
+
- Lemme 1: Le point $Q$ est sur le cercle circonscrit à $A B C$.
|
| 516 |
+
|
| 517 |
+
Preuve : Par construction de $\mathrm{B}_{1}, \mathrm{C}_{1}, \mathrm{~A}^{\prime} \mathrm{BQC}$ est un parallélogramme, donc $\widehat{\mathrm{BQC}}=\widehat{\mathrm{CA}^{\prime} \mathrm{B}}$. Mais par symétrie, $\widehat{C A^{\prime} B}=\widehat{B A C}$. Donc $\widehat{B A C}=\widehat{B_{Q C}}$ : par angle inscrit, $Q$ est bien sur le cercle circonscrit à $A B C$.
|
| 518 |
+
|
| 519 |
+
- Lemme 2: Les points $P, Q, A^{\prime}$ sont alignés.
|
| 520 |
+
|
| 521 |
+
Preuve : Le quadrilatère $\mathrm{BCC}_{1} \mathrm{~B}_{1}$ est un trapèze, donc la droite (PQ) passe par les milieux respectifs de $\left[B_{1} C_{1}\right]$ et $[B C]$. Donc la droite (PQ) passe par le milieu de $[B C]$. Or $A^{\prime} B Q C$ est un parallélogramme, donc $\left(Q A^{\prime}\right)$ passe également par le milieu de $[B C]$. On en déduit bien que $Q, P, A^{\prime}$ sont alignés.
|
| 522 |
+
|
| 523 |
+
- Lemme 3: Les points O, P, T sont alignés.
|
| 524 |
+
|
| 525 |
+
Preuve : Considérons la symétrie par rapport à la médiatrice de $[\mathrm{BC}]$ : elle fixe O , elle échange B et $C$. Elle échange également $A$ et $Q$, en effet $\widehat{Q_{C B}}=\widehat{A^{\prime} B C}=\widehat{C B A}$ par parallélisme et symétrie puis
|
| 526 |
+
$\widehat{C B Q}=\widehat{A C B}$. On pose à présent $X$ l'intersection de $(A B)$ avec $d$, et $Y$ l'intersection de $(A C)$ avec $d$. Alors comme $d$ est invariante par la symétrie, la symétrie échange $B_{1}$ et $Y, C_{1}$ et $X$. On en déduit que $\frac{\mathrm{OB}_{1}}{\mathrm{OC}_{1}}=\frac{\mathrm{OY}}{\mathrm{OX}}$. Or en appliquant le théorème de Thalès, on obtient $\frac{\mathrm{OY}}{\mathrm{OX}}=\frac{\mathrm{TC}}{\mathrm{TB}}$, d'où $\frac{\mathrm{TC}}{\mathrm{TB}}=\frac{\mathrm{OB}_{1}}{O C_{1}}$. Ceci entraîne $O, P, T$ alignés (en appliquant Thalès dans $\mathrm{OC}_{1} \mathrm{PBT}^{\prime}$ et dans $\mathrm{OB}_{1} \mathrm{BCT}^{\prime}$ où $\mathrm{T}^{\prime}$ est l'intersection de $(O P)$ et $(B C)$, on obtient $\frac{T B}{T C}=\frac{T^{\prime} B}{T^{\prime} C}$, d'où $T=T^{\prime}$ ). On a donc bien montré que $O, P, T$ (et donc $A, O, P, T)$ sont alignés.
|
| 527 |
+
|
| 528 |
+
- Lemme 4 : L'homothétie de centre P et de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$ envoie $\mathrm{QBC} \operatorname{sur} \mathrm{A}^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$.
|
| 529 |
+
|
| 530 |
+
Preuve: D'après le théorème de Thalès dans $\mathrm{QCPB}_{2} A^{\prime}$ et dans $\mathrm{QBPC}_{2} \mathrm{~A}^{\prime}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}}{\mathrm{PB}_{2}}=\frac{\mathrm{PB}}{\mathrm{PC}_{2}}$, donc l'homothétie de centre $P$ qui envoie $Q$ sur $A^{\prime}$ envoie également $B$ sur $C_{2}$ et $C$ sur $B_{2}$. Il reste à montrer qu'elle envoie O sur T . Or, d'après le théorème de Thalès dans $\mathrm{QC}_{1} \mathrm{PBA}^{\prime}$ puis dans $\mathrm{OC}_{1} \mathrm{PBT}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}_{1}}{\mathrm{~PB}}=\frac{\mathrm{PO}}{\mathrm{PT}}$, donc c'est bien l'homothétie de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$.
|
| 531 |
+
|
| 532 |
+
- On a à présent tous les éléments pour conclure : l'homothétie du lemme 4 envoie QBC sur $A^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$ et O sur T. Or par le lemme 1, O est le centre du cercle circonscrit de QBC. Donc T est le centre du cercle circonscrit de $A^{\prime} C_{2} B_{2}$. Mais comme $T$ est sur $(B C)$, on a $T A=T A^{\prime}$ donc $A$ est sur le cercle de centre $T$ et de rayon $T A^{\prime}$. Finalement, on a bien montré que $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques, et on a même trouvé le centre du cercle en question, qui est $T$.
|
| 533 |
+
Commentaire des correcteurs : Le problème est bien résolu par un bon nombre d'élèves. Les rédactions montrent une très bonne maitrise de la notion d'homothétie, qui permet de raconter l'exercice de façon parfois très efficace, avec le mérite de dévoiler les rôles des différents points, là où d'autres élèves ont proposé des approches plus terre-à-terre (des calculs de rapport) ou plus abstraites (solution en dynamique).
|
| 534 |
+
|
| 535 |
+
Exercice 18. Soient $A B C$ un triangle, avec $A C>A B$, et $\Gamma$ son cercle circonscrit. Soit $T$ le point d'intersection de la tangente à $\Gamma$ en $A$ avec (BC). Soient $M$ le milieu de $[B C]$ et $R$ le symétrique de $A$ par rapport à $B$. Soit $S$ le point tel que $S A B T$ est un parallélogramme. La parallèle à ( $A B$ ) passant par $M$ coupe (SB) en $P$. On suppose que $P$ est sur $\Gamma$, montrer que ( $A C$ ) est tangente au cercle circonscrit à SRT.
|
| 536 |
+
|
| 537 |
+
## Solution de l'exercice 18
|
| 538 |
+
|
| 539 |
+
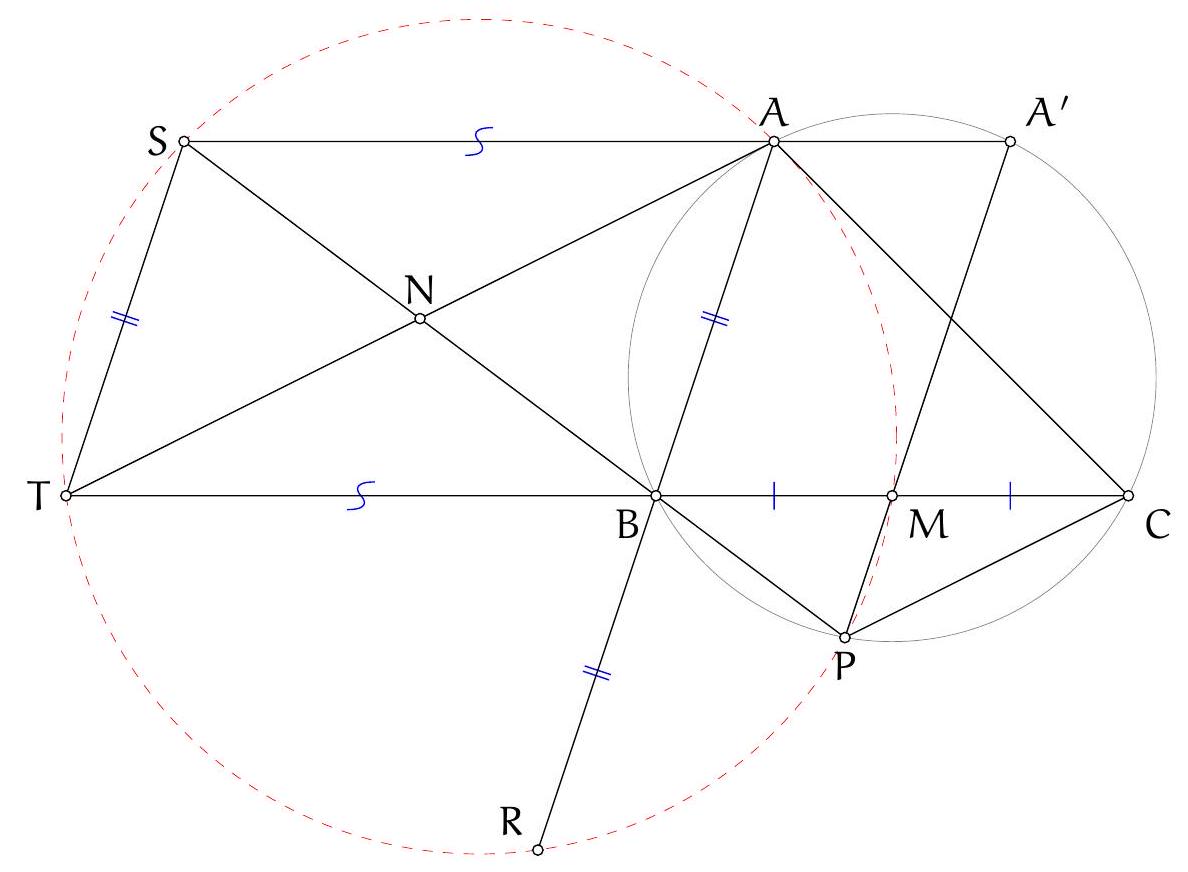
|
| 540 |
+
|
| 541 |
+
Soit $N$ le point d'intersection de $(A T)$ et ( $B S)$. On a $(P M) / /(A B) / /(S T)$ donc d'après le théorème de Thalès, $\frac{B P}{B S}=\frac{B M}{B T}$. Alors $\frac{B P}{B N}=\frac{B P}{\frac{B S}{2}}=2 \frac{B P}{B S}=\frac{2 B M}{B T}=\frac{B C}{B T}$, donc d'après la réciproque du théorème de Thalès, (NT) et (PC) sont parallèles. On a alors :
|
| 542 |
+
|
| 543 |
+
$$
|
| 544 |
+
\begin{aligned}
|
| 545 |
+
\widehat{S A^{\prime} P} & =\widehat{A A^{\prime} P} \\
|
| 546 |
+
& =\widehat{A C P} \text { par angle inscrit } \\
|
| 547 |
+
& =\widehat{A C B}+\widehat{B C P} \\
|
| 548 |
+
& =\widehat{\mathrm{TAB}}+\widehat{B T A} \text { par angle tangentiel et angles alternes-internes } \\
|
| 549 |
+
& =\widehat{\mathrm{CBA}} \\
|
| 550 |
+
& =\widehat{\mathrm{SAB}} \text { par angles alternes-internes. }
|
| 551 |
+
\end{aligned}
|
| 552 |
+
$$
|
| 553 |
+
|
| 554 |
+
Donc par angle correspondant, $(A B)$ et ( $A^{\prime} P$ ) sont parallèles. Or $(A B)$ et (MP) sont parallèles. Il découle que $P, M, A^{\prime}$ sont alignés.
|
| 555 |
+
On en déduit donc que $B T=B S, B M=B P$. En effet :
|
| 556 |
+
|
| 557 |
+
$$
|
| 558 |
+
\begin{aligned}
|
| 559 |
+
\widehat{\mathrm{TSB}} & =\widehat{\mathrm{BPA}^{\prime}} \text { par angle alterne-interne } \\
|
| 560 |
+
& =\widehat{\mathrm{AA}^{\prime} \mathrm{P}} \text { car } A A^{\prime} \mathrm{PB} \text { trapèze isocèle } \\
|
| 561 |
+
& =\widehat{\mathrm{CMA}^{\prime}} \text { par angle alterne-interne } \\
|
| 562 |
+
& =\widehat{\mathrm{BTS}^{2}} \text { par angle correspondants. }
|
| 563 |
+
\end{aligned}
|
| 564 |
+
$$
|
| 565 |
+
|
| 566 |
+
Donc $B T=B S$, et comme $(S T) / /(P M)$, alors $B P=B M$ de même.
|
| 567 |
+
Notamment STRA est un trapèze isocèle donc cyclique donc $A$ est sur (SRT). De plus, $\widehat{N A B}=\widehat{A C B}$ par angle tangentiel, et $\widehat{A B N}=\widehat{\mathrm{BST}}=\widehat{\mathrm{STB}}=\widehat{\mathrm{CBA}}$ par angle alterne-interne et correspondant. Donc $B A N \sim B C A$. En particulier $\widehat{B N A}=\widehat{B A C}$, donc par réciproque de l'angle tangentiel, (AC) est tangente à (ANB).
|
| 568 |
+
|
| 569 |
+
Or une homothétie de centre $A$ et de facteur 2 envoie N sur T , B sur R, fixe $A$ donc envoie ( $A N B$ ) sur le cercle $(A T R)=(S R T)$, et elle fixe $(A C)$. Donc $(S R T)$ est bien tangent à (AC) (les homothéties préservent les tangences), ce qui conclut.
|
| 570 |
+
|
| 571 |
+
Remarque. La condition "On suppose que $P$ est sur $\Gamma^{\prime \prime}$ est difficile à tracer. En fait, comme $(A B)$ est parallèle à $\left(A^{\prime} M\right)$ et $\left(A A^{\prime}\right)$ parallèle à $(B C), A A^{\prime} M B$ est un parallélogramme donc $A M=A^{\prime} M=A B$. Ainsi $A B M$ est isocèle en $A$. Cela signifie que le projeté de $A$ sur $[B C]$ est le milieu de $[B M]$, donc que l'abscisse de $A$ sur $[B C]$ est au quart du segment (en partant de $B$ ), et réciproquement une telle position de $A$ entraîne que $P$ est sur $\Gamma$. C'est donc la condition qui nous permet de tracer la figure.
|
| 572 |
+
|
| 573 |
+
Remarque. On peut montrer que $P$ et $M$ se situent aussi sur le cercle circonscrit à SRT, en utilisant que TSAM est un trapèze isocèle, puis que AMPR est un trapèze isocèle.
|
| 574 |
+
|
| 575 |
+
Commentaire des correcteurs : L'exercice était difficile, et a été traité avec des méthodes très différentes (barycentrique, homothétie, points harmoniques,...). Les solutions rendues étaient quasiment toutes complètes.
|
| 576 |
+
|
French_STS/md/fr-Corrige-envoi-5-2023-2024.md
ADDED
|
@@ -0,0 +1,396 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> Envoi 5 : Pot Pourri <br> À RENVOYER AU PLUS TARD LE 19 AVRIL 2024
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2009 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $\mathcal{A}$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $A^{\prime}$, I et $X$ sont alignés.
|
| 17 |
+
|
| 18 |
+
## Solution de l'exercice 1
|
| 19 |
+
|
| 20 |
+
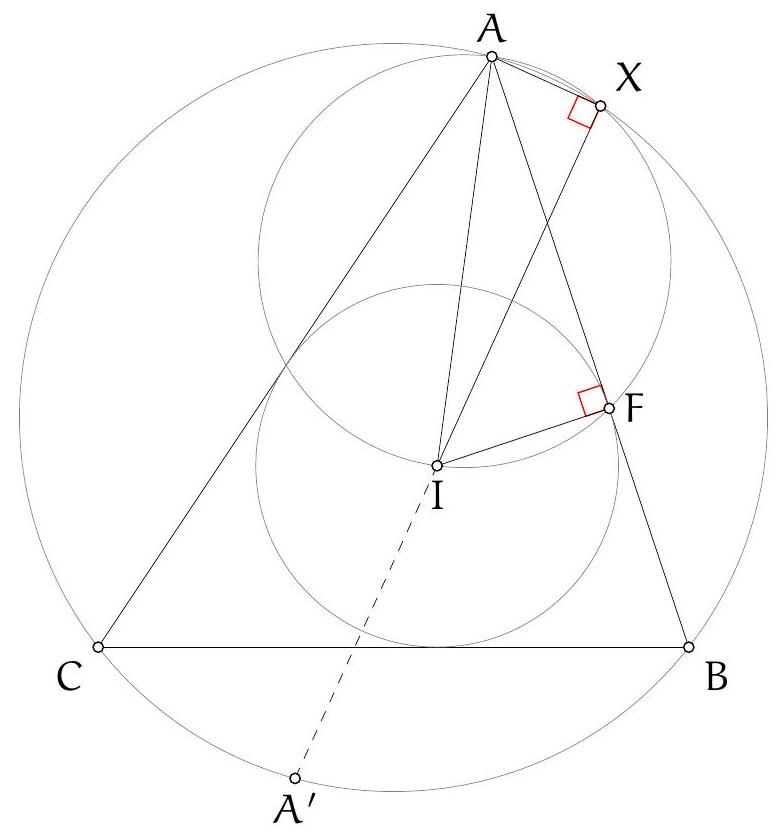
|
| 21 |
+
|
| 22 |
+
Puisque $F$ est le point de contact du cercle inscrit avec le côté $[A C$, l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
|
| 29 |
+
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
| 30 |
+
|
| 31 |
+
Exercice 2. $2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 n-1) \times(2 n-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
| 32 |
+
Solution de l'exercice 2 Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les n premières lignes, il doit y avoir n tours. Cependant, ces n tours doivent être dans les $\mathrm{n}-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde. Cela conclut.
|
| 33 |
+
|
| 34 |
+
Exercice 3. Déterminer tous les entiers N tels que $2^{\mathrm{N}}-2 \mathrm{~N}$ est un carré parfait.
|
| 35 |
+
Solution de l'exercice 3 Montrons que les solutions sont $\mathrm{N}=0,1$ ou 2.
|
| 36 |
+
On remarque déjà que $2^{0}-0=1^{2}, 2^{1}-2=0^{2}$ et $2^{2}-4=0^{2}$. Donc les entiers 0,1 et 2 sont solutions. Supposons par l'absurde qu'il existe N un autre entier solution. On dispose alors de $x \in \mathbb{N}$ tel que $2^{N}-2 \mathrm{~N}=x^{2}$. Puisque $2^{N}$ doit être entier, on doit avoir $N \geqslant 0$, et donc $N \geqslant 3$. En outre, $x$ est divisible par 2, donc $\chi^{2}$ est divisible par 4 . Puisque $N \geqslant 2,2^{N}$ est également divisible par 4 et donc $N$ est pair. On a
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
2 N=2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right)
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
En outre, on vérifie que $\mathrm{N}=4, \mathrm{~N}=6$ ou $\mathrm{N}=8$ ne sont pas des solutions car 8,52 et 240 ne sont pas des carrés parfaits. Donc $\mathrm{N} \geqslant 10$.
|
| 43 |
+
Enfin, puisque $2 \mathrm{~N}>0$, on doit avoir $2^{\frac{N}{2}}-x \geqslant 1$. Mais on montre par récurrence que $2^{\frac{N}{2}}>2 \mathrm{~N}$ pour tout $N$ pair $\geqslant 10$. En effet, $2^{5}=32>20$ et si $2^{\frac{N}{2}}>2 N$, avec $N$ pair $\geqslant 10$, alors
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
2^{\frac{N+2}{2}}=2 \cdot 2^{\frac{N}{2}}>4 \mathrm{~N}>2(\mathrm{~N}+2)
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Mais alors on a
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right) \geqslant 2^{\frac{N}{2}}+x>2 N
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
ce qui est absurde. Cela montre qu'il n'y a pas d'autre solution.
|
| 56 |
+
On a donc bien montré que les entiers solutions sont exactement 0,1 et 2 .
|
| 57 |
+
|
| 58 |
+
Exercice 4. Soient $a, b$ et $c$ des réels tels que $0 \leqslant a, b, c \leqslant 2$. Montrer que
|
| 59 |
+
|
| 60 |
+
$$
|
| 61 |
+
(a-b)(b-c)(a-c) \leqslant 2
|
| 62 |
+
$$
|
| 63 |
+
|
| 64 |
+
Solution de l'exercice 4 Notons qu'il y a 6 ordres possibles pour les variables $\mathrm{a}, \mathrm{b}$ et c .
|
| 65 |
+
Dans les trois cas $b \geqslant a \geqslant c, a \geqslant c \geqslant b$ et $c \geqslant b \geqslant a$, le produit $(a-b)(b-c)(c-a)$ est négatif, de sorte que l'inégalité est vérifiée.
|
| 66 |
+
Si $a \geqslant b \geqslant c$, l'inégalité des moyennes appliquée à $a-b$ et $b-c$ et le fait que $c-a \leqslant 2$ car $a, c \in[0,2]$ donne:
|
| 67 |
+
|
| 68 |
+
$$
|
| 69 |
+
(a-b)(b-c)(a-c) \leqslant\left(\frac{a-b+b-c}{2}\right)^{2}(a-c)=\frac{(a-c)^{3}}{4} \leqslant \frac{2^{3}}{4}=2
|
| 70 |
+
$$
|
| 71 |
+
|
| 72 |
+
De même, si $b \geqslant c \geqslant a$, alors
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
(a-b)(b-c)(a-c)=(b-a)(b-c)(c-a) \leqslant(b-a)\left(\frac{b-c+c-a}{2}\right)^{2} \leqslant \frac{(b-a)^{3}}{4} \leqslant 2
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Et enfin, si $c \geqslant a \geqslant b$, alors
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
(a-b)(b-c)(a-c)=(c-b)(c-a)(a-b) \leqslant(c-b)\left(\frac{c-a+a-b}{2}\right)^{2} \frac{(c-b)^{3}}{4} \leqslant 2
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Si bien que l'inégalité est vraie dans tous les cas.
|
| 85 |
+
|
| 86 |
+
Exercice 5. Déterminer tous les entiers $n$ ayant la propriété suivante : si l'on pose $a_{k}=\operatorname{ppcm}(k, k+$ $1, \ldots, k+n-1$ ), alors la suite ( $a_{k}$ ) est croissante.
|
| 87 |
+
Solution de l'exercice 5 Montrons que les naturels ayant cette propriété sont exactement 1 et 2 . Déjà, si $n=1, a_{k}=k$ est une suite croissante. Et si $n=2$, puisque deux entiers consécutifs sont premiers entre eux, $a_{k}=k(k+1)$ est une suite croissante également. Si $n=3$, on remarque que $a_{5}=210>a_{6}=168$, donc 3 n'a pas la propriété désirée.
|
| 88 |
+
|
| 89 |
+
Soit maintenant $n \geqslant 4$. L'idée pour montrer que $n$ ne vérifie pas la propriété est de trouver un $k$ tel que les $(k+i)_{0 \leqslant i \leqslant n-1}$ soient premiers entre eux, tandis que $k+1$ ait un grand facteur commun avec $k+n$, pour avoir $a_{k}>a_{k+1}$. C'est pourquoi on regarde $k=(n-1)!-1$.
|
| 90 |
+
Posons $\mathrm{D}=\operatorname{ppcm}(k+1, \ldots, k+n-1)$. On a alors $a_{k}=\operatorname{ppcm}(k, D)=k \cdot D$. En effet, pour $1 \leqslant i \leqslant n-1$, on a $\operatorname{pgcd}(k, k+i)=\operatorname{pgcd}(k, i)=1$ car $i \mid k+1=(n-1)!$.
|
| 91 |
+
En outre, $a_{k+1}=\operatorname{ppcm}(D, k+n)$. Or, $n-1$ divise à la fois $k+1$ (donc $\left.D\right)$ et $k+n$. Donc
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
a_{k+1} \leqslant D \cdot((n-2)!+1)<D \cdot((n-1)!-1)=a_{k}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
En effet, pour tout $n \geqslant 4,(n-1)!-(n-2)!=(n-2) \cdot(n-2)!\geqslant 4>2$, donc $(n-1)!-1>(n-2)!+1$.
|
| 98 |
+
|
| 99 |
+
Exercice 6. Démontrer, pour tous réels $\mathrm{a}, \mathrm{b}, \mathrm{c}$ strictement positifs, l'inégalité suivante :
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
\frac{a}{9 b c+1}+\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}} .
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
Solution de l'exercice 6 Vu la forme de l'inégalité, on est tenté d'appliquer l'inégalité des mauvais élèves. Seulement, si l'on applique l'inégalité en l'état, on trouve :
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
Pour conclure, il faudrait alors montrer que $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}$, mais cette inégalité n'est pas toujours vraie.
|
| 112 |
+
Pour faire apparaître $\mathrm{a}+\mathrm{b}+\mathrm{c}$ au numérateur du membre de droite de l'inégalité des mauvais élèves, on peut par exemple multiplier en haut et en bas par a dans la première fraction du membre de gauche (et de même avec b et c dans les deux autres fractions). Ceci donne, en appliquant l'inégalité des mauvais élèves:
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1}=\frac{a^{2}}{9 a b c+a}+\frac{b^{2}}{9 a b c+b} \frac{c^{2}}{9 a b c+c} \geqslant \frac{(a+b+c)^{2}}{27 a b c+a+b+c} .
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
Il suffit alors de montrer que
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
Pour cela, on peut appliquer l'inégalité des moyennes $27 \mathrm{abc} \leqslant(\mathrm{a}+\mathrm{b}+\mathrm{c})^{3}$ pour obtenir :
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{(a+b+c)^{2}}{(a+b+c)^{3}+(a+b+c)}=\frac{(a+b+c)}{(a+b+c)^{2}+1}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
comme voulu.
|
| 131 |
+
|
| 132 |
+
Exercice 7. Déterminer tous les entiers $x$ tels que $2^{x}+x^{2}+25$ est le cube d'un nombre premier.
|
| 133 |
+
|
| 134 |
+
## Solution de l'exercice 7 L'exercice va utiliser deux idées:
|
| 135 |
+
|
| 136 |
+
- Les modulos pour obtenir des informations sur $x$.
|
| 137 |
+
- Des encadrements comparant $2^{x}$ et $x^{2}$ afin de montrer que le membre de gauche est souvent strictement compris entre deux cubes consécutifs (et ne peut donc être un cube d'entier).
|
| 138 |
+
Soit $x$ un entier tel que $2^{x}+x^{2}+25$ est le cube d'un nombre premier $p$. Puisque $2^{x}=p^{3}-x^{2}-25$ est un entier, $x$ est positif. De plus $p^{3} \geqslant 25$ donc $p>2$ et $p$ est impair.
|
| 139 |
+
Si $x=0$, alors $2^{x}+x^{2}+25=26$ qui n'est pas un cube. Ainsi, $x \geqslant 1$. On déduit que $x^{2}+25$ est de la parité de $p^{3}$, c'est-à-dire impair. Ceci force $x$ à être pair. En particulier, $x \geqslant 2$ donc $p^{3}>27$ et $p>3$. Soit y l'entier tel que $x=2 y$. En regardant l'équation modulo 3 , on trouve
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
2^{2 y}+4 y^{2}+25 \equiv 1+y^{2}+25 \equiv 2+y^{2} \quad \bmod 3
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
Si y n'est pas divisible par 3 , son carré vaut 1 modulo 3 , ce qui implique que 3 divise $p$, ce qui est exclus. Ainsi, 3 divise $y$. Soit $z$ l'entier tel que $y=3 z$. L'équation devient
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
2^{6 z}+36 z^{2}+25=p^{3}
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
Si $z=1$, alors le membre de gauche vaut $125=5^{3}$. Ainsi, $x=6 \times 1$ est solution.
|
| 152 |
+
Montrons que si $z \geqslant 2$, on a $\left(2^{2 z}\right)^{3}<2^{6 z}+36 z^{2}+25<\left(2^{2 z}+1\right)^{3}$, ce qui montrera que le côté gauche ne peut être le cube d'un entier. L'inégalité de gauche est toujours vraie car $36 z^{2}+25>0$. Pour montrer l'inégalité de droite, il faut montrer que $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$.
|
| 153 |
+
D'une part, si $z \geqslant 2$, on a $3 \times 2^{2 z} \geqslant 3 \times 16>25$. D'autre part, on montre par récurrence sur $z$ que $2^{4 z}>12 z^{2}$.
|
| 154 |
+
Initialisation: $\operatorname{Si} z=2$, on a bien $2^{4 z}=256>48=12 z^{2}$.
|
| 155 |
+
Hérédité : On suppose que $2^{4 z}>12 z^{2}$ pour $z \geqslant 2$. Alors
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
2^{4(z+1)}=16 \times 2^{4 z}>16 \times 12 z^{2} \geqslant 12 \times 4 z^{2} \geqslant 12\left(z^{2}+2 z+1\right)=12(z+1)^{2}
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
où on a utilisé que $z^{2} \geqslant z$ et $z^{2} \geqslant 1$ pour $z \geqslant 2$. Ainsi, la propriété est vraie pour $z+1$, ce qui achève la récurrence.
|
| 162 |
+
On a donc bien $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$, ce qui implique que le membre de gauche $n$ 'est pas le cube d'un entier pour $z \geqslant 2$.
|
| 163 |
+
L'unique solution est donc $x=6$.
|
| 164 |
+
|
| 165 |
+
Exercice 8. Soit $A B C$ un triangle, $\omega$ son cercle inscrit et $D, E$ et $F$ les points de contact de $\omega$ avec les côtés $B C, C A$ et $A B$ respectivement. La perpendiculaire à ( $B C$ ) en $C$ coupe la droite ( $E F$ ) en $M$ et la perpendiculaire à (BC) en $B$ coupe la droite (EF) en $N$. La droite ( $D M)$ recoupe $\omega$ en $P$ et la droite $(\mathrm{DN})$ recoupe $\omega$ en Q . Montrer que $\mathrm{DP}=\mathrm{DQ}$.
|
| 166 |
+
|
| 167 |
+
## Solution de l'exercice 8
|
| 168 |
+
|
| 169 |
+
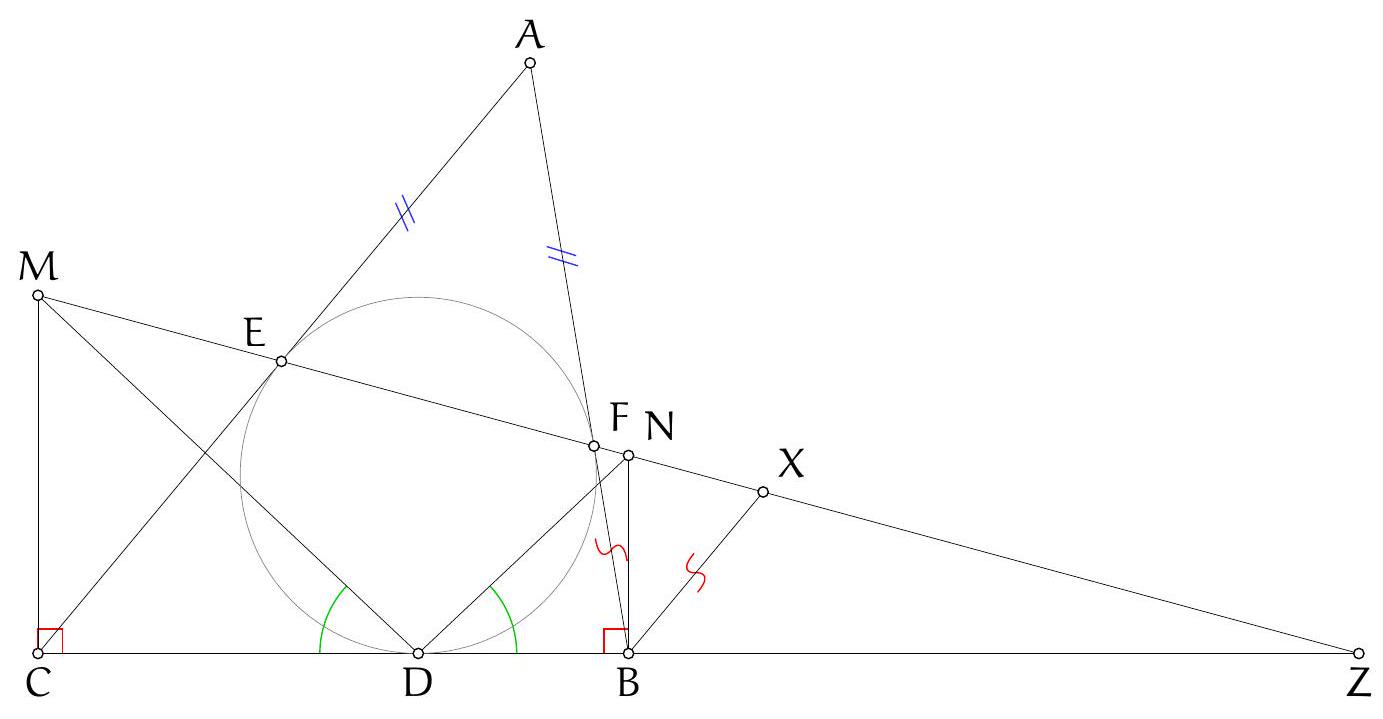
|
| 170 |
+
|
| 171 |
+
On commence par "éffacer" les points $P$ et $Q$ de la figure, c'est-à-dire qu'on commence par se ramener à un énoncé équivalent au problème original, mais qui n'implique pas les points P et Q .
|
| 172 |
+
Si l'énoncé est vrai, alors (DI) est la médiatrice du segment [PQ], de sorte que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$. Réciproquement, si on prouve que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$, les droites (DM) et (DN) seront alors symétriques par rapport à la droite (DI). Ainsi, puisque le cercle $\omega$ et ces droites sont symétriques par rapport à (DI), leurs intersections le sont aussi, et $P$ et Q seront symétriques par rapport à (DI) et $\mathrm{DP}=\mathrm{DQ}$. Il suffit donc de montrer que $\widehat{\mathrm{MDI}}=\widehat{\mathrm{NDI}}$ ou encore, puisque les droites (DI) et (BC) sont perpendiculaires, $\widehat{M D C}=\widehat{\mathrm{NDB}}$.
|
| 173 |
+
Cette égalité est en particulier vraie si les triangles MCD et NBD sont semblables. Comme ces deux triangles ont déjà un angle droit en commun, il suffit de montrer que $\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BN}}{\mathrm{CM}}$.
|
| 174 |
+
Soit $Z$ le point d'intersection des droites $(B C)$ et $(E F)$ et soit $X$ le point d'intersection de la parallèle à (AC) passant par B avec la droite (EF).
|
| 175 |
+
Les triangles $A E F$ et $F B X$ sont alors semblables, ainsi le triangle $F B X$ est isocèle en $B$. On a donc, en utilisant le théorème de Thalès pour les points $E, X, Z$ et $C, B, Z$ :
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
\frac{B D}{C D}=\frac{B F}{C E}=\frac{B X}{C E}=\frac{Z B}{Z C} .
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
En appliquant ensuite Thalès aux points $M, N, Z$ et $C, B, Z$, on trouve bien
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\frac{B D}{C D}=\frac{Z B}{Z C}=\frac{B N}{C M},
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
ce qui permet de conclure.
|
| 188 |
+
|
| 189 |
+
Exercice 9. On dispose de $\mathrm{a}+\mathrm{b}$ bols alignés sur une rangée. Les a premiers bols contiennent une pomme tandis que les $b$ derniers bols contiennent une poire.
|
| 190 |
+
Une opération consiste à déplacer une pomme du bol $i$ au bol $i+1$ et une poire du bol $j$ au bol $j-1$, où $i$ et $j$ sont deux entiers tels que $i-j$ est pair (Un bol peut contenir plusieurs fruits). On souhaite arriver à la situation finale où les $b$ premiers bols contiennent une poire et les $a$ derniers bols contiennent une pomme. Montrer que c'est possible si et seulement si ab est pair.
|
| 191 |
+
Solution de l'exercice 9 Commençons par montrer qu'il n'est pas possible d'y arriver lorsque a et b sont impairs tous les deux. Soit I la somme alternée des nombres de fruits dans les bols. Dans les positions initiales et finales décrites, on a alors $I=0$ car $a+b$ est pair. En outre, lors de chaque opération, I est augmenté de $\pm 2$ à cause de la condition $i-j$ pair.
|
| 192 |
+
Supposons par l'absurde qu'il soit possible de passer de la position intiale à la position finale décrite. Les pommes doivent passer des bols de numéros 1 à $a$ vers les bols de numéros $b+1$ à $a+b$, et au cours de chaque opération, une pomme augmente de un le numéro de son bol. Il faut donc
|
| 193 |
+
|
| 194 |
+
$$
|
| 195 |
+
\sum_{k=1}^{a}(b+k)-\sum_{k=1}^{a} k=a \cdot b
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
opérations pour passer de la position initiale à la position finale, avec ab impair par hypothèse. Ainsi, lorsque la position finale est atteinte, $\mathrm{I} \equiv 2 \mathrm{ab} \equiv 2(\bmod 4)$, ce qui est absurde car I est nul dans la position finale décrite.
|
| 199 |
+
|
| 200 |
+
Montrons maintenant par récurrence qu'il est possible de parvenir à la position finale lorsque a ou b est pair. Sans perte de généralité, nous traitons le cas où b est pair, l'autre cas s'obtenant directement par symétrie. Si $\mathrm{b}=0$, il n'y a rien à montrer. Supposons maintenant que la propriété soit vraie pour $\mathrm{b}=\mathrm{n}$ pair, et supposons $\mathrm{b}=\mathrm{n}+2$. Par hypothèse de récurrence, en ignorant les deux dernières poires, nous pouvons arriver en un nombre fini d'opérations à la situation où nous avons, dans l'ordre, n bols avec une poire, puis a bols avec une pomme, puis 2 bols avec une poire. Si nous faisons deux opérations, entre les bols de numéros $\mathfrak{i}=a+n$ et $\mathfrak{j}=a+n+2$, puis $\mathfrak{i}=\mathfrak{j}=a+n+1$, les trois derniers bols contiennent maintenant dans l'ordre : une poire puis une poire puis une pomme. On réitère ces opérations permettant d'échanger une pomme avec les deux poires qui suivent jusqu'à arriver à la situation finale désirée.
|
| 201 |
+
|
| 202 |
+
## Exercices Seniors
|
| 203 |
+
|
| 204 |
+
Exercice 10. Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $A$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $\mathcal{A}^{\prime}$, I et $X$ sont alignés.
|
| 205 |
+
Solution de l'exercice 10
|
| 206 |
+
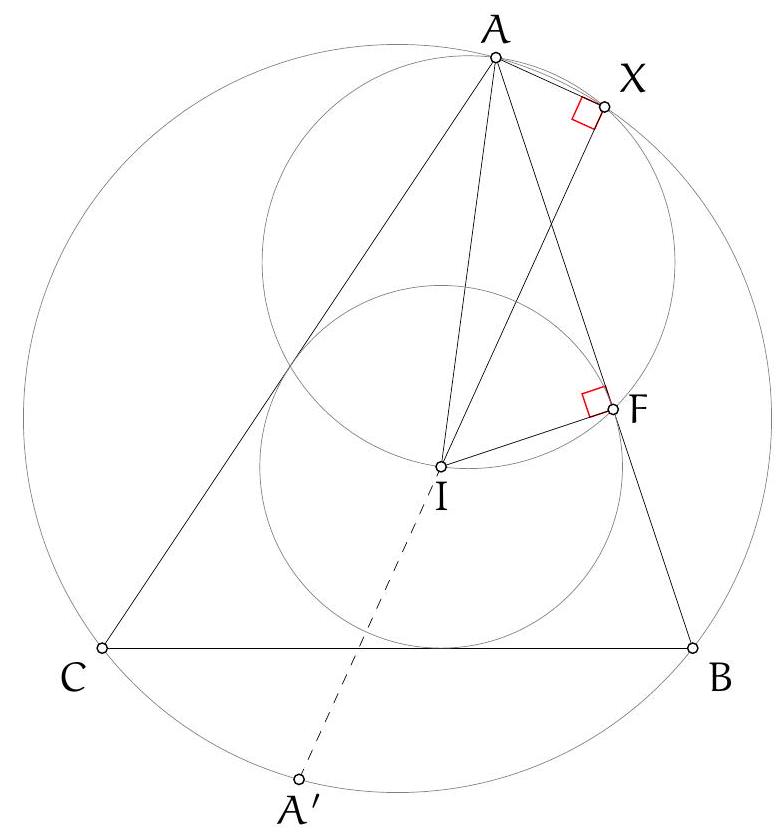
|
| 207 |
+
|
| 208 |
+
Puisque $F$ est le point de contact du cercle inscrit avec le côté [AC], l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
|
| 215 |
+
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
| 216 |
+
|
| 217 |
+
Exercice 11. $2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 \mathrm{n}-1) \times(2 \mathrm{n}-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
| 218 |
+
Solution de l'exercice 11 Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les $n$ premières lignes, il doit $y$ avoir $n$ tours. Cependant, ces $n$ tours doivent être dans les $n-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde.
|
| 219 |
+
|
| 220 |
+
## Exercice 12.
|
| 221 |
+
|
| 222 |
+
On définit la suite $\left(a_{n}\right)$ par $a_{0}=a_{1}=a_{2}=1$ et si $n \geqslant 3$ :
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
a_{n}=\left\lfloor\frac{n}{a_{n-1} a_{n-2} a_{n-3}}\right\rfloor
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
Déterminer $\mathrm{a}_{2022}$.
|
| 229 |
+
Solution de l'exercice 12 En calculant les premiers termes de la suite, on effectue la conjecture suivante, que l'on montre par récurrence sur $k$ :
|
| 230 |
+
|
| 231 |
+
$$
|
| 232 |
+
\text { Si } k \geqslant 1 \text {, alors } a_{4 k}=1, a_{4 k+1}=1, a_{4 k+2}=\left\lfloor\frac{4 k+2}{3}\right\rfloor \text { et } a_{4 k+3}=3 .
|
| 233 |
+
$$
|
| 234 |
+
|
| 235 |
+
Initialisation : On a $a_{3}=3, a_{4}=1, a_{5}=1, a_{6}=2$ et $a_{7}=3$, de sorte que la propriété est vérifiée pour $\mathrm{k}=1$.
|
| 236 |
+
Hérédité : Supposons la propriété vérifiée pour $k \geqslant 1$ fixée. Alors on a successivement :
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
a_{4(k+1)}=\left\lfloor\frac{4(k+1)}{a_{4 k+1} a_{4 k+2} a_{4 k+3}}\right\rfloor=\left\lfloor\frac{4(k+1)}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor,
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
or $\frac{4(\mathrm{k}+1)}{3}<2\left(\frac{4 \mathrm{k}+2}{3}-1\right)<2\left\lfloor\frac{4 \mathrm{k}+2}{3}\right\rfloor$ pour $k \geqslant 2$ et $\frac{8}{3}<2\left\lfloor\frac{4 \times 1+2}{3}\right\rfloor$, de sorte que $\mathrm{a}_{4(\mathrm{k}+1)}=1$.
|
| 243 |
+
|
| 244 |
+
$$
|
| 245 |
+
\mathbf{a}_{4(k+1)+1}=\left\lfloor\frac{4(k+1)+1}{a_{4 k+2} a_{4 k+3} a_{4(k+1)}}\right\rfloor=\left\lfloor\frac{4(k+1)+1}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
et là aussi, on a $\frac{4(k+1)}{3}<2\left\lfloor\frac{4 k+2}{3}\right\rfloor$, de sorte que $a_{4(k+1)+1}=1$.
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{a_{4 k+3} a_{4(k+1)} a_{4(k+1)+1}}\right\rfloor=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
donc $a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor$.
|
| 255 |
+
Enfin,
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
a_{4(k+1)+3}=\left\lfloor\frac{4(k+1)+3}{a_{4(k+1)} a_{4(k+1)+1} a_{4(k+1)+2}}\right\rfloor=\left\lfloor\frac{4(k+1)+3}{\lfloor(4(k+1)+2) / 3\rfloor}\right\rfloor .
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
Or on a bien
|
| 262 |
+
|
| 263 |
+
$$
|
| 264 |
+
4(k+1)+3 \geqslant 3\left(\frac{4(k+1)+2}{3}\right) \geqslant 3\lfloor(4(k+1)+2) / 3\rfloor
|
| 265 |
+
$$
|
| 266 |
+
|
| 267 |
+
et
|
| 268 |
+
|
| 269 |
+
$$
|
| 270 |
+
4(k+1)+3 \leqslant 4\left(\frac{4(k+1)+2}{3}-1\right)<4\lfloor(4(k+1)+2) / 3\rfloor
|
| 271 |
+
$$
|
| 272 |
+
|
| 273 |
+
pour $k \geqslant 1$, de sorte que $a_{4(k+1)+3}=3$. Ceci achève la récurrence.
|
| 274 |
+
Ainsi $\mathrm{a}_{2022}=\mathrm{a}_{4 \times 505+2}=\left\lfloor\frac{4 \times 505+2}{3}\right\rfloor=674$.
|
| 275 |
+
|
| 276 |
+
Exercice 13. Déterminer tous les entiers $n$ ayant la propriété suivante : si l'on pose $a_{k}=\operatorname{ppcm}(k, k+$ $1, \ldots, k+n-1)$, alors la suite ( $a_{k}$ ) est croissante.
|
| 277 |
+
Solution de l'exercice 13 Montrons que les naturels ayant cette propriété sont exactement 1 et 2 . Déjà, si $\mathrm{n}=1, \mathrm{a}_{\mathrm{k}}=\mathrm{k}$ est une suite croissante. Et si $\mathrm{n}=2$, puisque deux entiers consécutifs sont premiers entre eux, $a_{k}=k(k+1)$ est une suite croissante également. Si $n=3$, on remarque que $a_{5}=210>a_{6}=168$, donc 3 n'a pas la propriété désirée.
|
| 278 |
+
|
| 279 |
+
Soit maintenant $n \geqslant 4$. L'idée pour montrer que $n$ ne vérifie pas la propriété est de trouver un $k$ tel que les $(k+i)_{0 \leqslant i \leqslant n-1}$ soient premiers entre eux, tandis que $k+1$ ait un grand facteur commun avec $k+n$, pour avoir $a_{k}>a_{k+1}$. C'est pourquoi on regarde $k=(n-1)!-1$.
|
| 280 |
+
Posons $\mathrm{D}=\operatorname{ppcm}(k+1, \ldots, k+n-1)$. On a alors $a_{k}=\operatorname{ppcm}(k, D)=k \cdot D$. En effet, pour $1 \leqslant \mathfrak{i} \leqslant n-1$, on a $\operatorname{pgcd}(k, k+i)=\operatorname{pgcd}(k, \mathfrak{i})=1 \operatorname{car} \mathfrak{i} \mid k+1=(n-1)!$.
|
| 281 |
+
En outre, $a_{k+1}=\operatorname{ppcm}(D, k+n)$. Or, $n-1$ divise à la fois $k+1$ (donc $\left.D\right)$ et $k+n$. Donc
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
a_{k+1} \leqslant D \cdot((n-2)!+1)<D \cdot((n-1)!-1)=a_{k}
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
En effet, pour tout $n \geqslant 4,(n-1)!-(n-2)!=(n-2) \cdot(n-2)!\geqslant 4>2$, donc $(n-1)!-1>(n-2)!+1$.
|
| 288 |
+
|
| 289 |
+
Exercice 14. Soit $A B C$ un triangle et soit $J$ le centre de son cercle $A$-exinscrit. Soit K le symétrique du point $J$ par rapport au segment $[B C]$. Soient $E$ et $F$ les points sur les droites (BJ) et (CJ) tels que $\widehat{\mathrm{EAB}}=\widehat{\mathrm{CAF}}=90^{\circ}$. Montrer que $\widehat{\mathrm{FKE}}+\widehat{\mathrm{FJE}}=180^{\circ}$.
|
| 290 |
+
|
| 291 |
+
## Solution de l'exercice 14
|
| 292 |
+
|
| 293 |
+
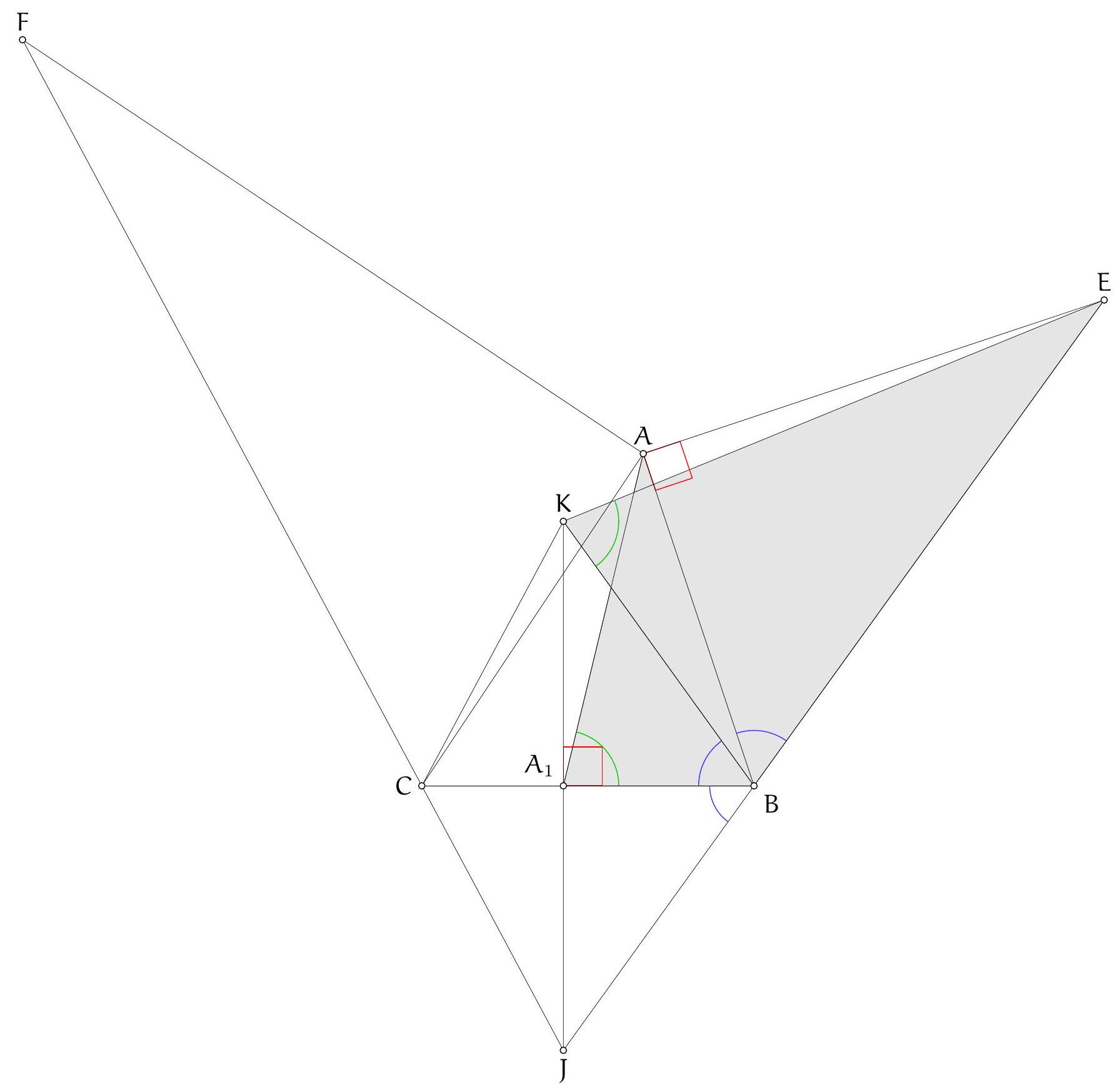
|
| 294 |
+
|
| 295 |
+
Puisque la droite (BJ) est la bissectrice extérieure de l'angle $\widehat{A B C}$, on a $\widehat{A B J}=\widehat{C B J}=90^{\circ}-\widehat{A B C} / 2$. Puisque la symétrie axiale préserve les angles, on a ainsi $\widehat{\mathrm{KBC}}=\widehat{\mathrm{ABE}}$.
|
| 296 |
+
Notons $A_{1}$ le projeté orthogonale du point $J$ sur le segment $[B C]$, de sorte que $A_{1}$ est également le milieu du segment $[J K]$. Les triangles $K A_{1} B$ et $B A E$ sont donc rectangles et ont un autre angle en commun, ils sont donc semblables. On a ainsi
|
| 297 |
+
|
| 298 |
+
$$
|
| 299 |
+
\frac{B K}{B E}=\frac{B A_{1}}{B A} .
|
| 300 |
+
$$
|
| 301 |
+
|
| 302 |
+
Cette égalité de rapport combinée avec l'égalité d'angle $\widehat{\mathrm{KBE}}=\widehat{\mathrm{ABE}}+\widehat{A B K}=\widehat{\mathrm{KBA}_{1}}+\widehat{A B K}=\widehat{\mathrm{ABA}_{1}}$ implique que les triangles $K B E$ et $A_{1} B A$ sont semblables (ce résultat peut également être formulé comme le fait que $B$ est le centre de la smilitude envoyant la paire $\left(A_{1}, K\right)$ sur la paire $(A, E)$ et donc aussi le centre de la similitude envoyant la paire $\left(A_{1}, \mathcal{A}\right)$ sur la paire $(K, E)$ ).
|
| 303 |
+
On déduit que $\widehat{\mathrm{BKE}}=\widehat{\mathrm{BA}_{1} A}$. De la même façon, $\widehat{\mathrm{CKF}}=\widehat{\mathrm{CA}_{1} A}$. On a alors, toujours puisque la symétrie préserve les angles:
|
| 304 |
+
|
| 305 |
+
$$
|
| 306 |
+
\widehat{\mathrm{EJF}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BJC}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BKC}}+\widehat{\mathrm{EKF}}=360^{\circ}-\widehat{\mathrm{BKE}}-\widehat{\mathrm{CKF}}=360^{\circ}-\widehat{\mathrm{BA} A_{1} A}-\widehat{\mathrm{CA} A_{1} \mathrm{~A}}=180^{\circ} .
|
| 307 |
+
$$
|
| 308 |
+
|
| 309 |
+
Exercice 15. Soit $a, b, c>0$ tels que $a^{2}<16 b c, b^{2}<16 a c$ et $c^{2}<16 a b$. Montrer que
|
| 310 |
+
|
| 311 |
+
$$
|
| 312 |
+
a^{2}+b^{2}+c^{2}<2(a b+b c+a c)
|
| 313 |
+
$$
|
| 314 |
+
|
| 315 |
+
$\underline{\text { Solution de l'exercice } 15}$ Remarquons tout d'abord que l'on a forcément $\sqrt{\mathrm{a}}<\sqrt{\mathrm{b}}+\sqrt{\mathrm{c}}$. En effet, dans le cas contraire, on aurait
|
| 316 |
+
|
| 317 |
+
$$
|
| 318 |
+
16 b c>a^{2}=\sqrt{a}^{4} \geqslant(\sqrt{b}+\sqrt{c})^{4} \geqslant 16 b c
|
| 319 |
+
$$
|
| 320 |
+
|
| 321 |
+
par IAG car $\sqrt{b}+\sqrt{c} \geqslant 2 \sqrt[4]{b c}$, absurde. Ainsi, $\sqrt{a}-\sqrt{b}<\sqrt{c}$. Mais par symétrie, on a aussi $\sqrt{b}-\sqrt{a}<\sqrt{c}$, et on a $\sqrt{c}<\sqrt{a}+\sqrt{b}$. Donc
|
| 322 |
+
|
| 323 |
+
$$
|
| 324 |
+
\begin{gathered}
|
| 325 |
+
|\sqrt{a}-\sqrt{b}|<\sqrt{c}<\sqrt{a}+\sqrt{b} \\
|
| 326 |
+
\Longrightarrow a+b-2 \sqrt{a b}<c<a+b+2 \sqrt{a b} \\
|
| 327 |
+
\Longrightarrow-2 \sqrt{a b}<c-a-b<2 \sqrt{a b} \\
|
| 328 |
+
\Longrightarrow(c-a-b)^{2}<4 a b \\
|
| 329 |
+
\Longrightarrow a^{2}+b^{2}+c^{2}<2(a b+b c+a c)
|
| 330 |
+
\end{gathered}
|
| 331 |
+
$$
|
| 332 |
+
|
| 333 |
+
Exercice 16. Avant un championnat, chaque équipe participante propose au plus $t$ couleurs différentes pour son maillot. Un ensemble $S$ d'équipes est dit identifiable si l'on peut assigner à chaque équipe de $S$ une couleur apparaissant dans son ensemble de propositions et n'apparaissant dans aucun ensemble de couleurs d'une autre équipe. Si l'on note n le nombre total de couleurs différentes proposées, déterminer le plus grand entier $\mathrm{g}(\mathrm{n}, \mathrm{t})$ tel que l'on puisse toujours trouver un ensemble d'équipes identifiable de taille au moins $\mathrm{g}(\mathrm{n}, \mathrm{t})$.
|
| 334 |
+
Solution de l'exercice 16 Montrons que le nombre recherché est $g(n, t)=\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$.
|
| 335 |
+
Si $n$ s'écrit sous la forme $k \cdot t+r$, avec $0 \leqslant r<t$, on peut considérer la situation où $k$ équipes demandent chacunes $t$ couleurs toutes distinctes deux à deux, puis une dernière équipe demandant $r$ nouvelles couleurs. Dans cette situation, il y a $\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$ équipes demandant au moins une couleur, donc cela montre déjà que $g(n, t) \leqslant\left\lceil\frac{n}{t}\right\rceil$.
|
| 336 |
+
Montrons maintenant avec une sorte d'algorithme glouton que $g(n, t) \geqslant\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$. On considère le graphe bipartite dont les sommets sont les équipes et les couleurs demandées, et où l'on relie chaque équipe à toutes ses couleurs demandées. Ainsi, le degré d'une équipe est par hypothèse inférieur ou égal à $t$, tandis que le degré d'une couleur est $>0$. Soit C la couleur de degré minimal $\mathrm{d}>0$ et soit $E$ une équipe reliée à C . On ajoute alors l'équipe E à notre ensemble identifiable $S$ en cours de construction, et on lui associe la couleur $C$. Ensuite, on supprime dans notre graphe toutes les équipes reliées à $C$ et on supprime également toutes les couleurs demandées par E. Ce faisant, si on ajoute une arête du graphe (c'est-à-dire une équipe et une couleur) à notre ensemble identifiable, il le restera car la nouvelle couleur n'aura été demandée par aucune équipe précédente, et la nouvelle équipe n'aura demandé aucune des couleurs précédentes. Il suffit maintenant de montrer que toutes les couleurs qui apparaissent encore dans notre graphe ont un degré $>0$. Puisqu'à chaque étape, on supprime au plus $t$ couleurs du graphe, cela permettra de conclure.
|
| 337 |
+
Supposons par l'absurde qu'il existe une couleur a apparaissant encore dans le graphe après l'ajout de E à l'ensemble identifiable, mais telle que son degré soit nul. Cela signifie que les $\mathrm{d}^{\prime}=\operatorname{deg}(\mathrm{a})$ équipes qui étaient reliées à a juste avant l'ajout de $E$ à $S$ avaient toutes demandé la couleur $C$. Or, puisque a est encore dans le graphe, cela signifie que $E$ n'avait pas demandé la couleur a. Cela montre que dans le graphe avant la suppression de $E, d=\operatorname{deg}(C) \geqslant d^{\prime}+1=\operatorname{deg}(a)+1$, ce qui contredit la minimalité du degré de C , et nous fournit la contradiction recherchéé.
|
| 338 |
+
|
| 339 |
+
Exercice 17. Montrer qu'il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 .
|
| 340 |
+
Solution de l'exercice 17 On montre un résultat un peu plus fort, qui se prête mieux à un raisonnement par récurrence : il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 , et tels que le premier et le dernier chiffre de l'écriture en base 4 de $n^{2}$ vaut 1 . Un premier exemple est le nombre $5^{2}=25=121_{4}$. Ensuite, on montre que si l'on a un tel n , on peut en construire un nouveau qui lui est strictement supérieur, ce qui montrera bien qu'il existe une infinité d'entiers ayant la propriété recherchée.
|
| 341 |
+
Soit donc n tel que l'écriture de $\mathrm{n}^{2}$ en base 4 ne contient que des 1 et des 2 , et commence et se termine par un 1 . On suppose que cette écriture contient $k$ chiffres. On pose alors $m=2^{2 k-1} \cdot n+n$. On a
|
| 342 |
+
|
| 343 |
+
$$
|
| 344 |
+
\mathrm{m}^{2}=4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}+4^{\mathrm{k}} \cdot \mathrm{n}^{2}+\mathrm{n}^{2}
|
| 345 |
+
$$
|
| 346 |
+
|
| 347 |
+
En base $4, m^{2}$ est donc constitué de trois copies de $n^{2}$, avec $n^{2}$ et $4^{k} \cdot n^{2}$ qui sont deux copies disjointes adjacentes, et $4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}$ et $4^{\mathrm{k}} \cdot \mathrm{n}^{2}$ qui ont exactement une puissance de 4 en commun dans leur écriture, à savoir $4^{2 k-1}$. Mais par hypothèse, les coefficients devant 1 et devant $4^{k-1}$ de $n^{2}$ sont des 1 , donc le coefficient devant $4^{2 \mathrm{k}-1}$ de $\mathrm{m}^{2}$ est un 2 . En outre, tous les autres coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$ apparaissaient dans celle de $\mathrm{n}^{2}$, et sont donc bien des 1 ou des 2 . Enfin, les premiers et derniers coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$, à savoir les coefficients devant $4^{0}$ et $4^{3 \mathrm{k}-2}$, sont bien des 1 par hypothèse de récurrence.
|
| 348 |
+
|
| 349 |
+
Exercice 18. Soit $A B C$ un triangle et soient $A_{1}, B_{1}$ et $C_{1}$ les points de contact resepctifs du cercle $A$-exinscrit, noté $\omega_{A}$, avec le côté $B C$ et les demi-droites $[A C)$ et $[A B$ ). Soit $P$ le milieu du segment $\left[B_{1} C_{1}\right]$. La droite $\left(A_{1} P\right)$ recoupe le cercle $\omega_{A}$ au point $X$. La tangente au cercle circonscrit au triangle $A B C$ au point $A$ et la tangente au cercle $\omega_{A}$ au point $X$ se coupent en $R$. Montrer que $R X=R P$.
|
| 350 |
+
|
| 351 |
+
## Solution de l'exercice 18
|
| 352 |
+
|
| 353 |
+
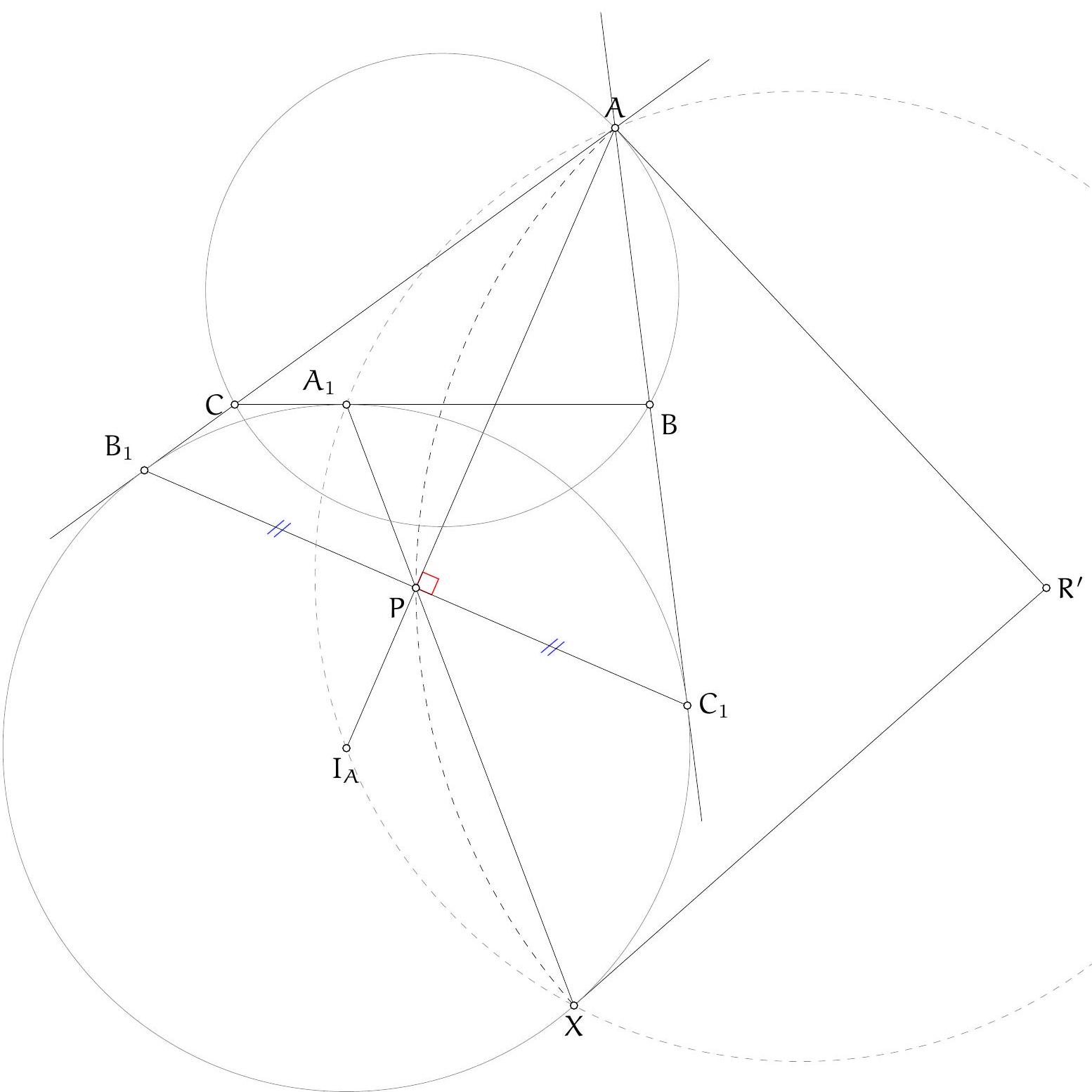
|
| 354 |
+
|
| 355 |
+
En traçant le cercle de centre $R$ de rayon $R A$, on s'aperçoit que celui-ci passe également par $P$. On va donc plutôt introduire $R^{\prime}$ le centre du cercle circonscrit au triangle $A P X$ et montre que les droites $\left(A R^{\prime}\right)$ et ( $X R^{\prime}$ ) sont respectivement tangentes aux cercles circonscrits au triangle $A B C$ et au triangle $A_{1} B_{1} C_{1}$.
|
| 356 |
+
Pour cela, notons que puisque $P$ est le milieu du segment $\left[B_{1} C_{1}\right]$ dont la droite $\left(A I_{A}\right)$ est la médiatrice, les points $A, P$ et $I_{A}$ sont alignés. De plus, puisque $\widehat{I_{A} B_{1} A}=90^{\circ}=180^{\circ}-\widehat{I_{A} C_{1} A}$, les points $B_{1}, I_{A}, C_{1}$ et $A$ sont cocycliques. Par puissance d'un point, on a :
|
| 357 |
+
|
| 358 |
+
$$
|
| 359 |
+
\mathrm{PA} \times \mathrm{PI}_{\mathrm{A}}=\mathrm{PB}_{1} \times \mathrm{PC}_{1}=\mathrm{PA}_{1} \times \mathrm{PX}
|
| 360 |
+
$$
|
| 361 |
+
|
| 362 |
+
de sorte que les points $A_{1}, I_{A}, X$ et $A$ sont cocycliques par la réciproque de la puissance d'un point.
|
| 363 |
+
|
| 364 |
+
Montrons à présent que $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$. D'une part, d'après le théorème de l'angle au centre :
|
| 365 |
+
|
| 366 |
+
$$
|
| 367 |
+
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PXA}} .
|
| 368 |
+
$$
|
| 369 |
+
|
| 370 |
+
Mais en utilisant la cocyclicité des points $A_{1}, I_{A}, X$ et $A$, on a trouve
|
| 371 |
+
|
| 372 |
+
$$
|
| 373 |
+
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathcal{A}_{1} X A}=90^{\circ}-\widehat{\mathcal{A}_{1} \mathrm{I}_{\mathrm{A}} A} .
|
| 374 |
+
$$
|
| 375 |
+
|
| 376 |
+
Soit alors $D$ le pied de la bissectrice de l'angle $\widehat{B A C}$ et $S$ le pôle Sud su sommet $A$ dans $A B C$. $D$ et $S$ sont alignés avec $A$ et $I_{A}$. Alors
|
| 377 |
+
|
| 378 |
+
$$
|
| 379 |
+
90^{\circ}-\widehat{A_{1} I_{A} A}=\widehat{C D I_{A}}=180^{\circ}-\widehat{A B C}-\frac{1}{2} \widehat{B A C}=\widehat{A B C}+\frac{1}{2} \widehat{A C B}=\widehat{A C P}
|
| 380 |
+
$$
|
| 381 |
+
|
| 382 |
+
Ainsi, $\widehat{P_{A R}}{ }^{\prime}=\widehat{A C P}$, donc la droite $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$.
|
| 383 |
+
Montrons que la droite ( $R^{\prime} X$ ) est tangente au cercle circonscrit au triangle $A_{1} B_{1} C_{1}$. On a là aussi par angle au centre :
|
| 384 |
+
|
| 385 |
+
$$
|
| 386 |
+
\widehat{A_{1} X R^{\prime}}=\widehat{\mathrm{PXR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PAX}}=90^{\circ}-\widehat{\mathrm{I}_{A} A X}
|
| 387 |
+
$$
|
| 388 |
+
|
| 389 |
+
Puis, par angle inscrit dans le cercle passant par $A, A_{1}, I_{A}$ et $X$, et en utilisant que le triangle $I_{A} \mathcal{A}_{1} X$ est isocèle en $\mathrm{I}_{\mathrm{A}}$, on a
|
| 390 |
+
|
| 391 |
+
$$
|
| 392 |
+
90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} A X}=90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} \mathrm{~A}_{1} X}=\frac{1}{2} \widehat{\mathrm{~A}_{1} \mathrm{I}_{A} X}=\widehat{\mathrm{A}_{1} \mathrm{~B}_{1} X}
|
| 393 |
+
$$
|
| 394 |
+
|
| 395 |
+
où l'on a utilisé le théorème de l'angle au centre dans le cercle $\omega_{A}$. Ainsi, la droite ( $\left.R^{\prime} X\right)$ est tangente à $\omega_{A}$ et $R=R^{\prime}$, ce qui conclut.
|
| 396 |
+
|
French_STS/md/fr-Corrige-envoi-algebre-2023-2024.md
ADDED
|
@@ -0,0 +1,722 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOI 2 : AlgèBre <br> À RENVOYER AU PLUS TARD LE 6 JANVIER 2024
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2009 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soient $x$ et $y$ deux réels positifs. Montrer que
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\left(x^{2}+x+1\right)\left(y^{2}+y+1\right) \geqslant 9 x y .
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Quels sont les cas d'égalité?
|
| 23 |
+
Solution de l'exercice 1 On applique l'inégalité arithmético-géométrique pour avoir
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
\begin{gathered}
|
| 27 |
+
x^{2}+x+1 \geqslant 3 \sqrt[3]{x^{3}}=3 x \\
|
| 28 |
+
y^{2}+y+1 \geqslant 3 \sqrt[3]{y^{3}}=3 y
|
| 29 |
+
\end{gathered}
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
En multipliant ces deux inégalités, qui sont à termes positifs, on obtient l'inégalité de l'énoncé. Comme $x^{2}+x+1$ et $y^{2}+y+1$ sont strictement positifs, on a égalité lorsque l'on a égalité dans les deux inégalités arithmético-géométriques. Mais ceci arrive lorsque $x^{2}=x=1$ et $y^{2}=y=1$, et on a donc égalité pour $x=y=1$.
|
| 33 |
+
|
| 34 |
+
Commentaire des correcteurs: De manière générale, l'exercice a été très bien résolu. Plusieurs personnes oublient de faire le cas d'égalité.
|
| 35 |
+
|
| 36 |
+
Exercice 2. Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
| 37 |
+
Solution de l'exercice 2 On réécrit l'égalité
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{gathered}
|
| 41 |
+
2 a-2 b=b^{2}-a^{2} \\
|
| 42 |
+
2(a-b)=-(a+b)(a-b)
|
| 43 |
+
\end{gathered}
|
| 44 |
+
$$
|
| 45 |
+
|
| 46 |
+
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
2=-a-b
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
d'où
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\mathrm{b}=-2-\mathrm{a}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
et $b$ est encore un entier.
|
| 59 |
+
Commentaire des correcteurs: Exercice bien traité dans l'ensemble, avec quelques erreurs de raisonnement. Presque tous les élèves ont évité le piège $a+1=-(b+1)$.
|
| 60 |
+
|
| 61 |
+
Exercice 3. Montrer qu'il n'existe pas de réels $x, y, z$ strictement positifs tels que
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right)=26 x^{2} y^{2} z^{2}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Solution de l'exercice 3 On pourrait essayer de simplement appliquer l'inégalité arithmético-géométrique sur chacun des facteurs du côté gauche, mais ceci donne que le terme de gauche est supérieur ou égal à $16 \sqrt{2} x^{2} y^{2} z^{2}$ ce qui ne suffit pas pour conclure (car $16 \sqrt{2}<26$ ). En fait, ceci vient du fait que l'on ne peut pas avoir égalité dans les trois inégalités arithmético-géométriques à la fois. On aimerait bien que le cas $x=y=z$ soit un cas d'égalité des inégalités arithmético-géométrique que l'on applique.
|
| 68 |
+
Prenons par exemple le premier terme $2 x^{2}+y z$. On le sépare en $x^{2}+x^{2}+y z$ (de façon à ce que chacun des termes soit égaux si $x=y=z$ ), on peut alors appliquer l'inégalité arithmético-géométrique :
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
2 x^{2}+y z \geqslant 3 \sqrt[3]{x^{2} \cdot x^{2} \cdot y z}=3 \sqrt[3]{x^{4} y z}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
En appliquant l'inégalité arithmético-géométrique sur tous les termes qui sont positifs, on a
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right) \geqslant 27 \sqrt[3]{x^{4} y z \cdot y^{4} x z \cdot z^{4} y z}=27 \sqrt[3]{x^{6} y^{6} z^{6}}=27 x^{2} y^{2} z^{2}
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
ce qui est strictement supérieur à $26 x^{2} y^{2} z^{2}$, on ne peut donc pas avoir égalité.
|
| 81 |
+
Commentaire des correcteurs: Exercice réussi dans l'ensemble. Bonnes utilsations de l'IAG, sauf quelques erreurs de raisonnement.
|
| 82 |
+
|
| 83 |
+
Exercice 4. Montrer que pour tous les réels $x, y, z$, on a
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leqslant 0 .
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Solution de l'exercice 4 On réécrit l'inégalité en
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\frac{x^{2}}{2 x^{2}+1}+\frac{y^{2}}{2 y^{2}+1}+\frac{z^{2}}{2 z^{2}+1} \leqslant \frac{y^{2}}{2 x^{2}+1}+\frac{z^{2}}{2 y^{2}+1}+\frac{x^{2}}{2 z^{2}+1} .
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
L'inégalité n'étant pas symétrique, on ne peut pas supposer sans perte de généralité que $x^{2} \leqslant y^{2} \leqslant$ $z^{2}$. Cependant, remarquons que les suites $\left(x^{2}, y^{2}, z^{2}\right)$ et $\left(\frac{1}{2 x^{2}+1}, \frac{1}{2 y^{2}+1}, \frac{1}{2 z^{2}+1}\right)$ sont rangées dans l'ordre inverse (le plus grand de la première suite correspond au plus petit de la deuxième suite par exemple). On peut donc appliquer l'inégalité de réordonnement qui implique directement l'inégalité de l'énoncé.
|
| 96 |
+
|
| 97 |
+
Commentaire des correcteurs: Les élèves ayant abordé le problème l'ont plutôt bien réussi. Ils ont proposé trois types de solutions. Certains passent par l'inégalité de réarrangement (aussi appelée inégalité du tourniquet), à l'instar du corrigé. L'erreur la plus fréquente est alors de dire que l'inégalité est symétrique, ce qui n'est manifestement pas le cas, et de supposer un ordre. Dans le cadre de l'inégalité de réarrangement ceci n'est pas dramatique, mais ce type d'imprécisions reste dangereux : quelques élèves, en supposant illégalement un ordre commode, se sont dispensés d'utiliser l'inégalité de réarrangement, et leur raisonnement est tout à fait erroné. D'autres utilisent directement et efficacement l'inégalité arithméticogéométrique après avoir un peu transformé le problème. Une regrettable moitié enfin, se débarasse des fractions, développe, puis utilise l'IAG termes à termes. Rappelons que cette stratégie est hasardeuse car une faute de calcul rend complètement invalide la solution, et que les problèmes un peu plus durs (comme le problème 6) sont difficiles à résoudre ainsi.
|
| 98 |
+
|
| 99 |
+
Exercice 5. Soit $n \geqslant 2$ et $a_{1}, \ldots, a_{n} \in[0,1]$ des réels. Déterminer la valeur maximale que peut prendre le plus petit des nombres
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
a_{1}-a_{1} a_{2}, a_{2}-a_{2} a_{3}, \ldots, a_{n}-a_{n} a_{1}
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
Solution de l'exercice 5 Soit $i$ tel que $a_{i}$ soit minimal. Alors on a $a_{i+1} \geqslant a_{i}$ (où $a_{n+1}=a_{1}$ ) et donc par inégalité arithmético-géométrique sur $a_{i}$ et $1-a_{i}$, on obtient
|
| 106 |
+
|
| 107 |
+
$$
|
| 108 |
+
a_{i}-a_{i} a_{i+1} \leqslant a_{i}-a_{i}^{2}=a_{i}\left(1-a_{i}\right) \leqslant \frac{1}{4}\left(a_{i}+1-a_{i}\right)^{2}=\frac{1}{4}
|
| 109 |
+
$$
|
| 110 |
+
|
| 111 |
+
donc le minimum des nombres vaut au plus $\frac{1}{4}$. Il reste à vérifier que l'on peut trouver des $a_{i}$ tel que le minimum soit égal à $\frac{1}{4}$. Si tous les $a_{i}$ valent $\frac{1}{2}$, alors tous les $a_{i}-a_{i} a_{i+1}$ valent $\frac{1}{4}$ et le minimum vaut bien $\frac{1}{4}$.
|
| 112 |
+
|
| 113 |
+
Commentaire des correcteurs : Le problème est bien réussi dans l'ensemble. Il contenait deux étapes: prouver que l'expresison est toujours plus petite que 0.25 et donner un exemple en lequel cette borne est atteinte. Quelques élèves oublient l'une ou l'autre de ces deux étapes et perdent alors de précieux points.
|
| 114 |
+
|
| 115 |
+
## Exercice 6.
|
| 116 |
+
|
| 117 |
+
Soient $a, b, c$ trois réels strictement positifs. Montrer que
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Solution de l'exercice 6 On commence par appliquer l'inégalité arithmético-géométrique aux trois termes de l'énoncé :
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \sqrt[3]{\frac{\left(a^{4}+1\right)\left(b^{4}+1\right)\left(c^{4}+1\right)}{\left(b^{3}+b^{2}+b\right)\left(c^{3}+c^{2}+c\right)\left(a^{3}+a^{2}+a\right)}}
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
On cherche donc à minorer les quotients $\frac{a^{4}+1}{a^{3}+a^{2}+a}$. Pour cela, on applique des inégalités arithméticogéométriques :
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
\begin{aligned}
|
| 133 |
+
a^{3}+a^{2}+a & \leqslant \frac{1}{2}\left(a^{4}+a^{2}\right)+a^{2}+\frac{1}{2}\left(a^{2}+1\right)=\frac{1}{2}\left(a^{4}+1\right)+2 a^{2} \\
|
| 134 |
+
& \leqslant \frac{1}{2}\left(a^{4}+1\right)+\left(a^{4}+1\right)=\frac{3}{2}\left(a^{4}+1\right)
|
| 135 |
+
\end{aligned}
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
et ainsi $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$. On a de même pour $b$ et $c$, et donc
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
\frac{\mathrm{a}^{4}+1}{\mathrm{~b}^{3}+\mathrm{b}^{2}+\mathrm{b}}+\frac{\mathrm{b}^{4}+1}{\mathrm{c}^{3}+\mathrm{c}^{2}+\mathrm{c}}+\frac{\mathrm{c}^{4}+1}{\mathrm{a}^{3}+\mathrm{a}^{2}+\mathrm{a}} \geqslant 3 \sqrt[3]{\left(\frac{2}{3}\right)^{3}}=2
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
## Solution alternative :
|
| 145 |
+
|
| 146 |
+
On peut également réfléchir avec l'inégalité de réarrangement. L'inégalité n'est pas symétrique, on ne peut donc pas supposer sans perte de généralités $a \geqslant b \geqslant c$ ou quelque chose de similaire.
|
| 147 |
+
Cependant, par stricte croissance, $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ est dans le même ordre que $(a, b, c)$. De même, $\left(a^{3}+a^{2}+a, b^{3}+b^{2}+b, c^{3}+c^{2}+c\right)$ est également dans le même ordre et $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$ est dans le sens inverse. Ainsi, par inégalité de réarrangement,
|
| 148 |
+
|
| 149 |
+
$$
|
| 150 |
+
\frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
est la valeur minimale que peut prendre une somme de produit de termes de $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ avec des termes de $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$. En particulier ici :
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
On peut maintenant comme précédemment montrer $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$ et conclure par
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \cdot \frac{2}{3}=2
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Commentaire des correcteurs : Le problème est très bien réussi. Cependant, beaucoup d'élèves croient qu'on peut supposer $a \geqslant b \geqslant c$ car 'l'inégalité est symétrique". Or l'inégalité n'est pas symétrique : si on change b et c l'inégalité est drastiquement changée. Heureusement qu'ici par chance, le raisonnement était rectifiable facilement (cf la solution 2 du corrigé). Cependant, les quelques copies qui ont tout multiplié et développé n'ont pas réussi, témoignant encore une fois du fait que réfléchir avant de tout développer hasardeusement est toujours une bonne idée.
|
| 166 |
+
|
| 167 |
+
Exercice 7. Soient $a, b, c, d$ quatre réels tels que $|a|>1,|b|>1,|c|>1$ et $|d|>1$. Supposons que $(a+1)(b+1)(c+1)(d+1)=(a-1)(b-1)(c-1)(d-1)$. Montrer que
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1}>0
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
$\underline{\text { Solution de l'exercice } 7}$ On sait d'après l'énoncé que aucun des $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ ne vaut 1 . La condition de l'énoncé s'écrit alors
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
\frac{a+1}{a-1} \frac{b+1}{b-1} \frac{c+1}{c-1} \frac{d+1}{d-1}=1
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
Remarquons que comme $|a|>1$, alors on a soit $a>1$ et donc $a+1>0$ et $a-1>0$, ou alors $a<-1$ et donc $a+1<0$ et $a-1<0$. Ainsi, dans tous les cas $\frac{a+1}{a-1}$ est positif, et de même pour $b, c, d$. On peut donc appliquer l'inégalité arithmético-géométrique sur le produit précédent pour avoir
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\frac{\mathrm{a}+1}{\mathrm{a}-1}+\frac{\mathrm{b}+1}{\mathrm{~b}-1}+\frac{\mathrm{c}+1}{\mathrm{c}-1}+\frac{\mathrm{d}+1}{\mathrm{~d}-1} \geqslant 4 \sqrt[4]{\frac{\mathrm{a}+1}{\mathrm{a}-1} \frac{\mathrm{~b}+1}{\mathrm{~b}-1} \frac{\mathrm{c}+1}{\mathrm{c}-1} \frac{\mathrm{~d}+1}{\mathrm{~d}-1}}=4
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
On réécrit ceci sous la forme
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
\left(1+\frac{2}{\mathrm{a}-1}\right)+\left(1+\frac{2}{\mathrm{~b}-1}\right)+\left(1+\frac{2}{\mathrm{c}-1}\right)+\left(1+\frac{2}{\mathrm{~d}-1}\right) \geqslant 4
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
et donc
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1} \geqslant 0
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Mais l'énoncé nous demande de montrer que l'inégalité est stricte, on s'intéresse donc au cas d'égalité dans l'inégalité arithmético-géométrique. On a égalité si et seulement si
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\frac{a+1}{a-1}=\frac{b+1}{b-1}=\frac{c+1}{c-1}=\frac{d+1}{d-1}
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
Comme le produit de ces quatre termes vaut 1 , nécessairement ces termes valent tous 1 ou tous -1 . Dans le premier cas, on a $a+1=a-1$ ce qui est impossible. Dans le deuxième cas, on a $a+1=1-a$ et donc $a=0$, ce qui est aussi impossible car $|a|>1$. Ainsi, on ne peut pas avoir égalité et l'inégalité est bien stricte comme dans l'énoncé.
|
| 204 |
+
|
| 205 |
+
Commentaire des correcteurs : Le problème est peu abordé. Certains se sont lancés dans des calculs compliqués, et étonnamment très peu ont réussi à faire fonctionner cela. En inégalité, il est crucial d'essayer de faire apparaître les hypothèses plutôt que de bourriner les calculs.
|
| 206 |
+
|
| 207 |
+
Exercice 8. Soit $\mathrm{n} \geqslant 1$ un entier et $\mathrm{x}_{1}, \ldots, \mathrm{x}_{\mathrm{n}}$ des réels positifs. Montrer que
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Quels sont les cas d'égalité?
|
| 214 |
+
Solution de l'exercice 8 L'astuce est d'appliquer une inégalité arithmético-géométrique au côté gauche de l'inégalité, mais avec des coefficients $\sqrt{n}$ et $\frac{1}{\sqrt{n}}$ :
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
\begin{aligned}
|
| 218 |
+
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots\right. & \left.+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right)=\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right) \frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}} \\
|
| 219 |
+
& \leqslant \frac{1}{4}\left(\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)+\frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}}\right)^{2}
|
| 220 |
+
\end{aligned}
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
Pour chaque $i$, le coefficient de $x_{i}$ est $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}}$. La fonction $t \mapsto t+\frac{1}{t}$ est décroissante pour $t<1$ et croissante pour $\mathrm{t}>1$. En effet, par exemple pour $1<x<y$, on a $x y>1$ et donc:
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
y-x>\frac{y-x}{x y}=\frac{1}{x}-\frac{1}{y}
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
Ainsi, le coefficient maximal est atteint en $i=1$ ou $i=n$. Dans chaque cas, on trouve un coefficient $\sqrt{n}+\frac{1}{\sqrt{n}}=\frac{n+1}{\sqrt{n}}$, et donc
|
| 230 |
+
|
| 231 |
+
$$
|
| 232 |
+
\begin{aligned}
|
| 233 |
+
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{1}{4}\left(\frac{n+1}{\sqrt{n}}\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right)^{2} \\
|
| 234 |
+
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
|
| 235 |
+
\end{aligned}
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
On s'intéresse aux cas d'égalité. Pour $1<i<n$, l'inégalité $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}} \leqslant \frac{n+1}{\sqrt{n}}$ est stricte, donc nécessairement $x_{i}$ doit être égal à 0 . Ensuite, il faut avoir égalité dans l'inégalité arithmético-géométrique, ce qui s'écrit
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
\begin{aligned}
|
| 242 |
+
\sqrt{n}\left(x_{1}+\frac{x_{n}}{n}\right) & =\frac{1}{\sqrt{n}}\left(x_{1}+n x_{n}\right) \\
|
| 243 |
+
\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{1} & =\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{n}
|
| 244 |
+
\end{aligned}
|
| 245 |
+
$$
|
| 246 |
+
|
| 247 |
+
Si $n=1$, on a toujours égalité (il n'y a qu'un seul $x_{i}$ ), sinon on a la condition $x_{1}=x_{n}$. Réciproquement, on peut vérifier que si $x_{1}=x_{n}$ et tous les autres $x_{i}$ sont nuls, on a bien égalité dans l'inégalité de l'énoncé.
|
| 248 |
+
|
| 249 |
+
Commentaire des correcteurs : Le problème est peu abordé, et encore moins résolu. Très peu de copies traitent les cas d'égalité, alors que cela fait partie de l'énoncé, et pouvait faire gagner des points. Veillez à bien connaître les énoncés des inégalités connues, mal appliquer une inégalité peut fausser toute une preuve.
|
| 250 |
+
|
| 251 |
+
Exercice 9. Soit c un entier positif ou nul. Trouver toutes les suites d'entiers strictement positifs $a_{1}, a_{2}, \ldots$ telles que pour tout entier strictement positif $n, a_{n}$ soit égal au nombre d'entiers $i$ vérifiant $a_{i} \leqslant a_{n+1}+c$.
|
| 252 |
+
Solution de l'exercice 9 Soit $\left(a_{n}\right)$ une suite vérifiant les conditions de l'énoncé pour la constante $c$. On commence par montrer que la suite est croissante. En effet, supposons par l'absurde qu'il existe un entier $n$ tel que $a_{n}>a_{n+1}$. Alors d'après l'hypothèse de l'énoncé, il y a strictement plus de $a_{i}$ inférieurs ou égaux à $a_{n+1}+c$ que de $a_{i}$ inférieurs ou égaux à $a_{n+2}+c$. Ceci signifie que nécessairement $a_{n+2}<a_{n+1}$. En continuant ainsi, on trouve que la suite des $a_{i}$ est strictement décroissante à partir du rang $n$. Comme elle est à valeurs entières strictement positives, c'est absurde.
|
| 253 |
+
Montrons maintenant que la suite est d'abord constante jusqu'à un certain rang, puis strictement croissante. Supposons en effet que $a_{i}=a_{j}$ avec $i<j$. Alors si $i>1, a_{i-1}$ et $a_{j-1}$ sont tous les deux les nombres de $a_{k}$ inférieurs ou égaux à $a_{i}+c=a_{j}+c$, et donc $a_{i-1}=a_{j-1}$. Comme on a $i \leqslant j-1<j$, on a $a_{j}=a_{i} \leqslant a_{j-1} \leqslant a_{j}$ et donc $a_{i-1}=a_{j-1}=a_{j}$ et donc $a_{i-1}=a_{j}$. On continue en diminuant successivement $i$ de 1 jusqu'à avoir $a_{j}=a_{1}$. Toute la suite ne peut pas être égale à $a_{1}$, car par hypothèse seulement $a_{1}$ termes de la suite sont inférieurs ou égaux à $a_{2}+c=a_{1}+c>a_{1}$. Ainsi, la suite est constante égale à $a_{1}$ jusqu'à un certain rang $N$, puis croît strictement.
|
| 254 |
+
Soit $n \geqslant N$, alors on sait qu'il y a $a_{n}$ éléments de la suite inférieurs ou égaux à $a_{n+1}+c$. Ces éléments sont les $n$ premiers $a_{i}$ (par croissance), ainsi que les éléments $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ pour un certain $k$. Ainsi, $k$ est donné par les inégalités $a_{n+k} \leqslant a_{n+1}+c$ et $a_{n+k+1}>a_{n+1}+c$. Comme la suite est strictement croissante après le rang N , nécessairement
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
a_{n+k} \geqslant a_{n+k-1}+1 \geqslant a_{n+k-2}+2 \geqslant \ldots \geqslant a_{n+1}+k-1
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
d'où $a_{n+1}+c \geqslant a_{n+k} \geqslant a_{n+1}+k-1$ et $k \leqslant c+1$. Ainsi, le nombre $a_{n}$ d'éléments de la suite inférieurs ou égaux à $a_{n+1}+c$ est au plus
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
a_{n}=n+k \leqslant n+c+1
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
D'un autre côté, on sait que $a_{n+k+1}$ vaut au moins $a_{n+1}+c+1 \geqslant a_{n}+c+2=n+k+c+2$. On a donc $a_{n+k+1} \geqslant n+k+c+2$ ce qui est la même borne que la borne supérieure ci-dessus mais pour $a_{n+k+1}$. Alors pour tout $m \geqslant n+k+1$, on a
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
m+c+1 \geqslant a_{m} \geqslant a_{n+k+1}+(m-(n+k+1)) \geqslant n+k+c+2+m-n-k-1=m+c+1
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
et donc $a_{m}=m+c+1$ pour tout $m$ suffisamment grand.
|
| 273 |
+
Montrons que cette égalité est vraie pour tout $m$. Si par l'absurde elle était fausse, soit $M$ maximal tel que $a_{M} \neq M+c+1$. Alors $a_{M}$ est le nombre de termes de la suite inférieurs ou égaux à $a_{M+1}+c=$ $M+2 c+2$, qui sont les $M$ termes $a_{1}, \ldots, a_{M}$ ainsi que les termes $a_{M+1}, \ldots, a_{M+c+1}=M+2 c+2$, et donc
|
| 274 |
+
|
| 275 |
+
$$
|
| 276 |
+
a_{M}=M+(c+1)
|
| 277 |
+
$$
|
| 278 |
+
|
| 279 |
+
ce qui est absurde. Ainsi, pour tout $\mathrm{n}, \mathrm{a}_{\mathrm{n}}=\mathrm{n}+\mathrm{c}+1$.
|
| 280 |
+
Vérifions que cette solution fonctionne bien. Soit $n \geqslant 1$ entier. Alors $a_{n+1}+c=n+2 c+2$ et les entiers $i$ tels que $a_{i}=\mathfrak{i}+\boldsymbol{c}+1 \leqslant n+2 c+2$ sont les $i$ inférieurs ou égaux à $n+c+1$, il y en a $n+c+1=a_{n}$, comme voulu.
|
| 281 |
+
|
| 282 |
+
Commentaire des correcteurs : Le problème est très peu abordé, et très rarement résolu. Les remarques sur le comportement de la suite valaient des points. Attention à bien vérifier les solutions candidates. Attention aussi à rester rigoureux dans la manipulation des inégalités.
|
| 283 |
+
|
| 284 |
+
## Exercices Seniors
|
| 285 |
+
|
| 286 |
+
Exercice 10. Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
| 287 |
+
Solution de l'exercice 10 On réécrit l'égalité
|
| 288 |
+
|
| 289 |
+
$$
|
| 290 |
+
\begin{gathered}
|
| 291 |
+
2 a-2 b=b^{2}-a^{2} \\
|
| 292 |
+
2(a-b)=-(a+b)(a-b)
|
| 293 |
+
\end{gathered}
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
|
| 297 |
+
|
| 298 |
+
$$
|
| 299 |
+
2=-a-b
|
| 300 |
+
$$
|
| 301 |
+
|
| 302 |
+
d'où
|
| 303 |
+
|
| 304 |
+
$$
|
| 305 |
+
\mathrm{b}=-2-\mathrm{a}
|
| 306 |
+
$$
|
| 307 |
+
|
| 308 |
+
et $b$ est encore un entier.
|
| 309 |
+
Commentaire des correcteurs: Le problème était réussi par presque tous. Attention aux erreurs de calcul pour ceux qui sont passés un peu vite.
|
| 310 |
+
|
| 311 |
+
Exercice 11. Pour un réel $x$, on note $\lfloor x\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\lfloor 2,7\rfloor=2,\lfloor\pi\rfloor=3$ et $\lfloor-1,5\rfloor=-2$ ). On note aussi $\{x\rfloor=x-\lfloor x\rfloor$.
|
| 312 |
+
Trouver tous les réels $x$ tels que
|
| 313 |
+
|
| 314 |
+
$$
|
| 315 |
+
\lfloor x\rfloor\{x\}<x-1
|
| 316 |
+
$$
|
| 317 |
+
|
| 318 |
+
Solution de l'exercice 11 On réécrit $x=\lfloor x\rfloor+\{x\}$ dans le terme de droite et on met tous les termes à gauche pour que l'inégalité devienne
|
| 319 |
+
|
| 320 |
+
$$
|
| 321 |
+
\lfloor x\rfloor\{x\}-\lfloor x\rfloor-\{x\}+1<0
|
| 322 |
+
$$
|
| 323 |
+
|
| 324 |
+
ou encore
|
| 325 |
+
|
| 326 |
+
$$
|
| 327 |
+
(\lfloor x\rfloor-1)(\{x\}-1)<0
|
| 328 |
+
$$
|
| 329 |
+
|
| 330 |
+
Remarquons que pour tout $x$ réel, on a $0 \leqslant\{x\}<1$ et donc $\{x\}-1<0$. Alors l'inégalité est équivalente à
|
| 331 |
+
|
| 332 |
+
$$
|
| 333 |
+
\lfloor x\rfloor-1>0
|
| 334 |
+
$$
|
| 335 |
+
|
| 336 |
+
ou encore $\lfloor x\rfloor>1$. Ceci veut précisément dire que $x \geqslant 2$. On peut vérifier que réciproquement, si $x \geqslant 2$, alors $x$ vérifie bien l'inégalié de l'énoncé.
|
| 337 |
+
|
| 338 |
+
Commentaire des correcteurs : L'exercice était difficile à aborder initialement car un terme en $\lfloor x\rfloor\{x\}$ est assez inhabituel, mais plutôt bien appréhendé par ceux qui l'ont traité. On pouvait raisonner par équivalence comme cela est fait dans le corrigé. Il faut faire attention dans ce cas à bien garder le résonnement par équivalence tout du long (ou expliquer que la réciproque est vraie). En particulier c'est un des cas où il faut mettre des signes $\Leftrightarrow$ entre chaque ligne mathématique. On pouvait également pour mieux se représenter les choses faire une disjonction de cas qui utilisait en général les mêmes idées.
|
| 339 |
+
|
| 340 |
+
Exercice 12. La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
|
| 341 |
+
|
| 342 |
+
$$
|
| 343 |
+
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
|
| 344 |
+
$$
|
| 345 |
+
|
| 346 |
+
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
| 347 |
+
Solution de l'exercice 12 On pose $P_{n}=\prod^{n} a_{k}$. On a
|
| 348 |
+
|
| 349 |
+
$$
|
| 350 |
+
\frac{P_{n}}{P_{n-1}}=\frac{1}{n}+\frac{1}{P_{n-1}}
|
| 351 |
+
$$
|
| 352 |
+
|
| 353 |
+
ce qui donne
|
| 354 |
+
|
| 355 |
+
$$
|
| 356 |
+
n P_{n}=P_{n-1}+n
|
| 357 |
+
$$
|
| 358 |
+
|
| 359 |
+
On pose alors $M_{n}=n!P_{n}$. On déduit
|
| 360 |
+
|
| 361 |
+
$$
|
| 362 |
+
M_{n}=M_{n-1}+n!
|
| 363 |
+
$$
|
| 364 |
+
|
| 365 |
+
On déduit que $M_{n}=\sum k!$. On déduit alors
|
| 366 |
+
|
| 367 |
+
$$
|
| 368 |
+
a_{n}=\frac{P_{n}}{P_{n-1}}=\frac{\frac{1}{n!} \sum k!}{\frac{1}{(n-1)!} \sum k!}
|
| 369 |
+
$$
|
| 370 |
+
|
| 371 |
+
Il reste à montrer que
|
| 372 |
+
|
| 373 |
+
$$
|
| 374 |
+
\sum_{k=1}^{n} k!\leqslant \sum_{k=1}^{n-1} n \times k!
|
| 375 |
+
$$
|
| 376 |
+
|
| 377 |
+
ce qui vient en utilisant $\mathrm{n} \geqslant 3$ pour avoir notamment $\mathrm{n} \geqslant 2+1$ et
|
| 378 |
+
|
| 379 |
+
$$
|
| 380 |
+
\sum_{k=1}^{n} k!\leqslant 1+2+\sum_{k=3}^{n} n \times(k-1)!\leqslant n+n \sum_{k=2}^{n-1} k!
|
| 381 |
+
$$
|
| 382 |
+
|
| 383 |
+
## Solution alternative:
|
| 384 |
+
|
| 385 |
+
A partir de l'équation sur les $P_{n}$, on veut donc montrer que $a_{n} \leqslant 1$ pour $n \geqslant 3$, c'est-à-dire que $P_{n} \leqslant P_{n-1}$. Ceci se réécrit
|
| 386 |
+
|
| 387 |
+
$$
|
| 388 |
+
\begin{gathered}
|
| 389 |
+
\frac{1}{n} P_{n-1}+1 \leqslant P_{n-1} \\
|
| 390 |
+
P_{n-1} \geqslant \frac{n}{n-1} .
|
| 391 |
+
\end{gathered}
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
On cherche donc à montrer cette inégalité par récurence. Pour $\mathrm{n}=3$, on a bien
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
\mathrm{P}_{2}=\frac{1}{2}+1=\frac{3}{2}=\frac{3}{3-1} .
|
| 398 |
+
$$
|
| 399 |
+
|
| 400 |
+
Si le résultat est vrai au rang n , on a, au rang $\mathrm{n}+1$,
|
| 401 |
+
|
| 402 |
+
$$
|
| 403 |
+
P_{n}=\frac{1}{n} P_{n-1}+1 \geqslant \frac{1}{n} \frac{n}{n-1}+1=\frac{n}{n-1} \geqslant \frac{n+1}{n}
|
| 404 |
+
$$
|
| 405 |
+
|
| 406 |
+
ce qui conclut la récurrence.
|
| 407 |
+
|
| 408 |
+
Solution alternative 2 :
|
| 409 |
+
On a $a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n}}$. Ainsi :
|
| 410 |
+
|
| 411 |
+
$$
|
| 412 |
+
a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n-1}} \frac{1}{a_{n}}=\left(a_{n}-\frac{1}{n-1}\right) \frac{1}{a_{n}}
|
| 413 |
+
$$
|
| 414 |
+
|
| 415 |
+
Dès lors $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n}$. On peut calculer les premiers termes pour avoir $a_{3}=1$. On peut ensuite prouver par récurrence sur $n$ que $a_{n} \leqslant 1$.
|
| 416 |
+
Si le résultat est vrai au rang $n, a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n} \leqslant 1-\frac{1}{n-1}+\frac{1}{n} \leqslant 1$. Ce qui conclut.
|
| 417 |
+
Commentaire des correcteurs : La plupart de ceux qui ont abordé l'exercice l'ont bien compris. Il s'agissait principalement de transformer la relation de récurrence forte en une relation de récurrence simple puis de faire une récurrence. Certains élèves ont donné des raisonnements qui demandaient de traiter les premiers termes à la main. Il ne faut pas oublier de le faire, surtout que cela peut permettre de déceler une erreur de raisonnement.
|
| 418 |
+
|
| 419 |
+
Exercice 13. Déterminer toutes les fonctions f de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous $x, y$ réels :
|
| 420 |
+
|
| 421 |
+
$$
|
| 422 |
+
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)
|
| 423 |
+
$$
|
| 424 |
+
|
| 425 |
+
Solution de l'exercice 13 Soit f une solution de l'équation.
|
| 426 |
+
Pour $x=y=0$, on $a$ :
|
| 427 |
+
|
| 428 |
+
$$
|
| 429 |
+
\mathbf{f}(0)^{3}=0
|
| 430 |
+
$$
|
| 431 |
+
|
| 432 |
+
Ainsi, $f(0)=0$. On exclut la fonction $f \equiv 0$ qui est effectivement solution du problème.
|
| 433 |
+
On considère maintenant, un nombre $x$ tel que $f(x)=0$. On a alors pour un $y$ quelconque :
|
| 434 |
+
|
| 435 |
+
$$
|
| 436 |
+
0=x^{2} f(y)-0
|
| 437 |
+
$$
|
| 438 |
+
|
| 439 |
+
Comme on a exclu le cas $f \equiv 0$, on peut trouver $y$ tel que $f(y) \neq 0$ et donc $x=0$. Ainsi, si $f(x)=0$, on $\mathrm{a} x=0$ 。
|
| 440 |
+
|
| 441 |
+
On peut maintenant remarquer qu'échanger $x$ et $y$ dans l'équation, change le terme de droite en son oppposé, on a donc:
|
| 442 |
+
|
| 443 |
+
$$
|
| 444 |
+
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)=-\left(y^{2} f(x)-x^{2} f(y)\right)=-f(y) f(x) f(y-x)
|
| 445 |
+
$$
|
| 446 |
+
|
| 447 |
+
Ainsi pour $x$ et $y$ non nuls, on a $f(x-y)=-f(y-x)$. En posant $y=2 x$ avec $x \neq 0$, on obtient que pour tout $x \neq 0, f(-x)=-f(x)$. Comme $f(0)=0, f$ est impaire.
|
| 448 |
+
|
| 449 |
+
On peut maintenant prendre $x=2 y$, l'égalité de l'énoncé avec l'imparité donnent :
|
| 450 |
+
|
| 451 |
+
$$
|
| 452 |
+
f(2 y) f(y)^{2}=4 y^{2} f(y)-y^{2} f(2 y)
|
| 453 |
+
$$
|
| 454 |
+
|
| 455 |
+
D'autre part, avec $x=-\mathrm{y}$ :
|
| 456 |
+
|
| 457 |
+
$$
|
| 458 |
+
f(y)^{2} f(2 y)=2 y^{2} f(y)
|
| 459 |
+
$$
|
| 460 |
+
|
| 461 |
+
En utilisant ces deux égalités, on a :
|
| 462 |
+
|
| 463 |
+
$$
|
| 464 |
+
f(2 y) y^{2}=2 y^{2} f(y)
|
| 465 |
+
$$
|
| 466 |
+
|
| 467 |
+
Si $y$ est non nul, on a $\mathrm{f}(\mathrm{y}) \neq 0$, et donc l'égalité précédente s'écrit $\mathrm{f}(2 \mathrm{y})=2 \mathrm{f}(\mathrm{y})$, et l'équation (1) s'écrit
|
| 468 |
+
|
| 469 |
+
$$
|
| 470 |
+
\begin{gathered}
|
| 471 |
+
2 f(y)^{3}=2 y^{2} f(y) \\
|
| 472 |
+
f(y)^{2}=y^{2}
|
| 473 |
+
\end{gathered}
|
| 474 |
+
$$
|
| 475 |
+
|
| 476 |
+
On trouve donc $f(y)= \pm y$. Attention, a priori, le signe pourrait dépendre de $y$. Soit, par l'absurde, a et $b$ deux réels non nuls tels que $f(a)=a$ et $f(b)=-b$. En prenant $x=b$ et $y=a$, on obtient:
|
| 477 |
+
|
| 478 |
+
$$
|
| 479 |
+
-a b f(a-b)=a b(a+b)
|
| 480 |
+
$$
|
| 481 |
+
|
| 482 |
+
Comme $a$ et $b$ sont non nuls, $f(a-b)=-(a+b)$. Mais $f(a-b)= \pm(a-b)$, et en fonction du signe on obtient soit $a=0$, soit $b=0$, ce qui est absurde. Pour $x=0$, on a à la fois $f(x)=x$ et $f(x)=-x$, donc nécessairement $f$ est de la forme : $f(x)=0$ pour tous $x$, ou $f(x)=-x$ pour tous $x$, ou $f(x)=x$ pour tous $x$.
|
| 483 |
+
|
| 484 |
+
Ces trois fonctions sont bien solutions.
|
| 485 |
+
Commentaire des correcteurs: Le problème a été tenté par un nombre important d'élèves, souvent avec les bonnes idées de substitutions. Un grand nombre doit faire plus attention à ne pas diviser par 0 , même quand ce 0 se cache dans un $f(x)$ ou autre valeur. Cela mène à des raisonnements qui souvent retombent sur leur pattes, mais pour les mauvaises raisons. Une autre erreur très fréquente est celle des "multigraphes" : si l'on sait que $\mathrm{f}(x)^{2}=x^{2}$ pour tout $x$, alors on ne peut pas immédiatement conclure que $f$ est plus ou moins la fonction identité. En effet la fonction pourrait alterner de façon arbitraire entre $+x$ et $-x$.
|
| 486 |
+
|
| 487 |
+
Exercice 14. Emile a créé un exercice pour Benoît. Il lui annonce qu'il a choisi secrètement un polynôme P unitaire de degré 2023 à coefficients entiers, c'est-à-dire de la forme
|
| 488 |
+
|
| 489 |
+
$$
|
| 490 |
+
P(X)=X^{2023}+a_{2022} X^{2022}+a_{2021} X^{2021}+\ldots+a_{1} X+a_{0}
|
| 491 |
+
$$
|
| 492 |
+
|
| 493 |
+
où $a_{0}, a_{1}, \ldots, a_{2022}$ sont des entiers relatifs. Il donne à Benoît $k$ entiers $n_{1}, n_{2}, \ldots, n_{k}$, où $k$ est un entier positif, ainsi que la valeur du produit $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)$. A partir de ces connaissances, Benoît doit essayer de retrouver le polynôme P .
|
| 494 |
+
Trouver l'entier $k$ minimal tel que Emile puisse trouver $P$ et $n_{1}, \ldots, n_{k}$ afin de s'assurer que le seul polynôme coincidant avec les informations données à Benoît soit P .
|
| 495 |
+
Solution de l'exercice 14 Montrons que le $k$ minimal est $k=2023$. En effet, supposons d'abord que $k<2023$ et qu'Emile choisisse $P$ et $n_{1}, \ldots, n_{k}$. Posons
|
| 496 |
+
|
| 497 |
+
$$
|
| 498 |
+
\mathrm{Q}=\mathrm{P}+\left(\mathrm{X}-\mathrm{n}_{1}\right)\left(\mathrm{X}-\mathrm{n}_{2}\right) \ldots\left(\mathrm{X}-\mathrm{n}_{\mathrm{k}}\right)
|
| 499 |
+
$$
|
| 500 |
+
|
| 501 |
+
qui est un polynôme à coefficients entiers, toujours unitaire de degré 2023, et différent de P . Alors P et $Q$ sont égaux en chaque $n_{i}$, et donc les produits $P\left(n_{1}\right) \ldots P\left(n_{k}\right)$ et $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ sont égaux, donc Benoît ne peut pas retrouver la valeur du polynôme $P$.
|
| 502 |
+
Supposons maintenant que $k=2023$. Emile peut alors choisir $n_{1}=3, n_{2}=6, \ldots, n_{2023}=3 \cdot 2023$ et poser
|
| 503 |
+
|
| 504 |
+
$$
|
| 505 |
+
P=(X-3)(X-6) \ldots(X-3 \cdot 2023)+1
|
| 506 |
+
$$
|
| 507 |
+
|
| 508 |
+
Alors le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)$ vaut 1 . Soit Q un polynôme à coefficients entiers, unitaire de degré 2023 tel que le produit $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ soit égal à 1 , il faut montrer que nécessairement $Q=P$. Comme tous les $Q\left(n_{i}\right)$ sont entiers, ils valent tous soit 1 , soit -1 . On peut cependant remarquer que comme les $n_{i}$ sont divisibles par 3 alors pour tout $i, Q\left(n_{i}\right)$ est congru au coefficient constant de $Q$. Comme 1 et -1 ne sont pas congrus modulos 3 , tous les $Q\left(n_{i}\right)$ sont égaux. Comme 2023 est impair, ils ne peuvent pas tous être égaux à -1 , donc ils valent tous 1 . Alors $P-Q$ est un polynôme de degré au plus 2022 (car les termes d'ordre 2023 s'annulent) et est nul en chacun des 2023 valeurs des $n_{i}$, donc $\mathrm{Q}=\mathrm{P}$, ce qui conclut.
|
| 509 |
+
|
| 510 |
+
Commentaire des correcteurs : L'exercice a été plutôt bien compris et beaucoup d'élèves ont penser à créer un polynome P dont le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)=1$ ce qui était la bonne façon de résoudre l'exercice. Attention cepandant à mieux justifier les arguments de division euclidienne sur les polynômes à coefficients entiers, certains sont allés un peu vite sur cette étape.
|
| 511 |
+
|
| 512 |
+
Exercice 15. Soit c un entier positif ou nul. Trouver toutes les suites d'entiers strictement positifs $a_{1}, a_{2}, \ldots$ telles que pour tout entier strictement positif $n, a_{n}$ soit égal au nombre d'entiers $i$ vérifiant $a_{i} \leqslant a_{n+1}+c$.
|
| 513 |
+
Solution de l'exercice 15 Soit ( $a_{n}$ ) une suite vérifiant les conditions de l'énoncé pour la constante $c$. On commence par montrer que la suite est croissante. En effet, supposons par l'absurde qu'il existe un entier $n$ tel que $a_{n}>a_{n+1}$. Alors d'après l'hypothèse de l'énoncé, il y a strictement plus de $a_{i}$ inférieurs ou égaux à $a_{n+1}+c$ que de $a_{i}$ inférieurs ou égaux à $a_{n+2}+c$. Ceci signifie que nécessairement $a_{n+2}<a_{n+1}$. En continuant ainsi, on trouve que la suite des $a_{i}$ est strictement décroissante à partir du rang n . Comme elle est à valeurs entières strictement positives, c'est absurde.
|
| 514 |
+
Montrons maintenant que la suite est d'abord constante jusqu'à un certain rang, puis strictement croissante. Supposons en effet que $a_{i}=a_{j}$ avec $i<j$. Alors si $i>1, a_{i-1}$ et $a_{j-1}$ sont tous les deux les nombres de $a_{k}$ inférieurs ou égaux à $a_{i}+c=a_{j}+c$, et donc $a_{i-1}=a_{j-1}$. Comme on $a i \leqslant j-1<j$, on a $a_{j}=a_{i} \leqslant a_{j-1} \leqslant a_{j}$ et donc $a_{i-1}=a_{j-1}=a_{j}$ et donc $a_{i-1}=a_{j}$. On continue en diminuant successivement $i$ de 1 jusqu'à avoir $a_{j}=a_{1}$. Toute la suite ne peut pas être égale à $a_{1}$, car par hypothèse seulement $a_{1}$ termes de la suite sont inférieurs ou égaux à $a_{2}+c=a_{1}+c>a_{1}$. Ainsi, la suite est constante égale à $a_{1}$ jusqu'à un certain rang N , puis croît strictement.
|
| 515 |
+
Soit $n \geqslant N$, alors on sait qu'il y a $a_{n}$ éléments de la suite inférieurs ou égaux à $a_{n+1}+c$. Ces éléments sont les $n$ premiers $a_{i}$ (par croissance), ainsi que les éléments $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ pour un certain $k$. Comme la suite est strictement croissante après le rang N , nécessairement
|
| 516 |
+
|
| 517 |
+
$$
|
| 518 |
+
a_{n+k} \geqslant a_{n+k-1}+1 \geqslant a_{n+k-2}+2 \geqslant \ldots \geqslant a_{n+1}+k-1
|
| 519 |
+
$$
|
| 520 |
+
|
| 521 |
+
d'où $a_{n+1}+c \geqslant a_{n+1}+k-1$ et $k \leqslant c+1$. Ainsi, le nombre $a_{n}$ d'éléments de ls suite inférieurs ou égaux à $a_{n+1}+c$ est au plus
|
| 522 |
+
|
| 523 |
+
$$
|
| 524 |
+
a_{n}=n+k \leqslant n+c+1
|
| 525 |
+
$$
|
| 526 |
+
|
| 527 |
+
D'un autre côté, on sait que $a_{n+k+1}$ vaut au moins $a_{n+1}+c+1 \geqslant a_{n}+c+2=n+k+c+2$. On a donc $a_{n+k+1} \geqslant n+k+c+2$ ce qui est la même borne que la borne supérieure ci-dessus mais pour $a_{n+k+1}$. Alors pour tout $m \geqslant n+k+1$, on $a$
|
| 528 |
+
|
| 529 |
+
$$
|
| 530 |
+
m+c+1 \geqslant a_{m} \geqslant a_{n+k+1}+(m-(n+k+1)) \geqslant n+k+c+2+m-n-k-1=m+c+1
|
| 531 |
+
$$
|
| 532 |
+
|
| 533 |
+
et donc $a_{m}=m+c+1$ pour tout $m$ suffisamment grand.
|
| 534 |
+
Montrons que cette égalité est vraie pour tout $m$. Si par l'absurde elle était fausse, soit $M$ maximal tel que $a_{M} \neq M+c+1$. Alors $a_{M}$ est le nombre de termes de la suite inférieurs ou égaux à $a_{M+1}+c=$ $M+2 c+2$, qui sont les $M$ termes $a_{1}, \ldots, a_{M}$ ainsi que les termes $a_{M+1}, \ldots, a_{M+c+1}=M+2 c+2$, et donc
|
| 535 |
+
|
| 536 |
+
$$
|
| 537 |
+
a_{M}=M+(c+1)
|
| 538 |
+
$$
|
| 539 |
+
|
| 540 |
+
ce qui est absurde. Ainsi, pour tout $\mathrm{n}, \mathrm{a}_{\mathrm{n}}=\mathrm{n}+\mathrm{c}+1$.
|
| 541 |
+
Vérifions que cette solution fonctionne bien. Soit $n \geqslant 1$ entier. Alors $a_{n+1}+c=n+2 c+2$ et les entiers $i$ tels que $a_{i}=\mathfrak{i}+\boldsymbol{c}+1 \leqslant n+2 c+2$ sont les $i$ inférieurs ou égaux à $n+c+1$, il y en a $n+c+1=a_{n}$, comme voulu.
|
| 542 |
+
|
| 543 |
+
Commentaire des correcteurs : Le problème, malgré sa position, n'a pas été beaucoup cherché ni résolu. La plupart des élèves ayant rendu une tentative ont bien compris la mécanique de la suite et ont les bons réflexes : chercher les variations (croissance, convexité) de la suite avant d'en déduire qu'elle est
|
| 544 |
+
arithmétique. En revanche, beaucoup d'élèves, victimes du même tropisme, pensent montrer que la suite est strictement croissante dès le début de la preuve alors qu'ils n'ont que montré que la suite est constante puis strictement croissante à partir d'un certain rang. Enfin, on déplore que beaucoup d'élèves ont oublié de vérifier que la suite qu'ils trouvent à la fin est bien solution du problème.
|
| 545 |
+
|
| 546 |
+
Exercice 16. Déterminer toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous $x, y$ réels, on ait
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
f\left(x^{2}+x y+f\left(y^{2}\right)\right)=x f(y)+f\left(x^{2}\right)+y^{2}
|
| 550 |
+
$$
|
| 551 |
+
|
| 552 |
+
Solution de l'exercice 16 En posant $y=0$, on trouve $f\left(x^{2}+f(0)\right)=x f(0)+f\left(x^{2}\right)$. En remplaçant $x$ par $-x$ dans cette équation, on trouve $f\left(x^{2}+f(0)\right)=-\chi f(0)+f\left(x^{2}\right)$, et en combinant on obtient donc $2 x f(0)=0$ pour tout $x$, soit $f(0)=0$.
|
| 553 |
+
En posant $x=0$, on trouve $f\left(f\left(y^{2}\right)\right)=y^{2}+f(0)=y^{2}$. En posant $y=-x$, on trouve cette fois-ci que $f\left(f\left(y^{2}\right)\right)=-y f(y)+y^{2}+f\left(y^{2}\right)$. On en déduit que
|
| 554 |
+
|
| 555 |
+
$$
|
| 556 |
+
f\left(y^{2}\right)=y f(y)
|
| 557 |
+
$$
|
| 558 |
+
|
| 559 |
+
D'autre part, en posant $x=-f\left(y^{2}\right) / y$, on trouve
|
| 560 |
+
|
| 561 |
+
$$
|
| 562 |
+
-\frac{f(y) f\left(y^{2}\right)}{y}+y^{2}=0
|
| 563 |
+
$$
|
| 564 |
+
|
| 565 |
+
On déduit que si $y$ est non nul, alors $y^{3}=f(y) f\left(y^{2}\right)=y f(y)^{2}$, ou encore $f(y)^{2}=y^{2}$. Puisque si $y=0$, alors $f(0)=0$, on a donc pour tout $y$ réel que $f(y)= \pm y$.
|
| 566 |
+
Dans la suite, on suppose qu'il existe $a$ et $b$ tels que $f(a)=a$ et $f(b)=-b$. Notons qu'alors $f\left(a^{2}\right)=a^{2}$ et $f\left(b^{2}\right)=-b^{2}$, puisque $f\left(x^{2}\right)=x f(x)$.
|
| 567 |
+
En remplaçant $x=a$ et $y=b$ dans l'équation, on trouve
|
| 568 |
+
|
| 569 |
+
$$
|
| 570 |
+
\pm\left(a^{2}+a b-b^{2}\right)=-a b+b^{2}+a^{2}
|
| 571 |
+
$$
|
| 572 |
+
|
| 573 |
+
Le cas où le signe du LHS (Left Hand Side = membre de gauche de l'équation) est un + donne que $b(a-b)=0$. Si $b \neq 0$, alors $a=b$ ce qui donne $a=f(a)=f(b)=-b=-a$ donc $a=b=0$. Dans tous les cas, $a$ ou $b$ est nul.
|
| 574 |
+
Le cas où le signe du LHS est un - donne que $a^{2}=0$ donc $a=0$.
|
| 575 |
+
On déduit que les seules solutions sont les fonction $f \equiv x$ et $f \equiv-x$.
|
| 576 |
+
Commentaire des correcteurs : Le problème a rencontré un certain succès. Cette équation fonctionnelle nécessitait de beaucoup jouer sur les "symétries" du problème, en particulier le fait que peu de termes changeaient si l'on changeait le signe d'un variable. Une fois cette remarque effectuée, on pouvait tenter les substitutions $(x, y),(-x, y),(x,-y)$ et $(-x,-y)$, qui donnaient que $f(0)=0$ et que $f$ est impaire. Plusieurs options étaient ensuite possibles, comme jouer sur le caractère involutif de fou tenter de compenser deux termes de l'équation (c'est ce qui motive la substitution $x=-\frac{f\left(y^{2}\right)}{y}$ dans le corrigé). La deuxième spécificité du problème est que la solution aboutissait à un problème de multigraphe : on a pour tout $x$ soit $f(x)=\chi$ soit $f(x)=-\chi$. Notez qu'à ce stade, l'identité et moins l'identité ne sont pas les seules fonctions avec cette propriété, par exemple la fonction valeur absolue vérifie aussi cette propriété (et il y a en fait une large famille de fonctions vérifiant cela). On aimerait alors "inverser" cette formule pour montrer qu'on a soit $f(x)=x$ pour tout $x$, soit $f(x)=-x$ pour tout $x$. Cette subitlité a échappé à plusieurs élèves.
|
| 577 |
+
Une autre erreur récurrente a été de déduire de $x f(x)=-x f(-x)$ que $f(x)=f(-x)$ pour tout $x$ non nul, d'en déduire que $f$ est impaire et donc que $f(0)=0$. Mais comme l'égalité $f(x)=-f(-x)$ n'est vraie que pour les $x$ non nuls, on ne peut substituer $x=0$ dans cette équation pour déduire $f(0)$.
|
| 578 |
+
|
| 579 |
+
Exercice 17. Soit $\mathrm{n} \geqslant 2$ un entier et $\mathrm{C}>0$ une constante réelle. On suppose qu'il existe une suite $x_{1}, x_{2}, \ldots, x_{n}$ de réels non tous nuls telle que :
|
| 580 |
+
$-x_{1}+x_{2}+\ldots+x_{n}=0$.
|
| 581 |
+
|
| 582 |
+
- Pour tout indice $1 \leqslant i \leqslant n$, on a soit $x_{i} \leqslant x_{i+1}$, soit $x_{i} \leqslant x_{i+1}+C x_{i+2}$ (où on définit $x_{n+1}=x_{1}$ et $x_{n+2}=x_{2}$ ).
|
| 583 |
+
|
| 584 |
+
1. Montrer que nécessairement $C \geqslant 2$.
|
| 585 |
+
2. On suppose que $C=2$, montrer que n est nécessairement pair.
|
| 586 |
+
|
| 587 |
+
Solution de l'exercice 17 Dans toute la solution, on considèrera tous les indices modulo n . Remarquons que la condition de l'énoncé signifie que pour tout $i$, si $x_{i+2} \leqslant 0$, alors $x_{i} \leqslant x_{i+1}$ car la condition $x_{i} \leqslant x_{i+1}+C x_{i+2}$ implique aussi $x_{i} \leqslant x_{i+1}$, De la même façon dans le cas contraire, $x_{i} \leqslant x_{i+1}+C x_{i+2}$ dès que $x_{i+1} \geqslant 0$. On s'intéresse donc au signe des différents termes $x_{k}$.
|
| 588 |
+
Commençons par montrer qu'il n'existe jamais deux termes négatifs ou nuls à la suite parmi les $x_{k}$. Supposons par l'absurde que ce soit le cas et qu'il existe donc $i$ avec $x_{i} \leqslant 0$ et $x_{i+1} \leqslant 0$. Alors on applique la propriété à l'indice $i-1$. Comme $x_{i+1} \leqslant 0$, on a donc $x_{i-1} \leqslant x_{i} \leqslant 0$. En réappliquant ceci à l'indice $i-1$, on trouve $x_{i-2} \leqslant 0$, et en continuant ainsi on trouve successivement que tous les $x_{k}$ sont négatifs ou nuls. Mais comme la somme des $x_{k}$ vaut 0 , ceci veut dire qu'ils sont tous nuls, ce qui est impossible d'après l'énoncé.
|
| 589 |
+
Soient $\mathfrak{i}_{1}, \ldots, \mathfrak{i}_{\mathrm{K}}$ les indices $i$ où $x_{i}$ est négatif ou nul. Maintenant, on peut écrire toutes les inégalités que l'on connait entre les $x_{i}$ : pour tout $j$,
|
| 590 |
+
|
| 591 |
+
$$
|
| 592 |
+
\begin{gathered}
|
| 593 |
+
x_{\mathfrak{i}_{j}+1} \leqslant x_{\mathfrak{i}_{j}+2}+C x_{\mathfrak{i}_{\mathfrak{j}}+3}, \quad x_{\mathfrak{i}_{\mathfrak{j}}+2} \leqslant x_{\mathfrak{i}_{\mathfrak{j}}+3}+C x_{\mathfrak{i}_{\mathfrak{j}}+4}, \ldots, \quad x_{\mathfrak{i}_{j+1}-3} \leqslant x_{\mathfrak{i}_{j+1}-2}+C x_{\mathfrak{i}_{j+1}-1} \\
|
| 594 |
+
x_{\mathfrak{i}_{j+1}-2} \leqslant x_{\mathfrak{i}_{j+1}-1}, \quad x_{\mathfrak{i}_{j+1}-1} \leqslant x_{\mathfrak{i}_{j+1}}+C x_{\mathfrak{i}_{j+1}+1}
|
| 595 |
+
\end{gathered}
|
| 596 |
+
$$
|
| 597 |
+
|
| 598 |
+
La seule inégalité intéressante faisant apparaître les termes négatifs $x_{i_{j}}$ est cette dernière, on a donc pour tout $j, x_{i_{j}} \geqslant x_{i_{j}-1}-C x_{i_{j}+1}$. Mais on sait que la somme des termes positifs doit se compenser avec la somme des termes négatifs car la somme de tous les $x_{k}$ vaut 0 , et on écrit donc
|
| 599 |
+
|
| 600 |
+
$$
|
| 601 |
+
-\left(x_{i_{1}}+x_{i_{2}}+\ldots+x_{i_{k}}\right) \leqslant\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\ldots+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)
|
| 602 |
+
$$
|
| 603 |
+
|
| 604 |
+
Le terme de gauche vaut la somme des termes positifs, et en réordonnant les termes à droite on trouve
|
| 605 |
+
|
| 606 |
+
$$
|
| 607 |
+
\begin{aligned}
|
| 608 |
+
\left(x_{i_{1}+1}+x_{i_{1}+2}\right. & \left.+\ldots+x_{i_{2}-1}\right)+\left(x_{i_{2}+1}+x_{i_{2}+2}+\ldots+x_{i_{3}-1}\right)+\ldots+\left(x_{i_{k}+1}+x_{i_{k}+2}+\ldots+x_{i_{1}-1}\right) \\
|
| 609 |
+
& \leqslant\left(C x_{i_{1}+1}-x_{i_{2}-1}\right)+\left(C x_{i_{2}+1}-x_{i_{3}-1}\right)+\ldots+\left(C x_{\mathfrak{i}_{k}+1}-x_{i_{1}-1}\right)
|
| 610 |
+
\end{aligned}
|
| 611 |
+
$$
|
| 612 |
+
|
| 613 |
+
La raison pour mettre les termes de cette manière est la suivante : les seules inégalités qui nous restent parmi les inégalités citées précédemment ne prennent qu'en compte les $\chi_{k}$ pour $k$ entre un $i_{j}+1$ et le $\mathfrak{i}_{j+1}-1$ suivant, c'est-à-dire dans une des suites de termes strictement positifs successifs. On va alors montrer que si $C<2$, alors on a nécessairement pour tout $\mathfrak{j}$,
|
| 614 |
+
|
| 615 |
+
$$
|
| 616 |
+
x_{i_{j}+1}+x_{i_{j}+2}+\ldots+x_{i_{j+1}-1}>C x_{i_{j}+1}-x_{i_{j+1}-1}
|
| 617 |
+
$$
|
| 618 |
+
|
| 619 |
+
On va alors montrer que pour toute suite $a_{1}, a_{2}, \ldots, a_{m}$ de termes strictement positifs vérifiant les inégalités
|
| 620 |
+
|
| 621 |
+
$$
|
| 622 |
+
a_{1} \leqslant a_{2}+C a_{3}, \quad a_{2} \leqslant a_{3}+C a_{4}, \ldots, \quad a_{m-2} \leqslant a_{m-1}+C a_{m}, \quad a_{m-1} \leqslant a_{m}
|
| 623 |
+
$$
|
| 624 |
+
|
| 625 |
+
alors nécessairement $a_{1}+\ldots+a_{m}>\mathrm{Ca}_{1}-a_{m}$. Pour cela, on écrit
|
| 626 |
+
|
| 627 |
+
$$
|
| 628 |
+
\begin{gathered}
|
| 629 |
+
C a_{1}-a_{m}=a_{1}+(C-1) a_{1}-a_{m} \leqslant a_{1}+(C-1) a_{2}+C(C-1) a_{3}-a_{m} \\
|
| 630 |
+
=a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{3}-a_{m} \leqslant a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{4}+C(C-1) a_{5}-a_{m} .
|
| 631 |
+
\end{gathered}
|
| 632 |
+
$$
|
| 633 |
+
|
| 634 |
+
On peut continuer ainsi jusqu'à obtenir, selon la parité de m,
|
| 635 |
+
|
| 636 |
+
$$
|
| 637 |
+
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+C(C-1) a_{m}-a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+C(C-1) a_{m-1}-a_{m} & \text { si m est pair }\end{cases}
|
| 638 |
+
$$
|
| 639 |
+
|
| 640 |
+
Dans le deuxième cas, on utilise la dernière inégalité $a_{m-1} \leqslant a_{m}$ pour obtenir
|
| 641 |
+
|
| 642 |
+
$$
|
| 643 |
+
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+(C(C-1)-1) a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+(C(C-1)-1) a_{m-1} & \text { si m est pair }\end{cases}
|
| 644 |
+
$$
|
| 645 |
+
|
| 646 |
+
Lorsque $C<2$, tous les coefficients devant les $a_{i}$ sont strictement inférieurs à 1 et donc $C a_{1}-a_{m}$ est strictement inférieur à $a_{1}+a_{2}+\ldots+a_{m}$. Ceci conclut alors la première partie de l'exercice par ce qu'on a vu précédemment.
|
| 647 |
+
Maintenant, supposons que $C=2$. Remarquons que dans l'étude de la suite $a_{i}$, on a toujours l'inégalité $C a_{1}-a_{m} \leqslant a_{1}+\ldots+a_{m}$, mais par ce que l'on a montré précédemment l'inégalité est toujours stricte dans le cas où $m$ est pair (car $a_{m}$ strictement positif). Ainsi, pour que $C=2$, il faut que les suites de termes positifs consécutifs soient toujours de taille impaire., ce qui signifie que tous les $i_{j+1}-\boldsymbol{i}_{j}$ sont pairs (car on compte aussi un terme négatif). Mais alors comme tous les $\mathfrak{i}_{j+1}-\mathfrak{i}_{\mathfrak{j}}$ sont pairs, ceci signifie en sommant sur $j$ que $n$ est nécessairement pair.
|
| 648 |
+
|
| 649 |
+
Commentaire des correcteurs : L'exercie a été très peu réussi. Le point clef était de séparer les éléments de la suite entre termes positifs et négatifs (voir la vidéo sur la chaîne sur le sujet). Malheuresement, un certain nombre d'entre vous ont pensé démontrer que deux termes consécutifs ne pouvaient pas être strictement positifs, or c'est tout à fait possible (on peut facilement trouver un contre-exemple pour $\mathrm{n}=4$ ). Souvent l'erreur était d'être trop optimiste dans l'utilisation des inégalités alors que l'énoncé est en fait assez miraculeux.
|
| 650 |
+
|
| 651 |
+
Exercice 18. Soit $\mathbb{Z}[\mathrm{X}]$ l'ensemble des polynômes à coefficients entiers. Trouver toutes les fonctions $f: \mathbb{Z}[X] \rightarrow \mathbb{Z}[X]$ telles que pour tous $P, Q \in \mathbb{Z}[X]$ et $r \in \mathbb{Z}$, on ait
|
| 652 |
+
|
| 653 |
+
$$
|
| 654 |
+
P(r)|Q(r) \Longleftrightarrow(f(P))(r)|(f(Q))(r)
|
| 655 |
+
$$
|
| 656 |
+
|
| 657 |
+
Solution de l'exercice 18 Soit f une fonction solution de l'énoncé. Commençons par remarquer que si $P, Q, r$ sont tels que $|P(r)|=|Q(r)|$, alors $f(P)(r)$ et $f(Q)(r)$ se divisent mutuellement, et donc $|f(P)(r)|=|f(Q)(r)|$.
|
| 658 |
+
Remarquons aussi que si $P$ et $Q$ sont deux polynômes tels que pour une infinité d'entiers $r, P(r) \mid Q(r)$, alors c'est aussi le cas pour $f(P)$ et $f(Q)$, et donc $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$. En effet, on écrit la division euclidienne $f(Q)=R f(P)+S$ avec $R, S \in \mathbb{Q}[X]$ et $\operatorname{deg}(S)<\operatorname{deg}(f(P))$. On multiplie par les dénominateurs des coefficients de $R$ et $S$ pour obtenir une égalité de la forme $a f(Q)=R^{\prime} f(P)+S^{\prime}$ avec a entier et $R^{\prime}, S^{\prime}$ deux polynômes à coefficients entiers. Alors pour une infinité de $r$ entiers, $a f(P)(r) \mid$ $S^{\prime}(r)$. Comme $|a f(P)(r)|$ croît plus rapidement que $\left|S^{\prime}(r)\right|$ lorsque $|r|$ tend vers l'infini, on obtient que nécessairement $S^{\prime}=0$ et donc que $f(P)=\operatorname{Rf}(Q)$ et $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$. Notamment, $f(Q)=0$ ou $\operatorname{deg}(f(Q)) \geqslant \operatorname{deg}(f(P))$. On utilisera souvent la conséquence suivante : si $P$ divise $Q$ dans $\mathbb{Z}[X]$, alors $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$.
|
| 659 |
+
Commençons par trouver les antécédents du polynôme nul par $f$. Soit $Q$ tel que $f(Q)=0$. Alors pour tout polynôme $P$, on a que pour tout $r, f(P)(r) \mid f(Q)(r)=0$, et alors $P(r) \mid Q(r)$. Par la remarque précédente, $Q=0$ ou $\operatorname{deg}(Q) \geqslant \operatorname{deg}(P)$. Comme on peut prendre $P$ quelconque, on a nécessairement $\mathrm{Q}=0$. Ainsi, $f(P) \neq 0$ pour tout $P \neq 0$.
|
| 660 |
+
On va s'intéresser à l'image des constantes par $f$. Pour toute constante $c$ non nulle, posons $P(X)=c$ et $Q(X)=X$, alors $P(k c) \mid Q(k c)$ pour tout entier $k$, et donc $f(c)$ doit diviser $f(Q)=f(X)$ dans $\mathbb{Q}[X]$. Notamment, $\operatorname{deg}(f(c)) \leqslant \operatorname{deg}(f(X))$. Comme les degrés des images des constantes sont bornés, il existe donc une constante $C \neq 0$ dont le degré est maximal. Alors pour tout entier $k, f(C)$ divise $f(k C)$ dans $\mathbb{Q}[X]$, mais $\operatorname{deg}(f(k C)) \leqslant \operatorname{deg}(f(C))$, et donc il existe un rationnel $g(k)$ tel que $f(k C)=g(k) f(C)$.
|
| 661 |
+
Montrons que la fonction $g$ ainsi définie est, au signe en chaque point près, un polynôme à coefficients rationnels. Pour cela, remarquons que pour tout entier $k$, on a $|k C|=|P(k C)|$ avec $P(X)=X$, et donc $|f(k C)(k C)|=|f(X)(k C)|$, et donc
|
| 662 |
+
|
| 663 |
+
$$
|
| 664 |
+
|\boldsymbol{f}(X)(k C)|=|\boldsymbol{g}(k)||f(C)(k C)|
|
| 665 |
+
$$
|
| 666 |
+
|
| 667 |
+
Mais on sait déjà que $f(C)$ divise $f(X)$ dans $\mathbb{Q}[X]$, soit $\hat{g}$ leur quotient (qui est un polynôme dans $\mathbb{Q}[X]$ ), alors on a
|
| 668 |
+
|
| 669 |
+
$$
|
| 670 |
+
\forall k \in \mathbb{Z},|g(k)|=|\hat{g}(C k)|
|
| 671 |
+
$$
|
| 672 |
+
|
| 673 |
+
Appliquons maintenant la propriété de l'énoncé avec $P(X)=k C$ et $Q(X)=X+a$ pour $k$, $a$ deux entiers. On sait que $|\mathrm{P}(\mathrm{r})|=|\mathrm{Q}(\mathrm{r})|$ en $r=k C-a$, et on a donc
|
| 674 |
+
|
| 675 |
+
$$
|
| 676 |
+
\begin{gathered}
|
| 677 |
+
|f(X+a)(k C-a)|=|f(k C)(k C-a)| \\
|
| 678 |
+
|f(X+a)(k C-a)|=|\hat{g}(k C)||f(C)(k C-a)| .
|
| 679 |
+
\end{gathered}
|
| 680 |
+
$$
|
| 681 |
+
|
| 682 |
+
Or, deux polynômes dont les valeurs absolues sont égales en une infinité d'entiers sont égaux au signe près. En faisant varier $k$, on trouve donc l'égalité polynomiale (au signe près)
|
| 683 |
+
|
| 684 |
+
$$
|
| 685 |
+
f(X+a)(T)= \pm \hat{g}(T+a) f(C)(T)
|
| 686 |
+
$$
|
| 687 |
+
|
| 688 |
+
où le signe ne dépend pas de $T$, mais peut dépendre de $a$. A présent, on peut calculer les valeurs de $f$ en toutes les constantes : soit $n$ un entier, on a pour tout a entier,
|
| 689 |
+
|
| 690 |
+
$$
|
| 691 |
+
|f(n)(a)|=|f(X+n-a)(a)|=|\hat{g}(n) f(C)(a)|
|
| 692 |
+
$$
|
| 693 |
+
|
| 694 |
+
et on a donc l'égalité polynomiale $f(n)= \pm \hat{g}(n) \cdot f(C)$. Enfin, pour un polynôme $P$ quelconque, on peut écrire pour tout $r$ entier,
|
| 695 |
+
|
| 696 |
+
$$
|
| 697 |
+
|f(P)(r)|=|f(P(r))(r)|=|\hat{g}(P(r)) f(C)(r)|
|
| 698 |
+
$$
|
| 699 |
+
|
| 700 |
+
et donc $f(P)= \pm \hat{g}(P) \cdot f(C)$. Il reste à trouver les formes de $\hat{g}$ qui conviennent. On sait que si $m \mid n$ sont deux entiers, alors pour tout entier $r, f(m)(r) \mid f(n)(r)$, et donc $\hat{g}(m) f(C)(r) \mid \hat{g}(n) f(C)(r)$. En choisissant $r$ tel que $f(C)(r) \neq 0$ (possible car $f(C) \neq 0$ ), on obtient $\hat{g}(m) \mid \hat{g}(n)$. Mais alors pour tout entier $k$, on sait que lorsque $n \rightarrow+\infty, \hat{g}(n k) / \hat{g}(n)$ est un entier qui doit tendre vers $k^{\text {deg }(\hat{g})}$. Ainsi, pour $n$ assez grand, $\hat{\boldsymbol{g}}(\mathrm{nk})=\mathrm{k}^{\mathrm{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{n})$, et donc les polynômes $\hat{\boldsymbol{g}}(\mathrm{kX})$ et $\mathrm{k}^{\operatorname{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{X})$ sont égaux. Ainsi, on trouve $\hat{g}(k)=\hat{g}(1) k^{\operatorname{deg}(\hat{g})}$ et $\hat{g}$ est donc un monôme de la forme $\hat{g}(X)=a X^{n}$ pour un rationnel a et un entier positif $n$.
|
| 701 |
+
Ainsi, on a montré qu'il existait un polynôme $A=\operatorname{af}(C) \in \mathbb{Q}[X]$ et un entier $n$ positif ou nul tel que pour tout $P \in \mathbb{Z}[X]$,
|
| 702 |
+
|
| 703 |
+
$$
|
| 704 |
+
f(P)(X)= \pm A(X) P(X)^{n}
|
| 705 |
+
$$
|
| 706 |
+
|
| 707 |
+
où le signe dans le $\pm$ peut dépendre de $P$, mais pas de $X$. Avec $P=1$, on obtient que $A$ est un polynôme à coefficients entiers. De plus, en posant $P=2, Q=3$ dans l'hypothèse de l'énoncé, on obtient que pour tout entier $r$,
|
| 708 |
+
|
| 709 |
+
$$
|
| 710 |
+
A(r) 2^{n}\left|A(r) 3^{n} \Longleftrightarrow 2\right| 3
|
| 711 |
+
$$
|
| 712 |
+
|
| 713 |
+
Ceci implique que $A(r) \neq 0$ pour tout $r$, et que $n \geqslant 1$.
|
| 714 |
+
Supposons maintenant que f soit de la forme ci-dessus, avec $A \in \mathbb{Z}[X]$ ne s'annulant en aucun entier et $n \geqslant 1$. Alors on a bien que pour tout $r$ entier et $P, Q \in \mathbb{Z}[X]$,
|
| 715 |
+
|
| 716 |
+
$$
|
| 717 |
+
\mathrm{P}(\mathrm{r})\left|\mathrm{Q}(\mathrm{r}) \Longleftrightarrow \pm \mathrm{A}(\mathrm{r}) \mathrm{P}(\mathrm{r})^{n}\right| \pm \mathrm{A}(\mathrm{r}) \mathrm{Q}(\mathrm{r})^{\mathrm{n}}
|
| 718 |
+
$$
|
| 719 |
+
|
| 720 |
+
et donc f vérifie la condition de l'énoncé.
|
| 721 |
+
Commentaire des correcteurs : L'exercice a été très peu réussi, mais certains ont réussi à avoir des avancées partielles sur le problème.
|
| 722 |
+
|
French_STS/md/fr-Corrige-envoi-arithmetique-2023-2024.md
ADDED
|
@@ -0,0 +1,232 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOI 3 : ARITHMÉTIQUE <br> À RENVOYER AU PLUS TARD LE 11 FÉVRIER 2024
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2009 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
| 17 |
+
Solution de l'exercice 1 Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3):$ tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
|
| 18 |
+
|
| 19 |
+
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
|
| 20 |
+
Commentaire des correcteurs : L'exercice a été très bien réussi dans l'ensemble, cependant pas mal d'élèves pourraient aller plus vite en utilisant des modulos plutôt que les écritures explicites des divisions euclidiennes, les calculs seraient de fait allégés.
|
| 21 |
+
|
| 22 |
+
Exercice 2. Soit $n$ un entier vérifiant $n \geqslant 2$. On note $d$ le plus grand diviseur de $n$ différent de $n$. On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
| 23 |
+
Solution de l'exercice 2 Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que $d$ divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de $2:$ on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme $d$ est différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
|
| 24 |
+
On trouve alors $\mathrm{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $n+d$ n'est pas une puissance de 2 .
|
| 25 |
+
|
| 26 |
+
Commentaire des correcteurs : L'exercice a été très bien réussi, mais plusieurs copies ont oublié que 1 est un diviseur impair d'une puissance de 2.
|
| 27 |
+
|
| 28 |
+
Exercice 3. Déterminer tous les entiers $n \geqslant 0$ tels que $2023+n$ ! est un carré parfait.
|
| 29 |
+
Solution de l'exercice 3 Soit $n \geqslant 0$ tel que $2023+n$ ! est un carré parfait. Si $n \geqslant 4$, alors 4 divise $n$ !, donc $2023+\mathrm{n}!\equiv 2023 \equiv 3(\bmod 4)$. Or 3 n'est pas un carré modulo 4 (les carrés modulo 4 sont 0 et 1 ), donc on a une contradiction. Ainsi $n \leqslant 3$.
|
| 30 |
+
Notons que $44^{2}=1936<2023+0!=2023+1!=2024<2023+2!=2025=45^{2}<2023+3!+2029<$ $2116=46^{2}$. Ainsi pour $\mathrm{n}=0,1,3,2023+\mathrm{n}$ ! n'est pas un carré, mais pour $\mathrm{n}=2$ c'est un carré. Ainsi $2023+\mathrm{n}$ ! est un carré si et seulement si $n=2$.
|
| 31 |
+
|
| 32 |
+
Commentaire des correcteurs : L'exercice a été très bien réussi. Quelques copies ont oublié le cas $\mathrm{n}=$ 0 .
|
| 33 |
+
|
| 34 |
+
Exercice 4. Déterminer tous les triplets $(p, q, r)$ de nombres premiers tels que $p+q^{2}=r^{4}$.
|
| 35 |
+
Solution de l'exercice 4 Notons que l'équation se réécrit $p=\left(r^{2}\right)^{2}-q^{2}=\left(r^{2}-q\right)\left(r^{2}+q\right)$. Come $r^{2}+q$ est strictement positif, et $p$ aussi, $r^{2}-q$ aussi. En particulier, d'après l'équation précédente, on a que $r^{2}-q=1$ et $r^{2}+q=p$. Si $r$ et $q$ sont impairs, alors $r^{2}-q$ est pair, ce qui est contradictoire. Ainsi parmi $r$ et $q$, un est pair, donc vaut 2 car $q$ et $r$ sont premiers.
|
| 36 |
+
Si $r=2$, alors $r^{2}-q=1$, donc $q=4-1=3$. De plus $p=q+r^{2}=7$, donc $(p, q, r)=(7,3,2)$ est une éventuelle solution.
|
| 37 |
+
Si $q=2$, alors $r^{2}=q+1=3$ ce qui est impossible.
|
| 38 |
+
Réciproquement, pour $(\mathfrak{p}, \mathbf{q}, \mathrm{r})=(7,3,2), \mathfrak{p}+\mathrm{q}^{2}=7+9=16=2^{4}$.
|
| 39 |
+
Commentaire des correcteurs : L'exercice est très bien résolu. Beaucoup d'approches différentes de celle proposée dans le corrigé étaient envisageables, et les élèves les ont toujours bien mises en oeuvre.
|
| 40 |
+
|
| 41 |
+
Exercice 5. Déterminer tous les quadruplets ( $a, b, c, d$ d'entiers positifs avec $a, b, c$ strictement positifs tels que
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
\begin{aligned}
|
| 45 |
+
& \operatorname{PPCM}(b, c)=a+d \\
|
| 46 |
+
& \operatorname{PPCM}(c, a)=b+d \\
|
| 47 |
+
& \operatorname{PPCM}(a, b)=c+d
|
| 48 |
+
\end{aligned}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Solution de l'exercice 5 Le système étant symétrique, on suppose que c est le maximum de $\mathrm{a}, \mathrm{b}$ et c . Comme c divise $\operatorname{PPCM}(\mathrm{b}, \mathrm{c}), \mathrm{c}$ divise $\mathrm{a}+\mathrm{d}$. Comme c divise $\operatorname{PPCM}(\mathrm{c}, \mathrm{a}), \mathrm{c}$ divise $\mathrm{b}+\mathrm{d}$, donc c divise $a+d-(b+d)=a-b$. Or $-c<a-b<c$ donc $a=b$. La dernière ligne donne alors $a=\operatorname{PPCM}(a, b)=c+d \geqslant c$. Pour avoir égalité, on a donc $d=0$ et $a=c$.
|
| 52 |
+
Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}$ et $\mathrm{d}=0$, chaque équation équivaut à $\mathrm{a}=\mathrm{a}+0$, qui est vrai. Les quadruplets solution sont donc les ( $\mathbf{a}, \mathrm{a}, \mathrm{a}, 0$ ) pour $a \in \mathbb{N}^{*}$.
|
| 53 |
+
|
| 54 |
+
Commentaire des correcteurs: L'exercice a été bien réussi dans l'ensemble. Cependant beaucoup d'élèves oublient que $A$ divise $B$ n'implique pas $A \leqslant B$ : cela ne marche que si $A$ est positif et $B$ strictement positif. Si B est uniquement positif, il peut être nul. Et beaucoup d'élèves raisonnent par implication, mais oublient de vérifier les solutions à la fin : en compétition cela coûte systématiquement un point.
|
| 55 |
+
|
| 56 |
+
Exercice 6. Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu' un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
| 57 |
+
|
| 58 |
+
Solution de l'exercice 6 Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} c_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
|
| 59 |
+
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, $d$ des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
|
| 60 |
+
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
|
| 61 |
+
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
|
| 62 |
+
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
|
| 63 |
+
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
|
| 64 |
+
|
| 65 |
+
Commentaire des correcteurs: L'idée du raisonnement derrière l'exercice a généralement été comprise, mais les solutions ont été assez mal rédigées dans leur ensemble, préférant des descriptions informelles à des énoncés précis et soigneusement démontrés. Rédiger de telles démonstrations au collège n'est certainement pas chose facile, mais est tout de même nécessaire pour éviter quelques écueils. Si ceux-ci étaient mineurs et relativement faciles à contourner dans ce problème (pour peu qu'on les vît, ce qui était rare), ce n'est pas toujours le cas et des conclusions 'intuitivement vraies" peuvent s'avérer complètement fausses parce que des étapes cruciales de raisonnement n'auraient pas été envisagées. Quelques élèves n'ont pas compris la question : il ne s'agissait pas ici de montrer que l'on pouvait choisir $p=3$ une infinité de fois avec un choix judicieux d'opérations. Il fallait montrer que quelle que soit la suite d'opérations choisie à partir de n'importe quel entier (et même si on essayait d'éviter de le faire), on doit choisir $p=3$ une infinité de fois. Les autres élèves ont, pour la plupart, compris que les facteurs premiers de $n$ devenaient de plus en plus petits, puisqu'un facteur $p>2$ était remplacé par le nombre pair $p+1$, dont tous les facteurs premiers étaient strictement inférieurs à $p$. Cette intuition est correcte, mais ne doit pas figurer telle quelle dans une copie, parce que cet énoncé n'est pas clair : en quel sens les facteurs premiers devenaient-ils de plus en plus petits? Leur maximum? Leur nombre? Une espèce de combinaison des deux, dirait-on intuitivement, mais encore faut-il la décrire! Tout le problème d'employer cette intuition informelle comme une étape de raisonnement est qu'il semble naturel d'en déduire qu'au bout d'un certain moment, l'entier écrit au tableau n'a plus que des 2 et des 3 comme facteurs premiers. Ceci n'est pas vrai, puisqu'on peut par exemple multiplier une suite valide par 5 . Cela peut paraître un contre-exemple trivial, mais cela montre qu'il existe des contre-exemples, et donc qu'il peut exister des contre-exemples plus subtils que celui-ci. Le corrigé permet de trouver une des façons de formaliser cette intuition, en explicitant une quantité entière qui ne peut que décroître (un "mono-variant") et qui doit donc être constante à partir d'un certain moment. Quelques élèves ont pris une autre approche, consistant essentiellement à raisonner par récurrence (forte) en se reposant sur l'observation suivante : si $\mathrm{n}=\mathrm{ab}$, alors on peut aussi considérer qu'on a chaque jour deux nombres $a$ et $b$ écrits sur deux tableaux différents, et qu'on effectue chaque jour l'opération sur l'un des deux tableaux. Partant, l'un ou l'autre des entiers est modifié selon l'opération une infinité de fois et on a donc par hypothèse de récurrence
|
| 66 |
+
utilisé $\mathrm{p}=3$ une infinité de fois.
|
| 67 |
+
|
| 68 |
+
Exercice 7. Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
|
| 69 |
+
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
| 70 |
+
Solution de l'exercice 7 Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
|
| 71 |
+
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
|
| 72 |
+
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
|
| 73 |
+
Notons c la couleur de n . On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
|
| 74 |
+
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
|
| 75 |
+
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
|
| 76 |
+
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur c ce qui conclut.
|
| 77 |
+
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
|
| 78 |
+
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
|
| 79 |
+
Ceci conclut l'hérédité.
|
| 80 |
+
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$. Il existe $\ell \in\{0 \ldots, \boldsymbol{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
|
| 81 |
+
|
| 82 |
+
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc).
|
| 83 |
+
|
| 84 |
+
Exercice 8. Déterminer tous les couples ( $a, p$ ) d'entiers strictement positifs, avec $p$ premier, tels que pour tout couple ( $m, n$ ) d'entiers strictement positifs, le reste de la division euclidienne de $a^{2^{n}}$ par $p^{n}$ est non nul, et est le même que celui de $a^{2^{m}}$ par $p^{m}$.
|
| 85 |
+
Solution de l'exercice 8 En prenant $\mathrm{n}=1$ dans l'énoncé, on obtient que pour tout entier m strictement positif, le reste de $a^{2^{m}}$ modulo $p^{m}$ vaut celui de $a^{2}$ modulo $p$, donc est constant. Notons $r$ ce reste : on a donc $r \neq 0$ ainsi $r \in\{1, \ldots, p-1\}$. On a $a^{2} \equiv r(\bmod p)$ et $a^{4} \equiv r\left(\bmod p^{2}\right)$, donc $a^{4} \equiv r(\bmod p)$, donc $r^{2} \equiv r(\bmod p)$. Ainsi comme $r$ est premier avec $p, r$ est inversible $\bmod p$, donc $r \equiv 1(\bmod p)$. On a donc $a^{2^{m}} \equiv 1\left(\bmod p^{m}\right)$ pour tout $m$. En particulier $a^{2} \equiv 1(\bmod p)$
|
| 86 |
+
Or
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
Si $p \geqslant 3$, pour tout $k \geqslant 1, a^{2^{k}}+1 \equiv 1^{2^{k-1}}+1 \equiv 2 \not \equiv 0(\bmod p)$, donc si $a \neq 1 V_{p}\left(a^{2^{m}}-1\right)=$ $V_{p}\left(a^{2}-1\right)$. Or pour tout $m, p^{m}$ divise $a^{2^{m}}-1$, donc $m \leqslant V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)$ ce qui est absurde car $V_{p}\left(a^{2}-1\right)$ est fini. Ainsi $a=1$. Réciproquement pour tout $p$ premier, $a=1$ est solution car le reste de $1^{2^{m}}$ modulo $p^{m}$ vaut toujours 1 et est non nul.
|
| 93 |
+
Si $p=2$ et $a \neq 1, a^{2} \equiv 1(\bmod 2)$, donc $a$ est impair. Réciproquement si a est impair, rappelons que
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
Le produit de droite contient $m$ termes tous pairs, donc est divisible par $2^{m}$. Ainsi pour tout $n$, le reste de $a^{2^{n}}$ modulo $2^{n}$ vaut 1 et est non nul, donc tous les couples de la forme ( $a, 2$ ) avec a impair sont solutions.
|
| 100 |
+
Ainsi les couples solutions sont ceux de la forme ( $1, \mathfrak{p}$ ) pour $p \geqslant 3$ et $(a, 2)$ pour a impair.
|
| 101 |
+
Solution alternative $A$ partir du fait que $a^{2^{m}} \equiv 1\left(\bmod p^{m}\right)$ pour tout $m$, on a comme $p$ divise $a^{2}-1$, par LTE si $p \geqslant 3$ que si $a>1, V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)+V_{p}\left(2^{m-1}\right)=V_{p}\left(a^{2}-1\right)$. En particulier, comme $V_{p}\left(a^{2^{m}}-1\right) \geqslant m$ pour tout $m \geqslant 1, V_{p}\left(a^{2}-1\right) \geqslant m$ pour tout $m$ ce qui est absurde donc $a=1$. Réciproquement, $a=1$ et $p \geqslant 3$ convient comme dans la solution précédente.
|
| 102 |
+
Pour le cas $p=2$, de même que précédemment on a $p$ impair, donc 4 divise $p^{2}-1=(p-1)(p+1)$, donc par LTE, comme 4 divise $a^{4}-1$, si $a>1 V_{2}\left(a^{2^{m}}-1\right)=V_{2}\left(a^{2}-1\right)+V_{2}\left(2^{m-1}\right) \geqslant 2+m-1=m+1$, ainsi $a^{2^{m}}-1$ est divisible par $2^{m}$ pour tout m , et on conclut de la même façon que précédemment.
|
| 103 |
+
|
| 104 |
+
Commentaire des correcteurs : L'exercice est résolu de manière inégale par ceux qui s'y sont essayés. En effet, certains loupent certaines solutions (soit le cas $p=2$ soit le cas $a=1$ : les petites valeurs devraient pourtant permettre de repérer ces solutions. Attention aussi aux utilisations du LTE : le théorème LTE a des hypothèses, il faut les vérifier sous peine d'écrire des choses fausses.
|
| 105 |
+
|
| 106 |
+
Exercice 9. Déterminer tous les quadruplets $(x, y, z, t)$ d'entiers strictement positifs tels que $2^{x} 3^{y}+$ $5^{z}=7^{\mathrm{t}}$ 。
|
| 107 |
+
Solution de l'exercice 9 Supposons $x \geqslant 2$, en regardant modulo $4,1 \equiv 2^{x} 3^{y}+5^{z} \equiv 7^{\mathrm{t}} \equiv(-1)^{\mathrm{t}}$ $(\bmod 4)$, donc $t$ est pair.
|
| 108 |
+
L'équation prise modulo 3 devient $0+(-1)^{z} \equiv 1(\bmod 3)$ donc $z$ est pair. En particulier, posons $z=$ $2 \mathrm{~b}, \mathrm{t}=2 \mathrm{c}$, on a alors $2^{\mathrm{x}} 3^{\mathrm{y}}=\left(7^{\mathrm{b}}-5^{\mathrm{c}}\right)\left(7^{\mathrm{b}}+5^{\mathrm{c}}\right)$. Le pgcd de $7^{\mathrm{b}}+5^{\mathrm{c}}$ et $7^{\mathrm{b}}-5^{\mathrm{c}}$ divise leur somme et leur produit, donc il divise $2^{x} 3^{y}$ et $2 \times 7^{\text {b }}$, ainsi il divise 2 . Or $7^{b}+5^{c}$ et $7^{b}-5^{c}$ sont égaux mod 2 donc ils ont la même parité, et leur produit est pair, donc chacune est pair, leur pgcd vaut 2 . Comme
|
| 109 |
+
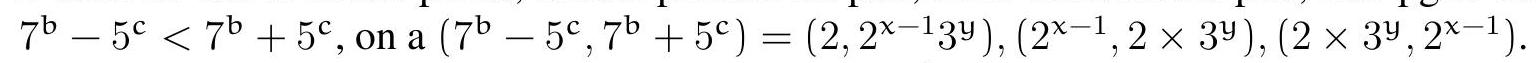
|
| 110 |
+
|
| 111 |
+
- Dans le premier cas, si $\mathrm{c} \geqslant 2$, modulo $25,7^{\mathfrak{b}} \equiv 2(\bmod 25)$. Or les puissances de 7 valent $1,7,-1,-7$ modulo 25 , mais jamais 2 . Comme $\mathrm{c} \neq 0$ car $z \neq 0$, on a donc $\mathrm{c}=1$, donc $7^{\mathrm{b}}=$ $5+2=7$, donc $b=1$. On a donc $12=2^{x-1} 3^{y}$ donc $(x, y, z, t)=(3,1,2,2)$, qui réciproquement est solution car $2^{3} \times 3+5^{2}=24+25=49=7^{2}$.
|
| 112 |
+
- Dans le second cas $\left(7^{\text {b }}-5^{\mathrm{c}}, 7^{\text {b }}+5^{\mathrm{c}}\right)=\left(2^{\mathrm{x}-1}, 2 \times 3^{y}\right)$. Par parité, on a $x \geqslant 2$, et comme le cas où $x=2$ est déjà couvert par le cas précédent, on peut supposer $x \geqslant 3$. On pose $x^{\prime}=x-1$, on a alors $7^{\mathrm{b}}=5^{\mathrm{c}}+2^{\mathrm{x}^{\prime}}$ avec $x^{\prime} \geqslant 2$. En regardant modulo $4,(-1)^{\mathrm{b}} \equiv 1(\bmod 4)$, donc b est pair. En regardant modulo $5,2^{\mathrm{b}} \equiv 2^{\mathrm{x}^{\prime}}(\bmod 5)$. Or les puissances de 2 alternent entre 1, 2, 4, $3 \bmod 5$, donc deux puissances de 2 ont même valeur modulo 5 si et seulement si leur exposant sont égaux modulo 4 , donc b et $x^{\prime}$ ont même parité. En regardant modulo $3,1 \equiv(-1)^{\mathfrak{c}}+(-1)^{x^{\prime}}(\bmod 3)$ donc c et $x^{\prime}$ sont impairs. Ceci contredit le fait que b et $x^{\prime}$ ont même parité.
|
| 113 |
+
Avant de traiter le dernier cas, résolvons l'équation dans le cas $x=1$ : on a $2 \times 3^{y}+5^{z}=7^{\mathrm{t}}$. Modulo 3 , on obtient comme avant que $z$ est pair, donc $5^{z} \equiv 25^{z / 2} \equiv 1(\bmod 8)$. En particulier modulo 8 , $(-1)^{\mathrm{t}} \equiv 1+2 \times 3^{y}$. Le terme de droite vaut 3 si $y$ est pair, -1 sinon, donc $t$ est impair et $y$ est impair $\left(\operatorname{car} 3^{2} \equiv 1(\bmod 8)\right)$. On a alors en regardant modulo 5 , comme les puissances de 7 valent $1,2,4,3,1$ et les puissances de 3 valent $1,3,4,2,1$, on a $7^{\mathrm{t}} \equiv 2$ ou 3 car t est impair, et 7 d'ordre 4 (qui est pair) modulo 5 . Comme y est impair, on a $2 \times 3^{y} \equiv 1$ ou 4 modulo 5 car l'ordre de 3 modulo 5 est pair. Or l'équation modulo 5 donne $2 \times 3^{y} \equiv 7^{\mathrm{t}}$ ce qui est impossible. Il n'y a donc pas de solution avec $x=1$. Pour le troisième cas $\left(7^{\mathfrak{b}}-5^{\mathfrak{c}}, 7^{\mathfrak{b}}+5^{\mathrm{c}}\right)=\left(2 \times 3^{y}, 2^{\mathrm{x}-1}\right)$, on a $7^{\mathrm{b}}-5^{\boldsymbol{c}}=2 \times 3^{y}$. Comme $\mathrm{c}>0$, on est ramené au cas précédent il n'y a pas de solution.
|
| 114 |
+
Ainsi la seule solution est $(x, y, z, t)=(3,1,2,2)$.
|
| 115 |
+
Commentaire des correcteurs : L'exercice était très difficile et a été très peu abordé. Il est tout de même regrettable que les quelques copies qui réussissent à trouver la factorisation ne pensent que rarement à considérer le pgcd de $7^{z}+5^{\mathrm{t}}$ et $7^{z}-5^{\mathrm{t}}$ (ou même simplement la parité de ces deux nombres!) et se lancent tête baissée dans de grandes disjonctions de cas ou dans des utilisations abusives du théorème de Zsigmondy, que beaucoup auraient pu s'épargner (un seul élève a su utiliser ce théorème vraiment efficacement).
|
| 116 |
+
|
| 117 |
+
|
| 118 |
+
## Exercices Seniors
|
| 119 |
+
|
| 120 |
+
Exercice 10. Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
| 121 |
+
Solution de l'exercice 10 Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3)$ : tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
|
| 122 |
+
|
| 123 |
+
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
|
| 124 |
+
Commentaire des correcteurs: Exercice très bien réussi.
|
| 125 |
+
|
| 126 |
+
Exercice 11. Soit n un entier vérifiant $\mathrm{n} \geqslant 2$. On note d le plus grand diviseur de n différent de n . On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
| 127 |
+
Solution de l'exercice 11 Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de 2 : on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme dest différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
|
| 128 |
+
On trouve alors $\boldsymbol{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
| 129 |
+
|
| 130 |
+
Commentaire des correcteurs: Exercice bien réussi, cependant quelques élèves vont un peu trop vite et oublient des étapes, essentielles pour aboutir à des contradictions, alors injustifiées.
|
| 131 |
+
|
| 132 |
+
Exercice 12. Déterminer tous les quadruplets ( $a, b, c, d$ ) d'entiers positifs avec $a, b, c$ strictement positifs tels que
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
\begin{aligned}
|
| 136 |
+
& \operatorname{PPCM}(b, c)=a+d \\
|
| 137 |
+
& \operatorname{PPCM}(c, a)=b+d \\
|
| 138 |
+
& \operatorname{PPCM}(a, b)=c+d
|
| 139 |
+
\end{aligned}
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
Solution de l'exercice 12 Le système étant symétrique, on suppose que c est le maximum de $\mathrm{a}, \mathrm{b}$ et c . Comme c divise $\operatorname{PPCM}(\mathrm{b}, \mathrm{c})$, c divise $a+d$. Comme c divise $\operatorname{PPCM}(\mathrm{c}, \mathrm{a})$, c divise $b+\mathrm{d}$, donc c divise $a+d-(b+d)=a-b$. Or $-c<a-b<c$ donc $a=b$. La dernière ligne donne alors $a=\operatorname{PPCM}(a, b)=c+d \geqslant c$. Pour avoir égalité, on a donc $d=0$ et $a=c$.
|
| 143 |
+
Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}$ et $\mathrm{d}=0$, chaque équation équivaut à $\mathrm{a}=\mathrm{a}+0$, qui est vrai. Les quadruplets solution sont donc les $(a, a, a, 0)$ pour $a \in \mathbb{N}^{*}$.
|
| 144 |
+
|
| 145 |
+
Commentaire des correcteurs: L'exercice est très bien réussi, cependant quelques élèves ont oublié de vérifier que les solutions trouvées étaient solutions du système ce qui les a pénalisés.
|
| 146 |
+
|
| 147 |
+
Exercice 13. Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu'un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
| 148 |
+
Solution de l'exercice 13 Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} \mathbf{c}_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
|
| 149 |
+
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, d des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
|
| 150 |
+
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
|
| 151 |
+
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
|
| 152 |
+
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
|
| 153 |
+
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
|
| 154 |
+
|
| 155 |
+
Commentaire des correcteurs : Certains élèves ont mal compris l'énoncé : il s'agissait de prouver que l'on était obligé de choisir $p=3$ une infinité de fois quels que soient les choix effectués, pas que l'on pouvait s'arranger pour que ce soit le cas. L'exercice est généralement bien abordé par ceux qui l'ont correctement interprété, mais de trop nombreux élèves manquent de rigueur. L'enjeu était de trouver un argument rigoureux (donc a priori un monovariant, que ce soit celui proposé par le corrigé, l'ordre lexicographique inversé des exposants ou beaucoup d'autres possibilités) pour clarifier la phrase lue dans de trop nombreuses copies : "les facteurs premiers décroissent". Cette phrase dénuée de sens mathématique ne constitue en aucun cas un argument recevable, il faut clarifier l'intuition qui se cache derrière. C'est un écueil que l'on croise souvent en combinatoire : il est parfois délicat de passer de l'intuition à l'argument rigoureux, et souvent une partie de la difficulté de l'exercice réside justement dans cette étape.
|
| 156 |
+
|
| 157 |
+
Exercice 14. Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
|
| 158 |
+
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
| 159 |
+
Solution de l'exercice 14 Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
|
| 160 |
+
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
|
| 161 |
+
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
|
| 162 |
+
Notons c la couleur de $\boldsymbol{n}$. On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
|
| 163 |
+
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
|
| 164 |
+
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
|
| 165 |
+
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur $c$ ce qui conclut.
|
| 166 |
+
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
|
| 167 |
+
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
|
| 168 |
+
Ceci conclut l'hérédité.
|
| 169 |
+
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$. Il existe $\ell \in\{0 \ldots, \mathfrak{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
|
| 170 |
+
|
| 171 |
+
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc). Il est crucial que les élèves se relisent à froid : certaines copies n'ont vraiment pas de sens en les relisant à froid, et plusieurs élèves auraient évité une déconvenue en relisant leur production à tête reposée.
|
| 172 |
+
|
| 173 |
+
Exercice 15. Soit $\left(P_{n}\right)_{n \in \mathbb{N}}$ une suite de polynômes à coefficients entiers. On suppose qu'il existe un polynôme $Q$ unitaire à coefficient entier tel que $P_{n+1}-P_{n}=Q$ pour tout $n \geqslant 0$. On suppose de plus que pour tout $\mathrm{n} \geqslant 0, \mathrm{P}_{\mathrm{n}}$ a une racine entière. Montrer qu'on est dans un des deux cas suivants :
|
| 174 |
+
|
| 175 |
+
- $P_{0}$ et $Q$ ont une racine entière en commun
|
| 176 |
+
- Il existe un polynôme à coefficients entiers R tel que $\mathrm{P}_{0}=R Q$ et le degré de R est 1 .
|
| 177 |
+
|
| 178 |
+
Solution de l'exercice 15 Supposons que $\mathrm{P}_{0}$ et Q n'ont pas de racines entière en commun. Notons que par récurrence immédiate $P_{n}=P_{0}+n Q$ pour tout $n \geqslant 0$. Notons $x_{n}$ une racine entière de $P_{n}$ pour tout $n \geqslant 0$, on a que $n Q\left(x_{n}\right)=-P_{0}\left(x_{n}\right)$, donc $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right)$.
|
| 179 |
+
Notons que si $x_{k}=x_{j}$ avec $k \neq j$, alors $P_{0}\left(x_{k}\right)+k Q\left(x_{k}\right)=0=P_{0}\left(x_{j}\right)+j Q\left(x_{j}\right)$, donc $(k-j) Q\left(x_{k}\right)=$ 0 , donc $Q\left(x_{k}\right)=0$. Ainsi $P_{0}\left(x_{k}\right)=0$, donc $P_{0}$ et $Q$ ont une racine entière en commun, ce qui est contradictoire. Ainsi la suite $\left(x_{k}\right)_{k \geqslant 0}$ est injective donc prend des valeurs arbitrairement grandes.
|
| 180 |
+
Faisons la division euclidienne de $\mathrm{P}_{0}$ par Q . Comme Q est unitaire à coefficient entier (et $\mathrm{P}_{0}$ à coefficients entiers), il existe des polynômes $R$ et $S$ à coefficients entiers tels que $P_{0}=Q R+S$ avec $S$ de degré inférieur ou égal à Q.
|
| 181 |
+
En évaluant en $x_{n}, P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)+S\left(x_{n}\right)$, donc comme $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right), Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)=P_{0}\left(x_{n}\right)-Q\left(x_{n}\right) R\left(x_{n}\right)$. Or pour tout entier $k$ avec $|k|$ assez grand, comme le degré de $S$ est strictement inférieur à celui de $\mathrm{Q},|S(k)|<|\mathrm{Q}(\mathrm{k})|$. Comme la suite ( $\mathrm{x}_{\mathrm{n}}$ ) prend des valeurs arbitrairement grande, il existe une infinité de $n$ tels que $\left|S\left(x_{n}\right)\right|<\left|Q\left(x_{n}\right)\right|$. Comme $Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)$, on en déduit qu'il existe une infinité de $n$ tels que $S\left(x_{n}\right)=0$. Comme la suite est injective, $S$ a une infinité de racine, donc $S=0$. Ainsi $P_{0}=Q R$.
|
| 182 |
+
De plus, en évaluant en $x_{n}$, on a $-n Q\left(x_{n}\right)=P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)$. Si $Q\left(x_{n}\right)=0$, alors $P_{0}\left(x_{n}\right)=0$ et $P_{0}$ et $Q$ ont une racine en commun, contradiction. Ainsi $Q\left(x_{n}\right) \neq 0$, donc $R\left(x_{n}\right)=-n$. Ainsi pour tout entier $N \geqslant 0$, il existe au moins $N$ entiers $y$ tels que $R(y) \in[-N, N]$.
|
| 183 |
+
Or si le degré de $R$ noté $d$ vaut au moins 2 , pour un $M$ assez grand et pour un $C>0$, on a pour tout $x$ vérifiant $|x| \geqslant M,|R(x)| \geqslant C|x|^{d}$. Ainsi pour $N$ assez grand, le nombre d'entier tel que $|R(x)| \leqslant N$ est plus petit que $2 M+1$ (le nombre d'entiers dans $[-M, M]$ ), auquel on ajoute le nombre d'entiers $|x| \geqslant M$ tel que $|P(x)| \leqslant N$. Pour ces $x$, on a $C|x|^{d} \leqslant N$ donc $|x| \leqslant(N / C)^{1 / d}$. Ainsi on a au plus $2 M+1+2(N / c)^{1 / d}+1$ entiers tels que $P(y) \in[-n, n]$, ce qui est strictement inférieurs à $N$ pour $N$ assez grand, ce qui est contradictoire.
|
| 184 |
+
Ainsi le degré de $R$ est au plus 1 . Comme on a $R\left(x_{n}\right)=-n$ pour tout $n$, le degré de $R$ vaut 1 .
|
| 185 |
+
Alternativement, pour prouver que le degré de $R$ valait $n$, on pouvait remarquer que pour tout $n, x_{n+1}-x_{n}$ divise $R\left(x_{n+1}\right)-R\left(x_{n}\right)=-1$. En particulier $x_{n+1}-x_{n}= \pm 1$ pour tout $n$. Comme la suite $\left(x_{n}\right)$ est injective, on ne peut avoir $x_{n+1}-x_{n}=1$ et $x_{n+2}-x_{n+1}=-1$, ou avoir $x_{n+1}-x_{n}=-1$ et $x_{n+2}-x_{n+1}=1$ sinon $x_{n}=x_{n+2}$. Ainsi on a facilement par récurrence que soit pour tout $n$, $x_{n+1}-x_{n}=1$, et donc $x_{n}=x_{0}+n\left(x_{1}-x_{0}\right)$, soit $x_{n+1}-x_{n}=-1$, et donc $x_{n}=x_{0}-n\left(x_{1}-x_{0}\right)$.
|
| 186 |
+
Dans le premier cas, en posant $S(X)=R\left(x_{0}+X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}+x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{y-x_{0}}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{y-x_{0}}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
|
| 187 |
+
Dans le second cas, en posant $S(X)=R\left(x_{0}-X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}-x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{x_{0}-y}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{x_{0}-y}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
|
| 188 |
+
|
| 189 |
+
Commentaire des correcteurs: L'exercice a été très bien traité par les élèves qui l'ont abordé. Presque tous ont bien vu qu'un R de degré au moins 2 " croirait et décroirait trop vite" pour attendre tous les entiers négatifs, mais certains n'ont pas rendu cette idée, certes vraie, rigoureuse. De plus, il faut garder
|
| 190 |
+
en tête qu'on peut considérer la divison euclidienne de $P_{0}$ par $Q$ dans $Z[X]$ seulement parce que $Q$ est unitaire. Enfin, ne jamais oublier les cas triviaux : il est dommage de voir des élèves perdre un point pour ne pas avoir préciser que $R$ ne pouvait être constant.
|
| 191 |
+
|
| 192 |
+
Exercice 16. Soit $p$ un nombre premier et $n$ un entier vérifiant $n \geqslant 2$.
|
| 193 |
+
|
| 194 |
+
- A quelle condition existe-t-il $n+1$ entiers (pas forcément distincts) tels que, pour tout choix de $n$ entiers parmi les $\mathrm{n}+1$, leur somme est une puissance de p ?
|
| 195 |
+
- A quelle condition existe-t-il $n+1$ entiers strictement positifs (pas forcément distincts) tels que, pour tout choix de $n$ entiers parmi les $n+1$, leur somme est une puissance de $p$ ?
|
| 196 |
+
Solution de l'exercice 16 Essayons d'analyser l'énoncé. Posons $x_{1}, \ldots, x_{n+1}$ les entiers tels que pour tout choix de $n$ entiers parmi les $n+1$ entiers, alors leur somme est une puissance de $p$. Il existe donc $\alpha_{1}, \ldots, \alpha_{n+1}$ des entiers positifs tels que $x_{2}+\cdots+x_{n+1}=p^{\alpha_{1}}, x_{1}+x_{3}+\cdots+x_{n+1}=p^{\alpha_{2}}, \ldots, x_{1}+$ $\cdots+x_{n}=p^{\alpha_{n+1}}$.
|
| 197 |
+
En particulier, notons déjà que $p^{\alpha_{i}}=x_{1}+\cdots+x_{n+1}-x_{i}$ pour tout $i \in\{1, \ldots, n+1\}$ et que $p^{\alpha_{1}}+$ $\cdots+p^{\alpha_{n+1}}=\mathfrak{n}\left(x_{1}+\cdots+x_{n+1}\right)$, donc pour tout $i \in\{1, \ldots, n+1\}, x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n^{2}}-p^{\alpha_{i}}$.
|
| 198 |
+
Réciproquement, si on se donne $\alpha_{1}, \ldots, \alpha_{n+1}$ des entiers positifs tels que $x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n}-p^{\alpha_{i}}$ pour tout $i \in\{1, \ldots, n+1\}$, alors on voit que $x_{1}+\cdots+x_{i-1}+x_{i+1}+\cdots+x_{n+1}=p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}-$ $p^{\alpha_{1}}-\cdots-p^{\alpha_{i-1}}-p^{\alpha_{i+1}}-\cdots-p^{\alpha_{n+1}}=p^{\alpha_{i}}$.
|
| 199 |
+
La question revient donc à la suivant : existe-t-il des entiers positifs $\alpha_{1}, \ldots, \alpha_{n+1}$ tels que $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$ pour la première question, et pour la seconde question tels que $\frac{\mathrm{p}^{\alpha_{1}+\cdots+p^{\alpha_{n+1}}}}{n}-\mathrm{p}^{\alpha_{i}}>0$, i.e. $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ pour tout $i$.
|
| 200 |
+
|
| 201 |
+
Essayons de répondre d'abord à la première partie de la question : à quelle condition sur n existe-t-il $\alpha_{1}, \ldots, \alpha_{n+1}$ tels que $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$ ? Déjà, modulo $p-1$, on a $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \equiv n+1$ $(\bmod p-1)$. Notons $d$ le pgcd de $p-1$ et $n$, alors si $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$, comme $d$ divise $p-1$, d divise aussi $n+1$. Comme divise $n$, on obtient que $d$ divise $n+1-n=1$, donc $d=1$. Ainsi il faut que $n$ et $p-1$ sont premiers entre eux.
|
| 202 |
+
Réciproquement si $n$ et $p-1$ sont premiers entre eux, soit $x \in\{1, \ldots, n+1\}$ on prend $\alpha_{1}=\cdots=\alpha_{x}=0$ et $\alpha_{x+1}=\cdots=\alpha_{n+1}=1$. On cherche donc un certain $x$ tel que $x$ tel que $n$ divise $x+(n+1-x) p$, i.e. $x$ tel que $x+p-x p \equiv 0\left(\bmod \mathfrak{n}\right.$ ), soit $x \equiv p(p-1)^{-1}(\bmod \mathfrak{n})$ (qui existe car $p-1$ et $n$ sont premiers entre eux). On peut prendre un tel $x$ dans $\{1, \ldots, n\}$ tel que la précédente congruence est vraie. Ainsi la condition pour la première question est exactement $n$ et $p-1$ sont premiers entre eux.
|
| 203 |
+
Pour la seconde question, on cherche de plus à avoir $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ pour tout $i$. Quitte à réordonner les $\alpha_{i}$, on peut supposer $\alpha_{1} \leqslant \alpha_{2} \leqslant \cdots \leqslant \alpha_{n+1}$, la condition est équivalente à $p^{\alpha_{1}}+\cdots+$ $p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$. Si $\alpha_{2}<\alpha_{n+1}$, on a:
|
| 204 |
+
|
| 205 |
+
$$
|
| 206 |
+
p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \leqslant 2 p^{\alpha_{2}}+(n-1) p^{\alpha_{n+1}} \leqslant p^{\alpha_{2}+1}+(n-1) p^{\alpha_{n+1}} \leqslant n p^{\alpha_{n+1}}
|
| 207 |
+
$$
|
| 208 |
+
|
| 209 |
+
Ainsi on a $\alpha_{2} \geqslant \alpha_{n+1}$, donc $\alpha_{2}=\cdots=\alpha_{n+1}$. Dans ce cas, il est clair que $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$ est vérifié. Il reste donc à chercher à quelle condition sur $n$ existe-t-il $\alpha_{1} \leqslant \alpha_{2}$ deux entiers positifs tels que $n$ divise $p^{\alpha_{1}}+n p^{\alpha_{2}}$ donc à quelle condition $n$ divise $p^{\alpha_{1}}$. Il est alors clair que les solutions sont les puissances de $p$. Ainsi la condition pour la seconde question est que $n$ soit une puissance de $p$.
|
| 210 |
+
|
| 211 |
+
Commentaire des correcteurs : Chacune des parties de cet exercice a été globalement réussie par les élèves qui l'ont abordée. Néanmoins, plusieurs élèves, après avoir réussi l'une des deux parties, ont cru que l'autre n'en était qu'un simple corollaire, ce qui n'était pas vrai ; ils l'ont donc mal traitée, aboutissant à des résultats incorrects. C'est dommage!
|
| 212 |
+
|
| 213 |
+
Exercice 17. Soient $a, b$ deux entiers tels que $\mathrm{pgcd}(\mathrm{a}, \mathrm{b}) \mathrm{a}$ au moins deux facteurs premiers distincts. Soit $S=\{x \in \mathbb{N} \mid x \equiv a[b]\}$. Un élément de $S$ est dit irréductible s'il ne peut pas s'écrire comme un produit d'au moins deux éléments de $S$ (pas forcément distincts).
|
| 214 |
+
Montrer qu'il existe $\mathrm{N}>0$ tel que tout élément de $S$ s'écrit comme produit d'au plus N éléments irréductibles de $S$ (pas forcément distincts).
|
| 215 |
+
$\underline{\text { Solution de l'exercice } 17}$ Soit $d=\operatorname{pgcd}(a, b)$, et écrivons $a=d a^{\prime}, b=d b^{\prime}$. Commençons par traiter le cas où $\operatorname{pgcd}\left(\mathrm{d}, \mathrm{b}^{\prime}\right)>1$. Si c'est le cas, alors on a $\operatorname{pgcd}\left(\mathrm{a}^{2}, \mathrm{~b}\right)=\operatorname{dpgcd}\left(\mathrm{da}^{\prime 2}, \mathrm{~b}^{\prime}\right)>\mathrm{d}$. Donc, pour tout $k \geqslant 2$, on a $a^{k} \not \equiv a[b]$. En particulier, tout élément de $S$ est irréductible, et donc $N=1$ convient.
|
| 216 |
+
Supposons à présent que $d$ et $b^{\prime}$ sont premiers entre eux. On a alors $a$ et $b^{\prime}$ premiers entre eux; soit $\omega$ l'ordre de a modulo $b^{\prime}$. On a alors que $\mathrm{a}^{\omega+1} \equiv \mathrm{a}[\mathrm{b}]$. Donc tout produit de $\omega+1$ éléments de $S$ est encore un élément de $S$. Ceci signifie en particulier que tout élément non irréductible de $S$ peut s'écrire comme un produit de $k$ éléments de $S$ pour un certain $k \in \llbracket 2, \omega \rrbracket$.
|
| 217 |
+
Soient $p$ et $q$ deux diviseurs premiers de d, et soit $x \in S$. Si $x$ est irréductible, c'est bon; sinon, écrivons $x=\mathfrak{u}_{1} \mathfrak{u}_{2} \ldots \mathfrak{u}_{k}$ avec $\mathfrak{u}_{1}, \ldots, \mathfrak{u}_{k} \in S$, pour un $k \in \llbracket 2, \omega \rrbracket$. Montrons d'abord qu'on peut supposer $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathfrak{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour tout $\boldsymbol{j}<\mathrm{k}$. Pour cela, on remarque que, si $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right) \geqslant \varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$, alors on peut remplacer $\mathfrak{u}_{j}$ par $\frac{\mathfrak{u}_{j}}{p^{\varphi\left(b^{\prime}\right)}}$ et $\mathfrak{u}_{k}$ par $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k}$. On a $p^{\varphi\left(b^{\prime}\right)} \equiv 1\left[b^{\prime}\right]$, donc $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv \mathfrak{u}_{k} \equiv a\left[b^{\prime}\right]$. D'autre part, $\mathrm{d} \mid \mathfrak{u}_{k}$ donc $\mathrm{p}^{\varphi\left(\mathrm{b}^{\prime}\right)} \mathfrak{u}_{\mathrm{k}} \equiv 0 \equiv \mathrm{a}[\mathrm{d}]$. Donc, d'après le théorème des restes chinois, on a $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv a[b]$. D'autre part, on a aussi $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a\left[b^{\prime}\right]$, et on a également (puisque $v_{\mathfrak{p}}\left(u_{j}\right) \geqslant$ $\left.\varphi\left(b^{\prime}\right)+v_{p}(d)\right)$ que $d \left\lvert\, \frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}}\right.$. Donc $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a[b]$.
|
| 218 |
+
On a à présent $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour $\boldsymbol{j}<\mathrm{k}$. De même, on peut supposer que $v_{\boldsymbol{q}}\left(\mathfrak{u}_{\mathrm{k}}\right)<$ $\varphi\left(b^{\prime}\right)+v_{q}(d)$. Toute écriture de $\boldsymbol{u}_{j}(j<k)$ sous forme de produit d'irréductibles fait apparaître seulement des multiples de $d$, donc de $p$, et comprend donc au plus $v_{p}\left(u_{j}\right)$ facteurs. De même pour $q$ avec $\mathfrak{u}_{k}$. Finalement, on a réussi à écrire $x$ sous la forme d'un produit d'au plus $(\omega-1)\left(\varphi\left(b^{\prime}\right)+v_{p}(d)-1\right)+$ $\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathrm{q}}(\mathrm{d})-1$ facteurs irréductibles, comme souhaité.
|
| 219 |
+
|
| 220 |
+
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Il semble que la notion d'irréductibilité a posé des problèmes de compréhension, montrer que tout nombre de $S$ peut s'écrire comme un nombre fini d'éléments irréductibles ne répondait pas à l'énoncé. Enfin, il est regrettable que pour certains, les copies rendues pour ce problème d'envoi soient pratiquement illisibles.
|
| 221 |
+
|
| 222 |
+
Exercice 18. Pour tout entier $k \geqslant 1$, on note $p(k)$ le plus petit nombre premier ne divisant pas $k$. Soit $\left(a_{n}\right)_{n \in \mathbb{N}}$ une suite telle que $a_{0} \in \mathbb{N}^{*}$ et pour tout $n \geqslant 0, a_{n+1}$ est le plus petit entier strictement positif différent de $a_{0}, \ldots, a_{n}$ tel que $a_{n}^{a_{n+1}}-1$ est divisible par $p\left(a_{n}\right)$. Démontrer que tout entier strictement positif apparaît une unique fois dans la suite $\left(a_{n}\right)_{n \in \mathbb{N}}$.
|
| 223 |
+
Solution de l'exercice 18 Déjà notons que la suite est bien définie: si $a_{1}, \ldots, a_{n}$ sont construits, comme $a_{n}$ est premier avec $p\left(a_{n}\right)$, il existe une infinité d'entiers $k$ tels que $a_{n}^{k} \equiv 1\left(\bmod p\left(a_{n}\right)\right)$ qui sont tous les multiples de l'ordre de $a_{n}$ modulo $p\left(a_{n}\right)$. En particulier, il existe au moins un de ces entiers $n$ 'apparaissant pas parmi $a_{1}, \ldots, a_{n}$, donc $a_{n+1}$ existe bien.
|
| 224 |
+
Notons que chaque entier apparaît au plus une fois dans la suite par construction. Il faut donc montrer que tous apparaissent au moins une fois. Supposons qu'il existe un entier $N$ qui n'apparaît pas dans la suite $\left(x_{n}\right)$, on prend alors $N$ minimal. On note $N_{0}$ un entier tel que si $n \geqslant N_{0}, a_{n}>N$.
|
| 225 |
+
Montrons que pour tout premier $q$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. Supposons que ce n'est pas le cas, et fixons $q$ un nombre premier tel que $p\left(a_{n}\right)=q$ pour une infinité de $n$. On se donne alors $\phi: \mathbb{N} \rightarrow \mathbb{N}$ strictement croissante telle que $p\left(a_{\phi(n)}\right)=q$. Notons alors que tout multiple de $q-1$ apparaît : en effet si on fixe $M$ un multiple de $q-1$, alors comme les $p\left(a_{\phi(n)+1}\right)$ sont deux à deux distincts, il existe $n$ tel que $a_{\phi(n)+1}>M$. Or comme $q-1$ divise $M, a_{\phi(n)}^{M} \equiv 1(\bmod q-1)$ par petit Fermat, ce qui contredit la définition de $a_{\phi(n)+1}$.
|
| 226 |
+
Ainsi tous les multiples de $\mathrm{q}-1$ apparaissent. on note $\mathrm{p}_{1}<\cdots<\mathrm{p}_{\mathrm{k}}$ les nombres premiers strictement inférieurs à $q$. On sait que pour tout $j \geqslant 1,\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ est congru à 1 modulo $q$, divisible par $q-1$ pour $j$ assez grand (car tous les facteurs de $q-1$ sont parmi $p_{1}, \ldots, p_{k}$ ) donc apparaît dans la suite, et vérifie $p\left(\left(p_{1} \ldots p_{k}\right)^{j(q-1)}\right)=q$. Comme il y a une infinité de tels termes, il existe $\mathrm{N}_{1}>\mathrm{N}_{0}$ tel que $a_{N_{1}}=\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ pour $j$ assez grand. Ainsi $a_{N_{1}}^{N} \equiv 1(\bmod q)$, ce qui contredit le fait que $a_{N_{1}+1}>N$.
|
| 227 |
+
Ainsi on a bien prouvé que pour tout premier $\mathbf{q}$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. En particulier, pour tout $M \in \mathbb{N}$, comme la suite $\left(p\left(a_{n}\right)\right)$ prend un nombre fini de fois chaque valeurs entre 1 et $M$, à partir d'un certain rang $p\left(a_{n}\right)>M$, donc $\left(p\left(a_{n}\right)\right)$ tend vers $+\infty$. En particulier, pour tout $k$, à partir d'un certain rang, $p_{1} \ldots, p_{k}$ divise $a_{n}$.
|
| 228 |
+
Soit $k$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant$ $m+1$. On a alors $p\left(a_{m}\right)=p_{k+1}$, et $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv 1\left(\bmod p_{k+1}\right)$. Or par Petit Fermat, $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv$ $a^{p_{1} \ldots p_{k}}\left(\bmod p_{k+1}\right)$, donc pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $a^{i p_{1} \ldots p_{k}} \equiv 1\left(\bmod p_{k+1}\right)$. Ainsi pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $i p_{1} \ldots p_{k}$ apparaît dans la suite $\left(a_{n}\right)$. En prenant $i$ un inverse de $p_{1} \ldots p_{\mathrm{k}}$ modulo $p_{\mathrm{k}+1}-1$ dans $\left\{1, \ldots, p_{\mathrm{k}+1}-1\right\}$, on a alors que $\left(i p_{1} \ldots \mathrm{p}_{\mathrm{k}}\right)^{\mathrm{N}} \equiv \mathrm{N}\left(\bmod \mathrm{p}_{\mathrm{k}+1}\right)$, donc si $a_{n}=i p_{1} \ldots p_{k}$, alors $a_{n+1}<N$, donc $n \leqslant N_{0}$. Ainsi si de tels $k$, $m$ existent, alors $p_{k}$ divise $a_{1} \ldots a_{n+1}$, donc $k$ est borné.
|
| 229 |
+
Or pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$. En effet, notons pour tout $k \geqslant 1 r_{k}$ le premier rang à partir duquel $p_{1} \ldots p_{k}$ divise $a_{n}$. La suite $\left(r_{j}\right)$ est croissante, et ne peut être stationnaire sinon un $a_{n}$ serait divisible par tous les nombres premiers. Donc elle tend vers $+\infty$, pour tout $K$, il existe $k \geqslant \mathrm{~K}$ tel que $r_{k+1}>r_{k}$. Ainsi $a_{r_{k+1}-1}$ est divisible par $p_{1} \ldots p_{k}$ car $r_{k+1}-1 \geqslant r_{k}$, et pas par $p_{k+1}$. Mais tous les termes après $r_{k+1}$ sont divisibles par $p_{1} \ldots p_{k+1}$, donc $m=r_{k+1}-1$ convient. On a donc bien obtenu que pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$, donc on a abouti à une contradiction.
|
| 230 |
+
Ainsi chaque entier apparaît une unique fois dans la suite.
|
| 231 |
+
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Certains ont utilisé des résultats moins élémentaires que le corrigé par exemple le postulat de Bertrand.
|
| 232 |
+
|
French_STS/md/fr-Corrigé-Envoi-5-2019.md
ADDED
|
@@ -0,0 +1,180 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+

|
| 4 |
+
|
| 5 |
+
ENVOI 4 : POT-POURRI
|
| 6 |
+
À RENVOYER AU PLUS TARD LE 14 MARS 2019
|
| 7 |
+
|
| 8 |
+
Les consignes suivantes sont à lire attentivement :
|
| 9 |
+
|
| 10 |
+
- Le groupe junior est constitué des élèves nés en 2004 ou après. Les autres élèves sont dans le groupe senior.
|
| 11 |
+
- Les exercices classés 'Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 12 |
+
- Les exercices classés 'Communs" sont à chercher par tout le monde.
|
| 13 |
+
- Les exercices classés 'Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 14 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 15 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 16 |
+
- Pour les exercices de géométrie, faire des figures sur des feuilles blanches séparées.
|
| 17 |
+
- Respecter la numérotation des exercices.
|
| 18 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 19 |
+
|
| 20 |
+
[^0]
|
| 21 |
+
## Exercices Juniors
|
| 22 |
+
|
| 23 |
+
Exercice 1. Au début, les 9 cases d'un échiquier $3 \times 3$ contiennent chacune un 0 . A chaque étape, Pedro choisit deux cases partageant un côté, et ajoute soit 1 aux deux cases, soit -1 aux deux cases. Montrer qu'il est impossible d'atteindre en un nombre fini de coups la situation où toutes les cases sont remplies par un 2.
|
| 24 |
+
|
| 25 |
+
Solution de l'exercice 1 L'idée ici est de faire apparaître un invariant I.
|
| 26 |
+
Colorions l'échiquier naturellement en noir et blanc de telle sorte qu'il y a 4 cases noires et 5 blanches. Soit donc I la somme des cases noires moins la somme des cases blanches. Au début, $\mathrm{I}=0$, et dans une hypothétique situation où toutes les cases sont remplies par un $2, \mathrm{I}=-2$.
|
| 27 |
+
Or I ne varie pas; en effet, à chaque étape on choisit deux cases partageant un côté commun, donc de couleur différente, et on leur ajoute le même nombre. Il en résulte que I n'est modifié lors de l'accomplissement d'une étape, d'où le résultat.
|
| 28 |
+
|
| 29 |
+
Exercice 2. Soient $m, n, k$ trois entiers positifs tels que $m^{2}+n=k^{2}+k$. Montrer que $m \leqslant n$.
|
| 30 |
+
Solution de l'exercice 2 On écrit $(2 k+1)^{2}=4\left(k^{2}+k\right)+1=4\left(m^{2}+n\right)+1=(2 m)^{2}+4 \mathfrak{n}+1$.
|
| 31 |
+
Or si $\mathrm{n}<\mathrm{m}$, on peut écrire
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
(2 \mathfrak{m})^{2}<(2 \mathfrak{m})^{2}+4 \mathfrak{n}+1<4 \mathfrak{m}^{2}+4 \mathfrak{m}+1=(2 \mathrm{~m}+1)^{2}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
ce qui est impossible puisque $(2 \mathrm{k}+1)^{2}=(2 \mathrm{~m})^{2}+4 \mathfrak{n}+1$ est un carré et ne peut donc pas être entre deux carrés consécutifs. D'où $n \geqslant m$.
|
| 38 |
+
Exercice 3. Soit $A B C$ un triangle dont les trois angles sont aigus, avec $A B>A C$, et soit $\Omega$ son cercle circonscrit. On note $M$ le milieu de [BC]. Les tangentes à $\Omega$ en $B$ et $C$ s'intersectent en $P$, et les droites $(A P)$ et $(B C)$ se coupent en $S$. On note $D$ le pied de la hauteur issue de $B$ dans $A B P$, et $\omega$ le cercle circonscrit à CSD. Enfin, on note K le second point d'intersection (après C ) de $\omega$ et $\Omega$.
|
| 39 |
+
Montrer que $\widehat{\mathrm{CKM}}=90^{\circ}$.
|
| 40 |
+
|
| 41 |
+
## Solution de l'exercice 3
|
| 42 |
+
|
| 43 |
+
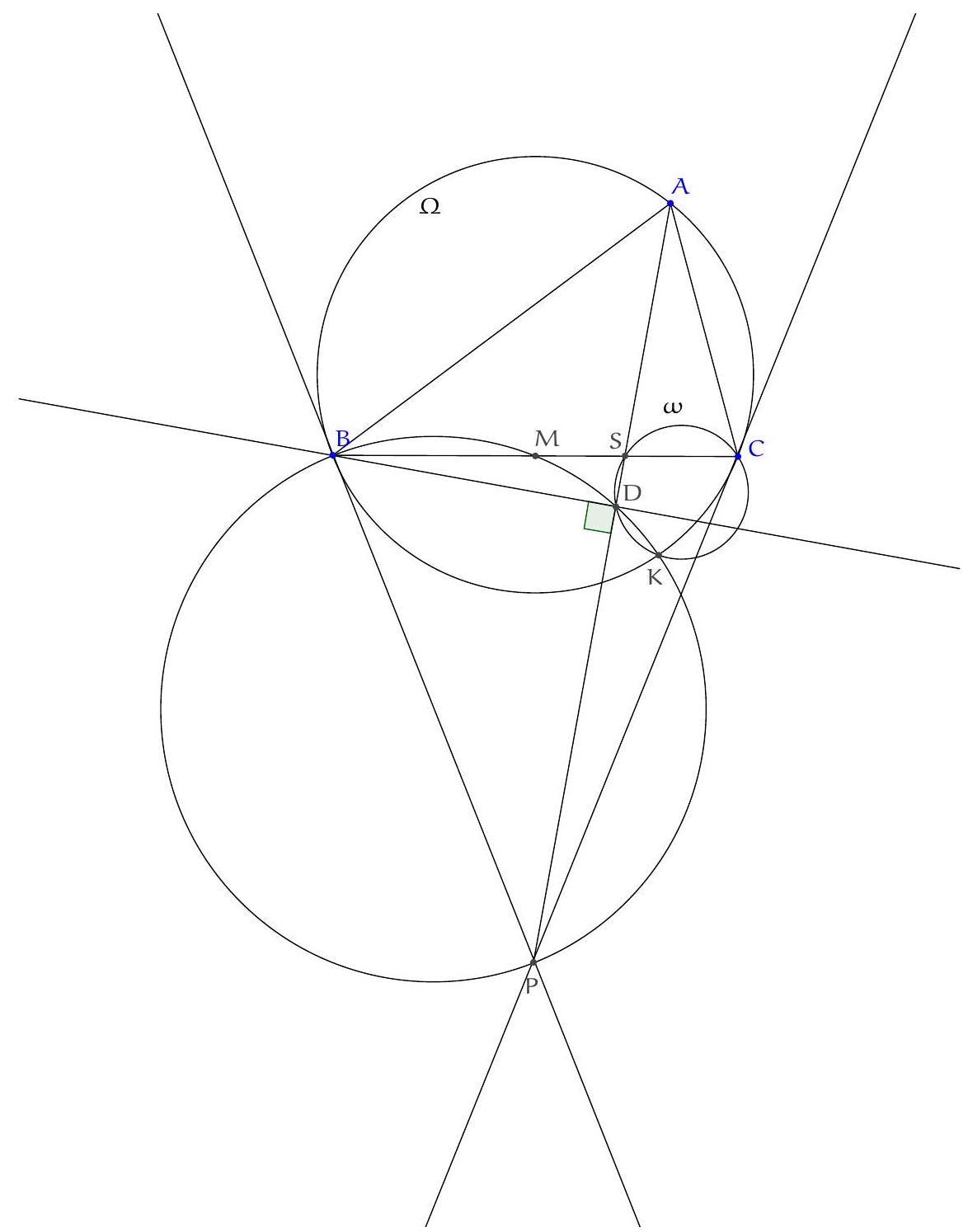
|
| 44 |
+
|
| 45 |
+
L'idée est de se rendre compte que la figure contient de nombreux points cocycliques. Pour commencer, on a $\mathrm{PB}=\mathrm{PC}$ donc (MP) est la médiatrice de $[\mathrm{BC}]$, et en particulier l'angle $\widehat{\mathrm{BMP}}$ est droit. Comme $\widehat{B D P}$ l'est aussi, les points $B, D, M$ et $P$ sont cocycliques sur le cercle $\Gamma$ de diamètre [BP]. Si on trace ce cercle sur notre figure, il semble que $\Gamma$ passe aussi par K . En effet, on va vérifier par chasse aux angles que $B, D, K$ et $P$ sont cocycliques. D'une part, en utilisant le théorème de l'angle inscrit, on a
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\widehat{\mathrm{KDP}}=180^{\circ}-\widehat{\mathrm{KDS}}=\widehat{\mathrm{KCS}}=\widehat{\mathrm{KCB}} .
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
D'autre part, en utilisant le cas limite du théorème de l'angle inscrit, on a
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
\widehat{\mathrm{KBP}}=\widehat{\mathrm{KCB}}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
donc les cinq points $B, D, K, M$ et $P$ sont cocycliques. On peut maintenant conclure en décomposant l'angle $\widehat{\mathrm{CKM}}$ en D pour pouvoir utiliser un maximum de cercles :
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\widehat{\mathrm{CKM}}=\widehat{\mathrm{CKD}}+\widehat{\mathrm{DKM}}=180^{\circ}-\widehat{\mathrm{CSD}}+\widehat{\mathrm{DBM}}=\widehat{\mathrm{BSD}}+\widehat{\mathrm{DBS}}=180^{\circ}-\widehat{\mathrm{BDS}}=90^{\circ}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
## Exercices Communs
|
| 64 |
+
|
| 65 |
+
Exercice 4. Soit $A B C$ un triangle isocèle en $A$ mais pas rectangle. Soit $D$ le point de ( $B C$ ) tel que $(A D)$ soit perpendiculaire à $(A B)$, et soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de [BC].
|
| 66 |
+
Montrer que $A H E$ est isocèle en H .
|
| 67 |
+
|
| 68 |
+
## Solution de l'exercice 4
|
| 69 |
+
|
| 70 |
+
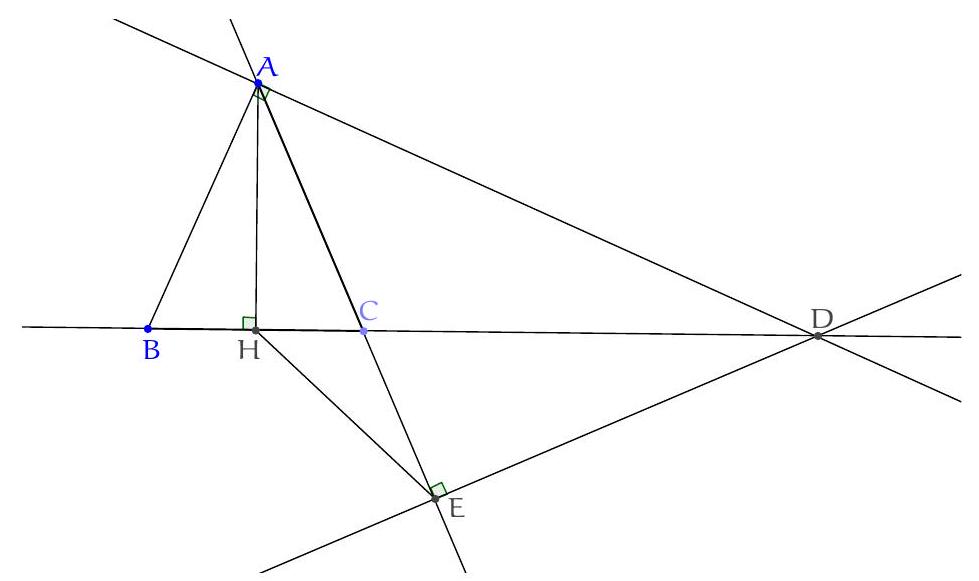
|
| 71 |
+
|
| 72 |
+
Commençons par remarquer que les points $A, D, E$ et $H$ sont cocycliques sur le cercle de diamètre [AD]. On en déduit par chasse au angles :
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\widehat{\mathrm{HEA}}=\widehat{\mathrm{HDA}}=90^{\circ}-\widehat{\mathrm{DBA}}=90^{\circ}-\widehat{\mathrm{BCA}}=\widehat{\mathrm{HAE}},
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
donc le triangle AHE est isocèle en H .
|
| 79 |
+
Exercice 5. Soit $n \geqslant 2$ et soient $x_{1}, x_{2}, \ldots, x_{n}$ des nombres réels tels que $x_{1}+x_{2}+\cdots+x_{n}=0$ et $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1$.
|
| 80 |
+
Montrer qu'il existe $i$ tel que $x_{i} \geqslant \frac{1}{\sqrt{n(n-1)}}$.
|
| 81 |
+
Solution de l'exercice 5 On note $\mathrm{N}^{+}$le nombre d'indices $i$ tels que $x_{i}>0$ et $N^{-}$le nombre d'indices $i$ tels que $x_{i} \leqslant 0$, de sorte que $\mathrm{N}^{+}+\mathrm{N}^{-}=\mathrm{n}$. On note également
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
S_{1}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i} \quad \text { et } \quad S_{1}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0}\left(-x_{i}\right)
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
ainsi que
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
S_{2}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i}^{2} \quad \text { et } \quad S_{2}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0} x_{i}^{2} .
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
L'intérêt de ces quantités est qu'elles permettent à la fois de reformuler les hypothèses et d'utiliser des inégalités bien connues comme celle de Cauchy-Schwarz. Les hypothèses de l'énoncé se réécrivent $S_{1}^{+}=$ $S_{1}^{-}$et $S_{2}^{+}+S_{2}^{-}=1$. Pour faire apparaître la racine dans le résultat, on va utiliser $S_{2}^{+}$. Plus précisément, on va montrer que $S_{2}^{+} \geqslant \frac{1}{n}$. Comme la somme $S_{2}^{+}$contient au maximum $n-1$ termes (les nombres ne peuvent pas être tous $>0)$, un de ces termes est plus grand que $\frac{1}{n(n-1)}$, soit $x_{i}^{2} \geqslant \frac{1}{\sqrt{n(n-1)}}$ pour un certain $i$ avec $x_{i}>0$, ce qui permet de conclure.
|
| 94 |
+
Pour montrer cela, on écrit :
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
1-S_{2}^{+}=S_{2}^{-} \leqslant\left(S_{1}^{-}\right)^{2}=\left(S_{1}^{+}\right)^{2} \leqslant N^{+} S_{2}^{+} \leqslant(n-1) S_{2}^{+} .
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
La première inégalité s'obtient en développant $\left(S_{1}^{-}\right)^{2}$ et en ne gardant que les termes $\chi_{i}^{2}$. La seconde est l'inégalité de Cauchy-Schwarz, et la troisième est le fait que les $x_{i}$ ne sont pas tous strictement positifs. On en déduit $S_{2}^{+} \geqslant \frac{1}{n}$, ce qui permet de conclure.
|
| 101 |
+
|
| 102 |
+
Exercice 6. Trouver tous les triplets ( $a, b, c$ ) d'entiers strictement positifs tels que
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
3^{a}-5^{b}=c^{2}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Solution de l'exercice 6 Comme $3^{a}$ et $5^{b}$ sont tous deux impairs, on a c pair donc $c^{2} \equiv 0[4]$. Comme $5^{b} \equiv 1[4]$, on doit avoir $3^{a} \equiv 1[4]$, donc a est pair. On écrit $a=2 a^{\prime}$, et l'équation devient
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
5^{b}=3^{2 a^{\prime}}-c^{2}=\left(3^{a^{\prime}}-c\right)\left(3^{a^{\prime}}+c\right) .
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Notons que la somme des deux facteurs vaut $2 \times 3^{a^{\prime}}$, donc elle n'est pas divisible par 5 , donc un des deux facteurs n'est pas divisible par 5 et ne peut valoir que 1 . C'est nécessairement le plus petit, donc on a
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
3^{a^{\prime}}-c=1 \quad \text { et } 3^{a^{\prime}}+c=5^{b}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
ou encore (en sommant les deux dernières égalités) $2 \times 3^{a^{\prime}}=5^{b}+1$.
|
| 121 |
+
On peut maintenant remarquer que $a^{\prime}=1$ est solution, mais qu'il ne semble plus y en avoir ensuite. Une manière naturelle de séparer le cas $a^{\prime}=1$ du reste est de regarder modulo 9 . En effet, dans ce cas, dès que $a^{\prime} \geqslant 2$, les deux membres doivent être divisibles par 9 , i.e. $5^{b} \equiv-1[9]$. Ceci implique que $b$ doit être divisible par 3. De plus, en regardant modulo 3, on obtient que b doit être impair. L'équation se réécrit donc
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
2 \times 3^{a^{\prime}}=5^{3 b^{\prime}}+1=125^{b^{\prime}}+1
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
avec $\mathbf{b}^{\prime}$ impair. Mais alors, le membre de droite se factorise par $125+1=126=2 \times 7 \times 9$. En particulier, il est divisible par 7 , ce qui n'est pas le cas du membre de gauche. Il est donc impossible d'avoir $a^{\prime} \geqslant 2$. On doit donc avoir $\boldsymbol{a}^{\prime}=1$, ce qui conduit à la solution $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,2)$ dans l'équation de départ.
|
| 128 |
+
|
| 129 |
+
## Exercices Seniors
|
| 130 |
+
|
| 131 |
+
Exercice 7. Soit $\left(a_{n}\right)_{n \geqslant 0}$ une suite de réels. On suppose que $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ pour tout entier naturel $n$. De plus, $a_{0}$ et $a_{1}$ sont strictement positifs et distincts. Montrer que la suite $\left(a_{n}\right)_{n \geqslant 0} n$ 'est pas bornée.
|
| 132 |
+
|
| 133 |
+
Solution de l'exercice 7 Il est clair que la suite ( $a_{n}$ ) est à termes positifs.
|
| 134 |
+
Soit $i$ tel que $a_{i}<a_{j}$ pour $j<i$. Supposons par l'absurde que $i \geqslant 4$. Alors $a_{i-2}=\left|a_{i}-a_{i-1}\right|=$ $a_{i-1}-a_{i}<a_{i-1}$ donc $a_{i-3}=\left|a_{i-2}-a_{i-1}\right|=a_{i-1}-a_{i-2}=a_{i}$, ce qui contredit l'hypothèse sur $i$.
|
| 135 |
+
Ainsi, si $m=\min \left\{a_{1}, a_{2}, a_{3}\right\}$, alors pour tout $i, a_{i} \geqslant m$. En effet, s'il existe $i$ avec $a_{i}<m$, choisissons $i$ minimal, alors $a_{i}$ est plus petit que tous les termes précédents, donc $i \leqslant 3$ ce qui contredit la définition de $m$.
|
| 136 |
+
De plus, $m>0$ car $a_{3} \geqslant 0$ et $a_{3}=0 \rightarrow a_{1}=a_{2}$.
|
| 137 |
+
Dès lors, on écrit $a_{i}=\left|a_{i+1}-a_{i+2}\right|$ pour tout $i$, donc
|
| 138 |
+
|
| 139 |
+
- Si $a_{i+1}>a_{i+2}$, d'où $a_{i+1}=a_{i}+a_{i+2} \geqslant a_{i}+m$
|
| 140 |
+
- Sinon, $a_{i+2}=a_{i+1}+a_{i} \geqslant a_{i}+m$
|
| 141 |
+
|
| 142 |
+
Dans tous les cas, il existe un terme de la suite $\geqslant a_{i}+m$. On peut donc prouver par une très simple récurrence sur $k$ l'existence de $i$ tel que $a_{i} \geqslant m k$, donc la suite ( $a_{i}$ ) n'est pas bornée.
|
| 143 |
+
Exercice 8. Soit $A B C D$ un trapèze avec $(A B)$ parallèle à $(C D)$. On suppose qu'il y a deux cercles $\omega_{1}$ et $\omega_{2}$ à l'intérieur du trapèze tels que $\omega_{1}$ est tangent aux côtés [DA], $\left.A B\right]$ et $[B C]$ et $\omega_{2}$ est tangent aux côtés $[B C],[C D]$ et $[D A]$. Soit $\left(d_{1}\right)$ la seconde tangente (après $\left.(A D)\right)$ à $\omega_{2}$ passant par $A$, et soit $\left(d_{2}\right)$ la seconde tangente (après $(B C)$ ) à $\omega_{1}$ passant par $C$.
|
| 144 |
+
Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
|
| 145 |
+
|
| 146 |
+
## Solution de l'exercice 8
|
| 147 |
+
|
| 148 |
+
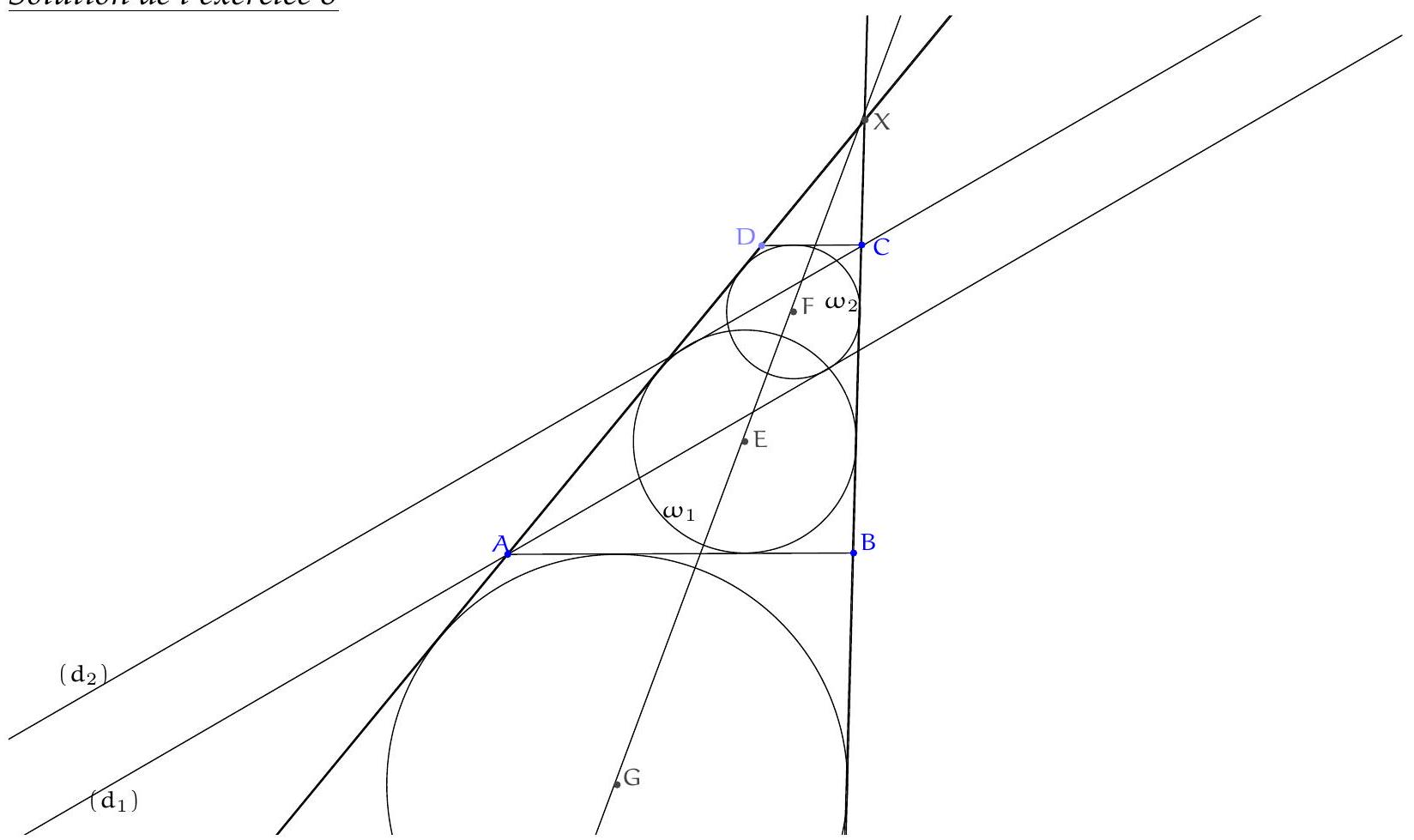
|
| 149 |
+
|
| 150 |
+
On note $X$ le point d'intersection de ( $A D$ ) et ( $B C$ ). On note respectivement $E$ et $F$ les centres de $\omega_{1}$ et $\omega_{2}$. Notons que $\omega_{1}$ est le cercle inscrit à $X A B$ et que $\omega_{2}$ est le cercle $X$-exinscrit à XCD. Enfin, on note $G$ le centre du cercle $X$-exinscrit à $X A B$.
|
| 151 |
+
On vérifie que les triangles XAG et $X E B$ sont semblables. En effet, on a $\widehat{A X G}=\widehat{E X B}=\frac{1}{2} \widehat{A X B}$. De plus, on a $\widehat{G A X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$ et $\widehat{B E X}=180^{\circ}-\frac{1}{2} \widehat{A X B}-\widehat{A B X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$, donc XAG et XEB sont bien semblables. Soit $s$ la similitude (directe) qui envoie $X$ sur $X, A$ sur $E$ et $G$ sur $B$. D'après l'homothétie décrite précédemment, on a $\frac{X C}{X B}=\frac{X F}{X G}$, donc $s(F)=C$.
|
| 152 |
+
Par similitude, on en déduit $\widehat{X A F}=\widehat{\mathrm{XEC}}$. La fin de l'exercice est maintenant une simple chasse aux angles, qui peut être menée de nombreuses manières différentes. Notons par exemple Y l'intersection de $\left(\mathrm{d}_{2}\right)$ avec $(A D)$. Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles revient à montrer $\widehat{X Y C}=\widehat{X_{A d}}$. Or, on a
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
\widehat{X Y C}=180^{\circ}-\widehat{A X B}-\widehat{X C Y}=\widehat{B C Y}-\widehat{A X B}=2 \widehat{B C E}-\widehat{A X B} .
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
De plus, on peut écrire
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
\widehat{\mathrm{BCE}}=180^{\circ}-\widehat{\mathrm{XCE}}=\frac{1}{2} \widehat{\mathrm{AXB}}+\widehat{\mathrm{XEC}}=\frac{1}{2} \widehat{A X B}+\widehat{\mathrm{XAF}}
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
ce qui donne $\widehat{X Y C}=2 \widehat{X A F}=\widehat{\mathrm{XAd}_{1}}$, d'où finalement le résultat.
|
| 165 |
+
|
| 166 |
+
Exercice 9. Soit $S=\{1, \ldots, n\}$, avec $n \geqslant 3$ un entier, et soit $k$ un entier strictement positif. On note $S^{k}$ l'ensemble des $k$-uplets d'éléments de $S$. Soit $f: S^{k} \rightarrow S$ telle que, si $x=\left(x_{1}, \ldots, \chi_{k}\right) \in S^{k}$ et $y=\left(y_{1}, \ldots, y_{k}\right) \in S^{k}$ avec $x_{i} \neq y_{i}$ pour tout $1 \leqslant i \leqslant k$, alors $f(x) \neq f(y)$.
|
| 167 |
+
Montrer qu'il existe $\ell$ avec $1 \leqslant \ell \leqslant k$ et une fonction $g: S \rightarrow S$ vérifiant, pour tous $x_{1}, \ldots, x_{k} \in S$, $f\left(x_{1}, \ldots, x_{k}\right)=g\left(x_{\ell}\right)$.
|
| 168 |
+
Solution de l'exercice 9 Nous montrerons le résultat par récurrence sur k. Le cas $k=1$ est trivial, supposons donc le résultat vrai pour $\mathrm{k}-1 \geqslant 1$ et montrons le pour k .
|
| 169 |
+
Supposons l'existence de $k-1$ éléments $a_{2}, \ldots, a_{k}$ de $S$ tels que la fonction $\phi: a \in S \mapsto f\left(a, a_{2}, \ldots, a_{k}\right) \in$ $S$ est injective. Par égalité de cardinal, elle est aussi bijective.
|
| 170 |
+
Dès lors, si $b_{2}, \ldots, b_{k}$ sont des éléments de $S$ avec $b_{i} \neq a_{i}$ pour tout $i \in\{2, \ldots, k\}$, et $b \in S$, alors $\phi(a) \neq f\left(b, b_{2}, \ldots, b_{k}\right)$ pour $S \ni a \neq b$. Par surjectivité de $\phi, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)$.
|
| 171 |
+
Soient $c_{2}, \ldots, c_{k}$ des éléments de $S$; puisque $n \geqslant 3$, il existe $b_{2}, \ldots, b_{k}$ tels que $a_{i} \neq b_{i} \neq c_{i}$ pour tout $i \in\{2, \ldots, k\}$. Dès lors le raisonnement précédent montre que, si $b \in S, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)=$ $\mathrm{f}\left(\mathrm{b}, \mathrm{c}_{2}, \ldots, \mathrm{c}_{\mathrm{k}}\right)$, et ainsi $\ell=1$, et $\mathrm{g}=\phi$ conviennent.
|
| 172 |
+
Nous supposons donc qu'il existe deux fonctions $\alpha, \beta: S^{k-1} \rightarrow S$ avec, pour tous $a_{2}, \ldots, a_{k}$ dans $S$, $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \beta\left(a_{2}, \ldots, a_{n}\right)=\beta$, et $f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$.
|
| 173 |
+
Montrons que $f^{\prime}:\left(a_{2}, \ldots, a_{k}\right) \in S^{k-1} \mapsto f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$ satisfait les conditions du problème. En effet, si $\left(a_{2}, \ldots, a_{k}\right)$ et $\left(b_{2}, \ldots, b_{k}\right)$ sont deux $(k-1)$-uplets dont les coordonnées sont toutes différentes, alors soit $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \alpha\left(b_{2}, \ldots, b_{k}\right)=\alpha^{\prime}$, auquel cas $g\left(a_{2}, \ldots, a_{k}\right)=$ $f\left(\alpha, a_{2}, \ldots, a_{k}\right) \neq f\left(\alpha^{\prime}, b_{2}, \ldots, b_{k}\right) g\left(b_{2}, \ldots, b_{k}\right)$ par hypothèse, soit $\alpha \neq \beta\left(b_{2}, \ldots, b_{k}\right)$ auquel cas on a de même $g\left(a_{2}, \ldots, a_{k}\right) \neq g\left(b_{2}, \ldots, b_{k}\right)$.
|
| 174 |
+
Dès lors par hypothèse de récurrence, et sans perte de généralité, on peut supposer l'existence de $h$ : $S \rightarrow S$ telle que $g\left(a_{2}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour $a_{2}, \ldots, a_{k}$ dans S. $h$ doit être injective car $h(a)=$ $g(a, a, \ldots, a) \neq g(b, \ldots, b)=h(b)$ si $a \neq b$ sont des éléments de S. Par égalité de cardinal, $h$ est surjective.
|
| 175 |
+
Montrons que $f\left(a_{1}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour tous $a_{1}, \ldots, a_{k} \in S$, ce qui conclura. Supposons par l'absurde l'existence d'un $k$-uplet $a=\left(a_{1}, \ldots, a_{k}\right) \in S^{k}$ tel que $f(a) \neq h\left(a_{2}\right)$. Par surjectivité, il existe $b_{2} \in S$ avec $h\left(b_{2}\right)=f(a)$ avec $b_{2} \neq a_{2}$ donc. Soient $b_{i} \neq a_{i}$ des éléments de $S$, pour $3 \leqslant i \leqslant k$. On a $\alpha=$ $\alpha\left(b_{2}, \ldots, b_{k}\right)$ et $\beta=\beta\left(b_{2}, \ldots, b_{k}\right)$ deux éléments de $S$ tels que $f\left(\alpha, b_{2}, \ldots, b_{k}\right)=f\left(\beta, b_{2}, \ldots, b_{k}\right)=$ $h\left(b_{2}\right)=f(a)$. L'hypothèse faite sur $f$ assure donc $\alpha=a_{1}=\beta$, ce qui est une contradiction d'après la définition de $\alpha$ et $\beta$.
|
| 176 |
+
|
| 177 |
+
|
| 178 |
+
[^0]: Animath, Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.
|
| 179 |
+
copies.ofm@gmail.com
|
| 180 |
+
|
French_STS/md/fr-corrige-envoi-1.md
ADDED
|
@@ -0,0 +1,228 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES<br><br>ENVOI 1 : GÉOMÉTRIE<br>CORRECTION
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2004 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Communs" sont à chercher par tout le monde.
|
| 8 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 9 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 10 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 11 |
+
- Pour les exercices de géométrie, faire des figures sur des feuilles blanches séparées.
|
| 12 |
+
- Respecter la numérotation des exercices.
|
| 13 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 14 |
+
|
| 15 |
+
Animath,<br>Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.<br>contact-pofm@animath.fr
|
| 16 |
+
|
| 17 |
+
## Exercices Juniors
|
| 18 |
+
|
| 19 |
+
Exercice 1. Soit $A B C D$ un trapèze isocèle avec (AD)//(BC).
|
| 20 |
+
(a) Montrer que $A B C D$ admet un cercle circonscrit.
|
| 21 |
+
(b) On note O le centre du cercle circonscrit de $A B C D$ et E l'intersection des diagonales. Montrer que O est sur le cercle circonscrit de AEB.
|
| 22 |
+
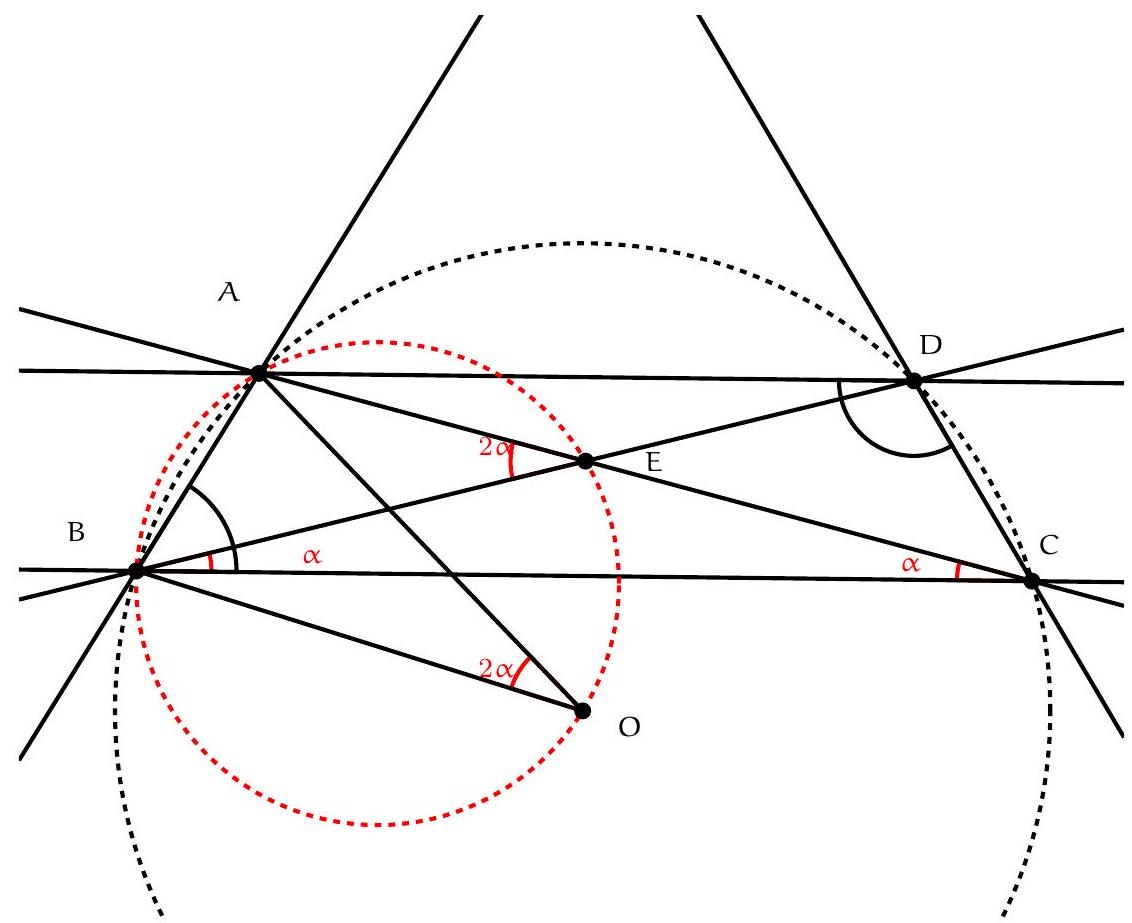
|
| 23 |
+
|
| 24 |
+
Démonstration. a) $A B C D$ est un trapèze isocèle, ainsi $\widehat{A B C}=\widehat{D C B}$. On sait également que $(A D) / /(C B)$, donc $\widehat{D C B}=180-\widehat{C D A}$. Avec ces deux égalités on trouve que $\widehat{A B C}+\widehat{C D A}=180$, ce qui montre bien que les points $A, B, C$ et $D$ sont sur le même cercle.
|
| 25 |
+
b) On va noter $\alpha$ l'angle $\widehat{A C B}$ et on va essayer de calculer différents angles afin d'arriver à la conclusion demandée. On trouve par symétrie que $\widehat{D B C}=\alpha$ également. Ainsi, dans le triangle EBC , sachant que la somme des angles vaut 180 , on trouve $\widehat{\mathrm{AEB}}=180-\widehat{\mathrm{BEC}}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}=2 \alpha$. Avec le théorème de l'angle au centre, sachant que l'angle inscrit $\widehat{A C B}=\alpha$, on a $\widehat{A O B}=2 \alpha$. Mais alors, $\widehat{A O B}=2 \alpha=\widehat{A E B}$ ce qui montre bien que les points $A, E, O$ et $B$ sont cocycliques.
|
| 26 |
+
|
| 27 |
+
Exercice 2. Soit $\omega_{1}$ et $\omega_{2}$ deux cercles de centre $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$, on suppose qu'ils se coupent en $A$ et $B$. Le cercle passant par les points $O_{1}, O_{2}$ et $B$ coupe le cercle $\omega_{1}$ en $C$. Montrer que les points $C$, $A$ et $O_{2}$ sont alignés.
|
| 28 |
+
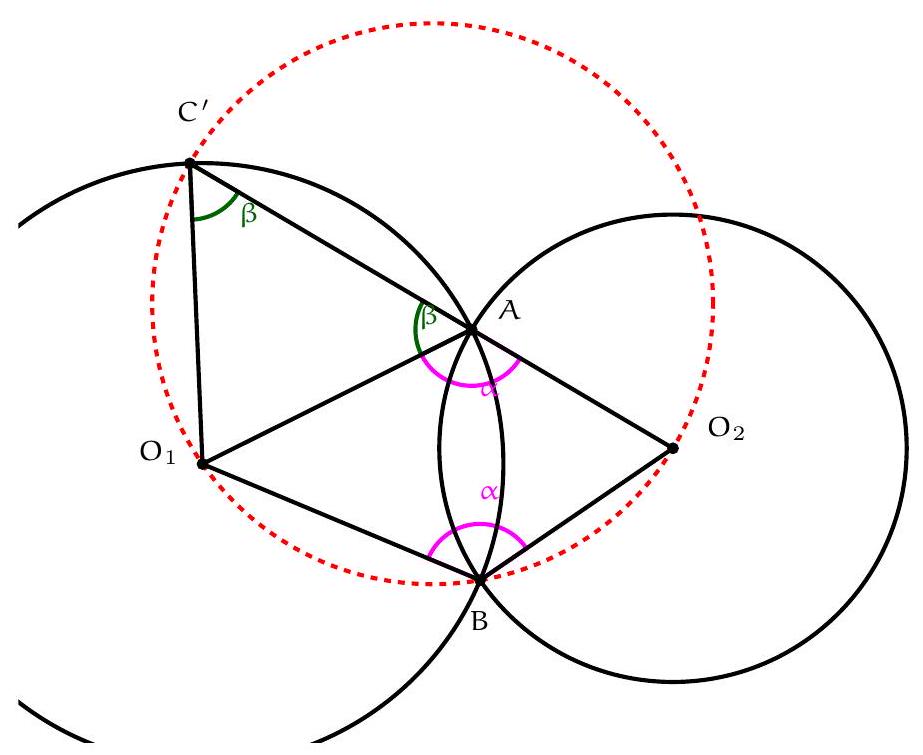
|
| 29 |
+
|
| 30 |
+
Démonstration. Pour résoudre cet exercice, on va plutôt introduire dans un premier temps $\mathrm{C}^{\prime}$ la deuxième intersection de la droite $\left(A O_{2}\right)$ avec le cercle $\omega_{1}$ puis on va montrer que $\mathrm{C}=\mathrm{C}^{\prime}$.
|
| 31 |
+
On peut décomposer l'angle plat $\widehat{\mathrm{O}_{2} \mathrm{AC}^{\prime}}$ en deux angles : $\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}$ et $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ dont la somme vaut donc 180 degrés. D'une part, en faisant une symétrie axiale d'axe $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, alors les points $A$ et $B$ sont échangés, mais alors l'angle $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ vaut l'angle $\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}$. D'autre part, $\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{1} \mathrm{C}^{\prime}$ comme $O_{1}$ est le centre du cercle $\omega_{1}$, ainsi le triangle $O_{1} A C^{\prime}$ est isocèle en $O_{1}$, et on trouve que ${\widehat{O_{2} \mathrm{C}^{\prime} O_{1}}}_{1}=\widehat{\mathrm{AC}^{\prime} \mathrm{O}_{1}}={\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}}_{1}=180-{\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}}_{2}=180-{\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}}_{2}$, donc en particulier, $\widehat{\mathrm{O}_{2} \mathrm{C}^{\prime} \mathrm{O}_{1}}=$ $180-{\widehat{\mathrm{O}_{2}} \mathrm{BO}_{1}}$, ce qui démontre bien que les points $\mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et $\mathrm{C}^{\prime}$ sont cocycliques. Ainsi, si on reprend la définition du point C , on obtient que $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{~B}$ et C sont cocycliques et que $\mathrm{C}^{\prime}$ est sur $\omega_{1}$, donc que $C^{\prime}=C$, mais comme les points $A, O_{2}$ et $C^{\prime}=C$ sont alignés on a entre autre que $A, O_{2}$ et $C$ sont alignés.
|
| 32 |
+
|
| 33 |
+
Exercice 3. Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.
|
| 34 |
+
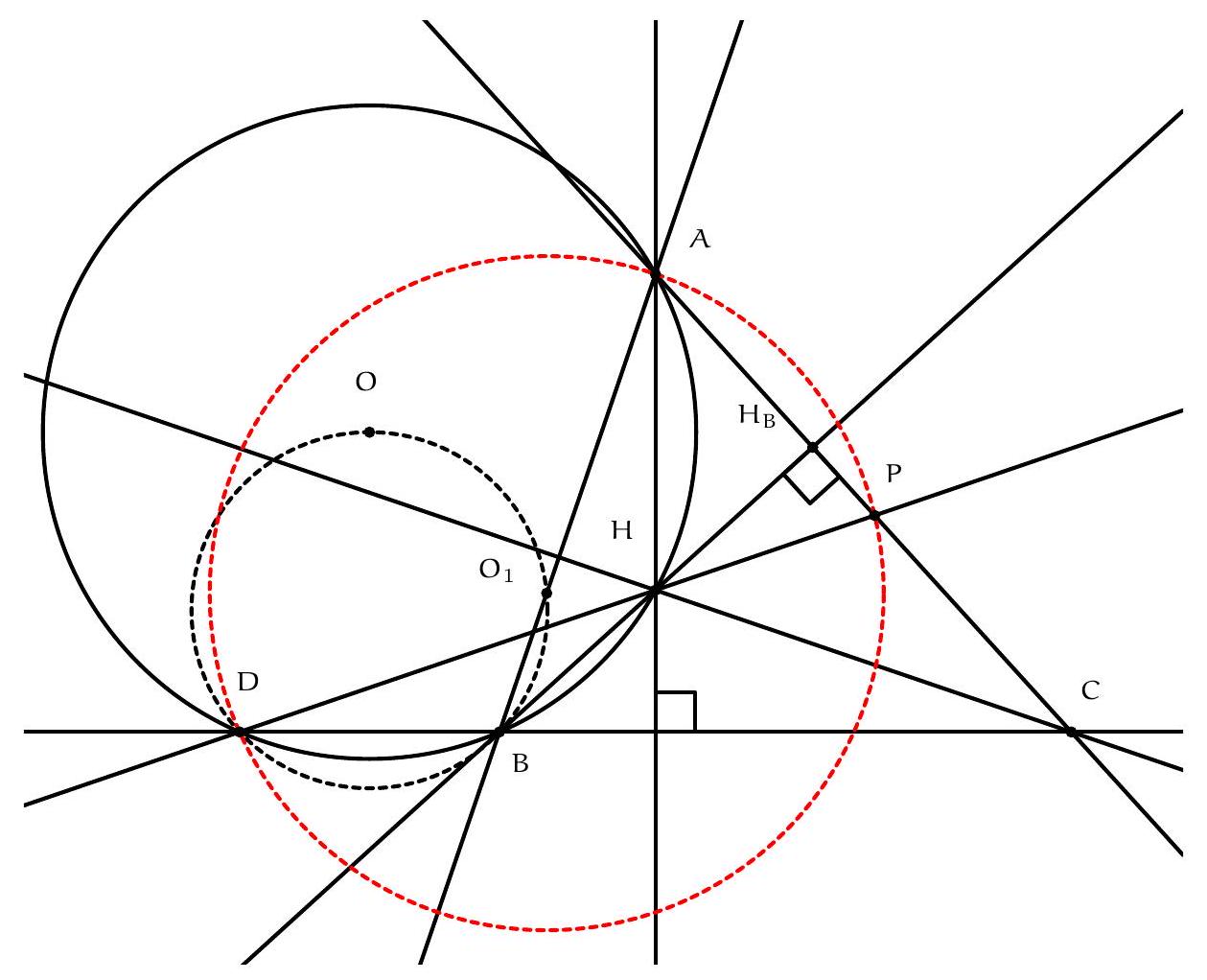
|
| 35 |
+
|
| 36 |
+
Démonstration. Une construction soigneuse nous permet de conjecturer que le centre du cercle APD est également sur la droite ( $A B$ ), c'est donc tout naturellement que l'on introduit $\mathrm{O}_{1}$, le point de la droite $(A B)$ qui est à égale distance de $A$ et de $D, c^{\prime}$ est alors un bon candidat pour être le centre du cercle APD.
|
| 37 |
+
Étape 1. $\mathrm{O}_{1}$ est le centre du cercle de APD.
|
| 38 |
+
Démonstration. On introduit $\mathrm{H}_{\mathrm{B}}$ le pied de la hauteur issue de B dans le triangle ABC , on pose alors $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}$. Comme le triangle $\mathrm{HH}_{\mathrm{B}} \mathrm{P}$ est droit en $\mathrm{H}_{\mathrm{B}}$, on a $\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{HP}}=90-\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}=90-x$. Mais d'autre part, $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{BP}}=\widehat{\mathrm{DHB}}$, ce dernier angle vaut l'angle $\widehat{\mathrm{DAB}}=x$ par cocyclicité des points $A, H, B$ et D.
|
| 39 |
+
On note $M$ le milieu du segment [AD], alors $M$ et $\mathrm{O}_{1}$ sont sur la médiatrice du segment [AD], donc $\left(\mathrm{MO}_{1}\right) \perp(\mathrm{AD})$, et ainsi $\widehat{M O_{1} \mathrm{~A}}=90-\widehat{\mathrm{MAO}_{1}}$.
|
| 40 |
+
Or $O_{1} A=O D$, donc $\widehat{A O_{1} D}=2 x=2 \widehat{A P D}$. On a maintenant d'une part que $\widehat{A O_{1} D}=2 \widehat{A P D}$ mais d'autre part que $O A=O_{1} \mathrm{D}$, on voudrait en déduire que $\mathrm{O}_{1}$ est bien le centre du cercle circonscrit de APD. Mais par angle au centre c'est bien le cas.
|
| 41 |
+
|
| 42 |
+
Étape 2. $\mathrm{O}_{1}$ est sur le cercle ODB.
|
| 43 |
+
Démonstration. On remarque que les points $\mathrm{O}, \mathrm{M}$ et $\mathrm{O}_{1}$ sont sur la (même) médiatrice de [AC], ils sont donc alignés. On trouve ainsi l'angle $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x$. Mais d'autre part, $\widehat{\mathrm{DOB}}=2 \widehat{\mathrm{DAB}}=$ $2(90-x)$. Comme le triangle ODB est isocèle en O , on peut calculer l'angle $\widehat{\mathrm{OBD}}$ qui vaut ainsi $x$. Mais alors, $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x=\widehat{\mathrm{OBD}}$, ce qui conclut l'étape 2 .
|
| 44 |
+
|
| 45 |
+
On sait que $\mathrm{O}_{1}$ est le centre du cercle APD et sur le cercle ODB, donc le centre du cercle de APD est bien sur le cercle ODB ce qui conclut.
|
| 46 |
+
|
| 47 |
+
## Exercices Communs
|
| 48 |
+
|
| 49 |
+
Exercice 4. Soit $A B C$ un triangle, $H$ le pied de la hauteur issue de $A$, $L$ le pied de la bissectrice issue de $B$ et $M$ le milieu de $[A B]$. On suppose que dans le triangle HLM on a les deux propriétés: $(A H)$ est une hauteur et ( BL ) est une bissectrice. Montrer que ( CM ) est une médiane.
|
| 50 |
+
|
| 51 |
+
Démonstration. On prend le triangle $A B C$, on va démontrer qu'il est équilatéral, en utilisant les deux propriétés, la troisième découlera.
|
| 52 |
+
|
| 53 |
+
On a $(A H) \perp(M L)$ et $(A H) \perp(B C)$, donc $(B C) / /(M L)$. On trouve ainsi que $L$ est le milieu de $[A C]$. Cependant, $\frac{A L}{L C}=\frac{A B}{B C}$ ce qui montre que $A B=B C$, et (BL) est une bissectrice, une hauteur et une médiane.
|
| 54 |
+
|
| 55 |
+
Il faut maintenant que (BL) bissecte $\widehat{M L H}$, ou encore (AC) comme bissectrice extérieure, donc par chasse aux angles $\beta=\widehat{\mathrm{HLC}}=\widehat{M L A}=\alpha$. Donc $\alpha=\beta$ et $A B C$ est équilatéral, donc en particulier (CM) est la médiane dans MHL.
|
| 56 |
+
|
| 57 |
+
Exercice 5. Soit $\omega_{1}$ et $\omega_{2}$ deux cercles qui se coupent en $P$ et $Q$. On suppose que la tangente commune à $\omega_{1}$ et $\omega_{2}$, la plus proche de P , touche les cercles $\omega_{1}$ et $\omega_{2}$ en $A$ et $B$ respectivement. Les tangentes en $P$ aux cercles $\omega_{1}$ et $\omega_{2}$ recoupe $\omega_{2}$ et $\omega_{1}$ en $D$ et $C$ respectivement. On pose $H$ et $K$ sur les segments $[A C]$ et $[B D]$ de tel sorte que $A H=A P$ et $B K=B P$. Montrer que les points $A, B, K, Q$ et $H$ sont sur le même cercle.
|
| 58 |
+
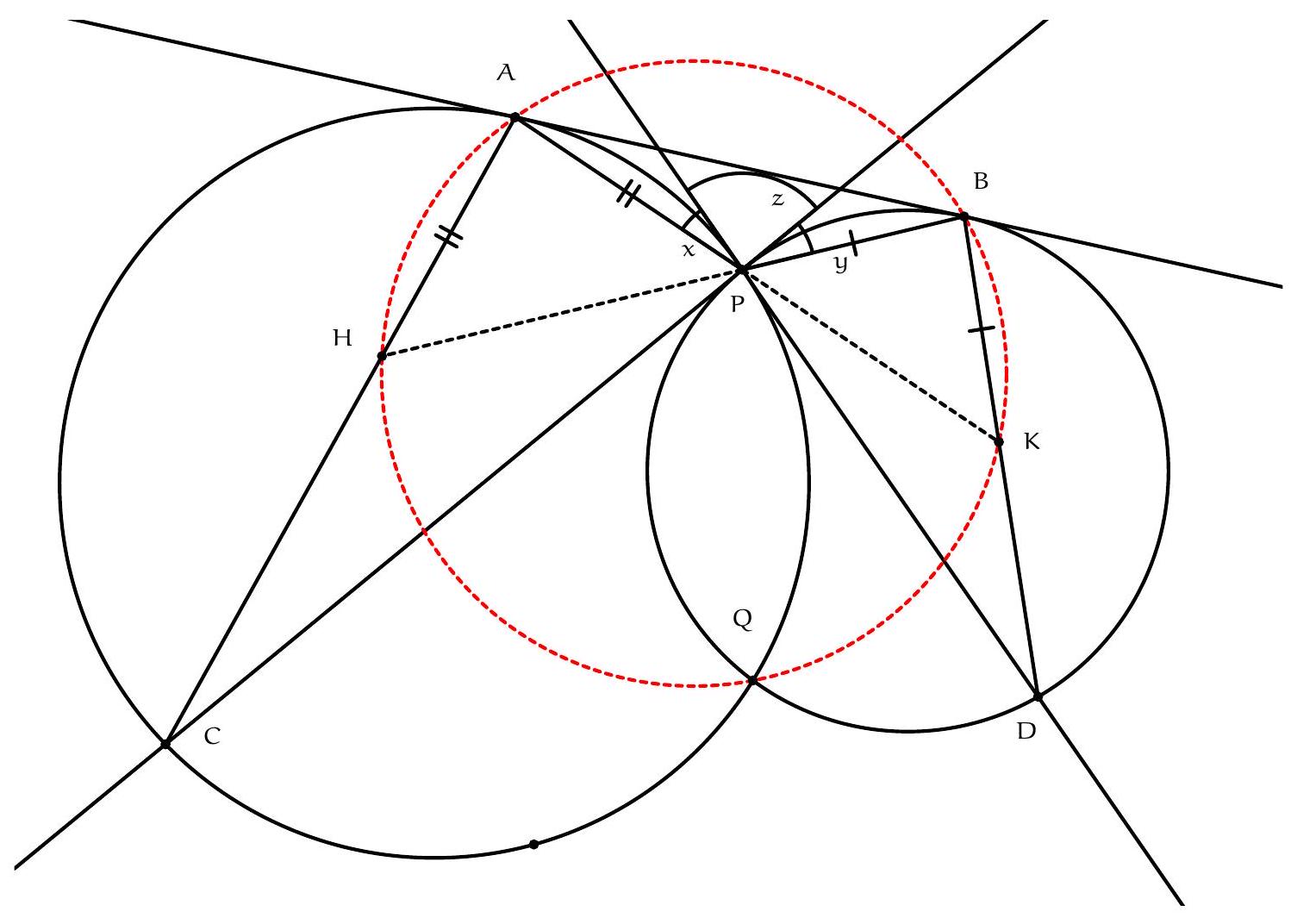
|
| 59 |
+
|
| 60 |
+
Démonstration. On conjecture sur une bonne figure que les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, de même pour les points $K, P$ et $A$.
|
| 61 |
+
|
| 62 |
+
Lemme. Les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, ainsi que les points $\mathrm{K}, \mathrm{P}$ et A .
|
| 63 |
+
On note $x=\widehat{\mathrm{PAB}}, y=\widehat{\mathrm{ABP}}$ et $z=\widehat{\mathrm{CPD}}$. Comme la droite ( PC$)$ est tangente à $\omega_{2}$ on sait que l'angle que la tangente forme avec la droite ( PB ) est également $x$, de la même manière l'angle entre (PC) et (AP) est y (il s'agit de choisir les bonnes orientations). $z$ est l'angle entre les deux tangentes. Dans ce cas $\widehat{A P B}=x+y+z$ et au total les angles du triangle $A B P$ sont $x, y$ et $x+y+z$, cela montre que $2 x+2 y+z=180$.
|
| 64 |
+
|
| 65 |
+
Par angle à la tangente l'angle $\widehat{C A P}=z$, mais $A H=A P$ donc les triangle $A H P$ est isocèle en $A$, et $\widehat{A H P}=\widehat{A P H}=\frac{180-z}{2}=\frac{2 x+2 y}{2}=x+y$, alors l'angle $\widehat{\mathrm{HPB}}=\widehat{\mathrm{HPA}}+\widehat{\mathrm{APB}}=x+y+x+z+y=$ $2 x+2 y+z=180$, ce qui montre bien que les points $H, P$ et $B$ sont alignés. Le raisonnement symétrique montre que $K, P$ et $A$ sont alignés.
|
| 66 |
+
|
| 67 |
+
On a trouvé dans la preuve du lemme que $\widehat{A H B}=\widehat{A H P}=x+y$, mais alors par symétrie $\widehat{B K A}=\widehat{B K P}=x+y$, et par angle à la tangente, $\widehat{P Q A}=x$ et $\widehat{P Q B}=y$, donc $\widehat{A Q B}=x+y$, on a ainsi $\widehat{A H B}=\widehat{B K A}=\widehat{B Q A}$ ce qui montre bien que les points $A, H, Q, K$ et $P$ sont cocycliques.
|
| 68 |
+
|
| 69 |
+
Exercice 6. Soit $A B C$ un triangle, $D$ est le milieu de l'arc $B C$ du cercle $A B C$ ne contenant pas $A, Z$ est l'unique point sur la bissectrice extérieure de $\widehat{B A C}$ tel que $Z A=Z C$. Montrer que le cercle $A D Z$ passe par le milieu du côté de $[A B]$.
|
| 70 |
+
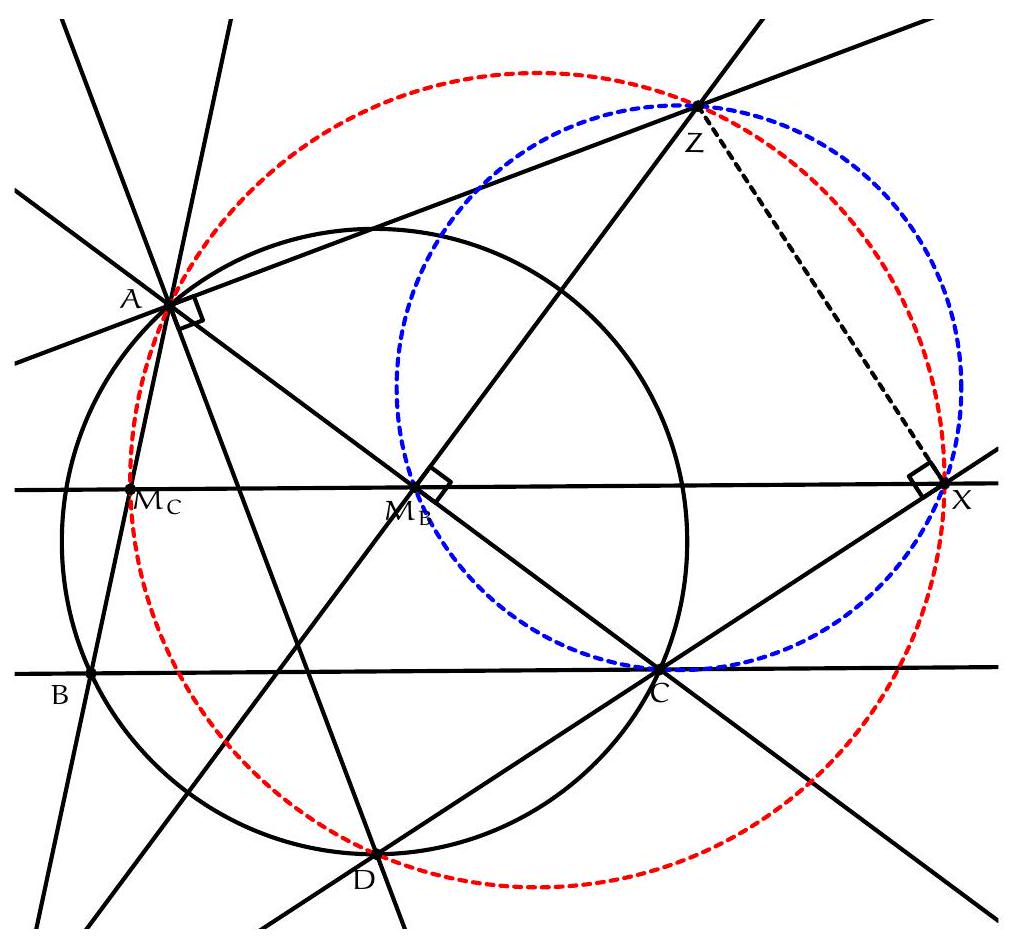
|
| 71 |
+
|
| 72 |
+
## Démonstration. Preuve 1:
|
| 73 |
+
|
| 74 |
+
On note $\alpha=\widehat{B A C}$, on pose $M_{B}$ le milieu de $[A B]$ et $M_{C}$ le milieu de $[A C]$. On note $X$ l'intersection des droites $\left(M_{B} M_{C}\right)$ et (DC).
|
| 75 |
+
|
| 76 |
+
Alors comme $\left(M_{B} M_{C}\right) / /(B C)$, on trouve $\widehat{M_{B} X C}=\widehat{B C D}=\widehat{B A D}=\frac{\alpha}{2}$, l'avant-dernière égalité découle du fait que les points $A, B, C$ et $D$ sont cocycliques et que $D$ est le pôle sud de $A$ dans le triangle $A B C$. On calcule maintenant que $\widehat{C A Z}=90-\frac{\alpha}{2}, Z$ et $M_{B}$ sont sur la médiatrice de $[A C]$ donc $\left(Z M_{B}\right) \perp(A C)$, et on trouve alors $\widehat{A Z M_{B}}=\widehat{C_{Z M}}=\frac{\alpha}{2}$, mais alors $\widehat{C_{Z M}}=\widehat{C_{B M}}$, ce qui montre que les points $Z, M_{B}, C$ et $X$ sont cocycliques.
|
| 77 |
+
|
| 78 |
+
Comme $Z, M_{B}, C$ et $X$ sont cocycliques et $\widehat{Z M_{B} C}=90$ on doit avoir $\widehat{Z C X}=90$. On a de plus, $\widehat{D A Z}=90$, ce qui montre que les points $A, Z, X$ et $D$ sont cocycliques.
|
| 79 |
+
|
| 80 |
+
On a également, $\widehat{M_{B} A D}=\frac{\alpha}{2}=\widehat{M_{B} X D}$ ce qui montre que les points $A, M_{B}, D$ et $X$ sont cocycliques. Mais dans ce cas : $A, M_{B}, D, X$ et $Z$ sont cocycliques. Donc en particulier, le cercle $A D Z$ passe par le milieu du segment $[A B]$.
|
| 81 |
+
|
| 82 |
+
## Preuve 2:
|
| 83 |
+
|
| 84 |
+
On va présenter ici une méthode un peu plus générale que la méthode précédente, il s'agit de composer trois similitudes et d'en trouver certaines propriétés.
|
| 85 |
+
|
| 86 |
+
On pose $S_{Z, \mu, r}$ la similitude directe de centre $Z, d^{\prime}$ angle $\mu$ (orienté) et de rapport r .
|
| 87 |
+
Alors, $S_{M_{B}, 180,1}$ fixe $M_{B}$ échange $A$ et $B$ elle échange également $D$ avec une point appelé $D^{\prime}$.
|
| 88 |
+
On trouve par chasse aux angles immédiate que $\widehat{A Z C}=\alpha$.
|
| 89 |
+
$S_{Z, \alpha, 1}$ fixe $Z$, envoie alors $A$ sur $C$.
|
| 90 |
+
On trouve par chasse aux angles que $\widehat{C D B}=180-\alpha$. Donc $S_{D, 180-\alpha, 1}$ fixe $D$ et envoie $C$ sur $B$.
|
| 91 |
+
On effectue alors $T=S_{M_{B}, 180,1}+S_{Z, \alpha, 1}+S_{D, 180-\alpha,}$, cette transformation est également une similitude directe de rapport $1 \times 1 \times 1$ et d'angle $180+180-\alpha+\alpha=360$, le résultat est donc une translation, mais $T$ envoie $B$ sur $B$, une translation qui a un point fixe est l'identité donc $T$ est en fait l'identité. Mais la transformation $T$ envoie $D$ sur $\mathrm{D}^{\prime}$ puis $\mathrm{D}^{\prime}$ sur $\mathrm{D}^{\prime \prime}$ et $\mathrm{D}^{\prime \prime}$ sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}, \mathrm{D}^{\prime \prime}$ est envoyé sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$ par la similitude de centre D donc $\mathrm{D}^{\prime \prime}=\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, ainsi la similitude de centre $Z$ envoie $D^{\prime}$ sur $D$, donc en particulier $Z D^{\prime}=Z D$ et $\widehat{D^{\prime} Z D}=\alpha$. Dans le triangle $A^{\prime} D Z$, le point $M_{B}$ est le pied de la hauteur, bissectrice, etc..., donc en particulier, $\widehat{M_{B} Z C}=\frac{\alpha}{2}=\widehat{M_{B} A D}$, ce qui conclut.
|
| 92 |
+
|
| 93 |
+
Cette deuxième approche peut sembler longue mais elle est beaucoup plus général et peut s'appliquer à d'autre configurations que le cas particulier que l'on vient de voir.
|
| 94 |
+
|
| 95 |
+
## Exercices Seniors
|
| 96 |
+
|
| 97 |
+
Exercice 7. Soit $A B C$ un triangle isocèle en $A, \Gamma$ est un cercle tangent à ( $A C$ ) en $C$ à l'extérieur du triangle $A B C$. On note $\omega$ le cercle passant par $A$ et $B$ et tangent intérieurement à $\Gamma$ en $D$. E est la seconde intersection de (AD) et de $\Gamma$, montrer que (BE) est tangente à $\Gamma$.
|
| 98 |
+
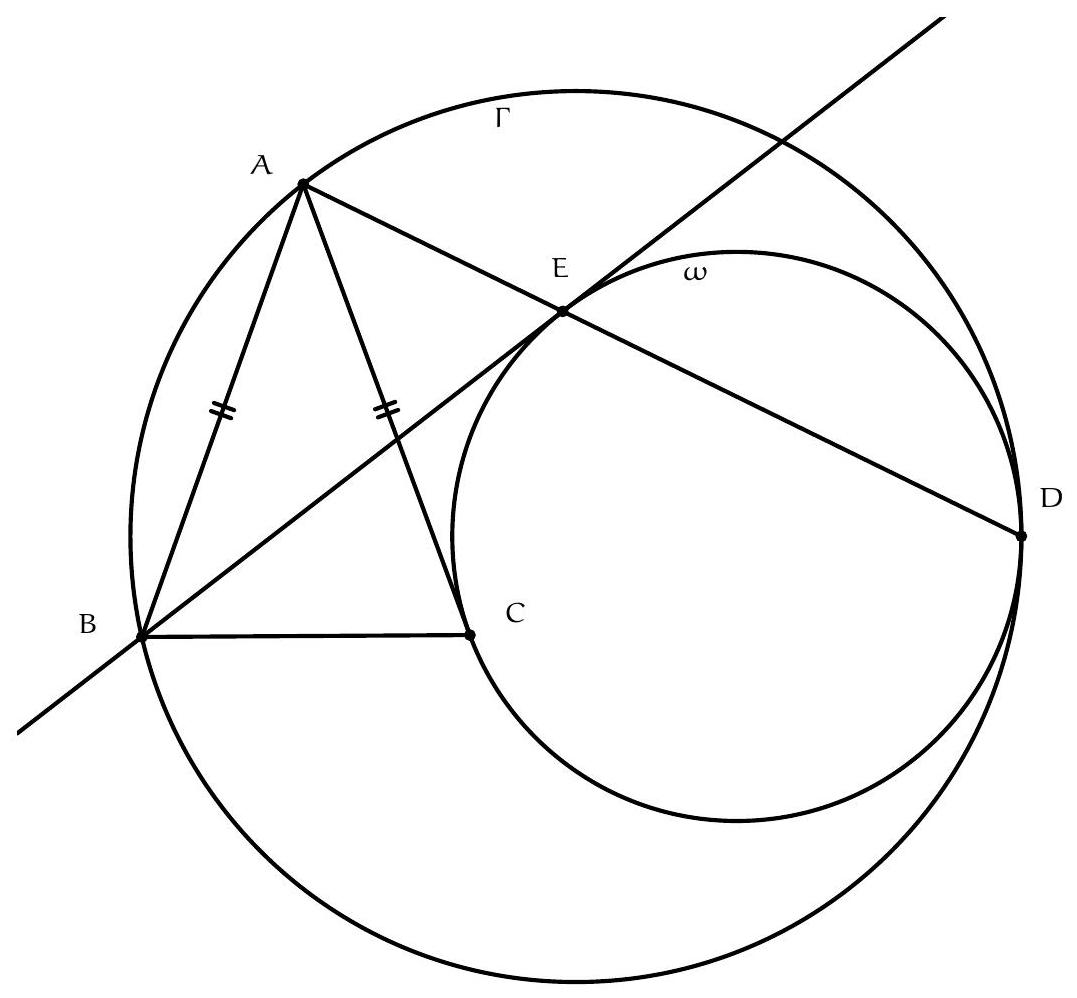
|
| 99 |
+
|
| 100 |
+
## Démonstration. Preuve 1:
|
| 101 |
+
|
| 102 |
+
On note $I_{A}$ l'inversion de centre $A$ et de rayon $r=A B=A C$, ainsi, $B$ et $C$ sont fixe par $I_{A}$, la puissance de $A$ par rapport au cercle $\omega$ est exactement le rayon au carré donc les cercle $\omega$ est fixe par inversion. Cela montre que $D$ et $E$ sont échangés dans $I_{A}$. Mais alors le cercle $\Gamma$ passant par $A, B$ et $D$ va être envoyé sur une droite passant par $B$ et $E$ et tangente au cercle $\omega$, cela conclut.
|
| 103 |
+
|
| 104 |
+
## Preuve 2:
|
| 105 |
+
|
| 106 |
+
On construit $B^{\prime}$, le deuxième point de $\Gamma$, tel que $A B=A B^{\prime}=A C$. Alors, on veut démontrer que $l^{\prime}$ intersection, $E^{\prime}$ des droites $\left(B B^{\prime}\right)$ et ( $\left.A D\right)$ est sur $\omega$.
|
| 107 |
+
|
| 108 |
+
On a $\widehat{B D A}=x$ et $\widehat{A B B^{\prime}}=x$. Par isocélité de $A B B^{\prime}$ en $A$, on trouve $\widehat{A B^{\prime} B}=x$. Donc les triangles $A B D$ et $A E B$ sont semblables, on trouve alors $A B^{2}=A E \times A D$. Donc $E^{\prime}$ est sur $\omega$, ce qui montre que $E^{\prime}=E$. L'homothetie de centre $D$ qui envoie le cercle $\omega$ sur le cercle $\Gamma$ envoie ainsi le point $E$ sur le point $A$ et donc la tangente en $E$ à $\omega$ sur la tangente en $A$ à $\Gamma$ ?. Il se trouve que comme $A B=A B^{\prime}$, la tangente en $A$ à $\Gamma$ est parallèle à la droite $\left(B^{\prime}\right)$, mais la tangente en $E$ à $\omega$ doit être parallèle à la tangente en $A$ à $\Gamma$. Cela montre que la tangente en $E$ à $\omega$ et ( $\left.\mathrm{BB}^{\prime}\right)$ ne sont en fait qu'une seule et même droite et cela conclut.
|
| 109 |
+
|
| 110 |
+
Exercice 8. Soit ADE un triangle isocèle en $A$. Soit le cercle $\omega$, tangent aux droites (AD) et (AE) en $D$ et $E$. Soit $B$ et $C$ deux points au delà de $D$ et $E$ sur les droites ( $A D$ ) et ( $A E$ ). On suppose que $B C>B D+C E$. Finalement, soit $F$ et $G$ deux points sur le segment $[B C]$ de tel sorte que $B D=B F$ et $C G=C E$, les droites $(D G)$ et $(F E)$ se coupent en $K$, la tangente à $\omega$ parallèle à ( $B C$ ) et entre $A$ et ( $B C$ ) touche $\omega$ en L. Montrer que le centre du cercle inscrit de ABC est sur (KL).
|
| 111 |
+
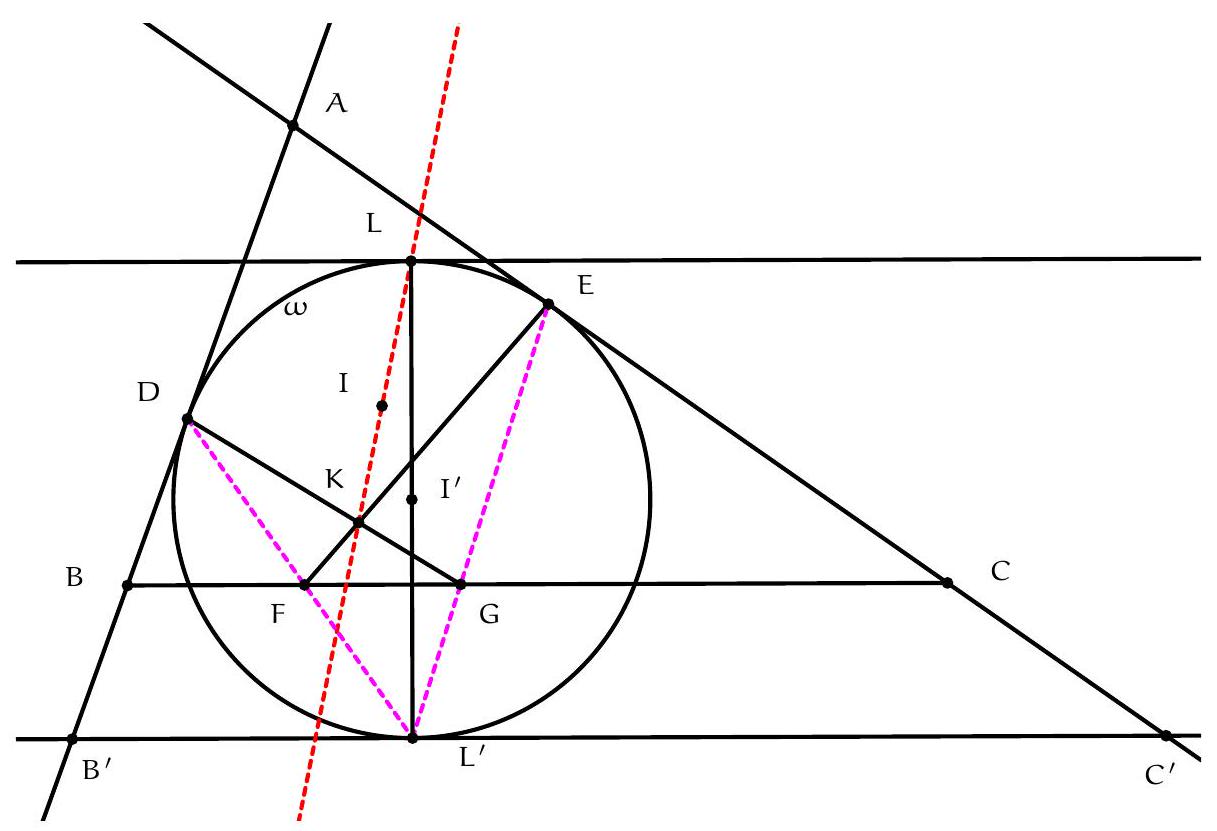
|
| 112 |
+
|
| 113 |
+
Démonstration. Soit $B^{\prime}$ et $C^{\prime}$ deux points sur les demi-droites $[A D]$ et $[A C]$ au delà de $D$ et $E$ de tel sorte que $\left(B^{\prime} C^{\prime}\right) / /(B C)$ et que $\left(B^{\prime} C^{\prime}\right)$ soit tangente à $\omega$ en $L^{\prime}$.
|
| 114 |
+
Lemme. $D, F$ et $L^{\prime}$ sont alignés de même pour $E, G$ et $L^{\prime}$.
|
| 115 |
+
On a $(B F) / /\left(B^{\prime} L^{\prime}\right)$ et $D B=B F$, ainsi que $\mathrm{DB}^{\prime}=\mathrm{B}^{\prime} \mathrm{L}^{\prime}$, donc $\mathrm{DBF} \sim \mathrm{DB}^{\prime} \mathrm{L}^{\prime}$, par Thalès. On obtient que $D, F$ et $L^{\prime}$ sont alignés, le raisonnement symétrique montre que $E, G$ et $L^{\prime}$ sont alignés.
|
| 116 |
+
|
| 117 |
+
On remarque que $\omega$ est le cercle inscrit de $A B^{\prime} C^{\prime}$. La tangente en $L$ et la tangente en $L^{\prime}$ sont deux droites parallèles, donc le segment [LL'] est un diamètre de $\omega$, ainsi $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
|
| 118 |
+
|
| 119 |
+
Comme I est le centre du cercle inscrit de $A B C$, I est l'intersection des bissectrices des angles $\widehat{A B C}, \widehat{B C A}$ et $\widehat{C A B}$ ou encore par isocélité des triangles $D B F, G C E$ et EAD que I est l'intersection des médiatrices de [DF], [GE] et [ED], le fait que ces médiatrices soient concourantes nous amène à dire que le quadrilatère DEFG est cyclique et de centre du cercle circonscrit I.
|
| 120 |
+
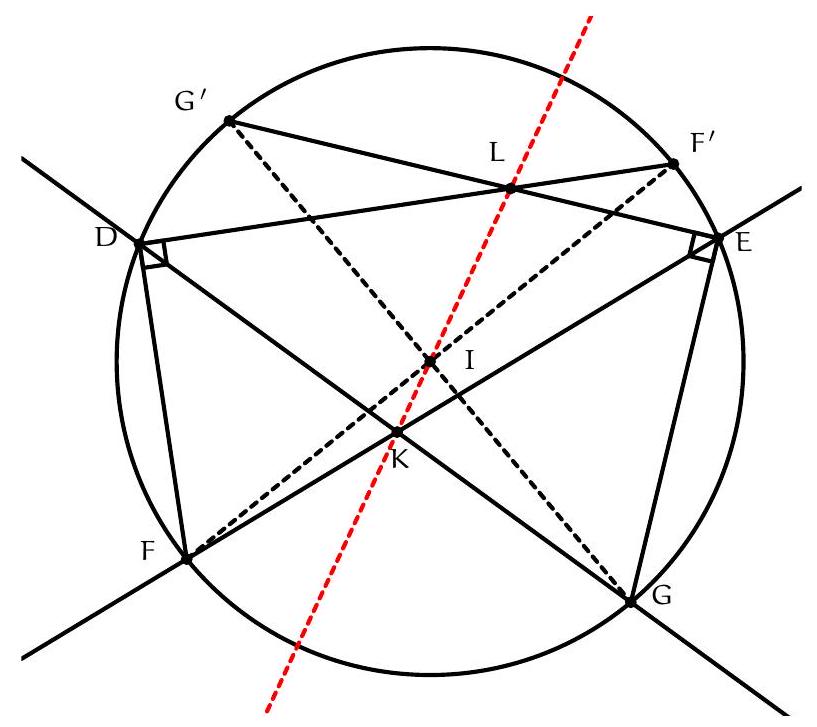
|
| 121 |
+
|
| 122 |
+
On va isoler maintenant le cercle DEFG, le point $I$, le point $L$ et le point $K$, en sachant que $I$ est le centre du cercle DEFG, que K est l'intersection des diagonales et que L est tel que $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
|
| 123 |
+
|
| 124 |
+
On intersecte maintenant la droite ( EL ) avec le cercle EDFG en $\mathrm{G}^{\prime}$, et la droite ( DL ) également avec le cercle EDG et en $F^{\prime}$. En sachant que $\widehat{L^{\prime} E L}=90$ et $\widehat{L^{\prime} D L}=90$ on trouve que $\mathrm{G}^{\prime}$ (resp. $\mathrm{D}^{\prime}$ ) est le point diamétralement opposé à G (resp. D) dans le cercle EDFG, donc I est l'intersection des droites $\mathrm{GG}^{\prime}$ et $\mathrm{DD}^{\prime}$. On numérote les points $\mathrm{G}^{\prime}, \mathrm{G}, \mathrm{D}, \mathrm{F}^{\prime}, \mathrm{F}$ et $E$ comme 1, 2, 3, 4,5 et 6 et appliquer Pascal comme les 6 points sont sur le même cercle, alors $\left(G^{\prime} G\right) \cap\left(F^{\prime} F\right),(G D) \cap(F E)$ et $\left(\mathrm{DF}^{\prime}\right) \cap\left(E G^{\prime}\right)((12) \cap(45),(23) \cap(56)$ et $(34) \cap(61))$ sont alignés ce qui démontre bien que les points K, I et L sont alignés.
|
| 125 |
+
|
| 126 |
+
Exercice 9. Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.
|
| 127 |
+

|
| 128 |
+
|
| 129 |
+
Démonstration. Dans cet exercice nous allons d'abord donner une preuve en chasse aux angles uniquement avant de faire un lien avec le point de Feuerbach. La preuve que nous allons don-
|
| 130 |
+
ner démontre en outre plusieurs propriétés du point de Feuerbach que nous énoncerons à la fin.
|
| 131 |
+
On note $A^{\prime}$, l'intersection des droites $(B C)$ et $\left(A_{B} A_{C}\right)$, on df́init de la même manière les points $B^{\prime}$ et $C^{\prime}$.
|
| 132 |
+
On note $T$ l'intersection des cercles circonscrits de $A B_{A} B^{\prime}$ et $A B C$, on veut démontrer au final que $T$ est le point de tangence des cercles $A^{*} B^{*} C^{*}$ et $A B C$.
|
| 133 |
+
|
| 134 |
+
Lemme 1. T est également sur le cercle circonscrit de $B^{\prime} B_{C} C$.
|
| 135 |
+
Démonstration. En chasse aux angles : $\left(B^{\prime} T, T C\right)=\left(B^{\prime} T, A T\right)+(A T, T C)$ d'après le relation de Chasles, en utilisant la cocyclicité des points $T, A, B_{A}$ et $B^{\prime}$ ainsi que celle des points $T, A, B$ et $C$, on trouve $\left(B^{\prime} T, A T\right)+(A T, T C)=\left(B^{\prime} B_{A}, A B_{A}\right)+(A B, B C)=\left(B^{\prime} B_{A}, A B\right)+(A B, B C)=$ $\left(B^{\prime} B_{A}, B C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, ainsi $\left(B^{\prime} T, T C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, donc les points $T, B^{\prime}, B_{C}$ et $C$ sont cocycliques, ce qui conclut la preuve du lemme.
|
| 136 |
+
|
| 137 |
+
Lemme 2. les points $B^{\prime}$, $B$ et $T$ sont alignés.
|
| 138 |
+
Démonstration. On regarde les cercles $B^{\prime} T C B_{C}, A B^{\prime} T B_{A}$ et $A C B_{A} B_{C}$ (tous ces points sont cocycliques d'après le lemme précédent), leurs axes radicaux sont ( $B^{\prime} T$ ), ( $B_{A} A$ ) et ( $B_{C} C$ ), ce qui montre par concourance des axes radicaux que les points $B, B^{\prime}$ et $T$ sont alignés.
|
| 139 |
+
|
| 140 |
+
Lemme 3. $\left(A A^{*}\right)$ est tangente au cercle circonscrit de $A B C$.
|
| 141 |
+
|
| 142 |
+
## Démonstration.
|
| 143 |
+
|
| 144 |
+
Lemme 3.1. $O, C_{A}$ et $B_{A}$ sont alignés.
|
| 145 |
+
Démonstration. On va démontrer que $C_{A}$ est sur la médiatrice de $[B C]$.
|
| 146 |
+
On a $\left(C_{A} O, B C\right)=\left(C_{A} O, A C\right)+(A C, B C)=\left(C_{A} O, A C_{A}\right)+(A C, B C)=(A B, A O)+(A C, B C)=$ 90 (car la hauteur issue d'un sommet d'un triangle et la droite reliant ce somet avec le centre du cercle circonscrit sont conjugués isogonales), ce qui montre que ( $C_{A} O$ ) et ( $B C$ ) sont perpendiculaires, mais O est sur le médiatrice de $[\mathrm{BC}]$ donc $\mathrm{C}_{A}$ également.
|
| 147 |
+
|
| 148 |
+
De manière symétrique, $B_{A}$ est sur la médiatrice de $[B C]$ et ainsi $O, B_{A}$ et $C_{A}$ sont alignés.
|
| 149 |
+
Lemme 3.2. Le triangle $A^{*} C_{A} B_{A}$ est isocèle en $A^{*}$.
|
| 150 |
+
Démonstration. $\left(A^{*} C_{A}, C_{A} B_{A}\right)=\left(C_{B} C_{A}, C_{A} O\right)=\left(C_{B} B, B O\right)=(C B, B O)=(O C, B C)=$ $\left(\mathrm{OB}_{A}, \mathrm{~B}_{\mathrm{C}} \mathrm{B}_{\mathrm{A}}\right)=\left(\mathrm{CB}_{\mathrm{A}}, \mathrm{B}_{\mathrm{A}} \mathrm{A}^{*}\right)$
|
| 151 |
+
|
| 152 |
+
Donc $A^{*} B_{A} C_{A}$ est isocèle en $A^{*}$.
|
| 153 |
+
De plus, les angles en $B_{A}$ et $B$ des triangles $A^{*} B_{A} C_{A}$ et $B C O$ sont égaux, ce qui montre en fait que $A^{*} B_{A} C_{A} \sim O B C$.
|
| 154 |
+
|
| 155 |
+
Ainsi, $\left(C_{A} A^{*}, A^{*} B_{A}\right)=2\left(C_{A} A, A B_{A}\right)$ et $A^{*}$ est le centre du cercle circonscrit de $A B_{A} C_{A}$. Mais dans ce cas $\left(A^{*} A, A C\right)=\left(A A^{*}, A C_{A}\right)=90-\left(C_{A} B_{A}, B_{A} A\right)=90-\left(B_{A}, B_{A} A\right)=90-$ $(O C, C A)=(A B, B C)$ (on utilise toujours le fait que la hauteur issue d'un sommet d'un triangle et la droite reliant ce somet avec le centre du cercle circonscrit sont conjugués isogonales)
|
| 156 |
+
|
| 157 |
+
Donc $\left(A A^{*}\right)$ est bien une tangente de $A B C$.
|
| 158 |
+
|
| 159 |
+
Lemme 4. Les points $C_{B}, B_{C}, T, A$ et $A^{*}$ sont cocycliques.
|
| 160 |
+
Démonstration.
|
| 161 |
+
Étape 1. $C_{B}, B_{C}, A$ et $A^{*}$ sont cocycliques.
|
| 162 |
+
Démonstration. On calcule l'angle $\left(C_{B} A, B_{C} A\right)$ :
|
| 163 |
+
$\left(C_{B} A, A B_{C}\right)=\left(C_{B} A, A O\right)+\left(A O, A B_{C}\right)=\left(C_{B} B, B O\right)+\left(C O, C B_{C}\right)$ par cocyclicité des points $\mathrm{C}_{\mathrm{B}} \mathrm{BAO}$ et $\mathrm{AOB}_{\mathrm{C}} \mathrm{C},\left(\mathrm{C}_{\mathrm{B}} \mathrm{B}, \mathrm{BO}\right)+\left(\mathrm{CO}, \mathrm{CB}_{\mathrm{C}}\right)=(\mathrm{CB}, \mathrm{BO})+(\mathrm{CO}, \mathrm{CB})=(\mathrm{CO}, \mathrm{BO})=2(\mathrm{CA}, \mathrm{AB})$, donc $\left(C_{B} A, A B_{C}\right)=2(C A, A B)$, on trouve également que $\left(C_{B} A^{*}, A^{*} B_{C}\right)=2(C A, A B)$ d'après le lemme 3.2, ainsi $\left(C_{B} A, A B_{C}\right)=\left(C_{B} A^{*}, A^{*} B_{C}\right)$, ainsi les points $C_{B}, B_{C}, A$ et $A^{*}$ sont cocycliques.
|
| 164 |
+
|
| 165 |
+
Étape 2. T est sur le cercle circonscrit de $C_{B}, B_{C}, A$ et $A^{*}$.
|
| 166 |
+
Démonstration. $\left(A^{*} B_{C}, B_{C} T\right)=\left(B^{\prime} B_{C}, B_{C} T\right)=\left(B^{\prime} C, C T\right)=\left(B^{\prime} C, C T\right)=(A C, C T)=(A A, A T)=$ $\left(A A^{*}, A T\right)$, où la droite $(A A)$ désigne ici la tangente en $A$ au cercle $A B C$, d'après les lemmes 1 et 3 , alors les points $A^{*}, B_{C}, T$ et $A$ sont cocycliques.
|
| 167 |
+
|
| 168 |
+
En conclusion, les points $C_{B}, B_{C}, T, A$ et $A^{*}$ sont cocycliques.
|
| 169 |
+
On a de manière symétrique $C^{*}, A_{B}, B_{A}, T$ et $C$.
|
| 170 |
+
Comme $T$ est sur le cercle $C_{B} B_{C} T A A^{*}$ on peut échanger les rôles de $B$ et $C$, de la même manière on peut échanger les rôles de $A$ et $B$ en sachant que les points $C^{*} A_{B} B_{A} T C$ sont cycliques. On peut trouver la cocyclicité des quadrilatères suivants : $A B^{\prime} \mathrm{TB}_{A}, \mathrm{BC}^{\prime} \mathrm{TC}_{A}, \mathrm{CA}^{\prime} \mathrm{TA}_{\mathrm{C}}, \mathrm{BA}^{\prime} \mathrm{TA}_{\mathrm{B}}$, $A C^{\prime} \mathrm{TC}_{A}, C B^{\prime} \mathrm{TB}_{C}$, on trouve la cyclicité des pentagones suivants: $A A^{*} \mathrm{TC}_{A} B_{A}, C C^{*} \mathrm{~TB}_{C} A_{C}$ et $B B^{*} T A_{B} C_{B}$, mais également $B, B^{\prime}$ et $T$ sont alignés, $A A^{\prime} T$ et $C C^{\prime} T$ alignés, ainsi que $O C_{A} B_{C}$, $O B_{C} A_{C}$ et $O C_{B} A_{B}$. Après avoir compris un peu mieux l'exercice et les différentes propriétés de la figure on peut conclure.
|
| 171 |
+
On rappelle avant tout le théorème de Miquel dont la démonstration en chasse aux angles est laissée au lecteur:
|
| 172 |
+
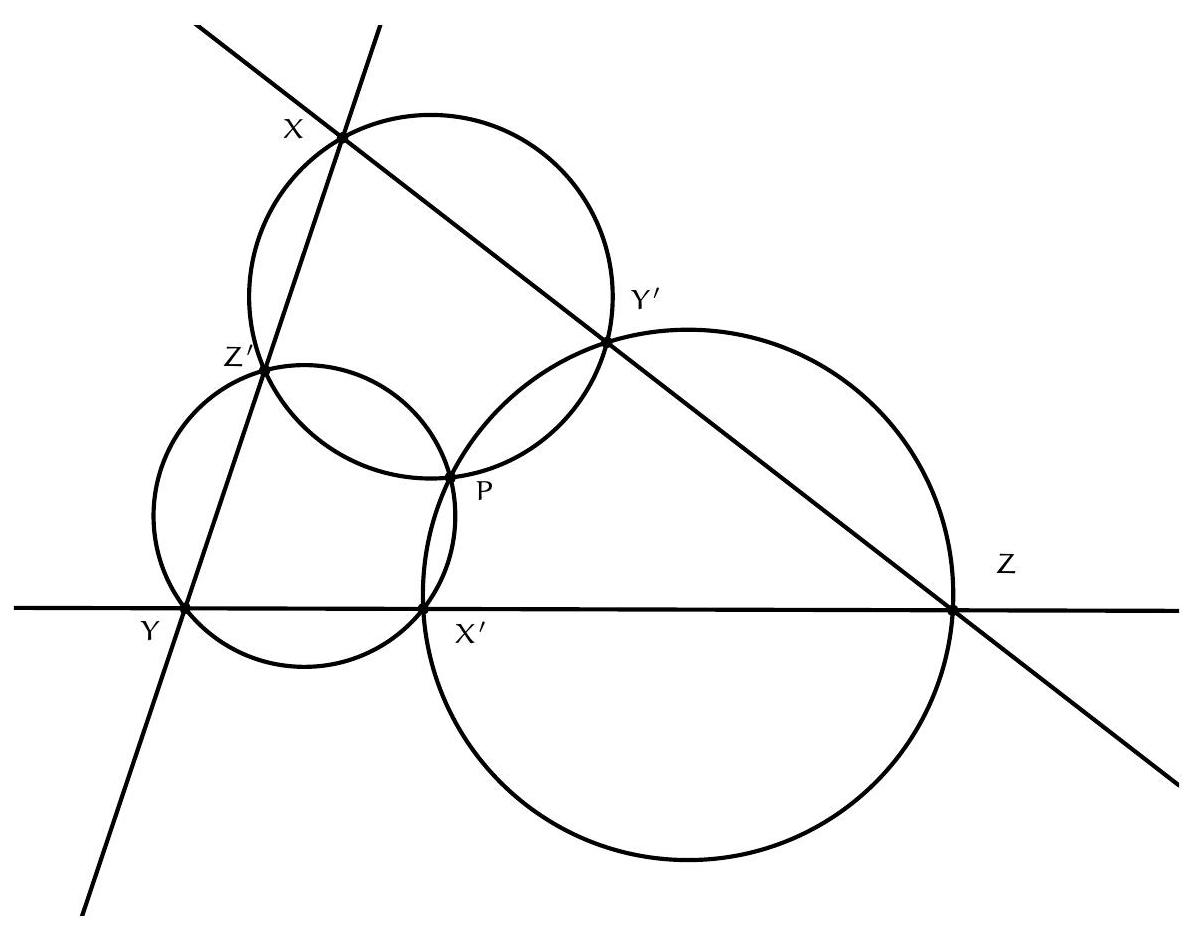
|
| 173 |
+
|
| 174 |
+
Soit $X Y Z$ un triangle, $X^{\prime}, Y^{\prime}$ et $Z^{\prime}$ des points sur les côtés $Y Z, X Y$ et $Z X$, alors les cercles $Y X^{\prime} Z^{\prime}$, $X Y^{\prime} Z^{\prime}$ et $X^{\prime} Y^{\prime} Z$ sont concourants en $P$.
|
| 175 |
+
|
| 176 |
+
On pose dans un premier temps: $X, Y, Z=A_{C}, B^{\prime}, C^{*}$ et $X^{\prime}, Y^{\prime}, Z^{\prime}=B_{C}, A^{\prime}, C$. Alors les cercles circonscrits de $C A_{C} A^{\prime}, B^{\prime} B_{C} C$ et $B_{C} C^{*} A^{\prime}$ se coupent en $T$, car $T$ est sur les cercles circonscrits $\operatorname{de} C A_{C} A^{\prime}$ et $B^{\prime} B_{C} C$. Ainsi, $T, B_{C}, C^{*}$ et $A^{\prime}$ sont cocycliques.
|
| 177 |
+
|
| 178 |
+
En posant $X, Y, Z=A^{\prime}, C_{B}, B^{*}$ et $X^{\prime}, Y^{\prime}, Z^{\prime}=A^{*}, C^{*}, B_{C}$. Alors $B_{C} C^{*} A^{\prime}, C_{B} B_{C} A^{*}$ et $A^{*} B^{*} C^{*}$ sont concourantes en $T$ également (car $T$ est déjà sur les cercles circonscrits de $B_{C} C^{*} A^{\prime}$ et $C_{B} B_{C} A^{*}$ ). Cela démontre ainsi que le point $T$ est sur le cercle circonscrit de $A^{*} B^{*} C^{*} T$.
|
| 179 |
+
|
| 180 |
+
On va maintenant démontrer que les cercles circonscrits de $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents en $T$. On introduit ( t ) la tangente en $T$ au cercle $A B C$, on va démontrer que ( $t$ ) est également tangente au cercle $A^{*} B^{*} C^{*}$.
|
| 181 |
+
On a $\left(C^{*} T, t\right)=\left(C^{*} T, T C\right)+(T C, t)=\left(C^{*} A_{B}, A_{B} C\right)+(T B, B C)$ (par cocyclicité et angle tangent). Or, $\left(C^{*} A_{B}, A_{B} C\right)=(B A, A C)+(A B, B C)$ par chasse au angle direct, mais $\left(B C^{\prime}, C^{\prime} C_{B}\right)=(B A, A C)+$ $(A B, B C)$ également. Ainsi, $\left(C^{*} \mathrm{~T}, \mathrm{t}\right)=\left(\mathrm{BC}^{\prime}, \mathrm{C}^{\prime} \mathrm{C}_{\mathrm{B}}\right)+(\mathrm{TB}, \mathrm{BC})=\left(\mathrm{BT}, \mathrm{TC}_{\mathrm{B}}\right)+(\mathrm{TB}, \mathrm{BC})=$ $\left(\mathrm{BC}, \mathrm{TC}_{\mathrm{B}}\right)=\left(\mathrm{TB}^{*}, \mathrm{~B}^{*} \mathrm{C}^{*}\right)$.
|
| 182 |
+
Ce qui conclut la preuve de l'exo.
|
| 183 |
+
Remarque. Il est également possible de démontrer, avec des outiles plus ava, cés, que les droites $(A B),(B C),(C A),\left(A^{*} B^{*}\right),\left(B^{*} C^{*}\right)$ et $\left(C^{*} A^{*}\right)$ sont tangentes à une même parabole $\mathcal{P}$ de foyer $T$ et de directrice la droite qui relie $O$ et le centre du cercle circonscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$.
|
| 184 |
+
|
| 185 |
+
Démonstration. On va commencer par quelques lemmes sur les paraboles
|
| 186 |
+
Lemme. pour toute parabole il existe un foyer et une directrice tel que pour tout point P de la parabole, la distance de $P$ au foyer et à la droite soit la même.
|
| 187 |
+
|
| 188 |
+
Démonstration. On va démontrer le résultat suivant sur les ellipses : chaque ellipse admet deux foyers, appelés $F_{1}$ et $F_{2}$ tel que pour chaque point $E$ de l'ellipse $F_{1} E+F_{2} E$ est constante.
|
| 189 |
+
on rappelle qu'une conique est une section conique c'est-à-dire que l'on coupe un cône avec un plan quelconque et que l'on regarde les points d'intersection du plan et de la conique dans le plan du plan en question.
|
| 190 |
+

|
| 191 |
+
|
| 192 |
+
On peut prendre les deux sphères tangentes au cône et au plan à la fois, la sphère du bas touche le plan en un point $F_{1}$ et la sphère du haut touche le plan en un point $F_{2}$, alors pour un point $E$ sur l'ellipse (en rouge sur le dessin), la droite $F_{1} E$ est une tangente à la sphère du bas, la droite $\mathrm{E}_{1} \mathrm{E}$ également car elle appartient au cône et que la phère est tangente au cône. Ainsi, $\mathrm{EF}_{1}=E \mathrm{E}_{1}$, de la même manière $\mathrm{EF}_{2}=\mathrm{EE}_{2}$, ainsi $\mathrm{EF}_{1}+\mathrm{EF}_{2}=\mathrm{E}_{1} \mathrm{E}_{2}$ et $\mathrm{E}_{1} \mathrm{E}_{2}$ est clairement une constante pour tout les points E . Donc $\mathrm{EF}_{1}+\mathrm{EF}_{2}$ est constant, ce qui conclut.
|
| 193 |
+
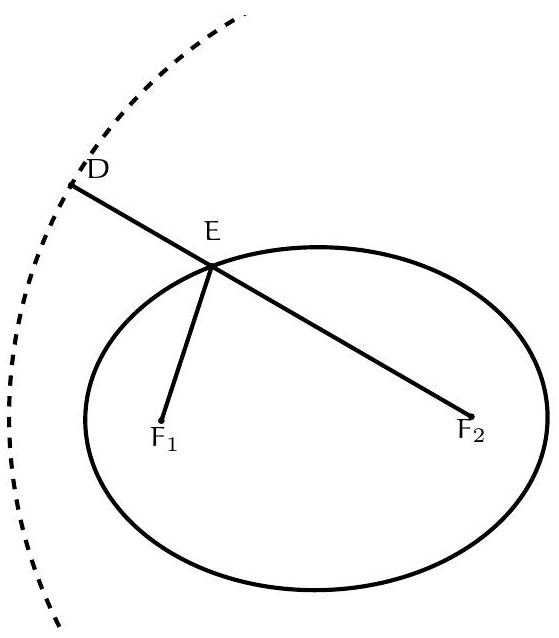
|
| 194 |
+
|
| 195 |
+
On contruit maintenant le point D tel que $E \mathrm{~F}_{1}=E D$ et que les points $\mathrm{D}, E$ te $\mathrm{F}_{2}$ soient alignés. Alors pour tout $E$ sur l'ellipse on trouve que $F_{2} D=F_{1} E+F_{2} E$ est une constante, donc quand $E$ bouge sur l'ellipse, le point D bouge sur une cercle de centre $F_{2}$.
|
| 196 |
+
|
| 197 |
+
On cherche maintenant à contruire une ellipse, pour construire une ellipse l'intersection du plan et de la conique ce fait de manière parallèle à un des "côtés" du cône, dans ce cas le point $\mathrm{F}_{2}$ est envoyé à l'infini. Regardons ce qu'il advient de notre point D précédent, il bouge sur un cercle de centre un point à l'infini donc une droite, pour construire le point $E$, il s'agit maintenant de prendre le point sur un rayon du cercle (c'est-à-dire une droite perpendiculaire au lieu des points D dans notre cas) et de prendre le point sur cette droite qui à la même distance à D et à $F_{1}$, autrement dit il existe un point $F_{1}$ et une droite ( d ) tel que pour tout point de la parabole la distance à la droite (appelée directrice) et au point soit la même.
|
| 198 |
+
|
| 199 |
+
Lemme. Soit $\mathcal{P}$ une parabole et $(t)$ une tangente à $\mathcal{P}$ en $E$, alors le symétrique de $F$ par rapport à $(t)$ est sur la directrice de la parabole.
|
| 200 |
+
|
| 201 |
+
Démonstration. Soit $\mathrm{E}_{1}$ la projection orthogonale de E sur la directrice, alors $\mathrm{FE}=\mathrm{EE}_{1}$, on note $\mathrm{E}^{\prime}$ le symétrique de F par rapport à ( t ), on a alors $\mathrm{EE}^{\prime}=\mathrm{EF}=\mathrm{EE} \mathrm{E}_{1}$, comme $\mathrm{EE}_{1}$ est la distance de E à la parabole la droite, le point $E^{\prime}$ est du même côté de la directrice que la parabole. On prend maintenant G le point de la parabole tel que ( $\mathrm{GE}^{\prime}$ ) est perpendiculaire à la directrice, alors en notant $\mathrm{G}_{1}$ la projection orthogonale de G sur la directrice, on a d'une part : $\mathrm{FG}=\mathrm{GG}_{1}=\mathrm{GE}^{\prime}$ donc $E^{\prime}=G_{1}$ est $E^{\prime}$ est sur la directrice. Ce qui conclut.
|
| 202 |
+
|
| 203 |
+
Lemme. Soit $\left(t_{1}\right),\left(t_{2}\right)$ et $\left(t_{3}\right)$ trois tangentes à une parabole $\mathcal{P}$ de foyer $F$, alors le cercle circonscrit du triangle formé par $\left(t_{1}\right),\left(t_{2}\right)$ et $\left(t_{3}\right)$ passe par $F$ également.
|
| 204 |
+
|
| 205 |
+
Démonstration. Les trois symétriques de F par rapport aux trois droites sont sur la directrice, donc alignés, ce qui montre d'après Steiner que le point $F$ est sur le cercle circonscrit du triangle induit par les trois tangentes et de plus que l'orthocentre de ce triangle est sur la directrice.
|
| 206 |
+
|
| 207 |
+
Il existe une unique conique tangente à cinq droites, en prenant la coniques tangentes aux droites $(A B),(B C),(C A)$ et $\left(B_{A} B_{C}\right)$ et la droite à l'infini on trouve une parabole tangente aux quatres premiers droites, d'après le lemme précédent le foyer est sur les cercles circonscrits de $B^{\prime} B_{C} C$ et $B^{\prime} A B_{A}$, il s'agit donc de $F\left(B^{\prime}\right.$ est sur les tangentes donc ne peut pas être le foyer de la parabole). De la même manière on arrive à démontrer que finalement les 6 droites $(A B)$, $(B C),(C A),\left(A^{*} B^{*}\right),\left(B^{*} C^{*}\right)$ et $\left(C^{*} A^{*}\right)$ sont tangentes à une même parabole $\mathcal{P}$ de foyer $T$ et de directrice la droite qui relie $O$ et le centre du cercle circonscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$.
|
| 208 |
+
|
| 209 |
+
## Lien avec le point de Feuerbach
|
| 210 |
+
|
| 211 |
+
On pose que l'intersection des tangentes en $B$ et $C$ sont $A^{\prime \prime}$. On définit de la même manière $B^{\prime \prime}$ et $C^{\prime \prime}$, alors le cercle $A B C$ est le cercle inscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, on va montrer que le cercle $A^{*} B^{*} C^{*}$ est le cercle d'Euler du triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, on va ici montrer que les points $A^{*}, B^{*}$ et $C^{*}$ sont les milieux des côtés de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. On sait déjà que les droites $\left(A A^{*}\right),\left(B B^{*}\right)$ et $\left(C C^{*}\right)$ sont des tangentes au cercle circonscrit de $A B C$, ce qui montre que les points $A^{*}, B^{*}$ et $C^{*}$ sont sur les côtés du triangles $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, il faut maintenant démontrer qu'ils sont les milieux des côtés.
|
| 212 |
+
Pour conclure on va démontrer les deux lemmes suivants.
|
| 213 |
+
|
| 214 |
+
Lemme 1. Soit $A B C$ un triangle, $D, E$ et $F$ les points de tangence du cercle inscrit sur les côtés, $B C, C A$ et $A B$. On note également les points $X$ la projection orthogonale de $C$ sur la bissectrice issue de $B$, alors les points $X, E$ et $F$ sont alignés.
|
| 215 |
+
|
| 216 |
+
Démonstration. Il y a une projection orthogonale donc on peut penser à la droite de Simson. On note alors $Y$ le point d'intersection des droites $(C X)$ et $(A B)$, on sait que le cercle passant par $A$, $C$ et I est le cercle antarctique et ainsi le symétrique de $C$ par rapport à la bissectrice issue de $B$ est également sur ce cercle par symétrie axiale le long de la bissectrice, qui passe par le centre, alors les points $A, Y, C$ et I sont cocycliques, donc d'après la droite de Simson, les projections orthogonales de I sur les trois côtés du triangle sont alignés, il s'agit alors des points $E, F$ et $X$ ce qui montre le lemme.
|
| 217 |
+
|
| 218 |
+
Lemme 2. On note toujours $D$ le point de tangence du cercle inscrit de $A B C$ sur $B C$ et $D^{\prime}$ le point de tangence du cercle $A$-exinscrit (de centre $I_{A}$ ) de $A B C$ sur $B C$, on note alors $X$ et $Y$ les projections respectives de $B$ et $C$ sur ( $A I$ ), alors les points $D, D^{\prime}, X$ et $Y$ sont cocycliques de diamètre $\left[\mathrm{DD}^{\prime}\right]$.
|
| 219 |
+
|
| 220 |
+
Démonstration. On va de ce fait montrer que $\widehat{\mathrm{DXD}^{\prime}}=90$, en prenant (AI) et (BC) comme droites de référence, on trouve par cocyclicité des points $D^{\prime}, B, X$ et $I_{A}$, grâce aux angles droits, que $\left(X D^{\prime}\right) \backslash \backslash\left(B I_{A}\right)$, de la même manière $(X D) \backslash \backslash(B I)$, par passage aux antiparallèle $\left(X D^{\prime}, X D\right)=$ $\left(\mathrm{BI}_{\mathrm{A}}, \mathrm{BI}\right)=90$ ce qui démontre bien que $X$ est sur le cercle de diamètre [ $\mathrm{DD}^{\prime}$ ], de la même manière $Y$ est sur le cercle de diamètre $\left[D^{\prime}\right]$, ce qui montre le lemme 2 . On remarque ici que le milieu du côté $[B C]$ est également le milieu de [DD'], et ainsi le centre du cercle passant par $D^{\prime}$, D, X et Y .
|
| 221 |
+
|
| 222 |
+
Nous pouvons maintenant conclure et montrer que cet exercice est équivalent au point de Feuerbach. En effet, d'après le lemme 1 , le point $A_{C}$ est la projection orthogonale de $A^{\prime \prime}$ sur ( $C^{\prime \prime} \mathrm{O}$ ), de la même manière $\mathrm{B}_{\mathrm{C}}$ est la projection orthogonale de $\mathrm{B}^{\prime \prime}$ sur $\left(\mathrm{C}^{\prime \prime} \mathrm{O}\right)$, cela montre, d'après le lemme 2 que le centre du cercle circonscrit de $B_{C} A_{C} C$ est le milieu de $A^{\prime \prime} B^{\prime \prime}$, or d'après la preuve précédente le centre du cercle $B_{C} A_{C} C$ est $C^{*}$ qui est ainsi le milieu de $A^{\prime \prime} B^{\prime \prime}$. Ainsi le cercle $A^{*} B^{*} C^{*}$ est le cercle d'Euler et ABC le cercle inscrit. L'exercice montre alors que le cercle d'Euler et le cercle inscrit sont tangents, le point de tangence est appelé point de Feuerbach.
|
| 223 |
+
|
| 224 |
+
## Propriétés du point de Feuerbach
|
| 225 |
+
|
| 226 |
+
On peut alors trouver les propriétés suivantes sur le point de Feuerbach : Soit $A B C$ un triangle, D, E et $G$ les points de tangence du cercle inscrit avec les côtés $B C, C A$ et $A B$. On note $M_{A}, M_{B}$ et $M_{C}$ les milieux des côtés $B C, C A$ et $A B$. Alors en posant $F$ le point de Feuerbach, on trouve que les droites (DF), (EG) et $M_{B} M_{C}$ sont concourantes. On trouve également la propriété suivante : le cercle passant par les points $D, F$ et $M_{A}$ passe également par $X$ et $Y$ intersections de (BI) et (CI) avec la droite (EG). La dernière remarque revient à dire que le point de Feuerbach est le foyer d'une conique tangente aux droites $\mathrm{DE}, \mathrm{EG}, \mathrm{GD}, \mathrm{M}_{\mathrm{A}} M_{B}, M_{B} M_{C}$ et $M_{C} M_{A}$, on a aussi vu que la directrice de cette conique est la droite passant par l'orthocentre du triangle $M_{A} M_{B} M_{C}$, (soit $O$ le centre du cercle circonscrit) de $A B C$ et l'orthocentre de DEG. Il est possible de démontrer que cette droite est en fait la droite (OI) (exercice laissé au lecteur).
|
| 227 |
+
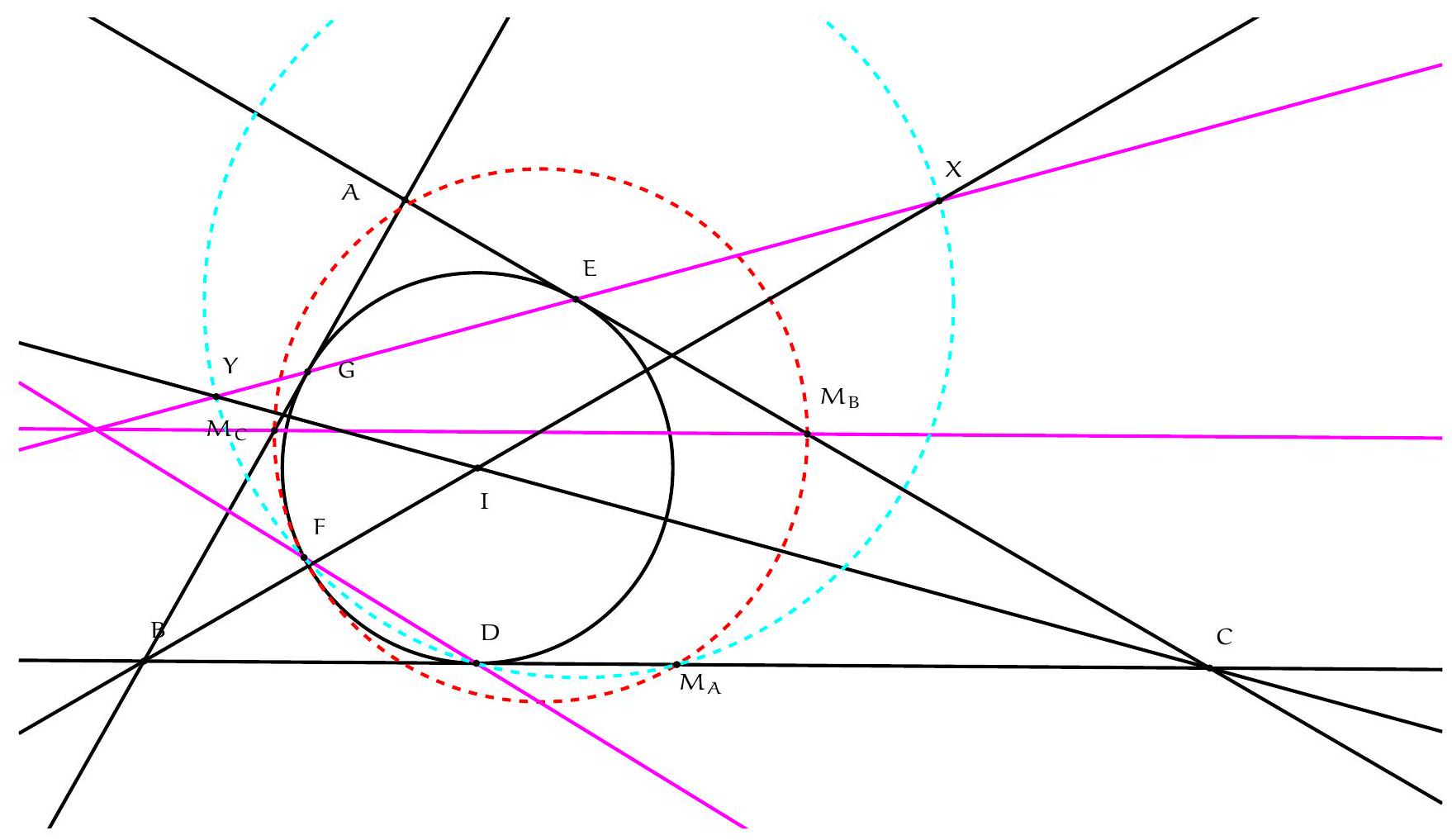
|
| 228 |
+
|
French_STS/md/fr-corrige-envoi-2.md
ADDED
|
@@ -0,0 +1,65 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+

|
| 4 |
+
|
| 5 |
+
Envoi 2 : ARITHMÉTIQUE
|
| 6 |
+
À RENVOYER AU PLUS TARD LE 14 DÉCEMBRE 2018
|
| 7 |
+
|
| 8 |
+
## Exercices Juniors
|
| 9 |
+
|
| 10 |
+
Exercice 1. Trouver le nombre de solutions de $n^{2} m^{6}=180 t+2$ pour $n, m$ et $t$ des entiers positifs.
|
| 11 |
+
Solution de l'exercice 1 On considère l'expression modulo 4. La gauche est un carré et est donc congru à 0 ou 1.180 est congru à 0 modulo 4 donc $180 t+2$ est congru à $0 * t+2=2$. L'équation n'a pas de solutions modulo 4 , elle n'en a donc pas non plus dans $\mathbb{N}$
|
| 12 |
+
Exercice 2. Trouver la somme des $n$ tels que $n^{2}+8 n+44$ soit un carré parfait.
|
| 13 |
+
Solution de l'exercice 2 Soit f la fonction étudiée, une idée dans ce genre d'exercice est de coincer $f(n)$ entre 2 carrés d'entiers consécutifs $k^{2}<f(n)<(k+1)^{2}$ et de dire par l'absurde que si $f(n)=\mathfrak{i}^{2}$ alors $k<i<k+1$ ce qui est impossible car on a des entiers.
|
| 14 |
+
Ici les calculs peuvent s'abréger en remarquant que f a même parité que $n+4$, ainsi si $(n+4)^{2}=n^{2}+8 n+16<f(n)<n^{2}+12 n+36=(n+6)^{2}$ ce qui est vrai dès que $n>2, f(n)$ n'est pas un carré. Pour les petits cas 2 est solution et 1 non.
|
| 15 |
+
Exercice 3. Un entier $n$ est parfait si la somme de ses diviseurs est 2 n . Soit n un entier parfait et $p$ son plus petit diviseur premier. Montrer que l'exposant de $p$ dans la décomposition en produit de puissances de nombres premiers de n est pair.
|
| 16 |
+
$\underline{\text { Solution de l'exercice } 3}$ Soit $n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}$ avec les $p_{i}$ premiers distincts. La somme des diviseurs de $n$ est $\sigma(n)=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$ (cf. la page 14 du cours d'arithmétique complet disponible sur maths-olympiques.fr).
|
| 17 |
+
Supposons par l'absurde que $a_{1}$ soit impair, alors $1+\cdots+p_{1}^{a_{1}}=\left(1+p_{1}\right)+p_{1}^{2}\left(1+p_{1}\right)+\cdots+$ $p_{1}^{a_{1}-1}\left(1+p_{1}\right)$. Alors $p_{1}+1$ divise $1+\cdots+p_{1}^{a_{1}}$, donc aussi $2 n=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$. Si $p_{1}+1$ $\mathrm{n}^{\prime}$ est pas premier: il a un plus grand diviseur premier $\mathrm{q}<\mathrm{p}_{1}$ qui vérifie $\mathrm{q} \mid 2 \mathrm{n}$; alors comme q est premier avec $\mathrm{n}, \mathrm{q}=2$; mais alors $\mathrm{q}^{2}\left|\mathrm{p}_{1}+1\right| 2 \mathrm{n}$ et donc $\mathrm{q} \mid \mathrm{n}$, contradiction.
|
| 18 |
+
Donc $p_{1}+1$ est premier et alors nécessairement $p_{1}=2$ et $p_{1}+1=p_{2}=3$. Alors $n, \frac{n}{2}, \frac{n}{3}$ et $\frac{n}{6}$ sont entiers et divisent de $n$. Comme $n>6$, ils sont différents de 1 . Ainsi $2 n=\sigma(n) \geqslant$ $n+\frac{n}{2}+\frac{n}{3}+\frac{n}{6}+1=2 n+1$, contradiction. Donc $a_{1}$ est pair.
|
| 19 |
+
|
| 20 |
+
## Exercices Communs
|
| 21 |
+
|
| 22 |
+
Exercice 4. Soit $n$ un entier strictement positif. Montrer qu'il existe $n$ entiers 2 à 2 distincts $r_{1}, \ldots, r_{n}$ tels que chaque $r_{i}$ divise $r_{1}+\cdots+r_{n}$.
|
| 23 |
+
Solution de l'exercice 4 La solution s'inspire des fractions égyptiennes, une fraction égyptienne est uplet d'entiers distincts $a_{1}, \ldots, a_{n}$ vérifiant $1 / a_{1}+\cdots+1 / a_{n}=1$, par exemple
|
| 24 |
+
$1 / 2+1 / 3+1 / 6=1$.
|
| 25 |
+
Alors en posant $r_{i}:=\prod_{j \neq i} a_{j}=\frac{a_{1} \cdots a_{n}}{a_{i}} \in \mathbb{Z}$, ils seront distinct et leur somme fera $a_{1} \cdots a_{n}$, que chaque $r_{i}$ divise.
|
| 26 |
+
On montre par récurrence qu'une fraction égyptienne existe pour chaque $\mathrm{n} \geqslant 3$. L'exemple fait l'initialisation.
|
| 27 |
+
Hérédité : supposons prouvé pour n prouvons pour $\mathrm{n}+1$, on écrit les coefficients triés dans l'ordre croissant, puis on écrit $a_{n}^{\prime}=1+a_{n}$ et $a_{n+1}^{\prime}=a_{n}\left(1+a_{n}\right)$ On remarque $1 / a_{n}^{\prime}+1 / a_{n+1}^{\prime}=1 / a_{n}$. En posant $a_{i}^{\prime}=a_{i}$ pour $i \in\{1, \ldots, n-1\}$, on dispose d'une fraction égyptienne de longueur $n+1$, ce qui conclut la récurrence (depuis l'exemple on a $1 / 7+1 / 42=1 / 6$ et cela donne : $1 / 2+1 / 3+1 / 7+1 / 42=1)$.
|
| 28 |
+
Exercice 5. Soit $n$ un entier positif. Montrer qu'il existe un entier positif $m$ tel que $n!=$ $\varphi(\mathrm{m})$, où $\varphi$ est la fonction indicatrice $d^{\prime}$ Euler. (On rappelle que si $m=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}}$ avec $p_{1}, \ldots, p_{\mathrm{k}}$ des nombres premiers 2 à 2 distincts, $\left.\varphi(m)=m\left(\left(1-\frac{1}{\mathfrak{p}_{1}}\right) \cdots\left(1-\frac{1}{\mathfrak{p}_{\mathrm{k}}}\right)\right)\right)$
|
| 29 |
+
$\underline{\text { Solution de l'exercice } 5}$ On procède par construction en partant des plus grands nombres premiers au plus petit.
|
| 30 |
+
L'idée est de contraindre la valeur de $\phi(m)$. La construction peut paraître un peu lourde mais il ne faut pas se laisser et impressionner et comprendre l'idée qui est derrière.
|
| 31 |
+
Soit $p_{1}, p_{2} \ldots$ les nombres premiers $p_{k} \leqslant n<p_{k+1}$
|
| 32 |
+
On montre par récurrence descendante que pour tout $i$ il existe $m_{i}$ tel que
|
| 33 |
+
|
| 34 |
+
- $m_{i}$ est un produit de $p_{j}$ avec $k \geqslant j \geqslant i$
|
| 35 |
+
- Pour tout $j \geqslant i, p_{j}$ a le même exposant dans $m_{i}$ et $n$ !
|
| 36 |
+
- $\phi\left(m_{i}\right) \mid n!$
|
| 37 |
+
|
| 38 |
+
L'initialisation se fait pour $\mathrm{i}=\mathrm{k}+1$ avec $\mathrm{m}_{\mathrm{k}+1}=1$.
|
| 39 |
+
Pour l'hérédité on multiplie $m_{i+1}$ par $p_{i}$ jusqu'à avoir autant de $p_{i}$ dans $\phi\left(m_{i}\right)$ que dans $n$ ! pour obtenir $m_{i}$ on respecte ainsi les 2 premières hypothèses sur $m_{i}$.
|
| 40 |
+
Vérifions que la dernière est aussi vérifiée, pour $j \geqslant i$ on sait que l'on n'a pas de problème, le risque est une trop grosse valuation pour un $p_{l}$ où $l$ petit or vu la construction si $p_{l}^{\alpha} \mid \phi\left(m_{i}\right)$, $p_{l}^{\alpha}\left|\left(p_{i}-1\right)\left(p_{i+1}-1\right) \cdots\left(p_{k}-1\right)\right| n!$ on est donc assuré que la récurrence marche. Avec $m=m_{1}$, on obtient une solution à l'exercice.
|
| 41 |
+
Exercice 6. Soit $n \geqslant 3$ un entier, montrer qu'il existe deux entier $x$ et $y$ tels que $7 x^{2}+y^{2}=2^{n}$.
|
| 42 |
+
|
| 43 |
+
## Solution de l'exercice 6 Encore une solution par récurrence! Initialisation: $x_{3}=y_{3}=1$.
|
| 44 |
+
|
| 45 |
+
Hérédité : On suppose prouvé par récurrence pour $n,\left(X=\left(x_{n}+y_{n}\right) / 2, Y=\left|7 x_{n}-y_{n}\right| / 2\right)$ $\left(X=\left|x_{n}-y_{n}\right| / 2, Y=\left(7 x_{n}+y_{n}\right) / 2\right)$ les 2 couples vérifient $7 X^{2}+Y^{2}=2^{n+1}$. Le premier couple est solution si $x_{n}$ et $y_{n}$ on même congruence modulo 4 ( $X$ et $Y$ impairs) sinon le second convient, ce qui conclut.
|
| 46 |
+
|
| 47 |
+
## Exercices Seniors
|
| 48 |
+
|
| 49 |
+
Exercice 7. Soit $p \geqslant 5$ un nombre premier. Montrer qu'il existe un entier $n$ tel que pour tout $x \in\{n-1, n, n+1\}, p^{2} \nmid x^{p-1}-1$ et $p \nmid x$.
|
| 50 |
+
Solution de l'exercice 7 Lemme : entre 0 et $p^{2}$ il y a exactement $p-1$ éléments dont la puissance $(p-1)$-ième est congrue à 1 modulo $p^{2}$.
|
| 51 |
+
preuve: On prend $\omega$ une racine primitive modulo $p^{2}$ (pour rappel $\omega$ une racine primitive modulo m signifie que les puissances de $\omega$ correspondent à tout les inversibles modulo m , ce qui existe dès que $m$ est $1,2,4$ ou une puissance de premier impair ou 2 fois une puissance de premier impair, lire les polycopiés pour plus de détail), les éléments d'ordre divisant
|
| 52 |
+
$p-1$, sont alors ce dont le logarithme discret (log vérifie que $\log (x)<\phi(m)$ et $\omega^{(\log (x))}=$ $x(\bmod m))$ est divisible par $p$, ce qui donne bien $p-1$ possibilités.
|
| 53 |
+
On utilise un principe des tiroirs : les chaussettes sont les $x$ entre 0 et $p^{2}$ d'ordre divisant $p-1$, il y en a $p-1$ par le lemme, les $p$ tiroirs sont les intervalles $k p+1 ;(k+1) p$, il y donc un tiroir vide d'où l'on peut tirer le n voulu en prenant par exemple $\mathrm{kp}+2$.
|
| 54 |
+
Exercice 8. Soit P un polynôme à coefficients rationnels de degré supérieur ou égal à 2 , et $\left(q_{n}\right)_{n \in \mathbb{N}}$ une suite de rationnels tels que pour tout $n \geqslant 0, q_{n}=P\left(q_{n+1}\right)$. Montrer que la suite $q_{n}$ est périodique à partir d'un certain rang.
|
| 55 |
+
Solution de l'exercice 8 Soit $u$ entier tel que $u_{1}$ soit entier. Soit $\tilde{P}(X)=u P\left(\frac{1}{u} X\right)$. Soit $v$ entier tel que $v \tilde{P}$ soit à coefficients entiers. Soit a le coefficient dominant de $v \tilde{P}$. On pose $Q(X)=$ $a \tilde{P}\left(\frac{1}{a} X\right), m=a^{\operatorname{deg}(P)-2} v$ et pour tout $n \in \mathbb{N}, r_{n}=u a q_{n}$.
|
| 56 |
+
Nous avons $m Q(X)$ unitaire à coefficients entiers et pour tout $n, r_{n}=Q\left(r_{n+1}\right) . r_{0}$ est entier, or comme pour tout $n, r_{n+1}$ est racine rationnelle du polynôme $m Q(X)-m r_{n}$ unitaire à coefficients entiers, par récurrence, $r_{n}$ est entier pour tout $n$.
|
| 57 |
+
Comme $\operatorname{deg}(Q)>1,|Q(x) / x|$ tend vers $+\infty$ quand $|x|$ tend vers $+\infty$. Donc il existe $M>\left|r_{0}\right|$ tel que pour tout $x,|Q(x)| \leqslant M \Rightarrow|x| \leqslant M$. Par récurrence immédiate, $\left|r_{n}\right| \leqslant M$ pour tout n . La suite r prend donc ses valeurs dans un ensemble fini. Soit $p$ minimal tel que $\left\{r_{0}, \ldots, r_{p-1}\right\}=\left\{r_{0}, r_{1}, \ldots\right\}$. Montrons par récurrence sur $n$ que $r_{n+p}=r_{n}$ pour tout $n$. Par hypothèse, $r_{n+p} \in\left\{r_{n}, \ldots, r_{n+p-1}\right\}=\left\{r_{0}, \ldots, r_{p-1}\right\}$. Donc $r_{n+p}=r_{n+k}$ avec $k \in\{0, \ldots, p-1\}$. Alors si $k>0, r_{p-1}=Q^{\circ(n+1)}\left(r_{n+p}\right)=Q^{\circ(n+1)}\left(r_{n+k}\right)=r_{k-1}$ et il y a contradiction avec la minimalité de $p$. Donc $k=0$ et $r_{n}=r_{n+p}$. Ce qui conclut la récurrence.
|
| 58 |
+
Nous venons de montrer que la suite est périodique de période $p$.
|
| 59 |
+
Exercice 9. Pour $m$ entier positif, on note $d(m)$ le nombre de diviseurs positifs de $m$ (1 et m compris). Soit k un entier strictement positif. Montrer qu'il existe une infinité d'entiers positifs $n$ tels que $n$ ait exactement $k$ diviseurs premiers distincts et tel que pour tout $a, b$ entiers strictement positifs avec $n=a+b, d(n)$ ne divise pas $d\left(a^{2}+b^{2}\right)$
|
| 60 |
+
Solution de l'exercice 9 Prouvons que chaque entier de la forme $n=m 2^{p-1}$ avec $p$ premier impair, possédant $k-1$ facteurs premiers strictement plus grand que 3 et vérifiant $(5 / 4)^{(p-1) / 2}>$ m est solution.
|
| 61 |
+
Si $a+b=n$ et $d(n) \mid d\left(a^{2}+b^{2}\right)$ alors $p \mid d\left(a^{2}+b^{2}\right)$. Donc il existe $q$ premier tel que $q$ ait un exposant $c p-1$ dans $a^{2}+b^{2}$. Si $q \geqslant 5, a^{2}+b^{2} \geqslant 5^{q-1}>n^{2}$, or $a^{2}+b^{2}=n^{2}-2 a b \leqslant n^{2}$. Donc $\mathrm{q}=2 \mathrm{ou} 3$.
|
| 62 |
+
Si $q=3$ en regardant $a^{2}+b^{2}$ modulo 3,3 divise $a$ et $b$ donc $n$, contradiction avec l'hypothèse.
|
| 63 |
+
Si $q=2$, si $a$ et $b$ ont des valuations 2 -adiques distinctes la plus petite est $p-1$ celle de la somme des carrés $2 p-2$, absurde.
|
| 64 |
+
S'ils ont même valuation 2-adique $a=2^{\mathrm{t}} a_{0} b=2^{\mathrm{t}} b_{0}$ avec $a_{0}$ et $b_{0}$ impaire $a_{0}^{2}+b_{0}^{2}=$ $x 2^{\text {cp-1-2t }}$ la gauche fait 1 modulo 4 , donc $\mathrm{cp}-1-2 \mathrm{t}=1$ or $\mathrm{t}<\mathrm{p}-1$, donc $\mathrm{c}=1$ est la seule solution, on a un problème de parité absurde, ce qui conclut.
|
| 65 |
+
|
French_STS/md/fr-corrige-envoi-4-2023-2024.md
ADDED
|
@@ -0,0 +1,309 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br> 
|
| 2 |
+
|
| 3 |
+
ENVOI 4 : COMBINATOIRE
|
| 4 |
+
À RENVOYER AU PLUS TARD LE 15 MARS 2024
|
| 5 |
+
|
| 6 |
+
Les consignes suivantes sont à lire attentivement :
|
| 7 |
+
|
| 8 |
+
- Le groupe junior est constitué des élèves nés en 2009 ou après. Les autres élèves sont dans le groupe senior.
|
| 9 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 10 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 11 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 12 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 13 |
+
- Respecter la numérotation des exercices.
|
| 14 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
## Exercices Juniors
|
| 18 |
+
|
| 19 |
+
Exercice 1. Antoine propose à Baptiste de jouer à l'"alphabet en folie" : Ils commencent par se mettre d'accord sur une lettre. Puis, à tour de rôle, chacun peut choisir de prononcer entre 1 et 2 lettres suivantes dans l'alphabet en partant de A. Celui qui prononce la lettre choisie a gagné. Si Antoine commence, pour quelles lettres de départ dispose-t-il d'une stratégie lui permettant de gagner la partie à coup sûr?
|
| 20 |
+
|
| 21 |
+
Voici un exemple de partie : la lettre choisie initialement est E. Antoine dit "A", Baptiste "BC", Antoine "CD" et Baptiste dit "E". Dans ce cas, Baptiste a gagné.
|
| 22 |
+
Solution de l'exercice 1 Montrons que Antoine a une stratégie gagnante si, et seulement si, le rang de la lettre choisie dans l'alphabet n'est pas un multiple de 3 . Colorons les lettres de l'alphabet en bleu-blanc-rouge dans l'ordre. Si la lettre d'arrivée est rouge (c'est à dire que son rang dans l'alphabet est un multiple de 3), Baptiste possède la stratégie suivante : à chaque fois qu'Antoine choisit de dire une lettre, Baptiste en dit deux et à chaque fois qu'Antoine décide de dire deux lettres il n'en dit qu'une. Selon cette stratégie, quels que soient ses choix passés, Antoine n'a le choix à chaque tour qu'entre une lettre bleue ou une lettre bleue et une blanche et ne dira pas la lettre finale rouge. En revanche, si la lettre choisie est blanche ou bleue, Antoine possède une stratégie gagnante : il lui suffit de prendre A si la lettre finale est bleue ou A et B si elle est blanche, puis d'appliquer la stratégie qui était celle de Baptiste dans le cas rouge.
|
| 23 |
+
|
| 24 |
+
Commentaire des correcteurs: L'exercice est compris dans l'ensemble des copies. Certains élèves perdent des points en oubliant de montrer qu'ils trouvent bien toutes les lettres pour lesquelles Antoine a une stratégie gagnante. Précisément, il était nécessaire d'expliquer pourquoi Antoine n'a pas de stratégie gagnante pour les lettres dont le rang est un multiple de 3. Outre cet écueil, beaucoup de rédactions sont laborieuses ou peu précises : cela n'a pas été pénalisé lorsque le raisonnement était manifestement compris. La rédaction d'un exercice de combinatoire est souvent source de difficulté, il s'agit toutefois d'une piste d'amélioration rapide et il est donc vivement conseillé de lire les corrigés des exercices afin de pouvoir s'inspirer de rédactions claires et efficaces à l'avenir.
|
| 25 |
+
|
| 26 |
+
Exercice 2. Aurélien découpe une feuille de papier en 7 morceaux. Une étape consiste ensuite à choisir un morceau et à le découper en 4,7 ou 10 morceaux. Aurélien peut-il obtenir ainsi 2021 morceaux ?
|
| 27 |
+
Solution de l'exercice 2 L'exercice décrit une suite d'opérations et demande s'il est possible de passer d'un état initial à un état final, on peut donc légitimement chercher un invariant du système.
|
| 28 |
+
Ici, nous allons montrer que le nombre de morceausx d'Aurélien est toujours de la forme $3 k+1$, avec $k$ un entier naturel.
|
| 29 |
+
C'est le cas dans la situation initiale, puisqu'Aurélien dispose de $7=3 \times 2+1$ morceaux. Puis, si c'est le cas lors d'une étape et qu'Aurélien dispose de $3 k+1$ morceaux avec $k$ un entier naturel, Aurélien remplace un morceau par $3 \times 1+1$ morceaux, par $3 \times 2+1$ morceaux ou par $3 \times 3+1$ morceaux, de sorte qu'il lui reste, à la fin de l'opération, $3(k+1)+1,3(k+2)+1$ ou $3(k+3)+1$ morceaux. De proche en proche, on a bien le résultat annoncé. Comme $2021=3 \times 673+2$ n'est pas de la forme indiquée, on ne peut jamais obtenir 2021 morceaux par le processus décrit.
|
| 30 |
+
|
| 31 |
+
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont abordé. Certains manquent un peu d'habitude pour bien justifier proprement, ce qui peut être dommageable dans des cas plus compliqués. Je vous conseille de regarder le corrigé pour quelque chose de parfaitement clair.
|
| 32 |
+
|
| 33 |
+
Exercice 3. On dispose de cinq couleurs et d'une grille $99 \times 99$. On colorie certains carrés de la grille avec l'une des cinq couleurs de sorte que
|
| 34 |
+
|
| 35 |
+
- Chaque couleur apparaît le même nombre de fois dans la grille.
|
| 36 |
+
- Aucune ligne et aucune colonne ne contient des cases de couleur différente.
|
| 37 |
+
|
| 38 |
+
Quelle est le plus grand nombre possible de cases que l'on peut colorier en suivant ces règles?
|
| 39 |
+
Solution de l'exercice 3 Réponse : $\mathrm{N}=5 \times 19 \times 20=1900$.
|
| 40 |
+
Comme chaque ligne ou colonne ne peut contenir qu'une couleur, on va réfléchir en partant des lignes. On dit qu'une ligne ou colonne est d'une couleur (disons rouge) quand la seule couleur que peuvent avoir des cases de cette ligne ou colonne est le rouge. Si une ligne ou colonne n'a pas de couleur, on lui assigne arbitrairement une couleur. Ainsi, une case rouge se trouve forcément à l'intersection d'une ligne rouge et d'une colonne rouge. Par conséquent, on peut majorer le nombre de case rouge par le produit du nombre de ligne rouges par le nombre de colonnes rouges. Introduisons maintenant des notations. On numérotes les couleurs disponibles de 1 à 5 et on note $x_{i}$ le nombre de lignes colorées de la i-ième couleur, et $y_{i}$ le nombre de colonnes colorées de cette couleur. Notons enfin N le nombre de cases coloriées par couleur. On veut maximiser le nombre total de cases coloriées, 5 N . Les arguments précédemment cités montrent que $\forall i: N \leqslant x_{i} y_{i}$. ON a évidemment aussi, $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. L'étude des petits cas nous montre que pour maximiser $N$ il faut que les $x_{i}$ et les $y_{i}$ soient tous environs égaux, valant tous $\frac{99}{5}$ arrondi soit par excès ou par défaut. Une étude plus approfondie des petits cas où on remplace 99 par un petit nombre congru à $4 \bmod 5$, comme 99 , nous permet de conjecturer que la construction suivante est optimale :
|
| 41 |
+
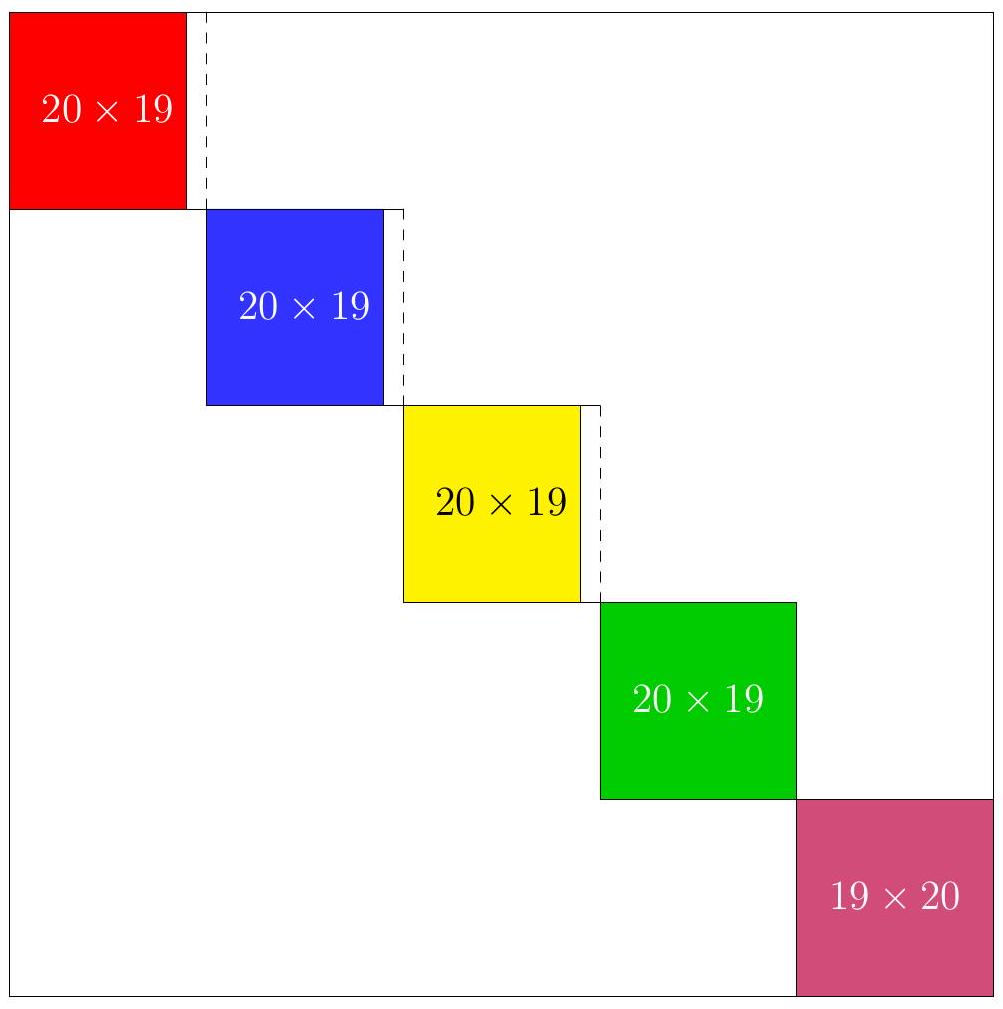
|
| 42 |
+
|
| 43 |
+
Ici, on a $N=19 \cdot 20$.
|
| 44 |
+
Prouvons maintenant l'optimalité. Supposons par l'absurde disposer d'une configuration valide où $\mathrm{N}>$ $19 \times 20$, donc $\forall i: x_{i} y_{i}>19 \times 20$. On remarque ensuite que $x_{i}+y_{i}>39$. En effet,
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Donc
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
Donc $38<x_{i}+y_{i}$. De plus, si $x_{i}+y_{i}=39$, alors $\left(x_{i}-y_{i}\right)^{2}<1$ Donc $x_{i}=y_{i}$, ce qui est impossible car 39 est impair. Donc $x_{i}+y_{i} \geqslant 40$.
|
| 57 |
+
Le compte final $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ est une contradiction et termine la preuve.
|
| 58 |
+
|
| 59 |
+
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu par les élèves qui l'ont abordé. Dans l'ensemble, une bonne partie des élèves ont trouvé une configuration qui marchait pour $\mathrm{N}=1900$, qui était bien la réponse maximale. Mais peu d'entre eux ont montré qu'on ne pouvait pas faire mieux, beaucoup se sont contentés de dire qu'en partant de la configuration qu'ils avaient donnés, on ne pouvait pas colorier plus de cases : mais ceci ne veut pas dire qu'on ne peut pas trouver une autre configuration, complètement différente (et qui ne part pas de la configuration à $\mathrm{N}=1900$ ), avec plus de cases coloriées. Enfin, un certain nombre d'élèves sont partis du principe qu'il devait forcément y avoir le même nombre de ligne et de colonne par couleur, et ont abouti à 1805 : mais la contrainte était d'avoir le même nombre de cases par couleur au total, aucune condition ne portait sur le nombre de lignes et de colonnes par couleur, et d'ailleurs les configurations optimales n'ont pas le même nombre de lignes et de colonnes par couleur. Enfin, certains élèves avaient le bon raisonnement, mais ont oublié de répondre à la question de l'énoncé, qui était "quel est le plus grand nombre de cases possibles à colorier dans la grille" : on souligne l'importance de bien se relire et d'être sûr qu'on a bien répondu à la question posée avant de rendre une copie.
|
| 60 |
+
|
| 61 |
+
Exercice 4. Une partie se joue sur un échiquier de taille $\mathrm{n} \times \mathrm{n}$. Au début, il y a 99 pierres sur chaque case. Tour à tour, Aimeric et Benoit choisissent une ligne ou une colonne et retirent une pierre de chaque case de la ligne ou de la colonne choisie. Ils ne peuvent choisir une ligne ou une colonne que si elle comporte au moins une pierre sur chaque case. Le premier joueur qui ne peut pas se déplacer perd la partie. Aimeric joue le premier tour. Déterminer tous les $n$ pour lesquels Benoit a une stratégie gagnante.
|
| 62 |
+
|
| 63 |
+
## Solution de l'exercice 4 Réponse : Les n pairs.
|
| 64 |
+
|
| 65 |
+
Dans la suite, on numérote les colonnes de gauche à droite et les lignes de haut en bas.
|
| 66 |
+
Nous allons montrer qu'il y a exactement 99 n tours de jeu, de sorte que si n est pair, Benoit aura eu le dernier tour de jeu (donc aura gagné), sinon c'est Aimeric.
|
| 67 |
+
|
| 68 |
+
Considérons les cases de l'une des grandes diagonales de la grille. Comme chaque ligne et chaque colonne contient exactement une de ces cases, à chaque étape, la somme du nombre de pierres sur ces cases diminue d'exactement 1 . Si toutes les cases de la grande diagonale sont vides, il n'est plus possible d'effectuer aucune action. Montrons que réciproquement, si l'une des cases de la grande diagonale contient au moins un caillou, il est encore possible de jouer.
|
| 69 |
+
Supposons que cette case soit à l'intersection de la ligne $i$ et de la colonne $i$. Si la ligne $i$ et ou la colonne i ne contiennent pas de case vide, alors il est encore possible de jouer sur cette colonne ou cette ligne. On peut donc supposer que la ligne $i$ contient une case vide, disons sur la colonne $a$, et que la colonne $i$ contient une case vide, disons sur la ligne $b$. Notons $r_{i}$ le nombre de fois que l'on a joué sur la ligne $i$, $r_{b}$ le nombre de fois que l'on a joué sur la ligne $b, c_{i}$ le nombre de fois que l'on a joué sur la colonne $i$ et enfin $c_{a}$ le nombre de fois que l'on a joué sur la colonne $a$.
|
| 70 |
+
Puisque la case à l'intersection de la ligne $i$ et de la colonne a est vie, on a $c_{a}+r_{i}=99$. De même, on a $r_{b}+c_{i}=99$. Mais puisque $r_{i}+c_{i}<99$ (car la case à l'intersection de la ligne et de la colonne $i$ est non vide), on a $\mathrm{r}_{\mathrm{b}}+\mathrm{c}_{\mathrm{a}}>99$, ce qui est absurde car la case à l'intersection de la ligne b et de la colonne a a perdu alors strictement plus que 99 caillous.
|
| 71 |
+
On déduit que la partie finit si et seulement si chaque case de la grande diagonale est vide, donc au bout d'exactement 99 n étapes, ce qui permet de conclure comme annoncé.
|
| 72 |
+
|
| 73 |
+
Commentaire des correcteurs: Beaucoup d'élèves ont compris l'importance de la parité du nombre de tours de jeu, mais certains d'entre eux supposent que toutes les cases doivent être vides lorsque plus aucun coup n'est jouable, sans le démontrer. Beaucoup de copies traitent le cas n pair avec une stratégie miroir, mais celle-ci n'est pas directement adaptable au cas n impair sans argument supplémentaire. Les dessins, malheureusement trop rares, ont été appréciés et ont facilité la compréhension des arguments combinatoires.
|
| 74 |
+
|
| 75 |
+
Exercice 5. Soit $n$ un entier naturel. Joseph peut tirer $2 n+1$ flèches. Chacun de ses tirs est un échec ou une réussite. Un tir est dit "équilibré" si le nombre d'échecs avant ce tir additionné au nombre de réussites après ce tir est égal à $n$. Déterminer si le nombre de tirs équilibrés est pair ou impair.
|
| 76 |
+
Solution de l'exercice 5 Montrons que le nombre de tirs équilibrés est impair.
|
| 77 |
+
Première remarque : considérons une succession de deux tirs telle que le premier est réussi et le suivant raté. Alors il y a autant de tirs ratés avant pour les deux et autant de tirs réussis après donc soit les deux tirs sont équilibrés, soit aucun des deux ne l'est. De même, si le premier est raté et le suivant réussi, en notant e le nombre d'échecs avant ces deux tirs et r le nombre de réussites après, le premier tir est équilibré si et seulement si $e+(1+r)=n$ et le deuxième est équilibré si et seulement si $(e+1)+r=n$. On remarque que ces deux conditions sont égales. Ainsi, puisque cela ne modifie pas l'équilibre des tirs précédents et suivants, supposer que pour une succession de 2 tirs dont l'un est réussi et l'autre est raté, c'est le premier qui est raté ne modifie pas la parité du nombre de tirs équilibrés. On peut donc se ramener au cas où Joseph commence par une succession d'échecs, puis de réussites. Dans l'ordre des tirs, le nombre de succès à venir additionné au nombre d'échecs passés débute au nombre de réussites total R , augmente strictement à chaque échec jusqu'à atteindre la valeur 2 n puis diminue à chaque réussite jusqu'à atteindre le nombre d'échec total E . Or $\mathrm{E}+\mathrm{R}=2 * \mathrm{n}+1$ donc exactement une de ces deux valeurs E et R est plus petite que n et l'autre est strictement plus grande. La valeur n n'est donc atteinte que pour un seul tir dans cette configuration, et elle est donc impair dans le cas général.
|
| 78 |
+
|
| 79 |
+
Commentaire des correcteurs : L'exercice était difficile et n'a été abordé que par un nombre assez faible d'étudiants. La solution a été intuitée la plupart du temps, mais rarement justifié de manière convaincante.
|
| 80 |
+
|
| 81 |
+
Exercice 6. Dans une école il y a n cours et n élèves. Les élèves sont inscrits dans plusieurs cours de sorte que deux élèves différents n'ont jamais exactement les même cours. Prouver qu'on peut supprimer un cours de sorte qu'aucune paire d'élèves ne se retrouve avec exactement les mêmes cours.
|
| 82 |
+
|
| 83 |
+
## Solution de l'exercice 6
|
| 84 |
+
|
| 85 |
+
On va montrer par récurrence forte sur n la propriété plus forte suivante :
|
| 86 |
+
$\mathcal{P}_{n}$ :Pour tout $m \geqslant n$, dans une classe à $n$ élèves et $m$ cours telle que deux élèves n'ont jamais exactement les mêmes cours, alors il est possible de retirer un cours de sorte que les élèves ne suivent pas exactement les mêmes cours parmi les cours restants.
|
| 87 |
+
|
| 88 |
+
Initialisation: $\mathrm{Si} \mathrm{n}=1$, il n'y a rien à démontrer.
|
| 89 |
+
Hérédité : Soit $n \geqslant 2$. Supposons que $\mathcal{P}_{k}$ est vraie pour tout $1 \leqslant k \geqslant n-1$. Soit $m \geqslant n$. Considérons alors une classe de $n$ élèves qui suivent $m$ cours notés $C_{1}, \ldots, C_{m}$. Si deux élèves ne suivent jamais les mêmes cours parmi les cours $C_{1}, \ldots, C_{m-1}$, alors on a démontré ce qu'il fallait. Sinon, il existe $k$ paires d'élèves $\left(A_{1}, B_{1}\right), \ldots,\left(A_{k}, B_{k}\right)$ avec $k \geqslant 1$, telles que les élèves $A_{i}$ et $B_{i}$ suivent les mêmes cours parmi $C_{1}, \ldots, C_{m-1}$ (et alors exactement l'un d'eux, disons $A_{i}$, suit le cours $C_{m}$ ). Notons $E_{1}, \ldots, E_{n-2 k}$ l'ensemble des élèves restant. Considérons le sous-ensemble de $n-k$ élèves $\left\{A_{1}, \ldots, A_{k}, E_{1}, \ldots, E_{n-2 k}\right\}$ et l'ensemble de cours $\left\{C_{1}, \ldots, C_{m-1}\right\}$. D'après l'hypothèse de récurrence, puisque $n-k \leqslant m-1$, on dispose d'un cours, disons $C_{m-1}$ qui, si on le retire, vérifie qu'aucune paire de deux élèves parmi les élèves considérés ne suivent les mêmes cours parmi $C_{1}, \ldots, C_{m-2}$. Alors, parmi ces $n-k$ élèves considérés, il n'y a pas de paire d'élèves ayant exactement les mêmes cours parmi $C_{1}, \ldots, C_{m-2}, C_{m}$. Mais alors un élève $B_{i}$ ne suit pas exactement les mêmes cours que $A_{i}$ (à cause du cours $C_{m}$ ou qu'un autre élève (car $A_{i}$ ne suit pas les mêmes cours qu'un autre élève parmi $C_{1}, \ldots, C_{m-2}$ ). Ceci achève la récurrence.
|
| 90 |
+
|
| 91 |
+
La propriété $\mathcal{P}_{n}$ est donc vraie pour tout n , en particulier, l'énoncé est vrai pour $\mathrm{m}=\mathrm{n}$ cours et n élèves.
|
| 92 |
+
|
| 93 |
+
## Solution alternative :
|
| 94 |
+
|
| 95 |
+
Notons $E_{1}, \ldots, E_{n}$ les $n$ élèves et $C_{1}, \ldots, C_{n}$ les $n$ cours.
|
| 96 |
+
On procède par l'absurde et l'on suppose l'inverse : quelque soit le cours $C_{i}$ que l'on supprime, il existe deux élèves $E_{i_{1}}$ et $E_{i_{2}}$ ayant exactement les mêmes cours en dehors du cours $C_{i}$. Si deux telles paires ou plus existent pour un même cours $C_{i}$, on n'en garde qu'une seule. Comme ces deux élèves ne suivent pas exactement les mêmes cours, l'un suit le cours $C_{i}$ et l'autre ne le suit pas. Leurs cours ne coïncident donc pas si l'on supprime un autre cours $C_{j}$.
|
| 97 |
+
Considérons alors le graphe dont les sommets sont les élèves et deux élèves sont reliés par une arêtes s'il existe un $i$ (qui est alors unique d'après le paragraphe précédent) tel que, si l'on supprime $C_{i}$, les deux élèves ont les mêmes cours. Comme chaque cours $C_{i}$ induit une paire d'élèves reliés par une arête, le graphe obtenu admet au moins un cycle, que l'on note $E_{i_{1}} \ldots E_{i_{k}} E_{i_{1}}$, avec $k \leqslant n$. Notons $j_{\ell}$ le numéro du cours qui induit l'arête $E_{i_{\ell}} E_{i_{\ell+1}}$. Les élèves $E_{i_{1}}$ et $E_{i_{k}}$ suivent alors les mêmes cours parmi ceux qui ne sont pas $C_{j_{1}}, \ldots, C_{j_{k-1}}$. En particulier, soient ils suivent tous les deux le cours $C_{j_{k}}$, soient ils ne le suivent pas tous les deux, ce qui contredit le fait que l'arête $E_{i_{k}} E_{i 1}$ appartient au graphe. On a la contradiction désirée.
|
| 98 |
+
|
| 99 |
+
Commentaire des correcteurs: Le problème a été très peu abordé et très peu résolu. Plusieurs élèves parviennent à modéliser le problème par un graphe, ce qui est excellent.
|
| 100 |
+
|
| 101 |
+
Exercice 7. Déterminer le plus grand entier $n$ pair ayant la propriété suivante : quelle que soit la façon de paver une grille $\mathrm{n} \times \mathrm{n}$ avec des dominos, il existe une ligne coupant le tableau en deux parties non vides et n'intersectant aucun domino.
|
| 102 |
+
|
| 103 |
+
## Solution de l'exercice 7 Réponse: $\mathrm{n}=6$
|
| 104 |
+
|
| 105 |
+
Mentionnons pour commencer que la réponse peut se deviner en essayant l'exercice pour des petites valeurs de n.
|
| 106 |
+
Le problème demande de trouver le plus grand entier n vérifiant une certaine propriété, il comporte donc nécessairement deux parties. Nous allons montrer d'abord que 6 vérifie la propriété, puis nous allons montrer que si $n \geqslant 8$, il existe une configuration de dominos ne respectant pas la propriété.
|
| 107 |
+
Cas $\mathrm{n}=\mathbf{6}$ : Supposons au contraire qu'il existe une configuration de dominos telle que chaque ligne coupant le tableau en deux parties non vides coupe au moins un domino. On ne va considérer que les lignes horizontales séparant deux rangées et les lignes verticales séparant deux colonnes du tableau, on appelle ces lignes des séparatrices, et les deux parties non vides du tableau obtenues avec une séparatrice des sections.
|
| 108 |
+
D'une part, un domino ne peut être intersecté que par au plus une séparatrice (et cette séparatrice coupe le domino en deux carrés égaux). D'autre part, une séparatrice intersecte un nombre pair de dominos, En effet, chaque section obtenue contient un nombre pair de cases (les sections sont des rectangles dont l'un des côtés est de longueur 6). Comme chaque domino sectionné recouvre exactement une case de la section et que les autres cases sont recouvertes par des dominos inclus dans la section et sont donc en nombre pair, on déduit bien qu'une séparatrice intersecte un nombre pari de dominos.
|
| 109 |
+
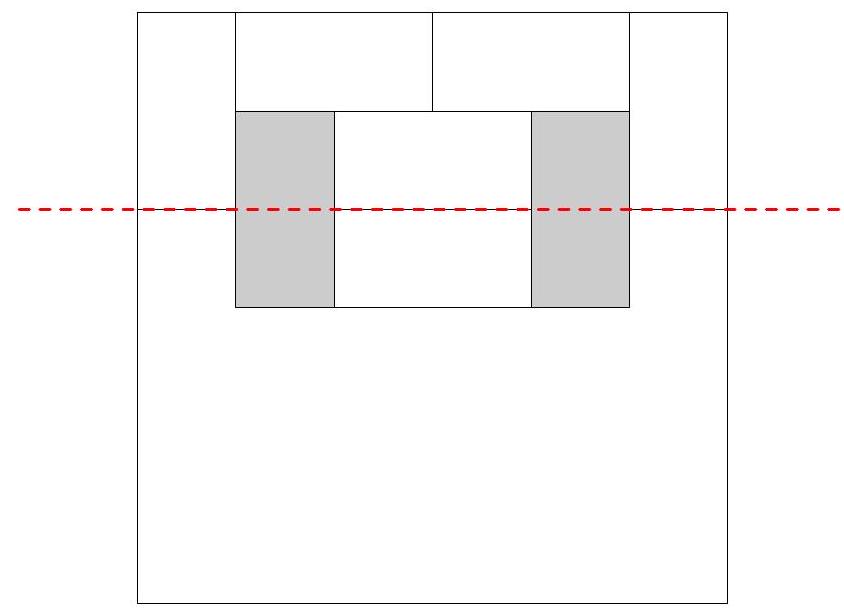
|
| 110 |
+
|
| 111 |
+
Par hypothèse, chaque séparatrice intersecte au moins un domino, donc elle en intersecte au moins 2 . Il y a 10 séparatrices, donc au moins 20 dominos du pavage sont intersectés par une séparatrice. Or, le pavage d'un carré $6 \times 6$ contient exactement 18 dominos. On a abouti à une contradiction.
|
| 112 |
+
Cas $n \geqslant 8$ : Nous allons donner pour tout entier $n \geqslant 8$ un pavage de la grille $n \times n$ tel que toute ligne coupant le tableau en deux parties non vides intersecte au moins un domino.
|
| 113 |
+
On considère le motif suivant:
|
| 114 |
+
|
| 115 |
+
|
| 116 |
+
On pave ensuite l'intérieur du carré grisé avec le motif suivant :
|
| 117 |
+
|
| 118 |
+
|
| 119 |
+
On obtient bien de cette façon un pavage qui vérifie la propriété de l'énoncé.
|
| 120 |
+
Commentaire des correcteurs : Le problème a été très peu abordé et en somme très peu résolu. Les élèves ayant rendu une tentative ont donné de bons arguments pour montrer que $\mathrm{n} \leqslant 6$ en proposant des constructions par récurrence.
|
| 121 |
+
|
| 122 |
+
Exercice 8. Aline et Elsa jouent au jeu suivant. Elles disposent de 100 pierres qu'elles séparent en deux piles (pas forcément de même taille) au début du jeu. Puis chacune à leur tour, en commençant par Aline, elles effectuent le mouvement suivant : elles choisissent une pile, puis un entier strictement positif inférieur ou égal à la moitié de la taille de la pile choisie et retirent ce nombre de pierres de la pile. La première joueuse qui ne peut plus effectuer de mouvement perd.
|
| 123 |
+
Déterminer toutes les configurations initiales pour lesquelles Elsa a une stratégie gagnante.
|
| 124 |
+
Solution de l'exercice 8 Dans la suite, on désigne par $(x, y)$ la configuration où la première pile est de taille $x$ et la deuxième pile est de taille $y$.
|
| 125 |
+
On observe sur le cas à une seule pile en commençant par la fin que les solutions perdantes pour Aline sont les piles à $2^{n}-1$ pierres.
|
| 126 |
+
Revenons au cas d'une configuration intiale générique $(\boldsymbol{a}, \boldsymbol{b}$ ). Par définition, la position $(1,1)$ est perdante. $(a, b)$ est perdante pour la personne qui doit jouer si $\frac{a+1}{b+1}$ est une puissance (positive ou négative) de 2. En effet, si $\frac{a+1}{b+1}=2^{n}$, si on pioche dans $a$, on diminue le quotient mais strictement de moins qu'un facteur 2. À l'inverse, si on pioche dans la pile $b$ on l'augmente mais strictement moins que d'un facteur 2 ce qui conserve bien une position gagnante pour la joueuse suivante.
|
| 127 |
+
Réciproquement, si $2^{\mathrm{n}}(b+1)<\mathrm{a}+1<2^{\mathrm{n}+1}(b+1)$ avec $\mathrm{n} \geqslant 0$ alors on prend le nombre nécessaire de pierres de la pile a de sorte qu'il en reste précisément $2^{n}(b+1)-1$. Cela est possible car $a<$ $2^{n+1}(b+1)-1$ donc $a \leqslant 2^{n+1}(b+1)-2$ d'où $\frac{a}{2} \leqslant 2^{n}(b+1)-1$ ce qui signifie qu'on en a laissé plus que la moitié.
|
| 128 |
+
|
| 129 |
+
Commentaire des correcteurs : L'exercice était difficile et n'a été rendu que par un élève.
|
| 130 |
+
|
| 131 |
+
Exercice 9. Soit $N$ un entier strictement positif. On suppose qu'il existe quatre sous-ensembles $A_{1}, A_{2}, A_{3}$ et $\boldsymbol{A}_{4}$ de $\{1, \ldots, \boldsymbol{N}\}$, chacun de cardinal 500 et on suppose que, pour tous $x, y$ dans $\{1, \ldots, N\}$, il existe un indice $i$ tel que $x$ et $y$ sont dans $A_{i}$. Déterminer la plus grande valeur de $N$ possible.
|
| 132 |
+
|
| 133 |
+
## Solution de l'exercice 9 Réponse : 833.
|
| 134 |
+
|
| 135 |
+
Nous allons traiter ce problème avec le langage des graphes. La modélisation du problème pousse à considérer le graphe dont les sommets sont les éléments de $S$, qui sont reliés par une arête de couleur $i$ si les deux sommets apprtiennent à l'ensemble $A_{i}$.
|
| 136 |
+
Dans la suite, on dira également qu'un graphe $G_{1}$ recouvre un graphe $G_{2}$ si toute arête de $G_{2}$ est une arête de $\mathrm{G}_{1}$.
|
| 137 |
+
|
| 138 |
+
On note $\mathrm{K}_{\mathrm{m}}$ le graphe constitué de m sommets et dont tous les sommets sont réliés. Un tel graphe est dit complet.
|
| 139 |
+
On note $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ le graphe constitué de 2 ensembles de sommets $S_{1}$ et $S_{2}$, tous les deux de cardinal m et dans lequel chaque sommet de $S_{1}$ est relié à tous les sommets de $S_{2}$. Un tel graphe est communément appelé bipartite complet, et on appellera $\mathrm{S}_{1}$ et $\mathrm{S}_{2}$ les équipes de $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$.
|
| 140 |
+
Lemme : Soit $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ un graphe bipartite complet et $S_{1}$ et $S_{2}$ ses équipes. Supposons qu'il est possible de recouvrir $K_{m, m}$ avec de graphes complets $K_{k}$ et $K_{\ell}$ de taille respective $k, \ell<2 \mathrm{~m}$. Alors $\mathrm{m}<\frac{\mathrm{k}+\ell}{3}$.
|
| 141 |
+
Preuve du lemme: Commençons par montrer que $\mathrm{K}_{\mathrm{k}}$ et $\mathrm{K}_{\ell}$ contiennent chacun soit $S_{1}$ soit $S_{2}$. En effet, soit $v \in S_{1}$ n' appartenant pas à $K_{\ell}$. Pour tout sommet $w$ de $S_{2}$, l'arête $v w$ appartient donc à $K_{k}$, mais alors $w$ appartient à $K_{k}$, donc $K_{k}$ contient tous les sommets de $S_{2}$. Mais alors, en raisonnant sur un sommet de $S_{1}$ n'appartenant pas à $K_{k}$, on obtient que $K_{\ell}$ contient aussi tous les éléments de $S_{2}$. Ainsi, chaque sommet de $S_{2}$ appartient à $K_{k}$ et à $K_{\ell}$ et chaque sommet de $S_{1}$ appartient à $K_{k}$ ou à $K_{\ell}$, de sorte que $k+\ell \geqslant\left|S_{1}\right|+2\left|S_{2}\right|=3 \mathrm{~m}$
|
| 142 |
+
|
| 143 |
+
Revenons au problème. On suppose par l'absurde que $\mathrm{N} \geqslant 834$. Remarquons que si on pouvait avoir N encore plus grand, on pourrait se ramener au cas $\mathrm{N}=834$ en ajoutant arbitrairement des éléments de $\{1, . .834\}$ qui n'y étaient pas encore aux ensembles.
|
| 144 |
+
Nous partitionnons notre ensemble de points comme suit:
|
| 145 |
+
|
| 146 |
+
- Z l'ensemble des points dans $A_{1}$ et $A_{2}$.
|
| 147 |
+
- Xl'ensemble des points dans $A_{1}$ mais pas $A_{2}$.
|
| 148 |
+
- Yl'ensemble des points dans $A_{2}$ mais pas $A_{1}$.
|
| 149 |
+
- $W$ le reste (ni dans $A_{1}$, ni dans $A_{2}$ ).
|
| 150 |
+
|
| 151 |
+
On a alors $|\mathrm{X}|+|\mathrm{Y}|+|\mathrm{Z}|+|\mathrm{W}|=834$ et $|\mathrm{X}|+|\mathrm{Z}|=|\mathrm{Y}|+|\mathrm{Z}|=500$ ce qui nous donne $|\mathrm{W}|-|\mathrm{Z}|=-166$.
|
| 152 |
+
Cas 1: $|W|=0$. Il vient $|Z|=166,|X|=|Y|=334$. Ceci contredit notre lemme car cela implique que nous pouvons couvrir $\mathrm{K}_{334,334}$ avec deux cliques de taille 500 .
|
| 153 |
+
Cas 2: $|W|>O$. Alors $Z \subset K_{2} \cap K_{3}$ (c'est-à-dire que chacun de ses éléments est dans $A_{3}$ ou $A_{4}$ ) pour que chacun de ses sommets soit connecté aux éléments de $|W|$ donc $\left|K_{3} \cap Z\right|+\left|K_{4} \cap Z\right| \geqslant|Z|$. Ainsi, nous pouvons voir que si $|W|>0$ : (En utilisant que $W \subset K_{3} \cap K_{4}$ )
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\left|K_{3} \cap(X \cup Y)\right|+\left|K_{4} \cap(X \cup Y)\right| \leqslant 1000-2|W|-|Z|
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
Alors, nous devons couvrir $K_{500-|Z|, 500-|Z|}$ (graphe formé à l'aide des ensembles $X$ et $Y$ ) avec deux cliques de tailles $\left|K_{3} \cap(X \cup Y)\right|, \mid K_{4} \cap(X \cup Y)$. Par notre lemme, $3(500-|Z|) \leqslant 1000-2|W|-|Z|$ or comme $|Z|=|W|+166$, on obtient une contradiction!
|
| 160 |
+
|
| 161 |
+
Par ailleurs, pour $\mathrm{N}=833$, on dispose d'une construction explicite : En reprenant nos notations $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$. Avec $|Z|=167$ et $|\mathrm{X}|=|\mathrm{Y}|=333$. On place tous les éléments de X dans $A_{3}$ et $A_{4}$ et un élément de $|\mathrm{Y}|$ dans les deux, la moitié des éléments de Y qu'il reste dans $A_{3}$ et l'autre dans $A_{4}$.
|
| 162 |
+
|
| 163 |
+
Commentaire des correcteurs : L'exercice a été peu traité, et résolu par un seul élève.
|
| 164 |
+
|
| 165 |
+
## Exercices Seniors
|
| 166 |
+
|
| 167 |
+
Exercice 10. Aurélien découpe une feuille de papier en 7 morceaux. Une étape consiste ensuite à choisir un morceau et à le découper en 4,7 ou 10 morceaux. Aurélien peut-il obtenir ainsi 2021 morceaux ?
|
| 168 |
+
|
| 169 |
+
Solution de l'exercice 10 L'exercice décrit une suite d'opérations et demande s'il est possible de passer d'un état initial à un état final, on peut donc légitimement chercher un invariant du système.
|
| 170 |
+
Ici, nous allons montrer que le nombre de morceausx d'Aurélien est toujours de la forme $3 k+1$, avec $k$ un entier naturel.
|
| 171 |
+
C'est le cas dans la situation initiale, puisqu'Aurélien dispose de $7=3 \times 2+1$ morceaux. Puis, si c'est le cas lors d'une étape et qu'Aurélien dispose de $3 k+1$ morceaux avec $k$ un entier naturel, Aurélien remplace un morceau par $3 \times 1+1$ morceaux, par $3 \times 2+1$ morceaux ou par $3 \times 3+1$ morceaux, de sorte qu'il lui reste, à la fin de l'opération, $3(k+1)+1,3(k+2)+1$ ou $3(k+3)+1$ morceaux.
|
| 172 |
+
De proche en proche, on a bien le résultat annoncé. Comme $2021=3 \times 673+2$ n'est pas de la forme indiquée, on ne peut jamais obtenir 2021 morceaux par le processus décrit.
|
| 173 |
+
|
| 174 |
+
Commentaire des correcteurs : Exercice très bien réussi. Notons tout de même un critère de réduction $\bmod 3$ permettant de ne pas faire de division euclidienne pour calculer $2021=2 \bmod 3$ : un nombre est congru à la somme de ces chiffres $\bmod 9$ et donc $\bmod 3$.
|
| 175 |
+
|
| 176 |
+
Exercice 11. On dispose de cinq couleurs et d'une grille $99 \times 99$. On colorie certains carrés de la grille avec l'une des cinq couleurs de sorte que
|
| 177 |
+
|
| 178 |
+
- Chaque couleur apparaît le même nombre de fois dans la grille.
|
| 179 |
+
- Aucune ligne et aucune colonne ne contient des cases de couleur différente.
|
| 180 |
+
|
| 181 |
+
Quelle est le plus grand nombre possible de cases que l'on peut colorier en suivant ces règles?
|
| 182 |
+
|
| 183 |
+
## Solution de l'exercice 11 Réponse : N = 5 $\times 19 \times 20=1900$.
|
| 184 |
+
|
| 185 |
+
Comme chaque ligne ou colonne ne peut contenir qu'une couleur, on va réfléchir en partant des lignes. On dit qu'une ligne ou colonne est d'une couleur (disons rouge) quand la seule couleur que peuvent avoir des cases de cette ligne ou colonne est le rouge. Si une ligne ou colonne n'a pas de couleur, on lui assigne arbitrairement une couleur. Ainsi, une case rouge se trouve forcément à l'intersection d'une ligne rouge et d'une colonne rouge. Par conséquent, on peut majorer le nombre de case rouge par le produit du nombre de ligne rouges par le nombre de colonnes rouges. Introduisons maintenant des notations. On numérotes les couleurs disponibles de 1 à 5 et on note $x_{i}$ le nombre de lignes colorées de la i-ième couleur, et $y_{i}$ le nombre de colonnes colorées de cette couleur. Notons enfin N le nombre de cases coloriées par couleur. On veut maximiser le nombre total de cases coloriées, 5 N . Les arguments précédemment cités montrent que $\forall i: N \leqslant x_{i} y_{i}$. ON a évidemment aussi, $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. L'étude des petits cas nous montre que pour maximiser N il faut que les $x_{i}$ et les $y_{i}$ soient tous environs égaux, valant tous $\frac{99}{5}$ arrondi soit par excès ou par défaut. Une étude plus approfondie des petits cas où on remplace 99 par un petit nombre congru à $4 \bmod 5$, comme 99 , nous permet de conjecturer que la construction suivante est optimale :
|
| 186 |
+
|
| 187 |
+
|
| 188 |
+
Ici, on a $N=19 \cdot 20$.
|
| 189 |
+
Prouvons maintenant l'optimalité. Supposons par l'absurde disposer d'une configuration valide où $\mathrm{N}>$ $19 \times 20$, donc $\forall i: x_{i} y_{i}>19 \times 20$. On remarque ensuite que $x_{i}+y_{i}>39$. En effet,
|
| 190 |
+
|
| 191 |
+
$$
|
| 192 |
+
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
|
| 193 |
+
$$
|
| 194 |
+
|
| 195 |
+
Donc
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
Donc $38<x_{i}+y_{i}$. De plus, si $x_{i}+y_{i}=39$, alors $\left(x_{i}-y_{i}{ }^{2}<1\right.$ Donc $x_{i}=y_{i}$, ce qui est impossible car 39 est impair. Donc $x_{i}+y_{i} \geqslant 40$.
|
| 202 |
+
Le compte final $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ est une contradiction et termine la preuve.
|
| 203 |
+
|
| 204 |
+
Commentaire des correcteurs : Le problème a été plutôt bien résolu par les élèves. On soulignera 2 erreurs courantes : aboutir à un résultat de $\mathrm{N}=1805$ et avoir le bon résultat mais ne donner que des arguments intuitifs pour démontrer qu'il est optimal. Les élèves devraient mieux se relire et profiter des envois pour travailler leur rigueur, surtout en combinatoire
|
| 205 |
+
|
| 206 |
+
Exercice 12. Soit $k$ un entier strictement positif et $P$ un point du plan. Déterminer le plus petit entier $n$ ayant la propriété suivante : on peut tracer $n$ droites ne passant pas par $P$ de sorte que toute demi-droite d'origine le point $P$ coupe au moins $k$ droites.
|
| 207 |
+
Solution de l'exercice 12 Réponse : $\mathrm{n}=2 \mathrm{k}+1$
|
| 208 |
+
L'énoncé demande de déterminer le plus petit entier n possédant une certaine propriété, il contient nécessairement deux parties. D'une part, on montre que si $n$ est inférieur à $2 k$, il ne vérifie pas la propriété, d'autre part on montre que $2 \mathrm{k}+1$ vérifie la propriété.
|
| 209 |
+
Soit $n$ un entier inférieur ou égal à $2 k$. Considérons un ensemble de $n$ droites ne passant pas par $P$. Prenons $d$ une droite passant par $P$ et parallèle à l'une des $n$ droites. La droite $d$ coupe au plus $n-1 \leqslant 2 k-1$ des autres droites. On peut répartir ces points d'intersection en deux groupes de points, de sorte que les points de chaque groupe sont situés du même côté sur d par rapport à $P$. L'un des groupes est de taille inférieure à $k-1$, de sorte qu'il existe une demi-droite issue de P coupent au plus $k-1$ droites.
|
| 210 |
+
|
| 211 |
+
Construction pour $n=2 k+1$ : Considérons un polygone régulier $A_{1} \ldots, A_{2 k+1}$ à $2 k+1$ côtés et dont le cercle circonscrit est de centre $P$ et dont on prolonge les côtés. On obtient un ensemble de $2 k+1$ droites. Considérons une demi-droite dissue du sommet $P$, et disons qu'elle intersecte le segment $\left[A_{1} A_{2}\right]$ (éventuellement en l'une de ses extrémités) en effectuant un angle de $\theta \leqslant \frac{360}{2 \mathrm{n}}$ avec sa médiatrice, et de sorte que le point d'intersection entre d et $\left[A_{1} A_{2}\right]$ soit plus proche de $A_{2}$ que de $A_{1}$. Alors la demi-droit coupe la droite $\left(A_{r} \mathcal{A}_{r+1}\right)$ si et seulement si elle forme un angle inférieur à $\pi / 2$ avec la médiatrice du segment $\left[A_{r} A_{r+1}\right]$. Cette condition induit l'inégalité suivante sur $r$
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
\frac{r}{n} 360^{\circ}-\theta \leqslant 90^{\circ} .
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
Cette inégalité est valable pour les $r \leqslant\left\lfloor\frac{k+1}{2}\right\rfloor$.
|
| 218 |
+
De la même façon, la demi-droite d coupe la droite $\left(A_{2 k+2-r} A_{2 k+1-r}\right)$ pour les $r$ satisfaisant $r \leqslant\left\lfloor\frac{k}{2}\right\rfloor-1$. Il vient que la droite $d$ coupe le segment $\left[A 1 A_{2}\right]$ et au moins $\left.\left\lfloor\frac{k+1}{2}\right\rfloor+\frac{k}{2}\right\rfloor-1=k-1$ droites, soit au moins $k$ droites.
|
| 219 |
+
|
| 220 |
+
Commentaire des correcteurs : Un bilan assez mitigé pour cet exercice. La plupart des élèves trouvent la bonne borne de $2 \mathrm{k}+1$ et la preuve qu'on ne peut pas faire moins, mais beaucoup ont du mal à trouver une construction ou bien à donner preuve de son bon fonctionnement. Il s'agissait ici surtout de bien comprendre sous quelle condition une droite donnée intersecte notre demi-droite partant de P .
|
| 221 |
+
|
| 222 |
+
Exercice 13. Soit $k \geqslant 1$ un nombre entier.
|
| 223 |
+
Considérons 4 k jetons, dont 2 k sont rouges et 2 k sont bleus. Une suite de ces 4 k jetons peut être transformée en une autre suite par un mouvement, consistant à interchanger un certain nombre (éventuellement un seul) de jetons rouges consécutifs avec un nombre égal de jetons bleus consécutifs. Par exemple, un mouvement permet de passer de rbbbrrrb à rrrbrbbb où $r$ désigne un jeton rouge et b désigne un jeton bleu.
|
| 224 |
+
|
| 225 |
+
Déterminer le plus petit nombre $n$ (comme fonction de $k$ ) tel que, partant de n'importe quelle suite initiale des 4 k jetons, il faut au plus n mouvements pour atteindre l'état dans lequel les 2 k premiers jetons sont rouges.
|
| 226 |
+
Solution de l'exercice 13 Réponse : $\mathrm{n}=\mathrm{k}$.
|
| 227 |
+
Le problème demande de déterminer le plus petit n vérifiant une certaine propriété, il contient donc nécessairement deux parties. Ici, dans un premier temps, on montre qu'étant donnée une configuration initiale de jetons, il est toujours possible d'arriver à la configuration finale décrite en au plus k étapes. Dans un second temps, on donne une configuration initiale à partir de laquelle il faut au moins $k$ étapes pour arriver à la situation finale.
|
| 228 |
+
On peut toujours atteindre la situation finale en au plus $k$ opérations: Considérons une configuration initiale de 4 k jetons. On appelle première moitié l'ensemble des 2 k jetons les plus à gauche et deuxième moitié l'ensemble des 2 k jetons les plus à droite. Parmi les 2 k jetons de la première moitié, il y a au moins $k$ jetons rouges ou au moins $k+1$ jetons bleus.
|
| 229 |
+
S'il y a au moins $k$ jetons rouges, alors on peut échanger chacun des jetons bleus de la première moitié avec un jeton rouge de la deuxième moitié. Comme à chaque étape, on enlève au moins un jeton bleu de la première moitié pour le placer dans la deuxième moitié, il faut au plus $k$ étapes pour échanger tous les jetons bleus.
|
| 230 |
+
S'il y au moins $k+1$ jetons bleus dans la première moitié, alors on peut, en au plus $k-1$ opérations, échanger tous les jetons rouges de la première moitié avec des jetons bleus de la deuxième moitié. A l'issue de ces étapes, les $2 k$ jetons bleus sont dans la première moitié et les $2 k$ jetons rouges sont la deuxième moitié. En échangeant alors les deux groupes de $2 k$ jetons consécutifs, on a atteint la situation finale voulue en au plus $k-1+1$ opérations.
|
| 231 |
+
|
| 232 |
+
Il existe une configuration initiale pour laquelle il faut au moins $k$ opérations : Considérons la configuration brbr...br (qui consiste en 2 k blocs de la forme br). Notons qu'à chaque opération, le nombre de blocs de jetons rouges consécutifs diminue d'au plus 2 . Comme il y a 2 k blocs de jetons rouges consécutifs dans la situation initiale et un seul bloc de jetons rouges consécutifs dans la situation finale voulue, on ne peut passer de l'une à l'autre en $k-1$ opérations ou moins. Il faut donc au moins $k$ opérations.
|
| 233 |
+
|
| 234 |
+
Commentaire des correcteurs : Le problème a été bien résolu dans l'ensemble. Une large majorité d'élèves parvient à montrer que l'on peut toujours atteindre l'objectif en $k$ mouvements. Mais Une moitié de ces élèves bacle la preuve que la configuration des jetons alternés nécessite au moins $k$ mouvements. Souvent les arguments ne sont pas quantifiés, ou alors ne prennent en compte que la configuration initiale. Par exemple, une erreur commune est de penser qu'un mouvement déplace au plus un jeton, ce qui est faux après plusieurs mouvements. Des élèves tentent alors de justifier que le nombre de mouvements utilisés pour créer un gros bloc compense le nombre de jetons alors déplacé, mais de tels arguments ne sont pas quantifiés et ne sont pas rigoureux.
|
| 235 |
+
|
| 236 |
+
Exercice 14. Aline et Elsa jouent au jeu suivant. Elles disposent de 100 pierres qu'elles séparent en deux piles (pas forcément de même taille) au début du jeu. Puis chacune à leur tour, elles effectuent le mouvement suivant : elles choisissent une pile, puis un entier strictement positif inférieur ou égal à la moitié de la taille de la pile choisie et retirent ce nombre de pierres de la pile. La première joueuse qui ne peut plus effectuer de mouvement perd.
|
| 237 |
+
Déterminer toutes les configurations initiales pour lesquelles Elsa a une stratégie gagnante.
|
| 238 |
+
Solution de l'exercice 14 Dans la suite, on désigne par $(x, y)$ la configuration où la première pile est de taille $x$ et la deuxième pile est de taille $y$.
|
| 239 |
+
On observe sur le cas à une seule pile en commençant par la fin que les solutions perdantes pour Aline sont les piles à $2^{n}-1$ pierres.
|
| 240 |
+
Revenons au cas d'une configuration intiale générique $(\boldsymbol{a}, \boldsymbol{b}$ ). Par définition, la position $(1,1)$ est perdante. $(a, b)$ est perdante pour la personne qui doit jouer si $\frac{a+1}{b+1}$ est une puissance (positive ou négative) de 2. En effet, si $\frac{a+1}{b+1}=2^{n}$, si on pioche dans $a$, on diminue le quotient mais strictement de moins qu'un facteur 2. À l'inverse, si on pioche dans la pile $b$ on l'augmente mais strictement moins que d'un facteur 2 ce qui conserve bien une position gagnante pour la joueuse suivante.
|
| 241 |
+
Réciproquement, si $2^{n}(b+1)<a+1<2^{n+1}(b+1)$ avec $n \geqslant 0$ alors on prend le nombre nécessaire de pierres de la pile a de sorte qu'il en reste précisément $2^{n}(b+1)-1$. Cela est possible car $a<$ $2^{n+1}(b+1)-1$ donc $a \leqslant 2^{n+1}(b+1)-2$ d'où $\frac{a}{2} \leqslant 2^{n}(b+1)-1$ ce qui signifie qu'on en a laissé plus que la moitié.
|
| 242 |
+
|
| 243 |
+
Commentaire des correcteurs : Le problème a été assez discriminant. Parmi le petit nombre d'élèves ayant proposé des solutions, celles-ci étaient soit entièrement juste et assez efficace, soit plutôt confuses, essayant trop d'adapter la stratégie pour une seule pile au cas des deux piles.
|
| 244 |
+
|
| 245 |
+
Exercice 15. Soit $n \geqslant 3$ un entier. On colorie 2 n sommets d'un $4 \mathrm{n}+1$-gone régulier. Montrer qu'il existe trois sommets coloriés qui forment un triangle isocèle.
|
| 246 |
+
Solution de l'exercice 15 On porcède par l'absurde en supposant qu'aucun triplet de sommets coloriés ne forme de triangle isocèle.
|
| 247 |
+
Dans un premier temps, fixons un sommet colorié O et notons $\mathrm{OP}_{1} \ldots \mathrm{P}_{2 n} \mathrm{P}_{-2 n} \ldots \mathrm{P}_{-1}$ le reste du polygone. Puisque le triangle $O P_{i} P_{-i}$ est isocèle pour $1 \leqslant i \leqslant 2 n$, au plus l'un des deux sommets $P_{i}$ et $P_{-i}$ est colorié.
|
| 248 |
+
Supposons que deux sommets consécutifs ne sont jamais tous les deux coloriés. En particulier, $\mathrm{P}_{1}$ et $\mathrm{P}_{-1}$ ne sont pas coloriés car ils sont adjacents à O qui est colorié. Mais alors chacune des $2 \mathrm{n}-1$ paires ( $\mathrm{P}_{i}, \mathrm{P}_{-i}$ ) de sommets restants contient au plus un point colorié, et au moins $2 \mathrm{n}-1$ sommets parmis les $P_{i}$ sont coloriés. On conclut que chaque paire $\left(P_{i}, P_{-i}\right)$ avec $i \geqslant 2$ contient exactement un sommet colorié. Ainsi, soit $P_{i}$ soit $P_{-i}$ est colorié pour $i \geqslant 2$.
|
| 249 |
+
Supposons que $\mathrm{P}_{2 n}$ est colorié. Alors $\mathrm{P}_{2 n-1}$ n'est pas colorié, donc $\mathrm{P}_{-2 n+1}$ est colorié. Mais alors $\mathrm{P}_{-2 n+2}$ n'est pas colorié, donc $P_{2 n-2}$ est colorié. Le triangle $P_{2 n-2}, P_{2 n}, P_{-2 n+1}$ étant isocèle et colorié, on trouve une contradiction.
|
| 250 |
+
On a montré qu'il existe deux sommets consécutifs coloriés, disons 0 et $P_{1}$. Les sommets $P_{-1}$ et $P_{2}$ ne sont alors pas coloriés, sous peine de créer un triangle isocèle avec $O$ et $P_{1}$. De même, le triangle $\mathrm{OP}_{1} \mathrm{P}_{-2 n}$ est isocèle en $\mathrm{P}_{-2 n}$ dont $\mathrm{P}_{-2 n} \mathrm{n}$ 'est pas colorié.
|
| 251 |
+
Considérons alors la suite de sommets suivante, de longueur $2(n-1): P_{3}, P_{-3}, \ldots, P_{2 i-1}, P_{-2 i+1}, \ldots, P_{2 n-1}, P_{-2 n+1}$
|
| 252 |
+
Deux sommets consécutifs de cette suite forment un triangle isocèle avec $O$ ou avec $P_{1}$, et ne peuvent pas être tous les deux coloriés.
|
| 253 |
+
Il en va de même pour la suite $P_{-2}, P_{4}, \ldots, P_{-2 i} P_{2 i+2}, \ldots, P_{-2 n+2}, P_{2 n}$.
|
| 254 |
+
Ces deux suites contiennent donc chacune au plus une moitié de sommets coloriés. Mais comme elles contiennent ensemble exactement $2 \mathrm{n}-2$ sommets coloriés, les inégalités précédents sont saturées et dans chaque suite, exactement un sommet sur deux est colorié.
|
| 255 |
+
Si $P_{3}$ est colorié, alors $\mathrm{P}_{5}$ est colorié et le triangle $\mathrm{P}_{1} \mathrm{P}_{3} \mathrm{P}_{5}$ est isocèle colorié. De même, si $\mathrm{P}_{-2}$ est colorié, alors $\mathrm{P}_{-4}$ est colorié et le triangle $\mathrm{OP}_{-2} \mathrm{P}_{-4}$ est isocèle colorié. On déduit que $\mathrm{P}_{-2 n+1}, \mathrm{P}_{2 n}$ et $\mathrm{P}_{2 n-2}$ sont coloriés et forment un triangle isocèle, ce qui conclut.
|
| 256 |
+
|
| 257 |
+
|
| 258 |
+
Commentaire des correcteurs : Le problème admettait de nombreuses solutions et a été, dans l'ensemble, bien résolu par ceux qui l'ont cherché.
|
| 259 |
+
|
| 260 |
+
Exercice 16. On considère un 2022-gone régulier de côté 1 . Les points sont numérotés $A_{1}, \ldots, A_{2022}$ dans un certain ordre. Au départ, Elie part du point $A_{1}$, puis saute de point en point vers le point $A_{2}$, puis de $A_{2}$ vers $A_{3}$ etc... chaque fois en prenant l'arc le plus court. Lorsqu'il atteint $A_{2022}$, il rejoint finalement $A_{1}$. Déterminer la valeur maximale de la somme des longueurs des arcs qu'a parcouru Elie, parmi toutes les numérotations de points possibles.
|
| 261 |
+
Solution de l'exercice 16 Réponse: $\mathrm{Si} N=1011$, La valeur maximale est $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$.
|
| 262 |
+
Le problème demande de trouver la valeur maximale d'une somme de longueurs, il contient nécessairement deux parties. Dans un premier temps, on montre que le chemin parcouru par Elie est forcément de longueur inférieure à $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$, cette partie s'appelle l'analyse. Dans un second temps, on donne l'exemple d'une numérotation pour laquelle le chemin parcouru est exactement de longueur $2\left(N^{2}-N+1\right)$, cette étape s'appelle la construction.
|
| 263 |
+
Analyse : Dans la suite, on garde la notation $N=1011$. On note également $\underline{P Q}$ la longueur de l'arc le plus court reliant P et Q et $\overline{\mathrm{PQ}}$ la longueur de l'arc le plus long. Considérons une numérotation $A_{1}, \ldots, A_{2 N}$ dans un ordre quelconque. On pose aussi $A_{2 N+1}=A_{1}$.
|
| 264 |
+
Puisque majorer chaque portion $A_{i} A_{i+1}$ par sa longueur minimale est une estimation trop grossière, on va plutôt minorer la somme $A_{1} \overline{A_{2}+\ldots}+A_{2 N} A_{1}$ en majorant des paquets de terme. Plus précisément, nous allons regarder le chemin parcouru entre deux sommets impairs consécutifs.
|
| 265 |
+
Soit $1 \leqslant i \leqslant N$. On désire montrer que $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$, autrement dit, que passer par $A_{2 i}$ est moins coûteux que prendre le grand arc $A_{2 i-1} \mathcal{A}_{2 i+1}$. La volonté de démontrer une telle inégalité peut venir de tentatives sur des petits cas.
|
| 266 |
+
Si $A_{2 i}$ est sur le petit arc $A_{2 i-1} A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\underline{A_{2 i-1} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$. Supposons désormais que $A_{2 i}$ est sur le grand arc $A_{2 i-1} A_{2 i+1}$. Si le petit arc $A_{2 i} A_{2 i+1}$ ne contient pas $A_{2 i-1}$ ou si le petit arc $A_{2 i-1} A_{2 i}$ ne contient pas $A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Si maintenant $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$, alors $A_{2 i+1}$ est sur le grand arc $A_{2 i-1} A_{2 i}$ et $A_{2 i-1} A_{2 i}+$ $\underline{A_{2 i} A_{2 i+1}} \leqslant \underline{A_{2 i-1} A_{2 i}}+\overline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Le cas où $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$ se traite de façon similaire.
|
| 267 |
+
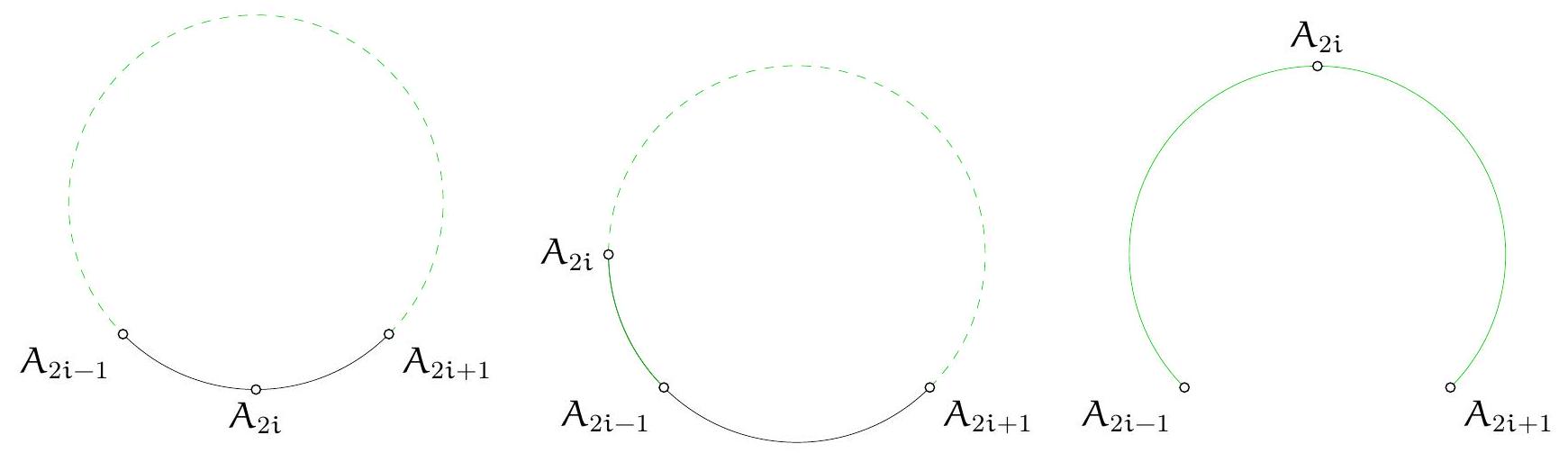
|
| 268 |
+
|
| 269 |
+
On a donc
|
| 270 |
+
|
| 271 |
+
$$
|
| 272 |
+
\begin{aligned}
|
| 273 |
+
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} & \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \\
|
| 274 |
+
& =\left(2 \mathrm{~N}-\underline{A_{1} A_{3}}\right)+\ldots+\left(2 N-\underline{A_{2 N-1} A_{1}}\right) \\
|
| 275 |
+
& \left.=2 N^{2}-\underline{\left(A_{1} A_{3}\right.}+\ldots+\underline{A_{2 N-1}} \overline{A_{1}}\right) .
|
| 276 |
+
\end{aligned}
|
| 277 |
+
$$
|
| 278 |
+
|
| 279 |
+
Il suffit donc de minimiser la somme $\underline{A_{1} A_{3}}+\ldots+\underline{A_{2 N-1} A_{1}}$. Pour cela, notons qu'il existe deux sommets $A$ et B de numéro impair à distance au moins $\mathrm{N}-1$ (car il y a N sommets impairs). Comme la somme
|
| 280 |
+
est cyclique, on peut supposer que $A=A_{1}$ (quitte à renuméroter les sommets). Mais alors le chemin $A_{1} \ldots A_{2 N-1} A_{1}$ nécessite de parcourir un arc $\underline{A_{1} B}$ pour aller de $A_{1}$ vers $B$ puis un arc $B A_{1}$ pour aller de $B$ vers $A_{1}$. Un tel chemin est donc de longueur au moins le double du petit arc $A B$, soit $2(N-1)$.
|
| 281 |
+
|
| 282 |
+
Il vient
|
| 283 |
+
|
| 284 |
+
$$
|
| 285 |
+
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \geqslant 2 N^{2}-2(N-1)=2\left(N^{2}-N+1\right)
|
| 286 |
+
$$
|
| 287 |
+
|
| 288 |
+
Construction : Réciproquement, numérotons les sommets dans l'ordre $A_{1} A_{3} \ldots A_{2 N-1} A_{2} \ldots A_{2 N}$. Le chemin d'Elie est alors de longueur
|
| 289 |
+
|
| 290 |
+
$$
|
| 291 |
+
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}}=\underbrace{N+N-1+\ldots+N+N-1}_{N-1 \text { fois }}+N+1=2 N^{2}-2 N+2
|
| 292 |
+
$$
|
| 293 |
+
|
| 294 |
+
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu. Beaucoup d'élèves ont trouvé une construction réalisant la bonne borne, mais parmi ceux qui ont cherché l'exercice, trop d'élèves encore tentent de justifier qu'on ne peut pas faire mieux par l'un des deux arguments :
|
| 295 |
+
|
| 296 |
+
- Soit en disant qu'à chaque étape on place le point $A_{k}$ à l'endroit "optimal". Mais effectuer la "meilleure" opération à chaque fois n'est pas gage d'arriver à la meilleure configuration. Ici, placer le point $A_{k}$ diamétralement opposé au point $A_{k+1}$ impose à la fin d'avoir $A_{2022}$ et $A_{1}$ adjacents. Qui nous dit que ne pas systématiquement placer les points $A_{k}$ et $A_{k+1}$ le plus éloigné possible ne permet pas d'augmenter la distance entre $A_{1}$ et $A_{2022}$ pour avoir une plus grande distance totale?
|
| 297 |
+
- Soit en disant que si l'on échange des points sur la configuration trouvée, on n'augmente pas la distance. Là aussi, ce raisonnement ne permet pas de prouver que la configuration est un maximum global, mais seulement de prouver que la configuration est un maximum local.
|
| 298 |
+
Nous espérons qu'à la lecture de ce commentaire, les élèves ne commettront plus ces deux erreurs communes de raisonnement.
|
| 299 |
+
|
| 300 |
+
Exercice 17. On considère 51 entiers strictement positifs de somme 100 sur une ligne. Montrer que pour tout entier $1 \leqslant k<100$, il existe des entiers consécutifs de somme $k$ ou $100-k$.
|
| 301 |
+
Solution de l'exercice 17 On reformule légèrement l'énoncé pour le rendre plus visuel : on se représente un cercle de périmètre 100 gradué (de 0 à 99 par exemple) sur-lequel on a marqué en noir 51 graduations et en pointillés les 49 autres. Sans perte de généralité on marque en noir la graduation 0. Nos entiers positifs correspondent aux longueurs entre les graduations noires. On vérifie facilement qu'il s'agit d'une représentation bijective du problème. Pour tout $k$, par principe des tiroirs, comme l'application qui à $j$ associe $j+k$ est injective (modulo 100), il existe une graduation marquée en noir $j$ telle que son image $j+k$ l'est aussi. Deux cas se présentent alors. Soit le segment $[j, j+k]$ ne coupe pas 0 et alors on a bien les entiers souhaités. Soit il coupe 0 et alors $[j+k, j]$ ne coupe pas 0 et est de longueur $n-k$. Dans les deux cas, on a trouvé des entiers consécutifs de somme $k$ ou $n-k$.
|
| 302 |
+
|
| 303 |
+
Commentaire des correcteurs: L'exercice est plutôt bien traité.
|
| 304 |
+
|
| 305 |
+
Exercice 18. Soient $\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots \mathrm{C}_{\mathrm{n}}$ des cercles de même rayon disposés dans le plan de sorte qu'ils ne soient jamais tangents 2 à 2 et qu'il existe toujours un chemin passant par les cercles pour aller d'un point de l'un d'entre eux à un autre (autrement dit, les cercles sont connectés). En notant S l'ensemble des points d'intersection des cercles, montrer que $|S| \geqslant n$.
|
| 306 |
+
Solution de l'exercice 18 Dans un premier temps, on reformule le problème en termes de graphes. On note C l'ensemble des centres des cercles et S l'ensemble des points d'intersections qui constituent les sommets d'un graphe $G$. On relie par une arête tout couple ( $c, s) \in C \times S$ si $s$ appartient au cercle de centre $c$. Remarquons alors que pour toute arête $(c, s), \operatorname{deg}(c) \geqslant \operatorname{deg}(s)$. En effet, d'après l'énoncé, à tout point $c_{i}$ relié à $s$ autre que c on peut associer un autre point d'intersection de $\mathrm{c}_{\mathrm{i}}$ avec c car les cercles ne sont pas tangents. Étant donnés $\boldsymbol{c}_{\boldsymbol{i}}$ et $\boldsymbol{c}_{\boldsymbol{j}}$ distincts, ces deuxièmes points $s_{i}$ et $s_{j}$ ne peuvent pas être confondus puisque tous les cercles sont de même rayons. Maintenant que le problème est reformulé, on peut raisonner uniquement sur le graphe : $G$ est un graphe bipartite entre $C$ et $S$ tel que pour toute arête $(c, s), \operatorname{deg}(c) \geqslant \operatorname{deg}(s)$. Il vient aisément que $|C| \leqslant|S|$ En effet, en notant A l'ensemble des arêtes et $a=\left(c_{a}, s_{a}\right)$ ces arêtes $:|C|=\sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}\left(c_{a}\right)} \leqslant \sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}\left(s_{a}\right)}=S$ ce qui conclut.
|
| 307 |
+
|
| 308 |
+
Commentaire des correcteurs : Le problème a été peu tenté, et résolu par un seul élève. Faire une récurrence était voué à l'échec : en effet, on peut rajouter un cercle, sans pour autant rajouter de point d'intersection à la figure formée.
|
| 309 |
+
|
French_STS/md/fr-corrige-envoi-5.md
ADDED
|
@@ -0,0 +1,424 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br> 
|
| 2 |
+
|
| 3 |
+
ENVOI 5 : Pot-POURRI
|
| 4 |
+
À RENVOYER AU PLUS TARD LE 28 AVRIL 2023
|
| 5 |
+
|
| 6 |
+
Les consignes suivantes sont à lire attentivement :
|
| 7 |
+
|
| 8 |
+
- Le groupe junior est constitué des élèves nés en 2008 ou après. Les autres élèves sont dans le groupe senior.
|
| 9 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 10 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 11 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 12 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 13 |
+
- Respecter la numérotation des exercices.
|
| 14 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
## Exercices Juniors
|
| 18 |
+
|
| 19 |
+
Exercice 1. Trouver toutes les triplets d'entiers positifs $(x, y, z)$ satisfaisant l'équation
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
x!+2^{y}=z!
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
## Solution de l'exercice 1
|
| 26 |
+
|
| 27 |
+
Soit ( $x, y, z$ ) un triplet solution.
|
| 28 |
+
On cherche dans un premier temps à réduire le nombre de valeurs que $x$ peut prendre. Pour ce faire notons que $x$ ! < $<$ ! donc $x<z$. En particulier, $x$ ! divise $z$ ! et $x$ !, donc $x$ ! divise $z$ ! $-x!=2^{y}$. Supposons par l'absurde que $x \geqslant 3$, dans ce cas 3 divise $x$ ! mais ne divise pas $2^{y}$, ce qui rend impossible le fait que $x$ ! divise $2^{y}$. Ainsi $x=0,1$ ou 2 .
|
| 29 |
+
On effectue maintenant une disjonction de cas entre $x!=1$ donc $x=0$ ou 1 , ou bien $x!=2$ donc $x=2$.
|
| 30 |
+
|
| 31 |
+
- Cas $x=0$ ou 1 : l'équation devient $1+2^{y}=z$ !. On effectue alors une deuxième disjonction de cas
|
| 32 |
+
- Cas $y=0$ : on trouve $z=2$. Réciproquement, $(0,0,2)$ et $(1,0,2)$ sont bien solution.
|
| 33 |
+
- Cas $y \geqslant 1$ : ainsi $1+2^{y} \geqslant 3$ et $1+2^{y}$ est impair. Or $z$ ! est pair si $z \geqslant 2$, et vaut 0 ou 1 si $z=1$, aucun des deux cas ne peut donc satisfaire notre équation. Ainsi, si on suppose que $y \geqslant 1$, il n'y a pas de solution.
|
| 34 |
+
- Cas $x=2$ : On distingue encore selon les valeurs de $y$ :
|
| 35 |
+
- Cas $\mathrm{y}=0$ : on obtient $3=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
|
| 36 |
+
- Cas $\mathrm{y}=1$ : on obtient $4=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
|
| 37 |
+
- Cas $y \geqslant 2$ : on obtient que 2 divise $2^{y}+2$, mais que 4 ne divise pas $2^{y}+2$. Ainsi 2 divise $z$ ! mais 4 ne divise pas $z$ !, donc $z=2$ ou 3 . Comme de plus $2^{y}+2 \geqslant 4+2=6$, on obtient $z=3$, donc $2+2^{y}=6$, donc $2^{y}=4$ donc $y=2$. Réciproquement, $(2,2,3)$ est bien solution $\mathrm{car} 2+4=6$.
|
| 38 |
+
Ainsi les solutions sont les triplets $(0,0,2),(1,0,2)$ et $(2,2,3)$.
|
| 39 |
+
Commentaire des correcteurs : L'exercice, plutôt simple, a été abordé par un grand nombre d'élèves. La plupart ont réussi à trouver le bon ensemble de solutions, et ont bien pensé à utiliser les modulos ou la divisibilité, ce qui est très bien. Cependant, de nombreuses erreurs ont été commises, consistant à négliger de traiter proprement les petits cas. Par exemple, de nombreuses copies affirmaient hâtivement qu'une puissance de 2 est paire, ce qui est faux pour $2^{0}=1$. Il faut faire attention à ce genre de détails. On rappelle également que 0 est un entier positif.
|
| 40 |
+
|
| 41 |
+
Exercice 2. Soit $A B C$ un triangle equilatéral et P un point sur le cercle circonscrit de ce triangle mais distincs de $A$, $B$ et $C$. Les droites passant par $P$ et parallèles à $(B C),(C A)$ et $(A B)$ intersectent les droites (CA), (AB) et (BC) en $M$, $N$ et $Q$ respectivement. Montrer que les points $M, N$ et $Q$ sont alignés.
|
| 42 |
+
|
| 43 |
+
## Solution de l'exercice 2
|
| 44 |
+
|
| 45 |
+
On se place dans le cas de la figure suivante :
|
| 46 |
+
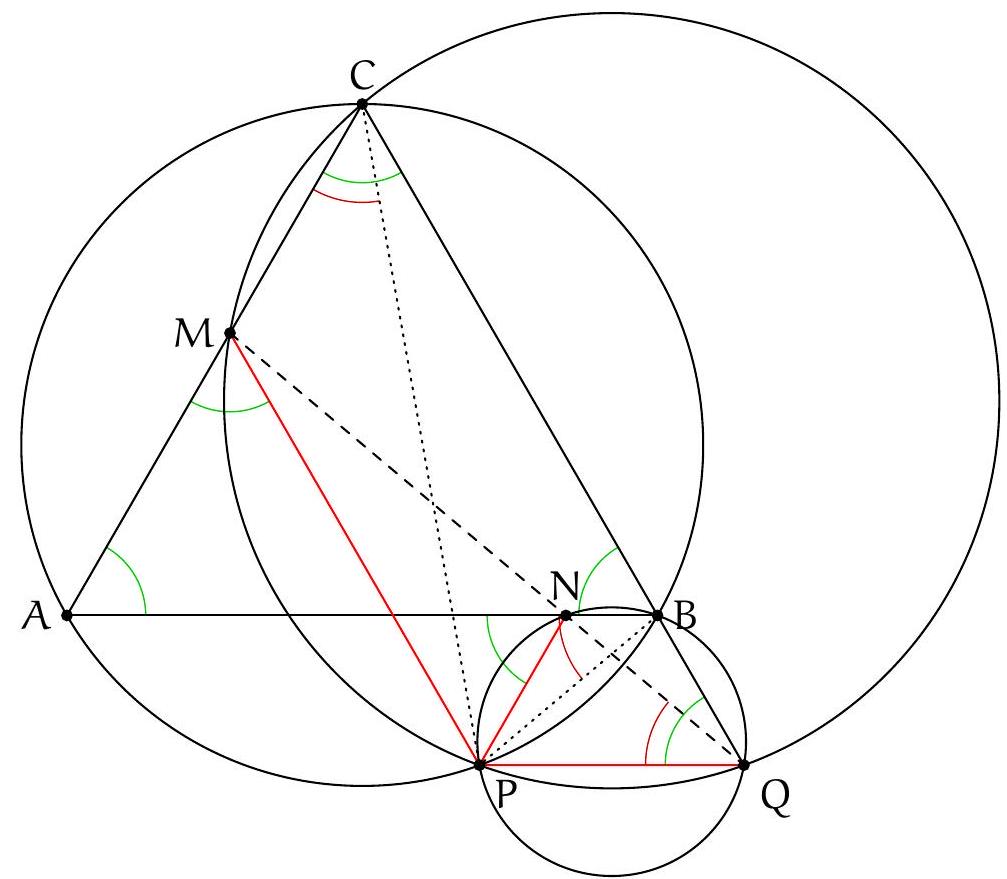
|
| 47 |
+
|
| 48 |
+
Montrons que $P, N, B, Q$ sont cocycliques. Comme $(P N)$ est parallèle à $(A C)$, et $(N B)$ est parallèle à $(\mathrm{AB}), \widehat{A N P}=\widehat{C A B}=60$. Comme $(\mathrm{PQ})$ est parallèle à $(\mathrm{AB}), \widehat{\mathrm{PQB}}=\widehat{A B C}=60$. Ainsi $\mathrm{P}, \mathrm{N}, \mathrm{B}, \mathrm{Q}$ sont cocycliques. Ainsi $\widehat{\mathrm{PQN}}=\widehat{\mathrm{PBN}}=\widehat{\mathrm{PBA}}$.
|
| 49 |
+
Montrons que $P, M, C, Q$ sont cocycliques. Comme $(P M)$ est parallèle à $(B C), \widehat{A M P}=\widehat{A C B}=60$. Or $\widehat{\mathrm{PQC}}=\widehat{\mathrm{PQB}}=60$. Ainsi $\mathrm{P}, \mathrm{M}, \mathrm{C}, \mathrm{Q}$ sont cocycliques. Ainsi $\widehat{\mathrm{PQM}}=\widehat{\mathrm{PCM}}=\widehat{\mathrm{PCA}}$. Par cocyclité de $A, P, B, C, \widehat{P Q M}=\widehat{P C A}=\widehat{P B A}=\widehat{P Q N}$ donc $Q, N, M$ sont alignés.
|
| 50 |
+
|
| 51 |
+
Commentaire des correcteurs : Bien résolu dans l'ensemble. Beaucoup de preuves qui sont un peu trop longues. Quelques erreurs de raisonnement (on ne peut pas utiliser que les points sont alignés pour montrer qu'ils le sont effectivement).
|
| 52 |
+
|
| 53 |
+
Exercice 3. Soit $x, y, z$ trois réels positifs, tel que $x \leqslant 1$. Démontrer que:
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
x y+y+2 z \geqslant 4 \sqrt{x y z}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Solution de l'exercice 3
|
| 60 |
+
Notons que comme $x \leqslant 1, x y+y \geqslant x y+x y=2 x y$. En particulier par inégalité arithmético-géométrique
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
x y+y+2 z \geqslant 2 x y+2 z=2(x y+z) \geqslant 4 \sqrt{x y z}
|
| 64 |
+
$$
|
| 65 |
+
|
| 66 |
+
ce qui donne l'inégalité voulue.
|
| 67 |
+
Commentaire des correcteurs : L'exercice était assez simple et a été abordé par de nombreux élèves, et réussi par presque chacun d'entre eux. J'invite toutefois les élèves à bien se relire lorsqu'ils soumettent une copie, afin de vérifier que les inégalités sont écrites correctement et que des cas n'ont pas été oubliés (par exemple en simplifiant une équation par $y z$ alors que $y z$ peut être nul).
|
| 68 |
+
|
| 69 |
+
Exercice 4. 2024 élèves, tous de taille différente, doivent se placer en file indienne. Cependant, chaque élève ne souhaite pas avoir à la fois devant lui et derrière lui un élève plus petit que lui. Combien y a-t-il de façons de former une telle file indienne?
|
| 70 |
+
|
| 71 |
+
## Solution de l'exercice 4
|
| 72 |
+
|
| 73 |
+
Regardons l'élève de plus grande taille : s'il n'est pas placé au tout début ou à la toute fin de la file, il est entre deux élèves plus petits que lui. Ainsi l'élève le plus grand doit être placé à la fin ou au début.
|
| 74 |
+
Via ce raisonnement, et en regardant les petits cas on peut conjecturer que si on doit placer $n \geqslant 1$ élèves tous de taille différente avec la contrainte de l'énoncé, il y a $2^{\text {n-1 }}$ possibilités. Montrons cela par récurrence sur n .
|
| 75 |
+
Initialisation : pour $\mathrm{n}=1$ élèves, il n'y a qu'une file possible et $1=2^{\mathrm{n}-1}$.
|
| 76 |
+
Hérédité : supposons l'hypothèse vraie au rang $n$ pour un $n \geqslant 1$, montrons qu'elle l'est au rang $n+1$. L'élève le plus grand est frocément placé soit au tout début, soit à la toute fin. Si on l'enlève de la file, la file de $n$ personnes vérifie toujours l'énoncé : il y a donc potentiellement $2^{n-1}$ possibilité pour la file sans la personne la plus grande. Si on rajoute la personne la plus grande devant ou derrière la file vérifie toujours l'énoncé (car la personne à côté du plus grand ne sera pas entre deux personnes plus petites), comme il y a deux choix de placements du plus grand, il y a $2^{\mathfrak{n}}=2^{\mathfrak{n + 1 - 1}}$ possibilités pour former la file, ce qui conclut la récurrence.
|
| 77 |
+
Ainsi en appliquant la propriété pour $\mathrm{n}=2024$, il y a $2^{2023}$ possibilités.
|
| 78 |
+
Commentaire des correcteurs: Exercice très bien réussi dans l'ensemble, avec peu d'erreurs. Deux méthodes de preuve principales ont été employées : la première est semblable à ce que fait l'énoncé, et consiste à voir comment placer les élèves, un par un. La seconde consiste à comprendre quelle va être la "forme" de la répartition des élèves, en V , et à compter ces configurations par divers arguments.
|
| 79 |
+
|
| 80 |
+
Exercice 5. Soient $A, B, C, D$ et $E$ cinq points dans cet ordre sur un cercle tels que $A E=D E$. Soit $P$ le point d'intersection de $(A C)$ et $(B D)$. Soit $Q$ le point de la demi-droite $[B A)$ tel que $A Q=D P$. Soit $R$ le point de la demi-droite $[C D)$ tel que $D R=A P$. Montrer que les droites $(P E)$ et $(Q R)$ sont perpendiculaires.
|
| 81 |
+
|
| 82 |
+
## Solution de l'exercice 5
|
| 83 |
+
|
| 84 |
+
On se place dans le cas de la figure suivante:
|
| 85 |
+
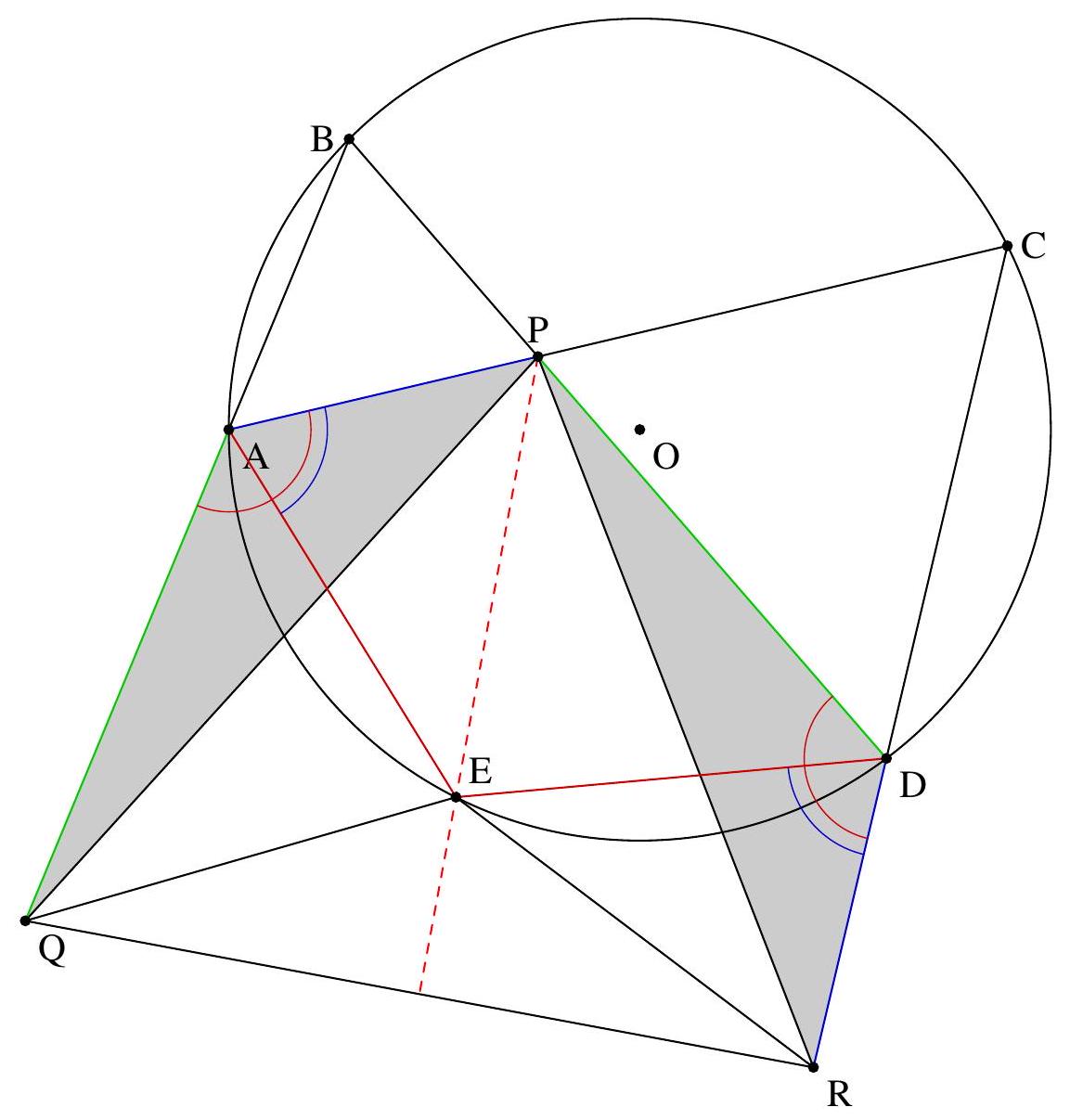
|
| 86 |
+
|
| 87 |
+
Dans cet énoncé on a de nombreuses égalités de longueur $(A Q=D P, D R=A P, A E=D E$. Comme sur la figure, il ne faut pas hésiter à colorier les longueurs égales pour voir des potentiels triangles isométriques, et avancer dans le problème).
|
| 88 |
+
Les triangles DRP et AQP ont l'air d'être isométriques : prouvons-le. Notons déjà que $\mathrm{DR}=A \mathrm{~A}$ et $\mathrm{DP}=\mathrm{AR}$ par hypothèse. De plus $\widehat{\mathrm{RDP}}=180-\widehat{\mathrm{CDP}}=180-\widehat{\mathrm{CDB}}=180-\widehat{\mathrm{CAB}}=180-\widehat{\mathrm{PAB}}=$ $\widehat{\mathrm{PAQ}}$. Ainsi les triangles DRP et AQP sont isométriques.
|
| 89 |
+
En particulier $P Q=P R$, donc $P$ est sur la médiatrice de $(Q R)$.
|
| 90 |
+
Les triangles $D E R$ et $A E P$ ont l'air d'être isométriques : prouvons-le. On a $D E=A E$ et $D R=A P$. De plus $\widehat{\mathrm{EDR}}=180-\widehat{\mathrm{EDC}}=\widehat{\mathrm{CAE}}=\widehat{\mathrm{PAE}}$. Ainsi les triangles DER et AEP sont isométriques et $E P=E R$.
|
| 91 |
+
De même les triangles $A E Q$ et $D E P$ sont isométriques ( $\operatorname{car} A, Q$ jouent un rôle symétrique à $D, R$ ), ainsi $E P=E Q$, donc $E R=E Q: E$ est sur la médiatrice de $(Q R)$.
|
| 92 |
+
Ainsi la médiatrice de ( $Q R$ ) est ( $E P$ ), donc ( $E P$ ) et $(Q R)$ sont perpendiculaires.
|
| 93 |
+
Commentaire des correcteurs : L'exercice est très bien réussi.
|
| 94 |
+
|
| 95 |
+
Exercice 6. Est-il possible de trouver un bloc de 1000 nombres entiers strictement positifs consécutifs qui contient exactement 5 nombres premiers?
|
| 96 |
+
|
| 97 |
+
## Solution de l'exercice 6
|
| 98 |
+
|
| 99 |
+
A première vue, il semble difficile de garantir exactement 5 nombre premier dans un bloc de 1000 entiers consécutifs : aucun théorème d'arithmétique élémentaire permet de s'assurer d'avoir des nombres premiers rapprochés, mais pas d'autres nombres premier entre eux. On peut donc essayer de se demander combien de nombres premiers on peut trouver dans un bloc de 1000 nombres consécutifs.
|
| 100 |
+
Déjà, il est relativement connu qu'on peut trouver 1000 nombres consécutifs dont aucun n'est premier. En effet, $1001!+2, \ldots, 1001!+1001$ ne sont pas premiers : si $2 \leqslant i \leqslant 1001,1001!+i$ est divisible par $i$ et strictement plus grand que $i$, donc il n'est pas premier.
|
| 101 |
+
On peut aussi remarquer qu'entre 1 et 1000 il y a beaucoup de nombres premiers : en tout cas strictement plus que 5 , vu que $2,3,5,7,11,13$ sont premiers.
|
| 102 |
+
Notons $\mathrm{P}(\mathrm{n})$ le nombre de nombres premiers dans l'ensemble $\{n, \ldots, n+999\}$. L'étape naturelle après nos deux remarques précédentes est de se demander comment évalue le nombre $P(n)$ lorsque $n$ parcourt $\mathbb{N}^{*}$. Pour passer de $\{n, \ldots, n+999\}$ à $\{n+1, \ldots, n+1+999\}$, on rajoute $n+1000$ et on enlève $n$. Ainsi on ajoute au plus un nombre premier, et on enlève au plus un nombre premier : on a donc
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Ainsi $P$ ne varie que de 1 en 1 , et on sait que $P(1)>5>P(1001!+2)$. Il semble assez intuitif que cela implique qu'il existe un entier k tel que $\mathrm{P}(\mathrm{k})=5$, nous allons prouver cela.
|
| 109 |
+
Soit $k$ le premier entier tel que $\mathrm{P}(\mathrm{k}) \leqslant 5$. On sait que $\mathrm{k}>1$, donc $\mathrm{P}(\mathrm{k}-1)>5$ par minimalité. Ainsi, on a forcément $P(k)=P(k-1)-1$ (pour avoir $P(k) \leqslant 5$ ), donc $P(k)>4$. Ainsi $P(k) \geqslant 5$, or par définition $P(k) \leqslant 5$, donc $P(k)=5$.
|
| 110 |
+
Ainsi la réponse à l'énoncé est oui : il existe bien un bloc de 1000 entiers consécutifs avec exactement cinq entiers premiers.
|
| 111 |
+
|
| 112 |
+
Commentaire des correcteurs : L'exercice a globalement été bien traité, mais peu d'élèves ont réussi à bien formuler le fait qu'il existe 1000 nombres composés consécutifs.
|
| 113 |
+
|
| 114 |
+
Exercice 7. On dit qu'un entier $k>1$ est superbe s'il existe $\mathrm{m}, \mathrm{n}, \mathrm{a}$ trois entiers strictement positifs tels que
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Déterminer le plus petit entier superbe.
|
| 121 |
+
|
| 122 |
+
## Solution de l'exercice 7
|
| 123 |
+
|
| 124 |
+
Supposons que $k=2$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}, \mathrm{a}$ tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{2}$. En regardant modulo $3,5^{\mathrm{m}}+1 \equiv 2^{\mathrm{m}}+1 \equiv \mathrm{a}^{2}(\bmod 3)$. Or les puissances de 2 modulo 9 valent alternativement 2 si m est impair, puis 1 si m est pair, donc $2^{\mathrm{m}}+1$ vaut soit 2 soit 0 modulo 3 . Comme les carrés modulo 3 sont 0 et 1 , on en déduit que $2^{\mathrm{m}}+1$ vaut 0 modulo 3 , donc que $m$ est impair. En regardant modulo 7 , on obtient que $5^{\mathrm{m}} \equiv \boldsymbol{a}^{2}(\bmod 7)$. Or les carrés modulo 7 sont $0,1,2,4$, et les puissances de 5 alternent entre $1,5,4,6,2,3$. Ainsi $5^{\mathrm{m}}$ vaut $0,1,2$ ou 4 si et seulement si $m$ vaut 0,2 ou 4 modulo 6 , ce qui est impossible car $m$ est pair. Ainsi $k \neq 2$.
|
| 125 |
+
Supposons que $\mathrm{k}=3$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{3}$. En regardant modulo $7,5^{\mathrm{m}} \equiv \mathrm{a}^{3}$. Or les cubes modulo 7 sont $0,1,6$. Et les puissances de 5 modulo 7 alternent entre $1,5,4,6,2,3$. Ainsi on obtient que $m \equiv 0(\bmod 6)$ ou $m \equiv 3(\bmod 6)$ : dans tous les cas 3 divise m . On regarde alors modulo 9 : on a $5^{\mathrm{m}}+4 \equiv \mathrm{a}^{3}$. Or comme m est divisible par 3 , $5^{m}$ et $a^{3}$ sont des cubes. Les cubes modulo 9 sont $0,1,8$. Ainsi $5^{m}-a^{3}$ peut valoir $0,1,2,7,8$ modulo 9 , mais pas 4 ce qui est contradictoire. Ainsi $k \neq 3$.
|
| 126 |
+
Supposons que $k=3$ est superbe : il existe trois entiers strictement positifs $\mathbf{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{4}=\left(a^{2}\right)^{2}$. En particulier, 2 est superbe ce qui est contradictoire.
|
| 127 |
+
Notons que 5 est superbe : en prenant $\mathbf{a}=3$, on a $\mathbf{a}^{\mathrm{k}}=3^{5}=243=5^{1}+63 \times 3+49$ donc 5 est superbe. Ainsi 5 est le plus petit entier superbe.
|
| 128 |
+
|
| 129 |
+
Commentaire des correcteurs : L'exercice a été traité par peu d'élèves, qui l'ont bien résolu.
|
| 130 |
+
|
| 131 |
+
Exercice 8. Soit $x, y, z$ trois nombres réels vérifiant $x+y+z=2$ et $x y+y z+z x=1$. Déterminer la valeur maximale que peut prendre $x-y$.
|
| 132 |
+
Solution de l'exercice 8
|
| 133 |
+
Soit ( $x, y, z$ ) un triplet vérifiant l'énoncé. Quitte à échanger $x$ et le maximum du triplet, puis $z$ et le minimum du triplet, on peut supposer $x \geqslant z \geqslant y$, tout en augmentant $x-y$.
|
| 134 |
+
Comme $x+y+z=2$, on a $4=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z)=x^{2}+y^{2}+z^{2}+2$, donc $x^{2}+y^{2}+z^{2}=2$.
|
| 135 |
+
En particulier $(x-y)^{2}+(y-z)^{2}+(x-z)^{2}=2\left(x^{2}+y^{2}+z^{2}\right)-2(x y+y z+x z)=2$. Or par inégalité arithmético quadratique, $(x-z)^{2}+(z-y)^{2} \geqslant \frac{(x-z+z-y)^{2}}{2}=\frac{(x-y)^{2}}{2}$, donc $2 \geqslant(x-y)^{2}+\frac{(x-y)^{2}}{2}=$ $\frac{3(x-y)^{2}}{2}$, donc $(x-y) \leqslant \frac{2}{\sqrt{3}}$.
|
| 136 |
+
Essayons de montrer que cette valeur est atteignable. Si on a $x-y=\frac{2}{\sqrt{3}}$, alors on a égalité dans l'inégalité arithmético quadratique : ainsi $x-z=z-y$, donc comme leur somme vaut $x-y, x-z=z-y=\frac{1}{\sqrt{3}}$. En particulier, comme $x+y+z=3 z+(z-x)+(z-y)=3 z$, on a $z=\frac{2}{3}, x=\frac{2}{3}+\frac{1}{\sqrt{3}}$ et $y=\frac{2}{3}-\frac{1}{\sqrt{3}}$. Réciproquement, pour ces valeurs de $x, y, z$, on a bien :
|
| 137 |
+
$-x+y+z=3 \times \frac{2}{3}=2$
|
| 138 |
+
$-x y+y z+z x=x y+(x+y) z=\left(\frac{2}{3}+\frac{1}{\sqrt{3}}\right)\left(\frac{2}{3}-\frac{1}{\sqrt{3}}+\frac{4}{3} \times \frac{2}{3}=\frac{4}{9}-\frac{1}{3}+\frac{8}{9}=\frac{9}{9}=1\right.$
|
| 139 |
+
$-x-y=2 \times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
|
| 140 |
+
Ainsi $(x, y, z)$ vérifie les conditions de l'énoncé, et $x-y=\frac{2}{\sqrt{3}}$, donc la valeur maximale que peut prendre $x-y$ est $\frac{2}{\sqrt{3}}$.
|
| 141 |
+
|
| 142 |
+
Commentaire des correcteurs : L'exercice a été assez peu abordé. La principale erreur est d'oublier de trouver des $x, y, z$ pour lesquels on a égalité.
|
| 143 |
+
|
| 144 |
+
Exercice 9. Soit $A B C$ un triangle et $I$ le centre du cercle inscrit. On note $D$ et $E$ les pieds des bissectrices issues de $B$ et $C$. Soit $X$ l'intersection des symétriques de $(A B)$ et $(A C)$ par rapport à $(C E)$ et $(B D)$. Montrer que les droites (XI) et (BC) sont perpendiculaires.
|
| 145 |
+
Solution de l'exercice 9
|
| 146 |
+
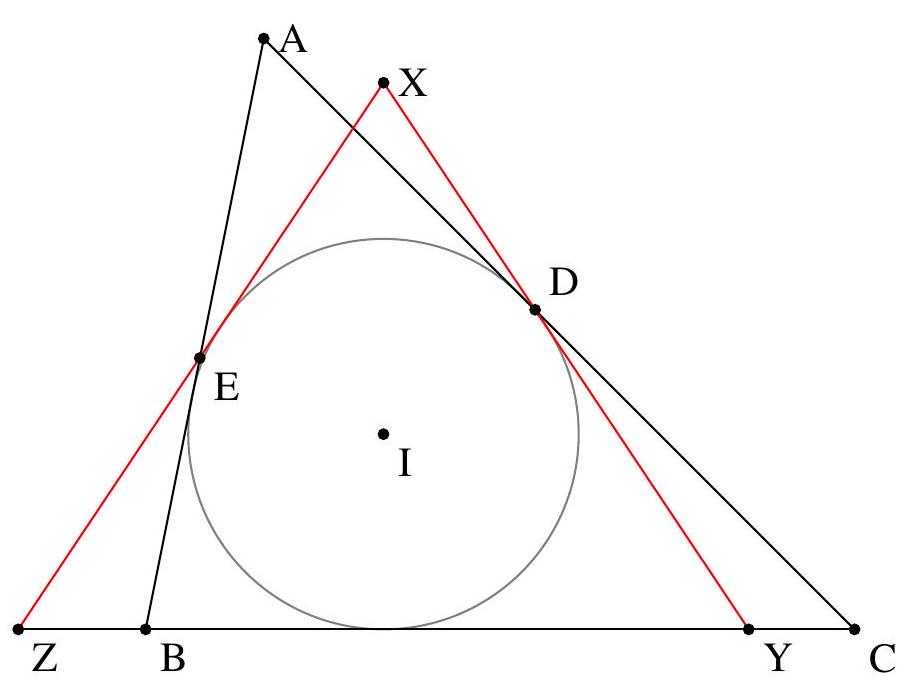
|
| 147 |
+
|
| 148 |
+
Notons $Y$ et $Z$ les intersections respectives de (DX) et (EX) avec la droite (BC). On va montrer que le triangle ZXY est isocèle en $X$ et que I est le centre de son cercle inscrit. Si on arrive à montrer ces propriétés, la conclusion de l'exercice suivrait. En effet, la droite (XI) est alors la bissectrice du triangle $X Y Z$ isocèle en $X$, donc en également la hauteur.
|
| 149 |
+
Soit $\omega$ le cercle inscrit du triangle $A B C$, on sait donc que la droite $(A B)$ est tangente à $\omega$, comme la droite $(\mathrm{CI})$ est un axe de symétrie de $\omega$ il suit que la droite (XE) est également tangente à $\omega$. De la même manière, la droite (DX) est tangente à $\omega$. Par définition la droite (YZ) est la droite (BC) donc également tangente à $\omega$. Cela montre que $\omega$ est le cercle inscrit du triangle XYZ. En particulier, la droite (XI) est la bissetrice issue de $X$.
|
| 150 |
+
On finit la preuve de l'exercice en montrant que $\widehat{X Z Y}=\widehat{X Y Z}$. On note $\alpha$ l'angle en $A$ dans le triangle ABC. On a alors,
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
\begin{aligned}
|
| 154 |
+
\widehat{\mathrm{XZY}} & =\widehat{\mathrm{EZC}} \\
|
| 155 |
+
& =\widehat{\mathrm{XEC}}-\widehat{\mathrm{ECZ}} \\
|
| 156 |
+
& =\widehat{\mathrm{AEC}}-\widehat{\mathrm{ECA}} \\
|
| 157 |
+
& =\widehat{\mathrm{EAC}}=\alpha .
|
| 158 |
+
\end{aligned}
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
De la même manière $\widehat{X Y Z}=\alpha$ ce qui montre bien que le triangle ZYX est isocèle en $X$ et conclut la preuve de l'exercice.
|
| 162 |
+
|
| 163 |
+
Commentaire des correcteurs : Cet exercice de géométrie a été abordé par très peu d'élèves. La plupart d'entre eux l'ont bien réussi, par diverses méthodes. Les méthodes de résolution les plus simples, dans cet exercice, étaient celles qui faisaient le plus appel aux arguments de symétrie. On ne peut que conseiller, face à une figure qui présente de telles symétries, de chercher à les exploiter.
|
| 164 |
+
|
| 165 |
+
## Exercices Seniors
|
| 166 |
+
|
| 167 |
+
Exercice 10. Trouver toutes les triplets d'entiers positifs $(x, y, z)$ satisfaisant l'équation
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
x!+2^{y}=z!
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
## Solution de l'exercice 10
|
| 174 |
+
|
| 175 |
+
Soit ( $x, y, z$ ) un triplet solution.
|
| 176 |
+
On cherche dans un premier temps à réduire le nombre de valeurs que $x$ peut prendre. Pour ce faire notons que $x!<z$ ! donc $x<z$. En particulier, $x$ ! divise $z$ ! et $x$ !, donc $x$ ! divise $z$ ! $-x!=2^{y}$. Supposons par l'absurde que $x \geqslant 3$, dans ce cas 3 divise $x$ ! mais ne divise pas $2^{y}$, ce qui rend impossible le fait que $x$ ! divise $2^{y}$. Ainsi $x=0,1$ ou 2 .
|
| 177 |
+
On effectue maintenant une disjonction de cas entre $x!=1$ donc $x=0$ ou 1 , ou bien $x!=2$ donc $x=2$.
|
| 178 |
+
|
| 179 |
+
- Cas $x=0$ ou 1 : l'équation devient $1+2^{y}=z$ !. On effectue alors une deuxième disjonction de cas
|
| 180 |
+
- Cas $y=0$ : on trouve $z=2$. Réciproquement, $(0,0,2)$ et $(1,0,2)$ sont bien solution.
|
| 181 |
+
- Cas $y \geqslant 1$ : ainsi $1+2^{y} \geqslant 3$ et $1+2^{y}$ est impair. Or $z$ ! est pair si $z \geqslant 2$, et vaut 0 ou 1 si $z=1$, aucun des deux cas ne peut donc satisfaire notre équation. Ainsi, si on suppose que $y \geqslant 1$, il n'y a pas de solution.
|
| 182 |
+
- $\boldsymbol{C a s} x=2$ : On distingue encore selon les valeurs de $y$ :
|
| 183 |
+
- Cas $y=0$ : on obtient $3=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
|
| 184 |
+
- Cas $y=1$ : on obtient $4=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
|
| 185 |
+
- Cas $y \geqslant 2$ : on obtient que 2 divise $2^{y}+2$, mais que 4 ne divise pas $2^{y}+2$. Ainsi 2 divise $z$ ! mais 4 ne divise pas $z$ !, donc $z=2$ ou 3 . Comme de plus $2^{y}+2 \geqslant 4+2=6$, on obtient $z=3$, donc $2+2^{y}=6$, donc $2^{y}=4$ donc $y=2$. Réciproquement, $(2,2,3)$ est bien solution car $2+4=6$.
|
| 186 |
+
Ainsi les solutions sont les triplets $(0,0,2),(1,0,2)$ et $(2,2,3)$.
|
| 187 |
+
Commentaire des correcteurs : La quasi-totalité des élèves ayant traité l'exercice l'ont bien compris. Mais résoudre l'équation sans faute était plus compliqué : bien des élèves ont oublié des cas (typiquement, le cas $x=0$; on rappelle d'ailleurs que $0!=1$ ), fait des généralisations hâtives (par exemple que $1+2^{y-1}$ était toujours impair - ce qui n'est vrai que si $y \geqslant 2$, et il faut traiter le cas $y \leqslant 1$ ), ou oublié de vérifier que les triplets qu'ils ont trouvés étaient des solutions (faute assez répandue; il faut toujours le faire, même s'il ne s'agit que de dire "on vérifie réciproquement que [...] sont bien des solutions"). Quelques élèves n'ont pas justifié certains arguments plus généraux ("les seules factorielles de différence 1 sont 2 et 1 ", ou "les seules factorielles qui sont des puissances de 2 sont 2 et 1 "), ou l'ont fait très vaguement (en parlant de "vitesse de croissance", qui n'est pas un concept applicable ici). Ce genre d'affirmation doit toujours être justifié (surtout dans la mesure où l'argument tient en une ou deux phrases). Enfin, un nombre surprenant de copies contient de légères incohérences ou des étourderies, en général non sanctionnées : nous invitons les candidats à bien se relire avant d'envoyer les copies.
|
| 188 |
+
|
| 189 |
+
Exercice 11. Félix souhaite colorier les entiers de 1 à 2023 tels que si $a, b$ sont deux entiers distincts entre 1 et 2023 et a divise $\mathbf{b}$, alors a et $b$ sont de couleur différentes. Quel est le nombre minimal de couleur dont Félix a besoin?
|
| 190 |
+
|
| 191 |
+
## Solution de l'exercice 11
|
| 192 |
+
|
| 193 |
+
On peut essayer de colorier de manière gloutonne les nombres : 1 peut être colorié d'une couleur qu'on note $a$, 2 et 3 de la même couleur $b$ (mais pas de la couleur $a$ ), puis 4,6 de la couleur $c$ (on peut aussi colorier 5 et 7 de la couleur c), etc. Il semble donc qu'une coloriation performante soit pour tout $k$ de colorier les nombres $n$ vérifiant $2^{k} \leqslant n<2^{k+1}$ de la couleur $k+1$, tant que $n \leqslant 2023$. Ainsi on colorie $[1,2[$ de couleur $1,[2,4[$ de couleur $2, \ldots,[1024,2023]$ de couleur 11 . Si $a \neq b$ sont de la même couleur $\mathrm{k} \in\{1, \ldots, 11\}$ alors $0<\frac{\mathrm{a}}{\mathrm{b}}<\frac{2^{k+1}}{2^{k}}=2$, donc si b divise a , alors $\frac{\mathrm{a}}{\mathrm{b}}$ est entier donc vaut 1 . On a alors $\mathrm{a}=\mathrm{b}$ ce qui est contradictoire. Ainsi notre coloriage vérifie bien la condition de l'énoncé, et nécessite 11 couleurs.
|
| 194 |
+
Réciproquement si un coloriage vérifie l'énoncé, les nombres $2^{0}=1,2^{1}, \ldots, 2^{10}$ sont entre 1 et 2023 , et si on prend $a \neq b$ parmi ces 11 nombres, soit $a$ divise $b$, soit $b$ divise $a$. Ainsi ces 11 nombres sont de couleurs différentes. Il faut donc au moins 11 couleurs.
|
| 195 |
+
Ainsi le nombre minimal de couleurs requises est 11.
|
| 196 |
+
Commentaire des correcteurs : L'exercice est très bien réussi. Comme dans tout exercice où on demande de trouver le nombre minimal tel que, il est important de découper la preuve en deux parties : pourquoi $n=11$ couleurs suffisent, et pourquoi si $n \leqslant 10, n$ couleurs ne suffisent pas.
|
| 197 |
+
|
| 198 |
+
Exercice 12. Soient $A, B, C, D$ et $E$ cinq points dans cet ordre sur un cercle tels que $A E=D E$. Soit $P$ le point d'intersection de ( $A C)$ et $(B D)$. Soit $Q$ le point de la demi-droite $[B A)$ tel que $A Q=D P$. Soit $R$ le point de la demi-droite [CD) tel que $D R=A P$. Montrer que les droites $(P E)$ et $(Q R)$ sont perpendiculaires.
|
| 199 |
+
|
| 200 |
+
## Solution de l'exercice 12
|
| 201 |
+
|
| 202 |
+
On se place dans le cas de la figure suivante :
|
| 203 |
+
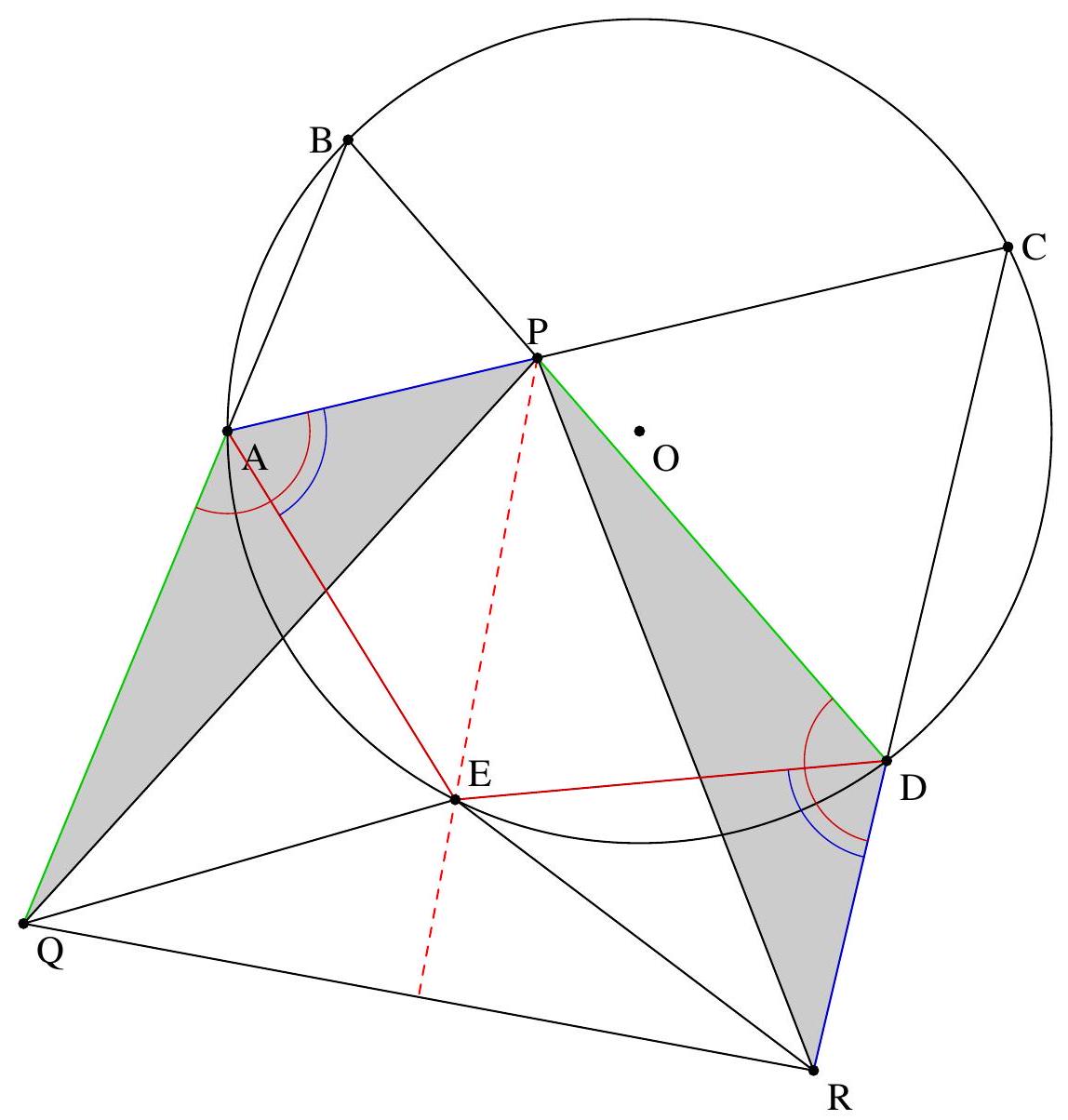
|
| 204 |
+
|
| 205 |
+
Dans cet énoncé on a de nombreuses égalités de longueur ( $A Q=D P, D R=A P, A E=D E$. Comme sur la figure, il ne faut pas hésiter à colorier les longueurs égales pour voir des potentiels triangles isométriques, et avancer dans le problème).
|
| 206 |
+
Les triangles DRP et $A Q P$ ont l'air d'être isométriques : prouvons-le. Notons déjà que $\mathrm{DR}=A Q$ et $\mathrm{DP}=A R$ par hypothèse. De plus $\widehat{\mathrm{RDP}}=180-\widehat{\mathrm{CDP}}=180-\widehat{\mathrm{CDB}}=180-\widehat{\mathrm{CAB}}=180-\widehat{\mathrm{PAB}}=$ $\widehat{P A Q}$. Ainsi les triangles DRP et AQP sont isométriques.
|
| 207 |
+
En particulier $P Q=P R$, donc $P$ est sur la médiatrice de $(Q R)$.
|
| 208 |
+
Les triangles DER et $A E P$ ont l'air d'être isométriques : prouvons-le. On a $D E=A E$ et $D R=A P$. De plus $\widehat{\mathrm{EDR}}=180-\widehat{\mathrm{EDC}}=\widehat{\mathrm{CAE}}=\widehat{\mathrm{PAE}}$. Ainsi les triangles DER et AEP sont isométriques et $E P=E R$.
|
| 209 |
+
De même les triangles $A E Q$ et $D E P$ sont isométriques (car $A, Q$ jouent un rôle symétrique à $D, R$ ), ainsi $E P=E Q$, donc $E R=E Q: E$ est sur la médiatrice de $(Q R)$.
|
| 210 |
+
Ains i la médiatrice de (QR) est (EP), donc (EP) et $(Q R)$ sont perpendiculaires.
|
| 211 |
+
Commentaire des correcteurs : Cet exercice a été réussi par une large majorité des élèves l'ayant traité. Le principal problème était une imprécision dans le vocabulaire : deux triangles dont toutes les longueurs
|
| 212 |
+
sont égales sont dits isométriques plutôt qu'égaux ou identiques. Quant à la notion de triangles semblables, elle est plus faible que la précédente, et traduit simplement l'égalité des angles (et donc aussi des rapports de longueurs, mais pas des longueurs elles-mêmes).
|
| 213 |
+
|
| 214 |
+
Exercice 13. On dit qu'un polynôme $P$ est fantabuleux s'il existe des réels $\mathrm{a}_{0}, \ldots, \mathrm{a}_{2022}$ tel que
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
P(X)=X^{2023}+a_{2022} X^{2022}+\cdots+a_{1} X+a_{0}
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
s'il a 2023 racines $r_{1}, \ldots, r_{2023}$ (non nécessairement distinctes) dans $[0,1]$, et si $P(0)+P(1)=0$. Déterminer la valeur maximale que peut prendre $\mathrm{r}_{1} \cdot \mathrm{r}_{2} \cdots \mathrm{r}_{2023}$ pour un polynôme fantabuleux.
|
| 221 |
+
|
| 222 |
+
## Solution de l'exercice 13
|
| 223 |
+
|
| 224 |
+
La réponse est $2^{-2023}$, on va montrer cela en deux temps, dans un premier temps on va montrer que l'on ne peut pas trouver de polynôme avec une valeur plus grand et dans un second temps exhiber un polynôme qui vérifie les conditions de l'énoncé et dont le produit de racine est bien égal à $2^{-2023}$.
|
| 225 |
+
Notons que par hypothèse, on peut réécrire $P(X)=\prod_{k=1}^{2023}\left(X-r_{k}\right)$. En particulier, $P(0)=-\prod_{k=1}^{2023} r_{k}$ et $\mathrm{P}(1)=\prod_{\mathrm{k}=1}^{2023}\left(1-\mathrm{r}_{\mathrm{k}}\right)$. L'hypothèse $\mathrm{P}(0)+\mathrm{P}(1)=0$ devient :
|
| 226 |
+
|
| 227 |
+
$$
|
| 228 |
+
\prod_{k=1}^{2023}\left(1-r_{k}\right)=\prod_{k=1}^{2023} r_{k}=r_{1} \cdot r_{2} \cdots r_{2023}
|
| 229 |
+
$$
|
| 230 |
+
|
| 231 |
+
Ainsi comme pour tout $k, r_{k} \geqslant 0$ et $1-\mathrm{r}_{\mathrm{k}} \geqslant 0$, par inégalité arithmético-géométrique,
|
| 232 |
+
|
| 233 |
+
$$
|
| 234 |
+
\left(r_{1} \cdot r_{2} \cdots r_{2023}\right)^{2}=\prod_{k=1}^{2023}\left(1-r_{k}\right) r_{k} \leqslant \prod_{k=1}^{2023}\left(\frac{\left(1-r_{k}\right)+r_{k}}{2}\right)^{2}=\frac{1}{4^{2023}}
|
| 235 |
+
$$
|
| 236 |
+
|
| 237 |
+
Ainsi $r_{1} \cdot r_{2} \cdots r_{2023} \leqslant 2^{-2023}$.
|
| 238 |
+
Notons de plus que si $\mathrm{P}(\mathrm{X})=\left(\mathrm{X}-\frac{1}{2}\right)^{2023}$, P est bien unitaire de degré 2023, a 2023 racines dans $[0,1]$, vérifie $\mathrm{P}(0)+\mathrm{P}(1)=\left(-\frac{1}{2}\right)^{2023}+\left(\frac{1}{2}\right)^{2023}=0$ donc P est fantabuleux. Le produit de ses racines vaut $2^{-2023}$. Ainsi la valeur maximale que peut prendre $r_{1} \cdot r_{2} \cdots r_{2023}$ pour un polynôme fantabuleux est $2^{-2023}$.
|
| 239 |
+
|
| 240 |
+
Commentaire des correcteurs: L'exercice demandait de trouver la valeur maximale que pouvait prendre un produit de racines pour une classe de polynômes particuliers. Presque tous les élèves ont trouvé le cas réalisant le maximum (et donc sa valeur), et une proportion satisfaisante de ces élèves ont mené la preuve jusqu'au bout, généralement en appliquant l'IAG. Les relations de Viète semblent bien maitrisées mais n'étaient absolument pas nécessaires à la résolution du problème. Une idée à retenir : l'IAG est souvent une inégalité judicieuse pour montrer qu'un produit de réels positifs est maximal lorsque tous ses termes sont égaux.
|
| 241 |
+
|
| 242 |
+
Exercice 14. Est-il possible de trouver un bloc de 1000 nombres entiers strictement positifs consécutifs qui contient exactement 5 nombres premiers?
|
| 243 |
+
|
| 244 |
+
## Solution de l'exercice 14
|
| 245 |
+
|
| 246 |
+
A première vue, il semble difficile de garantir exactement 5 nombre premier dans un bloc de 1000 entiers consécutifs : aucun théorème d'arithmétique élémentaire permet de s'assurer d'avoir des nombres premiers rapprochés, mais pas d'autres nombres premier entre eux. On peut donc essayer de se demander combien de nombres premiers on peut trouver dans un bloc de 1000 nombres consécutifs.
|
| 247 |
+
Déjà, il est relativement connu qu'on peut trouver 1000 nombres consécutifs dont aucun n'est premier. En effet, $1001!+2, \ldots, 1001!+1001$ ne sont pas premiers : si $2 \leqslant i \leqslant 1001,1001!+i$ est divisible par $i$ et strictement plus grand que $i$, donc il n'est pas premier.
|
| 248 |
+
On peut aussi remarquer qu'entre 1 et 1000 il y a beaucoup de nombres premiers : en tout cas strictement plus que 5 , vu que $2,3,5,7,11,13$ sont premiers.
|
| 249 |
+
Notons $\mathrm{P}(\mathrm{n})$ le nombre de nombre premier dans l'ensemble $\{\mathrm{n}, \ldots, n+999\}$. L'étape naturelle après nos deux remarques précédentes est de se demander comment évalue le nombre $P(n)$ lorsque $n$ parcourt $\mathbb{N}^{*}$. Pour passer de $\{n, \ldots, n+999\}$ à $\{n+1, \ldots, n+1+999\}$, on rajoute $n+1000$ et on enlève $n$. Ainsi on ajoute au plus un nombre premier, et on enlève au plus un nombre premier : on a donc
|
| 250 |
+
|
| 251 |
+
$$
|
| 252 |
+
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\} .
|
| 253 |
+
$$
|
| 254 |
+
|
| 255 |
+
Ainsi $P$ ne varie que de 1 en 1 , et on sait que $P(1)>5>P(1001!+2)$. Il semble assez intuitif que cela implique qu'il existe un entier $k$ tel que $\mathrm{P}(\mathrm{k})=5$, nous allons prouver cela.
|
| 256 |
+
Soit $k$ le premier entier tel que $\mathrm{P}(\mathrm{k}) \leqslant 5$. On sait que $\mathrm{k}>1$, donc $\mathrm{P}(\mathrm{k}-1)>5$ par minimalité. Ainsi, on a forcément $P(k)=P(k-1)-1$ (pour avoir $P(k) \leqslant 5$ ), donc $P(k)>4$. Ainsi $P(k) \geqslant 5$, or par définition $P(k) \leqslant 5$, donc $P(k)=5$.
|
| 257 |
+
Ainsi la réponse à l'énoncé est oui : il existe bien un bloc de 1000 entiers consécutifs avec exactement cinq entiers premiers.
|
| 258 |
+
|
| 259 |
+
Commentaire des correcteurs : L'exercice a été très réussi par les élèves qui l'ont cherché. Une erreur que j'ai retrouvée souvent est au niveau de la preuve de l'existence de 1000 entiers consécutifs non premiers. Certains écrivent que $1000!, 1000!+1, \ldots, 1000!+999$ ne sont pas premiers, alors que rien ne permet de voir a priori que $1000!+1$ n'est pas premier. Par ailleurs, d'autres élèves ont voulu utilisé le théorème des nombres premiers, ce qui n'était pas forcément une bonne idée, car mettant en jeu des concepts d'équivalents de suite qui ne sont pas bien maîtrisés. Même si ce raisonnement peut être justifié, je n'ai pas jugé suffisant de dire que la densité des nombres premiers étant nulle, il existe 1000 entiers consécutifs tous non premiers.
|
| 260 |
+
|
| 261 |
+
Exercice 15. On dit qu'un nombre rationnel strictement positif q est magnifique s'il existe quatre entiers strictement positifs $a, b, c, d$ tels que
|
| 262 |
+
|
| 263 |
+
$$
|
| 264 |
+
\mathrm{q}=\frac{\mathrm{a}^{2021}+\mathrm{b}^{2023}}{\mathrm{c}^{2022}+\mathrm{d}^{2024}}
|
| 265 |
+
$$
|
| 266 |
+
|
| 267 |
+
Existe-t-il un rationnel strictement positif qui n'est pas magnifique?
|
| 268 |
+
|
| 269 |
+
## Solution de l'exercice 15
|
| 270 |
+
|
| 271 |
+
La question posée est assez déroutante : il a l'air d'être dur de décider ou non si un nombre peut s'écrire de cette forme. On peut donc essayer de se fixe un rationnel strictement positif de la forme $r / s$ avec $r, s$ des entiers strictement positif, et chercher des bons $a, b, c, d$ pour avoir
|
| 272 |
+
|
| 273 |
+
$$
|
| 274 |
+
\frac{r}{s}=\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
|
| 275 |
+
$$
|
| 276 |
+
|
| 277 |
+
Cela permettra au moins de comprendre si tous les rationnels sont magnifique, ou de trouver un ensemble de rationnels qui pourraient être non magnifique. Ici le choix de $a, b, c, d$ n'est pas clair. Le plus naturel est de prendre $a=r^{r_{a}} \boldsymbol{s}^{s_{a}}, b=r^{r_{b}} s^{s_{b}}, c=r^{r_{c}} \boldsymbol{s}^{s_{c}}$ et $d=r^{r_{d}} \boldsymbol{s}^{s_{d}}$ avec les $r_{i}$ et $s_{i}$ des entiers positifs. On obtient alors :
|
| 278 |
+
|
| 279 |
+
$$
|
| 280 |
+
\frac{\mathrm{r}}{\mathrm{~s}}=\frac{\mathrm{r}^{2021 \mathrm{r}_{\mathrm{a}}} \mathrm{~s}^{2021 \mathrm{~s}_{\mathrm{a}}}+\mathrm{r}^{2023 r_{\mathrm{b}}} \mathrm{~s}^{2023 s_{\mathrm{b}}}}{\mathrm{r}^{2022 r_{\mathrm{c}}} \mathrm{~s}^{2022 s_{\mathrm{c}}}+\mathrm{r}^{2024 \mathrm{r}_{\mathrm{d}}} \mathrm{~s}^{2024 \mathrm{~s}_{\mathrm{d}}}}
|
| 281 |
+
$$
|
| 282 |
+
|
| 283 |
+
Pour espérer factoriser et simplifier ce terme, le plus simple est d'avoir $2021 r_{a}=2023 r_{b}$, i.e. de poser $r_{b}=2021 r_{1}$ et $r_{a}=2023 r_{1}$ pour un certain entier positif $r_{1}$. De même on pose $r_{c}=2024 r_{2}$ et $r_{d}=2022 r_{2}$ pour un certain entier positif $r_{2}, s_{a}=2023 s_{1}$ et $s_{b}=2021 s_{1}$ pour un certain entier positif $s_{1}$, et $s_{c}=2024 s_{2}$ et $s_{d}=2022 s_{2}$ pour un certain entier positif $r_{2}$.
|
| 284 |
+
On a alors
|
| 285 |
+
|
| 286 |
+
$$
|
| 287 |
+
\frac{r}{\mathrm{~s}}=\frac{\mathrm{r}^{2021 \times 2023 r_{1}} s^{2021 \times 2023 s_{1}}}{\mathrm{r}^{2022 \times 2024 \mathrm{r}_{2}} \mathrm{~s}^{2022 \times 2024 \mathrm{~s}_{2}}}=\mathrm{r}^{2021 \times 2023 \mathrm{r}_{1}-2022 \times 2024 \mathrm{r}_{2}} \mathrm{~s}^{2021 \times 2023 \mathrm{~s}_{1}-2022 \times 2024 \mathrm{~s}_{2}}
|
| 288 |
+
$$
|
| 289 |
+
|
| 290 |
+
Ainsi il suffit de trouver $r_{1}, r_{2}, s_{1}, s_{2}$ des entiers positifs tels que $2021 \times 2023 r_{1}-2022 \times 2024 r_{2}=1$ et $-2021 \times 2023 \mathrm{~s}_{1}+2022 \times 2024 \mathrm{~s}_{2}=1$. Pour cela, il suffit d'utiliser le théorème de Bézout. En effet, $2021 \times 2023$ et $2022 \times 2024$ sont premiers entre eux : si on raisonne par l'absurde en considérant $p$ un facteur premier de ces deux nombres, $p$ divise deux nombres entre 2021 et 2024, donc divise leur différence, donc $p=2$ ou 3 . Or $2021 \times 2023$ est impair, et non divisible par 3 , donc on a une contradiction. Ainsi il existe deux entiers $e, f$ tels que $2021 \times 2023 e-2022 \times 2024 f=1$. Quitte à rajouter $2022 \times 2024$ plusieurs fois à $e$, et $2021 \times 2023$ le même nombre de fois à $f$, on peut supposer $e, f$ positifs. De même il existe deux entiers positifs $g$ et $h$ tels que $-2021 \times 2023 g+2022 \times 2024 h=1$. Poser $s_{1}=g, s_{2}=h, r_{1}=$ $e, r_{2}=\mathrm{f}$ donne bien que $\mathrm{r} / \mathrm{s}$ est magnifique : ainsi tout rationnel strictement positif est magnifique.
|
| 291 |
+
|
| 292 |
+
Commentaire des correcteurs : L'exercice a été très réussi par les élèves qui l'ont cherché.
|
| 293 |
+
|
| 294 |
+
Exercice 16. Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
|
| 295 |
+
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
| 296 |
+
|
| 297 |
+
## Solution de l'exercice 16
|
| 298 |
+
|
| 299 |
+
On propose deux solutions : une première solution très élémentaire et uniquement combinatoire, et une seconde solution utilisant des idées de combinatoire analytique, couplées à de la théorie des nombres.
|
| 300 |
+
|
| 301 |
+
## Première solution :
|
| 302 |
+
|
| 303 |
+
Notons $a_{n}(k)$ le nombre de suites de $n$ mouvements tel que si Martin était initialement à la position 0 , il se retrouve à la position $k$ (par exemple, pour $n=2, a_{2}(0)=2$ et $a_{2}(2)=a_{2}(-2)=1$. Cela revient donc à compter le nombre de n uplets à valeurs dans $\{-1,0,1\}$ de somme $k$. On va essayer de comprendre $\left(a_{p}(k)\right)_{k}$ modulo $p$, et de trouver une relation de récurrence sur les $\left(a_{n}(k)\right)$ pour trouver le reste de $a_{p-1}(0)$ modulo $p$.
|
| 304 |
+
On va montrer le lemme suivant :
|
| 305 |
+
Lemme 1. $a_{p}(k)$ vaut 0 modulo $p$, sauf si $k=p, 0$ ou $-p$ : dans ce cas $a_{p}(k)$ vaut 1 modulo $p$.
|
| 306 |
+
Démonstration. On se fixe $k$ un entier différent de $\pm p$ (si $k= \pm p$, on voit bien que $a_{p}(k)=1$ ), on note $A$ l'ensemble des $p$ uplets de somme $k$. On définit $T: A \mapsto A$ l'application suivante : si $\left(a_{1}, \ldots, a_{p}\right)$ est dans $A, T\left(a_{1}, \ldots, a_{p}\right)=\left(a_{2}, \ldots, a_{p}, a_{1}\right)$. Il est clair que $T\left(a_{1}, \ldots, a_{p}\right)$ est bien dans $A$, et qu'en appliquant $p$ fois $T$ à un élément de $A$, on obtient le même élément de $A$. Notons que $T$ est clairement injective, donc bijective car $A$ est fini. Pour chaque $y$, on définit $\Omega_{y}:=\left\{T^{k}(y) \mid k \geqslant 0\right.$ où $T^{k}$ est la composée $k$ fois de $T$.
|
| 307 |
+
Soit $x, y$ deux éléments de $A$ tels que $\Omega_{y} \cap \Omega_{x}$ est non vide. Il existe $h, \ell$ positif tels que $T^{h}(x)=$ $T^{\ell}(y)$. En particulier en appliquant $\ell(p-1)$ fois $T, T^{h+\ell(p-1)}(x)=T^{\ell p}(y)=y$, donc pour tout entier j positif, $\mathrm{T}^{\mathrm{j}}(\mathrm{y})=\mathrm{T}^{\mathrm{h}+\ell(p-1)+\mathrm{j}}(\mathrm{x}) \in \Omega_{x}$ : on a donc $\Omega_{y} \subset \Omega_{x}$. De même on a l'inclusion réciproque, donc $\Omega_{x}=\Omega_{y}$. Ainsi les $\left(\Omega_{x}\right)$ partitionnent l'ensemble $A$.
|
| 308 |
+
Soit $x$ dans $A$, montrons que $\Omega_{x}$ est de cardinal $p$, sauf si $x=(0, \ldots, 0)$. Déjà, comme $T$ appliqué $p$ fois donne l'identité, on sait que $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ donc est au plus de cardinal $p$. Supposons qu'il existe $i \neq j$ deux éléments de $\{0, \ldots, p-1\}$ tels que $T^{i}(x)=T^{j}(x)$. Par symétrie, on peut supposer $i<j$, on a donc $T^{p-j+i}(x)=T^{p-j+j}(x)=x$, donc $x=T^{k}(x)$ avec $h=p-j+i \in\{1, \ldots, p-1\}$. Posons $x=\left(x_{1}, \ldots, x_{n}\right)$, l'équation $x=T^{h}(x)$ se retraduit par $x_{j}=x_{j+h}$ pour tout entier $j$ (en prenant les indices modulo $p$. En particulier, pour tout entier $\ell \geqslant 0, x_{j+h \ell}=x_{j}$. En prenant $\ell$ un inverse de $h$ modulo $p$, on a que pour tout $j, x_{j}=x_{j+1}$. Ainsi $x$ est de la forme $(1, \ldots, 1),(0, \ldots, 0)$ ou $(-1, \ldots,-1)$ ce qui est contradictoire avec le fait que $k \neq \pm p$ sauf si $x=(0, \ldots, 0)$. Ainsi $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ est bien de cardinal $p$ sauf si $x=(0, \ldots, 0)$.
|
| 309 |
+
Comme $A$ est partitionné en ensembles de cardinal $p$, sa taille est divisible par $p$ si $k \neq 0$. Si $k=0, A$ privé de $(0, \ldots, 0)$ est partitionné en ensembles de cardinal $p$, donc la taille de $A$ vaut 1 modulo p .
|
| 310 |
+
|
| 311 |
+
Maintenant, notons que pour tout entier $k$, et tout $n \geqslant 2, s_{n}(k)=s_{n-1}(k-1)+s_{n-1}(k)+s_{n-1}(k+1)$. En effet, un $n$-uplet de somme $k$ à valeurs dans $\{-1,0,1\}$ peut soit commencer par 1 et finir par un $n-1$-uplet de somme $k-1$, soit commencer par -1 et finir par un $n-1$-uplet de somme $k+1$, soit commencer par 0 et finir par un $n-1$-uplet de somme $k$. Donc il y a autant de $n$-uplets de somme $k$ que de $\mathrm{n}-1$-uplets de somme $k-1, k$ ou $k+1$.
|
| 312 |
+
|
| 313 |
+
Maintenant, à partir de ces observations essayons de conclure. Pour $p=3, s_{p}=3$, donc le reste de $s_{p}$ modulo $p$ est 0 . Via la formule précédente,
|
| 314 |
+
|
| 315 |
+
$$
|
| 316 |
+
\begin{aligned}
|
| 317 |
+
s_{\mathfrak{p}-1}(k)-s_{\mathfrak{p}-1}(k+3) & =s_{\mathfrak{p}-1}(k)+s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-\left(s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-s_{\mathfrak{p}-1}(k+3)\right) \\
|
| 318 |
+
& =s_{\mathfrak{p}}(k+1)-s_{\mathfrak{p}}(k+2)
|
| 319 |
+
\end{aligned}
|
| 320 |
+
$$
|
| 321 |
+
|
| 322 |
+
En sommant la formule précédente pour $k$ multiple de 3 entre 0 et $3(p-1)$, on obtient que :
|
| 323 |
+
|
| 324 |
+
$$
|
| 325 |
+
s_{\mathfrak{p}-1}(0)-s_{\mathfrak{p}-1}(3 p)=\sum_{k=0}^{p-1} s_{p}(3 k+1)-s_{p}(3 k+2)
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
Or on a $s_{\mathfrak{p}}(n)=0$ sauf pour $n= \pm p$ ou 0 . Et on a clairement $s_{p-1}(3 p)=0$, car $3 p>p-1$, donc un $p-1$-uplet de $\{-1,0,1\}$ ne peut pas avoir somme $3 p$. Ainsi la formule précédente donne que $s_{p-1}$ vaut 1 modulo $p$ et $p$ est de la forme $3 k+1, p-1$ si $p$ est de la forme $3 k+2$.
|
| 329 |
+
|
| 330 |
+
## Seconde solution :
|
| 331 |
+
|
| 332 |
+
L'énoncé peut être reformulé de la façon suivante : $s_{p}$ est le nombre de $p-1$ uplets dans $\{-1,0,1\}$ de somme nulle. En particulier, en ajoutant 1 à chaque pas, $s_{p}$ est le nombre de $p-1$ uplets dans $\{0,1,2\}$ de somme $p-1$. C'est donc également le coefficient de degré $p-1$ de $\left(1+X+X^{2}\right)^{p-1}$ d'après la théorie des séries génératrices : en effet, chaque terme du produit $\left(1+X+X^{2}\right) \ldots\left(1+X+X^{2}\right)$ correspond à $p-1$ choix de 0,1 ou 2 , et la somme des différents pas correspond à la puissance de $X$ dans le produit global.
|
| 333 |
+
Ainsi on cherche à comprendre ce que vaut le reste du $p-1$-ième coefficient de $Q(X):=\left(1+X+X^{2}\right)^{p-1}$ modulo $p$. On peut essayer de comprendre les valeurs de $Q$ modulo $p$ : si a est un entier, et $p$ ne divise pas $1+a+a^{2}, Q(a) \equiv 1(\bmod p)$ par le théorème de petit Fermat. Sinon $Q(a) \equiv 0(\bmod p)$.
|
| 334 |
+
En particulier $\sum_{a=0}^{p-1} Q(a) \equiv-n_{p}$ où $n$ est le nombre de solution de racines distinctes de $X^{2}+X+1$ modulo $p$. Pour $p=3$, il n'y a qu'une seule racine : 1 . Pour $p \neq 3,1$ n'est pas racine, donc ce sont les racines de $X^{3}-1$ différentes de 1 . Or il existe un élément d'ordre 3 modulo $p$ si et seulement si 3 divise $p-1$ : en effet, s'il existe un élément d'ordre 3 modulo $p$, par petit Fermat, 3 divise $p-1$. Si 3 divise $p-1$, soit $y$ une racine primitive modulo $p, y^{(p-1) / 3}$ est un élement d'ordre 3.
|
| 335 |
+
Ainsi $n_{3}=1$, si $p \neq 3$ et 3 ne divise pas $p-1, n_{p}=0$ et si $p \neq 3$ et 3 divise $p-1, X^{2}+X+1$ a une racine. Comme c'est un polynôme de degré 2 il a 2 racines. De plus celles-ci sont distinctes : sinon sont discrminant vaudrait 0 modulo $p$, or celui-ci vaut -3 . Ainsi si 3 divise $p-1, n=2$.
|
| 336 |
+
Or $Q$ est unitaire de degré $2(p-1)$. Ecrivons $Q$ sous la forme $\sum_{k=0}^{2(p-1)} a_{k} X^{k}$ avec $a_{2(p-1)}=1$ et $a_{p-1}=s_{p}$. Ona:
|
| 337 |
+
|
| 338 |
+
$$
|
| 339 |
+
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p)
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
Pour $k=0, \sum_{a=0}^{p-1} a^{k} \equiv 0(\bmod p)$. Pour $k>0,0^{k}=0$, donc si on se donne $y$ une racine primitive modulo p ,
|
| 343 |
+
|
| 344 |
+
$$
|
| 345 |
+
\sum_{a=0}^{p-1} a^{k} \equiv \sum_{a=1}^{p-1} a^{k} \equiv \sum_{n=0}^{p-2}\left(y^{n}\right)^{k} \equiv \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \quad(\bmod p)
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
Si $y^{k} \not \equiv 1(\bmod n)($ ce qui est le cas si $p-1$ ne divise pas $k)$, alors $\sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv \frac{y^{(p-1) k}-1}{y^{k}-1} \equiv 0(\bmod p)$ $\operatorname{car} y^{p-1} \equiv 1(\bmod p)$. Si $p-1$ divise $k, \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv p-1(\bmod p)$. Ainsi, on obtient
|
| 349 |
+
|
| 350 |
+
$$
|
| 351 |
+
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p) \equiv-a_{p-1}-a_{2(p-1)}=-a_{p-1}-1
|
| 352 |
+
$$
|
| 353 |
+
|
| 354 |
+
Donc $\mathrm{a}_{\mathrm{p}-1} \equiv \mathrm{n}-1(\bmod \mathrm{p})$
|
| 355 |
+
Ainsi :
|
| 356 |
+
|
| 357 |
+
- Si $p=3$, le reste de $s_{p}$ modulo $p$ vaut 0 ,
|
| 358 |
+
- si $p \neq 3$ et 3 ne divise pas $p-1$ (i.e. si $p \equiv 2(\bmod 3)$ ), le reste de $s_{p}$ modulo $p$ vaut $p-1$,
|
| 359 |
+
- si 3 divise $p-1$, le reste de $s_{p}$ modulo $p$ vaut 1 .
|
| 360 |
+
|
| 361 |
+
Commentaire des correcteurs: L'exercice a été très peu réussi. Les élèves l'ayant réussi ont suivi la première solution. Beaucoup ont essayé de calculer une somme, puis se sont retrouvés très vite bloqués par les coefficients binomiaux, qu'il était difficile de regarder $\bmod p$.
|
| 362 |
+
$\mathcal{E}_{x e r c i c e}$ 17. Déterminer toutes les fonctions f injective de $\mathbb{N}$ dans $\mathbb{N}$ telles que tout polynôme $\sum_{i=0}^{n} a_{i} x^{i}$, celui-ci a une racine réelle si et seulement si le polynôme $\sum_{i=0}^{n} a_{i} x^{f(i)}$ a une racine réelle.
|
| 363 |
+
|
| 364 |
+
## Solution de l'exercice 17
|
| 365 |
+
|
| 366 |
+
Il s'avère que la condition d'injectivité était inutile : nous allons prouver le résultat sans l'injectivité de f. Notons que le polynôme 1 n'a pas de racine réelle, la condition de l'énoncé nous apprend que $\chi^{f(0)}$ n'en a pas non plus: la seule possibilité pour $f(0)$ est donc $f(0)=0$. De même, $f(n) \neq 0$ si $n \neq 0$ car $X^{n}$ a une racine réelle, et 1 n'en a pas.
|
| 367 |
+
Montrons que $f(n)$ a la même parité que $n$ pour tout entier $n$. Notons que si $n$ est pair, $X^{n}+1 n$ 'a pas de racine réelle donc $X^{f(n)}+1$ non plus. Ceci implique que $f(n)$ est pair (sinon -1 serait une racine réelle ). De même si $n$ est impair, $f(n)$ est impair. Posons $\alpha=f(1), \alpha$ est donc impair.
|
| 368 |
+
Soit $t$ un réel. Pour la suite, nous aurons besoin de comprendre, pour tout $b$ réel vérifiant $b>1$, si l'équation $x^{b}-x=t$ sur $\mathbb{R}^{+}$. Pour tout $t>0$, on pose $f_{b}: \mathbb{R}^{+} \rightarrow \mathbb{R}$ qui à $x$ associe $x^{b}-x$.
|
| 369 |
+
Lemme 2. L'équation $x^{b}-x=t$ a une solution si et seulement si $t \geqslant f_{b}\left(x_{b}\right)$ où $x_{b}=\left(\frac{1}{b}\right)^{\frac{1}{b-1}}$.
|
| 370 |
+
Démonstration. La fonction $\mathrm{f}_{\mathrm{b}}$ est continue et dérivable sur $\mathbb{R}^{+}$. Lla dérivée de $\mathrm{f}_{\mathrm{b}}$ est $\mathrm{b} x^{\mathrm{b}-1}-1$, qui est négative jusqu'en $x_{b}$ puis positive. Ainsi f décroît puis croît. Comme f a pour limite $+\infty$ en $+\infty$, les valeurs prises par $f$ sur $\mathbb{R}^{+}$sont exactement $\left[f\left(x_{b}\right),+\infty[\right.$ par continuité, ce qui donne le résultat voulu.
|
| 371 |
+
|
| 372 |
+
On aura aussi besoin du lemme suivant :
|
| 373 |
+
Lemme 3. Soit $b>a$ deux entiers strictement positifs, avec $b$ pair. Si l'équation $x^{b}-x^{a}=t a$ une solution, alors cette équation a une solution positive.
|
| 374 |
+
|
| 375 |
+
Démonstration. Soit $x$ une solution de l'équation. Comme best pair, $|x|^{b}-|x|^{a} \leqslant x^{b}-x^{a}=t$. Or l'application qui à $y$ associe $y^{b}-y^{a}$ est continue, et tend vers $+\infty$ en $+\infty$, donc l'équation $y^{b}-y^{a}=t$ a une solution dans $[|x|,+\infty[$, donc une solution positive.
|
| 376 |
+
Maintenant appliquons l'hypothèse de l'énoncé au polynôme $X^{2 n}-X-t$. Celui-ci a une racine réelle si et seulement si $t \geqslant f_{2 n}\left(x_{2 n}\right)$. En particulier, le polynôme $X^{f(2 n)}-X^{\alpha}-t$ a une racine réelle si et seulement si $t \geqslant f_{2 n}\left(x_{2 n}\right)$.
|
| 377 |
+
|
| 378 |
+
- $\operatorname{Si} \mathrm{f}(2 \mathrm{n})<\alpha$, alors la fonction qui à $x$ associe $\chi^{f(2 n)}-\chi^{\alpha}$ tend vers $-\infty$ et $+\infty$, et $+\infty$ en $-\infty$ car $\alpha$ est impair. Ainsi par continuité, l'équation $x^{f(2 n)}-x^{\alpha}=\mathrm{t}$ a toujours une solution donc $X^{f(2 n)}-X^{\alpha}-t$ a toujours une racine ce qui est absurde.
|
| 379 |
+
$-\operatorname{Si} f(2 \mathrm{n})=\alpha$, alors le polynôme n'a une racine que pour $\mathrm{t}=0$ ce qui est absurde.
|
| 380 |
+
Ainsi $f(2 \mathfrak{n})>\alpha$. En particulier , par le lemme précédent le polynôme $X^{f(2 \mathfrak{n})}-X^{\alpha}-t$ a une racine réelle si et seulement s'il a une racine réelle positive, c'est-à-dire si et seulement si l'équation $\chi^{\mathrm{f}(2 \mathfrak{n})}-\chi^{\alpha}=\mathrm{t}$ a une solution positive. Comme $x \mapsto \chi^{\alpha}$ est bijectif de $\mathbb{R}^{+}$dans $\mathbb{R}^{+}$, le polynôme $X^{f(2 n)}-X^{\alpha}-t$ a une racine réelle si et seulement si l'équation $\chi^{f(2 n) / \alpha}-\chi=t$ a une racine positive, donc si et seulement si $t \geqslant f_{f(2 n) / \alpha}\left(x_{f(2 n) / \alpha}\right)$. Posons $u=f(2 n) / \alpha>1$, on a donc $f_{u}\left(x_{\mathfrak{u}}\right)=f_{2 n}\left(x_{2 n}\right)$.
|
| 381 |
+
- Si $2 n>u$, Comme $x_{u}<1, f_{u}\left(x_{u}\right)>f_{2 n}\left(x_{u}\right) \geqslant f_{2 n}\left(x_{2 n}\right)=f_{u}\left(x_{u}\right)$ (via les variations de $f_{2 n}$ ) ce qui est absurde.
|
| 382 |
+
- Si $2 n<u$, Comme $x_{2 n}<1, f_{2 n}\left(x_{2 n}\right)>f_{u}\left(x_{2 n}\right) \geqslant f_{u}\left(x_{u}\right)=f_{2 n}\left(x_{2 n}\right)$ (via les variations de $f_{u}$ ) ce qui est absurde.
|
| 383 |
+
Ainsi $u=2 \mathfrak{n}$, donc $\mathbf{f}(2 \mathfrak{n})=2 \mathfrak{n} \boldsymbol{\alpha}$.
|
| 384 |
+
Il reste alors à montrer que si n est impair, $\mathrm{f}(\mathrm{n})=\alpha \mathrm{n}$. Pour cela on fait de même que dans l'argument précédent : on regarde le polynôme $X^{2 n}-X^{n}-t$, on montre qu'il a une racine réelle si et seulement si
|
| 385 |
+
$t \geqslant f_{2 n / n}\left(x_{2 n / n}\right)=f_{2}\left(x_{2}\right)$. Ensuite on obtient que $X^{f(2 n)}-X^{f(n)}-t$ a une racine si et seulement si $t \geqslant f_{2}\left(x_{2}\right)$. Comme $f(n)$ est impair, et $f(2 n)$ pair, on en déduit que $f(2 n)>f(n)$, puis que $f_{2}\left(x_{2}\right)=$ $f_{f(2 n) / f(n)}\left(x_{f(2 n) / f(n)}\right)$. De même on prouve que $f(2 n) / f(n)=2$, donc $f(2 n)=2 f(n)$. Or $f(2 n)=$ $2 \mathrm{n} \alpha$, donc $\mathrm{f}(\mathrm{n})=\mathrm{n} \alpha$. Ainsi si f est solution, f est de la forme $\mathrm{f}: \mathrm{n} \mapsto$ an pour un certain a impair.
|
| 386 |
+
Réciproquement s'il existe a impair tel que $f(n)=$ an pour tout entier positif $n$, alors si le polynôme $\sum_{k=0}^{n} a_{k} X^{k}$ a une racine réelle $x_{0}$, le polynôme $\sum_{k=0}^{n} a_{k} X^{f(k)}=\sum_{k=0}^{n} a_{k} X^{a k}$ a pour racine $x_{0}^{1 / a}$. Réciproquement si $\sum_{k=0}^{n} a_{k} X^{a k}$ a une racine réelle $y_{0}, y_{0}^{a}$ est racine de $\sum_{k=0}^{n} a_{k} X^{k}$. Ainsi $f$ vérifie bien l'énoncé.
|
| 387 |
+
Les fonctions vérifiant l'énoncé sont les fonctions telles qu'il existe a impair tel que $f(n)=$ an pour tout entier positif n .
|
| 388 |
+
|
| 389 |
+
Commentaire des correcteurs : L'exercice a été très peu abordé, mais les élèves l'ayant abordé ont majoritairement réussi l'exercice avec des preuves variées. Attention aux expressions de la forme $\chi^{q}$ avec $q$ rationnel et $x$ négatif : cela n'a pas forcément un sens clair. Il faut être très précautionneux.
|
| 390 |
+
|
| 391 |
+
Exercice 18. Un quadrilatère convexe $A B C D$ admet un cercle inscrit de centre $I$. Soit $\mathrm{I}_{\mathrm{a}}, \mathrm{I}_{\mathrm{b}}, \mathrm{I}_{\mathrm{c}}$ et $\mathrm{I}_{\mathrm{d}}$ les centres des cercles inscrits de triangles $\mathrm{DAB}, \mathrm{ABC}, \mathrm{BCD}$ et $C D A$ respectivement. On suppose que les tangentes communes aux cercle circonscrits de $\mathrm{AI}_{\mathrm{b}} \mathrm{I}_{\mathrm{d}}$ et $\mathrm{Cl}_{\mathrm{b}} \mathrm{I}_{\mathrm{d}}$ se rencontrent en $X$ et que les tangentes commune extérieures des cercles circonscrits de $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$ et $\mathrm{DI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$ se rencontrent en $Y$. Montrer que $\widehat{\mathrm{XIY}}=90$.
|
| 392 |
+
|
| 393 |
+
## Solution de l'exercice 18
|
| 394 |
+
|
| 395 |
+
On note $\omega_{i}$ le cercle inscrit de centre $I_{i}$ et de rayon $r_{i}$ pour $i \in\{A, B, C, D\}$, on note également $O_{A}, O_{B}$, $O_{C}$ et $O_{D}$ les centres des cercles $A I_{b} I_{d}, B I_{a} I_{c}, C I_{b} I_{d}$ et $D I_{a} I_{c}$. On commence par démontrer le lemme suivant:
|
| 396 |
+
|
| 397 |
+
Lemme 4. Les cercles $\omega_{a}$ et $\omega_{c}$ sont tangents tous les deux en le même point sur (AC).
|
| 398 |
+
Preuve : (On référe également au Lemme 36 du cours de Géométrie D de Valbonne 2022).
|
| 399 |
+
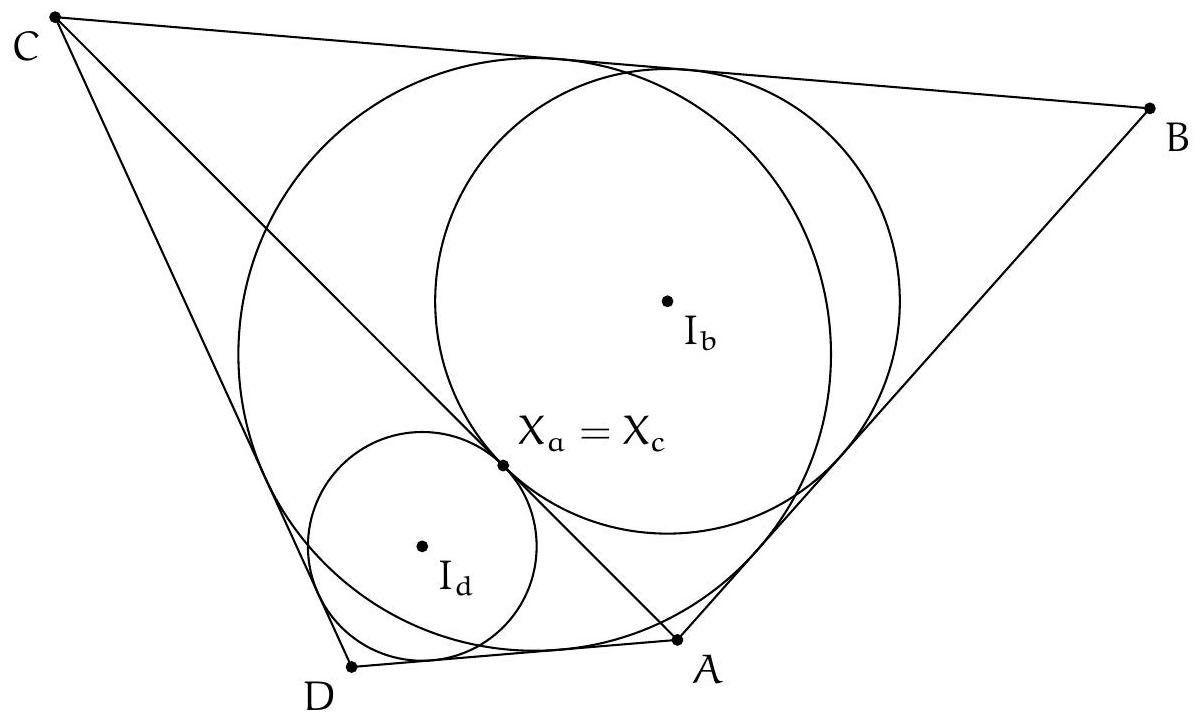
|
| 400 |
+
|
| 401 |
+
Soit $X_{a}$ le point de tangence de $\omega_{a}$ sur (BD) et $X_{c}$ le point de tangence de $\omega_{c}$ sur (BD). On sait que $A B C D$ est circonscriptible, cela implique que $A B-A D=B C-C D$. On Peut calculer la distance $B X_{a}$ elle vaut
|
| 402 |
+
|
| 403 |
+
$$
|
| 404 |
+
B X_{a}=\frac{A B-A D+B D}{2}=\frac{B C-C D+B D}{2}=B X_{c},
|
| 405 |
+
$$
|
| 406 |
+
|
| 407 |
+
ce qui montre que $X_{a}=X_{c}$.
|
| 408 |
+
On renomme $T$ le point de tangence. Alors les points $\mathrm{I}_{a}, T$ et $\mathrm{I}_{c}$ sont alignés et $\left(I_{a} I_{c}\right) \perp(B D)$. On note $\widehat{A B T}=2 \varphi$ et $\widehat{T B C}=2 \mu$, alors $\widehat{A B I}=\varphi+\mu$ et $\widehat{\mathrm{ABI}_{a}}=\varphi$, ce qui montre que $\widehat{I_{a} B I}=\mu$ et ainsi que les droites (BT) et (BI) sont conjuguées isogonales dans le triangle $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$, or (BT) est la hauteur dans ce même triangle et par un lemme classique on sait alors que la droite (BI) passe également par le centre du cercle circonscrit au triangle $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$. Donc $\mathrm{O}_{B}$ est sur la droite (BI). De la même manière $\mathrm{O}_{\mathrm{D}}$ se trouve sur la droite (DI). On sait aussi que $\left(O_{B} O_{D}\right) \perp\left(I_{a} I_{c}\right)$ donc $(D B) / /\left(O_{B} O_{D}\right)$. On va maintenant démontrer que la droite (IY) bissecte l'angle $\widehat{\text { BID. }}$. $X$ se trouve sur la droite $\mathrm{O}_{B} \mathrm{O}_{D}$ de telle sorte que $\frac{X O_{B}}{\mathrm{XO}_{\mathrm{D}}}=\frac{\mathrm{r}_{\mathrm{b}}}{\mathrm{r}_{\mathrm{d}}}$, par le lemme de la bissectrice on veut montrer que $\frac{\mathrm{IO}_{B}}{\mathrm{IO}}=\frac{\mathrm{r}_{\mathrm{b}}}{r_{d}}$, or comme $(\mathrm{DB}) / /\left(\mathrm{O}_{B} \mathrm{O}_{\mathrm{D}}\right)$
|
| 409 |
+
on a $\frac{\mathrm{IO}_{\mathrm{B}}}{\mathrm{IO}}=\frac{\mathrm{IB}}{\mathrm{ID}}$. On calcule maintenant
|
| 410 |
+
|
| 411 |
+
$$
|
| 412 |
+
X:=r_{b} \cdot \frac{1}{r_{d}}=\frac{\sin (\widehat{\mathrm{IAB}}) \cdot A \mathrm{II}}{\sin (\widehat{\mathrm{ABI}})} \frac{\sin (\widehat{\mathrm{ADI}})}{\sin (\widehat{\mathrm{IAD}}) \cdot \mathrm{AI}}
|
| 413 |
+
$$
|
| 414 |
+
|
| 415 |
+
d'après la loi des sinus dans les triangles IAB et IAD, on a d'une part $X=\frac{\sin (\widehat{A D I})}{\sin (\widehat{A B I})}$. On trouve d'autre part,
|
| 416 |
+
|
| 417 |
+
$$
|
| 418 |
+
X^{\prime}:=r_{b} \cdot \frac{1}{r_{d}}=\frac{2 I_{a} I_{c}}{\sin \left(\widehat{I_{a} D I_{c}}\right)} \cdot \frac{\sin \left(\widehat{I_{a} B I_{c}}\right)}{2 \mathrm{I}_{\mathrm{a}} \mathrm{I}_{c}}=\frac{\sin \left(\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{DI}_{\mathrm{c}}}\right)}{\sin \left(\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}}\right)},
|
| 419 |
+
$$
|
| 420 |
+
|
| 421 |
+
or, $\widehat{A D I}=\widehat{A D C} / 2=\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{DI}_{\mathrm{c}}}$ et également $\widehat{A B I}=\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{BI}_{\mathrm{c}}}$ ce qui montre que $X=\mathrm{X}^{\prime}$ et ainsi que la droite (IY) est la bissectrice extérieure de l'angle $\widehat{\text { BID }}$. On montre de la même manière que la droite (XI) est la bissectrice extérieure de l'angle $\widehat{A I C}$. Dans le but de démontrer que $\widehat{X I Y}=90$ il faut démontrer que les angles $\widehat{A I C}$ et $\widehat{\text { BID }}$ ont les même bissectrice. Si la proposition suivante est vraie alors, (DI, IC) $=$ $(A I, I B)$. Ou encore $(C I, I D)+(A I, I B) \equiv 0(\bmod 180)$. On va démontrer cette dernière relation, on appelle $E$ le point d'intersection des droites (AD) et (BC), Alors (AI, IB) $=90+\frac{(B E, E A)}{2}$ et $(C I, I D)=90-\frac{(B E, E A)}{2}, \operatorname{donc}(A I, I B)+(B E, E A)=180 \equiv 0(\bmod 180)$, ce qui conclut.
|
| 422 |
+
|
| 423 |
+
Commentaire des correcteurs: Bien résolu pour les quelques élèves qui ont rendu une copie.
|
| 424 |
+
|
French_STS/md/fr-corrigé-commenté-envoi-2.md
ADDED
|
@@ -0,0 +1,254 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+

|
| 2 |
+
|
| 3 |
+
## ENVOI 2 : AlgÈBRE <br> Corrigé
|
| 4 |
+
|
| 5 |
+
## Exercices Juniors
|
| 6 |
+
|
| 7 |
+
Exercice 1. Soient $x, y$ des réels strictement positifs. Montrer que:
|
| 8 |
+
|
| 9 |
+
$$
|
| 10 |
+
x+\frac{y^{2}}{x} \geqslant 2 y
|
| 11 |
+
$$
|
| 12 |
+
|
| 13 |
+
et trouver les cas d'égalité.
|
| 14 |
+
Solution de l'exercice 1 L'inégalité de la moyenne donne
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
x+\frac{y^{2}}{x} \geqslant 2 \sqrt{x \cdot \frac{y^{2}}{x}}=2 y
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
Supposons qu'on a égalité, alors $x=\frac{y^{2}}{x}$ donc $x^{2}=y^{2}$ donc $x=y$. Réciproquement si $x=y, x+\frac{y^{2}}{x}=$ $y+\frac{y^{2}}{y}=2 y$ on a bien égalité.
|
| 21 |
+
Commentaire des correcteurs Le problème est très bien réussi! Attention à bien justifier que les cas d'égalités annoncés sont bien les seuls cas d'égalité possibles.
|
| 22 |
+
|
| 23 |
+
Exercice 2. Soit $x \geqslant 0$ un réel. Montrer que :
|
| 24 |
+
|
| 25 |
+
$$
|
| 26 |
+
1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{4}
|
| 27 |
+
$$
|
| 28 |
+
|
| 29 |
+
et trouver les cas d'égalité.
|
| 30 |
+
Solution de l'exercice 2 On utilise l'inégalité arithmético-géométrique, dans le cas $\mathrm{n}=4$. On obtient $1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{\frac{2+6+8}{4}}=4 x^{4}$.
|
| 31 |
+
Supposons qu'on a égalité. D'après le cas d'égalité $\chi^{2}=1$, donc $x=1$. Réciproquement si $x=1$, on a $1+x^{2}+x^{6}+x^{8}=4=4 x^{4}$.
|
| 32 |
+
Commentaire des correcteurs Le problème très bien réussi! Certains élèves ont approché ce problème avec des polynômes plutôt qu'avec des inégalités.
|
| 33 |
+
|
| 34 |
+
Exercice 3. Soit $a, b, c$ des nombres réels. Montrer que:
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
2 a^{2}+20 b^{2}+5 c^{2}+8 a b-4 b c-4 a c \geqslant 0
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
et trouver les cas d'égalité.
|
| 41 |
+
Solution de l'exercice 3 L'inégalité est équivalente à $4 b c+4 a c-8 a b \leqslant 2 a^{2}+20 b^{2}+5 c^{2}$. Or on sait que $4 a c=2 \times a \times(2 c) \leqslant a^{2}+(2 c)^{2}=a^{2}+4 c^{2}$ et que $4 b c=2 \times c(2 b) \leqslant 4 b^{2}+c^{2}$. On a également $-8 \mathfrak{a b}=2 \times(-\mathfrak{a}) \times(4 b) \leqslant \mathfrak{a}^{2}+16 b^{2}$. En sommant toutes ces inégalités, on obtient $4 b c+4 a c-8 a b \leqslant 2 a^{2}+20 b^{2}+5 c^{2}$.
|
| 42 |
+
Supposons qu'on a égalité, dans ce cas on a égalité dans les trois inégalités utilisées : on a donc $\mathrm{a}=2 \mathrm{c}$, $c=2 b$ donc $a=4 b$ et $-a=4 b$. En particulier $-a=a$ donc $a=0$ donc $b$ et $c$ sont également nuls. Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$, on a bien égalité.
|
| 43 |
+
On aurait pu également remarquer que $2 a^{2}+20 b^{2}+5 c^{2}+8 a b-4 b c-4 a c=(a+4 b)^{2}+(a-2 c)^{2}+$ $(2 b-c)^{2} \geqslant 0$ et trouver de la même façon le cas d'égalité.
|
| 44 |
+
Commentaire des correcteurs Le problème est très bien réussi et tous les élèves ont trouvé la factorisation. Attention, le cas d'égalité était un peu élaboré dans cet exercice.
|
| 45 |
+
|
| 46 |
+
Exercice 4. Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
f(x) f(y)=f(x y)+x+y
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
Solution de l'exercice 4 En évaluant en $y=0$ on obtient $f(x) f(0)=f(0)+x$ pour tout réel $x$. Pour $x=1$, on obtient que $f(0) \neq 0$, sinon on aurait $1=0$. En évaluant en $x=0$ on obtient $f(0)^{2}=f(0)$ donc $f(0)=1$ donc $f(x)=1+x$ pour tout $x$ réel.
|
| 53 |
+
Réciproquement soit $f$ la fonction telle que $f(x)=1+x$ pour tout $x$ réel et soit $(x, y) \in \mathbb{R}^{2}$, alors $\mathrm{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ donc $f$ vérifie bien l'équation. L'unique solution de l'équation est donc la fonction $f$ telle que $f(x)=1+x$ pour tout $x$ réel.
|
| 54 |
+
Commentaire des correcteurs L'exercice est globalement bien réussi. Cependant, il faut bien distinguer deux parties dans une équation fonctionnelle :
|
| 55 |
+
|
| 56 |
+
- L'analyse qui consiste à choisir une fonction f vérifiant l'équation et déterminer les propriétés vérifiée par f . Ici, on établit que si f est une solution de l'équation, alors pour tout réel $\mathrm{x}, \mathrm{f}(\mathrm{x})=$ $x+1$.
|
| 57 |
+
- La synthèse qui consiste à vérifier que réciproquement, la fonction f qui à $x$ associe $x+1$ est bien solution de l'équation.
|
| 58 |
+
Certains élèves ont oublié la deuxième partie et ont été pénalisés.
|
| 59 |
+
|
| 60 |
+
Exercice 5. Trouver tous les triplets de réels ( $\mathrm{a}, \mathrm{b}, \mathrm{c}$ ) vérifiant le système d'égalités :
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
\left\{\begin{array}{l}
|
| 64 |
+
a\left(b^{2}+c\right)=c(c+a b) \\
|
| 65 |
+
b\left(c^{2}+a\right)=a(a+b c) \\
|
| 66 |
+
c\left(a^{2}+b\right)=b(b+a c)
|
| 67 |
+
\end{array}\right.
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Solution de l'exercice 5 Les égalités se réécrivent $a b(b-c)=c(c-a), b c(c-a)=a(a-b)$ et $\mathrm{ca}(\mathrm{a}-\mathrm{b})=\mathrm{b}(\mathrm{b}-\mathrm{c})$. En multipliant ces trois égalités, on obtient $(\mathrm{abc})^{2}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})=$ $\mathrm{abc}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})$. En particulier deux cas se présentent :
|
| 71 |
+
|
| 72 |
+
- Soit $\mathrm{abc}=0$. Les égalités étant cycliques, supposons $\mathrm{a}=0$. Par la première égalité $\mathbf{c}^{2}=0$ donc $\mathbf{c}=0$. Par la troisième égalité $\boldsymbol{b}^{2}=0$ donc $\mathrm{b}=0$
|
| 73 |
+
- Soit deux des éléments parmi $a, b, c$ sont égaux, on suppose $a=b$. Dans ce cas $b c(c-a)=0$. Si $\mathrm{b}=0$ ou $\mathrm{c}=0$ on retombe dans le cas précédent, sinon $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
|
| 74 |
+
- Soit $a b c=1$, dans ce cas $a, b, c$. sont non nuls Les égalités se réécrivent $: b-c=c^{2}(c-a)$, $c-a=a^{2}(a-b)$ et $a-b=b^{2}(b-c)$. En particulier $a-b, b-c$ et $c-a$ sont de même signe, mais de somme nulle et on a donc nécessairement $\mathrm{a}-\mathrm{b}=\mathrm{b}-\mathrm{c}=\mathrm{c}-\mathrm{a}=0$ i.e; $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
|
| 75 |
+
Commentaire des correcteurs Beaucoup d'élèves ont rendu une copie à ce problème mais rares sont ceux qui ont eu la totalité des points. En effet il y a eu plusieurs d'erreurs récurrentes :
|
| 76 |
+
- Si $a \geqslant b$ et $c \geqslant d$, on n'a pas nécessairement $a c \geqslant b d$. Cela est vrai pour des nombres réels positifs, mais pas pour des nombres réels négatifs : par exemple $2 \geqslant-1,0 \geqslant-1$ mais $0 \times 2=0<(-1) \times(-1)=1$.
|
| 77 |
+
- Plusieurs élèves ont supposé $a \geqslant b \geqslant c$. Pourtant on ne peut pas faire une telle supposition puisque le système n'est pas symétrique : échanger a et b change totalement le système. En revanche, le système est cyclique : remplacer a par $b, b$ par $c$ et $c$ par a ne le change pas. On peut donc supposer que a est le plus grand, mais on ne peut pas supposer d'inégalité supplémentaire sur bet c.
|
| 78 |
+
- Certains oublient de vérifier que $\mathrm{a}=\mathrm{b}=\mathrm{c}$ est une solution : il faut le faire.
|
| 79 |
+
|
| 80 |
+
Exercice 6. Soient $a, b, c>0$ tels que : $a+b+c=1$. Montrer que :
|
| 81 |
+
|
| 82 |
+
$$
|
| 83 |
+
\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6 \geqslant 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
et déterminer les cas d'égalité.
|
| 87 |
+
Solution de l'exercice 6 Le terme de droite de l'inégalité vaut $2 \sqrt{2}\left(\sqrt{\frac{b+c}{a}}+\sqrt{\frac{a+b}{c}}+\sqrt{\frac{a+c}{b}}\right)$. On utilise l'inégalité arithmético-géométrique : $2 \sqrt{2 \frac{b+c}{a}} \leqslant 2+\frac{b+c}{a}$. De même $2 \sqrt{\frac{b+a}{c}} \leqslant 2+\frac{b+a}{c}$ et $2 \sqrt{\frac{a+c}{b}} \leqslant 2+\frac{a+c}{b}$. En sommant ces trois inégalités, on obtient
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6 \geqslant 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
Supposons qu'on a égalité, alors en regardant le premier cas d'égalité, on a $\frac{b+c}{a}=2$ donc $1-a=2 a$ donc $\mathrm{a}=\frac{1}{3}$. En regardant les deux autres cas d'égalité on obtient $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{3}$. Réciproquement si $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{3}, \frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{a}}{\mathrm{c}}+\frac{\mathrm{b}}{\mathrm{a}}+\frac{\mathrm{b}}{\mathrm{c}}+\frac{\mathrm{c}}{\mathrm{a}}+\frac{\mathrm{c}}{\mathrm{b}}+6=12$ et $2 \sqrt{2}\left(\sqrt{\frac{1-\mathrm{a}}{\mathrm{a}}}+\sqrt{\frac{1-\mathrm{c}}{\mathrm{c}}}+\sqrt{\frac{1-\mathrm{b}}{\mathrm{b}}}\right)=2 \sqrt{2}(3 \times \sqrt{2})=12 ;$ on a bien égalité.
|
| 94 |
+
Commentaire des correcteurs Le problème est globalement bien réussi. Une minorité d'élèves ont employé des inégalités dans le mauvais sens ou effectué des manipulations superflues. Attention à ne pas oublier le cas d'égalité!
|
| 95 |
+
|
| 96 |
+
Exercice 7. Soit $a, b, c$ des réels strictement positifs tels que : $a b+b c+c a=a b c$. Montrer que :
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\frac{1}{a^{2}+b^{2}}+\frac{1}{b^{2}+c^{2}}+\frac{1}{c^{2}+a^{2}} \leqslant \frac{1}{6},
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
et trouver les cas d'égalité.
|
| 103 |
+
Solution de l'exercice 7 Posons $u=\frac{1}{a}, v=\frac{1}{b}, w=\frac{1}{c}$. En divisant par abc, la condition se réécrit $u+v+w=1$. L'inégalité voulue se réécrit $\frac{u^{2} v^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{\mathfrak{u}^{2} w^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$. On utilise l'inégalité arithmético-géométrique sur les dénominateurs: $\mathfrak{u}^{2}+v^{2} \geqslant 2 u v$ et similairement sur les deux autres. On obtient $\frac{u^{2} v^{2}}{u^{2}+w^{2}}+\frac{u^{2} w^{2}}{u^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{2}(u v+v w+u w)$. Or $1=(u+v+w)^{2}=u^{2}+v^{2}+w^{2}+2(u v+$ $v w+w u) \geqslant 3(u v+v w+u w)$ par lemme du tourniquet. En particulier $u v+v w+u w \leqslant \frac{1}{3}$ donc $\frac{\mathcal{u}^{2} v^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{\mathfrak{u}^{2} w^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$.
|
| 104 |
+
Pour les cas d'égalité, on a égalité dans le lemme du tourniquet, donc $u=v=w$ donc $\mathrm{a}=\mathrm{b}=\mathrm{c}$. En réinjectant dans la condition, $3 \mathrm{a}^{2}=\mathrm{a}^{3}$ donc $\mathrm{a}=\mathrm{b}=\mathrm{c}=3$. Réciproquement si $\mathrm{a}=\mathrm{b}=\mathrm{c}=3$, on a $\frac{1}{\mathrm{a}^{2}+\mathrm{b}^{2}}+\frac{1}{\mathrm{~b}^{2}+\mathrm{c}^{2}}+\frac{1}{\mathrm{c}^{2}+\mathrm{a}^{2}}=\frac{3}{2 \times 9}=\frac{1}{6}$ on a bien égalité.
|
| 105 |
+
Commentaire des correcteurs Le problème est bien réussi par les copies qui l'ont traité. Attention toutefois aux cas d'égalités : il faut préciser dans quelle inégalité utilisée vous regardez le cas d'égalité, calculer chaque variable (ce qui se fait avec la condition imposée sur les variables) et ne pas oublier alors de vérifier qu'on a égalité! Il faut également penser à énoncer les inégalités qu'on utilise. Attention à l'inégalité des mauvais élèves : certains se sont trompés de sens d'inégalité, d'autres l'ont utilisé pour des nombres négatifs et aboutissent à des résultats faux.
|
| 106 |
+
|
| 107 |
+
Exercice 8. Soient $a_{1}, \ldots, a_{2019}$ des entiers positifs. Montrer qu'il y a équivalence entre:
|
| 108 |
+
(i) il existe un réel $x$ tel que pour tout $i \in\{1, \ldots, 2019\}$, on a : $a_{i}=\lfloor i x\rfloor$
|
| 109 |
+
(ii) pour tous $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, 2019\}$ vérifiant $i+j \leqslant 2019$, on $a: a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
| 110 |
+
|
| 111 |
+
Solution de l'exercice 8 Prouvons tout d'abord le sens direct : s'il existe $x$ réel tel que pour tout $i$ entre 1 et $2019, a_{i}=\lfloor i x\rfloor$, et si on se donne $\boldsymbol{i}, \boldsymbol{j}$ entre 1 et 2019 tels que $\boldsymbol{i}+\mathfrak{j} \leqslant 2019$, alors $(\mathfrak{i}+\mathfrak{j}) \mathbf{x}=$ $i x+j x \geqslant\lfloor i x\rfloor+\lfloor j x\rfloor=a_{i}+a_{j}$ et $(i+j) x=i x+j x<\lfloor i x\rfloor+1+\lfloor j x\rfloor+1=a_{i}+a_{j}+2$, donc $a_{i}+a_{j} \leqslant a_{i+j}<a_{i}+a_{j}+2$. Comme les $a_{i}$ sont entiers, on a donc $a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
| 112 |
+
Réciproquement supposons que pour tout $i, j$ entre 1 et 2019 tels que $i+j \leqslant 2019, a_{i}+a_{j} \leqslant a_{i+j} \leqslant$ $a_{i}+a_{j}+1$. Trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i}=\lfloor i x\rfloor$ revient à trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i} \leqslant i x<a_{i}+1$, c'est-à-dire tel que pour tout $i, \frac{a_{i}}{i} \leqslant x<\frac{a_{i}+1}{i}$. Il suffit donc de montrer que le maximum des $\frac{a_{i}}{i}$ pour $i$ entre 1 et 2019 est strictement inférieur au minimum des $\frac{a_{j}+1}{j}$ pour $j$ entre 1 et 2019 , ou plus simplement que $\frac{a_{i}}{i} \leqslant \frac{a_{i}+1}{j}$ pour tout $i, j$ entre 1 et 2019.
|
| 113 |
+
Montrons cela par récurrence forte sur $\mathfrak{m}=\max (\mathfrak{i}, \mathfrak{j})$. Si $\mathfrak{m}=1, \mathfrak{i}=\mathfrak{j}=1$ donc l'inégalité est évidente. Pour l'hérédité, supposons l'inégalité vraie pour tout $i, j$ entre 1 et m . On veut montrer l'inégalité $\frac{\mathrm{a}_{i}}{\mathrm{i}}<$ $\frac{a_{j}+1}{j}$, où $1 \leqslant \mathfrak{i}, \mathfrak{j} \leqslant \mathfrak{m}+1$. Il y a trois cas à traiter :
|
| 114 |
+
|
| 115 |
+
- Si $i=$ j l'inégalité est évidente.
|
| 116 |
+
- Si $i<j$, en appliquant l'hypothèse de récurrence à $(i, j-i): a_{j} \geqslant a_{i}+a_{j-i}>a_{i}+(j-i) \frac{a_{i}}{i}-1=$ $a_{i} \times \frac{j}{i}-1$ donc $\frac{a_{j}+1}{j}>\frac{a_{i}}{i}$
|
| 117 |
+
- Si $\boldsymbol{i}>\mathfrak{j}$, en appliquant l'hypothèse de récurrence à $(\mathfrak{i}-\mathfrak{j}, \mathfrak{j}): a_{i} \leqslant a_{j}+a_{i-j}+1<a_{j}+$ $\frac{(i-j)\left(a_{j}+1\right)}{j}=a_{j} \frac{i}{j}+\frac{i-j}{j}<\left(a_{j}+1\right) \frac{i}{j}$ donc $\frac{a_{i}}{i}<\frac{a_{j}+1}{j}$
|
| 118 |
+
Commentaire des correcteurs L'exercice était difficile et seulement un nombre très réduit d'élèves sont parvenus à montrer la seconde implication. La première implication est dans l'ensemble bien abordée.
|
| 119 |
+
|
| 120 |
+
Exercice 9. Soit $a, b, c, d$ des réels strictement positifs tels que : $a+b+c+d=1$. Montrer que :
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\frac{a^{4}}{a^{3}+a^{2} b+a b^{2}+b^{3}}+\frac{b^{4}}{b^{3}+b^{2} c+b c^{2}+c^{3}}+\frac{c^{4}}{c^{3}+c^{2} d+c d^{2}+d^{3}}+\frac{d^{4}}{d^{3}+d^{2} a+d a^{2}+a^{3}} \geqslant \frac{1}{4}
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
et déterminer les cas d'égalité.
|
| 127 |
+
Solution de l'exercice 9 Dans cette solution, on va utiliser à plusieurs reprises l'inégalité $2\left(x^{2}+y^{2}\right) \geqslant$ $(x+y)^{2}(*)$, valable pour tous réels $x, y$ avec égalité si et seulement si $x=y$. Déjà notons que $a^{3}+$ $a^{2} b+a b^{2}+b^{3}=\left(a^{2}+b^{2}\right)(a+b)$. En particulier l'inégalité se réécrit $\sum_{\text {cycl. }} \frac{a^{4}}{\left(a^{2}+b^{2}\right)(a+b)} \geqslant \frac{1}{4}$. Notons $S$ la somme de gauche dans l'inégalité précédente. Chaque dénominateur des termes de $S$ est symétrique en les deux variables qu'il contient, on cherche donc une relation entre $S$ et $\sum_{c y c l} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}$. Calculons la différence des deux termes:
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
S-\sum_{c y c l .} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}=\sum_{c y c l .} \frac{a^{4}-b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}=\sum_{c y c l .} \frac{a^{2}-b^{2}}{(a+b)}=\sum_{c y c l .} a-b=0
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
En particulier $S=\sum_{\text {cycl. }} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}$ donc $2 S=\sum_{\text {cycl. }} \frac{a^{4}+b^{4}}{\left(a^{2}+b^{2}\right)(a+b)} . \operatorname{Par}(*), a^{4}+b^{4} \geqslant \frac{\left(a^{2}+b^{2}\right)^{2}}{2}$ donc en sommant $2 S \geqslant \sum_{\text {cycl. }} \frac{a^{2}+b^{2}}{2(a+b)} .(*)$ donne de nouveau $a^{2}+b^{2} \geqslant \frac{(a+b)^{2}}{2}$ donc en sommant $2 S \geqslant \sum_{\text {cycl. }} \frac{a+b}{4}=$ $\frac{2(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d})}{4}=\frac{1}{2}$ donc $S \geqslant \frac{1}{4}$.
|
| 134 |
+
Supposons qu'on a égalité. Dans ce cas on a les égalités cycliques $\mathrm{a}=\mathrm{b}$, soit $\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{d}$. Par la condition sur la somme $4 a=1$ donc $a=\frac{1}{4}$.
|
| 135 |
+
Réciproquement si $a=b=c=d=\frac{1}{4}$, alors $a+b+c+d=1$ et $S=\sum_{\text {cycl. }} \frac{a^{4}}{a^{3}+a^{2} b+b^{2}+b^{3}}=\sum_{\text {cycl. }} \frac{a^{4}}{4 a^{3}}=$ $\sum_{\text {cycl. }} \frac{\mathrm{a}}{4}=4 \frac{\mathrm{a}}{4}=\frac{1}{4}$ on a bien égalité.
|
| 136 |
+
Commentaire des correcteurs Le problème était difficile et peu sont ceux qui ont réussi à avoir une solution complète. Il était possible d'utiliser l'inégalité de Jensen appliquée à la fonction qui à $x$ associe $\frac{1}{1+x+x^{2}+x^{3}}$, mais les cas d'égalité étaient eux plus délicats : pour les cas d'égalité, si sa dérivée seconde $f^{\prime \prime}$ est strictement positive sur l'ensemble des valeurs que prennent les variables sur lesquelles on veut utiliser l'inégalité, alors on a égalité des variables (si $f^{\prime \prime}$ est strictement positive sauf sur un nombre fini de points le raisonnement se tient). Néanmoins la convexité stricte de la fonction en quesion n'était pas claire, on attendait donc une justification. Attention aux additions de fractions.
|
| 137 |
+
|
| 138 |
+
## Exercices Seniors
|
| 139 |
+
|
| 140 |
+
Exercice 10. Trouver toutes les fonctions f de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
f(x) f(y)=f(x y)+x+y
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
Solution de l'exercice 10 En évaluant en $y=0$ on obtient $\boldsymbol{f}(\mathrm{x}) \boldsymbol{f}(0)=\boldsymbol{f}(0)+x$ pour tout réel $x$. Pour $x=1$, on obtient que $f(0) \neq 0$, sinon on aurait $1=0$. En évaluant en $x=0$ on obtient $f(0)^{2}=f(0)$ donc $f(0)=1$ donc $f(x)=1+x$ pour tout $x$ réel.
|
| 147 |
+
Réciproquement soit $f$ la fonction telle que $f(x)=1+x$ pour tout $x$ réel et soit $(x, y) \in \mathbb{R}^{2}$, alors $\mathbf{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ donc $f$ vérifie bien l'équation. L'unique solution de l'équation est donc la fonction $f$ telle que $f(x)=1+x$ pour tout $x$ réel.
|
| 148 |
+
Commentaire des correcteurs L'exercice est globalement bien réussi. Attention, lorsque l'on divise par un nombre, à bien vérifier que ce nombre est non nul. Il ne faut pas non plus oublier de contrôler que les solutions trouvées vérifient bien l'équation fonctionnelle.
|
| 149 |
+
|
| 150 |
+
Exercice 11. Soit $x, y$ des réels. Montrer que:
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
|x|+|y| \leqslant|x-y|+|x+y| .
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
Solution de l'exercice 11 Si $x$ et $y$ sont positifs, $|x|+|y|=x+y=|x+y|$. Si $x$ et $y$ sont négatifs $|x|+|y|=-x-y=|x+y|$. Si $x$ est positif et $y$ négatif $|x|+|y|=x-y=|x-y|$. Si $x$ est négatif et $y$ positif $|x|+|y|=y-x=|x-y|$. Dans tous les cas par positivité de la valeur absolue $|x|+|y| \leqslant|x-y|+|x+y|$.
|
| 157 |
+
Commentaire des correcteurs Le nombre de cas traités dans les disjonctions de cas était très important (souvent 8), alors que ce nombre pouvait aisément être ramené à 2. Les preuves utilisant l'inégalité triangulaires sont parfaites et élégantes. Les preuves passant l'inégalité au carré étaient lourdes et n'étaient pas toujours justes.
|
| 158 |
+
|
| 159 |
+
Exercice 12. Trouver tous les polynômes $P$ à coefficients réels tels que pour tous réels $x, y$,
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
x P(x)+y P(y) \geqslant 2 P(x y)
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Solution de l'exercice 12 Si $P(X)=c X$ avec $c \geqslant 0, x P(x)+y P(y)=c\left(x^{2}+y^{2}\right) \geqslant 2 c x y=2 P(x y)$ par inégalité de la moyenne, les polynômes de la forme cX avec $\mathrm{c} \geqslant 0$ conviennent, montrons que ce sont les seuls. Supposons P non constant. En évaluant en ( $x, 0$ ) l'inégalité, on obtient $\mathrm{xP}(x) \geqslant 2 \mathrm{P}(0)$. En regardant la limite en $+\infty$, on obtient que le coefficient dominant de $P$ est forcément strictement positif (car $P$ ne peut tendre vers $-\infty)$. En évaluant en $(x, x)$, on obtient $x P(x) \geqslant P\left(x^{2}\right)$. Le polynôme $X P(X)$ est de degré $\operatorname{deg}(P)+1, P\left(X^{2}\right)$ est de degré $2 \operatorname{deg}(P)$. Si $2 \operatorname{deg}(P)>\operatorname{deg}(P)+1$, alors $P\left(X^{2}\right)-X P(X)$ est un polynôme de degré $2 \operatorname{deg}(P)$ de coefficient dominant strictement positif, donc il est strictement positif pour $x$ assez grand, contradiction. En particulier $2 \operatorname{deg}(\mathrm{P}) \leqslant \operatorname{deg}(\mathrm{P})+1$ donc P est un polynôme de degré au plus 1 et de coefficient dominant strictement positif.
|
| 166 |
+
Maintenant posons $\mathrm{P}(X)=\mathrm{aX}+\mathrm{b}$ avec $\mathrm{a} \geqslant 0$. En évaluant l'inégalité en $(x, x)$ on obtient $a x^{2}+b x \geqslant$ $\mathrm{a} x^{2}+\mathrm{b}$ donc $\mathrm{b} x \geqslant \mathrm{~b}$. Pour $x=2$, on obtient $\mathrm{b} \geqslant 0$, pour $x=0$ on obtient $\mathrm{b} \leqslant 0$ donc $\mathrm{b}=0$. Ainsi $P(X)=a X$ avec $a \geqslant 0$ ce qui conclut.
|
| 167 |
+
Commentaire des correcteurs Les élèves partaient souvent du principe que le coefficient dominant était positif, cependant il faut le vérifier au début. De même, il fallait justifier le calcul du degré du polynôme. Enfin, il ne faut pas oublier de vérifier que les polynômes trouvés satisfont bien l'énoncé.
|
| 168 |
+
|
| 169 |
+
Exercice 13. Trouver toutes les suites périodiques $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ de réels strictement positifs, et telles que pour tout $\mathrm{n} \geqslant 1$,
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
x_{n+2}=\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right) .
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
Solution de l'exercice 13 Soit $n \geqslant 1$. En multipliant la relation de récurrence par $x_{n+1}$, on obtient que $x_{n+2} x_{n+1}=\frac{1}{2}\left(1+x_{n+1} x_{n}\right)$. Ainsi $\left(x_{n+2} x_{n+1}-1\right)=\frac{1}{2}\left(x_{n+1} x_{n}-1\right)$. En particulier $x_{n+1} x_{n}-1=$ $\frac{1}{2^{n-1}}\left(x_{2} x_{1}-1\right)$. Si la suite $\left(x_{n}\right)$ est périodique, la suite $x_{n+1} x_{n}-1$ l'est aussi de même période, ce qui n'est possible d'après l'équation précédente que si $x_{2} x_{1}-1=0$. Dans ce cas pour tout $\mathrm{n} \geqslant 1$, $x_{n+1} x_{n}-1=0$, donc $x_{n+1}=\frac{1}{x_{n}}$. En réinjectant cela dans l'équation de récurrence, on obtient que pour tout $n \geqslant 1, x_{n+2}=\frac{1}{2}\left(x_{n+2}+x_{n}\right)$ donc $\frac{1}{2} x_{n+2}=\frac{1}{2} x_{n}$ soit $x_{n+2}=x_{n}$. En particulier ( $x_{n}$ ) est 2 -périodique et vérifie $x_{2}=\frac{1}{x_{1}}$. On a donc $x_{n}=x_{1}$ si $n$ est impair, $x_{n}=\frac{1}{x_{1}}$ si $n$ est pair.
|
| 176 |
+
Réciproquement soit $a \in \mathbb{R}^{+*}$ et $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ telle que $x_{n}=a$ si $n$ est impair, $x_{n}=\frac{1}{a}$ si $n$ est pair. Comme $\frac{1}{x_{n+1}}=x_{n}$, on a $\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right)=x_{n}=x_{n+2}$ pour tout $n \geqslant 1$. La suite $\left(x_{n}\right)$ est donc 2 -périodique et vérifie la relation de récurrence donnée.
|
| 177 |
+
Les suites vérifiant l'énoncé sont les suites $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ avec $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ telle que $x_{n}=a$ si $n$ est impair, $x_{n}=\frac{1}{a}$ si $n$ est pair pour $a>0$.
|
| 178 |
+
Commentaire des correcteurs Il y avait plusieurs solutions possibles. Plusieurs erreurs ont été faites avec les quantificateurs, notemment quelques confusion entre le $\forall$ et $\exists$. Il ne faut pas oublier de vérifier que les suites trouvées satisfont l'énoncé !
|
| 179 |
+
|
| 180 |
+
Exercice 14. Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
|
| 181 |
+
|
| 182 |
+
$$
|
| 183 |
+
f(x f(x)+f(y))=f(x)^{2}+y
|
| 184 |
+
$$
|
| 185 |
+
|
| 186 |
+
Solution de l'exercice 14 En évaluant l'égalité en $(0, \mathrm{y}), \mathbf{f}(\mathrm{f}(\mathrm{y}))=\mathrm{f}(0)^{2}+\mathrm{y}$. En particulier $\mathrm{f} \circ \mathrm{f}$ est bijective, donc $f$ est injective et surjective donc bijective. Soit a tel que $f(a)=0$. En évaluant en (a, a), $f(0)=f(a f(a)+f(a))=f(a)^{2}+a=a$ donc $f(0)=a$. En particulier on obtient que $f(f(0))=0$. Comme pour tout $y, f(f(y))=f(0)^{2}+y$, en évaluant en $y=0$, on obtient $f(0)^{2}=0$ donc $f(0)=0$. En particulier, pour tout $y, f(f(y))=y$.
|
| 187 |
+
Evaluons désormais l'égalité en $(x, 0)$, on obtient $f(x f(x))=f(x)^{2}$. En évaluant l'égalité précédente en $f(x)$ on obtient $f(f(x) f(f(x)))=f(f(x))^{2}$ donc $f(x f(x))=x^{2}$. En particulier $x^{2}=f(x)^{2}$ pour tout $x$ réel, donc pour tout réel $x, f(x)= \pm x$.
|
| 188 |
+
Montrons désormais que pour tout $x, f(x)=x$ ou pour tout $x, f(x)=-x$. Supposons qu'il existe $a$ et $b$ non nuls tels que $f(a)=a$ et $f(b)=-b$. En évaluant l'égalité initiale en $(a, b)$, on obtient que $f\left(a^{2}-b\right)=a^{2}+b$, donc $a^{2}+b$ vaut $a^{2}-b$ ou $b-a^{2}$, ainsi $a=0$ ou $b=0$ ce qui est absurde. On en déduit donc que pour tout $x, f(x)=x$ ou pour tout $x, f(x)=-x$.
|
| 189 |
+
Réciproquement si $f(x)=x$ pour tout réel $x, f(x f(x)+f(y))=f\left(x^{2}+y\right)=x^{2}+y=f(x)^{2}+y$ donc $f$ est solution. Si $f(x)=-x$ pour tout réel $x, f(x f(x)+f(y))=f\left(-x^{2}-y\right)=x^{2}+y=f(x)^{2}+y$ donc $f$ est solution. Les solutions sont donc la fonction identité et son opposé.
|
| 190 |
+
Commentaire des correcteurs L'erreur la plus fréquente à été de confondre " $\forall x, f(x)=x$ ou $f(x)=-\chi$ " et " $f(x)=x \forall x$ ou $f(x)=-x \forall x$ ".
|
| 191 |
+
|
| 192 |
+
Exercice 15. Soient $a_{1}, \ldots, a_{2019}$ des entiers positifs. Montrer qu'il y a équivalence entre :
|
| 193 |
+
(i) il existe un réel $x$ tel que pour tout $i \in\{1, \ldots, 2019\}$, on a : $a_{i}=\lfloor i x\rfloor$
|
| 194 |
+
(ii) pour tous $i, j \in\{1, \ldots, 2019\}$ vérifiant $i+j \leqslant 2019$, on $a: a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
| 195 |
+
|
| 196 |
+
Solution de l'exercice 15 Prouvons tout d'abord le sens direct: s'il existe x réel tel que pour tout $i$ entre 1 et $2019, a_{i}=\lfloor i x\rfloor$, et si on se donne $\boldsymbol{i}, \boldsymbol{j}$ entre 1 et 2019 tels que $\boldsymbol{i}+\mathfrak{j} \leqslant 2019$, alors $(\mathfrak{i}+\mathfrak{j}) \mathbf{x}=$ $i x+j x \geqslant\lfloor i x\rfloor+\lfloor j x\rfloor=a_{i}+a_{j}$ et $(i+j) x=i x+j x<\lfloor i x\rfloor+1+\lfloor j x\rfloor+1=a_{i}+a_{j}+2$, donc $a_{i}+a_{j} \leqslant a_{i+j}<a_{i}+a_{j}+2$. Comme les $a_{i}$ sont entiers, on a donc $a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
| 197 |
+
Réciproquement supposons que pour tout $i, j$ entre 1 et 2019 tels que $i+j \leqslant 2019, a_{i}+a_{j} \leqslant a_{i+j} \leqslant$ $a_{i}+a_{j}+1$. Trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i}=\lfloor i x\rfloor$ revient à trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i} \leqslant i x<a_{i}+1$, c'est-à-dire tel que pour tout $i, \frac{a_{i}}{i} \leqslant x<\frac{a_{i}+1}{i}$. Il suffit donc de montrer que le maximum des $\frac{a_{i}}{i}$ pour $i$ entre 1 et 2019 est strictement inférieur au minimum des $\frac{a_{j}+1}{j}$ pour $j$ entre 1 et 2019 , ou plus simplement que $\frac{a_{i}}{i}<\frac{a_{i}+1}{j}$ pour tout $i, j$ entre 1 et 2019.
|
| 198 |
+
Montrons cela par récurrence forte sur $\mathfrak{m}=\max (\mathfrak{i}, \mathfrak{j})$. Si $\mathfrak{m}=1, \mathfrak{i}=\mathfrak{j}=1$ donc l'inégalité est évidente. Pour l'hérédité, supposons l'inégalité vraie pour tout $i, j$ entre 1 et m . On veut montrer l'inégalité $\frac{\mathrm{a}_{i}}{\mathrm{i}}<$ $\frac{a_{i}+1}{j}$, où $1 \leqslant i, j \leqslant \mathfrak{m}+1$. Il y a trois cas à traiter :
|
| 199 |
+
|
| 200 |
+
- Si $i=$ j l'inégalité est évidente.
|
| 201 |
+
- Si $i<j$, en appliquant l'hypothèse de récurrence à $(i, j-i): a_{j} \geqslant a_{i}+a_{j-i}>a_{i}+(j-i) \frac{a_{i}}{i}-1=$ $a_{i} \times \frac{j}{i}-1$ donc $\frac{a_{j}+1}{j}>\frac{a_{i}}{i}$
|
| 202 |
+
- Si $\boldsymbol{i}>\mathfrak{j}$, en appliquant l'hypothèse de récurrence à $(\mathfrak{i}-\mathfrak{j}, \mathfrak{j}): a_{i} \leqslant \mathfrak{a}_{\mathfrak{j}}+\mathfrak{a}_{i-j}+1<\mathfrak{a}_{j}+$ $\frac{(i-j)\left(a_{j}+1\right)}{j}=a_{j} \frac{i}{j}+\frac{i-j}{j}<\left(a_{j}+1\right) \frac{i}{j}$ donc $\frac{a_{i}}{i}<\frac{a_{j}+1}{j}$
|
| 203 |
+
Commentaire des correcteurs Plusieurs élèves se sont compliqués la tâche en cherchant une solution trop compliquée, difficile à rédiger et ont donc fini par faire une erreur. Pour éviter cela, il aurait fallu chercher à reformuler le problème pour le simplifier.
|
| 204 |
+
|
| 205 |
+
Exercice 16. Soit $1<t<2$ un nombre réel. Montrer que pour tout entier $d$ suffisamment grand, il existe un polynôme $P(X)=\sum_{k=0}^{d} a_{k} X^{k}$, avec $a_{d}=1$ et $a_{0}, \ldots, a_{d-1} \in\{1,-1\}$, tel que :
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
|\mathrm{P}(\mathrm{t})-2019| \leqslant 1
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
Solution de l'exercice 16 Soient $d \geqslant 2019$ un entier et $a_{1}<\ldots<a_{k}$ les $d$-uplets de la forme $\left( \pm 1, \ldots, \pm 1\right.$ ), ordonnés par ordre lexicographique (en partant de la droite!, c'est-à-dire que $a_{i}>a_{j}$ si et seulement si le premier terme non nul de $a_{i}-a_{j}$ en partant de la droite est $>0$ ), avec $k=2^{d}$.
|
| 212 |
+
Pour passer de $a_{i}$ à $a_{i+1}$, on regarde le premier -1 en partant de la droite dans $a_{i}$, on le change par un 1 , et on remplace tous les 1 à sa droite par des -1 . Par exemple si $\mathrm{d}=3$, les triplets sont dans l'ordre $a_{1}=(-1,-1,-1), a_{2}=(-1,-1,1), a_{3}=(-1,1,-1), a_{4}=(-1,1,1) a_{5}=(1,-1,-1), a_{6}=$ $(1,-1,1), a_{7}=(1,1,-1)$ et $a_{8}=(1,1,1)$.
|
| 213 |
+
On associe à $a_{i}=\left(a_{i 1}, \ldots, a_{i d}\right)$ le polynôme $P_{i}(X)=\sum_{j=1}^{d} a_{i j} X^{j-1}$, de telle sorte que $M:=-P_{1}(t)=$ $P_{k}(t)=1+\ldots+t^{d-1}>d$.
|
| 214 |
+
Or $\left|P_{i+1}(t)-P_{i}(t)\right|=2\left|t^{\mathrm{l}}-\left(1+\ldots+t^{\mathrm{l}-1}\right)\right|$ pour un certain $l \geqslant 0$ (qui dépend de $i$ ) pour tout $i$.
|
| 215 |
+
Montrons $t^{\mathrm{l}}-\left(1+\ldots+\mathrm{t}^{\mathrm{l}-1}\right) \leqslant 1$ : cela équivaut à $\mathrm{t}^{\mathrm{l}+1}-\mathrm{t}^{\mathrm{l}}-\left(\mathrm{t}^{\mathrm{l}}-1\right) \leqslant \mathrm{t}-1$ après multiplication par $t-1$, soit après réarrangement $t^{l}(2-t)+t \geqslant 2$, ce qui est vrai car $t^{l} \geqslant 1$.
|
| 216 |
+
Dès lors, $P_{i+1}(t)$ est plus grand que $P_{i}(t)$ d'au plus 2 , ce qui montre que, puisque $2019-t^{d} \in[-M ; M]$, il existe $i$ tel que $\left|P_{i}(t)-\left(2019-t^{d}\right)\right| \leqslant 1$, ce qui conclut en posant $P=X^{d}+P_{i}$
|
| 217 |
+
Commentaire des correcteurs Les copies reçues étaient globalement bonnes. Cependant, la plupart des élèves oublient des éléments de rédactions importants. Quelques élèves ont proposé une preuve algorithmique alternative très jolie.
|
| 218 |
+
|
| 219 |
+
Exercice 17. Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous réels $x, y$,
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Solution de l'exercice 17 Clairement, $f(x)=x$ est une solution; on va montrer que c'est la seule. On pose dans la suite $a=f(0)$.
|
| 226 |
+
Avec $y=0$ on a $\mathbf{f}(\mathbf{f}(\boldsymbol{x}(\mathrm{x}+1)))=\mathbf{f}(\mathrm{x})(\mathbf{f}(\mathrm{x})+1)(*)$ pour tout x .
|
| 227 |
+
Si on prend $y=-f(x)$ on voit que la fonction $f$ admet des zéros.
|
| 228 |
+
Dès lors pour exploiter $(*)$ il est intéressant de choisir y tel que $f(f(x f(x+1))-y f(y-1))=f(f(x f(x+$ $1))$ ), ce qui est possible en prenant $y=z+1$ avec $f(z)=0$. On a alors $(f(x)+z+1)(f(x-z)+1)=$ $f(x)(f(x)+1)$, ce qui se simplifie avec $x=z:(z+1)(f(-1)+1)=0$.
|
| 229 |
+
Si $z=-1$, on a $f(-1)=0$, donc avec $x=0, y=1$, on a $a+1=a$, une évidente contradiction.
|
| 230 |
+
On a donc montré $f(-1)=-1$. On reprend $x=0, y=1$ pour avoir $f(0)=0$. Dès lors $y=1$ dans l'équation montre que $(f(x)+1)(f(x-1)+1)=f(x)(f(x)+1)$ (1) d'après $(*)$.
|
| 231 |
+
$x=0$ puis $x=-1$ dans l'équation originelle donne $y(f(-y)+1)=(y-1)(f(-y-1)+1)$ (2). Ainsi, si on avait $\left(1^{\prime}\right): f(x)=f(x-1)+1$, on pourrait déduire de (2) $y(f(-y)+1)=(y-1) f(-y)$, puis $f(-y)=-y$, ce qui montrerait que $f$ est l'identité.
|
| 232 |
+
Pour montrer $\left(1^{\prime}\right)$, commençons par prouver que $f(x)=0 \Longleftrightarrow x=0$.
|
| 233 |
+
Soit $t$ tel que $f(t)=0$; d'après (1), on a $f(t-1)=-1$. (2) donne alors, avec $y=-t, t=0$, comme voulu.
|
| 234 |
+
Montrons à présent $f(x)=-1 \Longleftrightarrow x=-1$.
|
| 235 |
+
Si $f(t)=-1,(*)$ donne $f(f(t f(t+1)))=0$ donc $t f(t+1)=0$. Or $t \neq 0$ car $f(0) \neq-1$, donc $f(t+1)=0$ et ainsi $t=-1$ comme voulu.
|
| 236 |
+
Pour montrer ( $1^{\prime}$ ) d'après (1), il suffit donc de voir que $f(-2)=f(-1)-1=-2$. Or $\boldsymbol{f}(2)=2$ en utilisant (1) donc $(*)$ avec $x=-2$ donne $2=f(-2)+f(-2)^{2}$ et donc $f(-2) \in\{-2,1\}$. Mais si $f(-2)=1$, (1) donne $f(-3)=0$, impossible d'après ce qu'on a montré. Cela conclut la preuve de ( $1^{\prime}$ ) et donc la solution.
|
| 237 |
+
Commentaire des correcteurs L'exercice était assez délicat. Quelques élèves courageux ont avancé de façon substantielle dans le problème, voire même l'ont résolu complètement. Plusieurs élèves se sont contentés de vérifier que la fonction identité était solution, mais cela ne rapportait aucun point. En revanche, des élèves ont montré que si f est solution alors f est l'identité mais ont oublié de signaler que réciproquement l'identité était solution. Ces élèves ont alors perdu un point, conformément à l'usage en compétition.
|
| 238 |
+
|
| 239 |
+
Exercice 18. Soient $\mathrm{P}, \mathrm{Q}$ deux polynômes à coefficients réels, non constants et premiers entre eux. Montrer qu'il existe au plus trois réels $\lambda$ tels que:
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
P+\lambda Q=R^{2}
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
où $R \in \mathbb{R}[X]$.
|
| 246 |
+
Solution de l'exercice 18 On procède par l'absurde en supposant l'existence de quatre réels distincts $\lambda_{1}, \ldots, \lambda_{4}$ et quatre polynômes $R_{1}, \ldots, R_{4}$ tels que $P+\lambda_{i} Q=R_{i}^{2}$ pour $i=1,2,3,4$.
|
| 247 |
+
On a $P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime}$ et donc $R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=P Q^{\prime}-Q^{\prime}$.
|
| 248 |
+
Remarquons que si $T \mid R_{i}, R_{j}$ alors $T \mid R_{i}^{2}-R_{j}^{2}=\left(\lambda_{i}-\lambda_{j}\right) Q$ puis $T \mid R_{i}^{2}-\lambda_{i} Q=P$ et donc $T$ est constant, car $\mathrm{P}, \mathrm{Q}$ sont premiers entre eux.
|
| 249 |
+
Dès lors les $R_{i}$ sont deux à deux premiers entre eux et ainsi $R_{1} R_{2} R_{3} R_{4} \mid P Q^{\prime}-P^{\prime} Q$.
|
| 250 |
+
Soient $A, B$ des polynômes non nuls ; le degré de $A+\lambda B$, si $\lambda \in \mathbb{R}$, est égal à $\max \{\operatorname{deg}(A), \operatorname{deg}(B)\}$, sauf si $\operatorname{deg}(A)=\operatorname{deg}(B)$ et $\lambda=-\frac{a}{b}$ où $a, b$ sont les coefficients dominants de $A$ et $B$ respectivement, auquel cas il est plus petit.
|
| 251 |
+
Si $A=P$ et $B=Q$, cela montre que, soit $\operatorname{deg} R_{i}=\frac{1}{2} \max \{\operatorname{deg}(P), \operatorname{deg}(Q)\}$ pour tout $i$, et donc que $\operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=2 \max \operatorname{deg}\{P, Q\}>\operatorname{deg}(P)+\operatorname{deg}(Q)-1 \geqslant \operatorname{deg}\left(P Q^{\prime}-P^{\prime} Q\right)$, soit il y a un $R_{i}$, tel que $\operatorname{deg}\left(R_{i}\right)<\operatorname{deg}\left(R_{j}\right)$ pour $j \neq i ;$ alors pour $A=P+\lambda_{i} Q=: P_{1}$ et $B=Q$ on voit que $\operatorname{deg}\left(R_{i}\right)=\frac{1}{2} \operatorname{deg}\left(P_{1}\right)$ et $\operatorname{deg} R_{j}=\frac{1}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}$ et $\operatorname{donc} \operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=\frac{3}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}+\frac{1}{2} \operatorname{deg}\left(P_{1}\right)>$ $\operatorname{deg}(\mathrm{Q})+\operatorname{deg}\left(\mathrm{P}_{1}\right)-1 \geqslant \operatorname{deg}\left(\mathrm{P}_{1} \mathrm{Q}^{\prime}-\mathrm{P}_{1}^{\prime} \mathrm{Q}\right)=\operatorname{deg}\left(\mathrm{PQ}^{\prime}-\mathrm{P}^{\prime} \mathrm{Q}\right)$.
|
| 252 |
+
Par un argument sur les degrés, on a donc nécessairement $P Q^{\prime}-P^{\prime} Q=0$ et ainsi $P \mid P^{\prime} Q$. Or $P$ et $Q$ sont premiers entre eux donc $P \mid P^{\prime}$, ce qui est une évidente contradiction à $P$ non constant.
|
| 253 |
+
Commentaire des correcteurs Les copies reçues étaient d'un très bon niveau (à part quelques petites erreurs). Etant donné la grande difficulté supposée de l'exercice, c'était une agréable surprise!
|
| 254 |
+
|
French_STS/md/fr-corrigé-commentaire-envoi-1.md
ADDED
|
@@ -0,0 +1,326 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
|
| 2 |
+
|
| 3 |
+
# ENVOI 1 : GÉOMÉTRIE Corrigé
|
| 4 |
+
|
| 5 |
+
## Exercices Juniors
|
| 6 |
+
|
| 7 |
+
Exercice 1. Soit $A B C D$ un quadrilatère et $M, N, P, Q$ les milieux respectifs de $[A B],[B C],[C D]$, [DA].
|
| 8 |
+
Montrer que le quadrilatère MNPQ est un parallélogramme.
|
| 9 |
+
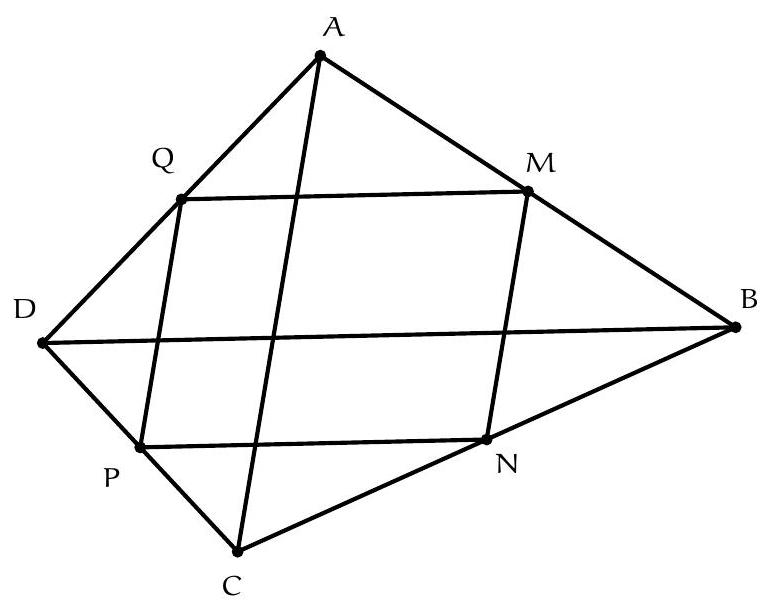
|
| 10 |
+
|
| 11 |
+
Solution de l'exercice 1 Puisque les points $M$ et $N$ sont les milieux respectifs des côtés $[A B]$ et $[B C]$, les droites (MN) et ( $A C$ ) sont parallèles. Puisque les points $P$ et $Q$ sont les milieux respectifs des côtés $[C D]$ et $[D A]$, les droites $(P Q)$ et ( $A C$ ) sont parallèles. Donc les droites ( $P Q)$ et $(M N)$ sont parallèles. On obtient de la même façon que les droites (NP) et (MQ) sont parallèles. Donc les côtés opposés deux à deux du quadrilatère MNPQ sont parallèles, ce qui en fait un parallélogramme.
|
| 12 |
+
Commentaire des correcteurs L'exercice est bien traité.
|
| 13 |
+
|
| 14 |
+
Exercice 2. Soit $A B C$ un triangle rectangle en $B$. Soit $M$ le point d'intersection de la médiane issue de $B$ avec la droite (AC), et (d) la perpendiculaire à la droite (BC) passant par le point $M$. Soit $U$ le milieu du segment $[A B]$, V le milieu du segment [AM], I le point d'intersection de la droite (UV) avec la droite (d), et J le point d'instersection de la droite (UV) avec la droite (BC).
|
| 15 |
+
|
| 16 |
+
Montrer que $A C=I J$.
|
| 17 |
+
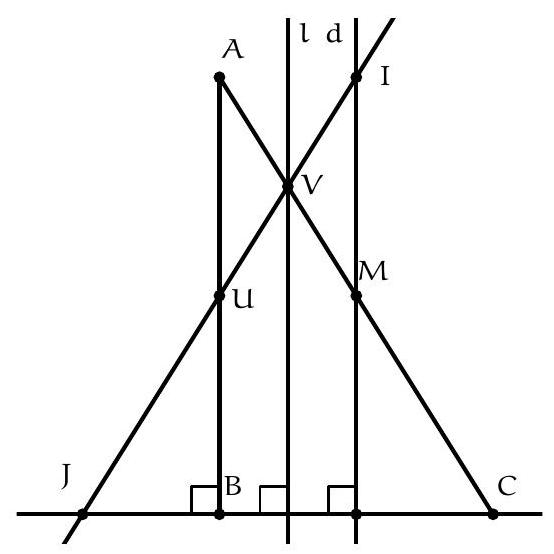
|
| 18 |
+
|
| 19 |
+
Solution de l'exercice 2 Les droites d et ( AB ) sont perpendiculaires à la droite ( BC ) donc elles sont parallèles. On obtient par le théorème de Thalès que $\frac{V I}{V U}=\frac{A V}{V M}=1$ donc $V$ est le milieu du segment [UI]. Le quadrilatère $A I M U$ a ses diagonales qui se coupent en leur milieu, c'est donc un parallélogramme. Les points $U$ et $M$ sont les milieux respectifs des segments $[A B]$ et $[A C]$ donc les droites (UM) et (BC) sont parallèles. Donc la droite (UM) est perpendiculaire au segment $[A B]$ et le quadrilatère AIMU est un rectangle.
|
| 20 |
+
Soit l la droite perpendiculaire au segment [BC] passant par V. Cette droite est la médiatrice du segment $[\mathrm{UM}]$ et du segment $[\mathrm{AI}]$ donc le point $U$ est le symétrique du point $M$ par rapport à la droite $l$ et le point $A$ est le symétrique du point I par rapport à la droite $l$ donc la droite $(A M)$ est la symétrique de la droite (UI) par rapport à la droite $l$. Puisque la droite $(B C)$ est sa propre symétrique par rapport à la droite $l$, le point d'intersection de la droite (BC) avec la droite (UI) est le symétrique du point d'intersection de la droite $(A M)$ avec la droite $B C$ donc les points C et J sont symétriques par rapport à la droite l . La symétrie conserve les longueurs, donc $A C=I J$.
|
| 21 |
+
Commentaire des correcteurs Même si l'argument semblait facile pour certains, on attendait une vraie justification, avec par exemple le théorème de Thalès. Attention à quelques confusions : une droite est bien la bissectrice d'un angle ou la médiatrice d'un segment, et non par exemple la bissectrice d'un segment.
|
| 22 |
+
|
| 23 |
+
Exercice 3. Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\prime}$ des points sur la droite $d_{1}, B, B^{\prime}$ des points sur la droite $d_{2}, C, C^{\prime}$ des points sur la droite $d_{3}$ tels que les droites $(A B)$ et $\left(A^{\prime} B^{\prime}\right)$ sont parallèles et les droites ( BC ) et ( $\mathrm{B}^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
|
| 24 |
+
Montrer que les droites $(A C)$ et $\left(A^{\prime} C^{\prime}\right)$ sont parallèles.
|
| 25 |
+
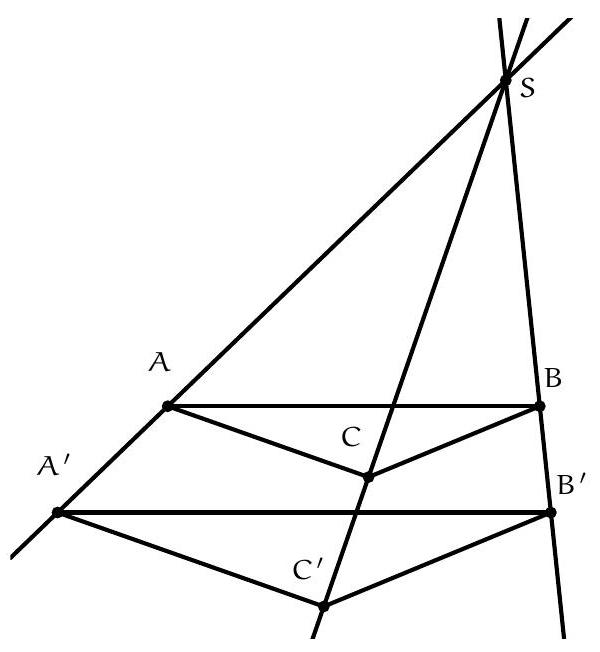
|
| 26 |
+
|
| 27 |
+
Solution de l'exercice 3 Soit $S$ le point de concours des trois droites. Puisque les droites $(A B)$ et $\left(A^{\prime} B^{\prime}\right)$ sont parallèles, d'après le théorème de Thalès,
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
De même on trouve
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
On déduit que
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
ce qui signifie, d'après le théorème de Thalès, que les droites $(A C)$ et $\left(A^{\prime} C^{\prime}\right)$ sont parallèles. Commentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.
|
| 46 |
+
|
| 47 |
+
Exercice 4. Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\Gamma$ le cercle de centre $B$ passant par $A$, et $\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\Omega$ qui n'est pas sur le segment $[B C]$.
|
| 48 |
+
Montrer que le triangle DFE est isocèle en $F$.
|
| 49 |
+
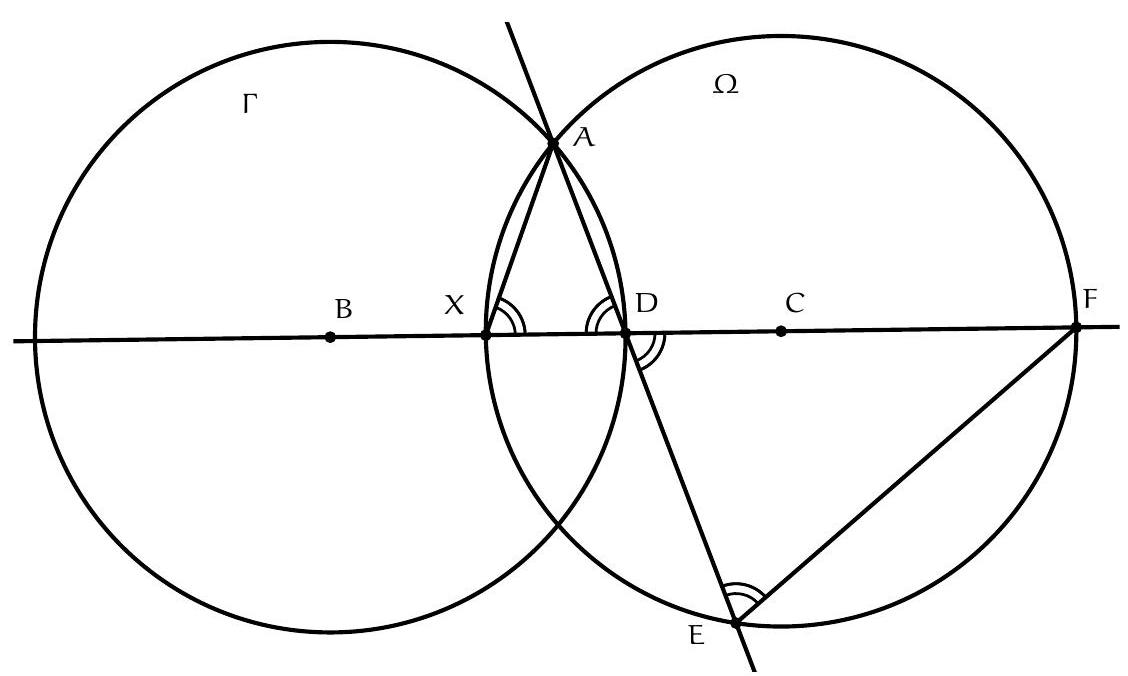
|
| 50 |
+
|
| 51 |
+
Solution de l'exercice 4 Soit $X$ le point d'intersection du cercle $\Omega$ avec le segment [BC]. Les points $B$ et C sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$ donc les cercles $\Gamma$ et $\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\widehat{A D X}=\widehat{A X D}$.
|
| 52 |
+
Les points $F, E, X$ et $A$ sont cocycliques donc $\widehat{F E A}=\widehat{F X A}$. On déduit
|
| 53 |
+
|
| 54 |
+
$$
|
| 55 |
+
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
Ce qui donne bien que le triangle FDE est isocèle en F .
|
| 59 |
+
Commentaire des correcteurs Certains élèves ont noté des symétries dans la figure, mais il fallait veiller à la justifier de façon rigoureuse.
|
| 60 |
+
|
| 61 |
+
Exercice 5. Soit $\Gamma$ un cercle, $P$ un point à l'extérieur du cercle. Les tangentes au cercle $\Gamma$ passant par le point $P$ sont tangentes au cercle $\Gamma$ en $A$ et $B$. Soit $M$ est le milieu du segment [BP] et $C$ le point d'intersection de la droite ( $A M$ ) et du cercle $\Gamma$. Soit D la deuxième intersection de la droite ( PC ) et du cercle $\Gamma$.
|
| 62 |
+
Montrer que les droites $(A D)$ et $(B P)$ sont parallèles.
|
| 63 |
+
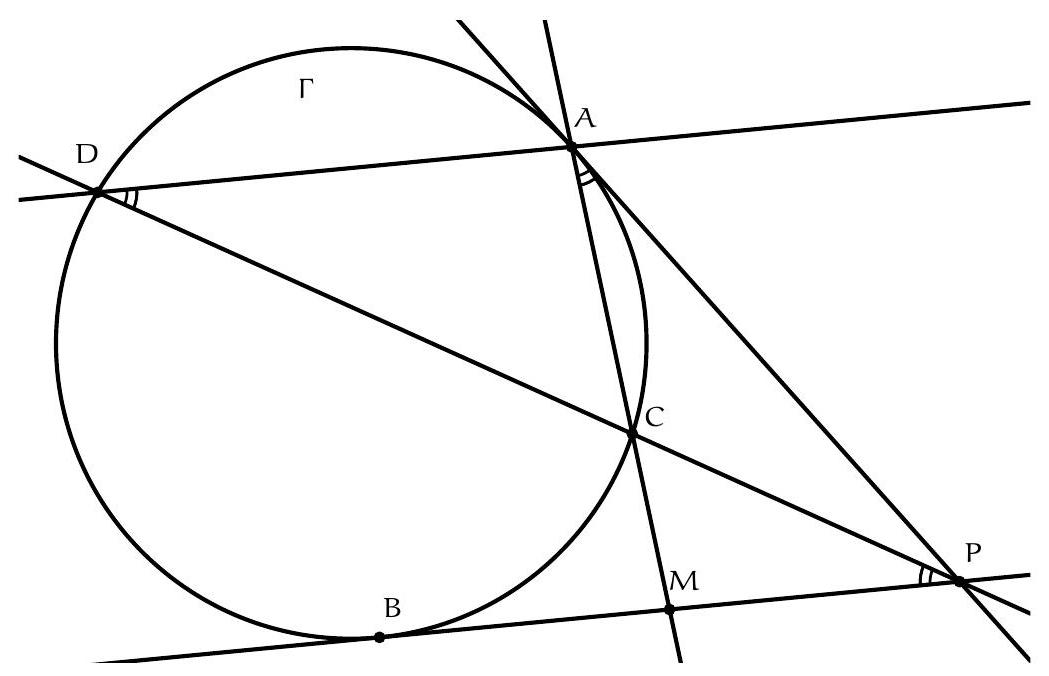
|
| 64 |
+
$\underline{\text { Solution de l'exercice } 5}$ En utilisant la puissance du point $M$ par rapport au cercle $\Gamma, \mathrm{MB}^{2}=M C \cdot M A$. Puisque $M$ est le milieu du segment $[B P], M P^{2}=M B^{2}$ donc $M P^{2}=M C \cdot M A$. On déduit de la réciproque de la puissance d'un point par rapport à un cercle que la droite ( PM ) est tangente au cercle circonscrit au triangle PAC. On obtient du théorème de l'angle tangent que $\widehat{M P C}=\widehat{P A C}$. Or la droite $(\mathrm{PA})$ est tangente au cercle $\Gamma$ donc à nouveau par le théorème de l'angle tangent, $\widehat{\mathrm{PAC}}=\widehat{\mathrm{ADC}}$. En résumé :
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
\widehat{\mathrm{BPD}}=\widehat{M P C}=\widehat{\mathrm{PAC}}=\widehat{A D C}=\widehat{A D P}
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
donc les droites $(A D)$ et (BP) sont parallèles.
|
| 71 |
+
Commentaire des correcteurs Quelques démonstrations proposées étaient fausses. Une bonne façon de vérifier que sa démonstration est correcte est de vérifier qu'on a utilisé toutes les hypothèses. Plusieurs élèves n'utilisent à aucun moment que le point $M$ est le milieu du segment [PB], ce qui est pourtant une hypothèse cruciale. Attention à se relire pour éviter des erreurs typographiques comme écrire un angle ou un triangle à la place d'un autre.
|
| 72 |
+
|
| 73 |
+
Exercice 6. Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B)$ et (CD), et $V$ le point d'intersection des droites (BC) et ( $D A$ ). Soit $K$ le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\mathrm{KU}]$ et de la médiatrice du segment [KV].
|
| 74 |
+
Montrer que les points $\mathrm{U}, \mathrm{V}$ et L sont alignés.
|
| 75 |
+
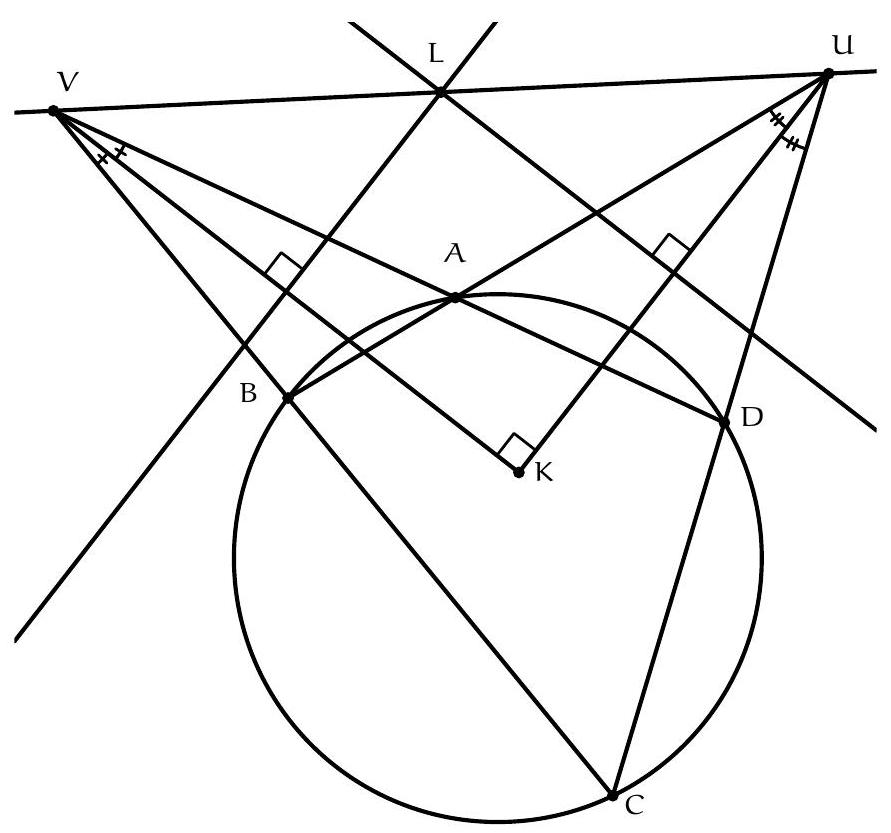
|
| 76 |
+
|
| 77 |
+
Solution de l'exercice 6 Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U, L et V sont alignés, il suffit de montrer que $\widehat{U L V}=180^{\circ}$. Par le théorème de l'angle au centre, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Il suffit donc de montrer que $\widehat{U K V}=90^{\circ}$.
|
| 78 |
+
La somme des angles du triangle UKV vaut $180^{\circ}$, donc il suffit de montrer que $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. D'une part $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. Or $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. On déduit
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
De la même manière, on obtient
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Or $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ et
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
Finalement
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\begin{aligned}
|
| 100 |
+
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
|
| 101 |
+
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
|
| 102 |
+
\end{aligned}
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
ce qui donne le résultat voulu.
|
| 106 |
+
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle.
|
| 107 |
+
|
| 108 |
+
Exercice 7. Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.
|
| 109 |
+
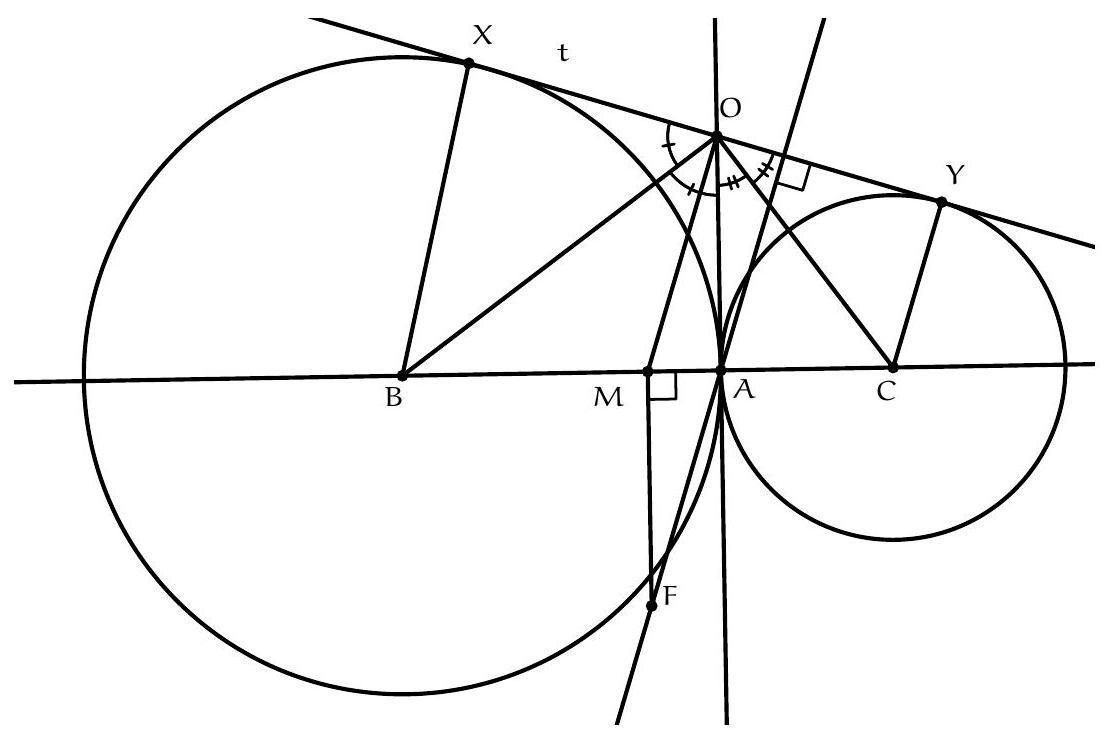
|
| 110 |
+
|
| 111 |
+
Solution de l'exercice 7 Soient $X$ et $Y$ les points de tangences de $t$ avec les cercles de centre B et $C$ respectivement. Soit $O$ le point d'intersection la droite $t$ avec la tangente commune au deux cercles en $A$. Les points $X$ et $A$ sont symétriques para rapport à la droite $(O B)$ et les points $Y$ et $A$ sont symétriques par rapport à la droite $(\mathrm{OC})$. On déduit $\widehat{\mathrm{BOA}}=\frac{1}{2} \widehat{\mathrm{XOA}}$ et $\widehat{\mathrm{COA}}=\frac{1}{2} \widehat{\mathrm{YOA}}$. On en déduit :
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
\widehat{\mathrm{BOC}}=\widehat{\mathrm{BOA}}+\widehat{\mathrm{AOC}}=\frac{1}{2} \widehat{\mathrm{XOA}}+\frac{1}{2} \widehat{\mathrm{AOY}}=\frac{1}{2} \widehat{\mathrm{XOY}}=90^{\circ}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
Soit $M$ le milieu de $[B C]$. Le triangle $B O C$ est rectangle $O$ donc $M$ est le centre du cercle circonscrit à ce triangle. Ceci donne $M O=M B=\frac{1}{2} B C$. Comme les droites $(O A)$ et ( $M F$ ) sont perpendiculaires à la droite (BC), elles sont donc parallèles. Enfin,
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
\widehat{M O Y}=\widehat{M O C}+\widehat{C O Y}=\widehat{M C O}+\widehat{A O C}=90^{\circ}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
donc les droites $(\mathrm{OM})$ et ( AF ) sont perpendiculaires à la droite $t$ donc elles sont parallèles. Donc le quadrilatère OMFA est un parallélogramme et $\mathrm{BC}=2 \mathrm{OM}=2 A \mathrm{~F}$.
|
| 124 |
+
Commentaire des correcteurs On a pu constaté plusieurs solutions intéressantes. L'exercice nécessitait plusieurs initiatives, ainsi plusieurs solutions étaient incomplètes. Quelques élèves ont tenté une solution calculatoire. Les calculs étaient alors souvent trop laborieux et chargés de notations un peu lourdes.
|
| 125 |
+
|
| 126 |
+
Exercice 8. Soit $A B C$ un triangle acutangle non isocèle en $A$. Soit $M$ le milieu du segment $[B C], H$ l'orthocentre du triangle $A B C, O_{1}$ le milieu du segment $[A H]$ et $O_{2}$ le centre du cercle circonscrit au triangle CBH . Montrer que le quadrilatère $\mathrm{O}_{1} \mathrm{AMO}_{2}$ est un parallélogramme.
|
| 127 |
+
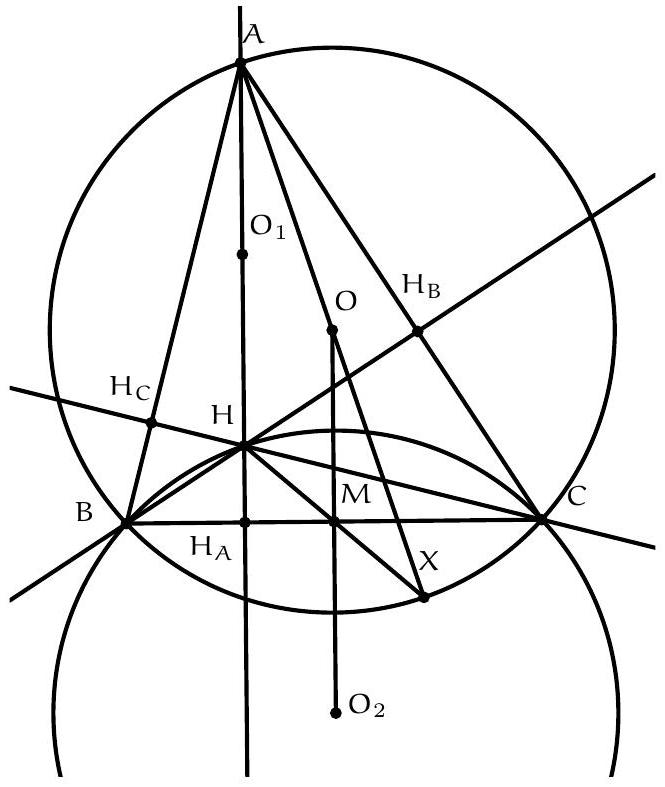
|
| 128 |
+
|
| 129 |
+
Solution de l'exercice 8 Soit $\mathrm{H}_{\mathrm{A}}$ le pied de la hauteur issue du sommet $A, \mathrm{H}_{\mathrm{B}}$ le pied de la hauteur issue du sommet B et O le centre du cercle circonscrit au triangle ABC .
|
| 130 |
+
On remarque déjà que $\mathrm{O}_{2}$ est sur la médiatrice de $[\mathrm{BC}]$ donc les droites $\left(\mathrm{MO}_{2}\right)$ et $(\mathrm{AH})$ sont parallèles car elles sont perpendiculaires à ( BC ). Il suffit donc de montrer que $\mathrm{MO}_{2}=A \mathrm{O}_{1}$.
|
| 131 |
+
Soit $X$ le symétrique du point $H$ par rapport au point $M$. Alors $M$ est le milieu de [BC] et $[\mathrm{XH}]$ donc BHCX est un parallélogramme et $\widehat{\mathrm{XBA}}=\widehat{\mathrm{XBC}}+\widehat{\mathrm{CBA}}=\widehat{\mathrm{HCB}}+\widehat{\mathrm{CBA}}=90^{\circ}$ (car le triangle $\mathrm{BCH}_{\mathrm{C}}$ est rectangle en $\mathrm{H}_{\mathrm{C}}$ ) et de même $\widehat{\mathrm{XCA}}=90^{\circ}$ donc $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$.
|
| 132 |
+
La symétrie de centre $M$ envoie $B$ sur $C, C$ sur $B$ et H sur $X$ donc elle envoie le cercle circonscrit à $B C H$ sur le cercle circonscrit à BCX donc elle envoie $\mathrm{O}_{2}$ sur O . En particulier, $\mathrm{MO}_{2}=\mathrm{MO}$.
|
| 133 |
+
Comme les points $O$ et $M$ sont les milieux respectifs des segments $[X A]$ et $[X H]$, d'après le théorème de Thalès,
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\frac{\mathrm{OM}}{\mathrm{AH}}=\frac{\mathrm{XM}}{\mathrm{XH}}=\frac{1}{2}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
donc $\mathrm{AH}=2 \mathrm{OM}$ donc
|
| 140 |
+
|
| 141 |
+
$$
|
| 142 |
+
\mathrm{MO}_{2}=\mathrm{MO}=\frac{1}{2} A \mathrm{H}=A \mathrm{O}_{1}
|
| 143 |
+
$$
|
| 144 |
+
|
| 145 |
+
ce qui conclut.
|
| 146 |
+
Commentaire des correcteurs Cet exercice demandait de connaître plusieurs propriétés de l'orthocentre, en particulier le fait que le symétrique de l'orthocentre H par rapport au milieu du côté [BC] appartient au cercle circonscrit au triangle $A B C$ et est également le symétrique du sommet $A$ par rapport au centre O. Plusieurs élèves ont remarqué la première étape du problème qui est que les droites $\left(\mathrm{MO}_{2}\right)$ et ( AH ) sont parallèles. Ceci montre un réel effort de recherche sur un problème difficile de la part des élèves, ce qui est encourageant.
|
| 147 |
+
|
| 148 |
+
Exercice 9. Soit $A B C$ un triangle, $\Gamma$ sont cercle circonscrit et $\omega$ le cercle de même centre que $\Gamma$ et tangent à la droite ( BC ). Les tangentes au cercle $\omega$ passant par $A$ coupent ( BC ) en un point $X$ du côté de $B$ et en un point $Y$ du côté de $C$. La tangente au cercle $\Gamma$ en $B$ et la parallèle à la droite $(A C)$ passant par $X$ se coupent en un point $S$ et la tangente au cercle $\Gamma$ en $C$ et la parallèle à la droite $(A B)$ passant par $Y$ se coupent en un point $T$.
|
| 149 |
+
Montrer que la droite (ST) est tangente au cercle $\Gamma$.
|
| 150 |
+
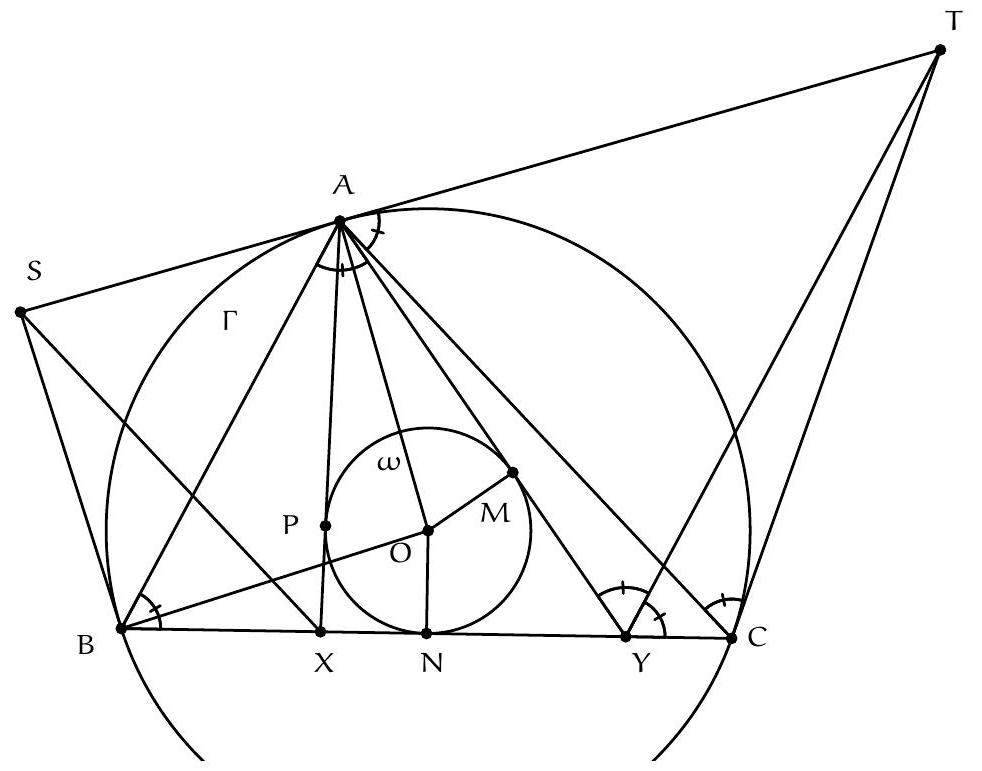
|
| 151 |
+
|
| 152 |
+
Solution de l'exercice 9 Afin d'éviter d'avoir à séparer les différents cas, en fonction de la position du point $Y$ par rapport au segment $[B C]$, nous allons utiliser les angles de droite orientés : ( $A B, C D$ ) désigne l'angle (relatif) dont il faut tourner la droite ( $A B$ ) pour qu'elle soit parallèle à la droite ( $C D$ ).
|
| 153 |
+
Nous allons montrer que la droite (TA) est tangente au cercle circonscrit au triangle $A B C$ et de même pour la droite (SA), ce qui donnera bien que la droite (ST) est tangente à ce cercle.
|
| 154 |
+
Pour montrer que la droite $(A T)$ est tangente au cercle $\Gamma$, il suffit de montrer que $(A C, A T)=(B C, B A)$. Les droites $(T Y)$ et $(A B)$ sont parallèles donc $(B C, B A)=(B C, Y T)=(Y C, Y T)$, donc on est ramené à montrer que $(A C, A T)=(Y C, Y T)$, autrement dit que les points $T, A, Y$ et $C$ sont cocycliques.
|
| 155 |
+
Pour cela, on peut montrer que $(Y T, Y A)=(C T, C A)$. En effet, $(Y T, Y A)=(A B, A Y)$ (par parallélisme de $(A B)$ et $(Y T))$ et $(C T, C A)=(B C, B A)$ donc il ne reste plus qu'à montrer que $(A B, A Y)=$ ( $B C, B A$ ), autrement dit que le triangle $A Y B$ est isocèle en $Y$.
|
| 156 |
+
Soit $O$ le centre du cercle $\Gamma$, qui est aussi le centre du cercle $\omega$, et soit $M$ et $N$ les points de contact respectifs du cercle $\omega$ avec les segments [YA] et [YB]. Alors les triangles OMA et ONB sont rectangles, $\mathrm{OA}=\mathrm{OB}$ et $\mathrm{OM}=\mathrm{ON}$ donc $\mathrm{MA}=\sqrt{\mathrm{OA}^{2}-\mathrm{OM}^{2}}=\sqrt{\mathrm{OB}^{2}-\mathrm{ON}}{ }^{2}=\mathrm{NB}$ et puisque $\mathrm{YM}=\mathrm{YN}$, on déduit $Y A=Y B$ et le triangle $Y A B$ est isocèle en $Y$ comme voulu.
|
| 157 |
+
Commentaire des correcteurs Il y avait malhreusement une imprécision dans l'énoncé puisqu'il fallait que le triangle $A B C$ ait des angles aigus. Cet oubli de notre part a provoqué quelques confusions pour certains élèves qui ont tracé une figure avec un angle obtu en $A$ et ont donc pensé que l'énoncé était faux. L'exercice restait plutôt difficile. Quelques élèves ont essayé de conclure avec les similitudes, mais les hypothèses n'étaient jamais assez fortes.
|
| 158 |
+
|
| 159 |
+
## Exercices Seniors
|
| 160 |
+
|
| 161 |
+
Exercice 10. Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\prime}$ des points sur la droite $d_{1}, B, B^{\prime}$ des points sur la droite $d_{2}, C, C^{\prime}$ des points sur la droite $d_{3}$ tels que les droites ( $A B$ ) et ( $A^{\prime} B^{\prime}$ ) sont parallèles et les droites $(B C)$ et ( $B^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
|
| 162 |
+
Montrer que les droites ( $A C$ ) et ( $A^{\prime} C^{\prime}$ ) sont parallèles.
|
| 163 |
+
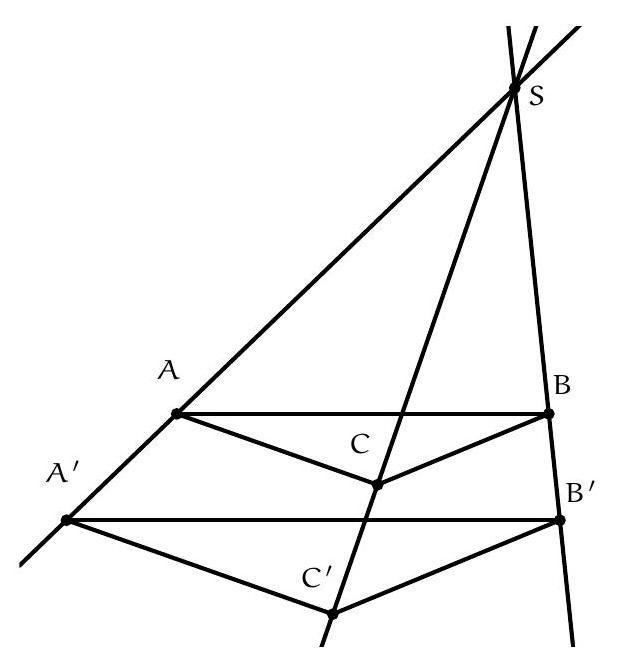
|
| 164 |
+
|
| 165 |
+
Solution de l'exercice 10 Soit $S$ le point de concours des trois droites. Puisque les droites ( $A B$ ) et ( $A^{\prime} B^{\prime}$ ) sont parallèles, d'après le théorème de Thalès,
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
De même on trouve
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
On déduit que
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
ce qui signifie, d'après le théorème de Thalès, que les droites ( $A C$ ) et ( $A^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
|
| 184 |
+
Commentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.
|
| 185 |
+
|
| 186 |
+
Exercice 11. Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\Gamma$ le cercle de centre $B$ passant par $A$, et $\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\Omega$ qui n'est pas sur le segment $[B C]$.
|
| 187 |
+
Montrer que le triangle DFE est isocèle en $F$.
|
| 188 |
+
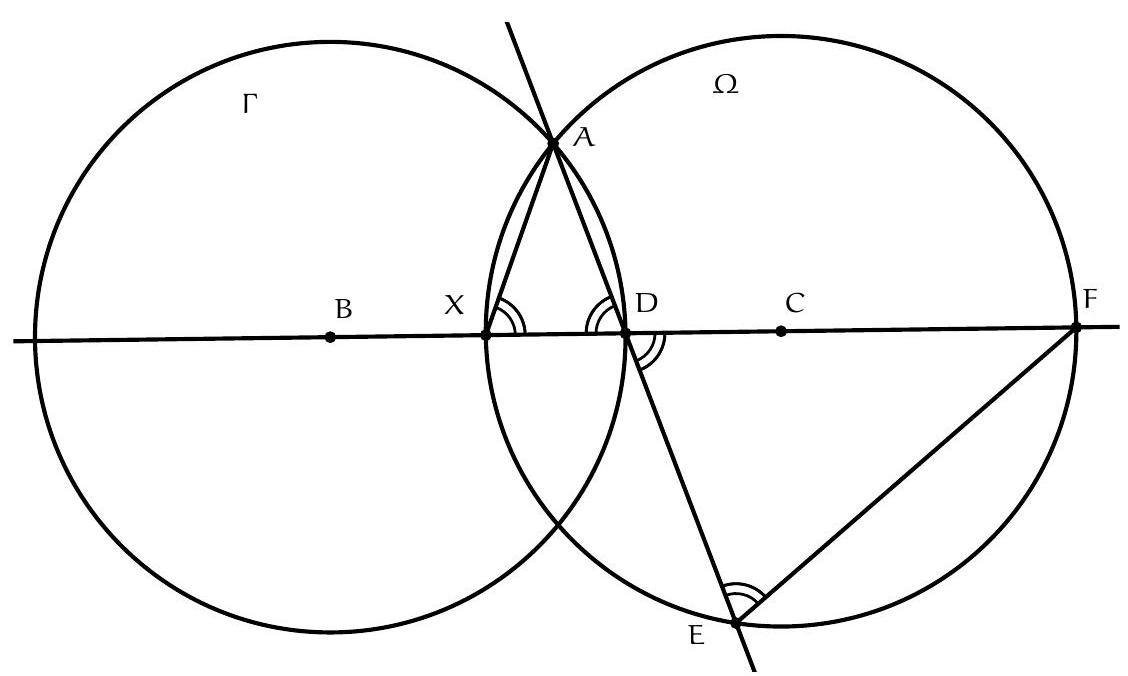
|
| 189 |
+
|
| 190 |
+
Solution de l'exercice 11 Soit $X$ le point d'intersection du cercle $\Omega$ avec le segment [BC]. Les points B et C sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$ donc les cercles $\Gamma$ et $\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\widehat{A D X}=\widehat{A X D}$.
|
| 191 |
+
Les points $F, E, X$ et $A$ sont cocycliques donc $\widehat{F E A}=\widehat{F X A}$. On déduit
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Ce qui donne bien que le triangle FDE est isocèle en F .
|
| 198 |
+
Commentaire des correcteurs On a observé pratiquement que des preuves complètes, même si certaines étaient très longues et calculatoires.
|
| 199 |
+
|
| 200 |
+
Exercice 12. Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $\Omega$ un autre cercle passant par les points $A$ et $B$. La droite (AC) coupe le cercle $\Omega$ en un point $D$ et la tangente à cercle $\Gamma$ en B coupe $\Omega$ en un point E .
|
| 201 |
+
Montrer que les droites $(B C)$ et ( $D E$ ) sont parallèles.
|
| 202 |
+

|
| 203 |
+
|
| 204 |
+
Solution de l'exercice 12 La droite ( BE ) est tangente au cercle $\Omega$ en $B$ donc par le théorème de l'angle tangent, $\widehat{\mathrm{EBA}}=\widehat{\mathrm{BCA}}$. Les points $\mathrm{D}, \mathrm{A}, \mathrm{B}$ et E sont cocycliques donc $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{EBA}}$. On déduit que $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{BCD}}$ ce qui donne bien que les droites ( BC ) et (ED) sont parallèles.
|
| 205 |
+
Commentaire des correcteurs La grande majorité des copies reçues ont fourni des preuves complètes. Cependant, beaucoup d'élèves font des chasses aux angles qui ne sont valides que dans leur cas de figure. Certains élèves ont traité tous les cas, ce qui a été récompensé.
|
| 206 |
+
|
| 207 |
+
Exercice 13. Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B$ ) et ( $C D$ ), et V le point d'intersection des droites (BC) et ( $D A$ ). Soit K le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\mathrm{KU}]$ et de la médiatrice du segment [KV].
|
| 208 |
+
Montrer que les points $\mathrm{U}, \mathrm{V}$ et L sont alignés.
|
| 209 |
+
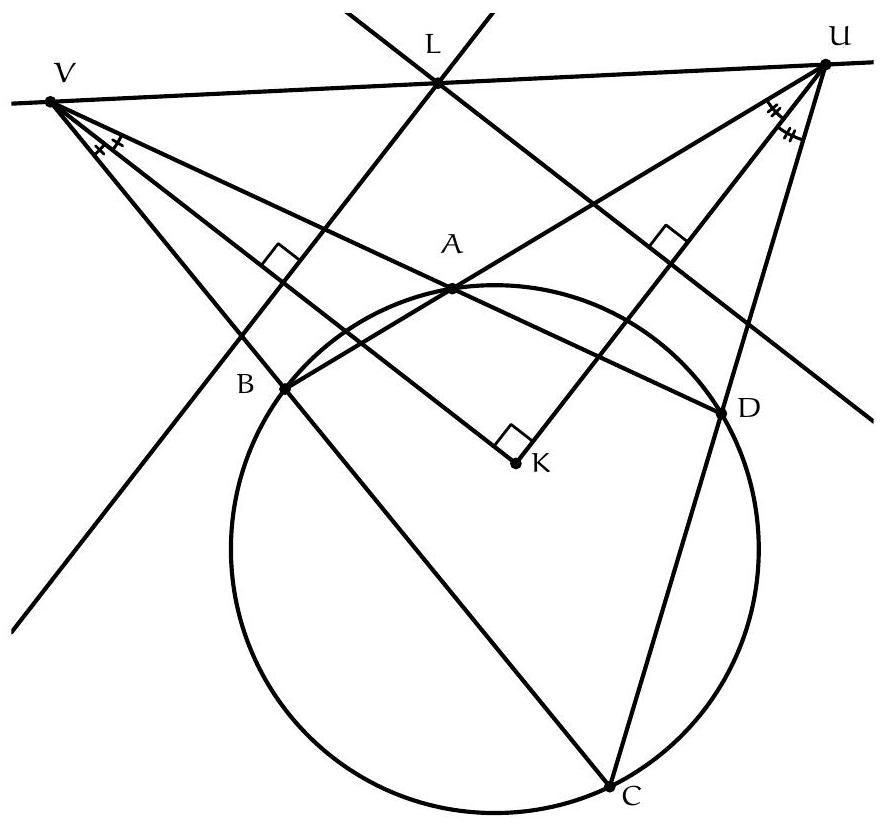
|
| 210 |
+
|
| 211 |
+
Solution de l'exercice 13 Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U , L et V sont alignés, il suffit de montrer que $\widehat{\mathrm{ULV}}=180^{\circ}$. Par le théorème de l'angle au centre, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Il suffit donc de montrer que $\widehat{U K V}=90^{\circ}$.
|
| 212 |
+
La somme des angles du triangle UKV vaut $180^{\circ}$, donc il suffit de montrer que $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. D'une part $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. Or $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. On déduit
|
| 213 |
+
|
| 214 |
+
$$
|
| 215 |
+
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
|
| 216 |
+
$$
|
| 217 |
+
|
| 218 |
+
De la même manière, on obtient
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
Or $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ et
|
| 225 |
+
|
| 226 |
+
$$
|
| 227 |
+
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
|
| 228 |
+
$$
|
| 229 |
+
|
| 230 |
+
Finalement
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
\begin{aligned}
|
| 234 |
+
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
|
| 235 |
+
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
|
| 236 |
+
\end{aligned}
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
ce qui donne le résultat voulu.
|
| 240 |
+
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle. Attention également à ne pas utiliser l'énoncé pour démontrer l'énoncé.
|
| 241 |
+
|
| 242 |
+
Exercice 14. Soit BCDE un carré et soit O son centre. Soit $A$ un point situé à l'extérieur du carré $B C D E$ tel que le triangle $A B C$ est rectangle en $A$. Montrer que le point $O$ appartiant à la bissectrice de l'angle $\widehat{B A C}$.
|
| 243 |
+
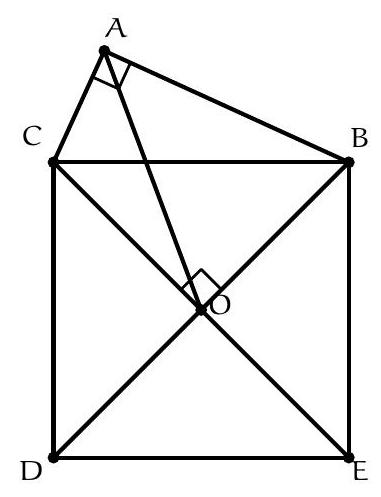
|
| 244 |
+
|
| 245 |
+
Solution de l'exercice 14 Les diagonales du carré BCDE se coupent perpendiculairement en O donc $\widehat{\mathrm{BOC}}=90^{\circ}=\widehat{\mathrm{BAC}}$ donc les points $\mathrm{A}, \mathrm{B}, \mathrm{O}$ et C sont cocycliques. Comme O est sur la médiatrice du segment $[B C]$, $O$ est le pôle Sud de $A$ dans le triangle $A B C$ donc $O$ est sur la bissectrice de l'angle $\widehat{B A C}$. Commentaire des correcteurs L'exercice est plutôt bien réussi, les solutions proposées sont intéressantes mais calculatoires pour certaines.
|
| 246 |
+
|
| 247 |
+
Exercice 15. Soit $\Omega$ et $\Gamma$ deux cercles sécants. On note $A$ une de leurs intersections. Soit d une droite quelconque passant par le point $A$. On note $P$ et $Q$ les intersections respectives de la droite $d$ avec les cercles $\Omega$ et $\Gamma$ différentes de $A$.
|
| 248 |
+
Montrer qu'il existe un point indépendant de la droite d choisie et qui appartient toujours à la médiatrie du segment $[\mathrm{PQ}]$.
|
| 249 |
+
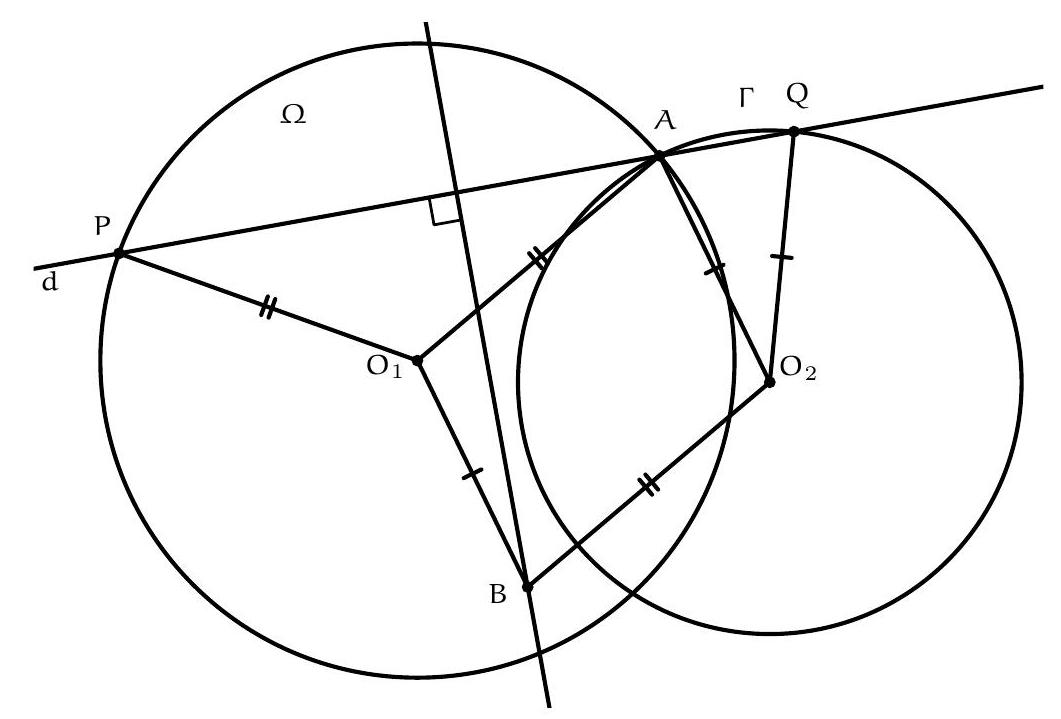
|
| 250 |
+
|
| 251 |
+
Solution de l'exercice 15 Par symétrie, on peut supposer que le rayon du cercle $\Omega$ est supérieur au rayon du cercle $\Gamma$.
|
| 252 |
+
Soit $\mathrm{O}_{1}$ le centre du cercle $\Omega$ et $\mathrm{O}_{2}$ le centre du cercle $\Gamma$. Soit B le point tel que le quadrilatère $\mathrm{AO}_{1} \mathrm{BO}_{2}$ soit un parallélogramme. On va montrer que le point B appartient à la médiatrice du segment $[\mathrm{PQ}]$. Comme le point B est indépendant du choix de la droite d, ceci montrera bien que les médiatrices des semgent $[\mathrm{PQ}]$ passent par un point fixe lorsque la droite $d$ varie.
|
| 253 |
+
Pour montrer que $B P=B Q$, on va montrer que les triangles $\mathrm{PO}_{1} B$ et $\mathrm{BO}_{2} \mathrm{Q}$ sont isométriques. On sait déjà que $\mathrm{O}_{1} \mathrm{P}=\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{2} \mathrm{~B}$ et $\mathrm{O}_{1} \mathrm{~B}=\mathrm{O}_{2} \mathrm{~A}=\mathrm{O}_{2} \mathrm{Q}$. Il reste donc à montrer que $\widehat{\mathrm{BO}_{1} \mathrm{P}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$.
|
| 254 |
+
D'une part
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\widehat{\mathrm{PO}_{1} \mathrm{~B}}=360^{\circ}-\widehat{\mathrm{PO}_{1} \mathrm{~A}}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}=360^{\circ}-\left(180^{\circ}-2 \widehat{\mathrm{O}_{1} \mathrm{AP}}\right)-\widehat{\mathrm{AO} O_{1} B}=180^{\circ}+2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{~B}}
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
D'autre part
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
\widehat{\mathrm{BO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\widehat{\mathrm{AO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\left(180^{\circ}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}\right)=180^{\circ}+\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{2 \mathrm{O}_{2} \mathrm{AQ}}
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
Mais $\widehat{O_{1} \mathrm{AP}}+\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+\widehat{\mathrm{O}_{2} \mathrm{AQ}}=180^{\circ}$ donc $2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+2 \widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360$ et $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}=$ $180^{\circ}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}$ donc
|
| 267 |
+
|
| 268 |
+
$$
|
| 269 |
+
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+180^{\circ}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}+180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360^{\circ}
|
| 270 |
+
$$
|
| 271 |
+
|
| 272 |
+
donc
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
On trouve bien $\widehat{\mathrm{PO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$ et le point B est bien sur la médiatrice de $[\mathrm{PQ}]$.
|
| 279 |
+
Commentaire des correcteurs L'exercice est bien résolu par ceux qui l'ont traité et on a pu observé plusieurs solutions différentes. Beaucoup d'élèves font des chasses aux angles non orientés mais ils n'ont pas été pénalisés.
|
| 280 |
+
|
| 281 |
+
Exercice 16. Soit $A B C$ un triangle, $H$ son orthocentre et $M$ le milieu du segment $[B C]$. Soit $d$ une droite passant par le point $M$. On suppose que $d$ coupe le cercle de diamètre $[A H]$ en $P$ et $Q$. Montrer que l'orthocentre du triangle $A P Q$ est sur le cercle circonscrit du triangle $A B C$.
|
| 282 |
+
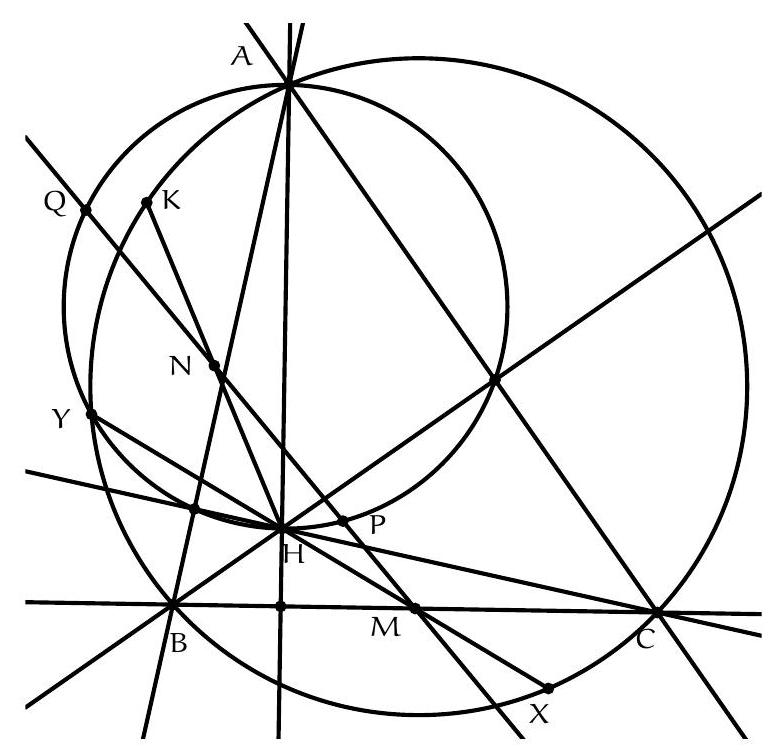
|
| 283 |
+
|
| 284 |
+
Solution de l'exercice 16 Soit N le milieu de $[\mathrm{PQ}]$ et K l'orthocentre du triangle APQ . Si on appelle $\mathrm{K}^{\prime}$ le symétrique de K par rapport au milieu $N$ du segment $[P Q]$, alors $[P Q]$ et $\left[K K^{\prime}\right]$ ont le même milieu $N$ donc $\mathrm{PKQK}^{\prime}$ est un parallélogramme donc $\widehat{\mathrm{K}^{\prime} \mathrm{PA}}=\widehat{\mathrm{K}^{\prime} \mathrm{PQ}}+\widehat{\mathrm{QPA}^{\prime}}=\widehat{\mathrm{PQK}}+\widehat{\mathrm{QPA}^{\prime}}=90^{\circ}(\mathrm{car}(\mathrm{PA})$ et (QK) sont perpendiculaires). De même, $\widehat{K^{\prime} Q A}=90^{\circ}$ donc $K^{\prime}$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A P Q$, autrement dit $K^{\prime}=\mathrm{H}$ : le symétrique de K par rapport au milieu N du segment $[\mathrm{PQ}]$ est H .
|
| 285 |
+
Soit X le symétrique de H par rapport à M et Y la seconde intersection de la droite ( MH ) avec le cercle circonscrit au triangle $A B C$. Par un raisonnement analogue à celui mené précédemment, on sait que $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$ donc $\widehat{H Y A}=\widehat{X Y A}=90^{\circ}$ donc $Y$ est sur le cercle de diamètre $[\mathrm{AH}]$. Puisque $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$, il suffit de montrer que $\widehat{X K A}=90^{\circ}$ pour finir l'exercice.
|
| 286 |
+
On décompose l'angle en trois morceaux : $\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{XKH}}-\widehat{\mathrm{HKQ}}-\widehat{\mathrm{QKA}}$
|
| 287 |
+
Les points $M$ et $N$ sont la milieux respectifs des segments $[H X]$ et $[H K]$ donc les droites (MN) et (KX) sont parallèles. On déduit $\widehat{\mathrm{XKH}}=\widehat{\mathrm{MNH}}=\widehat{\mathrm{PNH}}$.
|
| 288 |
+
Les segments $[\mathrm{PQ}]$ et $[\mathrm{KH}]$ se coupent en leur milieu donc le quadrilatère PHQK est un parallèlogramme. $\mathrm{D}^{\prime}$ où $\widehat{\mathrm{HKQ}}=\widehat{\mathrm{KHP}}=\widehat{\mathrm{NHP}}$.
|
| 289 |
+
Le point Q est l'orthocentre du triangle KPA donc $\widehat{\mathrm{QKA}}=180^{\circ}-\widehat{\mathrm{QPA}}$.
|
| 290 |
+
On déduit
|
| 291 |
+
$\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}-\left(180^{\circ}-\widehat{\mathrm{QPA}}\right)=180^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{NPH}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{APH}}=90^{\circ}$
|
| 292 |
+
car $P$ est sur le cercle de diamètre $[\mathrm{AH}]$. Ainsi, $\widehat{X K A}=90^{\circ}$ donc K est bien sur le cercle circonscrit à ABC.
|
| 293 |
+
Commentaire des correcteurs Ce problème nécessitait un peu de culture. La plupart des élèves ayant essayé le problème ont identifié l'intérêt du cercle d'Euler et des symétriques de l'orthocentre par rapport au milieu des côtés.
|
| 294 |
+
|
| 295 |
+
Exercice 17. Soit $A B C$ un triangle et $I$ le centre de son cercle inscrit. La perpendiculaire à la droite ( $A \mathrm{I}$ ) passant par le point I coupe la droite ( AB ) en un point D et la droite ( AC ) en un point E . On suppose qu'il existe deux points $F$ et $G$ sur le segment $[B C]$ tels que $B A=B F$ et $C A=C G$. Soit $T$ le point d'intersection des cercles circonscrits aux triangles ADF et AEG.
|
| 296 |
+
Montrer que le centre du cercle circonscrit au triangle AIT se trouve sur la droite (BC).
|
| 297 |
+
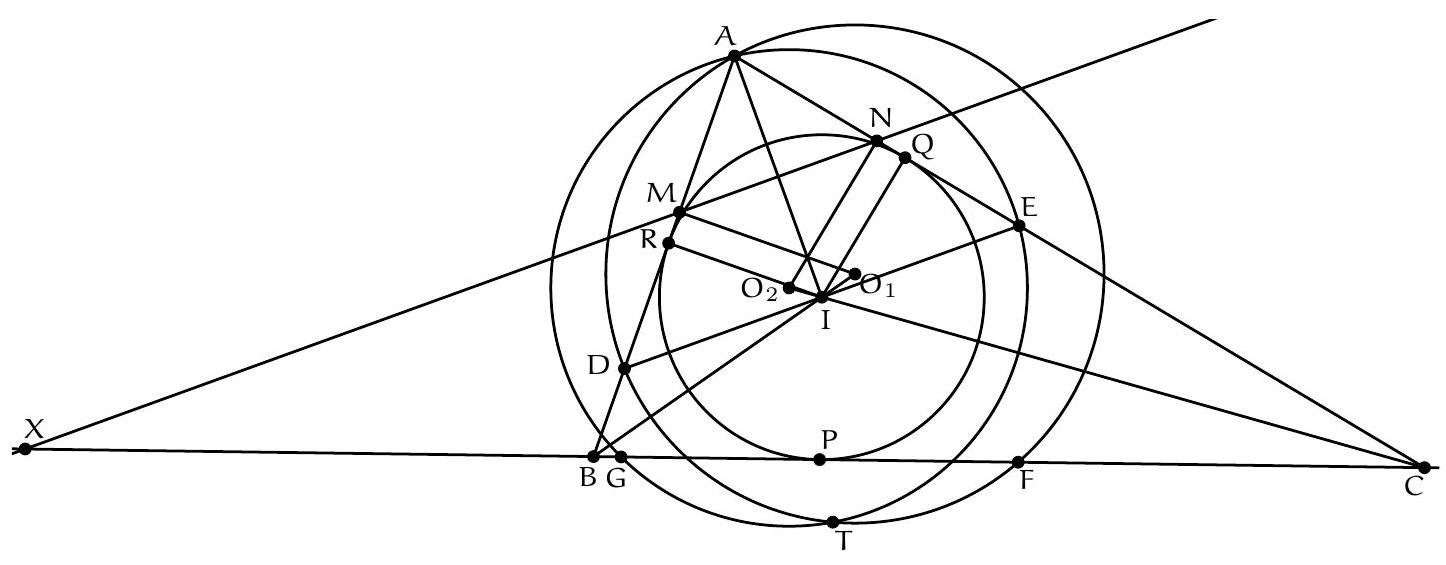
|
| 298 |
+
|
| 299 |
+
Solution de l'exercice 17 Soient $M$ et $N$ les milieux respectifs des segments [AD] et [AE] et soit $X$ le point d'intersection de la droite (MN) (qui est aussi la médiatrice du segment [AI]) avec la droite (BC). Soient $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$ les centres respectifs des cercles circonscrits aus triangles ADF et AEG. On souhaite montrer que le point $X$ est le centre du cercle circonscrit à AIT donc qu'il appartient à la médiatrice du segment [AT], c'est-à-dire à la droite $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$.
|
| 300 |
+
Soient $P, Q$ et $R$ les points de contact respectifs du cercle inscrit au triangle $A B C$ avec les côtés $[B C],[A C]$ et $[A B]$. Le point $O_{1}$ est sur la médiatrice du segment $[A D]$ donc la droite $\left(O_{1} M\right.$ ) est perpendiculaire à la droite ( $A B$ ). Les droites $\left(O_{1} M\right.$ ) et (IR) sont donc parallèles. D'après le théorème de Thalès, on déduit que $\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}$. On a de même $\frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$. De plus, le triangles ABF est isocèle en B donc la médiatrice de $[A F]$ est la bissectrice de $\widehat{A B F}$ donc $\mathrm{O}_{1}$ est sur (BI) et de même $\mathrm{O}_{2}$ est sur (CI).
|
| 301 |
+
D'après le théorème de Ménélaus appliquée aux points $\mathrm{M}, \mathrm{N}, \mathrm{X}$ dans le triangle $A B C$ :
|
| 302 |
+
|
| 303 |
+
$$
|
| 304 |
+
\frac{X B}{X C} \cdot \frac{N C}{N A} \cdot \frac{M A}{M B}=1
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
et en l'appliquant au triangle BIC, l'alignement des points $\mathrm{O}_{1}, \mathrm{O}_{2}$ et $X$ équivaut à $\frac{O_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{X \mathrm{C}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=1$. On souhaite donc montrer cette égalité.
|
| 308 |
+
On sait déjà $\frac{\mathrm{XB}}{\mathrm{XC}}=\frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}}, \frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}, \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$ donc
|
| 309 |
+
|
| 310 |
+
$$
|
| 311 |
+
\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{\mathrm{XC}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{MR}}{\mathrm{MB}} \cdot \frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}} \cdot \frac{\mathrm{NC}}{\mathrm{NQ}}=\frac{\mathrm{MR} \cdot \mathrm{NA}}{\mathrm{MA} \cdot \mathrm{NQ}}=1
|
| 312 |
+
$$
|
| 313 |
+
|
| 314 |
+
car $M A=\frac{1}{2} D A=\frac{1}{2} E A=N A$ et $A R=A Q$ donc $M R=N Q$. Ainsi, $O_{1}, O_{2}, X$ sont alignés.
|
| 315 |
+
Commentaire des correcteurs L'exercice était difficile et a donc été très peu abordé. Quelques élèves ont donné une reformulation intéressante de l'énoncé. Les élèves qui ont cherché l'exercice plus en profondeur ont fait preuve d'inventivité : certains ont utilise le théorème de Desargues, d'autres une inversion.
|
| 316 |
+
|
| 317 |
+
Exercice 18. Soit ABC un triangle, soit O le centre de son cercle circonscrit. Soit I le centre du cercle inscrit au triangle $A B C$ et D le point de tangence de ce cercle avec le segment [AC]. Les droites (OI) et $(A B)$ se coupent en un point $P$. Soit $M$ le milieu de l'arc $A C$ ne contenant pas $B$ et $N$ le milieu de l'arc $B C$ contenant $A$.
|
| 318 |
+
Montrer que les droites (MD) et (NP) se coupent sur le cercle circonscrit à ABC.
|
| 319 |
+
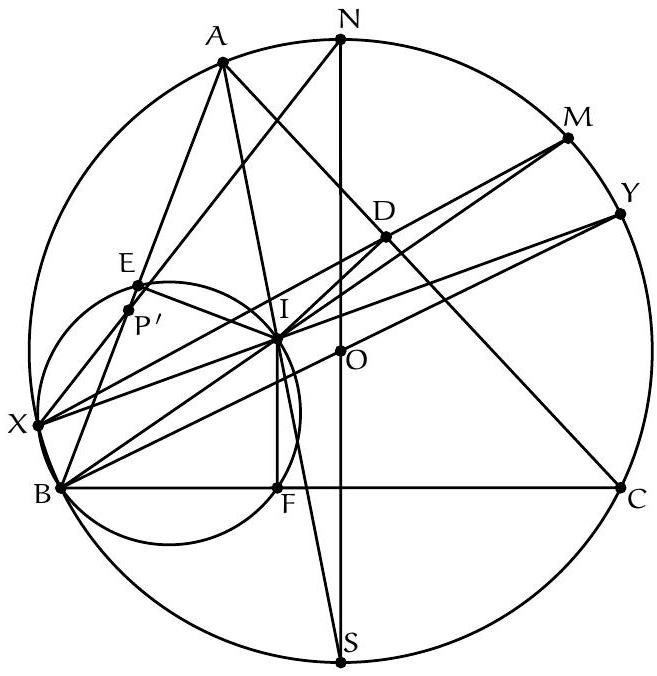
|
| 320 |
+
|
| 321 |
+
Solution de l'exercice 18 Soit $X$ le point d'intersection de la droite (MD) avec le cercle circonscrit au triangle $A B C$ et soit $P^{\prime}$ le point d'intersection de la droite $(X N)$ avec le segment $[A B]$. Soit $S$ le point d'intersection de la bissectrice de l'angle $\widehat{B A C}$ avec le cercle circonscrit au triangle $A B C$. On sait que les points $\mathrm{N}, \mathrm{O}$ et S sont alignés.
|
| 322 |
+
Soit $E$ et $F$ les points de contact respectifs du cercle inscrit au triangles $A B C$ avec les segment $[A B]$ et [BC].
|
| 323 |
+
Le point $M$ est le milieu de l'arc $C A$, il est donc sur la bissectrice de l'angle $\widehat{A X C}$. Le point $D$ est le pied de cette bissectrice. D' après le théorème de la bissectrice, $\frac{A X}{X C}=\frac{D A}{D C}=\frac{A E}{C F}$. Puisque $\widehat{E A X}=\widehat{B A X}=$ $\widehat{B C X}=\widehat{F C X}$, il vient que les triangles $A E X$ et $C F X$ sont semblables donc le point $X$ est le centre de la similitude qui envoie les points $E$ et $F$ sur les points $A$ et $C$, il est donc le point d'intersection des cercles circonscrits aux triangles $A B C$ et EFB. Puisque [BI] est un diamètre du cercle circonscrit au triangle EBF , on déduit $\widehat{\mathrm{IXB}}=90^{\circ}$. Soit $Y$ le point diamétralement opposé au point B dans le cercle circonscrit au triangle ABC . Alors $\widehat{\mathrm{YXB}}=90=\widehat{\mathrm{IXB}}$. Les points $X$, I et $Y$ sont donc alignés.
|
| 324 |
+
D'après le théorème de Pascal appliqué à l'hexagone SABYXN , les points $\mathrm{O}=(\mathrm{BY}) \cap(\mathrm{SN}), \mathrm{I}=$ $(Y X) \cap(A S)$ et $P^{\prime}=(A B) \cap(X N)$ sont alignés. Le point $P^{\prime}$ correspond donc au point d'intersection des droites (OI) et ( $A B$ ) donc $P=P^{\prime}$ ce qui donne bien que les droites (MD) et (NP) se coupent sur le cercle circonscrit au triangle $A B C$.
|
| 325 |
+
Commentaire des correcteurs Des solutions variées ont été proposées : utiliser une inversion de centre $M$ fixant les points $A$, I et $C$ pour montrer que les points $X$, I et $Y$ sont alignés, utiliser $Z$ le centre de l'homotétie positive envoyant le cercle inscrit sur le cercle circonscrit et considérer le cercle mixti-linéaire ou enocre utiliser les coordonnées barycentriques.
|
| 326 |
+
|
French_STS/md/fr-corrigé-commenté-envoi-3.md
ADDED
|
@@ -0,0 +1,393 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+

|
| 2 |
+
|
| 3 |
+
## ENVOi 3 : ARITHMÉTIQUE <br> Corrigé
|
| 4 |
+
|
| 5 |
+
## Exercices Juniors
|
| 6 |
+
|
| 7 |
+
Exercice 1. Trouver tous les entiers $p$ tels que $p, p+2$ et $p+4$ soient tous les 3 premiers?
|
| 8 |
+
Un nombre premier est un entier $\geqslant 2$ qui n'est divisible que par 1 et lui-même.
|
| 9 |
+
Solution de l'exercice 1 Tout d'abord, on peut s'attendre à ce qu'il n'y en ait que très peu. On souhaite obtenir des informations sur ces nombres premiers.
|
| 10 |
+
Notons qu'un nombre premier divisible par 3 est a fortiori égal à 3 . On considère 3 cas en fonction du reste de la division de $p$ par 3 (modulo 3 ):
|
| 11 |
+
$-p=3 k: p$ est divisible par 3 donc $p=3 .\{3,5,7\}$ est bien un triplet de nombres premiers.
|
| 12 |
+
$-p=3 k+1: p+2$ est divisible par 3 et premier donc $p=1$ (impossible).
|
| 13 |
+
$-p=3 k+2: p+4$ est divisible par 3 et premier donc $p=-1$ (impossible).
|
| 14 |
+
D'où $\mathrm{p}=3$.
|
| 15 |
+
Commentaire des correcteurs L'exercice est globalement très bien traité, à part quelques tentatives modulo 10 , l'argument modulo 3 a bien été compris. Attention à ne pas oublier le cas $\mathrm{p}=2$.
|
| 16 |
+
|
| 17 |
+
Exercice 2. Déterminer tous les couples d'entiers $(n, p)$ strictement positifs où $p$ est un nombre premier et tels que $n+p$ soit une puissance de $n$.
|
| 18 |
+
|
| 19 |
+
Une puissance de $n$ est de la forme $\mathrm{n}^{\mathrm{k}}$ pour k entier naturel.
|
| 20 |
+
|
| 21 |
+
Solution de l'exercice 2 Soit $(\mathfrak{p}, \mathfrak{n}$ ) un éventuel couple solution. On dispose d'un entier naturel $k$ tel que
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\mathrm{n}+\mathrm{p}=\mathrm{n}^{\mathrm{k}}
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
Tout d'abord, si $k=0$, alors $n+p=1$. Or $p$ étant premier, $p>1$ et $n \geqslant 0$ donc $n+p=1<p \leqslant p+n$ ce qui est absurde. On a donc $k \geqslant 1$.
|
| 28 |
+
On peut alors réécrire l'équation comme ceci :
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
p=n\left(n^{k-1}-1\right)
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
On obtient que $n$ divise $p$. Comme $p$ est premier, il faut donc que $n=1$ ou $n=p$.
|
| 35 |
+
Si $n=1$, alors $1+p=1$ ce qui est absurde puisque $p \neq 0$.
|
| 36 |
+
On a donc $\mathrm{n}=\mathrm{p}$. Alors $2 \mathrm{p}=\mathrm{p}^{\mathrm{k}}$ donc 2 divise p . Ainsi, $\mathrm{p}=2$ et l'équation devient $2+2=2^{k}$ donc $k=2$. Réciproquement, le couple $(2,2)$ vérifie bien que $2+2=2^{2}$ et donc que $2+2$ est une puissance de 2 .
|
| 37 |
+
|
| 38 |
+
Le seul couple solution est donc (2,2).
|
| 39 |
+
Commentaire des correcteurs L'exercice est bien réussi. Plusieurs approches pouvaient fonctionner. Il était cependant assez facile d'oublier des cas particuliers.
|
| 40 |
+
|
| 41 |
+
Exercice 3. On pose 23 allumettes sur une table et 2 joueurs jouent à un jeu : chacun, à son tour, retire entre 1 et 4 allumettes (inclus). Celui qui prend la dernière gagne. Existe-t-il une stratégie gagnante pour l'un des deux?
|
| 42 |
+
|
| 43 |
+
Une stratégie gagnante est une manière de jouer qui permet à l'un des deux de gagner peu importe comment son adversaire joue.
|
| 44 |
+
|
| 45 |
+
Solution de l'exercice 3 Le $1^{\text {er }}$ joueur possède une stratégie gagnante. La voici :
|
| 46 |
+
|
| 47 |
+
1. J1 prend 3 allumettes : il en reste un multiple de 5
|
| 48 |
+
2. J2 en retire $\mathrm{r} \in\{1,2,3,4\}$
|
| 49 |
+
3. J1 en enlève $5-\mathrm{r}$ : il en reste un multiple de 5
|
| 50 |
+
|
| 51 |
+
Et ainsi de suite. Donc à chaque fois que J 2 joue, il y a un nombre d'allumettes divisible par 5. A chaque fois que J1 joue, en revanche, il y en a un nombre non-divisible par 5 et donc en particulier non nul! Ce qui assure à J 1 de gagner.
|
| 52 |
+
Commentaire des correcteurs L'exercice est très bien réussi, il faut cependant penser à bien détailler la rédaction parfois un peu trop succincte.
|
| 53 |
+
|
| 54 |
+
Exercice 4. Déterminer tous les triplets d'entiers ( $a, b, \mathfrak{n}$ ) strictement positifs vérifiant:
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
a!+b!=2^{n}
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Solution de l'exercice 4 Les factorielles ayant beaucoup de facteurs impairs en commun, on se dit directement qu'obtenir une puissance de 2 va être très contraignant.
|
| 61 |
+
Supposons que $\mathrm{a}, \mathrm{b} \geqslant 3$, 3 divise donc la somme des factorielles et donc $2^{\mathrm{n}}$ : $\mathrm{c}^{\prime}$ est absurde.
|
| 62 |
+
C'est à dire que l'un des deux est dans $\{1,2\}$. Par symétrie, on ne traite que deux cas :
|
| 63 |
+
|
| 64 |
+
1. $a=1$ : encore deux petits cas de figure:
|
| 65 |
+
$-b=1: n=1$
|
| 66 |
+
|
| 67 |
+
- $b \geqslant 2$ : les deux membres n'ont pas la même parité, c'est impossible
|
| 68 |
+
|
| 69 |
+
2. $a=2: b \geqslant 2$ (comme vu au-dessus), quelques cas :
|
| 70 |
+
$-\mathrm{b}=2,3: \mathrm{n}=2,3$
|
| 71 |
+
|
| 72 |
+
- $\mathrm{b} \geqslant 4$ : il y a un problème modulo 4 , impossible
|
| 73 |
+
|
| 74 |
+
D'où : les seules solutions sont dans $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
|
| 75 |
+
Commentaire des correcteurs
|
| 76 |
+
L'exercice plutôt bien réussi. Il ne faut pas oublier de bien préciser que l'on peut supposer $a \geqslant b$ avant d'utiliser cette inégalité dans son raisonnement.
|
| 77 |
+
|
| 78 |
+
Exercice 5. Trouver tous les couples de nombres premiers ( $p, q$ ) tels que :
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\mathrm{p}^{2}\left(\mathrm{p}^{3}-1\right)=\mathrm{q}(\mathrm{q}+1)
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Solution de l'exercice 5 Si $p=q$, alors $p^{4}-p=p+1$. Or $p^{4}=p \cdot p^{3} \geqslant 8 p>2 p+1$ pour tout nombre premier $p$ car $p \geqslant 2$. On a donc $p \neq q$ et donc $p$ et $q$ sont premiers entre eux.
|
| 85 |
+
$p^{2}$ est premier avec $q$ donc d'après le lemme de Gauss, $p^{2} \mid q+1$. On dispose donc de $k \in \mathbb{N}^{*}$ tel que $\mathrm{q}+1=\mathrm{kp}^{2}$.
|
| 86 |
+
Comme q est premier avec $\mathrm{p}^{2}, \mathrm{q} \mid \mathrm{p}^{3}-1=(\mathrm{p}-1)\left(\mathrm{p}^{2}+\mathrm{p}+1\right)$. Donc $\mathrm{q} \mid \mathrm{p}-1$ ou $\mathrm{q} \mid \mathrm{p}^{2}+\mathrm{p}+1$.
|
| 87 |
+
Si $q \mid p-1$, alors
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
\mathrm{p}<\mathrm{kp} \mathrm{p}^{2}-1=\mathrm{q} \leqslant \mathrm{p}-1
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
ce qui est absurde.
|
| 94 |
+
On a donc $\mathrm{q} \mid \mathrm{p}^{2}+\mathrm{p}+1$ donc $\mathrm{kp}^{2}-1=\mathrm{q} \leqslant \mathrm{p}^{2}+\mathrm{p}+1$ soit $(\mathrm{k}-1) \mathrm{p}^{2} \leqslant \mathrm{p}+2$. Si $k=1$, alors $\mathrm{q}=\mathrm{p}^{2}-1=(p-1)(p+1)$ qui n'est premier que si $p=2$.
|
| 95 |
+
On a alors $q=3$ mais $2^{2}\left(2^{3}-1\right)=28 \neq 12=3(3+1)$.
|
| 96 |
+
On en déduit que $k \geqslant 2$ et $p>2$, donc $p+2<p^{2} \leqslant(k-1) p^{2} \leqslant p+2$ ce qui est également absurde.
|
| 97 |
+
Finalement il n'y a pas de solution.
|
| 98 |
+
Commentaire des correcteurs
|
| 99 |
+
Peu d'élèves ont entièrement réussi le problème. On a pu voir beaucoup d'erreurs de divisibilité et bien souvent, le cas $\mathrm{p}=\mathrm{q}$ n'a pas été considéré.
|
| 100 |
+
|
| 101 |
+
Exercice 6. Trouver tous les couples d'entiers strictement positifs ( $\mathrm{m}, \mathfrak{n}$ ) pour lesquels:
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
1+2^{n}+3^{n}+4^{n}=10^{m}
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Solution de l'exercice 6 Cette équation est valable pour tous $n$, $m$, elle est donc valable en la passant modulo un entier $k$, c'est-à-dire en ne considérant que les restes de la division par rapport à $k$.
|
| 108 |
+
On commence par la regarder modulo 3 :
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
1+(-1)^{n}+0+1^{n} \equiv 1^{\mathrm{m}}(\bmod 3) \operatorname{donc}(-1)^{n} \equiv-1
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
Donc n est impair : soit $\mathrm{k} \in \mathbb{N}$ tel que $\mathrm{n}=2 \mathrm{k}+1$.
|
| 115 |
+
On suppose à présent que $\mathrm{n}, \mathrm{m} \geqslant 3$ et on regarde modulo 8 :
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
1+0+3 \cdot 3^{2 k}+0 \equiv 0(\bmod 8) \text { ie } 1+3 \cdot 1 \equiv 0
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
Ce qui est absurde.
|
| 122 |
+
On en déduit que l'un des deux est dans $\{1,2\}$.
|
| 123 |
+
Il suffit alors de traiter les cas $n=1, n=2, m=1$ et $\mathrm{m}=2$.
|
| 124 |
+
Pour $\boldsymbol{n}=1$ on trouve $1+2+3+4=10,(1,1)$ est solution. Pour $n=2,1+4+9+16=30$ n'est pas une puissance de 10 (car 30 est divisible par 3). Comme l'application qui à $n$ associe $1+2^{n}+3^{n}+4^{n}$ est strictement croissante à $m$ fixé on a au plus une solution. Comme $(1,1)$ et $(3,2)$ sont solutions (car $1+2^{3}+3^{3}+4^{3}=1++27+64=100=10^{2}$ ), ce sont donc les seules solutions avec $\mathrm{m}=1$ ou 2 . L'ensemble des solutions est donc $\{(1,1),(2,3)\}$.
|
| 125 |
+
|
| 126 |
+
## Commentaire des correcteurs
|
| 127 |
+
|
| 128 |
+
Même si beaucoup d'élèves ont quasiment réussi l'exercice, peu se retrouvent avec la note maximale : en effet, plusieurs n'ont pas justifié pourquoi, pour $\mathrm{m}=2$, seul $\mathrm{n}=3$ était solution (ce qui pouvait se faire par encadrement ou en utilisant un argument de croissance). La rédaction n'est pas une course, il vaut mieux écrire une page et avoir tous les arguments bien expliqués que de compacter tout en 9 lignes et se retrouver avec une copie peu claire pour le correcteur et souvent incomplète (de plus, souvent les copies compactes sont bien plus compliquées à lire que des copies un peu longues mais bien détaillées). Il ne faut pas oublier de vérifier que les couples obtenus vérifient bien l'équation.
|
| 129 |
+
|
| 130 |
+
Exercice 7. Soit $p \geqslant 3$ un nombre premier. Pour $k \in \mathbb{N}$ vérifiant $1 \leqslant k \leqslant p-1$, le nombre de diviseurs de $\mathrm{kp}+1$ qui sont compris strictement entre $k$ et $p$ est noté $a_{k}$.
|
| 131 |
+
Que vaut $a_{1}+a_{2}+\ldots+a_{p-1}$ ?
|
| 132 |
+
$\underline{\text { Solution de l'exercice } 7}$ La réponse est $p-2$.
|
| 133 |
+
Nous allons montrer que chacun de $\{2, \ldots, \boldsymbol{p}-1\}$ contribue exactement une fois au comptage représenté $\operatorname{par} a_{1}+a_{2}+\ldots+a_{p-1}$.
|
| 134 |
+
Soit $2 \leqslant \mathrm{~m} \leqslant \mathrm{p}-1$ un entier, on se propose de montrer deux choses :
|
| 135 |
+
|
| 136 |
+
1. $m$ est compté au plus une fois
|
| 137 |
+
2. m est bien compté
|
| 138 |
+
m est compté au plus une fois :
|
| 139 |
+
Par l'absurde, on suppose qu'il existe $1 \leqslant i<j \leqslant p-1$ deux entiers vérifiant:
|
| 140 |
+
|
| 141 |
+
- $m \mid i p+1$ et $m>i$
|
| 142 |
+
- $m \mid j p+1$ et $m>j$
|
| 143 |
+
|
| 144 |
+
On a donc $m \mid p(j-i)$ or $\operatorname{pgcd}(m, p)=1$ donc $m \mid j-i$. Cependant, c'est impossible car $0<j-i<$ $j<m$ : m est compté au plus une fois
|
| 145 |
+
m est bien compté :
|
| 146 |
+
On considère les $m-1$ entiers $\{p+1,2 p+1, \ldots,(m-1) p+1\}$.
|
| 147 |
+
Exactement comme précédemment, on voit qu'ils sont 2 à 2 distincts modulo m. De plus, aucun d'entre eux n'est $\equiv 1(\bmod m)$ car si on retire les +1 aucun entier n'est divisible par $m$.
|
| 148 |
+
D'où $m$ est compté une et une fois et cela conclut.
|
| 149 |
+
Commentaire des correcteurs
|
| 150 |
+
Le chemin à suivre a été globalement compris, mais la formalisation de ce raisonnement n'était pas toujours rigoureuse.
|
| 151 |
+
|
| 152 |
+
Exercice 8. Déterminer tous les entiers $n \geqslant 1$ tels qu'il existe une permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ de $(1,2, \ldots, \mathbf{n})$ vérifiant la condition suivante :
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
\mathrm{k} \mid \mathrm{a}_{1}+\mathrm{a}_{2}+\ldots+\mathrm{a}_{\mathrm{k}}
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
pour tout $k \in\{1,2, \ldots, n\}$.
|
| 159 |
+
|
| 160 |
+
Solution de l'exercice 8 On commence par regarder ce qu'il se passe pour $\mathrm{n}=1,2,3: \mathfrak{n}=1,3$ sont solutions mais $\mathrm{n}=2$ ne l'est pas. Soit $\mathrm{n}>3$ vérifiant la propriété de l'énoncé.
|
| 161 |
+
On a $n \left\lvert\, a_{1}+a_{2}+\ldots+a_{n}=1+2+\ldots+n=\frac{n(n+1)}{2}\right.$ et donc $\frac{n+1}{2} \in \mathbb{Z}: n$ est impair.
|
| 162 |
+
Ensuite $n-1 \left\lvert\, a_{1}+a_{2}+\ldots+a_{n-1}=\frac{n(n+1)}{2}-a_{n}\right.$.
|
| 163 |
+
$\operatorname{Et} n-1 \left\lvert\, \frac{(n-1)(n+1)}{2}\right.$ donc $n-1 \left\lvert\, \frac{n+1}{2}-a_{n}\right.$.
|
| 164 |
+
Cependant, il y a un "problème de taille" : $-(n-1)<\frac{n+1}{2}-a_{n}<n-1$
|
| 165 |
+
ce qui $n$ 'est pas absurde, mais implique que $a_{n}=\frac{n+1}{2}$.
|
| 166 |
+
On poursuit (pas de souci, $\mathrm{n}>3$ ) :
|
| 167 |
+
$n-2 \left\lvert\, \frac{n(n+1)}{2}-\frac{n+1}{2}-a_{n-1}=\frac{(n-1)(n+1)}{2}-a_{n-1}\right.$.
|
| 168 |
+
Et $n-2 \left\lvert\, \frac{(n-2)(n+1)}{2}\right.$ donc $n-2 \left\lvert\, \frac{n+1}{2}-a_{n-1}\right.$.
|
| 169 |
+
Comme précédemment, $-(n-2)<\frac{n+1}{2}-a_{n-1}<n-2$ et donc $a_{n}=a_{n-1}=\frac{n+1}{2}$ : c'est absurde.
|
| 170 |
+
Les seules solutions sont donc bien 1 et 3 .
|
| 171 |
+
Commentaire des correcteurs
|
| 172 |
+
Peu d'élèves ont entièrement réussi le problème. Les solutions sont assez diverses dans l'ensemble même si elles tournent autour de la même idée.
|
| 173 |
+
|
| 174 |
+
Exercice 9. Existe-t-il des entiers $\mathbf{a}$ et $b$ pour lesquels : $\mathbf{a}^{5} \mathbf{b}+3$ et $\mathbf{a b}^{5}+3$ sont tous deux des cubes parfaits?
|
| 175 |
+
|
| 176 |
+
Un cube parfait est un entier $n$ pour lequel il existe $m \in \mathbb{Z}$ tel que : $n=m^{3}$.
|
| 177 |
+
|
| 178 |
+
Solution de l'exercice 9 Nous allons montrer qu'il n'y a pas d'entiers a et b satisfaisant les conditions du problème.
|
| 179 |
+
Soient $a$ et $b$ des entiers tels que $a^{5} b+3$ et $a b^{5}+3$ sont des cubes parfaits. Soit $m$ et $n$ des entiers tels que $a^{5} b+3=m^{3}$ et $a b^{5}+3=n^{3}$. Supposons que $3 \mid n$. Alors $27 \mid n$. De plus $3 \mid a b^{5}$ donc $3 \mid a$ ou $3 \mid b^{5}$. Si $3 \mid a$, alors $3^{5} \mid a^{5}$ donc $3 \mid a^{5} b+3=m^{3}$. Mais alors $27 \mid m^{3}$ et $27 \mid a^{5}$ donc $27 \mid m^{3}-a^{5} b=3$ ce qui est absurde. Si $3 \mid b$, alors $3^{5} \mid b^{5}$ et en particulier $27 \mid n^{3}-a b^{5}=3$ ce qui est aussi absurde. On déduit que 3 ne divise pas n et de même 3 ne divise pas m . Si $3 \mid \mathrm{a}$, alors $3 \mid \mathrm{m}$, n ce qui est exclut. On déduit donc que 3 ne divise pas non plus a et b. Notons que
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
m^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\left(a^{2}+b^{2}\right)
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
Comme $a$ et $b$ ne sont pas divisibles par $3, a^{2} \equiv b^{2} \equiv 1 \bmod 3$ donc $3 \mid a^{2}-b^{2}=(a-b)(a+b)$ et donc $3 \mid m^{3}-n^{3}$. D'après le théorème de Fermat, $m^{3} \equiv m \bmod 3$ et $n^{3} \equiv n \bmod 3$. On déduit que $\mathrm{m} \equiv \mathrm{m}^{3} \equiv \mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. Il vient que
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
m^{2}+m n+n^{2} \equiv 3 m^{2}=0 \quad \bmod 3
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
On déduit que 3 divise $m-n$ et 3 divise $m^{2}+m n+n^{2}$ donc $9 \mid(m-n)\left(m^{2}+m n+n^{2}\right)=m^{3}-n^{3}$. Il vient que $9 \mid a b(a-b)(a+b)\left(a^{2}+b^{2}\right)$. Mais 3 ne divise pas $a, b$ et $a^{2}+b^{2} \equiv 2 \bmod 3$ donc 3 ne divise pas non plus $a^{2}+b^{2}$ et donc 9 non plus. On déduit que $9 \mid a^{2}-b^{2}$, soit $a^{2} \equiv b^{2} \bmod 9$. Ainsi
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\mathrm{m}^{3}=\mathrm{a}^{5} \mathrm{~b}+3 \equiv \mathrm{a}^{3} \cdot \mathrm{a}^{2} \cdot \mathrm{~b}+3 \equiv \mathrm{a}^{3} \mathrm{~b}^{2} \cdot \mathrm{~b}+3 \equiv(\mathrm{ab})^{3}+3 \quad \bmod 9
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Or les cubes modulo 9 prennent uniquement les valeurs $-1,0$ et 1 . On ne peut donc avoir $\mathrm{m}^{3}-(a b)^{3} \equiv 3$ mod 9. La condition de l'énoncé ne peut donc pas être satisfaite, comme annoncé.
|
| 198 |
+
|
| 199 |
+
## Commentaire des correcteurs
|
| 200 |
+
|
| 201 |
+
Plusieurs élèves se sont contentés de tester tous les cas, d'autres ont fourni de bons raisonnements par l'absurde. Globalement le problème est bien réussi par ceux qui l'ont abordé.
|
| 202 |
+
|
| 203 |
+
## Exercices Seniors
|
| 204 |
+
|
| 205 |
+
Exercice 10. Trouver tous les triplets ( $\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
|p-q|,|q-r|,|r-p|
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
soient également des nombres premiers.
|
| 212 |
+
|
| 213 |
+
Solution de l'exercice 10 Notons que les trois nombres doivent être deux à deux distincts puisque 0 n'est pas un nombre premier. On peut donc supposer, quitte à échanger l'ordre des variables, que $p>q>r$. Un nombre premier est impair ou égal à 2 .
|
| 214 |
+
On suppose que $p, q$ et $r$ sont tous impairs. Alors $p-q, q-r$ et $r-p$ sont pairs. Comme leur valeur absolue est première, ces nombres valent tous 2 . Ainsi les entiers $p, p+2$ et $p+4$ sont premiers. Si $p$ est divisible par 3 , alors $\mathrm{p}=3$ et $\mathrm{q}=5$ et $\mathrm{r}=7$.
|
| 215 |
+
Cependant, le triplet $(3,5,7)$ n'est pas solution du problème : $7-3=4$ n'est pas premier.
|
| 216 |
+
Si $p$ n'est pas divisible par 3 , alors $p$ est de la forme $3 k+1$ ou $3 k+2$. Le premier cas implique que $p+2$ soit divisible par 3 donc $p+2=3$ mais $p=1$ n'est pas un nombre premier. Le deuxième cas implique que $p+4$ soit divisible par 3 , mais $p+4=3$ ne donne pas de solution strictement positive.
|
| 217 |
+
On suppose que $r=2$. Alors $p$ et $q$ sont impaires et $p-q$ est pair et premier donc égal à 2 . Il vient que $q+2$, $q$ et $q-2$ sont tous les trois des nombres premiers. D'après le cas précédent, cela implique que $\boldsymbol{q}-2=3$ donc $p=7$. Réciproquement, le triplet $(p, q, r)=(2,5,7)$ et ses permutations sont donc bien solutions au problème.
|
| 218 |
+
|
| 219 |
+
Les seuls triplets solutions sont donc $(2,5,7)$ ainsi que ses permutations.
|
| 220 |
+
Commentaire des correcteurs
|
| 221 |
+
Beaucoup d'élèves ont les idées majeures, mais perdent bêtement des points pour la rédaction. Il faut toujours vérifier que les solutions obtenues satisfont bien l'énoncé. Certains ont affirmé sans aucune justification que si $p, p+2$ et $p+4$ sont premiers alors $p=3$. De même certains ont dit qu'on ne peut pas avoir $|\mathrm{p}-\mathrm{q}|=|\mathrm{q}-\mathrm{r}|=|\mathrm{r}-\mathrm{p}|=2$ sans le justifier, ce qui était assez clair (on peut supposer $p>q>r$ par exemple). Il vaut mieux un peu plus détailler les points importants pour ne pas perdre de points.
|
| 222 |
+
|
| 223 |
+
Exercice 11. Trouver tous les nombres entiers $z \in \mathbb{Z}$ tels que
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
2^{z}+2=r^{2}
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
où $r \in \mathbb{Q}$ est un nombre rationnel.
|
| 230 |
+
Un nombre rationnel est un nombre qui s'écrit sous la forme $\frac{\mathrm{a}}{\mathrm{b}}$ avec $\mathrm{a}, \mathrm{b}$ des entiers et $\mathrm{b} \neq 0$.
|
| 231 |
+
Solution de l'exercice 11 Notons que si $(z, r)$ est un couple solution, $(z,-r)$ est également un couple solution. On peut donc supposer pour la suite que $r \geqslant 0$. Etant donné que $2^{z}+z>0$, on a même $r>0$. On pose $r=\frac{a}{b}$, avec $a$ et $b$ des entiers strictement positifs et premiers entre eux.
|
| 232 |
+
Si $z \geqslant 0$, alors $2^{z}+2$ est entier donc r est entier et $\mathrm{b}=1$. On doit désormais résoudre l'équation $2^{z}+2=a^{2}$ dans les entiers positifs. Si $z \geqslant 2$, alors l'équation vue modulo 4 donne $a^{2} \equiv 2 \bmod 4$ ce qui n'a pas de solution puisqu'un carré est toujours congru à 0 ou à 1 modulo 4 . On déduit que $z=0$ ou $z=1$. Dans le premier cas, on obtient $3=\mathfrak{a}^{2}$ qui n'admet pas de solution entière. Dans le deuxième cas on trouve $4=a^{2}$ soit $a=2$. Réciproquement, les couples $(1,-2)$ et $(1,2)$ satisfont bien l'équation.
|
| 233 |
+
$\mathrm{Si} z<0$, alors on pose $z^{\prime}=-z$, avec $z^{\prime}>0$. L'équation dévient $\frac{1}{2^{z^{\prime}}}+2=\frac{a^{2}}{b^{2}}$. En supprimant les dénominateurs on obtient
|
| 234 |
+
|
| 235 |
+
$$
|
| 236 |
+
b^{2}\left(1+2^{z^{\prime}+1}\right)=a^{2} \cdot 2^{z^{\prime}}
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
Puisque $1+2^{z^{\prime}+1}$ est premier avec $2^{z^{\prime}}$, par le lemme de Gauss on obtient que $2^{z^{\prime}+1}+1$ divise $a^{2}$. Comme $a$ et $b$ sont premiers entre eux, par le lemme de Gauss on obtient aussi que $a^{2}$ divise $1+2^{z^{\prime}+1}$. On déduit que $a^{2}=2^{z^{\prime}+1}+1$, que l'on réécrit $2^{z^{\prime}+1}=(a-1)(a+1)$. On déduit que $a+1$ et $a-1$ sont tous les deux des puissances de 2 dont la différence vaut 2 . On déduit donc que $a+1=4$ et $a-1=2$ soit $\mathrm{a}=3$ et $z^{\prime}=2$. Ainsi $\mathrm{b}=2$. Réciproquement, les couples $\left(-2,-\frac{3}{2}\right)$ et $\left(-2, \frac{3}{2}\right)$ sont bien solutions de l'équation. Les solutions sont donc $\left\{\left(-2,-\frac{3}{2}\right),\left(-2, \frac{3}{2}\right),(1,-2),(1,2)\right\}$.
|
| 240 |
+
Commentaire des correcteurs
|
| 241 |
+
Un tiers des élèves a écrit que $x^{2}=4$ implique que $x=2$ et oublie donc la solution $x=-2$. Quelques élèves n'ont pas vu que l'on se plaçait dans $\mathbb{Z}$ et $\mathbb{Q}$ et ont juste regardé l'équation sur les entiers positifs. Mis à part cela, l'exercice est assez bien réussi.
|
| 242 |
+
|
| 243 |
+
Exercice 12. Déterminer tous les triplets d'entiers $(\mathfrak{a}, \mathfrak{b}, \mathfrak{n}$ ) strictement positifs vérifiant:
|
| 244 |
+
|
| 245 |
+
$$
|
| 246 |
+
a!+b!=2^{n}
|
| 247 |
+
$$
|
| 248 |
+
|
| 249 |
+
Solution de l'exercice 12 Les factorielles ayant beaucoup de facteurs impairs en commun, on se dit directement qu'obtenir une puissance de 2 va être très contraignant.
|
| 250 |
+
Supposons que $\mathrm{a}, \mathrm{b} \geqslant 3,3$ divise donc la somme des factorielles et donc $2^{\mathrm{n}}$ : $\mathbf{c}^{\text {'est absurde. }}$ C'est à dire que l'un des deux est dans $\{1,2\}$. Par symétrie, on ne traite que deux cas :
|
| 251 |
+
|
| 252 |
+
1. $a=1$ : encore deux petits cas de figure :
|
| 253 |
+
$-\mathrm{b}=1: \mathrm{n}=1$
|
| 254 |
+
$-\mathrm{b} \geqslant 2$ : les deux membres n'ont pas la même parité, c 'est impossible
|
| 255 |
+
2. $a=2: b \geqslant 2$ (comme vu au-dessus), quelques cas :
|
| 256 |
+
$-\mathrm{b}=2,3: \mathbf{n}=2,3$
|
| 257 |
+
$-\mathrm{b} \geqslant 4$ : il y a un problème modulo 4 , impossible
|
| 258 |
+
D'où : les seules solutions sont dans $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
|
| 259 |
+
Commentaire des correcteurs
|
| 260 |
+
Il y a eu pas mal d'erreurs de logique. Ce n'est pas parce que l'on ne peut pas avoir $\mathbf{a} \geqslant 3$ et $\mathbf{b} \geqslant 3$ en même temps qu'on a forcément $\mathrm{a}<3$ et $\mathrm{b}<3$ (on a plutôt $\mathrm{a}<3$ ou $\mathrm{b}<3$ ). 1 est une puissance de 2 qu'il ne faut pas oublier et 0 n'est pas dans $\mathbb{N}^{*}$ et 1 est un diviseur impair de 2 qu'il ne faut pas oublier non plus. Ne pas oublier de rappeller les solutions symétriques si on suppose $a \geqslant b$.
|
| 261 |
+
|
| 262 |
+
Exercice 13. Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\operatorname{pgcd}(x, y, z)<\operatorname{pgcd}(x+y, y+z, z+x)
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
Solution de l'exercice 13 Notons que puisque $\operatorname{pgcd}(x, y, z)$ divise chacun des $x, y, z$, il divise également $\operatorname{pgcd}(x+y, y+z, z+x)$.
|
| 269 |
+
On remarque que si le triplet $(x, y, z)$ est solution, alors les triplets $(k x, k y, k z)$ sont solutions pour tout $k \in \mathbb{N}^{*}$. On peut donc supposer, quitte à diviser chaque variable par $\operatorname{pgcd}(x, y, z)$, que les entiers $x, y, z$ sont premiers entre eux dans leur ensemble. En particulier ils ne sont pas tous pairs.
|
| 270 |
+
Soit $d=\operatorname{pgcd}(x+y, y+z, z+x)$. Alors d divise $(x+y)+(x+z)-(y+z)=2 x$ et de même $d$ divise $2 y$ et $2 z$. Donc $d$ divise $\operatorname{pgcd}(2 x, 2 y, 2 z)=2 \operatorname{pgcd}(x, y, z)=2$. On déduit que $d=1$ ou $d=2$. Mais comme $\mathrm{d}>1, \mathrm{~d}=2$ donc les entiers $x, y, z$ sont tous de même parité. Comme ils ne sont pas tous paires, ils sont tous impaires.
|
| 271 |
+
Réciproquement, si $x, y$ et $z$ sont tous les trois impaires, étant donné que $\operatorname{pgcd}(x, y, z)$ et 2 sont premiers entre eux et divisent $\operatorname{pgcd}(x+y, y+z, z+x)$, on a bien
|
| 272 |
+
|
| 273 |
+
$$
|
| 274 |
+
\operatorname{pgcd}(x, y, z)<2 \operatorname{pgcd}(x, y, z) \leqslant \operatorname{pgcd}(x+y, y+z, z+x)
|
| 275 |
+
$$
|
| 276 |
+
|
| 277 |
+
Les triplets solutions sont donc les triplets $\left\{(k x, k y, k z), k \in \mathbb{N}^{*}, x, y, z\right.$ impaires $\}$. Commentaire des correcteurs
|
| 278 |
+
Les correcteurs étaient très satisfait des différentes approches des élèves. Quelques erreurs sont à noter : ce n'est pas parce que $2 \mathrm{n} \equiv k$ mod a que $k$ est pair et ce $n$ 'est pas parce que $\operatorname{pgcd}(x, y, z)=\operatorname{pgcd}(x+$ $y, y+z, z+x)$ que $(x, y, z)=(x+y, y+z, z+x)$.
|
| 279 |
+
|
| 280 |
+
Exercice 14. Existe-t-il des entiers $a$ et $b$ pour lesquels : $\mathbf{a}^{5} \mathbf{b}+3$ et $a^{5}+3$ sont tous deux des cubes parfaits?
|
| 281 |
+
|
| 282 |
+
Un cube parfait est un entier $n$ pour lequel il existe $m \in \mathbb{Z}$ tel que : $\mathfrak{n}=\mathrm{m}^{3}$.
|
| 283 |
+
|
| 284 |
+
Solution de l'exercice 14 Nous allons montrer qu'il n'y a pas d'entiers a et b satisfaisant les conditions du problème.
|
| 285 |
+
Soient $a$ et $b$ des entiers tels que $a^{5} b+3$ et $a b^{5}+3$ sont des cubes parfaits. Soit $m$ et $n$ des entiers tels que $a^{5} b+3=m^{3}$ et $a b^{5}+3=n^{3}$. Supposons que $3 \mid n$. Alors $27 \mid n$. De plus $3 \mid a b^{5}$ donc $3 \mid a$ ou $3 \mid b^{5}$. Si $3 \mid a$, alors $3^{5} \mid a^{5}$ donc $3 \mid a^{5} b+3=m^{3}$. Mais alors $27 \mid m^{3}$ et $27 \mid a^{5}$ donc $27 \mid m^{3}-a^{5} b=3$ ce qui est absurde. Si $3 \mid b$, alors $3^{5} \mid b^{5}$ et en particulier $27 \mid n^{3}-a b^{5}=3$ ce qui est aussi absurde. On déduit que 3 ne divise pas $n$ et de même 3 ne divise pas $m$. Si $3 \mid a$, alors $3 \mid \mathrm{m}$, n ce qui est exclut. On déduit donc que 3 ne divise pas non plus $a$ et $b$. Notons que
|
| 286 |
+
|
| 287 |
+
$$
|
| 288 |
+
m^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\left(a^{2}+b^{2}\right)
|
| 289 |
+
$$
|
| 290 |
+
|
| 291 |
+
Comme $a$ et $b$ ne sont pas divisibles par $3, a^{2} \equiv b^{2} \equiv 1 \bmod 3$ donc $3 \mid a^{2}-b^{2}=(a-b)(a+b)$ et donc $3 \mid \mathrm{m}^{3}-\mathrm{n}^{3}$. D'après le théorème de Fermat, $\mathrm{m}^{3} \equiv \mathrm{~m} \bmod 3$ et $\mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. On déduit que $\mathrm{m} \equiv \mathrm{m}^{3} \equiv \mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. Il vient que
|
| 292 |
+
|
| 293 |
+
$$
|
| 294 |
+
m^{2}+m n+n^{2} \equiv 3 m^{2}=0 \quad \bmod 3
|
| 295 |
+
$$
|
| 296 |
+
|
| 297 |
+
On déduit que 3 divise $m-n$ et 3 divise $m^{2}+m n+n^{2}$ donc $9 \mid(m-n)\left(m^{2}+m n+n^{2}\right)=m^{3}-n^{3}$. Il vient que $9 \mid a b(a-b)(a+b)\left(a^{2}+b^{2}\right)$. Mais 3 ne divise pas $a, b$ et $a^{2}+b^{2} \equiv 2 \bmod 3$ donc 3 ne divise pas non plus $a^{2}+b^{2}$ et donc 9 non plus. On déduit que $9 \mid a^{2}-b^{2}$, soit $a^{2} \equiv b^{2} \bmod 9$. Ainsi
|
| 298 |
+
|
| 299 |
+
$$
|
| 300 |
+
\mathrm{m}^{3}=\mathrm{a}^{5} \mathrm{~b}+3 \equiv \mathrm{a}^{3} \cdot \mathrm{a}^{2} \cdot \mathrm{~b}+3 \equiv \mathrm{a}^{3} \mathrm{~b}^{2} \cdot \mathrm{~b}+3 \equiv(\mathrm{ab})^{3}+3 \quad \bmod 9
|
| 301 |
+
$$
|
| 302 |
+
|
| 303 |
+
Or les cubes modulo 9 prennent uniquement les valeurs $-1,0$ et 1 . On ne peut donc avoir $\mathrm{m}^{3}-(a b)^{3} \equiv 3$ mod 9. La condition de l'énoncé ne peut donc pas être satisfaite, comme annoncé.
|
| 304 |
+
Commentaire des correcteurs
|
| 305 |
+
Beaucoup d'élèves ont une solution brutale qui consiste à regarder les paires $\left(\mathrm{ab}^{5}, \mathrm{ba}^{5}\right)$ modulo 9 d 'une façon ou d'une autre, ce n'est pas forcément une mauvaise chose mais il est plus subtil d'utiliser le petit théorème de Fermat en compétition pour ne pas perdre de temps (et parce que souvent les études ne sont pas exhaustives). La plupart des élèves ont une solution légèrement diff��rente du corrigé qui consiste à remarquer que $a^{5} b+3$ et $b^{5} a+3$ ne peuvent pas être congrus à des cubes en même temps $\bmod 9$.
|
| 306 |
+
|
| 307 |
+
Exercice 15. Soit $p$ un nombre premier impair, $h<p$ un entier, $e \in\{1,2\}$.
|
| 308 |
+
On pose $n=h \cdot p^{e}+1$ et on suppose que:
|
| 309 |
+
|
| 310 |
+
$$
|
| 311 |
+
\left\{\begin{array}{r}
|
| 312 |
+
n \mid 2^{n-1}-1 \\
|
| 313 |
+
n \nmid 2^{h}-1
|
| 314 |
+
\end{array}\right.
|
| 315 |
+
$$
|
| 316 |
+
|
| 317 |
+
Montrer que n est premier.
|
| 318 |
+
Solution de l'exercice 15 Soit $\omega$ l'ordre de 2 modulo $n$. Par hypothèse, $\omega$ divise $n-1$ mais $\omega$ ne divise pas $h=\frac{n-1}{p^{e}}$, donc $p$ divise $\omega$.
|
| 319 |
+
$\omega$ divise $\phi(n)$ par le théorème d'Euler donc $p$ divise $\phi(n)$. Evidemment, $p$ ne divise pas $n$ donc il existe q premier qui divise n avec $\mathrm{q}=1(\bmod \mathrm{p})$ (d'après la formule donnant $\phi)$
|
| 320 |
+
On écrit $\mathrm{n}=\mathrm{q}^{\mathrm{a}} \mathrm{N}$ où N est premier avec q . Modulo p on a $1=1^{\mathrm{a}} * \mathrm{~N}$ donc $\mathrm{N}=1(\bmod \mathrm{p})$. On va montrer que $\mathrm{n}=\mathrm{q}$.
|
| 321 |
+
Dès lors, si $n \neq q$, soit $a \geqslant 2$ soit $N \geqslant p+1$ et donc $n \geqslant(p+1)^{2}>p^{2}+1>p h+1$ donc $e=2$ et le raisonnement montre que soit $a=1$, soit $N=1$ et dans tous les cas $a \leqslant 2$ et $N<p^{2}$.
|
| 322 |
+
Traitons deux cas :
|
| 323 |
+
|
| 324 |
+
- Si $a=2, n \equiv q^{2} \equiv(1+p k)^{2} \equiv 1+2 k p(\bmod p)$ où $q=1+k p$. Or $n \equiv 1\left(\bmod p^{2}\right)$ donc $p$ divise $2 k ; p$ divise $k$ et donc $q \geqslant p^{2}+1$ et $n=q^{2}>p^{3}+1>p^{2} h+1=n$, contradiction
|
| 325 |
+
- Si $a=1, q=1+k p, N=1+l p$ avec $k, l>0(\operatorname{car} q \equiv N \equiv 1(\bmod p))$. On a obligatoirement $k, l<p$ car sinon $n=q N \geqslant\left(1+p^{2}\right)(1+p)>p^{3}+1>p^{2} h+1=n$. De plus $1+(k+l) p \equiv n \equiv 1$ $\left(\bmod p^{2}\right)$ donc $k+l=p$. Un parmi $k$ et $l$ est donc impair, ce qui oblige $q$ ou $N$ pair, donc dans tous les cas $n$ est pair, ce qui contredit $n \mid 2^{n-1}-1$.
|
| 326 |
+
|
| 327 |
+
Dans tous les cas $\mathrm{n}=\mathrm{q}$ est premier.
|
| 328 |
+
Commentaire des correcteurs
|
| 329 |
+
Les correcteurs ont noté beaucoup d'erreurs d'inattention et de mauvaises utilisations de l'ordre d'un élément modulo $n$. Certains élèves ont été surpris en train d'essayer d'arnaquer les correcteurs, ce qui est inutile et ne permettra sûrement pas de gagner des points en compétition.
|
| 330 |
+
|
| 331 |
+
Exercice 16. Soit $m, n \geqslant 2$ des entiers vérifiant la propriété suivante:
|
| 332 |
+
|
| 333 |
+
$$
|
| 334 |
+
a^{n} \equiv 1 \quad(\bmod m) \quad a=1, \ldots, n
|
| 335 |
+
$$
|
| 336 |
+
|
| 337 |
+
Prouver que $m$ est un nombre premier et que $\mathrm{n}=\mathrm{m}-1$.
|
| 338 |
+
|
| 339 |
+
Solution de l'exercice 16 Commençons par supposer que $m=p$ est un nombre premier. On doit donc montrer $n=p-1$. Si $n \geqslant p$, on a $p^{n} \equiv 1(\bmod p)$, une évidente contradiction. Donc $n<p$.
|
| 340 |
+
Considérons $T=X^{n}-1$ le polynôme de $\mathbb{Z} / p \mathbb{Z}[X]$. Il a pour racines par hypothèse $1, \ldots, n$, qui sont au nombre de $n$ et distinctes, et, puisque $\mathbb{Z} / p \mathbb{Z}$ est intègre, et que $T$ est de degré $n$, ce sont les seules. Donc $T=(X-1) \cdot \ldots \cdot(X-n)$. En regardant le coefficient en $X^{n-1}$ de $T$, on voit que $0 \equiv 1+\ldots+n(\bmod p)$ par les formules de Viète. Ainsi, $p \left\lvert\, \frac{n(n+1)}{2}\right.$, donc (puisque $n<p$ ) on a nécessairement $n=p-1$.
|
| 341 |
+
|
| 342 |
+
Revenons au cas général. Soit $p$ un diviseur premier de $m$. On a $n=p-1$ puisque l'hypothèse de l'énoncé reste vraie pour $m=p$. Dès lors, si $q$ est un autre diviseur premier de $m, q-1=n=p-1$ et $q=p$. Il reste à voir que $m$ ne peut pas être une puissance de $p$ autre que $p$. Il suffit clairement de le voir pour $\mathrm{m}=\mathrm{p}^{2}$. Or $(p-1)^{\mathrm{p}-1} \equiv(-1)^{\mathrm{p}-1}+\mathrm{p} \times(-1)^{\mathfrak{p}-2}\left(\mathrm{p}^{\mathrm{p}}\right)\left(\bmod \mathrm{p}^{2}\right)$ par le binôme de Newton. Puisque $p-1$ est pair, et que $p^{2} \nmid-p(p-1)$, on a bien $(p-1)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. Ceci achève la démonstration.
|
| 343 |
+
Commentaire des correcteurs
|
| 344 |
+
Il y avait pas mal de bonnes copies mais plein de petites erreurs donc les notes se trouvent majoritairement entre 4 et 7 .
|
| 345 |
+
|
| 346 |
+
Exercice 17. Soit $S$ un ensemble non vide d'entiers strictement positifs vérifiant la propriété suivante : Pour tous entiers $a, b \in S$, l'entier $a b+1$ appartient aussi à $S$.
|
| 347 |
+
Montrer que l'ensemble des nombres premiers ne divisant aucun des éléments de $S$ est fini.
|
| 348 |
+
Solution de l'exercice 17 Soit $p$ un nombre premier et soit $a_{1}, a_{2}, \ldots a_{k}$ les restes possibles des éléments de $S$ modulo $p$. On suppose que 0 n'appartient pas à $R=\left\{a_{1}, \ldots, a_{k}\right\}$, c'est-à-dire que $p$ ne divise aucun élément de $S$.
|
| 349 |
+
On sait que pour tout $i, j, a_{i} a_{j}+1 \in R$. Notons que si $j$ et $l$ sont distincts, alors $a_{i} a_{j}+1$ et $a_{i} a_{l}+1$ sont distincts. En effet
|
| 350 |
+
|
| 351 |
+
$$
|
| 352 |
+
a_{i} a_{j}+1-\left(a_{i} a_{l}+1-\equiv a_{i}\left(a_{j}-a_{l}\right) \neq 0 \quad \bmod p\right.
|
| 353 |
+
$$
|
| 354 |
+
|
| 355 |
+
Ainsi pour $i$ fixé, $R=\left\{a_{1}, \ldots, a_{k}\right\}=\left\{a_{i} a_{1}+1, \ldots, a_{i} a_{k}+1\right\}$. Il vient que
|
| 356 |
+
|
| 357 |
+
$$
|
| 358 |
+
a_{1}+\ldots+a_{k} \equiv a_{i} a_{1}+1+\ldots+a_{i} a_{k}+1 \equiv a_{i}\left(a_{1}+\ldots+a_{k}\right)+k \bmod p
|
| 359 |
+
$$
|
| 360 |
+
|
| 361 |
+
Si $a_{1}+\ldots+a_{k} \equiv 0 \bmod p$, alors $k \equiv 0 \bmod p$ donc $k=p$ et $0 \in R$ ce qui est contraire à l'hypothèse. On déduit que $a_{1}+\ldots+a_{k}$ est inversible modulo $p$ et
|
| 362 |
+
|
| 363 |
+
$$
|
| 364 |
+
a_{i} \equiv \frac{k}{a_{1}+\ldots+a_{k}} \bmod p
|
| 365 |
+
$$
|
| 366 |
+
|
| 367 |
+
Ce terme ne dépend pas de $i$. Donc les $a_{i}$ sont égaux et $R$ est un singleton noté $\{a\}$. Ainsi $a^{2}+1 \equiv a$ $\bmod p$ donc $p \mid a^{2}+1-a$ et $p \leqslant n^{2}-n+1$ pour tout $n$ dans $S$. Si $n_{0}$ est le plus petit élément de $S$, alors en particulier $p \leqslant \mathfrak{n}_{0}^{2}-\mathfrak{n}_{0}+1$.
|
| 368 |
+
En conclusion, si $p$ ne divise aucun élément de $S$, $p$ est borné par $n_{0}^{2}-n_{0}+1$. Ainsi l'ensemble des nombres premiers ne divisant aucun élément de $S$ est fini.
|
| 369 |
+
Commentaire des correcteurs
|
| 370 |
+
L'exercice a été bien résolu par les quelques élèves qui l'ont traité.
|
| 371 |
+
|
| 372 |
+
Exercice 18. Trouver tous les entiers $n \geqslant 1$ pour lesquels la fonction:
|
| 373 |
+
|
| 374 |
+
$$
|
| 375 |
+
x \longmapsto x^{x}
|
| 376 |
+
$$
|
| 377 |
+
|
| 378 |
+
prenne toutes les valeurs possibles modulo $n$ lorsque $x$ parcourt $\llbracket 0, n-1 \rrbracket$.
|
| 379 |
+
On dit que c'est une surjection dans $\mathbb{Z} / n \mathbb{Z}$.
|
| 380 |
+
Solution de l'exercice 18 Notons déjà que si $n$ vérifie la propriété, alors tout diviseur d de n la vérifie également. Posons f l'application qui à $x$ dans $\mathbb{N}^{*}$ dans $\mathbb{Z} / \mathfrak{Z} \mathbb{Z}$.
|
| 381 |
+
Pour $n=p^{2}$ avec $p$ premier, notons que $p$ n'est pas dans l'image de $f$. En effet, si $f(x) \equiv p\left(\bmod p^{2}\right)$, $p$ divise $x^{x}$ donc $p$ divise $x$. En particulier, comme $x \geqslant p \geqslant 2, p^{2}$ divise $x^{x}=f(x)$ contradiction. En particulier, si $n$ vérifie la propriété, dans sa décomposition en facteurs premiers toutes les valuations $p$ adiques valent au plus 1.
|
| 382 |
+
Pour $n=p$ premier, donnons nous $y \in \mathbb{N}$. On cherche $x$ entier positif tel que $x^{x} \equiv y(\bmod p)$. Pour cela, on utilise le petit théorème de Fermat: si $p-1$ divise $x-1, x^{x} \equiv x^{x-1} \times x \equiv x(\bmod p)$. En particulier, il suffit de prendre $x$ strictement positif tel que $x \equiv 1(\bmod p-1)$ et $x \equiv y(\bmod p)$. Ceci est possible par le théorème des restes chinois, car $p$ et $p-1$ sont premiers entre eux, donc $f$ est surjective.
|
| 383 |
+
|
| 384 |
+
Il reste à traiter le cas où $n$ est un produit de facteurs premiers deux à deux distincts : supposons $n=p_{1} \ldots p_{k}$ avec les ( $p_{i}$ ) premiers et deux à deux distincts. On peut réessayer d'utiliser l'argument précédent : soit $y \in \mathbb{N}$, on cherche $x$ entier strictement positif tel que $x^{x}=y(\bmod \boldsymbol{n})$, ceci est équivalent par théorème des restes chinois à $x^{x}=y\left(\bmod p_{i}\right)$ pour tout $i$ entre 1 et $k$. Il suffit de prendre $x$ tel que $x \equiv 1\left(\bmod p_{i}-1\right)$ et $x \equiv y\left(\bmod p_{i}\right)$ pour tout $i$, c'est à dire $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ et $x \equiv y$ $\left(\bmod p_{i}\right)$ pour tout $i$. Notons que les $\left(p_{i}\right)$ sont deux à deux premiers entre eux, mais à priori on ne peut pas affirmer que $p_{i}$ est premier $\prod_{i=1}^{k}\left(p_{i}-1\right)$ pour tout $i$.
|
| 385 |
+
Si pour tout $(\boldsymbol{i}, \mathfrak{j})$ entre 1 et $k, p_{i}$ ne divise pas $\mathfrak{p}_{\mathfrak{j}}-1$, dans ce cas $\mathfrak{p}_{\boldsymbol{i}}$ est premier $\prod_{i=1}^{k}\left(\mathfrak{p}_{\boldsymbol{i}}-1\right)$ pour tout $\boldsymbol{i}$, donc par théorème des restes chinois on peut trouver $x$ tel que $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ et $x \equiv y$ $\left(\bmod p_{i}\right)$ pour tout i , ainsi $x^{x} \equiv y(\bmod \boldsymbol{n})$.
|
| 386 |
+
|
| 387 |
+
Supposons qu'il existe $(i, j)$ tel que $p_{i}$ divise $p_{j}-1$. Comme $i \neq j$, il suffit dans ce cas de vérifier que $f$ n'est pas surjective modulo $m$ avec $m=p_{i} p_{j}$, supposons que $f$ est surjective modulo $m$. Soit $a \in \mathbb{N}, y$ tel que $y \equiv 0\left(\bmod p_{i}\right)$ et $y \equiv a\left(\bmod p_{j}\right)$ par théorème des restes chinois. Supposons qu'il existe $x$ tel que $x^{x} \equiv y\left(\bmod p_{i} p_{j}\right)$. Dans ce cas $x^{x} \equiv 0\left(\bmod p_{i}\right)$ donc $p_{i}$ divise $x$, posons alors $x=k p_{i}$. Dans ce cas, $x^{x} \equiv\left(x^{k}\right)^{\mathfrak{p}_{i}} \equiv a\left(\bmod \mathfrak{p}_{j}\right)$. On obtient, en élevant à la puissance $\frac{\mathfrak{p}_{j}-1}{\mathfrak{p}_{i}}, a^{\frac{p_{j}-1}{p_{i}}}=\left(x^{k}\right)^{\mathfrak{p}_{j}-1}=1$ $\left(\bmod \mathfrak{p}_{\mathfrak{j}}\right)$. En particulier, si a est une racine primitive modulo $\mathfrak{p}_{\mathfrak{j}}$, comme a est d'ordre exactement $\mathfrak{p}_{\mathfrak{j}}-1$, on obtient une contradiction, l'application f n'est pas surjective.
|
| 388 |
+
|
| 389 |
+
Ainsi l'application est surjective si et seulement si $\mathrm{n}=\mathrm{p}_{1} \ldots \mathrm{p}_{\mathrm{k}}$ avec les $\left(\boldsymbol{p}_{\boldsymbol{i}}\right)$ premiers et deux à deux distincts et pour tout $(\boldsymbol{i}, \mathfrak{j})$ entre 1 et $k, p_{i}$ ne divise pas $\mathfrak{p}_{\mathfrak{j}}-1$.
|
| 390 |
+
Commentaire des correcteurs
|
| 391 |
+
Les copies reçues sur ce problème sont de très bon niveau. Le problème était relativement difficile, mais nombreux sont ceux qui ont trouvé de bonnes avancées. Certaines copies ont voulu utiliser le lemme chinois, certes il pouvait être utile, mais il pouvait causer beaucoup d'erreurs : notamment ce n'est pas
|
| 392 |
+
parce que l'application est surjective modulo $p$ pour tout nombre $p$ premier qu'elle l'est pour tout nombre "squarefree" c'est-à-dire sans facteur premier avec multiplicité supérieure ou égale à 2 . Attention aussi à l'utilisation du théorème d'Euler $\left(a^{\phi(n)}=1(\bmod n)\right)$ : pour pouvoir l'utiliser, il faut que le nombre soit premier avec n .
|
| 393 |
+
|
French_STS/md/fr-corrigé-commenté-envoi-4.md
ADDED
|
@@ -0,0 +1,320 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br> 
|
| 2 |
+
|
| 3 |
+
ENVOI 3 : COMBINATOIRE
|
| 4 |
+
À RENVOYER AU PLUS TARD LE 15 FÉVRIER 2020
|
| 5 |
+
|
| 6 |
+
Les consignes suivantes sont à lire attentivement:
|
| 7 |
+
|
| 8 |
+
- Le groupe junior est constitué des élèves nés en 2004 ou après. Les autres élèves sont dans le groupe senior.
|
| 9 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 10 |
+
- Les exercices classés "Communs" sont à chercher par tout le monde.
|
| 11 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 12 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 13 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 14 |
+
- Pour les exercices de géométrie, faire des figures sur des feuilles blanches séparées.
|
| 15 |
+
- Respecter la numérotation des exercices.
|
| 16 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 17 |
+
|
| 18 |
+
Animath,<br>Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.<br>contact-pofm@animath.fr
|
| 19 |
+
|
| 20 |
+
## Exercices Juniors
|
| 21 |
+
|
| 22 |
+
Exercice 1. De combien de façons peut-on placer 7 tours sur un échiquier $7 \times 7$ telle qu'aucune tour ne puisse en attaquer une autre?
|
| 23 |
+
Une tour peut attaquer une autre tour si elle se situe sur la même ligne ou la même colonne.
|
| 24 |
+
|
| 25 |
+
## Solution de l'exercice 1
|
| 26 |
+
|
| 27 |
+
Si on place 7 tours de sorte que deux tours ne soient pas sur la même colonne, sachant qu'il y a 7 colonne, alors il y aura exactement une tour sur chaque colonne (et de même sur chaque ligne).
|
| 28 |
+
Il y a 7 positions possibles pour placer une tour sur la première colonne. Il y a ensuite 6 positions possibles pour placer une tour sur la seconde colonne sans qu'elle soit sur la même ligne que la première tour. Ainsi de suite, sur la $k$-ième colonne il y a $8-k$ manières de placer une tour sans qu'elle soit sur la même ligne qu'une tour déjà placée.
|
| 29 |
+
Ainsi il y a 7 ! $=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040$ manières de disposer les tours de cette manière.
|
| 30 |
+
Si on note $\sigma(i)$ le numéro de ligne de la tour présente sur la i-ième colonne dans une des configurations satisfaisant l'énoncé, alors $\sigma$ est ce que l'on appelle une permutation.
|
| 31 |
+
Commentaire des correcteurs
|
| 32 |
+
Le problème a été très bien réussi.
|
| 33 |
+
|
| 34 |
+
Exercice 2. Les entiers de 1 à 2020 sont écris au tableau. Jacques a le droit d'en effacer deux et d'écrire à la place leur différence ou leur somme, et de recommencer jusqu'à ce qu'il ne reste plus qu'un entier. Est-il possible que l'entier obtenu à la fin soit 321 ?
|
| 35 |
+
Solution de l'exercice 2 L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée à essayer dans ce cas est de chercher un invariant.
|
| 36 |
+
Une seconde idée est de tester le problème avec des plus petites valeurs. Par exemple, on peut tester l'énoncé pour les entiers écrits de 1 à 4 et regarder à quelles valeurs ont peut aboutir à la fin du processus décrit dans l'énoncé. On remarque que partant d'une valeur fixée n , les résultats possibles ont tous la même parité, celle de la somme des nombres de 1 à $n$. Après avoir testé cette conjecture pour les entiers écrits de 1 à 5 , on essaye donc de montrer que la parité de la somme des entiers écrits au tableau est invariante sous l'opération décrite.
|
| 37 |
+
Si un instant donné, la somme des entiers écrits au tableau vaut $S$ et que Jacques choisit les entiers $x$ et $y$, alors ces entiers seront remplacés par $x+y$ ou par $x-y$ et alors $S$ sera remplacé par $(S-x-y)+y-x=$ $S-2 x$ ou par $(S-y-x)+(x-y)=S-2 y$. Ces deux entiers ont la même parité, donc la somme des entiers écrits au tableau garde la même parité tout au long du processus. Puisque dans la situation initiale, la somme des entiers écrits au tableau est
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
1+2+3+\cdots+2020=\frac{2020 \cdot 2021}{2}=1010 \cdot 2021
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
et est paire, le nombre écrit au tableau dans la situation finale sera également pair et il ne peut donc pas s'agir du nombre 321.
|
| 44 |
+
Commentaire des correcteurs
|
| 45 |
+
Il était nécessaire dans ce problème d'évoquer la notion d'invariant. Les explications des élèves qui n'évoquaient pas explicitement l'invariant de parité n'étaient pas toujours très convaincantes. Attention à ne pas faire un raisonnement qui soit trop "avec les mains".
|
| 46 |
+
|
| 47 |
+
Exercice 3. Andréa, Baptiste et Camille jouent au foot à trois. Un des joueur est aux cages, les deux autres sont sur le terrain et essaient de marquer. Le joueur qui marque devient ensuite gardien pour le tir suivant.
|
| 48 |
+
Durant l'après-midi, Andréa a été sur le terrain 12 fois, Baptiste l'a été 21 fois et Camille a été aux cages 8 fois. Leur professeur sait qui a marqué le 6 -ième but. Qui était-ce?
|
| 49 |
+
|
| 50 |
+
## Solution de l'exercice 3
|
| 51 |
+
|
| 52 |
+
Si on note n le nombre de parties jouées, alors au total il y a eu n fois un gardien. On utilise à présent les hypothèses données par l'énoncé. Si Andréa a été 12 fois sur le terrain, il a donc été $\mathrm{n}-12$ fois aux cages. Si Baptiste a été 21 fois sur le terrain, il a été $\mathrm{n}-21$ fois aux cages. Ainsi $\mathrm{n}-12+\mathrm{n}-21+8=\mathrm{n}$, ce qui nous donne que $n=25$. Cela veut également dire que Andréa a été aux cages 13 fois. Mais il est impossible d'être aux cages deux fois d'affilée. Ainsi, on sait que Andréa était aux cages au début, et l'a été exactement une fois sur deux. En particulier, il a été aux cages à la septième partie et donc Andréa a marqué le 6-ième but.
|
| 53 |
+
|
| 54 |
+
## Commentaire des correcteurs
|
| 55 |
+
|
| 56 |
+
L'exercice a été largement réussi. Certaines preuves et rédaction sont particulièrement efficaces.
|
| 57 |
+
|
| 58 |
+
## Exercice 4.
|
| 59 |
+
|
| 60 |
+
On choisit 5 diviseurs positifs de $10^{2020}$. Montrer qu'il y en a deux dont le produit est un carré.
|
| 61 |
+
Solution de l'exercice 4 On commence par regarder la forme que peut prendre un éventuel diviseur de $10^{2020}$. Les diviseurs de $10^{2020}$ sont de la forme $2^{\mathrm{a}} 5^{\mathrm{b}}$. Le produit de deux diviseurs est donc également un nombre de la forme $2^{a} 5^{b}$ et c'est un carré parfait si et seulement si $a$ et $b$ sont tous les deux pairs. On est donc ramené à montrer le résultat suivant : si on a 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$ et les $a_{i}$ et $b_{i}$ tous les deux inférieurs ou égaux à 2020, alors on peut trouver deux indices $j$ et $k$ tels que $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ est un couple de deux nombres entiers pairs. On s'empresse de regarder si ce résultat est vrai pour quelques paires d'entiers et on cherche désormais à démontrer ce résultat. On est amené à regarder la parité des entiers considérés. Il y a 4 possibilités pour un couple ( $\mathrm{a}, \mathrm{b}$ ) : soit a et b sont pairs, soit $a$ et $b$ sont impairs, soit $a$ est pair et $b$ est pair, soit $a$ est impair et $b$ est pair. Ainsi par le principe des tiroirs, si on choisit 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$, il y a deux couples $\left(a_{j}, b_{j}\right)$ et $\left(a_{k}, b_{k}\right)$ possédant la même caractéristique, c'est-à-dire tels que $a_{j}$ et $a_{k}$ soient de le même parité et $b_{j}$ et $b_{k}$ soient de même parité. Alors $a_{j}+a_{k}$ et $b_{j}+b_{k}$ sont tous les deux paires. Ainsi, en choisissant 5 diviseurs de $10^{2020}$, on peut en trouver 2 tels que leur produit soit un carré.
|
| 62 |
+
Commentaire des correcteurs
|
| 63 |
+
Exercice globalement très bien réussi. Certains ont considéré que tout diviseur de $10^{2} 020$ était sous la forme $2^{x}, 5^{y}$ ou $10^{z}$ ce qui n'est pas vrai (par exemple 20 est un diviseur de $10^{2020}$ et n'a aucune des formes citées). Certains ont dit que si on avait deux diviseurs sous la forme $2^{b} 5^{c}$ et $2^{\mathrm{d}} 5^{f}$ avec b et d de même parité, c et f de même parité alors leur produit est un carré, il fallait justifier cela en disant que deux nombres de parité différente ont une somme paire. Attention au verbe falloir : beaucoup ont dit que pour que le produit de $2^{\mathrm{b}} 5^{\mathrm{c}}$ et $2^{\mathrm{d}} 5^{\mathrm{f}}$ soit un carré il fallait avoir $\mathrm{b}+\mathrm{d}$ pair et $\mathrm{c}+\mathrm{f}$ pair, ce qui est vrai. Néanmoins ils ont utilisé après que si on a $\mathrm{b}+\mathrm{d}$ pair et $\mathrm{c}+\mathrm{f}$ pair alors le produit de $2^{\mathrm{b}} 5^{\mathrm{c}}$ et $2^{\mathrm{d}} 5^{\mathrm{f}}$ est un carré, ce qui n'est pas la même chose que ce qui était dit. Quand on affirme "pour A il faut avoir B", on affirme que A implique B , c'est-à-dire que si on a A alors on a B . Pour dire que B implique A , on doit dire "pour A il suffit d'avoir B". "Il faut que" et "il suffit que" ont des sens différents.
|
| 64 |
+
|
| 65 |
+
Exercice 5. Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et n colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
| 66 |
+
Solution de l'exercice 5 Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que $c$ est bien le plus grand entier, on va d'une part montrer que si un entier $n$ satisfait la propriété, alors $n \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes. L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
|
| 67 |
+
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
|
| 68 |
+
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
|
| 69 |
+
|
| 70 |
+
- Si chaque lettre apparaît au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
|
| 71 |
+
- Si une lettre apparait exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
|
| 72 |
+
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
|
| 73 |
+
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $n \leqslant 7$.
|
| 74 |
+
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
|
| 75 |
+
|
| 76 |
+
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
|
| 77 |
+
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
| 78 |
+
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
|
| 79 |
+
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
|
| 80 |
+
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
|
| 81 |
+
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
|
| 82 |
+
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
|
| 83 |
+
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
|
| 84 |
+
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
|
| 85 |
+
|
| 86 |
+
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
|
| 87 |
+
Commentaire des correcteurs
|
| 88 |
+
L'exercice est globalement bien réussi, les élèves ont bien compris que la contrainte était que chaque colonne rajoutait 4 paires de lettres identiques, mais peu ont fait une preuve totalement rigoureuse de ce fait. Certains ont donné un ensemble de 7 colonnes et justifié le fait que 7 était optimal car il n'était pas possible de rajouter une colonne à ce qu'ils avaient faits. Mais cette justification n'est pas suffisante. En
|
| 89 |
+
effet, ce n'est pas parce que la construction ne peut être agrandie que pour autant sa taille est maximale : on peut imaginer qu'il existe une construction plus grande très différente de celle donnée.
|
| 90 |
+
|
| 91 |
+
Exercice 6. Dans 5 boites se trouvent respectivement 402,403, 404, 405 et 406 pierres. La seule opération autorisée est de prendre 4 pierres dans un tas ayant au moins 4 pierres et d'en mettre une dans chacun des autres tas. Quel est le plus grand nombre de pierre qu'il est possible d'avoir dans un seul tas?
|
| 92 |
+
|
| 93 |
+
Solution de l'exercice 6 L'énoncé présente une suite d'opérations et décrit une certaine situation initiale. Une première idée à essayer dans ce cas est de chercher un invariant.
|
| 94 |
+
Une deuxième idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour des tas de taille $0,1,2,3$ et 4 . Après plusieurs essais, on remarque que les tas ont toujours, à permutation près, les tailles $0,1,2,3$ et 4 . Après avoir testé sur des tas de taille $1,2,3,4$ et 5 , on s'aperçoit que les tas ont toujours des valeurs distinctes deux à deux modulo 5 . On s'empresse de démontrer cette conjecture.
|
| 95 |
+
Enlever 4 pierres d'un tas revient, modulo 5, à en ajouter 1. Comme on en ajoute une dans chacun des autres tas, les valeurs des tas augmentent toutes de 1 modulo 5 . Ainsi, si avant l'opération ces valeurs étaient distinctes deux à deux modulo 5 , après l'opération elles resteront distinctes deux à deux modulo 5 . On a donc déterminé notre invariant.
|
| 96 |
+
Ainsi la somme des tailles de 4 tas quelconques ne pourra jamais dépasser $0+1+2+3=6$ et donc un tas quelconque ne pourra jamais contenir plus que $2020-6=2014$ pierres.
|
| 97 |
+
Réciproquement, nous devons désormais démontrer que l'on peut toujours faire en sorte qu'un tas contienne 2014 pierres au bout d'un nombre fini d'opérations. Pour cela, il suffit de ne jamais toucher au tas contenant 404 pierres, et de faire l'opération sur les autres tas jusqu'à ce que ce ne soit plus possible de faire une seule opération. Ainsi les tas restants auront $0,1,2,3$ pierres à la fin du procédé, donc il y aura bien $2020-(0+1+2+3)=2014$ pierres sur le même tas.
|
| 98 |
+
|
| 99 |
+
## Commentaire des correcteurs
|
| 100 |
+
|
| 101 |
+
Un grand nombre d'élèves se contente de la construction de la borne sans montrer qu'elle est effectivement optimale. Dans de plus rares cas, certains élèves ne prouvent que la minimalité sans l'atteignabilité. La majorité des preuves d'optimalité se basent sur un travail modulo 5 , mais certaines preuves plus originales s'en passent, avec un travail sur les dernières opérations (travail rarement parfaitement exécuté).
|
| 102 |
+
|
| 103 |
+
Exercice 7. Un mauvais sorcier a enfermé $n$ mathématiciens. Il dispose de $n$ couleurs. Le sorcier place sur la tête de chaque mathématicien un chapeau d'une des $n$ couleurs; deux chapeaux peuvent avoir la même couleur. Chaque mathématicien peut voir la couleur du chapeau de chacun de ses collègues mais pas la sienne. Les mathématiciens doivent alors tous en même en temps annoncer la couleur de leur chapeau. Si au moins un des mathématiciens devine correctement, tous les mathématiciens sont libres. Ils peuvent bien sûr se concerter sur une stratégie avant de connaître la couleur des chapeaux des autres mathématiciens.
|
| 104 |
+
Proposez une stratégie qui assure que les mathématiciens soient libérés.
|
| 105 |
+
Solution de l'exercice 7 Tout d'abord, nous allons coder les différentes informations. Par exemple, on numérote les couleurs de 1 à $n$ et on numérote les mathématiciens de 1 à $n$ également. On note $i_{1}, \ldots i_{n}$ les couleurs des chapeaux des mathématiciens.
|
| 106 |
+
Puisqu'un mathématicien ne peut pas voir son propre chapeau mais uniquement les chapeaux des autres, il va devoir déclarer un nombre qui dépend des chapeaux qu'il observe. On peut par exemple chercher une expression qui va dépendre de façon symétrique de chacun des chapeaux.
|
| 107 |
+
Une information importante et qui dépend de façon symétrique de chacun des chapeaux est par exemple la somme des numéros de tous les chapeaux, à savoir $i_{1}+i_{2}+\ldots i_{n}$. Cette somme admet un certain reste $s$ modulo $n$. On a donc $i_{l} \equiv s-\sum_{j \neq l} i_{j} \bmod n$. On doit donc s'assurer qu'il existe un indice $l$ tel que le mathématicien $l$ déclare le numéro $s-\sum_{j \neq l} i_{j} \bmod n$. On reconnaît dans $\sum_{j \neq l} i_{j}$ la somme des numéros des chapeaux vus par le mathématicien $l$.
|
| 108 |
+
Ainsi, si chaque mathématicien de numéro $k$ déclare le nombre entre 1 et $n$ congru à $k-\sum_{j \neq k} \dot{i}_{j} \bmod n$, alors le mathématicien dont le numéro est congru à $s$ modulo $n$ déclarera le numéro $s-\sum_{j \neq s} \mathfrak{i}_{j}=i_{s}$ $\bmod n$ qui est la couleur de son chapeau. Tous les mathématiciens sont donc libérés !
|
| 109 |
+
|
| 110 |
+
Exercice 8. Un coloriage des entiers $\{1,2, \cdots, 2020\}$ en bleu et rouge est dit agréable s'il n'existe pas deux entiers distincts dans $\{1,2, \cdots, 2020\}$ de même couleur dont la somme est une puissance de 2 . Combien de tels coloriage existent-ils?
|
| 111 |
+
Solution de l'exercice 8 Une première idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour un coloriage des entiers de 1 à 7 .
|
| 112 |
+
Colorions dans l'ordre les nombres : pour colorier 1, on n'a pas de contrainte apparente, idem pour colorier 2 . Par contre comme $3+1=4$, la couleur de 3 est imposée. Pour colorier 4 , il n'y a pas de contrainte apparente car $4+3=7,4+2=6$ et $4+1=5$ ne sont pas des puissances de deux. Par contre comme $5+3=6+2=7+1=8$, la couleur de 5,6 et 7 est imposée. En testant tous les coloriages possibles, on voit que peu importe les couleurs choisies pour colorier 1, 2 et 4 , le coloriage obtenu est agréable. On peut donc supposer qu'un coloriage agréable est fixé une fois la couleur des puissances de 2 est choisie et que tout coloriage des puissances de 2 peut être prolonger en un coloriage agréable.
|
| 113 |
+
Nous allons montrer que pour tout coloriage des puissances de 2 entre 1 et 2020, il existe une unique manière de colorier les autres nombres de sorte à obtenir un coloriage agréable.
|
| 114 |
+
Pour cela nous allons procéder par récurrence. Montrons que si on colorie les puissances de 2 de 1 à N , alors il existe une unique manière agréable de colorier les autres entiers de 1 à N .
|
| 115 |
+
Le résultat est clair pour $N=1$.
|
| 116 |
+
Soit N tel que le résultat soit vrai pour $\mathrm{N}-1$. On colorie les puissances de 2 de 1 à N . Par hypothèse de récurrence, il existe une unique manière agréable de colorier les autres entiers de 1 à $\mathrm{N}-1$.
|
| 117 |
+
Si $\mathrm{N}=2^{\mathrm{k}}$ pour un certain entier k , alors N est déjà colorié et le coloriage est agréable : en effet si $1 \leqslant \ell<2^{k}$, alors $2^{k}+\ell$ n'est pas une puissance de 2 car $2^{k}<2^{k}+\ell<2^{k+1}$. Ainsi dans ce cas il y a une unique manière de compléter le coloriage.
|
| 118 |
+
Si $N$ n'est pas une puissance de 2 , alors $N=2^{k}+n$ avec $1 \leqslant n<2^{k}$ et $k$ un entier. Alors $N$ ne peut pas être colorié de la même couleur que $2^{k}-n$ car $N+2^{k}-n=2^{k+1}$. On colorie donc N de l'autre couleur, et c'est bien l'unique manière de compléter le coloriage de manière agréable. Le coloriage obtenu est agréable : en effet soit $t$ entier tel que $1 \leqslant t<N$ et $t+N$ est une puissance de 2 , on a $2^{k}<\mathrm{N} \leqslant \mathrm{t}+\mathrm{N}<2 \mathrm{~N}=2^{\mathrm{k}+1}+2 \mathrm{n}<2^{\mathrm{k}+1}+2^{\mathrm{k}+1}=2^{\mathrm{k}+2}$, donc $\mathrm{t}+\mathrm{N}=2^{\mathrm{k}+1}$. On a donc $\mathrm{t}=2^{\mathrm{k}+1}-2^{k}-\mathrm{n}=2^{k}-\mathrm{n}$. Comme on a colorié N et $2^{k}-\mathrm{n}$ de deux couleurs différentes, le coloriage est agréable.
|
| 119 |
+
Il y a 11 puissances de 2 entre 1 et 2020 qui sont $1=2^{0}, 2=2^{2}, \cdots, 1024=2^{10}$, et il y a $2^{11}$ manières de les colorier en bleu et rouge. Ainsi il y a $2^{11}$ coloriages agréables.
|
| 120 |
+
Commentaire des correcteurs
|
| 121 |
+
La majorité des élèves a vu l'importance des puissances de 2 . Certains ont proposé alternativement de regarder les éléments congrus à $2^{n}$ modulo $2^{n+1}$ ce qui fonctionnait aussi. Nombreux sont ceux qui ont prouvé qu'il y avait au plus 2048 coloriages, mais très peu ont vérifié que les coloriages ainsi produit convenaient, alors que c'était pourtant une partie importante de l'exercice. Il faut penser à détailler les arguments utilisés : par exemple faire une récurrence est une bonne idée quand on veut généraliser quelque chose.
|
| 122 |
+
|
| 123 |
+
Exercice 9. Soit n un entier. On dispose de n couleurs, et chaque point d'un cercle est colorié de l'une de ces couleurs. Montrer qu'il existe deux droites parallèles qui intersectent le cercle en 4 points distincts de même couleur
|
| 124 |
+
|
| 125 |
+
## Solution de l'exercice 9
|
| 126 |
+
|
| 127 |
+
L'énoncé nous demande de démontrer une existence, on peut essayer de montrer cette existence à l'aide du principe des tiroirs. Gardant cette information en tête, on essaye de traduire le résultat demandé.
|
| 128 |
+
Considérons deux droites parallèles coupant le cercle en 4 points distincts. Ces 4 points délimitent un quadrilatère dont deux côtés sont parallèles et les médiatrices de ces deux segments sont confondues : en effet, elles sont perpendiculaires à deux côtés parallèles donc elles sont parallèles et elles passent par le centre du cercle donc elles sont bien confondues. Le quadrilatère est donc un trapèze isocèle. il possède donc deux côtés égaux et deux diagonales de même longueur.
|
| 129 |
+
Réciproquement, si 4 points $A, B, C$ et $D$ sont dans cet ordre sur un cercle de centre $O$ et délimitent un quadrilatère tels que $A B=C D$, alors la médiatrice du segment $[\mathrm{BC}]$ est l'axe de la symétrie envoyant $B$ sur $C$. Cet axe de symétrie contient $O$ donc la symétrie conserve le cercle. Puisque $A B=C D$, cette symétrie envoye $A$ sur $D$ et donc la médiatrice du segment $[B C]$ est aussi celle du segment $[A D]$ et le quadrilatère $A B C D$ est un trapèze isocèle.
|
| 130 |
+

|
| 131 |
+
|
| 132 |
+
On suppose désormais que $A C=B D$. Alors les triangles $A O C$ et $D O B$ sont isométriques car l'un est obtenu en appliquant une rotation sur l'autre triangle. On déduit que $\mathrm{BC}=A D$ et que la quadrilatère $A B C D$ est un trapèze isocèle à nouveau.
|
| 133 |
+
On cherche donc désormais à montrer qu'il existe deux paires de points $(A, B)$ et $(C, D)$, tous de même couleur, telles que $A B=C D$. D'après la discussion précédente, ces points seraient alors les sommets d'un trapèze isocèle.
|
| 134 |
+
Pour un tel exercice, dit de géométrie combinatoire, il est bon de penser toujours à des objets réguliers, par exemple à des cercles ou des polygones réguliers. Ici, penser à de tels objets est pertinent puisque les polygones réguliers sont inscriptibles dans un cercle.
|
| 135 |
+
|
| 136 |
+
Pour combiner cette idée avec celle du principe des tiroirs, nous allons considérer des $\mathrm{n}+1$-gones réguliers. Un $(n+1)$-gone régulier sur le cercle, d'après le principe des tiroirs, possède deux sommets de même couleur. On a donc obtenu une paire de sommets de même couleur.
|
| 137 |
+
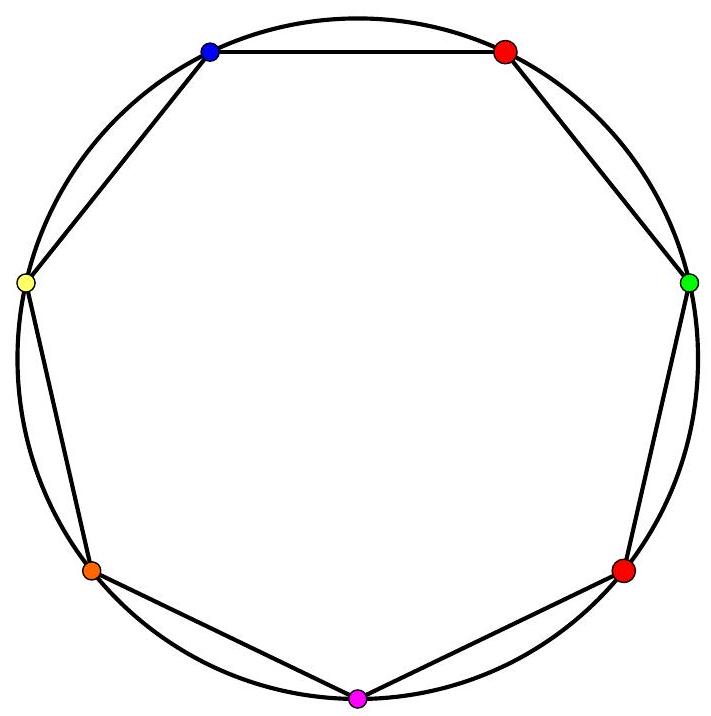
|
| 138 |
+
|
| 139 |
+
On appellera couleur de la paire la couleur commune des deux sommets et distance de la paire la distance entre ses deux sommets. On va créer plus de telles paires. N'oublions pas que nous aimerions que la distance des différentes paires que nous créons soit la même. Or, dans un $\mathrm{n}+1$-gone régulier, il y a $\left\lfloor\frac{\mathfrak{n}+1}{2}\right\rfloor$ distances distinctes possibles entre deux sommets quelconques. Pour obtenir deux paires de même distance, il faut donc $\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ polygones réguliers.
|
| 140 |
+
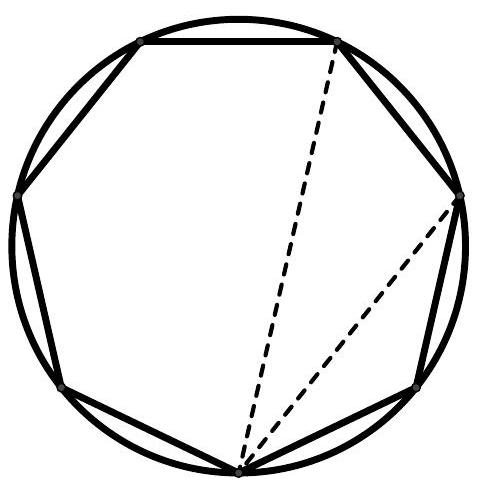
|
| 141 |
+
|
| 142 |
+
N'oublions pas que nous désirons également que les couleurs des paires soient identiques. Ainsi, on prend $\mathrm{n} \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1(\mathrm{n}+1)$-gones réguliers disjoints inscrits dans le cercle. On obtient alors $n \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ paires de sommets tous distincts et les sommets d'une même paire sont de même couleur et leur distance appartient à un ensemble de taille $\left\lfloor\frac{n+1}{2}\right\rfloor$. D'après le principe des tiroirs, il y a donc parmi ces paires $n+1$ paires de sommets de même distance. Comme il y a $n$ couleurs, à nouveau d'après le principe des tiroirs, parmi ces $n+1$ paires de même distance, il y en a au moins 2 de même couleur. On a donc obtenu deux paires de même distance et de même couleur, on a donc 4 points $A, B, C$ et $D$ de même couleur tels que $A B=C D$. Ainsi, on a bien deux droites parallèles coupant le cercle en 4 points de même couleur.
|
| 143 |
+
Commentaire des correcteurs
|
| 144 |
+
L'exercice, manifestement trop difficile, n'a été résolu par personne. Un seul élève a pensé à utiliser un $\mathrm{n}+1$-gone régulier pour appliquer le principe des tiroirs, mais il fallait poursuivre et compter correctement les différentes distances entre deux sommets quelconques d'un $n+1$-gone puis penser à considérer plusieurs $\mathrm{n}+1$-gones. Quelques élèves ont pensé à ramener la condition de parallélisme à une condition sur les longueurs d'arc.
|
| 145 |
+
|
| 146 |
+
## Exercices Seniors
|
| 147 |
+
|
| 148 |
+
## Exercice 10.
|
| 149 |
+
|
| 150 |
+
On choisit 5 diviseurs de $10^{2020}$. Montrer qu'il y en a deux dont le produit est un carré.
|
| 151 |
+
Solution de l'exercice 10 On commence par regarder la forme que peut prendre un éventuel diviseur de $10^{2020}$. Les diviseurs de $10^{2020}$ sont de la forme $2^{\mathrm{a}} 5^{\mathrm{b}}$. Le produit de deux diviseurs est donc également un nombre de la forme $2^{a} 5^{b}$ et c'est un carré parfait si et seulement si $a$ et $b$ sont tous les deux pairs. On est donc ramené à montrer le résultat suivant : si on a 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$ et les $a_{i}$ et $b_{i}$ tous les deux inférieurs ou égaux à 2020, alors on peut trouver deux indices $j$ et $k$ tels que $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ est un couple de deux nombres entiers pairs. On s'empresse de regarder si ce résultat est vrai pour quelques paires d'entiers et on cherche désormais à démontrer ce résultat. On est amené à regarder la parité des entiers considérés. Il y a 4 possibilités pour un couple $(a, b):$ soit $a$ et b sont pairs, soit $a$ et $b$ sont impairs, soit $a$ est pair et $b$ est pair, soit $a$ est impair et $b$ est pair. Ainsi par le principe des tiroirs, si on choisit 5 paires d'entiers ( $a_{i}, b_{i}$ ) avec $1 \leqslant i \leqslant 5$, il y a deux couples ( $a_{j}, b_{j}$ ) et $\left(a_{k}, b_{k}\right)$ possédant la même caractéristique, c'est-à-dire tels que $a_{j}$ et $a_{k}$ soient de le même parité et $b_{j}$ et $b_{k}$ soient de même parité. Alors $a_{j}+a_{k}$ et $b_{j}+b_{k}$ sont tous les deux paires. Ainsi, en choisissant 5 diviseurs de $10^{2020}$, on peut en trouver 2 tels que leur produit soit un carré.
|
| 152 |
+
Commentaire des correcteurs
|
| 153 |
+
L'exercice est très bien réussi. Une erreur récurrente est de mal identifier les diviseurs de $10^{2020}$.
|
| 154 |
+
|
| 155 |
+
Exercice 11. Lors d'une fête, 2019 personnes s'assoient autour d'une table ronde, en se répartissant de façon régulière. Après s'être assises, elles constatent qu'un carton indiquant un nom est posé à chacune des places et que personne n'est assis à la place où figure son nom. Montrer qu'on peut tourner la table de telle sorte que deux personnes se retrouvent assises en face de leur nom.
|
| 156 |
+
Solution de l'exercice 11 On commence par tester l'énoncé sur des valeurs plus petites, par exemple pour une fête de 5 personnes.
|
| 157 |
+
Ensuite, on essaye de coder l'information. On appelle rotation une configuration obtenue après avoir tourné la table depuis sa position d'origine. À une rotation $r$, on associe $n(r)$ le nombre de personnes assises face à leur nom après la rotation.
|
| 158 |
+
Comme pour toute personne il existe une unique rotation qui la rend assise face à son nom, $\sum_{r=0}^{2018} n(r)=$ 2019. Or il y a 2019 rotations et la rotation nulle vérifie $n(r)=0$. Donc comme 2018 entiers positifs ont pour somme 2019, l'un d'eux vaut donc au moins 2 par principe des tiroirs, ce qui signifie bien qu'une rotation amène deux noms en face des bonnes personnes.
|
| 159 |
+
Commentaire des correcteurs
|
| 160 |
+
Le problème est très bien réussi. Lorsque l'on applique le principe des tiroirs, il n'est pas nécessaire de préciser qui sont les chaussettes et qui sont les tiroirs lorsque la situation est suffisamment claire.
|
| 161 |
+
|
| 162 |
+
Exercice 12. Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et $n$ colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
| 163 |
+
Solution de l'exercice 12 Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \leqslant c$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes.
|
| 164 |
+
L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
|
| 165 |
+
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
|
| 166 |
+
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
|
| 167 |
+
|
| 168 |
+
- Si chaque lettre apparait au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
|
| 169 |
+
- Si une lettre apparaît exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
|
| 170 |
+
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
|
| 171 |
+
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $\mathrm{n} \leqslant 7$.
|
| 172 |
+
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
|
| 173 |
+
|
| 174 |
+
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
|
| 175 |
+
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
| 176 |
+
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
|
| 177 |
+
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
|
| 178 |
+
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
|
| 179 |
+
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
|
| 180 |
+
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
|
| 181 |
+
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
|
| 182 |
+
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
|
| 183 |
+
|
| 184 |
+
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
|
| 185 |
+
Commentaire des correcteurs
|
| 186 |
+
De nombreux élèves ont réussi à trouver la réponse $\mathrm{n}=7$ et ont exhibé un exemple. La plupart proposent un argument correct pour montrer que c'est optimal, mais parfois ce raisonnement est rédigé de façon peu claire.
|
| 187 |
+
|
| 188 |
+
Exercice 13. Soit $\mathrm{N}>1$. Alice et Bob jouent au jeu suivant. 2 N cartes numérotées de 1 à 2 N sont mélangées puis disposées dans une ligne, de manière à ce que les faces numérotées soient visibles. Chacun à leur tour, Alice et Bob choisissent une carte, soit celle tout à droite soit celle soit à gauche de la ligne, et la garde pour eux, jusqu'à ce que toutes les cartes aient été prises. Alice commence. A la fin du jeu, chaque joueur calcule la somme des numéros des cartes qu'il a prises. Le joueur ayant la plus grande somme gagne. Un joueur dispose-t-il d'une façon de ne pas perdre?
|
| 189 |
+
|
| 190 |
+
Solution de l'exercice 13 On commence par tester le jeu pour des petites valeurs, par exemple pour un jeu composé de $2 \cdot 3$ cartes. Après plusieurs essais, on s'aperçoit par exemple que la stratégie qui consiste à prendre toujours la plus grande carte parmi la carte située la plus à gauche et la carte située la plus à droite ne fonctionne pas toujours, pour aucun des deux joueurs.
|
| 191 |
+
Testons le cas $\mathrm{N}=2$. Chacun des deux joueurs ne pourra prendre que deux cartes. Dans ce type de problème, une première idée est d'essayer de chercher une stratégie qui permet à un joueur de jouer comme il le souhaite, quelque soit les coups de l'adversaire. Regardons donc les cartes qu'Alice et Bob peuvent s'assurer d'obtenir. On note XYZW les cartes étalées sur la rangée dans cet ordre. Supposons qu'Alice prenne la carte $X$. Si Bob choisit la carte Y, Alice a le choix entre les cartes Z et W. Si Bob choisit la carte $W$, Alice a le choix entre les cartes $Z$ et $Y$. Ainsi, en choisissant la carte X, Alice s'assure de pouvoir prendre la carte $Z$ si elle le souhaite. En revanche, avant le premier coup d'Alice, Bob ne peut pas garantir de prendre une des quatre cartes.
|
| 192 |
+
On désire désormais généraliser ce processus. On regarde alors le cas $N=3$. Les cartes sont XYZWUV. On s'aperçoit alors que si Alice prend la carte $X$ au premier tour, elle s'assure de pouvoir prendre les cartes $Z$ et $U$ si elle le veut. Ces remarques sont suffisantes pour penser qu' Alice dispose d'une stratégie gagnante en récupérant les cartes $X, Z, U$ si $X+Z+U>Y+W+V$ et en récupérant les cartes $Y, W, V$ dans le cas contraire. On prouve à présent que cette stratégie fonctionne dans le cas général.
|
| 193 |
+
Alice colorie une carte sur deux en noir (la carte toute à droite est blanche, celle toute à gauche est noire). Elle calcule la somme des numéros des cartes blanches et celle de numéros des cartes noires.
|
| 194 |
+
Si la somme des blanches est plus grande, elle choisit la carte blanche tout à droite. Bob prendra obligatoirement une carte noire ensuite. A chaque tour Alice peut choisir entre une carte blanche ou noire et en prenant la blanche, elle ne laisse pas la choix à Bob, qui prendra forcément une carte noire.
|
| 195 |
+
Ainsi à la fin Alice aura toutes les cartes blanches et Bob toutes les cartes noires. Donc elle aura un score supérieur ou égal à celui de Bob. Elle procède de même si la somme des cartes noires est plus grande.
|
| 196 |
+
Commentaire des correcteurs
|
| 197 |
+
La majorité des élèves a su trouver la bonne stratégie. Parmi ceux qui ne l'ont pas trouvée, beaucoup ont proposé une stratégie "au tour par tour", sans justifier qu'elle permettait de ne pas perdre. Une telle approche ne peut pas permettre de résoudre l'exercice.
|
| 198 |
+
|
| 199 |
+
Exercice 14. On considère une grille de taille $2019 \times 2019$. Sur cette grille sont posés des cailloux. Une configuration est dite belle s'il n'existe pas de parallélogramme formé par quatre cailloux $A B C D$, tels que $A, B, C$, et $D$ ne soient pas tous alignés.
|
| 200 |
+
Quel est le plus grand nombre de cailloux qu'il est possible de mettre dans une grille?
|
| 201 |
+
Solution de l'exercice 14 Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $\mathrm{n} \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver une grille possédant exactement c cailloux satisfaisant la propriété.
|
| 202 |
+
On s'empresse de tester l'énoncé pour des valeurs plus petites, par exemple pour une grille de taille $3 \times 3$, $4 \times 4$ ou même $5 \times 5$, afin de deviner la valeur. On trouve dans ces petits cas que les plus grands entiers sont respectivement 5, 7 et 9 . On peut conjecturer que la valeur recherchée sera donc $2 \times 2019-1=4037$. En testant ces petites valeurs, on a pu remarquer que la présence de cailloux sur une colonne forçait que certains emplacements soient vides. Nous allons donc essayer de formaliser ce raisonnement.
|
| 203 |
+
On considère les paires de cailloux qui sont sur la même colonne. S'il y a deux telles paires dont les cailloux sont à même distance sur des colonnes différentes alors on obtient un parallélogramme, ce que l'on veut éviter.
|
| 204 |
+
Soit $n_{i}$ le nombre de cailloux dans la $i$-ième colonne. Sur la colonne $i$ il y a par conséquent au moins $n_{i}-1$ paires à distances distinctes. Puisque pour deux colonnes fixées, la distance entre deux quelconques cailloux de la première colonne doit être différente de la distance entre deux quelconques cailloux de la deuxième colonne, toutes les distances entre deux paires de cailloux appartenant à la même colonne doivent être distinctes. Cela fait en tout $\left(n_{1}-1\right)+\left(n_{2}-1\right)+\cdots+\left(n_{2019}-1\right)=n-2019$ distances distinctes avec n le nombre total de cailloux. Or il y a au plus 2018 distances possibles, puisqu'il y a 2019 emplacements pour un cailloux dans une colonne. Ceci montre que $\mathrm{n} \leqslant 2018+2019=4037$.
|
| 205 |
+
Réciproquement, si on remplit chaque case de la première ligne par un caillou et chaque case de la première colonne par un caillou et on laisse les autres cases vides, on a alors placé $2 \times 2019-1=4037$ cailloux sans créer de parallélogrammes.
|
| 206 |
+
Le plus grand entier recherché est donc 4037.
|
| 207 |
+
Commentaire des correcteurs
|
| 208 |
+
Une grande partie des élèves a eu la bonne idée pour résoudre l'exercice, mais beaucoup ont eu du mal à formaliser le résultat correctement. Si on tente de résoudre cet exercice par récurrence, il faut expliciter les grilles que l'on manipule et faire attention au fait qu'une sous-grille d'une grille "maximale" n'est pas forcément maximale.
|
| 209 |
+
|
| 210 |
+
Exercice 15. Un lycée comporte un nombre impair de classes, et, dans chaque classe, un nombre impair d'élèves. Un élève est choisi dans chaque classe pour faire parti du comité des élèves. Si le nombre de classes avec le plus de garçons que de filles est impair, montrer que le nombre de façons de former un comité des élèves contenant un nombre impair de garçons excède le nombre de façons de former un comité d'élèves contenant un nombre impair de filles.
|
| 211 |
+
Solution de l'exercice 15 En l'absence d'idées face au problème, on peut essayer de démontrer le résultat par récurrence. Pour regarder si cela pourrait fonctionner, on peut regarder ce qu'il advient du résultat si l'on passe d'un lycée avec 3 élèves à un lycée avec 4 élèves. On vérifie également que les hypothèses de l'énoncé sont adaptées à une récurrence. On s'aperçoit que nous allons devoir distinguer plusieurs cas, selon la répartition garçon/filles dans les différentes classes. On démarre donc la récurrence.
|
| 212 |
+
Nous allons montrer le résultat par récurrence forte sur le nombre d'élèves au total. S'il n'y a aucun élève, alors le résultat est vrai, de même s'il n'y a qu'un élève dans le lycée.
|
| 213 |
+
Supposons qu'il y ait n élèves en tout dans des classes satisfaisant l'énoncé. Supposons que l'énoncé de l'exercice est vrai dès lors qu'il y a strictement moins que n élèves. Il y a deux cas à étudier :
|
| 214 |
+
|
| 215 |
+
- S'il n'y a de classe avec une fille et un garçon, alors il y a un nombre impair de classe avec que des garçons et les autres classes n'ont que des filles, donc le comité aura nécessairement un nombre impair de garçons, l'énoncé est vérifié.
|
| 216 |
+
- S'il existe une classe avec une fille et un garçon, appelons-les respectivement Alice et Bob. Si on enlève Alice et Bob de la classe alors il y a plus de manières de choisir le comité avec un nombre impair de garçons. Si on considère uniquement les comités avec soit Alice soit Bob, alors on a autant de comité avec un nombre impair de garçons qu'avec un nombre impair de filles : en effet, échanger Alice et Bob change la parité du nombre de garçons et de filles. Ainsi l'énoncé est vérifié.
|
| 217 |
+
Par récurrence forte, l'énoncé est vérifié quelque soit le nombre total d'élèves.
|
| 218 |
+
Une solution un peu plus astucieuse consiste à procéder différemment : soit $n$ le nombre de classes, et soient $f_{i}$ et $g_{i}$ les nombres de filles et garçons dans la classe $i$ pour $1 \leqslant i \leqslant n$. Alors la quantité suivante, lorsqu'on la développ,e compte le nombre de façons de faire un comité avec un nombre impair de garçons moins celui de faire un comité avec un nombre impair de filles :
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
\prod_{i=1}^{n}\left(g_{i}-f_{i}\right)
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
Mais ce produit est positif s'il y a un nombre impair de classes avec plus de garçons que de filles, ce qui donne bien le résultat voulu.
|
| 225 |
+
Commentaire des correcteurs
|
| 226 |
+
Les élèves ont pour la plupart procédé par récurrence sur le nombre de classes, en utilisant l'inégalité de réordonnement. La plupart ont procédé de manière correcte, mais certains ont écrit des inégalités strictes sans justifier pourquoi le cas d'égalité ne se présente pas (qui demande de citer une des hypothèses de l'énoncé : le nombre impair d'élèves par classe).
|
| 227 |
+
|
| 228 |
+
Exercice 16. On considère une grille $2019 \times 2019$. On note $C_{i, j}$ la case sur la i-ième colonne et la j-ième ligne pour $1 \leqslant \mathfrak{i}, \mathfrak{j} \leqslant 2019$. Un coloriage de la grille est formidable s'il n'existe pas $1 \leqslant \mathfrak{i}<\ell \leqslant 2019$ et $1 \leqslant j<k \leqslant 2019$ tels que les cases $C_{i, j}, C_{i, k}$ et $C_{\ell, j}$ soient de la même couleur. Quel est le plus petit entier N tel qu'il existe un coloriage formidable avec N couleurs?
|
| 229 |
+
Solution de l'exercice 16 Dans ce problème, on cherche le plus petit entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c est bien le plus petit entier recherché, on va d'une part montrer que si un entier $n$ satisfait la propriété, alors $n \geqslant c$ et d'autre part on va montrer que l'on peut trouver un coloriage avec exactement c couleurs satisfaisant la propriété.
|
| 230 |
+
On s'empresse de tester l'énoncé sur des plus petites valeurs, par exemple pour des grilles de taille $3 \times 3$, $4 \times 4$ ou même $5 \times 5$, afin de deviner la valeur minimale dans le cas général, ainsi qu'une éventuelle construction. On s'aperçoit que pour une grille $3 \times 3$, on a besoin d'au moins 2 couleurs pour une coloriage formidable. Pour une grille $5 \times 5$, on remarque que l'on a besoin de 3 couleurs au moins. On conjecture donc que pour N impair, on a besoin d'au moins $\frac{\mathrm{N}+1}{2}$.
|
| 231 |
+
La difficulté de l'exercice repose dans le fait qu'il faut d'abord essayer de deviner la valeur minimale avant de faire la preuve. En l'absence d'idée d'une preuve directe qu'il faut bien au moins $\frac{\mathrm{N}+1}{2}$ couleurs, on peut essayer de montrer par l'absurde qu'un coloriage possédant $\frac{\mathrm{N}-1}{2}$ ne sera pas formidable.
|
| 232 |
+
Pour cela, on remarque que la donnée de deux cases $C_{i, j} C_{l, j}$ (avec $i<l$ ) de couleur rouge sur une colonne $j$ empêche les cases de ligne $i$ et sur une colonne $k \geqslant j$ d'être de la couleur rouges. On peut dire que ces deux cases génèrent une interdiction sur la ligne $i$. On peut essayer de compter ces interdictions. Ce comptage dépend du nombre de couleurs que l'on utilise, ce qui nous encourage bien à résonner par l'absurde pour montrer qu'un coloriage avec $\frac{\mathrm{N}-1}{2}$ couleurs générera trop d'interdictions.
|
| 233 |
+
Où chercher les interdictions? On peut commencer par procéder manuellement : on regarde le nombre minimal d'interdictions générées par la colonne 1, puis les interdictions générées par la ligne 2 etc... Cette opération manuelle s'effectue à nouveau sur des petits cas, comme une grille $5 \times 5$ ou $7 \times 7$. On s'aperçoit au terme de ces opérations sur des petits cas que la contradiction s'obtient en regardant la colonne N , sur laquelle se trouvent toujours trop d'interdictions. Nous allons donc formaliser ce raisonnement en regardant le nombre d'interdictions.
|
| 234 |
+
On suppose donc que l'on dispose d'un coloriage formidable de la grille possédant 1009 couleurs (quitte à avoir des couleurs qui ne sont pas utilisées pour le coloriage en question).
|
| 235 |
+
Dans la suite, on dira que la paire $\left(C_{i, j}, C_{l, j}\right)$ génère une interdiction pour la case $C_{i, k}$ pour la couleur $c$ si les cases $C_{i, j}$ et $C_{l, j}$ sont de la couleur $c$, ce qui empêche la case $C_{i, k}$ d'être de la couleur c par hypothèse.
|
| 236 |
+
Soit $j \leqslant 2018$ une colonne fixée et soit $k_{j}$ le nombre de couleurs apparaissant sur au moins deux cases de la colonnes $j$. Pour une couleur de numéro c , on note $n_{c}$ le nombre de cases de la colonne $j$ coloriées avec la couleur c . Quitte à renuméroter les couleurs, on peut supposer que ce sont les couleurs $1, \ldots, \mathrm{k}_{\mathrm{j}}$ qui apparaissent au moins 2 fois et que les couleurs $k_{j+1}, \ldots, 1009$ apparaissent au plus une fois dans la colonne.
|
| 237 |
+
Etant donnée une couleur $\mathrm{c} \leqslant \mathrm{k}_{\mathrm{j}}$, il y a au moins $\mathrm{n}_{\mathrm{c}}-1$ paires de cases de la couleur c dans la colonne j. En effet, la case de la couleur c située la plus basse dans la colonne forme une paire avec chacune des $n_{c}-1$ autres cases de la colonne. Chacune de ces paires génère une interdiction pour l'une des cases de la colonne 2019 : la paire de cases $\left(C_{i, j}, C_{l, j}\right)(i<l)$ génère une interdiction pour la case $C_{i, 2019}$. Ainsi, les cases de la colonne $j$ génère $\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)$ interdictions dans la dernière colonne. Or, puisque les couleurs $k_{j+1}, \ldots, 1009$ occupent au plus une case dans la colonne $j$, on a au moins
|
| 238 |
+
|
| 239 |
+
$$
|
| 240 |
+
\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)=\sum_{c=1}^{k_{j}} n_{c}-k_{j} \geqslant 2019-\left(1009-k_{j}\right)-k_{j}=1010
|
| 241 |
+
$$
|
| 242 |
+
|
| 243 |
+
interdictions générées dans la colonne 2019.
|
| 244 |
+
Ainsi, chaque colonne de numéro $k \leqslant 2018$ génère au moins 1010 interdictions pour les cases de la colonne 2019, ce qui donne au total au moins 2018 - 1010 interdictions pour la colonne 2019.
|
| 245 |
+
A présent, on note que si la case de ligne $i$ de la colonne 2019 reçoit 2 interdictions pour la même couleur $c$, cela signifie qu'il existe des cases $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}$ avec $j<j^{\prime}$, toutes de couleurs $c$, dont les paires $\left(C_{i, j}, C_{l, j}\right),\left(C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}\right)$ génèrent la même interdiction pour la case $C_{i, 2019}$ pour la couleur $c$. Mais le fait que les cases $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}$ est interdit par hypothèses. Ainsi, si une case possède $m$ interdictions, ces interdictions concernent m couleurs différentes.
|
| 246 |
+
Enfin, ces interdictions ne peuvent pas concerner la case $\mathrm{C}_{2019,2019}$. Ainsi, d'après le principe des tiroirs, puisqu'il y a 2018 - 1010 interdictions sur la colonne 2019 au moins, il y a une case parmi les cases $\mathrm{C}_{1,2019}, \ldots, \mathrm{C}_{2018,2019}$ qui possède au moins 1010 interdictions, elle est donc interdite pour au moins 1010 couleurs différentes, ce qui est absurde puisque l'on ne peut utiliser que 1009 couleurs différentes. En conclusion, un coloriage formidable possède au moins 1010 couleurs différentes. Réciproquement, si l'on dispose de 1010 couleurs, on peut construire un coloriage formidable, en s'inspirant de la configuration suivante pour $\mathrm{N}=7$.
|
| 247 |
+

|
| 248 |
+
|
| 249 |
+
## Commentaire des correcteurs
|
| 250 |
+
|
| 251 |
+
Très peu d'élèves ont rendu une copie pour cet exercice. Quelques élèves ayant traité l'exercice ont mal compris l'énoncé et ont donné des explications peu claires. La construction a été assez largement trouvée parmi les élèves qui ont cherché l'exercice.
|
| 252 |
+
|
| 253 |
+
## Exercice 17.
|
| 254 |
+
|
| 255 |
+
Un super-domino est un pavé droit dans une grille en trois dimensions de l'une des trois formes suivantes : $1 \times 1 \times 2,1 \times 2 \times 1$ et $2 \times 1 \times 1$. Quels sont les entiers $a, b, c>1$ tels qu'il est possible de paver un pavé droit de dimensions $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ dans un grille en trois dimensions avec des super-dominos de sorte qu'il y ait autant de super-dominos de chacun des 3 types?
|
| 256 |
+
Solution de l'exercice 17 Dans ce problème, on cherche tous les entiers $a, b, c$ satisfaisant certaines propriétés. Nous allons donc établir que si $\mathrm{a}, \mathrm{b}$ et c satisfont la propriété alors $\mathrm{a}, \mathrm{b}$ et c sont d'une certaine forme, et d'autre part montrer que si $a, b$ et $c$ sont de la forme trouvée, alors ils satisfont bien la propriété.
|
| 257 |
+
On peut également noter qu'il s'agit d'un problème de pavage, nous pouvons donc nous attendre à devoir utiliser un coloriage adroit du pavé droit. Si l'on n'a à priori pas d'idée sur la forme des entiers $a, b$ et $c$, on peut commencer par effectuer quelques remarques.
|
| 258 |
+
Si on parvient à paver un pavé droit $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ avec N super-dominos de chacun des trois types, alors nécessairement il y aura $2 \mathrm{~N}+2 \mathrm{~N}+2 \mathrm{~N}=\mathrm{abc}$ cases pavées, donc 6 divise $a b c$. Ainsi une coordonnée est paire. Supposons donc sans perte de généralité que a est pair.
|
| 259 |
+
Pour simplifier, on supposera que le pavé est composé de abc cases de coordonnées $(i, j, k)$, où $i$ est l'abscisse, $j$ l'ordonnée de la case et $k$ la profondeur.
|
| 260 |
+
On cherche désormais un coloriage de notre pavé. Tout d'abord, les objets manipulés sont des dominos, composés de 2 cubes; On va donc chercher un coloriage à 2 couleurs, du type damier. Regardons les caractéristiques d'un éventuel coloriage. On peut commencer par se concentrer sur une face, par exemple sur les cases de profondeur 1 . Un domino $1 \times 1 \times 2$ occupe au maximum une case sur cette face tandis que les deux autres types de dominos occupent 0 ou 2 cases de cette face. On peut donc essayer d'adapter notre coloriage à cette remarque en appliquant le même coloriage à chacune des tranches (par tranche, on entend ici l'ensemble des cases possédant la même profondeur), c'est-à-dire un coloriage où la couleur d'une case ( $i, j, k$ ) dépend de $i$ et de $j$ mais pas de $k$. L'avantage sera que les deux cubes d'un quelconque domino $1 \times 1 \times 2$ seront de la même couleur. De ce constat, on peut chercher à faire en sorte que les 2 cubes des dominos $1 \times 2 \times 1$ et $2 \times 1 \times 1$ soient de couleur différentes. Ceci nous fait penser à un coloriage en damier, que l'on applique uniformément à chacune des tranches. Formalisons donc ce coloriage et voyons l'information qu'il nous apporte.
|
| 261 |
+
On colorie en blanc les cases $(i, j, k)$ telles que $i+j$ est paire, et en noir les autres. Ainsi, les cubes d'un super-domino $1 \times 1 \times 2$ sont de la même couleur, noir ou blanc, tandis qu'un super-domino $1 \times 2 \times 1$ contient exactement un cube blanc et un cube noir, de même pour un super-domino $2 \times 1 \times 1$. On déduit que lorsque l'on pave notre pavé droit avec le même nombre de super-domino de chaque type, le nombre total de cases blanches recouvertes est pair : en effet un super-domino $1 \times 1 \times 2$ en recouvre 2 ou 0 , et un super-domino d'un des deux autres type en recouvre 1 . Ainsi pour pouvoir paver le pavé droit $a \times b \times c$ avec autant de super-dominos de chaque type, il faut qu'il y ait un nombre pair de cases blanches. Or, la tranche constituée des cases de profondeur 1 contient exactement $\frac{\mathrm{ab}}{2}$ cases blanches et toutes les tranches sont coloriées de la même façon et il y a c tranches. Il y a donc $\frac{\mathrm{ab}}{2} \times \mathrm{c}$ cases blanches et ce nombre doit être pair. On déduit que 4 divise abc. Comme 6 et 4 divisent abc , on a que 12 divise abc si un pavé $a \times b \times c$ satisfait l'énoncé.
|
| 262 |
+
|
| 263 |
+
On s'attaque désormais à la réciproque en montrant que l'on peut paver correctement un pavé $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ si 12 divise abc. Pour trouver un tel pavage, on commence toujours par regarder les pavés de petites dimensions, par exemple un pavé $2 \times 2 \times 3$. Ces essais sont plus utiles qu'on ne le croit. En effet, si l'on parvient à paver ce pavé, on pourra paver correctement des pavés plus gros en découpant ces gros pavés en petits pavés de dimension $2 \times 2 \times 3$ par exemple. Or, on remarque qu'avec deux dominos de chaque type, on peut paver un pavé $2 \times 2 \times 3$ et $3 \times 4 \times 3$ (voir la figure, le pavage de droite est découpé en deux parties pour être plus lisible). De plus, cela permet de paver un pavé $2 \times 4 \times 3$ en recollant selon
|
| 264 |
+
la largeur deux pavés $2 \times 2 \times 3$ en recollant deux $3 \times 2 \times 3$ selon la largeur. Puisque tout entier $a>1$ s'écrit comme somme de 2 et de 3 , en recollant le bon nombre de pavés de la forme $2 \times 4 \times 3$ et $3 \times 4 \times 3$, on peut paver n'importe quel pavé $a \times 4 \times 3$ pour $a>1$. De même, on peut paver les pavés de la forme $a \times 2 \times 6$, avec $a>1$. Or si 12 divise $a b c$ alors il y a deux possibilités:
|
| 265 |
+
|
| 266 |
+
- Une dimension du pavé droit est divisible par 6 et une autre dimension est paire. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $a \times 2 \times 6, a>1$.
|
| 267 |
+
- Une dimension du pavé droit est divisible par 4 et une autre dimension est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $\mathbf{a} \times 4 \times 3$, $\boldsymbol{a}>1$.
|
| 268 |
+
- Deux dimensions du pavé sont paires, et la dernière est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $2 \times 2 \times 3$.
|
| 269 |
+
- Une dimension du pavé droit est divisible par 12 et les autres sont impaires, non divisibles par 3, supérieures ou égales à 5 . Alors on décompose le pavé droit $12 \mathrm{a} \times \mathrm{b} \times \mathrm{c}$ en un pavé $12 \mathrm{a} \times 3 \times \mathrm{c}$ et $12 a \times(b-3) \times c$, et on pave chacun comme précédemment cas $b-3$ est pair.
|
| 270 |
+
Ceci achève la construction et montre que les pavé droits qui peuvent être ainsi pavés sont ceux tels que 12 divise abc.
|
| 271 |
+
|
| 272 |
+
|
| 273 |
+
|
| 274 |
+
## Commentaire des correcteurs
|
| 275 |
+
|
| 276 |
+
L'exercice était difficile et a été résolu par un faible nombre d'élèves, mais un certain nombre d'élèves a réussi à avancer sur le problème, en montrant que certains pavés étaient pavables.
|
| 277 |
+
|
| 278 |
+
Exercice 18. 2019 élèves participent à un concours et répondent chacun à 6 questions. A la fin du concours, on remarque que, parmi les bonnes réponses données par un quelconque groupe de 3 élèves, il y a au moins une réponse correcte à au moins 5 des 6 questions du concours. Quelle est la valeur minimale du nombre total de réponses correctes aux questions du concours?
|
| 279 |
+
Solution de l'exercice 18 Dans ce problème, on cherche le plus petit entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c est bien le plus petit entier recherché, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \geqslant c$ et d'autre part on va montrer que l'on peut trouver une configuration avec exactement c réponses correctes données.
|
| 280 |
+
On peut commencer par ranger les données dans un tableau $2019 \times 6$, où les 2019 lignes représentent les 2019 élèves et les 6 colonnes les 6 problèmes. Dans la case ( $\boldsymbol{i}, \mathfrak{j}$ ), on inscrit un 1 si l'élève $\boldsymbol{i}$ a répondu correctement à la question $j$ et on inscrit un 0 sinon. Le problème nous invite à effectuer un doublecomptage, cette présentation sous forme de tableau permet de voir quel double-comptage est intéressant. Les hypothèses concernant les triplets d'élèves invitent à tenter d'effectuer un double comptage. Mais d'abord, on effectue quelques remarques simples. On peut noter que si trois élèves ont répondu tous les trois faux aux questions 5 et 6 , alors on a un triplet d'élèves dont les réponses ne sont pas correctes pour au moins 5 exercices. Ainsi, si $q_{1}$ et $\mathrm{q}_{2}$ sont deux questions du concours, il y a au plus 2 élèves qui ont répondu faux à ces questions. Comme il y a $\binom{6}{2}=15$ façons de choisir une paire de questions $\left\{\mathbf{q}_{1}, \mathbf{q}_{2}\right\}$, et pour chaque paire il y a au plus deux élèves qui ont mal répondu à ces deux questions donc il y a au plus $2 \cdot 15=30$ paires $\left(\left\{q_{1}, q_{2}\right\}, e\right)$ telles que l'élève $e$ a mal répondu aux questions $q_{1}$ et $q_{2}$. Dans le tableau, cela se traduit par le fait qu'il y a au plus 30 paires de 0 tels que les deux 0 appartiennent à la même ligne. Cette majoration du nombre de paires de 0 appartenant à la même ligne nous permet de deviner le double comptage que nous allons effectuer : nous allons compter de deux façons différentes le nombre N de paires de 0 tels que les deux 0 appartiennent à la même ligne. Une telle paire sera dite mauvaise dans la suite. On a déjà compté "selon les colonnes", ce qui nous a donné $\mathrm{N} \leqslant 30$. On va chercher à présent à compter "selon les lignes".
|
| 281 |
+
On note El 'ensemble des élèves qui ont répondu à au plus 4 questions. A chacun des élèves de E , on peut associer au moins un couple de réponses fausses donc $|E| \leqslant N \leqslant 30$
|
| 282 |
+
Pour un élève $e \in E$ on note $\mathrm{n}(e)$ le nombre de questions auxquelles il a répondu faux. Alors $\mathrm{N}=$ $\sum_{e \in E}\binom{\mathfrak{n}(e)}{2}$, puisque les seuls mauvaises paires appartiennent à des lignes associées à des éléments de E et que s'il y a $n(e) 0$ dans une lignes, il y a $\binom{n(e)}{2}$ façons de créer des paires de 0 de cette lignes. On utilise à présent la convexité de la fonction $x \mapsto \frac{x(x-1)}{2}=\binom{x}{2}$ pour appliquer l'inégalité de Jensen et obtenir une minoration de N :
|
| 283 |
+
|
| 284 |
+
$$
|
| 285 |
+
N=\sum_{e \in \mathrm{E}}\binom{\mathfrak{n}(e)}{2} \geqslant|\mathrm{E}|\binom{\frac{\sum_{e \in \mid} n(e)}{|E|}}{2}
|
| 286 |
+
$$
|
| 287 |
+
|
| 288 |
+
On note f le nombre total de réponses fausses proposées par les élèves de E , et $v$ le nombre total de réponses justes, de telles sorte que $\mathrm{f}+v=6|\mathrm{E}|$. On a donc $\sum_{e \in \mathrm{E}} \mathfrak{n}(e)=\mathrm{f}$. Ainsi :
|
| 289 |
+
|
| 290 |
+
$$
|
| 291 |
+
\begin{aligned}
|
| 292 |
+
& 30 \geqslant N \geqslant \frac{f(f-|E|)}{2|E|} \\
|
| 293 |
+
& \mathbf{f}^{2}-\mathbf{f}|\mathrm{E}|-60|\mathrm{E}| \leqslant 0
|
| 294 |
+
\end{aligned}
|
| 295 |
+
$$
|
| 296 |
+
|
| 297 |
+
Cette dernière équation fournit que $f \leqslant \frac{|E|+\sqrt{|E|^{2}+240|E|}}{2}$.
|
| 298 |
+
Soit $V$ le nombre total de réponses justes données par l'ensembe des élèves, alors $V$ est la somme du nombre de bonnes réponses des élèves de E et la somme des bonnes réponses des élèves qui ne sont pas
|
| 299 |
+
dans E. Par définition, les élèves qui ne sont pas dans E ont répondu correctement à au moins 5 questions. Donc
|
| 300 |
+
|
| 301 |
+
$$
|
| 302 |
+
\mathrm{V} \geqslant v+(2019-|\mathrm{E}|) 5=2019 \times 5-5|\mathrm{E}|+v=2019 \times 5-5|\mathrm{E}|+6|\mathrm{E}|-\mathrm{f}=5 \times 2019+|\mathrm{E}|-\mathrm{f}
|
| 303 |
+
$$
|
| 304 |
+
|
| 305 |
+
Mais en utilisant l'inégalité obtenue en f plus haut on obtient
|
| 306 |
+
|
| 307 |
+
$$
|
| 308 |
+
\mathrm{V} \geqslant 2019 \times 5+\frac{|\mathrm{E}|-\sqrt{|\mathrm{E}|^{2}+240|\mathrm{E}|}}{2}
|
| 309 |
+
$$
|
| 310 |
+
|
| 311 |
+
Le côté droit est décroissant en $|E|$ et puisque $|E| \leqslant 30$, donc $V \geqslant 2019 \times 5+\frac{30-\sqrt{30^{2}+240 \times 30}}{2}=10065$. Donc V $\geqslant 10065$.
|
| 312 |
+
|
| 313 |
+
Réciproquement, il est possible que 2019 - 30 élèves aient répondu à 5 problèmes, et que 30 élèves aient répondu à 4 problèmes : il suffit que pour chacun des 15 ensembles de 4 questions parmi les 6 il y ait deux élèves qui ont répondu exactement à celles là. Cette configuration satisfait l'énoncé, et est telle que le nombre de bonnes réponses est exactement 10065.
|
| 314 |
+
|
| 315 |
+
## Commentaire des correcteurs
|
| 316 |
+
|
| 317 |
+
L'exercice, difficile, n'a été résolu que par très peu d'élèves. Cependant, il est appréciable de voir que plusieurs élèves ont rendu quelques éléments de réponses même s'ils ne disposaient pas d'une preuve complète. Quelques erreurs à éviter :
|
| 318 |
+
|
| 319 |
+
1. Ce n'est pas parce qu'on dispose d'une configuration à 10065 bonnes réponses et qu'on ne peut pas enlever de bonne réponse dans cette configuration que c'est forcément la configuration optimale et que 10065 est la valeur optimale.
|
| 320 |
+
2. Ce n'est pas parce qu'on a un minimum de bonnes réponses sur les élèves qui ont répondu correctement à au plus 4 questions ET qu'on a un minimum de bonnes réponses sur les élèves ayant répondu correctement à au moins 5 questions que le minimum pour le nombre global d'élèves est la somme de ces deux minimums. Autrement dit, le minimum global n'est pas forcément la somme des deux minimums locaux, surtout lorsque les deux groupes d'élèves et leur taille ne sont pas indépendants.
|
French_STS/md/fr-corrigé-commenté-envoi-5.md
ADDED
|
@@ -0,0 +1,391 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br> 
|
| 2 |
+
|
| 3 |
+
Envoi 5 : Pot Pourri
|
| 4 |
+
À RENVOYER AU PLUS TARD LE 15 MARS 2020
|
| 5 |
+
|
| 6 |
+
Les consignes suivantes sont à lire attentivement :
|
| 7 |
+
|
| 8 |
+
- Le groupe junior est constitué des élèves nés en 2005 ou après. Les autres élèves sont dans le groupe senior.
|
| 9 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 10 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 11 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 12 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 13 |
+
- Pour les exercices de géométrie, faire des figures sur des feuilles blanches séparées.
|
| 14 |
+
- Respecter la numérotation des exercices.
|
| 15 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 16 |
+
|
| 17 |
+
Animath,<br>Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.<br>contact-pofm@animath.fr
|
| 18 |
+
|
| 19 |
+
## Exercices Juniors
|
| 20 |
+
|
| 21 |
+
Exercice 1. Martin et Théo jouent à un jeu : Martin écrit un nombre entier au tableau. Théo a ensuite le droit d'effacer le nombre et de lui ajouter 2 , ou d'effacer le nombre et de lui enlever 3 , ceci autant de fois qu'il veut. Théo gagne s'il arrive à obtenir 2020 après un nombre fini d'étapes, sinon Martin gagne. Quel joueur a une stratégie gagnante ?
|
| 22 |
+
Solution de l'exercice 1 On commence par tester l'énoncé pour des entiers proches de 2020. Par exemple, on remarque que si Martin écrit les entiers 2018, 2016, ... Théo peut écrire 2020 au tableau en rajoutant au nombre écrit par Martin un nombre suffisamment grand de 2 . On remarque aussi que si Martin écrit 2019, Théo peut aussi gagner en remplaçant 2019 par 2021 puis 2023 puis 2023 par 2020.
|
| 23 |
+
Cette remarque nous permet de conjecturer d'une part que Théo peut toujours gagner quelque soit le nombre écrit par Martin, d'autre part que si un nombre k est écrit au tableau, Théo peut écrire les nombres $k+1$ ou $k-1$ au bout d'un nombre fini d'opérations.
|
| 24 |
+
Nous montrons donc que Théo peut toujours gagner quelque soit le nombre écrit par Martin. Supposons qu'à un instant donné, le nombre $k$ est écrit au tableau. Alors en remplaçant $k$ par $k+2$ en ajoutant 2 , $k+2$ par $k+4$ en ajoutant 2 et enfin $k+4$ par $k+1$ en retranchant 3 , Théo a remplacé le nombre $k$ par le nombre $k+1$ en un nombre fini d'opération. Nous appellerons cette transformation l'opération A. D'autre part, toujours si l'entier $k$ est écrit au tableau à un instant donné, en remplaçant $k$ par $k+2$ et $k+2$ par $k-1$, Théo a remplacé l'entier $k$ par l'entier $k-1$. Nous appellerons cette transformation l'opération B.
|
| 25 |
+
Supposons désormais que Martin a écrit le nombre $k_{0}$ au tableau. Si $k_{0}=2020$, Théo a déjà gagné. Si $\mathrm{k}_{0}<2020$, alors en effectuant $2020-\mathrm{k}_{0}$ fois l'opération $A$, Théo peut remplacer l'entier $k_{0}$ par 2020 et gagner. Si $k_{0}>2020$, en effectuant $k_{0}-2020$ fois l'opération $B$, Théo peut remplacer à nouveau l'entier $k_{0}$ par 2020. Dans tous les cas, Théo gagne!
|
| 26 |
+
Commentaire des correcteurs : L'exercice a été résolu avec succès par tous les élèves qui l'ont abordé.
|
| 27 |
+
|
| 28 |
+
Exercice 2. Soit $A B C$ un triangle tel que $\widehat{B A C}=60^{\circ}$. Soit $O$ le centre du cercle circonscrit au triangle $A B C, H$ son orthocentre et $I$ le point d'intersection des bissectrices. Montrer que les points B, O, I, H et C sont cocycliques.
|
| 29 |
+
|
| 30 |
+
## $\underline{\text { Solution de l'exercice } 2}$
|
| 31 |
+
|
| 32 |
+
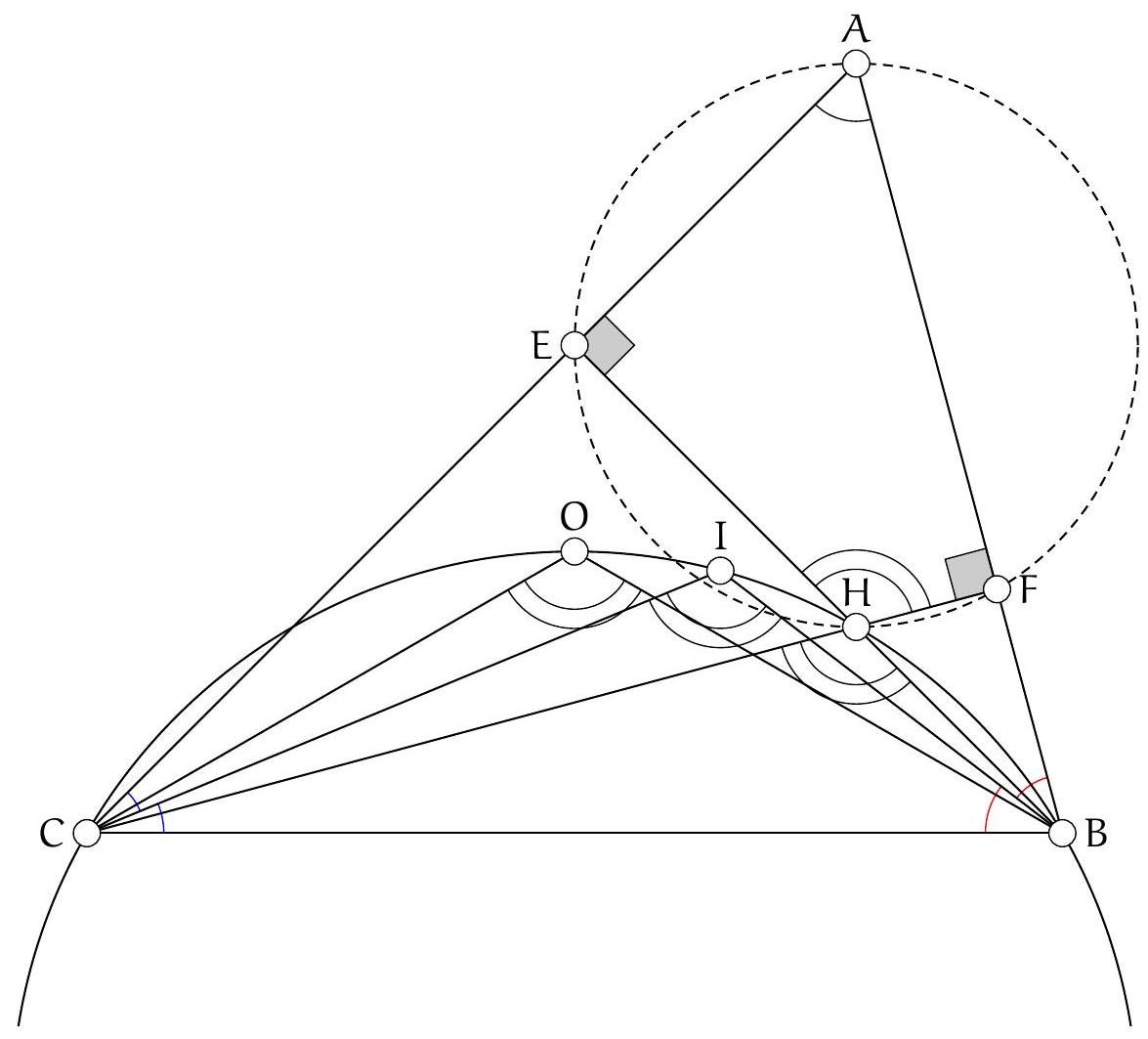
|
| 33 |
+
|
| 34 |
+
On traite le cas où les angles du triangle sont aigus.
|
| 35 |
+
Avant de se lancer dans une chasse aux angles, on se demande quelles égalités d'angles nous allons déterminer pour montrer que les 5 points sont sur un même cercle. Pour cela, on note qu'on a, à priori, plus facilement accès aux angles des triangles BOC, BHC et BIC qu'aux angles du triangle BOH par exemple. Ceci nous motive à montrer que $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}$.
|
| 36 |
+
Tout d'abord, d'après le théorème de l'angle inscrit, $\widehat{B O C}=2 \cdot \widehat{B A C}=120^{\circ}$. On sait donc que nous allons devoir montrer successivement $\widehat{\mathrm{BHC}}=120^{\circ}$ et $\widehat{\mathrm{BIC}}=120^{\circ}$.
|
| 37 |
+
Pour calculer $\widehat{\mathrm{BHC}}$, on utilise la définition du point H comme le point d'intersection des hauteurs du triangle $A B C$. On introduit donc $D, E$ et $F$ les pieds des hauteurs respectivement issues des sommets $A, B$ et $C$. On utilise alors le fait (classique) que $\widehat{\mathrm{HEA}}=180^{\circ}-\widehat{\mathrm{HFA}}=90^{\circ}$ pour obtenir que les points $A, E, H$ et $F$ sont cocycliques. Ainsi $\widehat{\mathrm{FHE}}=180^{\circ}-\widehat{\mathrm{EAF}}=120^{\circ}$ donc $\widehat{\mathrm{BHC}}=\widehat{\mathrm{EHF}}=120^{\circ}$
|
| 38 |
+
Enfin, pour montrer que $\widehat{\mathrm{BIC}}=120^{\circ}$, on se sert du fait que le point I est le point d'intersection des bissectrices du triangle. Cette définition nous donne en effet accès aux angles $\widehat{\mathrm{BCI}}$ et $\widehat{\mathrm{BCI}}$ en fonction des angles du triangle. On a donc:
|
| 39 |
+
$\widehat{\mathrm{BIC}}=180^{\circ}-\widehat{\mathrm{IBC}}-\widehat{\mathrm{ICB}}=180^{\circ}-\frac{1}{2} \widehat{\mathrm{ABC}}-\frac{1}{2} \widehat{\mathrm{ACB}}=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{BAC}}\right)=180^{\circ}-60^{\circ}=120^{\circ}$
|
| 40 |
+
En conclusion, $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}=120^{\circ}$ donc les 5 points $\mathrm{B}, \mathrm{O}, \mathrm{H}, \mathrm{I}$ et C sont cocycliques.
|
| 41 |
+
|
| 42 |
+
On peut traiter de façon similaire le cas où un des angles du triangle $A B C$ est obtus.
|
| 43 |
+
Commentaire des correcteurs: L'exercice est majoritairement bien réussi.
|
| 44 |
+
|
| 45 |
+
## Exercice 3.
|
| 46 |
+
|
| 47 |
+
1. Existe-t-il des nombres $a_{0}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \times a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times$ $a_{2020}+a_{2020} \times a_{0}=1010 ?$
|
| 48 |
+
2. Existe-t-il des nombres $a_{1}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times$ $a_{2020}+a_{2020} \times a_{1}=1010 ?$
|
| 49 |
+
|
| 50 |
+
## Solution de l'exercice 3
|
| 51 |
+
|
| 52 |
+
Déjà regardons l'énoncé : on veut savoir si on peut trouver des nombres $\left(a_{i}\right)_{1 \leqslant i \leqslant n}$ valant +1 ou -1 tels que $a_{1} a_{2}+\cdots+a_{n} a_{1}$ vaut 1010 avec dans la première question $n=2021$, dans la seconde $n=2020$. Pour cela on peut tester avec des $n$ petits quels sont les nombres qu'on peut écrire sous la forme $a_{1} a_{2}+\cdots+a_{n} a_{1}$. Pour $n=3$, on trouve 3 (si on ne prend que des 1 ) et -1 (si on prend $a_{1}=a_{2}=1, a_{3}=-1$ ). Pour $n=4$, on trouve $4,0,-4$ (pour avoir 4 on ne prend que des 1 , pour avoir 0 il suffit de prendre trois $a_{i}$ valant 1 et un valant -1 , pour avoir -4 , il suffit d'altener les $a_{i}$ valant 1 et ceux valant -1 . On peut continuer à tester les valeurs pour des $n$ petits. On peut remarquer que déjà les nombres qu'on peut obtenir ont l'air d'être régulièrement écartés de 4 , ils sont même congrus à $n$ modulo 4.
|
| 53 |
+
|
| 54 |
+
Notons également que si $a= \pm 1$ et $b= \pm 1$, alors $a b \pm 1$ et que $a b=1$ si $a=b$ et $a b=-1$ si $a=-b$ 。
|
| 55 |
+
|
| 56 |
+
1. Ici on est dans le cas où $n=2021$ et on veut obtenir une somme de 1010. Cela semble impossible à cause de la parité, on va donc regarder la parité de la somme. Soient $a_{0}, \ldots, a_{2020}$ des nombres valant -1 ou 1 . Pour simplifier on pose $a_{2021}=a_{0}$. Comme on a toujours $a_{i} a_{i+1}= \pm 1, a_{0} \times$ $a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}$ est une somme de 2021 nombres impairs, donc impaire. Elle ne peut donc pas valoir 1010 qui est pair. Il n'existe pas de nombres $a_{0}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \times a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}=1010$.
|
| 57 |
+
2. Dans ce cas $\mathrm{n}=2020$ est divisible par 4 . A priori vu les tests effectués pour des petites valeurs, on s'attend à ce que le nombre obtenu soit divisible par 4 , or $1010=2 \times 505$ n'est pas divisible par 4. On pourrait essayer de réutiliser l'argument de parité précédent, mais comme 2020 est pair, il prouverait que la somme est paire, or 1010 l'est aussi. Il va donc falloir plus précisément compter les moments où $a_{i} a_{i+1}=-1$ et ceux où $a_{i} a_{i+1}=1$. Or on sait que $a_{i} a_{i+1}=-1$ si et seulement si $a_{i}=-a_{i+1}$, il suffit donc de compter le nombre de changement de signes de la suite $a_{i}$ !
|
| 58 |
+
Soient $a_{1}, \ldots, a_{2020}$ des nombres valant -1 ou 1 tels que $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+$ $a_{2020} \times a_{1}=1010$. Posons $a_{2021}=a_{1}$. On note $N$ le nombre de $i$ tels que $1 \leqslant i \leqslant 2020$ tels que $a_{i}=-a_{i+1}$. En particulier dans la somme $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}$ il y a N valeurs -1 et $(2020-\mathrm{N})$ valeurs 1 . La somme vaut donc $2020-\mathrm{N}-\mathrm{N}=2020-2 \mathrm{~N}$, on a donc $2020-2 \mathrm{~N}=1010$ soit $2 \mathrm{~N}=1010$ donc $\mathrm{N}=505$. Or N est pair. En effet N est le nombre de changement de signs dans la suite $\left(a_{1}, \ldots, a_{2020}, a_{1}\right)$ et cette suite commence par $a_{1}$ et termine $a_{1}$ donc elle a nécessairement un nombre pair de changements de signe puisque $a_{1}$ est du même signe que lui-même. On ne peut donc pas avoir $N=505$, ce qui fournit une contradiction. Il n'existe pas de nombres $a_{1}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}=1010$.
|
| 59 |
+
Commentaire des correcteurs: L'exercice a été bien traité : la première question a été quasiment toujours réussie, pour la seconde question, la majorité des copies mentionne qu'un nombre impair de produits valant -1 est possible mais peu trouvent un argument rigoureux pour le prouver : on pouvait vérifier que changer $a_{i}$ en $-a_{i}$ ne changeait pas la parité du nombre de produits valant -1 et dire que dans la situation où tous les $a_{i}$ valent 1 , le nombre de produits valant -1 est pair, il ne pouvait donc être impair à la fin. On pouvait également interpréter les produits -1 comme les changements de parité de la suite ( $a_{i}$ ) composée de $a_{1}, \ldots, a_{2019}, a_{1}$. Comme elle commence à $a_{1}$ et termine à $a_{1}$, le nombre de changements de signe est forcément pair.
|
| 60 |
+
|
| 61 |
+
Exercice 4. Soit $A B C$ un triangle dont les angles sont aigus. La hauteur issue de $A$ recoupe le cercle circonscrit au triangle $A B C$ en un point $D$. La hauteur issue de $B$ recoupe le cercle circonscrit au triangle $A B C$ en un point $E$. La droite (ED) coupe les côtés $[A C]$ et $[B C]$ respectivement en les points $P$ et $Q$. Montrer que les points $P, Q, B$ et $A$ sont cocycliques.
|
| 62 |
+
|
| 63 |
+
## Solution de l'exercice 4
|
| 64 |
+
|
| 65 |
+
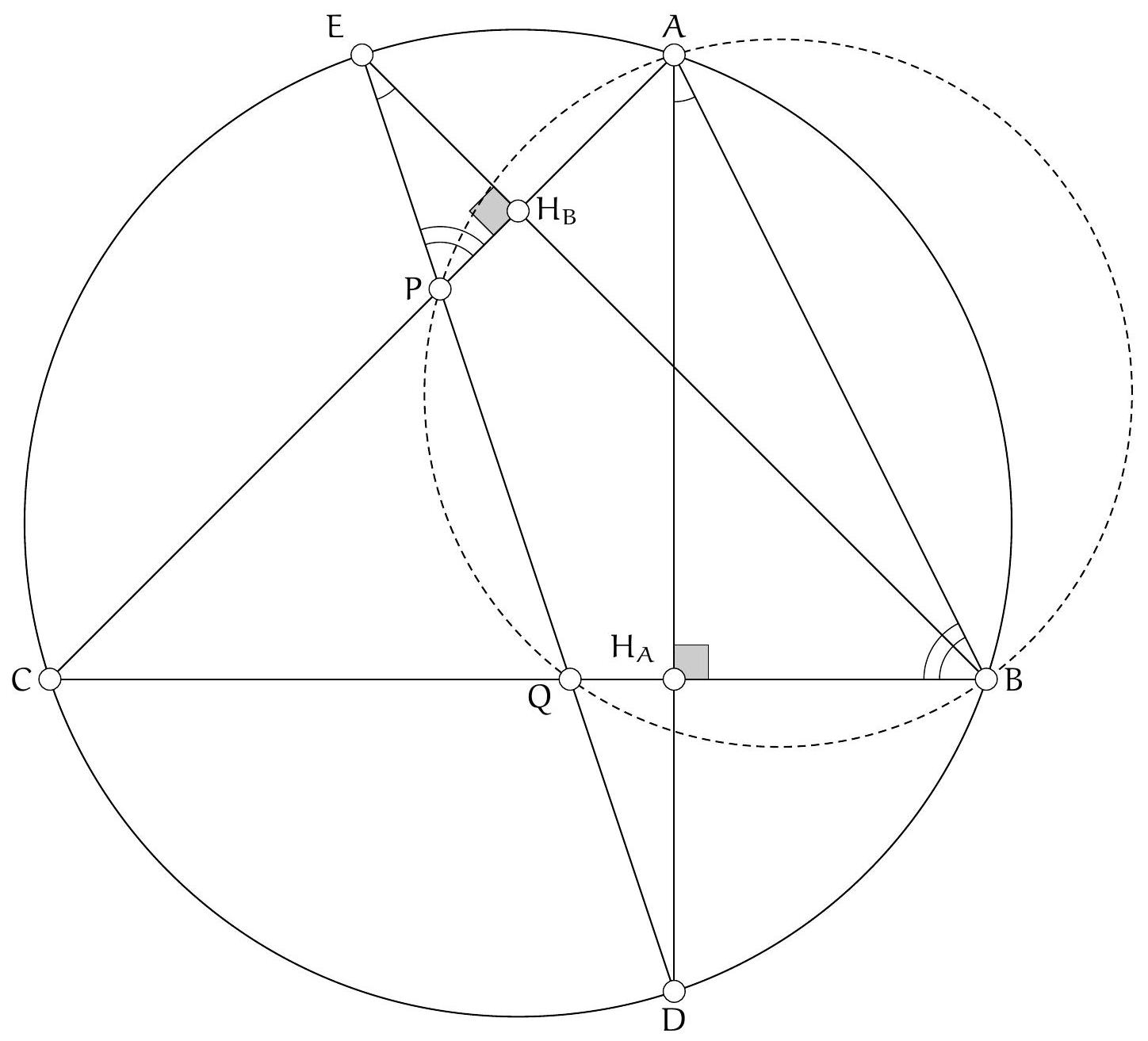
|
| 66 |
+
|
| 67 |
+
Déterminons quels sont les angles qui semblent faciles d'accès. Par exemple, il semble compliqué de pouvoir obtenir l'angle $\widehat{\mathrm{PBQ}}$ ou l'angle $\widehat{\mathrm{PBA}}$. En revanche, on connait déjà l'angle $\widehat{\mathrm{QBA}}$ donc il semble raisonnable d'essayer de montrer que $\widehat{\mathrm{QPA}}=180^{\circ}-\widehat{\mathrm{QBA}}$.
|
| 68 |
+
Or, $180^{\circ}-\widehat{\mathrm{QPA}}=\widehat{\mathrm{EPA}}$, on essaye donc de montrer que $\widehat{\mathrm{EPA}}=\widehat{\mathrm{QBA}}$. Deux angles droits nous sont donnés : si on pose $H_{B}$ le pied de la hauteur issue du sommet $B$ et $H_{A}$ le pied de la hauteur issue du sommet $A$, alors les angles $\widehat{A H_{A} B}$ et $\widehat{B H_{B} A}$ sont droits.
|
| 69 |
+
On n'a pas encore utilisé l'hypothèse que les points $E$ et $D$ étaient sur le cercle circonscrit au triangle $A B C$. Cette hypothèse se traduit par une égalité d'angle à l'aide du théorème de l'angle inscrit. Ceci donne notemment $\widehat{\mathrm{DEB}}=\widehat{\mathrm{DAB}}$.
|
| 70 |
+
|
| 71 |
+
En reportant ces différentes égalités d'angles sur la figure, on trouve donc que $\widehat{\mathrm{PEH}_{B}}=\widehat{\mathrm{H}_{\mathrm{A}} \mathrm{AB}}$ et $\widehat{\mathrm{PH}_{B} \mathrm{E}}=\widehat{\mathrm{BH}_{\mathrm{A}} \mathrm{A}}$. Les triangles $\mathrm{PEH}_{B}$ et $\mathrm{BAH}_{\mathrm{A}}$ sont donc sembables (il y a deux paires d'angles égaux deux à deux). Ainsi, $\widehat{\mathrm{EPH}_{\mathrm{B}}}=\widehat{\mathrm{ABH}_{\mathrm{A}}}$ qui est l'égalité que l'on souhaitait démontrer.
|
| 72 |
+
Commentaire des correcteurs: L'exercice est très bien réussi et les élèves ont montré plusieurs façons efficaces de voir les choses.
|
| 73 |
+
|
| 74 |
+
Exercice 5. Les cases d'un échiquier $8 \times 8$ sont blanches. Un coup consiste à échanger les couleurs des cases d'un rectangle $3 \times 1$ ou $1 \times 3$ (les cases blanches deviennent noires et les cases noires deviennent blanches). Est-il possible d'aboutir en un nombre fini de coups à la configuration où toutes les cases de l'échiquier sont noires?
|
| 75 |
+
Solution de l'exercice 5 L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée dans ce cas est de chercher un invariant.
|
| 76 |
+
On peut éventuellement essayer à la main de voir s'il est possible d'aboutir à une configuration où toutes les cases sont noires. Après plusieurs essais, on se rend compte qu' on n'arrive pas à aboutir la configuration désirée et on peut donc conjecturer que la réponse à l'exercice est négative.
|
| 77 |
+
Ici, le support de l'énoncé est un échiquier, on va donc chercher un invariant de coloriage, c'est-à-dire que nous allons chercher un coloriage astucieux de l'échiquier qui mette en évidence l'invariant. Quelles sont les caractéristiques d'un bon coloriage ? Tout d'abord, puisque les rectangles considérés possèdent 3 cases, on peut chercher un coloriage qui possède au plus 3 couleurs. Aussi, on peut chercher un coloriage tel que chaque rectangle $3 \times 1$ ou $1 \times 3$ possède une case de chaque couleur. On adopte donc le coloriage suivant (où on a remplacé les couleurs par des numéros, étant donné que l'exercice parle déjà de couleurs de cases).
|
| 78 |
+
|
| 79 |
+
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
|
| 80 |
+
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
| 81 |
+
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
|
| 82 |
+
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
|
| 83 |
+
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
|
| 84 |
+
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
|
| 85 |
+
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
|
| 86 |
+
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
|
| 87 |
+
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
|
| 88 |
+
|
| 89 |
+
Que nous apprend ce coloriage ? Chaque rectangle $3 \times 1$ ou $1 \times 3$ possède exactement une case de chaque numéro. Donc lorsque l'on change les couleurs d'un rectangle, exactement une case de chaque numéro change de couleur. Puisque les nombres de cases de numéro 1,2 et 3 ne sont pas identiques, ceci nous encourage à compter à chaque étape le nombre de cases blanches de chaque numéro.
|
| 90 |
+
Soit $\mathrm{N}_{1}$ le nombre de cases blanches contenant le numéro 1, dites de type $1, \mathrm{~N}_{2}$ le nombre de cases blanches de types 2 et $\mathrm{N}_{3}$ le nombre de cases blanches de type 3. Dans la situation initiale, $\mathrm{N}_{1}=\mathrm{N}_{3}=21$ et $\mathrm{N}_{2}=22$, ces nombres ne sont pas tous égaux. On va donc s'intéresser à l'évolution de la différence entre les nombres $N_{1}$ et $N_{2}$. Changer la couleur des cases d'un rectangle $3 \times 1$ ou $1 \times 3$ fait en même temps diminuer ou augmenter chacun des nombres $N_{1}, N_{2}$ et $N_{3}$. En particulier, la différence $N_{1}-N_{2}$, à chaque étape, augmente de $2,0 \mathrm{ou}-2$. En particulier, sa parité ne change pas. Or $\mathrm{N}_{1}-\mathrm{N}_{2}$ est impair au départ. Dans la situation finale demandée, $N_{1}-N_{2}=0.0$ est pair, donc le nombre $N_{1}-N_{2}$ ne peut être nul au bout d'un nombre fini d'étape. On ne peut donc pas arriver à un échiquier entièrement noir. Commentaire des correcteurs: L'exercice n'a pas été abordé par beaucoup d'élèves. L'exercice est cela dit un exercice d'invariant par coloriage très instructif.
|
| 91 |
+
|
| 92 |
+
Exercice 6. Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
2^{x}+3^{y}=z^{2}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Solution de l'exercice 6 Tout d'abord, analysons le problème : on a une équation diophantienne avec une puissance 2 , une puissance de 3 et un carré. On s'empresse donc de tester les petites valeurs de $z$ et de trouver la solution. On peut remarquer que $2^{0}+3^{1}=2^{2}, 2^{3}+3^{0}=3^{2}$ et $2^{4}+3^{2}=5^{2}$. A priori comme on a quelques solutions, on ne va pas trouver de contradictions immédiates simplement en regardant modulo quelque chose.
|
| 99 |
+
Néanmoins on a un carré, donc il est naturel de regarder modulo 4 ou modulo 3 et d'essayer d'obtenir des informations sur $x$ et $y$. Idéalement, on aimerait obtenir que soit $x$ soit $y$ est pair, comme ça on aurait un autre carré dans l'équation ce qui nous permettrait de factoriser. On va donc regarder modulo 4, pour cela on a envie de traitrer en premier le cas où 4 divise $2^{\mathrm{x}}$, i.e. le cas $x \geqslant 2$.
|
| 100 |
+
Supposons $x \geqslant 2$. Comme un carré est congru à 0 ou 1 modulo $4, z^{2}$ est congru à 0 ou 1 modulo 4 , donc $3^{y}$ aussi. Comme il n'est pas divisible par 4 , on a forcément $3^{y} \equiv 1(\bmod 4)$. Comme $3^{2} \equiv 9 \equiv 1$ $(\bmod 4)$, on a nécessairement $y$ pair $\left(\right.$ si $\left.y=2 k+1,3^{y} \equiv 9^{k} \times 3 \equiv 3(\bmod 4)\right)$. Posons $y=2 k$ avec $k$ entier, on obtient $2^{\mathrm{x}}=z^{2}-\left(3^{k}\right)^{2}=\left(z-3^{k}\right)\left(z+3^{k}\right)$. Notons que $z+3^{k}$ est strictement positif, donc
|
| 101 |
+
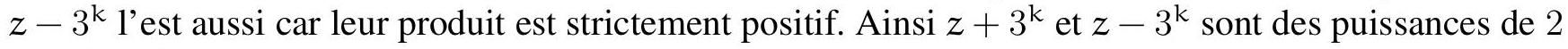 car elles divisent $2^{x}$.
|
| 102 |
+
Ici on a deux termes dont le produit vaut $2^{x}$, on aimerait montrer que l'un d'entre eux ne peut pas être très grand. Pour cela on va considérer le pgcd de $z+3^{k}$ et $z-3^{k}$ et le calculer en utilisant qu'il divise leur somme, différence et produit.
|
| 103 |
+
Soit d le pgcd de $\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$, alors $d$ divise $\left(z+3^{k}\right)-\left(z-3^{k}\right)=2 \times 3^{k}$, mais $d$ divise aussi $2^{\mathrm{x}}$ donc $d$ divise 2 . Comme $z+3^{k} \equiv z-3^{k}(\bmod 2)$, si d vaut $1,\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$ sont impairs donc $2^{\mathrm{x}}$ aussi, ce qui contredit le fait que $x \geqslant 2$. On a donc $\mathrm{d}=2$
|
| 104 |
+
En particulier comme $\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$ sont des puissances de 2 de pgcd 2 , le plus petit des deux vaut 2 donc comme $z+3^{k}>z-3^{k}, z=3^{k}+2$. Considérer le pgcd ici n'est pas nécessaire, on aurait pu directement aboutir à cela en posant $z+3^{\mathrm{k}}=2^{\mathrm{a}}, z-3^{\mathrm{k}}=2^{\mathrm{b}}$, observé que $\mathrm{a}>\mathrm{b}$ et écrit $2 \times 3^{\mathrm{k}}=2^{\mathrm{a}}-2^{\mathrm{b}}=2^{\mathrm{b}}\left(2^{\mathrm{a}-\mathrm{b}}-1\right)$, mais un bon réflexe quand on a un produit est de regarder le pgcd des facteurs.
|
| 105 |
+
De ceci, on déduit que $z+3^{k}=2^{x-1}$ et $z-3^{k}=2$, donc en faisant la différence $2 \times 3^{k}+2=2^{x-1}$ donc $3^{\mathrm{k}}+1=2^{\mathrm{x}-2}$. Cette équation est assez connue, mais si on ne la connait pas, comme on a des puissances de 2 et de 3 , il est pertinent de regarder modulo $2,4,8$ ou 3,9 . Comme $3+1=2^{2}$, regarder modulo 4 et 3 ne conclura pas tout de suite, on regarde donc modulo 8 .
|
| 106 |
+
Si $x \geqslant 5,8$ divise $2^{x-2}$ donc 8 divise $3^{x}+1$. Or les puissances de 3 modulo 8 valent 1 ou 3 donc $3^{x}-1$ vaut 2 ou 4 modulo 8 et n'est pas divisible par 8 , ce qui donne une contradiction. On a donc forcément $x=2,3$ ou 4 .
|
| 107 |
+
Pour $x=2,1=1+3^{k}$ donc $3^{k}=0$ ce qui est impossible. Pour $x=3,1+3^{k}=2$ donc $3^{k}=1$ donc $k=0$ et $y=0$. Pour $x=4,1+3^{k}=4$ donc $3^{k}=3$, on a donc $k=1$ soit $y=2$.
|
| 108 |
+
Réciproquement, si $(x, y)=(3,0), z^{2}=2^{x}+3^{y}=9=3^{2}$ donc $z= \pm 3$ et le triplet $(3,0,3)$ convient. Si $(x, y)=(4,2), z^{2}=2^{x}+3^{y}=25=5^{2}$ donc $z=5$ et le triplet $(4,2,5)$ convient.
|
| 109 |
+
Il reste donc à traiter le cas où $x=0$ et celui où $x=1$. Pour le cas où $x=0$, on a $2^{x}=1$ qui est un carré, on va donc factoriser et réutiliser la technique du pgcd. Si $x=0$, l'équation se réécrit $3^{y}=z^{2}-1=(z-1)(z+1)$. Le pgcd de $z-1$ et $z+1$ divise $3^{y}$ et divise $z+1-(z-1)=2$ donc il vaut nécessairement 1 . Comme $3^{y}=(z-1)(z+1), z-1$ et $z+1$ sont des puissances de 3 positives (car $z+1>0$ donc $z-1>0$ leur produit étant strictement positif) de pgcd 1 , le plus petit des deux
|
| 110 |
+
vaut nécessairement 1 donc $z-1=1, z=2$. On obtient $3^{y}=z^{2}-1=3$ donc $y=1$. Réciproquement $(0,1,2)$ est solution car $1+3=2^{2}$.
|
| 111 |
+
Pour le cas $x=1$, on ne voit pas de solution, il faut donc trouver un modulo pertinent pour évaluer l'équation, comme il y a une puissance de 3 et un carré, on peut regarder modulo 3 . $\mathrm{Si} x=1$ l'équation devient $2+3^{y}=z^{2}$. Si $y=0$ l'équation devient $z^{2}=3$ qui n'a pas de solution entière. On a donc $y>0$ donc $z^{2} \equiv 2(\bmod 3)$. Or un carré modulo 3 est congru à 0 ou 1 , il n'y a donc pas de solution pour $x=1$. Les solutions sont donc $(0,1,2),(3,0,3)$ et $(4,2,5)$.
|
| 112 |
+
Commentaire des correcteurs: Exercice globalement bien réussi. Il faut néanmoins penser à vérifier les solutions obtenues et justifier tout ce qui est affirmé : par exemple il faut justifier que si deux puissances de 2 sont distance de 2 ce sont forcément 2 et 4 (on peut le faire facilement en regardant modulo 4).
|
| 113 |
+
|
| 114 |
+
Exercice 7. Une grille de taille $\mathrm{n} \times \mathrm{n}$ contient $\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\{1, \ldots, n\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\sqrt{n}$ nombres différents.
|
| 115 |
+
|
| 116 |
+
Solution de l'exercice 7 Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\sqrt{n}$, donc $i$ apparait dans au moins $2 \sqrt{n}$ lignes et colonnes.
|
| 117 |
+
Bien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.
|
| 118 |
+
Notons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.
|
| 119 |
+
Notons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \times l_{i} \geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.
|
| 120 |
+
Notons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\sum_{c \in C \cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.
|
| 121 |
+
Maintenant il reste à relier le nombre d'apparitions de i dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.
|
| 122 |
+
On obtient ainsi $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
|
| 123 |
+
On en déduit que $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
|
| 124 |
+
En particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e. c contient au moins $\sqrt{\mathrm{n}}$ numéros différents.
|
| 125 |
+
|
| 126 |
+
Commentaire des correcteurs: L'exercice était très dur et seul un élève l'a réussi. Il fallait essayer de relier le nombre de numéros par ligne aux nombres de colonnes/lignes où apparait un numéro et rares sont ceux qui ont eu l'idée.
|
| 127 |
+
|
| 128 |
+
Exercice 8. Soit $A B C$ un triangle non isocèle en $B$. Soit $D$ le pied de la bissectrice de l'angle $\widehat{A B C}$. Soit $M$ le milieu de l'arc $\widehat{A C}$ contenant $B$ sur le cercle circonscrit au triangle $A B C$. Le cercle circonscrit au triangle $B D M$ coupe la segment $[A B]$ en un point $K$ distinct de $B$. Soit $J$ le symétrique du point $A$ par rapport au point K . La droite (DJ) intersecte la droite ( $A M$ ) en un point O . Montrer que les points $\mathrm{J}, \mathrm{B}, \mathrm{M}$ et O sont cocycliques.
|
| 129 |
+
|
| 130 |
+
## Solution de l'exercice 8
|
| 131 |
+
|
| 132 |
+
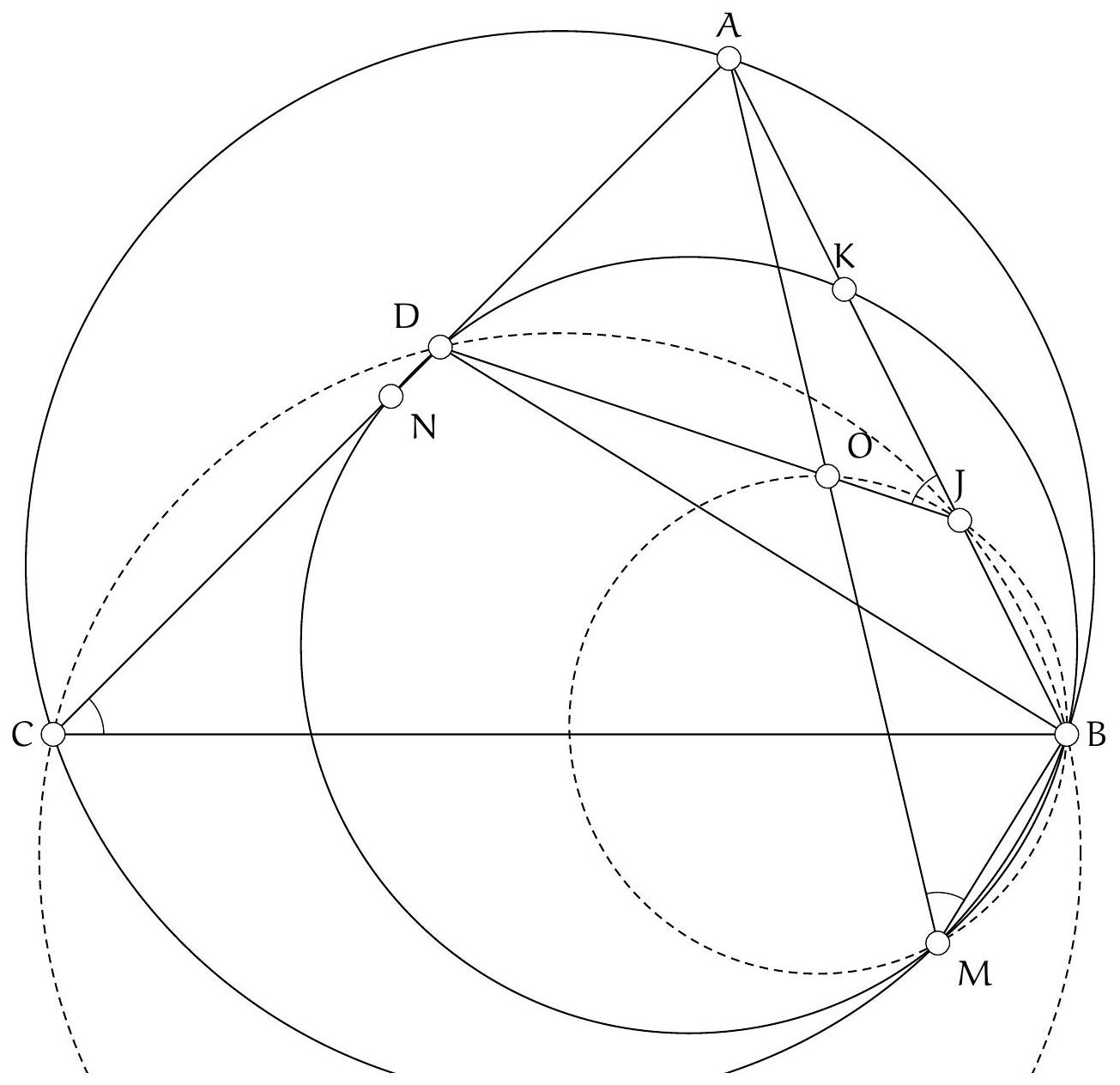
|
| 133 |
+
|
| 134 |
+
Tout d'abord, on reconnaît dans la figure quelques points connus : le point $M$ est le milieu de l'arc $A C$ contenant $B$, il s'agit donc du pôle Nord du point $B$ dans le triangle $A B C$, c'est-à-dire qu'il est le point d'intersection de la bissectrice extérieure de l'angle $\widehat{A B C}$, de la médiatrice du segment $[A C]$ et du cercle circonscrit au triangle $A B C$. On obtient donc que l'angle $\widehat{D B M}$ est droit (par définition de la bissectrice extérieure). Le fait que $M$ appartient à la médiatrice du segment $[A C]$ nous invite également à considérer cette médiatrice. Soit N le milieu du segment $[A C]$. Alors $\widehat{\mathrm{DNM}}=90^{\circ}$. On déduit donc que les points $B, M, N$ et $D$ sont cocycliques et $D$ appartient au cercle passant par les pointe $B, K$ et $D$.
|
| 135 |
+
De nouveaux points cocycliques apportent deux informations : une information sur les angles grâce au théorème de l'angle inscrit et une information sur les longueurs grâce à la puissance d'un point. Puisque la majorité des points se trouve sur deux droites se coupant en le sommet $A$, nous allons utiliser la puissance du point $A$ par rapport à divers cercles.
|
| 136 |
+
Notamment, par puissance d'un point $A K \cdot A B=A D \cdot A N$. Donc
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
A J \cdot A B=2 A K \cdot A B=2 A D \cdot A N=A D \cdot A C
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
donc les points $\mathrm{D}, \mathrm{C}, \mathrm{B}$ et J sont cocycliques d'après la réciproque de la puissance d'un point. Pour conclure, nous allons utiliser les angles orientés, pour éviter d'avoir à traiter séparément les différentes configurations possibles.
|
| 143 |
+
Nous avons à présent tous les outils pour effectuer une chasse aux angles. Des angles difficiles d'accès sont les angles $\widehat{\mathrm{OMJ}}, \widehat{\mathrm{OBJ}}, \widehat{M J B} \ldots$ En revanche, les angles $\widehat{\mathrm{DJB}}$ et $\widehat{\mathrm{OMB}}$ semblent plus faciles à obtenir à l'aide des cercles présents sur la figure.
|
| 144 |
+
Puisque les points D, C, B et O sont cocycliques, on trouve
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
(J B, J O)=(J B, J D)=(C B, C D)=(C B, C A)=(M B, M A)=(M B, M O)
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
donc le quadrilatère JBMO est bien cyclique.
|
| 151 |
+
Commentaire des correcteurs : L'exercice n'a pas été abordé par beaucoup d'élèves et il a été résolu par deux élèves. Quelques élèves ont noté que le point $M$ est le pôle Nord du point $B$, ce qui est un très bon réflexe.
|
| 152 |
+
|
| 153 |
+
Exercice 9. Déterminer le plus petit entier $\mathrm{n} \geqslant 2$ tel qu'il existe des entiers strictement positifs $a_{1}, \ldots, a_{n}$ tels que
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
Solution de l'exercice 9 Analysons le problème. Dans ce problème, on cherche le plus petit entier n satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c'est bien le plus petit entier, on doit d'une part montrer que si un entier n satisfait la propriété, alors $n \geqslant c$ et on doit montrer d'autre part que l'on peut trouver $c$ entiers satisfaisant la relation de divisibilité.
|
| 160 |
+
|
| 161 |
+
Pusiqu'il y a une relation de divisibilité, on peut s'attendre à utiliser divers idées :
|
| 162 |
+
|
| 163 |
+
- Si $a \mid b$ alors $a$ divise les combinaisons linéaires de $a$ et $b$
|
| 164 |
+
- Si $a \mid b$ et que $a$ et $b$ sont strictement positifs, alors $a \mid b$
|
| 165 |
+
- Si $a \mid b$, les diviseurs de $a$ divisent également $b$
|
| 166 |
+
|
| 167 |
+
Une fois cette première analyse effectuée, on peut commencer par regarder si on trouve des entiers $a_{i}$ satisfaisant la propriété pour des petites valeurs de $n$, par exemple pour $n=2,3$ ou même 4 si on est courageux, avant de se convaincre que cette méthode ne permettra pas de déterminer n .
|
| 168 |
+
|
| 169 |
+
Néanmoins, avoir cherché des $a_{i}$ pour des petites valeurs de $n$ nous permet de trouver d'éventuelles propriétés que doivent satisfaire les $a_{i}$. Par exemple, on a pu remarquer que les entiers $a_{i}$ ne peuvent pas tous être pairs, puisque dans ce cas la somme des $a_{i}^{2}$ serait paire mais $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est impair. On se rend alors compte que ce qui importe dans cet argument, ce n'est pas la parité des $a_{i}$ qui entre en jeu mais la parité de la somme.
|
| 170 |
+
|
| 171 |
+
On obtient que $a_{1}+a_{2}+\ldots+a_{n}$ est impair. Dans le cas contraire, puisque $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv$ $a_{1}+a_{2}+\ldots+a_{n} \bmod 2, a_{1}+\ldots+a_{n}$ est pair également mais alors $a_{1}^{2}+\ldots+a_{n}^{2}$ est pair et divise $\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1$ qui est impair, ce qui est absurde.
|
| 172 |
+
|
| 173 |
+
On déduit que $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est pair. L'argument de parité précédent nous invite à préciser cette étude. On va donc chercher si $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par $4,8 \ldots$. La présence des multiples carré nous invite à regarder chaque terme avec des modulos bien choisis.
|
| 174 |
+
|
| 175 |
+
Par exemple, modulo $4,\left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1$ donc 4 divise $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Ne nous arrêtons pas en si bon chemin, nous savons également que les carrés des nombres impairs ne peuvent que valoir 1 modulo 8. Ainsi, $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par 8 . Or 8 est premier avec $a_{1}^{2}+\ldots+a_{n}^{2}$ qui est impair. On déduit de tout cela que
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
Enfin, une autre remarque que l'on peut formuler sur l'énoncé est qu'il implique la somme des carrés de nombres d'un côté et le carré de la somme des nombres de l'autre côté. Ceci fait penser à l'inégalité de Cauchy-Schwarz, ou à l'inégalité des moyennes arithmétiques et quadratiques. On peut donc essayer de comparer les quantités $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)$ et $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$.
|
| 182 |
+
|
| 183 |
+
Cette idée de comparer les termes est cohérente avec ce que l'on cherche à montrer. La divisibilité obtenue donne que $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Or, dans l'inégalité des moyennes arithmétique et quadratique, le carré de la somme est plus petit que la somme des carrés des éléments multipliée par le
|
| 184 |
+
nombre de variables. On se doute donc que l'inégalité obtenue va être fausse pour n trop petit, ce qui va nous fournir la borne souhaitée. Plus précisement,
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-1<n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
où l'inégalité au milieu correspond à l'inégalité des moyennes arithmétiques et quadratiques. On obtient finalement que $\mathrm{n}>8$ donc $\mathrm{n} \geqslant 9$.
|
| 191 |
+
|
| 192 |
+
Réciproquement, on cherche 9 entiers satisfaisant la propriété. On peut s'attendre à ce que de petits entiers fonctionnent. On peut donc chercher des $a_{i}$ valant 1 ou 2 . Finalement, on trouve qu'en prenant $a_{1}=\cdots=a_{7}=1$ et $a_{8}=a_{9}=2$, on a bien 15 qui divise $11^{2}-1=120=15 \times 8$.
|
| 193 |
+
La réponse attendue est donc $\mathrm{n}=9$.
|
| 194 |
+
Commentaire des correcteurs: L'exercice n'a été résolu que par un élève. C'est un exercice instructif et très complet, faisant appel à des arguments arithmétiques et des inégalités.
|
| 195 |
+
|
| 196 |
+
## Exercices Seniors
|
| 197 |
+
|
| 198 |
+
Exercice 10. Soit $\left(x_{n}\right)_{n \in \mathbb{N}}$ une suite réelle telle que $x_{0}=0$ et $x_{1}=1$ et pour tout $n \geqslant 0, x_{n+2}=$ $3 x_{n+1}-2 x_{n}$. On pose également $y_{n}=x_{n}^{2}+2^{n+2}$ pour tout entier naturel $n$. Montrer que pour tout entier $n>0, y_{n}$ est le carré d'un entier impair.
|
| 199 |
+
Solution de l'exercice 10 On commence par tester l'énoncé pour des petites valeurs de n . On calcule donc les premières valeurs des suites $\left(x_{n}\right)$ et $\left(y_{n}\right)$. On trouve par exemple $x_{2}=3, x_{4}=7$, $x_{5}=15 \ldots$ On peut donc conjecturer que $x_{n}=2^{n}-1$. On s'empresse de le démontrer par récurrence.
|
| 200 |
+
Le résultat est déjà au rang 0 et 1 . Si on suppose $x_{n}=2^{n}-1$ et $x_{n+1}=2^{n+1}-1$, on a $x_{n+2}=$ $3 x_{n+1}-2 x_{n}=3 \times 2^{n+1}-3-2 \times 2^{n}+2=(3-1) \times 2^{n+1}-1=2^{n+2}-1$ ce qui achève la récurrence. On injecte alors cette expression de $x_{n}$ dans l'expression de $y_{n}$. Il ne nous reste plus qu'à manipuler algébriquement cette nouvelle expression :
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
y_{n}=\left(2^{n}-1\right)^{2}+2^{n+2}=2^{2 n}-2^{n+1}+1+2^{n+2}=2^{2 n}-2^{n+1}+1+2 \times 2^{n+1}=2^{2 n}+2^{n+1}+1=\left(2^{n}+1\right)^{2}
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
Ceci montre bien que $y_{n}$ est le carré d'un entier impair.
|
| 207 |
+
Commentaire des correcteurs: L'exercice a été résolu par tous les élèves qui l'ont abordé !
|
| 208 |
+
|
| 209 |
+
Exercice 11. Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tout couple $(x, y)$ de réels :
|
| 210 |
+
|
| 211 |
+
$$
|
| 212 |
+
f(f(x))+f(f(y))=2 y+f(x-y)
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
Solution de l'exercice 11 Analysons le problème : ici on est face à une équation fonctionnelle, avec deux variables. La première chose à faire est d'essayer les quelques substitutions classiques : $x=y=0$, $x=0, y=0, x=y$. Ici comme on a un $f(x-y)$, il est très tentant de regarder ce que ça donne pour $x=y$. Posons donc $C=f(0)$, pour $x=y$, on obtient $2 f(f(x))=2 x+C$ soit $f(f(x))=x+\frac{C}{2}$.
|
| 216 |
+
Maintenant qu'on a une expression plus maniable de $f(f(x))$, on peut la réinjecter dans l'équation et regarder ce que ça donne.
|
| 217 |
+
En réinjectant dans l'équation initiale, on a donc $x+y+C=2 y+f(x-y)$ soit $f(x-y)=x-y+C$, pour $y=0$ on a donc $f(x)=x+C$ pour tout réel $x$. Maintenant, il faudrait déterminer $C$ avant d'effectuer la vérification, on essaie donc de voir quelle contrainte l'équation $f(f(x))=x+\frac{C}{2}$ donne sur $C$.
|
| 218 |
+
En particulier $f(f(x))=f(x+C)=x+2 C$ donc $2 C=\frac{C}{2}$ donc $4 C=C, 3 C=0$ donc $C=0$, on a donc $f(x)=x$ pour tout réel $x$. Maintenant on n'oublie pas de vérifier que la fonction trouvée est bien solution ! Réciproquement la fonction identité convient car dans ce cas, $f(f(x))+f(f(y))=f(x)+f(y)=$ $x+y=2 y+x-y=2 y+f(x-y)$ pour tout $x, y$ réels.
|
| 219 |
+
Commentaire des correcteurs: L'exercice a été très bien réussi. Il faut faire attention à ne pas conclure que $f$ est l'identité lorsque l'on trouve $f(X)=X$ avec $X$ dépendant de $x$ et $y$ (il faut vérifier que $X$ peut prendre toutes les valeurs réelles).
|
| 220 |
+
|
| 221 |
+
Exercice 12. Trouver tous les couples d'entiers positifs $(x, y)$ tels que $2^{x}+5^{y}+2$ est un carré parfait. Solution de l'exercice 12 Ici on est face à un problème d'équation diophantienne avec un carré et une puissance de 2 . On peut se rendre compte en testant les petits cas que $(x, y)=(0,0)$ et $(1,1)$ sont solutions. Comme on a un carré et une puissance de 2 , on est très tenté de regarder modulo 4 ou 8 . Regardons déjà modulo 4 pour voir s'il y a une contradiction. Pour cela on va d'abord traiter le cas où $x \geqslant 2$.
|
| 222 |
+
Déjà notons que si $x \geqslant 2,2^{x}+5^{y}+2 \equiv 1+2 \equiv 3(\bmod 4)$ et 3 n'est pas un carré modulo 4 (les carrés sont 0 et 11 modulo 4). On a donc forcément $x=1$ ou $x=0$.
|
| 223 |
+
Maintenant réécrivons l'équation dans le cas $x=1$. Pour $x=1$ soit $y$ entier positif tel que $2+5^{y}+2=$ $5^{y}+4$ est un carré parfait. Notons que comme 4 est un carré, on va pouvoir factoriser.
|
| 224 |
+
Soit $k$ entier positif tel que $k^{2}=5^{y}+4$, on a donc $(k-2)(k+2)=5^{y}$. Notons que comme $k+2>0$, on a $k-2>0$ et $k+2$ et $k-2$ sont des puissances de 5 . Si $k-2>1$, alors 5 divise $k+2$ et $k-2$ donc 5 divise $k+2-(k-2)=4$ contradiction.
|
| 225 |
+
Ainsi $\mathrm{k}-2=1$ donc $\mathrm{k}=3$, donc $5^{y}+4=9$ donc $\mathrm{y}=1$. Réciproquement si $(\mathrm{x}, \mathrm{y})=(1,1)$, $2^{x}+5^{y}+2=9$ est un carré parfait.
|
| 226 |
+
Pour $x=0$, soit $y$ tel que $1+5^{y}+2=5^{y}+3$ est un carré, soit $k \geqslant 0$ tel que $k^{2}=5^{y}+3$. Ici comme on a des carrés et des puissances de 5 , on peut essayer de regarder modulo 5 . Si $y \geqslant 1$, alors on a $k^{2} \equiv 3$ $(\bmod 5)$, or les carrés modulo 5 sont 1 et 4 , ce qui est une contradiction. On a donc forcément $y=0$.
|
| 227 |
+
Réciproquement si $(\mathrm{x}, \mathrm{y})=(0,0), 2^{\mathrm{x}}+5^{\mathrm{y}}+2=4$ est un carré parfait.
|
| 228 |
+
Les solutions sont donc les couples $(0,0)$ et $(1,1)$.
|
| 229 |
+
Commentaire des correcteurs: Cet exercice a été très bien réussi dans l'ensemble. Pour le cas $x=0$, la majorité des élèves ont utilisé le fait qu'un carré n'est pas congrus à 3 modulo 5 , mais il ne fallait pas oublier de traiter à part le cas $y=0$ !
|
| 230 |
+
|
| 231 |
+
Exercice 13. Soit $A B C$ un triangle aux angles aigus. Soit $D$ le pied de la bissectrice de l'angle $\widehat{B A C}$. La perpendiculaire à la droite $(A D)$ passant par le point $B$ recoupe le cercle circonscrit au triangle $A D B$ en un point $E$. Soit $O$ le centre du cercle circonscrit au triangle $A B C$. Montrer que les points $A, O$ et $E$ sont alignés.
|
| 232 |
+
|
| 233 |
+
## Solution de l'exercice 13
|
| 234 |
+
|
| 235 |
+
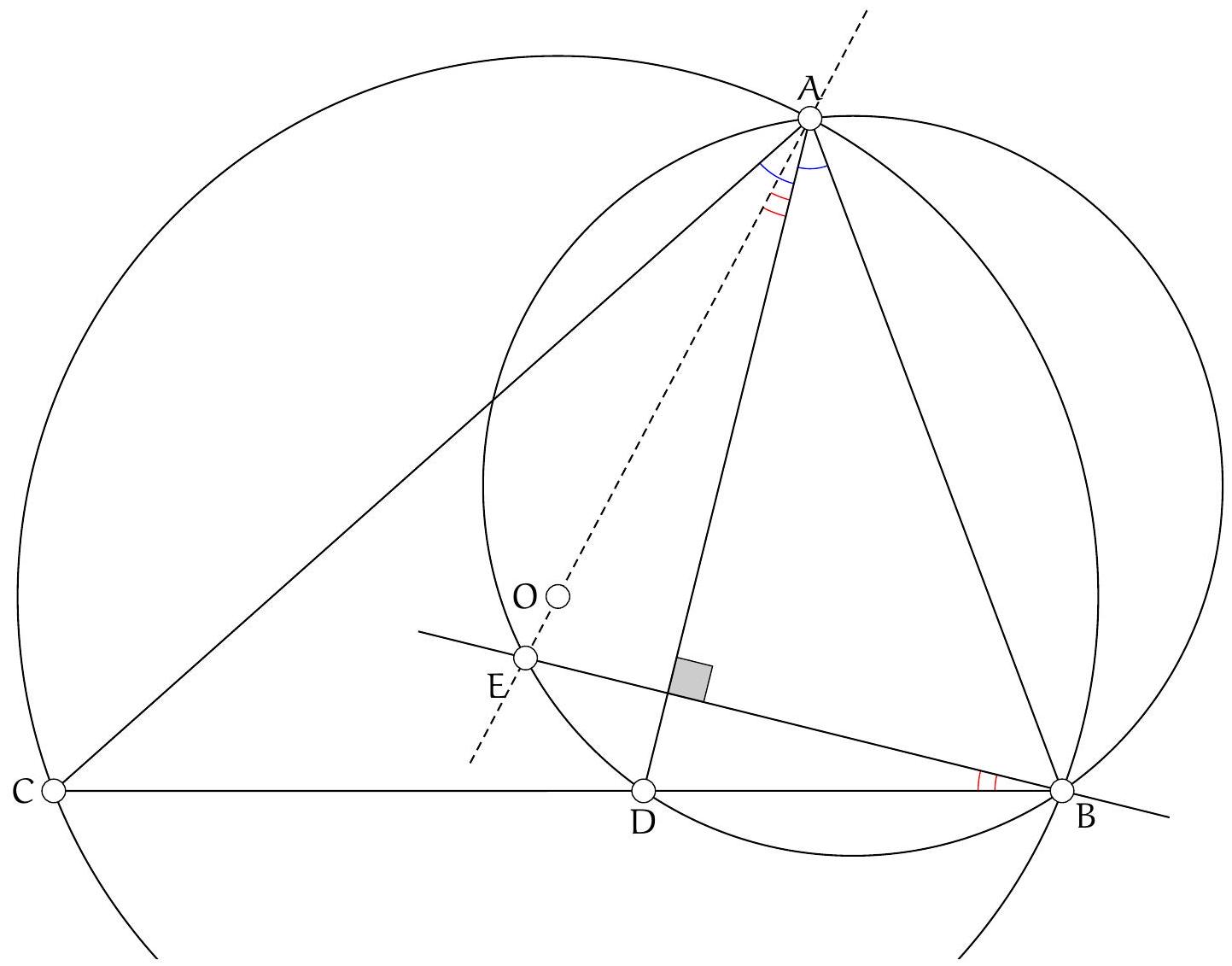
|
| 236 |
+
|
| 237 |
+
Examinons les angles que nous pouvons obtenir facilement. Puisque les points $A, E, D$ et $B$ sont sur un même cercle, on doit pouvoir utilise le théorème de l'angle inscrit pour avoir une égalité portant sur $\widehat{\mathrm{EAD}}$. Puisque la droite $(\mathrm{BE})$ est perpendiculaire à la droite $(\mathrm{AD})$, on doit pouvoir calculer l'angle $\widehat{\mathrm{EBA}}$. Enfin, on connaît bien sûr l'angle $\widehat{O A B}$. Il semble donc raisonnable de montrer l'alignement des points $A, O$ et $E$ en montrant que $\widehat{O A B}=\widehat{\mathrm{EAB}}$. On calcule séparément ces deux angles en fonction des angles du triangle $A B C$.
|
| 238 |
+
D'une part, d'après le théorème de l'angle au centre et puisque le triangle $A O B$ est isocèle en O , on a
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
\widehat{\mathrm{OAB}}=\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{AOB}}\right)=90^{\circ}-\widehat{\mathrm{ACB}}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
D'autre part, $\widehat{E A B}=\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}$. On utilise alors le théorème de l'angle inscrit et le fait que $\widehat{\mathrm{DAB}}=$ $\frac{1}{2} \widehat{\mathrm{BAC}}$, on obtient :
|
| 245 |
+
|
| 246 |
+
$$
|
| 247 |
+
\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}=\widehat{\mathrm{EBD}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}
|
| 248 |
+
$$
|
| 249 |
+
|
| 250 |
+
Or la somme des angles du triangle ADC fait $180^{\circ}$ donc $\widehat{\mathrm{BDA}}=\widehat{\mathrm{DCA}}+\widehat{\mathrm{DAC}}=\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}$. Ainsi
|
| 251 |
+
|
| 252 |
+
$$
|
| 253 |
+
90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\left(\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}\right)+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{ACB}}
|
| 254 |
+
$$
|
| 255 |
+
|
| 256 |
+
et on trouve bien que $\widehat{O A B}=90^{\circ}-\widehat{A C B}=\widehat{E A B}$ donc les points $A, O$ et $E$ sont alignés. Commentaire des correcteurs: L'exercice est bien réussi. Cependant, plusieurs élèves ont rendu un preuve très compliquée.
|
| 257 |
+
|
| 258 |
+
Exercice 14. Une grille de taille $\mathrm{n} \times \mathrm{n}$ contient $\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\{1, \ldots, n\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\sqrt{n}$ nombres différents.
|
| 259 |
+
|
| 260 |
+
Solution de l'exercice 14 Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\sqrt{n}$, donc $i$ apparait dans au moins $2 \sqrt{n}$ lignes et colonnes.
|
| 261 |
+
Bien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.
|
| 262 |
+
Notons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.
|
| 263 |
+
Notons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \times l_{i} \geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.
|
| 264 |
+
Notons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\sum_{c \in C \cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.
|
| 265 |
+
Maintenant il reste à relier le nombre d'apparitions de $i$ dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.
|
| 266 |
+
On obtient ainsi $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
|
| 267 |
+
On en déduit que $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
|
| 268 |
+
En particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e. c contient au moins $\sqrt{\mathrm{n}}$ numéros différents.
|
| 269 |
+
|
| 270 |
+
Commentaire des correcteurs: L'exercice a été globalement bien réussi par ceux qui l'ont traité, mais il faut faire attention à être clair dans ses explications et être précis dans les définitions des différents objets introduits.
|
| 271 |
+
|
| 272 |
+
Exercice 15. Trouver tous les entiers $n \geqslant 1$ tel que pour tout nombre premier $p<n, n-\left\lfloor\frac{n}{p}\right\rfloor p n$ 'est pas divisible par un carré différent de 1.
|
| 273 |
+
Solution de l'exercice 15 Analysons le problème : on cherche les entiers $n$ vérifiant une certaine propriété. On peut déjà commencer par chercher les petites valeurs de n qui conviennent : en testant les entiers $n$ entre 1 et 20 on trouve $\{1,2,3,5,7,13\}$.
|
| 274 |
+
Une des premières choses à faire devant ce problème est de réussir à donner un sens à $n-\left\lfloor\frac{n}{p}\right\rfloor p$. $\frac{n}{p}$ étant la division de $n$ par $p$ on peut essayer de regarder si cette quantité ne s'interprète pas à partir de la division euclidienne.
|
| 275 |
+
Notons que $n-\left\lfloor\frac{n}{p}\right\rfloor p$ est le reste de la division euclidienne de $n$ par $p$. En effet si $n=p q+r$ avec $q$ entier et $0 \leqslant r \leqslant p-1$, on a $\left\lfloor\frac{n}{p}\right\rfloor=\left\lfloor q+\frac{r}{p}\right\rfloor=q$ donc $n-\left\lfloor\frac{n}{p}\right\rfloor p=r$.
|
| 276 |
+
Ensuite, on note que toutes les solutions trouvées sauf 1 sont des nombres premiers : on va donc essayer de montrer qu'un entier $n$ vérifiant la propriété est forcément premier, par exemple en prenant $p$ un de ses diviseurs.
|
| 277 |
+
Soit $n>1$ un entier vérifiant la propriété. On déduit de ceci que si $n$ n'est pas premier, si $p<n$ est un diviseur premier de $n$, alors $n-\left\lfloor\frac{n}{p}\right\rfloor p=0$ est divisible par 4 qui est un carré parfait, contradiction.
|
| 278 |
+
Maintenant que peut-on faire pour avancer : analysons ce que la propriété peut nous donner. Si $\boldsymbol{n} \geqslant 12$, pour $p=2$ le reste de la division euclidienne vaut 1 , pour $p=3$ il vaut 1 ou 2 , donc cela n'apporte rien. Pour $p=5$, on obtient que le reste ne peut valoir 4 , pour $p=7$, le reste ne peut valoir 4 , pour $p=8$ le reste ne peut valoir ni 4 ni 8 ni 9 . A priori, continuer comme ça indéfiniment semble compliqué, vu qu'on aura juste un très gros système, qui admettra probablement des solutions (comme il y a une infinité de nombre congru à 1 modulo $p_{1} \times \ldots p_{k}$, le fait de regarder les restes par les $k$ premiers nombre premiers semble peu utile). Par contre, 4 semble jouer un rôle important : 4 ne peut pas être un reste de la divison de $n$ par $p$. En particulier si $p \geqslant 5, p$ ne peut diviser $n-4$ ! Il semble donc intéressant de regarder ce que peut valoir $n-4$, et de même ce que peuvent valoir $n-8$ et $n-9$ car ceux-ci ne peuvent pas avoir de facteur premier plus grand que 10 . Pour éviter les cas où ces quantités sont négatives, on supposer $n \geqslant 11$.
|
| 279 |
+
Soit n premier supérieur ou égal à 11 vérifiant l'énoncé. Soit p divisant $\boldsymbol{n}-4$, on a $\mathrm{p}<\mathrm{n}$. Si $\mathrm{p} \geqslant 5$, le reste de la division euclidienne de p par 5 vaut 4 et il est divisible par 4 qui est un carré différent de 1, ce qui donne une contradiction. De plus, $p$ ne peut valoir 2 car sinon 2 divise $n-4$ donc 2 divise $n, n$ 'est dans ce cas pas premier. Ainsi $\mathrm{n}-4=3^{x}$ avec $x$ un entier strictement positif car $\mathrm{n}-4>1$.
|
| 280 |
+
En faisant le même raisonnement $\mathrm{n}-8$ et $\mathrm{n}-9$ ne sont pas divisibles par $p$ si $p \geqslant 10$.
|
| 281 |
+
Maintenant analysons les facteurs premiers de $\boldsymbol{n}-8$ et $\mathrm{n}-9$ : ils peuvent être divisibles par 2, 3, 5, 7. Pour le facteur 3 , comme 3 divise $n-4, n \equiv 1(\bmod 3)$, donc $n-8 \equiv 2(\bmod 3)$ et $n-9 \equiv 1$ $(\bmod 3)$, ceux-ci ne sont pas divisibles par 3.
|
| 282 |
+
De plus $n-8$ n'est pas divisible par 2 car $n$ ne l'est pas. Comme $n-8$ et $n-9$ sont premiers entre eux, trois cas se présentent à nous : soit $\mathrm{n}-8$ est une puissance de 5 , soit c'est une puissance de 7 , soit $\mathrm{n}-8$ est divisible par 5 et 7 , dans ce cas $n-9$ est une puissance de 2 .
|
| 283 |
+
|
| 284 |
+
- $\operatorname{Sin}-8=5^{y}$ avec $y$ entier positif, on a $n-4=5^{y}+4=3^{x}$.
|
| 285 |
+
|
| 286 |
+
Ici 4 étant un carré, on aimerait montrer que $3^{x}$ est un carré pour factoriser l'équation. Pour cela, on regarde modulo 4 car on a des carrés et $5 \equiv 1(\bmod 4)$.
|
| 287 |
+
Regardons modulo 4 , on a $3^{x} \equiv 1^{y} \equiv(\bmod 4)$. Sinon comme l'ordre de 3 modulo 4 est 2 , 2 divise $x$ donc $x$ est pair. Posons $x=2 k$, on a $\left(3^{k}-2\right)\left(3^{k}+2\right)=5^{y}$ donc $3^{k}-2$ est positif et $3^{k}-2$ et $3^{k}+2$ sont des puissances de 5 . Ici on a un produit de terme valant une puissance de 2 , on essaie donc de calculer leur pgcd pour espérer borner un des termes. En particulier, le pgcd de $3^{\mathrm{k}}+2$ et $3^{\mathrm{k}}-2$ divise $\left(3^{\mathrm{k}}+2\right)-\left(3^{\mathrm{k}}-2\right)=4$ qui n'est pas divisible par 5 , et il divise leur produit c'est-à-dire $5^{y}$, il vaut donc 1 . Comme $3^{k}-2$ et $3^{k}+2$ sont des puissances de 2 de pgcd 1 , la plus petite vaut 1 , on a donc $3^{\mathrm{k}}-2=1$ soit $\mathrm{k}=1$ soit $\chi=2$. On obtient $\mathrm{n}=3^{\mathrm{x}}+4=9+4=13$.
|
| 288 |
+
|
| 289 |
+
- $\operatorname{Sin}-8=7^{y}$ avec $y$ entier positif, on a $\mathrm{n}-4=7^{y}+4=3^{x}$.
|
| 290 |
+
|
| 291 |
+
Comme 4 est un carré, on aimerait réussir à montrer que $x$ est pair pour factoriser, pour cela on regarde modulo 7 . Notons que si $y=0$, il n'y a pas de solution à cette équation. Sinon on a $3^{\mathrm{x}} \equiv 4(\bmod 7)$, or les puissances de 3 modulo 7 valent $1,3,2,6,4,5,1$, l'ordre de 3 vaut donc 6 et on a forcément $x \equiv 4(\bmod 6)$ donc $x$ est pair. Posons $x=2 k$, on a $\left(3^{k}-2\right)\left(3^{k}+2\right)=7^{y}$ donc $3^{k}-2$ est positif et $3^{k}-2$ et $3^{k}+2$ sont des puissances de 7 .
|
| 292 |
+
En particulier, le pgcd de $3^{l}+2$ et $3^{k}-2$ divise $\left(3^{k}+2\right)-\left(3^{k}-2\right)=4$ qui n'est pas divisible par 7 , il divise aussi $7^{y}$ et vaut donc 1 . Comme $3^{k}-2$ et $3^{k}+2$ sont des puissances de 2 de pgcd 1 , la plus petite vaut 1 , on a donc $3^{k}-2=1$ donc $k=1$ donc $x=2$, on a donc $7^{y}=3^{x}-4=5$ ce qui est impossible.
|
| 293 |
+
|
| 294 |
+
- Sinon $\boldsymbol{n}-9=2^{y}$ avec $y$ entier positif, on a $\boldsymbol{n}-4=2^{y}+5=3^{x}$. Notons que comme $\mathrm{n}-4 \geqslant 7$, on a $x \geqslant 1$ et $y \geqslant 1$
|
| 295 |
+
Ici on n'a pas de carré à priori, mais on peut essayer d'obtenir des informations sur la parité de $x$ et $y$. Vu qu'on a des puissances de 2 et 3 on va donc regarder modulo 3 et 4 . Notons que si $y=1$, l'équation devient $3^{x}=7$, il n'y a pas de solution. Comme $x \geqslant 1$ en regardant modulo 3 , on a $2^{y} \equiv-5 \equiv 1(\bmod 3)$ et l'ordre de 2 modulo 3 est 2 , on obtient que $y$ est pair. Comme $y \geqslant 2$, on a $3^{x} \equiv 1(\bmod 4)$ et comme l'ordre de 3 modulo 4 est 2 , $x$ est pair. On écrit donc $x=2 b$, $\mathrm{y}=2 \mathrm{c}$, on a $5=\left(3^{\mathrm{b}}-2^{\mathrm{c}}\right)\left(3^{\mathrm{b}}+2^{\mathrm{c}}\right)$ donc $3^{\mathrm{b}}-2^{\mathrm{c}}$ est positif et comme $3^{\mathrm{b}}-2^{\mathrm{c}}<3^{\mathrm{b}}+2^{\mathrm{c}}, 3^{\mathrm{b}}-2^{\mathrm{c}}$ et $3^{b}+2^{c}$ valent respectivement 1 et 5 . On en déduit que $3^{b} \times 2=\left(3^{b}+2^{c}\right)+\left(3^{b}-2^{c}\right)=6$ donc $\mathrm{b}=1$ donc $x=2$, on retombe dans le cas précédent $\mathrm{n}=13$.
|
| 296 |
+
En particulier, on a obtenu que $\mathrm{n}=13$ ou $\mathrm{n}<11$ et n premier, i.e. n vaut $2,3,5,7$ ou 13 . Vérifions que ce sont des solutions :
|
| 297 |
+
- Il n'y a pas de nombre premier strictement inférieur à 1 et 2 donc 1 et 2 sont solutions.
|
| 298 |
+
- Le reste de la division de 3 par 2 est 1 qui n'a pas de facteurs carrés, donc 3 est solution.
|
| 299 |
+
- Les restes des divisions euclidiennes de 5 par 2 et 3 sont 1 et 2 qui sont sans facteurs carrés donc 5 est solution.
|
| 300 |
+
- Les restes des divisions euclidiennes de 7 par 2, 3 et 5 sont 1,1 et 2 qui sont sans facteurs carrés donc 7 est solution.
|
| 301 |
+
- Les restes des divisions euclidiennes de 13 par 2, 3, 5, 7 et 11 sont 1, 1, 3, 6 et 2 qui sont sans facteurs carrés donc 13 est solution.
|
| 302 |
+
L'ensemble des solutions est donc $\{1,2,3,5,7,13\}$.
|
| 303 |
+
Commentaire des correcteurs: Cet exercice d'arithmétique a été résolu par peu d'élèves, qui ont tous montré qu'ils sont extrêmement à l'aise. Les autres élèves qui ont abordé le problème ont simplement remarqué que si $n \geqslant 2$ était solution alors il était premier, ce qui était un bon début, mais il manquait encore de nombreuses étapes avant d'arriver à la solution.
|
| 304 |
+
|
| 305 |
+
Exercice 16. Soient $\mathrm{P}, \mathrm{Q}$ des polynômes à coefficients réels tels que $\mathrm{P} \circ \mathrm{Q}=\mathrm{P}^{2019}$. On suppose que toutes les racines de P sont réelles. Montrer qu'elles sont toutes égales.
|
| 306 |
+
Solution de l'exercice 16 Face à un problème de polynôme, un premier réflexe peut être de regarder les différents degrés. Ici, on voit que $Q$ est un polynôme de degré 2019 car 2019deg $(P)=\operatorname{deg}\left(P^{2019}\right) \operatorname{deg}(\mathrm{P} \circ$ $Q)=\operatorname{deg}(P) \operatorname{deg}(Q)$.
|
| 307 |
+
Maintenant, il faut utiliser l'hypothèse du fait que les racines de $P$ sont réelles. On écrit $P(X)=\prod_{i=1}^{k}(X-$ $\left.x_{i}\right)^{a_{i}}$ où les racines $x_{1}, \ldots, x_{k}$ sont deux à deux distinctes.
|
| 308 |
+
Réécrivons ainsi l'équation: $\prod_{i=1}^{l}\left(Q(X)-x_{i}\right)^{a_{i}}=\prod_{i=1}^{k}\left(X-x_{i}\right)^{2019 a_{i}}$.
|
| 309 |
+
A priori, on sait que le terme de droite va être nul si on l'évalue en $x_{j}$, on regarde donc ce qu'on en déduit pour le terme de gauche. Posons $X=\left\{x_{1}, \ldots, x_{k}\right\}$, on a alors nécessairement $Q\left(x_{j}\right) \in\left\{x_{1}, \ldots, x_{k}\right\}=X$ pour tout $1 \leqslant j \leqslant k$.
|
| 310 |
+
De plus comme le terme de droite de l'égalité est un polynôme scindé réel, forcément pour tout $\mathfrak{j}$, comme le polynôme $\mathrm{Q}(\mathrm{X})-\mathrm{x}_{\mathrm{j}}$ divise un polynôme scindé, lui aussi est scindé et de degré 2019 donc admet 2019 racines réelles dans $X$.
|
| 311 |
+
Notons de plus que si $i \neq j, Q-x_{i}$ et $Q-x_{j}$ ont nécessairement des racines disjointes : en effet on ne peut avoir $Q(x)=x_{i}$ et $Q(x)=x_{j}$. Ainsi les polynômes $Q-x_{i}$ sont $|X|=k$ polynômes distincts scindés dont les racines sont dans $X$ et qui n'ont aucune racine en commun. Nécessairement, chacun de ces polynômes n'a qu'une racine : ainsi pour tout $i$ il existe $j(i)$ tel que $Q(X)-x_{i}=c\left(X-x_{j(i)}\right)^{2019}$ avec c le coefficient dominant de Q . De plus, l'application de $\{1, \ldots, \mathrm{k}\}$ dans $\{1, \ldots, \mathrm{k}\}$ quià $i$ associe $j(i)$ est bijective.
|
| 312 |
+
Maintenant on a une expression très précise des $\mathrm{Q}-x_{i}$, rappelons que l'on veut montrer qu'il n'y a qu'un seul $x_{i}$. Pour cela, on peut essayer de regarder les coefficients de $Q-x_{i}$ qui sont quasiment ceux de $Q$. Le coefficient de $X^{2018}$ dans $Q$ vaut donc celui de $Q-x_{i}$, c'est-à-dire $-2019 x_{j(i)} c$ pour tout i. Puisque $\mathfrak{i} \mapsto \mathfrak{j}(\mathfrak{i})$ est une bijection de $\{1, \ldots, k\}$, on a $x_{j}=x_{1}$ pour tout $1 \leqslant \mathfrak{j} \leqslant k$, et donc par hypothèse sur les $x_{i}, k=1$. C'est exactement ce que l'on voulait prouver.
|
| 313 |
+
Commentaire des correcteurs: Ce problème concernant des polynômes a été cherché peu cherché. Rares sont ceux qui ont eu la note de 7 , cependant certains avaient bien compris l'idée mais ont omis quelques détails dans leur copie.
|
| 314 |
+
|
| 315 |
+
Exercice 17. Soit $A B C$ un triangle, $\Omega$ son cercle circonscrit et $O$ le centre de $\Omega$. Soit $S$ le centre du cercle tangent aux côtés $A B$ et $A C$ et tangent intérieurement au cercle $\Omega$ en un point K . Le cercle de diamètre $[A S]$ recoupe le cercle $\Omega$ en un point $T$. Soit $M$ le milieu du segment [BC]. Montrer que les points K, T, M et O sont cocycliques.
|
| 316 |
+
Solution de l'exercice 17 Dans ce problème, nous allons utiliser divers résultats autour du cercle tangent aux côtés $A B$ et $A C$ au cercle $\Omega$. Ce cercle est appelé le cercle $A$-mixtilinéaire, on le notera $\omega$. On note U le point de contact de ce cercle avec le côté $A B$ et V le point de contact avec le côté $A C$. On note également I le centre du cercle inscrit du triangle $A B C$.
|
| 317 |
+
Résultat $n^{\circ} 1$ : La droite (KU) est la bissectrice de l'angle $\widehat{A K B}$.
|
| 318 |
+
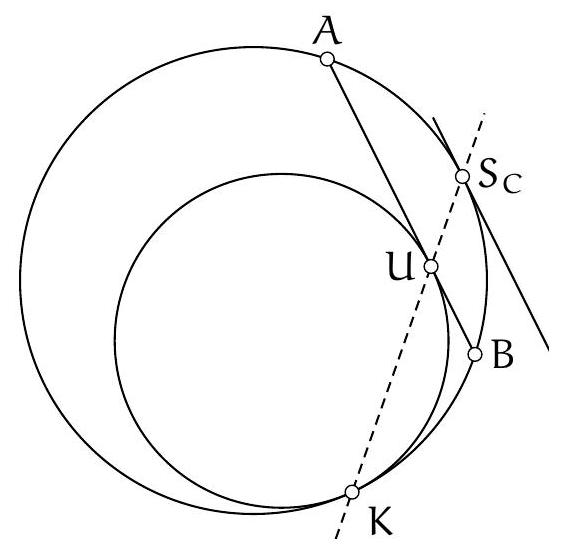
|
| 319 |
+
|
| 320 |
+
Pour montrer ce résultat, on peut par exemple considérer l'homothétie $h$ de centre K qui envoie $\omega$ sur $\Omega$. Soit $S_{C}$ l'image de $U$ par $h$. Alors $h((A B))$ est la droite tangente au cercle $\Omega$ en le point $S_{C}$, et cette droite est parallèle à la droite $(A B)$. Ceci signifie que le triangle $A S_{C} B$ est isocèle donc $S_{C}$ est le pôle sud de $K$ dans le triangle $A B K$ donc la droite (UK) est bien la bissectrice de l'angle $\widehat{A K B}$.
|
| 321 |
+
De même la droite ( VK ) est la bissectrice de l'angle $A K C$ et elle coupe le cercle $\Omega$ en un point noté $S_{B}$.
|
| 322 |
+
Résultat $n^{\circ} 2$ : Le point I est le milieu du segment [UV].
|
| 323 |
+
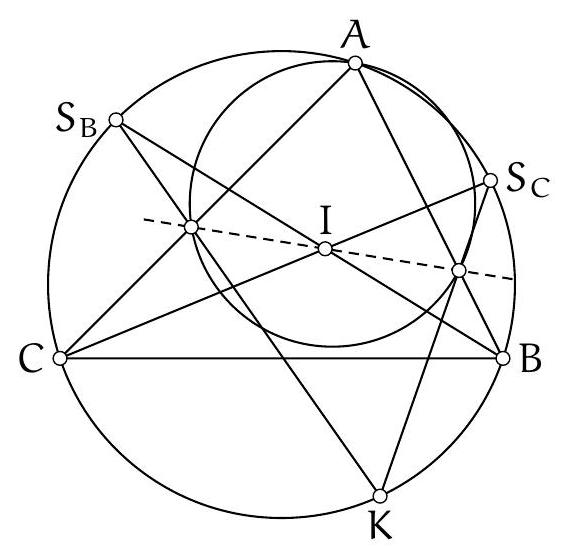
|
| 324 |
+
|
| 325 |
+
Notons que le triangle UAV est isocèle donc la droite (AI) est la médiatrice du segment [UV]. Dès lors, il suffit de démontrer que le point I appartient au segment [UV].
|
| 326 |
+
Pour cela, on applique le théorème de Pascal à l'hexagone $A C S_{C} K S_{B} B$. Ce théorème nous dit que les points $U=(A B) \cap\left(K S_{C}\right), V=(A C) \cap\left(K S_{B}\right)$ et $I=\left(B S_{B}\right) \cap\left(C S_{C}\right)$ sont alignés, comme nous le voulions. (On a ici utilisé le résultat $n^{\circ} 1$ pour avoir l'alignement des points $K, U$ et $S_{C}$ et $K, V$ et $S_{B}$.)
|
| 327 |
+
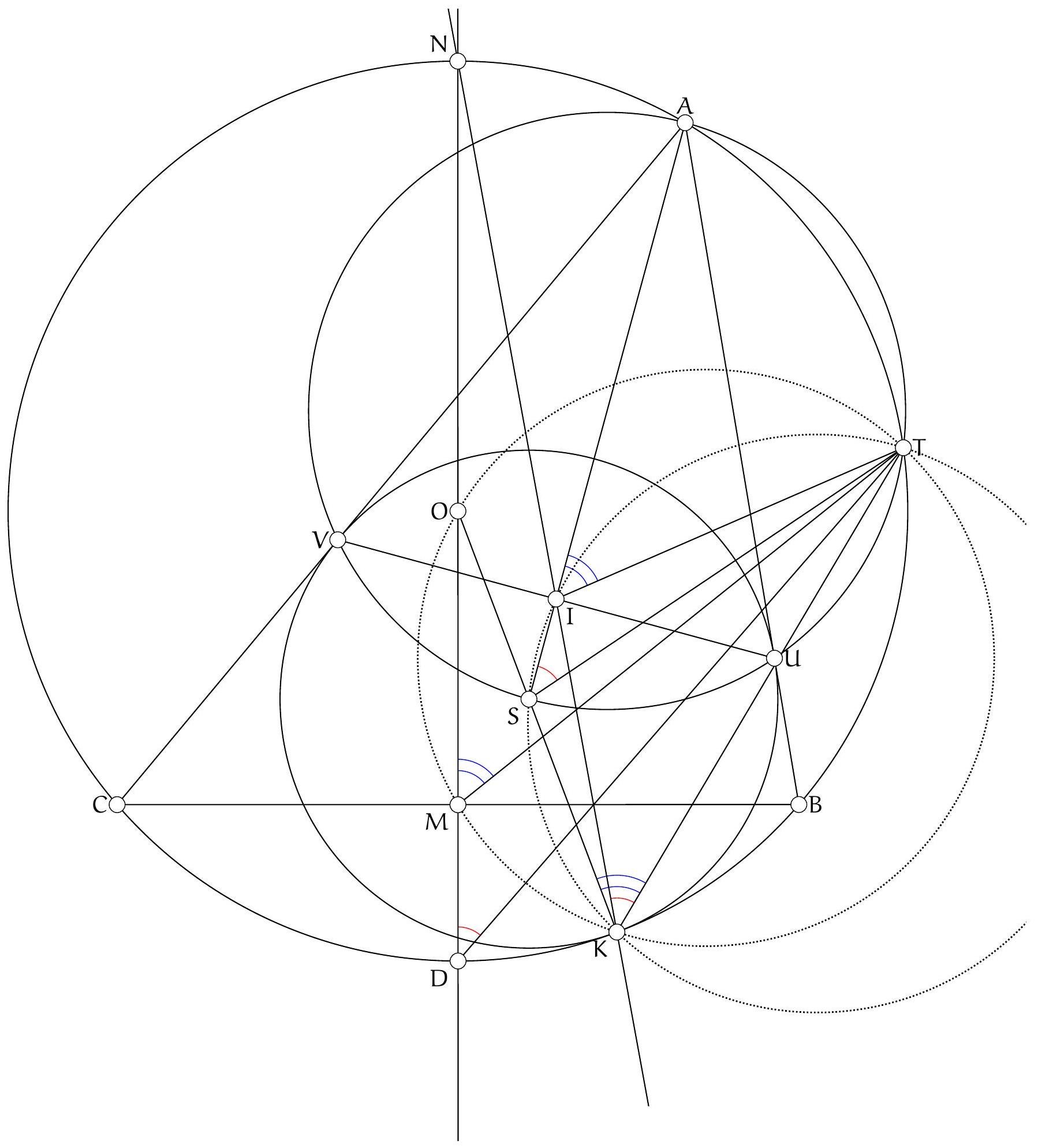
|
| 328 |
+
|
| 329 |
+
Nous pouvons désormais passer à la résolution de l'exercice, maintenant que ces rappels sont faits.
|
| 330 |
+
Tout d'abord, en traçant la figure on s'aperçoit que les points U et V appartiennent au cercle de diamètre [AS]. On s'empresse de démontrer ce résultat. Puisque la droite $(A B)$ au cercle $\omega$ de centre $S$ en le point U , on a $\widehat{S U A}=90^{\circ}$. De même $\widehat{S V A}=90^{\circ}$, les points $A, U, S$ et $V$ sont donc bien sur un même cercle dont $[A S]$ est un diamètre.
|
| 331 |
+
Une première idée qui nous vient ensuite à l'esprit est d'utiliser la définition du point T comme second point d'intersection des cercles circonscrits aux triangles $A B C$ et $A U V$. En effet, cette définition nous
|
| 332 |
+
indique que $T$ est le centre de la similitude qui envoie le point $U$ sur le point $B$ et le point $V$ sur le point $C$. Regardons ce qui deviennent les autres points après cette similitude. Le point I est le milieu du segment [UV], il est donc envoyé sur le milieu du segment [BC], à savoir $M$. Le point $S$ est le milieu de l'arc UV du cercle $\omega$, il est donc envoyé sur le milieu de l'arc BC du cercle $\Omega$, à savoir le pôle Sud du point $A$ dans le triangle $A B C$, que l'on notera $D$.
|
| 333 |
+
Le point $A$ devient le pôle Nord du point T dans le triangle TVU. Il est donc envoyé sur le pôle Nord du point T dans le triangle TBC, on notera N ce point.
|
| 334 |
+
Considérer cette similitude a donc permis d'introduire naturellement de nouveaux points qui seront sans doute utiles à la résolution du problème. On note de plus que si $s$ est cette similitude et $X$ et $Y$ deux points quelconques, alors les triangles $\mathrm{TXs}(\mathrm{X})$ et $\mathrm{TYs}(\mathrm{Y})$ sont semblables. On a donc obtenu de nombreux triangles semblables et donc de nombreuses égalités d'angles.
|
| 335 |
+
On a introduit le point N . Il semble aligné avec les points K et I , nous allons donc tenter de démontrer ce résultat. La façon la plus raisonnable de le faire est de procéder par chasse aux angles. Par exemple on peut essayer de démontrer que $\widehat{\mathrm{VKI}}=\widehat{\mathrm{VKN}}$. Cette idée a du sens puisque les points $\mathrm{S}_{\mathrm{B}}, \mathrm{V}$ et K sont alignés et cet alignement permettrait de passer d'un calcul d'angle dans le triangle UKV à un calcul d'angle dans le triangle $A B C$, que l'on connaît bien.
|
| 336 |
+
Comment calculer l'angle $\widehat{\mathrm{VKI}}$ ? Comme I est le milieu du segment [UV] et que l'on a déjà les tangentes au cercle $\omega$ en $U$ et $V$, on est fortement invités à utiliser la symédiane issue du sommet K , qui n'est autre que la droite $(A K)$. Ainsi, $\widehat{\mathrm{VKI}}=\widehat{\mathrm{UKA}}$. Les points $\mathrm{K}, \mathrm{U}, \mathrm{S}_{\mathrm{C}}$ sont alignés donc
|
| 337 |
+
|
| 338 |
+
$$
|
| 339 |
+
\widehat{U K A}=\widehat{S_{C} K A}=\widehat{A B S_{C}}=\frac{1}{2} \widehat{A C B}
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
On s'est donc débarrassé des points $\mathrm{U}, \mathrm{V}$ et K ce qui est encourageant. Il nous reste à montrer que $\frac{1}{2} \widehat{A C B}=\widehat{S_{B} K N}=\widehat{S_{B} B N}$, ce qui résulte de la chasse aux angles suivante :
|
| 343 |
+
|
| 344 |
+
$$
|
| 345 |
+
\widehat{S_{B} B N}=\widehat{C B N}-\widehat{S_{B} B C}=90^{\circ}-\frac{1}{2} \widehat{B A C}-\frac{1}{2} \widehat{A B C}=\frac{1}{2} \widehat{B C A}
|
| 346 |
+
$$
|
| 347 |
+
|
| 348 |
+
En résumé, $\widehat{\mathrm{VKI}}=\frac{1}{2} \widehat{\mathrm{ACB}}=\widehat{\mathrm{S}_{\mathrm{B}} \mathrm{BN}}=\widehat{\mathrm{S}_{\mathrm{B}} \mathrm{KN}}=\widehat{\mathrm{VKN}}$ donc les points K , I et N sont alignés.
|
| 349 |
+
Utilisons ce que nous venons de trouver. D'après cet alignement : $\widehat{\mathrm{IKT}}=\widehat{\mathrm{NKT}}=\widehat{\mathrm{NDT}}$. Or les triangles NDT et IST sont semblables, donc $\widehat{\mathrm{NDT}}=\widehat{\mathrm{IST}}$. On a obtenu $\widehat{\mathrm{IKT}}=\widehat{\mathrm{IST}}$ donc les points $\mathrm{T}, \mathrm{I}, \mathrm{S}$ et K sont cocycliques.
|
| 350 |
+
Un autre alignement que nous n'avons pas encore utilisé est celui des points $O, S$ et $K$, qui est vrai car l'homothétie de centre K envoyant le cercle $\omega$ sur $\Omega$ envoie le point $S$ sur le point O . Cet alignement ainsi que le fait que les points $T, I, S$ et $K$ sont cocycliques nous donne
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\widehat{\mathrm{OKT}}=\widehat{\mathrm{SKT}}=180^{\circ}-\widehat{\mathrm{SIT}}=\widehat{\mathrm{AIT}}
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
Mais les triangles AIT et NMT sont semblables. Ainsi :
|
| 357 |
+
|
| 358 |
+
$$
|
| 359 |
+
\widehat{\mathrm{OKT}}=\widehat{\mathrm{AIT}}=\widehat{\mathrm{NMT}}=\widehat{\mathrm{OMT}}
|
| 360 |
+
$$
|
| 361 |
+
|
| 362 |
+
et les points $\mathrm{O}, \mathrm{M}, \mathrm{K}$ et T sont bien cocycliques.
|
| 363 |
+
Commentaire des correcteurs : L'exercice était plutôt corsé. Les quelques élèves l'ayant résolu ont montré une belle maitrise de divers outils comme l'inversion, la manipulation de birapports, les théorèmes de Ménélaüs et Céva... et une bonne culture des propriétés du cercle mixti-linéaire. Quelques élèves, même s'ils n'ont pas résolu le problème, ont tout de même renvoyé leurs avancées dans le problème et cela a été très apprécié.
|
| 364 |
+
|
| 365 |
+
Exercice 18. Soit G un graphe fini non orienté, $\mathrm{n} \in \mathbb{N}^{*}, \mathrm{~d} \in \mathbb{N}^{*}$ tel que le degré de tout sommet de G est borné par $d, x$ un sommet de $G$. On note $a(n, x)$ le nombre de sous-graphes induits connexes de G contenant n sommets dont le sommet $x$ (un sous-graphe induit $U$ est un graphe dont les sommets sont des sommets de $G$ et si $x$ et $y$ sont des sommets de $U$, $x$ est relié par une arête à $y$ dans $U$ si et seulement si $x$ est relié par une arête à $y$ dans $G$ ).
|
| 366 |
+
|
| 367 |
+
1. Montrer que $a(n, x) \leqslant 2^{n d}$.
|
| 368 |
+
2. Montrer que $a(n, x) \leqslant\left(\frac{(d+1)^{d+1}}{d^{d}}\right)^{n}$
|
| 369 |
+
|
| 370 |
+
Solution de l'exercice 18 Ici, on est face à un problème de graphe, plus précisément on compter les sousgraphes induits contenant $n$ éléments dont un fixé. On aimerait majorer cela, autant la première question semble pouvoir se faire potentiellement en comptant, autant la seconde n'a pas l'air très interprétable : $\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}$ ne correspond à rien de spécial. A priori, il n'y a pas d'argument combinatoire clair pour faire apparaître cette quantité.
|
| 371 |
+
Comme à priori, on n'a pas de bonnes idées pour voir commencer avancer, on peut tenter de faire cela au hasard! On va donc essayer d'introduire des probabilités. On aimerait construire aléatoirement un sousgraphe induit connexe de G. On pourrait prendre des sommets au hasard mais ça se comporte très mal avec la connexité, il est difficile d'obtenir des informations faciles sur les composantes connexes d'un tel graphe. Plutôt que de choisir des sommets on va donc choisir des arêtes! Ici il sera plus facile de voir quels points sont reliés. L'objectif sera donc d'étudier la composante connexe de $\times$ dans le graphe formé des arêtes choisies.
|
| 372 |
+
On colorie chaque arête en blanc de G indépendamment avec probabilité $p \in[0,1]$. On note X l'ensemble des sommets reliés à $x$ dans le graphe dont les arêtes sont les blanches, i.e. la composante connexe de $x$ dans le graphe aléatoire. Posons $A_{n}(x)$ l'ensemble des sous-graphes induits connexes de $G$ contenant $n$ sommets dont le sommet $x$ (on peut voir un sous-graphe induit comme un ensemble de sommets). Notons que comme les évènements $X=H$ pour $H$ dans $A_{n}(x)$ sont disjoints $1 \geqslant \sum_{H \in A_{n}(x)} P(X=H)$.
|
| 373 |
+
A priori, il suffit donc d'estimer $P(X=G)$ pour avoir une borne sur $a(n, x)$, on va donc essayer de comprendre comment on peut avoir $\mathrm{X}=\mathrm{H}$. Une solution simple est que toutes les arêtes de H soient bien blanches, et les arêtes allant de H à son complémentaire ne le soient pas. Il va donc falloir évaluer la probabilité de cet évènement, en dénombrant le nombre d'arête de chaque catégorie
|
| 374 |
+
Soit H dans $A_{n}(x)$, on a $P(X=H) \geqslant \mathbb{P}\left(A_{H}\right)$ où $A_{H}$ est l'évènement "toutes les arêtes internes à $H$ sont coloriées, et les arêtes reliant H à l'extérieur ne sont pas coloriées". Par indépendance, si on note $l$ le nombre d'arêtes internes à $H$ et $k$ le nombre d'arêtes reliant $G$ à l'extérieur, $\mathbb{P}\left(A_{H}\right)=p^{l}(1-p)^{k}$. Or comme $G$ est de taille $n$ et le degré de chaque sommet est borné par $d, l+k \leqslant n d$.
|
| 375 |
+
Ici pour la première borne, il est assez naturel de prendre $p=\frac{1}{2}$ vu qu'on veut une borne par une puissance de 2.
|
| 376 |
+
Pour $p=\frac{1}{2}$, on obtient donc $\mathbb{P}\left(A_{G}\right)=2^{-(l+k)} \geqslant \frac{1}{2^{n d}}$. Ainsi, on a $1 \geqslant \sum_{G \in A_{n}(x)} \frac{1}{2^{n d}}=a(n, x) \frac{1}{2^{n d}}$, donc $a(n, x) \leqslant 2^{\text {nd }}$.
|
| 377 |
+
Ici le raisonnement effectué tient si on change sous-graphe induit par sous-graphe car la probabilité d'avoir comme composante connexe le sous-graphe H est la probabilité que les arêtes de H soient blanches, et les arêtes qui ne sont pas dans H ne le soient pas, on a au plus nd arêtes concernées, donc $\mathbb{P}\left(A_{H}\right) \geqslant 2^{-\mathrm{nd}}$ et on obtient le même résultat.
|
| 378 |
+
Pour la seconde inégalité, on aimerait avoir une meilleure minoration de $\mathbb{P}(\mathrm{X}=\mathrm{H})$. A priori, ce qu'on a fait dans la première partie était assez symétrique, on mettait autant de probabilité pour une arête blanche et une arête non blanche. On aimerait bien déséquilibrer cela, par exemple mettre une faible probabilité pour les arêtes blanches. Ainsi, on a envie d'avoir peu d'arêtes blanches à colorier pour obtenir H. A priori, à nombre de sommets fixé, le graphe ayant le minimum d'arête est un arbre : il est donc naturel de considérer un sous-arbre couvrant.
|
| 379 |
+
|
| 380 |
+
Pour cela, on va utiliser le fait que H contient un sous-arbre $T$ avec le même nombre de sommet (et $\mathrm{n}-1$ arêtes). En particulier, $P(X=H) \geqslant P\left(B_{H}\right)$ avec $B_{G}$ l'évènement: les arêtes de $T$ sont coloriées, les autres ne le sont pas. Comme il y a au plus dn arêtes avec une extrémité dans $H$, on a donc $P\left(B_{H}\right) \geqslant$ $p^{n-1}(1-p)^{d n} \geqslant p^{n}(1-p)^{d n}$.
|
| 381 |
+
Maintenant on aimerait obtenir l'inégalité voulue, pour cela il est naturel d'essayer d'optimiser la quantité précédente en $p$. Si on pose $f:[0,1] \mapsto \mathbb{R}$ qui à $p$ associe $p^{n}(1-p)^{\text {dn }}$, $f$ est $C^{1}$ et de dérivée $n p^{n-1}(1-$ $p)^{\mathrm{dn}}-\mathrm{dnp}^{\mathrm{n}}(1-p)^{\mathrm{d} n-1}=n^{\mathrm{n}-1}(1-p)^{\mathrm{dn}-1}(1-p-d p)$ qui $\mathrm{s}^{\prime}$ annule et admet un minimum pour $1-p-d p=0$ c'est-à-dire $p=\frac{1}{d+1}$.
|
| 382 |
+
Prenons donc $p=\frac{1}{d+1}$, on a $P\left(A_{H}\right) \geqslant(d+1)^{-n}\left(\frac{d}{d+1}\right)^{d n}=\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}$. On obtient
|
| 383 |
+
|
| 384 |
+
$$
|
| 385 |
+
1 \geqslant \sum_{G \in A_{n}(x)} P\left(B_{G}\right) \geqslant a(n, x) \times\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}
|
| 386 |
+
$$
|
| 387 |
+
|
| 388 |
+
Donc $a(n, x) \leqslant\left(\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}\right)^{n}$.
|
| 389 |
+
Notons que à d fixé, la seconde borne est bornée par $(e(\mathrm{~d}+1))^{n}$ donc bien meilleure pour d grand.
|
| 390 |
+
Commentaire des correcteurs: L'exercice était difficile, seuls 2 élèves ont réussi la deuxième question. Une approche non probabiliste était possible en se ramenant à compter les sous-abres de l'arbre d-aire complet.
|
| 391 |
+
|
French_STS/md/fr-corrigé-envoi-1.md
ADDED
|
@@ -0,0 +1,555 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOI 1 : GÉOMÉTRIE
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2008 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soient $\omega$ et $\Omega$ deux cercles concentriques (c'est-à-dire qu'ils ont le même centre) de sorte que le cercle $\omega$ soit à l'intérieur du cercle $\Omega$. Soient $X$ et $Y$ deux points sur le cercle $\omega$. On note $P$ et $Q$ les points d'intersection respectifs du cercle $\Omega$ avec les tangentes en $X$ et $Y$ à $\omega$, de telle sorte que $P$ et $Q$ soient du même côté par rapport à la droite $(\mathrm{XY})$. Montrer que les points $X, Y, P$ et $Q$ sont cocycliques.
|
| 17 |
+
|
| 18 |
+
## Solution de l'exercice 1
|
| 19 |
+
|
| 20 |
+
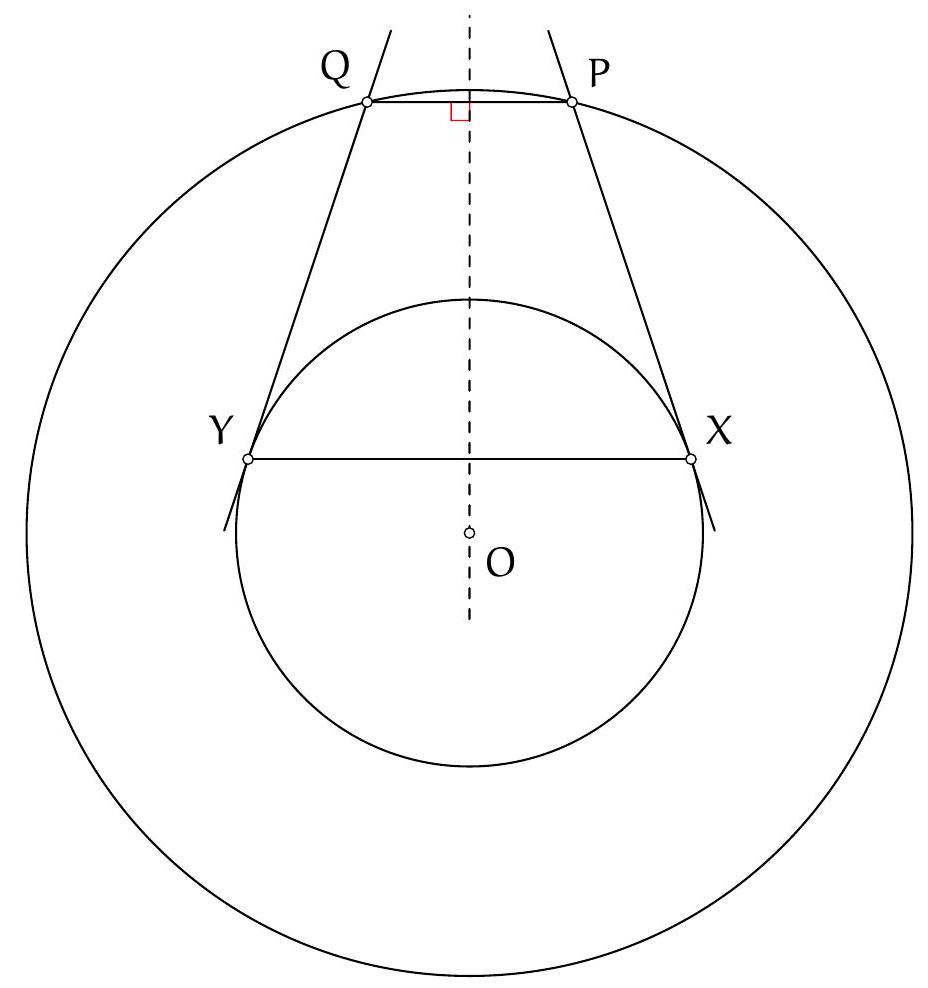
|
| 21 |
+
|
| 22 |
+
Le quadrilatère $X Y Q P$ semble être un trapèze isocèle sur la figure. On commence par le démontrer.
|
| 23 |
+
Soit d la médiatrice de $[\mathrm{XY}]$. Puisque O est le centre du cercle $\omega, \mathrm{O}$ appartient à d . Ainsi, les cercles centrés en $O$, et en particulier $\omega$ et $\Omega$, sont envoyés sur eux-mêmes par la symétrie d'axe $d$. On note $s$ cette symétrie.
|
| 24 |
+
|
| 25 |
+
On a $s(X)=\mathrm{Y}, \mathrm{s}(\omega)=\omega$ et $s(\Omega)=\Omega$, donc $s$ envoie la tangente à $\omega$ en $X$ sur la tangente à $s(\omega)=\omega$ en $s(X)=Y$. Le point d'intersection P de $\Omega$ avec la tangente à $\omega$ en $X$ est envoyé sur le point d'intersection de $s(\Omega)$ avec la tangente à $s(\omega)$ en $s(X)$.
|
| 26 |
+
|
| 27 |
+
Il s'agit du point d'intersection de $\Omega$ avec la tangente à $\omega$ en $Y$, à savoir le point $Q$. Autrement dit, $P$ et Q sont symétriques par rapport à la médiatrice de $[\mathrm{XY}]$. Les segments $[\mathrm{XY}]$ et $[\mathrm{PQ}]$ sont perpendiculaires à $d$ donc parallèles entre eux et les segments $[\mathrm{PX}]$ et $[\mathrm{QY}]$ sont symétriques par rapport à d . Ceci suffit à conclure que le quadrilatère PQYX est un trapèze isocèle.
|
| 28 |
+
|
| 29 |
+
Concluons qu'il s'agit d'un quadrilatère cyclique. Par angles correspondants, $\widehat{\mathrm{QPX}}=180^{\circ}-\widehat{\mathrm{PXY}}$ et puisque $s$ conserve les angles, $\widehat{\mathrm{YQP}}=\widehat{\mathrm{QPX}}$. On déduit que
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\widehat{Y Q P}=\widehat{Q P X}=180^{\circ}-\widehat{P X Y}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
donc les points $P, Q, Y$ et $X$ sont bien cocycliques d'après la réciproque du théorème de l'angle inscrit.
|
| 36 |
+
Commentaire des correcteurs : Le problème a été plutôt bien réussi, mais il y a eu trois problèmes récurrents :
|
| 37 |
+
|
| 38 |
+
- Plusieurs élèves utilisent allègrement que deux triangles avec deux côtés de même longueur et un angle en commun sont isométriques. Malheureusement ce fait est faux : ici on pouvait s'en sortir en utilisant que les triangles étaient rectangles (dans ce cas le critère est vrai par Pythagore). Mais dans un cas général c'est totalement faux : il faut que les côtés soient adjacents à l'angle. Ainsi il est nécessaire de bien préciser rectangle.
|
| 39 |
+
- Beaucoup d'élèves supposent que (QY) et (PX) s'intersectent. C'est le cas sauf quand les droites sont parallèles : il fallait donc aussi traiter ce cas. En olympiade, introduire un point qui n'existe pas dans un cas particulier coûte régulièrement 1 point à certains candidats : il faut donc être prudent et traiter le cas particulier à côté.
|
| 40 |
+
- Certains élèves parlent de symétrie sans vraiment d'argument rigoureux. Il est important de préciser pourquoi les objets sont envoyés l'un sur l'autre par symétrie.
|
| 41 |
+
|
| 42 |
+
Exercice 2. Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, $D$ et $E$ sont cocycliques.
|
| 43 |
+
|
| 44 |
+
## $\underline{\text { Solution de l'exercice } 2}$
|
| 45 |
+
|
| 46 |
+

|
| 47 |
+
|
| 48 |
+
On va faire une chasse aux angles pour démontrer que $\widehat{I D A}+\widehat{I E A}=180^{\circ}$. Notons $x=\widehat{A C E}=\widehat{E C B}$ ainsi que $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Comme la somme des angles d'un triangle vaut $180^{\circ}$ on a ainsi
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\begin{aligned}
|
| 52 |
+
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{ACB}} \\
|
| 53 |
+
& =60^{\circ}+2 y+2 x
|
| 54 |
+
\end{aligned}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
Ce qui implique que $x+y=60^{\circ}$. On peut donc exprimer tous les angles de la figure en fonction de $x$ et en particulier les deux angles qui nous intéressent, $\widehat{I D A}$ et $\widehat{I E A}$. On a $\widehat{I D A}=\widehat{B D A}=180^{\circ}-60^{\circ}-y$ ainsi que $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-x$. Donc la somme vaut
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Ce qui est l'égalité voulue.
|
| 64 |
+
|
| 65 |
+
## Solution alternative de l'exercice 2
|
| 66 |
+
|
| 67 |
+
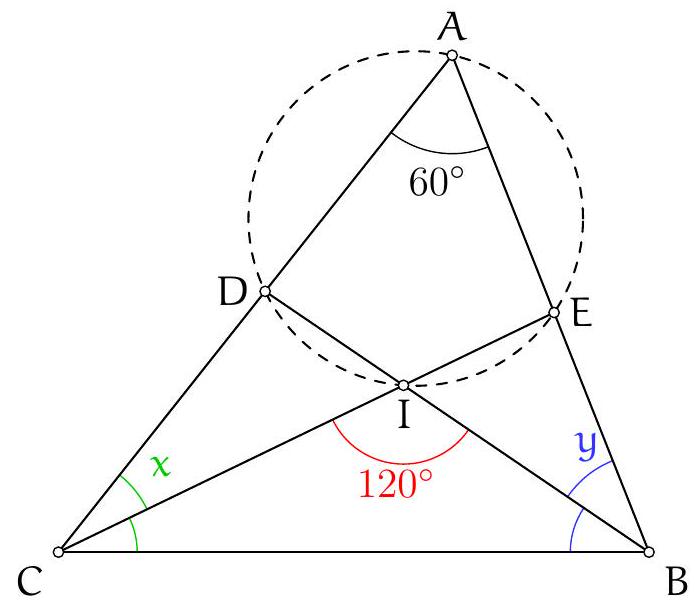
|
| 68 |
+
|
| 69 |
+
Une fois que l'on a obtenu que $x+y=60^{\circ}$, on peut conclure d'une autre façon, en démontrant que $\widehat{\mathrm{DAE}}+\widehat{\mathrm{DIE}}=180^{\circ}$. En effet, dans le triangle BCI, on a $\widehat{\mathrm{BIC}}=180^{\circ}-\mathrm{x}-\mathrm{y}=120^{\circ}$, de sorte que $\widehat{\mathrm{DIE}}+\widehat{\mathrm{DAE}}=\widehat{\mathrm{BIC}}+\widehat{\mathrm{BAC}}=120^{\circ}+60^{\circ}=180^{\circ}$.
|
| 70 |
+
|
| 71 |
+
Commentaire des correcteurs: Exercice très bien réussi dans l'ensemble. Même si l'exercice était relativement rapide, il faut bien penser à faire une belle figure propre et bien préciser les étapes de raisonnement.
|
| 72 |
+
|
| 73 |
+
Exercice 3. Soit ABC un triangle dont O est le centre du cercle circonscrit. On note $\ell$ une droite perpendiculaire à la droite $(A O)$. La droite $(\ell)$ intersecte les côtés $(A B)$ et $(A C)$ en les points $D$ et $E$. Montrer que les points $B, C, E$ et $D$ sont cocycliques.
|
| 74 |
+
|
| 75 |
+
## Solution de l'exercice 3
|
| 76 |
+
|
| 77 |
+
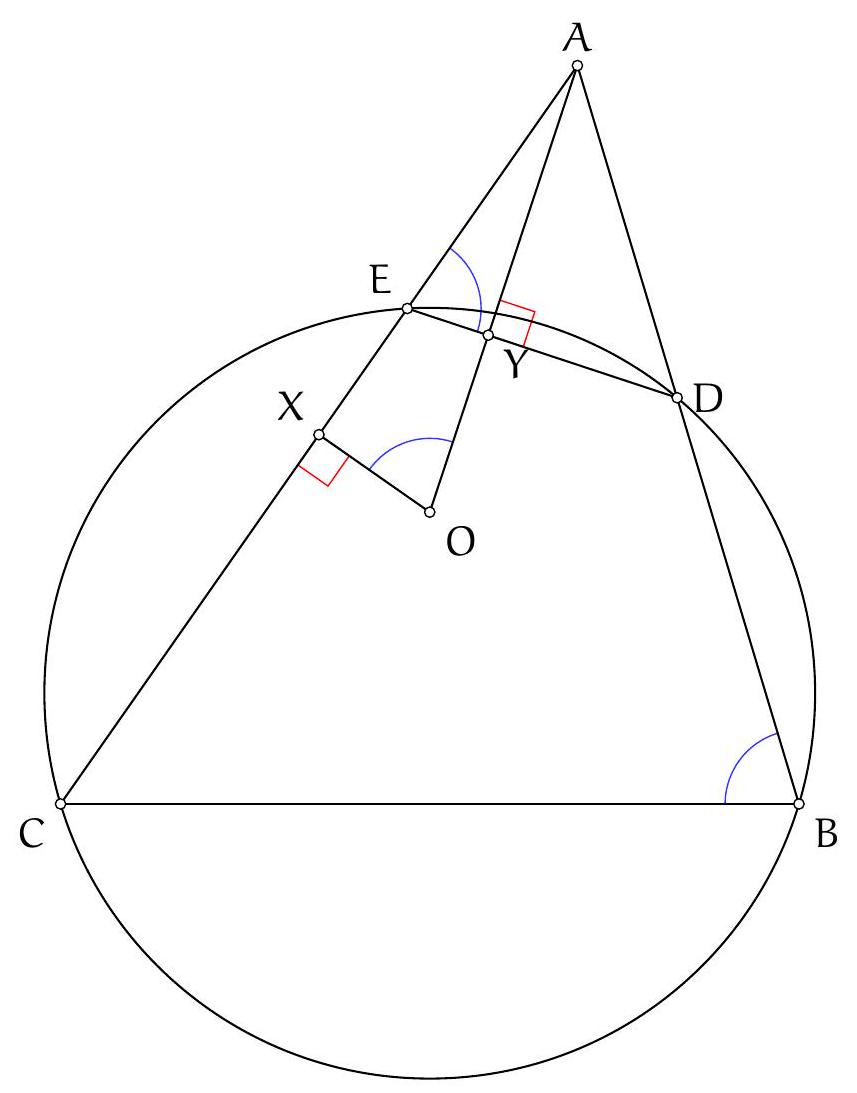
|
| 78 |
+
|
| 79 |
+
Posons $X$ et $Y$ les projetés orthogonaux de $O$ sur ( $A C$ ) et (DE) respectivement. Notons que $X$ est le milieu du segment $[A C]$ et aussi le pied de la bissectrice de l'angle $\widehat{\mathrm{COA}}$ dans le triangle $A O C$ isocèle en O.
|
| 80 |
+
|
| 81 |
+
Comme $\widehat{\mathrm{EXO}}=90^{\circ}=\widehat{\mathrm{EYO}}$, on en déduit que $\mathrm{E}, \mathrm{X}, \mathrm{O}$ et Y sont cocycliques par le théorème de l'angle inscrit. Par le théorème de l'angle au centre, on a alors :
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\widehat{\mathrm{CBA}}=\widehat{\mathrm{COA}} / 2=\widehat{\mathrm{XOA}}=180^{\circ}-\widehat{\mathrm{YEX}}=180^{\circ}-\widehat{\mathrm{CED}}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
On en déduit la cocyclicité des points $\mathrm{B}, \mathrm{C}, \mathrm{D}$ et E .
|
| 88 |
+
Commentaire des correcteurs: L'exercice est très bien réussi, néanmoins beaucoup de preuves se perdent dans de nombreux calculs quand il est possible de faire bien plus simple.
|
| 89 |
+
|
| 90 |
+
Exercice 4. Soient $\omega_{1}$ et $\omega_{2}$ deux cercles disjoints. Une tangente commune extérieure à ces deux cercles coupe $\omega_{1}$ en $A$ et $\omega_{2}$ en $B$. La deuxième tangente commune extérieure à ces deux cercles coupe $\omega_{1}$ en $D$ et $\omega_{2}$ en $C$. La droite (BD) coupe $\omega_{1}$ en le point $P$ autre que $D$ et $\omega_{2}$ en le point $Q$ autre que B. Montrer que BQ = DP.
|
| 91 |
+
|
| 92 |
+
## Solution de l'exercice 4
|
| 93 |
+
|
| 94 |
+
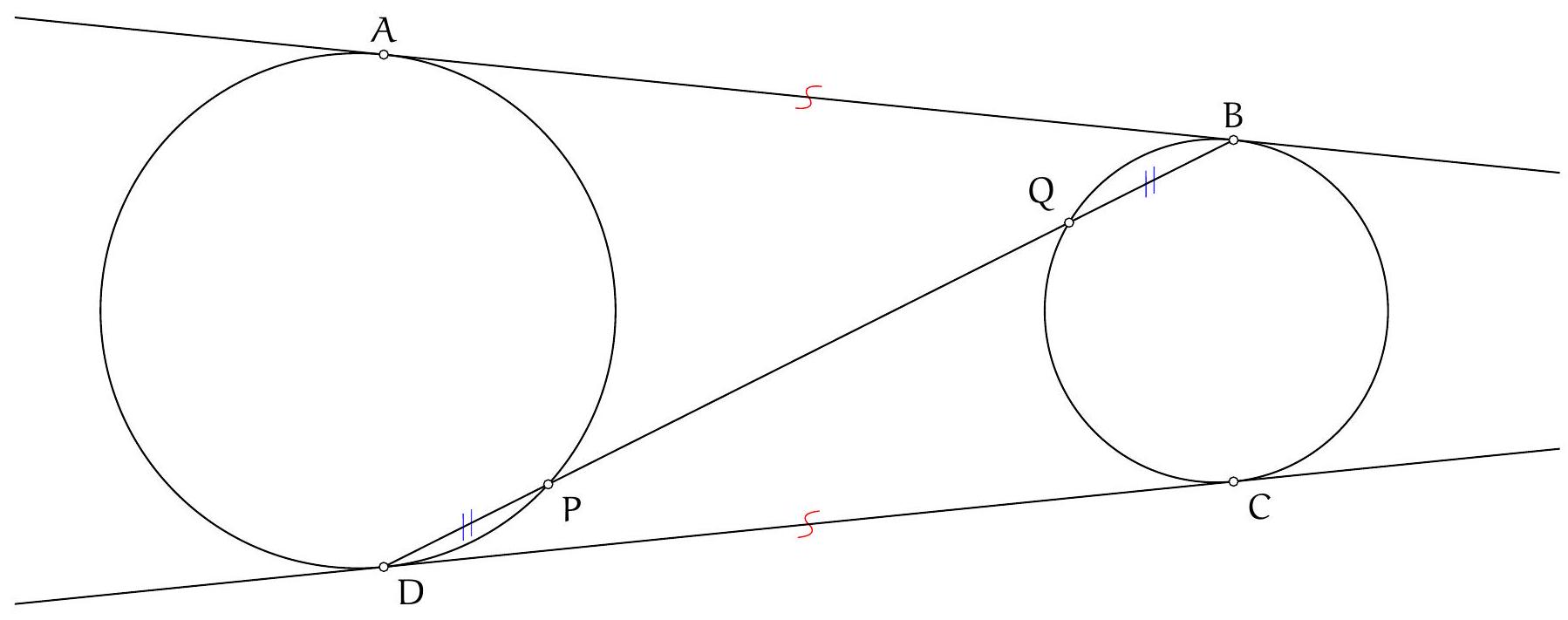
|
| 95 |
+
|
| 96 |
+
Une symétrie axiale par rapport à la droite joignant les centres des deux cercles échange $A$ et $D$ ainsi que $B$ et $C$. Donc, $A B=D C$. On pense alors à appliquer la puissance d'un point, on a alors :
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\mathrm{DQ} \cdot \mathrm{DB}=\mathrm{DC}^{2}=\mathrm{AB}^{2}=\mathrm{BP} \cdot \mathrm{BD}
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
où la première égalité vient de la puissance du point depuis D par rapport à $\omega_{2}$ et la troisième égalité vient de la puissance du point depuis B par rapport au cercle $\omega_{1}$. On peut réécrire cette identité de la manière suivante :
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
(B P-D Q) B D=0
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Cela implique que $\mathrm{BP}=\mathrm{DQ}$ et donc que $\mathrm{DP}=\mathrm{BQ}$, d'où la conclusion.
|
| 109 |
+
Commentaire des correcteurs: L'exercice a globalement été très bien réussi. Utiliser des puissances de points simplifiait l'exercice : certaines copies ont réussi à faire sans, mais il peut être bon d'ètudier la solution avec cette notion afin de voir comment elle simplifiait la résolution du problème. Signalons que très peu de copies ont pensé au fait que lorsque les cercles ont même rayon, alors les tangentes ne se coupent pas. Il faut donc traiter ce cas à part. Enfin si la nècessitè de faire une figure propre et grande est acquise pour la plupart des élèves, il y a encore quelques copies qui ne respectent pas cette consigne.
|
| 110 |
+
|
| 111 |
+
Exercice 5. Soit $A B C$ un triangle acutangle avec $A B<A C<B C$ et soit $\Omega$ son cercle circonscrit. Soient D et E les points diamètralement opposés respectivement aux points B et C dans le cercle $\Omega$. Le cercle de centre $A$ et de rayon $A E$ intersecte $[A C]$ en $K$. Le cercle de centre $A$ et de rayon $A D$ coupe $(B A)$ en $L$ (de telle sorte $A$ se trouve entre B et $L$ ). Montrer que les droites (EK) et (DL) se coupent sur le cercle $\Omega$.
|
| 112 |
+
|
| 113 |
+
## Solution de l'exercice 5
|
| 114 |
+
|
| 115 |
+
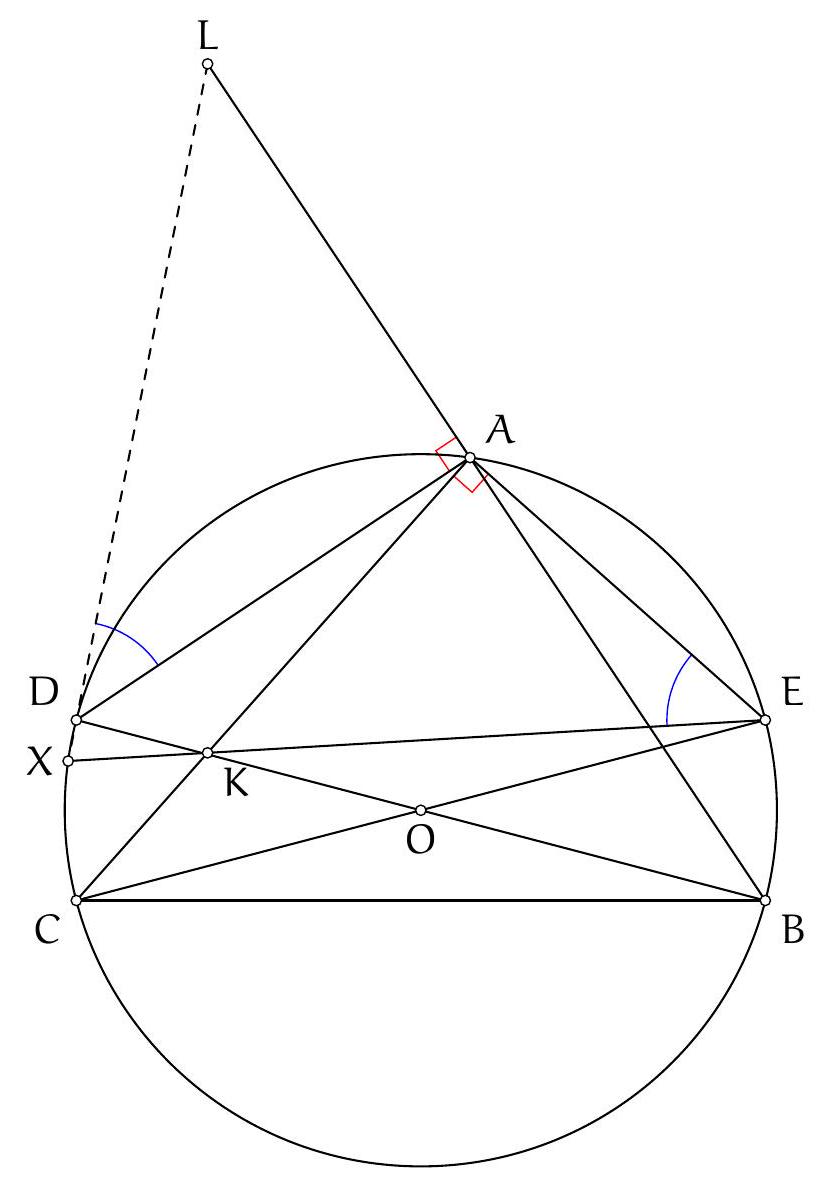
|
| 116 |
+
|
| 117 |
+
Notons $X$ le second point d'intersection de la droite (EK) avec le cercle $\Omega$. La première chose à comprendre est que les points K et L sont très peu importants et qu'ils ne sont là que pour créer des triangles rectangles isocèles.
|
| 118 |
+
|
| 119 |
+
Ainsi, on sait que $[C E]$ est un diamètre du cercle $\Omega$ et on obtient donc que $\widehat{\mathrm{EAK}}=90^{\circ}$. Le triangle EAK est isocèle en $A$ car $A K=A E$ d'après les hypothèses de l'énoncé, en combinant cela avec l'information que $\widehat{\mathrm{EAK}}=90^{\circ}$ cela montre que $\widehat{\mathrm{KEA}}=45^{\circ}$. De la même manière le triangle DAL est rectangle isocèle en $A$ et donc
|
| 120 |
+
|
| 121 |
+
$$
|
| 122 |
+
\widehat{\mathrm{XDA}}=180^{\circ}-\widehat{\mathrm{AEX}}=180^{\circ}-45^{\circ}=180^{\circ}-\widehat{\mathrm{LDA}}
|
| 123 |
+
$$
|
| 124 |
+
|
| 125 |
+
Ce qui montre bien que les points $X, D$ et $L$ sont alignés.
|
| 126 |
+
Commentaire des correcteurs : L'exercice est bien traité. En revanche, une quantité significative d'élèves a déployé une longue chasse aux angles quand il était possible d'avoir une solution directe.
|
| 127 |
+
|
| 128 |
+
Exercice 6. Soit $A B C$ un triangle avec $\widehat{A B C}=\widehat{A C B}=40^{\circ}$. La bissectrice issue du sommet $B$ coupe la droite ( $A C$ ) au point $D$. Montrer que $B D+D A=B C$.
|
| 129 |
+
|
| 130 |
+
## Solution de l'exercice 6
|
| 131 |
+
|
| 132 |
+
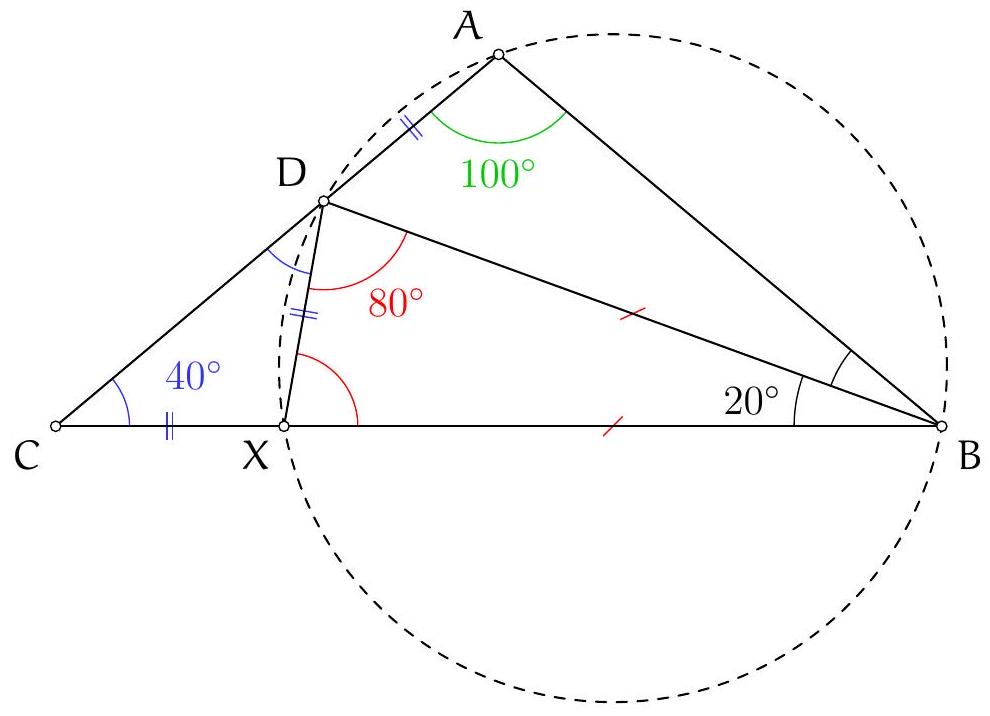
|
| 133 |
+
|
| 134 |
+
Pour résoudre ce genre d'exercice, une bonne idée est souvent d'essayer de reporter les longueurs qui nous intéressent à des endroits où les calculs seront plus faciles à faire. C'est pour cela que l'on introduit $X$ le point du segment $[B C]$ de telle sorte que $B D=B X$. On veut alors démontrer que $X C=A D$ pour conclure.
|
| 135 |
+
|
| 136 |
+
Une chasse aux angles rapide montre dans un premier temps que $\widehat{\mathrm{BXD}}=80^{\circ}$. En effet, on sait par construction du point $X$ que le triangle BDX est isocèle en B , on peut donc calculer $\widehat{\mathrm{BXD}}=\left(180^{\circ}-\right.$ $\left.20^{\circ}\right) / 2=80^{\circ}$. Cela donne ensuite que $\widehat{\mathrm{CDX}}=\widehat{\mathrm{DXB}}-\widehat{\mathrm{DCX}}=80^{\circ}-40^{\circ}=40^{\circ}=\widehat{\mathrm{DCX}}$ et donc que le triangle DXC est isocèle en X . Cela montre que $\mathrm{DX}=\mathrm{XC}$. Résoudre l'exercice revient donc à montrer que $A D=D X$.
|
| 137 |
+
|
| 138 |
+
En regardant très fort le quadrilatère BADX on remarque que la droite ( BD ) est la bissectrice de l'angle $\widehat{A B X}$ et comme on veut démontrer que $A D=D X$ on pense naturellement au théorème du pôle sud. Il suffit donc de démontrer que les points $B, A, D$ et $X$ sont cocycliques pour conclure, il s'agit alors d'une deuxième petite chasse aux angles.
|
| 139 |
+
|
| 140 |
+
En effet, $\widehat{\mathrm{BAD}}+\widehat{\mathrm{BXD}}=100^{\circ}+80^{\circ}=180^{\circ}$ ce qui montre bien que le quadriltère ADXB est cyclique, puis d'après le théorème du pôle Sud dans le triangle $B A X$ que $A D=D X$. Cela conclut ainsi la preuve de l'exercice.
|
| 141 |
+
|
| 142 |
+
## Solution alternative de l'exercice 6
|
| 143 |
+
|
| 144 |
+
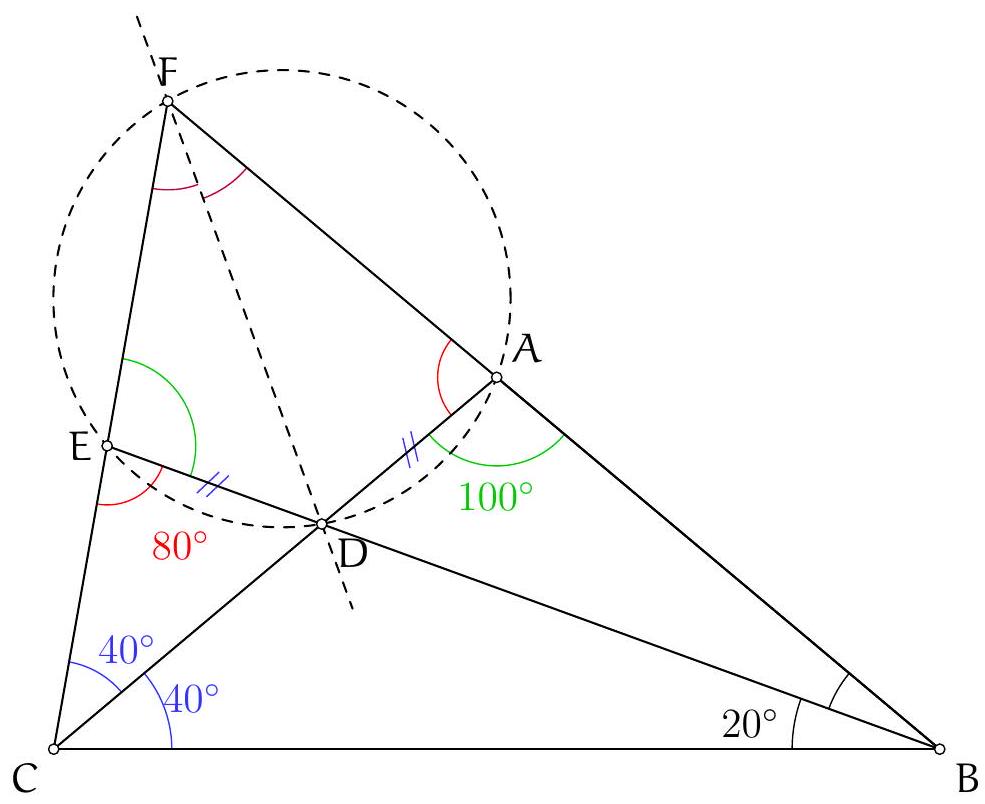
|
| 145 |
+
|
| 146 |
+
On présente une deuxième solution, correspondant à une deuxième façon de reporter les longueurs à étudier.
|
| 147 |
+
|
| 148 |
+
Soit $E$ le point de la demi-droite $[B D)$ tel que $B E=B C$. On cherche à montrer que $E D=D A$, de sorte que $B D+D A=B D+D E=B E=B C$. Le triangle $E B C$ est isocèle en $B$, de sorte que $180^{\circ}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}+\widehat{\mathrm{CEB}}=20^{\circ}+2 \widehat{\mathrm{CEB}}$. Ainsi, $\widehat{\mathrm{CEB}}=80^{\circ}$ et $\widehat{\mathrm{ECD}}=\widehat{\mathrm{ECB}}-\widehat{\mathrm{DCB}}=80^{\circ}-40^{\circ}=40^{\circ}$. Le point D est donc le pied de la bissectrice issue du sommet C dans le triangle ECB .
|
| 149 |
+
|
| 150 |
+
Soit désormais $F$ le point d'intersection des droites ( $E C$ ) et ( $A B$ ). L'idée derrière l'introduction de ce point est que l'on connait déjà deux bissectrices de ce triangle : la droite (BD) est la bissectrice de l'angle $\widehat{A B C}$ et la droite (CD) est la bissectrice de l'angle $\widehat{F C B}$. Ainsi, le point $D$ est le centre du cercle inscrit au triangle FCB. Il est donc sur la bissectrice de l'angle $\widehat{\mathrm{BFC}}$.
|
| 151 |
+
|
| 152 |
+
Or on a $\widehat{D E F}=180^{\circ}-\widehat{D E C}=100^{\circ}$ et $\widehat{D A F}=180^{\circ}-\widehat{D A B}=80^{\circ}$, de sorte que $\widehat{D E F}+\widehat{D A F}=180^{\circ}$ et les points $F, E, D$ et $A$ sont cocycliques. Le point $D$ est donc sur le cercle circonscrit au triangle $F E A$ et sur la bissectrice de l'angle $\widehat{E F A}$, il s'agit donc du pôle Sud du point F . A ce titre, D est sur la médiatrice du segment $[A E]$ et $D E=D A$ comme annoncé.
|
| 153 |
+
|
| 154 |
+
Commentaire des correcteurs: L'exercice est globalement bien réussi par les élèves l'ayant tenté : certains ont même trouvé des approches très différentes (mais souvent un peu plus laborieuses) que celles du corrigé. Un certain nombre d'élève ont essayé de calculer toutes les longueurs, en espérant que les expressions trigonométriques se simplifieraient bien à la fin. Il était possible de faire ainsi (le plus simple étant via la loi des sinus), mais attention, en compétition, essayer de calculer pleins de longueurs sans aboutir à rien rapporte habituellement très peu de points. Il faut donc éviter d'aboutir à des calculs trop compliqués.
|
| 155 |
+
|
| 156 |
+
Exercice 7. Soit $A B C$ un triangle. On note $D$ et $E$ les milieux respectifs des côtés $A B$ et $A C$. Soit $O$ le centre du cercle circonscrit du triangle $A B C$. On note K le point d'intersection des droites (OE) et (BC). On note L le deuxième point d'intersection de la droite (OD) avec le cercle circonscrit au triangle OKB. On note $F$ la projection orthogonale de $A$ sur le droite (KL). Montrer que les points D, $E$ et $F$ sont alignés.
|
| 157 |
+
|
| 158 |
+
## Solution de l'exercice 7
|
| 159 |
+
|
| 160 |
+
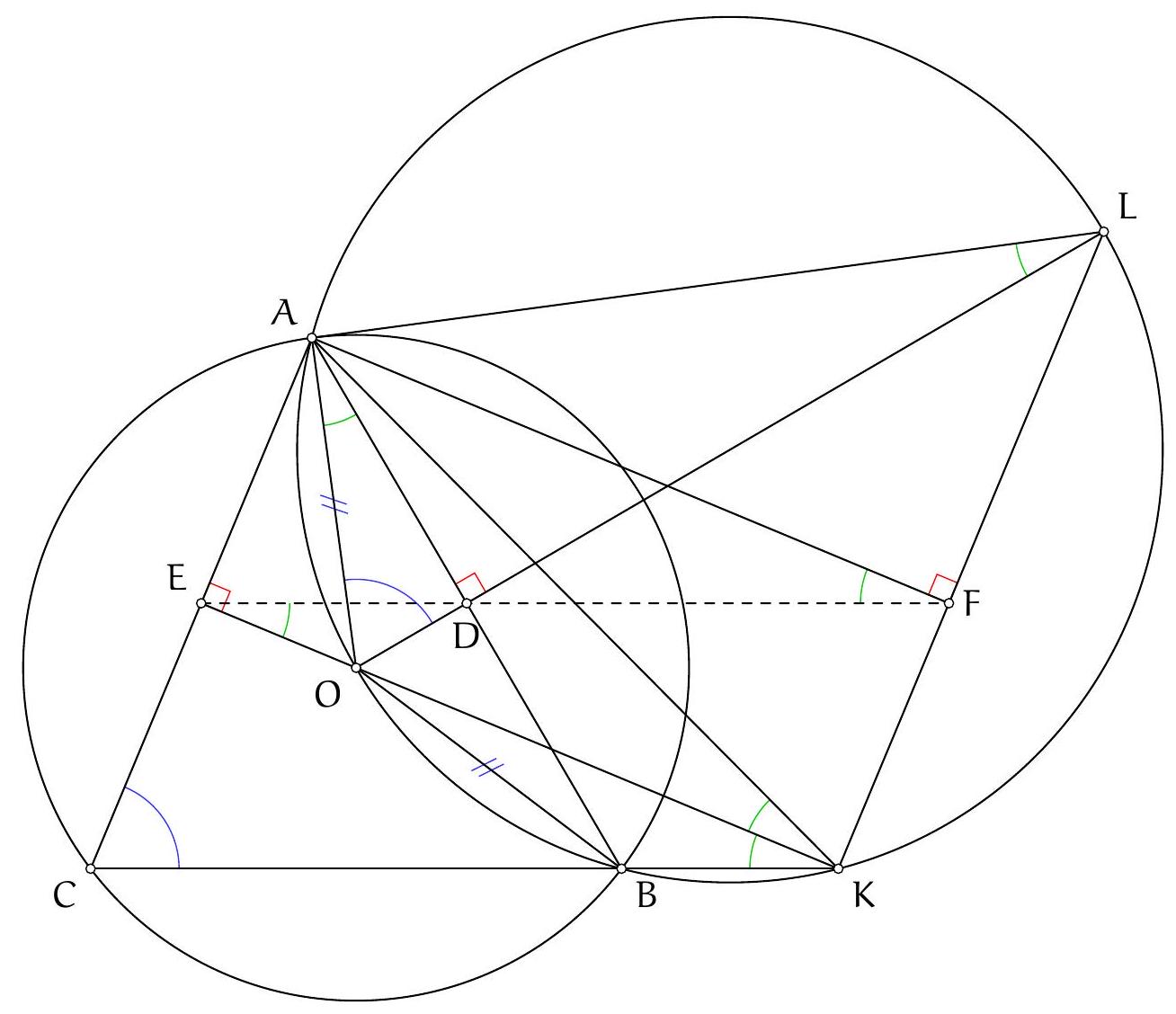
|
| 161 |
+
|
| 162 |
+
En traçant la figure, on s'aperçoit que le point $A$ appartient également au cercle passant $O, K$ et $B$. On commence par démontrer ce fait.
|
| 163 |
+
|
| 164 |
+
D'une part, d'après le théorème de Thalès les droites ( DE ) et ( BC ) sont parallèles, on a l'égalité des angles alternes-internes :
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
\widehat{\mathrm{OKB}}=\widehat{\mathrm{OED}} .
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
D'autre part, puisque $\widehat{\mathrm{ODA}}=90^{\circ}=180^{\circ}-\widehat{\mathrm{OEA}}$, les points $\mathrm{O}, \mathrm{E}, \mathrm{A}$ et D sont cocycliques, de sorte qu'avec le théorème de l'angle inscrit on obtient
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
\widehat{O A B}=\widehat{O A D}=\widehat{O E D}=\widehat{O K B} .
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
Ce qui prouve bien que le point $\mathcal{A}$ appartient au cercle passant par $\mathrm{O}, \mathrm{K}$ et B . Notons que O est le milieu de l'arc $A B$ dans le cercle circonscrit au triangle $A K B$. Le point $O$ est donc le pôle Sud du point $K$ dans le triangle $A B K$. En particulier, $\widehat{O K B}=\widehat{A K O}$.
|
| 177 |
+
|
| 178 |
+
Puisque $\widehat{A F K}=90^{\circ}=180^{\circ}-\widehat{A E K}$, les points $A, F, K$ et $E$ sont cocycliques. On a donc avec le théorème de l'angle inscrit:
|
| 179 |
+
|
| 180 |
+
$$
|
| 181 |
+
\widehat{A F E}=\widehat{A K E}=\widehat{A K O} .
|
| 182 |
+
$$
|
| 183 |
+
|
| 184 |
+
D'autre part, puisque $\widehat{A F L}=90^{\circ}=\widehat{A D L}$, les points $A, D, F$ et $L$ sont cocycliques. On a alors avec le théorème de l'angle inscrit dans le cercle passant par $A, D, F$ et $L$ puis dans celui passant par $A, L, K$ et O :
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
\widehat{A F D}=\widehat{A L D}=\widehat{A L O}=\widehat{A K O}
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
On déduit que $\widehat{A F D}=\widehat{A K O}=\widehat{A F E}$. Les points $F, D$ et $E$ sont donc alignés, comme voulu.
|
| 191 |
+
Remarque 1. Une fois que l'on a montré que le point A est sur le cercle passant par $\mathrm{O}, \mathrm{K}$ et B , on peut conclure directement en remarquant que les points $\mathrm{E}, \mathrm{D}$ et F sont les projetés orthogonaux du point A sur les côtés du triangle OKL. La propriété de la droite de Simson nous indique que ces points sont alignés. La propriété de la droite de Simson est un classique de la géométrie du triangle, que l'on pourra retrouver dans le polycopié de géométrie pour débutants de la POFM (Exercice 3.10). La fin de la preuve donnée ci-dessus redémontre en substance cette propriété.
|
| 192 |
+
|
| 193 |
+
Commentaire des correcteurs: L'exercice, pourtant difficile, est bien traité. Très peu d'élèves ont cependant penser à la droite de Simson pour conclure.
|
| 194 |
+
|
| 195 |
+
Exercice 8. Soit ABC un triangle dont les angles sont aigus, $\omega$ son cercle circonscrit et O le centre de $\omega$. La perpendiculaire issue de $A$ par rapport à $(B C)$ intersecte $(B C)$ en $D$ et $\omega$ en $E$. Soit $F$ un point sur le segment $[A E]$ tel que $2 \cdot F D=A E$. Soit $\ell$ la perpendiculaire à $(O F)$ passant par $F$. Montrer que la droite $\ell$, la droite $(B C)$ et la tangente à $\omega$ en $E$ sont concourantes.
|
| 196 |
+
|
| 197 |
+
## Solution de l'exercice 8
|
| 198 |
+
|
| 199 |
+
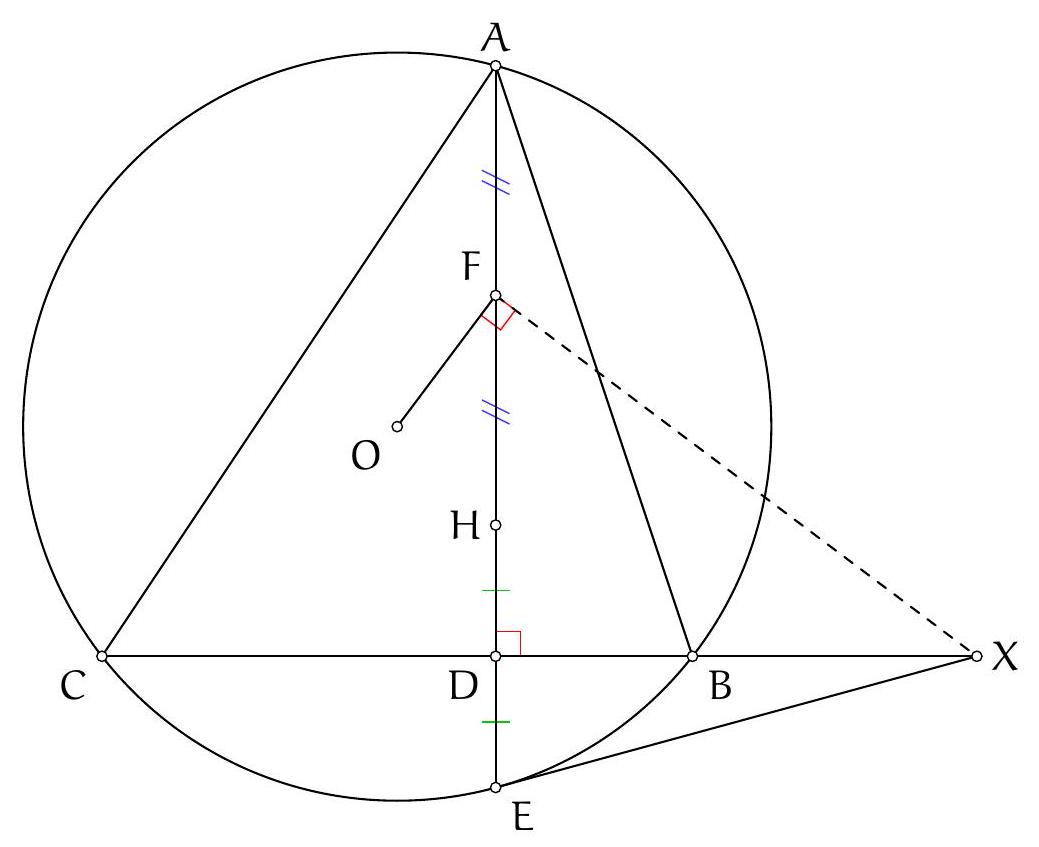
|
| 200 |
+
|
| 201 |
+
On désire montrer que trois droites sont concourantes. Une stratégie serait donc de considérer le point d'intersection de deux de ces droites et de montrer que ce point appartient à la troisième droite, c'est la stratégie que nous allons adopter ici.
|
| 202 |
+
|
| 203 |
+
Dans le cas de notre exercice, il était possible de choisir n'importe quelle paire de droites parmi les droites $(\ell),(B C)$ et la tangente à $\omega$ en $E$ et aboutir.
|
| 204 |
+
|
| 205 |
+
Soit $X$ le point d'intersection de la tangente à $\omega$ en $E$ avec la droite (BC). Nous allons montrer que $X$ est sur $\ell$ en montrant que les droites (FX) et (FO) sont perpendiculaires. Et pour montrer qu'elles sont bien perpendiculaires, on va utiliser la réciproque du théorème de Pythagore en montrant que $\mathrm{XO}^{2}=$ $\mathrm{OF}^{2}+\mathrm{FX}$. On notera dans la suite R le rayon de $\omega$.
|
| 206 |
+
|
| 207 |
+
D'une part, puisque ( $X E$ ) est tangente au cercle $\omega$, on a $X O^{2}=X E^{2}+O E^{2}=X E^{2}+R^{2}$. D'après le théorème de Pythagore dans le triangle $X D E$ rectangle en $D, X E^{2}=X D^{2}+D E^{2}$. On en déduit que
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
X O^{2}=X D^{2}+D E^{2}+R^{2}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
D'autre part, d'après le théorème de Pythagore dans le triangle FDX rectangle en $\mathrm{D}, \mathrm{XF}^{2}=\mathrm{XD}^{2}+\mathrm{FD}^{2}$. Pour calculer $\mathrm{OF}^{2}$, on utilise la formule de la puissance du point F par rapport au cercle $\omega$. En effet, cette formule nous dit que la puissance du point $F$ par rapport au cercle $\omega$ vaut $\mathrm{OF}^{2}-R^{2}$. Comme d'autre part elle vaut $-F A \times F E$, on déduit que $\mathrm{OF}^{2}=R^{2}-F A \times F E$. On a alors,
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
X F^{2}+O F^{2}=\left(X D^{2}+F D^{2}\right)+\left(R^{2}-F A \times F E\right)
|
| 217 |
+
$$
|
| 218 |
+
|
| 219 |
+
Pour montrer que $X O^{2}=X F^{2}+\mathrm{FO}^{2}$, il suffit donc de montrer que $\mathrm{DE}^{2}=\mathrm{FD}^{2}-\mathrm{FA} \times \mathrm{FE}$, ou encore $D^{2}+F A \times F E$. Il s'agit alors de faire apparaître l'hypothèse de longueur sur le point $F$.
|
| 220 |
+
|
| 221 |
+
Notons H l'orthocentre du triangle $A B C$. On sait que les points H et E sont symétriques par rapport à la droite $(\mathrm{BC})$ (résultat classique de géométrie du triangle que l'on pourra retrouver dans le polycopié
|
| 222 |
+
de géométrie pour débutant de la POFM, exercice 4.8). On déduit que $\mathrm{DE}=\mathrm{DH}$. Mais alors,
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
\mathrm{FH}=\mathrm{FD}-\mathrm{DH}=\frac{1}{2}(A E-\mathrm{HE})=\frac{1}{2} A H .
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
En particulier, F est le milieu du segment $[\mathrm{AH}]$. Il ne reste plus qu'à calculer $\mathrm{DE}^{2}+\mathrm{FA} \times \mathrm{FE}$ de la manière suivante
|
| 229 |
+
|
| 230 |
+
$$
|
| 231 |
+
\begin{aligned}
|
| 232 |
+
\mathrm{DE}^{2}+\mathrm{FA} \times \mathrm{FE} & =\mathrm{DE}^{2}+\mathrm{FA} \times(\mathrm{FH}+\underbrace{\mathrm{DH}+\mathrm{DE}}_{=2 \mathrm{DE}}) \\
|
| 233 |
+
& =\mathrm{DE}^{2}+\mathrm{FA}^{2}+2 \mathrm{DE} \times \mathrm{FA} \\
|
| 234 |
+
& =(\mathrm{FA}+\mathrm{DE})^{2} \\
|
| 235 |
+
& =(\mathrm{FH}+\mathrm{DH})^{2}=\mathrm{FD}^{2} .
|
| 236 |
+
\end{aligned}
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
Ce qui conclut bien que $\mathrm{XO}^{2}=\mathrm{XF}^{2}+\mathrm{FO}^{2}$ et termine la preuve du problème.
|
| 240 |
+
Commentaire des correcteurs: L'exercice était très difficile, et peu d'élèves ont réussi à avoir de bonnes avancées. L'approche la plus élémentaire était d'introduire le milieu de [BC], puis de remarquer un trapèze isocèle (ou un parallélogramme), pour pouvoir entamer une chasse aux angles.
|
| 241 |
+
|
| 242 |
+
Exercice 9. Soit $A B C$ un triangle équilatéral. Soit $X$ un point de la droite ( $B C$ ) différent de $B$ et $C$. Soient $Y$ et $Z$ deux points sur les droites $(A B)$ et $(A C)$ de telle sorte que les deux droites ( $B Z$ ) et ( $C Y$ ) sont parallèles à la droite $(A X)$. La droite $(X Y)$ intersecte la droite ( $A C)$ en $M$ et la droite ( $X Z$ ) intersecte la droite $(A B)$ en $N$. Montrer que la droite ( $M N$ ) est tangente au cercle inscrit de $A B C$.
|
| 243 |
+
Solution de l'exercice 9 On commence par énoncer deux lemmes qui vont être utiles dans la suite. Si l'utilité du premier lemme sautera aux yeux du lecteur l'intérêt du deuxième lemme paraîtra sans doute moins clair.
|
| 244 |
+
Lemme 1. Soit $A B C$ un triangle et $\omega$ le cercle $A$-exinscrit de ce triangle, on note J le centre de $\omega$ et $\alpha$ l'angle en A . Alors, $\widehat{\mathrm{BJC}}=90-\alpha / 2$, de plus il existe une forme d'unicité. Soit X un point de la droite (AB), si on effectue une rotation de la droite (JX) autour de J par un angle $90-\alpha / 2$ et que l'on note par Y l'intersection de cette droite avec la droite ( AB ), alors la droite ( YX ) est tangente à $\omega$.
|
| 245 |
+
Remarque 2. Le lecteur attentif remarquera que la rotation d'angle $90-\alpha / 2$ depuis J n'est pas unique, il faut faire attention au sens dans lequel on effectue la rotation (en fait il faut travailler avec des angles orientés).
|
| 246 |
+
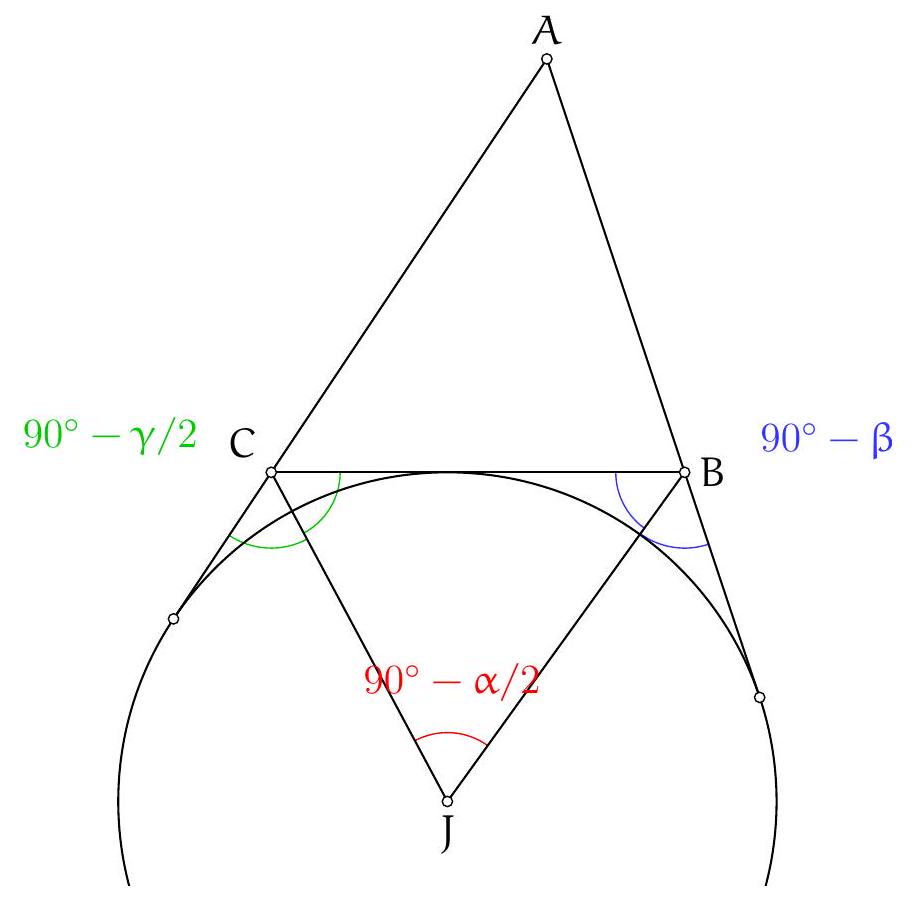
|
| 247 |
+
|
| 248 |
+
## Démonstration.
|
| 249 |
+
|
| 250 |
+
On remarque dans un premier temps que l'unicité découle de la première partie du lemme. En effet, le point $Y$ est défini de manière unique et vérifie alors bien la condition $\widehat{\mathrm{XJY}}=90-\alpha / 2$. Il ne nous reste plus qu'à démontrer la première partie du lemme. On note $\beta$ et $\gamma$ les angles en $B$ et $C$. Alors, ( $B J$ ) et (CJ) sont des bissectrices extérieures donc
|
| 251 |
+
|
| 252 |
+
$$
|
| 253 |
+
\widehat{\mathrm{JBC}}=(180-\beta) / 2=90-\beta / 2
|
| 254 |
+
$$
|
| 255 |
+
|
| 256 |
+
et
|
| 257 |
+
|
| 258 |
+
$$
|
| 259 |
+
\widehat{\mathrm{JCB}}=90-\gamma / 2
|
| 260 |
+
$$
|
| 261 |
+
|
| 262 |
+
Comme les angles dans le triangle BCJ ont pour somme 180 il faut donc que $\widehat{\mathrm{BJC}}=90-\alpha / 2$ comme annoncé.
|
| 263 |
+
|
| 264 |
+
Lemme 2. Soit ABCD un trapèze isocèle avec $(\mathrm{AB})$ parallèle à $(\mathrm{CD})$. On note X le point d'intersection des diagonales (AC) et (BD) ainsi que Y le point d'intersection des droites (AD) et (BC). La droite (XY) intersecte la droite (CD) au point Z. Le point Z est alors le milieu du segment [DC].
|
| 265 |
+
Remarque 3. Il est possible que les droites (AD) et (BC) soient parallèles dans ce cas on considère le point Y "à l'infini" (c'est en principe une notion bien définie mais on ne le fait pas proprement ici) dans la même direction que la droite (AD) et donc de la droite (BC) par hypothèses. Dans ce cas une droite qui passe par Y est juste une droite qui est parallèles à (AD) (et donc à (BC)). Moralement, passer par un point à l'infini c'est forcer une direction.
|
| 266 |
+
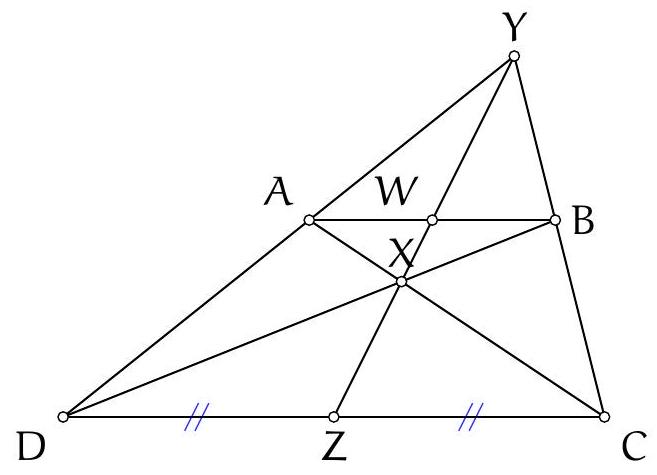
|
| 267 |
+
|
| 268 |
+
## Démonstration.
|
| 269 |
+
|
| 270 |
+
Il existe une preuve naturelle de ce lemme en utilisant des outils de la géométrie projective mais on va donner ici une preuve élémentaire. Soit $W$ l'intersection de la droite ( $X Y$ ) avec la droite ( $A B$ ), on peut alors écrire les identités suivantes qui découlent du théorème de Thalès.
|
| 271 |
+
|
| 272 |
+
Comme les trois droites $(A C),(B D)$ et $(W Z)$ sont concourantes en $Y$ et les droites $(A B)$ et (CD) sont parallèles, on a l'égalité
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
\frac{A W}{W B}=\frac{C Z}{Z D}
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
où l'on a pris soin des orientations de longueurs (ici les deux côtés de l'équation sont négatifs). De la même manière les trois droites ( $A D$ ), ( $B C$ ) et ( $W Z$ ) sont concourantes en $Z$ et que les droites $(A B)$ et $(C D)$ sont parallèles, on a donc l'égalité
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
\frac{B W}{W A}=\frac{C Z}{Z D}
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
En combinant ces deux égalités on obtient
|
| 285 |
+
|
| 286 |
+
$$
|
| 287 |
+
\left(\frac{C Z}{Z D}\right)^{2}=1
|
| 288 |
+
$$
|
| 289 |
+
|
| 290 |
+
Et donc, en prenant soin des signes
|
| 291 |
+
|
| 292 |
+
$$
|
| 293 |
+
\frac{C Z}{Z D}=-1
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
Ce qui conclut la preuve du lemme.
|
| 297 |
+
Revenons désormais au problème.
|
| 298 |
+
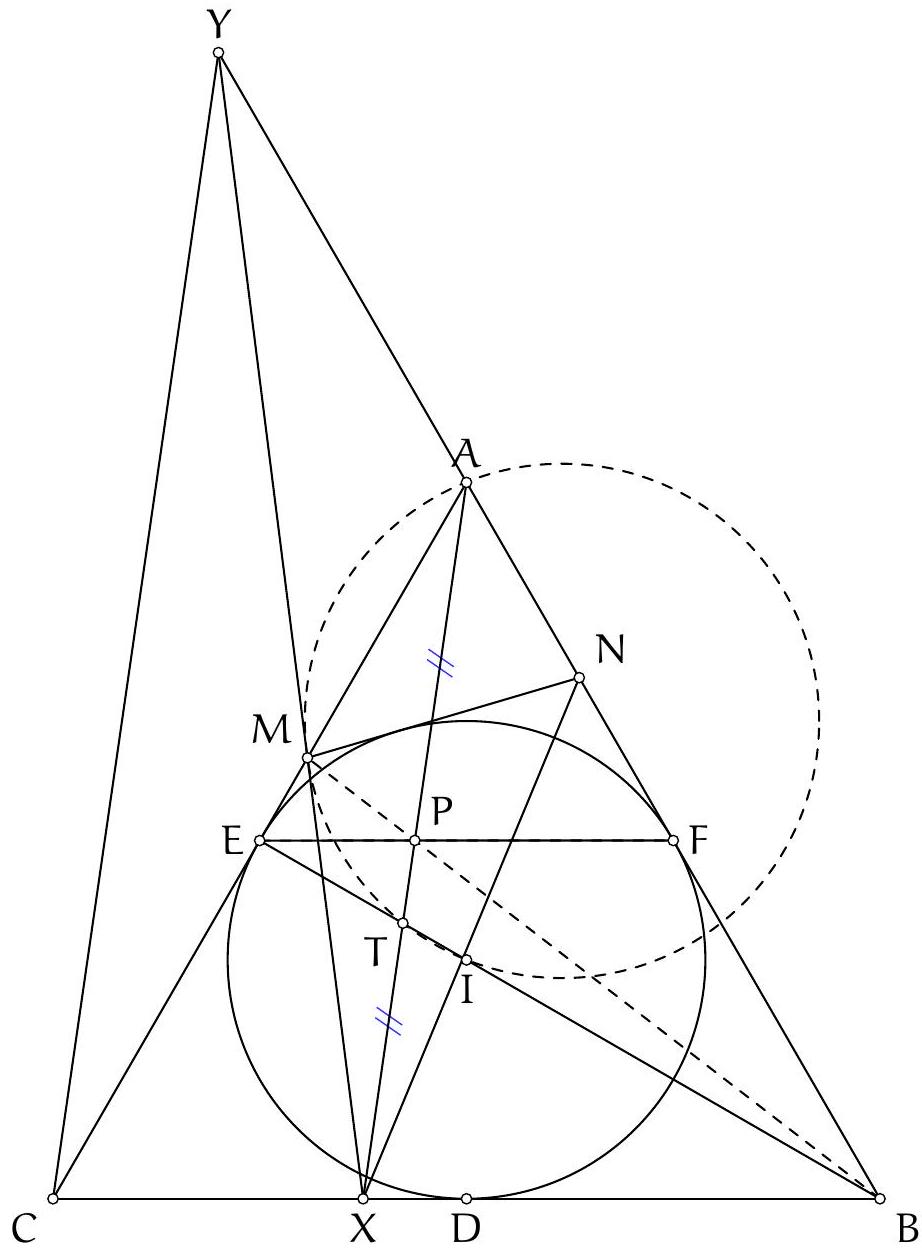
|
| 299 |
+
|
| 300 |
+
On note $D$, $E$ et $F$ les points de tangences du cercle inscrit dans le triangle $A B C$. On va montrer un résultat a priori plus fort. Si on note $x=\widehat{\mathrm{CAX}}$ on va démontrer que $\widehat{M I E}=x$. Cela conclurait alors car par symétrie on aurait $\widehat{M I F}=\widehat{B A X}=60-x$ et donc $\widehat{M I N}=120-(60-x)-x=60$ ce qui conclurait d'après le Lemme 1.
|
| 301 |
+
|
| 302 |
+
Soit $T$ le point d'intersection des droites $(A X)$ et $(B E)$, l'égalité $\widehat{M I E}=\widehat{E A T}$ est équivalente à la propriété que les points $A, M$, I et $T$ sont cocycliques. Une chasse aux angles immédiate montre que cette propriété est encore équivalente à ce que les droites $(M T)$ et $(A B)$ soient parallèles (par exemple on peut utiliser des parallèles/antiparallèles par rapport aux droites (EB) et (EA)). On note de plus $P$ l'intersection des droites (MB) et ( $A X$ ).
|
| 303 |
+
|
| 304 |
+
On applique alors le Lemme 2 dans un premier temps au trapèze $A X C Y$ pour montrer que le point $P$ et le milieu du segment $[A X]$. Ainsi, d'après la droite des milieux on a $F, P$ et $E$ alignés. On remarque alors que dans le quadrilatère $A M T B$ avec $P$ l'intersection des droites $(A T)$ et ( $M B$ ) ainsi que E l'intersection des droites ( $A M$ ) et (BT), la droite (EP) passe par le milieu du segment $[A B]$, il suit que l'on peut alors appliquer la réciproque du Lemme 2 (il y a une unicité laissée au lecteur) pour montrer que le quadrilatère AMTB est bien un trapèze avec $(A B) / /(M T)$ ce qui conclut.
|
| 305 |
+
|
| 306 |
+
Commentaire des correcteurs : L'exercice était très difficile. Une poignée d'élèves en est venue à bout, à l'aide de techniques essentiellement calculatoires (et parfois avancées) largement différentes de la solution proposée par le corrigé.
|
| 307 |
+
|
| 308 |
+
## Exercices Seniors
|
| 309 |
+
|
| 310 |
+
Exercice 10. Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, D et $E$ sont cocycliques.
|
| 311 |
+
|
| 312 |
+
## Solution de l'exercice 10
|
| 313 |
+
|
| 314 |
+
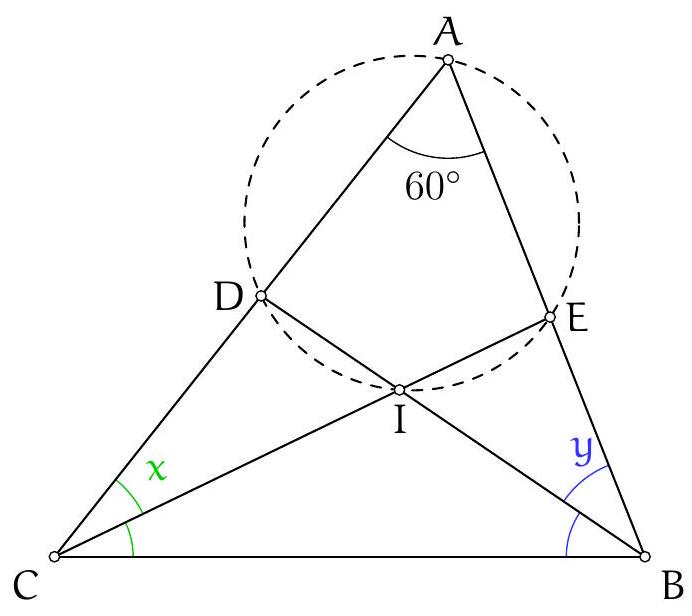
|
| 315 |
+
|
| 316 |
+
On va faire une chasse aux angles pour démontrer que $\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}$. Notons $x=\widehat{\mathrm{ACE}}=\widehat{\mathrm{ECB}}$ ainsi que $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Comme la somme des angles d'un triangle vaut $180^{\circ}$ on a ainsi
|
| 317 |
+
|
| 318 |
+
$$
|
| 319 |
+
\begin{aligned}
|
| 320 |
+
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{A B C}+\widehat{A C B} \\
|
| 321 |
+
& =60^{\circ}+2 y+2 x .
|
| 322 |
+
\end{aligned}
|
| 323 |
+
$$
|
| 324 |
+
|
| 325 |
+
Ce qui implique que $x+y=60^{\circ}$. On peut donc exprimer tous les angles de la figure en fonction de $x$ et en particulier les deux angles qui nous intéressent, $\widehat{\text { IDA }}$ et $\widehat{I E A}$. On a $\widehat{I D A}=\widehat{\mathrm{BDA}}=180^{\circ}-60^{\circ}-y$ ainsi que $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-\chi$. Donc la somme vaut
|
| 326 |
+
|
| 327 |
+
$$
|
| 328 |
+
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
|
| 329 |
+
$$
|
| 330 |
+
|
| 331 |
+
Ce qui est l'égalité voulue.
|
| 332 |
+
Solution alternative de l'exercice 10
|
| 333 |
+
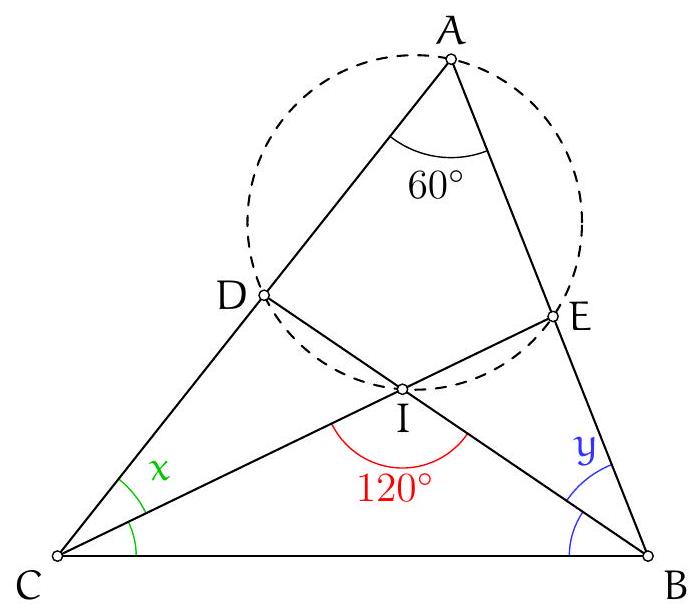
|
| 334 |
+
|
| 335 |
+
Une fois que l'on a obtenu que $x+y=60^{\circ}$, on peut conclure d'une autre façon, en démontrant que $\widehat{\mathrm{DAE}}+\widehat{\mathrm{DIE}}=180^{\circ}$. En effet, dans le triangle BCI, on a $\widehat{\mathrm{BIC}}=180^{\circ}-\mathrm{x}-\mathrm{y}=120^{\circ}$, de sorte que $\widehat{\mathrm{DIE}}+\widehat{\mathrm{DAE}}=\widehat{\mathrm{BIC}}+\widehat{\mathrm{BAC}}=120^{\circ}+60^{\circ}=180^{\circ}$.
|
| 336 |
+
|
| 337 |
+
Commentaire des correcteurs : Exercice très bien réussi. Il faut bien penser à faire une figure propre et à bien détailler son raisonnement.
|
| 338 |
+
|
| 339 |
+
Exercice 11. Soit $A B C$ un triangle, $L, M$ et $N$ les milieux respectifs des côtés $[B C],[C A]$ et $[A B]$. On suppose que $\widehat{A N C}=\widehat{A L B}$. Montrer que $\widehat{C A L}=\widehat{A B M}$.
|
| 340 |
+
|
| 341 |
+
## Solution de l'exercice 11
|
| 342 |
+
|
| 343 |
+
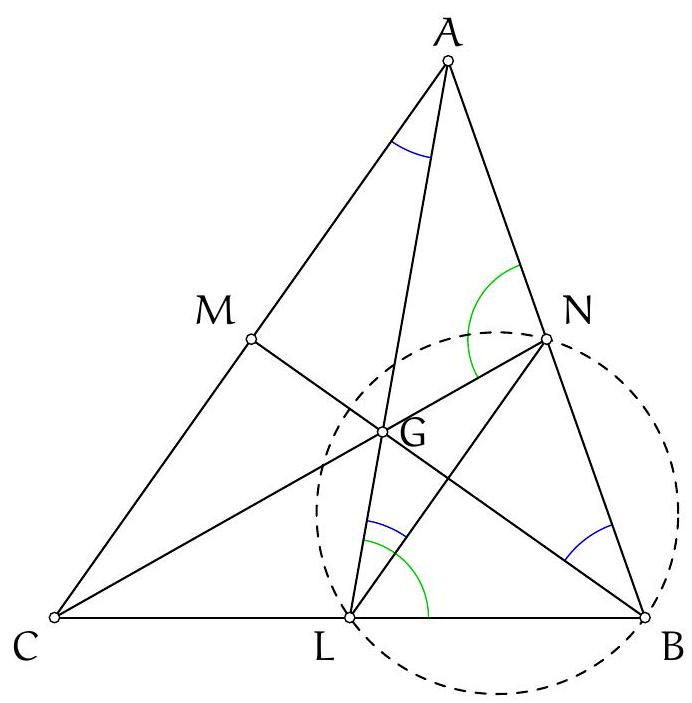
|
| 344 |
+
|
| 345 |
+
On essaie dans un premier temps d'interpréter la condition de l'énoncé $\widehat{A N C}=\widehat{A L B}$. Pour cela on commence par introduire G le centre de gravité du triangle $A B C$ (on rappelle que c'est aussi l'intersection des trois médianes ( $A L),(B M)$ et ( $C N)$ ). La condition de l'énoncé revient à dire que le quadrilatère NGBL est cyclique.
|
| 346 |
+
|
| 347 |
+
On a ainsi $\widehat{C A L}=\widehat{A L N}$ par angles alternes-internes. Puis comme le quadrilatère NGBL est cyclique on a $\widehat{C A L}=\widehat{A L N}=\widehat{G L N}=\widehat{G B N}=\widehat{A B M}$, ce qui conclut.
|
| 348 |
+
|
| 349 |
+
Commentaire des correcteurs : L'exercice est bien résolu. Une poignée d'élèves a cru que l'énoncé impliquait forcément que le triangle était isocèle voire même équilatéral, mais il n'en est rien.
|
| 350 |
+
|
| 351 |
+
Exercice 12. Soit $A B C$ un triangle acutangle. Soient $P$ et $Q$ deux points sur le segment [BC]. On note respectivement $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ et $\mathrm{O}_{4}$ les centres des cercles circonscrits des triangles ABP, ABQ, ACP et ACQ . Montrer que les points $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ et $\mathrm{O}_{4}$ sont cocycliques si et seulement si $\widehat{\mathrm{BAP}}=\widehat{\mathrm{QAC}}$.
|
| 352 |
+
|
| 353 |
+
## Solution de l'exercice 12
|
| 354 |
+
|
| 355 |
+
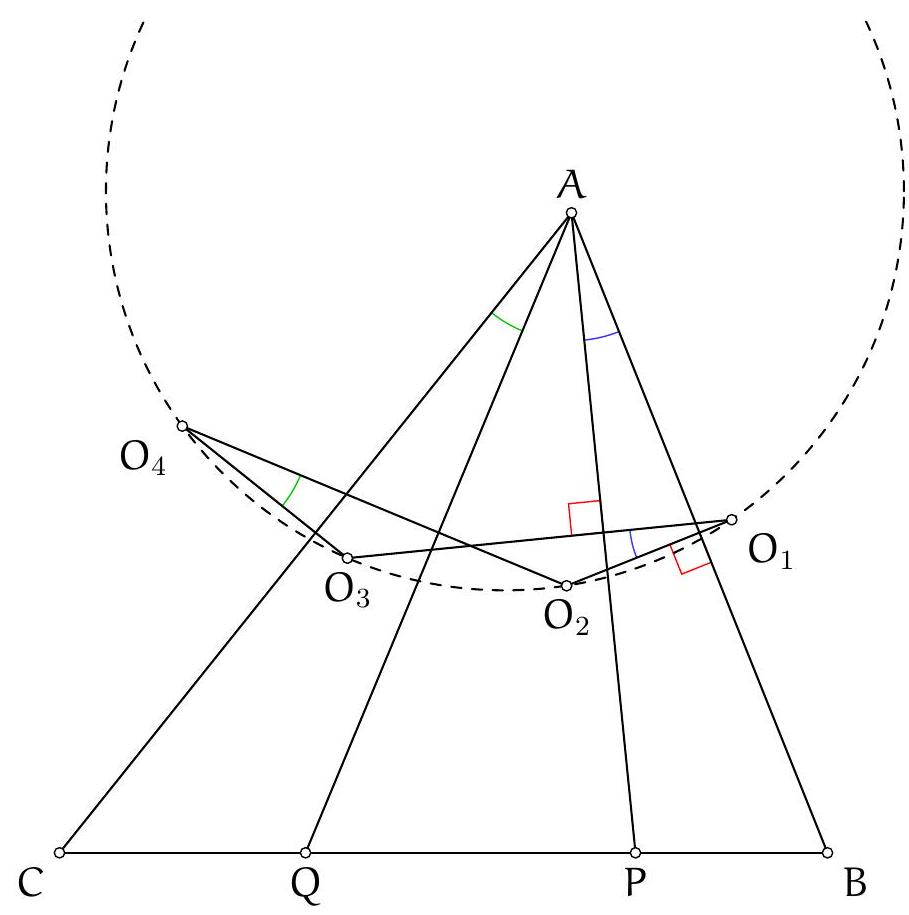
|
| 356 |
+
|
| 357 |
+
La figure comporte beaucoup d'objets on va donc essayer de la simplifier un peu. On remarque donc dans un premier temps qu'il y a beaucoup d'axes radicaux (les droites ( $A B$ ), ( $A P$ ), ( $A Q$ ) et ( $A C$ ) sur la figure et donc beaucoup d'angles droits avec les centres des cercles. On a les perpendicularités suivantes :
|
| 358 |
+
|
| 359 |
+
$$
|
| 360 |
+
\left(\mathrm{O}_{1} \mathrm{O}_{2}\right) \perp(A B),\left(\mathrm{O}_{1} \mathrm{O}_{3}\right) \perp(A P),\left(\mathrm{O}_{2} \mathrm{O}_{4}\right) \perp(A Q),\left(\mathrm{O}_{3} \mathrm{O}_{4}\right) \perp(A C)
|
| 361 |
+
$$
|
| 362 |
+
|
| 363 |
+
En particulier, on veut démontrer une relation de cocyclicité et il faut pour cela se préoccuper d'angles entre droites (et on n'a pas besoin de plus d'informations). En particulier :
|
| 364 |
+
|
| 365 |
+
$$
|
| 366 |
+
\left(\mathrm{O}_{1} \mathrm{O}_{3}, \mathrm{O}_{1} \mathrm{O}_{2}\right)=\left(\mathrm{O}_{1} \mathrm{O}_{3}, A \mathrm{AP}\right)+(A \mathrm{P}, \mathrm{AB})+\left(\mathrm{AB}, \mathrm{O}_{1} \mathrm{O}_{2}\right)=-\frac{\pi}{2}+(A P, A B)+\frac{\pi}{2}=(A P, A B)
|
| 367 |
+
$$
|
| 368 |
+
|
| 369 |
+
De la même manière,
|
| 370 |
+
|
| 371 |
+
$$
|
| 372 |
+
\left(\mathrm{O}_{4} \mathrm{O}_{3}, \mathrm{O}_{4} \mathrm{O}_{2}\right)=(\mathrm{AC}, \mathrm{AQ})
|
| 373 |
+
$$
|
| 374 |
+
|
| 375 |
+
Ainsi,
|
| 376 |
+
|
| 377 |
+
$$
|
| 378 |
+
\begin{array}{cl}
|
| 379 |
+
\left(\mathrm{O}_{1} \mathrm{O}_{2}, \mathrm{O}_{1} \mathrm{O}_{3}\right)=\left(\mathrm{O}_{2} \mathrm{O}_{4}, \mathrm{O}_{3} \mathrm{O}_{4}\right) & \left(\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3} \mathrm{O}_{4} \text { cyclique }\right) \\
|
| 380 |
+
\mathbb{\Downarrow} & \\
|
| 381 |
+
(\mathrm{AB}, \mathrm{AP})=(\mathrm{AQ}, \mathrm{AC}), & (\widehat{\mathrm{BAP}}=\widehat{\mathrm{QAC}})
|
| 382 |
+
\end{array}
|
| 383 |
+
$$
|
| 384 |
+
|
| 385 |
+
Ce qui conclut.
|
| 386 |
+
Commentaire des correcteurs: L'exercice a été en général bien résolu par les élèves qui l'ont tenté. Il y a des approches plus directes que d'autres. Le corrigé ci-dessus de la POFM donne un bon exemple de comment on pouvait arriver au résultat avec un minimum d'effort et chasse aux angles.
|
| 387 |
+
|
| 388 |
+
Exercice 13. Soit $A B C$ un triangle. Soit $t$ la tangente en $A$ au cercle circonscrit du triangle $A B C$. On note $A^{\prime}$ le point de $t$ de telle sorte que la droite ( $B C$ ) coupe le segment $\left[A A^{\prime}\right]$ en son milieu. On note $C^{\prime}$ le symétrique de C par rapport à $t$. Montrer que les points $B, A, C^{\prime}$ et $A^{\prime}$ sont cocycliques.
|
| 389 |
+
|
| 390 |
+
## Solution de l'exercice 13
|
| 391 |
+
|
| 392 |
+

|
| 393 |
+
|
| 394 |
+
On note $X$ le point d'intersection des droites ( $A A^{\prime}$ ) et ( $B C$ ). On note de plus $C^{*}$ le symétrique de C par rapport au point $X$. On va montrer que les points $B, A, C^{\prime}$ et $A^{\prime}$ sont cocycliques sur un cercle qui contient de plus le point $\mathrm{C}^{\star}$. On commence par utiliser les longueurs et la puissance du point depuis X .
|
| 395 |
+
|
| 396 |
+
$$
|
| 397 |
+
\begin{aligned}
|
| 398 |
+
X A \cdot X A^{\prime} & =-X A^{2} \\
|
| 399 |
+
& =-X B \cdot X C \\
|
| 400 |
+
& =X B \cdot X C^{\star} .
|
| 401 |
+
\end{aligned}
|
| 402 |
+
$$
|
| 403 |
+
|
| 404 |
+
Ce qui montre bien que les points $B, A, C^{*}$ et $A^{\prime}$ sont cocycliques. Il ne reste plus qu'à placer le point $C^{\prime}$ sur le cercle. Pour cela on remarque que $\widehat{A C^{\prime} A^{\prime}}=\widehat{A C A^{\prime}}$ par symétrie puis que $\widehat{A C^{*} A^{\prime}}=\widehat{A C A^{\prime}}$ comme le quadrilatère $A C A^{\prime} C^{\star}$ est une parallèlogramme. Cela conclut donc que $\widehat{A C^{\prime} A^{\prime}}=\widehat{A C^{\star} A^{\prime}}$. Et enfin que les points $B, A, C^{\star}, C^{\prime}$ et $A^{\prime}$ sont cocycliques.
|
| 405 |
+
|
| 406 |
+
Commentaire des correcteurs : L'exercice est bien réussi en général. Une chasse aux angles frontale ne suffisait pas. En général n'importe quelle autre idée supplémentaire permettait d'aboutir avec un peu d'astuce, ce qui explique la grande variété de solutions (triangles semblables, puissance d'un point, introduction d'un nouveau point, et même quelques solutions à partir d'inversions ou en analytique). Certains élèves se sont trompés en lisant l'énoncé.
|
| 407 |
+
|
| 408 |
+
Exercice 14. Soit $A B C$ un triangle non isocèle en $A$ et $I$ le centre de son cercle inscrit. On note D le point de la droite (BC) tel que $\widehat{\mathrm{DIA}}=90^{\circ}$. On note E le pied de la hauteur issue de I dans le triangle ADI. Montrer que le point $E$ est sur le cercle circonscrit du triangle $A B C$.
|
| 409 |
+
|
| 410 |
+
## Solution de l'exercice 14
|
| 411 |
+
|
| 412 |
+

|
| 413 |
+
|
| 414 |
+
On introduit $\Omega$ le cercle circonscrit du triangle $A B C$ ainsi que $\omega$ le cercle antarctique de centre $S$, le milieu de l'arc BC ne contenant pas $A$. $\omega$ passe ainsi par B, C et I. On note de plus $\gamma$ le cercle de diamètre $[A I]$, ce cercle recoupe $\Omega$ en $A$ et $H$.
|
| 415 |
+
|
| 416 |
+
Regardons les axes radicaux des cercles $\omega, \Omega$ et $\gamma$. Comme les cercles $\gamma$ et $\Omega$ sont tangents (leurs centres se trouvent sur la bissectrice depuis $A$ dans le triangles $A B C$ ) leur axe radical est la droite perpendiculaire à (AC) passant par I soit la droite (DI). Les deux autres axes radicaux sont $(B C)$ et $(A H)$. Comme les axes radicaux sont concourants, on a que la droite $(A H)$ passe par $D$, donc les points $A, H$ et D sont alignés. Le cercle $\gamma$ a pour diamètre $[A I]$ donc on a $\widehat{A H I}=90^{\circ}$, ce qui montre que H est le pied de la hauteur issue de I dans le triangle DAI , soit $\mathrm{H}=\mathrm{E}$. Mais par définition H est sur $\Omega$, ce qui conclut.
|
| 417 |
+
|
| 418 |
+
Commentaire des correcteurs: Le problème a été beaucoup traité et en général bien résolu, mais très peu d'élèves ont vu la solution directe adoptant le point de vue que D est le centre radical de trois cercles (ou même simplement qu'il est sur la tangente commune de deux cercles).
|
| 419 |
+
|
| 420 |
+
Exercice 15. Soit ABC un triangle et $\Omega$ son cercle circonscrit. On note X le point d'intersection des tangentes à $\Omega$ en $B$ et $C$. On note $\varphi$ l'angle $\widehat{B A X}$ et $\mu$ l'angle $\widehat{X A C}$. On note $Y$ le point de la droite ( $A X$ ) tel que $\widehat{A C Y}=\varphi$. Montrer que $\widehat{A B Y}=\mu$.
|
| 421 |
+
|
| 422 |
+
## Solution de l'exercice 15
|
| 423 |
+
|
| 424 |
+
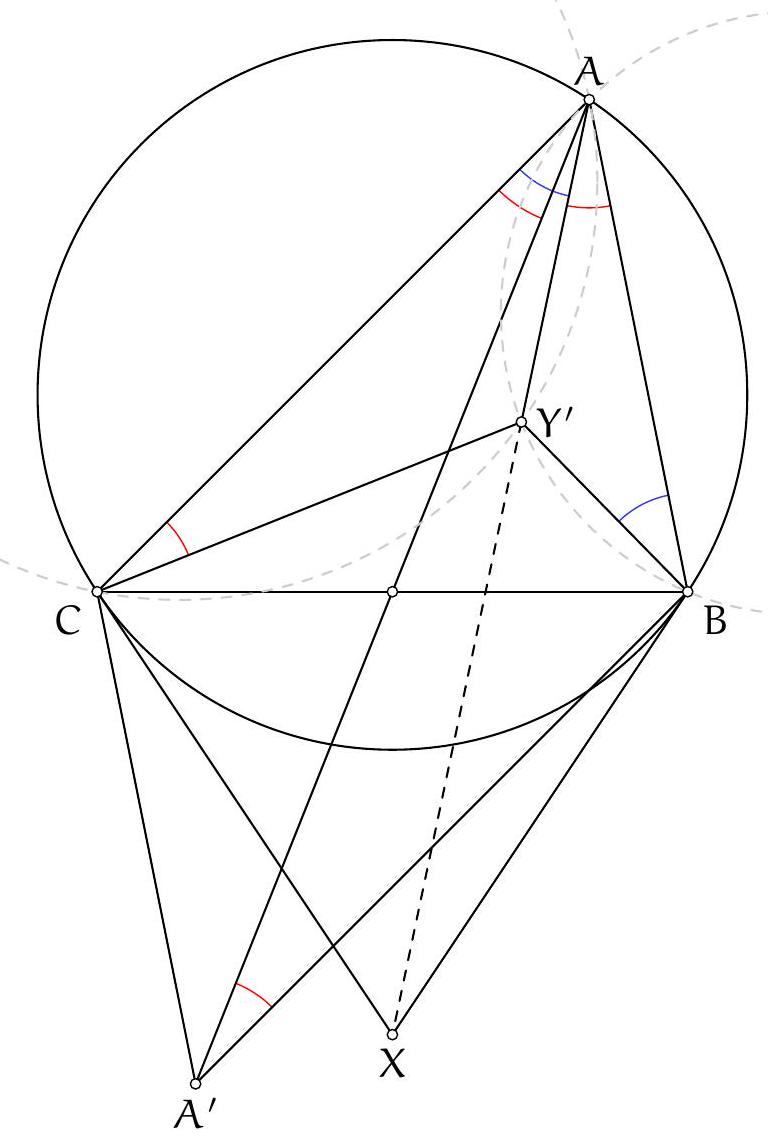
|
| 425 |
+
|
| 426 |
+
On redéfinit les points de l'énoncé de la manière qui nous arrange. On note $\omega_{1}$ (resp. $\omega_{2}$ ) le cercle passant par $A, B$ (resp. $A$ et $C$ ) et tangent en $A$ à ( $A C)$ (resp. ( $A B$ )). On note $Y^{\prime} l^{\prime}$ 'intersection des cercles $\omega_{1}$ et $\omega_{2}$ autre que $A$. Pour conclure il suffit de montrer que les points $Y^{\prime}, A$ et $X$ sont alignés. En effet, on a par théorème de l'angle tangent que $\widehat{\mathrm{BAY}}=\widehat{A C Y^{\prime}}$ ainsi que $\widehat{C A Y^{\prime}}=\widehat{A B Y^{\prime}}$.
|
| 427 |
+
|
| 428 |
+
Regardons maintenant $\mathfrak{J}$, l'inversion de centre $A$ composée avec une symétrie d'axe la bissectrice de l'angle $\widehat{B A C}$ qui échange $B$ et $C$ (il s'agit de ce que l'on appelle une involution projective). Les cercles $\omega_{1}$ et $\omega_{2}$ sont alors envoyés respectivement sur les droites parallèles à ( $A B$ ) et ( $A C$ ) passant par C et B. Le point $Y^{\prime}$ est donc envoyé sur le point $A^{\prime}$, le symétrique de $A$ par rapport au milieu de $[B C]$ par $l^{\prime}$ 'involution $\mathcal{J}$, la droite $\left(A Y^{\prime}\right)$ est échangée avec la médiane ( $A A^{\prime}$ ) dans le triangle $A B C$. Comme la droite $\left(A X\right.$ ) est la symédiane on a donc que la droite ( $A Y^{\prime}$ ) et la droite $(A X)$ sont la même droite ce qui conclut.
|
| 429 |
+
|
| 430 |
+
## Solution alternative de l'exercice 15
|
| 431 |
+
|
| 432 |
+
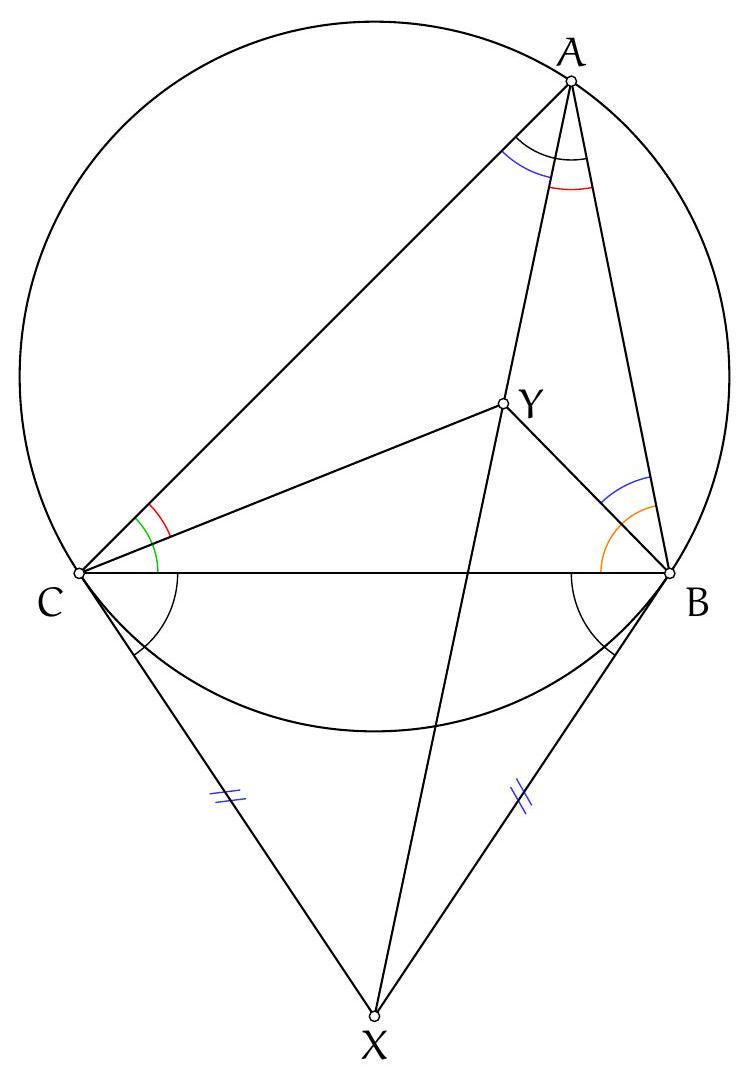
|
| 433 |
+
|
| 434 |
+
On pose $\alpha=\widehat{B A C}, \beta=\widehat{A B C}$ et $\gamma=\widehat{B C A}$. On va utiliser un autre outil classique lorsque qu'il y a des symédianes en jeu, la chasse aux sinus. On remarque dans un premier temps que d'après le théorème de l'angle tangent :
|
| 435 |
+
|
| 436 |
+
$$
|
| 437 |
+
\widehat{B C X}=\widehat{C B X}=\widehat{B A C}=\alpha
|
| 438 |
+
$$
|
| 439 |
+
|
| 440 |
+
Le triangle $B C X$ est donc isocèle en $X$. On a de plus $\widehat{A B X}=\alpha+\beta=180^{\circ}-\gamma$. De même, on a $\widehat{A C X}=180^{\circ}-\beta$. En appliquant la loi des sinus dans le triangle $A B X$, puis dans le triangle $A C X$, on trouve
|
| 441 |
+
|
| 442 |
+
$$
|
| 443 |
+
\frac{\sin (\gamma)}{\sin (\varphi)}=\frac{\sin \left(180^{\circ}-\gamma\right)}{\sin (\varphi)}=\frac{A X}{B X}=\frac{A X}{C X}=\frac{\sin (\beta)}{\sin (\mu)}
|
| 444 |
+
$$
|
| 445 |
+
|
| 446 |
+
En appliquant la loi des sinus cette fois-ci dans le triangle $A B Y$ puis dans le triangle $A B C$, on a
|
| 447 |
+
|
| 448 |
+
$$
|
| 449 |
+
\frac{Y C}{Y A}=\frac{\sin (\mu)}{\sin (\varphi)}=\frac{\sin (\beta)}{\sin (\gamma)}=\frac{A C}{B C}
|
| 450 |
+
$$
|
| 451 |
+
|
| 452 |
+
Cela montre que les triangles BYA et $A Y C$ sont semblables. En effet, ils ont un angle $\varphi$ en commun et un rapport en commun
|
| 453 |
+
|
| 454 |
+
$$
|
| 455 |
+
\frac{B A}{Y A}=\frac{A C}{C Y}
|
| 456 |
+
$$
|
| 457 |
+
|
| 458 |
+
Cette relation de similitude implique que $\widehat{A B Y}=\widehat{Y A C}$, ce qui conclut.
|
| 459 |
+
Commentaire des correcteurs: L'exercice est bien résolu. Il admettait en fait une solution élémentaire en chasse aux angles, qui a échappé à la vigilance des concepteurs du sujet mais aussi à plusieurs élèves qui ont développé l'arsenal de propriétés connues autour de la symédiane, victimes de la même déformation que les concepteurs du sujet.
|
| 460 |
+
|
| 461 |
+
Exercice 16. Soit $A B C D$ un quadrilatère convexe tel que $A C=B D$ et tel que les côtés $A B$ et $C D$ ne sont pas parallèles. Soit $P$ le point d'intersection des diagonales (AC) et (BD). Soient $E$ et $F$ des points respectivement sur les segments $[B P]$ et $[A P]$ tels que $\mathrm{PC}=\mathrm{PE}$ et $\mathrm{PD}=\mathrm{PF}$. Montrer que le cercle circonscrit au triangle formé par les droites (AB), (CD) et (EF) est tangent au cercle circonscrit au triangle ABP.
|
| 462 |
+
|
| 463 |
+
## Solution de l'exercice 16
|
| 464 |
+
|
| 465 |
+

|
| 466 |
+
|
| 467 |
+
On note dans un premier temps X l'intersection des droites (CD) et ( $F E$ ), Y l'intersection des droites $(A B)$ et (CD) ainsi que Zl'intersection des droites ( $A B$ ) et (FE).
|
| 468 |
+
|
| 469 |
+
La première idée de cet exercice est de considérer un point de Miquel (pour savoir ce qu'est un point de Miquel on fait référence au polycopié de T. Budzinski, Transformations Géométriques, Théorème 4.14), que l'on notera $M$ et qui intervient naturellement dans la configuration. En effet, les triangles plats AFC et BED sont isométriques. Ainsi si on considère la similitude directe qui envoie le segment [AF] sur le segment $[E B]$ il s'agit d'une rotation (comme $A F / E B=1$ ) et cette rotation envoie donc également le point C sur le point D . Comme annoncé, on note $M$ le centre de la rotation (le point de Miquel). $M$ est donc le point de Miquel des quadrilatères complets suivants : $A B F E, A B C D$ et $F E C D$. En principe l'ordre des points importe comme il y a 3 classes d'ordre pour 4 mêmes points qui donnent 3 points de Miquel différents pour les distinguer on adopte ici les notations du Théorème 4.14 cité précédemment.
|
| 470 |
+
|
| 471 |
+
Le point $M$ est donc sur les cercles circonscrits de plein de triangles et en particulier sur le cercle circonscrit des ABP, ZAF et BDY, c'est donc un bon candidat pour être notre point de tangence. Dans la suite on va donc montrer que $M$ est également sur le cercle circonscrit au triangle $X Y Z$ et que c'est le point de tangence entre les cercles circonscrits des triangles XYZ et $A B P$.
|
| 472 |
+
|
| 473 |
+
On remarque maintenant que le quadrilatère DCEF est un trapèze isocèle avec (CE)//(DF). $M$ étant le point d'intersection des cercles circonscrits à PFE et PCD autre que $P$, on en déduit que $M$ est sur l'axe de symétrie du trapèze FDCE. $M$ est donc sur la bissectrice extérieure issue de $P$ dans les triangles PFE et PCD, en particulier $M$ est le pôle Nord de ces triangles. Par les propriétés classique du point de Miquel, $M$ est également le centre de la similitude directe qui envoie $F$ sur $A$ et $E$ sur $B$. Donc MFE $\sim M A B$, en particulier $M A=M B$ et $M$ est alors le pôle Nord dans le triangle ABP.
|
| 474 |
+
|
| 475 |
+
Pour conclure il suffit de montrer que $M$ est le pôle Nord dans le triangle $X Y Z$. On montre dans un premier temps que cet assertion implique bien la fin de l'exercice.
|
| 476 |
+
|
| 477 |
+
Si $M$ est le pôle Nord du triangle $X Y Z$, alors il est bien sur le cercle circonscrit de ce triangle. Soit $t$ (resp. $t^{\prime}$ ) la tangente au cercle circonscrit de $A B P$ (resp. $X Y Z$ ) en $M$. On voudrait montrer que $t$ et $t^{\prime}$ sont la même droite. Comme $M$ est le pôle Nord, on a $t / /(A B)$. Mais de la même manière $t^{\prime} / /(Z Y)$. Ce qui montre bien que $t / / t^{\prime}$ et donc qu'il s'agit de la même droite.
|
| 478 |
+
|
| 479 |
+
Pour conclure on va montrer que $M$ est sur la médiatrice du segment [ZY]. Comme $M$ est sur la bissectrice extérieure issue de $X$ (car $M$ est sur la md́atrice commune de (DF) et (EC) et les droites (EF) et ( DC ) se coupent en $X$ ), cela conclurait bien. Il suffit donc de montrer que ( $M Z, M A$ ) $=(M B, M Y$ ). Or on a plein de cocyclicités qui apparaissent avec le point de Miquel et le trapèze DFEC.
|
| 480 |
+
|
| 481 |
+
$$
|
| 482 |
+
\begin{aligned}
|
| 483 |
+
(M Z, M A) & =(F Z, F A) \\
|
| 484 |
+
& =(F E, F C) \\
|
| 485 |
+
& =(D E, D C) \\
|
| 486 |
+
& =(M B, M Y)
|
| 487 |
+
\end{aligned}
|
| 488 |
+
$$
|
| 489 |
+
|
| 490 |
+
(ZAFM cyclique)
|
| 491 |
+
(angles opposés)
|
| 492 |
+
(FECD cyclique)
|
| 493 |
+
(MBYD cyclique).
|
| 494 |
+
Ce qui conclut.
|
| 495 |
+
Commentaire des correcteurs: Le problème est bien résolu par les élèves qui l'ont abordé. Les élèves ont pour la plupart utilisé les propriétés du point de Miquel de l'un ou l'autre des divers quadrilatères (tous les points de Miquel étaient confondus ici). Relativement peu d'élèves ont complété cette notion avec la notion de pôle Nord, qui aidait ici à simplifier les raisonnements (beaucoup d'élèves ont en fait redémontré l'une ou l'autre des propriétés à la main via des chasses aux angles plus ou moins compliquées).
|
| 496 |
+
|
| 497 |
+
Exercice 17. Soit $A B C$ un triangle et H son orthocentre. On note $\ell_{1}$ et $\ell_{2}$ deux droites passant par H et perpendiculaire entre elles. On note $X_{1}, Y_{1}$ et $Z_{1}$ les points d'intersection de $\ell_{1}$ avec les droites ( $B C$ ), $(C A)$ et $(A B)$ respectivement. On note également $X_{2}, Y_{2}$ et $Z_{2}$ les points d'intersection de $\ell_{2}$ avec les droites $(B C),(C A)$ et $(A B)$ respectivement. Montrer que les milieux des segments $\left[X_{1} X_{2}\right],\left[Y_{1} Y_{2}\right]$ et $\left[Z_{1} Z_{2}\right]$ sont alignés.
|
| 498 |
+
|
| 499 |
+
## Solution de l'exercice 17
|
| 500 |
+
|
| 501 |
+
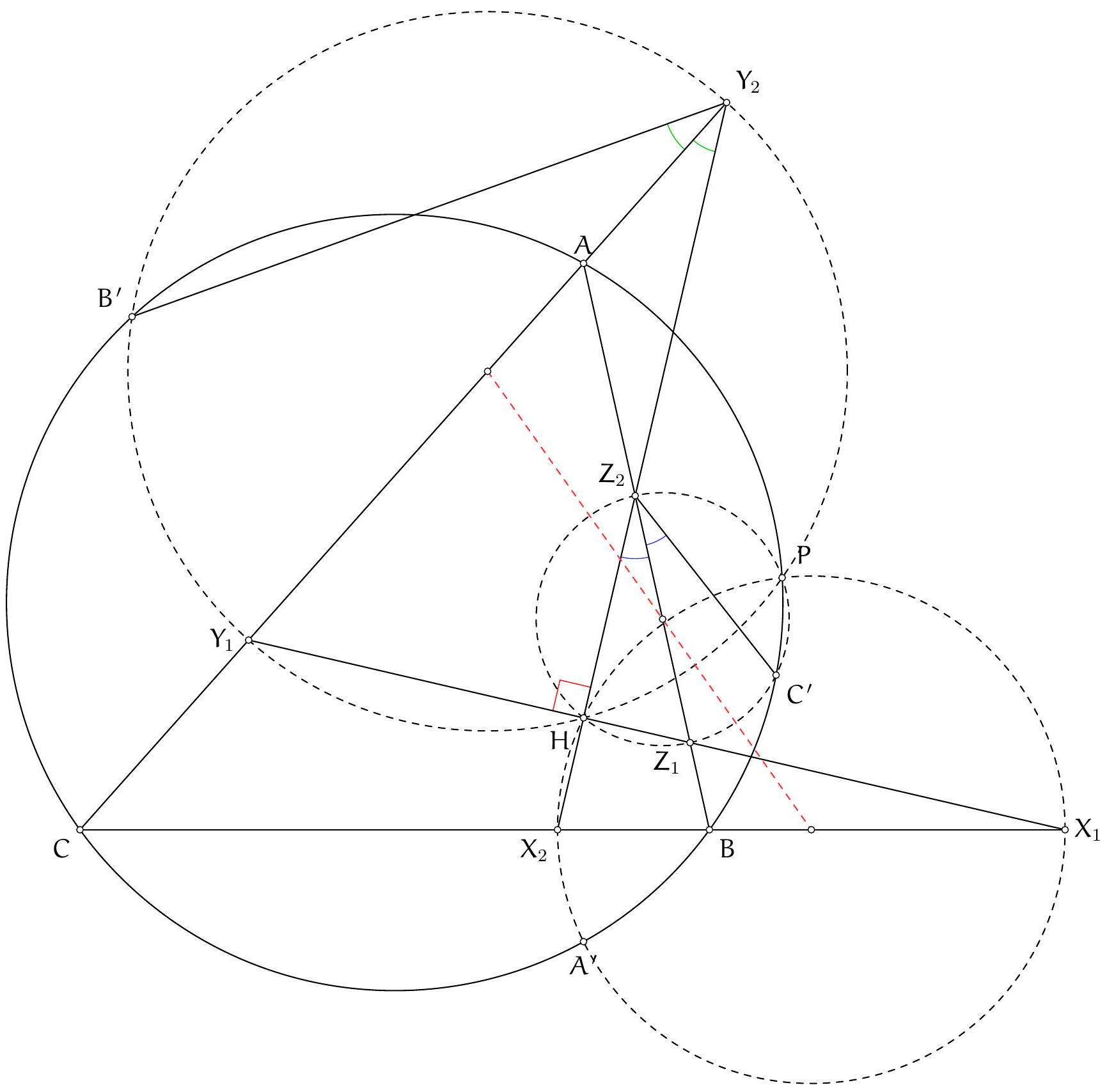
|
| 502 |
+
|
| 503 |
+
L'approche présentée dans ce corrigé est longue, mais purement élémentaire et les nombreuses étapes doivent toutes paraître naturelles.
|
| 504 |
+
Première étape : les milieux. L'introduction d'un milieu dans un exercice est toujours une épine dans notre pied car cette condition est difficile à utiliser avec notre outil favori : la chasse aux angles. On peut donc se demander comment retirer cette épine ; ici, une solution doit paraître raisonnable. Du fait de
|
| 505 |
+
l'angle droit $\widehat{\mathrm{X}_{1} \mathrm{HX}_{2}}$, le milieu de $\left[\mathrm{X}_{1} \mathrm{X}_{2}\right]$ est naturellement le milieu du diamètre du cercle circonscrit au triangle $\mathrm{HX}_{1} \mathrm{X}_{2}$, donc le centre de ce cercle, qui sera maintenant nommé $\Gamma_{\mathrm{A}}$.
|
| 506 |
+
|
| 507 |
+
Sur notre figure, on trace donc trois cercles $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$, où $\Gamma_{B}$ et $\Gamma_{C}$ sont définis de manière similaire. On peut ainsi arrêter de penser aux milieux comme des milieux et on y pense comme des centres de cercles.
|
| 508 |
+
Deuxième étape : Effacer les centres. Manipuler des centres de cercles est souvent plus agréable que manipuler des milieux de segments, mais ce n'est pas encore tout à fait satisfaisant. En traçant nos trois nouveaux cercles, on constate qu'ils ont l'air de se couper à nouveau en un autre point que H. Devant une telle observation, une première interrogation est de se demander ce qu' une telle information impliquerait par symétrie. Par exemple, sur ma figure, peut-être que $B$ semble se trouver sur $\Gamma_{A}$, mais si c'était toujours le cas, par symétrie, C devrait aussi se situer sur $\Gamma_{\mathrm{A}}$, et sur ma figure ce n'est pas du tout le cas, ma conjecture est donc à éliminer.
|
| 509 |
+
|
| 510 |
+
Ici pas de tel argument, la concourance des trois cercles n'entraîne rien par symétrie. Mieux, regardons maintenant ce qui découlerait de la concourance de ces trois cercles en un point P . Les trois centres seraient sur la médiatrice de $[\mathrm{HP}]$, corde commune aux trois cercles, ce qui conclurait! Dans l'autre sens, si les trois centres sont alignés, alors le symétrique de H par rapport à la droite des trois centres est sur chaque cercle, ils se recoupent donc bien. A la place de l'alignement des trois centres, on peut montrer la concourance des trois cercles, une propriété a priori bien plus agréable!
|
| 511 |
+
Interlude : Comment savoir si on est allé dans la bonne direction? C'est généralement une question difficile mais ici on peut répondre par l'affirmative car on peut effacer des morceaux de la figure (ici les trois milieux) et la simplifier. On a tracé le triangle, les deux droites et les 6 points d'intersection, préfère-t-on tracer trois milieux et montrer leur alignement ou trois cercles et montrer leur concourance? La deuxième option.
|
| 512 |
+
|
| 513 |
+
Même si les deux options semblent similaires en complexité (ce qui n'est pas la difficulté), un problème de géométrie olympique maximise sa difficulté par rapport à sa complexité donc un énoncé équivalent et de complexité comparable sera presque toujours plus facile, sinon cet énoncé aurait été posé à la place. On est maintenant convaincu d'aller dans la bonne direction, et on aura pas peur de s'éloigner encore plus de problème de base. C'est souvent une bonne chose, tant qu'on garde l'équivalence avec le problème de base bien sûr.
|
| 514 |
+
Troisième étape : Les propriétés du point P . Après une chasse aux angles naïve infructueuse, on cherche des propriétés des cercles $\Gamma$ ou du point $P$. Deux possibilités : on constate que $P$ est sur le cercle circonscrit à $\mathrm{ABC}, \Omega$, parce qu'on a tracé ce cercle. En effet, dans un tel exercice centré sur un triangle ABC , on trace toujours son cercle circonscrit sur au moins une figure, si ce n'est sur toutes. Une autre manière d'effectuer cette conjecture présuppose une certaine habitude avec le point de Miquel. Le point d'intersection de $\Gamma_{\mathrm{B}}$ et de $\Gamma_{\mathrm{C}}$ est le point de Miquel de $\ell_{1}, \ell_{2},(A B),(A C)$. Dire qu'il est sur $\Gamma_{\mathrm{A}}$ revient à dire que c'est un point de Miquel du pentalatère $\ell_{1}, \ell_{2},(A B),(A C),(B C)$ (tout cercle circonscrit au trilatère formé par 3 de ces droites passe par P ).
|
| 515 |
+
|
| 516 |
+
Une bonne manière de se représenter les points de Miquel de pentalatère (qui n'existent pas pour n'importe quel pentalatère) est de se rappeler de la droite de Simson (ou Steiner). Un point est sur le cercle circonscrit à un trilatère (ou triangle) si et seulement si ses projetés (orthogonaux) sur les trois côtés sont alignés, donc un point est le point de Miquel de 4 droites si et seulement ses 4 projetés sont alignés, et de 5 si et seulement si ses 5 projetés sont alignés. Avec cette vision des choses, en supposant $P$ sur les trois cercles $\Gamma$, les projetés de $P$ sur les côtés sont tous sur la droite reliant les deux projetés de P sur $\ell_{1}$ et sur $\ell_{2}$, ils sont donc alignés et $P$ est sur $\Omega$.
|
| 517 |
+
|
| 518 |
+
Pourquoi avoir choisi $\Omega$ alors que P est sur 10 cercles, littéralement? C'est le seul qui ne fait intervenir que des points déjà introduits et surtout qui conserve la symétrie entre $A, B$ et $C$. Pour montrer la concourance de $\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$, on peut montrer que $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$ se coupent sur $\Omega$, en un point qui sera alors
|
| 519 |
+
aussi sur $\Gamma_{\mathrm{A}}$.
|
| 520 |
+
Interlude : va-t-on dans la bonne direction? Que préfère-t-on, montrer la concourrance de $\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$, ou bien celle de $\Gamma_{\mathrm{B}}, \Gamma_{\mathrm{C}}$ et $\Omega$ ? Avantage du premier : cela conserve la symétrie. Avantage du deuxième : c'est plus loin de l'énoncé sans être plus complexe. Le deuxième gagne.
|
| 521 |
+
Quatrième étape : Il nous reste une hypothèse : $\ell_{1}$ et $\ell_{2}$ se coupent en l'orthocentre. J'avais oublié. Corrigeons ça. Comment utiliser l'hypothèse d'orthocentre? On ne souhaite surtout pas tracer des hauteurs qui ne passent par rien ici. Par contre, le cercle circonscrit est déjà tracé et important, et on sait que de nombreux symétriques de H s'y trouvent. Lesquels choisir? Par rapport aux côtés ou aux milieux des côtés? Cette fois, il suffit de se poser la question pour avoir la réponse : les symétriques par rapport aux côtés sont aussi sur les cercles $\Gamma$, car ceci sont stables par la symétrie axiale! Ils sont donc beaucoup plus intéressants : c'est clairement la bonne manière d'utiliser l'hypothèse de milieu. Nommons les $A^{\prime}, B^{\prime}$ et $C^{\prime}$ 。
|
| 522 |
+
Conclusion: On a reformulé tous les éléments de l'énoncé en des éléments équivalents ( H est bien le seul point dont les trois symétriques sont sur le cercle circonscrit du triangle $A B C$ ) et utilisables pour faire une chasse aux angles. On a conservé la symétrie entre B et C , essayons de la conserver encore pour la chasse aux angles (ce n'est pas toujours possible). On définit $P$ comme le point d'intersection autre que H de $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$. On veut montrer qu'il se trouve sur $\Omega$. Plutôt que de montrer qu'il est cocyclique avec $A, B, C$, montrons qu'il est cocyclique avec $A B^{\prime} C^{\prime}$. En effet, on ne sait rien de la direction de la droite PB ou PC , alors que $\mathrm{PB}^{\prime}$ et $\mathrm{PC}^{\prime}$ sont des cordes de $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$. De plus, l'angle $\widehat{\mathrm{B}^{\prime} \mathrm{AC}}$ ' est connu (c'est-à-dire qu'on peut l'exprimer avec des opérations simples en fonction des angles du triangle $A B C$ ).
|
| 523 |
+
|
| 524 |
+
On veut donc trouver la valeur connue de $\widehat{\mathrm{B}^{\prime} \mathrm{PC}^{\prime}}$. Pour exploiter la définition de P , on éclate cet angle en $\widehat{\mathrm{B}^{\prime} \mathrm{PH}}$ et $\widehat{\mathrm{HPC}^{\prime}}$. On cherche donc une relation simple entre ces deux angles. Ce sont des angles inscrits, qui interceptent un arc de deux fois la longueur de $\mathrm{HY}_{1}$ d'un côté de $\mathrm{HZ}_{1}$ de l'autre. On cherche donc une relation entre l'angle $\widehat{\mathrm{HY}_{2} \mathrm{Y}_{1}}$ et $\widehat{\mathrm{Z}_{1} \mathrm{Z}_{2} \mathrm{H}}$, mais ces deux angles sont entre la même droite $\ell_{2}$ et les côtés du triangle. On a donc une relation, qui, en remontant tout, donne une relation simple entre $\widehat{B^{\prime} A C^{\prime}}$ et $\widehat{\mathrm{B}^{\prime} \mathrm{PC}^{\prime}}$, qui ne peut être que la somme des deux valant $180^{\circ}$, ce qui terminerait. On est maintenant convaincu que cette petite chasse aux angles va terminer ce problème, il suffit de l'écrire pour finir la preuve de l'exercice.
|
| 525 |
+
|
| 526 |
+
Commentaire des correcteurs : Les élèves ont très bien vu comment réécrire l'énoncé pour se ramener à la concourance de trois cercles. Ensuite, les méthodes employées sont variées et utilisent principalement le point de Miquel. Une poignée d'élèves ont été plus que ravis d'appliquer des résultats invoquant des paraboles.
|
| 527 |
+
|
| 528 |
+
Si une telle technologie permettait en apparence d'annihiler l'exercice, elle ne donne ici qu'une réécriture des raisonnements autour du point de Miquel commun aux différents quadrilatères de la figure, des raisonnements plus élémentaires et, au goût des correcteurs, bien plus instructifs pour les élèves.
|
| 529 |
+
|
| 530 |
+
Exercice 18. Soit $A B C$ un triangle et $\omega$ son cercle inscrit dont les points de tangence sur [BC], [CA] et $[A B]$ sont respectivement $D$, $E$ et $F$. On note $\Omega$ le cercle tangent à $\omega$ et passant par $B$ et $C$ et $T$ le point de tangence de ces deux cercles. On note $X$ et $Y$ les milieux des segments [DE] et [DF]. On note $U$ et $V$ les seconds points d'intersection des droites (TX) et (TY) avec $\Omega$. On note également $Z$ et $W$ les seconds points d'intersection des droites (AB) et (AC) avec $\Omega$. Montrer que (ZU), (WV), (XY) et la bissectrice de l'angle $\widehat{B A C}$ sont concourantes.
|
| 531 |
+
|
| 532 |
+
## Solution de l'exercice 18
|
| 533 |
+
|
| 534 |
+
Pendant toute la preuve on va utiliser les résultats du lemme qui suit. On commence d'abord par une notation.
|
| 535 |
+
|
| 536 |
+
Soit ABC un triangle, on note $\Omega$ le cercle circonscrit à $A B C$, on note également $\omega$ le cercle tangent à (AB), (AC) et intérieurement à $\Omega$, on dit que ce cercle est le cercle mixtilinéaire (intérieur) du triangle $A B C$ depuis $A$.
|
| 537 |
+
Lemme 3. Soit ABC un triangle, on note I le centre de son cercle inscrit, on note de de plus, $\Omega$ le cercle circonscrit à ABC ainsi que $\omega$ le cercle mixtilinéaire depuis A . On note T (resp. D et F) le point de tangence de $\omega$ avec $\Omega$ (resp. (AC) et (AB)) ainsi que N le pôle nord (le milieu de l'arc BC qui contient A). Sous ces hypothèses et notation on sait alors que I est le milieu du segment [DF] et que les points T, I et N sont alignés.
|
| 538 |
+
|
| 539 |
+
## Démonstration.
|
| 540 |
+
|
| 541 |
+
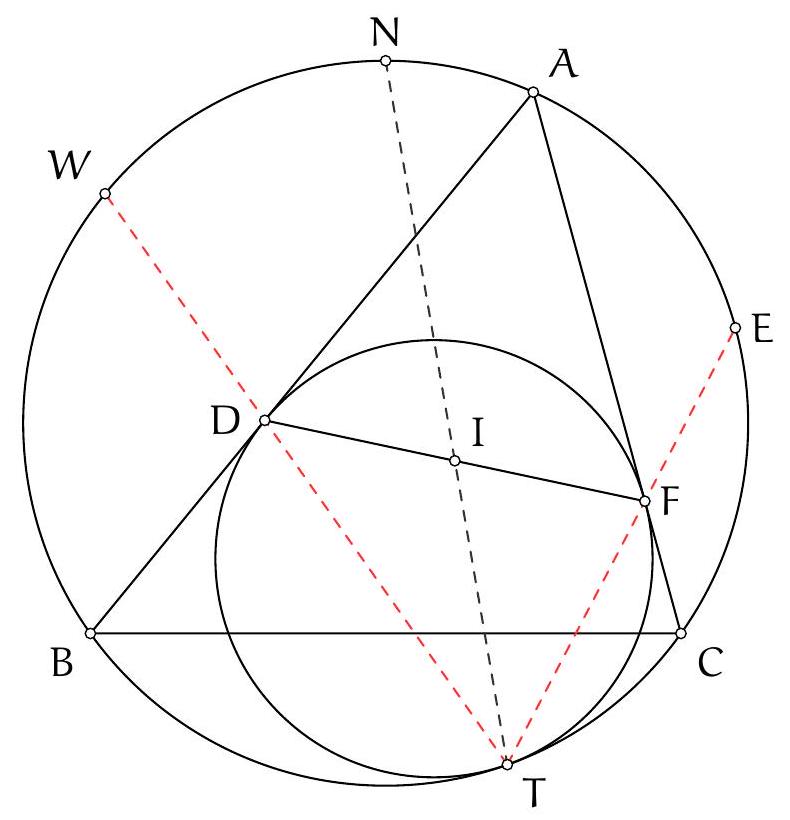
|
| 542 |
+
|
| 543 |
+
Notons E et $W$ les milieux respectifs des arcs $A C$ et $A B$. D'après le lemme du bocal on sait que les points $W$, D et T sont alignés ainsi que les points $\mathrm{T}, \mathrm{F}$ et E . On sait de plus d'après le théorème du pôle sud que les points $B$, I et $E$ sont alignés ainsi que les points $C$, $I$ et $W$. On peut alors appliquer le théorème de Pascal à l'hexagone BETWCA pour conclure que les points $D$, I et $F$ sont alignés. Comme l'axe (AI) est un axe de symétrie qui échange $(A B)$ avec $(A C)$ et $\omega$ avec lui-même on peut en déduire que le point I est bien le milieu du segment [EF].
|
| 544 |
+
|
| 545 |
+
Pour la deuxième partie du lemme, on note $\beta$ et $\gamma$ les angles en $B$ et $C$ respectivement dans le triangle $A B C$. Dans le triangle TDF on remarque que la droite (TI) est une médiane d'après la première partie du lemme. De plus, par des propriétés classique de la construction de la symédiane (voir par exemple le cours d'Alexander Semenov au stage de Valbonne 2022 ou bien celui de Thomas Budzinski à Montpellier
|
| 546 |
+
2016) la droite (TA) est la symédiane. Ainsi, $\widehat{\mathrm{ITC}}=\widehat{\mathrm{ITF}}+\widehat{\mathrm{FTC}}=\widehat{\mathrm{ATD}}+\widehat{\mathrm{FTC}}=\gamma / 2+\beta / 2=\widehat{\mathrm{BTI}}$ où la dernière égalité découle par symétrie. Cela conclut la deuxième partie du lemme.
|
| 547 |
+
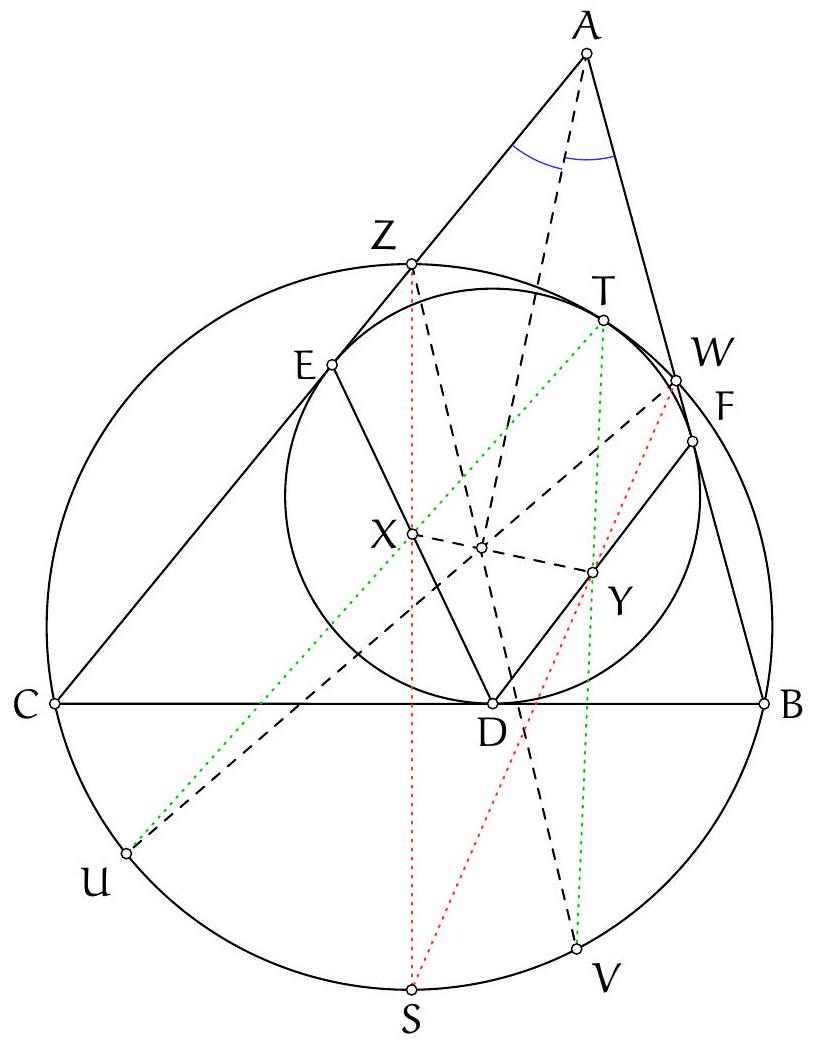
|
| 548 |
+
|
| 549 |
+
On peut maintenant passer à la preuve de l'exercice.
|
| 550 |
+
En se plaçant dans le triangle $Z B C$ on remarque que $\omega$ est le cercle mixtiliniéaire depuis B. Ainsi, d'après le Lemme 3, le point $Y$ est le centre du cercle inscrit de ce triangle et de plus, la droite (TY) passe par le pôle Nord issu de $B$ dans $Z B C$, ce point est le point $V$ de l'énoncé. De la même manière le point $X$ est le centre du cercle inscrit du triangle WBC et $U$ est le milieu de l'arc BW qui contient $C$. Cela montre en particulier que la droite ( $W \mathrm{~W}$ ) bissecte extérieurement l'angle $\widehat{A W Z}$, de la même manière la droite (ZU) est la bissectrice extérieure de l'angle $\widehat{W Z A}$. Ainsi il est maintenant clair que dans le triangle $A W Z$ les droites (WV), (ZU) et la bissectrice issue de $A$ sont concourantes en un point $P$.
|
| 551 |
+
|
| 552 |
+
On veut également démontrer que la droite ( $Y Z$ ) passe par ce point $P$. On veut pour cela appliquer le théorème de Pascal à l'hexagone TUZSWV, où $S$ dénote le milieu de l'arc $B C$ sur le cercle $\Omega$. Mais la droite (ZY) est bien la bissectrice de l'angle $\widehat{\mathrm{BZC}}$ comme $Y$ est le centre du cercle inscrit au triangle ZBC. De la même manière la droite $(W X)$ passe bien par le point $S$, on peut alors conclure en appliquant le théorème de Pascal.
|
| 553 |
+
|
| 554 |
+
Commentaire des correcteurs: Les élèves ayant abordé le problème ont presque tous résolu le problème. Ceux qui ont remarqué le cercle mixtilinéaires de la figure s'en sont sortis avec une preuve beaucoup plus courte. Il est conseillé d'énoncer les propriétés du cercle mixtilinéaires utilisées lors de la preuve pour rendre une copie plus agréable à lire.
|
| 555 |
+
|
French_STS/md/fr-corrigé-envoi-2.md
ADDED
|
@@ -0,0 +1,865 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOi 2 : Algèbre <br> À RENVOYER AU PLUS TARD LE 10 JANVIER 2023
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2008 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soient x, y deux réels strictement positifs. Montrer que
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 8
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Quand a-t-on égalité?
|
| 23 |
+
Solution de l'exercice 1
|
| 24 |
+
Dans cet exercice, on a affaire à des termes strictement positifs dont le produit $x \cdot \frac{2}{y} \cdot \frac{y}{x} \cdot 2=4$ est connu. On pense donc à utiliser l'inégalité arithmético-géométrique qui donne à la fois
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
x+\frac{2}{y} \geqslant 2 \sqrt{\frac{2 x}{y}}
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
et
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
\frac{y}{x}+2 \geqslant 2 \sqrt{\frac{2 y}{x}}
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
Les deux inégalités ne font intervenir que des termes positifs donc on peut les combiner pour avoir
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 2 \sqrt{\frac{2 x}{y}}\left(\frac{y}{x}+2\right) \geqslant 4 \sqrt{\frac{2 x \cdot 2 y}{y x}}=8 .
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
Cherchons les cas d'égalité. Pour ceci, il faut avoir égalité dans les deux inégalités précédentes. Comme $\frac{y}{x}+2>0$, on a égalité dans la première égalité si et seulement si on a égalité dans la première application de l'inégalité arithmético-géométrique, c'est-à-dire si $x=\frac{2}{y}$, soit $x y=2$.
|
| 43 |
+
De même, pour avoir égalité dans la deuxième inégalité, il faut que $\frac{y}{x}=2$. En multipliant les deux équations ensemble, on trouve $y^{2}=4$, donc $y=2$ car $y$ est positif. Ensuite, on obtient $x=1$. Réciproquement, $x=1$ et $y=2$ est un cas d'égalité, c'est le seul.
|
| 44 |
+
|
| 45 |
+
Commentaire des correcteurs : Si nle problème a été bien réussi dans l'ensemble, voilà quelques pistes de progression :
|
| 46 |
+
|
| 47 |
+
- Beaucoup d'élèves ne connaissent pas l'IAG et la redémontrent.
|
| 48 |
+
- Le cas d'égalité a souvent été oublié.
|
| 49 |
+
- Beaucoup d'élèves développent l'expression avant d'y appliquer l'IAG, plutôt que de l'appliquer directement dans les parenthèses.
|
| 50 |
+
|
| 51 |
+
Exercice 2. Trouver tous les réels $x, y$ tels que
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
x(x-2 y)+y(2 y-4)+4=0
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
## Solution de l'exercice 2
|
| 58 |
+
|
| 59 |
+
Développons l'équation pour obtenir
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
x^{2}-2 x y+2 y^{2}-4 y+4=0 .
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
Les termes $x^{2}-2 x y$ nous font penser à l'identité remarquable $x^{2}-2 x y+y^{2}=(x-y)^{2}$. On sépare alors le $2 y^{2}$ en $y^{2}+y^{2}$ pour écrire
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
(x-y)^{2}+y^{2}-4 y+4=0
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Mais on reconnait alors une deuxième identité remarquable $y^{2}-4 y+4=(y-2)^{2}$. En factorisant, ceci donne
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
(x-y)^{2}+(y-2)^{2}=0
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
Or, une somme de carrés de nombre réels est forcément positive, et ne peut être nulle que si les deux carrés sont tous les deux nuls. Ainsi, si $x$ et $y$ sont solution de l'équation, on a à la fois
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
x-y=0 \quad \text { et } \quad y-2=0
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Ainsi, l'unique solution possible de l'équation est $x=y=2$. On peut vérifier réciproquement que ceci est bien une solution, c'est donc la seule.
|
| 84 |
+
|
| 85 |
+
Commentaire des correcteurs : Les élèves ont en général trouvé la solution avec la méthode présentée dans le corrigé. Malheureusement, la plupart oublient de vérifier que la solution qu'ils ont trouvé est bien solution du problème. Il suffit en effet qu'à une seule étape, l'équivalence ne soit pas justifiée pour que la vérification soit nécessaire. Certains ont considéré l'expression comme un polynôme en $x$, dont il s'agit de trouver les racines, celles-ci n'existant que pour certianes valeurs de y .
|
| 86 |
+
|
| 87 |
+
Exercice 3. Pour un réel $x$, on note $\lfloor x\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\lfloor 2,7\rfloor=2,\lfloor\pi\rfloor=3$ et $\lfloor-1,5\rfloor=-2)$.
|
| 88 |
+
Soient $a, b$ deux réels tels que
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
a+\lfloor a\rfloor=b+\lfloor b\rfloor .
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
Montrer que $a=b$.
|
| 95 |
+
|
| 96 |
+
## Solution de l'exercice 3
|
| 97 |
+
|
| 98 |
+
Supposons par l'absurde $a \neq b$. Par symétrie (c'est-à-dire que $a$ et $b$ jouent le même rôle), on peut supposer $a<b$. On a alors
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
\lfloor a\rfloor \leqslant a<b
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
donc $\lfloor a\rfloor$ est un entier relatif inférieur ou égal à $b$, et donc par définition on a $\lfloor a\rfloor \leqslant\lfloor b\rfloor$. En ajoutant $a<b$, on obtient alors
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
a+\lfloor a\rfloor<b+\lfloor b\rfloor
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
ce est absurde. On a donc bien $a=b$.
|
| 111 |
+
|
| 112 |
+
## Solution alternative
|
| 113 |
+
|
| 114 |
+
Pour un réel $x$, posons $\{x\}$ la partie fractionnaire de $x$ donnée par $\{x\}=x-\lfloor x\rfloor$. C'est un nombre réel compris entre 0 inclus et 1 exclus.
|
| 115 |
+
On réécrit alors l'équation en posant $a=\lfloor a\rfloor+\{a\}$ et $b=\lfloor b\rfloor+\{b\}$ pour avoir
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
2\lfloor a\rfloor+\{a\}=2\lfloor b\rfloor+\{b\} .
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
En réarrangeant les termes, on obtient
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
2\lfloor a\rfloor-2\lfloor\mathbf{b}\rfloor=\{\mathbf{b}\}-\{\mathbf{a}\}
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
Mais on a
|
| 128 |
+
|
| 129 |
+
$$
|
| 130 |
+
\{b\}-\{a\} \leqslant\{b\}<1
|
| 131 |
+
$$
|
| 132 |
+
|
| 133 |
+
et
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
\{b\}-\{a\} \geqslant-\{a\}>-1
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Mais d'après l'égalité au-dessus, $\{b\}-\{a\}$ est un entier, et il est donc nul. On a donc $\{b\}-\{a\}=0$, ce qui donne ensuite $2\lfloor a\rfloor-2\lfloor b\rfloor=0$.
|
| 140 |
+
Ainsi, on a
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
\lfloor a\rfloor=\lfloor b\rfloor \text { et } \quad\{a\}=\{b\}
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
donc
|
| 147 |
+
|
| 148 |
+
$$
|
| 149 |
+
a=\lfloor a\rfloor+\{a\}=\lfloor b\rfloor+\{b\}=b
|
| 150 |
+
$$
|
| 151 |
+
|
| 152 |
+
Commentaire des correcteurs : Exercice très bien réussi, avec une certaine diversité dans les approches. Quelques rares points sont perdus par étourderie. Certains élèves semblent confus sur le fonctionnement de la partie entière dans les négatifs.
|
| 153 |
+
|
| 154 |
+
Exercice 4. Soit $\boldsymbol{n}$ un entier strictement positif et $x \geqslant \mathrm{n}$ un réel. Montrer que $x+\frac{\mathfrak{n}}{\boldsymbol{x}} \geqslant \mathrm{n}+1$ et donner les cas d'égalité.
|
| 155 |
+
|
| 156 |
+
## Solution de l'exercice 4
|
| 157 |
+
|
| 158 |
+
Le réel $x$ est strictement positif donc on peut multiplier l'équation par $x$ pour avoir que l'équation est équivalente à
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
x^{2}+n \geqslant(n+1) x
|
| 162 |
+
$$
|
| 163 |
+
|
| 164 |
+
ce qui donne, en réarrangeant les termes,
|
| 165 |
+
|
| 166 |
+
$$
|
| 167 |
+
x^{2}-(n+1) x+n \geqslant 0
|
| 168 |
+
$$
|
| 169 |
+
|
| 170 |
+
On reconnait alors une factorisation
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
(x-n)(x-1) \geqslant 0
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
Mais ceci est vrai car $x \geqslant \mathrm{n}$ et $x \geqslant 1$.
|
| 177 |
+
On a égalité lorsque $x=n$ ou $x=1$. Mais si $x=1$, alors $n=1$ et $x=n$. Ainsi, dans tous les cas, le seul cas d'égalité est $x=n$.
|
| 178 |
+
|
| 179 |
+
## Solution alternative de l'exercice 4
|
| 180 |
+
|
| 181 |
+
On repart de l'équation développée $x^{2}-(n+1) x+n \geqslant 0$.
|
| 182 |
+
La condition $x \geqslant n$ est très peu naturelle, on préfère des conditions de type $t \geqslant 0$. On pose donc $x=n+t$ $\operatorname{avec} t \geqslant 0$. L'équation se réécrit alors
|
| 183 |
+
|
| 184 |
+
$$
|
| 185 |
+
n^{2}+2 n t+t^{2}-(n+1)(n+t)+n \geqslant 0
|
| 186 |
+
$$
|
| 187 |
+
|
| 188 |
+
ou encore
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
t^{2}+(n-1) t \geqslant 0
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
Mais cette nouvelle équation est clairement vraie car $t \geqslant 0$ et $n \geqslant 1$. De plus, on a égalité si et seulement si $t=0$, ou encore $x=n$.
|
| 195 |
+
|
| 196 |
+
Commentaire des correcteurs : Le problème a été bien réussi par les élèves, les solutions rendues étaient presque toutes abouties et suivaient le même schéma que les solutions du corrigé. En revanche, la plupart de ses copies ont été pénalisées pour des manques de justifications, notamment des justifications de signes. On rappelle que lorsqu'on multiplie ou divise une inégalité par une quantité, il faut s'assurer du signe de cette quantité : si elle est strictement positive, ça conserve le sens de l'inégalité, si elle est strictement négative, ça change le sens de l'inégalité, et si on multiplie par une quantité nulle, on n'a pas équivalence. C'est donc un détail qui a toute son importance. En ce qui concerne le cas d'égalité, plusieurs élèves ont oublié de le traiter, et d'autres ont oublié la condition $x \geqslant \mathrm{n}$, de sorte qu'ils considéraient que pour tout $\mathrm{n} \in \mathbb{N}^{*}, x=1$ était un cas d'égalité. Ce n'était vrai que pour $\mathrm{n}=1$, et donc c'était déjà compté dans le cas $x=\mathrm{n}$.
|
| 197 |
+
|
| 198 |
+
Exercice 5. Trouver tous les triplets de réels positifs ou nuls ( $\mathrm{a}, \mathrm{b}, \mathrm{c})$ tels que
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
\left\{\begin{array}{l}
|
| 202 |
+
a^{2}+a b=c \\
|
| 203 |
+
b^{2}+b c=a \\
|
| 204 |
+
c^{2}+c a=b
|
| 205 |
+
\end{array}\right.
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
## Solution de l'exercice 5
|
| 209 |
+
|
| 210 |
+
Supposons d'abord qu'un des réels est nul, sans perte de généralité $a=0$. Alors la première équation donne $\mathrm{c}=0$ et la dernière équation donne $\mathrm{b}=0$. Réciproquement, le triplet $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ est bien solution, on suppose à présent que les trois réels sont non nuls.
|
| 211 |
+
Supposons maintenant que deux des réels soient égaux, sans perte de généralité $\mathrm{a}=\mathrm{b}$. On peut alors soustraire les deuxième et troisième équations pour avoir $b^{2}-c^{2}=0$. Comme $b$ et $c$ sont tous les deux positifs, on a donc $a=b=c$. Dans la première équation, on a alors $2 a^{2}=a$. Mais $a$ est non nul donc on peut diviser par $2 a$ pour avoir $a=\frac{1}{2}$. Réciproquement, le triplet $a=b=c=\frac{1}{2}$ est bien solution. On suppose désormais que les trois réels sont deux à deux distincts.
|
| 212 |
+
Faisons le produit des équations pour obtenir
|
| 213 |
+
|
| 214 |
+
$$
|
| 215 |
+
a(a+b) b(b+c) c(c+a)=a b c
|
| 216 |
+
$$
|
| 217 |
+
|
| 218 |
+
On a supposé précédememnt que les réels étaient tous non nuls donc on peut diviser par abc pour avoir
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
(a+b)(b+c)(c+a)=1
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
En faisant la différence des deux premières équations, on obtient $a^{2}-b^{2}+b a-b c=c-a$ ce qui se factorise en
|
| 225 |
+
|
| 226 |
+
$$
|
| 227 |
+
(a-b)(a+b)=(c-a)(b+1)
|
| 228 |
+
$$
|
| 229 |
+
|
| 230 |
+
En faisant de même avec les deuxième et troisième lignes puis avec les troisième et première lignes, on obtient en plus
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
\left\{\begin{array}{l}
|
| 234 |
+
(b-c)(b+c)=(a-b)(c+1) \\
|
| 235 |
+
(c-a)(c+a)=(b-c)(a+1)
|
| 236 |
+
\end{array}\right.
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
En faisant le produit de ces trois équations et en divisant par $(a-b)(b-c)(c-a)$ des deux côtés (qui est non nul car on a supposé $a, b, c$ deux à deux distincts), on obtient
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
(1+a)(1+b)(1+c)=(a+b)(b+c)(c+a)
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
Mais on a montré précédemment que ce deuxième terme vaut 1 , ce qui est absurde car
|
| 246 |
+
|
| 247 |
+
$$
|
| 248 |
+
(1+a)(1+b)(1+c)>1 \cdot 1 \cdot 1=1
|
| 249 |
+
$$
|
| 250 |
+
|
| 251 |
+
Ainsi, les seules solutions sont celles trouvées au début de la solution, c'est-à-dire $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ et $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{2}$.
|
| 252 |
+
Commentaire des correcteurs : Le problème a été abordé et plutôt bien réussi. Néanmoins, plusieurs erreurs sont récurrentes :
|
| 253 |
+
|
| 254 |
+
- Certains obtiennent les deux triplets solutions, mais ne vérifient pas qu'ils sont solution. Quand on raisonne à coup d'implication, il n'est pas du tout sûr que les triplets trouvés soient solution.
|
| 255 |
+
- Beaucoup supposent par exemple $a>b>c$. Deux problèmes : on oublie que plusieurs variables peuvent être égales. Mais surtout pour faire cela, il faut que le système soit symétrique : c'est-àdire que si on inverse deux variables, par exemple $a$ et $b$, alors le système ne change pas. Ce n'est pas du tout le cas : le système est complètement changé.
|
| 256 |
+
|
| 257 |
+
Exercice 6. Montrer que pour tous réels $\mathrm{a}, \mathrm{b}, \mathrm{c}$ strictement positifs:
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
\frac{b c}{a^{2}+2 b c}+\frac{c a}{b^{2}+2 c a}+\frac{a b}{c^{2}+2 a b} \leqslant 1 \leqslant \frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b}
|
| 261 |
+
$$
|
| 262 |
+
|
| 263 |
+
## Solution de l'exercice 6
|
| 264 |
+
|
| 265 |
+
Commençons par résoudre une des inégalités. Dans ce problème, l'inégalité la plus simple à étudier est celle de droite. On applique l'inégalité arithmético-géométrique sur les dénominateurs pour avoir $2 \mathrm{bc} \leqslant \mathrm{b}^{2}+\mathrm{c}^{2}$ par exemple, ce qui donne
|
| 266 |
+
|
| 267 |
+
$$
|
| 268 |
+
\frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b} \geqslant \frac{a^{2}}{a^{2}+b^{2}+c^{2}}+\frac{b^{2}}{a^{2}+b^{2}+c^{2}}+\frac{c^{2}}{a^{2}+b^{2}+c^{2}}=1 .
|
| 269 |
+
$$
|
| 270 |
+
|
| 271 |
+
Pour le côté gauche, on remarque que celui-ci ressemble beaucoup au côté droit. Appelons $G$ et $D$ les côtés gauche et droit de l'équation respectivement. On a alors
|
| 272 |
+
|
| 273 |
+
$$
|
| 274 |
+
\begin{gathered}
|
| 275 |
+
\mathrm{G}+2 \cdot \mathrm{D}=\frac{\mathrm{a}^{2}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{\mathrm{b}^{2}}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{\mathrm{c}^{2}}{\mathrm{c}^{2}+2 \mathrm{ab}}+\frac{2 \mathrm{bc}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{2 c a}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{2 a b}{\mathrm{c}^{2}+2 a b} . \\
|
| 276 |
+
\frac{\mathrm{a}^{2}+2 \mathrm{bc}}{\mathrm{a}^{2}+2 b c}+\frac{b^{2}+2 c a}{b^{2}+2 c a}+\frac{c^{2}+2 a b}{c^{2}+2 a b}=3 .
|
| 277 |
+
\end{gathered}
|
| 278 |
+
$$
|
| 279 |
+
|
| 280 |
+
On a donc
|
| 281 |
+
|
| 282 |
+
$$
|
| 283 |
+
\mathrm{G}=\frac{1}{2}(3-\mathrm{D}) \leqslant \frac{1}{2}(3-1)=1
|
| 284 |
+
$$
|
| 285 |
+
|
| 286 |
+
par l'inégalité de droite que l'on a montré précédemment.
|
| 287 |
+
Commentaire des correcteurs : L'exercice a été bien réussi. Un certain nombre d'élève n'a trouvé qu'une seule des deux inégalités : il est important d'envoyer tout ce qui a été trouvé sur l'envoi, même si on n'a trouvé que la moitié de l'exercice. Un certain nombre d'élèves ont juste tout mis au même dénominateur, et ensuite prouvé l'inégalité, ce qui n'était pas très élégant mais fonctionnait bien.
|
| 288 |
+
|
| 289 |
+
Exercice 7. Soient $x, y, z$ des réels strictement positifs tels que $x y+y z+z x=1$. Montrer que
|
| 290 |
+
|
| 291 |
+
$$
|
| 292 |
+
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 5
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
## Solution de l'exercice 7
|
| 296 |
+
|
| 297 |
+
Dans cet exercice, on aimerait bien appliquer l'inégalité arithmético-géométrique de façon à obtenir une minoration du type $\left(x^{2}+1\right)+\frac{1}{x^{2}+1} \geqslant 2$. Mais si on s'y prend mal, on n'arrive pas à conclure. En effet, on aurait pu s'en douter en étudiant le cas d'égalité de l'équation. Au vu de la condition $x y+y z+z x=1$, on se doute que l'égalité va se produire pour $x=y=z=\frac{1}{\sqrt{3}}$. En introduisant ces valeurs dans l'équation, on trouve bien que l'on a égalité, mais ceci n'est pas un cas d'égalité de l'inégalité arithméticogéométrique plus tôt.
|
| 298 |
+
Dans le cas d'égalité $x=y=z=\frac{1}{\sqrt{3}}$, on a $x^{2}+1=\frac{4}{3}$ et $\frac{1}{x^{2}+1}=\frac{3}{4}$. On applique donc l'inégalité arithmético-géométrique avec des coefficients appropriés pour avoir l'égalité des deux termes dans ce cas :
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
\frac{3}{4}\left(x^{2}+1\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}\right) \geqslant 2
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
En sommant ces trois équations, on a
|
| 305 |
+
|
| 306 |
+
$$
|
| 307 |
+
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}+3\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 6
|
| 308 |
+
$$
|
| 309 |
+
|
| 310 |
+
qui donne
|
| 311 |
+
|
| 312 |
+
$$
|
| 313 |
+
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}
|
| 314 |
+
$$
|
| 315 |
+
|
| 316 |
+
Par rapport à l'inégalité de l'énoncé, il nous reste un terme $\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right)$ à minorer. Mais on a, par l'inégalité arithmético-géométrique,
|
| 317 |
+
|
| 318 |
+
$$
|
| 319 |
+
\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right) \geqslant \frac{5}{4}(x y+y z+z x)=\frac{5}{4}
|
| 320 |
+
$$
|
| 321 |
+
|
| 322 |
+
En ajoutant cette inégalité à l'inégalité obtenue précédemment, on obtient bien
|
| 323 |
+
|
| 324 |
+
$$
|
| 325 |
+
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}+\frac{5}{4}=5
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
## Solution alternative de l'exercice 7
|
| 329 |
+
|
| 330 |
+
Posons $s=x^{2}+y^{2}+z^{2}$. Notons que par l'inégalité des mauvais élèves,
|
| 331 |
+
|
| 332 |
+
$$
|
| 333 |
+
\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{4}{3} \frac{(1+1+1)^{2}}{x^{2}+y^{2}+z^{2}+3}=\frac{12}{s+3}
|
| 334 |
+
$$
|
| 335 |
+
|
| 336 |
+
Ainsi il suffit de montrer que $2 s+\frac{12}{s+3} \geqslant 5$. En multipliant des deux côtés par $s+3$ qui est positif, il suffit de montrer que $2 s(s+3)+12 \geqslant 5(s+3)$. Ceci est équivalent à $2 s^{2}+6 s+12 \geqslant 5 s+15$ et donc à $2 s^{2}+s \geqslant 3$. Or par le lemme du tourniquet, $s \geqslant x y+y z+x z=1$, donc $2 s^{2}+s \geqslant 3$. On a bien le résultat voulu.
|
| 337 |
+
|
| 338 |
+
Commentaire des correcteurs : L'exercice a été bien résolu par les élèves l'ayant cherché. Attention à ne pas s'emmêler dans les inégalités. Ici on pouvait directement utiliser l'inégalité des mauvais élèves : poser $s=x^{2}+y^{2}+z^{2}$ permettait de conclure en multipliant par $s+3$. Notons qu'il n'est pas nécessaire de reprouver à chaque fois $x^{2}+y^{2}+z^{2} \geqslant x y+y z+x z$ pour l'utiliser : c'est le lemme du tourniquet, qui est présent dans le cours de la POFM.
|
| 339 |
+
|
| 340 |
+
Exercice 8. Soient $a$ et $b$ deux réels. On définit les suites $\left(a_{n}\right)$ et $\left(b_{n}\right)$ par $a_{0}=a, b_{0}=b$ et pour tout $n$ entier naturel, $a_{n+1}=a_{n}+b_{n}$ et $b_{n+1}=a_{n} b_{n}$. Déterminer toutes les paires $(a, b)$ telles que $\mathrm{a}_{2022}=\mathrm{a}_{0}$ et $\mathrm{b}_{2022}=\mathrm{b}_{0}$.
|
| 341 |
+
|
| 342 |
+
## Solution de l'exercice 8
|
| 343 |
+
|
| 344 |
+
Supposons que $(a, b)$ soit une solution de l'énoncé. On calcule
|
| 345 |
+
|
| 346 |
+
$$
|
| 347 |
+
\sum_{i=1}^{2022} a_{i}=\sum_{i=1}^{2022}\left(a_{i-1}+b_{i-1}\right)=\sum_{i=0}^{2021} a_{i}+\sum_{i=0}^{2021} b_{i}
|
| 348 |
+
$$
|
| 349 |
+
|
| 350 |
+
Mais on a
|
| 351 |
+
|
| 352 |
+
$$
|
| 353 |
+
\sum_{i=0}^{2021} a_{i}=a_{0}+\sum_{i=1}^{2021} a_{i}=a_{2022}+\sum_{i=1}^{2021} a_{i}=\sum_{i=1}^{2022} a_{i}
|
| 354 |
+
$$
|
| 355 |
+
|
| 356 |
+
donc on peut réécrire l'équation précédente comme
|
| 357 |
+
|
| 358 |
+
$$
|
| 359 |
+
\sum_{i=0}^{2021} b_{i}=0
|
| 360 |
+
$$
|
| 361 |
+
|
| 362 |
+
De la même manière, on a
|
| 363 |
+
|
| 364 |
+
$$
|
| 365 |
+
0=\sum_{i=1}^{2022} b_{i}=\sum_{i=1}^{2022} a_{i-1} b_{i-1}=\sum_{i=0}^{2021} a_{i} b_{i}
|
| 366 |
+
$$
|
| 367 |
+
|
| 368 |
+
Pour faire apparaître les produits $a_{i} b_{i}$, on élève l'équation $a_{i+1}=a_{i}+b_{i}$ au carré pour avoir $a_{i+1}^{2}=$ $a_{i}^{2}+b_{i}^{2}+2 a_{i} b_{i}$. On somme ceci entre $i=0$ et 2021 pour avoir
|
| 369 |
+
|
| 370 |
+
$$
|
| 371 |
+
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}+\sum_{i=0}^{2021} b_{i}^{2}+2 \sum_{i=0}^{2021} a_{i} b_{i}
|
| 372 |
+
$$
|
| 373 |
+
|
| 374 |
+
Mais encore une fois,
|
| 375 |
+
|
| 376 |
+
$$
|
| 377 |
+
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}
|
| 378 |
+
$$
|
| 379 |
+
|
| 380 |
+
donc
|
| 381 |
+
|
| 382 |
+
$$
|
| 383 |
+
\sum_{i=0}^{2021} b_{i}^{2}=0
|
| 384 |
+
$$
|
| 385 |
+
|
| 386 |
+
Une somme de carrés de nombres réels est nécessairement positive, et ne peut être nulle que si tous les $b_{i}$ sont nuls. Ceci implique notamment $b=0$. Réciproquement, si a est un réel, le couple ( $a, 0$ ) fonctionne car on montre par récurrence que pour tout $n, a_{n}=a$ et $b_{n}=0$, et alors $a_{2022}=a=a_{0}$.
|
| 387 |
+
|
| 388 |
+
Commentaire des correcteurs : L'exercice était très difficile, a été peu abordé, et encore moins réussi. Plusieurs élèves arrivent cependant à obtenir que $b_{0}+\cdots+b_{2021}=0$ ce qui est un bon début.
|
| 389 |
+
|
| 390 |
+
Exercice 9. Soient $b_{1}, \ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,
|
| 391 |
+
|
| 392 |
+
$$
|
| 393 |
+
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
|
| 394 |
+
$$
|
| 395 |
+
|
| 396 |
+
Montrer que l'on a
|
| 397 |
+
|
| 398 |
+
$$
|
| 399 |
+
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
|
| 400 |
+
$$
|
| 401 |
+
|
| 402 |
+
## Solution de l'exercice 9
|
| 403 |
+
|
| 404 |
+
Pour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire
|
| 405 |
+
|
| 406 |
+
$$
|
| 407 |
+
\begin{aligned}
|
| 408 |
+
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
|
| 409 |
+
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
|
| 410 |
+
\end{aligned}
|
| 411 |
+
$$
|
| 412 |
+
|
| 413 |
+
et
|
| 414 |
+
|
| 415 |
+
$$
|
| 416 |
+
\begin{aligned}
|
| 417 |
+
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
|
| 418 |
+
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j}
|
| 419 |
+
\end{aligned}
|
| 420 |
+
$$
|
| 421 |
+
|
| 422 |
+
Afin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .
|
| 423 |
+
Soit $m$ l'entier minimal tel que $\sum_{j=1}^{m} b_{j}>1$. On écrit alors
|
| 424 |
+
|
| 425 |
+
$$
|
| 426 |
+
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
|
| 427 |
+
$$
|
| 428 |
+
|
| 429 |
+
Pour $i<m$, on majore $a_{i}$ par $\sum_{j=1}^{i} b_{j}$, et pour $i \geqslant m$, on majore $a_{i}$ par $\sum_{j=i+1}^{n} b_{j}$ pour obtenir $\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}$.
|
| 430 |
+
Posons $x=\sum_{j=1}^{m-1} b_{j}$ et $y=\sum_{j=m+1}^{n} b_{j}$. Par définition de $m$, on a $x \leqslant 1$ et $y \leqslant 1$. Considérons la première somme dans le terme précédent. Dans celle-ci, on a un terme $b_{i}^{2}$ pour tout $i \leqslant m-1$ et un terme $2 b_{i} b_{j}$ pour tous $j<i \leqslant m-1$. Ainsi, cette somme n'est rien d'autre que $x^{2}$. De même, la somme de droite n'est rien d'autre que $y^{2}$. On peut donc écrire, comme $x+b_{m}+y=2$,
|
| 431 |
+
|
| 432 |
+
$$
|
| 433 |
+
\begin{aligned}
|
| 434 |
+
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
|
| 435 |
+
= & 2(x+y)-2 x y
|
| 436 |
+
\end{aligned}
|
| 437 |
+
$$
|
| 438 |
+
|
| 439 |
+
Il nous reste enfin à voir que $2(x+y)-2 x y \leqslant 2$ pour conclure, ou encore $x+y-x y \leqslant 1$. Mais ceci se réécrit, en passant tous les termes à droite de l'inégalité,
|
| 440 |
+
|
| 441 |
+
$$
|
| 442 |
+
(1-x)(1-y) \geqslant 0
|
| 443 |
+
$$
|
| 444 |
+
|
| 445 |
+
ce qui est vérifié car on a vu que $x \leqslant 1$ et $y \leqslant 1$.
|
| 446 |
+
Commentaire des correcteurs : L'exercice était très difficile, a été très peu abordé et résolu par personne. Il est dommage de voir que peu d'élèves ont écrit leur piste de recherche : typiquement à $\left(b_{i}\right)$ fixé de trouver les $\left(a_{i}\right)$ maximisant la somme.
|
| 447 |
+
|
| 448 |
+
## Exercices Seniors
|
| 449 |
+
|
| 450 |
+
Exercice 10. Soit $\left(u_{n}\right)_{n \in \mathbb{N}}$ une suite périodique de période 2022 et de période 5 . Montrer que $\left(u_{n}\right)$ est constante.
|
| 451 |
+
Une suite $\left(u_{n}\right)$ est dite périodique de période $t$ si, pour tout entier naturel $n, u_{n+t}=u_{n}$.
|
| 452 |
+
Solution de l'exercice 10
|
| 453 |
+
Commençons par remarquer que si une suite $\left(u_{n}\right)$ est $t$-périodique, alors on a pour tout $n, u_{n}=u_{n+t}=$ $u_{n+2 t}$ par exemple. Ainsi, on peut montrer par récurrence que pour tous les entiers naturels $k$ et $n$, $u_{n+k t}=u_{n}$ : la suite est kt-périodique pour tout $k$.
|
| 454 |
+
Soit $n$ un entier naturel. On a alors, comme la suite est 2022-périodique,
|
| 455 |
+
|
| 456 |
+
$$
|
| 457 |
+
u_{n+1}=u_{n+1+2 \times 2022}=u_{n+4045}=u_{n+5 \times 809}
|
| 458 |
+
$$
|
| 459 |
+
|
| 460 |
+
Mais la suite est 5 -périodique donc ceci vaut aussi $u_{n}$. Ainsi, pour tout entier naturel $n$, on a $u_{n+1}=u_{n}$. On en déduit par récurrence que pour tout $n, u_{n}=u_{0}$ et donc la suite ( $u_{n}$ ) est constante.
|
| 461 |
+
|
| 462 |
+
Commentaire des correcteurs : L'exo a été réussi par qusiment toutes les personnes l'ayant abordé, avec 3 méthodes principales :
|
| 463 |
+
|
| 464 |
+
- Montrer que $u_{0}=u_{1}=u_{2}=u_{3}=u_{4}$.
|
| 465 |
+
- Montrer que $u_{n}=u_{n+1}$.
|
| 466 |
+
- Utiliser le théorème de Bezout pour montrer $u_{0}=u_{n}$.
|
| 467 |
+
|
| 468 |
+
Les quelques élèves qui n'ont pas eu 7 points ont la plupart du temps utilisé des propriétés un peu fortes sans les justifier (même rapidement, cela aurait suffit).
|
| 469 |
+
|
| 470 |
+
Exercice 11. Soit $n$ un entier strictement positif et $x \geqslant n$ un réel. Montrer que $x+\frac{n}{x} \geqslant n+1$ et donner les cas d'égalité.
|
| 471 |
+
|
| 472 |
+
## Solution de l'exercice 11
|
| 473 |
+
|
| 474 |
+
Le réel $x$ est strictement positif donc on peut multiplier l'équation par $x$ pour avoir que l'équation est équivalente à
|
| 475 |
+
|
| 476 |
+
$$
|
| 477 |
+
x^{2}+n \geqslant(n+1) x
|
| 478 |
+
$$
|
| 479 |
+
|
| 480 |
+
ce qui donne, en réarrangeant les termes,
|
| 481 |
+
|
| 482 |
+
$$
|
| 483 |
+
x^{2}-(n+1) x+n \geqslant 0
|
| 484 |
+
$$
|
| 485 |
+
|
| 486 |
+
On peut chercher les racines de ce polynôme de degré 2 ou alors reconnaitre la factorisation
|
| 487 |
+
|
| 488 |
+
$$
|
| 489 |
+
(x-n)(x-1) \geqslant 0
|
| 490 |
+
$$
|
| 491 |
+
|
| 492 |
+
Mais ceci est vrai car $x \geqslant n$ et $x \geqslant 1$.
|
| 493 |
+
On a égalité lorsque $x=\mathfrak{n}$ ou $x=1$. Mais si $x=1$, alors $\mathfrak{n}=1$ et $x=n$. Ainsi, dans tous les cas, le seul cas d'égalité est $x=\mathrm{n}$.
|
| 494 |
+
|
| 495 |
+
## Solution alternative de l'exercice 11
|
| 496 |
+
|
| 497 |
+
On repart de l'équation développée $x^{2}-(n+1) x+n \geqslant 0$.
|
| 498 |
+
La condition $x \geqslant n$ est très peu naturelle, on préfère des conditions de type $t \geqslant 0$. On pose donc $x=n+t$ $\operatorname{avec} t \geqslant 0$. L'équation se réécrit alors
|
| 499 |
+
|
| 500 |
+
$$
|
| 501 |
+
\mathrm{n}^{2}+2 n t+\mathrm{t}^{2}-(n+1)(n+t)+n \geqslant 0
|
| 502 |
+
$$
|
| 503 |
+
|
| 504 |
+
ou encore
|
| 505 |
+
|
| 506 |
+
$$
|
| 507 |
+
\mathrm{t}^{2}+(n-1) \mathrm{t} \geqslant 0
|
| 508 |
+
$$
|
| 509 |
+
|
| 510 |
+
Mais cette nouvelle équation est clairement vraie car $\mathrm{t} \geqslant 0$ et $\mathrm{n} \geqslant 1$. De plus, on a égalité si et seulement si $t=0$, ou encore $x=n$.
|
| 511 |
+
|
| 512 |
+
Commentaire des correcteurs : Le problème a été bien réussi par les élèves, les solutions rendues étaient presque toutes abouties. Les solutions étaient assez variées, certaines passaient par l'étude d'un trinôme, d'autres par un calcul de dérivée, ou encore par l'inégalité arithmético-géométrique. Néanmoins, un certain nombre de copies ont été pénalisées pour des manques de justifications, notamment des justifications de signes. On rappelle que lorsqu'on multiplie ou divise une inégalité par une quantité, il faut s'assurer du signe de cette quantité : si elle est strictement positive, ça conserve le sens de l'inégalité, si elle est strictement négative, ça change le sens de l'inégalité, et si on multiplie par une quantité nulle, on n'a pas équivalence. C'est donc un détail qui a toute son importance. En ce qui concerne le cas d'égalité, plusieurs copies ont oublié de le traiter, et d'autres ont oublié la condition $x \geqslant n$, de sorte qu'elles considérées que pour tout $\mathrm{n} \in \mathbb{N}^{*}, x=1$ était un cas d'égalité. Ce n'était vrai que pour $\mathrm{n}=1$, et donc c'était déjà compté dans le cas $x=n$.
|
| 513 |
+
|
| 514 |
+
Exercice 12. Soit ( $a_{n}$ ) une suite de réels. On suppose que $a_{0}=1$ et que pour tout $n \geqslant 1, a_{n}$ est la plus petite solution strictement positive de
|
| 515 |
+
|
| 516 |
+
$$
|
| 517 |
+
\left(a_{n}-a_{n-1}\right)\left(a_{n}+a_{n-1}-2 \sqrt{n}\right)=2 .
|
| 518 |
+
$$
|
| 519 |
+
|
| 520 |
+
Trouver le plus petit entier $n$ tel que $a_{n} \geqslant 2022$.
|
| 521 |
+
Solution de l'exercice 12 Pour se donner une idée du problème, on calcule les premières valeurs de $a_{n}$ : pour $a_{1}$, l'équation s'écrit
|
| 522 |
+
|
| 523 |
+
$$
|
| 524 |
+
\left(a_{1}-1\right)\left(a_{1}-1\right)=2
|
| 525 |
+
$$
|
| 526 |
+
|
| 527 |
+
donc $a_{1}-1=\sqrt{2}$ ou $-\sqrt{2}$. Seul le premier cas donne une solution positive $a_{1}=1+\sqrt{2}$. Cherchons maintenant à calculer $a_{2}: 1$ 'équation devient
|
| 528 |
+
|
| 529 |
+
$$
|
| 530 |
+
\left(a_{2}-1-\sqrt{2}\right)\left(a_{2}+1-\sqrt{2}\right)=2
|
| 531 |
+
$$
|
| 532 |
+
|
| 533 |
+
ce que l'on peut développer en
|
| 534 |
+
|
| 535 |
+
$$
|
| 536 |
+
\left(a_{2}-\sqrt{2}\right)^{2}-1^{2}=2
|
| 537 |
+
$$
|
| 538 |
+
|
| 539 |
+
ou encore $a_{2}-\sqrt{2}= \pm \sqrt{3}$. Un seul signe donne une solution positive $a_{2}=\sqrt{2}+\sqrt{3}$.
|
| 540 |
+
A partir de ces premières valeurs, on fait l'hypothèse que la suite $a_{n}$ est donnée par $a_{n}=\sqrt{n}+\sqrt{n+1}$ et on montre ceci par récurrence. C'est vrai pour $n=0$. Supposons que ceci soit vrai pour $n-1$ et montrons le au rang $n$ : l'équation donnant $a_{n}$ est
|
| 541 |
+
|
| 542 |
+
$$
|
| 543 |
+
\left(a_{n}-\sqrt{n-1}-\sqrt{n}\right)\left(a_{n}+\sqrt{n-1}-\sqrt{n}\right)=2
|
| 544 |
+
$$
|
| 545 |
+
|
| 546 |
+
ce que l'on développe en
|
| 547 |
+
|
| 548 |
+
$$
|
| 549 |
+
\left(a_{n}-\sqrt{n}\right)^{2}-(\sqrt{n-1})^{2}=2
|
| 550 |
+
$$
|
| 551 |
+
|
| 552 |
+
et donc
|
| 553 |
+
|
| 554 |
+
$$
|
| 555 |
+
\left(a_{n}-\sqrt{n}\right)^{2}=n+1
|
| 556 |
+
$$
|
| 557 |
+
|
| 558 |
+
donc $a_{n}-\sqrt{n}= \pm \sqrt{n+1}$. Seul le signe + donne une solution positive, donc on a bien $a_{n}=\sqrt{n}+$ $\sqrt{n+1}$ ce qui conclut la récurrence.
|
| 559 |
+
On remarque immédiatement que la suite ( $a_{n}$ ) est croissante, et par conséquent si on trouve un $n$ tel que $a_{n-1}<2022 \leqslant a_{n}$, il s'agit du $n$ cherché. En effet, si on a $0 \leqslant m<n$, on a alors $m \leqslant n-1$ donc $a_{m} \leqslant a_{n-1}<2022$ comme voulu : $n$ est bien le plus petit indice tel que $a_{n} \geqslant 2022$.
|
| 560 |
+
Mais maintenant on a
|
| 561 |
+
|
| 562 |
+
$$
|
| 563 |
+
\mathrm{a}_{1011^{2}-1}=\sqrt{1011^{2}-1}+1011<2 \cdot 1011=2022<1011+\sqrt{1011^{2}+1}=a_{1011^{2}}
|
| 564 |
+
$$
|
| 565 |
+
|
| 566 |
+
donc le n cherché est $\mathrm{n}=1011^{2}$.
|
| 567 |
+
Commentaire des correcteurs : Le problème a été bien réussi par les élèves qui ont rendu une copie. Une très grande majorité a parfaitement conjecturé $a_{n}=\sqrt{n}+\sqrt{n+1}$ puis l'a montré par récurrence. On rappelle que calculer les premiers termes pour deviner une expression est une très bonne initiative à prendre au brouillon car ça peut être la première étape dans la résolution d'un problème (comme c'était le cas ici). À partir de là on pouvait rapidement conclure, mais il fallait faire attention à ne pas faire d'erreurs de calculs, et à bien justifier (notamment des arguments de croissance étaient pertinents). Ces points là manquaient dans certaines copies. On notera aussi qu'en test ou en compétition, il n'y a pas de calculatrice, il faut donc prendre l'habitude de chercher à faire des calculs efficaces à la main.
|
| 568 |
+
|
| 569 |
+
Exercice 13. Soit $n \geqslant 3$ et soient $x_{1}, \ldots, x_{n}$ des réels. Montrer que
|
| 570 |
+
|
| 571 |
+
$$
|
| 572 |
+
2\left(x_{1}+\cdots+x_{n}\right)^{2} \leqslant n\left(x_{1}^{2}+\cdots+x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
|
| 573 |
+
$$
|
| 574 |
+
|
| 575 |
+
## Solution de l'exercice 13
|
| 576 |
+
|
| 577 |
+
La difficulté de l'exercice est le fait que l'énoncé n'est pas symétrique. Au vu de celui-ci, on veut faire apparaître les produits $x_{i} x_{i+1}$; pour cela, on peut penser à utiliser le développement de $\left(x_{i}+x_{i+1}\right)^{2}$. On a
|
| 578 |
+
|
| 579 |
+
$$
|
| 580 |
+
\begin{gathered}
|
| 581 |
+
\left(x_{1}+x_{2}\right)^{2}+\cdots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}=\left(x_{1}^{2}+2 x_{1} x_{2}+x_{2}^{2}\right)+\cdots+\left(x_{n-1}^{2}+2 x_{n-1} x_{n}+x_{n}^{2}\right)+\left(x_{n}^{2}+2 x_{n} x_{1}+x_{1}^{2}\right) \\
|
| 582 |
+
=2\left(x_{1}^{2}+\ldots x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
|
| 583 |
+
\end{gathered}
|
| 584 |
+
$$
|
| 585 |
+
|
| 586 |
+
et on reconnaît le membre de droite de l'énoncé, avec un coefficient 2 au lieu de $n$. L'inégalité de l'énoncé se réécrit alors
|
| 587 |
+
|
| 588 |
+
$$
|
| 589 |
+
4\left(x_{1}+\ldots+x_{n}\right)^{2} \leqslant \mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)
|
| 590 |
+
$$
|
| 591 |
+
|
| 592 |
+
Mais ceci est alors une application de l'inégalité de Cauchy-Schwarz. En effet, on a
|
| 593 |
+
|
| 594 |
+
$$
|
| 595 |
+
\begin{gathered}
|
| 596 |
+
\mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)=\left(1^{2}+\ldots+1^{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}+\ldots+\left(x_{n}+x_{1}\right)^{2}\right) \\
|
| 597 |
+
\geqslant\left(1 \cdot\left(x_{1}+x_{2}\right)+1 \cdot\left(x_{2}+x_{3}\right)+\ldots+1 \cdot\left(x_{n}+x_{1}\right)\right)^{2} \\
|
| 598 |
+
=\left(2 x_{1}+2 x_{2}+\ldots+2 x_{n}\right)^{2}=4\left(x_{1}+\ldots+x_{n}\right)^{2} .
|
| 599 |
+
\end{gathered}
|
| 600 |
+
$$
|
| 601 |
+
|
| 602 |
+
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont tenté. L'erreur la plus fréquente était d'utiliser l'inégalité de Tchebychev en oubliant l'hypothèse sur l'ordre des termes. Les élèves ayant pensé à réécrire le terme de droite comme somme de $\left(x_{i}+x_{i+1}\right)^{2}$ ont réussi à conclure avec CauchySchwarz, AM-QM, Tchebychev, Jensen ou les mauvais élèves.
|
| 603 |
+
|
| 604 |
+
Exercice 14. Soient $a, b, c, x, y, z>0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \leqslant x<y<z \leqslant c$ et $a<b<c$. Montrer que $a=x, b=y, c=z$.
|
| 605 |
+
|
| 606 |
+
## Solution de l'exercice 14
|
| 607 |
+
|
| 608 |
+
Les termes $a+b+c$ et $a b c$ nous rappellent les formules de Viète qui lient les coefficients d'un polynôme à ses racines. Ceci nous invite à considérer les polynômes $P(X)=(X-a)(X-b)(X-c)$ et $Q(X)=$ $(X-x)(X-y)(X-z)$. Sous forme développée, on a
|
| 609 |
+
$P(X)=X^{3}-(a+b+c) X^{2}+(a b+b c+c a) X-a b c, \quad Q(X)=X^{3}-(x+y+z) X^{2}+(x y+y z+z x) X-x y z$
|
| 610 |
+
et l'énoncé nous assure que les coefficients de degrés 0 et 2 sont identiques pour les deux polynômes. Mais on peut considérer la différence $P(X)-Q(X)$ qui est alors un monôme de la forme $\alpha X$, pour un certain $\alpha$ réel.
|
| 611 |
+
Au vu de l'énoncé, il faut montrer que $P(X)=Q(X)$, ou encore que $\alpha=0$. Mais pour ceci, on évalue simplement $P(X)-Q(X)$ en $X=a$ et $X=c$. En ces deux points, on a $P(X)=0$, et alors
|
| 612 |
+
|
| 613 |
+
$$
|
| 614 |
+
\alpha a=-Q(a)=-(a-x)(a-y)(a-z) \geqslant 0
|
| 615 |
+
$$
|
| 616 |
+
|
| 617 |
+
car $a$ est inférieur à $x, y$ et $z$. Comme $a>0$, on en déduit $\alpha \geqslant 0$. Mais on a aussi
|
| 618 |
+
|
| 619 |
+
$$
|
| 620 |
+
\alpha c=-Q(c)=-(c-x)(c-y)(c-z) \leqslant 0
|
| 621 |
+
$$
|
| 622 |
+
|
| 623 |
+
car $c$ est supérieur à $x, y$ et $z$. Comme $c>0$, on en déduit $\alpha \leqslant 0$. Ainsi, on a $\alpha=0$ comme voulu, c'est-à-dire que $P(X)=Q(X)$.
|
| 624 |
+
Mais alors les deux polynômes doivent avoir les mêmes racines qui sont $a<b<c$ pour $P(X)$ et $x<y<z$ pour $Q(X)$. On a donc bien
|
| 625 |
+
|
| 626 |
+
$$
|
| 627 |
+
\mathrm{a}=\mathrm{x}, \mathrm{~b}=\mathrm{y}, \mathrm{c}=z
|
| 628 |
+
$$
|
| 629 |
+
|
| 630 |
+
Commentaire des correcteurs : L'exercice n'a pas été beaucoup abordé mais il a été dans l'ensemble très bien réussi par ceux qui l'ont tenté. La solution la plus courante était de passer par des polynômes de degré 3 comme dans le corrigé. D'autres solutions ont été trouvées, comme passer par des polynômes de degré 2 , faire des disjonctions de cas sur les signes ou encore utiliser l'inégalité de réarrangement. Notons que plusieurs copies ont évoqué le théorème des valeurs intermédiaires : lors de son utilisation il faut rappeler toutes les hypothèses, notamment l'hypothèse de continuité doit être écrite même si elle est évidente à vérifier. Une autre erreur faite plusieurs fois est celle du sens des inégalités : lorsqu'on utilise une inégalité, il faut vérifier qu'on l'utilise dans le bon sens. Parfois utiliser une inégalité dans le mauvais sens (donc fausse) peut donner l'impression d'aboutir, mais vu que l'inégalité utilisée initialement est fausse, la solution l'est aussi.
|
| 631 |
+
|
| 632 |
+
Exercice 15. Pour une fonction $f$ et $n$ un entier strictement positif, on note $f^{n}$ la composée $n$-ième de f définie par $\mathrm{f}^{\mathrm{n}}=\mathrm{f} \circ \mathrm{f} \circ \ldots \circ \mathrm{f}$ pù f apparaît n fois dans le membre de droite.
|
| 633 |
+
Trouver toutes les fonctions $\mathrm{f}: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ telles que
|
| 634 |
+
|
| 635 |
+
$$
|
| 636 |
+
f^{f(n)}(m)+m n=f(m) f(n)
|
| 637 |
+
$$
|
| 638 |
+
|
| 639 |
+
pour tous $\mathrm{m}, \mathrm{n} \in \mathbb{N}^{*}$.
|
| 640 |
+
|
| 641 |
+
## Solution de l'exercice 15
|
| 642 |
+
|
| 643 |
+
En $m=n$, on trouve que $f(m)^{2}=f^{f(m)}(m)+m^{2}>m^{2}$, ce qui donne $f(m)>m$ car $f(m)$ est positif, et donc comme $f(m)$ est entier, $f(m) \geqslant m+1$. Par une récurrence simple, on trouve que pour tous les entiers $k$, $m$ strictement positifs, $f^{k}(m) \geqslant m+k$.
|
| 644 |
+
Mais on remarque qu'à part le premier terme de l'énoncé, le reste est symétrique en $m$ et $n$, et on peut écrire que pour tous $m, n>0$,
|
| 645 |
+
|
| 646 |
+
$$
|
| 647 |
+
f^{f(n)}(m)+m n=f(m) f(n)=f^{f(m)}(n)+n m
|
| 648 |
+
$$
|
| 649 |
+
|
| 650 |
+
et donc $f^{f(n)}(m)=f^{f(m)}(n)$. On veut maintenant utiliser le fait que l'on a affaire à une composée, et on pose donc $n=f(a)$ afin que $f^{f(m)}(n)=f^{f(m)+1}(a)$. En évaluant l'équation précédente avec $a=m$, on a
|
| 651 |
+
|
| 652 |
+
$$
|
| 653 |
+
f^{f(\mathfrak{m})+1}(\mathfrak{m})=f^{f(f(\mathfrak{m}))}(\mathfrak{m})
|
| 654 |
+
$$
|
| 655 |
+
|
| 656 |
+
Mais ceci implique alors que $f(f(m))=f(m)+1$. En effet, sinon, soit $\alpha=\min (f(f(m)), f(m)+1)$ et $k=\max (f(f(m)), f(m)+1)-\alpha>0$ afin que l'équation s'écrive $f^{k}\left(f^{\alpha}(m)\right)=f^{\alpha}(m)$. Mais c'est absurde car $f^{k}\left(f^{\alpha}(m)\right) \geqslant f^{\alpha}(m)+k>f^{\alpha}(m)$.
|
| 657 |
+
On déduit que pour tout $m \in \mathbb{N}^{*} f(f(m))=f(m)+1$. Par une récurrence simple, pour tout $k \geqslant 1$, $f^{k}(m)=f(m)+k-1$. Ainsi l'équation de l'énoncé donne pour tous $m, n \in \mathbb{N}^{*}$,
|
| 658 |
+
|
| 659 |
+
$$
|
| 660 |
+
\mathbf{f}(\mathrm{m})+\mathrm{f}(\mathrm{n})-1+\mathrm{mn}=\mathbf{f}(\mathrm{m}) \mathbf{f}(\mathfrak{n})
|
| 661 |
+
$$
|
| 662 |
+
|
| 663 |
+
Si $n=m$, on obtient une équation liant simplement $f(n)$ et $n$ :
|
| 664 |
+
|
| 665 |
+
$$
|
| 666 |
+
2 \mathrm{f}(\mathrm{n})+\mathrm{n}^{2}-1=\mathrm{f}(\mathrm{n})^{2}
|
| 667 |
+
$$
|
| 668 |
+
|
| 669 |
+
C'est une équation du second degré que l'on peut par exemple factoriser en $(f(n)-1)^{2}=n^{2}$, donc $\mathrm{f}(\mathrm{n})=\mathrm{n}+1$ car $\mathrm{f}(\mathrm{n})$ est strictement positif.
|
| 670 |
+
Réciproquement, si $f(n)=n+1$ pour tout $n$, alors on peut écrire pour tous $m, n$ :
|
| 671 |
+
|
| 672 |
+
$$
|
| 673 |
+
f^{f(n)}(m)+m n=m+f(n)+m n=m n+m+n+1=(m+1)(n+1)=f(m) f(n)
|
| 674 |
+
$$
|
| 675 |
+
|
| 676 |
+
et cette fonction est bien solution de l'équation de l'énoncé.
|
| 677 |
+
Commentaire des correcteurs: Les élèves ayant résolu le problème on tous une solution étudiant les antécédents du plus petit élément de l'image de f. Il est excellent d'avoir su adapter ce genre d'argument à une équation fonctionnelle. C'était d'ailleurs là que résidait la difficulté, et quelques subtilités de l'argument ont échappé à la vigilance de quelques élèves. Par ailleurs, plusieurs élèves n'ont pas hésité à proposer leur preuve de propriétés élémentaires de f, ce sur quoi il est très bon de s'entraîner : l'injectivité de f , le fait que 1 n 'est pas atteint, la symétrie de l'équation fonctionnelle en $m$ et $n$...
|
| 678 |
+
|
| 679 |
+
Exercice 16. Soient $b_{1}, \ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,
|
| 680 |
+
|
| 681 |
+
$$
|
| 682 |
+
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
|
| 683 |
+
$$
|
| 684 |
+
|
| 685 |
+
Montrer que l'on a
|
| 686 |
+
|
| 687 |
+
$$
|
| 688 |
+
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
|
| 689 |
+
$$
|
| 690 |
+
|
| 691 |
+
## Solution de l'exercice 16
|
| 692 |
+
|
| 693 |
+
Pour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire
|
| 694 |
+
|
| 695 |
+
$$
|
| 696 |
+
\begin{aligned}
|
| 697 |
+
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
|
| 698 |
+
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
|
| 699 |
+
\end{aligned}
|
| 700 |
+
$$
|
| 701 |
+
|
| 702 |
+
et
|
| 703 |
+
|
| 704 |
+
$$
|
| 705 |
+
\begin{aligned}
|
| 706 |
+
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
|
| 707 |
+
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j} .
|
| 708 |
+
\end{aligned}
|
| 709 |
+
$$
|
| 710 |
+
|
| 711 |
+
Afin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .
|
| 712 |
+
Soit $m$ l'entier minimal tel que $\sum_{j=1}^{m} b_{j}>1$. On écrit alors
|
| 713 |
+
|
| 714 |
+
$$
|
| 715 |
+
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
|
| 716 |
+
$$
|
| 717 |
+
|
| 718 |
+
Pour $i<m$, on majore $a_{i}$ par $\sum_{j=1}^{i} b_{j}$, et pour $i \geqslant m$, on majore $a_{i}$ par $\sum_{j=i+1}^{n} b_{j}$ pour obtenir
|
| 719 |
+
|
| 720 |
+
$$
|
| 721 |
+
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}
|
| 722 |
+
$$
|
| 723 |
+
|
| 724 |
+
Posons $x=\sum_{j=1}^{m-1} b_{j}$ et $y=\sum_{j=m+1}^{n} b_{j}$. Par définition de $m$, on a $x \leqslant 1$ et $y \leqslant 1$. Considérons la première somme dans le terme précédent. Dans celle-ci, on a un terme $b_{i}^{2}$ pour tout $i \leqslant m-1$ et un terme $2 b_{i} b_{j}$ pour tous $j<i \leqslant m-1$. Ainsi, cette somme n'est rien d'autre que $x^{2}$. De même, la somme de droite n'est rien d'autre que $y^{2}$. On peut donc écrire, comme $x+b_{m}+y=2$,
|
| 725 |
+
|
| 726 |
+
$$
|
| 727 |
+
\begin{aligned}
|
| 728 |
+
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
|
| 729 |
+
= & 2(x+y)-2 x y
|
| 730 |
+
\end{aligned}
|
| 731 |
+
$$
|
| 732 |
+
|
| 733 |
+
Il nous reste enfin à voir que $2(x+y)-2 x y \leqslant 2$ pour conclure, ou encore $x+y-x y \leqslant 1$. Mais ceci se réécrit, en passant tous les termes à droite de l'inégalité,
|
| 734 |
+
|
| 735 |
+
$$
|
| 736 |
+
(1-x)(1-y) \geqslant 0
|
| 737 |
+
$$
|
| 738 |
+
|
| 739 |
+
ce qui est vérifié car on a vu que $x \leqslant 1$ et $y \leqslant 1$.
|
| 740 |
+
Commentaire des correcteurs : L'exercice a été très peu abordé, et c'est particulièrement dommage car c'était un bon prototype d'exercice pouvant tomber à des olympiades internationales, donc il est dommage de ne pas laisser au moins des pistes pour voir comment en test chacun aurait pu avancer sur le problème. Celui-ci témoigne d'erreurs récurrentes commises par les élèves dans de tels problèmes :
|
| 741 |
+
|
| 742 |
+
- Souvent des élèves affirment que si la suite $\left(a_{i}\right)$ vérifie telle propriété, on peut la changer pour agumenter la somme de l'énoncé, puis conclut directement qu'on se ramène au cas où la suite ne vérifie pas ça. Attention : cela n'est pas forcément vrai. En effet, si on dit que telle propriété est un problème, et qu'on compte le nombre de problèmes de la suite, celui-ci n'a aucune raison de décroître. Il faut donner un procédé permettant d'enlever les problèmes 1 par 1 , sans en créer de nouveau : souvent une bonne technique est d'introduire un variant (soit le nombre de problème, soit autre chose). Une autre option pour cela est de montrer qu'il y a un maximisant, mais cela est souvent compliqué. Ici cela pouvait se montrer, mais dépasse le cadre des théorèmes de mathématique olympique.
|
| 743 |
+
- Certains, sous prétexte que l'exercice est dur, ne prouvent pas leurs affirmations. Etonnamment, souvent ce qui n'est pas prouvé se révèle être faux, difficile ou incomplet : ce n'est pas parce que l'exercice est dur, qu'il faut se permettre moins de détail.
|
| 744 |
+
- Beaucoup d'élèves ont essayé de montrer directement qu'on pouvait supposer la suite croissante puis décroissante. C'était difficile à prouver proprement, et surtout ce n'était pas le premier réflexe à avoir. Ici utiliser une représentation graphique était utile : en fait on a forcément $a_{k} \leqslant b_{1}+\cdots+$ $b_{k}$ et $a_{k} \leqslant b_{k+1}+\cdots+b_{n}$. on peut donc représenter graphiquement les points $\left(k, b_{1}+\cdots+b_{k}\right)$ et $\left(k, b_{k+1}+\cdots+b_{n}\right)$ et relier les deux types de points pour obtenir une courbe. Il est naturel d'ensuite regarder le minimum de ces deux courbes et de poser $a_{k}$ la suite correspondant à cette courbe. C'est exactement ce qui est fait dans le corrigé, et il est récurrent que les élèves oublient de représenter graphiquement les contraintes pour essayer de comprendre ce qui se passe, et voir quel est vraiment la bonne façon d'aborder l'énoncé.
|
| 745 |
+
|
| 746 |
+
Exercice 17. Soit $\alpha \neq 0$. Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous réels $x, y$,
|
| 747 |
+
|
| 748 |
+
$$
|
| 749 |
+
f\left(x^{2}+y+f(y)\right)=f(x)^{2}+\alpha y
|
| 750 |
+
$$
|
| 751 |
+
|
| 752 |
+
## Solution de l'exercice 17
|
| 753 |
+
|
| 754 |
+
Posons $x=0$. Alors l'équation devient $f(y+f(y))=f(0)^{2}+\alpha y$ pour tout $y$. Comme $\alpha$ est non nul, le côté droit décrit tous les réels lorsque $y$ varie, et ainsi $f$ est surjective.
|
| 755 |
+
Posons $y=0$. Alors on peut écrire pour tout réel $x$,
|
| 756 |
+
|
| 757 |
+
$$
|
| 758 |
+
\mathbf{f}(\mathrm{x})^{2}=\mathbf{f}\left(\mathrm{x}^{2}+\mathrm{f}(0)\right)=\mathbf{f}\left((-\mathrm{x})^{2}+\mathbf{f}(0)\right)=\mathrm{f}(-\mathrm{x})^{2}
|
| 759 |
+
$$
|
| 760 |
+
|
| 761 |
+
On sait que f est surjective, soit donc c un antécédent de 0 . L'équation de l'énoncé $\operatorname{avec} x=0$ et $\mathrm{y}=\mathrm{c}$ donne
|
| 762 |
+
|
| 763 |
+
$$
|
| 764 |
+
\alpha \mathrm{c}+\mathrm{f}(0)^{2}=\mathrm{f}(0+\mathrm{c}+\mathrm{f}(\mathrm{c}))=\mathrm{f}(\mathrm{c})=0
|
| 765 |
+
$$
|
| 766 |
+
|
| 767 |
+
Mais on sait que $\mathrm{f}(-\mathrm{c})^{2}=\mathrm{f}(\mathrm{c})^{2}=0$ donc -c est aussi un antécédent de 0 . Par l'équation ci-dessus appliquée à c et à -c , on a donc $\alpha \mathrm{c}+\mathrm{f}(0)^{2}=0=-\alpha \mathrm{c}+\mathrm{f}(0)^{2}$. Comme $\alpha \neq 0$, on en déduit que nécessairement $\mathrm{c}=0$.
|
| 768 |
+
Maintenant que l'on sait que 0 est le seul antécédent de 0 , on annule le terme de droite dans l'équation de départ en choisissant $y=-\frac{f(x)^{2}}{\alpha}$, alors $f\left(x^{2}+y+f(y)\right)=0$, soit $x^{2}+y+f(y)=0$ ou encore
|
| 769 |
+
|
| 770 |
+
$$
|
| 771 |
+
\begin{gathered}
|
| 772 |
+
x^{2}-\frac{f(x)^{2}}{\alpha}+f\left(-\frac{f(x)^{2}}{\alpha}\right)=0 \\
|
| 773 |
+
x^{2}=\frac{f(x)^{2}}{\alpha}-f\left(-\frac{f(x)^{2}}{\alpha}\right)
|
| 774 |
+
\end{gathered}
|
| 775 |
+
$$
|
| 776 |
+
|
| 777 |
+
pour tout réel $x$. Dès lors, si $f(x)= \pm f\left(x^{\prime}\right)$, l'équation précédente donne $x^{2}=x^{\prime 2}$ donc $x= \pm x^{\prime}$.
|
| 778 |
+
Soit $x \neq 0$ un réel. Etudions l'équation $f\left(x^{\prime}\right)= \pm f(x)$. On a vu que celle ci avait exactement deux solutions, qui sont $x$ et $-x$ (qui sont distincts car $x \neq 0$ ). Mais il existe une solution à $f\left(x^{\prime}\right)=-f(x)$ par surjectivité de f. Comme $f(x) \neq 0$, cela ne peut pas être $x^{\prime}=x$, c'est donc $x^{\prime}=-x$. Ainsi, $f(-x)=-f(x)$, et la seule solution à $f\left(x^{\prime}\right)=f(x)$ est $x^{\prime}=x$. Comme en plus 0 est l'unique antécédent de 0 , f est à la fois impaire et injective.
|
| 779 |
+
L'équation initiale avec $y=0$ donne pour tout $x$ réel, $f\left(x^{2}\right)=f(x)^{2}$. Ainsi, l'équation de l'énoncé se réécrit
|
| 780 |
+
|
| 781 |
+
$$
|
| 782 |
+
\forall x, y \in \mathbb{R}, \quad f\left(x^{2}+y+f(y)\right)=f\left(x^{2}\right)+\alpha y
|
| 783 |
+
$$
|
| 784 |
+
|
| 785 |
+
donc $\operatorname{avec} z=x^{2}$,
|
| 786 |
+
|
| 787 |
+
$$
|
| 788 |
+
\forall y \in \mathbb{R}, z \geqslant 0, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
|
| 789 |
+
$$
|
| 790 |
+
|
| 791 |
+
Si maintenant $z \leqslant 0$, on calcule pour tout $y$, par imparité de f ,
|
| 792 |
+
|
| 793 |
+
$$
|
| 794 |
+
\begin{aligned}
|
| 795 |
+
f(z+y+f(y)) & =-f(-z-y-f(y))=-f((-z)+(-y)+f(-y)) \\
|
| 796 |
+
& =-(f(-z)+\alpha(-y))=f(z)+\alpha y
|
| 797 |
+
\end{aligned}
|
| 798 |
+
$$
|
| 799 |
+
|
| 800 |
+
C'est la même équation que pour $z \geqslant 0$, d'où
|
| 801 |
+
|
| 802 |
+
$$
|
| 803 |
+
\forall y, z \in \mathbb{R}, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
|
| 804 |
+
$$
|
| 805 |
+
|
| 806 |
+
Avec $z=0$, on a notamment pour tout $y, f(y+f(y))=\alpha y$. Posons $z=x+f(x)$ dans l'équation ci-dessus pour avoir pour tous $x, y \in \mathbb{R}$,
|
| 807 |
+
|
| 808 |
+
$$
|
| 809 |
+
f(x+f(x)+y+f(y))=f(x+f(x))+\alpha y=\alpha x+\alpha y=\alpha(x+y)=f(x+y+f(x+y))
|
| 810 |
+
$$
|
| 811 |
+
|
| 812 |
+
et donc, par injectivité, $f(x+y)=f(x)+f(y)$. Ainsi, $f$ est solution de l'équation de Cauchy. Mais $f$ est croissante car si $x>y$, on a
|
| 813 |
+
|
| 814 |
+
$$
|
| 815 |
+
f(x)=f(y)+f(x-y)=f(y)+f\left((\sqrt{x-y})^{2}\right)=f(y)+f(\sqrt{x-y})^{2} \geqslant f(y)
|
| 816 |
+
$$
|
| 817 |
+
|
| 818 |
+
donc $f$ est linéaire sur $\mathbb{R}$. D'après l'équation $f\left(x^{2}\right)=f(x)^{2}$, son coefficient dominant a vérifie $a^{2}=$ a donc $\mathrm{a}=0$ ou $\mathrm{a}=1$, c'est-à-dire que f est soit nulle, soit l'identité sur $\mathbb{R}$. f étant surjective, nécessairement, c'est l'identité : pour tout $x, f(x)=x$.
|
| 819 |
+
En réinjectant dans l'équation, on obtient
|
| 820 |
+
|
| 821 |
+
$$
|
| 822 |
+
\forall x, y \in \mathbb{R}, \quad x^{2}+2 y=x^{2}+\alpha y
|
| 823 |
+
$$
|
| 824 |
+
|
| 825 |
+
donc avec $x=0, y=1$, on a $\alpha=2$ nécessairement. Réciproquement, si $\alpha=2$, l'identité est bien solution par le calcul précédent. Ainsi, si $\alpha \neq 2$, il n'y a aucune solution, et si $\alpha=2$, l'identité est solution.
|
| 826 |
+
|
| 827 |
+
Commentaire des correcteurs : L'exercice a été très peu abordé, une poignée d'élèves l'ont résolu parfaitement. Certains ont tenté des débuts de solution assez naturels, en montrant notamment que f était surjective et que $f(0)=0$, mais ne sont pas allés plus loin. Attention à bien noter pour quelles valeurs les égalités obtenues sont effectivement vraies : lorsqu'on fait une substitution d'une variable en fonction d'une autre on perd de la généralité. Par exemple après avoir posé $y=f\left(-x^{2}\right)$, l'égalité qui en résute n'est pas vraie pour tout $x$ et pour tout $y$.
|
| 828 |
+
|
| 829 |
+
Exercice 18. Soit $\mathrm{P}(\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :
|
| 830 |
+
|
| 831 |
+
- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou
|
| 832 |
+
- le polynôme $\mathrm{P}(\mathrm{f}(\mathrm{X})$ ).
|
| 833 |
+
|
| 834 |
+
Trouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.
|
| 835 |
+
|
| 836 |
+
## Solution de l'exercice 18
|
| 837 |
+
|
| 838 |
+
On dit qu'un entier n fonctionne si quelque soit le polynôme P initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.
|
| 839 |
+
Commençons par faire la remarque simple qu'à chaque étape, quoique choisisse Emile, le polynôme écrit au tableau sera unitaire, de degré pair, et non constant.
|
| 840 |
+
On montre les points suivants :
|
| 841 |
+
|
| 842 |
+
1. $\underline{S i n}$ fonctionne, alors $\mathrm{n}+2$ aussi :
|
| 843 |
+
|
| 844 |
+
Soit $P(X)$ un polynôme comme dans l'énoncé. Supposons qu'Emile peut trouver une suite d'opérations qui lui permet d'obtenir un polynôme $f(X)$ avec $n$ racines réelles distinctes écrit au tableau.
|
| 845 |
+
On va chercher à trouver deux constantes $a$ et $b$ telles que le polynôme $g(X)=P(f(X)+a)+b$ ait exactement $n+2$ racines réelles distinctes. Alors Emile pourra simplement ajouter $a$, composer par P , puis ajouter b au polynôme obtenu pour avoir le polynôme voulu.
|
| 846 |
+
On souhaite utiliser le fait que $f(X)$ ait exactement $n$ racines en faisant en sorte qu'une racine de $f$ soit une racine de $g(X)=P(f(X)+a)+b$, ce qui impose $b=-P(a)$. Les racines de $g(X)$ sont alors les réels $x$ tels que $f(x)+a$ soit un antécédent de $P(a)$. Pour avoir le moins de cas possibles à traiter, on choisit |a| très grand pour que l'équation $P(X)=P(a)$ ait exactement deux solutions réelles : c'est possible car pour c assez grand, l'équation $\mathrm{P}(\mathrm{X})=\mathrm{c}$ a exactement deux solutions réelles.
|
| 847 |
+
Soient $a, a^{\prime}$ les deux solutions de $P(X)=P(a)$. Ainsi, les racines de $g(X)$ sont les racines de $f(X)$ et les solutions de $f(x)+a=a^{\prime}$, c'est-à-dire les antécédents par $f$ de $a^{\prime}-a$. Encore une fois, on veut le moins d'antécédents possibles (sans pour autant en avoir aucun), donc on voudrait que $a^{\prime}-a$ soit très grand. $f$ étant unitaire de degré pair, si $a^{\prime}-a$ est assez grand, $a^{\prime}-a$ exactement 2 antécédents par f , ce qui donne bien que $g(X)$ a exactement $n+2$ racines.
|
| 848 |
+
Vérifions que l'on peut bien choisir a comme voulu. Prenons a négatif tel que $|a|$ soit très grand. Lorsque $a$ tend vers $-\infty, P(a)$ tend vers $+\infty$ et $a^{\prime}$ est la solution la plus grande de $P(X)=P(a)$ qui tend vers $+\infty . S \mathrm{Si}|a|$ est assez grand, $a^{\prime}-a$ peut devenir arbitrairement grand, comme voulu.
|
| 849 |
+
2. $\underline{n}=0$ et $\mathrm{n}=2021$ fonctionnent:
|
| 850 |
+
|
| 851 |
+
Soit $P(X)$ un polynôme comme dans l'énoncé.
|
| 852 |
+
Le cas de $\mathrm{n}=0$ est simple. En effet, $\mathrm{P}(\mathrm{X})$ est unitaire de degré pair, donc il admet un minimum $\operatorname{sur} \mathbb{R}$. Si c est strictement supérieur à l'opposé de ce minimum, $\mathrm{P}(\mathrm{x})+\mathrm{c}=0 \mathrm{n}$ 'a aucune solution sur $\mathbb{R}$. Ainsi, si Emile remplace $P(X)$ par $P(X)+c$ au premier tour, il obtient un polynôme sans racines réelles comme voulu.
|
| 853 |
+
Pour $\mathfrak{n}=2021$, c'est un peu plus subtil. Comme $x \mapsto P(x)$ est décroissant pour $x$ assez petit et croissant pour x assez grand, P a un nombre impair d'extrema locaux. Ainsi il existe c tel qu'un nombre impair de ces extrema soient en des solutions de $\mathrm{P}(\mathrm{x})=\mathrm{c}$. En effet, supposons que les valeurs prises en ces extrema soient $c_{1}, \ldots, c_{k}$, et disons que $c_{i}$ est la valeur de $P$ en $n_{i}$ extrema distincts. Alors le nombre d'extrema de $P$ est $n_{1}+\cdots+n_{k}$ et est impair, donc il existe $i$ tel que $n_{i}$ soit impair, et c'est ce qu'on voulait.
|
| 854 |
+
|
| 855 |
+
Supposons maintenant qu'Emile remplace le polynôme $P(X)$ initial par $P(X)-c$. Celui-ci est positif en $-\infty$ et $+\infty$ donc change de signe un nombre pair de fois. Mais par définition de $c$, il a aussi un nombre impair de zéros qui sont des extrema locaux (c'est-à-dire où il ne change pas de signe), et donc $\mathrm{P}(\mathrm{X})-\mathrm{c}$ a un nombre impair de racines réelles distinctes. Ce nombre est nécessairement inférieur à 2022, donc à 2021 car il est impair. Par la partie précédente de la démonstration, en ajoutant 2 à plusieures reprises au nombre de racines distinctes, Emile peut toujours obtenir, après un certain nombre d'étapes, un polynôme avec exactement 2021 racines réelles distinctes.
|
| 856 |
+
En combinant les deux premières parties de la démonstration, on obtient que tous les n pairs et les n impairs supérieurs ou égaux à 2021 fonctionnent. Il reste à voir que les autres ne fonctionnent pas.
|
| 857 |
+
3. $\mathrm{n} \leqslant 2019$ impair ne fonctionne pas :
|
| 858 |
+
|
| 859 |
+
Soit $n \leqslant 2019$ impair. Dans cette partie de la démonstration, il faut exhiber un polynôme $P(X)$ qui empêche Emile d'obtenir $n$ racines réelles distinctes en un nombre fini d'étapes. D'après la preuve de la partie précédente, il faut trouver un polynôme $P(X)$ tel que si un nombre impair d'extrema locaux de $P$ vérifient $P(x)=c$, alors $P(X)-c$ a strictement plus de 2019 racines distinctes.
|
| 860 |
+
Considérons le polynôme $P(X)=X^{2}\left(X^{2}-1\right) \ldots\left(X^{2}-1010\right)$. Il est pair donc tous ses extrema locaux vont par paires, sauf celui en 0 qui est nul. Mais le polynôme $P(X)$ a 2021 racines distinctes, et il semble donc être un bon candidat pour cette partie. Comme $P(X)$ est pair, pour tout $\mathrm{c} \neq 0$, l'équation $\mathrm{P}(\mathrm{x})=\mathrm{c}$ a un nombre pair de solutions, et l'équation $\mathrm{P}(\mathrm{x})=0$ a un nombre impair de solutions (précisément 2021).
|
| 861 |
+
Supposons par l'absurde qu'au bout d'un certain nombre d'étapes, Emile arrive à obtenir un polynôme avec $n$ racines réelles distinctes, ce polynôme sera alors de la forme $f(P(X))$, avec $f(X)$ unitaire non constant. Soient $r_{1}, \ldots, r_{k}$ les racines de $f(X)$. Les racines de $f(P(X))$ sont exactement les réels solutions d'une équation de la forme $P(x)=r_{i}$. Soit $n_{i}$ le nombre de solutions à $P(x)=r_{i}$. On a $n_{1}+n_{2}+\ldots+n_{k}=n$. Comme $n$ est impair, un des $n_{i}$ est forcément impair. Mais le seul réel $r_{i}$ ayant un nombre impair d'antécédents par $P$ est 0 , qui en a 2021. Ainsi, $r_{i}=0$ et $n_{i}=2021$, ce qui donne $n \geqslant 2021$, absurde.
|
| 862 |
+
Pour conclure, les entiers n qui fonctionnent sont les entiers pairs et les entiers impairs supérieurs ou égaux à 2021.
|
| 863 |
+
|
| 864 |
+
Commentaire des correcteurs : L'exercice n'a été abordé que par une copie qui l'a réussi parfaitement. L'exercice était très difficile, néanmoins il est dommage qu'il n'y ait pas eu plus de copies proposant au moins des pistes de recherche. Il n'est pas nécessaire d'avoir résolu entièrement un problème pour rendre quelque chose, et ici il y avait plusieurs étapes intermédiaires importantes qui pouvaient rapporter des points même si la solution n'était pas aboutie.
|
| 865 |
+
|
French_STS/md/fr-corrigé-envoi-3.md
ADDED
|
@@ -0,0 +1,343 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES<br><br>ENVOI 3 : ARITHMÉTIQUE<br>À RENVOYER AU PLUS TARD LE 17 FÉVRIER 2022
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2007 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Montrer que pour tout entier n , le nombre $\mathrm{n}^{3}-7 \mathrm{n}$ est divisible par 6 .
|
| 17 |
+
$\underline{\text { Solution de l'exercice } 1}$ Une première approche est de regarder l'expression modulo 6 :
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\mathrm{n}^{3}-7 n \equiv \mathrm{n}^{3}-\mathrm{n} \equiv(\mathrm{n}-1) \mathrm{n}(\mathrm{n}+1) \quad \bmod 6
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
donc il suffit de montrer que 6 divise $(n-1) \mathfrak{n}(n+1)$. Or parmi trois nombres consécutifs, au moins un est divisible par 2 et au moins un est divisible par 3 . Ainsi comme 2 et 3 sont premiers entre eux, $6 \mid n^{3}-n$ et donc 6 divise $n^{3}-7 n$.
|
| 24 |
+
|
| 25 |
+
Une deuxième approche qui fonctionne aussi ici consiste aussi à regarder l'expression $n^{3}-7 n$ et de montrer à la main que celle-ci est toujours nulle en faisant une disjonction de cas sur les valeurs que peut prendre n modulo 6 .
|
| 26 |
+
|
| 27 |
+
| n | $\mathrm{n}^{3}-7 \mathrm{n}$ |
|
| 28 |
+
| :---: | :---: |
|
| 29 |
+
| 0 | $0^{3}-7 \cdot 0 \equiv 0+0 \equiv 0$ |
|
| 30 |
+
| 1 | $1^{3}-7 \cdot 1 \equiv 1-1 \equiv 0$ |
|
| 31 |
+
| 2 | $2^{3}-7 \cdot 2 \equiv 8-2 \equiv 0$ |
|
| 32 |
+
| 3 | $3^{3}-7 \cdot 3 \equiv 3-3 \equiv 0$ |
|
| 33 |
+
| $4 \equiv-2$ | $(-2)^{3}-7 \cdot(-2) \equiv-2+2 \equiv 0$ |
|
| 34 |
+
| $5 \equiv-1$ | $(-1)^{3}-7 \cdot(-1) \equiv-1+1 \equiv 0$ |
|
| 35 |
+
|
| 36 |
+
Ainsi, quelle que soit la valeur de n modulo $6, \mathrm{n}^{3}-7 \mathrm{n} \equiv 0$.
|
| 37 |
+
Commentaire des correcteurs: L'exercice est très bien résolu.
|
| 38 |
+
|
| 39 |
+
Exercice 2. Soient $a, b, c$ trois entier tels que 7 divise $a^{2}+b^{2}+c^{2}$. Montrer que 7 divise $a^{4}+b^{4}+c^{4}$. Solution de l'exercice 2
|
| 40 |
+
Les carrés modulo 7 valent $0,1,2,4$. On cherche donc toutes les sommes de trois de ces nombres étant divisible par 7. Après avoir testé toutes les possibilités, on s'aperçoit que les seuls ensembles de trois carrés modulo 7 dont la somme est divisible par 7 sont $\{0,0,0\}$ et $\{1,2,4\}$.
|
| 41 |
+
On alors $\mathrm{a}^{4}+\mathrm{b}^{4}+\mathrm{c}^{4} \equiv 0^{2}+0^{2}+0^{2} \equiv 0 \bmod 7$ ou $\mathrm{a}^{4}+\mathrm{b}^{4}+\mathrm{c}^{4} \equiv 1^{2}+2^{2}+4^{2} \equiv 1+4+16 \equiv 0 \bmod 7$
|
| 42 |
+
Dans les deux cas, $a^{4}+b^{4}+c^{4} \equiv 0 \bmod 7$, comme désiré.
|
| 43 |
+
Commentaire des correcteurs: L'exercice est très bien résolu.
|
| 44 |
+
|
| 45 |
+
Exercice 3. Soit $\mathrm{a}, \mathrm{b}, \mathrm{c} \geqslant 1$ des entiers tels que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ et $\mathrm{a}^{\mathrm{c}} \mid \mathrm{c}^{\mathrm{b}}$. Montrer que $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
| 46 |
+
|
| 47 |
+
## Solution de l'exercice 3
|
| 48 |
+
|
| 49 |
+
Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $a, b$ et $c$. En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{\mathfrak{p}}(\mathfrak{a})=v_{\mathfrak{p}}\left(\mathrm{a}^{2}\right) \leqslant v_{\mathfrak{p}}(\mathrm{bc})=v_{\mathfrak{p}}(b)+v_{\mathfrak{p}}(\mathfrak{c})$.
|
| 50 |
+
Soit $p$ un nombre premier. Lhypothèse que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ se traduit en terme de valuation p -adique par $b v_{p}(a) \leqslant c v_{p}(b)$, ou encore $v_{p}(a) \leqslant \frac{c}{b} v_{p}(b)$. De même, on obtient que $v_{p}(a) \leqslant \frac{b}{c} v_{p}(c)$.
|
| 51 |
+
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathfrak{a})^{2} \leqslant v_{\mathfrak{p}}(\mathrm{b}) v_{\mathfrak{p}}(\mathfrak{c})$. On a donc, d'après l'inégalité des moyennes:
|
| 52 |
+
|
| 53 |
+
$$
|
| 54 |
+
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
ce qui donne bien $2 v_{\mathfrak{p}}(\mathrm{a}) \leqslant v_{\mathfrak{p}}(\mathrm{b})+v_{\mathfrak{p}}(\mathrm{c})$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
| 58 |
+
|
| 59 |
+
Commentaire des correcteurs: L'exercice est très bien résolu.
|
| 60 |
+
|
| 61 |
+
Exercice 4. Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
3 \cdot 2^{x}+4=\mathrm{n}^{2}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
$\underline{\text { Solution de l'exercice } 4}$ Pour $x=0$, l'équation devient $n^{2}=7$ qui n'a pas de solution. Supposons $x>0$, on factorise : $3 \cdot 2^{x}=(n-2)(n+2)$. Le membre de gauche est pair donc le membre de droite est paire. Les deux facteurs du membre de droite sont de même parité donc ils sont tous les deux pairs et on a deux cas :
|
| 68 |
+
|
| 69 |
+
- Cas 1: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}-2$ et $2^{\mathrm{b}}=\mathrm{n}+2$, avec $\mathrm{a}+\mathrm{b}=\mathrm{x}$. On peut combiner ces deux équations pour trouver $2^{b}=3 \cdot 2^{a}+4$. Notons que $n+2$ et $n-2$ ont pour différence 4 donc ils ne peuvent pas être tous les deux divisibles par 8 . On a donc $a \leqslant 2$ ou $b \leqslant 2$. Or $2^{b}>4$, donc $b>2$ et on déduit que $a \leqslant 2$. Si $a=0,2^{b}=3+4=7$ ce qui n'est pas possible. Si $a=1,2^{b}=6+4=10$ ce qui n'est pas possible non plus. Si $\mathbf{a}=2$, alors $2^{b}=12+4=16$ donc $b=4$. On obtient $x=6$ et $n=14$. réciproquement, on vérifie que $3 \cdot 2^{6}+4=196=14^{2}$ et le couple $(6,14)$ est bien solution.
|
| 70 |
+
- Cas 2: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}+2$ et $2^{\mathrm{b}}=\mathrm{n}-2$, avec $\mathrm{a}+\mathrm{b}=\mathrm{x}$. Les deux équations combinées donnent $2^{\mathrm{b}}+4=3 \cdot 2^{\mathrm{a}}$. De même que précédemment, on a $\mathrm{a} \leqslant 2$ ou $\mathrm{b} \leqslant 2$.
|
| 71 |
+
|
| 72 |
+
1. Si $b \leqslant 2$, alors $b=0,1$ ou 2 . Si $b=0$, alors $5=3 \cdot 2^{a}$ ce qui $n$ 'est pas possible. Si $b=1$, $6=3 \cdot 2^{\mathrm{a}}$ et $\mathrm{a}=1$, soit $x=2$ et $\mathrm{n}=4$ et on vérifie que $3 \cdot 2^{2}+4=16=4^{2}$ et $(2,4)$ est bien solution. Si $b=2$, alors $8=3 \cdot 2^{a}$ ce qui n'est pas possible.
|
| 73 |
+
2. Si $a \leqslant 2$, alors $a=0,1$ ou 2 . Si $a=0,2^{b}+4=3<4$ ce qui $n$ 'est pas possible. Si $a=1$, on retombe sur le cas où $b=1$ et sur le couple $(2,4)$. Si $a=2,2^{b}+4=12$ donc $b=3$. Ceci donne $x=5$ et $\mathfrak{n}=10$. Réciproquement, on vérifie que $3 \cdot 2^{5}+4=100=10^{2}$ et $(5,10)$ est bien solution.
|
| 74 |
+
|
| 75 |
+
Ainsi l'ensemble des couples ( $\boldsymbol{x}, \mathrm{n}$ ) solutions est $\{(2,4),(5,10),(6,14)\}$
|
| 76 |
+
Commentaire des correcteurs: L'exercice est globalement bien résolu, mais de nombreux élèves oublient des cas, ou oublient tout simplement de vérifier les solutions trouvées, chose pourtant cruciale dans une équation diophantienne.
|
| 77 |
+
|
| 78 |
+
Exercice 5. Un ensemble E d'entiers strictement positifs est dit intéressant si pour tout $\mathrm{n} \geqslant 1$ et pour tous $x_{1}, \ldots, x_{n}$ des éléments de $E$ deux à deux distincts, leur moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ et leur moyenne géométrique $\left(x_{1} \cdot \ldots \cdot x_{n}\right)^{\frac{1}{n}}$ sont des entiers.
|
| 79 |
+
|
| 80 |
+
1. Existe-t-il un ensemble E intéressant contenant exactement 2022 éléments?
|
| 81 |
+
2. Existe-t-il un ensemble E intéressant infini?
|
| 82 |
+
|
| 83 |
+
## Solution de l'exercice 5
|
| 84 |
+
|
| 85 |
+
1) Pour commencer, on peut remarquer que si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous multiples de $n$, chacun des nombres $\frac{x_{k}}{n}$ est un entier, de sorte que leur somme $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. De même, si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous puissances $n$-ièmes parfaites, chacun des nombres $x_{k}^{1 / n}$ est entier, de sorte que leur produit $\left(x_{1} \times \ldots \times x_{n}\right)^{\frac{1}{n}}$ est un entier. Pour trouver un ensemble E intéressant contenant exactement 2022 éléments, il suffit donc que pour tout $1 \leqslant n \leqslant 2022$, tous les éléments de $E$ soient à la fois des multiples de $n$ et des puissances $n$-ièmes parfaites. Pour cela, il suffit que tous les éléments de E soient à la fois des multiples de 2022!, et des puissances 2022!-ièmes parfaites. Ainsi, $E=\left\{(2022!)^{k 2022!}, 1 \leqslant k \leqslant 2022\right\}$ convient.
|
| 86 |
+
2) Nous allons montrer qu'il n'existe pas d'ensemble intéressant infini. En fait, on va montrer qu'il n'existe même pas d'ensemble infini d'entiers strictement positifs vérifiant l'hypothèse sur les moyennes arithmétiques. En effet, supposons par l'absurde qu'un tel ensemble infini E existe, c'est-à-dire que pour tout $n \geqslant 1$ et $x_{1}, \ldots, x_{n} \in E$ deux à deux distincts, la moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. Soit $a<b$ deux éléments quelconques de $E$ et $n \geqslant 2$. Choisissons $x_{1}<\ldots<x_{n-1}$ des éléments deux à deux distincts de $E$, et distincts de plus de a et $b$. L'hypothèse appliquée successivement aux $n$-uplets $\left(x_{1}, \ldots, x_{n-1}, a\right)$ et $\left(x_{1}, \ldots, x_{n-1}, b\right)$ assure que $n$ divise à la fois $x_{1}+\ldots+x_{n-1}+a$ et $x_{1}+\ldots+x_{n-1}+b$. Ainsi, $n$ divise la différence de ces deux nombres qui vaut $a-b$. Ceci étant vrai pour tout $\mathrm{n} \geqslant 2$, l'entier $\mathrm{a}-\mathrm{b}$ admet un nombre infini de diviseurs. Il est donc nul, c'est-à-dire que $\mathrm{a}=\mathrm{b}$. Ceci est en contradiction avec notre hypothèse de départ, un tel ensemble $E$ n'existe donc pas.
|
| 87 |
+
|
| 88 |
+
Commentaire des correcteurs : La première question de l'exercice est plus souvent traitée que la deuxième. Attention, plusieurs élèves y construisent un ensemble dont les moyennes arithmétique et géométrique de tous les éléments de l'ensemble sont entièress, mais pas les moyennes des éléments de n'importe quel sous-ensemble.
|
| 89 |
+
|
| 90 |
+
Exercice 6. Soit $p$ un nombre premier. Montrer qu'il existe une permutation $\left(a_{1}, \ldots, a_{p}\right)$ de $(1, \ldots, p)$ telle que les entiers $a_{1}, a_{1} \cdot a_{2}, \ldots, a_{1} \cdot a_{2} \cdot \ldots \cdot a_{p}$ donnent $p$ restes deux à deux distincts lorsque qu'on réalise leur divison euclidienne par $p$.
|
| 91 |
+
Solution de l'exercice 6 On peut être très optimiste sur cet exercice et vouloir que $a_{1} a_{2} \cdots a_{k} \equiv k$ $\bmod p$ pour tout $k$ compris entre 1 et $p$. Il faut donc que $a_{1}=1$ et pour tout $k \neq 1$ :
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
a_{k} \equiv \frac{a_{1} \cdots a_{k}}{a_{1} \cdots a_{k-1}} \equiv \frac{k}{k-1} \quad \bmod p
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
où l'on note $\frac{\mathrm{a}}{\mathrm{b}}$ tout nombre entier dont le reste c par la division euclidienne par $p$ vérifie $\mathrm{cb} \equiv \mathrm{a} \bmod p$, qui existe toujours dès que $b$ est non nul. Ainsi, pour $k \neq 1$, on peut poser $a_{k}$ l'élément de $\{1, \ldots, p\}$ vérifiant $(k-1) a_{k} \equiv k \bmod p$.
|
| 98 |
+
Il reste juste à vérifier que tous les nombres $a_{k}$ que l'on a formés sont bien deux à deux distincts, et ainsi que $\left\{a_{1}, \ldots, a_{p}\right\}$ est bien une permutation de $\{1, \ldots, p\}$. Supposons qu'il existe $i<j$ tels que $a_{i} \equiv a_{j}$. Si $\mathfrak{i}=1$, pour tout $\mathfrak{j} \geqslant 2, \frac{\mathfrak{j}}{\mathfrak{j}-1} \neq 1 \bmod \boldsymbol{p}$. Sinon $\frac{i}{i-1} \equiv \frac{\mathfrak{j}}{\mathfrak{j}-1}$ implique que $\mathfrak{i}-\mathfrak{j} \equiv \mathfrak{i}-\mathfrak{i}$, soit $\mathfrak{i} \equiv \mathfrak{j}$ $\bmod p$, ce qui est en contradiction avec notre hypothèse de départ.
|
| 99 |
+
Ainsi tous les $a_{k}$ sont différents modulo $p$. Etant donné qu'il y a $p$ termes dans la suite et $p$ éléments dans $\{1,2, \cdots, p\},\left(a_{1}, a_{2}, \cdots, a_{p}\right)$ est une permutation de $(1,2, \cdots p)$.
|
| 100 |
+
|
| 101 |
+
Commentaire des correcteurs: L'exercice a été peu traité. Avoir l'idée de créer une permutation telle que $a_{1} a_{2} \ldots a_{i} \equiv i \bmod p$ était l'idée principale du problème. Pour la mettre en oeuvre, il fallait une bonne compréhension de la notion d'inverse modulo $p$, et c'était le cas de la plupart des élèves qui ont rendu une solution.
|
| 102 |
+
|
| 103 |
+
Exercice 7. Soit $n \geqslant 1$ un entier. Trouver tous les diviseurs $d \geqslant 1$ de $3 n^{2}$ tels que $n^{2}+d$ soit un carré parfait.
|
| 104 |
+
Solution de l'exercice 7 Soit $d \geqslant 1$ un diviseur de $3 n^{2}$ tel que $n^{2}+d$ soit un carré parfait. Puisque $n^{2}<n^{2}+d<=n^{2}+3 n^{2}=(2 n)^{2}$, il existe $k \in \llbracket 1, n \rrbracket$ tel que $n^{2}+d=(n+k)^{2}$. En simplifiant, on obtient $d=2 k n+k^{2}$, de sorte que $k(k+2 n) \mid 3 n^{2}$.
|
| 105 |
+
Notons $\alpha=\operatorname{gcd}(k, n) \geqslant 1$. On dispose d'entiers $\ell, m \geqslant 1$ premiers entre eux tels que avec $k=\alpha l$, $\mathrm{n}=\alpha \mathrm{m}$. La relation de divisibilité précédente s'écrit alors, après simplification, $\ell(\ell+2 \mathrm{~m}) \mid 3 \mathrm{~m}^{2}$. Or on $\operatorname{agcd}(\ell+2 \mathrm{~m}, \mathrm{~m})=\operatorname{gcd}(\ell+2 \mathrm{~m}-2 \mathrm{~m}, \mathrm{~m})=\operatorname{gcd}(\ell, \mathrm{m})=1$, c'est-à-dire $\ell+2 \mathrm{~m}$ premier avec m , donc avec $\mathrm{m}^{2}$. Comme $\ell+2 \mathrm{~m} \mid 3 \mathrm{~m}^{2}$, on a par le lemme de Gauss $\ell+2 \mathrm{~m} \mid 3$, c'est-à-dire $\ell+2 \mathrm{~m} \in\{1,3\}$. Mais $\ell, \mathrm{m} \geqslant 1$ donc $\ell+2 \mathrm{~m} \geqslant 3$. Autrement dit, $\ell+2 \mathrm{~m}=3$ et donc nécessairement, $\ell=\mathrm{m}=1$. Alors $k=n=\alpha$, et $d=k(k+2 n)=3 n^{2}$.
|
| 106 |
+
Réciproquement, $d=3 n^{2}$ convient puisque c'est un diviseur de $3 n^{2}$ et que $n^{2}+3 n^{2}=(2 n)^{2}$.
|
| 107 |
+
Commentaire des correcteurs: L'exercice est peu traité. Toutes les copies ont la bonne intuition de l'unique solution. D'autres démonstrations que celle du corrigé ont été proposées par des élèves (elles passent notamment par la parité des valuations $p$-adiques pour $p$ premier et en trouvant les $m$ tels que $\frac{\mathrm{m}+3}{\mathrm{~m}}$ est un carré de rationnel).
|
| 108 |
+
|
| 109 |
+
Exercice 8. Un ensemble $A$ d'entiers est dit admissible s'il vérifie la propriété suivante : pour tous $x, y \in A$ (non nécessairement distincts), et pour tout $k \in \mathbb{Z}$, on a $x^{2}+k x y+y^{2} \in A$.
|
| 110 |
+
Déterminer tous les couples d'entiers non nuls ( $\mathrm{m}, \mathrm{n}$ ) tels que le seul ensemble admissible contenant à la fois $m$ et $n$ soit $\mathbb{Z}$.
|
| 111 |
+
|
| 112 |
+
Solution de l'exercice 8 Remarquons que si $\mathrm{d}=\operatorname{gcd}(\mathrm{m}, \mathfrak{n})>1$ alors l'ensemble $A$ des multiples de d est un ensemble admissible contenant $n$ et $m$ mais $n$ 'étant pas égal à $\mathbb{Z}$. En effet, si $x$ et $y$ sont multiples de $d$, alors pour tout entier $k, x^{2}+k x y+y^{2}$ est bien divisible par $d$ et est dans $A$. On déduit que les couples $(m, n)$ recherchés doivent vérifier $\operatorname{gcd}(m, n)=1$.
|
| 113 |
+
Réciproquement, soient $m$ et $n$ des entiers tels que $\operatorname{gcd}(m, n)=1$. Montrons que tout ensemble admissible contenant $m$ et $n$ est $\mathbb{Z}$. Soit $A$ un ensemble admissible contenant $m$ et $n$. Remarquons que si $x \in A$, alors l'hypothèse nous donne que pour tout entier $k$, l'entier $x^{2}+k x \cdot x+x^{2}=(k+2) x^{2}$ est dans $A$. On déduit que tout multiple de $x^{2}$ est dans $A$ si $x$ est dans $A$.
|
| 114 |
+
Notons que si $\operatorname{gcd}(m, n)=1$, alors on a aussi $\operatorname{gcd}\left(m^{2}, n^{2}\right)=1$. D'après le théorème de Bezout, on dispose donc d'entiers $u, v \in \mathbb{Z}$ tels que $u^{2}+v n^{2}=1$. Comme $u m^{2}$ et $v n^{2}$ sont dans $A$, en appliquant l'hypothèse à $x=u m^{2}, y=v n^{2}$ et $k=2$, on a
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
\left(u m^{2}\right)^{2}+2 u m^{2} v n^{2}+\left(v n^{2}\right)^{2}=\left(u m^{2}+v n^{2}\right)^{2}=1^{2}=1 \in A
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
Par conséquent, $\forall k \in \mathbb{Z}, k \cdot 1^{2} \in A$. Ainsi $A=\mathbb{Z}$ et le seul ensemble admissible contenant $m$ et $n$ est $\mathbb{Z}$.
|
| 121 |
+
Les couples recherchés sont donc les couples d'entiers ( $m, n$ ) premiers entre eux.
|
| 122 |
+
Commentaire des correcteurs : Parmi les élèves ayant rendu une tentatives, on trouve beaucoup de solutions complètes. Parmi les solutions non complètes, la plupart des élèves ont deviné la nature des couples solutions et ont réussi à montrer que si 1 est dans $A$, alors $A=\mathbb{Z}$. Avoir été si loin dans ce problème difficile est déjà très bien!
|
| 123 |
+
|
| 124 |
+
Exercice 9. Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\mathrm{a}!+5^{\mathrm{b}}=7^{\mathrm{c}}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
$\underline{\text { Solution de l'exercice } 9}$ Un premier réflexe à avoir est de regarder les petites valeurs de $\mathrm{a}, \mathrm{b}$ et c que l'on peut trouver dans une solution ( $a, b, c$ ).
|
| 131 |
+
Tout d'abord, si $a=0$ ou $a=1$, alors $a!=1$, donc $0 \equiv a!+5^{b} \equiv 7^{c} \equiv 1(\bmod 2)$, ce qui est impossible. On en déduit que $a \geqslant 2$.
|
| 132 |
+
Puis, si $a \geqslant 7$, alors $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 5)$ et $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 7)$, donc $b=c=0$. Mais alors $\mathrm{a}!+5^{\mathrm{b}}=\mathrm{a}!+1 \neq 1=7^{\mathrm{c}}$, ce qui est impossible. On en déduit que $2 \leqslant \mathrm{a} \leqslant 6$.
|
| 133 |
+
Supposons maintenant que $\mathrm{b} \leqslant 1$. Alors
|
| 134 |
+
|
| 135 |
+
$$
|
| 136 |
+
7^{\mathfrak{c}}=\mathrm{a}!+5^{\mathrm{b}} \in\{2,6,24,120,720\}+\{1,5\}=\{3,7,11,25,29,121,125,721,725\}
|
| 137 |
+
$$
|
| 138 |
+
|
| 139 |
+
Dans ce dernier ensemble, seul 7 lui-même est une puissance de 7 . On en déduit les deux triplets solutions $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1)$ et $(3,0,1)$, qui sont les deux seules solutions pour $b \leqslant 1$.
|
| 140 |
+
On s'intéresse enfin aux cas où $b \geqslant 2$. Alors $a!\equiv a!+5^{b} \equiv 7^{\mathrm{c}}(\bmod 25)$. Or, comme $7^{2} \equiv-1$ $(\bmod 25)$, on sait que $7^{\mathrm{c}} \equiv 1,7,-1$ ou $-7(\bmod 25)($ selon que $\mathrm{c} \equiv 0,1,2$ ou $3(\bmod 4))$ et que $\mathrm{a}!\equiv 2,6,-1,-5$ ou $-5(\bmod 25)($ selon que $a$ vaut $2,3,4,5$ ou 6$)$. Cela signifie donc que $a=4$ et $\mathrm{c} \equiv 2(\bmod 4)$.
|
| 141 |
+
Mais alors $(-3)^{\mathrm{b}} \equiv \mathrm{a}!+5^{\mathrm{b}} \equiv(-1)^{\mathrm{c}} \equiv 1(\bmod 8)$, ce qui signifie que b est pair. On pose alors $\beta=\mathrm{b} / 2$ et $\gamma=\mathrm{c} / 2$, de sorte que
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
24=\mathrm{a}!=7^{\mathrm{c}}-5^{\mathrm{b}}=\left(7^{\gamma}+5^{\beta}\right)\left(7^{\gamma}-5^{\beta}\right) .
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
On en déduit notamment que $7^{\gamma}+5^{\beta} \leqslant 24$, donc que $\gamma \leqslant 1$ et $\mathrm{c} \leqslant 2$. Comme $\mathrm{c} \equiv 2(\bmod 4)$, cela signifie que $\mathrm{c}=2$, donc que $5^{\mathrm{b}}=7^{\mathrm{c}}-\mathrm{a}!=49-24=25=5^{2}$.
|
| 148 |
+
Les solutions recherchées sont donc les triplets $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1),(3,0,1)$ et $(4,2,2)$.
|
| 149 |
+
Commentaire des correcteurs: Globalement bien traité pour ceux qui l'ont rédigé, le principal souci de cet exercice consistait à bien se ramener à $a<7$, et à travailler modulo la bonne puissance de nombre premier, ici 25 , ce qui a été plutôt bien trouvé. Il faut bien faire attention aux cas limites $(\mathrm{b}=0, \mathrm{c}=0)$.
|
| 150 |
+
|
| 151 |
+
## Exercices Seniors
|
| 152 |
+
|
| 153 |
+
Exercice 10. Soit $a, b, c \geqslant 1$ des entiers tels que $a^{b} \mid b^{c}$ et $a^{c} \mid c^{b}$. Montrer que $a^{2} \mid b c$.
|
| 154 |
+
Solution de l'exercice 10 Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $\mathrm{a}, \mathrm{b}$ et c . En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{p}(a)=v_{p}\left(a^{2}\right) \leqslant$ $v_{p}(b c)=v_{p}(b)+v_{p}(c)$.
|
| 155 |
+
Soit $p$ un nombre premier. L'hypothèse que $a^{b} \mid b^{c}$ se traduit en terme de valuation $p$-adique par $\mathrm{b} v_{\mathfrak{p}}(\mathrm{a}) \leqslant \mathrm{c} v_{p}(\mathrm{~b})$, ou encore $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{c}}{\mathrm{b}} \nu_{p}(\mathrm{~b})$. De même, on obtient que $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{b}}{\mathrm{c}} \nu_{p}(\mathrm{c})$.
|
| 156 |
+
|
| 157 |
+
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathrm{a})^{2} \leqslant \nu_{p}(b) v_{p}(c)$. On a donc, d'après l'inégalité des moyennes:
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
ce qui donne bien $2 v_{p}(a) \leqslant v_{p}(b)+v_{p}(c)$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $a^{2} \mid b c$.
|
| 164 |
+
|
| 165 |
+
Commentaire des correcteurs : Le problème est globalement bien réussi. Une poignée d'élèves s'est trompée en affirmant que si $a$ divise $b^{c}$, alors $a$ divise $b$. Cette affirmation peut être réfutée en regardant $\mathrm{a}=25, \mathrm{~b}=10$ et $\mathrm{c}=2$.
|
| 166 |
+
|
| 167 |
+
Exercice 11. Trouver tous les entiers $n \geqslant 1$ tels que
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
6^{n}-1 \mid 7^{n}-1
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
Solution de l'exercice 11 Soit $n$ un éventuel entier vérifiant $6^{n}-1 \mid 7^{n}-1$.
|
| 174 |
+
On a $5=6-1 \mid 6^{n}-1^{n}$, donc $5 \mid 7^{n}-1$. On calcule donc les puissances de 7 modulo 5 :
|
| 175 |
+
|
| 176 |
+
| | $n$ | 0 | 1 | 2 | 3 | 4 |
|
| 177 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 178 |
+
| $7^{\mathrm{n}}(\bmod 5)$ | 1 | 2 | 4 | 3 | 1 | |
|
| 179 |
+
|
| 180 |
+
Ainsi, si on note $n=4 q+r$ la division euclidienne de $n$ par 4 , on a $7^{n} \equiv\left(7^{4}\right)^{q} \times 7^{r} \equiv 1^{q} 7^{r} \equiv 7^{r}$ $(\bmod 5)$. Donc pour que $5 \mid 7^{n}-1$, il faut que $r=0$, autrement dit $n$ est multiple de 4 .
|
| 181 |
+
En regardant alors modulo 7 , on obtient $6^{n} \equiv(-1)^{4 \mathrm{q}} \equiv 1(\bmod 7)$, donc $7\left|6^{n}-1\right| 7^{n}-1$, ce qui n'est pas possible.
|
| 182 |
+
Il n'y a donc aucun $n$ vérifiant $6^{n}-1 \mid 7^{n}-1$.
|
| 183 |
+
Commentaire des correcteurs: L'exercice est très bien résolu et a été traité par de nombreux élèves.
|
| 184 |
+
|
| 185 |
+
Exercice 12. Déterminer tous les couples d'entiers strictement positifs ( $\mathfrak{m}, \mathfrak{n}$ ) tels que
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
m n-1 \mid n^{3}-1
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
Solution de l'exercice 12 Remarquons que les couples $(1, \mathfrak{n})$ et $(\mathfrak{m}, 1)$ sont solutions pour tous les entiers strictement positifs $m$ et $n$. On suppose dans la suite que $m, n \geqslant 2$.
|
| 192 |
+
Notons que les nombres $m n-1, n^{3}-1$ sont strictement positifs. La condition de divisibilité implique donc que $\mathrm{mn}-1 \leqslant \mathrm{n}^{3}-1$, donc $\mathrm{m} \leqslant \mathrm{n}^{2}$.
|
| 193 |
+
On commence par ramener un peu de symétrie au problème en remarquant que $\mathrm{mn}-1$ divise $(\mathrm{mn})^{3}-1^{3}$, de sorte que $\mathfrak{m n}-1$ divise $(\mathfrak{m n})^{3}-1-\mathfrak{m}^{3}\left(\mathfrak{n}^{3}-1\right)=\mathfrak{m}^{3}-1$.
|
| 194 |
+
Maintenant que le problème est complètement symétrique en $m$ et $n$, on peut supposer sans perte de généralité que $m \geqslant n . m \geqslant n$. Puisque $m n-1$ divise $n^{3}-1$ et $m n-1$, il divise également $n^{3}-1-$ $(m n-1)=n\left(n^{2}-\mathfrak{m}\right)$. Comme $m n-1$ et $n$ sont premiers entre eux, on a par le lemme de Gauss que $m n-1$ divise $n^{2}-m$. Mais alors, si $n^{2}-m$ est non nul, puisque $m \geqslant n$ et $m \geqslant 1$,
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
0<\mathfrak{n}^{2}-\mathfrak{m}<\mathrm{mn}-1 \leqslant \mathfrak{n}^{2}-\mathrm{m}
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
ce qui est impossible. On a donc $n^{2}=m$. Réciproquement, le couple ( $\left.n^{2}, n\right)$ est bien solution $\left(n^{2}, n\right)$.
|
| 201 |
+
Ainsi, les couples solutions sont $\left\{(1, \mathfrak{n}),(\mathfrak{n}, 1),\left(\mathfrak{n}^{2}, \mathfrak{n}\right),\left(\mathfrak{n}, \mathfrak{n}^{2}\right)\right\}$.
|
| 202 |
+
|
| 203 |
+
## Solution alternative:
|
| 204 |
+
|
| 205 |
+
De même que précédemment, on se ramène au cas où $n \geqslant 2$.
|
| 206 |
+
Soit $(m, n)$ une solution. On a donc un entier a tel que $n^{3}-1=a(m n-1)$. En passant modulo $n$, on obtient $-1 \equiv-a(\bmod \mathfrak{n})$, soit $a \equiv 1(\bmod \mathfrak{n})$. Écrivons donc $a=k n+1$.
|
| 207 |
+
En réinjectant, on obtient $n^{3}-1=(k n+1)(m n-1)=k m n^{2}+(m-k) n-1$, ce qui se simplifie en $\mathrm{n}^{2}=\mathrm{kmn}+\mathrm{m}-\mathrm{k}$.
|
| 208 |
+
Repasser modulo $n$ nous donne $m \equiv k(\bmod n)$, donc si $m=n p+r$ et $k=n q+r^{\prime}$ sont les divisions euclidiennes de $m$ et $k$ par $n$, on a $r=r^{\prime}$. On réécrit donc l'égalité sous la forme $n^{2}=$ $(n p+r)(n q+r) n+n p+r-(n q+r)$, qu'on peut encore une fois simplifier:
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
n=p-q+n^{2} p q+n r(p+q)+r^{2}
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
Si $p \geqslant 1$, alors $n=p-q+n^{2} p q+n r(p+q)+r^{2} \geqslant n^{2} q-q=q\left(n^{2}-1\right)$. Ainsi si $q \geqslant 1$, il faut $n \geqslant n^{2}-1$, impossible car $n \geqslant 2$.
|
| 215 |
+
On vient de montrer qu'au moins un nombre parmi $p$ et $q$ doit être nul.
|
| 216 |
+
Si $p=0$ et $q \geqslant 1$, on a $n=q(n r-1)+r^{2}$. Comme $r=m \geqslant 1, \mathfrak{n r}-1 \geqslant 1$ donc $\mathbf{q}(\mathfrak{n r}-1) \geqslant \mathfrak{n r}-1$ donc $n=q(n r-1)+r^{2} \geqslant(\mathfrak{n r}-1)+1=n r \geqslant n$. Toutes ces inégalités sont donc des égalités, ce qui impose $\mathrm{q}=\mathrm{r}=1$. On obtient donc $\mathrm{m}=1$.
|
| 217 |
+
Si $q=0$ et $p \geqslant 1$, on a $n=p(n r+1)+r^{2}$. Ainsi, si $r \geqslant 1$, on a $n \geqslant n+2$, donc $r=0$, puis $n=r$ et finalement $m=n^{2}$.
|
| 218 |
+
Si $p=q=0$, on a $n=r^{2}$ et $m=r$.
|
| 219 |
+
Ainsi les solutions sont les couples $(1, n)$ et $\left(n^{2}, n\right)$ pour tout $n \geqslant 1$, ainsi que les couples $\left(r, r^{2}\right)$ avec $r \geqslant 1$. On vérifie réciproquement que tous ces couples sont solutions, et que $n=1$ donne bien les mêmes solutions (puisqu'a priori ce ne sont que les solutions avec $n \geqslant 2$ ).
|
| 220 |
+
|
| 221 |
+
Commentaire des correcteurs: L'exercice est globalement bien réussi. Pas mal d'élèves oublient de traiter les cas particuliers de leur raisonnement, alors que dans un tel problème c'est justement les cas particuliers/dégénérés qui donnent les solutions.
|
| 222 |
+
|
| 223 |
+
Exercice 13. Soit $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ une fonction telle que pour tout entier $\mathrm{n} \geqslant 1, \mathrm{f}(\mathrm{f}(\mathrm{n}))$ soit égal au nombre de diviseurs positifs de $n$. Montrer que si $p$ est un nombre premier, alors $f(p)$ est aussi un nombre premier.
|
| 224 |
+
|
| 225 |
+
## Solution de l'exercice 13
|
| 226 |
+
|
| 227 |
+
Dans la suite, on note $d(n)$ le nombre de diviseurs positifs de $n$. Si $p$ est premier, on a $f(f(p))=2$ par définition. En appliquant f des deux côtés de l'égalité, on voit que $f(2)=d(f(p))$. On veut donc montrer que $f(2)=2$, ce qui prouvera que $f(p)$ a exactement deux diviseurs et est donc premier. Or, on a aussi $f(2)=d(f(2))$. Or, pour qu'un entier $\boldsymbol{n} \geqslant 2$ soit égal à son nombre de diviseurs, tous les nombres inférieurs à $n$ doivent diviser $n$, y compris $n-1$ qui est toujours premier avec $n$, donc $n-1=1$ et $n=2$. On déduit que $f(2) \in\{1,2\}$. Si $f(2)=1$, alors $d(f(p))=1$ pour tout $p$ premier, donc $f(p)=1$ pour $p$ premier, puisque 1 est le seul entier à admettre un seul diviseur. Mais alors
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
1=\mathbf{f}(3)=\mathbf{f}\left(\mathrm{d}\left(2^{2}\right)\right)=\mathbf{f}\left(\mathbf{f}\left(\mathbf{f}\left(2^{2}\right)\right)\right)=\mathrm{d}\left(\mathbf{f}\left(2^{2}\right)\right)
|
| 231 |
+
$$
|
| 232 |
+
|
| 233 |
+
et l'on déduit que $f(4)=1$. Mais alors
|
| 234 |
+
|
| 235 |
+
$$
|
| 236 |
+
\mathbf{f}(\mathbf{f}(4))=\mathbf{f}(1)=\mathbf{f}(\mathbf{f}(2))=\mathrm{d}(2)=2 \neq \mathrm{d}(4)
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
ce qui fournit la contradiction désirée. On a donc bien $\boldsymbol{f}(2)=2$, ce qui conclut.
|
| 240 |
+
Commentaire des correcteurs : Une bonne partie des élèves ont résolu le problème, mais beaucoup d'autres sont allés bien trop vite. En effet, à partir de l'égalité $f(f(f(p)))=f(p)$, il est tentant de conclure immédiatemment que $\boldsymbol{f}(\mathfrak{p})=2$. Mais un autre cas possible est le cas où $f(2)=1$, puisque 1 vérifie aussi que $d(n)=n$. C'est traiter ce cas qui constituait la principale difficulté du problème. Il est donc dommage d'être passé à côté.
|
| 241 |
+
|
| 242 |
+
Exercice 14. On dit que deux entiers $a, b \in \mathbb{N}^{\star}$ sont reliés s'il existe un nombre premier $p$ tel que $\mathrm{a}=\mathrm{pb}$ ou $\mathrm{b}=\mathrm{pa}$.
|
| 243 |
+
Trouver tous les entiers $n \geqslant 1$ ayant la propriété suivante : on peut écrire tous les diviseurs positifs de $n$ (1 et n compris) exactement une fois sur un cercle de sorte que tout diviseur soit relié avec chacun de ses deux voisins?
|
| 244 |
+
Solution de l'exercice 14 Traitons d'abord le cas où $n$ n'a qu'un seul facteur premier, donc $\mathrm{n}=\mathrm{p}^{\alpha}$. Si $\alpha \leqslant 1$, n'importe quelle configuration marche. En revanche, si $\alpha \geqslant 2,1$ doit être placé à côté de deux nombres différents, et n'est relié qu'à un seul autre diviseur de $p^{\alpha}$ (celui-ci étant $p$ ), ce n'est donc pas possible.
|
| 245 |
+
Remarquons que la parité du nombre de diviseurs premiers comptés avec multiplicité change forcément entre un nombre et un nombre qui lui est relié. Ainsi, si $n$ a un nombre impair de diviseurs, l'existence d'une telle configuration impliquerait que 1 a à la fois un nombre pair et un nombre impair de diviseurs premiers, ce qui n'est pas possible. Les nombres ayant un nombre impair de diviseurs étant les carrés parfaits, ceux-ci ne vérifient pas non plus la propriété de l'énoncé.
|
| 246 |
+
Maintenant, essayons de résoudre le cas où on a deux facteurs premiers, mettons $n=p^{a} q^{b}$ avec l'un des nombres $a$ ou b étant impair, et l'on suppose sans perte de généralité qu'il s'agit de $a$.
|
| 247 |
+
L'arrangement suivant fonctionne :
|
| 248 |
+
|
| 249 |
+
$$
|
| 250 |
+
1, q, q^{2}, \ldots, q^{b}, p q^{b}, p q^{b-1}, \ldots, p q, p^{2} q, \ldots, p^{a-1} q^{b}, p^{a} q^{b}, p^{a} q^{b-1}, \ldots, p^{a} q, p^{a}, p^{a-1}, \ldots, p, 1
|
| 251 |
+
$$
|
| 252 |
+
|
| 253 |
+
On utilise le fait que a est impair pour dire qu'on a effectivement écrit $p^{a-1} q^{b}$ juste avant $p^{a} q^{b}$.
|
| 254 |
+
On procède maintenant par récurrence sur le nombre de diviseurs premiers : supposons avoir montré pour un $k \geqslant 2$ que tous les nombres de la forme $\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ avec au moins l'un des $\alpha_{i}$ impair vérifient la propriété de l'énoncé, et soit $n=\prod_{i=1}^{k+1} p_{i}^{\alpha_{i}}$ avec au moins l'un des $\alpha_{i}$ impairs, disons $\alpha_{1}$. Alors l'hypothèse de récurrence nous dit qu'on peut ordonner les diviseurs de $n^{\prime}=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ de la forme $d_{1}, \ldots d_{m}$ de sorte que $d_{i}$ et $d_{i+1}$ soient tous reliés, de même que $d_{m}$ et $d_{1}$. Alors l'arrangement suivant fonctionne pour $m$ (car mest pair) :
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
d_{1}, p_{k+1} d_{1}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{1}, p_{k+1}^{\alpha_{k+1}} d_{2}, \ldots p_{k+1} d_{2}, d_{2}, d_{3}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{m}, \ldots p_{k+1} d_{m}, d_{m}, d_{1}
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
Ainsi les nombres qui ne vérifient pas cette propriété sont les carrés (différents de 1 ) et le puissances (plus grandes que 2) de nombres premiers.
|
| 261 |
+
|
| 262 |
+
Commentaire des correcteurs: L'exercice, un peu combinatoire, est relativement peu traité mais globalement bien réussi par les élèves qui l'ont abordé. La plupart des élèves qui ont l'intuition de la construction à réaliser pour des nombres composés ont des difficultés à la formuler rigoureusement (par une récurrence).
|
| 263 |
+
|
| 264 |
+
Exercice 15. Soit $m, n \geqslant 2$ des entiers tels que $\operatorname{PGCD}(m, n)=\operatorname{PGCD}(m, n-1)=1$. On définit la suite $\left(n_{k}\right)_{k \in \mathbb{N}}$ par $n_{0}=m$ et $n_{k+1}=n \cdot n_{k}+1$ pour $k \in \mathbb{N}$. Montrer que les entiers $n_{1}, \ldots, n_{m-1}$ ne peuvent pas tous être des nombres premiers.
|
| 265 |
+
Solution de l'exercice 15 Tout d'abord, la suite ( $\mathrm{n}_{\mathrm{k}}$ ) est une suite arithmético-géométrique. On peut donc établir une formule close pour son terme général, à savoir $n_{k}=n^{k} m+\frac{n^{k+1}-1}{n-1}$, que l'on peut aussi obtenir par récurrence à partir du calcul des premiers termes. De cette expression on déduit en particulier que $n_{k}>m$ pour tout $k>0$. On va désormais montrer que l'un des nombres $n_{1}, \ldots, n_{m-1}$ est divisible par $m$, ce qui fera de ce nombre un nombre composé.
|
| 266 |
+
En passant modulo $m$, on déduit $n_{k} \equiv \frac{\mathfrak{n}^{k+1}-1}{n-1} \bmod m$ par récurrence, où l'on a utilisé que $n-1$ est inversible modulo $m$ car $n-1$ est premier avec $m$.
|
| 267 |
+
Soit $\omega$ l'ordre de $n \bmod m$ (celui-ci existe car $m$ et $n$ premiers entre eux). On a $\omega \leqslant \varphi(m) \leqslant m-1$ d'après le théorème d'Euler. On déduit que $m \mid n^{\omega}-1$, ce qui implique que $m$ divise $n_{\omega-1}-1$ comme voulu. Ainsi, les $n_{k}$ ne sont pas tous premiers.
|
| 268 |
+
|
| 269 |
+
Commentaire des correcteurs: L'exercice est très bien résolu. Les élèves ont pratiquement tous pensé à justifier le fait que $m<n_{k}$, ce qui est nécessaire pour conclure que $n_{k}$ est composé s'il est divisible par m.
|
| 270 |
+
|
| 271 |
+
Exercice 16. Soient $p$ un nombre premier impair et $x_{1}, \ldots, x_{p}$ des entiers relatifs.
|
| 272 |
+
On suppose que pour tout $k \geqslant 1$ entier, on a
|
| 273 |
+
|
| 274 |
+
$$
|
| 275 |
+
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
Montrer que les entiers $x_{1}, \ldots, x_{p}$ sont tous congrus modulo $p$.
|
| 279 |
+
Solution de l'exercice 16 Notons que la relation est également vrai pour $k=0$ car $\underbrace{1+\ldots+1}_{\mathrm{p} \text { fois }} \equiv 0$ $\bmod p$
|
| 280 |
+
Soit $\mathrm{Q}(\mathrm{X})=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} X^{\mathrm{k}}$ un polynôme à coefficients entiers. On a
|
| 281 |
+
|
| 282 |
+
$$
|
| 283 |
+
\mathrm{Q}\left(\mathrm{x}_{1}\right)+\ldots+\mathrm{Q}\left(\mathrm{x}_{\mathrm{p}}\right)=\sum_{\ell=1}^{p} \sum_{k=0}^{n} \mathrm{a}_{\mathrm{k}} x_{\ell}^{k}=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} \underbrace{\sum_{\ell=1}^{p} x_{\ell}^{k}}_{\equiv 0 \bmod p} \equiv 0 \bmod p
|
| 284 |
+
$$
|
| 285 |
+
|
| 286 |
+
On suppose par l'absurde que les $x_{i}$ ne donnent pas tous le même reste modulo $p$. Soit $\left\{y_{1}, \ldots, y_{r}\right\}$ l'ensemble des restes modulo $p$ généré par l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$, avec $y_{1} \equiv x_{1}$. On note $a_{1}$ le nombre d'éléments de l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$ qui ont pour reste $y_{1}$. Soit $P(X)=\left(X-y_{2}\right) \ldots\left(X-y_{r}\right)$. P est nul en chacun des $y_{i}$ pour $i \neq 0$. Notons que comme $y_{1} \neq y_{i} \bmod p, P\left(y_{1}\right) \neq 0 \bmod p$. La relation établie plus haut nous donne alors $a_{1} P\left(y_{1}\right) \equiv 0 \bmod p$, ce qui implique que $a_{1}=0 \bmod p$, c'est-à-dire que $a_{1}=p$. Cela est en contradiction avec notre supposition de départ, donc les $x_{i}$ sont tous égaux.
|
| 287 |
+
|
| 288 |
+
Solution alternative : On présente une solution un peu plus conceptuelle qui s'appuie sur la structure de corps de $\mathbb{Z} / p \mathbb{Z}$ et sur le fait que les sommes de Newton des racines d'un polynôme déterminent ses coefficients.
|
| 289 |
+
Soit $P(X)=\left(X-x_{1}\right) \ldots\left(X-x_{p}\right)$ le polynôme unitaire à coefficients entiers dont les racines sont les $x_{\ell}$. L'hypothèse de l'énoncé nous indique que les sommes de Newton des $x_{\ell}$ sont nulles modulo $p$.
|
| 290 |
+
Or il est possible de relier les coefficients du polynômes P aux sommes de Newton du polynôme P , via les formules suivantes: si $a_{k}$ est le coefficient devant $X^{k}$ dans l'écriture de $P$, alors pour tout $0 \leqslant k \leqslant p$ :
|
| 291 |
+
|
| 292 |
+
$$
|
| 293 |
+
k a_{p-k}=(-1)^{k-1} \sum_{\ell=1}^{k-1} a_{p-\ell}\left(x_{1}^{\ell}+\ldots+x_{p}^{\ell}\right)
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
On peut retrouver ces formules par récurrence à l'aide des relations de Viète.
|
| 297 |
+
On remarque alors que si $k \neq 0, p, k a_{p-k} \equiv 0 \bmod p$ car chacune des $x_{1}^{\ell}+\ldots+x_{p}^{\ell}$ est divisible par $p$. Ainsi, dans $\mathbb{Z} / p \mathbb{Z}[X]$, le polynôme $P$ est de la forme $P(X)=X^{p}-a=X^{p}-a^{p}=(X-a)^{p}$, où l'on a utilisé que $a^{p} \equiv a(\bmod p)$ par le petit théorème de Fermat et que dans la formule $(X-a)^{p}=$ $\sum_{k=0}^{p}\binom{p}{k} a^{p-k} X^{k}$, seuls les coefficients $\binom{p}{0}$ et $\binom{p}{p}$ sont non nuls modulo $p$. Cela implique que les $x_{i}$ sont tous égaux (à $a$ ) modulo $p$ comme voulu.
|
| 298 |
+
|
| 299 |
+
Commentaire des correcteurs : L'exercice est très bien réussi. Cet exercice demandait de la culture sur les polynômes modulo $p$, et les élèves ont présenté diverses preuves pour s'en sortir.
|
| 300 |
+
|
| 301 |
+
Exercice 17. Soit $n$ un entier strictement positif et soient $a, a_{1}, \ldots, a_{n}$ des entiers strictement positifs. On suppose que pour tout entier $k$ pour lequel l'entier $a k+1$ est un carré parfait, au moins l'un des entiers $a_{1} k+1, \ldots, a_{n} k+1$ est également un carré parfait.
|
| 302 |
+
Montrer qu'il existe un indice $1 \leqslant i \leqslant n$ tel que $a=a_{i}$.
|
| 303 |
+
Solution de l'exercice 17 Commençons par deux lemmes sur les résidus quadratiques.
|
| 304 |
+
Lemme 1 : Si $x$ est résidu quadratique modulo $p$ avec $p$ premier impair, il l'est aussi modulo $p^{2}$ (et même $\mathrm{p}^{\mathrm{m}}$, mais on n'en a pas besoin ici).
|
| 305 |
+
Démonstration: En effet, soit a tel que $a^{2} \equiv x(\bmod p)$, ce qu'on réécrit sous la forme $a^{2}-x=k p$. Mais alors on obtient $\left(a-2^{-1} k p\right)^{2} \equiv a^{2}-k p \equiv x\left(\bmod p^{2}\right)$, et 2 est inversible modulo $p^{2}$ car $p$ est impair. Ainsi, $x$ est bien un résidu quadratique modulo $p^{2}$.
|
| 306 |
+
Lemme 2: Sii $t$ est un entier non nul et $p$ est un nombre premier tel que $p \equiv 1(\bmod 8 \mathrm{t})$, alors $\left(\frac{\mathrm{t}}{\mathrm{p}}\right)=1$.
|
| 307 |
+
Démonstration : En effet, soit $q$ un diviseur premier de $t$ et $\alpha=\nu_{q}(t)$. Si $q=2,\left(\frac{2}{p}\right)=1$ car $p \equiv 1(\bmod 8)$. donc $q$ est résidu quadratique modulo $p$. Notons maintenant que $\alpha$ est pair, alors $q^{\alpha}$ est automatiquement un carré modulo $p$, et si $\alpha$ est impair, $q^{\alpha}$ est le produit de $q$ (qui est un carré) avec $q^{\alpha-1}$ qui est un carré, donc $q^{\alpha}$ est un carré modulo $p$. Si $q \geqslant 3$, comme $p \equiv 1(\bmod 4)$, la loi de réciprocité quadratique nous donne $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{1}{q}\right)=1$, De même que précédemment, on déduit que $\left(\frac{q^{\alpha}}{p}\right)=1$. La multiplicativité des symboles de Legendre permet de conclure que $\left(\frac{t}{p}\right)=1$.
|
| 308 |
+
On rappelle également un cas particulier du théorème de la progression arithmétique de Dirichlet : pour tout $t$ entier, il existe une infinité de nombres premiers $p$ tels que $p \equiv 1 \bmod 8 t$.
|
| 309 |
+
Revenons à l'exercice. Supposons par l'absurde que tous les $a_{i}$ sont différents de $a$.
|
| 310 |
+
Posons $M=\max \left\{a, a_{1}, \ldots, a_{n}\right\} \geqslant 2$. On construit alors une suite de nombres premiers $p_{1}, \ldots p_{n}$ par récurrence comme suit : par le théorème de la progression arithmétique de Dirichlet, il existe au moins un nombre premier $p_{1} \equiv 1\left(\bmod 8 a_{1}\left(a_{1}-a\right)\right)$ avec $p_{1}>M$. (On utilise ici le fait que $\left.a_{1}-a \neq 0\right)$.
|
| 311 |
+
Pour $2 \leqslant i \leqslant n$, on prend ensuite $p_{i}$ tel que $p_{i} \equiv 1\left(\bmod 8 a_{i}\left(a_{i}-a\right)\right.$ ) avec $p_{i}>p_{i-1}$ (qui existe pour les mêmes raisons que $p_{1}$ ).
|
| 312 |
+
En particulier les $p_{i}$ sont deux-à-deux distincts, et $p_{i} \equiv 1 \bmod 8 a_{i}$ et $p_{i} \equiv 1 \bmod 8\left(a_{i}-a\right)$, de sorte que d'après le deuxième lemme, pour tout $i,\left(\frac{a_{i}}{p_{i}}\right)=\left(\frac{a_{i}-a}{p_{i}}\right)=1$.
|
| 313 |
+
Par définition, pour tout $i$ il existe $n_{i}$ tel que $n_{i}^{2} \equiv a_{i}-a\left(\bmod p_{i}\right)$, et quitte à remplacer $n_{i}$ par $n_{i}+p_{i}$, on peut supposer $p_{i}^{2} \nmid n_{i}^{2}-\left(a_{i}-a\right)\left(p_{i} \neq 2\right)$. Ainsi, on peut écrire $n_{i}^{2} \equiv a c_{i} p_{i}+\left(a_{i}-a\right)\left(\bmod p_{i}^{2}\right)$ avec $p_{i} \nmid c_{i}$ puisque a et $p_{i}$ sont premiers entre eux $\left(a<p_{i}\right)$.
|
| 314 |
+
Ensuite, comme $a_{i}$ est inversible modulo $p_{i}$ pour tout $i$, le théorème des restes chinois indique que l'on peut trouver un entier $k$ vérifiant que pour tout $i, k \equiv\left(c_{i} p_{i}-1\right) a_{i}^{-1} \bmod p_{i}^{2}$, ou encore $a_{i} k+1 \equiv c_{i} p_{i}$ $\left(\bmod p_{i}^{2}\right)$.
|
| 315 |
+
Remarquons que, par construction,
|
| 316 |
+
|
| 317 |
+
$$
|
| 318 |
+
a k+1 \equiv a \frac{c_{i} p_{i}-1}{a_{i}}+1 \equiv \frac{a c_{i} p_{i}-a+a_{i}}{a_{i}} \equiv \frac{n_{i}^{2}}{a_{i}} \equiv a_{i}\left(\frac{n_{i}}{a_{i}}\right)^{2} \quad\left(\bmod p_{i}^{2}\right)
|
| 319 |
+
$$
|
| 320 |
+
|
| 321 |
+
Or $\left(\frac{a_{i}}{p_{i}}\right)=1$, donc $a_{i}$ est également un résidu quadratique modulo $p_{i}^{2}$ par le premier lemme, donc on a un entier, mettons $\mathrm{N}_{i}$, tel que $a k+1 \equiv \mathrm{~N}_{i}^{2}\left(\bmod p_{i}^{2}\right)$.
|
| 322 |
+
|
| 323 |
+
Alors le théorème des restes chinois nous donne un entier $x$ tel que $x \equiv N_{i}\left(\bmod p_{i}^{2}\right)$ pour tout $i$ et $x \equiv 1(\bmod a)\left(\operatorname{car} a\right.$ est premier avec les $\left.p_{i}\right)$. Mais alors $x^{2} \equiv N_{i}^{2} \equiv a k+1\left(\bmod p_{i}^{2}\right)$ pour tout $i$, et $x^{2} \equiv 1^{2} \equiv a k+1(\bmod a)$, donc $x^{2} \equiv a k+1\left(\bmod a P^{2}\right)$, où on a posé $P=\prod_{i=1}^{n} p_{i}$.
|
| 324 |
+
On réécrit maintenant la congruence sous la forme $x^{2}=a k+1+m a P^{2}=a\left(P^{2} m+k\right)+1$. On utilise enfin l'hypothèse de l'énoncé : il existe un indice $j$ tel que $a_{j}\left(P^{2} m+k\right)+1$ soit un carré parfait. Mais alors $a_{j}\left(P^{2} m+k\right)+1 \equiv a_{j} k+1 \equiv c_{j} p_{j}\left(\bmod p_{j}^{2}\right)$, et comme $p_{j} \nmid c_{j}, v_{p_{j}}\left(a_{j}\left(P^{2} m+k\right)+1\right)=1$, ce qui est en contradiction avec le fait que c'est un carré parfait. Notre affirmation de départ était donc fausse, et l'un des $a_{i}-a$ est non nul.
|
| 325 |
+
|
| 326 |
+
Commentaire des correcteurs : L'exercice est globalement bien réussi par les quelques élèves qui l'ont traité, et qui présentent des solutions très différentes de celle du corrigé.
|
| 327 |
+
|
| 328 |
+
Exercice 18. Déterminer tous les polynômes $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ tels que :
|
| 329 |
+
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ pour tout $n \geqslant 1$
|
| 330 |
+
(ii) $\mathrm{P}(\mathrm{mn})$ et $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ ont le même nombre de diviseurs premiers pour tous $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
| 331 |
+
|
| 332 |
+
Solution de l'exercice 18 Dans la suite, pour tout entier $\mathfrak{n} \in \mathbb{N}^{*}$, on note $\mathcal{D}(n)$ l'ensemble des diviseurs premiers de $n$, et $\delta(n)=|\mathcal{D}(n)|$. Soit $P \in \mathbb{Z}[X]$ un polynôme vérifiant les deux conditions.
|
| 333 |
+
On commence par montrer le résultat suivant :
|
| 334 |
+
Lemme : Soit $\mathrm{n} \geqslant 1$. Pour tout $k \in \mathbb{N}^{*}, \mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$.
|
| 335 |
+
Démonstration: On montre d'abord le résultat pour des petites valeurs de k .
|
| 336 |
+
Tout d'abord, par hypothèse, $\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\delta\left(\mathrm{P}(\mathrm{n})^{2}\right)=\delta(\mathrm{P}(\mathrm{n}))$. De même, $\delta\left(\mathrm{P}\left(\mathrm{n}^{4}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=$ $\delta(P(n))$. Mais $\delta\left(P\left(n^{4}\right)\right)=\delta\left(P\left(n^{3}\right) P(n)\right)$. $P\left(n^{4}\right)$ ayant le même nombre de diviseurs premiers que $P(n)$, cette dernière égalité assure que $\mathcal{D}\left(P\left(n^{3}\right)\right) \subset \mathcal{D}(P(n))$. Par ailleurs $\delta\left(P\left(n^{3}\right)\right)=\delta\left(P\left(n^{2}\right) P(n)\right) \geqslant$ $\delta(P(n))$. Par conséquent, l'inclusion précédente est saturée par cardinalité, et $\mathcal{D}\left(P\left(n^{3}\right)\right)=\mathcal{D}(P(n))$. Alors $\delta(P(n))=\delta\left(P\left(n^{3}\right)\right)=\delta\left(P\left(n^{2}\right) P(n)\right)$, donc nécessairement $\mathcal{D}\left(P\left(n^{2}\right)\right) \subset \mathcal{D}(P(n))$. Par égalité des cardinaux, $\mathcal{D}(\mathrm{P}(\mathrm{n}))=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)$.
|
| 337 |
+
Soit maintenant $k \geqslant 3$. On montre l'égalité $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ par récurrence. Supposons que $\mathcal{D}(P(n))=\mathcal{D}\left(P\left(n^{2}\right)\right)=\ldots=\mathcal{D}\left(P\left(n^{k}\right)\right)$. Alors $\delta\left(P\left(n^{k+1}\right)\right)=\delta\left(P\left(n^{k}\right) P(n)\right)$, où par hypothèse de récurrence, $P\left(n^{k}\right)$ et $P(n)$ ont exactement les mêmes diviseurs premiers, donc $\delta\left(P\left(n^{k}\right) P(n)\right)=\delta(P(n))$, et $\delta\left(P\left(n^{k+1}\right)\right)=\delta(P(n))$. Alors d'une part, $\delta\left(P\left(n^{k+2}\right)\right)=\delta\left(P\left(n^{k}\right) P\left(n^{2}\right)\right)=\delta\left(P\left(n^{2}\right)\right)$ puisque $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ (vu que $\mathrm{k} \geqslant 3$ ) d'où $\delta\left(P\left(\mathrm{n}^{\mathrm{k}+2}\right)\right)=\delta(\mathrm{P}(\mathrm{n}))$. Mais d'autre part, avec l'égalité $\delta\left(P\left(n^{k+2}\right)\right)=\delta\left(P\left(n^{k+1}\right) P(n)\right)$, on voit que nécessairement, $\mathcal{D}\left(P\left(n^{k+1}\right)\right) \subset \mathcal{D}(P(n))$. Par égalité des cardinaux, on a bien $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k+1}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$, ce qui achève l'hérédité.
|
| 338 |
+
|
| 339 |
+
On utilise désormais l'égalité $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ pour conclure l'exercice. On écrit $\mathrm{P}=\mathrm{X}^{\mathrm{d}} \mathrm{Q}$, où $d \in \mathbb{N}$ et $Q \in \mathbb{Z}[X]$ vérifie $Q(0) \neq 0$. Clairement $Q(n) \geqslant 1$ si $n \geqslant 1$. Fixons $p$ premier ne divisant pas $Q(0)$. Pour $k \geqslant 1, p \nmid Q\left(p^{k}\right)$ donc $\mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}(Q(p)) d$ 'après le point précédent. En effet, si $d=0$ cela correspond à l'égalité démontrée plus haut, et si $d \geqslant 1,\{p\} \cup \mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}\left(P\left(p^{k}\right)\right)=\mathcal{D}(P(p))=$ $\{p\} \cup \mathcal{D}(Q(p))$ où $p \nmid Q\left(p^{k}\right)$ et $p \nmid Q(p)$.
|
| 340 |
+
Supposons par l'absurde que $Q$ est non constant. $Q$ tend donc vers $+\infty$ à l'infini. Alors $\delta(Q(p)) \geqslant 1$ car dans le cas contraire $Q\left(p^{k}\right)$ serait égal à 1 pour tout $k \geqslant 1$, donc $Q(X)-1$ admettrait une infinité de racines et serait donc constant. Notons $\mathcal{D}(Q(p))=\left\{q_{1}, \ldots, q_{s}\right\}$ où $s \geqslant 1$ et $q_{1}<\ldots<q_{s}$ des nombres premiers. Soit $\alpha=\max _{r \text { premier }} \nu_{r}(Q(1)) \geqslant 0$. Il existe $k_{0} \geqslant 1$ tel que pour tout $k \geqslant k_{0}$, il existe $i(k) \in \llbracket 1, s \rrbracket$ avec $v_{q_{i(k)}}\left(Q\left(p^{k}\right)\right) \geqslant \alpha+1$ En effet, comme $Q$ tend vers $+\infty$ en $\infty$, pour $k$ assez grand, $Q\left(p^{k}\right)$ est strictement supérieur à $\left.\left(q_{1} \ldots q_{s}\right)^{\alpha}\right)$. Soit $\beta=\varphi\left(\left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right) \geqslant 1$, et $N \geqslant 1$ tel que $N \beta \geqslant k_{0}$. Alors $q_{i(N \beta)}^{\alpha+1} \mid Q\left(p^{N \beta}\right)$, mais $p^{N \beta} \equiv 1\left(\bmod \left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right)$ puisque $p \notin\left\{q_{1}, \ldots, q_{s}\right\}$. En particulier, $Q\left(p^{N \beta}\right) \equiv Q(1)\left(\bmod q_{i(N \beta)}^{\alpha+1}\right)$, et donc $q_{i(N \beta)}^{\alpha+1} \mid Q(1)$. Cela est en contradiction avec la maximalité de $\alpha$. Ainsi, $Q$ est constant égal à $a \in \mathbb{N}^{*}$, et $P=a X^{d}$ avec $d \in \mathbb{N}$.
|
| 341 |
+
On vérifie réciproquement que les polynômes de la forme $a X^{d}$ avec $d \in \mathbb{N}$ et $a \in \mathbb{N}^{*}$ sont solutions.
|
| 342 |
+
Commentaire des correcteurs: Seuls cinq élèves ont rendu une tentative sur cet exercice. Il était très agréable de lire les différentes (excellentes) idées des élèves, qu'elles aient mené à une solution complète ou pas. Les élèves ont pratiquement tous invoqué un résultat (attribué à Schür) sur le fait que l'ensemble des nombres premiers divisant l'un des $\mathrm{P}(\mathrm{n})$ est infini si P est non constant à coefficients entiers. Ce résultat, assez puissant et dont la preuve constituerait un exercice en soi, était d'une grande aide ici.
|
| 343 |
+
|
French_STS/md/fr-corrigé-envoi-4.md
ADDED
|
@@ -0,0 +1,279 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br> 
|
| 2 |
+
|
| 3 |
+
ENVOI 4 : COMBINATOIRE
|
| 4 |
+
À RENVOYER AU PLUS TARD LE 20 MARS 2023
|
| 5 |
+
|
| 6 |
+
Les consignes suivantes sont à lire attentivement:
|
| 7 |
+
|
| 8 |
+
- Le groupe junior est constitué des élèves nés en 2008 ou après. Les autres élèves sont dans le groupe senior.
|
| 9 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 10 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 11 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 12 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 13 |
+
- Respecter la numérotation des exercices.
|
| 14 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
## Exercices Juniors
|
| 18 |
+
|
| 19 |
+
Exercice 1. Six paniers à fruits contiennent des poires, des pêches et des pommes. Le nombre de pêches dans chaque panier est égal au nombre total de pommes dans les autres paniers. Le nombre de pommes dans chaque panier est égal au nombre total de poires dans les autres paniers. Montrez que le nombre total de fruits est un multiple de 31.
|
| 20 |
+
$\underline{\text { Solution de l'exercice } 1}$ Notons $p_{1}, p_{2}, \ldots, p_{6}$ le nombre de poires dans chaque panier, et $q_{1}, q_{2}, \ldots, q_{6}$ le nombre de pommes dans chaque panier. Notons également $P$ le nombre total de poires. On a:
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\begin{aligned}
|
| 24 |
+
& \mathrm{q}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{1} \\
|
| 25 |
+
& \mathrm{q}_{2}=\mathrm{p}_{1}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{2} \\
|
| 26 |
+
& \\
|
| 27 |
+
& \mathrm{q}_{6}=\mathrm{p}_{1}+\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}=\mathrm{P}-\mathrm{p}_{3}
|
| 28 |
+
\end{aligned}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
D'où: $q_{1}+q_{2}+\cdots+q_{6}=\left(P-p_{1}\right)+\left(P-p_{2}\right)+\cdots+\left(P-p_{6}\right)=6 P-\left(p_{1}+p_{2}+\cdots+p_{6}\right)=5 P$ Le nombre total de pommes est égal à 5 fois le nombre total de poires. De même, le nombre total de pêches est égal à 5 fois le nombre total de pommes, donc à 25 fois le nombre total de poires. Le nombre total de fruits est donc égal à $31=25+5+1$ fois le nombre total de poires, et est donc multiple de 31.
|
| 32 |
+
|
| 33 |
+
Commentaire des correcteurs : Exercice très bien réussi.
|
| 34 |
+
|
| 35 |
+
Exercice 2. Une ligne maritime Est-Ouest voit partir chaque matin 10 bateaux à des moments tous distincts, 5 bateaux partent du côté Ouest et 5 du côté Est. On suppose qu'ils naviguent tous à la même vitesse et que dès que deux bateaux se rencontrent ils se retournent et repartent chacun de leur côté, toujours à la même vitesse. Quel est le nombre possible de rencontres entre bateaux?
|
| 36 |
+
Solution de l'exercice 2 Le nombre de croisements ne change pas si on dit que les bateaux continuent tout droit au lieu de faire demi-tour lors d'une rencontre. Chaque bateau qui part d'un côté croise tous les autres bateaux qui partent de l'autre côté. Il y a donc $5 \times 5=25$ rencontres.
|
| 37 |
+
|
| 38 |
+
Commentaire des correcteurs: L'énoncé de cet exercice mal réussi a manifestement troublé les élèves, peut-être parce qu'il n'était pas assez précis. On considérait en effet que tous les bateaux étaient déjà à l'eau et partis avant la première rencontre. Il fallait alors déterminer combien il pouvait y avoir de rencontres entre bateaux (pas simplement le nombre maximal, mais bien tous les nombres de rencontres possibles).
|
| 39 |
+
Si beaucoup d'élèves ont donné le nombre correct (il y en a toujours 25), très peu semblent avoir compris (ou du moins expliqué) que cela ne dépendait effectivement pas des écarts entre les bateaux. Un certain nombre d'élèves ont reconnu que les changements de sens des bateaux suivaient des sortes de "phases", (les deux premiers bateaux se rencontrent, repartent dans des directions opposés, "transmettent" cela vers les bateaux extrêmes, qui repartent en sens opposé et "retransmettent" de proche en proche vers les bateaux centraux la bonne direction) et ont tenté de s'en servir pour aboutir au 25. Mais aucun n'a justifié l'existence de ces phases, ni pourquoi on pouvait les traiter séparément, alors que celles-ci ne se déroulent pas vraiment successivement! Pour s'en convaincre, on pourra considérer le cas où les trois bateaux venant de l'ouest et les cinq bateaux venant de l'est sont très proches les uns des autres, mais les deux derniers bateaux venant de l'ouest sont bien plus lointains. D'autres approches ont été tentées, avec des justifications en général insuffisantes. On rappelle que les affirmations, dans un exercice olympique, sont insuffisantes : celles-ci doivent être démontrées. Si l'on ne sait pas les démontrer, c'est un signe d'autant plus sûr qu'une preuve est nécessaire. Une meilleure approche (que quelques rares copies ont trouvée, sous diverses formes) consistait à remarquer, comme dans le corrigé, que du point de vue du nombre de rencontres, l'énoncé produit les mêmes résultats que si les deux bateaux poursuivaient leur chemin après un croisement. Dans ce cas, un croisement doit impliquer deux bateaux de directions opposées, chaque bateau venant de l'ouest doit croiser chaque bateau venant de l'est, d'où $5 \cdot 5=25$ croisements.
|
| 40 |
+
|
| 41 |
+
Exercice 3. Soit $n \geqslant 6$. Prouvez que chaque carré peut être découpé en exactement n carrés (pas nécessairement de même taille).
|
| 42 |
+
|
| 43 |
+
Solution de l'exercice 3 On peut le montrer par récurrence. Si on a un découpage du carré en $n$ carrés, on peut obtenir un découpage en $\mathrm{n}+3$ carrés en subdivisant l'un des carrés en 4 . Il suffit donc de montrer que l'on peut découper un carré en 6,7 et 8 carrés. Pour 6 , on subdivise le carré en une grille $3 \times 3$ et on fusionne les 4 carrés en haut-gauche. Pour 7 , on subdivise le carré en 4 , puis on subdivise l'un des carrés obtenus en 4 . Pour 8 , on subdivise le carré en une grille $4 \times 4$ et on fusionne les 9 carrés en haut-gauche.
|
| 44 |
+
|
| 45 |
+
Commentaire des correcteurs : Exercice très bien réussi. Deux méthodes sont apparues, soit avec une récurrence, soit une découpe selon la parité, mais elles étaient bien expliquées dans l'ensemble.
|
| 46 |
+
|
| 47 |
+
Exercice 4. Un certain nombre de diagonales divisent un polygone convexe en triangles. Ces segments ne peuvent s'intersecter que sur un sommet du polygone. Sur chaque sommet du polygone on écrit le nombre de triangles qui touchent ce sommet. Est-il possible de reconstruire les diagonales en connaissant seulement les nombres sur les sommets?
|
| 48 |
+
Solution de l'exercice 4 Il est toujours possible de reconstruire les diagonales en utilisant ce procédé :
|
| 49 |
+
|
| 50 |
+
- On considère un sommet "visible" $v$ qui ne touche qu'un seul triangle.
|
| 51 |
+
- On trace la diagonale qui relie les deux sommets $x$ et $y$ adjacents à $v$.
|
| 52 |
+
- On "cache" $v$ et on retire 1 au nombre de triangles adjacents de $x, y$.
|
| 53 |
+
- On continue jusqu'à ce qu'il ne reste plus que 3 sommets.
|
| 54 |
+
|
| 55 |
+
On utilise pour cela le fait que dans toute triangulation d'un polygone convexe, il existe un sommet adjacent à un seul triangle. Pour le montrer, on considère la diagonale d qui "saute" le moins de sommets : si $v$ est un sommet sauté, il n'est relié à aucune diagonale sinon elle serait plus courte que d (car elles ne peuvent pas s'intersecter). Il est donc adjacent à un unique triangle.
|
| 56 |
+
|
| 57 |
+
Commentaire des correcteurs : Exercice bien réussi. Attention, il fallait bien justifier l'existence du sommet avec un 1 qui n'est pas absolument évidente.
|
| 58 |
+
|
| 59 |
+
Exercice 5. Nimatha et Thanima jouent à un jeu sur un échiquier $8 \times 8$. Tour par tour en commençant par Nimatha, chaque joueur choisit une case qui n'a pas encore été choisie et la colorie dans sa couleur (rouge pour Nimatha, bleu pour Thanima). Montrez que Thanima peut toujours faire que Nimatha ne puisse colorier aucun carré $2 \times 2$ entièrement en rouge.
|
| 60 |
+
Solution de l'exercice 5 On considère le coloriage suivant :
|
| 61 |
+
|
| 62 |
+
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
|
| 63 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 64 |
+
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 5 |
|
| 65 |
+
| 9 | 9 | 10 | 10 | 11 | 11 | 12 | 12 |
|
| 66 |
+
| 13 | 14 | 14 | 15 | 15 | 16 | 16 | 13 |
|
| 67 |
+
| 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 |
|
| 68 |
+
| 21 | 22 | 22 | 23 | 23 | 24 | 24 | 21 |
|
| 69 |
+
| 25 | 25 | 26 | 26 | 27 | 27 | 28 | 28 |
|
| 70 |
+
| 29 | 30 | 30 | 31 | 31 | 32 | 32 | 29 |
|
| 71 |
+
|
| 72 |
+
Lorsque Nimatha joue sur un nombre $X$, Thanima réagit en jouant sur la seconde occurrence du nombre $X$. Tout carré $2 \times 2$ contient deux nombres identiques : si l'un est coloré en rouge, l'autre est coloré en bleu. Ainsi, il est impossible pour Nimatha de créer un carré $2 \times 2$ entièrement rouge si Thanima suit cette stratégie.
|
| 73 |
+
|
| 74 |
+
Commentaire des correcteurs: L'exercice est globalement bien réussi. Mais tous les élèves ayant voulu proposer une stratégie sans pavage n'ont pas réussi : en effet, souvent il est difficile de construire une stratégie marchant dasn tous les cas quand il y a 64 coups possibles au tout début.
|
| 75 |
+
|
| 76 |
+
Exercice 6. Au moins $\mathrm{n}\left(\sqrt{\mathrm{n}}+\frac{1}{2}\right)$ carrés d'un échiquier $\mathrm{n} \times \mathrm{n}$ ont été marqués. Montrer qu'il existe quatre cases marquées qui forment les coins d'un rectangle.
|
| 77 |
+
Solution de l'exercice 6 On essaye d'utiliser le principe des tiroirs. S'il y a deux cases marquées aux coordonnées $(i, j)$ et $(i, k)$, on met une chaussette dans le tiroir étiqueté $(\mathfrak{j}, k)$. Il y a $\frac{n(n-1)}{2}$ tiroirs possibles. $S^{\prime}$ il y a deux chaussettes dans le même tiroir $(\mathfrak{j}, k)$, c'est qu'il existe $i, i^{\prime}$ tels que $(i, j),(i, k),\left(i^{\prime}, j\right),\left(i^{\prime}, k\right)$ sont toutes marquées, et on a bien trouvé quatre cases marquées qui forment les coins d'un rectangle. Il ne reste plus qu'à montrer qu'il y a strictement plus de chaussettes de tiroirs. On note $d_{i}$ le nombre de cases marquées dans la i-ème colonne. On a :
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
\sum_{i=1}^{n} d_{i} \geqslant n\left(\sqrt{n}+\frac{1}{2}\right)
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
Le nombre de chaussettes vaut :
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
En utilisant Cauchy-Schwarz, on a :
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
\begin{aligned}
|
| 93 |
+
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2} & \geqslant \frac{1}{2}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-\sum_{i=1}^{n} d_{i}\right) \\
|
| 94 |
+
& \geqslant \frac{1}{2 n}\left(n\left(\sqrt{n}+\frac{1}{2}\right)\right)\left(n\left(\sqrt{n}+\frac{1}{2}\right)-n\right) \\
|
| 95 |
+
& =\frac{1}{2} n\left(\sqrt{n}+\frac{1}{2}\right)\left(\sqrt{n}-\frac{1}{2}\right) \\
|
| 96 |
+
& =\frac{1}{2} n\left(n-\frac{1}{4}\right)
|
| 97 |
+
\end{aligned}
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
Ce qui est effectivement strictement plus grand que le nombre de tiroirs.
|
| 101 |
+
Commentaire des correcteurs : Très peu de copies ont rendu l'exercice. Ici il était naturel d'essayer de regarder les paires de points par colonne : c'était l'idée clé du problème, et elle permettait ensuite d'écrire des inégalités comme dans le corrigé.
|
| 102 |
+
|
| 103 |
+
Exercice 7. Soit $n \geqslant 3$ un entier. Chaque ligne d'un tableau $(n-2) \times n$ contient les nombres de 1 à $n$ en un exemplaire chacun, on suppose de plus que dans chaque colonne tous les nombres sont différents. Montrer que l'on peut compléter le tableau en un tableau $\mathrm{n} \times \mathrm{n}$ de telle sorte que dans chaque ligne et dans chaque colonne il y ait tous les nombres de 1 à $n$.
|
| 104 |
+
Solution de l'exercice 7 Notons $a_{i}, b_{i}$ les deux nombres qu'il manque dans la colonne $i$. Chacun des nombres de 1 à $n$ apparaît en deux exemplaires parmi les $a_{i}, b_{i}$. Construisons un multigraphe dont les sommets sont les nombres de 1 à $n$, et pour chaque $i=1, \ldots, n$, on ajoute une arête entre $a_{i}$ et $b_{i}$. Chaque sommet de ce graphe est de degré 2 , il s'agit donc d'un ensemble de cycles disjoints. On peut donc orienter les arêtes de chaque cycle dans un sens arbitraire. On obtient alors un multigraphe orienté dont chaque sommet à un degré entrant de 1 et un degré sortant de 1 . Imaginons que l'arête de la i-ème colonne pointe de $u$ vers $v$, alors on écrit $u$ aux coordonnées $(i, n-1)$ et $v$ aux coordonnées ( $i, n$ ). La propriété des degrés donne que chaque nombre apparaît exactement une fois sur chaque ligne.
|
| 105 |
+
|
| 106 |
+
Commentaire des correcteurs : Bien dans l'ensemble, tous les élèves ont la construction. Néanmoins, peu proposent une justification complète de celle-ci.
|
| 107 |
+
|
| 108 |
+
Exercice 8. Dans un tournoi organisé entre 6 équipes, chaque équipe joue contre chaque autre équipe exactement une fois. Lorsqu'une équipe gagne, elle obtient 3 points, et l'équipe perdante reçoit 0 point. Si la partie est nulle, les deux équipes reçoivent un point. Déterminez les a pour lesquels il est possible que les scores finaux des équipes puissent être les six nombres consécutifs $a, a+1, \ldots, a+5$ ?
|
| 109 |
+
Solution de l'exercice 8 Lors de chaque match, entre deux et trois points sont attribués au total. Étant donné qu'il y a 15 matchs au total, il y a donc eu entre 30 et 45 points de répartis entre les équipes. On doit donc avoir:
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\begin{aligned}
|
| 113 |
+
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
|
| 114 |
+
& 30 \leqslant 6 a+15 \leqslant 45
|
| 115 |
+
\end{aligned}
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
Ce qui signifie que a peut seulement être 3,4 ou 5 .
|
| 119 |
+
Si $a=5$, aucun match n'a pu être nul donc tous les scores sont des multiples de 3. Il n'est donc pas possible d'avoir 6 nombres consécutifs pour les scores, et ce cas n'est pas possible.
|
| 120 |
+
Si $a=3$, les scores sont $3,4,5,6,7,8$. Les équipes qui ont 6 et 7 points ont chacune gagné au moins un match, et l'équipe qui a 8 points a gagné au moins 2 matchs, donc au moins 4 matchs n'ont pas fini par une partie nulle. Ainsi, le nombre total de points répartis entre les équipe vaut au moins 34 , or $3+4+5+6+7+8=33$, ce cas n'est donc pas possible.
|
| 121 |
+
Le cas $a=4$ est possible. Les scores sont $4,5,6,7,8,9$. Voici un tableau qui fonctionne :
|
| 122 |
+
|
| 123 |
+
| X | 3 | 1 | 0 | 0 | 0 |
|
| 124 |
+
| :---: | :---: | :---: | :---: | :---: | :---: |
|
| 125 |
+
| 0 | X | 1 | 0 | 3 | 1 |
|
| 126 |
+
| 1 | 1 | X | 3 | 0 | 1 |
|
| 127 |
+
| 3 | 3 | 0 | X | 1 | 0 |
|
| 128 |
+
| 3 | 0 | 3 | 1 | X | 1 |
|
| 129 |
+
| 3 | 1 | 1 | 3 | 1 | X |
|
| 130 |
+
|
| 131 |
+
Le nombre écrit sur la j-ème colonne de la i-ème ligne est le score obtenu par l'équipe i lors de son match contre l'équipe $j$.
|
| 132 |
+
|
| 133 |
+
Commentaire des correcteurs: L'exercice est très bien réussi par les élèves l'ayant traité.
|
| 134 |
+
|
| 135 |
+
Exercice 9. Plusieurs nombres sont écrits sur une ligne. Thanima a le droit de choisir deux nombres adjacents de telle sorte que le nombre de gauche soit strictement plus grand que le nombre de droite, elle échange alors ces deux nombres et les multiplie par 2. Montrer que Thanima ne peut effectuer qu'un nombre fini de telles opérations.
|
| 136 |
+
Solution de l'exercice 9 On commence par poser un jeton sur le minimum (si égalité, sur le nombre le plus à gauche). On bouge le jeton avec le nombre sur lequel il est posé. On va montrer que le jeton se déplace toujours vers la gauche.
|
| 137 |
+
Pour cela, supposons par l'absurde qu'à un moment, le jeton s'est déplacé vers la droite. Alors soit x la position du jeton avant l'échange, $i$ la position initiale du jeton, et $j$ la position initiale du nombre avec qui le jeton est échangé. $\mathrm{Si} i<j$, alors comme le jeton n'est jamais allé vers la droite avant, l'autre nombre a dû faire au moins autant de déplacements que le jeton; il a donc été multiplié par deux au moins autant de fois. Comme le jeton avait été posé sur le minimum, le nombre du jeton est plus petit (ou égal) au nombre à la position $x+1$. Le déplacement vers la droite n'était donc pas possible. $\mathrm{Si} j<i$, alors le jeton et le nombre qui était initialement sur $j$ ont déjà été échangés une fois; juste après cet échange, le nombre avec le jeton était plus petit que le nombre qui était initialement en j. Le même argument que le cas précédent s'applique : si le nombre initialement en $j$ est à nouveau juste à droite du jeton, il a du être doublé au moins autant de fois; il est donc resté plus grand et ne peut pas être échangé à nouveau. Ainsi, le jeton se déplace toujours vers la gauche.
|
| 138 |
+
Maintenant, on démontre le résultat par récurrence sur le nombre n de nombres écrits sur la ligne. Comme le jeton se déplace toujours vers la gauche, à partir d'un certain nombre de mouvements, il ne bouge plus. On remarque alors que les nombres à gauche et à droite du jeton forment deux instances séparées du problème initial, et on ne peut effectuer qu'un nombre fini d'opérations sur chaque instance par hypothèse de récurrence. On ne peut donc effectuer qu'un nombre fini d'opérations sur l'instance entière. L'initialisation en $n=0$ est évidente.
|
| 139 |
+
|
| 140 |
+
Commentaire des correcteurs: Très peu (4) de solutions rendues pour cet exercice difficile. Deux ne font qu'effleurer l'exercice, et les deux autres utilisent une solution ne figurant pas dans la correction, consistant à montrer que deux nombres ne peuvent être échangés qu'au plus une fois. Cependant, aucun ne parvient à développer les arguments de façon convaincante.
|
| 141 |
+
|
| 142 |
+
## Exercices Seniors
|
| 143 |
+
|
| 144 |
+
Exercice 10. Comptez le nombre de réarrangements $\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \ldots, \boldsymbol{a}_{2023}$ de la séquence $1,2, \ldots, 2023$ telle que $\mathrm{a}_{\mathrm{k}}>\mathrm{k}$ pour exactement une valeur de $k$.
|
| 145 |
+
Solution de l'exercice 10 À un réarrangement valide, on peut lui associer un sous-ensemble de 1, ..., 2023 de cardinal au moins $2: l$ 'ensemble des $k$ tels que $a_{k} \neq k$.
|
| 146 |
+
On peut montrer qu'à un sous-ensemble de cardinal au moins 2 de $1, \ldots, 2023$, on peut associer un unique réarrangement valide qui lui correspond. Si l'ensemble est $\mathrm{E}=\left\{e_{1}, \ldots, e_{n}\right\}$ avec $e_{1}<e_{2}<\cdots<e_{n}$, l'unique réarrangement qui a pour ensemble associé $E$ vérifie : $a_{e_{1}}=e_{n}, a_{e_{2}}=e_{1}, a_{e_{3}}=e_{2}, \ldots, a_{e_{n}}=$ $e_{n-1}$ et pour tout $k \notin E, a_{k}=k$.
|
| 147 |
+
Ainsi, le nombre de réarrangements valides est égal au nombre de sous-ensembles de $1, \ldots, 2023$ de cardinal au moins 2 . La réponse est donc :
|
| 148 |
+
|
| 149 |
+
$$
|
| 150 |
+
2^{2023}-2024
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
Commentaire des correcteurs: La plupart des copies rendues donnent une solution correcte. Seulement deux ont raisonné comme dans le corrigé. Les autres ont soit raisonné par récurrence en remplaçant 2023 par n, soit omt procédé par sommation (deux copies ont présenté la somme correcte mais n'ont pas su la calculer : peut-être qu'il ne connaissent pas la somme d'une suite géométrique)
|
| 154 |
+
|
| 155 |
+
Exercice 11. Un terrible groupe de bandits se prépare à se partager un butin. Chaque bandit vise deux autres bandits avec ses pistolets. Les bandits sont appelés dans un certain ordre. Lorsqu'un bandit est appelé, s'il est encore en vie, il tire sur les bandits qu'il visait. Après que tous les bandits ont été appelés, il y a eu 28 victimes. Montrez que quelque soit l'ordre dans lequel on avait appelé les bandits, il y aurait eu au moins 10 victimes.
|
| 156 |
+
Solution de l'exercice 11 Supposons par l'absurde qu'il existe un ordre qui cause 9 victimes ou moins. Il y a alors trois catégories de bandits :
|
| 157 |
+
|
| 158 |
+
- Ceux qui sont morts avant de tirer
|
| 159 |
+
- Ceux qui ont pu tirer puis sont morts
|
| 160 |
+
- Ceux qui sont encore en vie à la fin
|
| 161 |
+
|
| 162 |
+
Les bandits de 1ère et 2ème catégorie sont au total au plus 9 , car il y a au plus 9 victimes. Les bandits de 2ème et 3ème catégorie ne visent que des bandits de lère ou 2ème catégorie (s'ils ont tiré, leurs cibles sont mortes). Ils visent donc un sous-ensemble d'au plus 9 bandits. De plus, les bandits de 1ère catégorie ne visent qu'au plus $2 \times 9=18$ bandits : il y a au plus 9 bandits de cette catégorie et chacun vise au plus 2 bandits. Il y a finalement au plus $18+9=27$ bandits visés : il existe un bandit qui n'est visé par personne. Ce bandit survit quelque soit l'ordre d'appel, ce qui contredit l'énoncé.
|
| 163 |
+
|
| 164 |
+
Commentaire des correcteurs: Le principe était généralement compris mais il a été difficile pour plusieurs copies de justifier rigoureusement l'intuition. En particulier, certains considèrent les cas optimaux mais sans justifier qu'ils sont optimaux (ils peuvent par ailleurs ne pas être atteignables).
|
| 165 |
+
|
| 166 |
+
Exercice 12. Les nombres $0,1, \ldots, n$ sont écrits sur un tableau. À tout moment, Thanima peut effacer un nombre s'il est la moyenne arithmétique de deux nombres encore présents sur le tableau. L'objectif de Thanima est d'effacer le plus de nombre possible, et elle joue de façon optimale. En fonction de n, combien de nombres reste t-il à la fin sur le tableau?
|
| 167 |
+
|
| 168 |
+
## Solution de l'exercice 12 Si $n \leqslant 2$, la réponse est $n$.
|
| 169 |
+
|
| 170 |
+
Sinon, à la fin du procédé, il existe toujours au moins deux nombres : on ne peut effacer ni 0 ni n .
|
| 171 |
+
Si $n=2^{k}$ est une puissance de 2 , il est possible de n'avoir que deux nombres sur le tableau à la fin : on commence par effacer tous les nombres congrus à 1 modulo 2 , puis tous les nombres congrus à 2 modulo $4, \ldots$, puis tous les nombres congrus à $2^{i}$ modulo $2^{i+1}, \ldots$, puis $2^{k-1}$. Il ne reste alors plus que 0 et $2^{k}$.
|
| 172 |
+
Si n n'est pas une puissance de 2 , on peut toujours obtenir 3 nombres : on écrit $\mathrm{n}=2^{\mathrm{k}}+\mathrm{a}$ avec $0<\mathrm{a}<2^{\mathrm{k}}$. On efface dans l'ordre $\boldsymbol{n}-1, \boldsymbol{n}-2, \ldots, 2^{\mathrm{k}}+1$, puis on efface les nombres entre 1 et $2^{\mathrm{k}}-1$ en utilisant la même technique qui est utilisée pour $n=2^{k}$. À la fin, il reste $0,2^{k}$ et $n$.
|
| 173 |
+
Montrons maintenant que lorsque $\mathrm{n}>2$ n'est pas une puissance de 2 , on ne peut pas finir avec seulement 0 et n . Supposons par l'absurde qu'il existe une séquence de suppressions qui permet de ne finir qu'avec 0 et $n$. Soit $p$ un nombre premier impair qui divise $n$. En prenant la séquence des suppressions à l'envers, on obtient une séquence d'insertions où l'on part de 0 et $n$, et si $x$ et $y$ sont présents, on peut ajouter $\frac{x+y}{2}$ si c'est un nombre entier. Par récurrence, on démontre alors que tous les nombres obtenus sont divisibles par $p$, en particulier, on ne peut pas obtenir 1, ce qui est la contradiction recherchée.
|
| 174 |
+
|
| 175 |
+
Commentaire des correcteurs : Exercice globalement très réussi par ceux l'ayant traité ; quelques imprécisions, notamment des solutions qui ne précisent pas dans quel ordre enlever les entiers entre $2^{k}$ et n , alors que celui-ci est important.
|
| 176 |
+
|
| 177 |
+
Exercice 13. Un rectangle est divisé en dominos $1 \times 2$ et $2 \times 1$. Dans chaque domino, une diagonale est tracée. Deux diagonales n'ont jamais d'extrémité commune. Montrez que exactement deux coins du rectangle sont des extrémités de ces diagonales.
|
| 178 |
+
Solution de l'exercice 13 Remarquons que ce motif (ainsi que toutes ses rotations et symétries) est impossible :
|
| 179 |
+
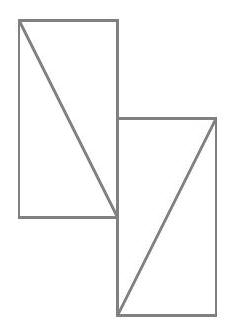
|
| 180 |
+
|
| 181 |
+
En effet, le seul moyen de compléter le carré bas-gauche est d'ajouter ce domino :
|
| 182 |
+
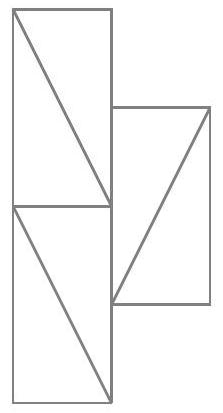
|
| 183 |
+
|
| 184 |
+
De même, le seul moyen de compléter le carré bas-droite est d'ajouter ce domino :
|
| 185 |
+
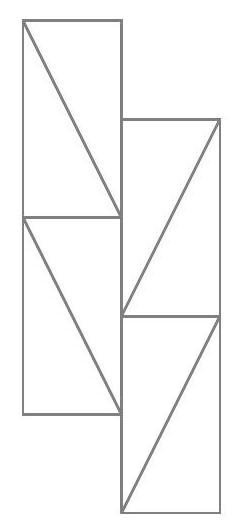
|
| 186 |
+
|
| 187 |
+
On ne peut pas continuer pour toujours, car on finit par atteindre le bord du rectangle.
|
| 188 |
+
Ce motif aussi est impossible (ainsi que toutes ses rotations et symétries) :
|
| 189 |
+
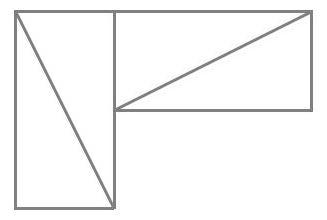
|
| 190 |
+
car le seul moyen de compléter le carré dans le coin est en ajoutant ce domino :
|
| 191 |
+
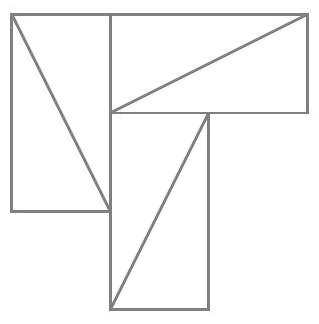
|
| 192 |
+
ce qui fait apparaître le motif interdit précédent. Grâce à une analyse minutieuse, ces deux cas démontrent qu'il n'est en fait pas possible que deux dominos qui partagent un bord aient leurs diagonales dans des sens différents (montantes ou descendantes). Si on forme le graphe G dont les sommets sont les dominos et où il y a une arête entre deux dominos s'ils partagent un bord en commun, $G$ est connexe. Ainsi, tous les dominos ont leur diagonale dans le même sens; on en déduit facilement la propriété demandée.
|
| 193 |
+
|
| 194 |
+
Commentaire des correcteurs: L'exercice a été peu traité. Ceux qui ont rendu une copie ont en général bien compris l'exercice et bien traité tous les cas et vu le motif du corrigé. Certains ont une argumentation différente en regardant un chemin entre les diagonales opposées, et d'autres utilisent un raisonnement de théorie des graphes.
|
| 195 |
+
|
| 196 |
+
Exercice 14. Soit $G$ un graphe à $n$ sommets. Une arête e de $G$ est un cul-de-sac s'il est possible de partitionner $G$ en deux ensembles $A$ et $B$ tels que :
|
| 197 |
+
|
| 198 |
+
- Il y a au plus 2023 arêtes de G ayant une extrémité dans A et une extrémité dans B.
|
| 199 |
+
- L'arête e a l'une de ses extrémités dans $A$ et l'autre dans B.
|
| 200 |
+
|
| 201 |
+
Montrez qu'il y a au plus 2023( $\mathrm{n}-1$ ) culs-de-sac.
|
| 202 |
+
Solution de l'exercice 14 On le démontre par récurrence forte sur n . Le cas $\mathrm{n}=1$ est immédiat. S'il n'existe aucun cul-de-sac dans G, la propriété est triviale. Sinon, soit e un cul-de-sac de G. On obtient une partition des sommets de $G$ en deux ensembles $A$, $B$ telle qu'il y a au plus 2023 arêtes entre $A$ et $B$. D'après l'hypothèse de récurrence, il y a au plus $2023(|A|-1)$ culs-de-sacs lorsque l'on ne considère que les sommets de $A$ et les arêtes qui relient ces sommets. De même, il y a au plus 2023(|B|-1) culs-de-sacs lorsque l'on ne considère que les sommets de $B$ et les arêtes qui les relient. On remarque que si une arête e n'est pas un cul-de-sac dans le graphe restreint à $A$ (de même pour $B$ ), alors elle n'est pas non plus un cul-de-sac dans G. Il y a donc au plus :
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
2023+2023(|A|-1)+2023(|B|-1)=2023(|\mathrm{G}|-1)
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
culs-de-sacs dans G, ce qui termine l'hérédité.
|
| 209 |
+
Commentaire des correcteurs : L'exercice est globalement bien réussi. Plusieurs élèves oublient de vérifier et même de mentionner qu'un cul-de-sac d'un graphe G appartenant à un sous-graphe $A$ de $G$ est un cul-de-sac pour $A$, c'est dommage car c'est un argument important de la preuve. En effet, être un cul-de-sac dans deux graphes différents n'est à priori pas lié.
|
| 210 |
+
|
| 211 |
+
Exercice 15. On place un certain nombre de segments ouverts dans le plan, aucun d'entre eux n'est parallèle aux axes $x$ et $y$. Ces segments sont disjoints. Thanima commence à se déplacer depuis $(0,0)$ parallèlement à l'axe $x$. À chaque fois qu'elle rencontre un mur, elle tourne de 90 degrés, et continue à se déplacer sans traverser le mur.
|
| 212 |
+
Démontrez qu'il est impossible que Thanima visite les deux côtés de tous les murs.
|
| 213 |
+
Solution de l'exercice 15 On commence par démontrer qu'il existe un mur qui est plus bas que tous les autres (c'est à dire que l'ensemble des points sous ce segment n'intersecte aucun segment). Supposons par l'absurde que ce $n$ 'est pas le cas. On peut alors construire un cycle $A_{1}, B_{1}, A_{2}, B_{2}, \ldots, A_{k}, B_{k}$ qui ne s'intersecte pas lui-même, où $A_{i}$ et $B_{i}$ sont sur le même mur, et $\left[B_{i}, A_{i+1}\right]$ est un segment vertical où $B_{i}$ est au dessus de $A_{i+1}$ (on considère les indices modulo $k$ ). On considère $l$, $r$ tel que $\left[B_{l}, A_{l+1}\right]$ soit le plus à gauche et $\left[B_{r}, A_{r+1}\right]$ soit le plus à droite. Le cycle donne une ligne brisée entre $B_{l}$ et $A_{r+1}$, et une autre entre $B_{r}$ et $A_{l+1}$. Cependant, les lignes brisées ne passent ni à gauche de $\left[B_{l}, A_{l+1}\right]$ ni à droite de $\left[B_{r}, A_{r+1}\right]$, et leurs extrémités sont "croisées", elles doivent donc s'intersecter. C'est une contradiction avec le fait que le cycle ne s'intersecte pas lui-même.
|
| 214 |
+
Similairement, il existe un mur plus haut que tous les autres. Si Thanima passe par le côté haut du mur le plus haut, elle continue à marcher vers l'infini en direction des y positifs. Si Thanima passe par le côté bas du mur le plus bas, elle continue à marcher vers l'infini en direction des y négatifs. Ces deux cas ne peuvent pas arriver simultanément, elle ne passe donc que par un seul de ces deux côtés. En particulier, elle ne peux pas passer par tous les côtés de tous les murs.
|
| 215 |
+
|
| 216 |
+
Commentaire des correcteurs: L'exercice a été peu traité. La plupart des solutions sont justes et proches de celle proposées dans le corrigé; néanmoins, elles présentaient un certain nombre d'imprécisions, auxquelles il faut être particulièrement attentif quand il s'agit de quelque chose d'aussi visuel que la géométrie combinatoire.
|
| 217 |
+
|
| 218 |
+
Exercice 16. Soit $k \geqslant 1$ un entier. Quel est le plus petit entier $n$ tel que, quelque soit la manière de placer n points dans le plan, il est possible de choisir un sous-ensemble $S$ constitué de $k$ de ces points qui vérifie "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est inférieure ou égale à 2 " ou "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est strictement plus grande que 1."
|
| 219 |
+
Solution de l'exercice 16 Commençons par montrer que $\mathrm{n}=(k-1)^{2}+1$ est possible. Pour cela, considérons le disque de rayon 1 centré sur un point $P_{1}$ de l'ensemble. S'il y a au moins $k$ points dans ce disque, on peut prendre pour $S$ ces $k$ points (les distances entre eux sont inférieures ou égales à 2 ). On peut donc supposer qu'il y a au plus $(k-1)$ points dans le disque.
|
| 220 |
+
Considérons alors un disque de rayon 1 centré sur un $P_{2}$ de l'ensemble qui n'est pas dans le disque précédent. Par le même argument, on peut supposer qu'il y a au plus $(k-1)$ points dans ce disque.
|
| 221 |
+
En continuant à choisir des points en dehors des disques précédents, et comme on exclut au plus ( $k-1)$ points à chaque étape, on arrive à construire $S=\left\{P_{1}, \ldots, P_{k}\right\}$ de telle manière à ce que les distances entre ces points soient toutes strictement supérieures à 1 .
|
| 222 |
+
Pour montrer que $\mathrm{n}=(\mathrm{k}-1)^{2}$ n'est pas possible, on place à distance très grande les uns des autres $k-1$ groupes, ou chaque groupe est constitué de $\mathrm{k}-1$ points à distance très petite.
|
| 223 |
+
|
| 224 |
+
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont traité, avec des méthodes très variées : certains ont utilisé la même technique que la correction, d'autres ont recouru à la théorie des graphes par exemples.
|
| 225 |
+
|
| 226 |
+
Exercice 17. Soit $k, n \geqslant 1$ deux entiers fixés. Thanima possédait 2 n bonbons de chaque couleur. Elle a donné deux bonbons de couleurs différentes à chacun des enfants de sa famille. Sachant que quelque soit la manière de choisir $k+1$ enfants, il y en a deux parmi eux qui ont reçu une couleur de bonbon en commun, trouvez le nombre maximum possible d'enfants.
|
| 227 |
+
Solution de l'exercice 17 On peut modéliser le problème par un graphe : chaque sommet de ce graphe est une couleur. Si Thanima a donné un bonbon d'une couleur $\mathrm{c}_{1}$ et un bonbon d'une couleur $\mathrm{c}_{2}$ à un enfant de sa famille, on ajoute une arête entre $\mathrm{c}_{1}$ et $\mathrm{c}_{2}$.
|
| 228 |
+
Comme Thanima n'a que 2 n bonbons de chaque couleur, le degré maximal de chaque sommet est 2 n . On sait de plus qu'il est impossible de choisir $k+1$ arêtes disjointes. On cherche le nombre maximal d'arêtes.
|
| 229 |
+
On voit qu'il est possible d'obtenir 3 kn arêtes. Pour cela, on crée un graphe dans lequel on met $k$ fois la structure suivante : on crée trois sommets, et entre chaque paire de ces trois sommets, on ajoute n arêtes. Montrons qu'il n'est pas possible de faire plus que 3 kn . Pour cela, on considère un ensemble C d'arêtes disjointes de plus grand cardinal. D'après l'énoncé, on a $|\mathrm{C}| \leqslant \mathrm{k}$. Ainsi, chaque arête du graphe doit intersecter l'une des arêtes de C , sinon cela contredirait la maximalité de C . Notons $\mathrm{V}_{\mathrm{C}}$ l'ensemble des sommets qui apparaissent dans l'une des arêtes de C. Le nombre d'arêtes du graphe vaut :
|
| 230 |
+
|
| 231 |
+
$$
|
| 232 |
+
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2}
|
| 233 |
+
$$
|
| 234 |
+
|
| 235 |
+
où $\mathrm{d}_{\text {ext }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets qui ne sont pas dans $V_{C}$, et $\mathrm{d}_{\text {int }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets de $\mathrm{V}_{\mathrm{C}}$. Soit $(\mathrm{a}, \mathrm{b}$ ) une arête de C , et soient $x, y$ deux sommets différents qui ne sont pas dans $\mathrm{V}_{\mathrm{C}}$, on ne peut pas à la fois avoir d'arêtes entre a et $x$ et entre $b$ et $y$, sinon remplacer $(a, b)$ par $(a, x)$ et $(b, y)$ dans $C$ donnerait un ensemble d'arêtes disjointes plus grand. Deux cas peuvent arriver :
|
| 236 |
+
|
| 237 |
+
- À la fois $a$ et $b$ ont des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas, toutes ces arêtes vont vers le même sommet, et la borne de degré sur ce sommet donnent $d_{\text {ext }}(a)+d_{\text {ext }}(b) \leqslant 2 n$.
|
| 238 |
+
- Soit il y a au plus un sommet parmi $a$ et $b$ qui a des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas on a aussi $\mathrm{d}_{\text {ext }}(a)+\mathrm{d}_{\text {ext }}(b) \leqslant 2 \mathrm{n}$.
|
| 239 |
+
Comme $\mathrm{d}_{\mathrm{int}}(v) \leqslant 2 \mathrm{n}-\mathrm{d}_{\text {ext }}(v)$ pour tout sommet $v$, on a :
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
\begin{aligned}
|
| 243 |
+
\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \leqslant d_{e x t}(a)+d_{e x t}(b)+\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\
|
| 244 |
+
& =2 n+\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\
|
| 245 |
+
& \leqslant 3 n
|
| 246 |
+
\end{aligned}
|
| 247 |
+
$$
|
| 248 |
+
|
| 249 |
+
Ainsi, en groupant les termes deux à deux, on obtient que le nombre d'arête dans le graphe est :
|
| 250 |
+
|
| 251 |
+
$$
|
| 252 |
+
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2} \leqslant 3 \mathrm{kn}
|
| 253 |
+
$$
|
| 254 |
+
|
| 255 |
+
Commentaire des correcteurs : L'exercice a été très peu abordé.
|
| 256 |
+
|
| 257 |
+
Exercice 18. Thanima possède un magnifique collier constitué de rubis, d'émeraudes et de saphirs, que l'on représente par une suite de $\mathrm{R}, \mathrm{E}$ et S . En une opération magique, elle peut faire l'une des actions suivantes :
|
| 258 |
+
|
| 259 |
+
- Remplacer un motif RR dans le collier par un motif ES (ou ES par RR).
|
| 260 |
+
- Remplacer un motif EEE par un motif SR (ou SR par EEE).
|
| 261 |
+
- Supprimer un motif SS, ou ajouter un motif SS n'importe où.
|
| 262 |
+
- Supprimer un motif RES, ou ajouter un motif RES n'importe où.
|
| 263 |
+
|
| 264 |
+
Il n'est pas possible de déplacer les lettres cycliquement à cause du fermoir. Elle ne peut pas non plus retourner le collier.
|
| 265 |
+
Est-il possible de passer d'un collier contenant uniquement un saphir à un collier contenant uniquement une émeraude avec des opérations magiques?
|
| 266 |
+
Solution de l'exercice 18 Supposons que Thanima dispose de trois objets numérotés 1,2 et 3 sur trois supports numérotés 1,2 et 3 . Au début, chaque objet se trouve sur le support qui porte le même numéro. Thanima peut lire les lettres du collier une par une de gauche à droite et faire les opérations suivantes :
|
| 267 |
+
|
| 268 |
+
- Si elle voit un E, elle échange les objets qui se trouvent sur les supports 1 et 2.
|
| 269 |
+
- Si elle voit un $S$, elle échange les objets qui se trouvent sur les supports 2 et 3.
|
| 270 |
+
- Si elle voit un R, elle déplace l'objet sur le support 1 sur le support 2, l'objet sur le support 2 sur le support 3 , et l'objet sur le support 3 sur le support 1 .
|
| 271 |
+
On remarque que :
|
| 272 |
+
- Lorsque l'on ajoute un motif SS quelque part, on échange deux fois de suite les objets sur les supports 2 et 3 , ce qui ne change pas la position finale des objets.
|
| 273 |
+
- Lorsque l'on ajoute un motif RES quelque part, l'objet qui était sur le support 1 à ce moment est déplacé sur le support 2 par $R$, puis sur le support 1 par $E$. L'objet qui était sur le support 2 est déplacé sur le support 3 par $R$, puis sur le support 2 par $S$. L'objet sur le support 3 est déplacé sur le support 1 par R, puis sur le support 2 par E puis à nouveau sur le support 3 par S . On ne change donc pas la position finale des objets.
|
| 274 |
+
- Lorsque l'on applique RR, l'objet sur le support 1 est déplacé sur le support 3 , l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . Lorsque l'on applique ES, l'objet sur le support 1 est déplacé sur le support 3, l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . On ne change donc pas la position finale des objets en remplaçant un motif RR par un motif RES.
|
| 275 |
+
- Lorsque l'on applique EEE, cela revient à échanger les objets sur les supports 1 et 2 . Lorsque l'on applique $S R$, l'objet sur le support 1 est envoyé sur le support 2 , l'objet 2 est envoyé sur le support 1 et l'objet sur le support 3 reste sur le support 3 . On ne change donc pas la position finale des objets en remplaçant un motif EEE par un motif SR.
|
| 276 |
+
On conclut qu'aucune opération magique ne permet de changer la position finale des objets. Or les colliers "S" et "E" ne donnent pas les mêmes positions finales des objets, il est donc impossible de passer de l'un à l'autre par des opérations magiques.
|
| 277 |
+
|
| 278 |
+
Commentaire des correcteurs : Très peu (3) de solutions rendues pour cet exercice très difficile; aucune n'a été concluante, mais les élèves ont eu de bonnes idées, ce qui est très encourageant. L'idée était effectivement de trouver un invariant, qui consistait ici en une interprétation des lettres R, E et S en tant qu'opérations sur un ensemble. Une fois cette idée en tête, une stratégie raisonnable consistait alors à chercher des simplifications produisant des mots que l'on pouvait identifier à l'opération identité.
|
| 279 |
+
|
French_STS/md/fr-corrigé-envoi-5.md
ADDED
|
@@ -0,0 +1,550 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES <br>  <br> ENVOI 5 : Pot POURRI <br> À RENVOYER AU PLUS TARD LE 21 AVRIL 2022
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2007 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## Exercices Juniors
|
| 15 |
+
|
| 16 |
+
Exercice 1. Déterminer tous les couples d'entiers $(x, y)$ tels que $x^{2}+73=y^{2}$.
|
| 17 |
+
Solution de l'exercice 1 Comme souvent pour une équation diophantienne, on cherche à réarranger l'équation de sorte à avoir des produits de facteurs des deux côtés de l'égalité. Lorsque l'on est en présence de carrés parfaits, on peut utiliser l'identité remarquable $y^{2}-x^{2}=(y-x)(y+x)$. Ceci permet de réécrire l'équation sous la forme :
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
73=(y-x)(y+x)
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Ainsi, le nombre $y-x$ est un diviseur de 73 . Or les diviseurs de 73 sont $73,1,-1,-73$. On distingue alors quatre cas:
|
| 24 |
+
|
| 25 |
+
Cas $\mathrm{n}^{\circ} 1: \mathrm{y}-\mathrm{x}=73$. Alors $\mathrm{x}+\mathrm{y}=1$. Ceci conduit à $\mathrm{y}=73+\mathrm{x}=73+(1-\mathrm{y})$, soit $\mathrm{y}=37$ et $x=-36$. Réciproquement, on a bien $(-36)^{2}+73=37^{2}$, donc le couple $(-36,37)$ est bien solution.
|
| 26 |
+
Cas $\mathrm{n}^{\circ} 2: y-x=1$. Alors $x+y=73$. Ceci conduit à $y=1+x=1+(73-y)$, soit $y=37$ et $x=36$. Réciproquement, on a bien $36^{2}+73=37^{2}$, donc le couple $(36,37)$ est bien solution.
|
| 27 |
+
Cas $\mathrm{n}^{\circ} 3: \mathrm{y}-\mathrm{x}=-1$. Alors $\mathrm{x}+\mathrm{y}=-73$. Ceci conduit à $\mathrm{y}=-1+\mathrm{x}=-1+(-73-\mathrm{y})$, soit $y=-37$ et $x=-36$. Réciproquement, on a bien $(-36)^{2}+73=(-37)^{2}$, donc le couple $(-36,-37)$ est bien solution.
|
| 28 |
+
$\underline{\text { Cas } \mathrm{n}^{\circ} 4:} \mathrm{y}-\mathrm{x}=-73$. Alors $\mathrm{x}+\mathrm{y}=-1$. Ceci conduit à $\mathrm{y}=-73+\mathrm{x}=-73+(-1-\mathrm{y})$, soit $y=-37$ et $x=36$. Réciproquement, on a bien $36^{2}+73=(-37)^{2}$, donc le couple $(36,-37)$ est bien solution.
|
| 29 |
+
Les couples solutions sont donc $(-36,-37),(-36,37),(36,-37)$ et $(36,37)$.
|
| 30 |
+
|
| 31 |
+
## Commentaires des correcteurs:
|
| 32 |
+
|
| 33 |
+
Exercice bien réussi dans l'ensemble, avec quelques erreurs récurrentes :
|
| 34 |
+
|
| 35 |
+
- Supposer que les entiers sont positifs.
|
| 36 |
+
- Oublier des cas dans la factorisation (oublier de prendre les opposés / d'échanger les facteurs)
|
| 37 |
+
|
| 38 |
+
Exercice 2. Soit a un réel strictement positif et $\mathrm{n} \geqslant 1$ un entier. Montrer que
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Solution de l'exercice 2 Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
L'idée derrière la solution qui suit est "d'homogénéiser" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \leqslant i \leqslant 2 n$, on a $a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\begin{aligned}
|
| 54 |
+
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
|
| 55 |
+
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text { termes }}+a^{n}}{a^{n}} \\
|
| 56 |
+
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
|
| 57 |
+
& =2 n+1 \\
|
| 58 |
+
& >2 n
|
| 59 |
+
\end{aligned}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
ce qui fournit l'inégalité voulue.
|
| 63 |
+
|
| 64 |
+
## Commentaires des correcteurs:
|
| 65 |
+
|
| 66 |
+
L'exercice est très bien résolu! Les élèves ont bien compris comment utiliser l'inégalité de la moyenne.
|
| 67 |
+
|
| 68 |
+
Exercice 3. Soient $\omega_{1}$ et $\omega_{2}$ deux cercles de centres respectifs $O_{1}$ et $O_{2}$. On suppose que $\omega_{1}$ et $\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\left(O_{1} A\right)$ recoupe le cercle $\omega_{2}$ en $C$ tandis que la droite $\left(O_{2} A\right)$ recoupe le cercle $\omega_{1}$ en D . Montrer que les points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et C appartiennent à un même cercle.
|
| 69 |
+
|
| 70 |
+
## Solution de l'exercice 3
|
| 71 |
+
|
| 72 |
+
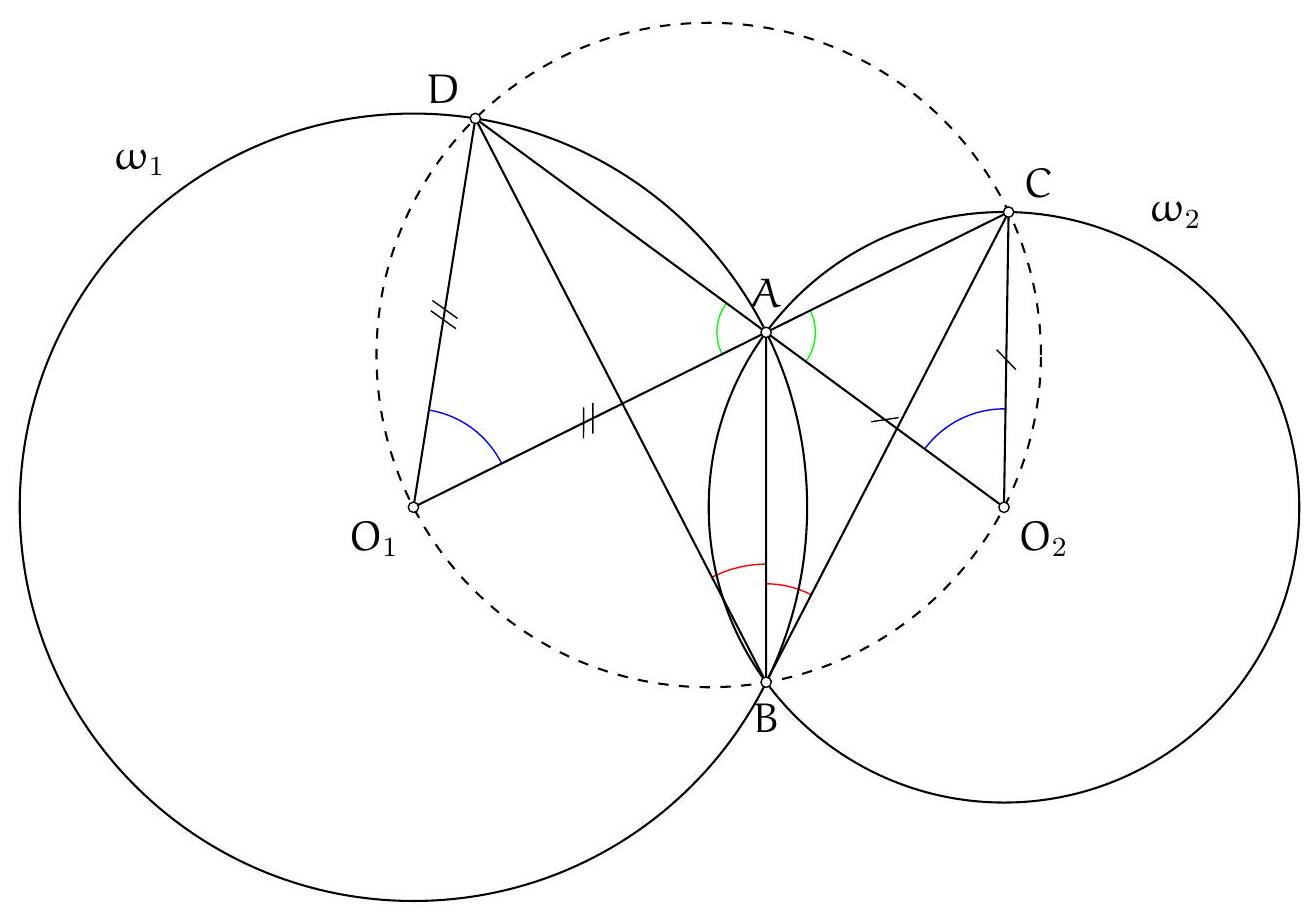
|
| 73 |
+
|
| 74 |
+
Notons que puisque les angles $\widehat{\mathrm{DAO}_{1}}$ et $\widehat{\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\mathrm{CO}_{2} A$ est isocèle en $\mathrm{O}_{2}$. Les triangles $\mathrm{DO}_{1} A$ et $\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} A}$, et donc que
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
|
| 78 |
+
$$
|
| 79 |
+
|
| 80 |
+
si bien que les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D sont cocycliques.
|
| 81 |
+
Par ailleurs, on peut découper l'angle $\widehat{\mathrm{DBC}}$ en la somme $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B C}=\frac{1}{2} \widehat{A_{2} C}$. Ainsi
|
| 82 |
+
|
| 83 |
+
$$
|
| 84 |
+
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
ce qui permet de conclure que le point B appartient au cercle passant par les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D .
|
| 88 |
+
|
| 89 |
+
## Commentaires des correcteurs:
|
| 90 |
+
|
| 91 |
+
Exercice très bien résolu.
|
| 92 |
+
|
| 93 |
+
Exercice 4. Aurélien écrit 11 entiers naturels au tableau. Montrer qu'il peut choisir certains de ces entiers et placer des signes + et - entre eux de telle sorte que le résultat soit divisible par 2021.
|
| 94 |
+
|
| 95 |
+
## Solution de l'exercice 4
|
| 96 |
+
|
| 97 |
+
On peut voir un choix de certains entiers avec des signes + et - comme un choix de certains entiers que l'on va compter positivement et de certains entiers que l'on va compter négativement. Les nombres qu'Aurélien peut obtenir sont des nombres qui s'écrivent comme la différence entre deux sommes de plusieurs entiers de départ. On peut remarquer que la réciproque est aussi vrai, si a et b s'écrivent comme somme de certains entiers, alors Aurélien peut obtenir $a-b$ en mettant un signe plus devant les entiers qui sont dans $a$ et un signe $b$ devant ceux qui sont dans $b$. Si le même entier de départ est utilisé pour obtenir à la fois a et $b$, Aurélien ne peut pas écrire devant un signe - et + , mais il peut simplement de pas écrire l'entier tout court, ce qui a le même effet que l'ajouter puis l'enlever. Toutes les différences entre deux sommes d'entiers du tableau sont donc des résultats qu'Aurélien peut obtenir. Dire qu'une différence entre deux sommes est dvisible par 2021 revient à dire que les deux sommes étaient congrues modulo 2021. On dispose de $2^{11}=2048>2021$ sommes, donc d'après le principe des tiroirs, deux sont congrues modulo 2021.
|
| 98 |
+
|
| 99 |
+
## Commentaires des correcteurs:
|
| 100 |
+
|
| 101 |
+
Exercice extrêmement bien réussi par ceux qui l'ont traité. Les solutions sont presque toutes analogues à celle du corrigé.
|
| 102 |
+
|
| 103 |
+
Exercice 5. Soient $x, y, z$ des réels strictement positifs tels que
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
x+\frac{y}{z}=y+\frac{z}{x}=z+\frac{x}{y}=2
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Déterminer toutes les valeurs possibles que peut prendre le nombre $x+y+z$.
|
| 110 |
+
Solution de l'exercice 5 Dans un tel problème, il faut chercher à examiner chaque équation séparément mais aussi à les mettre en relation. En pratique, cela consiste à regarder l'équation obtenue lorsque l'on effectue la somme ou le produit de deux ou plusieurs équations. Une autre idée est d'appliquer des inégalités connues d'un côté ou de l'autre de l'équation. En effet, souvent les égalités présentes dans les problèmes ne sont possibles que lorsque les variables vérifient le cas d'égalité d'une inégalité bien connue.
|
| 111 |
+
Commençons par un examen séparé. On considère la première équation $x+\frac{y}{z}=2$. D'après l'inégalité des moyennes, on a
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
2=x+\frac{y}{z} \geqslant 2 \sqrt{x \cdot \frac{y}{z}}
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
soit $\sqrt{\frac{x y}{z}} \leqslant 1$. De même, la deuxième équation $y+\frac{z}{x}=2$ donne $\sqrt{\frac{y z}{x}} \leqslant 1$. En multipliant ces deux inégalités, on obtient
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
1 \geqslant \sqrt{\frac{x y}{z}} \cdot \sqrt{\frac{y z}{x}}=y
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Ainsi $y \leqslant 1$, et de même on trouve que $x \leqslant 1$ et $z \leqslant 1$. On cherche désormais à appliquer ces estimations ou à prouver des estimations inverses (par exemple $y \geqslant 1$, ce qui imposerait que $y=1$ ).
|
| 124 |
+
Notons que la relation $x+\frac{y}{z}=2$ se réécrit $x z+y=2 z$. On obtient de même que $y x+z=2 x$ et $y z+x=2 y$. En sommant ces trois relations, on trouve que $x z+y x+y z+x+y+z=2(x+y+z)$, ou encore $x y+y z+z x=x+y+z$. Mais alors
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
x+y+z=x y+y z+z x \leqslant x \cdot 1+y \cdot 1+z \cdot 1=x+y+z
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
Notre inégalité est en fait une égalité. Et puisque $x, y$ et $z$ sont non nuls, chacune des inégalités utilisées dans la ligne ci-dessus est en fait une égalité. On a donc $x=y=z=1$ et $x+y+z=3$. Cette valeur est bien atteignable puisque le triplet $(1,1,1)$ vérifie bien le système de l'énoncé, ce qui termine notre problème.
|
| 131 |
+
|
| 132 |
+
## Commentaires des correcteurs:
|
| 133 |
+
|
| 134 |
+
Exercice plutôt bien réussi. Les méthodes de résolution sont extrêmement variées. Certains élèves ont commis l'erreur de considérer que le problème est symétrique, alors qu'il n'est que cyclique.
|
| 135 |
+
|
| 136 |
+
Exercice 6. Trouver tous les couples $(x, y)$ d'entiers strictement positifs tels que $x y \mid x^{2}+2 y-1$.
|
| 137 |
+
Solution de l'exercice 6 D'une part, on peut écrire $x|x y| x^{2}+2 y-1$ donc $x \mid 2 y-1$. Donc il existe n tel que $2 \mathrm{y}-1=\mathrm{nx}$. Forcément, n et $x$ sont impairs.
|
| 138 |
+
D'autre part, la relation de divisibilité de l'énoncé nous donne une inégalité : on sait que $x y>0$, donc
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
x y \leqslant x^{2}+2 y-1
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
En multipliant cette relation par 2 pour simplifier les calculs et en combinant les deux, on obtient
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
x(n x+1) \leqslant 2 x^{2}+2(n x+1)-2
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
En reorganisant les termes,
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
(n-2) x^{2} \leqslant(2 n-1) x
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
Soit, comme $x>0$
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
x \leqslant \frac{2 n-1}{n-2}=2+\frac{3}{n-2}
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
En se souvenant que n et $x$ sont forcément impairs, on distingue plusieurs cas.
|
| 163 |
+
Cas $\mathrm{n}^{\circ} 1: n \geqslant 7$. Alors
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
x \leqslant 2+\frac{3}{n-2}<3
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Donc $x=1$. Réciproquement, tous les couples $(1, y)$ sont solution.
|
| 170 |
+
Cas $\mathrm{n}^{\circ} 2: \mathrm{n}=5$. Alors
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
x \leqslant 2+\frac{3}{n-2}=3
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
Donc $x=1$ ou $x=3$. Tous les couples avec $x=1$ sont solutions. Si $x=3$, on a $2 y-1=\mathfrak{n} x=$ $5 \cdot 3=15$ donc $y=8$. On vérifie $(3,8)$ est solution : $24 \mid 24$.
|
| 177 |
+
$\underline{\text { Cas } \mathrm{n}^{\circ} 3:} \mathbf{n}=3$. Alors
|
| 178 |
+
|
| 179 |
+
$$
|
| 180 |
+
x \leqslant 2+\frac{3}{n-2}=5
|
| 181 |
+
$$
|
| 182 |
+
|
| 183 |
+
Donc $x=1$ ou $x=3$. Tous les couples avec $x=1$ sont solutions. Si $x=3$, on a $2 y-1=$ $\mathrm{n} x=3 \cdot 3=9$ donc $y=5$. On vérifie que $(3,5)$ n'est pas solution : $15 \nmid 24 . \operatorname{Si} x=5$ on a $2 \mathrm{y}-1=\mathrm{n} x=5 \cdot 3=15$ donc $y=8$. On vérifie que $(5,8)$ est solution : $40 \mid 40$.
|
| 184 |
+
Cas $\mathrm{n}^{\circ} 4: \mathbf{n}=1$. Alors $x=2 y-1$. Alors
|
| 185 |
+
|
| 186 |
+
$$
|
| 187 |
+
x y=2 y^{2}-y \mid 4 y^{2}-2 y=(2 y-1)^{2}+2 y-1=x^{2}+2 y+1
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
Donc tous les couples de la forme $(2 y-1, y)$ sont solutions.
|
| 191 |
+
|
| 192 |
+
## Commentaires des correcteurs:
|
| 193 |
+
|
| 194 |
+
L'exercice est plutôt bien réussi par les élèves qui l'ont traité. Malgré la disjonction de cas relativement fastidieuse, on relève très peu d'oublis. Certains ont encore du mal avec la notion de divisibilité, notamment comment interpréter une expression du type $a \mid b c$.
|
| 195 |
+
|
| 196 |
+
Exercice 7. Soit $n \geqslant 1$ un entier strictement positif. Sur un mur, $n$ clous sont plantés. Chaque paire de clous est reliée par une corde coloriée à l'aide d'une des n couleurs. On dit que le mur est coloré si pour tout triplet de couleurs deux à deux distinctes $a, b, c$, il existe trois clous tels que les trois cordes reliant ces clous soient de couleur $a, b$ et $c$.
|
| 197 |
+
|
| 198 |
+
- Existe-t-il un mur coloré pour $\mathrm{n}=6$ ?
|
| 199 |
+
- Existe-t-il un mur coloré pour $\mathrm{n}=7$ ?
|
| 200 |
+
|
| 201 |
+
|
| 202 |
+
## Solution de l'exercice 7
|
| 203 |
+
|
| 204 |
+
C'est en fait la parité de n qui est cruciale.
|
| 205 |
+
Cas n pair : Il y a $\frac{n(n-1)}{2}$ donc en moyenne il y a $\frac{n-1}{2}$ cordes de chaque couleur. Ce nombre n'étant pas entier, il y a des couleurs avec plus de cordes que la moyenne et des avec moins. On pourrait tout-à-fait choisir une couleur sous-représentée et comparer le nombre de triplets de couleurs comportant cette couleur avec le nombre de triplets de cordes comportant une corde de cette couleur pour obtenir un contradiction. On va ici choisir l'approche opposée : on considère une couleur sur-représentée. Il y a au moins $\frac{n+1}{2}$ cordes de cette couleur, donc au moins $n+1$ extrémités de cordes de cette couleur. D'après le principe des tiroirs, il existe un sommet ayant deux extrémités de cordes de cette couleur. Il existe donc un triplet de cordes comportant deux fois cette couleur, et ne correspondant donc à aucun triplet de couleur. Cependant il y a $\binom{n}{3}$ triplets de cordes qui doivent remplir les $\binom{n}{3}$ triplets de couleurs possibles, il n'y a aucune marge pour gâcher des triplets de cordes. Il est donc impossible d'obtenir un mur coloré pour $n$ pair.
|
| 206 |
+
Cas n impair : Ici le raisonnement précédent nous indique juste que pour chaque couleur il faut $\frac{\mathrm{n}-1}{2}$ cordes reliant $n-1$ points distincts et laissant un unique point ne relié par cette couleur. On trouve la construction suivante : on numérote les clous dans $\mathbb{Z} / \mathrm{n} \mathbb{Z}$ et les couleurs aussi. Ensuite, on donne à la corde entre le clou $i$ et le clou $j$ la couleur $i+j$. Cette construction semble prometteuse car elle est totalement symétrique et vérifie la propriété voulue. En effet, on vérifie facilement que le triplet de couleur de corde $\mathrm{a}, \mathrm{b}, \mathrm{c}$ est atteint en prenant les clous $\frac{\mathrm{a}+\mathrm{b}}{2}, \frac{\mathrm{a}+\mathrm{c}}{2}, \frac{\mathrm{~b}+\mathrm{c}}{2}$
|
| 207 |
+
|
| 208 |
+
Commentaires des correcteurs:
|
| 209 |
+
L'exercice est bien résolu. Certains n'ont trouvé qu'un cas sur les deux, mais ont été récompensé.
|
| 210 |
+
|
| 211 |
+
Exercice 8. Soit $\Gamma$ un cercle et P un point à l'extérieur de $\Gamma$. Les tangentes à $\Gamma$ issues de P touchent $\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle $P B K$ recoupe le cercle $\Gamma$ au point $T$. Soit $P^{\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
| 212 |
+
|
| 213 |
+
## Solution de l'exercice 8
|
| 214 |
+
|
| 215 |
+
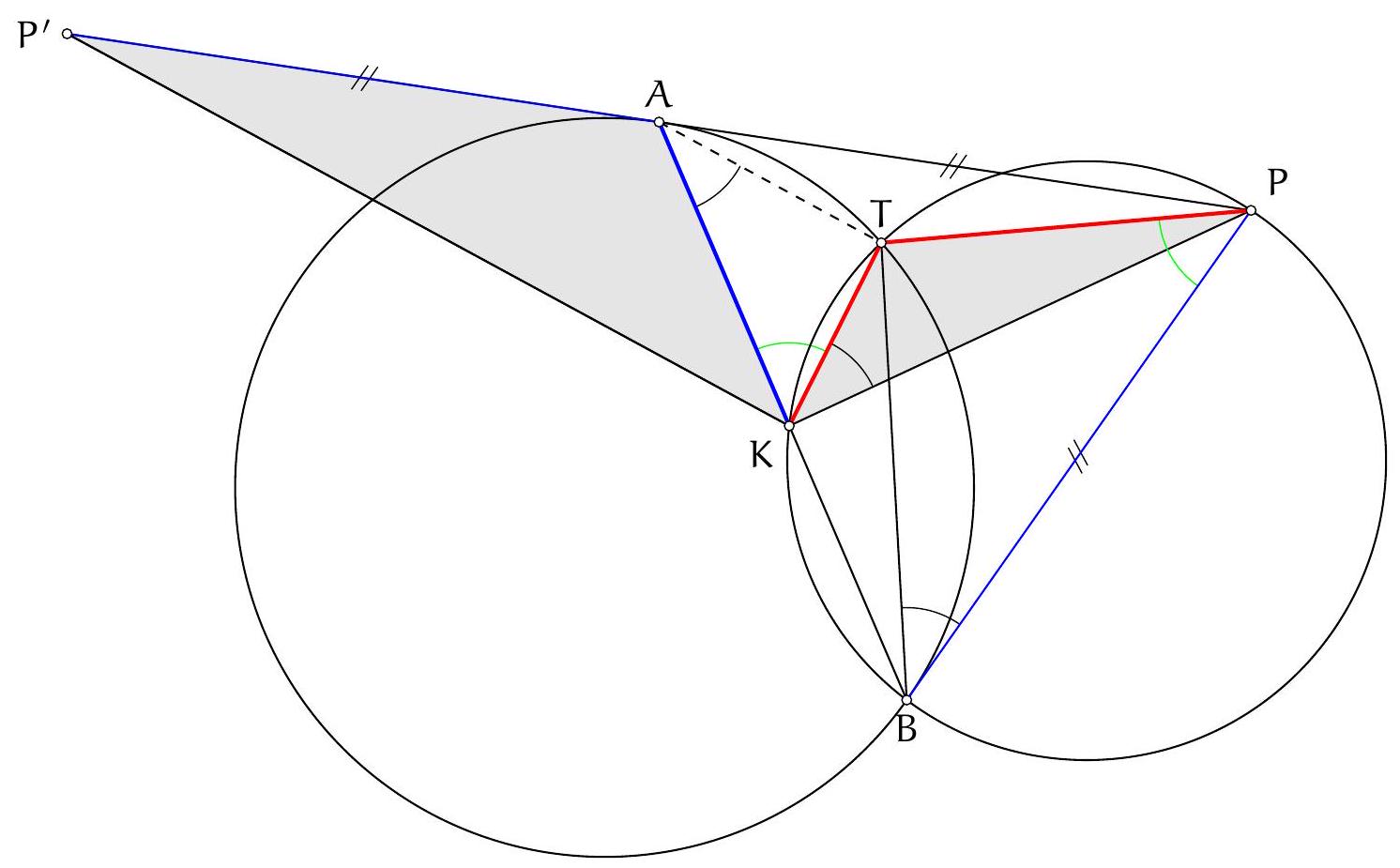
|
| 216 |
+
|
| 217 |
+
D'après le théorème de l'angle inscrit, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $P^{\prime}$ KA sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.
|
| 218 |
+
Pour montrer que $\triangle P K T \sim \triangle P^{\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\widehat{T P K}=$ $\widehat{K^{\prime} A}$ et $\widehat{\mathrm{KTP}}=\widehat{\mathrm{KAP}}$. Toutefois, lorsque l'on essaye de calculer l'angle $\widehat{\mathrm{TPK}}$, on se rend compte que l'égalité $\widehat{\mathrm{TPK}}=\widehat{\mathrm{KP}^{\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} \mathrm{AK}}$ et que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
|
| 219 |
+
Pour montrer que $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} A \mathrm{AK}}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passat par $P, B, K$ et $T$, on trouve :
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
\widehat{\mathrm{KTP}}=180^{\circ}-\widehat{\mathrm{KBP}}=180^{\circ}-\widehat{\mathrm{ABP}}=180^{\circ}-\widehat{\mathrm{BAP}}=\widehat{\mathrm{PAK}}
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Il reste donc à montrer que $\frac{K T}{K A}=\frac{T P}{A P^{\prime}}$. Puisque $A P^{\prime}=A P=B P$, il suffit de montrer que $\frac{K T}{K A}=\frac{T P}{B P}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.
|
| 226 |
+
D'une part, par angle inscrit, $\widehat{A K T}=180^{\circ}-\widehat{\mathrm{BKT}}=\widehat{\mathrm{TPB}}$. D'autre part par angle tangentiel, $\widehat{\mathrm{TAK}}=$ $\widehat{\mathrm{TAB}}=\widehat{\mathrm{TBP}}$.
|
| 227 |
+
Donc les triangles $A K T$ et BPT sont semblables comme voulu.
|
| 228 |
+
|
| 229 |
+
## Commentaires des correcteurs:
|
| 230 |
+
|
| 231 |
+
Une bonne réussite relativement à la difficulté estimée de l'exercice. Quelques élèves, qui n'ont pas résolu complètement l'exercice, on tenu à partager leurs idées sur le problème, ce qui a été grandement apprécié.
|
| 232 |
+
|
| 233 |
+
Exercice 9. Soient $a_{1}, \ldots, a_{101}$ des réels appartenant à l'intervalle $[-2 ; 10]$ tels que
|
| 234 |
+
|
| 235 |
+
$$
|
| 236 |
+
a_{1}+\ldots+a_{101}=0
|
| 237 |
+
$$
|
| 238 |
+
|
| 239 |
+
Montrer que
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
a_{1}^{2}+\ldots+a_{101}^{2} \leqslant 2020
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
Solution de l'exercice 9 Lorsque l'on effectue des inégalités sur des réels qui ne sont pas forcément positifs, il est essentiel de séparer les variables positives et négatives. Cette idée simple constitue souvent l'idée de départ dans la solution et peut mener à des développements intéressants, en plus de prévenir certaines erreurs lors de manipulations d'inégalités avec des nombres négatifs.
|
| 246 |
+
La deuxième idée, lorsque les variables jouent des rôles symétriques, est d'imposer un ordre aux réels. En plus de permettre, parfois, d'obtenir des résultats intéressants pour le problème, cela simplifie grandement la rédaction de la solution.
|
| 247 |
+
Quitte à renuméroter les variables, on suppose donc que $a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{100} \leqslant a_{101}$. Si tous les réels sont nuls, alors la somme de leur carré est nulle et donc bien inférieure à 2020. On suppose désormais que l'un des réels est non nul. Puisque la somme des $a_{i}$ est nulle, cela impose qu'au moins un réel est strictement positif et un autre strictement négatif. On note alors $p$ l'indice vérifiant $a_{p}<0 \leqslant a_{p+1}$.
|
| 248 |
+
Réécrivons dès à présent l'hypothèse de la somme nulle sous la forme
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
-\left(a_{1}+a_{2}+\ldots+a_{p}\right)=a_{p+1}+\ldots+a_{101}
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
On va désormais chercher à faire apparaître cette hypothèse dans la somme à calculer. Pour cela, on va également se servir du fait que si $1 \leqslant i \leqslant p$, alors $a_{i} \geqslant-2$ et que si $p+1 \leqslant i \leqslant 101$, alors $a_{i} \leqslant 10$. On a :
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\begin{aligned}
|
| 258 |
+
a_{1}^{2}+\ldots+a_{101}^{2} & =\underbrace{a_{1} \cdot a_{1}}_{\leqslant-2 a_{1}}+\ldots+\underbrace{a_{p} \cdot a_{p}}_{\leqslant-2 a_{p}}+\underbrace{a_{p+1} \cdot a_{p+1}}_{\leqslant 10 a_{p+1}}+\ldots+\underbrace{a_{101} \cdot a_{101}}_{\leqslant 10 a_{101}} \\
|
| 259 |
+
& \leqslant-2 a_{1}+\ldots+\left(-2 a_{p}\right)+10 a_{p+1}+\ldots+10 a_{101} \\
|
| 260 |
+
& =2\left(-\left(a_{1}+\ldots+a_{p}\right)\right)+10\left(a_{p+1}+\ldots+a_{101}\right) \\
|
| 261 |
+
& =2(\underbrace{a_{p+1}}_{\leqslant 10}+\ldots+\underbrace{a_{101}}_{\leqslant 10})+10(-(\underbrace{a_{1}}_{\geqslant-2}+\ldots+\underbrace{a_{p}}_{\geqslant-2})) \\
|
| 262 |
+
& \leqslant 2 \cdot 10 \cdot(101-p)+10 \cdot 2 \cdot p \\
|
| 263 |
+
& =2020
|
| 264 |
+
\end{aligned}
|
| 265 |
+
$$
|
| 266 |
+
|
| 267 |
+
ce qui est l'inégalité voulue.
|
| 268 |
+
|
| 269 |
+
## Commentaires des correcteurs :
|
| 270 |
+
|
| 271 |
+
Certains élèves ont remarqué que, pour $-2 \leqslant a_{i} \leqslant 10$, on a $\left(a_{i}+2\right)\left(a_{i}-10\right) \leqslant 0$, et s'en sont servi pour aboutir à une preuve de façon très efficace. D'autres ont choisi de construire les valeurs de $a_{i}$ maximisant la somme des carrés; dans ce cas, il était bien sûr indispensable de prouver l'optimalité de la construction pour obtenir la majorité des points.
|
| 272 |
+
|
| 273 |
+
## Exercices Seniors
|
| 274 |
+
|
| 275 |
+
Exercice 10. Soit a un réel strictement positif et $n \geqslant 1$ un entier. Montrer que
|
| 276 |
+
|
| 277 |
+
$$
|
| 278 |
+
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
Solution de l'exercice 10 Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
L'idée derrière la solution qui suit est "d'homogénéiser" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \leqslant i \leqslant 2 n$, on a $a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :
|
| 288 |
+
|
| 289 |
+
$$
|
| 290 |
+
\begin{aligned}
|
| 291 |
+
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
|
| 292 |
+
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text { termes }}+a^{n}}{a^{n}} \\
|
| 293 |
+
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
|
| 294 |
+
& =2 n+1 \\
|
| 295 |
+
& >2 n
|
| 296 |
+
\end{aligned}
|
| 297 |
+
$$
|
| 298 |
+
|
| 299 |
+
ce qui fournit l'inégalité voulue.
|
| 300 |
+
Commentaires des correcteurs:
|
| 301 |
+
Exercice très bien résolu dans l'ensemble. De nombreux élèves ont su appliquer l'IAG directement à $2 \mathrm{n}+1$ termes, les autres ont pour la plupart réussi à s'en sortir avec l'IAG à deux termes.
|
| 302 |
+
|
| 303 |
+
Exercice 11. Déterminer tous les entiers a tels que $a-3$ divise $a^{3}-3$.
|
| 304 |
+
Solution de l'exercice 11
|
| 305 |
+
On sait que $a-3 \mid a^{3}-3^{3}$, donc il divise la différence
|
| 306 |
+
|
| 307 |
+
$$
|
| 308 |
+
a-3 \mid a^{3}-3-\left(a^{3}-3^{3}\right)=27-3=24
|
| 309 |
+
$$
|
| 310 |
+
|
| 311 |
+
Réciproquement, il suffit que $a-3$ divise 24 pour qu'il divise $24+a^{3}-3^{3}=a^{3}-3$. Les solutions sont donc exactement les diviseurs de 24 auxquels on ajoute 3 . On a donc
|
| 312 |
+
|
| 313 |
+
$$
|
| 314 |
+
a-3 \in\{-24,-12,-8,-6,-4,-3,-2,-1,0,1,2,3,4,6,8,12,24\}
|
| 315 |
+
$$
|
| 316 |
+
|
| 317 |
+
et $a \in\{-21,-9,-5,-3,-1,0,1,2,3,4,5,6,9,11,15,27\}$.
|
| 318 |
+
|
| 319 |
+
## Commentaires des correcteurs:
|
| 320 |
+
|
| 321 |
+
Exercice très bien résolu dans l'ensemble ; l'erreur la plus fréquente est l'oubli de certains diviseurs de 24.
|
| 322 |
+
|
| 323 |
+
Exercice 12. Soient $\omega_{1}$ et $\omega_{2}$ deux cercles de centres respectifs $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$. On suppose que $\omega_{1}$ et $\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\left(O_{1} A\right)$ recoupe le cercle $\omega_{2}$ en $C$ tandis que la droite $\left(O_{2} A\right)$ recoupe le cercle $\omega_{1}$ en D . Montrer que les points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et C appartiennent à un même cercle.
|
| 324 |
+
|
| 325 |
+
## Solution de l'exercice 12
|
| 326 |
+
|
| 327 |
+
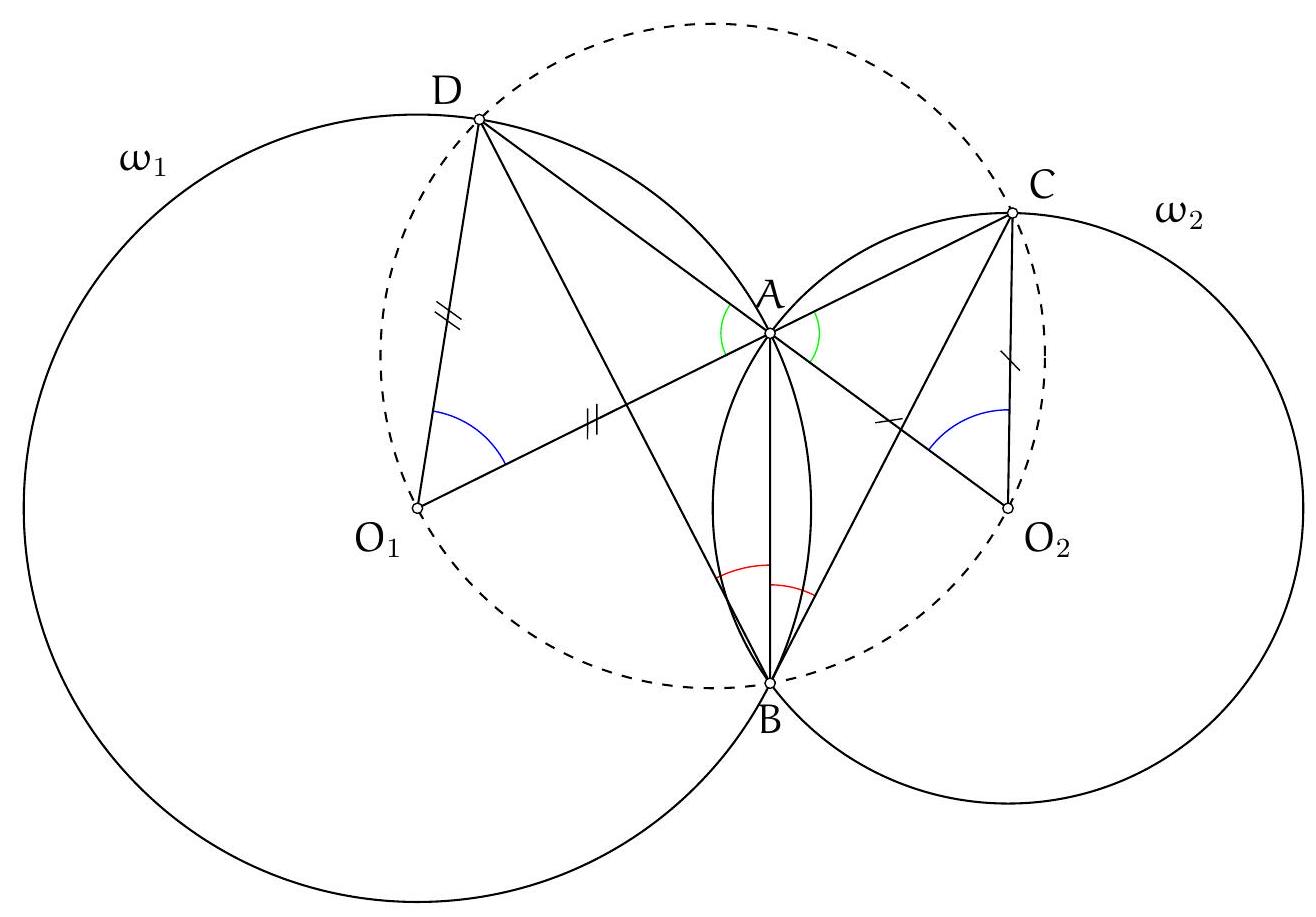
|
| 328 |
+
|
| 329 |
+
Notons que puisque les angles $\widehat{\mathrm{DAO}_{1}}$ et $\widehat{\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\mathrm{CO}_{2} A$ est isocèle en $\mathrm{O}_{2}$. Les triangles $\mathrm{DO}_{1} A$ et $\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}$, et donc que
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
si bien que les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D sont cocycliques.
|
| 336 |
+
Par ailleurs, on peut découper l'angle $\widehat{\mathrm{DBC}}$ en la somme $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B C}=\frac{1}{2} \widehat{A O_{2} C}$. Ainsi
|
| 337 |
+
|
| 338 |
+
$$
|
| 339 |
+
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
|
| 340 |
+
$$
|
| 341 |
+
|
| 342 |
+
ce qui permet de conclure que le point B appartient au cercle passant par les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D .
|
| 343 |
+
|
| 344 |
+
## Commentaires des correcteurs:
|
| 345 |
+
|
| 346 |
+
Exercice très bien résolu.
|
| 347 |
+
|
| 348 |
+
Exercice 13. Soit ( $a_{n}$ ) une suite strictement croissante d'entiers positifs telle que $a_{1}=1$ et pour tout $n \geqslant 1, a_{n+1} \leqslant 2 n$. Montrer que pour tout entier $n \geqslant 1$, il existe deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$.
|
| 349 |
+
|
| 350 |
+
## Solution de l'exercice 13
|
| 351 |
+
|
| 352 |
+
Soit $n \geqslant 1$ un entier. On va utiliser le principe des tiroirs. Construisons nos tiroirs deux sorte que si deux nombres sont dans un même tiroirs, ils vérifient la propriété de l'énoncé. Pour cela, on considère les tiroirs suivants : on réunit les entiers de 1 à $2 n$ en les couples de la forme $\{i, n+i\}$ pour $i$ entre 1 et $n$, ce qui constitue $n$ tiroirs. Ces tiroirs sont bien disjoints deux à deux, et si deux termes de la suite sont dans un même tiroir, cela donne les deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$, car tous les termes d'une suite strictement croissante sont distincts.
|
| 353 |
+
Or, puisque la suite ( $a_{m}$ ) est croissante et puisque $a_{n+1} \leqslant 2 n, a_{m} \in \llbracket 1,2 n \rrbracket$ pour $m \in \llbracket 1, n+1 \rrbracket$. Donc les $n+1$ premiers termes de la suites sont dans l'intervalle $\llbracket 1,2 n \rrbracket$. Par le principe des tiroirs, il y a deux termes distincts qui appartiennent au même ensemble $\{i, n+i\}$ pour un certain $i$, ce qui est le résultat voulu.
|
| 354 |
+
|
| 355 |
+
## Commentaires des correcteurs :
|
| 356 |
+
|
| 357 |
+
Exercice très bien traité.
|
| 358 |
+
|
| 359 |
+
Exercice 14. Soit $\Gamma$ un cercle et $P$ un point à l'extérieur de $\Gamma$. Les tangentes à $\Gamma$ issues de $P$ touchent $\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle PBK recoupe le cercle $\Gamma$ au point $T$. Soit $\mathrm{P}^{\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
| 360 |
+
|
| 361 |
+
## Solution de l'exercice 14
|
| 362 |
+
|
| 363 |
+
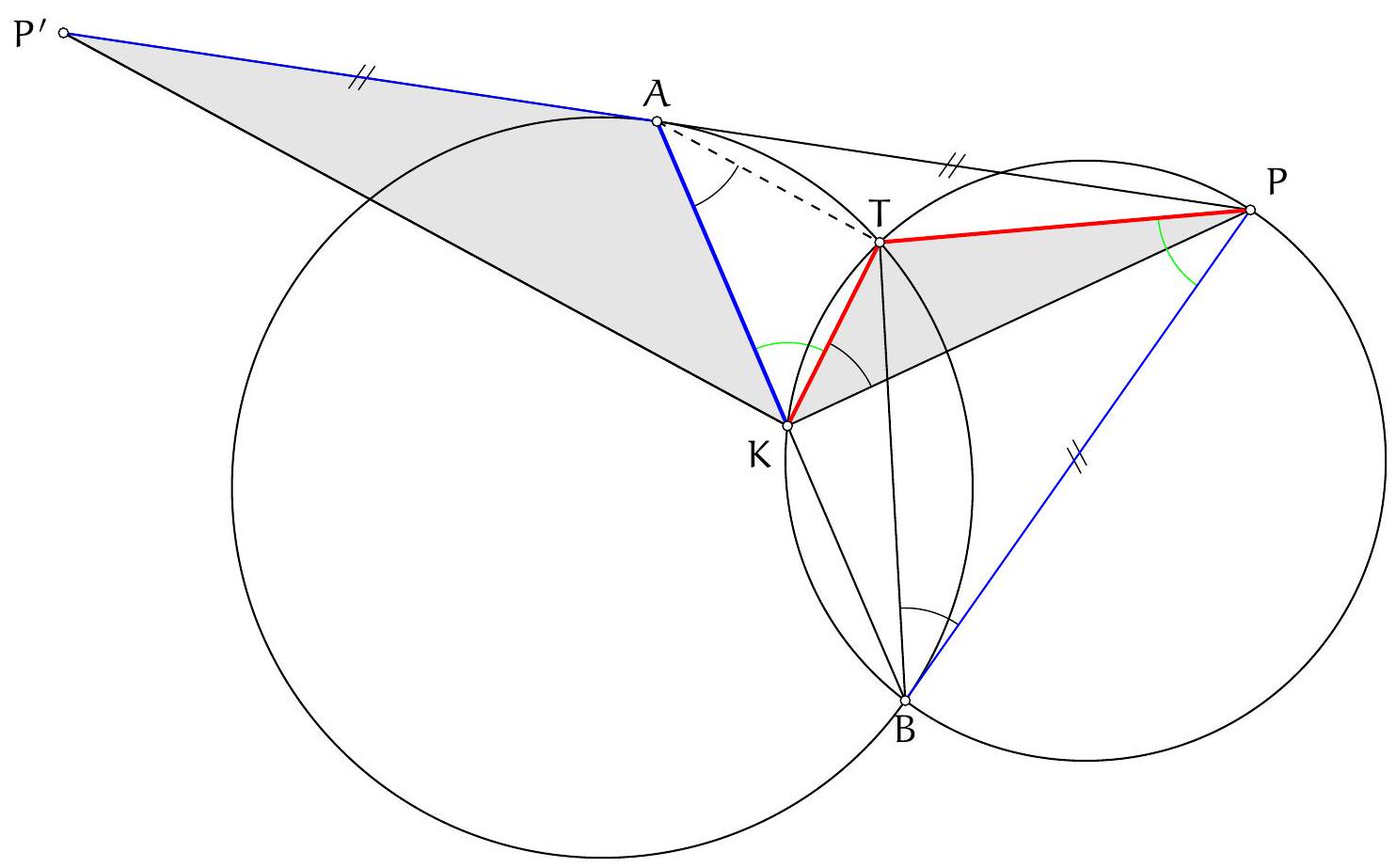
|
| 364 |
+
|
| 365 |
+
D'après le théorème de l'angle inscrit, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $\mathrm{P}^{\prime} \mathrm{KA}$ sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.
|
| 366 |
+
Pour montrer que $\triangle P K T \sim \triangle P^{\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\widehat{T P K}=$ $\widehat{K P^{\prime} A}$ et $\widehat{K T P}=\widehat{K A P}$. Toutefois, lorsque l'on essaye de calculer l'angle $\widehat{T P K}$, on se rend compte que l'égalité $\widehat{T P K}=\widehat{K P^{\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\widehat{K T P}=\widehat{P^{\prime} A K}$ et que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
|
| 367 |
+
Pour montrer que $\widehat{K T P}=\widehat{P^{\prime} A K}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passant par $\mathrm{P}, \mathrm{B}, \mathrm{K}$ et T , on trouve :
|
| 368 |
+
|
| 369 |
+
$$
|
| 370 |
+
\widehat{\mathrm{KTP}}=180^{\circ}-\widehat{\mathrm{KBP}}=180^{\circ}-\widehat{\mathrm{ABP}}=180^{\circ}-\widehat{\mathrm{BAP}}=\widehat{\mathrm{PAK}}
|
| 371 |
+
$$
|
| 372 |
+
|
| 373 |
+
Il reste donc à montrer que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{A \mathrm{P}^{\prime}}$. Puisque $A P^{\prime}=A P=B P$, il suffit de montrer que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{BP}}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.
|
| 374 |
+
D'une part, par angle inscrit, $\widehat{A K T}=180^{\circ}-\widehat{\mathrm{BKT}}=\widehat{\mathrm{TPB}}$. D' autre part, par angle tangentiel, $\widehat{\mathrm{TAK}}=$ $\widehat{\mathrm{TAB}}=\widehat{\mathrm{TBP}}$.
|
| 375 |
+
Donc les triangles AKT et BPT sont semblables comme voulu.
|
| 376 |
+
|
| 377 |
+
## Solution $n^{\circ} 2$ :
|
| 378 |
+
|
| 379 |
+
En cas d'allergie à la chasse aux angles, il est aussi possible de progresser dans le problème avec des idées avancées. Le problème se présente naturellement comme dynamique : en gardant fixe $\Omega, P, A, B, P^{\prime}$ on peut faire bouger K projectivement. Alors la T bouge aussi projectivement car le cercle PBK ayant deux points fixes P et B il a une intersection non fixe avec la droite $(\mathrm{AB})$ et avec $\Omega$, donc peut passer projectivement à $K$ ou à $T$. De plus, les angles à mesurer sont entre une droite fixe et une droite qui bouge projectivement chacun, l'égalité d'angle revient donc à dire que le point à l'infini de la première droite projective est envoyé sur le point à l'infini de la deuxième par une rotation bien choisie (ou par une symétrie si les angles avaient été dans l'autre sens). Le problème est bien projectif, cherchons trois cas particuliers.
|
| 380 |
+
On peut envoyer K à l'infini, alors par tangence $T$ se retrouve en $B$ et les deux angles qui doivent être égaux sont nuls.
|
| 381 |
+
On peut envoyer K sur $A$, alors T se retrouve aussi en $A$ et les deux angles qui doivent être égaux sont égaux car le triangle PAB est isocèle en P .
|
| 382 |
+
Il nous manque encore un cas particulier utilisant le fait que $\mathrm{P}^{\prime}$ soit non seulement sur la droite ( $P A$ ) mais bien symétrique. On peut placer K sur le symétrique de B par rapport à $A$ pour construire un parallélogramme. La chasse aux angles n'est alors pas tout à fait immédiate, mais plus facile que dans le problème original, car elle ne nécessite pas d'idée pour utiliser la condition de milieu puisqu'il suffit de considérer le parallélogramme. Elle est laissée en exercice au lecteur.
|
| 383 |
+
|
| 384 |
+
## Commentaires des correcteurs:
|
| 385 |
+
|
| 386 |
+
L'exercice a été très bien réussi, et les preuves utilisant les astuces autour des milieux de segments ont été particulièrement appréciées.
|
| 387 |
+
|
| 388 |
+
Exercice 15. Soient $\mathrm{m}, \mathrm{n}$ et $\times$ des entiers strictement positifs. Montrer que
|
| 389 |
+
|
| 390 |
+
$$
|
| 391 |
+
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)=\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
## Solution de l'exercice 15
|
| 395 |
+
|
| 396 |
+
Quitte à échanger $m$ et $n$, on peut supposer que $m \leqslant n$. On procède alors par récurrence sur $n$ à $m$ fixé.
|
| 397 |
+
Initialisation : Si $\mathrm{m}=\mathrm{n}$, l'égalité est triviale.
|
| 398 |
+
Hérédité : Supposons l'égalité vraie pour un certain $n \geqslant m$ et cherchons à montrer que l'égalité est vraie pour $n+1$. Le membre de gauche devient
|
| 399 |
+
|
| 400 |
+
$$
|
| 401 |
+
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)
|
| 402 |
+
$$
|
| 403 |
+
|
| 404 |
+
Examinons les termes du membre de droite, qui sont de la forme $\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)$. On a
|
| 405 |
+
|
| 406 |
+
$$
|
| 407 |
+
\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)-\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)= \begin{cases}1 & \text { si }\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1 \\ 0 & \text { sinon }\end{cases}
|
| 408 |
+
$$
|
| 409 |
+
|
| 410 |
+
Or, $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ si et seulement si $x \geqslant(n+1) i$, ou encore $i \leqslant\left\lfloor\frac{x}{n+1}\right\rfloor$. Donc le nombre de $i$ de $\llbracket 1, m \rrbracket$ pour lesquels $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ est précisément $\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)$. On déduit que
|
| 411 |
+
|
| 412 |
+
$$
|
| 413 |
+
\begin{aligned}
|
| 414 |
+
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right) & =\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
|
| 415 |
+
& =\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
|
| 416 |
+
& =\sum_{i=1}^{n+1} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
|
| 417 |
+
\end{aligned}
|
| 418 |
+
$$
|
| 419 |
+
|
| 420 |
+
où la deuxième égalité provient de l'hypothèse de récurrence. Ceci achève la récurrence et conclut l'exercice.
|
| 421 |
+
$\underline{\text { Solution alternative: }}$ Une solution très astucieuse consiste à procéder par double comptage, en remarquant que les deux membres de l'égalité servent à compter le même objet, à savoir le nombre de paires $(a, b)$ telles que $a \leqslant m, b \leqslant n$ et $a b \leqslant x$.
|
| 422 |
+
Cherchons en effet à compter ce nombre d'objet d'une première façon. Le choix d'une paire $(a, b) \in$ $\llbracket 1, \mathrm{~m} \rrbracket \times \llbracket 1, n \rrbracket$ telle que $\mathrm{ab} \leqslant x$ se caractérise dans un premier temps par le choix de $a$ dans $\llbracket 1, m \rrbracket$. Puis, puisque $a b \leqslant x$, on $a b \leqslant\left\lfloor\frac{x}{a}\right\rfloor$. Donc $b \leqslant \min (\lfloor x / a\rfloor, n)$ et il y a $\min (\lfloor x / a\rfloor, n)$ choix pour $b$ si a est fixé. On a donc en tout
|
| 423 |
+
|
| 424 |
+
$$
|
| 425 |
+
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
|
| 426 |
+
$$
|
| 427 |
+
|
| 428 |
+
telles paires $(a, b)$.
|
| 429 |
+
En commençant par choisir b plutôt que $a$, un raisonnement similaire nous permet d'affirmer qu'il y a
|
| 430 |
+
|
| 431 |
+
$$
|
| 432 |
+
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
|
| 433 |
+
$$
|
| 434 |
+
|
| 435 |
+
telles paires d'entiers $(a, b)$. Les deux termes sont donc égaux.
|
| 436 |
+
Commentaires des correcteurs:
|
| 437 |
+
L'exercice a été bien traité et par beaucoup d'élèves, relativement à sa difficulté estimée.
|
| 438 |
+
|
| 439 |
+
Exercice 16. Soit $A B C$ un triangle dans lequel $A B<A C$. Soit $\omega$ un cercle passant par $B$ et $C$ et on suppose que le point $A$ se trouve à l'intérieur du cercle $\omega$. Soient $X$ et $Y$ des points de $\omega$ tels que $\widehat{B X A}=\widehat{A Y C}$. On suppose que $X$ et $C$ sont situés de part et d'autre de la droite $(A B)$ et que $Y$ et $B$ sont situés de part et d'autre de la droite (AC). Montrer que, lorsque $X$ et $Y$ varient sur le cercle $\omega$, la droite (XY) passe par un point fixe.
|
| 440 |
+
Solution de l'exercice 16 Tout d'abord, nous allons chercher à tracer une figure exacte, en espérant que les raisonnements mis en oeuvre pour le tracé nous éclairerons sur la dynamique de la figure.
|
| 441 |
+
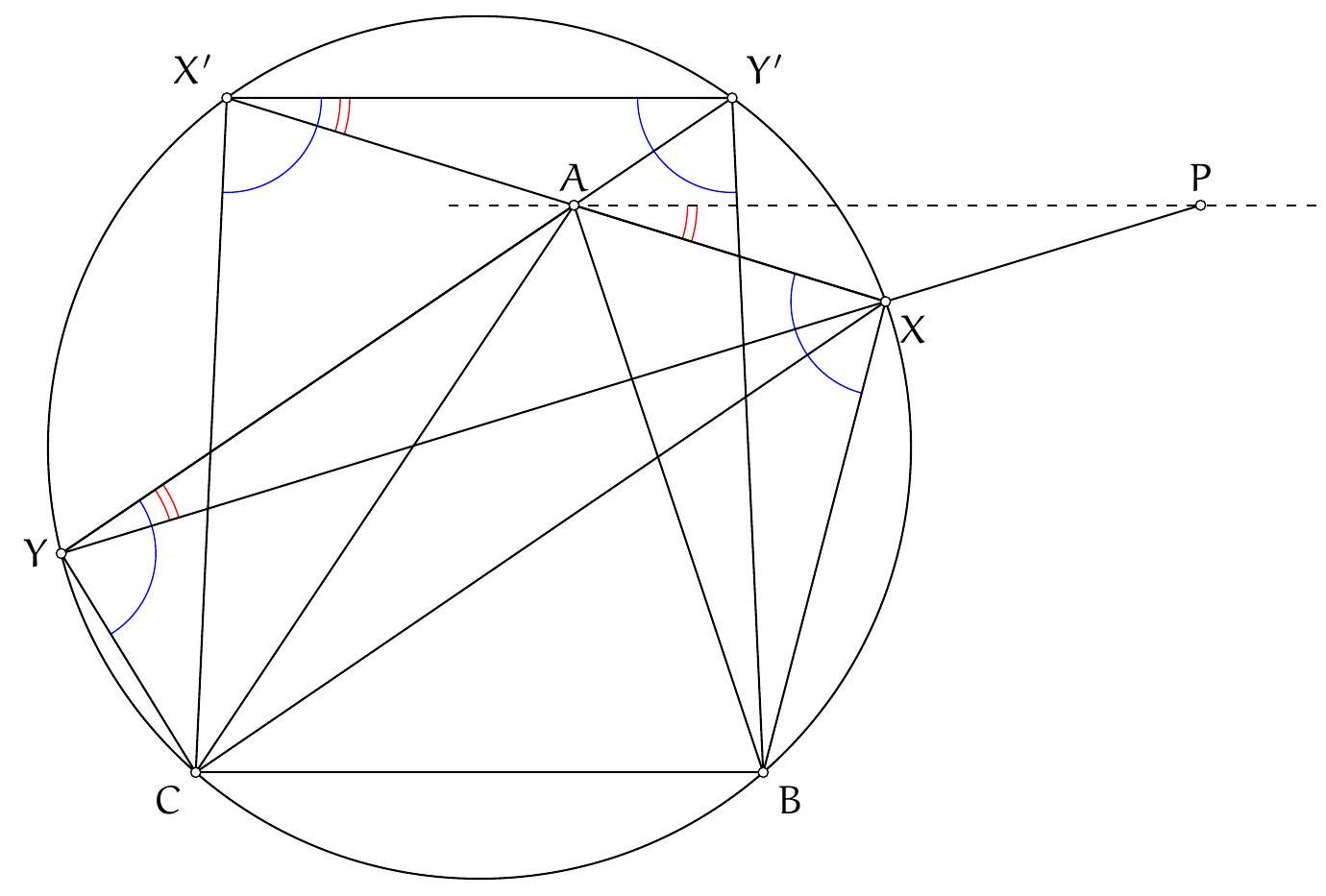
|
| 442 |
+
|
| 443 |
+
Pour tracer la figure, on cherche à tirer profit de l'hypothèse que les points $X, B, C$ et $Y$ sont sur un même cercle, à l'aide du théorème de l'angle inscrit. Supposons la figure tracée. On prolonge donc la droite ( $X A$ ) et on note $X^{\prime}$ le second point d'intersection de $(X A)$ avec $\omega$ et de même $Y^{\prime}$ le second point d'intersection de (YA) avec $\omega$.
|
| 444 |
+
Le théorème de l'angle inscrit et l'hypothèse sur $X$ et $Y$ nous impose l'égalité suivante :
|
| 445 |
+
|
| 446 |
+
$$
|
| 447 |
+
\widehat{C X^{\prime} Y^{\prime}}=\widehat{C Y^{\prime}}=\widehat{C Y^{\prime}}=\widehat{A X B}=\widehat{X^{\prime} X B}=\widehat{X^{\prime} Y^{\prime} B}
|
| 448 |
+
$$
|
| 449 |
+
|
| 450 |
+
de sorte que le quadrilatère $B C X^{\prime} Y^{\prime}$ est un trapèze isocèle, et les droites $\left(X^{\prime} Y^{\prime}\right)$ et ( $B C$ ) sont parallèles.
|
| 451 |
+
On en déduit un protocole pour tracer la figure : On place un point $X$ sur le cercle $\omega$ et on prolonge la droite $(A X)$ de sorte à obtenir le point $X^{\prime}$. Puis on obtient le point $Y^{\prime}$ en traçant la parallèle à la droite (BC) passant par $X^{\prime}$. On obtient enfin le point $Y$ en prolongeant la droite ( $Y^{\prime} A$ ).
|
| 452 |
+
Résolvons à présent l'exercice. Maintenant que l'on peut tracer un figure exacte, on peut tracer la figure pour deux positions différentes du point $X$, notées $X_{1}$ et $X_{2}$, tracer les points $Y_{1}$ et $Y_{2}$ associés et conjecturer la position du point fixe à l'aide du point d'intersection des droites $\left(X_{1} Y_{1}\right.$ et $\left(X_{2} Y_{2}\right)$. Il est frappant que le point d'intersection obtenu appartient à la parallèle à la droite $(B C)$ passant par le point $A$.
|
| 453 |
+
Soit donc $P$ le point d'intersection de la droite $(X Y)$ avec la parallèle à ( $B C$ ) passant par $A$. Puisque les droites $\left(X^{\prime} Y^{\prime}\right)$ et $(A P)$ sont parallèles, on trouve :
|
| 454 |
+
|
| 455 |
+
$$
|
| 456 |
+
\widehat{X A P}=\widehat{X X^{\prime} Y^{\prime}}=\widehat{X Y Y^{\prime}}=\widehat{X Y A}
|
| 457 |
+
$$
|
| 458 |
+
|
| 459 |
+
De sorte que la droite (AP) est tangente au cercle circonscrit au triangle $A X Y$. On a donc, d'après la puissance d'un point :
|
| 460 |
+
|
| 461 |
+
$$
|
| 462 |
+
\mathrm{PA}^{2}=\mathrm{PX} \cdot \mathrm{PY}=\mathcal{P}_{\omega}(\mathrm{P})
|
| 463 |
+
$$
|
| 464 |
+
|
| 465 |
+
La position du point $P$ sur la parallèle à $(B C)$ passant par $A$ est uniquement déterminée par la puissance du point $P$ par rapport au cercle $\omega$, qui ne dépend pas de $X$ et $Y$. C'est ce que nous voulions démontrer.
|
| 466 |
+
|
| 467 |
+
## Solution $n^{\circ} 2$ :
|
| 468 |
+
|
| 469 |
+
On propose une solution alternative utilisant des connaissances avancées. L'énoncé du problème nous invite à considérer le problème dynamiquement, puisque la partie fixe et la partie mobile de la figure a déjà été spécifiée dans l'énoncé. Si la construction de $X$ et $Y$ ne semble pas projective, l'énoncé nous demande en fait de montrer qu'elle l'est. En effet, passer à la seconde intersection avec la droite reliant à un point fixe hors du cercle revient à faire une inversion laissant le cercle globalement invariant et est une transformation projective, c'est même une involution projective du cercle. En fait, toutes les involutions projectives du cercle sont de cette forme : il suffit de prouver que passer de X à Y est une involution projective pour pouvoir en déduire l'existence de ce point $P$. En effet, si on construit $P$ comme ( $X_{1} \mathrm{Y}_{1}$ ) intersecté avec $\left(X_{2} \mathrm{Y}_{2}\right)$ pour deux positions de $X$ et $Y$, alors $P$ définit une involution qui, coïncidant en 4 points avec celle de l'énoncé, ne peut être que la même.
|
| 470 |
+
Maintenant qu'on a vu que ce problème était fondamentalement dynamique et que le point $P$ n'est qu'une excuse pour demander de démontrer l'existence d'une involution projective, faisons-le. Même si ce n'est initialement pas très visible, il est en fait assez facile de montrer que la transformation de $X$ à $Y$ est projective. Les angles de l'énoncé nous invitent à regarder les cercles $A X B$ et $A Y C$, vivant dans le faisceau de cercle ayant pour points fixes respectivement $A, B$ et $A, C$. Comme le cercle $A B X$ a une seule intersection non fixe avec le cercle $\omega$, il est bien projectif de passer de $X$ à ce cercle. De même de l'autre côté avec $Y$ et l'autre cercle. Enfin il faut prouver qu'on peut passer d'un cercle à l'autre. L'égalité des angles nous donne en fait que le cercle AYC est l'image du cercle AXB par la similitude indirecte de centre $A$ envoyant $B$ sur $C$. La transformation est donc bien projective.
|
| 471 |
+
Montrons que c'est une involution. On sait qu'une transformation projective est une involution dès qu'elle échange une paire de points. Cherchons donc un cas simple. Un cas particulièrement simple est celui où l'angle commun est nul : cela correspond au fait que $X, A, B$ soient alignés dans cet ordre et que $Y, A, C$ soient aussi alignés dans cet ordre. La transformation envoie alors bien $X$ sur $Y$. Vérifions qu'elle enverrait aussi $Y$ sur $X$. Cela revient à dire que $\widehat{A Y B}=\widehat{A X C}$, ce qui est immédiat d'après le théorème de l'angle inscrit.
|
| 472 |
+
|
| 473 |
+
## Commentaires des correcteurs:
|
| 474 |
+
|
| 475 |
+
Exercice abordé par quatre personnes, avec deux approches dynamiques et deux approches élémentaires.
|
| 476 |
+
|
| 477 |
+
Exercice 17. Une suite réelle $a_{1}, \ldots, a_{k}$ est casable dans l'intervalle $[b, c]$ si il existe des réels $x_{0}, \ldots, x_{k}$ dans $[b, c]$ tels que $\left|x_{i}-x_{i-1}\right|=a_{i}$ pour $k \geqslant i \geqslant 1$. La suite est normalisée si ses termes sont tous inférieurs ou égaux à 1 .
|
| 478 |
+
|
| 479 |
+
1) Montrer que pour tout entier $n \geqslant 1$, toute suite normalisée de longueur $2 \mathfrak{n}+1$ est casable dans [0, $\left.2-\frac{1}{2^{n}}\right]$.
|
| 480 |
+
2) Montrer que pour tout entier $\mathrm{n} \geqslant 1$, il existe une suite normalisée de longueur $4 \mathrm{n}+3$ qui n 'est pas casable dans $\left[0,2-\frac{1}{2^{n}}\right]$.
|
| 481 |
+
|
| 482 |
+
## Solution de l'exercice 17
|
| 483 |
+
|
| 484 |
+
1) Dans la suite, on dira qu'une suite de ( $x_{i}$ ) satisfaisant la propriété de l'énoncé case la suite ( $a_{i}$ ). On commence par se donner une idée du problème en essayant de montrer l'énoncé pour des petites valeurs de $n$. Si $n=0$, il faut montrer qu'existent $x_{0}, x_{1} \in[0,1]$ tels que $\left|x_{1}-x_{0}\right|=a_{1}$. On peut par exemple prendre $x_{0}=0$ et $x_{1}=a_{1}$. Si l'on cherche à montrer l'énoncé pour $\mathrm{n}=1$, on se retrouve rapidement à devoir distinguer plusieurs cas, ce qui nous pousse à vouloir procéder par récurrence sur n .
|
| 485 |
+
Avant d'attaquer la récurrence, il est important de noter l'idée suivante : si l'ensemble $\left\{x_{0}, \ldots, x_{2 n+1}\right\}$ case la suite ( $a_{i}$ ) dans l'intervalle $[b, c]$, alors l'ensemble $\left\{x_{0}+d, \ldots, x_{2 n+1}\right\}$ case la suite ( $a_{i}$ ) dans l'intervalle $[b+d, c+d]$. Ainsi, il suffit de montrer que la suite ( $a_{i}$ ) est casable dans un intervalle de longueur $2-\frac{1}{2^{n}}$.
|
| 486 |
+
Notons donc $\mathcal{P}_{\mathfrak{n}}$ la propriété suivante : toute suite $\left(a_{i}\right)$ normalisée de longueur $2 \mathfrak{n}+1$ est casable dans un intervalle de longueur $2-\frac{1}{2^{n}}$. On a déjà montré que la propriété $\mathcal{P}_{0}$ est vraie, on suppose maintenant que $\mathcal{P}_{2 n-1}$ est vraie pour un certain $n \geqslant 1$ fixé.
|
| 487 |
+
Soit ( $a_{i}$ ) une suite normalisée de longueur $2 \mathrm{n}+1$. D'après notre hypothèse de récurrence, la suite $\left(a_{i}\right)_{i \leqslant 2 n-1}$ est casable dans un intervalle de longueur $2-\frac{1}{2^{n-1}}$. D'après notre remarque ci-dessus, on peut supposer que cet intervalle est $\left[0,2-\frac{1}{2^{n-1}}\right]$. On dispose donc de $x_{0}, \ldots, x_{2 n-1}$ dans $\left[0,2-\frac{1}{2^{n-1}}\right]$ tels que $\left|x_{i}-x_{i-1}\right|=a_{i}$ pour $2 n-1 \geqslant i \geqslant 1$. Notons que si $\left(x_{i}\right)$ convient, alors $\left(2-1 / 2^{n-1}-x_{i}\right)$ vérifie les mêmes propriétés que la suite ( $x_{i}$ ). On peut donc supposer, quitte à remplacer ( $x_{i}$ ) par $\left(2-1 / 2^{n-1}-x_{i}\right)$, que $x_{2 n+1} \leqslant 1-\frac{1}{2^{n}}$.
|
| 488 |
+
Désormais, nous allons montrer qu'il existe $x_{2 n}$ et $x_{2 n+1}$ qui appartiennent tous les deux soit à l'intervalle $\left[0,2-1 / 2^{n}\right]$ soit à l'intervalle $\left[-1 / 2^{n}, 2-1 / 2^{n-1}\right]$ tels que $\left|x_{2 n}-x_{2 n-1}\right|=a_{2 n}$ et $\left|x_{2 n+1}-x_{2 n}\right|=a_{2 n+1}$. Dans le premier cas, on aura obtenu une suite ( $x_{i}$ ) qui case la suite ( $a_{i}$ ) dans l'intervalle $\left[0,2-1 / 2^{n}\right]$. Dans le deuxième cas, on aura obtenu une suite ( $x_{i}$ ) qui case la suite $\left(a_{i}\right)$ dans l'intervalle $\left[-1 / 2^{n}, 2-\right.$ $\left.1 / 2^{n-1}\right]$, qui est de longueur $2-1 / 2^{n}$. On aura gagné dans les deux cas.
|
| 489 |
+
Considérons les deux quantités $A=x_{2 n-1}+a_{2 n}+a_{2 n+1}$ et $B=x_{2 n-1}+a_{2 n}-a_{2 n+1}$. Notons qu'on ne peut avoir $A>2-1 / 2^{n}$ et $B<-1 / 2^{n}$, sans quoi on aurait $a_{2 n+1}>1$. On a donc $A \leqslant 2-1 / 2^{n}$ ou $B \geqslant-1 / 2^{n}$.
|
| 490 |
+
Si $A \leqslant 2-1 / 2^{n}$, on pose $x_{2 n}=x_{2 n-1}+a_{2 n}$ et $x_{2 n+1}=A$. On vérifie que la suite $\left(x_{i}\right)$ case la suite $\left(a_{i}\right)$ dans l'intervalle $\left[0,2-1 / 2^{\mathfrak{n}}\right]$.
|
| 491 |
+
On suppose que $B \geqslant-1 / 2^{n}$. On pose $x_{2 n}=x_{2 n-1}+a_{2 n}$ et $x_{2 n+1}=$ B. Si $x_{2 n} \leqslant 2-1 / 2^{n-1}$, alors $B \in\left[-1 / 2^{n}, 2-1 / 2^{n-1}\right]$ et la suite ( $x_{i}$ ) case la suite ( $a_{i}$ ) dans l'intervalle $\left[-1 / 2^{n}, 2-1 / 2^{n-1}\right]$. Si $x_{2 n}>2-1 / 2^{n-1}$, alors $B>2-1 / 2^{n-1}-1 \geqslant 0$, si bien que la suite $\left(x_{i}\right)$ case la suite $\left(a_{i}\right)$ dans l'intervalle $\left[0,2-1 / 2^{\mathfrak{n}}\right]$.
|
| 492 |
+
Cette disjonction de cas achève la récurrence.
|
| 493 |
+
2) L'idée est la suivante : on souhaite construire des $a_{i}$ de sorte à forcer les $x_{i}$ à se trouver au centre de l'intervalle. Pour cela, on souhaite que les $a_{i}$ soient très proches de 1 , afin d'écarter deux $x_{i}$ l'un de l'autre, et on souhaite également qu'ils ne soient pas trop proches de 1 , pour éloigner les $x_{i}$ des bornes de l'intervalle. Cette discussion motive la construction qui suit.
|
| 494 |
+
Soit $N=3 \cdot 2^{n}-1$. Considérons la suite suivante :
|
| 495 |
+
|
| 496 |
+
$$
|
| 497 |
+
1,1-\frac{1}{N}, 1,1-\frac{2}{N}, 1, \ldots, 1-\frac{2^{2}}{N}, 1, \ldots, 1-\frac{2^{n}}{N}, 1, \ldots, 1-\frac{2}{N}, 1,1-\frac{1}{N}, 1
|
| 498 |
+
$$
|
| 499 |
+
|
| 500 |
+
Nous allons montrer que cette suite n'est pas casable dans l'intervalle ] $-1+1 / 2 \mathrm{~N}, 1-1 / 2 \mathrm{~N}$ [, qui est un intervalle de longueur $2-1 / \mathrm{N}>2-1 / 2^{n}$, ce qui permettra de conclure. On suppose par l'absurde qu'il existe une suite ( $x_{i}$ ) qui case la suite ( $a_{i}$ ) donnée dans l'intervalle $]-1+1 / 2 \mathrm{~N}, 1-1 / 2 \mathrm{~N}[$ et on cherche à aboutir à une contradiction dans les estimations sur les $x_{i}$.
|
| 501 |
+
Quitte à remplacer $\left(x_{i}\right)$ par $\left(-x_{i}\right)$, on peut suppose que $x_{0} \geqslant 0$. Puisque $\left|x_{1}-x_{0}\right|=1$, on doit avoir $x_{1}=x_{0}-1$, et $x_{1} \leqslant 1-1 / 2 N-1=-1 / 2 N$, soit $\left|x_{1}\right|>1 / 2 N$. De manière générale, on va montrer pour $i \leqslant n$ que
|
| 502 |
+
|
| 503 |
+
$$
|
| 504 |
+
\left|x_{2 i}\right|<1-\frac{2^{i+1}-1}{2 N} \quad, \quad\left|x_{2 i+1}\right|>\frac{2^{i+1}-1}{2 N}
|
| 505 |
+
$$
|
| 506 |
+
|
| 507 |
+
La preuve s'effectue par récurrence sur $i$. On a montré le résultat pour $i=0$. Supposons le vrai pour $i \geqslant 0$ fixé. On a $\left|x_{2 i+2}-x_{2 i+1}\right|=a_{2 i+2}=1-2^{i} / N$. Si $x_{2 i+1}>0$, on a $x_{2 i+1}+\left(1-2^{i} / N\right)>1-\frac{2^{i}-1}{2 N}>$ $1-\frac{1}{2 \mathrm{~N}}$. On a donc forcément $x_{2 i+2}=x_{2 i+1}-\left(1-2^{i} / N\right)$. Comme $1-2^{i} / N>\left(2^{i+1}-1\right) / 2 N$, on a
|
| 508 |
+
|
| 509 |
+
$$
|
| 510 |
+
\left|x_{2 i+2}\right|=1-\frac{2^{i}}{N}-x_{2 i+1}<1-\frac{2^{i+2}-1}{2 N}
|
| 511 |
+
$$
|
| 512 |
+
|
| 513 |
+
On procède de même dans le cas où $x_{2 i+1}<0$.
|
| 514 |
+
On a ensuite $\left|x_{2 i+3}-x_{2 i+2}\right|=a_{2 i+3}=1$. Un raisonnement identique au précédent nous permet d'avoir, dans le cas où $x_{2 i+2}>0$ :
|
| 515 |
+
|
| 516 |
+
$$
|
| 517 |
+
\left|x_{2 i+3}\right|=1-x_{2 i+2}>1-\left(1-\frac{2^{i+2}-1}{2 \mathrm{~N}}\right)=\frac{2^{i+2}-1}{2 \mathrm{~N}}
|
| 518 |
+
$$
|
| 519 |
+
|
| 520 |
+
et on procède de même dans le cas où $x_{2 i+2}<0$.
|
| 521 |
+
On procède de même pour montrer par récurrence que si $\boldsymbol{i} \geqslant \mathrm{n}+1$ :
|
| 522 |
+
|
| 523 |
+
$$
|
| 524 |
+
\left|x_{2 i}\right|<\frac{2^{2(n+1)-\mathfrak{i}}-1}{2 N} \quad, \quad\left|x_{2 i+1}\right|>1-\frac{2^{2(n+1)-\mathfrak{i}}-1}{2 N}
|
| 525 |
+
$$
|
| 526 |
+
|
| 527 |
+
Mais alors $\left|\mathrm{x}_{4 \mathrm{n}+3}\right|>1-\frac{2-1}{2 \mathrm{~N}}>1-\frac{1}{2 \mathrm{~N}}$, ce qui contredit notre hypothèse de départ et permet de conclure.
|
| 528 |
+
|
| 529 |
+
## Commentaires des correcteurs:
|
| 530 |
+
|
| 531 |
+
L'exercice n'a été abordé que par deux élèves, qui ont correctement résolu la question 1). La question 2) attendait cependant beaucoup de rigueur dans la preuve que la suite donnée n'était pas casable.
|
| 532 |
+
|
| 533 |
+
Exercice 18. Un graphe G fini simple à $n$ sommets est dit divisible s'il est possible d'attribuer à chaque sommet $s$ de $G$ un numéro $n_{s}$ de sorte que deux sommets distincts possèdent toujours deux numéros distincts et deux sommets quelconques $s$ et $s^{\prime}$ sont reliés par une arête si et seulement si $n_{s} \mid n_{s^{\prime}}$ ou $n_{s^{\prime}} \mid n_{s}$.
|
| 534 |
+
Un graphe G fini simple à n sommets est dit permutable s'il est possible de numéroter les sommets de $G$ de 1 à $n$ et s'il existe une permutation $\sigma$ de $\{1, \ldots, n\}$ telle que les sommets ayant pour numéros $i$ et $j$ sont reliés par une arête si et seulement si $(\mathfrak{i}-\mathfrak{j})(\sigma(\mathfrak{i})-\sigma(\mathfrak{j}))<0$.
|
| 535 |
+
Montrer qu'un graphe G est permutable si et seulement si G et son complémentaire sont divisibles.
|
| 536 |
+
|
| 537 |
+
## Solution de l'exercice 18
|
| 538 |
+
|
| 539 |
+
Un graphe est de divisibilité ssi on peut l'orienter (dans le sens des divisibilités) de manière à ce que s'il y a un arc (arête orientée) de A vers B et un de B vers C, il y en a un de A vers C. En effet, on peut alors attribuer à chaque sommet un nombre premier différent, et le nombre attribué pour les relations de divisibilité est alors le produit de son nombre premier par ceux de chacun ds sommets ayant un arc arrivant sur lui. On a alors les bonnes relations de divisibilité si il y a un arc de A vers B tout premier divisant le nombre attribué à A est le premier d'un sommet C avec un arc de C vers A . Il y a alors aussi un arc de C vers B donc le premier divise aussi le nombre attribué à B .
|
| 540 |
+
Montrons qu'on peut orienter un graphe de permutation. On trace un arc de $a$ vers $b$ ssi $a<b$ et $\sigma(a)>\sigma(b)$. On a bien les arêtes du graphe de permutation attribué et la relation est transitive, on a donc bien un graphe de divisibilité. Son complémentaire est également de divisibilité car orientable en traçant un arc de a vers b ssi $\mathrm{a}<\mathrm{b}$ et $\sigma \mathrm{a}<\sigma \mathrm{b}$.
|
| 541 |
+
|
| 542 |
+
Réciproquement, on suppose un graphe orienté transitif dont le complémentaire est également orientable de manière transitive, montrons qu'il est de permutation. Choisir une numérotation et une permutation revient en fait à choisir librement deux numérotations des sommets, soit à ordonner deux fois les sommets. Deux sommets doivent alors être reliés si et seulement si leur position relative est différente selon les deux ordres. Pour le premier ordre, on place les éléments un à un, à chaque étape en rajoutant un élément n'ayant pas de prédécesseur selon le graphe complémentaire orienté. On considère donc tous les choix possibles, tous les sommets sans prédécesseur non choisi. Alors, tous ces éléments considérés forment une clique du graphe, il y en a donc un unique qui est sans antécédents dans cette clique pour le graphe orienté. C'est cet élément qu'on place en tout premier pour notre ordre. On l'enlève ensuite et on recommence jusqu'à ce que tous les sommets soient ordonnées. Pour le deuxième ordre, on fait presque la même chose. On rajoute aussi à chaque étape un sommet sans prédécesseur selon le graphe complémentaire, mais parmi cette clique de candidats potentiels, on va prendre celui sans successeur dans la clique.
|
| 543 |
+
Vérifions que cette construction fonctionne. Prenons $A$ et $B$ deux sommets non reliés. Supposons SPDG que dans le graphe complémentaire, $A$ est un prédécesseur de $B$. Si $B$ est choisi pour un des deux ordres, forcément $A$ n'a pas été considéré parmi les choix potentiels, soit il a déjà été choisi, soit il a lui-même un prédécesseur non choisi. Par transitivité, ce prédécesseur serait aussi un prédécesseur de $B$, ce qui empêcherait le choix de B. Donc pour les deux ordres, $A$ a été choisi avant B. Les deux ordres sont donc compatibles avec l'absence d'arêtes entre $A$ et $B$.
|
| 544 |
+
Prenons $A$ et $B$ reliés et supposons SPDG que $A$ est un antécédent de $B$ dans le graphe. Montrons d'abords que pour le premier ordre, quand B est choisi, $A$ a déjà été choisi. À ce moment-là, si $A$ n'avait pas déjà été choisi, il n'aurait pas pu être considéré comme choix potentiel, sinon il aurait été choisi préférentiellement à $B$. Donc il avait un antécédent non choisi dans le graphe complémentaire. On remonte des antécédents successifs en partant de $A$ jusqu'à arriver jusqu'à un sommet $C$, sans antécédents encore non choisis. Par transitivité du graphe complémentaire orienté, $C$ est un antécédent de $A$ pour
|
| 545 |
+
ce graphe complémentaire. C a été considéré comme choix potentiel, n'ayant pas d'antécédent dans le graphe complémentaire, mais B lui a été préféré, donc B est un antécédent de C pour le graphe normal (pas complémentaire). $A$ étant lui-même un antécédent de $B$, par transitivité, $A$ doit être un antécédent de $C$ dans le graphe normal donc une arête entre $A$ et $C$ existe. Or on a construit $C$ comme un antécédent de $\mathcal{A}$ dans le graphe complémentaire, donc une arête du graphe complémentaire existe en $\mathcal{A}$ et C . La contradiction montre que selon le premier ordre, $A$ arrive avant $B$. On prouve identiquement que selon le deuxième ordre, $B$ arrive avant $A$. Ces deux ordres sont donc compatibles avec l'existence d'une arête entre $A$ et $B$.
|
| 546 |
+
|
| 547 |
+
## Commentaires des correcteurs:
|
| 548 |
+
|
| 549 |
+
L'exercice n'a été abordé que par une personne, qui l'a brillamment résolu.
|
| 550 |
+
|
French_STS/md/fr-corrigé.md
ADDED
|
@@ -0,0 +1,274 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
PRÉPARATION OLYMPIQUE FRANÇAISE DE MATHÉMATIQUES<br><br>ENVOI 3 : ARITHMÉTIQUE<br>À RENVOYER AU PLUS TARD LE 13 FÉVRIER 2023
|
| 2 |
+
|
| 3 |
+
Les consignes suivantes sont à lire attentivement :
|
| 4 |
+
|
| 5 |
+
- Le groupe junior est constitué des élèves nés en 2008 ou après. Les autres élèves sont dans le groupe senior.
|
| 6 |
+
- Les exercices classés "Juniors" ne sont à chercher que par les élèves du groupe junior.
|
| 7 |
+
- Les exercices classés "Seniors" ne sont à chercher que par les élèves du groupe senior.
|
| 8 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 9 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 10 |
+
- Respecter la numérotation des exercices.
|
| 11 |
+
- Bien préciser votre nom en lettres capitales, et votre prénom en minuscules sur chaque copie.
|
| 12 |
+
|
| 13 |
+
|
| 14 |
+
## 1 Exercices junior
|
| 15 |
+
|
| 16 |
+
Exercice 1. Soient $a, b$ deux entiers. Montrer que $a b(a-b)$ est divisible par 2.
|
| 17 |
+
Solution de l'exercice 1 On s'intéresse à la parité d'un produit, il est donc pertinent de faire une disjonction de cas sur la parité des entiers en jeu, ici a et $b$. On remarque alors la chose suivante :
|
| 18 |
+
|
| 19 |
+
- Si $a$ ou best pair : alors $a b$ est pair (le produit d'un nombre pair par un entier quelconque étant pair) et donc $\mathrm{ab}(\mathrm{a}-\mathrm{b})$ est bien divisible par 2 .
|
| 20 |
+
- Sinon, si $a$ et $b$ sont tous les deux impairs, alors $a-b$ est pair (en tant que différence de deux impairs) et donc $a b(a-b)$ est divisible par 2
|
| 21 |
+
Finalement, dans tous les cas, si $a$ et $b$ sont des entiers, alors $a b(a-b)$ est divisible par 2.
|
| 22 |
+
Commentaire des correcteurs : Beaucoup d'élèves ont abordé cet exercice, et tous l'ont parfaitement réussi. L'idée consistait à faire des disjonctions de cas selon les parités de a et de b , ce qui pouvait se faire en deux cas : soit " $a$ ou b pair" et "a et b impairs", soit "a et b de même parité" et "a et b de parité différente". Certaines copies ont fait plus de cas, ce n'était pas nécessaire et parfois il y avait des cas qui étaient inclus dans d'autres cas déjà traités : cela rallongeait souvent les solutions, ce qui fait perdre en efficacité et peut faire perdre du temps qu'on aurait pu passer à chercher d'autres exercices plus difficiles.
|
| 23 |
+
|
| 24 |
+
Exercice 2. Montrer qu'il existe une infinité de couples ( $\mathrm{m}, \mathfrak{n}$ ) d'entiers strictement positifs distincts tels que m ! n soit un carré parfait.
|
| 25 |
+
$\underline{\text { Solution de l'exercice } 2}$ On aurait envie de prendre $\mathrm{m}=\mathrm{n}$ pour avoir $\mathrm{m}!\mathrm{n}!=(\mathrm{n}!)^{2}$ et avoir un carré parfait. Mais l'énoncé force $m \neq n$. Malgré cela, on voit déjà un moyen de faire apparaître naturellement des carrés parfaits.
|
| 26 |
+
Supposons sans perte de généralité $m>n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n) \operatorname{par}(n, m)$, ça ne pose pas de problème). Alors $m!n!=\mathfrak{m} \times(m-1) \times \ldots \times(n+1) \times n!\times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Alors $m!n!$ sera un carré parfait si et seulement si $m \times \ldots \times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \geqslant 2$ car on veut $m, n \geqslant 1$ ). En effet on a bien $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
|
| 27 |
+
Finalement, pour tout $k \geqslant 2$ entier, $(m, n)=\left(k^{2}, k^{2}-1\right)$ convient, ce qui nous fournit bien une infinité de couples de solutions.
|
| 28 |
+
|
| 29 |
+
Commentaire des correcteurs : Le problème a été abordé par beaucoup d'élèves et une large majorité l'a parfaitement réussi. D'autres ont eu des pistes intéressantes sans forcément aboutir, comme remarquer que, dans le cas $m>n$ par exemple, il est nécessaire et suffisant d'avoir $m \times(m-1) \times \ldots \times(n+1)$ qui est un carré parfait.
|
| 30 |
+
|
| 31 |
+
Exercice 3. Trouver les triplets d'entiers $(x, y, n)$ tels que $n^{2}=17 x^{4}-32 x^{2} y^{2}+41 y^{4}$.
|
| 32 |
+
Solution de l'exercice 3 On va montrer par descente infinie que ( $0,0,0$ ) est la seule solution.
|
| 33 |
+
Comme un carré ne vaut que 0 ou 1 modulo 3 (une façon de le voir est de faire une disjonction de cas sur les valeurs modulo 3), il est pertinent de tenter une étude modulo 3 pour essayer de voir où ça nous mène. Pour ce faire, on remarque que si $(x, y, n)$ est solution, alors modulo 3 , on a
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
n^{2} \equiv-x^{4}-2 x^{2} y^{2}-y^{4} \equiv-\left(x^{2}+y^{2}\right)^{2} \quad(\bmod 3)
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
Ainsi, $\mathfrak{n}^{2}+\left(x^{2}+y^{2}\right)^{2}$ est divisible par 3 . Or un carré vaut 0 ou 1 modulo 3 donc la seule manière qu'une somme de carrés soit divisible par 3 , c'est que chacun des termes le soit. Donc $n$ et $x^{2}+y^{2}$ sont divisibles par 3. De même il découle que $x$ et $y$ sont divisibles par 3.
|
| 40 |
+
En réinjectant dans l'équation, on en déduit que $3^{4}=81$ divise $n^{2}$ et donc 9 divise n , donc $\left(\frac{x}{3}, \frac{y}{3}, \frac{\mathfrak{n}}{9}\right)$ est une autre solution. Or si on avait une solution avec $x, y$ ou n non nul (et quitte à les changer en leurs opposés, ce qui ne change pas les valeurs des carrés, positifs), on pourrait obtenir une suite strictement décroissante d'entiers naturels, ce qui est absurde (c'est le principe de la descente infinie).
|
| 41 |
+
On en déduit que la seule solution potentielle est $(0,0,0)$. Et réciproquement, on remarque que $(x, y, \mathfrak{n})=$ $(0,0,0)$ convient (les deux membres donnent 0 ).
|
| 42 |
+
L'unique solution de l'équation est donc $(0,0,0)$.
|
| 43 |
+
Commentaire des correcteurs: Dans l'ensemble les copies qui ont abordé le problème l'ont plutôt bien réussi. Certaines ont tenté des pistes comme une étude modulo 8 ou une réécriture de l'équation, ici ça n'aboutissait pas mais c'étaient de bonnes idées qui peuvent tout de même être utiles sur d'autres problèmes similaires. Signalons des erreurs récurrentes sur le principe de la descente infinie : un certain nombre de copies concluent qu'il n'y a aucune solution par descente infinie. En réalité la descente infinie nous permet de conclure qu'il n'y a aucune solution non-nulle, mais rien n'exclut la solution $(0,0,0)$ a priori (et d'ailleurs elle marche). À ce sujet, un certain nombre de copies conclut que ( $0,0,0$ ) est la seule solution possible, sans pour autant penser à la vérifier. Même si elle a l'air évidente ici, une mention de la vérification de la solution est indispensable, car la descente infinie garantit que c'est la seule solution possible, mais pas que c'est bien une solution.
|
| 44 |
+
|
| 45 |
+
Exercice 4. Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.
|
| 46 |
+
Solution de l'exercice 4 Comme $21=3 \times 7$ et que 3 et 7 sont premiers entre eux, 21 divise $2^{2^{n}}+2^{n}+1$ si et seulement si 3 et 7 divisent $2^{2^{n}}+2^{n}+1$.
|
| 47 |
+
Éliminons de suite le cas $n=0$, qui donne $2^{2^{0}}+2^{0}+1=4$ qui n'est pas divisible par 21. On peut donc supposer $n>0$, en particulier $2^{n}$ est pair. Alors modulo $3: 2^{2^{n}}+2^{n}+1 \equiv(-1)^{2^{n}}+(-1)^{n}+1 \equiv$ $(-1)^{n}+2(\bmod 3)$. En particulier $2^{2^{n}}+2^{n}+1$ est divisible par 3 si est seulement si $n$ est pair. On suppose donc désormais que cette condition est vérifiée.
|
| 48 |
+
Reste à traiter le cas de la divisibilité par 7 . Modulo 7 , les puissances de 2 sont $2^{0} \equiv 1,2^{1} \equiv 2,2^{2} \equiv$ $4,2^{3} \equiv 1$ : il s'agit donc d'étudier l'exposant modulo 3. Comme $n$ est pair (par le cas précédent), on sait déjà que $2^{n} \equiv 1(\bmod 3)$ donc $2^{2^{n}} \equiv 2(\bmod 7)$. On veut donc $2^{n} \equiv-1-2 \equiv 4(\bmod 3)$, et donc $n \equiv 2(\bmod 3)$ (et réciproquement si $n \equiv 2(\bmod 3)$, comme $n$ est pair alors 7 divise $\left.2^{2^{n}}+2^{n}+1\right)$.
|
| 49 |
+
On doit avoir $n \equiv 0(\bmod 2), n \equiv 2(\bmod 3):$ comme 2 et 3 sont premiers entre eux, le théorème des restes chinois donne qu'il existe une unique solution modulo $2 \times 3=6$, et on remarque que c'est $n \equiv 2$ $(\bmod 6)$.
|
| 50 |
+
En conclusion, les entiers naturels $n$ qui conviennent sont exactement ceux qui vérifient $n \equiv 2(\bmod 6)$.
|
| 51 |
+
Commentaire des correcteurs : Les copies ont bien abordé le problème : presque tout le monde a pensé à étudier les cycles de puissances et beaucoup de gens ont pensé à se ramener à étudier la divisibilité par 3 et par 7 . Malheureusement, il y a eu beaucoup d'erreurs de calcul, raisonement, ou lecture de l'énoncé qui rendent une bonne partie de la preuve fausse, car il y a une erreur au début. Beaucoup de gens ont oublié le cas $n=0$ !
|
| 52 |
+
|
| 53 |
+
Exercice 5. Soit $n \in \mathbb{N}^{\star}$. Montrer que si $2 n+1$ et $3 n+1$ sont des carrés parfaits, alors $5 n+3$ n'est pas premier.
|
| 54 |
+
Solution de l'exercice 5 Supposons que $2 \mathrm{n}+1$ et $3 \mathrm{n}+1$ sont des carrés parfaits : on dispose de $\mathrm{a}, \mathrm{b}$ deux entiers strictement positifs $(2 n+1,3 n+1>0)$ tels que $2 \mathfrak{n}+1=a^{2}$ et $3 n+1=b^{2}$. Ici, il s'agit de remarquer que $5 \mathfrak{n}+3=4 \times(2 n+1)-(3 n+1)=4 a^{2}-b^{2}$. Pour trouver cette identité, on essaie d'exprimer 5 à partir de 2 et 3 : il est naturel de prendre $5=2+3$ mais cela ne donne pas $5 \mathrm{n}+3$, en revanche on voit que $5=4 \times 2-3$.
|
| 55 |
+
On peut donc écrire $5 n+3=(2 a-b)(2 a+b)$. Comme $a, b>02 a+b>2 a-b$, et $2 a+b>0$. Ceci force $2 a-b>0$ (sinon on aurait $5 n+3 \leqslant 0$, ce qui est exclu). Il suffit donc de montrer que $2 a-b>1$ pour conclure : on aura alors écrit $5 \mathrm{n}+3$ comme produit de deux entiers strictement plus grands que 1 , et il ne pourra pas être premier.
|
| 56 |
+
Mais si $2 \mathrm{a}=\mathrm{b}+1,5 \mathrm{n}+3=2 \mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ donc $\mathrm{a}^{2}=2 \mathrm{n}+1 \leqslant \frac{5 n+3}{2}<\frac{4 \mathrm{a}-1}{2}<2 \mathrm{a}$ donc $\mathrm{a}<2$. Mais $a=1$ donne $2 \mathrm{n}+1=1$ donc $\mathrm{n}=0$, absurde car $\mathrm{n}>0$. Ainsi $2 a-b \neq 1$.
|
| 57 |
+
On a donc bien montré que si $2 \mathfrak{n}+1$ et $3 \mathfrak{n}+1$ sont des carrés parfaits (avec $\mathfrak{n} \in \mathbb{N}^{\star}$ ), alors $5 \mathfrak{n}+3$ n'est pas un nombre premier.
|
| 58 |
+
$\underline{\text { Commentaire des correcteurs : Les élèves qui ont abordé le problème l'ont en général plutôt bien compris }}$ et ont trouvé la factorisation qui était intéressante ici. Néanmoins la plupart d'entre eux ont oublié de vérifier les signes de leurs termes : pour pouvoir conclure $2 \mathrm{a}-\mathrm{b}=1,2 \mathrm{a}+\mathrm{b}=5 \mathrm{n}+3 \mathrm{il}$ fallait avoir vérifié au préalable $2 a+b>2 a-b>0$, ce qui n'était pas très dur mais nécessaire pour que l'identification soit valide. Notons qu'un certain nombre de copies ont tenté d'exploiter des congruences : ici ça ne menait pas à grand chose d'intéressant, lorsqu'il s'agit des nombres premiers il est souvent plus intéressant de rechercher des factorisations plutôt que d'exploiter des congruences car ces dernières, à moins de trouver une divisibilité par un nombre particulier, ne nous renseignent pas sur le caractère premier ou non d'un entier.
|
| 59 |
+
|
| 60 |
+
Exercice 6. Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.
|
| 61 |
+
Solution de l'exercice 6 Ce qu'on connaît pour des nombres premiers, c'est leurs propriétés de divisibilité. Une expression développée n'est donc pas très pratique pour étudier cela : on va d'abord chercher à factoriser.
|
| 62 |
+
Remarquons que $p^{5}+p^{3}+2=p^{3}\left(p^{2}+1\right)+2$. On veut résoudre $p^{3}\left(p^{2}+1\right)=q^{2}-q-2$. Mais on reconnaît alors $q^{2}-q-2=(q-2)(q+1)$ (si on ne le voit pas directement, on peut le trouver en résolvant $\mathrm{q}^{2}-\mathrm{q}-2=0$ avec la méthode classique utilisant le discriminant).
|
| 63 |
+
On veut donc résoudre $p^{3}\left(p^{2}+1\right)=(q-2)(q+1)$. En particulier $p^{3} \mid(q-2)(q+1)$. Alors $\operatorname{pgcd}(q-$ $2, q+1)=\operatorname{pgcd}(q-2, q+1-(q-2))=\operatorname{pgcd}(q-2,3)$ vaut donc 1 ou 3. Cela suggère d'étudier d'abord le cas $p=3$ : on obtient $(q-2)(q+1)=270$, et en résolvant $q^{2}-q-2=270$ on trouve $q=17$ (qui est bien un nombre premier) et $q=-16$ (qui n'est pas solution car ce n'est pas un nombre premier). Donc lorsque $p=3$, il y a une unique solution $(p, q)=(3,17)$.
|
| 64 |
+
On peut donc supposer $p \neq 3$. En particulier, il ne divise pas $\operatorname{pgcd}(q-1, q+2)$, donc au moins un des nombres $q+1$ et $q-2$ est premier avec $p$, donc avec $p^{3}$. Or $p^{3} \mid(q+1)(q-2)$ : donc d'après le lemme de Gauss, $q+1$ ou $q-2$ est divisible par $p^{3}$. Or, $p^{3}$ ne peut pas diviser $q-2$ parce que sinon, on aurait $(q-2)(q+1) \geqslant p^{3} p^{3}>p^{3}\left(p^{2}+1\right)$, absurde. Ainsi $p^{3} \mid q+1$, et donc $q-2 \mid p^{2}+1$.
|
| 65 |
+
Mais les divisibilités qu'on vient d'obtenir montrent que $p^{3} \leqslant q+1=(q-2)+3 \leqslant p^{2}+1+3=p^{2}+4$, et donc $p^{2}(p-1) \leqslant 4$. Or $p^{2}(p-1)$ est strictement croissante en $p$, et en $p=2$ on a égalité, donc le seul cas possible est $p=2$ (autrement dit, pour $p>2$, on a $p^{2}(p-1)>4$ ).
|
| 66 |
+
Lorsque $p=2$, l'équation devient $q^{2}-q-2=40$, en résolvant on trouve $q=7$ (qui convient car 7 est premier) et $\mathrm{q}=-6$ (qui ne convient pas car n'est pas un nombre premier).
|
| 67 |
+
Finalement, il y a deux solutions qui sont $(\mathbf{p}, \mathbf{q})=(2,7)$ et $(\mathbf{p}, \mathbf{q})=(3,17)$.
|
| 68 |
+
Commentaire des correcteurs : L'exercice a été assez abordé, mais beaucoup d'erreurs ont été commises. Quand on a une équation du type $a b=c d$, on ne peut pas conclure que $c$ vaut $a$ ou $b$, ou que $c$ divise $a$ ou b. Beaucoup d'élèves utilisent donc des affirmations arithmétiques fausses, et donc se retrouvent avec peu de points car ne traitant qu'un cas très particulier.
|
| 69 |
+
|
| 70 |
+
Exercice 7. Soit $n \geqslant 2$. Montrer qu'il existe des entiers $a, b$ tels que, pour tout entier $m$, le nombre $m^{3}+a m+b$ ne soit pas un multiple de $n$.
|
| 71 |
+
Solution de l'exercice $7 \quad \mathrm{~m}^{3}+\mathrm{am}+\mathrm{b}$ est un multiple de n si et seulement si $\mathrm{m}^{3}+\mathrm{am} \equiv-\mathrm{b}(\bmod \mathrm{n})$. On remarque alors qu'il suffit de trouver a tel que $\mathrm{m}^{3}+\mathrm{am}$ ne prend pas toutes les valeurs possibles modulo $n$ (et de prendre pour $-b$ une des valeurs qui $n$ 'est pas prise). Comme $\mathrm{m}^{3}+a m$ modulo $n$ ne dépend que de $m$ modulo $n$, on peut se restreindre à $0 \leqslant m \leqslant n-1$.
|
| 72 |
+
Il s'agit de trouver un a tel que les $0^{3}+\mathrm{a} \cdot 0(\bmod n), 1^{3}+\mathrm{a} \cdot 1(\bmod n), \ldots,(n-1)^{3}+a(n-1)$ $(\bmod n) n$ 'atteignent pas $n$ valeurs distinctes $(\operatorname{modulo} n)$. Alors si on trouve $m_{1} \neq m_{2}$ entre 0 et $n-1$ tels que $m_{1}^{3}+a m_{1} \equiv m_{2}^{3}+a m_{2}(\bmod n)$, les $n-2$ autres valeurs de $m$ modulo $n$ donneront au plus $n-2$ valeurs de $m^{3}+$ am modulo $n$, donc au total, pour $0 \leqslant m \leqslant n-1, m^{3}+$ am prendra au plus $n-1$ valeurs sur mes $\boldsymbol{n}$ possibles : il y en aura bien une qui ne sera pas atteinte. Or $0^{3}+\mathrm{a} \times 0 \equiv 0(\bmod \mathfrak{n})$, $1^{3}+a \times 1 \equiv a+1(\bmod \mathfrak{n})$. Si $a+1 \equiv 0(\bmod \boldsymbol{n})$, on sera dans la situation décrite ci-dessus.
|
| 73 |
+
Posons alors $a=-1$ (ou $a=n-1$ si on veut $a>0)$. Alors $m^{3}+a m$ est nul si $m=0$ ou $m=1$. Donc il existe $c$ entier, $0 \leqslant c \leqslant n-1$, tel que pour tout $0 \leqslant m \leqslant n-1, m^{3}+a m \not \equiv c(\bmod n)$. Posons alors $b=-c\left(\right.$ ou $b=n-c$ si on veut $b>0$ ), alors pour tout $0 \leqslant m \leqslant n-1, m^{3}+a m+b$ sera non nul modulo $n$, donc pour tout $m$ entier, $m^{3}+a m+b$ ne sera pas un multiple de $n$.
|
| 74 |
+
Ainsi, il existe bien de tels entiers $a$ et $b$.
|
| 75 |
+
Commentaire des correcteurs : Le problème n'a pas beaucoup été abordé, et lorsque l'énoncé a été bien compris il a été bien réussi. Cependant, beaucoup n'ont pas compris l'énoncé, et on montré à la place que pour toute valeur de $m$ fixée, on pouvait trouver des $a$ et $b$ de sorte que $n$ ne divise pas $m^{3}+a m+b$. La différence ici est que a et bne sont pas fixés indépendamment de m , ce qui est une version sensiblement plus simple de l'exercice.
|
| 76 |
+
|
| 77 |
+
Exercice 8. Trouver tous les entiers $\mathrm{a}, \mathrm{b}, \mathrm{c} \in \mathbb{N}$ tels que $1517^{\mathrm{a}}+15^{\mathrm{b}}=1532^{\mathrm{c}}$.
|
| 78 |
+
Solution de l'exercice 8 On commence par traiter les petites valeurs de c.
|
| 79 |
+
Si $c=0,1517^{a}+15^{b}=1$ n'a pas de solution.
|
| 80 |
+
Si $c=1$, on doit trouver $a, b$ tels que $1517^{a}+15^{b}=1532$. Si $a \geqslant 2$ ou si $a=0$ il n'y a pas de solution. Si $\mathrm{a}=1$, alors $15^{\mathrm{b}}=1532-1517=15$ donc $\mathrm{b}=1$ : ceci fournit la solution $(1,1,1)$.
|
| 81 |
+
On suppose maintenant $\mathrm{c} \geqslant 2$. En particulier $16=4^{2}$ divise $1532^{c}$ : ceci invite à étudier l'équation modulo des puissances de 2 plus petites que 16 pour éliminer la dépendance en c . On obtient alors $1+(-1)^{\mathrm{b}} \equiv 0(\bmod 4)$ donc $b$ est impair (en particulier, $\left.\mathrm{b} \geqslant 1\right)$.
|
| 82 |
+
En réduisant modulo $8: 15^{b} \equiv-1(\bmod 8)\left(b\right.$ est impair). On a alors $1517^{a}-1 \equiv 5^{a}-1 \equiv 0(\bmod 8)$, donc a est pair.
|
| 83 |
+
En réduisant modulo 5 (comme 5 divise 15 , cela supprime la dépendance en $b)$, on a $2^{\mathrm{a}} \equiv 2^{\mathrm{c}}(\bmod 5)$, donc $a \equiv c(\bmod 4)$ (l'ordre de 2 modulo 5 , est 4$)$. Puisqu'on a montré que a était pair, c est pair. Notons $a=2 e$ et $c=2 d$, alors $d$ et $e$ ont la même parité $(\operatorname{car} 2 e \equiv 2 \mathrm{~d}(\bmod 4)$ donc $e \equiv d(\bmod 2)$, et en réinjectant dans l'équation de départ, on obtient $15^{\mathrm{b}}=\left(1532^{\mathrm{d}}-1517^{\mathrm{e}}\right)\left(1532^{\mathrm{d}}+1517^{\mathrm{e}}\right)$.
|
| 84 |
+
Remarquons alors que
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\left(1532^{\mathrm{d}}+1517^{e}\right)-\left(1532^{\mathrm{d}}-1517^{e}\right)=2 \times 1517^{e}=2 \times 37^{e} \times 41^{e}
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
Or ni 37 ni 41 ne divisent 1532 donc $1532^{\mathrm{d}}-1517^{e}$, et $1532^{\mathrm{d}}-1517^{e}$ est impair. Par conséquent, $1532^{\mathrm{d}}+1517^{e}$ et $1532^{\mathrm{d}}-1517^{e}$ sont premiers entre eux, donc l'un d'eux est $5^{\mathrm{b}}$ et l'autre est $3^{\mathrm{b}}$. Puisque $1532^{\mathrm{d}}+1517^{e}>1532^{\mathrm{d}}-1517^{e}$, il s'ensuit que $1532^{\mathrm{d}}+1517^{e}=5^{\mathrm{b}}$ et $1532^{\mathrm{d}}-1517^{e}=3^{\mathrm{b}}$. Alors $3^{\mathrm{b}}+5^{\mathrm{b}}=2 \cdot 1532^{\mathrm{d}}$. Si $\mathrm{d} \geqslant 2$, le membre de droite est divisible par 16 , mais on vérifie modulo 16 que le premier membre n'est jamais divisible par $16\left(3^{4} \equiv 5^{4} \equiv 1(\bmod 16)\right.$ donc il suffit de tester $3^{0}+5^{0} \equiv 2(\bmod 16), 3^{1}+5^{1} \equiv 8(\bmod 16), 3^{2}+5^{2} \equiv 2(\bmod 16)$ et $\left.3^{3}+5^{3} \equiv 5(\bmod 16)\right)$, ce qui implique que $\mathrm{d}=1(\operatorname{car} 2 \mathrm{~d}=\mathrm{c} \geqslant 2)$ et donc e impair $(\mathrm{d} \equiv e(\bmod 2))$. Comme $1532^{\mathrm{d}}>1517^{e}, \mathrm{il}$ s'ensuit que $e=1$, mais $1532^{\mathrm{d}}-1517^{\mathrm{d}}=15$ n'est pas une puissance de 3 , d'où une contradiction.
|
| 91 |
+
Finalement la seule solution est $(a, b, c)=(1,1,1)$.
|
| 92 |
+
Commentaire des correcteurs : Problème peu abordé mais bien compris par ceux ayant rendu une copie. Il s'agissait de trouver des propriétés sur $\mathrm{a}, \mathrm{b}$ et c en réduisant modulo des petits nombres jusqu'à arriver à une absurdité et de nombreux chemins ont été suivis. Attention cependant, il faut généralement traiter des petits cas à part. Par exemple ici, $15^{0}=1 \not \equiv 0[3]$ !
|
| 93 |
+
|
| 94 |
+
Exercice 9. Quentin et Timothé jouent à un jeu. D'abord, Quentin choisit un nombre premier $\mathrm{p}>2$, puis Timothé choisit un entier strictement positif $n_{0}$. Quentin choisit alors un entier $n_{1}>n_{0}$ et calcule $s_{1}=n_{0}^{n_{1}}+n_{1}^{n_{0}}$; puis Timothé choisit un entier $n_{2}>n_{1}$ et calcule $s_{2}=n_{1}^{n_{2}}+n_{2}^{n_{1}}$. Les joueurs continuent de jouer chacun à leur tour, en choisissant au tour $k$ un entier $n_{k}>n_{k-1}$ et en calculant $s_{k}=n_{k}^{n_{k-1}}+n_{k-1}^{n_{k}}$. Le premier joueur à choisir un entier $n_{k}$ tel que $p$ divise $s_{k}\left(s_{1}+2 s_{2}+3 s_{3}+\ldots+k s_{k}\right)$ gagne le jeu. Déterminer lequel de Quentin et Timothé possède une stratégie gagnante.
|
| 95 |
+
Solution de l'exercice 9 Nous allons montré que Timothé a une stratégie gagnante. Notons que Quentin va choisir les $n_{2 k+1}$ et Timothé va choisir les $n_{2 k}$. On fait d'abord quelques remarques.
|
| 96 |
+
|
| 97 |
+
- Remarque 1 : Remarquons d'abord que si l'un des joueurs choisit $n_{k} \equiv 0(\bmod p)$ et ne gagne pas à cette étape, alors le joueur suivant gagne en choisissant $\mathfrak{n}_{k+1} \equiv 0(\bmod \mathfrak{p})$, car alors $s_{k+1} \equiv 0(\bmod \mathfrak{p})$, et en particulier $p$ divise $s_{k+1}\left(s_{1}+2 s_{2}+\ldots+k s_{k}+(k+1) s_{k+1}\right)$.
|
| 98 |
+
- Remarque 2: Pour $a \not \equiv 0(\bmod p), a^{p-1} \equiv 1(\bmod p)(F e r m a t)$. Alors si $a, b \geqslant 1$ sont deux entiers tels que $a$ soit divisible par $p-1$ et congru à 1 modulo $p$ et $b$ n'est pas divisible par $p$, alors $\mathrm{a}^{\mathrm{b}}+\mathrm{b}^{\mathrm{a}} \equiv 1^{\mathrm{b}}+1 \equiv 2(\bmod \mathrm{p})$. On va donc chercher une stratégie de ce côté-là.
|
| 99 |
+
- Stratégie : On va montrer que la stratégie suivante fonctionne : pour $k \geqslant 0$, Timothé va distinguer deux cas.
|
| 100 |
+
- Si $k=0$ ou $n_{2 k-1}$ n'est pas divisible par $p$, alors Timothé choisit $n_{2 k}>n_{2 k-1}$ (resp. $n_{0}>0$ ) de telle sorte que $n_{2 k} \equiv 0(\bmod p-1)$ et $n_{2 k} \equiv 1(\bmod p)(p, p-1$ sont premiers entre eux donc par le théorème des restes chinois, il existe un unique reste modulo $p(p-1)$ qui convient, en particulier il existe bien de tels nombres aussi grands que l'on veut.)
|
| 101 |
+
- Si $n_{2 k-1}$ est divisible par $p$, alors Timothé choisit $n_{2 k}>n_{2 k-1}$ divisible par $p$.
|
| 102 |
+
|
| 103 |
+
Par la première remarque, dans le second cas si Quentin n'avait pas gagné, alors Timothé gagne à cet instant. Dans le premier cas, si $n_{2 k-1}$ n'est pas divisible par $p, s_{2 k} \equiv 2(\bmod p)$ (d'après la deuxième remarque). Donc si Timothé ne gagne pas à un instant donné, alors il a obtenu $s_{2 k} \equiv 2(\bmod p)$.
|
| 104 |
+
|
| 105 |
+
- On s'intéresse alors aux valeurs prises par $s_{2 k+1}$. On distingue deux cas.
|
| 106 |
+
- D'abord si à chaque étape, Quentin choisit $\mathfrak{n}_{2 \mathrm{k}+1}$ non divisible par p . Alors d'après la deuxième remarque, il obtient $s_{2 k+1} \equiv 2(\bmod p)$. Autrement dit, $s_{k} \equiv 2(\bmod p)$ pour tout $k$, et donc $1+2 s_{2}+\ldots+k s_{k} \equiv k(k+1)(\bmod p)$ et donc le premier $k$ tel que cette quantité est divisible par $p$ est $k=p-1$ (lemme d'Euclide), or $p-1$ est pair ( $p>2$ ), donc c'est Timothé qui vient de choisir, et c'est donc celui-ci qui gagne.
|
| 107 |
+
- Maintenant, si à un moment Quentin choisit $n_{2 k+1}$ divisible par $p$, (on considère que c'est la première fois que Quentin choisit un tel nombre), en particulier $2 k+1<p-1$ sinon on a vu audessus que Timothé gagne. Alors pour $\mathrm{m} \leqslant 2 \mathrm{k}$, on a $s_{\mathrm{m}} \equiv 2(\bmod \mathrm{p})$, et $s_{2 \mathrm{k}+1} \equiv 1(\bmod \mathrm{p})$. Alors
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
s_{1}+2 s_{2}+\ldots+(2 k+1) s_{2 k+1} \equiv 2 k(2 k+1)+(2 k+1) \equiv(2 k+1)^{2} \not \equiv 0 \quad(\bmod p)
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
(car $1 \leqslant 2 \mathrm{k}+1 \leqslant \mathrm{p}-1$ ), donc Quentin ne gagne pas à cette étape. Mais alors, comme évoqué précédemment, en choisissant $n_{2 k+2}$ divisible par $p$, on a $s_{2 k+2} \equiv 0(\bmod p)$ donc Timothé gagne.
|
| 114 |
+
|
| 115 |
+
- Dans tous les cas, avec cette stratégie, Timothé va gagner, donc c'est Timothé qui a une stratégie gagnante.
|
| 116 |
+
|
| 117 |
+
Commentaire des correcteurs: L'exercice a été peu traité car il était très difficile. Mais les quelques élèves ayant rendu une copie ont bien compris le problème, et vu comment bien choisir les $n_{k}$.
|
| 118 |
+
|
| 119 |
+
## Exercices Seniors
|
| 120 |
+
|
| 121 |
+
Exercice 10. Montrer qu'il existe une infinité de couples ( $\mathrm{m}, \mathrm{n}$ ) d'entiers distincts tels que $\mathrm{m}!n!$ soit un carré parfait.
|
| 122 |
+
|
| 123 |
+
Solution de l'exercice 10 On aurait envie de prendre $m=n$ pour avoir $m!n!=(n!)^{2}$ et avoir un carré parfait. Mais l'énoncé force $m \neq n$. Malgré cela, on voit déjà un moyen de faire apparaître naturellement des carrés parfaits.
|
| 124 |
+
Supposons sans perte de qénéralité $m>n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n)$ par $(n, m)$, ça ne pose pas de problème $)$. Alors $m!n!=m \times(m-1) \times \ldots \times(n+1) \times n!\times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Alors $m!n$ ! sera un carré parfait si et seulement si $m \times \ldots \times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \geqslant 2$ car on veut $m, n \geqslant 1)$. En effet on a bien $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
|
| 125 |
+
Finalement, pour tout $k \geqslant 2$ entier, $(m, n)=\left(k^{2}, k^{2}-1\right)$ convient, ce qui nous fournit bien une infinité de couples solutions.
|
| 126 |
+
|
| 127 |
+
Commentaire des correcteurs: L'ensemble des élèves ayant abordé l'exercice l'ont parfaitement réussi, même si certains détaillaient parfois plus que nécessaire.
|
| 128 |
+
|
| 129 |
+
Exercice 11. Déterminer tous les entiers naturels $n$ tels que 21 divise $2^{2^{n}}+2^{n}+1$.
|
| 130 |
+
Solution de l'exercice 11 Comme $21=3 \times 7$ et que 3 et 7 sont premiers entre eux, 21 divise $2^{2^{n}}+2^{\mathrm{n}}+1$ si et seulement si 3 et 7 divisent $2^{2^{n}}+2^{n}+1$.
|
| 131 |
+
Éliminons de suite le cas $n=0$, qui donne $2^{2^{0}}+2^{0}+1=4$ qui n'est pas divisible par 21. On peut donc supposer $n>0$, en particulier $2^{n}$ est pair. Alors modulo $3: 2^{2^{n}}+2^{n}+1 \equiv(-1)^{2^{n}}+(-1)^{n}+1 \equiv$ $(-1)^{n}+2(\bmod 3)$. En particulier $2^{2^{n}}+2^{n}+1$ est divisible par 3 si est seulement si $n$ est pair. On suppose donc désormais que cette condition est vérifiée.
|
| 132 |
+
Reste à traiter le cas de la divisibilité par 7 . Modulo 7 , les puissances de 2 sont $2^{0} \equiv 1,2^{1} \equiv 2,2^{2} \equiv$ $4,2^{3} \equiv 1$ : il s'agit donc d'étudier l'exposant modulo 3 . Comme n est pair (par le cas précédent), on sait déjà que $2^{n} \equiv 1(\bmod 3)$ donc $2^{2^{n}} \equiv 2(\bmod 7)$. On veut donc $2^{n} \equiv-1-2 \equiv 4(\bmod 3)$, et donc $n \equiv 2(\bmod 3)\left(\right.$ et réciproquement si $n \equiv 2(\bmod 3)$, comme $n$ est pair alors 7 divise $\left.2^{2^{n}}+2^{n}+1\right)$.
|
| 133 |
+
On doit avoir $\mathfrak{n} \equiv 0(\bmod 2), \mathfrak{n} \equiv 2(\bmod 3):$ comme 2 et 3 sont premiers entre eux, le théorème des restes chinois donne qu'il existe une unique solution modulo $2 \times 3=6$, et on remarque que c'est $\boldsymbol{n} \equiv 2$ $(\bmod 6)$.
|
| 134 |
+
En conclusion, les entiers naturels $n$ qui conviennent sont exactement ceux qui vérifient $\mathfrak{n} \equiv 2(\bmod 6)$.
|
| 135 |
+
Commentaire des correcteurs: Les élèves ayant abordé ce problème l'ont globalement bien compris et ont présenté des solutions en général abouties. Certains ont fait une étude directement modulo 21, d'autres ont décomposé en une étude modulo 3 et modulo 7. Ceux ayant choisi cette alternative ont pour la plupart oublié de préciser que 3 et 7 sont premiers entre eux, c'est pourtant nécessaire pour que l'étude modulo 21 soit équivalent aux études modulo 3 et modulo 7 . Certains ont aussi mal lu l'énoncé et considéré $2^{2 n}+2^{n}+1$ au lieu de $2^{2^{n}}+2^{n}+1$. On rappelle que $2^{2^{n}}=2^{\left(2^{n}\right)}$, autrement dit c'est $2^{k}$ avec $k=2^{n}$, à différencier de $\left(2^{2}\right)^{n}$.
|
| 136 |
+
|
| 137 |
+
Exercice 12. Soient $k, m, n>0$ des entiers tels que $m^{2}+n=k^{2}+k$. Montrer que $m \leqslant n$.
|
| 138 |
+
Solution de l'exercice 12 Il y a des carrés : on aimerait faire apparaître des expressions factorisées, et plus particulièrement des carrés parfaits. Remarquons alors que $(2 k+1)^{2}=4 k^{2}+4 k+1=4 m^{2}+4 \mathfrak{n}+1$. On a alors $4 m^{2}+n+1>4 m^{2}=(2 m)^{2}$. Alors $(2 k+1)^{2}>(2 m)^{2}$ donc $(2 k+1)^{2} \geqslant(2 m+1)^{2}$ (il n'y a pas de carré entre deux carrés consécutifs). D'où, en redéveloppant: $4 \mathrm{~m}^{2}+4 \mathrm{n}+1 \geqslant 4 \mathrm{~m}^{2}+4 \mathrm{~m}+1$. On obtient bien $\mathrm{m} \leqslant \mathrm{n}$, comme voulu.
|
| 139 |
+
|
| 140 |
+
Commentaire des correcteurs : Dans l'ensemble ce problème a été très bien réussi, à l'exception de de quelques rares exceptions relevant certainement de l'étourderie. Beaucoup ont raisonné par l'absurde en supposant $m>n$, et la plupart des autres ont fait une disjonction de cas selon si $m>k, m=k$ ou $m<k$. Attention dans ce dernier cas à ne pas oublier $m=k$ ! Un autre observation remarquable qui peut être faite est qu'aucun des élèves n'a donné la solution du corrigé.
|
| 141 |
+
|
| 142 |
+
Exercice 13. Trouver tous les nombres premiers $p, q$ vérifiant $p^{5}+p^{3}+2=q^{2}-q$.
|
| 143 |
+
Solution de l'exercice 13 En réarrangeant les termes et en factorisant, cela revient à résoudre $p^{3}\left(p^{2}+\right.$ $1)=(q-2)(q+1)$. En particulier $p^{3} \mid(q-2)(q+1)$. Or $(q+1)-(q-2)=3$ donc $\operatorname{pgcd}(q-2,3)$ vaut 1 ou 3. Cela suggère d'étudier d'abord le cas $p=3$ : on obtient $(q-2)(q+1)=270$, et en résolvant $\mathrm{q}^{2}-\mathrm{q}-2=270$ on trouve $\mathrm{q}=17$ (qui convient) et $\mathrm{q}=-16$ (qui ne convient pas). Donc lorsque $p=3$, il y a une unique solution $(p, q)=(3,17)$.
|
| 144 |
+
On peut donc supposer $p \neq 3$. En particulier, il ne divise pas $\operatorname{pgcd}(q-1, q+2)$, donc au moins un des nombres $q+1$ et $q-2$ est premier avec $p^{3}$. Or $p^{3} \mid(q+1)(q-2):$ donc $q+1$ ou $q-2$ est divisible par $p^{3}$ (Gauss). Or, $p^{3}$ ne peut pas diviser $q-2$ parce que sinon, on aurait $(q-2)(q+1) \geqslant p^{3} p^{3}>p^{3}\left(p^{2}+1\right)$, absurde. Ainsi $p^{3} \mid q+1$, et donc $q-2 \mid p^{2}+1$.
|
| 145 |
+
Mais $\mathrm{p}^{3} \leqslant \mathrm{q}+1=(\mathrm{q}-2)+3 \leqslant \mathrm{p}^{2}+1+3=\mathrm{p}^{2}+4$, et donc $\mathrm{p}^{2}(\mathrm{p}-1) \leqslant 4$. Or $\mathrm{p}^{2}(\mathrm{p}-1)$ est strictement croissante en $p$, et en $p=2$ on a égalité, donc le seul cas possible est $p=2$ (autrement dit, pour $p>2$, on a $p^{2}(p-1)>4$ ).
|
| 146 |
+
Lorsque $\mathrm{p}=2$, l'équation devient $\mathrm{q}^{2}-\mathrm{q}-2=40$, en résolvant on trouve $\mathrm{q}=7$ (qui convient) et $q=-6$ (qui ne convient pas).
|
| 147 |
+
Finalement, il y a deux solutions qui sont $(\mathbf{p}, \mathbf{q})=(2,7)$ et $(\mathbf{p}, \mathbf{q})=(3,17)$.
|
| 148 |
+
Commentaire des correcteurs: C'est bien réussi pour la plupart des élèves, qui ont presque tous trouvé la factorisation en $(q+1)(q-2)$ ou celle en $(x-3)(x+3)$ une fois le discriminant en $q$ considéré. En général le raisonnement a été bien mené. Attention à certaines utilisations frauduleuses du lemme de Gauss, et à vérifier rigoureusement tous les cas lors de la disjonction de cas. On peut rapidement oublier une solution!
|
| 149 |
+
|
| 150 |
+
Exercice 14. Anna et Elie jouent à un jeu. On leur donne à tous les deux le même ensemble $A$ composé d'un nombre fini d'entiers strictement positifs et distincts. Anna choisit un entier $a \in A$ secrètement. Si Elie choisit un entier b (pas forcément dans $\mathcal{A}$ ) et le donne à Anna, Anna lui donne le nombre de diviseurs strictement positifs de ab . Montrer que Elie peut choisir b de sorte à retrouver à coup sur l'entier choisi par Anna.
|
| 151 |
+
Solution de l'exercice 14 Notons P l'ensemble fini des nombres premiers divisant au moins un élément de $A$ et $n \geqslant 1$ le plus grand entier tel qu'il existe $a \in A$ et $p \in P$ tels que $p^{n} \mid a$. On peut remplacer A par l'ensemble des entiers $m$ dont les facteurs premiers sont tous dans $P$ et tels que pour tout $p \in P$, $v_{p}(m) \leqslant n$. Elie propose un entier $b$ de la forme $\prod_{p \in P} p^{b_{p}}$. Si Anna a choisi l'entier $a$, alors elle donne à Elie l'entier $\prod_{p \in P}\left(b_{p}+v_{p}(a)+1\right)$. Il suffit donc pour Elie de choisir les $b_{p}$ de sorte que tous les $\prod_{p \in P}\left(b_{p}+a_{p}\right)$ soient deux à deux distincts, pour tous les choix possibles de $a_{p}$ entre 1 et $n+1$ pour chaque $p \in P$.
|
| 152 |
+
|
| 153 |
+
On propose deux solutions.
|
| 154 |
+
|
| 155 |
+
## Première méthode :
|
| 156 |
+
|
| 157 |
+
L'idée de cette construction est de forcer les factorisations en produits de facteurs premiers des $\prod_{p}\left(b_{p}+a_{p}\right)$ à être différentes pour tous les choix possibles des $a_{p}$. On veut faire en sorte que chaque $b_{p}+i$ pour $1 \leqslant i \leqslant n+1$ possède un diviseur premier «distinctif», qui n'apparaît que dans la décomposition en produit de facteurs premiers de $b_{p}+i$, jamais dans celle d'un autre $b_{q}+j$.
|
| 158 |
+
Formellement, on choisit, pour chaque $p \in P$ et chaque $1 \leqslant i \leqslant n+1$, des nombres premiers deux à deux distincts $Q_{p, i}>n+1$. On construit les $b_{p}$ grâce au théorème chinois : pour chaque $q \in P$ distinct de $p$ et pour chaque $1 \leqslant i \leqslant n+1, Q_{q, i} \mid b_{p}$, et pour chaque $1 \leqslant i \leqslant n+1, b_{p} \equiv-\mathfrak{i}\left[Q_{p, i}\right]$.
|
| 159 |
+
Avec cette construction, si $q, p \in P$ et $1 \leqslant i, j \leqslant n+1$, alors $Q_{q, j} j b_{p}+i$ si et seulement si $i=j$ et $\mathrm{p}=\mathrm{q}$.
|
| 160 |
+
En particulier, étant donnés des $1 \leqslant a_{p} \leqslant n+1$ pour chaque $p \in P$, si $q \in P, \Pi=\prod_{p \in P}\left(b_{p}+a_{p}\right)$ est divisible par $Q_{q, j}$ si et seulement si $j=a_{q}$ : ainsi $\Pi$ détermine la famille $\left(a_{p}\right)$.
|
| 161 |
+
|
| 162 |
+
## Deuxième méthode :
|
| 163 |
+
|
| 164 |
+
La première construction était très arithmétique et utilisait des nombres premiers. Celle qu'on présente maintenant vient plus d'une idée de "taille". L'idée est que si l'on prend de gigantesques $b_{p}$, le produit $\prod_{p}\left(b_{p}+a_{p}\right)$ ressemblera à l'écriture d'un certain nombre en une certaine base, dont les chiffres donneront les $a_{i}$.
|
| 165 |
+
Passons à la construction proprement dite. Le problème tel que nous l'avons reformulé n'utilise plus le fait que $P$ soit constitué de nombres premiers : on renumérote ses éléments en $1, \ldots, r$. Montrons que pour $N>(n+1)^{r}$, $b_{i}=N^{2^{i}}$ convient. En effet, dans ce cas, on voit que le développement de $\Pi=\prod_{i=1}^{r}\left(N^{2^{i}}+a_{i}\right)$ écrit un nombre en base $N$ dont le chiffre devant $N^{2+1}-2-2^{i}$ est exactement $a_{i}$ : ainsi $\Pi$ détermine la famille des $\left(a_{i}\right)$.
|
| 166 |
+
|
| 167 |
+
Commentaire des correcteurs : Le problème a été peu abordé, et peu réussi. Le principal problème est que certains montrent comment si on fixe a et $c$, choisir un $b$ pour que ba n'ait pas le même nombre de diviseur que bc de manière correcte, puis prétendent que la généralisation se fait bien en itérant. Il s'avère que cette partie est totalement fausse : s'il y a au départ trois nombres $a, c, e$, on peut choisi un b pour que $a b$ et $b c$ n'ait pas le même nombre de diviseur. Mais il est possible que $c b$ et $e b n$ 'ait pas le même nombre de diviseur, dans ce cas si on multiplie par $\mathrm{b}^{\prime}$ pour que $\mathrm{cbb}^{\prime}$ et $\mathrm{ebb}^{\prime}$ ait un nombre différent de diviseur, il est possible que $\mathrm{abb}^{\prime}$ et $\mathrm{cbb}^{\prime}$ ait le même nombre de diviseur. Cela montre que le procédé peut boucler et ne pas aboutir: le problème ne se résumait donc pas à ce cas particulier!
|
| 168 |
+
|
| 169 |
+
Exercice 15. Pour tout entier $n \geqslant 1$, on pose $u_{n}=1!+2!+\ldots+n!$. Montrer qu'il existe une infinité de nombres premiers divisant au moins l'un des termes de la suite ( $\mathfrak{u}_{n}$ ).
|
| 170 |
+
Solution de l'exercice 15 Supposons l'inverse : alors il existe des nombres premiers $p_{1}<\ldots<p_{\mathrm{r}}$ tels que pour tout $n \geqslant 1, u_{n}:=1+2!+\ldots+n!$ soit le produit des $p_{i}^{a_{i}(n)}$, où les $a_{i}(n)$ sont des entiers positifs.
|
| 171 |
+
Si $n \geqslant 1$ est tel que $a_{i}(n)<v_{p_{i}}((n+1)!)$, alors
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
\mathfrak{a}_{\mathfrak{i}}(n+1)=v_{p_{\mathfrak{i}}}\left(u_{n+1}\right)=v_{p_{\mathfrak{i}}}\left(u_{n}+(n+1)!\right)=v_{p_{\mathfrak{i}}}\left(u_{n}\right)=a_{i}(n)
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
En particulier, $a_{i}(n+1)<v_{p_{i}}((n+2)!)$. En particulier, ou bien $a_{i}(n) \geqslant \nu_{p_{\mathfrak{i}}}((n+1)!)$ pour tout $n$, ou bien $\mathfrak{a}_{\mathfrak{i}}(\mathfrak{n})$ est constante à partir $\mathrm{d}^{\prime}$ un certain rang.
|
| 178 |
+
En particulier, en renommant et regroupant les $p_{i}$, on dispose d'entiers $\mathrm{N} \geqslant 1, \mathrm{C} \geqslant 1$ et de nombres premiers $q_{1}<\ldots<q_{s}$ ne divisant pas $C$ tels que pour tout $n>N, u_{n}=C \prod_{i=1}^{s} q_{i}^{b_{i}(n)}$ et $b_{i}(n) \geqslant$ $v_{q_{i}}((n+1)!)$.
|
| 179 |
+
Soit maintenant $n>N+C+1$ tel que $n+1$ soit divisible par le produit des $q_{i}$. Alors $u_{n}=u_{n-1}+n$ ! et $v_{q_{i}}\left(u_{n}\right)=b_{i}(n) \geqslant v_{q_{i}}((n+1)!)>v_{q_{i}}(n!)$, donc $v_{q_{i}}\left(u_{n-1}\right)=v_{q_{i}}(n!)$. D'autre part, si $p \mid C$, $v_{p}\left(u_{n-1}\right)=v_{p}(C) \leqslant v_{p}(\mathfrak{n}!)$, donc $u_{n-1} \mid n!$.
|
| 180 |
+
Il reste à montrer que pour tout $n$ assez grand, $u_{n}$ ne divise pas $(n+1)!$.
|
| 181 |
+
En effet, si $n \geqslant 2, n u_{n}>n \cdot n!+n \cdot(n-1)!=(n+1) \cdot n!=(n+1)!$. D'autre part, si $n \geqslant 4$,
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\begin{aligned}
|
| 185 |
+
(n-1) \mathfrak{u}_{n} & =(n-1) n!+(n-1)(n-1)!+(n-1)(n-2)!+(n-1) \sum_{k=1}^{n-3} k! \\
|
| 186 |
+
& =n \cdot n!+(n-1)(n-3) \cdot(n-3)!<(n+1) \cdot n! \\
|
| 187 |
+
& =(n+1)!
|
| 188 |
+
\end{aligned}
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
Commentaire des correcteurs : Le problème a été peu abordé et la majorité des copies rendues l'a résolu correctement, parfois d'une manière différente de celle du corrigé. L'idée était, pour chaque diviseur premier $p$ d'un terme de la suite, de contrôler $v_{p}\left(u_{n}\right)$ pour $n$ assez grand en utilisant le fait que $\mathfrak{u}_{n}-\mathfrak{u}_{n-1}=n$ ! (ce qui est aussi apparu dans des tentatives n'ayant pas abouti) et en choisissant judicieusement la valeur de $n$ (les copies ayant remarqué cela ont toutes résolu le problème).
|
| 192 |
+
|
| 193 |
+
Exercice 16. Soient $n \geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \ldots, a_{N}$ des éléments de $U$ telle que $\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\mathrm{p}^{\mathrm{n}}$.
|
| 194 |
+
|
| 195 |
+
## Solution de l'exercice 16
|
| 196 |
+
|
| 197 |
+
On commence par traiter le cas $p=3$, dont la solution est différente. Soit $\mathrm{g} \in \mathrm{U}$ un générateur modulo $p^{n}$, on pose $a_{i}=g^{i-1}\left(\bmod p^{n}\right)$. Comme $g^{2}-1$ est divisible par 3 , la somme considérée $S$ vérifie $\left(g^{2}-1\right) S \equiv \sum_{i=1}^{N}\left(g^{2 i+1}-g^{2 i-1}\right) \equiv g\left(g^{2 N}-1\right)\left[p^{n+1}\right]$. Donc pour que $v_{p}(S)=n-1$, il faut et suffit que $v_{p}\left(g^{2 N}-1\right)=n\left(g\right.$ est premier avec $p$ ). Puisque $g^{N} \equiv 1\left[p^{n}\right]$ (par Euler-Fermat), il suffit de montrer que $v_{p}\left(g^{N}-1\right)=n$. Mais par LTE, $v_{p}\left(g^{N}-1\right)=v_{p}\left(g^{N / p}-1\right)+1<n+1$, donc $v_{p}\left(g^{N}-1\right) \leqslant n$, de sorte que $v_{p}\left(g^{N}-1\right)=n$, ce qui conclut.
|
| 198 |
+
Supposons maintenant $p>3$ : Soient $b_{0}, \ldots, b_{m-1} \in U$ des entiers représentant exactement une fois chaque classe de congruence modulo $p^{n-1}$, ainsi $m=N / p=p^{n-2}(p-1)$ (et on pose $b_{m}=b_{0}$ ). On considère la permutation
|
| 199 |
+
|
| 200 |
+
$$
|
| 201 |
+
\begin{aligned}
|
| 202 |
+
& \mathrm{b}_{0}, \mathrm{~b}_{0}+\mathrm{p}^{\mathrm{n}-1}, \mathrm{~b}_{0}+2 p^{n-1}, \ldots, \mathrm{~b}_{0}+(p-1) p^{n-1} \\
|
| 203 |
+
& \mathrm{~b}_{1}, \mathrm{~b}_{1}+\mathrm{p}^{n-1}, \ldots, \mathrm{~b}_{1}+(p-1) p^{n-1} \\
|
| 204 |
+
& \mathrm{~b}_{2}, \ldots, b_{m-1}, \ldots, b_{m-1}+(p-1) p^{n-1}
|
| 205 |
+
\end{aligned}
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
(les additions sont toujours à effectuer modulo $\mathrm{p}^{\mathrm{n}}$ ).
|
| 209 |
+
Alors la somme correspondante $S$ est congrue modulo $p^{n}$ à
|
| 210 |
+
|
| 211 |
+
$$
|
| 212 |
+
S_{1}=\sum_{i=0}^{m-1} b_{i} b_{i+1}+\sum_{i=0}^{m-1}(p-1) p^{n-1} b_{i}+\sum_{i=0}^{m-1} \sum_{k=0}^{p-2} b_{i} p^{n-1}(2 k+1)+(p-1) \sum_{i=0}^{m-1} b_{i}^{2}
|
| 213 |
+
$$
|
| 214 |
+
|
| 215 |
+
. Comme la somme des $b_{i}$ est divisible par $p$ et la somme des $b_{i}^{2}$ par $p^{n-1}, S \equiv S_{2}\left[p^{n}\right]$, où $S_{2}=$ $\sum_{i=0}^{\mathfrak{m}-1} b_{i} b_{i+1}-\sum_{i=0}^{m-1} b_{i}^{2}$.
|
| 216 |
+
Soit alors $g \in U$ une racine primitive modulo $p^{n}:$ prenons $b_{i}=g^{i}\left(\bmod p^{n}\right)$. Alors $(g+1) S_{2} \equiv$ $(g+1) \sum_{i=0}^{m-1}\left(g^{2 i+1}-g^{2 i}\right) \equiv\left(g^{2 m}-1\right)\left[p^{n}\right]$. D'après LTE, $v_{p}\left(g^{2 m}-1\right) \geqslant 1+v_{p}\left(\frac{2 m}{p-1}\right)=n-1$ (puisque $p-1|m, p| g^{p-1}-1$ par Fermat, et $N=p^{n-1}(p-1)$, mais comme $2 m<N, v_{p}\left(g^{2 m}-1\right)<n$, donc $v_{p}\left(g^{2 m}-1\right)=n-1$. De plus, puisque $p>3, g+1$ est premier à $p$, et donc $v_{p}\left(S_{2}\right)=n-1$, d'où $\nu_{p}(S)=n-1$.
|
| 217 |
+
$\underline{\text { Commentaire des correcteurs : Le problème a été très peu abordé, sans doute à cause de la forme quelque }}$ peu intimidante de son énoncé. Il est important, devant de tels problèmes, de ne pas se laisser impressionner et continuer à réfléchir normalement. Tous les élèves ayant rendu une copie ont trouvé une solution correcte, en général plus simple que la construction proposée dans le corrigé. En fait, l'idée la plus naturelle (prendre les nombres dans l'ordre croissant) fournissait une solution, et il est étonnant qu'aussi peu d'élèves l'aient remarqué ou même essayé.
|
| 218 |
+
|
| 219 |
+
Exercice 17. Soit $\left(a_{n}\right)_{n \geqslant 1}$ une suite d'entiers strictement positifs telle que $a_{1}$ et $a_{2}$ soient premiers entre eux et, pour tout $n \geqslant 1, a_{n+2}=a_{n} a_{n+1}+1$. Montrer que pour tout entier $m>1$, il existe $n>m$ tel que $a_{m}^{m} \mid a_{n}^{n}$. Le résultat est-il encore vrai lorsque $m=1$ ?
|
| 220 |
+
|
| 221 |
+
## Solution de l'exercice 17 D'abord, $a_{n}>0$ pour tout $n>0$.
|
| 222 |
+
|
| 223 |
+
On commence par une observation : soit $n>m$ très grand (disons, $n>(m+1)\left(a_{m}+1\right)$ ). Alors $a_{m}^{m} \mid a_{n}^{n}$ si et seulement si pour chaque nombre premier $p\left|a_{m}, p\right| a_{n}$. Cette idée justifie le lemme qui va suivre :
|
| 224 |
+
|
| 225 |
+
Lemme : soit $\left(u_{n}\right)_{n \geqslant 0}$ la suite modulo un nombre premier $p$ telle que $u_{0}=0, u_{1}=1$ et pour tout $n \geqslant 0$, $u_{n+2}=u_{n} u_{n+1}+1$. Alors $u$ est périodique.
|
| 226 |
+
|
| 227 |
+
Preuve : soit $v_{n}=\left(u_{n}, u_{n+1}\right)$; alors $u$ est périodique dès que $v$ est périodique. Comme $v_{n+1}$ dépend uniquement de $\nu_{n}, v$ est périodique dès qu'il existe $N \geqslant 1$ tel que $\nu_{N}=v_{0}$. Si $N \geqslant 1$ est tel que $u_{N}=0$, alors la relation de récurrence montre que $u_{N+1}=1=u_{1}$ et donc $v_{N}=v_{0}$. Par conséquent, pour montrer que $u$ est périodique, il suffit de montrer qu'il existe $N \geqslant 1$ tel que $u_{N}=0$.
|
| 228 |
+
Supposons donc que le seul entier n tel que $u_{n}=0$ soit $n=0$. Alors comme $v$ est à valeurs dans un ensemble fini, il existe un entier $\mathrm{n} \geqslant 0$ minimal tel qu'il existe un entier $m>n$ tel que $v_{n}=v_{m}$. En particulier, $u_{m}=u_{n}$ et $m \neq 0$, donc $u_{m} \neq 0$, et donc $u_{n} \neq 0$ et donc $n>0$. Alors $m+1>n+1 \geqslant 2$ et $u_{n+1}=u_{m+1}$, donc $u_{n-1} u_{n}+1=u_{m-1} u_{m}+1$, donc $u_{n}\left(u_{n-1}-u_{m-1}\right)=0$, d'où, comme $u_{n} \neq 0$, $u_{n-1}=u_{m-1}$, de sorte que $v_{m-1}=v_{n-1}$, ce qui contredit la minimalité de $n$.
|
| 229 |
+
|
| 230 |
+
Revenons à notre preuve. Lorsque $m>1$, pour chaque facteur premier $p$ de $a_{m}, a_{m+1}=a_{m-1} a_{m}+1 \equiv$ $1[p],\left(a_{m+n}(\bmod p)\right)_{n \geqslant 0}$ satisfait les hypothèses du lemme, donc il existe $N_{p} \geqslant 1$ tel que que pour tout $n \geqslant 0, a_{m+n} \equiv a_{m+n+N_{p}}[p]$.
|
| 231 |
+
Soit $N$ le produit des $N_{p}$ (où $p$ parcourt les facteurs premiers de $a_{m}$ ) : alors, si $n \geqslant 0$, tout diviseur premier $p$ de $a_{m}$ divise $a_{m+n N}$. En particulier, si $n \geqslant m a_{m}, a_{m}^{m} \mid a_{m+n N}^{m+n N}$ (parce que si $p \mid a_{m}$, $\left.v_{p}\left(a_{m+n N}^{m+n N}\right) \geqslant m+n N \geqslant m a_{m} \geqslant v_{p}\left(a_{m}^{m}\right)\right)$.
|
| 232 |
+
Le résultat est faux pour $\mathrm{m}=1$ : prenons $\mathrm{a}_{1}=155, \mathrm{a}_{2}$ congru à 4 modulo 5 et congru à 29 modulo 31 . On vérifie alors que $a_{n}$ est divisible par 5 si et seulement si $n=1$ et $n \equiv 4[7]$, alors que $a_{n}$ est divisible par 31 si et seulement si $n=1$ ou $n \equiv 5[7]$, donc si $n>1, a_{n}$ n'est jamais divisible par 5 et 31 , et donc 155 ne divise pas $a_{n}^{n}$.
|
| 233 |
+
|
| 234 |
+
Commentaire des correcteurs : Le problème a été peu abordé et toutes les copies ont su traiter le cas $\mathrm{m}>1$, essentiellement par la méthode du corrigé. La plupart des élèves ont détecté que le cas $m=1$ ne fonctionnait pas et exhibé des contre-exemples, mais certains ont laissé complètement implicite l'endroit où était utilisée l'hypothèse $m>1$. Dans un problème, les hypothèses doivent être utilisées; si l'énoncé attire l'attention sur l'une d'entre elles, il faut d'autant plus soigneusement relever l'endroit où l'on s'en sert.
|
| 235 |
+
|
| 236 |
+
Exercice 18. Déterminer toutes les fonctions $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ telles que :
|
| 237 |
+
(i) Les entiers $f(1), f(2), \ldots$ sont premiers entre dans leur ensemble.
|
| 238 |
+
(ii) Il existe $N \geqslant 1$ tel que pour tout $n \geqslant N, f(n) \neq 1$ et pour tous $a, b \in \mathbb{N}^{\star}$,
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
f(a)^{n} \mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
Solution de l'exercice 18 Soit f une solution. Comme les valeurs de f sont premières entre elles dans leur ensemble, si f est constante, elle égale 1 , ce qui est exclu.
|
| 245 |
+
Avec $a=1$, on voit que $f(1)^{\mathfrak{n}} \mid \mathbf{f}(b+1)-f(b)$ pour tout $b \geqslant 1$ et tout $n$ assez grand. Comme $f$ est non constante, il existe $b$ tel que $f(b+1) \neq f(b)$. Il s'ensuit que $f(1)=1$.
|
| 246 |
+
Soit $a \geqslant 2$, il existe un $t \geqslant 0$ tel que $f(1+(t+1) a) \neq f(1+t a)$ (car, pour $t$ assez grand, $f(1+t a) \neq$ $1=f(1))$ : soit $b=1+$ ta. Pour tout $n \geqslant 1$ assez grand, $f(a)^{n} \mid f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$.
|
| 247 |
+
Soit $p$ un nombre premier divisant $f(a)$. Alors il existe un $l \geqslant 1$ tel que $p \mid f(a+b)^{a^{l}}-f(b)^{a^{l}}$. Pour $n>l$, par LTE, la valuation $p$-adique de $f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$ est $v_{p}\left(a^{n-1-l}\right)+C$ pour une certaine constante $C$ qui ne dépend que de $f, a, b, l$ (mais pas de $n$ ).
|
| 248 |
+
Donc pour $n>l$ assez grand, $v_{p}\left(a^{n-1-l}\right)+C \geqslant v_{p}\left(f(a)^{n}\right)$, donc $(n-1-l) v_{p}(a)+C \geqslant n v_{p}(f(a))$, d'où $v_{p}(f(a)) \leqslant v_{p}(a)$.
|
| 249 |
+
Par conséquent, pour tout $a \geqslant 1, f(a) \mid a$.
|
| 250 |
+
En particulier, si a est premier, $f(a)$ vaut 1 ou $a$, et est égal à a sauf pour un nombre fini de nombres premiers.
|
| 251 |
+
Soit $a$ un nombre premier tel que $f(a)=a$ : pour tout $b \geqslant 1$ et tout $n$ assez grand, $a^{n} \mid f(a+b)^{a^{n-1}}-$ $f(b)^{a^{n-1}}$. En particulier, $f(a+b) \equiv f(b)[a]$ : ainsi, la classe de congruence de $f(b)$ modulo a ne dépend que de $b$ modulo $a$.
|
| 252 |
+
On va montrer que $f$ est l'identité. Soit $u \geqslant 2$, soit $P$ l'ensemble fini des nombres premiers $p$ tels que $p \leqslant u$ ou $f(p)=1$. Supposons qu'il existe un nombre premier $q \notin P$ et un entier $n$ tels que $q \mid n-u$ et $\mathrm{f}(\mathrm{n})=\mathrm{n}$.
|
| 253 |
+
Alors $q \mid f(n)-f(u)$, et donc $q \mid n-f(u)$, d'où $q \mid u-f(u)$. Comme $0 \leqslant u-f(u) \leqslant u<q$, on en déduit que $f(u)=u$.
|
| 254 |
+
On propose trois méthodes, de la plus élémentaire à la moins élémentaire, d'exhiber un tel couple (q, $\mathfrak{n}$ ).
|
| 255 |
+
|
| 256 |
+
## Première méthode (complètement élémentaire):
|
| 257 |
+
|
| 258 |
+
Soit $\Pi$ le produit des nombres premiers de $P$, et soit $N \geqslant 1$ tel que pour tout $p \in P, p^{N}$ ne divise pas $\mathbf{u}-1$.
|
| 259 |
+
Supposons que $n>\Pi^{N}+u$ soit congru à 1 modulo $\Pi^{N}$ et tel que $f(n)=n$. Alors, si $p \in P, v_{p}(n-u)<$ $N$, et $n-u>\Pi^{N}$, de sorte que $n-u$ possède un diviseur premier $q \notin P$, et on a gagné.
|
| 260 |
+
Soit n un produit de nombres premiers deux à deux distincts, tous hors de $P$. Alors, si $\mathrm{p} \mid \mathrm{n}$ est un diviseur premier, $n \equiv p[p]$ et $f(p)=p$, donc $p \mid f(n)-f(p)$, d'où $p \mid f(n)$. Comme $f(n) \mid n$, on en déduit que $\mathrm{f}(\mathrm{n})=\mathrm{n}$.
|
| 261 |
+
Comme il existe une infinité de nombres premiers, il existe une progression arithmétique C de raison $\Pi^{N}$ et de premier terme premier à $\Pi$ et contenant une infinité de nombres premiers. En prenant pour n le produit de $\varphi\left(\Pi^{N}\right)$ premiers $q \in C$ tels que $q>\Pi^{N}+u, n$ convient.
|
| 262 |
+
|
| 263 |
+
Deuxième méthode (il y a des prérequis, mais ils sont élémentaires et relativement classiques) :
|
| 264 |
+
On reprend les notations et le raisonnement de ce qui précède : on cherche à construire un entier $\mathrm{n}>$ $\Pi^{N}+u$ congru à 1 modulo $\Pi^{N}$ tel que $f(n)=n$.
|
| 265 |
+
|
| 266 |
+
Il est connu (du moins, classique et relativement élémentaire) que si $\Phi_{\Pi^{N}}$ est le $\Pi^{\mathrm{N}}$-ième polynôme cyclotomique, il existe une infinité de nombres premiers n divisant une valeur de $\Phi_{\Pi^{\mathrm{N}}}$, et ceux qui ne sont pas dans $P$ sont congrus à 1 modulo $\Pi^{N}$ et vérifient $f(n)=n$. On peut en choisir un qui est strictement supérieur à $\Pi^{\mathrm{N}}+\mathrm{u}$.
|
| 267 |
+
|
| 268 |
+
Troisième méthode (utilise un théorème relativement classique, mais dont aucune démonstration accessible au niveau olympique n'est connue) :
|
| 269 |
+
|
| 270 |
+
Soit $\mathrm{q} \notin \mathrm{P}$ premier : alors $\mathrm{f}(\mathrm{q})=\mathrm{q}$. D’après le théorème de Dirichlet, il existe un nombre premier $p>u+q$ congru à $u$ modulo $q$ tel que $f(p)=p$. Alors le couple $(q, p)$ convient.
|
| 271 |
+
Ainsi, l'identité est la seule solution potentielle. Réciproquement, l'identité vérifie la première condition et si $a, b \geqslant 1$ et $n \geqslant 2$, alors par LTE, pour tout nombre premier $p \mid a, v_{p}\left((a+b)^{a^{n-1}}-b^{a^{n-1}}\right) \geqslant$ $v_{p}(a)+v_{p}\left(a^{n-1}\right)=v_{p}\left(a^{n}\right)$, donc $a^{n} \mid(a+b)^{a^{n-1}}-b^{a^{n-1}}$, et donc l'identité est solution.
|
| 272 |
+
|
| 273 |
+
Commentaire des correcteurs : L'exercice a été très peu abordé. Toutes les solutions fonctionnaient en deux temps : d'abord, utiliser LTE pour montrer que $f(a) \mid a$ pour tout entier a, éventuellement assez grand. Ensuite, utiliser cette information (souvent en conjonction avec le cas où a est un nombre premier assez grand, puisqu'alors $f(a)=a$ ) de diverses manières pour conclure. Si quelques élèves ont été hâtifs dans la deuxième partie, très peu ont songé à vérifier, en considérant la valuation $p$-adique de nombres de la forme $f(a+b)^{a^{n-1}}-f(b)^{a^{n-1}}$, que ce nombre était bien non nul. Non, ce cas n'est pas un détail! Signalons enfin que comme dans tout type d'équation, il est important de vérifier les solutions : si un raisonnement logique montre que seule l'identité peut être solution, il faut déterminer si oui ou non l'identité est bien solution.
|
| 274 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi1-corrige.md
ADDED
|
@@ -0,0 +1,241 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Olympiades Françaises de Mathématiques
|
| 2 |
+
2012-2013
|
| 3 |
+
|
| 4 |
+
Envoi $\mathcal{N u m e ́ r o ~} 1$ - Corrigé
|
| 5 |
+

|
| 6 |
+
|
| 7 |
+
## Exercices Juniors
|
| 8 |
+
|
| 9 |
+
Exercice 1. ABC est un triangle dont tous les angles sont aigus. À l'extérieur de ce triangle on construit les trois points $X, Y$ et $Z$ vérifiant :
|
| 10 |
+
|
| 11 |
+
- Le triangle $A X B$ est isocèle de base $A B$ et l'angle $\widehat{A X B}$ vaut $120^{\circ}$,
|
| 12 |
+
- Le triangle BYC est isocèle de base BC et l'angle $\widehat{B Y C}$ vaut $120^{\circ}$,
|
| 13 |
+
- Le triangle CZA est isocèle de base CA et l'angle $\widehat{C Z A}$ vaut $60^{\circ}$.
|
| 14 |
+
|
| 15 |
+
Montrer que les droites $(X Y)$ et (BZ) sont perpendiculaires.
|
| 16 |
+
Solution. Traçons le cercle de centre $X$ qui passe par $A$ et $B$ et celui de centre $Y$ qui passe par $B$ et $C$ et notons K leur autre point d'intersection :
|
| 17 |
+
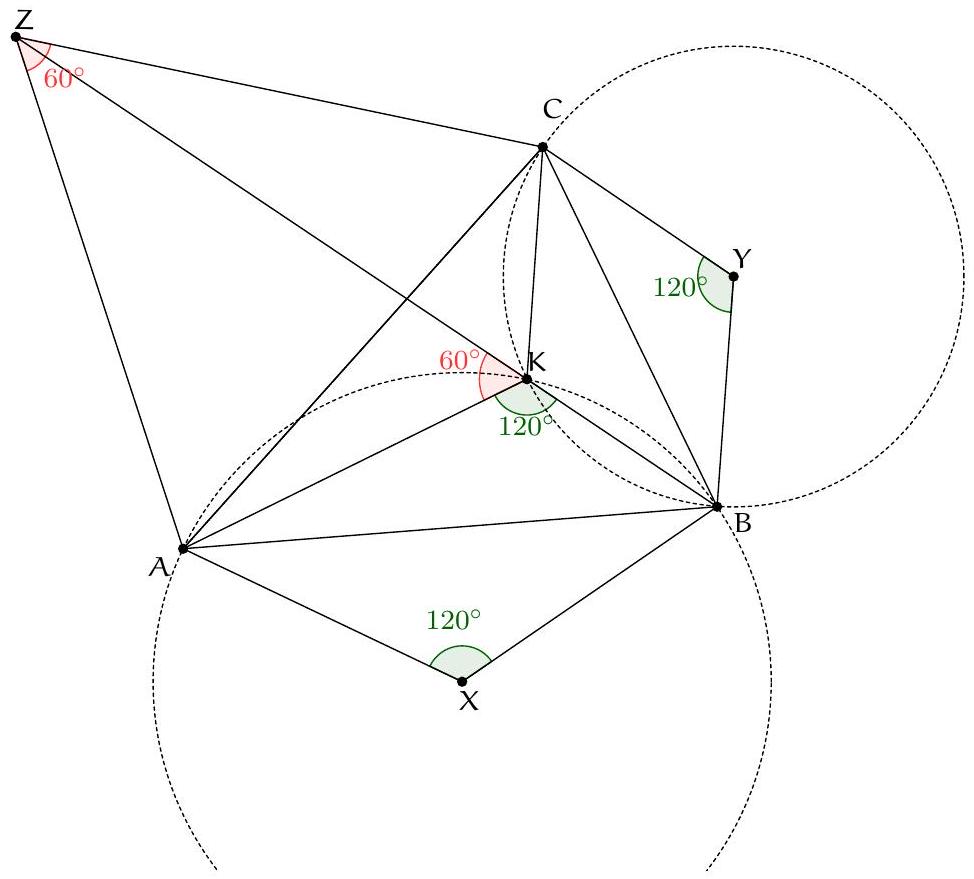
|
| 18 |
+
|
| 19 |
+
L'angle $\widehat{A K B}$ vaut la moitié de l'angle au centre, et l'angle au centre est le complémentaire de $120^{\circ}$, donc $\widehat{A K B}$ vaut $\frac{240}{2}=120^{\circ}$. De même, $\widehat{\mathrm{BKC}}=120^{\circ}$ et par conséquent, l'angle restant $\widehat{\mathrm{CKA}}=120^{\circ}$. Mais alors, comme $\widehat{C K A}+\widehat{A Z C}=120+60=180^{\circ}$, donc les points $A, Z, C, K$ sont cocycliques. Comme $A Z=Z C$, les arcs que ces deux cordes délimitent sont égaux et les angles inscrits sont égaux. Ainsi, $\widehat{A K Z}=\widehat{Z K C}=60^{\circ}$.
|
| 20 |
+
|
| 21 |
+
Maintenant regardons les points $B, K$ et $Z: \widehat{B K Z}=120+60=180^{\circ}$, donc les trois points sont alignés, la droite ( BZ ) est la droite qui passe par les deux points d'intersection des cercles, elle est perpendiculaire au segment qui relie les deux centres, ie $[\mathrm{XY}]$.
|
| 22 |
+

|
| 23 |
+
|
| 24 |
+
Exercice 2. $A B C D$ est un trapèze dans lequel les côtés $A D$ et $B C$ sont parallèles, $K$ est un point du côté $A B$ et $L$ un point du côté $C D$. Montrer que si les angles $\widehat{B A L}$ et $\widehat{C D K}$ sont égaux alors les angles $\widehat{\mathrm{BLA}}$ et $\overline{\mathrm{CKD}}$ le sont aussi.
|
| 25 |
+
|
| 26 |
+
Solution. On suppose les angles $\widehat{\mathrm{BAL}}$ et $\widehat{\mathrm{CDK}}$ ont la même valeur. Nous allons montrer que les angles KBL et KCL sont égaux (ceci impliquera que les triangles KDC et BAL ont deux angles identiques, et donc que $\widehat{\mathrm{BLA}}=\widehat{\mathrm{KCL}}$ ).
|
| 27 |
+
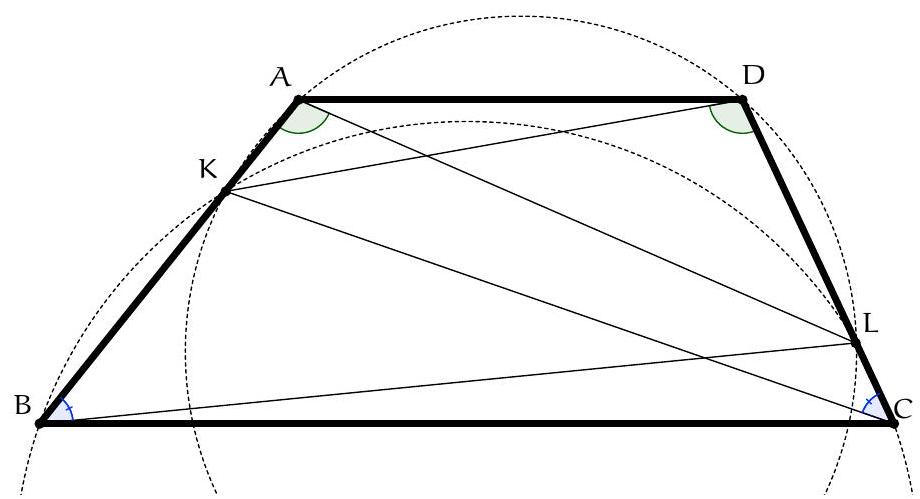
|
| 28 |
+
|
| 29 |
+
Je vais d'abord montrer un point amusant sur les trapèzes : si on place des points $K$ et $L$ sur les côtés $A B$ et $C D$ tels que $A, D, K, L$ soient cocycliques, alors les points $B, C, K, L$ sont aussi cocycliques. Il suffit d'utiliser la propriété qu'un quadrilatère est inscrit dans un cercles ssi la somme des angles opposés vaut $180^{\circ}$, et aussi que comme $A D$ et $B C$ sont parallèles, $\widehat{A}+\widehat{B}=\widehat{C}+\widehat{D}=180^{\circ}$.
|
| 30 |
+
|
| 31 |
+
L'hypothèse $\widehat{\mathrm{BAL}}=\widehat{\mathrm{CDK}}$ revient à dire que $\mathrm{A}, \mathrm{D}, \mathrm{K}, \mathrm{L}$ cocycliques par le théorème des angles inscrits, donc par le résultat précédent $\mathrm{B}, \mathrm{C}, \mathrm{K}, \mathrm{L}$ sont aussi cocycliques et les angles bleus sont égaux.
|
| 32 |
+
|
| 33 |
+
Exercice 3. ABC est un triangle dont tous les angles sont aigus. Soit respectivement H le pied de la hauteur de ce triangle issue de $C$ et K le milieu du côté $A C$. On suppose que $B K=C H$ et que les angles $\widehat{\mathrm{KBC}}$ et $\widehat{\mathrm{HCB}}$ sont égaux. Montrer que le triangle ABC est équilatéral.
|
| 34 |
+
|
| 35 |
+
Solution. Voici la figure :
|
| 36 |
+
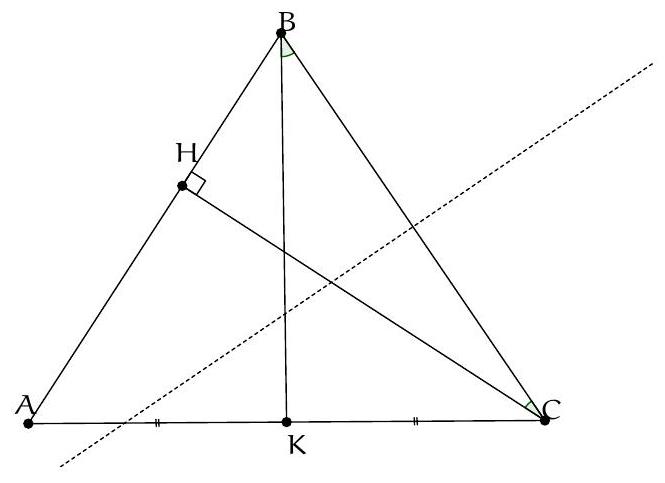
|
| 37 |
+
|
| 38 |
+
Maintenant considérons la médiatrice de $[\mathrm{BC}]$ (dessinée en pointillés sur la figure) et la symétrie par rapport à cet axe. Il est évident que par cette symétrie $B$ devient $C$ et vice-versa. Appelons $A^{\prime}$ l'image de $A$ par la symétrie. Les hypothèses que tous les angles sont aigus, $\mathrm{BK}=\mathrm{CH}$ et $\widehat{\mathrm{KBC}}=\widehat{\mathrm{HCB}}$ impliquent que $K$ est l'image de $H$ par la symétrie. Mais comme $A$ est l'intersection de $B H$ et $C K$, $A^{\prime}$ est l'intersection de l'image de $B H$ (c-à-d $C K$ ) et de l'image de $C K\left(c-a ̀-d B H\right.$ ), donc $A^{\prime}=A$, $A$ est sur la médiatrice de $B C$ et le triangle est isocèle en $A$.
|
| 39 |
+
|
| 40 |
+
Mais nous n'avons pas fini, comme $\mathrm{CH} \mapsto \mathrm{BK}$ et $\mathrm{BA} \mapsto \mathrm{CA}$, l'angle droit est conservé, et BK est à la fois une hauteur et une médiane. Donc le triangle est aussi isocèle en $B$, il est donc équilatéral.
|
| 41 |
+
|
| 42 |
+
## Exercices Communs
|
| 43 |
+
|
| 44 |
+
Exercice 4. ABCD est un rectangle et $M$ un point intérieur à ce rectangle. Montrer que l'aire de ce rectangle est inférieure ou égale à la somme $A M \times C M+B M \times D M$ ( $A M \times C M$ désigne le produit des longueurs des segments $A M$ et $C M$, de même pour $B M \times D M$ )
|
| 45 |
+
|
| 46 |
+
Solution.Nous allons travailler en analytique et tout passer aux coordonnées : $\mathrm{A}(0,0), \mathrm{B}(\mathrm{a}, 0), \mathrm{C}(\mathrm{a}, \mathrm{b})$, $\mathrm{D}(0, \mathrm{~b}), \mathrm{M}(\mathrm{x}, \mathrm{y})$.
|
| 47 |
+
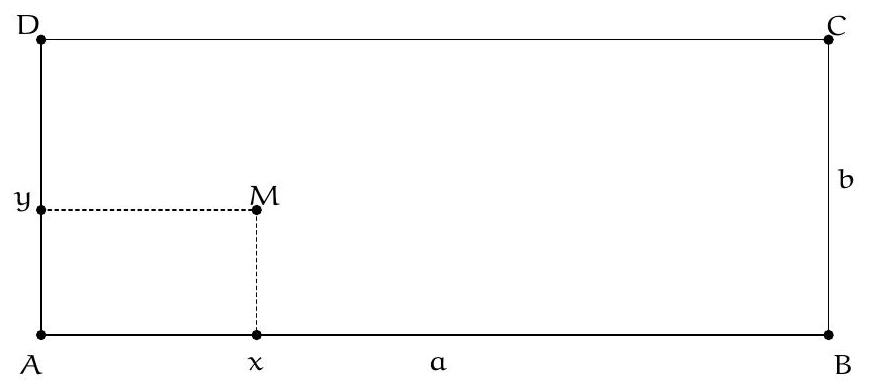
|
| 48 |
+
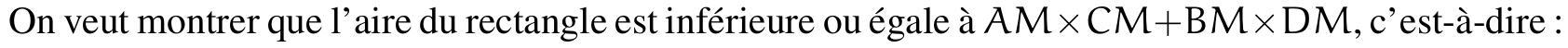
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\sqrt{x^{2}+y^{2}} \times \sqrt{(a-x)^{2}+(b-y)^{2}}+\sqrt{(a-x)^{2}+y^{2}} \times \sqrt{x^{2}+(b-y)^{2}} \geqslant a b
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Nous allons utiliser l'inégalité de Cauchy-Schwartz :
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
\begin{aligned}
|
| 58 |
+
& \sqrt{x^{2}+y^{2}} \times \sqrt{(b-y)^{2}+(a-x)^{2}} \geqslant x(b-y)+y(a-x) \\
|
| 59 |
+
& \sqrt{(a-x)^{2}+y^{2}} \times \sqrt{(b-y)^{2}+x^{2}} \geqslant(a-x)(b-y)+y x
|
| 60 |
+
\end{aligned}
|
| 61 |
+
$$
|
| 62 |
+
|
| 63 |
+
Et on finit en remarquant que $x(b-y)+y(a-x)+(a-x)(b-y)+y x=a b$.
|
| 64 |
+

|
| 65 |
+
|
| 66 |
+
Exercice 5. Soit $A B C D$ un trapèze dans lequel les côtés $A B$ et $C D$ sont parallèles. On considère un point $P$ de la droite ( $A C$ ) tel que $C$ soit intérieur au segment $[A P]$ et on désigne respectivement par $X$ et $Y$ les milieux des côtés $A B$ et $C D$. La droite ( PX ) rencontre la droite (BC) en $N$ et la droite (PY) rencontre la droite (AD) en $M$. Montrer que la droite ( $M N$ ) est parallèle à la droite ( $A B$ ).
|
| 67 |
+
|
| 68 |
+
Solution. Faisons une figure appropriée:
|
| 69 |
+
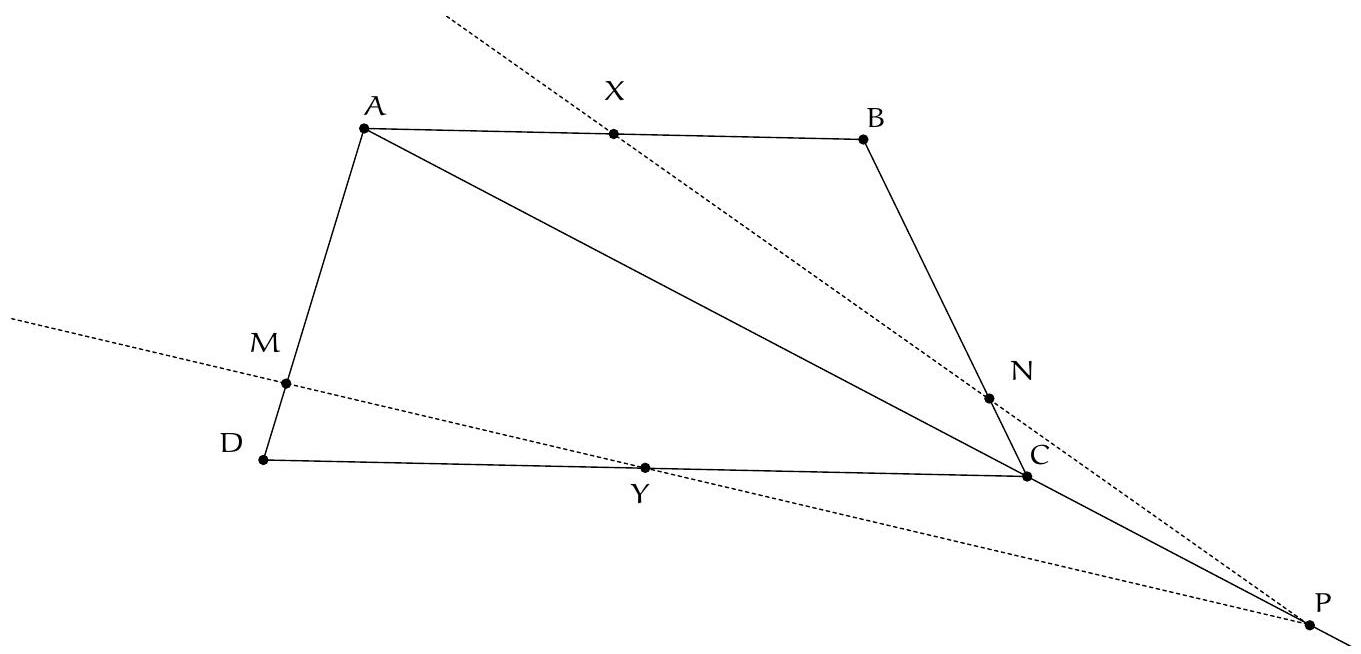
|
| 70 |
+
|
| 71 |
+
Tout d'abord considérez le cas où on prend $P$ "à l'infini", c'est au lieu de prendre $P X$ et $P Y$ on prend les droites parallèles à $A C$ passant par $X$ et $Y$. Dans ce cas, par Thalès les points $M$ et $N$ sont les milieux respectifs de $A D$ et $B C$, et par conséquent $(M N) \|(A B)$.
|
| 72 |
+
|
| 73 |
+
Revenons au cas général. Nous allons essayer de montrer que $\frac{B N}{N C}=\frac{A M}{M D}$, et ainsi nous aurons bien $(M N) \|(A B)$ (je laisse en exercice la démo de ce résultat pour ceux qui ont des doutes). Comme nous avons beaucoup de points alignés et que nous voulons calculer des quotients de longueur, le théorème de Menelaus vient à l'esprit. Dans le triangle $A B C$, les points $X, N, P$ sont alignés, donc :
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{A X}{X B} \cdot \frac{B N}{N C} \cdot \frac{C P}{P A}=-1
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
Mais comme $X$ est le milieu de $A B, \frac{A X}{X B}=1$, donc $\frac{B N}{N C}=-\frac{C P}{P A}$. Ensuite, en utilisant Menelaus dans le triangle $A D C$, on obtient $\frac{A M}{M D}=-\frac{C P}{P A}$, et les deux quotients sont égaux. Ensuite il n'est pas très dur de vérifier que l'on arrive bien au résultat attendu, $(M N) \|(A B)$.
|
| 80 |
+

|
| 81 |
+
|
| 82 |
+
Exercice 6. Soit ABC un triangle et O un point intérieur à ce triangle. D et E sont respectivement les pieds des perpendiculaires abaissées de $O$ sur les droites ( $B C$ ) et ( $A C$ ) et $F$ est le milieu du segment $A B$. Montrer que si $\mathrm{DF}=\mathrm{EF}$ alors les angles $\widehat{\mathrm{OBD}}$ et $\widehat{\mathrm{OAE}}$ sont égaux.
|
| 83 |
+
|
| 84 |
+
Solution. Dans cet exercice il y a une hypothèse superflue, à savoir que le point $O$ est à l'intérieur du triangle $A B C$. Nous allons résoure l'exercice sans cette hypothèse.
|
| 85 |
+
|
| 86 |
+
Commençons par tracer un angle droit $A E O$ et un segment $A B$ et plaçons $F$ au milieu du segment $A B$. Notre but maintenant est de trouver un point D tel que l'angle BDO soit droit et que l'on ait $\mathrm{FD}=\mathrm{FE}$.
|
| 87 |
+
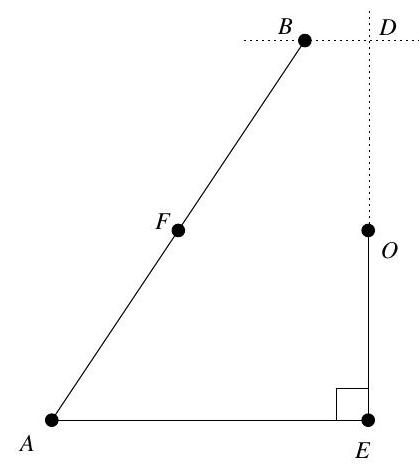
|
| 88 |
+
|
| 89 |
+
Comme la figure ci-dessus l'indique, il exite toujours une façon évidente de placer le point D : il suffit de tracer la droite parallèle à $A E$ passant par $B$ et de prendre le point d'intersection de cette droite avec la droite EO. L'angle BDO est alors droit par construction et on a bien $\mathrm{FD}=\mathrm{FE}$, car F est équidistant des deux droites parallèles. Une telle position du point $D$ ne peut pas apparaître dans l'exercice (et cela va nous servir par la suite) : en effet, l'exercice parle d'un triangle $A B C$, or ici les droites $A E$ et $B D$ ne se coupent pas et il n'y a donc pas de point $C$.
|
| 90 |
+
|
| 91 |
+
Rajoutons à notre figure le milieu $M$ du segment $A O$ et le milieu N du segment BO.
|
| 92 |
+

|
| 93 |
+
|
| 94 |
+
On a alors trois segments égaux représentés en gras sur la figure. En effet, $\mathrm{ME}=\mathrm{MO}$, car le triangle $A E O$ est rectangle en $E$; et $M O=F N$, car $F N O M$ est un parallélogramme, les lignes des mileux étant parallèles aux côtés du triangle $A O B$.
|
| 95 |
+
|
| 96 |
+
Revenons maintenant à l'exercice.
|
| 97 |
+
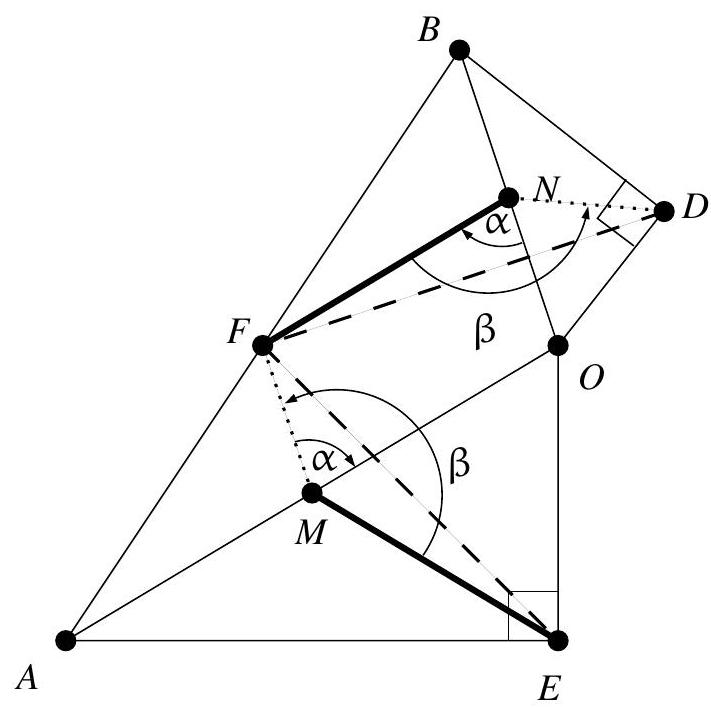
|
| 98 |
+
|
| 99 |
+
Nous venons de montrer que $\mathrm{ME}=\mathrm{FN}$ et on a de même $\mathrm{ND}=\mathrm{FM}$. Comme on a de plus $\mathrm{FD}=\mathrm{FE}$ par hypothèse, on conclut que les triangles NDF et MFE sont égaux. Il est important de distinguer deux cas : celui où ces triangles sont directement isométriques, comme sur la figure, et celui où ils sont indirectement isométrique (distinction qui n'a pas été faite correctement dans la solution initialement proposée).
|
| 100 |
+
|
| 101 |
+
Nous allons utiliser les angles orientés.
|
| 102 |
+
|
| 103 |
+
1er cas : triangles directement isométriques. Soit
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
\alpha=(M F, M O)=(N O, N F), \quad \beta=(M E, M F)=(N F, N D)
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Dans le triangle rectangle AEO on a
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
(A E, A O)=\frac{1}{2}(M E, M O) \bmod 180^{\circ}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
(L'égalité n'est vraie que modulo $180^{\circ}$ à cause de la division par 2.) On trouve donc, modulo $180^{\circ}$,
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
(A E, A O)=\frac{1}{2}(M E, M O)=\frac{1}{2}[(M E, M F)+(M F, M O)]=\frac{1}{2}(\alpha+\beta) .
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
De la même manière
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
(B O, B D)=\frac{1}{2}(N O, N D)=\frac{1}{2}[(N O, N F)+(N F, N D)]=\frac{1}{2}(\alpha+\beta) .
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
On a donc $(A E, A O)=(B O, B D)$ mod $180^{\circ}$. Or les deux angles font partie de triangles rectangles et sont donc aigus, ce qui implique qu'ils sont géométriquement égaux.
|
| 128 |
+
|
| 129 |
+
2ème cas : triangles indirectement isométriques. Les calculs sont exacement les mêmes que dans le cas précédent, sauf que cette fois-ci on a $(N F, N D)=-\beta$. On trouve donc
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
(A E, A O)=\frac{1}{2}(\alpha+\beta), \quad(B O, B D)=\frac{1}{2}(\alpha-\beta)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
modulo $180^{\circ}$. Ainsi ces angles ne sont pas égaux entre eux. Avons-nous trouvé une erreur dans l'exercice ? Non : en fait nous allons prouver que dans ce cas les droites $A E$ et $B D$ sont parallèles et nous sommes donc dans la configuration interdite mentionnée au début de la solution.
|
| 136 |
+
|
| 137 |
+
Pour cela il suffit de prouver que $(A E, A B)+(B A, B D)=0 \bmod 180^{\circ}$. On a
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
(A E, A B)+(B A, B D)=(A E, A O)+(A O, A B)+(B A, B O)+(B O, B D)
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
Nous savons déjà que, modulo $180^{\circ}$,
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
(A E, A O)+(B O, B D)=\frac{1}{2}(\alpha+\beta)+\frac{1}{2}(\alpha-\beta)=\alpha
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
De plus, dans le triangle $A O B$, on a
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
(A O, A B)+(B A, B O)=(O A, O B) \bmod 180^{\circ} .
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
Ce dernier angle vaut $180^{\circ}-\alpha=-\alpha \bmod 180^{\circ}$. On trouve donc bien que $(A E, A B)+(B A, B D)=$ $\alpha-\alpha=0 \bmod 180^{\circ}$. Par conséquent $A E$ et $B D$ sont parallèles. Le cas de triangles indirectement isométrique ne peut donc pas apparaître dans un triangle $A B C$.
|
| 156 |
+
|
| 157 |
+
## Exercices Olympiques
|
| 158 |
+
|
| 159 |
+
Exercice 7. Dans le triangle $A B C$ les bissectrices des angles en $A$ et $C$ rencontrent le cercle circonscrit au triangle $A B C$ respectivement en $A_{0}$ et $C_{0}$. La droite passant par I, centre du cercle inscrit dans le triangle $A B C$, et parallèle à la droite $(A C)$ rencontre la droite ( $A_{0} C_{0}$ ) en $P$.
|
| 160 |
+
|
| 161 |
+
Montrer que la droite (PB) est tangente au cercle circonscrit au triangle $A B C$.
|
| 162 |
+
$\underline{\text { Solution. Sur la figure on va rajouter } B_{0} \text { le point d'intersection de la bissectrice de } \widehat{A B C} \text { avec le cercle : }}$
|
| 163 |
+
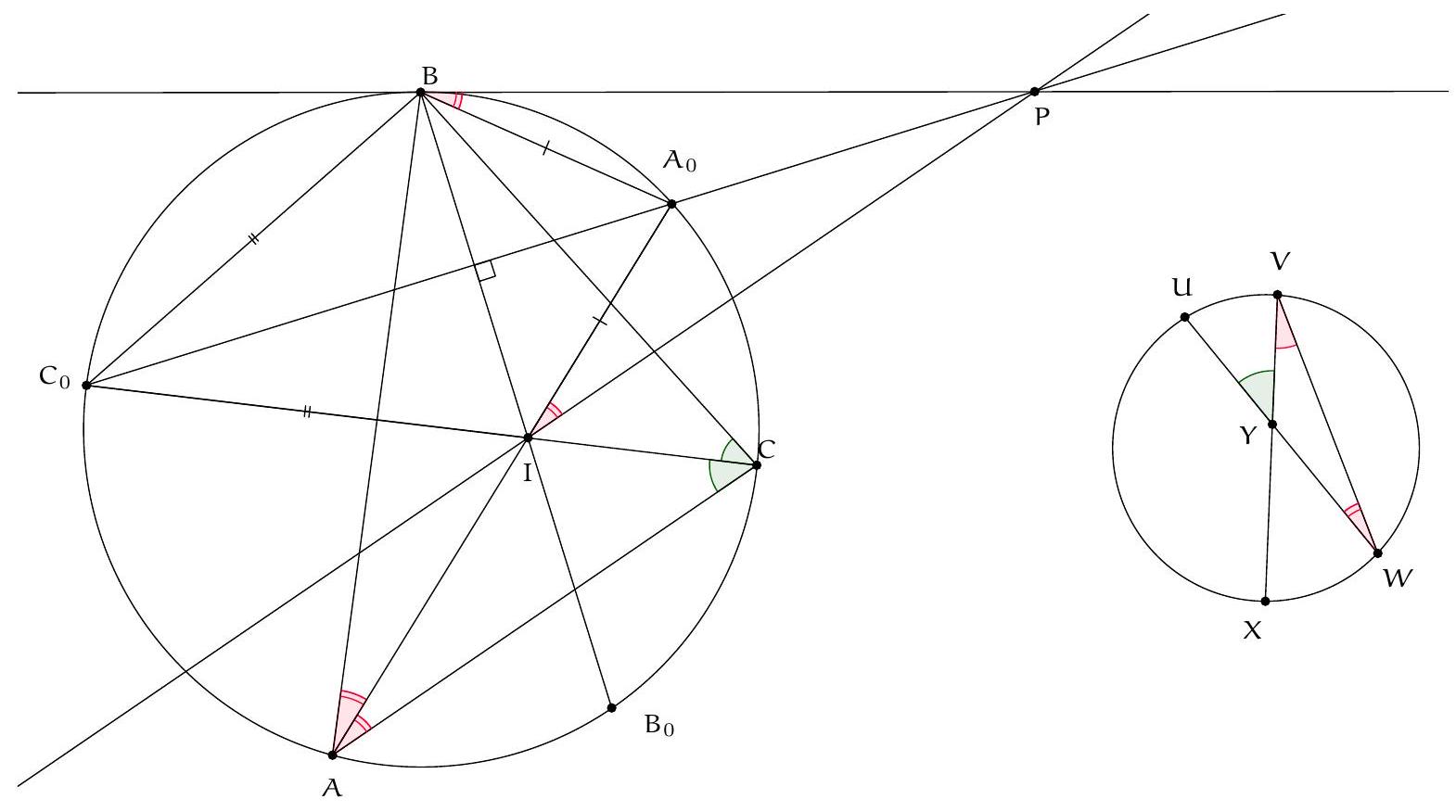
|
| 164 |
+
|
| 165 |
+
Avant de commencer, je veux démontrer un petit résultat sur les arcs. Regardez la figure de droite (je vais noter $\widehat{U V}$ l'arc délimité par U et V en radians):
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\widehat{U Y V}=\widehat{Y V W}+\widehat{Y X W}=\frac{1}{2} \widehat{W X}+\frac{1}{2} \widehat{U V} .
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
Revenons à nos moutons. Grâce à la formule précédente, on peut calculer :
|
| 172 |
+
|
| 173 |
+
$$
|
| 174 |
+
\widehat{\mathrm{BIC}_{0}}=\frac{1}{2} \widehat{\mathrm{BC}_{0}}+\frac{1}{2} \widehat{\mathrm{~B}_{0} \mathrm{C}}=\frac{1}{2} \widehat{\mathrm{C}_{0} \mathrm{~A}}+\frac{1}{2} \widehat{\mathrm{AB}_{0}}=\widehat{\mathrm{C}_{0} \mathrm{BI}} .
|
| 175 |
+
$$
|
| 176 |
+
|
| 177 |
+
Donc le triangle $\mathrm{BIC}_{0}$ est isocèle en $\mathrm{C}_{0}$. On prouve de même que $A_{0} B I$ est isocèle en $A_{0}$, donc $\left(A_{0} C_{0}\right)$ est la médiatrice du segment BI.
|
| 178 |
+
|
| 179 |
+
Par symétrie, $\widehat{A_{0} \mathrm{BP}}=\widehat{A_{0} \mathrm{IP}}$, et comme (IP) et ( AC ) sont parallèles, $\widehat{A_{0} \mathrm{IP}}=\widehat{\mathrm{A}_{\mathrm{O}} A C}=\widehat{\mathrm{BAA}_{0}}$. Comme $\widehat{A_{0} \mathrm{BP}}=\widehat{\mathrm{BAA}_{0}}$, on se retrouve avec le cas extrême du théorème de l'angle inscrit, et par la réciproque du théorème ( BP ) est tangente au cercle.
|
| 180 |
+
|
| 181 |
+
Exercice 8. Soit $A B C$ un triangle non isocèle en $A$; I et $O$ sont respectivement le centre du cercle inscrit et le centre du cercle circonscrit de ce triangle $A B C$ et le cercle inscrit touche le côté BC en D. La bissectrice intérieure de l'angle en $A$ dans le triangle $A B C$ rencontre le cercle circonscrit au point $M$ et la droite (DM) rencontre à nouveau le cercle circonscrit en P .
|
| 182 |
+
|
| 183 |
+
Montrer que l'angle $\widehat{A P I}$ est un angle droit.
|
| 184 |
+
Solution.On va placer E le point diamétralement opposé à A sur le cercle circonscrit. Si on arrive à prouver que les points $\mathrm{P}, \mathrm{I}$ et E sont alignés, alors l'angle $\widehat{A P I}$ sera droit.
|
| 185 |
+
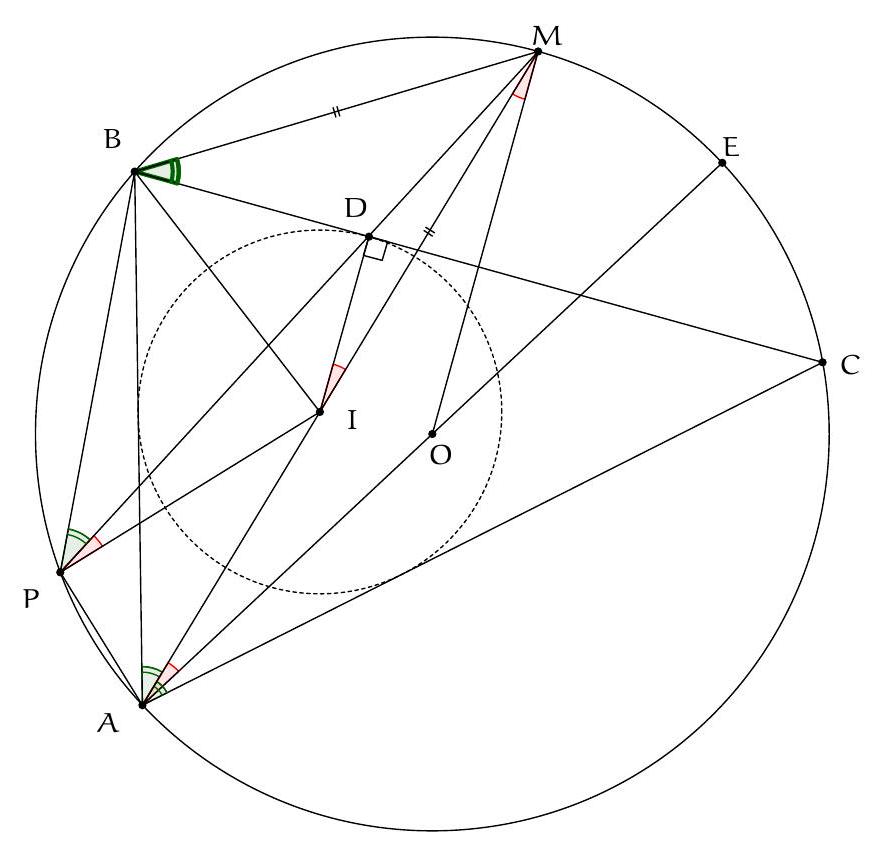
|
| 186 |
+
|
| 187 |
+
Tout d'abord, ramenez-vous au début de la preuve de l'exo 7 pour démontrer que $M I=M B$. Ensuite, $\widehat{M P B}=\widehat{C B M}$ puisque $M$ est le milieu de l'arc $\widehat{B C}$. Les triangles MPB et MBD sont semblables (ils ont l'angle $\widehat{M}$ en commun et ont un deuxième angle égal). Donc
|
| 188 |
+
|
| 189 |
+
$$
|
| 190 |
+
\frac{M P}{M B}=\frac{M B}{M D} \Longrightarrow M P \cdot M D=M B^{2}=M I^{2}
|
| 191 |
+
$$
|
| 192 |
+
|
| 193 |
+
Le cercle passant par les points P , I et D admet donc la droite MI comme tangente (par la théorie de la puissance d'un point part rapport à un cercle). On en déduit grâce au cas extrème du théorème de l'angle inscrit que
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
\widehat{\mathrm{DPI}}=\widehat{\mathrm{DIM}}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
Le point $M$ est le milieu de l'arc $\widehat{B C}$, donc la droite $O M$ est la médiatrice de $[B C]$, et les droites $O M$ et ID sont parallèles. De plus le triangle $A O M$ est isocèle en $O$. Ainsi
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
\widehat{\mathrm{DIM}}=\widehat{\mathrm{IMO}}=\widehat{\mathrm{MAE}}=\widehat{\mathrm{MPE}}
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
où la dernière égalité est simplement l'angle inscrit. On a montré que :
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
\widehat{\mathrm{MPI}}=\widehat{\mathrm{MPE}},
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
les points P, I, E sont bien alignés, la démonstration est achevée.
|
| 212 |
+

|
| 213 |
+
|
| 214 |
+
Exercice 9. On considère un cercle de centre $O$ et quatre points $A B C D$ de ce cercle tels que le point d'intersection $P$, autre que $O$, des cercles circonscrits aux triangles $A B O$ et $C D O$ soit intérieur au triangle OAD. On choisit un point $Q$ de la demi-droite [OP) à l'extérieur du segment $[O P]$ et on choisit un point $R$ de la demi-droite $[\mathrm{PO})$ à l'extérieur du segment $[\mathrm{OP}]$. Montrer que les angles $\widehat{\mathrm{QAP}}$ et $\widehat{\mathrm{OBR}}$ sont égaux si et seulement si les angles $\widehat{\mathrm{PDQ}}$ et $\widehat{\mathrm{RCO}}$ sont égaux.
|
| 215 |
+
|
| 216 |
+
Solution. Tout d'abord on remarque que les droites $\mathrm{AB}, \mathrm{CD}$ et OP sont concourantes, puisque ce sont les trois axes radicaux des cercles de la figure pris deux deux. Notons $M$ leur point d'intersection.
|
| 217 |
+
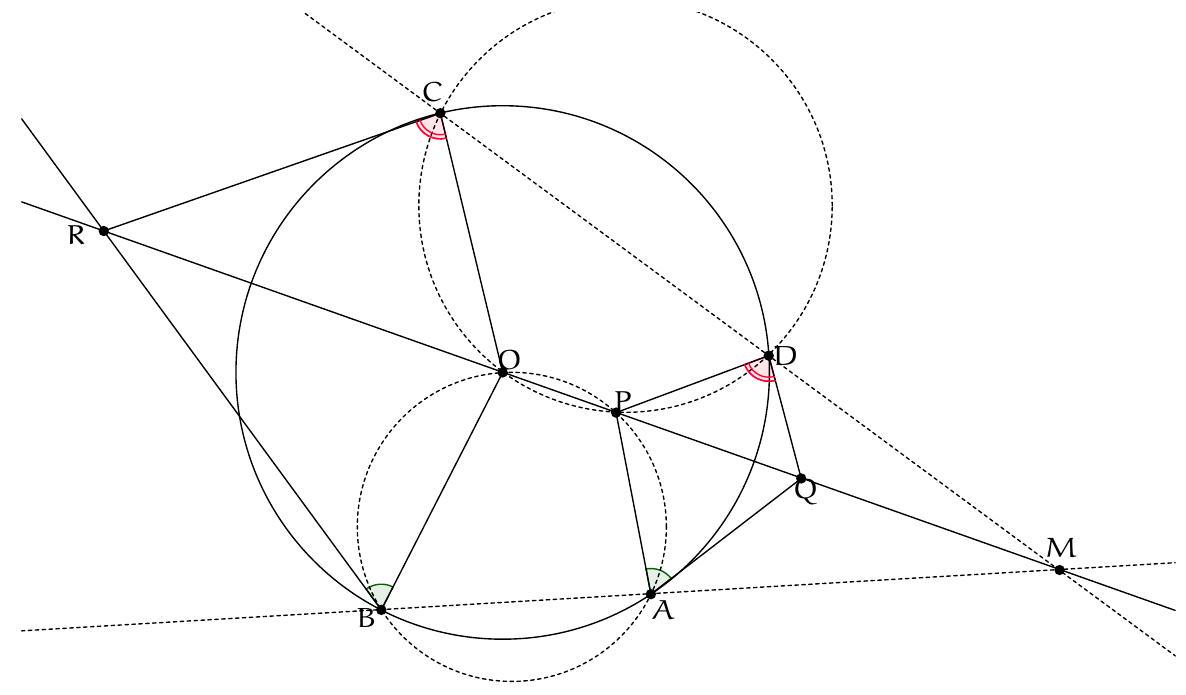
|
| 218 |
+
|
| 219 |
+
Comme $M$ est l'intersection des axes radicaux, on a
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
M O \cdot M P=M A \cdot M B=M C \cdot M D .
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Nous allons travailler dans les complexes. On notera $z_{A}$ l'affixe du point $A$ etc. On peut supposer que $M$ est l'origine, que la droite ( OM ) est l'axe des réels et que $z_{\mathrm{O}} z_{\mathrm{P}}=1$. Considérons l'inversion de centre $M$ qui échange $O$ et $P$, qui sera d'équation : $A \leftrightarrow A^{\prime}$ ssi $z_{A} \overline{z_{\mathcal{A}^{\prime}}}=1$. Grâce à la relation d'au dessus, cette inversion transforme $A$ en $B$ et $C$ en $D$. Plaçons un point $Q$ sur la droite $O P$ et notons $R$ son image par l'inversion. Nous allons montrer que $\widehat{\mathrm{QAP}}=\widehat{\mathrm{OBR}}$. Gardez en tête que $z_{\mathrm{O}}, z_{\mathrm{P}}, z_{\mathrm{Q}}, z_{\mathrm{R}}$ sont tous réels :
|
| 226 |
+
|
| 227 |
+
$$
|
| 228 |
+
\widehat{\mathrm{QAP}}=\arg \left(\frac{z_{\mathrm{Q}}-z_{\mathrm{A}}}{z_{\mathrm{P}}-z_{\mathrm{A}}}\right)=\arg \left(\frac{\frac{1}{z_{\mathrm{R}}}-\frac{1}{z_{\mathrm{z}}}}{\frac{1}{z_{\mathrm{O}}}-\frac{1}{z_{\mathrm{B}}}}\right)=\arg \left(\frac{z_{\mathrm{O}}}{z_{\mathrm{R}}} \frac{\overline{z_{\mathrm{B}}}-z_{\mathrm{R}}}{\overline{z_{\mathrm{B}}}-z_{\mathrm{O}}}\right) .
|
| 229 |
+
$$
|
| 230 |
+
|
| 231 |
+
Comme $z_{\mathrm{O}} / z_{\mathrm{R}}$ est réel, son argument vaut 0 à $\pi$ près. Ensuite on utilise la formule $\arg (\bar{z})=-\arg (z)$ pour finir le calcul :
|
| 232 |
+
|
| 233 |
+
$$
|
| 234 |
+
\widehat{\mathrm{QAP}}=-\arg \left(\frac{z_{\mathrm{B}}-z_{\mathrm{R}}}{z_{\mathrm{B}}-z_{\mathrm{O}}}\right)=\widehat{\mathrm{OBR}}
|
| 235 |
+
$$
|
| 236 |
+
|
| 237 |
+
De même on montre que $\widehat{P D Q}=\widehat{R C O}$. Ainsi, la seule façon de placer le point $R$ telle que $\widehat{\mathrm{QAP}}=\widehat{\mathrm{OBR}}$ est de le mettre sur l'image de Q par l'inversion, et on a dans ce cas $\widehat{\mathrm{PDQ}}=\widehat{\mathrm{RCO}}$.
|
| 238 |
+

|
| 239 |
+
|
| 240 |
+
Fin
|
| 241 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi2-corrige.md
ADDED
|
@@ -0,0 +1,142 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
Olympiades Françaises de Mathématiques
|
| 2 |
+
2012-2013
|
| 3 |
+
|
| 4 |
+
Envoi Numéro 2-Corrigé
|
| 5 |
+

|
| 6 |
+
|
| 7 |
+
## Exercices Juniors
|
| 8 |
+
|
| 9 |
+
Exercice 1. Peut-on numéroter les arêtes d'un cube de 1 à 12 en sorte que la somme des nombres sur les arêtes entrant dans un sommet du cube soit la même pour tous les sommets?
|
| 10 |
+
|
| 11 |
+
## Solution.
|
| 12 |
+
|
| 13 |
+
Nous allons prouver par l'absurde que la réponse à la question est négative.
|
| 14 |
+
Supposons qu'une telle numérotation existe et notons $k$ la somme dans chaque sommet. Sur chaque arête, écrivons son numéro deux fois : une fois à un bout de l'arête et l'autre fois à l'autre bout. Maintenant, calculons la somme des numéros ainsi écrits de deux manières différentes.
|
| 15 |
+
|
| 16 |
+
Première manière : on additionne les numéros arête par arête. On trouve alors $2(1+2+\cdots+12)$, car chaque numéro de 1 à 12 est écrit deux fois.
|
| 17 |
+
|
| 18 |
+
Deuxième manière : on additionne les numéros sommet par sommet. Par hypothèse, la somme vaut $k$ dans chaque sommet. Au total, on trouve donc 8 k .
|
| 19 |
+
|
| 20 |
+
Conclusion:
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
8 k=2(1+2+\ldots+12)=12 \times 13=4 \times 39
|
| 24 |
+
$$
|
| 25 |
+
|
| 26 |
+
d'où $k=39 / 2$, ce qui est impossible.
|
| 27 |
+

|
| 28 |
+
|
| 29 |
+
Exercice 2. Les sept dixièmes de la surface de la Terre sont couverts par l'océan. Montrer qu'il existe un diamètre de la Terre dont les deux extrémités baignent dans l'océan.
|
| 30 |
+
|
| 31 |
+
Solution. Soit $S$ la surface couverte par l'océan et $S^{\prime}$ son symétrique par rapport au centre de la Terre. Si les surfaces $S$ et $S^{\prime}$ étaient disjointes, elles occuperaient ensemble les 14/10 de la surface de la Terre, ce qui est impossible, car $14 / 10>1$. Donc $S$ et $S^{\prime}$ ont au moins un point d'intersection, qu'on appellera $P$. Soit $\mathrm{P}^{\prime}$ le symétrique de $P$ par rapport au centre de la Terre. On a donc $P \in S$ et $P \in S^{\prime}$, autrement dit $P \in S$ et $P^{\prime} \in S$. Par conséquent, les deux bouts du diamètre $P P^{\prime}$ baignent dans l'océan.
|
| 32 |
+

|
| 33 |
+
|
| 34 |
+
Exercice 3. Trouver cent entiers positifs distincts $n_{1}, \ldots, n_{100}$ tels que
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
1=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\cdots+\frac{1}{n_{100}}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Solution. Nous montrerons par récurrence la propriété suivante :
|
| 41 |
+
Pour tout entier $k \geqslant 3$ on peut trouver $k$ entiers positifs $n_{1}<n_{2}<\cdots<n_{k}$ tels que
|
| 42 |
+
|
| 43 |
+
$$
|
| 44 |
+
1=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\cdots+\frac{1}{n_{k}}
|
| 45 |
+
$$
|
| 46 |
+
|
| 47 |
+
et que $n_{k}$ soit pair.
|
| 48 |
+
Pour $k=3$, il suffit de prendre $n_{1}=2, n_{2}=3, n_{3}=6$. On a bien
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
1=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
et 6 est bien pair.
|
| 55 |
+
Pour passer de $k$ à $k+1$, nous allons garder tels quels les nombres $n_{1}, \ldots, n_{k-1}$ et remplacer $n_{k}$ par $n_{k}^{\prime}=3 n_{k} / 2$ (qui est entier car $n_{k}$ est pair) et $n_{k+1}^{\prime}=3 n_{k}$ (qui est pair car $n_{k}$ l'est). Les nombres
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\mathrm{n}_{1}, \ldots, \mathrm{n}_{\mathrm{k}-1}, \frac{3 \mathrm{n}_{\mathrm{k}}}{2}, 3 \mathrm{n}_{\mathrm{k}}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
sont toujours rangés dans l'ordre croissant; le nombre le plus grand est toujours pair; et la somme des inverses n'a pas changé car
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\frac{1}{n_{k}^{\prime}}+\frac{1}{n_{k+1}^{\prime}}=\frac{2}{3 n_{k}}+\frac{1}{3 n_{k}}=\frac{3}{3 n_{k}}=\frac{1}{n_{k}}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Ainsi, si la propriété est vraie pour $k$, elle est aussi vraie pour $k+1$.
|
| 68 |
+
Maintenant, en prenant $k=100$, nous obtenons l'affirmation demandée par l'exercice.
|
| 69 |
+

|
| 70 |
+
|
| 71 |
+
## Exercices Communs
|
| 72 |
+
|
| 73 |
+
Exercice 4. Ruby a effectué une série de mouvements avec son Rubik's cube. (Par exemple, elle peut tourner la face du haut dans le sens des aiguilles d'une montre, puis la face de fond de 180 degrés, puis la face de droite dans le sens contraire des aiguilles d'une montre. Ou n'importe quelle autre série de rotations de faces.) Ensuite elle répète inlassablement la même série de mouvements. Montrer qu'au bout d'un certain nombre de répétitions elle retrouvera la configuration de départ.
|
| 74 |
+
|
| 75 |
+
Solution. Notons $x_{0}$ la configuration de départ et $x_{n}$ la configuration après $n$ répétitions de la série de Ruby. Comme le nombre total de configurations d'un Rubik's cube est fini, à un moment une configuration va se répéter : $x_{n}=x_{m}$ avec $n<m$. Demandons maintenant à Ruby d'inverser sa série de mouvements, autrement dit d'exécuter les rotations dans l'ordre inverse et dans le sens inverse par rapport à sa série de mouvements initiale. En appliquant cette série inversée à la configuration $x_{n}$ nous obtenons $x_{n-1}$. De même, en l'appliquant à $x_{m}$ nous obtenons $x_{m-1}$. Comme $x_{n}=x_{m}$, on en déduit que $\mathrm{x}_{\mathrm{n}-1}=\mathrm{x}_{\mathrm{m}-1}$. En continuant à appliquer la série inversée, nous allons arriver au bout de n répétitions à l'égalité $x_{0}=x_{m-n}$.
|
| 76 |
+
|
| 77 |
+
Nous avons donc prouvé que la configuration de départ réapparaîtra au bout $\mathrm{m}-\mathrm{n}$ répétitions de la série de Ruby.
|
| 78 |
+

|
| 79 |
+
|
| 80 |
+
Exercice 5. Devant l'entrée de la grotte aux trésors se trouve un tonneau avec quatre trous indistinguables disposés aux sommets d'un carré sur le couvercle. À l'intérieur de chaque trou se trouve un hareng qui peut être placé soit la tête en bas soit la tête en haut. En insérant les mains dans deux trous Ali-Baba peut déterminer la position des deux harengs qui s'y trouvent. Il peut également en retourner un ou deux comme il le souhaite ou n'en retourner aucun. La porte de la grotte s'ouvre lorsque les quatre harengs sont soit tous la tête en bas soit tous la tête en haut. Le problème c'est que lorsque Ali-Baba sort ses mains des trous le tonneau commence à tourner sur lui-même à une grande vitesse, si bien que, lorsqu'il s'arrête de nouveau, il est impossible pour Ali-Baba de savoir dans quels trous il avait mis les mains la fois précédente. Aidez Ali-Baba à ouvrir la grotte en un nombre fini d'opérations.
|
| 81 |
+
|
| 82 |
+
Solution. En insérant les mains d'abord dans deux trous adjacents, puis dans deux trous en diagonale, on peut placer 3 harengs sur 4 la tête en haut. Si la porte ne s'ouvre pas, cela veut dire que le dernier hareng est placé la tête en bas.
|
| 83 |
+
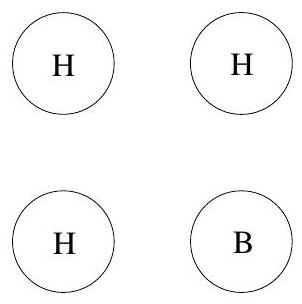
|
| 84 |
+
|
| 85 |
+
Insérons maintenant les mains en diagonale. Si l'on trouve un hareng la tête en bas, on le retourne et c'est gagné. Sinon, on retourne un des harengs au hasard pour obtenir deux harengs adjacents la tête en bas et deux autres adjacents la tête en haut.
|
| 86 |
+
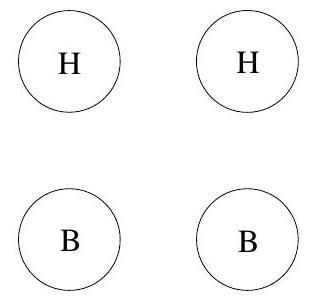
|
| 87 |
+
|
| 88 |
+
Insérons maintenant les mains dans deux trous adjacents et retournons les deux harengs. Soit la porte s'ouvre, soit les harengs sont maintenant en alternance.
|
| 89 |
+

|
| 90 |
+
|
| 91 |
+
Il suffit alors d'insérer les mains en diagonale une dernière fois et de retourner les deux harengs pour qu'ils soient tous placés de la même manière.
|
| 92 |
+

|
| 93 |
+
|
| 94 |
+
Exercice 6. Trois sauterelles se trouvent aux points $(0,0),(0,1)$ et $(1,0)$ d'une feuille quadrillée. Chaque minute une sauterelle saute sur un autre point de la grille d'une telle façon que son saut soit parallèle à la droite passant par les deux autres sauterelles. Est-il possible qu'au bout d'un certain temps les sauterelles se retrouvent aux points $(-1,0),(1,0)$ et $(0,1)$ ?
|
| 95 |
+
|
| 96 |
+
Solution. Si $A B$ et $C D$ sont deux droites parallèles, alors l'aire du triangle $A B C$ est égale à celle du triangle $A B D$, car ces deux triangles ont la même base $[A B]$ et la même hauteur. Il découle de cette remarque que l'aire du triangle formé par les trois sauterelles ne change pas lors de leurs sauts. Or l'aire du triangle de départ vaut $1 / 2$, tandis que celle du triangle qu'on souhaite obtenir à la fin vaut 1 . Il est donc impossible de passer de l'un à l'autre.
|
| 97 |
+

|
| 98 |
+
|
| 99 |
+
## Exercices Olympiques
|
| 100 |
+
|
| 101 |
+
Exercice 7. Chacun des 400 députés d'un parlement a giflé exactement un autre député. Montrer qu'on peut créer une commission parlementaire de 134 députés telle qu'aucun membre de la commission n'ait giflé aucun autre membre.
|
| 102 |
+
|
| 103 |
+
Solution. Appellons deux députés ennemis si l'un d'eux a giflé l'autre. Nous allons résoudre par récurrence un exercice plus général :
|
| 104 |
+
|
| 105 |
+
Dans un parlement d'au moins $3 n-2$ députés, chaque député a giflé 0 ou 1 autre député. Il est alors toujours possible de créer une commission parlementaire de n députés qui ne contienne aucun couple ennemi.
|
| 106 |
+
|
| 107 |
+
Pour $\mathrm{n}=1$ la propriété est évidente : on peut toujours former une commission à un député car un député n'est jamais son propre ennemi.
|
| 108 |
+
|
| 109 |
+
Montrons maintenant comment passer de n à $\mathrm{n}+1$. Considérons un parlement avec au moins
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
3(n+1)-2=3 n+1
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
députés. Comme le nombre total de gifles est inférieur ou égal au nombre de députés, il existe, par le principe des tiroirs, un député qui a été giflé au plus une fois et qui a donc au plus deux ennemis. Mettons ce député dans la commission d'office et écartons son ou ses deux ennemis. Il nous reste au moins $3 n-2$ députés parmi lesquels il n'y a aucun ennemi du député selectionné. Par hypothèse de récurrence, on peut compléter la commission en choisissant encore n députés parmi ceux qui restent sans qu'il y ait aucun couple ennemi parmi eux.
|
| 116 |
+

|
| 117 |
+
|
| 118 |
+
Exercice 8. Un digicode s'ouvre dès qu'on fait l'unique combinaison correcte de 4 chiffres (qui peut éventuellement contenir des répétitions). Par exemple, si l'on tape la suite des chiffres 000125 le digicode s'ouvrira si le code est soit 0001, soit 0012, soit 0125. Petit Pierre ne connaît pas le code. Combien de chiffres au minimum doit-il taper pour ouvrir le digicode à coup sûr?
|
| 119 |
+
|
| 120 |
+
Solution. Il est clair qu'il faut au moins 10003 chiffres, car il faut essayer toutes les 10000 combinaisons. Montrons que ce nombre est aussi suffisant.
|
| 121 |
+
|
| 122 |
+
Dessinons 1000 points correspondant à toutes les suites de 3 chiffres. Dessinons une flèche entre deux points si les deux derniers chiffres de la première combinaison coincident avec les deux premiers chiffres de la deuxième combinaison (et vont dans le même ordre). Par exemple, il y aura une flèche allant du point 200 vers le point 009 et une autre allant du point 201 vers le point 017 ; entre les points 303 et 030 il y aura deux flèches allant dans les deux sens; sur le point 777 il y aura une flèche en forme de boucle qui revient vers son point de départ. Ainsi, chaque flèche correspond à un unique code possible.
|
| 123 |
+
|
| 124 |
+
On voit facilement qu'il y a 10 flèches entrantes et 10 flèches sortantes dans chaque point. En effet, pour obtenir une flèche sortante, par exemple, il faut choisir un chiffre de 0 à 9 à rajouter aux derniers chiffres du numéro du point, ce qui fait exactement 10 choix.
|
| 125 |
+
|
| 126 |
+
Il est facile à voir également que le graphe formé par les points et les flèches est connexe. En effet, on passe d'un point $a b c$ au point def en trois flèches $a b c \rightarrow b c d \rightarrow c d e \rightarrow$ def.
|
| 127 |
+
|
| 128 |
+
Le théorème d'Euler bien connu (voir, par exemple, "Graphe Eulérien" dans wikipédia) assure alors qu'on peut parcourir toutes les flèches du graphe sans passer deux fois par la même flèche. Ce parcours donnera la suite de 10003 chiffres recherchée : il faudra taper les 3 chiffres du point de départ et ensuite juste le dernier chiffre de chaque point du parcours. Le fait qu'on passe une et une seule fois par chaque flèche du graphe signifie exactement que chaque code possible de 4 chiffres sera essayé une et une seule fois.
|
| 129 |
+

|
| 130 |
+
|
| 131 |
+
Exercice 9. On dispose de 500 emplacements à billes numérotés de 1 à 500 de gauche à droite. Des billes numérotées de 1 à 500 sont posées dans ces emplacements dans le désordre : leurs numéros ne coïncident pas nécessairement avec les numéros des emplacements. (Dans chaque emplacement il y a exactement une bille.) On dit que l'ordre des billes est plutôt croissant si la plus longue sous-suite décroissante des numéros des billes qu'on peut extraire de cet ordre ne dépasse pas 5 éléments. Montrer qu'il existe au plus $5^{1000}$ ordres plutôt croissants.
|
| 132 |
+
|
| 133 |
+
Solution. Montrons d'abord que si les billes sont disposées dans un ordre plutôt croissant alors on peut les colorier en 5 couleurs de telle sorte que la suite des billes de chaque couleur soit croissante. Pour cela nous allons ordonner les 5 couleurs dans un certain ordre et colorier les billes une par une de gauche à droite en utilisant à chaque fois la première couleur disponible, c'est à dire la première couleur telle que la précédente bille de cette couleur ait un numéro plus petit que celle que nous sommes en train de colorier. Montrons qu'avec cette méthode nous arriverons en effet à colorier toutes les billes. Supposons par l'absure que nous sommes arrivés à une bille pour laquelle aucune des 5 couleurs n'est disponible. En particulier cela veut dire qu'on a déjà utilisé la couleur numéro 5 pour colorier une bille dont le numéro était plus grand. Si pour cette bille-là nous avions choisi la couleur numéro 5, c'est que, d'après notre règle, la couleur numéro 4 n'était pas disponible. Autrement dit il y avait une bille encore plus tôt dans la suite qui avait un numéro encore plus grand et qu'on avait coloriée en couleur 4. En remontant de la même manière jusqu'à la couleur numéro 1 on découvrira une suite de 6 billes dont les numéros vont dans l'ordre décroissant. Ceci contredit l'hypothèse que notre ordre était plutôt croissant.
|
| 134 |
+
|
| 135 |
+
Considérons maintenant un ordre plutôt croissant et colorions les billes selon la règle ci-dissus. Colorions également chaque emplacement de la même couleur que la bille qu'il contient (il suffira de mettre beaucoup de peinture sur chaque bille, de sorte qu'elle coule aussi dans l'emplacement). Il est facile à voir que l'ordre des billes se rétablit d'une manière inambiguë si l'on connaît la couleur de toutes les billes et de tous les emplacements. En effet, les billes d'une couleur donnée vont dans les emplacements de cette même couleur et y sont rangées dans l'ordre croissant.
|
| 136 |
+
|
| 137 |
+
Or il y a $5^{500}$ coloriages possibles des billes et $5^{500}$ coloriages possibles des emplacements en 5 couleurs. Donc le nombre d'ordres plutôt croissants est au plus $5^{1000}$.
|
| 138 |
+
|
| 139 |
+
Remarque : d'après la formule de Stirling le nombre de permutations de 500 éléments, qui vaut 500 !, peut être estimé à $(500 / e)^{500}$. Comme $500 / e>25$, notre estimation montre que les ordres plutôt croissants sont beaucoup moins nombreux que tous les ordres possibles.
|
| 140 |
+

|
| 141 |
+
$\mathcal{F i n}$
|
| 142 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi3-corrige.md
ADDED
|
@@ -0,0 +1,189 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Mathématiques 2012-2013
|
| 2 |
+
|
| 3 |
+
Envoi $\mathcal{N u m e ́ r o ~} 3$ - Corrigé
|
| 4 |
+

|
| 5 |
+
|
| 6 |
+
## Exercices Juniors
|
| 7 |
+
|
| 8 |
+
Exercice 1. On appelle diviseur propre d'un entier $n$ un diviseur positif de $n$ qui est différent de 1 et de n.
|
| 9 |
+
|
| 10 |
+
Existe-t-il un entier n dont le produit des diviseurs propres est égal à 2013 ?
|
| 11 |
+
|
| 12 |
+
## Solution.
|
| 13 |
+
|
| 14 |
+
La décomposition en facteurs premiers de 2013 est $3 \times 11 \times 61$. Ainsi, si le produit des diviseurs stricts d'un entier n vaut 2013, cela implique que n est lui même divisible par 3, 11 et 61 . Or, dans ce cas, il compte parmi ses diviseurs stricts au moins les nombres suivants :
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
3,11,61,33,671
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
dont le produit surpasse 2013 (il vaut $2013 \times 33 \times 671=44573859$ ). Ainsi, un tel entier n n'existe pas.
|
| 21 |
+

|
| 22 |
+
|
| 23 |
+
Exercice 2. Chaque nombre rationnel strictement positif est colorié soit en rouge, soit en noir, de telle sorte que:
|
| 24 |
+
|
| 25 |
+
- les nombres $x$ et $x+1$ sont de couleurs différentes ;
|
| 26 |
+
- les nombres $x$ et $\frac{1}{x}$ sont de la même couleur;
|
| 27 |
+
- le nombre 1 est colorié en rouge.
|
| 28 |
+
|
| 29 |
+
Quelle est la couleur de $\frac{2012}{2013}$ ?
|
| 30 |
+
(On ne demande pas de démontrer l'existence d'un tel coloriage.)
|
| 31 |
+
|
| 32 |
+
## Solution.
|
| 33 |
+
|
| 34 |
+
On remarque que $\frac{2012}{2013}$ s'écrit:
|
| 35 |
+
|
| 36 |
+
$$
|
| 37 |
+
\frac{2012}{2013}=\frac{1}{1+\frac{1}{2012}}
|
| 38 |
+
$$
|
| 39 |
+
|
| 40 |
+
Ainsi, d'après les règles de l'énoncé, il a la couleur inverse de 2012. Or, ce dernier s'obtient en ajoutant 2011 fois 1 à 1 ; il a donc la couleur inverse de 1 (puisqu'on inverse 2011 fois la couleur), c'est-à-dire noir. Ainsi $\frac{2012}{2013}$ est rouge.
|
| 41 |
+

|
| 42 |
+
|
| 43 |
+
Exercice 3. La suite de Fibonacci est construite ainsi : chaque terme est la somme des deux précédents. Ses premiers termes valent:
|
| 44 |
+
|
| 45 |
+
$$
|
| 46 |
+
1,1,2,3,5,8,13,21,34,55,89, \ldots
|
| 47 |
+
$$
|
| 48 |
+
|
| 49 |
+
Montrer que la suite de Fibonacci contient un multiple de 1000.
|
| 50 |
+
|
| 51 |
+
## Solution.
|
| 52 |
+
|
| 53 |
+
Notons $F_{n}$ le $n$-ième terme de la suite de Fibonacci ( $F_{1}=1, F_{2}=1, F_{3}=2$, etc.) et notons $u_{n}$ le reste de la division euclidienne de $F_{n}$ par 1000 ( $u_{n}$ est donc le nombre formé par les trois derniers chiffres de $F_{n}$ ). Comme il n'y a qu'un nombre fini de couples ( $x, y$ ) d'entiers compris entre 0 et 999 (il $y$ en a exactement $1000^{2}=1000000$ ), il existe des entiers $n$ et $N$ tels que $N>0$ et
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
u_{n}=u_{n+N} \quad ; \quad u_{n+1}=u_{n+1+N}
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Or, $u_{n-1}$ (resp. $u_{n-1+N}$ ) s'obtient à partir de $u_{n}$ et $u_{n+1}$ (resp. $u_{n+N}$ et $u_{n+1+N}$ ) comme le reste de la division euclidienne de $u_{n+1}-u_{n}$ (resp. $u_{n+1+N}-u_{n+N}$ ) par 1000. Ainsi, des égalités (1), on déduit que $\mathfrak{u}_{n-1}=u_{n-1+N}$. En continuant ainsi, on obtient $u_{N+1}=u_{1}=1$ et $u_{N+2}=u_{2}=1$, d'où il résulte enfin $u_{N}=0$. L'entier $F_{N}$ est donc multiple de 1000.
|
| 60 |
+

|
| 61 |
+
|
| 62 |
+
Exercice 4. Montrer que l'équation
|
| 63 |
+
|
| 64 |
+
$$
|
| 65 |
+
x(x+2)=y(y+1)
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+
n'a pas de solution en nombres entiers strictement positifs.
|
| 69 |
+
|
| 70 |
+
## Solution.
|
| 71 |
+
|
| 72 |
+
Si le couple $(x, y)$ est solution, on a $x(x+1)<x(x+2)=y(y+1)$ et donc $x<y$. Mais de même, en supposant toujours $(x, y)$ solution, on peut écrire $(x+1)(x+2)>x(x+2)=y(y+1)$, d'où on déduit $x+1>y$. Ainsi, une solution ( $x, y$ ) hypothétique devrait donc vérifier $x<y<x+1$, ce qui ne peut se produire. On en déduit que l'équation proposée n'a pas de solution en nombres entiers strictement positifs.
|
| 73 |
+

|
| 74 |
+
|
| 75 |
+
## Exercices Communs
|
| 76 |
+
|
| 77 |
+
Exercice 5. Soient n et m deux entiers strictement positifs. Montrer que $5^{\mathrm{m}}+5^{n}$ s'écrit comme une somme de deux carrés si et seulement si $n$ et $m$ ont même parité.
|
| 78 |
+
|
| 79 |
+
## Solution.
|
| 80 |
+
|
| 81 |
+
Supposons pour commencer que $n$ et $m$ n'ont pas même parité. On étudie alors la quantité $5^{n}+5^{m}$ modulo 8 . Par récurrence, on démontre facilement que $5^{k}$ est congru à 1 (resp. 5) modulo 8 si k est pair (resp. impair). Ainsi, d'après notre hypothèse, on a toujours $5^{n}+5^{m} \equiv 6(\bmod 8)$. Or, par ailleurs, un carré est toujours congru à 0,1 ou 4 modulo 8 . Comme il n'y a aucune manière d'écrire 6 comme somme de deux de ces trois nombres, on en déduit que $5^{n}+5^{\mathrm{m}}$ ne peut s 'écrire comme somme de deux carrés.
|
| 82 |
+
|
| 83 |
+
Supposons maintenant que $n$ et $m$ ont même parité. Quitte à échanger $n$ et $m$, on peut supposer en outre que $\mathrm{m} \geqslant \mathrm{n}$. Ainsi, il existe un entier k positif ou nul tel que $\mathrm{m}=\mathrm{n}+2 \mathrm{k}$. On a alors $5^{\mathrm{m}}+5^{\mathrm{n}}=$ $5^{\mathrm{n}}\left(5^{2 \mathrm{k}}+1\right)$. Comme, manifestement $5=2^{2}+1^{2}$ et $5^{2 \mathrm{k}}+1$ s'écrivent comme sommes de deux carrés, il suffit pour conclure de montrer que, si $x$ et $y$ s'écrivent comme somme de deux carrés, alors il en va de même du produit xy . Ceci résulte directement de la formule :
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)=(a d-b c)^{2}+(a c+b d)^{2}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+

|
| 90 |
+
|
| 91 |
+
Exercice 6. Existe-t-il des nombres rationnels positifs ou nuls $x, y$ et $z$ tels que:
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
x^{5}+2 y^{5}+5 z^{5}=11
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Solution.
|
| 98 |
+
Nous allons montrer qu'il n'existe pas de tels rationnels $x, y, z$. On raisonne par l'absurde en supposant qu'il en existe. Soit $d$ le plus petit dénominateur commun de $x, y$ et $z$. On peut alors écrire $x=\frac{a}{d}$, $\mathrm{y}=\frac{\mathrm{b}}{\mathrm{d}}$ et $z=\frac{\mathrm{c}}{\mathrm{d}}$ pour certains entiers $\mathrm{a}, \mathrm{b}$ et c . L'équation que l'on cherche à résoudre devient alors :
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
a^{5}+2 b^{5}+5 c^{5}=11 d^{5}
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Étudions cette équation modulo 11. Une recherche exhaustive (ou l'utilisation du petit théorème de Fermat) montre qu'une puissance 5 -ième est congrue à 0,1 ou -1 modulo 11 . On en déduit que la congruence $a^{5}+2 b^{5}+5 c^{5} \equiv 0(\bmod 11)$ implique que $a, b$ et $c$ sont tous les trois multiples de 11. Ainsi, $a^{5}+2 b^{5}+5 c^{5}$ est divisible par $11^{5}$, d'où on déduit que $d$ est lui aussi divisible par 11. Les fractions $\frac{a}{d}, \frac{b}{d}$ et $\frac{c}{d}$ peuvent donc, toutes les trois, être simplifiées par 11. Ceci contredit la minimalité de $d$ et termine la démonstration.
|
| 105 |
+

|
| 106 |
+
|
| 107 |
+
## Exercices Olympiques
|
| 108 |
+
|
| 109 |
+
Exercice 7. Prouver qu'il existe une unique manière de colorier chaque nombre rationnel strictement positif soit en rouge, soit en bleu, de sorte que :
|
| 110 |
+
|
| 111 |
+
- les nombres $x$ et $x+1$ sont de couleurs différentes ;
|
| 112 |
+
- les nombres $x$ et $\frac{1}{x}$ sont de la même couleur;
|
| 113 |
+
- le nombre 1 est colorié en rouge.
|
| 114 |
+
|
| 115 |
+
|
| 116 |
+
## Solution.
|
| 117 |
+
|
| 118 |
+
Montrons tout d'abord qu'un tel coloriage est nécessairement unique. Pour cela, nous allons démontrer par récurrence sur $\max (\mathrm{a}, \mathrm{b})$ que la couleur de la fraction $\frac{\mathrm{a}}{\mathrm{b}}$ (supposée écrite sous forme irréductible) est entièrement déterminée. La conclusion est vraie lorsque $\max (a, b)=1$ puisque cela impose $a=b=1$ et que l'on sait, par hypothèse, que la couleur de 1 est rouge. Considérons maintenant une fraction irréductible $\frac{a}{b}$ et supposons que l'on ait déjà démontré que la couleur de toute fraction irréductible $\frac{a^{\prime}}{b^{\prime}}$ $\operatorname{avec} \max \left(\mathrm{a}^{\prime}, \mathrm{b}^{\prime}\right)<\max (\mathrm{a}, \mathrm{b})$ soit déterminée. Quitte à remplacer $\frac{\mathrm{a}}{\mathrm{b}}$ par son inverse $\frac{\mathrm{b}}{\mathrm{a}}$ (ce qui ne modifie ni $\max (a, b)$, ni la couleur de la fraction), on peut supposer que $a>b$. Par hypothèse, $\frac{a}{b}$ a la couleur inverse de $\frac{a}{b}-1=\frac{a-b}{b}$. De plus, $\max (a-b, b)<\max (a, b)=a$. Ainsi, la fraction $\frac{a-b}{b}$ relève de l'hypothèse de récurrence; sa couleur est donc entièrement déterminée et, par suite, celle de $\frac{\mathrm{a}}{\mathrm{b}}$ l'est également.
|
| 119 |
+
|
| 120 |
+
L'existence se démontre de la même façon : en reprenant les arguments précédents, on construit le coloriage par récurrence sur $\max (\mathrm{a}, \mathrm{b})$ en vérifiant que chaque identité entre couleurs est utilisée une et une seule fois lorsqu'on construit le coloriage avec cette méthode.
|
| 121 |
+
Remarque. Si $a$ et $b$ sont deux entiers premiers entre eux, notons $q_{1}(a, b), \ldots, q_{n}(a, b)$ la suite (finie) des quotients successifs obtenus lorsque l'on effectue l'algorithme d'Euclide à partir de a et b. On peut alors montrer que l'unique coloriage satisfaisant aux conditions de l'énoncé est celui qui attribue la couleur rouge (resp. bleue) à la fraction irréductible $\frac{a}{b}$ lorsque $\sum_{i} q_{i}(a, b)$ est impair (resp. pair).
|
| 122 |
+

|
| 123 |
+
|
| 124 |
+
Exercice 8 . Trouver tous les entiers naturels $\mathrm{k}>0$ tels que l'équation en $x$ et y :
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
x(x+k)=y(y+1)
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
ait une solution en entiers strictement positifs.
|
| 131 |
+
|
| 132 |
+
## Solution.
|
| 133 |
+
|
| 134 |
+
L'équation de l'énoncé s'écrit encore $\left(x+\frac{k}{2}\right)^{2}=\left(y+\frac{1}{2}\right)^{2}+\frac{k^{2}-1}{4}$, soit, en factorisant:
|
| 135 |
+
|
| 136 |
+
$$
|
| 137 |
+
\left(x-y+\frac{k-1}{2}\right) \cdot\left(x+y+\frac{k+1}{2}\right)=\frac{k^{2}-1}{4} .
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
Distinguons deux cas selon la parité de $k$. Si $k$ est impair, on écrit $k=2 a+1$ et l'équation précédente devient $(x-y+a)(x+y+a+1)=a(a+1)$. En écrivant que le premier facteur vaut 1 et le second $a(a+1)$, on obtient $x=\frac{a(a-1)}{2}$ et $y=x+(a-1)=\frac{(a-1)(a+2)}{2}$. Étant donné que le produit de deux entiers consécutifs est toujours pair, les valeurs que l'on vient d'obtenir forment une solution dès que a $>1$. Pour $\mathrm{a}=1$ (i.e. $k=3$ ), au contraire, il n'y a pas de solution, car l'égalité $(x-y+1)(x+y+2)=2$ ne peut être satisfaite étant donné que le deuxième facteur est toujours $>2$ lorsque $x$ et $y$ sont strictement positifs. Pour $a=0$, enfin, on a $k=1$ et, clairement, tous les couples ( $x, y$ ) conviennent.
|
| 141 |
+
|
| 142 |
+
On raisonne de manière analogue dans le cas où $k$ est pair. On pose $k=2 a$ et l'équation (2) devient $(2 x-2 y+2 a-1)(2 x+2 y+2 a+1)=4 a^{2}-1$. Comme précédemment, en demandant que le premier facteur vaille 1 , on obtient un système en $x$ et $y$ dont les solutions sont $x=a(a-1)$ et $y=$ $(a+1)(a-1)$. Cette solution est acceptable dès que $a>1$. Pour $a=1$, l'équation à résoudre devient $(2 x-2 y+1)(2 x+2 y+3)=3$ et elle n'a pas de solution avec $x, y>0$ étant donné que cette dernière condition implique que le deuxième facteur est $>3$.
|
| 143 |
+
|
| 144 |
+
En résumé, les entiers $k$ convenables sont $k=1$ et tous les entiers $k \geqslant 4$.
|
| 145 |
+
|
| 146 |
+
Exercice 9. Soit $p \geqslant 5$ un nombre premier. Montrer que 1 et 5 sont les seuls diviseurs positifs de $2^{p}+3^{p}$ qui soient inférieurs ou égaux à $p$.
|
| 147 |
+
|
| 148 |
+
## Solution.
|
| 149 |
+
|
| 150 |
+
La factorisation
|
| 151 |
+
|
| 152 |
+
$$
|
| 153 |
+
2^{\mathfrak{p}}+3^{\mathfrak{p}}=5 \cdot \sum_{i=0}^{p-1} 2^{\boldsymbol{i}}(-3)^{p-1-\mathfrak{i}}
|
| 154 |
+
$$
|
| 155 |
+
|
| 156 |
+
montre que 5 est bien un diviseur de $2^{p}+3^{\mathrm{p}}$.
|
| 157 |
+
Soit à présent $\mathrm{d} \in\{2, \ldots, \mathrm{p}\}$ un diviseur de $2^{\mathfrak{p}}+3^{\mathfrak{p}}$. On souhaite démontrer que $\mathrm{d}=5$. On considère pour cela $q$ un diviseur premier de d . Alors, manifestement, $q$ est aussi un diviseur de $2^{p}+3^{p}$ qui est $\leqslant p$. De plus, il est clair que l'on ne peut pas avoir $\mathbf{q}=2$. Ainsi $q$ est impair et de la congruence $2^{\mathfrak{p}}+3^{\mathfrak{p}} \equiv 0$ $(\bmod \mathbf{q})$, on déduit que $a^{p} \equiv 1(\bmod q)$ où $a$ un entier est tel que $2 a \equiv-3(\bmod q)($ un tel entier existe bien car $q$ est impair). Par ailleurs, par le petit théorème de Fermat, on sait également que $a^{q} \equiv a$ $(\bmod q)$ et donc $a^{q-1} \equiv 1(\bmod q)\left(\right.$ puisque $a n^{\prime}$ est pas un multiple de $\left.q\right)$. On en déduit que $a^{n} \equiv 1$ $(\bmod q)$ avec $n=\operatorname{PGCD}(p, q-1)$. Or, comme $q<p$ et $p$ est un premier, les entiers $p$ et $q-1$ sont nécessairement premiers entre eux. Autrement dit $\mathfrak{n}=1$ et, par suite, $a \equiv 1(\bmod \mathbf{q})$. En revenant à la définition de a , on obtient $2 \equiv-3(\bmod \mathbf{q})$, ce qui ne peut se produire que pour $\mathrm{q}=5$.
|
| 158 |
+
|
| 159 |
+
On a ainsi démontré que l'unique diviseur premier de dest 5 . Il suffit donc pour conclure de démontrer que d n'est pas divisible par 25. Cela est évident si $p \leqslant 25$. Supposant maintenant $p>25$, nous allons démontrer que $2^{\mathfrak{p}}+3^{\mathfrak{p}}$ n'est, lui-même, pas divisible par 25 (ce qui suffira à conclure). D'après l'équation (3), cela revient à prouver que $\sum_{i=0}^{\mathfrak{p}-1} 2^{\boldsymbol{i}}(-3)^{p-1-\boldsymbol{i}}$ n'est pas divisible par 5 . Or, un calcul modulo 5 montre que cette somme est congrue modulo 5 à
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
(-3)^{\mathrm{p}-1} \cdot \sum_{i=0}^{\mathrm{p}-1} 1=(-3)^{\mathrm{p}-1} \cdot \mathrm{p}
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Or, $(-3)^{p-1}$ est premier avec 5 et, comme $p>25$ est un nombre premier, les entiers $p$ et 5 sont premiers entre eux. On a ainsi bien démontré ce que l'on souhaitait.
|
| 166 |
+

|
| 167 |
+
|
| 168 |
+
Exercice 10. Soit $n \geqslant 5$ un entier. Soient $a_{1}, \ldots, a_{n}$ des entiers dans $\{1, \ldots, 2 n\}$ deux à deux distincts. Montrer qu'il existe des indices $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, \mathfrak{n}\}$ avec $\mathfrak{i} \neq \boldsymbol{j}$ tels que
|
| 169 |
+
|
| 170 |
+
$$
|
| 171 |
+
\operatorname{PPCM}\left(\mathfrak{a}_{\mathbf{i}}, \mathfrak{a}_{\mathbf{j}}\right) \leqslant 6\left(\mathrm{E}\left(\frac{\mathfrak{n}}{2}\right)+1\right)
|
| 172 |
+
$$
|
| 173 |
+
|
| 174 |
+
où $\mathrm{E}(\mathrm{x})$ désigne la partie entière du nombre x .
|
| 175 |
+
|
| 176 |
+
## Solution.
|
| 177 |
+
|
| 178 |
+
Supposons, pour commencer, qu'il existe un indice $i$ tel que $a_{i} \leqslant n$. S'il existe $j$ tel que $a_{j}=2 a_{i}$, on a alors
|
| 179 |
+
|
| 180 |
+
$$
|
| 181 |
+
\operatorname{PPCM}\left(a_{i}, a_{j}\right)=a_{j} \leqslant 2 n \leqslant 6 \cdot\left(E\left(\frac{n}{2}\right)+1\right)
|
| 182 |
+
$$
|
| 183 |
+
|
| 184 |
+
et on a trouvé un couple ( $i, j)$ convenable. Si , au contraire, l'entier $2 a_{i}$ n'apparaît pas parmi les $a_{j}$, définissons les entiers $b_{1}, \ldots, b_{n}$ en posant $b_{i}=2 a_{i}$ et $b_{j}=a_{j}$ pour $j \neq i$. Les $b_{j}$ sont encore deux à deux distincts et compris entre 1 et 2 n . De plus, on vérifie immédiatement que $\operatorname{PPCM}\left(b_{i}, b_{j}\right) \geqslant$ $\operatorname{PPCM}\left(a_{i}, a_{j}\right)$. Ainsi, il suffit de démontrer la propriété de l'énoncé pour la suite des $b_{j}$.
|
| 185 |
+
|
| 186 |
+
En appliquant à nouveau le raisonnement précédent — éventuellement plusieurs fois - on en vient à supposer que tous les $a_{j}$ sont strictement supérieurs à $n$. Autrement dit, l'ensemble des $a_{j} n^{\prime}$ 'est autre que $\{n+1, n+2, \ldots, 2 n\}$. Posons $k=E\left(\frac{n}{2}\right)+1$. Comme on a supposé $n \geqslant 5$, il est facile de vérifier que l'un des $a_{j}$ vaut $2 k$ et un autre vaut $3 k$. On conclut en remarquant que le PPCM de ces deux nombres est égal à 6 k .
|
| 187 |
+

|
| 188 |
+
$\mathcal{F i n}$
|
| 189 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi4-corrige.md
ADDED
|
@@ -0,0 +1,353 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Mathématiques 2012-2013
|
| 2 |
+
|
| 3 |
+
Envoi $\mathcal{N u m e ́ r o ~} 4$ - Corrigé
|
| 4 |
+

|
| 5 |
+
|
| 6 |
+
## Exercices Juniors
|
| 7 |
+
|
| 8 |
+
Exercice 1. Soient $x_{1}, x_{2}, \ldots, x_{5}$ des réels tels que
|
| 9 |
+
|
| 10 |
+
$$
|
| 11 |
+
\left|x_{2}-x_{1}\right|=2\left|x_{3}-x_{2}\right|=3\left|x_{4}-x_{3}\right|=4\left|x_{5}-x_{4}\right|=5\left|x_{1}-x_{5}\right| .
|
| 12 |
+
$$
|
| 13 |
+
|
| 14 |
+
Montrer que ces cinq réels sont égaux.
|
| 15 |
+
Solution.
|
| 16 |
+
Notons $\alpha=\left|x_{2}-\chi_{1}\right|$ et montrons par l'absurde que $\alpha=0$. D'après l'énoncé, il existe des signes $\varepsilon_{1}, \ldots$, $\varepsilon_{5}$ tels que
|
| 17 |
+
|
| 18 |
+
$$
|
| 19 |
+
x_{2}-x_{1}=\varepsilon_{1} \alpha, x_{3}-x_{2}=\varepsilon_{2} \frac{\alpha}{2}, x_{4}-x_{3}=\varepsilon_{3} \frac{\alpha}{3}, x_{5}-x_{4}=\varepsilon_{4} \frac{\alpha}{4}, x_{1}-x_{5}=\varepsilon_{5} \frac{\alpha}{5} .
|
| 20 |
+
$$
|
| 21 |
+
|
| 22 |
+
Alors, par télescopage,
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
0=x_{1}-x_{5}+x_{5}-x_{4}+x_{4}-x_{3}+x_{3}-x_{2}+x_{2}-x_{1}=\varepsilon_{1} \alpha+\varepsilon_{2} \frac{\alpha}{2}+\varepsilon_{3} \frac{\alpha}{3}+\varepsilon_{4} \frac{\alpha}{4}+\varepsilon_{5} \frac{\alpha}{5} .
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
Si $\alpha \neq 0$, il existe donc des signes $\varepsilon_{1}^{\prime}, \ldots, \varepsilon_{4}^{\prime}$ tels que
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
\frac{1}{5}=\varepsilon_{1}^{\prime}+\varepsilon_{2}^{\prime} \frac{1}{2}+\varepsilon_{3}^{\prime} \frac{1}{3}+\varepsilon_{4}^{\prime} \frac{1}{4}
|
| 32 |
+
$$
|
| 33 |
+
|
| 34 |
+
donc un entier n tel que $\frac{1}{5}=\frac{\mathfrak{n}}{12}$ ce qui est impossible car 5 ne divise par 12 .
|
| 35 |
+

|
| 36 |
+
|
| 37 |
+
Exercice 2. Soit $\left(u_{n}\right)_{n}$ une suite de réels telle que, pour tout entier $n$,
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\left|u_{n+1}-u_{n}\right| \leqslant 1 .
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
Montrer que la moyenne des $n$ premiers termes de la suite et la moyenne des $n+1$ premiers termes de la suite sont distantes d'au plus $\frac{1}{2}$.
|
| 44 |
+
|
| 45 |
+
## Solution.
|
| 46 |
+
|
| 47 |
+
Notons, pour tout entier $n$ strictement positif $v_{n}=\frac{1}{n}\left(u_{1}+\ldots+u_{n}\right)$.
|
| 48 |
+
$\triangleright$ Soit $\mathrm{m}>\mathrm{n}$. Remarquons tout d'abord que, par inégalité triangulaire,
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\begin{aligned}
|
| 52 |
+
\left|u_{m}-u_{n}\right| & \leqslant\left|u_{m}-u_{m-1}\right|+\left|u_{m-1}-u_{m-2}\right|+\ldots+\left|u_{n+1}-u_{n}\right| \\
|
| 53 |
+
& \leqslant m-n .
|
| 54 |
+
\end{aligned}
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
$\triangleright$ Pour tout entier n strictement positif,
|
| 58 |
+
|
| 59 |
+
$$
|
| 60 |
+
\begin{aligned}
|
| 61 |
+
\left|v_{n+1}-v_{n}\right| & =\left|\frac{(n+1)\left(u_{1}+\ldots+u_{n}\right)-n\left(u_{1}+\ldots+u_{n}+u_{n+1}\right)}{n(n+1)}\right| \\
|
| 62 |
+
& \leqslant\left|\frac{\left(u_{1}-u_{n+1}\right)+\ldots+\left(u_{n}-u_{n+1}\right)}{n(n+1)}\right| \\
|
| 63 |
+
& \leqslant \frac{\left|u_{1}-u_{n+1}\right|+\ldots+\left|u_{n}-u_{n+1}\right|}{n(n+1)} \\
|
| 64 |
+
& \leqslant \frac{n+\ldots+1}{n(n+1)}=\frac{1}{2}
|
| 65 |
+
\end{aligned}
|
| 66 |
+
$$
|
| 67 |
+
|
| 68 |
+

|
| 69 |
+
|
| 70 |
+
Exercice 3. Soit $E$ un ensemble fini de réels strictement positifs tels que, pour tout réel $x$ strictement positif, E contient autant d'éléments strictement supérieurs à $x$ que d'éléments strictement inférieurs à $\frac{1}{x}$. Déterminer le produit de tous les éléments de E.
|
| 71 |
+
|
| 72 |
+
## Solution.
|
| 73 |
+
|
| 74 |
+
Soit $x_{0} \in E$ tel que $x_{0}>1$. Alors, par hypothèse,
|
| 75 |
+
|
| 76 |
+
- les ensembles $\mathrm{E} \cap$ ] - $\infty, \frac{1}{x_{0}}$ [et $\left.\mathrm{E} \cap\right] \mathrm{x}_{0},+\infty[$ ont des cardinaux de même parité,
|
| 77 |
+
- les ensembles $\mathrm{E} \cap]-\infty, \mathrm{x}_{0}\left[\right.$ et $\mathrm{E} \cap \frac{1}{\mathrm{x}_{0}},+\infty[$ ont des cardinaux de même parité.
|
| 78 |
+
|
| 79 |
+
Par conséquent, les deux ensembles
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\begin{aligned}
|
| 83 |
+
\left.\mathrm{E} \cap] \frac{1}{x_{0}}, x_{0}\right] & =(\mathrm{E} \cap] \frac{1}{x_{0}},+\infty[) \backslash(\mathrm{E} \cap] \mathrm{x}_{0},+\infty[) \\
|
| 84 |
+
\mathrm{E} \cap\left[\frac{1}{x_{0}}, x_{0}[ \right. & =(\mathrm{E} \cap]-\infty, \mathrm{x}_{0}[) \backslash(\mathrm{E} \cap]-\infty, \frac{1}{x_{0}}[)
|
| 85 |
+
\end{aligned}
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
ont des cardinaux de même parité. Or, ils sont composés des mêmes éléments, sauf éventuellement $x_{0}$ et $\frac{1}{x_{0}}$, le premier ensemble contient $\chi_{0}$ mais pas $\frac{1}{x_{0}}$ : ainsi, le second ensemble contient un et un seul élément de $\left\{\frac{1}{x_{0}}, x_{0}\right\}$ mais ne peut contenir $x_{0}:$ il contient donc $\frac{1}{x_{0}}$.
|
| 89 |
+
On a ainsi établi que si $x_{0} \in E$, alors $\frac{1}{x_{0}} \in E$. Le produit de tous les éléments de $E$ donne donc 1 .
|
| 90 |
+

|
| 91 |
+
|
| 92 |
+
## Exercices Communs
|
| 93 |
+
|
| 94 |
+
Exercice 4. Soit $x, y, z>0$ tels que $x y z=8$. Montrer que
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
\frac{x-2}{x+1}+\frac{y-2}{y+1}+\frac{z-2}{z+1} \leqslant 0
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
## Solution.
|
| 101 |
+
|
| 102 |
+
Commençons par remarquer que $a-2=a+1-3$ pour tout réel a donc
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\frac{x-2}{x+1}+\frac{y-2}{y+1}+\frac{z-2}{z+1}=3-3\left(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\right)
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
L'inégalité à établir se réécrit donc
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} \geqslant 1
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
En mettant au même dénominateur, on obtient
|
| 115 |
+
|
| 116 |
+
$$
|
| 117 |
+
3+2(x+y+z)+x y+y z+z x \geqslant 1+x+y+z+x y+y z+z x+x y z
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
soit
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\frac{x+y+z}{3} \geqslant 2
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
Or, cette dernière égalité est simplement l'inégalité arithmético-géométrique.
|
| 127 |
+

|
| 128 |
+
|
| 129 |
+
Exercice 5. Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que, pour tous $x$ et $y$,
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
f(x y) \leqslant x f(y)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
## Solution.
|
| 136 |
+
|
| 137 |
+
$\triangleright \operatorname{Avec}(x, y)=(0,0)$, on obtient $f(0) \leqslant 0$ et avec $(x, y)=(2,0), f(0) \geqslant 0$. Par conséquent, $f(0)=0$.
|
| 138 |
+
$\triangleright \operatorname{Si} x>0$ et $y>0$, alors
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
f(x)=f\left(\frac{x}{y} y\right) \leqslant \frac{x}{y} f(y)
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
D'où
|
| 145 |
+
|
| 146 |
+
$$
|
| 147 |
+
\frac{f(x)}{x} \leqslant \frac{f(y)}{y}
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
et donc $\frac{f(x)}{x}=\frac{f(y)}{y}$ (par symétrie des rôles de $x$ et $y$ ).
|
| 151 |
+
$\triangleright$ De même, si $x<0$ et $y<0$, alors
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
f(x)=f\left(\frac{x}{y} y\right) \leqslant \frac{x}{y} f(y)
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
D'où
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\frac{f(x)}{x} \geqslant \frac{f(y)}{y}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
et donc $\frac{f(x)}{x}=\frac{f(y)}{y}$ (par symétrie des rôles de $x$ et $y$ ).
|
| 164 |
+
$\triangleright$ Notons $\alpha=\mathfrak{f}(1)$ et $\beta=-\mathbf{f}(-1)$ les constantes exhibées aux points précédents. Avec $(x, y)=$ $(-1,-1)$, l'inéquation donne $\alpha=f\left((-1)^{2}\right) \leqslant-f(-1)=\beta$.
|
| 165 |
+
$\triangleright$ On a obtenu qu'une solution est de la forme
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
x \mapsto\left\{\begin{array}{cl}
|
| 169 |
+
0 & \text { si } x=0 \\
|
| 170 |
+
\alpha x & \text { si } x>0 \\
|
| 171 |
+
\beta x & \text { si } x<0
|
| 172 |
+
\end{array}\right.
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
$\operatorname{avec} \alpha \leqslant \beta$. On vérifie que ces fonctions conviennent.
|
| 176 |
+

|
| 177 |
+
|
| 178 |
+
Exercice 6. Soient un entier $n$ et des réels $0<\mathfrak{u}_{1}<\mathfrak{u}_{2}<\ldots<\boldsymbol{u}_{\boldsymbol{n}}$ tels que
|
| 179 |
+
|
| 180 |
+
$$
|
| 181 |
+
\mathfrak{u}_{1}+\mathfrak{u}_{2}+\ldots+\mathfrak{u}_{n}=\frac{1}{\mathfrak{u}_{1}^{2}}+\frac{1}{\mathfrak{u}_{2}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}
|
| 182 |
+
$$
|
| 183 |
+
|
| 184 |
+
Montrer que, pour tout entier $k$ inférieur ou égal à $n$, il existe $k$ réels parmi $\mathfrak{u}_{1}, \mathfrak{u}_{2}, \ldots, \mathfrak{u}_{n}$ dont la somme est supérieure ou égale à $k$.
|
| 185 |
+
|
| 186 |
+
## Solution.
|
| 187 |
+
|
| 188 |
+
$\triangleright$ Commençons par montrer le résultat pour $k=n$. Notons $a=\frac{u_{1}+\ldots+u_{n}}{n}$ et $g=\left(u_{1} \ldots u_{n}\right)^{\frac{1}{n}}$ les moyennes arithmétique et géométrique de $u_{1}, \ldots, u_{n}$. Alors, l'inégalité classique entre moyenne arithmétique-géométrique-harmonique donne
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
\mathrm{a}=\frac{\frac{1}{\mathbf{u}_{1}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}}{\mathrm{n}} \geqslant \frac{1}{\mathrm{~g}^{2}} \geqslant \frac{1}{\mathrm{a}^{2}}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
Ainsi, $a \geqslant 1$ et, donc, $u_{1}+\ldots+u_{n} \geqslant n$.
|
| 195 |
+
$\triangleright$ Soit $k<n$. Supposons que $u_{1}+\ldots+u_{k}<k, u_{2}+\ldots+u_{k+1}<k, \ldots, u_{n}+\ldots+u_{k-1}<k$. Alors, en additionnant toutes ces inégalités, on obtient
|
| 196 |
+
|
| 197 |
+
$$
|
| 198 |
+
n\left(u_{1}+\ldots+u_{n}\right)<n k
|
| 199 |
+
$$
|
| 200 |
+
|
| 201 |
+
ce qui contredit le point précédent. Ainsi, l'une des sommes $\mathfrak{u}_{1}+\ldots+\mathfrak{u}_{\mathrm{k}}, \mathfrak{u}_{2}+\ldots+\mathfrak{u}_{\mathrm{k}+1}, \ldots$, $u_{n}+\ldots+u_{k-1}$ est supérieure ou égale à $k$.
|
| 202 |
+
|
| 203 |
+
## Exercices Olympiques
|
| 204 |
+
|
| 205 |
+
Exercice 7. Trouver les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que, pour tous $x, y \in \mathbb{R}$,
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
\mathrm{f}\left(\frac{\mathrm{x}+\mathrm{y}}{3}\right)=\frac{\mathrm{f}(\mathrm{x})+\mathrm{f}(\mathrm{y})}{2}
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
## Solution.
|
| 212 |
+
|
| 213 |
+
Soit $f$ une solution.
|
| 214 |
+
$\triangleright$ Commençons par remarquer que la fonction $g: x \mapsto f(x)-f(0)$ est aussi une solution de l'équation fonctionnelle.
|
| 215 |
+
$\triangleright$ Pour tous réels $x$ et $y$,
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
\mathrm{g}(x+y)=\mathrm{g}\left(\frac{3 \mathrm{x}+3 \mathrm{y}}{3}\right)=\frac{\mathrm{g}(3 \mathrm{x})+\mathrm{g}(3 \mathrm{y})}{2}
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
Or, pour tout réel $a$,
|
| 222 |
+
|
| 223 |
+
$$
|
| 224 |
+
g(3 a)=2 \cdot \frac{g(3 a)+g(0)}{2}=2 g\left(\frac{3 a+0}{3}\right)=2 g(a)
|
| 225 |
+
$$
|
| 226 |
+
|
| 227 |
+
En conclusion, $g(x+y)=g(x)+g(y)$.
|
| 228 |
+
$\triangleright$ On a montré que, pour tout $x, g(2 x)=2 g(x)$. Or, l'équation fonctionnelle avec $y=2 x$ donne
|
| 229 |
+
|
| 230 |
+
$$
|
| 231 |
+
\mathrm{g}\left(\frac{\mathrm{x}+2 \mathrm{x}}{3}\right)=\frac{\mathrm{g}(\mathrm{x})+\mathrm{g}(2 x)}{2}
|
| 232 |
+
$$
|
| 233 |
+
|
| 234 |
+
soit $\mathrm{g}(2 \mathrm{x})=\mathrm{g}(\mathrm{x})$. En combinant ces deux résultats, on obtient que g est nulle donc f est constante. La réciproque est évidente.
|
| 235 |
+

|
| 236 |
+
|
| 237 |
+
Exercice 8. Soient $x$, y et $z$ des réels strictement positifs tels que
|
| 238 |
+
|
| 239 |
+
$$
|
| 240 |
+
x+y+z \geqslant \frac{1}{x}+\frac{1}{y}+\frac{1}{z}
|
| 241 |
+
$$
|
| 242 |
+
|
| 243 |
+
Montrer que
|
| 244 |
+
|
| 245 |
+
$$
|
| 246 |
+
\frac{x}{y}+\frac{y}{z}+\frac{z}{x} \geqslant \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}
|
| 247 |
+
$$
|
| 248 |
+
|
| 249 |
+
## Solution.
|
| 250 |
+
|
| 251 |
+
En mettant au même dénominateur, l'inégalité recherchée se réécrit
|
| 252 |
+
|
| 253 |
+
$$
|
| 254 |
+
x^{2} z+y^{2} x+z^{2} y \geqslant x+y+z
|
| 255 |
+
$$
|
| 256 |
+
|
| 257 |
+
Montrons celle-ci en utilisant successivement l'hypothèse et l'inégalité de Cauchy-Schwarz :
|
| 258 |
+
|
| 259 |
+
$$
|
| 260 |
+
\begin{aligned}
|
| 261 |
+
& x+y+z \leqslant \frac{(x+y+z)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
|
| 262 |
+
& \leqslant \frac{\left(x \sqrt{z} \cdot \frac{1}{\sqrt{z}}+y \sqrt{x} \cdot \frac{1}{\sqrt{x}}+z \sqrt{y} \cdot \frac{1}{\sqrt{y}}\right)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
|
| 263 |
+
& \leqslant x^{2} z+y^{2} x+z^{2} y . \\
|
| 264 |
+
& \text { య̛or }
|
| 265 |
+
\end{aligned}
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
Exercice 9. Soient a, b et c des réels strictement positifs tels que
|
| 269 |
+
|
| 270 |
+
$$
|
| 271 |
+
a^{2}+b^{2}>c^{2}, \quad b^{2}+c^{2}>a^{2}, \quad c^{2}+a^{2}>b^{2}
|
| 272 |
+
$$
|
| 273 |
+
|
| 274 |
+
Montrer que
|
| 275 |
+
|
| 276 |
+
$$
|
| 277 |
+
\frac{a^{2} b^{2} c^{2}}{\left(a^{2}+b^{2}-c^{2}\right)\left(b^{2}+c^{2}-a^{2}\right)\left(c^{2}+a^{2}-b^{2}\right)}+2 \frac{(a+b-c)(b+c-a)(c+a-b)}{a b c} \geqslant 3
|
| 278 |
+
$$
|
| 279 |
+
|
| 280 |
+
## Solution.
|
| 281 |
+
|
| 282 |
+
## Notons
|
| 283 |
+
|
| 284 |
+
$$
|
| 285 |
+
\begin{aligned}
|
| 286 |
+
& A=\frac{a^{2} b^{2} c^{2}}{\left(a^{2}+b^{2}-c^{2}\right)\left(b^{2}+c^{2}-a^{2}\right)\left(c^{2}+a^{2}-b^{2}\right)} \\
|
| 287 |
+
& B=\frac{(a+b-c)(b+c-a)(c+a-b)}{a b c}
|
| 288 |
+
\end{aligned}
|
| 289 |
+
$$
|
| 290 |
+
|
| 291 |
+
On doit montrer que $A+2 B \geqslant 3$. Tout d'abord, on remarque que $a+b>c$ car $c^{2}<a^{2}+b^{2}<(a+b)^{2}$. On a de même $b+c>a$ et $c+a>b$, donc $a, b, c$ sont les côtés d'un triangle dont on notera $\alpha, \beta, \gamma$ les angles. Le fait que $a^{2}+b^{2}>c^{2}$, etc. signifie que le triangle est acutangle.
|
| 292 |
+
D'après l'inégalité arithmético-géométrique, on a $\frac{A+2 B}{3} \geqslant \sqrt[3]{A B^{2}}$, donc il suffit de montrer que $A B^{2} \geqslant$ 1, autrement dit que
|
| 293 |
+
|
| 294 |
+
$$
|
| 295 |
+
\frac{(a+b-c)^{2}(b+c-a)^{2}(c+a-b)^{2}}{\left(a^{2}+b^{2}-c^{2}\right)\left(b^{2}+c^{2}-a^{2}\right)\left(c^{2}+a^{2}-b^{2}\right)} \geqslant 1
|
| 296 |
+
$$
|
| 297 |
+
|
| 298 |
+
D'après la formule d'Al-Kashi, on a
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
a^{2}+b^{2}-c^{2}=2 a b \cos \alpha
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
D'autre part,
|
| 305 |
+
|
| 306 |
+
$$
|
| 307 |
+
(c+a-b)(b+c-a)=c^{2}-a^{2}-b^{2}+2 a b=2 a b(1-\cos \alpha)
|
| 308 |
+
$$
|
| 309 |
+
|
| 310 |
+
donc $\frac{(c+a-b)(b+c-a)}{a^{2}+b^{2}-c^{2}}=\frac{1-\cos \alpha}{\cos \alpha}$. En multipliant par les deux expressions similaires, l'inégalité à démontrer devient
|
| 311 |
+
|
| 312 |
+
$$
|
| 313 |
+
\frac{(1-\cos \alpha)(1-\cos \beta)(1-\cos \gamma)}{\cos \alpha \cos \beta \cos \gamma} \geqslant 1
|
| 314 |
+
$$
|
| 315 |
+
|
| 316 |
+
Traitons d'abord le cas particulier $\alpha=\beta$. Alors $\gamma=\pi-2 \alpha$. Comme $\gamma \leqslant \frac{\pi}{2}$, on a $\alpha \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right]$.
|
| 317 |
+
Comme $\frac{1-\cos \gamma}{\cos \gamma}=\frac{1+\cos 2 \alpha}{-\cos 2 \alpha}=\frac{2 \cos ^{2} \alpha}{1-2 \cos ^{2} \alpha}$, on a
|
| 318 |
+
|
| 319 |
+
$$
|
| 320 |
+
\begin{aligned}
|
| 321 |
+
\frac{(1-\cos \alpha)(1-\cos \beta)(1-\cos \gamma)}{\cos \alpha \cos \beta \cos \gamma} & =\frac{(1-\cos \alpha)^{2}\left(2 \cos ^{2} \alpha\right)}{\cos ^{2} \alpha\left(1-2 \cos ^{2} \alpha\right)} \\
|
| 322 |
+
& =\frac{2(1-\cos \alpha)^{2}}{1-2 \cos ^{2} \alpha}
|
| 323 |
+
\end{aligned}
|
| 324 |
+
$$
|
| 325 |
+
|
| 326 |
+
Cette expression est minoré par 1 si et seulement si $2(1-\cos \alpha)^{2} \geqslant 1-2 \cos ^{2} \alpha$. On développe et on passe tout dans le membre de gauche. L'inégalité devient $(2 \cos \alpha-1)^{2} \geqslant 0$, ce qui est vrai.
|
| 327 |
+
Traitons maintenant le cas général. On suppose par symétrie que $\alpha \geqslant \beta \geqslant \gamma$.
|
| 328 |
+
|
| 329 |
+
Posons $f(x)=\frac{1-\cos x}{\cos x}$ et $g(x)=\log f(x)$. On veut montrer que
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
f(\alpha) f(\beta) f(\gamma) \geqslant 1
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
ou encore que $\frac{g(\alpha)+g(\beta)+g(\gamma)}{3} \geqslant 0=g\left(\frac{\pi}{3}\right)=g\left(\frac{\alpha+\beta+\gamma}{3}\right)$. La difficulté est que $g$ n'est pas convexe. En effet, on calcule que
|
| 336 |
+
|
| 337 |
+
$$
|
| 338 |
+
g^{\prime \prime}(x)=\frac{(1-\cos x)\left(-\cos ^{2} x-\cos x+1\right)}{\cos ^{2} x(1-\cos x)^{2}}
|
| 339 |
+
$$
|
| 340 |
+
|
| 341 |
+
est positif sur $\left[x_{0}, \frac{\pi}{2}\right]$ et négatif sur $\left[0, x_{0}\right]$, où $x_{0}$ satisfait l'équation $\cos x_{0}=\frac{-1+\sqrt{5}}{2}$. On remarque que $x_{0}<\frac{\pi}{3}$ puisque $\frac{-1+\sqrt{5}}{2}>\frac{1}{2}$. On en déduit que $\alpha \geqslant x_{0}$. En effet, dans le cas contraire on aurait $\alpha+\beta+\gamma \leqslant 3 \alpha \leqslant 3 x_{0}<\pi$, ce qui est faux.
|
| 342 |
+
Premier cas: $\beta \geqslant x_{0}$. Alors $g(\alpha)+g(\beta) \geqslant 2 g\left(\frac{\alpha+\beta}{2}\right)$ par convexité de $g$ sur $\left[x_{0}, \frac{\pi}{2}\right]$ donc on se ramène au cas particulier $\alpha=\beta$ traité plus haut.
|
| 343 |
+
Deuxième cas: $\beta<x_{0}$. Notons que $\gamma>x_{0}-\beta$. En effet, dans le cas contraire on aurait $\alpha+\beta+\gamma \leqslant$ $\frac{\pi}{2}+\beta+\left(x_{0}-\beta\right)=\frac{\pi}{2}+x_{0}<\pi$, ce qui est faux.
|
| 344 |
+
Posons $\varphi(t)=g(\beta+t)+g(\gamma-t)$. Pour tout $t \in\left[0, x_{0}-\beta\right]$, on a
|
| 345 |
+
|
| 346 |
+
$$
|
| 347 |
+
\varphi^{\prime}(t)=g^{\prime}(\beta+t)-g^{\prime}(\gamma-t) \leqslant 0
|
| 348 |
+
$$
|
| 349 |
+
|
| 350 |
+
puisque $0<\gamma-t \leqslant \beta+t \leqslant x_{0}$. Donc $\varphi(0) \geqslant \varphi\left(x_{0}-\beta\right)$, ce qui s'écrit $g(\beta)+g(\gamma) \geqslant g\left(\beta^{\prime}\right)+g\left(\gamma^{\prime}\right)$ où $\beta^{\prime}=x_{0}$ et $\gamma^{\prime}=\gamma-\left(x_{0}-\beta\right)$. On est ainsi ramenés au premier cas.
|
| 351 |
+

|
| 352 |
+
$\mathcal{F i n}$
|
| 353 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi5-corrige.md
ADDED
|
@@ -0,0 +1,349 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Mathématiques 2012-2013
|
| 2 |
+
|
| 3 |
+
Envoi $\mathcal{N u m e ́ r o ~} 5$ - Corrigé
|
| 4 |
+

|
| 5 |
+
|
| 6 |
+
## Exercices Juniors
|
| 7 |
+
|
| 8 |
+
Exercice 1. Prouver que l'équation
|
| 9 |
+
|
| 10 |
+
$$
|
| 11 |
+
a^{3}+b^{5}+c^{7}+d^{11}=e^{13}
|
| 12 |
+
$$
|
| 13 |
+
|
| 14 |
+
admet une infinité de solutions en entiers strictement positifs.
|
| 15 |
+
|
| 16 |
+
## Solution.
|
| 17 |
+
|
| 18 |
+
Il convient de remarquer que si ( $a, b, c, d, e$ ) est une solution alors, pour tout entier $k>0$, le quintuplet
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
\left(a k^{5 \times 7 \times 11 \times 13}, \mathrm{bk}^{3 \times 7 \times 11 \times 13}, \mathrm{ck}^{3 \times 5 \times 11 \times 13}, \mathrm{dk}^{3 \times 5 \times 7 \times 13}, e k^{3 \times 5 \times 7 \times 11}\right)
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
en est une aussi.
|
| 25 |
+
Pour conclure, il suffit donc de trouver une solution. On peut penser à en trouver une telle que
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
a^{3}=b^{5}=c^{7}=d^{11}=\frac{1}{4} e^{13}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
où $e=2^{\mathrm{t}}$ pour un certain t à déterminer. Pour cela, t doit être choisi de sorte que $13 \mathrm{t}-2$ soit multiple commun de $3,5,7,11$ et 11 . En cherchant un peu, on voit que l'on peut prendre $13 \mathbf{t}-2=3 \times 5 \times 7 \times 11$, ou encore $\mathrm{t}=89$.
|
| 32 |
+
|
| 33 |
+
Exercice 2. Prouver que, pour tous entiers strictement positifs a, b, c, d, on a
|
| 34 |
+
|
| 35 |
+
$$
|
| 36 |
+
(2 a-1)(2 b-1)(2 c-1)(2 d-1) \geqslant 2 a b c d-1
|
| 37 |
+
$$
|
| 38 |
+
|
| 39 |
+
et déterminer les cas d'égalité.
|
| 40 |
+
|
| 41 |
+
## Solution.
|
| 42 |
+
|
| 43 |
+
Si $x$ et $y$ sont des entiers strictement positifs, on a $x \geqslant 1$ et $y \geqslant 1$, et ainsi $(x-1)(y-1) \geqslant 0$. Cela conduit à $x y-x-y+1 \geqslant 0$, et donc à $(2 x-1)(2 y-1) \geqslant 2 x y-1$. Notons que l'égalité a lieu si et seulement si $x=1$ ou $y=1$.
|
| 44 |
+
|
| 45 |
+
Si $a, b, c, d$ sont des entiers strictement positifs, on a donc $(2 a-1)(2 b-1) \geqslant 2 a b-1$ et $(2 c-$ 1) $(2 \mathrm{~d}-1) \geqslant 2 \mathrm{~cd}-1$, mais aussi $(2 a b-1)(2 c d-1) \geqslant 2 a b c d-1$. Ainsi :
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
(2 a-1)(2 b-1)(2 c-1)(2 d-1) \geqslant(2 a b-1)(2 c d-1) \geqslant 2 a b c d-1
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
D'après ci-dessus, l'égalité a lieu si et seulement si trois des nombres $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ sont égaux à 1 .
|
| 52 |
+

|
| 53 |
+
|
| 54 |
+
Exercice 3. Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).
|
| 55 |
+
|
| 56 |
+
Prouver que la droite (BP) passe par le milieu de [AL].
|
| 57 |
+
|
| 58 |
+
## Solution.
|
| 59 |
+
|
| 60 |
+
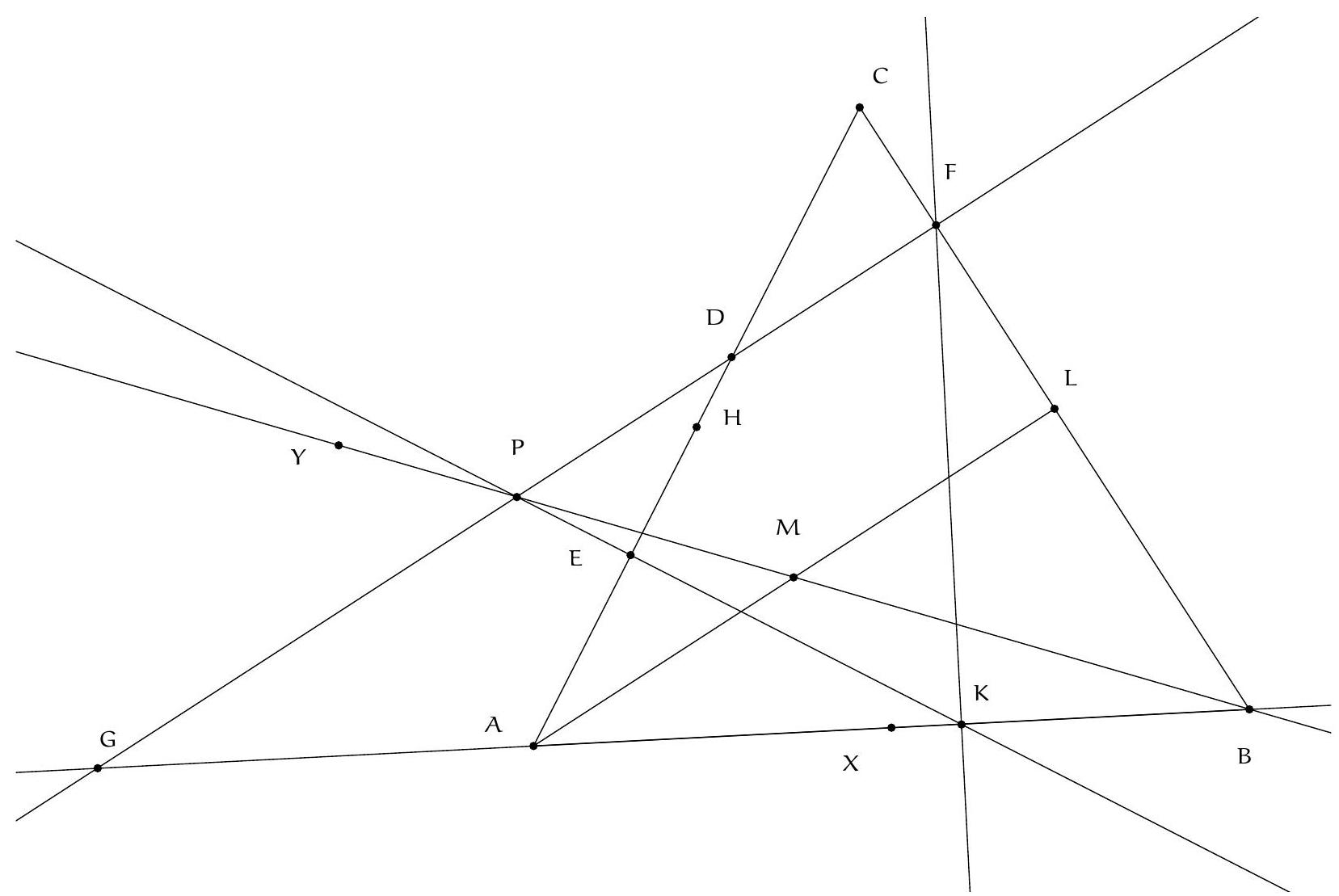
|
| 61 |
+
|
| 62 |
+
Première solution. Comme les côtés de PKF sont perpendiculaires aux côtés de ABC , le triangle PKF a les mêmes angles intérieurs que $A B C$ et est donc équilatéral, et donc $P F=K F$.
|
| 63 |
+
|
| 64 |
+
Notons $M$ l'intersection de (BP) et ( $A L$ ). Comme les triangles BLM et BFP sont semblables, on a
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
\frac{M L}{B L}=\frac{P F}{B F}=\frac{\mathrm{KF}}{B F}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
D'autre part, $\frac{A L}{B L}=\tan 60^{\circ}=\sqrt{3}$, donc $A L=2 M L$, ce qui prouve que $M$ est le milieu de [AL].
|
| 71 |
+
Deuxième solution. Posons que les côtés de $A B C$ soient de longueur 2 , et que $A D=2 a$ avec $a \in$ $[0,1]$. On en déduit que $\mathrm{DC}=2-2 \mathrm{a}, \mathrm{FC}=\mathrm{DC} \cos \left(60^{\circ}\right)=1-\mathrm{a}$, et $\mathrm{BF}=1+\mathrm{a}$ Par suite, on a
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
\mathrm{BK}=\mathrm{BF} \cos \left(60^{\circ}\right)=\frac{1+\mathrm{a}}{2} \quad \text { et } \quad \mathrm{KF}=\mathrm{BF} \sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}(1+\mathrm{a})
|
| 75 |
+
$$
|
| 76 |
+
|
| 77 |
+
Puisque les côtés de PKF sont perpendiculaires aux côtés de $A B C$, le triangle $P K F$ a les mêmes angles intérieurs que $A B C$ et est donc équilatéral. On a alors $P F=K F=\frac{\sqrt{3}}{2}(1+a)$.
|
| 78 |
+
|
| 79 |
+
Le point $L$ étant le milieu de $[B C]$ avec $A B C$ équilatéral, les droites $(A L)$ et $(B C)$ sont donc perpendiculaires, ce qui assure que ( $M L$ ) et ( PF ) sont parallèles, où $M$ est l'intersection de ( $B P$ ) et ( $A L$ ). D'après le théorème de Thalès, il vient alors
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\frac{\mathrm{ML}}{\mathrm{PF}}=\frac{\mathrm{BL}}{\mathrm{BF}}=\frac{1}{1+\mathrm{a}}
|
| 83 |
+
$$
|
| 84 |
+
|
| 85 |
+
d'où $M L=\frac{\sqrt{3}}{2}=\frac{1}{2} A L$, ce qui conclut.
|
| 86 |
+
Troisième solution. Comme ci-dessus, on remarque que PKF est équilatéral, et on note M l'intersection de (BP) et (AL). Soit Q l'intersection de (FP) et ( AB ). On a $\widehat{\mathrm{PKQ}}=\widehat{\mathrm{PQK}}=30^{\circ}$, donc PQK est isocèle en $P$ et on a $P Q=P K$. Mais, $P K=K F$ puisque $P K F$ est équilatéral, donc $P Q=K F$ ce qui assure que $P$ est le milieu de [QF]. Ayant leurs côtés communs ou parallèles, les triangles BPQ et BMA d'une part, et les triangles BPF et BML d'autre part, sont semblables. Cela conduit à
|
| 87 |
+
|
| 88 |
+
$$
|
| 89 |
+
\frac{P Q}{A M}=\frac{P M}{B M} \quad \text { et } \quad \frac{P F}{M L}=\frac{P M}{B M}
|
| 90 |
+
$$
|
| 91 |
+
|
| 92 |
+
d'où $\frac{A M}{M L}=\frac{P Q}{P F}=1$, et $M$ est bien le milieu de $[A L]$.
|
| 93 |
+
Quatrième solution. Soit $X$ le milieu de $[A B]$ et $Y$ tel que $A L C Y$ soit un rectangle. Alors $X C=A L=$ $C Y$ et $\widehat{Y C X}=60^{\circ}$, donc $X C Y$ est équilatéral. Deux de ses côtés étant perpendicualires à deux des côtés du triangle équilatéral $A B C$, il en est de même de son troisième côté. Soit $M$ l'intersection de (AL) et (BY). Puisque $(A L)$ et $(C Y)$ sont parallèles et que $B C=2 B L$, on a $A L=C Y=2 M L$, d'où $M$ est le milieu de [AL]. Comme ci-dessus, on remarque que KFP est équilatéral car ses côtés sont perpendiculaires à ceux de $A B C$. Or, il en est de même de $X Y C$, donc les triangles KFP et $X C Y$ ont leurs côtés parallèles. Puisque les points $B, F, C$ d'une part, et $B, K, X$ d'autre part sont alignés, il existe donc une homothétie de centre B qui envoie $X C Y$ sur KFP. En particulier, le point $P$ appartient à la droite (BY) qui passe par le milieu de [AL].
|
| 94 |
+
|
| 95 |
+
## Exercices Communs
|
| 96 |
+
|
| 97 |
+
Exercice 4. Soit $A B C D$ un quadrilatère convexe. Pour tout point $M$ à l'intérieur ou sur le bord de $A B C D$, on pose
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
f(M)=M A+M B+M C+M D .
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
Prouver que, pour tout $M$, on a
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
f(M) \leqslant \max (f(A), f(B), f(C), f(D))
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
## Solution.
|
| 110 |
+
|
| 111 |
+
Lemme. Si le point K est sur les bords ou à l'intérieur du triangle XYZ , on a
|
| 112 |
+
|
| 113 |
+
$$
|
| 114 |
+
X Y+X Z \geqslant K Y+K Z .
|
| 115 |
+
$$
|
| 116 |
+
|
| 117 |
+
Preuve du lemme. Si $\mathrm{K}=\mathrm{Y}$, le résultat est immédiat d'après l'inégalité triangulaire. Sinon, on note P l'intersection de (YK) avec le côté [XZ]. D'après l'inégalité triangulaire, on a alors
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
X Y+X Z=X Y+X P+P Z \geqslant Y P+P Z=Y K+K P+P Z \geqslant Y K+K Z .
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
Revenons à l'exercice, et considérons un point $M$ à l'intérieur ou sur le bord du quadrilatère convexe $A B C D$. On va commencer par prouver que l'on peut trouver un point $P$ du bord de $A B C D$ tel que $f(M) \leqslant f(P)$. Les diagonales $[A C]$ et $[B D]$ se coupent en $O$ et, sans perte de généralité, on peut supposer que $M$ est dans ou sur les bords du triangle $A D O$. Les droites ( $B M$ ) et ( $C M$ ) recoupent alors le côté [AD] respectivement en $X$ et $Y$. Soit $P$ un point de $[X Y]$. D'après le lemme, puisque $M$ est dans ou sur les bords du triangle BDP, on a $P B+P D \geqslant M B+M D$. Et, puisque $M$ est dans ou sur les bords du triangle $C A P$, on a $P A+P C \geqslant M A+M C$. En sommant, il vient $f(M) \leqslant f(P)$, avec $P \in[A D]$ comme désiré.
|
| 124 |
+
|
| 125 |
+
Toujours avec le point $P \in[A D]$ ci-dessus, on montre maintenant que $f(P) \leqslant f(A)$ ou $f(P) \leqslant$ $f(D)$, ce qui terminera la démonstration. En effet, puisque $P \in[A D]$, on a $P A+P D=A D$. On veut maximiser $\mathrm{PB}+\mathrm{PC}$. Pour cela, on construit le symétrique $\mathrm{B}^{\prime}$ de B par rapport à ( $A D$ ). On a donc $P B+P C=P B^{\prime}+P C$. De plus, puisque $A B C D$ est convexe, selon que la droite ( $B^{\prime} C$ ) rencontre ( $A D$ ) en un point de $[A D]$ ou non, le point $P$ est sur dans ou sur les bords de $A B^{\prime} C$ ou de $D^{\prime} C$. D'après le lemme, on a alors $\mathrm{PB}^{\prime}+P C \leqslant A B^{\prime}+A C=A B+A C$ ou $P B^{\prime}+P C \leqslant B^{\prime}+D C=D B+D C$. Ainsi, on a
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
f(P)=P A+P D+P B+P C \leqslant A D+A B+A C=f(A)
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
ou
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
f(P)=P A+P D+P B+P C \leqslant A D+D B+D C=f(D),
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
comme annoncé.
|
| 138 |
+
|
| 139 |
+
## Exercice 5. On considère une grille carrée de $4 \times 4$ cases.
|
| 140 |
+
|
| 141 |
+
Deux cases distinctes ayant un côté commun sont dites voisines. Initialement, toutes les cases sont rouges. Par la suite, une case pourra éventuellement changer de couleur et être soit rouge soit bleue. Effectuer une opération sur la case c signifie que l'on change simultanément la couleur de c ainsi que celles de toutes ses voisines (les cases rouges deviennent bleues et les cases bleues deviennent rouges).
|
| 142 |
+
|
| 143 |
+
Donner toutes les valeurs de $n$ pour lesquelles il existe un groupe de $n$ cases distinctes telles qu'après avoir effectué une opération sur chacune de ces n cases, on obtienne une grille entièrement bleue.
|
| 144 |
+
|
| 145 |
+
## Solution.
|
| 146 |
+
|
| 147 |
+
Regroupons les cases de la grille en quatre tuiles, contenant chacune une case marquée, comme indiqué dans la figure suivante :
|
| 148 |
+
|
| 149 |
+
|
| 150 |
+
Il est facile de vérifier qu'une opération quelconque change la couleur d'une et une seule de ces cases marquées et qu'une opération effectuée dans une tuile ne modifie pas la couleur des cases marquées des autres tuiles. Si l'on veut rendre la grille entièrement bleue, il faut donc que, dans chaque tuile, le nombre d'opérations effectuées soit impair. La somme de quatre nombres impairs étant paire, cela signifie que le nombre total n d'opérations doit être pair. De plus, puisque dans chaque tuile il y a quatre cases et que les opérations doivent être effectuées sur des cases distinctes, c'est que dans chaque tuile on a fait une ou trois opérations. Par suite, on a $4 \leqslant n \leqslant 12$.
|
| 151 |
+
|
| 152 |
+
Les seules valeurs de $n$ possibles sont donc $n=4,6,8,10,12$. Il reste à prouver que ces cinq valeurs sont bien des solutions. Pour cela, on pourra se reporter à la figure ci-dessus et ses quatre cases marquées et au figures ci-dessous (les points indiquent les cases sur lesquelles on effectue une opération).
|
| 153 |
+

|
| 154 |
+
|
| 155 |
+
## Remarques.
|
| 156 |
+
|
| 157 |
+
Plus généralement, on considère un graphe simple non orienté d'ordre $k$ dont chaque sommet a deux états possibles, rouge ou bleu, et on dispose d'une opération qui revient à changer simutanément l'état d'un sommet et celui de chacun de ses voisins (ici, les sommets sont les cases, deux reliées par une arête si et seulement si elles ont un côté en commun). On note que :
|
| 158 |
+
|
| 159 |
+
- l'ordre dans lequel sont effectuées les opérations n'a pas d'importance,
|
| 160 |
+
- si on effectue deux opérations sur un même sommet, cela revient à ne rien faire du tout. Par suite, on pourra toujours supposer qu'un sommet n'est concerné que par au plus une opération.
|
| 161 |
+
|
| 162 |
+
On dispose alors des deux théorèmes suivants :
|
| 163 |
+
|
| 164 |
+
## Théorème 1.
|
| 165 |
+
|
| 166 |
+
Pour tout graphe fini simple et non orienté, à partir d'une configuration où tous les sommets sont rouges, il existe un ensemble de sommets $E$ tel qu'en effectuant une opération sur chaque sommet de $E$, tous les sommets soient bleus.
|
| 167 |
+
|
| 168 |
+
Preuve.
|
| 169 |
+
On raisonne par récurrence sur le nombre $k$ de sommets, et on suppose directement le résultat vrai pour tout graphe de $k$ sommets. Pour un graphe d'ordre $k+1$, puisque chaque sommet peut-être soit rouge soit bleu, il y a donc $2^{k+1}$ états globaux possibles (il n'est pas ici supposé qu'ils soient tous accessibles par le jeu des opérations). De même, puisque chaque opération peut être effectuée ou non, il a $2^{k+1}$ ensembles possibles de sommets sur lesquels effectuer les opérations.
|
| 170 |
+
|
| 171 |
+
Raisonnons par l'absurde en supposant qu'il soit impossible d'atteindre l'état où tous les sommets sont bleus. C'est donc qu'il existe deux ensembles de sommets, disons $T_{1}$ et $T_{2}$, distincts et qui conduisent au même état final. Il est alors facile de vérifier que l'ensemble $S=T_{1} \Delta T_{2}$ (la différence symétrique) est un ensemble non vide de sommets pour lequel effectuer une opération sur chaque sommet de $S$ ne change pas l'état global de la configuration. En particulier, chaque sommet $L$ de $S$ doit être reliée à un nombre impair de sommets de $S$ (hors elle-même). Or, il est bien connu que, dans tout graphe simple non orienté, la somme des degrés est paire (c'est le double du nombre d'arêtes). En considérant le sous-graphe formé uniquement des sommets de $S$, on en déduit que $|S|$ est pair.
|
| 172 |
+
|
| 173 |
+
Par ailleurs, puisque chaque sommet du graphe initial qui n'est pas dans $S$ doit être relié à un nombre pair de sommets de $S$, effectuer n'importe quelle opération ne change pas la parité du nombre de sommets de $S$ qui sont rouges. Fixons maintenant un sommet L dans $S$. D'après l'hypothèse de récurrence, il est possible de rendre tous les sommets bleus sauf L, qui lui se doit de rester rouge sans quoi tous les sommets seraient bleus, en contradiction avec notre hypothèse. Mais alors, entre l'état initial et l'état final, la parité du nombre de sommets de $S$ qui sont bleus n'est pas conservée, ce qui fournit la contradiction attendue.
|
| 174 |
+
|
| 175 |
+
## Théorème 2.
|
| 176 |
+
|
| 177 |
+
Dans les conditions du théorème 1 , si deux suites d'opérations $S$ et $S^{\prime}$ permettent chacune de rendre tous les sommets bleus, alors $|S|=\left|S^{\prime}\right| \bmod [2]$, où $|s|$ désigne le nombre d'opérations effectuées dans la suite $s$.
|
| 178 |
+
|
| 179 |
+
## Preuve.
|
| 180 |
+
|
| 181 |
+
Comme précédemment, sans perte de généralité, on peut supposer qu'au plus une opération est effectuée par sommet (cela ne change pas la parité totale). Du coup, on peut raisonner sur l'ensemble des sommets concernés.
|
| 182 |
+
|
| 183 |
+
On reprend les notations de la preuve précédente, et on prouve un peu plus que souhaité en remarquant que si deux ensembles de sommets $\mathrm{T}_{1}$ et $\mathrm{T}_{2}$ distincts conduisent à un même état final (pas forcément celui où tous les sommets sont bleus), alors on a toujours $|S|$ est pair. Et, puisque $|S|=\left|T_{1}\right|+\left|T_{2}\right|-2\left|T_{1} \cap T_{2}\right|$, on a directement $\left|T_{1}\right|=\left|T_{2}\right| \bmod [2]$.
|
| 184 |
+
|
| 185 |
+
On retrouve évidemment les résultats démontrés dans le cas particulier de l'exercice.
|
| 186 |
+
Déterminer la parité commune des suites d'opérations qui rendent l'ensemble des sommets bleus dépend de la strucure du graphe, pas seulement du nombre de sommets etc... et il ne semble pas qu'il soit connu de résultat simple et général.
|
| 187 |
+

|
| 188 |
+
|
| 189 |
+
Exercice 6. Pour tout entier $n \geqslant 1$, on pose $S_{n}=x_{1}+x_{2}+\cdots+x_{n}$, où $x_{k}=\frac{k(k+1)}{2}$ pour tout $k \geqslant 1$. Prouver que, pour tout $n \geqslant 10$, il existe un entier $a_{n}$ tel que $S_{n-1}<a_{n}^{2}<S_{n}$.
|
| 190 |
+
|
| 191 |
+
## Solution.
|
| 192 |
+
|
| 193 |
+
Pour tout entier $\mathrm{n} \geqslant 1$, on a
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
S_{n}=\sum_{k=1}^{n} \frac{k(k+1)}{2}=\frac{1}{2} \sum_{k=1}^{n} k^{2}+\frac{1}{2} \sum_{k=1}^{n} k=\frac{n(n+1)(2 n+1)}{12}+\frac{n(n+1)}{4}=\frac{n(n+1)(n+2)}{6}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
Il suffit donc de prouver que, pour $n \geqslant 10$, on a $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$, car alors l'intervalle $] S_{n-1}, S_{n}[$ contiendra forcément un entier.
|
| 200 |
+
|
| 201 |
+
Or, d'après le calcul ci-dessus, l'inégalité $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$ est équivalente à
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\sqrt{\frac{n(n+1)(n+2)}{6}}-\sqrt{\frac{n(n+1)(n-1)}{6}}>1
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
ou encore
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
\sqrt{\frac{n(n+1)}{6}}(\sqrt{n+2}-\sqrt{n-1})>1
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Puisque
|
| 214 |
+
|
| 215 |
+
$$
|
| 216 |
+
\sqrt{n+2}-\sqrt{n-1}=\frac{3}{\sqrt{n+2}+\sqrt{n-1}}
|
| 217 |
+
$$
|
| 218 |
+
|
| 219 |
+
on veut prouver que
|
| 220 |
+
|
| 221 |
+
$$
|
| 222 |
+
\sqrt{3 n(n+1)}>\sqrt{2(n+2)}+\sqrt{2(n-1)}
|
| 223 |
+
$$
|
| 224 |
+
|
| 225 |
+
Pour cela, il suffit de montrer que $\sqrt{3 n(n+1)}>2 \sqrt{2(n+2)}$. Cette dernière inégalité s'écrit aussi $3 n^{2}-5 n-16>0$. Il est facile de vérifier qu'elle est satisfaite pour $n \geqslant 10$.
|
| 226 |
+

|
| 227 |
+
|
| 228 |
+
## Exercices Olympiques
|
| 229 |
+
|
| 230 |
+
Exercice 7. On considère un ensemble fini E de garçons et de filles.
|
| 231 |
+
Une partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.
|
| 232 |
+
|
| 233 |
+
Prouver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.
|
| 234 |
+
|
| 235 |
+
## Solution.
|
| 236 |
+
|
| 237 |
+
Première solution. On dira qu'un ensemble X de garçons est étranger à un groupe Y de filles si aucun garçon de X n'est connu d'une des filles de Y . De même, un ensemble Y de filles sera dit étranger à un groupe $X$ de garçons si aucune fille de $Y$ n'est connue d'un des garçons de $X$. Puisque la relation 'se connaître" est supposée symétrique, on en déduit que $X$ est étranger à $Y$ si et seulement si $Y$ est étranger à $X$. Cela ouvre la porte à un double-comptage :
|
| 238 |
+
|
| 239 |
+
On note $N$ le nombre de couples $(X, Y)$ de groupes $X$ de garçons et $Y$ de filles mutuellement étrangers. Soit $X$ un groupe de garçons. On note $Y_{X}$ le plus grand groupe de filles qui soit étranger à $X$. Clairement, tout groupe $Y$ de filles qui est étranger à $X$ est contenu dans $Y_{X}$ et, réciproquement, tout sous-ensemble de $Y_{X}$ est étranger à $X$. Par suite, le nombre de groupes $Y$ qui sont étrangers à $X$ est $2^{\left|{ }^{\mid}\right|} \mid$(où $|A|$ désigne le nombre déléments de l'ensemble $\mathcal{A}$ ). On en déduit que
|
| 240 |
+
|
| 241 |
+
$$
|
| 242 |
+
N=\sum_{X} 2^{\left|Y_{X}\right|}
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
Or, pour tout groupe $X$ de garçons, on a $X$ populaire si et seulement si $Y_{X}=\emptyset$, c.à.d. $2^{\left|Y_{X}\right|}=1$. Ainsi, le nombre de groupes populaires de garçons est congru à N modulo 2 .
|
| 246 |
+
|
| 247 |
+
Un raisonnement analogue montre que le nombre de groupes populaires de filles est lui aussi congru à N modulo 2 , ce qui conclut.
|
| 248 |
+
|
| 249 |
+
Deuxième solution. Soit G l'ensemble des garçons et F celui des filles. Nous allons prouver le résultat par récurrence sur $\mathrm{n}=|\mathrm{G}|$. On note tout d'abord que si F ou G est vide, la conclusion est immédiate (il n'existe aucun groupe populaire). Cela assure le résultat pour $\mathrm{n}=0,1$ et on considère maintenant un groupe de $\mathrm{n}+1 \geqslant 2$ personnes dans lequel il y a au moins une fille et au moins un garçon.
|
| 250 |
+
|
| 251 |
+
Soit $g$ un des garçons. On pose $\mathrm{G}^{\prime}=\mathrm{G}-\{\mathrm{g}\}$ et $\mathrm{F}^{\prime}$ l'ensemble des filles qui ne connaissent pas $g$. Alors :
|
| 252 |
+
|
| 253 |
+
- un groupe populaire de garçons dans $G^{\prime} \cup F$ l'est encore dans $G \cup F$,
|
| 254 |
+
- un groupe populaire de garçons dans $G \cup F$ qui ne l'est plus dans $G^{\prime} \cup F$ est la réunion d'un groupe populaire de garçons dans $G^{\prime} \cup F^{\prime}$ et de $\{g\}$.
|
| 255 |
+
|
| 256 |
+
Il en découle que le nombre $N(G, F)$ de groupes populaires de garçons dans $G \cup F$ est la somme du nombre $N\left(G^{\prime}, F\right)$ de groupes populaires de garçons dans $G^{\prime} \cup F$ et du nombre $N\left(G^{\prime}, F^{\prime}\right)$ de groupes populaires de garçons dans $G^{\prime} \cup F^{\prime}$, soit donc $N(G, F)=N\left(G^{\prime}, F\right)+N\left(G^{\prime}, F^{\prime}\right)$.
|
| 257 |
+
|
| 258 |
+
D'autre part :
|
| 259 |
+
|
| 260 |
+
- un groupe populaire de filles dans $G \cup F l^{\prime}$ est encore dans $G^{\prime} \cup F$,
|
| 261 |
+
- un groupe populaire de filles dans $G^{\prime} \cup F$ qui ne l'est plus dans $G \cup F$ est un groupe populaire de filles dans $G^{\prime} \cup F^{\prime}$.
|
| 262 |
+
|
| 263 |
+
Par conséquent, le nombre $M(G, F)$ de groupes populaires de filles dans $G \cup F$ est la différence entre le nombre $M\left(G^{\prime}, F\right)$ de groupes populaires de filles dans $G^{\prime} \cup F$ et le nombre $M\left(G^{\prime}, F^{\prime}\right)$ de groupes populaires de filles dans $G^{\prime} \cup F^{\prime}$, soit donc $M(G, F)=M\left(G^{\prime}, F\right)-M\left(G^{\prime}, F^{\prime}\right)$.
|
| 264 |
+
|
| 265 |
+
Or, d'après l'hypothèse de récurrence, on a $N\left(G^{\prime}, F\right)=M\left(G^{\prime}, F\right) \bmod [2]$ et $N\left(G^{\prime}, F^{\prime}\right)=M\left(G^{\prime}, F^{\prime}\right)=$ $-M\left(G^{\prime}, F^{\prime}\right) \bmod [2]$, d'où $N(F, G)=M(F, G) \bmod [2]$, ce qui achève la récurrence.
|
| 266 |
+
|
| 267 |
+
Troisième solution. On note toujours respectivement F et G l'ensemble des filles et celui des garçons. Pour chaque fille $f$ et chaque garçon $g$, on pose $h(f, g)=0$ si $f$ et $g$ se connaissent, et $h(f, g)=1$ sinon. Alors, un ensemble $X$ de garçons est populaire si et seulement si $\prod_{f \in F}\left(1-\prod_{g \in X} h(f, g)\right)=1$. Par suite, le nombre N de groupes populaires de garçons est
|
| 268 |
+
|
| 269 |
+
$$
|
| 270 |
+
\begin{aligned}
|
| 271 |
+
N & =\sum_{X \subseteq G} \prod_{f \in F}\left(1-\prod_{g \in X} h(f, g)\right) \\
|
| 272 |
+
& =\sum_{X \subseteq G} \prod_{f \in F}\left(1+\prod_{g \in X} h(f, g)\right) \bmod 2 \\
|
| 273 |
+
& =\sum_{X \subseteq G} \sum_{Y \subseteq F} \prod_{g \in X} \prod_{f \in Y} h(f, g) \bmod 2 .
|
| 274 |
+
\end{aligned}
|
| 275 |
+
$$
|
| 276 |
+
|
| 277 |
+
On a une égalité similaire pour le nombre $M$ de groupes populaires de filles, ce qui conclut.
|
| 278 |
+

|
| 279 |
+
|
| 280 |
+
Exercice 8 . Pour tout entier $k \geqslant 2$, on note $\mathrm{P}(\mathrm{k})$ le plus grand diviseur premier de $k$.
|
| 281 |
+
Prouver qu'il existe une infinité d'entiers $n$ tels que
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
\mathrm{P}(\mathrm{n})<\mathrm{P}(\mathrm{n}+1)<\mathrm{P}(\mathrm{n}+2)
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
## Solution.
|
| 288 |
+
|
| 289 |
+
Soit $p$ un nombre premier impair. Pour tout entier $k \geqslant 1$, on note $n_{k}=p^{2^{k}}-1$. On a évidemment $\mathrm{P}\left(\mathfrak{n}_{\mathrm{k}}+1\right)=\mathrm{p}$. D'autre part, pour tout entier $i$ tel que $0<i<k$, on a
|
| 290 |
+
|
| 291 |
+
$$
|
| 292 |
+
\mathrm{p}^{2^{k}}=\left(\mathfrak{p}^{2^{i}}\right)^{2^{k-i}}=(-1)^{2^{k-i}}=1 \quad \bmod p^{2^{i}}+1,
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
d'où $n_{k}+2=2 \bmod \left[n_{i}+2\right]$.
|
| 296 |
+
Les entiers $n_{k}+2$ et $n_{i}+2$ étant pairs, il vient alors $\operatorname{pgcd}\left(n_{k}+2, n_{i}+2\right)=2$. Or $n_{k}+2$ n'est pas uns puissance de 2 , car $p^{2^{k}}=1 \bmod 4$ pour $k \geqslant 1$ et donc $\mathfrak{n}_{k}=2 \bmod 4$. Puisque $n_{k}+2>1$, il existe donc un nombre premier impair $q_{k}$ qui divise $n_{k}+2$ et aucun des $n_{i}+2$ pour $i<k$. Cela assure qu'il existe une infinité de nombres premiers impairs qui divisent chacun au moins un des $n_{k}+2$, et donc que la suite $\left(\mathrm{P}\left(n_{k}+2\right)\right)_{k \geqslant 1} n^{\prime}$ 'est pas bornée. On peut donc considérer $k$ minimal tel que $P\left(n_{k}+2\right)>p$.
|
| 297 |
+
|
| 298 |
+
Pour conclure, il reste à prouver que, pour ce choix de $k$, on a $P\left(n_{k}\right)<p$. Or, on a
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
\mathfrak{n}_{k}=\left(\mathfrak{p}^{2^{k-1}}+1\right)\left(\mathfrak{p}^{2^{k-1}}-1\right)=\left(\mathfrak{n}_{k-1}+2\right) \mathfrak{n}_{k-1},
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
d'où, par une récurrence,
|
| 305 |
+
|
| 306 |
+
$$
|
| 307 |
+
n_{k}=(p-1) \prod_{i=1}^{k-1}\left(n_{i}+2\right)
|
| 308 |
+
$$
|
| 309 |
+
|
| 310 |
+
Puisque $n_{k}+1$ est divisible par $p$, ce ne peut être le cas pour $n_{k}$, et la minimalité de $k$ assure qu'aucun des facteurs $n_{i}+2$ n'est divisible par un nombre premier supérieur à $p$. Ainsi, $n_{k} n^{\prime}$ 'a pas de diviseur premier supérieur ou égal à $p$, et donc $\mathrm{P}\left(\mathfrak{n}_{\mathrm{k}}\right)<\mathrm{p}$, comme souhaité.
|
| 311 |
+
|
| 312 |
+
Exercice 9. On note I le centre du cercle inscrit $\gamma$ dans le triangle $A B C$ et $O$ le centre de son cercle circonscrit. Soit $\omega_{\text {A }}$ le cercle qui passe par B et $C$ et qui est tangent à $\gamma$. Les cercles $\omega_{B}$ et $\omega_{C}$ sont définis de manière analogue. On note $A^{\prime}$ l'autre point commun de $\omega_{B}$ et $\omega_{C}$. Les points $B^{\prime}$ et $C^{\prime}$ sont définis de façon semblable.
|
| 313 |
+
|
| 314 |
+
Prouver que les droites $\left(A A^{\prime}\right),\left(B B^{\prime}\right)$ et $\left(C C^{\prime}\right)$ sont concourantes en un point $K$, qui est aligné avec O et I.
|
| 315 |
+
|
| 316 |
+
## Solution.
|
| 317 |
+
|
| 318 |
+
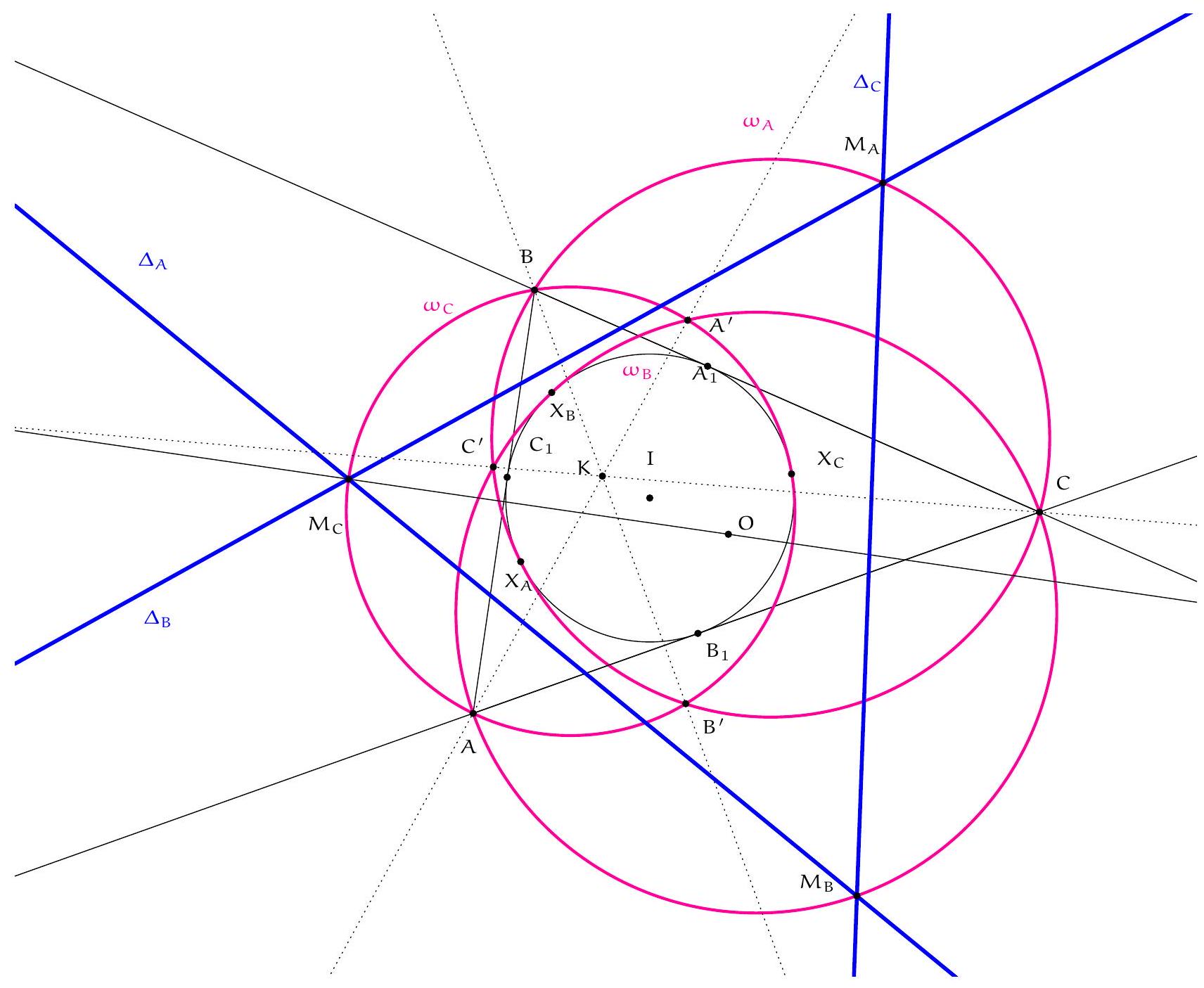
|
| 319 |
+
|
| 320 |
+
On note respectivement $A_{1}, B_{1}, C_{1}$ les points de contact de $\gamma$ avec les côtés $[B C],[C A],[A B]$. Soit $X_{A}$ le point de commun des cercles $\gamma$ et $\omega_{\mathrm{A}}$.
|
| 321 |
+
|
| 322 |
+
Le cercle $\omega_{A}$ est l'image de $\gamma$ par une homothétie de centre $X_{A}$, qui envoie $A_{1}$ en un point $M_{A}$ de $\omega_{\mathrm{A}}$ en lequel la tangente à $\omega_{\mathrm{A}}$ est parallèle à ( BC ). Par conséquent, ce point $M_{\mathrm{A}}$ est le milieu de l'arc $B C$ de $\omega_{A}$ qui ne contient pas $X_{A}$, ce qui assure que
|
| 323 |
+
|
| 324 |
+
$$
|
| 325 |
+
\widehat{M_{A} X_{A}} B=\widehat{M_{A} X_{A}} C=\widehat{M_{A} B C}=\widehat{M_{A} B A_{1}} .
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
Comme, on a évidemment $\widehat{A_{1} M_{A} B}=B{\widehat{M_{A}}}_{A}$, c'est que les triangles $M_{A} B A_{1}$ et $M_{A} X_{A} B$ sont semblables. Il vient alors
|
| 329 |
+
|
| 330 |
+
$$
|
| 331 |
+
\frac{M_{A} B}{M_{A} X_{A}}=\frac{M_{A} A_{1}}{M_{A} B},
|
| 332 |
+
$$
|
| 333 |
+
|
| 334 |
+
ou encore $M_{A} B^{2}=M_{A} A_{1} \cdot M_{A} X_{A}$.
|
| 335 |
+
Cette dernière relation signifie que $M_{A}$ appartient à l'axe radical $\Delta_{B}$ de $B$ et $\gamma$. De même, $M_{A}$ appartient à l'axe radical $\Delta_{\mathrm{C}}$ de C et $\gamma$. Notons que cet axe radical $\Delta_{\mathrm{C}}$ est perpendiculaire à la droite (CI). Or, puisque $A_{1}$ et $B_{1}$ sont les points de contact avec $\gamma$ des des deux tangentes à $\gamma$ issues de $C$, les droites $\left(A_{1} B_{1}\right)$ et $(C I)$ sont perpendiculaires, d'où l'on peut affirmer que $\Delta_{C}$ est parallèle à ( $\left.A_{1} B_{1}\right)$. De même, les droites $\Delta_{B}$ et ( $A_{1} C_{1}$ ) sont parallèles.
|
| 336 |
+
|
| 337 |
+
On définit les points $X_{B}, X_{C}, M_{B}, M_{C}$ et la droite $\Delta_{A}$ de façon analogue à ci-dessus, et on prouve de même que $M_{B}$ appartient à $\Delta_{A}$ et $\Delta_{C}$, que $M_{C}$ appartient à $\Delta_{A}$ et $\Delta_{B}$, et que les droites $\Delta_{A}$ et $\left(B_{1} C_{1}\right)$ sont parallèles. On remarque alors que $\Delta_{A}, \Delta_{B}$ et $\Delta_{C}$ portent les côtés du triangle $M_{A} M_{B} M_{C}$, et les parallélismes signalés ci-dessus assurent que le triangle $M_{A} M_{B} M_{C}$ est l'image de $A_{1} B_{1} C_{1}$ par une homothétie $\Phi$, dont on note K le centre et
|
| 338 |
+
|
| 339 |
+
$$
|
| 340 |
+
r=\frac{M_{A} K}{A_{1} K}=\frac{M_{B} K}{B_{1} K}=\frac{M_{C} K}{C_{1} K}
|
| 341 |
+
$$
|
| 342 |
+
|
| 343 |
+
le rapport. En particulier, les droites $\left(M_{A} A_{1}\right),\left(M_{B} B_{1}\right)$ et $\left(M_{C} C_{1}\right)$ sont concourantes en $K$.
|
| 344 |
+
Si l'on évalue la puissance de K par rapport à $\gamma$, il vient $\mathrm{KA}_{1} \cdot \mathrm{KX}_{A}=\mathrm{KB}_{1} \cdot \mathrm{KX} X_{B}$. Après multiplication des deux côtés par $r$, on obtient $M_{A} K \cdot K X_{A}=M_{B} K \cdot K X_{B}$. Cela signifie que $K$ appartient à l'axe radical $\left(C C^{\prime}\right)$ des cercles $\omega_{A}$ et $\omega_{B}$. On prouve de même que $K$ appartient à $\left(A A^{\prime}\right)$ et à ( $\left.B^{\prime}\right)$.
|
| 345 |
+
|
| 346 |
+
Soit $\mathrm{O}^{\prime}$ l'image de I par $\Phi$. Le point $\mathrm{O}^{\prime}$ appartient donc à la droite passant par $M_{A}$ et parallèle à $\left(A_{1} I\right)$ (et donc perpendiculaire à (BC)). Comme $M$ est le milieu d'un arc $B C$ de $\omega_{A}$, cette droite est donc la médiatrice de $[\mathrm{BC}]$. De même, le point $\mathrm{O}^{\prime}$ appartient à la médiatrice de $[A C]$, et finalement c'est que $\mathrm{O}^{\prime}=\mathrm{O}$. Par suite, les points $\mathrm{I}, \mathrm{O}, \mathrm{K}$ sont alignés.
|
| 347 |
+

|
| 348 |
+
$\mathcal{F i n}$
|
| 349 |
+
|
French_STS/md/fr-ofm-2012-2013-envoi6-corrige.md
ADDED
|
@@ -0,0 +1,207 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Envoi no. 6 : géométrie
|
| 2 |
+
|
| 3 |
+
Exercice 1. Soit $A B C$ un triangle rectangle isocèle en $B$. Soit $M$ un point de l'arc $A C$ du cercle de centre $B$ passant par $A$ et $C, H$ son projeté orthogonal sur $(A B)$. On note $I$ le centre du cercle inscrit à $B H M$ et $J$ le centre du cercle exinscrit dans l'angle $B$ ( $J$ est donc l'intersection de la bissectrice intérieure en $B$ avec les bissectrices extérieures en $H$ et $M)$. Montrer que $M I A J$ est un carré.
|
| 4 |
+
|
| 5 |
+
## Solution.
|
| 6 |
+
|
| 7 |
+
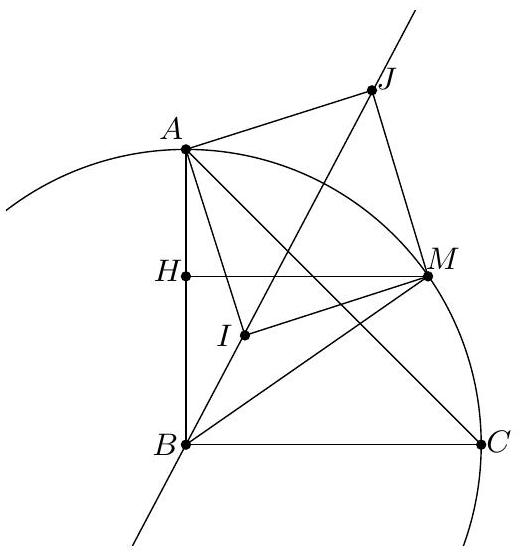
|
| 8 |
+
|
| 9 |
+
On observe d'abord que $(M I) \perp(M J)$ puisque dans un triangle, les bissectrices intérieure et extérieure en un point sont perpendiculaires.
|
| 10 |
+
|
| 11 |
+
D'autre part, $\widehat{M I J}=180^{\circ}-\widehat{B I M}=\widehat{I B M}+\widehat{B M I}=\frac{1}{2}(\widehat{H B M}+\widehat{B M H})=$ $45^{\circ}$. Comme $M I J$ est rectangle en $M$, on en déduit qu'il est rectangle isocèle en $M$.
|
| 12 |
+
|
| 13 |
+
De plus, $(I J)$ est la bissectrice de $\widehat{M B H}=\widehat{M B A}$, et $M B A$ est isocèle en $B$, donc $(I J)$ est la médiatrice de $[A M]$. On en déduit que $A I J$ est le symétrique du triangle rectangle isocèle $M I J$ par rapport à la droite $(I J)$, donc $M I A J$ est un carré.
|
| 14 |
+
|
| 15 |
+
Exercice 2. Soit $A B C D$ un quadrilatère convexe. Soit $M$ l'intersection entre les bissectrices intérieures des angles $B$ et $C$, et $N$ l'intersection entre les bissectrices intérieures des angles $A$ et $D$. Montrer que les droites $A B, C D$ et $M N$ sont concourantes.
|
| 16 |
+
|
| 17 |
+
Solution. Quitte à échanger les rôles de $A$ et de $B$ et les rôles de $C$ et de $D$, on peut supposer que $A$ et $D$ se trouvent sur les segments $[E B]$ et $[E C]$ respectivement.
|
| 18 |
+
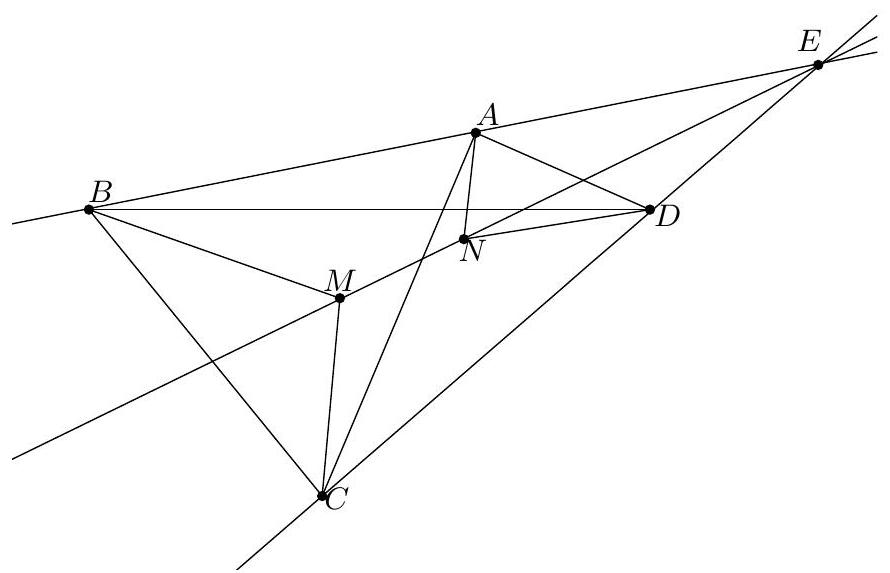
|
| 19 |
+
|
| 20 |
+
Notons $E$ le point d'intersection entre $(A B)$ et $(C D)$. Alors $M$ est l'intersection des bissectrices intérieures des angles $B$ et $C$ du triangle $E B C$, donc $M$ est le centre du cercle inscrit à $E B C$. En particulier il se trouve sur la bissectrice intérieure en $E$.
|
| 21 |
+
|
| 22 |
+
De même, $N$ est le point d'intersection des bissectrices extérieures en $A$ et $D$ du triangle $E A D$, donc $N$ est le centre du cercle exinscrit dans l'angle $E$ de $E A D$. En particulier, il se trouve sur la bissectrice intérieure en $E$. Ceci prouve que $E, M, N$ sont alignés.
|
| 23 |
+
|
| 24 |
+
Exercice 3. Soit $A B C D$ un quadrilatère inscriptible, $L=(A C) \cap(B D), J$ et $K$ les pieds des perpendiculaires à $(A D)$ et $(B C)$ passant par $L$ et $I$ le milieu de $[C, D]$. Montrer que $I J=I K$.
|
| 25 |
+
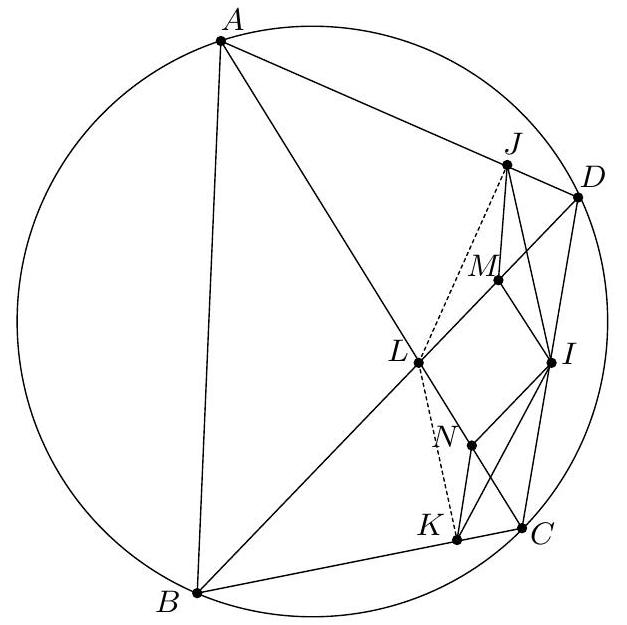
|
| 26 |
+
|
| 27 |
+
## Solution 1.
|
| 28 |
+
|
| 29 |
+
Il est facile de voir en utilisant le théorème de l'angle inscrit que $B L C$ et $A L D$ sont semblables, et que $C K L$ et $D J L$ sont semblables.
|
| 30 |
+
|
| 31 |
+
Notons $M$ et $N$ les milieux respectifs de $[L D]$ et $[L C]$. Alors $L N I M$ est un parallélogramme. On en déduit que $N L=I M$. Or, $C K L$ est un triangle rectangle en $K$ donc $N L=N K$, d'où $N K=I M$. De même, $M J=I N$.
|
| 32 |
+
|
| 33 |
+
Comme $M J L$ est isocèle en $M$, on a $\widehat{J M L}=180^{\circ}-2 \widehat{M L J}=180^{\circ}-$ $2\left(90^{\circ}-\widehat{L D J}\right)=2 \widehat{B D A}$, et de même $\widehat{K N L}=2 \widehat{B C A}$. Or, $\widehat{B D A}=\widehat{B C A}$ donc $\widehat{J M L}=\widehat{K N L}$. On en déduit que $\widehat{I M J}=360^{\circ}-\widehat{J M L}-\widehat{L M I}=$ $360^{\circ}-\widehat{K N L}-\widehat{L N I}=\widehat{K N I}$ (l'avant-dernière égalité découlant du fait que $L M I N$ est un parallélogramme).
|
| 34 |
+
|
| 35 |
+
Des égalités $\widehat{I M J}=\widehat{K N I}, N K=I M$ et $M J=I N$, on déduit que les triangles $I M J$ et $K N I$ sont isométriques, et en particulier que $I J=I K$.
|
| 36 |
+
|
| 37 |
+
## Solution 2.
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{aligned}
|
| 41 |
+
I J^{2}-I K^{2} & =\overrightarrow{I J} \cdot \overrightarrow{I J}-\overrightarrow{I K} \cdot \overrightarrow{I K}=(\overrightarrow{I J}+\overrightarrow{I K}) \cdot(\overrightarrow{I J}-\overrightarrow{I K}) \\
|
| 42 |
+
& =(\overrightarrow{I D}+\overrightarrow{D J}+\overrightarrow{I C}+\overrightarrow{C K}) \cdot \overrightarrow{K J}=(\overrightarrow{D J}+\overrightarrow{C K}) \cdot(\overrightarrow{L J}-\overrightarrow{L K}) \\
|
| 43 |
+
& =\overrightarrow{C K} \cdot \overrightarrow{L J}-\overrightarrow{D J} \cdot \overrightarrow{L K} \quad \operatorname{car}(D J) \perp(L J) \text { et }(C K) \perp(L K) \\
|
| 44 |
+
& =C K \cdot L J \cos (\overrightarrow{C K}, \overrightarrow{L J})-D J \cdot L K \cos (\overrightarrow{D J}, \overrightarrow{L K})
|
| 45 |
+
\end{aligned}
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
Or, $\overrightarrow{L K}$ fait un angle orienté de $+90^{\circ}$ par rapport à $\overrightarrow{C K}$, et $\overrightarrow{D J}$ fait un angle orienté de $+90^{\circ}$ par rapport à $\overrightarrow{L J}$, donc les deux cosinus sont égaux. Par conséquent, il suffit de montrer que $C K \cdot L J=D J \cdot L K$ : ceci découle du fait que
|
| 49 |
+
|
| 50 |
+
$$
|
| 51 |
+
\frac{C K}{L K}=\cot \widehat{K C L}=\cot \widehat{B C A}=\cot \widehat{B D A}=\cot \widehat{L D J}=\frac{D J}{L J}
|
| 52 |
+
$$
|
| 53 |
+
|
| 54 |
+
Exercice 4. Soit $A B C$ un triangle. On note $O$ le centre de son cercle circonscrit. Soient $D, E, F$ des points situés sur $[B, C],[C, A]$ et $[A, B]$ respectivement. On suppose que $F B=F D$ et $E D=E C$. Le cercle de centre $F$ et de rayon $F B$ et le cercle de centre $E$ et de rayon $E C$ se recoupent en $G$. Montrer que $A, F, O, E, G$ sont cocycliques.
|
| 55 |
+
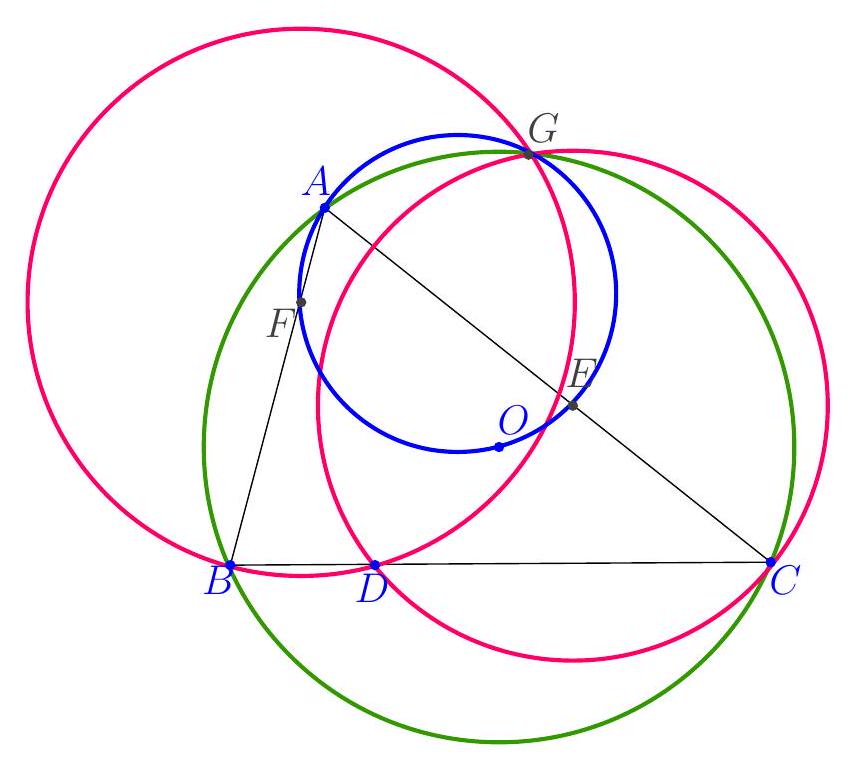
|
| 56 |
+
|
| 57 |
+
## Solution.
|
| 58 |
+
|
| 59 |
+
Les triangles $B F D$ et $C E D$ étant isocèles, on a $(D E, D F)=(D E, D C)+$ $(D B, D F)=(C D, C E)+(B F, B D)=(B C, A C)+(A B, B C)=(A B, A C)$.
|
| 60 |
+
|
| 61 |
+
Comme $E G=E D$ et $F G=F D$, les points $E$ et $F$ appartiennent à la médiatrice de $[G D]$ donc le quadrilatère $F G E D$ est symétrique par rapport à $(F E)$. On en déduit que $(D E, D F)=(G F, G E)$ donc $(G F, G E)=$ $(A B, A C)=(A F, A E)$. Il en résulte que $F, A, G, E$ sont cocycliques.
|
| 62 |
+
|
| 63 |
+
On a $2(\overrightarrow{G B}, \overrightarrow{G D})=(\overrightarrow{F B}, \overrightarrow{F D})=\Pi-2(\overrightarrow{B D}, \overrightarrow{B F})$ où $\Pi$ est l'angle plat (cette dernière égalité provenant du fait que $F B D$ est isocèle en $F$ ). On montre de même que $2(\overrightarrow{G D}, \overrightarrow{G C})=\Pi-2(\overrightarrow{C E}, \overrightarrow{C D})$. En additionnant ces deux égalités, on obtient
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
\begin{aligned}
|
| 67 |
+
2(\overrightarrow{G B}, \overrightarrow{G C}) & =-2(\overrightarrow{B D}, \overrightarrow{B F})-2(\overrightarrow{C E}, \overrightarrow{C D}) \\
|
| 68 |
+
& =-2(\overrightarrow{B C}, \overrightarrow{B A})-2(\overrightarrow{C A}, \overrightarrow{C B})-2(\overrightarrow{C B}, \overrightarrow{B C}) \\
|
| 69 |
+
& =-2(\overrightarrow{C A}, \overrightarrow{B A})=2(\overrightarrow{A B}, \overrightarrow{A C})
|
| 70 |
+
\end{aligned}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Donc $A, B, C, G$ sont cocycliques.
|
| 74 |
+
Comme $F G=F B$ et $O B=O G$, les points $G$ et $B$ sont symétriques par rapport à $(O F)$ donc $2(\overrightarrow{O G}, \overrightarrow{O F})=(\overrightarrow{O G}, \overrightarrow{O B})$. De même, $2(\overrightarrow{O E}, \overrightarrow{O G})=$ $(\overrightarrow{O C}, \overrightarrow{O G})$. En additionnant ces deux égalités, il vient $2(\overrightarrow{O E}, \overrightarrow{O F})=(\overrightarrow{O C}, \overrightarrow{O B})=$ $2(\overrightarrow{A C}, \overrightarrow{A B})=2(\overrightarrow{E A}, \overrightarrow{A F})$, donc $A, O, E, F$ sont cocycliques.
|
| 75 |
+
|
| 76 |
+
Exrercice 5. Soient $A, B, C, D, E$ des points dans cet ordre sur un demi-cercle de rayon 1. Démontrer que
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
A B^{2}+B C^{2}+C D^{2}+D E^{2}+A B \cdot B C \cdot C D+B C \cdot C D \cdot D E \leqslant 4
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
Solution. En remplaçant $E$ par le point diamétralement opposé à $A$, la quantité $D E$ augmente et les autres longueurs de la formule ne changent pas, donc on se ramène au cas où $[A E]$ est un diamètre.
|
| 83 |
+
|
| 84 |
+
D'après la formule d'Al-Kashi,
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\begin{aligned}
|
| 88 |
+
A B^{2}+B C^{2} & =A C^{2}+2 A B \cdot B C \cos \widehat{A B C} \\
|
| 89 |
+
C D^{2}+D E^{2} & =C E^{2}+2 C D \cdot D E \cos \widehat{C D E} \\
|
| 90 |
+
A C^{2}+C E^{2} & =A E^{2}
|
| 91 |
+
\end{aligned}
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
En additionnant ces trois égalités, compte tenu de $A E^{2}=4$, on obtient
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
A B^{2}+B C^{2}+C D^{2}+D E^{2}=4+2 A B \cdot B C \cos \widehat{A B C}+2 C D \cdot D E \cos \widehat{C D E},
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
donc on se ramène à montrer que
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\begin{gathered}
|
| 104 |
+
2 A B \cdot B C \cos \widehat{A B C}+2 C D \cdot D E \cos \widehat{C D E}+A B \cdot B C \cdot C D+B C \cdot C D \cdot D E \leqslant 0 . \\
|
| 105 |
+
\text { Or, } C D \leqslant C E=A E \cos \widehat{A E C}=2 \cos \left(180^{\circ}-\widehat{A B C}\right)=-2 \cos \widehat{A B C} \text {, donc } \\
|
| 106 |
+
A B \cdot B C \cdot C D+2 A B \cdot B C \cos \widehat{A B C} \leqslant 0
|
| 107 |
+
\end{gathered}
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
et de même
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
B C \cdot C D \cdot D E+2 C D \cdot D E \cos \widehat{C D E} \leqslant 0
|
| 114 |
+
$$
|
| 115 |
+
|
| 116 |
+
On conclut en additionnant ces deux dernières inégalités.
|
| 117 |
+
|
| 118 |
+
Exercice 6. Soit $A B C D E F$ un hexagone régulier et $M \in[A, C], N \in[C, E]$. On suppose que $\frac{A M}{A C}$ et $\frac{C N}{C E}$ sont égaux à un nombre $r>0$, et que $B, M, N$ sont colinéaires. Déterminer la valeur de $r$.
|
| 119 |
+
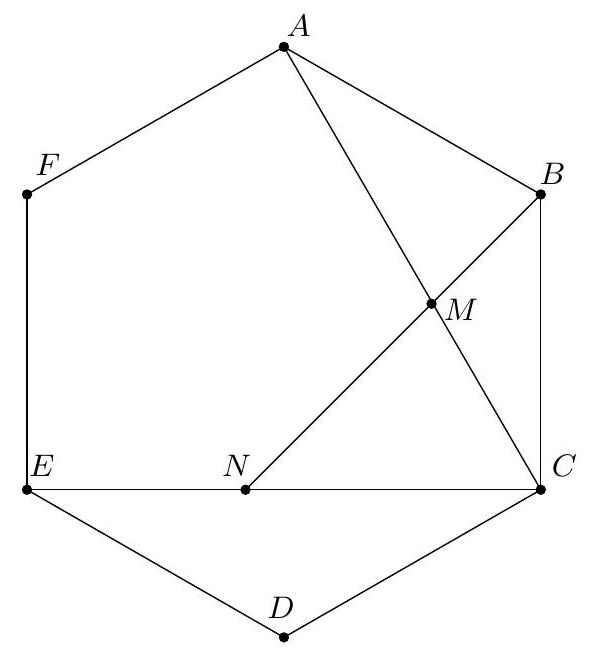
|
| 120 |
+
|
| 121 |
+
## Solution.
|
| 122 |
+
|
| 123 |
+
On peut supposer que l'hexagone est inscrit dans un cercle de rayon 1. On se place dans un repère tel que les coordonnées de $A, B, C$ sont respectivement $A=(0,1), B=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ et $C=\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$.
|
| 124 |
+
|
| 125 |
+
Comme $C E=\sqrt{3}$, on a $C N=r \sqrt{3}$ donc $\overrightarrow{C N}=(-r \sqrt{3}, 0)$. On en déduit que
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
N=\left(\frac{\sqrt{3}}{2}-r \sqrt{3},-\frac{1}{2}\right)
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
Comme $\overrightarrow{A C}=\left(\frac{\sqrt{3}}{2},-\frac{3}{2}\right)$, on a $\overrightarrow{A M}=\left(\frac{\sqrt{3}}{2} r,-\frac{3 r}{2}\right)$ donc
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
M=\left(\frac{\sqrt{3}}{2} r, 1-\frac{3 r}{2}\right)
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
On calcule aisément que
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
\overrightarrow{B M}=\left(\frac{\sqrt{3}}{2}(r-1), \frac{1}{2}-\frac{3 r}{2}\right), \quad \overrightarrow{B N}=(-r \sqrt{3},-1)
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
Le fait que $B, M, N$ sont alignés signifie que ces deux vecteurs sont colinéaires, ce qui équivaut à
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
\frac{\sqrt{3}}{2}(1-r)+r \sqrt{3}\left(\frac{1}{2}-\frac{3 r}{2}\right)=0
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
ce qui se simplifie en $r=\frac{1}{\sqrt{3}}$.
|
| 150 |
+
|
| 151 |
+
Exercice 7. Soit $A B C$ un triangle et $M$ un point de $[B, C]$. Soit $\omega$ un cercle tangent à $(A B)$ en $T$ et à $(B C)$ en $K$ et tangent au cercle circonscrit à $A M C$ en $P$. Montrer que si $(K T) / /(A M)$ alors les cercles circonscrits à $K P C$ et $A P T$ sont tangents en $P$.
|
| 152 |
+
|
| 153 |
+
## Solution.
|
| 154 |
+
|
| 155 |
+

|
| 156 |
+
|
| 157 |
+
Rappelons d'abord que si $A, B, C$ sont trois points d'un cercle $\Gamma$, et si $\delta$ est la tangente en $B$ à $\Gamma$, alors on a l'égalité d'angles de droites $(\delta, B C)=(A B, A C)$.
|
| 158 |
+
|
| 159 |
+
Soient $\delta$ et $\delta^{\prime}$ les tangentes en $P$ aux cercles $(K P C)$ et $(A P T)$ respectivement. On a
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
(\delta, P K)=(C P, C K)=(C P, C M)=(A P, A M)
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
et
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\begin{aligned}
|
| 169 |
+
\left(\delta^{\prime}, P K\right) & =\left(\delta^{\prime}, P T\right)+(P T, P K)=(A P, A T)+(T B, T K) \\
|
| 170 |
+
& =(A P, A M)+(A M, A T)+(T B, T K)=(A P, A M)
|
| 171 |
+
\end{aligned}
|
| 172 |
+
$$
|
| 173 |
+
|
| 174 |
+
puisque $(T B)=(A T)$ et $(A M)=(T K)$.
|
| 175 |
+
On en déduit que $\delta$ et $\delta^{\prime}$ sont parallèles. Or, elles ont un point commun, donc elles sont égales.
|
| 176 |
+
|
| 177 |
+
Exercice 8. Soient $\omega_{1}$ et $\omega_{2}$ deux cercles sécants en deux points $X$ et $Y$. Un cercle $\omega$ est tangent intérieurement à $\omega_{1}$ et $\omega_{2}$ en $P$ et $Q$ respectivement. Le segment $[X, Y]$ coupe $\omega$ en $M$ et $N$. Les demi-droites $[P, M)$ et $[P, N)$ coupent $\omega_{1}$ en $A$ et $D$; les demi-droites $[Q, M)$ et $[Q, N)$ coupent $\omega_{2}$ en $B$ et $C$. Montrer que $A B=C D$.
|
| 178 |
+
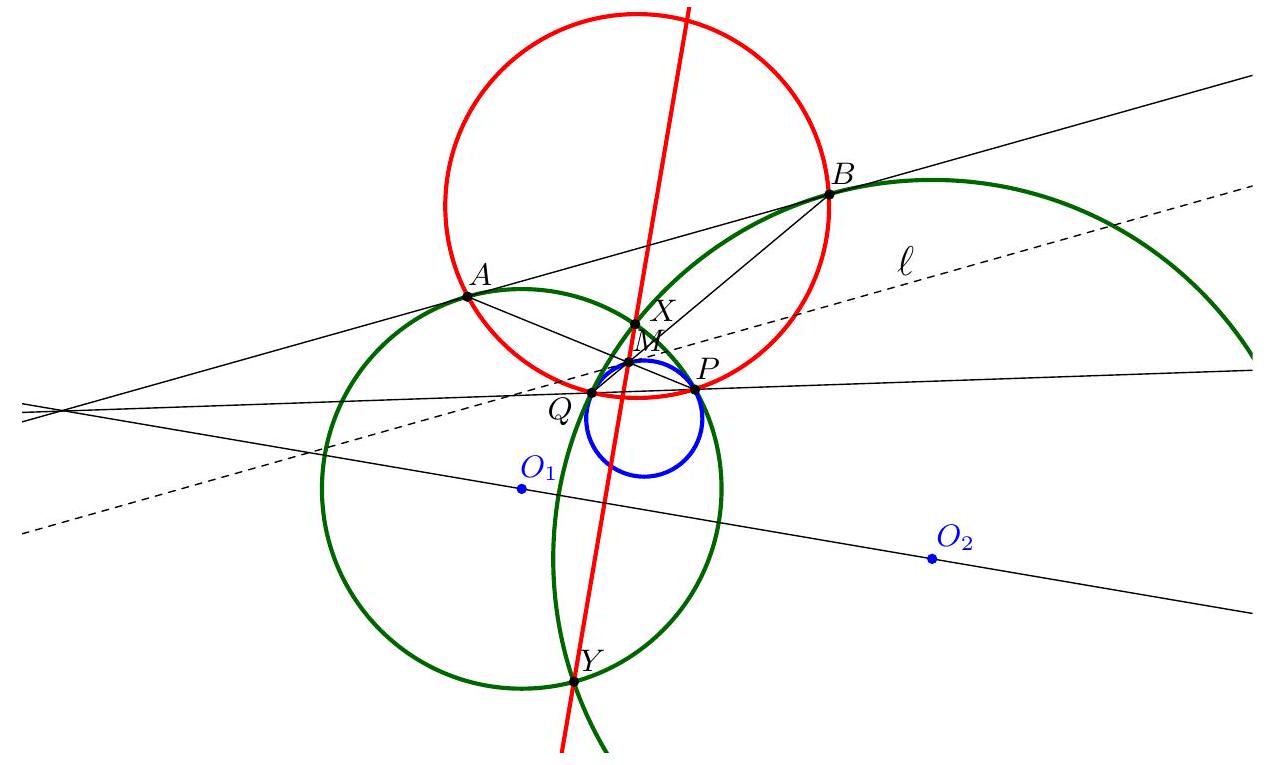
|
| 179 |
+
|
| 180 |
+
Soit $\ell$ la tangente en $M$ à $\omega$ et $\ell_{1}$ la tangente en $A$ à $\omega_{1}$. Comme $\omega$ est tangent en $P$ à $\omega_{1}$, il existe une homothétie $h$ de centre $P$ qui envoie $\omega \operatorname{sur} \omega_{1}$. Or, $P, M, A$ sont alignés donc $h(M)=A$. On en déduit que $h(\ell)=\ell_{1}$, et donc $\ell / / \ell_{1}$.
|
| 181 |
+
|
| 182 |
+
D'autre part, comme $M$ est sur l'axe radical de $\omega_{1}$ et $\omega_{2}$, on a $\overline{M A} \cdot \overline{M P}=$ $\overline{M B} \cdot \overline{M Q}$ donc $A, B, P, Q$ sont cocycliques. On en déduit que
|
| 183 |
+
|
| 184 |
+
$$
|
| 185 |
+
(A B, A P)=(Q B, Q P)=(Q M, Q P)=(\ell, M P)=\left(\ell_{1}, A P\right)
|
| 186 |
+
$$
|
| 187 |
+
|
| 188 |
+
d'où $(A B)=\ell_{1}$. Autrement dit, $(A B)$ est tangente en $A$ à $\omega_{1}$. Mais de même, $(A B)$ est tangente en $B$ à $\omega_{2}$, donc $(A B)$ est une tangente commune à $\omega_{1}$ et $\omega_{2}$. De même, $(C D)$ est une tangente commune à $\omega_{1}$ et $\omega_{2}$, donc $A B=C D$.
|
| 189 |
+
|
| 190 |
+
Exrtcice 9. Soit $A B C D$ un quadrilatère inscriptible. On note $K$ le point d'intersection des diagonales. Soient $M$ et $N$ les milieux de $[A, C]$ et $[B, D]$. Les cercles circonscrits à $A D M$ et $B C M$ se recoupent en un point $L$. Montrer que $K, L, M, N$ sont cocycliques.
|
| 191 |
+
|
| 192 |
+
## Solution.
|
| 193 |
+
|
| 194 |
+
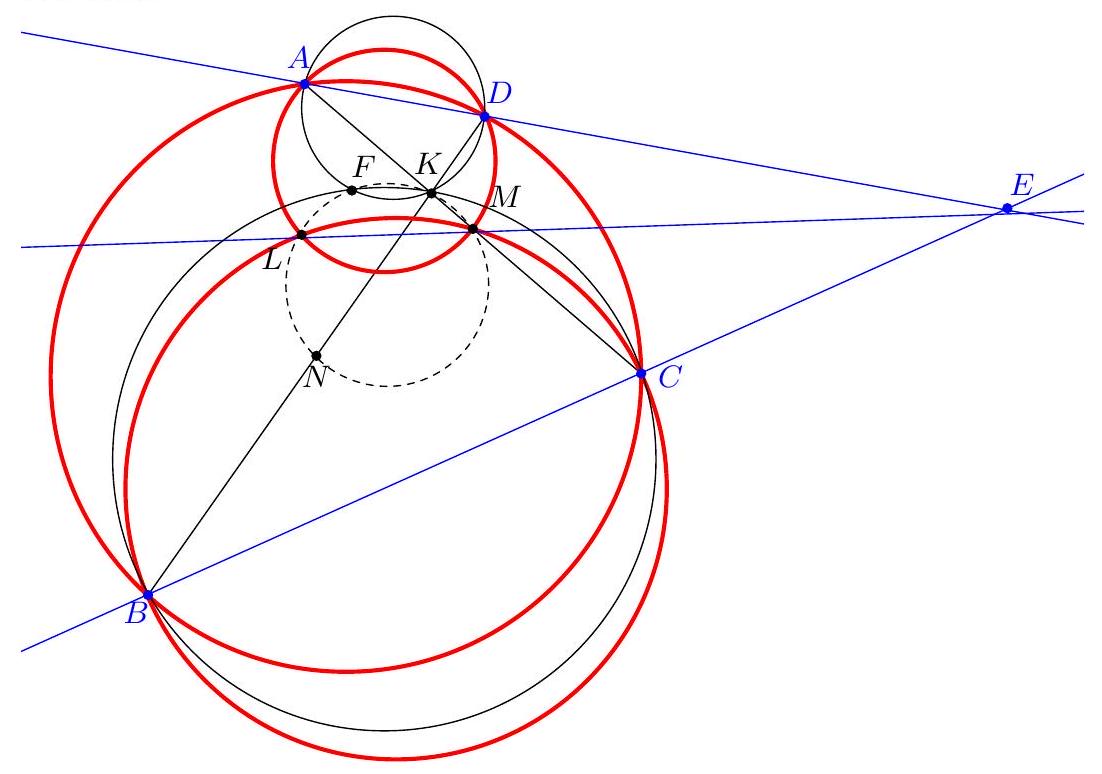
|
| 195 |
+
|
| 196 |
+
Notons $E$ le centre radical des trois cercles $A B C, A D M, B C M$. Les triplets $(E, A, D),(E, L, M)$ et $(E, B, C)$ sont alignés.
|
| 197 |
+
|
| 198 |
+
Soit $F$ le point où les cercles $A D K$ et $B C K$ se recoupent. On a $(F A, F D)=$ $(K A, K D)=(K C, K B)=(F C, F B)$ et $(A D, A F)=(K D, K F)=(K B, K F)=$ $(C B, C F)$, donc les triangles $F A D$ et $F C B$ sont semblables. Soit $s$ la similitude de centre $F$ qui envoie $A$ sur $D$ et $C$ sur $B$. Alors $s(M)=N$, donc l'angle de $s$ est à la fois égal à $(F M, F N)$ et à $(A C, D B)=(K M, K N)$. Par conséquent, $F, K, M, N$ sont cocycliques.
|
| 199 |
+
$E$ est l'intersection de $(A D)$ et de $(B C)$, donc il est le centre radical des cercles $A B C D, A D K$ et $B C K$. Par conséquent, $E, F, K$ sont alignés. En utilisant la puissance d'un point par rapport à un cercle, on a
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
\overline{E K} \cdot \overline{E F}=\overline{E A} \cdot \overline{E D}=\overline{E B} \cdot \overline{E C}=\overline{E M} \cdot \overline{E L},
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
donc $M, L, K, F$ sont cocycliques.
|
| 206 |
+
Finalement, $L$ et $N$ sont sur le cercle $M K F$ donc $K, L, M, N$ sont cocycliques.
|
| 207 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-1-solutions.md
ADDED
|
@@ -0,0 +1,302 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## OFM 2013-2014 : solution de l'envoi no. 1
|
| 2 |
+
|
| 3 |
+
## Exercices groupe B
|
| 4 |
+
|
| 5 |
+
Exercice 1. Soient $A, B, C, D$ quatre points sur un même cercle. Notons $A^{\prime}$ et $C^{\prime}$ les projetés orthogonaux de $A$ et $C$ sur $(B D)$, et $B^{\prime}$ et $D^{\prime}$ les projetés orthogonaux de $B$ et $D$ sur $(A C)$. Montrer que $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ sont cocycliques.
|
| 6 |
+
|
| 7 |
+
## Solution.
|
| 8 |
+
|
| 9 |
+
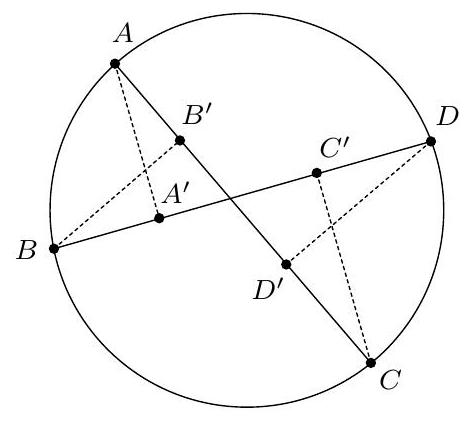
|
| 10 |
+
|
| 11 |
+
Comme $A, B, A^{\prime}, B^{\prime}$ sont cocycliques (sur le cercle de diamètre $[A B]$ ), les angles orientés de droites $\left(B A^{\prime}, B A\right)$ et $\left(B^{\prime} A^{\prime}, B^{\prime} A\right)$ sont égaux, donc $(B D, B A)=\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)$. De même, $(C D, C A)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$. Or, $(C D, C A)=(B D, B A)$ puisque $A, B, C, D$ sont cocycliques, donc $\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$, ce qui prouve que $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ sont cocycliques.
|
| 12 |
+
|
| 13 |
+
Exercice 2. Sur la diagonale $[B D]$ d'un carré $A B C D$ on a choisi un point $E$. Soient $O_{1}$ et $O_{2}$ les centres des cercles circonscrits aux triangles $A B E$ et $A D E$ respectivement. Montrer que $A O_{1} E O_{2}$ est un carré.
|
| 14 |
+
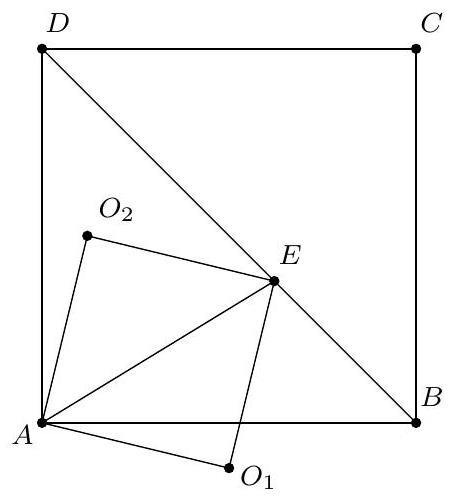
|
| 15 |
+
|
| 16 |
+
## Solution.
|
| 17 |
+
|
| 18 |
+
$\widehat{A O_{1} E}=2 \widehat{A B E}=90^{\circ}$ et $O_{1} A=O_{1} E$ donc $A O_{1} E$ est un triangle isocèle rectangle en $O_{1}$. De même, $A O_{2} E$ est un triangle isocèle rectangle en $O_{2}$.
|
| 19 |
+
|
| 20 |
+
Comme $O_{1}$ et $O_{2}$ ne sont pas dans le même demi-plan délimité par $(A E)$, on en déduit que $A O_{1} E O_{2}$ est un carré.
|
| 21 |
+
|
| 22 |
+
Exercice 3. Un quadrilatère $A B C D$ est inscrit dans un cercle. Ses diagonales se coupent au point $K$. Le cercle passant par $A, B, K$ croise les droites $(B C)$ et $(A D)$ aux points $M$ et $N$ respectivement. Montrer que $K M=K N$.
|
| 23 |
+
|
| 24 |
+
## Solution.
|
| 25 |
+
|
| 26 |
+
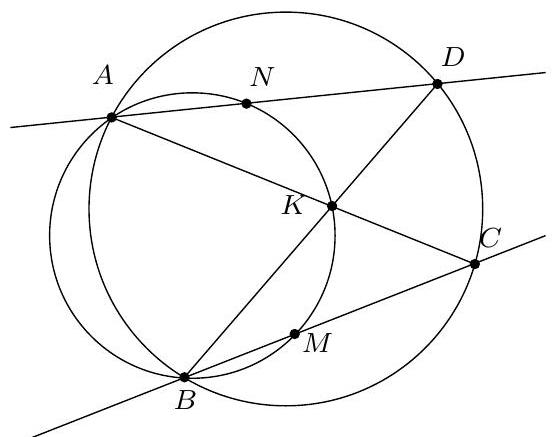
|
| 27 |
+
|
| 28 |
+
On a $(N M, N K)=(B M, B K)=(B C, B D)=(A C, A D)=(A K, A N)=(M K, M N)$ donc $M K N$ est isocèle en $K$.
|
| 29 |
+
|
| 30 |
+
## Exercices communs
|
| 31 |
+
|
| 32 |
+
Exercice 4. Soit $A B C$ un triangle dont tous les angles sont aigus, et dont l'angle $\widehat{B}$ est de 60 degrés ( $=\pi / 3$ radian). Les hauteurs $[A D]$ et $[C E]$ se coupent au point $H$. Prouver que le centre du cercle circonscrit au triangle $A B C$ est situé sur la bissectrice commune des angles $\widehat{A H E}$ et $\widehat{C H D}$.
|
| 33 |
+

|
| 34 |
+
|
| 35 |
+
## Solution.
|
| 36 |
+
|
| 37 |
+
Puisque $B, E, H, D$ sont sur le cercle de diamètre $[B H]$, on a $\widehat{D H E}=180^{\circ}-\widehat{E B D}=$ $120^{\circ}$, donc $\widehat{A H C}=120^{\circ}$. Comme $\widehat{A O C}=2 \widehat{A B C}=120^{\circ}$, on en déduit que $A, C, O, H$ sont cocycliques.
|
| 38 |
+
|
| 39 |
+
Par conséquent, $\widehat{C H O}=\widehat{C A O}=\frac{1}{2}(\widehat{C A O}+\widehat{O C A})=\frac{1}{2}\left(180^{\circ}-\widehat{A O C}\right)=90^{\circ}-\widehat{A B C}=$ $30^{\circ}$.
|
| 40 |
+
|
| 41 |
+
De plus, comme $(C H) \perp(A B)$ et $(A H) \perp(B C)$, on a $\widehat{C H D}=\widehat{A B C}=60^{\circ}$, donc $O$ est sur la bissectrice de $\widehat{C H D}$.
|
| 42 |
+
|
| 43 |
+
Exercice 5. A l'extérieur du triangle $A B C$ on construit les deux points $X$ et $Y$ vérifiant :
|
| 44 |
+
|
| 45 |
+
- le triangle $A X B$ est isocèle de base $[A B]$;
|
| 46 |
+
- le triangle $B Y C$ est isocèle de base $[B C]$;
|
| 47 |
+
$-\widehat{A X B}+\widehat{B Y C}=180^{\circ}$.
|
| 48 |
+
Soit $Z$ le milieu de $[A C]$. Montrer que les droites $(X Z)$ et $(Y Z)$ sont perpendiculaires.
|
| 49 |
+
|
| 50 |
+
Solution. Notons $D$ et $E$ les milieux de $[B C]$ et $[A B]$.
|
| 51 |
+
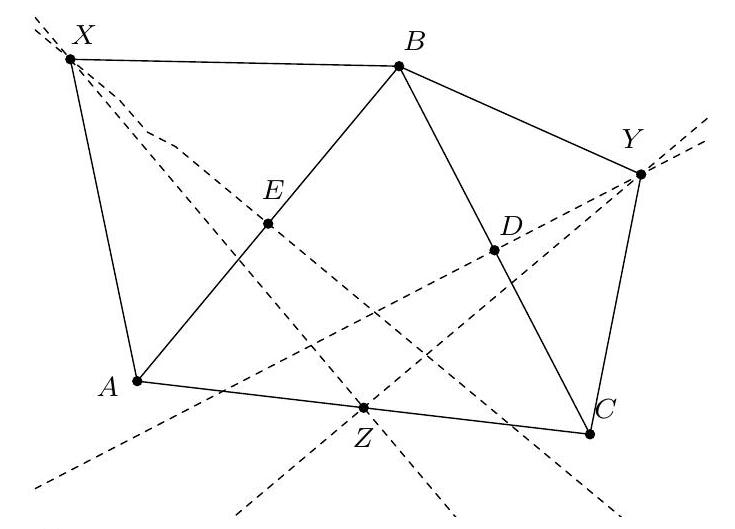
|
| 52 |
+
|
| 53 |
+
On a
|
| 54 |
+
|
| 55 |
+
- $(X E) \perp(D Z)$ car $(D Z) / /(A B)$
|
| 56 |
+
- $(E Z) \perp(D Y)$ car $(E Z) / /(B C)$
|
| 57 |
+
- $\frac{X E}{D Z}=\frac{X E}{E A}=\frac{C D}{D Y}=\frac{E Z}{D Y}$ (la deuxième égalité provient du fait que les triangles rectangles $X E A$ et $C D Y$ sont semblables)
|
| 58 |
+
donc $X E Z$ et $Z D Y$ sont semblables. Comme $(X E) \perp(D Z)$, on en déduit que $(X Z) \perp$ $(Z Y)$.
|
| 59 |
+
|
| 60 |
+
Exercice 6. Le sommet $B$ d'un angle $\widehat{A B C}$ se trouve à l'extérieur d'un cercle $\omega$ tandis que les demi-droites $[B A)$ et $[B C)$ le traversent. Soit $K$ un point d'intersection du cercle $\omega$ avec $[B A)$. La perpendiculaire à la bissectrice de l'angle $\widehat{A B C}$ passant par $K$ recoupe le cercle au point $P$, et la droite $(B C)$ au point $M$. Montrer que le segment $[P M]$ est deux fois plus long que la distance entre le centre de $\omega$ et la bissectrice de $\widehat{A B C}$.
|
| 61 |
+
|
| 62 |
+
## Solution.
|
| 63 |
+
|
| 64 |
+
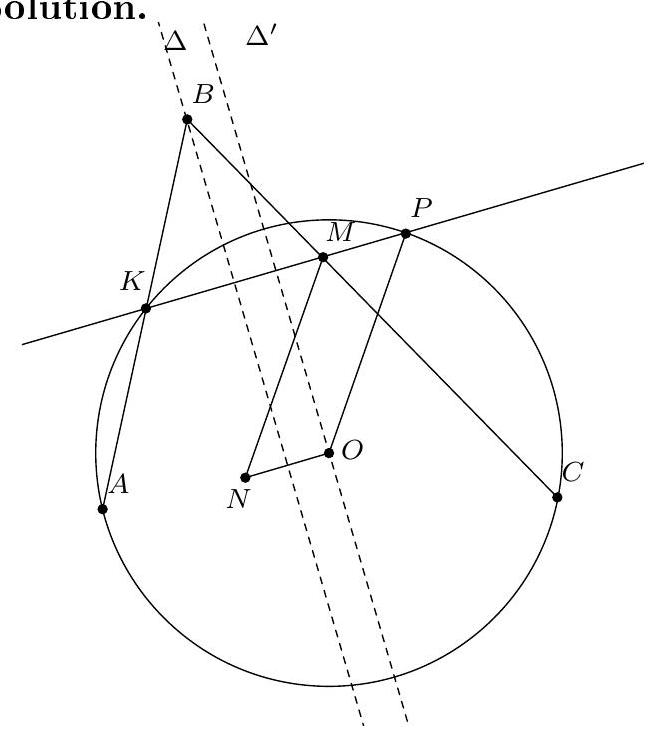
|
| 65 |
+
|
| 66 |
+
Soit $O$ le centre du cercle $\omega$. Notons $\Delta$ la bissectrice de $\widehat{A B C}, \Delta^{\prime}$ la parallèle à $\Delta$ passant par $O$ et $N$ le symétrique de $O$ par rapport à $\Delta$.
|
| 67 |
+
|
| 68 |
+
La symétrie $s_{\Delta^{\prime}}$ par rapport à $\Delta^{\prime}$ envoie $O$ sur $O$ et $P \operatorname{sur} K\left(\operatorname{car}(P K) \perp \Delta^{\prime}\right.$ et $\Delta^{\prime}$ passe par $O$ ).
|
| 69 |
+
|
| 70 |
+
La symétrie $s_{\Delta}$ par rapport à $\Delta$ envoie $O$ sur $N$ et $K$ sur $M$.
|
| 71 |
+
Par conséquent, la composée $s_{\Delta} \circ s_{\Delta^{\prime}}$ envoie $O$ sur $N$ et $P$ sur $M$. Or, $s_{\Delta} \circ s_{\Delta}^{\prime}$ est une translation, donc $M N O P$ est un parallélogramme. Il s'ensuit que $P M=O N=2 d(O, \Delta)$.
|
| 72 |
+
|
| 73 |
+
## Exercices groupe A
|
| 74 |
+
|
| 75 |
+
Exercice 7. Soit $A B C D$ un quadrilatère convexe. On considère les deux quadrilatères convexes $F_{1}$ et $F_{2}$, dont chacun a deux sommets opposés qui sont les milieux des diagonales $[A C]$ et $[B D]$, et dont les deux autres sommets sont les milieux des côtés opposés du quadrilatère $A B C D$. Montrer que les aires de $F_{1}$ et de $F_{2}$ sont égales si et seulement si au moins l'une des diagonales du quadrilatère $A B C D$ le divise en triangles d'aires égales.
|
| 76 |
+
|
| 77 |
+
Solution. Notons $I, J, K, L, M, N$ les milieux de $[A C],[B D],[A B],[B C],[C D]$ et $[D A]$.
|
| 78 |
+
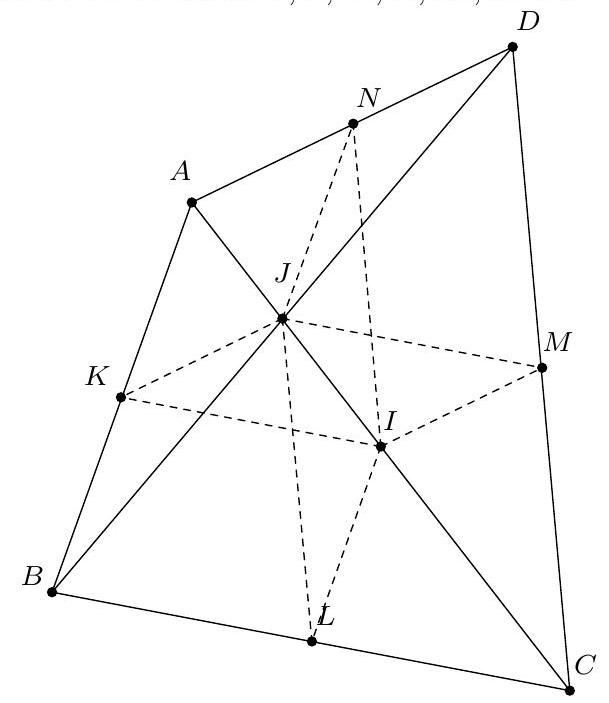
|
| 79 |
+
|
| 80 |
+
On remarque que $(I K)$ et $(J M)$ sont parallèles, puisqu'ils sont parallèles à $(B C)$. De même, $(I M) / /(J K)$. On en déduit que $I M J K$ est un parallélogramme, et de même $I N J L$ est un parallélogramme.
|
| 81 |
+
|
| 82 |
+
Notons $[\vec{u}, \vec{v}]$ le produit mixte des vecteurs $\vec{u}$ et $\vec{v}$. C'est l'aire d'un parallélogramme $X Y Z T$ tel que $\overrightarrow{X Y}=\vec{u}$ et $\overrightarrow{Y Z}=\vec{v}$, affectée d'un signe + si $X Y Z T$ est parcouru dans le sens direct et d'un signe - sinon.
|
| 83 |
+
|
| 84 |
+
On vérifie facilement les propriétés suivantes:
|
| 85 |
+
|
| 86 |
+
- $[\vec{u}, \vec{v}]=-[\vec{v}, \vec{u}]$
|
| 87 |
+
- $[\vec{u}, \vec{v}+\vec{w}]=[\vec{u}, \vec{v}]+[\vec{u}, \vec{w}]$
|
| 88 |
+
- $[\vec{v}+\vec{w}, \vec{u}]=[\vec{v}, \vec{u}]+[\vec{w}, \vec{u}]$.
|
| 89 |
+
(La deuxième propriété dit que si un parallélogramme $P$ est la réunion de deux parallélogrammes $P_{1}$ et $P_{2}$ alors l'aire de $P$ est la somme des aires de $P_{1}$ et de $P_{2}$; la troisième propriété découle des deux précédentes.)
|
| 90 |
+
|
| 91 |
+
Comme $I K=B C / 2$ et $K J=A D / 2$, l'aire de $I M J K$ est égale à $\pm \frac{1}{4}[\overrightarrow{A D}, \overrightarrow{B C}]$ et de même l'aire de $I N J M$ est égale à $\pm \frac{1}{4}[\overrightarrow{A B}, \overrightarrow{C D}]$. On en déduit que les aires de $F_{1}$ et de $F_{2}$ sont égales si et seulement si
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
[\overrightarrow{A B}, \overrightarrow{C D}]= \pm[\overrightarrow{A D}, \overrightarrow{B C}]
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
On a
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\begin{aligned}
|
| 101 |
+
& {[\overrightarrow{A B}, \overrightarrow{C D}]=[\overrightarrow{A D}, \overrightarrow{B C}]} \\
|
| 102 |
+
& \quad \Longleftrightarrow \quad[\overrightarrow{A B}, \overrightarrow{A D}]-[\overrightarrow{A B}, \overrightarrow{A C}]=[\overrightarrow{A D}, \overrightarrow{A C}]-[\overrightarrow{A D}, \overrightarrow{A B}] \\
|
| 103 |
+
& \quad \Longleftrightarrow \quad[\overrightarrow{A C}, \overrightarrow{A B}]=[\overrightarrow{A D}, \overrightarrow{A C}] \\
|
| 104 |
+
& \\
|
| 105 |
+
& \quad \Longleftrightarrow \quad(A C) \text { partage le quadrilatère en deux parties d'aires égales. }
|
| 106 |
+
\end{aligned}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
De même, $[\overrightarrow{A B}, \overrightarrow{C D}]=-[\overrightarrow{A D}, \overrightarrow{B C}]$ si et seulement $\mathrm{si}(B D)$ partage le quadrilatère en deux parties d'aires égales.
|
| 110 |
+
|
| 111 |
+
Autre solution. Comme ci-dessus, on remarque que $I M J K$ et que $I N J L$ sont des parallélogrammes.
|
| 112 |
+
|
| 113 |
+
Si $(A D) / /(B C)$ on obtient que l'aire de $I M J K$ est égale à 0 . Alors l'aire de $I N J L$ est égale à 0 si et seulement si $(A B) / /(C D)$, ce qui équivaut à ce que les diagonales du quadrilatère $A B C D$ le divisent en triangles d'aires égales.
|
| 114 |
+
|
| 115 |
+
On se ramène donc à traiter le cas où $(A D)$ et $(B C)$ se croisent. De même, on peut supposer que $(A B)$ et $(C D)$ se croisent. Sans perte de généralité, on peut supposer qu'ils se croisent comment sur la figure : $X=[D A) \cap[C B), Y=[B A) \cap[C D)$.
|
| 116 |
+
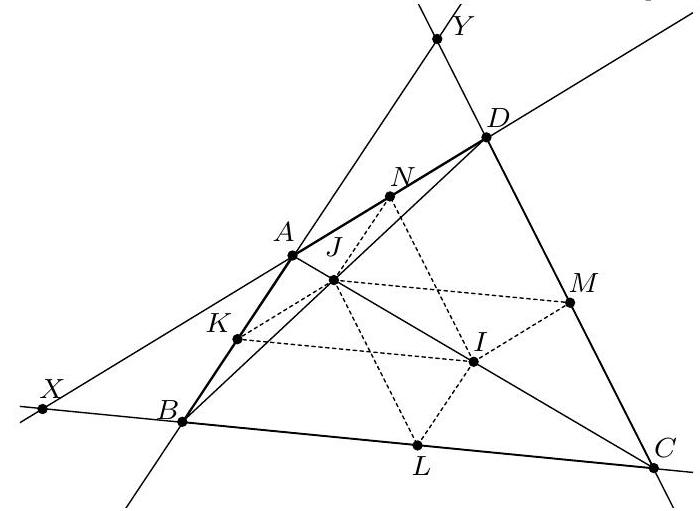
|
| 117 |
+
|
| 118 |
+
L'aire de $I M J K$ est égale à
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
K J \cdot K I \sin \widehat{I K J}=\frac{1}{4} B C \cdot A D \sin \widehat{A X B}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
L'aire de $I N J L$ est égale à
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
N J \cdot N I \sin \widehat{J N I}=\frac{1}{4} A B \cdot C D \sin \widehat{A Y D}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
D'après la loi des sinus pour les triangles $A X B$ et $A Y D$, on a
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
\frac{\sin \widehat{A X B}}{\sin \widehat{A Y D}}=\frac{A B \sin \widehat{X A B}}{B X} \frac{D Y}{A D \sin \widehat{Y A D}}=\frac{A B \cdot D Y}{B X \cdot A D}
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
En combinant (1), (2) et (3), on obtient que l'aire de $I M J K$ est égale à l'aire de $I N J L$ si et seulement si
|
| 137 |
+
|
| 138 |
+
$$
|
| 139 |
+
\frac{C B}{B X}=\frac{C D}{D Y}
|
| 140 |
+
$$
|
| 141 |
+
|
| 142 |
+
Cette dernière égalité équivaut à dire que $(X Y) / /(B D)$.
|
| 143 |
+
On a que $(A C)$ divise $A B C D$ en triangles d'aires égales si et seulement si $J$ se trouve qur $(A C)$ (puisque l'aire de $A J B$ est égale à celle de $A J D$ et l'aire de $C J B$ est égale à celle de $C J D)$.
|
| 144 |
+
|
| 145 |
+
Il ne reste plus qu'à noter que dans un quadrilatère $X B D Y$, la droite joignant $C=$ $(X B) \cap(D Y)$ et $A=(X D) \cap(B Y)$ passe par le milieu de $[B D]$ si et seulement si $(X Y)$ et $(B D)$ sont parallèles.
|
| 146 |
+
|
| 147 |
+
En effet, si $(X Y)$ et $(B D)$ sont parallèles, il existe une homothétie de centre $C$ qui envoie $B$ et $D$ sur $X$ et $Y$ respectivement. Cette homothétie envoie le milieu de $[B D]$ sur le milieu de $[X Y]$ donc ces deux milieux sont alignés avec $C$, et de même ils sont alignés avec $A$.
|
| 148 |
+
|
| 149 |
+
Réciproquement, supposons que $(A C)$ passe par le milieu $U$ de $[B D]$. Soit $Y^{\prime}$ le point d'intersection de $(C Y)$ avec la parallèle à $(B D)$ passant par $X$. Soit $A^{\prime}=\left(B Y^{\prime}\right) \cap(D X)$.
|
| 150 |
+
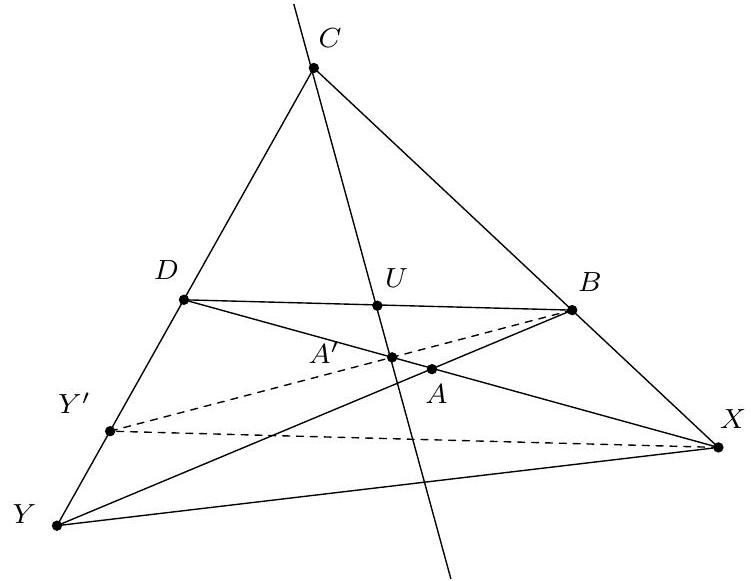
|
| 151 |
+
|
| 152 |
+
D'après le paragraphe précédent, $C, A^{\prime}$ et $U$ sont alignés, donc $A$ appartient à la droite $\left(C A^{\prime}\right)$. De plus, $A$ appartient à $(D X)$, donc $A=\left(C A^{\prime}\right) \cap(D X)=A^{\prime}$. On en déduit que $Y=Y^{\prime}$, et que $X B D Y$ est un parallélogramme.
|
| 153 |
+
|
| 154 |
+
Exercice 8. Le cercle $\omega$ passe par les sommets $B$ et $C$ du triangle $A B C$ et coupe les côtés $[A B]$ et $[A C]$ aux points $D$ et $E$ respectivement. Les segments $[C D]$ et $[B E]$ se coupent en un point $O$. Soient $M$ et $N$ les centres des cercles inscrits dans les triangles $A D E$ et $O D E$ respectivement. Montrer que le milieu de l'arc $D E$ (le plus petit des deux arcs) du cercle $\omega$ se trouve sur la droite ( $M N$ ).
|
| 155 |
+
|
| 156 |
+
## Solution.
|
| 157 |
+
|
| 158 |
+
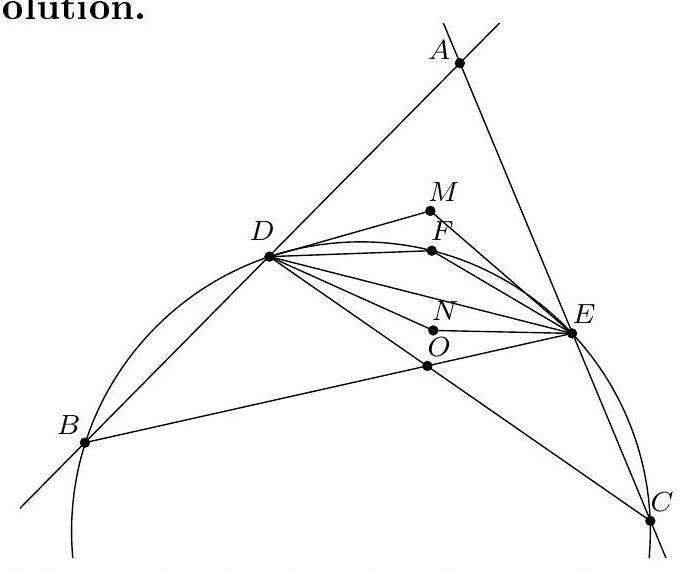
|
| 159 |
+
|
| 160 |
+
Notons $\theta=(D E, D F)=(E F, E D)$. On a $2(D F, D M)+2 \theta=2(D E, D M)=(D E, D A)=$ $\theta+(D F, D A)=\theta+(D F, D B)=\theta+(E F, E B)=2 \theta+(E D, E O)=\theta+2(E D, E N)$, donc $\widehat{F D M}=\widehat{D E N}$. De même, $\widehat{M E F}=\widehat{N D E}$. Notons $\beta$ et $\gamma$ ces angles.
|
| 161 |
+

|
| 162 |
+
|
| 163 |
+
Soient $P$ et $Q$ les seconds points d'intersection des droites $(D F)$ et $(E F)$ avec le cercle circonscrit au triangle DME. On a
|
| 164 |
+
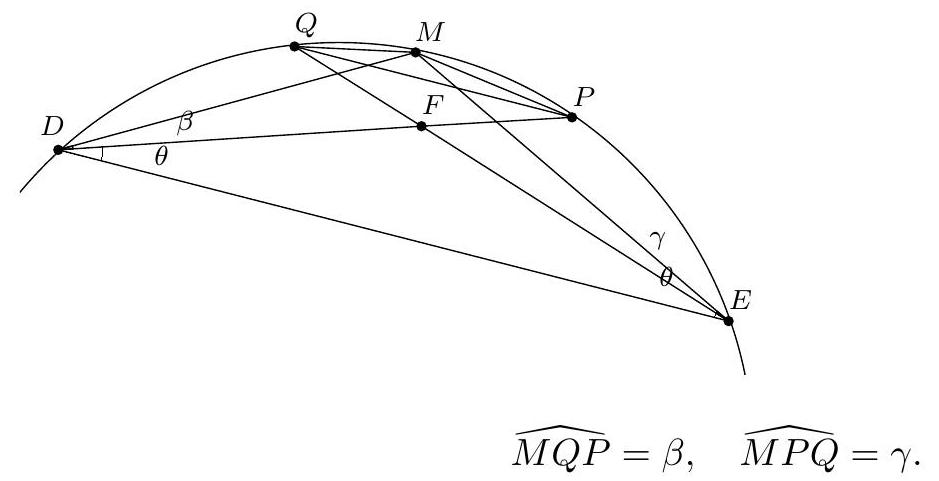
|
| 165 |
+
|
| 166 |
+
Comme $D F=D E$, on a $(P Q) / /(D E)$. Avec (4), cela implique que les triangles $D E N$ et $Q M P$ sont homothétiques. De plus, $F$ est le centre de l'homothétie (puisque c'est le point d'intersection des droites $(Q E)$ et $(P D)$ ). Donc la droite $(M N)$ traverse $F$.
|
| 167 |
+
|
| 168 |
+
Autre solution. Si on ne pense pas à introduire les points $P$ et $Q$, on peut terminer la démonstration moyennant des calculs trigonométriques un peu pénibles.
|
| 169 |
+
|
| 170 |
+
Notons $\varphi$ l'angle $(\overrightarrow{F M}, \overrightarrow{E D})$. D'après la loi des sinus dans les triangles $M D F$ et $M E F$, on a
|
| 171 |
+
|
| 172 |
+
$$
|
| 173 |
+
\begin{aligned}
|
| 174 |
+
\frac{M F}{\sin \beta} & =\frac{D F}{\sin (\beta+\varphi+\theta)} \\
|
| 175 |
+
\frac{M F}{\sin \gamma} & =\frac{E F}{\sin (\varphi-\gamma-\theta)}
|
| 176 |
+
\end{aligned}
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
Comme $D F=E F$, en divisant ces deux égalités on obtient
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi-\gamma-\theta)}{\sin (\beta+\varphi+\theta)}
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
En utilisant la formule $\sin (x+y)=\sin x \cos y+\cos x \sin y$, on en déduit
|
| 186 |
+
|
| 187 |
+
$$
|
| 188 |
+
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi) \cos (\gamma+\theta)-\cos \varphi \sin (\gamma+\theta)}{\sin (\varphi) \cos (\beta+\theta)+\cos \varphi \sin (\beta+\theta)}
|
| 189 |
+
$$
|
| 190 |
+
|
| 191 |
+
On chasse les dénominateurs et on rassemble les termes en $\sin \varphi$ et en $\cos \varphi$ :
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
\cos \varphi(\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)))=\sin \varphi(-\sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta))
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
Comme
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
\begin{aligned}
|
| 201 |
+
- & \sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta) \\
|
| 202 |
+
& =-\sin \gamma(\cos \beta \cos \theta-\sin \beta \sin \theta)+\sin \beta(\cos \gamma \cos \theta-\sin \gamma \sin \theta) \\
|
| 203 |
+
& =\cos \theta \sin (\beta-\gamma),
|
| 204 |
+
\end{aligned}
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
on obtient
|
| 208 |
+
|
| 209 |
+
$$
|
| 210 |
+
\tan \varphi=\frac{\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)}{\cos \theta \sin (\beta-\gamma)}
|
| 211 |
+
$$
|
| 212 |
+
|
| 213 |
+
Soit $\varphi^{\prime}=(F N, D E)$. Le calcul de $\tan \varphi^{\prime}$ est identique, en remplaçant $(\beta, \gamma, \theta)$ par $(\beta+\theta, \gamma+\theta,-\theta)$. Or, l'expression de $\tan \varphi$ est invariante par cette transformation, donc $\tan \varphi^{\prime}=\tan \varphi$, d'où $F, M, N$ sont alignés.
|
| 214 |
+
|
| 215 |
+
Exercice 9. Un cercle de centre $O$ est inscrit dans un quadrilatère $A B C D$ dont les côtés ne sont pas parallèles. Montrer que le point $O$ coïncide avec le point d'intersection des lignes médianes du quadrilatère si et seulement si $O A \cdot O C=O B \cdot O D$. (Une ligne médiane du quadrilatère est une droite reliant les milieux des côtés opposés.)
|
| 216 |
+
|
| 217 |
+
Solution. Soient $I$ et $J$ les milieux des côtés $[A B]$ et $[C D]$ respectivement. Les droites $(A B)$ et $(C D)$ se coupent au point $P$. Sans perte de généralité, on peut supposer que $P$ est le point d'intersection des demi-droites $[A B)$ et $[C D)$.
|
| 218 |
+
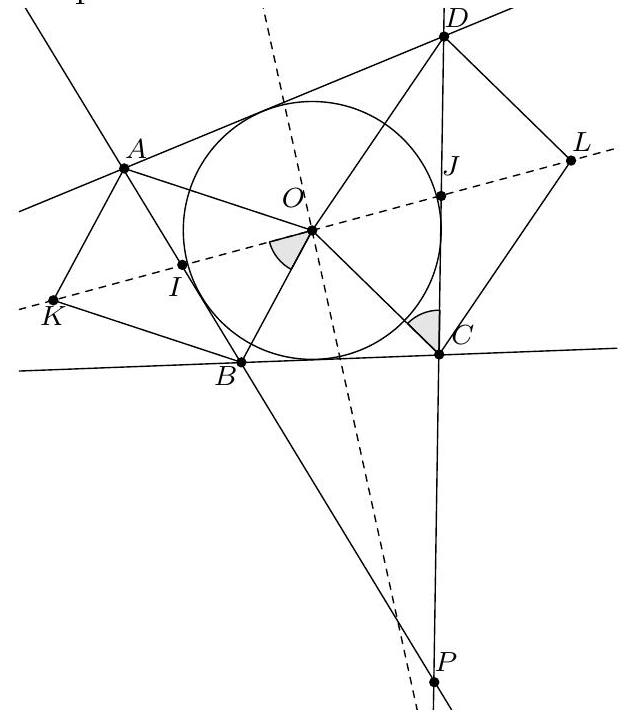
|
| 219 |
+
|
| 220 |
+
1) Supposons que $O$ est le point d'intersection des lignes médianes du quadrilatère $A B C D$. Alors $O$ est le milieu du segment $[I J]$, parce que les milieux des côtés d'un quadrilatère sont les sommets d'un parallélogramme. Puis, $[P O]$ est la bissectrice et la médiane issus de $P$ du triangle $I P J$, donc $I P J$ est isocèle en $P$ et $\widehat{B I O}=\widehat{C J O}$. En outre,
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
\widehat{I B O}+\widehat{J C O}=\frac{1}{2}(\widehat{A B C}+\widehat{B C D})=\frac{1}{2}(\pi+\widehat{B P C})=\pi-\widehat{P I J}=\widehat{I B O}+\widehat{I O B}
|
| 224 |
+
$$
|
| 225 |
+
|
| 226 |
+
Alors $\widehat{J C O}=\widehat{I O B}$ et les triangles $O I B$ et $C J O$ sont semblables. On obtient que $\frac{O B}{O C}=$ $\frac{I B}{J O}$. De même, on a $\frac{O A}{O D}=\frac{I A}{J O}$. Comme $I B=I A$, on obtient $O A \cdot O C=O B \cdot O D$.
|
| 227 |
+
2) On suppose maintenant que $O A \cdot O C=O B \cdot O D$. On note que
|
| 228 |
+
|
| 229 |
+
$$
|
| 230 |
+
\begin{aligned}
|
| 231 |
+
\widehat{A O B}+\widehat{C O D} & =(\pi-\widehat{O A B}-\widehat{O B A})+(\pi-\widehat{O C D}-\widehat{O D C}) \\
|
| 232 |
+
& =\pi-\frac{1}{2}(\widehat{D A B}+\widehat{A B C}+\widehat{B C D}+\widehat{C D A})=\pi
|
| 233 |
+
\end{aligned}
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
Par conséquent, si on construit les parallélogrammes $O A K B$ et $C O D L$ à partir des triangles $O A B$ et $O C D$, ces parallélogrammes seront semblables, parce que $\frac{O A}{A K}=\frac{O A}{O B}=$ $\frac{D O}{O C}=\frac{D O}{D L}$. En particulier, les triangles $O I B$ et $C J O$ sont également semblables, parce qu'ils se correspondent mutuellement dans les parallélogrammes semblables $O A K B$ et $C O D L . \mathrm{Il}$ vient
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
\widehat{I O B}=\widehat{O C J}=\widehat{O C B}, \quad \widehat{C O J}=\widehat{I B O}=\widehat{O B C}
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
On obtient que
|
| 243 |
+
|
| 244 |
+
$$
|
| 245 |
+
\widehat{I O B}+\widehat{B O C}+\widehat{C O J}=\widehat{O C B}+\widehat{B O C}+\widehat{O B C}=\pi,
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
donc $O$ se trouve sur $(I J)$. De même, $O$ se trouve sur l'autre ligne médiane du quadrilatère $A B C D$.
|
| 249 |
+
|
| 250 |
+
Autre solution. On peut résoudre l'exercice par une méthode analytique utilisant les nombres complexes. Les calculs sont longs mais pas impraticables.
|
| 251 |
+
|
| 252 |
+
Notons $U, V, W, X$ les points de contact des droites $(A B),(B C),(C D)$ et $(D A)$ avec le cercle. On peut supposer que le cercle est de centre 0 et de rayon 1 . Notons $a, b, c, d, u, v, w, x$ les affixes des points $A, B, C, D, U, V, W, X$.
|
| 253 |
+
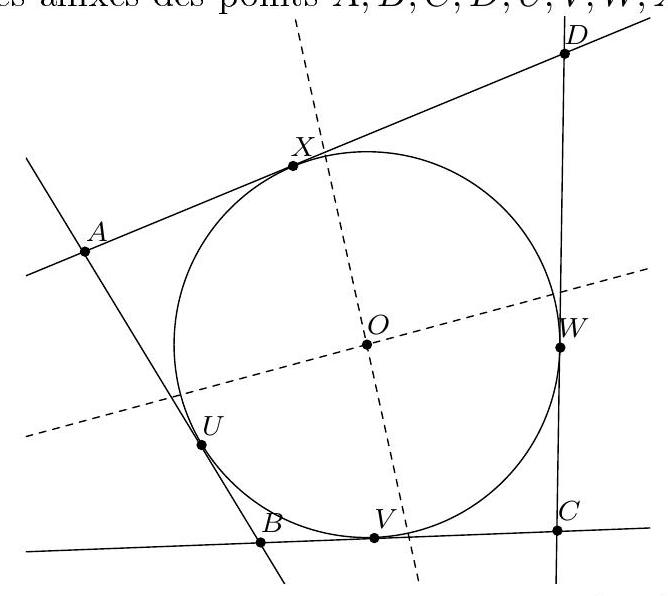
|
| 254 |
+
|
| 255 |
+
Un point d'affixe $z$ appartient à $(A B)$ si et seulement si $z-u$ est perpendiculaire à $u$, ce qui s'écrit $0=\bar{u}(z-u)+u(\bar{z}-\bar{u})$, ou encore $\bar{u} z+u \bar{z}=2$. Comme $\bar{u}=1 / u$, ceci s'écrit encore $z+u^{2} \bar{z}=2 u$. De même, l'équation de la droite $(A D)$ est $z+x^{2} \bar{z}=2 x$. En combinant ces deux équations, on trouve que
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
a=\frac{2 u x}{u+x} .
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
De même, on a $b=\frac{2 u v}{u+v}, c=\frac{2 v w}{v+w}$ et $d=\frac{2 w x}{w+x}$.
|
| 262 |
+
On calcule que $4 O A^{-2}=|u+x|^{2}=2+u \bar{x}+\bar{u} x$. On a des expressions analogues pour $4 O B^{-2}$, etc. Par conséquent,
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\begin{aligned}
|
| 266 |
+
O A \cdot O C & =O B \cdot O D \\
|
| 267 |
+
& \Longleftrightarrow \quad(2+u \bar{x}+\bar{u} x)(2+v \bar{w}+\bar{v} w)=(2+u \bar{v}+\bar{u} v)(2+w \bar{x}+\bar{w} x) \\
|
| 268 |
+
& \Longleftrightarrow \quad u x(2+u \bar{x}+\bar{u} x) v w(2+v \bar{w}+\bar{v} w)=u v(2+u \bar{v}+\bar{u} v) w x(2+w \bar{x}+\bar{w} x) \\
|
| 269 |
+
& \Longleftrightarrow \quad\left(2 u x+u^{2}+x^{2}\right)\left(2 v w+v^{2}+w^{2}\right)=\left(2 u v+u^{2}+v^{2}\right)\left(2 w x+x^{2}+w^{2}\right) \\
|
| 270 |
+
& \Longleftrightarrow \quad 2 u v^{2} x+2 u w^{2} x+2 u^{2} v w+u^{2} v^{2}+2 v w x^{2}+w^{2} x^{2} \\
|
| 271 |
+
& =2 u v x^{2}+2 u v w^{2}+2 u^{2} w x+u^{2} x^{2}+2 v^{2} w x+v^{2} w^{2} \\
|
| 272 |
+
& \Longleftrightarrow 2(u-w) v^{2} x-2(u-w) u w x+2(u-w) u v w \\
|
| 273 |
+
& \quad-2(u-w) v x^{2}+(u-w)(u+w) v^{2}-(u-w)(u+w) x^{2}=0 \\
|
| 274 |
+
& \Longleftrightarrow 2 v^{2} x-2 u w x+2 u v w-2 v x^{2}+u v^{2}+v^{2} w-u x^{2}-w x^{2}=0 \\
|
| 275 |
+
& \Longleftrightarrow \quad 2 v x(v-x)+(v-x) w(v+x)+2 u w(v-x)+u(v+x)(v-x)=0 \\
|
| 276 |
+
& \Longleftrightarrow 2 v x+v w+v x+2 u w+u v+u x=0 \\
|
| 277 |
+
& \Longleftrightarrow 2(u w+x v)+(x+v)(u+w)=0 .
|
| 278 |
+
\end{aligned}
|
| 279 |
+
$$
|
| 280 |
+
|
| 281 |
+
D'autre part, $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$ si et seulement si $0, \frac{a+d}{2}$ et $\frac{b+c}{2}$ sont alignés, ce qui se traduit par le fait que $\frac{a+d}{b+c}$ est réel, c'est-à-dire
|
| 282 |
+
|
| 283 |
+
$$
|
| 284 |
+
\frac{\frac{u x}{u+x}+\frac{x w}{x+w}}{\frac{u v}{u+v}+\frac{v w}{v+w}}=\frac{\frac{1}{u+x}+\frac{1}{w+x}}{\frac{1}{u+v}+\frac{1}{v+w}}
|
| 285 |
+
$$
|
| 286 |
+
|
| 287 |
+
On multiplie les numérateurs de chaque membre par $(u+x)(x+w)$ et les dénominateurs par $(u+v)(v+w)$, ce qui donne successivement
|
| 288 |
+
|
| 289 |
+
$$
|
| 290 |
+
\begin{aligned}
|
| 291 |
+
& \frac{x[u(x+w)+w(u+x)]}{v[u(v+w)+w(u+v)]}=\frac{2 x+(u+w)}{2 v+(u+w)} \\
|
| 292 |
+
& \quad \Longleftrightarrow \quad x[2 u w+u(u+w)][2 v+(u+w)]=v[2 u w+v(u+w)][2 x+(u+w)] \\
|
| 293 |
+
& \Longleftrightarrow \quad 2 x u w(u+w)+2 x^{2} v(u+w)+x^{2}(u+w)^{2} \\
|
| 294 |
+
& \quad=2 v u w(u+w)+2 x v^{2}(u+w)+v^{2}(u+w)^{2} \\
|
| 295 |
+
& \quad \Longleftrightarrow \quad 2(x-v) u w(u+w)+2(x-v) x v(u+w)+(x-v)(x+v)(u+w)^{2}=0
|
| 296 |
+
\end{aligned}
|
| 297 |
+
$$
|
| 298 |
+
|
| 299 |
+
Comme les côtés opposés ne sont pas parallèles, on a $u+w \neq 0$. En simplifiant par $(x-v)(u+w)$, on obtient la condition $2 u w+2 x v+(x+v)(u+w)=0$ qui est la même que la précédente.
|
| 300 |
+
|
| 301 |
+
On en conclut que $O A \cdot O C=O B \cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$. De même, on montre que $O A \cdot O C=O B \cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A B]$ et de $[C D]$.
|
| 302 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-2-solutions.md
ADDED
|
@@ -0,0 +1,96 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## OFM 2013-2014 : solutions de l'Envoi 2
|
| 2 |
+
|
| 3 |
+
## Exercices groupe B
|
| 4 |
+
|
| 5 |
+
Exercice 1 On dit qu'un nombre à 9 chiffres est intéressant si chaque chiffre de 1 à 9 y apparaît une unique fois, que les chiffres de 1 à 5 y apparaissent dans l'ordre mais pas les chiffres de 1 à 6 , par exemple 189236457 .
|
| 6 |
+
|
| 7 |
+
Combien y a-t-il de nombres intéressants?
|
| 8 |
+
Solution de l'exercice 1 Pour construire un nombre intéressant, on peut placer d'abord les chiffres de 1 à 5 , puis intercaler le 6 quelque part, puis le 7 , le 8 et le 9 . L'ordre des chiffres de 1 à 5 est imposé. Ensuite, le 6 peut être placé n'importe où sauf après le 5 car les chiffres de 1 à 6 ne sont pas dans l'ordre. Il y a donc 5 manières de placer le 6 . Ensuite, on peut placer le 7 n'importe où, donc il y a 7 manières de le placer, et de même 8 manières de placer le 8 et 9 pour le 9.
|
| 9 |
+
|
| 10 |
+
Il y a donc $5 * 7 * 8 * 9=2520$ nombres intéressants.
|
| 11 |
+
Exercice 2 Dans un pays, il y a n villes. Deux villes quelconques sont toujours reliées soit par une autoroute, soit par une ligne de train. Montrer qu'un des deux moyens de transport permet de relier n'importe quelle ville à n'importe quelle autre.
|
| 12 |
+
$\underline{\text { Solution de l'exercice } 2}$ On raisonne par récurrence sur $n$ : pour $n=1$ ou $n=2$, le résultat est immédiat. Supposons qu'on l'a montré au rang $n$, et considérons $n+1$ villes :
|
| 13 |
+
|
| 14 |
+
On isole une des villes, appelons-la par exemple Paris. Alors un des deux moyens de transports permet de relier entre elles toutes les villes sauf Paris. Supposons que c'est la voiture:
|
| 15 |
+
|
| 16 |
+
- si Paris est relié à une ville par une autoroute par exemple Lyon, on peut en voiture aller de Paris à Lyon, puis à n'importe quelle autre ville d'après l'hypothèse de récurrence.
|
| 17 |
+
- sinon, Paris est relié à toutes les villes par une ligne de train, donc on peut aller de n'importe quelle ville à n'importe quelle ville en train en passant par Paris.
|
| 18 |
+
|
| 19 |
+
Exercice 32014 scientifiques participent à un congrès, chaque scientifique étant soit un mathématicien, soit un physicien. Bien sûr, les physiciens mentent toujours et les mathématiciens disent toujours la vérité, sauf quand ils se trompent. Lors du dîner final, tous sont assis en rond autour d'une table, et chacun prétend se trouver entre un mathématicien et un physicien. Il se trouve qu'exactement un mathématicien distrait s'est trompé. Combien y a-t-il de physiciens au congrès?
|
| 20 |
+
|
| 21 |
+
Solution de l'exercice 3 Si 2 physiciens sont assis côté à côté, comme ils ont menti, ils ne sont pas entre un physicien et un mathématicien, donc chacun est entre deux physiciens, et ainsi de suite, donc le congrès n'accueille que des physiciens, ce qui est absurde car il y a au moins un mathématicien (celui qui s'est trompé...). Chaque physicien est donc entre deux mathématiciens.
|
| 22 |
+
|
| 23 |
+
D'autre part, chaque mathématicien est entre un mathématicien et un physicien, sauf celui qui s'est trompé. Appelons-le Thomas : si Thomas est entre deux physiciens, alors on a partout ailleurs une alternance de deux mathématiciens, un physicien... Mais alors, si il y a k paires de mathématiciens côte à côte, il y a $2 k+1$ mathématiciens et $k+1$ physiciens, donc $3 k+2$ scientifiques, ce qui est absurde car $3 k+2 \neq 2014$.
|
| 24 |
+
|
| 25 |
+
Thomas est donc entre deux mathématiciens, donc on a trois mathématiciens côté à côte, et les autres par paires. Si il y a $k$ paires, alors on a $2 k+3$ mathématiciens et $k+1$ physiciens donc $3 k+4=2014$ donc $k=670$ et il y a 671 physiciens.
|
| 26 |
+
|
| 27 |
+
## Exercices communs
|
| 28 |
+
|
| 29 |
+
Exercice 4 Montrer que tout polyèdre a deux faces qui ont le même nombre de sommets.
|
| 30 |
+
Solution de l'exercice 4 Soit $n$ le nombre de faces du polyèdre, et soit $F$ une face fixée : les arêtes de $F$ séparent $F$ de faces toutes différentes, donc le nombre d'arêtes de $F$ est inférieur ou égal au nombre de faces autres que $F$. De plus, $F$ a au moins 3 arêtes. Chaque face a autant d'arêtes que de sommet, donc toute face a un nombre de sommets compris entre 3 et $n-1$, soit $n-3$ possibilités. D'après le principe des tiroirs, il existe donc deux faces qui ont le même nombre de sommets.
|
| 31 |
+
|
| 32 |
+
Exercice 5 Sur un échiquier 5 sur 5, on a placé sur des cases différentes k cavaliers, de telle manière que chacun peut en prendre exactement 2 autres.
|
| 33 |
+
|
| 34 |
+
Quelle est la plus grande valeur possible de k? Solution de l'exercice 5 La configuration suivante donne un exemple avec 16 cavaliers :
|
| 35 |
+
|
| 36 |
+
|
| 37 |
+
On montre maintenant que c'est optimal : quitte à échanger les couleurs, on peut supposer le centre noir. Notons $k$ le nombre de cavaliers sur une case noire, $l$ le nombre de cavaliers sur une case blanche et $N$ le nombre de manière de choisir deux cavaliers en prise : sur deux tels cavaliers, un est sur une case noire donc il y a $k$ manières de le choisir, puis 2 manières de choisir un cavalier sur une case blanche qu'il peut prendre, donc $\mathrm{N}=2 \mathrm{k}$, mais le même raisonnement donne $N=2 l$ donc $k=l$.
|
| 38 |
+
|
| 39 |
+
Si il y a un cavalier au centre de l'échiquier, il a accès à 8 cases blanches donc au moins 6 cases blanches sont inoccupées donc $l \leqslant 12-6=6$ donc $k+l \leqslant 12$. On peut donc supposer le centre vide.
|
| 40 |
+
|
| 41 |
+
Si il y a un cavalier sur une case blanche qui touche le centre, il a accès à 6 cases, donc 4 d'entre elles sont inoccupées. Le centre l'est aussi, donc $k \leqslant 13-5=8$ et $k+l \leqslant 16$, ce qu'on veut montrer.
|
| 42 |
+
|
| 43 |
+
Si enfin le centre et ses voisins immédiats sont inoccupés, alors les coins le sont aussi car il ne peuvent avoir de cavaliers en prise, ce qui ne laisse que les 16 cases de la figure ci-dessus.
|
| 44 |
+
|
| 45 |
+
Exercice 6 Soit $\mathrm{n} \in \mathbb{N}^{*}$. Montrer qu'il est possible de partitionner $\{1,2, \ldots, \mathrm{n}\}$ en deux sousensembles $A$ et $B$ tels que la somme des éléments de $A$ soit égale au produit des éléments de B.
|
| 46 |
+
|
| 47 |
+
Solution de l'exercice 6 A priori, l'ensemble B doit être bien plus petit que A. On va donc chercher un $B$ avec un petit nombre d'éléments. En testant des petites valeurs de $n$, on peut penser à chercher $B$ sous la forme $\{1, a, b\}$ avec $a, b \neq 1$ et $a \neq b$.
|
| 48 |
+
|
| 49 |
+
On a alors $\prod_{x \in B} x=a b$, et :
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\begin{aligned}
|
| 53 |
+
\sum_{x \in \mathcal{A}} & =\sum_{x=1}^{n} x-1-a-b \\
|
| 54 |
+
& =\frac{n(n+1)}{2}-a-b-1
|
| 55 |
+
\end{aligned}
|
| 56 |
+
$$
|
| 57 |
+
|
| 58 |
+
On veut donc $\frac{n(n+1)}{2}=a b+a+b+1=(a+1)(b+1)$, donc il suffit d'écrire $\frac{n(n+1)}{2}$ comme un produit. Or, si $n$ est pair, on peut prendre $a+1=\frac{n}{2}$ et $b+1=n+1$, soit $a=\frac{n}{2}-1$ et $b=n$. Si $n$ est impair, on prend $a=\frac{n-1}{2}$ et $b=n-1$. Dans les deux cas, l'hypothèse $n \geqslant 5$ permet de vérifier facilement que 1, a et $b$ sont deux à deux distincts.
|
| 59 |
+
Exercice 7 On se donne $n$ points du plan, tels que trois quelconques d'entre eux ne sont jamais alignés. Chacun est colorié en rouge ou en bleu. On suppose qu'il y a exactement un point bleu à l'intérieur de chaque triangle dont les sommets sont rouges, et un point rouge à l'intérieur de chaque triangle dont les sommets sont bleus.
|
| 60 |
+
|
| 61 |
+
Quelle est la plus grande valeur possible de n?
|
| 62 |
+
|
| 63 |
+
## Exercices groupe A
|
| 64 |
+
|
| 65 |
+
Solution de l'exercice 7 On montre d'abord que les points bleus forment un polygone convexe: si ce n'était pas le cas, on pourrait trouver un point bleu à l'intérieur d'un polygone bleu, donc on en découpant ce polygone en triangles, on pourrait trouver un point bleu à l'intérieur d'un triangle bleu. Le grand triangle bleu doit contenir un unique point rouge, mais on peut le découper en trois triangles qui contiennent chacun un unique point rouge, ce qui est absurde.
|
| 66 |
+
|
| 67 |
+
Les points bleus forment donc un polygone convexe, de même que les rouges. De plus, il y a au maximum 2 points rouges à l'intérieur du polygone bleu, car s'il y en avait 3 ils formeraient un triangle sans point bleu à l'intérieur.
|
| 68 |
+
|
| 69 |
+
Enfin, si $k$ est le nombre de points bleus, on peut découper le polygone bleu en $k-2$ triangles, qui chacun doivent contenir un point rouge, donc $k-2 \leqslant 2$ et $k \leqslant 4$. De même, il y a au plus 4 points rouges donc $\mathrm{n} \leqslant 8$. On peut alors vérifier que la configuration à 8 points suivante convient:
|
| 70 |
+
|
| 71 |
+
|
| 72 |
+
Exercice 8 La ville de Gotham City est un grand rectangle, découpé en pâtés de maisons rectangulaires plus petits par des rues parallèles aux bords de la ville. On suppose qu'il y a au moins une rue, et qu'aucune rue ne traverse la ville de part en part.
|
| 73 |
+
|
| 74 |
+
Montrer qu'il existe un pâté de maison qui ne touche pas le bord de la ville. Solution de l'exercice 8
|
| 75 |
+
Batman explore la ville selon le procédé suivant : il part du bord de la ville (du point rouge sur la figure) et suit jusqu'au bout une rue (l'Avenue du Joker par exemple) qui s'enfonce à l'intérieur. Comme l'Avenue de Joker ne traverse pas la ville de part en part, elle débouche sur une autre (appelons-la Boulevard Double-Face). Mais le Boulevard Double-Face ne traverse pas non plus Gotham City de part en part, donc va déboucher sur une autre rue soit à gauche, soit à droite, soit éventuellement des deux côtés. Si le Boulevard débouche sur une nouvelle rue à gauche, Batman part vers la gauche. Sinon, il part vers la droite. Il continue ainsi...
|
| 76 |
+
|
| 77 |
+
Il est alors clair que Batman ne sortira jamais de Gotham. Mais le nombre de rues est fini, donc il finira forcément par passer deux fois par un même point. On suppose par exemple que le premier point où il passe deux fois de suite est la Place Ra's Al Ghul (en bleu sur la figure) : entre ses deux passages, il a fait le tour d'une certaine zone, sans toucher le bord de la ville. Tout pâté de maison dans cette zone convient, comme celui colorié en vert.
|
| 78 |
+
|
| 79 |
+
|
| 80 |
+
Exercice 9 Soient E un ensemble de cardinal n et $\mathscr{F}$ un ensemble de parties de E avec $|\mathscr{F}|=$ $2^{\text {n-1 }}$ tel que pour tous $A, B$ et $C$ dans $\mathscr{F}, A \cap B \cap C$ est non vide.
|
| 81 |
+
|
| 82 |
+
Montrer que l'intersection de tous les éléments de $\mathscr{F}$ est non vide.
|
| 83 |
+
Solution de l'exercice 9 Si $A \subset E$, on notera $A^{c}$ son complémentaire: l'ensemble des parties de $E$ est partitionné en $2^{n-1}$ doubletons de la forme $\left\{A, A^{c}\right\}$ où $A \subset E$. Or, il est impossible que les deux éléments d'un doubleton soient dans $\mathscr{F}$, car leur intersection est vide, donc $\mathscr{F}$ contient exactement un élément de chaque doubleton.
|
| 84 |
+
|
| 85 |
+
Soient donc $A$ et $B$ dans $\mathscr{F}$ : on va montrer que $A \cap B \in \mathscr{F}$. D'après ce qu'on vient de dire, il suffit de montrer $(A \cap B)^{c} \notin \mathscr{F}$. Or, ceci est vrai car $A \cap B \cap(A \cap B)^{c}$ est vide.
|
| 86 |
+
|
| 87 |
+
Par récurrence sur $k$, on en déduit que pour tous $A_{1}, A_{2}, \ldots, A_{k}$ de $\mathscr{F}, A_{1} \cap A_{2} \cap \ldots \cap A_{k} \in \mathscr{F}$. En effet, c'est vrai pour $k=2$ et si on l'a montré pour $k$, alors :
|
| 88 |
+
|
| 89 |
+
$$
|
| 90 |
+
A_{1} \cap A_{2} \cap \ldots \cap A_{k}=\left(A_{1} \cap A_{2} \cap \ldots \cap A_{k-1}\right) \cap A_{k}
|
| 91 |
+
$$
|
| 92 |
+
|
| 93 |
+
est l'intersection de deux éléments de $\mathscr{F}$, donc est dans $\mathscr{F}$.
|
| 94 |
+
|
| 95 |
+
Comme $\mathscr{F}$ est fini, l'intersection de tous les éléments de $\mathscr{F}$ est dans $\mathscr{F}$. Or, l'ensemble vide ne peut pas être dans $\mathscr{F}$ car son intersection avec lui-même est vide, donc l'intersection de tous les éléments de $\mathscr{F}$ n'est pas vide.
|
| 96 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-3-solutions.md
ADDED
|
@@ -0,0 +1,407 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Matfématiques 2013-2014
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## Envoi $\mathcal{N u m e ́ r o ~} 3$ - Corrigé
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe B
|
| 8 |
+
|
| 9 |
+
Exercice 1. Existe-t-il des réels $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}>0$ et $e, f, \mathrm{~g}, \mathrm{~h}<0$ vérifiant simultanément
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
a e+b c>0, e f+c g>0, f d+g h>0 \text { et } d a+h b>0 ?
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Solution de l'exercice 1 Non, il n'en existe pas. Par l'absurde : supposons qu'il existe de tels réels.On commence par réécrire les inégalités, mais avec uniquement des termes positifs. On a donc
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
b c>a(-e) \text { et }(-e)(-f)>c(-g) \text { et }(-g)(-h)>(-f) d \text { et da }>(-h) b
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Si l'on multiplie toutes ces inégalités membres à membres (et, comme tout est positif, il n'y a aucun danger), il vient abcdefgh > abcbdefgh, d'où la contradiction cherchée.
|
| 22 |
+

|
| 23 |
+
|
| 24 |
+
Exercice 2. Soit $a, b, c$ des réels tels que $-1 \leqslant a x^{2}+b x+c \leqslant 1$ pour $x=-1, x=0$ et $x=1$. Prouver que
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
-\frac{5}{4} \leqslant a x^{2}+b x+c \leqslant \frac{5}{4} \text { pour tout réel } x \in[-1,1]
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Solution de l'exercice 2 Posons $\mathrm{P}(\mathrm{x})=\mathrm{ax}{ }^{2}+\mathrm{bx}+\mathrm{c}$. Alors $\mathrm{P}(-1)=\mathrm{a}-\mathrm{b}+\mathrm{c}, \mathrm{P}(0)=\mathrm{c}$ et $\mathrm{P}(1)=$ $\mathrm{a}+\mathrm{b}+\mathrm{c}$. Et, d'après l'énoncé, on a $|\mathrm{P}(-1)| \leqslant 1,|\mathrm{P}(0)| \leqslant 1$ et $|\mathrm{P}(1)| \leqslant 1$.
|
| 31 |
+
Or, pour tout réel $\chi$, on vérifie directement que
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
P(x)=\frac{x(x+1)}{2} P(1)-\frac{x(1-x)}{2} P(-1)+\left(1-x^{2}\right) P(0)
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
- Soit $x \in[0 ; 1]$. D'après (1) et l'inégalité triangulaire, il vient
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
\begin{aligned}
|
| 41 |
+
|\mathrm{P}(x)| & \leqslant \frac{x(x+1)}{2}|\mathrm{P}(1)|+\frac{x(1-x)}{2}|\mathrm{P}(-1)|+\left(1-x^{2}\right)|\mathrm{P}(0)| \\
|
| 42 |
+
& \leqslant \frac{x(x+1)}{2}+\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
|
| 43 |
+
& =-x^{2}+x+1 \\
|
| 44 |
+
& =\frac{5}{4}-\left(x-\frac{1}{2}\right)^{2}
|
| 45 |
+
\end{aligned}
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
Et ainsi $|P(x)| \leqslant \frac{5}{4}$.
|
| 49 |
+
|
| 50 |
+
- Soit $x \in[-1 ; 0]$. D'après (1) et l'inégalité triangulaire, il vient cette fois
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
\begin{aligned}
|
| 54 |
+
& \leqslant-\frac{x(x+1)}{2}|P(1)|-\frac{x(1-x)}{2}|P(-1)|+\left(1-x^{2}\right)|P(0)| \\
|
| 55 |
+
& \leqslant-\frac{x(x+1)}{2}-\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
|
| 56 |
+
& =-x^{2}-x+1 \\
|
| 57 |
+
& =\frac{5}{4}-\left(x+\frac{1}{2}\right)^{2}
|
| 58 |
+
\end{aligned}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Et ainsi $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$, à nouveau.
|
| 62 |
+
Finalement, pour tout $x \in[-1 ; 1]$, on a $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$.
|
| 63 |
+

|
| 64 |
+
|
| 65 |
+
Exercice 3. Prouver que, pour tout réel $a \geqslant 0$, on a
|
| 66 |
+
|
| 67 |
+
$$
|
| 68 |
+
a^{3}+2 \geqslant a^{2}+2 \sqrt{a}
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Solution de l'exercice 3 Pour tout réel $a \geqslant 0$, on a
|
| 72 |
+
|
| 73 |
+
$$
|
| 74 |
+
\begin{aligned}
|
| 75 |
+
a^{3}-a^{2}-2 \sqrt{a}+2 & =a^{2}(a-1)-2(\sqrt{a}-1) \\
|
| 76 |
+
& =a^{2}(\sqrt{a}-1)(\sqrt{a}+1)-2(\sqrt{a}-1) \\
|
| 77 |
+
& =(\sqrt{a}-1)\left(a^{2}(\sqrt{a}+1)-2\right) .(1)
|
| 78 |
+
\end{aligned}
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
Or:
|
| 82 |
+
|
| 83 |
+
- Si $a \geqslant 1$ alors $\sqrt{a} \geqslant 1$ et $a^{2} \geqslant 1$. Ainsi, on a $\sqrt{a}-1 \geqslant 0$ et $a^{2}(\sqrt{a}+1) \geqslant 2$. Par suite, chacun des facteurs de (1) est positif, ce qui assure que le produit est positif.
|
| 84 |
+
- Si $a \leqslant 1$ alors $\sqrt{a} \leqslant 1$ et $a^{2} \leqslant 1$. Ainsi, on a $\sqrt{a}-1 \leqslant 0$ et $a^{2}(\sqrt{a}+1) \leqslant 2$. Par suite, chacun des deux facteurs de (1) est négatif, et le produit est donc encore positif.
|
| 85 |
+
|
| 86 |
+
Finalement, pour tout réel $a \geqslant 0$, on a $a^{3}-a^{2}-2 \sqrt{a}+2 \geqslant 0$ ou encore $a^{3}+2 \geqslant a^{2}+2 \sqrt{a}$.
|
| 87 |
+
|
| 88 |
+
## Exercices Communs
|
| 89 |
+
|
| 90 |
+
Exercice 4. Prouver que si $n$ est un entier strictement positif, l'expression
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
\frac{\sqrt{n+\sqrt{0}}+\sqrt{n+\sqrt{1}}+\sqrt{n+\sqrt{2}}+\cdots \sqrt{n+\sqrt{n^{2}-1}}+\sqrt{n+\sqrt{n^{2}}}}{\sqrt{n-\sqrt{0}}+\sqrt{n-\sqrt{1}}+\sqrt{n-\sqrt{2}}+\cdots \sqrt{n-\sqrt{n^{2}-1}}+\sqrt{n-\sqrt{n^{2}}}}
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
est indépendante de n .
|
| 97 |
+
Solution de l'exercice 4 En calculant le carré de chacun des deux membres, on déduit que, pour tous réels $a, b$ tels que $0 \leqslant b \leqslant a$, on a
|
| 98 |
+
|
| 99 |
+
$$
|
| 100 |
+
\sqrt{a+\sqrt{a^{2}-b^{2}}}=\sqrt{\frac{a+b}{2}}+\sqrt{\frac{a-b}{2}}
|
| 101 |
+
$$
|
| 102 |
+
|
| 103 |
+
En particulier, pour tous entiers naturels $n$ et $m$, avec $m \leqslant n^{2}$, on a
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
\sqrt{n+\sqrt{m}}=\sqrt{\frac{n+\sqrt{n^{2}-m}}{2}}+\sqrt{\frac{n-\sqrt{n^{2}-m}}{2}}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Soit $\mathrm{n}>0$ un entier. On a donc
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\sum_{m=0}^{n^{2}} \sqrt{n+\sqrt{m}}=\sum_{m=0}^{n^{2}} \sqrt{\frac{n+\sqrt{n^{2}-m}}{2}}+\sum_{m=0}^{n^{2}} \sqrt{\frac{n-\sqrt{n^{2}-m}}{2}}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
D'où, après réindexation :
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\begin{aligned}
|
| 119 |
+
\sum_{m=0}^{n^{2}} \sqrt{n+\sqrt{m}} & =\sum_{m=0}^{n^{2}} \sqrt{\frac{n+\sqrt{m}}{2}}+\sum_{m=0}^{n^{2}} \sqrt{\frac{n-\sqrt{m}}{2}} \\
|
| 120 |
+
& =\frac{1}{\sqrt{2}} \sum_{m=0}^{n^{2}} \sqrt{n+\sqrt{m}}+\frac{1}{\sqrt{2}} \sum_{m=0}^{n^{2}} \sqrt{n-\sqrt{m}}
|
| 121 |
+
\end{aligned}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
$\operatorname{Ainsi}\left(1-\frac{1}{\sqrt{2}}\right) \sum_{m=0}^{n^{2}} \sqrt{n+\sqrt{m}}=\frac{1}{\sqrt{2}} \sum_{m=0}^{n^{2}} \sqrt{n-\sqrt{m}}$
|
| 125 |
+
et donc $\frac{\sum_{m=0}^{n^{2}} \sqrt{n+\sqrt{m}}}{\sum_{m=0}^{n^{2}} \sqrt{n-\sqrt{m}}}=1+\sqrt{2}$, qui est bien une valeur
|
| 126 |
+
Exercice 5. Soit ( $a_{n}$ ) une suite définie par $a_{1}, a_{2} \in[0,100]$ et
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
a_{n+1}=a_{n}+\frac{a_{n-1}}{n^{2}-1} \quad \text { pour tout enter } n \geqslant 2
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
Existe-t-il un entier $n$ tel que $a_{n}>2013$ ?
|
| 133 |
+
Solution de l'exercice 5 La réponse est non.
|
| 134 |
+
|
| 135 |
+
Plus précisément, montrons par récurrence que l'on a $a_{n} \leqslant 400$, pour tout $n \geqslant 0$.
|
| 136 |
+
L'inégalité est vraie pour $\mathrm{n}=1$ et $\mathrm{n}=2$, d'après l'énoncé.
|
| 137 |
+
Supposons qu'elle soit vraie pour tout $k \leqslant n$ pour un certain entier $\mathrm{n} \geqslant 2$.
|
| 138 |
+
Pour tout $k \in\{2, \cdots, n\}$, on a $a_{k+1}=a_{k}+\frac{a_{k-1}}{k^{2}-1}$. En sommant, membre à membre, ces relations et après simplification des termes communs, il vient:
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
\begin{aligned}
|
| 142 |
+
a_{n+1} & =a_{2}+\sum_{k=2}^{n} \frac{a_{k-1}}{k^{2}-1} \\
|
| 143 |
+
& \leqslant 100+\sum_{k=2}^{n} \frac{400}{k^{2}-1}, \text { d'après l'hypothèse de récurrence et l'énoncé } \\
|
| 144 |
+
& =100+200 \sum_{k=2}^{n}\left(\frac{1}{k-1}-\frac{1}{k+1}\right) \\
|
| 145 |
+
& =100+200\left(1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}\right) \text { après simplification par dominos } \\
|
| 146 |
+
& =400-\frac{200}{n}-\frac{200}{n+1}
|
| 147 |
+
\end{aligned}
|
| 148 |
+
$$
|
| 149 |
+
|
| 150 |
+
et donc $a_{n+1} \leqslant 400$, ce qui achève la récurrence.
|
| 151 |
+

|
| 152 |
+
|
| 153 |
+
Exercice 6. Déterminer la plus grande valeur possible et la plus petite valeur possible de
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\sqrt{4-a^{2}}+\sqrt{4-b^{2}}+\sqrt{4-c^{2}}
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
lorsque $a, b, c$ sont des réels strictement positifs vérifiant $a^{2}+b^{2}+c^{2}=6$.
|
| 160 |
+
Solution de l'exercice 6 Tout d'abord, on note que si l'on veut que l'expression ait un sens, il faut $\mathrm{a}, \mathrm{b}, \mathrm{c} \in$ [0; 2].
|
| 161 |
+
|
| 162 |
+
D'après l'inégalité de Cauchy-Schwarz, on a
|
| 163 |
+
$\left(\sqrt{4-a^{2}}+\sqrt{4-b^{2}}+\sqrt{4-c^{2}}\right)^{2} \leqslant 3\left(4-a^{2}+4-b^{2}+4-c^{2}\right)=18$,
|
| 164 |
+
c.à.d. $\sqrt{4-\mathrm{a}^{2}}+\sqrt{4-\mathrm{b}^{2}}+\sqrt{4-\mathrm{c}^{2}} \leqslant 3 \sqrt{2}$, avec égalité pour $\mathrm{a}=\mathrm{b}=\mathrm{c}=\sqrt{2}$.
|
| 165 |
+
|
| 166 |
+
Ainsi, la plus grande valeur possible est $3 \sqrt{2}$.
|
| 167 |
+
Cherchons maintenant la valeur minimale :
|
| 168 |
+
Sans perte de généralité, on peut supposer que $a \leqslant b \leqslant c$.
|
| 169 |
+
De $a^{2}+b^{2}+c^{2}=6$, on déduit alors que $3 a^{2} \leqslant 6$, soit donc $0 \leqslant a^{2} \leqslant 2$.
|
| 170 |
+
D'autre part, si $x, y \geqslant 0$, on a clairement $\sqrt{x}+\sqrt{y} \leqslant \sqrt{x+y}$, avec égalité si et seulement si $x=0$ ou $\mathrm{y}=0$.
|
| 171 |
+
Il vient alors
|
| 172 |
+
$\sqrt{4-a^{2}}+\sqrt{4-b^{2}}+\sqrt{4-c^{2}} \geqslant \sqrt{4-a^{2}}+\sqrt{8-b^{2}-c^{2}}=\sqrt{4-a^{2}}+\sqrt{2+a^{2}}$,
|
| 173 |
+
et, puisque $0 \leqslant 4-\mathrm{c}^{2} \leqslant 4-\mathrm{b}^{2}$, égalité a lieu si et seulement si $4-\mathrm{c}^{2}=0$, c.à $\mathrm{d} . \mathrm{c}=2$.
|
| 174 |
+
Il reste donc à trouver le minimum de l'expression $\mathrm{f}(\mathrm{x})=\sqrt{4-\mathrm{x}}+\sqrt{2+\mathrm{x}}$, lorsque $x \in[0 ; 2]$. Or, puisque tout est positif, cela revient à trouver le minimum de $(f(x))^{2}=6+2 \sqrt{(4-x)(2+x)}$, sous les mêmes conditions.
|
| 175 |
+
|
| 176 |
+
Comme $(4-x)(2+x)=-x^{2}+2 x+8=9-(x-1)^{2}$, la valeur minimale de $\sqrt{(4-x)(2+x)}$ est $\sqrt{8}$, avec égalité pour $x=0$.
|
| 177 |
+
Ainsi, on a $(\mathrm{f}(\mathrm{x}))^{2} \geqslant 6+2 \sqrt{8}=(2+\sqrt{2})^{2}$, ou encore $\mathrm{f}(\mathrm{x}) \geqslant 2+\sqrt{2}$, avec égalité pour $\mathrm{x}=0$.
|
| 178 |
+
Par suite, on a $\sqrt{4-\mathrm{a}^{2}}+\sqrt{4-\mathrm{b}^{2}}+\sqrt{4-\mathrm{c}^{2}} \geqslant 2+\sqrt{2}$, avec égalité en particulier pour $(\mathrm{a}, \mathrm{b}, \mathrm{c})=$ $(0, \sqrt{2}, 2)$.
|
| 179 |
+
Cela assure que la plus petite valeur cherchée est $2+\sqrt{2}$.
|
| 180 |
+
|
| 181 |
+
## Exercices du groupe A
|
| 182 |
+
|
| 183 |
+
Exercice 7. Déterminer toutes les fonctions $\mathrm{f}: \mathbb{R} \longrightarrow \mathbb{R}^{+*}$ qui vérifient les trois conditions suivantes pour tous réels $x$ et $y$ :
|
| 184 |
+
i) $f\left(x^{2}\right)=f(x)^{2}-2 x f(x)$,
|
| 185 |
+
ii) $f(-x)=f(x-1)$,
|
| 186 |
+
iii) si $1<x<y$ alors $f(x)<f(y)$.
|
| 187 |
+
|
| 188 |
+
Solution de l'exercice 7 Nous allons prouver que la seule solution est $\mathrm{f}: x \longrightarrow x^{2}+x+1$.
|
| 189 |
+
Soit $f$ une solution éventuelle du problème.
|
| 190 |
+
De i ), pour $x=0$, on déduit que $f(0)=f^{2}(0)$. Et, comme $f(0)>0$, on a donc $f(0)=1$.
|
| 191 |
+
Soit $x$ un réel. En utilisant i) pour les valeurs $x$ et $-x$, il vient
|
| 192 |
+
$f(x)^{2}-2 x f(x)=f\left(x^{2}\right)=f(-x)^{2}+2 x f(-x)$,
|
| 193 |
+
ou encore $(f(x)-f(-x))(f(x)+f(-x))=2 x(f(x)+f(-x))$.
|
| 194 |
+
Puisque $f$ est à valeurs strictement positives, on a $f(x)+f(-x) \neq 0$,
|
| 195 |
+
et donc $f(x)-f(-x)=2 x$.
|
| 196 |
+
Finalement, et d'après ii), on a
|
| 197 |
+
|
| 198 |
+
$$
|
| 199 |
+
f(x)=f(x-1)+2 x \text {, pour tout réel } x .(1)
|
| 200 |
+
$$
|
| 201 |
+
|
| 202 |
+
En particulier, on déduit facilement de (1) que, pour tout entier $n \geqslant 0$, on a
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
\mathrm{f}(\mathrm{n})=\mathrm{f}(0)+2(\mathrm{n}+(\mathrm{n}-1)+\cdots+1)=\mathrm{n}^{2}+\mathrm{n}+1
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
De ii), on obtient alors que
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
f(n)=n^{2}+n+1 \text { pour tout entier } n
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
Soit $x$ un réel et $\mathrm{n} \geqslant 0$ un entier.
|
| 215 |
+
Pour tout entier $k$, on a $f(x+k)=2 x+2 k+f(x+k-1)$.
|
| 216 |
+
Après sommation membre à membre de toutes ces relations pour $k=0,1, \cdots, n$, et simplification des termes communs, il vient
|
| 217 |
+
$\mathbf{f}(\mathrm{x}+\mathfrak{n})=2 \mathbf{n} x+2(\mathfrak{n}+(\mathfrak{n}-1)+\cdots+1)+\mathbf{f}(\mathrm{x})$.
|
| 218 |
+
Et ainsi :
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
f(x+n)=f(x)+2 n x+n^{2}+n, \text { pour tout réel } x \text { et tout entier } n \geqslant 0 \text {. (2) }
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
Cela va nous permettre de conclure sur les rationnels positifs :
|
| 225 |
+
Soit $x=\frac{m}{n}$, avec $\mathrm{m}, \mathrm{n}>0$ entiers.
|
| 226 |
+
D'après (2), on a
|
| 227 |
+
|
| 228 |
+
$$
|
| 229 |
+
\begin{aligned}
|
| 230 |
+
\mathrm{f}\left((x+\mathrm{n})^{2}\right) & =\mathrm{f}\left(x^{2}+2 \mathrm{~m}+\mathrm{n}^{2}\right) \\
|
| 231 |
+
& =\mathrm{f}\left(x^{2}\right)+2\left(2 \mathrm{~m}+\mathrm{n}^{2}\right) \mathrm{x}^{2}+\left(2 \mathrm{~m}+\mathrm{n}^{2}\right)^{2}+2 \mathrm{~m}+\mathrm{n}^{2} \\
|
| 232 |
+
& =\mathrm{f}^{2}(x)-2 \mathrm{xf}(x)+2\left(2 \mathrm{~m}+\mathrm{n}^{2}\right) x^{2}+\left(2 \mathrm{~m}+\mathrm{n}^{2}\right)^{2}+2 \mathrm{~m}+\mathrm{n}^{2}
|
| 233 |
+
\end{aligned}
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
Mais, d'après i) et (2), on a également
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
\begin{aligned}
|
| 240 |
+
\mathbf{f}\left((x+n)^{2}\right) & =f^{2}(x+n)+2(x+n) f(x+n) \\
|
| 241 |
+
& =\left(f(x)+2 m+n^{2}+n\right)^{2}-2(x+n)\left(f(x)+2 m+n^{2}+n\right)
|
| 242 |
+
\end{aligned}
|
| 243 |
+
$$
|
| 244 |
+
|
| 245 |
+
En identifiant les deux dernières expressions de $f\left((x+n)^{2}\right)$, et après un calcul passionnant, on obtient que
|
| 246 |
+
|
| 247 |
+
$$
|
| 248 |
+
f(x)=x^{2}+x+1, \text { pour tout rationnel } x>0
|
| 249 |
+
$$
|
| 250 |
+
|
| 251 |
+
Soit $x>1$ un réel.
|
| 252 |
+
On sait qu'il existe deux suites de rationnels positifs, $\left(u_{n}\right)$ et $\left(v_{n}\right)$, qui convergent vers $x$ et telles que $u_{n} \leqslant w \leqslant v_{n}$ pour tout entier $n$.
|
| 253 |
+
Or, d'après iii), la fonction $f$ est strictement croissante sur $] 1 ;+\infty\left[\right.$ donc, pour tout entier $n$, on a $f\left(u_{n}\right)<$ $\mathrm{f}(\mathrm{x})<\mathrm{f}\left(v_{\mathrm{n}}\right)$,
|
| 254 |
+
ou encore $u_{n}^{2}+u_{n}+1<f(x)<v_{n}^{2}+v_{n}+1$.
|
| 255 |
+
En faisant tendre $n$ vers $+\infty$, et d'après le théorème des gendarmes, il vient alors $f(x)=x^{2}+x+1$.
|
| 256 |
+
|
| 257 |
+
$$
|
| 258 |
+
\text { Ainsi, on a } f(x)=x^{2}+x+1 \text {, pour tout réel } x>1 \text { (3) }
|
| 259 |
+
$$
|
| 260 |
+
|
| 261 |
+
Donnons maintenant le coup de grâce.
|
| 262 |
+
Soit $x$ un réel.
|
| 263 |
+
On choisit un entier $\mathrm{n}>0$ tel que $x+n>1$.
|
| 264 |
+
De (2) et (3), on déduit que
|
| 265 |
+
$\mathbf{f}(x+\mathfrak{n})=(x+\mathfrak{n})^{2}+(x+\mathfrak{n})+1$ et $\mathbf{f}(x+\mathfrak{n})=\mathbf{f}(\mathrm{x})+2 \mathfrak{n} x+\mathfrak{n}^{2}+\mathfrak{n}$.
|
| 266 |
+
En identifiant ces deux expressions, et après encore quelques calculs, il vient $f(x)=x^{2}+x+1$.
|
| 267 |
+
Et finalement, on a $f(x)=x^{2}+x+1$, pour tout réel $x$.
|
| 268 |
+
Ce n'est que routine que de vérifier que cette fonction est bien une solution du problème.
|
| 269 |
+

|
| 270 |
+
|
| 271 |
+
Exercice 8. Soit P et Q deux polynômes à coefficients réels, de degrés $\mathrm{n} \geqslant 0$. On suppose que le coefficient de $x^{n}$ de chacun de ces deux polynômes est égal à 1 et que, pour tout réel $x$, on a $P(P(x))=$ $\mathrm{Q}(\mathrm{Q}(\mathrm{x})$ ).
|
| 272 |
+
Prouver que $\mathrm{P}=\mathrm{Q}$.
|
| 273 |
+
Solution de l'exercice 8 Le résultat est évident si $\mathrm{n}=0$. Dans ce qui suit, on suppose donc que $\mathrm{n} \geqslant 1$.
|
| 274 |
+
|
| 275 |
+
Par l'absurde : supposons que le polynôme $\mathrm{R}=\mathrm{P}-\mathrm{Q}$ ne soit pas le polynôme nul.
|
| 276 |
+
Soit $k$ le degré de R.
|
| 277 |
+
Puisque $P$ et $Q$ sont tous deux de degré $n$, et de même coefficient dominant, on a $k \in\{0, \cdots, n-1\}$. De plus, on a
|
| 278 |
+
|
| 279 |
+
$$
|
| 280 |
+
P(P(x))-Q(Q(x))=[Q(P(x))-Q(Q(x))]+R(P(x))
|
| 281 |
+
$$
|
| 282 |
+
|
| 283 |
+
Posons $Q(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$.
|
| 284 |
+
On remarque qu'alors
|
| 285 |
+
|
| 286 |
+
$$
|
| 287 |
+
\mathrm{Q}(\mathrm{P}(\mathrm{x}))-\mathrm{Q}(\mathrm{Q}(\mathrm{x}))=\left[\mathrm{P}^{n}(x)-\mathrm{Q}^{n}(x)\right]+\mathrm{a}_{n-1}\left[\mathrm{P}^{n-1}(x)-\mathrm{Q}^{n-1}(x)\right]+\cdots+\mathrm{a}_{1}[\mathrm{P}(\mathrm{x})-\mathrm{Q}(\mathrm{x})]
|
| 288 |
+
$$
|
| 289 |
+
|
| 290 |
+
et chacun des termes de cette somme autre que $\left[P^{n}(x)-Q^{n}(x)\right]$ est de degré au plus $n(n-1)$. D'autre part, on a
|
| 291 |
+
|
| 292 |
+
$$
|
| 293 |
+
\left[P^{n}(x)-Q^{n}(x)\right]=R(x)\left[P^{n-1}(x)+P^{n-2}(x) Q(x)+\cdots+Q^{n-1}(x)\right]
|
| 294 |
+
$$
|
| 295 |
+
|
| 296 |
+
ce qui assure que $\left[P^{n}(x)-Q^{n}(x)\right]$ est de degré $n(n-1)+k$ et de coefficient dominant égal à $n$ (on rappelle que $P$ et $Q$ sont tous les deux de coefficient dominant égal à 1 ).
|
| 297 |
+
|
| 298 |
+
- On suppose que $k>0$.
|
| 299 |
+
|
| 300 |
+
Alors, le polynôme $Q(P(x))-Q(Q(x))$ est de degré $n(n-1)+k$.
|
| 301 |
+
D'autre part, le degré de $R(P(x))$ est $k n$, et on a $k n \leqslant n(n-1)<n(n-1)+k$.
|
| 302 |
+
De (1), on déduit que $P(P(x))-Q(Q(x))$ est de degré $n(n-1)+k$, et donc non nul, en contradiction avec l'énoncé.
|
| 303 |
+
|
| 304 |
+
- Il reste à étudier le cas où $k=0$, c'est-à-dire lorsque $R$ est constant.
|
| 305 |
+
|
| 306 |
+
Notons c cette constante. Notre hypothèse initiale assure que $c \neq 0$.
|
| 307 |
+
$\operatorname{De} P(P(x))=Q(Q(x))$, il vient $\mathrm{Q}(\mathrm{Q}(\mathrm{x})+\mathrm{c})=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))-\mathrm{c}$.
|
| 308 |
+
Puisque $Q$ n'est pas constant, c'est donc que l'égalité $Q(y+c)=Q(y)-c$ est vraie pour une infinité de réels $y$. S'agissant de polynômes, c'est donc qu'elle est vraie pour tout réel $y$.
|
| 309 |
+
|
| 310 |
+
Une récurrence immédiate conduit alors à $Q(j c)=a_{0}-j c$ pour tout entier $j \geqslant 0$.
|
| 311 |
+
Comme ci-dessus, l'égalité $Q(x)=-x+a_{0}$ étant vraie pour une infinité de valeurs (puisque $c \neq 0$ ), elle est donc vraie pour tout $x$. Cela contredit que $Q$ est de coefficient dominant égal à 1 .
|
| 312 |
+
|
| 313 |
+
Ainsi, dans tous les cas, on a obtenu une contradiction. Cela assure que $R$ est bien le polynôme nul, et achève la démonstration.
|
| 314 |
+
|
| 315 |
+
## Autre solution.
|
| 316 |
+
|
| 317 |
+
Le résultat est facile à montrer si $\mathfrak{n}=0$ ou $\mathfrak{n}=1$. Dans ce qui suit, on suppose donc que $\mathrm{n} \geqslant 2$. Notons $R=P-Q$ et supposons par l'absurde qu'il est non nul. Quitte à permuter les rôles de P et de Q , on peut supposer que le coefficient dominant de $R$ est strictement positif.
|
| 318 |
+
Lemme 1. Pour tout polynôme R ayant un coefficient dominant strictement positif, il existe un réel a tel que pour tout $x \geqslant a$ on a $R(x)>0$.
|
| 319 |
+
En effet, $R(x)$ peut s'écrire sous la forme $c x^{m}\left(1+\frac{c_{1}}{x}+\cdots+\frac{c_{m}}{x^{m}}\right)$ avec $c>0$. Le terme entre parenthèses tend vers 1 lorsque $x \rightarrow+\infty$, donc est strictement positif pour $x$ assez grand.
|
| 320 |
+
|
| 321 |
+
Lemme 2. Pour tout polynôme $P$ de degré $\geqslant 1$ ayant un coefficient dominant strictement positif, il existe a tel que P est strictement croissant sur [a, $+\infty$ [.
|
| 322 |
+
En effet, le polynôme dérivé $P^{\prime}$ vérifie les conditions du lemme 1 donc $P^{\prime}(x)$ est strictement positif pour $x$ assez grand.
|
| 323 |
+
Revenons à l'exercice. D'après les deux lemmes précédents, il existe a tel que sur [a, $+\infty[, P$ et $Q$ sont strictement croissants, et $R$ et $R \circ Q$ sont strictement positifs.
|
| 324 |
+
On a alors pour tout $x \geqslant a$ :
|
| 325 |
+
|
| 326 |
+
$$
|
| 327 |
+
\begin{aligned}
|
| 328 |
+
\mathrm{P}(\mathrm{P}(\mathrm{x})) & >\mathrm{P}(\mathrm{Q}(x)) \quad \text { puisque } \mathrm{P}(\mathrm{x})>\mathrm{Q}(\mathrm{x}) \\
|
| 329 |
+
& =\mathrm{Q}(\mathrm{Q}(\mathrm{x}))+\mathrm{R}(\mathrm{Q}(\mathrm{x})) \\
|
| 330 |
+
& >\mathrm{Q}(\mathrm{Q}(\mathrm{x}))
|
| 331 |
+
\end{aligned}
|
| 332 |
+
$$
|
| 333 |
+
|
| 334 |
+
ce qui contredit $\mathrm{P}(\mathrm{P}(\mathrm{x}))=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))$.
|
| 335 |
+

|
| 336 |
+
|
| 337 |
+
Exercice 9. Soit $n>0$ un entier et $x_{1}, \cdots, x_{n}$ des réels strictement positifs. Prouver que :
|
| 338 |
+
|
| 339 |
+
$$
|
| 340 |
+
\begin{gathered}
|
| 341 |
+
\max _{x_{1}>0, \cdots, x_{n}>0} \min \left(x_{1}, \frac{1}{x_{1}}+x_{2}, \cdots, \frac{1}{x_{n-1}}+x_{n}, \frac{1}{x_{n}}\right)= \\
|
| 342 |
+
\min _{x_{1}>0, \cdots, x_{n}>0} \max \left(x_{1}, \frac{1}{x_{1}}+x_{2}, \cdots, \frac{1}{x_{n-1}}+x_{n}, \frac{1}{x_{n}}\right)=2 \cos \left(\frac{\pi}{n+2}\right) .
|
| 343 |
+
\end{gathered}
|
| 344 |
+
$$
|
| 345 |
+
|
| 346 |
+
Solution de l'exercice 9 Soit Ul'ensemble des n -uplets de réels strictement positifs. Pour $x=\left(x_{1}, \cdots, x_{n}\right) \in U$, on pose
|
| 347 |
+
|
| 348 |
+
$$
|
| 349 |
+
\begin{aligned}
|
| 350 |
+
& \quad m(x)=\min \left(x_{1}, \frac{1}{x_{1}}+x_{2}, \cdots, \frac{1}{x_{n-1}}+x_{n}, \frac{1}{x_{n}}\right) \\
|
| 351 |
+
& \text { et } M(x)=\max \left(x_{1}, \frac{1}{x_{1}}+x_{2}, \cdots, \frac{1}{x_{n-1}}+x_{n}, \frac{1}{x_{n}}\right)
|
| 352 |
+
\end{aligned}
|
| 353 |
+
$$
|
| 354 |
+
|
| 355 |
+
Notre stratégie va consister à prouver qu'il existe $a \in U$ tel que $m(a)=M(a)$ et que, pour tout $x \in U$, on a $m(x) \leqslant m(a)$ et $M(a) \leqslant M(x)$.
|
| 356 |
+
|
| 357 |
+
Soit $a=\left(a_{1}, \cdots, a_{n}\right) \in U$.
|
| 358 |
+
La condition $m(a)=M(a)$ s'écrit
|
| 359 |
+
|
| 360 |
+
$$
|
| 361 |
+
a_{1}=\frac{1}{a_{1}}+a_{2}=\cdots=\frac{1}{a_{n-1}}+a_{n}=\frac{1}{a_{n}} .
|
| 362 |
+
$$
|
| 363 |
+
|
| 364 |
+
Mais, admettons pour le moment que l'on ait déjà trouvé $a \in U$ tel que $m(a)=M(a)$.
|
| 365 |
+
Par l'absurde : On suppose qu'il existe $x \in U$ tel que $m(x)>m(a)$.
|
| 366 |
+
On prouve alors par récurrence sur $k$ que $x_{k}>\mathfrak{a}_{k}$ pour tout $k \in\{1, \cdots, \mathfrak{n}\}$ :
|
| 367 |
+
Déjà, on a $x_{1} \geqslant m(x)>m(a)=a_{1}$.
|
| 368 |
+
D'autre part, si $x_{k}>a_{k}$ pour un certain $k \in\{1, \cdots, n-1\}$, alors
|
| 369 |
+
|
| 370 |
+
$$
|
| 371 |
+
\frac{1}{x_{k}}+x_{k+1} \geqslant m(x)>m(a)=\frac{1}{a_{k}}+a_{k+1}
|
| 372 |
+
$$
|
| 373 |
+
|
| 374 |
+
Or, d'après l'hypothèse de récurrence, on a $\frac{1}{x_{k}}<\frac{1}{a_{k}}$, d'où $x_{k+1}>a_{k+1}$, ce qui achève la récurrence.
|
| 375 |
+
En particulier, on a donc $x_{n}>a_{n}$.
|
| 376 |
+
Mais, $\frac{1}{x_{n}} \geqslant m(x)>m(a)=\frac{1}{a_{n}}$, d'où $x_{n}<a_{n}$. Contradiction.
|
| 377 |
+
Ainsi, pour tout $x \in U$, on a $m(x) \leqslant m(a)$.
|
| 378 |
+
On démontre de même que $M(a) \leqslant M(x)$, pour tout $x \in U$.
|
| 379 |
+
Dans ces conditions, on a $\max _{x \in U}\{m(x)\}=\mathfrak{m}(a)=M(a)=\min _{x \in U}\{M(x)\}$, comme désiré.
|
| 380 |
+
Pour conclure, il ne reste donc plus qu'à trouver $a \in U$ vérifiant (1).
|
| 381 |
+
Montrons comment trouver un tel a sans trop s'aider de l'énoncé :
|
| 382 |
+
Supposons qu'un tel a existe. On note $\alpha>0$ la valeur commune dans (1).
|
| 383 |
+
On vérifie sans difficulté qu'alors, pour tout $k$, on a $a_{k}=\frac{b_{k}}{b_{k-1}}$, où $b_{0}=1, b_{1}=\alpha$, et $b_{j}=\alpha b_{j-1}-b_{j-2}$ pour $j \geqslant 2$. (2)
|
| 384 |
+
|
| 385 |
+
Comme $\alpha=\frac{1}{a_{n}}$, on doit avoir $b_{n-1}=\alpha b_{n}$, ce qui signifie que $b_{n+1}=0$.
|
| 386 |
+
Revenons sur $\alpha$. En fait, on a même $\alpha<2$ :
|
| 387 |
+
En effet, supposons que $\alpha \geqslant 2$. Alors, $a_{1}=\alpha \geqslant 2$ et, par une récurrence sans difficulté, on déduit que $a_{k}=\alpha-\frac{1}{a_{k-1}} \geqslant 1+\frac{1}{k}$.
|
| 388 |
+
En particulier, on a $a_{n} \geqslant 1+\frac{1}{n}>1$ et $a_{n}=\frac{1}{\alpha}<1$, contradiction.
|
| 389 |
+
On peut donc poser $\alpha=2 \cos (t)$ où $t \in] 0, \frac{\pi}{2}[$.
|
| 390 |
+
Compte-tenu de la formule bien connue
|
| 391 |
+
|
| 392 |
+
$$
|
| 393 |
+
2 \cos (a) \sin (b)=\sin (b+a)+\sin (b-a)
|
| 394 |
+
$$
|
| 395 |
+
|
| 396 |
+
une autre récurrence sans difficulté à partir de (2) conduit alors à
|
| 397 |
+
|
| 398 |
+
$$
|
| 399 |
+
b_{k}=\frac{\sin ((k+1) t)}{\sin (t)} \text { pour tout } k \geqslant 0
|
| 400 |
+
$$
|
| 401 |
+
|
| 402 |
+
La condition $b_{n+1}=0$ impose alors $t=\frac{\pi}{n+2}$. Ainsi, on a $\alpha=2 \cos \left(\frac{\pi}{n+2}\right)$ et $a=\left(a_{1}, \cdots, a_{n}\right)$ où $a_{k}=\frac{\sin \left(\frac{(k+1) \pi}{n+2}\right)}{\sin \left(\frac{k \pi}{n+2}\right)}$.
|
| 403 |
+
|
| 404 |
+
Réciproquement, on vérifie aisément que, dans ces conditions, la chaîne d'égalités (1) est vraie.
|
| 405 |
+

|
| 406 |
+
$\mathcal{F i n}$
|
| 407 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-4-solutions.md
ADDED
|
@@ -0,0 +1,133 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Matfématiques 2013-2014
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
# Envoi $\mathcal{N u m e ́ r o ~} 4$ - Corrigé
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe B
|
| 8 |
+
|
| 9 |
+
Exercice 1. Combien existe-t-il de couples d'entiers strictement positifs ( $a, b$ ) tels que
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\frac{1}{a}+\frac{1}{b}=\frac{1}{2014} ?
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
Solution de l'exercice 1 Soient $a, b$ deux entiers strictement positifs tels que $1 / a+1 / b=1 / 2014$. On a en particulier $\mathrm{a}, \mathrm{b}>2014$. On peut donc multiplier l'équation $\mathrm{ab}:$ on cherche en fait les entiers $\mathrm{a}, \mathrm{b}>2014$ tels que $\mathrm{ab}-2014 \mathrm{a}-2014 \mathrm{~b}=0$ ou encore, de manière équivalente, tels que ( $a-$ $2014)(b-2014)=2014^{2}$. On en déduit que le nombre recherché est le nombre de couples d'entiers strictement positifs $(u, v)$ tels que $u v=2014^{2}$, autrement dit le nombre de diviseurs positifs de $2014^{2}$. Comme $2014^{2}=2^{2} \cdot 19^{2} \cdot 53^{2}, 2014^{2}$ possède $(2+1) \cdot(2+1) \cdot(2+1)=27$ diviseurs positifs.
|
| 16 |
+
|
| 17 |
+
La réponse est donc 27 .
|
| 18 |
+
Exercice 2. Trouver tous les entiers $\boldsymbol{n} \geqslant 1$ tels que $2^{n}+12^{n}+2014^{n}$ soit un carré parfait.
|
| 19 |
+
Solution de l'exercice 2 Regardons l'expression modulo $3: 2^{\mathfrak{n}}+12^{n}+2014^{n} \equiv(-1)^{n}+1 \bmod 3$. Comme un carré n'est jamais congru à 2 modulo 3, on en déduit que $n$ est impair. Regardons ensuite l'expression modulo 7 :
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
2^{n}+12^{n}+2014^{n} \equiv 2^{n}+(-2)^{n}+5^{n} \equiv 5^{n} \quad \bmod 7
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
car $n$ est impair. Lorsque $n$ est impair, $5^{n}$ ne peut être congru qu'à 3,5 ou 6 modulo 7 . Or un carré est congru à $0,1,2$ ou 4 modulo 7 . Il n'existe donc pas d'entiers $n \geqslant 1$ tels que $2^{n}+12^{n}+2014^{n}$ soit un carré parfait.
|
| 26 |
+
Exercice 3. Trouver tous les couples d'entiers relatifs $(x, y)$ tels que $x^{3}+y^{3}=(x+y)^{2}$.
|
| 27 |
+
Solution de l'exercice 3 Soit $(x, y)$ un couple solution. Comme $x^{3}+y^{3}=(x+y)\left(x^{2}-x y+y^{2}\right)$, on a donc soit $x+y=0$, soit $x^{2}-x y+y^{2}=x+y$. Dans le deuxième cas, on remarque qu'alors nécessairement
|
| 28 |
+
$(x-1)^{2}+(y-1)^{2}+(x-y)^{2}=2$. Parmi les trois entiers $x-1, y-1$ et $x-y$, deux sont donc égaux à $1 \mathrm{ou}-1$ et le troisième est nul. On vérifie que les seules possibilités sont $(2,2),(0,0),(1,2),(1,0),(2,1)$ et $(0,1)$.
|
| 29 |
+
|
| 30 |
+
Ainsi, les solutions sont les couples $(2,2),(1,2),(1,0),(2,1),(0,1)$ et $(x,-x)$ où $x$ est un entier relatif.
|
| 31 |
+
|
| 32 |
+
## Exercices Communs
|
| 33 |
+
|
| 34 |
+
Exercice 4. Trouver tous les couples d'entiers positifs $(m, n)$ tels que $1+(m+n) m$ divise $(m+$ $n)(n+1)-1$.
|
| 35 |
+
Solution de l'exercice 4 Soit $(m, n)$ un couple solution. Alors $1+(m+n) m$ divise $(m+n)(n+1)-1+$ $1+(m+n) m=(m+n)(m+n+1)$. Or, $1+(m+n) m$ est premier avec $m+n$. Ainsi, $1+(m+n) m$ divise $m+n+1$. Donc $m^{2}+m n+1 \leqslant m+n+1$. Donc $m=0$ ou $m=1$.
|
| 36 |
+
|
| 37 |
+
Réciproquement, on vérifie que les couples $(0, n)$ et $(1, n)$, où $\boldsymbol{n} \geqslant 0$ est un entier, conviennent.
|
| 38 |
+
Exercice 5. Montrer que si la somme de tous les diviseurs positifs d'un entier $n \geqslant 1$ est une puissance de deux, alors le nombre de diviseurs positifs de n est une puissance de deux.
|
| 39 |
+
Solution de l'exercice 5 Décomposons $n$ en produit de facteurs premiers : $n=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$. On voit aisément que la somme des diviseurs positifs de $n$, notée $\sigma(n)$, vaut
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\sigma(n)=\prod_{i=1}^{k}\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}\right)
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
Ainsi, si $1 \leqslant i \leqslant k, 1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}$ est une puissance de deux. Ceci implique clairement que $p_{i} \neq 2$. Supposons ensuite par l'absurde que $\alpha_{i}+1$ n'est pas une puissance de deux et choisissons $q$ un nombre premier impair divisant $\alpha_{i}+1$. Alors
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}=\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}\right) \cdot\left(1+p_{i}^{q}+p_{i}^{2 q}+\cdots+p_{i}^{\alpha_{i}+1-q}\right)
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
En effet, cette égalité découle du fait que $\left(p_{i}^{\alpha_{i}+1}-1\right) /(p-1)=\left(p_{i}^{q}-1\right) /(p-1) \cdot\left(p_{i}^{\alpha_{i}+1}-1\right) /\left(p^{q}-1\right)$. Ceci est absurde, car $1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}$ est impair. Ainsi, $\alpha_{i}+1$ est une puissance de deux pour tout $1 \leqslant i \leqslant k$. Ceci conclut, car le nombre de diviseurs (positifs) de $n$ est $\prod_{i=1}^{k}\left(\alpha_{i}+1\right)$.
|
| 52 |
+
Exercice 6. Trouver tous les nombres premiers $p$ et $q$ tels que $p$ divise $5^{q}+1$ et $q$ divise $5^{p}+1$.
|
| 53 |
+
Solution de l'exercice 6 Notons $\alpha$ l'ordre de 5 modulo $q$ et $\beta$ l'ordre de 5 modulo $p$. Comme $5^{2 p} \equiv 1$ $\bmod \mathrm{q}$, on en déduit que $\alpha$ divise $2 p$. Donc $\alpha=1,2, \mathrm{p}$ ou $2 p$.
|
| 54 |
+
|
| 55 |
+
Si $\alpha=1$, alors $5 \equiv 1 \bmod \mathbf{q}$, donc $\mathbf{q}=2$. Si $\alpha=2$, alors $25 \equiv 1 \bmod \mathbf{q}$, donc $\mathbf{q}=2$ ou $\mathbf{q}=3$.
|
| 56 |
+
Si $q=2$, alors $p$ divise $5^{2}+1$, donc $p=2$ ou $p=13$. Réciproquement, $(2,2)$ et $(13,2)$ conviennent.
|
| 57 |
+
Si $q=3$, alors $p$ divise $5^{3}+1$, donc $p=2,3$ ou 7 . Réciproquement, on vérifie que $(3,3),(7,3)$ conviennent, mais que $(2,3)$ ne convient pas.
|
| 58 |
+
|
| 59 |
+
De même, on a $\beta=1,2$, q ou 2 q. Si $\beta=1$ ou 2 , on obtient similairement les solutions $(2,13)$ et $(3,7)$.
|
| 60 |
+
|
| 61 |
+
Supposons maintenant que $\alpha=p$ ou $2 p$ et que $\beta=q$ ou $2 q$. D'après le petit théorème de Fermat, $5^{p-1} \equiv 1 \bmod p$ et $5^{q-1} \equiv 1 \bmod q$. Donc $\beta$ divise $p-1$ et $\alpha$ divise $q-1$. Donc $q$ divise $p-1$ et $p$ divise $\mathrm{q}-1$. Donc $\mathrm{q} \leqslant \mathrm{p}-1$ et $\mathrm{p} \leqslant \mathrm{q}-1$. Ainsi $\mathrm{q} \leqslant \mathrm{q}-2$, ce qui est absurde.
|
| 62 |
+
|
| 63 |
+
Les solutions sont donc $(2,2),(3,3),(13,2),(2,13),(3,7)$ et $(7,3)$.
|
| 64 |
+
|
| 65 |
+
## Exercices du groupe A
|
| 66 |
+
|
| 67 |
+
Exercice 7. Trouver toutes les fonctions $\mathrm{f}: \mathbb{N} \rightarrow \mathbb{N}$ telles que $2 m n+m f(m)+n f(n)$ est un carré parfait pour tous entiers positifs $m$ et $n$.
|
| 68 |
+
Solution de l'exercice 7 Pour simplifier, posons $F(m, n)=2 m n+m f(m)+n f(n)$. Alors $F(m, 0)=$ $\mathrm{mf}(\mathrm{m})$ est un carré pour tout $\mathrm{m} \geqslant 1$.
|
| 69 |
+
|
| 70 |
+
On peut donc écrire $f(p)=p a^{2}$ pour un nombre premier $p$. Supposons que $a \geqslant 2$. Alors $(a p)^{2}+2 p+$ $f(1)=F(p, 1)>\left(a p^{2}\right)$ est un carré, donc $(a p)^{2}+2 p+f(1) \geqslant(a p+1)^{2}$ et $2 p+f(1) \geqslant 2 a p+1 \geqslant 4 p+1$, de sorte que $p \leqslant(f(1)-1) / 2$. Ainsi $f(p)=p$ pour tous nombres premiers $p$ suffisamment grands.
|
| 71 |
+
|
| 72 |
+
Soit maintenant $k \geqslant 1$ et $p$ un nombre premier suffisamment grand pour que $f(p)=p, p>k f(k)$ et $\mathrm{p}>\mathrm{k}^{2}+1$. Alors
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\begin{gathered}
|
| 76 |
+
(k+p-1)^{2}=\left(k^{2}+1\right)+p^{2}-2 k-2 p+2 k p<p^{2}-p-2 k+2 k p<F(p, k) \text { et } \\
|
| 77 |
+
F(p, k)=p^{2}+2 k p+k f(k)<p^{2}+2 k p+p \leqslant(p+k+1)^{2} .
|
| 78 |
+
\end{gathered}
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
Comme $F(p, k)$ est un carré, ceci impose que $k f(k)+p^{2}+2 k p=(k+p)^{2}$ et donc que $f(k)=k$.
|
| 82 |
+
Réciproquement, on vérifie que la fonction identité convient.
|
| 83 |
+
Exercice 8. (Corée 2003) Trouver tous les triplets d'entiers ( $a, b, c$ ) tels que $a \neq 0$ et
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
2 a^{4}+2 a^{2} b^{2}+b^{4}=c^{2}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
Solution de l'exercice 8 Supposons qu'il exise un tel triplet : soit alors a $>0$ le plus petit entier tel que $(a, b, c)$ soit solution. Si $d=\operatorname{pgcd}(a, b)$, en divisant l'égalité par $d^{4}$ on voit que $\left(a / d, b / d, c / d^{2}\right)$ est également solution. On a donc $\mathrm{d}=1$.
|
| 90 |
+
|
| 91 |
+
Regardons l'expression $2 a^{4}+2 a^{2} b^{2}+b^{4}$ modulo 8 , et utilisons le fait qu'un carré est congru à 0,1 ou 4 modulo 8 : si a est impair, alors $2 a^{4}+2 a^{2} b^{2}+b^{4}$ est congru à 2 ou à 5 modulo $8 ; a$ est donc forcément pair, et b es impair. Réécrivons l'égalité de l'énoncé en
|
| 92 |
+
|
| 93 |
+
$$
|
| 94 |
+
\left(a^{2}\right)^{2}+\left(a^{2}+b^{2}\right)^{2}=c^{2}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Le triplet $\left(a^{2}, a^{2}+b^{2}, c\right)$ est donc pythagoricien. Comme $\operatorname{pgcd}(a, b)=1$, il existe des entiers $u, v$ premiers entre eux tels que $a^{2}=2 u v, a^{2}+b^{2}=u^{2}-v^{2}$ et $c=u^{2}+v^{2}$.
|
| 98 |
+
|
| 99 |
+
En regardant modulo 4 , on obtient $1 \equiv a^{2}+b^{2} \equiv u^{2}-v^{2}$. Puisqu'un carré est congru à 0 ou 1 modulo 4 , on en déduit que $u$ est impair et que $v$ est pair. Puisque $a^{2}=2 u v$ et que $u$ et $v$ sont premiers entre eux, on peut écrire $u=m^{2}$ et $v=2 n^{2}$ avec $m, n$ premiers entre eux et $m$ impair. De $b^{2}=u^{2}-v^{2}-2 u v$ il vient $2 v^{2}=(u-v+b)(u-v-b)$. Donc
|
| 100 |
+
|
| 101 |
+
$$
|
| 102 |
+
2 n^{4}=\left(\frac{m^{2}-2 n^{2}+b}{2}\right)\left(\frac{m^{2}-2 n^{2}-b}{2}\right) .
|
| 103 |
+
$$
|
| 104 |
+
|
| 105 |
+
Posons $x=\left(m^{2}-2 n^{2}+b\right) / 2$ et $y=\left(m^{2}-2 n^{2}-b\right) / 2$ : ce sont des entiers car $m^{2}$ et $b$ sont impairs. En outre, $0<a^{2}+b^{2}=(u-v)(u+v)$, et $u+v$ est positif, donc $u-v$ l'est également, et a fortiori $x=(u-v+b) / 2 \geqslant 0$, puis $y \geqslant 0$ également.
|
| 106 |
+
|
| 107 |
+
D'aute part, on obtient $x-y=b$ et $x y=2 \mathfrak{n}^{4}$. Comme $\operatorname{pgcd}(b, n)=1, x$ et $y$ sont forcément premiers entre eux. Puisque $x y=2 n^{4}$, on peut écrire $x$ et $y$ sous la forme $x=2 k^{4}$ et $y=l^{4}$, ou bien $x=l^{4}$ et $y=2 k^{4}$, avec $\operatorname{pgcd}(k, l)=1$ et $l$ impair.
|
| 108 |
+
|
| 109 |
+
Ainsi, $2 k^{4}+l^{4}=x+y=m^{2}-2 n^{2}$, et donc
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
m^{2}=2 k^{4}+l^{4}+2 n^{2}=2 k^{4}+2 k^{2} l^{2}+l^{4}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Or, $2 \mathrm{klm}=2 \mathrm{mn}=\mathrm{a}>0$, donc $\mathrm{lm} \geqslant 1$ et $0<\mathrm{k}<\mathrm{a}$, ce qui contredit la minimalité de a .
|
| 116 |
+
Il n'existe donc pas de triplet ( $a, b, c$ ) solution lorsque $a \neq 0$.
|
| 117 |
+
Exercice 9. Trouver le nombre de suites $\left(u_{n}\right)_{n \geqslant 1}$ d'entiers relatifs telles que $u_{n} \neq-1$ pour tout entier $n \geqslant 1$ et telles que
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
u_{n+2}=\frac{2014+u_{n}}{1+u_{n+1}}
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
pour tout entier $\mathrm{n} \geqslant 1$.
|
| 124 |
+
$\underline{\text { Solution de l'exercice } 9}$ La relation de l'énoncé impose que $\left(u_{n+1}-u_{n-1}\right)\left(u_{n}+1\right)=u_{n}-u_{n-2}$ pour $\mathrm{n} \geqslant 3$. Par récurrence, il vient
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\mathbf{u}_{3}-\mathbf{u}_{1}=\prod_{i=3}^{n}\left(u_{i}+1\right)\left(u_{n+1}-u_{n-1}\right)
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
Supposons par l'absurde que $u_{3} \neq u_{1}$. Ainsi $u_{n+1} \neq u_{n-1}$ pour tout $n \geqslant 2$. En faisant croitre $n$, on voit qu'il ne peut pas y avoir une infinité de termes $u_{i}$ tels que $u_{i} \neq 0,-2$. Ainsi, $u_{i}=0$ ou -2 à partir d'un certain rang (car $\mathfrak{u}_{3}-\mathfrak{u}_{1}$ a un nombre fini de diviseurs). On vérifie aisément à partir de la relation de récurence de l'énoncé que ceci n'est pas possible. Donc $u_{3}=u_{1}$, et par (1) on en déduit que $u_{n+2}=u_{n}$ pour tout entier $n \geqslant 1$.
|
| 131 |
+
|
| 132 |
+
Sous cette hypothèse, la relation à vérifier devient $\left(1+u_{n+1}\right) u_{n}=2014+u_{n}$, ou encore $u_{n} u_{n+1}=$ 2014, ce qui est équivalent à $u_{1} \mathfrak{u}_{2}=2014$. Ainsi, le nombre de suites $\left(u_{n}\right)_{n \geqslant 1}$ qui conviennent est le nombre paires d'entiers $(a, b)$ telles que $a b=2014$, avec $a \neq-1$ et $b \neq-1$ : c'est exactement le nombre de diviseurs (positifs ou négatifs) de 2014, moins 2. Comme $2014=2 \cdot 19 \cdot 53$, celui-ci a $2 \cdot(1+1) \cdot(1+1) \cdot(1+1)=16$ diviseurs (positifs ou négatifs), donc 14 suites conviennent.
|
| 133 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-5-solutions.md
ADDED
|
@@ -0,0 +1,222 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## OLYMPIADES FRANÇAISES DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
Envoi No. 5
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. Soit $A B C D$ un carré de côté 1. À l'intérieur du carré, on trace les arcs de cercles de centres $A, B, C, D$ et de rayon 1 . Déterminer l'aire de chaque portion délimitée à l'intérieur du carré.
|
| 12 |
+
|
| 13 |
+
## Solution de l'exercice 1
|
| 14 |
+
|
| 15 |
+
Considérons les aires $a, b, c$ des portions indiquées sur la figure.
|
| 16 |
+
|
| 17 |
+
|
| 18 |
+
Comme l'aire du carré est égale à 1 , on a
|
| 19 |
+
|
| 20 |
+
$$
|
| 21 |
+
a+4 b+4 c=1 .
|
| 22 |
+
$$
|
| 23 |
+
|
| 24 |
+
Comme l'aire du quart de cercle $A B C$ est égale à $\pi / 4$, on a
|
| 25 |
+
|
| 26 |
+
$$
|
| 27 |
+
a+3 b+2 c=\pi / 4 \text {. }
|
| 28 |
+
$$
|
| 29 |
+
|
| 30 |
+
Considérons maintenant le secteur angulaire $O M N$ de rayon 1 et d'angle $\pi / 3$. Il a pour aire $\pi / 6$. D'autre part, le triangle $O M N$ a pour aire $\frac{\sqrt{3}}{4}$, donc l'aire de la "lune" est égale à $\frac{\pi}{6}-\frac{\sqrt{3}}{4}$. On en déduit que
|
| 31 |
+
|
| 32 |
+
$$
|
| 33 |
+
a+2 b+c=2\left(\frac{\pi}{6}-\frac{\sqrt{3}}{4}\right)+\frac{\sqrt{3}}{4}=\frac{\pi}{3}-\frac{\sqrt{3}}{4} .
|
| 34 |
+
$$
|
| 35 |
+
|
| 36 |
+
En soustrayant les équations (1) et (2) et les équations (1) et (3), on en déduit
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
\begin{aligned}
|
| 40 |
+
b+2 c & =1-\frac{\pi}{4} \\
|
| 41 |
+
2 b+3 c & =1+\frac{\sqrt{3}}{4}-\frac{\pi}{3}
|
| 42 |
+
\end{aligned}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
ce qui donne facilement
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\begin{aligned}
|
| 49 |
+
b & =-1+\frac{\sqrt{3}}{2}+\frac{\pi}{12} \\
|
| 50 |
+
c & =1-\frac{\sqrt{3}}{4}-\frac{\pi}{6} \\
|
| 51 |
+
a & =1-\sqrt{3}+\frac{\pi}{3}
|
| 52 |
+
\end{aligned}
|
| 53 |
+
$$
|
| 54 |
+
|
| 55 |
+
Exercice 2. Dans un cercle $\mathcal{C}$ de centre $O$, on trace une corde $[C D]$. Soit $\Gamma$ le cercle de diamètre $[C D]$ et $O^{\prime}$ son centre. La médiatrice de $[C D]$ coupe le cercle $\mathcal{C}$ en deux points $A$ et $B$ tels que $A$ est extérieur à $\Gamma$. Notons $T$ et $T^{\prime}$ les points de contact des tangentes à $\Gamma$ passant par $A$. Soit $F$ le milieu de $\left[T T^{\prime}\right]$. Montrer que $O^{\prime}$ est le milieu de $[B F]$.
|
| 56 |
+
|
| 57 |
+
## Solution de l'exercice 2
|
| 58 |
+
|
| 59 |
+
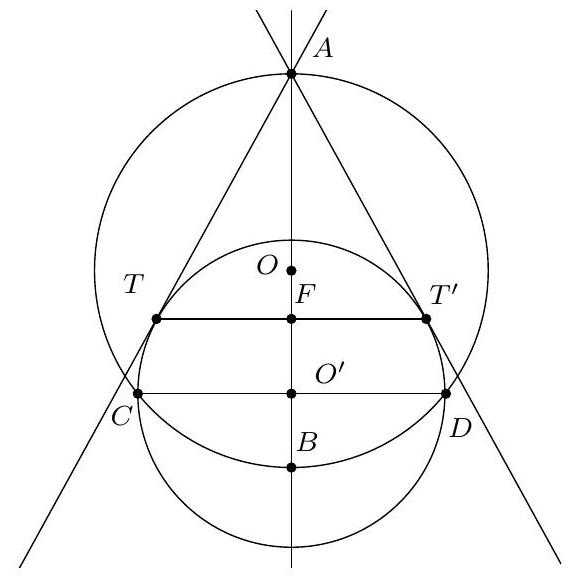
|
| 60 |
+
|
| 61 |
+
Comme les triangles $A F T$ et $A T O^{\prime}$ sont semblables, on a $\frac{A F}{A T}=\frac{A T}{A O^{\prime}}$. Or, $A T^{2}=A O^{\prime 2}-O^{\prime} T^{2}=$ $A O^{\prime 2}-O^{\prime} C^{2}$ donc $A F=\frac{A O^{\prime 2}-O^{\prime} C^{2}}{A O^{\prime}}$.
|
| 62 |
+
Comme les triangles $A C B$ et $A O^{\prime} C$ sont semblables, on a $\frac{A B}{A C}=\frac{A C}{A O^{\prime}}$. Or, $A C^{2}=A O^{\prime 2}+O^{\prime} C^{2}$ donc $A B=\frac{A O^{\prime 2}+O^{\prime} C^{2}}{A O^{\prime}}$.
|
| 63 |
+
En additionnant les égalités précédemment trouvées, on obtient $\frac{A F+A B}{2}=A O^{\prime}$.
|
| 64 |
+
|
| 65 |
+
Exercice 3. Soit $A B C$ un triangle isocèle en $A$. Soient $M$ et $N$ deux points de $[B C]$. Les droites $[A M]$ et $[A N]$ recoupent le cercle circonscrit à $A B C$ en $P$ et $Q$.
|
| 66 |
+
|
| 67 |
+
1) Montrer que $M, N, P, Q$ sont cocycliques.
|
| 68 |
+
2) Soient $R_{1}$ et $R_{2}$ les rayons des cercles circonscrits à $B M P$ et $C M P$. Calculer $R_{1}+R_{2}$ en fonction des longueurs $A B$ et $B C$.
|
| 69 |
+
|
| 70 |
+
## Solution de l'exercice 3
|
| 71 |
+
|
| 72 |
+
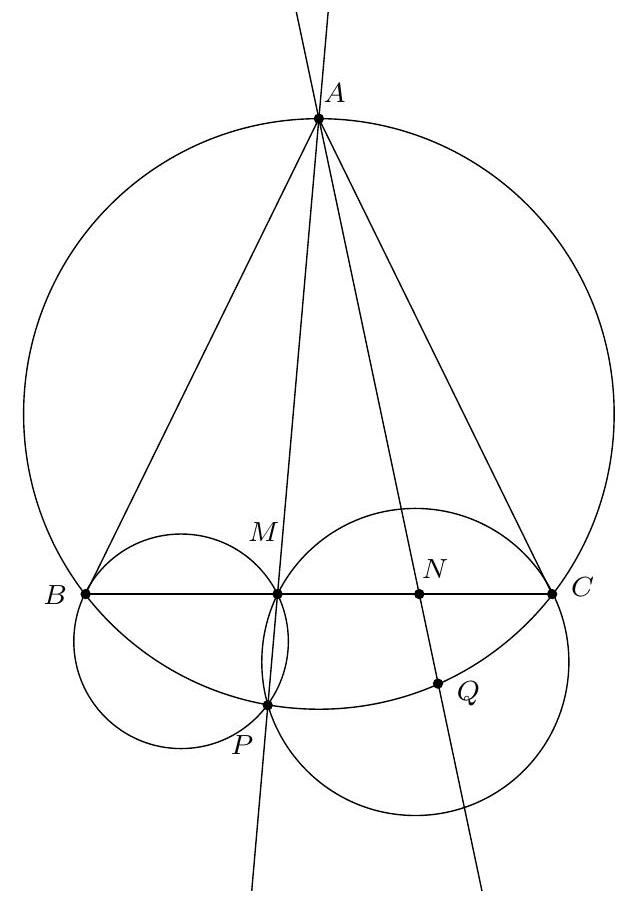
|
| 73 |
+
|
| 74 |
+
1) $\widehat{P M N}=\widehat{P M C}=\pi-\widehat{M C P}-\widehat{C P M}=\pi-\widehat{B C P}-\widehat{C P A}=\pi-\widehat{B C P}-\widehat{C B A}$, et $\widehat{N Q P}=\widehat{A Q P}=\widehat{A C P}=\widehat{A C B}+\widehat{B C P}=\widehat{C B A}+\widehat{B C P}$,
|
| 75 |
+
donc $\widehat{P M N}=\pi-\widehat{N Q P}$, ce qui prouve la cocyclicité de $M, N, P, Q$.
|
| 76 |
+
2) D'après la loi des sinus, on a
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
2\left(R_{1}+R_{2}\right)=\frac{B M}{\sin \widehat{M P B}}+\frac{C M}{\sin \widehat{C P M}}
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
Or, $\widehat{M P B}=\widehat{A P B}=\widehat{A C B}$ et de même $\widehat{C P M}=\widehat{A C B}$, donc
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
2\left(R_{1}+R_{2}\right)=\frac{B M+C M}{\sin \widehat{A C B}}=\frac{B C}{\sin \widehat{A C B}} .
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
D'autre part, soit $H$ le projeté orthogonal de $A \operatorname{sur}(B C)$. On a $\sin \widehat{A C B}=\frac{A H}{A B}=\frac{\sqrt{A B^{2}-(B C / 2)^{2}}}{A B}$, donc
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
R_{1}+R_{2}=\frac{A B \times B C}{2 \sqrt{A B^{2}-(B C / 2)^{2}}}
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
## Exercices communs
|
| 95 |
+
|
| 96 |
+
Exercice 4. Soit $A B C$ un triangle. Les bissectrices de $\widehat{A}, \widehat{B}$ et $\widehat{C}$ recoupent le cercle circonscrit en $A^{\prime}, B^{\prime}$ et $C^{\prime}$ respectivement. Soit $I$ le centre du cercle inscrit à $A B C$. Les cercles de diamètres $\left[I A^{\prime}\right],\left[I B^{\prime}\right]$ et $\left[I C^{\prime}\right]$ coupent respectivement les droites $(B C),(C A)$ et $(A B)$ en $A_{1}$ et $A_{2}, B_{2}$ et $B_{2}$, $C_{1}$ et $C_{2}$. Montrer que $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.
|
| 97 |
+
|
| 98 |
+
## Solution de l'exercice 4
|
| 99 |
+
|
| 100 |
+
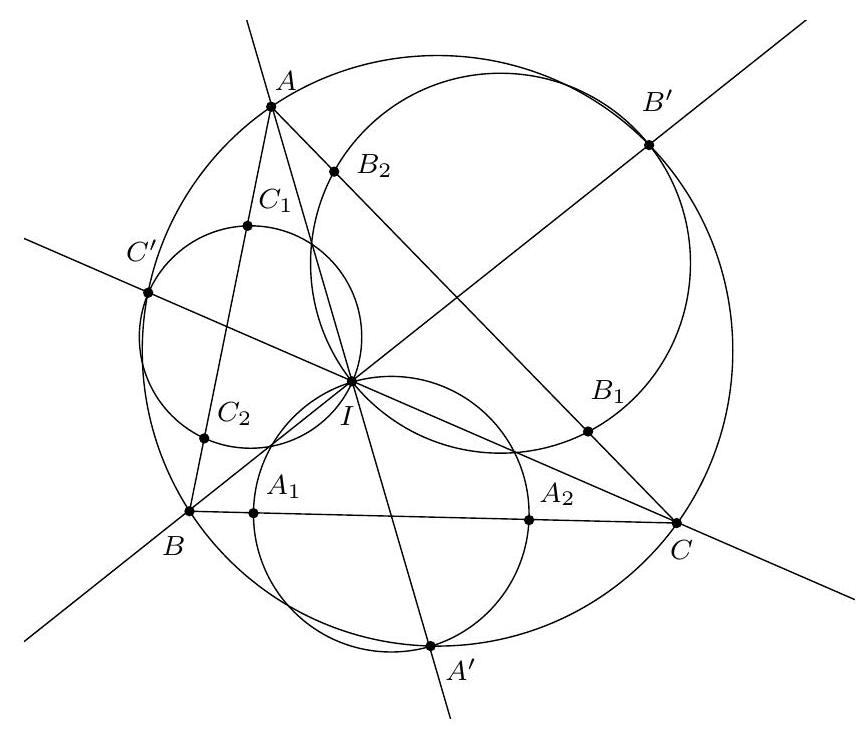
|
| 101 |
+
|
| 102 |
+
Notons $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$ les cercles de diamètres respectifs $\left[I A^{\prime}\right],\left[I B^{\prime}\right]$ et $\left[I C^{\prime}\right]$.
|
| 103 |
+
Remarquons d'abord que $I$ est l'orthocentre de $A^{\prime} B^{\prime} C^{\prime}$. Pour le voir, montrons par exemple que $\left(A^{\prime} C^{\prime}\right) \perp\left(B^{\prime} I\right)$ :
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
\begin{aligned}
|
| 107 |
+
\left(B^{\prime} I, A^{\prime} C^{\prime}\right) & =\left(B B^{\prime}, A^{\prime} C^{\prime}\right)=\left(B B^{\prime}, B A\right)+\left(A B, A A^{\prime}\right)+\left(A^{\prime} A, A^{\prime} C^{\prime}\right) \\
|
| 108 |
+
& =\left(B B^{\prime}, B A\right)+\left(A B, A A^{\prime}\right)+\left(C A, C C^{\prime}\right) \\
|
| 109 |
+
& =\frac{\widehat{B}+\widehat{A}+\widehat{C}}{2}=\frac{\pi}{2} \quad(\bmod \pi)
|
| 110 |
+
\end{aligned}
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
Soit $B^{\prime \prime}$ le pied de la hauteur de $A^{\prime} B^{\prime} C^{\prime}$ issue de $B^{\prime}$. Alors $B, B^{\prime \prime}$ et $I$ sont alignés d'après ce qui précède.
|
| 114 |
+
D'autre part, comme $\left(I B^{\prime \prime}\right) \perp\left(B^{\prime \prime} A^{\prime}\right), B^{\prime \prime}$ appartient à $\Gamma_{A}$. De même, il appartient à $\Gamma_{C}$, donc l'axe radical de ces deux cercles est $\left(I B^{\prime \prime}\right)$. On en déduit que $B$ appartient également à cet axe radical, ce qui entraîne que $B A_{1} \cdot B A_{2}=B C_{1} \cdot B C_{2}$ et donc $A_{1}, A_{2}, C_{1}, C_{2}$ sont cocycliques. Soit $\Gamma_{C A}$ le cercle passant par ces points.
|
| 115 |
+
On définit de même $\Gamma_{A B}$ et $\Gamma_{B C}$. Si ces trois cercles étaient deux à deux distincts, alors leurs axes radicaux pris deux à deux seraient $(A B),(B C)$ et $(C A)$ et ne seraient ni concourants ni parallèles, ce qui est impossible.
|
| 116 |
+
Donc deux de ces cercles sont confondus, et par conséquent $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.
|
| 117 |
+
|
| 118 |
+
Exercice 5. Soit $A B C D$ un quadrilatère cyclique. Un cercle passant par $A$ et $B$ coupe $[A C]$ et $[B D]$ en $E$ et $F$. Les droites $(A F)$ et $(B E)$ coupent $[B C]$ et $[A D]$ en $P$ et $Q$ respectivement. Montrer que $(P Q)$ est parallèle à $(C D)$.
|
| 119 |
+
|
| 120 |
+
Solution de l'exercice 5
|
| 121 |
+
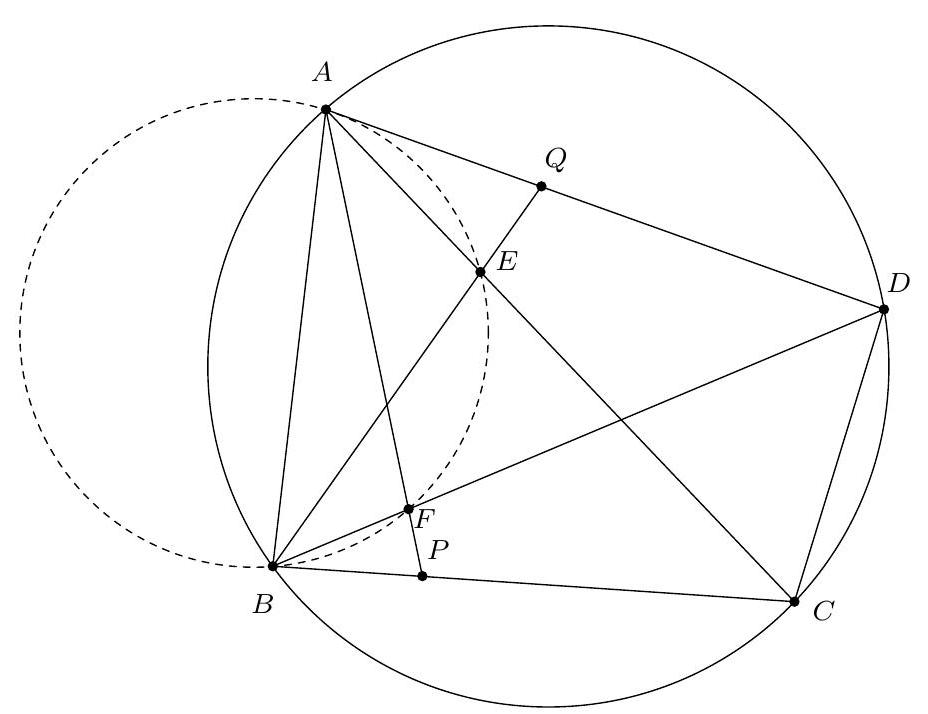
|
| 122 |
+
$\widehat{A Q B}=\widehat{A Q E}=\pi-\widehat{Q E A}-\widehat{E A Q}=\widehat{A E B}-\widehat{C A D}$ et de même, $\widehat{A P B}=\widehat{A F B}-\widehat{C B D}$. Or, $\widehat{A E B}=\widehat{A F B}$ et $\widehat{C A D}=\widehat{C B D}$, donc $\widehat{A Q B}=\widehat{A P B}$. On en déduit que $A, B, P, Q$ sont cocycliques. Il vient: $(A D, P Q)=(Q A, Q P)=(B A, B P)=(B A, B C)=(D A, D C)$, donc $(P Q)$ et $(D C)$ sont parallèles.
|
| 123 |
+
|
| 124 |
+
Exercice 6. Soit $A$ un point extérieur à un cercle $\Gamma$. On mène deux tangentes $[A T]$ et $\left[A T^{\prime}\right]$ issues de $A$. Soient $M$ et $M^{\prime}$ les milieux de $[A T]$ et $\left[A T^{\prime}\right]$. Soit $P$ un point de $\left(M M^{\prime}\right)$. Notons $[U V]$ la corde de $\Gamma$ telle que $(P U)$ et $(P V)$ soient tangentes à $\Gamma$. La droite $(U V)$ coupe $\left(M M^{\prime}\right)$ en $Q$. Montrer que le triangle $P A Q$ est rectangle.
|
| 125 |
+
|
| 126 |
+
## $\underline{\text { Solution de l'exercice } 6}$
|
| 127 |
+
|
| 128 |
+
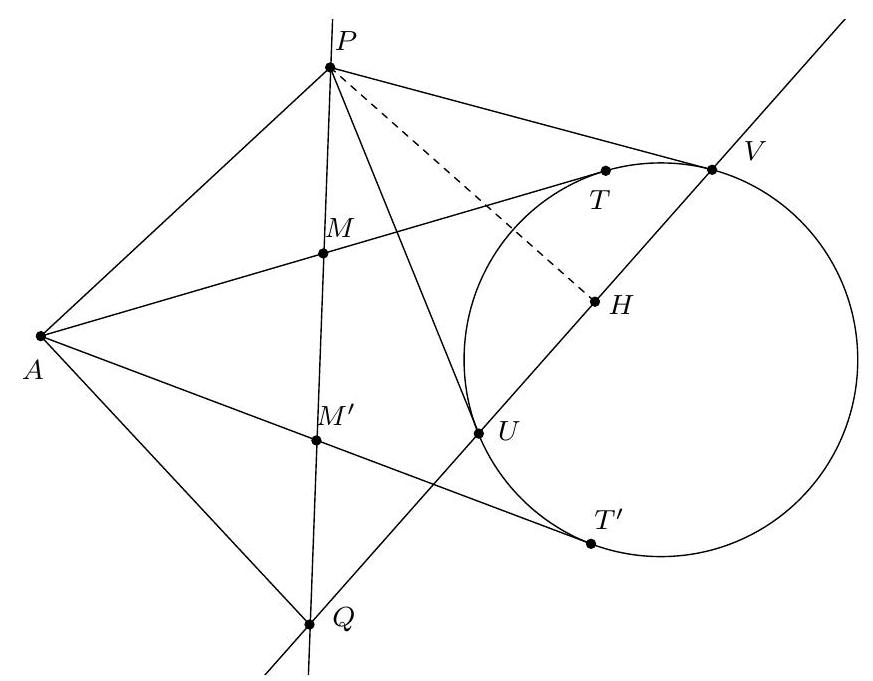
|
| 129 |
+
|
| 130 |
+
Comme $M A=M T, M$ appartient à l'axe radical de $A$ et $\Gamma$ ( $A$ étant considéré comme un cercle de rayon nul). De même, $M^{\prime}$ appartient à cet axe radical, donc $P$ et $Q$ également. On en déduit que $P A=P U=P V$ et que $Q A^{2}=Q U \cdot Q V$.
|
| 131 |
+
Notons $H$ le projeté orthogonal de $P$ sur ( $U V$ ). On a
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\begin{aligned}
|
| 135 |
+
P A^{2}+Q A^{2} & =P U^{2}+Q U \cdot Q V=P H^{2}+H U^{2}+(Q H-H U)(Q H+H U) \\
|
| 136 |
+
& =P H^{2}+H U^{2}+Q H^{2}-H U^{2}=P H^{2}+Q H^{2}=P Q^{2}
|
| 137 |
+
\end{aligned}
|
| 138 |
+
$$
|
| 139 |
+
|
| 140 |
+
donc $P A Q$ est rectangle en $A$.
|
| 141 |
+
|
| 142 |
+
## Exercices du groupe A
|
| 143 |
+
|
| 144 |
+
Exercice 7. Soit $A B C$ un triangle et $\omega$ son cercle inscrit. On note $P, Q, R$ les points de contact de $\omega$ avec $(B C),(C A)$ et $(A B)$. Un cercle passant par $B$ et $C$ est tangent en $X$ à $\omega$, un cercle passant par $C$ et $A$ est tangent en $Y$ à $\omega$ et un cercle passant par $A$ et $B$ est tangent en $Z$ à $\omega$. Montrer que les droites $(P X),(Q Y)$ et $(R Z)$ sont concourantes.
|
| 145 |
+
|
| 146 |
+
Solution de l'exercice 7
|
| 147 |
+
Rappelons d'abord quelques résultats sur la polarité que nous allons utiliser. Soit $\mathcal{C}$ un cercle de centre $O$ et de rayon $R$. Si $P$ est un point distinct de $O$, la polaire de $P$ par rapport à $\mathcal{C}$ est la droite formée des points $M$ tels que $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. Le pôle par rapport à $\mathcal{C}$ d'une droite $\mathcal{D}$ ne passant pas par $O$ est l'unique point $P$ tel que pour tout $M$ appartenant à $\mathcal{D}$ on a $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. À partir de cette définition, il est facile de montrer les propriétés suivantes:
|
| 148 |
+
(i) si $P$ est un point extérieur à $\mathcal{C}$ et $(P T),\left(P T^{\prime}\right)$ sont les deux tangentes à $\mathcal{C}$, alors la polaire de $P$ est la droite ( $T T^{\prime}$ );
|
| 149 |
+
(ii) trois points donnés sont alignés si et seulement si leurs polaires sont concourantes.
|
| 150 |
+
(Remarque : pour la propriété (ii), la droite sur laquelle se trouvent les trois points est la polaire du point de rencontre des trois droites.)
|
| 151 |
+
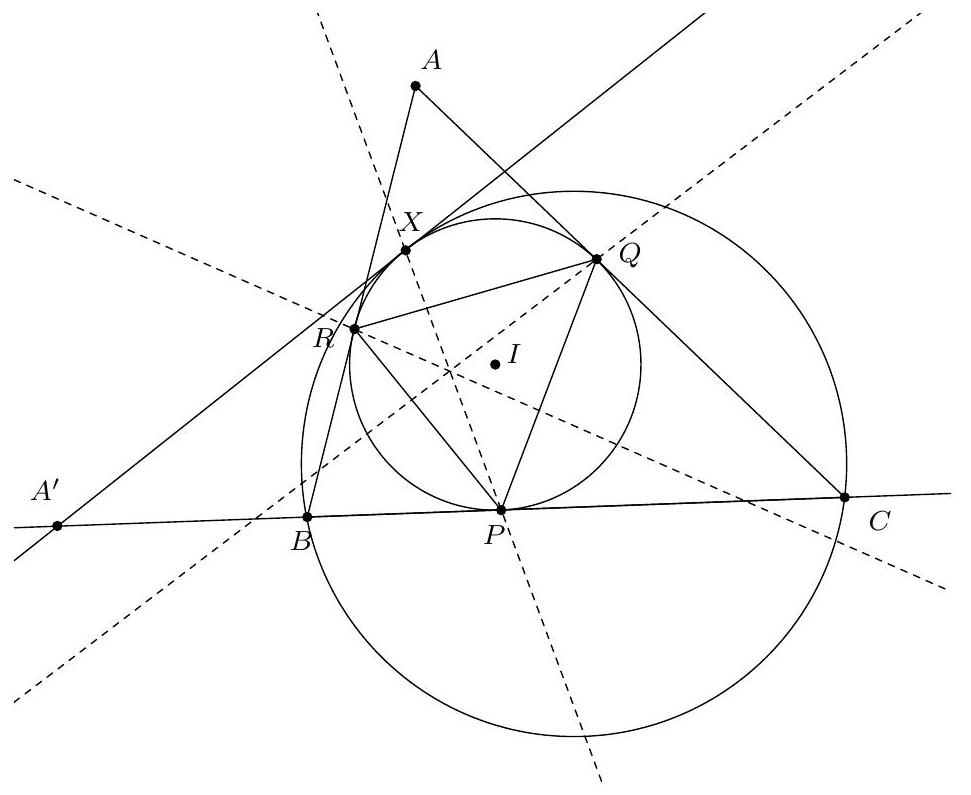
|
| 152 |
+
|
| 153 |
+
Revenons à l'exercice. Notons $\Gamma_{A}$ le cercle passant par $B, C$ et $X$. On définit de même les cercles $\Gamma_{B}$ et $\Gamma_{C}$. Soit $A^{\prime}$ le point de rencontre entre la tangente commune à $\omega$ et $\Gamma_{X}$, et la droite $(B C)$. On définit de même les points $B^{\prime}$ et $C^{\prime}$.
|
| 154 |
+
D'après la propriété (ii), la polaire de $A^{\prime}$ par rapport à $\omega$ est la droite $(P X)$. Il suffit donc d'après la propriété (i) de montrer que $A^{\prime}, B^{\prime}$ et $C^{\prime}$ sont alignés.
|
| 155 |
+
Soit $\Gamma$ le cercle circonscrit à $A B C$. Comme $A^{\prime}$ appartient à l'axe radical $(B C)$ de $\Gamma$ et $\Gamma_{A}$, on a $\mathcal{P}_{\Gamma}\left(A^{\prime}\right)=\mathcal{P}_{\Gamma_{A}}\left(A^{\prime}\right)=A^{\prime} X^{2}=\mathcal{P}_{\omega}\left(A^{\prime}\right)$. On en déduit que $A^{\prime}$ appartient à l'axe radical de $\Gamma$ et $\omega$. Il en va de même pour $B^{\prime}$ et $C^{\prime}$, ce qui prouve que $A^{\prime}, B^{\prime}$ et $C^{\prime}$ sont alignés.
|
| 156 |
+
|
| 157 |
+
Exercice 8. Soit $A B C$ un triangle. On note $P$ le milieu de l'arc du cercle circonscrit à $A B C$ contenant $A$. On suppose que la bissectrice de l'angle $\widehat{B A C}$ coupe le cercle de diamètre $[P C]$ en deux points $D$ et $E$. Soit $F$ le symétrique de $E$ par rapport à $(B C)$ et $I$ le milieu de $[B C]$. Montrer que $B, D, F, I$ sont cocycliques.
|
| 158 |
+
|
| 159 |
+
## Solution de l'exercice 8
|
| 160 |
+
|
| 161 |
+
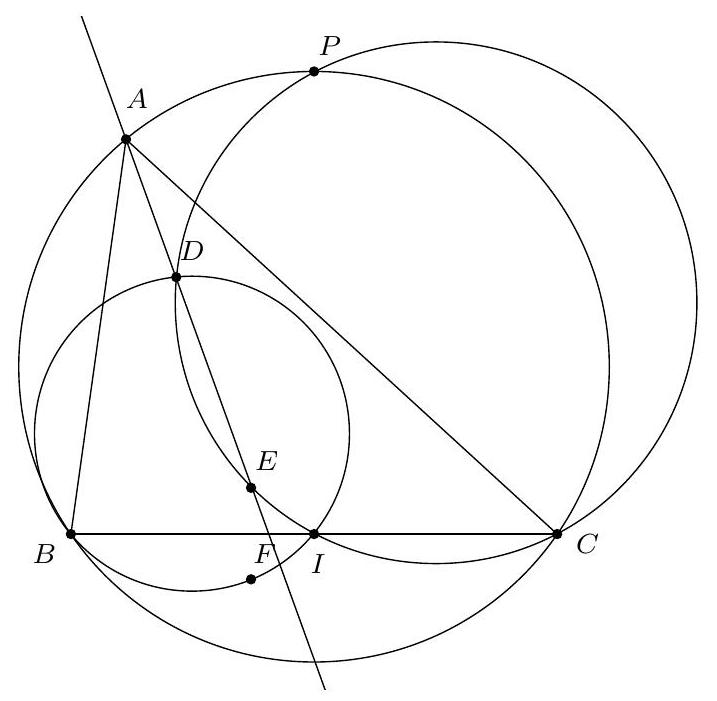
|
| 162 |
+
|
| 163 |
+
On applique l'inversion $i$ de pôle $I$ et de puissance $-I B \cdot I C$. Soit $Q$ le point diamétralement opposé à $P$. Alors $i$ échange $P$ et $Q$ d'une part, et $B$ et $C$ d'autre part. Comme le cercle de diamètre $[P C]$ passe par $I$, son image par $i$ est une droite. Or, $i(P)=Q$ et $i(C)=B$, donc $i$ transforme le cercle de diamètre $[P C]$ en la droite $(B Q)$.
|
| 164 |
+
La bissectrice de $\widehat{A}$ est transformée en un cercle passant par $I$ et par $P$.
|
| 165 |
+
Notons $K=i(D), L=i(E)$ et $M=i(F)$. D'après ce qui précède, les points $K$ et $L$ appartiennent à $(B Q)$, et $P, I, K, L$ sont cocycliques. De plus, $L$ et $M$ sont symétriques par rapport à $(B C)$.
|
| 166 |
+

|
| 167 |
+
|
| 168 |
+
Enfin, remarquons que $Q I \cdot Q P=Q B^{2}$ car $Q B I$ et $Q P B$ sont semblables. En utilisant la puissance par rapport au cercle $P I K L$, on obtient que $Q K \cdot Q L=Q B^{2}$, donc $K$ et $L$ sont inverses par rapport au cercle de centre $Q$ et de rayon $Q B$. On est ainsi ramenés à démontrer le lemme suivant :
|
| 169 |
+
Lemme: Soit $\mathcal{C}$ un cercle de centre $Q$. Soit $[B C]$ une corde de $\mathcal{C}$ et $L$ un point de $(Q B)$. Alors $C$, l'inverse de $L$ par rapport à $\mathcal{C}$ et le symétrique de $L$ par rapport à $(B C)$ sont alignés.
|
| 170 |
+
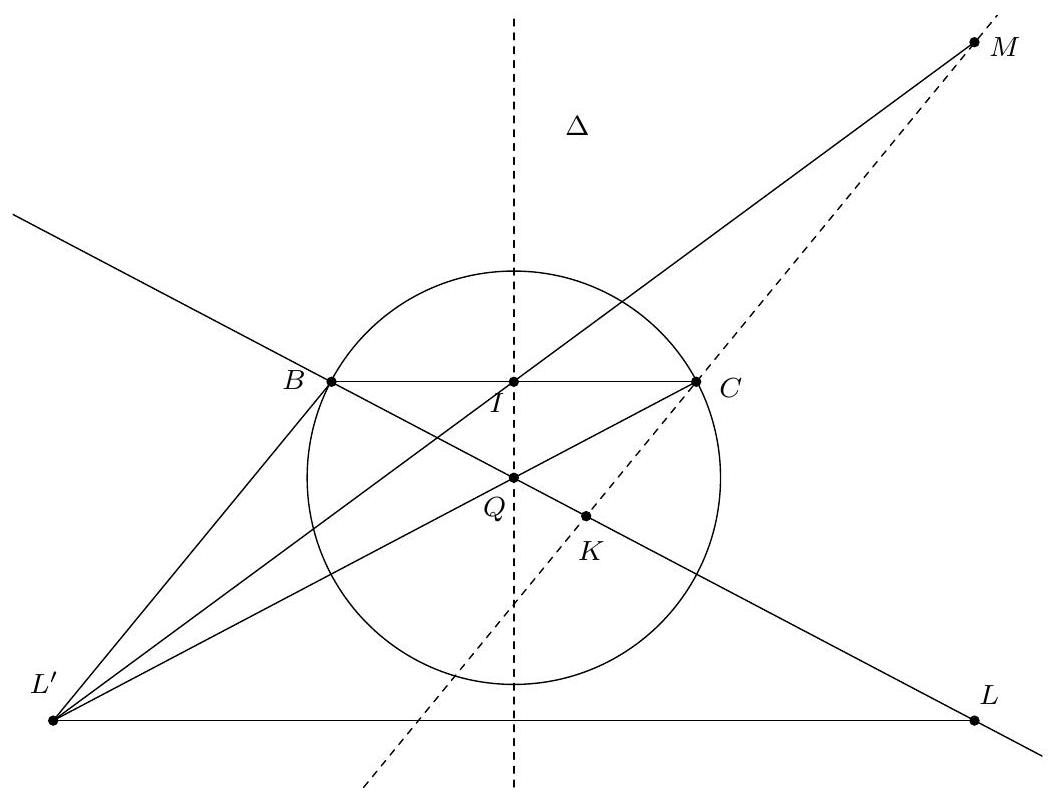
|
| 171 |
+
|
| 172 |
+
Première démonstration du lemme: on note toujours $I$ le milieu de $[B C]$. Soit $\Delta$ la médiatrice de $[B C]$ et $L^{\prime}$ le symétrique de $L$ par rapport à $\Delta$. On a
|
| 173 |
+
|
| 174 |
+
$$
|
| 175 |
+
\left[B L^{\prime}\right]=\operatorname{sym}_{\Delta}([C L])=\operatorname{sym}_{\Delta} \operatorname{sym}_{(B C)}([C M])=\operatorname{sym}_{I}([C M]),
|
| 176 |
+
$$
|
| 177 |
+
|
| 178 |
+
donc $(C M)$ et $\left(L^{\prime} B\right)$ sont parallèles.
|
| 179 |
+
D'autre part, $\frac{Q B}{Q K}=\frac{Q L}{Q B}=\frac{Q L^{\prime}}{Q C}$ donc $\left(L^{\prime} B\right)$ et $(C K)$ sont parallèles. Finalement, $(C M)$ et $(C K)$ sont parallèles, donc $C, K, M$ sont alignés.
|
| 180 |
+
Deuxième démonstration du lemme : on conserve les notations du paragraphe précédent. On note $b, c, k, \ell, \ell^{\prime}, m$ les affixes de $B, C, K, L, L^{\prime}, M$, et on peut supposer que $Q$ est l'origine, que $|b|=1$ et que $c=\bar{b}$.
|
| 181 |
+
Comme $L$ appartient à $(Q B)$, il existe $t \in \mathbb{R}$ tel que $\ell=t b$.
|
| 182 |
+
Comme $K$ et $L$ sont inverses par rapport au cercle, on a $k=\frac{1}{t} b$.
|
| 183 |
+
On a $\ell^{\prime}=\bar{\ell}$. Le fait que $L^{\prime}$ est le symétrique $M$ par rapport à $I$ se traduit par $\ell^{\prime}+m=b+c$. Il vient $m=b+c-\bar{\ell}=b+c-t c$.
|
| 184 |
+
On en déduit que $\overrightarrow{C M}=m-c=b-t c=t k-t c=t \overrightarrow{C K}$, par conséquent $C, K, M$ sont alignés.
|
| 185 |
+
|
| 186 |
+
Exercice 9. Soit $A B C$ un triangle isocèle en $A, D$ le pied de la hauteur issue de $A$ et $M$ un point intérieur à $A D C$ tel que $\widehat{A M B}$ est obtus et $\widehat{D B M}+\widehat{D A M}=\widehat{M C B}$. Les droites $(C M)$ et $(A D)$ se coupent en $P$, et les droites $(B M)$ et $(A D)$ se coupent en $Q$. Soit $S$ un point de $[A B]$ et $R$ un point de $[A M)$ qui n'est pas sur $[A M]$ tel que $\widehat{S Q B}=\widehat{D P C}$ et $\widehat{M R Q}=2 \widehat{Q A M}$. Montrer que $Q R S$ est isocèle.
|
| 187 |
+
|
| 188 |
+
## Solution de l'exercice 9
|
| 189 |
+
|
| 190 |
+
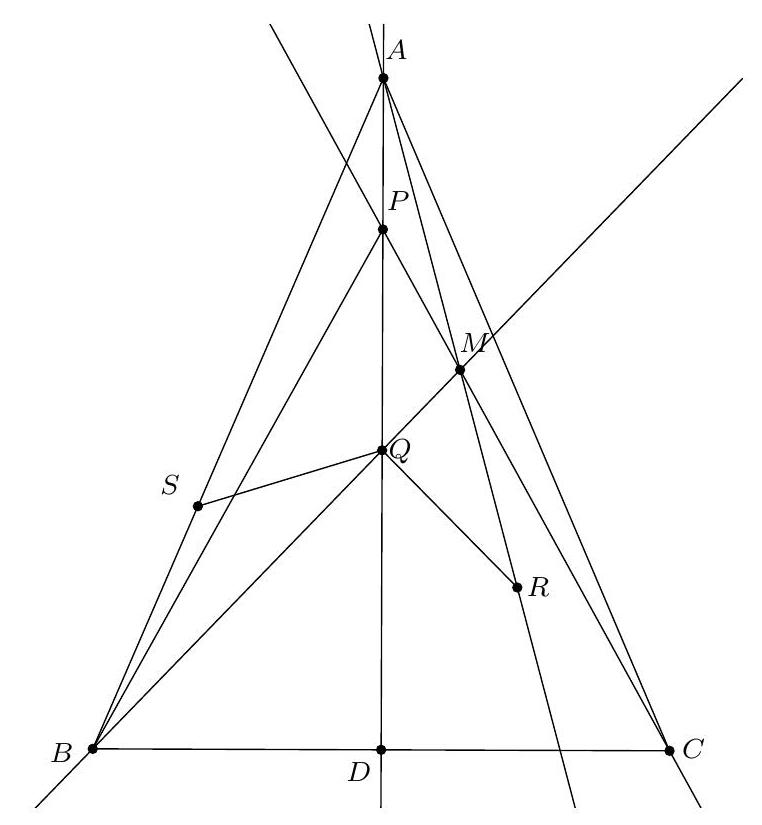
|
| 191 |
+
|
| 192 |
+
Notons $\alpha=\widehat{B A D}, \beta=\widehat{C B M}, \gamma=\widehat{M C B}$ et $\theta=\widehat{D A M}$. Par hypothèse, on a $\beta+\theta=\gamma$, $\widehat{S Q B}=\widehat{D P C}=\frac{\pi}{2}-\gamma$ et $\widehat{M R Q}=2 \theta$.
|
| 193 |
+
On a $\widehat{Q S A}=\pi-\widehat{B S Q}=\widehat{Q B S}+\widehat{S Q B}=\left(\frac{\pi}{2}-\alpha-\beta\right)+\left(\frac{\pi}{2}-\gamma\right)=\pi-(\alpha+\beta+\gamma)$.
|
| 194 |
+
D'après la loi des sinus pour les triangles $Q A S$ et $Q A R$, on a
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
\frac{Q S}{Q R}=\frac{Q S}{Q A} \times \frac{Q A}{Q R}=\frac{\sin \alpha}{\sin (\alpha+\beta+\gamma)} \frac{\sin 2 \theta}{\sin \theta}=\frac{2 \sin \alpha \cos \theta}{\sin (\alpha+\beta+\gamma)}
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
On doit montrer que ce rapport est égal à 1.
|
| 201 |
+
D'après le théorème de Ceva trigonométrique appliqué au point $M$ dans le triangle $A B C$, on a
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\frac{\sin (\alpha+\theta)}{\sin (\alpha-\theta)} \times \frac{\sin \beta}{\sin \left(\frac{\pi}{2}-\alpha-\beta\right)} \times \frac{\sin \left(\frac{\pi}{2}-\alpha-\gamma\right)}{\sin \gamma}=1
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
donc $\sin (\alpha+\theta) \sin \beta \cos (\alpha+\gamma)=\sin (\alpha-\theta) \cos (\alpha+\beta) \sin \gamma$.
|
| 208 |
+
En utilisant l'identité $2 \sin x \cos y=\sin (x+y)+\sin (x-y)$, on en déduit
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\gamma-\beta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\beta-\gamma)]
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
Compte tenu de $\gamma-\beta=\theta$,
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\theta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha-\theta)]
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
ou encore $(\sin (\alpha+\theta)-\sin (\alpha-\theta))[\sin (\alpha+\beta+\gamma)-(\sin (\alpha+\theta)+\sin (\alpha-\theta))]$.
|
| 221 |
+
Il vient $\sin (\alpha+\beta+\gamma)=\sin (\alpha+\theta)+\sin (\alpha-\theta))=2 \sin \alpha \cos \theta$.
|
| 222 |
+
|
French_STS/md/fr-ofm-2013-2014-envoi-6-solutions.md
ADDED
|
@@ -0,0 +1,343 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## OLYMPIADES FRANÇAISES DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
Envoi No. 6
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. Déterminer tous les entiers $a$ et $b$ tels que $(a+1)(b-1)=a^{2} b^{2}$.
|
| 12 |
+
|
| 13 |
+
## Solution de l'exercice 1
|
| 14 |
+
|
| 15 |
+
Soit $a, b$ des entiers tels que $(a+1)(b-1)=a^{2} b^{2}$.
|
| 16 |
+
Puisque d'une part $a$ et $a+1$ sont premiers entre eux, et d'autre part $b$ et $b-1$ sont premiers entre eux, c'est donc que $b-1= \pm a^{2}$ et que $a+1= \pm b^{2}$, où les signes sont les mêmes dans les deux relations.
|
| 17 |
+
|
| 18 |
+
- Si $b-1=a^{2}$ et $a+1=b^{2}$ :
|
| 19 |
+
|
| 20 |
+
Alors, $a=b^{2}-1=(b-1)(b+1)=a^{2}\left(a^{2}+2\right)$.
|
| 21 |
+
Si $a=0$, on obtient $b=1$, et on vérifie bien que $(a, b)=(0,1)$ est bien une solution du problème.
|
| 22 |
+
Si $a \neq 0$, après division par $a$, il vient donc $a\left(a^{2}+2\right)=1$. Comme $a$ et $a^{2}+2$ sont des entiers, avec $a^{2}+2>2$, cette dernière égalité ne peut être satisfaite.
|
| 23 |
+
|
| 24 |
+
- Si $b-1=-a^{2}$ et $a+1=-b^{2}$ :
|
| 25 |
+
|
| 26 |
+
Alors, $-a-1=b^{2}$ et $-b+1=a^{2}$. Ce sont les équations obtenues au cas précédent, où $(a, b)$ a été remplacé par $(-b,-a)$. Ainsi, la seule solution est $(a, b)=(-1,0)$.
|
| 27 |
+
|
| 28 |
+
Finalement, les solutions du problème sont $(a, b)=(0,1)$ et $(a, b)=(-1,0)$.
|
| 29 |
+
Exercice 2. Prouver que tout ensemble de 90 nombres choisis dans $\{1,2, \cdots, 100\}$ en contient 10 qui forment une progression arithmétique.
|
| 30 |
+
|
| 31 |
+
## Solution de l'exercice 2
|
| 32 |
+
|
| 33 |
+
On dispose les entiers de 1 à 100 dans un tableau carré $10 \times 10$ comme suit :
|
| 34 |
+
|
| 35 |
+
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 36 |
+
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
|
| 37 |
+
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|
| 38 |
+
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|
| 39 |
+
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|
| 40 |
+
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
|
| 41 |
+
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
|
| 42 |
+
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
|
| 43 |
+
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
|
| 44 |
+
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
|
| 45 |
+
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
|
| 46 |
+
|
| 47 |
+
Si l'on veut éliminer 10 nombres de sorte qu'avec les 90 restants on ne puisse former de suite arithmétique de longueur 10, il faut déjà éliminer au moins un nombre dans chacune des 10 lignes, et chacune des 10 colonnes. Comme il y a justement 10 lignes, et 10 colonnes, c'est donc que l'on doit éliminer exactement un nombre par ligne et par colonne.
|
| 48 |
+
|
| 49 |
+
De plus, si pour $1 \leqslant i \leqslant 9$, le nombre éliminé dans la ligne $i$ appartient à la colonne $k$, alors le nombre éliminé dans la ligne $i+1$ doit appartenir à une colonne $l$, avec $l<k$, sans quoi on aurait 10 entiers consécutifs parmi les 90 restants. Cela implique que l'on doit éliminer $10,19,28,37,46,55,64,73,82$ et 91.
|
| 50 |
+
Mais alors, il reste $11,20,29,38,47,56,65,74,83$ et 92 , qui forment une suite arithmétique de raison 9 , ce qui conclut.
|
| 51 |
+
|
| 52 |
+
Exercice 3. Les diagonales du quadrilatère convexe $A B C D$ sont perpendiculaires et se rencontrent en $O$. La perpendiculaire à $(A B)$ passant par $O$ rencontre $(A B)$ en $M$ et $(C D)$ en $M^{\prime}$. La perpendiculaire à $(B C)$ passant par $O$ rencontre $(B C)$ en $N$ et $(D A)$ en $N^{\prime}$. La perpendiculaire à $(C D)$ passant par $O$ rencontre $(C D)$ en $P$ et $(A B)$ en $P^{\prime}$. La perpendiculaire à $(D A)$ passant par $O$ rencontre ( $D A)$ en $Q$ et $(B C)$ en $Q^{\prime}$.
|
| 53 |
+
|
| 54 |
+
Prouver que les points $M, N, P, Q, M^{\prime}, N^{\prime}, P^{\prime}, Q^{\prime}$ sont cocycliques.
|
| 55 |
+
|
| 56 |
+
## Solution de l'exercice 3
|
| 57 |
+
|
| 58 |
+
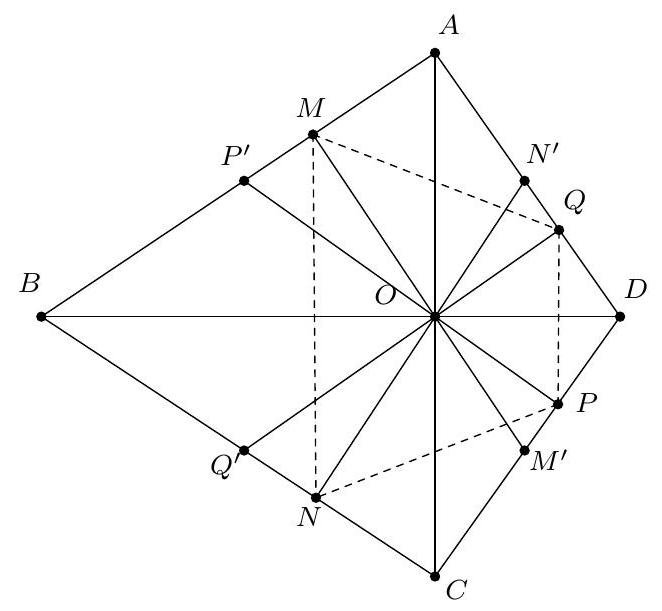
|
| 59 |
+
|
| 60 |
+
Commençons par prouver que le quadrilatère $M N P Q$ est inscriptible :
|
| 61 |
+
On note que le quadrilatère $B M O N$ à deux angles droits en $M$ et en $N$, donc il est inscrit dans le cercle de diamètre $[O B]$. De même, les quadrilatères $C N O P, D P O Q$ et $A Q O M$ sont inscrits respectivement dans les cercles de diamètres $[O C],[O D]$ et $[O A]$. On en déduit que $\widehat{O M N}=\widehat{O B N}$, que $\widehat{O M Q}=\widehat{O A Q}$, que $\widehat{O P Q}=\widehat{O D Q}$ et que $\widehat{O P N}=\widehat{O C N}$.
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\begin{aligned}
|
| 65 |
+
& \text { Il vient alors } \\
|
| 66 |
+
& \begin{aligned}
|
| 67 |
+
\widehat{Q M N} & =\widehat{Q M O}+\widehat{O M N} \\
|
| 68 |
+
& =\widehat{Q A O}+\widehat{O B N} \\
|
| 69 |
+
& =\widehat{D A C}+\widehat{D B C}
|
| 70 |
+
\end{aligned}
|
| 71 |
+
\end{aligned}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
Et d'autre part
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\begin{aligned}
|
| 78 |
+
\widehat{Q P N} & =\widehat{Q P O}+\widehat{O P N} \\
|
| 79 |
+
& =\widehat{Q D O}+\widehat{O C N} \\
|
| 80 |
+
& =\widehat{A D B}+\widehat{A C B}
|
| 81 |
+
\end{aligned}
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
Or, puisque $[A C]$ et $[D B]$ sont perpendiculaires, on a $\widehat{D A C}+\widehat{A D B}=90^{\circ}$, et de même $\widehat{D B C}+$ $\widehat{A C B}=90^{\circ}$. Ainsi $\widehat{Q M N}=180^{\circ}-\widehat{Q P N}$. Cela assure que $M N P Q$ est inscriptible.
|
| 85 |
+
|
| 86 |
+
On note $\Gamma$ le cercle circonscrit à $M N P Q$. Par symétrie des rôles, pour conclure, il suffit de prouver que $Q^{\prime}$ est sur $\Gamma$.
|
| 87 |
+
Supposons que $N \in\left[C Q^{\prime}\right]$, les autres cas se traitant de façons similaires.
|
| 88 |
+
Nous avons $\widehat{N Q^{\prime} Q}=\widehat{N Q^{\prime} O}=180^{\circ}-\widehat{Q^{\prime} C O}-\widehat{C O Q^{\prime}}$.
|
| 89 |
+
Mais $\widehat{Q^{\prime} C O}=\widehat{N C O}=\widehat{N P O}$, puisque $N C P O$ inscriptible.
|
| 90 |
+
|
| 91 |
+
D'autre part, comme les côtés sont perpendiculaires deux à deux, on a $\widehat{C O Q^{\prime}}=\widehat{O D Q}=\widehat{O P Q}$, la dernière égalité découlant du fait que $O P D Q$ est inscriptible.
|
| 92 |
+
Ainsi, on a $\widehat{N Q^{\prime} Q}=180^{\circ}-\widehat{N P O}-\widehat{O P Q}=180^{\circ}-\widehat{N P Q}$, ce qui assure que $Q^{\prime}$ appartient bien au cercle circonscrit à $N P Q$.
|
| 93 |
+
|
| 94 |
+
## Exercices communs
|
| 95 |
+
|
| 96 |
+
Exercice 4. A l'intérieur du cercle $\Gamma$ se trouvent trois cercles $\gamma_{1}, \gamma_{2}$ et $\gamma_{3}$, et tangents à $\Gamma$ respectivement en $A, B$ et $C$, tous distincts. Les cercles $\gamma_{2}$ et $\gamma_{3}$ ont un point commun $K$ qui appartient à $[B C]$, les cercles $\gamma_{3}$ et $\gamma_{1}$ ont un point commun $L$ qui appartient à $[C A]$, et les cercles $\gamma_{1}$ et $\gamma_{2}$ ont un point commun $M$ qui appartient à $[A B]$.
|
| 97 |
+
|
| 98 |
+
Prouver que le centre de $\Gamma$ appartient à $\gamma_{1}, \gamma_{2}$ et $\gamma_{3}$.
|
| 99 |
+
|
| 100 |
+
## Solution de l'exercice 4
|
| 101 |
+
|
| 102 |
+
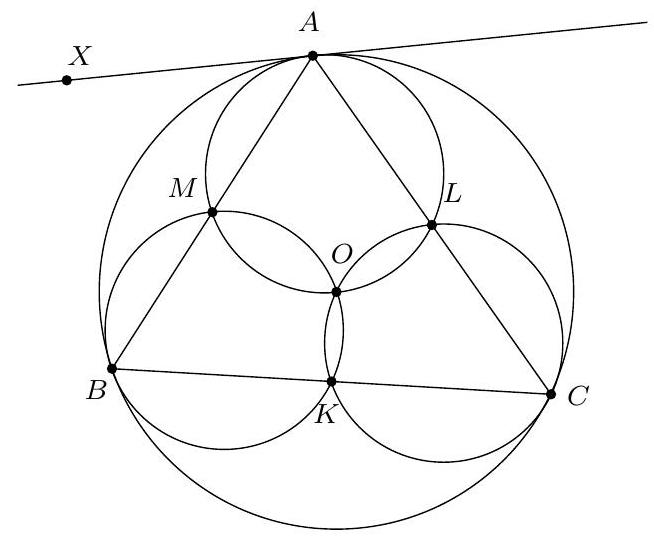
|
| 103 |
+
|
| 104 |
+
Soit $X$ un point de la tangente commune à $\Gamma$ et $\gamma_{1}$, et situé du côté opposé à $C$ par rapport à la droite $(A B)$. Alors $\widehat{A L M}=\widehat{X A M}=\widehat{X A B}=\widehat{A C B}$, ce qui assure que $(M L)$ et $(B C)$ sont parallèles. De même, on a $(K M)$ et $(A C)$ parallèles, ainsi que $(K L)$ et $(A B)$ parallèles.
|
| 105 |
+
|
| 106 |
+
Posons $x=\frac{A M}{A B}$. D'après le théorème de Thalès, on a alors :
|
| 107 |
+
|
| 108 |
+
$$
|
| 109 |
+
\frac{B K}{B C}=\frac{B M}{B A}=1-x \text { et } \frac{C L}{C A}=\frac{C K}{C B}=1-(1-x)=x
|
| 110 |
+
$$
|
| 111 |
+
|
| 112 |
+
Ainsi $x=\frac{A M}{A B}=\frac{A L}{A C}=1-x$, d'où $x=\frac{1}{2}$.
|
| 113 |
+
Les points $M, K, L$ sont donc les milieux respectifs des segments $[A B],[B C],[C A]$, et les triangles $A M L, M B K, L K C$ sont tous semblables à $A B C$ dans un rapport $\frac{1}{2}$. Si on note $r_{1}, r_{2}, r_{3}$ et $R$ les rayons respectifs des cercles $\gamma_{1}, \gamma_{2}, \gamma_{3}$ et $\Gamma$, on en déduit que $r_{1}=r_{2}=r_{3}=\frac{1}{2} R$.
|
| 114 |
+
D'autre part, puisque $\gamma_{1}$ et $\Gamma$ sont tangents en $A$ les diamètres issus de $A$ dans $\gamma_{1}$ et $\Gamma$ sont portés par la même droite. Ainsi, le centre de $\Gamma$ appartient à $\gamma_{1}$, et on prouve de même qu'il appartient également à $\gamma_{2}$ et $\gamma_{3}$.
|
| 115 |
+
Remarque: une autre manière d'exprimer le paragraphe précédent consiste utiliser l'homothétie $\overline{h \text { de centre } A}$ et de rapport $\frac{1}{2}$. Comme $h(A)=A, h(B)=M$ et $h(C)=L$, l'image par $h$ de $\Gamma$ est le cercle circonscrit à $A L M$, c'est-à-dire $\gamma_{1}$. Soit $A^{\prime}$ le point diamétralement opposé à $A$ dans
|
| 116 |
+
le cercle $\Gamma$ et soit $O$ le centre de $\Gamma$. Comme $h\left(A^{\prime}\right)=O$, le point $O$ appartient à $\gamma_{1}$, et de même il appartient à $\gamma_{2}$ et $\gamma_{3}$.
|
| 117 |
+
Exercice 5. Soit $n, m \geqslant 1$ des entiers, avec $m$ impair.
|
| 118 |
+
Prouver que $2^{m}-1$ et $2^{n}+1$ sont premiers entre eux.
|
| 119 |
+
|
| 120 |
+
## Solution de l'exercice 5
|
| 121 |
+
|
| 122 |
+
Par l'absurde : supposons qu'il existe un nombre premier $p$ qui divise à la fois $2^{m}-1$ et $2^{n}+1$.
|
| 123 |
+
Alors, on a $2^{m} \equiv 1 \bmod [p]$ et $2^{n} \equiv-1 \bmod [p]$,
|
| 124 |
+
d'où $2^{2 n} \equiv 1 \bmod [p]$.
|
| 125 |
+
Soit $\omega$ l'ordre de 2 modulo $p$. On sait qu'alors $\omega$ divise $m$ et $2 n$. Mais, comme $m$ est impair, $\omega$ est donc impair, ce qui assure qu'en fait $\omega$ divise $n$.
|
| 126 |
+
On a alors $2^{n} \equiv 1 \bmod [p]$, et toujours $2^{n} \equiv-1 \bmod [p]$.
|
| 127 |
+
Par suite, $p$ divise 2, et donc $p=2$.
|
| 128 |
+
Mais, on a $m \geqslant 1$, d'où $2^{m}-1$ est impair et n'est donc pas divisible par 2. Contradiction.
|
| 129 |
+
Finalement, $2^{m}-1$ et $2^{n}+1$ sont premiers entre eux.
|
| 130 |
+
Autre solution
|
| 131 |
+
Montrons d'abord par récurrence sur $a+b$ que le pgcd de $2^{a}-1$ et $2^{b}-1$ est $2^{\operatorname{pgcd}(a, b)}-1$. Si $a=0$ ou $b=0$ c'est clair. Supposons la propriété vraie pour tous les couples ( $a^{\prime}, b^{\prime}$ ) tels que $a^{\prime}+b^{\prime}<a+b$. On peut supposer $a \geqslant b>0$. On a
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
\begin{aligned}
|
| 135 |
+
\operatorname{pgcd}\left(2^{a}-1,2^{b}-1\right) & =\operatorname{pgcd}\left(2^{b}-1,2^{a}-1-\left(2^{b}-1\right)\right) \\
|
| 136 |
+
& =\operatorname{pgcd}\left(2^{b}-1,2^{b}\left(2^{a-b}-1\right)\right) \\
|
| 137 |
+
& =\operatorname{pgcd}\left(2^{b}-1,2^{a-b}-1\right) \quad \operatorname{car} 2^{b}-1 \text { et } 2^{b} \text { premiers entre eux } \\
|
| 138 |
+
& =2^{\operatorname{pgcd}(b, a-b)}-1 \quad \text { par hypothèse de récurrence } \\
|
| 139 |
+
& =2^{\operatorname{pgcd}(a, b)}-1
|
| 140 |
+
\end{aligned}
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
ce qui démontre notre assertion.
|
| 144 |
+
Revenons à l'exercice. Notons $d^{\prime}=\operatorname{pgcd}\left(2^{m}-1,2^{n}+1\right)$. Soit $d=\operatorname{pgcd}(m, n)$, alors ce qui précède montre que $2^{d}-1=\operatorname{pgcd}\left(2^{m}-1,2^{2 n}-1\right)$. Or, $2^{2 n}-1$ est un multiple de $2^{n}+1$, donc $d^{\prime}$ divise $2^{d}-1$. Comme $2^{d}-1$ divise $2^{n}-1$, $d^{\prime}$ divise aussi $\left(2^{n}+1\right)-\left(2^{n}-1\right)=2$. Or, $2^{m}-1$ est impair donc $d^{\prime}$ est impair. Il vient $d^{\prime}=1$.
|
| 145 |
+
Exercice 6. On désigne par $K$ la valeur maximale de
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right|
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
où $x_{1}, x_{2}, x_{3}, x_{4} \in[0 ; 1]$.
|
| 152 |
+
a) Prouver que $\frac{4}{243}<K<\frac{1}{27}$.
|
| 153 |
+
b) Déterminer $K$.
|
| 154 |
+
|
| 155 |
+
## Solution de l'exercice 6
|
| 156 |
+
|
| 157 |
+
a) Soit $x_{1}, x_{2}, x_{3}, x_{4} \in[0 ; 1]$.
|
| 158 |
+
|
| 159 |
+
On pose
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right| .
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
Si deux des nombres $x_{1}, x_{2}, x_{3}, x_{4}$ sont égaux, on a $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=0$, qui n'est clairement pas la valeur maximale de $f$. Sans perte de généralité, on peut donc supposer que $x_{1}>x_{2}>x_{3}>x_{4}$. D'après l'inégalité arithmético-géométrique, on a
|
| 166 |
+
|
| 167 |
+
$$
|
| 168 |
+
\sqrt[3]{\left(x_{1}-x_{2}\right)\left(x_{2}-x_{3}\right)\left(x_{3}-x_{4}\right)} \leqslant \frac{\left(x_{1}-x_{2}\right)+\left(x_{2}-x_{3}\right)+\left(x_{3}-x_{4}\right)}{3}=\frac{x_{1}-x_{4}}{3} \leqslant \frac{1}{3}
|
| 169 |
+
$$
|
| 170 |
+
|
| 171 |
+
et donc $\left|x_{1}-x_{2}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{3}-x_{4}\right| \leqslant \frac{1}{27}$.
|
| 172 |
+
D'autre part, on a $\left|x_{1}-x_{3}\right|<1,\left|x_{1}-x_{4}\right| \leqslant 1$ et $\left|x_{2}-x_{4}\right|<1$, d'où $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)<\frac{1}{27}$.
|
| 173 |
+
Et ainsi, on a $K<\frac{1}{27}$.
|
| 174 |
+
D'autre part, on vérifie facilement que $f\left(1, \frac{3}{4}, \frac{1}{4}, 0\right)=\frac{9}{512}>\frac{4}{243}$, d'où $K>\frac{4}{243}$.
|
| 175 |
+
b) Sans perte de généralité, on suppose toujours que $x_{1}>x_{2}>x_{3}>x_{4}$. Mais, il est facile de constater que $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \leqslant f\left(1, x_{2}, x_{3}, 0\right)$. Ainsi, en posant $x_{2}=y$ et $x_{3}=z$, on cherche la valeur maximale de
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
g(x, y)=(1-y)(1-z)(y-z) y z
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
sous la contrainte $0<z<y<1$.
|
| 182 |
+
Soit $s$ un réel.
|
| 183 |
+
On rappelle que si $a, b$ sont deux réels tels que $a+b=s$ alors $a b=\frac{1}{4} s^{2}-\left(a-\frac{s}{2}\right)^{2} \leqslant \frac{1}{4} s^{2}$, avec égalité si et seulement si $a=b=\frac{1}{2} s$.
|
| 184 |
+
|
| 185 |
+
Soit alors $t \in] 0,1[$, et considérons les couples $(y, z)$ pour lesquels $y-z=t$.
|
| 186 |
+
Dans ces conditions, les valeurs $(1-y)+z=1-t$ et $(1-z)+y=1+t$ sont fixées. D'après le rappel, le produit $(1-y) z$ est donc maximal pour $y+z=1$, et il en est de même pour le produit $(1-z) y$. Compte-tenu de $y-z=t$, cela correspond à $y=\frac{1+t}{2}$ et $z=\frac{1-t}{2}$ et, dans ces conditions, on a $g(y, z)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$.
|
| 187 |
+
|
| 188 |
+
Il s'agit donc de chercher la valeur maximale de $P(t)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$, lorsque $\left.t \in\right] 0,1[$.
|
| 189 |
+
Il est facile de vérifier que, pour tout $t \in] 0,1\left[\right.$, on a $P^{\prime}(t)=\frac{1}{16}\left(1-t^{2}\right)\left(1-5 t^{2}\right)$. Cela assure que la valeur maximale cherchée est $P\left(\frac{1}{\sqrt{5}}\right)=\frac{\sqrt{5}}{125}$.
|
| 190 |
+
|
| 191 |
+
Ainsi, on a $K=\frac{\sqrt{5}}{125}$.
|
| 192 |
+
|
| 193 |
+
## Exercices du groupe A
|
| 194 |
+
|
| 195 |
+
Exercice 7. Si $n>0$ est un entier, on désigne par $d(n)$ le nombre de diviseurs strictement positifs de $n$.
|
| 196 |
+
a) Existe-t-il une suite $\left(a_{i}\right)_{i \geqslant 1}$ strictement croissante d'entiers strictement positifs tels que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ soit divisible par exactement $d(i)-1$ termes de la suite (y compris lui-même)?
|
| 197 |
+
b) Existe-t-il une suite $\left(a_{i}\right)_{i \geqslant 1}$ strictement croissante d'entiers strictement positifs tels que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ soit divisible par exactement $d(i)+1$ termes de la suite (y compris lui-même)?
|
| 198 |
+
Solution de l'exercice 7
|
| 199 |
+
a) La réponse est oui.
|
| 200 |
+
|
| 201 |
+
Il suffit de trouver une suite $\left(a_{i}\right)$ qui vérifie les deux conditions suivantes :
|
| 202 |
+
|
| 203 |
+
- le nombre $a_{1}$ ne divise aucun autre terme de la suite,
|
| 204 |
+
- le nombre $i$ divise $j$ si et seulement si $a_{i}$ divise $a_{j}$, pour tous $i, j \geqslant 2$.
|
| 205 |
+
|
| 206 |
+
Or, il est bien connu que, pour tous entiers $i, j \geqslant 1$, on a $\operatorname{pgcd}\left(2^{i}-1,2^{j}-1\right)=2^{d}-1$, où $d=\operatorname{pgcd}(i, j)$. Par conséquent, la suite définie par $a_{1}=2$ et $a_{i}=2^{i}-1$ pour $i>1$ convient.
|
| 207 |
+
b) La réponse est également oui.
|
| 208 |
+
|
| 209 |
+
En fait, de façon plus générale, on va prouver que si $f: \mathbb{N}^{*} \longrightarrow \mathbb{N}^{*}$ est une fonction et qu'il existe un entier $N>0$ tel que $f(n) \leqslant n$ pour tout $n \geqslant N$, alors il existe une suite strictement croissante $\left(a_{i}\right)_{i \geqslant 1}$ d'entiers strictement positifs telle que, pour tout $i$ suffisamment grand, le nombre $a_{i}$ est divisible par exactement $f(i)$ termes de la suite.
|
| 210 |
+
Notons tout de suite que cela répond à la fois au a) et au b) puisque $d(n)<n$ pour tout $n \geqslant 3$ (le nombre $n-1$ ne divise pas $n$ pour $n \geqslant 3$ ).
|
| 211 |
+
|
| 212 |
+
Dans les conditions ci-dessus donc, on commence par choisir une suite strictement croissante $a_{1}, a_{2}, \cdots, a_{M}$ de $M$ nombres premiers. Puis, par récurrence sur $k>M$, si $a_{1}, a_{2}, \cdots, a_{k-1}$ sont définis avec $a_{1}<a_{2}<\cdots<a_{k-1}$, on choisit un nombre premier $p_{k}$ tel que $p_{k}>a_{k-1}$ et on pose $a_{k}=a_{1} a_{2} \cdots a_{f(k)-1} p_{k}$.
|
| 213 |
+
|
| 214 |
+
On a alors clairement $a_{k-1}<a_{k}$.
|
| 215 |
+
De plus, pour tout $i>M$, le nombre $a_{i}$ est divisible que par $a_{1}, a_{2}, \cdots, a_{f(i)-1}$ et par lui-même. Par contre, $a_{i}$ n'est divisible par aucun autre terme $a_{j}$, avec $j>f(i)-1$ et $j \neq i$, puisqu'un tel $a_{j}$ contient un facteur premier $p_{j}$ qui ne divise aucun des $a_{k}$ avec $k \leqslant f(i)-1$ et tel que $p_{j} \neq p_{i}$.
|
| 216 |
+
Exercice 8. Soit $A B C$ un triangle. On désigne par $D$ le pied de la bissectrice de $\widehat{B A C}$, et par $E$ le pied de la hauteur issue de $A$. La médiatrice de $[A D]$ rencontre les demi-cercles de diamètres respectifs $[A B]$ et $[A C]$ construits extérieurement à $A B C$, en $X$ et $Y$.
|
| 217 |
+
|
| 218 |
+
Prouver que les points $X, Y, D, E$ sont cocycliques.
|
| 219 |
+
Solution de l'exercice 8
|
| 220 |
+
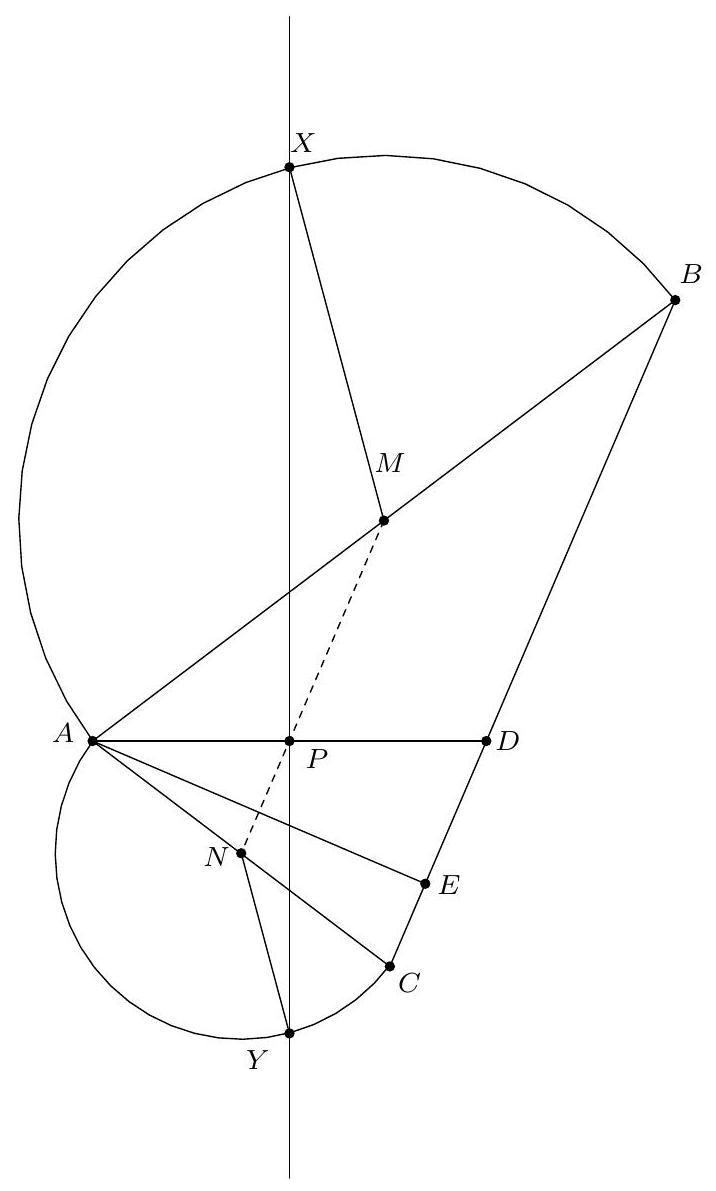
|
| 221 |
+
|
| 222 |
+
On désigne par $M, N$ et $P$ les milieux respectifs de $[A B],[A C]$ et $[A D]$. D'après le théorème des milieux, on a $N, P, M$ alignés et, compte-tenu de ce que $(A P)=(A D)$ est la bissectrice de $\widehat{B A C}$, on a
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
\frac{M P}{N P}=\frac{B D}{C D}=\frac{A M}{A N}=\frac{A B}{A C}=\frac{M X}{N Y} .
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
En particulier, il vient $\frac{M P}{M X}=\frac{N P}{N Y}$. En utilisant la loi des sinus dans $M P X$ et $N P Y$, et puisque $\widehat{N P Y}=\widehat{M P X}$, c'est donc que $\sin \widehat{P X M}=\sin \widehat{P Y N}$. (1)
|
| 229 |
+
Or, on a clairement $\widehat{P X M}<\widehat{B X A}=90^{\circ}$ et $\widehat{P Y N}<\widehat{A Y C}=90^{\circ}$, donc (1) donne $\widehat{P X M}=\widehat{P Y N}$. Comme $\widehat{M P X}=\widehat{N P Y}$, c'est donc que les triangles $P X M$ et $P Y N$ sont semblables, et que $\widehat{P M X}=\widehat{P N Y}$. (2)
|
| 230 |
+
|
| 231 |
+
Sans perte de généralité, on peut supposer qu'entre $M$ et $N$, c'est $N$ qui est du même côté que $A$ par rapport à $(X Y)$.
|
| 232 |
+
Ainsi (2) conduit à $\widehat{P M A}+\widehat{A M X}=\widehat{P N C}+\widehat{C N Y}$,
|
| 233 |
+
d'où $\widehat{C B A}+2 \widehat{A B X}=180^{\circ}-\widehat{B C A}+180^{\circ}-2 \widehat{A C Y}$
|
| 234 |
+
et donc
|
| 235 |
+
|
| 236 |
+
$$
|
| 237 |
+
\begin{aligned}
|
| 238 |
+
\widehat{A B X}+\widehat{A C Y} & =180^{\circ}-\widehat{A B C}-\widehat{B C A}+90^{\circ}-\widehat{A B X}+90^{\circ}-\widehat{A C Y} \\
|
| 239 |
+
& =\widehat{B A C}+\widehat{X A B}+\widehat{C A Y} \\
|
| 240 |
+
& =\widehat{X A Y} .
|
| 241 |
+
\end{aligned}
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
Mais, $\widehat{A E B}=\widehat{A E C}=90^{\circ}$ donc $E$ appartient aux cercles de diamètres $[A B]$ et $[A C]$, soit donc aux cercles circonscrits aux triangles $A B X$ et $A C Y$. Par suite, on a $\widehat{A B X}=\widehat{A E X}$ et $\widehat{A C Y}=\widehat{A E Y}$. (4)
|
| 245 |
+
|
| 246 |
+
De (3) et (4), on déduit que
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
\widehat{X E Y}=\widehat{X E A}+\widehat{A E Y}=\widehat{A B X}+\widehat{A C Y}=\widehat{X A Y}
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
D'autre part, puisque $(X Y)$ est la médiatrice de $[A D]$, on a $\widehat{X A Y}=\widehat{X D Y}$, et finalement $\widehat{X E Y}=$ $\widehat{X D Y}$, ce qui conclut.
|
| 253 |
+
|
| 254 |
+
Autre solution. On applique une inversion $i$ de pôle $A$. Rappelons que les cercles ne passant pas par $A$ sont transformés en des cercles ne passant pas par $A$, que les droites passant par $A$ sont conservées et que les cercles passant par $A$ sont transformés en des droites perpendiculaires à la droite reliant $A$ et le centre du cercle. D'autre part, toute inversion conserve les angles entre deux droites ou cercles sécants.
|
| 255 |
+
On en déduit que $i$ transforme le cercle de diamètre $[A B]$ en la perpendiculaire à $\left(A B^{\prime}\right)$ passant par $B^{\prime}$, transforme la droite $(B C)$ en le cercle $\left(A B^{\prime} C^{\prime}\right)$ de sorte que $D^{\prime}$ est le milieu de l'arc $B^{\prime} C^{\prime}$ ne contenant pas $A$ et $E^{\prime}$ est le point diamétralement opposé à $A$. De plus, $i$ envoie la médiatrice de $[A D]$ sur le cercle de centre $D^{\prime}$ passant par $A$. Enfin, comme $E$ sur le cercle de diamètre $[A B]$, les points $E^{\prime}, B, X^{\prime}$ sont alignés et de même $E^{\prime}, C, Y^{\prime}$ sont alignés.
|
| 256 |
+
Supposons que les angles en $B$ et en $C$ du triangle $A B C$ sont aigus (le raisonnement est analogue dans le cas contraire). Alors $E^{\prime}$ appartient à l'arc $B^{\prime} C^{\prime}$ ne contenant pas $A$. Quitte à échanger les rôles de $B$ et de $C$, on peut supposer que $E^{\prime}$ appartient à l'arc $C^{\prime} D^{\prime}$ comme sur la figure.
|
| 257 |
+
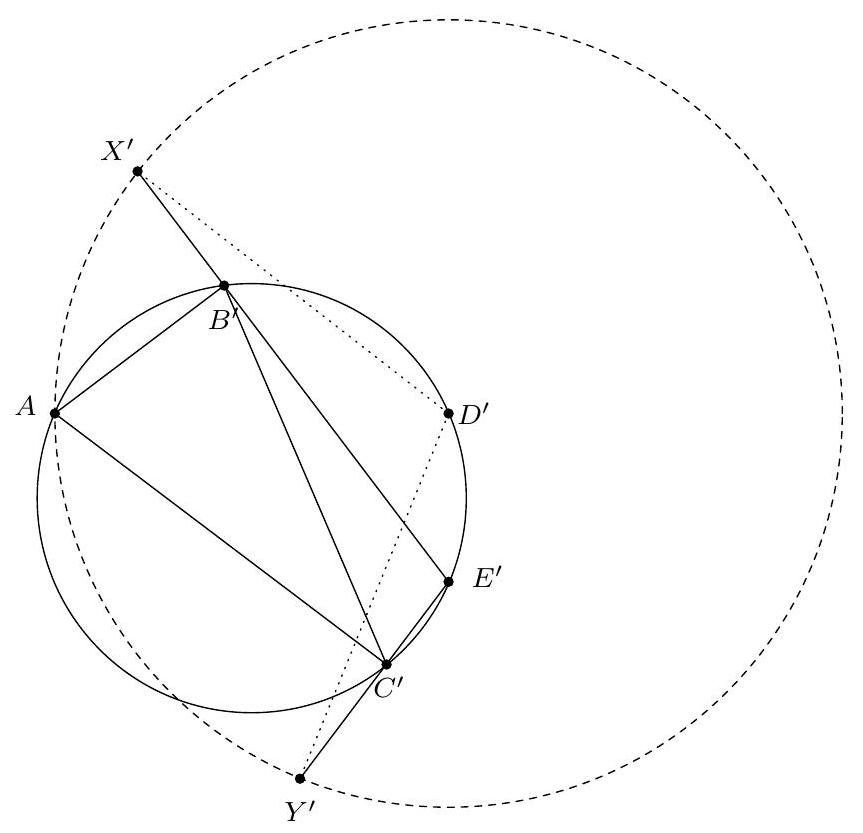
|
| 258 |
+
|
| 259 |
+
Le fait que $E$ ne se trouve pas sur le même demi-cercle de diamètre $[A B]$ que $X$ implique que $B^{\prime}$ se trouve entre $E^{\prime}$ et $X^{\prime}$. De même, $C^{\prime}$ se trouve entre $E^{\prime}$ et $Y^{\prime}$.
|
| 260 |
+
Remarquons d'abord que $\widehat{Y^{\prime} E^{\prime} D^{\prime}}$ et $\widehat{X^{\prime} E^{\prime} D^{\prime}}$ sont supplémentaires puisque $\widehat{Y^{\prime} E^{\prime} D^{\prime}}=\widehat{C^{\prime} E^{\prime} D^{\prime}}=$ $\pi-\widehat{C^{\prime} A D^{\prime}}=\pi-\widehat{D^{\prime} A B^{\prime}}=\pi-\widehat{D^{\prime} E^{\prime} B^{\prime}}=\pi-\widehat{D^{\prime} E^{\prime} X^{\prime}}$.
|
| 261 |
+
|
| 262 |
+
Appliquons maintenant le théorème de Ceva trigonométrique pour le point $D^{\prime}$ appartenant au triangle $E X^{\prime} Y^{\prime}$.
|
| 263 |
+
|
| 264 |
+
$$
|
| 265 |
+
\frac{\sin \left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} X^{\prime}}\right)}{\sin \left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} Y^{\prime}}\right)} \times \frac{\sin \left(\overrightarrow{X^{\prime} D^{\prime}}, \overrightarrow{X^{\prime} Y^{\prime}}\right)}{\sin \left(\overrightarrow{X^{\prime} D^{\prime}}, \overrightarrow{X^{\prime} E^{\prime}}\right)} \times \frac{\sin \left(\overrightarrow{Y^{\prime} D^{\prime}}, \overrightarrow{Y^{\prime} E^{\prime}}\right)}{\sin \left(\overrightarrow{Y^{\prime} D^{\prime}}, \overrightarrow{Y^{\prime} X^{\prime}}\right)}=-1 .
|
| 266 |
+
$$
|
| 267 |
+
|
| 268 |
+
Comme $\left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} X^{\prime}}\right)=\left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} B^{\prime}}\right)=\left(\overrightarrow{A D^{\prime}}, \overrightarrow{A B^{\prime}}\right)$ et $\left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} Y^{\prime}}\right)=\left(\overrightarrow{E^{\prime} D^{\prime}}, \overrightarrow{E^{\prime} C^{\prime}}\right)=\left(\overrightarrow{A D^{\prime}}, \overrightarrow{A C^{\prime}}\right)+$ $\pi$, la première fraction est égale à 1 .
|
| 269 |
+
De plus, comme $D^{\prime} X^{\prime} Y^{\prime}$ est isocèle en $D^{\prime}$, on a $\left(\overrightarrow{X^{\prime} D^{\prime}}, \overrightarrow{X^{\prime} Y^{\prime}}\right)=-\left(\overrightarrow{Y^{\prime} D^{\prime}}, \overrightarrow{Y^{\prime} X^{\prime}}\right)$. En reportant dans (1), on en conclut que
|
| 270 |
+
|
| 271 |
+
$$
|
| 272 |
+
\sin \left(\overrightarrow{X^{\prime} D^{\prime}}, \overrightarrow{X^{\prime} E^{\prime}}\right)=\sin \left(\overrightarrow{Y^{\prime} D^{\prime}}, \overrightarrow{Y^{\prime} E^{\prime}}\right)
|
| 273 |
+
$$
|
| 274 |
+
|
| 275 |
+
ce qui prouve que les angles $\widehat{D^{\prime} X^{\prime} E^{\prime}}$ et $\widehat{D^{\prime} Y^{\prime} E^{\prime}}$ sont égaux ou supplémentaires.
|
| 276 |
+
S'ils étaient supplémentaires, on aurait $\widehat{X^{\prime} E^{\prime} D^{\prime}}+\widehat{D^{\prime} X^{\prime} E^{\prime}}+\widehat{Y^{\prime} E^{\prime} D^{\prime}}+\widehat{D^{\prime} Y^{\prime} E^{\prime}}=2 \pi$, donc la somme des angles des triangles $D^{\prime} X^{\prime} E^{\prime}$ et $D^{\prime} Y^{\prime} E^{\prime}$ dépasserait $2 \pi$, ce qui est impossible. Par conséquent, $\widehat{D^{\prime} X^{\prime} E^{\prime}}$ et $\widehat{D^{\prime} Y^{\prime} E^{\prime}}$ sont égaux. D'après $(2)$, ceci montre que $\left(\overrightarrow{X^{\prime} D^{\prime}}, \overrightarrow{X^{\prime} E^{\prime}}\right)=\left(\overrightarrow{Y^{\prime} D^{\prime}}, \overrightarrow{Y^{\prime} E^{\prime}}\right)$, d'où la cocyclicité de $D^{\prime}, E^{\prime}, X^{\prime}, Y^{\prime}$.
|
| 277 |
+
Exercice 9. On considère une rangée de cases numérotées $0,1, \ldots, k$ de gauche à droite où, pour chaque $i \geqslant 1$, la case numéro $i$ contient $x_{i}$ jetons. Il n'y a initialement aucun jeton sur la case numéro 0 . A tour de rôle, Alice et Bob jouent alors selon les règles suivantes :
|
| 278 |
+
|
| 279 |
+
- Bob choisit un ensemble $S$ de jetons, pas forcément tous sur la même case.
|
| 280 |
+
- Alice peut ensuite soit éliminer tous les jetons qui ne sont pas dans $S$ mais alors déplacer chaque jeton de $S$ de la case qu'il occupe à la case voisine à sa gauche (un tel jeton passe donc d'une case numéro $i$ à la case numéro $i-1$, soit éliminer tous les jetons qui sont dans $S$ mais alors déplacer chaque jeton qui n'est pas dans $S$ de la case qu'il occupe à la case voisine à sa gauche.
|
| 281 |
+
Bob gagne la partie s'il arrive à amener un jeton sur la case numéro 0, et Alice gagne si elle arrive à éliminer tous les jetons.
|
| 282 |
+
|
| 283 |
+
1) Prouver qu'Alice possède une stratégie gagnante si $\sum_{i=1}^{k} 2^{-i} x_{i}<1$.
|
| 284 |
+
2) Est-il vrai que si $\sum_{i=1}^{k} 2^{-i} x_{i} \geqslant 1$ alors Bob possède une stratégie gagnante?
|
| 285 |
+
|
| 286 |
+
## Solution de l'exercice 9
|
| 287 |
+
|
| 288 |
+
Dans tout ce qui suit, on peut clairement supposer que Bob ne choisit jamais $S=\emptyset$ ou $S$ l'ensemble de tous les jetons non encore éliminés, sans quoi Alice gagne immédiatement. Du coup, le nombre de jetons diminue strictement après chaque fois qu'Alice joue, ce qui assure que le jeu se termine toujours en un nombre fini de tours, soit par élimination de tous les jetons, soit parce que l'un d'eux aura atteint la case numéro 0 . Ainsi, il n'y aura pas de partie nulle.
|
| 289 |
+
De plus, s'agissant d'un jeu à information parfaite, il est bien connu que l'un des deux joueurs a alors une stratégie gagnante. Reste à savoir lequel...
|
| 290 |
+
|
| 291 |
+
1) - Approche probabiliste : Fixons une stratégie pour Bob. Alice va alors jouer de façon aléatoire. Plus précisément, à chaque tour, après que Bob ait choisi son ensemble $S$ de jetons, Alice lance une pièce équilibrée. Si elle obtient Face, elle élimine les jetons de $S$ (et déplace donc ceux qui ne sont pas dans $S$ vers la gauche) et, si elle obtient Pile, elle fait le contraire.
|
| 292 |
+
|
| 293 |
+
Pour chaque jeton $j$, on note $X_{j}$ la variable aléatoire égale à 1 si le jeton $j$ est sur la case numéro 0 à la fin de la partie, et égale à 0 sinon.
|
| 294 |
+
Soit enfin $X=\sum_{j} X_{j}$, la somme portant sur l'ensemble des jetons de départ.
|
| 295 |
+
On remarque que $X$ représente le nombre total de jetons qui arrivent sur la case numéro 0 à la fin du jeu, et donc qu'Alice gagne si et seulement si $X<1$.
|
| 296 |
+
|
| 297 |
+
Soit $j$ un des jetons de départ. A chaque tour, Bob peut choisir $S$ de sorte que, si $j$ n'a pas encore été éliminé, on ait $j \in S$ ou $j \notin S$ mais, quoi qu'il en soit, la probabilité que $j$ soit alors déplacé vers la gauche est égale à $\frac{1}{2}$. Si, au début du jeu, le jeton $j$ se trouve sur la case numéro $i$, il arrive sur la case numéro 0 à la fin du jeu si et seulement si les $i$ premiers lancers de pièces ont tous conduit à des déplacements vers la gauche, ce qui arrive donc avec une probabilité $\frac{1}{2^{i}}$. Par suite, on a $E\left(X_{j}\right)=\frac{1}{2^{i}}$ pour tout jeton $j$.
|
| 298 |
+
Par linéarité de l'espérance, on a donc
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
E(X)=\sum_{j} E\left(X_{j}\right)=\sum_{i=1}^{k} 2^{-i} x_{i}<1
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
Cela assure que l'événement $[X<1]$ se réalise avec une probabilité non nulle. Ainsi, quelle que soit la stratégie de Bob, Alice a une probabilité non nulle de gagner, ce qui prouve que Bob n'a pas de stratégie gagnante. D'après notre remarque initiale, c'est donc Alice qui en possède une.
|
| 305 |
+
|
| 306 |
+
- Approche déterministe : Plaçons nous à un instant donné au cours de la partie, juste avant que ce soit à Bob de jouer, et considérons la configuration $C$ obtenue. Pour chaque $i$, on note $y_{i}$ le nombre de jetons qui sont alors sur la case numéro $i$, et on définit le poids de $C$ par $W(C)=\sum_{i=1}^{k} y_{i} 2^{-i}$.
|
| 307 |
+
|
| 308 |
+
Pour faire le lien avec l'approche probabiliste, on peut noter que $W(C)=E(Y)$, où $Y$ est le nombre de jetons qui vont arriver sur la case numéro 0 si Alice joue le reste de la partie, depuis la configuration $C$, de la façon aléatoire ci-dessus.
|
| 309 |
+
|
| 310 |
+
La stratégie d'Alice va consister alors à toujours choisir des configurations afin de minimiser les poids $W$ successifs :
|
| 311 |
+
Soit donc $C$ une configuration pour laquelle le jeu ne soit pas déjà terminé, de poids $W=W(C)$, et supposons que Bob choisisse l'ensemble $S$ de jetons.
|
| 312 |
+
On note $W^{+}$(resp. $W^{-}$) le poids de la configuration obtenue si Alice déplace les jetons de $S$ vers la gauche (resp. élimine les jetons de $S$ ).
|
| 313 |
+
Pour chaque jeton $j$, la contribution de $j$ est nulle ( $j$ a été éliminé) dans l'une des sommes $W^{+}$et $W^{-}$, et vaut le double de ce qu'elle est dans $W$ pour l'autre. Ceci étant vrai pour chaque jeton, on a donc $W=\frac{1}{2}\left(W^{+}+W^{-}\right)$.
|
| 314 |
+
En particulier, Alice peut alors choisir une configuration $C^{\prime}$ pour laquelle $W\left(C^{\prime}\right) \leqslant W(C)$. Or, puisqu'on débute le jeu avec une configuration de poids strictement inférieur à 1 , cela assure que, tout au long du jeu, Alice peut imposer des configurations de poids strictement inférieurs à 1 . Ceci empêche clairement Bob de gagner puisqu'un jeton sur la case numéro 0 donne, à lui seul, un poids égal à 1.
|
| 315 |
+
2) Supposons que $\sum_{i=1}^{k} 2^{-i} x_{i} \geqslant 1$.
|
| 316 |
+
|
| 317 |
+
On va prouver que Bob possède une stratégie gagnante. Compte-tenu de notre remarque préliminaire, il suffit de prouver qu'Alice n'a pas de stratégie gagnante.
|
| 318 |
+
|
| 319 |
+
Soit $C$ une configuration pour laquelle le jeu n'est pas encore terminé. On note $J$ l'ensemble des jetons de $C$.
|
| 320 |
+
Si $A \subset J$, on note $C_{A}$ la configuration obtenue à partir de $C$ en ne gardant que les jetons qui sont dans $A$ (sans les déplacer vers la gauche).
|
| 321 |
+
|
| 322 |
+
Lemme. Si $C$ est une configuration telle que $W(C) \geqslant 1$, il existe une partie $S$ de $J$ telle que
|
| 323 |
+
|
| 324 |
+
$$
|
| 325 |
+
W\left(C_{S}\right) \geqslant \frac{1}{2} \text { et } W\left(C_{\bar{S}}\right) \geqslant \frac{1}{2} \text {. }
|
| 326 |
+
$$
|
| 327 |
+
|
| 328 |
+
Preuve du lemme.
|
| 329 |
+
Tout d'abord, on remarque que si une configuration $C$ vérifie $W(C) \geqslant 1$ alors il existe $i$ tel que $y_{i} \geqslant 2$. En effet, dans le cas contraire, on aurait
|
| 330 |
+
|
| 331 |
+
$$
|
| 332 |
+
W(C) \leqslant \sum_{i=1}^{k} 2^{-i}=1-\frac{1}{2^{k}}<1
|
| 333 |
+
$$
|
| 334 |
+
|
| 335 |
+
On raisonne par récurrence sur le nombre $n$ de jetons de la configuration :
|
| 336 |
+
|
| 337 |
+
- Si la configuration considérée ne possède que deux jetons alors, d'après ci-dessus, ils sont tous les deux sur la même case. De plus, si l'on veut que $W(C) \geqslant 1$, il est facile de vérifier qu'ils sont en fait sur la case numéro 1. Ainsi, la partie $S$ formée par l'un des deux jetons convient.
|
| 338 |
+
- Soit $n \geqslant 3$ et supposons la conclusion assurée pour toute configuration de poids supérieur ou égal à 1 , et contenant $n-1$ jetons. Soit alors $C$ une configuration telle que $W(C) \geqslant 1$ et à $n$ jetons.
|
| 339 |
+
Si $y_{1} \geqslant 2$, une partie $S$ formée uniquement d'un des jetons qui sont sur la case numéro 1 convient. Sinon, soit $i \geqslant 2$ tel que $y_{i} \geqslant 2$ et soit $A$ et $B$ deux jetons qui sont sur la case numéro $i$. On considère alors la configuration $C^{\prime}$ identique à $C$ sauf pour $A$ et $B$ qui sont remplacés par un seul jeton $X$, placé sur la case numéro $i-1$. On a clairement $W\left(C^{\prime}\right)=W(C) \geqslant 1$, et $C^{\prime}$ ne contient que $n-1$ jetons. D'après l'hypothèse de récurrence, il existe donc une partie $S^{\prime}$ de l'ensemble des jetons de $C^{\prime}$ telle que $W\left(C_{S^{\prime}}^{\prime}\right) \geqslant \frac{1}{2}$ et $W\left(C_{\overline{S^{\prime}}}^{\prime}\right) \geqslant \frac{1}{2}$.
|
| 340 |
+
Il est alors facile de vérifier que si $S$ est la partie formée des jetons de $S^{\prime}$, et en remplaçant $X$ par $A$ et $B$, on a bien $W\left(C_{S}\right) \geqslant \frac{1}{2}$ et $W\left(C_{\bar{S}}\right) \geqslant \frac{1}{2}$, ce qui achève la récurrence et la preuve.
|
| 341 |
+
|
| 342 |
+
Revenons au jeu. Une fois que Bob a choisi un ensemble $S$ de jetons, quel que soit le choix d'Alice, celui-ci conduira à une configuration dont le poids sera le double de celui de la configuration formée uniquement par les jetons qui ne seront pas éliminés. Le lemme assure donc qu'à partir d'une configuration de poids supérieur ou égal à 1 , Bob peut choisir $S$ de sorte qu'après le choix d'Alice, on obtienne une configuration de poids supérieur ou égal à 1. Puisque la configuration initiale est supposée de poids supérieur ou égal à 1, Bob peut donc imposer que toute la partie se déroule sur de telles configurations. Cela empêche clairement Alice de gagner (elle cherche à obtenir une configuration de poids nul), d'où la conclusion.
|
| 343 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-1-solutions.md
ADDED
|
@@ -0,0 +1,133 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Envoi de combinatoire: quelques corrigés
|
| 2 |
+
|
| 3 |
+
29 octobre 2014
|
| 4 |
+
|
| 5 |
+
Exercice 1 On considère un échiquier classique $8 \times 8$. Un zigzag est un chemin sur les cases blanches, qui part d'une case (quelconque) de la ligne du bas, et monte de ligne en ligne jusqu'à atteindre celle du haut (sur n'importe quelle case) : à chaque étape, on monte d'une case en diagonale. Combien y a-t-il de zigzags?
|
| 6 |
+
|
| 7 |
+
Solution On écrit un 1 dans chacune des quatre cases blanches du bas. Puis dans la deuxième ligne, on écrit la somme des cases blanches qui y mènent : c'est le nombre de manières d'atteindre ces cases. On recommence dans la troisième ligne, etc. jusqu'à la huitième ligne : sur chacune des quatre cases, on a le nombre de zigzags qui arrivent à cette case. Le nombre total de zigzags est donc $69+103+35+89=296$.
|
| 8 |
+

|
| 9 |
+
|
| 10 |
+
Exercice 2 On prend 1008 entiers distincts compris (au sens large) entre 1 et 2014.
|
| 11 |
+
(i) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ divise $c$ (le pgcd ou Plus Grand Diviseur Commun de deux entiers est le plus grand entier naturel qui les divise tous les deux).
|
| 12 |
+
(ii) Montrer qu'il existe trois entiers $a, b, c$ tels que le pgcd de $a$ et $b$ ne divise pas $c$.
|
| 13 |
+
|
| 14 |
+
Solution (i) Groupons les entiers de 1 à 2014 en paires d'entiers consécutifs : (1, 2), (3, 4),..., (2013, 2014). Il y en a 1007. Par le principe des tiroirs, si on choisit 1008 entiers, il y en aura deux d'une même paire, $a$ et $b$, avec $b=a+1$. Leur pgcd vaut 1 (puisqu'il divise leur différence), donc divise n'importe lequel des 1006 autres nombres, que l'on peut prendre pour $c$.
|
| 15 |
+
(ii) Il y a 1007 entiers pairs prenables. Donc parmi 1008 nombres, il y a forcément un impair. S'il y a deux nombres pairs au moins parmi les 1008, notons-les $a$ et $b$. Soit $c$ un nombre impair parmi les 1008. Le $\operatorname{pgcd}$ de $a$ et $b$ est multiple de 2 , puisque 2 divise à la fois $a$ et $b$. (en fait, le $\operatorname{pgcd}$ de $a$ et $b$ vaut 2 fois le $\operatorname{pgcd}$ de $a / 2$ et $b / 2$ ). Donc s'il divise $c$, alors 2 divise $c$, ce qui est absurde.
|
| 16 |
+
S'il y a moins de 2 nombres pairs parmi les 1008, ça veut dire qu'on a pris les 1007 impairs, ainsi qu'un nombre pair, noté $c$. On peut trouver des triplets d'au moins deux manières.
|
| 17 |
+
|
| 18 |
+
- Solution courte : on dispose du triplet $(3,9,1)$, et il est clair que $\operatorname{pgcd}(3,9)$ ne divise pas 1.
|
| 19 |
+
- Solution moins courte : si $c$ est divisible par tous les pgcd de couples d'entiers impairs entre 1 et 2013, ça va lui faire beaucoup de diviseurs premiers : il sera divisible par le pgcd de 3 et 9 , le pgcd de 5 et 15, celui de 7 et 21 , celui de 11 et 33 , etc. Donc il est divisible par $3,5,7,11$ déjà (et par 2 , puisqu'il est pair). Le plus petit multiple commun de ces nombres est leur produit (puisqu'ils n'ont deux-à-deux aucun facteur commun). Il vaut $2 \times 3 \times 5 \times 7 \times 11=2310$ donc $c>2014$, ce qui n'est pas possible. Donc il existe deux nombres impairs $a$ et $b$ tels que leur pged ne divise pas $c$.
|
| 20 |
+
|
| 21 |
+
Exercice 3 Combien y a-t-il de nombres à six chiffres qui ont quatre chiffres pairs, deux chiffres impairs et qui sont multiples de 5 ? Note: un nombre ne commence pas par un 0 .
|
| 22 |
+
|
| 23 |
+
Solution Un tel nombre termine par 0 ou 5 . Nous allons compter séparément les nombres qui se terminent par 0 et ceux qui se terminent par 5 .
|
| 24 |
+
Nombres dont le dernier chiffre est 0 :
|
| 25 |
+
|
| 26 |
+
- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir (2,4,6,8, mais pas 0 ). Il reste à choisir les 4 chiffres du milieu. On a 6 manières de positionner les impairs :
|
| 27 |
+
|
| 28 |
+
$$
|
| 29 |
+
(p, p, i, i),(p, i, p, i),(p, i, i, p),(i, p, i, p),(i, i, p, p),(i, p, p, i)
|
| 30 |
+
$$
|
| 31 |
+
|
| 32 |
+
(où $p$ représente un chiffre pair et $i$ un chiffre impair). Ensuite, il y a 5 possibilités pour le choix de chaque chiffre. Donc $6 \times 4 \times 5^{4}$ possibilités.
|
| 33 |
+
|
| 34 |
+
- Si le premier chiffre est impair, nous avons 5 possibilités pour le choisir . Il reste 4 manières de positionner l'impair du milieu. Et de nouveau 5 choix pour chaque chiffre du milieu. Donc $4 \times 5^{5}$ nombres possibles.
|
| 35 |
+
Nombres dont le dernier chiffre est 5 :
|
| 36 |
+
- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir. Il y a 4 possibilités pour la place de l'impair du milieu, 5 choix pour chacun des chiffres du milieu, donc $16 \times 5^{4}$ possibilités.
|
| 37 |
+
- Si le premier chiffre est impair il y a 5 possibilités pour le choisir. Il reste alors simplement à déterminer les pairs du milieu : 5 choix à chaque fois, donc $5^{5}$ choix en tout.
|
| 38 |
+
Au total, il y a $24 \times 5^{4}+4 \times 5^{5}+16 \times 5^{4}+5^{5}=13 \times 5^{5}=40625$ possibilités.
|
| 39 |
+
|
| 40 |
+
Exercice 4 Soit $n$ un entier strictement positif. On considère $2 n+1$ entiers distincts compris au sens large entre $-2 n+1$ et $2 n-1$. Montrer qu'on peut en choisir 3 dont la somme soit nulle.
|
| 41 |
+
|
| 42 |
+
Solution On raisonne par récurrence sur $n$.
|
| 43 |
+
Initialisation : Pour $n=1$, on prend $2 n+1=3$ entiers distincts parmi $-1,0,1$, donc ces trois entiers. Leur somme est bien nulle.
|
| 44 |
+
Hérédité : Supposons l'énoncé vrai au rang $n$ : si on prend $2 n+1$ entiers distincts compris au sens large entre $-2 n+1$ et $2 n-1$, alors on peut en choisir 3 dont la somme soit nulle. Maintenant, on veut montrer que parmi $2 n+3$ entiers distincts entre $-2 n-1$ et $2 n+1$, il y en a toujours 3 de somme nulle.
|
| 45 |
+
Si parmi ces $2 n+3$ entiers, il y en a $2 n+1$ entre $-2 n+1$ et $2 n-1$, alors c'est gagné par hypothèse de récurrence. On peut donc supposer que 3 au moins de ces entiers sont parmi $\{-2 n-1,-2 n, 2 n, 2 n+1\}$. Par symétrie entre les positifs et les négatifs, on peut supposer qu'on dispose de $2 n$ et $2 n+1$, ainsi que de $-2 n-1$ ou $-2 n$, donc on peut supposer qu'on ne dispose pas de 0 , puisque $0+2 n+(-2 n)=0+(2 n+1)+(-2 n-1)=0$ et on aurait alors un triplet de somme nulle. Maintenant, considérons les $n$ paires
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\{-k,-2 n-1+k\}, \quad 1 \leq k \leq n
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
si l'une d'elles est incluse dans notre sélection de $2 n+3$ entiers, alors on a encore trois nombres de somme nulle : $-k+(-2 n-1+k)+(2 n+1)=0$ et on a terminé. Supposons donc que notre sélection ne contienne qu'au plus un élément de ces $n$ paires, donc il reste au moins $n+1$ nombres à choisir parmi $(\{1, \ldots, 2 n-1\}$ et $-2 n-1$ ). On pose $A=\{1, \ldots, 2 n-1\}$. On distingue 2 cas.
|
| 52 |
+
|
| 53 |
+
- Si on a pris $-2 n-1$, on doit prendre au moins $n$ éléments de $A$. On regarde cette fois les $n$ paires
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
\{k, 2 n+1-k\}, \quad 1 \leq k \leq n
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Si l'une d'elles est complète, on a un triplet à somme nulle avec $-2 n-1$. On a supposé au début que $2 n$ était pris, donc si on prend $1,\{1,2 n\}$ est complète. Sinon on prend $n$ nombres dans les $n-1$ paires restantes, donc par principe des tiroirs, on a une paire complète.
|
| 60 |
+
|
| 61 |
+
- Si on n'a pas pris $-2 n-1$, on doit prendre au moins $n$ éléments de $A$. Et on a pris $-2 n$ d'après le début du raisonnement. Et $A$ peut se découper en $n-1$ paires
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\{k, 2 n-k\}, 1 \leq k \leq n-1
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
De nouveau, par le principe des tiroirs on doit prendre une paire complète, donnant un triplet à somme nulle avec $-2 n$.
|
| 68 |
+
Ceci clôt la récurrence.
|
| 69 |
+
|
| 70 |
+
Exercice 5 On considère 6 points du plan, disposés de telle sorte que le triangle formé par trois quelconques d'entre eux ait trois côtés de longueurs distinctes. Montrer qu'il existe un triangle dont le plus court côté est également le côté le plus long d'un autre triangle.
|
| 71 |
+
|
| 72 |
+
Solution On colorie en rouge le plus court côté de chaque triangle. Il suffit de montrer qu'on a un triangle rouge. Appelons $P_{1}, \ldots, P_{6}$ les points. Parmi les cinq segments $P_{1} P_{2}, P_{1} P_{3}, P_{1} P_{4}, P_{1} P_{5}, P_{1} P_{6}$ ayant $P_{1}$ pour extrémité, il y en a au moins 3 rouges ou bien au moins 3 non coloriés.
|
| 73 |
+
|
| 74 |
+
- Supposons qu'il y en ait 3 rouges, disons $P_{1} P_{2}, P_{1} P_{3}$ et $P_{1} P_{4}$. Le triangle $P_{2} P_{3} P_{4}$ a au moins un côté rouge, disons $P_{2} P_{3}$, donc le triangle $P_{1} P_{2} P_{3}$ est rouge.
|
| 75 |
+
- Supposons qu'il y en ait 3 non coloriées, disons $P_{1} P_{2}, P_{1} P_{3}$ et $P_{1} P_{4}$. Chacun des trois triangles $P_{1} P_{2} P_{3}$, $P_{1} P_{3} P_{4}, P_{1} P_{4} P_{2}$ a au moins un côté rouge, et ce côté n'est pas l'un de ceux ayant $P_{1}$ pour extrémité, donc $P_{2} P_{3}, P_{3} P_{4}, P_{4} P_{2}$ sont rouges. Ainsi, le triangle $P_{2} P_{3} P_{4}$ est rouge.
|
| 76 |
+
|
| 77 |
+
Exercice 6 Dans un cirque, il y a plusieurs clowns. Chacun utilise au moins 5 couleurs, parmi 12 possibles, pour se peindre. Une même couleur est utilisée par au plus 20 clowns. Deux clowns n'ont jamais exactement les mêmes couleurs. Combien y a-t-il de clowns au maximum?
|
| 78 |
+
|
| 79 |
+
Solution Soit $n$ le nombre de clowns et $N$ le nombre de paires $(L, c)$ où $L$ est un cLown et $c$ une couleur qu'il porte. D'une part, chaque clown ayant au moins 5 couleurs, $N \geq 5 \times n$. D'autre part, chacune des 12 couleurs peut apparaître dans au plus 20 paires. Donc $N \leq 20 \times 12$. On en déduit que $5 n \leq 240$, donc $n \leq 48$.
|
| 80 |
+
|
| 81 |
+
Maintenant, on considère les quintuplets : $A=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}\right), B=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{6}\right), C=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{7}\right)$, $D=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{8}\right)$. On imagine que les 12 couleurs sont disposées dans l'ordre sur un cercle (comme les nombres sur une pendule par exemple), et on note $A_{i}$ le quintuplet obtenu en décalant les couleurs de $A$ de $i$ rangs dans le sens croissant $\left(A_{0}=A, A_{1}=\left(c_{1+1}, c_{2+1}, c_{3+1}, c_{4+1}, c_{5+1}\right)=\left(c_{2}, c_{3}, c_{4}, c_{5}, c_{6}\right)\right.$, $A_{9}=\left(c_{10}, c_{11}, c_{12}, c_{1}, c_{2}\right.$, etc. $)$, et on fait de même pour $B, C, D$. Concrètement, chaque tel quintuplet de couleurs consiste donc de quatre couleurs consécutives sur le cercle, puis fait un "saut" pour le numéro de la dernière couleur qui est de taille 1 pour les $A_{i}$, de 2 pour les $B_{i}$, de 3 pour les $C_{i}$ et de 4 pour les $C_{i}$.
|
| 82 |
+
|
| 83 |
+
Considérons l'ensemble des $K_{i}$ avec $K=A, B, C$ ou $D$ et $0 \leq i \leq 11$. Cela donne 48 paquets de 5 couleurs. Et on vérifie aisément que deux paquets ne peuvent être identiques : si pour certains $i$ et $j$ et certains $K$ et $K^{\prime}$ on avait $K_{i}=K_{j}^{\prime}$, alors $K=K^{\prime}$ pour avoir le même "saut" entre le "paquet" des quatre couleurs consécutives et la cinquième ( 1 pour $A, 2$ pour $B, 3$ pour $C, 4$ pour $D$ ), donc $K_{i}=K_{j}$, et on voit bien que $i=j$, pour que les deux paquets de quatre couleurs consécutives soient les mêmes.
|
| 84 |
+
Enfin, chaque couleur est utilisée exactement 20 fois. En effet, on peut remarquer que toutes les couleurs jouent ici le même rôle(puisqu'on a "décalé" cycliquement les ensembles $A, B, C, D$ ), donc chacune sera représentée autant que les autres. On a au total $5 \times 48=240$ utilisations de couleur, donc chacune des 12 couleurs est utilisée $240 / 12=20$ fois. Pour s'en convaincre plus concrètement, on peut fixer une couleur : elle apparaît une et une seule fois comme "première" couleur d'un paquet de type $A_{i}$, puis comme "deuxième", etc., donc 5 paquets $A_{i}$ utilisent cette couleur, et de même pour $B, C$ et $D$. Elle est donc utilisée 20 fois. Conclusion : on peut bien avoir $n=48$ clowns, en donnant à chaque clown un des 48 paquets de couleurs qu'on vient de construire.
|
| 85 |
+
|
| 86 |
+
Exercice 7 On considère $n^{2}+2 n+1$ points dans un carré de côté $n$. Montrer que trois d'entre eux sont les sommets d'un triangle (éventuellement dégénéré) d'aire au plus $1 / 2$.
|
| 87 |
+
|
| 88 |
+
Solution On raisonne sur l'enveloppe convexe des $(n+1)^{2}$ points : si elle contient beaucoup de points, il y aura 3 sommets voisins de cette enveloppe assez proches pour faire un triangle d'aire petite. Si elle n'en contient pas beaucoup, on la triangule et on regarde les nombreux points dans les petits triangles pour en former un suffisamment petit.
|
| 89 |
+
|
| 90 |
+
Concrètement, voici une démonstration : Soit $E$ l'enveloppe convexe de nos points. On vérifie aisément que son périmètre est inférieur à celui du carré, à savoir $4 n$. Si $E$ a au moins $4 n$ sommets, donc autant de côtés, il existe deux côtés consécutifs $c_{1}$ et $c_{2}$ vérifiant $c_{1}+c_{2} \leq 2$ donc $c_{1} c_{2} \leq 1$ par inégalité arithméticogéométrique. Si $h$ est la hauteur relative à $c_{1}$ dans le triangle formé par les extrémités de $c_{1}$ et $c_{2}, h \leq c_{2}$, donc l'aire du triangle est bien d'au plus $1 / 2$.
|
| 91 |
+
Si $E$ a $s \leq 4 n-1$ sommets, on la triangule en $s-2$ triangles. . Maintenant, prenons un point restant et relions-le aux sommets du triangle dans lequel il se trouve (ou des triangles s'il est sur le côté commun de deux triangles de la triangulation). On prend un autre point restant et on le relie de même aux sommets des triangles de la nouvelle triangulation dans lesquels il se trouve. On continue ainsi jusqu'à ce que tous les points soient intégrés à la triangulation. Ainsi, on a obtenu ce qu'on appelle une triangulation de notre ensemble de points. On avait $s-2$ triangles initialement, on en a rajouté au moins 2 à chaque étape (voire
|
| 92 |
+
3), donc on a au moins $s-2+2\left((n+1)^{2}-s\right) \geq 2 n^{2}+4 n-1-s \geq 2 n^{2}$ triangles disjoints, donc l'un d'eux est d'aire au plus $1 / 2$.
|
| 93 |
+
|
| 94 |
+
Exercice 8 On dispose de $n$ jetons portant chacun un numéro entier (qui peut être négatif). Si on trouve parmi eux deux jetons portant le même numéro $m$, on les enlève et on met à leur place un jeton portant le numéro $m-1$, et un autre portant le numéro $m+1$. Montrer qu'au bout d'un nombre fini de tels changements, tous les jetons porteront des numéros distincts.
|
| 95 |
+
|
| 96 |
+
Solution On commence par montrer le lemme suivant:
|
| 97 |
+
Soit $m_{0}$ le plus petit des numéros des jetons au début. On note $m_{1}^{(k)}, \ldots, m_{j_{k}}^{(k)}$ les numéros inférieurs ou égaux à $m_{0}$ qui sont portés par des jetons après $k$ changements, comptés avec multiplicité et rangés par ordre décroissant de sorte que $m_{j_{k}}^{(k)} \leq \ldots \leq m_{1}^{(k)} \leq m_{0}^{(k)}=m_{0}$. Alors pour tout $i \in\left\{0, \ldots, j_{k}-1\right\}$, on a $m_{i+1}^{(k)}-m_{i}^{(k)} \leq 2$.
|
| 98 |
+
|
| 99 |
+
Démonstration : on raisonne par récurrence sur $k$. Le cas $k=0$ est clair.
|
| 100 |
+
Supposons que le résultat soit vérifié pour un certain $k . \mathrm{Au}(k+1)$-ème changement, si nous remplaçons deux jetons portant un numéro strictement plus grand que $m_{0}$, aucun des $m_{i}^{(k)}$ ne change, donc la propriété est toujours vérifiée. Supposons maintenant que nous remplaçons deux jetons portant un numéro $m_{i}^{(k)}=$ $m_{i+1}^{(k)}=m$. Alors la suite $\left(m_{i}^{(k+1)}\right)$ s'obtient à partir de la suite $\left(m_{i}^{(k)}\right)$ en remplaçant deux occurrences de $m$ par une occurrence de $m-1$ et une occurrence de $m+1$. La différence entre ces dernières est exactement 2 , donc même s'il reste encore des termes égaux à $m$, leur distance aux termes autour d'eux sera inférieure ou égale à 1 . Celle entre $m-1$ et le terme suivant est inférieure strictement à celle entre $m$ et ce même terme suivant, donc inférieure à 2 par hypothèse de récurrence. Pour ce qui est de $m+1$, nous avons deux cas à distinguer. Soit $m=m_{0}$ et alors $m+1$ est strictement supérieur à $m_{0}$ et ne nous intéresse plus. Soit $m<m_{0}$, et alors $m+1$ a une distance au terme précédent inférieure à la distance entre $m$ et ce même terme suivant, donc inférieure à 2 par hypothèse de récurrence.
|
| 101 |
+
|
| 102 |
+
Conséquence du lemme : tous les numéros portés par des jetons sont supérieurs ou égaux à $m_{0}-2 n$ à tout moment. Quitte à ajouter $2 n-m_{0}+1$ à tous les numéros au départ, ce qui ne change pas l'exercice, on peut donc supposer qu'ils sont tous strictement positifs à tout moment.
|
| 103 |
+
|
| 104 |
+
On note alors $P_{k}$ le produit des numéros de tous les jetons après $k$ changements. D'après ce qu'on vient de montrer, $P_{k}$ est un entier strictement positif pour tout $k$. Supposons de le $k+1$-ème changement consiste à remplacer deux jetons portant le numéro $m$ par un jeton portant le numéro $m-1$ et un jeton portant le numéro $m+1$. Alors $P_{k}$ s'écrit $m^{2} c$ avec $c>0$, et $P_{k+1}$ s'écrit
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
P_{k+1}=(m-1)(m+1) c=\left(m^{2}-1\right) c<m^{2} c=P_{k}
|
| 108 |
+
$$
|
| 109 |
+
|
| 110 |
+
Ainsi, la suite des $\left(P_{k}\right)$ est une suite strictement décroissante d'entiers strictement positifs, elle est donc finie, c'est-à-dire qu'on arrive nécessairement à un moment où aucun changement n'est possible.
|
| 111 |
+
|
| 112 |
+
Exercice 9 On considère un quadrillage formé de tous les petits carrés de côté 1 entièrement inclus dans le disque donné par l'inéquation $x^{2}+y^{2} \leq 2014^{2}$ dans le plan muni d'un repère orthonormé $O x y$. A chaque étape du jeu, chaque carré contient le nombre 1 ou le nombre -1 . On suppose que chaque case du quadrillage contient un 1 au début. Un tour consiste à choisir une ligne, une colonne, ou une diagonale (c'est-à-dire un ensemble de cases maximal tel que les centres de ces dernières soient alignés sur une droite formant un angle de 45 degrés avec l'un des axes de coordonnées) du quadrillage, et à changer les signes du contenu de toutes les cases de celle-ci. Peut-on à la fin avoir un -1 dans une case, et des 1 dans toutes les autres?
|
| 113 |
+
|
| 114 |
+
Solution On raisonne par l'absurde en supposant qu'on peut arriver à avoir un seul -1 . On appelle $C_{1}$ le petit carré qui contiendra ce -1 . Par symétrie de la figure, on peut supposer que le centre de ce petit carré a pour coordonnées $\left(a-\frac{1}{2}, b-\frac{1}{2}\right)$ avec $a \geq b \geq 1$.
|
| 115 |
+
|
| 116 |
+
1ère étape: On montre que le petit carré de centre $\left(a-\frac{3}{2}, b+\frac{1}{2}\right)$ appartient également à la figure. Pour cela, il suffit de montrer que le coin supérieur droit de ce petit carré appartient à la figure, c'est-à-dire que $(a-1)^{2}+(b+1)^{2} \leq 2014^{2}$. On distingue deux cas :
|
| 117 |
+
|
| 118 |
+
- Si $a>b$ alors $(a-1)^{2}+(b+1)^{2} \leq a^{2}+b^{2} \leq 2014^{2}$.
|
| 119 |
+
- Si $a=b$, alors l'inégalité $a^{2}+b^{2}=2 a^{2} \leq 2014^{2}$ ne peut être une égalité car la valuation 2 -adique du côté gauche est impaire alors que celle du côté droit est paire. Nous avons donc $2 a^{2}+2 \leq 2014^{2}$, d'où $(a-1)^{2}+(a+1)^{2}=2 a^{2}+2 \leq 2014^{2}$.
|
| 120 |
+
|
| 121 |
+
On appelle $C_{2}$ ce petit carré de centre ( $a-\frac{3}{2}, b+\frac{1}{2}$ ).
|
| 122 |
+
2ème étape : Par des considérations de symétrie et de convexité, les petits carrés $C_{1}, \ldots, C_{8}$ suivants appartiennent tous à la figure :
|
| 123 |
+
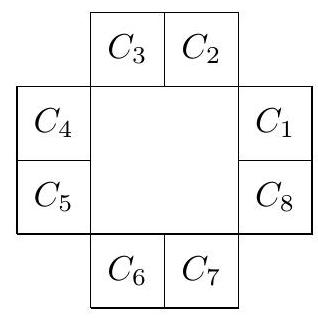
|
| 124 |
+
|
| 125 |
+
Or chaque ligne, chaque colonne et chaque diagonale contient soit aucun, soit deux de ces huit petits carrés. Ainsi, la parité du nombre de -1 parmi ces carrés ne change pas, contradiction.
|
| 126 |
+
|
| 127 |
+
Exercice 10 Soit $n \in \mathbb{N}^{*}$. On appelle $S$ l'ensemble des suites de $2 n$ chiffres comportant $n$ zéros et autant de uns. Deux suites de $S$ sont voisines lorsqu'il suffit de changer la position d'un chiffre de l'une pour obtenir l'autre. Par exemple, 11100010 et 10110010 sont voisines puisqu'en décalant le premier 0 de la deuxième suite de deux "pas" vers la droite, on obtient la première suite. Soit $T$ un sous-ensemble dense de cardinal minimal. Montrer que $\frac{1}{n^{2}+1}|S| \leq|T| \leq \frac{1}{n+1}|S|$. Remarque : on note $|A|$ le cardinal de $A$.
|
| 128 |
+
|
| 129 |
+
Solution On traite séparément les inégalités.
|
| 130 |
+
|
| 131 |
+
- Montrons que $\frac{1}{2 n^{2}+1}|S| \leq|T|$. Soit $s$ un élément de $S$. Soit $s_{i, j}$ la suite que l'on peut obtenir à partir de $s$, en déplaçant le $i$-ème chiffre de $s$ pour le mettre en position $j$. Si $s_{i, j} \neq s$, alors $j \neq i$. En outre, sans perte de généralité, on suppose que le $i$-ème chiffre de $s$ est un 0 ; si $j>i$ et si le $j$-ème chiffre de $s$ est un 0 , alors $s_{i, j}=s_{i, j-1}$; si $j<i$ et si le $j$-ème chiffre de $s$ est un 0 , alors $s_{i, j}=s_{i, j+1}$. Ainsi, toute suite $s_{i, j}$ distincte de $s$ peut s'écrire sous la forme $s_{i, k}$, telle que le $k$-ème chiffre de $s$ soit un 1 : à $i$ fixé, il existe au plus $n$ telles suites. Puisque $i$ peut prendre $2 n$ valeurs, la suite $s$ a donc, en effet, au plus $2 n^{2}$ voisins différents d'elle-même. Ainsi, il faut au moins $\frac{1}{2 n^{2}+1}|S|$ éléments pour faire un ensemble dense.
|
| 132 |
+
- Montrons que $|T| \leq \frac{1}{n+1}|S|$. Considérons les 0 comme des poteaux fixes, délimitant $n+1$ intervalles de 1 (on compte les extérieurs), certains éventuellement vides. Si $s \in S$, soit $r_{k}$ le nombre de 1 dans le $k$-ème intervalle en partant de la gauche. On introduit $N(s):=r_{1}+2 r_{2}+\cdots+n r_{n}$ et $R(s)$ la congruence de $N(s)$ modulo $n+1$. Si on déplace un 0 du $i$-ème intervalle (il y a bien un intervalle non vide) vers le $j$-ème, on obtient $s^{\prime}$ telle que $N\left(s^{\prime}\right)=N(s)+j-i$. En faisant varier $j$ entre 1 et $n+1$, on obtient toutes les congruences possibles pour $R\left(s^{\prime}\right)$. Si, pour tout $0 \leq k \leq n, S_{k}$ est l'ensemble des $s \in S$ telles que $R(s)=k$, toute suite de $S_{k}$ a une voisine dans $S_{k^{\prime}}$ pour tout $k^{\prime} \neq k$. Comme "être voisine" est une relation symétrique (si $s$ voisine de $s^{\prime}$, alors $s^{\prime}$ est voisine de $s$ ), toute suite $s$ qui n'est pas dans $S_{k}$ a une voisine dans $S_{k}$, donc $S_{k}$ est dense. Or les $S_{k}$ forment une partition de $S$ en $n+1$ sous-ensembles, donc il existe un $k_{0}$ tel que $\left|S_{k_{0}}\right| \leq \frac{1}{n+1}|S|$, ce qui conclut.
|
| 133 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-2-solutions.md
ADDED
|
@@ -0,0 +1,135 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Exercices du groupe B
|
| 2 |
+
|
| 3 |
+
Exercice 1. Soit $A B C D$ un quadrilatère convexe (c'est-à-dire que ses diagonales sont à l'intérieur de $A B C D$ ), et $P$ l'intersection de ses diagonales $[A C]$ et $[B D]$. On note $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ et $\mathrm{O}_{4}$ les centres des cercles circonscrits à $A B P, B C P, C D P$ et DAP.
|
| 4 |
+
Montrer que $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3} \mathrm{O}_{4}$ est un parallélogramme.
|
| 5 |
+
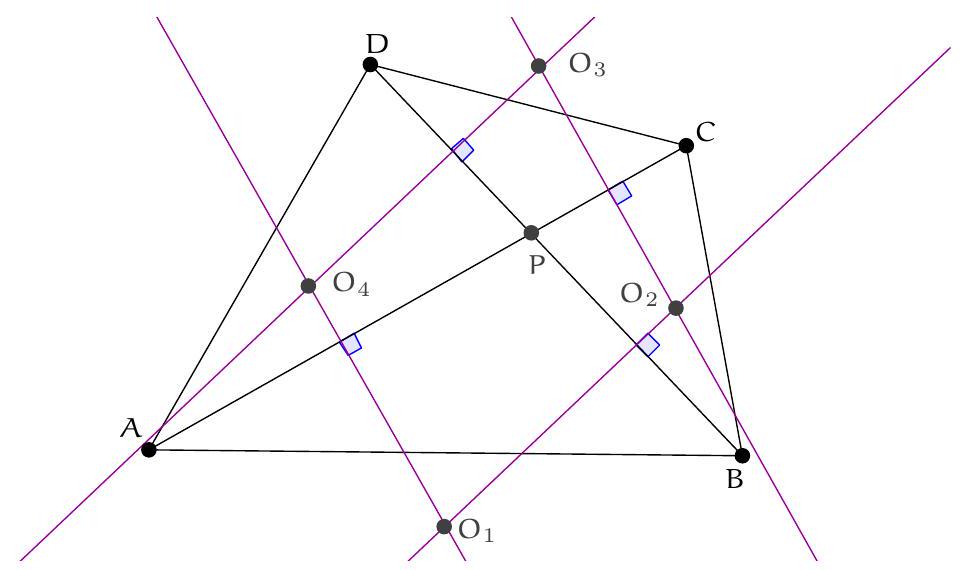
|
| 6 |
+
|
| 7 |
+
Solution de l'exercice $1 \quad \mathrm{O}_{1}$ et $\mathrm{O}_{2}$ sont sur la médiatrice de $[\mathrm{PB}]$, donc $\mathrm{O}_{1} \mathrm{O}_{2}$ est la médiatrice de [PB]. De même, $\left(\mathrm{O}_{3} \mathrm{O}_{4}\right)$ est la médiatrice de [PD], donc $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$ et $\left(\mathrm{O}_{3} \mathrm{O}_{4}\right)$ sont toutes deux perpendiculaires à ( BD$)$, donc elles sont parallèles. De même, $\left(\mathrm{O}_{2} \mathrm{O}_{3}\right)$ et $\left(\mathrm{O}_{4} \mathrm{O}_{1}\right)$ sont toutes deux perpendiculaires à (AC), donc elles sont parallèles.
|
| 8 |
+
ABCD a ses côtés opposés parallèles deux à deux, donc c'est un parallélogramme.
|
| 9 |
+
Exercice 2. Soit $A B C$ un triangle. $H$ son orthocentre et $P, Q$ et $R$ les pieds des hauteurs issues de $A, B$ et $C$.
|
| 10 |
+
Montrer que H est le centre du cercle inscrit à PQR .
|
| 11 |
+
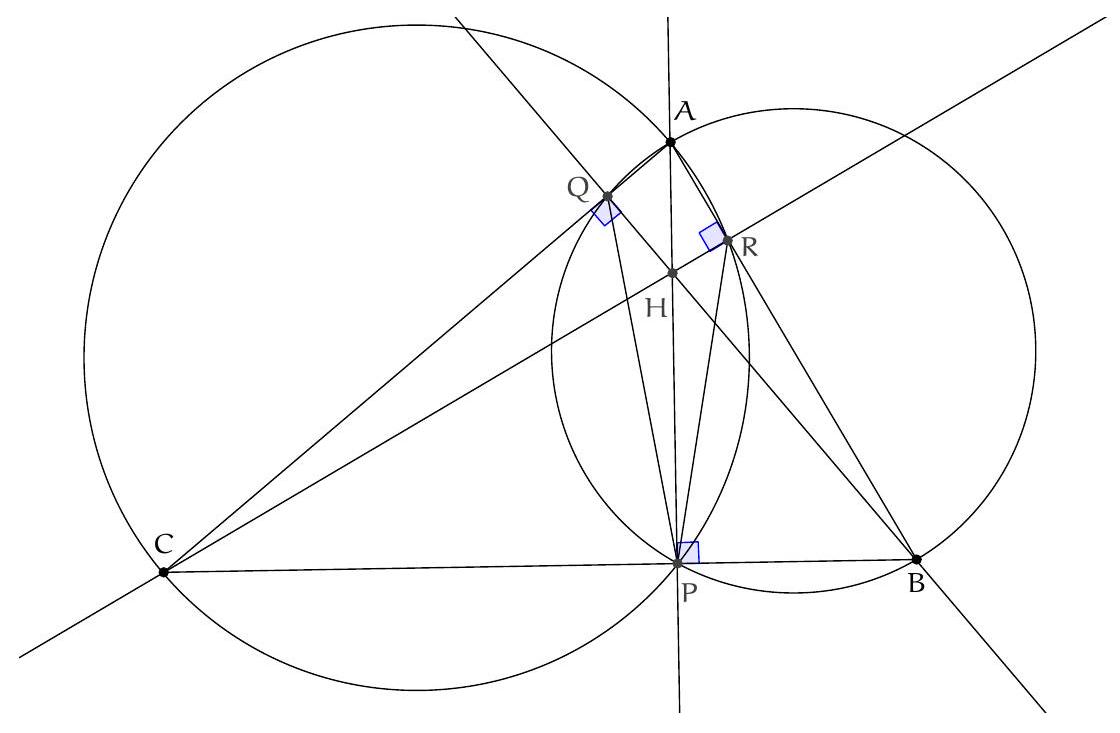
|
| 12 |
+
|
| 13 |
+
Solution de l'exercice 2 On sait que les points $A, B, P$ et $Q$ sont cocycliques sur le cercle de diamètre $[A B]$, donc :
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
\widehat{\mathrm{HPQ}}=\widehat{\mathrm{APQ}}=\widehat{\mathrm{ABQ}}=90^{\circ}-\widehat{\mathrm{BAQ}}=90^{\circ}-\widehat{\mathrm{BAC}}
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
De même, $A, C, P$ et $R$ sont cocycliques sur le cercle de diamètre $[A C]$ donc :
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
\widehat{H P R}=\widehat{A P R}=\widehat{A C R}=90^{\circ}-\widehat{C A R}=90^{\circ}-\widehat{B A C}
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
On a donc $\widehat{\mathrm{HPQ}}=\widehat{\mathrm{HPR}}$ donc $(\mathrm{PH})$ est la bissectrice de $\widehat{\mathrm{QPR}}$. On montre de même que $(\mathrm{QH})$ et $(\mathrm{RH})$ sont les bissectrices de $\widehat{\mathrm{PQR}}$ et $\widehat{\mathrm{PRQ}}$, donc $H$ est le centre du cercle inscrit à PQR .
|
| 26 |
+
Exercice 3. Soit $A B C D E F$ un hexagone ayant tous ses angles égaux à $120^{\circ}$. Montrer que $A B+$ $B C=D E+E F$.
|
| 27 |
+
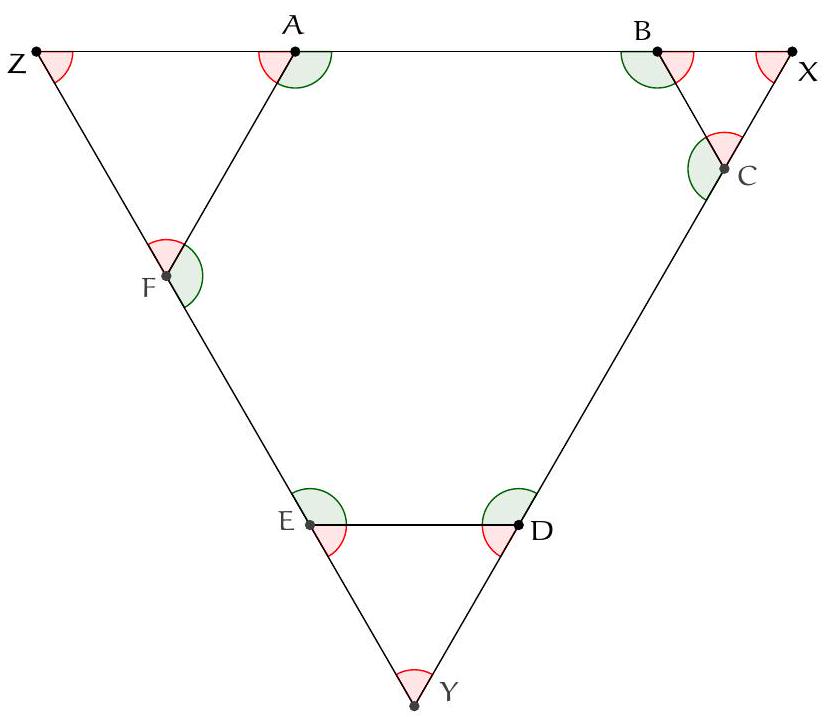
|
| 28 |
+
|
| 29 |
+
Solution de l'exercice 3 On prolonge les côtés [AB], [CD] et [EF], et on appelle Xl l'intersection de $\left(A B\right.$ ) et (CD), $Y$ celle de (CD) et (EF), et $Z$ celle de (EF) et $\left(A B\right.$ ). Alors $\widehat{X B C}=180^{\circ}-\widehat{A B C}=60^{\circ}$ et de même pour $\widehat{X C B}$, donc:
|
| 30 |
+
|
| 31 |
+
$$
|
| 32 |
+
\widehat{Z X Y}=\widehat{B X C}=180^{\circ}-\widehat{X B C}-\widehat{X C B}=180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}
|
| 33 |
+
$$
|
| 34 |
+
|
| 35 |
+
et de même pour les angles du triangle $X Y Z$ : on a représenté les angles de $120^{\circ}$ en vert et ceux de $60^{\circ}$ en rouge sur la figure.
|
| 36 |
+
Le triangle $X B C$ est donc équilatéral, donc $A B+B C=A B+B X=A X$ et de même $D E+E F=F Y$. Or, $X Y Z$ est équilatéral donc $Z X=Z Y$ et $Z A F$ est équilatéral donc $Z A=Z F$, d'où $A X=Z X-$ $Z A=Z Y-Z F=F Y$, d'où le résultat.
|
| 37 |
+
|
| 38 |
+
Exercice 4. Soit $A B C D$ un quadrilatère convexe. On note $P, Q, R$ et $S$ les milieux des côtés $[A B],[B C],[C D]$ et $[D A]$. Montrer que l'aire de PQRS est égale à la moitié de l'aire de $A B C D$.
|
| 39 |
+
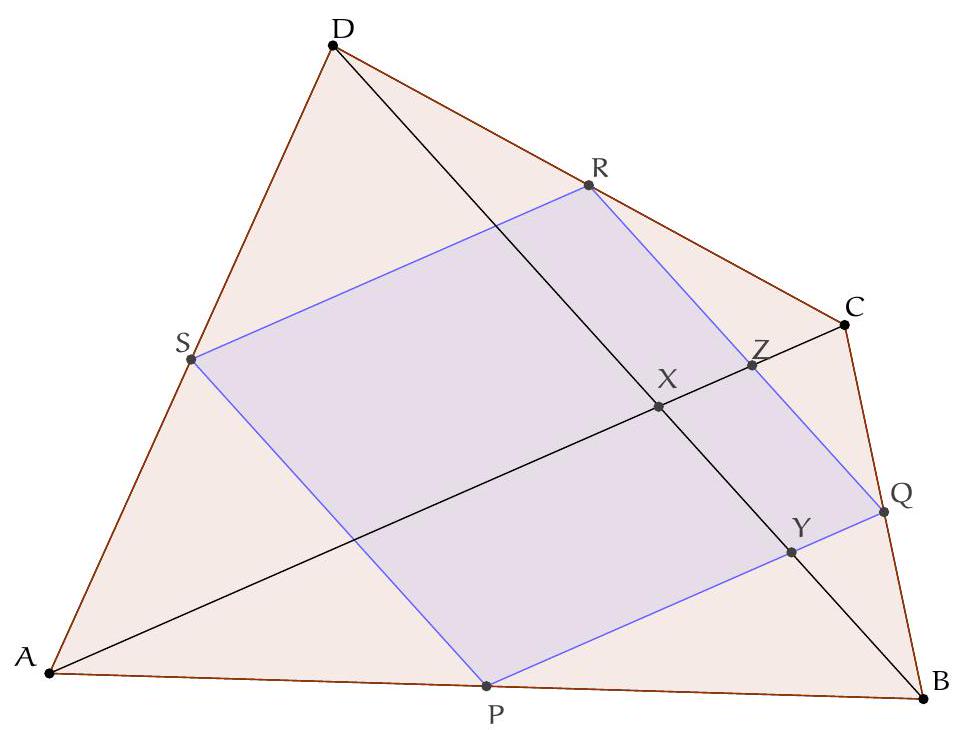
|
| 40 |
+
|
| 41 |
+
Solution de l'exercice 4 On note $X$ l'intersection des diagonales de $A B C D$. [PQ] coupe [BD] en $Y$, et $[Q R]$ coupe $[A C]$ en $Z$. D'après le théorème de la droite des milieux, ( $P Q$ ) est parallèle à ( $A C$ ), donc (QZ) est parallèle à ( $C X$ ) et, de nouveau d'après le théorème de la droite des milieux, Z est le milieu de $[B X]$, donc l'aire du triangle $X Q Z$ est la moitié de l'aire du triangle $X Q B$. De même, l'aire du triangle XQY est la moitié de celle du triangle XQC.
|
| 42 |
+
Le quadrilatère PQRS couvre donc la moitié du triangle XBC. De la même manière, il couvre la moitié des triangles $X C D, X D A$ et $X A B$, donc son aire est la moitié de celle de $A B C D$.
|
| 43 |
+
|
| 44 |
+
## Exercices Communs
|
| 45 |
+
|
| 46 |
+
Exercice 5. Soit $A B C$ un triangle rectangle en $C$. La bissectrice de $\widehat{B A C}$ coupe $[B C]$ en $P$, et celle de $\widehat{A B C}$ coupe $[A C]$ en $Q$. Soient $M$ et $N$ sur $[A B]$ tels que (MP) et (NQ) soient perpendiculaires à $(A B)$. Combien vaut l'angle $\widehat{M C N}$ ?
|
| 47 |
+
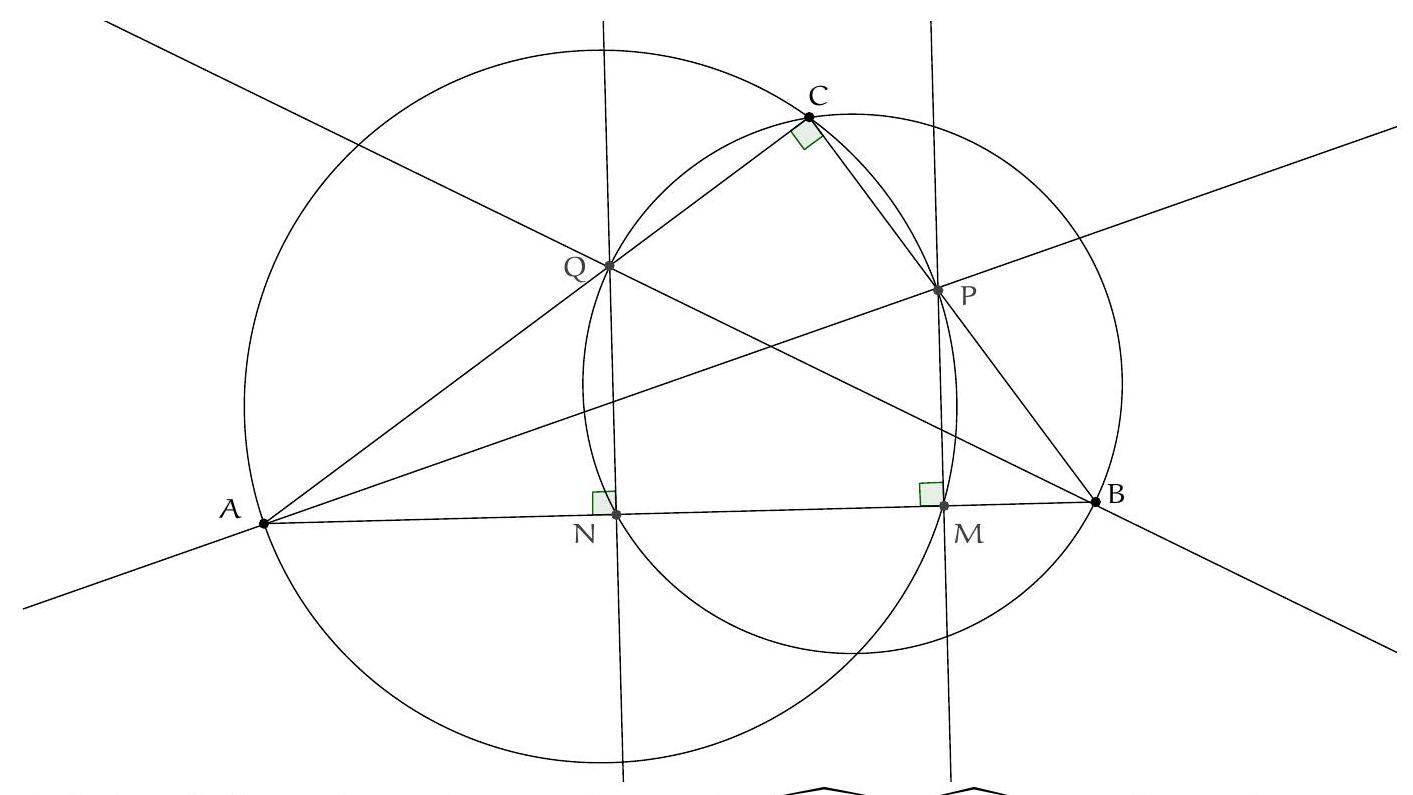
|
| 48 |
+
|
| 49 |
+
Solution de l'exercice 5 Comme les angles $\widehat{A M P}$ et $\widehat{A C P}$ sont droits, les points $A, C, P$ et $M$ sont cocycliques sur le cercle de diamètre $[A P]$. De même, les points $\mathrm{B}, \mathrm{C}, \mathrm{Q}$ et N sont cocycliques sur le cercle de diamètre $[B Q]$. On peut donc faire une chasse aux angles :
|
| 50 |
+
|
| 51 |
+
$$
|
| 52 |
+
\begin{aligned}
|
| 53 |
+
\widehat{M C N} & =90^{\circ}-\widehat{M C P}-\widehat{\mathrm{NCQ}} \\
|
| 54 |
+
& =90^{\circ}-\widehat{\mathrm{MAP}}-\widehat{\mathrm{NBQ}} \\
|
| 55 |
+
& =90^{\circ}-\frac{1}{2} \widehat{A B C}-\frac{1}{2} \widehat{\mathrm{BAC}} \\
|
| 56 |
+
& =\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{ABC}}-\widehat{\mathrm{BAC}}\right) \\
|
| 57 |
+
& =\frac{1}{2} \widehat{A C B} \\
|
| 58 |
+
& =45^{\circ}
|
| 59 |
+
\end{aligned}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Exercice 6. Soit $A B C$ un triangle ayant ses trois angles aigus, et $P$ le pied de la hauteur issue de $A$. On note $I_{1}$ et $I_{2}$ les centres de cercles inscrits à $A B P$ et $A C P$. Le cercle inscrit à $A B C$ touche $[\mathrm{BC}]$ en D . Combien valent les angles du triangle $\mathrm{I}_{1} \mathrm{I}_{2} \mathrm{D}$ ?
|
| 63 |
+
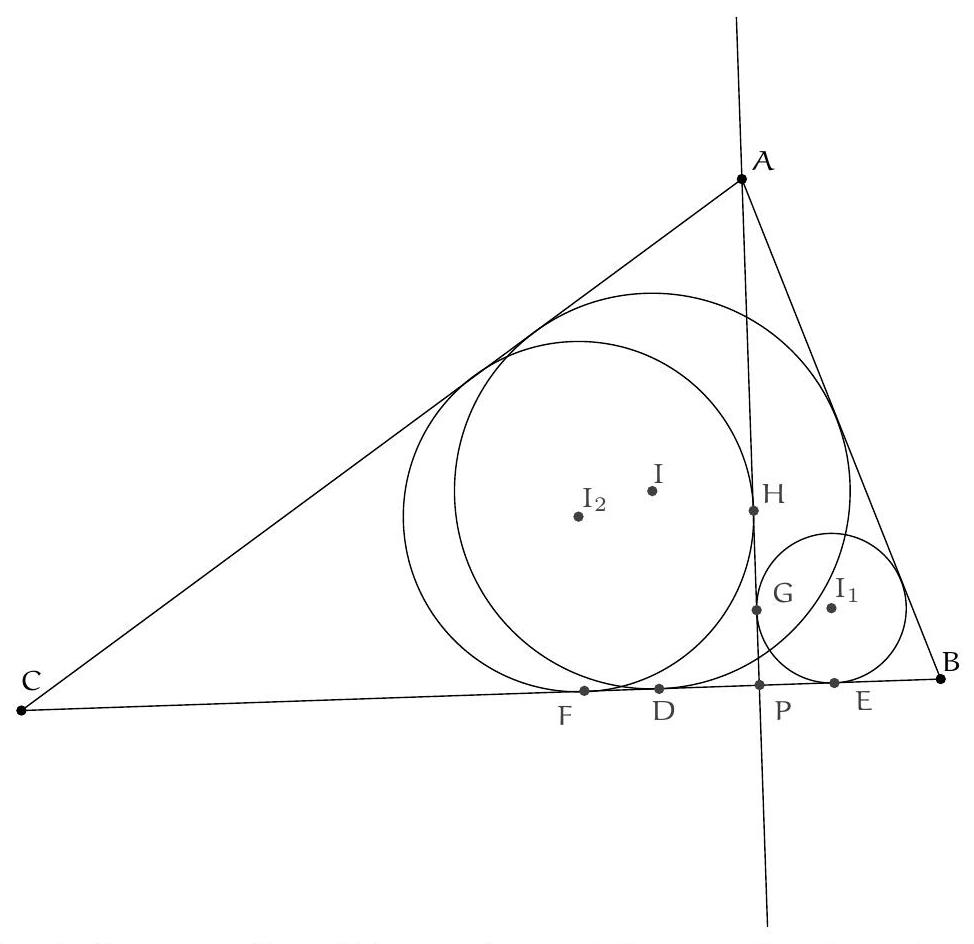
|
| 64 |
+
|
| 65 |
+
Solution de l'exercice 6 On note $E$ et $F$ les points où les cercles inscrits à ABP et ACP touchent $[B C]$, et G et H les points où ils touchent $[A P]: \mathrm{PEI}_{1} \mathrm{H}$ est un carré car les angles en $\mathrm{P}, \mathrm{E}$ et H sont droits, et $I_{1} E=I_{1} H$, donc $E P=E I_{1}$, et de même $F P=\mathrm{FI}_{2}$. On a donc:
|
| 66 |
+
$\mathrm{FD}=\mathrm{CD}-\mathrm{CF}=\frac{\mathrm{CA}+\mathrm{CB}-\mathrm{AB}}{2}-\frac{\mathrm{CA}+\mathrm{CP}-\mathrm{AP}}{2}=\frac{\mathrm{CB}-\mathrm{CP}+\mathrm{AP}-\mathrm{AB}}{2}=\frac{\mathrm{BP}+\mathrm{AP}-\mathrm{AB}}{2}=\mathrm{PE}=\mathrm{EI}_{1}$
|
| 67 |
+
et de même $\mathrm{ED}=\mathrm{FI}_{2}$. Comme de plus $\widehat{\mathrm{I}_{2} \mathrm{FD}}$ et $\widehat{\mathrm{I}_{1} \mathrm{ED}}$ sont droits, les triangles $\mathrm{I}_{1} \mathrm{ED}$ et $\mathrm{I}_{2} \mathrm{FD}$ sont isométriques donc $\mathrm{DI}_{1}=\mathrm{DI}_{2}$. De plus on a:
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\widehat{\mathrm{I}_{1} \mathrm{DI}_{2}}=180^{\circ}-\widehat{\mathrm{I}_{1} \mathrm{DE}}-\widehat{\mathrm{I}_{2} \mathrm{DF}}=180^{\circ}-\widehat{\mathrm{I}_{1} \mathrm{DE}}-\widehat{\mathrm{DI}_{1} \mathrm{E}}=\widehat{\mathrm{DEI}_{1}}=90^{\circ}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Le triangle est donc isocèle rectangle en D , donc ses angles valent $90^{\circ}, 45^{\circ}$ et $45^{\circ}$.
|
| 74 |
+
|
| 75 |
+
## Exercices du groupe A
|
| 76 |
+
|
| 77 |
+
Exercice 7. Deux cercles $\Gamma_{1}$ et $\Gamma_{2}$ de centres $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$ se coupent en P et Q . Une droite passant par $O_{1}$ coupe $\Gamma_{2}$ en $A$ et $B$, et une droite passant par $O_{2}$ coupe $\Gamma_{1}$ en $C$ et $D$. Montrer que s'il existe un cercle passant par $A, B, C$ et $D$, alors le centre de ce cercle est sur (PQ).
|
| 78 |
+
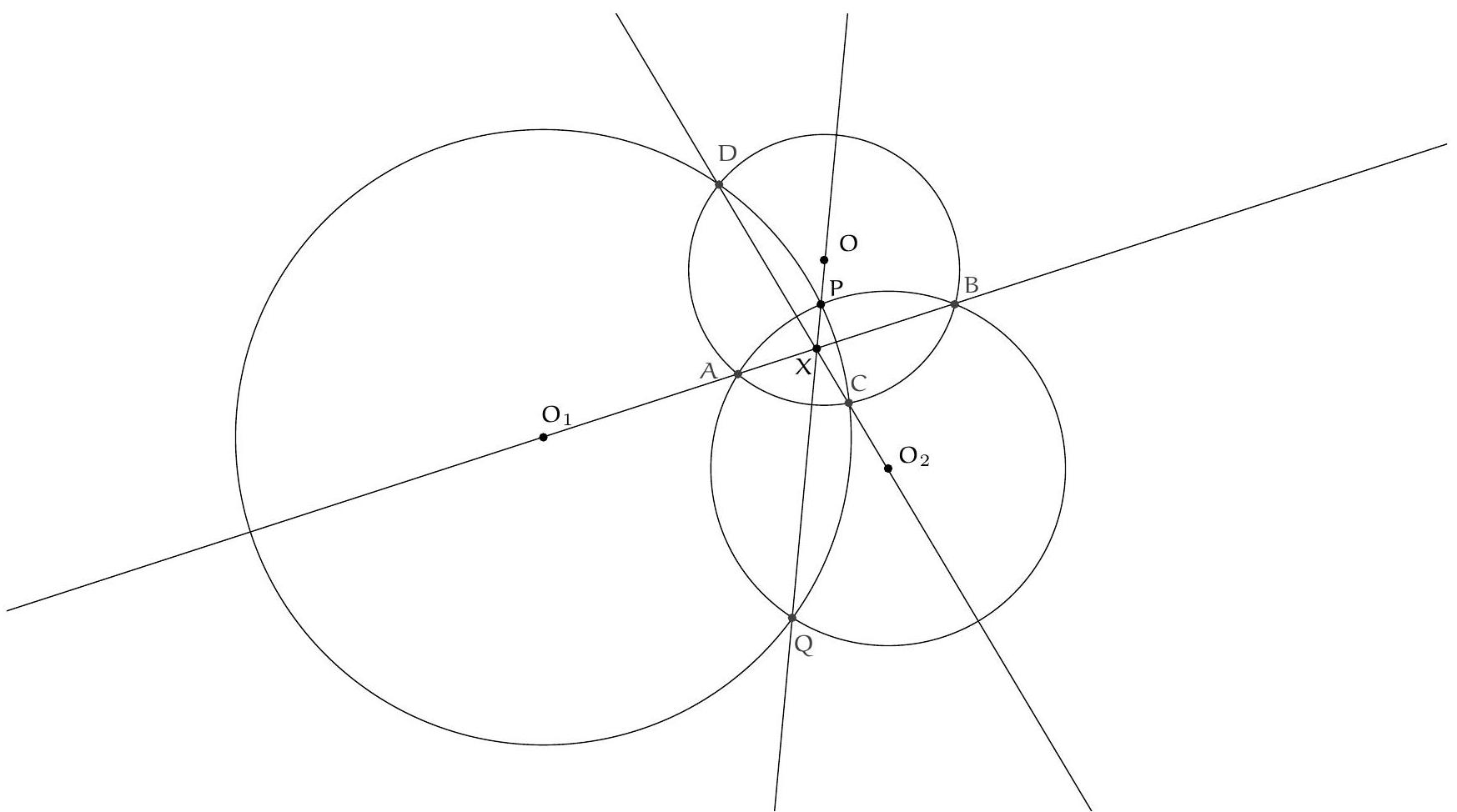
|
| 79 |
+
|
| 80 |
+
Solution de l'exercice 7 On note $\Gamma$ le cercle passant par $A, B, C$ et $D$. D'après le théorème des axes radicaux, $(\mathrm{AB}),(C D)$ et (PQ) sont concourrantes en un point qu'on appelle $X$. De plus, $(\mathrm{AB})$ est perpendiculaire à $\left(\mathrm{OO}_{2}\right)$, donc est la hauteur issue de $\mathrm{O}_{1}$ dans $\mathrm{OO}_{1} \mathrm{O}_{2}$. De même, (CD) est la hauteur issue de $\mathrm{O}_{2}$, donc $X$ est l'orthocentre de $\mathrm{OO}_{1} \mathrm{O}_{2}$. Par conséquent, ( OX ) est perpendiculaire à $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, mais on sait déjà que la perpendiculaire à $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$ passant par X est $(\mathrm{PQ})$, donc les droites $(\mathrm{OX})$ et ( PQ ) sont confondues, et $\mathrm{O} \in(\mathrm{PQ})$.
|
| 81 |
+
Exercice 8. Soit $A B C D$ un quadrilatère convexe. On suppose que les cercles inscrits aux triangles $A B C, B C D, C D A$ et $D A B$ ont un point commun. Montrer que $A B C D$ est un losange.
|
| 82 |
+
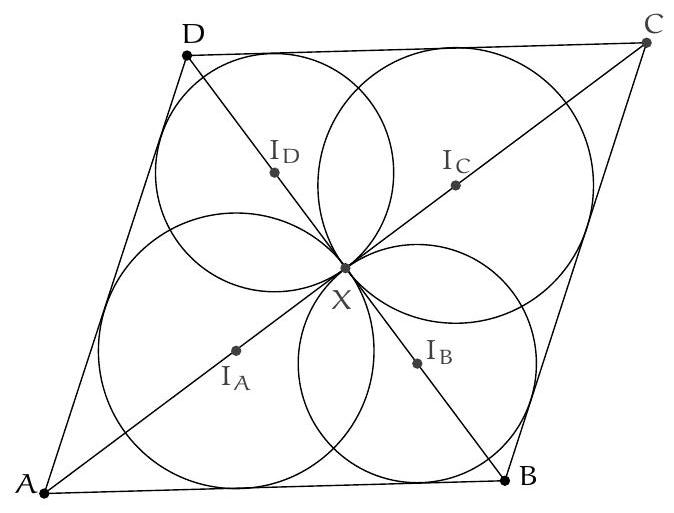
|
| 83 |
+
$\underline{\text { Solution de l'exercice } 8}$ On note $\omega_{A}$ le cercle inscrit à DAB et ainsi de suite: Les cercles $\omega_{B}$ et $\omega_{D}$ sont situés de part et d'autre de (AC), donc ils ne peuvent s'intersecter que sur ( $B C$ ). De même, $\omega_{\mathrm{A}}$ et $\omega_{\mathrm{c}}$ ne peuvent s'intersecter que sur (BD), donc l'intersection des 4 cercles ne peut être que l'intersection des diagonales, qu'on note $X$.
|
| 84 |
+
|
| 85 |
+
De plus, notons $R$ et $S$ les points de tangence du cercle inscrit à $A B C$ avec $[A B]$ et $[B C]$, et $T$ et $U$ les points de contact du cercle inscrit à CDA avec [CD] et [DA]. On a :
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
A B+C D=A R+B R+C T+D T=A X+B S+C X+D U=A U+B S+C S+D U=A D+B C
|
| 89 |
+
$$
|
| 90 |
+
|
| 91 |
+
donc $A B C D$ est circonscriptible : il existe un cercle à l'intérieur de $A B C D$ tangent à tous les côtés, qu'on note $\omega$.
|
| 92 |
+
Le centre de l'homothétie négative qui envoie $\omega_{A}$ sur $\omega_{C}$ est $X$, donc est sur ( $A C$ ). De plus, $A$ est le centre de l'homothétie positive qui envoie $\omega_{A}$ sur $\omega$, et $C$ est le centre de l'homothétie positive qui envoie $\omega$ sur $\omega_{C}$, donc le centre de l'homothétie positive qui envoie $\omega_{A}$ sur $\omega_{C}$ est aussi sur (AC), donc les centres de $\omega_{A}$ et $\omega_{C}$ sont sur ( $A C$ ), donc ( $A C$ ) est la bissectrice de $\widehat{B C D}$ et $\widehat{D A B}$, donc le quadrilatère est symétrique par rapport à $(A C)$ d'où $A B=A D$ et $C B=C D$. On a de même $B A=B C$ et $D A=D C$, donc $A B C D$ est un losange.
|
| 93 |
+
Exercice 9. Deux cercles $\omega_{1}$ et $\omega_{2}$ sont tangents en $S$, avec $\omega_{1}$ à l'intérieur de $\omega_{2}$. On note O le centre de $\omega_{1}$. Une corde $[A B]$ de $\omega_{2}$ est tangente à $\omega_{1}$ en $T$. Montrer que $(A O)$, la perpendiculaire à $(\mathrm{AB})$ passant par $B$ et la perpendiculaire à $(S T)$ passant par $S$ sont concourantes.
|
| 94 |
+
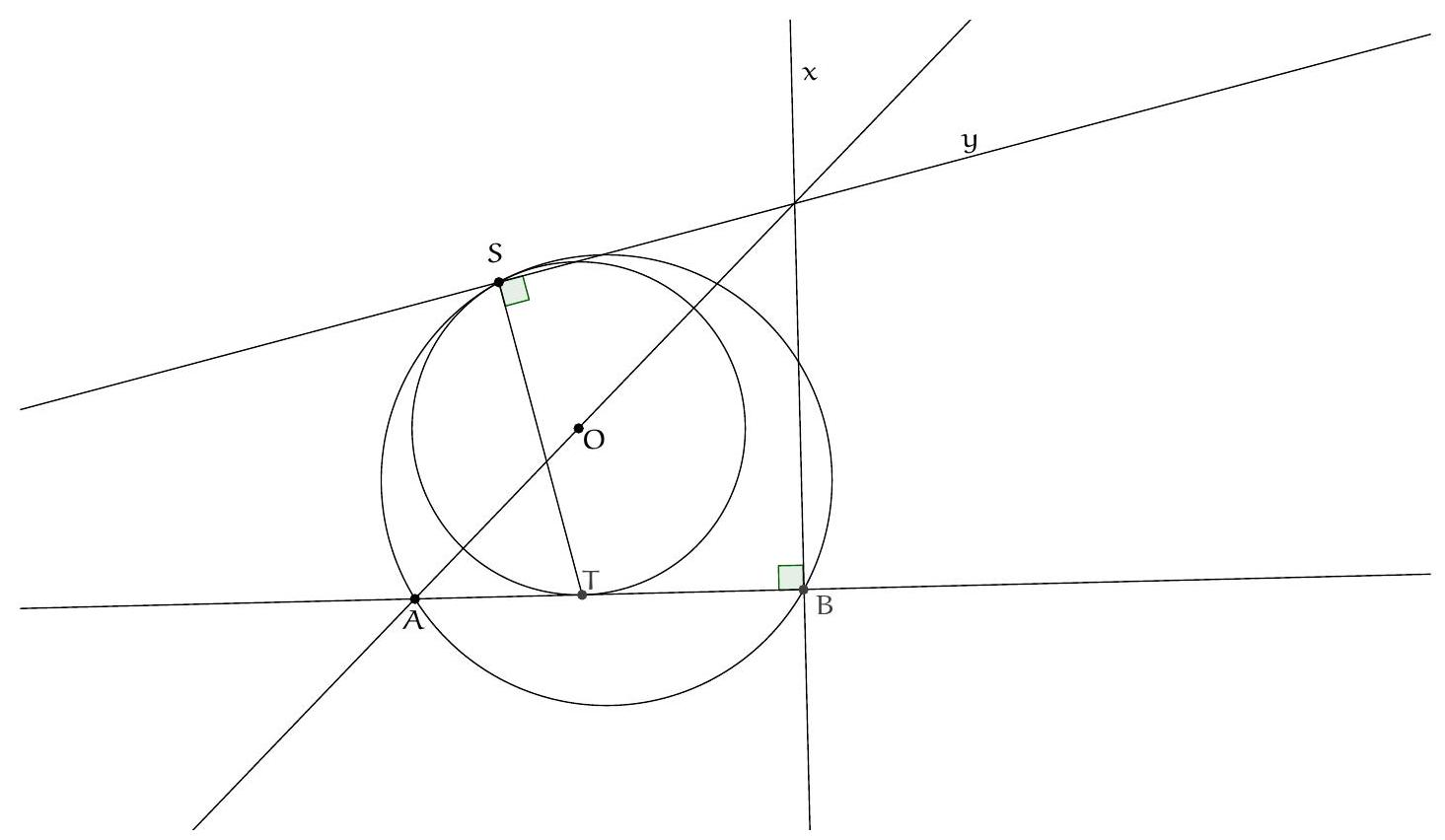
|
| 95 |
+
|
| 96 |
+
Solution de l'exercice 9 On note $(\mathrm{Bx})$ la perpendiculaire à ( AB ) passant par B, et (Sy) la perpendiculaire à (ST) passant par S. Pour obtenir le résultat grâce au théorème de Ceva trigonométrique dans le triangle ABS, on doit montrer :
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\frac{\sin \widehat{B A O}}{\sin \widehat{S A O}} \cdot \frac{\sin \widehat{A S y}}{\sin \widehat{B S y}} \cdot \frac{\sin \widehat{S B x}}{\sin \widehat{A B x}}=1
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
Or, on sait que $\sin A B x=1$. De plus, l'homothétie de centre $S$ qui envoie $\omega_{1}$ sur $\omega_{2}$ envoie $T$ sur le milieu de l'arc $\widehat{A B}$, donc (ST) est la bissectrice intérieure de $\widehat{A S B}$ et (Sy) est sa bissectrice extérieure, $\mathrm{d}^{\prime}$ où $\sin \widehat{\mathrm{ASy}}=\sin \widehat{\mathrm{BSy}}$. Il reste donc à montrer :
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\frac{\sin \widehat{\mathrm{BAO}}}{\sin \widehat{\mathrm{SAO}}} \cdot \sin \widehat{\mathrm{SBX}}=1
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Or, $\sin \widehat{\mathrm{BAO}}=\frac{\mathrm{OT}}{\mathrm{AO}}=\frac{\mathrm{OS}}{\mathrm{AO}}=\frac{\sin \widehat{O A S}}{\sin \widehat{A S O}}$, donc il ne reste plus qu'à montrer $\widehat{A S O}=\widehat{\mathrm{SBx}}$. Si on note $\mathrm{O}^{\prime}$ le centre de $\omega_{2}$, alors :
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
\widehat{\mathrm{ASO}}=\widehat{\mathrm{ASO}^{\prime}}=\frac{1}{2}\left(\pi-\widehat{\mathrm{AO}^{\prime} \mathrm{S}}\right)=\frac{\pi}{2}-\widehat{\mathrm{SBA}}=\widehat{\mathrm{SBx}}
|
| 112 |
+
$$
|
| 113 |
+
|
| 114 |
+
d'où le résultat.
|
| 115 |
+
Exercice 10. Soient $\Gamma$ un cercle de centre O , et ( d ) une droite qui n'intersecte pas $\Gamma$. On appelle $P$ le projeté orthogonal de $O$ sur (d). Soit $Q$ un point variable sur la droite (d), et $\left(t_{1}\right)$ et $\left(t_{2}\right)$ les tangentes à $\Gamma$ passant par $Q$. On note $A$ et $B$ les projetés orthogonaux de $P$ sur $\left(t_{1}\right)$ et $\left(t_{2}\right)$. Montrer que le point d'intersection de $(A B)$ et ( $O P)$ reste fixe quand $Q$ varie.
|
| 116 |
+
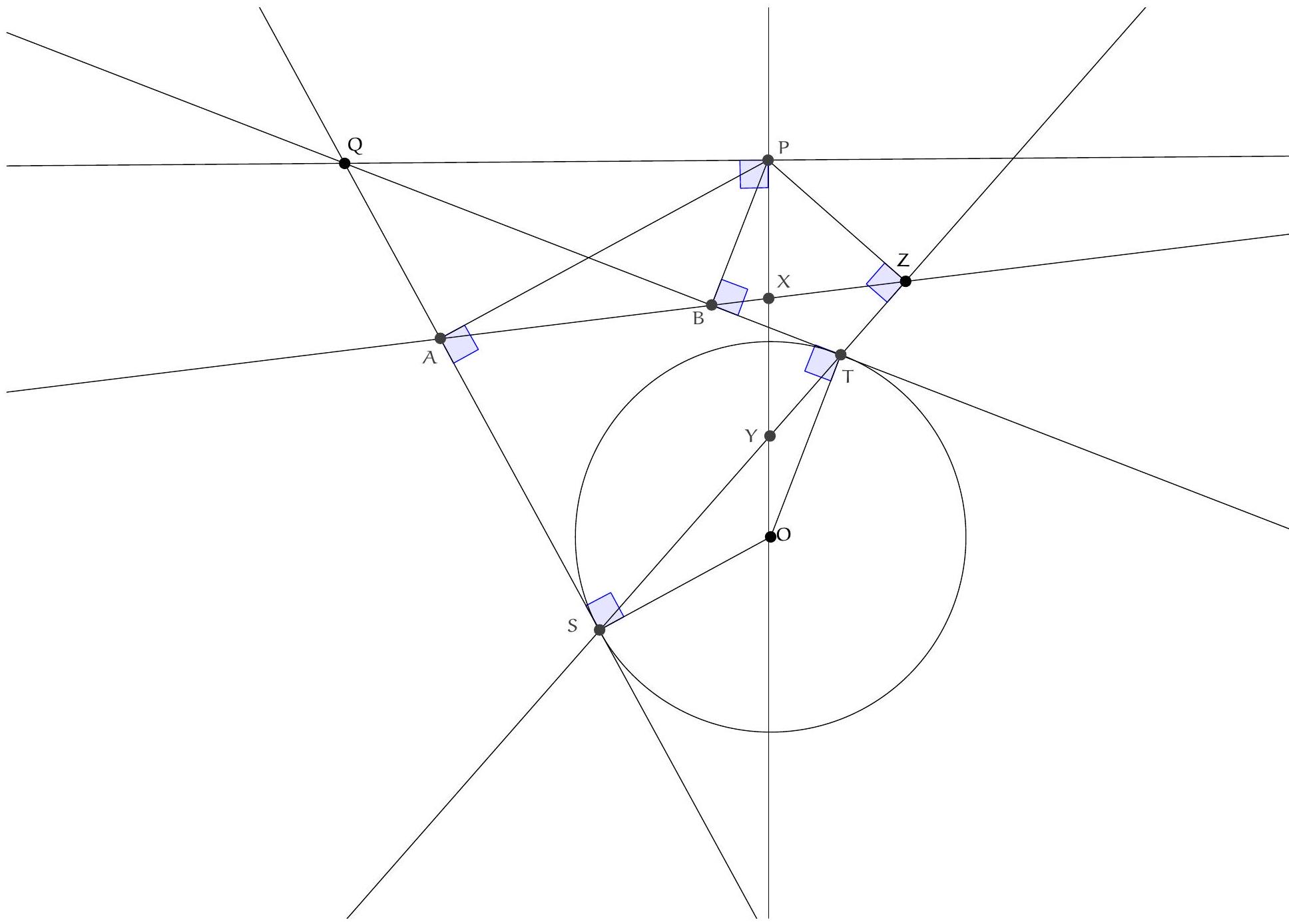
|
| 117 |
+
|
| 118 |
+
Solution de l'exercice 10 On note $X$ l'intersection de $(A B)$ et $(O P), S$ et $T$ les points où $\left(t_{1}\right)$ et $\left(t_{2}\right)$ touchent $\Gamma$, et $Y$ le point d'intersection de (ST) et (OP). Une première remarque qu'on peut faire est que $O, P, Q, S$ et $T$ sont cocycliques sur le cercle de diamètre [OQ]. Une bonne figure suggère que $Y$ ne dépend pas de $Q$. Et en effet, on a :
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
\widehat{\mathrm{OSY}}=\widehat{\mathrm{OST}}=\widehat{\mathrm{OQT}}=\widehat{\mathrm{OQS}}=\widehat{\mathrm{OPS}}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
donc les triangles OSY et OPS sont indirectement semblables donc $\frac{\mathrm{OY}}{\mathrm{OS}}=\frac{\mathrm{OS}}{\mathrm{OP}} \mathrm{d}^{\prime}$ où $\mathrm{OY}=\frac{\mathrm{r}^{2}}{\mathrm{OP}}$ où $r$ est le rayon de $\Gamma$, donc $O Y$ ne dépend pas de $Q$ et $Y$ est fixe (les amateurs de géométrie projective auront reconnu le pôle de (d) par rapport à $\Gamma$ ).
|
| 125 |
+
|
| 126 |
+
Soit maintenant $Z$ le projeté orthogonal de $P$ sur (ST) : comme $P$ est sur le cercle circonscrit à PST, la droite de Simson nous garantit que $Z \in(A B)$. Faisons maintenant un peu de chasse aux angles:
|
| 127 |
+
|
| 128 |
+
$$
|
| 129 |
+
\widehat{\mathrm{PZX}}=\widehat{\mathrm{PZA}}=\widehat{\mathrm{PSA}}=\widehat{\mathrm{PSQ}}=\widehat{\mathrm{POQ}}=\widehat{\mathrm{OPZ}}
|
| 130 |
+
$$
|
| 131 |
+
|
| 132 |
+
où on a utilisé successivement que $P, Z, A$ et $S$ sont cocycliques (sur le cercle de diamètre [PS]), que $O, P, Q, S$ sont cocycliques et enfin que (OQ) // (PZ). On a donc que XPZ est isocèle en $X$, donc $X$ est sur la médiatrice de $[P Z]$. Or, le centre du cercle circonscrit à PYZ est sur cette médiatrice, et est sur (PY) car PYZ est rectangle en Z.
|
| 133 |
+
$X$ est donc le centre du cercle circonscrit à PYZ, donc est le milieu de [PY] car PYZ est rectangle en $Z$. Comme $P$ et $Y$ ne dépendent pas de $Q, X$ non plus.
|
| 134 |
+
$\mathcal{F i n}$
|
| 135 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-3-solutions.md
ADDED
|
@@ -0,0 +1,231 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OLYMPIADES FRANÇAISES DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
ENVOI No. 3
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. Soit $n \geqslant 1$ un entier tel que le quotient de $2^{n}$ par $n$ est une puissance de 2 . Montrer que $n$ est une puissance de 2 .
|
| 12 |
+
Solution de l'exercice 1 Par hypothèse, $2^{\text {n }} / n$ est une puissance de 2 (ici, on parle bien de quotient, et non pas de quotient dans la division euclidienne). Il existe donc un entier $k \geqslant 0$ tel que $2^{\mathrm{n}}=2^{\mathrm{k}} n$. Ainsi, $n=2^{\mathrm{n}-\mathrm{k}}$, de sorte que n est bien une puissance de 2 .
|
| 13 |
+
Exercice 2. Trouver tous les entiers strictement positifs $m$ et $n$ tels que
|
| 14 |
+
|
| 15 |
+
$$
|
| 16 |
+
3 \cdot 2^{\mathrm{m}}+1=\mathrm{n}^{2} .
|
| 17 |
+
$$
|
| 18 |
+
|
| 19 |
+
Solution de l'exercice 2 Remarquons tout d'abord que la condition se réécrit $3 \cdot 2^{\mathrm{m}}=(n-1)(n+1)$.
|
| 20 |
+
$\triangleright \operatorname{Sin}$ est pair, les entiers $(n+1)$ et $(n-1)$ sont premiers entre eux donc égaux à $2^{m}$ et 3 ou à $3 \cdot 2^{\mathrm{m}}$ et 1 . Or, ils sont tous les deux impairs (et $\mathrm{m}>0$ ) : contradiction.
|
| 21 |
+
$\triangleright$ Si $n$ est impair, le pgcd de $(n+1)$ et $(n-1)$ est le pgcd de $(n+1)$ et $n+1-(n-1)=2$ donc 2 . Ainsi, ils sont égaux à 6 et $2^{\mathrm{m}-1}$, ou bien à 2 et $3 \cdot 2^{\mathrm{m}-1}$.
|
| 22 |
+
|
| 23 |
+
- Si $n-1=6$, alors $n=7$ et $2^{\mathrm{m-1}}=n+1=8$ d'où $m=4$.
|
| 24 |
+
- Si $n+1=6$, alors $n=5$ et $2^{\mathrm{m}-1}=\mathrm{n}-1=4$ d'où $m=3$.
|
| 25 |
+
- Si $n-1=2$ alors $n=3$ et $3 \cdot 2^{m}=n^{2}-1=8$, ce qui est impossible car 3 ne divise pas 8 .
|
| 26 |
+
- Si $n+1=2$ alors $n=1$ et $3 \cdot 2^{m}=n^{2}-1=0$, ce qui est impossible.
|
| 27 |
+
|
| 28 |
+
En conclusion, l'équation n'est vérifiée que pour les couples $(\mathfrak{m}, \mathfrak{n}) \in\{(4,7),(3,5)\}$.
|
| 29 |
+
Exercice 3. Soit $p$ un nombre premier. Trouver tous les entiers $n \geqslant 1$ tels que pour tout entier $a \geqslant 1$, si $a^{n}-1$ est divisible par $p$, alors $a^{n}-1$ est aussi divisible par $p^{2}$.
|
| 30 |
+
Solution de l'exercice 3 Montrons que les entiers $n$ qui conviennent sont exactement les multiples de $p$. Pour cela, nous allons d'abord prouver que lorsque $n=p m$ pour un entier $m \geqslant 1$, pour tout entier $a \geqslant 1$, si $a^{n}-1$ est divisible par $p$, alors $a^{n}-1$ est aussi divisible par $p^{2}$. Puis, réciproquement, nous allons prouver que si $p$ ne divise pas $n$, alors il existe un entier $a \geqslant 1$ tel que $a^{n}-1$ est divisible par $p$ mais tel que $a^{n}-1$ n'est pas divisible par $p^{2}$.
|
| 31 |
+
$\triangleright$ Si $n=p m$ pour un entier $m \geqslant 1$, alors $a^{n}=a^{p m} \equiv a^{m}(\bmod \mathfrak{p})$ d'après le petit théorème de Fermat pour tout entier a. Supposons dorénavant que l'entier a est tel que $a^{n}-1$ est divisible par $p$. D'après la ligne ci-dessus, $a^{\mathrm{m}}-1$ est divisible par $p$. Par ailleurs, la factorisation suivante est vérifiée:
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
a^{n}-1=a^{p m}-1=\left(a^{m}-1\right)\left(1+a^{m}+\cdots+a^{(p-1) m}\right)
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Comme $p$ divise $a^{m}-1, a^{m} \equiv 1(\bmod p)$ donc
|
| 38 |
+
|
| 39 |
+
$$
|
| 40 |
+
1+a^{m}+\cdots+a^{(\mathfrak{p}-1) m} \equiv 1+1+\cdots+1 \equiv p \equiv 0 \quad(\bmod \mathfrak{p})
|
| 41 |
+
$$
|
| 42 |
+
|
| 43 |
+
En conclusion, $a^{n}-1$ est le produit de deux entiers divisibles par $p$ donc est divisible par $p^{2}$.
|
| 44 |
+
$\triangleright$ Si $p$ ne divise pas $n$, alors avec l'entier $a=p+1$, on a que $a^{n}-1 \equiv 1^{n}-1 \equiv 0(\bmod \mathfrak{p})$ donc $p$ divise $a^{n}-1$. Or
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
1+a+\cdots+a^{(n-1)} \equiv 1+1+\cdots+1^{n-1} \equiv n \not \equiv 0(\bmod p)
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Ainsi, $p$ ne divise pas $1+a+\cdots+a^{(n-1)}$, et donc $p^{2}$ ne divise pas $p\left(1+a+\cdots+a^{(n-1)}\right)=$ $(a-1)\left(1+a+\cdots+a^{(n-1)}\right)=a^{n}-1$.
|
| 51 |
+
|
| 52 |
+
## Exercices communs
|
| 53 |
+
|
| 54 |
+
Exercice 4. Trouver tous les triplets d'entiers strictement positifs ( $a, b, c)$ tels que $6^{a}=1+2^{b}+$ $3^{\mathrm{c}}$.
|
| 55 |
+
Solution de l'exercice 4 Remarquons tout d'abord que 3 divise $2^{b}+1$ donc b est impair (car $2^{b}+$ $\left.1 \equiv(-1)^{\mathrm{b}}+1(\bmod 3)\right)$.
|
| 56 |
+
$\triangleright$ Si $\mathrm{b}=1$, l'équation se réécrit $1+3^{\mathrm{c}-1}=2 \cdot 6^{a-1}$ en divisant par 3 .
|
| 57 |
+
|
| 58 |
+
- Si $a>1$, alors 3 divise $1+3^{\mathrm{c}-1}$ ce qui est impossible.
|
| 59 |
+
- Sinon, $\mathrm{a}=1$ et par conséquent $\mathrm{c}=1$.
|
| 60 |
+
$\triangleright \mathrm{Si} \mathrm{b} \geqslant 3$, alors $\mathrm{a} \geqslant 2\left(\right.$ car $\left.6<1+2^{3}\right)$. En réduisant modulo 4 , on obtient la condition nécessaire $1+3^{c} \equiv 0(\bmod 4)$, et donc c est impair. En réduisant alors modulo 8 , on obtient la nouvelle condition $1+2^{\mathrm{b}}+3^{\mathrm{c}} \equiv 1+0+3(\bmod 8) \equiv 4(\bmod 8)$ donc $6^{\mathrm{a}} \equiv 4(\bmod 8)$ ce qui entraîne immédiatement $a=2\left(\right.$ en effet, pour $6^{a} \equiv 0(\bmod 8)$ pour $\left.a \geqslant 3\right)$. L'équation initiale devient alors $2^{\mathrm{b}}+3^{\mathrm{c}}=35$ et une étude exhaustive donne $\mathrm{b}=3$ et $\mathrm{c}=3$ ou $\mathrm{b}=5$ et $\mathrm{c}=1$.
|
| 61 |
+
|
| 62 |
+
En conclusion, les triplets solutions sont $(\mathbf{a}, \boldsymbol{b}, \boldsymbol{c}) \in\{(1,1,1),(2,3,3),(2,5,1)\}$.
|
| 63 |
+
Exercice 5. Soit n l'entier $4 \times 201420142014 \ldots 2014$ (où 2014 est écrit 117819 fois). Montrer que $2014^{3}$ divise n.
|
| 64 |
+
Solution de l'exercice 5 On peut écrire
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
4 \times 201420142014 \ldots 2014=4 \cdot 2014 \cdot \frac{10^{4 \cdot 117819}-1}{10^{4}-1}
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
Comme $2014=2 \cdot 19 \cdot 53$ et $10^{4}-1=3^{2} \cdot 11 \cdot 101$ sont premiers entre eux, il suffit de montrer que $19^{2}$ et $53^{2}$ divisent $10^{4 \cdot 117819}-1$. D'après le théorème d'Euler,
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
10^{\Phi\left(19^{2}\right)} \equiv 1 \quad\left(\bmod 19^{2}\right) \quad \text { et } \quad 10^{\Phi\left(53^{2}\right)} \equiv 1 \quad\left(\bmod 53^{2}\right),
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
où $\phi$ désigne la fonction indicatrice d'Euler. Il suffit donc de vérifier que $\phi\left(19^{2}\right)$ et $\phi\left(53^{2}\right)$ divisent tous les deux $4 \cdot 117819$. Ceci découle du fait que $\phi\left(19^{2}\right)=19^{2}-19=2 \cdot 3^{2} \cdot 19$, $\phi\left(53^{2}\right)=53^{2}-53=2^{2} \cdot 13 \cdot 53$ et $4 \cdot 117819=2^{2} \cdot 3^{2} \cdot 13 \cdot 19 \cdot 53$.
|
| 77 |
+
Exercice 6. Soient $m$ et $n$ deux entiers tels que $0 \leqslant \mathfrak{m} \leqslant 2 \boldsymbol{n}$. Prouver que le nombre entier
|
| 78 |
+
|
| 79 |
+
$$
|
| 80 |
+
2^{2 n+2}+2^{m+2}+1
|
| 81 |
+
$$
|
| 82 |
+
|
| 83 |
+
est un carré parfait $s i$, et seulement $\mathrm{si}, \mathrm{m}=\mathrm{n}$.
|
| 84 |
+
|
| 85 |
+
## Solution de l'exercice 6
|
| 86 |
+
|
| 87 |
+
$\triangleright$ Remarquons que si $\mathrm{m}=\mathrm{n}$, alors $2^{2 \mathrm{n}+2}+2^{\mathrm{m}+2}+1=\left(2^{\mathrm{m}+1}+1\right)^{2}$ est bien un carré parfait.
|
| 88 |
+
$\triangleright$ Réciproquement, supposons que $2^{2 n+2}+2^{\mathrm{m}+2}+1$ est un carré parfait. Comme il est strictement plus grand que $2^{2 \mathrm{n}+2}=\left(2^{\mathrm{n}+1}\right)^{2}$, il est supérieur ou égal au carré suivant, c'est-à-dire $2^{2 n+2}+2^{m+2}+1 \geqslant\left(2^{n+1}+1\right)^{2}$.
|
| 89 |
+
|
| 90 |
+
En développant, il vient $2^{\mathfrak{m}+2} \geqslant 2^{\mathfrak{n}+2}$, donc $\mathfrak{m} \geqslant n$. Supposons par l'absurde que $\mathrm{m}>n$ soit $2^{m}>2^{2 n-m}$.
|
| 91 |
+
|
| 92 |
+
Par hypothèse, la quantité $2^{2 n+2}+2^{m+2}+1$ est le carré d'un entier impair $2 k+1$ strictement plus grand que 1 , d'où
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
2^{2 \mathrm{n}+2}+2^{\mathrm{m}+2}+1=(2 \mathrm{k}+1)^{2}
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
pour un certain entier $k \geqslant 1$, ce qui se réécrit sous la forme $k(k+1)=2^{2 n}+2^{m}=2^{m}\left(2^{2 n-m}+1\right)$. Or les entiers $k$ et $k+1$ sont premiers entre eux. On en déduit que :
|
| 99 |
+
|
| 100 |
+
- soit $k=2^{m} p$ et $p(k+1)=2^{2 n-m}+1$ ce qui entraîne $(k+1) p<k / p+1$ : contradiction.
|
| 101 |
+
- soit $k+1=2^{m} p$ et $p k=2^{2 n-m}+1$ ce qui entraîne $k p<\frac{k+1}{p}+1$ donc $k p \leqslant \frac{k+1}{p}$, ou encore $k\left(p^{2}-1\right) \leqslant 1$, ce qui impose $p=1$ puisque $k \geqslant 1$. Alors, $2^{2 n-m}=2\left(2^{m-1}-1\right)$ donc $2 \mathrm{n}-\mathrm{m}=1$ et $\mathrm{m}=2:$ contradiction.
|
| 102 |
+
Ainsi, si $2^{2 \mathrm{n}+2}+2^{\mathrm{m}+2}+1=\left(2^{\mathrm{m}+1}+1\right)^{2}$ est un carré parfait, alors $\mathrm{m}=\mathrm{n}$.
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
## Exercices du groupe A
|
| 106 |
+
|
| 107 |
+
Exercice 7. Montrer qu'il existe une infinité de nombres entiers strictement positifs a tels que $a^{2}$ divise $2^{a}+3^{a}$.
|
| 108 |
+
Solution de l'exercice 7 Remarquons que $a=1$ convient puis construisons par récurrence une suite ( $u_{n}$ ) strictement croissante d'entiers impairs vérifiant la propriété.
|
| 109 |
+
$\triangleright$ Tout d'abord, on vérifie que $a=1$ et $a=5$ conviennent. Posons ainsi $u_{0}=1$ et $u_{1}=5$.
|
| 110 |
+
$\triangleright$ Considerons un entier $n \geqslant 1$ et supposons la suite définie jusqu'au rang $n$. Par définition de $u_{n}$, il existe un entier $q$ tel que $q u_{n}^{2}=2^{u_{n}}+3^{u_{n}}$. Comme $u_{n} \geqslant u_{1}=5$, on a $q>1$.
|
| 111 |
+
|
| 112 |
+
Soit $p \geqslant 3$ un facteur premier (impair) de $q$ et vérifions que $u_{n+1}=p u_{n}$ vérifie la propriété requise. Montrons que
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
p \quad \text { divise } \quad 3^{\mathfrak{u}_{n}(\mathfrak{p}-1)}-2^{\mathfrak{u}_{n}} 3^{\mathfrak{u}_{\mathfrak{n}}(\mathfrak{p}-2)}+\cdots+2^{\mathfrak{u}_{n}(p-1)} .
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
Ceci permet de conclure, car alors, étant donné que $p u_{n}^{2}$ divise $2^{u_{n}}+3^{\mathfrak{u}_{n}}$, il en découle que $p \cdot p u_{n}^{2}$ divise
|
| 119 |
+
ce qui achève la démonstration.
|
| 120 |
+
Pour établir (1), on remarque que $p$ divise $2^{u_{n}}+3^{\mathfrak{u}_{n}}$ (car $p$ divise $q$ ), de sorte qu'on a la congruence $2^{\mathfrak{u}_{n}} \equiv-3^{\mathfrak{u}_{n}}(\bmod p)$. Ainsi,
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
\begin{aligned}
|
| 124 |
+
3^{\mathfrak{u}_{n}(\mathfrak{p}-1)}-2^{\mathfrak{u}_{n}} 3^{\mathfrak{u}_{n}(\mathfrak{p}-2)}+\cdots+2^{\mathfrak{u}_{n}(\mathfrak{p}-1)} & \equiv 3^{\mathfrak{u}_{n}(\mathfrak{p}-1)}+3^{\mathfrak{u}_{n}(\mathfrak{p}-1)}+\cdots+3^{\mathfrak{u}_{n}(\mathfrak{p}-1)} \quad(\bmod p) \\
|
| 125 |
+
& \equiv p 3^{\mathfrak{u}_{n}(\mathfrak{p}-1)} \quad(\bmod p) \\
|
| 126 |
+
& \equiv 0 \quad(\bmod p) .
|
| 127 |
+
\end{aligned}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
Exercice 8. Soient $m, n \geqslant 1$ deux entiers impairs tels que $m$ divise $n^{2}+2$ et $n$ divise $m^{2}+2$. Prouver que $m$ et $n$ sont tous les deux des termes de la suite $\left(u_{n}\right)_{n \geqslant 1}$ définie par
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
\mathfrak{u}_{1}=\mathrm{u}_{2}=1, \quad \mathrm{u}_{\mathrm{n}}=4 \mathrm{u}_{n-1}-\mathrm{u}_{n-2} \quad \text { si } n \geqslant 3
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Solution de l'exercice 8 La structure de la solution est la suivante:
|
| 137 |
+
|
| 138 |
+
- On montre que mn divise $\mathrm{m}^{2}+\mathrm{n}^{2}+2$;
|
| 139 |
+
- On montre que $\mathrm{m}^{2}+\mathrm{n}^{2}+2=4 \mathrm{mn}$;
|
| 140 |
+
- On montre que la suite $\left(u_{n}\right)_{n \geqslant 1}$ est croissante;
|
| 141 |
+
- On conclut en montrant qu'en fait $m$ et $n$ sont deux termes consécutifs de la suite $\left(u_{n}\right)_{n \geqslant 1}$.
|
| 142 |
+
$\triangleright$ Soit $d$ le PGCD de $m$ et de $n$. Comme $m$ divise $n^{2}+2$, on en déduit que $d$ divise $n^{2}+2$ et donc que $d$ divise 2 . Comme $m$ et $n$ sont impairs, on en déduit que $d=1$, de sorte que $m$ et $n$ sont premiers entre eux. Ainsi, mn divise $\mathrm{m}^{2}+\mathrm{n}^{2}+2$.
|
| 143 |
+
$\triangleright$ Montrons que $\mathrm{m}^{2}+\mathrm{n}^{2}+2=4 \mathrm{mn}$ en utilisant la technique connue en anglais sous le nom de $\ll$ Vieta jumping $\gg$. Plus précisément, soit $k=\left(m^{2}+n^{2}+2\right) /(m n)$, et considérons tous les couples d'entiers strictement positifs $(x, y)$ tels que
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
x^{2}+y^{2}+2=k x y .
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
Parmi ces couples, choissisons-en un qui minimise la somme $x+y$. Nous allons montrer que $x=y$. Raisonnons par l'absurde en supposant, sans perte de généralité, que $x>y \geqslant 1$. On s'intéresse alors à l'équation du second degré
|
| 150 |
+
|
| 151 |
+
$$
|
| 152 |
+
t^{2}-k y t+y^{2}+2=0
|
| 153 |
+
$$
|
| 154 |
+
|
| 155 |
+
d'inconnue $t$. On sait déjà que $t_{1}=x$ est solution. D'après les formules de Viète,
|
| 156 |
+
|
| 157 |
+
$$
|
| 158 |
+
\mathrm{t}_{2}=\mathrm{ky}-\mathrm{x}=\frac{\mathrm{y}^{2}+2}{\mathrm{x}}
|
| 159 |
+
$$
|
| 160 |
+
|
| 161 |
+
est également solution. L'équation (2) montre que $t_{2}$ est un entier strictement positif. Comme $1 \leqslant y \leqslant x-1$, on a
|
| 162 |
+
|
| 163 |
+
$$
|
| 164 |
+
t_{2}=\frac{y^{2}+2}{x} \leqslant \frac{(x-1)^{2}+2}{x}<x=t_{1}
|
| 165 |
+
$$
|
| 166 |
+
|
| 167 |
+
où on a utilisé le fait que $x \geqslant 2$ pour la dernière inégalité. Ainsi, $t_{2}+y<t_{1}+y=x+y$, ce qui contredit la minimalité de $x+y$. Il en découle que $x=y$, et donc $x^{2}$ divise $2 x^{2}+2$. On en déduit que $x=1$, d'où
|
| 168 |
+
|
| 169 |
+
$$
|
| 170 |
+
\mathrm{k}=\frac{1^{2}+1^{2}+2}{1}=4
|
| 171 |
+
$$
|
| 172 |
+
|
| 173 |
+
Nous avons donc établi que
|
| 174 |
+
|
| 175 |
+
$$
|
| 176 |
+
m^{2}+n^{2}+2=4 m n
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
$\triangleright$ Vérifions que la suite $\left(u_{n}\right)_{n \geqslant 1}$ est strictement croissante, en écrivant que pour tout entier $n \geqslant 1$,
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
u_{n+1}-u_{n}=3 u_{n}-u_{n-1}>u_{n}-u_{n-1}
|
| 183 |
+
$$
|
| 184 |
+
|
| 185 |
+
Par récurrence, on en déduit que, pour tout entier $\boldsymbol{n} \geqslant 1, \mathfrak{u}_{n+1}-\boldsymbol{u}_{n}>\mathfrak{u}_{2}-\mathfrak{u}_{1}=0$.
|
| 186 |
+
$\triangleright$ Montrons finalement que $m$ et $n$ sont deux termes consécutifs de la suite $\left(u_{n}\right)_{n \geqslant 1}$ par récurrence forte sur $m+n$. L'initialisation ne pose pas de soucis: si $m+n=2$, on a $m=n=1$. Soit donc $k \geqslant 3$, supposons le résultat établi pour tous les couples ( $m, n$ ) d'entiers strictement positifs vérifiant (3) avec $m+n<k$, et considérons un couple d'entiers strictement positifs ( $m, n$ ) vérifiant (3) tels que $m+n=k$. Tout d'abord, $m \neq n$, car sinon $m=n=1$ d'après (3). Sans perte de généralité, supposons $\mathrm{m}>\mathrm{n}$. Mais, comme dans le paragraphe précédent, si $(m, n)$ est solution, alors $(n, 4 n-m)$ l'est également, avec $m+n>n+(4 n-m)$. D'autre part, on vérifie aisément que $2 n-\sqrt{3 n^{2}-2}<n<3 n<2 n+\sqrt{3 n^{2}-2}$ pour tout entier $n \geqslant 2$. Ainsi, par (3), on a $m=2 n+\sqrt{3 n^{2}-2}$ de sorte que $n>4 n-m$. Par hypothèse de récurrence, il existe un entier $i \geqslant 2$ tel que $u_{i-1}=n$ et $u_{i-2}=4 n-m$. Mais alors $u_{i}=4 n-(4 n-m)=m$, ce qui montre bien que $m$ et $n$ sont deux termes consécutifs de la suite $\left(u_{n}\right)_{n \geqslant 1}$.
|
| 187 |
+
Exercice 9. Trouver tous les entiers strictement positifs a tels que l'entier
|
| 188 |
+
|
| 189 |
+
$$
|
| 190 |
+
1-8 \cdot 3^{a}+2^{a+2}\left(2^{a}-1\right)
|
| 191 |
+
$$
|
| 192 |
+
|
| 193 |
+
soit un carré parfait.
|
| 194 |
+
Solution de l'exercice 9 La quantité (4) est égale à $\left(2^{\mathrm{a}+1}-1\right)^{2}-2^{3} \cdot 3^{\mathrm{a}}$. On remarque que cette quantité est un carré pour $a=3$ (elle vaut $9=3^{2}$ ) et $a=5$ (elle vaut $2025=45^{2}$ ) mais pas pour $a \in\{1,2,4,6,7\}$. On suppose dorénavant $a \geqslant 8$.
|
| 195 |
+
|
| 196 |
+
Supposons que la quantité (4) soit un carré, c'est-à-dire, puisqu'elle est impaire, qu'il existe un entier $k$ tel que
|
| 197 |
+
|
| 198 |
+
$$
|
| 199 |
+
\left(2^{a+1}-1\right)^{2}-2^{3} \cdot 3^{a}=(2 \mathrm{k}+1)^{2}
|
| 200 |
+
$$
|
| 201 |
+
|
| 202 |
+
Ainsi
|
| 203 |
+
|
| 204 |
+
$$
|
| 205 |
+
\left(2^{a+1}-1\right)^{2}-(2 k+1)^{2}=2^{3} \cdot 3^{a}
|
| 206 |
+
$$
|
| 207 |
+
|
| 208 |
+
soit encore $\left(2^{a}-k-1\right)\left(2^{a}+k\right)=2 \cdot 3^{a}$. Il existe alors un entier $b \geqslant 0$ tel que l'une des deux situations suivantes se produit (en discutant selon la parité de $k$ ):
|
| 209 |
+
|
| 210 |
+
- on a $2^{a}+\mathrm{k}=2 \cdot 3^{\mathrm{b}}$ et $2^{\mathrm{a}}-\mathrm{k}-1=3^{\mathrm{a}-\mathrm{b}}$ donc $2 \mathrm{k}+1=2 \cdot 3^{\mathrm{b}}-3^{\mathrm{a}-\mathrm{b}}$ (donc $\mathrm{b} \geqslant \mathrm{a}-\mathrm{b}$ );
|
| 211 |
+
- on a $2^{\mathrm{a}}+\mathrm{k}=3^{\mathrm{b}}$ et $2^{\mathrm{a}}-\mathrm{k}-1=2 \cdot 3^{\mathrm{a}-\mathrm{b}}$ donc $2 \mathrm{k}+1=3^{\mathrm{b}}-2 \cdot 3^{\mathrm{a}-\mathrm{b}}$ (donc $\mathrm{b} \geqslant \mathrm{a}-\mathrm{b}$ ). Ainsi, $3^{\mathrm{a}-\mathrm{b}}$ divise $2 \mathrm{k}+1$, et donc $3^{2(\mathrm{a}-\mathrm{b})}$ divise $(2 \mathrm{k}+1)^{2}+2^{3} \cdot 3^{\mathrm{a}}$. En utilisant (5), il vient $3^{\mathrm{a}-\mathrm{b}} \mid 2^{\mathrm{a}+1}-1$.
|
| 212 |
+
|
| 213 |
+
Dans la première situation, en additionnant les deux égalités on a $2 \cdot 3^{\mathbf{b}}=2^{a+1}-3^{a-b}-1<$ $2^{a+1}$ donc $3^{b}<2^{a+1}$. On montre de manière analogue que cette inégalité est valable aussi dans la deuxième situation.
|
| 214 |
+
|
| 215 |
+
Remarquons que $2^{9} \leqslant 3^{9-3}$ donc, pour tout $a \geqslant 8$,
|
| 216 |
+
|
| 217 |
+
$$
|
| 218 |
+
2^{a+1}=2^{9} \cdot 2^{a-8} \leqslant 2^{9} \cdot 3^{a-8} \leqslant 3^{6} \cdot 3^{a-8}=3^{a-2}
|
| 219 |
+
$$
|
| 220 |
+
|
| 221 |
+
En combinant les deux inégalités, $3^{\mathbf{b}}<3^{\mathbf{a}-2}$ donc $\mathbf{a}-\mathrm{b} \geqslant 3$.
|
| 222 |
+
Comme $3^{a-b}$ divise $2^{a+1}-1$ et $a-b \geqslant 3$, on a $2^{a+1} \equiv 1(\bmod 27)$ d'où 18 divise $a+1$ (en remarquant que le plus petit entier $k>0$ tel que $2^{k} \equiv 1(\bmod 27)$ est 18). Fort de cette condition, réduisons la quantité de l'énoncé modulo 19 en utilisant le théorème d'Euler ( $\chi^{18}=\chi^{\varphi(19)} \equiv 1$ $(\bmod 19)$ pour tout entier $x$ non divisible par 19$)$ et la relation $3 \cdot 13 \equiv 1(\bmod 19)$ :
|
| 223 |
+
|
| 224 |
+
$$
|
| 225 |
+
\left(2^{a+1}-1\right)^{2}-2^{3} \cdot 3^{a} \equiv(1-1)^{2}-2^{3} \cdot 13 \quad(\bmod 19) \equiv 10 \quad(\bmod 19)
|
| 226 |
+
$$
|
| 227 |
+
|
| 228 |
+
On conclut en remarquant alors que $(2 \mathrm{k}+1)^{18} \equiv 10^{9}(\bmod 19)=18(\bmod 19)$ ce qui contredit le théorème d'Euler. Il n'y a donc pas de solution $a \geqslant 9$.
|
| 229 |
+
|
| 230 |
+
En conclusion, les seules solutions sont 3 et 5 .
|
| 231 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-4-solutions.md
ADDED
|
@@ -0,0 +1,315 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Exercice 1.
|
| 2 |
+
|
| 3 |
+
Soit $a, b$ et $c$ des réels tels que
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
|a-b| \geq|c|,|b-c| \geq|a| \text { et }|c-a| \geq|b| .
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Prouver que l'un des trois nombres $a, b$ et $c$ est la somme des deux autres.
|
| 10 |
+
|
| 11 |
+
## Solution.
|
| 12 |
+
|
| 13 |
+
La première inégalité s'écrit $(a-b)^{2} \geq c^{2}$, ou encore $(a-b+c)(a-b-c) \geq 0$. De même, les deux autre inégalités conduisent à $(b-c+a)(b-c-a) \geq 0$ et $(c-a+b)(c-a-b) \geq 0$.
|
| 14 |
+
|
| 15 |
+
En multipliant membre à membre ces trois inégalités, il vient
|
| 16 |
+
|
| 17 |
+
$$
|
| 18 |
+
(a-b+c)^{2}(-a+b+c)^{2}(a+b-c)^{2} \leq 0
|
| 19 |
+
$$
|
| 20 |
+
|
| 21 |
+
Or, un carré étant toujours positif, c'est donc que l'un des facteurs est nul, ce qui conclut.
|
| 22 |
+
|
| 23 |
+
## Solution alternative.
|
| 24 |
+
|
| 25 |
+
Les variables $a, b$ et $c$ jouent des rôles symétriques. En outre, le problème est invariant si on change simultanément les signes de $a, b$ et $c$. Ainsi, il y a au moins deux variables parmi $a, b$ et $c$ qui ont le même signe ; on peut donc supposer, sans perte de généralité, que l'on est dans un des deux cas $a \geq b \geq c \geq 0$ ou $a \geq b \geq 0 \geq c$.
|
| 26 |
+
Montrons que la relation $b=a+c$ est vraie dans les deux cas, ce qui conclura le problème.
|
| 27 |
+
|
| 28 |
+
1. Si $a \geq b \geq c \geq 0$, alors $b \geq b-c=|b-c| \geq|a|=a$; chaque inégalité est donc une égalité, d'où la relation $b=b-c=|b-c|=|a|=a$.
|
| 29 |
+
2. Si $a \geq b \geq 0 \geq c$, alors $b-c=|b-c| \geq|a|=a$ et $a-b=|a-b| \geq|c|=-c$, d'où la relation $a+c \geq b \geq a+c$.
|
| 30 |
+
|
| 31 |
+
## Exercice 2.
|
| 32 |
+
|
| 33 |
+
Déterminer tous les nombres irrationnels $x$ pour lesquels les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.
|
| 34 |
+
|
| 35 |
+
## Solution.
|
| 36 |
+
|
| 37 |
+
Soit $x$ un nombre irrationnel pour lequel les deux nombres $x^{2}+x$ et $x^{3}+2 x^{2}$ sont des entiers.
|
| 38 |
+
|
| 39 |
+
On pose $x^{2}+x=a$ et $x^{3}+2 x^{2}=b$, où $a$ et $b$ sont des entiers. Alors $b-a x=x^{2}=a-x$, et ainsi $x(a-1)=b-a$. Si $a-1 \neq 0$, on aurait $x=\frac{b-a}{a-1}$, et $x$ serait rationnel, en contradiction avec l'énoncé.
|
| 40 |
+
|
| 41 |
+
Par suite, on a $a=1$ et donc $b=a=1$. Mais alors $x^{2}+x-1=0$ et $x^{3}+2 x^{2}-1=0$. On note que, si $x^{2}+x-1=0$, alors $x^{3}=-x^{2}+x$ et $x=-x^{2}+1$, d'où $x^{3}+2 x^{2}-1=0$.
|
| 42 |
+
|
| 43 |
+
Ainsi, les solutions du problème sont les solutions irrationnelles de l'équation du second degré $x^{2}+x-1=0$, c'est-à-dire les nombres $x_{1}=\frac{-1-\sqrt{5}}{2}$ et $x_{2}=\frac{-1+\sqrt{5}}{2}$. Puisque $\sqrt{5}$ n'est pas rationnel, ces deux nombres sont effectivement des solutions du problème.
|
| 44 |
+
|
| 45 |
+
## Exercice 3.
|
| 46 |
+
|
| 47 |
+
Soit $x$ un réel strictement positif tel que $x^{5}-x^{3}+x \geq 3$. Prouver que $x^{6} \geq 5$.
|
| 48 |
+
|
| 49 |
+
## Solution.
|
| 50 |
+
|
| 51 |
+
La clé du problème est la factorisation $x^{6}+1=\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)$, valable pour tout réel $x$.
|
| 52 |
+
|
| 53 |
+
Soit $x>0$ tel que $x^{5}-x^{3}+x \geq 3$. D'après l'identité ci-dessus, on a alors
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
x^{6}+1=\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)=\frac{x^{2}+1}{x}\left(x^{5}-x^{3}+x\right)=\left(x+\frac{1}{x}\right)\left(x^{5}-x^{3}+x\right)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
et donc $x^{6}+1 \geq 3\left(x+\frac{1}{x}\right)$.
|
| 60 |
+
Or, d'après l'inégalité arithmético-géométrique (IAG), on a $x+\frac{1}{x} \geq 2$, d'où $x^{6}+1 \geq 6$, et ainsi $x^{6} \geq 5$, comme souhaité.
|
| 61 |
+
|
| 62 |
+
## Exercice 4.
|
| 63 |
+
|
| 64 |
+
Déterminer tous les réels $t$ pour lesquels le polynôme
|
| 65 |
+
|
| 66 |
+
$$
|
| 67 |
+
P(x)=x^{3}+3 t x^{2}+(4 t-1) x+t
|
| 68 |
+
$$
|
| 69 |
+
|
| 70 |
+
possède deux racines réelles dont la différence est égale à 1 .
|
| 71 |
+
|
| 72 |
+
## Solution.
|
| 73 |
+
|
| 74 |
+
Si $t$ est un réel fixé, on pose $P_{t}(x)=x^{3}+3 t x^{2}+(4 t-1) x+t$.
|
| 75 |
+
La première chose à remarquer est que, pour tout $t$, on a $P_{t}(-1)=0$. Par suite, -1 est une racine du polynôme $P_{t}$, ce qui assure que $P_{t}(x)$ est factorisable par $x+1$. On trouve ainsi que
|
| 76 |
+
|
| 77 |
+
$$
|
| 78 |
+
P_{t}(x)=(x+1)\left(x^{2}+(3 t-1) x+t\right)
|
| 79 |
+
$$
|
| 80 |
+
|
| 81 |
+
pour tout réels $x$ et $t$.
|
| 82 |
+
Soit $t$ un réel pour lequel $P_{t}$ possède deux racines réelles dont la différence est égale à 1 , disons $a$ et $a+1$.
|
| 83 |
+
|
| 84 |
+
- Si $a=-1$ : il faut et il suffit que 0 soit également une racine de $P_{t}$. Comme $P_{t}(0)=t$, cela signifie que $t=0$.
|
| 85 |
+
- Si $a+1=-1$, il faut et il suffit que -2 soit également une racine de $P_{t}$. Comme $P_{t}(-2)=5 t-6$, cela signifie que $t=\frac{6}{5}$.
|
| 86 |
+
- Si -1 n'est ni $a$ ni $a+1$, c'est donc que $a$ et $a+1$ sont les racines de $x^{2}+(3 t-1) x+t$. On a donc $a^{2}+(3 t-1) a+t=0$ et $(a+1)^{2}+(3 t-1)(a+1)+t=0$. Par soustraction, il vient $2 a+1+3 t-1=0$, soit donc $a=-\frac{3 t}{2}$. En reportant dans la première équation ci-dessus, il vient alors $-9 t^{2}+10 t=0$, soit $t=0$ ou $t=\frac{10}{9}$.
|
| 87 |
+
Réciproquement, on a déjà vu que $t=0$ convenait et, pour $t=\frac{10}{9}$, les racines de $P_{t}$ sont $-1,-\frac{2}{3}$ et $-\frac{5}{3}$, ce qui prouve que $t=\frac{10}{9}$ est bien une solution du problème.
|
| 88 |
+
Finalement, les réels $t$ cherchés sont $\frac{10}{9}, \frac{6}{5}$ et 0 .
|
| 89 |
+
|
| 90 |
+
|
| 91 |
+
## Exercice 5 (Vietnam 2014).
|
| 92 |
+
|
| 93 |
+
Déterminer toutes les fonctions $f: \mathbb{Z} \mapsto \mathbb{Z}$ telles
|
| 94 |
+
|
| 95 |
+
$$
|
| 96 |
+
f(2 m+f(m)+f(m) f(n))=n f(m)+m
|
| 97 |
+
$$
|
| 98 |
+
|
| 99 |
+
pour tous les entiers $m$ et $n$.
|
| 100 |
+
|
| 101 |
+
## Solution.
|
| 102 |
+
|
| 103 |
+
Soit $f$ une éventuelle solution. On note $\mathbf{E}_{x, y}$ l'égalité de l'énoncé.
|
| 104 |
+
Posons $a=f(0)$. L'égalité $\mathbf{E}_{x, 0}$ indique que $f(2 x+(1+a) f(x))=x$, ce qui montre que $f$ est surjective. Puis, en choisissant un entier $b$ tel que $f(b)=-1$, l'égalité $\mathbf{E}_{b, y}$ indique que $f(2 b+1-f(y))=b-y$, ce qui montre que $f$ est injective, donc bijective.
|
| 105 |
+
Les égalités $\mathbf{E}_{b, b}$ et $\mathbf{E}_{0,0}$ indiquent respectivement que $f(2 b)=0$ et que $f\left(a+a^{2}\right)=0$. Il s'ensuit que $2 b=a+a^{2}$. De surcroît, l'égalité $\mathbf{E}_{a b, 0}$ indique que $f(0)=a b$, c'est-à-dire $0=a(a-1)(a+2)$. Ainsi, $a \in\{-2,0,1\}$.
|
| 106 |
+
Enfin, les égalités $\mathbf{E}_{0, y}$ et $\mathbf{E}_{a y, 0}$ indiquent respectivement que $f(a f(y)+a)=a y$ et que $f(2 a y+(a+1) f(a y))=a y$. Il s'ensuit que $a f(y)+a=2 a y+(a+1) f(a y)$, égalité que l'on note ( $\boldsymbol{\phi}$ ).
|
| 107 |
+
|
| 108 |
+
- Si $a=1$, alors l'égalité ( $\boldsymbol{\oplus}$ ) indique que $f(y)+1=2 y+2 f(y)$. Il s'ensuit que $f: y \mapsto 1-2 y$, qui n'est manifestement pas bijective.
|
| 109 |
+
- Si $a=0$, alors $b=0$, et l'égalité $\mathbf{E}_{x, 0}$ indique que $f(2 x)=x$. Cela prouve que $f$ n'est pas injective, puisque chaque entier a déjà un antécédent pair.
|
| 110 |
+
- Si $a=-2$, alors $b=1$, et l'égalité ( $\boldsymbol{\oplus}$ ) indique que $-2 f(y)-2=-4 y-f(-2 y)$. Or, l'égalité $\mathbf{E}_{x, 1}$ indique que $f(2 x)=f(x)+x$. En combinant ces deux égalités, on en déduit que $f(-x)-x=f(-2 x)=2 f(x)+2-4 x$, donc que $f(-x)=2 f(x)+2-3 x$. De manière symétrique, on sait que $f(x)=2 f(-x)+2+3 x$, d'où la relation $f: x \mapsto x-2$.
|
| 111 |
+
|
| 112 |
+
Réciproquement, il on vérifie aisément que la fonction $f: n \longmapsto n-2$ est bien une solution du problème : c'en est donc l'unique solution.
|
| 113 |
+
|
| 114 |
+
## Exercice 6 (Pays-Bas 2014).
|
| 115 |
+
|
| 116 |
+
Soit $P$ un polynôme à coefficients entiers, de degré $n$, avec $n \leq 10$. On suppose que $|P(10)-P(0)|<1000$ et que, pour tout $k \in\{1, \ldots, 10\}$, il existe un entier $m$ tel que $P(m)=k$. Montrer que, pour tout entier $k$ il existe un entier $m$ tel que $P(m)=k$.
|
| 117 |
+
|
| 118 |
+
## Solution.
|
| 119 |
+
|
| 120 |
+
Pour $i \in\{1, \ldots, 10\}$, on désigne par $c_{i}$ un entier tel que $P\left(c_{i}\right)=i$. Pour $i \in\{1, \ldots, 9\}$, puisque $P$ est à coefficients entiers, l'entier $c_{i+1}-c_{i}$ divise $P\left(c_{i+1}\right)-P\left(c_{i}\right)=i+1-i=1$, d'où $c_{i+1}-c_{i}= \pm 1$. De plus, pour $i, j \in\{1, \ldots, 10\}$ distincts, on a $P\left(c_{i}\right)=i \neq j=P\left(c_{j}\right)$, donc $c_{i} \neq c_{j}$. Ainsi, $c_{1}, c_{2}, \ldots, c_{10}$ sont, dans cet ordre, dix entiers consécutifs.
|
| 121 |
+
Quitte à étudier le polynôme $P(10-X)$ plutôt que le polynôme $P(X)$ lui-même, on peut supposer que $c_{1}<c_{2}<\cdots<c_{10}$ : on a donc $c_{i}=c_{1}+i-1$. Soit alors les polynômes $Q(X)=X+1-c_{1}$ et $R(X)=P(X)-Q(X)$. Le polynôme $Q$ est affine, donc de degré 1 , et $R$ est de degré au plus 10 .
|
| 122 |
+
En outre, pour $i=1,2, \ldots, 10$, on a $R\left(c_{i}\right)=P\left(c_{i}\right)-Q\left(c_{i}\right)=i-i=0$, donc $c_{1}, \ldots, c_{10}$ sont dix racines distinctes entières du polynôme $R$, à coefficients entiers. On peut donc factoriser $R$ sous la forme $R(X)=S(X) T(X)$, où $S(X)=\prod_{i=1}^{10}\left(X-c_{i}\right)$ et où $T$ est un polynôme à coefficients entiers. Remarquons que $T$ est de degré au plus 0 , ce qui signifie que $T$ est constant : il existe un entier $a$ tel que $R=a S$.
|
| 123 |
+
Si $a=0$, on a bien $P=Q$, donc $P$ est affine de coefficient $\pm 1$ et $P(\mathbb{Z})=\mathbb{Z}$ : on suppose désormais que $a \neq 0$. Notons alors que $S(n) \equiv 0(\bmod 10!)$ pour tout entier $n$. En effet, soit $k \geq 10$ un entier. Alors
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
S\left(c_{1}+k\right)=\prod_{i=0}^{9}(k-i)=10!\binom{k}{10} \equiv 0 \quad(\bmod 10!)
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
La relation $S\left(c_{1}+k\right) \equiv 0$ est donc vraie dans $\mathbb{Z} / 10!\mathbb{Z}$, ce qui signifie bien que $S(n) \equiv 0$ $(\bmod 10!)$ pour tout entier $n$.
|
| 130 |
+
En particulier, il s'ensuit que $R(n) \equiv 0(\bmod 10!)$ pour tout entier $n$. Or,
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
|R(10)-R(0)| \leq|P(10)-P(0)|+|Q(10)-Q(0)| \leq 1010<10!
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Ainsi, $R(10)=R(0)$, donc $S(10)=S(0)$. Le polynôme $S$ est strictement monotone sur $\left.]-\infty, c_{1}\right]$ et sur $\left[c_{10},+\infty\left[\right.\right.$, donc on ne peut avoir ni $10 \leq c_{1}$ ni $0 \geq c_{10}$. Ainsi, l'un des entiers 0 et 10 doit être une racine de $S$, mais alors l'autre aussi, ce qui est impossible car les racines de $S$ sont mutuellement distantes d'au plus 9 .
|
| 137 |
+
Le cas $a \neq 0$ est donc impossible, ce qui conclut le problème.
|
| 138 |
+
|
| 139 |
+
## Exercice 7.
|
| 140 |
+
Soit $n \geq 0$ un entier, et $x_{1}, x_{2}, \ldots, x_{n+1}$ des réels strictement positifs tels que $\prod_{k=1}^{n+1} x_{i}=1$. Prouver que
|
| 141 |
+
|
| 142 |
+
$$
|
| 143 |
+
\sqrt[x_{1}]{n}+\sqrt[x_{2}]{n}+\cdots+\sqrt[x_{n+1}]{n} \geq n \sqrt[n]{x_{1}}+n \sqrt[n]{x_{2}}+\cdots+n \sqrt[n]{x_{n+1}}
|
| 144 |
+
$$
|
| 145 |
+
|
| 146 |
+
## Solution.
|
| 147 |
+
|
| 148 |
+
Par IAG (deux fois), on a
|
| 149 |
+
|
| 150 |
+
$$
|
| 151 |
+
\begin{aligned}
|
| 152 |
+
n \cdot \sum_{i=1}^{n+1} \sqrt[x_{i}]{n} & =\sum_{j=1}^{n+1}\left(\sum_{i \neq j} n^{\frac{1}{x_{i}}}\right) \\
|
| 153 |
+
& \geq \sum_{j=1}^{n+1}\left(n \cdot n^{\frac{1}{n} \sum_{i \neq j} \frac{1}{x_{i}}}\right) \\
|
| 154 |
+
& \geq \sum_{j=1}^{n+1} n \cdot n \sqrt[n]{\prod_{i \neq j} \frac{1}{x_{i}}} \\
|
| 155 |
+
& =\sum_{j=1}^{n+1} n \cdot n \sqrt[{n \sqrt{x_{j}}}]{ } \operatorname{car} x_{1} x_{2} \cdots x_{n+1}=1
|
| 156 |
+
\end{aligned}
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
et il ne reste plus qu'à diviser par $n$ les premier et dernier membres pour obtenir l'inégalité demandée.
|
| 160 |
+
|
| 161 |
+
## Exercice 8 (Iran 2014).
|
| 162 |
+
|
| 163 |
+
Déterminer toutes les fonctions $f: \mathbb{R}_{+}^{*} \longmapsto \mathbb{R}_{+}^{*}$ telles que
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
f\left(\frac{y}{f(x+1)}\right)+f\left(\frac{x+1}{x f(y)}\right)=f(y)
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
pour tous $x, y \in \mathbb{R}_{+}^{*}$.
|
| 170 |
+
|
| 171 |
+
## Solution.
|
| 172 |
+
|
| 173 |
+
En cherchant un peu parmi les fonctions usuelles, on constate que la fonction $f: x \longmapsto \frac{1}{x}$ est une solution du problème. Nous allons maintenant prouver que c'est la seule.
|
| 174 |
+
Soit $f$ une solution du problème. Si $y>0$ est tel que $y f(y)>1$, posons $x=\frac{1}{y f(y)-1}$. La relation de l'énoncé donne
|
| 175 |
+
|
| 176 |
+
$$
|
| 177 |
+
f\left(\frac{y}{f(x+1)}\right)+f(y)=f(y)
|
| 178 |
+
$$
|
| 179 |
+
|
| 180 |
+
ce qui est impossible car $f$ est à valeurs strictement positives. Ainsi, $y f(y) \leq 1$.
|
| 181 |
+
Pour tous $x, y \in \mathbb{R}_{+}^{*}$, on a donc
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
f(y)=f\left(\frac{y}{f(x+1)}\right)+f\left(\frac{x+1}{x f(y)}\right) \leq \frac{f(x+1)}{y}+\frac{x f(y)}{x+1},
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
donc $y f(y) \leq(x+1) f(x+1)$. En particulier, pour tous les réels $a, b>1$, on a bien $a f(a) \leq b f(b) \leq a f(a)$ : il existe donc un réel $c \in] 0,1]$ tel que $x f(x)=c$ pour tout $x>1$.
|
| 188 |
+
Si $y>1$, alors $y>c$ donc $\frac{y(x+1)}{c}>x+1>1$ et $\frac{(x+1) y}{x c}>\frac{y}{c}>1$, et
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
\begin{aligned}
|
| 192 |
+
c & =y \cdot f(y)=y \cdot f\left(\frac{y}{f(x+1)}\right)+y \cdot f\left(\frac{x+1}{x f(y)}\right) \\
|
| 193 |
+
& =y \cdot f\left(\frac{(x+1) \cdot y}{c}\right)+y \cdot f\left(\frac{(x+1) \cdot y}{c \cdot x}\right) \\
|
| 194 |
+
& =\frac{c^{2} \cdot y}{(x+1) \cdot y}+\frac{c^{2} \cdot x \cdot y}{(x+1) \cdot y}=c^{2},
|
| 195 |
+
\end{aligned}
|
| 196 |
+
$$
|
| 197 |
+
|
| 198 |
+
donc $c=1$. On a donc $f(x)=\frac{1}{x}$ pour tout $x>1$.
|
| 199 |
+
On va maintenant prouver, par récurrence sur $k \in \mathbb{N}$, que $f(x)=\frac{1}{x}$ pour tout $x>2^{-k}$. Le résultat est déjà connu pour $k=0$. En outre, si on suppose le résultat connu pour $k \geq 0$, posons $x=1$. Si $y>2^{-1-k}$, alors $2 y>2^{-k}$ et $\frac{2}{f(y)} \geq 2 y>2^{-k}$. L'énoncé indique donc que
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
f(y)=f(2 y)+f\left(\frac{2}{f(y)}\right)=\frac{1}{2 y}+\frac{f(y)}{2}
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
c'est-à-dire $f(y)=\frac{1}{y}$. Le résultat est donc vrai aussi pour $k+1$.
|
| 206 |
+
Ceci montre que $f: x \longmapsto \frac{1}{x}$ est bien l'unique solution du problème.
|
| 207 |
+
|
| 208 |
+
## Exercice 9.
|
| 209 |
+
|
| 210 |
+
Soit $a \in] 0 ; 1\left[\right.$ et $n>0$ un entier. On note $f_{n}$ la fonction définie sur $\mathbb{R}$ par $f_{n}(x)=x+\frac{x^{2}}{n}$, pour tout réel $x$. Prouver que
|
| 211 |
+
|
| 212 |
+
$$
|
| 213 |
+
\frac{a(1-a) n^{2}+2 a^{2} n+a^{3}}{(1-a)^{2} n^{2}+a(2-a) n+a^{2}}<\underbrace{\left(f_{n} \circ f_{n} \circ \cdots \circ f_{n}\right)}_{n}(a)<\frac{a n+a^{2}}{(1-a) n+a} .
|
| 214 |
+
$$
|
| 215 |
+
|
| 216 |
+
## Solution.
|
| 217 |
+
|
| 218 |
+
Pour tout entier $k \geq 0$, posons $a_{k}=\underbrace{\left(f_{n} \circ f_{n} \circ \cdots \circ f_{n}\right)}_{k}(a)$. En particulier, $a_{0}=a$.
|
| 219 |
+
On remarque que, pour tout $k \geq 0$, on a $a_{k+1}=a_{k}+\frac{a_{k}^{2}}{n}>a_{k}$, donc la suite $\left(a_{k}\right)$ est strictement croissante. En particulier, $a_{k} \geq a>0$ pour tout $k \geq 0$.
|
| 220 |
+
De plus, pour tout $k \geq 0$, on a $a_{k+1}=\frac{a_{k}\left(a_{k}+n\right)}{n}$ et donc
|
| 221 |
+
|
| 222 |
+
$$
|
| 223 |
+
\frac{1}{a_{k+1}}=\frac{1}{a_{k}}-\frac{1}{a_{k}+n} .
|
| 224 |
+
$$
|
| 225 |
+
|
| 226 |
+
Ainsi, après sommation de ces égalités pour $k=0, \ldots, n-1$, on a
|
| 227 |
+
|
| 228 |
+
$$
|
| 229 |
+
\frac{1}{a_{n}}=\frac{1}{a}-\sum_{k=0}^{n-1} \frac{1}{a_{k}+n}
|
| 230 |
+
$$
|
| 231 |
+
|
| 232 |
+
Puisque $\left(a_{k}\right)$ est strictement croissante et à valeurs positives, on a
|
| 233 |
+
|
| 234 |
+
$$
|
| 235 |
+
\frac{n}{a_{n}+n}<\sum_{k=0}^{n-1} \frac{1}{a_{k}+n}<\frac{n}{a+n}
|
| 236 |
+
$$
|
| 237 |
+
|
| 238 |
+
et ainsi
|
| 239 |
+
|
| 240 |
+
$$
|
| 241 |
+
\frac{1}{a}-\frac{n}{a+n}<\frac{1}{a_{n}}<\frac{1}{a}-\frac{n}{a_{n}+n} .
|
| 242 |
+
$$
|
| 243 |
+
|
| 244 |
+
L'inégalité de gauche est équivalente à $a_{n}<\frac{a n+a^{2}}{(1-a) n+a}$, ce qui est l'inégalité de droite de l'encadrement demandé.
|
| 245 |
+
|
| 246 |
+
Reportons maintenant cette dernière inégalité dans l'inégalité de droite de (1). Il vient
|
| 247 |
+
|
| 248 |
+
$$
|
| 249 |
+
\frac{1}{a_{n}}<\frac{1}{a}-\frac{n}{\frac{a n+a^{2}}{(1-a) n+a}+n}
|
| 250 |
+
$$
|
| 251 |
+
|
| 252 |
+
ou encore
|
| 253 |
+
|
| 254 |
+
$$
|
| 255 |
+
\frac{a(1-a) n^{2}+2 a^{2} n+a^{3}}{(1-a)^{2} n^{2}+a(2-a) n+a^{2}}<a_{n}
|
| 256 |
+
$$
|
| 257 |
+
|
| 258 |
+
ce qui est l'inégalité de gauche de l'encadrement demandé.
|
| 259 |
+
|
| 260 |
+
## Exercice 10 (Iran 2014).
|
| 261 |
+
|
| 262 |
+
Déterminer tous les polynômes $P$ à coefficients entiers pour lesquels l'ensemble $P(\mathbb{N})$ contient une suite géométrique infinie de raison $a$ avec $a \notin\{-1,0,1\}$ et de premier terme non nul.
|
| 263 |
+
|
| 264 |
+
## Solution.
|
| 265 |
+
|
| 266 |
+
Tout d'abord, on note que si $P$ est un polynôme ayant les propriétés de l'énoncé, alors - $P$ les possède aussi (il suffit de changer le premier terme de la suite géométrique en son opposée). On peut donc supposer que le coefficient dominant de $P$ est strictement positif.
|
| 267 |
+
Soit $\left(u_{k}\right)=\left(u_{0} \cdot a^{k}\right)$ une suite géométrique infinie telle que décrite ci-dessus. Alors, quitte à la remplacer par la suite $\left(u_{2 k}\right)=\left(u_{0} \cdot\left(a^{2}\right)^{k}\right)$, on peut supposer que $a>0$.
|
| 268 |
+
De plus, notons que $a=\frac{u_{1}}{u_{0}}$ est rationnel. Si $a$ n'est pas entier, soit $p$ un facteur premier tel que la valuation $p$-adique de $a$ soit strictement négative c'est-à-dire que $v_{p}(a) \leq-1$. En posant $k=v_{p}\left(u_{0}\right)$, on constate alors que $v_{p}\left(u_{k+1}\right) \leq-1$, ce qui contredit le fait que $u_{k+1}$ soit entier, donc que $u_{k+1} \in P(\mathbb{N})$. Ainsi, on sait que $a$ est un entier tel que $a>1$.
|
| 269 |
+
Développons alors le polynôme $P$ sous la forme $P(x)=p_{n} x^{n}+p_{n-1} x^{n-1}+\cdots+p_{1} x+p_{0}$. Pour tout entier $b$, on a
|
| 270 |
+
|
| 271 |
+
$$
|
| 272 |
+
\begin{aligned}
|
| 273 |
+
P(a x+b) & =a^{n} p_{n} x^{n}+\left(n a^{n-1} p_{n} b+a^{n-1} p_{n-1}\right) x^{n-1}+\cdots \text { et } \\
|
| 274 |
+
a^{n} P(x) & =a^{n} p_{n} x^{n}+a^{n} p_{n-1} x^{n-1}+\cdots+a^{n} p_{0} .
|
| 275 |
+
\end{aligned}
|
| 276 |
+
$$
|
| 277 |
+
|
| 278 |
+
Le polynôme $P(a x+b)-a^{n} P(x)$ est un polynôme de degré au plus $n-1$ et dont le coefficient de degré $n-1$ est $a^{n-1}\left(n p_{n} b+p_{n-1}(1-a)\right)$. Notons que $P$ est non constant, donc que $n p_{n}>0$ : ce coefficient a donc une expression affine strictement croissante en $b$. Ainsi, il existe un entier $b$ tel que
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
n p_{n}(b+1)+p_{n-1}(1-a)>0>n p_{n}(b-1)+p_{n-1}(1-a) .
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
Par conséquent, il existe même un entier $N \geq 0$ tel que
|
| 285 |
+
|
| 286 |
+
- $P(a x+b-1)<a^{n} P(x)<P(a x+b+1)$ pour tout $x \geq N$, et
|
| 287 |
+
- $P$ est strictement croissante sur $[N,+\infty[$.
|
| 288 |
+
|
| 289 |
+
En outre, soit $M$ un entier tel que $M \geq N$ et $a M+b-1 \geq N$ : quitte à considérer une suite $\left(u_{k+\ell}\right)=\left(u_{\ell} \cdot a^{k}\right)$ au lieu de la suite $\left(u_{k}\right)$, on peut supposer que $\left|u_{0}\right|>\sum_{i=0}^{M}|P(i)|$. Pour tout entier $k \geq 0$, il existe donc un entier $v_{k}>M$ tel que $P\left(v_{k}\right)=u_{k}=u_{0} \cdot a^{k}$.
|
| 290 |
+
|
| 291 |
+
En particulier, notons que
|
| 292 |
+
|
| 293 |
+
$$
|
| 294 |
+
P\left(a v_{k}+b-1\right)<a^{n} P\left(v_{k}\right)=P\left(v_{k+n}\right)<P\left(a v_{k}+b+1\right),
|
| 295 |
+
$$
|
| 296 |
+
|
| 297 |
+
donc que $v_{k+n}=a v_{k}+b$ et que $a^{n} P\left(v_{k}\right)=P\left(a v_{k}+b\right)$. Ainsi, chaque entier $v_{k}$ est une racine du polynôme $a^{n} P(X)-P(a X+b)$, qui est donc nul. On a donc l'égalité de polynômes $a^{n} P(X)=P(a X+b)$.
|
| 298 |
+
Puisque $P$ est non constant, soit $r$ une racine de $P$. On pose alors
|
| 299 |
+
|
| 300 |
+
$$
|
| 301 |
+
\delta=\frac{b}{1-a} \text { et } \rho_{k}=a^{k}(r-\delta)+\delta
|
| 302 |
+
$$
|
| 303 |
+
|
| 304 |
+
Alors $\rho_{0}=r$ et $\rho_{k+1}=a\left(\rho_{k}-\delta\right)+\delta=a \rho_{k}+b$. Une récurrence immédiate montre donc que tous les termes $\rho_{k}$ sont des racines de $P$.
|
| 305 |
+
|
| 306 |
+
Or, si $r \neq \delta$, les termes $\rho_{k}$ sont deux à deux distincts, et $P$ se retrouve être nul, ce qui est impossible. donc $r=\delta$ est nécessairement la seule racine de $P$, de sorte que l'on peut écrire $P(X)=p_{n}(X-\delta)^{n}$. Puisque $P(X)=p_{n} X^{n}-n p_{n} \delta X^{n-1}+\cdots+(-1)^{n} p_{n} \delta^{n}$ est à coefficients entiers, alors $n p_{n} \delta$ est entier, donc $\delta$ est rationnel, et peut s'écrire sous forme irréductible $\delta=\frac{u}{v}$. Puis $p_{n} \delta^{n}$ est entier, donc $v^{n}$ divise $p_{n}$, et l'on peut factoriser $p_{n}$ sous la forme $p_{n}=w v^{n}$. On peut alors réécrire $P(X)=w(v X-u)^{n}$, avec $n, u, v$ et $w$ entiers et $n \geq 1, v \neq 0, w \neq 0$.
|
| 307 |
+
|
| 308 |
+
Réciproquement, supposons que $P(X)=w(v X-u)^{n}$ avec $n, u, v$ et $w$ entiers et $n \geq 1$, $v \neq 0, w \neq 0$.
|
| 309 |
+
|
| 310 |
+
- Si $u=0$, alors $P\left(2^{k}\right)=v^{n} \cdot w \cdot 2^{k n}$ décrit bien une suite géométrique de raison $2^{n} \notin\{-1,0,1\}$ et de premier terme $P(1)=v^{n} \cdot w$ non nul.
|
| 311 |
+
- Si $u \cdot v>0$, on pose $x_{k}=(3 u v-1)^{2 k+1}+1$ et $y_{k}=\frac{u}{v} x_{k}$. Alors $x_{k} \equiv 0(\bmod v)$, de sorte que $y_{k} \in \mathbb{N}$. En outre, $P\left(y_{k}\right)=w \cdot u^{n} \cdot(3 u v-1)^{(2 k+1) n}$ décrit bien une suite géométrique de raison $(3 u v-1)^{2 n} \notin\{-1,0,1\}$ et de premier terme $P\left(3 u^{2}\right)=w \cdot u^{n} \cdot(3 u v-1)^{n}$ non nul.
|
| 312 |
+
- Si $u \cdot v<0$, on pose $x_{k}=1-(3 u v+1)^{2 k}$ et $y_{k}=\frac{u}{v} x_{k}$. Alors $x_{k} \equiv 0(\bmod v)$, de sorte que $y_{k} \in \mathbb{N}$. En outre, $P\left(y_{k}\right)=w \cdot(-u)^{n} \cdot(3 u v+1)^{(2 k) n}$ décrit bien une suite géométrique de raison $(3 u v+1)^{2 n} \notin\{-1,0,1\}$ et de premier terme $P(0)=w \cdot(-u)^{n}$ non nul.
|
| 313 |
+
|
| 314 |
+
Les polynômes recherchés sont donc exactement ceux de la forme $P(x)=w(v x+u)^{n}$, avec $n, u, v$ et $w$ des entiers tels que $n>0, v \neq 0$ et $w \neq 0$.
|
| 315 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-5-solutions.md
ADDED
|
@@ -0,0 +1,266 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OLYMPIADES FRANÇAISES DE MATHÉMATIQUES
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
ENVOI NO. 5
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. Un polyèdre a 6 sommets et 12 arêtes. Montrer que chaque face est un triangle.
|
| 12 |
+
Solution de l'exercice 1 Notons $F$ le nombre de faces, $A$ le nombre d'arêtes et $S$ le nombre de sommets. La formule d'Euler donne $F-A+S=2$, donc $F=A-S+2=8$.
|
| 13 |
+
|
| 14 |
+
Notons $x_{i}(i=1,2, \ldots, 8)$ le nombre d'arêtes de la face $i$. On a $x_{1}+\cdots+x_{8}=2 A=24$ car chaque arête appartient à exactement deux faces. On en déduit que
|
| 15 |
+
|
| 16 |
+
$$
|
| 17 |
+
\frac{x_{1}+\cdots+x_{8}}{8}=3
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
autrement dit le nombre moyen d'arêtes par face est 3 . Or, chaque face possède au moins 3 arêtes, donc finalement chaque face est un triangle.
|
| 21 |
+
Exercice 2. Sept élèves d'une classe comparent leurs notes dans 12 épreuves, et remarquent qu'il n'existe pas deux élèves ayant des notes identiques dans chacune des 12 épreuves.
|
| 22 |
+
|
| 23 |
+
Montrer que l'on peut choisir 6 épreuves telles que deux élèves quelconques aient des notes différentes à au moins l'une de ces épreuves.
|
| 24 |
+
|
| 25 |
+
## Solution de l'exercice 2
|
| 26 |
+
|
| 27 |
+
Soit $m$ le plus petit entier tel que l'on peut choisit m épreuves $E_{1}, \ldots, E_{m}$ de sorte que deux élèves quelconques aient des notes différentes à au moins l'une de ces $m$ épreuves. On doit montrer que $m \leqslant 6$.
|
| 28 |
+
|
| 29 |
+
Comme $m$ est minimal, pour tout $i=1, \ldots, m$ il existe une paire $A_{i} d^{\prime}$ 'élèves ayant la même note à toutes les épreuves sauf $E_{i}$.
|
| 30 |
+
|
| 31 |
+
On forme un graphe dont les sommets sont les élèves, et dont les arêtes sont $A_{1}, \ldots, A_{m}$. Supposons que le graphe possède un cycle $\left(A_{i_{1}}, \ldots, A_{i_{r}}\right)$. Notons a et b les extrémités de $A_{i_{1}}$. Par hypothèse, a et $b$ obtiennent des notes différentes à l'épreuve $i_{1}$. Cependant, le chemin $\left(A_{i_{2}}, \ldots, A_{i_{r}}\right)$ montre que a et b obtiennent des notes identiques à l'épreuve $i_{1}$, ce qui est contradictoire.
|
| 32 |
+
|
| 33 |
+
Par conséquent, le graphe est un arbre. Comme un arbre a strictement plus de sommets de d'arêtes, on en déduit que $\mathrm{m}<7$.
|
| 34 |
+
|
| 35 |
+
Exercice 3. Jules et Jim, deux colocataires, reçoivent 10 autres paires de colocataires chez eux. Jules fait un petit sondage au cours de la soirée et interroge les 21 autres personnes. Parmi elles, aucune n'a serré la main de son colocataire, et il n'y en a pas deux qui ont serré le même nombre de mains. Combien de mains a serré Jim?
|
| 36 |
+
Solution de l'exercice 3 Au cours de la soirée, parmi les 21 , chaque personne serre entre 0 et 20 mains. Comme elles serrent toutes un nombre différent de mains, pour tout n compris entre 0 et 20 il existe une et une seule personne $A_{n}$ parmi les 21 qui a serré exactement n mains.
|
| 37 |
+
|
| 38 |
+
Comme $A_{20}$ a serré 20 mains, $A_{20}$ a serré la main à tout le monde sauf lui même et son colocataire. Or, $A_{0}$ n'a serré la main à personne, donc $A_{0}$ est le colocataire de $A_{20}$.
|
| 39 |
+
|
| 40 |
+
Comme $\AA_{19}$ a serré 19 mains, $\AA_{19}$ a serré la main à tout le monde sauf lui-même, son colocataire et $A_{0}$. Or, $A_{1}$ a serré la main à $A_{20}$ et à personne d'autre, donc n'a pas serré la main à $A_{19}$. On en déduit que $A_{1}$ est le colocataire de $A_{19}$.
|
| 41 |
+
|
| 42 |
+
En continuant le raisonnement, on montre que $A_{n}$ est le colocataire de $A_{20-n}$ pour tout $\boldsymbol{n}=0,1, \ldots, 9$, donc $A_{10}$ est le colocataire de Jules. Finalement, Jules a serré 10 mains.
|
| 43 |
+
|
| 44 |
+
## Exercices Communs
|
| 45 |
+
|
| 46 |
+
Exercice 4. 2015 droites deux à deux distinctes sont tracées dans le plan. On suppose qu'elles délimitent moins de 8000 régions (les régions peuvent être non bornées). Montrer que le nombre de régions est égal à 2016, 4030, 6042 ou 6043, et donner un exemple de configuration dans chaque cas.
|
| 47 |
+
|
| 48 |
+
## Solution de l'exercice 4
|
| 49 |
+
|
| 50 |
+
Notons $\mathrm{n}=2015$ le nombre de droites, f le nombre de régions, p le nombre maximal de droites parallèles et q le nombre maximal de droites concourantes.
|
| 51 |
+
|
| 52 |
+
Montrons d'abord que $\mathrm{f} \geqslant(\mathrm{p}+1)(\mathrm{n}-\mathrm{p}+1)$. En effet, plaçons d'abord les p droites parallèles. Elles forment $p+1$ régions. Il reste ensuite $n-p$ droites à placer, et chacune de ces droites crée au moins $p+1$ régions supplémentaires.
|
| 53 |
+
|
| 54 |
+
De même, montrons que $\mathrm{g} \geqslant \mathrm{q}(\mathrm{n}-\mathrm{q}+2)$. En effet, on place d'abord q droites concourantes. Chaque nouvelle droite crée au moins $q-1$ points d'intersection, donc au moins $q$ nouvelles régions. On en déduit que $f \geqslant(2 q)+(n-q) q=q(n-q+2)$.
|
| 55 |
+
|
| 56 |
+
Supposons que $3 \leqslant p \leqslant n-3$. Comme l'expression $g(p)=(p+1)(n-p+1)$ est égale à $(n+2)^{2} / 4-(p-n / 2)^{2}$, la fonction $g$ croît entre 0 et $n / 2$ et décroît entre $n / 2$ et $n$, donc $\boldsymbol{g}(\mathrm{p}) \geqslant \mathrm{g}(3)=4(n-2)>8000$. Impossible. On en déduit que $p \in\{1,2, n-2, n-1, n\}$ et de même $\mathbf{q} \in\{1,2,3, \mathfrak{n}-1, \mathfrak{n}\}$.
|
| 57 |
+
|
| 58 |
+
Si $\mathrm{p}=\mathrm{n}$ alors toutes les droites sont parallèles, et on a $\mathrm{f}=\mathrm{n}+1=2016$.
|
| 59 |
+
Si $p=n-1$ alors toutes les droites sauf une sont parallèles, et on a $f=2 n=4030$.
|
| 60 |
+
Si $p=n-2$ et les deux droites restantes sont parallèles, ou bien sécantes sur l'une des $n-2$ premières droites, alors $\mathrm{f}=3(\mathrm{n}-1)=6042$.
|
| 61 |
+
|
| 62 |
+
Si $p=n-2$ et les deux droites restantes sont sécantes ailleurs que sur les $n-2$ premières droites, alors $\mathrm{f}=3 \mathrm{n}-2=6043$.
|
| 63 |
+
|
| 64 |
+
Si $q=n$ alors $f=2 n$.
|
| 65 |
+
Si $\mathrm{q}=\mathrm{n}-1$ alors $\mathrm{f}=3 \mathrm{n}-3$ ou $3 \mathrm{n}-2$ selon que la dernière droite est parallèle ou non à l'une des premières droites.
|
| 66 |
+
|
| 67 |
+
Il reste à traiter le cas où $p \leqslant 2$ et $\mathrm{q} \leqslant 3$. Notons $\mathrm{D}_{1}, \ldots, \mathrm{D}_{2015}$ les droites. A chaque fois que l'on trace une droite $D_{i}(i>1000)$, celle-ci coupe au moins 999 des droites $D_{1}, \ldots, D_{1000}$, et chacun de ces points d'intersection est commun à au plus deux de ces droites, donc on obtient au moins 500 points d'intersection entre $D_{i}$ et l'une des 1000 premières droites. Par conséquent, $\mathrm{D}_{\mathrm{i}}$ crée au moins 501 régions supplémentaires. On en déduit que $\mathrm{f} \geqslant 1015 \times 501>8000$.
|
| 68 |
+
|
| 69 |
+
Exercice 5. Dans un club d'échecs de 20 personnes, 14 parties sont jouées et chaque joueur a joué au moins une partie. Montrer qu'il y a 6 parties auxquelles 12 joueurs différents ont participé.
|
| 70 |
+
Solution de l'exercice 5 Soit r le plus grand entier tel qu'il existe un ensemble $M$ de r parties faisant intervenir 2 r joueurs différents.
|
| 71 |
+
|
| 72 |
+
Notons J l'ensemble des 2 r personnes qui ont joué les parties de $M$. Par maximalité de $M$, si $a$ et $b$ sont deux joueurs n'appartenant pas à $J$, alors $a$ et $b$ n'ont pas joué entre eux. Par conséquent, ils ont joué une partie contre l'un des 2 r joueurs de $M$. On en déduit que le nombre total de parties est au moins égal à $r+(20-2 r)=20-r$. Or, par hypothèse le nombre de parties est 14 , donc $14 \geqslant 20-r$, ce qui entraîne $r \geqslant 6$.
|
| 73 |
+
Exercice 6. On considère un échiquier $2015 \times 2015$, auquel on a retiré le carré $2 \times 2$ en bas à droite. Montrer qu'on peut le paver par des pièces composées de 3 cases en forme de L (les pièces peuvent être pivotées).
|
| 74 |
+
|
| 75 |
+
Solution de l'exercice 6 Comme l'échiquier peut être décomposé en trois rectangles $2010 \times 2015$, $5 \times 2004$ et $5 \times 11$, et comme 2010 et 2004 sont divisibles par 6 , il suffit de montrer que
|
| 76 |
+
|
| 77 |
+
1) Pour tout $n \geqslant 2$ et tout entier $m$, un échiquier $6 m \times n$ peut être pavé par des pièces en forme de L;
|
| 78 |
+
2) L'échiquier $5 \times 11$ privé du carré $2 \times 2$ en bas à droite peut être pavé par des pièces en forme de L.
|
| 79 |
+
|
| 80 |
+
Pour le point 1), comme un tel échiquier est réunion d'échiquiers $6 \times \mathrm{n}$, on se ramène à traiter le cas $\mathrm{m}=1$.
|
| 81 |
+
|
| 82 |
+
Il est clair que l'on peut paver un échiquier $3 \times 2$, donc aussi des échiquiers $6 \times 2$ et $6 \times 3$. On peut donc paver tout échiquier de taille $6 \times 2 k$ ou $6 \times(2 k+3)$. Or, tout entier $n \geqslant 2$ s'écrit sous la forme $2 k$ s'il est pair, et $2 k+3$ s'il est impair, ce qui conclut.
|
| 83 |
+
|
| 84 |
+
Le point 2) se démontre en construisant un exemple de pavage:
|
| 85 |
+

|
| 86 |
+
|
| 87 |
+
## Exercices du groupe A
|
| 88 |
+
|
| 89 |
+
Exercice 7. n joueurs participent à un tournoi d'échecs. Chaque joueur fait exactement une partie avec chacun des autres joueurs. Une victoire rapporte 1 point, un match nul un demipoint et une défaite aucun point. Une partie est dite anormale si le gagnant de cette partie obtient un score au tournoi strictement plus faible que le perdant.
|
| 90 |
+
a) Montrer que la proportion de parties anormales est inférieure ou égale à $75 \%$.
|
| 91 |
+
b) Est-il possible qu'elle soit supérieure ou égale à $70 \%$ ?
|
| 92 |
+
$\underline{\text { Solution de l'exercice } 7}$ a) Soit $m=[n / 2]$. On classe les joueurs suivant leur score (parmi les joueurs ayant le même score, on les classe arbitrairement). On dira qu'un joueur classé parmi les $m$ meilleurs est fort; sinon, on dira qu'il est faible.
|
| 93 |
+
|
| 94 |
+
Soit x le nombre de parties normales entre les joueurs forts et les joueurs faibles. Les joueurs forts ont marqué au total $m(m-1) / 2$ points entre eux, et au plus $x$ lors de parties contre les joueurs faibles.
|
| 95 |
+
|
| 96 |
+
Notons $S_{1}$ le score total des joueurs forts et $S_{2}$ le score total des joueurs faibles. On a donc $S_{1} \leqslant \mathrm{~m}(\mathrm{~m}-1) / 2+x$ et $\mathrm{S}_{1}+\mathrm{S}_{2}=\mathrm{n}(\mathrm{n}-1) / 2$.
|
| 97 |
+
|
| 98 |
+
Le score moyen des joueurs forts, $\frac{\mathrm{S}_{1}}{\mathrm{~m}}$, est supérieur au score moyen de tous les joueurs: $\frac{S_{1}}{m}>\frac{n(n-1) / 2}{n}$, i.e. $S_{1}>m(n-1) / 2$. Par conséquent,
|
| 99 |
+
|
| 100 |
+
$$
|
| 101 |
+
x \geqslant S_{1}-m(m-1) / 2>\frac{m(n-m)}{2} \geqslant n(n-1) / 8
|
| 102 |
+
$$
|
| 103 |
+
|
| 104 |
+
Comme il y a au total $n(n-1) / 2$ parties, la proportion de parties normales est supérieure à $1 / 4$.
|
| 105 |
+
b) Considérons un tournoi constitué de $2 k+1$ groupes de $k$ joueurs (on a donc $n=k(2 k+1)$ ). On suppose que les joueurs du groupe $i$ font match nul entre eux, perdent contre les joueurs des groupes $i+1, \ldots, i+k$ et gagnent tous les autres matchs (ici, $i$ est pris modulo $k$ ). Alors tous les joueurs ont le même score.
|
| 106 |
+
|
| 107 |
+
On va modifier les parties des joueurs du $k+1$-ième groupe afin que les scores soient différents. Pour tout $i$, on remplace $i k$ victoires de joueurs du $(k+1)$-ième groupe contre des joueurs du $(k+1-i)$-ème groupe par des matchs nuls, de sorte que chaque joueur $\mathrm{du}(k+1)$ ième groupe voie son score décroître de $i / 2$ tandis que chaque joueur du ( $k+1-\mathfrak{i}$ )-ème score voie son score augmenter de $i / 2$.
|
| 108 |
+
|
| 109 |
+
De même, on remplace $i k$ défaites du $(k+1)$-ième groupe contre les $(k+1+i)$-ème groupe par des matchs nuls.
|
| 110 |
+
|
| 111 |
+
Alors les premières places dans le tournoi sont prises par les joueurs du premier groupe, puis du deuxième, etc.
|
| 112 |
+
|
| 113 |
+
Les joueurs des groupes $i \leqslant k$ ont perdu $k^{3}-i k$ parties, les joueurs des groupes $i>k+1$ perdu $(2 k+1-i) k^{2}$ parties anormales, et les joueurs du $(k+1)$-ième groupe ont perdu $k^{3}-$ $k\left(\frac{1}{2} k(k+1)\right)$ parties anormales. Tous calculs faits, on obtient en tout
|
| 114 |
+
|
| 115 |
+
$$
|
| 116 |
+
\frac{3}{2} k^{4}-\frac{1}{2} k^{3}-k^{2}
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
parties anormales.
|
| 120 |
+
Il y a au total $k(2 k+1)(k(2 k+1)-1) / 2$ parties. On vérifie que pour $k=100$, la proportion de parties anormales dépasse $70 \%$.
|
| 121 |
+
Exercice 8. Soient a et b deux entiers tels que $\mathrm{a}+\mathrm{b}$ n'est pas divisible par 3. Montrer que l'on ne peut pas colorier les entiers relatifs en trois couleurs de sorte que que pour tout entier $n$, les trois nombres $n, n+a$ et $n+b$ soient de couleurs différentes.
|
| 122 |
+
$\underline{\text { Solution de l'exercice } 8}$ Supposons par l'absurde qu'il existe un tel coloriage. On notera $x \sim y$ si $x$ et $y$ sont de la même couleur.
|
| 123 |
+
|
| 124 |
+
Pour tout $n$, les entiers $(n+a)+b$ et $x+a$ ne sont pas de la même couleur, et de même $n+a+b$ n'est pas de la même couleur que $n+b$, donc $n+a+b \sim n$. Il vient immédiatement $0 \sim p(a+b)$ pour tout entier $p$, et en particulier $0 \sim a(a+b)$.
|
| 125 |
+
|
| 126 |
+
D'autre part, $n+a, n+2 a$ et $n+a+b$ sont de couleurs différentes, donc $n, n+a$ et $n+2 a$ sont de couleurs différentes. En appliquant ce qui précède à $n+a$, on en déduit que $n+3 a$ est de même couleur que $n$, donc pour tout entier $j$, le nombre ja est de la même couleur que ra où $r$ est le reste de la division Euclidienne de j par 3.
|
| 127 |
+
|
| 128 |
+
En appliquant ceci à $j=a+b$, on en déduit que $0 \sim r a$ où $r$ est le reste de la division Euclidienne de $\mathrm{a}+\mathrm{b}$ par 3, ce qui est impossible puisque 0 , a et 2 a sont de couleurs différentes et $\mathrm{r} \in\{1,2\}$.
|
| 129 |
+
|
| 130 |
+
Exercice 9. Dans tout l'exercice, on s'intéresse à des tableaux $5 \times 5$, dont les lignes (resp. les colonnes) sont notées $\mathrm{L}_{0}, \mathrm{~L}_{1}, \mathrm{~L}_{2}, \mathrm{~L}_{3}, \mathrm{~L}_{4}$ du bas vers le haut (resp. $\mathrm{C}_{0}, \mathrm{C}_{1}, \mathrm{C}_{2}, \mathrm{C}_{3}, \mathrm{C}_{4}$, de gauche à droite).
|
| 131 |
+
|
| 132 |
+
Dans chacune des 25 cases d'un tel tableau, on écrit un nombre. Le nombre qui est dans la case située sur la ligne $L_{i}$ et la colonne $C_{j}$ est noté $f(i, j)$.
|
| 133 |
+
|
| 134 |
+
Un tableau est dit cohérent lorsque, pour tous $i$ et $j$ :
|
| 135 |
+
Le nombre $f(i, j)$ est le nombre de $i$ écrits dans les cases de la ligne $L_{j}$.
|
| 136 |
+
Déterminer tous les tableaux cohérents de taille $5 \times 5$.
|
| 137 |
+
Solution de l'exercice 9 On se donne un éventuel tableau cohérent. Commençons par dégager quelques unes de ses propriétés.
|
| 138 |
+
a) Pour tous $\boldsymbol{i}, \mathfrak{j}$, on a $\boldsymbol{f}(\mathfrak{i}, \mathfrak{j}) \in\{0,1,2,3,4,5\}$.
|
| 139 |
+
|
| 140 |
+
En effet, dans un tableau cohérent, chaque $f(i, j)$ représente le nombre de fois où $i$ apparaît sur $L_{j}$, donc $f(i, j)$ est un entier positif ou nul, et il ne peut dépasser 5 car c'est le nombre total de cases de $L_{j}$.
|
| 141 |
+
b) On a $f(0,0) \geqslant 1$.
|
| 142 |
+
|
| 143 |
+
Par l'absurde : Si $f(0,0)=0$ alors, il n'y a aucun 0 sur $L_{0}$. Mais, $f(0,0)$ est lui-même sur $L_{0}$. Contradiction.
|
| 144 |
+
|
| 145 |
+
Ainsi, $f(0,0) \geqslant 1$.
|
| 146 |
+
Pour tout $i$ (resp.j), on note $x_{i}$ (resp. $y_{j}$ ) la somme des nombres inscrits dans la colonne $C_{i}$ (resp. la ligne $\mathrm{L}_{\mathrm{j}}$ ).
|
| 147 |
+
c) On a $x_{i} \leqslant 5$ pour tout $i$.
|
| 148 |
+
|
| 149 |
+
Soit $i$ fixé. Pour tout $j$, on note $n_{j}$ le nombre de $j$ dans $L_{i}$. Alors :
|
| 150 |
+
$x_{i}=\mathbf{f}(0, \boldsymbol{i})+\mathbf{f}(1, \boldsymbol{i})+\mathbf{f}(2, \mathfrak{i})+\mathbf{f}(3, \mathfrak{i})+\mathbf{f}(4, \boldsymbol{i})$ $=\mathrm{n}_{0}+\mathrm{n}_{1}+\mathrm{n}_{2}+\mathrm{n}_{3}+\mathrm{n}_{4}$ $\leqslant$ nombre de cases de $\mathrm{L}_{i}$ (il pourrait y avoir un 5 sur $L_{i}$ ) $=5$.
|
| 151 |
+
|
| 152 |
+
Ainsi, on a $x_{i} \leqslant 5$, pour tout $i$.
|
| 153 |
+
d) Pour tous $i$ et $\mathfrak{j}$, on a $\boldsymbol{f}(\mathfrak{i}, \mathfrak{j}) \leqslant 4$.
|
| 154 |
+
|
| 155 |
+
Par l'absurde : supposons qu'il existe $i$ et $j$ tels que $f(i, j) \geqslant 5$.
|
| 156 |
+
D'après a), c'est donc que $f(i, j)=5$. Cela signifie que la ligne $L_{j}$ ne contient que des $i$. En particulier, on a $f(j, j)=i$.
|
| 157 |
+
|
| 158 |
+
Si $i>0$, la ligne $L_{j}$ doit donc contenir au moins un $\boldsymbol{j}$. Comme elle ne contient que des $\mathfrak{i}, c^{\prime}$ est que $\boldsymbol{i}=\mathfrak{j}$ et que $5=\boldsymbol{f}(\mathfrak{i}, \mathfrak{j})=\mathbf{f}(\mathfrak{j}, \mathfrak{j})=\mathfrak{i}$, en contradiction avec $\mathfrak{i} \leqslant 4$.
|
| 159 |
+
|
| 160 |
+
Ainsi, on a $i=0$ et il n'y a que des 0 sur la ligne $L_{j}$. Puisque $x_{j} \leqslant 5$, il n'y a que des 0 sur $C_{j}$ sauf $f(0, j)=5$. En particulier, chaque ligne $L_{k}$ contient au moins un 0 pour $k>0$. Cela assure que $f(0, k) \neq 0$ pour tout $k>0$. Mais, on a vu que $f(0,0)>0$ donc il doit $y$ avoir au moins un 0 sur $L_{0}$, alors qu'on vient de prouver qu'aucun des nombres sur $L_{0}$ n'est égal à 0 . Contradiction. $^{\prime}$.
|
| 161 |
+
|
| 162 |
+
Finalement, on a $f(i, j) \leqslant 4$, pour tous $i$ et $j$.
|
| 163 |
+
e) On a $x_{i}=5$ pour tout $i$.
|
| 164 |
+
|
| 165 |
+
Maintenant que l'on sait qu'il n'y a pas de 5 dans le tableau, on reprend le calcul et raisonnement du c), mais il n'y a plus d'inégalité...
|
| 166 |
+
|
| 167 |
+
Ainsi, on a $x_{i}=5$ pour tout $i$.
|
| 168 |
+
f) On a $y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}=25$.
|
| 169 |
+
|
| 170 |
+
Il suffit de remarquer que, pour tout $i$, le nombre $y_{i}$ est le nombre de $i$ qui apparaîssent dans le tableau. Donc $0 y_{0}+y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}$ est la somme de tous les nombres du tableau, et on a $y_{1}+2 y_{2}+3 y_{3}+4 y_{4}+5 y_{5}=x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=25$.
|
| 171 |
+
g) On a $f(0,1)=0$ et $f(0, i) \geqslant 1$ pour tout $i \geqslant 2$.
|
| 172 |
+
|
| 173 |
+
Par l'absurde : Supposons qu'il existe $i \geqslant 3$ tel que $f(0, i)=0$.
|
| 174 |
+
Alors, il n'y a aucun 0 sur $L_{i}$, ce qui entraine que chaque ligne contient au moins un $i$. Alors, on a $y_{j} \geqslant i \geqslant 3$.
|
| 175 |
+
|
| 176 |
+
D'après f), il vient alors $25 \geqslant(0+1+2+3+4) \times 3=30$. Contradiction.
|
| 177 |
+
Ainsi, on a $f(0,3)>0$ et $f(0,4)>0$.
|
| 178 |
+
Par l'absurde: Supposons que $f(0,2)=0$.
|
| 179 |
+
Comme ci-dessus, cela signifie que chaque ligne contient au moins un 2. Mais alors, chacun des nombres $0,1,3,4$ ( 2 aussi, mais il va avoir un traitement particulier) apparaît au moins deux fois dans le tableau, d'où $y_{i} \geqslant 2$ pour $i=0,1,3,4$.
|
| 180 |
+
|
| 181 |
+
D'autre part, il y a 5 cases sur $\mathrm{L}_{2}$, aucune ne contenant 0 et au moins une contenant un 2, d'où $y_{2} \geqslant 6$. En utilisant f ), il vient
|
| 182 |
+
$25 \geqslant(0+1+3+4) \times 2+2 \times 6=28$. Contradiction.
|
| 183 |
+
Par suite, on a $f(0,2)>0$.
|
| 184 |
+
Or, on a vu que $f(0,0)>0$ et donc qu'il y a au moins un 0 sur $L_{0}$. Comme $f(0, i)>0$ pour tout $i \neq 1$, $c^{\prime}$ est que $f(0,1)=0$.
|
| 185 |
+
|
| 186 |
+
Finalement, on a $f(0,1)=0$ et $f(0, i) \geqslant 1$ pour tout $i \geqslant 2$.
|
| 187 |
+
Il n'y a donc qu'un seul nombre non nul sur $L_{0}$, d'où $f(0,0)=1$.
|
| 188 |
+
h) On a $y_{1} \geqslant 8$.
|
| 189 |
+
|
| 190 |
+
Puisque $f(0,1)=0$, il n'y a aucun 0 sur $L_{1}$. En particulier, $f(1,1) \geqslant 1$ donc il y a au moins un 1 sur $L_{1}$.
|
| 191 |
+
|
| 192 |
+
- Il ne peut y avoir que des 1 sur $L_{1}$, car alors $f(1,1)=1$ et $f(1,1)=5$, ce qui est impossible.
|
| 193 |
+
- S'il y a quatre 1 , on a $\mathrm{f}(1,1)=4$ et tous les autres sont des 1 , d'où $y_{1}=8$.
|
| 194 |
+
- S'il y a trois 1 , alors $\mathrm{f}(1,1)=3$ et un autre des nombres est supérieur ou égal à 2 , donc $y_{1} \geqslant 3+1+1+1+2=8$.
|
| 195 |
+
- S'il y a deux 1 , le même raisonnement conduit à $y_{1} \geqslant 2+1+1+2+2=8$.
|
| 196 |
+
- S'il n'y a qu'un seul 1 , alors c'est $\mathrm{f}(1,1)=1$ et les autres sont supérieurs ou égaux à 2 , donc $y_{1} \geqslant 1+4 \times 2=9$.
|
| 197 |
+
|
| 198 |
+
Ainsi, on a $y_{1} \geqslant 8$.
|
| 199 |
+
i) On a $f(4,2)=f(4,3)=f(4,4)=0$, et donc que $f(0,4) \geqslant 3$.
|
| 200 |
+
|
| 201 |
+
Il n'y a aucun 0 dans $L_{1}$ donc chaque ligne contient au moins un 1.
|
| 202 |
+
Par l'absurde: supposons qu'il y ait un 4 sur $\mathrm{L}_{2}, \mathrm{~L}_{3}$ ou $\mathrm{L}_{4}$.
|
| 203 |
+
|
| 204 |
+
- S'il y a un 4 sur $L_{4}$, comme il y a aussi au moins un 1 , on a $y_{4} \geqslant 5$. Compte-tenu de $y_{1} \geqslant 8$, la formule du f) conduit à $25 \geqslant 28$, ce qui est impossible. Il n'y a donc pas de 4 sur $\mathrm{L}_{4}$.
|
| 205 |
+
- S'il y a un 4 sur $L_{3}$, comme il y a aussi au moins un 1 , on a $y_{3} \geqslant 5$. Compte-tenu de $y_{1} \geqslant 8$ et $y_{4} \geqslant 1$, la formule du f) conduit à $25 \geqslant 27$, ce qui est encore impossible. Il n'y a donc pas de 4 sur $\mathrm{L}_{3}$.
|
| 206 |
+
- S'il y a un 4 sur $L_{2}$ : dans chaque colonne, sauf $C_{1}$, les lignes $L_{0}$ et $L_{1}$ ont toutes les deux un nombre non nul. Or, la somme des termes d'une colonne vaut 5 d'après e), donc le $4 \mathrm{de} \mathrm{L}_{2}$ ne peut être que dans $C_{1}$, c'est-à-dire $f(2,1)=4$. Il y a donc quatre 2 dans $L_{1}$, d'où $y_{1} \geqslant 9$. Comme on a $y_{2} \geqslant 5, y_{3} \geqslant 1$ et $y_{4} \geqslant 1$, la formule du f) conduit à $25 \geqslant 26$, ce qui est encore impossible. Il n'y a donc pas de 4 sur $\mathrm{L}_{3}$.
|
| 207 |
+
|
| 208 |
+
Finalement, il n'y a aucun 4 dans les cases des lignes $L_{2}, L_{3}$ et $L_{4}$.
|
| 209 |
+
Cela prouve que $\mathbf{f}(4,2)=\mathbf{f}(4,3)=\mathbf{f}(4,4)=0$, et donc que $\mathbf{f}(0,4) \geqslant 3$.
|
| 210 |
+
j) On a $\boldsymbol{f}(3,2)=\boldsymbol{f}(3,3)=\mathfrak{f}(3,4)=0$, et donc que $f(0,3) \geqslant 3$.
|
| 211 |
+
|
| 212 |
+
Par l'absurde : supposons qu'il y ait un 3 dans les lignes $\mathrm{L}_{2}, \mathrm{~L}_{3}$ ou $\mathrm{L}_{4}$.
|
| 213 |
+
|
| 214 |
+
- S'il y a un 3 sur $L_{4}$, compte-tenu des 1 sur chaque ligne et de $h$ ), on a $y_{4} \geqslant 4$ et $y_{1} \geqslant 8$. Comme au i), la formule du f) conduit alors à une contradiction. Il n'y a donc pas de 3 sur $\mathrm{L}_{4}$.
|
| 215 |
+
- S'il y a un 3 sur $L_{3}$, compte-tenu des 1 sur chaque ligne et de $h$ ), on a cette fois $y_{4} \geqslant 1, y_{3} \geqslant$ $4, y_{2} \geqslant 1$ et $y_{1} \geqslant 8$. Comme au i), la formule du f) conduit alors à une contradiction. Il n'y a donc pas de 3 sur $L_{3}$.
|
| 216 |
+
- S'il y a un 3 sur $\mathrm{L}_{2}$ : notons que l'on a $\mathrm{f}(0,4) \geqslant 3$ et $\mathrm{f}(1,4) \geqslant 1$. Puisque $x_{4}=5$, il est impossible que $f(2,4)=3$.
|
| 217 |
+
|
| 218 |
+
De même pour $C_{3}$, comme $\mathrm{f}(0,3) \geqslant 2$ et $\mathrm{f}(1,3) \geqslant 1$, on ne peut avoir $\mathrm{f}(2,3)=3$.
|
| 219 |
+
Si $\mathrm{f}(2,2)=3$ alors $y_{2} \geqslant 7$. Avec $y_{4} \geqslant 1, y_{3} \geqslant 1$ et $y_{1} \geqslant 8$, on obtient le même type de contradiction que ci-dessus par utilisation de c).
|
| 220 |
+
|
| 221 |
+
Si $\mathrm{f}(2,0)=3$ alors, puisque $\mathrm{f}(0,0)=1$ et $\mathrm{f}(0,1)=0$, la ligne $\mathrm{L}_{0}$ est déterminée et, en particulier, on a $f(0,4)=2$, en contradiction avec les trois 0 que l'on a déjà identifiés sur $L_{4}$.
|
| 222 |
+
|
| 223 |
+
Reste à étudier le cas $\mathrm{f}(2,1)=3$.
|
| 224 |
+
On sait que $y_{4} \geqslant 1, y_{3} \geqslant 1, y_{2} \geqslant 4$ et $y_{1} \geqslant 8$. En l'état, le f) n'apporte pas de contradiction, mais permet de voir que si $y_{4} \geqslant 2$ ou $y_{3} \geqslant 2$, on en obtiendrait une. Donc, on doit avoir $y_{4}=y_{3}=1$, ce qui permet de remplir $L_{3}$ et donc $C_{3}$, et de savoir que $f(0,3)=f(0,4)=4$ ainsi que $\mathrm{f}(1,4)=\mathrm{f}(1,3)=1$. Comme $x_{4}=\mathrm{x}_{3}=5$, les colonnes $C_{3}$ et $C_{4}$ sont complètes. Les trois 2 sur $L_{1}$ permettent de compléter $L_{1}$ et donc $C_{1}$. Ces mêmes 2 sur $L_{1}$ permettent aussi de remplir
|
| 225 |
+
les trous sur $L_{0}$ et $L_{2}$ et de finir de remplir le tableau. On obtient
|
| 226 |
+
|
| 227 |
+
| 1 | 0 | 0 | 0 | 0 |
|
| 228 |
+
| :--- | :--- | :--- | :--- | :--- |
|
| 229 |
+
| 0 | 0 | 1 | 0 | 0 |
|
| 230 |
+
| 1 | 3 | 1 | 0 | 0 |
|
| 231 |
+
| 2 | 2 | 2 | 1 | 1 |
|
| 232 |
+
| 1 | 0 | 1 | 4 | 4 |
|
| 233 |
+
|
| 234 |
+
En particulier, on a $f(2,0)=1$ et pas de 2 sur $\mathrm{L}_{0}$. Contradiction.
|
| 235 |
+
Finalement, il n'y a aucun 3 dans les cases des lignes $\mathrm{L}_{2}, \mathrm{~L}_{3}$ et $\mathrm{L}_{4}$.
|
| 236 |
+
Cela prouve que $\mathbf{f}(3,2)=\mathbf{f}(3,3)=\mathbf{f}(3,4)=0$, et donc que $\mathbf{f}(0,3) \geqslant 3$.
|
| 237 |
+
k) On trouve tous les tableaux cohérents.
|
| 238 |
+
|
| 239 |
+
D'après ce qui précède, on part d'un tableau de la forme
|
| 240 |
+
|
| 241 |
+
| . | . | 0 | 0 | 0 |
|
| 242 |
+
| :--- | :--- | :--- | :--- | :--- |
|
| 243 |
+
| . | . | 0 | 0 | 0 |
|
| 244 |
+
| . | . | . | . | . |
|
| 245 |
+
| . | . | . | . | . |
|
| 246 |
+
| 1 | 0 | . | a | b |
|
| 247 |
+
|
| 248 |
+
avec $\boldsymbol{a}, \boldsymbol{b} \geqslant 3$, et aucun terme nul sur $\mathrm{L}_{1}$. Comme $\boldsymbol{a}, \boldsymbol{b} \in\{3,4\}$ et que la somme par colonne doit toujours donner 5 , on tombe assez rapidement sur les deux seuls tableaux cohérents, à savoir :
|
| 249 |
+
|
| 250 |
+
| 1 | 0 | 0 | 0 | 0 |
|
| 251 |
+
| :--- | :--- | :--- | :--- | :--- |
|
| 252 |
+
| 2 | 1 | 0 | 0 | 0 |
|
| 253 |
+
| 0 | 1 | 0 | 1 | 0 |
|
| 254 |
+
| 1 | 3 | 2 | 1 | 1 |
|
| 255 |
+
| 1 | 0 | 3 | 3 | 4 |
|
| 256 |
+
|
| 257 |
+
|
| 258 |
+
| 2 | 1 | 0 | 0 | 0 |
|
| 259 |
+
| :--- | :--- | :--- | :--- | :--- |
|
| 260 |
+
| 1 | 0 | 0 | 0 | 0 |
|
| 261 |
+
| 0 | 0 | 0 | 0 | 1 |
|
| 262 |
+
| 1 | 4 | 1 | 1 | 1 |
|
| 263 |
+
| 1 | 0 | 4 | 4 | 3 |
|
| 264 |
+
|
| 265 |
+
Remarque. Pour information, en affinant un peu ce qui précède, on peut prouver qu'il n'existe de tableau $n \times n$ cohérent que pour $n=5$.
|
| 266 |
+
|
French_STS/md/fr-ofm-2014-2015-envoi-6-solutions.md
ADDED
|
@@ -0,0 +1,245 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OLYMPIADES FRANÇAISES DE MATHÉMATIQUES <br>  <br> TEST D'ENTRAINEMENT (envoi 6) <br> Corrigé
|
| 2 |
+
|
| 3 |
+
Exercice 1. Calculer
|
| 4 |
+
|
| 5 |
+
$$
|
| 6 |
+
\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}+\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}+\cdots+\sqrt{1+\frac{1}{2014^{2}}+\frac{1}{2015^{2}}}
|
| 7 |
+
$$
|
| 8 |
+
|
| 9 |
+
Solution de l'exercice 1 On réduit au même dénominateur
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\begin{aligned}
|
| 13 |
+
1+\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}} & =\frac{n^{2}(n+1)^{2}+(n+1)^{2}+n^{2}}{n^{2}(n+1)^{2}} \\
|
| 14 |
+
& =\frac{n^{4}+n^{2}(2 n+1)+n^{2}+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
|
| 15 |
+
& =\frac{n^{4}+2 n^{2}(n+1)+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
|
| 16 |
+
& =\frac{\left(n^{2}+(n+1)\right)^{2}}{n^{2}(n+1)^{2}}
|
| 17 |
+
\end{aligned}
|
| 18 |
+
$$
|
| 19 |
+
|
| 20 |
+
On en déduit que la somme recherchée vaut
|
| 21 |
+
|
| 22 |
+
$$
|
| 23 |
+
\begin{aligned}
|
| 24 |
+
\sum_{n=1}^{2014} \frac{n^{2}+n+1}{n(n+1)} & =\sum_{n=1}^{2014} 1+\frac{1}{n(n+1)} \\
|
| 25 |
+
& =2014+\sum_{n=1}^{2014} \frac{1}{n(n+1)} \\
|
| 26 |
+
& =2014+\sum_{n=1}^{2014} \frac{1}{n}-\frac{1}{n+1} \\
|
| 27 |
+
& =2014+\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2014}-\frac{1}{2015}\right)
|
| 28 |
+
\end{aligned}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
On reconnaît une somme télescopique. Les termes se simplifient deux à deux, sauf 1 et $\frac{1}{2015}$, donc la somme vaut
|
| 32 |
+
|
| 33 |
+
$$
|
| 34 |
+
2014+1-\frac{1}{2015}=2015-\frac{1}{2015}
|
| 35 |
+
$$
|
| 36 |
+
|
| 37 |
+
Exercice 2. Soient $p$ et $q$ deux nombres premiers supérieurs ou égaux à 7 . Soit $x=\frac{p^{2012}+q^{2016}}{120}$. Calculer $x-[x]$, où $[x]$ désigne la partie entière de $x$, c'est-à-dire le plus grand entier inférieur ou égal à $x$.
|
| 38 |
+
Solution de l'exercice 2 Si a est un entier non divisible par 2,3 et 5 , on vérifie facilement que a ${ }^{4}$ est congru à 1 modulo 3,5 et 8 . Autrement dit, a ${ }^{4}-1$ est divisible par 3,5 et 8 , donc par $3 \times 5 \times 8=$ 120 . On en déduit que $p^{4}$ et $q^{4}$ sont congrus à 1 modulo 120 , donc $p^{2012}+q^{2016} \equiv 1+1 \equiv 2$ $(\bmod 120)$.
|
| 39 |
+
On en déduit que $x-[x]=\frac{2}{120}=\frac{1}{60}$.
|
| 40 |
+
Exercice 3. Soit $A B C$ un triangle. On dessine des triangles équilatéraux $A B E$ et $A C F$ à l'extérieur de $A B C$. Soit $G$ le centre de gravité de $A B E$ et K le milieu de $[E F]$. Déterminer les angles du triangle KCG.
|
| 41 |
+
|
| 42 |
+
## $\underline{\text { Solution de l'exercice } 3}$
|
| 43 |
+
|
| 44 |
+
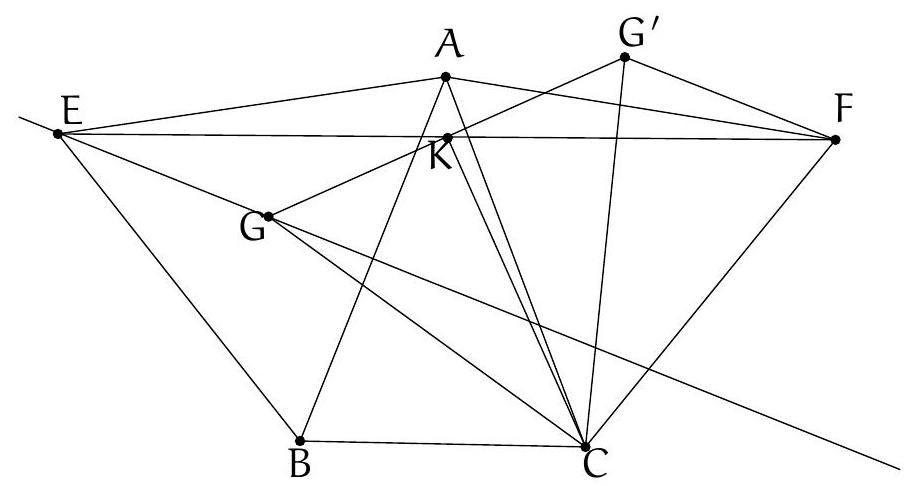
|
| 45 |
+
|
| 46 |
+
Montrons que GKC est rectangle en $K$ avec $\widehat{C G K}=60^{\circ}$. Pour cela, considérons le symétrique $\mathrm{G}^{\prime}$ de $G$ par rapport à $K$ : il suffit de montrer que $\mathrm{GCG}^{\prime}$ est équilatéral.
|
| 47 |
+
Comme EGFG' est un parallélogramme, on a $G^{\prime} F=E G$, et comme $G$ est le centre du cercle circonscrit à $A B E$, on a $G A=G E$, donc $G A=G^{\prime} F$.
|
| 48 |
+
$\mathrm{D}^{\prime}$ autre part, $\mathrm{AC}=\mathrm{FC}$ car $A F C$ est équilatéral.
|
| 49 |
+
Enfin, $\widehat{\mathrm{GAC}}=30^{\circ}+\widehat{\mathrm{BAC}}$ et $(\overrightarrow{\mathrm{FG}}, \overrightarrow{\mathrm{FC}})=(\overrightarrow{\mathrm{GE}}, \overrightarrow{\mathrm{FC}})=(\overrightarrow{\mathrm{GE}}, \overrightarrow{A G})+(\overrightarrow{A G}, \overrightarrow{A C})+(\overrightarrow{A C}, \overrightarrow{F C})=$ $60^{\circ}+(\overrightarrow{A G}, \overrightarrow{A C})-60^{\circ}=(\overrightarrow{A G}, \overrightarrow{A C})$, donc $G A C$ et $G^{\prime} F C$ sont isométriques.
|
| 50 |
+
Or, F est obtenu à partir de $A$ en effectuant une rotation de $60^{\circ}$ sutour de C , donc cette rotation envoie le triangle GAC sur $\mathrm{G}^{\prime} \mathrm{FC}$. En particulier, $\mathrm{GC}=\mathrm{G}^{\prime} \mathrm{C}$ et $\widehat{\mathrm{GCG}^{\prime}}=60^{\circ}$, ce qui conclut.
|
| 51 |
+
|
| 52 |
+
Autre méthode. Si on connaît les nombres complexes, il est facile de résoudre l'exercice par une méthode analytique systématique.
|
| 53 |
+
On prend un repère tel que $A$ soit l'origine. On nomme $b, c, e, f, g, k$ les affixes de $B, C, E, F, G, K$. On a alors $e=e^{-i \pi / 3} \mathrm{~b}, \mathrm{f}=e^{i \pi / 3} \mathrm{c}, \mathrm{k}=(e+\mathrm{f}) / 2, \mathrm{~g}=(\mathrm{b}+\mathrm{e}) / 3$. Il est alors facile de vérifier que $\mathrm{c}-\mathrm{k}=\mathrm{i} \sqrt{3}(\mathrm{~g}-\mathrm{k})$, ce qui montre que $(\mathrm{CK}) \perp(\mathrm{GK})$ et que $\mathrm{CK}=\mathrm{GK} \times \sqrt{3}$, ce qui conclut.
|
| 54 |
+
Exercice 4. Soit $\mathrm{n} \geqslant 1$ un entier.
|
| 55 |
+
On considère un ensemble de $4 \mathrm{n}+5$ points du plan, trois jamais alignés, et chacun coloré soit en rouge soit en bleu.
|
| 56 |
+
|
| 57 |
+
Prouver qu'il existe $n$ triangles dont les sommets sont tous d'une même couleur (la même pour tous les triangles), et dont les intérieurs respectifs sont deux à deux disjoints et ne contiennent aucun point coloré.
|
| 58 |
+
|
| 59 |
+
## Solution de l'exercice 4
|
| 60 |
+
|
| 61 |
+
Lemme. Soit $\mathrm{n} \geqslant 3$ et $\mathrm{m} \geqslant 1$ des entiers.
|
| 62 |
+
On considère un n-gone convexe $P$ et $m$ de ses points intérieurs, trois des $n+m$ points jamais alignés. Alors, on peut trianguler $P$ en $n+2 m-2$ triangles dont les somments sont tous parmi les $n+m$ points, aucun de ces triangles ne contenant un des $m$ points en son intérieur.
|
| 63 |
+
|
| 64 |
+
## Preuve du lemme. On procède par récurrence sur m.
|
| 65 |
+
|
| 66 |
+
Pour $\mathrm{m}=1$, il suffit de joindre le point intérieur à chacun des sommets, ce qui donne une triangulation adéquate de $P$ en $k$ triangles.
|
| 67 |
+
Supposons que l'affirmation soit vraie pour la valeur $m$ et donnons-nous $m+1$ points intérieurs à $P$. Soit I un de ces points intérieurs. A l'aide des m autres points intérieurs, d'après l'hypothèse de récurrence, on peut trianguler $P$ de la façon souhaitée en $k+2 m-2$ triangles. Comme I est intérieur à $P$, il est donc intérieur à l'un de ces triangles. En joignant I à chacun des trois sommets de ce triangle, on obtient ainsi une triangulation adéquate en $k+2 \mathrm{~m}-2+2=\mathrm{k}+$ $2(m+1)-2$ triangles, ce qui achève la preuve.
|
| 68 |
+
|
| 69 |
+
Revenons à l'exercice. Notons $r$ (resp. b) le nombre de points rouges (resp. bleus). On a donc $r+b=4 n+5$.
|
| 70 |
+
Sans perte de généralité, on peut supposer que $r \geqslant b$ et donc $r \geqslant 2 \mathfrak{n}+3$.
|
| 71 |
+
Soit $P$ l'enveloppe convexe des points rouges, et on suppose que $P$ est un k-gone. En particulier, il n'existe aucun point rouge en dehors de $P$, donc il y a $m$ points rouges intérieurs à $P$, avec $\mathrm{k}+\mathrm{m}=\mathrm{r} \geqslant 2 \mathrm{n}+3$. (1)
|
| 72 |
+
On note $w$ le nombre points bleus intérieurs à $P$.
|
| 73 |
+
D'après le lemme, en ne considérant que les points rouges, on peut obtenir une triangulation de $P$ en $k+2 m-2$ triangles à sommets rouges et ne contenant intérieurement aucun point rouge. Si au moins n de ces triangles ne contiennent aucun point bleu, c'est fini.
|
| 74 |
+
Sans quoi, au plus $n-1$ des triangles à sommets rouges ne contiennent pas de point bleu. Cela assure qu'au moins $k+2 m-2-(n-1)=k+2 m-(n+1)$ triangles à sommets rouges contiennent chacun au moins un point bleu et, ces triangles étant d'intérieurs deux à deux disjoints, on a donc $w \geqslant k+2 m-(n+1)$.
|
| 75 |
+
Soit $Q$ l'enveloppe convexe de ces $w$ points bleus intérieurs à $P$. Comme ci-dessus, on peut trianguler $Q$ en au moins $w-2$ triangles ne contenant aucun point bleu en leurs intérieurs.
|
| 76 |
+
Par l'absurde : supposons qu'au plus $n-1$ de ces triangles bleus ne contiennent pas de point rouge.
|
| 77 |
+
Alors, au moins $w-2-(n-1)$ triangles bleus contiennent au moins un point rouge et on a $m \geqslant w-(n+1)$. Par suite, on a $m \geqslant k+2 m-(n+1)-(n+1)$, d'où $k+m \leqslant 2 n+2$, en contradiction avec (1).
|
| 78 |
+
|
| 79 |
+
Ainsi, au moins $n$ de ces triangles à sommets bleus ne contiennent aucun point rouge, ce qui conclut.
|
| 80 |
+
Exercice 5. Soit $A B C$ un triangle non isocèle inscrit dans un cercle $\Gamma$ de rayon $R$. Le cercle passant par $A$ et tangent en $C$ à $[B C]$ recoupe le cercle passant par $B$ et tangent en $C$ à $[A C]$ au point D .
|
| 81 |
+
a) Montrer que $C D \leqslant R$.
|
| 82 |
+
b) Montrer que lorsque $C$ se déplace sur $\Gamma$, la droite (CD) passe par un point fixe.
|
| 83 |
+
|
| 84 |
+
## Solution de l'exercice 5
|
| 85 |
+
|
| 86 |
+
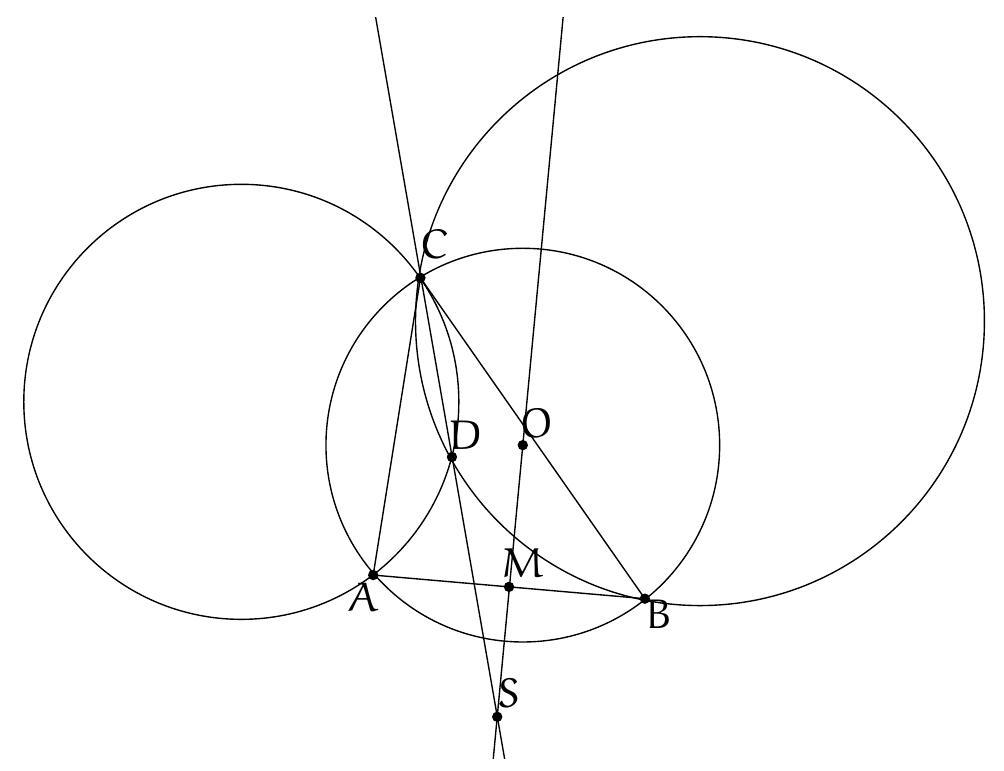
|
| 87 |
+
a) On observe d'abord que $(A D, A C)=(C D, C B)$ et $(B C, B D)=(C A, C D)$, donc $D A C$ et $D C B$ sont directement semblables. On en déduit que $D^{2}=D A \cdot D B$.
|
| 88 |
+
De plus, en notant $\gamma=(\overrightarrow{C A}, \overrightarrow{C B})$, on a $(\overrightarrow{D C}, \overrightarrow{D A})=\pi-\gamma$ et de même $(\overrightarrow{D B}, \overrightarrow{D C})=\pi-\gamma$, donc $(\overrightarrow{D A}, \overrightarrow{D B})=2 \gamma$. Il vient
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
\begin{aligned}
|
| 92 |
+
A^{2} & =D^{2}+D^{2}-2 D A \cdot D B \cos 2 \gamma=D A^{2}+D^{2}-2 D A \cdot D B\left(1-2 \sin ^{2} \gamma\right) \\
|
| 93 |
+
& =(D A-D B)^{2}+4 D A \cdot D B \sin ^{2} \gamma \geqslant 4 D A \cdot D B \sin ^{2} \gamma=(2 D C \sin \gamma)^{2} .
|
| 94 |
+
\end{aligned}
|
| 95 |
+
$$
|
| 96 |
+
|
| 97 |
+
Or, $2 R=\frac{A B}{\sin \gamma}$, donc $R \geqslant C D$.
|
| 98 |
+
b) On va montrer que (CD) passe par le point de rencontre des tangentes en $A$ et $B$ au cercle circonscrit, que nous appellerons $S$. Il est connu que (CS) est la symédiane du triangle passant par C, donc il suffit de montrer que (CD) est une symédiane.
|
| 99 |
+
Notons $M$ le milieu de $[A B]$. Comme les aires de $A C M$ et $B C M$ sont égales, on a $\frac{1}{2} C A \times C M \times$ $\sin \widehat{A C M}=\frac{1}{2} C B \times C M \times \sin \widehat{M C B}$, donc $C A \sin \widehat{A C M}=C B \sin \widehat{M C B}$.
|
| 100 |
+
On en déduit que si $\Delta$ est la symédiane et $\theta$ est l'angle entre $(C A)$ et $\Delta$, alors $\frac{\sin \theta}{\sin (\gamma-\theta)}=$ $\frac{\sin \widehat{M C B}}{\sin \widehat{A C M}}=\frac{C A}{C B}$. Il suffit donc de montrer que $\frac{\sin \widehat{A C D}}{\sin \widehat{D C B}}=\frac{C A}{C B}$.
|
| 101 |
+
|
| 102 |
+
$$
|
| 103 |
+
\begin{aligned}
|
| 104 |
+
\frac{\sin \widehat{A C D}}{\sin \widehat{D C B}} & =\frac{\sin \widehat{A C D}}{A D} \times \frac{D B}{\sin \widehat{D C B}} \times \frac{D A}{D B} \\
|
| 105 |
+
& =\frac{\sin \widehat{C D A}}{A C} \times \frac{B C}{\sin \widehat{B D C}} \times \frac{D A}{D B}
|
| 106 |
+
\end{aligned}
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Or, $\widehat{C D A}=\widehat{B D C}=\pi-\gamma$ et $\frac{B C}{A C}=\frac{D C}{D A}=\frac{D B}{D C}$, donc
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\frac{\sin \widehat{A C D}}{\sin \widehat{D C B}}=\frac{B C}{A C} \times \frac{D A}{D C} \times \frac{D C}{D B}=\frac{D C}{D B}=\frac{C A}{C B}
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Exercice 6. Existe-t-il des entiers strictement positifs $a$ et $b$ tels que $a^{n}+n^{b}$ et $b^{n}+n^{a}$ soient premiers entre eux pour tout entier $n \geqslant 0$ ?
|
| 116 |
+
|
| 117 |
+
## Solution de l'exercice 6
|
| 118 |
+
|
| 119 |
+
Par l'absurde : supposons qu'il existe de tels entiers a et b.
|
| 120 |
+
Par symétrie, on peut supposer que $a \geqslant b$.
|
| 121 |
+
Si $d=\operatorname{pgcd}(a, b)$ alors, pour $n=d$, il est clair que $d$ divise $a^{d}+d^{b}$ et $b^{d}+d^{a}$. Or ces deux nombres étant censés être premiers entre eux, c'est que $d=1$.
|
| 122 |
+
|
| 123 |
+
Soit $N=a^{a}+b^{b}$. On a $N>1$ donc il existe un nombre premier $p$ qui divise $N$. De plus, $p$ ne peut diviser a sans quoi il devrait diviser également $b$, en contradiction avec $d=1$. Ainsi, $a$ est inversible modulo $p$ et il existe un entier $k \in\{0, \cdots, p-1\}$ tel que $k a=b \bmod [p]$.
|
| 124 |
+
|
| 125 |
+
On choisit alors $n=k+p(a-b-k+p-1)$. D'après le petit théorème de Fermat, il vient :
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
a^{n}+n^{b} \equiv a^{k} \cdot a^{a-b-k+p-1}+k^{b} \equiv a^{a-b}+k^{b} \bmod [p]
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
$d^{\prime}$ où $a^{b}\left(a^{n}+n^{b}\right) \equiv a^{a}+b^{b} \equiv 0 \bmod [p]$,
|
| 132 |
+
et, puisque $p$ ne divise par $a$, on a alors $a^{n}+n^{b} \equiv 0 \bmod [p]$.
|
| 133 |
+
On prouve de même, on a $b^{n}+n^{a} \equiv 0 \bmod [p]$.
|
| 134 |
+
Mais, alors $p$ divise à la fois $a^{n}+n^{b}$ et $b^{n}+n^{a}$, ce qui contredit qu'ils soient premiers entre eux.
|
| 135 |
+
|
| 136 |
+
Finalement, il n'existe pas de tels entiers.
|
| 137 |
+
Exercice 7. Les Xantiens sont les habitants, en nombre éventuellement infini, de la planète Xanta. Vis-à-vis d'eux-mêmes et de leurs semblables, les Xantiens sont capables de ressentir deux types d'émotions, qu'ils appellent amour et respect. Il a été observé que:
|
| 138 |
+
|
| 139 |
+
- Chaque Xantien aime un et un seul Xantien, et respecte un et un seul Xantien.
|
| 140 |
+
- Si $A$ aime $B$, alors tout Xantien qui respecte $A$ aime également $B$.
|
| 141 |
+
- Si $A$ respecte $B$, alors tout Xantien qui aime $A$ respecte également $B$.
|
| 142 |
+
- Chaque Xantien est aimé d'au moins un Xantien.
|
| 143 |
+
|
| 144 |
+
Est-il vrai que chaque Xantien respecte le Xantien qu'il aime?
|
| 145 |
+
|
| 146 |
+
## Solution de l'exercice 7
|
| 147 |
+
|
| 148 |
+
Pour chaque Xantien $x$, désignons respectivement par $f(x)$ et $g(x)$ les Xantiens aimés et respectés par $x$.
|
| 149 |
+
La première condition assure que l'on a bien défini des fonctions $f$ et $g$ de l'ensemble $X$ des Xantiens sur lui-même.
|
| 150 |
+
Il s'agit de savoir si, pour tout $x$, on a $f(x)=g(x)$.
|
| 151 |
+
En fait, nous allons même prouver que, pour tout $x$, on a $f(x)=g(x)=x$.
|
| 152 |
+
Soit $x$ un Xantien.
|
| 153 |
+
Il respecte $g(x)$ qui, de son côté, aime $f(g(x))$.
|
| 154 |
+
La seconde condition assure donc que $f(g(x))=f(x)$ pour tout $x$. (1)
|
| 155 |
+
De même, la troisième condition conduit à $g(f(x))=g(x)$ pour tout $x$. (2)
|
| 156 |
+
Enfin, la quatrième condition signifie que f est surjective.
|
| 157 |
+
Soit $x$ un Xantien. Il existe donc un Xantien $y$ tel que $f(y)=x$.
|
| 158 |
+
Or, on a $f(g(f(y)))=f(g(y))$ d'après (2)
|
| 159 |
+
et ainsi, d'après (1), il vient $f(f(y))=f(y)$, ou encore $f(x)=x$.
|
| 160 |
+
De (1), on déduit alors immédiatement que $g(x)=x$.
|
| 161 |
+
Finalement, pour tout $x$, on a bien $f(x)=g(x)=x$.
|
| 162 |
+
Exercice 8. Déterminer tous les entiers strictement positifs a et $b$ tels que $4 \boldsymbol{a}+1$ et $4 \boldsymbol{b}-1$ soient premiers entre eux, et tels que $a+b$ divise $16 a b+1$.
|
| 163 |
+
Solution de l'exercice 8 Notons (C) la condition de l'énoncé. Les entiers $4 \mathbf{a}+1$ et $4 \mathrm{~b}-1$ sont premiers entre eux si et seulement si $4 \boldsymbol{a}+1$ est premier avec $(4 a+1)+(4 b-1)=4(a+b)$. Or, $4 \boldsymbol{a}+1$ est impair donc il est automatiquement premier avec 4 . On en déduit que $4 \boldsymbol{a}+1$ et $4 \boldsymbol{b}-1$ sont premiers entre eux si et seulement si $4 a+1$ est premier avec $a+b$.
|
| 164 |
+
D'autre part, $16 a b+1=16 a(a+b)+\left(1-16 a^{2}\right)=16 a(a+b)-(4 a-1)(1+4 a)$, donc $a+b$ divise $16 a b+1$ si et seulement si $a+b$ divise $(4 a-1)(1+4 a)$. Or, si $a+b$ est premier avec $1+4 a$ alors ceci équivaut à $a+b \mid 4 a-1$.
|
| 165 |
+
On en déduit que (C) équivaut à ce que $\operatorname{pgcd}(a+b, 4 a+1)=1$ et $a+b \mid 4 a-1$.
|
| 166 |
+
D'autre part, montrons que si $a+b \mid 4 a-1$ alors on a automatiquement $\operatorname{pgcd}(a+b, 4 a+1)=1$. En effet, si un nombre premier $p$ divise $a+b$ et $4 a+1$, alors il divise $4 a-1$ et $4 a+1$, donc il divise $(4 a+1)-(4 a-1)=2$. Il vient $p=2$, puis $2 \mid 4 a-1$. Impossible.
|
| 167 |
+
Finalement, (C) équivaut à $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$.
|
| 168 |
+
Or, $\mathrm{a}+\mathrm{b}>\mathrm{a}>\frac{4 \mathrm{a}-1}{4}$, donc $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$ ne peut se produire que si $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{2}$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$.
|
| 169 |
+
Le deuxième cas ne peut pas se produire car $4 a-1$ est impair.
|
| 170 |
+
(C) équivaut donc à $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$, $\mathrm{c}^{\prime}$ est-à-dire $\mathrm{b}=3 \mathrm{a}-1$ ou $\mathrm{a}=3 \mathrm{~b}+1$.
|
| 171 |
+
|
| 172 |
+
Exercice 9. Soit $A B C$ un triangle tel que $\widehat{A}=40^{\circ}$ et $\widehat{B}=60^{\circ}$. Soient $D$ et $E$ des points de [AC] et $[\mathrm{AB}]$ tels que $\widehat{\mathrm{CBD}}=40^{\circ}$ et $\widehat{\mathrm{ECB}}=70^{\circ}$. On note F l'intersection de (BD) et (CE). Monter que $(A F) \perp(B C)$.
|
| 173 |
+
|
| 174 |
+
## Solution de l'exercice 9
|
| 175 |
+
|
| 176 |
+
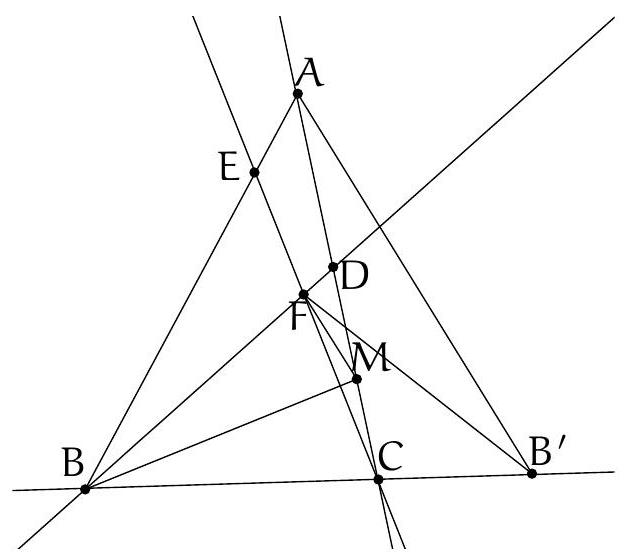
|
| 177 |
+
|
| 178 |
+
On a $\widehat{\mathrm{BFC}}=180^{\circ}-\widehat{\mathrm{CBF}}-\widehat{\mathrm{FCB}}=180^{\circ}-40^{\circ}-70^{\circ}=70^{\circ}=\widehat{\mathrm{FCB}}$ donc BCF est isocèle en B . Il vient $B C=B F$.
|
| 179 |
+
Soit $M$ le point d'intersection entre la bissectrice de $\widehat{C B F}$ et ( $A C$ ). On a $\widehat{B M A}=40^{\circ}=\widehat{B A M}$ donc $M A=M B$.
|
| 180 |
+
D'autre part, $\widehat{B M C}=180^{\circ}-\widehat{C B M}-\widehat{M C B}=180^{\circ}-20^{\circ}-80^{\circ}=80^{\circ}=\widehat{M C B}$ donc $B C=B M$.
|
| 181 |
+
On déduit de ce qui précède que $M A=B F$.
|
| 182 |
+
|
| 183 |
+
Soit $\mathrm{B}^{\prime} \in(\mathrm{BC})$ tel que $A B^{\prime}$ est équilatéral. Soit $\Delta$ la bissectrice de $\widehat{\mathrm{B}^{\prime} \mathrm{BA}}$. Comme $\mathrm{BF}=\mathrm{BM}$ et $\widehat{\mathrm{FBA}}=\widehat{\mathrm{CBM}}$, les points $M$ et $F$ sont symétriques par rapport à $\Delta$. Or, $A$ et $B^{\prime}$ sont aussi symétriques par rapport à $\Delta$, donc $M A=\mathrm{FB}^{\prime}$.
|
| 184 |
+
Finalement, $\mathrm{FB}^{\prime}=\mathrm{FB}$, donc $F$ appartient à la médiatrice de $\left[\mathrm{BB}^{\prime}\right]$, qui est aussi la hauteur ( $A F$ ) du triangle $A B B^{\prime}$.
|
| 185 |
+
Autre solution. Notons $H$ le projeté de $F$ sur $[B C]$ et $H^{\prime}$ le projeté de $A$ sur [BC]. Il s'agit de montrer que $\mathrm{H}=\mathrm{H}^{\prime}$. Pour cela, il suffit de voir que $\mathrm{BH}=\mathrm{BH}^{\prime}$.
|
| 186 |
+
On a $B^{\prime}=A B \cos 60$ et $B H=B F \cos 40=B C \cos 40$. Comme $\frac{A B}{B C}=\frac{\sin 80}{\sin 40}$, il suffit de montrer que $\sin 80 \cos 60=\sin 40 \cos 40$, c'est-à-dire (compte tenu de $\cos 60=\frac{1}{2}$ ) que $\sin 80=$ $2 \sin 40 \cos 40$, ce qui est vrai d'après la formule générale $\sin 2 x=2 \sin x \cos x$.
|
| 187 |
+
Exercice 10. Pour tout entier strictement positif $x$, on note $S(x)$ la somme des chiffres de son écriture décimale.
|
| 188 |
+
Soit $k>0$ un entier. On définit la suite $\left(x_{n}\right)$ par $x_{1}=1$ et $x_{n+1}=S\left(k x_{n}\right)$ pour tout $n>0$.
|
| 189 |
+
Prouver que $x_{n}<27 \sqrt{k}$, pour tout $n>0$.
|
| 190 |
+
|
| 191 |
+
## Solution de l'exercice 10
|
| 192 |
+
|
| 193 |
+
Lemme. Pour tout entier $s \geqslant 0$, on a $10^{s} \geqslant(s+1)^{3}$.
|
| 194 |
+
Preuve du lemme. On raisonne par récurrence sur s.
|
| 195 |
+
Pour $s=0$, on a $10^{0}=1=(0+1)^{3}$.
|
| 196 |
+
Supposons l'inégalité vraie pour la valeur s. Alors :
|
| 197 |
+
$10^{\mathrm{s}+1} \geqslant 10(\mathrm{~s}+1)^{3}$ d'après l'hypothèse de récurrence
|
| 198 |
+
$=10 s^{3}+30 s^{2}+30 s+10$
|
| 199 |
+
$\geqslant \mathrm{s}^{3}+6 \mathrm{~s}^{2}+12 \mathrm{~s}+8$
|
| 200 |
+
$=(s+2)^{3}$, ce qui achève la preuve.
|
| 201 |
+
Si $x>0$ est un entier dont l'écriture décimale utilise $s+1$ chiffres, on a $S(x) \leqslant 9(s+1)$ et $10^{s} \leqslant x<10^{s+1}$. Or, d'après le lemme, on a $s+1 \leqslant 10^{\frac{s}{3}}$, donc $s+1 \leqslant x^{\frac{1}{3}}$ et ainsi $S(x) \leqslant 9 x^{\frac{1}{3}}$.
|
| 202 |
+
Montrons maintenant par récurrence que $x_{n}<27 \sqrt{k}$ pour tout $n$. L'assertion est claire pour $n=1$. Supposons $x_{n}<27 \sqrt{k}$, alors $x_{n+1}=S\left(k x_{n}\right) \leqslant 9\left(k x_{n}\right)^{\frac{1}{3}}<9(27 k \sqrt{k})^{\frac{1}{3}}=9 \times 3 \times \sqrt{k}=$ $27 \sqrt{\mathrm{k}}$, d'où le résultat.
|
| 203 |
+
Exercice 11. Soient $a, b, c$ trois nombres réels strictement positifs tels que $a+b+c=9$. Montrer que
|
| 204 |
+
|
| 205 |
+
$$
|
| 206 |
+
\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 9
|
| 207 |
+
$$
|
| 208 |
+
|
| 209 |
+
Solution de l'exercice 11 On cherche une minoration de la forme $\frac{a^{3}+b^{3}}{a b+9} \geqslant u(a+b)+v, c^{\prime}$ est-àdire $f(a) \geqslant 0$ où $f(a)=a^{3}+b^{3}-(u(a+b)+v)(a b+9)$.
|
| 210 |
+
En sommant les trois inégalités, on en déduirait $\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 2 u(a+b+c)+3 v=$ $3(6 u+v)$, donc il suffit que $6 u+v=3$.
|
| 211 |
+
D'autre part, si une telle minoration existe, comme l'inégalité devient une égalité lorsque $\mathrm{a}=$ $\mathrm{b}=\mathrm{c}=3$, on doit avoir $\mathrm{f}(3)=0$ si $\mathrm{b}=3$. Comme de plus $\mathrm{f}(\mathrm{a}) \geqslant 0$ pour tout a , on doit nécessairement avoir $\mathrm{f}^{\prime}(3)=0$ pour $\mathrm{b}=3$.
|
| 212 |
+
Ceci impose la condition $0=f^{\prime}(3)=27-18 \mathbf{u}-(6 \mathbf{u}+\boldsymbol{v}) \times 3=18(1-\mathfrak{u})$, donc $\mathbf{u}=1$ et $v=-3$.
|
| 213 |
+
|
| 214 |
+
Montrons donc $\frac{a^{3}+b^{3}}{a b+9} \geqslant(a+b)-3$. Comme $a^{3}+b^{3} \geqslant \frac{(a+b)^{3}}{4}$ et $a b+9 \leqslant\left(\frac{a+b}{2}\right)^{2}+9$, il suffit de montrer que
|
| 215 |
+
|
| 216 |
+
$$
|
| 217 |
+
\frac{s^{3}}{s^{2}+36} \geqslant s-3
|
| 218 |
+
$$
|
| 219 |
+
|
| 220 |
+
où $s=a+b$. On réduit au même dénominateur; l'inégalité se simplifie en $3 s^{2}-36 s+108 \geqslant 0$, ou encore en $3(s-6)^{2} \geqslant 0$, ce qui est vrai.
|
| 221 |
+
Exercice 12. Déterminer tous les entiers $\mathrm{n}>0$ ayant la propriété suivante: "tout nombre strictement positif qui s'écrit comme la somme des carrés de $n$ entiers multiples de $n$ peut également s'écrire comme la somme des carrés de $n$ entiers dont aucun n'est un multiple de $\mathrm{n}^{\prime \prime}$.
|
| 222 |
+
|
| 223 |
+
## Solution de l'exercice 12
|
| 224 |
+
|
| 225 |
+
Un entier n ayant la propriété désirée sera dit bon.
|
| 226 |
+
Soit $\mathrm{n} \geqslant 2$ un entier bon. Alors 2 n est également bon : en effet, soit $\mathrm{m}=2 \mathrm{n}$ et soit $x_{1}, \cdots, x_{m}$ des entiers divisibles par m. Si deux de ces entiers sont non nuls, on peut supposer sans perte de généralité qu'il s'agit de $x_{1}$ et $x_{m}$. Puisque $n$ est bon, il existe alors des entiers $y_{i}$ non divisibles par $n$ (donc non divisibles par $m$ ) tels que $\sum_{i=1}^{n} x_{i}^{2}=\sum_{i=1}^{n} y_{i}^{2}$ et $\sum_{i=n+1}^{2 n} x_{i}^{2}=\sum_{i=n+1}^{2 n} y_{i}^{2}$. Ainsi, $\sum_{i=1}^{m} x_{i}^{2}=\sum_{i=1}^{m} y_{i}^{2}$ avec chaque $y_{i}$ non divisible par $m$.
|
| 227 |
+
Si un et un seul des $x_{i}$ est non nul, alors $\sum_{i=1}^{m} x_{i}^{2}$ est de la forme $(2 a)^{2}=a^{2}+a^{2}+a^{2}+a^{2}$ où $a>0$ est divisible par n et on raisonne de la même manière.
|
| 228 |
+
|
| 229 |
+
Lemme. Soit $\mathrm{n}>0$ un entier impair et $x_{1}, \cdots, x_{n}$ des entiers dont au moins un n'est pas divisible par $n$. Alors il existe des entiers $y_{1}, \cdots, y_{n}$ non divisibles par $n$ tels que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$.
|
| 230 |
+
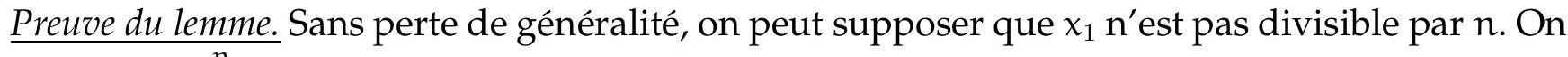 pose $X=2 \sum_{i=1}^{n} x_{i}$.
|
| 231 |
+
Si $n$ divise $X$, on remplace $x_{1}$ par $-x_{1}$. La nouvelle valeur $X^{\prime}$ vérifie $X^{\prime}=X-4 x_{1}$. Comme $n$ divise $X$ mais pas $4 x_{1}$ (rappelons que $n$ est supposé impair), il ne divise pas $X^{\prime}$. Ainsi, sans perte de généralité, on peut supposer que $n$ ne divise pas $X$.
|
| 232 |
+
Il est facile de vérifier que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n}\left(X-n x_{i}\right)^{2}$. En posant $y_{i}=X-n x_{i}$ pour tout $i$, la conclusion souhaitée en découle.
|
| 233 |
+
|
| 234 |
+
On peut maintenant prouver que tout $n \geqslant 3$ impair est bon. En effet, si $a>0$ est un entier qui peut s'écrire comme la somme de $n$ carrés d'entiers tous divisibles par $n$ alors, en considérant la plus grande puissance de $n$ qui divise ces entiers, il existe donc un entier $r>0$ et des entiers $x_{1}, \cdots, x_{n}$ dont au moins un n'est pas divisible par $n$ tels que $a=\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}$.
|
| 235 |
+
|
| 236 |
+
D'après le lemme, il existe des entiers $y_{1}, \cdots, y_{n}$ non divisibles par $n$ tels que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$, et donc $\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}=\sum_{i=1}^{n}\left(n^{r-1} y_{i}\right)^{2}$. Ainsi, en appliquant le lemme $r$ fois de suite, on est assuré de l'existence d'entiers $z_{1}, \cdots, z_{n}$ non divisibles par $n$ tels que $a=\sum_{i=1}^{n} z_{i}^{2}$. Cela prouve que $n$ est bon.
|
| 237 |
+
|
| 238 |
+
Puisque le double de tout entier bon est bon, tout entier qui n'est pas une puissance de 2 est bon.
|
| 239 |
+
|
| 240 |
+
On prouve maintenant que 8 est bon : En effet, si a est la somme de 8 carrés d'entiers divisibles par 8 alors a est divisible par 64 . En particulier $a \geqslant 64 \mathrm{et}$, d'après le théorème des quatre carrés de Lagrange, il existe des entiers $x_{1}, x_{2}$, $x_{3}, x_{4}$ tels que $a=1^{2}+4^{2}+4^{2}+4^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$. Notons que, puisque $a \equiv 0 \bmod [8]$, on a $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2} \equiv 7 \bmod$ [8]. Or, un carré étant congru à 0,1 ou 4 modulo 8 , la seule façon d'obtenir une somme de quatre carrés congrue à 7 modulo 8 est d'avoir $1,1,1,4$ à l'ordre près. Ainsi, aucun des $x_{i}$ n'est divisible par 8 , ce qui conclut.
|
| 241 |
+
|
| 242 |
+
Enfin, on prouve que 4 n'est pas bon. Pour cela, il suffit de constater que $32=4^{2}+4^{2}+0^{2}+0^{2}$. D'autre part, pour obtenir $32=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$, on doit avoir $\left|x_{i}\right| \leqslant 5$ pour tout i. De plus, si l'on veut éviter les multiples de 4 , il ne reste plus que $\left|x_{i}\right|=1,2,3$ ou 5 . Or, comme ci-dessus en raisonnant modulo 8 , la seule possibilités est d'avoir $\left|x_{i}\right|=2$ pour tout $i$. Mais, on a $32 \neq$ $2^{2}+2^{2}+2^{2}+2^{2}$, ce qui assure que $4 \mathrm{n}^{\prime}$ est pas bon.
|
| 243 |
+
Ainsi, tout diviseur de 4 ne peut être bon.
|
| 244 |
+
Finalement, tous les entiers $\mathrm{n}>0$ sont bons sauf 1,2 et 4 .
|
| 245 |
+
|
French_STS/md/fr-ofm-2015-2016-envoi-1-solutions.md
ADDED
|
@@ -0,0 +1,164 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Corrigé de l'envoi 1
|
| 2 |
+
|
| 3 |
+
## 1 Exercices groupe B
|
| 4 |
+
|
| 5 |
+
Exercice 1 Prouver qu'il n'existe qu'un nombre fini de nombres premiers s'écrivant sous la forme $n^{3}+2 n+3$ avec $n \in \mathbb{N}$.
|
| 6 |
+
Solution de l'exercice 1: Remarquons que $n^{3}-n=n(n-1)(n+1)$ est un produit de trois entiers consécutifs. Puisque parmi trois entiers consécutifs il y a toujours un multiple de 3 , on obtient que $n^{3}-n$ est divisible par 3, c'est-à-dire $n^{3} \equiv n(\bmod 3)$. (On peut le voir aussi en utilisant le petit théorème de Fermat.) On a donc $n^{3}+2 n+3 \equiv n+2 n+3 \equiv 3 n+3 \equiv 0(\bmod 3)$, donc $n^{3}+2 n+3$ est toujours divisible par 3 . D'autre part, il ne peut être égal à 3 que pour un nombre fini de valeurs de $n$.
|
| 7 |
+
|
| 8 |
+
Exercice 2 Résoudre $x^{4}-6 x^{2}+1=7 \times 2^{y}$ pour $x$ et $y$ entiers.
|
| 9 |
+
Solution de l'exercice 2: L'équation se réécrit $\left(x^{2}-3\right)^{2}=7 \times 2^{y}+8$. Si $y \geq 3$, alors le côté droit s'écrit $8\left(7 \times 2^{y-3}+1\right)$. Le côté gauche étant un carré, sa valuation 2 -adique est paire. Ainsi, $7 \times 2^{y-3}+1$ doit être pair, donc $y=3$. Dans ce cas $x^{2}-3=8$ donc $x^{2}=11$, impossible. Donc $y \leq 2$. Si $y=2$, on trouve $x= \pm 3$. Pour $y<0$, ainsi que pour $y=0$ ou $y=1$ il n'y a pas de solution. Les seuls couples de solutions sont donc $(x, y)=(3,2)$ et $(-3,2)$.
|
| 10 |
+
Exercice 3 Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \in \mathbb{N}$.
|
| 11 |
+
Solution de l'exercice 3: Soit E l'ensemble des entiers strictement positifs s'écrivant sous cette forme. Commençons par remarquer que
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \frac{2^{a-b}-1}{2^{c-d}-1}
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
Ainsi, si $x>0$ s'écrit $x=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, alors $b-d=v_{2}(x)$ et si on appelle $y$ l'entier impair tel que $x=2^{v_{2}(x)} y$, alors $y$ s'écrit sous la forme $\frac{2^{n}-1}{2^{m}-1}$. En particulier, l'entier que nous cherchons est nécessairement impair. D'autre part, on peut tout de suite exclure les entiers de la forme $2^{n}-1$, atteints avec $m=1$.
|
| 18 |
+
|
| 19 |
+
Il est classique que si $2^{m}-1$ divise $2^{n}-1$, alors $m$ divise $n$. Ainsi, en écrivant $n=m d, y$ est de la forme
|
| 20 |
+
|
| 21 |
+
$$
|
| 22 |
+
y=\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\ldots+2^{m}+1
|
| 23 |
+
$$
|
| 24 |
+
|
| 25 |
+
Autrement dit, en notant $u=\underbrace{0 \ldots 0}_{m-1 \text { zéros }} 1$, l'écriture en base 2 de $y$ est de la forme $\overline{1 u \ldots u}^{2}$, avec $u$ apparaissant $d-1$ fois. Les entiers impairs appartenant à $E$ sont exactement ceux ayant une telle écriture binaire pour $m$ et $d$ bien choisis. Les écritures binaires des premiers entiers impairs qui ne sont pas de la forme $2^{n}-1$ sont
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
5=\overline{101}^{2}, 9={\overline{1001}^{2}}^{2}, 11={\overline{1011}^{2}}^{2}
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
D'après le critère ci-dessus, le plus petit entier cherché est 11.
|
| 32 |
+
Remarque : cet exercice peut aussi se faire en trouvant des manières d'écrire les entiers 1 à 10 sous cette forme, puis en montrant que 11 ne s'écrit pas sous cette forme : en effet, vu que 11 est impair, on peut supposer $b=d=1$. Ensuite
|
| 33 |
+
|
| 34 |
+
$$
|
| 35 |
+
\left(2^{a}-1\right)=11\left(2^{c}-1\right)
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
se réécrit
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
10=2^{c} \times 11-2^{a}
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Puisque $10=2 \times 5$, nous avons $a=1$ ou $c=1$. Si $a=1$, on trouve $2^{c} \times 11=12$, qui n'a pas de solution, et si $c=1$, on trouve $2^{a}=12$, qui n'a pas de solution non plus. Donc 11 est l'entier cherché.
|
| 45 |
+
|
| 46 |
+
## 2 Exercices communs
|
| 47 |
+
|
| 48 |
+
Exercice 4 Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.
|
| 49 |
+
Solution de l'exercice 4: Si $p=2$ alors on a $3(q+2)(r+3)=8 q r$ ce qui implique $q=3$ ou $r=3$. On a alors la solution $(2,3,5)$.
|
| 50 |
+
|
| 51 |
+
Si $q=2$ et $p, r>2$ alors on a $(p+1)(r+3)=2 p r$. Puisque $p$ et $r$ sont impairs, le membre de gauche est divisible par 4 , alors que le membre de droite est divisible par 2 , mais pas par 4 , contradiction. Donc $p$ ou $r$ vaut 2 mais aucune solution valide n'en découle.
|
| 52 |
+
|
| 53 |
+
Si $r=2$ alors $5(p+1)(q+2)=8 p q$ et donc $p$ ou $q$ vaut 5 . On obtient la solution $(7,5,2)$.
|
| 54 |
+
Sinon, $(p+1)$ est pair et $(r+3)$ est pair. Donc on se ramène à
|
| 55 |
+
|
| 56 |
+
$$
|
| 57 |
+
\left(\frac{p+1}{2}\right)(q+2)\left(\frac{r+3}{2}\right)=p q r .
|
| 58 |
+
$$
|
| 59 |
+
|
| 60 |
+
Nous avons donc écrit pqr comme un produit de trois facteurs strictement plus grands que 1. On en déduit que $\left(\frac{p+1}{2}, q+2, \frac{r+3}{2}\right)$ est une permutation de $(p, q, r)$.
|
| 61 |
+
|
| 62 |
+
Clairement, $p \neq \frac{p+1}{2}$ puisque $p>\frac{p+1}{2}$.
|
| 63 |
+
Si $p=\frac{r+3}{2}$, alors puisque $q \neq q+2$, nous avons nécessairement $q=\frac{p+1}{2}=\frac{r+5}{4}$. Alors $r=q+2=\frac{r+13}{4}$, et donc $r$ n'est pas entier.
|
| 64 |
+
|
| 65 |
+
Si $p=q+2$, alors il y a deux cas à considérer :
|
| 66 |
+
$-r=\frac{p+1}{2}=\frac{q+3}{2}$ et $q=\frac{r+3}{2}=\frac{q+9}{4}$. Donc $q=3$ et on obtient la solution $(5,3,3)$.
|
| 67 |
+
$-r=\frac{r+3}{2}$ et $q=\frac{p+1}{2}=\frac{q+3}{2}$, ce qui donne $r=q=3$. On obtient alors cette même solution $(5,3,3)$.
|
| 68 |
+
Finalement, les seules solutions sont $(2,3,5),(7,6,2)$ et $(5,3,3)$.
|
| 69 |
+
Exercice 5 Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.
|
| 70 |
+
Solution de l'exercice 5: On veut résoudre $2^{n-1} n+1=m^{2}$, c'est-à-dire $2^{n-1} n=(m-1)(m+1)$. Puisque $n=1$ n'est pas solution, on a $n \geq 2$, et donc $m$ est nécessairement impair, et $m-1$ et $m+1$ sont pairs (en particulier $n \geq 3$ ). On pose $k=\frac{m-1}{2}$. Il suffit alors de résoudre $2^{n-3} n=k(k+1)$. Parmi les entiers $k$ et $k+1$ exactement un est pair, et donc ils sont de la forme $2^{n-3} d$ et $\frac{n}{d}$ avec $d$ un diviseur de $n$. Or un diviseur de $n$ ne peut pas être à distance 1 d'un entier supérieur à $2^{n-3}$ si $n$ est trop grand. Plus précisément, on a $2^{n-3} d \geq 2^{n-3} \geq n+2$ si $n \geq 6$, donc on a nécessairement $n \leq 5$. Pour $n=5$, on trouve $2^{4} \times 5+1=9^{2}$, donc 5 est solution. On vérifie que $2,3,4$ ne sont pas solutions. Donc $n=5$ est la seule solution.
|
| 71 |
+
Exercice 6 Soient $x>1$ et $y$ des entiers vérifiant $2 x^{2}-1=y^{15}$. Montrer que $x$ est divisible par 5 .
|
| 72 |
+
Solution de l'exercice 6: L'entier $y$ est clairement impair et strictement plus grand que 1. On factorise l'équation sous la forme
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
x^{2}=\left(\frac{y^{5}+1}{2}\right)\left(y^{10}-y^{5}+1\right)
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Remarquons que
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
y^{10}-y^{5}+1 \equiv 3\left(\bmod y^{5}+1\right)
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
et que donc $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)$ est égal à 1 ou à 3 . S'il valait 1 , alors $y^{10}-y^{5}+1$ serait un carré. Or pour $y>0$ nous avons
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\left(y^{5}-1\right)^{2}=y^{10}-2 y^{5}+1<y^{10}-y^{5}+1<y^{10}=\left(y^{5}\right)^{2},
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
c'est-à-dire que $y^{10}-y^{5}+1$ est strictement compris entre deux carrés consécutifs, et ne peut pas être lui-même un carré. Donc $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)=3$, de sorte qu'il existe des entiers $a$ et $b$ tels que
|
| 91 |
+
|
| 92 |
+
$$
|
| 93 |
+
y^{5}+1=6 a^{2} \quad \text { et } \quad y^{10}-y^{5}+1=3 b^{2} .
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
On peut factoriser $(y+1)\left(y^{4}-y^{3}+y^{2}-y+1\right)=6 a^{2}$. Puisque $y^{5} \equiv-1(\bmod 3)$, on a nécessairement $y \equiv-1$ $(\bmod 3)$, donc $y+1$ est divisible par 6 . De même que plus haut, on a
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
y^{4}-y^{3}+y^{2}-y+1 \equiv 5(\bmod y+1)
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
et donc $\operatorname{pgcd}\left(y+1, y^{4}-y^{3}+y^{2}-y+1\right)$ est égal à 1 ou à 5 . S'il vaut 5 , alors $a$ est divisible par 5 et donc $x$ aussi, et nous avons terminé. Supposons donc qu'il vaut 1. Alors $y^{4}-y^{3}+y^{2}-y+1$ est un carré. Dans ce cas, $4\left(y^{4}-y^{3}+y^{2}-y+1\right)$ est aussi un carré, ce qui est impossible, car pour $y>1$, on a
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\left(2 y^{2}-y\right)^{2}=4 y^{4}-4 y^{3}+y^{2}<4\left(y^{4}-y^{3}+y^{2}-y+1\right)<4 y^{4}-4 y^{3}+5 y^{2}-2 y+1=\left(2 y^{2}-y+1\right)^{2}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
## 3 Exercices groupe A
|
| 109 |
+
|
| 110 |
+
Exercice 7 Caractériser les entiers $n \geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\bmod n)$.
|
| 111 |
+
Solution de l'exercice 7: Voici les $n$ vérifiant cette propriété : $2,2 \cdot 3,2 \cdot 3 \cdot 7,2 \cdot 3 \cdot 7 \cdot 43$.
|
| 112 |
+
Pour prouver que c'est exhaustif on procède de la façon suivante : on commence par remarquer que $n$ n'a pas de facteur carré. En effet, si $p^{2}$ divise $n$, alors $p^{n+1}-p$ est divisible par $p^{2}$, ce qui n'est pas possible. Ainsi, $n$ est forcément un produit $p_{1} \ldots p_{k}$ de nombres premiers distincts. Par conséquent, par le lemme chinois la condition de l'énoncé est équivalente à $a^{n+1} \equiv a(\bmod p)$ pour tout entier $a$ et tout $p \in\left\{p_{1}, \ldots, p_{k}\right\}$. En choisissant $a$ d'ordre $p-1$ modulo $p$, on obtient que cela est équivalent à ce que $p-1$ divise $n$ pour tout $p \in\left\{p_{1}, \ldots, p_{k}\right\}$.
|
| 113 |
+
|
| 114 |
+
En résumé : $n$ est produit de premiers distincts $p_{1}, \ldots, p_{k}$, et $p_{i}-1$ divise $n$ pour tout $i$. On en déduit que pour tout $i, p_{i}-1$ est sans facteur carré et $p_{i}-1=q_{1} \ldots q_{m}$ où les $q_{j}$ sont des nombres premiers pris parmi les $p_{r}, r \neq i$.
|
| 115 |
+
|
| 116 |
+
Quitte à re-numéroter les $p_{i}$, on peut supposer que $p_{1}<p_{2}<\ldots<p_{k}$. D'après la condition ci-dessus, nous avons nécessairement $p_{1}=2$. Si $k=1$, cela nous donne l'entier $n=2$. Si $k>1$, alors $p_{2}-1$ est nécessairement égal à 2 , donc $p_{2}=3$. Si $k=2$, cela nous donne la solution $n=6$. Si $k>2$ on continue en disant que $p_{3}-1$ ne peut être égal à 2 ou 3 , donc il est égal à $p_{1} p_{2}=6$, d'où $p_{3}=7$. Si $k=3$, cela donne la solution $n=2 \cdot 3 \cdot 7=42$. Si $k>3$, on voit que de même la seule valeur possible pour $p_{4}$ est $2 \times 3 \times 7+1=43$. Pour $k=4$, cela donne la solution $n=2 \cdot 3 \cdot 7 \cdot 43$. Enfin, supposons que $k>4$. Alors $p_{5}-1$ doit être pair et strictement supérieur à 43 , donc les seules valeurs possibles sont $2 \cdot 43,2 \cdot 3 \cdot 43,2 \cdot 7 \cdot 43,2 \cdot 3 \cdot 7 \cdot 43$. On vérifie qu'aucune de ces possibilités ne fournit un $p_{5}$ premier. Ainsi on a nécessairement $k \leq 4$ et les solutions que nous avons trouvées sont les seules.
|
| 117 |
+
|
| 118 |
+
Exercice 8 Soit $k \geq 3$ un entier. On définit la suite $\left(a_{n}\right)_{n \geq k}$ par $a_{k}=2 k$, et
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
a_{n}= \begin{cases}a_{n-1}+1 & \text { si } \operatorname{pgcd}\left(a_{n-1}, n\right)=1 \\ 2 n & \text { sinon. }\end{cases}
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
Montrer que la suite $\left(a_{n+1}-a_{n}\right)_{n \geq k}$ a une infinité de termes qui sont des nombres premiers.
|
| 125 |
+
Solution de l'exercice 8: Partons d'un entier $n$ tel que $a_{n}=2 n$. Montrons par récurrence que si $p$ est le plus petit facteur premier de $n-1$, alors pour tout $i \in\{0, \ldots, p-2\}, a_{n+i}=2 n+i$. En effet, c'est vrai pour $i=0$, et si c'est vrai pour un certain $i<p-2$, alors
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
\operatorname{pgcd}(n+i+1,2 n+i)=\operatorname{pgcd}(n+i+1, n-1)=\operatorname{pgcd}(i+2, n-1)=1
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
car $i+2<p$, et donc $i+2$ est premier avec $n-1$ par définition de $p$, ce qui conclut la récurrence. De même, $\operatorname{pgcd}(n+p-1,2 n+p-2)=\operatorname{pgcd}(p, n-1)=p \neq 1$, et donc $a_{n+p-1}=2(n+p-1)$. En particulier,
|
| 132 |
+
|
| 133 |
+
$$
|
| 134 |
+
a_{n+p-1}-a_{n+p-2}=2 n+2 p-2-(2 n+p-2)=p
|
| 135 |
+
$$
|
| 136 |
+
|
| 137 |
+
est premier.
|
| 138 |
+
Puisque $a_{k}=2 k$, avons donc montré qu'il existe une infinité de $n$ satisfaisant $\operatorname{pgcd}\left(a_{n-1}, n\right) \neq 1$, et que pour de telles valeurs de $n, a_{n}-a_{n-1}$ est premier.
|
| 139 |
+
Exercice 9 Soit $t$ un entier naturel non-nul. Montrer qu'il existe un entier $n>1$ premier avec $t$ tel que pour tout entier $k \geq 1$, l'entier $n^{k}+t$ ne soit pas une puissance (c'est-à-dire qu'il ne soit pas de la forme $m^{r}$ avec $m \geq 1$ et $r \geq 2$ ).
|
| 140 |
+
|
| 141 |
+
Solution de l'exercice 9: Pour que $n$ soit premier avec $t$, on va le chercher sous la forme $1+t s$ où $s$ est entier. On aura alors $n^{k}+t \equiv 1+t(\bmod s)$. En particulier, si $s$ est divisible par $(t+1)$, alors $n^{k}+t$ l'est également.
|
| 142 |
+
|
| 143 |
+
On va d'abord traiter le cas où $t+1$ n'est pas une puissance. Dans ce cas, il suffirait de s'assurer qu'on peut choisir $s$ de telle sorte que $n^{k}+t$ soit divisible par $t+1$, et que le quotient soit premier avec $t+1$. Pour cela, prenons $s=(t+1)^{2}$. Alors $n=1+t(t+1)^{2}$, et
|
| 144 |
+
|
| 145 |
+
$$
|
| 146 |
+
n^{k}+t=\underbrace{\sum_{i=1}^{k}\binom{k}{i} t^{i}(t+1)^{2 i}}_{\text {termes divisibles par }(t+1)^{2}}+1+t=(t+1)(a(t+1)+1)
|
| 147 |
+
$$
|
| 148 |
+
|
| 149 |
+
pour un certain entier $a$, donc on a gagné.
|
| 150 |
+
|
| 151 |
+
Supposons maintenant que $t+1$ soit une puissance : $t+1=m^{r}$ avec $m$ qui n'est pas une puissance. Si on garde le même $n$ que ci-dessus, on voit que si $n^{k}+t=b^{d}$ est une puissance (avec $d \geq 2$ ), alors $t+1$ est nécessairement une puissance $d$-ième, et donc $d$ divise $r$. Ainsi, nous avons une borne sur les $d$ tels que $n^{k}+t$ est puissance $d$-ième pour un certain $k$. On constate alors qu'en remplaçant $n$ par sa puissance $r$-ième, c'est-à-dire en posant $n=n_{0}^{r}$ où $n_{0}=1+t(t+1)^{2}$ (ce qui ne change pas le fait que $t+1$ divise $n^{k}+t$, que le quotient soit premier avec $t+1$, et que donc $n^{k}+t=b^{d}$ implique $d \mid r$ comme ci-dessus), on arrive à écrire $t$ comme une différence de deux puissances $d$-ièmes :
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
t=b^{d}-\left(n_{0}^{k e}\right)^{d}
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
où $e$ est l'entier naturel tel que $r=d e$. Cela n'est pas possible car $n_{0}$ est grand par rapport à $t$. Plus précisément, nous avons:
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
t=b^{d}-\left(n_{0}^{k e}\right)^{d}=\left(b-n_{0}^{k e}\right)\left(b^{d-1}+b^{d-2} n_{0}^{k e}+\ldots+b n_{0}^{k e(d-2)}+n_{0}^{k e(d-1)}\right) \geq n_{0}>t
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
contradiction. Donc pour tout $k$ et pour tout $d, n^{k}+t$ n'est pas une puissance $d$-ième et nous avons terminé.
|
| 164 |
+
|
French_STS/md/fr-ofm-2015-2016-envoi-2-solutions.md
ADDED
|
@@ -0,0 +1,99 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Matfématiques 2015-2016
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## ENVOI NUMÉro 2 : CORRIGÉ
|
| 6 |
+
|
| 7 |
+
Exercice 1. Soit $A$ un point extérieur à un cercle $\mathscr{C}$ de centre $O$. Un point $P$ se déplace sur $\mathscr{C}$. Soit $M$ le point d'intersection entre $(A P)$ et la bissectrice de $\widehat{P O A}$. Montrer que $M$ se déplace sur un cercle que l'on décrira.
|
| 8 |
+
Solution de l'exercice 1
|
| 9 |
+
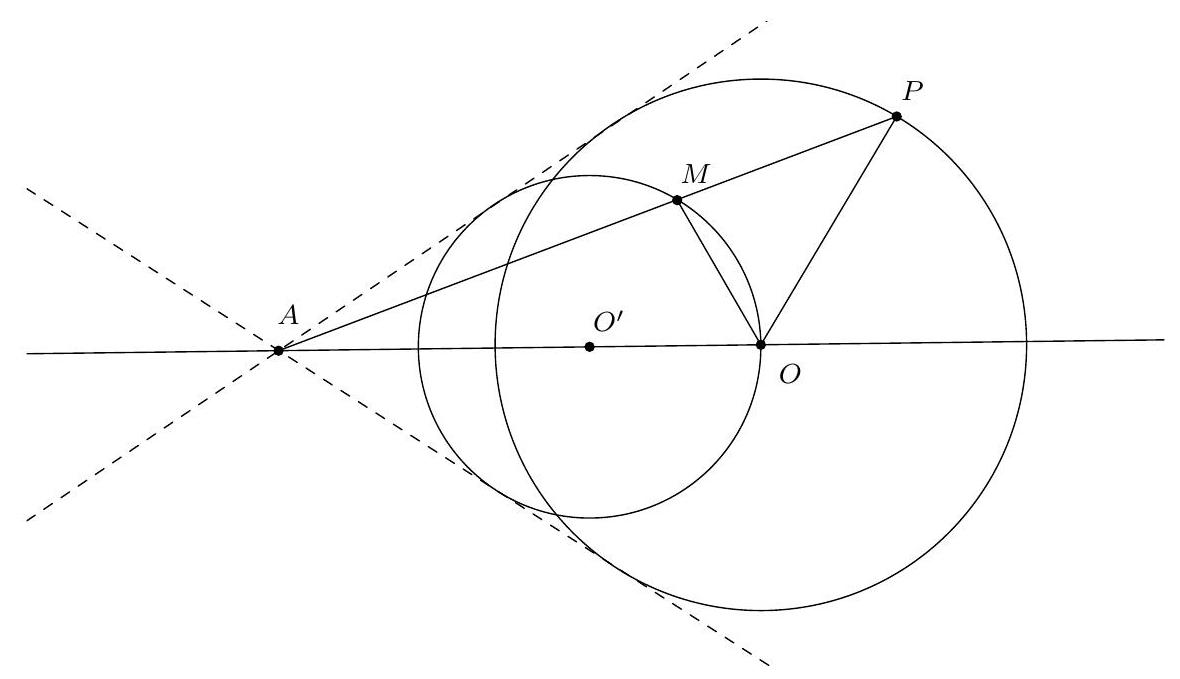
|
| 10 |
+
|
| 11 |
+
Notons $d=O A$ et $R$ le rayon du cercle.
|
| 12 |
+
D'après le théorème de la bissectrice, on a $M P / M A=O P / O A$, donc $\frac{M A}{A P}=\frac{M A}{M A+M P}=$ $\frac{1}{1+\frac{M P}{M A}}=\frac{1}{1+\frac{O P}{O A}}=\frac{O A}{O A+O P}=\frac{d}{d+R}$. Notons $k$ cette valeur. Soit $O^{\prime}$ le point de $[A O]$ tel que $A O^{\prime}=k A O$. D'après le théorème de Thalès, les droites $\left(O^{\prime} M\right)$ et $(O P)$ sont parallèles, donc $\frac{O^{\prime} M}{O P}=\frac{A M}{A P}=k$, donc $O^{\prime} M=k R$. Ceci prouve que $M$ décrit le cercle de centre $O^{\prime}$ et de rayon kR.
|
| 13 |
+
Remarquons que $A O^{\prime}+k R=k(d+R)=d$, donc ce cercle passe par $O$.
|
| 14 |
+
Exercice 2. Soit $A B C$ un triangle tel que $\widehat{A}=60^{\circ}$. On note $O$ le centre du cercle circonscrit, $I$ le centre du cercle inscrit et $H$ l'orthocentre. Montrer que
|
| 15 |
+
|
| 16 |
+
1) $B, C, O, I, H$ sont cocycliques
|
| 17 |
+
2) $O I H$ est isocèle.
|
| 18 |
+
|
| 19 |
+
## Solution de l'exercice 2
|
| 20 |
+
|
| 21 |
+
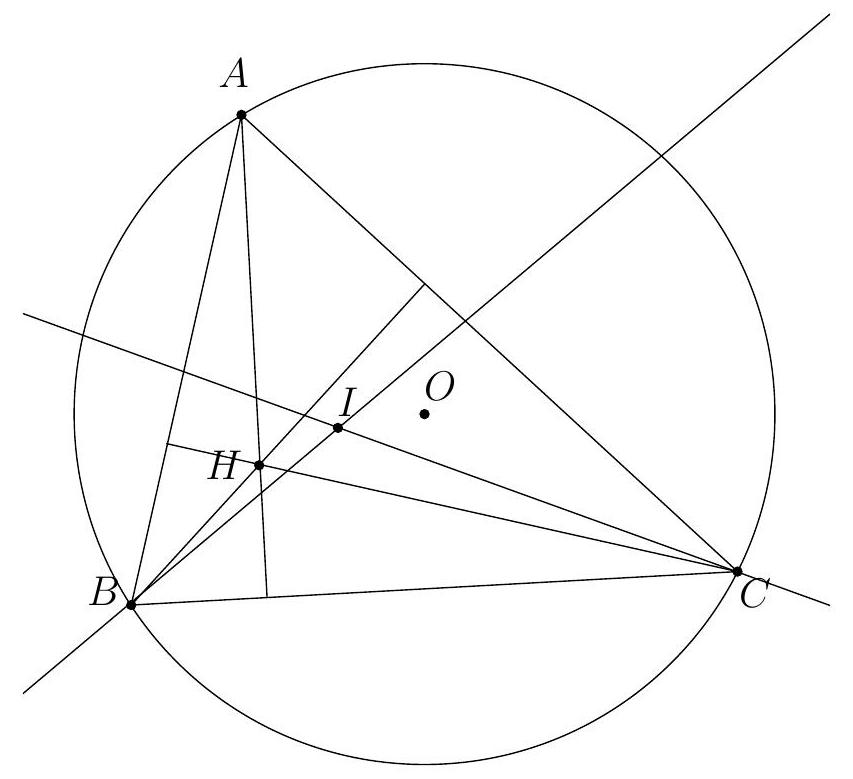
|
| 22 |
+
|
| 23 |
+
On utilise les angles de droites. Les angles sont modulo $180^{\circ}$.
|
| 24 |
+
|
| 25 |
+
1) $(H B, H C)=(H B, A C)+(A C, A B)+(A B, H C)=D-(A B, A C)+D=-(A B, A C)=-60^{\circ}=$ $120^{\circ}=(O B, O C)$ (où on a noté $D$ l'angle droit), donc $B, H, O, C$ sont cocycliques.
|
| 26 |
+
$(I B, I C)=(I B, B C)+(B C, I C)=-\widehat{B} / 2-\widehat{C} / 2=-120 / 2=-60^{\circ}=120^{\circ}$, donc $I$ se trouve également sur ce cercle.
|
| 27 |
+
2) $(C O, C I)-(C I, C H)=(C O, C B)+(C B, C I)-(C I, C B)-(C B, C H)=(C O, C B)+$ $(C H, C B)+2(C B, C I)=(90-\widehat{A})+(90-\widehat{B})-\widehat{C}=0$, donc $(C O, C I)=(C I, C H)$. On a donc $(O I, O H)=(C I, C H)=(C O, C I)=(H O, H I)$, donc $O I H$ est isocèle en $I$.
|
| 28 |
+
Exercice 3. Par un point $A$ d'un cercle de centre $O$, on mène une tangente à ce cercle, et on prend deux points $B$ et $C$ sur cette tangente, avec $C$ entre $A$ et $B$. De $B$ et $C$, on mène $(B D)$ et $(C E)$ tangentes au cercle. Démontrer que $\widehat{B O C}=\widehat{D A E}$.
|
| 29 |
+
Solution de l'exercice 3
|
| 30 |
+
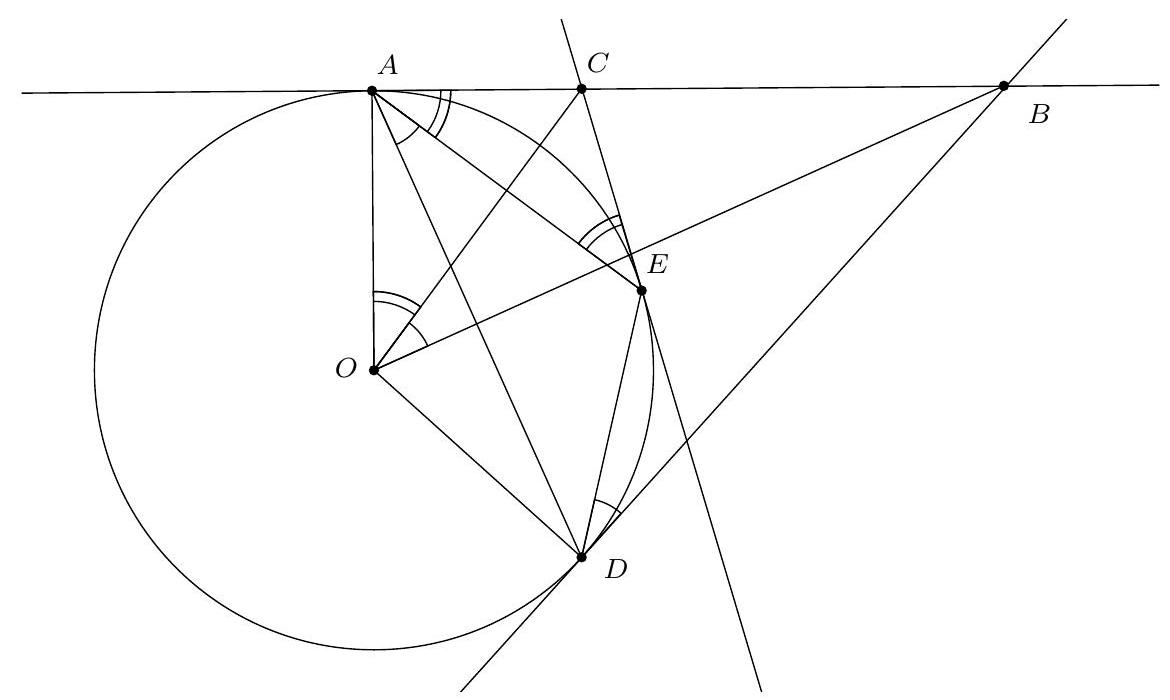
|
| 31 |
+
|
| 32 |
+
Notons $\alpha=\widehat{B D E}$ et $\beta=\widehat{C E A}$. D'après le théorème de l'angle inscrit, on a $\alpha=\widehat{D A E}$.
|
| 33 |
+
Comme $(C A)$ et $(C E)$ sont les deux tangentes menées à partir de $C$, on a $\widehat{E A C}=\widehat{C E A}=\beta$. $\widehat{B O C}=\widehat{B O A}-\widehat{C O A} . \mathrm{Or},(B O) \perp(A D)$ et $(O A) \perp(A C)$, donc $\widehat{B O A}=\widehat{D A C}=\alpha+\beta$, et de même $\widehat{C O A}=\beta$, donc $\widehat{B O C}=\alpha=\widehat{D A E}$.
|
| 34 |
+
Exercice 4. Soit $A B C$ un triangle. Soit $P$ appartenant au cercle circonscrit. On sait que les projetés de $P$ sur $(B C),(C A)$ et $(A B)$ sont alignés sur la droite dite de Simson. On suppose que cette droite passe par le point diamétralement opposé à $P$. Montrer qu'elle passe également par le centre de gravité de $A B C$.
|
| 35 |
+
|
| 36 |
+
## Solution de l'exercice 4
|
| 37 |
+
|
| 38 |
+
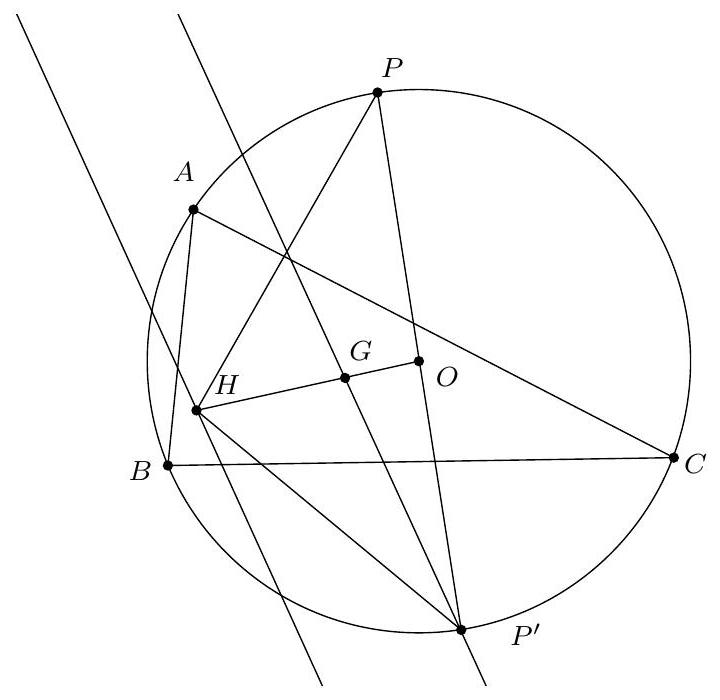
|
| 39 |
+
|
| 40 |
+
Notons $P^{\prime}$ le point diamétralement opposé à $P$. Soit $\Delta$ la droite de Simson. Soit $h$ l'homothétie de centre $P$ et de rapport 2. Alors $h(\Delta)$ est la droite de Steiner. On sait qu'elle passe par l'orthocentre $H$, donc $\Delta$ passe par le milieu de $[P H]$. On en déduit que $\Delta$ est la médiane de $P P^{\prime} H$ issue de $P^{\prime}$.
|
| 41 |
+
Par ailleurs, (HO) est la médiane de $P P^{\prime} H$ issue de $H$. Comme $\overrightarrow{H G}=\frac{2}{3} \overrightarrow{H O}$, le point $G$ est le centre de gravité de $P H P^{\prime}$, donc $\Delta$ passe par $G$.
|
| 42 |
+
Exercice 5. Soit $A B C$ un triangle. On suppose que la médiane $(B M)$ et la bissectrice $(C D)$ se coupent en un point $J$ tel que $J B=J C$. Soit $H$ le pied de la hauteur issue de $A$. Montrer que $J M=J H$.
|
| 43 |
+
|
| 44 |
+
## $\underline{\text { Solution de l'exercice } 5}$
|
| 45 |
+
|
| 46 |
+
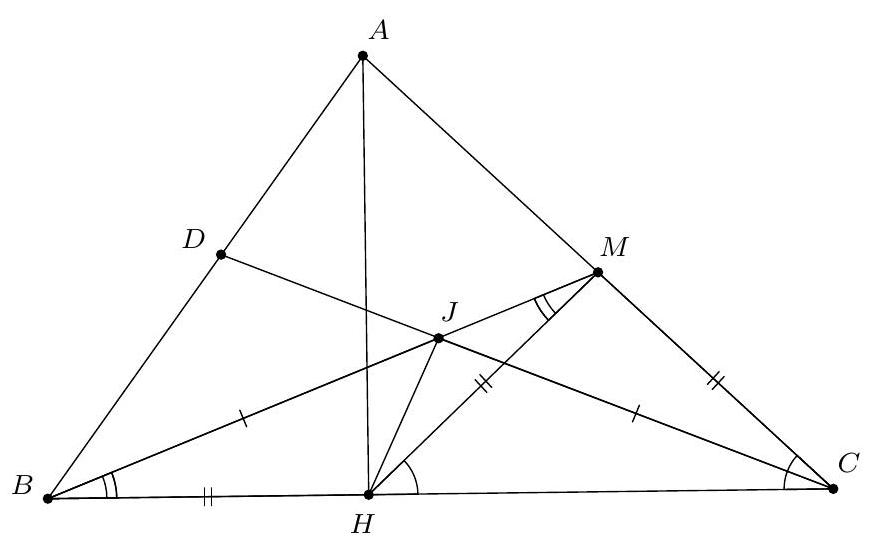
|
| 47 |
+
|
| 48 |
+
Notons $\gamma=\widehat{A C B}$. On a $M A=M C=M H$, donc $\widehat{C H M}=\gamma$.
|
| 49 |
+
On a aussi $\widehat{C H M}=180^{\circ}-\widehat{M H B}=\widehat{H B M}+\widehat{B M H}$.
|
| 50 |
+
De plus, $\widehat{H B M}=\widehat{D C B}=\gamma / 2$, donc $\widehat{B M H}=\widehat{H M B}=\gamma / 2$.
|
| 51 |
+
On en déduit que $B H=H M=M C$. Les triangles $B H J$ et $C M J$ vérifient $B J=C J, \widehat{H B J}=$ $\widehat{M C J}$ et $B H=C M$ donc sont isométriques. Par conséquent, $J H=H M$.
|
| 52 |
+
Exercice 6. Soit $A B C$ un triangle, et $D, E, F$ les pieds des hauteurs de $A, B, C$ respectivement. On définit aussi $H$ l'orthocentre de $A B C, O$ le centre de son cercle circonscrit, et $X$ le point de la droite $(E F)$ qui vérifie $X A=X D$. Montrer que les droites $(A X)$ et $(O H)$ sont perpendiculaires.
|
| 53 |
+
|
| 54 |
+
## Solution de l'exercice 6
|
| 55 |
+
|
| 56 |
+
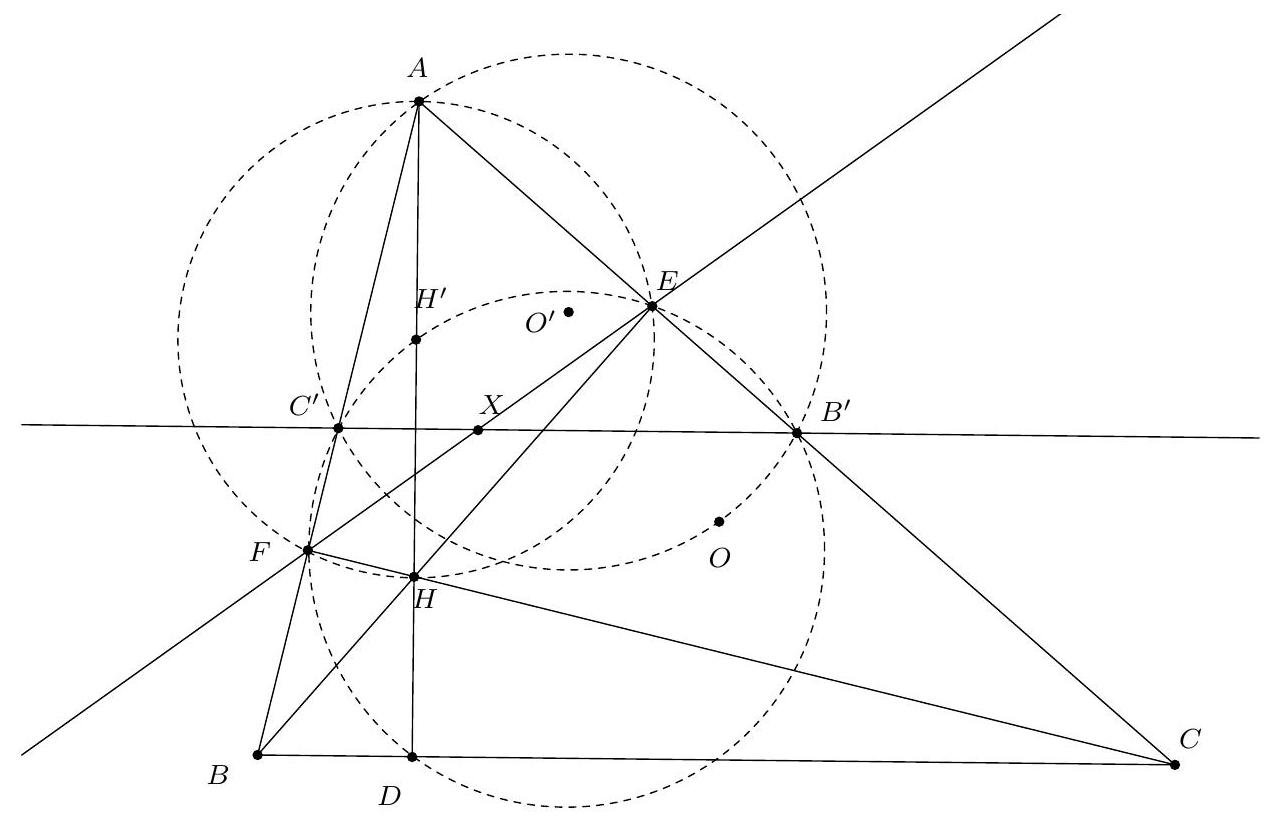
|
| 57 |
+
|
| 58 |
+
On sait que l'axe radical de deux cercles est une droite perpendiculaire à la droite passant par les centres des deux cercles.
|
| 59 |
+
La condition $X A=X D$ signifie que X est sur la médiatrice de $[A D]$, qui n'est autre que le droite des milieux $\left(B^{\prime} C^{\prime}\right)$ (avec $B^{\prime}$ et $C^{\prime}$ les milieux de $[A C]$ et de $[A B]$ ). On sait aussi que les points
|
| 60 |
+
$A, E, F, H$ sont cocycliques d'après la réciproque du théorème de l'angle inscrit. De, plus $[A H]$ étant un diamètre du cercle passant par ces quatre points, le milieu $H^{\prime}$ de $[A H]$ est le centre de ce cercle.
|
| 61 |
+
Le centre du cercle passant par $A, B^{\prime}, C^{\prime}$ est le milieu $O^{\prime}$ de $[A O]$ (par propriété de l'homothétie de centre $A$ et de rapport 1/2). On sait que $\left(O^{\prime} H^{\prime}\right)$ et $(O H)$ sont parallèles. Le problème revient donc à montrer que $(A X)$ et $\left(O^{\prime} H^{\prime}\right)$ sont perpendiculaires. Nous allons montrer ici que $(A X)$ est en fait l'axe radical des deux cercles évoqués précédemment, ce qui terminera l'exercice d'après la propriété évoquée au début de la preuve.
|
| 62 |
+
$A$ étant sur les deux cercles, est bien sur leur axe radical. On sait de plus que $B^{\prime}, C^{\prime}, E, F$ sont cocycliques sur le cercle d'Euler du triangle $A B C$. Ainsi on a l'égalité de longueurs : $X C^{\prime} \times X B^{\prime}=X E \times X F$, ce qui signifie que $X$ est bien sur l'axe radical de nos deux cercles.
|
| 63 |
+
Ainsi on a bien $(A X)$ et $(O H)$ qui sont perpendiculaires.
|
| 64 |
+
Exercice 7. Soit $A B C$ un triangle, et $\Gamma$ son cercle circonscrit. Soit $M$ le milieu de l'arc $B C$ ne contenant pas $A$. Un cercle $\mathscr{C}$ est tangent à $[A B),[A C)$ en $D$ et $E$ respectivement, et tangent intérieurement à $\Gamma$ en $F$. Montrer que $(D E),(B C)$ et $(F M)$ sont concourantes.
|
| 65 |
+
Solution de l'exercice 7
|
| 66 |
+
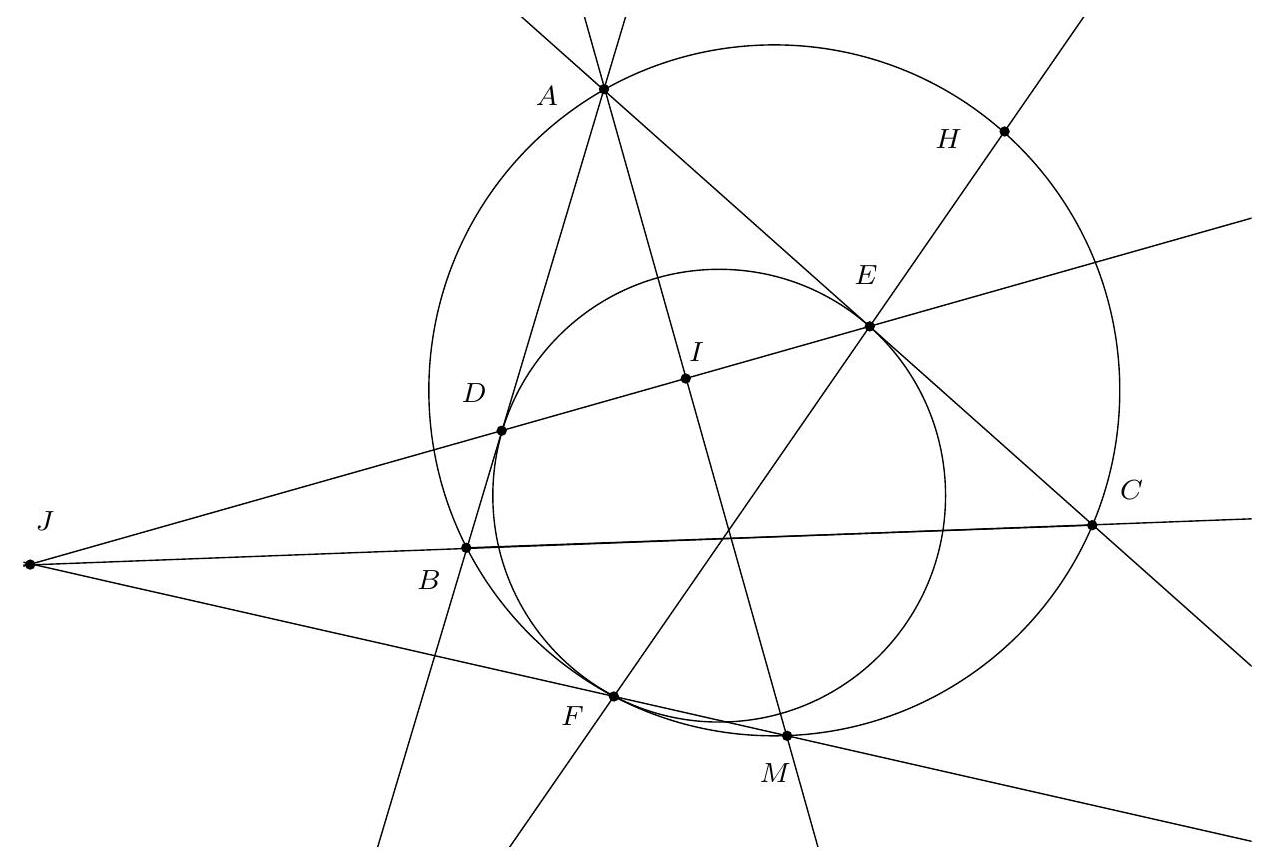
|
| 67 |
+
|
| 68 |
+
Soit $I$ le centre du cercle inscrit dans $A B C$. La droite $(E F)$ recoupe $\Gamma$ en un point $H$. Soit $J$ le point d'intersection de $(B C)$ avec $(F M)$.
|
| 69 |
+
Il est facile de voir que $H$ est le milieu de l'arc $A C$ ne contenant pas $B$ : en effet, l'homothétie de centre $F$ qui envoie $\mathscr{C}$ sur $\Gamma$ envoie $(A C)$ sur la tangente en $H$ à $\Gamma$; celle-ci est parallèle à $(A C)$, ce qui entraîne que $H$ est le milieu de l'arc, et par conséquent $B, I, H$ sont alignés.
|
| 70 |
+
En appliquant le théorème de Pascal à l'hexagone $A M F H B C$, on obtient que $I, E, J$ sont alignés. De même, $D, I, J$ sont alignés. Ainsi, $(D E),(B C)$ et $(F M)$ se rencontrent en $J$.
|
| 71 |
+
Exercice 8. Soit $A B C$ un triangle, $D, E, F$ les points de tangence du cercle inscrit sur les côtés $(B C),(A C)$ et $(A B), M$ le milieu de $[B C], I$ le centre du cercle inscrit de $A B C . G$ et $H$ sont définis comme les symétriques de $E$ et $F$ par rapport à $I$. On note $Q$ l'intersection entre les droites $(B C)$ et $(G H)$. Montrer que les droites $(I Q)$ et $(I M)$ sont perpendiculaires.
|
| 72 |
+
|
| 73 |
+
## Solution de l'exercice 8
|
| 74 |
+
|
| 75 |
+
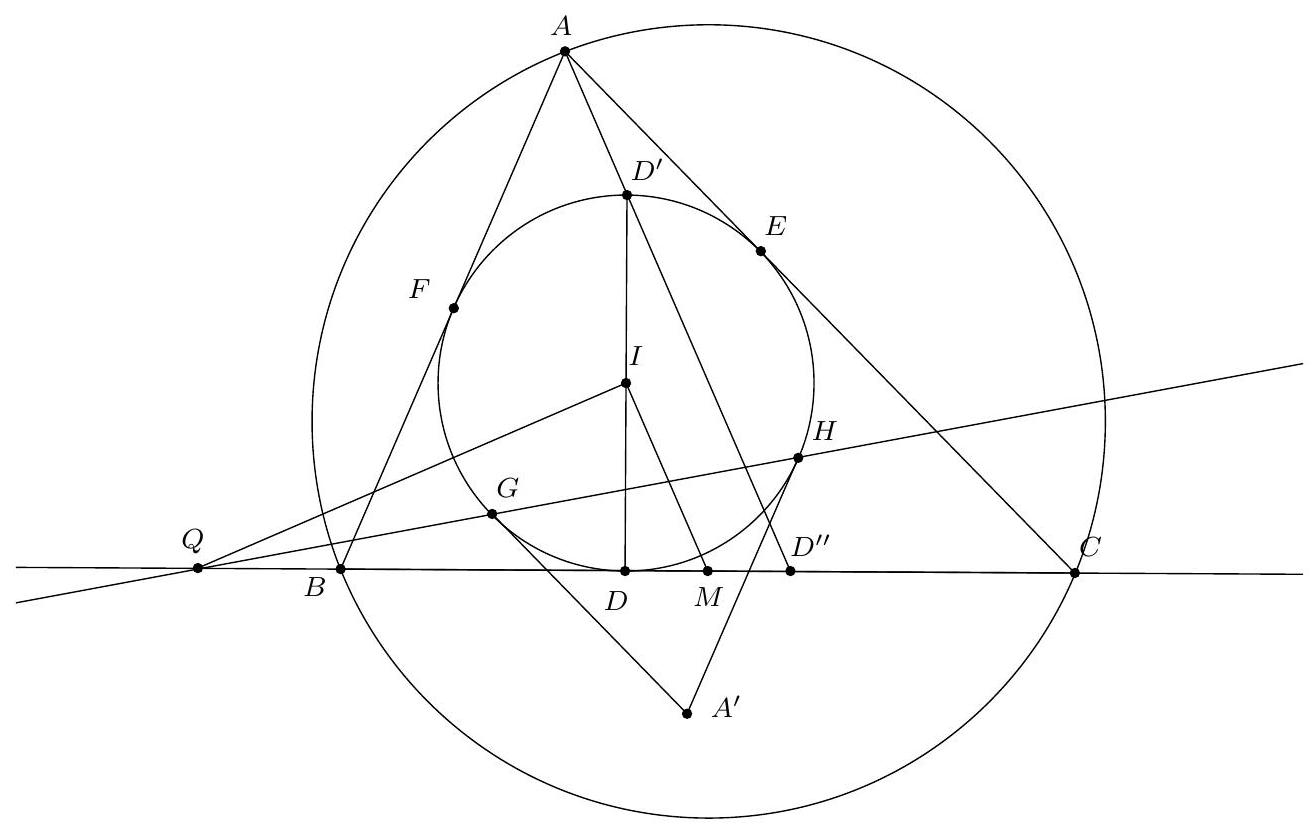
|
| 76 |
+
|
| 77 |
+
Soit $\omega$ le cercle inscrit de $A B C$.
|
| 78 |
+
On notera pour tout point $X$ du plan $p(X)$ la polaire de $X$ par rapport à $\omega$. On sait que pour tout point $X$ du plan, $p(X)$ est une droite perpendiculaire à $(I X)$. Nous allons donc montrer que $p(Q)$ et $(I M)$ sont parallèles pour en déduire le résultat.
|
| 79 |
+
On sait que $p(D)=(B C)$, et que $Q \in(B C)$ donc $Q \in p(D)$. Ainsi par propriété des polaires (par rapport à un cercle fixé), on en déduit que $D \in p(Q)$. De plus par construction de la polaire, on sait que $A^{\prime}$ le point d'intersection des tangentes à $\omega$ en $G$ et $H$ est aussi sur la polaire de $Q$. Ainsi on a : $p(Q)=\left(D A^{\prime}\right)$. Par symétrie de la construction, on sait que $A$ et $A^{\prime}$ sont symétriques par rapport à $I$.
|
| 80 |
+
Soit maintenant $D^{\prime}$ le symétrique de $D$ par rapport à $I$ (qui est donc sur $\omega$ ) et $D^{\prime \prime}$ le point de $(B C)$ tel que $M$ soit le milieu de [ $\left.D D^{\prime \prime}\right]$. Une homothétie envoyant une droite sur une droite qui lui est parallèle, on sait que les droites $\left(D A^{\prime}\right)$ et $\left(D^{\prime} A\right)$ sont parallèles, ainsi que les droites $(I M)$ et $\left(D^{\prime} D^{\prime \prime}\right)$. Or il est connu que les points $A, D^{\prime}, D^{\prime \prime}$ sont alignés (se montre par une homothétie de centre $A$ ).
|
| 81 |
+
Ainsi les droites $\left(D A^{\prime}\right)$ et $(I M)$ sont parallèles, et $\left(D A^{\prime}\right)$ et $(Q I)$ étant perpendiculaires, on en déduit que $(I Q)$ et $(I M)$ sont bien perpendiculaires.
|
| 82 |
+
|
| 83 |
+
Autre solution. Notons $\alpha, \beta$ et $\gamma$ les angles de $D E F$ et $R$ le rayon du cercle circonscrit à $D E F$. On a $B D=R \tan \beta, C D=R \tan \gamma$ donc
|
| 84 |
+
|
| 85 |
+
$$
|
| 86 |
+
2 D M=B C-2 B D=R(\tan \gamma-\tan \beta)=R \frac{\sin \gamma \cos \beta-\sin \beta \cos \gamma}{\cos \beta \cos \gamma}=R \frac{\sin (\gamma-\beta)}{\cos \beta \cos \gamma} .
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
D'autre part, la loi des sinus dans $Q D H$ donne $D Q=D H \frac{\cos \gamma}{\sin (\beta-\gamma)}=2 R \frac{\cos \beta \cos \gamma}{\sin (\beta-\gamma)}$ donc $Q D . D M=R^{2}=D I^{2}$. Or, $[I D]$ est la hauteur de $I Q M$ issue de $I$, donc $I Q M$ est rectangle en $I$.
|
| 90 |
+
Exercice 9. Soit $A B C$ un triangle non-isocèle en $A$. On note $D, E, F$ les points de tangence du cercle inscrit sur les côtés $(B C),(A C)$ et $(A B), I$ le centre du cercle inscrit de $A B C$. Soient $P$ et $Q$ les intersections de la droite $(E F)$ avec le cercle $\Omega$ circonscrit à $A B C$. Soient enfin $O_{1}$ et $O_{2}$ les centres des cercles circonscrits à $A I B$ et $A I C$. Montrer que le centre du cercle circonscrit à $D P Q$ se situe sur la droite $\left(O_{1} O_{2}\right)$.
|
| 91 |
+
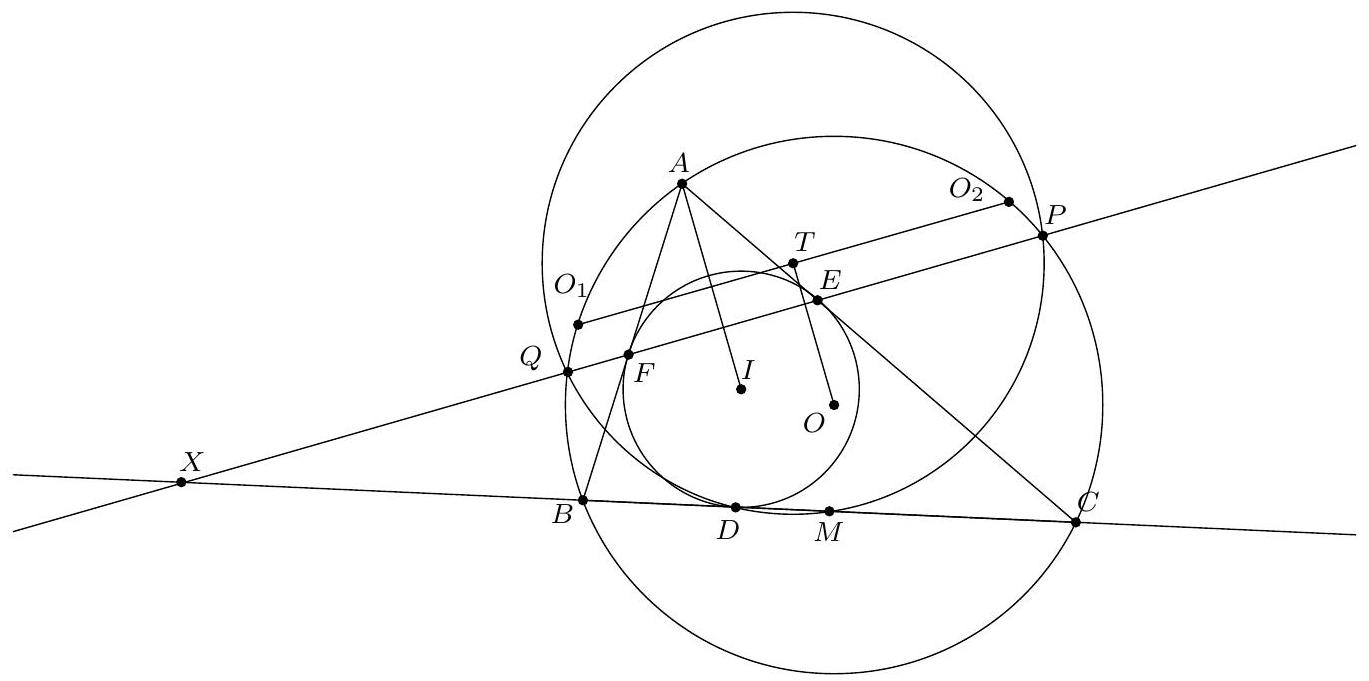
|
| 92 |
+
|
| 93 |
+
On peut déjà remarquer que $O_{1}$ et $O_{2}$ sont les pôles sud de $C$ et de $B$ respectivement dans le triangle $A B C$. La droite $\left(O_{1} O_{2}\right)$ est la médiatrice de $[A I]$. Or les droites $(A I)$ et $(E F)$ sont perpendiculaires. On en déduit alors que les droites $(P Q)$ et $\left(O_{1} O_{2}\right)$ sont parallèles. Comme $[P Q]$ et $\left[O_{1} O_{2}\right]$ sont aussi des cordes de $\Omega$, ces segments ont la même médiatrice. En particulier l'intersection entre la médiatrice de $[P Q]$ et $\left(O_{1} O_{2}\right)$ est le milieu de $\left[O_{1} O_{2}\right]$, disons $T$.
|
| 94 |
+
Ainsi si l'énoncé est vrai, alors le centre du cercle circonscrit à $D P Q$ doit être $T$.
|
| 95 |
+
Dans cette situation, on contrôle alors assez mal les deux autres médiatrices du triangle $P Q D$. On peut alors chercher un quatrième point appartenant au cercle. En particulier, définir un point comme seconde intersection entre un cercle et une droite peut souvent s'avérer utile.
|
| 96 |
+
Ici on peut s'intéresser à la seconde intersection de notre cercle avec la droite $(B C)$ : c'est en fait le milieu de $[B C]$. En effet, si on définit $X$ comme l'intersection entre les droites $(P Q)$ et $(B C)$, alors on sait que $X P \times X Q=X B \times X C$ et, comme les droites $(A D),(B E),(C F)$ sont concourantes (en le point de Gergonne du triangle $A B C$ ), la division $(X, D, B, C)$ est harmonique et donc on peut en déduire d'après la relation de Mac Laurin que : $X B \times X C=X D \times X M$. On trouve donc $X P \times X Q=X D \times X M$, ce qui implique que les points $P, Q, D, M$ sont cocycliques. Il suffit maintenant de montrer que la médiatrice de $[D M]$ passe par $T$. Pour cela, nous allons montrer que le projeté orthogonal de $T$ sur $(B C)$ est le milieu de $[D M]$. On associe à présent à chaque point $Z$ du plan le vecteur $\overrightarrow{O Z}$ qu'il forme avec une origine $O$ quelconque du plan (fixée). On notera $Z$ ce vecteur pour ne pas alourdir les notations.
|
| 97 |
+
Soit $N_{A}$ le pôle nord de $A$ dans $A B C$. Par définition, on sait que : $T=\frac{O_{1}+O_{2}}{2}$. De, plus, il est connu que $O_{1}$ est le milieu de $\left[I I_{C}\right]$ (centre du cercle exinscrit de $C$ ) et de même $O_{2}$ est le milieu de $\left[I I_{B}\right]$. Ainsi on trouve : $T=\frac{I+\frac{I_{B}+I_{C}}{2}}{2}$. Or on sait aussi que $N_{A}$ est le milieu de $\left[I_{B} I_{C}\right]$ et donc on trouve que $T$ est le milieu de $\left[I N_{A}\right]$. Le projeté orthogonal de $T$ sur $(B C)$ est le milieu des projetés orthogonaux de $I$ et $N_{A}$ sur $(B C)$, à savoir $D$ et $M$ respectivement.
|
| 98 |
+
Ainsi on en déduit que le centre du cercle circonscrit à $D P Q$ est $T$, qui est bien sur la droite $\left(O_{1} O_{2}\right)$.
|
| 99 |
+
|
French_STS/md/fr-ofm-2015-2016-envoi-3-solutions.md
ADDED
|
@@ -0,0 +1,313 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OLYMPIADES FRANÇAISES DE MATHÉMATIQUES 2015-2016
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
ENVOI No. 3
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(x) f(y)-f(x y)=x+y$ pour tous $x, y \in \mathbb{R}$.
|
| 12 |
+
|
| 13 |
+
Solution de l'exercice 1 Soit f une fonction vérifiant la condition de l'énoncé. En prenant $x=y=$ 0 , on obtient $f(0)(f(0)-1)=0$ donc $f(0)=0$ ou $f(0)=1$.
|
| 14 |
+
|
| 15 |
+
Premier cas : supposons que $f(0)=0$. En prenant $y=0$ dans l'équation initiale, on obtient $0=\chi$ pour tout $x \in \mathbb{R}$, ce qui est absurde.
|
| 16 |
+
|
| 17 |
+
Deuxième cas : supposons que $f(0)=1$. En prenant $y=0$ dans l'équation initiale, on obtient $f(x)=x+1$ pour tout $x \in \mathbb{R}$.
|
| 18 |
+
Réciproquement, on vérifie que la fonction $f(x)=x+1$ pour tout $x \in \mathbb{R}$ est solution car on a bien $(x+1)(y+1)-(x y+1)=x+y$ pour tous $x, y, \in \mathbb{R}$.
|
| 19 |
+
|
| 20 |
+
Remarque. Il est important de vérifier que réciproquement, la fonction $f(x)=x+1$ convient. En effet, nous avons raisonné par implications successives et non pas par équivalences. Par exemple, si l'énoncé était "Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(x) f(y)-f(x y)=$ $x+y$ pour tous $x, y \in \mathbb{R}$ et $f(2)=2$ ", nous aurions conclu que réciproquement, la fonction $f(x)=x+1$ ne convient pas $(\operatorname{car} f(2)=3)$ et que dans ce cas il n'y a pas de solution.
|
| 21 |
+
|
| 22 |
+
Exercice 2. Soit $n \geqslant 3$ un nombre entier et $a_{1}, a_{2}, \ldots, a_{n}$ des nombres réels.
|
| 23 |
+
(a) On suppose que $a_{i}<\max \left(a_{i-1}, a_{i+1}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$. Montrer que $a_{i}<$ $\max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$.
|
| 24 |
+
(b) On suppose que $a_{i} \leqslant \max \left(a_{i-1}, a_{i+1}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$. Est-il vrai que $a_{i} \leqslant \max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$ ?
|
| 25 |
+
N.B. Si $x$ et y sont deux nombres réels, on note $\max (x, y)$ le plus grand des deux.
|
| 26 |
+
|
| 27 |
+
Solution de l'exercice 2 (a) Soit $i \in\{1,2, \ldots, n\}$ un entier tel que $a_{i}=\max \left(a_{1}, \ldots, a_{n}\right)$. L'énoncé indique que $i \notin\{2,3, \ldots, n-1\}$. Cela montre à la fois que $i \in\{1, n\}$, donc que $a_{i}=\max \left(a_{1}, a_{n}\right)$, et que $a_{k}<a_{i}$ si $k \in\{2,3, \ldots, n-1\}$, ce qui était l'inégalité demandée.
|
| 28 |
+
(b) Le résultat est clairement vrai pour $\mathrm{n}=3$. Montrons qu'il n'est pas toujours vrai pour $\mathrm{n} \geqslant 4$ en exhibant un contre-exemple : prenons $a_{1}=a_{n}=1$ et $a_{i}=2$. La consigne de l'énoncé est respectée mais $a_{i}>\max \left(a_{1}, a_{n}\right)$ pour tout $2 \leqslant i \leqslant n-1$.
|
| 29 |
+
|
| 30 |
+
Autre solution pour (a). L'idée est de regarder où la suite "remonte" pour la première fois. Pour cela, nous allons distinguer deux cas :
|
| 31 |
+
|
| 32 |
+
Premier cas : il existe un plus petit entier $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ tel que $a_{i_{0}} \leqslant a_{i_{0}+1}$. Ainsi, $a_{1}>\cdots>a_{i_{0}}$ et $a_{i_{0}} \leqslant a_{i_{0}+1}$. En particulier, si $i_{0}=n-1$, on remarque qu'on a bien le résultat voulu (car alors $a_{n-1}<a_{1}$ at $a_{n-1} \leqslant a_{n}$ ). Supposons maintenant que $\mathfrak{i}_{0}<n-1$ et montrons que $a_{j}<a_{j+1}$ pour tout entier $\mathfrak{i}_{0}+1 \leqslant j \leqslant n-1$ par récurrence sur $j$.
|
| 33 |
+
|
| 34 |
+
Initialisation : on a $a_{i_{0}+1}<\max \left(a_{i_{0}}, a_{i_{0}+2}\right)$. Comme $a_{i_{0}} \leqslant a_{i_{0}+1}$, on doit avoir max $\left(a_{i_{0}}, a_{i_{0}+2}\right)=$ $a_{i_{0}+2}$, ce qui implique que $a_{i_{0}+1}<a_{i_{0}+2}$.
|
| 35 |
+
Hérédité : soit $\mathfrak{i}_{0}+1 \leqslant \mathfrak{j}<n-1$ un entier tel que $a_{j}<a_{j+1}$. Montrons que $a_{j+1}<a_{j+2}$. Comme $a_{\mathfrak{j}+1}<\max \left(a_{\mathfrak{j}}, a_{\mathfrak{j}+2}\right)$ et $a_{\mathfrak{j}}<\mathfrak{a}_{\mathfrak{j}+1}$, on doit avoir $\max \left(a_{j}, a_{j+2}\right)=a_{j+2}$, ce qui implique que $a_{j+1}<a_{j+2}$.
|
| 36 |
+
On a donc:
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
a_{1}>\cdots>a_{i_{0}} \leqslant a_{i_{0}+1}<a_{i_{0}+2}<a_{i_{0}+3}<\cdots<a_{n}
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
ce qui implique que $a_{i}<\max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$.
|
| 43 |
+
Deuxième cas : il n'existe pas d'entier $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ tel que $a_{i_{0}} \leqslant a_{i_{0}+1}$. Alors $a_{1}>a_{2}>\cdots>$ $a_{n}$ et on a bien le résultat voulu.
|
| 44 |
+
|
| 45 |
+
Exercice 3. Soient $0 \leqslant a, b, c, d, e \leqslant 1$ des nombres réels. Montrer que
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
Solution de l'exercice 3 L'idée est d'utiliser l'inégalité $(x+y)^{2} \geqslant 4 x y$ pour $x=1$ et une valeur particulière de $y$.
|
| 52 |
+
|
| 53 |
+
Plus précisément, pour tous $x, y \geqslant 0$, on a $(x-y)^{2} \geqslant 0$, et donc $(x+y)^{2} \geqslant 4 x y$ (cette inégalité est aussi l'inégalité arithmético-géométrique à deux variables). En évaluant cette inégalité avec $x=1$ et $y=a+b+c+d+e$, on obtient:
|
| 54 |
+
|
| 55 |
+
$$
|
| 56 |
+
(1+a+b+c+d+e)^{2} \geqslant 4(a+b+c+d+e)
|
| 57 |
+
$$
|
| 58 |
+
|
| 59 |
+
Or pour tout nombre réel $x$ tel que $0 \leqslant x \leqslant 1$, on a $x \geqslant x^{2}$. Donc
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
4(a+b+c+d+e) \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
ce qui montre finalement que $(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)$.
|
| 66 |
+
|
| 67 |
+
## Exercices communs
|
| 68 |
+
|
| 69 |
+
Exercice 4. Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(f(x)+3 y)=12 x+f(f(y)-x)$ pour tous $x, y \in \mathbb{R}$.
|
| 70 |
+
Solution de l'exercice 4 Soit f une fonction satisfaisant à la condition de l'énoncé. L'idée est de montrer que f est injective en utilisant le fait qu'elle est surjective. Montrons d'abord que f est surjective. En prenant $y=-f(x) / 3$ dans l'équation fonctionnelle, on obtient $f(f(y)-x)=$ $f(0)-12 x$. En faisant varier $x$, on voit que le membre de droite de cette dernière égalité peut prendre pour valeur n'importe quel nombre réel, et donc le membre de gauche aussi, ce qui implique que f est surjective.
|
| 71 |
+
|
| 72 |
+
Montrons que $f$ est injective. Soient $a, b \in \mathbb{R}$ tels que $f(a)=f(b)$. Nous allons montrer que $a=b$. En prenant $y=a$ et $y=b$ dans l'équation fonctionnelle, on obtient pour tout $x \in \mathbb{R}$
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
\mathbf{f}(\mathbf{f}(\mathrm{x})+3 \mathbf{a})=12 x+f(f(a)-x)=12 x+f(f(b)-x)=f(f(x)+3 b)
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
où on a utilisé le fait que $\mathrm{f}(\mathrm{a})=\mathrm{f}(\mathrm{b})$ pour la deuxième égalité. Ceci implique que pour tout $y \in \mathbb{R}$,
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
f(y)=f(y+3(b-a))
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
En effet, si on fixe $y \in \mathbb{R}$, par surjectivité il existe $x$ tel que $f(x)=y-3 a$ et en injectant dans (1), ceci donne (2). En particulier, $f(0)=f(3(b-a))$. Alors
|
| 85 |
+
|
| 86 |
+
$$
|
| 87 |
+
\mathbf{f}(\mathbf{f}(0))=\mathbf{f}(\mathbf{f}(3(b-a))+3 \cdot 0)=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0)-3(b-a))=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0))
|
| 88 |
+
$$
|
| 89 |
+
|
| 90 |
+
où pour la première égalité on utilise le fait que $f(0)=f(3(b-a))$, pour la deuxième on utilise l'équation fonctionnelle de l'énoncé (avec $x=3(b-a)$ et $y=0$ ), pour la troisième égalité on utilise (2) $(\operatorname{avec} y=f(0)-3(b-a)$ ). Donc $3(b-a)=0$ et $a=b$.
|
| 91 |
+
|
| 92 |
+
Pour conclure, en prenant $x=0$ dans l'équation de départ et en utilisant l'injectivité de f , on obtient
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
f(y)=f(0)+3 y
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
pour tout réel $y$.
|
| 99 |
+
Réciproquement, on vérifie que les fonctions de la forme $f(x)=a+3 x$ pour tout $x \in \mathbb{R}$ avec $a \in \mathbb{R}$ vérifient l'équation fonctionnelle de l'énoncé.
|
| 100 |
+
|
| 101 |
+
Exercice 5. Soient a, b, $c>0$. Montrer que
|
| 102 |
+
|
| 103 |
+
$$
|
| 104 |
+
\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}}>2 .
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Solution de l'exercice 5 L'idée est d'utiliser inégalité arithmético-géométrique pour minorer $\frac{1}{\sqrt{x+y}}$. Plus précisément, on a, par inégalité arithmético-géométrique :
|
| 108 |
+
|
| 109 |
+
$$
|
| 110 |
+
\sqrt{\frac{a}{b+c}}=\frac{a}{\sqrt{a(b+c)}} \geqslant \frac{a}{(a+b+c) / 2} \geqslant \frac{2 a}{a+b+c}
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
On procède de même pour montrer que $\sqrt{\frac{b}{c+a}} \geqslant \frac{2 b}{a+b+c}$ et que $\sqrt{\frac{c}{a+b}} \geqslant \frac{2 c}{a+b+c}$. On en déduit que
|
| 114 |
+
|
| 115 |
+
$$
|
| 116 |
+
\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}} \geqslant 2
|
| 117 |
+
$$
|
| 118 |
+
|
| 119 |
+
Il y a égalité seulement si et seulement si on est dans le cas d'égalité de chacune des trois inégalités arithmético-géométrique utilisées, soit : $a=b+c, b=a+c$ et $c=a+b$, ce qui est impossible.
|
| 120 |
+
|
| 121 |
+
Exercice 6. Soit $n>1$ un entier. Trouver tous les polynômes $P$ non constants à coefficients réels tels que
|
| 122 |
+
|
| 123 |
+
$$
|
| 124 |
+
P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=P\left(x^{\frac{n(n+1)}{2}}\right)
|
| 125 |
+
$$
|
| 126 |
+
|
| 127 |
+
pour tout nombre réel $x$.
|
| 128 |
+
Solution de l'exercice 6 Nous allons montrer que les solutions sont de la forme $\mathrm{P}(\mathrm{x})=\mathrm{x}^{\mathrm{a}}$ avec $a \geqslant 0$ un entier si $n$ est pair, et $P(x)=x^{a}$ ou $P(x)=-x^{a}$ avec $a \geqslant 0$ un entier si $n$ est impair. Comme $1+2+\cdots+n=\frac{n(n+1)}{2}$, on vérifie tout d'abord que ces polynômes vérifient l'équation de l'énoncé.
|
| 129 |
+
Soit maintenant $P$ un polynôme solution. Écrivons d'abord $P$ sous la forme $P(x)=x^{a} Q(x)$ avec $a \geqslant 0$ un entier et $Q$ un polynôme tel que $c=Q(0) \neq 0$. Écrivons $Q^{\prime}$ sous la forme $Q^{\prime}=x^{b} S(x)$ avec $b \geqslant 0$ un entier et $S$ un polynôme tel que $S(0) \neq 0$ (et donc $S$ n'est pas divisible par le polynôme $x$ ), et posons
|
| 130 |
+
|
| 131 |
+
$$
|
| 132 |
+
R(x)=Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)
|
| 133 |
+
$$
|
| 134 |
+
|
| 135 |
+
L'idée est de considérer la quantité $R^{\prime}(x) / R(x)$, où $R^{\prime}$ est le polynôme dérivé de R. En effet, comme $1+2+\cdots+n=\frac{\mathfrak{n}(\boldsymbol{n}+1)}{2}$, Q doit aussi vérifier l'égalité
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)=Q\left(x^{\frac{n(n+1)}{2}}\right) .
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
En faisant $x=0$, on trouve $\boldsymbol{c}^{n-1}=1$, de sorte que $\mathrm{c}=1$ si n est pair et $\mathrm{c}= \pm 1$ si n est impair. Supposons par l'absurde que $Q$ n'est pas constant (de sorte que $Q^{\prime} n^{\prime}$ est pas le polynôme nul), et dérivons (3) :
|
| 142 |
+
|
| 143 |
+
$$
|
| 144 |
+
R(x)\left(\frac{Q^{\prime}(x)}{Q(x)}+2 x \frac{Q^{\prime}\left(x^{2}\right)}{Q\left(x^{2}\right)}+\cdots+n x^{n-1} \frac{Q^{\prime}\left(x^{n}\right)}{Q\left(x^{n}\right)}\right)=\frac{n(n+1)}{2} x^{\frac{n(n+1)}{2}-1} Q^{\prime}\left(x^{\frac{n(n+1)}{2}}\right) .
|
| 145 |
+
$$
|
| 146 |
+
|
| 147 |
+
Notons que $R(0)=c^{n} \neq 0$ (et donc $R n^{\prime}$ est pas divisible par le polynôme $x$ ). La plus grande puissance de $x$ qui divise le membre de droite de (4) est $x^{\frac{n(n+1)}{2}-1+b \frac{n(n+1)}{2}}$ tandis que la plus grande puissance de $x$ qui divise celui de gauche est $x^{b}$ (car tous les termes de la somme sont divisibles par $x^{\mathrm{b}+1}$ sauf $\frac{\mathrm{Q}^{\prime}(x)}{\mathrm{Q}(x)}$ ). Donc
|
| 148 |
+
|
| 149 |
+
$$
|
| 150 |
+
\mathrm{b}=\frac{\mathrm{n}(\mathrm{n}+1)}{2}-1+\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}
|
| 151 |
+
$$
|
| 152 |
+
|
| 153 |
+
Or $n \geqslant 2$, donc
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\mathrm{b}<\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}<\frac{\mathrm{n}(\mathrm{n}+1)}{2}-1+\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}
|
| 157 |
+
$$
|
| 158 |
+
|
| 159 |
+
ce qui est absurde. Donc $Q$ est constant, ce qui conclut.
|
| 160 |
+
|
| 161 |
+
## Exercices du groupe A
|
| 162 |
+
|
| 163 |
+
Exercice 7 . Soit $n \geqslant 2$ un nombre entier et soient $x_{1}, \ldots, x_{n}$ des nombres réels positifs tels que $x_{1} x_{2} \cdots x_{n}=1$. Montrer que
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\frac{1}{n-1+x_{1}}+\frac{1}{n-1+x_{2}}+\cdots+\frac{1}{n-1+x_{n}} \leqslant 1
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
$\underline{\text { Solution de l'exercice } 7}$ En réduisant au même dénominateur, il s'agit de montrer que
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right) \leqslant \prod_{k=1}^{n}\left(x_{k}+n-1\right)
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
On note
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
\sigma_{k}=\sum_{1 \leqslant i_{1}<\cdots<i_{k} \leqslant n} x_{i_{1}} x_{i_{2}} \cdots x_{i_{k}}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
le $k$-ème polynôme élémentaire (de degré $k$ donc) en $x_{1}, \cdots, x_{n}$. Alors, en développant les deux côtés de (5), on voit que le coefficient de $\sigma_{k}$ est $(n-1)^{n-k}$ dans celui de droite pour $1 \leqslant k \leqslant n$, et $(n-k)(n-1)^{n-k-1}$ dans celui de gauche pour $1 \leqslant k \leqslant n-1$. Le coefficient constant vaut $(n-1)^{n}$ à droite et $n(n-1)^{n-1}$ à gauche. Autrement dit,
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
\prod_{k=1}^{n}\left(x_{j}+n-1\right)=\sum_{k=1}^{n}(n-1)^{n-k} \sigma_{k}+(n-1)^{n}
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
et
|
| 188 |
+
|
| 189 |
+
$$
|
| 190 |
+
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)=\sum_{k=1}^{n-1}(n-k)(n-1)^{n-k-1} \sigma_{k}+n(n-1)^{n-1}
|
| 191 |
+
$$
|
| 192 |
+
|
| 193 |
+
En notant $D=\prod_{k=1}^{n}\left(x_{k}+n-1\right)-\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)$, on a donc
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
D=x_{1} x_{2} \cdots x_{n}+\sum_{k=1}^{n-1}(k-1)(n-1)^{n-k-1} \sigma_{k}-(n-1)^{n-1}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
Or $\sigma_{k} \geqslant\binom{ n}{k}$ par l'inégalité arithmético-géométrique ( $\operatorname{car} x_{1} x_{2} \cdots x_{n}=1$,) de sorte que :
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
D \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{n-k-1}\binom{n}{k}-(n-1)^{n-1}
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
ou encore, en divisant les deux côtés par $(\mathrm{n}-1)^{\mathrm{n}-1}$,
|
| 206 |
+
|
| 207 |
+
$$
|
| 208 |
+
\frac{D}{(n-1)^{n-1}} \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{-k}\binom{n}{k}-1=\sum_{k=1}^{n} k(n-1)^{-k}\binom{n}{k}-\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}-1 .
|
| 209 |
+
$$
|
| 210 |
+
|
| 211 |
+
Or
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
\sum_{k=1}^{n} k\binom{n}{k}(n-1)^{-k}=\frac{n}{n-1} \sum_{k=1}^{n}\binom{n-1}{k-1} \cdot\left(\frac{1}{n-1}\right)^{k-1}=\frac{n}{n-1} \times\left(\frac{n}{n-1}\right)^{n-1}=\left(\frac{n}{n-1}\right)^{n}
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
et
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}=\sum_{k=0}^{n}(n-1)^{-k}\binom{n}{k}-1=\left(\frac{n}{n-1}\right)^{n}-1 .
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
On en déduit que $D \geqslant 0$, ce qui conclut.
|
| 224 |
+
Exercice 8. On note $S(k)$ la somme des chiffres d'un nombre entier $k$. On dit qu'un entier a est d'ordre $n$ s'il existe une suite d'entiers $a_{0}, a_{1}, \ldots, a_{n}$ tels que $a_{n}=a$ et $a_{i+1}=a_{i}-S\left(a_{i}\right)$ pour tout $i=0,1, \ldots, n-1$. Montrer que pour tout entier $n \geqslant 1$ il existe un entier $b$ qui soit d'ordre $n$ mais qui ne soit pas d'ordre $n+1$.
|
| 225 |
+
|
| 226 |
+
Solution de l'exercice 8 On pose $F(x)=x-S(x)$, et on considère la suite définie par $u_{0}=1$ et $u_{i+1}=10^{u_{i}}$ pour $i \geqslant 0$. Soit $n \geqslant 1$ fixé, et considérons un entier $N>u_{n+1}$. Nous allons montrer que $X=F^{(n)}\left(10^{N}-5 N\right.$ ) (on itère $n$ fois $F$ ) est d'ordre $n$ mais pas $n+1$. Pour cela, il suffit de montrer que X n'est pas d'ordre $\mathrm{n}+1$.
|
| 227 |
+
|
| 228 |
+
On remarque pour commencer que $F(a)-F(b)$ est toujours divisible par 9, et que si $a$ et $b$ ne différent que sur leurs $k$ derniers chiffres, alors $|a-b| \leqslant 10^{k}$.
|
| 229 |
+
|
| 230 |
+
Établissons maintenant une sorte de réciproque à cette remarque. Soient $a, b$ deux entiers et écrivons $a=\sum_{i \geqslant 0} c_{i} 10^{i}$ et $b=\sum_{i \geqslant 0} c_{i}^{\prime} 10^{i}$. On a $F(a)-F(b)=\sum_{i \geqslant 0}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right)$. Si $j$ est le plus grand indice tel que $c_{j}>c_{j}^{\prime}$, alors
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
F(a)-F(b) \geqslant\left(10^{j}-1\right)+\sum_{i=0}^{j-1}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right) \geqslant\left(10^{j}-1\right)-9 \sum_{i=0}^{j-1}\left(10^{i}-1\right)=9 j
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
On en déduit que si $|F(a)-F(b)|=9 k$, alors $j \leqslant k$, et donc
|
| 237 |
+
si $|F(a)-F(b)|=9 k, \quad$ alors $a$ et $b$ ne peuvent différer que sur leurs $k+1$ derniers chiffres. (6)
|
| 238 |
+
Montrons maintenant le lemme suivant:
|
| 239 |
+
Lemme. Si $F^{(n)}(a)=F^{(n)}(b)$ alors $a$ et b ne peuvent différer que sur leurs $u_{n}$ derniers chiffres.
|
| 240 |
+
Revenons maintenant à la preuve du lemme en raisonnant par récurrence sur n . L'initialisation pour $n=1$ provient de (6) appliqué avec $k=0$. Pour l'hérédité, soit $n \geqslant 1$ tel que le lemme est vrai jusqu'au rang $n$. Soient $a, b$ deux entiers tels que $F^{(n+1)}(a)=F^{(n+1)}(b)$. Alors $F^{(n)}(F(a))=$ $F^{(n)}(F(b))$, et donc $|F(a)-F(b)| \leqslant 10^{u_{n}}$ par hypothèse de récurrence. Comme $|F(a)-F(b)|$ est divisible par 9 , écrivons $|F(a)-F(b)|=9 k$ (avec $9 k \leqslant 10^{u_{n}}$ ). Alors d'après (6), a et b ne peuvent différer que sur leurs $k+1$ derniers chiffres. Comme $k+1 \leqslant 10^{u_{n}} / 9+1 \leqslant 10^{u_{n}}$, a et b ne peuvent différer que sur leurs $10^{u_{n}}=u_{n+1}$ derniers chiffres, ce qui conclut.
|
| 241 |
+
|
| 242 |
+
Revenons à l'exercice. Raisonnons par l'absurde en supposant l'existence d'un entier y tel que $X=F^{(n+1)}(y)=F^{(n)}\left(10^{N}-5 N\right)$. Alors
|
| 243 |
+
|
| 244 |
+
$$
|
| 245 |
+
F^{(n)}\left(10^{N}-5 N\right)=F^{(n)}(F(y))
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
et donc d'après le lemme
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
\left|10^{\mathrm{N}}-5 \mathrm{~N}-\mathrm{F}(\mathrm{y})\right| \leqslant 10^{\mathbf{u}_{\mathrm{n}}} \leqslant \mathrm{~N} .
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
Donc
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
10^{\mathrm{N}}-4 \mathrm{~N} \leqslant \mathrm{~F}(\mathrm{y}) \leqslant 10^{\mathrm{N}}-6 \mathrm{~N}
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
Or on constate que si $\mathrm{y} \geqslant 10^{\mathrm{N}}$, alors $\mathrm{F}(\mathrm{y}) \geqslant 10^{\mathrm{N}}-1$ (en effet, on vérifie aisément que F est croissante et que $\left.F\left(10^{N}\right)=10^{N}-1\right)$. De plus, si $y \leqslant 10^{N}-1$, alors $F(y) \leqslant 10^{N}-9 \mathrm{~N}-1$; en effet si $y=\sum_{i=0}^{N-1} c_{i} 10^{i}$, alors
|
| 261 |
+
|
| 262 |
+
$$
|
| 263 |
+
F(y)=\sum_{i=0}^{N-1} c_{i}\left(10^{i}-1\right) \leqslant \sum_{i=0}^{N-1} 9\left(10^{i}-1\right)=10^{N}-9 N-1
|
| 264 |
+
$$
|
| 265 |
+
|
| 266 |
+
Ceci contredit (7), et $X$ vérifie bien la condition cherchée.
|
| 267 |
+
Autre solution, un peu plus courte : Comme ci-dessus, on pose $F(x)=x-S(x)$. Il vient immédiatement que $F(a+1)=F(a)$ si $a \not \equiv 9(\bmod 10)$ et que $F(a+1)>F(a)$ si $a \equiv 9(\bmod 10)$. Par conséquent, tout entier k a au plus 10 antécédents par F , et a fortiori il a au plus $10^{\mathrm{n}}$ antécédents par $F^{(n)}$, où $F^{(n)}$ est la $n^{\text {ème }}$ itérée de $F$. Il s'ensuit que $F^{(n)}\left(k+10^{n}\right)>F^{(n)}(k)$ pour tout entier $k \geqslant 1$ (en effet, si $F^{(n)}\left(k+10^{n}\right)=F^{(n)}(k)$ pour un certain entier $k \geqslant 1$, on aurait $F^{(n)}(k)=F^{(n)}(i)$ pour tout $k \leqslant i \leqslant k+10^{n}$, de sorte que $l^{\prime}$ entier $F^{(n)}(k)$ aurait au moins $10^{n}+1$ antécédents qui sont $\left.k, k+1, k+2, \ldots, k+10^{n}\right)$.
|
| 268 |
+
|
| 269 |
+
Maintenant, soit $\ell$ un entier tel que $9 \ell \geqslant 2 \cdot 10^{n}$. On observe que $F\left(10^{\ell}\right)=10^{\ell}-1$ et que $F\left(10^{\ell}-1\right)=10^{\ell}-1-9 \ell$, puis on pose $a_{k}=F^{(k)}\left(10^{\ell}-10^{n}-1\right)$ et $b_{k}=F^{(k)}\left(10^{\ell}-1\right)$, pour $k \geqslant 0$. Puisque $b_{0} \geqslant a_{0}+10^{n}$, on en déduit que $b_{n}>a_{n}$. De même, puisque $a_{0} \geqslant b_{1}+10^{n}$, on en déduit que $a_{n}>b_{n+1}$. Cela montre que $b_{0}>i>b_{1}$ pour tout entier $i$ tel que $a_{n}=F^{(n)}(i)$.
|
| 270 |
+
|
| 271 |
+
Or, on a $F(k) \geqslant b_{0}$ pour tout $k \geqslant 10^{\ell}$ et $F(k) \leqslant b_{1}$ pour tout $k \leqslant 10^{\ell}-1$, ce qui montre que les éléments de l'ensemble $\left\{b_{1}+1, \ldots, b_{0}-1\right\}$ sont tous d'ordre 0 mais pas d'ordre 1 . Il s'ensuit que $a_{n}$ est d'ordre $n$ mais pas d'ordre $n+1$, ce qui conclut.
|
| 272 |
+
|
| 273 |
+
Exercice 9. Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que
|
| 274 |
+
|
| 275 |
+
$$
|
| 276 |
+
f(x) f(y f(x)-1)=x^{2} f(y)-f(x)
|
| 277 |
+
$$
|
| 278 |
+
|
| 279 |
+
pour tous $x, y \in \mathbb{R}$.
|
| 280 |
+
Solution de l'exercice 9 Tout d'abord, on remarque que la fonction nulle est solution.
|
| 281 |
+
Soit maintenant une fonction f solution. En prenant $x=0$, on obtient $f(0)(f(y f(0)-1)+1)=0$. Si $f(0) \neq 0$, alors $f(y f(0)-1)=-1$ pour tout $y \in \mathbb{R}$. Comme $y f(0)-1$ parcourt $\mathbb{R}$ quand
|
| 282 |
+
y parcourt $\mathbb{R}$, on en déduit qu'alors f est constante égale à -1 . En prenant $x=1$, on obtient $(-1)^{2}=-1^{2}+1$, ce qui est absurde. Donc $f(0)=0$.
|
| 283 |
+
|
| 284 |
+
Supposons maintenant que $f n^{\prime}$ est pas la fonction nulle. Il existe alors $a \in \mathbb{R}^{*}$ tel que $f(a) \neq 0$. En prenant $x=a$ et $y=0$, on obtient $f(-1)=-1$.
|
| 285 |
+
|
| 286 |
+
Si $f(x)=0$, en prenant $y=a$, on obtient $x^{2} f(a)=0$, et donc $x=0$. Ainsi, $f(x)=0$ si et seulement si $x=0$.
|
| 287 |
+
|
| 288 |
+
En prenant $x=y=1$, on obtient $f(1) f(f(1)-1)=0$, et donc, comme $f(1) \neq 0, f(1)=1$.
|
| 289 |
+
En prenant $x=1$, on obtient $f(y-1)=f(y)-1$, et en utilisant ceci dans l'équation initiale on obtient
|
| 290 |
+
|
| 291 |
+
$$
|
| 292 |
+
f(x) f(y f(x))=x^{2} f(y)
|
| 293 |
+
$$
|
| 294 |
+
|
| 295 |
+
En prenant $x=-1$ dans cette dernière équation, on obtient $f(-y)=-f(y)$, et donc $f$ est impaire. Combiné avec le fait que $\mathrm{f}(\mathrm{y}-1)=\mathrm{f}(\mathrm{y})-1$, on en déduit par récurrence que
|
| 296 |
+
|
| 297 |
+
$$
|
| 298 |
+
f(y-n)=f(y)-n
|
| 299 |
+
$$
|
| 300 |
+
|
| 301 |
+
pour tout entier $n \geqslant 0$, puis que $f(n)=n$ pour tout nombre entier relatif $n$. En prenant $x=n$ dans (8), on obtient
|
| 302 |
+
|
| 303 |
+
$$
|
| 304 |
+
\mathrm{f}(\mathrm{yn})=\mathfrak{n f}(\mathrm{y})
|
| 305 |
+
$$
|
| 306 |
+
|
| 307 |
+
et on en déduit que $f(r)=r$ pour tout nombre rationnel $r$.
|
| 308 |
+
En prenant $y=1$ dans (8), on obtient $f(x) f(f(x))=x^{2}$. En prenant $x=y=f(x)$ dans (8), on obtient $f(f(x)) f\left(f(x) f(f(x))=f(x)^{2} f(f(x))\right.$. Pour $x \neq 0, f(f(x)) \neq 0$, et donc en simplifiant par $f(f(x))$ on obtient $f\left(x^{2}\right)=f\left(f(x) f(f(x))=f(x)^{2}\right.$. Ainsi, $f(x)>0$ pour $x>0$.
|
| 309 |
+
|
| 310 |
+
Soit maintenant $z>0$ un nombre irrationnel, et supposons par l'absurde que $f(z)>z$. Soit $r=n / m$ un nombre rationnel tel que $f(z)>r>z$. Comme $m(r-z)>0$, on a $f(m(r-z))>0$. Or f est impaire (prendre $n=-1$ dans (10)), donc $m f(z)-n=f(m z)-n=f(m z-n)<0$, ce qui contredit le fait que $f(z)>r$. Le cas où $f(z)<z$ se traite de la même manière. Donc $f(x)=x$ pour tout $x \in \mathbb{R}$. Réciproquement, on vérifie qu'elle convient.
|
| 311 |
+
|
| 312 |
+
Les solutions sont donc la fonction nulle et la fonction identité.
|
| 313 |
+
|
French_STS/md/fr-ofm-2015-2016-envoi-4-solutions.md
ADDED
|
@@ -0,0 +1,135 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OCympiades Françaises de Mathématiques 2015-2016
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## Corrigé de l'envoi Numéro 4 - Combinatoire
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe B
|
| 8 |
+
|
| 9 |
+
Exercice 1. Soit $n \geqslant 2$. On place une pièce sur chaque case d'un échiquier $n \times n$. Un mouvement consiste à déplacer chaque pièce sur une case qui touche la case de départ par un coin exactement (plusieurs pièces peuvent se retrouver sur la même case).
|
| 10 |
+
Quel est le plus petit entier $k$ tel qu'il est possible qu'après un certain nombre de mouvements, seules $k$ cases contiennent au moins une pièce?
|
| 11 |
+
|
| 12 |
+
## Solution de l'exercice 1 La réponse est 4.
|
| 13 |
+
|
| 14 |
+
On note $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D les quatre cases quif forment le carré $2 \times 2$ en haut à droite :
|
| 15 |
+
|
| 16 |
+
|
| 17 |
+
Chaque pièce peut être amenée sur une des cases $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D , puis osciller à chaque mouvement entre $A$ et $D$ ou entre $B$ et $C$. Il est donc possible qu'après un certain nombre de mouvements, toutes les pièces soient sur une des quatre cases $A, B, C$ et $D$.
|
| 18 |
+
Il reste à montrer qu'on ne peut pas faire mieux que 4 . On considère le coloriage suivant de l'échiquier (ici pour $\mathrm{n}=4$ ) :
|
| 19 |
+
|
| 20 |
+
|
| 21 |
+
Comme $n \geqslant 2$, il y a au début au moins une pièce sur une case de chaque couleur. Mais à chaque mouvement, les pièces qui se trouvent sur des cases bleues passent sur des cases rouges, celles sur des cases rouges passent sur des bleues, celles sur des jaunes passent sur des vertes et celles sur des vertes passent sur des jaunes. A chaque étape, il y a donc des pièces sur au moins une case de chaque couleur, donc il y a toujours au moins 4 cases qui contiennent au moins une pièce.
|
| 22 |
+
Exercice 2. Soit A un ensemble de 13 entiers entre 1 et 37 . Montrer qu'il existe quatre nombres deux à deux distincts dans $A$ tels que la somme de deux d'entre eux est égale à la somme des deux autres.
|
| 23 |
+
Solution de l'exercice 2 A contient 13 entiers, donc il y a $\frac{13 \times 12}{2}=78$ manières de choisir deux nombres de A différents ( 13 manières de choisir le premier, 12 manières de choisir le deuxième et on divise par 2 car on a compté deux fois chaque ensemble de 2 nombres). Or, la somme de deux nombres de $\mathcal{A}$ vaut toujours au moins $1+2=3$ et au plus $36+37=73$, donc elle peut prendre 71 valeurs différentes. D'après le principe des tiroirs, il existe donc $\mathrm{a} \neq \mathrm{d}$ et $\mathrm{b} \neq \mathrm{c}$ dans $A$ tels que $\mathrm{a}+\mathrm{d}=\mathrm{b}+\mathrm{c}$, et l'ensemble $\{a, d\}$ est différent de $\{b, c\}$. Pour conclure, il suffit de s'assurer que $a, b, c$ et $d$ sont deux à deux distincts.
|
| 24 |
+
|
| 25 |
+
Mais si par exemple $a=b$, alors comme $a+d=b+c$, on doit avoir $d=c$ donc $\{a, d\}=\{b, c\}$, ce qui est faux. On a donc bien trouvé 4 nombres qui vérifient la propriété voulue.
|
| 26 |
+
Exercice 3. Les sept nains ont des tailles deux à deux distinctes. Ils se rendent à la mine en colonne dans un certain ordre, de telle manière que le nain en tête est plus grand que le deuxième, qui est plus petit que le troisième, qui est plus grand que le quatrième et ainsi de suite...
|
| 27 |
+
Combien y a-t-il de telles manières d'arranger les nains?
|
| 28 |
+
Solution de l'exercice 3 On note $u_{3}$ le nombre de manières d'arranger 3 nains de manière à ce que le premier est plus grand que le second, qui est plus grand que le troisième, $\mathfrak{u}_{5}$ le nombre de manières similaires d'arranger 5 nains et $u_{7}$ la solution de l'exercice.
|
| 29 |
+
Avec 3 nains, on est obligé de mettre le nain le plus petit au milieu et on peut ensuite placer comme on veut les deux autres.
|
| 30 |
+
Avec 5 nains, le nain le plus petit peut être en deuxième ou quatrième position :
|
| 31 |
+
|
| 32 |
+
- S'il est en position 2, n'importe quel nain peut être en premier, donc on a 4 choix pour le premier nain. Il reste à ordonner les trois derniers : il y a $\mathfrak{u}_{3}$ manières de le faire, donc on obtient $4 \mathfrak{u}_{3}$ arrangements.
|
| 33 |
+
- S'il est en position 4 , on a de même $4 u_{3}$ arrangements (en choisissant d'abord le cinquième).
|
| 34 |
+
|
| 35 |
+
On a donc $\mathfrak{u}_{5}=4 u_{3}+4 u_{3}=8 \times 2=16$.
|
| 36 |
+
Avec 7 nains, le nain le plus petit peut être en position 2, 4 ou 6 :
|
| 37 |
+
|
| 38 |
+
- S'il est en position 2 , n'importe quel nain peut être en premier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq derniers, soit $6 \mathbf{u}_{5}$ ordres possibles.
|
| 39 |
+
- S'il est en position 6 , n'importe quel nain peut être en dernier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq premiers, soit $6 \mathfrak{u}_{5}$ ordres possibles.
|
| 40 |
+
- S'il est en position 4, on peut d'abord trier les nains qui seront devant lui de ceux qui seront derrière. Il y a $\binom{6}{3}=20$ manières de faire ce tri. Puis il y a $u_{3}$ manières d'ordonner les trois nains de devant et $u_{3}$ manières d'ordonner les trois de derrière, soit $20 u_{3}^{2}$ ordres popssibles.
|
| 41 |
+
On a donc $\mathfrak{u}_{7}=6 \mathfrak{u}_{5}+6 \mathfrak{u}_{5}+20 \mathfrak{u}_{3}^{2}=6 \times 16+6 \times 16+20 \times 2^{2}=272$.
|
| 42 |
+
|
| 43 |
+
|
| 44 |
+
## Exercices communs
|
| 45 |
+
|
| 46 |
+
Exercice 4. Soit $n \geqslant 1$. On a un nombre fini de bouteilles, chacune contenant une quantité d'eau inférieure à 1 litre, telles que la quantité totale d'eau est de $\frac{\mathfrak{n}}{2}$ litres. On dispose également de n seaux vides.
|
| 47 |
+
|
| 48 |
+
Montrer qu'il est possible de vider chaque bouteille dans un seau (on peut vider plusieurs bouteilles dans le même seau, mais pas vider une bouteille en partie dans un seau et en partie dans un autre) de manière à avoir au plus 1 litre d'eau dans chaque seau.
|
| 49 |
+
Solution de l'exercice 4 On raisonne par récurrence sur $n$ : pour $\mathrm{n}=1$, il suffit de tout vider dans l'unique seau.
|
| 50 |
+
Supposons le résultat vrai au rang n : si on arrive à vider dans un seau un certain nombre de bouteilles représentant au total au moins $\frac{1}{2}$ litre et au plus 1 litre, alors il restera $\frac{\mathrm{n}-1}{2}$ litres à vider dans les $\mathrm{n}-1$ seaux restants, et on pourra appliquer l'hypothèse de récurrence pour conclure.
|
| 51 |
+
|
| 52 |
+
Si il existe une bouteille contenant au moins $\frac{1}{2}$ litre, on peut donc la vider dans le premier seau. Sinon, toutes les bouteilles contiennent moins de $\frac{1}{2}$ litre. On les vide donc une par une dans le premier seau, et on s'arrête dès que le contenu du seau dépasse $\frac{1}{2}$ litre : le seau contient alors plus de $\frac{1}{2}$ litre. De plus, juste avant de vider la dernière bouteille, il contenait moins de $\frac{1}{2}$ litre, et on a ajouté une bouteille, donc moins de $\frac{1}{2}$ litre. Le seau contient donc moins de 1 litre, et on peut conclure par hypothèse de récurrence.
|
| 53 |
+
Exercice 5. On note $S$ l'ensemble des entiers de 1 à 2016. Combien y a-t-il de manières de partitionner $S$ en deux sous-ensembles $A$ et $B$ de telle manière que ni $A$ ni $B$ ne contient deux entiers dont la somme est une puissance de 2 ?
|
| 54 |
+
|
| 55 |
+
Remarque. On dit que $A$ et $B$ forment une partition de $S$ si ni $A$ ni $B$ n'est vide, $A$ et $B$ sont d'intersection vide et si leur union est égale à $S$.
|
| 56 |
+
|
| 57 |
+
Solution de l'exercice 5 La réponse est $2^{11}=2048$. Plus précisément, on va montrer qu'il est possible de répartir comme on veut les nombres $1,2,4,8, \ldots, 1024=2^{10}$ comme on veut entre $A$ et $B$ et qu'une fois ces nombres placés il existe une unique manière de répartir les autres. On peut alors conclure car il y a $2^{11}=2048$ manières de répartir ces 11 nombres entre $A$ et $B$.
|
| 58 |
+
Le fait que la répartition de $1,2,4,8, \ldots, 1024$ impose la position de $k$ se montre par récurrence forte sur k : la position de 1 et 2 a déjà été fixée, et 3 doit être dans l'ensemble qui ne contient pas $1 \mathrm{car} 3+1=2^{2}$. Supposons maintenant que toutes les positions de nombres de 1 à $k-1$ soient fixées : si $k$ est une puissance de 2, alors la position de $k$ est fixée par hypothèse. Sinon, il existe a tel que $2^{a-1}<k<2^{a}$. Mais alors $0<2^{a}-k<k$ donc $2^{a}-k$ est dans $A$ ou $B$, et sa position a déjà été fixée. $k$ est donc nécessairement dans l'autre ensemble. Il existe donc au plus une partition qui convient une fois fixée la répartition des puissances de 2 .
|
| 59 |
+
Il reste à montrer qu'une telle répartition existe bien. Mais la preuve précédente fournit un algorithme qui permet de répartir les entiers qui ne sont pas des puissances de 2 entre $\mathcal{A}$ et $B$ de telle manière que pour tous $k$ et $a$ tel que $2^{a-1}<k<2^{a}$, les nombres $k$ et $2^{a}-k$ ne sont pas dans le même ensemble. Or, si deux nombres $x \neq y$ ont pour somme une puissance de 2 notée $2^{a}$, on peut supposer $x>y$. On a alors $x>\frac{x+y}{2}=2^{a-1}$, donc $2^{a-1}<x<2^{a}$ et $y=2^{a}-x$, donc $x$ et $y$ ne sont pas dans le même ensemble, donc il existe bien toujours une répartition qui convient.
|
| 60 |
+
Exercice 6. Sur chaque sommet d'un n-gone régulier on place un signe $+\mathrm{ou}-$. A chaque étape, on a le droit de changer les signes de trois sommets consécutifs du n-gone.
|
| 61 |
+
Quels sont les n pour lesquels quelle que soit la configuration de départ on peut obtenir en un nombre fini d'étapes des + sur tous les sommets?
|
| 62 |
+
Solution de l'exercice 6 On va montrer que ce sont exactement les n qui ne sont pas divisibles par 3.
|
| 63 |
+
Si $n$ est divisible par 3 , on note $A_{1}, \ldots, A_{n}$ les sommets du polygone, et on note $P$ le nombre de $k$ qui ne sont pas divisibles par 3 et tels qu'il y a un signe $-\operatorname{sur} A_{k}$. On montre qu'à chaque étape la parité de $P$ ne change pas : à chaque étape, on change les signes de 3 sommets consécutifs $A_{k}, A_{k-1}$ et $A_{k+1}$ (avec la convention $A_{0}=A_{n}$ et $A_{n+1}=A_{1}$ ). Exactement un de des nombres $k-1, k$ et $k+1$ est divisible par 3, donc on change exactement les signes de 2 sommets non divisibles par 3. P peut donc varier de -2 (si deux - deviennent des + ), de 0 (si un - devient un + et un + devient un - ) ou de 2 (si deux +
|
| 64 |
+
deviennent deux -), donc sa parité ne change jamais. En particulier, si $P=1$ au départ, il est impossible d'obtenir $\mathrm{P}=0$ donc il est impossible de n'avoir que des + .
|
| 65 |
+
Si $n$ n'est pas divisible par 3, on montre qu'il est possible de modifier exactement un signe. On peut alors facilement conclure car il suffit de modifier un par un les signes - :
|
| 66 |
+
|
| 67 |
+
- Si $n$ est de la forme $3 k-1$, on peut modifier les signes de $A_{1}, A_{2}, A_{3}$ puis de $A_{4}, A_{5}, A_{6}$ et ainsi de suite jusqu'à $A_{3 \mathrm{k}-2}, A_{3 \mathrm{k}-1}, A_{1}$, ce qui modifie le signe de tout le monde sauf $A_{1}$ (qui a été touché deux fois). On peut ensuite modifier le signe de tout le monde sauf $A_{2}$, puis modifier les signes de $A_{1}, A_{2}, A_{3}$. Cela revient à ne changer que le signe de $A_{3}$.
|
| 68 |
+
- Si $n$ et de la forme $3 k+1$, on peut modifier les signes de $A_{1}, A_{2}, A_{3}$ puis de $A_{4}, A_{5}, A_{6}$ et ainsi de suite jusqu'à $A_{3 k-2}, A_{3 k-1}, A_{3 k}$, ce qui modifie le signe de tout le monde sauf $A_{3 k+1}$ et on conclut comme ci-dessus.
|
| 69 |
+
|
| 70 |
+
|
| 71 |
+
## Exercices du groupe A
|
| 72 |
+
|
| 73 |
+
Exercice 7. Soit $n \geqslant 2$. On trace un circuit sur un échiquier $n \times n$ qui passe exactement une fois par chaque case et revient à son point de départ (deux cases consécutives sur le circuit doivent avoir un côté commun).
|
| 74 |
+
Montrer qu'il existe deux cases voisines sur l'échiquier telles que, si on "coupe" le circuit en ces deux cases, les deux chemins obtenus ont pour longueur au moins le quart de la longueur du circuit de départ.
|
| 75 |
+
|
| 76 |
+
Remarque. La longueur d'un chemin est le nombre de fois où il change de case. En particulier, si le circuit est découpé en deux chemins, la somme des longueurs des deux chemins vaudra toujours $\mathrm{n}^{2}$.
|
| 77 |
+
|
| 78 |
+
Solution de l'exercice 7 Remarquons tout d'abord que si l'échiquier est pavé en noir et blanc de la manière habituelle, le circuit doit alterner des cases noires et blanches et revenir à sa case de départ donc sa longueur doit être paire donc $n^{2}$ et pair. On écrit donc $n=2 m$.
|
| 79 |
+

|
| 80 |
+
|
| 81 |
+
On considère l'ensemble des coins des carrés qui se trouvent à l'intérieur du circuit (ce sont les points bleus sur la figure), et on relie deux de ces points quand ils sont à distance 1 l'un de l'autre (ce sont les
|
| 82 |
+
arêtes bleues sur la figure). Le graphe obtenu est un arbre : il est connexe car le circuit l'est, et il n'a pas de cycle car un cycle soit créerait un deuxième circuit à l'intérieur du premier, soit enfermerait le centre d'une case qui ne serait donc pas dans le circuit rouge. De plus, dans cet arbre, chaque sommet a au plus 4 voisins.
|
| 83 |
+
Le lemme suivant permet de faire le lien entre la longueur du chemin rouge et le nombre de sommets de l'arbre bleu :
|
| 84 |
+
|
| 85 |
+
Lemme (Lemme 1). Soit $T$ un arbre dont les sommets sont sur les coins d'un quadrillage, et $C$ un circuit passant par les centres des cases et faisant le tour de l'arbre. On note $|\mathrm{C}|$ la longueur de ce circuit. Alors $|C|=2|T|+2$.
|
| 86 |
+
|
| 87 |
+
Preuve du lemme 1. Chaque sommet de l'arbre est le centre d'un carré de côté 1. On calcule de deux manières différentes la somme $S$ des périmètres de ces carrés. D'un part on a $S=4|T|$. Mais d'autre part, pour calculer $S$, on prend en compte une fois chaque arête de $C$, et deux fois chaque arête qui sépare deux sommets de l'arbre. Comme l'arbre a $|\mathrm{T}|-1$ arêtes, on a donc $S=|C|+2(|T|-1)$. On en déduit le lemme.
|
| 88 |
+
|
| 89 |
+
On sait que $|C|=n^{2}=4 m^{2}$. On en déduit $|T|=\frac{1}{2}(|C|-1)=2 m^{2}-1$. De plus, couper le circuit en deux cases voisines revient essentiellement à couper une arête de l'arbre. On va donc montrer le lemme suivant:
|
| 90 |
+
|
| 91 |
+
Lemme (Lemme 2). On note |T| le nombre de sommets d'un arbre. Soit T un arbre ayant au moins deux sommets et dont tous les sommets sont de degré au plus 4. Il existe une arête e de T telle qu'en coupant l'arête $e$, l'arbre $T$ est coupé en deux arbres $T_{1}$ et $T_{2}$ tels que $\left|T_{1}\right| \geqslant \frac{1}{4}(|T|-1)$ et $\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)$.
|
| 92 |
+
|
| 93 |
+
Preuve du lemme 2. On raisonne par l'absurde. On fixe $\mathrm{x}_{0}$ un sommet de T : supprimer $\mathrm{x}_{0}$ divise T en $\mathrm{T}_{1}, \mathrm{~T}_{2}, \mathrm{~T}_{3}$ et $\mathrm{T}_{4}$ (si $\times$ n'a pas quatre voisins, certains de ces arbres ont un nombre de sommets nul). D'après le principe des tiroirs, il existe $i$ tel que $\left|T_{i}\right| \geqslant \frac{1}{4}(|T|-1)$. On suppose que c'est $T_{1}$, et on note $x_{1}$ le sommet de $T_{1}$ qui est relié à $x_{0}$. Mais si $T$ ne vérifie pas le lemme, alors $\left|\mathrm{T}_{1}\right|>|\mathrm{T}|-\frac{1}{4}(|\mathrm{~T}|-1)=\frac{3}{4}(|\mathrm{~T}|-1)+1$.
|
| 94 |
+
On peut maintenant effectuer le même raisonnement avec $x_{1}$ : il a au plus trois voisins différents de $x_{0}$ qui correspondent à trois arbres $\mathrm{T}_{1}^{\prime}, \mathrm{T}_{2}^{\prime}$ et $\mathrm{T}_{3}^{\prime}$, et le nombre total de sommets de ces trois arbres vaut au moins $\frac{3}{4}(|T|-1)$. Par le principe des tiroirs il existe $i$ tel que $\left|T_{i}^{\prime}\right| \geqslant \frac{1}{4}(|T|-1)$ donc, comme $T$ ne vérifie pas le lemme, $\left|\mathrm{T}_{1}^{\prime}\right|>\frac{3}{4}(|\mathrm{~T}|-1)+1$. On note $x_{2}$ le sommet par lequel $\mathrm{T}_{1}^{\prime}$ est relié à $x_{1}$. Comme on n'a considéré que les voisins de $x_{1}$ qui sont différents de $x_{0}$, on a $x_{2} \neq x_{0}$. On peut alors itérer cet argument. Comme T ne vérifie pas le lemme, le procédé ne s'arrête jamais et on construit une suite $\left(x_{n}\right)$ de sommets telle que $x_{n+2} \neq x_{n}$ pour tout $n$. Comme $T$ est un arbre, $\left(x_{n}\right)$ ne passe jamais deux fois par le même sommet donc $T$ est infini, ce qui est absurde.
|
| 95 |
+
|
| 96 |
+
D'après le lemme 2, il existe donc une arête $e$ de l'arbre (en vert sur la figure) telle que, si on coupe $e$, on obtient $T_{1}$ et $T_{2}$ tels que $\left|T_{1}\right|,\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)=\frac{\mathrm{m}^{2}-1}{2}$. Si on note $C_{1}$ et $C_{2}$ les circuits qui font le tour
|
| 97 |
+
de $T_{1}$ et de $T_{2}$, on a donc d'après le lemme 1 les inégalités $\left|C_{1}\right|,\left|C_{2}\right| \geqslant m^{2}+1$. Mais les deux parties du circuit obtenues en le coupant ont pour longueurs $\left|C_{1}\right|-1$ et $\left|C_{2}\right|-1$ (on retire l'arête orange) qui valent au moins $\mathrm{m}^{2}$, d'où le résultat.
|
| 98 |
+
|
| 99 |
+
Exercice 8. Soit $n \in \mathbb{N}^{*}$. On place des rectangles $1 \times n$ et $n \times 1$ sur un échiquier $2 n \times 2 n$, de telle manière que deux rectangles ne s'intersectent jamais et que chaque rectangle recouvre exactement n cases. Un ensemble de tels rectangles est dit saturé s'il est impossible d'ajouter un rectangle sans intersecter un rectangle déjà en place.
|
| 100 |
+
Trouver le plus petit $k$ tel qu'il existe un ensemble saturé de $k$ rectangles.
|
| 101 |
+
Solution de l'exercice 8 Commençons par le cas $n \geqslant 3$ : la réponse est $k=2 n+1$. L'ensemble suivant (dans le cas $\mathrm{n}=5$, la construction se généralisant facilement) convient :
|
| 102 |
+
|
| 103 |
+
|
| 104 |
+
Il reste à montrer qu'avec 2 n rectangles il est toujours possible d'en ajouter un qui ne les intersecte pas. Si les 2 n rectangles sont orientés dans le même sens, par exemple tous horizontaux, alors il doit y en avoir exactement un sur chaque ligne (sinon il y aurait une ligne vide), et il ne peut pas être tout au bout de la ligne (s'il était tout à gauche, on pourrait ajouter un rectangle à sa droite). Par conséquent, la première et la dernière colonne sont vides, et il est possible d'ajouter un rectangle vertical.
|
| 105 |
+
S'il y a des rectangles dans les deux sens, on peut supposer qu'il y a au plus n rectangles verticaux. Supposons que la configuration soit saturée. Soit $1 \leqslant k \leqslant n$ tel que la colonne $k$ contient un rectangle vertical noté $r$. En décalant $r$ d'une case vers la gauche, on doit intersecter un rectangle déjà en place, noté $r^{\prime}$ (sinon on pourrait ajouter un rectangle). Cependant, si $r^{\prime}$ était horizontal, il devrait intersecter $r$ car il n'y a pas assez de place pour un rectangle horizontal à gauche de $r$. Le rectangle $r^{\prime}$ est donc vertical, donc la colonne $k-1$ contient un rectangle vertical et de même pour les colonnes $k-2, \ldots, 2,1$.
|
| 106 |
+
De même, si $\mathrm{n}+1 \leqslant \mathrm{k} \leqslant 2 \mathrm{n}$ est tel que la colonne k contient un rectangle vertical, alors toutes les colonnes à sa droite contiennent un rectangle vertical. L'ensemble des colonnes ne contenant pas de rectangle vertical est donc un ensemble d'au moins n colonnes consécutives. Il y a donc un rectangle $\mathrm{n} \times 2 \mathrm{n}$ qui ne rencontre aucun des rectangles verticaux. Si la configuration est saturée, il faut donc 2 n rectangles horizontaux pour "bloquer" chaque ligne dans ce rectangle $\mathrm{n} \times 2 \mathrm{n}$. Comme on a supposé qu'il y avait au moins un rectangle vertical, il y a donc au moins $2 \mathrm{n}+1$ rectangles, ce qui est absurde.
|
| 107 |
+
Passons aux cas $n=1$ et $n=2$ : le cas $n=1$ est trivial et la réponse est 4 (il faut tout couvrir, sinon on pourrait ajouter un carré 1 . Pour $n=2$, il n'y a pas d'ensemble saturé de 5 rectangles.
|
| 108 |
+
|
| 109 |
+
Pour le montrer, on peut soit effectuer une disjonction de cas un peu fastidieuse, soit adapter la preuve précédente : si tous les rectangles ont la même direction, ce n'est pas possible (une seule ligne contient 2 rectangles donc un seul rectangle peut intersecter la première colonne donc il reste la place pour un domino vertical dans la première colonne). Sinon, on peut supposer qu'il y a au plus 2 dominos verticaux. La preuve pour $n \geqslant 3$ montre qu'il y a deux colonnes consécutives libres, donc au moins 4 dominos horizontaux, donc un seul vertical. De plus, les colonnes sans domino vertical sont consécutives donc on peut supposer que le domino vertical est dans la colonne 1. Il doit être au milieu de la colonne pour ne pas laisser une place, et il est alors facile de voir qu'il est impossible de "boucher tous les trous" avec 4 dominos horizontaux.
|
| 110 |
+
Enfin, la configuration suivante marche avec $\mathrm{k}=6$ :
|
| 111 |
+
|
| 112 |
+
|
| 113 |
+
Exercice 9. Soient $n \geqslant 2$ et $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$ des réels strictement positifs. Les $a_{i}$ sont supposés deux à deux distincts, de même que les $b_{i}$. On suppose qu'il est possible de séparer les $a_{i}$ en deux sous-ensembles de même somme, et de même pour les $b_{i}$.
|
| 114 |
+
Montrer qu'il existe un 2 n -gone simple ayant exactement n côtés horizontaux et n côtés verticaux, dont les longueurs des côtés horizontaux sont exactement les $a_{i}$ et dont les longueurs des côtés verticaux sont exactement les $b_{i}$.
|
| 115 |
+
|
| 116 |
+
Remarque. Un polygone simple est un polygone dont les côtés ne s'intersectent pas, sauf bien sûr deux côtés consécutifs en leur extrémité commune.
|
| 117 |
+
|
| 118 |
+
Solution de l'exercice 9 Quitte à changer les indices et éventuellement à échanger les rôles de $a$ et $b$, on peut supposer qu'il existe $\ell \leqslant m \leqslant \frac{n}{2}$ tels que $a_{1}+\cdots+a_{\ell}=a_{\ell+1}+\cdots+a_{n}=S_{a}$ et $b_{1}+\cdots+b_{m}=$ $b_{m+1}+\cdots+b_{n}$, que $b_{1} \geqslant \cdots \geqslant b_{m}$ et que $b_{m+1} \leqslant \cdots \leqslant b_{n}$. Quand on fait le tour de notre polygone dans le sens horaire, les $a_{i}$ avec $i \leqslant \ell$ correspondront aux longueurs des côtés où on va vers la droite, les $a_{i}$ avec $i \geqslant \ell+1$ à ceux où on va vers la gauche, les $b_{i}$ avec $i \leqslant m$ à ceux où on va vers le haut et les $b_{i}$ avec $i \geqslant m+1$ à ceux où on va vers le bas. Il reste à placer ces côtés correctement les uns par rapport aux autres, de manière à ce qu'ils ne s'intersectent pas.
|
| 119 |
+
On note $b_{i}^{\prime}=b_{i}$ pour $i \leqslant m$ et $b_{i}^{\prime}=-b_{i}$ pour $i \geqslant m+1$, de manière à avoir $\sum_{i=1}^{n} b_{i}^{\prime}=0$ (ce changement de notation permettra de mesurer la variation d'ordonnée quand on passe d'un sommet du polygone à un autre). Les $b_{i}^{\prime}$ sont alors rangés dans l'ordre décroissant.
|
| 120 |
+
|
| 121 |
+
Lemme. Il existe un sous-ensemble $\mathrm{I} \subset \llbracket 2, n-1 \rrbracket$ de cardinal $\ell-1$ tel que $b_{1}^{\prime}+\sum_{i \in I} b_{i}^{\prime}>0$ et $b_{n}^{\prime}+\sum_{i \in \mathrm{I}} \mathrm{b}_{\mathrm{i}}^{\prime}<0$.
|
| 122 |
+
|
| 123 |
+
Preuve du lemme. L'énoncé du lemme revient à trouver I de cardinal $\ell-1$ avec $\left.\sum_{i \in I} b_{i}^{\prime} \in\right]-$ $\mathrm{b}_{1}^{\prime},-\mathrm{b}_{n}^{\prime}\left[\right.$. Soient $\mathrm{I}_{\max }=\{2, \ldots, \ell\}$ et $\mathrm{I}_{\min }=\{\mathrm{n}-\ell+1, \ldots, \mathrm{n}-1\}$. Il est clair que $\sum_{i \in \mathrm{I}_{\max }} \mathrm{b}_{\mathrm{i}}^{\prime}>-\mathrm{b}_{1}^{\prime}$ (si on a $n$ nombres de somme nulle, la somme des $\ell$ plus grand est positive) et que $\sum_{i \in \mathrm{I}_{\mathrm{min}}} b_{i}^{\prime}<$ $-b_{n}^{\prime}$.
|
| 124 |
+
Si on remplace un par un les éléments de $I_{\min }$ par ceux de $I_{\max }$, la somme augmente à chaque étape d'un nombre de la forme $b_{i}^{\prime}-b_{j}^{\prime}<b_{1}^{\prime}-b_{n}^{\prime}$ (l'inégalité est stricte car les $b_{i}$ sont deux à deux distincts). On passe donc d'un nombre inférieur à $-b_{n}^{\prime}$ à un nombre supérieur à $-b_{1}^{\prime}$ en augmentant à chaque étape $d^{\prime}$ un nombre strictement inférieur à $b_{1}^{\prime}-b_{n}^{\prime}$ donc à un moment la somme se trouvera strictement entre $-b_{1}^{\prime}$ et $-b_{n}^{\prime}$.
|
| 125 |
+
|
| 126 |
+
On veut construire notre polygone de la manière suivante : $b_{1}$ sera la longueur du côté vertical le plus à gauche (on note $A$ le sommet en bas et $B$ le sommet en haut de ce côté) et $b_{n}$ celle du côté vertical le plus à droite (on nomme C le sommet en haut et D le sommet en bas de ce côté), et l'écart horizontal entre ces deux côtés vaut $S_{a}$. Pour passer de $B$ à $C$, on utilise les côtés horizontaux de longueur $a_{i}$ avec $1 \leqslant i \leqslant \ell$ entre lesquels on intercale les $\ell-1$ côtés de longueurs $b_{i}$ avec $i \in I$, en commençant par ceux tels que $i \leqslant m$. On obtient ainsi une ligne brisée (en bleu) qui relie le haut de $b_{1}$ au haut de $b_{n}$ en alternant les déplacements vers la droite et vers le haut, puis les déplacements vers la droite et vers le bas.
|
| 127 |
+
Puis, pour relier $D$ à $A$, on utilise les $n-\ell$ côtés horizontaux de longueur $a_{i}$ avec $\ell+1 \leqslant i \leqslant n$, entre lesquels on intercale les $b_{i}$ restants, cette fois en commençant par les $i \geqslant m+1$ pour descendre avant de remonter (cela correspond à la ligne verte sur la figure).
|
| 128 |
+
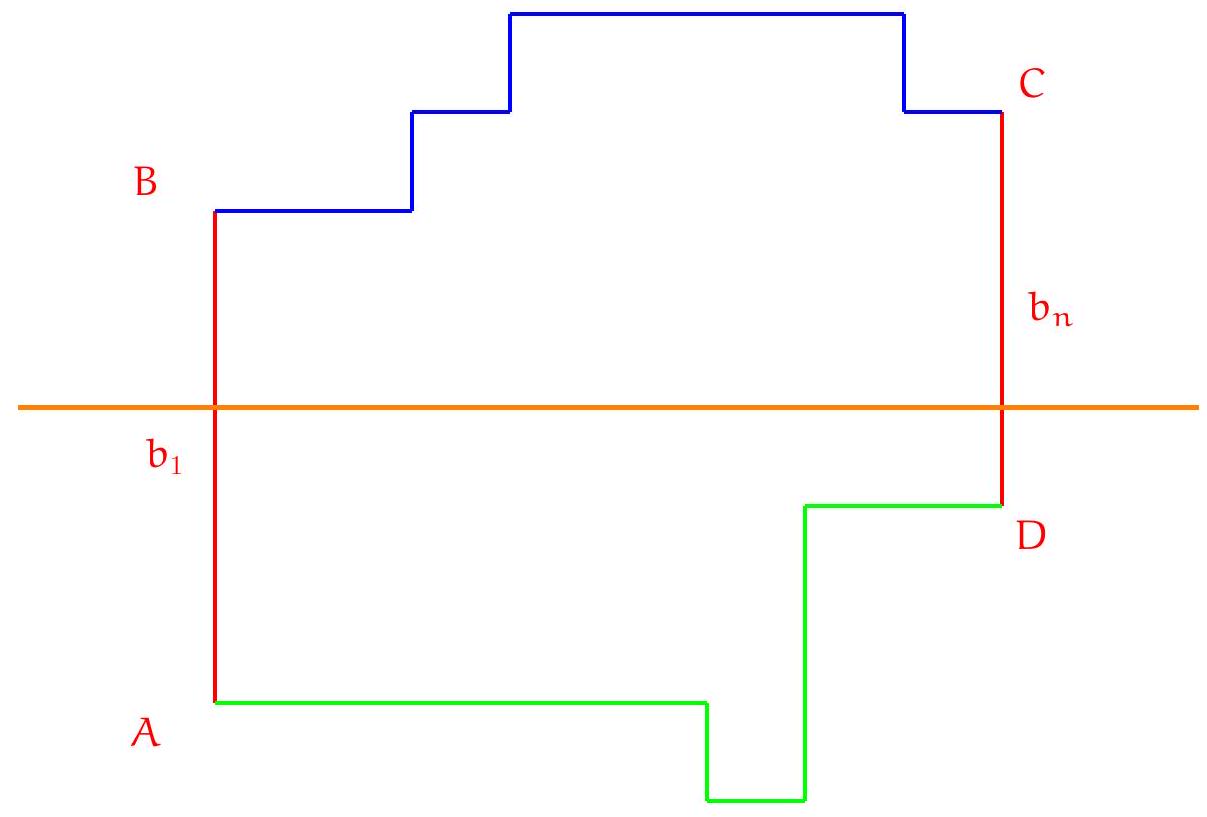
|
| 129 |
+
|
| 130 |
+
Le polygone ainsi construit a bien les longueurs de côtés voulues. il reste à vérifier que ces côtés ne s'intersectent pas. Les deux côtés rouges n'en coupent aucun autre car par construction, ils sont respec-
|
| 131 |
+
tivement plus à gauche et plus à droite que tous les autres. De plus, deux côtés bleus ne peuvent pas s'intersecter car il y en a toujours un plus à gauche que l'autre, et de même pour deux côtés verts.
|
| 132 |
+
Il suffit donc de vérifier qu'un côté bleu ne peut pas intersecter un sommet vert. On va montrer qu'en fait, la ligne bleue est entièrement située au-dessus de la ligne verte. Comme la ligne bleue monte puis redescend, son ordonnée est partout supérieure à $\min \left\{\mathrm{y}_{\mathrm{B}}, \mathrm{y}_{\mathrm{C}}\right\}$. De même, l'ordonnée sur la ligne verte est partout inférieure à $\max \left\{y_{A}, y_{D}\right\}$. Il suffit donc de montrer que $\min \left\{y_{B}, y_{C}\right\}>\max \left\{y_{A}, y_{D}\right\}$. Comme il est évident que $y_{B}>y_{A}$ et $y_{C}>y_{D}$, il suffit de montrer $y_{C}>y_{A}$ et $y_{B}>y_{D}$. Or, $y_{C}-y_{A}=$ $b_{1}+\sum_{i \in I} b_{i}^{\prime}$, qui est strictement positive d'après le lemme. De même, $y_{D}-y_{B}=\sum_{i \in I} b_{i}^{\prime}-b_{n}^{\prime}$ qui est strictement négative d'après le lemme. On peut donc tracer une ligne horizontale (en orange sur la figure) telle que la ligne bleue soit strictement au-dessus et la verte strictement en-dessous.
|
| 133 |
+
|
| 134 |
+
Remarque. L'énoncé original omettait la condition "les $b_{i}$ sont deux à deux distincts". Un contre-exemple assez simple sans cette hypothèse est le suivant: $n=4$ avec $a_{1}=a_{2}=a_{3}=a_{4}$ et $b_{1}=b_{2}=b_{3}=b_{4}$. En revanche, la preuve ci-dessus peut être adaptée dès que les $a_{i}$ ne sont pas tous égaux ou que les $b_{i}$ ne sont pas tous égaux.
|
| 135 |
+
|
French_STS/md/fr-ofm-2015-2016-envoi-5-solutions.md
ADDED
|
@@ -0,0 +1,256 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Mathématiques 2015-2016
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
# Envoi Numéro 5 - Pot-Pourri
|
| 6 |
+
|
| 7 |
+
Solutions
|
| 8 |
+
|
| 9 |
+
Exercice 1. Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\mathbf{p}, \mathbf{q}, \mathrm{r}$, pas forcément distincts, tels que
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
$\underline{\text { Solution de l'exercice } 1}$ Tout d'abord, si $p=q=r$, alors on obtient $\mathrm{a}=6$, qui est bien une solution. Montrons qu'il s'agit de la seule solution, et supposons qu'il existe une solution $a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}$ avec $p, q, r$ premiers et non tous égaux.
|
| 16 |
+
|
| 17 |
+
- Si deux des nombres $p, q, r$ sont égaux, disons $p=q \neq r$, alors:
|
| 18 |
+
|
| 19 |
+
$$
|
| 20 |
+
\mathrm{a}=2\left(\frac{\mathrm{p}}{\mathrm{r}}+\frac{\mathrm{r}}{\mathrm{p}}\right)+2=\frac{2\left(\mathrm{p}^{2}+\mathrm{r}^{2}\right)}{\mathrm{pr}}+2
|
| 21 |
+
$$
|
| 22 |
+
|
| 23 |
+
Ainsi, $\frac{2\left(\mathfrak{p}^{2}+r^{2}\right)}{p r}$ est un entier. On en déduit que le nombre premier $p$ divise $2 r^{2}$ tout en étant premier avec $r$, et donc que $p=2$. Le raisonnement $s^{\prime}$ adapte mot pour mot pour prouver que $r=2$, ce qui contredit que $r \neq p$. Il n'y a donc pas de solution dans ce cas.
|
| 24 |
+
|
| 25 |
+
- Si $p, q, r$ sont deux à deux distincts alors, sans perte de généralité, on peut supposer que $p>q>$ $r$ (on note qu'alors $p$ et $q$ sont impairs), et alors
|
| 26 |
+
|
| 27 |
+
$$
|
| 28 |
+
\operatorname{apqr}=\mathrm{pq}(\mathrm{p}+\mathrm{q})+\mathrm{qr}(\mathbf{q}+\mathrm{r})+\mathrm{rp}(\mathrm{r}+\mathrm{p})
|
| 29 |
+
$$
|
| 30 |
+
|
| 31 |
+
Ainsi, $p$ divise $q r(q+r)$. Puisque $p$ est premier avec $q r$, il divise donc $q+r$. Mais $0<q+r<2 p$ donc $p=q+r$. Cela implique que $r$ est pair, et donc que $r=2$. On a alors $p=q+2$ et $a=(q+1)+1+\frac{q+4}{q}=q+3+\frac{4}{q}$. En particulier, $\frac{4}{q}$ soit être un entier, ce qui est impossible pour $\mathrm{q}>1$ impair. Il n'y a ainsi pas de solution dans ce cas, ce qui conclut.
|
| 32 |
+
|
| 33 |
+
Exercice 2. Au club théâtre d'un lycée, on a formé 14 groupes de 4 élèves afin de travailler les scènes d'une pièce. Deux groupes différents ont toujours un et un seul élève en commun.
|
| 34 |
+
a) Prouver qu'il existe un élève qui appartient à au moins 5 groupes.
|
| 35 |
+
b) Chaque élève du club théâtre est membre d'au moins un groupe. Combien y a-t-il d'élèves dans ce club?
|
| 36 |
+
|
| 37 |
+
## Solution de l'exercice 2
|
| 38 |
+
|
| 39 |
+
a) Soit G un des groupes. Chacun des 13 autres groupes a un élève en commun avec G. Or $13=3 \times 4+1$ donc, d'après le principe des tiroirs, un des quatre élèves de G, disons $x$, appartient à au moins 4 des neuf autres groupes. Avec G, cela signifie que $x$ appartient à au moins 5 groupes.
|
| 40 |
+
b) Prouvons que $x$ appartient à tous les groupes. On note $\mathrm{G}=\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ des groupes auxquels appartient $x$, puis on procède par l'absurde : supposons qu'il existe un groupe $\mathrm{G}^{\prime}$ tel que $x \notin \mathrm{G}^{\prime}$.
|
| 41 |
+
Puisque $\mathrm{G}^{\prime}$ a un élève en commun avec chacun des groupes $\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ et, comme $\mathrm{G}^{\prime}$ ne contient que quatre élèves, c'est que l'un des membres de $G^{\prime}$, disons $y$, appartient à deux de ces cinq groupes, disons $G_{i}$ et $G_{j}$, avec $1 \leqslant i<j \leqslant 5$. Clairement, on a $x \neq y$, car $x \notin G^{\prime}$ et $y \in G^{\prime}$. Mais alors les groupes $G_{i}$ et $G_{j}$ ont $x$ et $y$ en commun, en contradiction avec l'hypothèse de l'énoncé.
|
| 42 |
+
Ainsi, $x$ appartient à tous les groupes. En enlevant $x$ de chacun de ces 14 groupes, on obtient alors 14 groupes deux à deux disjoints de 3 élèves, soit $14 \times 3=42$ élèves. Il faut encore y ajouter $x$ et, puisque chaque membre du club appartient à un des groupes, les membres sont alors bien tous comptés une et une seule fois.
|
| 43 |
+
Il y a donc exactement 43 membres dans le club.
|
| 44 |
+
|
| 45 |
+
Exercice 3. Soit $A B C D$ un quadrilatère convexe dont les diagonales ne sont pas perpendiculaires et tel que les droites $(A B)$ et $(C D)$ ne sont pas parallèles. On note O le point d'intersection de $[A C]$ et $[B D]$. Soit $\mathrm{H}_{1}$ et $\mathrm{H}_{2}$ les orthocentres respectifs des triangles $A O B$ et $C O D$. On désigne par $M$ et $N$ les milieux respectifs de $[A B]$ et [CD].
|
| 46 |
+
|
| 47 |
+
Prouver que les droites $\left(H_{1} H_{2}\right)$ et $(M N)$ sont parallèles si et seulement si $A C=B D$.
|
| 48 |
+
Solution de l'exercice 3 Soit $A^{\prime}$ et $B^{\prime}$ les pieds des hauteurs issues respectivement de $A$ et $B$ dans $A O B$. Soit $\mathrm{C}^{\prime}$ et $\mathrm{D}^{\prime}$ les pieds des hauteurs issues respectivement de C et D dans COD.
|
| 49 |
+
Les points $A^{\prime}$ et $D^{\prime}$ appartiennent donc au cercle $\Gamma_{1}$ de diamètre $[A D]$, et les points $B^{\prime}$ et $C^{\prime}$ appartiennent au cercle $\Gamma_{2}$ de diamètre $[B C]$. Les points $A^{\prime}$ et $B^{\prime}$ appartiennent donc au cercle $\Gamma_{3}$ de diamètre $[A B]$. En utilisant la puissance de $H_{1}$ par rapport à $\Gamma_{3}$, il vient $H_{1} A \cdot H_{1} A^{\prime}=H_{1} B \cdot H_{1} B^{\prime}$.
|
| 50 |
+
On en déduit que $\mathrm{H}_{1}$ a la même puissance par rapport à $\Gamma_{1}$ et $\Gamma_{2}$, donc que $\mathrm{H}_{1}$ appartient à l'axe radical de ces deux cercles, que l'on note $\Delta$. De même, on a $\mathrm{H}_{2} \in \Delta$. Or, l'axe radical de deux cercles étant perpendiculaire à la droite qui relie leur centres, on a $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right) \perp(\mathrm{PQ})$, où $P$ et $Q$ sont les milieux respectifs de $[A D]$ et $[B C]$.
|
| 51 |
+
|
| 52 |
+
Ainsi, $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right) / /(\mathrm{MN})$ si et seulement si $(\mathrm{MN}) \perp(\mathrm{PQ})$. Or, d'après le théorème des milieux, il est facile de vérifier que $P M Q N$ est un parallélogramme et que $M P=\frac{1}{2} B D$ et $M Q=\frac{1}{2} A C$. Par suite, $(M N) \perp(P Q)$ si et seulement si $P M Q N$ est un losange, ce qui équivaut à $M P=M Q$, c'est-à-dire $A C=B D$.
|
| 53 |
+
|
| 54 |
+
Solution alternative Les points considérés étant définis uniquement par des intersections de droite et de relations d'orthogonalité (mais ne faisant intervenir ni égalités d'angles ni intersections de cercles ou de cercle et droite), on peut tenter une approche analytique, qui sera pénible mais humainement faisable.
|
| 55 |
+
Plaçons-nous dans un repère orthonormé de centre $O$ et tel que les points $A, B, C, D, O$ aient pour coordonnées respectives
|
| 56 |
+
|
| 57 |
+
$$
|
| 58 |
+
\binom{-a}{0},\binom{-1}{-b},\binom{c}{0},\binom{d}{b \mathrm{~d}},\binom{0}{0}
|
| 59 |
+
$$
|
| 60 |
+
|
| 61 |
+
Alors les points $\mathrm{H}_{1}, \mathrm{H}_{2}, \mathrm{M}, \mathrm{N}$ ont pour coordonnées respectives
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
\binom{-1}{y_{1}}, \quad\binom{d}{y_{2}}, \quad\binom{-(a+1) / 2}{-b / 2}, \quad\binom{(c+d) / 2}{b d / 2}
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
avec $\overrightarrow{\mathrm{AH}_{1}} \cdot \overrightarrow{\mathrm{OB}}=-(\mathrm{a}-1)-\mathrm{y}_{1} \mathrm{~b}=0$ et $\overrightarrow{\mathrm{CH}_{2}} \cdot \overrightarrow{\mathrm{OD}}=(\mathrm{d}-\mathrm{c}) \mathrm{d}+\mathrm{y}_{2} \mathrm{bd}=0$, c'est-à-dire
|
| 68 |
+
|
| 69 |
+
$$
|
| 70 |
+
\mathrm{y}_{1}=\frac{1-\mathrm{a}}{\mathrm{~b}} \text { et } \mathrm{y}_{2}=\frac{\mathrm{c}-\mathrm{d}}{\mathrm{~b}}
|
| 71 |
+
$$
|
| 72 |
+
|
| 73 |
+
Les droites $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right)$ et $(\mathrm{MN})$ sont parallèles si et seulement si elles ont même pente, c'est-à-dire si l'égalité
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\frac{y_{2}-y_{1}}{d+1}=\frac{b d+b}{c+d+a+1}
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
est vérifiée. On calcule donc que
|
| 80 |
+
|
| 81 |
+
$$
|
| 82 |
+
\text { (1) } \begin{aligned}
|
| 83 |
+
& \Leftrightarrow b(d+1)^{2}=(c+d+a+1)\left(y_{2}-y_{1}\right)=\frac{1}{b}(c+d+a+1)(c-d+a-1) \\
|
| 84 |
+
& \Leftrightarrow b^{2}(d+1)^{2}=(c+a)^{2}-(d+1)^{2} \\
|
| 85 |
+
& \Leftrightarrow B D^{2}=(d+1)^{2}\left(b^{2}+1\right)=(c+a)^{2}=A C^{2}
|
| 86 |
+
\end{aligned}
|
| 87 |
+
$$
|
| 88 |
+
|
| 89 |
+
ce qui permet de conclure.
|
| 90 |
+
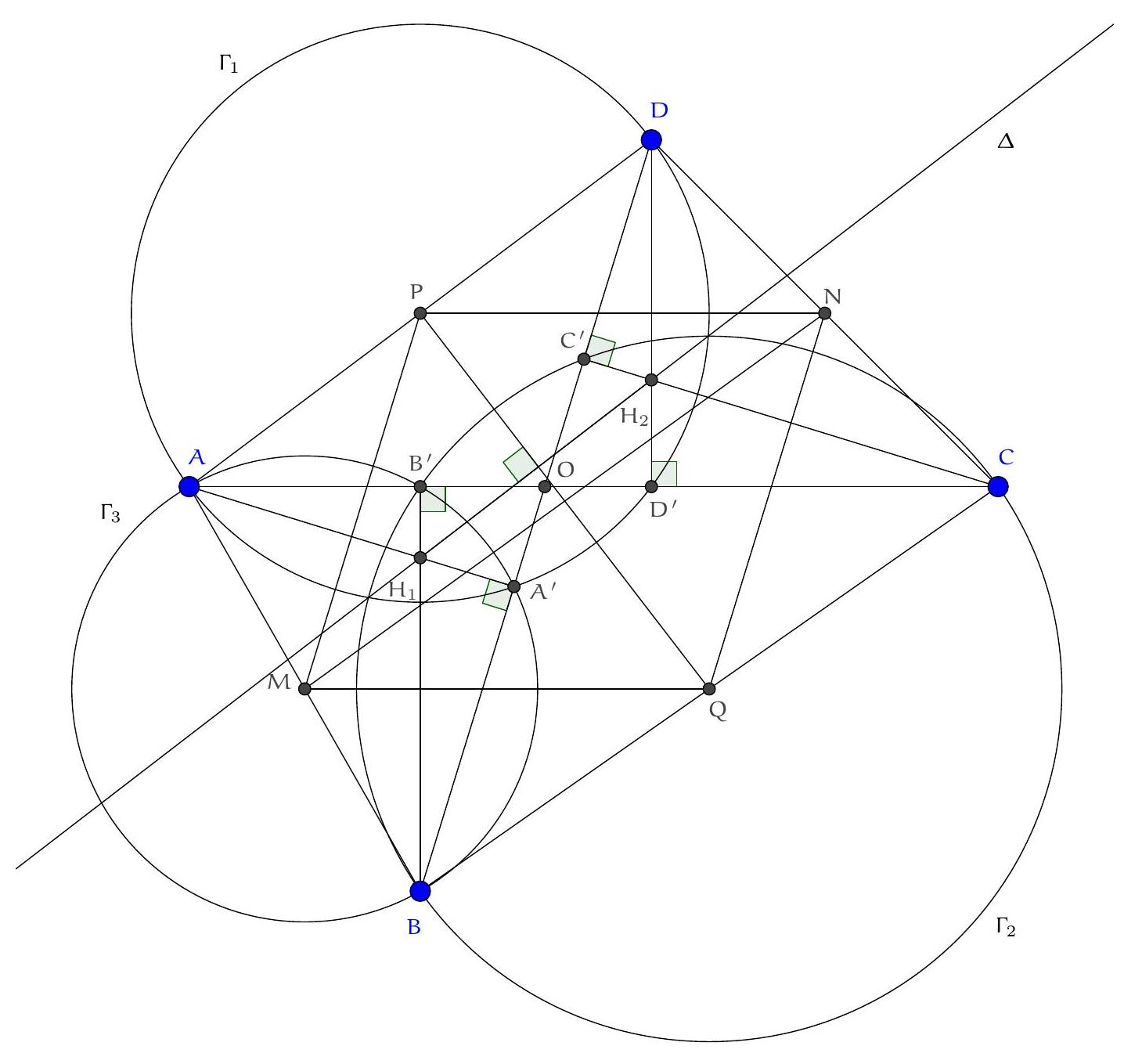
|
| 91 |
+
|
| 92 |
+
Exercice 4. Soit $S$ un ensemble d'entiers strictement positifs tel que
|
| 93 |
+
|
| 94 |
+
$$
|
| 95 |
+
\lfloor\sqrt{x}\rfloor=\lfloor\sqrt{y}\rfloor \text { pour tous } x, y \in S
|
| 96 |
+
$$
|
| 97 |
+
|
| 98 |
+
Prouver que si $x, y, z, t \in S$ avec $(x, y) \neq(z, t)$ et $(x, y) \neq(t, z)$, alors $x y \neq z t$.
|
| 99 |
+
( $\lfloor.$.$\rfloor désigne la partie entière.)$
|
| 100 |
+
Solution de l'exercice 4 Supposons tout d'abord qu'il existe des entiers $x_{1}, x_{2}, x_{3}, x_{4}$ dans $S$ tels que $x_{1} x_{2} \leqslant x_{3} x_{4}$ et $x_{1}+x_{2}>x_{3}+x_{4}$. Puisqu'il s'agit d'entiers, on a donc $x_{1}+x_{2}-x_{3}-x_{4} \geqslant 1$. Soit $n=\left\lfloor\sqrt{x_{1}}\right\rfloor$. Par définition de $S$, pour $i=1,2,3,4$, il existe donc un entier $w_{i}$ tel que $0 \leqslant w_{i} \leqslant 2 n$ et $x_{i}=n^{2}+w_{i}$.
|
| 101 |
+
|
| 102 |
+
Les inégalités $x_{1} x_{2} \leqslant x_{3} x_{4}$ et $x_{1}+x_{2}>x_{3}+x_{4}$ deviennent respectivement
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
w_{1}+w_{2}-w_{3}-w_{4} \geqslant 1 \quad \text { et } \quad\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2}
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
En particulier, on doit avoir $\boldsymbol{w}_{3}>0$, et donc
|
| 109 |
+
|
| 110 |
+
$$
|
| 111 |
+
\begin{aligned}
|
| 112 |
+
\mathrm{n}^{2} & \leqslant\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2} \\
|
| 113 |
+
& <w_{3}\left(w_{1}+w_{2}-w_{3}\right)-w_{1} w_{2}=\left(w_{1}-w_{3}\right)\left(w_{3}-w_{2}\right) \\
|
| 114 |
+
& <\frac{\left(\left(w_{1}-w_{3}\right)+\left(w_{3}-w_{2}\right)\right)^{2}}{4}=\frac{\left(w_{1}-w_{2}\right)^{2}}{4} \leqslant n^{2}
|
| 115 |
+
\end{aligned}
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
d'où la contradiction.
|
| 119 |
+
Soit alors $x_{1}, x_{2}, x_{3}, x_{4}$ dans $S$ tels que $x_{1} x_{2}=x_{3} x_{4}=a$. D'après le lemme ci-dessus, on a donc $x_{1}+x_{2}=$ $x_{3}+x_{4}=b$. Les nombres $x_{1}$ et $x_{2}$ d'une part, $x_{3}$ et $x_{4}$ d'autre part, sont alors les racines du polynôme $X^{2}-a X+b$. On a alors $x_{1}=x_{3}$ et $x_{2}=x_{4}$, ou $x_{1}=x_{4}$ et $x_{2}=x_{3}$, ce qui conclut.
|
| 120 |
+
|
| 121 |
+
Exercice 5. Soit $n \geqslant 5$ un entier, et $\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}=\{1,2, \cdots, n\}$. Prouver que les nombres $a_{1}, a_{1}+$ $a_{2}, a_{1}+a_{2}+a_{3}, \cdots, a_{1}+a_{2}+\cdots+a_{n}$ donnent au moins $\lfloor\sqrt{n}\rfloor+1$ restes distincts modulo $n$.
|
| 122 |
+
( $\lfloor.$.$\rfloor désigne la partie entière.)$
|
| 123 |
+
Solution de l'exercice 5 Pour $i=1, \cdots, n$, on pose $b_{i}=a_{1}+\cdots+a_{i}$. Procédons par l'absurde et supposons que les nombres $b_{1}, \cdots, b_{n}$ ne donnent qu'au plus $\sqrt{n}$ restes distincts modulo $n$.
|
| 124 |
+
Notons que, pour $i=1, \cdots, n-1$, on a $a_{i+1}=b_{i+1}-b_{i}$, et seul celui des $a_{i}$ qui vaut $n$ peut donc conduire à $b_{i+1}-b_{i} \equiv 0(\bmod n)$. Les nombres $b_{i+1}-b_{i}$ ne peuvent donc prendre, modulo $n$, qu'au plus $\sqrt{n}(\sqrt{n}-1)$ valeurs non nulles distinctes. En tenant compte du $a_{i}$ qui est égal à $n$ et de $a_{n}$ (qui n'est pas de la forme $b_{i+1}-b_{i}$ ), et puisque $n \geqslant 5$, les $a_{i}$ prennent donc au plus
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
\mathrm{n}-\sqrt{\mathrm{n}}+2 \leqslant \mathrm{n}-\sqrt{5}+2<\mathrm{n}
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
valeurs distinctes modulo $n$. Or, les $a_{i}$ forment une permutation de $\{1, \cdots, n\}$ donc ils représentent tous les restes modulo n : il y a là une contradiction.
|
| 131 |
+
Les nombres $b_{1}, \cdots, b_{n}$ donnent donc au moins $\lfloor\sqrt{n}\rfloor+1$ restes distincts modulo $n$.
|
| 132 |
+
|
| 133 |
+
Exercice 6. Soit H le pied de la hauteur issue de $A$ dans le triangle acutangle $A B C$, et $\mathrm{H}^{\prime}$ le symétrique de $H$ par rapport au milieu de $[B C]$. Les tangentes au cercle circonscrit à $A B C$ en $B$ et en $C$ se rencontrent en $X$. La perpendiculaire à $\left(\mathrm{XH}^{\prime}\right)$ en $\mathrm{H}^{\prime}$ rencontre la droite $(A B)$ en $Y$, et la droite $(A C)$ en $Z$.
|
| 134 |
+
Prouver que $\widehat{\mathrm{YXB}}=\widehat{\mathrm{ZXC}}$.
|
| 135 |
+
Solution de l'exercice 6 Soit $P, Q$ et $M$ les projetés orthogonaux respectifs de $X \operatorname{sur}(A B),(A C)$ et (BC). Clairement $M$ est le milieu de $[B C]$. Les points $X, H^{\prime}, Y, P$ sont sur le cercle de diamètre $[X Y]$, et les points $\mathrm{X}, \mathrm{H}^{\prime}, \mathrm{Z}, \mathrm{Q}$ sont sur le cercle de diamètre $[\mathrm{XZ}]$ donc
|
| 136 |
+
|
| 137 |
+
$$
|
| 138 |
+
\widehat{\mathrm{H}^{\prime} \mathrm{XY}}=\widehat{\mathrm{YPH}^{\prime}}=\widehat{\mathrm{APH}^{\prime}} \text { et } \widehat{\mathrm{H}^{\prime} \mathrm{XZ}}=\widehat{\mathrm{ZQH}^{\prime}}=\widehat{\mathrm{AQH}^{\prime}} \text {, }
|
| 139 |
+
$$
|
| 140 |
+
|
| 141 |
+
ce qui montre que $\widehat{Z X Y}=\widehat{\mathrm{ZXH}^{\prime}}+\widehat{\mathrm{H}^{\prime} X Y}=\widehat{\mathrm{AQH}^{\prime}}+\widehat{\mathrm{APH}^{\prime}}=\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}-\widehat{\mathrm{ABC}}$.
|
| 142 |
+
Puisque $\widehat{\mathrm{BXC}}=180^{\circ}-2 \widehat{\mathrm{BAC}}$, pour conclure il suffit donc de prouver que $\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}=180^{\circ}-\widehat{\mathrm{BAC}}$. Or, les points $B, P, X, M$ sont sur le cercle de diamètre $[B X]$, donc
|
| 143 |
+
|
| 144 |
+
$$
|
| 145 |
+
\widehat{A P M}=\widehat{B P M}=\widehat{B X M}=90^{\circ}-\widehat{B A C},
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
ce qui montre que $(P M) \perp(A Q)$.
|
| 149 |
+
De même, $(Q M)$ est perpendiculaire à ( $A P)$, et $M$ est donc l'orthocentre du triangle $A P Q$. Cela assure que $(A M) \perp(P Q)$ et que $A M=2 r \cos (\widehat{P A Q})$, où $r$ est le rayon du cercle circonscrit à $A P Q$.
|
| 150 |
+
Soit $R$ le projeté orthogonal de $A$ sur ( $X M$ ). Alors $A R M H$ est un parallélogramme, donc $A R H^{\prime} M$ est aussi un parallélogramme. Les droites $\left(\mathrm{RH}^{\prime}\right)$ et $(A M)$ sont alors parallèles, et ainsi $\left(\mathrm{RH}^{\prime}\right)$ et $(P Q)$ sont perpendiculaires. D'autre part, puisque $A, R, Q, X$ et $P$ sont tous sur le cercle de diamètre $[A X]$, on a $\widehat{\mathrm{PRQ}}=\widehat{\mathrm{PAQ}}=\widehat{\mathrm{BAC}}$. Par suite $\mathrm{RH}^{\prime}=\mathrm{AM}=2 \mathrm{r} \cos (\widehat{\mathrm{PAQ}})=2 \mathrm{r} \cos (\widehat{\mathrm{PRQ}})$, ce qui prouve que $\mathrm{H}^{\prime}$ est en fait l'orthocentre de PRQ.
|
| 151 |
+
En particulier, on a $\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}=180^{\circ}-\widehat{\mathrm{PRQ}}=180^{\circ}-\widehat{\mathrm{BAC}}$, ce qui achève la démonstration.
|
| 152 |
+
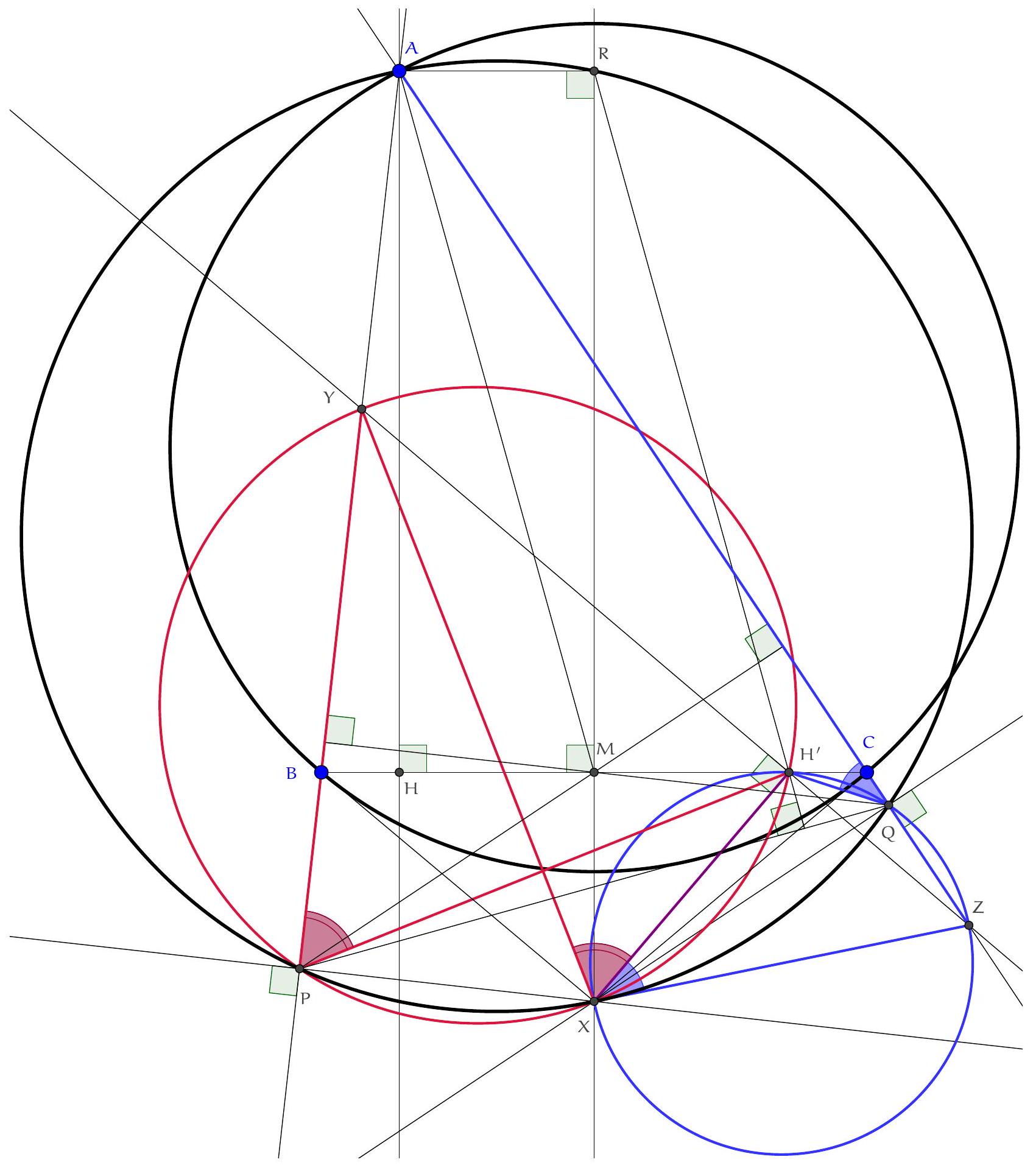
|
| 153 |
+
|
| 154 |
+
Exercice 7. Soit $a_{1}, a_{2} a_{3}$ des entiers strictement positifs. Pour tout entier $n \geqslant 3$, on pose
|
| 155 |
+
|
| 156 |
+
$$
|
| 157 |
+
a_{n+1}=\operatorname{ppcm}\left(a_{n}, a_{n-1}\right)-\operatorname{ppcm}\left(a_{n-1}, a_{n-2}\right)
|
| 158 |
+
$$
|
| 159 |
+
|
| 160 |
+
étant entendu que l'on a $\operatorname{ppcm}(0, x)=0$ pour tout entier $x$.
|
| 161 |
+
Prouver qu'il existe un entier naturel $k$ tel que $k \leqslant a_{3}+4$ et $a_{k} \leqslant 0$.
|
| 162 |
+
Solution de l'exercice 7 Si $x$ et $y$ sont des entiers, on note $x \vee y=\operatorname{ppcm}(x, y)$ et $x \wedge y=\operatorname{pgcd}(x, y)$, avec $\operatorname{pgcd}(0, x)=x$ pour tout $x$. On rappelle qu'alors $x y=(x \vee y)(x \wedge y)$.
|
| 163 |
+
Pour tout entier $n \geqslant 3, a_{n-1}$ divise $a_{n} \vee a_{n-1}$ et $a_{n-1} \vee a_{n-2}$, donc que $a_{n-1}$ divise $a_{n+1}$ également. Mais alors, pour tout $n \geqslant 4$, le nombre $a_{n-2}$ divise $a_{n}$, donc divise $a_{n} \vee a_{n-1}$ et $a_{n-1} \vee a_{n-2}$, et enfin divise $a_{n+1}$. Le nombre $a_{n+1}$ est donc divisible par $a_{n-1} \vee a_{n-2}$. On pose maintenant $c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}$. Montrons alors l'égalité ( $E_{n}$ ) suivante pour tout entier $n \geqslant 4$ tel que $a_{4}, \ldots, a_{n}>0$ :
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\left(a_{n-1} \vee a_{n-2}\right)\left(4+c_{4}-n\right)=a_{n+1}
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
Tout d'abord, par construction, l'égalité ( $E_{4}$ ) est vraie. Supposons maintenant que l'égalités ( $E_{n-1}$ ) est vraie, et déduisons-en que, si $a_{4}, \ldots, a_{n}>0$, alors ( $E_{n}$ ) est vraie aussi. Puisque $a_{n-3}$ divise $a_{n-1}$, on observe que
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
\begin{aligned}
|
| 173 |
+
\left(a_{n-1} \wedge a_{n}\right)\left(a_{n-1} \vee a_{n-2}\right) & =\left(a_{n-1} \wedge\left(a_{n-1} \vee a_{n-2}-a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee a_{n-2} \vee a_{n-3}\right) \\
|
| 174 |
+
& =\left(a_{n-1} \wedge\left(a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee\left(a_{n-2} \vee a_{n-3}\right)\right) \\
|
| 175 |
+
& =a_{n-1}\left(a_{n-2} \vee a_{n-3}\right) .
|
| 176 |
+
\end{aligned}
|
| 177 |
+
$$
|
| 178 |
+
|
| 179 |
+
Or, puisque
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\begin{aligned}
|
| 183 |
+
\left(E_{n}\right) & \Leftrightarrow \frac{a_{n+1}}{a_{n-1} \vee a_{n-2}}=4+c_{4}-n=\frac{a_{n}}{a_{n-2} \vee a_{n-3}}-1 \\
|
| 184 |
+
& \Leftrightarrow \frac{a_{n} \vee a_{n-1}}{a_{n-1} \vee a_{n-2}}=\frac{a_{n}}{a_{n-1} \vee a_{n-2}}+1=\frac{a_{n}}{a_{n-2} \vee a_{n-3}} \\
|
| 185 |
+
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}=\left(a_{n-2} \vee a_{n-3}\right)\left(a_{n} \vee a_{n-1}\right) \\
|
| 186 |
+
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}\left(a_{n} \wedge a_{n-1}\right)=\left(a_{n-2} \vee a_{n-3}\right) a_{n} a_{n-1},
|
| 187 |
+
\end{aligned}
|
| 188 |
+
$$
|
| 189 |
+
|
| 190 |
+
on en déduit que ( $E_{n}$ ) est bien vraie.
|
| 191 |
+
Il s'ensuit qu'il existe un entier naturel $k$, minimal, tel que $k \leqslant c_{4}+5$ et $a_{k} \leqslant 0$. Si $k \leqslant 5$, alors on a bien $k \leqslant a_{3}+4$. Sinon, alors $0<a_{5}<a_{3} \vee a_{4}$ et $0<a_{4}<a_{2} \vee a_{3}$, donc
|
| 192 |
+
|
| 193 |
+
$$
|
| 194 |
+
c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}<\frac{a_{3} \vee a_{4}}{a_{2} \vee a_{3}} \leqslant \frac{a_{3} a_{4}}{a_{2} \vee a_{3}}<a_{3},
|
| 195 |
+
$$
|
| 196 |
+
|
| 197 |
+
donc $k \leqslant \mathrm{c}_{4}+5 \leqslant \mathrm{a}_{3}+4$, ce qui conclut.
|
| 198 |
+
|
| 199 |
+
Exercice 8. Un ensemble E fini et non vide de réels strictement positifs est dit puissant lorsque, pour tous $a, b \in E$ distincts, l'un au moins des nombres $a^{b}$ et $b^{a}$ appartient aussi à $E$. Déterminer le nombre maximal d'éléments que peut contenir un ensemble puissant.
|
| 200 |
+
|
| 201 |
+
## Solution de l'exercice 8 Tout d'abord, l'ensemble
|
| 202 |
+
|
| 203 |
+
$$
|
| 204 |
+
\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{16}\right\}
|
| 205 |
+
$$
|
| 206 |
+
|
| 207 |
+
est un ensemble puissant qui contient quatre éléments. Soit S un ensemble puissant, et n son cardinal : nous allons montrer que $\mathrm{n} \leqslant 4$.
|
| 208 |
+
Démontrons d'abord le lemme suivant : il n'existe pas d'éléments a et b de $S$ tels que $\mathrm{a}<1<\mathrm{b}$. En effet, si l'on avait $a<1<b$, alors $a^{b}<a<1<b^{a}<b$; en prenant $a=\min S$ et $b=\min \{s \in S: 1<s\}$, on s'assurerait donc que ni $a^{b}$ ni $b^{a}$ n'appartient à $S$, contredisant le fait que $S$ est puissant.
|
| 209 |
+
D'autre part, si $S$ est un ensemble puissant, alors $S \cup\{1\}$ l'est aussi. Notre recherche d'un ensemble puissant de cardinal maximal nous amène donc à considérer deux cas.
|
| 210 |
+
|
| 211 |
+
1. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $1=a_{1}<a_{2}<\cdots<a_{n}$, alors on observe que
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
a_{n}<a_{n}^{a_{2}}<a_{n}^{a_{3}}<\ldots<a_{n}^{a_{n-1}}
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
donc que $S$ contient les éléments
|
| 218 |
+
|
| 219 |
+
$$
|
| 220 |
+
a_{2}<a_{2}^{a_{n}}<a_{3}^{a_{n}}<\ldots<a_{n-1}^{a_{n}} .
|
| 221 |
+
$$
|
| 222 |
+
|
| 223 |
+
Cela montre que $a_{i+1}=a_{i}^{a_{n}}$ pour tout $i \in\{2, \ldots, \mathfrak{n}-1\}$. On remarque cependant que
|
| 224 |
+
|
| 225 |
+
$$
|
| 226 |
+
\mathrm{a}_{2}<\mathrm{a}_{2}^{\mathrm{a}_{3}}<\mathrm{a}_{2}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{3}<\mathrm{a}_{3}^{\mathrm{a}_{2}}<\mathrm{a}_{3}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{4}
|
| 227 |
+
$$
|
| 228 |
+
|
| 229 |
+
ce qui montre que ni $a_{2}^{a_{3}} n i a_{3}^{a_{2}} n$ 'appartient à $S$, qui ne peut donc pas être puissant.
|
| 230 |
+
2. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $a_{1}<a_{2}<\cdots<a_{n}=1$, alors on observe que
|
| 231 |
+
|
| 232 |
+
$$
|
| 233 |
+
a_{n-1}<a_{n-1}^{a_{n-2}}<a_{n-1}^{a_{n-3}}<\ldots<a_{n-1}^{a_{1}}<a_{n}
|
| 234 |
+
$$
|
| 235 |
+
|
| 236 |
+
donc que $S$ contient les éléments
|
| 237 |
+
|
| 238 |
+
$$
|
| 239 |
+
a_{1}<a_{1}^{a_{n-1}}<a_{2}^{a_{n-1}}<\ldots<a_{n-2}^{a_{n-1}}<a_{n}=1
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
Cela montre que $a_{i+1}=a_{i}^{a_{n-1}}$ pour tout $i \in\{1, \ldots, n-2\}$. De même, on observe que
|
| 243 |
+
|
| 244 |
+
$$
|
| 245 |
+
a_{n-1}=a_{n-2}^{a_{n-1}}<a_{n-2}^{a_{n-3}}<\ldots<a_{n-2}^{a_{1}}<a_{n}=1
|
| 246 |
+
$$
|
| 247 |
+
|
| 248 |
+
donc que $S$ contient les éléments
|
| 249 |
+
|
| 250 |
+
$$
|
| 251 |
+
a_{2}=a_{1}^{a_{n-1}}<a_{1}^{a_{n-2}}<a_{2}^{a_{n-2}}<\ldots<a_{n-3}^{a_{n-2}}<a_{n}=1 .
|
| 252 |
+
$$
|
| 253 |
+
|
| 254 |
+
Cela montre aussi que $a_{i+2}=a_{i}^{a_{n-2}}=a_{i}^{a_{n-1}^{2}}$ pour tout $i \in\{1, \ldots, n-3\}$.
|
| 255 |
+
On en déduit que $a_{n-1}=a_{n-2}^{a_{n-1}}=a_{n-1}^{2 a_{n-1}}$ puis que $1=2 a_{n-1}$, donc que $a_{n-i}=2^{-2^{i}}$ pour $i \in\{1, \ldots, n-1\}$. Cependant, puisque $n \geqslant 5$, alors $a_{n-4}^{a_{n-3}}=2^{-2^{-4}}$ et $a_{n-3}^{a_{n-4}}=2^{-2^{-13}}$, donc $S$ ne contient ni $a_{n-4}^{a_{n-3}}$ et $a_{n-3}^{a_{n-4}}$ et ne peut pas être puissant.
|
| 256 |
+
|
French_STS/md/fr-ofm-2016-2017-envoi-1-solutions.md
ADDED
|
@@ -0,0 +1,206 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OCympiades Françaises de Mathématiques 2016-2017
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
Corrigé de L'envoi $\mathcal{N u m e ́ r o ~} 1$ - Aritfimétique
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe B
|
| 8 |
+
|
| 9 |
+
Exercice 1. On définit une suite ainsi:
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
\left\{\begin{array}{l}
|
| 13 |
+
u_{0}=15, u_{1}=57 \\
|
| 14 |
+
u_{n}=u_{n-1}+u_{n-2} \text { pour tout } n \geq 2
|
| 15 |
+
\end{array}\right.
|
| 16 |
+
$$
|
| 17 |
+
|
| 18 |
+
Trouver le plus grand entier $k$ tel que $3^{k} \mid u_{2017}$.
|
| 19 |
+
Solution de l'exercice 1 Soit $k$ l'entier cherché. Les premiers termes de la suite sont 15, 57, 72, 129, 201, 330, 541,... apparemment tous divisibles par 3 . En effet, $u_{0}$ et $u_{1}$ sont multiples de 3 , donc $u_{2}=u_{0}+u_{1}$ aussi. De même, $u_{3}$ est divisible par 3. Plus généralement, si $u_{n-1}$ et $u_{n-2}$ sont multiples de 3, alors $u_{n}$ aussi. On prouve ainsi de proche en proche (par récurrence, en fait) que pour tout entier $n$, $u_{n}$ est divisible par 3, donc $3 \mid u_{2017}$ et $k \geq 1$.
|
| 20 |
+
Raisonnons maintenant modulo 9 pour voir si $k \geq 2$. On trouve :
|
| 21 |
+
$u_{0} \equiv 6(\bmod 9)$
|
| 22 |
+
$u_{1} \equiv 3(\bmod 9)$
|
| 23 |
+
$u_{2} \equiv 0(\bmod 9)$
|
| 24 |
+
$u_{3} \equiv 3(\bmod 9)$
|
| 25 |
+
$u_{4} \equiv 3(\bmod 9)$
|
| 26 |
+
$u_{5} \equiv 6(\bmod 9)$
|
| 27 |
+
$u_{6} \equiv 0(\bmod 9)$
|
| 28 |
+
$u_{7} \equiv 6(\bmod 9)$
|
| 29 |
+
$u_{8} \equiv 6(\bmod 9)$
|
| 30 |
+
$u_{9} \equiv 3(\bmod 9)$
|
| 31 |
+
On constate que $u_{8} \equiv u_{0}(\bmod 9)$ et $u_{9} \equiv u_{1}(\bmod 9)$, donc $u_{10} \equiv u_{2}(\bmod 9)$, car les modulos s'additionnent. Plus généralement, on établit comme précédemment que $u_{n+8} \equiv u_{n}(\bmod 9)$ pour tout $n \in \mathbb{N}$. Ainsi, la suite $\left(u_{n}(\bmod 9)\right)$ est périodique de période 8 . Or $2017=252 \times 8+1$, donc $u_{2017} \equiv u_{1} \equiv 3(\bmod 9)$. Donc $k<2$. Conclusion : $k=1$.
|
| 32 |
+
|
| 33 |
+
Remarque. Si $l$ est un entier naturel quelconque, alors la suite $\left(v_{n}\right)$ définie par $v_{n}=u_{n}(\bmod l)$ est périodique artir d'un certain rang. En effet, il y a $l \times l=l^{2}$ possibilités pour le couple $\left(v_{n}, v_{n+1}\right)$. Donc, si on regarde $\left(v_{0}, v_{1}\right),\left(v_{1}, v_{2}\right), \cdots,\left(v_{l^{2}}, v_{l^{2}+1}\right)$, cela fait $l^{2}+1$ couples. D'après le principe des tiroirs (ie si on range $c+1$ chaussettes dans $c$ tiroirs, un tiroir contiendra au moins 2 chaussettes), deux couples sont égaux, il existe donc $0 \leqslant i<j \leqslant l^{2}$ tels que $\left(v_{i}, v_{i+1}\right)=$ $\left(v_{j}, v_{j+1}\right)$. Autrement dit, $u_{i} \equiv u_{j}(\bmod l)$ et $u_{i+1} \equiv u_{j+1}(\bmod l)$. Donc $u_{i+2} \equiv u_{j+2}(\bmod l)$, soit $\left(v_{i+1}, v_{i+2}\right)=\left(v_{j+1}, v_{j+2}\right)$. On en déduit de même que $v_{i+3}=v_{j+3}, v_{i+4}=v_{j+4}$, etc. Ainsi, $\left(v_{n}\right)$ est périodique artir du rang $i$ (au plus tard), de période $i-j$.
|
| 34 |
+
Elle peut toutefois avoir une période plus petite (exercice : montrer que la période minimale divise $i-j$ ).
|
| 35 |
+
|
| 36 |
+
Exercice 2. Trouver tous les entiers naturels $n$ pour lesquels $2^{n}+12^{n}+2011^{n}$ est un carré parfait.
|
| 37 |
+
|
| 38 |
+
Solution de l'exercice 2 Posons $u_{n}=2^{n}+12^{n}+2011^{n}$. On regarde modulo 3: $2 \equiv-1(\bmod 3), 12 \equiv 0$ $(\bmod 3)$ et $2011 \equiv 1(\bmod 3)$, donc
|
| 39 |
+
|
| 40 |
+
$$
|
| 41 |
+
u_{n} \equiv(-1)^{n}+0^{n}+1^{n} \equiv(-1)^{n}+1 \quad(\bmod 3)
|
| 42 |
+
$$
|
| 43 |
+
|
| 44 |
+
Si $n$ est pair, $u_{n} \equiv 2(\bmod 3)$. Or aucun carré ne peut être congru 2modulo3: eneffet, six $\equiv 0$ $(\bmod 3), x^{2} \equiv 0(\bmod 3)$, si $x \equiv 1(\bmod 3), x^{2} \equiv 1(\bmod 3)$, et si $x \equiv 2(\bmod 3), x^{2} \equiv 1(\bmod 3)$. Si $n$ est impair, on remarque que $u_{1}=2+12+2011=2025=45^{2}$ donc $n=1$ convient. Si $n \geq 3$, $2^{n} \equiv 12^{n} \equiv 0(\bmod 4)$. Et $2011 \equiv 3(\bmod 4)$. En écrivant $n=2 k+1, k \in \mathbb{N}$, on a
|
| 45 |
+
|
| 46 |
+
$$
|
| 47 |
+
u_{n} \equiv 3^{2 k+1} \equiv\left(3^{2}\right)^{k} \times 3 \equiv 9^{k} \times 3 \equiv 1^{k} \times 3 \equiv 3 \quad(\bmod 4) .
|
| 48 |
+
$$
|
| 49 |
+
|
| 50 |
+
Or un carré n'est jamais congru 3 modulo 4 , sionfaituntableaudecongruence :
|
| 51 |
+
|
| 52 |
+
| $x(\bmod 4)$ | $x^{2}(\bmod 4)$ |
|
| 53 |
+
| :---: | :---: |
|
| 54 |
+
| 0 | 0 |
|
| 55 |
+
| 1 | 1 |
|
| 56 |
+
| 2 | 0 |
|
| 57 |
+
| 3 | 1 |
|
| 58 |
+
|
| 59 |
+
Doncu $_{n}$ ne peut pas être un carré si $n \geq 3$ est impair. Conclusion : $n=1$ est la seule solution.
|
| 60 |
+
Exercice 3. Montrer que pour tout entier $n \geq 1$, il existe $m$ un multiple de $n$ tel que la somme des chiffres de $m$ fasse $n$.
|
| 61 |
+
Solution de l'exercice 3 La suite des puissances de 10, donc $1,10,100, \cdots$ contient une infinité de termes, qui peuvent prendre un nombre fini de résidus modulo $n$. Il existe donc un résidu $k$ tel qu'une infinité de puissances de 10 soient congrues kmodulon.Soientdonc $0 \leqslant a_{1}<a_{2}<a_{n}$ des entiers tels que
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
10^{a_{i}} \equiv k \quad(\bmod n)
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
pour tout $i \in\{1,2, \cdots, n\}$. On pose $m=10^{a_{n}}+10^{a_{n-1}}+\cdots+10^{a_{2}}+10^{a_{1}}$. $m$ s'écrit avec $n$ chiffres "1" et un certain nombre de zéros, donc sa somme des chiffres vaut $n$.
|
| 68 |
+
Et $m \equiv k+\cdots+k \equiv k n \equiv 0(\bmod n)$, donc $m$ est divisible par $n$, donc cet entier satisfait aux conditions de l'énoncé.
|
| 69 |
+
|
| 70 |
+
## Exercices Communs
|
| 71 |
+
|
| 72 |
+
Exercice 4. On dit qu'un entier naturel $d$ est sympathique si, pour tout couple d'entiers $(x, y)$,
|
| 73 |
+
|
| 74 |
+
$$
|
| 75 |
+
d\left|(x+y)^{5}-x^{5}-y^{5} \Longleftrightarrow d\right|(x+y)^{7}-x^{7}-y^{7}
|
| 76 |
+
$$
|
| 77 |
+
|
| 78 |
+
Montrer qu'il existe une infinité de nombres sympathiques. Est-ce-que 2017, 2018 sont sympathiques ? Solution de l'exercice 4 On remarque que :
|
| 79 |
+
|
| 80 |
+
$$
|
| 81 |
+
\begin{aligned}
|
| 82 |
+
& (x+y)^{5}-x^{5}-y^{5}=5 x y(x+y)\left(x^{2}+x y+y^{2}\right) \\
|
| 83 |
+
& (x+y)^{7}-x^{7}-y^{7}=7 x y(x+y)\left(x^{2}+x y+y^{2}\right)^{2}
|
| 84 |
+
\end{aligned}
|
| 85 |
+
$$
|
| 86 |
+
|
| 87 |
+
Ainsi, si on prend $p$ un nombre premier différent de 5 et de 7 :
|
| 88 |
+
|
| 89 |
+
- si $p$ divise $(x+y)^{5}-x^{5}-y^{5}$, comme $p$ et 5 sont premiers entre eux, d'après le lemme de Gauß, $p$ divise aussi $x y(x+y)\left(x^{2}+x y+y^{2}\right)$, a fortiori $p$ divise $(x+y)^{7}-x^{7}-y^{7}$.
|
| 90 |
+
- si $p$ divise $(x+y)^{7}-x^{7}-y^{7}$, comme $p$ et 7 sont premiers entre eux, $p$ divise également $x y(x+$ $y)\left(x^{2}+x y+y^{2}\right)^{2}$. Si $p$ divise $x^{2}+x y+y^{2}$, alors $p$ divise $(x+y)^{5}-x^{5}-y^{5}$ (car c'est bien un multiple de $x^{2}+x y+y^{2}$ ). Sinon, comme $p$ premier, cela signifie que $p$ et $x^{2}+x y+y^{2}$ sont premiers entre eux, donc d'après le lemme de Gauß, $p$ divise $x y(x+y)$, d'où l'on déduit que $p$ divise $(x+y)^{5}-x^{5}-y^{5}$.
|
| 91 |
+
|
| 92 |
+
Donc un tel nombre $p$ est sympathique
|
| 93 |
+
Comme il y a une infinité de nombres premiers différents de 5 et de 7 , il y a bien une infinité de nombres sympathiques.
|
| 94 |
+
En particulier, le nombre 2017 est premier, différent de 5 et de 7 , donc sympathique.
|
| 95 |
+
De plus, si $a$ et $b$ sont deux entiers sympathiques premiers entre eux, comme on a en général, pour tout entier $n$,
|
| 96 |
+
|
| 97 |
+
$$
|
| 98 |
+
a b \text { divise } n \Leftrightarrow a \text { divise } n \text { et } b \text { divise } n \text {, }
|
| 99 |
+
$$
|
| 100 |
+
|
| 101 |
+
$a b$ est aussi sympathique. Donc $2018=2 \cdot 1009$ est sympathique.
|
| 102 |
+
Exercice 5. Soit $m, n$ des entiers positifs tels que $\operatorname{pgcd}(m, n)=1$, où $a \wedge b$ désigne le plus grand diviseur commun de $a$ et $b$. Quelle(s) valeur(s) peut prendre
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
\left(2^{m}-2^{n} \wedge 2^{m^{2}+m n+n^{2}}-1\right) ?
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
Solution de l'exercice 5 On utilise la propriété suivante : si $m \geq 1$ et $a, b \in \mathbb{N}$, alors $\left(m^{a}-1\right) \wedge\left(m^{b}-1\right)=$ $m^{a \wedge b}-1$. On se ramène ainsi tudier $\left(m^{2}+m n+n^{2}\right) \wedge(m-n)$. Si $d \mid m^{2}+m n+n^{2}$ et $d \mid m-n$, alors $d \mid m^{2}+m n+n^{2}-(m-n)^{2}=3 m n$. Donc $d \mid 3 m n-3 n(m-n)=3 n^{2}$ et $d \mid 3 m n+3 m(m-n)=3 m^{2}$, donc $d \mid\left(3 m^{2}, 3 n^{2}\right)$, donc $d \mid 3$. Ainsi, $\left(m^{2}+m n+n^{2}\right) \wedge(m-n) \mid 3$, et ne peut prendre qu'au plus deux valeurs, 1 et 3 . Vérifions qu'elles sont réalisées.
|
| 109 |
+
Si $m=2$ et $n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=1$ et
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=1
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
Si $m=n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=3$ et
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=7 .
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
Donc les valeurs possibles sont 1 et 7 .
|
| 122 |
+
Preuve de la propriété : on peut supposer $a \geq b$. On écrit $a=b q+r$ la division euclidienne de $a$ par b. Soit $d:=\left(m^{a}-1\right) \wedge\left(m^{b}-1\right) . d \mid\left(m^{b}-1\right)+\left(m^{2 b}-m^{b}\right)+\left(m^{3 b}-m^{2 b}\right)+\cdots+\left(m^{q b}-m^{(q-1) b}\right)$, soit $d \mid m^{q b}-1$. Donc $d \mid m^{a}-m^{q b}$. Or $m^{a}-m^{q b}=m^{q b}\left(m^{r}-1\right)$. Comme $d$ est un diviseur de $m^{b}-1$ qui est premier avec $m$, alors $d$ est premier avec $m^{q b}$. D'après le lemme de Gauss, $d \mid m^{r}-1$. Ainsi, $d \mid\left(m^{b}-1\right) \wedge\left(m^{r}-1\right)$. On procède de même en faisant la division euclidienne de $b$ par $r$ et ainsi de
|
| 123 |
+
suite. On reproduit ainsi l'algorithme d'Euclide. Ce dernier termine sur $a \wedge b$, donc on obtient a fin que $d$ divise $m^{a \wedge b}-1$. Pour conclure, il reste rouver que $m^{a \wedge b}-1$ est un diviseur de $m^{b}-1$ et de $m^{a}-1$. Or, si $i=k j$ pour des entiers $i, j, k, m^{j}-1$ divise $m^{i}-1$, car :
|
| 124 |
+
|
| 125 |
+
$$
|
| 126 |
+
m^{i}-1=\left(m^{j}\right)^{k}-1=\left(m^{j}-1\right)\left(\left(m^{j}\right)^{k-1}+\left(m^{j}\right)^{k-2}+\cdots+m^{j}+1\right)
|
| 127 |
+
$$
|
| 128 |
+
|
| 129 |
+
Ceci permet de conclure.
|
| 130 |
+
Exercice 6. Trouver tous les triplets d'entiers naturels $(x, y, z)$ tels que :
|
| 131 |
+
|
| 132 |
+
$$
|
| 133 |
+
x^{2}+y^{2}=3 \cdot 2016^{z}+77 \text {. }
|
| 134 |
+
$$
|
| 135 |
+
|
| 136 |
+
Solution de l'exercice 6 Soit un triplet solution $(x, y, z)$. Que peut-on en dire de façon nécessaire ?
|
| 137 |
+
Si $z=0$, on a $x^{2}+y^{2}=80$. On fait une table de congruence modulo 4 : on montre ainsi que, si une somme de deux carrés est congrue modulo 4 , c'est que les deux carrés en question sot tous les deux pairs. On peut donc poser $x=2 x_{0}, y=2 y_{0}$ avec $x_{0}, y_{0}$ entiers et $x_{0}^{2}+y_{0}^{2}=20$. Par le même argument modulo 4 , on arrive $\mathrm{x}=4 \mathrm{x}_{1}, y=4 y_{1}$ avec $x_{1}, y_{1}$ entiers et $x_{1}^{2}+y_{1}^{2}=5$. Les seuls couples vérifiant cela sont $\left(x_{1}, y_{1}\right)=(1,2)$ ou $(2,1)$.
|
| 138 |
+
Si $z>0$, comme $7 \mid 2016$, on a modulo $7 x^{2}+y^{2}=0$, ce qui donne, en écrivant la table des carrés modulo 7, $x$ et $y$ congrus modulo 7. On peut donc poser $x=7 x_{1}$ et $y=7 y_{1}$ avec $x_{1}, y_{1}$ entiers. Donc $49 \mid x^{2}+y^{2}$, c'est-dire $49 \mid 3 \cdot 2016^{z}+77$ donc $z=1$. Il vient alors $x_{1}^{2}+y_{1}^{2}=125$. On teste les cas restants un par un pour voir ceux qui marchent a main : $\left(x_{1}, y_{1}\right)=(5,10),(2,11),(10,5),(11,2)$. Ainsi, tous les triplets solutions sont dans l'ensemble :
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
\{(4,8,0),(8,4,0),(35,70,1),(70,35,1),(14,77,1),(77,14,1)\}
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
et on vérifie que, réciproquement, tous ces triplets sont bien des solutions.
|
| 145 |
+
|
| 146 |
+
## Exercices du groupe A
|
| 147 |
+
|
| 148 |
+
Exercice 7. Soit $p$ un nombre premier, $m$ un entier naturel. Trouver le plus petit entier $d$ tel qu'il existe un polynôme unitaire $Q$ de degré $d$ à coefficients entiers tel que, pour tout entier $n, p^{m} \mid Q(n)$.
|
| 149 |
+
$\underline{\text { Solution de l'exercice } 7}$ Montrons que $d$ est le plus petit entier tel que $p^{m} \mid d$ !. Soit $k$ le plus petit entier tel que $p^{m} \mid k$ !.
|
| 150 |
+
Tout d'abord, montrons que $k \geq d$. On considère le polynôme $Q(x)=X(X+1) \cdots(X+k-1)$ : il est unitaire, de degré $k$, oefficients entiers. Qui plus est, pour tout $n \in \mathbb{N}, Q(n)=k!\binom{n}{k}$ (c'est une propriété des coefficients binomiaux), d'où $p^{m}|k!| Q(n)$. Donc $k$ est un entier pour lequel on dispose d'un polynôme $Q$ unitaire oefficients entiers de degré $k$ tel que pour tout $n \in \mathbb{N}, p^{m} \mid Q(n)$. Donc $k \geq d$. Reste ontrer le sens réciproque. Autrement dit, soit $Q$ un polynôme unitaire oefficients entiers de degré $l$ tel que pour tout entier $n, p^{m} \mid Q(n)$. Montrons que $k \leq l$. Il suffit de montrer que $p^{m} \mid l$ ! (car, par définition, $k$ est le plus petit entier érifier cela).
|
| 151 |
+
|
| 152 |
+
On introduit la famille des polynômes $P_{i}:=X(X+1) \cdots(X+i-1)$ pour $i \in\{0, \ldots l\}\left(P_{0}:=1\right)$. En effectuant les divisions euclidiennes successives de $Q$ par $P_{l}, P_{l-1}, \ldots, P_{0}$, on montre que $Q$ s'écrit :
|
| 153 |
+
|
| 154 |
+
$$
|
| 155 |
+
Q=\sum_{i=0}^{l} c_{i} P_{i}
|
| 156 |
+
$$
|
| 157 |
+
|
| 158 |
+
où $c_{i} \in \mathbb{Z}$ pour tout $i$.
|
| 159 |
+
On montre alors par récurrence sur $i \in\{0 \ldots l\}$ la propriété suivante :
|
| 160 |
+
|
| 161 |
+
$$
|
| 162 |
+
p^{m}\left|c_{i} P_{i}(-i)\right| c_{i} P_{i}(n) \text { pour tout } n \in \mathbb{Z}
|
| 163 |
+
$$
|
| 164 |
+
|
| 165 |
+
- pour $i=0$, le seul des $P_{i}$ qui ne s'annule pas en zéro est $P_{0}$, donc $Q(0)=c_{0}$, d'où $p^{m} \mid c_{0}=$ $c_{0} P_{0}(n)$ pour tout $n \in \mathbb{Z}$.
|
| 166 |
+
- soit $i<l$. Supposons que la propriété est vraie pour tous les éléments de $\{0, \ldots, i\}$ et montrons-la pour $i+1$. On constate que si $j>i+1,(X+i+1) \mid P_{j}$ donc $P_{j}(-i-1)=0$. Ainsi,
|
| 167 |
+
|
| 168 |
+
$$
|
| 169 |
+
\underbrace{Q(-i-1)}_{p^{m} \mid}=\underbrace{\sum_{j=0}^{i} c_{j} P_{j}(-i-1)}_{p^{m} \mid}+c_{i+1} P_{i+1}(-i-1)
|
| 170 |
+
$$
|
| 171 |
+
|
| 172 |
+
par hypothèse de récurrence et par définition de $Q$. Donc $p^{m} \mid c_{i+1} P_{i+1}(-i-1)$, et comme $P_{i+1}(-i-1)=(i+1)!$ divise tout produit de $i+1$ entiers consécutifs (on peut encore le voir grâce aux coefficients binomiaux), il divise $P_{i+1}(n)$ pour tout $n \in \mathbb{Z}$.
|
| 173 |
+
|
| 174 |
+
Ainsi, on obtient en particulier $p^{m} \mid P_{l}(n)$ pour tout $n \in \mathbb{N}$, donc $p^{m} \mid l$ !. Donc $k \leq l$, d'où $k \leq d$. Par double encadrement, on a donc bien montré que $k=d$.
|
| 175 |
+
Exercice 8. Si $n \in \mathbb{N}^{*}$, on note $d(n)$ son nombre de diviseurs. Quels sont les entiers strictement positifs tels que $d(n)^{3}=4 n$ ?
|
| 176 |
+
Solution de l'exercice 8 Soit $f(n):=\frac{d(n)^{3}}{n}$, l'énoncé revient rouver les antécédents de 4 par $f$. On remarque que $f(a b)=f(a) f(b)$ si $a$ et $b$ sont premiers entre eux. Ceci nous incite écomposer $n$ en produit de facteurs premiers :
|
| 177 |
+
|
| 178 |
+
$$
|
| 179 |
+
n=p_{1}^{a_{1}} \times p_{2}^{a_{2}} \times \cdots \times p_{l}^{a_{l}},
|
| 180 |
+
$$
|
| 181 |
+
|
| 182 |
+
où les $p_{i}, 1 \leqslant i \leqslant l$, sont premiers et $a_{i} \geqslant 1$. On a donc $f(n)=\prod_{i=1}^{l} f\left(p_{i}^{a_{i}}\right)$.
|
| 183 |
+
Soit $n \in \mathbb{N}^{*}$ vérifiant l'énoncé, $n^{3}=2 \times(d(n) / 2)^{3}$ est le double d'un cube parfait ( $d(n)$ est nécessairement pair). On en déduit que $v_{p}(n) \equiv 0(\bmod 3)$ pour $p$ nombre premier impair, et $v_{2}(n) \equiv 1(\bmod 3)$. Ici, $v_{p}(n)$ désigne la valuation $p$-adique de $n$, soit le plus grand entier $k$ tel que $p^{k} \mid n$, donc $v_{p_{i}}(n)=a_{i}$ avec nos notations. On peut écrire
|
| 184 |
+
|
| 185 |
+
$$
|
| 186 |
+
f(n)=\frac{\left(\left(a_{1}+1\right)\left(a_{2}+1\right) \cdots\left(a_{l}+1\right)\right)^{3}}{p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{l}^{a_{l}}}
|
| 187 |
+
$$
|
| 188 |
+
|
| 189 |
+
D'après la remarque précédente, le numérateur n'est pas divisible par 3, donc aucun des $p_{i}$ ne peut valoir 3. Et $n$ est le produit de puissances de cubes de nombres premiers impairs que multplie le double d'une puissance de $2^{3}$.
|
| 190 |
+
On montre aisément que si $m$ est puissance du cube d'un nombre premier strictement plus grand que 3 , alors $f(m) \geqslant \frac{64}{125}$ avec égalité si et seulement si $m=5^{3}$. On prouve ette fin que pour tout premier $p \geqslant 5$, $k \rightarrow f\left(p^{3 k}\right)$ est strictement décroissante, et que pour tout $k \geqslant 1, p \rightarrow f\left(p^{3 k}\right)$ l'est aussi. Pour avoir $f(n)=4$, il faut donc utiliser des puissances de 2 . On a $f(2)=f\left(2^{7}\right)=4, f\left(2^{4}\right)=\frac{125}{16}$ et $f\left(2^{3 k+1}\right)<1$ pour $k>2$.
|
| 191 |
+
Ainsi, 2 et 128 sont solution. Et pour en avoir une autre, il faut trouver $m$ un produit de puissances de cubes de nombres premiers impairs tel que $f(m)=\frac{64}{125}$. D'après l'étude précédente, seul $m=5^{3}$ convient. Donc il y a 3 entiers $n$ solution au problème : $n=2, n=2^{7}$ et $n=2^{4} \times 5^{3}$.
|
| 192 |
+
Exercice 9. Prouver qu'il existe une infinité d'entiers $n$ tels que $2^{2^{n}+1}+1$ est divisible par $n$, mais $2^{n}+1$ ne l'est pas.
|
| 193 |
+
|
| 194 |
+
Solution de l'exercice 9 Pour $m \geqslant 1$, posons $a_{m}=2^{3^{m}}+1$. On a
|
| 195 |
+
$a_{m}=\left(2^{3^{m-1}}+1\right)\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)=a_{m-1}\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)$.
|
| 196 |
+
Notons que pour $a \in \mathbb{N}^{*}$, si $p \mid a+1$ et $p \mid a^{2}-a+1$, alors $p \mid 2 a-1$ car $2 a-1=a(a+1)-\left(a^{2}-a+1\right)$. Et $p \mid 2 a+2$, donc $p \mid 3$. Donc $\left(a_{m-1} \wedge a_{m}\right) \mid 3$ pour tout $m \in \mathbb{N} *$. Donc $a_{m}$ possède un facteur premier impair (car $a_{m}$ impair) autre que 3 qui ne divise pas $a_{m-1}$, sauf éventuellement si $a_{m}$ est une puissance de 3 , auquel cas $a_{m+1}$ possède un facteur premier que n'a pas $a_{m}$.
|
| 197 |
+
Donc pour une infinité d'entiers $m \in \mathbb{N}^{*}, a_{m}$ possède un facteur premier $p_{m}>3$ qui ne divise pas $a_{m-1}$. Posons $b_{m}=3^{m-1} p_{m}$. D'après le petit théorème de Fermat,
|
| 198 |
+
|
| 199 |
+
$$
|
| 200 |
+
2^{b_{m}}+1 \equiv 2^{3^{m-1}}+1 \equiv a_{m-1} \quad(\bmod p)_{m}
|
| 201 |
+
$$
|
| 202 |
+
|
| 203 |
+
Donc $p_{m} \nmid 2^{b_{m}}+1$, donc $b_{m} \nmid 2^{b_{m}}+1$.
|
| 204 |
+
Comme $p_{m}$ et 3 sont premiers entre eux, il suffit de montrer que $p_{m} \mid 2^{2^{b m}+1}+1$ et que $3^{m_{1}} \mid 2^{2^{b_{m}}+1}+1$. Cela se fait assez directement avec LTE mais on peut peut-être trouver une solution alternative. Recherche en cours.
|
| 205 |
+
Ainsi, une infinité d'entiers $b_{m}$ satisfont la condition de l'énoncé.
|
| 206 |
+
|
French_STS/md/fr-ofm-2016-2017-envoi-2-solutions.md
ADDED
|
@@ -0,0 +1,400 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
## Olympiades Françaises de Mathématiques 2016-2017
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## Solutions à l'envoi $\mathfrak{N}$ (uméro 2 - Algèbre
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe $\mathcal{B}$
|
| 8 |
+
|
| 9 |
+
## Exercice 1.
|
| 10 |
+
|
| 11 |
+
Déterminer la valeur minimale de
|
| 12 |
+
|
| 13 |
+
$$
|
| 14 |
+
\left\lfloor\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{~d}}\right\rfloor+\left\lfloor\frac{\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{a}}\right\rfloor+\left\lfloor\frac{\mathrm{c}+\mathrm{d}+\mathrm{a}}{\mathrm{~b}}\right\rfloor+\left\lfloor\frac{\mathrm{d}+\mathrm{a}+\mathrm{b}}{\mathrm{c}}\right\rfloor
|
| 15 |
+
$$
|
| 16 |
+
|
| 17 |
+
lorsque $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ décrivent $\mathbb{N}^{*}$.
|
| 18 |
+
|
| 19 |
+
## Solution de l'exercice 1
|
| 20 |
+
|
| 21 |
+
Le minimum cherché est 9.
|
| 22 |
+
En effet, si a, b, c, d sont des entiers naturels non nuls, on pose
|
| 23 |
+
|
| 24 |
+
$$
|
| 25 |
+
f(a, b, c, d)=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor .
|
| 26 |
+
$$
|
| 27 |
+
|
| 28 |
+
On rappelle que, pour tout réel $x$, on a $\lfloor x\rfloor>x-1$. Ainsi, pour tous entiers $a, b, c, d>0$, on a
|
| 29 |
+
|
| 30 |
+
$$
|
| 31 |
+
\begin{aligned}
|
| 32 |
+
f(a, b, c, d)+4 & >\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c} \\
|
| 33 |
+
& >\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right) \\
|
| 34 |
+
& >6 \times 2 \text { car } t+\frac{1}{t} \geqslant 2 \text { pour tout réel } t>0 .
|
| 35 |
+
\end{aligned}
|
| 36 |
+
$$
|
| 37 |
+
|
| 38 |
+
Ainsi, $f(a, b, c, d)>8$. Or, $f(a, b, c, d)$ étant clairement un entier, $c^{\prime}$ est donc que $f(a, b, c, d) \geqslant$ 9. Il reste à vérifier que $f(5,5,5,4)=9$ pour conclure.
|
| 39 |
+
|
| 40 |
+
## Exercice 2.
|
| 41 |
+
|
| 42 |
+
Soit $m$ et $n$ des entiers naturels non nuls. Prouver que
|
| 43 |
+
|
| 44 |
+
$$
|
| 45 |
+
\frac{(m+n)!}{(m+n)^{m+n}}<\frac{m!}{m^{m}} \frac{n!}{n^{n}}
|
| 46 |
+
$$
|
| 47 |
+
|
| 48 |
+
## Solution de l'exercice 2
|
| 49 |
+
|
| 50 |
+
D'après la formule du binôme, on a
|
| 51 |
+
|
| 52 |
+
$$
|
| 53 |
+
(m+n)^{m+n}=\sum_{k=0}^{m+n}\binom{m+n}{k} m^{k} n^{m+n-k}
|
| 54 |
+
$$
|
| 55 |
+
|
| 56 |
+
Le membre de droite étant une somme de $m+n+1$ nombres strictement positifs, elle est strictement plus grande que n'importe lequel de ces nombres. En particulier, pour $k=m$, on a donc
|
| 57 |
+
|
| 58 |
+
$$
|
| 59 |
+
(m+n)^{m+n}>\binom{m+n}{m} m^{m} n^{n}
|
| 60 |
+
$$
|
| 61 |
+
|
| 62 |
+
Puisque $\binom{m+n}{m}=\frac{(m+n)!}{m!n!}$, cela conclut.
|
| 63 |
+
Remarque L'inégalité demandée peut s'interpréter en termes probabilistes. En effet, considérons une urne contenant $m$ boules blanches et $n$ boules noires indiscernables au toucher, et de laquelle on tire successivement $m+n$ boules avec remise. Il est facile de vérifier que la probabilité $p_{m}$ d'obtenir exactement $m$ boules blanches au cours de ces $m+n$ tirages est
|
| 64 |
+
|
| 65 |
+
$$
|
| 66 |
+
p_{m}=\binom{m+n}{m}\left(\frac{m}{m+n}\right)^{m}\left(\frac{n}{m+n}\right)^{n}
|
| 67 |
+
$$
|
| 68 |
+
|
| 69 |
+
Si on note $q_{m}$ la probabilité de ne pas obtenir exactement $m$ boules blanches, on a $q_{m}>0$ et $p_{m}+q_{m}=1$, d'où $p_{m}=1-q_{m}<1$.
|
| 70 |
+
|
| 71 |
+
## Exercice 3.
|
| 72 |
+
|
| 73 |
+
Soit $a_{0}<a_{1}<a_{2}<\ldots$ une suite infinie d'entiers strictement positifs. Prouver qu'il existe un unique entier $n \geqslant 1$ tel que
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
a_{n}<\frac{a_{0}+a_{1}+a_{2}+\cdots+a_{n}}{n} \leqslant a_{n+1} .
|
| 77 |
+
$$
|
| 78 |
+
|
| 79 |
+
## Solution de l'exercice 3
|
| 80 |
+
|
| 81 |
+
Pour $n \geqslant 1$, on pose $d_{n}=a_{0}+a_{1}+\cdots+a_{n}-n a_{n}$.
|
| 82 |
+
Clairement, l'inégalité de gauche de l'encadrement souhaité est équivalente à $\mathrm{d}_{\mathrm{n}}>0$.
|
| 83 |
+
D'autre part, on a $d_{n+1}=a_{0}+\cdots+a_{n}-n a_{n+1}$, donc l'inégalité de droite est équivalente à $d_{n+1} \leqslant 0$. Il s'agit donc de prouver qu'il existe un unique $n \geqslant 1$ tel que $d_{n+1} \leqslant 0<d_{n}$, ce qui nous pousse naturellement à étudier les variations de la suite ( $d_{i}$ ).
|
| 84 |
+
Pour tout $n \geqslant 1$, on a $d_{n+1}-d_{n}=n\left(a_{n}-a_{n+1}\right)<0$ car la suite $\left(a_{i}\right)$ est strictement croissante. De plus, on a $d_{1}=a_{0}>0$.
|
| 85 |
+
Ainsi, la suite ( $\mathrm{d}_{\mathrm{i}}$ ) est une suite strictement décroissante $\mathrm{d}^{\prime}$ entiers, ce qui assure qu'elle ne prendra des valeurs négatives ou nulles qu'à partir d'un certain rang, et de premier terme strictement positif. Il existe donc bien un unique indice $n$ pour lequel $d_{n+1} \leqslant 0<d_{n}$, à savoir le plus grand entier tel que $d_{n}>0$.
|
| 86 |
+
|
| 87 |
+
Remarque La conclusion n'est plus assurée sans l'hypothèse que les $a_{i}$ sont tous des entiers. Un contre-exemple est donné par $a_{n}=2-\frac{1}{2^{n}}$ pour tout $n \geqslant 0$.
|
| 88 |
+
|
| 89 |
+
## Exercices communs
|
| 90 |
+
|
| 91 |
+
## Exercice 4.
|
| 92 |
+
|
| 93 |
+
Déterminer tous les entiers $n \geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.
|
| 94 |
+
|
| 95 |
+
## Solution de l'exercice 4
|
| 96 |
+
|
| 97 |
+
Prouvons que seul $n=3$ a la propriété désirée.
|
| 98 |
+
Tout d'abord, en posant $\mathrm{P}_{1}(x)=3 x^{2}+3$ et $\mathrm{P}_{2}(x)=P_{3}(x)=-x^{2}-2$, on vérifie aisément que les polynômes $P_{1}(x)+P_{2}(x)=P_{1}(x)+P_{3}(x)=2 x^{2}+1$ et $P_{2}(x)+P_{3}(x)=-2 x^{2}-4$ n'ont aucune racine réelle, tandis que $P_{1}(x)+P_{2}(x)+P_{3}(x)=x^{2}-1$ admet 1 et -1 comme racines. Ainsi, $n=3$ est une solution du problème.
|
| 99 |
+
Remarquons maintenant que si $n \geqslant 4$ polynômes $\mathrm{P}_{1}, \ldots, \mathrm{P}_{n}$ vérifient les conditions requises, alors $\mathrm{P}_{1} \mathrm{P}_{2}, \mathrm{P}_{3}$ et $\mathrm{P}_{4}$ vérifient déjà ces conditions. Pour conclure, il suffit donc de prouver que $n=4 n^{\prime}$ est pas une solution.
|
| 100 |
+
La clé est alors de noter que si P et Q sont des polynômes tels que $\mathrm{P}+\mathrm{Q}$ n'a pas de racine rélle, alors $\mathrm{P}+\mathrm{Q}$ garde un signe constant sur $\mathbb{R}$.
|
| 101 |
+
On procède donc par l'absurde : supposons que $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}$ et $\mathrm{P}_{4}$ soient des polynômes tels que, pour tous $i, j, k$ distincts, $P_{i}+P_{j}$ n'a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.
|
| 102 |
+
Traçons alors le graphe complet dont les sommets sont les polynômes $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}, \mathrm{P}_{4}$ et colorons l'arête $P_{i} P_{j}$ en rouge si $P_{i}+P_{j}$ est strictement positif, et en vert si $P_{i}+P_{j}$ est strictement négatif. Chaque arête est nécessairement colorée. De plus, ce graphe ne peut contenir de triangles dont les trois arêtes sont de la même couleur, ce sans quoi la somme des trois polynômes qui sont les sommets de ce triangle n'aurait pas de racine réelle.
|
| 103 |
+
Quitte à changer chaque $P_{i}$ en $-P_{i}$, on peut supposer que deux des trois arêtes issues de $P_{1}$ sont rouges et, quitte à renuméroter, on peut supposer que $P_{1} P_{2}$ et $P_{1} P_{4}$ sont rouges. Pour éviter le triangle rouge $P_{1} P_{2} P_{4}$, $c^{\prime}$ est donc que $P_{2} P_{4}$ est verte. Puisque $P_{2} P_{3} P_{4}$ ne peut avoir ses trois arêtes vertes, $c^{\prime}$ est donc que $P_{2} P_{3}$ ou $P_{4} P_{3}$ est rouge. Par symétrie des rôles, on peut supposer que $\mathrm{P}_{2} \mathrm{P}_{3}$ est rouge. Mais alors $\mathrm{P}_{1} \mathrm{P}_{3}$ est verte.
|
| 104 |
+
Ainsi, pour tout réel $x$, on a simultanement
|
| 105 |
+
|
| 106 |
+
$$
|
| 107 |
+
\begin{aligned}
|
| 108 |
+
& P_{1}(x)+P_{4}(x)>0 \text { et } P_{2}(x)+P_{3}(x)>0 \text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)>0 \text {, et } \\
|
| 109 |
+
& P_{1}(x)+P_{3}(x)<0 \text { et } P_{2}(x)+P_{4}(x)<0 \text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)<0,
|
| 110 |
+
\end{aligned}
|
| 111 |
+
$$
|
| 112 |
+
|
| 113 |
+
ce qui est absurde. Ainsi, $n=4$ n'est pas une solution, ce qui conclut.
|
| 114 |
+
|
| 115 |
+
## Exercice 5.
|
| 116 |
+
|
| 117 |
+
a) Déterminer toutes les fonctions $f: \mathbb{R} \longrightarrow \mathbb{Z}$ telles que
|
| 118 |
+
|
| 119 |
+
$$
|
| 120 |
+
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
|
| 121 |
+
$$
|
| 122 |
+
|
| 123 |
+
pour tous réels $x$ et $y$.
|
| 124 |
+
b) Déterminer toutes les fonctions $f: \mathbb{R} \longrightarrow \mathbb{R}$ telles que
|
| 125 |
+
|
| 126 |
+
$$
|
| 127 |
+
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
|
| 128 |
+
$$
|
| 129 |
+
|
| 130 |
+
pour tous réels $x$ et $y$.
|
| 131 |
+
|
| 132 |
+
## Solution de l'exercice 5
|
| 133 |
+
|
| 134 |
+
a) Soit f une éventuelle solution du problème. Notons $\mathrm{P}(\mathrm{x}, \mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0)$.
|
| 135 |
+
Pour tout $x$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, d'où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Il s'ensuit que $f(x) \geqslant c^{2} \geqslant 0$.
|
| 136 |
+
Pour $x=0$, cela donne $c=c^{2}+(f(c)-c)^{2}$, d'où $c(1-c)=(f(c)-c)^{2} \geqslant 0$. Puisque $c$ est un entier, il vient $c=0$ ou $c=1$. Dans les deux cas, cela montre que $f(c)-c=0$. Ainsi, on sait que $f(c)=c$.
|
| 137 |
+
Enfin, pour tout $x$, de $P(x, 0)$ on déduit que
|
| 138 |
+
|
| 139 |
+
$$
|
| 140 |
+
f(c-x)^{2}+f(x)^{2}+c^{2}=c(1+2 c)
|
| 141 |
+
$$
|
| 142 |
+
|
| 143 |
+
- Si $\mathrm{c}=0$, l'égalité ci-dessus se réécrit comme $f(-x)^{2}+f(x)^{2}=0$, donc $f(x)=0$.
|
| 144 |
+
- Si $\mathrm{c}=1$, elle se réécrit comme $f(1-x)^{2}+f(x)^{2}=2$. Or, $f(1-x)$ et $f(x)$ sont entiers naturels, donc $f(x)=f(1-x)=1$.
|
| 145 |
+
Réciproquement, les fonctions $\mathrm{f}: x \longmapsto 0$ et $\mathrm{f}: x \longmapsto 1$ sont clairement solutions du problème.
|
| 146 |
+
b) Soit $f$ une éventuelle solution du problème. Notons $\mathrm{P}(\mathrm{x}, \mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0), d=f(c)$ et $\mathcal{F}=\{f(x) \mid x \in \mathbb{R}\}$.
|
| 147 |
+
Pour tout $x \in \mathbb{R}$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, $d^{\prime}$ où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Par conséquent, pour tout $x \in \mathcal{F}$, on a $x \geqslant c^{2} \geqslant 0$ et $f(x)=x \pm \sqrt{x-c^{2}}$.
|
| 148 |
+
Il s'ensuit que $c \geqslant c^{2}$, c'est-à-dire que $c(1-c) \geqslant 0$, donc que $0 \leqslant c \leqslant 1$. On procède alors par l'absurde, et on suppose que $0<c<1$.
|
| 149 |
+
Par inégalité arithmético-géométrique, il vient $0<\mathrm{c}(1-\mathrm{c}) \leqslant\left(\frac{\mathrm{c}+1-\mathrm{c}}{2}\right)^{2}=\frac{1}{4}$. D'autre part, de manière générale, pour tout réel $x \in] 0 ; 1[$, on sait que $x<\sqrt{x}$.
|
| 150 |
+
|
| 151 |
+
Or, on a prouvé ci-dessus que $d=c+\epsilon \sqrt{c-c^{2}}$, avec $\epsilon= \pm 1$. Si $\epsilon=-1$, alors $d-c^{2}=$ $\left(c-c^{2}\right)-\sqrt{c-c^{2}}<0$, ce qui est impossible. Il vient donc $\epsilon=1$, et $d=c+\sqrt{c-c^{2}}$. Puis on trouve $f(d)=d+\varepsilon \sqrt{d-c^{2}}$, avec $\varepsilon= \pm 1$. Observons que
|
| 152 |
+
|
| 153 |
+
$$
|
| 154 |
+
0<c-c^{2} \leqslant d-c^{2} \leqslant\left(c-c^{2}\right)+\sqrt{c-c^{2}} \leqslant \frac{1}{4}+\frac{1}{2}=\frac{3}{4}<1 .
|
| 155 |
+
$$
|
| 156 |
+
|
| 157 |
+
Par conséquent, si $\varepsilon=-1$, alors $f(d)-c^{2}=\left(d-c^{2}\right)-\sqrt{d-c^{2}}<0$, ce qui est encore une fois impossible. Il vient donc $\varepsilon=1$, et $f(d)=d+\sqrt{d-c^{2}}$.
|
| 158 |
+
Enfin, $P(d, 0)$ indique que
|
| 159 |
+
|
| 160 |
+
$$
|
| 161 |
+
\begin{aligned}
|
| 162 |
+
0 & =f(c-d)^{2}+f(d)^{2}+c^{2}-c(1+2 d)=f(c-d)^{2}+\left(d+\sqrt{d-c^{2}}\right)^{2}+c^{2}-c(1+2 d) \\
|
| 163 |
+
& \geqslant c^{4}+d^{2}+d-c^{2}+c^{2}-c(1+2 d)=c^{4}+(d-c)^{2}+(d-c)-c^{2} \\
|
| 164 |
+
& \geqslant c^{4}+c-c^{2}+\sqrt{c-c^{2}}-c^{2} \geqslant c^{4}+c-c^{2}+c-c^{2}-c^{2}=c(c-1)^{2}(c+2)
|
| 165 |
+
\end{aligned}
|
| 166 |
+
$$
|
| 167 |
+
|
| 168 |
+
ce qui est impossible.
|
| 169 |
+
Il s'ensuit que $c=0$ ou $c=1$, donc que $c=c^{2}$ et que $f(c)=c \pm \sqrt{c-c^{2}}=c$. Par conséquent, pour tout $x, P(x, 0)$ indique que
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
f(c-x)^{2}+f(x)^{2}+c^{2}=c(1+2 c)
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
- Si $\mathrm{c}=0$, l'égalité ci-dessus se réécrit comme $f(-x)^{2}+f(x)^{2}=0$, donc $f(x)=0$.
|
| 176 |
+
- Si $\mathrm{c}=1$, elle se réécrit comme $\mathrm{f}(1-x)^{2}+\mathrm{f}(\mathrm{x})^{2}=2$. Or, on a vu plus haut que $f(1-x) \geqslant c^{2}=1$ et que $f(x) \geqslant c^{2}=1$, ce qui montre que $f(x)=f(1-x)=1$.
|
| 177 |
+
Réciproquement, les fonctions $\mathrm{f}: x \longmapsto 0$ et $\mathrm{f}: \mathrm{x} \longmapsto 1$ sont clairement solutions du problème.
|
| 178 |
+
|
| 179 |
+
|
| 180 |
+
## Exercice 6.
|
| 181 |
+
|
| 182 |
+
a) Soit $x_{1} \geqslant x_{2}>0$ et $y_{1} \geqslant y_{2}>0$ des réels tels que
|
| 183 |
+
|
| 184 |
+
$$
|
| 185 |
+
x_{1} \geqslant y_{1} \text { et } x_{1} x_{2} \geqslant y_{1} y_{2}
|
| 186 |
+
$$
|
| 187 |
+
|
| 188 |
+
Prouver que
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
x_{1}+x_{2} \geqslant y_{1}+y_{2}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
b) Soit $x_{1} \geqslant x_{2} \geqslant \ldots \geqslant x_{n}>0$ et $y_{1} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}>0$ des réels tels que
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
x_{1} x_{2} \cdots x_{i} \geqslant y_{1} y_{2} \cdots y_{i} \text { pour } i=1, \ldots, n
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
Prouver que
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
x_{1}+x_{2}+\cdots+x_{n} \geqslant y_{1}+y_{2}+\cdots+y_{n}
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
## Solution de l'exercice 6
|
| 207 |
+
|
| 208 |
+
a) Procédons par l'absurde: supposons que $y_{1}+y_{2}>x_{1}+x_{2}$. Alors $y_{2}>x_{1}+x_{2}-y_{1}$ et on a
|
| 209 |
+
|
| 210 |
+
$$
|
| 211 |
+
0 \geqslant y_{1} y_{2}-x_{1} x_{2}>y_{1}\left(x_{1}+x_{2}-y_{1}\right)-x_{1} x_{2}=\left(x_{1}-y_{1}\right)\left(y_{1}-x_{2}\right)
|
| 212 |
+
$$
|
| 213 |
+
|
| 214 |
+
Puisque $x_{1} \geqslant y_{1}$, alors $y_{1}<x_{2}$. Mais alors $x_{1}+x_{2} \geqslant 2 y_{1} \geqslant y_{1}+y_{2}$, ce qui contredit notre hypothèse. On a donc bien $y_{1}+y_{2} \leqslant x_{1}+x_{2}$.
|
| 215 |
+
b) Procédons par récurrence forte sur $n$. Tout d'abord, le résultat est évident pour $n=1$, et on vient de le prouver pour $\mathrm{n}=2$. On suppose donc $\mathrm{n} \geqslant 3$.
|
| 216 |
+
Soit $\lambda=\min _{1 \leqslant k<n} \frac{x_{1}+\ldots+x_{k}}{y_{1}+\ldots+y_{k}}$, et soit $\ell$ un entier tel que $1 \leqslant \ell<n$ et tel que
|
| 217 |
+
|
| 218 |
+
$$
|
| 219 |
+
x_{1}+\ldots+x_{\ell}=\lambda\left(y_{1}+\ldots+y_{\ell}\right)
|
| 220 |
+
$$
|
| 221 |
+
|
| 222 |
+
On pose alors $y_{1}^{\prime}=\lambda y_{1}, y_{n}^{\prime}=\frac{y_{n}}{\lambda}$ et $y_{k}^{\prime}=y_{k}$ pour $k=2, \ldots, n-1$. Par construction, on a bien $y_{1}^{\prime} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}^{\prime}$ et, pour $k=1, \ldots, n$, on a également $x_{1} \ldots x_{k} \geqslant y_{1}^{\prime} \ldots y_{k}^{\prime}$, avec égalité quand $k=\ell<n$. Par hypothèse de récurrence, on sait que $x_{1}+\ldots+x_{\ell} \geqslant$ $y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}$.
|
| 223 |
+
En outre, remarquons que $y_{1}^{\prime} \geqslant y_{n}^{\prime}, y_{1} \geqslant y_{n}, y_{1}^{\prime} \geqslant y_{1}$ et $y_{1}^{\prime} y_{n}^{\prime}=y_{1} y_{n}$. En appliquant l'hypothèse de récurrence (pour $n=2$ ), on obtient donc $y_{1}^{\prime}+y_{n}^{\prime} \geqslant y_{1}+y_{n}$, et même $y_{1}^{\prime}+y_{2}^{\prime}+\ldots+y_{n}^{\prime} \geqslant y_{1}+y_{2}+\ldots+y_{n}$.
|
| 224 |
+
Enfin, posons $\bar{x}_{i}=x_{\ell+i}$ et $\bar{y}_{i}=y_{\ell+1}^{\prime}$, pour $i=1, \ldots, n-\ell$. Alors $\bar{x}_{1} \geqslant \ldots \geqslant \bar{x}_{n-\ell}>0$ et $\bar{y}_{1} \geqslant \ldots \geqslant \bar{y}_{n-\ell}>0$. En outre, pour $i=1, \ldots, n-\ell$, on a
|
| 225 |
+
|
| 226 |
+
$$
|
| 227 |
+
\left(x_{1} \ldots x_{\ell}\right)\left(\bar{x}_{1} \ldots \bar{x}_{i}\right)=x_{1} \ldots x_{\ell+i} \geqslant y_{1}^{\prime} \ldots y_{\ell+i}^{\prime}=\left(y_{1}^{\prime} \ldots y_{\ell}^{\prime}\right)\left(\bar{y}_{1} \ldots \bar{y}_{i}\right)
|
| 228 |
+
$$
|
| 229 |
+
|
| 230 |
+
Puisque $x_{1} \ldots x_{\ell}=y_{1}^{\prime} \ldots y_{\ell}^{\prime}>0$, cela montre que $\bar{x}_{1} \ldots \bar{x}_{i} \geqslant \bar{y}_{1} \ldots \bar{y}_{i}$. On a $n-\ell<n$, et l'hypothèse de récurrence montre donc que $\bar{x}_{1}+\ldots+\bar{x}_{n-\ell} \geqslant \bar{y}_{1}+\ldots+\bar{y}_{n-\ell}$.
|
| 231 |
+
|
| 232 |
+
Mises bout à bout, ces inégalités montrent que
|
| 233 |
+
|
| 234 |
+
$$
|
| 235 |
+
\begin{aligned}
|
| 236 |
+
x_{1}+\ldots+x_{n} & =\left(x_{1}+\ldots+x_{\ell}\right)+\left(\bar{x}_{1}+\ldots+\bar{x}_{n-\ell}\right) \\
|
| 237 |
+
& \geqslant y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}+\bar{y}_{1}+\ldots+\bar{y}_{n-\ell}=y_{1}^{\prime}+\ldots+y_{n}^{\prime} \\
|
| 238 |
+
& \geqslant y_{1}+\ldots+y_{n} .
|
| 239 |
+
\end{aligned}
|
| 240 |
+
$$
|
| 241 |
+
|
| 242 |
+
## Solution alternative
|
| 243 |
+
|
| 244 |
+
On pose
|
| 245 |
+
|
| 246 |
+
$$
|
| 247 |
+
x_{n+1}=\min \left(x_{n}, y_{n}\right) \frac{y_{1} \cdots y_{n}}{x_{1} \cdots x_{n}} \text { et } y_{n+1}=\min \left(x_{n}, y_{n}\right)
|
| 248 |
+
$$
|
| 249 |
+
|
| 250 |
+
On a alors $0<x_{n+1} \leqslant x_{n}, 0<y_{n+1} \leqslant y_{n}, x_{n+1} \leqslant y_{n+1}$ et $x_{1} \cdots x_{n} x_{n+1}=y_{1} \cdots y_{n} y_{n+1}$. Tout étant homogène, quitte à multiplier les $x_{i}$ et les $y_{i}$ par une même constante, on peut supposer que $x_{i}, y_{i}>1$ pour tout $i$. On pose ensuite $\alpha_{i}=\ln \left(x_{i}\right)$ et $\beta_{i}=\ln \left(y_{i}\right)$, pour tout i. On a alors:
|
| 251 |
+
$-\alpha_{1} \geqslant \ldots \geqslant \alpha_{n+1}>0$ et $\beta_{1} \geqslant \ldots \geqslant \beta_{n+1}>0 ;$
|
| 252 |
+
$-\beta_{1}+\cdots+\beta_{i} \leqslant \alpha_{1}+\cdots+\alpha_{i}$, pour $i=1, \ldots, n$;
|
| 253 |
+
$-\beta_{1}+\cdots \beta_{n+1}=\alpha_{1}+\cdots+\alpha_{n+1}$.
|
| 254 |
+
On peut donc utiliser l'inégalité de Muirhead, qui assure que, pour tous réels $\mathrm{x}_{1}, \ldots, \chi_{n+1}$ strictement positifs, on a
|
| 255 |
+
|
| 256 |
+
$$
|
| 257 |
+
\sum_{\text {sym. }} x_{1}^{\beta_{1}} \cdots x_{n+1}^{\beta_{n+1}} \leqslant \sum_{\text {sym. }} x_{1}^{\alpha_{1}} \cdots x_{n+1}^{\alpha_{n+1}} .
|
| 258 |
+
$$
|
| 259 |
+
|
| 260 |
+
En particulier, si $x_{1}=e$ et $x_{i}=1$ pour $i \geqslant 2$, il vient $\sum_{i=1}^{n+1} y_{i} \leqslant \sum_{i=1}^{n+1} x_{i}$. Puisque $x_{n+1} \leqslant y_{n+1}$, il s'ensuit en fait $\sum_{i=1}^{n} y_{i} \leqslant \sum_{i=1}^{n} x_{i}$.
|
| 261 |
+
|
| 262 |
+
Remarque Une fois introduits les nombres $\alpha_{i}$ et $\beta_{i}$, au lieu d'utiliser l'inégalité de Muirhead, on aurait pu directement utiliser l'inégalité de Karamata à la fonction exponentielle (qui est convexe sur $\mathbb{R}$ ).
|
| 263 |
+
|
| 264 |
+
## Exercices du groupe $\mathcal{A}$
|
| 265 |
+
|
| 266 |
+
## Exercice 7.
|
| 267 |
+
|
| 268 |
+
Soit $a_{0}$ et $b_{0}$ des entiers strictement positifs. Pour tout $i \geqslant 0$, on pose
|
| 269 |
+
|
| 270 |
+
$$
|
| 271 |
+
a_{i+1}=a_{i}+\left\lfloor\sqrt{b_{i}}\right\rfloor \text { et } b_{i+1}=b_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor \text {. }
|
| 272 |
+
$$
|
| 273 |
+
|
| 274 |
+
Prouver qu'il existe un entier $n \geqslant 0$ tel que $a_{n}=b_{n}$.
|
| 275 |
+
|
| 276 |
+
## Solution de l'exercice 7
|
| 277 |
+
|
| 278 |
+
Pour tout $i \geqslant 0$, posons $c_{i}=b_{i}-a_{i}, \alpha_{i}=\left\lfloor\sqrt{a_{i}}\right\rfloor$ et $\beta_{i}=\left\lfloor\sqrt{b_{i}}\right\rfloor$. Sans perte de généralité, on suppose que $c_{0} \geqslant 0$. On montre tout d'abord par récurrence que $c_{i} \geqslant 0$ pour tout $i \geqslant 0$. En effet, pour tout $n \geqslant 0$, on a $\lfloor\sqrt{n+1}\rfloor \leqslant\lfloor\sqrt{n}\rfloor+1$. La fonction $f: n \longmapsto n-\lfloor\sqrt{n}\rfloor$ est donc croissante sur $\mathbb{N}$, car
|
| 279 |
+
|
| 280 |
+
$$
|
| 281 |
+
f(n+1)-f(n)=n+1-\lfloor\sqrt{n+1}\rfloor-n+\lfloor\sqrt{n}\rfloor \geqslant n+1-\lfloor\sqrt{n}\rfloor-1-n+\lfloor\sqrt{n}\rfloor=0
|
| 282 |
+
$$
|
| 283 |
+
|
| 284 |
+
pour tout $n \geqslant 0$. Par conséquent, si $c_{i} \geqslant 0$, alors $b_{i} \geqslant a_{i}$, donc
|
| 285 |
+
|
| 286 |
+
$$
|
| 287 |
+
c_{i+1}=\left(b_{i}-\left\lfloor\sqrt{b_{i}}\right\rfloor\right)-\left(a_{i}-\left\lfloor\sqrt{a_{i}}\right\rfloor\right)=f\left(b_{i}\right)-f\left(a_{i}\right) \geqslant 0
|
| 288 |
+
$$
|
| 289 |
+
|
| 290 |
+
Ceci conclut la récurrence, et montre bien que $\boldsymbol{c}_{\boldsymbol{i}} \geqslant 0$ pour tout $i \geqslant 0$.
|
| 291 |
+
D'autre part, si $c_{i} \geqslant 0$, et toujours puisque $b_{i} \geqslant a_{i}$, on a aussi $c_{i+1}=c_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor-\left\lfloor\sqrt{b_{i}}\right\rfloor \leqslant$ $c_{i}$. La suite $\left(c_{i}\right)_{i \geqslant 0}$ est donc décroissante, à valeurs dans les entiers naturels. Il existe donc un entier $n \geqslant 0$ tel que $c_{i}=c_{n}$ pour tout $i \geqslant n$. Il suffit donc de prouver que $c_{n}=0$.
|
| 292 |
+
Procédons par l'absurde : supposons que $c_{n} \geqslant 1$. Pour tout $i \geqslant n$, on sait que $c_{i}=c_{i+1}=$ $c_{i}+\alpha_{i}-\beta_{i}$, donc que $\alpha_{i}=\beta_{i}$. La suite $\left(b_{i}-\beta_{i}^{2}\right)_{i \geqslant n}$ est à valeurs entières positives ; il existe donc un entier $m \geqslant n$ tel que $b_{i}-\beta_{i}^{2} \geqslant b_{m}-\beta_{m}^{2}$ pour tout $i \geqslant n$. Quitte à augmenter la valeur de $n$, on suppose en outre que $m=n$.
|
| 293 |
+
Notons enfin que les suites $\left(a_{i}\right)_{i \geqslant 0}$ et $\left(\alpha_{i}\right)_{i \geqslant 0}$ sont clairement croissantes. Deux cas sont alors possibles :
|
| 294 |
+
— Si $\alpha_{n}=\alpha_{n+1}$, alors
|
| 295 |
+
|
| 296 |
+
$$
|
| 297 |
+
\begin{aligned}
|
| 298 |
+
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1} \geqslant a_{n}+c_{n}+2 \beta_{n} \geqslant \beta_{n}^{2}+2 \beta_{n}+1=\left(\beta_{n}+1\right)^{2} \text { et } \\
|
| 299 |
+
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1}<\left(\beta_{n}+1\right)^{2}+2 \beta_{n}<\left(\beta_{n}+2\right)^{2}
|
| 300 |
+
\end{aligned}
|
| 301 |
+
$$
|
| 302 |
+
|
| 303 |
+
donc $\beta_{n+2}=\beta_{n}+1$. Ceci montre que
|
| 304 |
+
|
| 305 |
+
$$
|
| 306 |
+
b_{n+2}-\beta_{n+2}^{2}=b_{n}+2 \beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-1<b_{n}-\beta_{n}^{2}
|
| 307 |
+
$$
|
| 308 |
+
|
| 309 |
+
ce qui contredit notre hypothèse.
|
| 310 |
+
|
| 311 |
+
|
| 312 |
+
- Si $\alpha_{n}<\alpha_{n+1}$, alors
|
| 313 |
+
|
| 314 |
+
$$
|
| 315 |
+
\begin{aligned}
|
| 316 |
+
& b_{n+1} \geqslant \beta_{n+1}^{2}=\alpha_{n+1}^{2} \geqslant\left(\alpha_{n}+1\right)^{2}=\left(\beta_{n}+1\right)^{2} \text { et } \\
|
| 317 |
+
& b_{n+1}=b_{n}+\alpha_{n}<\left(\beta_{n}+1\right)^{2}+\beta_{n}<\left(\beta_{n}+2\right)^{2}
|
| 318 |
+
\end{aligned}
|
| 319 |
+
$$
|
| 320 |
+
|
| 321 |
+
donc $\beta_{n+1}=\beta_{n}+1$. Ceci montre que
|
| 322 |
+
|
| 323 |
+
$$
|
| 324 |
+
b_{n+1}-\beta_{n+1}^{2}=b_{n}+\beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-\beta_{n}-1<b_{n}-\beta_{n}^{2}
|
| 325 |
+
$$
|
| 326 |
+
|
| 327 |
+
ce qui contredit une fois encore notre hypothèse.
|
| 328 |
+
Notre hypothèse selon laquelle $c_{n} \geqslant 1$ était donc fausse, ce qui montre que $c_{n}=0$, concluant donc l'exercice.
|
| 329 |
+
|
| 330 |
+
## Exercice 8.
|
| 331 |
+
|
| 332 |
+
Un polynôme est dit «unitaire » si le coefficient de son monôme de plus haut de degré vaut 1. Soit $a<b$ des réels, et soit $P$ un polynôme unitaire non constant tel que $\max _{x \in[a, b]}|P(x)|<2$.
|
| 333 |
+
|
| 334 |
+
Prouver qu'il existe un polynôme $Q$, unitaire et non constant, tel que $\max _{x \in[\mathbf{a}, \mathbf{b}]}|\mathrm{Q}(\mathrm{x})|<\frac{1}{2017}$.
|
| 335 |
+
|
| 336 |
+
## Solution de l'exercice 8
|
| 337 |
+
|
| 338 |
+
Si Q désigne un polynôme, on pose
|
| 339 |
+
|
| 340 |
+
$$
|
| 341 |
+
\|Q\|=\frac{1}{2} \max _{x \in[a, b]}|Q(x)| \text { et } T(Q)(x)=Q(x)^{2}-2\|Q\|^{2}
|
| 342 |
+
$$
|
| 343 |
+
|
| 344 |
+
Il est clair que si Q est un polynôme unitaire non constant, alors $\mathrm{T}(\mathrm{Q})$ l'est également. De plus, on a $\|T(Q)\|=\|Q\|^{2}$. Si $l^{\prime}$ on note $T^{n}$ la $n$-ieme itérée de $T$, alors une récurrence immédiate assure que pour tout entier $n \geqslant 0, T^{n}(Q)$ est un polynôme non constant dont le coefficient du monôme de plus haut de degré vaut 1 et que $\left\|T^{\mathrm{n}}(Q)\right\|=\|Q\|^{2^{n}}$. Soit donc P un polynôme unitaire non constant, tel que $\max _{\mathrm{x} \in[\mathrm{a}, \mathbf{b}]}|\mathrm{P}(\mathrm{x})|<2$. Puisque $0<$ $\|P\|<1$, on a $\lim _{n \rightarrow+\infty}\left\|T^{n}(P)\right\|=0$. En particulier, il existe $n \geqslant 0$ suffisamment grand pour que $\left\|\mathrm{T}^{\mathrm{n}}(\mathrm{P})\right\|<\frac{1}{2 \times 2017}$, et le polynôme $\mathrm{Q}=\mathrm{T}^{\mathrm{n}}(\mathrm{P})$ répond alors à la question.
|
| 345 |
+
|
| 346 |
+
## Exercice 9.
|
| 347 |
+
|
| 348 |
+
a) Prouver qu'il existe des entiers $\mathbf{a}, \boldsymbol{b}$, $\mathbf{c}$ tels que $(\mathbf{a}, \mathbf{b}, \mathbf{c}) \neq(0,0,0)$ et $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}|<10^{6}$ pour lesquels
|
| 349 |
+
|
| 350 |
+
$$
|
| 351 |
+
|a+b \sqrt{2}+c \sqrt{3}|<10^{-11}
|
| 352 |
+
$$
|
| 353 |
+
|
| 354 |
+
b) Soit $\mathbf{a}, \mathbf{b}, \mathrm{c}$ des entiers tels que $(\mathbf{a}, \boldsymbol{b}, \mathrm{c}) \neq(0,0,0)$ et $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}|<10^{6}$. Prouver que
|
| 355 |
+
|
| 356 |
+
$$
|
| 357 |
+
|a+b \sqrt{2}+c \sqrt{3}|>10^{-21}
|
| 358 |
+
$$
|
| 359 |
+
|
| 360 |
+
## Solution de l'exercice 9
|
| 361 |
+
|
| 362 |
+
a) Soit E l'ensemble des $10^{18}$ nombres de la forme $a+b \sqrt{2}+c \sqrt{3}$, avec $a, b, c$ entiers naturels et $a, b, c<10^{6}$. On pose $d=(1+\sqrt{2}+\sqrt{3}) 10^{6}$.
|
| 363 |
+
Pour tout $x \in \mathrm{E}$, on a $0 \leqslant x<\mathrm{d}$. De plus $0<\mathrm{d}<(1+2+3) \times 10^{6}<10^{7}-10^{-11}$. On divise alors l'intervalle [0; d[ en $10^{18}-1$ intervalles
|
| 364 |
+
|
| 365 |
+
$$
|
| 366 |
+
\left[\frac{(\mathrm{k}-1) \mathrm{d}}{10^{18}-1} ; \frac{\mathrm{kd}}{10^{18}-1}[,\right.
|
| 367 |
+
$$
|
| 368 |
+
|
| 369 |
+
pour $k=1, \ldots, 10^{18}-1$. D'après le principe des tiroirs, au moins deux des $10^{18}$ élements de $E$, disons $x$ et $y$, appartiennent à un même de ces intervalles. Leur différence $z=x-y$ est bien de la forme $z=a+b \sqrt{2}+c \sqrt{3}$ avec $a, b, c$ entiers et $|a|,|b|,|c|<10^{6}$. De plus, $|z|=|x-y|<\frac{d}{10^{18}-1}<10^{-11}$.
|
| 370 |
+
b) Soit $a, b, c$ des entiers tels que $(a, b, c) \neq(0,0,0)$ et $|a|,|b|,|c|<10^{6}$. Pour $\epsilon= \pm 1$ et $\varepsilon= \pm 1$, on pose
|
| 371 |
+
|
| 372 |
+
$$
|
| 373 |
+
F_{\epsilon, \varepsilon}=a+\epsilon b \sqrt{2}+\varepsilon c \sqrt{3} .
|
| 374 |
+
$$
|
| 375 |
+
|
| 376 |
+
Comme ci-dessus, on a $\left|\mathrm{F}_{\epsilon, \varepsilon}\right|<10^{7}$.
|
| 377 |
+
On vérifie facilement que
|
| 378 |
+
|
| 379 |
+
$$
|
| 380 |
+
\begin{aligned}
|
| 381 |
+
F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1} & =\left((a+b \sqrt{2})^{2}-3 c^{2}\right)\left((a-b \sqrt{2})^{2}-3 c^{2}\right) \\
|
| 382 |
+
& =\left(a^{2}+2 b^{2}-3 c^{2}+2 a b \sqrt{2}\right)\left(a^{2}+2 b^{2}-3 c^{2}-2 a b \sqrt{2}\right) \\
|
| 383 |
+
& =\left(a^{2}+2 b^{2}-3 c^{2}\right)^{2}-2(2 a b)^{2}
|
| 384 |
+
\end{aligned}
|
| 385 |
+
$$
|
| 386 |
+
|
| 387 |
+
est un entier.
|
| 388 |
+
Afin de montrer qu'il est non nul, on procède par l'absurde, et on suppose que
|
| 389 |
+
|
| 390 |
+
$$
|
| 391 |
+
\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}=0
|
| 392 |
+
$$
|
| 393 |
+
|
| 394 |
+
Il s'ensuit que $x^{2}=2 y^{2}$, avec $x=a^{2}+2 b^{2}-3 c^{2}$ et $y=2 a b$. Si $x$ et $y$ sont non nuls, en considérant la valuation 2-adique, il vient $2 v_{2}(x)=1+2 v_{2}(\mathrm{y})$. C'est absurde, ce qui montre que $x=y=0$. Puis :
|
| 395 |
+
— si $a=0$, et puisque $x=0$, on a $2 b^{2}=3 c^{2}$, et la valuation 2 -adique montre de nouveau que $\mathrm{b}=\mathrm{c}=0$;
|
| 396 |
+
|
| 397 |
+
- si $b=0$, et puisque $x=0$, on a $a^{2}=3 c^{2}$, et la valuation 3-adique montre aussi que $a=c=0$.
|
| 398 |
+
Par conséquent, si $(a, b, c) \neq 0$, l'entier $F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1}$ est non nul.
|
| 399 |
+
Ainsi, $\left|\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right| \geqslant 1$, donc $\left|\mathrm{F}_{1,1}\right| \geqslant \frac{1}{\left|\mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right|}>10^{-21}$.
|
| 400 |
+
|
French_STS/md/fr-ofm-2016-2017-envoi-3-solutions.md
ADDED
|
@@ -0,0 +1,210 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Matfématiques 2016-2017
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## Envoi $\mathcal{N u m e ́ r o ~} 3$
|
| 6 |
+
|
| 7 |
+
## ג̀ renvoyer au plus tard le 15 Janvier
|
| 8 |
+
|
| 9 |
+
Les consignes suivantes sont à lire attentivement:
|
| 10 |
+
|
| 11 |
+
Le groupe B est constitué des élèves nés en 2002 ou après, avec les exceptions suivantes :
|
| 12 |
+
|
| 13 |
+
* les élèves de Terminale sont dans le groupe A,
|
| 14 |
+
* les élèves de Seconde et Première qui étaient à l'OFM en 2015-2016 sont dans le groupe A.
|
| 15 |
+
|
| 16 |
+
Les autres élèves sont dans le groupe A .
|
| 17 |
+
|
| 18 |
+
- Les exercices classés Groupe Bne sont à chercher que par les élèves du groupe B.
|
| 19 |
+
- Les exercices classés communs sont à chercher par tout le monde.
|
| 20 |
+
- Les exercices classés Groupe A ne sont à chercher que par les élèves du groupe A.
|
| 21 |
+
- Les exercices doivent être cherchés de manière individuelle.
|
| 22 |
+
- Utiliser des feuilles différentes pour des exercices différents.
|
| 23 |
+
- Respecter la numérotation des exercices.
|
| 24 |
+
- Bien préciser votre nom sur chaque copie.
|
| 25 |
+
|
| 26 |
+
|
| 27 |
+
## Exercices du groupe B
|
| 28 |
+
|
| 29 |
+
Exercice 1. Soit $A B C D$ un quadrilatère convexe (c'est-à-dire que ses diagonales sont à l'intérieur de $A B C D)$, et $P$ l'intersection de ses diagonales $[A C]$ et $[B D]$. On note $O_{1}, O_{2}, O_{3}$ et $O_{4}$ les centres des cercles circonscrits à $A B P, B C P, C D P$ et $D A P$.
|
| 30 |
+
Montrer que $O_{1} O_{2} O_{3} O_{4}$ est un parallélogramme.
|
| 31 |
+
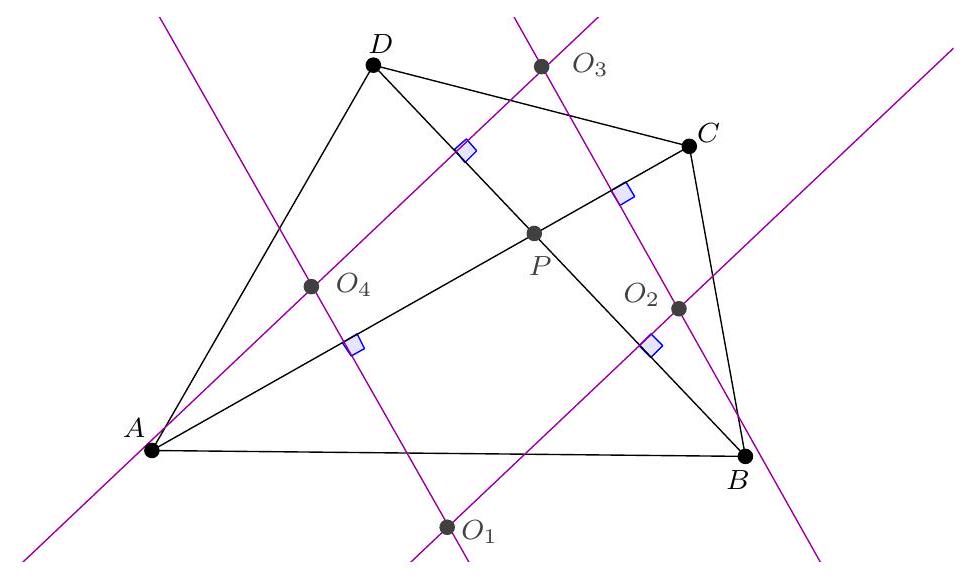
|
| 32 |
+
|
| 33 |
+
Solution de l'exercice $1 O_{1}$ et $O_{2}$ sont sur la médiatrice de $[P B]$, donc $O_{1} O_{2}$ est la médiatrice de $[P B]$. De même, $\left(O_{3} O_{4}\right)$ est la médiatrice de $[P D]$, donc $\left(O_{1} O_{2}\right)$ et $\left(O_{3} O_{4}\right)$ sont toutes deux perpendiculaires à $(B D)$, donc elles sont parallèles. De même, $\left(O_{2} O_{3}\right)$ et $\left(O_{4} O_{1}\right)$ sont toutes deux perpendiculaires à $(A C)$, donc elles sont parallèles.
|
| 34 |
+
$A B C D$ a ses côtés opposés parallèles deux à deux, donc c'est un parallélogramme.
|
| 35 |
+
Exercice 2. Soit $A B C$ un triangle. $H$ son orthocentre et $P, Q$ et $R$ les pieds des hauteurs issues de $A$, $B$ et $C$.
|
| 36 |
+
Montrer que $H$ est le centre du cercle inscrit à $P Q R$.
|
| 37 |
+
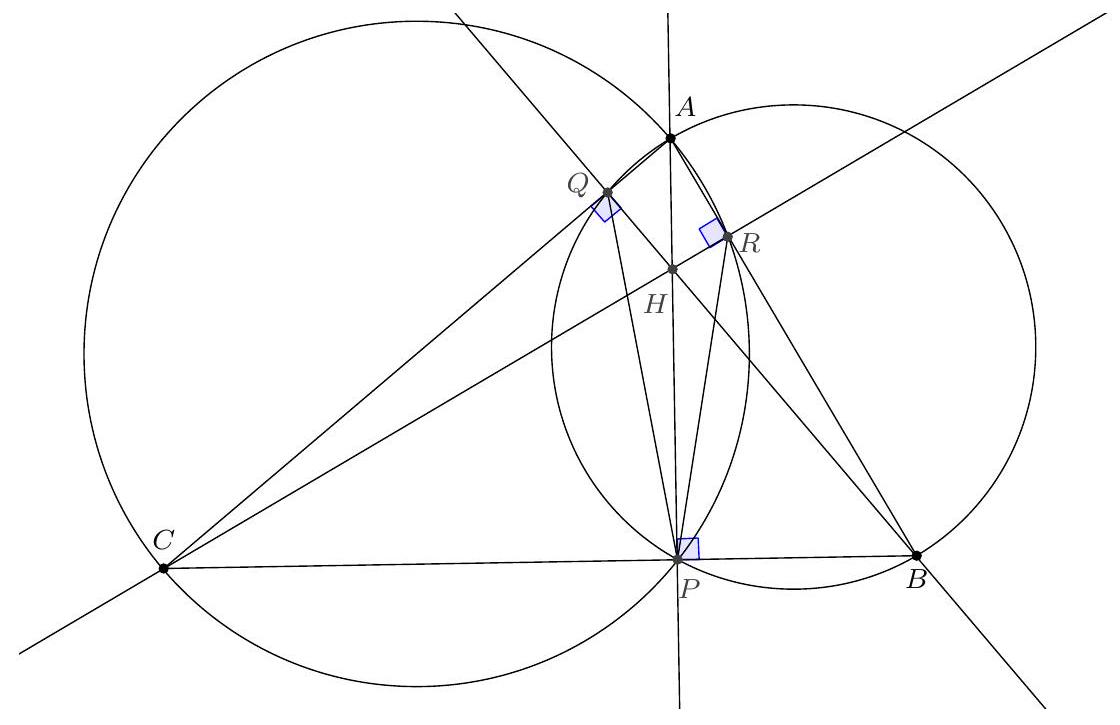
|
| 38 |
+
|
| 39 |
+
Solution de l'exercice 2 On sait que les points $A, B, P$ et $Q$ sont cocycliques sur le cercle de diamètre $[A B]$, donc :
|
| 40 |
+
|
| 41 |
+
$$
|
| 42 |
+
\widehat{H P Q}=\widehat{A P Q}=\widehat{A B Q}=90-\widehat{B A Q}=90-\widehat{B A C}
|
| 43 |
+
$$
|
| 44 |
+
|
| 45 |
+
De même, $A, C, P$ et $R$ sont cocycliques sur le cercle de diamètre $[A C]$ donc:
|
| 46 |
+
|
| 47 |
+
$$
|
| 48 |
+
\widehat{H P R}=\widehat{A P R}=\widehat{A C R}=90-\widehat{C A R}=90-\widehat{B A C}
|
| 49 |
+
$$
|
| 50 |
+
|
| 51 |
+
On a donc $\widehat{H P Q}=\widehat{H P R}$ donc $(P H)$ est la bissectrice de $\widehat{Q P R}$. On montre de même que $(Q H)$ et $(R H)$ sont les bissectrices de $\widehat{P Q R}$ et $\widehat{P R Q}$, donc $H$ est le centre du cercle inscrit à $P Q R$.
|
| 52 |
+
Exercice 3. Les points $D$ et $E$ divisent le côté $[A B]$ d'un triangle équilatéral en trois parties égales, de telle manière que $D$ est situé entre $A$ et $E$. Le point $F$ est situé sur $[B C]$ de sorte que $C F=A D$. Calculer la somme des angles $\widehat{C D F}+\widehat{C E F}$.
|
| 53 |
+
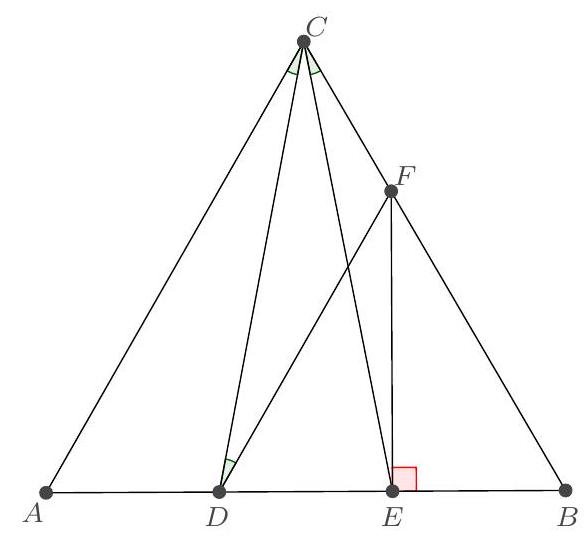
|
| 54 |
+
|
| 55 |
+
Solution de l'exercice 3 On a $B F=B D$ et $\widehat{D B F}=60^{\circ}$, donc le triangle $D B F$ est équilatéral. On a donc $\widehat{B A C}=\widehat{B D F}=60^{\circ}$ donc $(D F) \|(A C)$, donc $\widehat{C D F}=\widehat{A C D}$.
|
| 56 |
+
D'autre part, $\widehat{A C D}=\widehat{B C E}$ par symétrie, donc $\widehat{C D F}=\widehat{B C E}=\widehat{F C E}$. La somme qui nous intéresse vaut donc $\widehat{F C E}+\widehat{C E F}=\widehat{B F E}$ d'après la somme des angles du triangle $F C E$. Comme $(F E)$ est une médiane du triangle équilatéral $D B F$, c'est aussi une bissectrice, donc $\widehat{B F E}=\frac{1}{2} \widehat{B F D}=30^{\circ}$ et notre somme est égale à $30^{\circ}$.
|
| 57 |
+
|
| 58 |
+
## Exercices communs
|
| 59 |
+
|
| 60 |
+
Exercice 4. Deux cercles $\mathcal{C}$ et $\mathcal{C}^{\prime}$ de centres $O$ et $O^{\prime}$ sont tangents extérieurement en $B$. Une tangente commune extérieure touche $\mathcal{C}$ en $M$ et $\mathcal{C}^{\prime}$ en $N$. La tangente commune à $\mathcal{C}$ et $\mathcal{C}^{\prime}$ en $B$ coupe $(M N)$ en $A$. On note $C$ l'intersection de $(O A)$ et $(B M)$, et $D$ l'intersection de $\left(O^{\prime} A\right)$ et $(B N)$.
|
| 61 |
+
Montrer que $(C D)$ est parallèle à $(M N)$.
|
| 62 |
+
Solution de l'exercice 4 Comme $(A M)$ et $(A B)$ sont tangents au cercle de centre $O$, on a $A M=A B$. On a aussi $O M=O B$, donc $(O A)$ est la médiatrice de $[M B]$, et donc $C$ est le milieu de $[M B]$. De même, $D$ est le milieu de $[B N]$, donc $(C D)$ est parallèle à ( $M N$ ).
|
| 63 |
+
|
| 64 |
+
Exercice 5. Soit $A B C$ un triangle dont les trois angles sont aigus et $\Gamma$ son cercle circonscrit. La tangente à $\Gamma$ en $A$ recoupe $(B C)$ en $P$. On note $M$ le milieu de $[A P]$. La droite $(B M)$ recoupe $\Gamma$ en $R$ et la droite $(P R)$ recoupe $\Gamma$ en $S$.
|
| 65 |
+
Montrer que $(A P)$ et $(C S)$ sont parallèles.
|
| 66 |
+
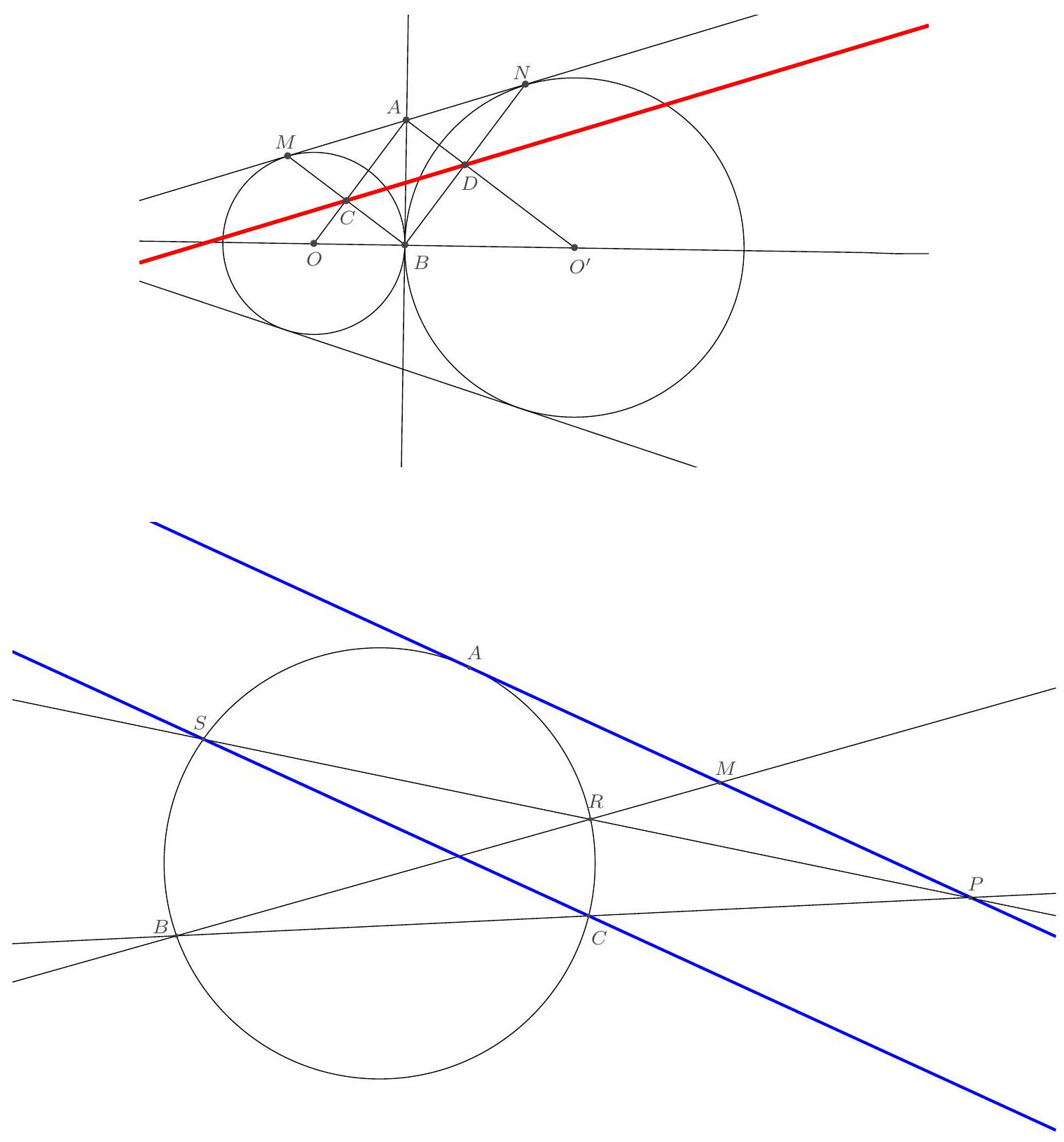
|
| 67 |
+
|
| 68 |
+
Solution de l'exercice 5 En écrivant la puissance de $M$ par rapport à $\Gamma$ puis le fait que $M$ est le milieu de $[A P]$, on obtient
|
| 69 |
+
|
| 70 |
+
$$
|
| 71 |
+
M R \times M B=M A^{2}=M P^{2}
|
| 72 |
+
$$
|
| 73 |
+
|
| 74 |
+
Les triangles $M R P$ et $M P B$ sont donc indirectement semblables, donc $\widehat{R P M}=\widehat{P B M}$. On a donc
|
| 75 |
+
|
| 76 |
+
$$
|
| 77 |
+
\begin{aligned}
|
| 78 |
+
\widehat{C S P} & =\widehat{C S R} \\
|
| 79 |
+
& =\widehat{C B R} \\
|
| 80 |
+
& =\widehat{P B M} \\
|
| 81 |
+
& =\widehat{R P M} \\
|
| 82 |
+
& =\widehat{S P A},
|
| 83 |
+
\end{aligned}
|
| 84 |
+
$$
|
| 85 |
+
|
| 86 |
+
où $\widehat{C S R}=\widehat{C B R}$ par le théorème de l'angle inscrit. Par angles alternes-internes, les droites $(C S)$ et $(A P)$ sont donc parallèles.
|
| 87 |
+
|
| 88 |
+
Exercice 6. Soit $A B C$ un triangle et $(I)$ le centre de son cercle inscrit. La droite ( $A I)$ recoupe $[B C]$ en $D$. La médiatrice de $[A D]$ recoupe $(B I)$ en $M$ et $(C I)$ en $N$.
|
| 89 |
+
Montrer que $A, M, N$ et $I$ sont cocycliques.
|
| 90 |
+
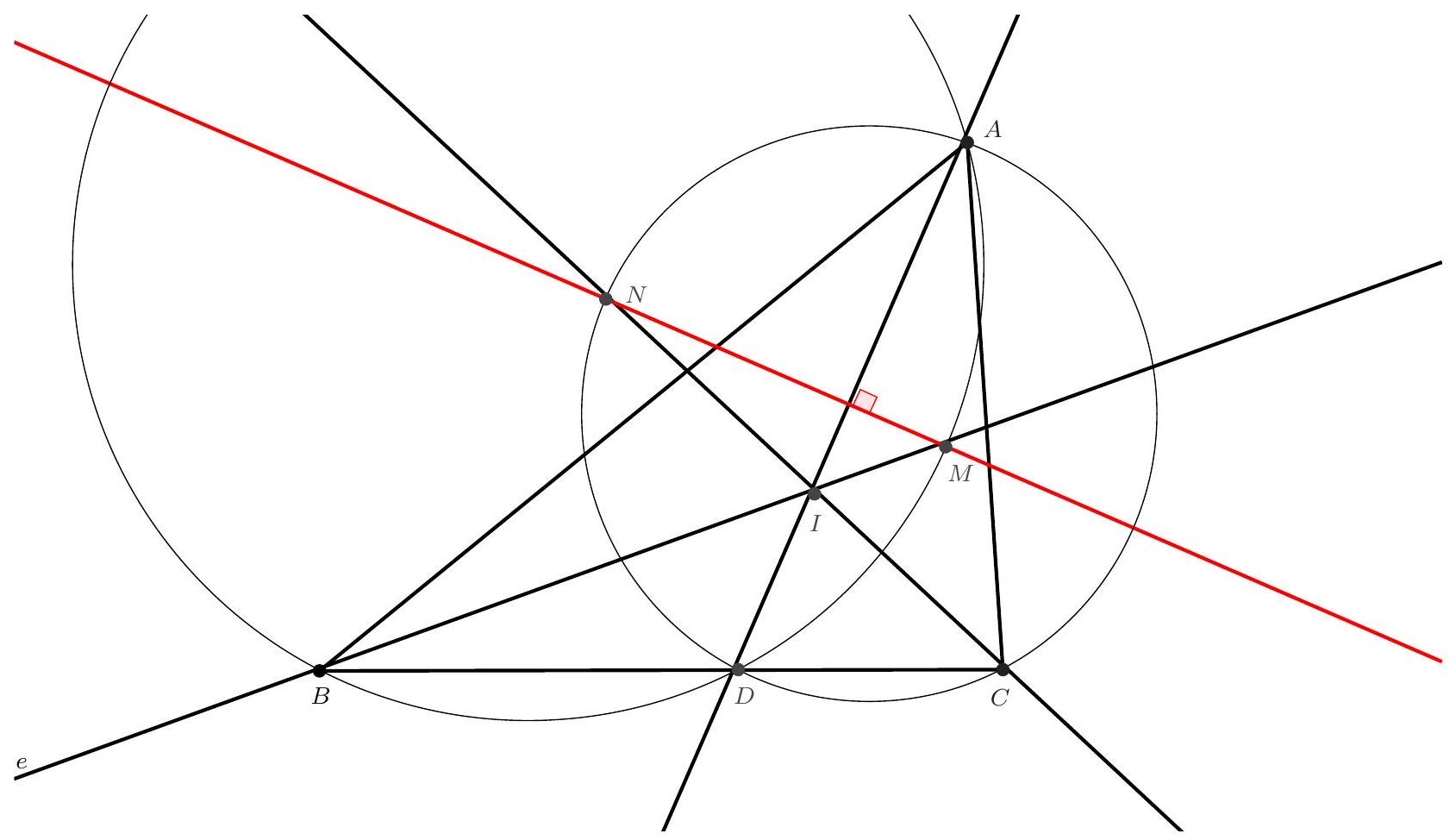
|
| 91 |
+
|
| 92 |
+
Solution de l'exercice 6 On commence par rappeler le théorème du Pôle Sud :
|
| 93 |
+
Lemme 1 (Théorème du Pôle Sud). Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $I$ le centre de son cercle inscrit. Soit $S$ le second point d'intersection de la bissectrice de $\widehat{B A C}$ avec $\Gamma$. Alors $S B=S C$. Le point $S$ est appelé Pôle Sud de $A$ dans le triangle $A B C$.
|
| 94 |
+
Preuve du lemme. Le théorème de l'angle inscrit dans $\Gamma$ donne $\widehat{S B C}=\widehat{S A C}$ et $\widehat{S C B}=\widehat{S A B}$. Or, comme $S$ est sur la bissectrice de $\widehat{B A C}$ on a $\widehat{S A C}=\widehat{S A B}$, d'où $\widehat{S B C}=\widehat{S C B}$, donc $S C B$ est isocèle en $S$ et $S B=S C$.
|
| 95 |
+
|
| 96 |
+
Revenons à notre exercice. Notons que le pôle Sud de $A$ dans un triangle $A B C$ est sur la bissectrice de $\widehat{B A C}$ et sur la médiatrice de $[B C]$, donc il peut être défini comme l'intersection de ces deux droites. On commence par montrer que $A, B, D$ et $M$ sont cocycliques. Le point $M$ est sur la médiatrice de $[A D]$ et sur la bissectrice de $\widehat{A B D}$. C'est donc le pôle Sud de $B$ dans $A B D$, donc il est sur le cercle circonscrit à $A B D$. De même, les points $A, C, D$ et $N$ sont cocycliques. On peut maintenant faire une chasse aux angles:
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\widehat{A M I}=\widehat{A M B}=\widehat{A D B}=180^{\circ}-\widehat{A D C}=180^{\circ}-\widehat{A N C}=180^{\circ}-\widehat{A N I}
|
| 100 |
+
$$
|
| 101 |
+
|
| 102 |
+
Les points $A, I, M$ et $N$ sont donc cocycliques.
|
| 103 |
+
|
| 104 |
+
## Exercices du groupe A
|
| 105 |
+
|
| 106 |
+
Exercice 7. Soit $A B C$ un triangle dont l'orthocentre $H$ est distinct des sommets ainsi que du centre du cercle circonscrit $O$. On désigne par $M, N, P$ les centres des cercles circonscrits aux triangles $H B C, H C A$ et $H A B$.
|
| 107 |
+
Montrer que les droites $(A M),(B N),(C P)$ et $(O H)$ sont concourantes.
|
| 108 |
+
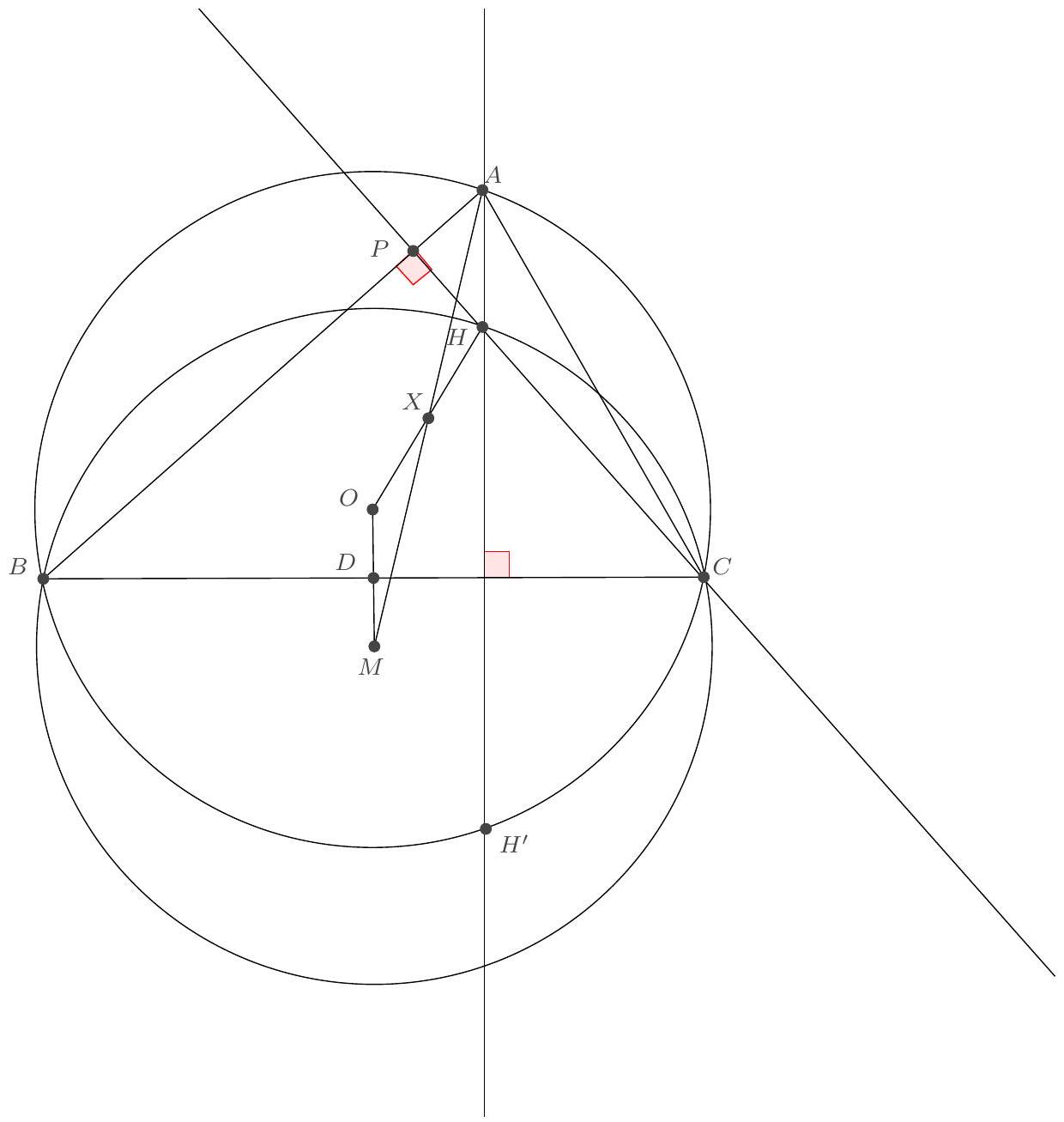
|
| 109 |
+
|
| 110 |
+
Solution de l'exercice 7 Soit $H^{\prime}$ le symétrique de $H$ par rapport à $(B C)$. On sait que $H^{\prime}$ est sur le cercle circonscrit à $A B C$ (il est facile de vérifier $\widehat{B H^{\prime} C}=\widehat{B H C}=180^{\circ}-\widehat{B A C}$ ). Le centre du cercle circonscrit à $H^{\prime} B C$ est donc 0 . Par symétrie par rapport à $(B C)$, le centre du cercle circonscrit à $B H C$ est donc le symétrique de 0 par rapport à $(B C)$, donc $M$ est le symétrique de $O$ par rapport à $(B C)$. On va maintenant montrer que $A H M O$ est un parallélogramme. Si c'est bien vrai, alors $[A M]$ et $[O H]$ se coupent en leur milieu, donc le milieu de $[O H]$ est sur $(A M)$ et, par le même raisonnement, il est aussi $\operatorname{sur}(B N)$ et $(C P)$. Si on note $D$ le milieu de $[B C]$, alors $\overrightarrow{O D}=\frac{1}{2}(\overrightarrow{O B}+\overrightarrow{O C})=\frac{1}{2}(\overrightarrow{O H}-\overrightarrow{O A})=\frac{1}{2} \overrightarrow{A H}$, donc $\overrightarrow{O M}=\overrightarrow{A H}$. En utilisant la relation $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$, qui est équivalente à $\overrightarrow{O H}=3 \overrightarrow{O G}$ (droite d'Euler).
|
| 111 |
+
On donne également une autre manière, moins rapide mais nécessitant moins de connaissances, de montrer que $A H M O$ est un parallélogramme. Les droites $(A H)$ et $(O M)$ sont parallèles, donc il suffit de montrer que $A H=O M$. Pour cela, on peut utiliser la trigonométrie. D'une part, en notant $R$ le rayon
|
| 112 |
+
du cercle circonscrit à $A B C$ et $\alpha, \beta, \gamma$ ses angles, on a
|
| 113 |
+
|
| 114 |
+
$$
|
| 115 |
+
O M=2 O D=2 O B \sin \widehat{O B C}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
|
| 116 |
+
$$
|
| 117 |
+
|
| 118 |
+
D'autre part, en notant $P$ le pied de la hauteur issue de $C$, on a
|
| 119 |
+
|
| 120 |
+
$$
|
| 121 |
+
A H=\frac{A P}{\cos \widehat{P A H}}=\frac{A P}{\sin \beta}=\frac{A C \sin \widehat{A C P}}{\sin \beta}=2 R \sin \widehat{A C P}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
|
| 122 |
+
$$
|
| 123 |
+
|
| 124 |
+
en utilisant la loi des sinus.
|
| 125 |
+
Exercice 8. Soit $A B C$ un triangle dont les trois angles sont aigus. Soit $D \in[B C]$ tel que $\widehat{B A C}=$ $\widehat{A D B}$. Soit $H$ le pied de la hauteur issue de $B$ dans $A B C$. La perpendiculaire à $(B C)$ passant par $H$ coupe $(A D)$ en $K$. On suppose que $K$ est à l'intérieur du triangle $A B C$. Soit $M$ le milieu de $[A C]$. Montrer que $M H=M K$.
|
| 126 |
+
|
| 127 |
+
Solution de l'exercice 8 Notons que $\widehat{A B H}=90^{\circ}-\widehat{B A C}=90^{\circ}-\widehat{A D B}=\widehat{A K H}$. Les points $A, B, K$, $H$ sont donc cocycliques. Soit $T$ le pied de la hauteur issue de $A$ dans $A B C$. Alors $\widehat{B T A}=\widehat{B H A}=90^{\circ}$ donc $A, B, H$ et $T$ sont cocyliques et le cercle qui passe par ces points passe aussi par $K$. On en déduit $\widehat{A T K}=180^{\circ}-\widehat{A H K}=\widehat{K H C}$.
|
| 128 |
+
On va maintenant montrer que $M, K$ et $T$ sont alignés. On a $(A T) \|(H K)$ car ces deux droites sont perpendiculaires à $(B C)$, donc $\widehat{A T K}=\widehat{K H C}=\widehat{T A C}$. Mais le triangle $A T C$ est rectangle en $T$ donc $M A=M C=M T$ et $\widehat{T A M}=\widehat{A T M}$. On en déduit $\widehat{A T M}=\widehat{A T K}$ donc $T, K$ et $M$ sont alignés. Enfin, $M H=M K$ parce que $A T \| H K$ et $M A=M T$.
|
| 129 |
+
|
| 130 |
+
Exercice 9. Soit ABC un triangle d'orthocentre H. Soient $\left(d_{1}\right)$ et $\left(d_{2}\right)$ deux droites perpendiculaires se coupant en $H$. Soit $A_{1}$ (respectivement $B_{1}, C_{1}$ ) l'intersection de $\left(d_{1}\right)$ avec $(B C)$ (respectivement $(C A),(A B)$ ). Soit $A_{2}$ (respectivement $B_{2}, C_{2}$ ) l'intersection de $\left(d_{2}\right)$ avec $(B C)$ (respectivement $(C A)$, $(A B)$ ). Soient $A_{3}, B_{3}, C_{3}$ des points dans le plan tels que $A_{1} A_{2} A_{3}, B_{1} B_{2} B_{3}, C_{1} C_{2} C_{3}$ soient des triangles directement semblables.
|
| 131 |
+
Montrer que $A_{3}, B_{3}, C_{3}$ sont alignés.
|
| 132 |
+
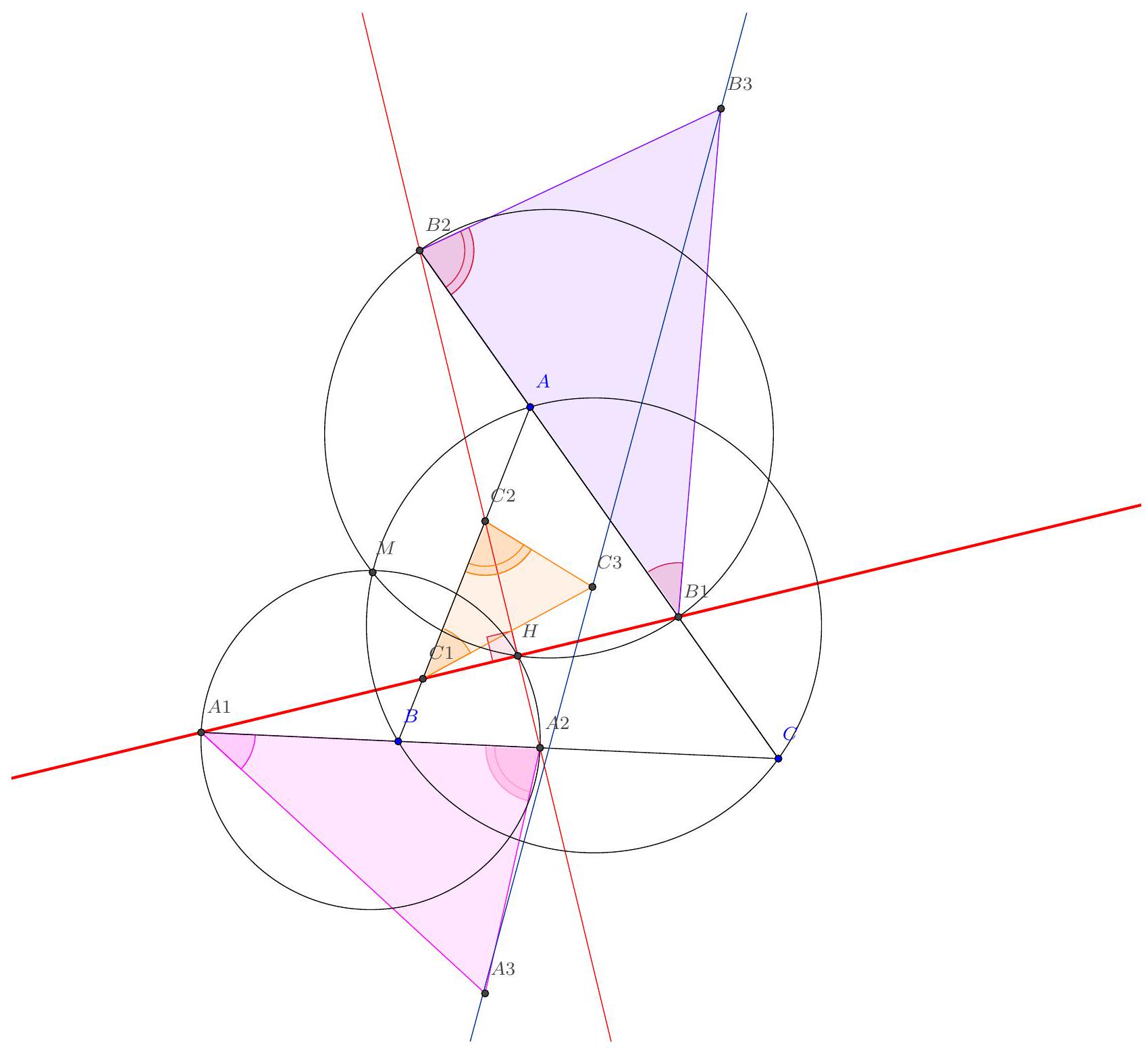
|
| 133 |
+
|
| 134 |
+
Solution de l'exercice 9 Nous donnons une preuve avec des similitudes directes. Il existe d'autres preuves, un peu plus courtes, qui utilisent des nombres complexes.
|
| 135 |
+
Rappelons tout d'abord le résultat suivant :
|
| 136 |
+
Lemme 2. Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $H$ son orthocentre. Alors les symétriques $H_{A}, H_{B}$ et $H_{C}$ de H par rapport à $(\mathrm{BC}),(\mathrm{CA})$ et $(\mathrm{AB})$ appartiennent à $\Gamma$.
|
| 137 |
+
|
| 138 |
+
Proof. Soit $H_{A}^{\prime}$ l'intersection de $A H$ et $\Gamma$. Par le théorème de l'angle inscrit, on a :
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
\begin{aligned}
|
| 142 |
+
\widehat{H_{A}^{\prime} B C} & =\widehat{H_{A}^{\prime} A C} \\
|
| 143 |
+
& =90-\widehat{B C A} \\
|
| 144 |
+
& =\widehat{H B C}
|
| 145 |
+
\end{aligned}
|
| 146 |
+
$$
|
| 147 |
+
|
| 148 |
+
Ainsi, $\left(H_{A}^{\prime} B\right)$ et $(H B)$ sont symétriques par rapport à $(B C)$. On en déduit que $H_{A}^{\prime}=H_{A} \in \Gamma$. De même $H_{B}, H_{C} \in \Gamma$.
|
| 149 |
+
|
| 150 |
+
Reprenons les notations de l'exercice et introduisons $H_{A}, H_{B}$ et $H_{C}$ comme dans le lemme précédent.
|
| 151 |
+
Lemme 3. Soit S l'intersection de $\left(A_{1} H_{A}\right)$ et de $\left(B_{1} H_{B}\right)$. Alors $S \in \Gamma$.
|
| 152 |
+
|
| 153 |
+
Proof. On note $\mathcal{S}_{y z}$ la symétrie d'axe $(Y Z)$. Alors
|
| 154 |
+
|
| 155 |
+
$$
|
| 156 |
+
\begin{aligned}
|
| 157 |
+
\mathcal{S}_{\mathcal{A C}}\left(\mathcal{S}_{\mathcal{B C}}\left(H_{A} A_{1}\right)\right) & =\mathcal{S}_{\mathcal{A C}}\left(A_{1} H\right) \text { car } H_{A} \text { et } H \text { sont symétriques par rapport à }(B C) \\
|
| 158 |
+
& =\mathcal{S}_{\mathcal{A C}}\left(B_{1} H\right) \\
|
| 159 |
+
& =\left(H_{B} B_{1}\right) \text { car } H \text { et } H_{B} \text { sont symétriques par rapport à }(A C) .
|
| 160 |
+
\end{aligned}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
Notons ( $\mathrm{XY}, \mathrm{ZW}$ ) l'angle de droite formé par les droites XY et ZW . De la proposition 1, on déduit que $\left(H_{A} A_{1}\right)$ et $\left(H_{B} B_{1}\right)$ sont images l'une de l'autre par la rotation d'angle $2 \cdot(C B, C A)$ de centre $C:\left(S H_{A}, S H_{B}\right)=2 \cdot(C B, C A)$. Ainsi,
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
\begin{aligned}
|
| 167 |
+
\left(S H_{A}, S H_{B}\right) & \equiv 2 \cdot(C B, C A) \\
|
| 168 |
+
& \equiv(C B, C A)+(C B, C H)+(C H, C A) \\
|
| 169 |
+
& \equiv(C B, C A)+\left(C H_{A}, C B\right)+\frac{\pi}{2}-(A C, A B) \\
|
| 170 |
+
& \equiv\left(C H_{A}, C A\right)+(B A, B H) \\
|
| 171 |
+
& \equiv\left(B H_{A}, B A\right)+\left(B A, B H_{B}\right) \\
|
| 172 |
+
& \equiv\left(B H_{A}, B H_{B}\right)[\pi]
|
| 173 |
+
\end{aligned}
|
| 174 |
+
$$
|
| 175 |
+
|
| 176 |
+
Ainsi, $S \in \Gamma$.
|
| 177 |
+
Lemme 4. Les cercles de diamètre $\left[A_{1} A_{2}\right],\left[B_{1} B_{2}\right],\left[C_{1} C_{2}\right]$ sont concourants en un point $M$ appartenant à $\Gamma$.
|
| 178 |
+
|
| 179 |
+
Proof. Soit $M^{\prime}$ le point d'intersection des cercles de diamètre $\left[A_{1} A_{2}\right]$ (passant donc par $H$ et $H_{A}$ ) et $\left[B_{1} B_{2}\right]$ (passant donc par $H$ et $H_{B}$ ) différent de $H$. On a :
|
| 180 |
+
|
| 181 |
+
$$
|
| 182 |
+
\begin{aligned}
|
| 183 |
+
\left(M^{\prime} H_{A}, M^{\prime} H_{B}\right) & \equiv\left(M^{\prime} H_{A}, M^{\prime} H\right)+\left(M^{\prime} H, M^{\prime} H_{B}\right) \\
|
| 184 |
+
& \equiv\left(A_{1} H_{A}, A_{1} H\right)+\left(B_{1} H, B_{1} H_{B}\right) \\
|
| 185 |
+
& \equiv 2 \cdot\left(A_{1} B, A_{1} H\right)+2 \cdot\left(B_{1} H, B_{1} A\right) \\
|
| 186 |
+
& \equiv 2 \cdot\left(\frac{\pi}{2}+\left(H H_{A}, H A_{1}\right)\right)+2 \cdot\left(H B_{2}, H H_{B}\right) \\
|
| 187 |
+
& \equiv 2 \cdot\left(H H_{A}, H A_{1}\right)+2 \cdot \frac{\pi}{2}+2 \cdot\left(H B_{2}, H H_{B}\right) \\
|
| 188 |
+
& \equiv 2 \cdot\left(H H_{A}, H H_{B}\right) \\
|
| 189 |
+
& \equiv 2 \cdot(C B, C A) \\
|
| 190 |
+
& \equiv\left(S H_{A}, S H_{B}\right)[\pi] .
|
| 191 |
+
\end{aligned}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
Ainsi, $M^{\prime} \in \Gamma$ par le théorème de l'angle inscrit. De la même façon, on montre que l'intersection des cercles de diamètre $\left[B_{1} B_{2}\right]$ et $\left[C_{1} C_{2}\right]$ est un point $M^{\prime \prime} \in \Gamma$. Comme l'intersection du cercle de diamètre $\left[B_{1} B_{2}\right]$ et de $\Gamma$ est unique, on en déduit que $M^{\prime}=M^{\prime \prime}=M$, c'est-à-dire que les quatre cercles sont concourants en $M$.
|
| 195 |
+
|
| 196 |
+
Nous pouvouns maintenant terminer l'exercice :
|
| 197 |
+
|
| 198 |
+
$$
|
| 199 |
+
\begin{aligned}
|
| 200 |
+
\left(C_{1} M, C_{1} C_{2}\right) & \equiv\left(H M, H C_{2}\right) \text { car } M, C_{1}, H, C_{2} \text { sont cocycliques } \\
|
| 201 |
+
& \equiv\left(H M, H B_{2}\right) \\
|
| 202 |
+
& \equiv\left(B_{1} M, B_{1} B_{2}\right)[\pi] \text { car } M, B_{1}, H, B_{2} \text { cocycliques. }
|
| 203 |
+
\end{aligned}
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
De la même façon, on prouve que $\left(B_{1} M, B_{1} B_{2}\right) \equiv\left(C_{1} M, C_{1} C_{2}\right)$. Donc, comme $\left(M A_{1}, M A_{2}\right) \equiv$ $\left(M B_{1}, M C_{2}\right) \equiv\left(M C_{1}, M C_{2}\right) \equiv \frac{\pi}{2} \quad[\pi]$, on obtient que $M A_{1} A_{2}, M B_{1} B_{2}$ et $M C_{1} C_{2}$ sont directement semblables, ce que l'on notera désormais $M A_{1} A_{2} \sim M B_{1} B_{2} \sim M C_{1} C_{2}$. En outre, $A_{1} A_{2} A_{3} \sim$ $B_{1} B_{2} B_{3} \sim C_{1} C_{2} C_{3}$ par hypothèse. Donc $M A_{1} A_{2} A_{3} \sim M B_{1} B_{2} B_{3} \sim M C_{1} C_{2} C_{3}$.
|
| 207 |
+
|
| 208 |
+
L'utilisation de similitudes directes permet alors de conclure directement : une similitude directe $\mathcal{S}$ de centre $M$ envoie $A_{1}$ sur $A_{3}$, et également $B_{1}$ sur $B_{3}$ et $C_{1}$ sur $C_{3}$. Comme $A_{1}, B_{1}$ et $C_{1}$ sont alignés, on en déduit que $A_{3}, B_{3}$ et $C_{3}$ le sont également.
|
| 209 |
+
$\mathcal{F i n}$
|
| 210 |
+
|
French_STS/md/fr-ofm-2016-2017-envoi-4-solutions.md
ADDED
|
@@ -0,0 +1,294 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Olympiades Françaises de Mathématiques 2016-2017
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
## Solutions à l'envoi $\mathfrak{N}$ (uméro 4 - Combinatoire
|
| 6 |
+
|
| 7 |
+
## Exercices du groupe $\mathcal{B}$
|
| 8 |
+
|
| 9 |
+
## Exercice 1.
|
| 10 |
+
|
| 11 |
+
On place quatre points dans le plan, trois jamais alignés, et on les relie tous deux à deux. On colorie chacun des six segments obtenus soit en bleu soit en rouge. Montrer qu'il existe deux triangles différents coloriés de la même façon. Par exemple, dans l'exemple suivant (où l'on a remplacé rouge par épais et bleu par pointillé), ABD et ACD sont coloriés de la même façon.
|
| 12 |
+
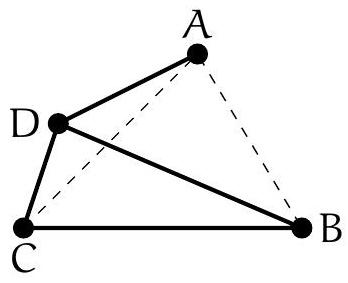
|
| 13 |
+
|
| 14 |
+
## Solution de l'exercice 1
|
| 15 |
+
|
| 16 |
+
Il y a quatre façons différentes de colorier un triangle (avec zéro, un, deux ou trois segments rouges) et il y a quatre triangles dessinés. Donc, soit deux triangles sont coloriés de la même façon, soit tous les triangles sont différents. Montrons que le deuxième cas n'est pas possible. En effet, deux triangles différents partagent toujours deux sommets en commun, donc un côté en commun. Or, si tous les triangles sont différents, il y a un triangle entièrement bleu, et un autre entièrement rouge. Leur côté commun serait alors à la fois rouge et bleu, impossible. Finalement, on a bien deux triangles coloriés de la même façon.
|
| 17 |
+
|
| 18 |
+
## Exercice 2.
|
| 19 |
+
|
| 20 |
+
Pour quel $n \geqslant 1$ peut-on remplir un échiquier $n \times n$ avec des pièces de la forme
|
| 21 |
+
|
| 22 |
+
sans qu'elles se recouvrent? (Les rotations sont autorisées).
|
| 23 |
+
|
| 24 |
+
## Solution de l'exercice 2
|
| 25 |
+
|
| 26 |
+
Supposons que nous avons réussi à recouvrir un échiquier $\mathrm{n} \times \mathrm{n}$. Une pièce recouvre 4 cases. Donc clairement 4 divise $n^{2}$ donc $n$ est pair. Maintenant, chaque pièce recouvre soit trois cases noires et une case blanche de l'échiquier, soit l'inverse. Or, comme n est pair, il y a autant de cases noires que de cases blanches. Il faut donc autant de pièces recouvrant trois cases noires que de pièces recouvrant trois cases blanches. Par conséquent, il y a un nombre pair de pièces, d'où 8 divise $n^{2}$. Donc, si l'on parvient à couvrir un échiquier $n \times n$, alors 4 divise n .
|
| 27 |
+
Réciproquement, si 4 divise $n$, on peut facilement recouvrir l'échiquier avec des blocs $4 \times 4$.
|
| 28 |
+
|
| 29 |
+
|
| 30 |
+
Exercice 3.
|
| 31 |
+
Soient $A_{1}, A_{2}, \ldots, A_{m}$ des sous-ensembles distincts de $\{1,2, \ldots, n\}$ tels que pour tout $1 \leqslant$ $\boldsymbol{i}, \mathbf{j} \leqslant \mathrm{n}$ on a $A_{i} \cap A_{j} \neq \emptyset$. Montrer $m \leqslant 2^{n-1}$.
|
| 32 |
+
|
| 33 |
+
## Solution de l'exercice 3
|
| 34 |
+
|
| 35 |
+
Considérons toutes les paires d'ensembles $\left\{A, A^{c}\right\}$ pour tout $A \subset\{1,2, \ldots, n\}$. Puisqu'il y a $2^{n-1}$ telles paires, si $m>2^{n-1}$ on aurait $1 \leqslant i<j \leqslant m$ tels que $A_{i}, A_{j} \in\left\{A, A^{c}\right\}$ pour un $A \subset\{1,2, \ldots, n\}$. Donc $A_{i} \cap A_{j}=\emptyset$ ce qui contredit notre hypothèse.
|
| 36 |
+
|
| 37 |
+
## Exercices communs
|
| 38 |
+
|
| 39 |
+
## Exercice 4.
|
| 40 |
+
|
| 41 |
+
Combien de tableaux $3 \times 3$ peut-on construire en les remplissant avec les nombres de 1 à 3 tels qu'il n'y ait pas deux fois le même nombre dans une ligne ni dans une colonne. Et de tableaux $4 \times 4$ avec les nombres de 1 à 4 ?
|
| 42 |
+
|
| 43 |
+
## Solution de l'exercice 4
|
| 44 |
+
|
| 45 |
+
Nous présentons ci-dessous une preuve complète de l'exercice. Il n'était pas nécessaire d'être aussi précis pour avoir tous les points mais il est bon, lorsque que l'on compte des objets, d'avoir une idée de la preuve pour démontrer que nous n'avons rien oublié ni compté en double.
|
| 46 |
+
|
| 47 |
+
Nous avons six façons de remplir la première rangée (trois façons de placer le 1 puis deux de placer le 2 puis une seule possibilité pour placer le 3). Ensuite, il nous reste deux façons de remplir la colonne contenant déjà un 1 (ce qui fait douze en tout). On se retrouve avec, par exemple, le tableau
|
| 48 |
+
|
| 49 |
+
$$
|
| 50 |
+
\left[\begin{array}{lll}
|
| 51 |
+
2 & 1 & 3 \\
|
| 52 |
+
& 2 & A \\
|
| 53 |
+
& 3 &
|
| 54 |
+
\end{array}\right] .
|
| 55 |
+
$$
|
| 56 |
+
|
| 57 |
+
On se rend compte qu'il n'y a qu'une seule façon de remplir la case $A$, c'est-à-dire celle qui est dans la rangée contenant un 2 et dans la colonne contenant un 3 . Puis on complète le tableau de la seule manière possible.
|
| 58 |
+
On a donc douze façons de remplir un tableau $3 \times 3$ comme dans l'énoncé.
|
| 59 |
+
|
| 60 |
+
Pour les tableaux $4 \times 4$, c'est à peu près la même idée. Nous avons vingt-quatre façons de remplir la première rangée et six façons de remplir la colonne contenant un 1 . Nous obtenons un tableau ressemblant à
|
| 61 |
+
|
| 62 |
+
$$
|
| 63 |
+
\left[\begin{array}{cccc}
|
| 64 |
+
2 & 1 & 4 & 3 \\
|
| 65 |
+
& 4 & & \\
|
| 66 |
+
A_{3,2} & 3 & & \\
|
| 67 |
+
& 2 & &
|
| 68 |
+
\end{array}\right] .
|
| 69 |
+
$$
|
| 70 |
+
|
| 71 |
+
Maintenant, notons $A_{k, l}, k, l \in\{2,3,4\}$, la case dans la rangée contenant $k$ et la colonne contenant l. Nous voyons qu'il y a deux possibilités pour remplir $A_{3,2}$ :
|
| 72 |
+
|
| 73 |
+
- si l'on remplit $A_{3,2}$ avec 1 , nous n'aurons plus qu'une seule possibilité pour $A_{4,2}$ puis, dans l'ordre, $A_{2,2}, A_{3,4}, A_{3,3}, A_{4,4}, A_{4,3}, A_{2,4}$ et $A_{2,3}$. On obtient l'unique tableau
|
| 74 |
+
|
| 75 |
+
$$
|
| 76 |
+
\left[\begin{array}{llll}
|
| 77 |
+
2 & 1 & 4 & 3 \\
|
| 78 |
+
3 & 4 & 1 & 2 \\
|
| 79 |
+
1 & 3 & 2 & 4 \\
|
| 80 |
+
4 & 2 & 3 & 1
|
| 81 |
+
\end{array}\right]
|
| 82 |
+
$$
|
| 83 |
+
|
| 84 |
+
- si l'on remplit $A_{3,2}$ avec 4 nous avons de nouveau deux possibilités:
|
| 85 |
+
* on remplit $A_{4,2}$ avec 1 puis on remplit les autres cases de la seule façon possible.
|
| 86 |
+
|
| 87 |
+
$$
|
| 88 |
+
\left[\begin{array}{llll}
|
| 89 |
+
2 & 1 & 4 & 3 \\
|
| 90 |
+
1 & 4 & 3 & 2 \\
|
| 91 |
+
4 & 3 & 2 & 1 \\
|
| 92 |
+
3 & 2 & 1 & 4
|
| 93 |
+
\end{array}\right] .
|
| 94 |
+
$$
|
| 95 |
+
|
| 96 |
+
* on remplit $A_{4,2}$ avec 3 puis on remplit $A_{2,2}, A_{2,4}$ et $A_{2,3}$ de la seule façon possible. Il reste deux façons de remplir le tableau obtenu.
|
| 97 |
+
|
| 98 |
+
$$
|
| 99 |
+
\left[\begin{array}{llll}
|
| 100 |
+
2 & 1 & 4 & 3 \\
|
| 101 |
+
3 & 4 & & \\
|
| 102 |
+
4 & 3 & & \\
|
| 103 |
+
1 & 2 & 3 & 4
|
| 104 |
+
\end{array}\right] .
|
| 105 |
+
$$
|
| 106 |
+
|
| 107 |
+
Remarque que toutes les affirmations sont toujours vraies, pas seulement dans l'exemple. Donc, quelque soit la façon de remplir la première rangée et la colonne contenant un 1, il reste toujours quatre façons de remplir le tableau. Il y a donc en tout $24 \cdot 6 \cdot 4=576$ façons de remplir un tableau $4 \times 4$ selon l'énoncé.
|
| 108 |
+
|
| 109 |
+
## Exercice 5.
|
| 110 |
+
|
| 111 |
+
Peut-on arranger les nombres $1,1,2,2, \ldots, 50,50$ tels que, pour tout $1 \leqslant k \leqslant 50$, entre les deux nombres $k$ il y ait exactement $k$ éléments.
|
| 112 |
+
|
| 113 |
+
## Solution de l'exercice 5
|
| 114 |
+
|
| 115 |
+
La réponse est non. Supposons, par l'absurde, qu'on le peut. Pour tout $1 \leqslant k \leqslant 50$, soit $a_{k}$ un entier tel que $a_{k}$ et $a_{k}+k+1$ sont les positions des deux $k$. Évidemment, on a
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
\sum_{k=1}^{50}\left(a_{k}+a_{k}+k+1\right)=1+2+\ldots+100
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
En regardant l'égalité précédente modulos 2 , on doit avoir $51 \times 26-1 \equiv 50 \times 101(\bmod 2)$ ce qui est faux.
|
| 122 |
+
|
| 123 |
+
## Exercice 6.
|
| 124 |
+
|
| 125 |
+
Soient $n \geqslant 2$ un entier et $X$ un ensemble à $n$ éléments. Montrer que le nombre de fonctions $f: X \rightarrow X$ telles que $f \circ f$ soit une fonction constante est égale à
|
| 126 |
+
|
| 127 |
+
$$
|
| 128 |
+
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
|
| 129 |
+
$$
|
| 130 |
+
|
| 131 |
+
Solution de l'exercice 6
|
| 132 |
+
Soit $\mathrm{f}: \mathrm{X} \rightarrow \mathrm{X}$ telle que f o $\mathrm{f}=\mathrm{c}$ pour un $\mathrm{c} \in X$. D'abord on a $\mathrm{f}(\mathrm{c})=\mathrm{c}$ parce que
|
| 133 |
+
|
| 134 |
+
$$
|
| 135 |
+
f \circ f(c)=c \Rightarrow f \circ f \circ f(c)=f(c),
|
| 136 |
+
$$
|
| 137 |
+
|
| 138 |
+
et selon la définition $\mathrm{f} \circ \mathrm{f} \circ \mathrm{f}(\mathrm{c})=\mathrm{f} \circ \mathrm{f}(\mathrm{f}(\mathrm{c}))=\mathrm{c}$, ce qui nous donne $\mathrm{f}(\mathrm{c})=\mathrm{c}$. Posons l'ensemble
|
| 139 |
+
|
| 140 |
+
$$
|
| 141 |
+
A=\{x \in X \mid f(x)=c\}
|
| 142 |
+
$$
|
| 143 |
+
|
| 144 |
+
On a montré qu'il contient $c$. Selon la définition, on a $f(x) \in A \backslash\{c\}$ pour tout $x \in A^{c}$ où $A^{c}$ est le complémentaire de $A$.
|
| 145 |
+
Donc, pour déterminer toutes les fonctions $f: X \rightarrow X$ telles que $f \circ f$ est constante, on doit d'abord choisir un $c \in X$ ( $n$ manières de faire) puis un $A \subset X$ contenant $c\left(\binom{n-1}{i}\right.$ manières de faire si $|A|=i+1)$ et ensuite choisir les valeurs $f(x)$ pour chaque $x \in A^{c}$ dans $A \backslash\{c\}$ ( $i^{n-i-1}$ manières de faire). Alors le nombre de telles fonctions sera
|
| 146 |
+
|
| 147 |
+
$$
|
| 148 |
+
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
|
| 149 |
+
$$
|
| 150 |
+
|
| 151 |
+
## Exercice 7.
|
| 152 |
+
|
| 153 |
+
Un constructeur de jouets crée au moins un jouet par jour. Il n'est pas capable de créer plus de 725 jouets par an. Pour tout $\mathrm{n} \in \mathbb{N}$, montrer qu'il existe des jours consécutifs pendant lesquels il a créé exactement n jouets.
|
| 154 |
+
|
| 155 |
+
## Solution de l'exercice 7
|
| 156 |
+
|
| 157 |
+
Soit $x_{i} \in \mathbb{N}$ le nombre de jouets qu'il a crée pendant le $i-$ ème jour. Si
|
| 158 |
+
|
| 159 |
+
$$
|
| 160 |
+
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{n}}<2 \mathrm{n}
|
| 161 |
+
$$
|
| 162 |
+
|
| 163 |
+
étudions les nombres suivants :
|
| 164 |
+
|
| 165 |
+
$$
|
| 166 |
+
1 \leqslant x_{1}<x_{1}+x_{2}<\ldots<x_{1}+x_{2}+\ldots+x_{n}<2 n .
|
| 167 |
+
$$
|
| 168 |
+
|
| 169 |
+
On a deux cas. Soit ils représentent tous les résidus modulo $n$, soit il existe $1 \leqslant i<j \leqslant n$ tels que
|
| 170 |
+
|
| 171 |
+
$$
|
| 172 |
+
x_{1}+x_{2}+\ldots+x_{i} \equiv x_{1}+x_{2}+\ldots+x_{j} \quad(\bmod n)
|
| 173 |
+
$$
|
| 174 |
+
|
| 175 |
+
Ce dernier cas nous donne
|
| 176 |
+
|
| 177 |
+
$$
|
| 178 |
+
\mathrm{n} \mid \mathrm{x}_{\mathrm{i}+1}+\ldots+\mathrm{x}_{\mathrm{j}}
|
| 179 |
+
$$
|
| 180 |
+
|
| 181 |
+
puis
|
| 182 |
+
|
| 183 |
+
$$
|
| 184 |
+
x_{i+1}+\ldots+x_{j}=n
|
| 185 |
+
$$
|
| 186 |
+
|
| 187 |
+
Dans le premier cas, il existe $1 \leqslant \mathfrak{j} \leqslant n$ tel que
|
| 188 |
+
|
| 189 |
+
$$
|
| 190 |
+
\mathrm{n} \mid \mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}
|
| 191 |
+
$$
|
| 192 |
+
|
| 193 |
+
donc
|
| 194 |
+
|
| 195 |
+
$$
|
| 196 |
+
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}=\mathrm{n}
|
| 197 |
+
$$
|
| 198 |
+
|
| 199 |
+
Dans les deux cas, le problème est résolu. Étudions maintenant ce qui se passe si, pour tous n jours consécutifs, le nombre total de jouets est plus grand que 2 n . Alors
|
| 200 |
+
|
| 201 |
+
$$
|
| 202 |
+
2 \mathrm{n} \times 365 \leqslant \sum_{i=1}^{365 n} x_{i} \leqslant 725 n
|
| 203 |
+
$$
|
| 204 |
+
|
| 205 |
+
on aboutit à une contradiction.
|
| 206 |
+
|
| 207 |
+
## Exercices dugroupe $\mathcal{A}$
|
| 208 |
+
|
| 209 |
+
## Exercice 8.
|
| 210 |
+
|
| 211 |
+
Soient $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$ des ensembles de kéléments. Montrer que $\sin <2^{k-1}$ alors il existe des éléments $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ tels que:
|
| 212 |
+
|
| 213 |
+
$$
|
| 214 |
+
a_{i} \in A_{i}, b_{j} \in B_{j}, a_{i} \neq b_{j}
|
| 215 |
+
$$
|
| 216 |
+
|
| 217 |
+
pour tout $1 \leqslant i, j \leqslant n$.
|
| 218 |
+
Solution de l'exercice 8
|
| 219 |
+
Soit $X$ l'union de tous les $A_{i}$ et $B_{j}$ pour tous $1 \leqslant i, j \leqslant n$ et soit $m=|X|$. On veut montrer qu'il y a un coloriage des éléments de $X$ en rouge et bleu telle que
|
| 220 |
+
|
| 221 |
+
- Aucun des $A_{1}, A_{2}, \ldots, A_{n}$ ne soit totalement rouge,
|
| 222 |
+
- Aucun des $B_{1}, B_{2}, \ldots, B_{n}$ ne soit totalement bleu.
|
| 223 |
+
|
| 224 |
+
Pour chaque $A_{i}$, le nombre de coloriages tels que $A_{i}$ soit tout en rouge est égal $2^{m-k}$. Donc, puisque $2 \mathrm{n}\left(2^{\mathrm{m}-\mathrm{k}}\right)<2^{\mathrm{m}}$, on aura un coloriage avec la propriété précédente. Avec un tel coloriage, on choisit chaque $a_{i}$ parmi les éléments bleus de $A_{i}$ et chaque $b_{j}$ parmi les éléments rouges de $B_{j}$. Ce qui convient.
|
| 225 |
+
|
| 226 |
+
## Exercice 9.
|
| 227 |
+
|
| 228 |
+
Soit $n$ un entier positif. Montrer que dans un ensemble $A$ de $2^{n}$ nombres strictement positifs, on peut choisir un sous-ensemble B de taille $n+1$ tel que la somme de deux nombres différents dans $B$ ne soit jamais dans $A$.
|
| 229 |
+
|
| 230 |
+
## Solution de l'exercice 9
|
| 231 |
+
|
| 232 |
+
Soient $n$ et $A$ comme dans l'énoncé. Nous allons montrer, par récurrence sur $m \leqslant n+1$, que l'algorithme glouton consistant à toujours prendre le plus grand nombre qui ne pose pas de problème convient.
|
| 233 |
+
Posons $A_{0}=A$, et $B_{0}=B$. Supposons que, pour $m<n+1$, on a construit $A_{m}$ et $B_{m}$ des sous-ensembles de $A$ tels que :
|
| 234 |
+
|
| 235 |
+
1. la somme de deux éléments différents de $B_{m}$ ne soit jamais dans $A$,
|
| 236 |
+
2. la somme d'un élément de $A_{m}$ et d'un élément de $B_{m}$ ne soit jamais dans $A$,
|
| 237 |
+
3. $A_{m}$ et $B_{m}$ sont disjoints,
|
| 238 |
+
4. $\operatorname{card}\left(A_{m}\right) \geqslant 2^{n}-2^{m}+1$ et
|
| 239 |
+
5. $\operatorname{card}\left(B_{m}\right)=m$.
|
| 240 |
+
|
| 241 |
+
Dans ce cas, $A_{m}$ est non vide car $m \leqslant n$ donc $2^{n}-2^{m}+1 \geqslant 1$. Soit $b_{m+1}$ le plus grand élément de $A_{m}$. On pose $B_{m+1}=B_{m} \cup\left\{b_{m+1}\right\}$. Par l'hypothèse 3 pour l'ordre $m$, on obtient 5 pour l'ordre $m+1$. De même, les hypothèses 1 et 2 nous donne 1 pour l'ordre supérieur. Maintenant, on pose
|
| 242 |
+
|
| 243 |
+
$$
|
| 244 |
+
A_{m+1}=\left\{a \in A_{m} \mid a \neq b_{m+1} \text { et } a+b_{m+1} \notin A\right\} .
|
| 245 |
+
$$
|
| 246 |
+
|
| 247 |
+
Par définition, et par l'hypothèse $2, A_{m+1}$ vérifie 2 et 3 . Le seul point moins évident est 4 . Nous voulons montrer que $\operatorname{card}\left(A_{m}\right)-\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$. Or,
|
| 248 |
+
|
| 249 |
+
$$
|
| 250 |
+
\begin{aligned}
|
| 251 |
+
A_{\mathfrak{m}} \backslash A_{\mathfrak{m}+1} & =\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left\{a \in A_{\mathfrak{m}} \mid a+b_{\mathfrak{m}+1} \in A\right\} \\
|
| 252 |
+
& \subset\left\{b_{\mathfrak{m}+1}\right\} \cup\left\{a \in A \mid a>b_{\mathfrak{m}+1}\right\} \\
|
| 253 |
+
& \subset\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left(A \backslash A_{\mathfrak{m}}\right) .
|
| 254 |
+
\end{aligned}
|
| 255 |
+
$$
|
| 256 |
+
|
| 257 |
+
Or ce dernier ensemble est de taille au plus $1+\left(2^{n}-\left(2^{n}-2^{m}+1\right)\right)=2^{m}$. Donc, $\operatorname{card}\left(A_{m}\right)-$ $\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$, puis on obtient 4 à l'ordre $m+1$. Ce qui conclut la récurrence.
|
| 258 |
+
Maintenant, on applique la récurrence jusqu'à $m=n+1$ et on obtient un ensemble $B_{n+1}$ de taille $n+1$ qui vérifie l'hypothèse 1 , donc qui est bien solution de l'exercice.
|
| 259 |
+
|
| 260 |
+
## Exercice 10.
|
| 261 |
+
|
| 262 |
+
On possède une liste infinie de cases, les cases étant numérotées par $1,2, \ldots$. Au départ, toutes les cases contiennent le nombre 1 . À chaque étape, on choisit un nombre $a \in \mathbb{N}^{*}$ tel que:
|
| 263 |
+
|
| 264 |
+
- soit toutes les cases numérotées par un multiple de a contiennent 1 auquel cas on remplace ces 1 par des 0 ,
|
| 265 |
+
- soit toutes les cases numérotées par un multiple de a contiennent 0 auquel cas on remplace ces 0 par des 1 .
|
| 266 |
+
Montrer que, pour tout $n \geqslant 2$, on peut faire en sorte que toutes les cases de numéro au plus n contiennent un 0 sauf la première case qui contient un 1.
|
| 267 |
+
|
| 268 |
+
|
| 269 |
+
## Solution de l'exercice 10
|
| 270 |
+
|
| 271 |
+
Nous allons d'abord reformuler le problème. On se place dans $\mathbb{N}^{*}$. Si $A$, B sont deux ensembles (dans $\mathbb{N}^{*}$ ), on note
|
| 272 |
+
|
| 273 |
+
- $A \oplus B:=A \cup B$ si $A \cap B=\emptyset$, sinon l'opération est interdite, et
|
| 274 |
+
- $A \ominus B:=A \backslash B$ si $B \subset A$, sinon l'opération est interdite.
|
| 275 |
+
|
| 276 |
+
On ajoute la convention que $\oplus$ et $\ominus$ sont associatives à gauche, c'est-à-dire que les opérations sont effectuées de la gauche vers la droite. Par exemple, $\{1\} \oplus\{2\} \ominus\{1,2\}=(\{1\} \oplus$ $\{2\}) \ominus\{1,2\}=\emptyset$, par contre $\{1\} \oplus\{1,2\} \ominus\{1\}$ est interdit.
|
| 277 |
+
Le problème se reformule donc par : montrer que, pour $n \in \mathbb{N}^{*}$, il existe une formule commençant par $\mathbb{N}^{*}$, contenant que des ensembles de multiples d'entiers et utilisant les opérations $\oplus$ et $\ominus$ aboutissant à un ensemble $E$ tel que $E \cap\{1, \ldots, \mathbf{n}\}=\{1\}$. Pour montrer cela, nous allons utiliser un lemme, que nous démontrerons plus tard, et qui n'est rien d'autre qu'une variante améliorée du principe d'inclusion-exclusion.
|
| 278 |
+
|
| 279 |
+
Lemme: Si $m \in \mathbb{N}^{*}$ et $A_{1}, \ldots, A_{m}$ sont des ensembles, alors il existe une formule utilisant les opérations $\oplus$ et $\ominus$ et constituée uniquement d'intersections quelconques des ensembles $A_{1}, \ldots, A_{m}$ dont la valeur est $A_{1} \cup \cdots \cup A_{m}$.
|
| 280 |
+
Par exemple, dans le cas $m=2, A_{1} \cup A_{2}=A_{1} \ominus\left(A_{1} \cap A_{2}\right) \oplus A_{2}$.
|
| 281 |
+
Maintenant, notons $\mathrm{p}_{1}, \mathrm{p}_{2}, \ldots$ les nombres premiers dans l'ordre. Notons $A_{i}$ l'ensemble des multiples (strictement positifs) de $p_{i}$, pour tout $i \in \mathbb{N}^{*}$. Prenons $n \geqslant 2$ et soit $m$ le nombre de nombres premiers inférieurs ou égaux à $n$. D'après le lemme, il existe une formule dont la valeur est $A_{1} \cup \cdots \cup A_{m}$. Or cette union est l'ensemble des nombres qui sont multiples d'au moins un nombre parmi $p_{1}, p_{2}, \ldots$ et $p_{m}$. Il contient donc tous les nombres inférieurs ou égaux à $n$ sauf 1 . En remplaçant les $\oplus$ par des $\ominus$ et vice-versa dans la formule et en ajoutant $\mathbb{N}^{*} \ominus$ devant, nous obtenons donc une formule autorisée dont la valeur vérifie ce que nous voulons. Il reste à ajouter pour conclure que, si $1 \leqslant \mathrm{l} \leqslant \mathrm{m}$ et si $1 \leqslant \mathfrak{i}_{1}<\mathfrak{i}_{2}<\cdots<\mathfrak{i}_{l} \leqslant \mathfrak{m}$, alors $A_{i_{1}} \cap A_{i_{2}} \cap \cdots \cap A_{i_{l}} n^{\prime}$ est rien d'autre que l'ensemble des multiples de $p_{i_{1}} p_{i_{2}} \ldots p_{i_{l}}$. Donc la formule que l'on a obtenue n'est constituée que d'ensembles de multiples d'entier et donc convient.
|
| 282 |
+
|
| 283 |
+
Montrons maintenant le lemme par récurrence sur $m$. Le cas $m=1$ est trivial. De plus, nous avons traité le cas $m=2$, pour l'exemple, ci-dessus. Soit $m \geqslant 2$ et supposons le théorème vrai pour $m$ ensembles. Soient $A_{1}, \ldots, A_{m+1} m+1$ ensembles. On a
|
| 284 |
+
|
| 285 |
+
$$
|
| 286 |
+
\begin{aligned}
|
| 287 |
+
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cup \cdots \cup A_{m}\right) \cap A_{m+1}\right) \oplus A_{m+1} \\
|
| 288 |
+
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cap A_{m+1}\right) \cup \cdots \cup\left(A_{m} \cap A_{m+1}\right)\right) \oplus A_{m+1}
|
| 289 |
+
\end{aligned}
|
| 290 |
+
$$
|
| 291 |
+
|
| 292 |
+
Par hypothèse de récurrence, il existe une formule pour le deuxième terme constituée uniquement d'intersections quelconques de $A_{1} \cap A_{m+1}, \ldots, A_{m} \cap A_{m+1}$; donc uniquement d'intersections quelconques de $A_{1}, \ldots, A_{m+1}$. Maintenant, on peut insérer la formule du deuxième terme dans la grosse formule en remplaçant, dans la formule du deuxième terme, les $\oplus$ par des $\ominus$ et vice-versa. En remplaçant directement le premier terme par la formule obtenue par l'hypothèse de récurrence, on obtient la formule voulue.
|
| 293 |
+
On conclut la preuve du lemme par récurrence.
|
| 294 |
+
|
French_STS/md/fr-ofm-2016-2017-envoi-5-solutions.md
ADDED
|
@@ -0,0 +1,226 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# OLYMPIADES FRANÇAISES DE MATHÉMATIQUES 2016-2017
|
| 2 |
+
|
| 3 |
+
|
| 4 |
+
|
| 5 |
+
ENVOI NO. 5
|
| 6 |
+
|
| 7 |
+
Corrigé
|
| 8 |
+
|
| 9 |
+
## Exercices du groupe B
|
| 10 |
+
|
| 11 |
+
Exercice 1. On considère un échiquier $3 \times 3$. Au début, on écrit le chiffre 0 dans chacune des 9 cases. Ensuite, à chaque étape, on effectue l'opération suivante : on choisit deux cases ayant un côté commun, puis on rajoute 1 au nombre écrit dans ces deux cases, ou bien on retranche 1 au nombre écrit dans ces deux cases. Est-il possible d'obtenir une configuration où le nombre 2017 est écrit dans les 9 cases?
|
| 12 |
+
|
| 13 |
+
Solution de l'exercice 1 Ce n'est pas possible. On colorie l'échiquier $3 \times 3$ en noir et blanc de manière usuelle (de sorte qu'une case noire n'ait que des cases blanches comme voisins et qu'une case blanche n'ait que des cases noires comme voisins). On vérifie que la somme des nombres sur les cases noires est toujours égale à la somme des nombres sur les cases blanches. En effet, c'est le cas au début, et si la somme des nombres sur les cases noires est égale à la somme des nombres sur les cases blanches, alors c'est toujours le cas après avoir effectué l'opération de l'énoncé.
|
| 14 |
+
|
| 15 |
+
Lorsque le nombre 2017 est écrit dans les 9 cases, ces deux sommes ne sont pas égales, d'où le résultat.
|
| 16 |
+
|
| 17 |
+
Exercice 2. Soit $A B C$ un triangle acutangle. On note O le centre de son cercle circonscrit. On considère le cercle $\Gamma_{B}$ passant par $A$ et $B$ et qui est tangent à ( $A C$ ), ainsi que le cercle $\Gamma_{C}$ passant par $A$ et $C$ qui est tangent à $(A B)$. Une droite $\Delta$ passant par $A$ recoupe $\Gamma_{B}$ en $X$ et $\Gamma_{C}$ en $Y$. Montrer que $\mathrm{OX}=\mathrm{OY}$.
|
| 18 |
+
|
| 19 |
+
## Solution de l'exercice 2
|
| 20 |
+
|
| 21 |
+
Soit $Z$ le point d'intersection du cercle circonscrit de $A B C$ avec $\Delta$. En faisant une chasse aux angles, on trouve que $\widehat{X B A}=\widehat{Z A C}=\widehat{Z B C}$. On en déduit que $\widehat{X B Z}=\widehat{A B C}$. Or, comme $\widehat{B C A}=$ $\widehat{B Z A}$, on en déduit que les triangles $A B C$ et $X B Z$ sont semblables. Donc
|
| 22 |
+
|
| 23 |
+
$$
|
| 24 |
+
\frac{X Z}{A C}=\frac{B Z}{B C} .
|
| 25 |
+
$$
|
| 26 |
+
|
| 27 |
+
On montre de même que les triangles CAY et CBZ sont semblables, de sorte que
|
| 28 |
+
|
| 29 |
+
$$
|
| 30 |
+
\frac{A Y}{B Z}=\frac{A C}{B C}
|
| 31 |
+
$$
|
| 32 |
+
|
| 33 |
+
On en déduit que $A Y=X Z$, puis que $A X=Z Y$. Ceci implique que les médiatrices des segments $[X Y]$ et $[A Z]$ sont les mêmes. Donc $O$ appartient à la médiatrice de $[X Y]$. Donc $O X=O Y$.
|
| 34 |
+
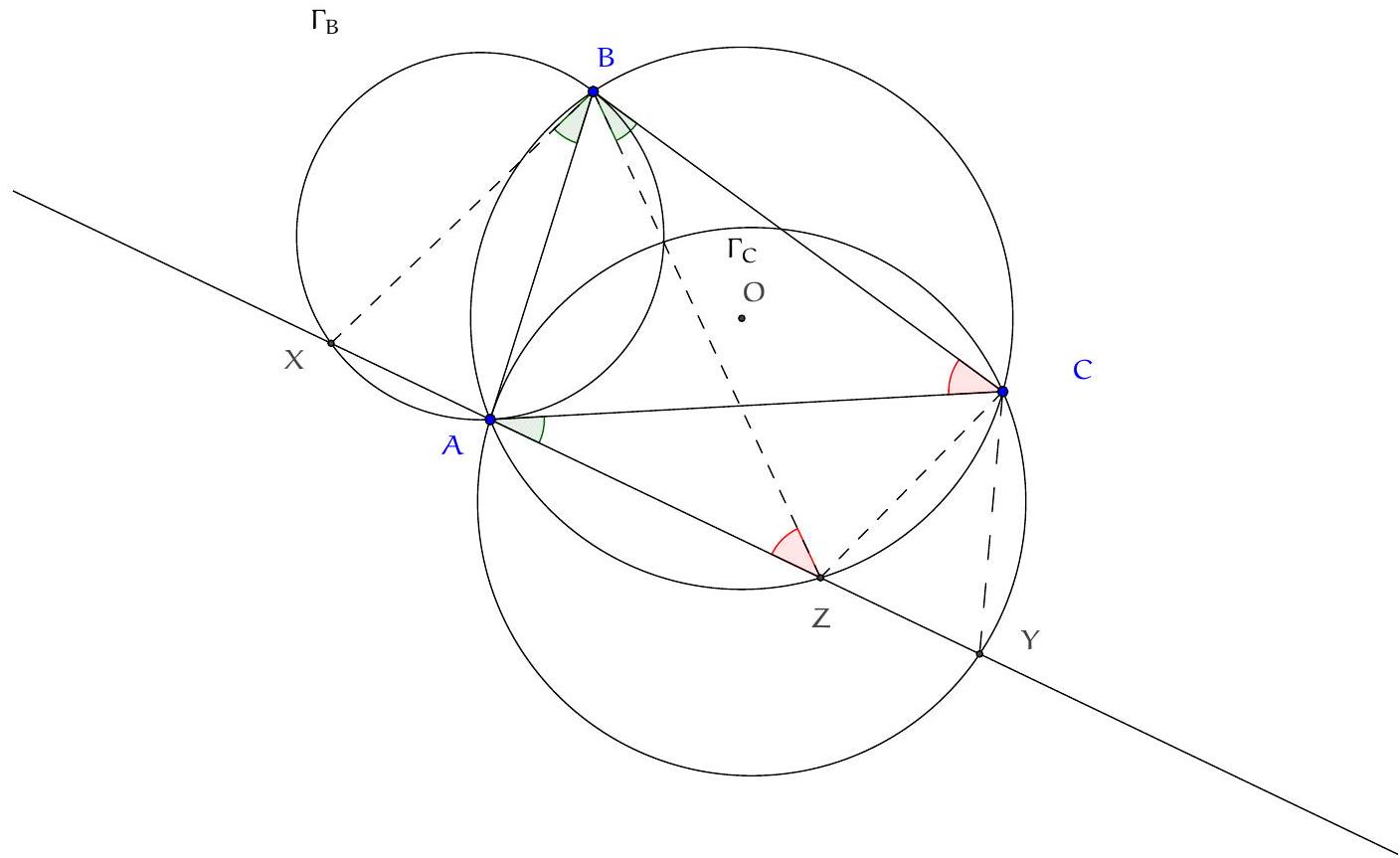
|
| 35 |
+
|
| 36 |
+
Exercice 3. Trouver tous les entiers strictement positifs $a, b$ et $c$ tels que $\operatorname{PGCD}(a, b, c)=1$,
|
| 37 |
+
|
| 38 |
+
$$
|
| 39 |
+
a\left|(b-c)^{2}, \quad b\right|(a-c)^{2}, \quad c \mid(a-b)^{2}
|
| 40 |
+
$$
|
| 41 |
+
|
| 42 |
+
et tels qu'il est possible de construire un triangle non aplati dont les côtés ont pour longueurs $\mathrm{a}, \mathrm{b}$ et c .
|
| 43 |
+
|
| 44 |
+
## Solution de l'exercice 3
|
| 45 |
+
|
| 46 |
+
Tout d'abord, vérifions que $\operatorname{PGCD}(a, b)=1$. Raisonnons par l'absurde en supposant que $p$ est un nombre premier qui divise à la fois $a$ et $b$. Alors $p$ divise $a$, qui lui même divise
|
| 47 |
+
|
| 48 |
+
$$
|
| 49 |
+
(b-c)^{2}=b(b-2 c)+c^{2}
|
| 50 |
+
$$
|
| 51 |
+
|
| 52 |
+
donc $p$ divise $c^{2}$ et donc $p$ divise $c$. Ceci contredit le fait que $\operatorname{PGCD}(a, b, c)=1$.
|
| 53 |
+
Supposons tout d'abord que deux des nombres sont égaux, par exemple $a=b$ par symétrie. Comme $a$ et $b$ sont premiers entre eux, on $a \mathrm{a}=\mathrm{b}=1$. La seule possibilité pour construire un triangle non-aplati est de prendre $\mathrm{c}=1$.
|
| 54 |
+
|
| 55 |
+
Supposons maintenant que $a, b, c$ sont deux à deux différents. Raisonnons par l'absurde, en supposant qu'il est possible de construire un triangle non aplati dont les côtés ont pour longueur a, b et c. Par symétrie, supposons que $c>b>a$.
|
| 56 |
+
|
| 57 |
+
Montrons que $a$ divise $(a+b-c)^{2}$ et que $b$ divise $(a+b-c)^{2}$. On $a(a+b-c)^{2}=a^{2}+2 a(b-$ $c)+(b-c)^{2}$, donc a divise $(a+b-c)^{2}$. De même $b$ divise $(a+b-c)^{2}$.
|
| 58 |
+
|
| 59 |
+
Comme $a$ et $b$ sont premiers entre eux, on en déduit que $a b$ divise $(a+b-c)^{2}$. Or $0<$ $a+b-c<a$, donc
|
| 60 |
+
|
| 61 |
+
$$
|
| 62 |
+
a b>a^{2}>(a+b-c)^{2}
|
| 63 |
+
$$
|
| 64 |
+
|
| 65 |
+
ce qui est absurde.
|
| 66 |
+
Ainsi, la seule solution est $\mathrm{a}=\mathrm{b}=\mathrm{c}=1$.
|
| 67 |
+
|
| 68 |
+
## Exercices communs
|
| 69 |
+
|
| 70 |
+
Exercice 4. Soient $\mathrm{a}, \mathrm{b}$ et c trois nombres strictement positifs tels que $\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{abc}=4$. Montrer que
|
| 71 |
+
|
| 72 |
+
$$
|
| 73 |
+
\left(1+\frac{\mathrm{a}}{\mathrm{~b}}+\mathrm{ca}\right)\left(1+\frac{\mathrm{b}}{\mathrm{c}}+\mathrm{ab}\right)\left(1+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{bc}\right) \geqslant 27
|
| 74 |
+
$$
|
| 75 |
+
|
| 76 |
+
Solution de l'exercice 4 En utilisant l'inégalité arithmético-géométrique, on trouve que
|
| 77 |
+
|
| 78 |
+
$$
|
| 79 |
+
4=a+b+c+a b c \geqslant 4\left((a b c)^{2}\right)^{\frac{1}{4}}
|
| 80 |
+
$$
|
| 81 |
+
|
| 82 |
+
et donc $a b c \leqslant 1$. Ensuite, en utilisant encore l'inégalité arithmético-géométrique,
|
| 83 |
+
|
| 84 |
+
$$
|
| 85 |
+
\left(1+\frac{a}{b}+c a\right)\left(1+\frac{b}{c}+a b\right)\left(1+\frac{c}{a}+b c\right)=\frac{(4-a)(4-b)(4-c)}{a b c}=15+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)
|
| 86 |
+
$$
|
| 87 |
+
|
| 88 |
+
et en utilisant encore l'inégalité arithmético-géométrique on en déduit que
|
| 89 |
+
|
| 90 |
+
$$
|
| 91 |
+
\left(1+\frac{\mathrm{a}}{\mathrm{~b}}+\mathrm{ca}\right)\left(1+\frac{\mathrm{b}}{\mathrm{c}}+\mathrm{ab}\right)\left(1+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{bc}\right) \geqslant 15+12\left(\frac{1}{\mathrm{abc}}\right)^{1 / 3} \geqslant 27
|
| 92 |
+
$$
|
| 93 |
+
|
| 94 |
+
Exercice 5. Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous nombres réels $x, y \in \mathbb{R}$ on ait
|
| 95 |
+
|
| 96 |
+
$$
|
| 97 |
+
f(x+y)+f(x) f(y)=f(x y)+f(x)+f(y)
|
| 98 |
+
$$
|
| 99 |
+
|
| 100 |
+
Solution de l'exercice 5 En prenant $y=0$, on trouve que $f(0)(f(x)-2)=0$ pour tout $x \in \mathbb{R}$. Si $f(0) \neq 0$, on en déduit que $f(x)=2$ pour tout $x \in \mathbb{R}$. Supposons donc dans la suite que $f(0)=0$ et notons $a=f(1)$.
|
| 101 |
+
|
| 102 |
+
En prenant $y=1$, on obtient
|
| 103 |
+
|
| 104 |
+
$$
|
| 105 |
+
f(x+1)=(2-a) f(x)+a
|
| 106 |
+
$$
|
| 107 |
+
|
| 108 |
+
pour tout $x \in \mathbb{R}$.
|
| 109 |
+
|
| 110 |
+
En prenant $y+1$ à la place de $y$ dans l'équation fonctionnelle, on obtient
|
| 111 |
+
|
| 112 |
+
$$
|
| 113 |
+
\begin{aligned}
|
| 114 |
+
(2-a) f(x+y)+a+f(x)((2-a) f(y)+a) & =f(x+y+1)+f(x) f(y+1) \\
|
| 115 |
+
& =f(x y+x)+f(x)+f(y+1) \\
|
| 116 |
+
& =f(x y+x)+f(x)+(2-a) f(y)+x
|
| 117 |
+
\end{aligned}
|
| 118 |
+
$$
|
| 119 |
+
|
| 120 |
+
En retranchant $(2-a) f(x+y)+(2-a) f(x) f(y)=(2-a) f(x y)+(2-a) f(x)+(2-a) f(y)$ à cette égalité, on obtient
|
| 121 |
+
|
| 122 |
+
$$
|
| 123 |
+
f(x)+(2-a) f(x y)=f(x y+x)
|
| 124 |
+
$$
|
| 125 |
+
|
| 126 |
+
En prenant $y=-1$, on en déduit que $f(x)=-(2-a) f(-x)$, et donc $f(x)=(2-a)^{2} f(x)$ pour tout $x \in \mathbb{R}$. Si f n'est pas la fonction nulle, en choisissant $x$ tel que $f(x) \neq 0$, on obtient que $a=1$ ou a $=3$.
|
| 127 |
+
|
| 128 |
+
Premier cas. On suppose que $a=1$. Alors $f(x y+x)=f(x y)+f(x)$ pour tous $x, y \in \mathbb{R}$. On en déduit que
|
| 129 |
+
|
| 130 |
+
$$
|
| 131 |
+
f(x+y)=f(x)+f(y)
|
| 132 |
+
$$
|
| 133 |
+
|
| 134 |
+
pour tout $x, y \in \mathbb{R}$. En injectant ceci dans l'équation fonctionnelle, on obtient que $f(x y)=$ $f(x) f(y)$. En prenant $x=y$, on en déduit que $f(x) \geqslant 0$ pour $x \geqslant 0$, et avec (1) on en déduit que $f$ est croissante. Il est alors classique que (1) et la croissance de $f$ entraînent que $f$ est de la forme $f(x)=\operatorname{ax}$ avec $x \in \mathbb{R}$, et donc $f(x)=x$ pour tout $x \in \mathbb{R}$.
|
| 135 |
+
|
| 136 |
+
Deuxième cas. On suppose que $a=3$. Partant de $\mathbf{f}(x+1)=(2-a) f(x)+\boldsymbol{a}$, on en déduit que $f(x+2)=f(x)$ pour tout $x \in \mathbb{R}$. En prenant $y+2$ à la place de $y$ dans l'équation fonctionnelle, on en déduit que
|
| 137 |
+
$f(x+y)+f(x) f(y)=f(x+y+2)+f(x) f(y+2)=f(x y+2 x)+f(x)+f(y+2)=f(x y+2 x)+f(x)+f(y)$
|
| 138 |
+
pour tous $x, y \in \mathbb{R}$. En comparant avec l'équation fonctionnelle initiale, on en déduit que $f(x y+$ $2 x)=f(x y)$ pour tous $x, y \in \mathbb{R}$, et donc que $f$ est constante, ce qui contredit le fait que $f(0)=0$ et $f(1)=3$.
|
| 139 |
+
|
| 140 |
+
Réciproquement, on vérifie que les trois solutions $f(x)=0$ pour tout $x \in \mathbb{R}, f(x)=2$ pour tout $x \in \mathbb{R}$ et $f(x)=x$ pour tout $x \in \mathbb{R}$ conviennent.
|
| 141 |
+
|
| 142 |
+
Exercice 6. On considère un quadrilatère convexe ABCD dont les diagonales sont perpendiculaires et se coupent en $E$. Soit $P \in[A D]$ un point tel que $P \neq A$ et $P E=E C$. On suppose que le cercle circonscrit du triangle $B C D$ recoupe $[A D]$ en un point $Q$ différent de $A$. On note $R$ le deuxième point d'intersection de $[A C]$ avec le cercle passant par $A$ et tangent à (EP) en $P$. On suppose que les points $B, R, Q$ sont alignés. Montrer que $\widehat{B C D}=90^{\circ}$.
|
| 143 |
+
|
| 144 |
+
Solution de l'exercice 6 Introduisons $F$, le point d'intersection du cercle circonscrit du triangle ARD et du segment [DE]. La puissance de E par rapport au cercle passant par $A, R, F, D$ est $E R \cdot E A=E F \cdot E D$. Par ailleurs, la puissance de $E$ par rapport au cercle passant par $A, R, P$ est
|
| 145 |
+
$E R \cdot E A=E P^{2}=E C^{2}$. On en déduit que $E D \cdot E F=E C^{2}$, ce qui montre que le cercle passant par $\mathrm{F}, \mathrm{C}, \mathrm{D}$ est tangent à (CE).
|
| 146 |
+
|
| 147 |
+
On en déduit que $\widehat{E C F}=\widehat{\mathrm{EDC}}$. Par ailleurs, comme $A, R, F, D$ sont cocycliques, on a $\widehat{A D E}=$ $\widehat{\mathrm{ERF}}$. On en déduit que $\widehat{\mathrm{QDB}}+\widehat{\mathrm{BDC}}=\widehat{\mathrm{FRC}}+\widehat{\mathrm{RCF}}$, ce qui implique que $\widehat{\mathrm{RBC}}=\widehat{\mathrm{RFC}}$. Comme $(B F)$ et $(C R)$ sont perpendiculaires, ceci implique que $F$ est le symétrique de $B$ par rapport à la droite ( $A C$ ). Il en découle que $\widehat{B C R}=\widehat{R C F}=\widehat{\mathrm{BDC}}$. Comme $\widehat{\mathrm{BEC}}=90^{\circ}$, on a $\widehat{\mathrm{ECD}}=90^{\circ}-\widehat{\mathrm{BCE}}$ et conclut que $\widehat{B C D}=90^{\circ}$.
|
| 148 |
+
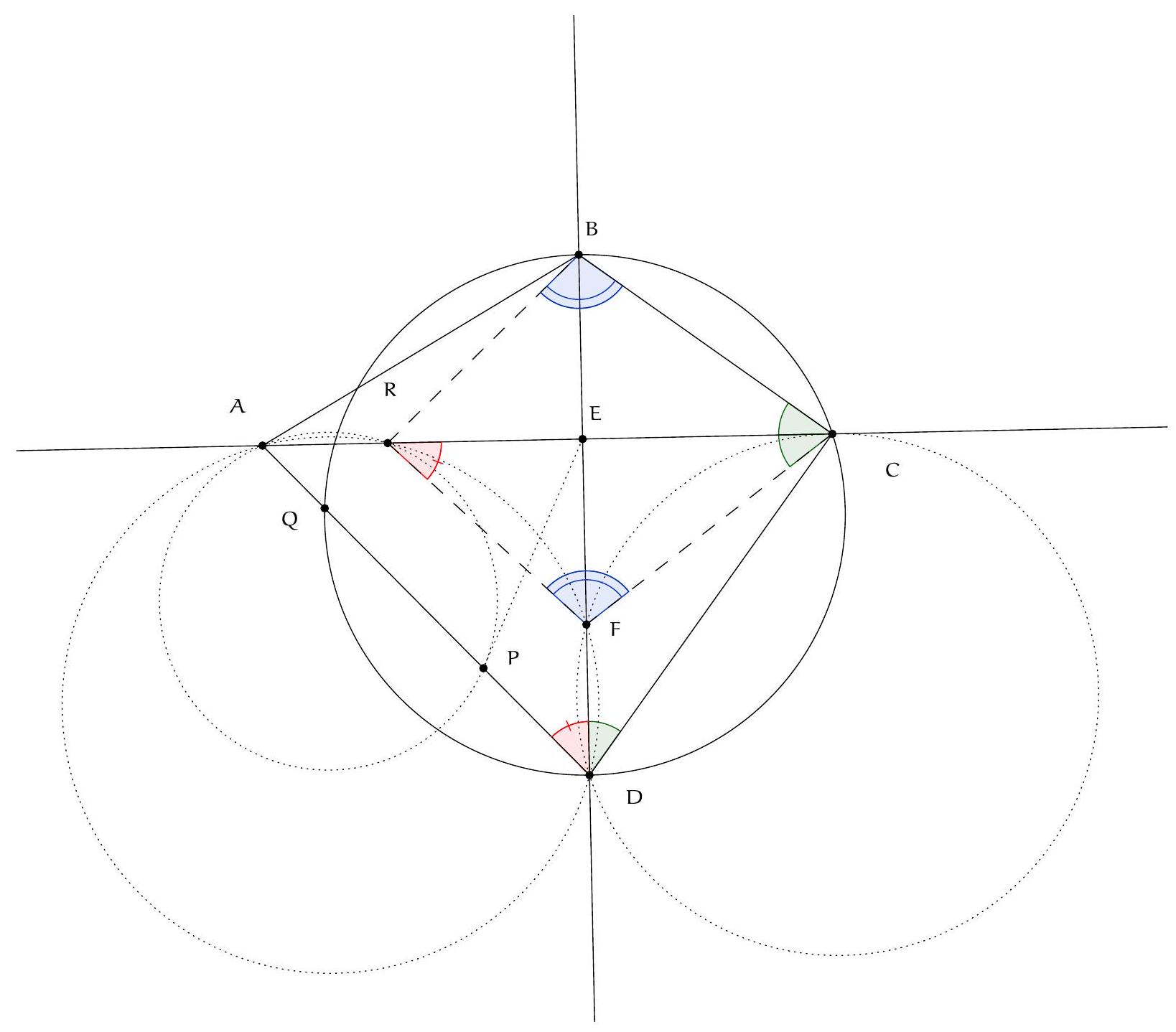
|
| 149 |
+
|
| 150 |
+
Exercice 7. Trouver tous les entiers strictement positifs $a, b$ et $c$ tels que $\left(a^{3}+b\right)\left(b^{3}+a\right)=2^{c}$. Solution de l'exercice 7 Soit $(a, b, c)$ un triplet solution. Si $a=b$, on a $a^{2}\left(a^{2}+1\right)^{2}=2^{c}$, ce qui implique $\mathrm{a}=\mathrm{b}=1$ et $\mathrm{c}=2$.
|
| 151 |
+
|
| 152 |
+
Si $a \neq b$, supposons par symétrie que $a>b$. On voit aisément que $a$ et $b$ sont impairs et premiers entre eux. Il existe deux entiers $x, y \geqslant 1$ tels que $2^{x}=a^{3}+b$ et $2^{y}=b^{3}+a$. Par croissance stricte de la fonction $f(x)=x^{3}-x \operatorname{sur}\left[1, \infty\left[\right.\right.$, on $a^{3}+b>b^{3}+a$, de sorte que $x>y$.
|
| 153 |
+
|
| 154 |
+
Si $b=1$, on a $2^{x}=\left(2^{y}-1\right)^{3}+1$, et donc $2^{x-y}=3-3 \cdot 2^{y}+2^{2 y}$, ce qui est absurde.
|
| 155 |
+
Si $b>1$, comme $b^{3}+a$ divise $\left(b^{3}\right)^{3}+a^{3}=b^{9}+a^{3}, b^{3}+a$ divise $b^{9}+a^{3}-\left(a^{3}+b\right)=b^{9}-b$.
|
| 156 |
+
Comme $a$ et $b$ sont premiers entre eux, on en déduit que $b^{3}+a$ divise
|
| 157 |
+
|
| 158 |
+
$$
|
| 159 |
+
b^{8}-1=\left(b^{4}+1\right)\left(b^{2}+1\right)\left(b^{2}-1\right)
|
| 160 |
+
$$
|
| 161 |
+
|
| 162 |
+
Comme $b^{4}+1$ et $b^{2}+1$ sont congrus à 2 modulo 4 , on en déduit que $2^{y-2}$ divise $b^{2}-1$, ce qui implique que $b^{2}-1 \geqslant 2^{y-2}$. Or $2^{y}>b^{3}$. Ceci implique que $4\left(b^{2}-1\right)>b^{3}$, ce qui force $b=3$. Alors $2^{y-2}$ divise 8 , donc $y=3,4$ ou 5 . On vérifie aisément que cela implique $(\mathfrak{a}, \boldsymbol{b})=(5,3)$.
|
| 163 |
+
|
| 164 |
+
Réciproquement, on vérifie que les seules solutions sont $(a, b, c)=(1,1,2),(a, b, c)=(3,5,12)$ et $(\mathbf{a}, \mathrm{b}, \mathrm{c})=(5,3,12)$.
|
| 165 |
+
|
| 166 |
+
## Exercices du groupe A
|
| 167 |
+
|
| 168 |
+
Exercice 8. Trouver tous les polynômes P à coefficients entiers tels que $\mathrm{P}(\mathrm{P}(\mathrm{n})+\mathrm{n})$ est un nombre premier pour une infinité d'entiers n .
|
| 169 |
+
|
| 170 |
+
Solution de l'exercice 8 Soit P un polynôme solution qui n'est pas constant. On peut écrire $\mathrm{P}(\mathrm{X}+$ $P(X))=P(X) Q(X)$, avec $Q$ un polynôme à coefficients entiers. En effet, si $P(X)=\sum_{i=0}^{k} a_{i} X^{i}$, avec $a_{i} \in \mathbb{Z}$, on a
|
| 171 |
+
$P(P(X)+X)=\sum_{i=0}^{k} a_{i}(P(X)+X)^{i}=a_{0}+\sum_{i=1}^{k} a_{i}\left(P(X) Q_{i}(X)+X^{i}\right)=P(X)+P(X) \sum_{i=1}^{k} a_{i} Q_{i}(X)=P(X) Q(X)$,
|
| 172 |
+
où les $\mathrm{Q}_{i}$ sont des polynômes à coefficients entiers, et donc $Q$ également.
|
| 173 |
+
Comme $P(X)+1$ et $P(X)-1$ ont un nombre fini de racines et que $P(n+P(n))$ est premier pour une infinité de nombres entiers $n$, on en déduit que $Q(n)=1$ ou $Q(n)=-1$ pour une infinité d'entiers $n$, ce qui implique que $Q$ est constant. En notant $k$ le degré de $P$, on a $\operatorname{deg}(P(P(X)+$ $X))=k^{2}$, ce qui implique $k=k^{2}$ et donc $k=1$. Si $P(X)=a X+b$ avec $a \neq 0$, on a $P(P(n)+n)=$ $(a+1)(a n+b)$. Comme $a \neq 0$, pour que ce nombre soit premier pour une infinité d'entiers $n$, on doit avoir $|a+1|=1$, ce qui implique que $a=-2$. Pour que $2 \mathfrak{n}-\mathrm{b}$ soit un nombre premier pour une infinité de nombres entiers $n$, il faut et il suffit que $b$ soit impair.
|
| 174 |
+
|
| 175 |
+
Ainsi, les solutions sont les polynômes constants égaux à un nombre premier et les polynômes $P$ de la forme $P(X)=-2 X+b$ avec $b$ un entier impair.
|
| 176 |
+
|
| 177 |
+
Exercice 9. Soient $A B C D$ un quadrilatère inscrit dans un cercle. On note $\Delta_{1}$ la droite parallèle à $(B C)$ passant par $A$ et $\Delta_{2}$ la droite parallèle à $(A D)$ passant par $B$. On note $E$ le point d'intersection de $\Delta_{1}$ avec (CD) et $F$ le point d'intersection de $\Delta_{2}$ avec (CD). La droite perpendiculaire à $\Delta_{1}$ passant $A$ coupe $(B C)$ en $P$, et la droite perpendiculaire à $\Delta_{2}$ passant par $B$ coupe ( $\left.A D\right)$ en Q. On note $\Gamma_{1}$ le cercle circonscrit du triangle $A D E$ et $\Gamma_{2}$ le cercle circonscrit du triangle BFC. Montrer que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents si et seulement si (DP) et (CQ) sont perpendiculaires.
|
| 178 |
+
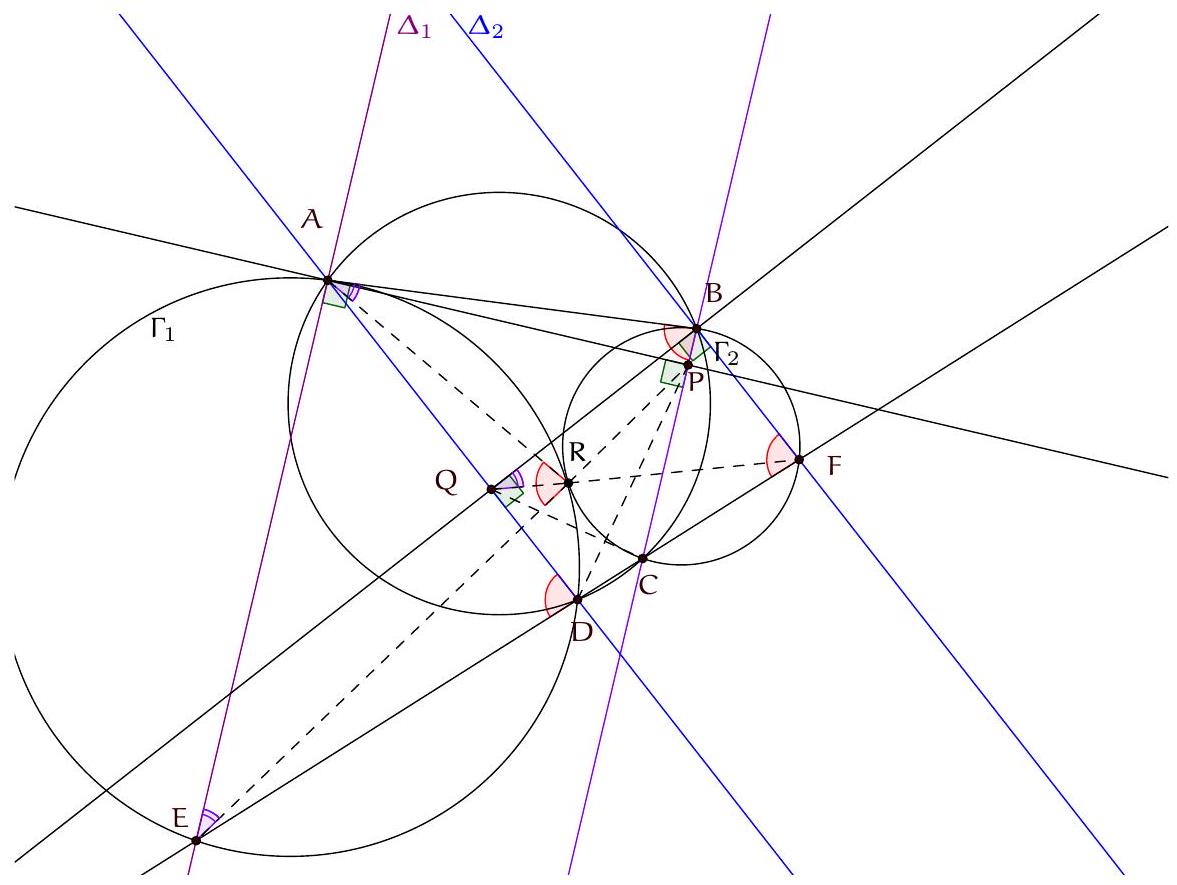
|
| 179 |
+
|
| 180 |
+
FIGURE 1 - Preuve de la première implication
|
| 181 |
+
|
| 182 |
+
## Solution de l'exercice 9
|
| 183 |
+
|
| 184 |
+
On commence par quelques remarques préliminaires. On a $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{ADC}}=\widehat{\mathrm{ABC}}=$ $180^{\circ}-\widehat{\mathrm{EAB}}$, donc $(\mathrm{AB})$ et $\Gamma_{1}$ sont tangents. De même, $\Gamma_{2}$ et $(A B)$ sont tangents. Ensuite, comme $(A P) \perp(B C)$ et $(A D) \perp(B Q)$, on a $(P D) \perp(C Q)$ si et seulement si les triangles $A P D$ et $B C Q$ sont semblables, c'est-à-dire si et seulement si $\frac{A P}{A D}=\frac{B C}{C O}$. Or les triangles $A D E$ et $B F C$ sont semblables, donc $\frac{A D}{A E}=\frac{B F}{B C}$. On en déduit que $\frac{A P}{A D}=\frac{B C}{C Q}$ si et seulement si $\frac{A P}{A E}=\frac{B F}{B Q}$ si et seulement si PAE et FBQ sont semblables ( $\operatorname{car} \widehat{\mathrm{PAE}}=\widehat{\mathrm{FBQ}}=90^{\circ}$ ).
|
| 185 |
+
|
| 186 |
+
Supposons maintenant que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents en $R$. On vois facilement que $\widehat{A R B}=90^{\circ}$, ce qui implique que les points $A, Q, P, B, R$ appartiennent tous au cercle de diamètre $[A B]$. On en déduit que $\widehat{A R P}=180^{\circ}-\widehat{A B P}=180^{\circ}-\widehat{A B C}=180^{\circ}-\widehat{A D E}=180^{\circ}-\widehat{A R E}$. Donc E, $R, P$ sont alignés. On montre de même que $F, R$, $Q$ sont alignés. Ainsi, $\widehat{P E A}=\widehat{R E A}=\widehat{R A B}=\widehat{R Q B}=\widehat{F Q B}$. On en déduit que $P E A$ et $F Q B$ sont semblables.
|
| 187 |
+
|
| 188 |
+
Supposons maintenant que PEA et FQB sont semblables. Soit $S$ le point d'intersection de (PE) et (QF). Nous allons montrer que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents en $S$. On a l'égalité des angles
|
| 189 |
+
|
| 190 |
+
$$
|
| 191 |
+
\widehat{\mathrm{SQB}}=\widehat{\mathrm{FQB}}=\widehat{\mathrm{PEA}}=\widehat{\mathrm{EPC}}=180^{\circ}-\widehat{\mathrm{SPB}}
|
| 192 |
+
$$
|
| 193 |
+
|
| 194 |
+
On en déduit que $S, Q, B, P$ sont cocycliques. Ainsi, $A, Q, P, B, S$ sont cocycliques. Il en découle que
|
| 195 |
+
|
| 196 |
+
$$
|
| 197 |
+
\widehat{A S E}=180^{\circ}-\widehat{A S P}=\widehat{A B P}=\widehat{A B C}=180^{\circ}-\widehat{A D C}=\widehat{A D E}
|
| 198 |
+
$$
|
| 199 |
+
|
| 200 |
+
Donc $S \in \Gamma_{1}$. On montre de même que $S \in \Gamma_{2}$. Pour conclure, on écrit
|
| 201 |
+
|
| 202 |
+
$$
|
| 203 |
+
\widehat{B S A}=90^{\circ}=\widehat{S A B}+\widehat{A B S}=\widehat{S D A}+\widehat{B C S}
|
| 204 |
+
$$
|
| 205 |
+
|
| 206 |
+
$\qquad$
|
| 207 |
+
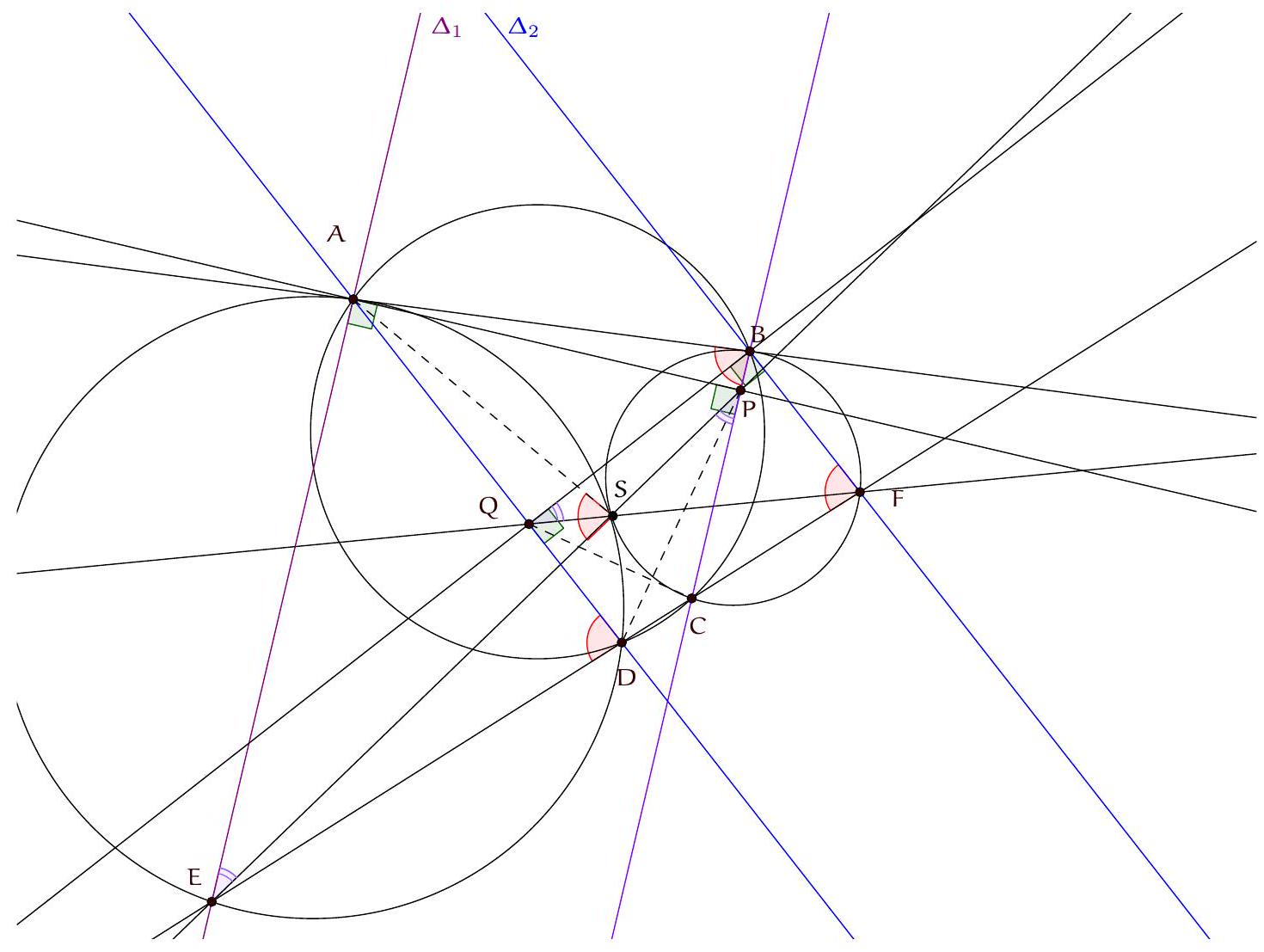
|
| 208 |
+
|
| 209 |
+
Figure 2 - Preuve de la deuxième implication.
|
| 210 |
+
|
| 211 |
+
Ceci entraîne aisément que la tangente à $\Gamma_{1}$ passant par $S$ est tangente à $\Gamma_{2}$.
|
| 212 |
+
Exercice 10. Soit $n \geqslant 2$ un nombre entier. On dispose les $n^{2}$ nombres entiers $1,2, \ldots, n^{2}$ dans les $n^{2}$ cases d'un échiquier $n \times n$ comme suit : la première ligne contient les nombres $1,2, \ldots, n$ (de gauche à droite), la deuxième ligne contient les nombres $n+1, n+2, \ldots, 2 n$ et ainsi de suite. À chaque étape, on peut choisir deux cases ayant un côté commun, et ajouter ou soustraire un même entier aux deux nombres dans ces deux cases.
|
| 213 |
+
|
| 214 |
+
Trouver toutes les valeurs de $n$ pour lesquelles il est possible d'obtenir la configuration où il n'y a que des 0 , et dans ce cas trouver le nombre minimal d'étapes nécessaires pour y parvenir. Solution de l'exercice 10 Tout d'abord, on vérifie que la parité de la somme des nombres écrits ne change pas lorsqu'on effectue une étape. La somme des $n^{2}$ premiers entiers vaut $n^{2}\left(n^{2}+1\right) / 2$, qui est paire si et seulement $n$ est pair. Comme on veut obtenir la configuration où il n'y a que des 0 (dont la somme des nombres est paire), on voit que n doit être pair.
|
| 215 |
+
|
| 216 |
+
Réciproquement, si $n$ est pair, montrons qu'il est possible d'atteindre la configuration où il n'y a que des 0 , et qu'il faut au moins $3 n^{2} / 4$ étapes pour y arriver. Supposons qu'on ait réussi à attendre cette configuration en un certain nombre d'étapes. Considérons alors le graphe G dont les sommets sont les cases et deux sommets sont adjacents si on a modifié leur contenu à une même étape. Soit $C$ une composante connexe de G. Alors $C$ possède au moins deux sommets (car tous les nombres sont non nuls au départ). De plus, C ne peut pas avoir exactement deux sommets (car tous les nombres sont différents au départ). Supposons que C a trois sommets. Dans ce cas, deux de ces sommets ont degré 1 et un a degré 2 (à cause de la géométrie de l'échiquier), et le nombre inscrit au départ dans la case correspondant à celle de degré 2 doit être la somme des nombres correspondant à celles de degré 1 . On vérifie aisément que ce n'est possible. Ainsi, chaque composante connexe a au moins 4 sommets, ce qui montre que G a au plus $\frac{\mathfrak{n}^{2}}{4}$ composantes connexes.
|
| 217 |
+
|
| 218 |
+
Notons $C_{1}, C_{2}, \ldots, C_{k}$ les composantes connexes de $G$ ainsi que $s_{i}$ et $a_{i}$ respectivement le nombre de sommets et d'arêtes de $C_{i}$. Comme $a_{i} \geqslant s_{i}-1$ pour tout $1 \leqslant i \leqslant k$, on en déduit que le nombre total d'arêtes $A$ de $G$ vérifie
|
| 219 |
+
|
| 220 |
+
$$
|
| 221 |
+
A \geqslant \sum_{i=1}^{k}\left(s_{i}-1\right)=\left(\sum_{i=1}^{k} s_{i}\right)-k=n^{2}-k \geqslant \frac{3 n^{2}}{4}
|
| 222 |
+
$$
|
| 223 |
+
|
| 224 |
+
ce qu'il montre qu'il faut au moins $3 \mathrm{n}^{2} / 4$ étapes.
|
| 225 |
+
Lorsque n est pair, en subdivisant l'échiquier en petits carrés $2 \times 2$ (chacun contiendra les nombres $\mathfrak{i}, \mathfrak{i}+1, \mathfrak{i}+\mathfrak{n}, \mathfrak{i}+\mathfrak{n}+1$ ) on vérifie aisément qu'il est possible d'obtenir des 0 dans chacun de ces petits carrés en utilisant 3 opérations par petit carré (on enlève $i$ aux deux de gauche, on enlève $i+1$ aux deux de gauche puis on enlève $n$ aux deux du bas).
|
| 226 |
+
|
French_STS/md/fr-pofm-2017-2018-envoi1-corrige.md
ADDED
|
@@ -0,0 +1,123 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Corrigé de l'envoi 1: Arithmétique
|
| 2 |
+
|
| 3 |
+
November 16, 2017
|
| 4 |
+
|
| 5 |
+
## Exercices Groupe B
|
| 6 |
+
|
| 7 |
+
Exercice 1 Une cellule peut se diviser en 42 ou en 44 petites cellules. Combien de divisions faut-il pour obtenir, à partir d'une cellule, exactement 2017 cellules?
|
| 8 |
+
|
| 9 |
+
Solution Une division augmente de 41 ou 43 le nombre de cellules. Soit $a$ le nombre de divisions en 42 cellules, et $b$ le nombre de divisions en 44 cellules. On veut trouver $a+b$, sachant que
|
| 10 |
+
|
| 11 |
+
$$
|
| 12 |
+
2017=1+41 a+43 b=1+41(a+b)+2 b=1+43(a+b)-2 b
|
| 13 |
+
$$
|
| 14 |
+
|
| 15 |
+
On voit que $41(a+b) \leq 2016$, donc $a+b<50$.
|
| 16 |
+
De même, $43(a+b) \geq 2016$, donc $a+b>46$.
|
| 17 |
+
Or $2017=1+41 \times 49+7=1+41 \times 48+48=1+41 \times 47+89$. Comme $2 b$ est pair, la seule solution est $a+b=48$ (avec $2 b=48$ donc $a=b=24$ ).
|
| 18 |
+
|
| 19 |
+
Exercice 2 On a $n$ lampes, chacune avec un interrupteur. Chaque lampe fonctionne normalement, appuyer sur son interrupteur l'éteint si elle est allumée, et l'allume si elle est éteinte. Toutes les minutes on touche aux interrupteurs.
|
| 20 |
+
|
| 21 |
+
À la première minute : on appuie sur tous les interrupteurs $(1,2,3, \ldots, n)$.
|
| 22 |
+
À la deuxième minute : on appuie sur tous les interrupteurs dont la lampe a un numéro pair $(2,4,6, \ldots)$.
|
| 23 |
+
|
| 24 |
+
À la troisième minute : on appuie sur tous les interrupteurs dont la lampe a un numéro divisible par $3(3,6,9, \ldots)$.
|
| 25 |
+
|
| 26 |
+
Et ainsi de suite, à la $k$-ième minute, on appuie sur les interrupteurs avec un numéro divisible par $k$.
|
| 27 |
+
|
| 28 |
+
Quelles sont les lampes qui sont allumées après $n$ minutes sachant qu'au début toutes les lampes sont éteintes ?
|
| 29 |
+
|
| 30 |
+
Solution Soit $i \in\{1, \ldots, n\}$ le numéro d'une des lampes. On appuie sur l'interrupteur $i$ à la $k$-ième minute si et seulement si $k$ est un diviseur de $i$, donc on a appuyé $d(i)$ fois sur l'interrupteur $i$, avec $d(i)$ le nombre de diviseurs de $i$. Décomposons $i$ en facteurs premiers : $i=p_{1}^{\alpha_{1}} \times \cdots \times p_{r}^{\alpha_{r}}$, avec $p_{1}, \ldots, p_{r}$ des nombres premiers distincts et $\alpha_{1}, \ldots, \alpha_{r}$ des entiers. Les diviseurs de $i$ sont les entiers
|
| 31 |
+
de la forme $p_{1}^{\beta_{1}} \times \cdots \times p_{r}^{\beta_{r}}$, avec $\beta_{1} \in\left\{0,1, \ldots, \alpha_{1}\right\}, \ldots, \beta_{r} \in\left\{0,1, \ldots, \alpha_{r}\right\}$, il y en a donc $d(i)=\left(\alpha_{1}+1\right) \ldots\left(\alpha_{r}+1\right)$ (nombres de choix de $\left.\beta_{1}, \ldots, \beta_{r}\right)$.
|
| 32 |
+
|
| 33 |
+
Pour que la lampe $i$ soit allumée à la fin, il faut et il suffit qu'on ait appuyé un nombre impair de fois sur l'interrupteur, donc que $d(i)$ soit impair, donc que tous les $\alpha_{j}, j \in\{1, \ldots, r\}$, soient pairs, c'est-à-dire que $i$ soit un carré parfait.
|
| 34 |
+
|
| 35 |
+
Ainsi, les lampes allumées après $n$ minutes sont celles dont le numéro est un carré parfait.
|
| 36 |
+
|
| 37 |
+
Exercice 3 On considère 5 nombres entiers positifs. En les ajoutant deux à deux de toutes les façons possibles, on génère 10 entiers. Montrer que ces 10 entiers ne peuvent pas être 10 entiers consécutifs.
|
| 38 |
+
|
| 39 |
+
Solution On suppose que les 10 entiers sont consécutifs, et on note $n$ le plus petit. Leur somme est $n+(n+1)+\cdots+(n+9)=10 n+45$. Mais c'est aussi la somme des 5 nombres de départ, comptés 4 fois chacun, donc c'est un multiple de 4. C'est impossible car pour tout entier $n, 10 n+45$ est impair. On aboutit à une contradiction, donc les 10 entiers ne peuvent pas être consécutifs.
|
| 40 |
+
|
| 41 |
+
## Exercices Communs
|
| 42 |
+
|
| 43 |
+
Exercice 1 Dans la région reculée de Torturie, le vizir dispose en cercle $n$ condamnés, numérotés dans l'ordre entre 1 et $n$. Implacablement, il envoie au bourreau un condamné sur deux : les condamnés $2,4, \ldots$ et ainsi de suite en tournant autour du cercle, en sautant une personne entre deux supplices, jusqu'au moment où il n'en reste plus qu'un. Calculer en fonction de $n$ le numéro du dernier condamné restant.
|
| 44 |
+
|
| 45 |
+
Solution On note $f(n)$ le numéro du survivant. Traitons d'abord le cas où $n$ est une puissance de 2 . Montrons par récurrence que dans ce cas, $f(n)=1$. Si $n=1$, c'est bien le cas. Si $n=2^{a}$, avec $a \geq 1$, le vizir élimine d'abord tous les numéros pairs. Il reste alors $\frac{n}{2}=2^{a-1}$ condamnés, et le prochain à être envoyé au bourreau est le numéro 3, qui est la deuxième personne restante. Par hypothèse de récurrence, le survivant sera la première personne restante, c'est-à-dire le numéro 1 . Ainsi $f\left(2^{a}\right)=1$ pour tout entier $a$.
|
| 46 |
+
|
| 47 |
+
Traitons maintenant le cas général. On écrit $n=2^{a}+b$, où $a$ et $b$ sont des entiers tels que $0 \leq b<2^{a}$. Le vizir envoie d'abord au bourreau les numéros $2,4, \ldots, 2 b$. Il reste alors $2^{a}$ condamnés. D'après le cas précédent, le survivant est celui situé juste avant la prochaine victime, à savoir le numéro $2 b+1$, car $2 b+1 \leq n$. Ainsi $f\left(2^{a}+b\right)=2 b+1$.
|
| 48 |
+
|
| 49 |
+
Exercice 2 Trouver tous les entiers $\mathrm{m}, \mathrm{n} \geq 0$ tels que $n^{3}-3 n^{2}+n+2=5^{m}$.
|
| 50 |
+
Solution On peut factoriser $n^{3}-3 n^{2}+n+2=(n-2)\left(n^{2}-n-1\right)$. Pour que l'équation soit vraie, il faut que les deux facteurs soient, au signe près, des puissances de 5.
|
| 51 |
+
|
| 52 |
+
Si $n-2$ est négatif, comme $n$ est positif, pour que $-(n-2)$ soit une puissance de 5 , il faut prendre $n=1$, et dans ce cas $n^{3}-3 n^{2}+n+2=1$, donc $m=0$, $n=1$ est solution.
|
| 53 |
+
|
| 54 |
+
Sinon, $\left(n^{2}-n-1\right)-(n-2)=n^{2}-2 n+1=(n-1)^{2}>0$, donc $n^{2}-n-1$ est une puissance de 5 plus grande que $n-2$, donc $n-2$ divise $n^{2}-n-1=(n-2)(n+1)+1$, donc $n-2$ divise 1 , donc $n=3$, et dans ce cas $n^{3}-3 n^{2}+n+2=5$, donc $m=1, n=3$ est solution.
|
| 55 |
+
|
| 56 |
+
Ainsi les seules solutions sont $m=0, n=1$ et $m=1, n=3$.
|
| 57 |
+
Exercice 3 Montrer que $n!=1 \times 2 \times \cdots \times n$ est divisible par $2^{n-1}$ si et seulement si $n$ est une puissance de 2 .
|
| 58 |
+
|
| 59 |
+
Solution On définit, pour tout nombre premier $p$, la valuation $p$-adique d'un entier $n$ comme le plus grand entier, noté $v_{p}(n)$, tel que $p^{v_{p}(n)}$ divise $n$. La valuation $p$-adique d'un produit d'entiers est la somme de leurs valuations $p$ adiques. Pour $x$ un nombre réel, on note $\lfloor x\rfloor$ la partie entière de $x$, c'est-à-dire le plus grand entier inférieur à $x$.
|
| 60 |
+
|
| 61 |
+
On observe que $\{1, \ldots, n\}$ contient $\left\lfloor\frac{n}{p}\right\rfloor$ multiples de $p,\left\lfloor\frac{n}{p^{2}}\right\rfloor$ multiples de $p^{2}$, etc. On en déduit la formule de Legendre :
|
| 62 |
+
|
| 63 |
+
$$
|
| 64 |
+
v_{p}(n!)=\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\ldots
|
| 65 |
+
$$
|
| 66 |
+
|
| 67 |
+
Pour cet exercice, on prend $p=2$, et on définit $k$ l'entier tel que $2^{k} \leq n<2^{k+1}$. Alors
|
| 68 |
+
$v_{2}(n!)=\left\lfloor\frac{n}{2}\right\rfloor+\left\lfloor\frac{n}{4}\right\rfloor+\cdots+\left\lfloor\frac{n}{2^{k}}\right\rfloor \leq \frac{n}{2}+\frac{n}{4}+\cdots+\frac{n}{2^{k}}=n\left(1-\frac{1}{2^{k}}\right) \leq n-1$.
|
| 69 |
+
Pour que $n$ ! soit divisible par $2^{n-1}$, c'est-à-dire pour que $v_{2}(n!) \geq n-1$, il faut être dans les cas d'égalité. En particulier, il faut que $n\left(1-\frac{1}{2^{k}}\right)=n-1$, donc que $n=2^{k}$.
|
| 70 |
+
|
| 71 |
+
Réciproquement, si $n=2^{k}$, alors on est dans les cas d'égalité, donc $2^{n-1}$ divise $n$ !.
|
| 72 |
+
|
| 73 |
+
## Exercices Groupe A
|
| 74 |
+
|
| 75 |
+
Exercice 1 Trouver les couples d'entiers $(x, y) \in \mathbb{Z}$ solutions de l'équation $y^{2}=x^{5}-4$.
|
| 76 |
+
|
| 77 |
+
Solution Par le petit théorème de Fermat, pour tout entier $x$ premier avec $11, x^{10} \equiv 1[11]$. Donc 11 divise $x^{10}-1=\left(x^{5}-1\right)\left(x^{5}+1\right)$. Par le lemme de Gauss, 11 divise $x^{5}-1$ ou $x^{5}+1$. Donc pour tout entier $x, x^{5}-4 \equiv-5[11]$ ou $x^{5}-4 \equiv-3[11]$ ou, dans le cas où 11 divise $x, x^{5}-4 \equiv-4[11]$.
|
| 78 |
+
|
| 79 |
+
Pour le terme de gauche, on calcule les résidus quadratiques modulo 11: $0^{2} \equiv 0[11], 1^{2}=(-1)^{2} \equiv 1[11], 2^{2}=(-2)^{2} \equiv 4[11], 3^{2}=(-3)^{2} \equiv-2[11]$, $4^{2}=(-4)^{2} \equiv 5[11]$, et $5^{2}=(-5)^{2} \equiv 3[11]$.
|
| 80 |
+
|
| 81 |
+
Ainsi $y^{2} \not \equiv x^{5}-4[11]$, donc l'équation n'a pas de solution.
|
| 82 |
+
|
| 83 |
+
Exercice 2 Existe-t-il un sous-ensemble infini $A$ de $\mathbb{N}$ qui vérifie la propriété suivante : toute somme finie d'éléments distincts de $A$ n'est jamais une puissance d'un entier (c'est-à-dire un entier de la forme $a^{b}$ avec $a$ et $b$ entiers supérieurs ou égaux à 2) ?
|
| 84 |
+
|
| 85 |
+
Solution On cherche à construire un tel ensemble $A=\left\{a_{0}, a_{1}, \ldots\right\}$, avec $\left(a_{0}, a_{1}, \ldots\right)$ une suite croissante d'entiers. On choisit comme premier élément $a_{0}=0$.
|
| 86 |
+
|
| 87 |
+
Soit $n \in \mathbb{N}$. On suppose qu'on a déjà trouvé $a_{0}<\cdots<a_{n}$ tels que l'ensemble B des somme d'éléments distincts ne contienne pas de puissance d'un entier. On veut choisir $a_{n+1}>a_{n}$ tel que l'ensemble des sommes d'éléments distincts de $\left\{a_{0}, \ldots a_{n+1}\right\}$ ne contienne pas de puissance d'un entier. Il suffit qu'aucun des $a_{n+1}+b$, avec $b \in B$, ne soit une puissance d'un entier.
|
| 88 |
+
|
| 89 |
+
Soit $N \in \mathbb{N}$. Majorons la proportion $p(N)$ de puissances d'entiers dans $\left\{a_{n}+1, \ldots, N\right\}$. Il y a moins de $\sqrt{N}$ carrés, moins de $\sqrt[3]{N}$ cubes, et ainsi de suites jusqu'aux racines $k$-ièmes, avec $k=\left\lfloor\log _{2}(N)\right\rfloor$. On peut s'arrêter à $k$ car pour tout $b>k, 2^{b}>N$ donc il n'y a pas de puissance $b$-ième dans $\left\{a_{n}+1, \ldots, N\right\}$. Donc
|
| 90 |
+
|
| 91 |
+
$$
|
| 92 |
+
p(N) \leq \frac{\sqrt{N}+\sqrt[3]{N}+\cdots+\sqrt[k]{N}}{N-a_{n}} \leq \frac{\sqrt{N} \log _{2}(N)}{N-a_{n}} \underset{N \rightarrow+\infty}{\longrightarrow} 0 .
|
| 93 |
+
$$
|
| 94 |
+
|
| 95 |
+
Ainsi, pour $N$ assez grand, on peut trouver $1+\max B$ nombres consécutifs dans $\left\{a_{n}+1, \ldots, N\right\}$ qui ne sont pas des puissances d'entiers. On choisit pour $a_{n+1}$ le plus petit d'entre eux. Alors aucun des $a_{n+1}+b$, avec $b \in B$, n'est une puissance d'un entier.
|
| 96 |
+
|
| 97 |
+
Finalement, on a bien construit un ensemble $A$ satisfaisant la propriété demandée.
|
| 98 |
+
|
| 99 |
+
Exercices 3 On note $P(n)$ le plus grand diviseur premier de $n$. Montrer qu'il existe une infinité d'entiers $n$ tels que $P(n-1)<P(n)<P(n+1)$.
|
| 100 |
+
|
| 101 |
+
Solution Soit $p$ un nombre premier impair. On cherche un entier $n$ de la forme $p^{2^{k}}$, avec $k$ entier, tel que $P(n-1)<P(n)<P(n+1)$.
|
| 102 |
+
|
| 103 |
+
Soit $k>l \geq 0$, on a
|
| 104 |
+
|
| 105 |
+
$$
|
| 106 |
+
\frac{p^{2^{k}}+1}{2}=\frac{p^{2^{l}}+1}{2}\left(p^{2^{k}-2^{l}}-p^{2^{k}-2 \cdot 2^{l}}+\cdots-p^{2 \cdot 2^{l}}+p^{2^{l}}-1\right)+1 .
|
| 107 |
+
$$
|
| 108 |
+
|
| 109 |
+
Donc les $\frac{p^{2^{k}}+1}{2}, k \in \mathbb{N}$, sont deux à deux premiers entre eux. Cela implique que les $P\left(\frac{p^{2^{k}}+1}{2}\right)=P\left(p^{2^{k}}+1\right)$ sont des entiers distincts. En particulier, on peut trouver $k$ tel que $P\left(p^{2^{k}}+1\right) \geq p=P\left(p^{2^{k}}\right)$. Soit $k_{p}$ le plus petit $k \geq 0$ vérifiant cette propriété. On choisit $n=p^{2^{k_{p}}}$. On voit que $P(n+1) \geq P(n)$, or $n$ et $n+1$ sont premiers entre eux, donc $P(n+1)>P(n)$. Il reste à montrer que $P(n-1)<P(n)$. On écrit
|
| 110 |
+
|
| 111 |
+
$$
|
| 112 |
+
n-1=p^{2^{k_{p}}}-1=\left(p^{2^{k_{p}-1}}+1\right)\left(p^{2^{k_{p}-2}}+1\right) \ldots\left(p^{2}+1\right)(p+1)(p-1)
|
| 113 |
+
$$
|
| 114 |
+
|
| 115 |
+
donc
|
| 116 |
+
|
| 117 |
+
$$
|
| 118 |
+
P(n-1)=\max \left(P\left(p^{2^{k_{p}-1}}+1\right), \ldots, P(p+1), P(p-1)\right)<p=P(n)
|
| 119 |
+
$$
|
| 120 |
+
|
| 121 |
+
par minimalité de $k_{p}$ et parce que $P(p-1) \leq p-1<p$.
|
| 122 |
+
Finalement, pour tout nombre premier impair $p$, on peut trouver $n$ une puissance de $p$ telle que $P(n-1)<P(n)<P(n+1)$. Comme il y a une infinité de nombres premiers impairs, et comme les puissances de nombres premiers distincts sont distinctes, il existe une infinité de tels entiers $n$.
|
| 123 |
+
|