problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7.4.1. (12 points) How many integer roots of the equation
$$
\cos 2 \pi x + \cos \pi x = \sin 3 \pi x + \sin \pi x
$$
lie between the roots of the equation $x^{2} + 10 x - 17 = 0$?
|
# Answer: 7.
Solution. If $x=2 k, k \in \mathbb{Z}$, then $\cos 2 \pi x+\cos \pi x=\cos 4 \pi k+\cos 2 \pi k=2, \sin 3 \pi x+\sin \pi x=$ $\sin 6 \pi k+\sin 2 \pi k=0$, so there are no even numbers among the roots of the first equation.
If, however, $x=2 k+1, k \in \mathbb{Z}$, then $\cos 2 \pi x+\cos \pi x=\cos (4 \pi k+2 \pi)+\cos (2 \pi k+\pi)=0, \sin 3 \pi x+\sin \pi x=$ $\sin (6 \pi k+3 \pi)+\sin (2 \pi k+\pi)=0$, so all odd numbers are roots of the first equation.
The roots of the second equation are $-5 \pm \sqrt{42}$; the smaller one lies between -12 and -11, and the larger one lies between 1 and 2. Thus, between the roots of the second equation lie 7 odd numbers $-11,-9,-7,-5,-3,-1,1$, which are 7 integer roots of the first equation.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1.1. (12 points) Among the first hundred elements of the arithmetic progression $3,7,11, \ldots$ find those that are also elements of the arithmetic progression $2,9,16, \ldots$ In your answer, indicate the sum of the found numbers.
|
Answer: 2870.
Solution.
$$
\begin{gathered}
a_{n}=a_{1}+(n-1) d_{1}=3+(n-1) \cdot 4 \\
b_{m}=b_{1}+(m-1) d_{2}=2+(m-1) \cdot 7 \\
3+(n-1) \cdot 4=2+(m-1) \cdot 7 \\
4(n+1)=7 m, \quad m=4 k, \quad n=7 k-1
\end{gathered}
$$
Consider the sequence of coinciding terms of the progressions $A_{k}$. For $k=1$, we find $n=6$, $m=4$. For $k=2$, we find $n=13$, $m=8$. The first term $A_{1}=a_{6}=23$, the difference $d=a_{13}-a_{6}=$ $51-23=28$. There are a total of $[100: 7]=14$ terms in the sequence, and their sum is
$$
S=\frac{2 \cdot 23+13 \cdot 28}{2} \cdot 15=2870
$$
|
2870
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2.1. (12 points) Find the greatest integer value of $a$ for which the equation
$$
\sqrt[3]{x^{2}-(a+7) x+7 a}+\sqrt[3]{3}=0
$$
has at least one integer root.
|
Answer: 11.
Solution. For the desired values of $a$, the numbers $x-a$ and $x-7$ are integers, and their product is -3, so there are 4 possible cases:
$$
\left\{\begin{array} { l }
{ x - a = 1 , } \\
{ x - 7 = - 3 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = 3 , } \\
{ x - 7 = - 1 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = - 1 , } \\
{ x - 7 = 3 ; }
\end{array} \quad \left\{\begin{array}{l}
x-a=-3 \\
x-7=1
\end{array}\right.\right.\right.\right.
$$
from which we find respectively
$$
\left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 4 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 6 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 1 1 , } \\
{ x = 1 0 ; }
\end{array} \quad \left\{\begin{array}{l}
a=11 \\
x=8
\end{array}\right.\right.\right.\right.
$$
Thus, the desired values are $a=3$ and $a=11$, of which the largest is 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3.1. (12 points) The curve given by the equation $y=2^{p} x^{2}+5 p x-2^{p^{2}}$ intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. Find the sum of all values of the parameter $p$ for which the center of the circle circumscribed around triangle $A B C$ lies on the $O x$ axis.
|
Answer: -1.
Solution. Let $x_{1}$ and $x_{2}$ be the roots of the quadratic trinomial $a x^{2}+b x+c (c \neq 0)$, the graph of which intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. Then $A\left(x_{1} ; 0\right), B\left(x_{2} ; 0\right), C(0 ; c)$. The fact that the center of the circle circumscribed around triangle $A B C$ lies on the $O x$ axis is equivalent to the angle $A C B$ being a right angle. It is not difficult to find that the slope of the line $A C$ is $k_{1}=-\frac{c}{x_{1}}$, and the slope of the line $B C$ is $k_{2}=-\frac{c}{x_{2}}$. The perpendicularity of these lines is equivalent to the condition $k_{1} \cdot k_{2}=-1$, that is, $x_{1} x_{2}=-c^{2}$, which, taking into account Vieta's theorem, can be rewritten as $a c=-1$.
For the trinomial from the problem statement, the condition $a c=-1$ becomes $2^{p+p^{2}}=1$, from which $p=0$, $p=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4.1. (12 points) Find all pairs of integers $(x, y)$ that are solutions to the equation
$$
7 x y-13 x+15 y-37=0 \text {. }
$$
In your answer, indicate the sum of the found values of $x$.
|
Answer: 4.
Solution. Multiplying both sides of the equation by 7, we get
$$
7 \cdot 7 x y - 13 \cdot 7 x + 15 \cdot 7 y - 37 \cdot 7 = 0
$$
Rewriting this equation, we have
$$
(7 x + 15)(7 y - 13) = 64
$$
If $x$ and $y$ are integers, then the numbers $7 x + 15$ and $7 y - 13$ are also integers and leave a remainder of 1 when divided by 7. All possible factorizations of the number 64 into the product of two integers are as follows:
$$
64 = 1 \cdot 64 = 2 \cdot 32 = 4 \cdot 16 = 8 \cdot 8 = -1 \cdot (-64) = -2 \cdot (-32) = -4 \cdot (-16) = -8 \cdot (-8)
$$
Among these factors, the numbers that leave a remainder of 1 when divided by 7 are 1, 8, and 64. Therefore, the possible cases are
$$
\begin{gathered}
7 x + 15 = 1, 7 y - 13 = 64 \Rightarrow (x, y) = (-2, 11) \\
7 x + 15 = 8, 7 y - 13 = 8 \Rightarrow (x, y) = (-1, 3) \\
7 x + 15 = 64, 7 y - 13 = 1 \Rightarrow (x, y) = (7, 2)
\end{gathered}
$$
Thus, the sum of the possible values of $x$ is $-2 - 1 + 7 = 4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The sequence $a_{1}, a_{2}, \ldots$ is defined by the equalities
$$
a_{1}=100, \quad a_{n+1}=a_{n}+\frac{1}{a_{n}}, \quad n \in \mathbb{N}
$$
Find the integer closest to $a_{2013}$.
|
# Answer: 118.
Solution.
\[
\begin{aligned}
a_{2013}^{2}=\left(a_{2012}+\frac{1}{a_{2012}}\right)^{2}=a_{2012}^{2}+2+\frac{1}{a_{2012}^{2}}=a_{2011}^{2} & +2 \cdot 2+\frac{1}{a_{2011}^{2}}+\frac{1}{a_{2012}^{2}}=\ldots \\
& =a_{1}^{2}+2 \cdot 2012+\frac{1}{a_{1}^{2}}+\ldots+\frac{1}{a_{2011}^{2}}+\frac{1}{a_{2012}^{2}}
\end{aligned}
\]
Therefore, on one hand,
\[
a_{2013}^{2}>a_{1}^{2}+2 \cdot 2012=10000+4024=14024>118^{2}=13924
\]
on the other hand,
\[
a_{2013}^{2}<a_{1}^{2}+2 \cdot 2012+\frac{2012}{100^{2}}<14024+1<118.5^{2}
\]
Therefore, \(118<a_{2013}<118.5\), and the nearest integer is 118.
|
118
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The quiz participants were asked four questions: 90 participants answered the first question correctly, 50 answered the second, 40 answered the third, and 20 answered the fourth, and no one was able to answer more than two questions correctly. What is the minimum number of participants in the quiz under these conditions?
|
Answer: 100.
Solution. The total number of answers is 200. Since no one answered more than two questions, the minimum possible number of participants in the quiz is 100, and in this case, each participant in the quiz must answer exactly 2 questions correctly. We will provide an example of a quiz where the described situation is realized. Number the participants from 1 to 100. Let participants numbered from 1 to 90 answer the first question, from 91 to 100 and from 1 to 40 answer the second question, from 41 to 80 answer the third question, and from 81 to 100 answer the fourth question.
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the minimum value of the discriminant of a quadratic trinomial, the graph of which has no common points with the regions located below the x-axis and above the graph of the function $y=\frac{1}{\sqrt{1-x^{2}}}$.
|
Answer: -4.
Solution. Since the discriminant of a quadratic trinomial
$$
D=b^{2}-4 a c
$$
we will find the maximum value of the product $a c$. Since for all $x$ the inequality $a x^{2}+b x+c \geqslant 0$ holds, then $a \geqslant 0, c \geqslant 0$. Let
$$
f(x)=\frac{1}{\sqrt{1-x^{2}}}-\left(a x^{2}+b x+c\right)
$$
Since for all $|x|<1$ it is true that $f(x) \geqslant 0$, then
$$
0 \leqslant f\left(\frac{1}{\sqrt{2}}\right)+f\left(-\frac{1}{\sqrt{2}}\right)=2 \sqrt{2}-(a+2 c)
$$
Thus, $a+2 c \leqslant 2 \sqrt{2}$, so from the inequality between the arithmetic mean and the geometric mean, we get:
$$
2 \sqrt{2} \geqslant a+2 c \geqslant 2 \cdot \sqrt{a \cdot 2 c}=2 \sqrt{2} \sqrt{a c}
$$
Therefore, $a c \leqslant 1$.
We will prove that 1 is the maximum of $a c$. Indeed, let $a=2 c=\sqrt{2}, b=0$, then the original inequality takes the form:
$$
\sqrt{2} x^{2}+\frac{1}{\sqrt{2}} \leqslant \frac{1}{\sqrt{1-x^{2}}} \Leftrightarrow\left\{\begin{array}{l}
\left(2 x^{2}-1\right)^{2}\left(x^{2}+1\right) \geqslant 0 \\
|x|<1
\end{array}\right.
$$
Therefore, for the discriminant of the quadratic trinomial, the following inequalities hold:
$$
D=b^{2}-4 a c \geqslant-4 a c \geqslant-4
$$
and its minimum value is -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. In triangle $ABC$, the bisectors $AL, BM$, and $CN$ are drawn, and $\angle ANM = \angle ALC$. Find the radius of the circumcircle of triangle $LMN$, two sides of which are equal to 3 and 4.
|
Answer: 2
Solution.
The following statement is true:
Let $A L, B M$ and $C N$ be the bisectors of the internal angles of a triangle. If $\angle A N M = \angle A L C$, then $\angle B C A = 120^{\circ}$.
Proof. Draw $M D \| A L$, then $\angle C M D = \frac{\alpha}{2}$. The angle $\angle A L C$ is an external angle of triangle $A L B$, so $\angle A N M = \angle A L C = \frac{\alpha}{2} + \beta$. The angle $\angle B M C$ is an internal angle of triangle $B M C$, so $\angle B M C = \pi - \frac{\beta}{2} - \gamma = \alpha + \frac{\beta}{2}$. Therefore, $\angle B M D = \alpha + \frac{\beta}{2} - \frac{\alpha}{2} = \frac{\alpha + \beta}{2}$. The angle $\angle N M C$ is an external angle of triangle $A N M$, so $\angle N M C = \frac{3 \alpha}{2} + \beta$. Therefore, $\angle B M N = \frac{3 \alpha}{2} + \beta - \frac{\alpha + \beta}{2} - \frac{\alpha}{2} = \frac{\alpha + \beta}{2}$. This means triangles $B M N$ and $B M D$ are congruent, so $N M = M D$ and $\angle M D N = \frac{\pi - (\alpha + \beta)}{2} = \frac{\gamma}{2}$. Therefore, points $N, M, C$ and $D$ lie on the same circle, and since $N M$ and $N D$ are chords subtending equal arcs, $N M = N D$, i.e., triangle $N M D$ is equilateral, so $\frac{\gamma}{2} = \frac{\pi}{3}$. Therefore, $\angle B C A = 120^{\circ}$ (see Fig. 4).
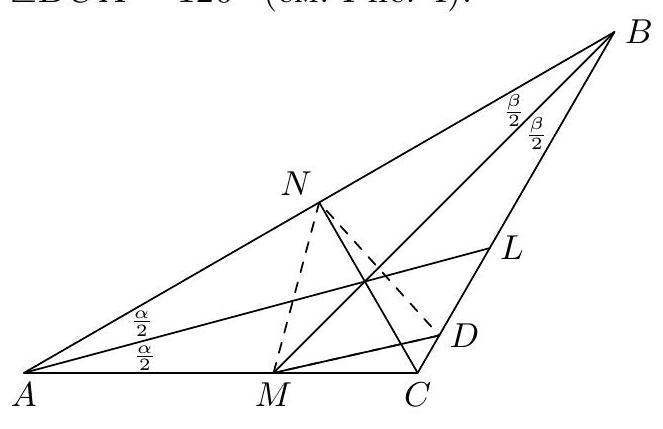
Fig. 4
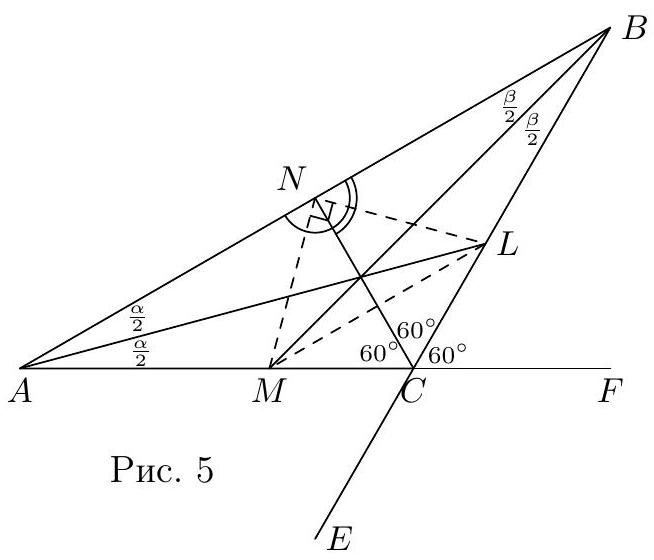
Remark. The converse statement is also true: if $\angle B C A = 120^{\circ}$ and $A L, B M$ and $C N$ are the bisectors of the internal angles of the triangle, then $\angle A N M = \angle A L C$.
The line $C B$ is the bisector of angle $N C F$ ( $\Rightarrow$ point $L$ is equidistant from lines $C N$ and $C F$ ), and the line $A L$ is the bisector of angle $B A F$ ( $\Rightarrow$ point $L$ is equidistant from lines $A N = N B$ and $A F = C F$). Therefore, point $L$ is equidistant from lines $N C$ and $N B$, i.e., line $N L$ is the bisector of angle $B N C$. Similarly, the line $C A$ is the bisector of angle $E C N$ ( $\Rightarrow$ point $M$ is equidistant from lines $C N$ and $C E$ ), and the line $B M$ is the bisector of angle $A B C$ ( $\Rightarrow$ point $M$ is equidistant from lines $B A = N A$ and $B E = C E$). Therefore, point $M$ is equidistant from lines $N A$ and $N C$, i.e., line $N M$ is the bisector of angle $A N C$. Therefore, $\angle M N L = 90^{\circ}$ (see Fig. 5).
Let's estimate the values that the tangents of the acute angles of $\triangle L M N$ can take.
From $\triangle A N C$ we get that $\angle A N C = 120^{\circ} - \alpha \Rightarrow \angle M N C = 60^{\circ} - \frac{\alpha}{2} \Rightarrow \angle N M C = 60^{\circ} + \frac{\alpha}{2}$.
From $\triangle B N C$ we get that $\angle B N C = 120^{\circ} - \beta \Rightarrow \angle L N C = 60^{\circ} - \frac{\beta}{2} \Rightarrow \angle N L C = 60^{\circ} + \frac{\beta}{2}$.
By the Law of Sines for $\triangle N M C$ we get: $\frac{N C}{\sin \angle N M C} = \frac{N M}{\sin \angle N C M} \Rightarrow N C = \frac{2 N M \sin \left(60^{\circ} + \frac{\alpha}{2}\right)}{\sqrt{3}}$.
By the Law of Sines for $\triangle N L C$ we get: $\frac{N C}{\sin \angle N L C} = \frac{N L}{\sin \angle N C L} \Rightarrow N C = \frac{2 N L \sin \left(60^{\circ} + \frac{\beta}{2}\right)}{\sqrt{3}}$.
Considering the equality $\frac{\alpha}{2} + \frac{\beta}{2} = 30^{\circ}$ from the last two relations, we get that
$$
\operatorname{tg} \angle N L M = \frac{N M}{N L} = \frac{\sin \left(90^{\circ} - \frac{\alpha}{2}\right)}{\sin \left(60^{\circ} + \frac{\alpha}{2}\right)}
$$
Since $\frac{\alpha}{2} \in (0^{\circ}, 30^{\circ})$ and the function $y = \sin t$ is increasing in the first quadrant, then $\operatorname{tg} \angle N L M \in \left(\frac{\sqrt{3}}{2} ; \frac{2}{\sqrt{3}}\right)$. If 3 and 4 are the lengths of the legs of $\triangle N L M$, then either $\operatorname{tg} \angle N L M = \frac{3}{4}$ or $\operatorname{tg} \angle N L M = \frac{4}{3}$. But since $\frac{3}{4} < \frac{\sqrt{3}}{2} = \sqrt{\frac{3}{4}}$, this case is impossible. Therefore, only the case where $M L = 4$ (hypotenuse) and 3 is the length of one of the legs is possible. The length of the other leg by the Pythagorean theorem is $\sqrt{7}$. Since the inequalities $\frac{\sqrt{3}}{2} < \frac{\sqrt{7}}{3} < \frac{2}{\sqrt{3}} \Leftrightarrow \frac{3}{4} < \frac{7}{9} < \frac{4}{3}$ hold, this case is realized. Since in a right triangle the radius of the circumscribed circle is half the hypotenuse, then
$$
R = \frac{M L}{2} = 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The numbers $a, b$, and $c$ satisfy the equation $\sqrt{a}=\sqrt{b}+\sqrt{c}$. Find $a$, if $b=52-30 \sqrt{3}$ and $c=a-2$.
|
Answer: $a=27$.
Solution. We have
$$
\sqrt{b}=\sqrt{52-30 \sqrt{3}}=\sqrt{27-2 \cdot 5 \cdot 3 \sqrt{3}+25}=3 \sqrt{3}-5
$$
Therefore, $\sqrt{a}-\sqrt{a-2}=3 \sqrt{3}-5, \frac{2}{\sqrt{a}+\sqrt{a-2}}=\frac{2}{3 \sqrt{3}+5}, \sqrt{a}+\sqrt{a-2}=\sqrt{27}+\sqrt{25}$. Since the function $f(a)=\sqrt{a}+\sqrt{a-2}$ is increasing and $f(27)=0$, the only solution to this equation is $a=27$.
Answer to variant 2: $c=16$.
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Lёsha's cottage plot has the shape of a nonagon, which has three pairs of equal and parallel sides (see figure). Lёsha knows that the area of the triangle with vertices at the midpoints of the remaining sides of the nonagon is 12 acres. Help him find the area of the entire cottage plot.
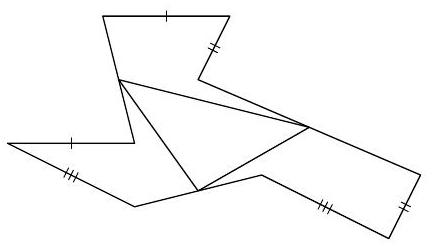
|
Answer: 48 acres.
Solution. Let $D E F G H I K L M$ be the given nonagon, and $A B C$ be the triangle with vertices at the midpoints of the remaining (unmarked) sides. From the condition, it follows that the quadrilateral $D F G E$ is a parallelogram, since its opposite sides $D E$ and $F G$ are equal and parallel. In a parallelogram, the diagonals bisect each other, so points $D, A, G$ lie on the same line. Moreover, $D A=A G$.
Similarly, considering the quadrilaterals $H G I K$ and $K M D L$, we get that point $B$ lies on the line $G K$, point $C$ lies on the line $D K$, and $G B=B K, K C=C D$.
The area of the nonagon $D E F G H I K L M$ is equal to the area of the triangle $D G K$, since triangles $A F G, B I K$ and $C M D$ are equal to triangles $A E D, B H G$ and $C L K$, respectively. Finally, $A, B, C$ are the midpoints of the sides of triangle $D G K$, which means,
its area is four times the area of triangle $A B C$. Thus, the area of the entire plot is
$$
S_{D E F G H I K L M}=4 S_{A B C}=48 \text { acres. }
$$
Answer to variant 2: 32 acres.
|
48
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. In a right triangle $ABC$ with a right angle at $C$, points $P$ and $Q$ are the midpoints of the angle bisectors drawn from vertices $A$ and $B$. The inscribed circle of the triangle touches the hypotenuse at point $H$. Find the angle $PHQ$.
|
Answer: $90^{\circ}$.
Solution. First, let's prove the following lemma.
Lemma. Let $ABC (\angle C=90^{\circ})$ be a right triangle, $I$ the intersection point of the angle bisectors $AM$ and $BK$, $S$ the midpoint of $KM$, and the inscribed circle of the triangle touches the hypotenuse at point $H$. Then the points $S, I$, and $H$ lie on the same line.

Proof. Let $D$ and $E$ be the projections of points $K$ and $M$ onto the hypotenuse $AB$ (see figure). Then $\triangle DKB = \triangle CKB$ by the hypotenuse and an acute angle, so $\angle DKB = \angle CKB$, which means $KB$ is the bisector of the external angle of $\triangle AKD$, and $AI$ is the bisector of its internal angle. Therefore, $I$ is the center of the excircle of $\triangle AKD$, so $DI$ is the bisector of angle $KDE$. Similarly, it can be shown that $EI$ is the bisector of angle $MDE$. Thus, $\triangle DIE$ is a right and isosceles triangle, meaning $IH$ is the perpendicular bisector of $DE$. The point $S$, being the midpoint of the lateral side of the right trapezoid $DKME$, also lies on the perpendicular bisector of $DE$. Therefore, the points $S, I$, and $H$ lie on the same line. The lemma is proved.
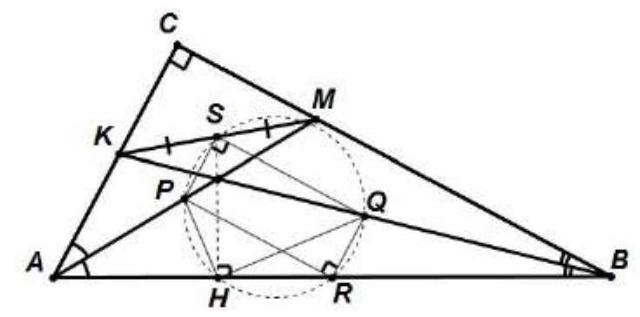
Using the lemma, we will now prove that $\angle PHQ = 90^{\circ}$. Let $R$ be the midpoint of the hypotenuse $AB$. Then $PS$ and $RQ$ are the midlines of triangles $\triangle AKM$ and $\triangle AKB$, so $PS \parallel AK \parallel QR$ and $PS = \frac{1}{2} AK = QR$, meaning $PSQR$ is a parallelogram. Moreover, $\angle PSQ = 90^{\circ}$, as its sides are parallel to the sides of angle $\angle ACB = 90^{\circ}$. Therefore, $PSQR$ is a rectangle.
Let $\Omega$ be the circle circumscribed around the rectangle $PSQR$. From the lemma, it follows that $\angle SHR = 90^{\circ}$. Since $\angle SPR = \angle SHR$, point $H$ lies on the circle $\Omega$. Consequently, $\angle PHQ = \angle PRQ = 90^{\circ}$ (as inscribed angles subtending the diameter $PQ$).
Answer to variant 2: $90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Find the number of natural numbers not exceeding 2022 and not belonging to either the arithmetic progression $1,3,5, \ldots$ or the arithmetic progression $1,4,7, \ldots$
|
Answer: 674.
Solution. These two progressions define numbers of the form $1+2n$ and $1+3n$. This indicates that the desired numbers are of the form $6n$ and $6n-4, n \in \mathbb{N}$. Since 2022 is divisible by 6, the numbers of the form $6n$ will be $\frac{2022}{6}=337$, and there will be as many numbers of the form $6n-4$. Therefore, the total number of numbers is $337 \cdot 2=674$.
|
674
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. Find the three last digits of the number $10^{2022}-9^{2022}$.
|
Answer: 119.
Solution. Since $A=10^{2022}-(10-1)^{2022}=10^{2022}-10^{2022}+2022 \cdot 10^{2021}-C_{2022}^{2} \cdot 10^{2022}+\ldots+$ $C_{2022}^{3} \cdot 10^{3}-C_{2022}^{2} \cdot 10^{2}+C_{2022}^{1} \cdot 10-1$, then $A(\bmod 1000) \equiv-C_{2022}^{2} \cdot 100+C_{2022}^{1} \cdot 10-1(\bmod 1000) \equiv$ $-\frac{2022 \cdot 2021 \cdot 100}{2}+20220-1(\bmod 1000) \equiv-100+220-1 \equiv 119$.
|
119
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The Dursleys are hiding Harry Potter on an island that is 9 km from the shore. The shore is straight. On the shore, 15 kilometers from the point on the shore closest to the island, Hagrid is on a magical motorcycle and wants to reach Harry as quickly as possible. The motorcycle travels along the shore at a speed of $50 \mathrm{km} /$ hour, and over the sea at a speed of 40 km/hour. Hagrid's plan is: first travel $X$ kilometers along the shore, and then head straight for the island. What value of $X$ is best suited for Hagrid's purposes?
|
# Answer: 3.
Solution. Let $A$ be the point from which Hagrid starts, $B$ be the island, and $C$ be the point where the motorcycle crashes into the sea. The travel time is $t=\frac{A C}{50}+\frac{B C}{40}=p A C+q B C=q\left(\frac{p}{q} A C+B C\right)$, where $p=\frac{1}{50}, q=\frac{1}{40}$. Thus, we aim to minimize $\frac{p}{q} A C+B C$. Mark an arbitrary point $D$ on the shore, construct a circle with $A D$ as the diameter and radius $q \cdot s: 2$ (where $s$ is arbitrary). Draw a circle centered at $D$ with radius $p \cdot s$, and let this circle intersect the first on land at point $E$. Drop a perpendicular $B F$ from $A E$, and it will intersect the shoreline at the optimal point $C$.
We will prove that $\frac{p}{q} A C+B C$ is minimal. From the similarity of triangles $A F C$ and $A E D$, it follows that $C F / A C=D E / A D=\frac{p}{q}, C F=\frac{p}{q} A C$, which means $\frac{p}{q} A C+B C=B F$. If we take any other point $M$ on the shore and calculate $\frac{p}{q} A M+B M$, we get the following: $\frac{p}{q} A M+B M=K M+M B$, where $K M$ is the perpendicular from $K$ to $A E$. And in turn, $K M+M B>B K>B F$.
Let $L$ be the point on the shore closest to the island. Triangles $B C L$ and $A C F$ are similar, from which $C L=\frac{B L \cdot C F}{A F}$. Therefore, $C L=12$ and $A C=X=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. There is a certain number of identical plastic bags that can be placed inside each other. If all the other bags end up inside one of the bags, we will call this situation a "bag of bags." Calculate the number of ways to form a "bag of bags" from 10 bags.
Explanation. Denote the bag with parentheses.
If we had one bag, there is only one way to form a "bag of bags": (). Two bags can also be arranged in only one way: (()).
Three bags can be arranged in two different ways: $(()())$ and $((()))$, and so on.
The order of the bags inside a bag does not matter. For example, the variant $(())())$ does not differ from $(()(()))$.
|
Answer: 719.
Solution. If $\Pi_{n}$ denotes the number of ways for $n$ packages, then:
$$
\begin{gathered}
\Pi_{1}=1, \Pi_{2}=1, \Pi_{3}=2, \Pi_{4}=4, \Pi_{5}=9, \Pi_{6}=20, \Pi_{7}=48, \Pi_{8}=115, \Pi_{9}=286 \\
\Pi_{10}=719
\end{gathered}
$$
The problem is solved by enumerating the cases. For example, if we take $\Pi_{5}$:
$\Pi_{5}=P_{4}+P_{3}+P_{2}+P_{1}$, where $P_{k}$ is the number of ways corresponding to the case when the root package contains $k$ packages.
$P_{4}=1$, there is only one way: $\left.(0)(0)\right)$.
$P_{3}=1$, there is also only one way: $((())(0))$.
$P_{2}=3$, there are three ways to split 4 packages into 2 groups: 3 and 1, 2 and 2. The first way corresponds to $\left(\Pi_{3}()\right)$ - two variants, the second way - one variant, $((())(0))$.
$P_{4}=\Pi_{4}$ ways: $\left(\Pi_{4}\right)$.
In total, it is $1|1|(2|1)|4=9$.
As $n$ increases, cases arise where one must be careful with combinatorics. For example, 8 packages can be arranged as $\left(\Pi_{3} \Pi_{3} \Pi_{1}\right)$, or as $\left(\Pi_{3} \Pi_{2} \Pi_{2}\right)$. In the second case, this is $\Pi_{3} \cdot \Pi_{2} \cdot \Pi_{2}=2 \cdot 1 \cdot 1=2$ ways, while in the first case, it is not $\Pi_{3} \cdot \Pi_{3} \cdot \Pi_{1}=2 \cdot 2 \cdot 1=4$, but actually only three, because the order of the triple packages does not matter.
|
719
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Propose a word problem that reduces to solving the inequality
$$
\frac{11}{x+1.5}+\frac{8}{x} \geqslant \frac{12}{x+2}+2
$$
Write the problem statement, its solution, and the answer.
Example of the required problem. Points A and B are connected by two roads: one is 19 km long, and the other is 12 km long. At 12:00, a pedestrian left point A on the longer road and walked the first 11 km at a constant speed, and then, getting tired, walked the remaining distance to point B at an average speed 1.5 km/h slower. At 14:00, a second pedestrian left point A on the shorter road and walked the entire distance at an average speed 0.5 km/h faster than the first pedestrian initially. What was the average speed of the first pedestrian for the last 8 km of the journey, if it is known that he arrived at point B no earlier than the second pedestrian?
Brief solution. If \( x \) is the required average speed of the first pedestrian (in km/h) on the second part of the journey, then \( x+1.5 \) is his speed on the first part, and \( (x+1.5)+0.5 = x+2 \) is the average speed of the second pedestrian. Then, by calculating the time each pedestrian spent on the journey, we obtain the required inequality. Since by the problem's condition \( x > 0 \), both sides of the inequality can be multiplied by the quantity \( x(x+1.5)(x+2) > 0 \), then we get \( 11x(x+2) + 8(x+1.5)(x+2) \geqslant 12x(x+1.5) + 2x(x+1.5)(x+2) \), or, after transformations, \( (x-4)(x+1)(x+3) \leqslant 0 \). Therefore, \( 0 < x \leqslant 4 \), and all found values of \( x \) satisfy the problem's condition.
|
Answer: no more than 4 km/h.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) How many roots does the equation $x^{2}-x \sqrt{5}+\sqrt{2}=0$ have?
|
Answer: 0.
Solution. Since $D=5-4 \sqrt{2}<0$, the equation has no roots.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (12 points) In trapezoid $A B C D$ with bases $A D=17$ and $B C=9$, points $E$ and $F$ are marked on the bases respectively such that $M E N F$ is a rectangle, where $M$ and $N$ are the midpoints of the diagonals of the trapezoid. Find the length of segment $E F$.
|
Answer: 4.
Solution. The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases, so $M N=\frac{A D-B C}{2}=4$. Since $M E N F$ is a rectangle, its diagonals are equal. Therefore, $E F=M N=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (12 points) A guard has detained a stranger and wants to drive him away. But the person caught said that he had made a bet with his friends for 100 coins that the guard would not drive him away (if the guard does, he has to pay his friends 100 coins, otherwise they pay him), and, deciding to bribe the guard, offered him to name a sum. What is the largest number of coins the guard can ask for so that the stranger, acting solely in his own interest, would definitely pay the guard?
|
Answer: 199.
Solution. If the guard asks for 199 coins, then the outsider, agreeing, will give him this amount, but will win the dispute and receive 100 coins. In total, he will lose 99 coins. If the outsider refuses, he will lose the dispute and lose 100 coins, which is less favorable (by 1 coin) for the one caught. If the guard demands 200, the outsider might refuse, as there is no difference in profit. If the guard demands more, it is more profitable for the outsider to refuse. The guard can ask for less, but the problem requires finding the largest amount. Thus, the answer is 199 coins.
|
199
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. (12 points) Find the smallest natural number such that after multiplying it by 9, the result is a number written with the same digits but in some different order.
|
Answer: 1089.
Solution. Note that the number must start with one, otherwise multiplying by 9 would increase the number of digits. After multiplying 1 by 9, we get 9, so the original number must contain the digit 9. The number 19 does not work, so two-digit numbers do not work. Let's consider three-digit numbers. The second digit (after the one) of the original number does not exceed 1, otherwise we get an increase in the number of digits. Therefore, there are only two such numbers: $\overline{1 a 9}$, where $a=0$ or $a=1$. Both numbers 109 and 119 do not meet the requirement of the problem. Let's consider three-digit numbers of the form $\overline{1 a b 9}$, where $a=0$ or $a=1$. Among them, we need to find the smallest one that satisfies the condition of the problem. But already at $a=0$ we get the number 1089, this is the answer ( $1089 \cdot 9=9801$ ).
|
1089
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. (12 points) The surface of a round table is divided into $n$ identical sectors, in which numbers from 1 to $n (n \geqslant 4)$ are written sequentially clockwise. Around the table sit $n$ players with numbers $1,2, \ldots, n$, going clockwise. The table can rotate around its axis in both directions, while the players remain in place. The players are seated at equal distances from each other, so when the table stops rotating, exactly one player is opposite each sector and receives the number of coins written on that sector. After $m$ rotations of the table, player №1 received 74 fewer coins than player №4, and player №2 received 50 fewer coins than player №3. Find $m$, given that player №4 received 3 coins twice as often as 2 coins, but half as often as 1 coin.
|
Answer: 69.
Solution. Let player No. 3 get one coin exactly $k$ times, then we get the equation $(m-k)-(n-1) k=50$. Exactly in $7 k$ cases, one coin was received by someone from players $2,3,4$, then we get the equation $3(m-7 k)-7 k(n-3)=74$. We expand the brackets, combine like terms, and get a system of two equations $m-n k=50,3 m-7 n k=74$. We multiply the first equation by 7, subtract the second from it, and get $m=69$.
|
69
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the area of a right triangle if the height drawn from the right angle divides it into two triangles, the radii of the inscribed circles of which are 3 and 4.
|
Answer: 150.
Solution. The ratio of the radii of the inscribed circles is equal to the similarity coefficient of the right triangles into which the height divides the original triangle. This coefficient is equal to the ratio of the legs of the original triangle. Let these legs be denoted as $3x$ and $4x$. By the Pythagorean theorem, the hypotenuse of the original triangle is $5x$, and the radius of the inscribed circle, due to similarity, is 5. Using the equality $2r = a + b - c$ for the radius of the inscribed circle (where $a$ and $b$ are the legs, and $c$ is the hypotenuse), we get the equation: $10 = 3x + 4x - 5x$, from which $x = 5$. Thus, the legs of the original triangle are 15 and 20, and its area is $S = \frac{1}{2} \cdot 15 \cdot 20 = 150$.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the minimum value of the expression $\frac{1}{1-x^{2}}+\frac{4}{4-y^{2}}$ under the conditions $|x|<1,|y|<2$ and $x y=1$.
Answer: 4.
|
Solution. Using the inequality between the arithmetic mean and the geometric mean, under the given conditions on $x$ and $y$, we obtain
$$
\frac{1}{1-x^{2}}+\frac{4}{4-y^{2}} \geqslant 2 \sqrt{\frac{1}{1-x^{2}} \cdot \frac{4}{4-y^{2}}}=\frac{4}{\sqrt{5-4 x^{2}-y^{2}}}=\frac{4}{\sqrt{1-(2 x-y)^{2}}} \geqslant 4
$$
and all inequalities become equalities if $2 x=y$ and $x y=1$, i.e., $x=\frac{1}{\sqrt{2}}, y=\sqrt{2}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. All natural numbers, the sum of the digits of each of which is equal to 5, were arranged in ascending order. What number is in the 125th place
#
|
# Answer: 41000.
Solution. Let's calculate the number of $n$-digit numbers, the sum of the digits of each of which is equal to 5, for each natural $n$. Subtract 1 from the leading digit, we get a number (which can now start with zero), the sum of the digits of which is equal to 4. Represent the digits of this number as cells, in each of which there is a number of balls equal to the digit in the corresponding place. Distributing 4 balls into $n$ cells is the same as placing $n-1$ partitions between 4 balls (there may be no balls between some partitions). This can be done in $C_{n+3}^{4}=\frac{(n+3)(n+2)(n+1) n}{24}$ ways, which is also the number of the desired $n$-digit numbers.
For $n=1,2,3,4,5$, we get $C_{4}^{4}=1, C_{5}^{4}=5, C_{6}^{4}=15, C_{7}^{4}=35, C_{8}^{4}=70$, totaling 126 numbers. The 126th place is occupied by the largest such five-digit number, i.e., 50000. Therefore, the 125th place is occupied by the previous one - 41000.
|
41000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Having walked $2 / 5$ of the length of a narrow bridge, a pedestrian noticed that a car was approaching the bridge from behind. Then he walked back and met the car at the beginning of the bridge. If the pedestrian had continued walking forward, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the pedestrian's speed.
|
Answer: 5.
Solution. In the time $t$ that the pedestrian walked towards the car until they met at the beginning of the bridge, he covered $2 / 5$ of the bridge's length. Therefore, if the pedestrian continued walking forward, in time $t$ he would have covered another $2 / 5$ of the bridge's length, and he would have $1 / 5$ of the bridge's length left to walk, while according to the problem, the car would have reached the beginning of the bridge in time $t$ and would have the entire bridge left to travel before meeting the pedestrian. Thus, the ratio of the car's speed to the pedestrian's speed is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many solutions does the equation
\[
\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}=\frac{2}{x^{2}} ?
\]
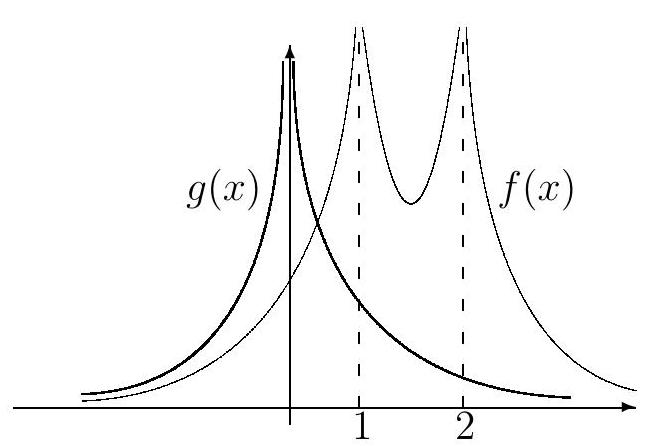
|
Answer: 1.
Solution. Let's introduce the functions $f(x)=\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}$ and $g(x)=\frac{2}{x^{2}}$.
For $x<0$, both functions $f$ and $g$ are positive, but $f(x)$ increases from $+\infty$ to 2 (not inclusive), since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}<0 \quad \text { for } \quad x \in(-\infty ; 0)$, while $g(x)$ decreases from $+\infty$ to 2 (not inclusive), since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(-\infty ; 0)$. Therefore, for $x<0$, the equation $f(x)=g(x)$ has no solutions.
For $0<x<1$, the function $f$ decreases from $+\infty$ to 2 (not inclusive), since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}<0 \quad \text { for } \quad x \in(0 ; 1)$, while the function $g$ decreases from $+\infty$ to 2 (not inclusive), since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(0 ; 1)$. However, for $0<x<1$, the inequality $f(x)>g(x)$ holds, because $\frac{1}{(x-1)^{2}}>\frac{1}{x^{2}}$ and $\frac{1}{(x-2)^{2}}>\frac{1}{x^{2}}$, so $f(x)>g(x)$. Therefore, for $0<x<1$, the equation has no solutions.
For $x>2$, the function $f$ increases from 2 (not inclusive) to $+\infty$, since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}>0 \quad \text { for } \quad x \in(2 ; +\infty)$, while the function $g$ decreases from 2 (not inclusive) to 0, since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(2 ; +\infty)$. For $x>2$, the inequalities $0<\frac{1}{(x-1)^{2}}<\frac{1}{x^{2}}$ and $\frac{1}{(x-2)^{2}}<\frac{1}{x^{2}}$ hold, so $f(x)<g(x)$. Therefore, for $x>2$, the equation has no solutions.
## Second Solution.
The original equation, under the conditions $x \neq 0, x \neq 1, x \neq 2$, is equivalent to the equation $6 x^{3}-21 x^{2}+24 x-8=0$. Consider the function $f(x)=6 x^{3}-21 x^{2}+24 x-8$. Since $f^{\prime}(x)=18 x^{2}-42 x+24$, $x=1$ is a point of maximum, and $x=\frac{4}{3}$ is a point of minimum. The function $f$ is increasing on the domain $(-\infty, 1) \cup\left(\frac{4}{3} ;+\infty\right)$ and decreasing on the interval $\left(1 ; \frac{4}{3}\right)$. Since $f(0)=-8, f(1)=1, f\left(\frac{4}{3}\right)=\frac{8}{9}$, the equation $f(x)=0$ has a unique root, which lies in the interval $(0 ; 1)$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Given three points, the distances between which are 4, 6, and 7. How many pairwise distinct triangles exist for which each of these points is either a vertex or the midpoint of a side?
|
Answer: 11.
Solution. Let's list all the constructions of triangles that satisfy the condition of the problem, with
| | Description of the triangle | | Side lengths |
| :---: | :---: | :---: | :---: |
| №1 | All points are vertices | | $4,6,7$ |
| | One point is a vertex, two are midpoints of sides | | |
| №2 | | The vertex is at the extension of both sides of lengths 4 and 6 | $8,12,14$ |
| №3 | | The extension of the side of length 4 | $8,14,2 \sqrt{94}$ |
| №4 | | The extension of the side of length 6 | $12,14,2 \sqrt{154}$ |
| №5 | | The vertex is at the extension of both sides of lengths 4 and 7 | $8,12,14$ |
| №6 | | The extension of the side of length 4 | $8,12,2 \sqrt{55}$ |
| №7 | | The extension of the side of length 7 | $12,14,2 \sqrt{154}$ |
indicating the lengths of the sides.
| №8 | | The vertex is at the extension of both sides of lengths 6 and 7 | $8,12,14$ |
| :---: | :---: | :---: | :---: |
| №9 | | The extension of the side of length 6 | $8,12,2 \sqrt{55}$ |
| $\overline{№ 10}$ | | The extension of the side of length 7 | $8,14,2 \sqrt{94}$ |
| | Two points are vertices, one is the midpoint of a side | | |
| №11 | | The vertices are on the side of length 4, the side of length 7 is extended | $4,14, \sqrt{154}$ |
| $\overline{№ 12}$ | | The side of length 6 is extended | $4,12, \sqrt{154}$ |
| №13 | | The vertices are on the side of length 6, the side of length 4 is extended | $6,8, \sqrt{94}$ |
| №14 | | The side of length 7 is extended | $6,14, \sqrt{94}$ |
| №15 | | The vertices are on the side of length 7, the side of length 4 is extended | $7,8, \sqrt{55}$ |
| №16 | | The side of length 6 is extended | $7,12, \sqrt{55}$ |
| №17 | All points are midpoints of sides | | $8,12,14$ |
Thus, there are 17 ways of construction, leading to 11 different triangles.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. To what power must the root $x_{0}$ of the equation $x^{11} + x^{7} + x^{3} = 1$ be raised to obtain the number $x_{0}^{4} + x_{0}^{3} - 1 ?$
|
Answer: 15.
Solution. If $x_{0}=1$, then $x_{0}^{4}+x_{0}^{3}-1=1$, so in this case the degree can be any. But the number $x_{0}=1$ does not satisfy the equation $x^{11}+x^{7}+x^{3}=1$, therefore $x_{0} \neq 1$.
Since $1=x_{0}^{11}+x_{0}^{7}+x_{0}^{3}$, we get
$$
x_{0}^{4}+x_{0}^{3}-1=x_{0}^{4}+x_{0}^{3}-x_{0}^{11}-x_{0}^{7}-x_{0}^{3}=x_{0}^{4}\left(1-x_{0}^{7}-x_{0}^{3}\right)=x_{0}^{4}\left(x_{0}^{11}+x_{0}^{7}+x_{0}^{3}-x_{0}^{7}-x_{0}^{3}\right)=x_{0}^{15} .
$$
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At the disco, 42 people arrived: boys and girls. Each girl danced with all the boys, except for four, and each boy danced with all the girls, except for three. How many boys were at the dance? (Folklore)
|
Answer: 24. Solution: Let $m$ be the number of boys and $d$ be the number of girls who came to the disco. Denote the boys by blue dots, the girls by red dots, and connect the boys and girls who did not dance with each other by segments. Let there be a total of $k$ segments. Since 4 segments come out of each red dot and 3 segments come out of each blue dot, and each segment connects a red and a blue dot, the equations $4 d=k=3 m$ are satisfied, from which $d=3 m / 4$. According to the condition, $m+d=m+3 m / 4=7 m / 4=42$, from which $m=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The divisors of a natural number $n$ (including $n$ and 1), which has more than three divisors, were listed in ascending order: $1=d_{1}<d_{2} \ldots<d_{k}=n$. The differences $u_{1}=d_{2}-d_{1}, u_{2}=d_{3}-d_{2}, \ldots, u_{k-1}=d_{k}-d_{k-1}$ turned out to be such that $u_{2}-u_{1}=u_{3}-u_{2}=\ldots=u_{k-1}-u_{k-2}$. Find all such $n$. (S. Berlov)
|
Answer: 10. Solution: Let $n$ be odd. Then $u_{k-1}=d_{k}-d_{k-1} \geq n-n / 3=2 n / 3$. In this case, $u_{k-2}=d_{k-1}-d_{k-2}n / 3$, but $u_{k-1}-u_{k-2}=u_{k-2}-u_{k-3}<u_{k-2}<n / 3$ - a contradiction. In the case of even $n$, we get $u_{k-1}=d_{k}-d_{k-1}=n / 2, u_{k-2}=d_{k-1}-d_{k-2}=n / 2-d_{k-2}$, so $u_{k-1}-u_{k-2}=d_{k-2}$. But $u_{2}-u_{1}=d_{3}-2 d_{2}+d_{1}=d_{3}-3$, which can only equal $d_{k-2}$ when $k=4$. Then $d_{k-2}=d_{2}=2, d_{3}=n / 2=d_{2}+3=5$ and $n=10$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numbers from 1 to 2150 are written on a board. Every minute, each number undergoes the following operation: if the number is divisible by 100, it is divided by 100; if it is not divisible by 100, 1 is subtracted from it. Find the largest number on the board after 87 minutes.
|
Answer: 2012. Solution. All numbers, the last two digits of which are 86 or less, will transform into numbers ending in 00 within 87 minutes, and in the next step, they will decrease by a factor of 100. In the end, all such numbers will be no more than $2100 / 100=21$ after 87 minutes. Those numbers that end in 87 or more will decrease by 87 over 87 minutes. The largest of such numbers is 2099, and it will turn into 2012 after 87 minutes.
|
2012
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. 99 wise men sat at a round table. They know that fifty of them are wearing hats of one of two colors, and the other forty-nine are wearing hats of the other color (but it is not known in advance which of the two colors 50 hats are, and which 49 are). Each wise man can see the colors of all the hats except his own. All the wise men must simultaneously write down (each on their own piece of paper) the color of their hat. Can the wise men agree in advance to answer in such a way that at least 74 of them give the correct answer? (U. Feige, proposed by K. Knop)
|
Solution. Let there be 50 white and 49 black hats among the hats. It is clear that the 49 sages who see 50 white and 48 black hats know that they are wearing black hats. Now let each of those who see 49 white and black hats name the color that predominates among the 49 people following them clockwise. If A is one of these sages, and B is the 25th sage from A clockwise wearing a white hat. If there are no more than 48 people between A and B, A will say that he is wearing a white hat; otherwise, B will say that he is wearing a white hat. Since all 50 sages in white hats are divided into 25 such pairs (A, B), 25 of them will correctly name the color of their hat, and in the end, there will be at least $49+25=74$ correct answers.
|
74
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Let's call two positive integers almost adjacent if each of them is divisible (without a remainder) by their difference. During a math lesson, Vova was asked to write down in his notebook all numbers that are almost adjacent to $2^{10}$. How many numbers will he have to write down?
|
Answer: 21. Solution. The number $2^{10}$ is divisible only by powers of two: from $2^{0}$ to $2^{10}$. Therefore, the numbers that are almost adjacent to it can only be $2^{10}-2^{9}, 2^{10}-2^{8}, \ldots, 2^{10}-2^{0}, 2^{10}+2^{0}, \ldots, 2^{10}+2^{10}$ (the number $0=2^{10}-2^{10}$ does not count, as it is not positive). On the other hand, it is easy to see that all these numbers are indeed almost adjacent to $2^{10}$. Note. Due to problems with the correct display of formulas, many participants read " $2^{10}$ " as "210" in the problem statement. The problem for this number is solved similarly, the answer is 31.
|
21
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. From the odd natural numbers from 1 to 47, 12 fractions less than 1 were formed, using each number exactly once. The resulting fractions were divided into groups of equal values. What is the smallest number of groups that could have been obtained? (I. Rubanov)
|
Answer: 7. Solution: Evaluation. A fraction containing at least one of the prime numbers 17, 19, 23, 29, 31, 37, 41, 43, 47 cannot equal any of our other fractions, because already $17 \cdot 3 > 47$. Since there are no more than nine such "lonely" fractions, among the constructed fractions there are some that are not equal to them. Therefore, if there are at least six "lonely" fractions, there are no fewer than seven groups of equal fractions. Suppose there are five "lonely" fractions (obviously, there cannot be fewer). Replace one of the remaining fractions with an equivalent irreducible fraction $\mathrm{m} / \mathrm{n}$. Since all fractions are less than 1, then $n \geq 3$. The denominators of fractions equal to $m / n$ are odd, multiples of $n$, and do not exceed 47. If $n \geq 5$, then there are no more than five such denominators, and among the seven remaining fractions, there will be two that are not equal; the evaluation is proven. For $n=3$, there are eight odd numbers that are multiples of 3 and do not exceed 47: $3, 9, 15, 21, 27, 33, 39, 45$. But all the remaining fractions after reduction should give $1 / 3$, and in one set, fractions $1 / 3$ and $3 / 9$, as well as fractions $5 / 15$ and $15 / 45$, cannot coexist, so there are no more than six fractions equal to $1 / 3$. Thus, in this case, among the seven remaining fractions, there will be two that are not equal. Example when there are exactly 7 classes: $\{1 / 3, 5 / 15, 7 / 21, 9 / 27, 11 / 33, 13 / 39\}, \{25 / 41\}, \{35 / 43\}, \{45 / 47\}, \{17 / 19\}, \{23 / 29\}, \{31 / 37\}$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Among the natural numbers $a_{1}, \ldots, a_{k}$, there are no identical ones, and the difference between the largest and the smallest of them is less than 1000. For what largest $k$ can it happen that all quadratic equations $a_{i} x^{2}+2 a_{i+1} x+a_{i+2}=0$, where $1 \leq i \leq k-2$, have no roots? (I. Bogdanov)
|
Answer. For $k=88$. Solution. Let the sequence $a_{1}, \ldots, a_{k}$ satisfy the condition of the problem. The absence of roots in the equations specified in the condition is equivalent to the inequality $\left(a_{i+1}\right)^{2}0$, from which $e-d>0$.
Let $a_{m}$ be the smallest number in the sequence. Obviously, one of the numbers $a_{m-1}$ and $a_{m+1}$ is not less than $a_{m}+1$, and the other is not less than $a_{m}+2$. Without loss of generality, we assume that $a_{m-1} \geq a_{m}+1$, and $a_{m+1} \geq a_{m}+2$. Then, by the lemma, $a_{m-2}>a_{m-1}+1$, that is, $a_{m-2} \geq a_{m-1}+2$. Similarly, $a_{m-3} \geq a_{m-2}+3, \ldots, a_{1} \geq a_{2}+(m-1)$. Going in the other direction, we similarly obtain $a_{m+2} \geq a_{m+1}+3, \ldots, a_{k} \geq a_{k-1}+(k-m+1)$. From this, $a_{1} \geq a_{m}+1+2+\ldots+(m-1)=a_{m}+m(m-1) / 2$ and $a_{k} \geq a_{m}+2+3+\ldots+(k-m+1)=a_{m}+(k-m)(k-m+3) / 2$.
Since the difference between any two numbers in our sequence is less than
1000, from the obtained inequalities we have $m(m-1) / 2<1000$ and $(k-m) \cdot(k-m+3) / 2<1000$, from which $m \leq 45, k-m \leq 43$ and $k \leq 88$.
Example. Let $a_{45}=10000, \quad a_{i}=10000+1+2+\ldots+(45-i) \quad$ for $1 \leq i \leq 44$, $a_{i}=10000+2+\ldots+(i-44) \quad$ for $46 \leq i \leq 88$. It is not difficult to verify that $a_{45}<a_{44}<a_{46}<a_{43}<a_{47}<\ldots<a_{88}<a_{1}$, so all numbers $a_{i}$ are distinct, and that $a_{1}-$ $a_{45}=1+2+\ldots+44=990<1000$. It remains to check the fulfillment of the inequality $(*)$. If $i=44$, the inequality is obvious. Otherwise, let $b=a_{i+1}-a_{i}$. Then, by construction, $a_{i+2}=a_{i}+2 b+1$, and the inequality $(*)$ is written in the form $\left(a_{i}+b\right)^{2}<a_{i}\left(a_{i}+2 b+1\right)$. Expanding the brackets and combining like terms, we get the inequality $b^{2}<a_{i}$, which is satisfied, since $b^{2} \leq 44^{2}<10000 \leq a_{i}$.
|
88
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. For what largest $n$ can the numbers $1,2, \ldots, 14$ be colored red and blue so that for any number $k=1,2, \ldots, n$ there exist a pair of blue numbers whose difference is $k$, and a pair of red numbers whose difference is also $k$? (D. Khramtsov)
|
Answer: $n=11$. Solution. Obviously, $\mathrm{n} \leq 12$, since there is only one pair of numbers with a difference of 13. Suppose the required is possible for $n=12$. The number 12 can be represented as the difference of numbers from 1 to 14 in exactly two ways: 13-1 and 14-2. Let the number 1 be red for definiteness. Then the number 13 is also red, and the numbers 2 and 14 are blue. Next, there are three pairs with a difference of 11: 12-1, 13-2, 14-3. The pair 13 and 2 is bicolored, so the other two pairs are monochromatic, which means the number 12 is red (like 1), and the number 3 is blue. Continuing in this way to consider differences of $10, 9, 8$, and 7, at each step we will find that all possible pairs, except for two, are already bicolored, and therefore the colors of two more numbers are uniquely determined. In the end, we will find that the numbers from 2 to 7 inclusive are blue, and the numbers from 8 to 13 are red. But in this case, the number 6 cannot be represented as the difference of either red or blue numbers - a contradiction. Therefore, $n \leq 11$. It remains to show that $n$ can equal 11. One example looks like this: the numbers $1,2,4,6,8,10,12$ are red, and the numbers 14, 13, 11, 9, 7, 5, 3 are blue (the arrangement of blue and red numbers is symmetric relative to the midpoint of the segment [1, 14]). There are other examples as well.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. For four different integers, all their pairwise sums and pairwise products were calculated and written on the board. What is the smallest number of different numbers that could have appeared on the board? (I. Rubanov)
|
Answer: 6. Solution: If we take the numbers $-1,0,1,2$, it is easy to verify that each of the numbers written on the board will be equal to -2, -1, 0, 1, 2, or 3 - a total of 6 different values. We will show that fewer than six different numbers could not appear on the board. Let the taken numbers be $ac+d$. If $ac+d$. Variant for completing the solution. Let $u$ and $v$ be the two largest numbers in absolute value, with $|u| \leq|v|$. If $|u| \geq 2$, then $|uv| \geq 2|v|$, which is greater than any sum. If $|u| \leq 1$, then among the original numbers there must be $-1,0$, 1. If $v>0$, at least 6 different numbers are written on the board: $-1,0,1, v,-v, v+1$. The case $v<0$ is handled similarly.
Criteria. Only the answer - 0 points.
A correct example for 6 - 2 points.
Proved that there are no fewer than five values, with no further substantial progress - 1 point.
Proved that there are no fewer than 6 different numbers, but no example - 3 points.
A correct example for 6 and proof that there are no fewer than five values, without further substantial progress - 3 points.
The same plus substantial, but incomplete progress in proving the existence of a sixth value - 4 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 2009 piles, each containing 2 stones. It is allowed to take the largest pile from those in which the number of stones is even (if there are several, then any of them), and move exactly half of the stones from it to any other pile. What is the maximum number of stones that can be obtained in one pile using such operations?
|
Answer: 2010. Solution. The operations described in the condition do not reduce the numbers of stones in the heaps, so at any moment, there is at least one stone in each of them. Therefore, it is impossible to accumulate more than $2009 \cdot 2$ $2008=2010$ stones in one heap.
We will show how to obtain a heap with 2010 stones. Take five heaps of two stones each and perform the following transformations: $(2,2,2,2,2) \rightarrow(3,1,2,2,2) \rightarrow$ $(3,1,3,1,2) \rightarrow(3,1,4,1,1) \rightarrow(5,1,2,1,1)$. Set aside three heaps of one stone each, replace them with three heaps of two stones each, and perform the following transformations: $(5,2,2,2,2) \rightarrow(5,1,3,2,2) \rightarrow(5,1,4,1,2) \rightarrow(7,1,2,1,2)$. Now set aside two heaps of one stone each, replace them with two heaps of two stones each, and similarly obtain $(9,1,2,1,2)$. When the large heap accumulates 2007 stones, there will still be three heaps of 2 stones and 2005 heaps of one stone. Proceed as follows: $(2007,2,2,2) \rightarrow(2007,1,3,2) \rightarrow(2007,1,4,1) \rightarrow(2009,1,2,1) \rightarrow$ $(2010,1,1,1)$.
Grading instructions. Only the answer - 0 points. The answer with a proof that there can be no more than 2010 stones in one heap, but without an example of how to get 2010 - 2 points. The answer with a justified example, but without a proof that more than 2010 stones in one heap is impossible - 4 points.
|
2010
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On each side of the square, 100 points are chosen, and from each chosen point, a segment perpendicular to the corresponding side of the square is drawn inside the square. It turns out that no two of the drawn segments lie on the same line. Mark all the intersection points of these segments. For what largest $k<200$ can it happen that exactly $k$ marked points lie on each drawn segment? (N. Avilov, I. Bogdanov)
|
Answer. For $k=150$. Solution. Estimation. Suppose there is an example with $k>150$. We will associate it with a $200 \times 200$ table, the rows of which correspond to horizontal segments (ordered from bottom to top), and the columns to vertical segments (ordered from left to right). In the cell of the table, there is a 1 if the corresponding segments intersect, and 0 if they do not. According to our assumption, in each row and each column, there are $200-k<50$ zeros. Note that among the rows from 51 to 150, there is at least one that starts and ends with 1 (otherwise, we would have at least 100 zeros in the first and last columns together). The corresponding horizontal segment $T$ intersects both the leftmost and the rightmost vertical segments. But there are zeros in this row, which means that some segment $X$ "falls short" of $T$ either above or below. Then in the column corresponding to segment $X$, either
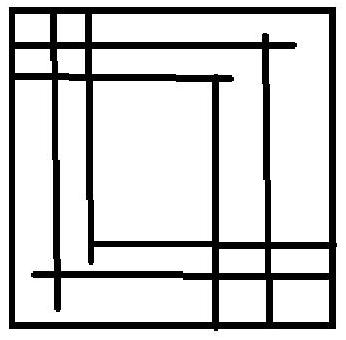
above, or below our row, there are only zeros, meaning there are at least 50 of them. Contradiction. Example. On the right in the figure. Each of the segments represents 50 parallel and equal segments of the example.
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the side AB of triangle ABC with an angle of $100^{\circ}$ at vertex C, points $P$ and $Q$ are taken such that $A P=B C$ and $B Q=A C$. Let $M, N, K-$ be the midpoints of segments $A B, C P, C Q$ respectively. Find the angle NМК. (M. Kungozhin + jury)
|
Answer: $40^{\circ}$. Solution: Extend the triangle to form a parallelogram $A C B D$. Then $M$ is the midpoint of segment $C D$.
Since $A P = B C = A D$ and $B Q = A C = B D$, triangles $A P D$ and $B Q D$ are isosceles. Therefore, $\angle Q D P = \angle A D P + \angle B D Q - \angle A D B = \left(90^{\circ} - \frac{\angle D A B}{2}\right) + \left(90^{\circ} - \frac{\angle D B A}{2}\right) - 100^{\circ} = 80^{\circ} - \frac{(\angle D A B + \angle D B A)}{2} = 40^{\circ}$. It remains to note that $\angle Q D P = \angle K M N$, since $M K$ and $M N$ are the midlines of triangles $D Q C$ and $D P C$ respectively.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the hundredth year of his reign, the Immortal Treasurer decided to start issuing new coins. In this year, he put into circulation an unlimited supply of coins with a value of $2^{100}-1$, the following year - with a value of $2^{101}-1$, and so on. As soon as the value of the next new coin can be exactly matched using the previously issued new coins, the Treasurer will be removed from office. In which year of his reign will this happen? (I. Bogdanov)
|
Answer. On the two hundredth. Solution. Let on the $k$-th year of reign $2^{k}-1$ can be made up of previously issued coins: $2^{k}-1=a_{1}+\ldots+a_{n}=N-n$, where $N$ is the sum of powers of two, each of which is divisible by $2^{100}$. Since $2^{k}$ is also divisible by $2^{100}$, the number $n-1$ must be divisible by $2^{100}$. Since, obviously, $n>1$, we get $n \geq 2^{100}+1$, from which $2^{k}-1 \geq\left(2^{100}-1\right)\left(2^{100}+1\right) \geq 2^{200}-1$, that is, $k \geq 200$, and the Treasurer will not be removed earlier than the 200th year. But on the 200th year, he will be removed, since $2^{200}-1=\left(2^{100}+1\right)\left(2^{100}-1\right)$.
|
200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In a convex quadrilateral $ABCD$, angles $A$ and $C$ are both 100°. Points $X$ and $Y$ are chosen on sides $AB$ and $BC$ respectively such that $AX = CY$. It turns out that line $YD$ is parallel to the bisector of angle $ABC$. Find angle $AXY$. (A. Kuznetsov, S. Berlov)
|
Solution. Draw a line through point $Y$ parallel to $AB$. Let it intersect $AD$ at point $K$. Then $\angle DYC = \angle DYK$ and $\angle C = 100^{\circ} = \angle BAD = \angle YKD$, so triangles $DYC$ and $DYK$ are congruent by two angles and a side. Therefore, $YK = YC = AX$ and $AXYK$ is a parallelogram. Hence, $\angle AXY = \angle AKY = 80^{\circ}$.
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $ABC$, $AC=1$, $AB=2$, $O$ is the point of intersection of the angle bisectors. A segment passing through point $O$ parallel to side $BC$ intersects sides $AC$ and $AB$ at points $K$ and $M$ respectively. Find the perimeter of triangle $AKM$.
|
Answer: 3. Solution. Note that $\angle K C O=\angle B C O=\angle K O C$ (alternate interior angles). Therefore, $O K=K C$. Similarly, $B M=O M$. Therefore, $A K+A M+K M=A K+K C+A M+B M=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. It is allowed to cut out any 18 cells from a $20 \times 20$ chessboard, and then place several rooks on the remaining cells so that they do not attack each other. What is the maximum number of rooks that can be placed in this way? Rooks attack each other if they stand on the same row or column of the board and there are no cut-out cells between them. (O. Dmitriev, R. Zhenodarov)
|
Answer: 38 rooks. Solution: Let's call the cut-out cells holes. In addition to them, add a hole at the bottom of each vertical line of the board, and a hole to the right of each horizontal line; a total of $2 \cdot 20=40$ holes are added. Suppose several rooks are placed on the board, not attacking each other. We will temporarily assume that a rook only attacks to the right and down. Then each rook attacks one hole to the right and one hole below itself (i.e., there are no other holes or rooks between it and these holes). On the other hand, each of the 18 original holes on the board is attacked by no more than two rooks (at most one from above and one from the left), and each of the 40 added holes is attacked by no more than one rook. Therefore, the total number of rooks on the board is no more than $(18 \cdot 2+40) / 2=38$.
It remains to provide an example of placing 38 rooks that satisfy the condition. For this, cut out all the cells of one of the main diagonals of the board, except for the two corner cells, and place the rooks on all cells adjacent to the cut-out ones. The figure on the right shows an example of such a placement on a $6 \times 6$ board.

|
38
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Viewers rate a movie with an integer number of points from 0 to 10. At any given time, the movie's rating is calculated as the sum of all the given ratings divided by their number. At some point in time $T$, the rating was an integer, and then with each new voting viewer, it decreased by one. What is the maximum number of viewers who could have voted after moment $T$? (O. Dmitriev, R. Zhenodarov)
|
Answer: 5. Solution: Consider a moment when the rating has decreased by 1. Suppose that before this, $n$ people had voted, and the rating was an integer $x$. This means the sum of the scores was $n x$. Let the next viewer give a score of $y$. Then the sum of the scores becomes $n x + y = (n + 1)(x - 1)$, from which we get $y = x - n - 1$. The maximum possible value of $x$ is 10, and the minimum possible value of $n$ is 1; therefore, the maximum value of $y$ (on the first such step) is 8. With each subsequent step, the value of $x$ decreases by 1, and the value of $n$ increases by 1. Thus, on the second step, the value of $y$ does not exceed 6, on the third step - 4, and so on. Since any rating is not less than 0, the number of steps does not exceed 5.
It remains to show that five steps are possible. Suppose the rating at moment $T$ is 10 (with one voter), then the second viewer gives 8 points, the third - 6, the fourth - 4, the fifth - 2, and the sixth - 0. Then the rating sequentially takes the values $9, 8, 7, 6$, and 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In quadrilateral $A B C D$, side $A B$ is equal to diagonal $A C$ and is perpendicular to side $A D$, and diagonal $A C$ is perpendicular to side $C D$. A point $K$ is taken on side $A D$ such that $A C=A K$. The bisector of angle $A D C$ intersects $B K$ at point $M$. Find the angle $A C M$. (R. Zhenodarov)
|
Answer: $\angle A C M=45^{\circ}$. Solution. Since triangle $B A K$ is a right isosceles triangle, $\angle A K B=45^{\circ}$. Let the bisector of angle $C A D$ intersect segment $B K$ at point $N$. Triangles $A N K$ and $A N C$ are equal: $A N$ is common, $A C=A K, \angle C A N=\angle K A N$. Therefore, $\angle N C A=\angle N K A=45^{\circ}$. Therefore, $C N$ is the bisector of the right angle $A C D$, and $N$ is the point of intersection of the bisectors of triangle $A C D$. Thus, point $N$ lies on the bisector of angle $A C D$ and on segment $B K$, that is, it coincides with point $M$. Therefore, $\angle A C M=\angle A C N=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. At the vertices of a cube, the numbers $1^{2}, 2^{2}, \ldots, 8^{2}$ (one number per vertex) are placed. For each edge, the product of the numbers at its ends is calculated. Find the maximum possible sum of all these products.
|
Answer: 9420. Solution. Let's color the vertices of the cube in two colors so that the ends of each edge are of different colors. Let the numbers $a_{1}, a_{2}, a_{3}, a_{4}$ be placed in the vertices of one color, and the numbers $b_{1}, b_{2}, b_{3}, b_{4}$ in the vertices of the other color, with numbers having the same indices placed in opposite vertices. Then, as it is easy to verify, the specified sum of products will be equal to $\left(a_{1}+a_{2}+a_{3}+a_{4}\right)\left(b_{1}+b_{2}+b_{3}+b_{4}\right)-$ $\left(a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}+a_{4} b_{4}\right)$. By the inequality of means,
$$
\left(a_{1}+a_{2}+a_{3}+a_{4}\right)\left(b_{1}+b_{2}+b_{3}+b_{4}\right) \leq\left(a_{1}+a_{2}+a_{3}+a_{4}+b_{1}+b_{2}+b_{3}+b_{4}\right)^{2} / 4=\left(1^{2}+2^{2}+\ldots+8^{2}\right)^{2} / 4=10404
$$
with equality achieved only when $a_{1}+a_{2}+a_{3}+a_{4}=b_{1}+b_{2}+b_{3}+b_{4}$ (1). On the other hand, the sum $a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}+a_{4} b_{4}$, where $a_{i}$ and $b_{i}$ are the numbers $1^{2}, 2^{2}, \ldots, 8^{2}$, is minimal when $8^{2}$ is multiplied by $1^{2}$, $7^{2}$ by $2^{2}$, $6^{2}$ by $3^{2}$, and $5^{2}$ by $4^{2}$ (2). Indeed, if $8^{2}$ is multiplied by $a^{2} \neq 1^{2}$, and $1^{2}$ by $b^{2}$, it is clear that multiplying $8^{2}$ by $1^{2}$ and $a^{2}$ by $b^{2}$ will decrease the sum $a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}+a_{4} b_{4}$. Then, similarly, we show that we will decrease the sum by multiplying $7^{2}$ by $2^{2}$, and so on.
Surprisingly, it is possible to achieve the simultaneous satisfaction of the condition of maximality (1) and the condition of minimality (2): for this, we need to place the numbers $1^{2}, 4^{2}, 6^{2}$, and $7^{2}$ in the vertices of one color, and the others in the vertices of the other color such that $8^{2}$ and $1^{2}$, $7^{2}$ and $2^{2}$, $6^{2}$ and $3^{2}$, $5^{2}$ and $4^{2}$ are in opposite vertices. It is clear that such an arrangement will give the desired maximum sum of products, equal to $\left(1^{2}+4^{2}+6^{2}+7^{2}\right)^{2}-\left(8^{2} \cdot 1^{2}+7^{2} \cdot 2^{2}+6^{2} \cdot 3^{2}+5^{2} \cdot 4^{2}\right)=102^{2}-984=9420$. Remark. The fact that the numbers $1^{2}, 2^{2}, \ldots, 8^{2}$ can be divided into two groups of 4 numbers with equal sums of numbers is not accidental. Note that $(n+1)^{2}-n^{2}=2 n+1$, so $\left((n+3)^{2}-(n+2)^{2}\right)-\left((n+1)^{2}-n^{2}\right)=(2 n+5)-(2 n+1)=4$ for any $n$. Therefore, $\left(1^{2}-2^{2}-3^{2}+4^{2}\right)-\left(5^{2}-6^{2}-7^{2}+8^{2}\right)=1^{2}-2^{2}-3^{2}+4^{2}-5^{2}+6^{2}+7^{2}-8^{2}=4-4=0$.
|
9420
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (I. Bogdanov) On an infinite tape, numbers are written in a row. The first is one, and each subsequent number is obtained from the previous one by adding to it the smallest non-zero digit of its decimal representation. How many digits are in the decimal representation of the number standing in this sequence at the $9 \cdot 1000^{1000}$-th position?
|
Answer: 3001. Solution. Since each number in the sequence, starting from the second, is at least one greater than the previous one, the $9 \cdot 1000^{1000}$-th number in the sequence is greater than $9 \cdot 1000^{1000}$, meaning it has at least 3001 digits. Let's denote the $n$-th number in the sequence by $a_{n}$, and let $k$ be the smallest index such that the number $a_{k}$ has 3002 digits. If we prove that $k > 9 \cdot 1000^{1000}$, then we will have that the $9 \cdot 1000^{1000}$-th number in the sequence has no more than 3001 digits, meaning it has exactly 3001 digits.
Consider the numbers from 0 to $10^{3001}-1$ that do not contain the digit 1 in their decimal representation. By padding each of these numbers with leading zeros to 3001 digits, we obtain all sequences of length 3001 consisting of digits other than 1. There are $9^{3001}$ such sequences. Therefore, among the numbers $a_{1}, \ldots, a_{k-1}$, there are no more than $9^{3001}$ numbers that do not contain the digit 1 (since all of them are less than or equal to $10^{3001}-1$).
Now consider the process of obtaining the number $a_{k}$ from $a_{1}$. On each of the $k-1$ steps, a number from 1 to 9 is added, and the number of steps on which a number other than 1 is added does not exceed $9^{3001}$. Therefore,
$$
10^{3001}-1 \leq a_{k}-a_{1} \leq 9 \cdot 9^{3001} + 1 \cdot (k-1-9^{3001}) = k-1 + 8 \cdot 9^{3001}
$$
from which $k \geq 10^{3001} - 8 \cdot 9^{3001}$. It remains to show that $10^{3001} - 8 \cdot 9^{3001} > 9 \cdot 10^{3000}$. To do this, it is sufficient to prove that $9^{3002} < 10^{3000}$. Note that $9^{7} = 4782969 < 5 \cdot 10^{6}$, from which $9^{28} < 5^{4} \cdot 10^{24} < 10^{27}$ and $9^{56} < 10^{54}$. Therefore, $9^{3002} = 9^{56} \cdot 9^{2946} < 10^{54} \cdot 10^{2946} = 10^{3000}$.
|
3001
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given two numbers (not necessarily integers), not equal to 0. If each of them is increased by one, their product will double. By what factor will their product increase if each of the original numbers is squared and then decreased by one? (D. Shiryayev, I. Rubanov)
|
Answer. 4 times. Solution. Let the numbers be denoted by $a$ and $b$. According to the condition, $(a+1)(b+1)=a b+a+b+1=2 a b$. By combining like terms in the last equality, we get $a b-a-b-1=0$, from which $(a-1)(b-1)=a b-a-b+1=2$ and $\left(a^{2}-1\right)\left(b^{2}-1\right)=(a-1)(b-1)(a+1)(b+1)=2 \cdot 2 a b=4 a b$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Squares with sides of 11, 9, 7, and 5 are arranged approximately as shown in the figure. It turned out that the area of the gray parts is twice the area of the black parts. Find the area of the white parts.
|
Answer: 42. Solution: Let the area of the white parts be $x$, and the area of the black parts be $y$. The total area of the white and black parts is $9^{2}+5^{2}=106=x+y$, and the total area of the white and gray parts is $11^{2}+7^{2}=170=x+2 y$. By subtracting the first equation from the second, we find that $y=64$, from which $x=106-y=42$.
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a football tournament where each team played against each other once, teams $A$, B, V, G, D, and E participated. Teams received 3 points for a win, 1 point for a draw, and 0 points for a loss. In the end, it turned out that teams $A$, B, V, G, and D each scored 7 points. What is the maximum number of points that team E could have scored?
|
Answer: 7 points. Solution: In a match where one of the teams won, the teams together score 3 points, in a match that ended in a draw - 2 points. Since 7 is not divisible by 3, the team that scored 7 points must have at least one draw. Since there are five such teams, there were at least three draws in the tournament. In total, as is easy to check, 15 matches were played. Therefore, all teams together scored no more than $2 \times 3 + 3 \times 12 = 42$ points. Of these, 35 points were scored by teams A, B, V, G, and D. Therefore, team $\mathrm{E}$ scored no more than 42-35 = 7 points. How it could-
| | $A$ | $B$ | $B$ | $\Gamma$ | $D$ | $E$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $A$ | $\mathrm{x}$ | 3 | 3 | 1 | 0 | 0 |
| $B$ | 0 | $\mathrm{x}$ | 3 | 3 | 1 | 0 |
| $B$ | 0 | 0 | $\mathrm{x}$ | 3 | 3 | 1 |
| $\Gamma$ | 1 | 0 | 0 | $\mathrm{x}$ | 3 | 3 |
| $D$ | 3 | 1 | 0 | 0 | $\mathrm{x}$ | 3 |
| $E$ | 3 | 3 | 1 | 0 | 0 | $\mathrm{x}$ |
have scored exactly 7 points is shown in the table on the right.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. 10 runners start simultaneously: five in blue T-shirts from one end of the running track, and five in red T-shirts from the other. Their speeds are constant and different, with each runner's speed being greater than 9 km/h but less than 12 km/h. Upon reaching the end of the track, each runner immediately turns around and runs back, and upon returning to their starting point, they finish running. The coach marks a check in the notebook each time two runners in different colored T-shirts meet (face to face or one overtakes the other), and no more than two runners meet at the same point during the run. How many checks will the coach have marked by the time the fastest runner finishes running? (I. Rubanov)
|
Answer: 50. Solution: We will show that by the time the fastest runner finishes, any two runners of different colors have met exactly twice, from which the answer 2$\cdot$5$\cdot$5 = 50 will follow.
Let $s$ (km) be the length of the track. Set $T=2 s / 12$ (hours). Since the speed of the fastest runner is less than 12 km/h, he will run the track twice in a time greater than $T$. We will show that all possible meetings of runners will occur before $T$ hours have passed since the start.
Take two runners of different colors. Their first meeting will occur when they have together run the length of the track, and this will happen in less than $s / 18 = T / 3 < T$ hours. When the faster of the two has run the entire track, the slower one, whose speed is more than 9/12 = 3/4 of the faster one's speed, will have already run more than $3 / 4$ of the track length and thus the faster one, turning around, will not catch up (for this he would have to run at least four times faster than the slower one). Therefore, the second meeting of these two will occur when both are running back. By this time, they will have together run a distance of $3 s$, and this will happen in less than $3 s / 18 = T$ hours, which completes the proof.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Twenty-two people are standing in a circle, each of them is either a knight (who always tells the truth) or a liar (who always lies). Each of them said: "The next 10 people clockwise after me are liars." How many of these 22 people are liars?
|
Answer: 20 liars
Solution: If more than 10 liars stand in a row, then one of them is telling the truth, which is impossible. There are 22 people in total, so there must be a knight among them. Consider the knight, who tells the truth, meaning that the 10 people following him are liars. Since 11 liars cannot stand in a row, there must be a knight after the 10 liars, followed by another 10 liars. In total, there are 2 knights and 20 liars.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Before starting to solve the problem, Kolya looked at the clock. It was two o'clock. Spending exactly an hour on solving it, Kolya looked at the clock again and noticed that the angle between the hour and minute hands remained the same. When did Kolya start solving the problem?
|
Answer. At 1 hour $8^{2} /{ }_{11}$ min or at 1 hour $40^{10} / 11$ min. Solution. Let it be $x$ minutes past two when Petya looked at the clock. Since the minute hand moves $6^{\circ}$ per minute, and the hour hand $-0,5^{\circ}$, the hour hand at this moment formed an angle of $30^{\circ}+0,5 x^{\circ}$ with the 12 o'clock direction, and the minute hand - an angle of $6 x^{\circ}$. In one hour, the minute hand made a full revolution and returned to its original position, while the hour hand turned $30^{\circ}$. Clearly, the minute hand will be directed along the line bisecting the angle between the two positions of the hour hand. Thus, $6 x^{\circ}=\left(\left(30^{\circ}+0,5 x^{\circ}\right)+\left(60^{\circ}+0,5 x^{\circ}\right)\right) / 2$, if the minute hand lies inside the angle formed by the two positions of the hour hand, or $6 x^{\circ}-180^{\circ}=\left(\left(30^{\circ}+0,5 x^{\circ}\right)+\left(60^{\circ}+0,5 x^{\circ}\right)\right) / 2$, if not. Solving these two equations, we get the two answers given above.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We took four natural numbers. For each pair of these numbers, we wrote down their greatest common divisor. Six numbers were obtained: 1, 2, 3, 4, 5, N, where $N>5$. What is the smallest value that the number $N$ can take? (O. Dmitriev)
|
Answer: 14. Solution: The number $N$ can equal 14, as shown, for example, by the quartet of numbers 4, $15, 70, 84$. It remains to show that $N \geq 14$.
Lemma. Among the pairwise GCDs of four numbers, there cannot be exactly two numbers divisible by some natural number $k$. Proof. If among the original four numbers there are no more than two numbers divisible by $k$, then among the pairwise GCDs, no more than one is divisible by $k$. If, however, three of the original numbers are divisible by $k$, then all three of their pairwise GCDs are divisible by $k$.
Applying the lemma to $k=2$, we get that the number $N$ is even. Applying it to $k=3, k=4$ and $k=5$, we get that $N$ is not divisible by 3, 4, and 5. Therefore, $N$ cannot equal $6, 8, 10$, and 12.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On a grid board of size $2014 \times 2014$, several (no less than one) cells are colored such that in each $3 \times 3$ square, an even number of cells are colored. What is the smallest possible number of colored cells? (M. Antipov)
|
Answer: 1342. Solution: Example. We will color the second, third, fifth, sixth, ..., 2012th, and 2013th cells in the first vertical column of the board. Then, in all 3x3 squares adjacent to the left edge of the board, exactly two cells are colored, and in all other colored cells, there are none. In this case, a total of $2 \cdot 2013 / 3=1342$ cells are colored.
Estimate: Suppose fewer than 1342 cells are colored on the board. We will call a triplet of consecutive horizontal rows of the board weak if at least two of these rows do not contain any colored cells. We will show that weak triplets exist. Indeed, if we divide all horizontal rows of the board, except the first one, into triplets of consecutive rows, we get 671 triplets. If none of them are weak, then each triplet contains at least two colored cells, and a total of at least $671 \cdot 2=1342$ cells are colored - a contradiction.
Note that there will be a weak triplet that contains colored cells. Indeed, take any weak triplet. If it does not contain any colored cells, then by moving it towards one of the colored cells, we will eventually encounter a row with colored cells and obtain the desired triplet. Fix it, remove the three rightmost cells from the rectangle $2014 \times$, formed by its horizontal rows, and divide the remaining rectangle $2013 \times 3$ into 671 squares $3 \times 3$. In each of these squares, either two cells are colored or none. If each has two, then a total of at least 1342 cells are colored - a contradiction. Therefore, there will be a square without any colored cells. We will move it horizontally towards the nearest colored cell. When it first encounters a colored cell, we will get a square with exactly one colored cell - a contradiction.
|
1342
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle $ABC$, the angle bisectors $BK$ and $CL$ are drawn. A point $N$ is marked on segment $BK$ such that $LN \parallel AC$. It turns out that $NK = LN$. Find the measure of angle $ABC$. (A. Kuznetsov)
|
Answer: $120^{\circ}$. Solution. In the isosceles triangle $L N K$, $\angle K L N = \angle L K N$. Moreover, the angles $\angle K L N$ and $\angle L K A$ are equal as alternate interior angles when the lines $L N$ and $A C$ are parallel. Thus, $\angle K L N = \angle L K A$, which means that the ray $K L$ is the bisector of angle $A K B$. Therefore, the point $L$ lying on it is equidistant from the lines $K A$ and $K B$. Additionally, it is equidistant from the lines $C A = K A$ and $C B$, as it lies on the bisector of angle $A C B$. This means that the point $L$ is equidistant from the lines $C B$ and $K B$, and therefore must lie on the bisector of one of the angles formed by these lines, in which it is contained. This is the angle $K B C_{1}$, where $C_{1}$ is a point on the extension of the segment $C B$ beyond point $B$, and its bisector must be the ray $B L = B A$. From this, we get that $\angle A B C_{1} = \angle A B K = \angle C B K$. Since these three angles together form a straight angle, each of them is $60^{\circ}$, from which $\angle A B C = \angle A B K + \angle C B K = 120^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For what largest $p$ does there exist a convex $n$-gon in which the lengths of the diagonals take on no more than two distinct values? (I. Rubanov)
|
Answer. For $n=7$. Solution. Example. A regular heptagon. It has diagonals of exactly two types: connecting vertices one apart and two apart. Evaluation. Let $A B$ be a side of a convex polygon $M$, which has diagonals of only two possible lengths $x$ and $y$. Then for any vertex $C$, not adjacent to $A$ and $B$, the sides $C A$ and $C B$ of triangle $A C B$ can only equal $x$ and $y$. The choice of these side lengths uniquely determines the vertex $C$, as it must lie on the same side of the line $A B$ as the entire polygon $M$. However, there are only four such combinations of sides: $C A=C B=x ; C A=C B=y ; C A=x, C B=y$; $C A=y, C B=y$. Of these, only one of the first two combinations is possible: otherwise, the corresponding vertices $C_{1}$ and $C_{2}$ of the polygon $M$ would lie on the perpendicular bisector of the side $A B$, and the one closer to $A B$ would be inside the triangle with vertices at $A, B$, and the other of these vertices, which contradicts the convexity of $M$. Thus, the polygon $M$ has no more than three vertices not adjacent to vertices $A$ and $B$, meaning it has no more than 7 vertices.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Vintik and Shpuntik built a machine called "Tug-Push," which moves forward on syrup with a fuel consumption of Zl/km, and backward on orange juice with a fuel consumption of 5l/km. Leaving home, they drove the machine in turns. Vintik drove 12 km in both directions. Shpuntik drove forward half as much as Vintik, and backward twice as much, after which the 75 liters of fuel they had ran out. How many kilometers will Vintik and Shpuntik have to walk back home?
|
Answer: 9 km. Solution: Let Vintik travel $2 x$ km forward and $y$ km back, then $2 x+y=12$ and $9 x+15 y=75$ (since together they traveled $3 x$ km forward and $3 y$ km back). Solving the system, we get $x=5, y=2$. It remains to calculate $3 x-3 y=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the city of liars and knights, there are 366 residents, all born on different days of a leap year. All residents of the city answered two questions. To the question “Were you born in February?” 100 people answered affirmatively, and to the question “Were you born on the 30th?” 60 people answered affirmatively. How many knights were born in February?
|
Answer: 29. Solution: To the first question, knights born in February and liars born in other months answered affirmatively. Let $x$ be the number of knights born in February, where $x$ does not exceed 29. Then, $29-x$ liars were born in February, and $100-x$ liars were born in other months. The total number of liars is $129-2x$, which means from 71 to 129 people.
To the second question, knights born on the 30th and liars born on other days answered affirmatively. Let $c$ be the number of knights born on the 30th, where $c$ does not exceed 11. Then, $11-c$ liars were born on the 30th, and $60-c$ liars were born on other days. The total number of liars is $71-2c$, which means from 49 to 71 people.
Therefore, the number of liars is 71, from which $x=29$.
|
29
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Triangles are inscribed in some cells of an $8 \times 8$ board, with one side coinciding with the side of the cell, and the third vertex lying on the opposite side of the cell. The triangles have no common points. What is the least possible number of empty cells?
|
Answer: 24. Solution: Estimation. On each side of a triangle, there are no fewer than two vertices of cells, with a total of $9 * 9=81$ vertices. Then, the total number of triangles is no more than 40, and the number of free cells is no less than 24. Example. Filled and unfilled concentric rings alternate (see figure).

|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A rectangular grid with sides 629 and 630 is cut into several squares (all cuts follow the grid lines). What is the smallest number of squares with an odd side that can be in such a partition? Don't forget to explain why there cannot be a smaller number of squares with an odd side in the partition.
|
Answer: Two. Solution. An example when there are exactly two squares: two squares with a side of 315 adjoin the side of the rectangle with a length of 630, and the remaining rectangle $630 \times 314$ is cut into squares $2 \times 2$. A smaller number of squares with an odd side cannot be: to each of the sides of length 629, at least one square with an odd side adjoins, and this cannot be the same square, as then its side would be at least 630, which is impossible. Note. One square with an odd side cannot exist also because the area of the rectangle is even, while the total area of all squares in this case would be odd.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A mad constructor created a clock with 150 hands. The first hand rotates at a speed of one revolution per hour, the second hand makes 2 revolutions per hour, ..., the 150th hand makes 150 revolutions per hour. The clock was started from a position where all hands were pointing straight up. When two or more hands meet during the operation of the clock, these hands immediately fall off. After how much time from the start will the hand rotating at a speed of 74 revolutions per hour fall off?
|
Answer: In 20 minutes. Solution. The first meeting of the hands will occur when the fastest 150th hand catches up with the slowest first hand. After this, they will fall off, and we can forget about them. The second meeting will happen when the fastest of the remaining, the 149th, catches up with the slowest of the remaining second. Reasoning similarly further, we realize that the 74th hand will fall off together with the 77th. Since the 77th hand makes three more revolutions per hour than the 74th, it catches up with the 74th at a speed of 3 revolutions per hour and will first catch up with it after $1 / 3$ of an hour.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the election in Sunny City, one could vote for Vintik, Shpuntik, or Knopochka. After the results were announced, it turned out that all candidates together received $146\%$ of the votes. The vote counter, Neznaika, explained that by mistake he calculated the percentage of votes for Vintik not from the total number of voters, but only from the number of voters for Vintik or Shpuntik (he calculated the other percentages correctly). It is known that more than 1,000 voters voted for Shpuntik. Prove that Vintik received more than 850 votes.
|
Solution. Let Shpuntik receive $a$ votes, Vintik - $k a$ votes, and Knopochka - $b$ votes. According to the condition, $k a /(a+k a)+(a+b) /(a+k a+b)=1.46 \Rightarrow k a /(a+k a)>0.46 \Rightarrow k>0.46(1+k) \Rightarrow k>46 / 54>0.85$. Since Shpuntik received more than 1000 votes, Vintik received $k a>1000 k>1000 \cdot 0.85=850$ votes, which is what we needed to prove.
|
850
|
Logic and Puzzles
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. In a convex quadrilateral $A B C D$, the bisector of angle $B$ passes through the midpoint of side $A D$, and $\angle C=\angle A+\angle D$. Find the angle $A C D$. (S. Berlov)
|
Answer. $\angle A C D=90^{\circ}$. Solution. Let $E$ be the midpoint of side $A D$, and $F$ be the
intersection point of $B E$ and $A C$. From the given condition, we have: $\angle B=360^{\circ}-2(\angle A+\angle D)$, from which $\angle A E B=180^{\circ}-\angle A-$ $\angle B / 2=\angle D$. Therefore, $B E \| C D$, and $E F$ is the midline of triangle $A C D$, meaning $A F=F C$. Thus, $B F$ is the bisector and median of triangle $A B C$, and therefore its altitude. Consequently, line $C D$, parallel to $B F$, is also perpendicular to $A C$, from which the answer follows.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At 9:00, a pedestrian set off on a journey. An hour later, a cyclist set off after him from the same starting point. At 10:30, the cyclist caught up with the pedestrian and continued on, but after some time, the bicycle broke down. After $3a$ minutes of repair, the cyclist resumed his journey, following the pedestrian, and caught up with him again at 13:00. How many minutes did the repair take? (The pedestrian's speed is constant, and he moved without stopping. The cyclist's speed is also constant, and he moved with only one break for repair.) (I. Rubanov)
|
Answer: 100 minutes. Solution: The cyclist caught up with the pedestrian half an hour after his start and one and a half hours after the pedestrian's start. This means he is moving three times faster than the pedestrian. By the time of the second meeting with the cyclist, the pedestrian had been walking for 4 hours = 240 minutes. If the cyclist had been riding without stopping for repairs, he would have reached this place in $240: 3=80$ minutes. In reality, he spent 3 hours = 180 minutes on this. Therefore, he spent $180-80=100$ minutes on repairs.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. We will call two numbers almost equal to each other if they are equal to each other or differ from each other by no more than one. A rectangular grid with sides of natural numbers a and b is such that it is impossible to cut out a rectangle along the grid lines, the area of which is almost equal to half the area of the original rectangle. What is the smallest value that the number $|a-b|$ can take? (E. Molchanov, S. Berlov)
|
Answer: 4. Solution: If one of the sides of the rectangle is even, a rectangle of half the area can be cut from it along the midline. Therefore, it is sufficient to consider the case where both sides are odd. In this case, $|b-a|$ is even. If $|b-a|=0$, then $a=b=2n+1$, half the area of the rectangle is $2n^2+2n+0.5$, and we can cut from it a rectangle of almost this area, $2n \times (n+1)$, with an area of $2n(n+1)$, and when $a=1$ - the square $1 \times 1$ with an area almost equal to $1/2$. If $|b-a|=2$, then $a=2n+1$, $b=2n-1$, half the area of the rectangle is $2n^2-0.5$, and we can cut from it a rectangle $2n \times n$ with an area almost equal to this number, $2n^2$. Thus, $|a-b| \geq 4$. Assuming $a=2n+3, b=2n-1$, we get a rectangle whose half area is $2n^2+2n-1.5$. Almost equal to it are the integer areas $2n^2+2n-1$ and $2n^2+2n-2$. For $n=3$, $2n^2+2n-1=23$ and $2n^2+2n-2=22=2 \cdot 11$. The prime numbers 23 and 11 are greater than the sides of the resulting rectangle $9 \times 5$ when $n=3$, so it is impossible to cut from it a rectangle along the grid lines with an area almost equal to half its area. Thus, the minimum possible value of $|a-b|$ is 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $ABC$, the bisector $BD$ is drawn, and in triangles $ABD$ and $CBD$ - the bisectors $DE$ and $DF$ respectively. It turned out that $EF \parallel AC$. Find the angle $DEF$. (I. Rubanov)
|
Answer: 45 degrees. Solution: Let segments $B D$ and $E F$ intersect at point $G$. From the condition, we have $\angle E D G = \angle E D A = \angle D E G$, hence $G E = G D$. Similarly, $G F = G D$. Therefore, $G E = G F$, which means $B G$ is the bisector and median, and thus the altitude in triangle $B E F$. Therefore, $D G$ is the median and altitude, and thus the bisector in triangle $E D F$, from which $\angle D E G = \angle E D G = \angle F D G = \angle G F D$. Since the sum of the four angles in the last equality is 180 degrees, each of them is 45 degrees.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A square with a side of 100 was cut into squares (not necessarily the same) with sides parallel to the sides of the original square and less than 10. Prove that the sum of the perimeters of the resulting squares is not less than 4400. (I. Rubanov)
|
Solution. Draw 11 parallel segments, two of which are sides of the $100 \times 100$ square, and the other nine divide this square into rectangles $10 \times 100$. Then each square of our dissection intersects exactly one of these segments with a segment equal to its side. Therefore, the sum of the sides of the squares in the dissection is no less than $11 \cdot 100=1100$, and the sum of the perimeters is no less than $1100 \cdot 4=4400$.
|
4400
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. On each of five cards, a number is written. The cards lie on the table numbers down. We can, by paying a ruble, point to any three cards, and we will be told the sum of the numbers written on them. For what minimum price can we surely find out the sum of all five numbers? (I. Rubanov)
|
Answer: For 4 rubles. Solution: Let the numbers written be $a, b, c, d, e$. We ask about the sums $a+b+c, a+b+d$, $a+b+e, c+d+e$. Then, by adding the first three sums and subtracting the fourth from the result, we get $3(a+b)$, then $a+b$ and, by adding $c+d+e$ to the result, the sum of all five numbers.
Suppose we managed to get by with three questions. Let's call the presence of a card in a question an occurrence. If there is a card with three occurrences, then we increase the number on it by 2, and decrease all other numbers by 1. Then the answers to all three questions will not change, but the sum of all numbers will decrease by 2. Therefore, it is impossible to determine this sum with such three questions. This means that each card has no more than two occurrences, and this is only possible if four cards have two occurrences each, and one has one. By changing the notation if necessary, we can assume that the single occurrence is on card $e$, and one of the questions is $-a+b+c$. Then in another question without card $e$, two of the three cards $a, b, c$ must be present. By changing the notation if necessary, we can assume that this is the question $a+b+d$. Then in the third question, neither of the cards $a$ and $b$ can be present, so this is the question $c+d+e$. But then, by increasing each of the numbers $a$ and $e$ by 2 and simultaneously decreasing each of the numbers $b, c$, and $d$ by 1, the answers to all three questions will not change, but the sum of all five numbers will increase by 1. Therefore, in this case, it is also impossible to determine the sum of all five numbers.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the side AC of triangle ABC with an angle of 120 degrees at vertex B, points D and E are marked such that $AD = AB$ and $CE = CB$. A perpendicular $DF$ is dropped from point D to the line BE. Find the ratio $BD / DF$.
|
Answer. 2. Solution. Let $\angle C A B=\alpha, \angle A C B=\beta$. Since $A D=A B$ and $C E=C B$, we have
$\angle D B E=\angle D B A+\angle E B C-\angle A B C=\left(180^{\circ}-\alpha\right) / 2+\left(180^{\circ}-\beta\right) / 2-120^{\circ}=60^{\circ}-(\alpha+\beta) / 2=30^{\circ}$.
Thus, in the right triangle $B F D$, the angle at vertex $B$ is $30^{\circ}$, from which $B D / D F=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. 30 people are lined up in six rows of five people each. Each of them is either a knight, who always tells the truth, or a liar, who always lies, and they all know who among them is a knight and who is a liar. A journalist asked each of them: “Is it true that there will be at least 4 rows in which liars are in the majority?”. What is the maximum number of "yes" answers he could hear?
|
Answer: 21. Solution: Let's call a row blue if it contains more than half (that is, no less than three) liars and red if there are no more than two liars in it.
Suppose the knights said "yes." Then we have no more than two red and no less than four blue rows. In the red rows, there are no more than 10 knights, and in the blue rows - no more than $2 \cdot 4=8$ knights. Therefore, in this case, the number of "yes" answers is no more than 18.
Suppose the liars said "yes." Then we have no more than three blue rows and no less than three red rows. In the blue rows, there are no more than 15 liars, and in the red rows - no more than $2 \cdot 3=6$ liars, in total - no more than 21 liars, that is, no more than 21 "yes" answers in this case. Exactly 21 "yes" answers are possible if in three rows there are 5 liars each, and in the other three rows, there are 2 liars each.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Misha and Masha were traveling by train to Kirov. Misha was lying on the bunk, while Masha was looking out the window. "How far is it to Kirov?" Misha asked Masha at 12:00. "73 kilometers," Masha replied. To the same question asked at 12:15 and 12:45, Masha answered: "62 kilometers" and "37 kilometers." It is known that if the distance was not a whole number of kilometers, Masha rounded it to the nearest whole number each time (and if there were two such numbers, she rounded to either one at her discretion). Find the speed of the train, given that it was constant. List all possibilities and prove that there are no others.
|
Answer: 48 km/h. Solution: Since Masha rounded the distance to the nearest whole number each time, at 12:00 the distance to Kirov was no less than 72.5 and no more than 73.5 km, at 12:15 - no less than 61.5 and no more than 62.5 km, and at 12:45 - no less than 36.5 and no more than 37.5 km. Therefore, in 15 minutes from 12:00 to 12:15, the train traveled no less than 10 and no more than 12 km, and in 30 minutes from 12:15 to 12:45 - no less than 24 and no more than 26 km. Since 15 minutes is a quarter of an hour and 30 minutes is half an hour, the first indicates that the speed of the train is no less than \(10 \times 4 = 40\) km/h and no more than \(12 \times 4 = 48\) km/h, and the second - that it is no less than \(24 \times 2 = 48\) km/h and no more than \(26 \times 2 = 52\) km/h. The only speed that satisfies both conditions is 48 km/h.
|
48
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. During the physical education lesson, all students of grade 8 lined up. It turned out that boys and girls alternated in the line. It is known that exactly $52\%$ of the students in grade 8 are boys. Find the number of girls in grade 8. Don't forget to justify your answer.
|
Answer: 12. Solution. If there were an even number of students in the row, the number of boys and girls would be equal. But according to the condition, there are more boys. Therefore, the number of students in the row is odd, and boys stand in odd positions. Let there be $n$ girls in the class. Then there are $n+1$ boys, and from the condition, we get that $n+1=0.52(2n+1)$, from which $n=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On an island, there are 1000 villages, each with 99 residents. Each resident of the island is either a knight, who always tells the truth, or a liar, who always lies. It is known that there are exactly 54054 knights on the island. One fine day, every resident of the island was asked the question: "Who is more in your village: knights or liars?" It turned out that in each village, 66 people answered that there were more knights, and 33 that there were more liars. How many villages on the island have more knights than liars?
|
Answer: 638. Solution. There cannot be an equal number of knights and liars in any village, because then all its inhabitants would have lied. If there are more knights in a village, then obviously 66 people told the truth and 33 people lied, and if there are more liars - then the opposite. Let there be $n$ villages where there are more knights. Then, from the condition, it follows that $66 n+33(1000-n)=54054$. Solving this equation, we get the answer.
|
638
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A square $15 \times 15$ is divided into $1 \times 1$ squares. Some of these squares were chosen, and one or two diagonals were drawn in each of the chosen squares. It turned out that no two drawn diagonals share a common endpoint. What is the maximum number of diagonals that can be drawn? (In your solution, provide the answer, a way to draw the diagonals, and a proof that this number of diagonals is indeed the maximum possible.)
|
Answer: 128. Solution. Let's number the rows and columns of the square in order with numbers from 1 to 15 and draw two diagonals in the cells located at the intersection of odd-numbered rows with odd-numbered columns. There are 64 such cells, meaning 128 diagonals will be drawn. On the other hand, the diagonals should not share endpoints, and there are a total of $16 x 16=256$ vertices in the 15x15 square. Therefore, the number of diagonals that can be drawn is no more than $256: 2=128$.
|
128
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a row, 2011 consecutive five-digit numbers are written. It turned out that the sum of the digits of the 21st number is 37, and the sum of the digits of the 54th number is 7. Find the sum of the digits of the 2011th number. (Provide all possible answers and prove that there are no other answers).
|
Answer: 29. Solution. When transitioning from the 21st number to the 54th, the sum of the digits decreases by 30. It is easy to verify that this is possible only if there is a transition through a number divisible by 10000 along the way. This means that the thousands and hundreds places of the 21st number are nines, and the tens place is at least a six. Therefore, the tens digit of the 11th number listed is one less than that of the 21st, while the other digits are the same, and the sum of the digits of the 11th number is 36. The 2011th number is exactly 2000 more than the 11th, and there is a number divisible by 10000 between them. Therefore, the 11th and 2011th numbers coincide in the last three places, and the sum of the digits in the thousands and ten-thousands places of the 2011th number is 7 less (it fell by 8 when transitioning through a number divisible by 10000, and increased by 1 when transitioning through the next number divisible by 1000), from which we get the answer.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The numbers 1, 2, 3, ..., 10 are written in a circle in some order. Petya calculated 10 sums of all triples of adjacent numbers and wrote the smallest of the calculated numbers on the board. What is the largest number that could have been written on the board?
|
Answer: 15. Solution: First, we prove that the written number is not greater than 15. We single out the number 10, and divide the remaining 9 numbers into three groups of three consecutive numbers. The sum of the numbers in these three groups is $1+2+3+\ldots+9=45$, so in at least one of the considered groups, the sum of the numbers is not greater than 45: $3=15$. An example of the arrangement of numbers, in which the number written by Petya is 15, is as follows: 1-5-9-2-7-6-8-3-4-10-(1). The given example is not the only one!
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In a football tournament, 8 teams participated, and each played against each other exactly once. It is known that any two teams that drew with each other ended up with a different number of points. Find the maximum possible total number of draws in this tournament. (A team earns 3 points for a win, 1 point for a draw, and 0 points for a loss.) (S. Tokarev)
|
Answer: 22. Solution: We will prove that no more than two teams can have exactly 6 draws. Indeed, any such team has either 6 or $6+$ 3 points (depending on whether they won or lost their decisive match). If there are three such teams, then two of them have the same number of points, meaning they did not play to a draw against each other; this is impossible because both either did not win or did not lose any matches. It is also clear that at most one team played all 7 of their matches to a draw. Thus, the sum of the number of draws for all 8 teams does not exceed $7+6+6+5+5+5+5+5=44$, and since each draw is counted twice, the total number of draws in the tournament does not exceed $44 / 2=22$. It can equal 22, as shown in the table on the right.
| | A | B | C | D | E | F | G | H |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| A | X | 1 | 1 | 1 | 1 | 1 | 3 | 3 |
| B | 1 | X | 1 | 1 | 1 | 1 | 1 | 3 |
| C | 1 | 1 | X | 3 | 0 | 1 | 1 | 1 |
| D | 1 | 1 | 0 | X | 3 | 1 | 1 | 1 |
| E | 1 | 1 | 3 | 0 | X | 1 | 1 | 1 |
| F | 1 | 1 | 1 | 1 | 1 | X | 1 | 1 |
| G | 0 | 1 | 1 | 1 | 1 | 1 | X | 1 |
| H | 0 | 0 | 1 | 1 | 1 | 1 | 1 | X |
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A car is driving at a constant speed in one direction along a straight road, near which there are two houses. At noon, when the car had not yet reached the houses, the sum of the distances from it to these houses was 10 km. After 10 minutes, when the car had already passed both houses, it turned out that the sum of the distances from it to the houses was again 10 km. What is the speed of the car? (Problem author - I. Rubanov)
|
Answer: 60 km/h. Solution: Let the houses be at points $A$ and $B$, the car was at point $C$ at noon, and at point $D$ 10 minutes later (see figure). According to the problem, $C A + C B = D A + D B = 10$. Note that $C A + C B = 2 C A + A B$, and $D A + D B = 2 D B + A B$, from which we get $C A = D B$.

Therefore, $C D = C A + A B + B D = 2 C A + A B = 10$ km. This means that in 10 minutes, the car traveled 10 kilometers. Therefore, in 60 minutes, it will travel 60 km.
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For what largest natural $\mathrm{k}$ can the cells of a $5 \times 5$ table be filled with zeros and ones (each cell must contain exactly one number) so that there are $k$ rows, in each of which the sum of the numbers is at least 3, and $k$ columns, in each of which the sum of the numbers is at most 2? (O. Nechaeva, I. Rubanov)
|
Answer. For $k=4$. Solution. For $k=5$, it is impossible to fill the table in the required manner, since when calculating the sum of the numbers in the table by adding the sums of the rows, it turns out that it is not less than $3 \cdot 5=15$, while when calculating the same sum by the columns, it turns out that it is not
| 1 | 1 | 0 | 0 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
more than $2 \cdot 5=10$. An example of filling the table that satisfies the condition of the problem for $k=4$ is shown on the right.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all natural numbers $n$ for which the number $n^{7}+n^{6}+n^{5}+1$ has exactly three natural divisors. (O. Nechaeva, I. Rubanov)
|
Answer. 1. Solution. For $n=1, n^{7}+n^{6}+n^{5}+1=4$. The number 4 has exactly three divisors: 1, 2, 4. Notice further that $n^{7}+n^{6}+n^{5}+1=\left(n^{7}+n^{5}\right)+\left(n^{6}+1\right)=n^{5}\left(n^{2}+1\right)+\left(n^{2}+1\right)\left(n^{4}-n^{2}+1\right)=\left(n^{2}+1\right)\left(n^{5}+n^{4}-n^{2}+1\right)=\left(n^{2}+1\right)(n+1)\left(n^{4}-n+1\right) . \quad$ For $n>1$, the inequalities $n^{2}+1>n+1>1$ are satisfied, and the number $\left(n^{2}+1\right)(n+1)\left(n^{4}-n+1\right)$ has at least four distinct divisors: $1, n+1, n^{2}+1$ and $\left(n^{2}+1\right)(n+1)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A smaller square was cut out from a larger square, one of its sides lying on the side of the original square. The perimeter of the resulting octagon is $40 \%$ greater than the perimeter of the original square. By what percentage is its area less than the area of the original square?
|
Answer: By $64 \%$. Solution. Let $ABCD$ be the original square with side 1 (and area 1), $KLMN$ be the cut-out square with side $x$, where $KL$ lies on $AB$ (point $K$ is closer to $A$ than $L$). Then the perimeter of the octagon $AKNMLBCD$ exceeds the perimeter of the square $ABCD$ by $KN + LM = 2x = 0.4 \cdot 4AB = 1.6AB$. That is, $x = 0.8AB$, and the area of the cut-out square is $0.64$ of the area of the original.
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are three consecutive even numbers. For the first one, we found the largest even proper divisor, for the second one - the largest odd proper divisor, and for the third one - again the largest even proper divisor. Can the sum of the three obtained divisors be equal to 2013? (A divisor of a natural number is called proper if it is different from 1 and the number itself)
|
Answer: Yes, it can. Solution. Here is an example: 1340, 1342, and 1344. For the first number, the largest even divisor is 670, for the third number, it is 672, and for the second number, the largest odd divisor is 671. $670+671+672=2013$. Remark. There are two natural ways to come up with this example. One can try to select a triplet so that the first number in it is divisible by 4, i.e., has the form $4 n$. Then the next number is $4 n+2$, and the third is $4 n+4$. But then it is clear that the divisors in question are $2 n, 2 n+1,2 n+2$. It remains to solve the equation $2 n+(2 n+1)+(2 n+2)=2013$. Or one can simply write the number 2013 as $670+671+672=2013$ and double each of the addends.
|
2013
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In parallelogram $A B C D$ with side $A B=1$, point $M$ is the midpoint of side $B C$, and angle $A M D$ is 90 degrees. Find the side $B C$.
|
Answer: 2. First solution. Draw the median $M N$ in triangle $A M D$. $A B M N$ is a parallelogram since $B M$ and $A N$ are equal and parallel, thus $M N = B C = 1$. But the median $M N$ is half the hypotenuse $A D$ in the right triangle $A M D$, from which it follows that $B C = A D = 2$. Second solution. Extend the segment $A M$ and side $C D$ until they intersect at point $K$. Consider triangle $A D K$. Segment $M C$ is parallel to the base $A D$ and equal to half of it. Therefore, $M C$ is the midline, $A M = M K$, and $K D = 2 C D = 2$. But in the considered triangle, the median $D M$ coincides with the altitude, so it is isosceles and $A D = 2 A B = 2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Sharik and Matroskin are skiing on a circular track, half of which is an uphill climb and the other half is a downhill descent. Their speeds on the climb are the same and four times slower than their speeds on the descent. The minimum distance by which Sharik lags behind Matroskin is 4 km, and the maximum distance is 13 km. Find the length of the track.
|
Answer: 24 km. Solution. The minimum lag of Sharik behind Matroskin occurs when Sharik is at the lowest point of the track, and Matroskin is climbing the hill (if Matroskin were descending at this time, it would mean that half of the track is less than 4 km, which is obviously impossible). And it remains until Matroskin reaches the highest point. After that, Sharik climbs another 4 km uphill, while Matroskin descends. If Matroskin had been descending all this time, he would have moved away from Sharik (or rather, from the highest point) by 16 km. But the distance stopped increasing when Matroskin was 13 km ahead of Sharik, which means Matroskin had reached the lowest point of the track and started climbing the hill. Since the lag increased by 3 km for each kilometer Sharik traveled, and it increased by a total of 9 km, Sharik had 4-(13-4)/(4-1) = 1 km left to the highest point when Matroskin reached the lowest point. Therefore, the length of the descent is 13-1 = 12 km, and the entire track is 24 km.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the rebus UHA = LCM(UX, UA, HA). Here U, X, A are three different digits. Two-digit and three-digit numbers cannot start with zero. Recall that the LCM of several natural numbers is the smallest natural number that is divisible by each of them.
|
Answer. $150=\operatorname{HOK}(15,10,50)$. Solution. Since UHA is divisible by UX, A $=0$, that is, the number has the form UX0. Since UX0 is divisible by U0 and X0, UX is divisible by U and X, from which it follows that X is divisible by U, and 10 U is divisible by X. Let $\mathrm{X}=\mathrm{M} \cdot \mathrm{U}$. Then $10 \mathrm{~V}$ is divisible by $M \cdot U$, from which 10 is divisible by M, that is, $M=2$ or $\mathrm{M}=5$. The condition $\mathrm{X}=2$ U is satisfied only by the numbers 120, 240, 360, 480, and the condition $\mathrm{X}=5 \mathrm{~V}$ - only by the number 150. Verification shows that only the number 150 fits.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The robbers filled a chest to the brim with gold and silver sand, with twice as much gold sand by volume as silver sand. Ali-Baba calculated that if half of the silver sand were removed and the chest topped up with gold sand, the value of the chest would increase by 20 percent. By what percentage and how would the value of the chest change if half of the gold sand were removed and the chest topped up with silver sand?
|
Answer. It will decrease by $40 \%$. Solution. Let the initial volume of silver sand in the chest be $A$, the cost of a unit volume of gold sand be $x$, and the cost of a unit volume of silver sand be $y$. Then the initial cost of the chest is $2 A x+A y$. The cost of the chest according to Ali-Baba's calculations is $2.5 A x+0.5 A y$, which leads to the equation $1.2(2 A x+A y)=2.5 A x+0.5 A y$ and the ratio $x=7 y$. Then in the second case, the cost of the chest will be $A x+2 A y=9 A y$, which, relative to the initial cost, equal to $2 A x+A y=15 A y$, constitutes $60 \%$.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of two-digit numbers that can be written in a row so that any two adjacent numbers are not coprime, while any two non-adjacent numbers are coprime?
|
Answer: 10. Solution: Ten numbers can be written: 11, 77, 91, 65, 85, 51, 57, 38, 46, 23. Suppose we managed to write 11 such numbers. Let's list the common divisor, different from 1, for each pair of adjacent numbers. This will result in 10 numbers, any two of which are coprime. All these numbers are either single-digit or double-digit. But it is impossible to choose more than four single-digit numbers, different from 1, any two of which are coprime. Therefore, in the constructed sequence of 10 numbers, there will be no fewer than six double-digit numbers. This means that some two of them will be adjacent, and some number in the original sequence will be divisible by each of them. Since they are coprime, it is also divisible by their product. But a double-digit number cannot be divisible by the product of two double-digit numbers.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The sides of 100 identical equilateral triangles are painted in 150 colors such that exactly two sides are painted in each color. If two triangles are placed with their same-colored sides together, the resulting rhombus will be called good. Petya wants to form as many good rhombi as possible from these triangles, with each triangle being used in no more than one rhombus. What is the maximum number of good rhombi that Petya can guarantee himself, regardless of the coloring method? (S. Berlov, I. Rubanov)
|
Answer: 25. Solution: Why is it always possible to get 25 good rhombuses? Let's construct the maximum possible number of good rhombuses. Suppose there are fewer than 25. Then there are at least 52 triangles that have not entered any good rhombus. Let's call such triangles single. For each triangle, choose a color, exactly one side of which belongs to the given triangle. We will call such colors highlighted. Thus, we have at least 52 highlighted colors. Note that for each highlighted color, one of the sides of this color does not belong to a single triangle (otherwise, we could glue two single triangles along the sides of the given color and increase the number of good rhombuses). Then one of the sides of each highlighted color is a side of a good rhombus. Since there are at least 52 highlighted colors, and no more than 24 good rhombuses, there will be a good rhombus with at least 3 sides having highlighted colors. Then two of these sides are in different triangles. Consequently, we can split this rhombus into two triangles and each of them can be glued to a single triangle along the side of the highlighted color. The number of good rhombuses has increased again. Contradiction. Why can't we get more than 25 good rhombuses? Let's divide our triangles into 25 quartets, and colors into 25 sextets, and match each quartet of triangles with a sextet of colors so that all sextets are used. We will color the sides of the quartet of triangles, which are matched with colors 1,2,3,4,5,6, as follows: 123,144,255,366. Since any good rhombus from these triangles includes the triangle 123, we cannot form two good rhombuses from them. By doing this with each quartet, we get a coloring that does not allow forming more than 25 good rhombuses.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Foma and Yerema were walking in the same direction along a road with kilometer markers. In one hour, Foma passed by five markers, while Yerema passed by six. Could Foma's speed have been greater than Yerema's?
|
Answer. Could. Solution. Let Erema be 50 m from the first of the poles he passed at the beginning of the hour, and 50 m beyond the sixth pole at the end of the hour. Then he walked 5100 m in an hour. Let Foma be 600 m from the first of the poles he passed at the beginning of the hour, and 600 m beyond the fifth pole he passed at the end of the hour. Then he walked $600+4000+600=5200$ m - more than Erema.
|
5200
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $p_{1}, p_{2}, \ldots, p_{100}$ be one hundred distinct prime numbers. Natural numbers $a_{1}, \ldots, a_{k}$, greater than 1, are such that each of the numbers $p_{1} p_{2}^{3}, p_{2} p_{3}^{3}, \ldots, p_{99} p_{100}^{3}, p_{100} p_{1}^{3}$ is equal to the product of some two of the numbers $a_{1}, \ldots, a_{k}$. Prove that $k \geq 150$. (I. Rubanov)
|
Solution. We will call a natural number white if it is divisible by the square of some prime number, and black otherwise. Let's say that the number $a_{i}$ serves a number from the list $p_{1} p_{2}^{3}, p_{2} p_{3}^{3}, \ldots, p_{99} p_{100}^{3}, p_{100} p_{1}^{3}(*)$, if it gives it in the product with some $a_{j}$. Obviously, in this case, one of the numbers $a_{i}, a_{j}$ is white, and the other is black. Since a white number can serve no more than one number from the list (*), there are no fewer than 100 white numbers among $a_{i}$. Moreover, if a black number serves the number $p_{k-1} p_{k}^{3}$, then it equals $p_{k-1}, p_{k}$, or $p_{k-1} p_{k}$, and therefore can serve no more than two numbers from the list (*). Thus, there are no fewer than 50 black numbers among $a_{i}$. Therefore, $k \geq 100+50=150$, which is what we needed to prove.
|
150
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. In the cells of a $10 \times 10$ table, the natural numbers 1, 2, ..., 99, 100 are arranged. Let's call a corner the figure that results from removing one cell from a 2x2 square. We will call a corner good if the number in its cell, which borders by sides with two other cells, is greater than the numbers in these two other cells. What is the maximum possible number of good corners? (Each corner is counted independently of how it is positioned relative to others, different corners can partially overlap). (A. Gолованов)
|
Answer: 162. Solution: Let's call the center of a corner the cell that borders by sides with two other cells of the corner. In any $2 \times 2$ square, no more than two of the four corners contained in it can be good: those with the two largest numbers in the center of this square. There are 81 $2 \times 2$ squares in our table, as the top-left cells of all such squares form a $9 \times 9$ square. Therefore, there are no more than $2 \times 81=162$ good corners. Let's provide an example where there are exactly 162. We will color the cells of the table in two colors in a checkerboard pattern, and arbitrarily place the numbers from 51 to 100 on the black cells, and the numbers from 1 to 50 on the white cells. It is easy to see that in this case, in each $2 \times 2$ square, there will be exactly two good corners with centers in the black cells.
|
162
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the side $A C$ of triangle $A B C$, a point $E$ is chosen. The bisector $A L$ intersects the segment $B E$ at point $X$. It turns out that $A X=X E$ and $A L=B X$. What is the ratio of the angles $A$ and $B$ of the triangle? (S. Berlov)
|
Answer. 2. Solution. Let the line passing through point $E$ parallel to $A L$ intersect lines $B C$ and $B A$ at points $P$ and $Q$ respectively. From the similarity of triangles $A B L$ and $Q B P$, we have $P Q / A L = B E / B X = B E / A L$, from which it follows that $P Q = B E$. Due to the parallelism of lines $A L$ and $P Q$, we have $\angle A Q E = \angle B A X = \angle X A E = \angle A E Q$, from which it follows that $A E = A Q$. Moreover, from the equality $A X = X E$, it follows that $\angle A E B = \angle A E X = \angle X A E$, from which it follows that $\angle A E B = \angle A Q E$. Thus, triangles $A Q P$ and $A E B$ are equal by two sides and the angle between them. Therefore, $A P = A B$ and $\angle B A E = \angle P A Q = 2 \angle C B A$, from which we obtain the answer.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Ninety-nine positive numbers are arranged in a circle. It turns out that for any four consecutive numbers, the sum of the first two of them in a clockwise direction is equal to the product of the last two of them in a clockwise direction. What can the sum of all 99 arranged numbers be? (S. Berlov)
|
Answer: 198. Solution: Let the consecutive numbers be $a, b, c, d, e$. Notice that if $a > c$, then $a + b > b + c$, which implies $c < a$. Similarly, if $c d > d e$, then $c > e$. Continuing this reasoning, we get that each number is greater than the number that is two positions clockwise from it. However, writing a chain of 99 such inequalities starting from some number $a$, we get that $a > a$ - a contradiction. Therefore, all 99 placed numbers must be equal to the same number $a$, such that $2a = a^2$, from which $a = 2$, and the desired sum is $2 \times 99 = 198$.
|
198
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A row of 100 coins is laid out. All the coins look the same, but somewhere among them are 50 counterfeit ones (and the rest are genuine). All genuine coins weigh the same, and the counterfeit ones may weigh differently, but each counterfeit is lighter than a genuine one. Can at least 34 genuine coins be found with a single weighing on a balance scale without weights? (O. Dmitriev, R. Zhenodarov)
|
Answer. It is possible. Solution. Number the coins from left to right with numbers from 1 to 100. Compare coins 17 and 84. At least one of them is genuine. Therefore, if the scales are in balance, both coins are genuine; in this case, 34 coins with numbers 1-17 and 84-100 will be genuine, since 50 counterfeit coins do not fit in these intervals. Now let's assume that coin 17 outweighs. Then it is genuine, and coin 84 is counterfeit. Since the numbers of any two counterfeit coins differ by no more than 49, in this case, the smallest number of a counterfeit coin is no less than $84-49=35$, that is, coins $1-34$ are definitely genuine. If coin 84 outweighs, similar reasoning shows that coins 67-100 are genuine.
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given two non-zero numbers. If you add one to each of them, as well as subtract one from each of them, then the sum of the reciprocals of the four resulting numbers will be equal to 0. What number can result if you subtract the sum of their reciprocals from the sum of the original numbers? Find all possibilities. (S. Berlov)
|
Answer: 0. Solution: Let the given numbers be a and b. We transform the sum of the four numbers given in the condition: $0=\frac{1}{a+1}+\frac{1}{a-1}+\frac{1}{b+1}+\frac{1}{b-1}=\frac{2 a}{a^{2}-1}+\frac{2 b}{b^{2}-1}$. Let $x=\frac{a}{a^{2}-1}=-\frac{b}{b^{2}-1}$. Then
$$
a-\frac{1}{a}+b-\frac{1}{b}=\frac{a^{2}-1}{a}+\frac{b^{2}-1}{b}=\frac{1}{x}-\frac{1}{x}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Inside parallelogram $A B C D$, a point $E$ is chosen such that $A E=D E$ and $\angle A B E=90^{\circ}$. Point $M$ is the midpoint of segment $BC$. Find the angle $DME$. (A. Kuznetsov)
|
Answer: $90^{\circ}$. Solution: Let $N$ be the midpoint of segment $A D$. Since triangle $A E D$ is isosceles, $E N \perp A D$. Since $A B \| M N$ and $\angle A B E=90^{\circ}$, then $B E \perp M N$. Therefore, $E$ is the orthocenter of triangle $B M N$. This means $M E \perp B N$. Since $B M D N$ is a parallelogram, $B N \| D M$, hence $\angle D M E=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The school table tennis championship was held according to the Olympic system. The winner won 6 matches. How many participants in the championship won more matches than they lost? (In the first round of the championship held according to the Olympic system, participants are paired. Those who lost the first game are eliminated from the championship, while those who won in the first round are paired again to play the second round. The losers are eliminated again, the winners are paired for the third round, and so on, until only one champion remains. It is known that in each round of our championship, a pair was found for each participant.)
|
Answer: 16. Solution. Since in each round every player found a partner and in each pair one of the players was eliminated, the total number of players decreased by half after each round. The winner participated in every round and won, so there were a total of six rounds. Since the winner was determined unequivocally after the sixth round, the total number of participants was $2^{6}=64$. Those who lost in the first round have one loss and zero wins, those who lost in the second round have one win and one loss. All those who advanced to the third round will have at least two wins and no more than one loss (after which they were eliminated), meaning the number of their wins is greater than the number of losses. Since the number of participants decreased by half after each round, 16 participants advanced to the third round.
Grading Instructions. The solution relies on two facts: (1) there were a total of 64 participants in the tournament; (2) the number of participants decreased exactly by half after each round. For the correct answer without any explanation - 1 point. For the correct answer with reasoning, explicitly or implicitly relying on facts (1) and (2), without justifying both of these facts - no more than 3 points. Without justifying fact (1) - no more than 5 points. Without justifying fact (2) - no more than 6 points.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.