problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. In triangle $ABC$, the median $BM$ is twice as short as side $AB$ and forms an angle of 40 degrees with it. Find angle $ABC$.
|
Answer: $110^{\circ}$. Solution. Extend the median $B M$ beyond point $M$ by its length and obtain point $D$. Since $A B=2 B M$, then $A B=B D$, which means triangle $A B D$ is isosceles. Therefore, angles $B A D$ and $B D A$ are each equal to $\left(180^{\circ}-40^{\circ}\right): 2=70^{\circ}$. $A B C D$ is a parallelogram because its diagonals are bisected by their point of intersection. Thus, angle $C B D$, like $A D B$, is $70^{\circ}$, and angle $A B C$, which is the sum of $C B D$ and $A B D$, is $110^{\circ}$.
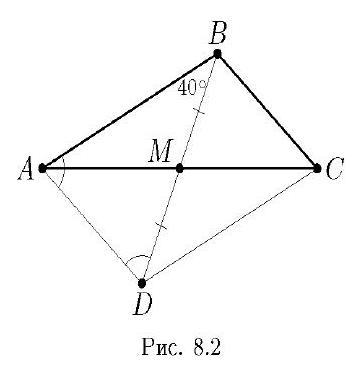
Grading Guidelines. Correct answer without justification - 0 points. The idea of extending the triangle to a parallelogram without further substantial progress - 2 points.
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Tom Sawyer took on the task of painting a very long fence, adhering to the condition: any two boards, between which there are exactly two, exactly three, or exactly five boards, must be painted in different colors. What is the smallest number of different colors he can manage with.
|
Answer: Three. Solution. Note that between the first and fourth, and the fourth and seventh boards, there are two boards each, and between the first and seventh boards, there are five boards. Therefore, the first, fourth, and seventh boards of the fence must be painted in different colors, so Tom will need at least three different paints. On the other hand, three colors will be enough for him, for example, if he paints like this: AAABBBCCCAAABBBCCC...: here, between any two same-colored boards, there are at least 6 boards.
Grading Guidelines. Only the answer - 0 points. Proven that two colors are not enough, but no example for three colors - 3 points. Only a correct example for three colors without explanation of why it works - no more than 3 points (3 points if the explanation is obvious, as in our example, and from 0 to 2 points otherwise, depending on the complexity of the justification). Proven that two colors are not enough and provided a correct example, but without explanation of why it works - from 5 to 7 points, depending on the complexity of the justification.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The length of a rectangle was reduced by $10 \%$, and the width was reduced by $20 \%$. As a result, the perimeter of the rectangle decreased by $12 \%$. By what percentage will the perimeter of the rectangle decrease if its length is reduced by $20 \%$ and its width is reduced by $10 \%$?
|
Answer: By 18%. Solution. Let the length be $a$, and the width be $b$. According to the condition, $2(0.1 a + 0.2 b) = 0.12(2 a + 2 b)$, from which we get $a = 4 b$. If the length is reduced by $20\%$, and the width by $10\%$, then the perimeter will decrease by $2(0.2 a + 0.1 b) = 1.8 b$, and it was $10 b$. Therefore, the perimeter will decrease by $18\%$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a coffee shop, 55 Indians and Turks met, each drinking tea or coffee. All Indians tell the truth when drinking tea and lie when drinking coffee, while all Turks do the opposite. When asked "Are you drinking coffee?" 44 people answered "yes," when asked "Are you a Turk?" 33 people answered "yes," and 22 people agreed with the statement "It is raining outside." How many Indians in the coffee shop are drinking tea?
|
Answer: 0. Solution. Let $h_{\psi}, h_{\kappa}$ be the number of Indians drinking tea and coffee, respectively. Similarly, define the quantities $T_{4}$ and $T_{k}$. Then from the first question, it follows that $T_{4}+T_{\kappa}=44$, and from the second question, it follows that $h_{\kappa}+T_{\kappa}=33$. Suppose that "It is raining outside" is a false statement. Then $h_{k}+T_{4}=22$. Adding the first two equations and subtracting the third, we get $2 T_{\kappa}=55$, a contradiction. Therefore, it is raining, from which $h_{4}+T_{\kappa}=22$. Adding all three equations and subtracting the obvious equation $h_{4}+h_{k}+T_{4}+T_{\kappa}=55$, we get $2 T_{\kappa}=44$, from which $T_{\kappa}=22$ and $h_{4}=0$.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the table, there are 100 identical-looking coins, of which 85 are counterfeit and 15 are genuine. You have a miracle tester, into which you can place two coins and get one of three results - "both coins are genuine," "both coins are counterfeit," and "the coins are different." Can you find all the counterfeit coins in 64 such tests? (K. Knop)
|
Answer. Yes. Solution. We will present one of the possible ways to define the fake coins. Divide the coins into 50 pairs and check all pairs except one. We will learn the number of fake coins in each pair. Since the total number of fake coins is known, we will also learn how many are fake in the remaining pair. We need to determine which coin is fake in each of the pairs consisting of different coins. For this, note that there is a pair where both coins are fake, because there are more than 50 fake coins. Take a coin from such a pair and test it with one coin from each pair where both coins are different. There are no more than 15 such pairs, since we have only 15 genuine coins. Therefore, we used no more than 49+15=64 tests.
Criteria. 1. Only the answer "yes" - 0 points. 2. The solution has two key ideas. The first: divide 100 into 50 pairs, perform 49 pairwise weighings, and show that this is enough to place each pair (including the unweighed 50th) into one of three classes - "2F", "2G", "FG". The second: show how all genuine coins can be found in no more than 15 operations, if the coins are already divided into 50 pairs, and it is known for each pair how many genuine coins it contains. If the solution contains exactly one of these two ideas, it is rated 1 point (even if the answer 64 is given as 65). 3. The fact that among 50 pairs of coins there will definitely be a pair of two fakes, and that the "worst case" when finding genuine coins is when all of them are in different pairs, is considered obvious, and we do not reduce the score for the lack of justification for these statements. The exception is the situation where the "worst case" is considered using the specifics of the number 15, and the reasoning does not transfer without changes to the case of 14 and 13 pairs: in such a case, 1 point is deducted. If the solution involves weighing coins from pairs FG arranged in a cycle, and the solution does not work for the case of one pair FG - no more than 4 points.
|
64
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Black and white balls are arranged in a circle, with black balls being twice as many as white ones. It is known that among pairs of adjacent balls, there are three times as many monochromatic pairs as polychromatic ones. What is the smallest number of balls that could have been arranged? (B. Trushin)
|
Answer: 24. Solution: Since the number of black balls is twice the number of white balls, the total number of balls is divisible by three. Let's denote it by $n$. All the balls are divided into alternating groups of consecutive balls of the same color (a group can consist of just one ball). Since the colors of the groups alternate, the total number of groups is even. Let the number of groups of each color be $k$. Then the number of adjacent balls of different colors will be $2k$, and the number of adjacent balls of the same color will be $n-2k$. From the condition of the problem, we get that $n-2k = 3 \cdot 2k$. Therefore, $n = 8k$. Thus, the total number of balls is divisible by both three and eight. Hence, $n$ is divisible by 24, and so $n \geq 24$. An example can be any circle of 8 white and 16 black balls, in which there are three white and black groups. For example, white - black - white - black - six white - fourteen black.
Criteria: Only the answer - 0 points. The answer with an example of 24 balls without proof that fewer than 24 balls is impossible - 2 points. Proof that fewer than 24 balls is impossible without an example of 24 balls - 4 points. Using the fact that the number of different-colored pairs is even without proper justification reduces the score by 1 point. Proving that the number of balls is divisible by 12 without further substantial progress - 1 point.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest natural $k$ such that for some natural number $a$, greater than 500,000, and some natural number $b$, the equality $\frac{1}{a}+\frac{1}{a+k}=\frac{1}{b}$ holds. (I. Bogdanov)
|
Answer. $k=1001$. Solution. Estimation. Let $a+k=c$ and $\text{GCD}(a, c)=d$. Then $a=d a_{1}, c=d c_{1}$ and $\frac{1}{a}+\frac{1}{c}=\frac{a_{1}+c_{1}}{d a_{1} c_{1}}$. Since the numbers $a_{1} c_{1}$ and $a_{1}+c_{1}$ are coprime, $d$ must divide $a_{1}+c_{1}$. Therefore, $d \geq a_{1}+c_{1}$ and $d^{2} \geq d\left(a_{1}+c_{1}\right)=a+c>10^{6}$, from which $d \geq 1001$ and $k=d\left(c_{1}-a_{1}\right) \geq 1001$. Example. $a=500500, k=1001$ : $\frac{1}{500500}+\frac{1}{501501}=\frac{1}{250500}$.
|
1001
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the vertices of a regular 300-gon, numbers from 1 to 300 are placed once each in some order. It turns out that for each number a, among the 15 nearest numbers to it in the clockwise direction, there are as many numbers less than a as there are among the 15 nearest numbers to it in the counterclockwise direction. A number that is greater than all 30 nearest numbers to it is called huge. What is the smallest possible number of huge numbers? (S. Berlov)
|
Answer: 10. Solution: Estimation. To prove that there are no fewer than 10 huge numbers, it is sufficient to prove that among any 30 consecutive numbers, there will be a huge one. Indeed, suppose this is not the case. Then consider the largest of these 30 numbers. On one side of it, all 15 nearest numbers will be part of this set of thirty, and therefore will be less than it. But then, according to the condition, the 15 nearest numbers on the other side of it will also be less than it, meaning it will be huge. Contradiction. Example. All numbers ending in 0 can be arranged in the following order: 300, 280, 260, 240, ..., 20, 290, 270, 250, ..., 10. After them, in a similar order, we can arrange the numbers ending in 1: 291, 271, ..., 11, 281, ..., 1, and then similarly arrange the numbers ending in 2, and so on until the cycle is complete. It is not difficult to verify that all conditions will be met, and the huge numbers will be only those from 291 to 300.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Wrote down two numbers - the first and the second. Added the second to the first - got the third, added the third to the second - got the fourth, and so on. The sum of the first six numbers is 2008. What is the fifth number?
|
Answer: 502. Solution: Let the first number be $a$, the second - $b$. Then the third number is $a+b$, the fourth $-a+2b$, the fifth $-2a+3b$, the sixth $-3a+5b$, and the sum of all six numbers is $8a+12b$. Thus, the fifth number is a quarter of the sum of all six numbers, that is, $2008: 4=502$.
Grading Guidelines. Answer without justification - 0 points. Answer obtained by considering a numerical example - 0 points. Noted that $2a+3b=(8a+12b)/4$, but division of 2008 by 4 is incorrect - 4 points.
|
502
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a right triangle, the height dropped to the hypotenuse is four times shorter than the hypotenuse. Find the acute angles of the triangle.
|
Answer: 15 and 75 degrees. Solution. Let $A B C$ be the given right-angled triangle with the right angle at vertex $C$. As is known, the median $C M$ is half the hypotenuse $A B$. The height $C H$ is given to be $A B / 4$. Therefore, in the right-angled triangle $C H M$, the hypotenuse $C M$ is twice the length of the leg $C H$. Consequently, the angle $C M H$ is 30 degrees, and the adjacent angle (let's call it $\angle B M C$) is 150 degrees. Since this is the angle at the vertex of the isosceles triangle $B M C$, $\angle A B C = \angle M B C = (180^{\circ} - \angle B M C) / 2 = 15^{\circ}$, from which we obtain the answer.
Grading Guidelines. Answer without justification - 0 points. Referring to the converse of the statement that if a leg is half the hypotenuse, it lies opposite a 30-degree angle - -3 points. Trigonometric solution without justification of the values of the necessary functions for angles of 15 and 71 degrees - no more than 3 points.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The decimal representation of a natural number $N$ consists only of ones and twos. It is known that by erasing digits from this number, any of the 10000 numbers consisting of 9999 ones and one two can be obtained. Find the smallest possible number of digits in the representation of $N$. (G. Chelnokov)
|
Answer: 10198. Solution: Example. The number 1...121...12...21...121...1, where there are 100 twos, 99 ones at the beginning and end, and 100 ones between adjacent twos. The number consisting of 9999 ones and a two, where before the two there are $100 m+n$ ones ($0 \leq m, n \leq 99$), is obtained by deleting all twos except the $(m+1)$-th, 99 ones before it, and $n$ ones after it. Estimation. Note that in the number $N$ there are no two consecutive twos - otherwise, it can be shortened by deleting one of these twos. Let the number $N$ have $k$ twos, with $a_{0}$ ones before the first two, $a_{1}$ ones between the first and second, ..., and $a_{k}$ ones after the last two. Let $s=a_{0}+\ldots+a_{k}$. To obtain a number where there is one one before the two, we will have to delete at least $a_{0}-1$ ones. Therefore, the number $s-\left(a_{0}-1\right)$ must be at least 9999, i.e., $s-a_{0} \geq 9998$. To obtain a number where there are $a_{0}+1$ ones before the two, we will have to delete the first two and at least $a_{1}-1$ ones, from which we get the inequality $s-a_{1} \geq 9998$. To obtain a number where there are $a_{0}+a_{1}+1$ ones before the two, we will have to delete the first two twos and at least $a_{2}-1$ ones, from which we get the inequality $s-a_{2} \geq 9998$. Reasoning similarly, we get that the inequality $s-a_{i} \geq 9998$ holds for all $i$ from 0 to $k-1$; in addition, to obtain a number where the two is the last, it is required that $s-a_{k} \geq 9999$. Adding all these inequalities, we get the inequality $(k+1) s-s \geq 9998(k+1)+1 \Rightarrow k s>9998(k+1) \Rightarrow$
$s>9998+9998 / k$. Since the desired number also has $k$ twos, the number of digits in it is greater than $9998+9998 / k+k \geq 9998+2 \sqrt{9998}>10197$, which is what we needed to prove.
|
10198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a $100 \times 100$ chessboard, 1975 rooks were placed (each rook occupies one cell, different rooks stand on different cells). What is the maximum number of pairs of rooks that could be attacking each other? Recall that a rook can attack any number of cells along a row or column, but does not attack a rook that is blocked by another rook. (I. Rubanov)
|
Answer: 3861. Solution: Sequentially remove from the $100 \times 100$ board the verticals and horizontals that do not contain rooks, each time gluing the edges of the removed strip. We will get a rectangle $\pi$, in each vertical and each horizontal of which there is at least one rook (obviously, the number of pairs of rooks attacking each other does not change in the process). Let there be $a$ horizontals and $b$ verticals in it. Note that if there are $k>0$ rooks in a horizontal or vertical, then there are exactly $k-1$ pairs of rooks attacking each other in it. Summing over all horizontals and verticals, we get that the number of pairs of rooks attacking each other is $1975 \cdot 2-(a+b)$ (*). At the same time, the area of the rectangle $\pi$ is not less than the number of rooks. We get that $a+b \geq 2 \sqrt{a b} \geq 2 \sqrt{1975}>2 \sqrt{1936}=88$, from which $a+b \geq 89$. Thus, the number of pairs of rooks attacking each other is no more than $1975 \cdot 2-89=3861$. To get an example where there are exactly 3861, it is sufficient to arbitrarily place 1975 rooks in some rectangle of size $45 \times 44$. This is possible since $45 \times 44=1980>1975$.
|
3861
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Zeus has scales that allow him to find out the weight of the load placed on them, and a bag with 100 coins, among which there are 10-gram and 9-gram coins. Zeus knows the total number $N$ of 10-gram coins in the bag, but it is unknown which ones weigh how much. He would like to make four weighings on the scales and as a result, guaranteed to find at least one 9-gram coin. For what largest $N$ is this possible? (K. Knop)
|
Answer. For $N=15$. Solution. First, let's outline Zeus's algorithm for $N=15$. By weighing a certain number of coins, he immediately determines the number of heavy coins among the weighed ones. Since he only needs to identify one light coin, he can weigh just 8 coins in the first weighing. If there are light coins among them, he continues to weigh these same coins (and forgets about all the others), otherwise, Zeus concludes that there are no more than seven heavy coins among the remaining coins, and he proceeds to weigh other coins. In any case, on the second weighing, he only needs to weigh four coins, on the third - two, and on the fourth - one.
Now let's prove that the task for Zeus is unsolvable when $N>15$. For this, consider Anti-Zeus, who, after Zeus places some coins on the scales during the first weighing, decides what the weight of these coins will be. Anti-Zeus tries to hinder Zeus, so his actions are as follows:
- if Zeus weighs no fewer than 8 and no more than $108-N$ coins, then Anti-Zeus makes exactly 8 of them heavy;
- if Zeus weighs fewer than 8 coins, then Anti-Zeus makes all these coins heavy,
- if Zeus weighs more than $108-N$ coins, then Anti-Zeus makes all the unweighed coins heavy.
Clearly, when $N>15$, Anti-Zeus achieves the following: no matter how Zeus divides the coins into two groups (weighed/unweighed), in each group consisting of at least 8 coins, there are at least 8 heavy coins.
On the second move, Anti-Zeus acts similarly: now each of the previous groups is divided into two parts (those that participated in the second weighing and those that did not), and Anti-Zeus ensures that in each of the four groups there are at least four heavy coins (or all are heavy if the group has fewer than 4 coins). After the third weighing, Anti-Zeus similarly tracks the 8 groups of coins that Zeus has, ensuring that in each group consisting of at least two coins, there are at least two heavy coins. Finally, on the fourth move, Anti-Zeus ensures that at least one heavy coin ends up in each non-empty group (of which there are no more than 16). Since Zeus knows nothing about each such group except its total weight, he cannot distinguish a heavy coin from a light one in this group, and therefore cannot reliably identify any light coin.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. What is the maximum number of white and black pawns that can be placed on a 9x9 grid (a pawn, regardless of its color, can be placed on any cell of the board) so that no pawn attacks any other (including those of the same color)? A white pawn attacks two diagonally adjacent cells on the next higher horizontal row, while a black pawn attacks two diagonally adjacent cells on the next lower horizontal row (see the figure). (A. Antropov)
|
Answer: 56. Solution: An example with 56 pawns is shown in the figure. Evaluation: Note that in each rectangle of three rows and two columns, there are no more than 4 pawns. Indeed, if there are at least 5, then on one of the colors, all three cells are occupied, and the pawn in the middle row attacks one of the two remaining ones. Therefore, in any rectangle of 9 rows and 8 columns, there are no more than 48 pawns (since it can be divided into 12 rectangles $3 \times 2$). Suppose we managed to place 57 pawns. Then in the ninth column, there must be at least 9 pawns, i.e., exactly 9. But then in the eighth column, there are no more than 2 pawns (otherwise, there would be a pawn not in the first and not in the last row that would attack some pawn in the ninth column). Then in the eighth and ninth columns together, there are no more than 11 pawns, and in the 2nd to 7th columns - no more than 36 pawns (they can be divided into 9 rectangles $3 \times 2$). It follows that in the first column, there should be 10 pawns - a contradiction.

|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In each cell of a $2 \times 2$ table, one number is written. All numbers are distinct, the sum of the numbers in the first row is equal to the sum of the numbers in the second row, and the product of the numbers in the first column is equal to the product of the numbers in the second column. Find the sum of all four numbers.
|
Answer: 0. Solution: Let the numbers in the top row of the table be (from left to right) $a$ and $b$, and the numbers in the bottom row (from left to right) be $c$ and $d$. By the condition, $a+b=c+d$ and $a c=b d$. Expressing $c$ from the first equation and substituting into the second, we get $a(a+b-d)=b d \Leftrightarrow(a+b)(a-d)=0$, from which, since $a-d \neq 0$, we obtain $a=-b$. Similarly, $d=-c$, from which we get the answer.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. 200 people are standing in a circle. Each of them is either a liar or a conformist. Liars always lie. A conformist who stands next to two conformists always tells the truth. A conformist who stands next to at least one liar can either tell the truth or lie. 100 of those standing said: "I am a liar," and the other 100 said: "I am a conformist." Find the maximum possible number of conformists among these 200 people. (R. Zhendarov, S. Berlov)
|
Answer: 150. Solution: A liar cannot say, "I am a liar." Therefore, 100 people who said, "I am a liar," are conformists. All of them lied, so next to each of them stands a liar. Since next to a liar there can be a maximum of two conformists, there are no fewer than 50 liars. Thus, there are no more than 150 conformists. Example. Place 50 liars in a circle. In each of the 50 gaps between the liars, place three conformists. The middle one of these three tells the truth, the two at the ends lie that they are liars, and all liars lie that they are conformists.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In pentagon $A B C D E A B=B C=C D=D E, \angle B=96^\circ$ and $\angle C=\angle D=108^\circ$. Find angle $E$.
|
Answer: $102^{\circ}$. Solution. Draw segments $B D$ and $C E$. Let them intersect at point $O$. Note that triangles $B C D$ and $C D E$ are isosceles with an angle of $108^{\circ}$ at the vertex, so the base angles are $36^{\circ}$ (they are marked on the diagram with one arc). Then $\angle B C E = \angle B D E = 72^{\circ}$. Angle $C O D$ is $108^{\circ}$ (since in triangle $C O D$ there are two angles of $36^{\circ}$). Therefore, $\angle C O B = 180^{\circ} - 108^{\circ} = 72^{\circ}$. Angles of $72^{\circ}$ are marked on the diagram with two arcs. We get that triangles $C B O$ and $D E O$ are isosceles. Thus, $A B = B O = B C = C D = D E = E O = x$. Note that $\angle O B A = 96^{\circ} - 36^{\circ} = 60^{\circ}$. Therefore, triangle $O B A$ is isosceles with an angle of $60^{\circ}$ at the vertex, i.e., equilateral. Hence, $A O = x$. Calculate angle $A O E$ $\angle A O E = \angle E O B - \angle A O B = 108^{\circ} - 60^{\circ} = 48^{\circ}$. Triangle $A O E$ is isosceles with an angle of $48^{\circ}$ at the vertex. Therefore, $\angle O E A = (180^{\circ} - 48^{\circ}) / 2 = 66^{\circ}$. We get that angle $E$ of the pentagon is $\angle A E D = \angle A E O + \angle O E D = 66^{\circ} + 36^{\circ} = 102$.
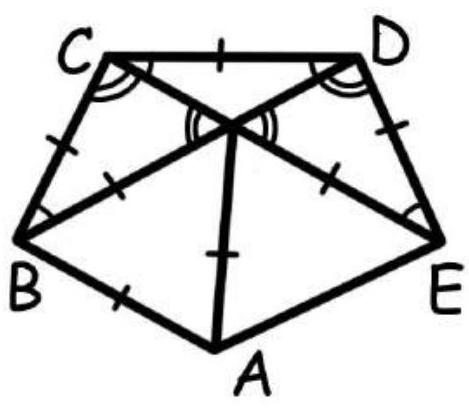
|
102
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $ABC$, angle $C$ is three times larger than angle $A$, and side $AB$ is twice as long as side $BC$. Prove that angle $ABC$ is 60 degrees.
|
Solution. Let $D$ be the midpoint of side $A B$. Since $B D=B C$, triangle $B C D$ is isosceles. Let $\angle C A D=x, \angle A C D=y$. Then $\angle D C B=3 x-y$, and $\angle C D B=x+y$. Since $\angle D C B=\angle C D B$, we have $3 x-y=x+y$, from which $y=x$. Therefore, $D C=D A=D B=B C$, which means triangle $B C D$ is equilateral, and thus angle $B$ is 60 degrees.
|
60
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. In the Thirtieth Kingdom, there are 100 cities, and no more than one road connects any two cities. One day, the tsar ordered that one-way traffic be introduced on each road, and at the same time, each road should be painted either white or black. The Minister of Transport proudly reported that after the order was carried out, from any city to any other, one could travel by alternating the colors of the roads, and in such a way that the first road in the journey would be white. What is the minimum number of roads that could have been in this country? When traveling from city to city, one can pass through intermediate cities any number of times. (M. Antipov)
|
Answer: 150. Solution: Example. Arrange the cities on a circle so that they divide it into equal arcs, and declare these arcs to be roads directed clockwise. Paint these 100 arcs in white and black colors so that the colors alternate on the circle. Direct another 50 white roads along the chords from the cities where black roads originate to the cities located one step away from them in the clockwise direction. Clearly, the described construction satisfies the emperor's order. Evaluation: We will prove a more general fact: if the kingdom has $2k$ cities, then there must be no fewer than $3k$ roads. Suppose this is not the case. Take the smallest natural $k$ such that in a kingdom of $2k$ cities, one can manage with fewer than $3k$ roads. Here $k>1$, since for two cities the order is clearly unfulfillable. Note that there are no fewer than $2k$ white roads among them, as a white road must leave each city. Therefore, there are no more than $k-1$ black roads, and hence there are at least two cities without black roads. Remove them along with the roads connected to them. In doing so, we will remove no fewer than three roads, since from each of the two cities one could leave and one could enter, and no more than one such road is counted twice. Thus, we now have $2(k-1)$ cities and fewer than $3(k-1)$ roads. Since no route with alternating road colors could pass through the removed cities, the remaining cities and roads still satisfy the emperor's condition, which contradicts the minimality of the number $k$.
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. At the vertices of a regular 100-gon, 100 chips numbered $1, 2, \ldots, 100$ were placed, in exactly that order clockwise. In one move, it is allowed to swap two adjacent chips if their numbers differ by no more than $k$. For what smallest $k$ can a series of such moves result in a configuration where each chip is shifted one position clockwise relative to its initial position? (S. Berlov)
|
Answer: 50. Solution: Example: The chip 50 is sequentially exchanged 99 times with the next one counterclockwise.
Evaluation. We reason by contradiction. Let $k<50$. First proof. We will consider the shifts of the chips relative to their initial positions, with shifts clockwise counted as positive and counterclockwise as negative. Then, when two chips are exchanged, 1 is added to the shift of one and 1 is subtracted from the shift of the other. Suppose after several moves all chips have shifted one position clockwise. Then the total shift of the chip numbered $k$ is $100 t_{k} + 1$, where $t_{k}$ is the number of complete revolutions of this chip (clockwise revolutions are counted with a plus sign, and counterclockwise with a minus sign). Since $k<50$, chips numbered 1 and 51 could not have exchanged places, and therefore they must have made the same number of complete revolutions, i.e., $t_{1} = t_{51}$. Similarly, $t_{2} = t_{52}, \ldots, t_{50} = t_{100}$. Therefore, the sum of all shifts of all chips is $100(2 t_{1} + \ldots + 2 t_{50} + 1)$. This sum must be 0, as the sum of shifts is 0 for each move. But it is not 0, since the sum in parentheses is odd. Contradiction.
Second proof. At any moment, we consider the \{lit painted\} arc from chip 100 to chip 1 clockwise. Since chips 100 and 1 cannot be exchanged in one move, any specific chip $\mathrm{m}$ $(2 \leq m \leq 99)$ could only enter the painted arc or leave the painted arc by exchanging with one of the chips 1 or 100. Since initially and at the end, chip $m$ was not on the painted arc, it must have made an equal number of \{lit entries\} to the painted arc and \{lit exits\} from the painted arc. For $m \leq 50$, chip $m$ could not have exchanged with chip 100, so it could only make \{lit entries\} or \{lit exits\} by exchanging with chip 1. On \{lit entry\}, chip 1 makes a shift of 1 clockwise, and on \{lit exit\}, 一 1 counterclockwise. We conduct similar reasoning for chips $m \geq 51$, which cannot exchange with chip 1. Thus, we find that chips 1 and 100 will make the same number of shifts clockwise and counterclockwise, so they will remain in their positions. Contradiction.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Each of the 10 people is either a knight, who always tells the truth, or a liar, who always lies. Each of them thought of some natural number. Then the first said: “My number is greater than 1”, the second said: “My number is greater than 2”, ..., the tenth said: “My number is greater than 10”. After that, they, in a different order, said (each one phrase): “My number is less than 1”, “My number is less than 2”, ..., “My number is less than 10”. What is the maximum number of knights that could have been among these 10 people? (O. Podlipsky)
|
Answer: 8. Solution: Those who in the first series of answers said that their numbers are greater than 9 and 10 are definitely liars, because these answers are incompatible with any of the answers in the second series. Therefore, there are no more than eight knights. An example when there are exactly 8 knights: the first eight in the first series of answers thought of the numbers $2, \ldots, 9$ respectively, and they give the answers "My number is less than 3", ..., "My number is less than 10" in the second series of answers. Each of the two liars thought of the number 5, and they give the last two answers of the first series and the first two answers of the second series.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There is a cube, each face of which is divided into 4 identical square cells. Oleg wants to mark 8 cells with invisible ink so that no two marked cells share a side. Rustem has detectors. If a detector is placed in a cell, the ink on it becomes visible. What is the minimum number of detectors Rustem can place in the cells so that, no matter which cells Oleg marks afterward, all the marked cells can be identified? (R. Zhinodarov, O. Dmitriev)
|
Answer: 16. Solution: Example. Let's divide all 24 cells into eight triples, where each triple consists of three cells adjacent to one vertex of the cube. Any two cells in the same triple share a common side. Since the number of marked cells is the same as the number of triples, there must be exactly one marked cell in each triple. Place 16 detectors such that there are two detectors in each triple. If one of the detectors in a given triple triggers, we have found the marked cell in that triple; if neither detector triggers, the marked cell is the one without a detector. Evaluation: Suppose we place fewer than 16 detectors. Then there will be a triple with at least two cells without detectors (let's call them "free cells")—mark these cells on the unfolded cube diagram with a dark background. On the same unfolded diagram, mark 7 cells with the letter A as shown in the figure. Now note that if we mark the seven cells A and one of the free cells with invisible ink, the detectors will not allow us to determine which of the free cells is marked. Therefore, it is not possible to get by with fewer than 16 detectors.
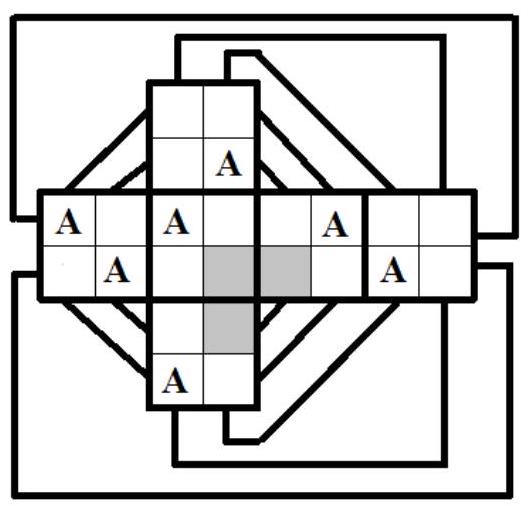
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given an equilateral triangle ABC. Point $D$ is chosen on the extension of side $A B$ beyond point $A$, point $E$ is on the extension of $B C$ beyond point $C$, and point $F$ is on the extension of $A C$ beyond point $C$ such that $C F=A D$ and $A C+E F=D E$. Find the angle BDE. (A. Kuznetsov)
|
Answer: 60 - . Solution: Complete triangle $A C E$ to parallelogram $A C E G$. Since $C F=A D$, $C E=A G$ and $\cdot F C E=\cdot D A G=60 \cdot$, triangles $D A G$ and $F C E$ are equal, from which $G D=E F$. Therefore, $D E=A C+E F=G E+G D$. This means that point $G$ lies on segment $D E$, and thus $D E \| A C$, from which $\cdot B D E=\cdot B A C=60$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. It is known that among 100 balls, exactly 51 are radioactive. There is a device into which two balls can be placed, and if both are radioactive, a light will turn on (if at least one of the two balls is not radioactive, the light will not turn on). Can all the radioactive balls be found using the device no more than 145 times?
|
Answer. Yes. Solution. Let's divide the balls into 50 pairs and test them. Consider two possible cases.
1) Exactly one of these tests revealed two radioactive balls. Then in each of the remaining 49 pairs, there is exactly one radioactive ball. Testing one of the found radioactive balls with one ball from each of the remaining pairs, we can identify all 98 remaining balls. In total, we conducted $50+49=99$ tests.
2) At least two tests revealed two radioactive balls each. Then we have already found 4 radioactive balls. Testing one of the found radioactive balls with 95 balls from the remaining 48 pairs, we will know about 99 balls whether they are radioactive or not. If there are 50 such balls, the remaining ball is radioactive, and if there are 51, it is not. We have found all the radioactive balls in $50+95=145$ tests.
Remark. More subtle reasoning can improve the estimate of 145.
|
145
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numbers 1, 2, 3, 4, 5, 6, 7 were written in a circle in some order. We will call a written number good if it is equal to the sum of the two numbers written next to it. What is the maximum possible number of good numbers among the written ones? (E. Bakayev)
|
Answer: 3. Solution: If the numbers are written, for example, in the order 2, 7, 5, 6, 1, 4, 3, then the numbers 7, 6, and 4 will be good. It remains to show that there cannot be more than three good numbers.
Note that a good number is greater than both of its neighbors, so two good numbers cannot stand next to each other. Therefore, the number following a good number clockwise should not be good, and the numbers following different good numbers should be different and not good. Consequently, among all the written numbers, the good ones do not exceed half, and thus, there are no more than three.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. On a white checkered board of size $25 \times 25$ cells, several cells are painted black, with exactly 9 cells painted black in each row and each column. What is the smallest $k$ such that it is always possible to repaint $k$ cells to white in such a way that it is impossible to cut out a black $2 \times 2$ square? (S. Berlov)
|
Solution. Evaluation. Note that if 9 cells are shaded in a row, then four of them can be repainted so that no two shaded cells are adjacent: it is enough to renumber the shaded cells from left to right and repaint the cells with even numbers. If such repainting is done with all even rows, then 48 cells will be repainted and there will be no shaded $2 \times 2$ squares, since there will be no two adjacent shaded cells in one even row.
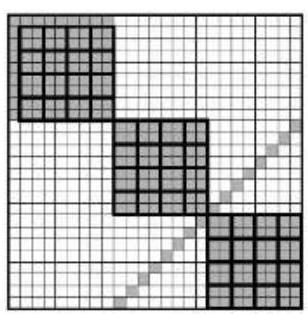
Example. Let's shade non-overlapping squares along the main diagonal: the first with a side of 9 and two with a side of 8 - and the cells located along the unshaded main diagonal of the $16 \times 16$ square containing the $8 \times 8$ squares. Then on the board, it will be possible to highlight 48 non-overlapping $2 \times 2$ squares, all cells of which are shaded. Therefore, in this example, at least 48 cells need to be repainted.
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From the natural numbers from 1 to 25, Dasha chose six such that the difference between any two chosen numbers is divisible by 4. What is the maximum number of prime numbers that Dasha could have chosen?
|
Answer: Five. First solution. The difference of two numbers is divisible by 4 if and only if these numbers have the same remainder when divided by 4. Let's list all prime numbers less than 25 and their remainders when divided by 4: 2-2, 3-3, 5-1, 7-3, 11-3, 13-1, 17-1, 19-3, 23-3. The most common remainder is 3, which appears five times, giving us the answer. Second solution. Since $5-2=3,13-11=19-17=2$, from the groups of prime numbers $\{2,3,5\},\{11,13\},\{17,19\}$ Dasha could choose no more than one number from each. Among the primes less than 25, the only numbers not in these groups are 7 and 23, so the number of prime numbers Dasha could choose is no more than five. An example where there are exactly five is given in the first solution.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle ABC, the median BM is drawn. It is known that $\angle A B M=40^{\circ}$, and $\angle C B M=70^{\circ}$. Find the ratio $A B: B M$.
|
Answer: 2. First solution. Complete the triangle $A B C$ to a parallelogram $A B C D$. Since the diagonals of a parallelogram bisect each other, point $M$ is the point of their intersection and $B D=2 B M$. On the other hand, $\angle B D A=\angle C B D=70^{\circ}$, and $\angle B A D=180^{\circ}-\angle B D A-\angle A B D=70^{\circ}=\angle B D A$, from which $A B=B D=2 B M$ and $A B: B M=2 B M: B M=2$. Second solution. Note that $B C$ is the bisector of the external angle at vertex $B$ of triangle $A B M$. Therefore, $A B: B M=A C: C M=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The cells of an $n \times n$ square are colored black and white with the condition that no four cells, located at the intersection of two rows and two columns, can all be the same color. What is the largest possible value of $n$?
|
Solution. An example for $n=4$ is shown in the figure on the right. We will prove by contradiction that it is impossible to color a $5 \times 5$ square in this way. Let's call a row predominantly black if it has more black squares than white, and predominantly white otherwise. Among the five rows, there will be either three predominantly black rows or three predominantly white rows; without loss of generality, let's assume we have found three predominantly black rows. In these rows, there are at least nine black cells.
| B | W | B | W |
| :---: | :---: | :---: | :---: |
| B | B | W | W |
| W | B | B | W |
| W | W | W | B |
Now we consider only these three rows. If in some column (let's call it A) there are three black cells, then the remaining four columns have at least six black cells. Therefore, there will be a column (let's call it B) where there are two black cells. Then, taking columns A and B and the two rows where the two black cells of column B are located, we get a contradiction.
Thus, in each column, there are no more than two black cells. But this is only possible if there are at least two black cells in at least four columns. Since there are only three ways to color two out of three cells black, in some two columns the coloring is the same, and we again get a contradiction.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A two-digit number $N$ was multiplied by 2, the digits of the result were swapped, and then the number was divided by 2. The result was the same number $N$. How many such numbers $N$ exist?
Answers:
A) none (-) B) exactly 4 (-) C) at least 10 (+) D) at least 14 (+) E) at least 15 (-)
|
Solution. Since the result turned out to be the same number, two identical digits were swapped. This means that $2 \mathrm{~N}$ should have two such digits. Let's consider several cases:
1) When multiplying by 2, there was no carry-over to the next place value. Obviously, as $N$, the numbers 11, 22, 33, 44 fit and only they do.
2) When multiplying by 2, there was a carry-over to the tens place. Then the first digit of the number $2 \mathrm{~N}$ is 1. The last digit is always even. Note that if there was a carry-over in the units place during multiplication, then in $2 \mathrm{~N}$ only the last digit (the units digit) will be even. This means that in this case $2 \mathrm{~N}=11 *$, so $N$ can be 55, 56, 57, 58, or 59.
3) Now let's assume there was only a carry-over to the tens place. Then the number $2 \mathrm{~N}$ has two identical even last digits. That is, $2 \mathrm{~N}$ is equal to 100, 122, 144, 166, or 188. Then $N$ is equal to 50, 61, 72, 83, or 94.
Thus, there are a total of 14 different numbers.
|
14
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A numerical sequence is given:
$x_{0}=\frac{1}{n} ; x_{k}=\frac{1}{n-k}\left(x_{0}+x_{1}+\ldots+x_{k-1}\right) ; k=1,2, \ldots, n-1$.
Find $S_{n}=x_{0}+x_{1}+\ldots+x_{n-1}$, if $n=2021$.
|
# Solution.
We will prove by mathematical induction that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$. For $k=0$, this equality holds. For $k=1$, $x_{0}+x_{1}=\frac{1}{n}+\frac{1}{n-1} \cdot \frac{1}{n}=\frac{1}{n-1}$. Suppose this equality holds for all $m \leq k$, then it should also hold for $k+1$. Let's check this:
$$
\begin{aligned}
& \left(x_{0}+x_{1}+\ldots+x_{k}\right)+x_{k+1}=\frac{1}{n-k}+x_{k+1}=\frac{1}{n-k}+\frac{1}{n-(k+1)}\left(x_{0}+x_{1}+\ldots+x_{k}\right)= \\
& =\frac{1}{n-k}+\frac{1}{(n-k-1)(n-k)}=\frac{1}{n-(k+1)} .
\end{aligned}
$$
Thus, this equality also holds for $k+1$. Therefore, our assumption that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$ is correct.
Then, for $n=2021$ and $k=n-1=2020: S_{2021}=x_{0}+x_{1}+\ldots+x_{2020}=\frac{1}{2021-2020}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The function $f(x)$ satisfies the condition: for any real numbers $a$ and $b$, the equality $f\left(\frac{a+2 b}{3}\right)=\frac{f(a)+2 f(b)}{3}$ holds. Find the value of the function $f(2021)$, if $f(1)=5, f(4)=2$.
|
# Solution.
Substituting the pairs of numbers \(a=4, b=1\) and \(a=1, b=4\) into the given equation, respectively, we get
If \(a=4, b=1\), then \(f\left(\frac{4+2}{3}\right)=\frac{f(4)+2 f(1)}{3}, f(2)=\frac{2+2 \cdot 5}{3}=4, f(2)=4\).
If \(a=1, b=4\), then \(f\left(\frac{1+2 \cdot 4}{3}\right)=\frac{f(1)+2 f(4)}{3}, f(3)=\frac{5+2 \cdot 2}{3}=3, f(3)=3\).
If we take \(a=0, b=3\), we get \(f\left(\frac{0+2 \cdot 3}{3}\right)=\frac{f(0)+2 f(3)}{3}, f(2)=\frac{f(0)+2 f(3)}{3}\).
Thus, \(f(0)=3 f(2)-2 f(3), f(0)=3 \cdot 4-2 \cdot 3, f(0)=6\).
Therefore, we have \(f(0)=6, f(1)=5, f(2)=4, f(3)=3, f(4)=2\).
We can form a chain of equalities
\[
\begin{aligned}
& f\left(\frac{2021+2 \cdot 2}{3}\right)=\frac{f(2022)+2 f(2)}{3}=f(675) \\
& f\left(\frac{675+2 \cdot 0}{3}\right)=\frac{f(675)+2 f(0)}{3}=f(225) \\
& f\left(\frac{225+2 \cdot 0}{3}\right)=\frac{f(225)+2 f(0)}{3}=f(75) \\
& f\left(\frac{75+2 \cdot 0}{3}\right)=\frac{f(75)+2 f(0)}{3}=f(25) \\
& f\left(\frac{25+2 \cdot 1}{3}\right)=\frac{f(25)+2 f(1)}{3}=f(9) \\
& f\left(\frac{9+2 \cdot 0}{3}\right)=\frac{f(9)+2 f(0)}{3}=f(3)
\end{aligned}
\]
Calculating in reverse order, we get:
\[
\begin{aligned}
& f(9)=3 f(3)-2 f(0) \text {, i.e., } f(9)=3 \cdot 3-2 \cdot 6=-3 ; \\
& f(25)=3 f(9)-2 f(1) \text {, i.e., } f(25)=3 \cdot(-3)-2 \cdot 5=-19 ; \\
& f(75)=3 f(25)-2 f(0) \text {, i.e., } f(75)=3 \cdot(-19)-2 \cdot 6=-69 ; \\
& f(225)=3 f(75)-2 f(0) \text {, i.e., } f(225)=3 \cdot(-69)-2 \cdot 6=-219 ; \\
& f(675)=3 f(225)-2 f(0) \text {, i.e., } f(675)=3 \cdot(-219)-2 \cdot 6=-669 ; \\
& f(2021)=3 f(675)-2 f(2) \text {, i.e., } f(2021)=3 \cdot(-669)-2 \cdot 4=-2015 \text {. }
\end{aligned}
\]
Answer. -2015.
|
-2015
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A numerical sequence is given:
$$
x_{0}=\frac{1}{n} ; x_{k}=\frac{1}{n-k}\left(x_{0}+x_{1}+\ldots+x_{k-1}\right) ; k=1,2, \ldots, n-1
$$
Find $S_{n}=x_{0}+x_{1}+\ldots+x_{n-1}$, if $n=2022$.
|
# Solution.
We will prove by mathematical induction that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$. For $k=0$, this equality holds. For $k=1$, $x_{0}+x_{1}=\frac{1}{n}+\frac{1}{n-1} \cdot \frac{1}{n}=\frac{1}{n-1}$. Suppose this equality holds for all $m \leq k$, then it should also hold for $k+1$. Let's check this:
$$
\begin{aligned}
& \left(x_{0}+x_{1}+\ldots+x_{k}\right)+x_{k+1}=\frac{1}{n-k}+x_{k+1}=\frac{1}{n-k}+\frac{1}{n-(k+1)}\left(x_{0}+x_{1}+\ldots+x_{k}\right)= \\
& =\frac{1}{n-k}+\frac{1}{(n-k-1)(n-k)}=\frac{1}{n-(k+1)} .
\end{aligned}
$$
Thus, this equality also holds for $k+1$. Therefore, our assumption that $x_{0}+x_{1}+\ldots+x_{k-1}+x_{k}=\frac{1}{n-k}$ is correct.
Then, for $n=2022$ and $k=n-1=2021: S_{2022}=x_{0}+x_{1}+\ldots+x_{2021}=\frac{1}{2022-2021}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The function $f(x)$ satisfies the condition: for any real numbers $a$ and $b$, the equality $f\left(\frac{a+2 b}{3}\right)=\frac{f(a)+2 f(b)}{3}$ holds. Find the value of the function $f(2021)$, if $f(1)=1, f(4)=7$.
#
|
# Solution.
Substituting the pairs of numbers $a=4, b=1$ and $a=1, b=4$ into the given equation, respectively, we get
If $a=4, b=1$, then $f\left(\frac{4+2}{3}\right)=\frac{f(4)+2 f(1)}{3}, f(2)=\frac{7+2 \cdot 1}{3}=3, f(2)=3$.
If $a=1, b=4$, then $f\left(\frac{1+2 \cdot 4}{3}\right)=\frac{f(1)+2 f(4)}{3}, f(3)=\frac{1+2 \cdot 7}{3}=5, f(3)=5$.
If we take $a=0, b=3$, we get $f\left(\frac{0+2 \cdot 3}{3}\right)=\frac{f(0)+2 f(3)}{3}, f(2)=\frac{f(0)+2 f(3)}{3}$.
Thus, $f(0)=3 f(2)-2 f(3), f(0)=3 \cdot 3-2 \cdot 5, f(0)=-1$.
Therefore, we have $f(0)=-1, f(1)=1, f(2)=3, f(3)=5, f(4)=7$.
Let's form a chain of equalities
$$
\begin{aligned}
& f\left(\frac{2021+2 \cdot 2}{3}\right)=\frac{f(2021)+2 f(2)}{3}=f(675) \\
& f\left(\frac{675+2 \cdot 0}{3}\right)=\frac{f(675)+2 f(0)}{3}=f(225) \\
& f\left(\frac{225+2 \cdot 0}{3}\right)=\frac{f(225)+2 f(0)}{3}=f(75) \\
& f\left(\frac{75+2 \cdot 0}{3}\right)=\frac{f(75)+2 f(0)}{3}=f(25) \\
& f\left(\frac{25+2 \cdot 1}{3}\right)=\frac{f(25)+2 f(1)}{3}=f(9) \\
& f\left(\frac{9+2 \cdot 0}{3}\right)=\frac{f(9)+2 f(0)}{3}=f(3)
\end{aligned}
$$
Calculating in reverse order, we get:
$$
\begin{aligned}
& f(9)=3 f(3)-2 f(0) \text {, i.e., } f(9)=3 \cdot 5-2 \cdot(-1)=17 ; \\
& f(25)=3 f(9)-2 f(1) \text {, i.e., } f(25)=3 \cdot 17-2 \cdot 1=49 ; \\
& f(75)=3 f(25)-2 f(0) \text {, i.e., } f(75)=3 \cdot 49-2 \cdot(-1)=149 ; \\
& f(225)=3 f(75)-2 f(0) \text {, i.e., } f(225)=3 \cdot 149-2 \cdot(-1)=449 ; \\
& f(675)=3 f(225)-2 f(0) \text {, i.e., } f(675)=3 \cdot 449-2 \cdot(-1)=1349 \\
& f(2021)=3 f(675)-2 f(2) \text {, i.e., } f(2021)=3 \cdot 1349-2 \cdot 3=4041
\end{aligned}
$$
Answer. 4041.
|
4041
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$ is inscribed in a sphere. Segment $C D$ is the diameter of this sphere, and point $K$ is the midpoint of edge $A A_{1}$. Find the volume of the prism if $C K=2 \sqrt{6}, D K=4$.
|
# Solution.
The planes of the bases $ABC$ and $A_1B_1C_1$ of the prism intersect the sphere along the circumcircles of the equilateral triangles $ABC$ and $A_1B_1C_1$; let their centers be points $O$ and $O_1$ respectively.
It is easy to show that the midpoint $M$ of the segment $OO_1$ is the center of the sphere (Fig. 3).
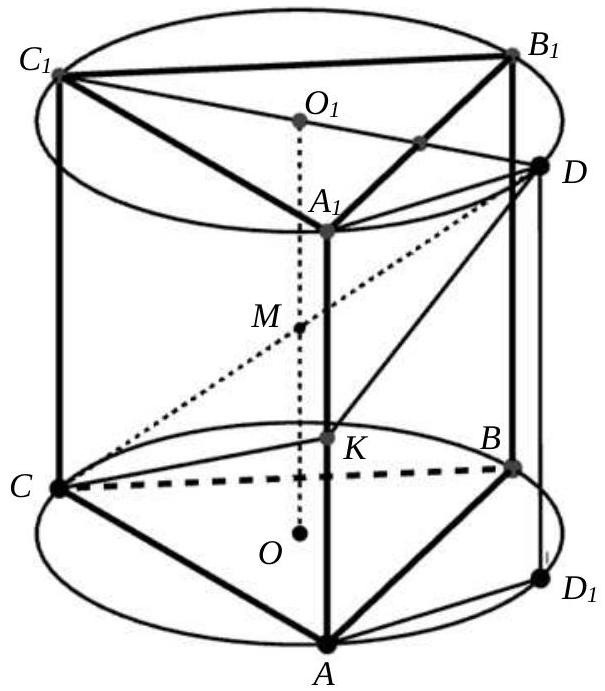
Fig. 3.
Draw the diameter $C_1D$ of the circle centered at point $O_1$ through point $C_1$. We will show that $CD$ is the diameter of the sphere. Indeed, the plane $CC_1D$ is perpendicular to the planes of the bases and, therefore, contains the segment $OO_1$ along with point $O_1$. Since $C_1D = 2DO_1$, the line $CD$ intersects the segment $OO_1$ at its midpoint, i.e., at the center $M$ of the given sphere.
Let $D_1$ be the projection of point $D$ onto the plane of the base $ABC$, the height of the prism is $h$, and the radii of the circles centered at $O$ and $O_1$ are $r$. Consider triangles $CAK$ and $KA_1D$. Given that $A_1D = AD_1 = r$ (triangle $A_1O_1D$ is equilateral), $AC = r\sqrt{3}$, $AK = KA_1 = \frac{h}{2}$, by the Pythagorean theorem, we obtain the system of equations:
$$
\left\{\begin{array}{l}
\frac{h^2}{4} + 3r^2 = (2\sqrt{6})^2 \\
\frac{h^2}{4} + r^2 = 4^2
\end{array}\right.
$$
Solving the system, we find that $r = 2$, $h = 4\sqrt{3}$. Then the side of the base is $2\sqrt{3}$, its area $S = 3\sqrt{3}$, and, consequently, the volume of the prism $V = S \cdot h = 36$.
Answer. 36.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are equal to 55 and 31, respectively, and its diagonals are perpendicular to each other. Find the scalar product of vectors $\overrightarrow{AD}$ and $\overrightarrow{BC}$.
|
# Solution.
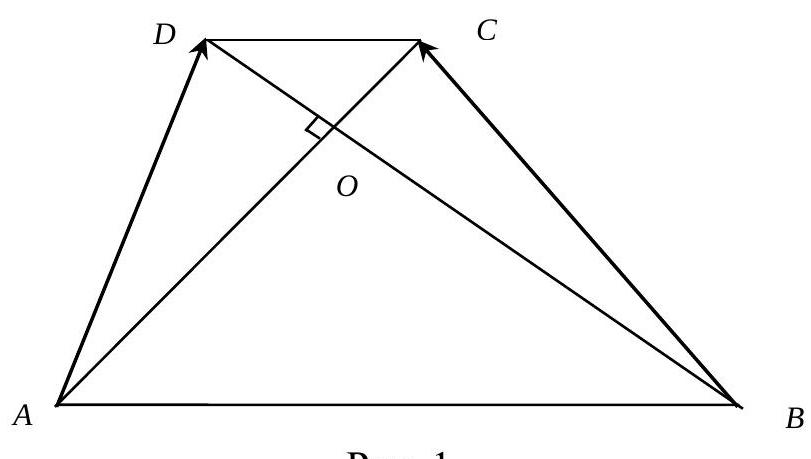
Fig. 1
Let the point of intersection of the diagonals be $O$ (Fig. 1).
Consider the vectors $\overrightarrow{A O}=\bar{a}$ and $\overrightarrow{B O}=\bar{b}$.
From the similarity of triangles $A O B$ and $D O C$, we have:
$\frac{A O}{O C}=\frac{55}{31}$ and $\overrightarrow{O C}=\frac{31}{55} \overrightarrow{A O}=\frac{31}{55} \vec{a}$
$\frac{B O}{O D}=\frac{55}{31}$ and $\overrightarrow{O D}=\frac{31}{55} \overrightarrow{B O}=\frac{31}{55} \vec{b}$.
Then
$\overrightarrow{A D}=\vec{a}+\frac{31}{55} \vec{b}$ and $\overrightarrow{B C}=\vec{b}+\frac{31}{55} \vec{a}$
Let's find the dot product
$\overrightarrow{A D} \cdot \overrightarrow{B C}=\left(\vec{a}+\frac{31}{55} \vec{b}\right) \cdot\left(\vec{b}+\frac{31}{55} \vec{a}\right)=\overrightarrow{a b}+\frac{31}{55} \vec{a} \cdot \vec{a}+\frac{31}{55} \vec{b} \cdot \vec{b}+\left(\frac{31}{55}\right)^{2} \vec{a} \vec{b}$.
Since $\vec{a} \perp \vec{b}$, then $\vec{a} \vec{b}=0$.
By the definition of the dot product of vectors, we get $\vec{a} \cdot \vec{a}=|\vec{a}| \cdot|\vec{a}| \cdot \cos 0^{0}=|\vec{a}|^{2}$ and $\vec{b} \cdot \vec{b}=|\vec{b}|^{2}$. Triangle $AOB$ is a right triangle, so $|\vec{a}|^{2}+|\vec{b}|^{2}=|A B|^{2}=55^{2}$.
Thus, $\overrightarrow{A D} \cdot \overrightarrow{B C}=\frac{31}{55}\left(|\vec{a}|^{2}+|\vec{b}|^{2}\right)=\frac{31}{55} \cdot 55^{2}=1705$.
Answer. 1705.
|
1705
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are equal to 41 and 24, respectively, and its diagonals are perpendicular to each other. Find the scalar product of vectors $\overrightarrow{AD}$ and $\overrightarrow{BC}$.
|
Solution.
Let the point of intersection of the diagonals be $O$ (Fig. 1).
Consider the vectors $\overrightarrow{A O}=\bar{a}$ and $\overrightarrow{B O}=\bar{b}$.
From the similarity of triangles $A O B$ and $D O C$, we have:
$\frac{A O}{O C}=\frac{41}{24}$ and $\overrightarrow{O C}=\frac{24}{41} \overrightarrow{A O}=\frac{24}{41} \vec{a}$.
$\frac{B O}{O D}=\frac{41}{24}$ and $\overrightarrow{O D}=\frac{24}{41} \overrightarrow{B O}=\frac{24}{41} \vec{b}$.
Then
$\overrightarrow{A D}=\vec{a}+\frac{24}{41} \vec{b}$ and $\overrightarrow{B C}=\vec{b}+\frac{24}{41} \vec{a}$.
Let's find the dot product
$\overrightarrow{A D} \cdot \overrightarrow{B C}=\left(\vec{a}+\frac{24}{41} \vec{b}\right) \cdot\left(\vec{b}+\frac{24}{41} \vec{a}\right)=\vec{a} \vec{b}+\frac{24}{41} \vec{a} \cdot \vec{a}+\frac{24}{41} \vec{b} \cdot \vec{b}+\left(\frac{24}{41}\right)^{2} \vec{a} \vec{b}$.
Since $\vec{a} \perp \vec{b}$, then $\vec{a} \vec{b}=0$.
By the definition of the dot product of vectors, we get $\vec{a} \cdot \vec{a}=|\vec{a}| \cdot|\vec{a}| \cdot \cos 0^{0}=|\vec{a}|^{2}$ and $\vec{b} \cdot \vec{b}=|\vec{b}|^{2}$.
Triangle $AOB$ is a right triangle, so $|\vec{a}|^{2}+|\vec{b}|^{2}=|A B|^{2}=41^{2}$.
Thus, $\overrightarrow{A D} \cdot \overrightarrow{B C}=\frac{24}{41}\left(|\vec{a}|^{2}+|\vec{b}|^{2}\right)=\frac{24}{41} \cdot 41^{2}=984$.
Answer. 984.
|
984
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A finite increasing sequence $a_{1}, a_{2}, \ldots, a_{n}$ ( $n \geq 3$ ) of natural numbers is given, and for all $k \leq n-2$ the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds. The sequence must contain a term $a_{k}=2021$. Determine the maximum number of three-digit numbers, divisible by 25, that this sequence can contain.
#
|
# Solution.
The final sequence can contain all three-digit numbers, as it can consist of a given number of natural numbers starting from the chosen number $a_{i}$.
We will prove that for any term of the arithmetic progression $1,2,3, \ldots$ defined by the formula for the $n$-th term $a_{n}=n$, the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds.
Indeed, for any value of $k$, the equalities
$a_{k}=k, a_{k+1}=k+1, a_{k+2}=k+2$ are valid, from which it follows that
$3 a_{k+1}-2 a_{k}-1=3(k+1)-2 k-1=k+2=a_{k+2}$, i.e., the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds, which is what we needed to prove.
For example, the sequence containing 2021: 3,4,5,6,.., 2018, 2019,2020,2021.
Thus, the sequence can contain all three-digit numbers from 100 to 999. Among them, the numbers divisible by $25: 100,125,150,175,200,225,250,275, \ldots, 900,925$, 950,975 - 4 in each of the nine hundreds, i.e., 36 numbers.
Answer. 36.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The function $f(x)$ satisfies the condition: for any real numbers $a$ and $b$, the equality $f\left(\frac{a+2 b}{3}\right)=\frac{f(a)+2 f(b)}{3}$ holds. Find the value of the function $f(2022)$, if $f(1)=1, f(4)=7$.
#
|
# Solution.
Substituting the pairs of numbers \(a=4, b=1\) and \(a=1, b=4\) into the given equation, respectively, we get
If \(a=4, b=1\), then \(f\left(\frac{4+2}{3}\right)=\frac{f(4)+2 f(1)}{3}, f(2)=\frac{7+2 \cdot 1}{3}=3, f(2)=3\).
If \(a=1, b=4\), then \(f\left(\frac{1+2 \cdot 4}{3}\right)=\frac{f(1)+2 f(4)}{3}, f(3)=\frac{1+2 \cdot 7}{3}=5, f(3)=5\).
If we take \(a=0, b=3\), we get \(f\left(\frac{0+2 \cdot 3}{3}\right)=\frac{f(0)+2 f(3)}{3}, f(2)=\frac{f(0)+2 f(3)}{3}\).
Thus, \(f(0)=3 f(2)-2 f(3), f(0)=3 \cdot 3-2 \cdot 5, f(0)=-1\).
Therefore, we have \(f(0)=-1, f(1)=1, f(2)=3, f(3)=5, f(4)=7\).
Let's form a chain of equalities
\[
\begin{aligned}
& f\left(\frac{2022+2 \cdot 0}{3}\right)=\frac{f(2022)+2 f(0)}{3}=f(674) \\
& f\left(\frac{674+2 \cdot 2}{3}\right)=\frac{f(674)+2 f(2)}{3}=f(226) \\
& f\left(\frac{226+2 \cdot 1}{3}\right)=\frac{f(226)+2 f(1)}{3}=f(76) \\
& f\left(\frac{76+2 \cdot 1}{3}\right)=\frac{f(76)+2 f(1)}{3}=f(26) \\
& f\left(\frac{26+2 \cdot 2}{3}\right)=\frac{f(26)+2 f(2)}{3}=f(10) \\
& f\left(\frac{10+2 \cdot 1}{3}\right)=\frac{f(10)+2 f(1)}{3}=f(4)
\end{aligned}
\]
Calculating in reverse order, we get:
\[
\begin{aligned}
& f(10)=3 f(4)-2 f(1) \text {, i.e., } f(10)=3 \cdot 7-2 \cdot 1=19 \\
& f(26)=3 f(10)-2 f(2) \text {, i.e., } f(26)=3 \cdot 19-2 \cdot 3=51 \\
& f(76)=3 f(26)-2 f(1) \text {, i.e., } f(76)=3 \cdot 51-2 \cdot 1=151 \\
& f(226)=3 f(76)-2 f(1) \text {, i.e., } f(226)=3 \cdot 151-2 \cdot 1=451 \\
& f(674)=3 f(226)-2 f(2) \text {, i.e., } f(674)=3 \cdot 451-2 \cdot 3=1347 \\
& f(2022)=3 f(674)-2 f(0) \text {, i.e., } f(2022)=3 \cdot 1347-2 \cdot(-1)=4043
\end{aligned}
\]
Answer. 4043.
|
4043
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. (20 points) At the first deposit, equipment of the highest class was used, and at the second deposit, equipment of the first class was used, with the highest class being less than the first. Initially, $40 \%$ of the equipment from the first deposit was transferred to the second. Then, $20 \%$ of the equipment that ended up on the second deposit was transferred back to the first, with half of the transferred equipment being of the first class. After this, the equipment of the highest class on the first deposit was 26 units more than on the second, and the total amount of equipment on the second deposit increased by more than $5 \%$ compared to the initial amount. Find the total amount of equipment of the first class.
|
# Solution.
Let there initially be $x$ units of top-class equipment at the first deposit and $y$ units of first-class equipment at the second deposit $(x1.05 y$, from which $y48 \frac{34}{67} .\end{array}\right.\right.$
This double inequality and the condition "x is divisible by 5" is satisfied by the unique value $x=50$. Then $y=130-70=60$. Thus, there were 60 units of first-class equipment.
Answer: 60.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1} \mathrm{c}$ is inscribed in a sphere with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. Segment $C D$ is the diameter of this sphere, point $K$ and $L$ are the midpoints of edge $A A_{1}$ and $A B$ respectively. Find the volume of the prism if $D L=\sqrt{2}, D K=\sqrt{3}$.
|
# Solution.
The planes of the bases $ABC$ and $A_1B_1C_1$ of the prism intersect the sphere along the circumcircles of the equilateral triangles $ABC$ and $A_1B_1C_1$, with their centers at points $O$ and $O_1$ respectively.
It is easy to show that the midpoint $M$ of the segment $OO_1$ is the center of the sphere (Fig. 5).
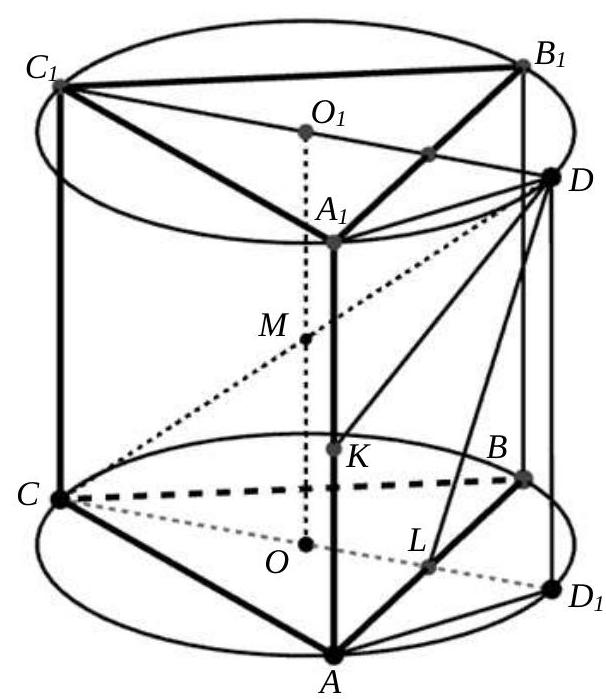
Fig. 5.
Draw a diameter $C_1D$ of the circle centered at point $O_1$ through point $C_1$. We will show that $CD$ is a diameter of the sphere. Indeed, the plane $CC_1D$ is perpendicular to the planes of the bases and, therefore, contains the segment $OO_1$ along with point $O_1$. Since $C_1D = 2DO_1$, the line $CD$ intersects the segment $OO_1$ at its midpoint, i.e., at the center $M$ of the given sphere.
Let $D_1$ be the projection of point $D$ onto the plane of the base $ABC$, the height of the prism is $h$, and the radii of the circles centered at $O$ and $O_1$ are $r$. Consider triangles $KA_1D$ and $LDD_1$. Given that $A_1D = AD_1 = r$ (triangle $A_1O_1D$ is equilateral), $LD_1 = \frac{r}{2}$, $DD_1 = h$, $KA_1 = \frac{h}{2}$, by the Pythagorean theorem, we obtain the system of equations
$$
\left\{\begin{array}{l}
\frac{h^2}{4} + r^2 = (\sqrt{3})^2 \\
h^2 + \frac{r^2}{4} = (\sqrt{2})^2
\end{array}\right.
$$
Solving the system, we find that $r = \frac{2\sqrt{6}}{3}$, $h = \frac{2\sqrt{3}}{3}$. Then the side of the base is $2\sqrt{2}$, its area $S = 2\sqrt{3}$, and consequently, the volume of the prism $V = S \cdot h = 4$.
Answer. 4.
## Mathematics. Variant-32 $10-11$ grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A finite increasing sequence $a_{1}, a_{2}, \ldots, a_{n}$ ( $n \geq 3$ ) of natural numbers is given, and for all $k \leq n-2$, the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-2$ holds. The sequence must contain $a_{k}=2022$. Determine the maximum number of three-digit numbers, divisible by 4, that this sequence can contain.
|
# Solution.
Since it is necessary to find the largest number of three-digit numbers that are multiples of 4, the deviation between the members should be minimal. Note that an arithmetic progression with a difference of $d=2$, defined by the formula $a_{k}=2 k$, satisfies the equation $a_{k+2}=3 a_{k+1}-2 a_{k}-2$.
Indeed,
$a_{k}=2 k, \quad a_{k+1}=2 k+2, a_{k+2}=2 k+4$, or by the formula
$a_{k+2}=3 a_{k+1}-2 a_{k}-2=3(2 k+2)-2 \cdot 2 k-2=2 k+4$
The sequence containing 2022: 4, 6,
This finite sequence can contain all even three-digit numbers from 100 to 999. Among them, the numbers divisible by 4 are: 100, 104, 108, 112, ..., 992, 925, 950, 996 - 25 in each of the nine hundreds, i.e., 225 numbers.
Answer. 225.
|
225
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The function $f(x)$ satisfies the condition: for any real numbers $a$ and $b$, the equality $f\left(\frac{a+2 b}{3}\right)=\frac{f(a)+2 f(b)}{3}$ holds. Find the value of the function $f(2022)$, if $f(1)=5, f(4)=2$.
|
# Solution.
Substituting the pairs of numbers $a=4, b=1$ and $a=1, b=4$ into the given equation, respectively, we get
If $a=4, b=1$, then $f\left(\frac{4+2}{3}\right)=\frac{f(4)+2 f(1)}{3}, f(2)=\frac{2+2 \cdot 5}{3}=4, f(2)=4$.
If $a=1, b=4$, then $f\left(\frac{1+2 \cdot 4}{3}\right)=\frac{f(1)+2 f(4)}{3}, f(3)=\frac{5+2 \cdot 2}{3}=3, f(3)=3$.
If we take $a=0, b=3$, we get $f\left(\frac{0+2 \cdot 3}{3}\right)=\frac{f(0)+2 f(3)}{3}, f(2)=\frac{f(0)+2 f(3)}{3}$.
Thus, $f(0)=3 f(2)-2 f(3), f(0)=3 \cdot 4-2 \cdot 3, f(0)=6$.
Therefore, we have $f(0)=6, f(1)=5, f(2)=4, f(3)=3, f(4)=2$.
Let's form a chain of equalities
$$
\begin{aligned}
& f\left(\frac{2022+2 \cdot 0}{3}\right)=\frac{f(2022)+2 f(0)}{3}=f(674) \\
& f\left(\frac{674+2 \cdot 2}{3}\right)=\frac{f(674)+2 f(2)}{3}=f(226) \\
& f\left(\frac{226+2 \cdot 1}{3}\right)=\frac{f(226)+2 f(1)}{3}=f(76) \\
& f\left(\frac{76+2 \cdot 1}{3}\right)=\frac{f(76)+2 f(1)}{3}=f(26) \\
& f\left(\frac{26+2 \cdot 2}{3}\right)=\frac{f(26)+2 f(2)}{3}=f(10) \\
& f\left(\frac{10+2 \cdot 1}{3}\right)=\frac{f(10)+2 f(1)}{3}=f(4)
\end{aligned}
$$
Calculating in reverse order, we get:
$$
\begin{aligned}
& f(10)=3 f(4)-2 f(1) \text {, i.e., } f(10)=3 \cdot 2-2 \cdot 5=-4 ; \\
& f(26)=3 f(10)-2 f(2) \text {, i.e., } f(26)=3 \cdot(-4)-2 \cdot 4=-20 \\
& f(76)=3 f(26)-2 f(1) \text {, i.e., } f(76)=3 \cdot(-20)-2 \cdot 5=-70 \\
& f(226)=3 f(76)-2 f(1) \text {, i.e., } f(226)=3 \cdot(-70)-2 \cdot 5=-220 \\
& f(674)=3 f(226)-2 f(2) \text {, i.e., } f(674)=3 \cdot(-220)-2 \cdot 4=-668 ; \\
& f(2022)=3 f(674)-2 f(0) \text {, i.e., } f(2022)=3 \cdot(-668)-2 \cdot 6=-2016
\end{aligned}
$$
Answer. -2016.
|
-2016
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ is inscribed in a sphere with the base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. The segment $C_{1} D$ is the diameter of this sphere, and point $K$ is the midpoint of edge $C C_{1}$. Find the volume of the prism if $D K=2, D A=\sqrt{6}$.
|
# Solution.
The planes of the bases $ABC$ and $A_1B_1C_1$ of the prism intersect the sphere along the circumcircles of the equilateral triangles $ABC$ and $A_1B_1C_1$, with their centers at points $O$ and $O_1$ respectively.
It is easy to show that the midpoint $M$ of the segment $OO_1$ is the center of the sphere (Fig. 5).
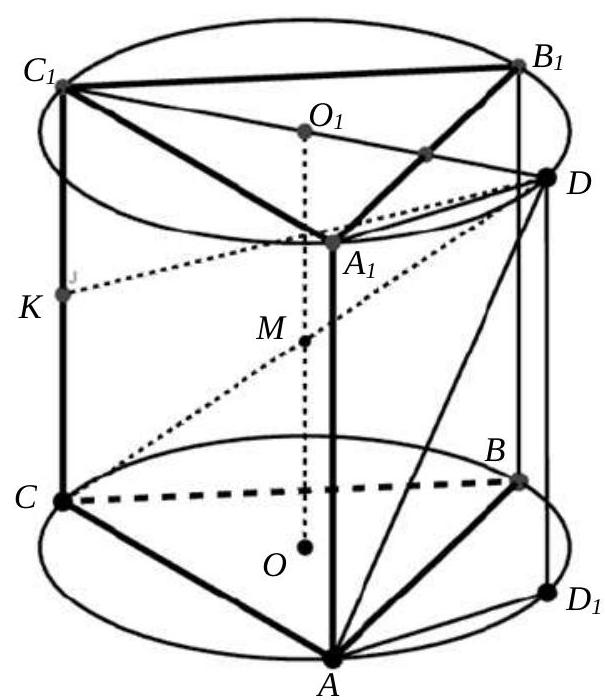
Fig. 5
Draw a diameter $C_1D$ of the circle centered at point $O_1$ through point $C_1$. We will show that $CD$ is a diameter of the sphere. Indeed, the plane $CC_1D$ is perpendicular to the planes of the bases and, therefore, contains the segment $OO_1$ along with point $O_1$. Since $C_1D = 2DO_1$, the line $CD$ intersects the segment $OO_1$ at its midpoint, i.e., at the center $M$ of the given sphere.
Let $D_1$ be the projection of point $D$ onto the plane of the base $ABC$, the height of the prism is $h$, and the radii of the circles centered at $O$ and $O_1$ are $r$. Consider the triangles $KC_1D$ and $ADD_1$. Given that $C_1D = 2r$, $AD_1 = r$ (triangle $A_1O_1D$ is equilateral), $DD_1 = h$, $KC_1 = \frac{h}{2}$, by the Pythagorean theorem, we obtain the system of equations
$$
\left\{\begin{array}{l}
\frac{h^2}{4} + 4r^2 = 2^2 \\
h^2 + r^2 = (\sqrt{6})^2
\end{array}\right.
$$
Solving the system, we find that $r = \frac{\sqrt{6}}{3}$, $h = \frac{4\sqrt{3}}{3}$. Then the side of the base is $\sqrt{2}$, its area $S = \frac{\sqrt{3}}{2}$, and consequently, the volume of the prism $V = S \cdot h = 2$.
Answer. 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are equal to 367 and 6, respectively, and its diagonals are perpendicular to each other. Find the scalar product of vectors $\overrightarrow{AD}$ and $\overrightarrow{BC}$.
|
# Solution.
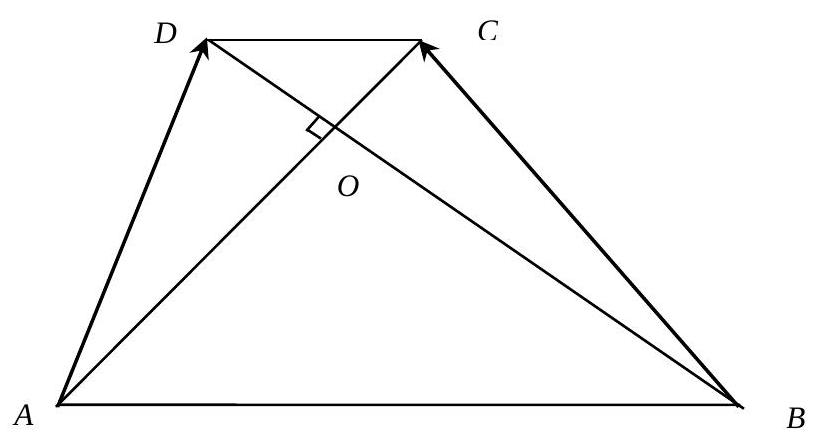
Fig. 1
Let the point of intersection of the diagonals be $O$ (Fig. 1).
Consider the vectors $\overrightarrow{A O}=\bar{a}$ and $\overrightarrow{B O}=\bar{b}$.
From the similarity of triangles $A O B$ and $D O C$, we have:
$\frac{A O}{O C}=\frac{367}{6}$ and $\overrightarrow{O C}=\frac{6}{367} \overrightarrow{A O}=\frac{6}{367} \vec{a}$.
$\frac{B O}{O D}=\frac{367}{6}$ and $\overrightarrow{O D}=\frac{6}{367} \overrightarrow{B O}=\frac{6}{367} \vec{b}$.
Then
$\overrightarrow{A D}=\vec{a}+\frac{6}{367} \vec{b}$ and $\overrightarrow{B C}=\vec{b}+\frac{6}{367} \vec{a}$.
Let's find the dot product
$\overrightarrow{A D} \cdot \overrightarrow{B C}=\left(\vec{a}+\frac{6}{367} \vec{b}\right) \cdot\left(\vec{b}+\frac{6}{367} \vec{a}\right)=\vec{a} \vec{b}+\frac{6}{367} \vec{a} \cdot \vec{a}+\frac{6}{367} \vec{b} \cdot \vec{b}+\left(\frac{6}{367}\right)^{2} \vec{a} \vec{b}$.
Since $\vec{a} \perp \vec{b}$, then $\vec{a} \vec{b}=0$.
By the definition of the dot product of vectors, we get $\vec{a} \cdot \vec{a}=|\vec{a}| \cdot|\vec{a}| \cdot \cos 0^{0}=|\vec{a}|^{2}$ and $\vec{b} \cdot \vec{b}=|\vec{b}|^{2}$
Triangle $AOB$ is a right triangle, so $|\vec{a}|^{2}+|\vec{b}|^{2}=|A B|^{2}=367^{2}$.
Thus, $\overrightarrow{A D} \cdot \overrightarrow{B C}=\frac{6}{367}\left(|\vec{a}|^{2}+|\vec{b}|^{2}\right)=\frac{6}{367} \cdot 367^{2}=2202$.
Answer. 2202.
|
2202
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are equal to 101 and 20, respectively, and its diagonals are perpendicular to each other. Find the scalar product of vectors $\overrightarrow{AD}$ and $\overrightarrow{BC}$.
|
Solution.
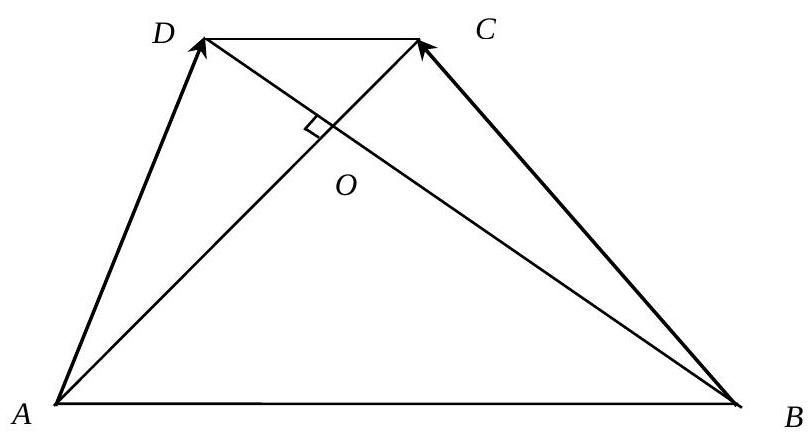
Fig. 1
Let the point of intersection of the diagonals be $O$ (Fig. 1).
Consider the vectors $\overrightarrow{A O}=\bar{a}$ and $\overrightarrow{B O}=\bar{b}$.
From the similarity of triangles $A O B$ and $D O C$, we have:
$\frac{A O}{O C}=\frac{101}{20}$ and $\overrightarrow{O C}=\frac{20}{101} \overrightarrow{A O}=\frac{20}{101} \vec{a}$
$\frac{B O}{O D}=\frac{101}{20}$ and $\overrightarrow{O D}=\frac{20}{101} \overrightarrow{B O}=\frac{20}{101} \vec{b}$.
Then
$\overrightarrow{A D}=\vec{a}+\frac{20}{101} \vec{b}$ and $\overrightarrow{B C}=\vec{b}+\frac{20}{101} \vec{a}$.
Let's find the dot product
$\overrightarrow{A D} \cdot \overrightarrow{B C}=\left(\vec{a}+\frac{20}{101} \vec{b}\right) \cdot\left(\vec{b}+\frac{20}{101} \vec{a}\right)=\vec{a} \vec{b}+\frac{20}{101} \vec{a} \cdot \vec{a}+\frac{20}{101} \vec{b} \cdot \vec{b}+\left(\frac{20}{101}\right)^{2} \vec{a} \vec{b}$.
Since $\vec{a} \perp \vec{b}$, then $\vec{a} \vec{b}=0$.
By the definition of the dot product of vectors, we get $\vec{a} \cdot \vec{a}=|\vec{a}| \cdot|\vec{a}| \cdot \cos 0^{0}=|\vec{a}|^{2}$ and $\vec{b} \cdot \vec{b}=|\vec{b}|^{2}$
Triangle $AOB$ is a right triangle, so $|\vec{a}|^{2}+|\vec{b}|^{2}=|A B|^{2}=101^{2}$.
Thus, $\overrightarrow{A D} \cdot \overrightarrow{B C}=\frac{20}{101}\left(|\vec{a}|^{2}+|\vec{b}|^{2}\right)=\frac{20}{101} \cdot 101^{2}=2020$.
Answer. 2020.
|
2020
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. If we now take into account that after reflections in the mirrors, the ray EC' has entered the eyepiece, that is, the direction of the ray after two deflections coincides with the direction of DA, it follows that the total deflection of the ray EC' is equal to the angle between the rays EC' and DA
$$
\mathrm{psi}_{\text {total }}=2 \mathrm{phi}=\text { alpha }
$$
from which
$$
\text { phi }=0.5 \mathrm{alpha}=15^{\circ}
$$
Thus, we have shown that if the ray $\mathrm{EC}$' after deflections overlaps with the ray $\mathrm{DA}$, then the angle between the mirrors must be equal to half the angle alpha, and this equality will not change after the platform is rotated: the angle alpha will remain the same, and therefore, the angle between the mirrors, which is 15 degrees, must be maintained.
|
Answer: There is no need to rotate mirror C relative to point C. The angle of rotation of mirror C relative to the platform is $0^{\circ}$.
## Solution Method 2.
|
0
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. (6 points) In an ideal gas, a thermodynamic cycle consisting of two isochoric and two adiabatic processes is carried out. The ratio of the initial and final absolute temperatures in the isochoric cooling process is \( k = 1.5 \). Determine the efficiency of this cycle, given that the efficiency of the Carnot cycle with the same ratio of maximum to minimum temperature as in the considered cycle is \( 50\% \).
## Possible solution.
In the graph of the cyclic process, it is clear that the absolute temperatures \( T_{1} = T_{\max} \), and \( T_{3} = T_{\min} \). By definition, the efficiency is the ratio of the work done by the gas in the cycle to the amount of heat transferred to the gas. In the studied cycle, work is performed in adiabatic processes, while energy is transferred in the form of heat in isochoric processes. Using the first law of thermodynamics, we obtain for the work of
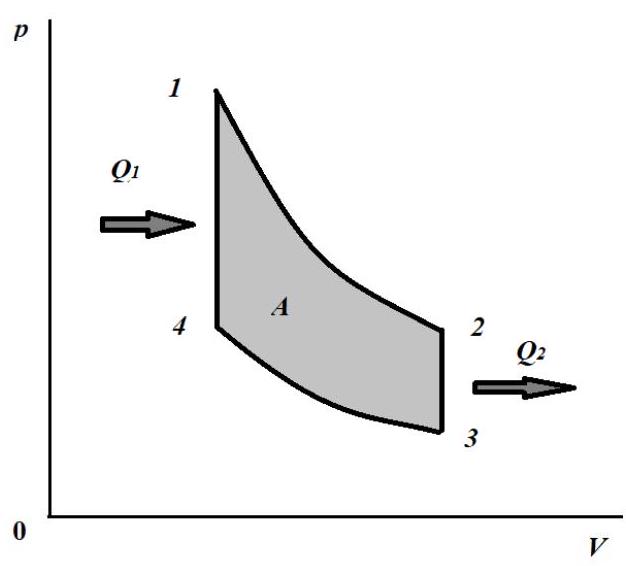
the gas in adiabatic processes:
$$
\begin{gathered}
A_{12} = -\Delta U_{12} = \frac{i}{2} v R \left( T_{\max} - T_{2} \right) > 0 \\
A_{34} = -\Delta U_{34} = \frac{i}{2} v R \left( T_{\min} - T_{4} \right) < 0
\end{gathered}
$$
where \(\Delta U\) is the change in internal energy of the gas, \(i\) is the number of degrees of freedom of the gas molecule, \(v\) is the amount of substance, and \(R\) is the universal gas constant.
The work done by the gas in the cycle:
$$
A = A_{12} + A_{34} = \frac{i}{2} v R \left[ \left( T_{\max} - T_{2} \right) - \left( T_{4} - T_{\min} \right) \right].
$$
The amount of heat transferred to the gas in the isochoric process \(4-1\):
$$
Q_{1} = \Delta U_{41} = \frac{i}{2} v R \left( T_{\max} - T_{4} \right)
$$
The efficiency
$$
\eta = \frac{\left( T_{\max} - T_{4} \right) - \left( T_{2} - T_{\min} \right)}{T_{\max} - T_{4}} = 1 - \frac{T_{2} - T_{\min}}{T_{\max} - T_{4}}
$$
According to Poisson's equation for adiabatic processes
$$
\begin{aligned}
p_{1} V_{1}^{\gamma} & = p_{2} V_{2}^{\gamma} \\
p_{4} V_{1}^{\gamma} & = p_{3} V_{1}^{\gamma} \\
\frac{p_{1}}{p_{4}} & = \frac{p_{2}}{p_{3}}.
\end{aligned}
$$
Here \(\gamma\) is the adiabatic index. By Charles's law
$$
\begin{aligned}
& \frac{p_{1}}{p_{4}} = \frac{T_{\max}}{T_{4}} \\
& \frac{p_{2}}{p_{3}} = \frac{T_{2}}{T_{\min}}
\end{aligned}
$$
We obtain that
$$
\frac{T_{\max}}{T_{4}} = \frac{T_{2}}{T_{\min}} = k
$$
Considering the obtained equality, we can write:
$$
\eta = 1 - \frac{T_{2} - T_{\min}}{T_{\max} - T_{4}} = 1 - \frac{T_{\min} (k - 1)}{T_{\max} \left( 1 - \frac{1}{k} \right)} = 1 - k \frac{T_{\min}}{T_{\max}}
$$
For the Carnot cycle
$$
\eta_{\mathrm{K}} = 1 - \frac{T_{\min}}{T_{\max}}
$$
Then
$$
\eta = 1 - k \left( 1 - \eta_{\mathrm{K}} \right) = 0.25 = 25\%.
$$
|
Answer: $\eta=1-k\left(1-\eta_{C}\right)=0.25=25 \%$.
## Evaluation Criteria
| Performance | Score |
| :--- | :---: |
| Participant did not start the task or performed it incorrectly from the beginning | $\mathbf{0}$ |
| Expression for work in the cycle is written | $\mathbf{1}$ |
| Expression for the amount of heat received is written | $\mathbf{1}$ |
| Expression for the efficiency coefficient in terms of temperatures in the cycle states is written | $\mathbf{1}$ |
| Expression for the temperature ratios in isochoric processes is obtained | $\mathbf{1}$ |
| Expression for the efficiency of the Carnot cycle is written | $\mathbf{1}$ |
| Necessary transformations are performed and a numerical answer is obtained | $\mathbf{1}$ |
| :---: | :---: | :---: |
| Total points | $\mathbf{6}$ |
|
25
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Finally, let's calculate the change in resistance when the switch is closed:
$$
\Delta R=R_{p}-R_{3}=33[\text { Ohms] }-30[\text { Ohms] }=3[\text { Ohms] }
$$
|
Answer: 3.0 Ohms
Criteria (maximum 10 points)
|
3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. By how many units can the city's fleet of natural gas vehicles be increased in 2022, assuming that the capacity of each of the old CNG stations in the city is equal to the capacity of the new station on Narodnaya Street, and that the city's fleet constitutes only $70 \%$ of all vehicles refueling at CNG stations in St. Petersburg. Assume that the stations are used at $100 \%$ of their capacity.
|
Task 2. There are a total of 15 stations: 4 new ones and 11 old ones.
The throughput capacity of the old stations is 11 x $200=2200$ vehicles per day, and for the new ones: $200+700=900$ vehicles per day. In total, the stations can refuel: $2200+900=3100$ vehicles per day.
Vehicles from the city fleet account for only $70 \%$ of all vehicles refueled at the CNG stations in St. Petersburg, so $3100 x 0.7=2170$ vehicles can be refueled. Currently, there are 1000 vehicles in the city fleet, so the city fleet of gas-powered vehicles can be increased by 1170 units.
|
1170
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}+4096}{64 a^{6}}$, if $\frac{a}{2}-\frac{2}{a}=5$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}+4096}{64 a^{6}}=\frac{a^{6}}{64}+\frac{64}{a^{6}}=\frac{a^{6}}{64}-2+\frac{64}{a^{6}}+2=\left(\frac{a^{3}}{8}-\frac{8}{a^{3}}\right)^{2}+2= \\
& =\left(\frac{a^{3}}{8}-3 \cdot \frac{a}{2}+3 \cdot \frac{2}{a}-\frac{8}{a^{3}}+3\left(\frac{a}{2}-\frac{2}{a}\right)\right)^{2}+2= \\
& =\left(\left(\frac{a}{2}-\frac{2}{a}\right)^{3}+3\left(\frac{a}{2}-\frac{2}{a}\right)\right)^{2}+2=\left(5^{3}+3 \cdot 5\right)^{2}+2=19602
\end{aligned}
$$
Answer. 19602.
|
19602
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}+729^{2}}{729 a^{6}}$, if $\frac{a}{3}-\frac{3}{a}=4$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}+729^{2}}{729 a^{6}}=\frac{a^{6}}{729}+\frac{729}{a^{6}}=\frac{a^{6}}{729}-2+\frac{729}{a^{6}}+2=\left(\frac{a^{3}}{27}-\frac{27}{a^{3}}\right)^{2}+2= \\
& =\left(\frac{a^{3}}{27}-3 \cdot \frac{a}{3}+3 \cdot \frac{3}{a}-\frac{27}{a^{3}}+3\left(\frac{a}{3}-\frac{3}{a}\right)\right)^{2}+2= \\
& =\left(\left(\frac{a}{3}-\frac{3}{a}\right)^{3}+3\left(\frac{a}{3}-\frac{3}{a}\right)\right)^{2}+2=\left(4^{3}+3 \cdot 4\right)^{2}+2=5778
\end{aligned}
$$
Answer. 5778.
|
5778
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}+729^{2}}{729 a^{6}}$, if $\frac{a}{3}-\frac{3}{a}=2$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{12}+729^{2}}{729 a^{6}}=\frac{a^{6}}{729}+\frac{729}{a^{6}}=\frac{a^{6}}{729}-2+\frac{729}{a^{6}}+2=\left(\frac{a^{3}}{27}-\frac{27}{a^{3}}\right)^{2}+2= \\
& =\left(\frac{a^{3}}{27}-3 \cdot \frac{a}{3}+3 \cdot \frac{3}{a}-\frac{27}{a^{3}}+3\left(\frac{a}{3}-\frac{3}{a}\right)\right)^{2}+2= \\
& =\left(\left(\frac{a}{3}-\frac{3}{a}\right)^{3}+3\left(\frac{a}{3}-\frac{3}{a}\right)\right)^{2}+2=\left(2^{3}+3 \cdot 2\right)^{2}+2=14^{2}+2=198
\end{aligned}
$$
Answer. 198.
|
198
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches the extensions of two sides $A B$ and $A D$ of square $A B C D$ with side $2 \sqrt{3} \mathrm{~cm}$. Two tangents are drawn from point $C$ to this circle. Find the radius of the circle if the angle between the tangents is $30^{\circ}$, and it is known that $\sin 15^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}$.
#
|
# Solution.
Fig. 1
The segment cut off from vertex $A$ by the point of tangency of the circle is equal to the radius of this circle. The diagonal of the square $A B C D A C=2 \sqrt{6}$. If radii of the circle are drawn to the points of tangency, a square with side $R$ is formed. Then $O A=R \sqrt{2}$, $O C=\frac{O K}{\sin 15^{\circ}}=\frac{2 \sqrt{2} R}{\sqrt{3}-1}$. As a result, we get the equation $\frac{2 \sqrt{2} R}{\sqrt{3}-1}=R \sqrt{2}+2 \sqrt{6}$, from which $R=\frac{2 \sqrt{6}}{\sqrt{6}+\sqrt{2}-\sqrt{2}}=2$.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}+4096}{64 a^{6}}$, if $\frac{a}{2}-\frac{2}{a}=3$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}+4096}{64 a^{6}}=\frac{a^{6}}{64}+\frac{64}{a^{6}}=\frac{a^{6}}{64}-2+\frac{64}{a^{6}}+2=\left(\frac{a^{3}}{8}-\frac{8}{a^{3}}\right)^{2}+2= \\
& =\left(\frac{a^{3}}{8}-3 \cdot \frac{a}{2}+3 \cdot \frac{2}{a}-\frac{8}{a^{3}}+3\left(\frac{a}{2}-\frac{2}{a}\right)\right)^{2}+2= \\
& =\left(\left(\frac{a}{2}-\frac{2}{a}\right)^{3}+3\left(\frac{a}{2}-\frac{2}{a}\right)\right)^{2}+2=\left(3^{3}+3 \cdot 3\right)^{2}+2=1298
\end{aligned}
$$
Answer. 1298.
|
1298
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}-729}{27 a^{6}}$, if $\frac{a^{2}}{3}-\frac{3}{a^{2}}=4$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}-729}{27 a^{6}}=\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\frac{a^{4}}{9}+1+\frac{9}{a^{4}}\right)=\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\frac{a^{4}}{9}-2+\frac{9}{a^{4}}+3\right)= \\
& =\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)^{2}+3\right)=4 \cdot\left(4^{2}+3\right)=76
\end{aligned}
$$
Answer. 76.
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}-4096}{64 a^{6}}$, if $\frac{a^{2}}{4}-\frac{4}{a^{2}}=3$.
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}-4096}{64 a^{6}}=\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\frac{a^{4}}{16}+1+\frac{16}{a^{4}}\right)=\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\frac{a^{4}}{16}-2+\frac{16}{a^{4}}+3\right)= \\
& =\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\left(\frac{a^{2}}{16}-\frac{16}{a^{2}}\right)^{2}+3\right)=3 \cdot\left(3^{2}+3\right)=36
\end{aligned}
$$
Answer. 36.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}-729}{27 a^{6}}$, if $\frac{a^{2}}{3}-\frac{3}{a^{2}}=6$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{12}-729}{27 a^{6}}=\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\frac{a^{4}}{9}+1+\frac{9}{a^{4}}\right)=\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\frac{a^{4}}{9}-2+\frac{9}{a^{4}}+3\right)= \\
& =\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)\left(\left(\frac{a^{2}}{3}-\frac{3}{a^{2}}\right)^{2}+3\right)=6 \cdot\left(6^{2}+3\right)=234
\end{aligned}
$$
Answer. 234.
|
234
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{12}-4096}{64 a^{6}}$, if $\frac{a^{2}}{4}-\frac{4}{a^{2}}=5$.
|
# Solution.
$$
\begin{aligned}
& \frac{a^{12}-4096}{64 a^{6}}=\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\frac{a^{4}}{16}+1+\frac{16}{a^{4}}\right)=\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\frac{a^{4}}{16}-2+\frac{16}{a^{4}}+3\right)= \\
& =\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right)\left(\left(\frac{a^{2}}{16}-\frac{16}{a^{2}}\right)^{2}+3\right)=5 \cdot\left(5^{2}+3\right)=140
\end{aligned}
$$
Answer. 140.
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (6 points) In an ideal gas, a thermodynamic cycle consisting of two isochoric and two adiabatic processes is carried out. The ratio of the initial and final absolute temperatures in the isochoric cooling process is \( k = 1.5 \). Determine the efficiency of this cycle, given that the efficiency of the Carnot cycle with the same ratio of maximum to minimum temperature as in the considered cycle is \( 50\% \).
## Possible solution.
In the graph of the cyclic process, it is clear that the absolute temperatures \( T_{1} = T_{\max} \), and \( T_{3} = T_{\min} \). By definition, the efficiency is the ratio of the work done by the gas in the cycle to the amount of heat transferred to the gas. In the studied cycle, work is performed in the adiabatic processes, while energy is transferred in the form of heat in the isochoric processes. Using the first law of thermodynamics, we obtain for the work of
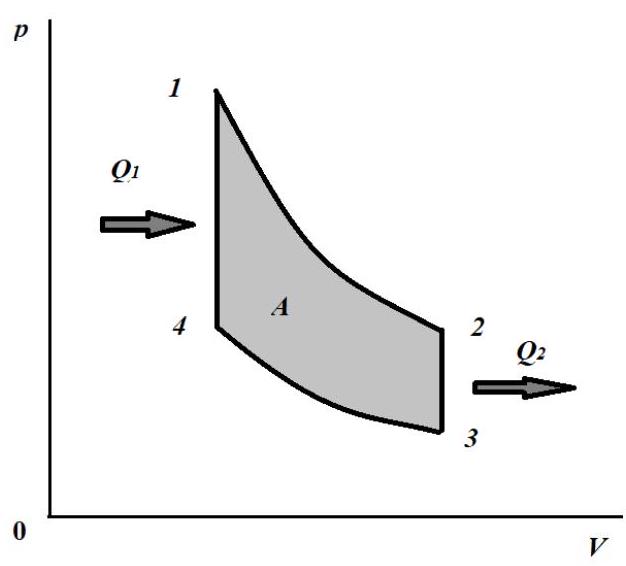
the gas in the adiabatic processes:
$$
\begin{gathered}
A_{12} = -\Delta U_{12} = \frac{i}{2} v R \left( T_{\max} - T_{2} \right) > 0 \\
A_{34} = -\Delta U_{34} = \frac{i}{2} v R \left( T_{\min} - T_{4} \right) < 0
\end{gathered}
$$
where \(\Delta U\) is the change in internal energy of the gas, \(i\) is the number of degrees of freedom of the gas molecule, \(v\) is the amount of substance, and \(R\) is the universal gas constant.
The work done by the gas in the cycle:
$$
A = A_{12} + A_{34} = \frac{i}{2} v R \left[ \left( T_{\max} - T_{2} \right) - \left( T_{4} - T_{\min} \right) \right].
$$
The amount of heat transferred to the gas in the isochoric process \(4-1\):
$$
Q_{1} = \Delta U_{41} = \frac{i}{2} v R \left( T_{\max} - T_{4} \right)
$$
The efficiency
$$
\eta = \frac{\left( T_{\max} - T_{4} \right) - \left( T_{2} - T_{\min} \right)}{T_{\max} - T_{4}} = 1 - \frac{T_{2} - T_{\min}}{T_{\max} - T_{4}}
$$
According to Poisson's equation for adiabatic processes
$$
\begin{aligned}
p_{1} V_{1}^{\gamma} & = p_{2} V_{2}^{\gamma} \\
p_{4} V_{1}^{\gamma} & = p_{3} V_{1}^{\gamma} \\
\frac{p_{1}}{p_{4}} & = \frac{p_{2}}{p_{3}}.
\end{aligned}
$$
Here \(\gamma\) is the adiabatic index. By Charles's law
$$
\begin{aligned}
& \frac{p_{1}}{p_{4}} = \frac{T_{\max}}{T_{4}} \\
& \frac{p_{2}}{p_{3}} = \frac{T_{2}}{T_{\min}}
\end{aligned}
$$
We obtain that
$$
\frac{T_{\max}}{T_{4}} = \frac{T_{2}}{T_{\min}} = k
$$
Considering the obtained equality, we can write:
$$
\eta = 1 - \frac{T_{2} - T_{\min}}{T_{\max} - T_{4}} = 1 - \frac{T_{\min} (k - 1)}{T_{\max} \left( 1 - \frac{1}{k} \right)} = 1 - k \frac{T_{\min}}{T_{\max}}
$$
For the Carnot cycle
$$
\eta_{\mathrm{K}} = 1 - \frac{T_{\min}}{T_{\max}}
$$
Then
$$
\eta = 1 - k \left( 1 - \eta_{\mathrm{K}} \right) = 0.25 = 25\%.
$$
|
Answer: $\eta=1-k\left(1-\eta_{C}\right)=0.25=25 \%$.
## Evaluation Criteria
| Performance | Score |
| :--- | :---: |
| Participant did not start the task or performed it incorrectly from the beginning | $\mathbf{0}$ |
| Expression for work in the cycle is written | $\mathbf{1}$ |
| Expression for the amount of heat received is written | $\mathbf{1}$ |
| Expression for the efficiency coefficient in terms of temperatures in the cycle states is written | $\mathbf{1}$ |
| Expression for the temperature ratios in isochoric processes is obtained | $\mathbf{1}$ |
| Expression for the efficiency of the Carnot cycle is written | $\mathbf{1}$ |
| Necessary transformations are performed and a numerical answer is obtained | $\mathbf{1}$ |
| :---: | :---: | :---: |
| Total points | $\mathbf{6}$ |
|
25
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Determine the amount of substance of sodium carbonate
According to the chemical reaction equation:
$$
\mathrm{n}\left(\mathrm{CO}_{2}\right)=\mathrm{n}\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=0.125 \text { mol }
$$
Determination of the amount of substance - 2 points
19. Calculate the mass of sodium carbonate
$$
m\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=n \cdot M=0.125 \cdot 106=13.25 \text { g }
$$
Determination of the mass of the substance - 2 points
20. Determine the mass fraction of sodium carbonate in the initial solution:
$$
\omega\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)=\frac{m\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right) \cdot 100 \%}{m_{\mathrm{p}-\mathrm{pa}}\left(\mathrm{Na}_{2} \mathrm{CO}_{3}\right)}=\frac{13.25 \cdot 100 \%}{132.5}=10 \%
$$
Determination of the mass fraction of the substance in the solution - 2 points
|
Answer: $10 \%$
## TOTAL 10 points
## TASK № 2
Aluminum oxide was melted with potash. The resulting product was dissolved in hydrochloric acid and treated with excess ammonia water. The precipitate that formed was dissolved in excess sodium hydroxide solution. Write the equations for the four reactions described.
## Solution:
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. Let's determine the amount of sulfur substance
According to the chemical reaction equation:
$$
\mathrm{n}(\mathrm{S})=\mathrm{n}\left(\mathrm{SO}_{2}\right)=1 \text { mole }
$$
29. Let's calculate the mass of pure sulfur:
$$
m(S)=n \cdot M=1 \cdot 32=32 \text { g }
$$
Determination of the mass of the substance - 2 points
30. Thus, in a sample of natural sulfur weighing 38 g, there are 32 g of pure substance.
Let's calculate the mass of the impurity:
$m($ impurity $)=38-32=6$ g
Determination of the mass of the impurity - 2 points
|
Answer: 6 g.
## TOTAL 10 points
## TASK № 2
Potassium phosphate was calcined with coke in the presence of river sand. The simple substance formed reacted with excess chlorine. The resulting product was added to an excess of potassium hydroxide solution. The formed solution was treated with lime water. Write the equations for the four described reactions.
## Solution:
|
6
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. Let's calculate the volume of carbon dioxide.
According to Avogadro's law, the following rule applies: in equal volumes of different gases taken at the same temperatures and pressures, the same number of molecules is contained.
From the chemical reaction equation, it follows that the ratio of the amount of substance (in moles) is $2: 1$, which means the volume of carbon dioxide is half the volume of oxygen.
$V\left(\mathrm{CO}_{2}\right)=\frac{1}{2} V\left(\mathrm{O}_{2}\right)=\frac{1}{2} \cdot 14=7$ liters
Determining the volume of carbon dioxide - 4 points
|
Answer: 7 l.
## TOTAL 10 points
## TASK № 2
Chromium (III) oxide was melted with potassium sulfite. The resulting product was added to water. To the precipitate formed, a mixture of bromine and sodium hydroxide was added, resulting in a yellow solution. Upon adding hydrogen sulfide water to the obtained solution, a precipitate formed. Write the equations for the four described reactions.
## Solution:
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}+256}{16 a^{4}}$, if $\frac{a}{2}+\frac{2}{a}=5$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{8}+256}{16 a^{4}}=\frac{a^{4}}{16}+\frac{16}{a^{4}}=\frac{a^{4}}{16}+2+\frac{16}{a^{4}}-2=\left(\frac{a^{2}}{4}+\frac{4}{a^{2}}\right)^{2}-2= \\
& =\left(\frac{a^{2}}{4}+2+\frac{4}{a^{2}}-2\right)^{2}-2=\left(\left(\frac{a}{2}+\frac{2}{a}\right)^{2}-2\right)^{2}-2=\left(5^{2}-2\right)^{2}-2=527
\end{aligned}
$$
Answer. 527.
|
527
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) Laboratory engineer Sergei received an object for research consisting of about 200 monoliths (a container designed for 200 monoliths, which was almost completely filled). Each monolith has a specific name (sandy loam or clayey loam) and genesis (marine or lake-glacial deposits). The relative frequency (statistical probability) that a randomly selected monolith will be sandy loam is $\frac{1}{9}$. The relative frequency that a randomly selected
monolith will be marine clayey loam is $\frac{11}{18}$. How many monoliths of lake-glacial genesis does the object contain, if there are no marine sandy loams among the sandy loams?
|
# Solution.
Let's determine the exact number of monoliths. It is known that the probability of a monolith being loamy sand is $\frac{1}{9}$. The number closest to 200 that is divisible by 9 is 198. Therefore, there are 198 monoliths in total. Monoliths of lacustrine-glacial origin consist of all loamy sands $(198: 9=22)$ and part of the clay loams. Let's find out how many monoliths of lacustrine-glacial origin are among the clay loams: The total number of clay loams is 198:9$\cdot$8=176. Among them, marine clay loams constitute $\frac{11}{18}$ of the total, which is 121. Therefore, the number of clay loams of lacustrine-glacial origin is 55. Thus, the total number of monoliths of lacustrine-glacial origin is: $22+55=77$.
Answer. 77.
|
77
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. (20 points)
Find $x_{0}-y_{0}$, if $x_{0}$ and $y_{0}$ are the solutions to the system of equations:
$$
\left\{\begin{array}{l}
x^{3}-2023 x=y^{3}-2023 y+2020 \\
x^{2}+x y+y^{2}=2022
\end{array}\right.
$$
|
# Solution.
Rewrite the system as
$$
\left\{\begin{array}{l}
x^{3}-y^{3}+2023 y-2023 x=2020 \\
x^{2}+x y+y^{2}=2022
\end{array}\right.
$$
Let $x_{0}$ and $y_{0}$ be the solution to the system of equations. Then
$\left\{\begin{array}{l}x_{0}{ }^{3}-y_{0}{ }^{3}+2023 y_{0}-2023 x_{0}=2020, \\ x_{0}{ }^{2}+x_{0} y_{0}+y_{0}{ }^{2}=2022 .\end{array}\right.$
Rewrite the first equation of the system as
$\left\{\begin{array}{l}\left(x_{0}-y_{0}\right)\left(x_{0}^{2}+x_{0} y_{0}+y_{0}{ }^{2}\right)-2023\left(x_{0}-y_{0}\right)=2020, \\ x_{0}{ }^{2}+x_{0} y_{0}+y_{0}{ }^{2}=2022 ;\end{array}\right.$
$\left\{\begin{array}{l}2022\left(x_{0}-y_{0}\right)-2023\left(x_{0}-y_{0}\right)=2020, \\ x_{0}^{2}+x_{0} y_{0}+y_{0}^{2}=2022 ;\end{array}\right.$
Then $x_{0}-y_{0}=-2020$.
Answer. -2020.
|
-2020
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}-256}{16 a^{4}} \cdot \frac{2 a}{a^{2}+4}$, if $\frac{a}{2}-\frac{2}{a}=3$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{8}-256}{16 a^{4}} \cdot \frac{2 a}{a^{2}+4}=\left(\frac{a^{4}}{16}-\frac{16}{a^{4}}\right) \cdot \frac{2 a}{a^{2}+4}=\left(\frac{a^{2}}{4}+\frac{4}{a^{2}}\right)\left(\frac{a^{2}}{4}-\frac{4}{a^{2}}\right) \cdot \frac{2 a}{a^{2}+4}= \\
& =\left(\frac{a^{2}}{4}-2+\frac{4}{a^{2}}+2\right)\left(\frac{a}{2}-\frac{2}{a}\right)\left(\frac{a}{2}+\frac{2}{a}\right) \cdot \frac{2 a}{a^{2}+4}= \\
& =\left(\left(\frac{a}{2}-\frac{2}{a}\right)^{2}+2\right)\left(\left(\frac{a}{2}-\frac{2}{a}\right)=\left(3^{2}+2\right) \cdot 3=33 .\right.
\end{aligned}
$$
Answer. 33.
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) Lab engineer Dasha received an object for research consisting of about 100 monoliths (a container designed for 100 monoliths, which was almost completely filled). Each monolith has a specific name (sandy loam or clayey loam) and genesis (marine or lake-glacial deposits). The relative frequency (statistical probability) that a randomly selected monolith will be sandy loam is $\frac{1}{7}$. The relative frequency that a randomly selected monolith will be marine clayey loam is $\frac{9}{14}$. How many monoliths of lake-glacial genesis does the object contain, if there are no marine sandy loams among the sandy loams?
#
|
# Solution.
Let's determine the exact number of monoliths. It is known that the probability of a monolith being loamy sand is $\frac{1}{7}$. The number closest to 100 that is divisible by 7 is 98. Therefore, there are 98 monoliths in total. Monoliths of lacustrine-glacial origin consist of all loamy sands ($98: 7=14$) and part of the clay loams. Let's find out how many monoliths of lacustrine-glacial origin are among the clay loams: The total number of clay loams is $98: 7 \cdot 6=84$. Among them, marine clay loams constitute $\frac{9}{14}$ of the total, which is 63. Therefore, the number of clay loams of lacustrine-glacial origin is 21. Thus, the total number of monoliths of lacustrine-glacial origin is: $14+21=35$.
Answer. 35.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) At the research institute, a scientific employee, Ivan Ivanovich, received an object for research containing about 300 oil samples (a container designed for 300 samples, which was almost completely filled). Each sample has certain characteristics in terms of sulfur content - either low-sulfur or high-sulfur, and density - either light or heavy. The relative frequency (statistical probability) that a randomly selected sample will be a heavy oil sample is $\frac{1}{8}$. The relative frequency that a randomly selected sample will be a light low-sulfur oil sample is $\frac{22}{37}$. How many high-sulfur oil samples does the object contain, if there were no low-sulfur samples among the heavy oil samples?
|
# Solution.
Let's determine the exact number of oil samples. It is known that the relative frequency of a selected sample being a heavy oil sample is $\frac{1}{8}$, and the number closest to 300 that is divisible by $8-296$. Therefore, the total number of samples in the container is 296. The samples of high-sulfur oil consist of all heavy oil samples (296:8=37) and part of the light oil samples. Let's find out how many high-sulfur oil samples are among the light oil samples. The total number of light oil samples is 296:8.7=259. Among them, the samples of low-sulfur oil constitute $\frac{22}{37}$ of the total, which is 176. Therefore, the number of high-sulfur light oil samples is 83. Then the total number of high-sulfur oil samples is: $37+83=120$.
Answer. 120.
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) Find the smallest natural solution of the inequality $\left(\frac{2023}{2022}\right)^{27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{72}$.
|
Solution.
$\left(\frac{2023}{2022}\right)^{27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{72}$
We transition to an equivalent inequality
$27+18+12+8+\ldots+27 \cdot\left(\frac{2}{3}\right)^{n}>72$
$27\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\left(\frac{2}{3}\right)^{3}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>72$
$\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\left(\frac{2}{3}\right)^{3}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>\frac{8}{3}$
The left side of the inequality represents the sum of a geometric progression
$\frac{1-\left(\frac{2}{3}\right)^{n+1}}{1-\frac{2}{3}}>\frac{8}{3}, 1-\left(\frac{2}{3}\right)^{n+1}>\frac{8}{9}, \frac{1}{9}>\left(\frac{2}{3}\right)^{n+1},\left(\frac{2}{3}\right)^{n}\frac{1}{6},\left(\frac{2}{3}\right)^{5}=\frac{32}{243}=\frac{64}{486}=\frac{1}{6} \cdot \frac{64}{81}<\frac{1}{6}$.
Thus, the smallest natural value of $n=5$.
Answer. 5.
|
5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Calculate
$$
\left(\frac{10001}{20232023}-\frac{10001}{20222022}\right) \cdot 4090506+\sqrt{4092529}
$$
|
# Solution.
$$
\begin{aligned}
& \left(\frac{10001}{20232023}-\frac{10001}{20222022}\right) \cdot 4090506+\sqrt{4092529} \\
& =\left(\frac{10001}{2023 \cdot 10001}-\frac{10001}{2022 \cdot 10001}\right) \cdot 4090506+\sqrt{2023^{2}}= \\
& \quad=\left(\frac{1}{2023}-\frac{1}{2022}\right) \cdot 2022 \cdot 2023+2023=\frac{2022-2023}{2022 \cdot 2023} \cdot 2022 \cdot 2023+2023=-1+2023=2022
\end{aligned}
$$
Answer. 2022.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) At the research institute, a scientific employee, Tatyana Vasilyevna, received an object for research containing about 150 oil samples (a container designed for 150 samples, which was almost completely filled). Each sample has certain characteristics in terms of sulfur content - either low-sulfur or high-sulfur, and density - either light or heavy. The relative frequency (statistical probability) that a randomly selected sample will be a heavy oil sample is $\frac{2}{11}$. The relative frequency that a randomly selected sample will be a light low-sulfur oil sample is $\frac{7}{13}$. How many high-sulfur oil samples does the object contain, if there were no low-sulfur samples among the heavy oil samples?
|
# Solution.
Let's determine the exact number of oil samples. It is known that the relative frequency of a sample being a heavy oil sample is $\frac{2}{11}$, and the number closest to 150 that is divisible by $11-143$. Therefore, the total number of samples in the container is 143. Samples of high-sulfur oil consist of all heavy oil samples ( $143: 11 \cdot 2=26$ ) and part of the light oil samples. Let's find out how many high-sulfur oil samples are among the light oil samples. The total number of light oil samples is 143:11.9=117. Among them, samples of low-sulfur oil constitute $\frac{7}{13}$ of the total, which is 77. Therefore, the number of high-sulfur light oil samples is 40. Then the total number of high-sulfur oil samples is: $26+40=66$.
Answer. 66.
|
66
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) Find the smallest natural solution of the inequality $\left(\frac{2023}{2022}\right)^{36+24+16+\ldots+36\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{96}$.
|
Solution.
$\left(\frac{2023}{2022}\right)^{36+24+16+\ldots+36\left(\frac{2}{3}\right)^{n}}>\left(\frac{2023}{2022}\right)^{96}$.
$36+24+16+. .+36 \cdot\left(\frac{2}{3}\right)^{n}>96$
$36\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>96$
$\left(1+\frac{2}{3}+\left(\frac{2}{3}\right)^{2}+\ldots+\left(\frac{2}{3}\right)^{n}\right)>\frac{8}{3}$
The left side of the inequality represents the sum of a geometric progression
$\frac{1-\left(\frac{2}{3}\right)^{n+1}}{1-\frac{2}{3}}>\frac{8}{3}, 1-\left(\frac{2}{3}\right)^{n+1}>\frac{8}{9}, \frac{1}{9}>\left(\frac{2}{3}\right)^{n+1},\left(\frac{2}{3}\right)^{n}\frac{1}{6},\left(\frac{2}{3}\right)^{5}=\frac{32}{243}=\frac{64}{486}=\frac{1}{6} \cdot \frac{64}{81}<\frac{1}{6}$.
Thus, the smallest natural value of $n=5$.
Answer. 5.
|
5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}+1296}{36 a^{4}}$, if $\frac{a}{\sqrt{6}}+\frac{\sqrt{6}}{a}=5$.
#
|
# Solution.
$$
\begin{aligned}
& \frac{a^{8}+1296}{36 a^{4}}=\frac{a^{4}}{36}+\frac{36}{a^{4}}=\frac{a^{4}}{36}+2+\frac{36}{a^{4}}-2=\left(\frac{a^{2}}{6}+\frac{6}{a^{2}}\right)^{2}-2= \\
& =\left(\frac{a^{2}}{6}+2+\frac{6}{a^{2}}-2\right)^{2}-2=\left(\left(\frac{a}{\sqrt{6}}+\frac{\sqrt{6}}{a}\right)^{2}-2\right)^{2}-2=\left(5^{2}-2\right)^{2}-2=527
\end{aligned}
$$
Answer. 527.
|
527
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle with a radius of 15 touches two adjacent sides $AB$ and $AD$ of the square $ABCD$. On the other two sides, the circle intersects at points, cutting off segments of 6 cm and 3 cm from the vertices, respectively. Find the length of the segment that the circle cuts off from vertex $B$ at the point of tangency.
|
# Solution.

Fig. 1
Let $X$ be the desired segment, then $X+15$ is the side of the square. The segment $K L=15+X-6-3=X+6$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
15^{2}=X^{2}+\left(\frac{X+6}{2}\right)^{2}
$$
This is a quadratic equation in terms of $X$, which has only one positive root 12.
Answer. 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) At the quality control department of an oil refinery, Engineer Pavel Pavlovich received a research object consisting of about 100 oil samples (a container designed for 100 samples, which was almost completely filled). Each sample has certain characteristics in terms of sulfur content - either low-sulfur or high-sulfur, and density - either light or heavy. The relative frequency (statistical probability) that a randomly selected sample will be a heavy oil sample is $\frac{1}{7}$. The relative frequency that a randomly selected sample will be a light low-sulfur oil sample is $\frac{9}{14}$. How many high-sulfur oil samples does the object contain, if there were no low-sulfur samples among the heavy oil samples?
|
# Solution.
Let's determine the exact number of oil samples. It is known that the relative frequency of a sample being a heavy oil sample is $\frac{1}{7}$. The number closest to 100 that is divisible by $7$ is $98$. Therefore, there are 98 samples in total in the container. The samples of high-sulfur oil include all the heavy oil samples ($98: 7=14$) and a portion of the light oil samples. Let's find out how many high-sulfur oil samples are among the light oil samples. The total number of light oil samples is $98:7 \cdot 6=84$. Among them, the samples of low-sulfur oil constitute $\frac{9}{14}$ of the total, which is 63. Therefore, the number of high-sulfur light oil samples is 21. Thus, the total number of high-sulfur oil samples is: $14+21=35$.
Answer. 35.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) For the numerical sequence $\left\{x_{n}\right\}$, all terms of which, starting from $n \geq 2$, are distinct, the relation $x_{n}=\frac{x_{n-1}+298 x_{n}+x_{n+1}}{300}$ holds. Find $\sqrt{\frac{x_{2023}-x_{2}}{2021} \cdot \frac{2022}{x_{2023}-x_{1}}}-2023$.
|
# Solution.
From the given relations in the problem, it is easily deduced that for all $n \geq 2$, $x_{n}-x_{n-1}=x_{n+1}-x_{n}$, which implies that the sequence is an arithmetic progression. Indeed,
$$
\begin{gathered}
x_{n}=\frac{x_{n-1}+298 x_{n}+x_{n+1}}{300} \\
2 x_{n}=x_{n-1}+x_{n+1} \\
x_{n}-x_{n-1}=x_{n+1}-x_{n}
\end{gathered}
$$
Let the common difference of this progression be $d, d \neq 0$ (as per the condition).
Then $\sqrt{\frac{x_{2023}-x_{2}}{2021} \cdot \frac{2022}{x_{2023}-x_{1}}}-2023=\sqrt{\frac{x_{1}+2022 d-x_{1}-d}{2021} \cdot \frac{2022}{x_{1}+2022 d-x_{1}}}-2023=$ $=\sqrt{\frac{2021 d}{2021} \cdot \frac{2022}{2022 d}}-2023=1-2023=-2022$.
Answer. -2022.
|
-2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}-6561}{81 a^{4}} \cdot \frac{3 a}{a^{2}+9}$, if $\frac{a}{3}-\frac{3}{a}=4$.
|
Solution.
$\frac{a^{8}-6561}{81 a^{4}} \cdot \frac{3 a}{a^{2}+9}=\left(\frac{a^{4}}{81}-\frac{81}{a^{4}}\right) \cdot \frac{3 a}{a^{2}+9}=\left(\frac{a^{2}}{9}+\frac{9}{a^{2}}\right)\left(\frac{a^{2}}{9}-\frac{9}{a^{2}}\right) \cdot \frac{3 a}{a^{2}+9}=$
$=\left(\frac{a^{2}}{9}-2+\frac{9}{a^{2}}+2\right)\left(\frac{a}{3}-\frac{3}{a}\right)\left(\frac{a}{3}+\frac{3}{a}\right) \cdot \frac{3 a}{a^{2}+9}=$
$=\left(\left(\frac{a}{3}-\frac{3}{a}\right)^{2}+2\right)\left(\frac{a}{3}-\frac{3}{a}\right)=\left(4^{2}+2\right) \cdot 4=72$.
Answer. 72.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle with a radius of 10 touches two adjacent sides $AB$ and $AD$ of the square $ABCD$. On the other two sides, the circle intersects at points, cutting off segments of 4 cm and 2 cm from the vertices, respectively. Find the length of the segment that the circle cuts off from vertex $B$ at the point of tangency.
|
Solution.
Fig. 1
Let $X$ be the desired segment, then $X+10$ is the side of the square. The segment $K L=10+X-4-2=X+4$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
10^{2}=X^{2}+\left(\frac{X+4}{2}\right)^{2}
$$
This is a quadratic equation in terms of $X$, which has only one positive root 8.
Answer. 8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) At the quality control department of an oil refinery, Engineer Valentina Ivanovna received a research object consisting of about 200 oil samples (a container designed for 200 samples, which was almost completely filled). Each sample has certain characteristics in terms of sulfur content - either low-sulfur or high-sulfur, and density - either light or heavy. The relative frequency (statistical probability) that a randomly selected sample will be a heavy oil sample is $\frac{1}{9}$. The relative frequency that a randomly selected sample will be a light low-sulfur oil sample is $\frac{11}{18}$. How many high-sulfur oil samples does the object contain, if there were no low-sulfur samples among the heavy oil samples?
|
# Solution.
Let's determine the exact number of oil samples. It is known that the relative frequency of a sample being a heavy oil sample is $\frac{1}{9}$. The number closest to 200 that is divisible by 9 is 198. Therefore, the total number of samples in the container is 198. The samples of high-sulfur oil consist of all heavy oil samples ($198: 9=22$) and a portion of the light oil samples. Let's find out how many high-sulfur oil samples are among the light oil samples. The total number of light oil samples is $198: 9 \cdot 8=176$. Among them, the samples of low-sulfur oil constitute $\frac{11}{18}$ of the total, which is 121. Therefore, the number of high-sulfur light oil samples is 55. Thus, the total number of high-sulfur oil samples is: $22+55=77$.
Answer. 77.
|
77
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) For the numerical sequence $\left\{x_{n}\right\}$, all terms of which, starting from $n \geq 2$, are distinct, the relation $x_{n}=\frac{x_{n-1}+398 x_{n}+x_{n+1}}{400}$ holds. Find $\sqrt{\frac{x_{2023}-x_{2}}{2021} \cdot \frac{2022}{x_{2023}-x_{1}}}+2021$.
|
# Solution.
From the given relations in the problem, it is easily deduced that for all $n \geq 2$, $x_{n}-x_{n-1}=x_{n+1}-x_{n}$, which implies that the sequence is an arithmetic progression. Indeed,
$$
\begin{gathered}
x_{n}=\frac{x_{n-1}+398 x_{n}+x_{n+1}}{400} \\
2 x_{n}=x_{n-1}+x_{n+1} \\
x_{n}-x_{n-1}=x_{n+1}-x_{n}
\end{gathered}
$$
Let the common difference of this progression be $d, d \neq 0$ (as per the condition).
Then $\sqrt{\frac{x_{2023}-x_{2}}{2021} \cdot \frac{2022}{x_{2023}-x_{1}}}+2021=\sqrt{\frac{x_{1}+2022 d-x_{1}-d}{2021} \cdot \frac{2022}{x_{1}+2022 d-x_{1}}}+2021=$ $=\sqrt{\frac{2021 d}{2021} \cdot \frac{2022}{2022 d}}+2021=1+2021=2022$
Answer. 2022.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}-256}{16 a^{4}} \cdot \frac{2 a}{a^{2}+4}$, if $\frac{a}{2}-\frac{2}{a}=5$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{8}-256}{16 a^{4}} \cdot \frac{2 a}{a^{2}+4}=\left(\frac{a^{4}}{16}-\frac{16}{a^{4}}\right) \cdot \frac{2 a}{a^{2}+4}=\left(\frac{a^{2}}{4}+\frac{4}{a^{2}}\right)\left(\frac{a^{2}}{16}-\frac{16}{a^{2}}\right) \cdot \frac{2 a}{a^{2}+4}= \\
& =\left(\frac{a^{2}}{4}-2+\frac{4}{a^{2}}+2\right)\left(\frac{a}{2}-\frac{2}{a}\right)\left(\frac{a}{2}+\frac{2}{a}\right) \cdot \frac{2 a}{a^{2}+4}= \\
& =\left(\left(\frac{a}{2}-\frac{2}{a}\right)^{2}+2\right)\left(\frac{a}{2}-\frac{2}{a}\right)=\left(5^{2}+2\right) \cdot 3=81
\end{aligned}
$$
Answer. 81.
|
81
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches two adjacent sides $AB$ and $AD$ of square $ABCD$ and cuts off segments of length 4 cm from vertices $B$ and $D$ at the points of tangency. On the other two sides, the circle intersects and cuts off segments of 2 cm and 1 cm from the vertices, respectively. Find the radius of the circle.
|
# Solution.
Fig. 1
Let $R$ be the radius of the circle, then $R+4$ is the side of the square. The segment $K L=4+R-2-1=R+1$. Consider the triangle $O N L$. By the Pythagorean theorem, the following equality holds:
$$
R^{2}=4^{2}+\left(\frac{1+R}{2}\right)^{2}
$$
This is a quadratic equation in terms of $R$, which has only one positive root 5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) In the educational center "Young Geologist," an object consisting of about 150 monoliths (a container designed for 150 monoliths, which was almost completely filled) was delivered. Each monolith has a specific name (sandy loam or clayey loam) and genesis (marine or lake-glacial deposits). The relative frequency (statistical probability) that a randomly selected monolith will be sandy loam is $\frac{2}{11}$. The relative frequency that a randomly selected monolith will be marine clayey loam is $\frac{7}{13}$. How many monoliths of lake-glacial genesis does the object contain, if there are no marine sandy loams among the sandy loams? #
|
# Solution.
Let's determine the exact number of monoliths. It is known that the relative frequency of a monolith being loamy sand is $\frac{2}{11}$. The number closest to 150 that is divisible by 11 is 143. Therefore, there are 143 monoliths in total. Monoliths of lacustrine-glacial origin make up all loamy sands ( $143: 11 \cdot 2=26$ ) and part of the loams. Let's find out how many monoliths of lacustrine-glacial origin are among the loams: The total number of loams is 143:11$\cdot$9=117. Among them, marine loams constitute $\frac{7}{13}$ of the total, which is 77. Therefore, the number of loams of lacustrine-glacial origin is 40. Thus, the total number of monoliths of lacustrine-glacial origin is: $26+40=66$.
Answer. 66.
|
66
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) For the numerical sequence $\left\{x_{n}\right\}$, all terms of which, starting from $n \geq 2$, are distinct, the relation $x_{n}=\frac{x_{n-1}+98 x_{n}+x_{n+1}}{100}$ holds. Find $\sqrt{\frac{x_{2023}-x_{1}}{2022} \cdot \frac{2021}{x_{2023}-x_{2}}}+2021$.
|
# Solution.
From the given relations in the problem, it is easily deduced that for all $n \geq 2$, $x_{n}-x_{n-1}=x_{n+1}-x_{n}$, which implies that the sequence is an arithmetic progression. Indeed,
$$
\begin{gathered}
x_{n}=\frac{x_{n-1}+98 x_{n}+x_{n+1}}{100} \\
2 x_{n}=x_{n-1}+x_{n+1} \\
x_{n}-x_{n-1}=x_{n+1}-x_{n}
\end{gathered}
$$
Let the common difference of this progression be $d, d \neq 0$ (as per the condition).
Then $\sqrt{\frac{x_{2023}-x_{1}}{2022} \cdot \frac{2021}{x_{2023}-x_{2}}}+2021=\sqrt{\frac{x_{1}+2022 d-x_{1}}{2022} \cdot \frac{2021}{x_{1}+2022 d-x_{1}-d}}+2021=$ $=\sqrt{\frac{2022 d}{2022} \cdot \frac{2021}{2021 d}}+2021=1+2021=2022$.
Answer. 2022.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (5 points) Find $\frac{a^{8}+256}{16 a^{4}}$, if $\frac{a}{2}+\frac{2}{a}=3$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{8}+256}{16 a^{4}}=\frac{a^{4}}{16}+\frac{16}{a^{4}}=\frac{a^{4}}{16}+2+\frac{16}{a^{4}}-2=\left(\frac{a^{2}}{4}+\frac{4}{a^{2}}\right)^{2}-2= \\
& =\left(\frac{a^{2}}{4}+2+\frac{4}{a^{2}}-2\right)^{2}-2=\left(\left(\frac{a}{2}+\frac{2}{a}\right)^{2}-2\right)^{2}-2=\left(3^{2}-2\right)^{2}-2=47
\end{aligned}
$$
Answer. 47.
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points) A circle touches two adjacent sides $AB$ and $AD$ of square $ABCD$ and cuts off segments of length 8 cm from vertices $B$ and $D$ at the points of tangency. On the other two sides, the circle intersects and cuts off segments of 4 cm and 2 cm from the vertices, respectively. Find the radius of the circle.
|
# Solution.
Fig. 1
Let $R$ be the radius of the circle, then $R+8$ is the side of the square. The segment $K L=8+R-4-2=R+2$. Consider $\triangle O N L$. By the Pythagorean theorem, the following equality holds:
$$
R^{2}=8^{2}+\left(\frac{2+R}{2}\right)^{2}
$$
This is a quadratic equation in terms of $R$, which has only one positive root 10.
Answer. 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) An educational center "Young Geologist" received an object for research consisting of about 300 monoliths (a container designed for 300 monoliths, which was almost completely filled). Each monolith has a specific name (sandy loam or clayey loam) and genesis (marine or lake-glacial deposits). The relative frequency (statistical probability) that a randomly selected monolith will be sandy loam is $\frac{1}{8}$. The relative frequency that a randomly selected monolith will be marine clayey loam is $\frac{22}{37}$. How many monoliths of lake-glacial genesis does the object contain, if there are no marine sandy loams among the sandy loams?
|
# Solution.
Let's determine the exact number of monoliths. It is known that the relative frequency of a monolith being loamy sand is $\frac{1}{8}$. The number closest to 300 that is divisible by $8-296$. Therefore, there are 296 monoliths in total. Monoliths of lacustrine-glacial origin consist of all loamy sands $(296: 8=37)$ and part of the clays. Let's find out how many monoliths of lacustrine-glacial origin are among the clays: The total number of clays is 296:8$\cdot$7=259. Among them, marine clays constitute $\frac{22}{37}$ of the total number, which is 176. Therefore, the number of clays of lacustrine-glacial origin is 83. Thus, the total number of monoliths of lacustrine-glacial origin is: $37+83=120$.
Answer. 120.
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) For the numerical sequence $\left\{x_{n}\right\}$, all terms of which, starting from $n \geq 2$, are distinct, the relation $x_{n}=\frac{x_{n-1}+198 x_{n}+x_{n+1}}{200}$ holds. Find $\sqrt{\frac{x_{2023}-x_{1}}{2022} \cdot \frac{2021}{x_{2023}-x_{2}}}+2022$.
|
# Solution.
From the given relations in the problem, it is easily deduced that for all $n \geq 2$, $x_{n}-x_{n-1}=x_{n+1}-x_{n}$, which implies that the sequence is an arithmetic progression. Indeed,
$$
\begin{gathered}
x_{n}=\frac{x_{n-1}+198 x_{n}+x_{n+1}}{200} \\
2 x_{n}=x_{n-1}+x_{n+1} \\
x_{n}-x_{n-1}=x_{n+1}-x_{n}
\end{gathered}
$$
Let the common difference of this progression be $d, d \neq 0$ (as per the condition).
Then $\sqrt{\frac{x_{2023}-x_{1}}{2022} \cdot \frac{2021}{x_{2023}-x_{2}}}+2022=\sqrt{\frac{x_{1}+2022 d-x_{1}}{2022} \cdot \frac{2021}{x_{1}+2022 d-x_{1}-d}}+2022=$ $=\sqrt{\frac{2022 d}{2022} \cdot \frac{2021}{2021 d}}+2022=1+2022=2023$.
Answer. 2023.
|
2023
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Development of a Method for Optimizing a Mathematical Problem
Problem Statement. At Unit 3 of an oil and gas company, the task is to optimize the operation of the navigation system elements. The task of this unit is to receive encrypted signals from Unit 1 and Unit 2, synthesize the incoming data packets, and further transmit them to the Data Processing Center. Write a program that receives one natural number from each unit as input, and returns a third number calculated by raising the value received from the first unit to the power of the number received from the second unit. Only the last digit of the resulting value will be sent to the Center. Use the following test values:
- From the first unit: 954950230952380948328708
- From the second unit: 470128749397540235934750230
|
Solution to the problem. Solving the problem "head-on" by raising one number to the power of another is bound to exceed the computational power not only of a single computer but even a data center would require a certain amount of time to perform the calculations. Since we only need to send the last digit, let's focus on calculating just that. Note that when raising numbers to a certain power, the last digit always has a certain cycle from a limited set of elements. For example: $2^{2}=4,2^{3}=8,2^{4}=16,2^{5}=32,2^{4}=64$.
Thus, we only need to take the last digit of the first number and the remainder of the second number divided by 4, and only then raise the first number to the power of the second.
Example of program implementation in Python
```
number = input()
degree = input()
number = int(str(number)[-1])
degree = int(str(degree)[-2] + str(degree)[-1]) % 4
if degree == 0:
degree = 4
print((number ** degree))
```
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) In a sequence of natural numbers, each subsequent number, starting from the third, is equal to the absolute difference of the two preceding ones. Determine the maximum number of elements such a sequence can contain if the value of each of them does not exceed 2022.
#
|
# Solution.
To maximize the length of the sequence, the largest elements should be at the beginning of the sequence. Let's consider the options:
1) $n, n-1,1, n-1, n-2, n-3,1, n-4, n-5,1, \ldots, 2,1,1$;
2) $n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
3) $1, n, n-1,1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
4) $n-1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
Thus, the length of the sequence that satisfies the condition of the problem will be the greatest if the largest member is the second, and the first is one less. This sequence will look like:
$$
n-1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1
$$
For $1<n \leq 4$, the length of such a sequence can be determined by direct counting $\left(l_{2}=4, l_{3}=6, l_{4}=7\right)$, and for larger $n$, we will prove that $l_{n+2}=l_{n}+3$.
Let's form a sequence with the largest member $n+2$:
$$
n+1, n+2,1, n+1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1 .
$$
That is, the length of such a sequence will be:
$$
\begin{gathered}
l_{n}=\frac{3 n}{2}+1=\frac{3 n+2}{2} \text { for even } n, \\
l_{n}=\frac{3(n-1)}{2}+3=\frac{3 n+3}{2} \text { for odd } n .
\end{gathered}
$$
Then, for $n=2022$
$$
l_{2022}=\frac{3 \cdot 2022+2}{2}=3034
$$
Answer. 3034.
|
3034
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) In a sequence of natural numbers, each subsequent number, starting from the third, is equal to the absolute difference of the two preceding ones. Determine the maximum number of elements such a sequence can contain if the value of each of them does not exceed 2021.
#
|
# Solution.
To maximize the length of the sequence, the largest elements should be at the beginning of the sequence. Let's consider the options:
1) $n, n-1,1, n-1, n-2, n-3,1, n-4, n-5,1, \ldots, 2,1,1$;
2) $n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
3) $1, n, n-1,1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
4) $n-1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1$.
Thus, the length of the sequence that satisfies the condition of the problem will be the greatest if the largest member is the second, and the first is one less. Then this sequence will look like:
$$
n-1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1
$$
For $1<n \leq 4$, the length of such a sequence can be determined by direct counting $\left(l_{2}=4, l_{3}=6, l_{4}=7\right)$, and for larger $n$, we will prove that $l_{n+2}=l_{n}+3$. Let's form a sequence with the largest member $n+2$:
$$
n+1, n+2,1, n+1, n, 1, n-1, n-2,1, n-3, n-4,1, \ldots, 2,1,1 .
$$
That is, the length of such a sequence will be:
$$
\begin{gathered}
l_{n}=\frac{3 n}{2}+1=\frac{3 n+2}{2} \text { for even } n, \\
l_{n}=\frac{3(n-1)}{2}+3=\frac{3 n+3}{2} \text { for odd } n .
\end{gathered}
$$
Then, for $n=2021$
$$
l_{2021}=\frac{3 \cdot 2021+3}{2}=3033
$$
Answer. 3033.
|
3033
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. (20 points) A finite increasing sequence $a_{1}, a_{2}, \ldots, a_{n}$ ( $n \geq 3$ ) of natural numbers is given, and for all $k \leq n-2$, the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds. The sequence must contain a term $a_{k}=2021$. Determine the maximum number of three-digit numbers, divisible by 25, that this sequence can contain.
|
# Solution.
The final sequence can contain all three-digit numbers, as it can consist of a given number of natural numbers starting from the chosen number $a_{i}$.
We will prove that for any term of the arithmetic progression $1,2,3, \ldots$ defined by the formula for the $n$-th term $a_{n}=n$, the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds.
Indeed, for any value of $k$, the equalities
$a_{k}=k, a_{k+1}=k+1, a_{k+2}=k+2$ are valid, from which it follows that
$3 a_{k+1}-2 a_{k}-1=3(k+1)-2 k-1=k+2=a_{k+2}$, i.e., the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-1$ holds, which is what we needed to prove.
For example, the sequence containing 2021: 3,4,5,6,..., 2018, 2019,2020,2021.
Thus, the sequence can contain all three-digit numbers from 100 to 999. Among them, the numbers divisible by $25: 100,125,150,175,200,225,250,275, \ldots, 900,925$, 950,975 - 4 in each of the nine hundreds, i.e., 36 numbers.
Answer. 36.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6. (30 points) At the first deposit, equipment of the highest class was used, and at the second deposit, equipment of the first class was used, with the highest class being less than the first. Initially, $40 \%$ of the equipment from the first deposit was transferred to the second. Then, $20 \%$ of the equipment that ended up on the second deposit was transferred back to the first, with half of the transferred equipment being of the first class. After this, the equipment of the highest class on the first deposit was 26 units more than on the second, and the total amount of equipment on the second deposit increased by more than $5 \%$ compared to the initial amount. Find the total amount of equipment of the first class.
|
# Solution.
Let there initially be $x$ units of top-class equipment at the first deposit and $y$ units of first-class equipment at the second deposit $(x1.05 y$, from which $y48 \frac{34}{67} .\end{array}\right.\right.$
This double inequality and the condition “x is divisible by 5” is satisfied by the unique value $x=50$. Then $y=130-70=60$. Thus, there were 60 units of first-class equipment.
Answer: 60.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. (20 points) A finite increasing sequence of natural numbers $a_{1}, a_{2}, \ldots, a_{n}(n \geq 3)$ is given, and for all $\kappa \leq n-2$ the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-2$ holds. The sequence must contain $a_{k}=2022$. Determine the maximum number of three-digit numbers, divisible by 4, that this sequence can contain.
|
# Solution.
Since it is necessary to find the largest number of three-digit numbers that are multiples of 4, the deviation between the members should be minimal. Note that the arithmetic
progression with a difference of $d=2$, defined by the formula $a_{k}=2 k$, satisfies the equality $a_{k+2}=3 a_{k+1}-2 a_{k}-2$.
Indeed,
$$
a_{k}=2 k, a_{k+1}=2 k+2, a_{k+2}=2 k+4, \text { or by the formula }
$$
$$
a_{k+2}=3 a_{k+1}-2 a_{k}-2=3(2 k+2)-2 \cdot 2 k-2=2 k+4
$$
The sequence containing 2022: 4, 6,
This finite sequence can contain all even three-digit numbers from 100 to 999. Among them, the numbers divisible by 4 are: 100, 104, 108, 112, ..., 992, 925, 950, 996 - 25 in each of the nine hundreds, i.e., 225 numbers.
Answer. 225.
|
225
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (15 points) The bases $AB$ and $CD$ of trapezoid $ABCD$ are 41 and 24, respectively, and its diagonals are perpendicular to each other. Find the scalar product of vectors $\overrightarrow{AD}$ and $\overrightarrow{BC}$.
|
# Solution.
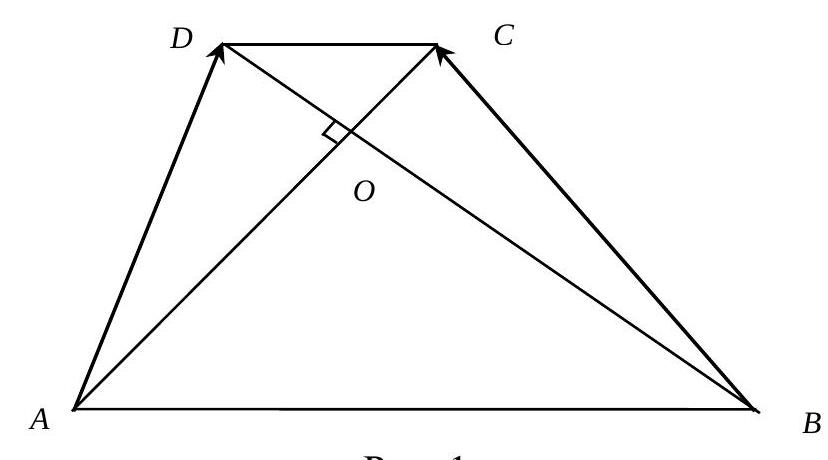
Fig. 1
Let the point of intersection of the diagonals be $O$ (Fig. 1).
Consider the vectors $\overrightarrow{A O}=\bar{a}$ and $\overrightarrow{B O}=\bar{b}$.
From the similarity of triangles $A O B$ and $D O C$, we have:
$\frac{A O}{O C}=\frac{41}{24}$ and $\overrightarrow{O C}=\frac{24}{41} \overrightarrow{A O}=\frac{24}{41} \vec{a}$
$\frac{B O}{O D}=\frac{41}{24}$ and $\overrightarrow{O D}=\frac{24}{41} \overrightarrow{B O}=\frac{24}{41} \vec{b}$
Then
$\overrightarrow{A D}=\vec{a}+\frac{24}{41} \vec{b}$ and $\overrightarrow{B C}=\vec{b}+\frac{24}{41} \vec{a}$
Let's find the dot product
$\overrightarrow{A D} \cdot \overrightarrow{B C}=\left(\vec{a}+\frac{24}{41} \vec{b}\right) \cdot\left(\vec{b}+\frac{24}{41} \vec{a}\right)=\vec{a} \vec{b}+\frac{24}{41} \vec{a} \cdot \vec{a}+\frac{24}{41} \vec{b} \cdot \vec{b}+\left(\frac{24}{41}\right)^{2} \vec{a} \vec{b}$
Since $\vec{a} \perp \vec{b}$, then $\vec{a} \vec{b}=0$.
By the definition of the dot product of vectors, we get $\vec{a} \cdot \vec{a}=|\vec{a}| \cdot|\vec{a}| \cdot \cos 0^{0}=|\vec{a}|^{2}$ and $\vec{b} \cdot \vec{b}=|\vec{b}|^{2}$.
Triangle $AOB$ is a right triangle, so $|\vec{a}|^{2}+|\vec{b}|^{2}=|A B|^{2}=41^{2}$.
Thus, $\overrightarrow{A D} \cdot \overrightarrow{B C}=\frac{24}{41}\left(|\vec{a}|^{2}+|\vec{b}|^{2}\right)=\frac{24}{41} \cdot 41^{2}=984$.
Answer. 984.
|
984
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Development of a Method for Optimizing a Mathematical Problem
Problem Statement. At Unit 3 of an oil and gas company, the task is to optimize the operation of the navigation system elements. The task of this unit is to receive encrypted signals from Unit 1 and Unit 2, synthesize the incoming data packets, and further transmit them to the Data Processing Center. Write a program that takes one natural number from each unit as input and returns a third number, calculated by raising the value received from the first unit to the power of the number received from the second unit. Only the last digit of the resulting value will be sent to the Center. Use the following test values:
- From the first unit: 954950230952380948328708
- From the second unit: 470128749397540235934750230
|
Solution to the problem. Solving the problem "head-on" by raising one number to the power of another is bound to exceed the computational power not only of a single computer but even a data center would require a certain amount of time to perform the calculations. Since we only need to send the last digit, let's focus on calculating just that. Note that when raising numbers to a certain power, the last digit always has a certain cycle from a limited set of elements. For example: $2^{2}=4,2^{3}=8,2^{4}=16,2^{5}=32,2^{4}=64$.
Thus, we only need to take the last digit of the first number and the remainder of the second number divided by 4, and only then raise the first number to the power of the second.
Example of program implementation in Python
```
number = input()
degree = input()
number = int(str(number)[-1])
degree = int(str(degree)[-2] + str(degree)[-1]) % 4
if degree == 0:
degree = 4
print((number ** degree))
```
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Does there exist a natural number that, when divided by the sum of its digits, gives both a quotient and a remainder of 2014? If there is more than one such number, write their sum as the answer. If no such numbers exist, write 0. (12 points)
#
|
# Solution:
Suppose there exists a natural number $\boldsymbol{n}$ with the sum of its digits $\boldsymbol{s}$, such that $n=2014 s+2014$, from which we get $n-s=2013 s+2014$. By the divisibility rule, $n-s$ is divisible by 3. However, the number $2013 s+2014$ is not divisible by 3, since the number $2013s$ is a multiple of 3, while the number 2014 is not. This is a contradiction.
Answer: 0.
| Points | Criteria for evaluating the performance of task № $\mathbf{5}$ |
| :---: | :--- |
| $\mathbf{1 2}$ | A correct and justified sequence of all steps of the solution is provided. All transformations and calculations are performed correctly. The correct answer is obtained. |
| $\mathbf{1 0}$ | A correct sequence of all steps of the solution is provided. There are gaps in the justification of divisibility by 3 or a computational error or typo that does not affect the further course of the solution. As a result of this error or typo, an incorrect answer may be obtained. |
| $\mathbf{5}$ | The problem is not solved, but its solution is significantly advanced, i.e.: - a significant part of the solution is performed correctly, possibly inaccurately (for example, the equation for the desired number is correctly written); - the other part is either not performed or performed incorrectly, possibly even with logical errors (for example, the desired number is found or its absence is incorrectly justified). The solution may be incomplete. |
| $\mathbf{0}$ | All cases of the solution that do not correspond to the above criteria for scoring 5, 10, and 12 points. |
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Calculating Samson loves to have lunch at the Italian restaurant "At Pablo's". During his next visit to the restaurant, Samson was offered to purchase a loyalty card for a period of 1 year at a price of 30000 rubles, which gives the client a $30 \%$ discount on the bill amount.
(a) Suppose that during the week Samson visits the restaurant three times (regardless of whether he has a loyalty card or not) with an average bill amount of 900 rubles without the discount. Is it profitable for him to buy the loyalty card?
(b) According to data from the information portal, the average bill amount per person in this restaurant is 600 rubles. On average, how many visits per year does a customer need to make to be indifferent about buying the restaurant's card or not?
(c) Recently, many stores and organizations operating in the service sector have been issuing so-called customer cards. Some of these cards are cumulative and provide discounts only after accumulating a certain amount on the card's account, while others immediately provide the customer with a discount that can be used with any purchase. Provide at least two strong reasons and substantiate why it is profitable for trading and service enterprises to issue such cards and use them in their work with customers. (10 points)
|
# Solution:
(a) After purchasing the card, one lunch will cost the client $900 * 0.3 = 270$ rubles less. Since there are 52 full weeks in a year $(365 / 7 = 52.14)$, Samson will save $270 * 3 * 52 = 42120$ rubles on discounts over the year, which is more than the cost of the card. Therefore, it is beneficial for him to buy the card.
(b) On average, a lunch with the card will be $600 * 0.3 = 180$ rubles cheaper. Then, from the condition of equal expenses, we determine that one needs to visit $30000 / 180 = 166$,(6), i.e., it will be beneficial to purchase the card if the restaurant is visited 167 times a year or more, and it will be unprofitable to purchase the card if the restaurant is visited 166 times or less.
(c) The use of cards with a cumulative discount system allows firms to "retain" regular customers, thereby preventing them from "switching" to the services of other firms.
The use of cards that provide discounts without a cumulative system also helps to attract new and "retain" old customers with discounts.
Often, providing such cards to customers requires their authorization in the company's databases. In this case, companies can inform their customers about planned promotions and also provide customer databases to their partners, albeit not without a cost. Additionally, issuing such cards requires additional expenses from the company owners. Therefore, it can signal to customers about the stability of the company, its concern for its customers, and its willingness to provide them with discounts.
## Grading Criteria:
(a) Correct calculations allowing for a comparison of expenses - 3 points, Correct conclusion about the profitability of purchasing the card
(b) Correctly found number of visits - 3 points, (c) 2 points each (total 4 points) for the reason and corresponding explanation.
|
167
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. Maximum 15 points
A company that produces educational materials for exam preparation incurs average costs per textbook of $100+\frac{100000}{Q}$, where $Q$ is the number of textbooks produced annually. What should be the annual production volume of the textbook to reach the break-even point if the planned price of the textbook is 300 monetary units?
#
|
# Solution
At the break-even point $\mathrm{P}=\mathrm{ATC}=\mathrm{MC}$
Form the equation $100+10000 / Q=300$
$100 \mathrm{Q}+100000=300 \mathrm{Q}$
$100000=200 \mathrm{Q}$
$\mathrm{Q}=100000 / 200=500$
## Evaluation Criteria
1. The correct answer is justified: 15 points
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.