problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. Find the largest natural number consisting of distinct digits such that the product of the digits of this number is 2016.
|
Answer: 876321.
Solution: Factorize the number 2016. $2016=2^{5} \cdot 3^{2} \cdot 7$. To make the number as large as possible, it should contain the maximum number of digits. Notice that the number must include the digit 1. Therefore, the number should consist of the digits $1,2,3,6,7,8$.
Grading Criteria. 20 points for the correct answer. 0 points for any other answer.
|
876321
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Ten consecutive natural numbers are written on the board. What is the maximum number of them that can have a digit sum equal to a perfect square?
|
Answer: 4.
Solution: Note that the sums of the digits of consecutive natural numbers within the same decade are consecutive natural numbers. Since there are 10 numbers, they span two decades. Also note that among ten consecutive natural numbers, there can be no more than 3 perfect squares, and three perfect squares can only occur if there are 9 numbers. Therefore, among the 10 consecutive natural numbers written on the board, there cannot be more than 4 numbers with a sum of digits equal to the square of a natural number. We can provide an example where there are exactly 4 such numbers: $\{1,2,3,4,5,6,7,8,9,10\}$.
Grading criteria. Full solution - 20 points. Only the estimate - 12 points. Answer + example - 9 points. Only the answer - 3 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all real roots of the equation
$(x+1)^{5}+(x+1)^{4}(x-1)+(x+1)^{3}(x-1)^{2}+(x+1)^{2}(x-1)^{3}+(x+1)(x-1)^{4}+(x-1)^{5}=0$
|
Solution. Multiply both sides of the equation by $(x+1)-(x-1)$ (this factor equals 2). Use the formula $a^{6}-b^{6}=(a-b)\left(a^{5}+a^{4} b+a^{3} b^{2}+a^{2} b^{3}+a b^{4}+b^{5}\right)$.
$$
\begin{gathered}
(x+1)^{6}-(x-1)^{6}=0 \\
(x+1)^{6}=(x-1)^{6}
\end{gathered}
$$
The equation
$$
x+1=x-1
$$
has no solutions. The equation
$$
x+1=-(x-1)
$$
has the solution $x=0$. Since we multiplied the equation by the number 2, we did not obtain any extraneous roots.
Answer. 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four points $A, B, C, D$ are on a plane. It is known that $A B=1, B C=$ $2, C D=\sqrt{3}, \angle A B C=60^{\circ}, \angle B C D=90^{\circ}$. Find $A D$.
|
Solution. Let's construct the diagram. Let the line $CD$ intersect the line $AB$ at point $O$

(according to the condition, these lines are not parallel). There are two possible positions for point $D$ on the line $CD$ - on the segment $CO$ and outside this segment. Triangle $BOC$ is a right triangle, with the angle at vertex $O$ equal to $30^{\circ}$. We find $AB=4$, $OA=3$, $OC=2\sqrt{3}$. For $OD$, considering $CD=\sqrt{3}$, we get two possible values, $OD=\sqrt{3}$ or $OD=3\sqrt{3}$. In triangle $AOD$, two sides and the angle at vertex $O$ are known. Using the cosine rule, we find $AD$. We get two values: $AD=3$ or $AD=\sqrt{3}$. Answer. 3 and $\sqrt{3}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The parabolas in the figure are obtained by shifting the parabola $f(x)=x^{2}$ and are arranged such that the points of their intersections with the $O X$ axis respectively coincide in pairs, and all vertices lie on the same straight line. There are a total of 2020 parabolas. The length of the segment on the $O X$ axis enclosed between the roots of the first parabola is 1; the length of the segment enclosed between the roots of the second parabola is 2. Find the length of the segment on the $O X$ axis enclosed between the roots of the last parabola.
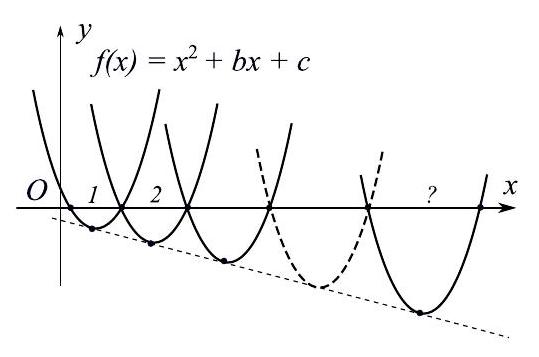
|
Solution. Note that the arrangement of parabolas can be changed by shifting the entire set to the left or right (the lengths of the segments on the $O X$ axis, enclosed between the roots of the parabolas, do not change with the shift). The intersection point of the line drawn through the vertices of the parabolas will not be needed. The lengths of the segments are determined by the angle of inclination of the drawn line.
Let's recall the expression for the distance between the roots of a parabola. Let $x_{1}$ and $x_{2}$ be the roots of the quadratic polynomial $x^{2}+b x+c$. Then
$$
\left|x_{2}-x_{1}\right|=\frac{-b+\sqrt{D}}{2}-\frac{-b-\sqrt{D}}{2}=\sqrt{D}
$$
Here $D$ is the discriminant of this polynomial.
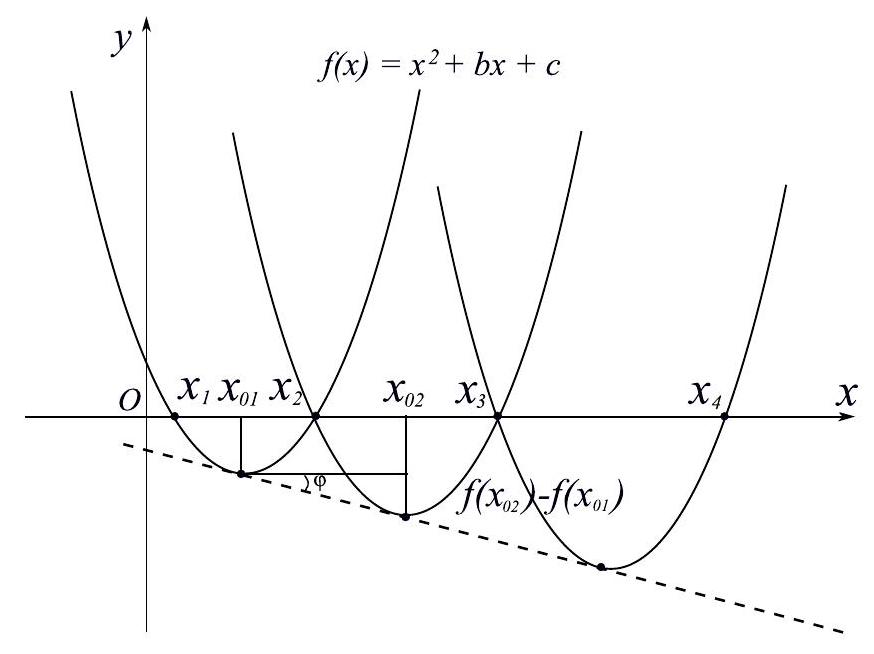
Let $x_{0}=-\frac{b}{2}$ be the abscissa of the vertex of the parabola $f(x)=x^{2}+b x+c$. The value of the polynomial at this point is
$$
f\left(x_{0}\right)=x_{0}^{2}+b x_{0}+c=\frac{b^{2}}{4}-b \cdot \frac{b}{2}+c=-\frac{D}{4}=-\frac{\left(x_{2}-x_{1}\right)^{2}}{4}
$$
In our problem, we need to calculate the tangent of the angle of inclination of the drawn line (the angle between the positive direction of the $O X$ axis and the line). Let this angle be $\varphi$. Let $x_{01}$ and $x_{02}$ be the abscissas of the vertices of the first and second parabolas, and $x_{1}, x_{2}, x_{3}$ be their roots in ascending order (see the figure).
$$
\operatorname{tg} \varphi=\frac{f\left(x_{02}\right)-f\left(x_{01}\right)}{x_{02}-x_{01}}
$$
We have
$$
\begin{gathered}
x_{02}-x_{01}=x_{02}-x_{2}+x_{2}-x_{01}=\frac{1}{2}\left(\left(x_{3}-x_{2}\right)+\left(x_{2}-x_{1}\right)\right)=\frac{1}{2}(2+1)=\frac{3}{2} \\
f\left(x_{02}\right)-f\left(x_{01}\right)=-1-\left(-\frac{1}{4}\right)=-\frac{3}{4}
\end{gathered}
$$
We get
$$
\operatorname{tg} \varphi=\frac{-\frac{3}{4}}{\frac{3}{2}}=-\frac{1}{2}
$$
Now let's find how the lengths of the segment on the $O X$ axis between the roots of the parabolas with numbers $n+1$ and $n$ are related, expressing this length through the roots $x_{n}, x_{n+1}, x_{n+2}$, the values at the vertices $f\left(x_{0 n}\right)$ and $f\left(x_{0 n+1}\right)$, the discriminants $D_{n}$ and $D_{n+1}$, and the found tangent. We use the fact that the distance between the abscissas of the vertices is the sum of half the distances between the roots of adjacent parabolas.
$x_{0 n+1}-x_{0 n}=x_{0 n+1}-x_{n+1}+x_{n+1}-x_{0 n}=\frac{x_{n+2}-x_{n+1}}{2}+\frac{x_{n+1}-x_{n}}{2}=\frac{\sqrt{D_{n+1}}}{2}+\frac{\sqrt{D_{n}}}{2}$
$$
\begin{gathered}
\operatorname{tg} \varphi=-\frac{1}{2}=\frac{f\left(x_{0 n+1}\right)-f\left(x_{0 n}\right)}{x_{0 n+1}-x_{0 n}}=\frac{-\frac{D_{n+1}}{4}+\frac{D_{n}}{4}}{\frac{\sqrt{D_{n+1}}}{2}+\frac{\sqrt{D_{n}}}{2}}= \\
=\frac{D_{n}-D_{n+1}}{2\left(\sqrt{D_{n+1}}+\sqrt{D_{n}}\right)}
\end{gathered}
$$
From this equation
$$
\sqrt{D_{n+1}}-\sqrt{D_{n}}=1
$$
Hence
$$
\begin{gathered}
\sqrt{D_{n+1}}=\sqrt{D_{n}}+1 \\
x_{n+2}-x_{n+1}=\left(x_{n+1}-x_{n}\right)+1
\end{gathered}
$$
That is, the length of the segment between the roots of each subsequent parabola increases by 1. From this, we get that the length of the segment on the $O X$ axis, enclosed between the roots of the parabola with number 2020, is 2020.
Answer. 2020.
|
2020
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Three numbers are stored in a computer's memory. Every second, the following operation is performed: each number in this triplet is replaced by the sum of the other two. For example, the triplet $(1 ; 3 ; 7)$ turns into $(10 ; 8 ; 4)$. What will be the difference between the largest and smallest number in the triplet obtained from the triplet (20; 1; 6) after 2016 seconds?
|
5. Answer: 19. Solution. Let the initial triplet be ( $a ; b ; c$). Since all numbers in the triplet are distinct, we will assume that $a<b<c$. In the next second, the triplet of numbers will look like this: $(b+c$; $a+c ; a+b)$. The largest number in this triplet is $b+c$, and the smallest is $a+b$. Their difference is $b+c-(a+b)=c-a$, i.e., it coincides with the initial difference between the largest and smallest numbers. Therefore, after 2016 seconds, the difference between the largest and smallest numbers in the triplet will be equal to the corresponding difference in the initial triplet of numbers, i.e., $20-1=19$. Grading criteria: correct reasoning provided, correct answer obtained - 7 points. Key pattern noticed, correct answer given, but no justification - 2 points.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Find the largest four-digit number in which all digits are different and which is divisible by any of its digits (don't forget to explain why it is the largest).
|
Answer: 9864.
Firstly, the desired number cannot have the form $\overline{987 a}$, because divisibility by the digit 7 would mean that $a$ is 0 or 7. This means the desired number is smaller. Secondly, consider numbers of the form $\overline{986 a}$. Divisibility by the digit 9 would mean that $9+8+6+a=a+23$ is divisible by 9. Therefore, $a=4$. Thus, we get the number 9864. The sum of its digits is 27, so it is divisible by 9, and since the number 864 is divisible by 8, the number itself is divisible by 8. Therefore, it is divisible by 6 and 4.
|
9864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. To some number $\kappa$, the sum of its digits was added and the result was 2014. Provide an example of such a number.
|
Answer: 1988 or 2006.
Grading Criteria:
+ a correct example is provided (one is sufficient)
$\pm$ a correct example is provided along with an incorrect one
- the problem is not solved or solved incorrectly
|
1988
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. The Wolf, the Hedgehog, the Chizh, and the Beaver were dividing an orange. The Hedgehog got twice as many segments as the Chizh, the Chizh got five times fewer segments than the Beaver, and the Beaver got 8 more segments than the Chizh. Find out how many segments were in the orange, if the Wolf only got the peel.
|
Answer: 16 segments.
Solution. First method. Let the number of orange segments given to Chizh be $x$, then Hedgehog received $2x$ segments, and Beaver received $5x$ segments (Wolf - 0 segments). Knowing that Beaver received 8 more segments than Chizh, we set up the equation: $5x - x = 8$. The solution to this equation is: $x = 2$.
The total number of segments in the orange was $x + 2x + 5x + 0 = 8x$. Substituting $x = 2$, we get 16 segments.
Second method. Let the number of orange segments given to Chizh be one part, then Hedgehog received two parts, Beaver received five parts, and Wolf received zero parts. Beaver received 4 parts more than Chizh, which is 8 segments. Therefore, one part is 2 segments. Since there are 8 parts in total, the number of segments is 16.
## Grading criteria:
+ the correct answer and a fully justified solution (by any method) are provided
$\pm$ the equation is correctly set up and the number of segments for one of the animals is correctly and justifiedly found, but the correct answer is missing
$\mp$ the equation is correctly set up, but it is not solved or is solved incorrectly
干 only the correct answer is provided and it is verified that it satisfies the condition
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. In a seven-story building, domovoi (Russian house spirits) live. The elevator travels between the first and the last floors, stopping at every floor. On each floor, starting from the first, one domovoi entered the elevator, but no one exited. When the thousandth domovoi entered the elevator, it stopped. On which floor did this happen? Explain your answer.
|
Answer: on the fourth floor.
Solution. First, let's find out how many housekeepers ended up in the elevator after the first trip from the first to the seventh floor and back, until the elevator returned to the first floor. One housekeeper entered on the first and seventh floors, and on all other floors, two housekeepers entered. Thus, in one such trip, 12 housekeepers ended up in the elevator.
Now, let's find out how many such complete trips the elevator managed to make. When dividing 1000 by 12, the quotient is 83 and the remainder is 4. This means that after 83 ascents and descents, 4 more housekeepers can still enter the elevator: on the first, second, third, and fourth floors.
## Grading criteria:
+ correct answer and a fully justified solution
$\pm$ correct answer and a generally correct solution, but there are gaps and deficiencies in the justification
干 correct answer only
干 correct answer is missing, but the correct idea of dividing the elevator trips into "cycles" of 12 housekeepers is indicated
- the problem is not solved or solved incorrectly
(Note: The "干" characters in the grading criteria should be replaced with appropriate English terms, such as "partially correct" or "incomplete.")
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the maximum possible area of a quadrilateral in which the product of any two adjacent sides is 1.
|
1. Find the maximum possible area of a quadrilateral for which the product of any two adjacent sides is 1.
OTBET: 1.
SOLUTION.
Let the quadrilateral have sides $a, b, c, d$. Then $a b=b c=c d=d a=1$. From the equality $a b=b c$, it follows that $a=c$, and from the equality $b c=c d$, we get that $b=d$. Therefore, the given quadrilateral is a parallelogram. Let $\alpha$ be the angle between sides $a$ and $b$. Then $S=a \cdot b \sin \alpha$, and the area is maximized if $\sin \alpha=1$. Thus, $S=a \cdot b=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Yura was walking down the road and met a tractor pulling a long pipe. Yura decided to measure the length of the pipe. For this, he walked along it "against the direction of the tractor" and counted 20 steps. After that, he walked along the pipe "in the direction of the tractor" and counted 140 steps. Knowing that his step is 1 m, Yura was able to find the length of the pipe. What is its length? Justify your answer.
|
Answer: 35 m.
Let's say that in the time it takes Yura to make 20 steps, the train travels $x$ meters. Denoting the length of the train by $L$, we get: $20=L-x, 140=L+7 x$. From this, $L=(140+20 \cdot 7): 8=35$.
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The graph of the linear function $y=k x+k+1(k>0)$ intersects the $O x$ axis at point $A$, and the $O y$ axis at point $B$ (see the figure). Find the smallest possible value of the area of triangle $A B O$.
|
Answer: 2.
Solution. The abscissa of point $A$ of intersection with the $O x$ axis: $0=k x+k+1 ; x=$
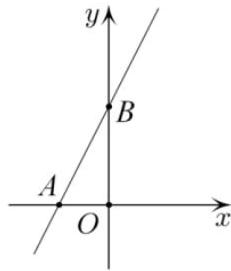
$-\left(1+\frac{1}{k}\right)$. The ordinate of point $B$ of intersection with the $O y$ axis: $y=k \cdot 0+k+1 ; y=k+1$. Therefore, $S_{A B O}=\frac{1}{2} \cdot O A \cdot O B=\frac{1}{2}(k+1)\left(1+\frac{1}{k}\right)=\frac{1}{2}\left(2+k+\frac{1}{k}\right)$. By the inequality between the arithmetic mean and the geometric mean, $k+\frac{1}{k} \geq 2$, and equality is achieved when $k=1$, so the minimum value of $S_{A B O}$ is also achieved when $k=1$. Thus, the smallest possible area of triangle $A B O$ is 2.
Comment. The correct answer is found based on the consideration of an example, and the minimality is not proven - 1 point. The expression for the area of the triangle in terms of $k$ is found - 5 points. If the logic is correct but errors in transformations prevent obtaining the correct answer - 4 points. The statement that the minimum value of the expression $k+\frac{1}{k}$ is achieved when $k=1$ can be used without proof.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. In the quarry, there are 120 granite slabs weighing 7 tons each and 80 slabs weighing 9 tons each. A railway platform can load up to 40 tons. What is the minimum number of platforms required to transport all the slabs?
|
Answer: 40 platforms
It is impossible to load 6 slabs onto one platform, even if they weigh 7 tons each. Therefore, at least $200 / 5=40$ platforms are needed. Forty platforms are sufficient: on each platform, you can load 3 slabs weighing 7 tons and 2 slabs weighing 9 tons.
Comment. The necessity of at least 40 platforms is justified - 3 points. An example of distributing the slabs on 40 platforms is provided - 3 points.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. All seats at King Arthur's round table are numbered clockwise. The distances between adjacent seats are the same.
One day, King Arthur sat at seat number 10, and Sir Lancelot sat directly opposite him at seat number 29. How many seats are there in total at the round table?
|
Answer: 38.
Solution. Along one side of the table between Arthur and Lancelot are seats numbered $11,12, \ldots, 28$ - a total of exactly 18 seats. Since these two are sitting directly opposite each other, there are also 18 seats on the other side of the table. Therefore, the total number of seats at the table is $18+18+1+1=38$.
|
38
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. At the festival of namesakes, 45 Alexanders, 122 Borises, 27 Vasily, and several Gennady arrived. At the beginning of the festival, all of them stood in a row so that no two people with the same name stood next to each other. What is the minimum number of Gennady that could have arrived at the festival?
|
Answer: 49.
Solution. Since there are a total of 122 Boris, and between any two of them stands at least one non-Boris (Alexander/Vasily/Gennady), there are at least 121 non-Boris. Since there are a total of 45 Alexanders and 27 Vasilies, there are at least $121-45-27=49$ Gennadys.
Note that there could have been exactly 49 Gennadys at the festival. Suppose in the line stood 122 Boris. Then 121 gaps between them were filled by other people: the first 45 gaps were filled by one Alexander each, the next 27 by one Vasily each, and the next 49 by one Gennady each. It is easy to see that all conditions of the problem are satisfied.
|
49
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. Dasha calls a natural number special if four different digits are used to write it. For example, the number 3429 is special, while the number 3430 is not special.
What is the smallest special number greater than 3429?
|
Answer: 3450.
Solution. Note that all numbers of the form $343 \star$ and $344 \star$ are not special. And the next number after them, 3450, is special.
|
3450
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.2. At first, the magical island was divided into three counties: in the first county lived only elves, in the second - only dwarves, in the third - only centaurs.
- During the first year, each county where non-elves lived was divided into three counties.
- During the second year, each county where non-dwarves lived was divided into four counties.
- During the third year, each county where non-centaurs lived was divided into six counties.
How many counties were there on the magical island after all these events?
|
Answer: 54.
Solution. Initially, there was 1 county of each kind.
After the first year, there was 1 elven county, 3 dwarf counties, and 3 centaur counties.
After the second year, there were 4 elven counties, 3 dwarf counties, and 12 centaur counties.
After the third year, there were 24 elven counties, 18 dwarf counties, and 12 centaur counties. In total, $24+18+12=54$ counties.
|
54
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
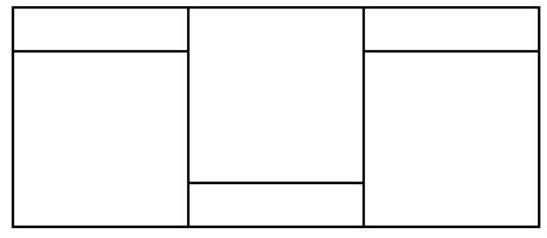
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.7. In a magic shop, for 20 silver coins you can buy an invisibility cloak and get 4 gold coins as change. For 15 silver coins you can buy an invisibility cloak and get 1 gold coin as change. How many silver coins will you get as change if you buy an invisibility cloak for 14 gold coins?
|
Answer: 10.
Solution. In the first case, compared to the second, by paying 5 extra silver coins, one can receive 3 extra gold coins in change. Therefore, 5 silver coins are equivalent to 3 gold coins.
In the second case, by paying 15 silver coins (which is equivalent to $3 \cdot 3=9$ gold coins), one can get the cloak and 1 gold coin in change. Therefore, the cloak costs 8 gold coins.
In the third case, by paying 14 gold coins for a cloak worth 8 coins, one would receive 6 gold coins in change, which is equivalent to $5 \cdot 2=10$ silver coins.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Each of the 33 bogatyrs (Russian epic heroes) either always lies or always tells the truth. It is known that each bogatyr has exactly one favorite weapon: a sword, spear, axe, or bow.
One day, Ded Chernomor asked each bogatyr four questions:
- Is your favorite weapon a sword?
- Is your favorite weapon a spear?
- Is your favorite weapon an axe?
- Is your favorite weapon a bow?
To the first question, 13 bogatyrs answered affirmatively, to the second question - 15 bogatyrs, to the third - 20 bogatyrs, and to the fourth - 27 bogatyrs.
How many bogatyrs always tell the truth?
|
Answer: 12.
Solution. Note that each of the truth-telling heroes answers affirmatively to only one question, while each of the lying heroes answers affirmatively to exactly three questions. Let the number of truth-telling heroes be $x$, and the number of lying heroes be $-(33-x)$. Then the total number of affirmative answers was $13+15+20+27=x+3 \cdot(33-x)$, from which we get $75=99-2 x$ and $x=12$. Note also that the number of truth-telling heroes can be exactly 12. Suppose 8 lying heroes love the sword the most, another 6 lying heroes love the spear, another 1 lying hero loves the axe, another 6 lying heroes love the bow, and another 12 truthful heroes love the bow. It is not difficult to verify that all conditions of the problem are satisfied in this case.
## 6th grade
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
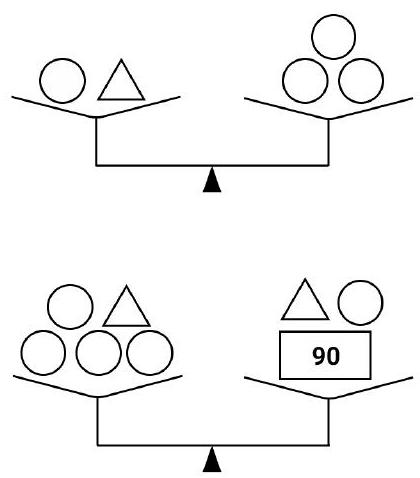
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.3. In a new math textbook, there are a total of 91 problems. Yura started solving them in the mornings, beginning on September 6.
Every morning, starting from September 7, he solves one fewer problem than the previous morning (until the problems run out).
By the evening of September 8, Yura realized that there were still 46 problems left to solve in the textbook. On which day of September will he finish solving the textbook?
|
Answer: 12.
Solution. In the first 3 days, Yura solved $91-46=45$ problems. Let's say on September 7th, he solved $z$ problems, then on September 6th, he solved $(z+1)$ problems, and on September 8th, he solved $(z-1)$ problems. We get that $45=(z+1)+z+(z-1)=3 z$, from which $z=15$.
Since $91=16+15+14+13+12+11+10$, Yura will solve problems for exactly 7 days, from September 6th to September 12th.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.6. Ksyusha runs twice as fast as she walks (both speeds are constant).
On Tuesday, when she left home for school, she first walked, and then, when she realized she was running late, she started running. The distance she walked was twice the distance she ran. In the end, it took her exactly 30 minutes to get from home to school.
On Wednesday, Ksyusha left home even later, so she had to run twice the distance she walked. How many minutes did it take her to get from home to school on Wednesday?
|
# Answer: 24.
Solution. Let the distance from home to school be $3 S$, Ksyusha's walking speed be $v$, and her running speed be $-2 v$ (distance is measured in meters, and speed in meters per minute). Then on Tuesday, Ksyusha walked a distance of $2 S$ and ran a distance of $S$. And on Wednesday, she walked a distance of $S$ and ran a distance of $2 S$.
According to the condition, $30=\frac{2 S}{v}+\frac{S}{2 v}=\frac{4 S}{2 v}+\frac{S}{2 v}=\frac{5 S}{2 v}$, from which we get $\frac{S}{v}=30 \cdot \frac{2}{5}=12$.
Then on Wednesday, Ksyusha got to school in $\frac{2 S}{2 v}+\frac{S}{v}=\frac{S}{v}+\frac{S}{v}=12+12=24$ minutes.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. In the country of Dragonia, there live red, green, and blue dragons. Each dragon has three heads, each of which always tells the truth or always lies. Moreover, each dragon has at least one head that tells the truth. One day, 530 dragons sat around a round table, and each of them said:
- 1st head: “To my left is a green dragon.”
- 2nd head: “To my right is a blue dragon.”
- 3rd head: “There is no red dragon next to me.”
What is the maximum number of red dragons that could have been at the table?
|
Answer: 176.
Solution. Consider an arbitrary red dragon. To the right of this dragon, at least one head must tell the truth. Note that the 1st and 3rd heads cannot tell the truth (since there is a red dragon to the left), so the 2nd head must tell the truth, and to the right of this dragon, there must be a blue dragon. Now consider the dragon to the left of the chosen red dragon. By similar reasoning, we understand that only the 1st head can tell the truth, and to the left of this dragon, there must be a green one.
From the previous reasoning, we get that for any red dragon, one position to the right there is definitely a blue dragon, and one position to the left - a green one. For each red dragon, we combine these three dragons into one group. Note that any dragon can be in at most one such group. Then we get that there are no more than $530 / 3$ < 177, i.e., no more than 176 such groups. Therefore, there are no more than 176 red dragons.
Now let's provide an example. Arrange 176 red dragons in a circle, and in 175 gaps between them, place a green and a blue dragon: ...RGRB..., and in one gap, place two blue and two green dragons: ...RBGBGR.... It is easy to check that all conditions are met: each dragon has at least one head that will tell the truth, and there are exactly 530 dragons in total.
## 7th grade
|
176
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. Petya bought himself shorts for football at the store.
- If he had bought shorts with a T-shirt, the cost of the purchase would have been twice as much.
- If he had bought shorts with cleats, the cost of the purchase would have been five times as much.
- If he had bought shorts with shin guards, the cost of the purchase would have been three times as much.
How many times greater would the cost of the purchase have been if Petya had bought shorts, a T-shirt, cleats, and shin guards?
|
Answer: 8.
Solution. Let the shorts cost $x$. Since the shorts with a T-shirt cost $2x$, the T-shirt also costs $x$. Since the shorts with boots cost $5x$, the boots cost $4x$. Since the shorts with shin guards cost $3x$, the shin guards cost $2x$. Then, if Petya bought shorts, a T-shirt, boots, and shin guards, his purchase would amount to $x+x+4x+2x=8x$, which is 8 times more than $x$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
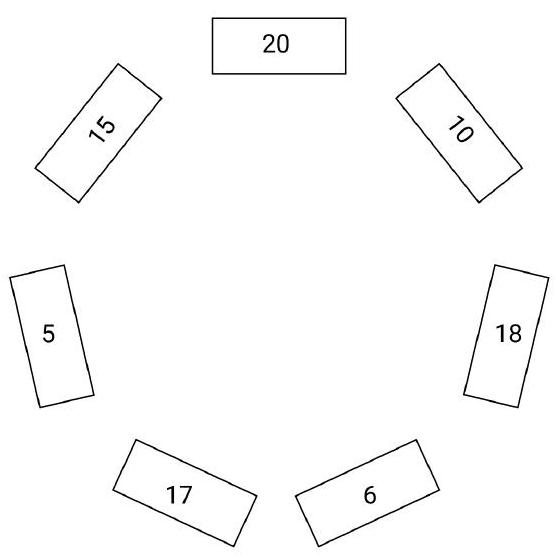
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?
|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (which then becomes 13), and 4 coins to the box with 15 (which then becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (which then becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (which then becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.
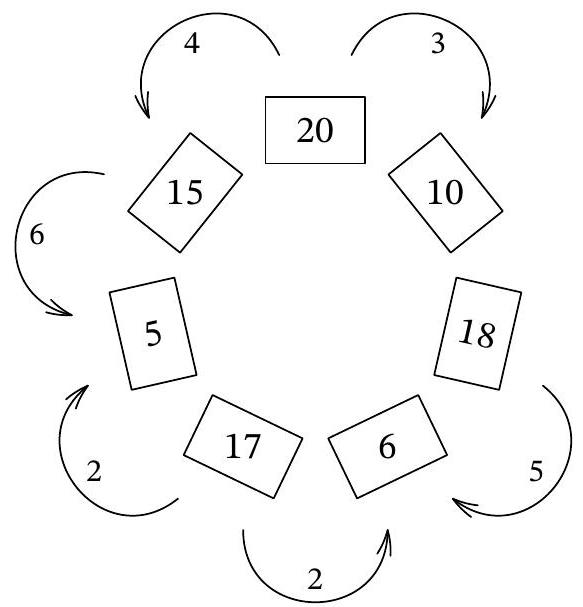
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. A circle of 130 trees has been planted: birches and lindens (both species are present). On each tree, there is a sign that reads: "Two different trees grow next to me." It is known that among all the trees, the statement is false on all lindens and on exactly one birch. How many birches could have been planted? List all possible options.
|
Answer: 87.
Solution. Let's divide all the trees into alternating groups of consecutive birches and consecutive lindens (by the condition, there are groups of both types).
Suppose there exists a group of at least 2 lindens. Then the truth would be written on the outermost of them (since it is between a birch and a linden) - a contradiction. Therefore, all groups of lindens consist of 1 tree. Then each linden is between two birches, and the lie is indeed written on it.
Now let's consider how many groups of birches there can be in terms of quantity.
- If a group has at least 4 birches, then on all non-edge (at least two) the lie is written (since each of them is between two birches) - a contradiction, since there is only one such birch.
- If a group has 3 birches, then only the middle one has the lie written on it.
- If a group has 2 birches, then the truth is written on each of them.
- If a group has 1 birch, then the lie is written on it (since it is between two lindens).
Therefore, there are several groups of 2 birches and exactly one group of 1 or 3 birches.
If there is a group of 1 birch, temporarily forget about it and one neighboring linden. Then the remaining $130-2=128$ trees will be divided into blocks of 3 trees: two birches and one linden. But 128 is not divisible by 3 - a contradiction.
If there is a group of 3 birches, temporarily forget about one of the birches in this group. Then the remaining $130-1=129$ trees will be divided into blocks of 3 trees: two birches and one linden. There are $\frac{129}{3}=43$ such blocks, and the total number of birches in them is $43 \cdot 2=86$. Returning the forgotten birch, we get that the total number of birches is $86+1=87$.
|
87
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In front of a pessimist and an optimist, there are glasses (the glasses are identical). Each of them was given water in their glass such that the pessimist's glass turned out to be $60\%$ empty, while the optimist's glass, on the contrary, was $60\%$ full. It turned out that the amount of water in the pessimist's glass was 46 milliliters less than in the optimist's glass. What is the volume of the glass in milliliters?
|
Answer: 230.
Solution. The pessimist's glass is $40 \%$ full, while the optimist's is $60 \%$ full. The pessimist has $20 \%$ less water than the optimist, which is $\frac{1}{5}$ of the total volume of the glass. Since this difference is 46 milliliters according to the problem, the total volume of the glass is $46 \cdot 5=230$ milliliters.
|
230
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. On the board, 23 signs are drawn - some pluses and some minuses. If any 10 of them are chosen, there will definitely be at least one plus among them. If any 15 of them are chosen, there will definitely be at least one minus among them. How many pluses are there in total?
|
Answer: 14.
Solution. Since among any 10 signs there is a plus, the number of minuses on the board is no more than 9 (otherwise, we could choose 10 minuses).
Since among any 15 signs there is a minus, the number of pluses on the board is no more than 14 (otherwise, we could choose 15 pluses).
Then the total number of signs on the board is no more than $9+14=23$. Since there are exactly 23 according to the condition, we get that the number of minuses on the board is exactly 9, and the number of pluses is exactly 14.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In the grove, there are 140 chameleons - blue and red. One day, several blue chameleons changed their color to red. As a result, the number of blue chameleons decreased by 5 times, and the number of red chameleons increased by 3 times. How many chameleons changed their color?
|
Answer: 80.
Solution. Let the number of blue chameleons become $x$. Then initially, there were $5 x$ blue chameleons. Accordingly, the number of red chameleons initially was $140-5 x$. Then the number of red chameleons became $3 \cdot(140-5 x)$. Since the total number of chameleons remained the same, we get the equation
$$
x+3 \cdot(140-5 x)=140
$$
Solving it, we find $x=20$. Then the number of chameleons that changed color is $5 x-x=4 x=4 \cdot 20=80$ chameleons.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
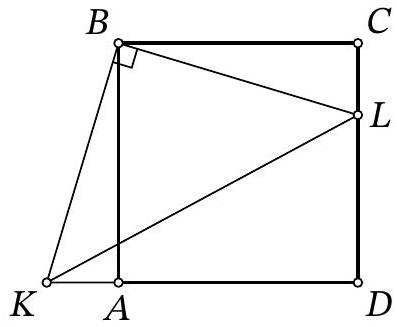
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.
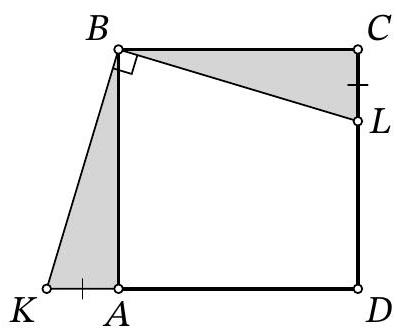
Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
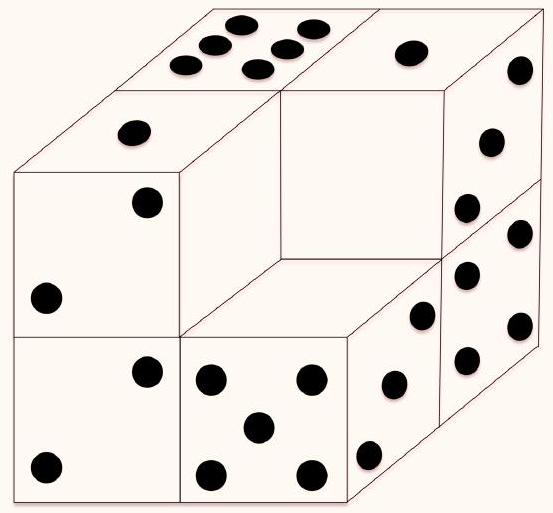
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?
|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
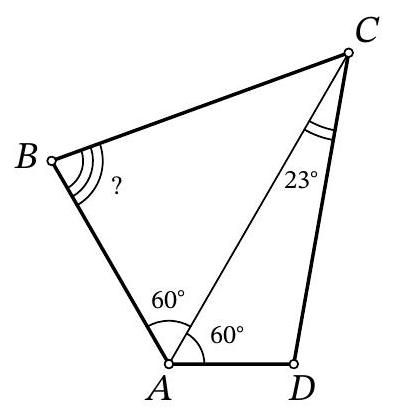
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. Vanya runs from home to school at a constant speed. If he had initially increased his speed by 2 m/s, he would have arrived at school 2.5 times faster. How many times faster would he have arrived at school if he had initially increased his speed by 4 m/s?
#
|
# Answer: 4.
Solution. Let Vasya's initial speed be $v$ m/s. If he ran at a speed of $(v+2)$ m/s, he would cover the same distance to school 2.5 times faster. This means that $\frac{v+2}{v}=2.5$, from which we find $v=\frac{4}{3}$. If he had initially run at a speed of $(v+4)$ m/s, he would have arrived at school $\frac{v+4}{v}$ times faster. Substituting $v=\frac{4}{3}$ into this expression, we get the answer 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. In city $\mathrm{N}$, there are exactly three monuments. One day, a group of 42 tourists arrived in this city. Each of them took no more than one photo of each of the three monuments. It turned out that any two tourists together had photos of all three monuments. What is the minimum number of photos that all tourists could have taken in total?
|
Answer: 123.
Solution. Let's number the three monuments. Note that the photo of the first monument is missing from no more than one tourist (otherwise, we could choose two tourists who, in total, have photos of no more than two monuments), so at least $42-1=41$ photos of the first monument were taken. Similarly, at least 41 photos of the second and third monuments were taken. Therefore, a total of at least $41 \cdot 3=123$ photos were taken.
Exactly 123 photos could have been taken, for example, if 1 tourist did not take any photos, and the other 41 each took one photo of each monument. It is clear that in this case, all conditions of the problem are satisfied.
|
123
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
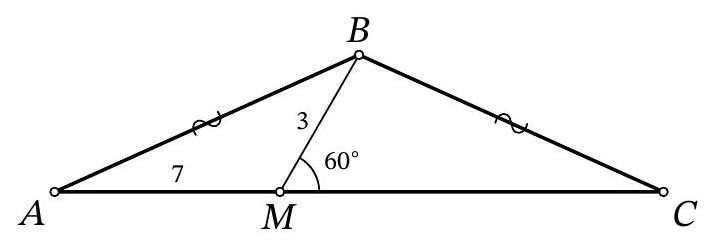
|
Answer: 17.
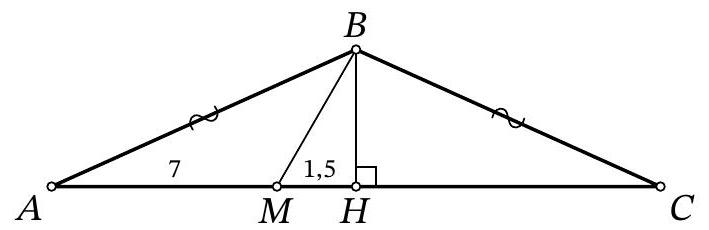
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
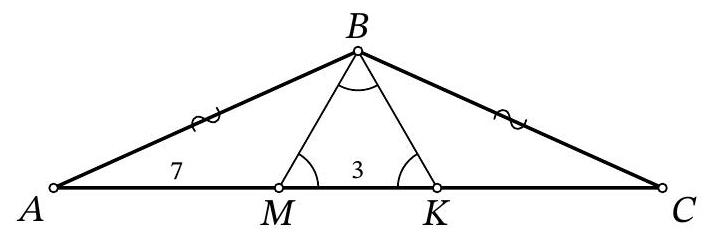
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
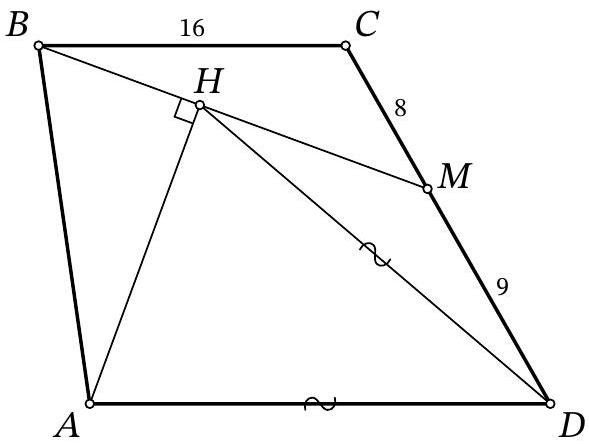
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we obtain $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.
Fig. 5: to the solution of problem 9.8
In the isosceles triangle $A D H$, draw the height and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. The entire surface of a cube $13 \times 13 \times 13$ was painted red, and then this cube was sawn into smaller cubes $1 \times 1 \times 1$. All the faces of the smaller cubes $1 \times 1 \times 1$ that were not painted red were painted blue. By what factor is the total area of the blue faces greater than the total area of the red faces?
|
Answer: 12.
Solution. Each face of the original cube consists of exactly $13^{2}$ $1 \times 1$ squares, so a total of $6 \cdot 13^{2}$ $1 \times 1$ squares were painted red. Since there are exactly $13^{3}$ $1 \times 1 \times 1$ cubes, and each has 6 faces, the number of $1 \times 1$ squares painted blue is $6 \cdot 13^{3}-6 \cdot 13^{2}$. Therefore, the answer to the problem is
$$
\frac{6 \cdot 13^{3}-6 \cdot 13^{2}}{6 \cdot 13^{2}}=13-1=12
$$
Remark. The same answer could have been obtained in a different way, by understanding that each $1 \times 1$ red square on the surface of the original cube corresponds to exactly 12 blue $1 \times 1$ squares inside the cube. These 12 blue squares are obtained from the red one by applying a parallel translation of length 1 "into the cube," perpendicular to the face of the red square.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.2. Given a natural number $n$. Roma wrote down three numbers $n, n+1, n+2$ on the board one after another, without spaces. He obtained a certain sequence of digits, in which there are consecutive digits 6474. Find the smallest possible value of $n$.
|
Answer: 46.
Solution. It is clear that for $n=46$ the condition is satisfied.
Suppose there exists $n<46$. One of the three numbers that Roma has should contain the digit 6, and for $n<46$, it must be in the units place. By a simple enumeration, one can verify that the corresponding values $n=4,5,6,14,15,16,24,25,26,34,35,36,44,45$ do not work.
|
46
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.
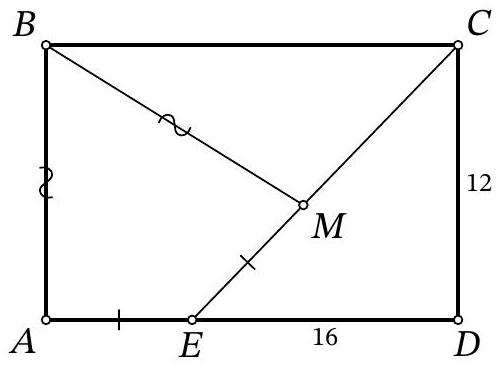
|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.
Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. Greedy Vovochka has 25 classmates. For his birthday, he brought 200 candies to the class. Vovochka's mother, to prevent him from eating them all himself, told him to distribute the candies so that any 16 of his classmates would collectively have at least 100 candies. What is the maximum number of candies Vovochka can keep for himself while fulfilling his mother's request?
|
Answer: 37.
Solution. Among all 25 classmates, select 16 people with the smallest number of candies given. Note that among them, there is a person who received no less than 7 candies (otherwise, if they all received no more than 6 candies, then in total they received no more than $16 \cdot 6=96$ candies, which is less than 100). Then the remaining $25-16=9$ classmates received no fewer than 7 candies. Thus, in total, at least $100+9 \cdot 7=163$ candies were given out. Accordingly, Vovochka left himself no more than $200-163=37$ candies.
Note also that Vovochka could have left himself exactly 37 candies if he gave the other 163 to his classmates as follows: 13 classmates received 7 candies each, and 12 classmates received 6 candies each. Then any 16 people together have at least $6 \cdot 12+7 \cdot 4=100$ candies, and Vovochka indeed gave out a total of $13 \cdot 7+12 \cdot 6=163$ candies.
|
37
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
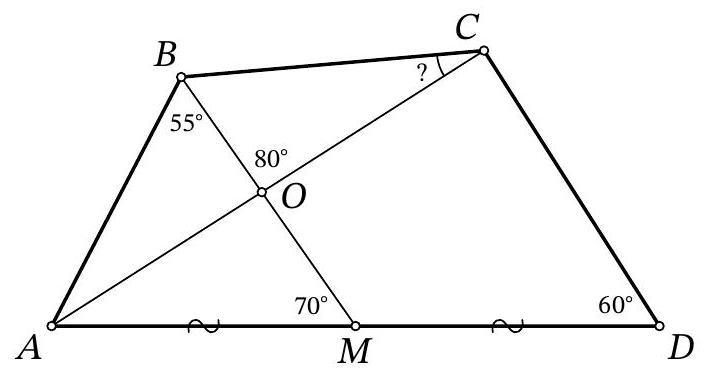
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.

Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. A square board $30 \times 30$ was cut along the grid lines into 225 parts of equal area. Find the maximum possible value of the total length of the cuts.
|
Answer: 1065.
Solution. The total length of the cuts is equal to the sum of the perimeters of all figures, minus the perimeter of the square, divided by 2 (each cut is adjacent to exactly two figures). Therefore, to get the maximum length of the cuts, the perimeters of the figures should be as large as possible.
The area of each figure is $\frac{900}{225}=4$. There are 5 four-cell figures in total:

The perimeter of the square is 8, and the perimeter of all other figures is 10. Therefore, the maximum length of the cuts does not exceed ( $225 \cdot 10 - 120$ )/ $2 = 1065$.
It remains to provide an example. From the above, it follows that this answer will be obtained if we cut the $30 \times 30$ square into any four-cell figures except the square. First, fill the $28 \times 30$ rectangle with $1 \times 4$ strips, leaving a $2 \times 30$ rectangle. The $2 \times 24$ rectangle can also be cut into $1 \times 4$ strips. A $2 \times 6$ rectangle will remain empty, which can easily be cut into two figures in the shape of the letter G and one $1 \times 4$ strip, as shown in Fig. 8.

Fig. 8: to the solution of problem 10.7
|
1065
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. A natural number $1 \leqslant n \leqslant 221$ is called lucky if the remainder of 221
divided by $n$ is divisible by the quotient (in this case, the remainder can be equal to 0). How many lucky numbers are there?
|
Answer: 115.
Solution. Let for some successful number $n$ the quotient be $k$, and the remainder be $k s$, by definition it is non-negative and less than the divisor $n$ (from the condition it follows that $k$ is a natural number, and $s$ is a non-negative integer.) Then
$$
221=n k+k s=k(n+s)
$$
Since $221=13 \cdot 17$ is divisible by the natural number $k$, we get several cases.
- Let $k=1$, then $n+s=221$. Since $0 \leqslant s110$. Notice that all such $n \in\{111,112,113, \ldots, 221\}$ are successful (and there are exactly 111 such numbers). Indeed, in all these cases $221=n \cdot 1+(221-n)$ the remainder (221-n) is non-negative, less than the corresponding $n$, and also divisible by the corresponding quotient 1.
- Let $k=13$, then $n+s=17$. Since $0 \leqslant 13 s14 s$, i.e., either $s=0$ and $n=17$, or $s=1$ and $n=16$. Notice that the numbers $n=16$ and $n=17$ are successful. Indeed, in both cases $221=16 \cdot 13+13$ and $221=17 \cdot 13+0$ the remainder is non-negative, less than the corresponding $n$, and also divisible by the corresponding quotient.
- Let $k=17$, then $n+s=13$. Since $0 \leqslant 17 s18 s$, i.e., $s=0$ and $n=13$. Notice that $n=13$ is successful. Indeed, in the case $221=$ $13 \cdot 17+0$ the remainder is non-negative, less than the corresponding $n$, and also divisible by the corresponding quotient.
- Let $k=221$, then $n+s=1$. Since $0 \leqslant 221 s222 s$, i.e., $s=0$ and $n=1$. Notice that $n=1$ is successful. Indeed, in the case $221=$ $1 \cdot 221+0$ the remainder is non-negative, less than the corresponding $n$, and also divisible by the corresponding quotient.
In total, there are $111+2+1+1=115$ successful numbers.
## 11th grade
|
115
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. Petya wrote down ten natural numbers in a row as follows: the first two numbers he wrote down arbitrarily, and each subsequent number, starting from the third, was equal to the sum of the two preceding ones. Find the fourth number if the seventh is 42 and the ninth is 110.
|
Answer: 10.
Solution. From the condition, it follows that the eighth number is equal to the difference between the ninth and the seventh, i.e., $110-42=68$. Then the sixth is $68-42=26$, the fifth is $42-26=16$, and the fourth is $26-16=10$.
Remark. In fact, the numbers on the board are the doubled Fibonacci numbers.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. In the store, there are 9 headphones, 13 computer mice, and 5 keyboards. In addition, there are 4 sets of "keyboard and mouse" and 5 sets of "headphones and mouse". In how many ways can you buy three items: headphones, a keyboard, and a mouse? Answer: 646.
|
Solution. Let's consider the cases of whether any set was purchased.
- Suppose the set "keyboard and mouse" was purchased, then headphones were added to it. This results in exactly $4 \cdot 9=36$ ways to make the purchase.
- Suppose the set "headphones and mouse" was purchased, then a keyboard was added to it. This results in exactly $5 \cdot 5=25$ ways to make the purchase.
- Suppose no set was purchased, then headphones, mouse, and keyboard were purchased separately. This results in exactly $9 \cdot 13 \cdot 5=585$ ways to make the purchase. In total, there are exactly $36+25+585=646$ desired ways.
|
646
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
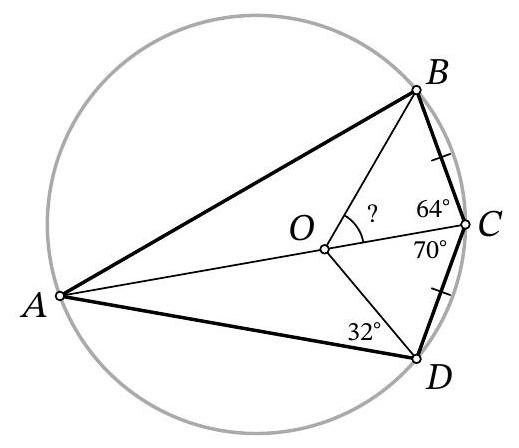
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the point of intersection of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the point of intersection of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Oleg wrote down several composite natural numbers less than 1500 on the board. It turned out that the greatest common divisor of any two of them is 1. What is the maximum number of numbers that Oleg could have written down?
|
Answer: 12.
Solution. Prime numbers less than $\sqrt{1500}$ will be called small. There are exactly 12 such numbers: $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37$.
Note that each of Oleg's numbers has a small divisor (otherwise it would be not less than $43^{2} > 1500$), and different numbers have different small divisors (otherwise the GCD of these numbers would be greater than 1). Therefore, the number of Oleg's numbers is no less than the total number of small numbers, i.e., no less than 12.
An example with 12 numbers is easy to construct: these are the numbers $2^{2}, 3^{2}, 5^{2}, 7^{2}, 11^{2}, 13^{2}, 17^{2}, 19^{2}, 23^{2}, 29^{2}, 31^{2}, 37^{2}$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.7. An archipelago consists of $N \geqslant 7$ islands. Any two islands are connected by no more than one bridge. It is known that from each island, no more than 5 bridges lead, and among any 7 islands, there are definitely two connected by a bridge. What is the largest value that $N$ can take?
|
Answer: 36.
Solution. There can be 36 islands in the archipelago, for example, as follows: they form 6 groups of 6 islands each, and two islands are connected by a bridge if and only if they are in the same group. It is clear that from each island, exactly 5 bridges lead out, and among any 7 islands, there are necessarily two that are in the same group, and they are connected to each other by a bridge.

Suppose there can be $N \geqslant 37$ islands. Choose any of the islands, call it $A$, it is connected to no more than five other islands. Temporarily forget about these no more than 6 islands, and consider the remaining at least $N-6$ islands (among which none are connected to $A$). Choose any of these islands, call it $B$, it is connected to no more than five other islands. Temporarily forget about these no more than 6 islands, and consider the remaining at least $N-12$ islands (among which none are connected to $A$ and $B$), and so on. Forgetting the sixth island $F$ and the no more than 5 islands connected to it, at least $N-36 \geqslant 1$ islands will remain (among which none are connected to $A, B, C, D, E, F$). Choose any of these islands, call it $G$. Then among the islands $A, B, C, D, E, F, G$, there are no islands connected by a bridge. Contradiction.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. In the quadrilateral pyramid $S A B C D$
- the lateral faces $S A B, S B C, S C D, S D A$ have areas 9, 9, 27, 27 respectively;
- the dihedral angles at the edges $A B, B C, C D, D A$ are equal;
- the quadrilateral $A B C D$ is inscribed, and its area is 36.
Find the volume of the pyramid $S A B C D$.
|
Answer: 54.
Solution. Let the angle between the lateral face and the base of the pyramid be denoted as $\alpha$.

Fig. 10: to the solution of problem 11.8
Draw the height $S H$ to the base of the pyramid, and denote its length as $h$ (Fig. 10). Also, draw the heights $S H_{a}, S H_{b}, S H_{c}, S H_{d}$ to the edges $D A, A B, B C, C D$ respectively. Since $S H_{a} \perp D A$ and (by the theorem of three perpendiculars) $H H_{a} \perp D A$, we have $\angle S H_{a} H=\alpha$. From the right triangle $S H_{a} H$, we get $S H_{a}=S H / \sin (\alpha)$.
Similarly, we find that the heights $S H_{b}, S H_{c}$, and $S H_{d}$ also have the same value. Denote their length as $h_{1}=h / \sin (\alpha)$. Using the areas of the lateral faces, we get $D A=27 x, A B=9 x, B C=9 x, C D=27 x$, where $x=2 / h_{1}$.
Since triangles $B A D$ and $B C D$ are equal by three sides, the quadrilateral $A B C D$ is a kite (symmetric with respect to the diagonal $B D$). In the inscribed quadrilateral $A B C D$, the angles $D A B$ and $D C B$ are equal and supplement each other to $180^{\circ}$, so they are each $90^{\circ}$. The area of the right triangle $D A B$ is thus $\frac{1}{2} \cdot 27 x \cdot 9 x=\frac{1}{2} 243 x^{2}$; the area of the entire base is twice this, and equals $243 x^{2}$. According to the problem, it is equal to 36, from which we find $x=\sqrt{36 / 243}=2 /(3 \sqrt{3})$, so $h_{1}=2 / x=3 \sqrt{3}$.
Now we find $\alpha$. For this, consider how the areas of the lateral faces change when projected onto $A B C D$. The heights of the lateral faces, drawn from the vertex $S$, are multiplied by $\cos (\alpha)$, while the corresponding bases of the triangles remain unchanged; thus, the areas are multiplied by $\cos (\alpha)$. On the other hand, the union of the projections of the lateral faces is exactly the quadrilateral $A B C D$, from which we get $36=(9+9+27+27) \cdot \cos (\alpha)$. Therefore, $\cos (\alpha)=\frac{1}{2}$, so $\alpha=\pi / 3$.
Finally, we find $h=h_{1} \sin (\alpha)=4.5$ and the volume of the pyramid $\frac{1}{3} \cdot S_{A B C D} \cdot h=\frac{1}{3} \cdot 36 \cdot 4.5=54$.
|
54
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers from 1 to 8 are arranged in a circle. A number is called large if it is greater than its neighbors, and small if it is less than its neighbors. Each number in the arrangement is either large or small. What is the smallest possible sum of the large numbers?
|
Answer: 23.
Instructions. Adjacent numbers cannot be of the same type, so larger and smaller numbers alternate, and there are four of each. 8 is large. 7 is also large, since a small number must be less than two numbers, and seven is less than only one. 1 and 2 are small. 3 and 4 cannot both be large, as there are only two larger numbers, and they cannot be adjacent in this case. Therefore, the sum of the two other large numbers (besides 7 and 8) is at least 8. And the sum of the large numbers is at least 23. Example: $8,6,7,1,3,2,5,4$.
Criteria. Only the correct answer and example: 2 points.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The circle inscribed in the right triangle ABC touches the legs CA and CB at points P and Q, respectively. The line PQ intersects the line passing through the center of the inscribed circle and parallel to the hypotenuse at point N. M is the midpoint of the hypotenuse. Find the measure of angle MCN.
|
Answer: $90^{\circ}$.
Instructions. Let the center of the inscribed circle be denoted by I. The points of intersection of the line,

parallel to the hypotenuse and passing through I, with the legs AC and BC, are denoted by K and T, respectively. We will assume that point N lies on the extension of segment KT beyond point K (see figure). It is easy to see that IPCQ is a square. PQ is the axis of symmetry of the square, and point N lies on it, which means that triangles NPI and NPC are symmetric and, therefore, equal. We have $\angle NCP = \angle NIP$. Angles NIP and ABC are equal as acute angles with respectively parallel sides. Angles MBC and MCB are equal, as angles at the base of an isosceles triangle (property of the median drawn to the hypotenuse). Combining the obtained angle equalities, we have $\angle MCB = \angle NCA$. Adding angle ACM to each of them, on one side we get a right angle, and on the other - $\angle NCM$. Hence the answer.
Criteria. Only answer: 0 points.
Noted that IPCQ is a square: 1 point.
Proved the equality of triangles NPI and NPC: 2 points.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. There are 22 batteries, 15 of which are charged and 7 are discharged. The camera works with three charged batteries. You can insert any three batteries into it and check if it works. How can you guarantee to turn on the camera in 10 such attempts?
|
Solution. Let's number the batteries: $1,2, \ldots, 22$. The first six tests will involve inserting batteries into the camera as follows: $1,2,3 ; 4,5,6 ; \ldots, 16,17,18$. If at least one of these groups turns on the camera, everything is fine. If not, then among the first 18 batteries, there are at least 6 discharged ones, which means that among the last four batteries, there is at most one discharged one. The next four tests will involve trying all combinations of the remaining batteries: $19,20,21 ; 19,20,22 ; 19,21,22 ; 20,21,22$ - and we will definitely find a group of three charged batteries.
- See also problem 1 for 10th grade.
- For an answer without justification - 0 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Inside triangle ABC, two points are given. The distances from one of them to the lines AB, BC, and AC are 1, 3, and 15 cm, respectively, and from the other - 4, 5, and 11 cm. Find the radius of the circle inscribed in triangle ABC.
|
Answer: 7 cm. First solution. Let $M_{1}$ and $M_{2}$ be the first and second given points, and let point $O$ be such that point $M_{2}$ is the midpoint of segment $O M_{1}$. Drop perpendiculars $M_{1} N_{1}, M_{2} N_{2}$, and $O N_{3}$ to line $A B$. Then segment $M_{2} N_{2}$ will be the midline of trapezoid $O N_{3} N_{1} M_{1}$. Therefore, $M_{2} N_{2}=\left(O N_{3}+M_{1} N_{1}\right) / 2 \Rightarrow 4=\left(O N_{3}+1\right) / 2$, from which $O N_{3}=7$. Similarly, we find that the perpendiculars $O M_{3}$ and $O K_{3}$ from point $O$ to lines $B C$ and $A C$ respectively are also equal to 7. Thus, point $O$ is the center of the inscribed circle of triangle $A B C$, which has a radius of 7. Second solution. Let $A B=c, B C=a$, $A C=b$. Then $3 a+15 b+c=5 a+11 b+4 c=r(a+b+c)=2 S_{A B C}$. From the first equality, we get $a=(4 b-3 c) / 2$. Substituting the found $a$ into the second equality $5 a+11 b+4 c=r(a+b+c)$, we find $r=7$.
- For an answer without justification - 0 points.
Problem 6. On the board, there are five "equations" of the form $x^{2}+\ldots x+\ldots=0$. Two players take turns writing natural numbers from 1 to 10 in place of the ellipses, with each number being used only once. The game ends when all numbers are written. The player who makes the first move wants to have as few equations with two distinct roots as possible at the end, while his opponent wants to have as many as possible. What is the best result the first player can achieve regardless of the second player's moves?
Answer. The first player can ensure that there are no more than three equations with two distinct roots on the board. This result cannot be improved. Solution. To create two equations without roots, the first player needs to use the first two moves to write the smallest of the numbers not yet written in the coefficient of $x$ in an "equation" where no numbers have been written yet. This is possible because if no more than two pairs of moves have been made, then at least one coefficient has been written in no more than four "equations". Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the first player on one of the first two moves. Then, obviously, $p \leq 3$ and $q \geq p+1$, from which $p^{2}-4 q \geq p^{2}-4(p+1)=p(p-4)-40$.
- For an answer without justification - 0 points. If there is a strategy for only one of the players, the solution is scored out of 4 points: 2 points for describing the strategy and 2 points for justifying it.
## SOURCES AND AUTHORS OF THE PROBLEMS
XII Tournament of Mathematical Flash Battles "League of Discoveries", Kazan, 2022: 6-4, 7-4.
Based on problems from Kostroma olympiads: 7-2, 9-2.
District-city round of the Chelyabinsk Region Olympiad 1999/2000: 9-1.
District-city round of the Chelyabinsk Region Olympiad 1998/1999: 11-5.
Third Kostroma City Tournament of Mathematical Battles, 1998 (numerical data changed): $9-3$.
Tatarstan, Olympiad for 6th grade, final round, 2014: 10-1.
Udmurtia, district round, 1979: 11-1
Folklore: $5-4=6.3,11-4$.
All other problems were composed by I.S. Rubanov specifically for this olympiad.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A teacher fills in the cells of a class journal of size $7 \times 8$ (7 rows, 8 columns). In each cell, she puts one of three grades: 3, 4, or 5. After filling in the entire journal, it turns out that in each row, the number of threes is not less than the number of fours and not less than the number of fives, and in each column, the number of fours is not less than the number of fives and not less than the number of threes. How many fives could the teacher have put?
|
Answer: 8 fives.
## Solution.
First step.
In each row, there are no fewer threes than fours, so in the entire journal, there are no fewer threes than fours. In each column, there are no fewer fours than threes, so in the entire journal, there are no fewer fours than threes. Therefore, the number of threes and fours in the journal is the same.
Second step.
Suppose in some column, there are more fours than threes. Since in the other columns, there are no fewer fours than threes, we would get that in the entire journal, there are more fours than threes. This is a contradiction. Therefore, in each column, the number of fours and threes is the same.
Third step.
Consider all possible distributions of threes, fours, and fives in a column: 1) $0,0,7 ; 2) 1,1,5 ; 3) 2,2,3$ - these do not work, as then there would be more fives. The only remaining case is $3,3,1$. Then, in the entire journal, there can be 8 fives.
Fourth step.
Such a distribution is possible (we need to consider that in the rows, the number of fours and threes is also the same),
| $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{5}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{5}$ | $\mathbf{5}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
| $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ |
| $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{3}$ | $\mathbf{4}$ |
see the example in the figure.
Criteria. If the solution is incorrect - 0 points.
If only the correct example is given - 3 points.
If only the correct estimate is given - 4 points.
If the solution is correct (any correct example and justification of the estimate) - 7 points.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The function $y=f(x)$ is such that for all values of $x$, the equality $f(x+1)=f(x)+2x+3$ holds. It is known that $f(0)=1$. Find $f(2018)$.
|
Solution. Rewrite the condition of the problem as $f(x+1)-f(x)=2 x+3$. Substituting sequentially instead of $x$ the numbers $0,1,2, \ldots, 2017$, we get the following equalities
$$
\begin{aligned}
& f(1)-f(0)=2 \cdot 0+3 \\
& f(2)-f(1)=2 \cdot 1+3 \\
& f(3)-f(2)=2 \cdot 2+3
\end{aligned}
$$
$$
f(2018)-f(2017)=2 \cdot 2017+3
$$
Add these equalities term by term: $f(2018)-f(0)=2 \cdot(0+1+2+\ldots+2017)+3 \cdot 2018$. Using the formula for finding the sum of an arithmetic progression, we get
$$
\begin{gathered}
f(2018)=1+2 \cdot \frac{1+2017}{2} \cdot 2017+3 \cdot 2018=1+2018 \cdot 2017+3 \cdot 2018= \\
=1+2 \cdot 2018+2018^{2}=2019^{2}=4076361
\end{gathered}
$$
Answer: $2019^{2}$ or 4076361.
|
4076361
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A car left point A for point B, which are 10 km apart, at 7:00. After traveling $2 / 3$ of the way, the car passed point C, from which a cyclist immediately set off for point A. As soon as the car arrived in B, a bus immediately set off from there in the opposite direction and arrived in point A at 9:00. At what distance from B did the bus catch up with the cyclist, if the cyclist arrived in point A at 10:00 and the speed of each participant in the movement was constant?
|
Solution. Let $v_{a}$ be the speed of the car, $v_{\varepsilon}$ be the speed of the cyclist, and $v_{a \varepsilon}$ be the speed of the bus. From the problem statement, we derive the following system of equations:
$$
\left\{\begin{array}{l}
\frac{20 / 3}{v_{a}}+\frac{20 / 3}{v_{s}}=3 \\
\frac{10}{v_{a}}+\frac{10}{v_{a \varepsilon}}=2
\end{array}\right.
$$
We need to find $\frac{\frac{10}{3}+\frac{10}{3 v_{a}} v_{g}}{v_{a \varepsilon}-v_{s}} v_{a \varepsilon}=\frac{\frac{10}{3 v_{s}}+\frac{10}{3 v_{a}}}{1 / v_{b}-1 / v_{a \varepsilon}}$.
From the system of equations, we get
$$
\left\{\begin{array} { l }
{ \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { s } } = \frac { 3 } { 2 } , } \\
{ \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { a \varepsilon } } = \frac { 2 } { 3 } , \quad \frac { 1 0 } { 3 v _ { a } } + \frac { 1 0 } { 3 v _ { s } } = \frac { 3 } { 2 } , \quad \frac { 1 0 } { 3 v _ { s } } - \frac { 1 0 } { 3 v _ { a \varepsilon } } = \frac { 5 } { 6 } }
\end{array} \left\{\begin{array}{l}
\frac{10}{3 v_{a}}+\frac{10}{3 v_{s}}=\frac{3}{2} \\
\frac{1}{v_{s}}+\frac{1}{v_{a \varepsilon}}=\frac{1}{4}
\end{array}\right.\right.
$$
Substituting the obtained values into expression (*), we get $\frac{3 / 2}{1 / 4}=\frac{3}{2} \cdot 4=6$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In city $\mathrm{N}$, only blondes and brunettes live. Blondes always lie, while brunettes always tell the truth. Every day, the residents dye their hair the opposite color. On one Monday in October, everyone born in the fall was asked: "Were you born this month?" - and 200 residents answered "yes," while no one answered "no." On Friday of the same week, everyone born in the fall was asked again: "Were you born this month?" - and this time only 50 of them gave an affirmative answer. How many "yes" answers were given to the same question on the last Monday of September, if there were exactly four Mondays in October of that year and no one in the city $\mathrm{N}$ was born in November?
|
4. Answer. 0.
Solution. Note that on Monday and Friday of the same week, the residents have the same hair color: Monday - Tuesday - Wednesday - Thursday - Friday. Then, if the same people answer differently on Monday and Friday, it means that the month has changed, and the brunettes will answer "no" to the same question.
If the month has changed, then it is the last Monday of October. Since there were 4 Mondays in October, the residents will have the same hair color again on the last Monday of September: M (September) - M1 - M2 - M3 - M4 (October) (since the hair color changes each subsequent Monday). The first time all brunettes answered "yes," it means that all residents who were brunettes on that day were born in October. On the following Friday and the last Monday of September, they will also be brunettes, but since the month will change, all of them will answer "no."
Let's pay attention to the blondes. The first time all of them answered "yes," it means that none of them were born in October. We also know that no one was born in November. Therefore, all blondes were born in September and will also answer "no" on the last Monday of September.
Thus, on the last Monday of September, 0 residents will answer "yes."
## Grading Criteria:
Correct and justified solution - 7 points. In all other cases - $\mathbf{0}$ points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A tournament of dodgeball was held at school. In each game, two teams competed. 15 points were awarded for a win, 11 for a draw, and no points for a loss. Each team played against each other once. By the end of the tournament, the total number of points scored was 1151. How many teams were there?
|
5. Answer: 12 teams.
Solution. Let there be $\mathrm{N}$ teams. Then the number of games was $\mathrm{N}(\mathrm{N}-1) / 2$. For each game, a total of 15 or 22 points are scored. Therefore, the number of games was no less than 53 $(1151 / 22)$ and no more than $76(1151 / 15)$.
Note that if there were no more than 10 teams, then the number of games would not exceed 45. And if there were no fewer than 13 teams, then the number of games would be no less than 78.
Thus, the number of teams was 11 (55 games) or 12 (66 games). In each game, teams score exactly 15 points in total! And 7 additional points if there was a draw. Therefore, the total number of draws is (1151-55*15)/7 (a non-integer - this could not have been the case) or (1151-66*15)/7=23. Therefore, the only option is that there were 12 teams.
## Grading Criteria.
Correct and justified solution - 7 points.
Justified that the number of teams is 11 or 12 without further progress - 3 points. Justified that the number of games was no less than 53 and no more than 76 without further progress - $\mathbf{2}$ points. Correct answer with a constructed example - $\mathbf{2}$ points. Just the correct answer - $\mathbf{0}$ points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. In a basket, there are 41 apples: 10 green, 13 yellow, and 18 red. Alyona sequentially takes one apple at a time from the basket. If at any point she has pulled out fewer green apples than yellow ones, and fewer yellow ones than red ones, she will stop taking apples from the basket.
(a) (1 point) What is the maximum number of yellow apples Alyona can take from the basket?
(b) (3 points) What is the maximum number of apples Alyona can take from the basket?
|
Answer: (a) 13 apples. (b) 39 apples.
Solution. (a) Alyona can take all 13 yellow apples from the basket, for example, if the first 13 apples turn out to be yellow. Since at no point do the yellow apples become fewer than the red ones, Alyona can indeed do this.
(b) We will show that Alyona can take all the apples except for two yellow ones. Let her take 10 green apples first, then 18 red ones, and then 11 yellow ones. Note that until the number of yellow apples reaches 11, the condition that there are fewer green apples than yellow ones will not be violated. Thus, Alyona can indeed take 39 apples.
Now we will prove that Alyona cannot take more than 39 apples. Suppose the opposite: Alyona managed to take 40 apples at some point. Before taking the 40th apple, she already had at least 11 yellow apples. She had taken no more than 10 green apples by this point, so the first condition is definitely satisfied. On the other hand, she had taken no more than 13 yellow apples and at least 16 red ones, so the second condition is also definitely satisfied. But then she would not take the 40th apple, a contradiction.
|
39
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. A polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-8$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -24. (b) 6.
Solution. (a) Since the graph of $G(x)$ is symmetric with respect to the line $x=-8$, the points at which it takes the same value must be divided into pairs of symmetric points, except possibly one point that lies on the axis of symmetry. Therefore, the middle of the five given points should lie on the axis of symmetry, i.e., $x_{3}=-8$. The first and fifth points should be symmetric with respect to the line $x=-8$, so $x_{1}+x_{5}=2 \cdot(-8)=-16$. Therefore, $x_{1}+x_{3}+x_{5}=-24$.
(b) Consider the auxiliary polynomial $F(x)=G(x-8)-2022$. Clearly, the degree of $F(x)$ coincides with the degree of $G(x)$. The graph of $F(x)$ is obtained by a parallel shift of the graph of $G(x)$ 8 units to the right and 2022 units down. Then this graph is symmetric with respect to the line $x=0$, and at five points $F(x)$ takes the value 0. It is clear that $F(x)$ has exactly 5 distinct roots, so its degree is at least 5. On the other hand, since the graph of $F(x)$ is symmetric with respect to the line $x=0$, the function $F(x)$ is even, so the degree of $F(x)$ is also even. Therefore, the degree of $F(x)$, and hence the degree of $G(x)$, is at least 6.
As an example of a polynomial of degree 6, we can take $F(x)=(x+2)(x+1)x^{2}(x-1)(x-2)$. It corresponds to $G(x)=(x+10)(x+9)(x+8)^{2}(x+7)(x+6)+2022$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. On a horizontal floor, there are three volleyball balls with a radius of 18, each touching the other two. Above them, a tennis ball with a radius of 6 is placed, touching all three volleyball balls. Find the distance from the top point of the tennis ball to the floor. (All balls are spherical.)
|
Answer: 36.
Fig. 9: to the solution of problem 11.4
Solution. Let the centers of the volleyballs be denoted by $A, B, C$, and the center of the tennis ball by $D$; the top point of the tennis ball is denoted by $X$.
Consider the section of the volleyballs by the plane $A B C$ (Fig. 9). This is three mutually tangent circles with a radius of 18. Therefore, the points $A, B, C$ are located at the vertices of an equilateral triangle with a side length of 36. Let the center of this triangle be denoted by $O$; then $O A=18 / \cos \left(30^{\circ}\right)=12 \sqrt{3}$ (from the right triangle $O A M$, where $M-$ is the midpoint of $A B$).
By symmetry, it is clear that the points $X, D$, and $O$ lie on the same vertical line. Consider the section of the tennis ball and one of the volleyballs by the plane $A D O$ (Fig. 10). The triangle $A D O$ is a right triangle, $A D=18+6=24$, by the Pythagorean theorem we have
$$
O D=\sqrt{A D^{2}-O A^{2}}=12
$$
The point $O$, as well as the entire plane $A B C$, is at the height of the radius of the volleyball, which is 18; the point $D$, as we found, is 12 units higher; and the point $X$ is 6 units higher than point $D$, which is the radius of the tennis ball. In total, we get $18+12+6=36$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Point $M$ is the midpoint of the base $B C$ of trapezoid $A B C D$. A point $P$ is chosen on the base $A D$. Ray $P M$ intersects ray $D C$ at point $Q$. The perpendicular to base $A D$, drawn through point $P$, intersects segment $B Q$ at point $K$.
It is known that $\angle K Q D=64^{\circ}$ and $\angle K D Q=38^{\circ}$. How many degrees does the angle $K B C$ measure?
|
Answer: $39^{2}$.
Fig. 11: to the solution of problem 11.6
Solution. From the condition, it follows that $\angle B K D=\angle K Q D+\angle K D Q=64^{\circ}+38^{\circ}=102^{\circ}$.
Let the lines $Q B$ and $A D$ intersect at point $X$ (Fig. 11). Triangles $Q X P$ and $Q B M$ are similar with a coefficient of $Q P / Q M$, and triangles $Q D P$ and $Q C M$ are similar with the same coefficient. Then, from the equality $M B=M C$, it follows that $P X=P D$. Therefore, point $K$ lies on the perpendicular bisector of segment $X D$, so $\angle K X D=\angle K D X=\frac{1}{2}\left(180^{\circ}-102^{\circ}\right)=39^{\circ}$. Since $B C \| A D$, we get that $\angle K B C=\angle K X D=39^{\circ}$.
Remark. The equality $P X=P D$ could also have been established using a homothety with center $Q$, which maps triangle $Q B C$ to triangle $Q X D$.
|
39
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Real numbers $a, b, c$ are such that
$$
\left\{\begin{array}{l}
a^{2}+a b+b^{2}=11 \\
b^{2}+b c+c^{2}=11
\end{array}\right.
$$
(a) (1 point) What is the smallest value that the expression $c^{2}+c a+a^{2}$ can take?
(b) (3 points) What is the largest value that the expression $c^{2}+c a+a^{2}$ can take?
|
Answer: (a) 0; (b) 44.
Solution. (a) Note that if $a=c=0$, and $b=\sqrt{11}$, then the given system of equalities is satisfied, and $c^{2}+c a+a^{2}$ equals 0. On the other hand,
$$
c^{2}+c a+a^{2}=\frac{c^{2}}{2}+\frac{a^{2}}{2}+\frac{(c+a)^{2}}{2} \geqslant 0
$$
Thus, the smallest value of the expression $c^{2}+c a+a^{2}$ is 0.
(b) We will use the formula $x^{3}-y^{3}=(x-y)\left(x^{2}+x y+y^{2}\right)$. Multiply the first equation by $a-b$, and the second by $b-c$, we get
$$
\left\{\begin{array}{l}
a^{3}-b^{3}=11(a-b) \\
b^{3}-c^{3}=11(b-c)
\end{array}\right.
$$
Adding these two equations, we get $a^{3}-c^{3}=11(a-c)$, from which it follows that $a^{2}+a c+c^{2}=11$ if $a \neq c$. It remains to determine what happens if $a=c$.
In the case $a=c$, both equalities in the system are the same, and we need to maximize the expression $3 a^{2}$.
The case $a=c=0$ has already been considered in the previous part, so we will consider $a \neq 0$ from now on. Let $b=k a$ for some real $k$. Then from the condition we have
$$
a^{2}+k a^{2}+k^{2} a^{2}=11 \quad \text { and } \quad a^{2}=\frac{11}{1+k+k^{2}}
$$
Note that
$$
1+k+k^{2}=\frac{3}{4}+\left(\frac{1}{2}+k\right)^{2} \geqslant \frac{3}{4}
$$
Thus,
$$
a^{2} \leqslant \frac{11}{3 / 4}=\frac{44}{3} \quad \text { and } \quad 3 a^{2} \leqslant \frac{44}{3} \cdot 3=44
$$
It is clear that this value is achieved if $a=c=\sqrt{44 / 3}, b=-\sqrt{11 / 3}$.
Another solution for part (b). We complete the squares in the left-hand sides of the given equations:
$$
\left\{\begin{array}{l}
\frac{3}{4} a^{2}+\left(\frac{1}{2} a+b\right)^{2}=11 \\
\frac{3}{4} c^{2}+\left(\frac{1}{2} c+b\right)^{2}=11
\end{array}\right.
$$
From the fact that $\left(\frac{1}{2} a+b\right)^{2}$ and $\left(\frac{1}{2} c+b\right)^{2}$ are non-negative, it follows that $\frac{3}{4} a^{2} \leqslant 11$ and $\frac{3}{4} c^{2} \leqslant 11$. Thus, $|a| \leqslant \sqrt{44 / 3}$ and $|c| \leqslant \sqrt{44 / 3}$.
We estimate the desired expression:
$$
c^{2}+a c+a^{2} \leqslant c^{2}+|a| \cdot|c|+a^{2} \leqslant \frac{44}{3}+\sqrt{\frac{44}{3}} \cdot \sqrt{\frac{44}{3}}+\frac{44}{3}=44
$$
Thus, the desired expression does not exceed 44, and this value is achieved when $a=c=\sqrt{44 / 3}$ and $b=-a / 2=-\sqrt{11 / 3}$.
Another solution. Mark a point $O$ on the plane and draw three coordinate lines $O a, O b, O c$ through it at angles of $120^{\circ}$ to each other (Fig. 12a). Considering $O$ as the origin on each of the lines, mark points $A, B, C$ on them with coordinates equal to the given numbers $a, b, c$.
(a)
(b)
Fig. 12: to the solution of problem 11.8
Note that $A B^{2}=a^{2}+a b+b^{2}$. Indeed, in the case $a, b>0$ this is simply the cosine rule for triangle $A O B$ with sides $a$ and $b$ and an angle of $120^{\circ}$ between them. But this equality holds in all other cases as well. For example, if $a>0$ and $b<0$ (Fig. 12b), we have $O B=-b$ and $\angle A O B=60^{\circ}$, from which
$$
A B^{2}=A O^{2}+B O^{2}-2 \cos \left(60^{\circ}\right) \cdot A O \cdot B O=a^{2}+b^{2}+a b
$$
Similarly, we get $B C^{2}=b^{2}+b c+c^{2}$ and $C A^{2}=c^{2}+c a+a^{2}$. Now it is not difficult to rephrase the original problem:
On three lines intersecting at one point at angles of $60^{\circ}$ to each other, points $A, B, C$ are marked respectively (possibly coinciding). Given $A B=B C=\sqrt{11}$; we need to find the smallest and largest possible value of $A C^{2}$.
(a) It is clear that the smallest value is 0, which is achieved when $A=C=O$ (Fig. 13a).
(b) On the other hand, from the triangle inequality we have $A C \leqslant A B+B C=2 \sqrt{11}$, which is achieved if the points $A, B, C$ lie on the same line (Fig. 13b).
(a)
(b)
Fig. 13: to the solution of problem 11.8
## 11th Grade
|
44
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.1.1. In a basket, there are 41 apples: 10 green, 13 yellow, and 18 red. Alyona sequentially takes one apple at a time from the basket. If at any point she has pulled out fewer green apples than yellow ones, and fewer yellow ones than red ones, she will stop taking apples from the basket.
(a) (1 point) What is the maximum number of yellow apples Alyona can take from the basket?
(b) (3 points) What is the maximum number of apples Alyona can take from the basket?
|
Answer: (a) 13 apples. (b) 39 apples.
|
39
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.1.2. In a basket, there are 38 apples: 9 green, 12 yellow, and 17 red. Alyona sequentially takes one apple at a time from the basket. If at any point she has pulled out fewer green apples than yellow ones, and fewer yellow ones than red ones, she will stop taking apples from the basket.
(a) (1 point) What is the maximum number of yellow apples Alyona can take from the basket?
(b) (3 points) What is the maximum number of apples Alyona can take from the basket?
|
Answer: (a) 12 apples. (b) 36 apples.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.1.3. In a basket, there are 35 apples: 8 green, 11 yellow, and 16 red. Alyona sequentially takes one apple at a time from the basket. If at any point she has pulled out fewer green apples than yellow ones, and fewer yellow ones than red ones, she will stop taking apples from the basket.
(a) (1 point) What is the maximum number of yellow apples Alyona can take from the basket?
(b) (3 points) What is the maximum number of apples Alyona can take from the basket?
|
Answer: (a) 11 apples. (b) 33 apples.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.1.4. In a basket, there are 44 apples: 11 green, 14 yellow, and 19 red. Alyona sequentially takes one apple at a time from the basket. If at any point she has pulled out fewer green apples than yellow ones, and fewer yellow ones than red ones, she will stop taking apples from the basket.
(a) (1 point) What is the maximum number of yellow apples Alyona can take from the basket?
(b) (3 points) What is the maximum number of apples Alyona can take from the basket?
|
Answer: (a) 14 apples. (b) 42 apples.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.3.1. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-8$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -24 . (b) 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.3.3. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-7$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -21 . (b) 6.
|
-21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.3.4. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-6$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have?
|
Answer: (a) -18 . (b) 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 11.7.4. Let $N$ be the least common multiple of ten different natural numbers $a_{1}<a_{2}<a_{3}<\ldots<a_{10}$.
(a) (2 points) What is the smallest value that $N / a_{6}$ can take?
(b) (2 points) Identify all possible values of $a_{6}$ in the interval $[1 ; 2000]$, for which the value of $N / a_{1}$ can take its smallest value.
|
Answer: (a) 5. (b) $504,1008,1512$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. $\left(225-4209520: \frac{1000795+(250+x) \cdot 50}{27}\right)=113$
4209520: $\frac{1000795+(250+x) \cdot 50}{27}=112$
$\frac{1000795+(250+x) \cdot 50}{27}=37585$
$1000795+(250+x) \cdot 50=1014795$
$250+x=280$
$x=30$
|
Answer: $\boldsymbol{x}=30$.
Criteria. Correct solution - 7 points. $3 a$ for each computational error minus 1 point. Error in the algorithm for solving the equation - 0 points
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. 11088 is $110\%$ of the containers in December compared to November. This means that in November, $11088: 1.10=10080$ containers were manufactured, which is $105\%$ compared to October. This means that in October, $10080: 1.05=9600$ containers were manufactured, which is $120\%$ compared to September. Therefore, in September, $9600: 1.20=8000$ containers were manufactured.
|
Answer: in September 8000, in October 9600, in November 10080 containers.
|
8000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In one lyceum, $76 \%$ of the students have at least once not done their homework, and $\frac{5}{37}$ sometimes forget their second pair of shoes. Find the number of students in the lyceum, if it is more than 1000 but less than 2000.
|
Solution. Since $76 \%=\frac{76}{100}=\frac{19}{25}$, and the numbers 25 and 37 are coprime, the number of students is a multiple of $25 \cdot 37$, i.e., $925 \mathrm{k}$, where k is a natural number. Since $1000<925 k<2000$, then $\mathrm{k}=2$, and the number of students $925 \cdot 2$ $=1850$.
Answer. 1850
Recommendations for checking. Only the correct answer - 0 points. Answer with verification - 1 point. If there is no reference to the coprimality of the numbers 25 and 37, deduct 1 point. Computational errors - deduct no less than 2 points (depending on the impact on the solution).
|
1850
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Denis housed chameleons that can change color only to two colors: red and brown. Initially, the number of red chameleons was five times the number of brown chameleons. After two brown chameleons turned red, the number of red chameleons became eight times the number of brown chameleons. Find out how many chameleons Denis has.
|
Solution. Let $t$ be the number of brown chameleons Denis had. Then the number of red chameleons was $5t$. From the problem statement, we get the equation $5 t+2=8(t-2)$. Solving this, we find $t=6$. Therefore, the total number of chameleons is $6 t$, which is 36.
Answer. 36
Recommendations for checking. Only the correct answer - 0 points. Answer with verification - 1 point. Correctly formulated equation, but incorrectly solved not due to arithmetic - no more than 4 points. No justification for the formulation of the equation, but it is clear from the context what the author meant - do not deduct.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. An odd six-digit number is called "simply cool" if it consists of digits that are prime numbers, and no two identical digits stand next to each other. How many "simply cool" numbers exist?
|
Solution. There are four single-digit prime numbers in total - 2, 3, 5, 7. We will place the digits starting from the least significant digit. In the units place, three of them can stand $-3, 5, 7$. In the tens place, there are also three out of the four (all except the one placed in the units place). In the hundreds place, there are also three out of the four (all except the one placed in the tens place). And so on. As a result, the number of "prime cool" numbers is $3^{2}$, i.e., 729.
Answer. 729.
Recommendations for checking. Only the correct answer - 1 point. All 4 numbers are included in the units place - 3 points. The number 1 is considered a prime number, and the subsequent solution is correct based on this - 5 points.
|
729
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the $3000-$th year, the World Hockey Championship will be held under new rules: 12 points will be awarded for a win, 5 points will be deducted for a loss, and no points will be awarded for a draw. If the Brazilian national team plays 38 matches in this championship, scores 60 points, and loses at least once, how many victories can they achieve? Provide all possible options and explain why there cannot be any others.
|
Solution. Let Brazil win in x matches and lose in y matches. We form the equation $12 x-5 y=60$. We see that $12 \mathrm{x} \vdots 12$ and $60 \vdots 12$. GCD(5, 12)=1, i.e., $y \vdots 12$. Possible: a) $y=12$. Then we get the equation $12 x-60=60$. Thus, $x=10$. This is possible. b) $y=24$. We get the equation: $12 x-120=60$. Hence, $x=15$. This is impossible, as the number of matches already exceeds 38. c) $y=36$. We get $12 x-180=60$. Hence, $x=20$, which is also impossible. Larger values of x do not fit, as the number of matches played will already exceed 38.
Answer. 10 wins.
Recommendations for checking. Only the correct answer - 0 points. Only the correct answer with verification - 1 point. The equation is correctly set up, but there is no further progress (even with the correct answer and verification) - 2 points. The equation is set up, there is an idea of divisibility, but there is no further progress - 3 points. After setting up the equation, there is an idea of divisibility, only the first case is considered, and the correct answer is obtained - 4 points. After setting up the equation, there is an idea of divisibility, only the first and second cases are considered, and the correct answer is obtained - 5 points. After considering the second case without explanation, it is written that the number of matches increases further - do not deduct points. Full enumeration with one computational error and the correct answer - 5 points. One case is missed in the full enumeration - no more than 4 points. More than one case is missed in the full enumeration with the correct answer - 1 point, with the wrong answer - 0 points.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Three boys and 20 girls stood in a row. Each child counted the number of girls who were to the left of them, the number of boys who were to the right of them, and added the results. What is the maximum number of different sums that the children could have obtained? (Provide an example of how such a number could be obtained and prove that a greater number of different sums is not possible.)
|
Solution. Let's consider how the number changes when moving from left to right by one person. If the adjacent children are of different genders, the number does not change. If we move from a girl to a girl, the number increases by 1, and if from a boy to a boy, it decreases by 1. Thus, the smallest number in the row could have increased by no more than 19, which means there are no more than 20 different numbers. Let's provide an example with 20 different numbers: place all the boys first, then all the girls in sequence from left to right. Then the numbers in the row will be: 2, $1,0,0,1,2, \ldots, 19$, a total of 20 different numbers.
Answer. 20.
Grading Recommendations. Only the correct answer - 0 points. Correct example with the correct answer - 2 points (a). Verification that with this arrangement, indeed 20 different numbers are obtained - 1 point (b). Estimation that more than 20 different numbers cannot exist - 4 points (c). Points for items a, b, c are cumulative.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Find all natural $k$ such that the product of the first $k$ prime numbers, decreased by 1, is a perfect power of a natural number (greater than the first).
(V. Senderov)
|
Answer. $k=1$.
Solution. Let $n \geqslant 2$, and $2=p_{1}<p_{2}<\ldots<p_{k}$; then $k>1$. The number $a$ is odd, so it has an odd prime divisor $q$. Then $q>p_{k}$, otherwise the left side of the equation $(*)$ would be divisible by $q$, which is impossible. Therefore, $a>p_{k}$.
Without loss of generality, we can assume that $n$ is a prime number (if $n=s t$, then we can replace $n$ with $t$, and $a$ with $a^{s}$). Note that $n>2$, since $a^{2}+1$ cannot be divisible by $3=p_{2}$.
We will now show that $n>p_{k}$. Otherwise, we have $n=p_{i}$ for some $1<p_{i} \leqslant p_{k}$. Since $a>p_{k}$ and $n>p_{k}$, it follows that $a^{n}+1>p_{k}^{p_{k}}>p_{1} p_{2} \ldots p_{k}$, which contradicts the equation $(*)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Petya wrote ten natural numbers on the board, none of which are equal. It is known that among these ten numbers, three can be chosen that are divisible by 5. It is also known that among the ten numbers written, four can be chosen that are divisible by 4. Can the sum of all the numbers written on the board be less than $75$?
(P. Kozhevnikov)
|
Answer. It can.
Solution. Example: $1,2,3,4,5,6,8,10,12,20$. In this set, three numbers $(5,10,20)$ are divisible by 5, four numbers $(4,8,12,20)$ are divisible by 4, and the total sum is 71.
Remark. It can be proven (but, of course, this is not required in the problem), that in any example satisfying the problem's conditions, the numbers $1,2,3,4,5,8,10,12$ and 20 must necessarily be present, and instead of the number 6, one can take 7 or 9.
Comment. To receive full marks (7 points for the problem), it is sufficient to have a correct example without specifying which numbers are divisible by 4 and 5, and an explicit calculation of the sum is also not required. Any non-working example is scored 0 points.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On the board, a certain natural number $N$ was written nine times (one under the other). Petya appended a non-zero digit to the left or right of each of the 9 numbers; all the appended digits are different. What is the maximum number of prime numbers that could result among the 9 obtained numbers?
(I. Efremov)
|
Answer: 6.
Solution. Let $S$ be the sum of the digits of the number $N$. Then the sums of the digits of the obtained numbers will be $S+1, S+2, \ldots, S+9$. Three of these sums will be divisible by 3. By the divisibility rule for 3, the corresponding three numbers on the board will also be divisible by 3. Since these numbers will be greater than 3, they will be composite. Therefore, more than 6 prime numbers cannot appear on the board.
Six prime numbers can appear even when $N=1$ - for example, if Petya gets, among others, the numbers 11, 13, 41, 61, 17, and 19.
Remark. Petya can get six prime numbers even if he only appends digits to one side, for example, from the number $N=3$ he can get the numbers 13, 23, 43, 53, 73, and 83.
Comment. Only an example is provided where 6 prime numbers appeared on the board - 2 points.
Only proven that more than six prime numbers could not appear - 5 points.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In the company, some pairs of people are friends (if $A$ is friends with $B$, then $B$ is also friends with $A$). It turned out that among any 100 people in the company, the number of pairs of friends is odd. Find the largest possible number of people in such a company.
(E. Bakayev)
|
Answer: 101.
Solution: In all solutions below, we consider the friendship graph, where vertices are people in the company, and two people are connected by an edge if they are friends.
If the graph is a cycle containing 101 vertices, then any 100 vertices will have exactly 99 edges, so such a company satisfies the conditions of the problem. It remains to show that there cannot be a company of 102 people (then a company of more than 102 people cannot exist either). Below we provide several different ways to do this; in each way, we assume, for the sake of contradiction, that such a company has been found.
First solution. Consider an arbitrary set of 101 vertices and the induced subgraph on these vertices, let it have $k$ edges. By removing an arbitrary vertex from this subgraph (say, of degree $d$), we get 100 vertices with an odd number of edges $k-d$. Thus, the degree of any vertex in our subgraph has a parity different from the parity of $k$, meaning that the degrees of all vertices in the subgraph have the same parity. However, as is well known, in a graph with an odd number of vertices, all vertices cannot have an odd degree. Therefore, all these degrees are even, and the number of edges $k$ is odd.
Now let the entire graph with 102 vertices have $\ell$ edges. When any vertex (say, of degree $d$) is removed, we get a subgraph with an odd number of edges $\ell-d$; similarly to the above reasoning, we get that in the entire graph, all vertices have the same parity of degrees. Note that our graph cannot be empty (i.e., have no edges) or complete (i.e., have all $C_{102}^{2}$ edges), otherwise, on any 100 vertices, there will be either 0 or $C_{100}^{2}=99 \cdot 50$ edges, which is an even number. Therefore, there is a vertex connected to at least one other vertex but not to all. In other words, there are vertices $u, v_{1}$, and $v_{2}$ such that $u$ is connected to $v_{1}$ but not to $v_{2}$. The degrees of vertices $v_{1}$ and $v_{2}$ in the original graph have the same parity, so after removing $u$, they will have different parities. This is impossible by the above proof.
Second solution. There are $n=C_{102}^{2}=51 \cdot 101$ ways to remove two vertices from 102, leaving 100. Number these ways from 1 to $n$. Let $a_{i}$ be the number of edges on the remaining 100 vertices in the $i$-th way; by assumption, all numbers $a_{i}$ are odd, and thus their sum $S$ is also odd (since the number $n$ is odd).
On the other hand, consider any edge $uv$. This edge is counted in the number $a_{i}$ exactly when vertices $u$ and $v$ are not removed in the $i$-th way, i.e., when some pair of the remaining 100 vertices is removed. This happens in $k=C_{100}^{2}=50 \cdot 99$ ways. Thus, each edge is counted in $S$ an even number of times $k$, so $S$ must be even. Contradiction.
Third solution. Call a vertex even if its degree is even, and odd otherwise. Consider two cases.
Case 1. Suppose the total number of edges in the graph is odd. Then, by removing any pair of vertices, we must remove an even number of edges (to leave an odd number). On the other hand, if we remove vertices with degrees $d_{1}$ and $d_{2}$, the number of removed edges is $d_{1}+d_{2}$ if these vertices are not connected by an edge, and $d_{1}+d_{2}-1$ if they are connected. Therefore, vertices of the same parity are never connected by an edge, and vertices of different parities are always connected.
Thus, if the graph has $k$ even vertices and $\ell$ odd vertices, even vertices have (even) degree $\ell$, and odd vertices have (odd) degree $k$. This is impossible, since $k+\ell=102$.
Case 2. Suppose the total number of edges in the graph is even. Similarly, we get that vertices of the same parity are always connected by an edge, and vertices of different parities are never connected. Therefore, if the graph has $k$ even vertices and $\ell$ odd vertices, even vertices have (even) degree $k-1$, and odd vertices have (odd) degree $\ell-1$. This again contradicts the equality $k+\ell=102$.
Remark. Of course, there are other examples of a company of 101 people satisfying the condition.
Comment. The statement that in any graph, the number of vertices of odd degree is even, is accepted without proof.
Only the answer -0 points.
Only an example of a company of 101 people satisfying the condition is provided -1 point.
Noting only that to complete the solution, it is sufficient to show that the company cannot have exactly 102 people does not add points. If this observation is missed in the solution, points are not deducted.
Proving only that the company cannot have 102 people -6 points.
Below are some advances in proving this fact. Points for different advances do not add up; 1 point can be added for a correct example of a company of 101 people.
Proving only that in any company of 101 people satisfying the condition, all vertex degrees have the same parity -2 points.
In addition to this, proving that in the entire company of 102 people, all vertices have the same parity -4 points.
Proving that the graph is either a complete bipartite graph or the union of two complete graphs (as shown in the third solution) -4 points.
If one of the above cases is missed (without sufficient reason) -3 points instead of 4.
Only one of the two cases from the third solution is fully resolved -4 points.
|
101
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The numbers $1,2,3, \ldots, 29,30$ were written in a row in a random order, and partial sums were calculated: the first sum $S_{1}$ equals the first number, the second sum $S_{2}$ equals the sum of the first and second numbers, $S_{3}$ equals the sum of the first, second, and third numbers, and so on. The last sum $S_{30}$ equals the sum of all the numbers. What is the maximum possible number of odd numbers among the sums $S_{1}, S_{2}, \ldots, S_{30}$?
|
Answer: 23.
Solution: Evaluation: adding an odd number changes the parity of the sum, there are 15 odd numbers, so the parity of the sums changes at least 14 times. Therefore, there will be at least 7 even sums, and thus no more than 23 odd sums.
Implementation: arrange the numbers as follows: 1, then all even numbers, then all remaining odd numbers (except 1). We get the sequence: $1,2,4,6, \ldots, 30,3,5, \ldots 29$. The odd sums are the first sum (equal to 1), the next 15 (since they are formed by adding an even number to 1), and 7 of the last 14 sums $\left(S_{18}, S_{20}, \ldots, S_{30}\right)$. In total, there are $1+15+7=23$ odd sums.
Comment: The implementation is proposed - 3 points, the evaluation is made - 4 points, the points are summed. For potentially useful ideas and approaches in the absence of a solution - 2-3 points. Answer without justification - 0 points.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
113. In the forest, there grew pines, cedars, and larches, and there were cones on all the trees, and they were equal in number. A gentle breeze blew, and several cones fell to the ground. It turned out that $11\%$ of the cones fell from each pine, $54\%$ from each cedar, and $97\%$ from each larch. At the same time, exactly $30\%$ of all the cones hanging on the trees fell from all the trees together. Prove that the total number of trees in the forest is divisible by 43.
|
11.3. Let $m$ be the number of cones on each tree, $s, k, l-$ the number of pines, cedars, and deciduous trees in the forest. Then the condition of the problem corresponds to the equation $0.3 m(s+k+l)=0.11 m s+0.54 m k+0.97 m l$. This is equivalent to $19(s+k+l)=43 k+86 l$. The right side of this expression is divisible by 43, so the left side must be as well. Since 43 is a prime number, $s+k+l$ must be divisible by 43.
|
43
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
115. In how many non-empty subsets of the set $\{1,2,3, \ldots, 10\}$ will there be no two consecutive numbers?
|
115. 143.
Let $A_{n}$ denote the set of non-empty subsets of the set $\{1,2,3, \ldots, n\}$ that do not contain two consecutive numbers, and let $a_{n}$ be the number of such subsets. Clearly, the set $A_{1}$ consists of the subset $\{1\}$, and the set $A_{2}$ consists of the subsets $\{1\}$ and $\{2\}$. Thus, $a_{1}=1$ and $a_{2}=2$. For $n \geq 3$, we can partition the sets in $A_{n}$ into two classes. The first class consists of sets that do not contain the number $n$, which coincides with $A_{n-1}$ and contains $a_{n-1}$ sets. The second class consists of sets that contain $n$. Among these sets, there is the set $\{n\}$, and the rest have two or more elements. By removing the element $n$ from these sets, we obtain the set $A_{n-2}$. Thus, we get the formula $a_{n}=a_{n-1}+a_{n-2}+1$ for finding the answer. Therefore, we sequentially find the values of $a_{n}: 4,7,12$, $20,33,54,88$ and 143.
|
143
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Lёsha colors cells inside a $6 \times 6$ square drawn on graph paper. Then he marks the nodes (intersections of the grid lines) to which the same number of colored and uncolored squares are adjacent. What is the maximum number of nodes that can be marked?
|
Answer: 45.
## Reasoning.
Evaluation. Each grid node belongs to one, two, or four squares.
The corner vertices of the original square are adjacent to only one small square each, so Lёsha will not be able to mark them. Therefore, the maximum number of marked nodes does not exceed $7 \cdot 7-4=45$.

With a chessboard coloring, Lёsha will be able to mark all nodes except the points described above.
## Criteria.
3 points. A correct example is provided.
3 points. The evaluation is proven.
7 points. A complete and correct solution.
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. On the sides $B C$ and $A D$ of a convex quadrilateral $A B C D$, their midpoints - points $M$ and $N$ respectively - are marked. Segments $M N$ and $A C$ intersect at point $O$, and $M O=O N$. It is known that the area of triangle $A B C$ is 2019. Find the area of quadrilateral $A B C D$.
|
Answer: 4038.
Solution. Let $K$ and $L$ be the midpoints of sides $AB$ and $CD$ respectively. Then $KMLN$ is a parallelogram, the diagonals of which intersect at point $O$.
Let $S_{BKM}=S$. Then $S_{OKM}=S$, since triangles $OKM$ and $BKM$ have the same bases and equal heights. Similarly,

$S_{DNL}=S_{ONL}$. But triangles $ONL$ and $OKM$ are equal (for example, $KO=OL$, $ON=OM$ (as diagonals of parallelogram $KMLN$), $\angle KOM=\angle NOL$ (as vertical angles)). Therefore, $S_{DNL}=S_{ONL}=S_{OKM}=S_{BKM}=S$.
Further, from the similarity of triangles $BKM$ and $ABC$ (with a coefficient of $\frac{1}{2}$), it follows that $S_{ABC}=4S_{BKM}=4S$. Similarly, $S_{ADC}=4S_{NDL}=4S$.
Thus, triangles $ABC$ and $ADC$ have equal areas. $S_{ABCD}=2S_{ABC}$.
## Criteria.
2 points. It is proven that the midpoints of the sides form a parallelogram, the diagonals of which intersect at point $O$.
Comment. It is necessary to prove that KLMN is a parallelogram, as well as the equality of all pairs of triangles mentioned in the solution.
|
4038
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. The teacher wrote four different natural numbers in Petya's notebook. For each pair of these numbers, Petya found their greatest common divisor. He got six numbers: 1, 2, 3, 4, 5, and \( N \), where \( N > 5 \). What is the smallest value that \( N \) can have?
(O. Dmitriev)
#
|
# Answer: 14.
Solution. The number $N$ can equal 14, as shown, for example, by the quartet of numbers $4, 15, 70, 84$. It remains to show that $N \geqslant 14$.
Lemma. Among the pairwise GCDs of four numbers, there cannot be exactly two numbers divisible by some natural number $k$.
Proof. If among the original four numbers there are no more than two numbers divisible by $k$, then among the pairwise GCDs, no more than one is divisible by $k$. If, however, three of the original numbers are divisible by $k$, then all three of their pairwise GCDs are divisible by $k$. The lemma is proved.
Applying the lemma to $k=2$, we get that the number $N$ is even. Applying it to $k=3, k=4$, and $k=5$, we get that $N$ is not divisible by 3, 4, and 5. Therefore, $N$ cannot equal $6, 8, 10$, and 12.
Comment. Only the answer - 0 points.
Only the answer and an example where $N=14-2$ points.
Proved only that $N \leqslant 14-4$ points.
If this is not proved, but it is proved that $N$ is even - 2 points (these points can be combined with points for the answer).
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. All cells of a $100 \times 100$ square table are numbered in some order with numbers from 1 to 10000. Petya colors the cells according to the following rules. Initially, he colors $k$ cells at his discretion. Then, on each move, Petya can color one more uncolored cell with number $a$ if at least one of the two conditions is met: either there is an already colored cell with a number less than $a$ in the same row; or there is an already colored cell with a number greater than $a$ in the same column. What is the smallest $k$ such that, regardless of the initial numbering, Petya can color all the cells of the table in several moves?
(S. Berlov)
|
Answer. $k=1$.
Solution. First, let's prove the following statement.
Lemma. For any two cells $A$ and $B$, there exists a cell $C$ such that by coloring it, one can then color both $A$ and $B$ (possibly $C$ coincides with $A$ or $B$).
Proof. We can assume that the number $a$ of cell $A$ is less than the number $b$ of cell $B$. Let $D$ be the cell in the same column as $A$ and in the same row as $B$, and let $d$ be its number (possibly $D=A$ or $D=B$). Then, if $d < a$, after coloring $A$, one can sequentially color $D$ and $B$. If $d > b$, after coloring $B$, one can sequentially color $D$ and $A$. Therefore, in any case, one can choose $C$ as one of the cells $A$, $B$, or $D$. The lemma is proved.
Now, let's proceed to the solution of the problem. It is clear that $k \geqslant 1$; hence, it is sufficient to prove that when $k=1$, the coloring is always possible.
Fix an arbitrary numbering of the cells. Consider all ways of coloring the cells according to the condition (for $k=1$) and choose the one in which the number of colored cells is maximal. Let $A$ be the first colored cell in this way. Suppose that in this way, some cell $B$ remains uncolored. Then, by choosing the corresponding cell $C$ according to the Lemma and starting the coloring from it, we can then color $B$, $A$, and, consequently, all the cells that were colored in the chosen way. Thus, we will color at least one more cell. The contradiction with the choice of the way shows that in fact, all cells will be colored in our way. This means that $k=1$ works.
## 10th grade
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. On the board, the expression $\frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f}$ is written, where $a, b, c, d, e, f$ are natural numbers. If the number $a$ is increased by 1, then the value of this expression increases by 3. If in the original expression the number $c$ is increased by 1, then its value increases by 4; if in the original expression the number $e$ is increased by 1, then its value increases by 5. What is the smallest value that the product $b d f$ can have?
(N. Agakhanov)
|
# Answer: 60.
First solution. Let the value of the original expression be $A$. Then, as a result of the first operation, the product will take the value $\frac{a+1}{a} \cdot A=A+3$, from which $A=3a$. This means that $A$ is a natural number. Moreover, from this equality, it follows that it is divisible by 3. Similarly, it is proven that the number $A$ is divisible by 4 and by 5, and that $A=4c=5e$. From the pairwise coprimality of the numbers 3, 4, and 5, it follows that $A$ is divisible by $3 \cdot 4 \cdot 5=60$. Therefore, $A \geqslant 60$.
Rewriting the equality $\frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f}=A$ as $\frac{A}{3b} \cdot \frac{A}{4d} \cdot \frac{A}{5f}=A$, we get $A^{2}=60bdf$, from which $bdf=\frac{A^{2}}{60} \geqslant 60$. It remains to provide an example showing that the product of the denominators can be equal to 60. One possible example is: $\frac{20}{3} \cdot \frac{15}{4} \cdot \frac{12}{5}$.
Second solution. As in the first solution, we get $A=3a=4c=5m$, from which
$$
\frac{1}{b} \cdot \frac{c}{d} \cdot \frac{e}{f}=3, \quad \frac{a}{b} \cdot \frac{1}{d} \cdot \frac{e}{f}=4, \quad \frac{a}{b} \cdot \frac{c}{d} \cdot \frac{1}{f}=5
$$
Multiplying the first equation by the second and dividing by the third, we get that $\frac{e^{2}}{bdf}=\frac{12}{5}$; since the fraction on the right is irreducible, the denominator $bdf$ is divisible by 5. Similarly, it is proven that it is divisible by 3 and by 4, from which it follows that it is divisible by 60, that is, it is not less than 60.
Comment. Only the answer - 0 points.
An example is provided where $bdf=60-1$ point.
It is only proven that $bdf \geqslant 60-4$ points.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. $\mathrm{ABCD}$ is a rhombus. Points $E$ and $F$ lie on sides $AB$ and $BC$ respectively, such that $\frac{AE}{BE}=\frac{BF}{CF}=5$. Triangle $DEF$ is equilateral. Find the angles of the rhombus. Solution.
The notation is shown in the figure. The situation where angle $D$ of the rhombus is acute is impossible (see below). Mark point $P$ on side $AB$ such that $AP=EB=FC$. Triangles $CDF$ and $ADP$ are congruent, as they have equal angles $\angle A=\angle C$ and corresponding equal sides $AD=DC, AP=FC$. Considering that triangle $FED$ is equilateral by the condition, we get that triangle $EDP$ is isosceles $(ED=FD=PD)$. (At this point, note that if angle $\angle A$ of the rhombus is obtuse, then angle $\angle APD$ is acute, and in the isosceles triangle $EDP$, the angle at the base is obtuse,

which is impossible). Mark the equal angles $x=\angle A=\angle C$ and $y=\angle ADP=\angle CDF$. We find $\angle EPD=x+y$ (the exterior angle of triangle $ADP$) and $\angle PDE=180^{\circ}-2(x+y)$. Summing all the angles at vertex $D$ of the rhombus ($\left.\angle D=180^{\circ}-x\right)$, we get the equation
$$
y+180^{\circ}-2(x+y)+60^{\circ}+y=180^{\circ}-x
$$
From this, $x=60^{\circ}$, the angles of the rhombus are $60^{\circ}$ and $120^{\circ}$.
The end of the solution can be different. After proving that triangle $EDP$ is isosceles, note that its exterior angles are equal: $\angle APD=\angle BED$. From this, triangles $ADP$ and $BED$ are congruent by the two indicated angles and sides $(AP=EB, PD=ED)$. Therefore, $BD=AD$, and triangle $ABD$ is equilateral. Thus, $\angle BAD=60^{\circ}$.
|
Answer. The angles of the rhombus are $60^{\circ}$ and $120^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 About numbers a and b, it is known that the system of equations
$$
\left\{\begin{array}{l}
y^{2}=x^{2}+a x+b \\
x^{2}=y^{2}+a y+b
\end{array}\right.
$$
has no solutions. Find a.
|
Solution: Since the system has no solutions, in particular, there are no solutions with $x=y$. When $x=y$, both equations of the system are equivalent to the equation $a x+b=0$. This linear equation has no roots only when its slope coefficient $a$ is zero.
## Criteria:
- Points are not deducted for the absence of an example of a system with $a=0$ that has no solutions.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 Another participant in the competition for meaningless activity marked the centers of 13 cells in a grid rectangle of size $(N-1) \times(N+1)$ such that the distance between any two marked points is greater than 2. What is the smallest value that $N$ can take?
|
Solution: We will show that it is impossible to mark cells in a $6 \times 8$ rectangle (and thus in any smaller size) in such a way. Indeed, let's divide the rectangle into $2 \times 2$ squares. In each of them, the pairwise distances between the centers of the cells do not exceed $\sqrt{2}$, so no more than one cell is marked in each. Therefore, the total number of marked cells does not exceed 12.
Example for a $7 \times 9$ rectangle:
| | | | $\mathrm{X}$ | | | | | $\mathrm{X}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | $\mathrm{X}$ | | | | | $\mathrm{X}$ | | |
| | | | | $\mathrm{X}$ | | | | |
| $\mathrm{X}$ | | $\mathrm{X}$ | | | | | $\mathrm{X}$ | |
| | | | | | $\mathrm{X}$ | | | |
| | $\mathrm{X}$ | | $\mathrm{X}$ | | | | | $\mathrm{X}$ |
Criteria:
- Only proved that $N>7-3$ points;
- Only provided an example for $N=8-3$ points;
- No points are deducted for the lack of justification in the example.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. In pentagon $M N P Q S: \quad M N=N P=P Q=Q S=S M$ and $\angle M N P=2 \angle Q N S$. Find the measure of angle $M N P$.
|
Answer: $60^{\circ}$
Solution. Since $\angle S N Q=\angle M N S+\angle P N Q$, we can take a point $T$ on the side $S Q$ such that $\angle S N T=\angle M N S=\angle M S N$, i.e., $N T \| M S$.
Then $\angle T N Q=\angle S N Q-\angle S N T=\angle P N Q=\angle N Q P$, i.e., $N T \| P Q$. Therefore, $M S \| P Q$, and since $M S=P Q$, $P Q S M$ is a parallelogram. Thus, $M P=S Q$, which means triangle $M N P$ is equilateral and $\angle M N P=60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. The teams participating in the quiz need to answer 50 questions. The cost (in integer points) of a correct answer to each question was determined by experts after the quiz, the cost of an incorrect answer - 0 points. The final score of the team was determined by the sum of points received for correct answers. When summarizing the results, it was found that the costs of correct answers could be assigned in such a way that the teams could take places according to any wishes of the experts. What is the maximum number of teams that could have participated in the quiz
|
Answer: 50.
Solution: We will prove that with 50 teams, such a distribution of points can exist. The example is obvious - let the $k$-th team answer only the $k$-th question. Then, by assigning the costs of the questions as $a_{1}, a_{2}, \ldots, a_{50}$, where $\left\{a_{1}, a_{2}, \ldots, a_{50}\right\}=\{1,2, \ldots, 50\}$, the jury will place the $k$-th team at position $50+1-a_{k}$.
Suppose there are 51 teams. Imagine that we have cloned each team, meaning we have an unlimited number of teams of each of the 51 types (all teams within a type answer questions the same way). We will prove that it is possible to form two groups from them, different in composition (at least for one type, the number of teams of this type in the first group is not equal to the number of teams of this type in the second group), but having the same results (that is, on each question, the same number of teams in the first group answered as in the second).
Indeed, let's write a system of linear equations, where the $i$-th equation states that the difference in the number of teams in the first and second groups that answered the $i$-th question is zero; here $x_{j}$ is the number of teams of the $j$-th type (in the first group if $x_{j}$ is positive, in the second if negative). The coefficients - zeros and ones - are determined by whether the team of the $j$-th type answered the $i$-th question. This is a system of 50 homogeneous equations with 51 unknowns. It has a non-zero solution, and since all coefficients are rational, there exists a non-zero rational solution. Since the equations are homogeneous, the solution vector can be multiplied by a constant. Multiply it so that all $x_{j}$ values become integers. The required groups are found. In this case, teams of each type are present in no more than one group. Let the number of teams in the first group be no less than in the second. Then it is impossible to assign points to the questions in such a way that the positions of all teams in the first group are higher than the positions of the teams in the second group, because the sum of the points of the teams in the first group is always equal to the sum of the points of the teams in the second group.
In the case where there are more than 51 teams, we can consider only 51 teams, and for them, the condition of the problem does not hold.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-3-1. The numbers from 1 to 217 are divided into two groups: one group has 10 numbers, and the other has 207. It turns out that the arithmetic means of the numbers in the two groups are equal. Find the sum of the numbers in the group of 10 numbers.
|
Answer: 1090.
Solution Variant 1. The shortest solution to this problem is based on the following statement:
If the arithmetic means of the numbers in two groups are equal, then this number is also equal to the arithmetic mean of all the numbers.
A formal proof of this is not difficult: it is sufficient to denote the arithmetic mean by $S$, the quantities of numbers in the groups by $n$ and $k$; then the sums of the numbers in the groups are $S n$ and $S k$, the sum of all the numbers is $S(n+k)$, i.e., their arithmetic mean is again $S$.
However, we urge the reader to understand why this statement is "intuitively obvious." For example, informally, one can think of it this way: in the first group, the numbers are "on average" $S$, and in the second - also. Therefore, if we combine both groups into one, the numbers will be "on average" $S$.
Let's move on to solving the problem. According to our statement, the arithmetic mean in each group is equal to the arithmetic mean of the numbers from 1 to 217, and it is not difficult to check that it is 109. Therefore, the answer is $109 \cdot 10=1090$.
|
1090
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-4-1. In the figure, $O$ is the center of the circle, $A B \| C D$. Find the degree measure of the angle marked with a «?».
|
Answer: $54^{\circ}$.
Solution variant 1. Quadrilateral $A D C B$ is an inscribed trapezoid in a circle. As is known, such a trapezoid is isosceles, and in an isosceles trapezoid, the angles at the base are equal: $\angle B A D=\angle C B A=63^{\circ}$. Triangle $D O A$ is isosceles ($O A$ and $O D$ are equal as radii), so its base angles $D A O$ and $A D O$ are equal. Therefore,
$$
\angle D O A=180^{\circ}-\angle D A O-\angle A D O=180^{\circ}-63^{\circ}-63^{\circ}=54^{\circ}
$$
|
54
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.