problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
9-6-1. Six pirates - a captain and five members of his crew - are sitting around a campfire facing the center. They need to divide a treasure: 180 gold coins. The captain proposes a way to divide the treasure (i.e., how many coins each pirate should receive: each pirate will receive a non-negative integer number of coins; different pirates may receive different numbers of coins). After this, the other five pirates vote on the captain's proposal. A pirate will vote "for" only if they receive more coins than each of their two neighbors. The proposal is accepted if at least three out of the five crew members vote "for."
What is the maximum number of coins the captain can get with this method of dividing the treasure?
|
Answer: 59.
Solution variant 1. Let's number the pirates clockwise, starting from the captain: First, Second, ..., Fifth. The main observation in this problem is:
two pirates sitting next to each other cannot both vote "for": one of them will not vote "for" because the captain offers no more to him than to his neighbor.
Therefore, for three to vote "for," they must be the First, Third, and Fifth - the proof of this fact is detailed in the comment. Then, if the captain keeps $x$ coins for himself, he must offer at least $x+1$ coins to the First and Fifth, and at least 1 coin to the Third, so they vote "for." Thus, the total number of coins should be at least $3x+3$, from which $3x+3 \leqslant 180, x \leqslant 59$.
Note that so far we have only proven that the captain cannot get more than 59 coins. From our reasoning, it is easy to construct an example where he can get exactly 59: it is sufficient to offer 60 coins to the First and Fifth, one coin to the Third, and nothing to the Second and Fourth.
Comment. The intuitive statement about the First, Third, and Fifth is rigorously proven through partitioning into pairs. From the pair First-Second, no more than one will vote "for," just as from the pair Third-Fourth. Therefore, the Fifth must definitely vote "for." Similarly, the First must vote "for." But then the Second and Fourth do not vote "for," so the Third votes "for."
|
59
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-8-1. In Midcity, houses stand along one side of a street, each house can have $1,2,3, \ldots, 9$ floors. According to an ancient law of Midcity, if two houses on one side of the street have the same number of floors, then no matter how far apart they are from each other, there must be a house with more floors between them. What is the maximum possible number of houses on one side of the street in Midcity?
|
Answer: 511.
Solution Variant 1. Estimation. Let $a_{k}$ be the maximum number of houses if all of them have no more than $k$ floors. Clearly, $a_{1}=1$. Let's find $a_{k}$. Consider the tallest house with $k$ floors, which is only one by the condition. Both to the left and to the right of it stand houses with $1,2,3, \ldots, k-1$ floors, and for the houses on each side, the ancient law of Mezhdugrad for $(k-1)$-floor houses is satisfied. Therefore, the total number of houses is no more than $a_{k-1}+1+a_{k-1}$ (houses to the left, the tallest house with $k$ floors, houses to the right). Thus, $a_{k} \leqslant 1+2 a_{k-1}$. Let's calculate using this formula: $a_{2} \leqslant 1+2 \cdot 1=3 ; a_{3} \leqslant 1+2 \cdot 3=7 ; a_{4} \leqslant 1+2 \cdot 7=15, \ldots$ One can notice the pattern $a_{m} \leqslant 2^{m}-1$, from which $a_{9} \leqslant 2^{9}-1=511$.
Example. Along the street, houses can stand as follows:
$$
12131214121312151213121412131216 \ldots
$$
a total of $2^{2}-1=511$ houses.
This example is constructed from the estimation: place the 9-floor house in the center, and to the left and right of it, write examples for no more than 8-floor houses. These examples for no more than 8-floor houses are constructed similarly: place the 8-floor house in the center, and to the left and right of it, write examples for no more than 7-floor houses, and so on. In the end, the example above is obtained.
|
511
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a finite set of cards. On each of them, either the number 1 or the number -1 is written (exactly one number on each card), and there are 100 more cards with -1 than cards with 1. If for each pair of different cards, the product of the numbers on them is found, and all these products are summed, the result is 1000. How many cards have the number 1?
|
Answer: 3950.
Solution: Let the number of cards with 1 be $m$, and the number of cards with -1 be $k$. Then, among all pairs, there are $\frac{m(m-1)}{2}$ pairs of two 1s, $\frac{k(k-1)}{2}$ pairs of two -1s, and $m k$ pairs of 1 and -1. Therefore, the sum in the condition is $\frac{m(m-1)}{2}+\frac{k(k-1)}{2}-m k$, from which we get $m^{2}-2 m k+k^{2}=2000+m+k, (m-k)^{2}=2000+m+k$. According to the condition $k-m=100$, so $m+k=8000$ and $2 m=7900, m=3950$.
Comment: The correct relationship between $k$ and $m$ (in addition to $k-m=100$) has been obtained, but without further progress - 3 points.
|
3950
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Consider natural numbers $a, b$, and $c$ such that the fraction
$$
k=\frac{a b+c^{2}}{a+b}
$$
is a natural number less than $a$ and $b$. What is the smallest number of natural divisors that the number $a+b$ can have?
(P. Kozlov)
|
Answer. Three divisors.
First solution. Since the number $a+b$ is greater than one, it has at least two distinct divisors. We will prove that there cannot be exactly two, i.e., that the number $a+b$ cannot be prime. Multiplying the equality from the condition by the denominator, we get $a b+c^{2}=k a+k b$ or, equivalently, $a b-k a-k b+k^{2}=k^{2}-c^{2}$. Factoring both sides, we arrive at the relation
$$
(a-k)(b-k)=(k-c)(k+c)
$$
Since $k<a$ and $k<b$, both parentheses on the left side are positive, and thus, $c<k$. Then there exist natural numbers $x, y, z$ and $t$ such that
$$
a-k=x y, \quad b-k=z t, \quad k-c=x z \quad \text { and } \quad k+c=y t .
$$
For example, we can set $x=\text{GCD}(a-k, k-c), t=\text{GCD}(b-k, k+c), y=(a-k) / x$ and $z=(b-k) / t$. Then the first two equalities are satisfied by definition; on the other hand, $k-c$ divides $x z$, and $k+c$ divides $y t$, so the written equalities follow from the equality of the products.
Therefore,
$$
\begin{aligned}
& a+b=(a-k)+(b-k)+(k-c)+(k+c)= \\
& =x y+z t+x z+y t=(x+t)(y+z)
\end{aligned}
$$
Thus, the number $a+b$ can be represented as the product of two natural numbers greater than 1, and therefore, it is not prime.
Finally, it is not difficult to see that $a+b$ can have exactly three distinct divisors. For example, if $a=10, b=15, c=5$, then $k=\frac{10 \cdot 15+5^{2}}{10+15}=7$, and $a+b=25=5^{2}$ has three divisors.
Remark. For no $a$ and $b$ can the sum $a+b$ equal $2^{2}$ or $3^{2}$. But for any prime number $p \geqslant 5$, there exist numbers $a, b$ and $c$ satisfying the condition of the problem such that $a+b=p^{2}$. For the case $a \leqslant b$, all suitable $a, b, c$ and $k$ have the form $a=n p$, $b=(p-n) p, c=m p$ and $k=n p-n^{2}+m^{2}$, where $2 \leqslant n \leqslant \frac{p-1}{2}$, $1 \leqslant m \leqslant n-1$. In particular, for $p=5$ the example is unique up to the permutation of the numbers $a$ and $b$.
Second solution. We will provide another proof that the number $p=a+b$ cannot be prime. Assume the contrary.
Assume $a \leqslant b$. Then the number $k p=a b+c^{2}=a(p-a)+c^{2}=a p+c^{2}-a^{2}$ is divisible by $p$ and less than $a p$. Therefore, the number $a^{2}-c^{2}=(a-c)(a+c)$ is positive and divisible by $p$. Then the first parenthesis is positive and $a-c<a+b=p$, so it does not divide $p$. The second parenthesis is also positive and $a+c<2 a \leqslant a+b=p$, so it also does not divide $p$. We have reached a contradiction, so the assumption is false. Thus, $a+b$ is a composite number and, therefore, it has at least three divisors.
Comment. Only the answer - 0 points.
Only the answer and an example where $a+b$ is the square of a prime number (i.e., it has three divisors) - 2 points.
Only the proof that the number $a+b$ cannot be prime (i.e., it has more than two divisors) - 4 points.
It is well known that the number of divisors of a natural number $n$, having a prime factorization of the form $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}$, is $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \ldots\left(\alpha_{k}+1\right)$. If this formula is used without proof - points are not deducted.
In the first solution, the representation (*) is known. If it is used without proof - points are not deducted. If it is used with an incorrect proof - 1 point is deducted.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Natural numbers starting from 1 are written in a row. This results in a sequence of digits: 1234567891011121314... What digit is in the 2021st position?
|
Answer. 1.
Solution. Note that the sum of the digits of all single-digit and two-digit numbers is $1892021$. Therefore, the digit in the 2021st position belongs to the recording of some three-digit number.
Let $x$ be some three-digit number, then the sum of the digits in the sequence from 1 to $x$ is $n=189+3(x-99)$. We have $189+3(x-99)<2021, 3x<2129, x<709 \frac{2}{3}$. The sequence of numbers from 1 to 709 contains $189+3 \cdot(709-99)=2019$ digits. Therefore, the digit in the 2021st position is the second digit of the number 710, which is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The bathtub fills with cold water in 6 minutes 40 seconds, with hot water - in 8 minutes. In addition, if the plug is removed from a full bathtub, the water will drain in 13 minutes 20 seconds. How long will it take to fill the bathtub completely, provided that both taps are open, but the bathtub is not plugged?
|
Solution: First, we will convert the time in seconds to minutes: 6 minutes 40 seconds will be replaced by $6+2 / 3$, or $20 / 3$, and 13 minutes 20 seconds will be replaced by $13+1 / 3$, or $40 / 3$. Then, in one minute, the cold water will fill $3 / 20$ of the bathtub, the hot water will fill $1 / 8$ of the bathtub, and $3 / 40$ of the bathtub will drain. Therefore, in one minute, the bathtub will fill $3 / 20+1 / 8-3 / 40$, i.e., $1 / 5$ of the bathtub. Thus, the entire bathtub will be filled in 5 minutes.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The sides of a rectangle were reduced: the length - by $10 \%$, the width - by $20 \%$. As a result, the perimeter of the rectangle decreased by $12 \%$. By what percentage will the perimeter of the rectangle decrease if its length is reduced by $20 \%$ and its width is reduced by $10 \%$?
|
Answer: by $18 \%$.
Solution. Let $a$ and $b$ be the length and width of the rectangle. After decreasing the length by $10 \%$ and the width by $20 \%$, we get a rectangle with sides $0.9 a$ and $0.8 b$, the perimeter of which is $0.88$ of the perimeter of the original rectangle. Therefore, $2(0.9 a + 0.8 b) = 0.88 \cdot 2(a + b)$, from which $a = 4 b$. If now the length is decreased by $20 \%$ and the width by $10 \%$, we get a rectangle with a perimeter of $2(0.8 \cdot 4 b + 0.9 b) = 8.2 b$, which is $8.2 b : 10 b = 0.82$ or $82 \%$ of the perimeter of the original rectangle. Therefore, the perimeter decreased by $18 \%$ the second time.
Remark. Correct solution with arithmetic errors - 5 points, solution with specific side lengths - 2 points.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a six-digit number, one digit was crossed out to obtain a five-digit number. The five-digit number was subtracted from the original number, and the result was 654321. Find the original number.
|
Answer: 727023.
Solution. Note that the last digit was crossed out, as otherwise the last digit of the number after subtraction would have been zero. Let $y$ be the last digit of the original number, and $x$ be the five-digit number after crossing out. Then the resulting number is $10 x + y - x = 9 x + y = 654321$. Dividing this number by 9 with a remainder (and considering that $y$ does not exceed 9), we get the remainder $y=3$ and the quotient $x=72702$.
|
727023
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each of the three friends either always tells the truth or always lies. They were asked the question: "Is there at least one liar among the other two?" The first answered: "No," the second answered: "Yes." What did the third answer?
|
Solution Since the first and second friends gave different answers, one of them is a liar, and the other is a knight. Moreover, the knight could not have answered “No” to the question posed, as in that case, he would have lied (there is definitely a liar among the two remaining). Therefore, the first one is a liar. He lied, which means that among the two remaining, there must be a liar, and it can only be the third friend. Thus, the third one answered “No”.
Answer: “No”.
2 A team consisting of Petya, Vasya, and a one-person scooter is participating in a race. The distance is divided into 42 segments of equal length, each with a checkpoint. Petya runs a segment in 9 minutes, Vasya in 11 minutes, and either of them can ride a segment on the scooter in 3 minutes. They start simultaneously, and the team's time is determined by the time of the last person to finish. They agreed that one will ride the first part of the way on the scooter and walk the rest, while the other will do the opposite (the scooter can be left at any checkpoint). How many segments should Petya ride on the scooter to ensure the team achieves the best possible time?
Solution If Petya rides 18 segments and runs the remaining $42-18=24$, he will spend $18 \cdot 3+24 \cdot 9=270$ minutes. In this case, Vasya, on the contrary, will have to ride 24 segments and run 18, which will take $24 \cdot 3+18 \cdot 11=270$ minutes - the same amount of time. If Petya rides fewer segments, his time (and thus the team's time) will increase. If Petya rides more segments, Vasya's time (and the team's time) will increase.
It is sufficient to denote the number of segments Petya rides as \( x \) and solve the equation
$$
x \cdot 3+(42-x) \cdot 9=(42-x) \cdot 3+11 x
$$
Answer: 18.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Tourists arrived at the campsite. For lunch, each of them ate half a can of soup, a third of a can of stew, and a quarter of a can of beans. In total, they ate 39 cans of food. How many tourists were there? Answer: 36.
|
Solution. Note that 12 tourists ate 6 cans of soup, 4 cans of stew, and 3 cans of beans - that is, a total of 13 cans of food.
39 cans is 3 sets of 13 cans. One set is eaten by 12 people. Therefore, the total number of tourists is 36.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Six people are standing in a circle, each of whom is either a knight - who always tells the truth, or a liar - who always lies. Each of them said one of two phrases: "There is a liar next to me" or "There is a liar opposite me." What is the minimum number of liars among them? Provide an example and prove that there cannot be fewer liars.
|
Answer: 2.
Solution. Let's number all the people standing clockwise (this way, people with numbers 1 and 4, 2 and 5, 3 and 6 will stand opposite each other).
Zero liars is obviously impossible (then there would be only knights and no one could say any of the phrases).
If there is one liar, let's say his number is 1, then the knight with number 3 has two knight neighbors and a knight standing opposite him. This means he cannot say either of these two phrases.
Example with two liars. Liars have numbers 1 and 2 and say "There is a liar opposite me," which is also said by knights 4 and 5. The remaining knights (3 and 6) say "There is a liar next to me."
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In Solar City, 6 dwarfs eat donuts daily, 8 dwarfs eat donuts every other day, and the rest do not eat donuts at all. Yesterday, 11 dwarfs ate donuts. How many dwarfs will eat donuts today?
|
Answer: 9.
Solution: Of the 11 dwarfs who ate donuts yesterday, 6 dwarfs eat them daily, so the remaining $11-6=5$ eat them every other day. Therefore, these five will not eat donuts today, while the other $8-5=3$ from those who eat every other day will. So today, these three will eat donuts, as well as the six who always eat donuts. We get the answer $3+6=9$.
Comment: Correct answer without justification -2 points.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Given nine cards with the numbers $5,5,6,6,6,7,8,8,9$ written on them. From these cards, three three-digit numbers $A, B, C$ were formed, each with all three digits being different. What is the smallest value that the expression $A+B-C$ can have?
|
# Answer: 149.
Solution. By forming the smallest sum of numbers $A$ and $B$, and the largest number $C$, we get the smallest value of the expression $A+B-C$. This is $566+567-988=145$. However, this partition is not valid: two numbers have the same digits. By swapping the digits 6 and 8 in the units place, we get the required partition: $568+567-986=149$. Why is this partition the best? With any other arrangement of the hundreds place digits, we will get a contribution from the hundreds place equal to 200, or 300, etc. In the tens and units places, we will get positive values because the sum of any two of the digits is greater than any third digit. Therefore, the number $A+B-C$ will be greater than 200. Thus, $A$ and $B$ start with the digit 5, and $C$ starts with the digit 9. Similarly, we find that the second digits of numbers $A$ and $B$ should be 6, and the second digit of $C$ should be 8. The units place has been discussed above.
Comment. The correct answer and an example of numbers $A, B, C$ without justification of minimality - 4 points.
|
149
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. A round table was sat by 10 people - liars and knights. Liars always lie, while knights always tell the truth. Each of them was given a coin. Then each of those sitting passed their coin to one of their two neighbors. After that, 5 people said: “I have one coin,” while the other 5 said: “I have no coins.” What is the maximum number of knights that could have been sitting at the table?
|
# Answer: 7.
Solution. After passing the coins, each person sitting at the table can have 0, 1, or 2 coins. The total number of coins will be 10. Note that if a person lies, they will state a number of coins that differs from the actual number by 1 or 2. Since the total number of coins based on the answers differs from the actual total by $10-5=5$, at least 3 people must have lied. Therefore, there are no more than 7 knights at the table. Suppose the knights sitting at the table pass the coins as follows (arrows indicate the direction of the coin transfer; the number of coins after the transfer is in parentheses): $\leftarrow \mathrm{P}(0)-\mathrm{P}(0) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{L}(1) \rightarrow$ $\mathrm{L}(2) \leftrightarrow \mathrm{L}(2) \leftarrow$. In this case, all knights tell the truth, while the liars lie, saying they have 0 coins.
Comment. It is proven that there are no more than 7 knights at the table - 5 points. It is proven that there can be 7 knights at the table - 2 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Little kids were eating candies. Each one ate 7 candies less than all the others together, but still more than one candy. How many candies were eaten in total?
|
Answer: 21 candies.
Solution: Let $S$ denote the total number of candies eaten by the children. If one of the children ate $a$ candies, then according to the condition, all the others ate $a+7$ candies, and thus together they ate $S=a+(a+7)=2a+7$ candies. This reasoning is valid for each child, so all the children ate the same number of candies: $a=(S-7)/2$ each.
Now let $N$ denote the number of children. Then the condition can be written as $a=a \cdot (N-1)-7$, from which $7=a \cdot (N-2)$. The number 7 is prime, so one of the factors is 1, and the other is 7. But by the condition $a>1$, so $a=7, N-2=1$. Thus, $N=3$, and a total of $S=a \cdot N=21$ candies were eaten.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3 In triangle $A B C$, the median $A M$ is drawn (point $M$ lies on side $\mathrm{BC}$). It is known that angle $C A M$ is $30^{\circ}$, and side $A C$ is 2. Find the distance from point $B$ to the line $A C$.
Omвem: 1.
|
Solution: See fig.
Triangle СKM is equal to triangle ВHM (these are right triangles, the hypotenuses СM and ВM of which are equal, and the angles are the same).
Therefore, $\mathrm{BH}=$ СK. But in triangle СKA, the leg СK lies opposite the angle $30^{\circ}$ and is equal to half the hypotenuse АC: СK=1.
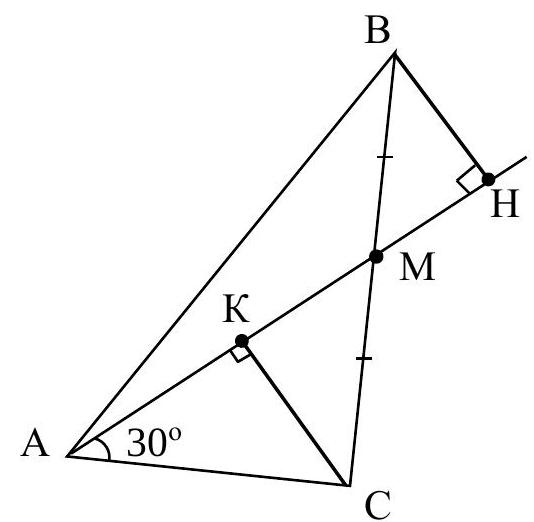
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Given natural numbers $M$ and $N$, both greater than ten, consisting of the same number of digits, and such that $M = 3N$. To obtain the number $M$, one of the digits of $N$ must be increased by 2, and each of the other digits must be increased by an odd digit. What digit could the number $N$ end with? Find all possible answers.
(n. Agakhanov)
|
Answer. The digit 6.
Solution. By the condition, $M=3 N$, so the number $A=M-$ $-N=2 N$ is even. However, by the condition, the number $A$ is composed of odd digits and the digit 2. Therefore, $A$ ends in 2. Thus, the number $N$, which is half of $A$, ends in either 1 or 6.
We will show that $N$ cannot end in 1. If $N$ ends in 1, then when it is doubled, there is no carry from the last digit to the second-to-last digit. This means that the second-to-last digit of the number $A=2 N$ will be even, but it must be odd. This is a contradiction.
Remark. Pairs of numbers $N$ and $M$ that satisfy the condition do exist, for example, $N=16, M=48$. Moreover, there are infinitely many such pairs. All suitable numbers $N$ can be described as follows: the first digit is 1 or 2, followed by several (possibly zero) digits, each of which is 5 or 6, and the last digit is 6.
Comment. The correct answer and an example of a number $N$ ending in the digit 6 - 1 point.
It is established that the last digit of the number $M$ is 2 more than the last digit of the number $N$ - 1 point.
It is shown that the last digit of the number $N$ can only be 1 or 6 - 2 points.
Points for different advancements are cumulative.
Note that the problem does not require providing an example of such a number. It is sufficient to prove that no digit other than 6 can be the last digit.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
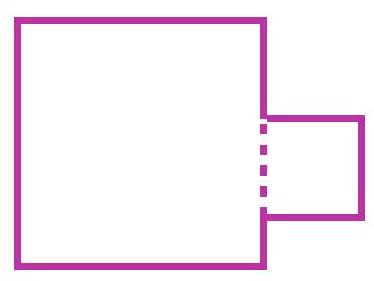
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-5. Given a figure consisting of 33 circles. You need to choose three circles that are consecutive in one of the directions. In how many ways can this be done? The image shows three of the desired ways.

|
Answer: 57.
Solution. The number of options along the long side is $1+2+3+4+5+6=21$. Along each of the other two directions, it is $-4+4+4+3+2+1=18$. The total number of options is $21+18 \cdot 2=57$
|
57
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-8. In a chess club, 90 children attend. During the session, they divided into 30 groups of 3 people, and in each group, everyone played one game with each other. No other games were played. In total, there were 30 games of "boy+boy" and 14 games of "girl+girl". How many "mixed" groups were there, that is, groups where there were both a boy and a girl?
|
Answer: 23.
Solution: There were a total of 90 games, so the number of games "boy+girl" was $90-30-14=46$. In each mixed group, two "boy+girl" games are played, while in non-mixed groups, there are no such games. In total, there were exactly $46 / 2=23$ mixed groups.
## Grade 5
|
23
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
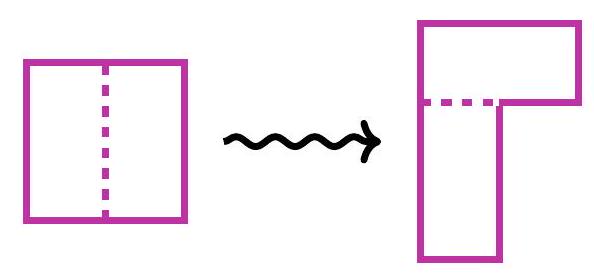
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-2. In a sports tournament, a team of 10 people participates. The regulations stipulate that 8 players from the team are always on the field, changing from time to time. The duration of the match is 45 minutes, and all 10 participants on the team must play an equal number of minutes. How many minutes will each player be on the field during the game?
|
Answer: 36.
Solution. In total, the players will spend $8 \cdot 45=360$ minutes on the field. This time needs to be divided equally among 10 players, so each will be on the field $360 / 10=36$ minutes.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-3. How many two-digit numbers exist where at least one of the digits is smaller than the corresponding digit in the number $35?$
For example, the numbers 17 and 21 are valid, while the numbers 36 and 48 are not.
|
Answer: 55.
Solution. First, let's find the number of two-digit numbers that do not meet the condition. In the units place, any digit from 5 to 9 can stand, and in the tens place, from 3 to 9. The total number of numbers that do not suit us will be exactly $7 \cdot 5=35$. Now we can count the number of two-digit numbers that meet the condition: we need to subtract the number of unsuitable numbers from their total number, which is 90: $90-35=55$.
|
55
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
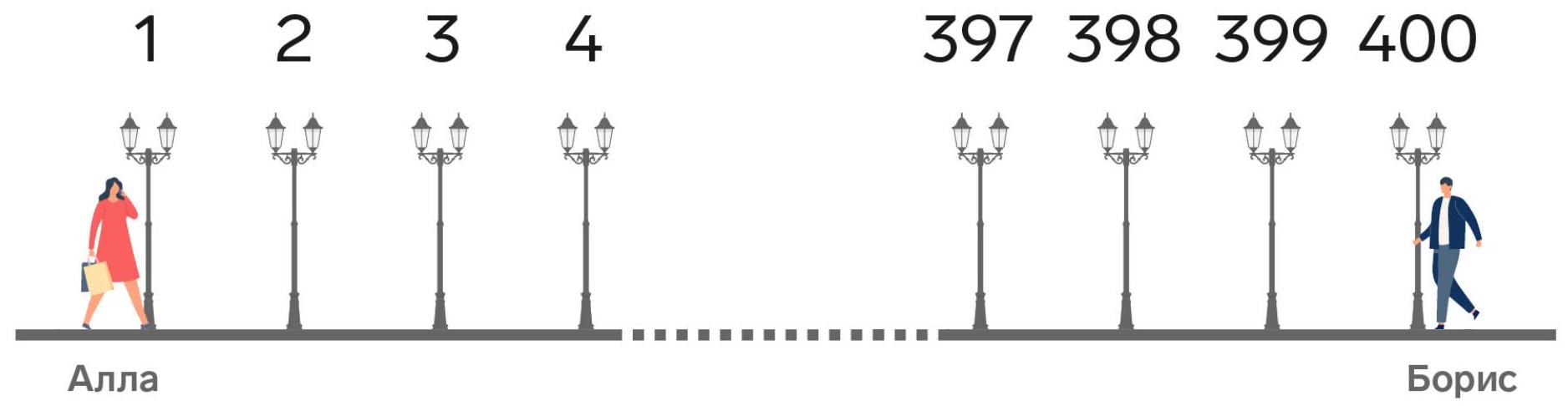
|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-6. On a rectangular table of size $x$ cm $\times 80$ cm, identical sheets of paper of size 5 cm $\times 8$ cm are placed. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
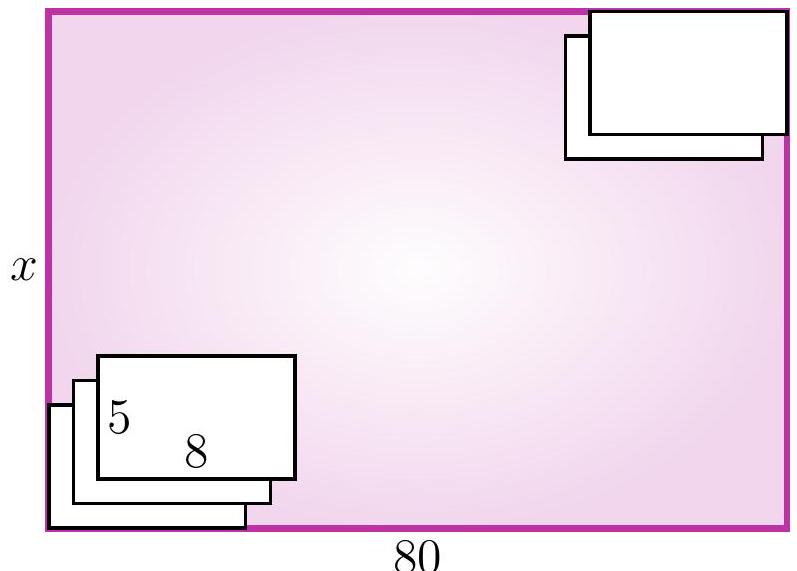
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
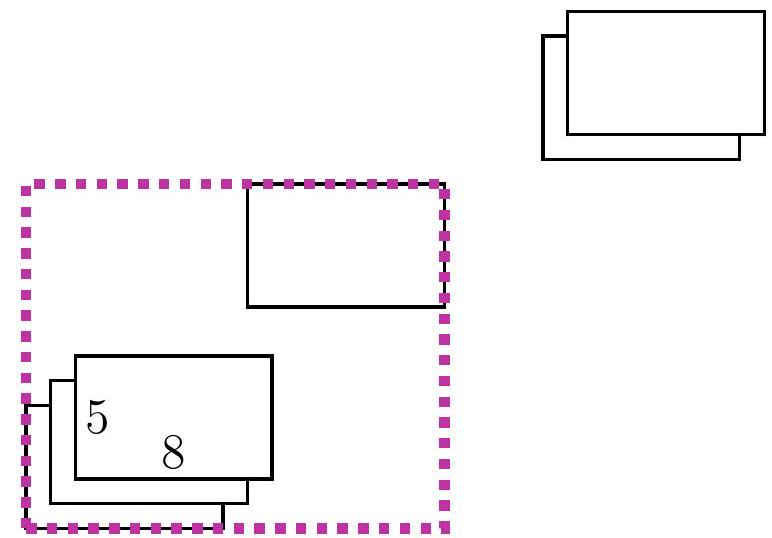
Let's call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-8. In the "Young Photographer" club, 300 children attend. During the class, they divided into 100 groups of 3 people, and in each group, each person took one photo of the other two in their group. No one took any other photos. In total, there were 100 photos of "boy+boy" and 56 photos of "girl+girl". How many "mixed" groups were there, that is, groups that had both a boy and a girl?
|
Answer: 72.
Solution: There were a total of 300 photos, so the number of photos of "boy+girl" was $300-100-56=144$. Each mixed group provides two photos of "boy+girl", while non-mixed groups do not provide such photos. Therefore, there were exactly $144 / 2=72$ mixed groups.
## 6th grade
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6-1. The physical education teacher lined up the class so that everyone was facing him. To the right of Kolya, there are 12 people, to the left of Sasha - 20 people, and to the right of him - 8 people. How many people are standing to the left of Kolya?
|
Answer: 16.
Solution: Since there are 20 people to the left of Sasha and 8 people to the right of him, there are a total of 28 people in the row, not counting Sasha. Therefore, including Sasha, there are 29 people in the class. Then, to the left of Kolya, there are $29-12-1=16$ people (first subtracting the 12 people who are to the right of Kolya, and then Kolya himself).
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6-5. Grandma baked 21 batches of dumplings, with $N$ dumplings in each batch, $N>70$. Then she laid out all the dumplings on several trays, with 70 dumplings on each tray. What is the smallest possible value of $N$?
|
Answer: 80.
Solution: The total number of baked buns is $21 \cdot N$. This number must be divisible by 70 to be able to distribute them into several trays of 70 each. $70=2 \cdot 5 \cdot 7$, and 21 is already divisible by 7. Therefore, $N$ must be divisible by 10, and the smallest such $N$ is 80.
|
80
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6-7. In a confectionery store, the saleswoman laid out 91 candies of several varieties in a row on the counter. It turned out that between any two candies of the same variety, there was an even number of candies. What is the smallest number of varieties there could have been?
|
Answer: 46.
Solution. We will prove that there could not have been three or more candies of the same type. Indeed, let candies of the same type $A, B$, and $C$ lie in that exact order. Suppose there are $2x$ candies between $A$ and $B$, and $2y$ candies between $B$ and $C$, then there are $2x + 2y + 1$ candies between $A$ and $C$, which is an odd number of candies, contradicting the condition.
Since there are no more than 2 candies of each type, there must be at least 46 types. Let's provide an example where there could be 46 types. For instance, the candies can be arranged in pairs: two of the first type, two of the second type, and so on for 45 pairs, with one more candy of the 46th type at the end. There are many other examples.
|
46
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-1. Petya has stickers. If he gives 5 stickers to each of his friends, he will have 8 stickers left. If he wants to give 6 stickers to each of his friends, he will be short of 11 stickers. How many friends does Petya have?
|
Answer: 19.
Solution I. Suppose Petya gave 5 stickers to each of his friends. Next, he wants to give each friend one more sticker. For this, he needs to spend $8+11=19$ stickers, and he gives one sticker to each friend, so he has 19 friends.
Solution II. Let Petya have $x$ friends. Then $5 x+8=6 x-11$, from which $x=19$.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-3. A secret object is a rectangle measuring $200 \times 300$ meters. Outside the object, there is a guard at each of the four corners. An intruder approached the perimeter of the secret object from the outside, and all the guards ran to him by the shortest paths along the external perimeter (the intruder remained in place). Three of the guards ran a total of 850 meters to reach the intruder. How many meters did the fourth guard run to reach the intruder?
|
Answer: 150.
Solution. Note that no matter where the violator is, two guards in opposite corners will run a distance equal to half the perimeter in total.

Therefore, all four guards will run a total distance equal to the perimeter (two in diagonally opposite corners will run a total of half the perimeter, and the other two will also run half the perimeter). Therefore, the fourth guard will run a distance that complements 850 to the perimeter, which is 1000, i.e., 150 meters.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-4. In a giraffe beauty contest, two giraffes, Tall and Spotted, made it to the final. 135 voters are divided into 5 districts, each district is divided into 9 precincts, and each precinct has 3 voters. The majority of voters on each precinct choose the winner in their precinct; in the district, the giraffe that wins the majority of precincts in the district wins; finally, the giraffe that wins the majority of districts is declared the winner of the final. The giraffe Tall won. What is the minimum number of voters who could have voted for him?
|
Answer: 30.
Solution: For High to win the final, he must win in 3 districts. To win in a district, High must win in 5 precincts of that district. In total, he needs to win in at least $3 \cdot 5=15$ precincts. To win in a precinct, at least 2 voters must vote for him. Therefore, at least 30 voters are needed.
Comment: In problems with questions like "what is the greatest" and "what is the least," the solution usually consists of two parts: estimation and example. Estimation is the proof that a greater (or lesser, depending on the question) answer cannot be achieved, and the example is the proof that the given answer can be achieved.
In the solution above, we did not provide an example (i.e., did not prove) that 30 voters are sufficient. For completeness, the solution is missing the phrase: "From the above reasoning, it is clear that 30 voters for High can be sufficient: 2 voters per 5 precincts in any 3 districts."
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-5. In a row, there are 1000 toy bears. The bears can be of three colors: white, brown, and black. Among any three consecutive bears, there is a toy of each color. Iskander is trying to guess the colors of the bears. He made five guesses:
- The 2nd bear from the left is white;
- The 20th bear from the left is brown;
- The 400th bear from the left is black;
- The 600th bear from the left is brown;
- The 800th bear from the left is white.
It turned out that exactly one of his guesses is incorrect. What could be the number of the bear whose color Iskander did NOT guess correctly? Select all possible answers.
|
Answer: 20.
Solution: Since among any three consecutive bears there is a bear of each color, the numbers of all bears of a certain color have the same remainder when divided by 3. Indeed, let's look at the bears with numbers $n, n+1$, and $n+2$, as well as with numbers $n+1, n+2$, and $n+3$. In both cases, there will be bears of all three colors only if the bears with numbers $n$ and $n+3$ are of the same color.
At least one of the guesses "the 20th bear is brown" and "the 600th bear is brown" is incorrect: since the numbers 200 and 600 give different remainders when divided by 3. Also, at least one of the guesses "the 2nd bear is white" and "the 20th bear is brown" is incorrect: since the numbers 2 and 20 give the same remainder when divided by 3, therefore, the bears with these numbers must be of the same color. Thus, the guess "the 20th bear is brown" is definitely incorrect.
Comment: As follows from the solution, the situation described in the problem is possible: all bears with numbers giving a remainder of 1 when divided by 3 must be black, a remainder of 2 - white, and a remainder of 0 - brown. This is the only possible situation.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-6. In an ornithological park, there are several species of birds, a total of 2021 individuals. The birds sat in a row, and it turned out that between any two birds of the same species, there was an even number of birds. What is the smallest number of bird species that could have been there?
|
Answer: 1011.
Solution. Estimation. We will prove that there could not have been three or more birds of the same species. Indeed, suppose birds of the same species $A, B$, and $C$ sit in that exact order. Let there be $2x$ birds between $A$ and $B$, and $2y$ birds between $B$ and $C$, then there are $2x + 2y + 1$ birds between $A$ and $C$, which is an odd number of birds, contradicting the condition. Since there are no more than 2 birds of each species, there must be at least 1011 species.
Example. We will provide an example where 1011 species could have been present. For instance, the birds could sit in pairs: two of the first species, two of the second species, and so on up to the 1010th species, with one more bird of the 1011th species at the end. There are many other examples.
|
1011
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-7. The recruits stood in a row, facing the same direction. Among them were three brothers: Peter, Nikolai, and Denis. In front of Peter were 50 people, in front of Nikolai 100, and in front of Denis 170. On the command "About face!" everyone turned to face the opposite direction. As a result, it turned out that in front of one of the brothers there are now four times as many people as in front of another. How many recruits could there be, including the brothers? List all possible options.
|
Answer: 211.
Solution. Let there be $x$ people in front of Peter, $y$ people in front of Nicholas, and $z$ people in front of Denis. There are three possible cases.

- $x=4 y$. Then $4 y+50=y+100$, from which $y$ is not an integer, which is impossible.
- $y=4 z$. Then $4 z+100=z+170$, from which $z$ is not an integer, which is impossible.
- $x=4 z$. Then $4 z+50=z+170$, from which $z=40$. In total, there are 211 recruits.
|
211
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
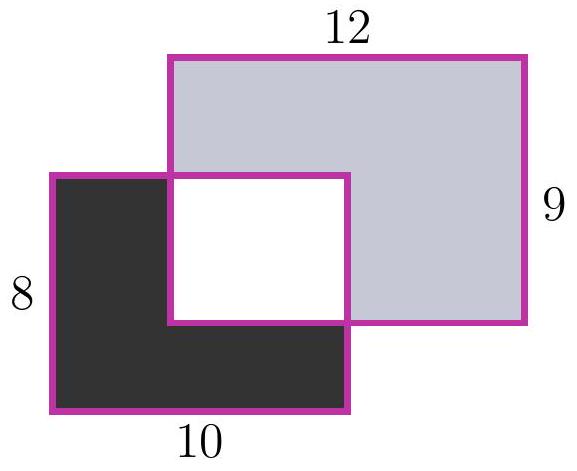
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.

|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
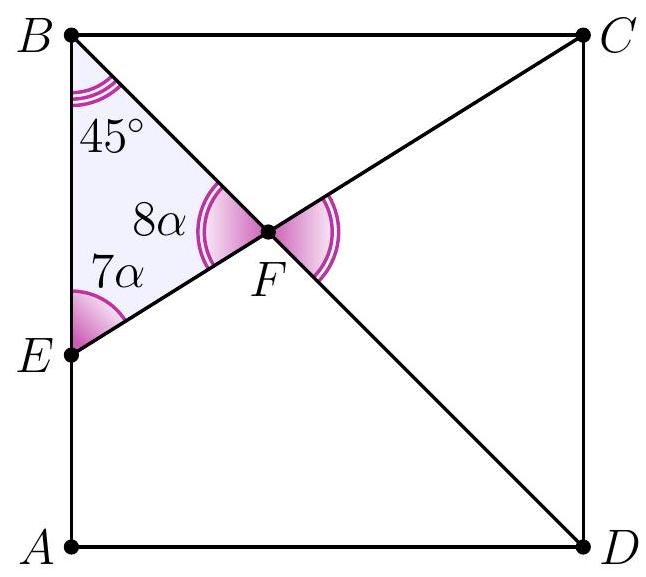
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-4. In a giraffe beauty contest, two giraffes, Tall and Spotted, made it to the final. 105 voters are divided into 5 districts, each district is divided into 7 precincts, and each precinct has 3 voters. The majority of voters on each precinct choose the winner of their precinct; in a district, the giraffe that wins the majority of precincts wins the district; finally, the giraffe that wins the majority of districts is declared the winner of the final. The giraffe Tall won. What is the minimum number of voters who could have voted for him?
|
Answer: 24.
Solution. For High to win the final, he must win in 3 districts. To win a district, High must win in 4 precincts of that district. In total, he needs to win in at least $3 \cdot 4=12$ precincts. To win in a precinct, at least 2 voters must vote for him. Therefore, at least 24 voters are needed.
Comment. In problems with questions like "what is the greatest" and "what is the least," the solution usually consists of two parts: estimation and example. Estimation is the proof that a greater (or lesser, depending on the question) answer cannot be achieved, and the example is the proof that the given answer can be achieved.
In the solution above, we did not provide an example (i.e., did not prove) that 24 voters are sufficient. For completeness, the solution is missing the phrase: "From the above reasoning, it is clear that 24 voters for High can be sufficient: 2 voters per 4 precincts in any 3 districts."
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-5. In a tournament, 6 teams $P, Q, R, S, T$ and $U$ participate, and each team must play against every other team exactly once. Each day, they are divided into 3 pairs, and all three matches are played simultaneously. The "Sports" channel has chosen which match it will broadcast each day:
$$
\begin{array}{c|c|c|c|c}
1 \text { day } & 2 \text { day } & 3 \text { day } & 4 \text { day } & 5 \text { day } \\
\hline P-Q & R-S & P-T & T-U & P-R
\end{array}
$$
On which day can teams $S$ and $U$ play against each other? Mark all possible options.
|
Answer. Only in the 1st.
Solution. Let's look at team $P$: on the 1st, 3rd, and 5th days, it will play against teams $Q, T$, and $R$. Therefore, in the remaining two days, it must play against teams $S$ and $U$. Since on the 2nd day $S$ plays against $R$, $P$ has no choice but to play against $U$ on the 2nd day, and against $S$ on the 4th day.
$$
\begin{array}{l|l|l|l|l}
1 \text { day } & 2 \text { day } & 3 \text { day } & 4 \text { day } & 5 \text { day } \\
\hline P-Q & R-S & P-T & T-U & P-R \\
& P-U & & P-S &
\end{array}
$$
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ $P-U$ | $P-T$ | $T-U$ $P-S$ | $P-R$ |
| | $T-Q$ | | $Q-R$ | |
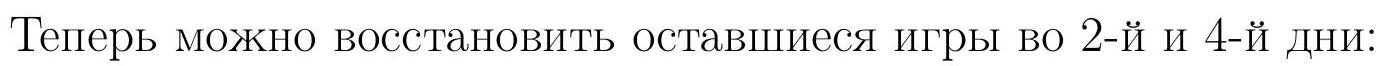
Similarly, let's look at team $T$. On the 5th day, it must play either against $R$ or $S$; $R$ is already playing against $P$, so $T$ will play against $S$. Therefore, the match $T-R$ must take place on the 1st day:
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ | $P-T$ | $T-U$ | $P-R$ |
| $T-R$ | $P-U$ | | $P-S$ | $T-S$ |
| | $T-Q$ | | $Q-R$ | |
Thus, the remaining match on the 1st day is the match $S-U$, which is what we were looking for.
Comment. The situation described in the problem is indeed possible:
| 1 day | 2 day | 3 day | 4 day | 5 day |
| :---: | :---: | :---: | :---: | :---: |
| $P-Q$ | $R-S$ | $P-T$ | $T-U$ | $P-R$ |
| $T-R$ | $P-U$ | $Q-S$ | $P-S$ | $T-S$ |
| $S-U$ | $T-Q$ | $R-U$ | $Q-R$ | $Q-U$ |
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-8. A chess tournament is held according to the following system: each of the 15 students from the "White Rook" school must play one game with each of the 20 students from the "Black Bishop" school, i.e., a total of 300 games should be played. At any given time, no more than one game is played.
After $n$ games, a spectator named Sasha, who has watched all the games and knows all the participants, exclaims: "I can definitely name one of the participants of the next game!" What is the smallest $n$ for which this could happen?
|
Answer: 280.
Solution: Estimation. Suppose fewer than 280 games have passed, i.e., more than 20 games remain. Then, among the participants of the "White Rook" school, there are at least two students who have not yet played all their games. In this case, Sasha cannot accurately name the participant of the next game from the "White Rook" school. Similarly, Sasha cannot name the participant of the next game from the "Black Bishop" school. Therefore, $n$ must be at least 280.
Example. We have just proven that if $n<280$, Sasha cannot name either of the participants of the next game. But is there a situation when $n=280$ where Sasha can still name someone who will play in the next game? It turns out, yes! For this, the 14 students of the "White Rook" school must play all their games, which is exactly 280 games. Then, in the next game, the remaining student from the "White Rook" school will definitely participate - and this is the one Sasha will name.
## 9th Grade
|
280
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-1. Segment $P Q$ is divided into several smaller segments. On each of them, a square is constructed (see figure).
What is the length of the path along the arrows if the length of segment $P Q$ is 73? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 219.
Solution. Note that in each square, instead of going along one side, we go along three sides. Therefore, the length of the path along the arrows is 3 times the length of the path along the segment, hence the answer $73 \cdot 3=219$.
|
219
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-3. Arina wrote down all the numbers from 71 to 81 in a row without spaces, forming a large number 717273...81. Sofia started appending the next numbers to it (i.e., she first appended 82, then 83, ...). She stopped when the large number became divisible by 12. The last number she appended was $N$. What is $N$?
|
Answer: 88.
Solution. A number is divisible by 12 if and only if it is divisible by 3 and by 4. For a number to be divisible by 4, the number formed by its last two digits must also be divisible by 4. Therefore, the last number that Sofia writes must be divisible by 4.
The nearest number that is divisible by 4 is 84, but the number 71727374...84 has a sum of digits equal to 158, which means it is not divisible by 3. The next number that is divisible by 4 is 88. The sum of the digits of the number 71727374...88 is 216, which means the entire number is divisible by 3.
|
88
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-5. A circle is divided into 100 equal arcs by 100 points. Next to the points, numbers from 1 to 100 are written, each exactly once. It turns out that for any number $k$, if a diameter is drawn through the point with the number $k$, then the number of numbers less than $k$ on either side of this diameter will be equal. What number can be written at the point diametrically opposite the point with the number $83?$
|
Answer: Only 84.
Solution: Consider the odd number $2 m+1$. Let's mentally discard it and the number diametrically opposite to it. According to the condition, among the remaining numbers, all numbers less than $2 m+1$ are divided into two groups of equal size. Therefore, among the remaining numbers, there is an even number of numbers less than $2 m+1$. In total, the number of numbers less than $2 m+1$ is also even - there are $2 m$ of them. From this, it follows that the number diametrically opposite to $2 m+1$ must be greater than it!
Then, opposite 99 can only be 100, opposite 97 - only 98 (since the numbers 99 and 100 are already opposite each other), opposite 95 - only 96 (since all larger numbers are already opposite each other), and so on. Therefore, opposite 83 stands 84.
Comment: Note that any variant where for all $m=1,2, \ldots, 50$ the numbers $2 m-1$ and $2 m$ are in diametrically opposite positions, is suitable.
|
84
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-6. Petya wants to place 99 coins in the cells of a $2 \times 100$ board so that no two coins are in cells that share a side, and no more than one coin is in any cell. How many ways are there to place the coins?
|
Answer: 396.
Solution. Note that there will be exactly 1 empty column. Then, to the left of it, there are exactly two ways to arrange the tiles, and to the right of it, there are also exactly two ways to arrange the tiles.
In total, there are $2 \cdot 2=4$ ways to arrange the tiles for a fixed empty column - each way on the left side of the picture must be combined with each way on the right side of the picture.
However, this reasoning does not work when the empty column is the farthest left or the farthest right - in those cases, there are not 4, but only 2 ways to arrange the tiles. Therefore, in total, there will be $98 \cdot 4 + 2 + 2 = 396$ ways.
|
396
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-8. All digits in the notation of 6-digit natural numbers $a$ and $b$ are even, and in the notation of any number between them, there is an odd digit. Find the largest possible value of the difference $b-a$.
---
Translation:
9-8. All digits in the notation of 6-digit natural numbers $a$ and $b$ are even, and in the notation of any number between them, there is an odd digit. Find the largest possible value of the difference $b-a$.
|
Answer: 111112.
Solution. Estimation. We will prove that to a 9-digit number $a$, less than 888 888, all digits of which are even, one can add a number not exceeding 111112 so that all its digits will again be even. If among the digits of the number $a$, except for the first one, there is a digit less than 8, then it can be increased by 2. Otherwise, the number has the form $A 88888$. Since $A<8$, one can add 111112 to it, and the result will be $(A+2) 00000$. If, however, $a=888$ 888, then all larger 6-digit numbers contain an odd digit, so there cannot be a suitable number $b$ among them.
Example. It remains to check that the difference 111112 is possible. The reasoning from the estimation suggests that examples could be the numbers $a=288888$ and $b=400$ 000. Indeed: any number between them has either the digit 3 or the digit 9.
|
111112
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-1. There are several bowls on the table, each containing several grapes. Different bowls may contain different numbers of grapes. If 12 bowls are each added 8 more grapes, the average number of grapes in all the bowls will increase by 6. How many bowls are on the table
|
Answer: 16.
Solution: Let the number of bowls be $n$. The total number of berries increased by $12 \cdot 8=96$. Since the average number of berries increased by 6, the total number of berries should have increased by $6n$. Therefore, $6n=96$, from which we find $n=16$.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-2. The large rectangle in the figure consists of 20 identical smaller ones. The perimeter of figure $A$ is 56 cm, the perimeter of figure $B$ is 56 cm. What is the perimeter of figure $C$? Provide your answer in cm.
| | $A$ | | |
| ---: | :--- | :--- | :--- |
| | | | |
| | | | |
| $B$ | | | $C$ |
| | | | |
|
Answer: 40.
Solution: Let the horizontal size of the rectangle be $x$, and the vertical size be $y$. From the condition, we get the system of equations
$$
\left\{\begin{array}{l}
6 x+2 y=56 \\
4 x+6 y=56
\end{array}\right.
$$
We need to find what $2 x+6 y$ equals. Solving the system, we find $x=8, y=4$, from which $2 x+6 y=40$.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
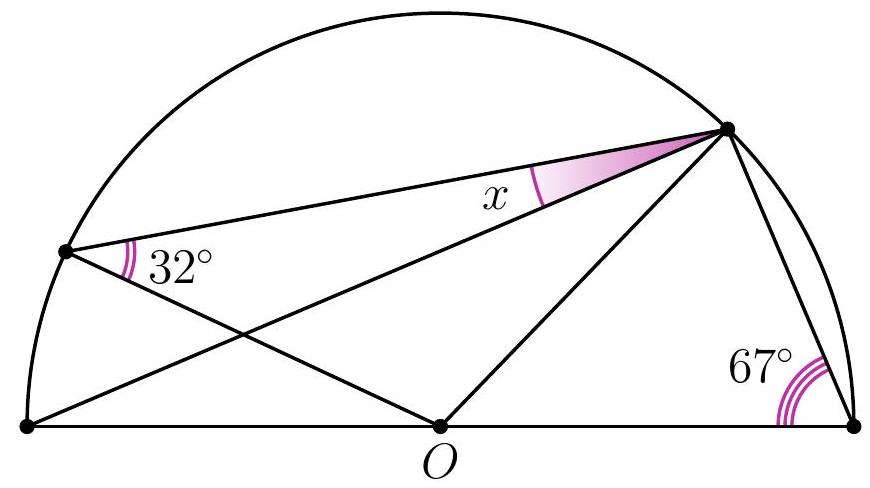
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
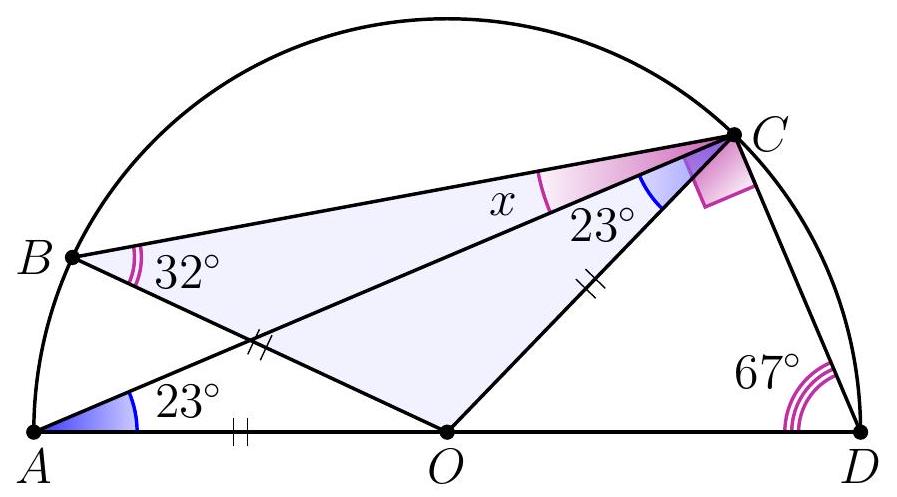
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-4. Initially, a natural number was displayed on the calculator screen. Each time, Olya added a natural number to the current number \( n \) on the calculator screen, which \( n \) did not divide. For example, if the screen showed the number 10, Olya could add 7 to get 17.
Olya repeated this operation five times, and the number 200 appeared on the screen. What is the largest initial number for which this could have happened?
|
Answer: 189.
Solution. Estimation. Note that Olya increased the number on the screen by at least 2 each time, because any number is divisible by 1. If Olya added two five times, the initial number would have been 190, and it would not have been possible to add two to it. Therefore, Olya must have added a number greater than two at least once. Consequently, she increased the number by at least 11 in total, from which $n \leqslant 189$.
Estimation. For $n=189$, this is possible: $200=189+2+2+2+2+3$.
|
189
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-5. For each natural number from 1 to 999, Damir subtracted the last digit from the first digit and wrote all 1000 differences on the board. For example, for the number 7, Damir wrote the number 0 on the board, for the number 105 he wrote $(-4)$, and for the number 61 he wrote 5.
What is the sum of all the numbers on the board
|
Answer: 495.
Solution: Note that for single-digit numbers, zeros are recorded on the board, which do not affect the sum. For numbers where the first and last digit are the same, zeros are also recorded on the board, which do not affect the sum.
Almost all other numbers can be paired: a number and the number obtained by swapping the first and last digit. For example, 17 and 71, 122 and 221, 103 and 301. If for one number in the pair, the number $x$ is recorded on the board, then for the other number in the pair, $-x$ is recorded, resulting in a zero contribution to the sum of all numbers on the board from $x$ and $-x$.
It remains to consider the numbers that do not have a pair. These are numbers ending in 0! For these, everything needs to be calculated directly. Numbers of the form $a 0$ (where $a=1,2, \ldots 9$) will contribute $a$ to the calculated sum, and there is one such number for each $a$. Numbers of the form $a * 0$ will also contribute $a$ to the calculated sum, and there are 10 such numbers. In total, there are 11 addends, each equal to $a$, in the calculated sum.
Therefore, the calculated sum is
$$
1 \cdot 11+2 \cdot 11+3 \cdot 11+\ldots+9 \cdot 11=45 \cdot 11=495
$$
|
495
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-7. Parabola $\Pi_{1}$ with branches directed upwards passes through points with coordinates $(10,0)$ and $(13,0)$. Parabola $\Pi_{2}$ with branches directed upwards also passes through the point with coordinates $(13,0)$. It is also known that the vertex of parabola $\Pi_{1}$ bisects the segment connecting the origin and the vertex of parabola $\Pi_{2}$. At what abscissa does parabola $\Pi_{2}$ intersect the $O x$ axis again?
|
Answer: 33.
Solution. We will use the following fact twice: if $x_{1}$ and $x_{2}$ are the x-coordinates of the points where the parabola intersects the x-axis, then the x-coordinate of the vertex is $\frac{x_{1}+x_{2}}{2}$ (the x-coordinate of the vertex is the midpoint of the segment with endpoints $x_{1}$ and $x_{2}$).
Applying this fact, we get that the x-coordinate of the vertex of the parabola $\Pi_{1}$ is $\frac{10+13}{2}=11.5$, and then the x-coordinate of the vertex of the parabola $\Pi_{2}$ is $2 \cdot 11.5$.
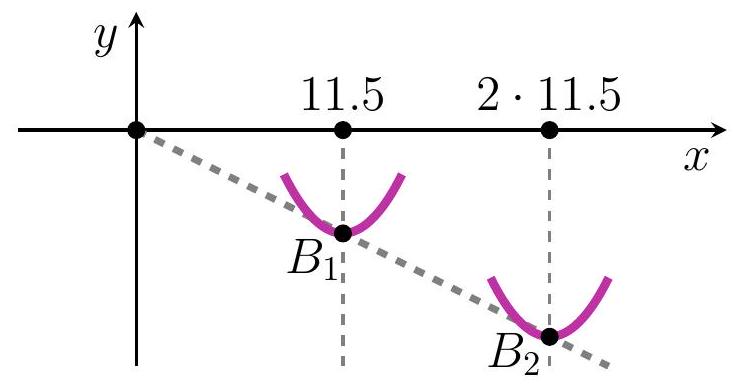
If we denote by $t$ the sought x-coordinate of the second point of intersection of the parabola $\Pi_{2}$ with the x-axis, then, applying the fact again, we get $\frac{13+t}{2}=2 \cdot 11.5$, from which $t=33$.
Comment. The condition that the branches of the parabolas are directed upwards was not used in the solution.
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-8. In trapezoid $A B C D$, the bases $A D$ and $B C$ are 8 and 18, respectively. It is known that the circumcircle of triangle $A B D$ is tangent to the lines $B C$ and $C D$. Find the perimeter of the trapezoid.
|
Answer: 56.
Solution. Let's make the following observation. Through point $B$ on the circle, a line passes parallel to the chord $AD$. It is clear that then $B$ is the midpoint of the arc $AD$, that is, $BA = BD$ (indeed, $\angle 1 = \angle 2$ as alternate interior angles, $\angle 1 = \angle 3$ by the theorem on the angle between a tangent and a chord, therefore, $\angle 2 = \angle 3$).

Next, from point $C$, two tangents are drawn to the circle; hence, they are equal: $CD = CB = 18$.
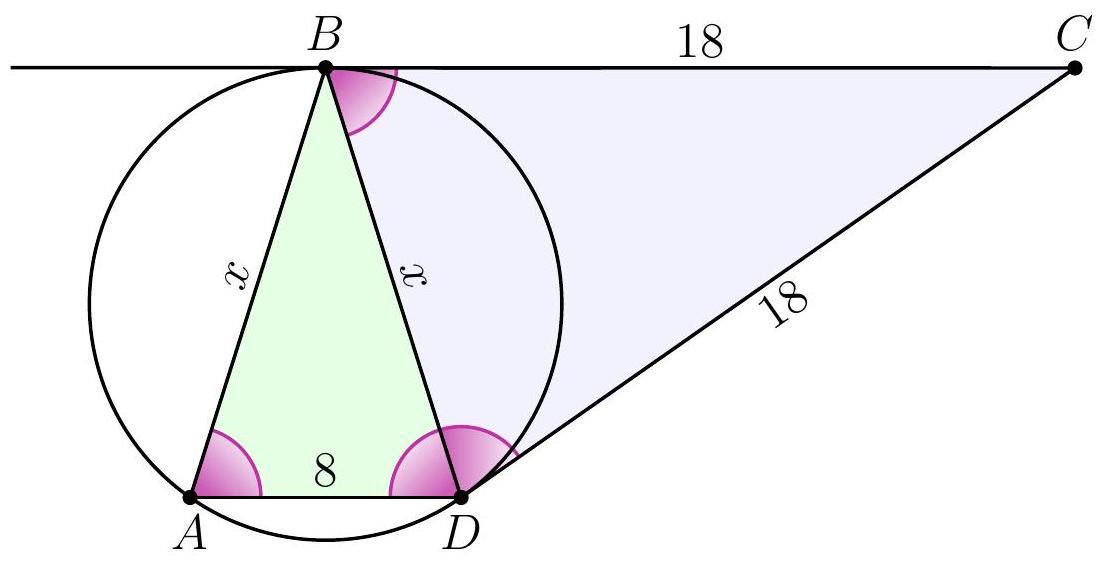
It remains to find the length of side $AB$, which we will denote as $x$. For this, note that $\angle CBD = \angle BDA$ as alternate interior angles. Therefore, isosceles triangles $CBD$ and $BDA$ are similar as isosceles triangles with equal angles at the base. From the similarity, we get $\frac{x}{8} = \frac{18}{x}$, from which $x = 12$. Thus, the perimeter of the trapezoid is $12 + 18 + 18 + 8 = 56$.
## 11th Grade
|
56
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-1. Twins Paolo and Sevilla are celebrating their birthday at a cafe with friends. If the final bill amount is divided equally among everyone, then each person should pay 12 euros. But if the bill is divided equally among everyone except Paolo and Sevilla, then each person should pay 16 euros. How many friends came to Paolo and Sevilla's birthday?
|
Answer: 6.
Solution. Let $n$ be the number of friends who arrived. Then we get the equation $12(n+2)=16n$, from which $n=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
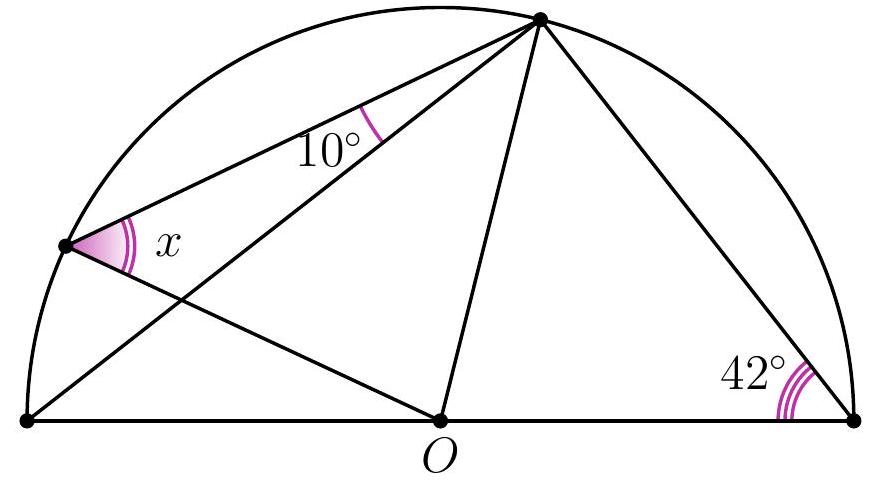
|
Answer: 58.
Solution. Angle $ACD$ is a right angle since it subtends the diameter of the circle.
Therefore, $\angle CAD = 90^{\circ} - \angle CDA = 48^{\circ}$. Also, $AO = BO = CO$ as they are radii of the circle, so $\angle OCA = \angle ACO = 48^{\circ}$ and $x = \angle OBC = \angle OCB = 48^{\circ} + 10^{\circ} = 58^{\circ}$.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-4. At first, a natural number was displayed on the calculator screen. Each time, Tanya added to the current number \( n \) on the screen a natural number that \( n \) did not divide. For example, if the screen showed the number 10, Tanya could add 7 to get 17.
Tanya repeated this operation five times, and the number 100 appeared on the screen. What is the largest initial number for which this could have happened?
|
Answer: 89.
Solution. Estimation. Note that Tanya increased the number on the screen by at least 2 each time, because any number is divisible by 1. If Tanya added two five times, the initial number would have been 90, and it would not have been possible to add two to it. Therefore, Tanya must have added a number greater than two at least once. Consequently, she increased the number by at least 11 in total, from which $n \leqslant 89$.
Estimation. For $n=89$, this is possible: $100=89+2+2+2+2+3$.
|
89
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-6. Petya uses all possible ways to place the signs + and - in the expression $1 * 2 * 3 * 4 * 5 * 6$ in the places of the asterisks. For each arrangement of the signs, he calculates the resulting value and writes it on the board. On the board, some numbers may appear multiple times. Petya adds up all the numbers on the board. What is the sum obtained by Petya?
|
Answer: 32.
Solution. Note that each of the digits $2,3,4,5,6$ will contribute zero to Petya's sum: each will equally often appear with a + sign and with a - sign. The digit 1 will appear in all sums with a + sign as many times as there are addends in total. Since each of the asterisks can take two values, there will be $2^{5}=32$ addends. Therefore, Petya's sum is 32.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-7. Given a parallelogram $A B C D$, where $\angle B=111^{\circ}$ and $B C=B D$. On the segment $B C$, a point $H$ is marked such that $\angle B H D=90^{\circ}$. Point $M$ is the midpoint of side $A B$. Find the angle $A M H$. Give your answer in degrees.
|
Answer: $132^{\circ}$.
Solution. Note that $\angle D M B=90^{\circ}$, since $D A=D B$, and in the isosceles triangle $B D A$, the median $D M$ is also the altitude. Since angles $D H B$ and $D M B$ are right angles, points $M, B, H$, and $D$ lie on the same circle. It is clear that we need to find the angle $D M H$, as $\angle A M H=\angle D M H+90^{\circ}$.
Angles $D M H$ and $D B H$ are equal, as these angles subtend the same arc $D H$ in the circle. Therefore, we need to find the angle $D B H$. This can be easily found from the isosceles triangle $D B C$ if we know the angle $C$ at the base of this triangle: $\angle D B C=180^{\circ}-2 \angle C$. But the angle $C$ is equal to $180^{\circ}-111^{\circ}=69^{\circ}$. Thus, $\angle D B C=42^{\circ}$, and $\angle A M H=\angle D M H+90^{\circ}=42^{\circ}+90^{\circ}=132^{\circ}$.
|
132
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-8. In a caravan, there are 100 camels, both one-humped and two-humped, and there are at least one of each. If you take any 62 camels, they will have at least half of the total number of humps in the caravan. Let $N$ be the number of two-humped camels. How many values (in the range from 1 to 99) can $N$ take?
|
Answer: 72.
Solution. If there were $N$ two-humped camels in total, then there were $100-N$ one-humped camels, and there were $100+N$ humps in total. Let's line up the camels: first the one-humped ones, and then the two-humped ones. It is clear that if the condition for 62 camels is met for the first 62 camels, then it is met for any 62 camels. There are two possible cases: the first 62 camels are all one-humped, or there is at least one two-humped camel among them.
1) Suppose the first 62 camels are one-humped. Then, by the condition, $62 \geqslant \frac{1}{2}(100+N)$, from which $N \leqslant 24$.
2) Among the first 62 camels, there are two-humped ones, let their number be $y$. Then, by the condition, $62+y \geqslant \frac{1}{2}(100+38+y)$, from which $y \geqslant 14$. Then $N \geqslant 14+38=52$.
Thus, the number of two-humped camels lies in the ranges from 1 to 24 inclusive or from 52 to 99 inclusive. This gives $24+48=72$ options.
|
72
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
When multiplying two two-digit numbers, a four-digit number $A$ is obtained, where the first digit matches the second, and the second-to-last digit matches the last. Find the smallest $A$, given that $A$ is divisible by 51.
|
Answer: 1122.
Solution.
Notice that $A=\overline{x x y y}=x \cdot 11 \cdot 100+y \cdot 11=11 \cdot(100 x+y)$. Since 51 and 11 are coprime, then $100 x+y$ is divisible by 51. The minimum $x=1$, so $y=2$ (the only number from 100 to 109 divisible by 51 is 102).
|
1122
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Variant 1.
Find the number of four-digit numbers for which the last three digits form an increasing arithmetic progression (numbers cannot start with zero).
|
Answer: 180.
Solution: The difference of the progression cannot be greater than 4.
For $d=1$ - there are eight suitable progressions of digits: from 012 to 789.
For $d=2$ - six: from 024 to 579.
For $d=3$ - four: from 036 to 369.
For $d=4$ - two: 048 and 159.
In total, $8+6+4+2=20$ options for the last three digits. By choosing the first digit in nine ways for each of them, we get the answer $20 \cdot 9=180$.
|
180
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Variant 1.
Find the ratio $\frac{16 b^{2}}{a c}$, given that one of the roots of the equation $a x^{2}+b x+c=0$ is 4 times the other.
|
Answer: 100.
Solution.
By Vieta's theorem, $-\frac{b}{a}=x_{1}+x_{2}=5 x_{2}$ and $\frac{c}{a}=x_{1} \cdot x_{2}=4 x_{2}^{2}$. Express $x_{2}=-\frac{b}{5 a}$ from the first equation and substitute it into the second: $\frac{c}{a}=\frac{4 b^{2}}{25 a^{2}}$. Then find $\frac{b^{2}}{a c}=\frac{25}{4}$.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Variant 1.
It is known that
$$
\frac{1}{\cos (2022 x)}+\operatorname{tg}(2022 x)=\frac{1}{2022}
$$
Find $\frac{1}{\cos (2022 x)}-\operatorname{tg}(2022 x)$.
|
Answer: 2022.
Solution 1.
\[
\begin{aligned}
& \frac{1}{\cos 2A} + \tan 2A = \frac{1 + \sin 2A}{\cos 2A} = \frac{\cos^2 A + \sin^2 A + 2 \sin A \cdot \cos A}{\cos^2 A - \sin^2 A} = \frac{(\cos A + \sin A)^2}{(\cos A - \sin A)(\cos A + \sin A)} = \frac{\cos A + \sin A}{\cos A - \sin A} \\
& \frac{1}{\cos 2A} - \tan 2A = \frac{1 - \sin 2A}{\cos 2A} = \frac{\cos^2 A + \sin^2 A - 2 \sin A \cdot \cos A}{\cos^2 A - \sin^2 A} = \frac{(\cos A - \sin A)^2}{(\cos A - \sin A)(\cos A + \sin A)} = \frac{\cos A - \sin A}{\cos A + \sin A}
\end{aligned}
\]
Therefore, if \(\frac{1}{\cos (2022x)} + \tan (2022x) = \frac{1}{2022}\), then \(\frac{1}{\cos (2022x)} - \tan (2022x) = 2022\).
Solution 2.
Consider the product \(\left(\frac{1}{\cos \alpha} + \tan \alpha\right)\left(\frac{1}{\cos \alpha} - \tan \alpha\right) = \frac{1}{\cos^2 \alpha} - \tan^2 \alpha = 1\). Therefore, the desired expression is 2022.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Variant 1.
It is known that
$$
\left(x^{2}-x+3\right)\left(y^{2}-6 y+41\right)\left(2 z^{2}-z+1\right)=77
$$
Find $\frac{x y}{z}$.
|
# Answer: 6.
Solution.
$$
\begin{aligned}
& x^{2}-x+3=(x-0.5)^{2}+2.75 \geq 2.75 \\
& y^{2}-6 y+41=(y-3)^{2}+32 \geq 32 \\
& 2 z^{2}-z+1=2(z-0.25)^{2}+0.875 \geq 0.875
\end{aligned}
$$
Therefore, $\left(x^{2}-x+3\right)\left(y^{2}-6 y+41\right)\left(2 z^{2}-z+1\right) \geq 77$ and if at least one of the three inequalities is strict, then the left side is greater than 77. Thus, all three inequalities must be equalities. This occurs when $x=0.5, y=3, z=0.25$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Variant 1.
In the district, there are three villages $A, B$, and $C$ connected by dirt roads, with any two villages being connected by several (more than one) roads. Traffic on the roads is two-way. We will call a path from one village to another either a road connecting them or a chain of two roads passing through a third village. It is known that villages $A$ and $B$ are connected by 34 paths, and villages $B$ and $C$ by 29 paths. What is the maximum number of paths that can connect villages $A$ and $C$?
|
Answer: 106.
Solution.
Let there be $k$ roads between cities $A$ and $B$, $m$ roads between cities $B$ and $C$, and $n$ roads between cities $A$ and $C$. Then the number of paths from $A$ to $B$ is $k + mn$, and the number of paths from $B$ to $C$ is $m + kn$. We have the system of equations $k + mn = 34$, $m + kn = 29$, where the unknowns are natural numbers greater than 1. Subtracting the second equation from the first, we get: $(m - k)(n - 1) = 5$. We need to check all divisors of 5: 1 and 5. Therefore, $n = 2$ or $n = 6$. For each of them, we find $m$ and $k$ by solving the corresponding system of linear equations. If $n = 2$, then $k = 8$ and $m = 13$. If $n = 6$, then $k = 4$ and $m = 5$. The number of paths connecting cities $A$ and $B$ is $n + km$. In the first case, $n + km = 2 + 8 \cdot 13 = 106$, and in the second case, $-n + km = 6 + 4 \cdot 5 = 26$. Therefore, the desired answer is 106.
|
106
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1.
103 natural numbers are written in a circle. It is known that among any 5 consecutive numbers, there are at least two even numbers. What is the minimum number of even numbers that can be in the entire circle?
|
Answer: 42.
Solution.
We will show that there will be 3 consecutive numbers, among which there are at least 2 even numbers. This can be done, for example, as follows. Consider 15 consecutive numbers. They can be divided into 3 sets of 5 consecutive numbers, so among them there are at least 6 even numbers. But these 15 numbers can also be divided into 5 sets of 3 consecutive numbers. Therefore, by the Pigeonhole Principle, in one of these triplets there are at least 2 even numbers.
Let's fix these 3 numbers. Among them, there are at least 2 even numbers. The remaining 100 numbers can be divided into 20 sets of 5 consecutive numbers. In each such set, there will be at least 2 even numbers. Thus, the total number of even numbers is at least $2 + 2 \cdot 20 = 42$. Such a situation is possible. We can number the numbers in a circle. The even numbers can be those with numbers $1, 2, 6, 7, \ldots, 96, 97, 101, 102$. (Other examples are also possible.)
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Variant 1.
Given a parallelogram $A B C D$. Let $B P$ and $C Q$ be the perpendiculars dropped from vertices $B$ and $C$ to diagonals $A C$ and $B D$ respectively (point $P$ lies on segment $A C$, and point $Q$ lies on segment $B D$). Find the ratio $\frac{10 B D}{A C}$, if $\frac{A P}{A C}=\frac{4}{9}$ and $\frac{D Q}{D B}=\frac{28}{81}$.
|
Answer: 6.
Solution: Let $O$ be the point of intersection of the diagonals. Note that points $B, C, Q, P$ lie on the same circle (segment $B C$ is seen from points $P$ and $Q$ at a right angle). Therefore, triangles $B O P$ and $C O Q$ are similar. Let $A C=2 a, B D=2 b$. Then $P O=a-\frac{8 a}{9}=\frac{a}{9}, Q O=$ $b-\frac{56 b}{81}=\frac{25 b}{81}$. From the similarity of triangles $B O P$ and $C O Q$, we have $\frac{P O}{Q O}=\frac{B O}{C O} \cdot \frac{a}{9}: \frac{25 b}{81}=\frac{b}{a} \cdot \frac{81 a}{9 \cdot 25 b}=\frac{b}{a}$, from which $\frac{b}{a}=\frac{3}{5}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Draw a row of 11 circles, each of which is either red, blue, or green. Moreover, among any three consecutive circles, there should be at least one red, among any four consecutive circles, there should be at least one blue, and there should be more than half green. How many red circles did you get?
|
Answer: 3 red circles
Hint. The circles are arranged only as follows: ZZKSKZKSKZZ.
Solution. (1) Three non-overlapping triplets of circles can be identified, each containing at least one red circle. Therefore, there are no fewer than three red circles. (2) Two non-overlapping quartets of circles can be identified, each containing at least one blue circle. Therefore, there are no fewer than two blue circles. (3) According to the condition, there are no fewer than six green circles. (4) Since $3+2+6=11$, all the constraints must turn into equalities. In particular, there are 3 red circles.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Represent the number 32 as the product of three integer factors, the sum of which is 3. What is the smallest of the factors?
|
Answer: -4.
Example: $32=(-4) \cdot(-1) \cdot 8$.
Solution. The given factorization is unique. This can be proven.
If all three factors are positive, then the largest of them is not less than 4, and the sum is greater than 3, which contradicts the condition. Therefore, two of the factors are negative, and the third is positive.
The number 32 has only one odd factor, and the sum of the three factors is odd. Therefore, one of them is +1 or -1. From the previous remark, it follows that this factor is -1. It is not difficult to enumerate: $32=(-1) \cdot(-2) \cdot 16=(-1) \cdot(-4) \cdot$ $8=(-1) \cdot(-16) \cdot 2=(-1) \cdot(-8) \cdot 4$. Only the second option fits.
|
-4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. In a table containing $A$ columns and 100 rows, natural numbers from 1 to $100 \cdot A$ were written in ascending order, starting from the first row. The number 31 is in the fifth row. In which row is the number 100?
|
Answer: in the 15th row.
Solution. From the condition, it follows that $A \leq 7$, since for $A \geq 8$ the number 31 would be located before the fifth row. Similarly, we get that $A \geq 7$, otherwise the number 31 would be located after the fifth row. Therefore, $A=7$. Since $100=7 \cdot 14+2$, the number 100 is located in the 15th row.
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. In the village of Matitika, along a straight road, five friends live in the following order: Alya, Bella, Valya, Galina, and Dilya. Each of them found the sum of the distances (in meters) from her house to the houses of the others. Bella named the number 700, Valya - 600, Galina - 650. How many meters are there between Bella's and Galina's houses?
|
Answer: 150 meters.
Solution. Let's denote the houses of the friends with the letters A, B, V, G, D.
It is easy to see that the total distance from B to the other houses is AB + 3BV + 2VG + GD, and from V to the other houses is AB + 2BV + 2VG + GD. These values differ by BV, so the distance between the houses B and V is $700-600=100$ meters.
Similarly, the distance between the houses V and G is $650-600=50$ meters.
Therefore, the distance between the houses B and G is $100+50=150$ meters.
Comment. By similar reasoning, the following result can be obtained: if Bella named the number $x$, Vanya $-y$, Galya $-z$, then the distance between Bella's and Galya's houses is $x+z-2y$ meters.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.7. Petya told Misha that in his class exactly two thirds of all the girls are blondes, exactly one seventh of the boys are blonds, and in total, a third of the class has light hair. Misha said: "You once told me that there are no more than 40 people in your class. 0 ! I know how many girls are in your class!" How many?
|
Answer: 12 girls
Solution. Let there be $x$ girls and $y$ boys in the class. From the problem statement, we have the following relationship:
$\frac{2}{3} x+\frac{1}{7} y=\frac{1}{3}(x+y)$,
which, after transformation, becomes $7 x=4 y$.
From the condition and the derived relationship, it follows that the number $x$ is divisible by 3 and 4, so it is divisible by 12. Let $x=12 n$, where $n$ is a natural number. From the derived equation, it follows that $y=21 n$.
Therefore, there are $x+y=12 n+21 n=33 n$ students in the class. According to the condition, this number is no more than 40, so $n=1$. In the class, there are $x=12 n=12$ girls.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Represent the number 36 as the product of three integer factors, the sum of which is 4. What is the smallest of the factors?
|
Answer: -4.
Example: $36=(-4) \cdot(-1) \cdot 9$.
Solution. The given factorization is unique. This can be proven.
If all three factors are positive, then the largest of them is not less than 4 (since $3^{3}<36$), and the sum is greater than 4, which contradicts the condition. Therefore, two of the factors are negative, and the third is positive.
Then the positive factor is 9. Indeed, if it is not more than 6, then the sum of the absolute values of the other two is greater than 2; if it is not less than 12, then the sum of the absolute values of the other two is less than 8. Then the two negative factors are either -4 and -1, or -2 and -2. Only the first variant satisfies the condition.
|
-4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Given a parallelogram $A B C D, \angle D=100^{\circ}, B C=12$. On side $A D$ there is a point $L$ such that $\angle A B L=50^{\circ}, L D=4$. Find the length of $C D$.
|
Answer: 8.
Solution. By the property of a parallelogram, $\angle A B C=\angle D=100^{\circ}, A D=B C=12$ and $C D=A B$. Therefore, $\angle C B L=\angle A B C-\angle A B L=100^{\circ}-50^{\circ}=50^{\circ}$ and $A L=A D-L D=12-4=8$. Since $\angle A L B=\angle C B L$ (as alternate interior angles when $A D$ and $B C$ are parallel and $B L$ is the transversal) and $\angle C B L=\angle A B L=50^{\circ}$, we get that $\angle A L B=\angle A B L$, so triangle $A B L$ is isosceles and $A B=A L=8$. Therefore, $C D=A B=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Four boys and three girls went to the forest to pick mushrooms. Each found several mushrooms, in total they collected 70. No two girls collected the same amount, and any three boys together brought no fewer than 43 mushrooms. The number of mushrooms collected by any two children differed by no more than 5 times. Masha collected the most among the girls. How many mushrooms did she bring?
|
Answer: 5 mushrooms.
Solution. Any three boys collected at least 43 mushrooms together, so there is a boy who collected no less than 15 mushrooms (since $14 \cdot 3 < 43$). Therefore, this boy and the other three collected no less than $15 + 43 = 58$ pieces.
If there is a boy who collected no less than 15 pieces, then any girl collected no less than $15 \div 5 = 3$ mushrooms. Therefore, the girls collected different numbers of mushrooms, meaning they collected at least $3 + 4 + 5 = 12$ pieces together.
Since $58 + 12 = 70$ is the total number of mushrooms collected, the girls must have collected 3, 4, and 5 mushrooms, so Masha brought 5 pieces.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. In a convex quadrilateral $A B C D$, side $B C$ is half the length of $A D$. Diagonal $A C$ is perpendicular to side $C D$, and diagonal $B D$ is perpendicular to side $A B$. Find the larger acute angle of this quadrilateral, given that the smaller one is $36^{\circ}$.
|
Answer: $84^{\circ}$.
Solution. Let point $M$ be the midpoint of side $A D$. Since angles $A B D$ and $A C D$ are right angles, angles $B$ and $C$ of quadrilateral $A B C D$ are obtuse, and angles $A$ and $D$ are acute, as angles of right triangles $A B D$ and $A C D$. Let $\angle A=\alpha$ be the given angle, and $\angle D=\beta$ be the angle to be found.
Triangles $A B D$ and $A C D$ are right triangles, so their medians to $A D$ are equal to half the hypotenuse, thus $A M=B M=C M=D M=B C$. From this, it follows that (1) $\angle A B M=\alpha$ (since $\triangle A M B$ is isosceles), (2) $\angle D C M=\beta$ (since $\triangle C M D$ is isosceles), (3) $\angle C B M=\angle B C M=60^{\circ}$ (since $\triangle B M C$ is equilateral).
The sum of the angles of quadrilateral $A B C D$ is $360^{\circ}$, so the equation $\alpha+\left(\alpha+60^{\circ}\right)+\left(\beta+60^{\circ}\right)+\beta=360^{\circ}$ holds, from which it follows that $\alpha+\beta=120^{\circ}$ or $\beta=120^{\circ}-\alpha$.
In this case, if $\alpha=36^{\circ}$, then $\beta=120^{\circ}-\alpha=120^{\circ}-36^{\circ}=84^{\circ}$.
|
84
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.7. In the city of Bukvinsk, people are acquainted only if their names have the same letters, otherwise - they are not. Several residents of Bukvinsk were asked how many acquaintances they have in the city. Martin said 20, Klim - 15, Inna - 12, Tamara - 12. What did Camilla answer?
|
Answer: 15 acquaintances
Solution. Note that all five students listed in the condition are acquainted with each other. Therefore, Martin has 16 acquaintances outside this group, while Inna and Tamara each have 8. However, all of Inna's acquaintances are acquainted with Martin, and all of Tamara's acquaintances are also, with no other acquaintances for Martin. Since $16=8+8$, there are no common acquaintances of Inna and Tamara outside our group. Their common acquaintances can only be people with the letter A in their name, so there are no such people outside the considered group. In this case, Camilla is acquainted with exactly the same people as Klim (and they are also acquainted with each other), meaning she has 15 acquaintances.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.8. In the cells of an $8 \times 8$ board, natural numbers from 1 to 64 (each appearing once) are placed such that numbers differing by 1 are in adjacent side-by-side cells. What is the smallest value that the sum of the numbers on the diagonal from the bottom left to the top right corner can take?
|
Answer: 88.
Solution. We will color the cells of the board in a checkerboard pattern. Let the considered diagonal be black. We will move through the cells according to the numbers placed. Consider the moment when we occupy the last cell on the diagonal. Before this, we must have visited all the cells on one side of it, so we have visited at least 19 black cells (7 on the diagonal and 12 on this side). Since white and black cells alternate during the traversal of the board, we have also visited at least 19 white cells, so the number of the current cell is no less than \(2 \cdot 19 + 1 = 39\). Since all cells on the diagonal have numbers of the same parity, the numbers in the other cells are no less than \(1, 3, \ldots, 13\). Thus, the sum of the numbers on the diagonal is no less than \(1 + 3 + \ldots + 13 + 39 = 88\). The diagram shows that this value is achievable.
| 58 | 57 | 48 | 47 | 42 | 41 | 40 | 39 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 59 | 56 | 49 | 46 | 43 | 12 | 13 | 38 |
| 60 | 55 | 50 | 45 | 44 | 11 | 14 | 37 |
| 61 | 54 | 51 | 8 | 9 | 10 | 15 | 36 |
| 62 | 53 | 52 | 7 | 18 | 17 | 16 | 35 |
| 63 | 4 | 5 | 6 | 19 | 20 | 21 | 34 |
| 64 | 3 | 26 | 25 | 24 | 23 | 22 | 33 |
| 1 | 2 | 27 | 28 | 29 | 30 | 31 | 32 |
|
88
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2.1. Condition:
In the campus, rooms are numbered consecutively $1,2,3,4 \ldots, 10,11, \ldots$ For room numbering, stickers with digits were purchased, with the digits 1, 2, and 3 being purchased in equal quantities, and the digit 5 being purchased three more than the digit 6. How many rooms are there in the campus, given that there are fewer than 100?
|
# Answer: 66
## Solution.
In each decade up to the sixth, the digits "5" and "6" are equal, so there are at least 50 rooms. Since the digits "1", "2", and "3" are equal, they must appear in each decade, meaning the number of rooms will be at least 53. Then the digit "5" will be four more than the digit "6". Therefore, the minimum number of rooms will reach 60, and the digit "5" will be ten more than the digit "6", as there are 11 fives among the numbers from 50 to 59 (but note one digit "6" in the number 56). Among the numbers from 60 to 66, there will be seven digits "6" and one digit "5", so the difference will decrease by 6, and the number of digits "5" will exceed the number of digits "6" by exactly four. Note that the difference in the number of digits "5" and "6" will decrease further until they are equal at number 69. If we take numbers from the next decades, the difference in the number of digits "5" and "6" will not exceed one when reaching the numbers 75, 76, or 85, 86, or 95, 96. Therefore, there is only one answer.
|
66
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3.1. Condition:
Vanya bought balloons, red ones were 7 times more than blue ones. While Vanya was walking home, some of the balloons burst, and among the burst balloons, there were 3 times fewer red ones than blue ones. What is the smallest number of balloons Vanya could have bought?
|
# Answer: 24
## Solution.
Notice that at least one red balloon has burst, which means at least three blue balloons have burst. Therefore, there are at least three blue balloons, which means there are at least $7 \cdot 3=21$ red balloons, so the total number of balloons must be at least 24. For example, Vanya could have been carrying 21 red balloons and 3 blue ones, and 1 red balloon and all 3 blue balloons could have burst.
#
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6.1. Condition:
Petya thought of a natural number and wrote down the sums of each pair of its digits on the board. After that, he erased some of the sums, and the numbers $2,0,2,2$ remained on the board. What is the smallest number Petya could have thought of?
|
Answer: 2000
## Solution.
Since among the sums there is a 0, the number must contain at least two digits 0. If the number has only three digits, there will be three pairwise sums, while the condition states there are at least four. Therefore, the number must have at least four digits. A sum of 2 can be obtained either as $1+1$ or as $2+0$. If the number contains the digit 2, then it will have four digits, three of which are $-2,0,0$, which means the number cannot be less than 2000. At the same time, 2000 meets the condition. If 2 is obtained as $1+1$, then at least four digits $-1,1,0,0$ are required. With these, it is impossible to get pairwise sums of $2,0,2$, 2, which means there must be at least 5 digits, i.e., the number will definitely be greater than 2000.
|
2000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.1. Condition:
A carpenter took a wooden square and cut out 4 smaller equal squares from it, the area of each of which was $9 \%$ of the area of the larger one. The remaining area of the original square was $256 \mathrm{~cm}^{2}$.
Find the side of the original square. Express your answer in centimeters.
|
Answer: 20
Solution.
Let the side of the larger square be 10x. The area of the smaller square is $9 \%$ of the area of the larger square, which is $9 / 100 \cdot 100 x^{2}=9 x^{2}$. After removing four smaller squares, the remaining area is $100 x^{2}-4 \cdot 9 x^{2}=64 x^{2}=256 \text{ cm}^{2}$. Therefore, $x^{2}=4$. Hence, $x=2$ cm, and the entire side is $10 x=20$ cm.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7.2 (7 points)
There are 22 kg of blueberries in a box. How can you measure out 17 kg of blueberries using a two-kilogram weight and a balance scale in two weighings.
|
# Solution:
Place the weight on one pan and balance the scales using all the blueberries $12=10+2$, then divide the 10 kg into equal parts of 5 kg each. And we get $12+5=17$ kg.
| Criteria | Points |
| :--- | :---: |
| Correct algorithm of actions | 7 |
| Incorrect solution | 0 |
Answer: 17 kg.
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7.3 (7 points)
A piece has fallen out of a dictionary, the first page of which is numbered 213, and the number of the last page is written with the same digits in some other order. How many pages are in the missing piece?
|
# Solution:
The number of the last page is 312 (it must be even). Then the number of pages is 312 - 212 = 100.
| Criteria | Points |
| :--- | :---: |
| Correct solution | 7 |
| Calculated 312 - 213 + 1 = 100, without explaining why 1 is added | 6 |
| Obtained the answer 99 | 4 |
| Noted the different parity of the first and last pages, without further progress | 2 |
| Incorrectly determined the number of the last page | 0 |
Answer: 100 pages (50 sheets)
|
100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7.5 (7 points)
On a plane, 6 lines are drawn and several points are marked. It turned out that on each line exactly 3 points are marked. What is the minimum number of points that could have been marked?
|
# Solution:
The vertices of the triangle, the midpoints of its sides, and the point of intersection of the medians - 7 points lying in threes on 6 lines (3 sides and 3 medians).
P.S. It doesn't have to be medians specifically.
Proof of the estimate: If we have a point through which at least 4 lines pass, then we will have no fewer than $1+4 \cdot 2=9$ marked points (on these 4 lines, there are 2 other marked points each). If we have
a point through which exactly 3 lines pass, then we will have no fewer than $1+3 \cdot 2=7$ marked points. If, however, through each marked point, no more than two lines pass, then the number of marked points will be no less than $6 \cdot 3 / 2=9$ (6 lines with 3 points each, each point is counted no more than twice). Therefore, we will have no fewer than 7 marked points.
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Proof of the estimate without an example | 4 |
| Example without the estimate | 3 |
| Incorrect answer | 0 |
## Answer: 7 points
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Misha has a $7 \times 7$ square of paper, all cells of which are white. Misha wants to color $N$ cells black. What is the smallest $N$ for which Misha can color the cells so that after coloring, no completely white rectangle with at least ten cells can be cut out from the square?
|
Answer: 4.
Solution. Divide the $7 \times 7$ square into 5 rectangles: four $3 \times 4$ rectangles (each corner of such a rectangle coincides with one of the corners of the $7 \times 7$ square) and a $1 \times 1$ square. If only three cells are colored, there will be a white rectangle consisting of 12 cells. Example for 4 cells: color $b 4, d 2, d 6, f 4$ in chess notation.
Criteria. Only the answer - 0 points. Correct example for 4 cells - 3 points. Proof that 3 black cells are not enough - 4 points. Points for parts of this problem are summed.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.6. On the board, 2011 numbers are written. It turns out that the sum of any three written numbers is also a written number. What is the smallest number of zeros that can be among these numbers?
|
Answer: 2009.
Solution. Let $n=2011$. Arrange the written numbers in non-decreasing order: $a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{n}$. Since the number $a_{1}+a_{2}+a_{3}$ is written, then $a_{1}+a_{2}+a_{3} \geqslant a_{1}$, hence $a_{2}+a_{3} \geqslant 0$. Similarly, we get $a_{n-2}+a_{n-1}+a_{n} \leqslant a_{n}$, hence $a_{n-2}+a_{n-1} \leqslant 0$. Therefore, $0 \geqslant a_{n-2}+a_{n-1} \geqslant a_{2}+a_{3} \geqslant 0$; thus, $a_{2}+a_{3}=a_{n-2}+a_{n-3}=0$. Since $a_{2} \leqslant a_{3} \leqslant a_{n-2} \leqslant a_{n-1}$, it follows that $a_{2}=a_{3}=a_{n-2}=a_{n-1}$, and therefore, $a_{2}=a_{3}=\ldots=a_{n-1}=0$. Thus, among the written numbers, there are at least 2009 zeros.
An example with 2009 zeros and the numbers $1, -1$ shows that there can be exactly 2009 zeros.
Comment. Only the answer - 0 points.
Provided an example showing that there can be exactly $2009-1$ points.
Proved only that there must be at least 2009 zeros - 5 points.
Only shown that $a_{2}+a_{3} \geqslant 0$ (or $\left.a_{n-1}+a_{n-2} \leqslant 0\right)-$ 1 point.
Only shown that among the written numbers, there are no more than two positive and/or no more than two negative - 3 points.
|
2009
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.8. A straight rod 2 meters long was sawn into $N$ sticks, the length of each of which is expressed in whole centimeters.
For what smallest $N$ can it be guaranteed that, using all the resulting sticks, one can, without breaking them, form the contour of some rectangle?
(A. Magazinov)
|
Answer. $N=102$.
Solution. First solution. Let $N \leqslant 101$. Cut the stick into $N-1$ sticks of 1 cm each and one stick of $201-N$ cm. It is impossible to form a rectangle from this set, as each side of the rectangle is less than half the perimeter, and thus the stick of length $201-N \geqslant 100$ cm cannot be part of any side. Therefore, $N \geqslant 102$.
We will show that for $N=102$, the desired rectangle can be found. To do this, note that among all the sticks, there will be two sticks of 1 cm each. Indeed, if this were not the case, the total length of the sticks would be at least $2 \cdot 101 + 1 = 203$ cm, which is incorrect.
Set aside these two sticks. Let the lengths of the remaining sticks be $a_{1}, a_{2}, \ldots, a_{100}$ cm, then we have $a_{1} + a_{2} + \ldots + a_{100} = 198$. Among the 100 numbers $A_{1} = a_{1}, A_{2} = a_{1} + a_{2}, A_{3} = a_{1} + a_{2} + a_{3}, \ldots, A_{100} = a_{1} + a_{2} + \ldots + a_{100}$, there will be two that give the same remainder when divided by 99. Let these be $A_{k}$ and $A_{\ell}, k < \ell$. The number $A_{\ell} - A_{k}$ is strictly greater than zero and strictly less than 198, and it is divisible by 99. Thus, $A_{\ell} - A_{k} = 99 = a_{k+1} + a_{k+2} + \ldots + a_{\ell}$.
Thus, we have found several sticks with a total length of 99 cm. Set these aside as well. The remaining sticks also have a total length of 99 cm. Therefore, we can form a rectangle of $1 \times 99$ cm.
Second solution. We will provide another proof that for $N=102$, it is possible to form a rectangle.
Let the lengths of the sticks in the set, expressed in centimeters, be $a_{1}, a_{2}, \ldots, a_{102}$. We have $a_{1} + a_{2} + \ldots + a_{102} = 200$. Consider a circle of length 200 and divide it into 102 red points, forming arcs of lengths $a_{1}, a_{2}, \ldots, a_{102}$. These points are some 102 vertices of a regular 200-gon $T$ inscribed in this circle. The vertices of $T$ are paired into opposite pairs. There are 100 such pairs, and 102 red points, so among the red points, there will be two pairs of opposite points.
These two pairs of points divide the circle into two pairs of equal arcs. Thus, we have divided all the sticks into four groups $A, B, C, D$, where the total lengths in groups $A$ and $C$, as well as in groups $B$ and $D$, are equal. Therefore, it is possible to form a rectangle using each group to form one of its sides.
Comment. Only the correct answer - 0 points.
An example is provided showing that $N \geqslant 102 - 1$ point. It is proven that $N=102$ works, but its minimality is not justified - 5 points.
|
102
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the side $A D$ of the square $A B C D$, point $K$ is marked, and on the extension of ray $A B$ beyond point $B$ - point $L$. It is known that $\angle L K C=45^{\circ}, A K=1, K D=2$. Find $L B$.
|
Answer: $L B=2$.
Fig. 1: to the solution of problem 5
Solution. Note that $\angle L A C=45^{\circ}=\angle L K C$, which implies that quadrilateral $L A K C$ is cyclic. Then $\angle K C L=90^{\circ}$ (Fig. 1). Therefore, triangle $L C K$ is an isosceles right triangle, i.e., $L C=K C$. Right triangles $B L C$ and $D K C$ are congruent by hypotenuse and leg, so $B L=K D=2$.
Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used
3 6. The cyclic nature of quadrilateral $L A K C$ is proven, but there is no further progress.
1 6. The correct answer is provided, but there is no justification.
06. The problem is not solved or is solved incorrectly.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. An excursion group of 6 tourists is visiting attractions. At each attraction, three people take photos, while the others photograph them. After what minimum number of attractions will each tourist have photos of all other participants in the excursion?
Answer: after 4 attractions.
|
Solution. Evaluation. A total of $6 \cdot 5=30$ photographs need to be taken (considering only photographs between two people $A$ and $B$, that is, if person $A$ photographs 3 other participants $B, C, D$ in one photograph - this counts as 3 photographings $A \rightarrow B, A \rightarrow C, A \rightarrow D$).
At one landmark, no more than $3 \cdot 3=9$ new photographings can occur. Thus, three landmarks are insufficient.
We can provide an example of how to organize the photographings around four landmarks. Let's number the people from 1 to 6. Then we can organize everything as follows:
- $(123) \rightarrow(456)$
- $(145) \rightarrow(236)$
- $(256) \rightarrow(134)$
- $(346) \rightarrow(125)$.
It is not difficult to verify that each person will photograph every other person at least once.
## Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used:
2 6. It is proven that the tourists need to visit at least 4 landmarks, but the method of photographing is not specified
2 6. A method of photographing at four landmarks is specified to meet the conditions of the problem, but the evaluation is not proven
0 6. The correct answer is provided, but there is no justification
0 6. The problem is not solved or is solved incorrectly.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of the numbers $1-2+3-4+5-6+\ldots+2013-2014$ and $1+2-3+4-5+6-\ldots-2013+2014$.
|
1. Answer: 2.
Notice that for each term of the first sum, except for 1, there is an opposite term in the second sum. The sum of opposite numbers is 0. Therefore, the total sum is $1+1=2$.
Grading criteria:
Correct answer with proper justification: 7 points.
Incorrect answer with the right idea in the justification: 2 points. Correct answer only: 1 point.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many natural numbers exist such that the product of all digits of such a number, multiplied by their quantity, equals 2014?
|
2. Answer: 1008.
Solution. The number 2014 is divisible only by the digits 1 and 2, so the number can only contain the digits 1 and 2. Moreover, the digit 2 can only appear once. If the number consists only of 1s, there are 2014 of them, and there is only one such number. If there is a 2, then there are 1007 digits of 1, and the 2 can be in any position, resulting in 1007 such numbers. Hence the answer.
Grading criteria:
Correct answer with proper justification: 7 points. Incorrect answer with correct idea of justification: 2 points. Only the correct answer provided: 1 point.
3) Answer: AC can be 6 cm, 8 cm, 12 cm, 16 cm, 18 cm.
4) C is the midpoint of AB. There are two cases: D is the midpoint of AC or D is the midpoint of BC, in each case AC = 12 cm.

$\xrightarrow[A C=12]{A} B$
2) D is the midpoint of AB. There are two cases: C is the midpoint of AD or C is the midpoint of BD; in the first case AC = 6 cm, and in the second case AC = 18 cm.
3) D is the midpoint of AC and C is the midpoint of BD. In this case AC = 16 cm.
4) D is the midpoint of BC and C is the midpoint of AD. In this case AC = 8 cm.

BC and C is the midpoint of AD. In this case AC = 8 cm.

Grading criteria:
Correct answer and all necessary diagrams provided: 7 points. Four answers with justification provided: 4 points. Three answers with justification provided: 2 points. Only the correct answer provided with no justification: 1 point.
|
1008
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Misha painted all integers in several colors such that numbers whose difference is a prime number are painted in different colors. What is the smallest number of colors that Misha could have used? Justify your answer.
|
5. Answer: 4 colors
Evaluation. Consider the numbers $1,3,6,8$. The difference between any two of them is a prime number, which means that all of them must be of different colors, and at least four colors are needed.
Example. Paint numbers of the form $4 \mathrm{k}$ in the first color, numbers of the form $4 \mathrm{k}+1$ in the second color, numbers of the form $4 \mathrm{k}+2$ in the third color, and numbers of the form $4 \mathrm{k}+3$ in the fourth color ( $\mathrm{k}$ - an integer). The difference between any two numbers of the same color is a multiple of 4 and cannot be a prime number.
Grading criteria:
Correct example provided: 3 points. Correct evaluation provided: 3 points.
Only the correct answer provided: 0 points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the fraction
$$
\frac{2 \cdot 2020}{1+\frac{1}{1+2}+\frac{1}{1+2+3}+\ldots+\frac{1}{1+2+3+\ldots+2020}}
$$
|
Solution. Let's denote the denominator of the fraction by $q$. By repeatedly applying the formula for the sum of an arithmetic progression, we get that
$$
q=\frac{2}{1 \cdot 2}+\frac{2}{2 \cdot 3}+\frac{2}{3 \cdot 4}+\ldots+\frac{2}{2020 \cdot 2021}
$$
Now, using the identity $\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$, we get
$$
q=\frac{2}{1}-\frac{2}{2}+\frac{2}{2}-\frac{2}{3}+\frac{2}{3}-\frac{2}{4}+\frac{2}{4}-\ldots+\frac{2}{2020}-\frac{2}{2021}=\frac{2 \cdot 2020}{2021}
$$
Substituting this expression into the original fraction and simplifying it, we get the answer: 2021.
|
2021
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How to measure 8 liters of water when you are near a river and have two buckets with a capacity of 10 liters and 6 liters? (8 liters of water should end up in one bucket).
|
Solution. Let's write the sequence of filling the buckets in the form of a table:
| | Bucket with a capacity of 10 liters | Bucket with a capacity of 6 liters | Comment |
| :--- | :--- | :--- | :--- |
| Initially | 0 liters | 0 liters | |
| Step 1 | 10 liters | 0 liters | Filled the first bucket from the river |
| Step 2 | 4 liters | 6 liters | Poured from the first bucket into the second until it was full |
| Step 3 | 4 liters | 0 liters | Poured the second bucket back into the river |
| Step 4 | 0 liters | 4 liters | Poured from the first bucket into the second bucket |
| Step 5 | 10 liters | 4 liters | Filled the first bucket from the river again |
| Step 6 | 8 liters | 6 liters | Poured from the first bucket into the second until it was full |
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Snow White entered a room where there were 30 chairs around a round table. Some of the chairs were occupied by dwarfs. It turned out that Snow White could not sit down without having someone next to her. What is the minimum number of dwarfs that could have been at the table? (Explain how the dwarfs should have been seated and why, if there were fewer dwarfs, there would be a chair with no one sitting next to it).
|
Answer: 10.
Solution: If there were three consecutive empty chairs at the table in some place, Snow White could sit down in such a way that no one would sit next to her. Therefore, in any set of three consecutive chairs, at least one must be occupied by a dwarf. Since there are 30 chairs in total, there cannot be fewer than 10 dwarfs. We will show that it is possible to seat 10 dwarfs in such a way that the condition of the problem is satisfied: we will seat the dwarfs every three chairs: on the first chair, on the fourth chair, on the seventh chair, and so on. Then the condition of the problem will be met.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Papa, Masha, and Yasha are going to school. While Papa takes 3 steps, Masha takes 5 steps. While Masha takes 3 steps, Yasha takes 5 steps. Masha and Yasha counted that together they made 400 steps. How many steps did Papa take?
|
Answer: 90 steps.
Solution. 1st method. Let's call the distance equal to 3 steps of Masha and 5 steps of Yasha a Giant's step. While the Giant makes one step, Masha and Yasha together make 8 steps. Since they made 400 steps together, the Giant would have made 400:8=50 giant steps in this time. If the Giant made 50 steps, then Masha made 150 steps. Now let's count them in "fives." 150 is 30 times 5 steps. This means that the father made 30 times 3 steps, that is, 90 steps.
2nd method. While Masha makes 3$\cdot$5=15 steps, the father makes $3 \cdot 3=9$ steps, and Yasha makes $5 \cdot 5=25$ steps. Together, in this time, Masha and Yasha will make $15+25=40$ steps. And while they make 400 steps, the father will also make 10 times more steps, that is, 9$\cdot$10=90 steps.
## 5th grade. Recommendations for checking.
Each problem is scored out of 7 points. Each score is an integer from 0 to 7. Some guidelines for checking are provided below. Naturally, the creators cannot foresee all cases. When evaluating a solution, it is important to determine whether the provided solution is generally correct (although it may have flaws) - in which case the solution should be scored no less than 4 points. Or if it is incorrect (although it may have significant progress) - in which case the score should not exceed 3 points.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How to measure 2 liters of water when you are near a river and have two buckets with a capacity of 10 liters and 6 liters? (2 liters of water should end up in one bucket).
|
Solution. Let's write the sequence of filling the buckets in the form of a table:
| | Bucket with a capacity of 10 liters | Bucket with a capacity of 6 liters | Comment |
| :---: | :---: | :---: | :---: |
| Initially | 0 liters | 0 liters | |
| Step 1 | 10 liters | 0 liters | The first bucket is filled from the river |
| Step 2 | 4 liters | 6 liters | Poured from the first bucket into the second until it is full |
| Step 3 | 4 liters | 0 liters | Poured the second bucket back into the river |
| Step 4 | 0 liters | 4 liters | Poured from the first bucket into the second |
| Step 5 | 10 liters | 4 liters | The first bucket is filled from the river |
| Step 6 | 8 liters | 6 liters | Poured from the first bucket into the second until it is full |
| Step 7 | 8 liters | 0 liters | Poured the second bucket back into the river |
| Step 8 | 2 liters | 6 liters | Poured from the first bucket into the second until it is full |
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dad, Masha, and Yasha are going to school. While Dad takes 3 steps, Masha takes 5 steps. While Masha takes 3 steps, Yasha takes 5 steps. Masha and Yasha counted that together they made 400 steps. How many steps did Dad take?
|
Answer: 90 steps.
Solution. 1st method. Let's call the distance equal to 3 steps of Masha and 5 steps of Yasha a Giant's step. While the Giant makes one step, Masha and Yasha together make 8 steps. Since they made 400 steps together, the Giant would have made 400:8=50 giant steps in this time. If the Giant made 50 steps, then Masha made 150 steps. Now let's count them in "fives." 150 is 30 times 5 steps. This means that the father made 30 times 3 steps, which is 90 steps.
2nd method. While Masha makes 3*5=15 steps, the father makes 3*3=9 steps, and Yasha makes 5*5=25 steps. Together, Masha and Yasha will make 15+25=40 steps in this time. And while they make 400 steps, the father will also make 10 times more steps, i.e., 9*10=90 steps.
In the museum, there are 16 halls arranged as shown in the diagram. In half of them, paintings are exhibited, and in the other half, sculptures. From any hall, you can go to any adjacent one (having a common wall). During any tour of the museum, the halls alternate: a hall with paintings - a hall with sculptures - a hall with paintings, and so on. The tour starts in hall A, where paintings are displayed, and ends in hall B.
a) Mark with crosses all the halls where paintings are displayed. Solution. See the diagram.
b) A tourist wants to visit as many halls as possible (travel from hall A to hall B), but visit each hall no more than once. What is the maximum number of halls he can visit? Draw one of his longest routes and prove that he could not visit more halls.
Answer: 15.
Solution. One of the possible routes is shown in the diagram. Let's prove that if the tourist wants to visit each hall no more than once, he cannot visit more than 15 halls. Note that the route starts in a hall with paintings (A) and ends in a hall with paintings (B). This means that the number of halls with paintings that the tourist has passed is one more than the number of halls with sculptures. Since the number of halls with paintings that the tourist could pass is no more than 8, the number of halls with sculptures is no more than 7. Therefore, the route cannot pass through more than
15 halls.
## 6th Grade. Recommendations for Checking.
Each problem is scored out of 7 points. Each score is an integer from 0 to 7. Some guidelines for checking are provided below. Naturally, the creators cannot foresee all cases. When evaluating a solution, it should be determined whether the provided solution is generally correct (although it may have flaws) - in which case the solution should be scored no less than 4 points. Or if it is incorrect (although it may have significant progress) - in which case the score should be no higher than 3 points.
|
90
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The clock shows half past eight. What is the angle between the hour and minute hands?
|
Answer: $75^{\circ}$.
Solution. At the moment when the clock shows half past eight, the minute hand points to the number 6, and the hour hand points to the midpoint of the arc between the numbers 8 and 9 (see figure). If two rays are drawn from the center of the clock to the adjacent
6 numbers on the clock face, the angle between them is $360^{\circ} \div 12 = 30^{\circ}$. The angle between the clock hands when they show half past eight is two and a half times larger. Therefore, it is $75^{\circ}$.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We will call a number palindromic if it reads the same from left to right as it does from right to left. For example, the number 12321 is palindromic.
a) Write any palindromic five-digit number that is divisible by 5.
b) How many five-digit palindromic numbers are there that are divisible by 5?
a) Solution. Any palindromic number ending in 5. For example, 51715.
b) Answer. 100.
|
Solution. A number that is divisible by 5 must end in 5 or 0. A palindromic number cannot end in 0, as then it would have to start with 0. Therefore, the first and last digits are 5. The second and third digits can be anything - from the combination 00 to the combination 99 - a total of 100 options. Since the fourth digit repeats the second, there will be 100 different numbers in total.
|
100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.