problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. What can the value of the expression $p^{4}-3 p^{3}-5 p^{2}+16 p+2015$ be if $p$ is a root of the equation $x^{3}-5 x+1=0$?
Answer: 2018
|
Solution: $\mathrm{p}^{4}-3 \mathrm{p}^{3}-5 \mathrm{p}^{2}+16 \mathrm{p}+2015=\left(\mathrm{p}^{3}-5 \mathrm{p}+1\right)(\mathrm{p}-3)+2018$. Since $\mathrm{p}$ is a root of the polynomial in the first parenthesis, the entire expression equals 2018.
|
2018
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are 400 students in a school. For New Year, each student sent 200 greetings to other students. What is the minimum number of pairs of students who could have greeted each other? Answer: 200.
|
Solution: The total number of greetings was $200 * 400=80000$. And the number of different pairs of students is $-400 * 399 / 2=79800$, which is 200 less than the number of greetings. Therefore, at least 200 pairs had 2 greetings. We can show that exactly 200 pairs can be: Let the 1st student greet everyone from the 2nd to the 201st, the 2nd student greet from the 3rd to the 202nd, ... the 200th student greet everyone from the 201st to the 400th, and then the 201st student greet everyone from the 202nd to the 400th and the 1st, the 202nd student greet from the 203rd to the 400th and from the 1st to the 2nd, and so on. Then the paired greetings will only be between students whose numbers differ by exactly 200.
5. Several schoolchildren have 128 identical tokens among them. They play a game according to the following rule: if someone has no less than half of all the tokens, then each of the others takes from this player as many tokens as they already have (if there are two such players, they choose by lot). Seven such exchanges occurred. Prove that now all 128 tokens are with one schoolchild.
Solution: Note that the number of tokens for those who take tokens doubles. Therefore, after the first transfer of tokens, they had a number of tokens that is a multiple of 2, but then the first player also had a number of tokens that is a multiple of two, since their total number is even. Similarly, after the second transfer of tokens, everyone will have a number of tokens that is a multiple of 4. After the 7th exchange, everyone will have a number of tokens that is a multiple of 128, that is, either 0 or 128.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. A merchant bought several bags of salt in Tver and sold them in Moscow with a profit of 100 rubles. With all the money earned, he again bought salt in Tver (at the Tver price) and sold it in Moscow (at the Moscow price). This time the profit was 120 rubles. How much money did he spend on the first purchase?
|
Answer: 500 rubles.
First method. Let the cost of a kilogram of salt in Tver be $x$ rubles, and in Moscow $-y$ rubles, and let the merchant buy $a$ kg of salt the first time. Then, according to the condition, $a(y-x)=100$.
The revenue amounted to $ay$ rubles, so the second time the merchant was able to buy $\frac{ay}{x}$ kg of salt. In this case, the profit was $\frac{ay}{x} \cdot y - ay = \frac{ay(y-x)}{x}$ rubles. According to the condition, $\frac{ay(y-x)}{x}=120$.
From the two equations obtained, it follows that $\frac{100y}{x}=120$, that is, $y=\frac{6}{5}x$. Substituting this result into the first equation, we get $ax=500$.
Second method. Let the merchant pay $x$ rubles for the salt during the first purchase in Tver. Then he sold it in Moscow for $x+100$ rubles. The second time he spent $x+100$ rubles in Tver, and received $x+100+120=x+220$ rubles in Moscow. Since the ratio of Moscow and Tver prices did not change, we set up the proportion: $\frac{x}{x+100}=\frac{x+100}{x+220}$. Solving the equation, we get $x=500$.
+ complete justified solution
$\pm$ correct solution with minor gaps or unclear places
干 correct answer obtained based on reasoning with specific numerical data
干 correct answer provided and only verified that it satisfies the condition
- only the answer is provided or the answer with unclear calculations without explanations
If the student assumes that the same number of whole bags was always bought and considers the price of one bag, the grade is not reduced.
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Sixteen boys gathered for fishing. It is known that every boy who put on boots also put on a cap. Without boots, there were 10 boys, and without a cap - two. Which boys are more and by how many: those who wore a cap but no boots, or those who put on boots? Be sure to explain your answer.
|
Answer. Those who were in caps but without boots were 2 more than those who were in boots.
Solution. Out of 16 boys, 10 were without boots, which means 6 were in boots. Two were without caps, so 14 were in caps. Since everyone who wore boots also wore a cap, out of the 14 who wore caps, 6 also wore boots, and the remaining 8 did not wear boots. Therefore, those who were in caps and without boots (8 people) are 2 more than those who were in boots (6 people).
This reasoning can be conducted based on the diagram:
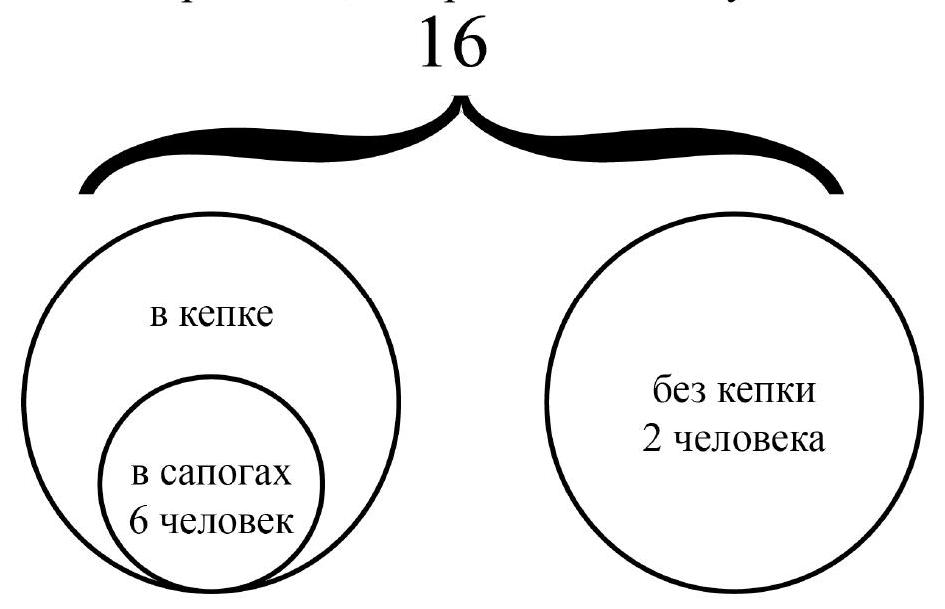
## Grading Criteria.
- Complete and justified solution - 7 points.
- Correct reasoning was conducted, but the final step was not taken (the number of those in caps and without boots and those in boots were given separately), 6 points.
- A correct diagram was drawn or correct reasoning was started, but the solution was not completed - 2 points.
- Correct answer without explanation (but with verification that everything matches) 2 points.
- Only the correct answer - 1 point.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Rectangle $A B C D$ was divided into four
smaller rectangles with equal perimeters (see figure). It is known that $A B=18$ cm, and $B C=16$ cm. Find the lengths of the sides of the other rectangles. Be sure to explain your answer.
|
Answer. 2 cm and 18 cm are the lengths of the sides of rectangle $A B L E$, 6 cm and 14 cm are the lengths of the sides of the other rectangles.
Solution. Since the perimeters of the three vertical rectangles are equal and the segments $E D, F G, K H$ and $L C$ are also equal, the segments $E F$, $F K$ and $K L$ are also equal. Therefore, each of
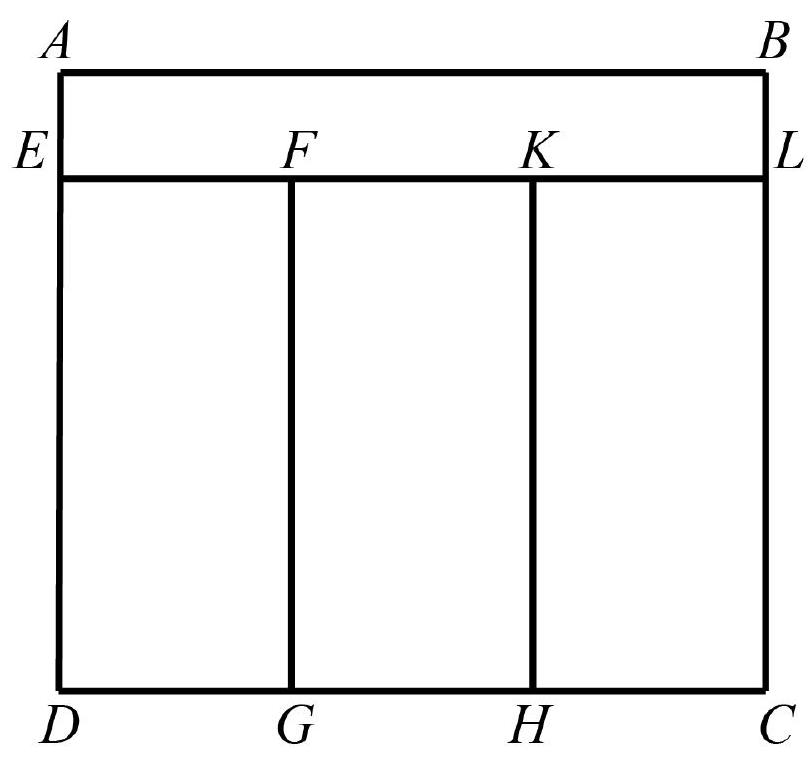
the segments $E F, F K$ and $K L$ is
$$
18 \text { cm : } 3=6 \text { cm. }
$$
The perimeter of rectangle $A B L E$ is equal to the perimeter of rectangle $D E F G$. We can solve this by setting up an equation or by trying to solve it without one.
Method 1. Let $A E=x$ cm, then $18+18+x+x=6+6+16-x+16-x$. From this, we find $x=2$. Therefore, $A E=2$ cm, and $E D=14$ cm.
Method 2. From the condition, it follows that $D E+E F=A E+A B$, that is, $D E+6=A E+18$. Then the difference in the lengths of segments $D E$ and $A E$ is 12 cm, and their sum is 16 cm according to the condition. Therefore, $A E=2$ cm, and $D E=14$ cm.
## Grading Criteria.
- Correct answer and complete explanation - 7 points.
- Correct answer with incomplete explanation - 5-6 points.
- Correct reasoning but with an arithmetic error - 3 points.
- Something is written on the picture, and the correct answer is obtained - 1-2 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
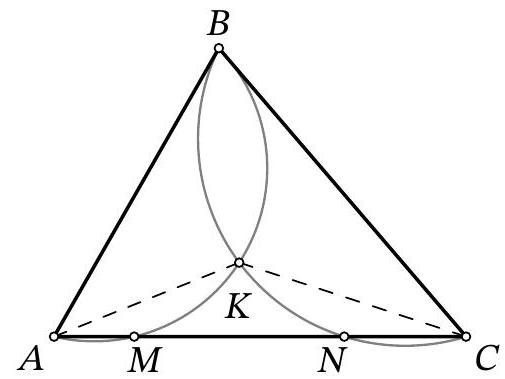
3. A point in a triangle is connected to the vertices by three segments. What is the maximum number of these segments that can equal the opposite side?
#
|
# Answer: One.
## Solution:
Let $B M = A C$ and $A B = M C$ (see fig.). Triangles $A B M$ and $M C A$ are equal by three sides. Therefore, angle $B A M$ is equal to angle $A M C$, which means $A B \parallel M C$.
Similarly, $A C \parallel M B$.
Thus, $A B M C$ is a parallelogram, but this is not the case, because angle $B M C$, lying in this parallelogram, is greater than a straight angle.
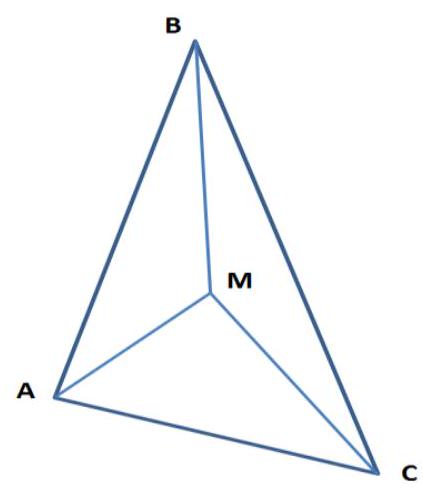
## Comment on the interpretation of the condition:
The words "Point in the triangle" imply "inside the triangle." Indeed, the solution remains valid even if point $M$ is on the boundary of the triangle. If point $M$ is chosen at a vertex, we consider this to not meet the condition of the problem ("A point in the triangle is connected to the vertices by three segments" - if the point coincides with a vertex, the segment becomes degenerate).
In other words, by default, it is assumed that the point is chosen strictly inside the triangle.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $p(x)=2 x^{3}-3 x^{2}+1$. How many squares of integers are among the numbers $p(1), p(2), \ldots$, $p(2016) ?$
#
|
# Answer: 32.
## Solution:
Notice that $p(x)=(x-1)^{2}(2 x+1)$.
For an integer $x(1 \leq x \leq 2016)$, the number $p(x)=(x-1)^{2}(2 x+1)$ is a perfect square of an integer either when $x=1(p(1)=0)$, or (for $x \geq 2$) when the number $2 x+1$ is a perfect square.
Note that for $x \geq 2$, the inequality holds: $5 \leq 2 x+1 \leq 4033$, and also that $2 x+1$ is odd.
Such squares are the numbers 9 (for $x=4$), 25 (for $x=12$), 49 (for $x=24$), and so on up to $63^{2}=3969$ (for $x=1984$) - that is, we have considered the squares of odd numbers from $3^{2}$ to $63^{2}$ (a total of 31). Together with the previously found square at $x=1$, we get 32 perfect squares among the numbers of the specified form.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. Find the largest five-digit number, the product of whose digits is 120.
|
Answer: 85311.
Solution. The largest single-digit divisor of the number $120-8$, so the desired number definitely starts with this digit. The product of all the remaining digits is 15.
The largest single-digit divisor of the number $15-5$, so the digit in the thousands place will be this digit. The product of the last three digits is three 3, so the largest number will end with 311.
|
85311
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.2. During the first half of the year, lazy Pasha forced himself to solve math problems. Every day he solved no more than 10 problems, and if on any day he solved more than 7 problems, then for the next two days he solved no more than 5 problems per day. What is the maximum number of problems Pasha could solve in 7 consecutive days?
|
Answer: 52.
Solution. Suppose Pasha solved at least 8 tasks (but no more than 10) in one of the first five days, then in the next two days he solved no more than 5 tasks per day. Thus, in these three days, he solved no more than $20(10+5+5)$ tasks. If he solved 7 tasks each day, it would be more.
It turns out that in the first five days, Pasha solved no more than 35 tasks. It remains to note that in the last two days, he solved no more than 17 tasks (since he could not exceed the limit of 7 tasks on both days), and he could solve 17 tasks (7 tasks on the sixth day and 10 tasks on the seventh day).
|
52
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. Given a convex quadrilateral $ABCD$, $X$ is the midpoint of diagonal $AC$. It turns out that $CD \parallel BX$. Find $AD$, if it is known that $BX=3, BC=7, CD=6$.

|
Answer: 14.
Solution. Double the median $B X$ of triangle $A B C$, to get point $M$. Quadrilateral $A B C M$ is a parallelogram (Fig. 1).
Notice that $B C D M$ is also a parallelogram, since segments $B M$ and $C D$ are equal in length (both 6) and parallel. This means that point $M$ lies on segment $A D$, since $A M \| B C$ and $M D \| B C$.
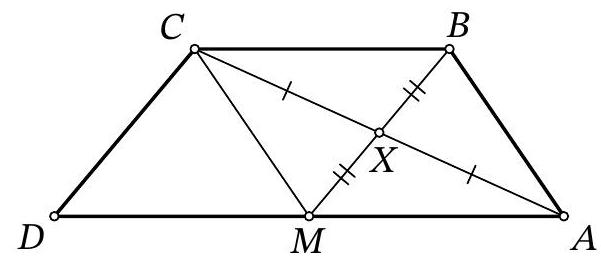
Fig. 1: to the solution of problem 9.3
Now it is easy to find the desired segment:
$$
A D=A M+M D=B C+B C=14
$$
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. A white checkered $8 \times 8$ table is given. In it, 20 cells are painted black. What is the minimum number of pairs of adjacent white cells that could remain?
|
Answer: 34.
Solution. We will call a pair of cells that are adjacent by side simply a pair. Let's first count the total number of pairs. There are 7 pairs in each row and column, so there are a total of $7 \cdot 8 \cdot 2 = 112$ pairs.
We will call cells that touch the border of the table boundary cells, and those that do not touch the border middle cells. Among the 20 black cells, consider the maximum number of middle black cells, no two of which are adjacent by side. We will call these black cells main, and let there be $s$ of them. Since all the middle cells of the table can be divided into $\frac{6^2}{2} = 18$ non-overlapping pairs (dominoes $1 \times 2$), in each of which there is no more than one main black cell, then $s \leqslant 18$.
In the initially white table, we will color the cells black one by one until there are 20, starting with $s$ main black cells. We will say that a black cell ruins a pair of adjacent cells if it is in it. Each of the main black cells ruins 4 pairs, so in total they ruin $4s$ pairs. Next, we color in black, in any order, the middle non-main cells (which are already contained in at least one ruined pair) and the boundary cells (which in principle are contained in three or two pairs). The remaining $20-s$ black cells ruin no more than 3 pairs each, so in total they ruin no more than $3(20-s) = 60 - 3s$ new pairs. In total, no more than $4s + 60 - 3s = 60 + s \leqslant 60 + 18 = 78$ pairs are ruined. Then, the number of unruined pairs, consisting only of white cells, is no less than $112 - 78 = 34$.
An example with 34 pairs of white cells is constructed as follows: consider 18 main black cells and 2 more boundary cells, each of which does not form a pair with other black cells (Fig. 3).
| | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
Fig. 3: to the solution of problem 9.6
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. The sides of the square $A B C D$ are parallel to the coordinate axes, with $A B$ lying on the y-axis, and the square is positioned as shown in the figure. The parabola defined by the equation
$$
y=\frac{1}{5} x^{2}+a x+b
$$
passes through points $B$ and $C$. Additionally, the vertex of this parabola (point $E$) lies on the segment $A D$. Find the sum of the roots of the quadratic trinomial whose graph is the parabola.
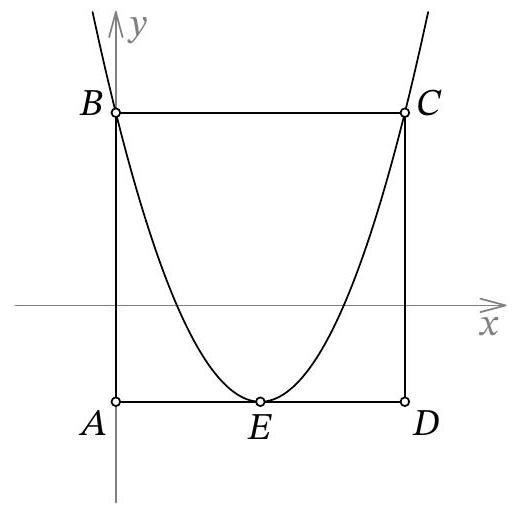
|
Answer: 20.
Solution. Note that the parabola is symmetric with respect to the vertical axis passing through its vertex, point $E$. Since points $B$ and $C$ are on the same horizontal line, they are symmetric with respect to this axis. This means that this axis passes through the midpoint of $B C$, and therefore, through the midpoint of $A D$.
Now that we have established that $E$ is the midpoint of $A D$, let's find the length of the side of the square $A B C D$. By completing the square in the quadratic polynomial, we get
$$
y=\frac{1}{5}\left(x-x_{E}\right)^{2}+y_{E}
$$
where $\left(x_{E}, y_{E}\right)$ are the coordinates of the vertex of the parabola (we will similarly denote the coordinates of other marked points). Substituting $x=x_{B}, y=y_{B}$ (the equality will hold since $B$ lies on the parabola) and moving $y_{E}$ to the left side, we get:
$$
y_{B}-y_{E}=\frac{1}{5}\left(x_{B}-x_{E}\right)^{2}
$$
If we denote the unknown side length of the square by $L$, then $y_{B}-y_{E}=L$ and $x_{B}-x_{E}=L / 2$. We obtain the relation $L=\frac{1}{5}(L / 2)^{2}$, from which it is not difficult to extract $L=20$.
It remains to recall that the points on the graph corresponding to the roots of the polynomial are also symmetric with respect to the axis of the parabola, which means that the semi-sum of the roots is equal to the abscissa of the vertex $x_{E}=L / 2$. Therefore, the sum of the roots is $L=20$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. 73 children are standing in a circle. A mean Father Frost walks around the circle clockwise and distributes candies. At first, he gave one candy to the first child, then skipped 1 child, gave one candy to the next child, then skipped 2 children, gave one candy to the next child, then skipped 3 children, and so on.
After distributing 2020 candies, he left. How many children did not receive any candies?
|
Answer: 36.
Solution. Let's number the children clockwise from 0 to 72. Initially, Santa Claus gives a candy to the child with number 1.
Consider the sequence of numbers $a_{n}=1+2+3+\ldots+n$, where $n=1,2,3, \ldots, 2020$. Notice that the $n$-th candy is given to the child whose number is the remainder of the division of $a_{n}$ by 73. We need to determine how many different remainders there are among these.
Consider the difference $a_{k}-a_{l}$ (for $k \geqslant l$). This is the sum of an arithmetic progression:
$$
a_{k}-a_{l}=(l+1)+(l+2)+\ldots+k=\frac{1}{2}(k+l+1)(k-l)
$$
The remainders of the division of $a_{k}$ and $a_{l}$ by 73 will coincide if this difference is divisible by 73. Since 73 is a prime number, either $k-l$ or $k+l+1$ must be divisible by 73.
First, note that all candies starting from the 74th will go to the children who have already received them in previous steps, since $k-(k-73)$ is divisible by 73, and therefore the numbers $a_{k}$ and $a_{k-73}$ give the same remainders when divided by 73. Thus, it is sufficient to consider $a_{k}$ for $k=1, \ldots, 73$.
For different natural numbers $k$ and $l$, not exceeding 73, the difference $k-l$ will not be divisible by 73. For the sum $k+l+1$ to be divisible by 73, it must be either 73 or $2 \cdot 73$. In the first case, we get $l=72-k$, where $k=1, \ldots, 71$ and $k \neq 36$, and in the second case only $k=72$ and $l=73$ (and vice versa).
This means that the same remainders will be in pairs $\left(a_{1}, a_{71}\right),\left(a_{2}, a_{70}\right), \ldots,\left(a_{35}, a_{37}\right),\left(a_{72}, a_{73}\right)$. The remainders between the pairs are different (and also different from the number $a_{36}$). In total, there are 37 different remainders.
Thus, among the 73 children, only 37 will receive candies. Therefore, 36 children will be left without candies.
## 10th grade
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.2. How many roots does the equation
$$
\overbrace{f(f(\ldots f}^{10 \text { times } f}(x) \ldots))+\frac{1}{2}=0
$$
have, where $f(x)=|x|-1$?
|
Answer: 20.
Solution. Let
$$
f_{n}(x)=\overbrace{f(f(\ldots(f}^{n \text { times } f}(x) \ldots))
$$
We will solve the equation $f_{10}(x)=-\frac{1}{2}$ graphically.
We will use the fact that the graph of $y=f_{k}(x)$ can be obtained from the graph of $y=f_{k-1}(x)$, based on the relation $f_{k}(x)=\left|f_{k-1}(x)\right|-1$. Specifically, to construct the next graph, we need to take the previous one, reflect all points with negative ordinates relative to the x-axis (obtaining $y=\left|f_{k-1}(x)\right|$), and then shift the entire graph down by 1.
We start with the graph of $y=f(x)$ (the gray line represents $y=|x|$):
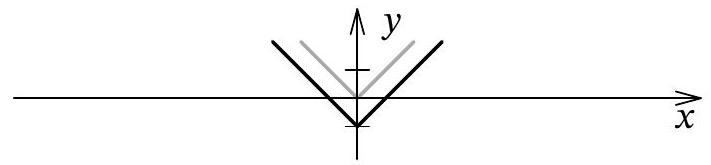
Reflecting its lower part relative to the x-axis, we get $y=|f(x)|$ (depicted below in gray), and shifting it down by 1, we get $y=f_{2}(x)$:
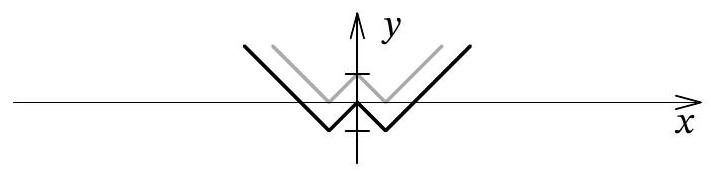
Repeating this process 8 more times, we arrive at the following graph:
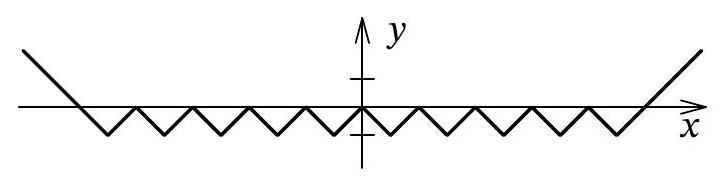
It is clear that it has exactly 20 intersections with the line $y=-\frac{1}{2}$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. Anton wrote three natural numbers $a, b$, and $c$ on the board. Ira drew three rectangles $a \times b, a \times c$, and $b \times c$ on the board. It turned out that the difference in the areas of one pair of rectangles is 1, and the difference in the areas of another pair of rectangles is 49. What can $a+b+c$ be? List all possible options.
|
Answer: 16.
Solution. Without loss of generality, we assume that $1=ac-ab=a(c-b)$, then $a=1$, $c=b+1$. Thus, the numbers written on the board were $1, b, b+1$.
Notice that either $b(b+1)-b \cdot 1=49$, or $b(b+1)-(b+1) \cdot 1=49$.
In the first case, we get $b^{2}=49, b=7$, and $a+b+c=1+b+(b+1)=16$.
In the second case, we get $b^{2}=50$. Such natural $b$ does not exist.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
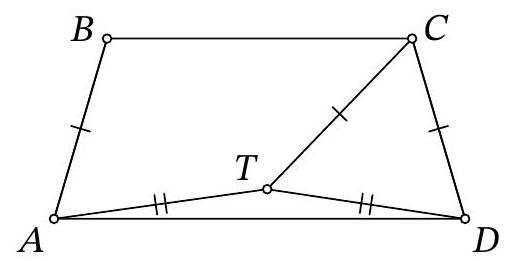
Problem 10.4. An isosceles trapezoid $ABCD$ with bases $BC$ and $AD$ is such that $\angle ADC = 2 \angle CAD = 82^{\circ}$. Inside the trapezoid, a point $T$ is chosen such that $CT = CD, AT = TD$. Find $\angle TCD$. Give your answer in degrees.
|
Answer: $38^{\circ}$.
Solution. Let $a$ be the length of the lateral side of the trapezoid. Note that point $T$ lies on the perpendicular bisector of the bases of the trapezoid, that is, on its axis of symmetry. From symmetry, we get that $B T=T C=a$ (Fig. 5).
Fig. 5: to the solution of problem 10.4
Next, note that $\angle B A D=\angle C D A=2 \angle C A D$, so $A C$ is the bisector of angle $B A D$. Since $\angle C A D=\angle A C B$ due to parallelism, triangle $A B C$ is isosceles. Therefore, $B C$ is also equal to $a$.
We have obtained that triangle $B T C$ is equilateral, and its angles are each $60^{\circ}$. Now it is not difficult to calculate the required angle:
$$
\angle T C D=\angle B C D-\angle B C T=\left(180^{\circ}-\angle A D C\right)-60^{\circ}=120^{\circ}-\angle A D C=38^{\circ} .
$$
|
38
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. On an island, there are two tribes: knights and liars. Knights always tell the truth, while liars always lie. One day, 80 people sat around a round table, and each of them stated: "Among the 11 people sitting after me in a clockwise direction, there are at least 9 liars." How many knights are sitting at the round table? List all possible options.
|
Answer: 20.
Solution. First, we prove that among 12 consecutive people, there are no more than 3 knights. Suppose this is not the case. Consider the first knight in this group. Among the 11 people sitting after him in a clockwise direction, there are at least 3 knights, which contradicts the problem's condition.
Next, suppose there are 4 consecutive liars. Number all people clockwise from 1 to 80 so that these liars have numbers from 1 to 4.
Consider the first liar. From his statement, it follows that among people with numbers from 2 to 12, there are at least 3 knights, but from the above proof, we know there are no more than 3 knights. Since the first three of them are definitely liars, among people with numbers from 5 to 12, there are exactly 3 knights.
Now consider the group of people with numbers from 5 to 16. Among them, there are no more than 3 knights, but among people with numbers from 5 to 12, there are exactly 3 knights. Therefore, people with numbers from 13 to 16 are liars. Thus, we have found a new set of 4 consecutive liars, shifted by 12 people in a clockwise direction from the original set.
Continuing similar reasoning for the new set of 4 consecutive liars, we will get another such set, then another, and so on. Since the greatest common divisor (GCD) of 80 and 12 is 4, all people at the table will fall into such sets. But they cannot all be liars, which is a contradiction.
Thus, our assumption was incorrect, and in any set of 4 consecutive people, there is at least one knight. But we know that among 12 consecutive people, there are no more than 3 knights. Therefore, in any set of 4 consecutive people, there is exactly one knight, meaning there are exactly 20 knights at the table.
It remains to construct an example of such a seating arrangement of knights and liars. Let all people with numbers divisible by 4 be knights, and all others be liars. It is not difficult to verify that this example satisfies the problem's condition.
Another solution. Let's call the sorrow of a certain person the number of liars among 12 people, including himself and 11 others sitting consecutively after him in a clockwise direction. According to the problem, the sorrow of each knight is at least 9, and the sorrow of each liar is at most 9. We will prove that the sorrow of all people is exactly 9.
First, note that the sorrow of adjacent people cannot differ by more than 1. Indeed, when moving to the next person in a clockwise direction, one person is removed from their set of 12, and one is added. Therefore, the number of liars can decrease by no more than 1 and increase by no more than 1.
Now suppose that a certain knight has a sorrow greater than 9. Then the sorrow of the next person is no less: from their set of 12 people, this knight is removed, and an unknown person is added, i.e., the number of liars does not decrease. Therefore, a liar cannot follow such a knight, and we have found another knight with a sorrow greater than 9. Clearly, we can continue this process in a circle and arrive at a contradiction: all at the table cannot be knights.
Similarly, it can be proven that a liar cannot have a sorrow less than 9. Indeed, the sorrow of the next person after such a liar cannot be greater than the liar's; therefore, this must also be a liar with a sorrow less than 9; continuing this, we arrive at the conclusion that all at the table are liars, which is also impossible.
Now it is clear that the number of liars among any 12 consecutive people is equal to the sorrow of the first of them, i.e., 9. From this, it is easy to understand that two people at a distance of 12 (i.e., with 11 others between them) have the same type (knight or liar), since adding either of them to the 11 intermediate people should result in 9 liars. This means that the sequence of knights and liars is periodic with a period of 12; but since the GCD of 80 and 12 is 4, it is also periodic with a period of 4.
Dividing the entire table into identical sets of four, it is easy to see that in each of them there are 3 liars (otherwise, in a group of three adjacent sets of four, there would not be 9). Therefore, there is one knight in each, meaning there are 20 knights in total.
A periodic seating arrangement of knights with three liars in between, as is easy to verify, satisfies the condition.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
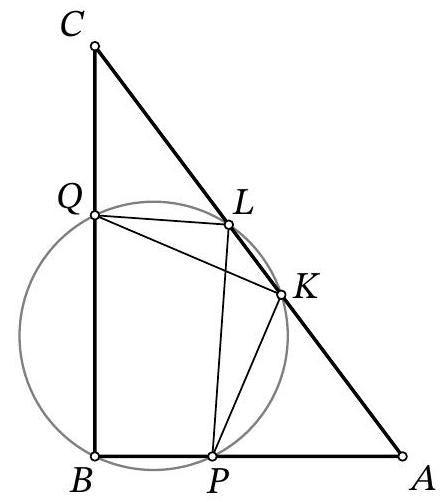
Problem 10.7. Given a right triangle $ABC$ with legs $AB=42$ and $BC=56$. A circle passing through point $B$ intersects side $AB$ at point $P$, side $BC$ at point $Q$, and side $AC$ at points $K$ and $L$. It is known that $PK=KQ$ and $QL: PL=3: 4$. Find $PQ^2$.
|
Answer: 1250.
Solution. Since in a cyclic quadrilateral the sum of opposite angles is $180^{\circ}$, then $\angle P K L=\angle P L Q=90^{\circ}$. From the condition, it also follows that right triangles $A B C$ and $Q L P$ are similar (Fig. 6). From this similarity and the cyclic nature of the pentagon
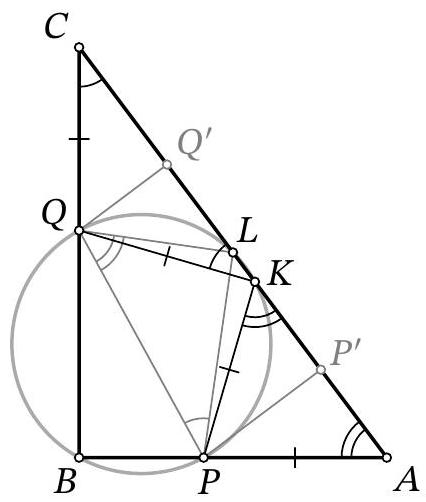
Fig. 6: to the solution of problem 10.7
$B Q L K P$, we get that $\angle C=\angle Q P L=\angle Q K L$, so triangle $C Q K$ is isosceles and $C Q=Q K$. Similarly, $\angle A=\angle P Q L=180^{\circ}-\angle P K L=\angle A K P$, so $A P=P K$. Also, by the condition, $P K=K Q$.
Thus, $C Q=Q K=P K=A P=x$. From the condition, we have
$$
A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{14^{2}\left(3^{2}+4^{2}\right)}=14 \cdot 5=70
$$
and also $\cos A=\frac{3}{5}$ and $\cos C=\frac{4}{5}$. Drop perpendiculars $P P^{\prime}$ and $Q Q^{\prime}$ to the hypotenuse $A C$. Then
$$
70=A C=A K+K C=2 A P^{\prime}+2 C Q^{\prime}=2 x \cos A+2 x \cos C=2 x\left(\frac{3}{5}+\frac{4}{5}\right)=\frac{14}{5} x
$$
from which $x=25$. By the Pythagorean theorem in triangle $P K Q$, we get
$$
P Q^{2}=P K^{2}+Q K^{2}=25^{2}+25^{2}=1250
$$
Another solution. As in the previous solution, by the Pythagorean theorem, we find $A C=70$. Also, from the similarity and the cyclic nature, we get $\angle C=\angle Q P L=\angle Q B L$, so triangle $C L B$ is isosceles and $C L=L B$. Similarly, $\angle A=\angle P Q L=\angle P B L$, so $A L=B L=C L$, i.e., $L$ is the midpoint of the hypotenuse.
Point $K$ is equidistant from points $P$ and $Q$, i.e., it is the midpoint of the arc $P L Q$ of the given circle and lies on the angle bisector of $\angle B$. Then, by the property of the angle bisector, we get $A K: K C=$ $A B: B C=3: 4$, which gives us $A K=\frac{3}{7} A C=30$ and $C K=\frac{4}{7} A C=40$. From the properties of secants to a circle drawn from the same point, we get $A K \cdot A L=A B \cdot A P$ and $C K \cdot C L=C Q \cdot C B$, from which respectively
$$
A P=\frac{A K \cdot A L}{A B}=\frac{30 \cdot 35}{42}=25 \quad \text { and } \quad C Q=\frac{C K \cdot C L}{C B}=\frac{40 \cdot 35}{56}=25
$$
Then $B P=A B-A P=17$ and $B Q=B C-C Q=31$, from which by the Pythagorean theorem in triangle $P B Q$ we get $P Q^{2}=P B^{2}+B Q^{2}=17^{2}+31^{2}=1250$.
|
1250
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. Two bandits stole 300 gold coins. They decided to divide them as follows: the first bandit puts some coins (possibly all) into a bag, and the second bandit chooses who gets this bag; then this action is repeated several times. The division ends when
- either all the money is gone,
- or someone gets 11 bags - in this case, all the remaining money immediately goes to the other bandit.
What is the maximum number of coins that the first bandit can guarantee to get?
|
Answer: 146.
Solution. First, we will show that the first bandit can get at least 146 coins. His strategy will be to put 14 coins in each bag. First, note that he will always be able to do this: since $21 \cdot 14=294$, he will do this at least 21 times, and when the coins start to run out, the process will certainly be over (one of the bandits will get 11 bags).
Let's analyze how the game can end. If the first bandit has accumulated 11 bags, that's already 154 coins. In the other case, the second bandit, on the contrary, has no more than 11 bags, that is, no more than 154 coins. Therefore, the remaining coins are with the first bandit, which is at least 146.
Now we will show how the second bandit can guarantee himself 154 coins. His strategy is as follows: take bags with 14 coins or more for himself, and give bags with 13 coins or less to the first bandit.
Similarly, let's analyze how the game can end. If the second bandit finishes with 11 bags, he will have at least 154 coins. In the other case, the first bandit will finish with no more than 11 bags, which is no more than $11 \cdot 13=143$ coins. Then the second bandit will have at least 157 coins.
Remark. Let's indicate how to get the answer in the general case. Suppose there are $N$ coins in total, and each bandit can get no more than $k$ bags ($N \geqslant 2 k$). We will divide the coins into $2 k$ almost equal groups, so that either all groups have the same number of coins (if $N \vdots 2 k$), or the number of coins in the groups differs by no more than 1 (such a division is unique). We will order the groups in ascending order. By reasoning similar to the one provided above, we can show that the first bandit can guarantee himself the sum of the $k$ smaller groups of the division, and the second bandit can guarantee the sum of the $k$ larger groups.
## 11th Grade
|
146
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. The teacher wrote a two-digit number on the board. Each of the three boys made two statements.
- Andrey: “the number ends with the digit 6” and “the number is divisible by 7”.
- Borya: “the number is greater than 26” and “the number ends with the digit 8”.
- Sasha: “the number is divisible by 13” and “the number is less than 27”.
It is known that each boy was right once and wrong once. What number could have been written on the board? List all possible options.
|
Answer: 91.
Solution. Let's consider Sasha's statements. If his second statement that the number is less than 27 is true, then Borya's first statement is definitely false, so the number must end in 8. The only two-digit number that meets these conditions is 18, but then none of Andrei's statements are true. Contradiction.
Therefore, the first statement of Sasha that the number is divisible by 13 must be true; then his second statement is false, and the number is not less than 27. But in this case, Borya's first statement that the number is greater than 26 is true, and his second statement that the number ends in 8 is false. Among the two-digit numbers divisible by 13, greater than 26, and not ending in 8, only the number 91 fits (the numbers $39,52,65$ do not fit because both of Andrei's statements would be false).
|
91
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. Vera has a set of weights of different masses, each weighing an integer number of grams. It is known that the lightest weight in the set weighs 71 times less than all the other weights combined. It is also known that the two lightest weights in the set together weigh 34 times less than all the other weights combined. What is the smallest number of grams the lightest weight can weigh?
|
Answer: 35.
Solution. All weights in the solution are expressed in grams.
Let the lightest weight be $m$, then the other weights are $71 m$, and the total weight is $72 \mathrm{~m}$. Let also the two lightest weights together weigh $n$, then the other weights weigh $34 n$, and the total weight is $35 n$, which is divisible by 35. Therefore, $72 m$ is divisible by 35, i.e., $m$ is divisible by 35, since 72 and 35 are coprime.
Thus, $m \geqslant 35$. Now let's provide an example of a possible set of weights where $m=35$. For the set of weights with different weights $35,37,48,2400$, all conditions are met: $35 \cdot 71=$ $2485=37+48+2400,(35+37) \cdot 34=2448=48+2400$.
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. On the coordinate plane, all points $(x, y)$ such that $x$ and $y$ are integers satisfying the inequalities $0 \leqslant x \leqslant 2$ and $0 \leqslant y \leqslant 26$ are marked. How many lines exist that pass through exactly 3 of the marked points?
|
Answer: 365.
Solution. All marked points are located on three vertical lines $x=0, x=1, x=2$. Let's call these lines the left, middle, and right lines, respectively.
Consider any three marked points lying on one line. If at least two of them lie on a vertical line, then there are more than 3 marked points on such a line, which does not fit our criteria. Therefore, on each of the three vertical lines, exactly one point must be chosen.
Notice that when choosing point $A(0, a)$ on the left line and point $B(2, b)$ on the right line, the point on the middle line is uniquely determined - it is the midpoint of segment $AB$, and it has coordinates $(1, \frac{a+b}{2})$. It has integer coordinates if and only if the numbers $a$ and $b$ have the same parity. Consequently, the number of lines passing through exactly three marked points is equal to the number of pairs $(a, b)$ for which $a$ and $b$ are integers of the same parity from 0 to 26 inclusive (it is clear that each triplet of integers $\left(a, \frac{a+b}{2}, b\right)$ corresponds to its own line containing exactly three marked points). On the segment $[0 ; 26]$, there are 14 even and 13 odd numbers, so the answer to the problem is the number $14 \cdot 14 + 13 \cdot 13 = 365$.
|
365
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. On the side $AC$ of triangle $ABC$, points $M$ and $N$ are marked ($M$ lies on the segment $AN$). It is known that $AB = AN$, $BC = MC$. The circumcircles of triangles $ABM$ and $CBN$ intersect at points $B$ and $K$. How many degrees does the angle $AKC$ measure if $\angle ABC = 68^\circ$?
|
Answer: 124.
Solution. From the given in the problem, it follows that $68^{\circ}+\alpha+\gamma=180^{\circ}$, where $\alpha$ and $\gamma$ denote the measures of angles $A$ and $C$ of the triangle, respectively. Since triangle $BAN$ is isosceles, $\angle BNA=90^{\circ}-\frac{1}{2} \alpha$, so $\angle BNC=90^{\circ}+\frac{1}{2} \alpha$. Similarly, $\angle BMA=90^{\circ}+\frac{1}{2} \gamma$.
From the fact that these angles are inscribed in the corresponding circles, we get $\angle BKA=90^{\circ}+\frac{1}{2} \alpha$ and $\angle BKC=90^{\circ}+\frac{1}{2} \gamma$ (Fig. 7). It remains
$$
\angle AKC=360^{\circ}-\angle BKA-\angle BKC=180^{\circ}-\frac{1}{2}(\alpha+\gamma)=90^{\circ}+\frac{1}{2} \cdot 68^{\circ}=124^{\circ}
$$

Fig. 7: to the solution of problem 11.4
Remark. Point $K$ is the incenter of triangle $ABC$.
|
124
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. In a chess tournament, a team of schoolchildren and a team of students, each consisting of 15 people, are competing against each other. During the tournament, each schoolchild must play against each student exactly once, and each person must play no more than one game per day. The number of games played on different days may vary.
At some point in the tournament, the organizer noticed that the schedule for the next day can be arranged in exactly 1 way with 15 games, and in $N$ ways with 1 game (the order of the games in the schedule does not matter, only who plays against whom). Find the maximum possible value of $N$.
|
Answer: 120.
Solution. Note that $N$ is the total number of games that remain to be played in the tournament.
Let's describe an example where $N=120$. Number the students and schoolchildren from 1 to 15. Suppose the schoolchild with number $k$ needs to play with students numbered from 1 to $k$. Then the total number of games remaining to be played is
$$
1+2+3+\ldots+15=120
$$
games. It is not hard to verify that there is exactly one way to schedule 15 games in one day (the first schoolchild must play with the first student, the second with the second, the third with the third, ..., the fifteenth with the fifteenth).
Now we will prove that $N \leqslant 120$. Without loss of generality, we will assume that the only way to play 15 games is when the first schoolchild plays with the first student, the second schoolchild with the second student, ..., the fifteenth schoolchild with the fifteenth student. These 15 pairs will be called direct, and pairs of players with different numbers will be called cross.
Note that we cannot have a situation where the $k$-th schoolchild needs to play with the $m$-th student, and the $m$-th schoolchild needs to play with the $k$-th student (otherwise, there is another way to play 15 games). Thus, for each pair of numbers $k$ and $m$, no more than one cross game is scheduled. The total number of cross games is then no more than $\frac{15 \cdot 14}{2}=105$. Adding the direct games, we get no more than 120.
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Given a convex quadrilateral $A B C D$. It is known that $\angle C=57^{\circ}, \sin \angle A+$ $\sin \angle B=\sqrt{2}$ and $\cos \angle A+\cos \angle B=2-\sqrt{2}$. How many degrees does angle $D$ measure?
|
Answer: 168.
Solution. We transform the given sums of trigonometric functions:
\[
\begin{aligned}
\sqrt{2} & =\sin \angle A+\sin \angle B=2 \sin \left(\frac{\angle A+\angle B}{2}\right) \cos \left(\frac{\angle A-\angle B}{2}\right) \\
2-\sqrt{2} & =\cos \angle A+\cos \angle B=2 \cos \left(\frac{\angle A+\angle B}{2}\right) \cos \left(\frac{\angle A-\angle B}{2}\right)
\end{aligned}
\]
Since both expressions are not equal to 0, we divide the first by the second and cancel the common factor \(\cos \left(\frac{\angle A-\angle B}{2}\right)\), which is not equal to 0. We get
\[
\frac{\sqrt{2}}{2-\sqrt{2}}=\operatorname{tg}\left(\frac{\angle A+\angle B}{2}\right)
\]
from which it is not difficult to extract \(\operatorname{tg}\left(\frac{\angle A+\angle B}{2}\right)=\sqrt{2}+1\), by eliminating the irrationality in the denominator.
Applying the double-angle tangent formula \(\operatorname{tg} 2 x=\frac{2 \operatorname{tg} x}{1-\operatorname{tg}^{2} x}\), we obtain
\[
\operatorname{tg}(\angle A+\angle B)=\frac{2(\sqrt{2}+1)}{1-(\sqrt{2}+1)^{2}}=\frac{2 \sqrt{2}+2}{-2 \sqrt{2}-2}=-1
\]
i.e., \(\angle A+\angle B=180^{\circ} \cdot k-45^{\circ}\) for some integer \(k\).
The angles \(\angle A\) and \(\angle B\) are less than \(180^{\circ}\), since the quadrilateral is convex; and since the sum of their cosines is positive, they cannot both be obtuse. Therefore, \(\angle A+\angle B<270^{\circ}\), leaving the only solution \(\angle A+\angle B=135^{\circ}\). Then the angle \(D\) is equal to \(360^{\circ}-57^{\circ}-135^{\circ}=168^{\circ}\).
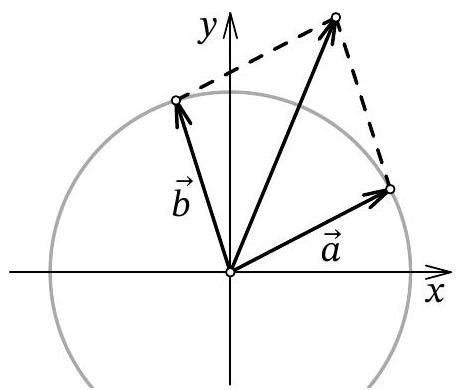
Figure 8: to the remark in the solution of problem 11.6
Remark. Consider the vectors \(\vec{a}=(\cos \angle A, \sin \angle A)\) and \(\vec{b}=(\cos \angle B, \sin \angle B)\) (Figure 8) and their sum, which is equal to \((2-\sqrt{2}, \sqrt{2})\) by the given condition. If we draw the parallelogram corresponding to this sum, it turns out to be a rhombus, and its diagonal is the bisector between \(\vec{a}\) and \(\vec{b}\). This provides a geometric explanation for why the angle between the x-axis and the vector \(\vec{a}+\vec{b}\) is \(\frac{1}{2}(\angle A+\angle B)\), which is why, when dividing one coordinate of the vector by the other in the solution, we obtained \(\operatorname{tg}\left(\frac{\angle A+\angle B}{2}\right)\).
|
168
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.7. Natural numbers $a$ and $b$ are such that $a^{a}$ is divisible by $b^{b}$, but $a$ is not divisible by $b$. Find the smallest possible value of the number $a+b$, given that the number $b$ is coprime with 210.
|
Answer: 374.
Solution. Obviously, $b \neq 1$. Let $p$ be a prime divisor of the number $b$; then $p \geqslant 11$, since $b$ is coprime with $210=2 \cdot 3 \cdot 5 \cdot 7$. Since $a^{a}$ is divisible by $b^{b}$, which is divisible by $p$, then $a$ is also divisible by $p$. From this, it immediately follows that the number $b$ is not a prime.
We will prove that $a+b \geqslant 253+121=374$. If $b$ can be represented as the product of at least three prime factors (not necessarily distinct), then it is not less than $11^{3}>374$, and thus $a+b$ is greater than 374. Now let $b$ be representable as exactly two prime factors. If $b=q r$ for distinct prime numbers $q$ and $r$, then by the above, $a$ is divisible by both $q$ and $r$, but then it is divisible by $b$, which is impossible.
The only case left to consider is when $b=s^{2}$ for some prime $s \geqslant 11$. The number $a$ is divisible by $s$; let $a=s k$ for some natural number $k$. The number $k$ is coprime with $s$, since $a$ is not divisible by $b$.
Since $a^{a}=(s k)^{s k}=s^{s k} \cdot k^{s k}$ is divisible by $b^{b}=\left(s^{2}\right)^{s^{2}}=s^{2 s^{2}}$, then $s^{s k}$ is divisible by $s^{2 s^{2}}$, i.e., $s k \geqslant 2 s^{2}$, and $k \geqslant 2 s$. The number $k$ is coprime with $s$, so it is not equal to $2 s$, i.e., $k \geqslant 2 s+1$.
Then $a+b=s k+s^{2} \geqslant s(2 s+1)+s^{2} \geqslant 11 \cdot 23+11^{2}=253+121=374$.
It is easy to verify that for $a=253=11 \cdot 23$ and $b=121=11^{2}$ all conditions are satisfied: $a^{a}=11^{253} \cdot 22^{253}$ is divisible by $b^{b}=11^{242}$, $a$ is not divisible by $b$, and the number $b$ is coprime with 210.
|
374
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Inside the tetrahedron $ABCD$, points $X$ and $Y$ are given. The distances from point $X$ to the faces $ABC, ABD, ACD, BCD$ are $14, 11, 29, 8$ respectively. And the distances from point $Y$ to the faces $ABC, ABD, ACD, BCD$ are $15, 13, 25, 11$ respectively. Find the radius of the inscribed sphere of the tetrahedron $ABCD$.
|
Answer: 17.
Solution. Consider a point $Z$ lying on the ray $XY$ such that $XY: YZ = 1: 2$. We will prove that this point is the center of the inscribed sphere of the tetrahedron.
Drop perpendiculars $X_{\alpha}, Y_{\alpha}, Z_{\alpha}$ from points $X, Y, Z$ to the plane $\alpha$ - obviously, they will lie in the same plane perpendicular to $\alpha$ (Fig. 9a). Also, draw a line through $X$ parallel to $X_{\alpha} Y_{\alpha}$, and denote its intersections with the lines $Y Y_{\alpha}$ and $Z Z_{\alpha}$ as $Y^{\prime}$ and $Z^{\prime}$, respectively (Fig. 9b).
Since triangles $X Y Y^{\prime}$ and $X Z Z^{\prime}$ are similar with a ratio of 3, and $Z^{\prime} Z_{\alpha} = Y^{\prime} Y_{\alpha} = X X_{\alpha}$, we have $Z Z_{\alpha} = X X_{\alpha} + 3(Y Y_{\alpha} - X X_{\alpha}) = 3 Y Y_{\alpha} - 2 X X_{\alpha}$. (The difference $Y Y_{\alpha} - X X_{\alpha}$ can be either positive, as shown in the figure, or negative.)
We obtain that the distances from $Z$ to the faces $ABC, ABD, ACD, BCD$ are respectively $3 \cdot 15 - 2 \cdot 14 = 17, 3 \cdot 13 - 2 \cdot 11 = 17, 3 \cdot 25 - 2 \cdot 29 = 17, 3 \cdot 11 - 2 \cdot 8 = 17$. Moreover, it is clear that point $Z$ is on the same side of each face as points $X$ and $Y$ (otherwise, the formula would give us a negative distance), meaning it also lies inside the tetrahedron.
A point inside the tetrahedron, the distances from which to its faces are equal, is unique - it is the center of the inscribed sphere. The radius of the sphere is equal to the distance from the center to the faces, which is 17.

(a) tetrahedron
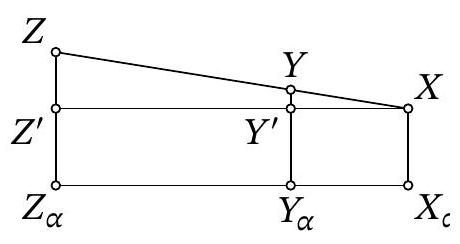
(b) section $X Y Y_{\alpha} X_{\alpha}$
Fig. 9: to the solution of problem 11.8
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Misha and Masha had the same multi-digit integer in their notebooks, ending in 9876. Masha placed a plus sign between the third and fourth digits from the right, while Misha placed a plus sign between the fourth and fifth digits from the right. To the surprise of the schoolchildren, both resulting sums turned out to be the same. What number was originally written by the schoolchildren? Provide all possible answers and prove that there are no others.
|
Solution. Let the written number have the form $\overline{x 9876}$, where $x$ is also some natural number. Then Misha got the sum $x+9876$, and Masha got the sum $10 x+9+876$. From the equality $x+9876=10 x+9+876$ we find that $x$ $=999$.
Answer: 9999876 and there is no other number.
## CONDITION
|
9999876
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Buratino buried two ingots on the Field of Wonders: a gold one and a silver one. On the days when the weather was good, the gold ingot increased by $30 \%$, and the silver one by $20 \%$. On the days when the weather was bad, the gold ingot decreased by $30 \%$, and the silver one by $20 \%$. After a week, it turned out that one of the ingots had increased, while the other had decreased. How many days was the weather good?
|
Solution. Increasing a number by $20 \%$ is equivalent to multiplying it by 1.2, and decreasing a number by $20 \%$ is equivalent to multiplying it by 0.8 (for $30 \%$ - by 1.3 and 0.7, respectively). Therefore, the result does not depend on the sequence of good and bad weather days, but only on the number of good and bad days.
After one good and one bad day, both ingots decrease: $1.2 \cdot 0.81$, while $1.3^{4} \cdot 0.7^{3}<1$. On the other hand, after two good and one bad day, the gold ingot increases. Therefore, it also increases after four good and two bad days, and even more so after five good and two bad days. Thus, if there are five or more good days, the gold ingot grows. Therefore, only when there are four good days does one ingot grow while the other decreases. Answer: four.
Comment. If the fact that the answer does not depend on the sequence of good and bad days is used without justification, no more than 4 points are awarded.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all positive roots of the equation $x^{x}+x^{1-x}=x+1$.
#
|
# Solution
Since $x>0$, then
$0=x^{2 x}+x-x^{x+1}-x^{x}=x^{x}\left(x^{x}-1\right)-x\left(x^{x}-1\right)=x\left(x^{x}-1\right)\left(x^{x-1}-1\right)$.
Thus, $x=1$.
## Answer $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the first day, Masha collected $25 \%$ fewer berries than Vanya, and on the second day, $20 \%$ more than Vanya. Over the two days, Masha collected $10 \%$ more berries than Vanya. What is the smallest number of berries they could have collected together?
|
# Solution
Masha collected $3 / 4$ on the first day and $-6 / 5$ of the number of berries collected by Vanya over these days. Let Vanya collect $4 x$ berries on the first day and $5 y$ on the second day, then Masha collected $3 x$ and $6 y$ berries respectively. According to the condition, $3 x + 6 y = 11 / 10 (4 x + 5 y)$. This equality can be easily transformed into $14 x = 5 y$. Now it is clear that $x$ is a multiple of 5, and $y$ is a multiple of 14, so the smallest natural numbers satisfying this equality are: $x = 5, y = 14$, and the total number of berries is $21 / 10 (4 x + 5 y) = 189$.
Answer: 189 berries
|
189
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task No. 1.1
# Condition:
The figure shows 4 circles.
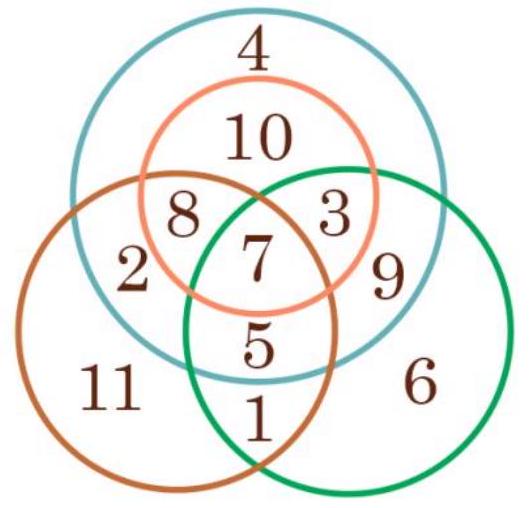
Find the sum of the numbers that are in exactly two circles.
#
|
# Answer: 22
## Exact match of the answer -1 point
## Solution.
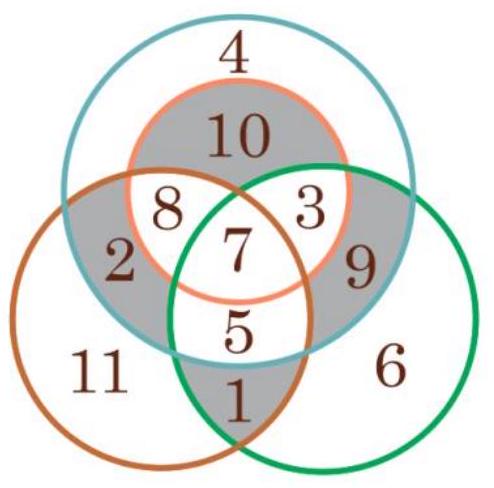
The gray areas on the diagram represent the regions that are included in exactly two circles. The number 10 is in the orange and blue circles, the number 2 is in the blue and brown circles, the number 1 is in the green and brown circles, and the number 9 is in the blue and green circles. $1+2+9+10=22$.
## Condition:
In the diagram, there are 4 circles.
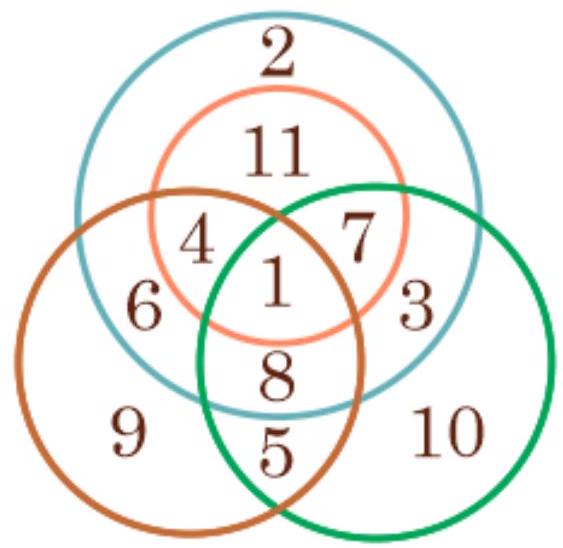
Find the sum of the numbers that are included in exactly two circles.
Answer: 25
Exact match of the answer -1 point
Solution by analogy with problem №1.1.
## Condition:
In the diagram, there are 4 circles.
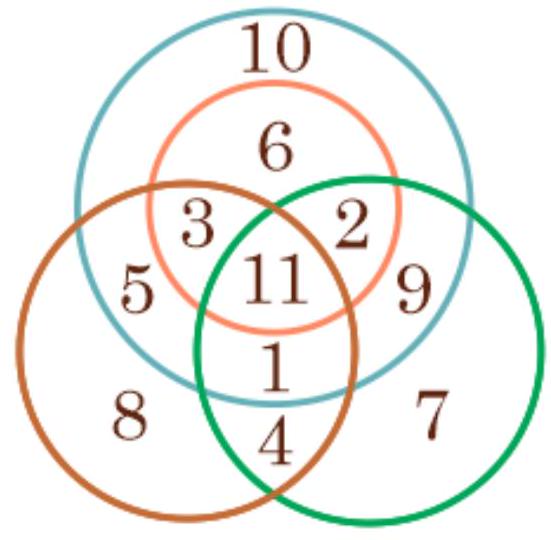
Find the sum of the numbers that are included in exactly two circles.
Answer: 24
Exact match of the answer -1 point
Solution by analogy with problem №1.1.
## Condition:
In the diagram, there are 4 circles.
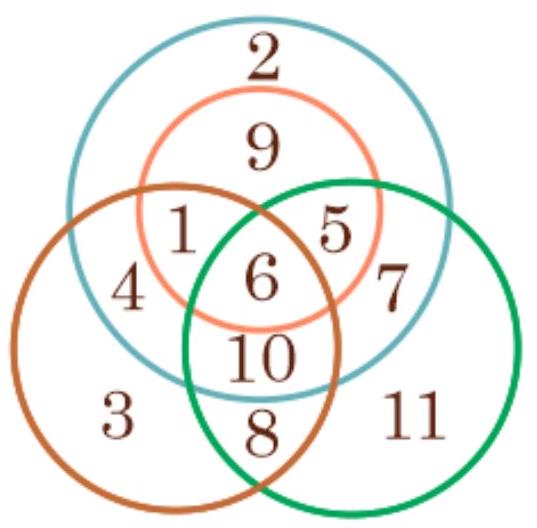
Find the sum of the numbers that are included in exactly two circles.
Answer: 28
Exact match of the answer -1 point
Solution by analogy with problem №1.1.
## Condition:
The father giraffe has four times as many spots as the son giraffe, and the son has 20 fewer spots than the mother giraffe. The mother giraffe has 2 more spots than the father giraffe.
How many spots do the three giraffes have in total?
Answer: 56
Exact match of the answer -1 point

## Solution.
The son has 20 fewer spots than the mother giraffe, and the mother giraffe has 2 more spots than the father giraffe, so the son has 18 fewer spots than the father. At the same time, the son has four times fewer spots than the father, so the difference is three times the number of spots the son has. Therefore, $18: 3=6$ spots for the son, $18+6=24$ spots for the father, and $24+2=26$ spots for the mother. In total, $6+24+26=56$.
## Condition:
The father giraffe has four times as many spots as the son giraffe, and the son has 28 fewer spots than the mother giraffe. The mother giraffe has 4 more spots than the father giraffe.
How many spots do the three giraffes have in total?
Answer: 76
Exact match of the answer -1 point

Solution by analogy with problem №2.1.
## Condition:
The father giraffe has five times as many spots as the son giraffe, and the son has 27 fewer spots than the mother giraffe. The mother giraffe has 3 more spots than the father giraffe.
How many spots do the three giraffes have in total?
Answer: 69
Exact match of the answer -1 point

Solution by analogy with problem №2.1.
## Condition:
The father giraffe has five times as many spots as the son giraffe, and the son has 24 fewer spots than the mother giraffe. The mother giraffe has 4 more spots than the father giraffe.
How many spots do the three giraffes have in total?
Answer: 59
Exact match of the answer -1 point

Solution by analogy with problem №2.1.
#
|
59
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Several numbers are written on the board. It is known that the square of any written number is greater than the product of any two other written numbers. What is the maximum number of numbers that can be on the board
#
|
# Answer. 3 numbers.
Solution. Suppose there are at least four numbers, and $a-$ is the number with the smallest absolute value. Among the remaining numbers, at least two have the same sign (both non-negative or both non-positive). Let these numbers be $b$ and $c$; then $bc = |bc| \geqslant |a|^2 = a^2$, which contradicts the condition.
It remains to provide an example of three numbers that satisfy the condition. For example, the numbers $1, 2, -3$ work.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. (a) (2 points) A natural number $n$ is less than 120. What is the largest remainder that the number 209 can give when divided by $n$?
(b) (2 points) A natural number $n$ is less than 90. What is the largest remainder that the number 209 can give when divided by $n$?
|
Answer: (a) 104. (b) 69.
Solution. Let $209=n k+r$, where $k-$ is the quotient, and $r$ is the remainder of the division. Since $rn k+r=209=n k+r>r k+r=r(k+1)$, hence
$$
k+1>\frac{209}{n} \quad \text { and } \quad r\frac{209}{119}$, i.e., $k \geqslant 1$. Then $r\frac{209}{89}$, i.e., $k \geqslant 2$. Then $r<\frac{209}{3}$, i.e., $r \leqslant 69$. The value $r=69$ is possible when $n=70$ and $k=2$.
|
104
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the board, natural numbers $a, b, c, d$ are written. It is known that among the six sums
$$
a+b, \quad b+c, c+d, d+a, a+c, b+d
$$
three are equal to 23, and the other three are equal to 34.
(a) (1 point) What is the value of $a+b+c+d$?
(b) (3 points) What is the smallest of the numbers $a, b, c, d$?
|
Answer: (a) 57. (b) 6.
Solution. (a) Let's add all 6 sums $a+b, b+c, c+d, d+a, a+c, b+d$. Since three of them are equal to 23 and the other three are equal to 34, we get $23 \cdot 3 + 34 \cdot 3$. On the other hand, we get $3(a+b+c+d)$. Therefore,
$$
a+b+c+d=\frac{23 \cdot 3 + 34 \cdot 3}{3}=57
$$
(b) Suppose that among the numbers $a, b, c, d$ there are at least three different ones. Without loss of generality, let's assume these are $a, b$, and $c$, with $a < b < c$. Then $a+b < a+c < b+c$, which contradicts the problem's condition.
Suppose all numbers $a, b, c, d$ are the same. Then all their pairwise sums are also the same, which again contradicts the problem's condition.
Therefore, among the numbers $a, b, c, d$ there are exactly two different ones. Without loss of generality, we only need to consider three cases:
- $a=b=c<d$
- $a=b<c=d$
- $a<b=c=d$.
Case 1. Let $a=b=c<d$. Then
$$
2a = a+b = a+c = b+c < a+d = b+d = c+d
$$
We get the system
$$
\left\{\begin{array}{l}
2a = 23 \\
a+d = 34
\end{array}\right.
$$
but it is not solvable in natural numbers.
Case 2. Let $a=b<c=d$. Then $a+b < b+c < c+d$, which contradicts the problem's condition.
Case 3. Let $a<b=c=d$. Then
$$
a+b = a+c = a+d < b+d = b+c = c+d = 2d
$$
We get the system
$$
\left\{\begin{array}{l}
a+d = 23 \\
2d = 34
\end{array}\right.
$$
the solution of which is $a=6, b=c=d=17$. Therefore, the smallest of the numbers is 6.
|
57
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. Given a parallelogram $A B C D$, point $M$ is the midpoint of side $B C$. On side $A D$, there is a point $K$ such that $B K=B M$ and the quadrilateral $K B M D$ is cyclic.
(a) (2 points) What is the length of segment $M D$, if $A D=17$?
(b) (2 points) How many degrees does the angle $K M D$ measure, if $\angle B A D=46^{\circ}$?
|
Answer: (a) 8.5. (b) 48.
Solution. (a) Note that KBMD is a cyclic trapezoid, so it is isosceles, i.e., $M D=K B$. Therefore,
$$
M D=K B=\frac{B C}{2}=\frac{A D}{2}=8.5
$$
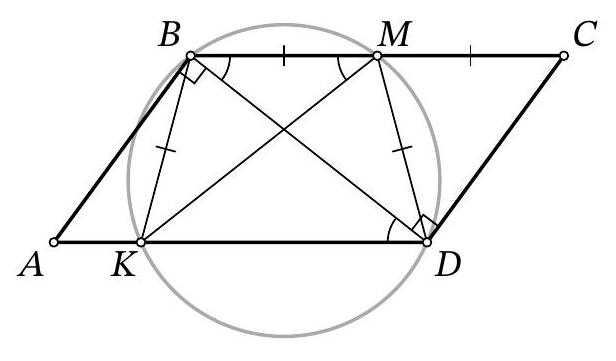
Fig. 7: to the solution of problem 10.4
(b) Since $M D=M B=M C$, angle $B D C$ is a right angle (as is known, if in a triangle the median is equal to half the side to which it is drawn, then it is drawn from a right angle). From the fact that $A B \| C D$, it follows that angle $A B D$ is also a right angle (Fig. 7).
Thus, $\angle B D K=90^{\circ}-\angle B A D$, and from the cyclic nature of quadrilateral $K B M D$ it follows that $\angle B M K=\angle B D K=90^{\circ}-\angle B A D$.
Moreover, from the parallelism it follows that $\angle M B D=\angle B D K$, and from the isosceles nature of triangle $B M D$ that $\angle B M D=180^{\circ}-2 \angle M B D=2 \angle B A D$.
We obtain
$$
\begin{aligned}
\angle K M D & =\angle B M D-\angle B M K=2 \angle B A D-\left(90^{\circ}-\angle B A D\right)= \\
& =3 \angle B A D-90^{\circ}=3 \cdot 46^{\circ}-90^{\circ}=48^{\circ} .
\end{aligned}
$$
|
48
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. One winter day, 43 children were throwing snowballs at each other. Each of them threw exactly one snowball at someone else. It is known that:
- the first threw a snowball at the one who threw a snowball at the second,
- the second threw a snowball at the one who threw a snowball at the third,
- the forty-third threw a snowball at the one who threw a snowball at the first.
What is the number of the one who threw a snowball at the third?
|
# Answer: 24.
Solution. First, note that not only did each throw exactly one snowball, but each was hit by exactly one snowball. Indeed, from the phrase "the first threw a snowball at the one who threw a snowball at the second," it follows that someone threw a snowball at the second; similarly, it is established that each was hit by at least one snowball. But since the total number of snowballs is the same as the number of children, each must have been hit by exactly one snowball.
Let's represent each child as a point; draw an arrow from point $A$ to point $B$ if child $A$ threw a snowball at $B$. Since exactly one arrow enters each point and exactly one arrow leaves each point, the arrows form one or several cycles.
Consider the cycle that includes the first child. Let the first child throw a snowball at child number $x$. Then child number $x$ threw a snowball at the second, the second at child number $x+1$, and so on. Thus, this cycle is structured as follows:
$$
\ldots \rightarrow 1 \rightarrow x \rightarrow 2 \rightarrow (x+1) \rightarrow 3 \rightarrow (x+2) \rightarrow 4 \rightarrow \ldots
$$
If we follow it with a step of two arrows, we get the numbers $1, 2, 3, 4, \ldots$ - all numbers from 1 to 43. Therefore, the cycle includes all 43 children, and there are no other cycles.
Notice that if we start from 1 and take 22 steps of two arrows, we will complete the entire cycle and one more arrow, that is, we will land on $x$. Therefore, $x=23$. Then the number of the one who threw a snowball at the third is $x+1=24$.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. A pair of natural numbers ( $a, p$ ) is called good if the number $a^{3}+p^{3}$ is divisible by $a^{2}-p^{2}$, and $a>p$.
(a) (1 point) Indicate any possible value of $a$ for which the pair $(a, 13)$ is good.
(b) (3 points) Find the number of good pairs for which $p$ is a prime number less than 20.
|
Answer: (a) any of the numbers $14, 26, 182$. (b) 24.
Solution. Since $a^{3}+p^{3}=(a+p)\left(a^{2}-a p+p^{2}\right)$, and $a^{2}-p^{2}=(a+p)(a-p)$, the condition of divisibility is equivalent to $a^{2}-a p+p^{2}=a(a-p)+p^{2}$ being divisible by $a-p$. Note that $a(a-p)$ is divisible by $a-p$, so $p^{2}$ must be divisible by the natural number $a-p$, i.e., $a-p$ is a divisor of $p^{2}$. Since $p$ is a prime number, $p^{2}$ has only 3 natural divisors: $1, p$, and $p^{2}$. Therefore, for any prime $p$, there are exactly 3 options for the number $a$: these are $1+p, p+p$, and $p^{2}+p$ (obviously, each of these numbers is greater than $p$).
(a) For $p=13$, we get $a=14,26,182$.
(b) Let's find the number of prime numbers less than 20. There are exactly 8: $2,3,5,7,11,13,17,19$. Thus, the total number of good pairs is $3 \cdot 8=24$.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. At one meal, Karlson can eat no more than 5 kg of jam. If he opens a new jar of jam, he must eat it completely during this meal. (Karlson will not open a new jar if he has to eat more than 5 kg of jam together with what he has just eaten.)
Little Boy has several jars of raspberry jam weighing a total of 50 kg, each weighing no more than 1 kg. In the least number of meals, how many meals will Karlson definitely be able to eat all the jam?
|
Answer: 12.
Solution. We will prove that in 12 meals, Karlson will always be able to eat all the jam.
We will distribute the jars into piles according to the following algorithm. In each pile (starting with the first, then the second, and so on), we will place jars one by one until the pile contains more than 5 kg of jam. The last jar we place in the pile will be called the extra jar. Since Little has 50 kg of jam, there will be no more than 10 such piles.
Obviously, if we remove the extra jar from a pile, Karlson will be able to eat all the remaining jam in one meal. That is, Karlson will eat all the jam except the extra jars in 10 meals. And he will spend no more than 2 meals on the extra jars, as there are no more than 10 of them, and each weighs no more than 1 kg.
Now we will show that Karlson will not always be able to eat all the jam in 11 meals. Suppose there are a total of $5 \cdot 11 + 1 = 56$ jars, and each contains $\frac{25}{28}$ kg of jam. If Karlson managed to eat all of this in 11 meals, then by the pigeonhole principle, there would be a meal during which he ate at least 6 jars of jam. But $6 \cdot \frac{25}{28} = \frac{150}{28} > 5$, a contradiction.
Another construction example. We will demonstrate that Karlson will be able to eat at least $\frac{25}{6}$ kg of jam in one meal if there is at least that much jam left.
First, we will select jars one by one until we accumulate more than $\frac{25}{6}$ kg of jam. Then we will start returning the selected jars one by one so that the total remains at least $\frac{25}{6}$ kg of jam.
Suppose we can no longer return any of the selected jars, but the total amount of jam in them is still more than 5 kg. Clearly, then we have at least 6 jars, and the smallest of them contains no more than $\frac{1}{6}$ of the total mass of jam. We will select and return it; then there will be at least $\frac{5}{6} \cdot 5 = \frac{25}{6}$ kg of jam left. Contradiction. Therefore, Karlson can open and eat the remaining selected jars in one meal.
Thus, Karlson will be able to eat at least $\frac{25}{6}$ kg of jam in one meal, except for the last time when he finishes the remaining. Then, obviously, in $\frac{50}{\frac{25}{6}} = 12$ meals, he will manage.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 10.4.2. Given a parallelogram $A B C D$, point $M$ is the midpoint of side $B C$. On side $A D$, there is a point $K$ such that $B K = B M$ and quadrilateral $K B M D$ is cyclic.
(a) (2 points) What is the length of segment $M D$, if $A D = 19$?
(b) (2 points) How many degrees does angle $K M D$ measure, if $\angle B A D = 44^{\circ}$?
|
Answer: (a) 9.5. (b) 42.
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 10.6.1. A pair of natural numbers $(a, p)$ is called good if the number $a^{3}+p^{3}$ is divisible by $a^{2}-p^{2}$, and $a>p$.
(a) (1 point) Indicate any possible value of $a$ for which the pair $(a, 13)$ is good.
(b) (3 points) Find the number of good pairs for which $p$ is a prime number less than 20.
|
Answer: (a) any of the numbers $14,26,182$. (b) 24.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 10.6.2. A pair of natural numbers $(a, p)$ is called good if the number $a^{3}+p^{3}$ is divisible by $a^{2}-p^{2}$, and $a>p$.
(a) (1 point) Indicate any possible value of $a$ for which the pair $(a, 17)$ is good.
(b) (3 points) Find the number of good pairs for which $p$ is a prime number less than 18.
|
Answer: (a) any of the numbers $18,34,306$. (b) 21.
|
21
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 10.6.3. A pair of natural numbers ( $a, p$ ) is called good if the number $a^{3}+p^{3}$ is divisible by $a^{2}-p^{2}$, and $a>p$.
(a) (1 point) Indicate any possible value of $a$ for which the pair $(a, 19)$ is good.
(b) (3 points) Find the number of good pairs for which $p$ is a prime number less than 24.
|
Answer: (a) any of the numbers $20,38,380$. (b) 27.
|
27
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 10.6.4. A pair of natural numbers $(a, p)$ is called good if the number $a^{3}+p^{3}$ is divisible by $a^{2}-p^{2}$, and $a>p$.
(a) (1 point) Indicate any possible value of $a$ for which the pair $(a, 11)$ is good.
(b) (3 points) Find the number of good pairs for which $p$ is a prime number less than 16.
|
Answer: (a) any of the numbers $12, 22, 132$. (b) 18.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Several consecutive natural numbers are written on the board. Exactly $52 \%$ of them are even. How many even numbers are written on the board
|
# Answer: 13.
Solution. Since the natural numbers written down are consecutive, even and odd numbers alternate. According to the condition, there are more even numbers, which means the sequence starts and ends with even numbers.
First method. Let $n$ be the number of even numbers, then the number of odd numbers is $(n-1)$. Thus, the even numbers constitute $\frac{n}{2 n-1} \cdot 100 \%$ of all the numbers written on the board. We get the equation $100 n=52(2 n-1)$, from which $n=13$.
Second method. Let a total of $x$ numbers be written. Then among them, $\frac{13}{25} x$ are even and $\frac{12}{25} x$ are odd, and there are exactly one more even numbers. Therefore, $\frac{13}{25} x-\frac{12}{25} x=1$, from which $x=25$. Thus, $\frac{13}{25} x=13$.
Third method. There is one more even number, which means one number constitutes ( $52-48$ ) \% of their total quantity. Therefore, the number of even numbers is $\frac{52}{52-48}=13$.
## Grading criteria:
+ the correct answer and a complete solution (by any method) are provided
$\pm$ correct, overall, reasoning is provided, but the answer is given to the wrong question (for example, only the total number of written numbers is found)
Ғ correct reasoning is provided, but a computational error is made
- only the answer is provided
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The graph of the function $y=x^{2}+a x+b$ is shown in the figure. It is known that the line $A B$ is perpendicular to the line $y=x$. Find the length of the segment $O C$.
---
The text has been translated while preserving the original formatting and line breaks.
|
Answer: 1.
Solution. Since $y(0)=b$, then $B(0 ; b)$. Now let's find the length of the segment $O A$.
First method. Since the line $A B$ is perpendicular to the line $y=x$, it is parallel to the line $y=-x$. Moreover, this line passes through the point $B(0 ; b)$. Therefore,
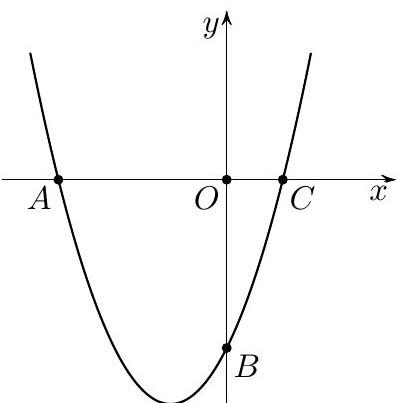
it is described by the equation $y=-x+b$. Since $y=0$ when $x=b$, then $O A=-b$.
Second method. From the problem statement, it follows that the bisector of triangle $A O B$, drawn to the side $A B$, lies on the line $y=x$, and therefore coincides with the height of this triangle. Consequently, $O A=O B=-b$.
Thus, the number $b$ and the desired length $c$ of the segment $O C$ are the roots of the quadratic equation $x^{2}+a x+b=0$. By Vieta's theorem: $b c=b$. Since $b \neq 0$, then $c=1$.
## Grading criteria: + correct answer and complete justified solution $\pm$ correct answer and solution with minor gaps in justification 干 only proved that $O A=O B$, with no further progress Ғ used the equality $O A=$ OB without proof, and then obtained the correct answer in a justified manner 干 the correct answer was obtained based on specific numerical values of a and b - only the answer is provided
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In a square table of size $100 \times 100$, some cells are shaded. Each shaded cell is the only shaded cell either in its column or in its row. What is the maximum number of cells that can be shaded?
|
Answer: 198.
Solution. Example. We will color all the cells of one row and all the cells of one column, except for their common cell. In this case, the condition of the problem is satisfied, and exactly 198 cells are colored.
Estimate. We will prove that no more than 198 cells could have been colored in the required manner. For each colored cell, we will highlight the line (row or column) in which it is the only colored cell. In such highlighting, no more than 99 rows can be highlighted. Indeed, if 100 rows are highlighted, then each colored cell is the only one in its row, but then there are no more than 100 colored cells. Similarly, no more than 99 columns can be highlighted. Therefore, the number of highlighted lines, and thus the number of colored cells, is no more than 198.
## Grading criteria:
+ a complete and justified solution is provided
Ғ the correct answer and an example of coloring are provided, but the estimate is missing or conducted incorrectly
- only the answer is provided
|
198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. The heights $A D$ and $B E$ of an acute-angled triangle $A B C$ intersect at point $H$. The circumcircle of triangle $A B H$ intersects sides $A C$ and $B C$ at points $F$ and $G$ respectively. Find $F G$, if $D E=$ $=5$ cm.
|
Answer: 10 cm.
Solution. Let $\angle H B F=\alpha$ (see Fig. 9.5). Then $\angle F A H=\angle H B F=\alpha$ (inscribed angles subtending the same arc). From the right triangle $A D C: \angle C=90^{\circ}-\alpha$, and from the right triangle $E C B: \angle E B C=90^{\circ}-\angle C=\alpha$.
Thus, $B E$ is the height and the angle bisector of triangle $F B C$, which means this triangle is isosceles and $B E$ is its median, i.e., $F E = E C$. Similarly, it can be shown that $C D = D G$. Therefore, $E D$ is the midline of triangle $F C G$. Hence, $F G = 2 D E = 10$ (cm).
## Grading Criteria:
+ - a complete and well-reasoned solution
- only the answer provided
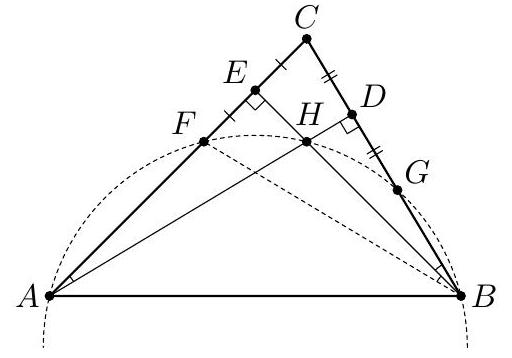
Fig. 9.5
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. Twenty-five coins are arranged into piles as follows. First, they are arbitrarily divided into two groups. Then any of the existing groups is again divided into two groups, and so on until each group consists of one coin. Each time a group is divided into two, the product of the number of coins in the two resulting groups is recorded. What can the sum of all recorded numbers be?
|
Answer: 300.
Solution. First method. Let's represent the coins as points and connect each pair of points with a segment. We will get $\frac{25(25-1)}{2}$ $=300$ segments. With each division of one group of coins into two, we will erase all segments connecting points corresponding to coins that end up in different groups. Suppose at some step we divide the coins of one of the already existing groups into two groups of $x$ and $y$ coins. Then we erase $x y$ segments. This is the number we record. Thus, the sum of the recorded numbers is the total number of erased segments. Since there were initially 300 segments, and in the end, all segments are erased, the total number of erased segments is 300.
Second method. Consider the variable quantity $S$, equal at each moment to half the sum of the squares of the number of coins in the piles. Initially, $S=\frac{25^{2}}{2}=312.5$, and at the very end, $S=\frac{1^{2}+1^{2}+\ldots .+1^{2}}{2}=\frac{25}{2}=12.5$. If a pile with $x+y$ coins is divided into two piles of $x$ and $y$ coins, then $S$ decreases by $\frac{(x+y)^{2}}{2}-$ $-\frac{x^{2}+y^{2}}{2}=x y$. Thus, with each division, the quantity $S$ decreases by the next recorded number. Therefore, the sum of all recorded numbers is equal to the total decrease in the quantity $S$, which is 312.5 $-12.5=300$.
Third method. We will prove by induction that if there are initially $n$ coins, then the desired sum is $\frac{n(n-1)}{2}$.
Base of induction. For $n=2$, after the first step, we get two piles with one coin each and record the number $1 \cdot 1=1$. Since the equality $\frac{2(2-1)}{2}=1$ is true, the statement is true for $n=2$.
Induction step. Assume the statement is true for all $n<k$ and prove that it is also true for $n=k$. Suppose on the first step $k$ coins are divided into two groups of $x$ and $y$ coins ( $k=x+y$ ). For $x$ and $y$ coins, the statement is true by the induction hypothesis.
If in such a division $x \geqslant 2$ and $y \geqslant 2$, then the recorded sum is
$$
x y+\frac{x(x-1)}{2}+\frac{y(y-1)}{2}=\frac{x^{2}-x+y^{2}-y+2 x y}{2}=\frac{(x+y)^{2}-(x+y)}{2}=\frac{k^{2}-k}{2}=\frac{k(k-1)}{2}
$$
If, however, $x=1$ and $y \geqslant 2$, then $k=y+1$ and the recorded sum in this case is $1 \cdot y+\frac{y(y-1)}{2}=\frac{(y+1)^{2}-(y+1)}{2}=$ $=\frac{k(k-1)}{2}$. According to the principle of mathematical induction, the statement is proven for any natural $n \geqslant 2$. In particular, for 25 coins, we get: $\frac{25(25-1)}{2}=300$.
## Grading criteria:
+ a complete and well-reasoned solution is provided
$\pm$ the correct answer and a generally correct solution with minor inaccuracies or gaps is provided
- only the answer is provided
|
300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. To a natural number $N$, the largest divisor of $N$ less than $N$ was added, and the result was a power of ten. Find all such $N$. (N. Agakhanov)
|
Answer: 75.
Solution. Let $m$ be the greatest divisor of the number $N$, less than $N$. Then $n=mp$, where $p$ is the smallest prime divisor of the number $N$. We have $N+m=10^{k}$, that is, $m(p+1)=10^{k}$. The number on the right side is not divisible by 3, so $p>2$. From this, it follows that $N$ is an odd number, and therefore $m$ is also odd. Thus, since $10^{k}$ is divisible by $m$, we get $m=5^{s}$. If $m=1$, then $N=p=10^{k}-1$, which is impossible since $10^{k}-1$ is divisible by 9, and thus is not a prime. Therefore, $s \geqslant 1$, the number $N$ is divisible by 5, and hence $p \leqslant 5$. If $p=3$, we get the equation $4 \cdot 5^{s}=10^{k}$, from which $k=2, m=25$, and $N=75$. If $p=5$, then $p+1=6$, and the number $10^{k}$ is divisible by 3, which is impossible.
|
75
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. To a natural number $N$, the largest divisor of $N$ less than $N$ was added, and the result was a power of ten. Find all such $N$.
(N. Agakhanov)
|
Answer: 75.
Solution. Let $m$ be the greatest divisor of the number $N$, less than $N$. Then $n=m p$, where $p$ is the smallest prime divisor of the number $N$. We have $N+m=10^{k}$, that is, $m(p+1)=10^{k}$. The number on the right side is not divisible by 3, so $p>2$. From this, it follows that $N$ is an odd number, and therefore $m$ is also odd. Since $10^{k}$ is divisible by $m$, we get $m=5^{s}$. If $m=1$, then $N=p=10^{k}-1$, which is impossible since $10^{k}-1$ is divisible by 9, and thus is not a prime. Therefore, $s \geqslant 1$, the number $N$ is divisible by 5, and hence $p \leqslant 5$. If $p=3$, we get the equation $4 \cdot 5^{s}=10^{k}$, from which $k=2, m=25$, and $N=75$. If $p=5$, then $p+1=6$, and the number $10^{k}$ is divisible by 3, which is impossible.
|
75
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A natural number $n$ is called good if each of its natural divisors, increased by 1, is a divisor of the number $n+1$. Find all good natural numbers.
(S. Berlov)
|
Answer. One and all odd prime numbers.
Solution. It is clear that $n=1$ satisfies the condition. Also, all odd primes satisfy it: if $n=p$, then its divisors increased by 1 are 2 and $p+1$; both of them divide $p+1$. On the other hand, any number $n$ that satisfies the condition has a divisor 1; hence, $n+1$ is divisible by $1+1$, which means $n$ is odd.
Now suppose that some composite $n$ satisfies the condition. We have $n=a b$, where $a \geqslant b \geqslant 2$. Then the number $n+1$ is divisible by $a+1$; moreover, the number $n+b=(a+1) b$ is also divisible by $a+1$. Therefore, the number $b-1=(n+b)-(n+1)$ is also divisible by $a+1$. Since $b-1>0$, we get that $b-1 \geqslant a+1$. But this contradicts the inequality $b \leqslant a$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the sum $\sin x + \sin y + \sin z$, given that $\sin x = \tan y$, $\sin y = \tan z$, $\sin z = \tan x$
|
Answer: 0.
First solution. From $\sin x = \operatorname{tg} y$, we get $\sin x \cos y = \sin y$. Therefore, $|\sin x| \cdot |\cos y| = |\sin y|$. This means $|\sin x| \geq |\sin y|$, and the inequality becomes an equality only if either $\sin y = \sin x = 0$ or $|\cos y| = 1$ (which again implies $\sin y = \sin x = 0$). Similarly, from the remaining equations, we obtain the inequalities $|\sin y| \geq |\sin z|$ and $|\sin z| \geq |\sin x|$. Thus, $|\sin x| \geq |\sin y| \geq |\sin z| \geq |\sin x|$. Therefore, $|\sin x| = |\sin y| = |\sin z|$. Since all inequalities have become equalities, we have $\sin x = \sin y = \sin z = 0$, and $\sin x + \sin y + \sin z = 0$.
Second solution. If one of the sines is zero, then the tangent equal to it is also zero, which means the sine in the numerator of the tangent is zero. Consequently, the other sines and tangents are also zero. In this case, $\sin x + \sin y + \sin z = 0$.
Suppose none of the sines are zero. Multiplying all three equations, we get $\sin x \sin y \sin z = \operatorname{tg} y \operatorname{tg} z \operatorname{tg} x = \frac{\sin x \sin y \sin z}{\cos x \cos y \cos z}$. Since $\sin x \sin y \sin z \neq 0$, we have $\cos x \cos y \cos z = 1$. This is only possible if $|\cos x| = |\cos y| = |\cos z| = 1$, which means the sines are zero, and the considered case is impossible.
Comment. A correct answer without justification - 0 points.
An answer obtained by considering an example - 1 point.
At least one case is incorrectly considered (or omitted) - no more than 3 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. In the castle, there are 16 identical square rooms forming a $4 \times 4$ square. Sixteen people, who are either liars or knights (liars always lie, knights always tell the truth), have settled in these rooms, one person per room. Each of these 16 people said: "At least one of the rooms adjacent to mine is occupied by a liar." What is the maximum number of knights that could be among these 16 people? Rooms are considered adjacent if they share a wall.
|
Answer: 12 knights.
Solution: Note that for each knight, at least one of their neighbors must be a liar. We will show that there must be no fewer than 4 liars (thus showing that there are no more than 12 knights). Suppose there are no more than 3 liars, then there will be a "vertical row" of rooms where only knights live. However, each of these knights must have a neighbor who is a liar (and these neighbors are different). Therefore, there must be at least 4 liars.
The diagram below shows how 12 knights and 4 liars could be accommodated.
| $\mathrm{P}$ | L | $\mathrm{P}$ | $\mathrm{P}$ |
| :--- | :--- | :--- | :--- |
| $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ | L |
| L | $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ |
| $\mathrm{P}$ | $\mathrm{P}$ | L | $\mathrm{P}$ |
Comment: A correct answer without justification - 0 points.
Example of accommodating 4 liars and 12 knights - 2 points.
Proved that there are no more than 12 knights - 5 points.
Note 1: In the example, liars should not be neighbors.
Note 2: The estimate can be obtained by noting that in three rooms - a corner room and the two adjacent to it - at least one liar must reside.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. First, we will calculate the number of ways to choose three points out of the 60 available. The first point can be chosen in 60 ways, the second in 59 ways, and the third in 58 ways; as a result, we get $205320=60 \cdot 59 \cdot 58$ options. Since the selections of vertices ABC, ACB, CBA, CAB, BAC, and BCA all give the same triangle, the number of ways to choose three points without considering the order of selection is 205320:6=34220. We will not be satisfied with the sets of three points that lie on the same straight line. There are exactly 30 such sets. Therefore, there are $34220-30=34190$ ways to construct the given triangles.
|
Answer: 34190
Recommendations for evaluating solutions: to determine the number of triplets of points, one can use the combination formula $C_{60}^{3}=\frac{60!}{3!57!}=34220$.
|
34190
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the quadratic function $f(x)=x^{2}+a x+b$ has zeros $x_{1}$, $x_{2}$ and $f(2014)=f(2016)$. Find $\frac{x_{1}+x_{2}}{2}$.
|
# Answer: 2015
## First Solution.
Since the graph of the quadratic function $f(x)$ is symmetric with respect to the line $x=-a / 2$ and $f(2014)=f(2016), f\left(x_{1}\right)=f\left(x_{2}\right)=0$, then
$-\frac{a}{2}=\frac{x_{1}+x_{2}}{2}=\frac{2014+2016}{2}=2015$.
## Second Solution.
Since $f(2014)=f(2016)$, then $2014^{2}+2014 a+b=2016^{2}+2016 a+b \Leftrightarrow$ $2 a=-2 \cdot 4030 \Leftrightarrow a=-4030$. By Vieta's theorem $x_{1}+x_{2}=-a \Rightarrow$ $\frac{X_{1}+X_{2}}{2}=-\frac{a}{2}=2015$
Recommendations for Checking
Only the answer is given: 0 points.
Only the value of $a$ is found: 4 points.
|
2015
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a square grid of cells, some cells are painted black. It turned out that no black cell shares a side with more than one other black cell? What is the maximum number of cells that could be painted black?
In a square of cells, some cells are painted black. It turned out that no black cell shares a side with more than one other black cell? What is the maximum number of cells that could be painted black?
|
Solution. An example of properly coloring 8 squares is shown in Fig. 1a. Suppose more than 8 were colored, then at least one of the four $2 \times 2$ squares would have at least three cells colored (Fig. 1b). But then at least one of them would share adjacent sides with two other black cells. This contradiction completes the proof.

a)
b)
Fig. 1
Answer: 8.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Three bees collect nectar from 88 garden flowers. Each flower was visited by at least one bee. Each bee visited exactly 54 flowers. We will call a flower sweet if it was visited by all three bees, and bitter if it was visited by exactly one. Which of these 88 flowers are more: sweet or bitter, and by how many?
|
Solution. Let among the 88 garden flowers, $s$ be sweet and $g$ be bitter. Then the number of flowers visited by two bees is exactly $88-s-g$. On one hand, the total number of bee landings on the flowers is $3 \cdot 54=162$ (each bee visited 54 flowers), and on the other hand, it is $3s + 2(88-s-g) + g = s - g + 176$. We have the equation $162 = s - g + 176$, from which $s - g = -14$. This means that there are 14 more bitter flowers. Answer: there are 14 more bitter flowers.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the tournament, 15 volleyball teams are playing, and each team plays against all other teams only once. Since there are no draws in volleyball, there is a winner in each match. A team is considered to have performed well if it loses no more than two matches. Find the maximum possible number of teams that performed well.
|
Answer: 5.
Solution.
Evaluation. If the number of teams that played well is not less than 6, then consider six of them. They could have lost no more than $6 \times 2=12$ matches. But the games between them amounted to $6 \times 5 / 2=15$. Thus, they lost no fewer than 15 matches in total. Contradiction.
Example. Place the captains of 5 teams in a circle facing the center. Let each team lose to the two teams whose captains are to the right of their captain in the circle, and win against the two teams whose captains are to the left, and also win against the remaining 10 teams. The games between the 10 teams can end in any way. The five teams whose captains stand in the circle performed well. The rest lost no fewer than five matches.
Criteria. Any correct solution: 7 points.
The evaluation that 6 or more teams cannot be good: 4 points.
An example for 5 good teams is provided: 2 points.
Only the answer: 0 points.
## Grading Criteria:
| Points | Correctness (incorrectness) of the solution |
| :---: | :---: |
| 7 | Complete correct solution. |
| 6-7 | Correct solution. There are minor flaws that do not significantly affect the solution. |
| 5-6 | The solution is generally correct. However, it contains several errors or the omission of individual cases, but can become correct with minor corrections or additions. |
| 4 | One of the two (more complex) significant cases is correctly considered, or in a problem of the type "evaluation + example," the evaluation is correctly obtained. |
| 2-3 | Auxiliary statements that help in solving the problem are proven, or in a problem of the type "evaluation + example," a correct example is constructed. |
| 1 | Individual important cases are considered in the absence of a solution (or in the case of an incorrect solution). |
| 0 | The solution is incorrect, and there is no progress. |
| 0 | The solution is absent. |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let there be $x$ seventh-graders participating in the tournament, who together scored $n$ points. Then the number of eighth-graders participating in the tournament is $10 * x$ people, and the total points they scored is $4.5 * n$ points. Therefore, a total of $11 * x$ students participated in the tournament, and they collectively scored $5.5 * n$ points. The total number of points scored by all participants is equal to the number of games played. We get the equation:
$$
\begin{gathered}
5.5 * n = \frac{11 * x * (11 x - 1)}{2} \\
n = x * (11 x - 1)
\end{gathered}
$$
Each seventh-grader played $11 x - 1$ games (since there are a total of $11 x$ participants). Therefore, $x$ seventh-graders could collectively score $n$ points, i.e., $x * (11 x - 1)$ points, only if each of them won all their games. This is only possible when $x = 1$ (two seventh-graders cannot simultaneously win against each other).
|
Answer: 1 student from 7th grade participated in the tournament and scored 10 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The bisectors $\mathrm{AD}$ and $\mathrm{BE}$ of triangle $\mathrm{ABC}$ intersect at point I. It turns out that the area of triangle ABI is equal to the area of quadrilateral CDIE. Find the greatest possible value of angle ACB.
|
Answer: $60^{\circ}$.
Solution. Let $\mathrm{S}(\mathrm{CDIE})=\mathrm{S}_{1}, \mathrm{~S}(\mathrm{ABI})=\mathrm{S}_{2}$, $S(B D I)=S_{3}, S(A I E)=S_{4}$ (see figure). Since the ratio of the areas of triangles with a common height is equal to the ratio of the bases, and the angle bisector divides the opposite side in the ratio of the adjacent sides, we have $\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\mathrm{CD} / \mathrm{BD}=$ $\mathrm{AC} / \mathrm{AB}$. Similarly, $\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right)$
$=A E / E C=A B / B C$. Since $S_{1}=S_{2}$, then
$\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right)$, from which
$\mathrm{AB} / \mathrm{BC}=\mathrm{AC} / \mathrm{AB}$. Or $\mathrm{c}^{2}=\mathrm{ab}$. By the cosine theorem,
$\cos C=\left(a^{2}+b^{2}-c^{2}\right) /(2 a b)=\left(a^{2}+b^{2}\right) /(2 a b)-c^{2} /(2 a b)=\left(a^{2}+b^{2}\right) /(2 a b)-1 / 2 \geq 1-1 / 2=1 / 2$.
We obtained $\cos \mathrm{C} \geq 1 / 2$. Therefore, the measure of angle C does not exceed $60^{\circ}$.
Equality is achieved in an equilateral triangle.
Criteria.
The relationship between the sides $c^{2}=a b$ is obtained, but the estimate is not made or is incorrect: 2 points.
It is proven that the angle is no more than 60 degrees, but an example where the estimate is achieved is not provided: 6 points.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) In Sun City, they exchange a honey cake for 6 pretzels, and for 9 pretzels, they give 4 doughnuts. How many doughnuts will they give for 3 honey cakes? Explain your answer.
|
Answer: 8.
Solution.
If for one cookie you get 6 pretzels, then for 3 cookies you will get $3 \times 6=18$ pretzels. 18 pretzels is 2 times 9 pretzels. Therefore, for them, you will get 2 times 4 gingerbread cookies, i.e., 8 gingerbread cookies.
## Grading Criteria.
- Any correct and justified solution - 7 points.
- Correct initial reasoning is provided, but incorrect conclusions are drawn or no conclusions are made - 2 points.
- The solution is complete, but one arithmetic error is made - 2 points.
- Only the correct answer - 1 point.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In the cells of an $8 \times 8$ board, the numbers 1 and -1 are placed (one number per cell). Consider all possible placements of a four-cell figure
$\square$ on the board (the figure can be rotated, but its cells must not go beyond the board's boundaries). A placement is called unsuccessful if the sum of the numbers in the four cells of the figure is not equal to 0. Find the smallest possible number of unsuccessful placements. (M. Antipov)
|
Answer: 36. Solution: We will show that in each "cross" of five cells on the board, there will be at least one unsuccessful placement. Suppose the opposite; let the numbers in the outer cells of the cross be \(a, b, c, d\), and in the central cell be \(e\); denote the sum of all these five numbers by \(S\). Then, according to our assumption, \(S-a=S-b=S-c=S-d=0\), from which it follows that \(a=b=c=d\). But in this case, \(e=-(a+b+c)=-3a\), which is impossible. Since each placement of the figure lies in no more than one cross, it follows that in 36 crosses (with centers in all non-edge cells), there will be at least 36 unsuccessful placements. On the other hand, the example arrangement on the right shows that the number of unsuccessful placements can be exactly 36 (the sign of the corresponding number is indicated in each cell). Indeed, in any cross, there is exactly one unsuccessful placement, and all placements adjacent to the long side of the board are successful.
Criteria: Answer without justification - 0 points. Proved that there are at least 36 unsuccessful placements, no example of 36 - 4 points. Provided an example where there are exactly 36 unsuccessful placements, no proof that there cannot be fewer than 36 - 3 points. Proved that at least one of the four placements of the figure in a "cross" is unsuccessful, no further substantial progress - 2 points.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the day when Dima's brother and sister were congratulating him on his birthday, Dima said: "Look how interesting, I am now twice as old as my brother and three times as old as my sister!" - "And your average age is 11 years," - added Dad. How old did Dima turn?
|
Answer: 18 years.
Solution. The first method. According to the problem, we can form an equation. Let Dima's age be $x$ years, then his sister's age is $x / 3$, and his brother's age is $-x / 2 ;(x+x / 3+x / 2): 3=11$. After solving this equation, we get that $x=18$. Dima is 18 years old.
It will be useful to provide another solution, "in parts."
The second method. If the ages of Dima, his brother, and sister are represented by segments, then "Dima's segment" consists of two "brother's segments" or three "sister's segments." Then, if Dima's age is divided into 6 parts, the sister's age is two such parts, and the brother's age is three such parts. Thus, the sum of their ages is 11 such parts. On the other hand, if the average age is 11 years, then the sum of the ages is 33 years. From this, it follows that one part is three years. Therefore, Dima is 18 years old.
## Grading criteria.
- Complete correct solution - 7 points.
- The equation is correctly set up, but errors are made in solving it - 3 points.
- The correct answer is provided and a check is performed - 2 points.
- Only the correct answer is provided - $\mathbf{0}$ points.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many three-digit numbers exist that are 5 times the product of their digits?
|
Answer. One number is 175.
Solution. First method. The digits that make up the number do not include the digit 0, otherwise the condition of the problem cannot be met. The given three-digit number is obtained by multiplying 5 by the product of its digits, so it is divisible by 5. Therefore, its notation ends with the digit 5. We get that the product of the digits, multiplied by 5, must be divisible by 25. Note that there cannot be any even digits in the notation of the number, otherwise the product of the digits would be zero. Thus, the three-digit number must be divisible by 25 and not contain even digits. There are only five such numbers: $175, 375, 575, 775$, and 975. The product of the digits of the desired number must be less than 200, otherwise, when multiplied by 5, it would give a four-digit number. Therefore, the numbers 775 and 975 are definitely not suitable. Among the remaining three numbers, only 175 satisfies the condition of the problem.
Second method. Note (similar to the first method of solving) that the last digit of the desired number is 5. Let $a, b, 5$ be the consecutive digits of the desired number. According to the problem, we have: $100a + 10b + 5 = a \cdot b \cdot 5 \cdot 5$. Dividing both sides of the equation by 5, we get: $20a + 2b + 1 = 5ab$. After subtracting $20a$ from both sides of the equation and factoring out the common factor on the right side, we get: $2b + 1 = 5a(b - 4a)$ (1). Considering that $a$ and $b$ can take natural values from 1 to 9, we get that the possible values of $a$ are only 1 or 2. But $a = 2$ does not satisfy equation (1), as the left side is an odd number, and the right side, when substituting $a = 2$, is even. Therefore, the only possibility is $a = 1$. Substituting this value into (1), we get: $2b + 1 = 5b - 20$, from which $b = 7$. Answer: the only desired number is 175.
## Grading Criteria.
- Complete correct solution - 7 points.
- Correct answer obtained and there are arguments that significantly reduce the number of cases to check, but the full solution is not provided - 4 points.
- The equation is correctly set up and transformations and arguments are provided that allow solving the problem, but the solution is not completed - 4 points.
All-Russian School Olympiad 2014-2015.
- The number of cases to check is reduced, but there are no explanations why, and the correct answer is given - 3 points.
- The equation is correctly set up, but the problem is not solved - 2 points.
- There are arguments in the solution that allow excluding certain numbers or considering numbers with certain properties (for example, ending in the digit 5), but there is no further significant progress in solving the problem - 1 point.
- Only the correct answer or the answer with verification is provided - 1 point.
|
175
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a circle, a diameter $A B$ and a chord $C D$ parallel to it were drawn such that the distance between them is half the radius of this circle (see figure). Find the angle $CAB$.
|
Answer: $75^{\circ}$.
Solution. Consider triangle $A O C$, where $O$ is the center of the circle. This triangle is isosceles because $O C$ and $O A$ are radii. Therefore, by the property of isosceles triangles, angles $A$ and $C$ are equal. Draw the perpendicular $C M$ to side $A O$ and consider the right triangle $O M C$. According to the problem, the leg $C M$ is half the hypotenuse $O C$. Therefore, the measure of angle $C O M$ is $30^{\circ}$.
Then, by the theorem on the sum of the angles of a triangle, we get that angle $C A O$ (or $C A B$) is $75^{\circ}$.
## Grading Criteria.
- Correct and justified solution to the problem - 7 points.
- Correct reasoning that constitutes a solution to the problem but results in an incorrect answer (e.g., angle $C O A$ is given instead of angle $C A O$) - 6 points.
- Generally correct reasoning with minor errors that do not fundamentally affect the solution, and the correct answer is given - 5 points.
- Correct solution to the problem without justifications: all intermediate conclusions are stated without indicating the connections between them (references to theorems or definitions) - 4 points.
- Additional constructions and markings on the diagram that clearly show the solution process, the correct answer is given, but the reasoning is not provided - 3 points.
- Correct answer given with incorrect reasoning - 0 points.
- Only the correct answer is given - 0 points.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. For a natural number $a$, the product $1 \cdot 2 \cdot 3 \cdot \ldots \cdot a$ is denoted as $a$ !.
(a) (2 points) Find the smallest natural number $m$ such that $m$ ! is divisible by $23 m$.
(b) (2 points) Find the smallest natural number $n$ such that $n$ ! is divisible by $33n$.
|
# Answer:
(a) (2 points) 24.
(b) (2 points) 12.
Solution. (a) The condition is equivalent to $(m-1)!$ being divisible by 23. Since 23 is a prime number, at least one of the numbers $1, 2, \ldots, m-1$ must be divisible by 23, so $m-1 \geqslant 23$ and $m \geqslant 24$. Clearly, $m=24$ works, since in this case $\frac{24!}{23 \cdot 24}=22!$.
(b) The condition is equivalent to $(n-1)!$ being divisible by $33=3 \cdot 11$. Since 3 and 11 are prime numbers, at least one of the numbers $1, 2, \ldots, n-1$ must be divisible by 11, so $n-1 \geqslant 11$ and $n \geqslant 12$. Clearly, $n=12$ works, since in this case $\frac{12!}{33 \cdot 12}=\frac{10!}{3}=8! \cdot 3 \cdot 10$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.2. In four classes of a school, there are more than 70 children, all of whom came to the grade meeting (no other children were present at the meeting).
Each girl who came was asked: "How many people from your class, including you, came to the meeting?"
Each boy who came was asked: "How many boys from your class, including you, came to the meeting?"
Among the answers, the numbers $7,9,10,12,15,16,19$ and 21 were encountered (all children answered correctly).
(a) (1 point) How many children are there in the largest class of the grade?
(b) (3 points) How many girls came to the grade meeting?
|
# Answer:
(a) (1 point) 21 students.
(b) (3 points) 33 girls.
Solution. (a) Since all 8 numbers listed in the condition are distinct, exactly 4 of them represent the number of children in the classes, and the other 4 represent the number of boys in the classes. The number 21, being the largest of the listed numbers, cannot be the number of boys in any class (otherwise, there would be no number corresponding to the total number of students in that class). Therefore, the largest class has 21 students.
(b) It follows that the number of students in the second largest class does not exceed 19, in the third largest does not exceed 16, and in the fourth largest does not exceed 15. Then the total number of students does not exceed $15+16+19+21=71$, and according to the problem, more than 70 students attended the grade meeting. Therefore, the class sizes are exactly $15, 16, 19, 21$, and the total number of students is 71.
Then the total number of boys in the classes is $7+9+10+12=38$, and the total number of girls is $71-38=33$.
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. The numbers $1, 2, 3, \ldots, 57$ are written on a board. What is the maximum number of these numbers that can be chosen so that no two chosen numbers differ exactly by a factor of 2.5?
|
Answer: 48.
Solution. Consider sequences of natural numbers that satisfy the following set of conditions: in each sequence
- each number does not exceed 57
- there are at least two numbers, and they all go in ascending order;
- each subsequent number is 2.5 times the previous one.
Let's list them all.
- 2,5
- $4,10,25$
- 6,15
- $8,20,50$
- 12,30
- 14,35
- 16,40
- 18,45
Notice that in each of these nine sequences, there should be at least one unselected number. Then the number of selected numbers is no more than $57-9=48$.
An example where the number of selected numbers is exactly 48 is not hard to construct: it is sufficient to select all numbers from 1 to 57, except for the second numbers from the nine sequences listed above.
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On a plane, 36 points are marked, no three of which lie on the same line. Some pairs of marked points are connected by segments such that no more than 3 segments emanate from each marked point.
What is the maximum number of different closed 4-segment broken lines that can result?
The vertices of the broken line can only be the marked points, and the segments can only be the drawn segments. It does not matter where the broken line starts or how it is oriented: for example, if for some 4 marked points \( A, B, C, D \) the segments \( AB, BC, CD, DA \) are drawn, then \( ABCD, BCDA, CDAB, DABC, ADCB, BADC, CBAD, DCBA \) are considered the same broken line.
|
# Answer: 54.
Solution. First, let's prove that there are no more than 54 broken lines.
Consider a "tick" structure, consisting of three points $A, B$, and $C$, as well as two segments $AB$ and $AC$ (the segment $BC$ may or may not be present; point $A$ will be called the vertex of the tick). Since from $B$ and $C$ no more than two segments can extend, each tick can be contained in no more than two 4-segment broken lines (Fig. 5a). Furthermore, point $A$ can be the vertex of no more than three ticks, so it can be part of no more than six 4-segment broken lines.
(a)
(b)
Fig. 5: Solution to problem 9.8
Now let's estimate the number of broken lines. There are 36 points in total, and each point can be part of no more than 6 broken lines, with each broken line involving exactly 4 points. Therefore, the number of broken lines is no more than $36 \cdot 6 / 4 = 54$.
Now let's prove that there could be exactly 54 broken lines.
Describe a construction consisting of 6 points: $A_1, A_2, A_3, B_1, B_2, B_3$ (Fig. 5b). Connect these points with segments such that for all $i, j \in \{1, 2, 3\}$, point $A_i$ is connected to point $B_j$ (thus, from each point, exactly 3 segments extend). Then any pair of vertices $A_{i_1}, A_{i_2}$ together with any pair of vertices $B_{j_1}, B_{j_2}$ will form a 4-segment broken line. Thus, there will be exactly 9 broken lines. To construct the example required in the problem, it is sufficient to consider 6 such constructions, all points of which are distinct.
|
54
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2.1. Points $A, B, C, D$ are marked on a line, in that exact order. Point $M$ is the midpoint of segment $A C$, and point $N$ is the midpoint of segment $B D$. Find the length of segment $M N$, given that $A D=68$ and $B C=20$.
## 68
|
Answer: 24.
Solution. Let $A C=x$, then $A M=\frac{x}{2}$. Now we calculate the length of $N D$:
$$
N D=\frac{B D}{2}=\frac{20+C D}{2}=\frac{20+(68-x)}{2}=44-\frac{x}{2}
$$
Now it is not difficult to calculate $M N$:
$$
M N=A D-A M-N D=68-\frac{x}{2}-\left(44-\frac{x}{2}\right)=24
$$
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.1. Along the road connecting Masha's and Sasha's houses, there are 17 apple trees and 18 poplars. When Masha was going to visit Sasha, she took photos of all the trees. Right after the tenth apple tree, Masha's phone memory ran out, and she couldn't photograph the remaining 13 trees. The next day, when Sasha was going to visit Masha, starting from the eighth apple tree, he picked one leaf from each tree. How many leaves did Sasha pick?
|
Answer: 22.
Solution. Note that the tenth apple tree, counting from Masha's house, is the eighth apple tree, counting from Sasha's house. Therefore, Sasha will not pick a leaf from exactly 13 trees. We get that he will pick a total of $17+18-13=22$ leaves.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.4. Along the road connecting Masha's and Sasha's houses, there are 17 apple trees and 20 poplars. When Masha was going to visit Sasha, she took photos of all the trees. Right after the tenth apple tree, Masha's phone memory ran out, and she couldn't photograph the remaining 13 trees. The next day, when Sasha was going to visit Masha, starting from the eighth apple tree, he picked one leaf from each tree. How many leaves did Sasha pick?
|
Answer: 24.
## 7th grade, problem 5
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. At a physical education class, 27 seventh-graders arrived, some of them brought one ball each. Sometimes during the class, one of the seventh-graders would give their ball to another seventh-grader who didn't have one.
At the end of the class, $N$ seventh-graders said: "I received balls less frequently than I gave them away!". Find the maximum possible value of $N$, given that none of the students lied.
|
Answer: 13.
Solution. If a seventh-grader received the ball less frequently than he gave it away, then he originally had the ball, but no longer had it at the end. Thus, at the beginning of the lesson, the students collectively had at least $N$ balls, which ultimately ended up with some of the remaining $27-N$ students. Therefore, $N \leqslant 27-N$, from which we get that $N \leqslant 13$ (since $N$ is an integer). It remains to show that the value $N=13$ is possible. For convenience, let's number the seventh-graders from 1 to 27. Suppose students with numbers $1,2, \ldots, 13$ brought a ball to the lesson, and during the lesson, the seventh-grader with number $i$ passed the ball to the seventh-grader with number $13+i$ (for all $i=1,2, \ldots, 13$). It is clear that the condition of the problem is satisfied.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. For a physical education class, 29 seventh-graders came, some of them brought one ball each. Sometimes during the class, one of the seventh-graders would give their ball to another seventh-grader who didn't have one.
At the end of the class, \( N \) seventh-graders said: “I received balls less frequently than I gave them away!”. Find the maximum possible value of \( N \), given that none of the students lied.
|
Answer: 14.
## 7th grade, problem 6
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. Let $s(n)$ denote the sum of all odd digits of the number $n$. For example, $s(4)=0$, $s(173)=11, s(1623)=4$.
Calculate the value of the sum $s(1)+s(2)+s(3)+\ldots+s(321)$.
|
Answer: 1727.
Solution. We will separately count the sum of odd digits by place value.
## Units place.
Among the numbers from 1 to 321, there are 32 complete tens:
- from 1 to 10;
- from 11 to 20;
- from 21 to 30;
- ...
- from 311 to 320.
In each ten, the sum of the odd digits in the units place is $1+3+5+7+9=25$. Considering also the last number 321 with the digit 1 in the units place, we get that the sum of all odd digits in the units place is
$$
25 \cdot 32 + 1 = 801
$$
## Tens place.
Consider which numbers have odd digits in the tens place.
- The digit 1 in the tens place appears in 40 numbers: from 10 to 19, from 110 to 119, from 210 to 219, from 310 to 319.
- The digit 3 in the tens place appears in 30 numbers: from 30 to 39, from 130 to 139, from 230 to 239.
- The digit 5 in the tens place appears in 30 numbers: from 50 to 59, from 150 to 159, from 250 to 259.
- The digit 7 in the tens place appears in 30 numbers: from 70 to 79, from 170 to 179, from 270 to 279.
- The digit 9 in the tens place appears in 30 numbers: from 90 to 99, from 190 to 199, from 290 to 299. Therefore, the sum of all odd digits in the tens place is
$$
1 \cdot 40 + 3 \cdot 30 + 5 \cdot 30 + 7 \cdot 30 + 9 \cdot 30 = 760
$$
## Hundreds place.
Consider which numbers have odd digits in the hundreds place.
- The digit 1 in the hundreds place appears in 100 numbers: from 100 to 199.
- The digit 3 in the hundreds place appears in 22 numbers: from 300 to 321.
Therefore, the sum of all odd digits in the hundreds place is
$$
1 \cdot 100 + 3 \cdot 22 = 166
$$
It remains to find the total sum:
$$
801 + 760 + 166 = 1727
$$
|
1727
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In the morning, 5 foreign cars were parked along the road. By noon, 2 domestic cars were parked between each pair of foreign cars. And by evening, a motorcycle was parked between each pair of adjacent cars. How many motorcycles were parked in total $?$
Answer: 12 .
|
Solution. Between 5 foreign cars there are 4 gaps, so there were $4 \cdot 2=8$ domestic cars parked there; that is, a total of $5+8=13$ cars were parked. Between them, 12 motorcycles were parked.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. At an open evening at the conservatory, four quartets, five duets, and six trios were supposed to perform (a quartet consists of four musicians, a trio of three, and a duet of two; each musician is a member of only one musical group). However, one quartet and two duets unexpectedly went on tour, and a soloist from one of the trios fell ill, so the members of this trio had to perform as a duo. How many musicians performed at the conservatory that evening?
|
Answer: 35.
Solution. If no one was absent, then at the evening there would have been
$4 \cdot 4(4$ quartets $)+5 \cdot 2(5$ duets $)+6 \cdot 3$ ( 6 trios $)=44$ people.
But $4(1$ quartet) $+2 \cdot 2$ (2 duets) +1 (a soloist from one of the trios) $=9$ people were absent. Thus, at the evening, $44-9=35$ people performed.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Dima stood on one of the steps of the staircase and suddenly noticed that there were an equal number of steps above and below him. Then he climbed up 7 steps, and after that, he went down 15 steps. In the end, he found himself on the 8th step of the staircase (counting from the bottom). How many steps does the staircase consist of?
|
Answer: 31.
Solution. Since Dima ended up on the 8th step at the end, before that he was on the $8+15=23$ step. He got there by climbing up 7 steps, so he started from the $23-7=16$ step. Thus, we have that the 16th step is the middle of the ladder. Therefore, the ladder consists of 31 steps.
|
31
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. On the table, there were cards with digits from 1 to 9 (a total of 9 cards). Katya chose four cards such that the product of the digits on two of them equals the product of the digits on the other two. Then Anton took one more card from the table. In the end, the cards with the digits $1,4,5,8$ remained on the table. Which card did Anton take?
|
# Answer: 7.
Solution. One of the cards that is not currently on the table has the number 7. Note that Katya could not have taken the 7, because then one of her products would be divisible by 7, while the other would not. Therefore, Anton took the 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Yulia thought of a number. Dasha added 1 to Yulia's number, and Anya added 13 to Yulia's number. It turned out that the number obtained by Anya is 4 times the number obtained by Dasha. What number did Yulia think of?
|
Answer: 3.
Solution. Note that since Anya's number is 4 times greater than Dasha's number, the difference between these numbers is 3 times greater than Dasha's number. Thus, Dasha's number is $(13-1): 3=4$. Therefore, Yulia's number is 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. Aся, Borya, Vasilina, and Grisha bought tickets to the cinema for one row. It is known that:
- There are a total of 9 seats in the row, numbered from 1 to 9.
- Borya did not sit in seat 4 or 6.
- Aся sat next to Vasilina and Grisha, and no one sat next to Borya.
- There were no more than two seats between Aся and Borya.
In which seat, with what number, was someone definitely sitting?
Answer: 5.
|
Solution. Note that Asey, Vasilina, and Grisha occupy three seats in a row, and Borya sits one seat away from them. Let's seat another child, Dima, in the free seat. Then, 5 children sit in a row. Thus, someone is sitting in the central seat of the row (that is, seat number 5). For any other seat, we can come up with an arrangement such that it is not occupied.
What if Dima is sitting in the 5th seat? Then Borya (since they are sitting next to each other) must sit either in seat 4 or 6, but this contradicts the condition. Therefore, in seat 5, either Asey, Borya, Vasilina, or Grisha is sitting.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. Masha braided her dolls: half of the dolls got one braid each, a quarter of the dolls got two braids each, and the remaining quarter of the dolls got four braids each. She tied a ribbon in each braid. How many dolls does Masha have if she needed 24 ribbons in total?
|
Answer: 12.
Solution. Note that since a quarter of the dolls have four braids, the total number of ribbons used on them is the same as the total number of dolls. Half of the dolls have one braid, so the number of ribbons used on them is half the total number of dolls. And a quarter of the dolls have two braids, so the number of ribbons used on them is also half the total number of dolls.
This means that the number of ribbons is twice the number of dolls. Therefore, Masha has a total of 12 dolls.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Electronic clocks display time from 00.00.00 to 23.59.59. How much time during the day does the number on the display that reads the same from left to right and from right to left light up?
|
Answer: 96 seconds.
Solution. If the digits on the display are $a b . c d . m n$, then $a=0,1,2,0 \leq b \leq 9,0 \leq c \leq 5$, $0 \leq d \leq 9,0 \leq m \leq 5,0 \leq n \leq 9$. Therefore, if $a=n, b=m, c=d$, the symmetrical number on the display is uniquely determined by the digits $a, b$ and $c$, where $a=0,1,2,0 \leq b \leq 5,0 \leq c \leq 5$. In this case, if $a=0$ or 1, then $b$ and $c$ can be any digits from 0 to 5, the number of such number sets is $2 \cdot 6 \cdot 6=72$. If $a=2$, then $b=0,1,2,3 ; 0 \leq c \leq 5$ and the number of such sets is $4 \cdot 6=24$. In total, $72+24$ $=96$ sets of numbers, each of which is displayed for 1 second.
|
96
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. $A L$ and $B M$ are the angle bisectors of triangle $A B C$. The circumcircles of triangles $A L C$ and $B M C$ intersect again at point $K$, which lies on side $A B$. Find the measure of angle $A C B$.
|
Answer. $\angle A C B=60^{\circ}$.
Solution. Draw the segment $C K . \angle L C K=\angle L A K$ (these angles are inscribed in the circle and subtend the same arc). Similarly, $\angle M C K$ $=\angle M B K$. Since $\angle A C B=\angle L C K+\angle M C K$, the desired angle $A C B$ is one-third of the sum of the angles of triangle $A B C$, that is, it is equal to $60^{\circ}$.
## Criteria and methodology for evaluating the performance of olympiad tasks
At the olympiad, a 7-point scale should be used: each problem is scored with an integer from 0 to 7. The final score is the sum of the points earned by the participant.
The main principles of evaluation are presented in the table.
| Points | Correctness (incorrectness) of the solution |
| :---: | :--- |
| 7 | Complete correct solution. |
| $6-7$ | Correct solution. There are minor flaws, which do not significantly affect the solution. |
| $5-6$ | The solution contains minor errors, gaps in reasoning, but is generally correct and can become fully correct after minor corrections or additions. |
| $2-3$ | Auxiliary statements that help in solving the problem have been proven. |
| $0-1$ | Important individual cases have been considered in the absence of a solution (or in the case of an incorrect solution). |
| 0 | The solution is incorrect, no progress has been made. |
| 0 | The solution is absent. |
a) any correct solution is scored 7 points. It is not permissible to deduct points for the solution being too long, or for the solution differing from the one provided in the methodological materials or from other solutions known to the jury; when checking the work, it is important to understand the logic of the participant's reasoning, assessing the degree of its correctness and completeness;
b) the olympiad work is not a participant's test, so any corrections in the work, including crossing out previously written text, are not grounds for deducting points; it is not permissible to deduct points for untidiness in writing solutions;
c) points are not awarded "for the participant's effort," including for writing a large volume of text that does not contain progress in solving the problem.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Option 1
On the sheet, three rectangles A, B, and C are drawn.
A
5
B
Rectangles A and B have the same width, and rectangles B and C have the same length (width - top to bottom, length - left to right). The length of rectangle B is 2 cm longer than the length of rectangle A, and the area of B is 22 cm² larger than the area of rectangle A. The width of rectangle C is 4 cm less than the width of rectangle B, and the area of C is 40 cm² less than the area of B. Find the area of rectangle A in square centimeters.
|
Answer: 88.
Solution: Let rectangle A have a length of $a$ cm and a width of $b$ cm. If the length is increased by 2 cm, the area will increase by $2 b$ cm $^{2}$. Therefore, $2 b=22, b=11$. The area of rectangle B is 40 cm $^{2}$ less than that of rectangle B, so the length of rectangle B is $40: 4=10$ cm. Therefore, the length of rectangle A is $a=10-2=8$ cm. Its area is $a b=88$ cm $^{2}$.
## Variant 2
Three rectangles A, B, and C are drawn on a sheet.

A

B
Rectangles A and B have the same width, and rectangles B and C have the same length (width - top to bottom, length - left to right). The length of rectangle B is 3 cm longer than that of rectangle A, and the area of B is 21 cm $^{2}$ larger than that of A. The width of rectangle C is 3 cm less than that of rectangle B, and the area of C is 60 cm $^{2}$ less than that of B. Find the area of rectangle A in square centimeters.
Answer: 119.
## Variant 3
Three rectangles A, B, and C are drawn on a sheet.

A

B
Rectangles A and B have the same width, and rectangles B and C have the same length (width - top to bottom, length - left to right). The length of rectangle B is 4 cm longer than that of rectangle A, and the area of B is 48 cm $^{2}$ larger than that of A. The width of rectangle C is 3 cm less than that of rectangle B, and the area of C is 39 cm $^{2}$ less than that of B. Find the area of rectangle A in square centimeters.
Answer: 108.
## Variant 4
Three rectangles A, B, and C are drawn on a sheet.
Rectangles A and B have the same width, and rectangles B and C have the same length (width - top to bottom, length - left to right). The length of rectangle B is 3 cm longer than that of rectangle A, and the area of B is $33$ cm $^{2}$ larger than that of A. The width of rectangle C is 4 cm less than that of rectangle B, and the area of C is 52 cm $^{2}$ less than that of B. Find the area of rectangle A in square centimeters.
Answer: 110.
## Variant 5
Three rectangles A, B, and C are drawn on a sheet.
Rectangles A and B have the same width, and rectangles B and C have the same length (width - top to bottom, length - left to right). The length of rectangle B is 4 cm longer than that of rectangle A, and the area of B is 36 cm $^{2}$ larger than that of A. The width of rectangle C is 5 cm less than that of rectangle B, and the area of C is 75 cm $^{2}$ less than that of B. Find the area of rectangle A in square centimeters.
Answer: 99.
|
88
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Option 1
There are candies in three boxes. It is known that there are 2 times fewer candies in the first box than in the second. It is also known that there are a total of 24 candies in the first and third boxes, and a total of 34 candies in the second and third boxes. How many candies are there in total in the boxes?
|
Answer: 44.
Solution: From the condition, it follows that in the second box there are $34-24=10$ more candies than in the first. And this difference is equal to the number of candies in the first box. Therefore, there are 10 candies in the first box, 20 in the second, and 14 in the third.
## Variant 2
In three boxes, there are candies. It is known that there are twice as few candies in the first box as in the second. It is also known that there are 26 candies in total in the first and third boxes, and 36 candies in total in the second and third boxes. How many candies are there in total in the boxes?
Answer: 46.
## Variant 3
In three boxes, there are candies. It is known that there are twice as few candies in the first box as in the second. It is also known that there are 27 candies in total in the first and third boxes, and 39 candies in total in the second and third boxes. How many candies are there in total in the boxes?
Answer: 51.
## Variant 4
In three boxes, there are candies. It is known that there are twice as few candies in the first box as in the second. It is also known that there are 22 candies in total in the first and third boxes, and 36 candies in total in the second and third boxes. How many candies are there in total in the boxes?
Answer: 50.
## Variant 5
In three boxes, there are candies. It is known that there are twice as few candies in the first box as in the second. It is also known that there are 28 candies in total in the first and third boxes, and 40 candies in total in the second and third boxes. How many candies are there in total in the boxes?
Answer: 52.
|
44
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Variant 1.
A square piece of paper is folded as follows: the four corners are folded to the center so that they meet at one point (see figure),
resulting in a square again. After performing this operation several times, a square with a side length of 3 cm and a thickness of 16 sheets of paper is obtained. Find the side length of the original square in centimeters.
|
Answer: 12.
Solution: After each operation, the thickness of the square doubles, and the area is halved. Since the thickness has become 16 sheets, the operation was applied 4 times. In this process, the area decreased by a factor of 16 and became equal to 9 square centimeters. Therefore, the area of the original square was $16 \times 9 = 12 \times 12 = 144$ square centimeters. Thus, the side length of the original square is 12 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Variant 1
Given nine cards with the numbers $5,5,6,6,6,7,8,8,9$ written on them. From these cards, three three-digit numbers $A$, B, V were formed, each of which has all three digits different. What is the smallest value that the expression A + B - V can have?
|
Answer: 149.
Solution. By forming the smallest sum of numbers A and B, as well as the largest number C, we get the smallest value of the expression A + B - C: $566 + 567 - 988 = 145$. However, this combination is not suitable: two numbers have the same digits. By swapping the digits 6 and 8 in the units place, we get the required combination: $568 + 567 - 986 = 149$. Why is this combination the best? With any other arrangement of digits in the hundreds place, we will get a contribution from the hundreds equal to 200, or $300, \ldots$. And in the tens and units places, we will get positive values, as the sum of any two of the digits is greater than any third digit. Therefore, the number A + B - C will be greater than 200. Thus, A and B start with the digit 5, and C starts with the digit 9. Similarly, we get that the second digits of numbers A and B should be 6, and the second digit of number C should be 8. The units place has been discussed above.
## Variant 2
Given nine cards with the numbers $5,5,6,6,7,7,8,8,9$ written on them. From these cards, three three-digit numbers A, B, C were formed, each of which has all three digits different. What is the smallest value that the expression A + B - C can take?
Answer: 148.
## Variant 3
Given nine cards with the numbers $4,4,5,5,5,6,7,7,8$ written on them. From these cards, three three-digit numbers A, B, C were formed, each of which has all three digits different. What is the smallest value that the expression A + B - C can take?
Answer: 38.
## Variant 4
Given nine cards with the numbers $4,4,5,5,6,6,7,7,8$ written on them. From these cards, three three-digit numbers A, B, C were formed, each of which has all three digits different. What is the smallest value that the expression A + B - C can take?
Answer: 37.
## Variant 5
Given nine cards with the numbers $5,5,6,6,6,7,7,8,9$ written on them. From these cards, three three-digit numbers A, B, C were formed, each of which has all three digits different. What is the smallest value that the expression A + B - C can take?
Answer: 148.
|
149
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Variant 1
Given the road map of the kingdom. The cities are marked with numbers, and the segments represent roads. One day, a traveling knight started his journey from one of the cities in the kingdom and managed to construct his route in such a way that he traveled each road exactly once. In which city, marked with a number, could he have started his journey? List all possible options.
|
Answer: 2, 5.
Solution: If a city is not the beginning or the end of the knight's journey, then every time he enters through one road, he must exit through another road. This means that the roads from such a city come in "pairs," and there is an even number of them in total. Therefore, cities 2 and 5, from which an odd number of roads lead out, will be the start and end of the journey (in some order), while the other cities cannot be the start or end of the journey. The required paths exist. For example, for 5, the path $5-6-1-2-3-4-5-7-1-8-3-7-8-2$ works, and for 2, the reverse path works.
## Variant 2
Given a map of the kingdom's roads. The cities are marked with numbers, and the segments represent roads. One day, a traveling knight started his journey in one of the cities of the kingdom and managed to construct his route so that he traveled each road exactly once. In which city, marked with which number, could he have started his journey? List all possible options.
Answer: $1,6$.
## Variant 3
Given a map of the kingdom's roads. The cities are marked with numbers, and the segments represent roads. One day, a traveling knight started his journey in one of the cities of the kingdom and managed to construct his route so that he traveled each road exactly once. In which city, marked with which number, could he have started his journey? List all possible options.
Answer: $7,8$.
## Variant 4
Given a map of the kingdom's roads. The cities are marked with numbers, and the segments represent roads. One day, a traveling knight started his journey in one of the cities of the kingdom and managed to construct his route so that he traveled each road exactly once. In which city, marked with which number, could he have started his journey? List all possible options.
Answer: 2, 4.
## Variant 5
Given a map of the kingdom's roads. The cities are marked with numbers, and the segments represent roads. One day, a traveling knight started his journey in one of the cities of the kingdom and managed to construct his route so that he traveled each road exactly once. In which city, marked with which number, could he have started his journey? List all possible options.
Answer: $2,6$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1.
Each of the 10 students came up with 5 natural numbers. It turned out that each number was thought of by at least three students. What is the maximum number of different numbers that could have been thought of?
|
Answer: 16.
Solution: In total, the students came up with 50 numbers, with each number being counted at least 3 times. We will prove that there could not have been more than 16 different numbers. If at least 17 different numbers were thought of and each by at least three students, then a total of no less than $17 \cdot 3=51$ numbers were thought of. This is a contradiction. An example where 16 numbers were thought of: Suppose the numbers 1 and 2 were thought of by 4 students each, and numbers 3 to 16 were thought of by 3 students each. Then a total of $2 \cdot 4 + 14 \cdot 3 = 8 + 42 = 50$ numbers were thought of, and each by at least 3 students.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Twelve pencils are sharpened so that they all have different lengths. Masha wants to put the pencils in a box in two rows of 6 each, so that in each row the lengths of the pencils decrease from left to right, and each pencil in the second row lies on a longer pencil. In how many ways can she do this?
Answer: 132.
|
A layout of pencils that satisfies the conditions in the problem will be called correct. We will stack the pencils in a box in descending order of length. The order of placement will be recorded in the form of a broken path from the point (0,0) in a rectangular Cartesian coordinate system on a plane to the point $(6,6)$. The path will be constructed according to the following rules. If a pencil is placed in the lower row, we draw the next segment of the broken line of length 1 parallel to the Ox axis; if a pencil is placed in the second row, we draw a segment of length 1 parallel to the Oy axis. As a result, a broken path is formed consisting of 12 segments, each of which has a unit length and is parallel to one of the coordinate axes, and there are exactly 6 segments parallel to each axis. In addition, for each node with coordinates (x, y), the inequality $\mathrm{x} \geq \mathrm{y}$ holds. Such a path is also called correct, and the nodes through which a correct path can pass are called admissible. Each correct layout is uniquely associated with a correct path. The reverse is also true: each correct path is uniquely associated with a correct layout of pencils. Therefore, it is necessary to find the number of correct broken paths from the origin to the point $(6,6)$. All such paths are located within a square with a side of 6, the sides of which lie on the coordinate axes or are parallel to them. We will draw a square, marking the nodes of the coordinate grid. Admissible nodes are marked with a circle, in which we will place the number of possible continuations of the path from the marked node to the end. The node with coordinates $(6,6)$, corresponding to the end of all correct paths, is marked with the number 1.
The rule for filling in subsequent values: in the marked node ( $x, y)$, we place a number equal to the sum of the numbers in the nodes ( $x+1, \mathrm{y})$ and ( $x, y+1)$, if these nodes are admissible. The filling of the diagram occurs sequentially from the top right corner to the bottom left. The filled diagram is shown in the figure.

The number 132 in the lower left corner of the figure is the answer to the problem.
|
132
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the sequence of numbers $a_{1}, a_{2}, \ldots$, is an arithmetic progression, and the sequence of numbers $a_{1} a_{2}, a_{2} a_{3}, a_{3} a_{4} \ldots$, is a geometric progression. It is known that $a_{1}=1$. Find $a_{2017}$.
|
Answer: $a_{2017}=1$;
Trunov K.V.
## Solution:
Since the sequence of numbers $a_{1} a_{2}, a_{2} a_{3}, a_{3} a_{4} \ldots$, is a geometric progression, then $\left(a_{n} a_{n+1}\right)^{2}=\left(a_{n-1} a_{n}\right)\left(a_{n+1} a_{n+2}\right)$ for $n \geq 2$. From this, we obtain that $a_{n} a_{n+1}=a_{n-1} a_{n+2}$ (since $a_{n} \neq 0$ for any $n$, otherwise the geometric progression would contain an infinite number of zeros, which would mean that the arithmetic progression $a_{1}, a_{2}, \ldots$, contains an infinite number of zeros, which is impossible). Since $a_{1}, a_{2}, \ldots$, is an arithmetic progression, we can write $a_{n} a_{n+1}=a_{n-1} a_{n+2}$ as $a_{n}\left(a_{n}+d\right)=\left(a_{n}-d\right)\left(a_{n}+2 d\right) \Leftrightarrow$
$\Leftrightarrow a_{n}^{2}+a_{n} d=a_{n}^{2}+a_{n} d-2 d^{2} \Leftrightarrow-2 d^{2}=0 \Leftrightarrow d=0 \Rightarrow a_{2017}=1$.
## Recommendations for checking.
Only the answer is given without justification - 0 points.
#
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of triples of natural numbers $a, b$, and $c$ not exceeding 2017 such that the polynomial $x^{11} + a x^{7} + b x^{3} + c$ has a rational root.
Trunov K.V.
|
Answer: 2031120
Solution: Since all coefficients of the polynomial are natural and the leading coefficient is 1, any rational root must be an integer.
Notice that for $x \geq 0$, $x^{11} + a x^{7} + b x^{3} + c \geq c \geq 1$. Therefore, there are no integer roots for $x \geq 0$. If $x \leq -2$, then $x^{11} + a x^{7} + b x^{3} + c \leq -2^{11} - 2^{7} a - 2^{3} b + c \leq -2^{11} - 2^{7} - 2^{3} + 2017 < 0$, so there are no integer roots for $x \leq -2$. Therefore, only $x = -1$ can be an integer root of the polynomial $x^{11} + a x^{7} + b x^{3} + c$, and $x = -1$ is a root of the polynomial if the condition $-1 - a - b + c = 0 \Rightarrow c = 1 + a + b$ is satisfied. Since $a$, $b$, and $c$ are natural numbers and do not exceed 2017, $a$ can take values from 1 to 2015. For $a = 1$, $b$ can take values from 1 to 2015; for $a = 2$, $b$ can take values from 1 to 2014; ..., for $a = 2015$, $b$ can take only the value 1. Therefore, the total number of such triples is $1 + 2 + 3 + 4 + \ldots + 2015 = \frac{1 + 2015}{2} \cdot 2015 = 2031120$.
## Recommendations for checking.
Proved that all rational roots are integers - 1 point.
Proved that there are no integer roots for $x \geq 0$ - +1 point.
Proved that there are no integer roots for $x \leq -2$ - +3 points.
|
2031120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. Nadya baked pies with raspberries, blueberries, and strawberries. The number of pies with raspberries was half of the total number of pies; the number of pies with blueberries was 14 less than the number of pies with raspberries. And the number of pies with strawberries was half the number of pies with raspberries and blueberries combined. How many pies of each kind did Nadya bake?
|
Answer: 21 raspberry pies, 7 blueberry pies, and 14 strawberry pies.
Solution. First method. Since the number of raspberry pies is half of the total, the number of blueberry and strawberry pies together is the same as the number of raspberry pies (see Fig. 5.3). Moreover, there are 14 fewer blueberry pies than raspberry pies, so these 14 pies are strawberry pies. Therefore, the number of raspberry and blueberry pies: \(14 \cdot 2 = 28\), which means a total of \(28 + 14 = 42\) pies were baked. Thus, the number of raspberry pies is \(42 : 2 = 21\), blueberry pies - 7, and strawberry pies - 14.
Fig. 5.3
Second method. Let \(x\) be the number of raspberry pies. Then the total number of pies baked is \(2x\), of which \(x - 14\) are blueberry pies, so the number of strawberry pies is \(2x - x - (x - 14) = 14\). Knowing that the number of strawberry pies is half the number of raspberry and blueberry pies together, we set up the equation: \(x + x - 14 = 2 \cdot 14\), from which \(x = 21\).
Thus, there are 21 raspberry pies, and the number of blueberry pies is \(21 - 14 = 7\).
## Grading Criteria:
+ Correct answer and correct solution provided
\(\pm\) Correct and justified reasoning provided, but one arithmetic error
\(\pm\) The number of pies of only one type or the total number of pies is correctly found, but the complete answer is not obtained
\(\mp\) The equation is correctly set up, but not solved
干 Correct answer provided, verified that it satisfies the condition, but not proven that other answers are impossible
- Only the answer is provided
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Postman Pechkin delivers mail by bicycle to four villages: Prostokvashino, Smetanino, Tvorozhnoye, and Molochnoye (see figure). He knows that the distance from Prostokvashino to Tvorozhnoye is 9 km, from Prostokvashino to Smetanino is 13 km, from Tvorozhnoye to Smetanino is 8 km, and from Tvorozhnoye to Molochnoye is 14 km. Find the distance from Prostokvashino to Molochnoye.
|
Answer: 19 km.
Solution. The distance from Prostokvashino to Smetanino with a detour to Tvorozhnoye is $9+8=17$ (km), and without the detour - 13 km. Therefore, the detour to Tvorozhnoye (from the highway and back) is 4 km. The distance from Prostokvashino to Molochnoye with a detour to Tvorozhnoye is $9+14=23$ (km), and without the detour: $23-4=19$ (km).
You can also introduce variables and set up equations.
## Grading Criteria:
+ correct answer and correct solution provided
$\pm$ correct and justified reasoning provided, but one arithmetic error is made
干 all necessary equations are correctly set up, but not solved
干 only the correct answer is provided
- incorrect solution provided
|
19
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. The teacher is going to give the children a problem of the following type. He will inform them that he has thought of a polynomial $P(x)$ of degree 2017 with integer coefficients, the leading coefficient of which is 1. Then he will tell them $k$ integers $n_{1}, n_{2}, \ldots, n_{k}$, and separately inform them of the value of the expression $P\left(n_{1}\right) \cdot P\left(n_{2}\right) \cdot \ldots \cdot P\left(n_{k}\right)$. Based on this data, the children are supposed to find the polynomial that the teacher could have thought of. For what smallest $k$ can the teacher formulate a problem of this type so that the polynomial found by the children necessarily coincides with the one thought of?
(G. Zhukov)
|
Answer. For $k=2017$.
Solution. First, we prove that $k>2016$. Suppose the teacher used some $k \leqslant 2016$, thinking of the polynomial $P(x)$. Consider the polynomial $Q(x)=P(x)+\left(x-n_{1}\right)\left(x-n_{2}\right) \ldots(x-n_{k})$. Note that the degree of the polynomial $Q(x)$ is also 2017, and its leading coefficient is also 1. Meanwhile, $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)=Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)$, but $P(x) \neq Q(x)$. Therefore, the children could have found the polynomial $Q(x)$ instead of $P(x)$, meaning the teacher did not achieve the required result.
It remains to prove that for $k=2017$ the teacher can come up with the required problem.
Lemma. Let $P(x)$ be a polynomial with integer coefficients, and let $a$ and $b$ be different integers. Then $P(a)-P(b)$ is divisible by $a-b$.
Proof. In the difference $P(a)-P(b)$, we group the terms by powers: if $P(x)=p_{n} x^{n}+p_{n-1} x^{n-1}+\ldots+p_{1} x+p_{0}$, then $P(a)-P(b)=p_{n}\left(a^{n}-b^{n}\right)+p_{n-1}\left(a^{n-1}-b^{n-1}\right)+\ldots+p_{1}(a-b)$, where each term is divisible by $a-b$.
Let $k=2017$. Set $n_{i}=4 i$ for $i=1,2, \ldots, k$; suppose the teacher informs the children that $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)=1$. Then the polynomial $P(x)=\left(x-n_{1}\right)\left(x-n_{2}\right) \ldots\left(x-n_{k}\right)+1$ fits the condition. Suppose there is another polynomial $Q(x)$ that also fits the condition. Then, since $Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)=1$ and the coefficients of the polynomial $Q(x)$ are integers, $Q\left(n_{i}\right)= \pm 1$ for any $i=1,2, \ldots, k$.
If there exist $i$ and $j$ such that $Q\left(n_{i}\right)=1$ and $Q\left(n_{j}\right)=-1$, then the difference $Q\left(n_{i}\right)-Q\left(n_{j}\right)=2$ is not divisible by $n_{i}-n_{j}$, which contradicts the lemma. Therefore, all values $Q\left(n_{i}\right)$ are equal to each other and are all equal to either 1 or -1. However, all values cannot be -1, as the product $Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)$ has an odd number of factors and the product would be -1. Thus, $Q\left(n_{i}\right)=1$ for any $i=1,2, \ldots, k$. Then the difference $P(x)-Q(x)$ is a polynomial of degree less than $k$, having at least $k$ roots, meaning this polynomial is identically zero, and $P(x)=Q(x)$. Contradiction.
Remark. Using the lemma, it can be shown that the polynomial $P(x)=\left(x-n_{1}\right)\left(x-n_{2}\right) \ldots\left(x-n_{2017}\right) \pm 1$ fits for any different integers $n_{1}, n_{2}, \ldots, n_{2017}$.
Comment. Only the correct answer - 0 points.
A complete solution to the problem consists of two parts:
(a) proving that the required cannot be achieved for $k \leqslant 2016$ - evaluated out of 2 points;
(b) proving that for $k=2017$ the required can be achieved - evaluated out of 5 points.
If in part (b) the polynomial $P(x)=\left(x-n_{1}\right)(x-n_{2}) \ldots\left(x-n_{k}\right) \pm 1$ (for some different integers $n_{1}, n_{2}, \ldots, n_{k}$) is presented, but it is not proven that no other polynomial $Q(x)$ satisfies the condition - 2 points (out of five).
Using the lemma about the divisibility of $P(a)-P(b)$ by $a-b$ without proof does not result in point deductions.
|
2017
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Petya wrote ten natural numbers on the board, none of which are equal. It is known that among these ten numbers, three can be chosen that are divisible by 5. It is also known that among the ten numbers written, four can be chosen that are divisible by 4. Can the sum of all the numbers written on the board be less than $75$?
(P. Kozhevnikov)
|
Answer. It can.
Solution. Example: $1,2,3,4,5,6,8,10,12,20$. In this set, three numbers $(5,10,20)$ are divisible by 5, four numbers $(4,8,12,20)$ are divisible by 4, and the total sum is 71.
Remark. It can be proven (but, of course, this is not required in the problem), that in any example satisfying the problem's conditions, the numbers $1,2,3,4,5,8,10,12$ and 20 must necessarily be present, and instead of the number 6, one can take 7 or 9.
Comment. To receive full marks (7 points for the problem), it is sufficient to have a correct example without specifying which numbers are divisible by 4 and 5, and an explicit calculation of the sum is also not required. Any non-working example is scored 0 points.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. In a company, some pairs of people are friends (if $A$ is friends with $B$, then $B$ is also friends with $A$). It turned out that for any selection of 101 people from this company, the number of pairs of friends among them is odd. Find the largest possible number of people in such a company.
(E. Bakayev, I. Bogdanov)
|
Answer: 102.
Solution: In all solutions below, we consider the friendship graph, where vertices are people in the company, and two people are connected by an edge if they are friends.
Consider 102 vertices, and construct the following graph on them. Connect one vertex $x$ to three others $v_{1}, v_{2}, v_{3}$. Divide the remaining 98 vertices into pairs and connect the vertices in each pair. The resulting graph has $98 / 2 + 3 = 52$ edges. When any vertex is removed, an odd number of edges is removed, so an odd number of edges remains. Therefore, the company described in the problem can consist of 102 people.
It remains to show that there is no such company of 103 people (then a company of more than 103 people is also impossible). Below we provide several different ways to do this; in each way, we assume, to the contrary, that such a company has been found.
First solution. There are $n = C_{103}^{2} = 51 \cdot 103$ ways to discard two vertices from 103, leaving 101. Number these ways from 1 to $n$. Let $a_{i}$ be the number of edges on the remaining 101 vertices in the $i$-th way; by assumption, all numbers $a_{i}$ are odd, and thus their sum $S$ is also odd (since the number $n$ is odd).
On the other hand, consider any edge $uv$. This edge is counted in the number $a_{i}$ exactly when vertices $u$ and $v$ are not discarded in the $i$-th way, that is, when some pair of the remaining 101 vertices is discarded. This happens in $k = C_{101}^{2} = 50 \cdot 101$ ways. Thus, each edge is counted in $S$ an even number of times $k$, so $S$ must be even. Contradiction.
Second solution. Call a vertex even if its degree is even, and odd otherwise. Consider two cases.
Case 1. Suppose the total number of edges in the graph is odd. Then, by discarding any pair of vertices, we must discard an even number of edges (to leave an odd number). On the other hand, if we discard vertices with degrees $d_{1}$ and $d_{2}$, the number of discarded edges is $d_{1} + d_{2}$ if these vertices are not connected by an edge, and $d_{1} + d_{2} - 1$ if they are connected. It follows that vertices of the same parity are never connected by an edge, and vertices of different parity are always connected.
Thus, if the graph has $k$ even vertices, the total number of edges is $k(103 - k)$, which is even. But we assumed that this number is odd - contradiction.
Case 2. Suppose the total number of edges in the graph is even. Similarly, we get that vertices of the same parity are always connected by an edge, and vertices of different parity are never connected. Therefore, if the graph has $k$ even vertices, the number of missing edges is $k(103 - k)$, which is even. Therefore, the total number of edges is $C_{103}^{2} - k(103 - k) = 103 \cdot 51 - k(103 - k)$, which is odd. But we assumed that this number is even.
Remark 1. Of course, there are other examples of a company of 102 people that satisfy the condition.
Remark 2. There is also another variation of the second solution.
Consider any 102 vertices and the induced subgraph on these vertices, let it have $k$ edges. By discarding any vertex from them (say, of degree $d$), we get 101 vertices with an odd number of edges $k - d$. Thus, the degree of any vertex in our subgraph has a parity different from the parity of $k$, that is, the degrees of all 102 vertices have the same parity.
Now consider the entire graph on 103 vertices. Call a vertex even if after its removal, the remaining graph has all vertex degrees even, and odd otherwise. Then two vertices of the same parity are connected to the same set of the remaining vertices, and two vertices of different parity are connected to sets of vertices that complement each other to the entire set of 101 remaining vertices. From this, it is not difficult to determine, as in the second solution, that the graph is either a complete bipartite graph or the union of two complete graphs. Further, one can proceed as in this solution.
Comment. The statement that in any graph, the number of vertices of odd degree is even, is accepted without proof.
Only the answer - 0 points.
Only an example of a company of 102 people satisfying the condition is provided - 1 point.
Noted only that to complete the solution, it is sufficient to show that a company cannot have exactly 103 people - no points are added. If this observation is missed in the solution - no points are deducted.
Proved only that a company cannot have 103 people - 6 points.
Below are some advances in proving this fact. Points for different advances do not add up; 1 point can be added for a correct example of a company of 102 people.
Proved only that in any company of 102 people satisfying the condition, all vertex degrees have the same parity - 2 points.
Proved that the graph is either a complete bipartite graph or the union of two complete graphs (as shown in the second solution) - 4 points.
If one of the above cases is missed (without sufficient reason) - 3 points instead of 4.
Only one of the two cases from the second solution is fully resolved - 4 points.
|
102
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. Let $S$ be a 100-element set consisting of natural numbers not exceeding 10000. Mark all points in space where each of the coordinates belongs to the set $S$. Attach to each of the 1000000 marked points $(x, y, z)$ a ball with the number $\frac{x^{2}+y^{2}+z^{2}}{x y+y z+z x}$ written on it. What is the maximum number of balls on which the number $2$ can be written?
(P. Kozlov)
|
Answer. $3 \cdot C_{100}^{2}=14850$.
Solution. Let's call a triplet of natural numbers $(x, y, z)$, whose elements belong to $S$, good if
$$
x^{2}+y^{2}+z^{2}=2(x y+y z+z x)
$$
Thus, we need to find the maximum possible number of good triplets.
Let's determine when a triplet is good. Rewrite (*) as a quadratic equation in $x$,
$$
x^{2}-2 x(y+z)+(y-z)^{2}=0
$$
Solving it, we get
$$
x=(y+z) \pm 2 \sqrt{y z}=(\sqrt{y} \pm \sqrt{z})^{2}
$$
from which $\sqrt{x}= \pm \sqrt{y} \pm \sqrt{z}$. In other words, a triplet is good if and only if one of the numbers $\sqrt{x}, \sqrt{y}$, and $\sqrt{z}$ is equal to the sum of the other two.
Let $s_{1}<s_{2}<\ldots<s_{100}$ be all the elements of the set $S$. Let $t_{i}=\sqrt{s_{i}}$. Estimate the number of good triplets $(x, y, z)$ in which $z$ is the largest number, i.e., $\sqrt{z}=\sqrt{x}+\sqrt{y}$. Note that for any $1 \leqslant i<j \leqslant 100$ there is at most one such triplet where $\sqrt{x}=t_{i}$ and $\sqrt{z}=t_{j}$ (from these values, $\sqrt{y}=\sqrt{z}-\sqrt{x}$ is restored). Therefore, the estimated number does not exceed the number of such pairs of numbers $(i, j)$, which is $C_{100}^{2}$.
Similarly, the number of good triplets in which the largest are $x$ and $y$ does not exceed $C_{100}^{2}$. Therefore, the total number of good triplets does not exceed $3 \cdot C_{100}^{2}$.
This estimate is achieved if we set $s_{i}=i^{2}$, i.e., $t_{i}=i$: indeed, then for any $i<j$ there is a good triplet $\left(s_{i}, s_{j-i}, s_{j}\right)$.
Remark 1. It can be shown that for the estimate to be achieved, it is necessary that $t_{i}=i t_{1}$ for all $i$. Since $1 \leqslant t_{i} \leqslant 100$, the example given above is unique.
Remark 2. It can be shown that the equality $\sqrt{z}=\sqrt{x}+\sqrt{y}$ for natural $x, y, z$ is possible only if the ratios $x / z$ and $y / z$ are squares of rational numbers, i.e., when $x=a^{2} t, y=b^{2} t$, and $z=c^{2} t$ for some natural $a, b, c$, and $t$ (where $a+b=c$).
This fact is not used in the solution provided above, but some students may rely on it in their work.
Comment. It is proven that a triplet is good if and only if one of the numbers $\sqrt{x}, \sqrt{y}$, and $\sqrt{z}$ is equal to the sum of the other two - 2 points (these points do not add to the points given below!).
Proving the fact mentioned in Remark 2 does not add 2 points.
If the further correct solution uses this fact without proof, 1 point is deducted.
It is proven that there are no more than 14850 good triplets - 6 points.
Only providing an example where there are exactly 14850 good triplets - 2 points.
|
14850
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.