problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. Let's call a four-digit number accompanying the year $\overline{20 a b}$ if it also ends in $\overline{a b}$ and, in addition, is divisible by $\overline{a b}$ (a two-digit number), for example, the number 4623 accompanies the year 2023. How many numbers accompany the year $2022?$
|
Solution. $\overline{m n 22}=\overline{m n} \cdot 100+22 \Rightarrow \overline{m n} \cdot 100: 22 \Rightarrow \overline{m n}: 11: 11,22,33,44,55,66,77$, 88,99 - 9 numbers.
Answer 9.
## Grading Criteria.
Correct answer with valid reasoning - 7 points.
Valid reasoning for divisibility by 11 and description of the set of numbers, but incorrect answer - 5 points.
Valid reasoning for divisibility by 11 - 3 points.
Valid reasoning for divisibility by 22, leading to answers $22,44,66,88$ - 4 numbers - 1 point.
Incorrect solution or only the answer - 0 points.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many solutions does the rebus $\frac{B+O+C+b+M+O+\breve{U}}{K+J+A+C+C}=\frac{22}{29}$ have, where different letters represent different digits, and the same letters represent the same digits? It is known that the digit 0 is not used.
|
Solution. In the rebus, 9 different letters are used, i.e., all non-zero digits are used. $1+2+3+0+0 \leq K+Л+A+C+C \leq 6+7+8+9+9$, i.e.
$$
6 \leq K+Л+A+C+C \leq 39 . \quad \text { Since the fraction } \frac{22}{29} \text { is irreducible, the number }
$$
$K+Л+A+C+C$ must be divisible by 29, the only case that satisfies all conditions is $K+Л+A+C+C=29$. Therefore, $B+O+C+b+M+O+\breve{И}=22$, in the word, 6 different letters are used (O is repeated twice). Note that $1+2+3+4+5+6=21$, doubling 1 gives 22, so $\mathrm{O}=1$. The unused digits form the word КЛА, so $7+8+9+\mathrm{C}+\mathrm{C}=29,2 \mathrm{C}=5$, but C cannot be non-integer. There are no solutions.
## Answer 0
## Grading Criteria.
Correct answer obtained with justification - 7 points.
Correctly shown that the numerator is 22 and the denominator is 29 without further progress - $\underline{2}$ points.
Shown that O must be equal to 1 - $\underline{\mathbf{1} \text { point. }}$
Underlined points are summed.
Incorrect solution or only the answer - 0 points.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Different positive numbers $x, y, z$ satisfy the equations
$$
x y z=1 \quad \text{and} \quad x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}
$$
Find the median of them. Justify your answer.
|
# Solution:
Method 1. Consider the polynomial $P(t)=(t-x)(t-y)(t-z)$. The numbers $x, y, z$ are its roots. Expanding the brackets or using Vieta's theorem for cubic polynomials, we get $P(t)=t^{3}+a t^{2}+b t+c$, where $a=-(x+y+z)$, $b=xy+xz+yz$, and $c=-xyz$. The condition of the problem shows that $a=-b$ and $c=-1$. Then we have $P(t)=t^{3}-b t^{2}+b t-1=(t-1)(t^{2}-b t+1)$. This means that one of the roots of the polynomial $P(t)$ is 1, and the other two are the roots of the quadratic trinomial $t^{2}-b t+1$. By Vieta's theorem, their product is 1. Since both are positive numbers, one of them is greater than 1, and the other is less than 1.
Method 2. Express $z$ from the first equation and substitute it into the second: $z=\frac{1}{xy}$, and then
\[
\begin{gathered}
x+y+\frac{1}{xy}=\frac{1}{x}+\frac{1}{y}+xy \\
x^{2}y+xy^{2}+1=y+x+x^{2}y^{2} \\
x^{2}(y-y^{2})+x(y^{2}-1)+1-y=0 \\
(1-y)(x^{2}y-xy-x+1)=0 \\
(1-y)(x-1)(xy-1)=0
\end{gathered}
\]
Thus, either $x=1$, or $y=1$, or $xy=1 \Leftrightarrow z=1$. In any of these cases, the product of the other two numbers is 1, as follows from the first condition. Since the numbers are distinct and positive, one of them is less than 1, the second is equal to 1, and the third is greater than 1.
Answer: 1.
Note: Reference to Vieta's theorem is accepted without proof.
| in progress | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| The problem is reduced to finding the roots of a cubic equation | 2 points |
| The problem is reduced to an equation with two variables | 1 point |
| An example of numbers satisfying the conditions of the problem is provided | 0 points |
| Incorrect solution or its absence | 0 points |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A company is called public if it has at least 15 shareholders. A shareholder of a company is called a minority shareholder if they own no more than $25 \%$ of the shares of that company. On the stock exchange where the shares are traded, one sixth of the companies are public. Prove that among all shareholders participating in the stock exchange, no less than $20 \%$ are minority shareholders. In the stock exchange, it is assumed that each shareholder owns shares of only one company.
|
Solution. Let the number of firms on the exchange be N. We will call a shareholder who owns more than $25 \%$ of a firm's shares a real shareholder. The number of real shareholders in one firm cannot exceed three. (If there are four, then one of them cannot own more than $25 \%$ of the shares). Therefore, the total number of real shareholders on the exchange cannot exceed $3 \mathrm{~N}$. Now consider a public company. Among its shareholders, there are no more than three real ones. This means that among the shareholders of a public company, there are at least 12 - minorities. The number of minorities on the exchange is no less than $12 \cdot \frac{1}{6} N$, i.e., no less than 2N. Thus, the number of minorities is no less than $2 \mathrm{~N}$, the number of real shareholders is no more than $3 \mathrm{~N}$, which means that minorities constitute no less than one fifth, i.e., no less than $20 \%$.
|
20
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Kolya, Seryozha, and Vanya regularly go to the cinema: Kolya goes there every 4th day, Seryozha - every 5th day, and Vanya - every 6th day. Today all the boys were at the cinema. When will all three meet at the cinema again?
|
1. Answer: 60.
Let's start numbering the days beginning with tomorrow (today's day is "zero"). Kolya will go to the cinema on the days whose numbers are divisible by 4, Seryozha - on the days whose numbers are divisible by 5, Vanya - on the days whose numbers are divisible by 6. For them to all be at the cinema together, the day number must be divisible by 4, 5, and 6. This will first happen on the day with the number $\operatorname{LCM}(4,5,6)=60$
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Four friends came back from fishing. Every two of them counted the sum of their catches. Six numbers were obtained: $7,9,14,14,19,21$. How many fish were caught in total?
|
4. 28 fish.
Note that the catch of each person is counted in exactly three sums. Therefore, if we add up all six numbers, we get the tripled total catch. Thus, the total number of fish caught is $(7+9+14+14+19+21): 3=28$ fish.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. From a $7 \times 7$ square grid, an equal number of $2 \times 2$ squares and $1 \times 4$ rectangles were cut out along the grid lines. What is the maximum number of these figures that could have been cut out?
|
Answer: 12.
Solution: Both the square and the rectangle consist of 4 cells. Therefore, the number of cut-out figures is no more than 49/4, that is, no more than 12. There are an equal number of figures of both types, so there are no more than 6 squares $2 \times 2$ and rectangles $1 \times 4$. The diagram shows how to cut out 6 squares $2 \times 2$ and 6 rectangles $1 \times 4$ from the square.
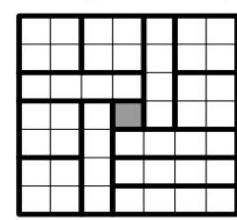
Comment: Only proved that there are no more than twelve figures - 3 points. Only provided an example of placing 12 figures - 6 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Find the value of the expression $a^{3}+12 a b+b^{3}$, given that $a+b=4$.
|
Answer: 64.
Solution. $a^{3}+12 a b+b^{3}=a^{3}+b^{3}+12 a b=(a+b)\left(a^{2}-a b+b^{2}\right)+12 a b=4 a^{2}-4 a b+4 b^{2}+12 a b=4(a+b)^{2}=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. A natural number is called interesting if all its digits are different, and the sum of any two adjacent digits is a square of a natural number. Find the largest interesting number.
|
Answer: 6310972.
Solution. Let's mark 10 points on the plane, representing the digits from 0 to 9, and connect those points whose sum is a square of a natural number.
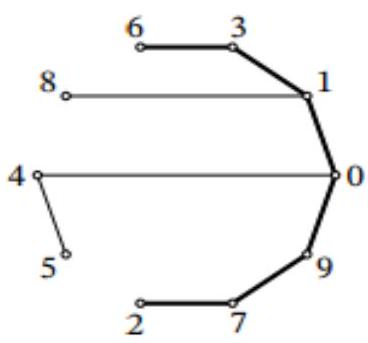
On this diagram, we need to find the path of maximum length, as the largest number should have the maximum number of digits. It is easy to notice that this path is $2-7-9-0-1-3-6$. To make the number as large as possible, the first digit should be as large as possible, i.e., the answer is the number 6310972.
Internet resources: http://www.problems.ru, https://olimpiada.ru.
|
6310972
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. In an intergalactic hotel, there are 100 rooms with capacities of
$101, 102, \ldots, 200$ people. In these rooms, a total of $n$ people live. A VIP guest has arrived at the hotel, and a whole room needs to be vacated for them. To do this, the hotel manager selects one room and relocates all its occupants to another single room. For what largest $n$ can the hotel manager always free up a room regardless of the current occupancy? (D. Belov, A. Safiullina)
|
Answer: 8824.
Solution: Suppose that with 8824 guests, the director cannot carry out the relocation. Let's divide the rooms into pairs by capacity: $101-200, 102-199, \ldots, 150-151$. Note that for each pair of rooms, the total number of people living in the two rooms is greater than the capacity of the larger room in the pair; otherwise, all the people from this pair could be gathered in the room with the larger capacity. Thus, the total number of people is no less than $201+200+199+\ldots+152=353 \cdot 25=8825$. Therefore, with 8824 guests, the director can free up a room.
Now let's provide an example proving that with 8825 or more guests, there exists a distribution in which it is impossible to free up a room in the specified manner.
Order the rooms by increasing capacity. Let there be 76 people in the first fifty rooms, and in the room with capacity $k$ for $151 \leqslant k \leqslant 200$, there are $k-75$ people. Let's calculate the number of people living in the hotel:
\[
\begin{aligned}
& 76 \cdot 50 + (76 + 77 + 78 + \ldots + 125) = \\
& \quad = 3800 + 201 \cdot 25 = 3800 + 5025 = 8825
\end{aligned}
\]
Consider any two arbitrary rooms with capacities $a < b$. If the number of people in the room with capacity $a$ is $a-75$ and the number of people in the room with capacity $b$ is $b-75$, then the total number of people in these two rooms is $(a-75) + (b-75) = a + b - 150$. Since $a + b \geq 301$, we have $a + b - 150 \geq 151$, which is greater than the capacity of the room with capacity $a$. Therefore, it is impossible to move all the people from these two rooms into the room with capacity $a$.
If the number of people in the hotel is greater than 8825, then it is sufficient to house the remaining people alternately in any rooms where there are still free spaces.
|
8824
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The beetle is 3 times heavier than the cat, the mouse is 10 times lighter than the cat, the turnip is 60 times heavier than the mouse. How many times heavier is the turnip than the beetle? Justify your answer.
|
# Answer. 2 times.
Solution. Cat $=10$ mice, turnip $=60$ mice. Therefore, the turnip is 6 times heavier than the cat. That is, the turnip $=6$ cats. According to the condition, Zhuchka $=3$ cats. Therefore, the turnip is 2 times heavier than Zhuchka.
## Grading Criteria.
- Correct solution - 7 points.
- Correct answer, partial explanations (some of the relationships are found), but no full justification - 3 points.
- Correct answer without explanations, how it was obtained - 2 points.
- Partial progress, for example, found that the turnip is 6 times heavier than the cat - up to 2 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. In some cells of a $200 \times 200$ square, there is one chip - either red or blue; the other cells are empty. A chip can see another if they are in the same row or column. It is known that each chip sees exactly five chips of the other color (and possibly some chips of its own color). Find the maximum possible number of chips in the cells.
(I. Bogdanov)
|
Answer: 3800 chips.
Solution: An example containing 3800 chips can be constructed as follows. Highlight the "border" of width 5 in a $200 \times 200$ square. This border consists of four corner squares $5 \times 5$ and four rectangles $5 \times 190$. Place the chips in these four rectangles: red chips in the left and top rectangles, and blue chips in the right and bottom rectangles. It is easy to see that this example meets all the requirements and contains 1900 red and 1900 blue chips.
It remains to prove that there cannot be more than 3800 chips. Consider an arbitrary arrangement of chips that meets the requirements. Call a row (a row or a column) multicolored if it contains chips of both colors.
Let's make two useful observations. First, each chip sees some chip of the other color, so each chip lies in at least one multicolored row. Moreover, since a multicolored row contains a red chip, it cannot have more than five blue chips (otherwise, the red chip would see all of them). Similarly, a multicolored row cannot have more than five red chips, so it contains no more than 10 chips in total.
Now it is not difficult to obtain the required estimate. If there are 191 multicolored rows, then they contain no more than $191 \cdot 10 = 1910$ chips, and the remaining nine rows contain no more than $9 \cdot 200 = 1800$ chips, totaling no more than $1910 + 1800 = 3710$ chips. Then in $b$ rows, there are at most 10 chips each; on the other hand, each chip must lie in a multicolored row, so in the intersection of $n-a$ monochromatic columns and $n-b$ monochromatic rows, chips cannot be placed. Therefore, in $n-b$ monochromatic rows, there are no more than $a (\leqslant b)$ chips each, and the total number of chips is no more than $10b + (n-b)b = (n+10-b)b \leqslant 20(n-10)$ (the last inequality holds because $(n+10-b) + b = 20 + (n-10)$ and $n+10-b \leqslant 20 \leqslant n-10 \leqslant b)$.
|
3800
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.7. Initially, a natural number $N$ is written on the board. At any moment, Misha can choose a number $a>1$ on the board, erase it, and write down all natural divisors of $a$, except for $a$ itself (the same numbers can appear on the board). After some time, it turned out that there are $N^{2}$ numbers on the board. For which $N$ could this have happened?
(M. Fadin, K. Kovalenko)
|
Answer. Only for $N=1$.
Solution. Lemma. For any natural $n>1$, the inequality holds
$$
\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{n^{2}}<1
$$
Proof. Consider the function $f(t) = \frac{1}{t^{2}}$ for $t > 1$. The function $f(t)$ is decreasing for $t > 1$. Let $1 = d_{1} < d_{2} < \ldots < d_{k} < d_{k+1} = N$ be the divisors of the number $N$. Then the numbers $N / d_{1} > N / d_{2} > \ldots > N / d_{k} > N / d_{k+1}$ are also divisors of the number $N$. Therefore, they are equal to the numbers $d_{k+1}, d_{k}, \ldots, d_{2}, d_{1}$ respectively. Taking the lemma into account, we get that the total number of numbers on the board will not exceed the number
$$
\begin{aligned}
d_{1}^{2}+d_{2}^{2} & +\ldots+d_{k}^{2}=\frac{N^{2}}{d_{k+1}^{2}}+\frac{N^{2}}{d_{k}^{2}}+\ldots+\frac{N^{2}}{d_{2}^{2}}= \\
& =N^{2}\left(\frac{1}{d_{2}^{2}}+\frac{1}{d_{3}^{2}}+\ldots+\frac{1}{d_{k+1}^{2}}\right) \leqslant \\
& \leqslant N^{2}\left(\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{N^{2}}\right)<N^{2} \cdot 1=N^{2}
\end{aligned}
$$
which is what we needed to prove.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A square $10 \times 10$ is divided into unit squares. How many triangles are formed after drawing one diagonal?
|
Answer: 110.
Solution. The figure shows one of the obtainable triangles. All such triangles are right-angled, with the right angle vertex being any lattice node except those lying on the diagonal. There are a total of $11 \times 11$ nodes, and 11 of them are on the diagonal, so the number of triangles is $11 \times 11-11=110$.
Criteria. Any correct solution: 7 points.
Incorrectly accounting for nodes on the diagonal: 4 points.
Correct answer: 2 points.
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Find the largest six-digit number, all digits of which are different, and each of the digits, except for the extreme ones, is either the sum or the difference of the adjacent digits.
|
Answer: 972538.
Solution. Let $A$ be the desired number. Let's try to find the number $A$ with the first digit being 9. We will try different options for the second digit. If the second digit is 8, then we get: $A=98176-$ it does not form a six-digit number. If the second digit is 7, then we get: $A=972538-$ a six-digit number.
Comment. Just the correct answer, but attempts to find the maximum number are missing - 4 points.
Any incorrect answer - 0 points.
|
972538
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. In the castle, there are 16 identical square rooms forming a $4 \times 4$ square. Sixteen people, who are either liars or knights (liars always lie, knights always tell the truth), moved into these rooms, one person per room. Each of these 16 people said: "At least one of the rooms adjacent to mine is occupied by a liar." What is the maximum number of liars that could be among these 16 people? Rooms are considered adjacent if they share a wall.
|
Answer: 8 liars.
Solution: Note that liars cannot live in adjacent rooms (otherwise, they would be telling the truth). Let's divide the rooms into 8 pairs of adjacent rooms. Then, in each pair, there can be no more than one liar. Therefore, there can be no more than 8 liars in total. Consider a chessboard coloring of the rooms in black and white. If we place 8 liars in the "black" rooms and 8 knights in the "white" rooms, the condition of the problem will be satisfied (all liars will be lying, and all knights will be telling the truth).
Comment: A correct answer without justification - 0 points.
Example of placing 8 liars and 8 knights - 2 points.
Proven that there are no more than 8 liars - 5 points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Initially, there were 10 piles of candies on the table, containing $1, 2, \ldots, 10$ candies respectively. The Child decided to redistribute the candies. On each odd minute, he chooses one pile and divides it into two piles, each containing at least one candy. On each even minute, he chooses two piles and merges them into one (thus, his first action is to divide a pile into two). Can it happen at some point that all piles on the table contain the same number of candies?
(N. Agakhanov, jury)
|
Answer: Yes.
Solution. We will provide an example of how Little One can achieve such a distribution. On the first minute, he divides the pile of 10 candies into two piles of 5 candies each. Then, on the 2nd, 4th, 6th, and 8th minutes, he combines the piles of 1+9, 2+8, 3+7, 4+6 respectively, and on the 3rd, 5th, 7th, and 9th minutes, he divides the pile of 10 candies he just received into two equal parts. By the 9th minute, he has 11 piles of 5 candies each.
Remark. There are other ways to get 11 piles of 5 candies. On the other hand, the number of piles on the table is always 10 or 11; from this, it is not hard to see that if the required result occurs, then there are exactly 11 piles of 5 candies each on the table.
Comment. Answer only - 0 points.
Any correct algorithm leading to the goal - 7 points.
|
11
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On the board, there are $n$ different integers, any two of which differ by at least 10. The sum of the squares of the three largest of them is less than three million. The sum of the squares of the three smallest of them is also less than three million. For what largest $n$ is this possible?
|
Answer. For $n=202$.
Solution. Notice immediately that $990^{2}+1000^{2}+1010^{2}=(1000-10)^{2}+1000^{2}+(1000+10)^{2}=3 \cdot 1000^{2}+2 \cdot 10^{2}$, which is greater than three million. On the other hand, $989^{2}+999^{2}+1009^{2}=(1000-11)^{2}+(1000-1)^{2}+(1000+9)^{2}=3 \cdot 1000^{2}-6 \cdot 1000+(9^{2}+1^{2}+11^{2})$, which is less than three million.
If there are not fewer than 102 non-negative numbers on the board, then the three largest of them are not less than $99 \cdot 10=990$, $100 \cdot 10=1000$, and $101 \cdot 10=1010$ respectively. Then, by the above observation, the sum of their squares is greater than three million, which is impossible. Therefore, there are no more than 101 non-negative numbers on the board. Similarly, there are no more than 101 negative numbers. Thus, the total number of numbers is no more than $101+101=202$.
An example for $n=202$ is given by the numbers $-1009, -999, -989, \ldots, -9$, $9, 19, \ldots, 999, 1009$. From the above observation, this example works.
Remark. Other examples that work include, for instance, the numbers $-1005, -995, -985, \ldots, -5, 5, 15, \ldots, 995, 1005$.
Comment. Only the proof that $n \leqslant 202$ is worth 5 points.
Only a correct example for $n=202$ (without justification of optimality or with incorrect justification) is worth 2 points. A correct example with $n=201$ numbers does not add points.
It may happen that a participant provides a correct example and a correct proof of optimality for exactly this example, but incorrectly counts the numbers in the example (for example, by counting that the sequence $5, 15, 25, \ldots, 1005$ contains exactly 100 numbers). In this case, 1 point should be deducted for the arithmetic error. (If this error leads to the participant incorrectly proving the estimate $n \leqslant 200$, no points are added for this part).
Works may be encountered where the authors believe that all numbers on the board are positive (or non-negative). In this case, the following criteria apply.
Only the proof that there are no more than $101$ positive (non-negative) numbers is worth 3 points.
An example consisting of non-negative numbers in this case does not add points.
|
202
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Scheherazade tells the Shah mathematical tales. A mathematical tale is an equation of the form $a x+b y=c$, where $a, b, c$ are natural numbers ranging from 1 to 17 (inclusive). A tale is sad if the corresponding equation has no solutions in integers (for example, the tale $2 x+4 y=7$ is sad, while the tale $3 x+5 y=2$ is not: this equation has a solution $x=-1, y=1$). Can Scheherazade invent 1001 different sad tales?
|
Answer: will be able to.
Solution. The following fairy tales will be sad:
a) a and b are even, c is odd. There are 8$\cdot$8$\cdot$9=576 such fairy tales.
b) a and b are divisible by 3, c is not divisible by 3. There are 5$\cdot$5$\cdot$12 such fairy tales. However, we need to account for the overlap with a): a and b are divisible by 6, c is odd and not divisible by 3. There are $2 \cdot 2 \cdot 6=24$ such fairy tales.
In total, a) and b): $576+300-24=852$
c) a and b are divisible by 5, c is not divisible by 5: there are 3$\cdot$3$\cdot$14=126 such. However, among them, $1 \cdot 1 \cdot 7$ have already been counted in a), and $1 \cdot 1 \cdot 10$ - in b). In total, new ones - 109
d) Fairy tales of the form $a=b=p, c \neq p$, where $p$ is one of the numbers 11, 13, 17. There are 3$\cdot$16=48 such fairy tales.
In total, there are already $852+109+48=1009$.
Evaluation. Full solution - 7 points. For errors related to the overlap of series, and arithmetic errors - deduct 1-3 points, depending on their severity.
|
1009
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $ABC$ (angle B is obtuse), the altitude $BH$ and the bisector $AK$ are drawn. Find the angle $AKB$, if the angle $KHC$ is $45^{\circ}$.
|
Answer: $45^{\circ}$.
Solution. Point K is equidistant from lines AB and AC (since AK is the bisector), and from lines HB and HC (since HK is the bisector of the right angle). Therefore, point K is equidistant from lines AB and BH. This means that BK is the bisector of the angle external to angle ABH. Therefore, angle HBC is half of this external angle: $90^{\circ}$ - $C=\frac{1}{2}\left(A+90^{\circ}\right)$, from which $C+\frac{1}{2} A=45^{\circ}$. But this is precisely the angle AKC we are looking for (it is the external angle in triangle AKC).
Grading. Full solution - 7 points. For a "trigonometric" solution - full credit. For a correctly set up but unsolved equation - 2 points. For the correct answer (without solution) - 0 points.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3 A weirdo chose 677 different natural numbers from the list $1,2,3, \ldots, 2022$. He claims that the sum of no two of the chosen numbers is divisible by 6. Did he go too far with his claim?
|
Solution: Suppose the eccentric is right. From the list specified in the condition, there are exactly 377 remainders of division by 6 of each type from 0 to 5. Numbers with remainders 0 and 3 can be taken no more than one each. It is impossible to take numbers with remainders 1 and 5 simultaneously, so in the eccentric's set, there are either those with a remainder of 1 or 5, and therefore no more than 337 numbers with a remainder of 1 or 5. Similarly, with a remainder of 2 or 4, there are no more than 337 numbers in total. In total, to ensure that the sum of no two numbers is divisible by 6, the eccentric could choose no more than $1+1+337+337=676$ numbers. Contradiction.
## Criteria:
- It is noted that no more than one number divisible by 3 and no more than one number with a remainder of 3 can be taken - 1 point.
|
676
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dwarves Glóin, Óin, and Thráin found 70 identical precious stones and want to divide them among themselves so that each of them gets no less than 10 stones. In how many ways can the dwarves do this?
|
Answer: 861.
Solution: Give each dwarf 9 stones, and lay out the remaining 43 stones in a row. To distribute the remaining stones among the dwarves, it is sufficient to place two dividers in the 42 spaces between the stones. Gloin will receive the stones to the left of the first divider, Oin will receive the stones between the two dividers, and Thrain will receive the stones to the right of the second divider. The number of ways to place these two dividers is $\frac{42 \cdot 41}{2}=861$.
Comment: Deduct 1 point for a computational error with correct reasoning. Deduct 1-2 points for potentially useful but unimplemented ideas.
|
861
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a $101 \times 101$ grid, all cells of which are painted white. It is allowed to choose several rows and repaint all cells in these rows to black. Then, choose exactly the same number of columns and repaint all cells in these columns to the opposite color (i.e., white to black, and black to white). What is the maximum number of black cells that the grid can contain after this operation?
|
Answer: 5100.
Solution. Let $k$ rows be repainted first, then $k$ columns. After the first stage of repainting, each column will contain $k$ black and $101-k$ white cells. Since $101-k$ columns will remain untouched, the total number of black cells in these columns will be $k(101-k)$. In each of the repainted columns, there will be $101-k$ black cells, so the total number of black cells in these columns will be $(101-k)k$. Therefore, the total number of black cells is $f(k) = 2k(101-k)$. It is clear that the graph of the function $f(x) = 2x(101-x)$ is a parabola with branches pointing downwards. This means that the maximum value of the function $f(x) = 2x(101-x)$ is achieved at the point $a = \frac{101}{2}$, and the function increases up to this point and then decreases. Therefore, for any integer $k$, $f(k) \leq f(50)$ for $0 \leq k \leq 50$ and $f(k) \leq f(51)$ for $51 \leq k \leq 101$. It remains to note that $f(50) = f(51) = 5100$.
Remark. The analysis of the behavior of the function $f(x)$ can be conducted using the derivative. From the fact that the maximum value of the function $f(x)$ is achieved at the point $a = \frac{101}{2}$, it does not follow that the function $f(k)$ (for integer $k$) must achieve its maximum value at one of the nearest integer points to $a$. Although this is true for our function, in general, there is a counterexample. For a valid conclusion, a reference to monotonicity is needed.
Comment. Only the answer - 1 point.
In the solution, an explicit formula for the number of black cells (in terms of $k$) is obtained - no less than 3 points.
An unproven conclusion that the maximum value is $f(50)$ or $f(51)$ - no more than 4 points.
|
5100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) In an $8 \times 8$ frame with a width of 2 cells (see figure), there are a total of 48 cells. How many cells are in a $254 \times 254$ frame with a width of 2 cells?

|
Answer: 2016.
Solution. First method. Cut the frame into four identical rectangles as shown in the figure. The width of the rectangles is equal to the width of the frame, i.e., 2 cells. The length of each rectangle is 2 less than the side of the frame: $254-2=252$ cells. Then the area of one rectangle is $2 \cdot 252=504$. Therefore, the total number of cells in the frame is $4 \cdot 504=2016$.

Second method. The area of the frame can be obtained by subtracting the area of the inner square from the area of the large square $254 \times 254$. The side of the inner square is 4 cells shorter than the side of the large square. Therefore, the area of the frame is
$$
254^{2}-250^{2}=(254-250)(254+250)=4 \cdot 504=2016.
$$
Remark. If the side of the frame is denoted by $n$, it can be proven (for example, by the methods described above) that its area will be $8 n-16$ cells.
## Grading Criteria.
- Any complete correct solution - 7 points.
- Correct approach, but an arithmetic error was made - 3 points.
- Correct reasoning, but an error was made in estimating the dimensions (for example, in the second method, it is incorrectly assumed that the side of the inner square is 2 cells shorter than the large one) - 2 points.
- Only the correct answer - 1 point.
|
2016
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) Anya multiplied 20 twos, and Vanya multiplied 17 fives. Now they are going to multiply their huge numbers. What will be the sum of the digits of the product?
|
Answer: 8.
Solution. In total, 20 twos and 17 fives are multiplied. Let's rearrange the factors, alternating twos and fives. This results in 17 pairs of $2 \cdot 5$ and three additional twos, which multiply to 8. Thus, the number 8 needs to be multiplied by 10, 17 times. This results in a number consisting of the digit 8 followed by 17 zeros. The sum of the digits is 8. Another way to write the same reasoning using the properties of exponents is:
$$
2^{20} \cdot 5^{17}=2^{3} \cdot 2^{17} \cdot 5^{17}=8 \cdot(2 \cdot 5)^{17}=8 \cdot 10^{17}=800000000000000000 .
$$
## Grading Criteria.
- Any complete and correct solution - 7 points.
- Correct solution approach, correct product obtained, but the sum of digits not indicated - 5 points.
- Grouping of twos and fives into pairs that give tens, but the answer is not obtained or is incorrect - 2 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
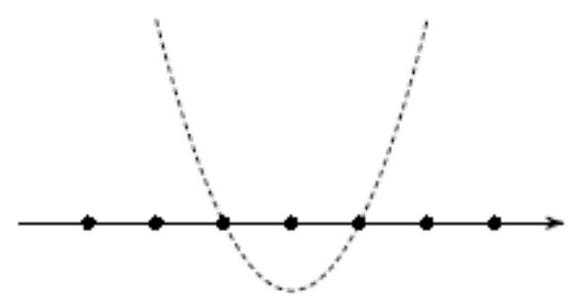
3. (7 points) The graph of a reduced quadratic trinomial is shown in the figure (the y-axis is erased, the distance between adjacent marked points is 1). What is the discriminant of this trinomial?
|
Solution. Let $x_{1}$ and $x_{2}$ be the roots of the given quadratic ( $x_{1}<x_{2}$ ). From the condition, it follows that $x_{2}-x_{1}=2$. Since $x_{2}=\frac{-b+\sqrt{D}}{2}, x_{1}=\frac{-b-\sqrt{D}}{2}$, we get that $x_{2}-x_{1}=\sqrt{D}$, hence $D=4$.
## Answer. 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) Replace each letter with a digit so that the operations performed horizontally and vertically are valid.
| $a b$ | + | $c d$ | $=$ | $e f$ |
| :---: | :---: | :---: | :---: | :---: |
| $\times$ | | $:$ | | + |
| $k$ | $:$ | $m$ | $=$ | $m$ |
| $m n d$ | $:$ | $e$ | $=$ | $e m$ |
Identical letters correspond to identical digits.
|
# Solution.
| 42 | + | 18 | $=$ | 60 |
| :---: | :---: | :---: | :---: | :---: |
| $\times$ | | $:$ | | + |
| 9 | $:$ | 3 | $=$ | 3 |
| 378 | $:$ | 6 | $=$ | 63 |
|
63
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) The graphs of the functions $y=k x+b$ and $y=b x+k$ intersect. Find the x-coordinate of the point of intersection.
#
|
# Solution.
Method 1. The desired abscissa is the solution to the equation $k x + b = b x + k$. This equation can be reduced to $(k - b) x = k - b$. Since the given graphs intersect (do not coincide), $k \neq b$, so $x = 1$.
Method 2. Notice that $x = 1$ is a solution to the problem, because when $x = 1$, both given linear functions take the same value $y = k + b$. Since their graphs intersect, meaning these lines have exactly one common point, there are no other solutions.
Answer. $x = 1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A three-digit number, all digits of which are different, will be called balanced if it is equal to the sum of all possible two-digit numbers formed from the different digits of this number. Provide an example of any balanced number. Justify your answer.
|
Solution: For example, the number $132=13+12+32+21+31+23$ is balanced (there are other options).
Grading criteria: Any suitable number with verification - 7 points, incorrect solution or only answer - 0 points.
|
132
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the tournament, each participant was supposed to play exactly one game with each of the remaining participants, but two participants dropped out during the tournament, having played only 4 games each. In the end, the total number of games played turned out to be 62. How many participants were there in total?
|
Answer: 13.
Solution: Let the total number of participants be $n$. Then, excluding the two who dropped out, the remaining participants played $\frac{(n-2)(n-3)}{2}$ matches. If these two managed to play against each other, then 7 matches were played with their participation, and if they did not, then 8 matches. Thus, we have two cases: $\frac{(n-2)(n-3)}{2}+8=62$ or $\frac{(n-2)(n-3)}{2}+7=62$. Solving these equations, we find that
## MATHEMATICS 10th GRADE
the first equation has no integer solutions, while the second has one positive integer solution $n=13$.
Grading criteria: A correct and justified solution - 7 points. A correct approach but an incorrect answer due to an arithmetic error - 5 points. Noticing the two cases but not completing the second, obtaining the correct answer - $\mathbf{4}$ points. In a trial-and-error solution, not all cases are considered, but the correct answer is obtained - $\mathbf{3}$ points. Only the correct answer with justification that it fits - $\mathbf{2}$ points. Incorrect solution or only the answer - $\mathbf{0}$ points.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $\mathrm{ABC}$ with sides $\mathrm{AB}=5, \mathrm{BC}=\sqrt{17}$, and $\mathrm{AC}=4$, a point $\mathrm{M}$ is taken on side $\mathrm{AC}$ such that $\mathrm{CM}=1$. Find the distance between the centers of the circumcircles of triangles $\mathrm{ABM}$ and $\mathrm{BCM}$.
|
Answer: 2.
Solution: Draw the height BH to side AC. Let $\mathrm{CH}=x$, then $\mathrm{BH}=$ 4 - $x$. By the Pythagorean theorem from two triangles, we have $B H^{2}=B C^{2}-C H^{2}=17-x^{2}$ and $B H^{2}=A B^{2}-A H^{2}=25-(4-x)^{2}$. Equating the right sides of both equations, we get $x=1$, which means points M and H coincide. Then triangles ABM and BCM are right triangles, the centers of the circumscribed circles lie on the midpoints of the hypotenuses AB and BC. The distance between the centers is equal to the length of the midline parallel to side AC, i.e., it is equal to 2.
## MATHEMATICS
10th GRADE
Grading criteria: Correct and justified solution - 7 points, incorrect solution or only answer $-\mathbf{0}$ points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In a school quiz, 100 students participated. After the results were tallied, it turned out that any 66 of them together earned no less than $50 \%$ of the total prize points. What is the highest percentage of points that one participant could have earned?
|
Answer: $25 \%$.
Solution: Suppose participant $\mathrm{X}$ scored the highest percentage of points $-x \%$. Divide the remaining participants into three groups A, B, and C, each with 33 people. Let the total percentages of points scored by these groups be $a, b$, and $c$ respectively. Then,
$$
2(100-x)=2(a+b+c)=(a+b)+(a+c)+(b+c) \geq 50+50+50=150.
$$
Therefore, $x \leq 25$.
Let's provide an example where the maximum percentage is 25. If each participant, except for $\mathrm{X}$, earned $\frac{75}{99}=\frac{25}{33} \%$ of all points, then any 66 of them would collectively score $50 \%$, while $\mathrm{X}$ would score $25 \%$ of all points.
Grading criteria: Correct and justified solution - 7 points, only the estimate "not more than $25 \%$ " is proven - $\mathbf{4}$ points, only a suitable example is provided - $\mathbf{3}$ points, the solution is incorrect or only the answer is given - $\mathbf{0}$ points.
|
25
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. CONDITION
There is an unlimited number of chips in six colors. What is the smallest number of chips that need to be arranged in a row so that for any two different colors, there are two adjacent chips of these colors in the row?
|
Solution. From the condition, it follows that for each fixed color A, a chip of this color must be paired with a chip of each of the other 5 colors. In a row, a chip has no more than two neighbors, so a chip of color A must appear at least 3 times. Similarly for each other color. Thus, there should be no less than $3 \cdot 6=18$ chips. Here is one example of the desired arrangement of chips: 123456246325164135.
Answer. 18 chips.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
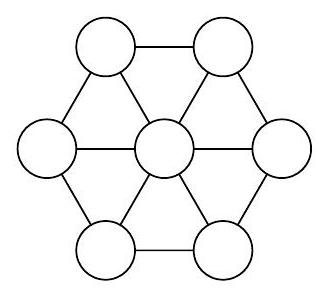
Problem 8.1. Gleb placed the numbers $1,2,7,8,9,13,14$ at the vertices and the center of a regular hexagon such that in any of the 6 equilateral triangles, the sum of the numbers at the vertices is divisible by 3. What number could Gleb have written in the center? It is sufficient to provide one suitable example.
|
Answer: 9.
Solution. Let's add the sums of the numbers in all six triangles; denote this value by $X$. On the one hand, $X$ is divisible by 3, since each term was divisible by 3 according to the condition. On the other hand, each number at the vertex of the hexagon entered $X$ twice (from two triangles), and the central number entered it 6 times. Subtracting from $X$ twice the sum of all numbers, which is $2 \cdot 54$, we get the quadrupled central number.
Divisibility by 3 is preserved in this process. This means that the number in the center is a multiple of 3. We have only one such number, which is 9.
The other numbers can be arranged around the perimeter of the hexagon so that their remainders when divided by 3 alternate; for example, in the order $1,2,7,8,13,14$.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. Misha suggested that Yulia move a chip from cell $A$ to cell $B$. In one step, you can move the chip to an adjacent cell by side or by corner. To make it more interesting, Misha put 30 candies in the prize fund, but said that he would take 2 candies for each horizontal or vertical move and 3 candies for each diagonal move. The remaining candies Yulia gets as a reward. What is the maximum number of candies Yulia can win?
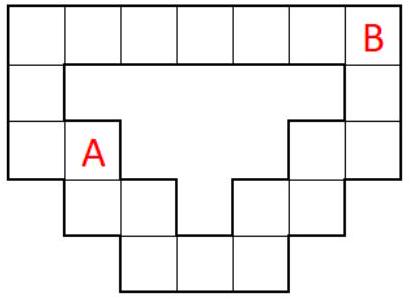
|
Answer: 14.
Solution. From $A$ to $B$, one can get through the top or the bottom. If going through the top, the first 2 moves are diagonal (a diagonal move is more advantageous than 2 horizontal moves), and the next 5 moves are horizontal. Misha will take $2 \cdot 3 + 5 \cdot 2 = 16$ candies, and Yulia will win 14. If going through the bottom, the first 5 moves are diagonal, and the last move is vertical. In this case, Misha will take $5 \cdot 3 + 1 \cdot 2 = 17$ candies, and Yulia will win 13 candies. We get that the first option is more advantageous, and the win will be 14 candies.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. The diagonals of quadrilateral $A B C D$ intersect at point $K$. It turns out that $A B=B K=K D$. On segment $K C$, a point $L$ is marked such that $A K=L C$. Find $\angle B L A$, given that $\angle A B D=52^{\circ}$ and $\angle C D B=74^{\circ}$.
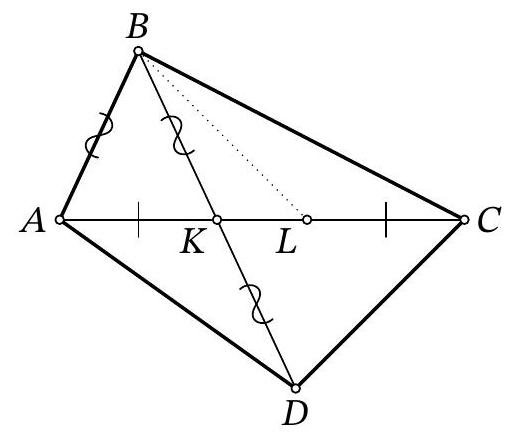
|
Answer: 42.
Solution. Triangle $ABL$ is equal to triangle $KDC$ ($AL=KC$, $AB=KD$ and $\angle BAK=$ $\angle BKA=\angle DKC$). We have
$$
\begin{aligned}
\angle BLA & =180^{\circ}-\angle BAL-\angle ABL=180^{\circ}-\frac{180^{\circ}-\angle ABD}{2}-\angle CDB= \\
& =90^{\circ}+\frac{1}{2} \angle ABD-\angle CDB=42^{\circ}
\end{aligned}
$$
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. A field was partially planted with corn, oats, and millet. If the remaining part is completely planted with millet, then millet will occupy half of the entire field. If the remaining part is equally divided between oats and corn, then oats will occupy half of the entire field. By what factor will the amount of corn increase if the remaining part is completely planted with corn?
|
Answer: 3.
Solution. Let the area of the entire field be 1, and the empty part be $x$. Then, from the first condition, millet occupies $\frac{1}{2}-x$, and from the second condition, oats occupy $\frac{1}{2}-\frac{1}{2} x$.
Corn is left with $1-x-\left(\frac{1}{2}-x\right)-\left(\frac{1}{2}-\frac{1}{2} x\right)=\frac{1}{2} x$. If we add $x$ to this, we get $\frac{3}{2} x$, which means the area planted with corn will triple.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. Six princesses have a magic chest. Every minute, a dress of one of 10 colors and one of 9 styles can be taken out of it. However, within one hour, it is impossible to take out two dresses from the chest that match both in color and style. What is the minimum number of dresses the princesses will have to take out of the chest to guarantee getting 6 dresses of different colors in one style?
|
Answer: 46.
Solution. Note that 45 dresses would not be enough, as the chest can issue exactly 5 dresses of each of the 9 styles.
We will prove that if the princesses take out 46 dresses, there will definitely be 6 dresses of the same style, and thus of different colors (identical dresses could not have occurred over the 46 minutes). Indeed, if this were not the case, then there would be no more than 5 dresses of each style, meaning there would be no more than 45 dresses in total; a contradiction.
|
46
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Along an alley, maples and larches were planted in one row, a total of 75 trees. It is known that there are no two maples between which there are exactly 5 trees. What is the maximum number of maples that could have been planted along the alley?
|
Answer: 39.
Solution. Let's divide all the trees into groups of 12 standing in a row. There will be 6 complete groups and 3 more trees at the end. In each group, we will divide the trees into 6 pairs: the first with the seventh, the second with the eighth, ..., the sixth with the twelfth. Note that there are exactly 5 other trees between the trees in one pair, which means that there is at most one maple tree in this pair. Therefore, in each group of 12 consecutive trees, there are no more than 6 maple trees, so in total there are no more than $6 \cdot 6+3=39$ maple trees.
It remains to show that 39 maple trees could have been planted. We will alternate groups of 6 maple trees with groups of 6 deciduous trees; at the end, we will plant a group of three maple trees. Then it is clear that there will be no more than 4 trees between two maple trees in one group, and no less than 6 trees between two maple trees in different groups.
|
39
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.8. In trapezoid $A B C D(A D \| B C) \angle A B C=108^{\circ}$ and $\angle A D C=54^{\circ}$. On ray $B A$ beyond point $A$, point $K$ is marked such that $A K=B C$. Find the angle $D K C$, given that $\angle B K C=27^{\circ}$.
|
Answer: 18.
Solution. We will prove that triangles $B K C$ and $A D C$ are equal. We have $\angle K B C=\angle D A K$ and $B C=$ $A K$; it remains to show that $B K=A D$.
Fig. 1: to the solution of problem 8.8
For this, we extend $A B$ and $D C$ until they intersect at point $E$ (Fig. 1). Triangle $B E C$ is isosceles, since $\angle B E C=\angle A B C-\angle B C E=\angle A B C-\angle A D C=54^{\circ}=\angle E C B$. Triangle $A E D$ is then also isosceles, as its angles are equal to the angles of triangle $B E C$ due to parallelism. We get $A D=A E=A B+B E=A B+B C=A B+A K=B K$, which completes the justification of the equality of triangles $B K C$ and $A D C$.
Now, knowing that $\angle A K D=\angle B C K$, it is not difficult to calculate the required angle:
$$
\begin{aligned}
\angle D K C & =\angle A K D-\angle B K C=\angle B C K-\angle B K C=\left(180^{\circ}-\angle K B C-\angle B K C\right)-\angle B K C= \\
& =180^{\circ}-\angle A B C-2 \angle B K C=18^{\circ} .
\end{aligned}
$$
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Semyon has 20 numbers: $1,2,3, \ldots, 19,20$. He formed 10 fractions by writing ten of these numbers in some order as numerators, and the remaining ten in some order as denominators. What is the maximum number of integers Semyon could obtain after simplifying all the written fractions?
|
Answer: 8 numbers.
## Solution:
For the fractions to have an integer value, the prime numbers $11, 13, 17, 19$ can only be numerators with a denominator of 1. Therefore, to form fractions equal to an integer, no more than 17 numbers can be used, meaning no more than 8 fractions can be formed. Example: 20/10, 19/1, $18 / 9, 16 / 8, 15 / 5, 14 / 7, 12 / 6, 4 / 2$.
## Criteria:
Correct answer without a correct example of fractions - 1 point.
Correct answer with an example of 8 fractions - 3 points.
The idea that each of the numbers 11, 13, 17, and 19 can only be present in one reducible fraction - 2 points.
(If all the above is present, only a correct conclusion remains to be drawn - and to get a full 7 points.)
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Before the lesson, Nestor Petrovich wrote several words on the board. When the bell rang for the lesson, he noticed a mistake in the first word. If he corrects the mistake in it, the words with mistakes will make up $24 \%$, and if he erases the first word from the board altogether, the words with mistakes will make up $25 \%$. What percentage of the total number of words written did the words with mistakes constitute before the lesson started?
|
Answer: $28 \%$.
## Solution:
Let there be $n$ words written on the board before the lesson, of which $x$ have errors. If the error in the first word is corrected, then there will be $x-1$ words with errors out of $n$, and by the condition $x-1=0.24 n$. If a word with an error is erased, then there will be $x-1$ words with errors out of $n-1$, and by the condition $x-1=0.25(n-1)$. Then $0.24 n=0.25(n-1)$, from which $0.01 n=0.25$.
Thus, $n=25$, and $x=0.24 n+1=0.24 \cdot 25+1=7$.
Therefore, before the lesson, words with errors made up $7 / 25$ of the total number of words, which is $28 \%$.
## Criteria:
A correct answer without a correct justification and without an example of how many words and words with errors it was obtained for, -1 point.
A correct answer without a correct justification, but with an example of how many words and words with errors it was obtained for, - 2 points.
Finding a suitable example of words without justification of why there cannot be another option (and if this justification does not follow from the solution), does not add points to the correct answer.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. The integer 23713 has the following two properties:
(1) any two adjacent digits form a prime two-digit number,
(2) all these prime two-digit numbers are pairwise distinct.
Find the largest of all integers with properties (1) and (2).
|
Answer: 617371311979.
Solution. Since even digits and the digit 5 can only be in the highest place (and only one of these digits can form a single prime number), and the remaining prime two-digit numbers are $11, 13, 17, 19, 31, 37, 71, 73, 79$, 97, the maximum number of digits in the desired number is 12. In the desired number, the numbers 19, 79, 97 will only appear if the number formed by the last four digits is 1979. The digit 7, besides the numbers 97 and 79, appears in four other numbers, which means the digit 7 must appear in the desired number two more times, and not in the second position from the left. In one case, the neighbors of the digit 7 are two 1s, and in the other case, two 3s. There are also four numbers with the digit 3. Therefore, the digit 3 cannot be in the second position from the left either. Consequently, the digit in this position must be 1. Then, the maximum desired number should start with 6. The remaining digits can be easily selected. The maximum number is 617371311979.

twelve - $\underline{2 \text { points. }}$
|
617371311979
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 Find the smallest positive integer $k$, for which in any coloring of the numbers of the set $M=\{1,2,3, \ldots, k\}$ in two colors, there will be ten not necessarily distinct numbers of the same color from the set $M$
|
Answer: 109.
Solution. Let $k \geq 100$. Suppose that for any 10 numbers of one color, their sum is either a number of the other color or does not belong to M. Let the number 1 be of the first color, and the number 2 be of the second color. Then the numbers 10 and 20 are of the second and first colors, respectively. Next, the number $28=10+9 \cdot 2$ is of the first color, and $29=20+9 \cdot 1$ is of the second color, $47=29+9 \cdot 2$ is of the first color, and $37=28+9 \cdot 1$ is of the second color. If 3 is of the first color, then $20+9 \cdot 3=47$ is of the second color. Contradiction. If 3 is of the second color, then $10+9 \cdot 3=37$ is of the first color. Contradiction. Let the numbers $1,2, \ldots, k$ be numbers of the first color $(9 \geq k \geq 2)$. Then the numbers $10,11, \ldots, 10 k$ are of the second color, and the numbers $100,101, \ldots 100 k$ are of the first color. Then the number $100+$ $9 \cdot 1=109$ should be a number of the second color. Contradiction. We will show that there is a coloring of the numbers such that for $k=108$ the specified 10 numbers will not exist. Color the numbers $1,2, \ldots, 9$ in the first color, the numbers 10, 11, .., 99 in the second color, and the numbers 100, 101, .., 108 in the first color. The sum of any 10 numbers of one color is either a number of the other color or is not a number from the set M.
Comments. Only the correct answer - $\underline{0 \text { points. A correct example with } k=109-\underline{3 \text { points }} .}$
|
109
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
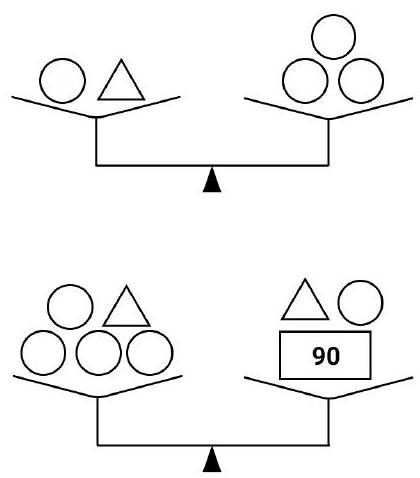
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. What is the total number of emeralds in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?
|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (which then becomes 13), and 4 coins to the box with 15 (which then becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (which then becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (which then becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.
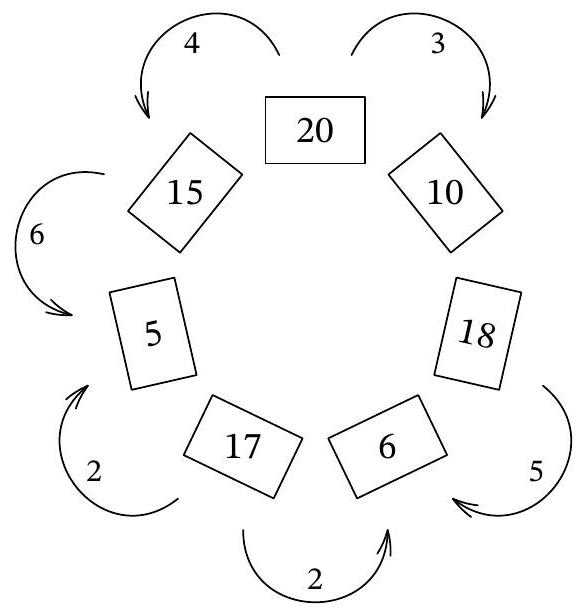
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB=BC=CD=AD$.
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots marked is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?

|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
|
Answer: 17.
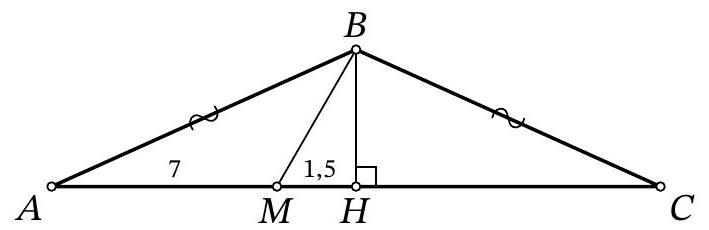
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
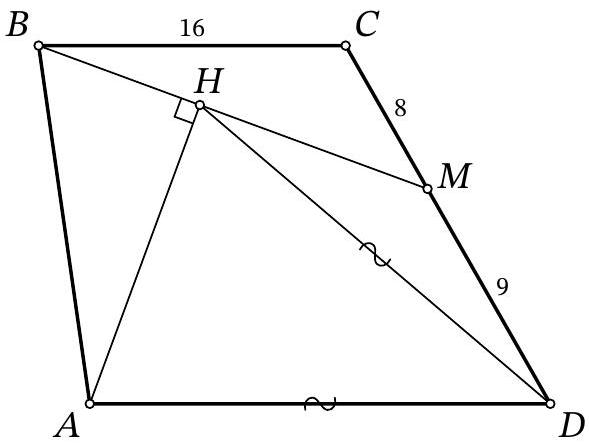
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we obtain $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.

Fig. 5: to the solution of problem 9.8
In the isosceles triangle $A D H$, draw the height and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.
|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.

Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
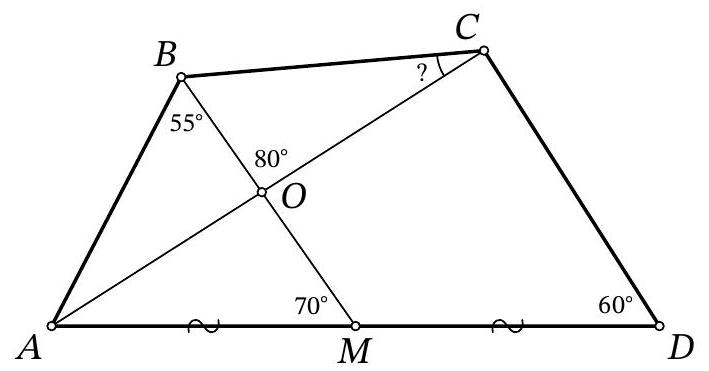
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.
Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
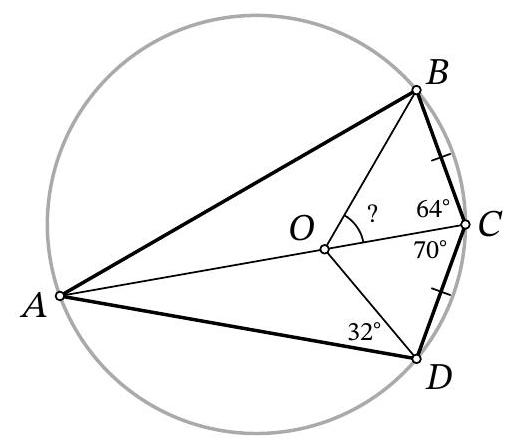
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the point of intersection of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the point of intersection of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. If there are several piles of stones on the table, it is considered that there are many stones on the table if one can find 50 piles and number them from 1 to 50 such that the first pile has at least one stone, the second pile has at least two stones, ..., the fiftieth pile has at least fifty stones. Suppose initially there are 100 piles, each with 100 stones. Find the largest \( n \leqslant 10000 \) such that after removing any \( n \) stones from the initial piles, there will still be many stones on the table. (When removing stones, a pile does not split into several.) (D. Khramov)
|
Answer. $n=5099$.
Solution. If 51 piles are completely removed, obviously, there will not be many stones left. Therefore, the desired value of $n$ is less than 5100. (Alternatively, one can remove 51 stones from each pile.)
It remains to show that after removing any $n=5099$ stones, there will still be many stones left. Let $a_{1}, a_{2}, \ldots$, $a_{100}$ be the number of stones left in the piles, respectively; we can assume that $0 \leqslant a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{100} \leqslant 100$. We need to show that $a_{i+50} \geqslant i$ for $i=1,2, \ldots, 50$, meaning that the piles from 51 to 100 meet the requirements.
Suppose this is not the case, i.e., $a_{i+50} \leqslant i-1$ for some $i \leqslant 50$. This means that each of the first $i+50$ piles contains no more than $i-1$ stones, so at least $101-i$ stones have been removed from each of them. Therefore, the total number of removed stones is at least $(i+50)(101-i)=5100-(i-1)(i-50) \geqslant 5100$. This is a contradiction.
Comment. An example of how removing 5100 stones can result in no many stones left - 1 point.
Proof that removing any 5099 stones will still leave many stones - 6 points.
|
5099
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle is inscribed in trapezoid $A B C D$, touching the lateral side $A D$ at point $K$. Find the area of the trapezoid if $A K=16, D K=4$ and $C D=6$.
|
Answer: 432.
Solution. Let $L, M, N$ be the points of tangency of the inscribed circle with the sides $BC, AB, CD$ respectively; let $I$ be the center of the inscribed circle. Denote the radius of the circle by $r$. Immediately note that $DN = DK = 4$ (the first equality follows from the equality of the segments of tangents), hence $CL = CN = CD - DN = 2$ (the second is obvious). Since $I$ is the point of intersection of the bisectors of the internal angles of the trapezoid, then $\angle IAD + \angle IDA = \frac{\angle DAB + \angle DAC}{2} = \frac{180^{\circ}}{2} = 90^{\circ}$, where the penultimate equality follows from the parallelism of the lines $AB$ and $CD$. Therefore, triangle $AID$ is right-angled and $\angle AID = 90^{\circ}$. Similarly, triangle $BIC$ is also right-angled. Further, since $IK$ and $IL$ are radii drawn to the points of tangency, then $\angle IKD = 90^{\circ}$ and $\angle ILB = 90^{\circ}$. Therefore, $IK$ and $IL$ are altitudes in triangles $AID$ and $BIC$ respectively.
We use the known fact that in a right-angled triangle, the square of the altitude dropped to the hypotenuse equals the product of the segments into which it divides the hypotenuse. Then $IK^2 = AK \cdot KD = 16 \cdot 4 = 64 = 8^2$, i.e., $r = IK = 8$, and also $8^2 = IL^2 = CL \cdot LB = 2 \cdot LB$, i.e., $LB = 32$. Now we have everything to find the area. Note that $MN$ is the height of the trapezoid and $MN = 2r = 16$, $AB + CD = (AM + MB) + 6 = (AK + BL) + 6 = 16 + 32 + 6 = 54$, hence the answer $\frac{16 \cdot 54}{2} = 432$.
Comment. A complete and justified solution - 7 points. A generally correct reasoning containing minor gaps or inaccuracies - up to 5 points. If the solution is not completed, 1-2 points are given for proving useful auxiliary statements.
|
432
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let's call a natural number "remarkable" if all its digits are different, it does not start with the digit 2, and by erasing some of its digits, the number 2018 can be obtained. How many different seven-digit "remarkable" numbers exist?
|
Answer: 1800.
Solution: To correctly count the number of options, it is necessary to follow the rule: before the digit 2, there must be one of the six digits $-3,4,5,6,7$ or 9. Let's assume for definiteness that this is 3, then two different digits from the remaining five ( $\frac{5 \cdot 4}{2}=10$ options) can be in the positions marked by dots: ..32..0..1..8.., i.e., either both numbers are in one interval $5 \cdot 2=10$ ways, or in different intervals, then $\frac{5 \cdot 4}{2} \cdot 2=20$ ways. Therefore, the total number of different options is $10 \cdot 30=300$. Similarly, the options for pairs $42,52,62,72$ and 92 are calculated, i.e., finally we get: $6 \cdot 300=$ 1800 options.
Comment: For a computational error with correct reasoning, deduct 1 point. For potentially useful but unimplemented ideas - 1-2 points.
|
1800
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Lena downloaded a new game for her smartphone, where it is allowed to conduct alchemical reactions of two types. If she combines one "fire" element and one "stone" element, she gets one "metal" element. And if she combines one "metal" element and one "stone" element, she gets three "stone" elements. Lena has 50 "fire" elements and 50 "stone" elements. To prepare element $X$, one "metal" element, two "fire" elements, and three "stone" elements are required. What is the maximum number of elements $X$ that Lena can obtain?
|
Answer: 14 elements.
Solution. Consider the expression $S=2 x+y+z$, where $x$ is the number of "metal" elements, $y$ is the number of "fire" elements, and $z$ is the number of "stone" elements. It is easy to see that this expression does not change with each of the two alchemical operations:
$$
\begin{aligned}
& 2(x+1)+y-1+z-1=2 x+y+z \\
& 2(x-1)+y+z-1+3=2 x+y+z
\end{aligned}
$$
Initially, $S=100$. To obtain $t$ elements of $X$, $t$ elements of "metal", $2 t$ elements of "fire", and $3 t$ elements of "stone" are required, so $S=7 t \leq 100$. Therefore, $t$ does not exceed 14. Fourteen elements of $X$ can be obtained: by combining 21 elements of "fire" and 21 elements of "stone", we get 21 elements of "metal", 29 elements of "fire", and 29 elements of "stone". Then, by combining 7 elements of "metal" and 7 elements of "stone", we obtain 14 elements of "metal", 29 elements of "fire", and 43 elements of "stone". This is enough to prepare 14 elements of $X$.
Comment. The proposed implementation - 3 points, the estimate made - 4 points, the points are summed. For potentially useful ideas and approaches in the absence of a solution - 2-3 points. Answer without justification - 0 points.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A three-digit number is 56 times greater than its last digit. How many times greater is it than its first digit? Justify your answer.
#
|
# Solution:
Method 1. The last digit is such that when multiplied by 6, the resulting number ends with the same digit. By exhaustive search, we confirm that this can be any even digit (and only it). Therefore, this three-digit number is either 112, 224, 336, or 448 (the option with the last digit 0 is not valid, as it would not be a three-digit number). In all cases, the answer is 112.
Method 2. Let the number be of the form $\overline{a b c}$. Then, by the condition, $100 a + 10 b + c = 56 c$, from which $20 a + 2 b = 11 c$. The number $11 c$ is therefore divisible by 2, meaning the digit $c$ is even, $c = 2d (d \leqslant 4)$. Thus, $10 a + b = 11 d$. But $10 a + b = \overline{a b}$. Since this number is divisible by 11 without a remainder, $a = b$. Then $d = a$ and the original number has the form $\overline{a a (2a)} = a \cdot \overline{112}$, meaning it is 112 times its first digit.
Answer: 112.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct answer obtained and its uniqueness justified | 7 points |
| Correct answer obtained with justification, but none of the numbers implementing it are provided | points are not deducted |
| All possible numbers (112, 224, 336, and 448) found, but it is not justified that there are no other numbers | 3 points |
| Not all cases are considered in the exhaustive search method | 2 points |
| Some of the numbers 112, 224, 336, and 448 are found or the correct answer is given without justification | 1 point |
|
112
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. On the way from city $A$ to city $B$, there are kilometer markers every kilometer. On each marker, one side shows the distance to $A$, and the other side shows the distance to $B$. In the morning, a tourist passed by a marker where one number was twice the other. After walking another 10 km, the tourist saw a marker where the two numbers differed by a factor of three. What is the distance from $A$ to $B$? Provide all possible answers and prove that there are no others.
|
Solution: Let $C_{1}$ and $C_{2}$ be the poles mentioned in the problem ($C_{1}$ - the pole near which the tourist was in the morning). Without loss of generality, assume the tourist was walking from $A$ to $B$. Then there are two possible situations: 1) $C_{1} A = 2 C_{1} B$ or 2) $C_{1} B = 2 C_{1} A$. Since $C_{2} A > C_{1} A$, the situation $C_{2} B = 3 C_{2} A$ is impossible, so the situation $C_{2} A = 3 C_{2} B$ must hold.
To the solution of problem 6.3
1) If $C_{1} A = 2 C_{1} B$, then $C_{1} A$ constitutes $\frac{2}{3}$ of the total distance $A B$. Then the distance from the second pole to $A$ is $\frac{3}{4}$ of the distance $A B$, meaning the tourist has walked $\frac{3}{4} - \frac{2}{3} = \frac{1}{12}$ of this distance. Therefore, $A B = 120$ km.
2) If $C_{1} B = 2 C_{1} A$, then $C_{1} A = \frac{1}{3} A B$. Then the tourist has walked $\frac{3}{4} - \frac{1}{3} = \frac{5}{12}$ of the entire distance in one day. Therefore, $A B = 24$ km.
Answer: either 120 km or 24 km.
Grading criteria:
| present in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The solution process is entirely correct, but there are computational errors, possibly leading to an incorrect answer | 6 points |
| Only one of the two cases is correctly considered; (one of the two answers is correctly obtained and justified) | 3 points |
| Both answers (120 km and 24 km) are correctly stated, but either without justification or with incorrect justification | 2 points |
| Only an example that realizes one of the two cases is provided | 1 point |
| Various reasoning and calculations that did not lead to a solution | 0 points |
|
120
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. 101 people bought 212 balloons of four colors, and each of them bought at least one balloon, but no one had two balloons of the same color. The number of people who bought 4 balloons is 13 more than the number of people who bought 2 balloons. How many people bought only one balloon? Provide all possible answers and prove that there are no others.
|
# Solution:
Method 1. First, exclude the 13 people who bought 4 balloons. There will be 88 people left, who bought a total of 160 balloons, with each person buying between 1 and 4 balloons, and the number of people who bought 2 and 4 balloons is now equal. Suppose now that each person who bought 4 balloons gives one balloon to someone who bought 2. Now everyone has either 1 or 3 balloons, and the total number of people and balloons remains the same. Suppose now that everyone releases one balloon into the sky; 72 balloons will remain, with each person having either 2 balloons or none. Therefore, there are now 36 people with balloons, and the remaining 52 people have no balloons. These are the people who initially had one balloon.
Method 2. Let \( x_{i} (1 \leqslant i \leqslant 4) \) be the number of people who bought exactly \( i \) balloons. According to the problem, we have the system
\[
\left\{\begin{aligned}
x_{1}+x_{2}+x_{3}+x_{4} & =101 \\
x_{1}+2 x_{2}+3 x_{3}+4 x_{4} & =212 \\
x_{4}-x_{2} & =13
\end{aligned}\right.
\]
By adding the third equation to the first, we get \( x_{1}+x_{3}+2 x_{4}=114 \) (so \( x_{3}+2 x_{4}=114-x_{1} \)), and by adding twice the third equation to the second, we find that \( x_{1}+3 x_{3}+6 x_{4}=238 \). Then
\[
238=x_{1}+3\left(x_{3}+2 x_{4}\right)=x_{1}+3\left(114-x_{1}\right)=342-2 x_{1} \text{. }
\]
From this, \( x_{1}=52 \).
Answer: 52 people.
Note: By solving the system from the second method, all possible distributions of balloons among people can be found: \( x_{1}=52, x_{2}=a, x_{3}=36-2 a, x_{4}=a+13 \) (where \( a \) is an integer from the interval \([0 ; 18]\)).
Recommendations for checking:
| included in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| There are arithmetic errors in the correct solution process, possibly leading to an incorrect answer | -1 point for each error |
| The system of equations describing the conditions of the problem is correctly set up, but the problem is not fully solved | 3 points |
| A correct specific case (or cases, but not all) of the distribution of balloons among people is provided | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
52
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. The numbers 7, 8, 9, 10, 11 are arranged in a row in some order. It turned out that the sum of the first three of them is 26, and the sum of the last three is 30. Determine the number standing in the middle.
|
Answer: 11
Solution. If we add the sum of the first three and the sum of the last three, we get the sum of all four numbers once and the middle number twice. Since the sum of all five numbers is $7+8+9+10+11=45$, and the sum of 26 and 30 is 56, then the number counted twice is 11.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Every day, a sweet tooth buys one more candy than the previous day. In one week, on Monday, Tuesday, and Wednesday, he bought a total of 504 candies. How many candies did he buy on Thursday, Friday, and Saturday in total for the same week?
|
Answer: 513
Solution. On Thursday, 3 more candies were bought than on Monday, on Friday - 3 more than on Tuesday, and on Saturday - 3 more than on Wednesday. In total, 9 more candies were bought on Thursday, Friday, and Saturday compared to Monday, Tuesday, and Wednesday, i.e., $504+9=513$ candies.
|
513
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. In an $11 \times 11$ square, the central cell is painted black. Maxim found a rectangular grid of the largest area that is entirely within the square and does not contain the black cell. How many cells does it have?
|
Answer: 55
Solution. If both sides of the rectangle are not less than 6, then it must contain the central cell, since the distance from the painted cell to the sides is 5 cells. If one of its sides is not more than 5, then the other is definitely not more than 11, and therefore its area is not more than 55.
|
55
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Alina travels to school by bus. The bus runs on a schedule every 15 minutes. It always takes the girl the same number of minutes to get to the bus stop. If she leaves home at 8:20, she will be at school at 8:57, but if she leaves home at 8:21, she will be late for school. Classes start at 9:00. How many minutes will Alina be late for school if she leaves home at 8:23?
|
Answer: 12
Solution. Since Alina is late for school if she leaves home one minute after 8:20, leaving 1, 2, ... 15 minutes after 8:20, she will catch the next bus, which means she will arrive at school 15 minutes later than 8:57, i.e., she will arrive at school at 9:12.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Each of the 37 hexagonal cells has 3, 4, or 6 neighbors. Some of the cells were filled with chips. After that, in each free cell that is adjacent to at least two cells containing chips, the number of these neighboring chips was written. Then the chips were removed, and only the numbers remained on the diagram. How many chips were there?
#
|
# Answer: 8
Solution. Let's look at the picture on the left. Consider the triplet and the central pair. We understand that the chips must be placed at the positions of the yellow crosses. Next, we understand the red minuses - the absence of chips. Then we place the chips at the positions of the green crosses. And the blue minuses - the absence of chips. The purple question mark - can a chip be placed here? We understand that no, because otherwise, at the position of the adjacent blue minus, there should be a 2, but there isn't one. Therefore, we place the chips at the positions of the purple crosses (also considering that no empty cells should be adjacent to two chips, otherwise, there would be numbers in them).
In the end, the chips are placed as shown in the picture on the right.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In a rectangle of size $5 \times 18$, numbers from 1 to 90 were placed. This resulted in five rows and eighteen columns. In each column, the median number was selected, and from these median numbers, the largest one was chosen. What is the smallest value that this largest number can take?
Recall that among 99 numbers, the median is the one that is greater than 49 others and less than 49 others.
|
Answer: 54
Solution. The largest of the average numbers $N$ is not less than each of the eighteen selected averages. Each of the eighteen averages, in turn, is not less than three numbers from its column (including itself). In total, $N$ is not less than some 54 numbers in the table. Therefore, $N$ is at least 54.
To construct an example where $N$ equals 54, it is sufficient to fill the table with numbers row by row: first, the first row with numbers from 1 to 18, the second row with numbers from 19 to 36, and the third row with numbers from 37 to 54, and the rest can be placed arbitrarily. Note that the average numbers in the rows will be the numbers from 37 to 54 (each of them is greater than any of the numbers from 1 to 36 and less than any of the numbers from 55 to 90). The number 54 is the largest of them.
|
54
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8.2
For a natural number $N$, all its divisors were listed, and then the sum of digits for each of these divisors was calculated. It turned out that among these sums, all numbers from 1 to 9 were found. Find the smallest value of $\mathrm{N}$.
## Number of points 7
|
Answer:
288
## Solution
Note that the number 288 has divisors $1,2,3,4,32,6,16,8,9$. Therefore, this number satisfies the condition of the problem. We will prove that there is no smaller number that satisfies the condition.
Indeed, since $\mathrm{N}$ must have a divisor with the sum of digits 9, $\mathrm{N}$ is divisible by 9.
Now consider the divisor $\mathrm{d}$ with the sum of digits $8. \mathrm{d}$ is not divisible by 3, so the numbers $\mathrm{d}$ and 9 are coprime, which means $\mathrm{N}$ is divisible by 9d. At the same time, if $\mathrm{d} \geq 32$, then $9 \mathrm{~d} \geq 288$, that is, $3 \mathrm{~N} \geq$ 288. Therefore, it remains to check $\mathrm{d}=26, \mathrm{~d}=17$ and $\mathrm{d}=8$.
If $\mathrm{d}=26$, then $9 \mathrm{~d}=234$. This number does not have a divisor with the sum of digits 5, and any number that is a multiple of it is greater than 288.
If $\mathrm{d}=17$, then $9 \mathrm{~d}=153$. This number does not have a divisor with the sum of digits 2, and any number that is a multiple of it is greater than 288.
If $\mathrm{d}=8$, then $9 \mathrm{~d}=72$. The multiples of it and less than 288 are 144 and 216. But these numbers do not have a divisor with the sum of digits 5.
Additional criteria for checking.
"2 or 3 points" Only the correct answer is provided
#
|
288
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8.5
On the Island of Liars and Knights, a circular arrangement is called correct if each person standing in the circle can say that among their two neighbors, there is a representative of their tribe. Once, 2019 natives formed a correct arrangement in a circle. A liar approached them and said: "Now we can also form a correct arrangement in a circle together." How many knights could there have been in the initial arrangement?
## Number of points 7
|
Answer:
1346
## Solution
We will prove that a correct arrangement around a circle is possible if and only if the number of knights is at least twice the number of liars.
Indeed, from the problem's condition, it follows that in such an arrangement, each liar has two knights as neighbors, and among the neighbors of any knight, there is at least one knight. Therefore, the correct arrangement should look like this: a group of knights, a liar, a group of knights, a liar, and so on (with at least two knights in each group). This means that in such an arrangement, there are at least twice as many knights as liars.
In the reverse direction: if there are at least twice as many knights as liars, then we can make an arrangement of the form RRKRRK..., and place any remaining knights (if they exist) between any two knights. Thus, if this condition is met, a correct arrangement is possible.
Let \( P \) be the number of knights and \( L \) be the number of liars in the correct arrangement specified in the problem. Then \( P \geq 2L \). The liar who arrived told a lie, so together with him, a correct arrangement is impossible, hence \( P \leq 2L + 1 \). Therefore, \( P = 2L \) or \( P = 2L + 1 \). In the first case, in the initial arrangement, there are \( 2019 \cdot \frac{2}{3} = 1346 \) knights, and the second case is impossible because the number \( (2019 - 1) \cdot \frac{2}{3} \) would not be an integer.
Additional criteria for evaluation.
"4 or 5 points: A generally correct reasoning is provided, containing minor gaps or inaccuracies (for example, only the necessary condition for the existence of a correct arrangement is proven or a computational error is made at the end)."
"2 or 3 points: The answer is obtained based on the assumption that there are twice as many knights as liars, but this is not proven."
|
1346
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the largest even three-digit number $x$ that gives a remainder of 2 when divided by 5 and satisfies the condition $\operatorname{GCD}(30, \operatorname{GCD}(x, 15))=3$.
|
Solution. From the condition, we get that there exist such $a, b \in \mathbb{N}$ that $3a=30$, GCD $(x, 15)=3b$, and GCD $(a, b)=1$.
Consider the equality GCD $(x, 15)=3b$. This means that $\exists c, d \in \mathbb{N}$ such that $x=3bc$ and $15=3bd$, and GCD $(c, d)=1$.
From the equality $15=3bd$ it follows that $bd=5$, i.e., $\left[\begin{array}{l}b=1, d=5 \\ b=5, d=1\end{array}\right.$.
Let $b=1, d=5$. Then $x=3c$. Considering that $x$ is even, we get $x=6m$. From the condition GCD $(c, d)=1$ it follows that $c$ does not divide 5, which means that $6m$ does not divide 5, i.e., $x$ can be any of the following numbers: $30l+6, 30l+12, 30l+18, 30l+24$, where $l$ is any natural number. Considering that $x$ when divided by 5 gives a remainder of 2,
only $30l+12$ fits.
Let $b=5, d=1$. Then $x=15c$, i.e., $x=30t$, but then GCD $(x, 15)=$ 15 and GCD $(30$, GCD $(x, 15))=15-$ contradiction.
Therefore, the problem has been reduced to finding the largest three-digit number of the form $30l+12$. This is 972.
|
972
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. A hundred people are standing in a circle, each of whom is either a knight or a liar (liars always lie, and knights always tell the truth). Each of those standing said: “I have a liar as a neighbor.” Find the minimum possible number of liars among these 100 people.
|
Answer: 34.
Solution: Note that 3 knights cannot stand next to each other, as in this case, the middle knight would be lying. Therefore, among any 3 standing next to each other, there is a liar. Take any liar, and divide the remaining 99 people into 33 groups of three standing next to each other. Since there is at least one liar in each group of three, the total number of liars in the circle is no less than $1+33=34$.
Exactly 34 liars can stand, for example, as follows: -L(KLK)(KLK)... (KLK)-.
Comment: It is only proven that the number of liars is no less than $34-4$ points.
Only an example of an arrangement with 34 liars is given -2 points.
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a football tournament where each team played against each other once, teams A, B, C, D, E, and F participated. Teams received 3 points for a win, 1 point for a draw, and 0 points for a loss. In the end, it turned out that teams A, B, C, D, and E each had 7 points. What is the maximum number of points that team $\mathrm{E}$ could have?
|
4. In a match where one of the teams won, the teams together score 3 points; in a match that ended in a draw, - 2 points. Since 7 is not divisible by 3, a team that scored 7 points must have at least one draw. Since there are five such teams, there were at least three draws in the tournament. In total, as is easy to check, 15 matches were played. Therefore, all teams together scored no more than $2 \cdot 3 + 3 \cdot 12 = 42$ points. Of these, 35 points were scored by teams A, B, V, G, and D. Therefore, team $\mathrm{E}$ scored no more than $42 - 35 = 7$ points. How it could have scored exactly 7 points is shown in the table.
| | A | B | V | G | D | E |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| A | X | 3 | 3 | 1 | 0 | 0 |
| B | 0 | X | 3 | 3 | 1 | 0 |
| V | 0 | 0 | X | 3 | 3 | 1 |
| G | 1 | 0 | 0 | X | 3 | 3 |
| D | 3 | 1 | 0 | 0 | X | 3 |
| E | 3 | 3 | 1 | 0 | 0 | X |
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the Island of Misfortune, only knights, who always tell the truth, and liars, who always lie, live. The island is governed by a group of 101 people. At the last meeting, it was decided to reduce this group by 1 person. But each member of the group stated that if they were removed from the group, the majority of the remaining would be liars. How many knights and how many liars are in the group?
|
2. 50 knights and 51 liars. Let there be $k$ knights in the group, then there are $101-k$ liars. Each one said that if they were removed, there would be no less than 51 liars among the remaining 100 people. Since the knights told the truth, then $k-1 \leq 49$ and
$k=50$.
|
50
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Sasha invited Dima to visit, saying that he lives in entrance 10, apartment No. 333, but forgot to mention the floor. Approaching the building, Dima noticed that the building is nine-story. Which floor should he go to?
|
3. $333=9 \cdot 37=10 \cdot 33+3$. Therefore, the number of apartments in the entrance is less than 37 but more than 33. In this range, only 36 is divisible by 9. So, there are 36 apartments in the entrance, and 4 on each floor. Since $333=9 \cdot 36+2 \cdot 4+1$, apartment 333 is on the third floor.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The graphs of the functions $y=a x^{2}+b x+1$ and $y=x^{2}+c x+d$ intersect at the point with coordinates ( $2 ; 4$ ). What is the value of the expression $4 a+d$, if $b+c=1$ ?
|
Answer: 1.
Solution: Since the graphs pass through the point with coordinates (2; 4), then $4=4a+2b+1$ and $4=4+2c+d$. Therefore, $4a+2b=3$, and $2c+d=0$, or $4a=3-2b, d=-2c$. Summing up the obtained expressions: $4a+d=3-2b-2c=3-2(b+c)=3-2=1$. Note: The condition is satisfied by the functions $y=ax^2+bx+1$ and $y=x^2+cx+d$ when $a=1, b=-1/2, c=3/2, d=-3$.
Criteria: Only the answer - 0 points. If the solution is found by selecting suitable values of $a, b, c$ and $d-3$ points. Correctly found values of the expressions $4a+2b=3$ and $2c+d=0$, but no further progress in the solution (or incorrect further solution) - 4 points. 7 points for a complete and correct solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Given a trapezoid $A B C D$, where $A D \| B C, B C=A C=5$, and $A D=6$. The angle $A C B$ is twice the angle $A D B$. Find the area of the trapezoid.
|
# Answer: 22.
Solution: Drop a perpendicular CH from vertex C to the base AD. Denote the intersection of BD and CH as E.
Let $\angle \mathrm{ADB}=\alpha=\angle \mathrm{CBD}$ (alternate interior angles), then $\angle A C B=2 \alpha=\angle C A D$ (alternate interior angles). Triangle ACB is isosceles by condition, so $\angle A B C=\angle B A C=90 \circ-\alpha, \angle B A D=$ $\angle B A C+\angle C A D=90 \circ-\alpha+2 \alpha=90 \circ+\alpha$.
Angle $\angle \mathrm{ABE}=\angle \mathrm{ABD}=\angle \mathrm{ABC}-\angle \mathrm{CBD}=90^\circ - 2 \alpha=\angle \mathrm{BCH}-\angle \mathrm{ACB}=\angle \mathrm{ACH}=\angle \mathrm{ACE}$. That is, quadrilateral $\mathrm{ABCE}$ is inscribed in a circle ( $\angle \mathrm{ABE}=\angle \mathrm{ACE}$ ), and $\mathrm{BE}$ is the diameter of this circle ( $\angle \mathrm{BCE}=\angle \mathrm{BCH}=$ $90 \circ$ ), so $\angle \mathrm{BAE}=90 \circ$, and $\angle \mathrm{EAD}=\angle \mathrm{BAD}-\angle \mathrm{BAE}=90 \circ+\alpha-90 \circ=\alpha=\angle \mathrm{ADB}=\angle \mathrm{ADE}$. Therefore, triangle AED is isosceles, EH is the altitude and median, so $\mathrm{AH}=\mathrm{HD}=\mathrm{AD}: 2=3$.
The height CH is found from the right triangle $\mathrm{ACH}: C H=\sqrt{A C^{2}-A H^{2}}=\sqrt{25-9}=\sqrt{16}=4$. The area of the trapezoid is $\frac{B C+A D}{2} \cdot C H=\frac{5+6}{2} \cdot 4=22$.
Criteria: Only the answer - 0 points. 7 points - correct answer with a correct solution. Partially correct progress in the solution - $3-5$ points.
|
22
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. In a six-digit number, the first digit, which is 2, was moved to the last place, leaving the other digits in the same order. The resulting number turned out to be three times larger than the original. Find the original number.
|
Answer: 285714.
Solution. According to the condition, the desired number has the form $\overline{2 a b c d e}$, then we have: $\overline{a b c d e 2}=$ $3 \cdot \overline{2 a b c d e}$, or $\overline{a b c d e} \cdot 10+2=3 \cdot(200000+\overline{a b c d e})$. Let $\overline{a b c d e}=X$ - a five-digit number, then $10 X+2=3 \cdot(200000+X)$, or $7 X=600000-2, X=85714$, then the original number will be $\overline{2 a b c d e}=\overline{2 X}=285714$.
|
285714
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Clone 1
The figure is divided into 7 equal squares and several rectangles. The perimeter of rectangle A is 112 cm. What is the perimeter of rectangle B? Express your answer in centimeters.
#
|
# Answer: 168
## Solution
1st method. Rectangles A and B are composed of identical squares: Rectangle A consists of three, and Rectangle B consists of four. Let's call the side of such a square a "stick" and count the perimeter in sticks. The perimeter of Rectangle B is four sticks more than the perimeter of Rectangle A. Also, note that four sticks are half the perimeter of Rectangle A. Therefore, the perimeter of Rectangle B is $112 / 2 + 112 = 168$ cm.
2nd method. Rectangles A and B are composed of identical squares: Rectangle A consists of three, and Rectangle B consists of four. Let's call the side of such a square a "stick" and count the perimeter in sticks. The perimeter of Rectangle A is 8 sticks, and the perimeter of Rectangle B is 12 sticks. The length of one stick is $112 / 8 = 14$ cm. Therefore, the perimeter of Rectangle B is $12 \cdot 14 = 168$ cm.
## Clone 2
The figure is divided into 7 equal squares and several rectangles. The perimeter of Rectangle A is 116 cm. What is the perimeter of Rectangle B? Express your answer in centimeters.
Answer: 174
## Clone 3
The figure is divided into 7 equal squares and several rectangles. The perimeter of Rectangle A is 122 cm. What is the perimeter of Rectangle B? Express your answer in centimeters.
Answer: 183
## Clone 4
The figure is divided into 7 equal squares and several rectangles. The perimeter of Rectangle A is 126 cm. What is the perimeter of Rectangle B? Express your answer in centimeters.
Answer: 189
#
|
168
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Clone 1
A rope was divided into 19 equal parts and arranged in a snake-like pattern. After that, a cut was made along the dotted line. The rope split into 20 pieces: the longest of them is 8 meters, and the shortest is 2 meters. What was the length of the rope before it was cut? Express your answer in meters.
|
Answer: 114
Solution
Let's find the length of each of the 19 equal parts into which the rope was divided. To do this, we need to add the shortest piece to half of the longest piece obtained after the cut. We get $8 / 2 + 2 = 6$. Then the total length of the rope is $19 \cdot 6 = 114$ meters.
## Clone 2
A rope was divided into 19 equal parts and laid out in a snake-like pattern. After that, a cut was made along the dotted line. The rope split into 20 pieces: the longest of which is 8 meters, and the shortest is 1 meter. What was the length of the rope before it was cut? Express your answer in meters.
Answer: 95
## Clone 3
A rope was divided into 19 equal parts and laid out in a snake-like pattern. After that, a cut was made along the dotted line. The rope split into 20 pieces: the longest of which is 10 meters, and the shortest is 2 meters. What was the length of the rope before it was cut? Express your answer in meters.
## Answer: 133
## Clone 4
A rope was divided into 19 equal parts and laid out in a snake-like pattern. After that, a cut was made along the dotted line. The rope split into 20 pieces: the longest of which is 10 meters, and the shortest is 3 meters. What was the length of the rope before it was cut? Express your answer in meters.
Answer: 152
|
152
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Clone 1
From 125 sugar cubes, a cube of $5 \times 5 \times 5$ was formed. Donut selected all the cubes that have an odd number of neighbors and ate them (neighbors are those cubes that share a common face). How many cubes did Donut eat in total?
|
# Answer: 62
## Solution
Consider the possible cases of the cube's placement inside the larger cube:
|
62
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A cube is a vertex of a larger cube, in which case it has 3 neighbors.
Cases 2 and 4 are suitable. For each face of the cube, the number of cubes that satisfy case 2 is: $3 \times 3=9$. Since the cube has 6 faces, the total is 54 cubes. The cube has 8 vertices, so in total, Donut ate $54+8=62$ cubes.
## Clone 2
A cube $5 \times 5 \times 5$ was formed from 125 sugar cubes. Donut ate all the cubes that have an even number of neighbors (neighbors are those cubes that share a face). How many cubes did Donut eat in total?
|
Answer: 63
## Clone 3
A cube of $6 \times 6 \times 6$ was formed using 216 sugar cubes. Donut selected all the sugar cubes that have an odd number of neighbors and ate them (neighbors are those cubes that share a face). How many sugar cubes did Donut eat in total?
## Answer: 104
## Clone 4
A cube of $6 \times 6 \times 6$ was formed using 216 sugar cubes. Donut selected all the sugar cubes that have an even number of neighbors and ate them (neighbors are those cubes that share a face). How many sugar cubes did Donut eat in total?
## Answer: 112
|
112
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Clone 1
In the expression OL $*$ IM $* P *$ IA * DA, it is required to replace the asterisks with two plus signs and two minus signs, and to replace the letters with digits according to the rules of a cryptarithm (identical letters with identical digits, and different letters with different digits). What is the maximum value of the expression that can be obtained in this way? The first digit in a two-digit number must be different from zero.
#
|
# Answer: 263
## Solution
The value of the expression will be the greatest if the addends with a plus sign are as large as possible, and the addends with a minus sign are as small as possible. Pluses should be placed before the two-digit numbers IM and IP, then we will get the maximum possible sum because we can use the maximum digit 9 twice in the tens place.
Next, we maximize the value of the expression
$$
\text{OL} + \text{IM} - P + \text{IA} - DA = 10 \cdot (2I + O - D) + (M + L - P).
$$
From the last equality, it is clear that I is multiplied by 20, O by 10, and M and L by 1. To get the maximum sum, the largest digit should be multiplied by the largest number. Then \( I = 9, O = 8, M = 7 \) and \( L = 6 \) (we can take 6 and 7 in the opposite order). Similarly, we get the digits with a minus sign. The smallest should be D, as it is multiplied by 10. But D cannot be zero, as it is the first digit of a two-digit number. Then \( D = 1, P = 0 \). The digit A can be any of the remaining digits, as it does not affect the result. Let, for example, \( A = 5 \). The maximum value of the expression will be \( 86 + 97 - 0 + 95 - 15 = 263 \).
## Clone 2
In the expression \(\mathrm{KP} * \mathrm{OC} * \mathrm{CB} * \mathrm{OP} *\) D, two plus signs and two minus signs need to be placed instead of the asterisks, and the letters need to be replaced by digits according to the rules of a cryptarithm (identical letters - identical digits, different letters - different digits). What is the greatest value of the expression that can be obtained in this way? The first digit in a two-digit number must be different from zero.
Answer: 263
## Clone 3
In the expression \(\mathrm{K} * \mathrm{AR} * \mathrm{TI} * \mathrm{NN} * \mathrm{AY}\), two plus signs and two minus signs need to be placed instead of the asterisks, and the letters need to be replaced by digits according to the rules of a cryptarithm (identical letters - identical digits, different letters - different digits). What is the greatest value of the expression that can be obtained in this way? The first digit in a two-digit number must be different from zero.
Answer: 170
|
263
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The numbers 20 and 21 are written on the board. Every minute, another number is written on the board, equal to the sum of any two of the already written numbers. Is it possible to eventually obtain the number $2020$ this way?
|
4. Answer: Yes, it is possible. Since the numbers 20 and 21 are already present on the board, we can obtain any number of the form 20a + 21b. Note that $2020=$ $101 * 20=(101-21) * 20+21 * 20=20 * 80+21 * 20$.
Grading recommendations: only answer - 0 points.
|
2020
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. Given the function $f(x)=\left(1-x^{3}\right)^{-1 / 3}$. Find $f(f(f \ldots f(2018) \ldots))$ (the function $f$ is applied 2019 times)
|
Solution: Let's carry out equivalent transformations (for $x \neq 1$ and $x \neq 0$):
$$
\begin{gathered}
f(f(x))=\left(1-f(x)^{3}\right)^{-1 / 3}=\left(1-\left(1-x^{3}\right)^{-1}\right)^{-1 / 3}=\left(1-\frac{1}{1-x^{3}}\right)^{-1 / 3}= \\
=\left(\frac{-x^{3}}{1-x^{3}}\right)^{-1 / 3}=\frac{-x^{-1}}{\left(1-x^{3}\right)^{-1 / 3}}=-\frac{\left(1-x^{3}\right)^{1 / 3}}{x} \\
f(f(f(x)))=f\left(-\frac{\left(1-x^{3}\right)^{1 / 3}}{x}\right)=\left(1+\frac{1-x^{3}}{x^{3}}\right)^{-1 / 3}=\left(\frac{1}{x^{3}}\right)^{-1 / 3}=x
\end{gathered}
$$
Thus, applying the function three times does not change the value of the variable. Since 2019 is divisible by three, applying the function 2019 times will also not change this value.
Answer: 2018.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Periodicity of the operation of applying the function with a step of 3 is found; no conclusion is drawn from this, or an incorrect conclusion is drawn | 5 points |
| Only $f(f(x))$ is correctly found | 2 points |
| Answer without justification and/or incorrect answer | 0 points |
|
2018
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A rectangular parallelepiped with edge lengths $\sqrt{70}, \sqrt{99}, \sqrt{126}$ is orthogonally projected onto all possible planes. Find the maximum value of the projection area. Justify your answer.
|
Solution: The projection represents a hexagon with pairwise parallel sides (some angles may be degenerate). It is divided into three parallelograms, so its area is twice the area of the triangle $M N P-$ see the figure.
This area - the area of the projection of the triangle - is maximal when the projection is made perpendicular to the projected triangle. In this case, the triangle is equal to its projection, and the area of the projection, consequently, is equal to the area of the triangle itself. The lengths of the sides of the triangle are easily found using the Pythagorean theorem: $\sqrt{70+99}=13, \sqrt{70+126}=14$ and $\sqrt{99+126}=15$. It remains to find the area of the triangle with sides $13,14,15$. By Heron's formula, it is $\sqrt{21 \cdot(21-13) \cdot(21-14) \cdot(21-15)}=84$. Then the maximum area
of the projection is 168.
Answer: 168.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Arithmetic errors in the solution (possibly leading to an incorrect answer) | deduct 1 point |
| There is an unproven statement about the relationship between the area of the triangle $M N P$ and the maximum projection area; with this, the problem is solved. | 5 points |
| The lengths of segments or areas of figures are incorrectly (using incorrect formulas) found; all steps of the solution are performed and a numerical value of the projection area (possibly incorrect) is obtained | 3 points |
| The diagonals of all faces of the parallelepiped (or other parameters of the triangle $M N P$ that allow finding its area) are correctly found | 2 points |
| Answer without justification and/or incorrect answer | 0 points |
|
168
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. In a round-robin chess tournament (each chess player plays one game against each other), 20 chess players participated, 6 of whom were from Russia. It is known that Vladimir, who scored more points than anyone else, took first place. Levon from Armenia took second place, also outscoring each of the other 18 chess players. What is the maximum total number of points that the Russian chess players could have scored? (In chess, one point is awarded for a win, half a point for a draw, and no points for a loss.)
|
Solution: Let's provide an example showing that Russian chess players could collectively score 96 points. Suppose Vladimir won all his games except the one against Levon, which ended in a draw. Additionally, suppose Levon drew all his games with the other Russians and consistently won against non-Russians. Finally, suppose all other games between Russians ended in draws, and all Russians defeated all other non-Russians except Levon. Then, Vladimir scored $18 \cdot 1 + 1 \cdot 0.5 = 18.5$ points, Levon scored $13 \cdot 1 + 6 \cdot 0.5 = 16$ points, each of the other Russians scored $13 \cdot 1 + 5 \cdot 0.5 = 15.5$ points, and each of the other thirteen players scored no more than 12 points. In this case, the condition of the problem is satisfied, and the total points scored by all Russians is $18.5 + 5 \cdot 15.5 = 96$.
We will show by contradiction that the Russians cannot score more points. Suppose they collectively scored 96.5 points or more. In the 15 games among themselves, they collectively scored 15 points, and the remaining (at least 81.5) points were scored in games with players from other countries. There were $6 \cdot 14 = 84$ games between a Russian and a non-Russian, and a total of 84 points were at stake in these games. Therefore, all non-Russians, including Levon, scored no more than 2.5 points in games with Russians, and no one, including Levon, could score more than $13 + 2.5 = 15.5$ points in total. The five Russians he outperformed scored no more than 15 points each, and thus Vladimir must have scored at least $96.5 - 15 \cdot 5 = 21.5$ points. However, he played only 19 games and could not score more than 19 points. This is a contradiction.
Answer: 96 points.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Proved that Russians cannot collectively score 96.5 points or more, but no example of 96 points is provided | 4 points |
| Provided a correct example where Russians collectively scored 96 points; however, it is not proved that they could not score more points. | 2 points |
| Correct answer without justification (or with incorrect justification) | 1 point |
| Incorrect answer and/or reasoning that did not lead to the answer or precise estimate | 0 points |
|
96
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. Inside a large square, there is a small square, the corresponding sides of which are parallel. The distances between some sides of the squares are marked on the diagram. By how much is the perimeter of the large square greater than the perimeter of the small square?
|
Answer: 32.
Solution. Let the side of the small square be $x$, then the side of the large square, if measured horizontally, is $2+x+6=x+8$. The perimeter of a square is four times its side, so it is not difficult to calculate the difference in perimeters:
$$
4(x+8)-4x=32
$$
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. Each of the natural numbers $1,2,3, \ldots, 377$ is painted either red or blue (both colors are present). It is known that the number of red numbers is equal to the smallest red number, and the number of blue numbers is equal to the largest blue number. What is the smallest red number?
|
Answer: 189.
Solution. Let $N$ be the largest blue number. Then only numbers from 1 to $N$ can be painted blue. Since there are a total of $N$ blue numbers, we get that all numbers from 1 to $N$ are blue. Accordingly, all numbers from $N+1$ to 377 are red. Since the number of red numbers equals the smallest red number, we get the equation $N+1=377-N$, from which we find $N=188$. Therefore, the smallest red number is 189.
|
189
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. Krosh and Yozhik decided to check who would run faster along a straight road from Kopyatych's house to Losyash's house. When Krosh had run 20 meters, Yozhik had run only 16 meters. And when Krosh had 30 meters left, Yozhik had 60 meters left. How many meters is the length of the road from Kopyatych's house to Losyash's house? (Krosh and Yozhik started running at the same time, each running at their own constant speed.)
|
Answer: 180.
Solution. When Krosh ran 20 meters, Yozhik ran only 16 meters, so their speeds are in the ratio of $5: 4$.
When Krosh had 30 meters left to run, let him have already run $5 x$ meters (where $x$ is not necessarily an integer). Then by this point, Yozhik had run $4 x$ meters. Therefore, the total length of the entire path in meters is on one side $5 x+30$, and on the other side $4 x+60$. We get the equation $5 x+30=4 x+60$, from which we find $x=30$.
Therefore, the desired length is $5 \cdot 30+30=180$ meters.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Consider seven-digit natural numbers, in the decimal representation of which each of the digits $1,2,3,4,5,6,7$ appears exactly once.
(a) (1 point) How many of them have the digits from the first to the sixth in ascending order, and from the sixth to the seventh in descending order?
(b) (3 points) How many of them have the digits from the first to the fifth in ascending order, and from the fifth to the seventh in descending order?
|
Answer: (a) 6. (b) 15.
Solution. (a) From the condition, it follows that the sixth digit is the largest, so it is 7. The last digit can be any digit from 1 to 6, and this uniquely determines the entire number (since the first five digits must be in ascending order). Therefore, there are exactly 6 such seven-digit numbers.
(b) From the condition, it follows that the fifth digit is the largest, so it is 7. The last two digits can be two different digits from 1 to 6, and this uniquely determines the entire number (since the first four digits must be in ascending order). Also, the sixth digit must be greater than the seventh, so there are exactly 15 possible pairs of the last two digits:
$$
65,64,63,62,61,54,53,52,51,43,42,41,32,31,21
$$
Accordingly, there are also 15 such seven-digit numbers.
Remark. The number of pairs in part (b) is equal to the number of ways to choose two digits from a set of 6 digits, i.e., $\mathrm{C}_{6}^{2}=\frac{6 \cdot 5}{2}=15$.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. In the forest, there live elves and gnomes. One day, 60 inhabitants of this forest lined up facing the same direction, at which point some of them might have been wearing hats. (There could have been from 0 to 60 elves, and inhabitants wearing hats could also have been from 0 to 60 inclusive.)
Each of the 60 inhabitants said one of the following phrases:
- "My neighbor on the right is an elf."
- "My neighbor on the right is wearing a hat."
It is known that elves without hats always tell the truth, while elves with hats always lie. Gnomes are the opposite: gnomes without hats always lie, while gnomes with hats always tell the truth.
(a) (2 points) What is the maximum number of elves without hats that could have been in the row?
(b) (2 points) What is the maximum number of elves with hats that could have been in the row?
|
Answer: (a) 59. (b) 30.
Solution. (a) Note that the rightmost resident cannot be telling the truth, since there is no one to the right of him. This means he cannot be a hatless elf, so the total number of hatless elves is no more than 59.
Now let's provide an example where there are exactly 59 hatless elves. Suppose the rightmost resident is an elf with a hat, and the other 59 are hatless elves. Let everyone say the phrase “My neighbor to the right is an elf.” Then the hatless elves are telling the truth, while the elf with the hat is lying.
(b) Note that among any two neighbors, there cannot be two elves with hats. Indeed, if this were the case, the left one would definitely have told the truth. But this cannot be, since elves with hats always lie.
Let's divide all residents into 30 pairs of neighbors. In each of these pairs, there is no more than one elf with a hat, so the total number of elves with hats is no more than 30.
Now let's provide an example where there are exactly 30 elves with hats. Suppose that gnomes with hats and elves with hats alternate, with the leftmost resident being a gnome. Let everyone say the phrase “My neighbor to the right is an elf.” Then the gnomes with hats are telling the truth, while the elves with hats are lying.
|
59
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. The cells of a $50 \times 50$ table are colored in $n$ colors such that for any cell, the union of its row and column contains cells of all $n$ colors. Find the maximum possible number of blue cells if
(a) (1 point) $n=2$
(b) (3 points) $n=25$.
|
Answer: (a) 2450. (b) 1300.
Solution. We will prove that the number of cells of any color $A$ present in the coloring is no less than 50. Suppose this is not the case, and the number of cells of color $A$ is no more than 49. Then there exists a row without cells of color $A$, and there also exists a column without cells of color $A$. But then for the cell at the intersection of these row and column, the condition is not satisfied, which is a contradiction. Therefore, the number of cells of any color $A$ is no less than 50.
(a) Since the number of cells not blue is no less than 50, the number of blue cells is no more than $50 \cdot 50 - 50 = 2450$. Exactly 2450 blue cells can be present, for example, if all cells in the bottom row are red, and all other cells in the table are blue.
(b) Since the number of cells of any non-blue color is no less than 50, the number of blue cells is no more than $50 \cdot 50 - 24 \cdot 50 = 1300$. Exactly 1300 blue cells can be present, for example, if all cells in the first 26 rows of the table are blue, and each of the remaining 24 rows consists of cells of a single color, and the colors of these 24 rows are different.
## 7th grade
|
1300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 7.8.1. The cells of a $50 \times 50$ table are colored in $n$ colors such that for any cell, the union of its row and column contains cells of all $n$ colors. Find the maximum possible number of blue cells if
(a) (1 point) $n=2$;
(b) (3 points) $n=25$.
|
Answer: (a) 2450. (b) 1300.
|
1300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 7.8.2. The cells of a $40 \times 40$ table are colored in $n$ colors such that for any cell, the union of its row and column contains cells of all $n$ colors. Find the maximum possible number of blue cells if
(a) (1 point) $n=2$;
(b) (3 points) $n=20$.
|
Answer: (a) 1560. (b) 840.
|
840
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 7.8.3. The cells of a $30 \times 30$ table are colored in $n$ colors such that for any cell, the union of its row and column contains cells of all $n$ colors. Find the maximum possible number of blue cells if
(a) $(1$ point) $n=2$;
(b) $(3$ points) $n=15$.
|
Answer: (a) 870. (b) 480.
|
480
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 7.8.4. The cells of a $20 \times 20$ table are colored in $n$ colors such that for any cell, the union of its row and column contains cells of all $n$ colors. Find the maximum possible number of blue cells if
(a) (1 point) $n=2$;
(b) (3 points) $n=10$.
|
Answer: (a) 380. (b) 220.
|
380
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two candles of different thickness, each 24 cm long, are lit simultaneously. The thin candle burns out in 4 hours, the thick one in 6 hours. After what time will one candle be half the length of the other? It is assumed that each candle burns uniformly, meaning it decreases by the same height over equal time intervals. The comparison is made between the unburned portions of the candles.
|
Solution. Let $x$ hours $(x<4)$ have passed since the candles were lit. Since the thin candle decreases by $24: 4=6$ cm every hour, it will decrease by a length of $6 x$ in this time, leaving an unburned stub of length $24-6 x$. Similarly, the stub of the second candle will have a length of $24-4 x$. For one candle to become half the length of the other, the condition $2(24-6 x)=24-4 x$ must be satisfied, from which $x=3$. Answer: in 3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. On a sheet of paper, three intersecting circles are drawn, forming 7 regions. We will call two regions adjacent if they share a common boundary. Regions that border at exactly one point are not considered adjacent.
Two regions already have numbers written in them. Write integers in the remaining 5 regions so that the number in each region equals the sum of all numbers in adjacent regions. What number should be in place of the question mark?
|
Answer: -8.
Solution. Let the unknown number be $x$. Then we can place the numbers in the other regions as follows:
The sum of the numbers in the regions surrounding $x$ should be equal to $x$. We can write this as:
$$
(x+15)+(x+8)+(x-7)=x
$$
Solving the equation, we get $x=-8$. It is easy to verify that the condition of the problem is also satisfied for the other regions.
|
-8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.