problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
24. In a $100 \times 100$ square table, some cells are shaded. Each shaded cell is the only shaded cell either in its column or in its row. What is the maximum number of cells that can be shaded?
## 10th grade
|
75.24. Answer: 198. Let's mark for each shaded cell the line in which it is the only one. Then among the marked lines - not all columns, otherwise there would be no more than 100 shaded cells. Similarly, not all rows are marked. Therefore, the number of marked lines is no more than 198. On the other hand, if we shade all cells in any row and in any column, except for the cell at their intersection, we get the required coloring with 198 cells.
|
198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. In a group of 30 people, each person likes exactly $k$ people in the group. What is the minimum $k$ for which we can assert that there will definitely be two people who like each other?
|
75.35. For $k=15$. Indeed, if we consider a graph with 30 vertices, each of which is connected by an edge, and place an arrow on edge $A B$ from $A$ to $B$ if person $B$ likes person $A$, then we should place $30 \cdot 15=$ $=450$ arrows, while the total number of edges is $30 \times$ $\times 29 / 2=435$. Therefore, on some edge, two arrows will appear (of course, in opposite directions). An example for $k<15$ is constructed as follows: arrange all people in a circle, after which we will assume that each person likes exactly $k$ people following them in a clockwise direction.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44 *. The sequence of integers $x_{0}, x_{1}, x_{2}, \ldots$ is such that $x_{0}=0$, and $\left|x_{n}\right|=\left|x_{n-1}+1\right|$ for each natural $n$. What is the smallest possible value of the expression $\mid \mathrm{x}_{1}+x_{2}+\ldots$ $\ldots+x_{1975} \mid$?
|
75.44. Answer. 20. Since $x_{1}^{2}=1, x_{2}^{2}=x_{1}^{2}+2 x_{1}+1, \ldots$ $\ldots, x_{1976}^{2}=x_{1975}^{2}+2 x_{1975}+1$, then, adding all these equalities, we get
$$
\sum_{i=1}^{1975} x_{i}=\left(x_{1976}^{2}-1976\right) / 2
$$
Since the closest square to 1976 of an even number ( $x_{1976}$ is even!) is $44^{2}=1936$, then $\left|\sum_{i=1}^{1975} x_{i}\right| \geqslant 20$. The reader can easily verify that this is the exact value, as constructing the sequence $\left\{x_{i}\right\}$ for which $x_{1976}=44$ is quite straightforward.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a grid paper, a square of $11 \times 11$ cells is drawn. It is required to mark the centers of some cells in such a way that the center of any other cell is located on a segment connecting some two marked points lying on the same vertical or on the same horizontal. What is the smallest number of cells that need to be marked?
|
76.5. Answer. 22 cells.
76,6. Let $a_{1}, a_{2}, \ldots, a_{m}$ be the sizes of the smaller square plots, $n$ be the side length of the larger square, and $S$ be the sum of the lengths of the internal fences. Then, obviously, $4 \sum a_{i}=2 S+4 n$, $\sum a_{i}^{2}=n^{2}$. From the second equality, it follows that $\sum a_{i}$ and $n$ have the same parity, and therefore, $2 \sum a_{i}$ and $2 n$ have the same remainders when divided by four. We get that $S=2 \sum a_{i}-2 n$ is divisible by four, and thus, the sum of the lengths of all fences $S+4 n$ is divisible by four.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The number 197719771977 is represented as
$$
a_{0}+a_{1} \cdot 10^{1}+a_{2} \cdot 10^{2}+\ldots+a_{11} \cdot 10^{11}
$$
where $a_{0}, a_{1}, \ldots, a_{11}$ are non-negative integers, the sum of which does not exceed 72. Find these numbers.
|
77.8. Consider the record of the number 197719771977, for which the sum of the numbers $a_{i}$ is minimal. If one of the numbers $a_{i}$ is greater than 10, then it can be replaced by $a_{i}-10$, while adding one to $a_{i+1}$ (for $i<11$). From this, it follows that in this case we will have the decimal representation of the number 197719771977 with the sum of the digits being 72. Therefore, the answer is: these are the numbers $1,9,7,7,1,9$, $7,7,1,9,7,7$.
|
197719771977
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. We consider all possible broken lines that follow the sides of the cells and connect the two opposite corners of a square sheet of grid paper measuring $100 \times 100$ by the shortest path. What is the smallest number of such broken lines needed so that their union contains all the vertices of the cells?
|
77.16. Answer. 101 broken lines. The fact that there are no fewer than 101 broken lines follows from the fact that if we consider all the vertices lying on the diagonal connecting two other opposite vertices of the square (there are 101 of them), then no broken line of the specified type can contain two vertices from this set. An example for 101 broken lines is obvious.
|
101
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. What is the greatest number of natural numbers less than 50 that can be chosen so that any two are coprime?
|
79.10. Answer. 16. Hint. Replace each number, except 1, with any of its prime divisors.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. For what least $n$ in the decimal representation of the fraction $m / n$ can the digit sequence ...501... appear after the decimal point?
|
80.25. We can consider that $m / n=0.501 \ldots$ Let's examine the difference $m / n-1 / 2$. On one hand, $m / n-1 / 2 < 0.001$. On the other hand, $m / n-1 / 2 = (2m-n) / 2n$. Since $2m-n$ is an integer, the fraction $(2m-n) / 2n$ can only take values of the form $1 / 2n, 2 / 2n, 3 / 2n, \ldots$. Therefore, $1 / 2n < 0.001$, which implies $n > 500$. For $n=251$, the required fraction exists - it is $126 / 251$.
|
251
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24*. On an $8 \times 8$ chessboard, the squares are colored in two colors in a checkerboard pattern. A token moves on the black squares, and in one move, it can transition to any diagonally adjacent square. What is the minimum number of moves required to visit all the black squares?
## 9th grade
|
81.24. We will paint all black cells below the diagonal connecting the top left and bottom right corners of the board in red and blue as follows: if the sum of the row number and column number (numbers are counted from the bottom and left) is divisible by four, we paint the cell red; if it is not divisible by four, we paint it blue. Now we will reflect this coloring symmetrically relative to the aforementioned diagonal and paint all cells above it. Each move, except for moves crossing the diagonal, the piece moves from a blue cell to a red one and vice versa. Since there are eight more blue cells than red ones, and there are only four moves from a blue cell to a blue cell, the piece must make at least three moves to cells it has already visited. Therefore, the answer: the minimum number of moves is \(31+3=34\).
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. The angle $A$ at the vertex of the isosceles triangle $A B C$ is $100^{\circ}$. On the ray $A B$, a segment $A M$ is laid off, equal to the base $B C$. Find the measure of angle $B C M$.
|
83.40. Answer. $10^{\circ}$. Indeed, let's lay off on the ray $A M$ a segment $B N$, equal in length to $B C$. Then, in the isosceles triangle $B N C$, the line $C M$ is the bisector of angle $C$. This follows from the fact that $B M / B N = C B / C N$. Since $\angle B C N = 20^{\circ}$, then $\angle B C M = 10^{\circ}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. The number 1584 has the following properties:
a) it is not a square of an integer;
b) it is different from its reverse 4851;
c) the product of the numbers 1584 and 4851 is a square of an integer.
Find a 20-digit number with the same properties.
|
85.37. For example, the number 15841584158415841584 fits.
|
15841584158415841584
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. 15 volleyball teams played a round-robin tournament, where each team won exactly seven matches. How many triplets of teams are there in this tournament where each team has exactly one win against the other two?
|
85.39. All triples of teams can be divided into two types: those that scored one point in matches against each other, and those that scored 2, 1, and 0 points in matches against each other. If the number of triples of the first type is $-a$, and the number of triples of the second type is $-b$, then $a+b=455$. On the other hand, the number of triples in which a given team scored exactly 1 point is obviously 49; in each triple of the first type, there are three such teams, and thus each such triple is counted three times, while each triple of the second type is counted exactly once. Therefore, $3a+b=49 \cdot 15=735$. From this, we get $a=140$.
|
140
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. a) Find a seven-digit number, all digits of which are different and which is divisible by all these digits.
b) Does such an eight-digit number exist?
## 6th grade
|
86.6. a) 7639128. b) It is clear that the record should not contain zero. Since our number is obviously even, it cannot be divisible by five - otherwise it would end in zero. There are eight digits left, the sum of which is not divisible by three, and the digit 3 must be included in the number's record - a contradiction. Therefore, such a number does not exist.
Fig. 61
|
7639128
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. A pile of 25 stones is arbitrarily divided into two piles, any of the existing piles is again divided into two, and so on, until each pile consists of one stone. Each time a pile is divided into two, the product of the number of stones in the resulting two piles is recorded. Prove that the sum of all recorded numbers is 300.
## 8th grade
|
86.19. Let's consider the quantity $S$ as the half-sum of the squares of the number of stones in the piles. Initially, $S=312.5$, and at the end, $S=12.5$. If a pile containing $x+y$ stones is split into two piles with $x$ and $y$ stones respectively, then $S$ decreases by $x y$. Therefore, the amount by which $S$ decreases coincides with the recorded number. Consequently, the sum of all recorded numbers is equal to the total decrease in the value of $S$, which is $312.5-12.5=300$.
|
300
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
25*. 200 football teams are holding a championship. On the first day, all teams played one game, on the second day, they all played one game again, and so on. Prove that after the sixth day, it is possible to indicate 34 teams, no two of which have played against each other.
## 9th grade
|
86.25. We will prove that for any $n=1,2, \ldots, 33$ it is possible to construct two non-intersecting groups of teams - the first with $n$ teams, and the second with $5 n+1$ teams - such that all teams that played against teams in the first group are in the second group (this means, in particular, that the teams in the first group did not play against each other). For $n=1$, we include any team in the first group, and in the second group, we include the six teams that played against it.
Suppose now that for some $n<33$ such groups have been constructed. Since the total number of teams in both groups is odd, there is a team $A$ that does not belong to either of these groups and played a match on the first day with one of the teams in the second group. There will also be no more than five teams, not included in our groups, that played against team $A$. Now, add team $A$ to the first group, and these five (or fewer) teams to the second group. Now, if necessary, add a few more teams (from those not included in either group) to the second group so that it contains exactly $5 n+6 = 5(n+1)+1$ teams. Since $n<33$, this is possible, and thus we have constructed the required groups for $n+1$.
Now consider both constructed groups for $n=33$. Since $6 n+1=199<200$, there is still one team that does not belong to either group. Adding it to the 33 teams in the first group, we get 34 teams that did not play against each other.
|
34
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
35. Find all positive solutions of the equation
$$
x^{1986} + 1986^{1985} = x^{1985} + 1986^{1988}
$$
|
86.35. Let's rewrite the equation as $x^{1985}(x-1)=$ $=1986^{1985}(1986-1)$. Since $x=1986$ is a solution to the equation, and the left side is an increasing function for $x>1$, there are no other solutions.
|
1986
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. Compute the integral
$$
\int_{-1}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}
$$
|
86.58. The main idea of the solution is to use the "non-evenness" of the function \( 1 /\left(1+x^{3}+\sqrt{1+x^{6}}\right) \), specifically:
\[
\begin{aligned}
& \text { of the function } 1 /\left(1+x^{3}+\sqrt{1+x^{6}}\right) \text {, specifically: } \\
& \int_{-1}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}=\int_{-1}^{0} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}+\int_{0}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}= \\
& =\int_{0}^{1} \frac{d x}{1-x^{3}+\sqrt{1+x^{6}}}+\int_{0}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}= \\
& =\int_{0}^{1}\left[\frac{1}{1-x^{3}+\sqrt{1+x^{6}}}+\frac{1}{1+x^{3}+\sqrt{1+x^{6}}}\right] d x= \\
& =\int_{0}^{1} \frac{\left(2+2 \sqrt{1+x^{6}}\right) d x}{\left(1+\sqrt{1+x^{6}}\right)^{2}-x^{6}}=\int_{0}^{1} 1 d x=1
\end{aligned}
\]
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Two players take turns placing crosses and noughts in the cells of a $9 \times 9$ square (the first player places crosses, and the opponent places noughts). At the end, the number of rows and columns where there are more crosses than noughts is counted - these are the points scored by the first player. The number of rows and columns where there are more noughts - the points scored by the second player. How can the first player win (score more points)?
## 6th grade
|
87.6. Hint. The first one needs to use central symmetry. The maximum guaranteed number of his points is 10, i.e., he can guarantee to win two points over the second one.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find the smallest natural number greater than 1 that is at least 600 times greater than each of its prime divisors.
|
89.12. Answer. This number is $1944=2^{3} \cdot 3^{5}$.
|
1944
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54*. In the language of the Tru-la-la tribe, a word is any sequence of 10 digits 0 and 1. It is known that two words are synonyms if and only if one can be obtained from the other by a series of operations of the following kind: from the word, several consecutive digits, the sum of which is even, are erased, after which the erased digits are written back in the same place, but in reverse order. How many words of the Tru-la-la language can be written that differ in meaning?
|
89.54. Answer. 56 words. Instruction. Consider all words of the Tru-lya-ya tribe language of the form $11 \ldots 100 \ldots 0100 \ldots 0$. Prove that any word can be brought to such a form. To prove that these words are distinct, use the following quantity defined for any word in the Tru-lya-ya language: the number of zeros to the right of which there is an odd number of ones. Prove that this quantity does not change when performing the operations described in the problem conditions.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. How many pairs of natural numbers ( $m, n$ ) exist such that $m, n \leqslant 1000$ and
$$
\frac{m}{n+1}<\sqrt{2}<\frac{m+1}{n} ?
$$
## 9th grade
|
90.20. Answer. 1706. Hint. The pair ( $m, n$ ) satisfies the inequalities from the condition if and only if the line $y=\sqrt{2 x}$ intersects a cell on the coordinate grid plane, the lower left corner of which has coordinates $(m, n)$.
|
1706
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56*. On a shelf, a 100-volume collection of L. N. Tolstoy's works stands in a random order. It is allowed to take any two volumes with numbers of different parity and swap their places. What is the minimum number of such swaps required to always arrange the volumes in order?
|
90.56. Answer. 124 permutations. Hint. Break down the entire permutation of volumes into cycles. We will call the operation of exchanging volumes from different cycles merging, and the operation of exchanging volumes from the same cycle - breaking. Prove that by applying no more than 25 merging operations and no more than 99 breaking operations, the volumes can be arranged in the correct order. An example where it is impossible to arrange the volumes in the correct order in fewer than 124 exchanges is as follows: the permutation consists of one cycle of length 50, composed entirely of volumes with even numbers, and 25 cycles of length 2, composed of volumes with odd numbers.
|
124
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49*. On the board, there are 128 ones. In one move, you can replace a pair of numbers $a$ and $b$ with the number $a b + 1$. Let $A$ be the maximum number that can appear on the board after 127 such operations. What is its last digit?
## 11th grade
|
92.49. Hint. Prove that to obtain the maximum number, you can act according to the following scheme: at each moment, perform the operation on the two smallest numbers.
By now, carrying out the calculations in accordance with the derived algorithm, we get that the last digit of the maximum number is two.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the table, there are several boys and five girls, and on the table, on a plate, there are 30 buns. Each girl gave a bun (from the plate) to each boy she knew, and then each boy gave a bun (from the plate) to each girl he did not know. After this, it turned out that all the buns were given out. How many boys were there?
|
93.3. Let the number of boys be $n$. Then there are $5 n$ different boy-girl pairs. Each such pair corresponds to
one passed bun: if the boy and girl are acquainted, the bun was passed by the girl, and if they are not acquainted - by the boy. Hence $5 n=30$. Answer. $n=6$.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. What is the greatest value that the expression
$$
a e k-a f h+b f g-b d k+c d h-c e g
$$
can take if each of the numbers $a, \ldots, k$ is equal to 1 or -1?
|
93.11. Each of the six terms of the given sum is equal to 1 or -1, so this sum is even. It cannot take the value six, since in this case the terms $a e k, b f g, c d h$ must be equal to 1 and, therefore, their product is 1, and the terms $a f h, b d k, c e g$ must be equal to -1, and their product is -1. However, these products obviously coincide. The value 4 is achieved, for example, when $a=b=c=e=h=1, d=f=g=-1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. A chip is placed on one of the squares of a $7 \times 7$ board. It is allowed to sequentially place new chips on empty squares, but in such a way that each square on which the next chip is placed shares a side with no more than one already occupied square. What is the maximum number of chips that can be on the board after several such operations?
## 9th grade
|
93.20. Answer. 36 chips.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The fifth power of a natural number $n$ consists of the digits $1,2,3,3,7,9$. Find this number.
|
Solution. Let's form several six-digit numbers (including the smallest and largest) from the given digits and extract their fifth roots using a microcalculator: $\sqrt[5]{123379} \approx 10.42914$; $\sqrt[5]{173923} \approx 11.17047$; $\sqrt[5]{213379} \approx 11.63672$; $\sqrt[5]{337912} \approx 12.75735$; $\sqrt[5]{733921} \approx 14.89807$; $\sqrt[5]{973321} \approx 15.76345$. From this, it is clear that $11 \leqslant n < 15$. But the number $n$ cannot be 15 because the number $15^5$ ends in the digit 5, which is not among the given digits. Therefore, $11 \leqslant n \leqslant 14$.
The number $14^5$ ends in the digit 4, which is also not among the given digits. Therefore, $11 \leqslant n \leqslant 13$.
The number $11^5$ starts and ends with the digit 1, and among the given digits, there is only one 1. Therefore, $n=12$ or $n=13$.
By calculating, we get:
$$
12^5 = 248832, 13^5 = 371293
$$
Thus, $n=13$.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. Find the integer part of the expression
$a=\sqrt{1981+\sqrt{1981+\sqrt{1981+\ldots+\sqrt{1981+\sqrt{1981}}}},}$ if the number 1981 appears in it $n$ times ( $n \geqslant 2$ ).
|
Solution. Using a calculator, we obtain:
$$
\begin{aligned}
& a_{1}=\sqrt{1981} \approx 44.508426 \\
& a_{2}=\sqrt{1981+\sqrt{1981}} \approx 45.005648 \\
& a_{3}=\sqrt{1981+\sqrt{1981+\sqrt{1981}}} \approx 45.011173 \\
& a_{4}=\sqrt{1981+\sqrt{1981+\sqrt{1981+\sqrt{1981}}}} \approx \\
& \approx 45.011234 \\
& a_{5} \approx 45.011234
\end{aligned}
$$
From this, we hypothesize that the integer part of the number \( a \) is 45, i.e., \([a]=45\).
Let's verify this hypothesis as follows: Suppose,
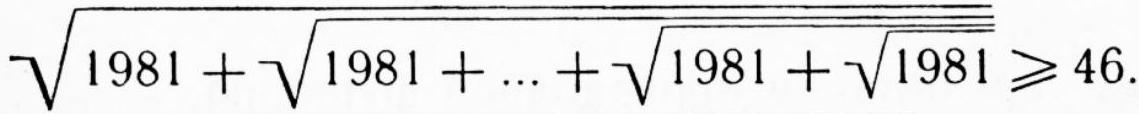
$$
\begin{aligned}
& \text{Then } \sqrt{1981+\ldots+\sqrt{1981+\sqrt{1981}}}>135 \text{ and } \\
& 1981+\ldots+\sqrt{1981+\sqrt{1981}}>135^{2}
\end{aligned}
$$
Continuing this process, we arrive at an obviously false inequality. Therefore, \([a]=45\).
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.
Find all natural numbers $n$ such that the sum $S(n)$ of the digits in the decimal representation of the number $2^{n}$ is 5.
|
Solution. To find the solution, we will construct a table of values for the expression $2^{n}$:
| $n$ | $2^{n}$ | $S(n)$ | $n$ | $2^{n}$ | $S(n)$ |
| :---: | ---: | ---: | :---: | ---: | :---: |
| 1 | 2 | 2 | 16 | 65536 | 25 |
| 2 | 4 | 4 | 17 | 131072 | 14 |
| 3 | 8 | 8 | 18 | 262144 | 19 |
| 4 | 16 | 7 | 19 | 524288 | 29 |
| 5 | 32 | 5 | 20 | 1048576 | 31 |
| 6 | 64 | 10 | 21 | 2097152 | 26 |
| 7 | 128 | 11 | 22 | +194304 | 25 |
| 8 | 256 | 13 | 23 | 8388608 | 41 |
| 9 | 512 | 8 | 24 | 16777216 | 37 |
| 10 | 1024 | 7 | 25 | 33554432 | 29 |
| 11 | 2048 | 14 | 26 | 67108864 | 40 |
| 12 | 4096 | 19 | 27 | 134217728 | 35 |
| 13 | 8192 | 20 | 28 | 268435456 | 43 |
| 14 | 16384 | 22 | 29 | 536870912 | 41 |
| 15 | 32768 | 26 | | | |
Careful examination of this table leads to the conjecture that
$$
S(k+6 n)=S(k)+9 m
$$
where $n, k$ are natural numbers; $m$ is a natural number or zero.
But why, when multiplying the number $2^{n}$ by $2^{6}$, do we get a number whose sum of digits is either equal to the sum of the digits of the number $2^{n}$, or differs from it by $9 m$? What property does the number $2^{6}$ and its sum of digits possess?
We notice that $S(6)=10$ and $2^{6}=64=63+1=9 \cdot 7+1$.
But what follows from this? Let's consider an example:
$2^{14} \cdot 2^{6}=16384(9 \cdot 7+1)=9 \cdot 7 \cdot 16384+16384$
The number $9 \cdot 7 \cdot 16384$ is divisible by 9. Therefore, the sum of its digits is also divisible by 9. Now it is clear why equation (1) is true.
So, $S(5)=5$. But why are there no other solutions?
By equation (1), they should be sought among $S(11), S(17), S(23), S(29), \ldots$. But $S(11), S(23), S(35), \ldots$ end in the digit 8. Therefore, we are only interested in $S(17), S(29), S(41), \ldots$, i.e., $S(5+12 k)$, where $k$ is a natural number.
It is easy to show that all $S(5+(2 k+1) 12)$ end in the digits 7 and 2, i.e., $S(5+(2 k+1) 12) \geqslant 9$. Therefore, we are only interested in $S(5+24 k)$, which end in the digits 1 and 2 for $k \geqslant 1$. But numbers of the form $2^{5}+24 k \quad(k \geqslant 1, \quad k$ - a natural number) are greater than 1000000012. The number 2000000012 (its sum of digits $S=5$) after division by $2^{2}$ becomes odd, but $2^{3}+24 k$ is even.
The numbers $1100000012, \quad 1010000012, \quad 1001000012$, $1000100012,1000010012,1000001012$ also give an odd number when divided by $2^{2}$. The number 1000000112 is not divisible by $2^{5}$.
Thus, we get the answer: $n=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 Task 1. For which natural $n(n \geqslant 2)$ is the equality
$$
-\sqrt[2]{17 \sqrt{5}+38}+\sqrt[2]{17 \sqrt{5}-38}=\sqrt{20} ?
$$
|
Solution. Using a calculator, we find:
$$
\begin{gathered}
17 \sqrt{5}+38 \approx 38.013154+38 \approx 76.013154>1 \\
17 \sqrt{5}-38 \approx 0.0131541$, and the function $\varphi(n)=\sqrt[n]{17 \sqrt{5}-38}$ is increasing, and $\varphi(n)<1$. To discover some properties of the function $\psi(n)=f(n)+\varphi(n)$, we will perform a mathematical experiment (construct a table of values of the function $\psi(n)$):
| $n$ | $f(n)$ | $\varphi(n)$ | $\varphi(n)$ |
| :---: | :---: | :---: | :---: |
| 2 | 8.7185522 | 0.1146908 | 8.8332422 |
| 3 | 4.2358226 | 0.2360586 | 4.4718813 |
| 4 | 2.952194 | 0.3386604 | 3.2913798 |
| 5 | 2.3777310 | 0.4205441 | 2.8002750 |
Now it is clear that equation (1) has a unique solution $n=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In trapezoid $A B C D$, segments $B C$ and $A D$ are the bases. $B C=9.5 ; A D=20 ; A B=5$; $C D=8.5$. Find its area.
|
Solution. To solve the problem, it is necessary to find the length of the height of this trapezoid. Place the trapezoid $ABCD$ relative to a rectangular coordinate system as shown in Figure 8. Then $A(0; 0)$, $D(20; 0)$, $B(x; y)$, $C(x+9.5; y)$. According to the problem's conditions,
$$
\begin{gathered}
AB^2 = (x-0)^2 + (y-0)^2 = 25 \\
CD^2 = (x+9.5-20)^2 + (y-0)^2 = 72.25
\end{gathered}
$$
After simplification, the system of equations (1) and (2) becomes:
$$
\left\{\begin{array}{l}
x^2 + y^2 = 25 \\
(x-10.5)^2 + y^2 = 72.25
\end{array}\right.
$$
Fig. 7
Fig. 8
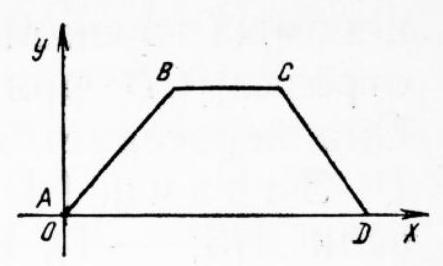
Fig. 9
After subtracting equation (3) from equation (4) term by term, we get:
$$
(x-10.5)^2 - x^2 = 47.25
$$
From this, $x=3$. Since the trapezoid $ABCD$ is located in the upper half-plane (Fig. 8), then $y=4$, i.e., the height of the trapezoid $ABCD$ is 4.
Thus, $S_{ABCD} = 0.5(9.5 + 20) \cdot 4 = 59$.
|
59
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 17. The side of a regular triangle $ABC$ is 4. Point $D$ is the midpoint of side $BC$. A line passing through $B$ intersects side $AC$ at point $M$. Perpendiculars from points $D$ and $A$ to line $BM$ are $DH$ and $AK$. Calculate the length of segment $AM$, if
$$
AK^4 - DH^4 = 15
$$
|
Instruction. Equation (1) has a unique solution. Let $\angle A B M=x$. Then $D H=2 \sin \left(60^{\circ}-x\right)$, $A K=4 \sin x$. Equation (1) takes the form:
$$
256 \sin ^{4} x-16 \sin ^{4}\left(60^{\circ}-x\right)=15
$$
Solving equation (2) on a microcalculator, we get $x=30^{\circ}$, and therefore, $A M=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Find all values of $a$ for which the equation
$$
2 \lg (x+3)=\lg (a x)
$$
has a unique solution.
|
The first solution. Obviously, $x>-3, a x>0$, $x \neq 0$. From equation (1) we get:
$$
(x+3)^{2}=a x, a=\frac{(x+3)^{2}}{x}=\left(\sqrt{x}+\frac{3}{\sqrt{x}}\right)^{2}, \text { if } x>0
$$
Obviously,
$$
\left(\sqrt{x}+\frac{3}{\sqrt{x}}\right)=\left(\sqrt{x}-\frac{3}{\sqrt{x}}\right)^{2}+12
$$
From here it is clear that for positive $x$ the minimum value of the function
$$
a=\frac{(x+3)^{2}}{x}
$$
is 12. If $-3-3$. Now it is clear that for all $a>0$, the line $y=a x$ has a unique common point with the curve $y=(x+3)^{2}$ for $x>-3$ only when $y=a x$ is tangent to this curve. From this we get $a=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. How many solutions does the equation
$$
\arcsin 2x + \arcsin x = \frac{\pi}{3} ?
$$
|
Solution. The function $f(x)=\arcsin 2 x$ is defined on the interval $[-0.5 ; 0.5]$, and the function $\varphi(x)=\arcsin x$ is defined on the interval $[-1 ; 1]$. Therefore, the left side of equation (1) is defined on the interval $[-0.5 ; 0.5]$. The monotonic and continuous function $y=\arcsin 2 x+\arcsin x$ changes on the interval $[-0.5 ; 0.5]$ from $\left(-\frac{\pi}{2}-\frac{\pi}{6}\right)$ to $\left(\frac{\pi}{2}+\frac{\pi}{6}\right)$, i.e., from $-\frac{2}{3} \pi$ to $\frac{2}{3} \pi$. But $\frac{\pi}{3}<\frac{2}{3} \pi$. Therefore, equation (1) has a unique solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 13. Find the minimum value of the function
$$
\psi(x)=\sqrt{15-12 \cos x}+\sqrt{7-4 \sqrt{3} \sin x}
$$
on the interval $[0 ; 0.5 \pi]$.
|
Solution. Since $|\cos x| \leqslant 1$ and $|\sin x| \leqslant 1$, the function $\psi(x)$ is defined on the entire interval $[0 ; 0.5 \pi]$. To find the properties of the functions $f(x)=\sqrt{15-12 \cos x}$, $\varphi(x)=\sqrt{7-4 \sqrt{3} \sin x}, \quad \psi(x)=f(x)+\varphi(x) \quad$, we create a table of their values using a calculator:
| $x^{0}$ | $f(x)$ | $\varphi(x)$ | $\varphi(x)$ |
| ---: | :---: | :---: | :---: |
| 0 | 1.7320508 | 2.6457513 | 4.3778021 |
| 5 | 1.7451827 | 2.5290645 | 4.2742472 |
| 10 | 1.783921 | 2.407616 | 4.1915837 |
| 15 | 1.8463179 | 2.2818523 | 4.1281702 |
| 20 | 1.9296859 | 2.1518401 | 4.0815260 |
| 25 | 2.030887 | 2.017937 | 4.0487624 |
| 30 | 2.1465542 | 1.8803984 | 4.0269526 |
| 35 | 2.2738018 | 1.7395827 | 4.0133843 |
| 40 | 2.409884 | 1.5958185 | 4.0056669 |
| 45 | 2.5523945 | 1.4494896 | 4.0018841 |
| 50 | 2.6993608 | 1.3010333 | 4.0003941 |
| 55 | 2.8490493 | 1.1509769 | 4.0000262 |
| 60 | 3.000020 | 0.9999899 | 4.0000001 |
| 65 | 3.1509650 | 0.84906731 | 4.0000323 |
| 70 | 3.3008723 | 0.69972737 | 4.0003597 |
| 75 | 3.4487282 | 0.5548598 | 4.0036527 |
| 80 | 3.5939145 | 0.42077535 | 4.0146899 |
| 85 | 3.7355228 | 0.31330512 | 4.0488279 |
| 90 | 3.8729833 | 0.26794924 | 4.1409325 |
Based on the table, we can hypothesize that on the interval $[0 ; 0.5 \pi]$, the function $\psi(x) \geqslant 4$, and $\psi\left(\frac{\pi}{3}\right)=4$.
Thus, let's try to prove that
$$
\sqrt{15-12 \cos x}+\sqrt{7-4 \sqrt{3} \sin x} \geqslant 4
$$
Let $\sqrt{7-4 \sqrt{3} \sin x}=t$.
From this, $\sin x=\frac{7-t^{2}}{4 \sqrt{3}}, \cos x=\sqrt{1-\frac{\left(7-t^{2}\right)^{2}}{48}}$ and the inequality (2) takes the form:
$$
\sqrt{15-\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}}} \geqslant 4-t
$$
Both sides of the inequality (3) are non-negative, so after squaring both sides, we get an equivalent inequality:
$$
15-\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}} \geqslant(4-t)^{2}
$$
or
$$
\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}} \leqslant 8 t-1-t^{2}
$$
From here, $t^{4}-4 t^{3}+6 t^{2}-4 t+1 \geqslant 0$.
Applying the theorem of Bezout, we get $(t-1) \cdot\left(t^{3}-\right.$ $\left.-3 t^{2}+3 t-1\right) \geqslant 0$ or $(t-1)^{4} \geqslant 0$.
Thus, it is proven that the minimum value of the function $\psi(x)$ is 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 16. Solve the equation
$$
\lg \left(x^{2}+9\right)-3 \cdot 2^{x}+5=0
$$
|
Solution. The equation does not have negative roots because on $(-\infty ; 0)$ the function $P(x)=\lg \left(x^{2}+\right.$ $+9)+5$ is decreasing, the function $K(x)=3 \cdot 2^{x}$ is increasing, and $P(0)>K(0)$. To hypothesize about the number of roots of the given equation, we construct tables of the functions $P(x)$ and $K(x)$:
| $x$ | $P(x)$ | $K(x)$ | $x$ | $P(x)$ | $K(x)$ |
| :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | |
| 0 | 5.954 | 3 | 1.6 | 6.062 | 9.09 |
| 0.2 | 5.956 | 3.45 | 1.8 | 6.087 | 10.4 |
| 0.4 | 5.961 | 3.95 | 2 | 6.113 | 12 |
| 0.6 | 5.971 | 4.55 | 2.2 | 6.141 | 13.8 |
| 0.8 | 5.984 | 5.22 | 2.4 | 6.169 | 15.8 |
| 1 | 6 | 6 | 2.6 | 6.197 | 18.2 |
| 1.2 | 6.018 | 6.89 | 2.8 | 6.226 | 20.9 |
| 1.4 | 6.039 | 7.92 | 3 | 5.255 | 24 |
Now we can hypothesize that if $x>2$, then $\lg \left(x^{2}+9\right)<2^{x}$ (this inequality is easily proven using the derivative). After this, it becomes clear that all roots of the given equation belong to the interval $[0 ; 2]$. The number 1 is a root of the equation.
From the table, it is clear that the intervals $[0 ; 0.8]$ and $[1.2 ; 2]$ cannot contain roots of the equation (1).
To prove that 1 is the only root of the equation (1), we construct tables of the functions $P^{\prime}(x)$ and $K^{\prime}(x)$:
| $x$ | $P^{\prime}(x)$ | $K^{\prime}(x)$ | $x$ | $P^{\prime}(x)$ | $K^{\prime}(x)$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0.8 | 0.072 | 3.6 | 1.1 | 0.093 | 4.4 |
| 0.9 | 0.079 | 3.8 | 1.2 | 0.099 | 4.7 |
| 1 | 0.080 | 4.1 | | | |
Now it is clear that on the interval $(0.8 ; 1.2)$ the function $y=P(x)-K(x)$ is decreasing.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 a d a c h a 19. A circle with radius 1 and center at point $O$ is circumscribed around an equilateral triangle $A B C$. Prove that the sum of the squares of the distances from any point $M$ on the circle to the vertices of this triangle is equal to 6 (Fig. 9).
|
Solution. Obviously,
$\overline{C M}^{2}+\overline{M A}^{2}+\overline{M B}^{2}=(\overline{O M}-\overline{O C})^{2}+(\overline{O A}-\overline{O M})^{2}+$ $+(\overline{O B}-\overline{O M})^{2}=\overline{O M}^{2}+\overline{O C}^{2}-2 \overline{O M} \cdot \overline{O C}+\overline{O A}^{2}+$ $+\overline{O M}^{2}-2 \overline{O A} \cdot \overline{O M}+\overline{O B}^{2}+\overline{O M}^{2}-2 \overline{O B} \cdot \overline{O M}=6-$ $-2 \overline{O M}(\overline{O C}+\overline{O A}+\overline{O B})=6-2 \overline{O M} \cdot \bar{O}=6$.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
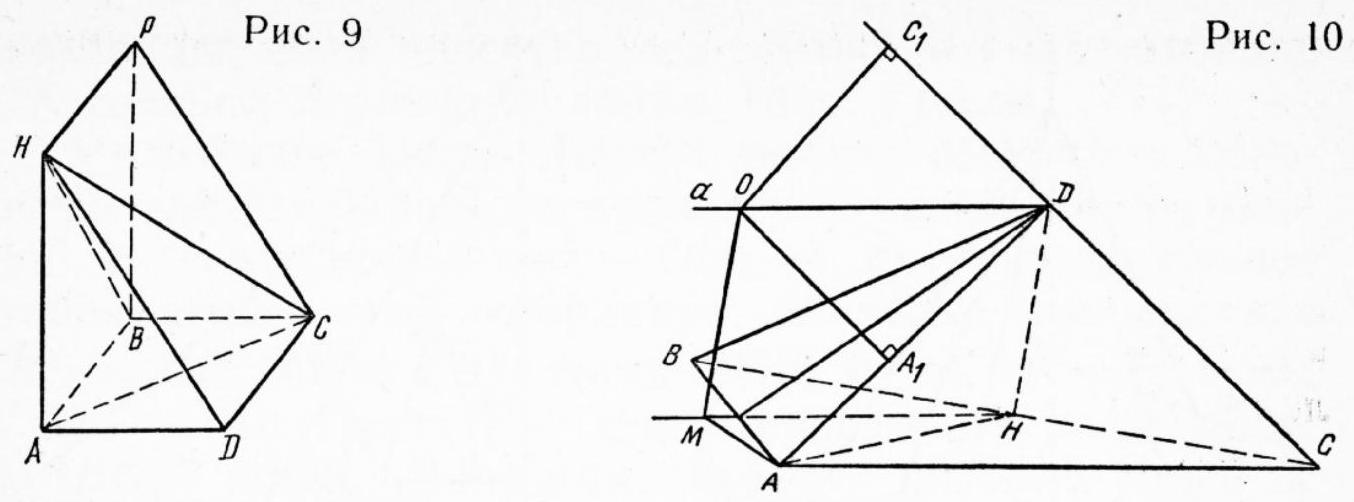
Problem 5. $DABC$ is a triangular pyramid (Fig. 5). $\overline{AK}=\overline{KD}, \overline{BP}=\overline{PC}, \overline{DM}=0.4 \overline{DC}$. Find the area $S$ of the section of the pyramid by the plane $KMP$, if the vertex $A$ is at a distance $h=1$ from the plane $KMP$ and the volume of the pyramid $DABC$ is 5.
|
Solution. We construct the section of the pyramid $DABC$ using the method of parallel projections. We choose the line $KP$ as the direction of projection. In this case, the pyramid $\dot{D}ABC$ is represented by the parallelogram $ABDC$ (Fig. 6), and the cutting plane is represented by the line $KM$, which intersects the edge $AB$ at point $E$. Point $K=P$ is the center of symmetry of the parallelogram $ABDC$, so $AE: EB = DM: MC = 2: 3$.
Thus, the section of the pyramid $DABC$ by the plane $KMP$ is the quadrilateral $KMPE$ (Fig. 5).
The quadrilateral pyramids $AEKMP$ and $DEKMP$ have the same base $KMPE$ and $AK = KD$. Therefore, their volumes are equal. The area of triangle $AMD$ is 0.4 of the area of triangle $ACD$, and the distance from point $P$ to the plane $ACD$ is half the distance from point $B$ to this plane. Therefore, the volumes of pyramids $PAMC$ and $DEPB$ constitute 0.6 of the volume of pyramid $DABC$. This means that the volume of pyramid $AKMPE$ is 0.2 of the volume of pyramid $DABC$, i.e., it is equal to 1.
Thus, $\frac{1}{3} S h = 1$. But $h = 1$, so $S = 3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. The base of the pyramid $HABCD$ is a square $ABCD$, and the edge $HA$ is perpendicular to the base plane. $AB=3, HA=4$. Prove that a sphere can be inscribed in the pyramid, and find its radius.
For comparison, we will provide two solutions to this problem.
|
The first solution. First, we find the radius of the sphere. Then we prove its existence. For this, we apply the formula $3 v = S r$. Clearly, $V = \frac{1}{3} \cdot 3 \cdot 3 \cdot 4 = 12$; $H B = 5$; $S(ABCD) = 9$; $S(BAH) = S(HAD) = 0.5 \cdot 3 \cdot 4 = 6$; $S(HBC) = S(HDC) = 0.5 \cdot 3 \cdot 5 = 7.5$. Therefore, $S = 9 + 2 \cdot 6 + 2 \cdot 7.5 = 36$. We get $r = 1$.
The planes $ABH$, $AHD$, and $ABD$ are mutually perpendicular. Therefore, the point $O$, which is 1 unit away from these planes, is the vertex of the cube $AB'C'D'A_1B_1OD_1$ (Fig. 8). We will prove that the point $O$ is 1 unit away from the planes $HBC$ and $HDC$.
Since the line $B_1O$ is parallel to the line $BC$, the distance from points $B_1$ and $O$ to the plane $HBC$ is the same. The planes $ABH$ and $BHC$ are perpendicular. Therefore, the distance from $B_1$ to the plane $HBC$ is equal to the distance from $B_1$ to the line $BH$.
Thus, the problem reduces to proving that the point $B_1$ is the center of the circle inscribed in the right triangle $HAB$. Since the area of the triangle $AHB$ and its semiperimeter are both 6, the radius of the inscribed circle is 1.
The second solution. We complete the given pyramid $HABCD$ to form a right triangular prism $HADPBC$ (Fig. 9). The right triangle $HAD$ is an orthogonal cross-section of this prism. Therefore, the radius of the sphere $\omega$, which touches the planes $HAB$, $ABD$, $HDC$, and $HAD$, is equal to the radius $r$ of the circle inscribed in the triangle $HAD$.
We already know that $r = 1$. Clearly, the center $O$ of the sphere $\omega$ is inside the pyramid $HABCD$. Therefore, the sphere $\omega$ touches the faces $ABCD$, $HAB$, $HAD$, and $HCD$ of this pyramid. The plane $HAC$ is a plane of symmetry of the pyramid $HABCD$. Therefore, the sphere $\omega$ also touches the face $HBC$, which is symmetric to the face $HDC$ relative to the plane $HAC$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. On this cuneiform tablet, divisors and quotients are placed, which, according to the sexagesimal system used by the Babylonians, is written as:
$$
60^{8}+10 \cdot 60^{7}
$$
Express this number in the decimal system.
## 1 -st Senkere table.
|
1. 195955200000000 .
|
195955200000000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Determine the volume of a truncated square pyramid if its height is 6, the side of the lower base is 4, and the upper base is 2.
|
10. Using the formula for the volume of a truncated pyramid
$$
V=\frac{H}{3}(B+b+\sqrt{B b})
$$
we get:
$$
V=\frac{6}{3}(16+4+\sqrt{16 \cdot 4})=2(16+4+8)=56
$$
It is interesting to see the solution of the Egyptian mathematician. We will translate the text from the papyrus verbatim:
"Problem to solve the pyramid (a drawing is attached on the side) as if it were said: 4 at the bottom, 2 at the top. Do as it is done: the square of 4 gives 16. Double 4 gives 8. Do as it is done: the square of 2 gives 4. Add 16, add 8, add 4, which gives 28. Do as it is done: take one third of 6, which makes 2. Do as it is done: take 28 twice, which makes 56. This is 56. You will find it correct."
|
56
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Two thirds in addition (to the unknown), $\frac{1}{3}$ in subtraction, 10 remains (i.e., two thirds of the unknown are added to it, and one third is subtracted from the resulting sum. The remainder is 10).
|
17. The equation will be:
$$
x+\frac{2}{3} x-\frac{1}{3}\left(x+\frac{2}{3} x\right)=10 ; x=9
$$
$\begin{array}{ll}\text { 18. } x=\frac{3}{10} ; x=\frac{15}{53} & \text { 19. } 4 \frac{1}{6} \text {. }\end{array}$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. Seven people have seven cats; each cat eats seven mice, each mouse eats seven ears of barley, and from each ear can grow seven measures of grain. What are the numbers in this series and what is their sum? (The problem is reconstructed according to Rodet.)
## Problems from the Akhmim Papyrus.
|
25. $7,49,343,2401,16807$, sum 19607.
|
19607
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. In the Akhmim papyrus, the area of a circle, the circumference of which is the arithmetic mean of two given circumferences, is taken as the arithmetic mean of their areas. Show that this is incorrect, and find how large the error is in percentage, where the radii of the given circles \( r=5 \); \( R=10 \).

Problems attributed to Pythagoras.
|
28. For $r=5$ and $R=10$, the error is about $11\%$.
Greek mathematics reached its peak by the 3rd century BC (the Alexandrian period). From this time, a number of mathematical treatises (by Euclid, Archimedes, and Apollonius) have survived to the present day. Our knowledge of the preceding period is based primarily on reports from later authors, which are not always reliable. Following the period of prosperity, there was a decline in Greek mathematics, which was due to the decline of Greek culture as a whole. Although significant works in mathematics continued to appear until the 6th century AD, none of them could compare with the works of the Alexandrian period in terms of content or rigor of exposition.
Greek mathematicians brought the logical construction of mathematics, especially geometry, to a high level of perfection. It was not until the 19th century that this logical construction was raised to a higher level. The Greeks brought trigonometry (primarily spherical, the development of which was driven by the needs of astronomy) to a high level of perfection. Theoretical mechanics (particularly statics, hydrostatics, and the theory of machines) was developed using rigorous mathematical methods. The Greeks achieved significant success in solving problems that are now part of higher mathematics (integral calculus). Here, methods were created that were forgotten in later times and only re-emerged in the 17th century among Western European mathematicians.
We also find a well-developed theory of conic sections among the Greeks, which in terms of factual material is little different from the modern one.
The Greeks laid the foundations of algebraic methods; however, although they solved a number of difficult problems in this area, they did not develop a method as advanced as in the aforementioned fields.
The name of Pythagoras (6th century BC) is associated with a number of unreliable reports. In particular, the so-called "Pythagorean theorem" was undoubtedly known to the peoples of the ancient East, from whom the Greeks could have borrowed both the theorem and its proof.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. The number 100 needs to be divided twice so that the larger part from the first division is twice the smaller part from the second division, and the larger part from the second division is three times the smaller part from the first division.
|
64. Diophantus' Solution. Let the smaller part of the second division be $x$. Then the larger part of the first division will be $2 x$. The smaller part of the first division is $100-2 x$, and the larger part of the second division is $300-6 x$. Both parts of the second division should add up to 100, hence $300-5 x=$ $=100$, from which $x=40$.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
79. - Tell me, famous Pythagoras, how many students attend your school and listen to your discourses?
- In all, 一 replied the philosopher: - half study mathematics, a quarter study music, a seventh part remains in silence, and, in addition, there are three women.
|
79. We form the equation:
$$
\frac{1}{2} x+\frac{1}{4} x+\frac{1}{7} x+3=x
$$
from which $x=28$. We can solve the following problems arithmetically as well.
|
28
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. Find the number of all trees planted at five-foot intervals from each other on a rectangular plot of land, the sides of which are 120 ft. and 70 ft.
|
90. The solution of Epaphroditus. $\frac{120}{5}=24$ and $\frac{70}{5}=14$, therefore, along the base of the plot, 25 trees are planted, and along the height, 15 trees, and in total $25 \cdot 15=375$ trees. The quotients 24 and 14 represent the number of intervals, hence the number of trees in each row is one more. Generally, if the dimensions of the plot are $a$ and $b$, and the interval is $d$, then the number of trees on the plot is:
$$
N=\left(\frac{a}{d}+1\right)\left(\frac{b}{d}+1\right)
$$
|
375
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Given a right triangle with sides 9, 12, 15. Find the diameter of the circle inscribed in this triangle.
## Problems of Marcus Junius Nipsus.
From the Erfurt Codex.
|
92. Solution: $A B=A E+R ; A E=A D$,
$$
B C=F C+R ; F C=D C
$$
therefore,
$$
A B+B C=2 R+A C
$$
from which
$$
2 R=A B+B C-A C
$$
in this case
$$
2 R=9+12-15=6
$$
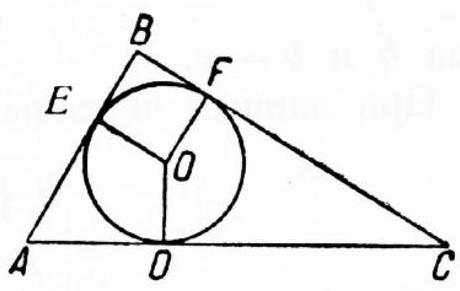
Fig. 33.
The Erfurt Codex is a manuscript of later origin (possibly from the 11th century), representing a collection of excerpts, sometimes more complete than the Arzeryan Codex: it contains a series of stereometric problems that are almost absent in ancient lists.
Marcus Junius Nipsus (lived no later than the 2nd century). Roman writer - surveyor.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
95. The sides of the triangle are $6, 8, 10$. Find its area (using Heron's formula).
20
## Junius Moderatus Columella's Problem.
From the work "De re rustica".
|
95. Solution of Niphus
\[
\Delta=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{12 \cdot 6 \cdot 4 \cdot 2}=24
\]
It would have been simpler, of course, to take half the product of the legs.
Junius Moderatus Columella (1st century AD) in his treatise "On Agriculture," when discussing land surveying, indicates 9
land measures and solutions to nine geometric problems with numerical data.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
98. In a cage, there is an unknown number of pheasants and rabbits. It is only known that the entire cage contains 35 heads and 94 feet. The task is to determine the number of pheasants and the number of rabbits.
|
98. If there were only pheasants in the cage, the number of legs would be 70, not 94. Therefore, the 24 extra legs belong to the rabbits, 2 per each. It is clear that there were 12 rabbits and, consequently, 23 pheasants.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
113. Find the number which, when increased by 5 or decreased by 11, becomes a perfect square.
## Problems of Apastamba.
From the collection "Sulva-sutra“.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
113. According to the condition, we have: $N+5=u^{2}$ and $N-11=v^{2}$, from which $16=u^{2}-v^{2}=(u+v)(u-v)$, thus, we get two combinations:
I) $\left.\begin{array}{l}u+v=8 \\ u-v=2\end{array}\right\} u=5 ; v=3$ and $N=20$
II) $\left.\begin{array}{r}u+v=16 \\ u-v=1\end{array}\right\} u=\frac{17}{2} ; \quad v=\frac{15}{2}$ and $N=67 \frac{1}{4}$.
"Sulva-sutras" or "Rules of the Cord" - collections of rules concerning the construction of altars, their shapes, sizes, and orientations.
Fig. 35. Currently, 3 such collections are known. Their authors are Baudhayana (6th or 7th century BCE), Katyayana, and Apastamba (4th or 5th century).
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
121. (Rule XXI). Determine the number of layers in a triangular heap.
## Problem of Paramadisvara.
From the commentary on the treatise of Aryabhata.
|
121. This task represents the summation of so-called triangular numbers of the form: $\frac{n(n+1)}{2}$.
Let's write the natural series: $1,2,3,4,5,6,7,8,9 \ldots$
The series of triangular numbers will be:
$$
1,3,6,10,15,21,28,36,45,55 \ldots
$$
It is clear that the sum of any two consecutive numbers always represents a perfect square. Denoting any triangular number by the symbol $T$, we will have:
$$
\begin{aligned}
& T_{n}+T_{n-1}=n^{2} \\
& T_{n-1}+T_{n-2}=(n-1)^{2} \\
& \dot{-} \dot{\bullet} \cdot \bullet \cdot \cdot ・ \\
& T_{3}+T_{2}=3^{2} \\
& T_{2}+T_{1}=2^{2}
\end{aligned}
$$
Let's denote the sum $T_{1}+T_{2}+T_{3}+\ldots+T_{n}$ by $\Sigma_{n}$. Then the addition of the previous equations will give:
$$
\begin{gathered}
T_{n}+2\left(T_{n-1}+T_{n-2}+\ldots+T_{2}\right)+T_{1}= \\
n^{2}+(n-1)^{2}+\ldots+3^{2}+2^{2}
\end{gathered}
$$
or
$$
\Sigma_{n}+\Sigma_{n}-\left(T_{1}+T_{n}\right)=S_{n}-1
$$
where $S_{n}$ is the sum of the squares of natural numbers,
$$
2 \Sigma_{n}=S_{n}-1+1+T_{n}=\frac{n(n+1)(2 n+1)}{6}+\frac{n(n+1)}{2}
$$
$\left(T_{1}=1\right)$ or
$$
\begin{gathered}
2 \Sigma_{n}=\frac{n(n+1)(2 n+1)+3 n(n+1)}{6} \\
2 \Sigma_{n}=\frac{n(n+1)(2 n+4)}{6} \\
\Sigma_{n}=\frac{n(n+1)(n+2)}{6}
\end{gathered}
$$
For example,
$$
\Sigma_{10}=\frac{10 \cdot 11 \cdot 12}{6}=220
$$
Paramadisvara, an Indian mathematician, of whom only that he commented on the work of Aryabhata is known.
|
220
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
122. Find the number which, when multiplied by 3, then divided by 5, increased by 6, after which the square root is extracted, one is subtracted, and the result is squared, will give 4.
## Problem of Sridhara.
From the treatise "The Essence of Calculation."
|
122. The method of inverse actions involves approaching the unknown by performing actions on numbers in the reverse order of those specified in the problem, and, obviously, all actions are replaced by their inverses. Sometimes this technique is called the "method of inversion."
$$
\sqrt{4}=2 ; 2+1=3 ; 3^{2}=9 ; 9-6=3 ; 3 \cdot 5=15 ; \frac{15}{3}=5
$$
calculations. Bhaskara-Acharya refers to it and even borrows problems from it. The time of his life is not precisely known, but it was certainly in the period between the 6th and 10th centuries AD.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
123. A fifth part of the swarm of bees is on the kadamba flower, one third on the silindhara flowers. The tripled difference of the last two numbers has gone to the kutaja flowers. And there is still one bee flying to and fro, attracted by the wonderful fragrance of jasmine and pandanus. Tell me, charming one, how many bees are there in all?
## Problems of Brahmagupta.
From the treatise, "The Improved System of Brahman".
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
123. We form the equation:
$$
\frac{1}{5} x+\frac{1}{3} x+3\left(\frac{1}{3} x-\frac{1}{5} x\right)+1=x
$$
from which \( x=15 \).
Brahmagupta, a famous Indian mathematician (born in 598 AD). His astronomical treatise "Brahma-sphutasiddhanta" consists of 20 books. Book XII contains arithmetic, and Book XVIII contains algebra. In the arithmetic section, several chapters are devoted to interesting geometric questions. The algebraic section primarily deals with first and second-degree equations, both determinate and indeterminate.
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
131. If a certain number is multiplied by 5, subtract its third from the product, divide the remainder by 10 and add to this sequentially $1 / 3, 1 / 2$ and $1 / 4$ of the original number, the result is 68. What is the number?
|
131. Bhaskara's Solution. If the required number were 3, then according to the condition $3 \cdot 5=15$, one third of 15 is 5. Since $15-5=10$, if we divide 10 by 10, we get one. If we add to it $\frac{1}{3}, \frac{1}{2}$ and $\frac{1}{4}$ of 3, we will have $1+1+\frac{3}{2}+\frac{3}{4}$, i.e., $\frac{17}{4}$, but it should be 68, i.e., in $68: \frac{17}{4}=$ $=16$ times more. therefore, the required number $3 \cdot 16=48$.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
133. From a bunch of pure lotus flowers, one third, one fifth, and one sixth parts were respectively offered to the gods: Shiva, Vishnu, and the Sun. One quarter went to Bhavani. The remaining 6 lotuses were given to the deeply revered teacher. Count the total number of flowers quickly.
|
133. We form the equation: $\frac{x}{3}+\frac{x}{4}+\frac{x}{5}+\frac{x}{6}+6=x$, from which $x=120$
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. The square root of half the bee swarm flew to a jasmine bush. Eight ninths of the swarm stayed at home. One bee flew after the male, worried by his buzzing in a lotus flower, where he had ended up at night, attracted by the pleasant fragrance, and cannot get out as the flower has closed. Tell me the number of bees in the swarm.
|
136. Bhaskara's Solution. Let the number of bees in the swarm be $2 x^{2}$. Then the square root of half this number is $x$, and $\frac{8}{9}$ of the entire swarm equals $\frac{16}{9} x^{2}$, therefore,
$$
\begin{aligned}
2 x^{2} & =x+\frac{16}{9} x^{2}+2 \\
2 x^{2}-9 x & =18 ; x=6 \text { and } 2 x^{2}=72
\end{aligned}
$$
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
145. Three friends had a monkey. They bought a certain number of mango fruits and hid them. At night, one of the friends wanted to indulge, went to the storeroom, and wanted to take a third of the fruits, but it turned out that one fruit was left over, and he gave it to the monkey, and ate his share. After some time, the second one came and, not suspecting that the first one had already taken his share, divided the remainder into three equal parts, and again one fruit was left over, and he gave it to the monkey and ate his share. Finally, the third one came and also divided the remainder into three equal parts, and again one fruit was left over, which he gave to the monkey, and ate his share.
The next morning, all three came to the storeroom and divided the remaining fruits equally among themselves, and again one fruit was left over, which they gave to the monkey.
Determine the smallest number of fruits that satisfies the above conditions of distribution.


## Problem from the tractate "Bava Batra".
Talmud.
|
145. This problem was proposed by an Indian professor to Delbo.
Solution: Let $x$ be the number of fruits each received in the morning. Then $3x + 1$ is what remained in the morning. The third one took $\frac{1}{2}(3x + 1)$, so he found $\frac{3}{2}(3x + 1) + 1$. The second one took $\frac{1}{2}\left[\frac{3}{2}(3x + 1) + 1\right]$, and found $\frac{3}{2}\left[\frac{3}{2}(3x + 1) + 1\right] + 1$; the first one took $\frac{3}{4}\left[\frac{3}{2}(3x + 1) + 1\right] + \frac{1}{2}$, or $\frac{27x + 19}{8} = 3x + 2 + \frac{3(x + 1)}{8}$, which must be an integer. The smallest value of $x$ that satisfies this condition is 7. Therefore, the first one took 26 fruits and gave 1 to the monkey, the second one took 17 fruits and gave 1 to the monkey. The third one took 11 fruits and gave 1 to the monkey. In the morning, each received 7 fruits, i.e., a total of 21, and one was given to the monkey. The total number of fruits: $26 + 17 + 11 + 21 + 4 = 79$.


The culture of precise knowledge among the ancient Jews developed under the influence of Babylon and Egypt.
The influence of the former was particularly evident in Jewish metrology. Initial geometric knowledge was of a narrowly practical nature, such as measuring fields, determining the capacity of vessels, etc. Arithmetic knowledge was necessary for keeping household accounts. The main monument of rabbinical writing is the "Talmud" (i.e., teaching, explanation), which was created between 300 BC and 500 AD. This is a kind of huge encyclopedia, where a number of treatises contain a lot of information on astronomy, mathematics, and metrology. A significant number of scholars, translators, and commentators in the field of exact knowledge worked at the courts of caliphs during the later periods of the flourishing of Arab rule, with many Jews becoming Arabized. The Middle Ages also produced several names. In modern times, when mathematical creativity became a common human heritage, Jewish mathematical thought usually merged into the sphere of the nationality with which the Jews were territorially connected. Astronomical and calendar research and works dedicated to the study of ancient written monuments stood apart.
|
79
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
156. What number, when added to nine, gives its own square root?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The last sentence is a note to the translator and should not be included in the translated text. Here is the final version:
156. What number, when added to nine, gives its own square root?
|
156. $x^{2}+9=6 x ; x=3$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
156. $x^{2}+9=6 x ; x=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. Determine the segments into which the base $A C$ is divided by the perpendicular dropped from the opposite vertex $B$ of triangle $A B C$, if the sides of the triangle are given: $A B=15 ; B C=13$; $A C=14$.
|
162. Let $O C=x$ (Fig. 45), $O B^{2}=169-x^{2}$;
$$
A O^{2}=(14-x)^{2}=196-28 x+x^{2}
$$
$O B^{2}=225-A O^{2}=225-196+28 x-x^{2}=29+28 x-x^{2}$, therefore, $169-x^{2}=29+28 x-x^{2} ; \quad 140=28 x ; \quad x=5$.
$A O=9 ; \quad O B=\sqrt{169-25}=12$.
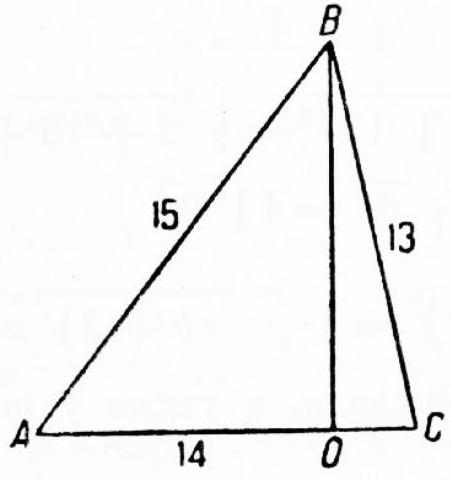
Fig. 45.
Fig. 46.
|
95
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
169. $x^{2}+10 x=39$.
169. $x^{2}+10 x=39$.
(Note: The equation is the same in both languages, so the translation is identical to the original text.)
|
169. Al-Karaji is looking for a number which, when added to $x^{2}+10 x$, would make a complete square. Such a number is 25. Then
$x^{2}+10 x+25=(x+5)^{2}=39+25=64 ; x+5=8$ and $x=3$.
He calls this method the "method of solving in the manner of Diophantus".
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
172. Find the last term and the sum of 20 terms of the progression:
$$
3,7,11,15 \ldots
$$
|
172. $a_{20}=19 \cdot 4+3=79 ; S_{20}=\frac{(3+79) \cdot 20}{2}=820$.
|
820
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
173. Find the sum of the first ten numbers in the natural number series.
|
173. $S_{10}=\frac{(1+10) \cdot 10}{2}=55$.
The above text is translated into English as follows, retaining the original text's line breaks and format:
173. $S_{10}=\frac{(1+10) \cdot 10}{2}=55$.
|
55
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. On two opposite banks of the river, there stands a palm tree on each. The height of one is 20 cubits, and the other is 30. The width of the river is 50 cubits. At the top of each palm tree, there sits a bird. Both birds see a fish in the river and simultaneously fly in a straight line to it, reaching the water surface at the same time at a point on the line connecting the roots of the palms. Determine the length of the paths flown by the birds and the point of their meeting.
|
179. Al-Karhi's Solution: Let $x$ be the distance from the meeting point to the roots of the taller palm, square it, you get $x^{2}$. Add to this 900, i.e., the square of the height of the taller palm, and set this sum equal to the square of $50-x$, i.e., $2500+x^{2}-100 x$, increased by the square of the height of the other palm, 400:
$$
x^{2}+900=2500+x^{2}-100 x+400
$$
you get $x=20$. The distance from the meeting point to the roots of the shorter palm is 30. The straight line each bird flew will be $\sqrt{1300}=10 \sqrt{13}$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
181. Find the area of a rectangle where the base is twice the height, and the area is numerically equal to the perimeter.
|
181. If the width is $x$, then the length is $2 x$. Thus, the area is $2 x^{2}$, and the perimeter is $6 x$. According to the condition, $2 x^{2}=6 x$, therefore, $x=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
192. If a number, when divided by 9, gives a remainder of 2 or 7, then the square of the number, when divided by 9, gives a remainder of 4.
|
192. Let $N=9 k+2, \quad$ then $N^{2}=81 k^{2}+18 k+4=$ $=$ multiple of 9 +4 ; let $N_{1}^{2}=9 k+7$, then $N_{1}^{2}=81 k^{2}+$ $+126 k+49=9\left(9 k^{2}+14 k+5\right)+4$.
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
203. $\frac{1}{x^{2}}+2 \frac{1}{x}=1 \frac{1}{4}$.
## Problems of Begh-Edin.
From the treatise "The Essence of the Art of Calculation".
|
203. Omar's Solution: $z=\frac{1}{x} ; \quad z^{2}+2 z=\frac{5}{4} ;$
$$
\begin{aligned}
& z^{2}+2 z+1=\frac{9}{4} ;(z+1)^{2}=\frac{9}{4} ; z+1=\frac{3}{2} ; z=\frac{1}{2} \\
& z^{2}=\frac{1}{4}, \text { therefore, } x^{2}=4 \text { and } x=2
\end{aligned}
$$
Bega Ed-Din (16th century), a Persian mathematician, author of the treatise "Kolasa-tal-Hisab" ("The Essence of the Art of Calculation"), which served as a guide for the study of mathematics in schools of Hindustan and Persia until the beginning of the 19th century.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
205. It is required to find a number which, when multiplied by itself, added to two, then doubled, added to three again, divided by 5, and finally multiplied by 10, results in 50.
|
205. $\frac{50}{10}=5 ; 5 \cdot 5=25 ; 25-3=22 ; 11-2=9 ; \sqrt{9}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
207. Zaimu is promised a reward in the form of the larger of two parts, which add up to 20, and the product of these parts is 96. How great is the reward?
|
207. The ordinary solution: Let the larger part be $x$. Then the smaller one is $20-x$. According to the condition, $x(20-x)=96$, or $x^{2}-20 x+96=0 ; x=10 \pm \sqrt{100-96}=10 \pm 2 ; x_{1}=12 ; x_{2}=8$. But Al-Baghdadi's solution is simpler: put one number as $10+x$, then the other is $10-x$. Their product is $100-x^{2}=96$, from which $x^{2}=4$ and $x=2$, therefore, $10+x=12$, $10-x=8$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
214. A dog is chasing a rabbit that is 150 feet ahead of it. It makes a leap of 9 feet every time the rabbit jumps 7 feet. How many jumps must the dog make to catch the rabbit?
## Herbert's Problem.
|
214. With each jump, the dog gains 2 feet, therefore, the entire distance of 150 feet will be covered in 75 jumps.
Herbert (died 1003), bishop of Reims, later Pope Sylvester II, author of two arithmetical treatises ("Calculations with the Abacus" and "On the Division of Numbers").
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
252. $\frac{x}{10-x}+\frac{10-x}{x}=25$.
|
252. $10 x=x^{2}+\frac{100}{27} ; x=5-\sqrt{21 \frac{8}{27}}$. But Regiomontanus also gives another solution, assuming $\frac{x}{10-x}=y$. Then $y+\frac{1}{y}=25 ; y=\frac{25}{2}-\sqrt{\frac{621}{4}}$. In both cases, Regiomontanus takes the roots with a minus sign.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
253. Find a number which, when divided by 17, 13, and 10, gives remainders of 15, 11, and 3, respectively.
From the treatise "De triangulis omnimodis libri quinque".
|
253. The problem is reduced to solving the system:
$$
17 x+15=13 y+11=10 z+3
$$
The smallest values: $x=64 ; y=84 ; z=110$.
The sought number is 1103.
This problem was proposed by Regiomontanus to the astronomer Bianchini. The latter, by trial and error, found two solutions: 1103 and 3313.
Ch. 57. Then Regiomontanus indicated that 1103 is the smallest value, and subsequent values are obtained by adding $17 \cdot 13 \cdot 10=2210$, so the second value will be $1103+$ $+2210=3313$ and so on.
|
1103
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
268. Someone has workers and money. If he gives each worker 5 (coins), he will have 30 left, but if 7, then he will be short of 30. The question is, how many workers does he have?
Problems by N. Chuquet from the treatise “Triparty...”.
|
268. If each person is given two more coins, the difference turns out to be 60 coins, therefore, there were 30 workers.
Shyukе Nicolas (died in 1500), French mathematician, author of the treatise "Le Triparty en la science des nombres" (1484), in which zero and negative exponents are used for the first time.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
269. $3 x^{2}+12=12 x$
|
269. Two equal roots $(x=2)$.
270. $x=5 \pm \sqrt{21}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
309. 26 persons together spent 88 coins, with each man spending 6, each woman 4, and each girl 2 coins. How many were men, women, and girls?
|
309. 10 solutions; from $x+y+z=26$
and
$$
6 x+4 y+2 z=88
$$
we get:
$$
2 x+y=18
$$
from which
$$
y=18-2 x
$$
therefore,
$$
2 x \leqslant 18
$$
H
$$
x \leqslant 9
$$
T. e
$$
\begin{aligned}
& x=0, \quad 1, \quad 2, \quad 3, \quad 4, \quad 5, \quad 6, \quad 7, \quad 8, \quad 9 \\
& y=18,16,14,12,10, \quad 8, \quad 6, \quad 4, \quad 2, \quad 0 \\
& z=8, \quad 9,10,11,12,13,14,15,16,17
\end{aligned}
$$
If we exclude the cases $x=0, y=0$, then 8 solutions.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
314. Divide $\sqrt[3]{216}$ by $\sqrt[4]{16}$.
|
314. Rudolf's Solution:
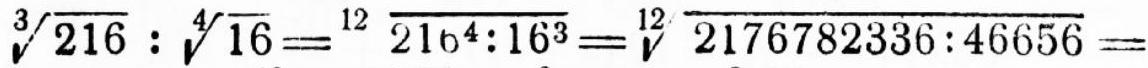
$$
\begin{aligned}
& =\sqrt[12]{531441}=\sqrt[6]{729}=\sqrt[3]{27}=3
\end{aligned}
$$
Indeed: $\quad \sqrt[3]{216}: \sqrt[4]{16}=6: 2=3$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
340. Find the positive root of the equation by construction:
$$
x^{2}+6 x=91
$$
|
340. Cardano's Solution: Let the square $F D$ (Fig. 74) be $x^{2}$, hence its side $F H=x$. $D G=D B=3$ (half the coefficient of $x$). Construct the square $A F E C$. The rectangle $A D$ equals the rectangle $D E$, i.e., equals $3 x$. The sum of the square $F D$ and the two rectangles equals $x^{2}+6 x$, which, by the condition, is 91. The small square $B C G D=9$, hence the square $A F E C=100$. Therefore, $A C=10$; but $A C=x+3$, so $x=7$. The usual method:
$x^{2}+6 x-91=0 ; x=-3 \pm \sqrt{9+91}=$
Fig. 74.
$=-3 \pm 10 ; \quad x_{1}=7 ; \quad x_{2}=-13$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
351. Show that
$$
\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}=4
$$
|
351. $\sqrt[3]{2+v \overline{-121}}=\sqrt[3]{2+11 i}=\sqrt[3]{8+12 i-6-i}=$
$$
\begin{aligned}
& =\sqrt[3]{2^{3}+3 \cdot 2^{2} i+3 \cdot 2 \cdot i^{2}+i^{3}}=\sqrt[3]{(2+i)^{3}}=2+i \\
& \sqrt[3]{2-\sqrt{-121}}=\sqrt[3]{2-11 i}=\sqrt[3]{8-12 i-6+i}= \\
& =\sqrt[3]{2^{3}-3 \cdot 2^{2} \cdot i+3 \cdot 2 i^{2}-i^{3}}=\sqrt[3]{(2-i)^{3}}=2-i
\end{aligned}
$$
therefore,
$$
\begin{aligned}
& 13 \overline{2+11 i}+\sqrt[3]{2-11 i}=2+i+2-i=4 \\
& x^{3}-4 x^{2}+4 x^{2}-16 x+x-4=0 \\
& x^{2}(x-4)+4 x(x-4)+(x-4)=0 \\
& (x-4)\left(x^{2}+4 x+1\right)=0 \\
& x_{1}=4 ; x_{2,3}=-2 \pm \sqrt{3}
\end{aligned}
$$
156
## 17th century.
Thomas Harriot (1560-1621), English algebraist, author of the treatise "Artis analyticae Praxis," published posthumously in 1631. He was familiar with the relationships between the coefficients and roots of equations.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
382. What is the smallest number of weights and of what weight can be used to weigh any whole number of pounds from 1 to 40 on a balance scale, given that during weighing, weights can be placed on both pans of the scale.
|
382. The solution to the problem is based on the properties of the ternary system of numeration, which can express any numbers; since the number $40=27+9+3+1=3^{3}+3^{2}+3+1$, it is possible with four weights of $27, 9, 3$ and 1 pound, as is easy to verify by checking, to weigh any load up to forty pounds. It is sufficient to take any load and express it in the ternary system: for example,
$$
23=27-(3+1) ; 31=27+3+1
$$
and so on.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
393. Several people had dinner together and had to pay 175 shillings for the bill. It turned out that two of them had no money, so each of the rest had to pay 10 shillings more than their share. How many people had dinner?
|
393. Let $x$ be the number of people who had lunch. It is easy to form the equation
$$
\frac{175}{x-2}-\frac{175}{x}=10
$$
from which
$$
x^{2}-2 x=35
$$
Maclaurin would solve it as follows:
$$
\begin{gathered}
x^{2}-2 x+1=36 \\
(x-1)^{2}=36 ; x-1= \pm 6 ; x_{1}=7 \text { or } x_{2}=-5
\end{gathered}
$$
The second root is not valid.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
409. Several merchants contributed to a common fund 100 times as many rubles as there were merchants. They sent a trusted person to Venice, who received a number of rubles from each hundred rubles, twice the number of merchants. The question is: how many merchants were there, if the trusted person received 2662 rubles?
|
409. Let the number of merchants be $x$. Each contributed $100 x$, and the total capital is $100 x^{2}$. The profit on the capital is $2 x^{3}=2662$, from which $x^{3}=1331$, hence $x=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
426. A lazy worker was told that he would receive 24 su for each day he worked, with the condition of deducting 6 su for each day he skipped. After 30 days, it turned out that he did not receive anything. The question is: how many days did he work?
|
426. We form the equation $24 x=6(30-x)$, from which $x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
430. A man, on his death, left a will according to which the eldest son receives 100 francs and one-tenth of the remainder, the second son - 200 francs and one-tenth of the new remainder, the third - 300 francs and one-tenth of the new remainder, and so on until the last. In this way, the shares of all the sons should be equal. Find the size of the inheritance left, the number of sons, and the share of each.
## Francker's Problems.
|
430. Let the entire inheritance be $x$ francs. The first one, according to the condition, receives
$100+\frac{1}{10}(x-100)=\frac{1}{10} x+9$.
The remainder will be $\frac{9}{10} x-90$. The second one receives
$$
200+\frac{1}{10}\left(\frac{9}{10} x-290\right)
$$
But the shares of the first and second are equal, therefore,
$$
\frac{1}{10} x+90=171+\frac{9}{100} x
$$
from which $x=8100$. Each share in this case is 900 francs, and the number of sons is 9.
Franeker, a French mathematician, professor at the "Faculté des sciences" in Paris, author of "A Complete Course of Pure Mathematics," which was widely distributed and translated into Russian.
|
8100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
433. Several people have to pay 800 francs for the production of a lawsuit. But three of them have no money, so the rest have to add 60 francs to their share. How many participants are there in the payment of legal costs?
|
433. We form the equation $\frac{80}{x+3}=\frac{800}{x}-60$, where $x-$ is the number of participants in the payment. $x^{2}+3 x=40$, from which $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
436. What is the cost of $15 \frac{13}{16}$ ells of material, if one ell costs 42 livres 17 sous 11 deniers?
Note. Livre - an ancient French coin; one livre $=20$ sous; 1 sou $=12$ deniers.
|
436. Answer: 678 livres 5 sous $9 \frac{11}{16}$ deniers.
|
678
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
438. How many myriameters will a traveler cover in 17 days, spending 10 hours a day on this, if in 29 days he has already traveled 112 myriameters, spending 7 hours each day on the road?
|
438. The desired number of miriameters is equal to $\frac{112 \cdot 17 \cdot 10}{29 \cdot 7}$.
Damn. 97.
|
97
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
448. A regiment of cuirassiers buys a certain number of horses for 11250 francs. A regiment of dragoons buys fifteen more horses for 16000 francs. Each dragoon horse is 50 francs cheaper than a cuirassier horse. Determine the number of horses of each type and their cost.
|
448. If there are $x$ cuirassier horses, then there are $x+15$ dragoon horses. The cost of the former is $\frac{11250}{x}$, and the cost of the latter is $\frac{16000}{15+x}$. According to the condition,
$$
\frac{11250}{x}=\frac{16000}{x+15}+50
$$
The authors solve it as follows: after simplification,
$$
x^{2}+110 x=335
$$
they add $55^{2}$ to both sides:
$$
(x+55)^{2}=6400
$$
from which $x=25$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
464. A number consists of three digits; the sum of these digits is 11; the digit in the units place is twice the digit in the hundreds place. If you add 297 to the desired number, you get a number written with the same digits as the desired number, but in reverse order. What number has these properties?
|
464. The question boils down to solving the system:
$$
\left\{\begin{array}{l}
x+y+z=11 \\
z=2 x \\
100 x+10 y+z+297=100 z+10 y+x
\end{array}\right.
$$
$x=3 ; y=2 ; z=6$. The desired number is 326.
|
326
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
471. Someone has twelve pints of wine and wants to give away half of it, but he does not have a six-pint container. He has two containers, one holds 8 pints and the other 5 pints; the question is: how can he pour six pints into the eight-pint container?
## Lebesgue's Problem.
|
471. Regarding this problem, Arago tells that it decided the fate of Poisson, as, by becoming interested in it, he thereby discovered his vocation and devoted his whole life to mathematics. We have already seen a similar problem (336). This one also has 2 solutions:
| 12 | 8 | 5 |
| ---: | ---: | ---: |
| 12 | 0 | 0 |
| 4 | 8 | 0 |
| 4 | 3 | 5 |
| 9 | 3 | 0 |
| 9 | 0 | 3 |
| 1 | 8 | 3 |
| 1 | 6 | 5 |
| 6 | 6 | 0 |
| 12 | 8 | 5 |
| ---: | ---: | ---: |
| 12 | 0 | 0 |
| 7 | 0 | 5 |
| 0 | 7 | 5 |
| 0 | 8 | 4 |
| 8 | 0 | 4 |
| 8 | 4 | 0 |
| 3 | 4 | 5 |
| 3 | 8 | 1 |
| 11 | 0 | 1 |
| 11 | 1 | 0 |
| 6 | 1 | 5 |
| 6 | 6 | 0 |
For more theoretical details, one can refer to the book by W. Ahrens "Mathematische Spiele".
Lebesgue, V. A., a French mathematician, professor at the Faculty of Sciences in Bordeaux. This problem is taken from his "Exercices d'analyse numérique," dedicated to indeterminate analysis and number theory (1859).
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
472. Solve the system in integers:
$$
\begin{aligned}
& 2 x+3 y+7 z=131 \\
& 2 x+3 y+8 z=140
\end{aligned}
$$
60
## Schläfli Problems.
|
472. Immediately find $z=9$ and $2 x+3 y=68$, from which in the usual way: $y=0,2,4, \ldots, 22$. In total, there are 12 solutions.
Schlömilch, Oscar (1823--1901), a well-known German mathematician, whose name is associated with the expression for the remainder term of a Taylor series. Author of the very useful course “Kompendium d. höheren Mathematik” (2 volumes).
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
475. Prove that
$$
\sqrt[3]{20+1+\sqrt{2}}+\sqrt[3]{20-14 \sqrt{ } 2}=4
$$
|
475. Cubing:
$$
\begin{gathered}
20+14 \sqrt{2}+20-14 \sqrt{2}+ \\
+3 \sqrt[3]{20+14 \sqrt{2}} \sqrt[3]{20-14 \sqrt{2}} \cdot 4=64 \\
40+12 \sqrt[3]{40-392}=40+24
\end{gathered}
$$
Another method:
$$
\begin{gathered}
\sqrt[3]{20+14 \sqrt{2}}=\sqrt[3]{8+12+12 \sqrt{2}+2 \sqrt{2}}= \\
=\sqrt[3]{2^{3}+3 \cdot 2} \cdot(\sqrt{2})^{2}+3 \cdot 2^{2} \cdot \sqrt{2}+(\sqrt{2})^{3}=2+\sqrt{2}
\end{gathered}
$$
Similarly:
$$
\sqrt[3]{20-14 \sqrt{2}}=2-\sqrt{2}
$$
The sum of (1) and (2) $=4$.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
490. Five bandits took a wallet filled with ducats from a passerby. The strongest of them took 81 ducats, and each of the other four took a different amount. Due to the unequal division, a dispute arose, and the ataman who arrived at that time ordered the one who took the most to double the number of ducats each of the others had, and then the one who took the second largest amount to do the same, followed by the one who took the third, fourth, and fifth largest amounts. As a result, each of the five bandits ended up with the same number of ducats. Determine how many ducats were in the wallet and how many each took initially.
## Problems from "Traitè de Géometrie" by E. Rouché et Ch. de-Comberousse.
|
490. Instruction. At the end of the section, each has $\frac{1}{5}$ of the total, so before doubling, four have $\frac{1}{10}$ each, and the fifth has $\frac{6}{10}$; before the second doubling, the first three have $\frac{1}{20}$ each, the fourth has $\frac{11}{20}$, and the fifth has $\frac{6}{20}$; before the third doubling, the first two have $\frac{1}{40}$ each, the third has $\frac{21}{40}$, the fourth has $\frac{11}{40}$, and the fifth has $\frac{6}{40}$; before the fourth doubling, the first has $\frac{1}{80}$, the second has $\frac{41}{80}$, the third has $\frac{21}{80}$, the fourth has $\frac{11}{80}$, and the fifth has $\frac{6}{80}$; before the fifth doubling, the first has $\frac{81}{160}$, the second has $\frac{41}{160}$, the third has $\frac{21}{160}$, the fourth has $\frac{11}{16 \text { i) }}$, and the fifth has $\frac{6}{160}$. But since the first has 81 ducats, the total was 160 ducats.
Rouché, E. and Comberousse, Ch. - French mathematicians who collaborated on the preparation of courses and textbooks, which enjoy well-deserved fame.
|
160
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.8. Let $n>1$ be a natural number. Find all positive solutions of the equation $x^{n}-n x+n-1=0$.
## 2.3. Equations with Radicals
In problems $2.9-2.15$, it is assumed that the values of square roots are non-negative. We are interested only in the real roots of the equations.
|
2.8. A n s w e r: $x=1$. It is clear that
$$
x^{n}-n x+n-1=\left(1+x+\ldots+x^{n-1}-n\right)(x-1)
$$
If $x>1$, then $1+x+\ldots+x^{n-1}-n>0$, and if $0<x<1$, then $1+x+\ldots$ $\cdots+x^{n-1}-n<0$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.9. Solve the equation $\sqrt{2 x-6}+\sqrt{x+4}=5$.
### 2.10. Solve the equation
$$
\sqrt[m]{(1+x)^{2}}-\sqrt[m]{(1-x)^{2}}=\sqrt[m]{1-x^{2}}
$$
|
2.9. Let $y=\sqrt{x+4}$. Then $x=y^{2}-4$, so $2 x-6=2 y^{2}-$ -14. Therefore, we get the equation $\sqrt{2 y^{2}-14}+y=5$. Move $y$ to the right side and square both sides. As a result, we get the equation $y^{2}+10 y-39=0$. Its roots are 3 and -13. But $y \geqslant 0$, so only the root $y=3$ remains, which corresponds to $x=5$. It is easy to verify that $x=5$ is indeed a root of the given equation.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.11. Solve the equation
$$
3 \sqrt{x^{2}-9}+4 \sqrt{x^{2}-16}+5 \sqrt{x^{2}-25}=\frac{120}{x}
$$
|
2.11. The expression on the left side increases as $x$ increases, while the expression on the right side decreases. Therefore, the equation has no more than one solution. It is easy to verify that $x=5$ is a solution.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.12. Solve the equation $x+\sqrt{3+\sqrt{x}}=3$.
|
2.12. If $x>1$, then $x+\sqrt{3+\sqrt{x}}>3$, and if $x<1$, then $x+$ $+\sqrt{3+\sqrt{x}}<3$. Only the root $x=1$ remains.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.13. $\left\{\begin{array}{l}\left(x_{3}+x_{4}+x_{5}\right)^{5}=3 x_{1}, \\ \left(x_{4}+x_{5}+x_{1}\right)^{5}=3 x_{2}, \\ \left(x_{5}+x_{1}+x_{2}\right)^{5}=3 x_{3}, \\ \left(x_{1}+x_{2}+x_{3}\right)^{5}=3 x_{4}, \\ \left(x_{2}+x_{3}+x_{4}\right)^{5}=3 x_{5} .\end{array}\right.$
## 3.3. Positive solutions
|
3.13. After cyclic renumbering of the unknowns, we can assume that $x_{1} \geqslant x_{i}(i=2,3,4,5)$. The function $f(x)=x^{5}$ is monotonically increasing, so $3 x_{2}=\left(x_{4}+x_{5}+x_{1}\right)^{5} \geqslant\left(x_{3}+x_{4}+x_{5}\right)^{5}=3 x_{1}$. Therefore, $x_{1}=x_{2}$ and $x_{3}=x_{1}$. Moreover, $3 x_{4}=\left(x_{1}+x_{2}+x_{3}\right)^{5} \geqslant$ $\geqslant\left(x_{5}+x_{1}+x_{2}\right)^{5}=3 x_{3}$. Therefore, $x_{4}=x_{3}$ and $x_{5}=x_{3}$.
We have obtained that $x_{1}=x_{2}=x_{3}=x_{4}=x_{5}=x$. This number $x$ must satisfy the equation $(3 x)^{5}=3 x$. We get three solutions: $x=0$ or $\pm 1 / 3$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.35. How many zeros does the product of all integers from 1 to 100 inclusive end with?
|
4.35. Answer: 24. Among the numbers from 1 to 100, there are 20 numbers divisible by 5, and among the numbers divisible by 5, there are 4 numbers divisible by 25 (there are no numbers divisible by 125 among the given numbers). Therefore, the considered product is divisible by $5^{24}$ and not divisible by $5^{25}$. It is also clear that it is divisible by $2^{24}$.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.43. Find the smallest natural number that:
a) When divided by 5 gives a remainder of 4, when divided by 6 gives a remainder of 5, and when divided by 7 gives a remainder of 6.
b) When divided by 5 gives a remainder of 4, when divided by 6 gives a remainder of 5, and when divided by 8 gives a remainder of 7.
|
4.43. a) Answer: 209. Let $n$ be the desired number. Then $n+1$ is divisible by $5 \cdot 6 \cdot 7=210$. Therefore, $n=209$.
b) Answer: 119. Let $n$ be the desired number. Then $n+1$ is divisible by $\operatorname{LCM}(5,6,8)=120$. Therefore, $n=119$.
|
119
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.46. Find a four-digit number that, when divided by 131, gives a remainder of 112, and when divided by 132, gives a remainder of 98.
|
4.46. Answer: 1946. Let $N$ be the desired number. By the condition, $N=131 k+112=132 l+98$, where $k$ and $l$ are natural numbers. Moreover, $N<10000$, so $l=\frac{N-98}{132}<\frac{10000-98}{132} \leqslant 75$. Further, $131 k+112=132 l+98$, therefore $131(k-l)=l-14$. Consequently, if $k \neq l$, then $|l-14| \geqslant 131$. But $l \leqslant 75$, so $k=l$ and $l-14=0$. Thus, $N=131 \cdot 14+112=132 \cdot 14+98=1946$.
|
1946
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.