problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
5. In Ali-Baba's cave, there is a lot of gold and diamonds. A full bag of gold weighs 200 kg, a full bag of diamonds 40 kg.
75 What is better?
Ali-Baba can carry 100 kg at a time. One kilogram of gold is worth 20 dinars, one kilogram of diamonds is worth 60 dinars. How much money can he get for the gold and diamonds he carries in one bag (in one trip)?
|
5. First, note that 5 kg of gold has the same volume as 1 kg of diamonds, but is more expensive. We will prove that: 1. Ali-Baba can get 3000 dinars for the treasures. Indeed, the bag can hold 40 kg of diamonds. If we replace 15 kg of diamonds with 75 kg of gold, the volume of the bag will remain the same, and its value will be 3000 dinars. 2. Now we will prove that 3000 dinars is the maximum amount that can be obtained for the treasures. If we remove some diamonds from the bag containing 25 kg of diamonds and 75 kg of gold, they can be replaced with the same amount of gold (to avoid exceeding the weight limit), which will reduce the total value, as diamonds are more expensive. If we remove some gold, the total value will also decrease, as the weight of the diamonds taken in place of it will be five times less (otherwise, there will be an excess in volume!). For example, if we take $5 x$ kg of gold and replace it with $x$ kg of diamonds, the value of the treasures will decrease by $40 x$ dinars. Answer: 3000 dinars.
|
3000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Satisfied Pikes. 40 pikes were released into the pond. A pike is satisfied if it has eaten three other pikes (satisfied or hungry). What is the maximum number of pikes that can be satisfied?
|
9. We will feed the pikes in three stages. Initially, we will feed 9 pikes, after which there will be 9 full and 4 hungry pikes left. Then, with the nine full pikes, we will feed three hungry pikes, and with three "newly" full pikes, we will feed the last hungry pike. In total, 13 pikes have been fed. Note that as each new full pike appears,
How best? 78
the total number decreases by 3, so we cannot feed more than 13 pikes.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From Alcuin's problems. How many jumps will it take for the hound to catch up with the hare if initially they are separated by a distance of 150 feet, the hare moves away from the dog by 7 feet with each jump, and the dog runs faster than the hare and gets 9 feet closer with each jump?
|
1. For each jump, the greyhound gets 2 feet closer to the hare. Therefore, she will catch up to it in 75 jumps.
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is average speed? A car travels from point $A$ to point $B$ at a speed of 40 km/h, and returns at a speed of 60 km/h. What is the average speed of the car?
|
2. If the distance from $A$ to $B$ is $n$, then the average speed on the path $2 A B$ is $V_{\text {avg }}=2 n:\left(\frac{n}{40}+\frac{n}{60}\right)=\frac{240 n}{5 n}=48 \mathrm{km} /$ h.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. From Nizhny Novgorod to Astrakhan, a steamboat takes 5 days, and on the return trip - 7 days. How long will it take for rafts to float from Nizhny Novgorod to Astrakhan?
|
3. When the steamboat goes from Nizhny Novgorod to Astrakhan (downstream), it covers $\frac{1}{5}$ of the distance in a day, and when it goes back - $\frac{1}{7}$ of the distance. Therefore, $\frac{1}{5}-\frac{1}{7}=\frac{2}{35}$ - two current speeds. From this, $\frac{1}{35}$ of the distance per day is the speed of the current. Consequently, rafts will take 35 days to float from Nizhny to Astrakhan.
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Two pedestrians are walking towards each other along a straight road at a speed of 5 km/h. The initial distance between them is 10 kilometers. A fly, which flies at a speed of $14 \mathrm{km} / \mathrm{h}$, takes off from the first pedestrian, flies straight to the second, lands on him, and without losing a second, flies back to the first pedestrian, then again to the second, and so on. What distance will the fly have flown by the time the pedestrians meet?
|
6. If the pedestrians walk at a speed of $5 \mathrm{km} / \mathrm{h}$, they will meet in one hour. In this time, the fly will fly $14 \times 1=14$ km.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Train and Pole. A train 18 m long passes by a pole in 9 seconds. How much time will it need to pass a bridge 36 m long?
|
7. Draw a picture! The lead car will pass the bridge in 18 seconds, and the last car will still be traveling on the bridge for another 9 seconds. Answer: 27 seconds.
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Task by L. Carroll. Couriers from places $A$ and $B$ move towards each other uniformly, but at different speeds. After meeting, one needed another 16 hours, and the other needed another 9 hours to reach their destination. How much time does it take for each to travel the entire distance from $A$ to $B$?
|
8. Let $t$ be the time it took for the couriers to reach the meeting point, and $v_1$ and $v_2$ be the speeds of the couriers. Then $\left(v_{1}+v_{2}\right) t=v_{1}(16+t)=v_{2}(9+t) ; 16 v_{1}=v_{2} t$ and $v_{1} t=9 v_{2} ; \frac{16 v_{1}}{v_{1} t}=\frac{v_{2} t}{9 v_{2}}$ or $\frac{16}{t}=\frac{t}{9}$ and $t^{2}=16 \cdot 9$, from which $t=4 \cdot 3=12$ hours. Therefore, the first traveled to the destination for 28 hours, and the second for 21 hours.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Draw a diagram! Two ferries leave simultaneously from opposite banks of a river and cross it perpendicular to the banks. The speeds of the ferries are constant. The ferries meet each other 720 meters from the nearest bank. Upon reaching the bank, they immediately head back. On the return trip, they meet 400 meters from the other bank. What is the width of the river?
|
10. The total distance they traveled by the time of their first meeting (720 m from one of the banks) is equal to the width of the river. When they meet for the second time, the total distance is three times the width of the river, which required three times the time. By the time of the first meeting, one of the ferries had traveled 720 m, and by the time of the second meeting - 2160 m (three times the distance). But this distance exceeds the width of the river by 400 m. Therefore, the width of the river is 1760 m.
|
1760
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. A Trip for Milk. Anton went to a dairy store. He had no money, but he had empty bottles - six one-liter bottles (worth 20 kopecks each) and six half-liter bottles (worth 15 kopecks each). In the store, there was milk sold by the liter for 22 kopecks. What is the maximum amount of milk he could bring home? He had no other containers besides the empty bottles.
|
11. By returning six half-liter bottles and one liter bottle, Anton will receive 1 ruble 10 kopecks, which will be the cost of 5 liters of milk. The 5 liters of milk he buys can be carried home in the remaining liter bottles. Let's ensure that he won't be able to carry more than 5 liters. If he returns not one liter bottle, but more, then to gather the cost of at least 5 liters of milk, he will need to return at least 5 more half-liter bottles, and the capacity of the remaining bottles will not exceed 4.5 liters (this is verified by enumeration).
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. How many parts should a worker produce to exceed the plan by 40 parts by no less than $47 \%$?
|
12. Let's pay attention to the fact that $1 \%$ of the plan for 40 parts is 0.4 parts. Next, $47 \% - 18.8$ parts. But you can't make 0.8 of a part, so the worker must make no less than 59 parts.
|
59
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Balls. In a box, there are 100 black and 100 white balls. What is the smallest number of balls that need to be taken out, without looking into the box, to ensure that among them there are 2 balls of the same color? To ensure there were 2 white balls?
|
2. Out of three balls, there will definitely be 2 of the same color. Therefore, three balls are sufficient. Note that two balls are not enough, as they can be of different colors. It may happen that we initially draw 100 black balls, and only then - 2 white ones. In total: 102 balls.
|
102
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. A three-digit number is thought of, which with any of the numbers 543, 142, and 562, matches one digit in the same place, while the other two do not match. What is the number thought of?
|
11. If the first digit of the desired number is 5, then either the second digit is 4 or the third is 2 (since a match with the second number is required). Both cases lead to a contradiction: a match with either the first or the third number will be in two digits, so the first digit cannot be 5. Reasoning similarly, we can see that the second digit of the desired number is not 4, and the third is not 2. The only remaining possibility is that the desired number is 163.
87 The Pigeonhole Principle
|
163
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Given a 1998-digit number, every two adjacent digits of which form a two-digit number divisible by 17 or 23. The last digit of the number is 1. What is the first?
|
12. Let's start recording this number from the end. At some point, we will notice that the number has the form ...92346...9234692346851. Further, we see that the digits 92346 are repeating, so we subtract from 1998 the number of digits that do not belong to this cycle - 3. We divide the resulting number by 5 (the number of digits in the cycle). This number will divide evenly. Therefore, the first digit is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. The warehouse has nails in boxes weighing $24, 23, 17$ and 16 kg. Can the warehouse keeper issue 100 kg of nails from the warehouse without opening the boxes?
|
13. For example: 4 boxes - at 17 kg each and 2 boxes - at 16 kg each.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. Find the sum: $1+2+3+\ldots+1999$.
|
15. Let $S=1+2+3+\ldots+1999$. Then: $S=1999+1998+\ldots+3+2+1$ and $2 S=(1+1999)+(2+1998)+\ldots+(1999+1)=2000 \cdot 1999$. Therefore: $S=1000 \cdot 1999$. Answer: 1999000.
|
1999000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. Find the sum: $1+3+5+\ldots+1999$.
|
16. Let $S=1+3+5+\ldots+1999$. Rewrite it as: $S=1999+1997+\ldots+1$. Then $2 S=2000 \cdot 1000 . S=1000000$.
|
1000000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. Find the number that when divided by 2 gives a remainder of 1, when divided by 3 gives a remainder of 2, when divided by 4 gives a remainder of 3, and when divided by 5 gives a remainder of 4.
|
25. A number greater than the desired one by 1 will be divisible by $2,3,4,5$, that is, by 60. The smallest suitable number is 59.
|
59
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. For a three-digit number $x$, it is known that if you subtract 7 from it, the result will be divisible by 7, if you subtract 8, the result will be divisible by 8, and if you subtract 9, the result will be divisible by 9. What is this number?
|
26. The desired number is divisible by 7, 8, and 9. Therefore, this number is 504. There are no other such three-digit numbers.
|
504
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. What digit does the number $3^{100}$ end with?
|
30. The number $3^{100}=81^{25}$, and therefore, ends in 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. What is the remainder when the number $2^{99}$ is divided by 7?
95 More problems!
|
31. Note that $2^{99}=8^{33}=(7+1)^{33}=(7+1) \ldots(7+1)$. Expand the brackets. The resulting terms will be divisible by 7, except for 1. Thus, $2^{99}$ can be written in the form: $7 x$ +1 . Answer: 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. How many diagonals does a thirty-four-sided polygon have?
|
35. Each vertex of the polygon is connected by diagonals to all other vertices, except for two, which it is connected to by a side. Thus, each vertex of the thirty-four-sided polygon is connected by diagonals to 31 vertices. Note that in this counting system, each diagonal is counted twice. In total: 527 diagonals.
|
527
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. In two boxes, there are 70 coins. It is known that in the first box, $\frac{5}{9}$ of the total number of coins are gold, and the rest are silver, in the second box, $\frac{7}{17}$ of the number of coins are silver, and the rest are gold. How many coins are in each box
|
37.Let $9 x$ be the number of coins in the first box, and $17 y$ be the number in the second, then $9 x + 17 y = 70$, where $x$ and $y$ are natural numbers, and $1 \leq y \leq 4$. By enumeration, we find that $y=2$, and $x=4$. Answer: in the first -36 coins, in the second -34.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. Calculate: $2379 \cdot 23782378-2378 \cdot 23792379$.
|
39. Let $a=2378$, then the desired expression is: $(a+1)(10000 a+a)-a(10000(a+1)+(a+1))=$ $=(a+1) \cdot 10001 a-a \cdot 10001 \cdot(a+1)=0$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41.On the farmyard, geese and piglets were wandering around. A boy counted the number of heads, there were 30, then he counted the total number of legs, there were 84. Can you find out how many geese and how many piglets were on the farmyard?
|
41.If only geese were wandering around the farmyard, there would be 60 legs in total, the "extra" legs, which number 24, belong to the piglets - two for each. Therefore, there were 12 piglets, and 18 geese.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42.A brick weighs 2 kg and half a brick. How much does the brick weigh?
|
42.It follows from the condition that half a brick weighs 2 kg. Therefore, a whole brick weighs 4 kg.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. A cup and a saucer cost 2500 rubles, while 4 cups and 3 saucers cost 8870 rubles. Find the price of a cup and the price of a saucer.
|
43.4 cups and 4 saucers cost 10000 rubles, while 4 cups and 3 saucers cost 8870 rubles, therefore, the price of one saucer: $10000-8870=1130$ rubles, the price of one cup: $2500-1130=1370$ rubles.
|
1370
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47. 6 carps are heavier than 10 perches, but lighter than 5 pikes; 10 carps are heavier than 8 pikes. What is heavier: 2 carps or 3 perches?
|
47. Since 6 carp are heavier than 10 perch, it is clear that 6 carp are even heavier than 9 perch. Therefore, 2 carp are heavier than 3 perch. This means that two of the three conditions in the problem are redundant.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
50.What is the 1997th digit in the decimal expansion of the fraction $\frac{1}{7}=0.142857 \ldots ?$
|
50.If we divide 1 by 7 using long division, we get that $\frac{1}{7}=0.(142857)$. The remainder of 1997 divided by 6 is 5, Therefore, the digit at the 1997th place is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. Little One eats a jar of jam in six minutes, while Karlson is twice as fast. How long will it take them to eat the jam together
|
51. The question of the problem can also be formulated as follows: "How long would it take for three Little Ones to eat the jam?" (According to the condition of the problem, Carlsson can be equated to two Little Ones). It is clear that three Little Ones would finish the jam three times faster than one. Answer: in 2 minutes.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. 180 g of gold with a fineness of 920 was alloyed with 100 g of gold with a fineness of 752. What is the fineness of the resulting alloy?
|
56. Assay of an alloy: $p=\frac{a}{b} \cdot 1000$, where $a$ is the weight of gold in the alloy, and $b$ is the weight of the alloy. That is: $p=\frac{100 \cdot 0.752 + 180 \cdot 0.920}{280} \cdot 1000=\frac{100 \cdot 752 + 180 \cdot 920}{280}=860$.
|
860
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60.Yura left the house for school 5 minutes later than Lena, but walked at twice her speed. How long after leaving will Yura catch up to Lena?
|
60.Let Lena walk $s$ km in 5 minutes. Then in the next 5 minutes, Yura will walk $2 s$ km, and Lena will walk another $s$ km, that is, a total of $2 s$ km. Therefore, in 5 minutes, Yura will catch up with Lena.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
61.If a cyclist rides at a speed of 10 km/h, he will be 1 hour late. If he rides at a speed of 15 km/h, he will arrive 1 hour early. At what speed should he ride to arrive on time?
|
61.If there were two cyclists, with the first one's speed being $10 \mathrm{km} / \mathrm{h}$ and the second one's speed being $15 \mathrm{km} / \mathrm{h}$. Then, according to the problem, if the first cyclist started 2 hours earlier than the second, they would arrive at the destination simultaneously. In this case, in 2 hours, the first cyclist would cover 20 km, and the second cyclist would be able to catch up in 4 hours - already at the final destination. Therefore, the entire distance is 60 km. The question of the problem can be rephrased as: "At what speed should a cyclist travel to cover the entire distance in 5 hours?". Answer: 12 km/h.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64.A motorboat travels 90 km downstream in the same time it takes to travel 70 km upstream. What distance can a raft drift in the same time?
|
64.Let in $t$ hours the motorboat covers 90 km downstream and 70 km upstream. Then the speed of the motorboat downstream is $\frac{90}{t}$ km/hour, and the speed upstream is $\frac{70}{t}$ km/hour. From this, the doubled speed of the current will be $\frac{90}{t}-\frac{70}{t}=\frac{20}{t}$ km/hour. The speed of the current (and therefore the rafts) will be $\frac{10}{t}$ km/hour, and in $t$ hours they will cover 10 km.
## 107 More problems!
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. Someone has 12 pints of wine and wants to pour out half, but he does not have a 6-pint container. However, he has two containers with capacities of 5 and 8 pints. How can he measure exactly 6 pints of wine?
|
69. The solution is visible from the table:
| steps: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 12 l | 12 | 4 | 4 | 9 | 9 | 1 | 1 | 6 |
| 8 l | 0 | 8 | 3 | 3 | 0 | 8 | 6 | 6 |
| 5 l | 0 | 0 | 5 | 0 | 3 | 3 | 5 | 0 |
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. A biologist discovered an amazing variety of amoebas. Each of them divided into two every minute. The biologist puts an amoeba in a test tube, and exactly an hour later, the test tube is filled with amoebas. How much time would it take for the entire test tube to be filled with amoebas if, instead of one, two amoebas were placed in it at the beginning?
|
71. At the beginning of the experiment, there is one amoeba in the test tube, after one minute there are already two, so 2 amoebas will fill the test tube in 59 minutes.
|
59
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
75. When Vanya was asked how old he was, he thought for a moment and said: “I am three times younger than Dad, but three times older than Seryozha.” At this point, little Seryozha ran up and reported that Dad is 40 years older than him. How old is Vanya?
|
75. Dad is 3 times older than Vanya, who, in turn, is 3 times older than Seryozha, so Dad is 9 times older than Seryozha. Therefore, Dad is 8 times older than Seryozha, which is 40 years. Hence, Seryozha's age is 5 years. Vanya is three times older than Seryozha, so he is 15 years old.
109 Such problems!
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
76. In the box, there are 100 white, 100 red, 100 blue, and 100 black balls. What is the smallest number of balls that need to be pulled out, without looking into the box, to ensure that among them there are at least 3 balls of the same color?
|
76. Answer: 9 balls. If we randomly draw 8 balls, there might not be three balls of the same color (2 white + 2 red + 2 blue + 2 black). If we add one more ball, then there will definitely be 3 balls of the same color.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
78. How many circles of radius 1 are needed to cover a square with a side length of $2$?
|
78. A circle of radius 1 can only cover one vertex of a $2 \times 2$ square, so at least four circles are required. However, a circle of unit radius can completely cover a $1 \times 1$ square, so four circles are sufficient. Answer: 4 circles.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. In the box, there are pencils: 7 red and 5 blue. In the dark, pencils are taken. How many pencils need to be taken to ensure that there are at least two red and at least three blue among them?
|
81. In order to definitely take no less than two red pencils, you need to take no less than 7 pencils, and to definitely take no less than 3 blue ones, you need to take no less than 10 pencils. Therefore, to definitely take no less than two red and no less than 3 blue, you need to take no less than 10 pencils.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. The distance between points $A B=30, B C=80, C D=236$, $D E=86, E A=40$. What is the distance $E C ?$
|
86. Since $D E+E A+A B+B C=D C$, the points $E, A$ and $B$ lie on the segment $D C$ in the given order. Therefore, $E C=150$.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11. Find the maximum value of the function $y=3 x+4 \sqrt{1-x^{2}}$
$$
|
\text { S o l u t i o n. }
$$
First, let's find the domain of the given function: $D(f)=$ $=\left\{x \mid 1-x^{2} \geqslant 0\right\}=\{x \mid-1 \leqslant x \leqslant 1\} ; \quad E(f)=\{y \mid \quad$ the equation $y=3 x+4 \sqrt{1-x^{2}}$ has a solution on $\left.[-1 ; 1]\right\}=\{y \mid$ the equation $y-3 x=4 \sqrt{1-x^{2}}$ has a solution on $\left.[-1 ; 1]\right\}=\{y \mid$ the equation $25 x^{2}-6 x y+\left(y^{2}-16\right)=0, \quad$ where $y \geqslant 3 x$, has a solution on $[-1 ; 1]\}=$
$$
\begin{gathered}
=\left\{y \mid\left(y \geqslant 3 x \cap y^{2}-25 \leqslant 0\right) \cap-1 \leqslant x \leqslant 1\right\}= \\
=\{y \mid(y \geqslant 3 x \cap-5 \leqslant y \leqslant 5) \cap-1 \leqslant x \leqslant 1\}= \\
=\{y \mid-3 \leqslant y \leqslant 5\}
\end{gathered}
$$
16
Therefore, $\quad y_{\text {max }}=5$ (achieved when $\left.\quad x=\frac{3}{5}\right)$.
Let's explain the solution of the system $\left\{\begin{array}{l}y \geqslant 3 x \\ -5 \leqslant y\end{array}\right.$ $\left\{\begin{array}{l}-5 \leqslant y \leqslant 5 \\ -1 \leqslant x \leqslant 1\end{array}\right.$ graphically (Fig. 19).
3 p r o b l e m 12. A cylindrical rod is being turned. The length of the rod is $l$, the diameter of the base is $D, h$-the thickness of the layer being turned. Find the maximum displacement of the center of gravity during the turning of the cylinder ${ }^{1}$.
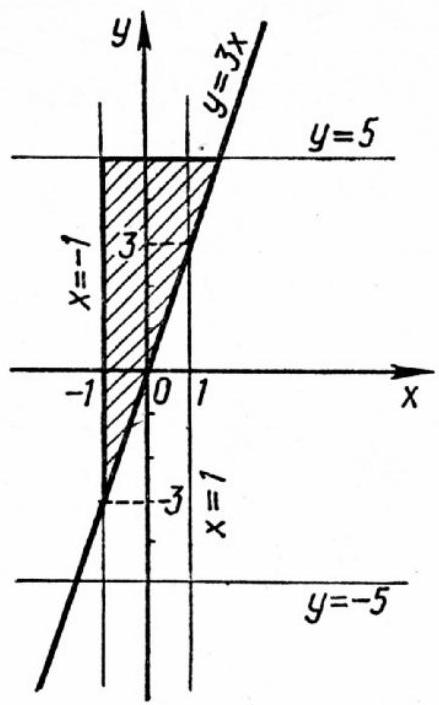
Fig. 19
$$
\text { S o l u t i o n. }
$$
Introduce a rectangular coordinate system as shown in Fig. 20; $x$ - the length of the turned layer at some moment in time $t$ :
$$
0 \leqslant x \leqslant l
$$
Before turning, the center of gravity of the cylinder was at point $C\left(\frac{l}{2} ; 0\right)$. Then, as the turning progresses, point $C$ will start moving to the left. When a layer of thickness $h$ is turned from the entire surface of the cylinder, the center of gravity will return to its original position. At the beginning of the experiment, $x_{C}=\frac{l}{2}$, the mass of the cylinder $m=\frac{\pi D^{2} l}{4} \rho$, where $\rho$ is the density of the material the cylinder is made of.
After some time, the turning body will consist of two cylinders of different diameters: $D-2 h$ and $D$. The mass of the first cylinder $m_{1}=\frac{\pi(D-2 h)^{2} x}{4} \rho$, the abscissa of the center of gravity of the first cylinder $x_{1}=\frac{x}{2}$. The mass of the second cylinder $m_{2}=$ $=\frac{\pi D^{2}(l-x)}{4} \rho$, the abscissa of the center of gravity of the second cylinder $x_{2}=\frac{l-x}{2}+x=\frac{l+x}{2}$.[^0]
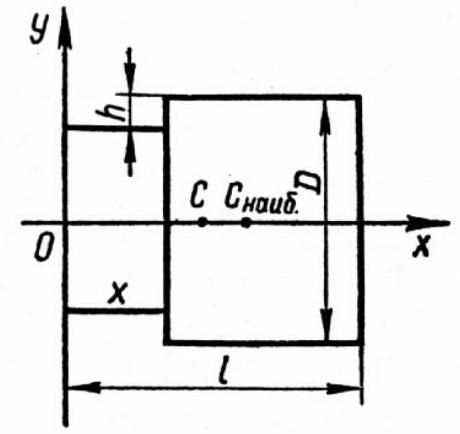
Fig. 20
Then the abscissa of the center of gravity of the system of two cylinders is
$$
\begin{gathered}
x_{C}=\frac{m_{1} x_{1}+m_{2} x_{2}}{m_{1}+m_{2}}= \\
=\frac{\frac{\pi(D-2 h)^{2} x^{2} \rho}{8}+\frac{\pi D^{2}(l-x) \rho(l+x)}{8}}{\frac{\pi(D-2 h)^{2} x \rho}{4}+\frac{\pi D^{2}(l-x) \rho}{4}}= \\
=\frac{(D-2 h)^{2} x^{2}+D^{2}\left(l^{2}-x^{2}\right)}{2\left((D-2 h)^{2} x+D^{2}(l-x)\right)}=\frac{4 h(h-D) x^{2}+D^{2} l^{2}}{8 h(h-D) x+2 D^{2} l}
\end{gathered}
$$
The problem has been reduced to finding the maximum value of the function
$$
y=\frac{4 h(h-D) x^{2}+D^{2} l^{2}}{8 h(h-D) x+2 D^{2} l}
$$
Let's find the range of values of this function:
$E(f)=\left\{y \left\lvert\, y=\frac{4 h(h-D) x^{2}+D^{2} l^{2}}{8 h(h-D) x+2 D^{2} l}\right.\right.$ has a solution in $[0 ; l[\}=$ $=\left\{y \mid 4(h-D) h x^{2}-8 h(h-D) y x+D^{2} l^{2}-2 D^{2} l y=0\right.$ has a solution in $\left[0 ; l[\}=\left\{y \left\lvert\,\left(y \geqslant \frac{D l}{2 h} \cup y \leqslant \frac{D l}{2(D-h)}\right) \cap 0 \leqslant y \leqslant l\right.\right\}=\{y \mid 0 \leqslant\right.$ $\left.\leqslant y \leqslant \frac{D l}{2(D-h)}\right\}$
Let's explain the last conclusion: $D>2 h \Rightarrow \frac{D}{2 h}>1 \Rightarrow \frac{D l}{2 h}>l$. Therefore, we have $0 \leqslant y \leqslant \frac{D l}{2(D-h)}$.
$$
\begin{gathered}
y_{\text {max }}=\frac{D l}{2(D-h)} ; \quad x_{\text {max }}=\frac{D l}{2(D-h)} \\
C C_{\text {max }}^{\prime}=\frac{D l}{2(D-h)}-\frac{l}{2}=\frac{l h}{2(D-h)}
\end{gathered}
$$
A series of problems reduces to finding the maximum or minimum value of a quadratic trinomial.
T h e o r e m. A quadratic trinomial $y=a x^{2}+b x+c$ has a maximum or minimum value, which is taken at $x=-\frac{b}{2 a}$; the value is minimum if $a>0$, and maximum if $a<0$. If $a>0$, the first term $a\left(x+\frac{b}{2 a}\right)^{2}$ cannot be negative; it becomes zero at $x=-\frac{b}{2 a}$. In this case, $y$ takes its minimum value $y=c-\frac{b^{2}}{4 a}$ and the function does not have a maximum value. If $a<0$, then $a\left(x+\frac{b}{2 a}\right)^{2} \leqslant 0$, but at $x=-\frac{b}{2 a}$ it becomes zero. Therefore, $y$ reaches its maximum value $y=c-\frac{b^{2}}{4 a}$. In this case, there is no minimum value.
Corollary. The product of two positive factors, whose sum is constant, reaches its maximum value when these factors are equal ${ }^{1}$.
Proof. Let $p$ be the sum of these two factors. If the first factor is $x$, then the second is $p-x$. The product of the considered factors $y=x(p-x)=-x^{2}+p x$, as follows from the proven theorem, takes its maximum value, equal to $y=\frac{p^{2}}{4}$, at $x=\frac{p}{2}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 16. Points $\boldsymbol{A}$ and $\boldsymbol{B}$ are located on a straight highway running from west to east. Point B is 9 km east of A. A car departs from point A heading east at a speed of 40 km/h. Simultaneously, a motorcycle departs from B in the same direction with a constant acceleration of 32 km/h².
Fig. 21 Determine the maximum distance that can be between the car and the motorcycle during the first two hours of travel.
|
## S o l u t i o n.
At time $t$, the car is at a distance of $40 t$ km from point $A$, and the motorcycle is at a distance of $\left(16 t^{2}+9\right)$ km.
20
The distance between them is the absolute value of the difference between $16 t^{2}+9$ and $40 t$. Let's denote this distance by $y$:
$$
y=\left|16 t^{2}+9-40 t\right|
$$
We need to find the maximum value of $y$ if $t$ varies in $[0 ; 2]$.
Let's plot the graph of the function $y=$ $=\left|16 t^{2}-40 t+9\right|$ (Fig. 22). If $t$ varies from 0 to 2, then the point on the graph with the greatest ordinate has an abscissa of $\frac{5}{4}$:
$$
y_{\text {max }}=16 \text { (km). }
$$
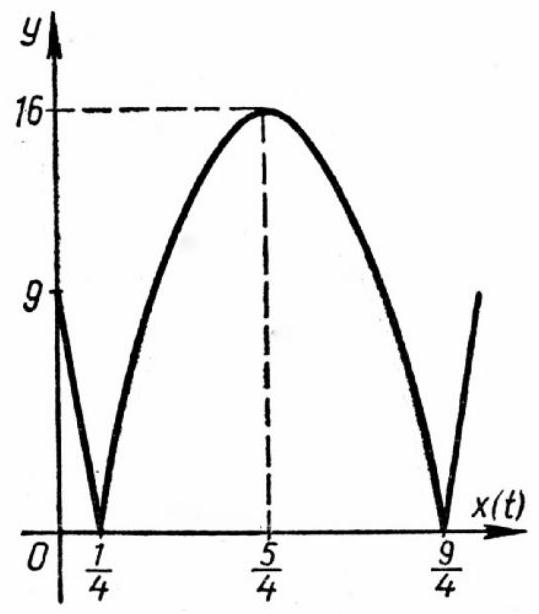
Fig. 22
Let's trace the graph to see how the distance between the car and the motorcycle changed during the first two hours. At the start of the journey, when $t=0$, the distance between them was 9 km. Over the first 15 minutes, the car was catching up to the motorcycle and at a distance of 1 km from point $B$, it overtook the motorcycle. Then the car started to pull ahead, and the distance between them began to increase. At $t=\frac{5}{4}$ hours, the distance between them reached its maximum value of 16 km. Thereafter, the car continued to lead, but the distance began to decrease as the motorcycle's speed increased and it approached the car. For example, at $t=2$ hours, $y=7$ km, and at $t=\frac{9}{4}$ hours, the motorcycle caught up with the car. If $t>\frac{9}{4}$, the distance between the car and the motorcycle increases again, but this time the motorcycle is in the lead. For instance, at $t=3$ hours, $y=33$ km.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 26. A company has 2 workshops and 3 warehouses. It is necessary to determine the most profitable organization of transportation.
| Warehouses | No. 1 | No. 2 | No. 3 | Produced |
| :---: | :---: | :---: | :---: | :---: |
| I | 3 | 3 | 2 | 10000 |
| II | 6 | 5 | 1 | 5000 |
| Required to deliver | 4000 | 8000 | 3000 | |
|
## S o l u t i o n.
Let $x$ units be transported from workshop I to warehouse 1, and $y$ units to warehouse 2. Then, from workshop I to warehouse 3, $(10000-x-y)$ units will be transported, and from workshop II to warehouses 1, 2, and 3, $4000-x$, $8000-y$, and $x+y-7000$ units will be transported, respectively (Table 13).
| | № 1 | № 2 | № 3 | |
| :---: | :---: | :---: | :---: | :---: |
| I | 个 | 3 | 2 | 10000 |
| | $x$ | $y$ | $\|10000-x-y\|$ | |
| II | 6 | $\mid 5$ | 1 | 5000 |
| | $4000-x$ | $8000-y$ | $x+y-7000$ | |
| | 4000 | 8000 | 3000 | |
Table 13
The total transportation cost $F$ under this assumption will be:
$$
\begin{gathered}
F=3 x+3 y+2 \cdot(10000-x-y)+6 \cdot(4000-x)+ \\
+5 \cdot(8000-y)+1 \cdot(x+y-7000)= \\
=-x-3(x+y)+77000
\end{gathered}
$$
Since $x+y=10000$, then $F=x-30000+77000=-x+47000$. We see that reducing $F$ is possible by increasing $x$ (where $x$ is an integer from $[0 ; 4000]$). Therefore, when $x=4000$, $F$ reaches its minimum value. The remaining 6000 units in workshop I can be transported to warehouse 2, which has a capacity of 8000 units. This means that when $x=4000$, the variable $y$ takes its maximum value, which is 6000. Thus, the function $F$ reaches its minimum value when $x=4000$ and $y=6000$.
The optimal transportation plan is shown in Table 14.
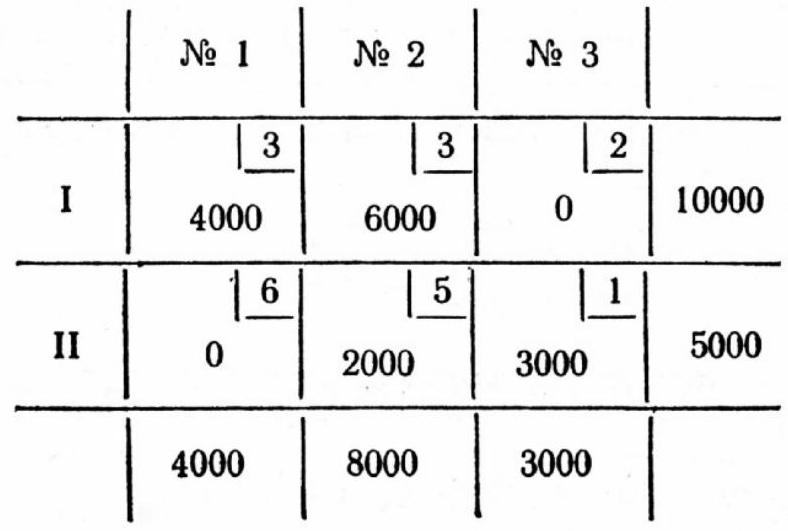
32
The minimum transportation cost for all 15000 units will be 43000 monetary units:
$$
F_{\text {min }}=43000
$$
|
43000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 35. For the fattening of animals, two types of feed I and II are used. Each kilogram of feed I contains 5 units of nutrient $\boldsymbol{A}$ and 2.5 units of nutrient B, while each kilogram of feed II contains 3 units of nutrient A and 3 units of nutrient B. Experimental data has shown that the fattening of animals will be economically beneficial when each animal receives at least 30 units of nutrient $A$ and at least 22.5 units of nutrient B in their daily diet. It is known that the cost of 1 kg of feed I and 1 kg of feed II is the same and equals 1 monetary unit. What should be the daily consumption of each type of feed to minimize the cost of feeding while meeting the above nutritional requirements?
|
## S o l u t i o n.
1. Let's construct a mathematical model of this problem. Let $x$ and $y$ be the number of kilograms of feed of types I and II, respectively, consumed daily. Then the system of constraints is:
$$
\left\{\begin{array}{l}
5 x+3 y \geqslant 30 \quad(a) \\
2.5 x+3 y \geqslant 22.5 \\
x \geqslant 0, y \geqslant 0
\end{array}\right.
$$
50
The objective function to be minimized is $F=x+y$.
2. Let's construct the set of feasible plans (on Fig. 33, this set is shaded). It is clear that $F$ achieves its minimum value at point $M$.
To find its coordinates, we solve the system
$$
\left\{\begin{array}{l}
5 x+3 y=30 \\
2.5 x+3 y=22.5
\end{array}\right.
$$
We get $(3 ; 5) ; F_{\text {min }}=8$ (monetary units).
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 37. On the set of solutions of the system of constraints
$$
\left\{\begin{array}{l}
2-2 x_{1}-x_{2} \geqslant 0 \\
2-x_{1}+x_{2} \geqslant 0 \\
5-x_{1}-x_{2} \geqslant 0 \\
x_{1} \geqslant 0, \quad x_{2} \geqslant 0
\end{array}\right.
$$
find the minimum value of the function $F=x_{2}-x_{1}$.
|
S o l u t i o n.
The set of feasible plans is the polygon $A B C D E$ (Fig. 35). The line $2-$ $-x_{1}-x_{2}=0$ is parallel to the level lines of the function $F=x_{2}$ $-x_{1}$. Therefore, all points on the segment $C D$ give the same minimum value of the objective function $F=x_{2}-x_{1}$ on the set of points of the pentagon $A B C D E$: $F=-2$.
|
-2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 39. Minimize $\boldsymbol{F}=\boldsymbol{x}_{2}-\boldsymbol{x}_{1}$ for non-negative $x_{1}$ and $x_{2}$, satisfying the system of constraints:
$$
\left\{\begin{aligned}
-2 x_{1}+x_{2}+x_{3} & =2 \\
x_{1}-2 x_{2}+x_{4} & =2 \\
x_{1}+x_{2}+x_{5} & =5
\end{aligned}\right.
$$
56
|
## S o l u t i o n.
These constraints can be considered as derived from inequalities, since each of the variables $x_{3}, x_{4}, x_{5}$ appears only in one equation.
1. Write the constraints as equations expressing the basic variables in terms of the non-basic variables:
$$
\left\{\begin{array}{l}
x_{3}=2+2 x_{1}-x_{2} \\
x_{4}=2-x_{1}+2 x_{2} \\
x_{5}=5-x_{1}-x_{2}
\end{array}\right.
$$
The basis B consists of the variables $x_{3}, x_{4}, x_{5}$. It corresponds to the basic non-negative solution $(0 ; 0 ; 2 ; 2 ; 5)$.
Now we need to express $F$ in terms of the non-basic variables. In our specific case, this has already been done.
2. Check if the objective function has reached its minimum value. The coefficient of $x_{1}$ in the expression for $F$ is negative. Therefore, increasing $x_{1}$ will further decrease $F$. However, as the value of $x_{1}$ increases, the values of $x_{4}$ and $x_{5}$ will decrease, and it is necessary to ensure that none of them become negative. Since increasing the value of $x_{1}$ leads to an increase in the value of $x_{3}$, there is no such danger for this variable. From the analysis of the other variables, we find that the value of $x_{1}$ can only be increased to 2. Such an increase gives $x_{4}=0, x_{3}=6, x_{5}=3$.
The new basis B consists of $x_{1}, x_{3}, x_{5}$.
3. To proceed to the next step, express these variables and the objective function in terms of the non-basic variables $x_{2}$ and $x_{4}$. For this, first solve the second equation of the system (2) for the new basic variable $x_{1}$:
$$
x_{1}=2+2 x_{2}-x_{4}
$$
Substituting this expression into the other equations and the objective function gives:
$$
\begin{aligned}
& x_{3}=6+3 x_{2}-2 x_{4} \\
& x_{5}=3-3 x_{2}+x_{4} \\
& F=-2-x_{2}+x_{4}
\end{aligned}
$$
4. We can further decrease the objective function $F$ by increasing the value of $x_{2}$. However, $x_{2}$ can only be increased to 1: this follows from the equation $x_{5}=3-3 x_{2}+x_{4}$. Substituting $x_{2}=1$ into the other equations gives $x_{1}=4, x_{3}=9$. Once again, express the basic variables and $F$ in terms of the non-basic variables:
$$
\begin{aligned}
& \left\{\begin{array}{l}
x_{1}=4-\frac{1}{3} x_{4}-\frac{2}{3} x_{5} \\
x_{2}=1+\frac{1}{3} x_{4}-\frac{1}{3} x_{5} \\
x_{3}=9-x_{4}-x_{5}
\end{array}\right. \\
& F=-3+\frac{2}{3} x_{4}+\frac{1}{3} x_{5}
\end{aligned}
$$
The basis B consists of the variables $x_{1}, x_{2}, x_{3}$.
5. By increasing the values of $x_{4}$ and $x_{5}$, we can no longer achieve a further decrease in $F$. Therefore, we have obtained the optimal solution.
The minimum value of $F$, equal to -3, is achieved at $x_{1}=4$, $x_{2}=1, x_{3}=9$.
Compare the values of the objective function corresponding to different bases:
$$
\begin{gathered}
F_{\mathrm{B}}=5, F_{\mathrm{b}^{\prime}}=-2, F_{\mathrm{E}^{\prime \prime}}=-3 \\
-3<-2<5
\end{gathered}
$$
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
To find the maximum value of $F=4 x_{1}+6 x_{2}$
subject to
$$
\left\{\begin{array}{c}
x_{1}+x_{2} \leqslant 18 \\
0.5 x_{1}+x_{2} \leqslant 12 \\
0 \leqslant x_{1} \leqslant 12 \\
0 \leqslant x_{2} \leqslant 9
\end{array}\right.
$$
|
S o l u t i o n.
This problem has already been solved graphically (see problem 32).
When solving by the simplex method, the system of constraints, consisting of inequalities, must be transformed into a system of linear equations by introducing additional variables:
$$
\begin{gathered}
x_{1}+x_{2}+x_{3}=18 \\
0.5 x_{1}+x_{2}+x_{4}=12 \\
x_{1}+x_{5}=12 \\
x_{2}+x_{6}=9 \\
x_{1} \geqslant 0, \ldots, 6 \\
i=1, \ldots, 6
\end{gathered}
$$
1. Find the basic non-negative solution of the system of constraints. Let variables $x_{3}, x_{4}, x_{5}, x_{6}$ be the basic ones, then $x_{1}$ and $x_{2}$ are non-basic:
$$
\left\{\begin{array}{l}
x_{3}=18-x_{1}-x_{2} \\
x_{4}=12-0.5 x_{1}-x_{2} \\
x_{5}=12-x_{1} \\
x_{6}=9-x_{2} \\
x_{l} \geqslant 0, i=1, \ldots, 6
\end{array}\right.
$$
The basis B consists of variables $x_{3}, x_{4}, x_{5}, x_{6}$. The basic solution is $(0 ; 0 ; 18 ; 12 ; 12 ; 9)$
$$
F_{\text {B }}=4 \cdot 0+6 \cdot 0=0
$$
2. $F$ can be increased by increasing $x_{1}$ or $x_{2}$. Let's increase, for example, $x_{2}$. From system (4), it is clear that the maximum allowable value that $x_{2}$ can take is 9. Let's transition to the basis B, consisting of $x_{3}, x_{4}, x_{5}, x_{6}$. For this, we will move the non-basic variable $x_{6}$ to the non-basic variables and introduce $x_{2}$ into the basic variables:
$$
\left\{\begin{array}{l}
x_{3}=9-x_{1}+x_{6} \\
x_{4}=3-0.5 x_{1}+x_{6} \\
x_{5}=12-x_{1} \\
x_{2}=9-x_{6} \\
x_{i} \geqslant 0, i=1, \ldots, 6
\end{array}\right\}
$$
The basic solution is $(0 ; 9 ; 9 ; 5 ; 12 ; 0), F_{\mathrm{b}^{\prime}}=54$.
3. Further increasing $F$ is only possible by increasing $x_{1}$. Analysis of system (5) shows that $x_{1}$ can be no more than 6 (otherwise,
\begin{array}{|c|c|c|c|c|}
\hline
A & 3 & 15 & 8 & 70 \\
\hline
B & 6 & 3 & 12 & 80 \\
\hline
Shipped & 20 & 40 & 30 & \\
\hline
\end{array}
11. Solve graphically the following linear programming problem. On the set of solutions of the system
$$
\left\{\begin{array}{l}
x_{1}+x_{2} \leqslant 1 \\
x_{1} \leqslant x_{2} \leqslant 1 \\
x_{1} \geqslant 0, x_{2} \geqslant 0
\end{array}\right.
$$
find the maximum value of $F=x_{1}+2 x_{2}$.
12. Find the minimum value of $F=x_{1}-x_{2}$ given
$$
\left\{\begin{array}{c}
x_{1}+x_{2} \leqslant 1 \\
x_{1}+2 x_{2} \leqslant 1 \\
2 x_{1}+3 x_{2} \leqslant 2 \\
3 x_{1}+2 x_{2} \leqslant 3 \\
x_{1}+x_{2} \leqslant \frac{1}{2} \\
x_{1} \geqslant 0, x_{2} \geqslant 0
\end{array}\right.
$$
13. Find the maximum value of $F=x_{1}-x_{2}$ given
$$
\left\{\begin{array}{l}
1 \leqslant x_{1}+x_{2} \leqslant 2 \\
2 \leqslant x_{1}-2 x_{2} \leqslant 3 \\
1 \leqslant 2 x_{1}-x_{2} \leqslant 2 \\
x_{1} \geqslant 0, x_{2} \geqslant 0 .
\end{array}\right.
$$
14. Find the minimum value of $F=x_{1}+x_{2}-x_{3}$ given
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3} \leqslant 4 \\
x_{1}-x_{2}+x_{3} \leqslant 2 \\
x_{1} \geqslant 0, x_{2} \geqslant 0, x_{3} \geqslant 0
\end{array}\right.
$$
Solve the following linear programming problems analytically and, where possible, provide a geometric interpretation.
15. $2 x_{1}+x_{2}-x_{3}+x_{4}=3$
$\left\{\begin{array}{c}-2 x_{1}+x_{2}+x_{3}-x_{4}=-1 \\ x_{i} \geqslant 0, i=1,2,3,4,\end{array}\right.$
$$
F_{\min }=x_{1}+x_{2}+x_{3}+x_{4} .
$$
16. $x_{1}+x_{3}=2$
$\left\{\begin{array}{l}x_{2}-x_{3}+x_{4}=1 \\ x_{i} \geqslant 0, i=1,2,3,4,\end{array}\right.$
$F_{\max }=x_{1}+x_{2}$.
17. $\left(x_{1}-3 x_{2}+x_{3}=5\right.$
$\left\{\begin{array}{l}x_{2}-x_{3}=2 \\ x_{1} \geqslant 0, x_{2} \geqslant 0, x_{3} \geqslant 0,\end{array}\right.$
$F_{\max }=x_{2}+x_{3}$.
18. $\left(2 x_{1}+x_{2}+x_{3}=4\right.$
$\left\{\begin{array}{l}x_{1}-x_{2}-x_{3} \leqslant 2 \\ x_{1} \geqslant 0, x_{2} \geqslant 0, x\end{array}\right.$
$F_{\max }=x_{1}-4 x_{2}+5 x_{3}$.
19. $10 x_{1}+x_{3} \leqslant 10$
$\left\{\begin{array}{l}10 x_{2}+x_{3} \leqslant 10 \\ x_{1} \geqslant 0, x_{2} \geqslant 0\end{array}\right.$
$F_{\max }=x_{1}-x_{2}+x_{3}$.
In preparing this manual, the authors used the following literature:
1. R. Courant, H. Robbins. What is Mathematics? Moscow, "Prosveshchenie", 1967.
2. N. P. Natanson. Simplest Problems on Maximum and Minimum. Moscow, Fizmatgiz, 1960.
3. D. O. Shklyarsky, N. N. Chentsov, I. M. Yaglom. Geometric Inequalities and Problems on Maximum and Minimum, Moscow, "Nauka", 1970.
## CONTENTS
Introduction ..... 3
§1. On the History of the Development of the Theory of Extreme Values of Quantities. ..... 6
§2. Analysis of the Set of Values of a Function ..... 15
§3. Using the Property of the Inequality Connecting the Arithmetic and Geometric Means of Two Non-Negative Numbers ..... 24
§4. Practical Problems Leading to a Linear Objective Function ..... 26
§5. Concept of Linear Programming Problems ..... 36
5.1. Types of Linear Programming Problems
5.2.
|
54
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5 (1246). By what percentage will the area of a rectangle increase if its length is increased by $20 \%$ and its width by $10 \%$?
|
Solution. Let the length of the rectangle be $x$, and the width be $y$, then its area is $x y$. After increasing the length and width of the rectangle by $20 \%$ and $10 \%$ respectively, its area became $1.2 x \cdot 1.1 y = 1.32 x y$, i.e., the area of the rectangle increased by $0.32 x y$, which is $32 \%$ of $x y$.
Answer: the area of the rectangle increased by $32 \%$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6 (1247). Three boxes are filled with nuts. In the second box, there are $10 \%$ more nuts than in the first, and $30 \%$ more than in the third. How many nuts are in each box if there are 80 more nuts in the first box than in the third?
|
Solution. Let there be $x$ nuts in the first box and $y$ in the third. Then in the second box, there were $x+0.1 x=1.1 x$ or $y+0.3 y=1.3 y$. Considering that there were 80 more nuts in the first box than in the third, we form the system of equations:
$$
\left\{\begin{array}{l}
1.1 x=1.3 y \\
x-y=80
\end{array}\right.
$$
from which $y=440, x=520, 1.1 x=572$.
42
Remark. This problem can be solved without forming a system of equations. Let there be $x$ nuts in the first box, then in the third $-x-80$, in the second box $-1.1 x$, or $1.3(x-80)$. We have the equation: $1.1 x=1.3(x-80)$, from which $x=520$.
Answer: there were 520 nuts in the first box, 572 in the second, and 440 in the third.
|
520
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13(1254). To a certain two-digit number, a one was added to the left and right. As a result, a number was obtained that is 23 times greater than the original. Find this two-digit number.
|
Solution. Let the desired two-digit number be $\bar{a} \bar{b}$. According to the problem, we form the equation: $\overline{\mid a b 1}=23 \cdot \overline{a b}$. We have $1000+$ $+10 \overline{a b}+1=23 \cdot \overline{a b}$, from which $13 \cdot \overline{a b}=1001, \overline{a b}=77$.
Answer: 77.
Remark 1. The unknown two-digit number can also be found by selecting its digits, if we take into account that only by multiplying 7 by 3 we get a number ending in one.
Remark 2. It is advisable to consider problems 805-808 from the textbook [4] simultaneously with this problem.
$\triangle 14$ (1255). In a two-digit number, one digit was erased. The resulting number is 31 times smaller than the original. Which digit and in which number was erased?
Solution. From the two-digit numbers that are multiples of $31 (31, 62, 93)$, we select the numbers that satisfy the condition of the problem: after erasing one digit, we get a number that is 31 times smaller than the original. This condition is satisfied by all two-digit numbers that are multiples of 31. Indeed, by erasing the tens digit in them, we will have the numbers 1, 2, and 3, which are 31 times smaller than the numbers 31, 62, and 93, respectively.
Answer: $31, 62, 93$; the first digit needs to be erased.
$\triangle 15$ (1256). The first digit of a three-digit number is 8. If this digit is moved to the last place, the number increases by 18. Find the original number.
Solution. Method I. Let $a$ be the tens digit of the desired number, and $b$ be its units digit. Then, according to the problem, we have:
$$
\begin{gathered}
\overline{a b 8}-\overline{8 a b}=18, \text { from which } 10 \overline{a b}+8-800-\overline{a b}=18, \\
9 \overline{a b}=810, \overline{a b}=90
\end{gathered}
$$
the original number is 890.
Method II. The problem can be easily solved by selecting digits, rephrasing it as follows: find out which digits are represented by the letters, if each letter represents only one digit:
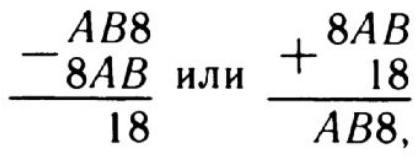
from which $B=0, A=9$.
Remark. Before solving problems 13 and 15 using equations, it is advisable to offer students the following auxiliary problems.
|
77
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If a zero is appended to the right of the thought number and the result is subtracted from 143, the result will be three times the thought number. What number was thought of?
|
Solution. Let the number be $x$. We have the equation $143-10 x=3 x$, from which $x=11$. A n s w e r: 11 .
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. If to a given number we append the digit 9 on the right and add to the resulting number twice the given number, the sum will be equal to 633. Find the given number.
|
Solution. The problem boils down to solving the equation $10 x+$ $+9+2 x=633$, where $x$ is the given number; $x=52$. A n s w e r: 52 .
|
52
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19(1260). Find the smallest natural number that, when multiplied by 2, becomes a square, and when multiplied by 3, becomes a cube of a natural number.
|
Solution. Let $x$ be the smallest natural number such that $2 x=b^{2}, 3 x=c^{3}$, where $b$ and $c$ are natural numbers. From the equation $2 x=b^{2}$, it follows that $x$ is divisible by 2. Since $3 x=c^{3}$, $x$ is divisible by $2^{3}=8$ and by $3^{2}=9$, i.e., $x=2^{3} \cdot 3^{2} a^{6}=72 a^{6}$, where $a$ is any natural number. The smallest $x$ is obtained when $a=1$. Answer: 72.
|
72
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41(1283). The path from $A$ to $B$ goes 3 km uphill, 6 km downhill, and 12 km on flat ground. The motorcyclist covered this path in 1 hour and 7 minutes, and the return path in 1 hour and 16 minutes. Find the motorcyclist's speed uphill and downhill, if his speed on flat ground was 18 km/h. (Note that the motorcyclist traveled at constant speeds both uphill and downhill, both on the path $A B$ and on the return path.)
|
Solution. I method. On a flat surface in one direction, the motorcyclist traveled $\frac{2}{3}$ hours $\left(12: 18=\frac{2}{3}\right)$, or 40 minutes. Then, 3 km uphill and 6 km downhill, the motorcyclist traveled 27 minutes, and 6 km uphill and 3 km downhill, the motorcyclist traveled 36 minutes. If we denote the motorcyclist's speed uphill and downhill as $v_{1}$ (km/min) and $v_{2}$ (km/min) respectively, we will have the system of equations:
$$
\left\{\begin{array}{l}
\frac{3}{v_{1}}+\frac{6}{v_{2}}=27 \\
\frac{3}{v_{2}}+\frac{6}{v_{1}}=36
\end{array}\right.
$$
56
from which $v_{1}=\frac{1}{5}$ km/min, or 12 km/h, $v_{2}=\frac{1}{2}$ km/min, or 30 km/h.
II method. The problem can also be solved without setting up a system of equations.
Indeed, if 3 km uphill and 6 km downhill took the motorcyclist 27 minutes, then by doubling the distance, we find that for a distance of 6 km uphill and 12 km downhill, the motorcyclist would need 54 minutes. Since the motorcyclist, according to the problem, spent 36 minutes on 6 km uphill and 3 km downhill, it would take 18 minutes $(54-36=18)$ for 9 km $(12-3=9)$ downhill. Therefore, the motorcyclist's speed downhill is $\frac{9}{18}=\frac{1}{2}$ km/min, or 30 km/h.
Similarly, we find that for a distance of 12 km uphill and 6 km downhill, the motorcyclist would need 72 minutes $(36 \cdot 2=72)$. Then, for a distance of 9 km uphill, it would take 45 minutes $(72-27=45)$. Therefore, the motorcyclist's speed uphill is $\frac{9}{45}=$ $=\frac{1}{5}$ km/min, or 12 km/h.
Answer: 12 km/h, 30 km/h.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42 (1284). How old is the brother and how old is the sister if 2 years ago the brother was twice as old as the sister, and 8 years ago - five times as old?
|
Solution. Method I. Let the current age of the sister be $x$ years, and the brother's age be $y$ years. According to the problem, we set up the system of equations:
$$
\left\{\begin{array}{l}
y-2=2(x-2) \\
y-8=5(x-8)
\end{array}\right.
$$
from which we find $x=10, y=18$.
Method II. Let 2 years ago the sister was $x$ years old, and the brother was $2x$ years old. Eight years ago, the sister was $(x-6)$ years old, and the brother was $(2x-6)$ years old. According to the problem, we have:
$$
2 x-6=5(x-6), \text { from which } x=8, 2 x=16
$$
Therefore, the sister is currently 10 years old $(8+2=10)$, and the brother is 18 years old $(16+2=18)$.
Answer: 18 years, 10 years.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43 (1285). From two cities $A$ and $B$, the distance between which is 180 km, a bus and a car set out towards each other at 6:20 AM. Their meeting occurred at 7:50 AM. If the bus had left 1 hour and 15 minutes earlier, and the car 15 minutes later, they would have met at 7:35 AM. What are the speeds of the bus and the car?
|
Solution. Let the speed of the bus be $v_{1}$ km/h, and the speed of the car be $v_{2}$ km/h. Since they met after 1.5 hours, we have the equation:
$$
1.5 v_{1} + 1.5 v_{2} = 180
$$
If the bus had left 1 hour and 15 minutes earlier, it would have been on the road for 2 hours and 30 minutes (7:35 - 5:05 = 2 hours 30 minutes).
If the car had left 15 minutes later, it would have been on the road for 1 hour (7:35 - 6:35 = 1 hour).
We get the equation:
$$
2.5 v_{1} + v_{2} = 180
$$
Thus, we have a system of two equations with two unknowns:
$$
\left\{\begin{array}{l}
1.5 v_{1} + 1.5 v_{2} = 180 \\
2.5 v_{1} + v_{2} = 180
\end{array}\right.
$$
from which $v_{1} = 40$ km/h, $v_{2} = 80$ km/h.
Answer: 40 km/h, 80 km/h.
44(1286). From city $A$ to city $B$, two buses left at 8:50. At the same time, a cyclist left from city $B$ to city $A$. One bus he met at 10:10, and the other at 10:50. The distance between the cities is 100 km. Find the speed of the cyclist if the speed of one bus is $1 \frac{5}{7}$ times the speed of the other.
Solution. Let the speed of one bus be $v_{1}$ km/h, the speed of the other bus $\frac{12}{7} v_{1}$ km/h, and the speed of the cyclist $v_{2}$ km/h.
Since the bus with the higher speed met the cyclist after $\frac{4}{3}$ hours (10:10 - 8:50 = 1 hour 20 minutes), and the other bus met the cyclist after 2 hours (10:50 - 8:50 = 2 hours), we have the system of equations:
$$
\left\{\begin{array}{l}
\frac{4}{3} \cdot \frac{12}{7} v_{1} + \frac{4}{3} v_{2} = 100 \\
2 v_{1} + 2 v_{2} = 100
\end{array}\right.
$$
Solving the system of equations, we find $v_{1} = 35$ km/h, $v_{2} = 15$ km/h. The speed of the second bus is $\frac{12}{7} v_{1} = 60$ km/h.
Answer: the speed of the cyclist is $15$ km/h.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45 (1287). A rider and a pedestrian simultaneously set off from point $A$ to point $B$. The rider, arriving in $B$ 50 minutes earlier than the pedestrian, returned back to $A$. On the return trip, he met the pedestrian 2 kilometers from $B$. The rider spent 1 hour and 40 minutes on the entire journey. Find the distance from $A$ to $B$ and the speed of the rider and the pedestrian.
|
S o l u t i o n. Since the rider spent 1 hour 40 minutes on the entire journey, he spent 50 minutes on the journey from $A$ to $B$ (1 hour 40 minutes: $2=50$ minutes). Then the pedestrian spent 1 hour 40 minutes on the journey from $A$ to $B$, as he arrived in $B$ 50 minutes later than the rider. Therefore, the pedestrian's speed is half the rider's speed. This means that when the rider was in $B$, the pedestrian was halfway through the journey. Since they met 2 km from $B$ on the return journey, the pedestrian had traveled 1 km from the halfway point (2 km $: 2=1$ km). Therefore, the distance from the halfway point to $B$ is 3 km, and the total distance between $A$ and $B$ is 6 km. Since the rider covered this distance in 50 minutes $\left(\frac{5}{6}\right.$ hours $)$, his speed is 7.2 km/h $\left(6: \frac{5}{6}=7.2\right)$; the pedestrian's speed is half of that: $7.2: 2=3.6$ km/h.
A n s w e r: 6 km; 7.2 km/h; 3.6 km/h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46 (1288). Freshly mined coal contains $2 \%$ water, and after two weeks of exposure to air, it contains $12 \%$ water. By how many kilograms has the mass of a ton of coal increased after the coal has been lying in the air for two weeks?
|
Solution. Since the freshly mined coal contains $2 \%$ water, in one ton of such coal, there are 20 kg of water and 980 kg of dry matter.
After two weeks of exposure to the air, the 980 kg of dry matter constitutes $88 \% (100 \% - 12 \% = 88 \%)$, meaning the total weight of the coal will be approximately 1114 kg $\left(\frac{980 \cdot 100}{88} \approx 1114\right)$.
Thus, the weight of the mined ton of coal has increased by about 114 kg.
Answer: by 114 kg.
|
114
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47 (1289). Two brothers walk together from school to home at the same speed. One day, 15 minutes after leaving school, the first brother ran back to school and, upon reaching it, immediately set off to catch up with the second. Left alone, the second continued walking home at half his usual speed. When the first brother caught up with the second, they resumed their initial speed and arrived home 6 minutes later than usual. How many times faster is the first brother's running speed compared to their usual walking speed?
|
Solution. Let the initial speed of the brothers be denoted by $v$ (m/min), and the segment of the path that the second brother traveled at a speed of $\frac{v}{2}$ be denoted by $s$. For this segment, he spent $\frac{2 s}{v}$ minutes $\left(s: \frac{v}{2}\right)$, which is 6 minutes more than the usual time spent (at speed $v$). We have the equation:
$$
\frac{2 s}{v}-\frac{s}{v}=6 \text {, i.e., } \frac{s}{v}=6, s=6 v \text {. }
$$
The first brother, in the same time $\left(\frac{2 s}{v}=\frac{2 \cdot 6 v}{v}=12\right.$ minutes), ran a distance of $15 v+15 v+s=30 v+6 v=36 v$. His running speed is $36 v: 12=3 v$, i.e., three times the usual walking speed of the brothers.
Answer: three times.
■ 48(1134)'. In a school mathematics olympiad, 9 sixth-grade students participated. For each solved problem, a student received 2 points, and for each unsolved problem, 1 point was deducted. A total of 10 problems were offered. Prove that among the participants from the sixth grade, there were at least 2 students who scored the same number of points. (It is assumed that a student who received more penalty points than earned points scored zero points.)
Solution. To prove this, we will create a table showing the number of points scored depending on the number of solved problems.
| Number of solved problems | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Number of points scored | 20 | 17 | 14 | 11 | 8 | 5 | 2 | 0 | 0 | 0 |
From the table, it is clear that there are only 8 different possibilities for scoring points. Since there were 9 students, at least two of them must have scored the same number of points.
49(1135). Two tourists, with one bicycle, need to travel a distance of 12 km in 1.5 hours. On the bicycle, each can reach a speed of 20 km/h, and on foot, 5 km/h. Can the tourists complete the entire journey without being late, if they cannot ride the bicycle together? (The bicycle can be left unattended.)
Solution. Let the first tourist ride the bicycle for $x$ km and walk the remaining $12-x$ km. Then the second tourist will ride the bicycle for $12-x$ km and walk $x$ km. Since the tourists will gain the most time if they arrive at the final destination simultaneously, we have the equation:
$$
\frac{x}{20}+\frac{12-x}{5}=\frac{x}{5}+\frac{12-x}{20}, \text { from which } x=6
$$
Thus, the tourists can complete the entire journey without being late if each of them rides the bicycle for half the distance (6 km) and walks the other half. They can switch modes of transportation, for example, every 100 meters.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52 (1138). In a box, there are multicolored balls: 5 white, 12 red, and 20 black. What is the smallest number of balls that need to be taken out of the box without looking inside, to ensure that among them there will be: a) at least one ball of each of the specified colors; b) 10 balls of one color?
|
Solution. a) In the worst case, 20 black and 12 red balls can be drawn, then the next ball drawn (white) will ensure the presence of balls of all the specified colors. Therefore, it is sufficient to draw 33 balls $(20+12+1=33)$ to ensure that there is at least one ball of each of the specified colors among them.
b) In the worst case, all white balls (5), 9 red, and 9 black balls can be drawn, then any ball drawn (red or black) will ensure the presence of 10 balls of one color (red or black). Therefore, it is sufficient to draw 24 balls to ensure that among the drawn balls there are 10 balls of one color.
62

Fig. 16
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53(1139). I have thought of an integer not exceeding 1000. How can you find out what number I have thought of by asking no more than 10 questions, to which I will only answer “yes” or “no”?
|
Solution. When solving the problem, it is convenient to use a table of powers with base 2, as the number not exceeding 1000 is in the numerical interval $\left[2^{0}, 2^{10}\right)$. Questions should be asked in such a way that after each answer, the interval is reduced by half. (The found intervals will be marked on Figure 16.)
Let, for example, the number $300(x=300)$ be thought of.
Question 1. Is the number $x$ greater than 512? $\left(512=2^{9}\right)$.
Answer. No.
Question 2. Is the number $x$ greater than 256? $\left(256=2^{9}: 2=2^{8}\right)$. Answer. Yes.
Question 3. Is the number $x$ greater than 384? $\left(384=\frac{2^{8}+2^{9}}{2}\right)$.
Answer. No.
Question 4. Is the number $x$ greater than 320? $\left(320=\frac{256+384}{2}\right)$.
Answer. No.
Question 5. Is the number $x$ greater than 288? $\left(288=\frac{256+320}{2}\right)$.
Answer. Yes.
Question 6. Is the number $x$ greater than 304? $\left(304=\frac{288+320}{2}\right)$.
Answer. No.
Question 7. Is the number $x$ greater than 296? $\left(296=\frac{288+304}{2}\right)$.
Answer. Yes.
Question 8. Is the number $x$ greater than 300? $\left(300=\frac{296+304}{2}\right)$.
Answer. No.
Question 9. Is the number $x$ greater than 298? $\left(298=\frac{296+300}{2}\right)$.
Answer. Yes.
Question 10. Is the number $x$ greater than 299? $\left(299=\frac{298+300}{2}\right)$.
Answer. Yes.
Therefore, the number thought of is 300 (the only integer 300 is greater than 299 but not greater than 300).
$54(1140)$. In 5 years, the brother's age will be to the sister's age as 7:5. How old is each of them now if a year ago the brother was twice as old as the sister? Solution. I method. Let the sister be $x$ years old a year ago, and the brother be $2x$ years old. In 5 years, the sister will be $(x+6)$ years old, and the brother will be $(2x+6)$ years old. According to the problem, we have:
$$
\frac{2 x+6}{x+6}=\frac{7}{5}
$$
from which $x=4, 2x=8$, i.e., the sister is 5 years old now, and the brother is 9 years old.
II method. Let the brother be $7x$ years old in 5 years, and the sister be $5x$ years old. A year ago, they were $(7x-6)$ years and $(5x-6)$ years old, respectively. According to the problem, we have the equation:
$$
7 x-6=2(5 x-6)
$$
from which $x=2$.
The brother is 9 years old now $(7x-6+1)$, and the sister is 5 years old $(5x-6+1)$.
III method. Let the sister be $x$ years old now, and the brother be $y$ years old. According to the problem, we form the system of equations:
$$
\left\{\begin{array}{l}
\frac{y-1}{x-1}=2 \\
\frac{y+5}{x+5}=\frac{7}{5}
\end{array}\right.
$$
from which we find $x=5, y=9$.
Answer: the sister is 5 years old now, and the brother is 9 years old.
$55(1150)$. The first digit of a four-digit number is 7. If this digit is moved to the last place, the resulting number is 864 less than the original number. Find the original number.
Solution. I method. Let the required number be $\overline{7 a b c}$. According to the problem, we have:
$$
\overline{7 a b c}-\overline{a b c 7}=864
$$
If $\overline{a b c}=x$, then we have the equation:
$$
7000+x-(10 x+7)=864
$$
from which $x=681$, and the required number is 7681.
II method. The problem can be easily solved by selecting digits, rephrasing it as follows: find out what digits the letters represent, if each letter represents only a digit.
$$
\begin{array}{r}
7 a b c \\
-\frac{a b c 7}{864}
\end{array} \quad \text { or }+\frac{864}{7 a b c}
$$
from which $c=1, b=8, a=6$.
Answer: the required number is 7681.
|
300
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64(1168). Can: a) the sum of five consecutive natural numbers be a prime number; b) the sum of the squares of five consecutive natural numbers be a prime number?
|
Solution. a) Let's check on specific examples whether the sum of five consecutive natural numbers is a prime or composite number: $1+2+3+4+5=15 ; 2+3+4+5+6=$ $=20 ; 3+4+5+6+7=25 ; \ldots ; 10+11+12+13+14=60$.
The numbers $15,20,25,60$ are composite numbers. We get the hypothesis: the sum of five consecutive natural numbers is a composite number. Let's prove it. We have:
$$
A=n+(n+1)+(n+2)+(n+3)+(n+4)=5 n+10=5(n+2) .
$$
Since by condition $n \in \boldsymbol{N}$, then $n+2 \in \boldsymbol{N}$ and $5(n+2) \in \boldsymbol{N}$, and $5(n+2)>5$. Therefore, the specified sum is divisible by 5, but not equal to 5, i.e., $A$ is a composite number.
b) Let's check on specific examples that the sum of the squares of five consecutive natural numbers is a composite number:
$$
\begin{gathered}
1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55,2^{2}+3^{2}+4^{2}+5^{2}+6^{2}=90 \\
3^{2}+4^{2}+5^{2}+6^{2}+7^{2}=135,10^{2}+11^{2}+12^{2}+13^{2}+14^{2}=730
\end{gathered}
$$
The numbers $55,90,135,730$ are composite.
To prove this fact in general, let's write five consecutive natural numbers as: $n-2, n-1, n, n+1$, $n+2$, where $n$ is any natural number greater than 2. Then we have:
$$
\begin{gathered}
B=(n-2)^{2}+(n-1)^{2}+n^{2}+(n+1)^{2}+(n+2)^{2}= \\
=5 n^{2}+10=5\left(n^{2}+2\right) .
\end{gathered}
$$
Since $n \in \boldsymbol{N}$, then $5\left(n^{2}+2\right) \in \boldsymbol{N}$ and $5\left(n^{2}+2\right)>5$. Therefore, the number $B$ is divisible by 5, but not equal to 5, i.e., $B$ is a composite number.
$\square$ 65(1181). If the thought number is divided by the sum of its digits, the quotient is 4 and the remainder is 3. If the thought number is reduced by twice the sum of its digits, the result is 25. What is the thought number?
$\mathrm{Pe}$ solution. Let the desired number be $\overline{a b}=10 a+b$. According to the problem, we form a system of equations:
$$
\left\{\begin{array}{c}
10 a+b=4(a+b)+3 \\
10 a+b-2(a+b)=25
\end{array}\right.
$$
which, after simplification, has the form:
$$
\left\{\begin{array}{l}
2 a-b=1 \\
8 a-b=25
\end{array}\right.
$$
from which $a=4, b=7$.
Answer: the desired number is 47.
|
47
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
67 (1183). One vessel contains 49 liters of water, and the other contains 56 liters. If the first vessel is filled to the top with water from the second vessel, the second vessel will be only half full. If the second vessel is filled to the top with water from the first, the first vessel will be only one-third full. What is the capacity of each vessel?
|
Solution. Method I. Let the capacity of the first vessel be $(49+x)$ liters, and the capacity of the second vessel be $(56+y)$ liters. If $x$ liters are poured from the second vessel into the first, then $(56-x)$ liters will remain in the second vessel, or $\frac{1}{2}(56+y)$. We have the equation:
$$
56-x=\frac{1}{2}(56+y)
$$
| $y$ |
| :---: |
| 56 |
If $y$ liters are poured from the first vessel into the second, then $(49-y)$ liters will remain in the first vessel. By the condition, $49-y = \frac{1}{3}(49+x)$.
We obtain the system of equations:
$$
\left\{\begin{array}{l}
56-x=\frac{1}{2}(56+y) \\
49-y=\frac{1}{3}(49+x)
\end{array}\right.
$$
After simplification, we have:
$$
\left\{\begin{array}{l}
2 x+y=56 \\
x+3 y=98
\end{array}\right.
$$
from which $x=14, y=28$.
The capacity of the first vessel is 63 liters, and the capacity of the second vessel is 84 liters.
Method II. Let the capacity of the first vessel be $x$ liters, and the capacity of the second vessel be $y$ liters. If the first vessel is filled to the top, i.e., $(x-49)$ liters are added, then $(56-(x-49))$ liters, or $(105-x)$ liters, will remain in the second vessel. By the condition, $105-x=\frac{y}{2}$.

If the second vessel is filled to the top, i.e., $(y-56)$ liters are added, then $(49-(y-56))$ liters, or $(105-y)$ liters, will remain in the first vessel. By the condition, $105-y=\frac{x}{3}$.
We have the system of equations:
$$
\left\{\begin{array}{l}
105-x=\frac{y}{2} \\
105-y=\frac{x}{3}
\end{array}\right.
$$
from which $x=63, y=84$.
Answer: 63 liters, 84 liters.
$\square$ 68(1184). A bus and a minibus, which leave $M$ and $K$ at 8:40 AM according to the schedule, usually meet at 8:52 AM. One day, the minibus left 8 minutes late and met the bus at 8:57 AM. Find the speed of the bus and the minibus, given that the distance from $M$ to $K$ is 24 km.
Solution. Let the speed of the bus be $v_{1}$ km/min, and the speed of the minibus be $v_{2}$ km/min. Since the bus and the minibus usually meet after 12 minutes (8:52 AM - 8:40 AM = 12 minutes), we have the equation $12 v_{1} + 12 v_{2} = 24$.
In the case when the minibus left late, it traveled for 9 minutes (8:57 AM - 8:48 AM = 9 minutes) before meeting the bus, and the bus traveled for 17 minutes (8:57 AM - 8:40 AM = 17 minutes) before meeting the minibus. By the condition, $17 v_{1} + 9 v_{2} = 24$.
We obtain the system of equations:
$$
\left\{\begin{array}{l}
12 v_{1} + 12 v_{2} = 24, \\
17 v_{1} + 9 v_{2} = 24,
\end{array}\right.
$$
from which $v_{1} = \frac{3}{4}$ km/min, or 45 km/h; $v_{2} = \frac{5}{4}$ km/min, or 75 km/h.
Remark. If the speed of the bus $v_{1}$ and the speed of the minibus $v_{2}$ are expressed in kilometers per hour, the solution of the problem reduces to the system:
$$
\left\{\begin{array}{l}
\frac{1}{5} v_{1} + \frac{1}{5} v_{2} = 24 \\
\frac{17}{60} v_{1} + \frac{3}{20} v_{2} = 24
\end{array}\right.
$$
Answer: the speed of the bus is 45 km/h, the speed of the minibus is 75 km/h.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69 (1185). From $A$ to $B$, the distance between which is 37 km, two buses with the same speed left at 7:18 AM and 7:48 AM, respectively. A cyclist, who left $B$ for $A$ at 7:28 AM, met the first bus at 7:58 AM and the second bus at 8:19 AM. Find the speeds of the cyclist and the buses.
|
Solution. Let the speed of the buses be $v_{1}$ km/min, and the speed of the cyclist be $v_{2}$ km/min. Since the first bus traveled for 40 minutes (7:58 AM - 7:18 AM = 40 minutes) before meeting the cyclist, the second bus for 31 minutes (8:19 AM - 7:48 AM = 31 minutes), and the cyclist spent 30 minutes (7:58 AM - 7:28 AM = 30 minutes) and 51 minutes (8:19 AM - 7:28 AM = 51 minutes) before meeting the buses, we have the system of equations:
$$
\left\{\begin{array}{l}
40 v_{1}+30 v_{2}=37 \\
31 v_{1}+51 v_{2}=37
\end{array}\right.
$$
from which $v_{1}=0.7$ km/min, or 42 km/h; $v_{2}=0.3$ km/min, or 18 km/h.
Remark. If the speed of the buses $v_{1}$ and the speed of the cyclist $v_{2}$ are expressed in kilometers per hour, the solution of the problem reduces to the system:
$$
\left\{\begin{array}{l}
\frac{2}{3} v_{1}+\frac{1}{2} v_{2}=37 \\
\frac{31}{60} v_{1}+\frac{51}{60} v_{2}=37
\end{array}\right.
$$
Obviously, the numerical data of this system complicate its solution.
Answer: the speed of the bus is 42 km/h, the speed of the cyclist is 18 km/h.
|
42
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71 (1187). A tourist left from $A$ to $B$. After 1 hour and 20 minutes, a cyclist left from $A$ in the same direction and overtook the tourist after 30 minutes. Upon arriving at $B$, the cyclist, without stopping, turned back and met the tourist 1.5 hours after the first meeting. Find the speeds of the tourist and the cyclist, given that the distance $A B$ is 24 km.
72
|
Solution. Let the speed of the cyclist be $v_{1}$ km/h, and the speed of the tourist be $v_{2}$ km/h. Since the cyclist overtook the tourist 30 minutes $\left(\frac{1}{2}\right.$ hours) after departure and traveled $\frac{1}{2} v_{1}$ km, while the tourist walked 1 hour 20 minutes longer than the cyclist $\left(1 \frac{1}{3} \text{ hours} + \frac{1}{2} \text{ hours} = 1 \frac{5}{6} \text{ hours}\right)$ and walked a distance of $\frac{11}{6} v_{2}$ km during this time, we have the equation $\frac{1}{2} v_{1} = \frac{11}{6} v_{2}$.
Until the second meeting, the tourist walked $3 \frac{1}{3}$ hours $\left(1 \frac{5}{6} \text{ hours} + 1 \frac{1}{2} \text{ hours} = 3 \frac{1}{3} \text{ hours}\right)$, and the cyclist - 2 hours $\left(\frac{1}{2} \text{ hours} + 1 \frac{1}{2} \text{ hours} = 2 \text{ hours}\right)$. Since the sum of the distances traveled by the tourist and the cyclist until the second meeting is 48 km $(24 \cdot 2 = 48)$, we have the equation $2 v_{1} + \frac{10}{3} v_{2} = 48$.
We obtain the system of equations:
$$
\left\{\begin{array}{l}
2 v_{1} + \frac{10}{3} v_{2} = 48 \\
\frac{1}{2} v_{1} - \frac{11}{6} v_{2} = 0
\end{array}\right.
$$
Multiplying both sides of the second equation by 4, we can easily solve this system:
$$
\left\{\begin{array}{l}
2 v_{1} - \frac{22}{3} v_{2} = 0 \\
2 v_{1} + \frac{10}{3} v_{2} = 48
\end{array}\right.
$$
from which $\frac{32}{3} v_{2} = 48$, i.e., $v_{2} = 4.5$ km/h, $v_{1} = 16.5$ km/h.
Answer: the speed of the cyclist is 16.5 km/h, the speed of the tourist is 4.5 km/h.
$\triangle 72$ (1192). A train traveled from $A$ to $B$ at a speed of 60 km/h, and returned from $B$ to $A$ at a speed 20 km/h less. What is the average speed of the train?
Solution. Let the distance from $A$ to $B$ be $s$ kilometers. Then the train traveled from $A$ to $B$ in $\frac{s}{60}$ hours, and from $B$ to $A$ in $\frac{s}{40}$ hours. Since the average speed is the quotient of the distance divided by the time, we have:
$$
v_{\mathrm{cp}} = \frac{2 s}{\frac{s}{60} + \frac{s}{40}} = 48 \text{ (km/h)}
$$
Note. Draw the students' attention to the fact that the average speed is not equal to the arithmetic mean of the speeds on different segments of the journey.
Answer: 48 km/h.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85 (954). Prove that the value of the numerical expression $11^{11}+$ $+12^{12}+13^{13}$ is divisible by 10.
|
Solution. It is sufficient to prove that the value of the numerical expression ends in zero. Indeed, the number $11^{11}$ ends in the digit 1. To determine which digit the number $12^{12}$ ends in, it is advisable to represent $12^{12}$ as $\left(12^{4}\right)^{3}$ and note that $12^{4}$ ends in the digit 6. Therefore, the number $12^{12}$ also ends in the digit 6. Let's calculate which digit the number $13^{13}$ ends in. The number $13^{2}$ ends in the digit 9, the number $13^{4}$ ends in the digit 1, and the number $13^{13}$ ends in the digit 3, since $13^{13} = 13^{4 \cdot 3} \cdot 13$. Therefore, the sum $11^{11} + 12^{12} + 13^{13}$ ends in the digit 0.
$\square 86(955)$. Prove that the value of the expression $n^{3} + 3 n^{2} + 5 n + 3$ is divisible by 3 for any natural $n$.
Solution. Method 1.
$$
\begin{aligned}
n^{3} + 3 n^{2} + 5 n + 3 & = n^{3} + 3 n^{2} + 6 n - n + 3 = \\
= (n^{3} - n) + (3 n^{2} + 6 n) + 3 & = (n-1) n (n+1) + 3 n (n+2) + 3.
\end{aligned}
$$
Since each of the three terms is divisible by 3 (the first term is the product of three consecutive natural numbers), the sum is also divisible by 3.
Method 2. $n^{3} + 3 n^{2} + 5 n + 3 = n (n^{2} + 5) + 3 (n^{2} + 1)$. Since the second term is divisible by 3, it remains to prove the divisibility by 3 of the value of the expression $n (n^{2} + 5)$. We will prove this by complete induction, dividing the set of natural numbers into 3 classes:
1) $n = 3 k$; 2) $n = 3 k + 1$; 3) $n = 3 k + 2$, where $k \in \mathbb{N}$.
If $n = 3 k$, the divisibility of the value of the expression $n (n^{2} + 5)$ by 3 is obvious. (If one of the factors is divisible by some number, then the product is also divisible by that number.)
If $n = 3 k + 1$, then $n^{2} + 5 = 9 k^{2} + 6 k + 6$, i.e., the value of the expression $n^{2} + 5$, and therefore the value of the expression $n (n^{2} + 5)$, is divisible by 3.
Similarly, the divisibility by 3 of the value of the expression $n (n^{2} + 5)$ is proved for $n = 3 k + 2$.
Since the divisibility by 3 of the value of the expression $n (n^{2} + 5)$ has been proved in each of the three possible cases, the statement is proved for any natural $n$.
$\triangle 87$ (956). What digit does the number $1982^{1982}$ end in?
Solution. We will establish the pattern in which the last digits of the natural powers of the number 1982 repeat. The number 1982 ends in the digit 2, the number $1982^{2}$ ends in the digit 4, the number $1982^{3}$ ends in the digit 8, the number $1982^{4}$ ends in the digit 6, and the number $1982^{5}$ ends in the digit 2. Clearly, the last digit of the natural powers of the number 1982 will repeat every four powers. Since $1982^{1982} = 1982^{495 \cdot 4 + 2}$, $1982^{1982}$, like $1982^{2}$, ends in the digit 4.
Answer: the digit 4.
$\square 88(957)$. Find a five-digit number if it is known that when this number is multiplied by 9, the result is a five-digit number written with the same digits but in reverse order.
Solution. Let $\overline{a b c d e}$ be the desired five-digit number. By the condition, we have $\overline{a b c d e} \cdot 9 = \overline{e d c b a}$.
We will solve the problem by selecting the digits. Clearly, $a = 1$, because otherwise, multiplying a five-digit number by 9 would not result in a five-digit number. Therefore, $e = 9$. We have:
$$
\times \overline{\overline{1 b c d 9}}
$$
Next, by selection, we find that $b = 0$. We get:
$$
\times \begin{array}{r}
\overline{10 c d 9} \\
\overline{9 d c 01}
\end{array}
$$
Therefore, $d$ is either 2 or 8. If $d = 2$, we check and find that none of the remaining digits (3, 4, 5, 6, 7, 8) for $c$ fit. Therefore, $d = 8$. We have:
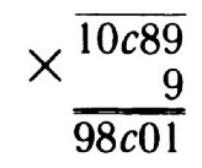
Therefore, $c = 9; \overline{a b c d e} = 10989$.
Answer: 10989.
|
10989
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
91 (960). Prove the validity of the equality:
1) $(n-2)(n-1) n(n+1)+1=\left(n^{2}-n-1\right)^{2}$;
2) $n(n+1)(n+2)(n+3)+1=\left(n^{2}+3 n+1\right)^{2}$.
|
Solution.
1) $(n-2)(n-1) n(n+1)+1=(n-2)(n+1)(n-1) n+1=$ $\left(n^{2}-n-2\right)\left(n^{2}-n\right)+1=\left(n^{2}-n\right)^{2}-2\left(n^{2}-n\right)+1=$ $\left(n^{2}-n-1\right)^{2}$
2) $n(n+1)(n+2)(n+3)+1=n(n+3)(n+1)(n+2)+1=$ $=\left(n^{2}+3 n\right)\left(n^{2}+3 n+2\right)+1=\left(n^{2}+3 n\right)^{2}+2\left(n^{2}+3 n\right)+1=$ $=\left(n^{2}+3 n+1\right)^{2}$.
3 remark. It is advisable to draw students' attention to the fact that from the proven equalities follows the theorem: the product of four consecutive natural numbers, increased by one, is equal to the square of some natural number.
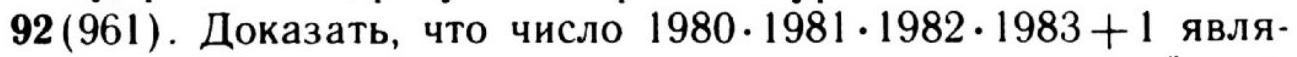
is the square of some natural number $x$, and find $x$.
Solution. Method I. You can use the identity proven in the previous problem.
From the identity of problem 91 (1) it follows that $1980 \cdot 1981 \cdot 1982 \times$ $\times 1983+1=\left(1982^{2}-1982-1\right)^{2}=3926341^{2}$.
From the identity of problem $91(2)$ it follows that
$1980 \cdot 1981 \cdot 1982 \cdot 1983+1=\left(1980^{2}+3 \cdot 1980+1\right)^{2}=3926341^{2}$.
Method II. Without using the identities of the previous problem, transform the given expression. Let $n=1980$. Then
$1980 \cdot 1981 \cdot 1982 \cdot 1983+1=n(n+1)(n+2)(n+3)+1=\left(n^{2}+3 n\right) \times$
$$
\times\left(n^{2}+3 n+2\right)+1=\left(n^{2}+3 n+1\right)^{2}=\left(1980^{2}+3 \cdot 1980+1\right)^{2}=
$$
$$
=3926341^{2} \text {. }
$$
Answer: $x=3926341$.
$93(962)$. Factorize:
1) $\cdot a^{2}-2 a-3$; 2) $b^{2}-7 b+12$; 3) $a^{3}+a^{2}-12$;
2) $x^{3}-7 x+6$; 5) $n^{2}-7 n+10$; 6) $\cdot n^{2}-n-2$.
Solution.
1) $a^{2}-2 a-3=a^{2}+a-3 a-3=a(a+1)-3(a+1)=$ $=(a+1)(a-3)$.
2) $b^{2}-7 b+12=b^{2}-3 b-4 b+12=b(b-3)-4(b-3)=$ $=(b-3)(b-4)$.
3) $a^{3}+a^{2}-12=\left(a^{3}-8\right)+\left(a^{2}-4\right)=(a-2)\left(a^{2}+2 a+4\right)+$ $+(a-2)(a+2)=(a-2)\left(a^{2}+2 a+4+a+2\right)=$ $=(a-2)\left(a^{2}+3 a+6\right)$.
4) $x^{3}-7 x+6=\left(x^{3}-1\right)-7 x+7=(x-1)\left(x^{2}+x+1\right)-$ $-7(x-1)=(x-1)\left(x^{2}+x-6\right)=(x-1)\left(\left(x^{2}-4\right)+(x-2)\right)=$ $=(x-1)(x-2)(x+3)$.
5) $n^{2}-7 n+10=n^{2}-2 n-5 n+10=n(n-2)-5(n-2)=$ $=(n-2)(n-5)$.
6) $n^{2}-n-2=\left(n^{2}-1\right)-n-1=(n-1)(n+1)-(n+1)=$ $=(n+1)(n-2)$.
|
3926341
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
105(974). Determine the value of $b$, if the graph of the function defined by the formula passes through the point with coordinates $(3 ; 10)$:
1) $y=x+b$;
2) $y=3 x+b$
3) $y=-\frac{1}{3} x+b$;
4) $y=-\frac{1}{2} x+b$.
A n s w e r: 1) $b=7$; 2) $b=1$; 3) $b=11$; 4) $b=11.5$.
106(975). Define the function by a formula whose graph is a straight line passing through points $A$ and $B$:
1) $A(-6 ;-3), B(2 ;-3)$
2) $A(-4 ;-4), B(3,3)$
3) $A(2 ; 2), B(0 ; 4)$;
4) $A(3 ;-8), B(-5 ; 32)$.
A n s w e r: 1) $y=-3$; 2) $y=x$; 3) $y=-x+4$; 4) $y=-5 x+7$.
N o t e. During club sessions, students can be introduced to the equation of a straight line passing through two points with given coordinates. Otherwise, solving such types of problems reduces to solving a system of two linear equations with two unknowns, which we obtain by substituting the coordinates of the given points into the equation of the line $y=k x+b$. Thus, solving problem (4) we get the system:
$$
\left\{\begin{array}{l}
-8=3 k+b \\
32=-5 k+b
\end{array}\right.
$$
solving which we find $k=-5, b=7$, hence $y=-5 x+7$.
$\triangle$ 107(976). A cylindrical helical spring of height 122 mm is to be made from steel wire with a diameter of 5 mm. Find the number of turns of the spring, if the gap between the turns of the unloaded spring should be 8 mm.
|
Solution. Let $x$ be the number of turns in the spring. Considering that the number of gaps in the spring is one less than the number of turns, according to the problem, we set up the equation $5x + 8(x-1) = 122$, from which $x = 10$.
Answer: 10 turns.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108(977). A person, living in a cottage near a railway station, usually manages to walk from the cottage to the station in time for the train departure in 18 minutes. Once, this person was delayed at home before leaving by several minutes. Although after that, he walked 1.2 times faster than usual, he still missed the train by 2 minutes. How many minutes was he delayed at home before leaving?
|
Solution. If the usual speed of the gardener is $v$ m/min, then the distance from the garden to the station is $18 v$ meters. When the gardener walked at a speed of $1.2 v$ m/min, it took 15 minutes to travel from home to the garden $(18 v: 1.2 v=15)$. Since the gardener was 2 minutes late, the train left 13 minutes after the gardener left home $(15-2=13)$. Therefore, he was delayed at home for 5 minutes $(18-13=5)$.
Answer: 5 minutes.
$\triangle 109(978)$. At 13:00, water started to be filled into a swimming pool from one pipe to fill it by 16:00 the next day. After some time, another identical pipe was turned on because the pool needed to be filled by 12:00 the next day. At what time was the second pipe turned on?
Solution. Since the pool needed to be filled 4 hours earlier $(16-12=4)$, the second pipe (identical to the first) was turned on 4 hours earlier. Therefore, the second pipe was turned on at 8:00 AM $(12-4=8)$.
Answer: at 8:00 AM.
$\triangle 110(979)$. An electric train passed a signal light in 5 seconds and a platform 150 meters long in 15 seconds. What is the length of the train and its speed?
Solution. Method I. Let the speed of the train be $x$ m/s. Then the length of the train is $5 x$ meters. In 15 seconds, the train travels a distance of $15 x$ meters, or $(150+5 x)$ meters. We have the equation $15 x=150+5 x$, from which $x=15$, i.e., the speed of the train is $15 \mathrm{~m} / \mathrm{s}$, and its length is 75 meters.
Method II. Since the time it takes for any point on the train to pass the platform is 10 seconds $(15-5=10)$, the speed of the train is 15 m/s $(150: 10=15)$, and its length is 75 meters $(15 \cdot 5=75)$.
Answer: $75 \mathrm{~m} ; 15 \mathrm{~m} / \mathrm{s}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
113(982). A cyclist arrived from point $A$ to point $B$ at the appointed time, moving at a certain speed. If he had increased this speed by 3 km/h, he would have arrived at the destination one hour earlier, and if he had traveled 2 km less per hour than he actually did, he would have been an hour late. Determine the distance between points $A$ and $B$, the speed of the cyclist, and the time of his journey.
$\mathrm{P}$ e shen i e. Let the cyclist, arriving from point $A$ to point $B$ at the appointed time, move at a speed of $v$ kilometers per hour and spend $t$ hours on the entire journey. Then the distance between points $A$ and $B$ is $v t$ kilometers, which, according to the problem, is equal to $(v+3)(t-1)$ or $(v-2)(t+1)$ km.
We have the system of equations:
$$
\left\{\begin{array}{l}
(v+3)(t-1)=v t \\
(v-2)(t+1)=v t
\end{array}\right.
$$
from which $t=5$ (hours), $v=12$ (km/h), the distance from $A$ to $B$ is 60 km. Answer: 60 km, 12 km/h, 5 hours.
$114(983)$. A reserve of hay was made for a certain number of horses for a certain period of time. If there were two fewer horses, the reserve of hay would have lasted for 10 more days; if there were two more horses, the reserve of hay would have lasted for 6 days less than the planned period. How many horses were there and for how many days was the reserve of hay made?
$\mathrm{Pe}$ e n i e. Let there be $x$ horses and the reserve of hay was made for $y$ days. If there were $x-2$ horses, the reserve of hay would have lasted for $(y+10)$ days. If there were $x+2$ horses, the reserve of hay would have lasted for $(y-6)$ days. If we denote the mass of the stored hay by $m$ (in kg), then one horse requires $\frac{m}{x y}$ kilograms per day, or $\frac{m}{(x-2)(y+10)}$, or $\frac{m}{(x+2)(y-6)}$.
We have the system of equations:
$$
\left\{\begin{array}{l}
(x-2)(y+10)=x y \\
(x+2)(y-6)=x y
\end{array}\right.
$$
from which $x=8, y=30$.
Answer: 8 horses, for 30 days.
$\square 115(984)$. The first pipe fills the pool in half the time it takes the second pipe to fill $\frac{2}{3}$ of this pool. The second pipe fills the pool alone 6 hours longer than the first pipe alone. How long does each pipe take to fill the pool separately?
|
Solution. Let the first pipe fill the pool in $x$ hours, then the second pipe - in $(x+6)$ hours; $\frac{2}{3}$ of the pool the second pipe will fill in $\frac{2}{3}(x+6)$ hours.
According to the problem, we have the equation
$$
x=\frac{1}{2} \cdot \frac{2}{3}(x+6)
$$
from which $x=3, x+6=9$.
Answer: the first pipe fills the pool in 3 hours, the second in 9 hours.
$116(985)$. A copper and zinc alloy contained 640 g more copper than zinc. After $\frac{6}{7}$ of the copper and $60\%$ of the zinc were extracted from the alloy, the mass of the alloy became 200 g. What was the original weight of the alloy?
Solution. Let the alloy contain $x$ g of zinc and $(x+640)$ g of copper. Since $\frac{1}{7}$ of the copper and $\frac{2}{5}$ of the zinc remained in the alloy, we have the equation
$$
\frac{1}{7}(x+640)+\frac{2}{5} x=200
$$
from which $x=200$.
Thus, the alloy originally contained 200 g of zinc and 840 g of copper $(200+640=840)$, and the alloy weighed 1040 g $(200+$ $+840=1040)$, or 1 kg 40 g.
Answer: 1 kg 40 g.
|
1040
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
119(988). In a flask, there is a solution of table salt. From the flask, $\frac{1}{5}$ of the solution is poured into a test tube and evaporated until the percentage of salt in the test tube doubles. After this, the evaporated solution is poured back into the flask. As a result, the salt content in the flask increases by $3 \%$. Determine the initial percentage of salt.
|
Solution. Before solving the problem, it is reasonable to clarify how the expression "percentage content of salt" should be understood (this is the ratio of the mass of salt to the mass of the solution, expressed as a percentage).
Let the initial mass of the solution in the flask be $m$ grams, the mass of salt in it be $m_{\text {s }}$ grams, and the initial percentage content of salt be $x \%$, i.e.,
$$
x=\frac{m_{s}}{m} \cdot 100
$$
According to the problem, $\frac{1}{5}$ of the solution was poured out from the flask, i.e., $\frac{m}{5}$ grams, so $\frac{4}{5} m$ grams remained. Since the amount of salt does not change during evaporation, to double the percentage content of salt in the test tube, the solution after evaporation should be $\frac{m}{10}$ grams, and a total of $\frac{9}{10}$ grams $\left(\frac{4}{5} m+\frac{m}{10}=\frac{9}{10} m\right)$.
Since the percentage content of salt increased by $3 \%$, we have:
$$
x+3=\frac{m_{s} \cdot 100}{\frac{9}{10} m}
$$
From equations (1) and (2), we get the equation
$$
x+3=\frac{10}{9} x, \text { from which } x=27
$$
Answer: $27 \%$.
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
120 (989). The road from point $A$ to point $B$ is 11.5 km long and goes first uphill, then on flat ground, and finally downhill. The pedestrian spent 2 hours and 54 minutes on the journey from $A$ to $B$, and 3 hours and 6 minutes on the return journey. The pedestrian's walking speed uphill was 3 km/h, on flat ground - 4 km/h, and downhill - 5 km/h. How many kilometers does the part of the road that goes on flat ground constitute?
|
Solution. Let the length of the road uphill be $x$ kilometers, on the plain be $y$ kilometers, and downhill be $z$ kilometers. According to the problem, we form a system of three linear equations with three unknowns:
88
$$
\left\{\begin{array}{l}
\frac{x}{3}+\frac{y}{4}+\frac{z}{5}=2.9 \\
\frac{z}{3}+\frac{y}{4}+\frac{x}{5}=3.1 \\
x+y+z=11.5
\end{array}\right.
$$
By adding the first two equations of the system, we get the equation
$$
\frac{8}{15}(x+z)+\frac{y}{2}=6 .
$$
Substituting the value of $x+z$ from the third equation of the system into this equation, we get the equation
$$
\frac{8}{15}\left(\frac{23}{2}-y\right)+\frac{y}{2}=6
$$
from which $y=4$.
Remark. The solution to the problem can be reduced to forming and solving a system of two linear equations with two unknowns if the length of the road on the plain is expressed as the difference between the total length of the road (11.5 km) and the lengths of the roads uphill and downhill.
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
125. A steamship from Kyiv to Kherson takes three days, and from Kherson to Kyiv - four days (without stops). How long will it take for rafts to float from Kyiv to Kherson?
|
Solution. To answer the question of the problem, the distance from Kyiv to Kherson needs to be divided by the speed of the Dnieper current. If $s$ is the distance from Kyiv to Kherson, then the speed of the steamboat downstream is $-\frac{s}{3}$ (km/day), and the speed of the steamboat upstream is $-\frac{s}{4}$ (km/day). Then, the speed of the Dnieper current, which is half the difference between the downstream and upstream speeds, is
$\left(\frac{s}{3}-\frac{s}{4}\right): 2=\frac{s}{24}$ (km/day). Therefore, the required time is $s: \frac{s}{24}=24$ (days).
Answer: 24 days.
$\triangle$ 126. The brother says to the sister: “When Aunt Katya was as old as we are together now, you were as old as I am now. And when Aunt Katya was as old as you are now, you were then ... . How old was the sister then
Answer: the sister was born that year.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
127. We collected 100 kg of mushrooms. It turned out that their moisture content was $99 \%$. When the mushrooms were dried, the moisture content decreased to $98 \%$. What was the mass of these mushrooms after drying?
|
Solution. According to the condition, in 100 kg of mushrooms, there is 1 kg of dry matter $(100-0.99 \cdot 100=1)$. Since the mass of dry matter in the total mass of mushrooms is constant (1 kg) and after drying it became $2 \%(100-98=2)$, the mass of mushrooms after drying became 50 kg (if $2 \%-1$ kg, then $100 \%-50$ kg $).$
Answer: 50 kg.
Remark. It is advisable to solve this problem simultaneously with problem 1188 from [1].
$\triangle$ 128. In how many ways can a list of 9 students be compiled?
Answer: 9 !
$\triangle$ 129. There are 35 students in the 6th grade. They exchanged photographs with each other. How many photographs were distributed in total? Answer: $35 \cdot 34=1190$.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
130. How many four-digit numbers can be formed from the digits $0,1,2,3,4,5$, if the numbers must be odd and digits may be repeated?
|
S o l u t i o n. For the first position, we can choose any of the five digits (excluding zero). For the second and third positions, we can choose any of the six digits, as digits can be repeated. For the last position, we can choose any of the three odd digits. Therefore, the total number of four-digit numbers is $5 \cdot 6 \cdot 6 \cdot 3=540$
A n s w e r: 540.
|
540
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
139. On a meadow, grass grows. If 9 cows were let onto the meadow, they would empty it in 4 days. If 8 cows were let onto the meadow, they would eat all the grass in 6 days. How many cows can graze on the meadow all the time while the grass grows?
|
Solution. Let $x$ kilograms of grass grow on the meadow per day, and one cow eats $y$ kilograms of grass per day. We have the system of equations:
$$
\left\{\begin{array}{l}
a+4 x-9 \cdot 4 y=0 \\
a+6 x-8 \cdot 6 y=0
\end{array}\right.
$$
where $a$ is the amount of grass that grew on the meadow before the cows were let in. Subtracting the first equation from the second, we find $x=6 y$. If the desired number of cows is $n$, then $n y=x$, from which $n=\frac{x}{y}=6$.
Remark. This problem can also be solved without setting up a system of equations. Indeed, if $a$ kilograms is the initial amount of grass, and $x$ kilograms is the amount of grass that grows on the meadow per day, then in one day one cow eats $\frac{a+4 x}{36}$ or $\frac{a+8 x}{48}$ kilograms of grass. We have the equation
$$
\frac{a+4 x}{36}=\frac{a+8 x}{48},
$$
from which $a=2 x$. Therefore, one cow eats $\frac{x}{6}$ kilograms of grass per day, where $x$ kilograms is the amount of grass that grows on the meadow per day. Therefore, 6 cows can be fed on the meadow.
Answer: 6 cows.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
158. It is known that the number $a$ is $n$ times greater than the number $b$, and the sum of the numbers $a$ and $b$ is $m$ times greater than their difference. Find the sum of the numbers $m$ and $n$, if $m$ and $n$ are natural numbers.
94
|
Given the problem, we set up the system of equations:
$$
\left\{\begin{array}{l}
\frac{a}{b}=n \\
\frac{a+b}{a-b}=m
\end{array}\right.
$$
From the second equation, express $\frac{a}{b}$. We have:
$$
\begin{gathered}
a+b=m a-m b, a(1-m)=-b(m+1) \\
\frac{a}{b}=\frac{m+1}{m-1}=\frac{m-1+2}{m-1}=1+\frac{2}{m-1} .
\end{gathered}
$$
Therefore,
$$
\frac{a}{b}=n=1+\frac{2}{m-1}
$$
Since $m$ and $n$ are natural numbers, then $n=3$ when $m=2$, $n=2$ when $m=3$, and $m+n=5$.
Answer: $m+n=5$.
$\triangle$ 159. Justify the rule for multiplying two-digit numbers by 11.
Solution.
$$
\overline{a b} \cdot 11=(10 a+b)(10+1)=100 a+10(a+b)+b
$$
where $a$ is the hundreds digit, $a+b$ is the tens digit, and $b$ is the units digit.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
173. In the Olympiad, 55 schoolchildren participated. All of them submitted their work. During the checking of each problem, one of three grades was given: «+» - the problem was solved, «-» - the problem was attempted, «0» - the problem was not attempted. After checking all the works, it turned out that in no two works did the number of «+» grades and the number of «-» grades coincide simultaneously. What is the smallest number of problems that could have been offered at the Olympiad?
|
Instruction. If the number of tasks was $a$, then
$$
\frac{(a+1)(a+2)}{2}=55 \text { when } a=9 .
$$
A n s w e r: 9 tasks.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
176. Among 150 schoolchildren, only boys collect stamps. 67 people collect stamps of the USSR, 48 people - of Africa, and 32 people - of America, 11 people only collect stamps of the USSR, 7 people - only of Africa, 4 people - only of America, and only Ivanov collected stamps of the USSR, Africa, and America. Find the maximum number of girls.
|
Solution. Let's represent the condition of the problem using Euler circles (Fig. 17).
We have a system of three equations:
\[
\begin{cases}
x + y + 1 = 56 & (56 = 67 - 11), \\
x + z + 1 = 41 & (41 = 48 - 7), \\
y + z + 1 = 28 & (28 = 32 - 4)
\end{cases}
\]
From this, \(2(x + y + z) = 122\), i.e., \(x + y + z = 61\).
Therefore, 84 boys collect stamps \((61 + 11 + 7 + 4 + 1)\), and the maximum number of girls is 66 \((150 - 84 = 66)\).
Answer: 66 girls.
Remark. From the system of equations obtained during the solution, it is easy to find \(x, y\), and \(z (x = 34, y = 21, z = 6)\), but for solving the problem, it is sufficient to find the sum \(x + y + z\). To reinforce the methods of solving systems of equations, it is advisable to suggest that students solve the obtained system, as well as problem 1279 from \([4]\).
|
66
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15(1091). Prove that the value of the expression $\sqrt{11+6} \sqrt{ } 2+$ $+\sqrt{11-6 \sqrt{2}}$ is a natural number.
|
Proof. I method. Let
$$
\sqrt{11+6 \sqrt{2}}+\sqrt{11-6 \sqrt{2}}=A
$$
Then
$$
A^{2}=11+6 \sqrt{2}+11-6 \sqrt{2}+2 \sqrt{121-72}=36
$$
from which
$$
\sqrt{A^{2}}=|A|=6, \text { i.e. }|\sqrt{11+6 \sqrt{2}}+\sqrt{11-6 \sqrt{2}}|=6
$$
Since under the modulus sign is the sum of two radicals, each of which is a positive number, then
$$
|\sqrt{11+6 \sqrt{2}}+\sqrt{11-6 \sqrt{2}}|=\sqrt{11+6 \sqrt{2}}+\sqrt{11-6 \sqrt{2}}=6
$$
Since $6 \in \boldsymbol{N}$, the statement is proved.
II method. Since $11+6 \sqrt{2}=9+2 \cdot 3 \sqrt{2}+2=(3+\sqrt{2})^{2}$, $11-6 \sqrt{2}=(3-\sqrt{2})^{2}$, then $\sqrt{11+6 \sqrt{2}}+\sqrt{11-6 \sqrt{2}}=\sqrt{(3+\sqrt{2})^{2}}+$ $+\sqrt{(3-\sqrt{2})^{2}}=|3+\sqrt{2}|+|3-\sqrt{2}|=3+\sqrt{2}+3-\sqrt{2}=6$.
Remark. The equalities $11+6 \sqrt{2}=(3+\sqrt{2})^{2}$ and $11-6 \sqrt{2}=(3-\sqrt{2})^{2}$ can also be obtained using the method of undetermined coefficients. Indeed, if $11+6 \sqrt{2}=(a+b \sqrt{2})^{2}$, where $a \in \boldsymbol{N}$ and $b \in \boldsymbol{N}$, then from the equality $\left(a^{2}+2 b^{2}\right)+2 a b \sqrt{2}=11+6 \sqrt{2}$ we conclude that $a^{2}+2 b^{2}=11, a b=3$, from which $a=3, b=1$, i.e. $11+6 \sqrt{2}=(3+\sqrt{2})^{2}$. Similarly, it is established that $11-$ $-6 \sqrt{2}=(3-\sqrt{2})^{2}$.
|
6
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
23(1099). A bus left city $M$ for city $N$ at a speed of 40 km/h. A quarter of an hour later, it met a car traveling from city $N$. This car reached city $M$, 15 minutes later it set off back to city $N$ and overtook the bus 20 km from city $N$. Find the distance between cities $M$ and $N$, if the speed of the car is 50 km/h.
|
Solution. Since the bus traveled 10 km in a quarter of an hour $(40: 4=10)$, the bus met the car 10 km from city $M$. If the distance between the cities is $s$ kilometers, then by the time the car overtook the bus, the bus had traveled $(s-30)$ kilometers from the moment of the meeting, spending $\frac{s-30}{40}$ hours on this. By that time, the car had traveled 20 km more, i.e., $(s-10)$ kilometers, spending $\frac{s-10}{50}$ hours on the entire journey (from the moment of the meeting). Considering that the car stood in city $M$ for 15 minutes $\left(\frac{1}{4} \text{ hours}\right)$, we get the equation
$$
\frac{s-10}{50}+\frac{1}{4}=\frac{s-30}{40}
$$
from which $s=160$ km.
Answer: 160 km.
$24(1100)$. Two boys started on a running track 50 m long with a 1-second interval. The boy who started second caught up with the first 10 m from the starting line, ran to the end of the track, and then ran back at the same speed. At what distance from the end of the track did he meet the first boy, if it is known that this meeting occurred 10 seconds after the first boy started?
Solution. Let the speed of the boy who started first be $v_{1}$ meters per second, and the speed of the boy who started second be $v_{2}$ meters per second $\left(v_{2}>v_{1}\right)$. The distance of 10 m, each of the starters ran in $\frac{10}{v_{1}}$ seconds and $\frac{10}{v_{2}}$ seconds, respectively. Since one boy caught up with the other 10 m from the starting line, and they started with a 1-second interval, we have the equation
$$
\frac{10}{v_{1}}-\frac{10}{v_{2}}=1
$$
Since, according to the problem, the boys met 10 seconds after the first boy started (9 seconds after the second boy started) and by the time of the meeting, both had run a distance equal to twice the length of the running track ( $50 \cdot 2=100$ ), we have the equation
$$
10 v_{1}+9 v_{2}=100
$$
Thus, we have a system of two equations with two unknowns:
$$
\left\{\begin{array}{l}
\frac{10}{v_{1}}-\frac{10}{v_{2}}=1 \\
10 v_{1}+9 v_{2}=100
\end{array}\right.
$$
From the first equation, express one of the unknowns (for example, $v_{2}$) and substitute its value into the second equation. We have $v_{2}=\frac{10 v_{1}}{10-v_{1}}, v_{1}^{2}-29 v_{1}+100=0$, from which $v_{1}^{\prime}=4 \text{ m/s}, v_{1}^{\prime \prime}=25 \text{ m/s}$.
Obviously, the condition of the problem is satisfied by one root $v_{1}=$ $=4 \text{ m/s}$.
Thus, the speed of the first boy is $4 \text{ m/s}$. The second boy met the first at a distance of 10 m from the end of the track $(10=50-10 \cdot 4)$.
Remark. To verify, it is advisable to find the speed of the second boy $\left(v_{2}=\frac{10 v_{1}}{10-v_{1}}=\frac{10 \cdot 4}{10-4}=6 \frac{2}{3} \text{ m/s}\right)$ and calculate the required distance in another way:
$$
9 v_{2}-50=9 \cdot \frac{20}{3}-50=10 \text{ m}
$$
Answer: 10 m.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25(1101). The distance between the ports $A$ and $B$ is covered by the steamboat downstream in 5 hours, and upstream in 6 hours. How many hours will it take for a raft to drift downstream this distance?
|
Solution. I method. To answer the question of the problem, the distance $AB$ needs to be divided by the speed of the current. Let $AB = s$ kilometers. Then the speed of the steamer downstream is $\frac{s}{5}$ kilometers per hour, the speed upstream is $-\frac{s}{6}$ kilometers per hour, the speed of the current is $-\left(\frac{s}{5}-\frac{s}{6}\right): 2=\frac{s}{60}$ kilometers per hour. The required time is $-s: \frac{s}{60}=60$ hours.
II method. Let the speed of the steamer in still water be $v_{1}$ kilometers per hour, and the speed of the current be $v_{2}$ kilometers per hour. Then, according to the condition, the distance $AB$ is equal to $5\left(v_{1}+v_{2}\right)$ kilometers, or $6\left(v_{1}-v_{2}\right)$ kilometers. From the equation $5\left(v_{1}+v_{2}\right)=6\left(v_{1}-v_{2}\right)$, we find $v_{1}=11 v_{2}$. Then the distance $AB$ is equal to $60 v_{2}$ kilometers, and the required time is $-60 v_{2}: v_{2}=60$ hours.
Answer: 60 hours.
$\square$ 26(1102). A motorboat traveled 90 km downstream in a certain time. In the same time, it would have traveled 70 km upstream. What distance would a log float in this time?
I method. Let $t$ hours be the time it takes for the motorboat to travel 90 km downstream (and also 70 km upstream). Then the speed of the motorboat downstream is $\frac{90}{t}$ kilometers per hour, the speed upstream is $\frac{70}{t}$ kilometers per hour, the speed of the current is $\left(\frac{90}{t}-\frac{70}{t}\right): 2=\frac{10}{t}$ kilometers per hour, and the required distance is $\frac{10}{t} \cdot t=10$ km.
II method. Let $v$ kilometers per hour be the motorboat's own speed, and $v_{1}$ kilometers per hour be the speed of the current. Then $\left(v+v_{1}\right)$ kilometers per hour is the speed of the motorboat downstream, and $\left(v-v_{1}\right)$ kilometers per hour is the speed of the motorboat upstream.
Downstream, the motorboat covers a distance of 90 km in $\frac{90}{v+v_{1}}$ hours. To cover a distance of 70 km upstream, the motorboat needs $\frac{70}{v-v_{1}}$ hours.
According to the condition, we have $\frac{90}{v+v_{1}}=\frac{70}{v-v_{1}}$, from which $v=8 v_{1}$.
Thus, the speed of the current is 9 times less than the speed of the motorboat downstream $\left(v+v_{1}=8 v_{1}+v_{1}=9 v_{1}\right)$. Therefore, in the same time, a log will float a distance 9 times less than the motorboat downstream. Thus, the required distance is 10 km $(90: 9=10)$.
Answer: 10 km.
$\square 27(1103)$. From points $A$ and $B$, two cyclists simultaneously set off towards each other and met 30 km from $B$.
Upon arriving at $A$ and $B$, they turned back. The second meeting occurred 18 km from $A$. Find the distance between $A$ and $B$.
Solution. I method. It is not difficult to understand that from the start of the movement to the first meeting, both cyclists together traveled a distance equal to $AB$, and by the time of the second meeting, they traveled three times the distance ( $3AB$ ). Thus, each of them traveled three times more by the second meeting than by the first. The cyclist who set off from $B$ traveled 30 km to the first meeting. Therefore, by the second meeting, he traveled 90 km ( $30 \cdot 3=90$ ). Therefore, the distance from $A$ to $B$ is 72 km $(90-18=72)$.
II method. Let $AB = s$ (in km). Since the speeds of both cyclists are constant, the ratios of the distances traveled by the cyclists to the first and second meetings are equal. Thus, we have the equation
$$
\frac{s-30}{30}=\frac{2s-18}{s+18}
$$
from which $s=72$ km.
Answer: 72 km.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33(1109). Find the members of the proportion $x_{1}: x_{2}=x_{3}: x_{4}$, where the first term is 6 more than the second, and the third is 5 more than the fourth. The sum of the squares of all terms is 793.
|
Solution. By the condition $x_{1}=x_{2}+6, x_{3}=x_{4}+5,\left(x_{2}+6\right): x_{2}=$ $=\left(x_{4}+5\right): x_{4}$.
We have a system of two equations with two unknowns:
$$
\left\{\begin{array}{l}
\left(x_{2}+6\right)^{2}+x_{2}^{2}+\left(x_{4}+5\right)^{2}+x_{4}^{2}=793 \\
\left(x_{2}+6\right) \cdot x_{4}=x_{2} \cdot\left(x_{4}+5\right)
\end{array}\right.
$$
from which
$$
\left\{\begin{array}{l}
x_{2}^{2}+6 x_{2}+x_{4}^{2}+5 x_{4}-366=0 \\
6 x_{4}=5 x_{2}
\end{array}\right.
$$
Substituting the value $x_{4}=\frac{5 x_{2}}{6}$ from the second equation of the system into the first, we get:
$$
\begin{aligned}
& x_{2}^{2}+6 x_{2}-216=0 \\
& x_{2}^{\prime}=-18, x_{2}^{\prime \prime}=12
\end{aligned}
$$
Since $x_{1}=x_{2}+6$, then $x_{1}^{\prime}=-12, x_{1}^{\prime \prime}=18$.
$$
x_{4}^{\prime}=\frac{5 x_{2}^{\prime}}{6}=-15, x_{4}^{\prime \prime}=\frac{5 x_{2}^{\prime \prime}}{6}=10, x_{3}^{\prime}=x_{4}^{\prime}+5=-10, x_{3}^{\prime \prime}=15
$$
We obtained two proportions:
$$
(-12):(-18)=(-10):(-15) \text { and } 18: 12=15: 10 .
$$
Answer: $18: 12=15: 10 ;(-12):(-18)=(-10):(-15)$.
$\triangle 34$ (1110). From a city, two pedestrians set out at different times along two mutually perpendicular roads. The speed of one of them is 4 km $/ h$, and the other's is 5 km $/ h$. Currently, the pedestrian walking at 4 km $/ h$ is 7 km from the city, and the second is 10 km away. In how many hours will the distance between the pedestrians be 25 km?
Solution. Let the distance of 25 km between the pedestrians be after $t$ hours. Then, based on the Pythagorean theorem, we can form the equation $(7+4 t)^{2}+(10+5 t)^{2}=25^{2}$, from which
$$
41 t^{2}+156 t-476=0, t=2
$$
By checking, we easily confirm that the problem is solved correctly. Indeed, after 2 hours, the first pedestrian was 15 km from the city $(7+2 \cdot 4=15)$, and the second - 20 km from the city $(10+2 \cdot 5=20)$. The distance between the pedestrians $\sqrt{15^{2}+20^{2}}=$ $=\sqrt{625}=25$, which meets the condition of the problem.
Answer: in 2 hours.
3 remark. After this problem, it is advisable to solve problem $69 \$ 8$ (No. 1003 from [2]).
$\triangle 1111$. Prove that if $z=\frac{2}{\frac{1}{a}+\frac{1}{b}}(a \neq 0, \quad b \neq 0$, $a+b \neq 0, a-b \neq 0)$, then $\frac{1}{z-a}+\frac{1}{z-b}=\frac{1}{a}+\frac{1}{b}$.
Proof. Transform the given expression $z$ :
$$
z=\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2 a b}{a+b}
$$
Substitute the value $z=\frac{2 a b}{a+b}$ into the left side of the identity to be proven. We will have:
$$
\begin{gathered}
\frac{1}{z-a}+\frac{1}{z-b}=\frac{1}{\frac{2 a b}{a+b}-a}+\frac{1}{\frac{2 a b}{a+b}-b}= \\
=\frac{a+b}{2 a b-a^{2}-a b}+\frac{a+b}{2 a b-a b-b^{2}}=\frac{a+b}{a b-a^{2}}+\frac{a+b}{a b-b^{2}}= \\
=\frac{a+b}{a(b-a)}+\frac{a+b}{b(a-b)}=\frac{a+b}{a(b-a)}-\frac{a+b}{b(b-a)}=\frac{a b+b^{2}-a^{2}-a b}{a b(b-a)}= \\
=\frac{b^{2}-a^{2}}{a b(b-a)}=\frac{b+a}{a b}=\frac{1}{a}+\frac{1}{b} .
\end{gathered}
$$
We obtained the expression on the right side of the identity. The statement is proven.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46(1122). Several points are marked on a plane, no three of which lie on the same line. A line is drawn through every two points. How many points are marked on the plane if it is known that a total of 45 lines have been drawn?
|
Solution. The problem reduces to solving the equation $\frac{x(x-1)}{2}=45$ in natural numbers, where $x$ is the number of points marked on the plane. We have $x^{2}-x-90=0$, from which $x_{1}=10, x_{2}=-9$. Only the root $x=10$ satisfies the condition of the problem.
Answer: 10 points.
$\triangle 47(969)$ '. Prove that to find the square of a two-digit number ending in the digit 5 and having $n$ tens, it is sufficient to multiply the number of tens $n$ by $n+1$ and append 25 (see problem 1091 from [4]).
Solution. Let's square the two-digit number $a 5=10 a+5$. We have:
$$
(10 a+5)^{2}=100 a^{2}+100 a+25=100 a(a+1)+25
$$
We obtained that the square of the number $\overline{a 5}$ ends with the number 25, and the number of its hundreds is $a(a+1)$, which is what we needed to prove.
Remark. It is also advisable to solve problem 856 from $[4]$.
' For problems 47-77, the numbers in parentheses indicate the exercise numbers in the textbook [2] 122
$\triangle$ 48(970). Find a two-digit number whose square is written using the digits $0 ; 2 ; 3$ and 5.
$\mathrm{Pe}$ solution. Since the square of an integer cannot end in the digit 2, 3, or a single zero, the square of an integer can only end in the digit 5 from the four given digits. Then the second-to-last digit is 2. Considering that the first digit cannot be zero, we establish that the square of a two-digit number is 3025, and the sought number is 55. (To find the sought number, it is useful to use the previous problem.)
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51 (974). What is the last digit of the difference $43^{43}-17^{17}$?
|
Solution. Let's determine the last digits of various powers of the numbers 43 and 17. The number 43 ends with the digit $3, 43^2$ ends with the digit $9, 43^3$ ends with the digit $7, 43^4$ ends with the digit 1. Therefore, the last digits in subsequent powers of the number 43 will repeat: $3, 9, 7, 1$, and so on. Since $43^{43} = 43^{4 \cdot 10 + 3} = (43^4)^{10} \cdot 43^3$, and $(43^4)^{10}$ ends with the digit 1, $43^{43}$, like $43^3$, ends with the digit 7.
Similarly, we establish that the last digits of the powers $17^1, 17^2, 17^3, 17^4$ are $7, 9, 3, 1$, respectively, i.e., the last digits of consecutive powers of the number 17 will also repeat every four powers. Since $17^{17} = 17^{4 \cdot 4 + 1} = (17^4)^4 \cdot 17^1$, the number $17^{17}$, like $17^1$, ends with the digit 7 (just like the number $43^{43}$). Therefore, the difference $43^{43} - 17^{17}$ ends with zero.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
55 (978). There are 4 balls of different masses. Using a balance scale without weights, how many weighings are needed to arrange these balls in order of decreasing mass?
|
Solution. Let $m_{A}, m_{B}, m_{C}, m_{D}$ be the masses of four different balls. We will use a graph to show how the weighings are performed (the arrow points from the heavier ball to the lighter one).
Suppose, for example, after two weighings, we have $m_{A}>m_{B}$ and $m_{C}>m_{D}$ (Fig. $29, a$ ). Next, we will compare $m_{A}$ and $m_{C}$ (the two heavier balls) and $m_{B}$ and $m_{D}$ (the two lighter balls). In this case, there are two possible scenarios (Fig. $29, b, c$ ).
In the first case (when the smaller of $m_{A}$ and $m_{C}$ is greater than the larger of $m_{B}$ and $m_{D}$, Fig. 29, b), no further weighings are needed: if $m_{A}>m_{C}$, and $m_{C}>m_{D}$, then $m_{A}>m_{D}$; if $m_{C}>m_{D}$, and $m_{D}>m_{B}$, then $m_{C}>m_{B}$ (by the transitive property of inequalities). Therefore, $m_{A}>m_{C}>m_{D}>m_{B}$.
In the second case (when the smaller of $m_{A}$ and $m_{C}$ is greater than the smaller of $m_{D}$ and $m_{B}$, Fig. 29, c), one more weighing is needed to compare the masses of $m_{A}$ and $m_{D}$ ( $m_{C}$ and $m_{D}$ can be easily compared using the transitive property of inequalities). (On the diagram, dashed arrows show the relationships between the masses of the balls established without weighing, based on the transitive property of inequalities.)
Answer: no more than 5 weighings.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
59(982). In the cabinet, there are books that need to be packed. If they are bundled in groups of 4, 5, or 6, there will always be one extra book left each time, but if they are bundled in groups of 7, there will be no extra books left. What is the number of books in the cabinet, given that there are no more than 400 books?
|
Solution. The problem reduces to finding a natural number that is a multiple of seven, not exceeding 400, which gives a remainder of 1 when divided by 4, 5, and 6. This number, obviously, has the form $60 n+1$, where 60 is the least common multiple of the numbers $4,5,6, n \in \boldsymbol{N}$, $n<7$. By trial, we find $n=5$. Answer: 301.
126
|
301
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60(983). There is a sheet of paper. It is cut into 4 pieces, then some (or all) of the resulting pieces are again cut into 4 pieces, and so on. Prove that it is impossible to obtain 50 pieces of the sheet in this way.
|
Solution. It is easy to understand that after each cut, the number of pieces of the sheet increases by 3. Thus, after $m$ cuts, the number of pieces will be $1+3 m$, where $m \in \boldsymbol{N}$. Since $1+3 m \neq 50$, it is impossible to obtain 50 pieces of the sheet in the manner specified in the problem.
$61(984)$. a) How many four-digit numbers are there that are written using only: 1) odd digits; 2) even digits?
b) How many four-digit numbers contain both even and odd digits in their notation?
Solution. a) 1) Each digit of a four-digit number can be any of the five odd digits, i.e., in five ways. Therefore, there are 5 one-digit numbers written with odd digits, 25 two-digit numbers $-5^{2}=25$, 125 three-digit numbers $-5^{3}=125$, and 625 four-digit numbers $-5^{4}=625$.
2) Since the digit zero cannot be at the beginning of a number, the highest place of the number can be written with any of the four even digits - $2,4,6,8$, and the other places can be any of the five even digits. Thus, there are 5 one-digit numbers written with even digits, 20 two-digit numbers $-4 \cdot 5=20$, 100 three-digit numbers $4 \cdot 5 \cdot 5=100$, and 500 four-digit numbers $-4 \cdot 5 \cdot 5 \cdot 5=500$.
b) To solve the problem, from the total number of four-digit numbers, we need to subtract the number of four-digit numbers written only with odd digits (625) and only with even digits (500). Since there are 10 one-digit numbers in total, 90 two-digit numbers $9 \cdot 10=90$ (the digit zero cannot be in the first place), 900 three-digit numbers $-9 \cdot 10^{2}=900$, and 9000 four-digit numbers $-9 \cdot 10^{3}=9000$, the number of four-digit numbers containing both even and odd digits in their notation is $9000-625-500=7875$.
|
7875
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
62 (985). In a chess tournament, more than 9 but fewer than 25 grandmasters and masters participated. At the end of the tournament, it turned out that each participant scored half of their points against grandmasters. How many people participated in the tournament? How many of them were masters?
|
Solution. Let $n$ be the number of chess players in the tournament, of which $m$ are grandmasters, and thus $n-m$ are masters. Therefore, all participants played $\frac{n(n-1)}{2}$ games and scored $\frac{n(n-1)}{2}$ points (both games and points). Among them, the grandmasters played $\frac{m(m-1)}{2}$ games (and scored the same number of points) against each other, while the masters played $\frac{(n-m)(n-m-1)}{2}$ games and scored $\frac{(n-m)(n-m-1)}{2}$ points among themselves.
Since each participant scored half of their points against the grandmasters, the grandmasters also scored half of their points against each other, meaning the grandmasters scored a total of $m(m-1)$ points.
Since the masters scored half of their points against the grandmasters, they also scored half of their points against each other, meaning they scored a total of $2 \cdot \frac{(n-m)(n-m-1)}{2} = (n-m)(n-m-1)$ points. The total number of points scored by all participants is $m(m-1) + (n-m)(n-m-1)$, or $\frac{n(n-1)}{2}$. We have the equation
$$
m(m-1) + (n-m)(n-m-1) = \frac{n(n-1)}{2}
$$
After simplification, we get:
$$
n^{2} - 4 n m + 4 m^{2} = n
$$
which simplifies to $(n-2 m)^{2} = n$, meaning $n$ is a perfect square. Since $9 < n < 25$, we have $n = 16$. Solving the equation $(16-2 m)^{2} = 16$, we get $m_{1} = 6, m_{2} = 10$. Therefore, 16 people participated in the tournament, among whom there were 6 or 10 grandmasters.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65 (998). An alloy consists of zinc and copper, entering into it in a ratio of $1: 2$, and another alloy contains the same metals in a ratio of $2: 3$. From how many parts of both alloys can a third alloy be obtained, containing the same metals in a ratio of 17:27?
|
S o l u t i o n. Let the third alloy contain $x$ kg of the first alloy and $y$ kg of the second alloy. We need to find the ratio $\frac{x}{y}$. Since zinc and copper are in the ratio $1:2$ in the first alloy and in the ratio $2:3$ in the second alloy, $x$ kg of the first alloy contains $\frac{1}{3} x$ (kg) of zinc and $\frac{2}{3} x$ (kg) of copper, and $y$ kg of the second alloy contains $\frac{2}{5} y$ (kg) of zinc and $\frac{3}{5} y$ (kg) of copper. In total, the third alloy contains $\left(\frac{1}{3} x+\frac{2}{5} y\right)$ kg of zinc and $\left(\frac{2}{3} x+\frac{3}{5} y\right)$ kg of copper.
By the condition
$$
\frac{\frac{1}{3} x+\frac{2}{5} y}{\frac{2}{3} x+\frac{3}{5} y}=\frac{17}{27}
$$
from which $35 x=9 y, \frac{x}{y}=\frac{9}{35}$, i.e., the third alloy can be obtained from 9 parts of the first alloy and 35 parts of the second alloy.
$66(1000)$. A tourist left from $M$ to $N$, the distance between which is 41 km, walking at a speed of 5 km per hour. After 2 hours, a rider set out after him, who, overtaking the tourist, arrived in $N$ and immediately turned back. Find the speed of the rider's movement if it is known that he met the tourist 2 hours and 45 minutes after overtaking him.
Solution. Let the speed of the rider be $v$ kilometers per hour. The rider caught up with the tourist (made up 10 km) due to the difference in speeds $(v-5)$ kilometers per hour, spending $\frac{10}{v-5}$ hours to catch up with the tourist.
By the time of the meeting, the rider had been traveling for $\left(\frac{10}{v-5}+2 \frac{3}{4}\right)$ hours and had traveled $\left(\frac{10}{v-5}+2 \frac{3}{4}\right) v$ kilometers. The tourist, by the time of the meeting, had been traveling for 2 hours longer $\left(\left(\frac{10}{v-5}+4 \frac{3}{4}\right)\right.$ hours $)$ and had traveled $\left(\frac{10}{v-5}+4 \frac{3}{4}\right) \cdot 5$ kilometers.
Since the sum of the distances traveled by the tourist and the rider by the time of the meeting is equal to twice the distance $M N$, we have the equation
$$
\left(\frac{10}{v-5}+\frac{19}{4}\right) \cdot 5+\left(\frac{10}{v-5}+\frac{11}{4}\right) v=82
$$
which reduces to the quadratic equation $11 v^{2}-248 v+1365=0$.
The roots of the equation are $v_{1}=13$ and $v_{2}=9 \frac{6}{11}$. Both roots satisfy the condition of the problem ( $v>5$ ).
A n s w e r: 13 km $/ h$ or $9 \frac{6}{11}$ km $/$ h.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69(1003). A cyclist and a motorcyclist are moving towards an intersection along two mutually perpendicular roads. At a certain moment, the cyclist is 8 km away, and the motorcyclist is 15 km away from the intersection. After how many minutes will the distance between them be 5 km, if the cyclist's speed is $\frac{1}{3}$ km/min, and the motorcyclist's speed is 1 km/min?
|
Solution. Let $OA=8$ km, $OB=15$ km (Fig. 30). If the distance of 5 km between the motorcyclist and the cyclist will be in $t$ minutes $\left(A_{1} B_{1}=5\right.$ km), then $A A_{1}=\frac{1}{3} t$ (km), $B B_{1}=t$ (km). Then $O A_{1}=O A-\frac{1}{3} t=$
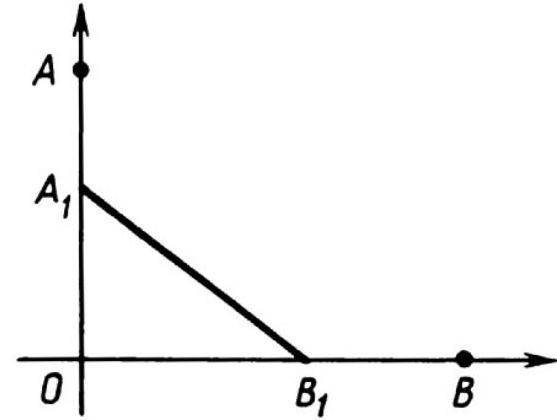
Fig. 30
$=8-\frac{1}{3} t, O B_{1}=O B-t=15-t$. By the Pythagorean theorem from
$\triangle O A_{1} B_{1}$ we have:
$$
\left(8-\frac{1}{3} t\right)^{2}+(15-t)^{2}=25
$$
After transformations, we get:
$$
\begin{gathered}
5 t^{2}-159 t+1188=0 \\
t_{1}=12\left(\text { min), }, t_{2}=19.8(\text { min }) .\right.
\end{gathered}
$$
Both roots satisfy the condition of the problem: in the first case ($t=12$ min) the motorcyclist and the cyclist have not yet reached the intersection, in the second case ($t=19.8$ min) the motorcyclist will have crossed the intersection.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
73(1007). A master and his apprentice were supposed to complete a job by a certain deadline. However, when half of the work was done, the apprentice fell ill, and the master, left alone, finished the job 2 days late. How many days would it take for each of them to complete the entire job working alone, if the master would need 5 fewer days than the apprentice?
|
Solution. Let the master be able to complete the entire job in $x$ days, then the apprentice - in $(x+5)$ days. In one day, the master completed $\frac{1}{x}$ of the work, the apprentice completed $\frac{1}{x+5}$ of the work; when working together, the master and the apprentice completed $\frac{2 x+5}{x(x+5)}$ of the work per day $\left(\frac{1}{x}+\frac{1}{x+5}=\frac{2 x+5}{x(x+5)}\right)$. For half the work, the master and the apprentice spent $\frac{x(x+5)}{2(2 x+5)}$ days $\left(\frac{1}{2}: \frac{2 x+5}{x(x+5)}\right)$, which is 2 days less than the time spent by the master alone on half the work.
Considering that the master, working alone, spent $\frac{x}{2}$ days on half the work, we set up the equation
$$
\frac{x}{2}-\frac{x(x+5)}{2(2 x+5)}=2
$$
After simplifications, we get:
$$
\begin{gathered}
x^{2}-8 x-20=0 \\
x_{1}=10, x_{2}=-2
\end{gathered}
$$
Only the positive root satisfies the condition of the problem: the master could complete the work in 10 days; therefore, the apprentice in 15 days.
Answer: 10 days, 15 days.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74 (1008). A tourist who set out from $A$ to $B$ walked the first half of the distance at a speed of $v_{1}$, and the second half at a speed of $v_{2}\left(v_{1} \neq v_{2}\right)$. On the return trip, he walked half of the total time at a speed of $v_{1}$, and the other half at a speed of $v_{2}$. In which case did the tourist spend more time: when walking from $A$ to $B$ or when walking from $B$ to $A$?
|
Solution. I method. Let the time spent by the tourist on the journey from $B$ to $A$ be $2 t$. Then half of the time ($t$) he walked at a speed of $v_{1}$, and the second half of the time at a speed of $v_{2}$. The entire distance, therefore, is $v_{1} t + v_{2} t$, and half the distance is $\frac{v_{1} t + v_{2} t}{2}$.
The tourist spent $\frac{v_{1} t + v_{2} t}{2 v_{1}} = \frac{1}{2} + \frac{v_{2} t}{2 v_{1}}$ units of time on the first half of the distance at a speed of $v_{1}$, and $\frac{v_{1} t + v_{2} t}{2 v_{2}} = \frac{1}{2} + \frac{v_{1} t}{2 v_{2}}$ units of time on the second half of the distance at a speed of $v_{2}$. The total time spent on the journey from $A$ to $B$ is
$$
\frac{t}{2} + \frac{v_{2} t}{2 v_{1}} + \frac{t}{2} + \frac{v_{1} t}{2 v_{2}} = t + \frac{t}{2} \left( \frac{v_{2}}{v_{1}} + \frac{v_{1}}{v_{2}} \right)
$$
which is more than $2 t$, since $\frac{v_{2}}{v_{1}} + \frac{v_{1}}{v_{2}} > 2$ when $v_{1} \neq v_{2}$
$$
\left( \frac{v_{2}^{2} - 2 v_{1} v_{2} + v_{1}^{2}}{v_{1} v_{2}} = \frac{(v_{2} - v_{1})^{2}}{v_{1} v_{2}} > 0 \text{ when } v_{1} > 0, v_{2} > 0, v_{1} \neq v_{2} \right)
$$
Thus, the tourist spent more time on the journey from $A$ to $B$ than on the journey from $B$ to $A$.
II method. Let the distance $A B$ be denoted by $s$. Then the time spent by the tourist on the journey from $A$ to $B$ is $t_{1} = \frac{s}{2 v_{1}} + \frac{s}{2 v_{2}} = \frac{s}{2} \cdot \frac{v_{1} + v_{2}}{v_{1} \cdot v_{2}}$. If the time spent by the tourist on the return journey is denoted by $t_{2}$, then $s = v_{1} \frac{t_{2}}{2} + v_{2} \frac{t_{2}}{2}$, from which $t_{2} = \frac{2 s}{v_{1} + v_{2}}$. Let's compare $t_{1}$ and $t_{2}$.
$$
\frac{s}{2} \cdot \frac{v_{1} + v_{2}}{v_{1} v_{2}} \vee \frac{2 s}{v_{1} + v_{2}}
$$
Since $s > 0$, by canceling $s$, we get:
$$
\begin{gathered}
\frac{v_{1} + v_{2}}{2 v_{1} v_{2}} \vee \frac{2}{v_{1} + v_{2}} \\
(v_{1} + v_{2})^{2} \bigvee 4 v_{1} v_{2}, \\
(v_{1} - v_{2})^{2} > 0
\end{gathered}
$$
Therefore, $t_{1} > t_{2}$.
Answer: the tourist spent more time on the journey from $A$ to $B$ than on the journey from $B$ to $A$.
Remark. This problem can be given in a more general formulation: which is faster - to walk half the distance at a speed of $v_{1}$ and the other half at a speed of $v_{2} (v_{1} \neq v_{2})$ or to walk half the total time at a speed of $v_{1}$ and the other half at a speed of $v_{2}$?
$75(1009)$. One dump truck can transport construction materials 24 hours faster than the other. If the first dump truck transports two-thirds of all materials and then the second transports the remaining part, it will take 33 hours longer than if both dump trucks work simultaneously. How many hours can each dump truck transport the construction materials?
Solution. Let the first dump truck transport the construction materials in $t$ hours, then the second in $(t + 24)$ hours. In 1 hour, the first dump truck can transport $\frac{1}{t}$ of the materials, and the second in 1 hour $\frac{1}{t + 24}$ of the materials. When working simultaneously, in 1 hour the dump trucks can transport $\frac{2 t + 24}{t(t + 24)}$ of the materials $\left(\frac{1}{t} + \frac{1}{t + 24}\right)$, spending $\frac{t(t + 24)}{2 t + 24}$ hours on the entire work $\left(1 : \frac{2 t + 24}{t(t + 24)} = \frac{t(t + 24)}{2 t + 24}\right)$.
The first dump truck can transport $\frac{2}{3}$ of all materials in $\frac{2 t}{3}$ hours $\left(\frac{2}{3} : \frac{1}{t} = \frac{2}{3} t\right)$, and the remaining part $\left(\frac{1}{3}\right)$ the second dump truck can transport in $\frac{t + 24}{3}$ hours $\left(\frac{1}{3} : \frac{1}{t + 24} = \frac{t + 24}{3}\right)$. According to the problem, we form the equation
$$
\frac{2 t}{3} + \frac{t + 24}{3} - 33 = \frac{t(t + 24)}{2 t + 24}
$$
from which
$$
\begin{gathered}
t + 8 - 33 = \frac{t(t + 24)}{2 t + 24} \\
(t - 25)(2 t + 24) = t(t + 24) \\
t^{2} - 50 t - 600 = 0 \\
t_{1} = 60, t_{2} = -10
\end{gathered}
$$
136
The only positive root of the equation that satisfies the problem is $t = 60$. Therefore, the first dump truck can transport the construction materials in 60 hours, and the second in 84 hours $(60 + 24 = 84)$.
Answer: 60 hours, 84 hours.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
76(1010). A collective farm team must harvest a potato crop by a certain deadline. After 60% of the potatoes were harvested, a combine was sent to assist the team, which reduced the harvesting time by 5 days. How many days would it have taken to harvest the potatoes without the combine's help, if it is known that the combine could have completed the entire job 8 days faster than the team?
|
Let's solve it. Let the brigade need $t$ days to harvest potatoes without the help of a combine, then the combine needs $(t-8)$ days to complete the entire work.
In one day, the brigade can complete $\frac{1}{t}$ of the entire work, and the combine can complete $\frac{1}{t-8}$ of the entire work in one day. With the help of the combine, the brigade completes $\frac{2 t-8}{t(t-8)}$ of the work in one day $\left(\frac{1}{t}+\frac{1}{t-8}=\right.$ $\left.=\frac{2 t-8}{t(t-8)}\right) \cdot 60\% \left(\frac{3}{5}\right)$ of the potatoes are harvested by the brigade in $\frac{3 t}{5}$ days $\left(\frac{3}{5} : \frac{1}{t}=\frac{3 t}{5}\right)$, and the remaining $40\% \left(\frac{2}{5}\right)$ of the potatoes are harvested by the brigade with the help of the combine in $\frac{t(t-8)}{5(t-4)}$ days $\left(\frac{2}{5} : \frac{2 t-8}{t(t-8)}=\right.$ $\left.=\frac{t(t-8)}{5(t-4)}\right)$. According to the condition, we have:
$$
t-5=\frac{3 t}{5}+\frac{t(t-8)}{5(t-4)}
$$
from which
$$
\begin{gathered}
t^{2}-25 t+100=0 \\
t_{1}=20, t_{2}=5
\end{gathered}
$$
The condition of the problem ( $t>5$ ) is satisfied by one root $t=20$. Answer: 20 days.
$\square$ 77(1011). Two riders set out simultaneously from $A$ and $B$ towards each other, and one arrives at $B$ after 27 minutes, while the other arrives at $A$ after 12 minutes after the meeting. How many minutes did each rider take to travel the path $A B$?
Solution. Let $A B=s$ (in meters), and the time until the riders meet is $t$ (in minutes). Then the solution of the problem reduces to solving one of the three equations (see the solution of problem 28, p. 112):
$$
\begin{aligned}
& \frac{s}{t+27} \cdot 27=\frac{s}{t+12} \cdot t \\
& \frac{s}{t+27} \cdot t=\frac{s}{t+12} \cdot 12 \\
& \frac{s}{t+27} \cdot t+\frac{s}{t+12} \cdot t=s
\end{aligned}
$$
Answer: the first rider traveled the path $A B$ in 45 minutes, the second in 30 minutes.
$\triangle$ 78. Simplify the expression
$$
70 \cdot\left(71^{9}+71^{8}+71^{7}+\ldots+71^{2}+72\right)+1
$$
Solution. Let's denote the number 71 for brevity as $a$. Then
$$
\begin{gathered}
(a-1)\left(a^{9}+a^{8}+a^{7}+\ldots+a^{2}+a+1\right)+1= \\
=\left(a^{10}+a^{9}+a^{8}+\ldots+a^{3}+a^{2}+a\right)-\left(a^{9}+a^{8}+a^{7}+\ldots+\right. \\
\left.+a^{2}+a+1\right)+1=a^{10}
\end{gathered}
$$
Therefore, the given expression equals $71^{10}$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
79. Calculate the sum
$$
1^{2}-2^{2}+3^{2}-4^{2}+\ldots+99^{2}-100^{2}+101^{2}
$$
|
$$
\begin{gathered}
1^{2}-2^{2}+3^{2}-4^{2}+\ldots+101^{2}= \\
=1+(101^{2}-100^{2})+(99^{2}-98^{2})+\ldots+(3^{2}-2^{2})= \\
=201+197+\ldots+9+5+1= \\
=\frac{1}{2}(201+1) \cdot 51=101 \cdot 51=5151
\end{gathered}
$$
Answer: 5151.
|
5151
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
84. Nine identical books cost 11 rubles and some kopecks, while 13 such books cost 15 rubles and some kopecks. Determine the exact cost of one book
|
S o l u t i o n. It is clear that each book costs 1 r. $m$ k., where $m$ is an integer, and $m<100$. From the first condition of the problem, it follows that $200<9 m<300$, i.e., $23 \leqslant m \leqslant 33$. From the second condition, $200<13 m<300$, i.e., $16 \leqslant m \leqslant 23$. Therefore, $m=23$.
A n s w e r: 1 r. 23 k.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. The percentage of VII grade students attending gymnastics classes is between 2.9 and $3.1 \%$. Determine the smallest possible number of students in this class.
|
Solution. If there are $x$ students in the class and $y$ of them do gymnastics, then by the condition $2.9 < 100 \cdot \frac{y}{x} < 3.1$, or $29x < 1000y < 31x$. If $x \leqslant 32$, then $31x \leqslant 992 \leqslant 1000y$, so $x \geqslant 33$. Since $29 \cdot 33 < 1000 \cdot y < 31 \cdot 33$, the number of students sought is 33
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
89. Calculate the value of the expression $\frac{2 a-b}{3 a-b}+\frac{5 b-a}{3 a+b}$, given that $10 a^{2}-3 b^{2}+5 a b=0$ and $9 a^{2}-b^{2} \neq 0$.
|
Solution. Since $5 a b=3 b^{2}-10 a^{2}$, then
$$
\begin{aligned}
& \quad \frac{2 a-b}{3 a-b}+\frac{5 b-a}{3 a+b}=\frac{3 a^{2}+15 a b-6 b^{2}}{9 a^{2}-b^{2}}=\frac{3 a^{2}+3\left(3 b^{2}-10 a^{2}\right)-6 b^{2}}{9 a^{2}-b^{2}}= \\
& \text { Answer: }-3 . \\
& =\frac{-3\left(9 a^{2}-b^{2}\right)}{9 a^{2}-b^{2}}=-3 .
\end{aligned}
$$
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. If the first digit of a four-digit number, which is a perfect square, is decreased by 3, and the last digit is increased by 3, the result is also a perfect square. Find this number.
|
S o l u t i o n. Let the given number be $a^{2}$, and the modified number $b^{2}$, then $a^{2}-3000+3=b^{2}$, or $a^{2}-b^{2}=2997$, from which $(a-b) \times$ $\times(a+b)=2997=3 \cdot 3 \cdot 3 \cdot 3 \cdot 37$. Clearly, $a+b$ is greater than 37, and from the problem statement, it follows that $a+b$ is less than 200 ( $a$ and $b$ are two-digit numbers). Therefore, $a+b=3 \cdot 37=111, a-b=3 \cdot 3 \cdot 3=27$. Then $2 a=138, a=69, a^{2}=4761$.
A n s w e r: 4761 .
|
4761
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.