problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
5. Given a square table of size $2023 \times 2023$. Each of its cells is colored in one of $n$ colors. It is known that for any six cells of the same color located in the same row, there are no cells of the same color above the leftmost of them and below the rightmost of them. What is the smallest $n$ for which this is possible?
|
Answer: 338.
Solution. Consider some specific color (say, blue). In each row, mark the five leftmost blue cells with a cross, and the rest with a zero (if there are fewer than six blue cells in the row, mark all cells with a cross). Note that in any column, there is no more than one blue cell with a zero (otherwise, for the topmost one, the condition of the problem is violated). Therefore, there are no more than 2023 blue cells with a zero. In addition, the number of blue cells with a cross does not exceed $5 \cdot 2023$. Thus, the total number of blue cells does not exceed $2023 + 5 \cdot 2023 = 6 \cdot 2023$. These arguments are valid for any color. Therefore, the total number of colors is no less than
$$
\frac{2023^{2}}{6 \cdot 2023} = \frac{2023}{6} = 337 \frac{1}{6}
$$
Thus, $n \geqslant 338$.
We will show that $n=338$ is achievable. Sequentially number all diagonals from top to bottom, running from southwest to northeast, with numbers from 1 to 4045. Paint the first six diagonals in the first color, the next six in the second color, and so on in a cycle (so after the 338th color, the first color will follow again). We will check that this coloring satisfies the condition of the problem. Note that no color is used more than twice, since $338 \cdot 6 \cdot 2 = 4056 > 4045$. Let the $k$-th color appear twice. In the first block, the rightmost cell of this color will be in the column with number $6k$. In the second block, the leftmost cell of this color is in the column with number
$$
6(338+k-1)+1-2022 = 6k+1
$$
Thus, cells of the same color from different blocks cannot be in the same column.
|
338
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Nastya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the difference \( a - b \) must be coprime with \( n \), and if they are connected, then \( a - b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
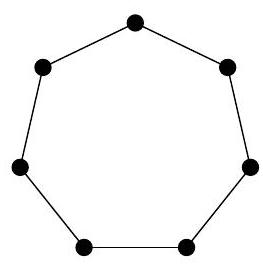
|
Answer: $n=5 \cdot 7 \cdot 11=385$.
Solution. We will make two observations.
1) $n$ is not divisible by 2 and 3. Among seven numbers, there are always three numbers of the same parity. If $n$ is even, then they must be pairwise connected. Moreover, among seven numbers, there will be three numbers that give the same remainder when divided by 3. If $n$ is divisible by 3, then these numbers also form a three-link cycle. But such cycles do not exist in the picture.
2) If $p$ is a prime divisor of $n$, then among three consecutively connected numbers, there exists a pair of adjacent numbers whose difference is not divisible by $p$. Let $(a, b, c)$ be a chain of consecutively connected numbers where $a-b$ and $b-c$ are divisible by $p$. Then $a-c=(a-b)+(b-c) \vdots p$. This means that $(a, b, c)$ forms a three-link cycle, which is impossible.
We will show that the number $n$ has at least three distinct prime divisors. Let $p$ be a prime divisor of $n$. There are no more than three distinct pairs $(a, b)$ for which $a-b \vdots p$. If there were 4 such pairs, then some two of them would intersect, which contradicts 2). But in total, 7 pairs of numbers are connected by segments, so $n$ has at least three distinct prime divisors. In view of 1), the minimal possible values for them are $5, 7, 11$, that is, $n \geqslant 5 \cdot 7 \cdot 11=385$. The arrangement for $n=385$ is shown in the figure.
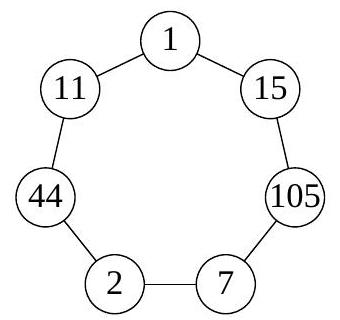
|
385
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Kostya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \), and if they are connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?

|
Answer: $n=15$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among any five numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) $n$ has at least two distinct prime divisors. Suppose $n$ is a power of a prime number $p$. Take a chain $(a, b, c, d)$ of sequentially connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which is not there.
Thus, the number $n$ has at least two distinct odd prime divisors, hence $n \geqslant 15$. The arrangement for $n=15$ is shown in the figure.
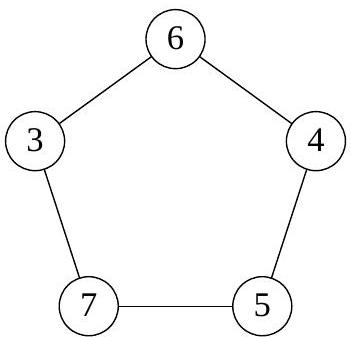
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Kostya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \); if connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
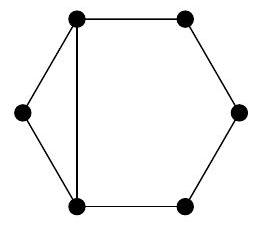
|
Answer: $n=15$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. If there are three even and three odd numbers, then each of these triples forms a cycle. Suppose there are four numbers $a, b, c, d$ of the same parity. Then all of them are pairwise connected, and we again get two three-link cycles - for example, $(a, b, c)$ and $(a, d, c)$. But there is only one such cycle in the picture.
2) $n$ has at least two distinct prime divisors. Suppose $n$ is a power of a prime number $p$. Consider a chain $(a, b, c, d)$ of sequentially connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means that there is a cycle of length 4 in the picture, which is not there.
Thus, the number $n$ has at least two distinct odd prime divisors, hence $n \geqslant 15$. The arrangement for $n=15$ is shown in the figure.
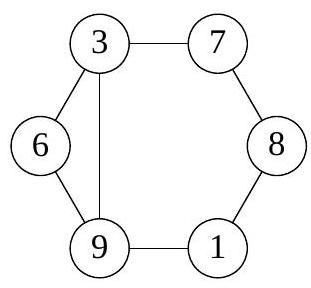
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On 2016 cards, numbers from 1 to 2016 were written (each one once). Then $k$ cards were taken. What is the smallest $k$ such that among them there will be two cards with numbers, the difference of whose square roots is less than 1?
|
Answer: 45.
Solution. We will show that $k=45$ works. Let's divide the numbers from 1 to 2016 into 44 groups:
\[
\begin{aligned}
& (1,2,3), \quad(4,5,6,7,8), \quad(9,10, \ldots, 15), \ldots, \quad\left(k^{2}, k^{2}+1, \ldots, k^{2}+2 k\right), \ldots, \\
& (1936,1937, \ldots, 2016)
\end{aligned}
\]
Since there are 45 numbers, some two of them (let's call them $a$ and $b$) will end up in the same group. Suppose for definiteness that $a<b$. Then $k^{2} \leqslant a<b<(k+1)^{2}$ and, consequently, $\sqrt{b}-\sqrt{a}<(k+1)-k=1$.
Now let's present 44 numbers, all differences between the square roots of which are at least 1:
\[
\begin{array}{llllll}
1^{2}, & 2^{2}, & 3^{2}, & 4^{2}, & \ldots, & 44^{2} .
\end{array}
\]
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the maximum number of different numbers from 1 to 1000 that can be chosen so that the difference between any two chosen numbers is not equal to any of the numbers 4, 5, 6.
|
Answer: 400.
Solution. Consider ten consecutive natural numbers. We will prove that no more than four of them are selected. If at least five numbers are selected, then three of them have the same parity, but then their pairwise differences cannot be only 2 and 8. Indeed, if $a<b<c$, then $b-a=2$ and $c-a=8$, but then $c-b=6$, which is impossible. Therefore, in each set of ten, no more than four numbers are selected, and in the first thousand numbers, there are no more than 400, since there are a hundred sets of ten in a thousand.
If we take all the numbers ending in $1, 2, 3$ or 4, then there will be exactly 400, but no difference will be equal to 4, 5 or 6.
|
400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. What is the maximum number of chess kings that can be placed on a $12 \times 12$ board so that each king attacks exactly one of the others?
|
Answer: 56.
Solution. Note that two kings attack each other if and only if their cells share at least one vertex. For each pair of attacking kings, mark the vertices of the cells they occupy. In this case, no fewer than six vertices are marked for each such pair. Since different pairs of kings mark different vertices (otherwise, some king would attack more than one king), the total number of pairs of kings is no more than $\left[13^{2} / 6\right]=28$, and the number of kings is no more than 56.
The arrangement of 56 kings is shown in the figure.
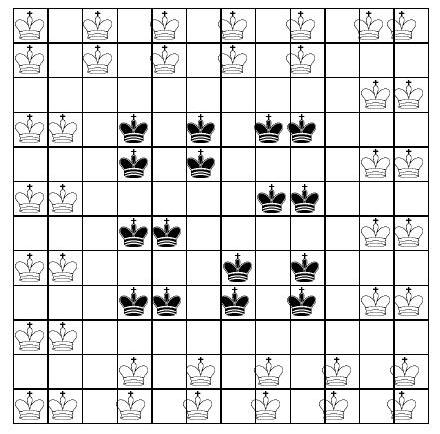
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From the numbers 1, 2, 3, ..., 2016, $k$ numbers are chosen. What is the smallest $k$ such that among the chosen numbers, there will definitely be two numbers whose difference is greater than 672 and less than 1344?
|
Answer: 674.
Solution. Let $n=672$. Then $2 n=1344$ and $3 n=2016$. Suppose it is possible to choose $674=n+2$ numbers such that no required pair of numbers can be found among them. Let $m$ be the smallest of the chosen numbers. Then the numbers $m+n+1, m+n+2$, $\ldots, m+2 n-1$ are not chosen. Remove them and the number $m$ from the set $\{1, \ldots, 3 n\}$, and denote the remaining set by $E$. Consider the pairs of numbers
\[
\begin{aligned}
& (1, n+2), \quad(2, n+3), \quad \ldots(m-1, m+n) \\
& (m+1, m+2 n), \quad(m+2, m+2 n+1), \quad \ldots, \quad(n+1,3 n) .
\end{aligned}
\]
There are $(m-1)+(n-m+1)=n$ such pairs. Note that the union of the left and right parts of these pairs gives the set $E$. Then any chosen number coincides with the left or right part of one of the pairs. By assumption, there are exactly $n+1$ such numbers, so there will be two of them, say $a$ and $b$, belonging to the same pair. Then their difference is $n+1$ or $2 n-1$. Thus, $a$ and $b$ satisfy the condition of the problem, which is impossible.
If the numbers $1,2,3, \ldots, 673$ are chosen, then it will not be possible to find the required two numbers.
|
674
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. At a cactus lovers' meeting, 80 cactus enthusiasts presented their collections, each consisting of cacti of different species. It turned out that no species of cactus is present in all collections at once, but any 15 people have cacti of the same species. What is the smallest total number of cactus species that can be in all the collections?
|
Answer: 16.
Solution. We will show that 16 cacti were possible. Number the cacti from 1 to 16. Let the 1st cactus lover have all cacti except the first; the 2nd cactus lover have all except the second cactus; the 15th cactus lover have all except the fifteenth cactus; and the cactus lovers from the 16th to the 80th have all cacti except the sixteenth. Then, any 15 cactus lovers will have a common cactus.
Now, we will establish that they must have more than 15 cacti. Suppose the opposite: let there be a total of $k \leqslant 15$ cacti. Number the cacti from 1 to $k$. For the cactus with number $i$, there exists a cactus lover $A_{i}$ who does not have it. But then, for the cactus lovers $A_{1}, A_{2}, \ldots, A_{k}$, there is no cactus that all of them have. And, even more so, there is no such cactus if we add a few more cactus lovers to them so that their number becomes 15. Contradiction.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On 2016 cards, numbers from 1 to 2016 were written (each one once). Then $k$ cards were taken. What is the smallest $k$ such that among them there will be two cards with numbers $a$ and $b$ such that $|\sqrt[3]{a}-\sqrt[3]{b}|<1$?
|
Answer: 13.
Solution. We will show that $k=13$ works. Divide the numbers from 1 to 2016 into 12 groups:
\[
\begin{aligned}
& (1,2,3,4,5,6,7), \quad(8,9, \ldots, 26), \quad(27,28, \ldots, 63), \ldots \\
& \left(k^{3}, k^{3}+1, \ldots,(k+1)^{3}-1\right), \ldots,(1728,1729, \ldots, 2016)
\end{aligned}
\]
Since there are 13 numbers, some two of them (let's call them $a$ and $b$) will end up in the same group. Let's assume for definiteness that $a<b$. Then $k^{3} \leqslant a<b<(k+1)^{3}$ and, consequently, $0<\sqrt[3]{b}-\sqrt[3]{a}<(k+1)-k=1$.
Now let's present 12 numbers, all differences between the cube roots of which are at least 1:
\[
1^{3}, \quad 2^{3}, \quad 3^{3}, \quad 4^{3}, \quad \ldots, \quad 12^{3} .
\]
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The cells of a $9 \times 9$ board are painted in black and white in a checkerboard pattern. How many ways are there to place 9 rooks on the same-colored cells of the board so that they do not attack each other? (A rook attacks any cell that is in the same row or column as itself.)
|
Answer: $4!5!=2880$.
Solution. Let the upper left corner of the board be black for definiteness. Note that black cells come in two types: cells with both coordinates even, and cells with both coordinates odd. If a rook is on a black cell with both even coordinates, then all black cells it attacks also have even coordinates. Similarly, a rook standing on a black cell with both odd coordinates attacks only black cells with both odd coordinates. Therefore, we need to count the number of ways to place 9 rooks on two boards: $4 \times 4$ and $5 \times 5$ (a board consisting only of black cells with both even coordinates, and a board consisting only of black cells with both odd coordinates). For the first board, this number is 4!, and for the second, it is 5!. Therefore, the total number of ways to place the rooks on black cells is $4!5!=2880$.
Now let's show that it is impossible to place 9 rooks on white cells in the required manner. Consider the cells whose first coordinate is odd and the second is even. No more than four rooks can be placed on such cells, as they are contained in four rows. Similarly, no more than four rooks can be placed on white cells whose first coordinate is even and the second is odd, as they are contained in four columns.
|
2880
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there live only knights, who always tell the truth, and liars, who always lie. One fine day, 30 islanders sat around a round table. Each of them can see everyone except themselves and their neighbors. Each person in turn said the phrase: "All I see are liars." How many liars were sitting at the table?
|
Answer: 28.
Solution. Not all of those sitting at the table are liars (otherwise they would all be telling the truth). Therefore, there is at least one knight sitting at the table. Everyone he sees is a liar. Let's determine who his neighbors are. Both of them cannot be liars (otherwise they would be telling the truth). Also, both of them cannot be knights, since they see each other. Therefore, one of them is a knight, and the other is a liar. It remains to note that the situation where two knights sit next to each other, and all the others are liars, is possible.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the cells of a $2015 \times n$ table, non-negative numbers are arranged such that in each row and each column there is at least one positive number. It is known that if a cell contains a positive number, then the sum of all numbers in its column is equal to the sum of all numbers in its row. For which $n$ is this possible?
|
Answer: $n=2015$.
Solution. We will prove by induction on $m+n$ that for an $m \times n$ table, the specified arrangement is possible only when $m=n$. For $m+n=2$, the statement is obvious. Consider an $m \times n$ table. Let the sum of the numbers in the first row be $a$. Consider all rows and columns whose sum of numbers is also $a$. If these are all the rows and all the columns, then the sum of all numbers in the table, calculated by rows, is $m a$, and calculated by columns, is $n a$. Therefore, $m=n$. If these are not all the rows and all the columns, then consider any row with a different sum. Then at the intersection of this row with a column with sum $a$, there is a zero. The same conclusion is true for a column with a sum different from $a$. Now, let's strike out from the table all rows and columns whose sum of numbers is different from $a$. After striking out, there cannot be any zero rows and columns, since from the rows and columns that remained, only zeros were struck out. Repeating the reasoning with the calculation of the sum of the numbers in the table, we understand that there will be an equal number of rows and columns left (let there be $k$ of each). Now, let's strike out from the original table all rows and columns whose sum of numbers is equal to $a$. We will get a table of size $(m-k) \times (n-k)$, satisfying the condition of the problem. Then, by the inductive hypothesis, $m-k=n-k$. Therefore, $m=n$.
|
2015
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many ways are there to color the cells of a $10 \times 10$ board in blue and green so that in each $2 \times 2$ square there are two blue and two green cells?
|
Answer: $2^{11}-2=2046$.
Solution. Note that if the colors of three cells in a $2 \times 2$ square are known, the color of the remaining cell is uniquely determined. Also, the colors of the two remaining cells are uniquely determined if there are two adjacent cells of the same color in a $2 \times 2$ square.
Consider the first row of the table. Suppose there are no adjacent cells of the same color in this row. Then the color of the first cell in the second row uniquely determines the colors of the other cells in the second row: they either all match the colors of the cells in the first row or are opposite to them. Therefore, the second row can be painted in two ways. In any of these ways, there are also no adjacent cells of the same color. Similarly, the color of the first cell in the third row uniquely determines its coloring. Thus, the third row can also be painted in two ways, and so on. Therefore, the number of ways to paint the table with such a fixed first row is exactly $2^{9}$. The number of ways to paint the table so that there are no adjacent cells of the same color in the first row is $2^{10}$.
Suppose there are two adjacent cells of the same color in the first row. Let's assume for definiteness that they are green. Then there must be two blue cells under them. Then the colors of the cells in the second row are uniquely determined. Therefore, there must be two green cells under the two adjacent blue cells. Thus, the colors of the cells in the third row are also uniquely determined, and so on. Therefore, the first row with adjacent cells of the same color uniquely determines the coloring of the entire table. The number of ways to paint the first row in two colors is $2^{10}$, but in two of them there are no adjacent cells of the same color. Therefore, the number of colorings of the table with such first rows is $2^{10}-2$, and the total number of colorings is $2^{10}+\left(2^{10}-2\right)=2^{11}-2=2046$.
|
2046
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an island, there live only knights, who always tell the truth, and liars, who always lie, and there are at least two knights and at least two liars. One fine day, each islander, in turn, pointed to each of the others and said one of two phrases: "You are a knight!" or "You are a liar!" The phrase "You are a liar!" was heard exactly 230 times. How many times was the phrase "You are a knight!" heard?
|
Answer: 526.
Solution. Let $r$ and $\ell$ denote the number of knights and liars, respectively. Note that a knight will say to another knight and a liar will say to another liar: "You are a knight!", while a knight will say to a liar and a liar will say to a knight: "You are a liar!" Therefore, the number of liar-knight pairs is $\frac{230}{2}=115=r \ell$. Since $r \ell=115=5 \cdot 23$ and $r, \ell \geqslant 2$, either $r=5$ and $\ell=23$, or $r=23$ and $\ell=5$. In either case, the number of knight-knight and liar-liar pairs is $\frac{5 \cdot 4}{2}+\frac{23 \cdot 22}{2}=263$. Therefore, the phrase "You are a knight!" was said 526 times.
|
526
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In an $8 \times 8$ table, natural numbers are arranged. The numbers in cells symmetric with respect to both diagonals of the table are equal. It is known that the sum of all numbers in the table is 1000, and the sum of the numbers on the diagonals is 200. For what smallest number $M$ can we assert that the sum of the numbers in each row does not exceed $M$?
|
Answer: $M=288$.
Solution. Consider the upper half of the table. Let the numbers be arranged as shown in the figure. Due to symmetry, the marked numbers completely determine the placement of the remaining numbers in the table.
| $a_{1}$ | $b_{1}$ | $b_{2}$ | $b_{3}$ | $c_{3}$ | $c_{2}$ | $c_{1}$ | $d_{1}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | $a_{2}$ | $b_{4}$ | $b_{5}$ | $c_{5}$ | $c_{4}$ | $d_{2}$ | |
| | | $a_{3}$ | $b_{6}$ | $c_{6}$ | $d_{3}$ | | |
| | | | $a_{4}$ | $d_{4}$ | | | |
Let
$$
\begin{array}{ll}
A=a_{1}+a_{2}+a_{3}+a_{4}, & B=b_{1}+b_{2}+b_{3}+b_{4}+b_{5}+b_{6} \\
D=d_{1}+d_{2}+d_{3}+d_{4}, & C=c_{1}+c_{2}+c_{3}+c_{4}+c_{5}+c_{6}
\end{array}
$$
By the condition, $2(A+D)=200$ and $2(A+D)+4(B+C)=1000$. Therefore, $A+D=100$ and $B+C=200$. Since the numbers are natural, $a_{i}+d_{j} \leqslant A+D-6=94$, and the sum of any three numbers $b_{i}$ and any three numbers $c_{j}$ does not exceed $B+C-6=194$. It remains to note that in each row there is one number of the form $a_{i}$ and $d_{j}$, and three numbers of the form $b_{i}$ and $c_{j}$, so their sum does not exceed $94+194=288$. Therefore, $M=288$ fits. We will show that smaller $M$ do not work. Consider the table
| 47 | 95 | 1 | 1 | 1 | 1 | 95 | 47 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 95 | 1 | 1 | 1 | 1 | 1 | 1 | 95 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 95 | 1 | 1 | 1 | 1 | 1 | 1 | 95 |
| 47 | 95 | 1 | 1 | 1 | 1 | 95 | 47 |
The sum of the numbers in it is $8 \cdot 95+4 \cdot 47+52=1000$, on the diagonals $4 \cdot 47+12=200$, and in the first row $-2 \cdot 47+2 \cdot 95+4=288$.
|
288
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Real numbers $a, b, c$ and $d$ satisfy the condition $a^{6}+b^{6}+c^{6}+d^{6}=64$. Find the maximum value of the expression $a^{7}+b^{7}+c^{7}+d^{7}$.
|
Answer: 128
Solution. By the condition $a^{6} \leqslant a^{6}+b^{6}+c^{6}+d^{6}=64$, therefore $a \leqslant 2$. Similarly, we get that $b \leqslant 2, c \leqslant 2$ and $d \leqslant 2$. Consequently,
$$
a^{7}+b^{7}+c^{7}+d^{7}=a \cdot a^{6}+b \cdot b^{6}+c \cdot c^{6}+d \cdot d^{6} \leqslant 2\left(a^{6}+b^{6}+c^{6}+d^{6}\right)=2 \cdot 64=128
$$
Equality is achieved when $a=2, b=c=d=0$. Therefore, $a^{7}+b^{7}+c^{7}+d^{7}$ does not exceed 128 and can be equal to it.
|
128
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On an island, there live liars and knights, a total of 2021 people. Knights always tell the truth, and liars always lie. Every resident of the island knows whether each person is a knight or a liar. One fine day, all the residents of the island lined up. After that, each resident of the island stated: "The number of liars standing to the right of me is greater than the number of knights standing to the left of me." How many knights are there on the island? Provide all possible options and prove that there are no others.
|
Answer: 1010
Solution. The rightmost islander cannot be telling the truth, since there is no one to the left of him, and in particular, there are no liars. Therefore, he is a liar. The leftmost islander cannot be lying, since there is at least one liar to the left of him, and there is no one to the right of him, and in particular, there are no knights. Therefore, he is a knight. Temporarily remove these two from the row. For all the others, the number of liars to the right and the number of knights to the left has decreased by one, so the truthfulness and falsity of their statements have not changed. Therefore, by repeating the same reasoning, we establish that the rightmost islander is a liar, and the leftmost is a knight. Remove the two outermost islanders again, and continue this process until only one resident remains. He is lying and therefore is a liar. Thus, in the middle of the row stands a liar, all to the right of him are also liars, and all to the left of him are knights. Therefore, there are 1010 knights.
|
1010
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (15 points) If all the trees on one hectare of forest are cut down, then 100 cubic meters of boards can be produced. Assuming that all the trees in the forest are the same, are evenly distributed, and that 0.4 m$^{3}$ of boards can be obtained from each tree, determine the area in square meters on which one tree grows. In your answer, write the integer part of the obtained number. (The integer part of a number is the greatest integer not exceeding the given number.)
|
Answer: 40.
Solution. Let's find out how many trees grow on one hectare of forest: $\frac{100 \mathrm{m}^{3}}{0.4 \mathrm{M}^{3}}=250$. Let's recall that 1 ha is $100 \mathrm{~m} \times 100 \mathrm{~m}=10000 \mathrm{~m}^{2}$. Thus, one tree grows on $\frac{10000 \mathrm{M}^{2}}{250}=40 \mathrm{M}^{2}$.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) Witch Gingema enchanted the wall clock so that the minute hand moves in the correct direction for five minutes, then three minutes in the opposite direction, then again five minutes in the correct direction, and so on. How many minutes will the hand show after 2022 minutes from the moment it pointed exactly at 12 o'clock before the start of the five-minute correct movement interval?
|
Answer: 28.
Solution. In 8 minutes of magical time, the hand will move 2 minutes in the clockwise direction. Therefore, in 2022 minutes, it will complete 252 full eight-minute cycles and have 6 minutes left. Since $252 \cdot 2=60 \cdot 8+24$, the hand will travel 8 full circles, plus 24 minutes, and then 5 minutes in the correct direction and 1 minute in the opposite direction. In total, $24+5-1=28$.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (50 points) Two multiplication examples of two natural numbers were written on the board, and in one of the examples, the numbers were the same. The troublemaker Petya erased both the original numbers and almost all the digits of the multiplication results, leaving only the last three digits: ... 689 and ... 759. Can the excellent student Misha determine which of these three digits belong to the number that resulted from the multiplication of the same numbers?
|
Answer: It could be 689.
First solution. Statement: at least one of the two last digits of the square of a natural number is necessarily even. Then the second number is eliminated. Example for the first number: $133 \cdot 133=17689$.
Proof of the statement: the statement is true for even numbers, let's consider the squares of odd numbers. Let the second-to-last digit of the original number be $n$, the last digit be $m$, where $m \in\{1,3,5,7,9\}$, and all other digits of the number be $k$. Then
$$
\left[\begin{array}{l}
(100 k+10 n+1)^{2}=100 \cdot(\ldots)+10 \cdot 2 n+1 \\
(100 k+10 n+3)^{2}=100 \cdot(\ldots)+10 \cdot 6 n+9 \\
(100 k+10 n+5)^{2}=100 \cdot(\ldots)+10 \cdot 2+5 \\
(100 k+10 n+7)^{2}=100 \cdot(\ldots)+10 \cdot(4 n+4)+9 \\
(100 k+10 n+9)^{2}=100 \cdot(\ldots)+10 \cdot(8 n+8)+1
\end{array}\right.
$$
In all cases, the second-to-last digit of the square is even.
Second solution. We will base our reasoning on the following statement: the square of a natural number is either divisible by 4 or gives a remainder of 1 when divided by 8. Indeed, if the original number is even, then its square is divisible by 4, and if the original number is odd, then it can be represented as $8 q+r$, where $r \in\{1,3,5,7\}$. Then $(8 q+$ $+r)^{2}=8 \cdot(\ldots)+1$. Having the last three digits of the number in front of us, we can check the divisibility rule by 4 or find the remainder when the number is divided by 8.
|
689
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many ways are there to color the cells of a $10 \times 10$ board in blue and green such that in each $2 \times 2$ square there are two blue and two green cells?
|
Answer: $2^{11}-2=2046$.
Solution. Note that if the colors of three cells in a $2 \times 2$ square are known, the color of the remaining cell is uniquely determined. Also, the colors of the two remaining cells are uniquely determined if there are two adjacent cells of the same color in a $2 \times 2$ square.
Consider the first row of the table. Suppose there are no adjacent cells of the same color in this row. Then the color of the first cell in the second row uniquely determines the colors of the other cells in the second row: they either all match the colors of the cells in the first row or are opposite to them. Therefore, the second row can be painted in two ways. In any of these ways, there are also no adjacent cells of the same color. Similarly, the color of the first cell in the third row uniquely determines its coloring. Thus, the third row can also be painted in two ways, and so on. Therefore, the number of ways to paint the table with such a fixed first row is exactly $2^{9}$. The number of ways to paint the table so that there are no adjacent cells of the same color in the first row is $2^{10}$.
Suppose there are two adjacent cells of the same color in the first row. Let's assume for definiteness that they are green. Then there must be two blue cells under them. Then the colors of the cells in the second row are uniquely determined. Therefore, there must be two green cells under the two adjacent blue cells. Thus, the colors of the cells in the third row are also uniquely determined, and so on. Therefore, the first row with adjacent cells of the same color uniquely determines the coloring of the entire table. The number of ways to paint the first row in two colors is $2^{10}$, but in two of them there are no adjacent cells of the same color. Therefore, the number of colorings of the table with such first rows is $2^{10}-2$, and the total number of colorings is $2^{10}+\left(2^{10}-2\right)=2^{11}-2=2046$.
|
2046
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) We will say that a number has the form $\overline{a b a}$ if its first and third digits are the same; the second digit does not have to be different. For example, 101 and 222 have this form, while 220 and 123 do not. Similarly, we define the form of the number $\overline{\overline{b a b c}}$. How many numbers of the form $\overline{a b a b c}$ are divisible by 5?
|
Answer: 180.
Solution. Numbers divisible by $5$ are those ending in 0 or 5, so we have two options for $c$. For $a$, we have 9 options, as the number cannot start with zero, and the value of $b$ can be anything.
Thus, we get that the total number of such numbers is $2 \cdot 9 \cdot 10=180$.
|
180
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) Nезнayka came up with a password for his email consisting of five characters. Deciding to check the reliability of this password, he calculated all possible combinations that can be formed from these five characters. In the end, he got 20 different combinations. Is a password with this number of combinations possible, or did Nезнayka make a mistake in his calculations? If it is possible, provide an example of a suitable password.
|
For example, error.
Solution. The maximum number of different combinations that can be formed from 5 symbols equals $5!(n!=1 \cdot 2 \cdots n$ - the factorial of number $n$, i.e., the product of all natural numbers from 1 to $n$ inclusive). This number is obtained when all 5 symbols are distinct.
Suppose among the given 5 symbols there are $k \leqslant 5$ identical ones. Consider an arbitrary combination of these symbols. Clearly, swapping any two identical symbols in the considered combination while keeping the other symbols in their places does not yield a new combination. There can be $k!$ such permutations among the identical symbols. Thus, each combination of symbols that are not identical repeats $k!$ times. Therefore, the total number of different combinations is $5!/ k!$. Similarly, if in addition to $k$ identical symbols there are also $n$ other identical symbols, then the total number of different combinations is $5!/(k!\cdot n!)$.
It is not hard to see that 20 different combinations are obtained when $k=3, n=1$.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Masha has 1000 beads in 50 different colors, 20 beads of each color. What is the smallest $n$ such that for any way of making a necklace from all the beads, one can choose $n$ consecutive beads, among which there are beads of 25 different colors?
|
Answer: $n=462$.
First solution. Let's call a segment of the necklace of length $m$ a set of $m$ consecutive beads. If the beads in the necklace are arranged in groups of 20 of the same color, then a segment of length 461 cannot contain more than 24 different colors. Therefore, $n \geqslant 462$. Consider a segment of the necklace of length 462. Suppose that in this segment, 25 beads of different colors do not appear. Number the beads of the necklace counterclockwise so that the first beads are those of the chosen segment. Let $m$ be the number of the first bead of a color that is not present in the segment (say, yellow). We will show that the segment of the necklace from $m-461$ to $m$ contains 25 colors. Indeed, the yellow color is present in it. In the remaining part of the segment, the yellow color cannot appear by construction. But there are beads of at least 24 colors in it, since $461 > 23 \cdot 20$.
Second solution. Let's call a segment of the necklace 462 consecutive beads. We will show that in some segment, there will be 25 different colors. Suppose the opposite. Then in any segment, there are no more than 24 different colors. Consider all possible pairs consisting of a segment of the necklace and some color present in it. In each segment, there are no more than 24 different colors, and the total number of segments of the necklace is 1000. Therefore, the number of pairs does not exceed $24 \cdot 1000 = 24000$. Now consider some specific color (say, blue). There are 20 blue beads in total, and between the farthest blue beads $A$ and $B$, there are always at least 18 beads (exactly 18 only when all blue beads are consecutive). Thus, there are at least 19 segments containing $B$ and not containing $A$. The bead $A$ itself is included in 462 segments. Therefore, blue beads are contained in at least 481 segments. These arguments are valid for any color. Therefore, the total number of pairs is at least $481 \cdot 50 = 24050 > 24000$, which is impossible.
|
462
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. What is the minimum number of chips that can be placed in the cells of a $99 \times 99$ table so that in each $4 \times 4$ square there are at least eight chips?
|
Answer: 4801.
Solution. Add a row and a column with number 100 to the table. Place a chip in each of their cells. Divide the expanded table into 625 squares $4 \times 4$. In each square, there can be no more than eight empty cells, so there are no more than 5000 empty cells in the entire table. Therefore, the total number of chips must be at least $99^{2}-5000=4801$.
Now, place chips in the cells of the expanded table where the product of the coordinates is divisible by four. In this case, each of the 625 squares $4 \times 4$ will have exactly 8 chips. Moreover, the added row and column will be completely filled with chips. Therefore, in the original table, there will be $625 \cdot 8-199=4801$ chips.
|
4801
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Boy Tolya loves to swim. When he comes to one grandmother's cottage, he swims in the Volkhov and floats downstream from one beach to another in 18 minutes. On the way back, it takes him exactly 1 hour. When he came to another grandmother's cottage, he swam the same distance downstream in the Luga River in 20 minutes. How much time will it take him to return back?
|
Answer: 45 minutes.
Solution. Let the distance between the beaches be $x$ km. Then in Volkhov, Tolya swims downstream at a speed of $x / 18$ km/min, and upstream at a speed of $x / 60$ km/min. Therefore, Tolya's own speed is $\frac{1}{2}(x / 60 + x / 18) = 13 x / 360$ km/min. In Luga, Tolya swims downstream at a speed of $x / 20$ km/min. Thus, the speed of the current in Luga is $x / 20 - 13 x / 360 = 5 x / 360$ km/min. Therefore, Tolya's speed against the current in Luga is $13 x / 360 - 5 x / 360 = x / 45$ km/min. Hence, Tolya will swim $x$ km against the current in Luga in 45 minutes.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The cells of a $20 \times 20$ table are painted in $n$ colors, and there are cells of each color. In each row and each column of the table, no more than six different colors are used. What is the largest $n$ for which this is possible?
|
Answer: 101.
Solution. Suppose there is a coloring with 102 colors. Then there are two rows that together use at least 12 colors (otherwise, the total number of colors does not exceed $11+5 \cdot 18=101$). Let's assume for definiteness that these are the first and second rows. By the condition, no more than six different colors are present in each row. Therefore, exactly six colors are used in both the first and second rows, and all these colors are different. We will call the colors used in the first two rows dark, and the rest light. Now consider the columns of the table. In each of them, there are no more than four light colors, since the two top cells are painted in different dark colors. Then the total number of light colors used in the table does not exceed $4 \cdot 20=80$ and 12 dark colors. Thus, the total number of colors does not exceed $80+12=92<102$, which is impossible.
A coloring with 101 colors is given below. Empty cells are painted in the 100th color.
| 0 | 1 | 2 | 3 | 4 | | | | | | | | | | | | | | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | 5 | 6 | 7 | 8 | 9 | | | | | | | | | | | | | | |
| | | 10 | 11 | 12 | 13 | 14 | | | | | | | | | | | | | |
| | | | 15 | 16 | 17 | 18 | 19 | | | | | | | | | | | | |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ |
| | | | | | | | | | | | | | | | 75 | 76 | 77 | 78 | 79 |
| 80 | | | | | | | | | | | | | | | | | 81 | 82 | 83 | 84 |
| 85 | 86 | | | | | | | | | | | | | | | | 87 | 88 | 89 |
| 90 | 91 | 92 | | | | | | | | | | | | | | | | | 93 | 94 |
| 95 | 96 | 97 | 98 | | | | | | | | | | | | | | | | | 99 |
|
101
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) Several positive numbers are written on the board. The sum of the five largest of them is 0.29 of the sum of all the numbers, and the sum of the five smallest is 0.26 of the sum of all the numbers. How many numbers are written on the board?
|
Answer: 18.
Solution. Let the total number of numbers be $k+10$. From the condition, it is clear that $k>0$. We can assume that the sum of all numbers is 1 (otherwise, we divide each number by this sum, and the condition of the problem remains). We order the numbers in ascending order:
$$
a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5} \leqslant a_{5+1} \ldots \leqslant a_{5+k} \leqslant a_{6+k} \leqslant a_{7+k} \leqslant a_{8+k} \leqslant a_{9+k} \leqslant a_{10+k}
$$
Then
$$
0.26=a_{1}+\ldots+a_{5} \leqslant 5 a_{5} \leqslant 5 a_{6} \Longrightarrow a_{6} \leqslant 0.26 / 5
$$
Moreover,
$$
0.29=a_{k+6}+\ldots+a_{k+10} \geqslant 5 a_{k+6} \geqslant 5 a_{k+5} \Longrightarrow a_{k+5} \geqslant 0.26 / 5
$$
Let $s=a_{6}+\ldots+a_{k+5}$. Note that $s=1-0.26-0.29=0.45$. Therefore,
$$
0.45=s \geqslant k \cdot a_{6} \geqslant \frac{0.26 k}{5}, \quad 0.45=s \leqslant k \cdot a_{k+5} \leqslant \frac{0.29 k}{5}
$$
Thus,
$$
\frac{0.45 \cdot 5}{0.29} \leqslant k \leqslant \frac{0.45 \cdot 5}{0.26} \Longleftrightarrow 7.75<\frac{225}{29} \leqslant k \leqslant \frac{225}{26}<8.65
$$
The only integer $k$ that satisfies this double inequality is 8. Therefore, the total number of numbers written on the board is $8+10=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) Students' written work is evaluated on a two-point grading system, i.e., a work will either be credited if it is done well, or not credited if it is done poorly. The works are first checked by a neural network, which gives an incorrect answer in $10 \%$ of cases, and then all works deemed uncredited are rechecked manually by experts, who do not make mistakes. The neural network can both incorrectly classify a good work as uncredited and a bad work as credited. It is known that among all the works submitted by students, $20 \%$ are actually bad. What is the smallest percentage of bad works that can be among those that experts recheck after the neural network's selection? Provide the integer part of the number.
|
Answer: 66.
Solution. We will represent the students' works in the diagram below.
Neural network errors can:
a) classify all 10% of good works as bad;
b) classify part of the good works as bad and part of the bad works as good;
c) classify all 10% of bad works as good.
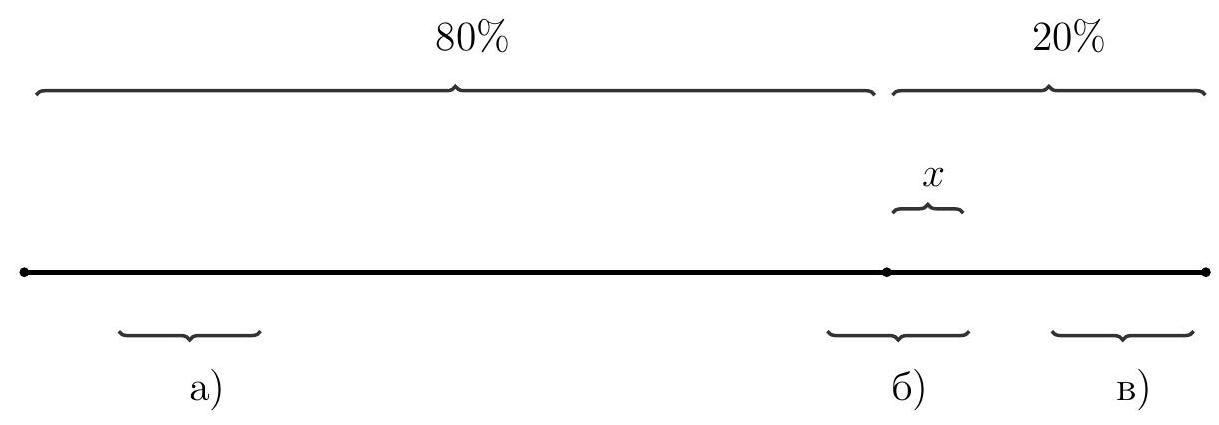
Let's analyze the general case. Let \( x \) be the percentage of all works that are incorrectly classified as good (these are the bad works that will not be reviewed by experts); \( 0 \leqslant x \leqslant 10 \). Then the experts will receive for rechecking (in percentages of all works): bad works that the neural network did not misclassify - these are \((20-x) \% \);
good works that were incorrectly classified as bad - these are \((10-x) \% \).
Thus, the percentage of bad works to be rechecked is
\[
\frac{(20-x) \times 100}{(20-x)+(10-x)} = \frac{(20-x) \times 100}{30-2x} = 50 + \frac{500}{30-2x}
\]
This function is increasing over its entire domain, so under the conditions of the problem, it takes the smallest value when \( x = 0 \). This value is \( 66 \frac{2}{3} \), and its integer part is 66.
|
66
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (30 points) Point $M$ is the midpoint of the hypotenuse $A C$ of the right triangle $A B C$. Points $P$ and $Q$ on lines $A B$ and $B C$ respectively are such that $A P = P M$ and $C Q = Q M$. Find the measure of angle $\angle P Q M$, if $\angle B A C = 17^{\circ}$.
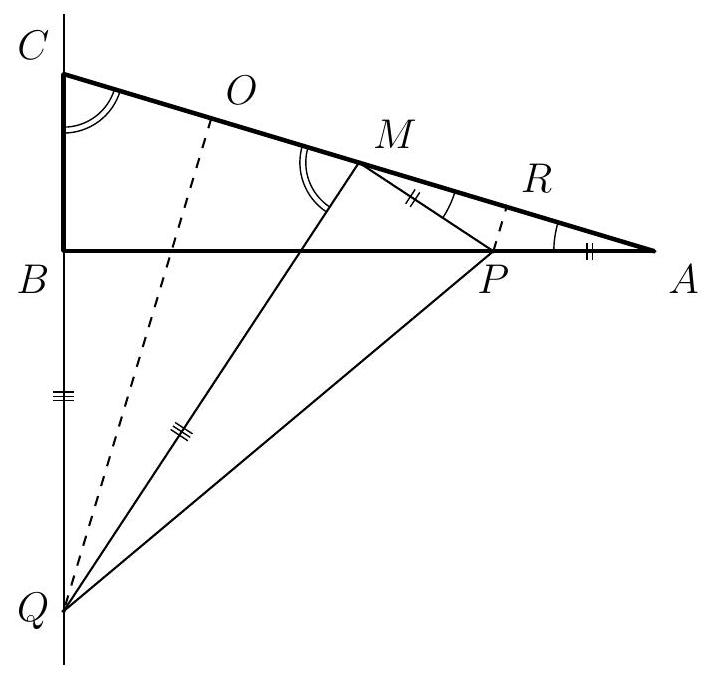
|
Answer: $17^{\circ}$.
Solution. Since in the right triangle $ABC$ the angle $BAC=17^{\circ}$, the angle $BCA=73^{\circ}$. Note that triangle $QMC$ is isosceles with base $MC$, as by condition $QM=QC$. Similarly, triangle $PMA$ is isosceles with base $MA$. Therefore, the angles at the bases of these triangles are equal. From this, we get that $\angle QMP=180^{\circ}-\angle PMA-\angle QMC=180^{\circ}-17^{\circ}-73^{\circ}=90^{\circ}$.
Let points $O$ and $R$ be the feet of the perpendiculars dropped from points $Q$ and $P$ to the line $AC$, respectively. It is easy to notice that triangles $QOM$ and $MRP$ are similar by two angles. Since $CM=MA$, from the isosceles nature of triangles $QCM$ and $PMA$, it follows that
$$
MO=\frac{1}{2} CM=\frac{1}{2} MA=MR
$$
Let $x=MO$. From the right triangles $QOM$ and $PMR$, we get that $MQ=\frac{x}{\cos 73^{\circ}}$ and $MP=\frac{x}{\cos 17^{\circ}}$ respectively. Thus, for triangle $MQP$ we have
$$
\operatorname{tg} \angle PQM=\frac{MP}{MQ}=\frac{x}{\cos 17^{\circ}} \cdot \frac{\cos 73^{\circ}}{x}=\frac{\cos \left(\pi / 2-17^{\circ}\right)}{\cos 17^{\circ}}=\operatorname{tg} 17^{\circ}
$$
Since in the right triangle $MQP$ the angle $PQM$ is acute, from the last equality it follows that $\angle PQM=17^{\circ}$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (40 points) Let's call the tail of a natural number any number that is obtained from it by discarding one or several of its first digits. For example, 234, 34, and 4 are tails of the number 1234. Does there exist a six-digit number without zeros in its decimal representation that is divisible by each of its tails?
|
Answer: Yes (721875 fits).
Solution. Suppose the required number exists. Let's write it as $A=$ $=\overline{a_{5} a_{4} \ldots a_{0}}$. Then $A$ is divisible by its five-digit tail, that is, by $\overline{a_{4} \ldots a_{0}}$. Therefore, $\overline{a_{4} \ldots a_{0}}$ divides the difference between $A$ and its tail, which is $a_{5} \cdot 10^{5}$. Thus, we need to check the five-digit divisors of $a_{5} \cdot 10^{5}$ without zeros in their decimal representation. Any divisor of the number $a_{5} \cdot 10^{5}$ is the product of $a_{5}$ and some powers of five and two. Since this product should not end in zero, it cannot contain both two and five simultaneously. If we take only twos, we get a number not exceeding $a_{5} \cdot 2^{5} \leqslant 9 \cdot 2^{5}=288$, which is not a five-digit number. Therefore, we need the number $a_{5} \cdot 5^{n}$, where $a_{5}$ is odd. Note that $n=5$, otherwise $a_{5} \cdot 5^{n} \leqslant 9 \cdot 625=5625$, and this number is also not five-digit. Finally, $a_{5}>3$, since the number $3 \cdot 5^{5}=9375$ is four-digit.
Considering the constraints, we get three possible options: $5 \cdot 5^{5}$, $7 \cdot 5^{5}, 9 \cdot 5^{5}$. The second one gives the number 721875, which fits:
$$
\begin{gathered}
721875 / 21875=33 ; 721875 / 1875=385 ; 721875 / 875=825 ; \\
721875 / 75=9625 ; 721875 / 5=144375
\end{gathered}
$$
It is not difficult to check that the other two options do not work. However, this is not necessary, as the answer has already been obtained.
|
721875
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (15 points) In a bookstore, there is a rule for "summing" discounts: "if different types of discounts apply to an item, they are applied sequentially one after another." For example, if two discounts A% and B% apply to an item, the first discount is applied to the original price, and the second discount is applied to the result of the first discount. Currently, two discounts are in effect in the store: "Autumn" at $25 \%$ and "Random" - a non-zero discount of a whole number of percent, determined at the moment of purchase. Someone with a loyalty card, which gives a $20 \%$ discount on all items, bought a book for 69 rubles, the original price of which was 230 rubles. What was the size of the "Random" discount?
|
Answer: $50 \%$.
Solution. Note that the sequence of applying discounts is irrelevant, since applying a discount of A\% is equivalent to multiplying the cost of the item by ( $1-\frac{A}{100}$ ). Let $R$ be the magnitude of the "random" discount. Then, as a result of "summing" the three discounts, we get
$$
230 \cdot\left(1-\frac{25}{100}\right) \cdot\left(1-\frac{20}{100}\right) \cdot\left(1-\frac{R}{100}\right)=69 \Longleftrightarrow R=50
$$
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) We will call a word any finite sequence of letters of the Russian alphabet. How many different four-letter words can be formed from the letters of the word КАША? And from the letters of the word ХЛЕБ? In your answer, indicate the sum of the found numbers.
|
Answer: 36.
Solution. In the word ХЛЕБ, all letters are different. Therefore, by rearranging the letters, we get $4 \cdot 3 \cdot 2 \cdot 1=24$ words. From the word КАША, we can form 12 words. Indeed, for the letters K and Ш, there are $4 \cdot 3=12$ positions, and we write the letters А in the remaining places. Thus, in total, we get $24+12=36$ words.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (35 points) Journalists have found out that
a) in the lineage of Tsar Pafnuty, all descendants are male: the tsar himself had 2 sons, 60 of his descendants also had 2 sons each, and 20 had 1 son each;
b) in the lineage of Tsar Zinovy, all descendants are female: the tsar himself had 4 daughters, 35 of his descendants had 3 daughters each, and another 35 had 1 daughter each.
The rest of the descendants of both tsars had no children. Who had more descendants?
|
Answer: At Zinovy.
Solution. We need to find the total number of children in the lineage of Pafnuty, including the children of the king himself. It is equal to $60 \cdot 2+20 \cdot 1+2=142$. The total number of children in the lineage of King Zinovy is $4+35 \cdot 3+35 \cdot 1=144$.
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (50 points) From the numbers 1 to 200, one or several were selected into a separate group with the following property: if there are at least two numbers in the group, then the sum of any two numbers in this group is divisible by 5. What is the maximum number of numbers that can be in a group with this property?
|
Answer: 40.
Solution. Suppose that the group selected a number $A$, which gives a remainder $i \neq 0$ when divided by 5. If there is another number $B$ in the group, then it must give a remainder $5-i$ when divided by 5, so that $A+B$ is divisible by 5. We will show that there cannot be any other numbers in this group. Suppose there is another number $C$, and $j=C \bmod 5$. Then the numbers $i+j$ and $5-i+j$ are divisible by 5, as well as their difference, which is $2 i-5$, which is impossible for $i \neq 0$.
Now consider the alternative case, where all numbers in the group are divisible by 5. In the given range, there are exactly 40 numbers that are multiples of 5, and all these numbers can be included in the group simultaneously.
|
40
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
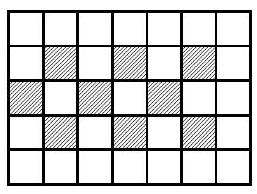
1. On a $5 \times 7$ grid, 9 cells are marked. We will call a pair of cells with a common side interesting if exactly one cell in the pair is marked. What is the maximum number of interesting pairs that can be?
|
Answer: 35.
Solution. Let's call two cells adjacent if they share a side. The number of interesting pairs containing a given marked cell is no more than 4, and for a boundary cell, it is no more than 3. Then the total number of interesting pairs does not exceed $9 \cdot 4 = 36$. At the same time, if there are two adjacent marked cells, the interesting pair containing them is counted twice. Note that among the 9 cells in the $3 \times 5$ rectangle, there are necessarily two adjacent cells. Therefore, among the marked cells, there is either a boundary cell or two adjacent cells. Thus, the total number of interesting pairs does not exceed 35. An example of a marking with 35 interesting pairs is provided below.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given positive numbers $a, b, c, d$. Find the minimum value of the expression
$$
A=\left(\frac{a+b}{c}\right)^{4}+\left(\frac{b+c}{d}\right)^{4}+\left(\frac{c+d}{a}\right)^{4}+\left(\frac{d+a}{b}\right)^{4}
$$
|
Answer: 64.
Solution. By Cauchy's inequality for means,
$$
A \geqslant 4 \cdot \frac{(a+b)(b+c)(c+d)(d+a)}{a b c d}=64 \cdot \frac{a+b}{2 \sqrt{a b}} \cdot \frac{b+c}{2 \sqrt{b c}} \cdot \frac{c+d}{2 \sqrt{c d}} \cdot \frac{d+a}{2 \sqrt{d a}} \geqslant 64
$$
Equality is achieved when $a=b=c=d=1$.
|
64
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a $7 \times 7$ checkerboard, 14 cells are marked. We will call a pair of cells with a common side interesting if at least one cell in the pair is marked. What is the maximum number of interesting pairs that can be?
|
# Answer: 55.
Solution. Let's call two cells adjacent if they share a side. The number of interesting pairs containing a given marked cell is no more than 4, and for a boundary cell, no more than 3. Then the total number of interesting pairs does not exceed $14 \cdot 4 = 56$. At the same time, if there are two adjacent marked cells, the interesting pair containing them is counted twice. Note that among the 14 cells in a $5 \times 5$ square, there are necessarily two adjacent ones. Therefore, among the marked cells, there is either a boundary cell or two adjacent ones. Thus, the total number of interesting pairs does not exceed 55. An example of a marking with 55 interesting pairs is provided below.

|
55
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given positive numbers $a, b, c, d$. Find the minimum value of the expression
$$
A=\left(\frac{a^{2}+b^{2}}{c d}\right)^{4}+\left(\frac{b^{2}+c^{2}}{a d}\right)^{4}+\left(\frac{c^{2}+d^{2}}{a b}\right)^{4}+\left(\frac{d^{2}+a^{2}}{b c}\right)^{4}
$$
|
Answer: 64.
Solution. By the Cauchy inequalities for means,
$$
A \geqslant 4 \cdot \frac{\left(a^{2}+b^{2}\right)\left(b^{2}+c^{2}\right)\left(c^{2}+d^{2}\right)\left(d^{2}+a^{2}\right)}{c d \cdot a d \cdot a b \cdot b c}=64 \cdot \frac{a^{2}+b^{2}}{2 a b} \cdot \frac{b^{2}+c^{2}}{2 b c} \cdot \frac{c^{2}+d^{2}}{2 c d} \cdot \frac{d^{2}+a^{2}}{2 d a} \geqslant 64
$$
Equality is achieved when $a=b=c=d=1$.
|
64
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle $\omega$ is circumscribed around triangle $A B C$. Tangents to the circle, drawn at points $A$ and $B$, intersect at point $K$. Point $M$ is the midpoint of side $A C$. A line passing through point $K$ parallel to $A C$ intersects side $B C$ at point $L$. Find the angle $A M L$.
|
Answer: $90^{\circ}$.
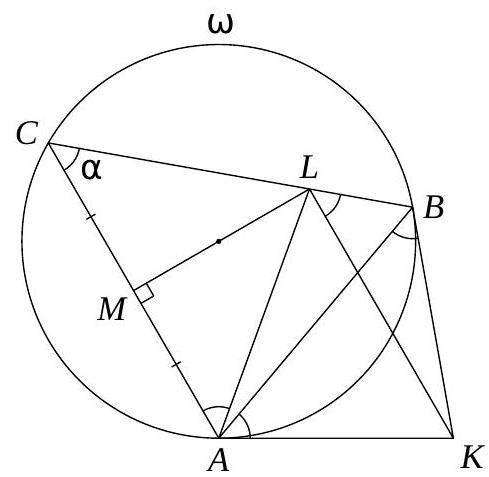
Solution. Let $\alpha=\angle A C B$. The angle between the tangent $A K$ and the chord $A B$ of the circle $\omega$ is equal to the inscribed angle that subtends $A B$, hence $\alpha=\angle B A K=\angle A B K$. Since
$A C \| K L$, we get $\angle B L K=\angle A C B=\angle B A K$. Therefore, the quadrilateral $A L B K$ is cyclic. Then
$$
\angle A L C=180^{\circ}-\angle A L B=\angle A K B=180^{\circ}-2 \alpha \quad \text { and } \quad \angle L C A=\alpha=180^{\circ}-\angle A L C-\alpha=\angle L A C .
$$
Thus, triangle $A L C$ is isosceles, and its median $L M$ is also an altitude. Therefore, $\angle A M L=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the table, there are three spheres and a cone (with its base $k$ on the table), touching each other externally. The radii of the spheres are 20, 40, and 40, and the radius of the base of the cone is 21. Find the height of the cone.
|
Answer: 28.
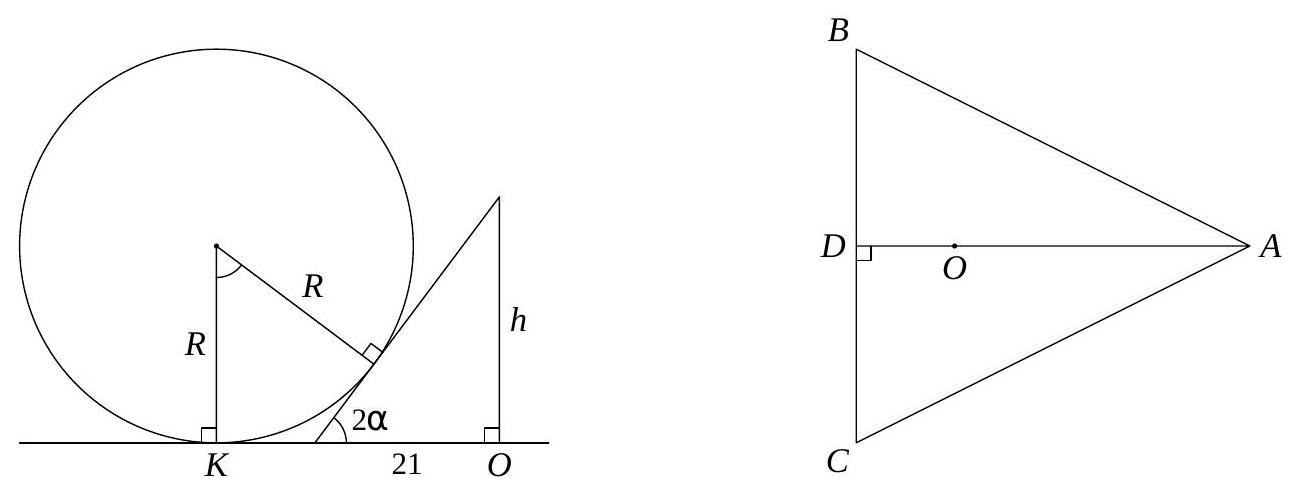
Solution. Let $O$ be the center of the base of the cone, $h$ be its height, and $2 \alpha$ be the angle of inclination of the cone's generators to the table. Consider the section passing through the axis of symmetry of the cone and the center of one of the spheres (see the left figure). Let $K$ be the point of contact of the sphere with the table, and $R$ be the radius of the sphere. Then
$$
O K=R \cdot \operatorname{tg} \alpha+21
$$
Let $A, B, C$ be the points of contact of the spheres with the table (see the right figure). From the condition of the spheres touching, $B C=80$ and
$$
A B=A C=\sqrt{(40+20)^{2}-(40-20)^{2}}=40 \sqrt{2}
$$
Thus, the height $A D$ of the triangle $A B C$ is the perpendicular bisector of $B C$. From (*) it follows that the point $O$ is equidistant from $B$ and $C$, i.e., it lies on $A D$, and $O A=20 \operatorname{tg} \alpha+21$. Note that
$$
B D=40, \quad A D=\sqrt{A B^{2}-B D^{2}}=40, \quad O D=A D-O A=19-20 \operatorname{tg} \alpha
$$
The equality (*) gives $O B=40 \operatorname{tg} \alpha+21$, and by the Pythagorean theorem
$O B^{2}=O D^{2}+B D^{2} \Longleftrightarrow(40 \operatorname{tg} \alpha+21)^{2}=(19-20 \operatorname{tg} \alpha)^{2}+40^{2} \Longleftrightarrow 30 \operatorname{tg}^{2} \alpha+61 \operatorname{tg} \alpha-38=0 \Longleftrightarrow \operatorname{tg} \alpha=\frac{1}{2}$.
From this,
$$
\operatorname{tg} 2 \alpha=\frac{2 \operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha}=\frac{4}{3} \quad \text { and } \quad h=21 \cdot \operatorname{tg} 2 \alpha=28
$$
## Variant 3
|
28
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
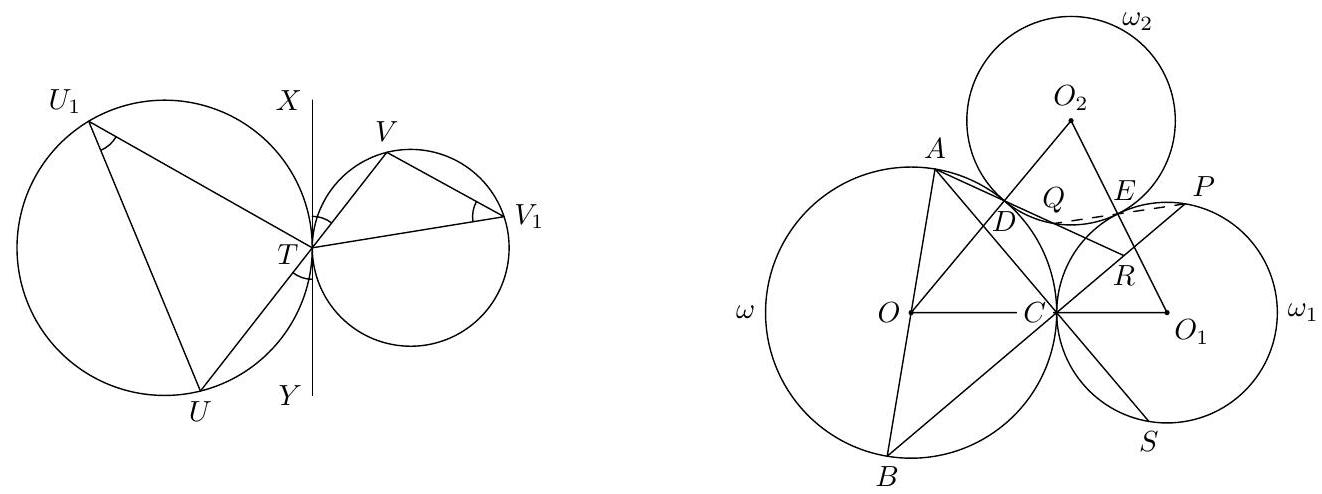
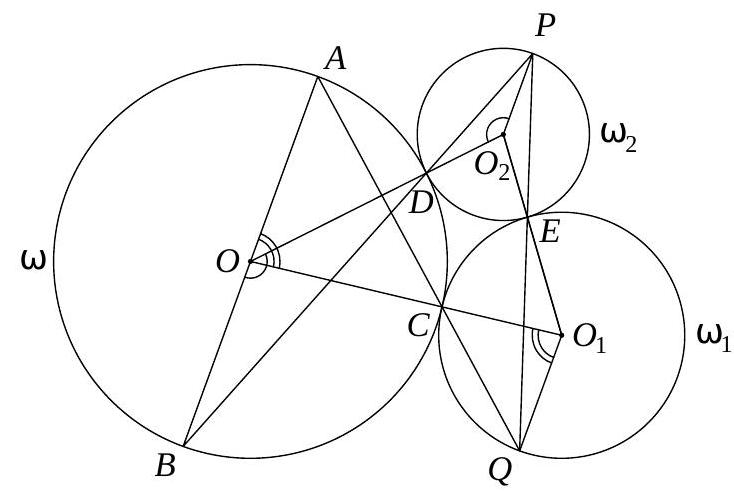
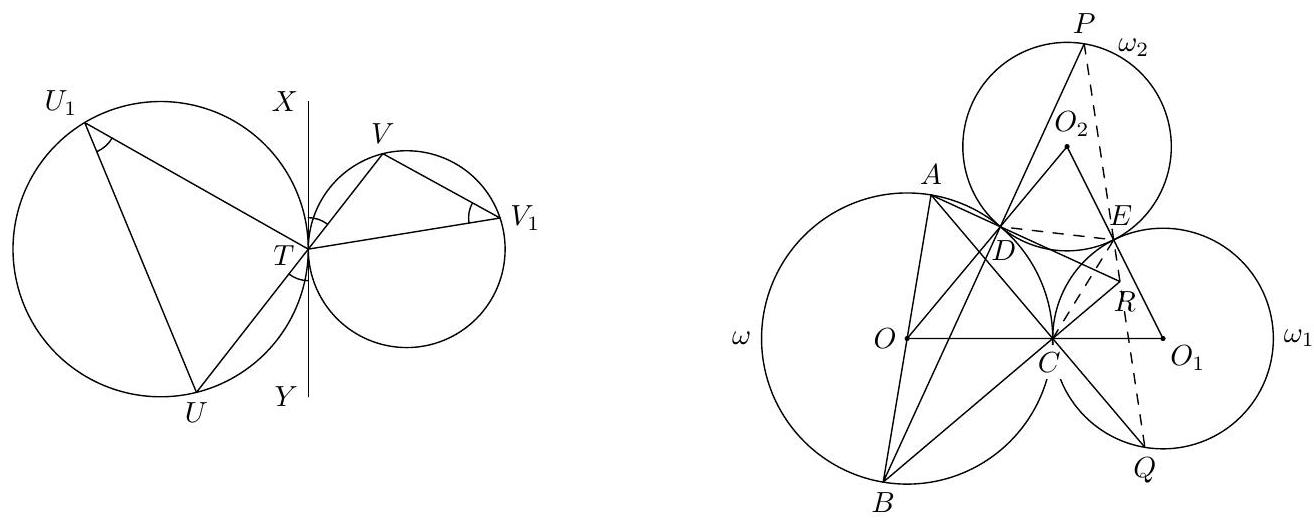
3. Quadrilateral $ABCD$ is inscribed in circle $\omega$, the center of which lies on side $AB$. Circle $\omega_{1}$ is externally tangent to circle $\omega$ at point $C$. Circle $\omega_{2}$ is tangent to circles $\omega$ and $\omega_{1}$ at points $D$ and $E$ respectively. Line $BC$ intersects circle $\omega_{1}$ again at point $P$, and line $AD$ intersects circle $\omega_{2}$ again at point $Q$. It is known that points $P, Q$, and $E$ are distinct. Find the angle $PEQ$.
|
Answer: $180^{\circ}$.
Solution 1. Since $\angle B C O=\angle P C O_{1}$, the isosceles triangles $B O C$ and $P O_{1} C$ are similar, from which $\angle B O C=\angle P O_{1} C$. Similarly, it can be verified that $\angle A O D=\angle Q O_{2} D$. Then the segments $O_{1} P$ and $O_{2} Q$ are parallel to the line $A B$ and, therefore, to each other. Hence, $\angle P O_{1} E=\angle Q O_{2} E$. Thus, the isosceles triangles $P O_{1} E$ and $Q O_{2} E$ are similar, from which $\angle O_{1} E P=\angle O_{2} E Q$. Therefore, the point $E$ lies on the segment $P Q$, which gives the answer.
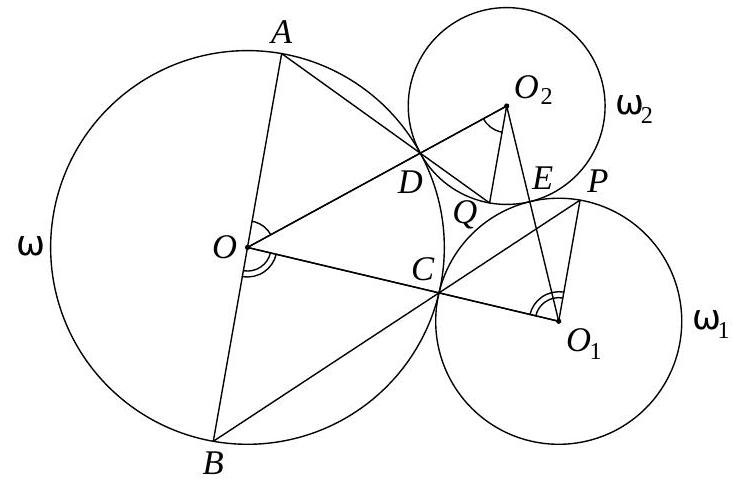
Solution 2. Note a useful property of tangent circles: if a secant $U V$ passes through the point $T$ of tangency of two circles, then the inscribed angles subtended by the arcs it intercepts are equal. Indeed, since an inscribed angle is equal to the angle between the tangent and the secant, the equalities $\angle U U_{1} T=\angle U T Y=\angle X T V=\angle V V_{1} T$ hold (see the left figure below).
Let the intersection of $A D$ and $B C$ be $R$, and the second intersection of $A C$ with the circle $\omega_{1}$ be $S$. Let $\angle O O_{1} O_{2}=2 \alpha$ and $\angle O O_{2} O_{1}=2 \beta$. From the isosceles triangles $O_{1} C E$ and $O_{2} D E$, we get that
$$
\angle O_{1} E C=90^{\circ}-\alpha, \quad \angle O_{2} E D=90^{\circ}-\beta \quad \text { and } \quad \angle C E D=180^{\circ}-\angle O_{1} E C-\angle O_{2} E D=\alpha+\beta
$$
On the other hand, from the sum of the angles of triangle $O O_{1} O_{2}$, we find that $\angle C O D=180^{\circ}-2 \alpha-2 \beta$. The inscribed angle $\angle C A D$ is half the central angle $\angle C O D$. Then
$$
\angle C A D=90^{\circ}-\alpha-\beta, \quad \angle A C R=\angle A C B=90^{\circ}, \quad \text { from which } \quad \angle C R D=\alpha+\beta
$$
Thus, $\angle C R D=\angle C E D$. From the cyclic quadrilateral $P E C S$, it follows that
$$
\angle P E C=180^{\circ}-\angle P S C=180^{\circ}-\angle C A B=90^{\circ}+\angle R B A
$$
Moreover, $\angle D E Q=\angle D B A=90^{\circ}-\angle R A B$. Now we can find the angle $P E Q$:
$$
\begin{aligned}
& \angle P E Q=\angle P E C+\angle C E D-\angle D E Q=\angle P E C+\angle C R D-\angle D E Q= \\
& =\left(90^{\circ}+\angle R B A\right)+\left(180^{\circ}-\angle R A B-\angle R B A\right)-\left(90^{\circ}-\angle R A B\right)=180^{\circ}
\end{aligned}
$$
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Quadrilateral $ABCD$ is inscribed in circle $\omega$, the center of which lies on side $AB$. Circle $\omega_{1}$ is externally tangent to circle $\omega$ at point $C$. Circle $\omega_{2}$ is tangent to circles $\omega$ and $\omega_{1}$ at points $D$ and $E$ respectively. Line $BD$ intersects circle $\omega_{2}$ again at point $P$, and line $AC$ intersects circle $\omega_{1}$ again at point $Q$. Find the angle $PEQ$.
|
Answer: $180^{\circ}$.
Solution 1. Since $\angle A C O=\angle Q C O_{1}$, the isosceles triangles $A O C$ and $Q O_{1} C$ are similar, from which $\angle A O C=\angle Q O_{1} C$. Similarly, it can be verified that $\angle B O D=\angle P O_{2} D$. Then the segments $O_{1} Q$ and $O_{2} P$ are parallel to the line $A B$ and, therefore, to each other. Hence, $\angle O_{1} Q E=\angle O_{2} P E$, which is equivalent to $\angle O_{1} E Q=\angle O_{2} E P$. This means that point $E$ lies on the segment $P Q$, from which $\angle P E Q=180^{\circ}$.
Solution 2. Note a useful property of tangent circles: if a secant $U V$ passes through the point $T$ of tangency of two circles, then the inscribed angles subtending the arcs cut by it are equal. Indeed, since the inscribed angle is equal to the angle between the tangent and the secant, the equalities $\angle U U_{1} T=\angle U T Y=\angle X T V=\angle V V_{1} T$ hold (see the left figure below).
Let the intersection of $A D$ and $B C$ be $R$. Let $\angle O O_{1} O_{2}=2 \alpha$ and $\angle O O_{2} O_{1}=2 \beta$. Then, from the isosceles triangles $O_{1} C E$ and $O_{2} D E$, we get that
$$
\angle O_{1} E C=90^{\circ}-\alpha, \quad \angle O_{2} E D=90^{\circ}-\beta \quad \text { and } \quad \angle C E D=180^{\circ}-\angle O_{1} E C-\angle O_{2} E D=\alpha+\beta .
$$
On the other hand, from the sum of the angles of triangle $O O_{1} O_{2}$, we find that $\angle C O D=180^{\circ}-2 \alpha-2 \beta$. The inscribed angle $\angle C A D$ is half of the central angle $\angle C O D$. Then
$$
\angle D A C=90^{\circ}-\alpha-\beta, \quad \angle A C R=\angle A C B=90^{\circ}, \quad \text { from which } \angle D R C=\alpha+\beta .
$$
Thus, $\angle D R C=\angle D E C$. By the proven statement,
$$
\angle P E D=\angle B A D=\angle R A B \quad \text { and } \quad \angle C E Q=\angle A B C=\angle R B A .
$$
Now we can find the angle $P E Q$ :
$$
\begin{aligned}
\angle P E Q & =\angle P E D+\angle D E C+\angle C E Q=\angle P E D+\angle D R C+\angle C E Q= \\
& =\angle P E D+180^{\circ}-\angle R A B-\angle R B A+\angle C E Q=180^{\circ} .
\end{aligned}
$$
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the cells of a $5 \times 5$ table, natural numbers are arranged such that all ten sums of these numbers in the rows and columns of the table are distinct. Find the smallest possible value of the sum of all the numbers in the table.
|
Answer: 48.
Solution. Since the elements of the table are natural numbers, the sums of the rows and columns of the table are no less than 5. Since all these sums are distinct, the minimal possible set of their values is $\{5,6, \ldots, 13,14\}$. By adding the sums of the rows and columns of the table, we get twice the sum $S$ of all the numbers in the table, as each of them is counted twice - in the row and in the column. Then
$$
S \geqslant \frac{1}{2}(5+6+\ldots+13+14)=\frac{1}{2} \cdot 95=47 \frac{1}{2}, \quad \text { that is } \quad S \geqslant 48 .
$$
An example for $S=48$ is given below.
| 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 3 | 3 |
| 1 | 2 | 2 | 3 | 3 |
| 2 | 3 | 3 | 3 | 4 |
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given positive numbers $a, b, c, d$. Find the minimum value of the expression
$$
A=\left(a+\frac{1}{b}\right)^{3}+\left(b+\frac{1}{c}\right)^{3}+\left(c+\frac{1}{d}\right)^{3}+\left(d+\frac{1}{a}\right)^{3}
$$
|
Answer: 32.
Solution 1. We will use the Cauchy inequality for means first in each parenthesis, and then for the entire sum. We get
$$
A \geqslant\left(2 \sqrt{\frac{a}{b}}\right)^{3}+\left(2 \sqrt{\frac{b}{c}}\right)^{3}+\left(2 \sqrt{\frac{c}{d}}\right)^{3}+\left(2 \sqrt{\frac{d}{a}}\right)^{3} \geqslant 32\left(\frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{d} \cdot \frac{d}{a}\right)^{3 / 8}=32
$$
Equality is achieved when $a=b=c=d=1$.
Solution 2. We will use the inequality $x^{3}+y^{3} \geqslant \frac{1}{4}(x+y)^{3}$, which is true for $x, y>0$. Applying it three times, we get
$$
x^{3}+y^{3}+z^{3}+w^{3} \geqslant \frac{1}{4}\left((x+y)^{3}+(z+w)^{3}\right) \geqslant \frac{1}{16}(x+y+z+w)^{3} \quad \text { for } \quad x, y, z, w>0
$$
Then, by the Cauchy inequality for means,
$$
A \geqslant \frac{1}{16}\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{d}+d+\frac{1}{a}\right)^{3} \geqslant \frac{1}{16}\left(8 \sqrt[8]{a \cdot \frac{1}{b} \cdot b \cdot \frac{1}{c} \cdot c \cdot \frac{1}{d} \cdot d \cdot \frac{1}{a}}\right)^{3}=\frac{8^{3}}{16}=32
$$
Equality is achieved when $a=b=c=d=1$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given an acute-angled triangle $A B C$. A circle with diameter $B C$ intersects sides $A B$ and $A C$ at points $D$ and $E$ respectively. Tangents drawn to the circle at points $D$ and $E$ intersect at point $K$. Find the angle between the lines $A K$ and $B C$.
|
Answer: $90^{\circ}$.
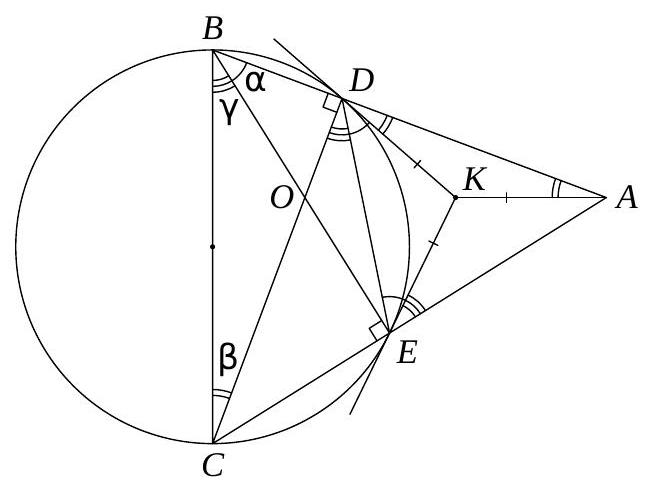
Solution 1. Let $\alpha=\angle D B E, \beta=\angle B C D, \gamma=\angle C B E, O$ - the intersection point of segments $C D$ and $B E$. The angle between the tangent $D K$ and the chord $D E$ is equal to the inscribed angle that subtends
$$
\angle D E K=\angle E D K=\alpha
$$
Moreover, $\angle C D E=\gamma$. Due to the cyclic nature of quadrilateral $B D E C$
$$
\angle A E K=\angle A E D-\alpha=\angle C B D-\alpha=\gamma \quad \text { and, similarly } \quad \angle A D K=\beta .
$$
Since $\alpha+\beta+\gamma=\angle A D C=90^{\circ}$, we get
$$
\angle D A E=180^{\circ}-2 \alpha-\beta-\gamma=90^{\circ}-\alpha=\frac{1}{2}\left(180^{\circ}-2 \alpha\right)=\frac{1}{2} \angle D K E
$$
Note that a circle $\omega$ can be circumscribed around quadrilateral $A D O E$. Then the angle $D A E$ is inscribed in $\omega$, and point $K$ lies on the perpendicular bisector of chord $B E$, i.e., on the diameter of $\omega$. Therefore, $K$ is the center of $\omega$, from which
$$
\angle D A K=\angle A D K=\beta=90^{\circ}-\alpha-\gamma=90^{\circ}-\angle C B D
$$
Thus, $A K \perp B C$.
Solution 2. Let
$$
\alpha=\angle D B E, \quad \beta=\angle B C D, \gamma=\angle C B E, \varphi=\angle D A K, \quad \psi=\angle E A K
$$
The angle between the tangent $D K$ and the chord $D E$ is equal to the inscribed angle that subtends $D E$, hence
$$
\angle D E K=\angle E D K=\alpha
$$
Moreover, $\angle C D E=\gamma$. Due to the cyclic nature of quadrilateral $B D E C$
$$
\angle A E K=\angle A E D-\alpha=\angle C B D-\alpha=\gamma \quad \text { and, similarly } \quad \angle A D K=\beta .
$$
Since $\alpha+\beta+\gamma=\angle A D C=90^{\circ}$, we get
$$
\gamma=90^{\circ}-\alpha-\beta, \quad \psi=180^{\circ}-2 \alpha-\beta-\gamma-\varphi=90^{\circ}-\alpha-\varphi
$$
The Law of Sines for triangles $D A K$ and $E A K$ gives
$$
\frac{A K}{\sin \beta}=\frac{D K}{\sin \varphi}, \quad \frac{A K}{\sin \gamma}=\frac{E K}{\sin \psi}
$$
Since $D K=E K$, we can eliminate the sides from these equations. We get
$$
\begin{aligned}
& \sin \gamma \sin \varphi=\sin \beta \sin \psi \Longleftrightarrow \cos (\alpha+\beta) \sin \varphi=\sin \beta \cos (\alpha+\varphi) \Longleftrightarrow \\
& \Longleftrightarrow \sin (\alpha+\beta+\varphi)+\sin (\varphi-\alpha-\beta)=\sin (\alpha+\beta+\varphi)+\sin (\beta-\alpha-\varphi) \Longleftrightarrow 2 \sin (\varphi-\beta) \cos \alpha=0
\end{aligned}
$$
Then
$$
\angle D A K=\varphi=\beta=90^{\circ}-\alpha-\gamma=90^{\circ}-\angle C B D
$$
from which $A K \perp B C$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the cells of a $4 \times 6$ table, natural numbers are arranged such that all ten sums of these numbers in the rows and columns of the table are distinct. Find the smallest possible value of the sum of all the numbers in the table.
|
Answer: 43.
Solution. Since the elements of the table are natural numbers, the sums of the rows and columns of the table are no less than 4. Since all these sums are different, the minimal possible set of their values is $\{4,5, \ldots, 12,13\}$. By adding the sums of the rows and columns of the table, we get twice the sum $S$ of all the numbers in the table, since each of them is counted twice - in the row and in the column. Then
$$
S \geqslant \frac{1}{2}(4+5+\ldots+12+13)=\frac{1}{2} \cdot 85=42 \frac{1}{2}, \quad \text { that is } \quad S \geqslant 43
$$
An example for $S=43$ is given below.
| 1 | 1 | 1 | 1 | 1 | 2 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 1 | 2 | 2 | 3 |
| 1 | 1 | 2 | 3 | 3 | 2 |
| 1 | 2 | 2 | 2 | 3 | 4 |
|
43
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given positive numbers $a, b, c, d$. Find the minimum value of the expression
$$
A=\left(a^{2}+\frac{1}{b c}\right)^{3}+\left(b^{2}+\frac{1}{c d}\right)^{3}+\left(c^{2}+\frac{1}{d a}\right)^{3}+\left(d^{2}+\frac{1}{a b}\right)^{3}
$$
|
Answer: 32.
Solution. We will use the Cauchy inequality for means first in each parenthesis, and then for the entire sum. We get
$$
A \geqslant\left(\frac{2 a}{\sqrt{b c}}\right)^{3}+\left(\frac{2 b}{\sqrt{c d}}\right)^{3}+\left(\frac{2 c}{\sqrt{d a}}\right)^{3}+\left(\frac{2 d}{\sqrt{a b}}\right)^{3} \geqslant 32\left(\frac{a^{2}}{b c} \cdot \frac{b^{2}}{c d} \cdot \frac{c^{2}}{d a} \cdot \frac{d^{2}}{a b}\right)^{3 / 8}=32
$$
Equality is achieved when $a=b=c=d=1$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $M$ is the midpoint of side $AB$ of triangle $ABC$. A circle $\omega_{1}$ is drawn through points $A$ and $M$, tangent to line $AC$, and a circle $\omega_{2}$ is drawn through points $B$ and $M$, tangent to line $BC$. Circles $\omega_{1}$ and $\omega_{2}$ intersect again at point $D$. Point $E$ lies inside triangle $ABC$ and is symmetric to point $D$ with respect to line $AB$. Find the angle $CEM$.
|
Answer: $180^{\circ}$
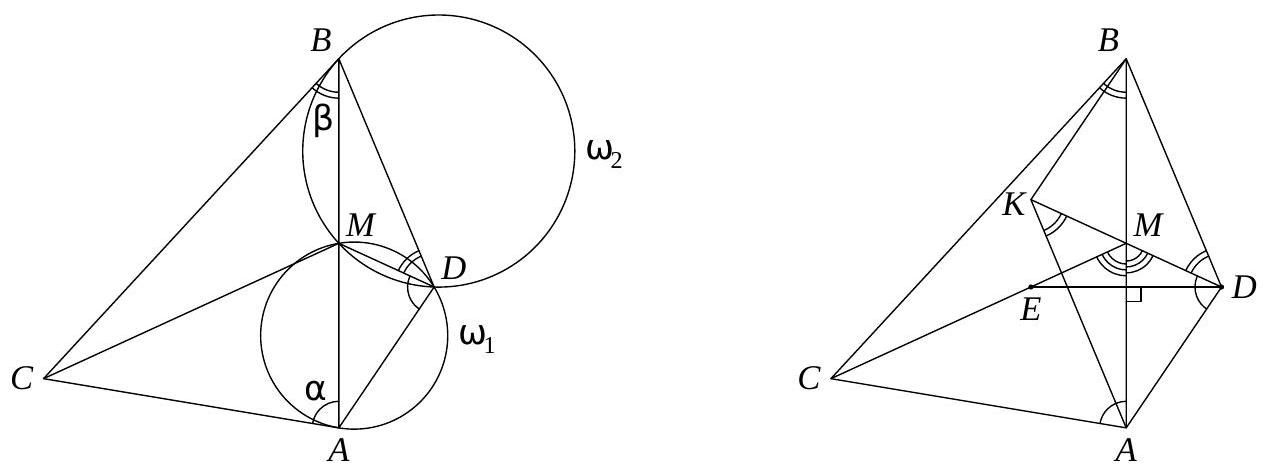
Solution 1. The angle between the tangent $A C$ and the chord $A M$ of circle $\omega_{1}$ is equal to the inscribed angle in $\omega_{1}$ that subtends $A M$, i.e., $\angle C A B = \angle A D M$. Similar reasoning for $\omega_{2}$ gives $\angle A B C = \angle B D M$. Extend triangle $A D B$ to parallelogram $A D B K$ (see the right figure). Triangles $A C B$ and $D A K$ are similar by two angles. Point $M$ is the midpoint of segments $A B$ and $D K$, so triangles $A C M$ and $D A M$ are also similar (by angle and proportional sides). Therefore, $\angle A M C = \angle A M D$. Moreover, from the symmetry of points $D$ and $E$ with respect to $A B$, it follows that $\angle A M E = \angle A M D$. Thus, point $E$ lies on segment $C M$.
Solution 2. By the properties of tangents, $\angle A D M = \angle C A M$ and $\angle M D B = \angle C B M$. Therefore,
$$
\angle A D B = \angle A D M + \angle M D B = \angle C A M + \angle C B M = 180^{\circ} - \angle A C B
$$
and quadrilateral $A C B D$ is cyclic. Then
$$
\angle B D C = \angle B A C = \angle M D A \quad \text{and} \quad \angle B C D = \angle B A D = \angle M A D.
$$
Thus, triangles $B D C$ and $M D A$ are similar by two angles, so
$$
\frac{B D}{M D} = \frac{B C}{M A} = \frac{C B}{M B}
$$
Therefore, triangles $B D M$ and $C B M$ are similar by angle and ratio of sides, and in particular, angles $\angle C M B$ and $\angle D M B$ are equal. Due to the symmetry of points $D$ and $E$ with respect to $A B$, we get
$$
\angle E M B = \angle D M B = \angle C M B
$$
Thus, point $E$ lies on line $C M$, from which $\angle C E M = 180^{\circ}$.
Solution 3. Let
$$
\alpha = \angle C A B, \quad \beta = \angle A B C, \varphi = \angle A M D, \psi = \angle A M C
$$
The angle between the tangent $A C$ and the chord $A M$ of circle $\omega_{1}$ is equal to the inscribed angle in $\omega_{1}$ that subtends $A M$, i.e., $\angle C A B = \angle A D M$. Similar reasoning for $\omega_{2}$ gives $\angle A B C = \angle B D M$. Note that
$$
\angle D A M = 180^{\circ} - \alpha - \varphi \quad \angle D M B = 180^{\circ} - \beta - (180^{\circ} - \varphi) = \varphi - \beta
$$
Then the Law of Sines for triangles $A D M$ and $D M B$ gives
$$
\frac{A M}{\sin \alpha} = \frac{D M}{\sin (\alpha + \varphi)}, \quad \frac{B M}{\sin \beta} = \frac{D M}{\sin (\varphi - \beta)}
$$
Since $A M = B M$, we can eliminate the sides from these equations. We get
$$
\frac{\sin \beta}{\sin \alpha} = \frac{\sin (\varphi - \beta)}{\sin (\alpha + \varphi)}
$$
Similar reasoning for triangles $A C M$ and $C M B$ gives
$$
\frac{\sin \beta}{\sin \alpha} = \frac{\sin (\psi - \beta)}{\sin (\alpha + \psi)}
$$
Eliminating the left side of these relations, we get
$$
\begin{aligned}
\sin (\varphi - \beta) \sin (\psi + \alpha) = & \sin (\psi - \beta) \sin (\varphi + \alpha) \Longleftrightarrow \cos (\varphi - \beta - \alpha - \psi) - \cos (\varphi - \beta + \alpha + \psi) = \\
& = \cos (\psi - \beta - \alpha - \varphi) - \cos (\varphi - \beta + \alpha + \psi) \Longleftrightarrow 2 \sin (\alpha + \beta) \sin (\varphi - \psi) = 0
\end{aligned}
$$
from which $\varphi = \psi$. Moreover, from the symmetry of points $D$ and $E$ with respect to $A B$, it follows that $\angle A M E = \varphi$. Thus, point $E$ lies on segment $C M$.
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the minimum number of cells that need to be marked in a $9 \times 9$ table so that each vertical or horizontal strip $1 \times 5$ contains at least one marked cell?
|
Answer: 16.
Solution. Consider a more general problem when the table has size $(2 n-1) \times(2 n-1)$, and the strip is $-1 \times n$. Let's call the $n$-th row and the $n$-th column central, and the marked cells on them, except for the center of the board, - axial. Suppose there are $k$ axial cells in the central row and $m$ axial cells in the central column. In rows and columns that do not contain axial cells, there should be at least two marked cells. In total, in such rows, there will be at least $2 \cdot(2 n-2-m)=4(n-1)-2 m$ marked cells, and in columns - at least $4(n-1)-2 k$ cells. At the same time, each cell will be counted no more than twice. Taking into account the axial cells, we get that there are at least
$$
\frac{1}{2}(4(n-1)-2 m+4(n-1)-2 k)+k+m=4(n-1) \text { cells. }
$$
The value $4(n-1)$ is achieved if all cells of the central row and column, except for the center of the board, are marked. Assuming $n=5$, we get the answer.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle $\omega$ with center at point $O$ is circumscribed around triangle $ABC$. Circle $\omega_{1}$ touches the line $AB$ at point $A$ and passes through point $C$, while circle $\omega_{2}$ touches the line $AC$ at point $A$ and passes through point $B$. A line through point $A$ intersects circle $\omega_{1}$ again at point $X$ and circle $\omega_{2}$ again at point $Y$. Point $M$ is the midpoint of segment $XY$. Find the angle $OMX$.
|
Answer: $90^{\circ}$.
Solution 1. Let $\alpha=\angle B A C$. The angle between the tangent $A B$ and the chord $A C$ of circle $\omega_{1}$ is equal to the inscribed angle that subtends $A C$, i.e., $\angle A X C=\angle B A C=\alpha$. Similarly, we get $\angle A Y B=\alpha$. Extend quadrilateral $C X Y B$ to form triangle $X Y Z$ (see figure). Note that
$$
\angle B O C=2 \angle B A C=2 \alpha=\angle Z X Y+\angle Z Y X=180^{\circ}-\angle X Z Y
$$
which means quadrilateral $O B Z C$ is cyclic. Then
$$
\angle O Z B=\angle O C B=\angle O B C=\angle O Z C
$$
Therefore, ray $Z O$ is the angle bisector of isosceles triangle $X Z Y$, which is also the median and altitude. Thus, point $M$ lies on ray $Z O$ and $\angle O M X=90^{\circ}$.
Solution 2. Let line $X Y$ intersect circle $\omega$ again at point $K$. Since line $A C$ is tangent to circle $\omega_{2}$,
$$
\angle B Y K=\angle B Y A=\angle B A C
$$
Angle $Y B A$ subtends arc $Y A$ of circle $\omega_{2}$, not containing point $B$. Therefore, it is equal to the angle between chord $Y A$ and the tangent to $\omega_{2}$ at point $A$, i.e., angle $X A C$. Considering the cyclic quadrilateral $A B C K$, we get
$$
\angle Y B A=\angle X A C=\angle K A C=\angle K B C
$$
which implies $\angle Y B K=\angle A B C$. Therefore, triangles $Y B K$ and $A B C$ are similar by two angles. Then
$$
\frac{Y K}{A C}=\frac{B K}{B C} \Longleftrightarrow Y K=\frac{A C \cdot B K}{B C}
$$
Similarly, it can be verified that triangles $C A X$ and $C B K$ are similar and $\frac{A X}{B K}=\frac{A C}{B C}$. Thus,
$$
A X=\frac{A C \cdot B K}{B C}=Y K
$$
From this, it follows that point $M$ is the midpoint of segment $A K$. Note that point $O$ is the circumcenter of triangle $A K B$ and, therefore, lies on the perpendicular bisector of side $A K$. Hence, $\angle O M X=\angle O M K=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given nine-digit numbers $m$ and $n$, obtained from each other by writing the digits in reverse order. It turned out that the product $mn$ consists of an odd number of digits and reads the same from left to right and from right to left. Find the largest number $m$ for which this is possible.
|
Answer: 220000001.
Solution. Let $m=\overline{a_{8} \ldots a_{0}}, n=\overline{a_{0} \ldots a_{8}}$. Since the number $m n$ contains an odd number of digits, it is a seventeen-digit number. Write $m n=\overline{b_{16} \ldots b_{0}}$. We will show by induction that
$$
b_{k}=a_{0} a_{8-k}+a_{1} a_{9-k}+\ldots+a_{k-1} a_{7}+a_{k} a_{8} \quad \text { for any } \quad k \in\{0, \ldots, 8\}
$$
Clearly, $b_{0}=a_{0} a_{8} \bmod 10$. Since $10^{17}>m n \geqslant a_{0} a_{8} \cdot 10^{16}$, we get $a_{0} a_{8} \leqslant 9$, which means $b_{0}=a_{0} a_{8}$. Suppose that for some $k0$, we get $a_{0}=1$ and $a_{k}=0$ for $k=1, \ldots, 6$. The number $m=220000001$ clearly satisfies the condition of the problem.
|
220000001
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of the circumcircle of triangle $ABC$. On the circumcircle of triangle $BOC$, outside triangle $ABC$, point $X$ is chosen. On the rays $XB$ and $XC$ beyond points $B$ and $C$, points $Y$ and $Z$ are chosen respectively such that $XY = XZ$. The circumcircle of triangle $ABY$ intersects side $AC$ at point $T$. Find the angle $\angle Y T Z$.
|
Answer: $180^{\circ}$.
Solution. Note that $\angle B Y T=\angle B A T$ as inscribed angles subtending the same arc. Since quadrilateral $B O C X$ is cyclic, we get
$$
180^{\circ}-\angle B X C=\angle B O C=2 \angle B A C=2 \angle B Y T
$$
On the other hand, triangle $Y X Z$ is isosceles, so $180^{\circ}-\angle Y X Z=2 \angle X Y Z$. Therefore, $\angle X Y T=\angle X Y Z$, which means point $T$ lies on segment $Y Z$.
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of the circumcircle of triangle $A B C$. Points $Q$ and $R$ are chosen on sides $A B$ and $B C$ respectively. Line $Q R$ intersects the circumcircle of triangle $A B R$ again at point $P$ and intersects the circumcircle of triangle $B C Q$ again at point $S$. Lines $A P$ and $C S$ intersect at point $K$. Find the angle between lines $K O$ and $Q R$.
|
Answer: $90^{\circ}$.
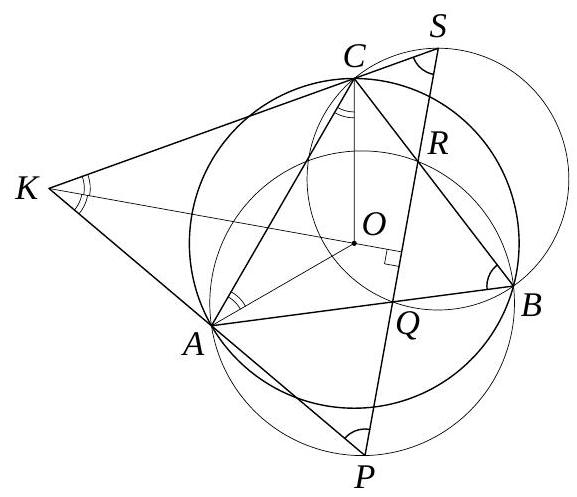
Solution. Note that $\angle C S Q=\angle C B Q$ and $\angle A P R=\angle A B R$ as inscribed angles subtending the same arc. Therefore, $\angle K S P=\angle K P S$, which means triangle $P K S$ is isosceles. Since
$$
180^{\circ}-\angle A K C=2 \angle K S P=2 \angle A B C=\angle A O C
$$
quadrilateral $A O C K$ is cyclic. Since triangle $A O C$ is isosceles, we have
$$
\angle A K O=\angle A C O=\angle C A O=\angle C K O.
$$
Therefore, line $K O$ is the angle bisector of isosceles triangle $P K S$, and thus also its altitude. Hence, $K O \perp Q R$.
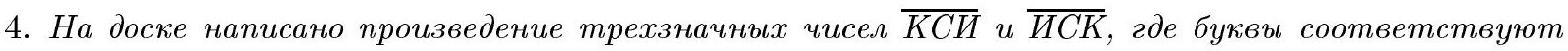
different decimal digits. This product is a six-digit number, its extreme digits are equal, and between them are two pairs of identical adjacent digits. What is written on the board?
Answer: $633556=847 \cdot 748$.
Solution. Since the problem does not change when I and K are swapped, we will assume $I \geqslant K \cdot 10000 > m \cdot 100000$.
From this, $d \geqslant m$, and equality is not possible, otherwise $I \cdot K \vdots 11$. Additionally, the inequality $p < (I+1)(K+1) \cdot 10000$ holds, from which we get
$$
m < d \leqslant \left[\frac{I \cdot K + I + K + 1}{10}\right] = m + \left[\frac{d + I + K + 1}{10}\right]
$$
From the condition, it follows that $p$ is divisible by 11. Then $\overline{KC I}$ or $\overline{I C K}$ is divisible by 11, which is equivalent to $I + K - C \vdots 11$. Therefore, either $C = I + K$ or $C = I + K - 11$. Let's consider these cases.
1) Suppose $C = I + K$. Since $d + I + K + 1 = d + 1 + C < 20$, from (*) we get $d = m + 1$, which means $I \cdot K = 11m + 1$. Additionally, $I + K \leqslant 9$, from which $I \cdot K \leqslant 20$. Therefore, $I \cdot K = 12$, and the pair (I, K) is $(2,6)$ or $(3,4)$. Since $682 \cdot 286 = 195052$ and $473 \cdot 374 = 176902$, these cases do not fit.
2) Suppose $C = I + K - 11$. Since $d + I + K + 1 \leqslant 27 < 30$, from (*) we get $d = m + 1$ or $d = m + 2$, from which $I \cdot K \bmod 11$ is 1 or 2. Additionally, $I + K \geqslant 11$, from which $I \cdot K \geqslant 18$. Therefore, $I \cdot K$ can take values $24, 35, 45, 56$, and the pair (I, K) can be $(3,8), (5,7), (5,9), (7,8)$. Since
$$
308 \cdot 803 = 247324, \quad 715 \cdot 517 = 369655, \quad 935 \cdot 539 = 503965 \quad 847 \cdot 748 = 633556
$$
only the last case fits.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (20 points) On the board, all two-digit numbers divisible by 5, where the number of tens is greater than the number of units, were written down. There turned out to be $A$ such numbers. Then, all two-digit numbers divisible by 5, where the number of tens is less than the number of units, were written down. There turned out to be $B$ such numbers. What is $100 B+A$?
|
Answer: 413.
Solution: We will write two-digit numbers in the form $\overline{x y}$, where $x$ is the number of tens, and $y$ is the number of units.
Let's calculate what $A$ is. We need two-digit numbers divisible by 5, i.e., numbers where $y$ is either 0 or 5. Note that if $y=0$, then $x$ can take any value from 1 to 9, giving us 9 numbers. And if $y=5$, then $x$ can take values only from 6 to 9, giving us another 4 numbers. In total, we get 13 numbers.
Let's calculate $B$. Here, there can only be the case where $y=5$, because $x$ cannot be less than 0. So, $x$ can take values from 1 to 4. Therefore, $B=4$. From this, we get that $100 B+A=400+13=413$.
|
413
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (20 points) The pensioners of one of the planets in the Alpha Centauri system enjoy spending their free time solving cybrow solitaire puzzles: they choose natural numbers from a certain interval $[A, B]$ in such a way that the sum of any two of the chosen numbers is not divisible by a given number $N$. Last week, the newspaper "Alphacentauri Panorama" offered its readers a solitaire puzzle with the values $A=1353, B=2134, N=11$. What is the maximum number of numbers that can be a solution to such a solitaire puzzle?
|
Answer: 356.
Solution: For $k=0,1, \ldots, 10$, let $I_{k}$ be the set of all numbers in $[A, B)$ that give a remainder of $k$ when divided by 11. Since $A$ and $B$ are multiples of 11, all sets $I_{k}$ contain an equal number of elements. Therefore, all numbers in $[A, B)$ that are not multiples of 11 can be paired as $(x, y)$, where $x \in I_{k}, y \in I_{11-k}$ for some $k$ from $\{1, \ldots, 5\}$. The number of such pairs is $\frac{2134-1353}{11} \cdot 5=355$. Clearly, from each pair, at most one number can be included in the final set. Additionally, this set can contain at most one number that is a multiple of 11. Thus, the solution includes no more than 356 numbers.
Now, we will show that a set of 356 numbers is possible. Include $A$ and all numbers that give an odd remainder when divided by 11 in this set. Take two distinct numbers $x$ and $y$ from this set, different from each other and from $A$. Then $(x \bmod 11) + (y \bmod 11)$ is an even number between 2 and 18. Therefore, it is not divisible by 11, and thus $x+y$ is also not divisible by 11. Clearly, $A+x$ is also not
divisible by 11. This means that such a set satisfies the problem's conditions. It remains to note that this set contains $\frac{2134-1353}{11} \cdot 5 + 1 = 356$ numbers.
|
356
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) Before the geometry lesson, the teacher wrote on the board the values of all the angles (in degrees) of a certain convex polygon. However, the duty students erased one of the written numbers. When the lesson began, it turned out that the sum of the remaining numbers was 1703. What number did the duty students erase?
|
Answer: 97.
Solution: Let the polygon have $n$ vertices. Since the $n$-gon is convex, each of its angles is less than $180^{\circ}$, and the sum of all angles is $(n-2) \cdot 180^{\circ}$. Therefore, the sum of all angles of the polygon minus one lies in the interval from $180(n-3)$ to $180(n-2)$. Then
$$
180(n-3)<1703<180(n-2), \quad \text { hence } \quad n=\left[\frac{1703}{180}\right]+3=12 \text {. }
$$
Therefore, the missing angle is $180 \cdot 10-1703=97$ degrees.
|
97
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In each cell of a $100 \times 100$ table, a natural number is written. In each row, there are at least 10 different numbers, and in any four consecutive rows, there are no more than 15 different numbers. What is the maximum number of different numbers that can be in the table?
|
Answer: 175
Solution. In one line, there are no less than 10 different numbers, so in the next three lines together, there appear no more than 5 new numbers. Therefore, the first four lines contain no more than 15 different numbers, and each of the following three lines adds no more than 5 new numbers, making the total number of numbers no more than $15+32 \cdot 5=175$.
Let's provide an example with 175 numbers. We will number the lines from 1 to 100. In the first line, we will place numbers from 1 to 10, and in the lines with numbers from $3k-1$ to $3k+1$, we will place numbers 1 to 5 and numbers from $5k+6$ to $5k+10$. Then, in each line, there will be 5 unique numbers and numbers from 1 to 5, i.e., exactly 10 different numbers, and in every four lines, there will be exactly 15 different numbers. Thus, in the table, there will be numbers from 1 to $5 \cdot 33 + 10 = 175$.
Remark. It can also be proven by induction that the number of different numbers in the table does not exceed 175. Specifically, it can be proven that in any $3n+1$ consecutive lines, there are no more than $5(n+2)$ different numbers. The base case $n=1$ is true by the condition. We will establish the transition from $n$ to $n+1$. Consider $3n+4$ consecutive lines. Suppose the fourth line from the bottom contains $k \geqslant 10$ different numbers. Then, in the three lowest lines, there are no more than $15-k$ different numbers. And in the remaining $3n+1$ lines, by the inductive hypothesis, there are no more than $5(n+2)$ numbers. Therefore, the total number of different numbers will be more than $5(n+2)+15-k=5(n+5)-k \leqslant 5(n+3)$.
|
175
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In each cell of a $75 \times 75$ table, a natural number is written. In each row, there are at least 15 different numbers, and in any three consecutive rows, there are no more than 25 different numbers. What is the maximum number of different numbers that can be in the table?
|
# Answer: 385
Solution. In one line, there are no less than 15 different numbers, so in the next two lines together, there appear no more than 10 new numbers. Therefore, the first three lines contain no more than 25 different numbers, and each of the following two lines adds no more than 10 new numbers, making the total number of numbers no more than $25 + 36 \cdot 10 = 385$.
Let's provide an example with 385 numbers. We will number the lines from 1 to 75. In the first line, we will place numbers from 1 to 15, and in the line with number $k$, we will place numbers from 1 to 10 and numbers from $5k + 6$ to $5k + 10$. Then, in each line, there will be 5 unique numbers and numbers from 1 to 10, i.e., exactly 15 different numbers, and in every three lines, there will be exactly 25 different numbers.
Remark. We can also prove that the number of different numbers in the table does not exceed 385 by induction. Specifically, we can prove that in any $2n + 1$ consecutive lines, there are no more than $5(2n + 3)$ different numbers. The base case $n=1$ is true by the problem statement. We will establish the transition from $n$ to $n+1$. Consider $2n + 3$ consecutive lines. Suppose the third line from the bottom contains $k \geq 15$ different numbers. Then, in the two lowest lines, there are no more than $25 - k$ different numbers. And in the remaining $2n + 1$ lines, by the inductive hypothesis, there are no more than $5(2n + 3)$ numbers. Therefore, the total number of different numbers will be more than $5(2n + 3) + 25 - k = 5(2n + 8) - k \leq 5(2n + 5)$.
|
385
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In an acute-angled triangle $A B C$, the altitudes $A A_{1}, B B_{1}$, and $C C_{1}$ are dropped. A point $T$ is chosen on the plane such that the lines $T A$ and $T B$ are tangents to the circumcircle of triangle $A B C$, and point $O$ is the center of this circle. The perpendicular dropped from point $T$ to the line $A_{1} B_{1}$ intersects the line $C C_{1}$ at point $K$, and the line passing through point $C_{1}$ parallel to $O K$ intersects the segment $C O$ at point $L$. Find the angle $\angle C L A_{1}$.
|
Answer: $90^{\circ}$
Solution. Let $\angle B A C=\alpha$ and $\angle A C B=\gamma$. Triangles $A O T$ and $B O T$ are congruent by three sides, and the inscribed angle $\angle A C B$ subtends the same arc as the central angle $\angle A O B$, so $\gamma=\angle A C B=\frac{1}{2} \angle A O B=\angle T O B$. Therefore, $\frac{O B}{O T}=\cos \gamma$. Similarly, $\angle B O C=2 \angle B A C$ and from the isosceles property of triangle $B O C$, it follows that $\angle B C O=90^{\circ}-\frac{1}{2} \angle B O C=90^{\circ}-\angle B A C$. Since $\angle A B_{1} B=90^{\circ}=\angle A A_{1} B$, quadrilateral $A B_{1} A_{1} B$ is cyclic. Therefore, $\angle B A C=\angle C A_{1} B_{1}$. Thus, $\angle B C O=90^{\circ}-\angle B A C=90^{\circ}-\angle C A_{1} B_{1}$ and lines $A_{1} B_{1}$ and $C O$ are perpendicular. Therefore, lines $C O$ and $T K$ are parallel, and quadrilateral $C O T K$ is a parallelogram, in particular, $C K=O T$. Then, by Thales' theorem, $\frac{C L}{C C_{1}}=\frac{C O}{C K}=\frac{O B}{O T}=\cos \gamma$. Therefore,
$$
C L=C C_{1} \cos \gamma=A C \sin \alpha \cos \gamma=C A_{1} \sin \alpha=C A_{1} \sin \angle C A_{1} B_{1} .
$$
Thus, point $L$ is the foot of the perpendicular dropped from $C$ to line $A_{1} B_{1}$, meaning $\angle C L A_{1}=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the minimum number of cells that need to be marked in a $15 \times 15$ table so that each vertical or horizontal strip $1 \times 10$ contains at least one marked cell.
|
Answer: 20
Solution. Let's cut the $15 \times 15$ table without the central $5 \times 5$ square into 20 rectangles of $1 \times 10$ (see the left figure). Therefore, we will need to mark at least 20 cells. An example with 20 cells: all cells of two parallel diagonals of length 10 are marked (see the right figure).
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the minimum number of cells that need to be marked in a $20 \times 20$ table so that each vertical or horizontal strip of $1 \times 12$ contains at least one marked cell.
|
Answer: 32
Solution. Let's cut the $20 \times 20$ table without the central $4 \times 4$ square into 32 rectangles of $1 \times 12$ (see the left figure). Therefore, we will need to mark at least 32 cells. An example with 32 cells: all cells of three parallel diagonals of lengths 4, 16, and 12 are marked (see the right figure).
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the leg $AC$ of the right triangle $ABC$ with hypotenuse $AB$, a point $P$ is marked. Point $D$ is the foot of the perpendicular dropped from vertex $A$ to the line $BP$, and point $E$ is the foot of the perpendicular dropped from point $P$ to the side $AB$. On the plane, a point $T$ is chosen such that the lines $TA$ and $TP$ are tangents to the circumcircle of triangle $PAB$, and point $O$ is the center of this circle. The perpendicular dropped from point $T$ to the line $DE$ intersects the line $BC$ at point $Q$, and the line passing through point $C$ parallel to $OQ$ intersects the segment $BO$ at point $K$. Find the angle $\angle OKE$.
|
Answer: $90^{\circ}$
Solution. Let $\angle A B P=\varphi$ and $\angle C B P=\psi$. Triangles $A O T$ and $P O T$ are equal by three sides, and the inscribed angle $\angle A B P$ subtends the same arc as the central angle $\angle A O P$, so $\gamma=\angle A B P=\frac{1}{2} \angle A O P=\angle A O T$. Therefore, $\frac{O A}{O T}=\cos \varphi$. The central angle $\angle A O B$ subtends the smaller arc $A B$, while the inscribed angle $\angle A P B$ subtends the larger arc $A B$, so $\angle A P B+\frac{1}{2} \angle A O B=180^{\circ}$. From the isosceles triangle $A O B$, we have
$$
\angle A B O=90^{\circ}-\frac{1}{2} \angle A O B=90^{\circ}-\left(180^{\circ}-\angle A P B\right)=\angle A P B-90^{\circ}=\angle P B C=\psi
$$
Since $\angle A D P=90^{\circ}=\angle A E P$, quadrilateral $A D P E$ is cyclic, in particular, $\angle E A P=\angle E D P=\angle B D E$. Therefore,
$$
\angle B D E+\angle D B O=\angle B D E+\angle D B A+\angle A B O=\angle E A P+\angle A O T+\angle B A O=90^{\circ}
$$
Thus, lines $D E$ and $B O$ are perpendicular, and lines $B O$ and $Q T$ are parallel. Points $O$ and $T$ lie on the perpendicular bisector of segment $A P$, so lines $A P$ and $O T$ are perpendicular. Therefore, lines $B C$ and $O T$ are parallel, and quadrilateral $B O T Q$ is a parallelogram, in particular, $B Q=O T$. By Thales' theorem for parallel lines $C K$ and $O Q$, we have $\frac{B K}{B C}=\frac{B O}{B Q}=\frac{O A}{O T}=\cos \varphi$. Therefore,
$$
B K=B C \cos \varphi=B P \cos \psi \cos \varphi=B E \cos \psi=B E \cos \angle E B K
$$
Thus, point $K$ is the foot of the perpendicular dropped from $E$ to line $B O$, meaning $\angle B K E=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The diagonals of the inscribed quadrilateral $A B C D$ intersect at point $P$, and triangle $A P D$ is acute-angled. Points $E$ and $F$ are the midpoints of sides $A B$ and $C D$ respectively. A perpendicular is drawn from point $E$ to line $A C$, and a perpendicular is drawn from point $F$ to line $B D$, these perpendiculars intersect at point $Q$. Find the angle between the lines $P Q$ and $B C$.
|
Answer: $90^{\circ}$
First solution. Let $E^{\prime}$ and $F^{\prime}$ be the points of intersection of $E Q$ with $A P$ and $F Q$ with $D P$, respectively, and let $T$ be the point of intersection of the lines $P Q$ and $B C$. Since the angles $\angle B A C$ and $\angle B D C$ subtend the same arc, they are equal. Therefore, the right triangles $A E^{\prime} E$ and $B F^{\prime} F$ are similar. Then, $\frac{E E^{\prime}}{F F^{\prime}}=\frac{A E}{D F}=\frac{B E}{C F}$, the last equality because points $E$ and $F$ are the midpoints of segments $A B$ and $C D$. Moreover, $\angle B E E^{\prime}=\angle C F F^{\prime}$, so triangles $B E E^{\prime}$ and $C F F^{\prime}$ are similar, and in particular, $\angle A B E^{\prime}=\angle D C F^{\prime}$. The angles $\angle A B D$ and $\angle A C D$ subtend the same arc and are therefore equal. Thus, $\angle E^{\prime} B F^{\prime}=\angle A B D-\angle A B E^{\prime}=\angle A C D-\angle D C F^{\prime}=\angle E^{\prime} C F^{\prime}$. Therefore, the quadrilateral $B E^{\prime} F^{\prime} C$ is cyclic and
$$
\angle P B T=\angle C B F^{\prime}=\angle C E^{\prime} F^{\prime}=\angle P E F^{\prime}=\angle P Q F^{\prime}
$$
(the last equality of angles follows from the cyclic nature of the quadrilateral $P E^{\prime} Q F^{\prime}$). It remains to calculate the angles:
$$
\angle P T B=180^{\circ}-\angle P B T-\angle B P T=180^{\circ}-\angle P Q F^{\prime}-\angle Q P F^{\prime}=90^{\circ}
$$
Second solution. Let $E^{\prime}$ and $F^{\prime}$ be the points of intersection of $E Q$ with $A P$ and $F Q$ with $D P$, respectively, and let $K$ and $L$ be the midpoints of segments $A P$ and $D P$, and $T$ be the point of intersection of the lines $P Q$ and $B C$. Let $O$ be the center of the circumcircle of triangle $A P D$, then $O K$ and $O L$ are the perpendicular bisectors of segments $A P$ and $D P$, respectively. Let $\angle B A P=\varphi$ for brevity. Then $\angle C D P=\varphi$, since the angles $\angle B A P$ and $\angle C D P$ subtend the same arc. Therefore, triangles $B A P$ and $C D P$ are similar by two angles and, hence,
$$
\frac{A P}{D P}=\frac{A B}{C D}=\frac{A E}{D F}=\frac{A E \cos \varphi}{D F \cos \varphi}=\frac{A E^{\prime}}{D F^{\prime}}
$$
Thus,
$$
\frac{P E^{\prime}}{P F^{\prime}}=\frac{A P-A E^{\prime}}{D P-D F^{\prime}}=\frac{A P}{D P}=\frac{P K}{P L}
$$
Let the lines $K O$ and $P Q$ intersect at point $K^{\prime}$, and the lines $L O$ and $P Q$ intersect at point $L^{\prime}$. Then triangles $P E^{\prime} Q$ and $P K K^{\prime}$ are similar with the ratio $\frac{P E^{\prime}}{P K}=\frac{P F^{\prime}}{P L}$, and with the same ratio of similarity, triangles $P F^{\prime} Q$ and $P L L^{\prime}$ are similar. Therefore, $P K^{\prime}=P L^{\prime}$ and, hence, points $K^{\prime}, L^{\prime}$, and $O$ coincide. Thus, the line $P Q$ passes through the point $O$. It remains to calculate the angles:
$\angle P T B=180^{\circ}-\angle C B D-\angle B P T=180^{\circ}-\angle C A D-\angle O P D=180^{\circ}-\angle P O L-\angle O P D=90^{\circ}$.
In the penultimate equality, it was used that the central angle $\angle P O D$ is equal to twice the inscribed angle $\angle C A D$ on one side and to twice the angle $\angle P O L$ on the other side.
Third solution. Draw a line $\ell$ from point $P$ perpendicular to side $B C$, let $T$ be its point of intersection with $B C$. Draw lines through points $A$ and $D$ perpendicular to diagonals $A C$ and $B D$, respectively. Let $S$ be their point of intersection. Since $\angle P A S=90^{\circ}=\angle P D S$, points $A, P, D$, and $S$ lie on a circle with diameter $P S$. Then (the equality $\angle D A P=\angle D B C$ follows from the cyclic nature of quadrilateral $A B C D$)
$$
\angle D P S=\angle D A S=90^{\circ}-\angle D A P=90^{\circ}-\angle D B C=\angle B P T
$$
Therefore, point $S$ lies on line $\ell$.
Let $H$ be the orthocenter of triangle $P B C$. Clearly, it also lies on line $\ell$. Then the lines $A S, B H$, and $E Q$ are parallel, and since $A E=E B$, line $E Q$ is the midline of trapezoid $A B H S$. Therefore, $E Q$ intersects line $\ell$ at the midpoint of segment $S H$. Similarly, line $F Q$ also intersects line $\ell$ at the midpoint of segment $S H$. But then lines $E Q, F Q$, and $\ell$ intersect at the midpoint of segment $S H$ and this point is point $Q$. Thus, $Q$ also lies on line $\ell$. In particular, lines $P Q$ and $B C$ intersect at a right angle.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The diagonals of the inscribed quadrilateral $A B C D$ intersect at point $P$, and the angle $A P B$ is obtuse. Points $E$ and $F$ are the midpoints of sides $A D$ and $B C$ respectively. A perpendicular is drawn from point $E$ to the line $A C$, and a perpendicular is drawn from point $F$ to the line $B D$, these perpendiculars intersect at point $Q$. Find the angle between the lines $P Q$ and $C D$.
|
Answer: $90^{\circ}$
First solution. Let $E^{\prime}$ and $F^{\prime}$ be the points of intersection of $E Q$ with $A P$ and $F Q$ with $B P$, respectively, and let $T$ be the point of intersection of the lines $P Q$ and $C D$. Since the angles $\angle C A D$ and $\angle C B D$ subtend the same arc, they are equal. Therefore, the right triangles $A E^{\prime} E$ and $D F^{\prime} F$ are similar. Then, $\frac{E E^{\prime}}{F F^{\prime}}=\frac{A E}{B F}=\frac{D E}{C F}$, the last equality because points $E$ and $F$ are the midpoints of segments $A D$ and $B C$. Moreover, $\angle D E E^{\prime}=\angle C F F^{\prime}$, so triangles $D E E^{\prime}$ and $C F F^{\prime}$ are similar, and in particular, $\angle A D E^{\prime}=\angle B C F^{\prime}$. The angles $\angle A C B$ and $\angle A D B$ subtend the same arc and are therefore equal. Thus, $\angle E^{\prime} B F^{\prime}=\angle A B D-\angle A B E^{\prime}=\angle A C D-\angle D C F^{\prime}=\angle E^{\prime} C F^{\prime}$. Therefore, the quadrilateral $B E^{\prime} F^{\prime} C$ is cyclic and
$$
\angle T D P=\angle C D F^{\prime}=\angle C E^{\prime} F^{\prime}=\angle P E^{\prime} F^{\prime}=\angle P Q F^{\prime}
$$
(the last equality of angles follows from the cyclic nature of the quadrilateral $P E^{\prime} Q F^{\prime}$). It remains to calculate the angles:
$$
\angle P T D=180^{\circ}-\angle T D P-\angle D P T=180^{\circ}-\angle P Q F^{\prime}-\angle Q P F^{\prime}=90^{\circ}
$$
Second solution. Let $E^{\prime}$ and $F^{\prime}$ be the points of intersection of $E Q$ with $A P$ and $F Q$ with $B P$, respectively, and let $K$ and $L$ be the midpoints of segments $A P$ and $B P$, and $T$ be the point of intersection of the lines $P Q$ and $C D$. Let $O$ be the center of the circumcircle of triangle $A P B$, then $O K$ and $O L$ are the perpendicular bisectors of segments $A P$ and $B P$, respectively. Let $\angle D A P=\varphi$ for brevity. Then $\angle C B P=\varphi$, since the angles $\angle D A P$ and $\angle C B P$ subtend the same arc. Therefore, triangles $C B P$ and $D A P$ are similar by two angles and, hence,
$$
\frac{A P}{B P}=\frac{A D}{B C}=\frac{A E}{B F}=\frac{A E \cos \varphi}{B F \cos \varphi}=\frac{A E^{\prime}}{B F^{\prime}}
$$
Thus,
$$
\frac{P E^{\prime}}{P F^{\prime}}=\frac{A P-A E^{\prime}}{B P-B F^{\prime}}=\frac{A P}{B P}=\frac{P K}{P L}
$$
Let the lines $K O$ and $P Q$ intersect at point $K^{\prime}$, and the lines $L O$ and $P Q$ intersect at point $L^{\prime}$. Then triangles $P E^{\prime} Q$ and $P K K^{\prime}$ are similar with the ratio $\frac{P E^{\prime}}{P K}=\frac{P F^{\prime}}{P L}$, and with the same ratio of similarity, triangles $P F^{\prime} Q$ and $P L L^{\prime}$ are similar. Therefore, $P K^{\prime}=P L^{\prime}$ and, hence, points $K^{\prime}, L^{\prime}$, and $O$ coincide. Thus, the line $P Q$ passes through the point $O$. It remains to calculate the angles:
$\angle P T C=180^{\circ}-\angle A C B-\angle C P T=180^{\circ}-\angle A B D-\angle A P O=180^{\circ}-\angle P O K-\angle A P O=90^{\circ}$.
In the penultimate equality, it was used that the central angle $\angle A O P$ is equal to twice the inscribed angle $\angle A B D$ on one side and to twice the angle $\angle P O K$ on the other side.
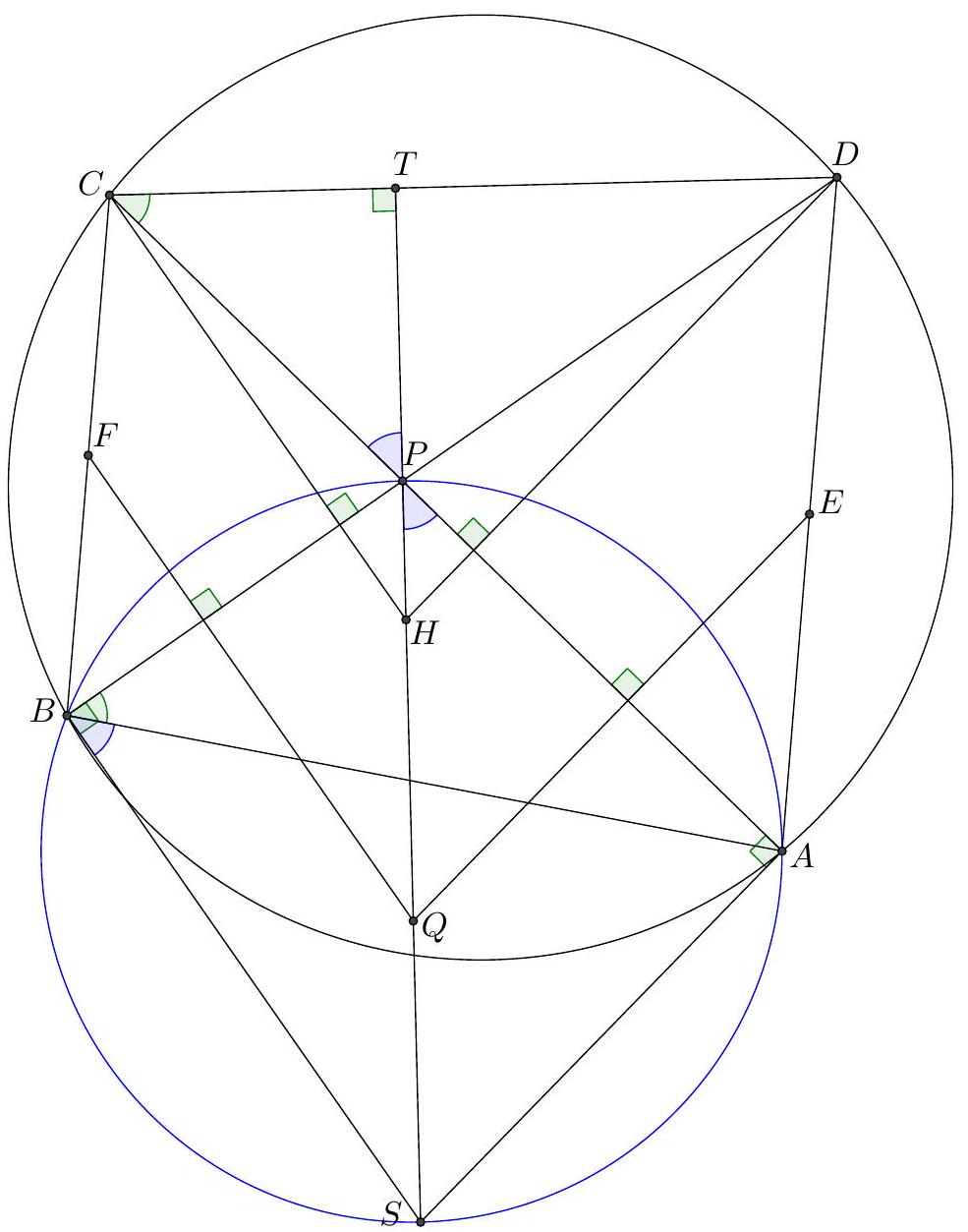
Third solution. Draw a line $\ell$ from point $P$ perpendicular to side $C D$, let $T$ be its point of intersection with $C D$. Draw lines through points $A$ and $B$ perpendicular to diagonals $A C$ and $B D$, respectively. Let $S$ be their point of intersection. Since $\angle P A S=90^{\circ}=\angle P B S$, points $A, P, B$, and $S$ lie on a circle with diameter $P S$. Then (the equality $\angle A B P=\angle A C D$ follows from the cyclic nature of quadrilateral $A B C D$)
$$
\angle A P S=\angle A B S=90^{\circ}-\angle A B P=90^{\circ}-\angle A C D=\angle C P T .
$$
Therefore, point $S$ lies on line $\ell$.
Let $H$ be the orthocenter of triangle $C P D$. Clearly, it also lies on line $\ell$. Then the lines $A S, D H$, and $E Q$ are parallel, and since $A E=E D$, line $E Q$ is the midline of trapezoid $A D H S$. Therefore, $E Q$ intersects line $\ell$ at the midpoint of segment $S H$. Similarly, line $F Q$ also intersects line $\ell$ at the midpoint of segment $S H$. But then lines $E Q, F Q$, and $\ell$ intersect at the midpoint of segment $S H$ and this point is point $Q$. Therefore, $Q$ also lies on line $\ell$. In particular, lines $P Q$ and $C D$ intersect at a right angle.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (30 points) Point $M$ is the midpoint of the hypotenuse $A C$ of the right triangle $A B C$. Points $P$ and $Q$ on lines $A B$ and $B C$ respectively are such that $A P = P M$ and $C Q = Q M$. Find the measure of angle $\angle P Q M$, if $\angle B A C = 17^{\circ}$.
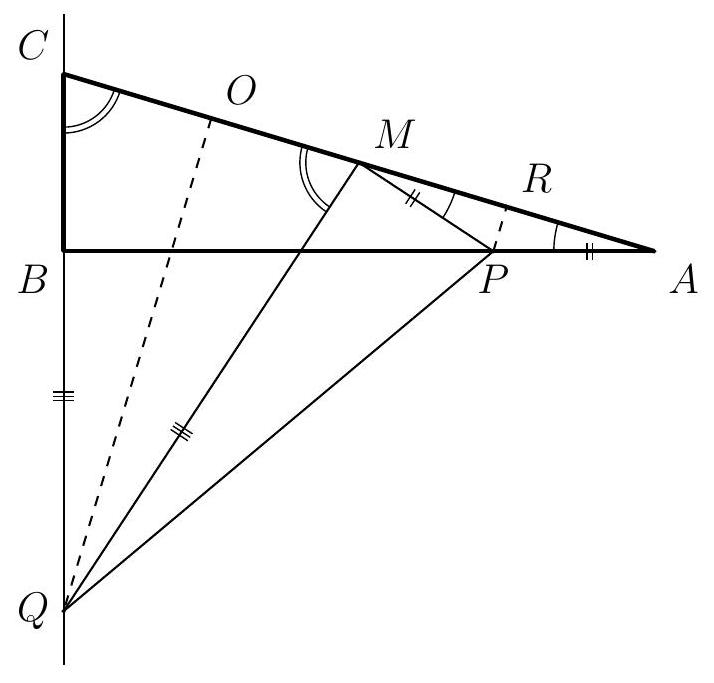
|
Answer: $17^{\circ}$.
Solution. Since in the right triangle $ABC$ the angle $BAC=17^{\circ}$, the angle $BCA=73^{\circ}$. Note that triangle $QMC$ is isosceles with base $MC$, as by condition $QM=QC$. Similarly, triangle $PMA$ is isosceles with base $MA$. Therefore, the angles at the bases of these triangles are equal. From this, we get that $\angle QMP=180^{\circ}-\angle PMA-\angle QMC=180^{\circ}-17^{\circ}-73^{\circ}=90^{\circ}$.
Let points $O$ and $R$ be the feet of the perpendiculars dropped from points $Q$ and $P$ to the line $AC$, respectively. It is easy to notice that triangles $QOM$ and $MRP$ are similar by two angles. Since $CM=MA$, from the isosceles nature of triangles $QCM$ and $PMA$, it follows that
$$
MO=\frac{1}{2} CM=\frac{1}{2} MA=MR
$$
Let $x=MO$. From the right triangles $QOM$ and $PMR$, we get that $MQ=\frac{x}{\cos 73^{\circ}}$ and $MP=\frac{x}{\cos 17^{\circ}}$ respectively. Thus, for triangle $MQP$ we have
$$
\operatorname{tg} \angle PQM=\frac{MP}{MQ}=\frac{x}{\cos 17^{\circ}} \cdot \frac{\cos 73^{\circ}}{x}=\frac{\cos \left(\pi / 2-17^{\circ}\right)}{\cos 17^{\circ}}=\operatorname{tg} 17^{\circ}
$$
Since in the right triangle $MQP$ the angle $PQM$ is acute, from the last equality it follows that $\angle PQM=17^{\circ}$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (30 points) On the sides $B C$ and $A C$ of the isosceles triangle $A B C (A B = A C)$, points $D$ and $E$ were found respectively such that $A E = A D, \angle E D C = 18^{\circ}$. Find the measure of the angle $\angle B A D$.
|
Answer: $36^{\circ}$.
Solution. Denote the angles as indicated in the figure. The angle $A D C$ is an exterior angle for triangle $A D B$; hence, $\beta+18^{\circ}=\alpha+x$. Angles $A B C$ and $A C B$ are the base angles of isosceles triangle $A B C$; hence, $\alpha=\frac{180^{\circ}-(x+y)}{2}$. Angles $A D C$ and $A E D$ are the base angles of isosceles triangle $A D E$; hence, $\beta=\frac{180^{\circ}-y}{2}$. Substitute these expressions into the relation for angle $A D C$:
$$
\frac{180^{\circ}-y}{2}+18^{\circ}=\frac{180^{\circ}-(x+y)}{2}+x
$$
Simplifying the expression, we get $18^{\circ}=\frac{x}{2}$, which means $x=36^{\circ}$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the cells of an $11 \times 11$ square, zeros and ones are arranged in such a way that in any figure of four cells in the shape of $\square$, the sum of the numbers is odd. (The figure can be rotated and flipped). What is the minimum number of ones that can be in such an arrangement?
|
Answer: 25
Solution. Place 25 figures in the square without any common cells (see the left figure). Each of them contains at least one unit, so the total number of units is no less than 25. A suitable arrangement of 25 units: in all cells with even coordinates (see the right figure).


|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In each cell of a $15 \times 15$ square, there is a natural number not exceeding 4, and the sum of the numbers in each $2 \times 2$ square is 7. What is the maximum value that the sum of the numbers in the entire table can take?
|
Answer: 417
Solution. Note that the sum of the numbers in two adjacent cells does not exceed five, since otherwise the sum of the numbers in the $2 \times 2$ square containing these two cells would be at least eight, which is impossible according to the condition.
Divide the table into 49 squares of $2 \times 2$ and a corner of width 1. Divide the corner into a corner cell and 14 dominoes of $1 \times 2$. The sum of the numbers in each $2 \times 2$ square is 7, the sum of the numbers in each domino does not exceed 5, and the number in the corner cell does not exceed 4, so the sum of all the numbers in the table does not exceed $49 \cdot 7 + 14 \cdot 5 + 4 = 417$.
Example. Number the rows and columns of the table from 1 to 15 from left to right and from bottom to top. Place fours in the cells at the intersections of odd-numbered rows and columns, and ones in the other cells (see the figure). The sum of all the numbers is $64 \cdot 4 + (225 - 64) \cdot 1 = 417$.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 | 4 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|
417
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Sasha chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \), while if they are connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?

|
Answer: $n=35$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, let $n$ be even. Among seven numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $q$ is a prime divisor of $n$, then among four consecutively connected numbers, there exists a pair of adjacent numbers whose sum is not divisible by $q$. Take a chain $(a, b, c, d)$ of consecutively connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two distinct odd prime divisors. Let there be exactly two of them (say, $p$ and $q$). We will show that they are different from 3. Suppose, for example, that $p=3$. No more than two numbers are divisible by 3 (if there are three, they form a cycle). The remaining numbers can be divided into two groups, giving remainders 1 and 2 when divided by 3. One of these groups is empty, otherwise any number from the smaller group will be connected to at least three numbers from the other group, which is impossible. The sum of the numbers in one group is not divisible by 3. Therefore, there exists a three-link chain in which the sum of any pair of connected numbers is not divisible by 3 and, hence, is divisible by $q$. But this contradicts 2).
Thus, if $n$ has exactly two distinct odd prime divisors, then $n \geqslant 5 \cdot 7=35$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>35$. The arrangement for $n=35$ is shown in the figure.
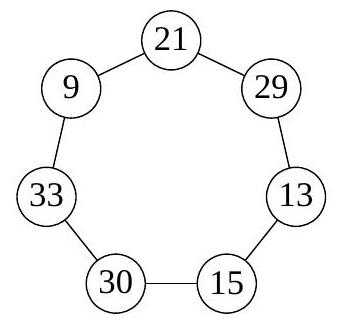
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Sasha chooses a natural number $n$ and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers $a$ and $b$ are not connected by a segment, then the sum $a+b$ must be coprime with $n$; if connected, then the numbers $a+b$ and $n$ must have a common natural divisor greater than 1. For what smallest $n$ does such an arrangement exist?
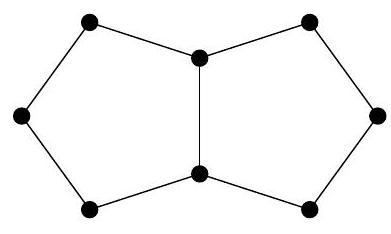
|
Answer: $n=35$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, let $n$ be even. Among eight numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $q$ is a prime divisor of $n$, then among four consecutively connected numbers, there exists a pair of adjacent numbers whose sum is not divisible by $q$. Consider a chain $(a, b, c, d)$ of consecutively connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two distinct odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from 3. Suppose, for example, that $p=3$. No more than two numbers are divisible by 3 (if there are three, they form a cycle). The remaining numbers (at least 6) can be divided into two groups, giving remainders 1 and 2 when divided by 3. We will show that one of these groups is empty. If this is not the case, then each number from one group is connected to any number from the other. But then there are no more than three numbers in one group and no more than two in the other, which is impossible. The sum of the numbers in one group is not divisible by 3. Therefore, there exists a three-link chain in which the sum of any pair of connected numbers is not divisible by 3 and, hence, is divisible by $q$. But this contradicts 2).
Thus, if $n$ has exactly two distinct odd prime divisors, then $n \geqslant 5 \cdot 7=35$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>35$. The arrangement for $n=35$ is shown in the figure.
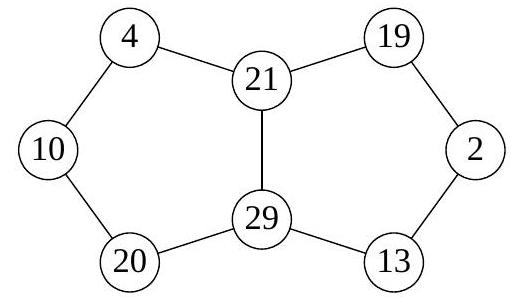
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Tanya chooses a natural number n and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers a and b are not connected by a segment, then the sum $a^{2}+b^{2}$ must be coprime with n; if connected, then the numbers $a^{2}+b^{2}$ and n must have a common natural divisor greater than 1. For what smallest $n$ does such an arrangement exist?

|
Answer: $n=65$.
Solution. First, let's make three observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among five numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $d$ is a divisor of $n$, then no more than two numbers are divisible by $d$. Suppose there are three such numbers. Then they must be pairwise connected, and thus form a three-link cycle.
3) If $q$ is a prime divisor of $n$, then among four sequentially connected numbers, there exists a pair of adjacent numbers whose sum of squares is not divisible by $q$. Suppose there is a chain $(a, b, c, d)$ of sequentially connected numbers such that the sum of squares of any pair of adjacent numbers is divisible by $q$. Then
$$
a^{2}+d^{2}=\left(a^{2}+b^{2}\right)-\left(b^{2}+c^{2}\right)+\left(c^{2}+d^{2}\right) \vdots q
$$
This means that the numbers $a$ and $d$ are connected, so there is a cycle of length 4 in the picture, which does not exist.
From 1) and 3), it follows that the number $n$ has at least two different odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from $3, 7, 11$. Suppose, for example, that $p \in\{3,7,11\}$. Note that for any natural number $a$
$$
a^{2} \bmod 3 \in\{0,1\}, \quad a^{2} \bmod 7 \in\{0,1,2,4\}, \quad a^{2} \bmod 11 \in\{0,1,3,4,5,9\}
$$
Therefore, $a^{2}+b^{2}$ is divisible by $p$ if and only if $a^{2}$ and $b^{2}$ are divisible by $p$, which means that $a$ and $b$ are divisible by $p$. By 2), this condition can be satisfied by only one pair. From the remaining four pairs of connected numbers, a three-link chain can be formed in which the sum of squares of each pair of adjacent numbers is divisible by $q$. But this contradicts 3).
Thus, if $n$ has exactly two different odd prime divisors, then $n \geqslant 5 \cdot 13=65$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>65$. The arrangement for $n=65$ is shown in the figure.
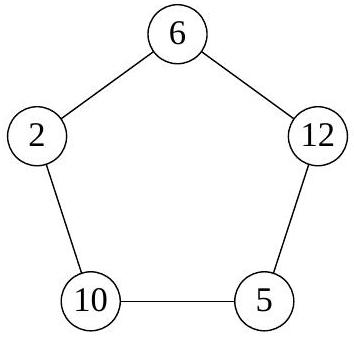
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Tanya chooses a natural number $n$ and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers $a$ and $b$ are not connected by a segment, then the sum $a^{2}+b^{2}$ must be coprime with $n$; if $a$ and $b$ are connected, then the numbers $a^{2}+b^{2}$ and $n$ must have a common natural divisor greater than 1. For what smallest $n$ does such an arrangement exist?
|
Answer: $n=65$.
Solution. First, let's make three observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among six numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) If $d$ is a divisor of $n$, then no more than two numbers are divisible by $d$. Suppose there are three such numbers. Then they must be pairwise connected and, therefore, form a three-link cycle.
3) If $q$ is a prime divisor of $n$, and in the chain $(a, b, c, d)$ of sequentially connected numbers, the sum of the squares of any pair of adjacent numbers is divisible by $q$, then $(a, b, c, d)$ forms a cycle. Indeed,
$$
a^{2}+d^{2}=\left(a^{2}+b^{2}\right)-\left(b^{2}+c^{2}\right)+\left(c^{2}+d^{2}\right) \vdots q
$$
that is, the numbers $a$ and $d$ are also connected.
From 1) and 3), it follows that the number $n$ has at least two different odd prime divisors. Let there be exactly two (say, $p$ and $q$). We will show that they are different from $3, 7, 11$. Suppose, for example, that $p \in\{3,7,11\}$. Note that for any natural number $a$
$$
a^{2} \bmod 3 \in\{0,1\}, \quad a^{2} \bmod 7 \in\{0,1,2,4\}, \quad a^{2} \bmod 11 \in\{0,1,3,4,5,9\}
$$
Therefore, $a^{2}+b^{2}$ is divisible by $p$ if and only if $a^{2}$ and $b^{2}$ are divisible by $p$, and hence $a$ and $b$ are divisible by $p$. By 2), this condition can be satisfied by only one pair. From the remaining six pairs of connected numbers, one can form a non-cyclic three-link chain (for example, passing along the left and top or the right and bottom sides of the large rectangle). In this chain, the sum of the squares of each pair of adjacent numbers is divisible by $q$, which contradicts 3).
Thus, if $n$ has exactly two different odd prime divisors, then $n \geqslant 5 \cdot 13=65$. If there are more than two such divisors, then $n \geqslant 3 \cdot 5 \cdot 7=105>65$. The arrangement for $n=65$ is shown in the figure.
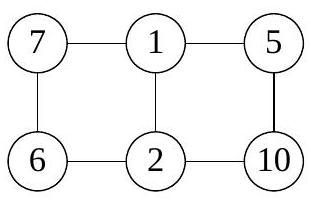
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The board has the number 5555 written in an even base $r$ ($r \geqslant 18$). Petya found out that the $r$-ary representation of $x^{2}$ is an eight-digit palindrome, where the difference between the fourth and third digits is 2. (A palindrome is a number that reads the same from left to right and from right to left). For which $r$ is this possible?
|
Answer: $r=24$.
Solution. Let's agree to write $u \equiv v(\bmod w)$ if $(u-v) \vdots w$. According to the condition, there exist such $r$-ary digits $a, b, c, d$ that $d-c=2$ and
$$
25(r+1)^{2}\left(r^{2}+1\right)^{2}=a\left(r^{7}+1\right)+b\left(r^{6}+r\right)+c\left(r^{5}+r^{2}\right)+d\left(r^{4}+r^{3}\right)
$$
Let's make some observations.
1) Since $r^{6} \equiv-1\left(\bmod \left(r^{2}+1\right)\right)$, the following equalities hold:
$$
r^{7}+1 \equiv 1-r\left(\bmod \left(r^{2}+1\right)\right) \quad \text { and } \quad r^{6}+r \equiv r-1\left(\bmod \left(r^{2}+1\right)\right)
$$
Moreover, $r^{4} \equiv 1\left(\bmod \left(r^{2}+1\right)\right)$, hence
$$
r^{5}+r^{2} \equiv r-1\left(\bmod \left(r^{2}+1\right)\right) \quad \text { and } \quad r^{4}+r^{3} \equiv 1-r\left(\bmod \left(r^{2}+1\right)\right)
$$
Then, by $(*)$
$$
0 \equiv(a-b-c+d)(1-r)\left(\bmod \left(r^{2}+1\right)\right)
$$
Note that $r^{2}+1+(1-r)(r+1)=2$, and the numbers $1-r$ and $r^{2}+1$ are odd. Therefore, they are coprime, which implies $a-b-c+d \vdots\left(r^{2}+1\right)$. But
$$
|a-b-c+d| \leqslant 2(r-1)<2 r<r^{2}+1
$$
Thus, $b-a=d-c=2$.
2) Since $r^{n} \equiv 1(\bmod (r-1))$ for any natural $n$, from $(*)$ and 1$)$ it follows that
$$
25 \cdot 16 \equiv 2(a+b+c+d)=4(b+c)(\bmod (r-1))
$$
Since $r-1$ is odd, $r-1$ divides the number $100-(b+c)$.
3) For any natural $n$
$$
r^{n}=(r+1-1)^{n} \equiv(-1)^{n}(1-n(r+1))\left(\bmod (r+1)^{2}\right)
$$
The right-hand side of $(*)$ is divisible by $(r+1)^{2}$, hence
$$
0 \equiv(7 a-5 b+3 c-d)(r+1)\left(\bmod (r+1)^{2}\right)
$$
Thus, $r+1$ divides the number
$$
7 a-5 b+3 c-d=7(b-2)-5 b+3 c-(c+2)=2(b+c)-16
$$
Then $b+c-8 \vdots(r+1)$ due to the oddness of $r+1$. Therefore, $b+c=8$ or $b+c=8+r+1$. In the second case,
$$
0 \equiv 92-(r+1) \equiv 90(\bmod (r-1))
$$
Since $r$ is even and $r-1 \geqslant 17$, we get $r=46$. Then $a=25$ and $b=27$, which is impossible, as $b=50 \bmod 46=4$. Thus, $b+c=8$. By 2$) 92 \vdots(r-1)$, hence $r=24$.
Remark. If $b+c=8$ and $r=24$, then
$$
a=25 \bmod 24=1, \quad b=a+2=3, \quad c=8-b=5, \quad d=c+2=7
$$
The equality $5555_{24}^{2}=13577531_{24}$ is verified by direct computation.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Nastya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the difference \( a - b \) must be coprime with \( n \), and if they are connected, then \( a - b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
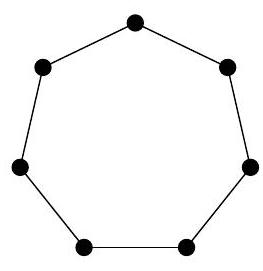
|
Answer: $n=5 \cdot 7 \cdot 11=385$.
Solution. We will make two observations.
1) $n$ is not divisible by 2 and 3. Among seven numbers, there are always three numbers of the same parity. If $n$ is even, then they must be pairwise connected. Moreover, among seven numbers, there will be three numbers that give the same remainder when divided by 3. If $n$ is divisible by 3, then these numbers also form a three-link cycle. But such cycles do not exist in the picture.
2) If $p$ is a prime divisor of $n$, then among three consecutively connected numbers, there exists a pair of adjacent numbers whose difference is not divisible by $p$. Let $(a, b, c)$ be a chain of consecutively connected numbers where $a-b$ and $b-c$ are divisible by $p$. Then $a-c=(a-b)+(b-c) \vdots p$. This means that $(a, b, c)$ forms a three-link cycle, which is impossible.
We will show that the number $n$ has at least three distinct prime divisors. Let $p$ be a prime divisor of $n$. There are no more than three distinct pairs $(a, b)$ for which $a-b \vdots p$. If there were 4 such pairs, then some two of them would intersect, which contradicts 2). But in total, 7 pairs of numbers are connected by segments, so $n$ has at least three distinct prime divisors. By 1), the smallest possible values for them are $5, 7, 11$, that is, $n \geqslant 5 \cdot 7 \cdot 11=385$. The arrangement for $n=385$ is shown in the figure.
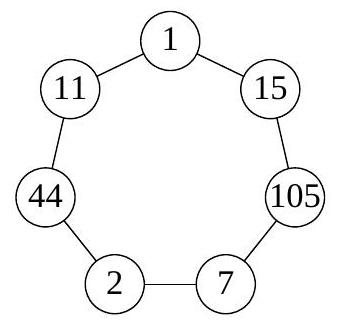
|
385
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Nastl chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the difference \( a - b \) must be coprime with \( n \), and if they are connected, then the numbers \( a - b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
|
Answer: $n=3 \cdot 5 \cdot 7=105$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among the six numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the diagram.
2) If $p$ is a prime divisor of $n$, then among three consecutively connected numbers, there exists a pair of adjacent numbers whose difference is not divisible by $p$. Suppose $(a, b, c)$ is a chain of consecutively connected numbers where $a-b$ and $b-c$ are divisible by $p$. Then $a-c=(a-b)+(b-c) \vdots p$. Therefore, $(a, b, c)$ forms a three-link cycle, which is impossible.
We will show that the number $n$ has at least three distinct prime divisors. Let $p$ be a prime divisor of $n$. There are no more than three distinct pairs $(a, b)$ for which $a-b \vdots p$. If there were 4 such pairs, then some two of them would intersect, which contradicts 2). But in total, 7 pairs of numbers are connected by segments, so $n$ has at least three distinct prime divisors. By 1), the smallest possible values for them are $3, 5, 7$, that is, $n \geqslant 3 \cdot 5 \cdot 7=105$. The arrangement for $n=105$ is shown in the figure.
|
105
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The picture shows several circles connected by segments. Kostya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \), and if they are connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
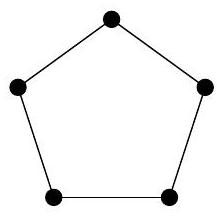
|
Answer: $n=15$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. Among any five numbers, there are always three numbers of the same parity, and by the condition, they must be pairwise connected. But there are no cycles of length 3 in the picture.
2) $n$ has at least two distinct prime divisors. Suppose $n$ is a power of a prime number $p$. Take a chain $(a, b, c, d)$ of sequentially connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means there is a cycle of length 4 in the picture, which is not there.
Thus, the number $n$ has at least two distinct odd prime divisors, hence $n \geqslant 15$. The arrangement for $n=15$ is shown in the figure.
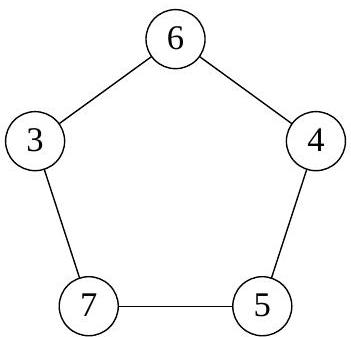
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the picture, several circles are drawn, connected by segments. Kostya chooses a natural number \( n \) and places different natural numbers in the circles so that for all these numbers the following property holds:
if numbers \( a \) and \( b \) are not connected by a segment, then the sum \( a + b \) must be coprime with \( n \); if connected, then the numbers \( a + b \) and \( n \) must have a common natural divisor greater than 1. For what smallest \( n \) does such an arrangement exist?
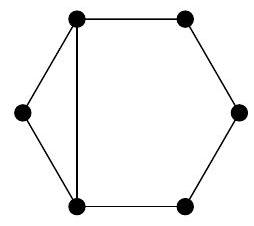
|
Answer: $n=15$.
Solution. We will make two observations.
1) $n$ is odd. Indeed, suppose $n$ is even. If there are three even and three odd numbers, then each of these triples forms a cycle. Suppose there are four numbers $a, b, c, d$ of the same parity. Then all of them are pairwise connected, and we again get two three-link cycles - for example, $(a, b, c)$ and $(a, d, c)$. But there is only one such cycle in the picture.
2) $n$ has at least two distinct prime divisors. Suppose $n$ is a power of a prime number $p$. Consider a chain $(a, b, c, d)$ of sequentially connected numbers. By the condition,
$$
a+d=(a+b)-(b+c)+(c+d) \vdots p
$$
Then the numbers $a$ and $d$ are also connected, which means that there is a cycle of length 4 in the picture, which is not there.
Thus, the number $n$ has at least two distinct odd prime divisors, hence $n \geqslant 15$. The arrangement for $n=15$ is shown in the figure.
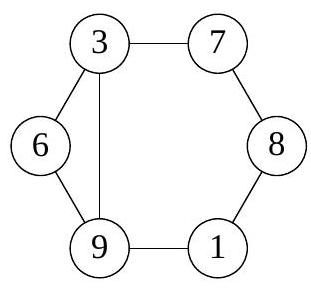
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$
|
Solution. Let $O$ be the center of $\omega$, $M$ be the intersection point of lines $A B$ and $C D$. Note that
$$
\angle A O C=2\left(180^{\circ}-\angle A B C\right)=2\left(180^{\circ}-135^{\circ}\right)=90^{\circ} .
$$
Then quadrilateral $A O C D$ is a square, and thus $\angle A D C=90^{\circ}$. By the tangent-secant theorem,
$$
D M^{2}=M C^{2}=B M \cdot A M, \quad \text { that is } \quad \frac{D M}{A M}=\frac{B M}{D M} .
$$
Therefore, triangles $D B M$ and $A D M$ are similar, from which
$$
\angle A B D=180^{\circ}-\angle M B D=180^{\circ}-\angle A D M=90^{\circ}
$$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (10 points) In each cell of a $50 \times 50$ square, a number is written that is equal to the number of $1 \times 16$ rectangles (both vertical and horizontal) in which this cell is an end cell. In how many cells are numbers greater than or equal to 3 written?
|
Answer: 1600.
Solution. We will denote the cells of the square by pairs $(i, j)$, where $i=1, \ldots, 50, j=$ $=1, \ldots, 50$. We will start the numbering from the bottom left corner of the square.
The cell $(i, j)$ is the rightmost for a horizontal rectangle if $16 \leqslant$ $\leqslant i-$ inequality (1), and the leftmost if $i \leqslant 50-15=35-$ inequality (2). The cell $(i, j)$ is the topmost for a vertical rectangle if $16 \leqslant j-$ inequality (3), and the bottommost if $j \leqslant 50-15=35-$ inequality (4). We are interested in the number of cells of the square for which at least three of the inequalities (1)-(4) are satisfied.
First, we will find the number of cells for which all inequalities are true. These are the cells for which $16 \leqslant i \leqslant 35$ and $16 \leqslant j \leqslant 35$. There are $(35-15) \times(54-15)=20 \times 20=400$ such cells.
Now we will calculate the number of cells for which inequality (1) is not true, but (2)-(4) are true. That is, $i<16$ and $16 \leqslant j \leqslant 35$. There are $15 \times(35-15)=15 \times 20=300$ such cells. It is easy to see that due to the symmetry (of the square) the number of cells for which other sets of three inequalities are true will be the same.
In total, we get $400+3 \cdot 300=1600$.
|
1600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (40 points) What is the maximum number of numbers that can be chosen among the natural numbers from 1 to 3000 such that the difference between any two of them is different from 1, 4, and 5?
|
Answer: 1000.
Solution. Let's provide an example. We can choose all numbers divisible by 3. Then the difference between any two numbers will also be divisible by 3, while the numbers 1, 4, and 5 are not divisible by 3.
The estimate is based on the consideration that among 6 consecutive numbers, 3 numbers cannot be chosen. Let's prove this statement. Take any chosen number and the five numbers following it. Then the second, fifth, and sixth numbers are definitely not chosen. The third and fourth numbers remain, but they cannot both be chosen at the same time. It is even more impossible to choose 3 numbers among five or fewer consecutive numbers.
|
1000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$

|
Solution. Let $O$ be the center of $\omega$, $M$ be the intersection point of lines $A B$ and $C D$. Note that
$$
\angle A O C=2\left(180^{\circ}-\angle A B C\right)=2\left(180^{\circ}-135^{\circ}\right)=90^{\circ} .
$$
Then quadrilateral $A O C D$ is a square, and thus $\angle A D C=90^{\circ}$. By the tangent-secant theorem,
$$
D M^{2}=M C^{2}=B M \cdot A M, \quad \text { that is } \quad \frac{D M}{A M}=\frac{B M}{D M} .
$$
Therefore, triangles $D B M$ and $A D M$ are similar, from which
$$
\angle A B D=180^{\circ}-\angle M B D=180^{\circ}-\angle A D M=90^{\circ}
$$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate:
$$
\frac{2 \cdot 2018}{1+\frac{1}{1+2}+\frac{1}{1+2+3}+\cdots+\frac{1}{1+2+\cdots+2018}}
$$
|
Answer: 2019.
Solution: a similar solution to this problem is present in variant 1 under the same number.
|
2019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find $g(2022)$, if for any real $x, y$ the equality holds
$$
g(x-y)=g(x)+g(y)-2021(x+y)
$$
#
|
# Answer: 4086462.
Solution. Substitute $x=y=0$, we get
$$
g(0)=g(0)+g(0)-2021(0+0) \Rightarrow g(0)=0
$$
Substitute $x=y$, we get
$$
\begin{gathered}
g(0)=g(x)+g(x)-2021(x+x) \Rightarrow g(x)=2021 x \Rightarrow \\
g(2022)=2021 \cdot 2022=4086462
\end{gathered}
$$
|
4086462
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find $g$(2021), if for any real $x, y$ the equality holds
$$
g(x-y)=g(x)+g(y)-2022(x+y)
$$
|
Answer: 4086462.
Solution. Substitute $x=y=0$, we get
$$
g(0)=g(0)+g(0)-2022(0+0) \Rightarrow g(0)=0
$$
Substitute $x=y$, we get
$$
\begin{gathered}
g(0)=g(x)+g(x)-2022(x+x) \Rightarrow g(x)=2022 x \Rightarrow \\
g(2021)=2022 \cdot 2021=4086462 .
\end{gathered}
$$
|
4086462
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two math teachers are conducting a geometry test, checking each 10th-grade student's ability to solve problems and their knowledge of theory. The first teacher spends 5 and 7 minutes per student, respectively, while the second teacher spends 3 and 4 minutes per student. What is the minimum time they will need to interview 25 students?
|
# Answer: 110 minutes.
## Solution: (estimation + example)
Let the first teacher accept the test on problems from $X$ students, and on theory from $Y$ students. Then the second teacher accepts the test on problems from (25-X) students, and on theory from (25-Y) students. Let $T$ be the minimum time required for them to interview 25 students. Then, considering the condition of the problem, we can set up the following system of inequalities:
$$
\left\{\begin{array} { c }
{ 5 X + 7 Y \leq T , } \\
{ 3 ( 2 5 - X ) + 4 ( 2 5 - Y ) \leq T . }
\end{array} \Rightarrow \left\{\begin{array} { c }
{ 5 X + 7 Y \leq T } \\
{ - 3 X - 4 Y \leq T - 1 7 5 . }
\end{array} \Rightarrow \left\{\begin{array}{c}
15 X+21 Y \leq 3 T \\
-15 X-20 Y \leq 5 T-875
\end{array}\right.\right.\right.
$$
$$
\text { Hence } 0 \leq Y \leq 8 T-875 \Rightarrow 8 T \geq 875 \Rightarrow T \geq 110 \text {. }
$$
Therefore, it is impossible to accept the test from 25 students in less than 110 minutes.
Let's provide an example (of achieving the boundary):
The first teacher accepts tests on problems from 22 students, spending 110 minutes on this; the second teacher accepts tests on problems from the remaining three students, spending 9 minutes on this, and accepts tests on theory from all 25 students, spending 100 minutes on this, thus spending 109 minutes.
|
110
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two math teachers are conducting a geometry test, checking each 10th-grade student's ability to solve problems and their knowledge of theory. The first teacher spends 5 and 7 minutes per student, respectively, while the second teacher spends 3 and 4 minutes per student. What is the minimum time required for them to interview 25 students?
#
|
# Answer: 110 minutes.
Solution: fully corresponds to the solution of problem 2, option 1.
|
110
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In an isosceles trapezoid \(ABCD\) with bases \(AD\) and \(BC\), perpendiculars \(BH\) and \(DK\) are drawn from vertices \(B\) and \(D\) to the diagonal \(AC\). It is known that the feet of the perpendiculars lie on the segment \(AC\) and \(AC=20\), \(AK=19\), \(AH=3\). Find the area of trapezoid \(ABCD\).
(10 points)
|
Solution. Note that right triangles $D K A$ and $B H C$ are similar, since
$\angle B C H=\angle D A K$. Let $D K=x, B H=y$. Due to similarity $\frac{D K}{K A}=\frac{B H}{H C}, \frac{x}{19}=\frac{y}{17}$. On the other hand, $C D$
$=\mathrm{AB}$ and by the Pythagorean theorem
$$
C D^{2}=D K^{2}+K C^{2}=x^{2}+1, A B^{2}=B H^{2}+H A^{2}=y^{2}+9
$$
From this, $x^{2}-y^{2}=8$. Since $y=\frac{17 x}{19}$, substituting $y$ into the last equation, we get $\mathrm{x}=19 / 3, \mathrm{y}$ $=17 / 3, S_{A B C D}=A C \cdot(D K+B H) / 2=20 \cdot(19 / 3+17 / 3)=120$.
Answer: 120.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In an isosceles trapezoid $A B C D$ with lateral sides $A B$ and $C D$, the lengths of which are 10, perpendiculars $B H$ and $D K$ are drawn from vertices $B$ and $D$ to the diagonal $A C$. It is known that the bases of the perpendiculars lie on segment $A C$ and $A H: A K: A C=5: 14: 15$. Find the area of trapezoid $A B C D$.
|
Solution. Let $x = BH$, $y = DK$. From the similarity of right triangles $DKA$ and $BHC$, since $\angle BHC = \angle DAK$, we get
$$
\frac{x}{y} = \frac{CH}{AK} = \frac{10}{14} = \frac{5}{7}, \quad 5y = 7x, \quad y = \frac{7x}{5}.
$$
By the condition $AH : AK : AC = 5 : 14 : 15$, therefore $AH : CK = 5 : 1$. By the Pythagorean theorem,
$$
AH^2 = AB^2 - BH^2 = 100 - x^2, \quad CK^2 = CD^2 - DK^2 = 100 - y^2
$$
Thus, $\frac{25}{1} = \frac{AH^2}{CK^2} = \frac{100 - x^2}{100 - y^2}$. Since $y = \frac{7x}{5}$, substituting $y$ into the last equation, we find that $x = \sqrt{50}$, $y = \frac{7\sqrt{50}}{5}$, $AH = \sqrt{50}$, $AC = 3\sqrt{50}$, $S_{ABCD} = AC \cdot (DK + BH) / 2 = AC \cdot (x + y) / 2 = 180$.
Answer: 180. 6. Can the number $\left(x^2 + x + 3\right)^2 + \left(y^2 + y + 3\right)^2$ be a perfect square for some integers $x$ and $y$?
Solution. Since $x^2 + x + 3 = x(x + 1) + 3$, the value of each expression in parentheses is an odd number for any integers $x$ and $y$. The square of an odd number, when divided by 4, leaves a remainder of 1, since $(2n + 1)^2 = 4n^2 + 4n + 1 = 4n(n + 1) + 1$. Thus, the value of the given expression is an even number and leaves a remainder of 2 when divided by 4.
Suppose it is a perfect square, then it is the square of an even number. But the square of any even number is divisible by 4 - a contradiction.
Answer: No, it cannot.
Answer:
Attention! The problem is considered solved if, in addition to the correct answer, necessary explanations are provided.
## Wishing you success!
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find $g(2022)$, if for any real $x, y$ the equality holds
$$
g(x-y)=2022(g(x)+g(y))-2021 x y .
$$
|
Answer: 2043231.
Solution. Substitute $x=y=0$, we get
$$
g(0)=2022(g(0)+g(0))-2021 \cdot 0 \Rightarrow g(0)=0
$$
Substitute $x=y$, we get
$$
\begin{gathered}
g(0)=2022(g(x)+g(x))-2021 \cdot x^{2} \Rightarrow g(x)=\frac{2021 x^{2}}{2 \cdot 2022} \Rightarrow \\
g(2022)=\frac{2021 \cdot 2022^{2}}{2 \cdot 2022}=\frac{2021 \cdot 2022}{2}=2021 \cdot 1011=2043231
\end{gathered}
$$
|
2043231
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find $g(2021)$, if for any real $x, y$ the equality holds
$$
g(x-y)=2021(g(x)+g(y))-2022 x y
$$
|
Answer: 2043231.
Solution. Substitute $x=y=0$, we get
$$
g(0)=2021(g(0)+g(0))-2022 \cdot 0 \Rightarrow g(0)=0
$$
Substitute $x=y$, we get
$$
\begin{gathered}
g(0)=2021(g(x)+g(x))-2022 \cdot x^{2} \Rightarrow g(x)=\frac{2022 x^{2}}{2 \cdot 2021}=\frac{1011 x^{2}}{2021} \Rightarrow \\
g(2021)=\frac{1011 \cdot 2021^{2}}{2021}=1011 \cdot 2021=2043231
\end{gathered}
$$
|
2043231
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. An equilateral triangle $M N K$ is inscribed in a circle. A point $F$ is taken on this circle. Prove that the value of $F M^{4}+F N^{4}+F K^{4}$ does not depend on the choice of point $F$.
#
|
# Solution:
Without loss of generality, we can assume that point \( \mathrm{M} \) lies on the arc \( M N \) of the circumscribed circle with center \( O \) and radius \( R \). Let \( \angle M O F = \alpha \). Then,
\[
\begin{aligned}
F M &= 2 R \sin (\alpha / 2), \\
F N &= 2 R \sin ((\angle M O N - M O F) / 2) = 2 R \sin \left(60^{\circ} - \alpha / 2\right), \\
F K &= 2 R \sin ((\angle M O K + M O F) / 2) = 2 R \sin \left(60^{\circ} + \alpha / 2\right).
\end{aligned}
\]
We will show that the value \( F M^{4} + F N^{4} + F K^{4} \) does not depend on the choice of point \( F \). Let's find
\[
\begin{gathered}
\frac{F M^{4} + F N^{4} + F K^{4}}{R^{4}} = 16 \left( \sin^{4}(\alpha / 2) + \sin^{4}\left(60^{\circ} - \alpha / 2\right) + \sin^{4}\left(60^{\circ} + \alpha / 2\right) \right) = \\
= 4 \left( (1 - \cos \alpha)^{2} + \left(1 - \cos \left(120^{\circ} - \alpha\right)\right)^{2} + \left(1 - \cos \left(120^{\circ} + \alpha\right)\right)^{2} \right) =
\end{gathered}
\]
\[
\begin{gathered}
= 12 - 8 \cos \alpha - 16 \cos \alpha \cos 120^{\circ} + 2 \left( (1 - \cos 2 \alpha) + \left(1 - \cos \left(240^{\circ} - 2 \alpha\right) + \left(1 - \cos \left(240^{\circ} + 2 \alpha\right) \right) \right) = \right. \\
= 12 - 8 \cos \alpha + 8 \cos \alpha + 6 - 2 \cos 2 \alpha - 4 \cos 2 \alpha \cos 240^{\circ} = 18
\end{gathered}
\]
Therefore, the value \( F M^{4} + F N^{4} + F K^{4} \) does not depend on the choice of point \( F \).
## Evaluation criteria are provided in the table:
| Points | Evaluation criteria for one problem. Maximum score per ticket - 35. |
| :---: | :--- |
| **7** | Complete and justified solution. |
| **6** | Justified solution with minor flaws. |
| **5 - 6** | The solution contains minor errors, gaps in justification, but is generally correct and can become fully correct after minor corrections or additions. |
| **4** | The problem is more solved than not, for example, one of the two (more complex) significant cases is correctly considered. |
| **2 - 3** | The problem is not solved, but formulas, drawings, considerations, or auxiliary statements relevant to the solution of the problem are provided. |
| **1** | The problem is not solved, but an attempt to solve it has been made, for example, individual (partial) cases have been considered in the absence of a solution or in the case of an incorrect solution. |
| **0** | The solution is absent, or the solution does not meet any of the criteria listed above. |
|
18
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. The function $f$ satisfies the equation $(x-1) f(x)+f\left(\frac{1}{x}\right)=\frac{1}{x-1}$ for each value of $x$, not equal to 0 and 1. Find $f\left(\frac{2018}{2019}\right)$.
(7 points).
|
Answer: 2019.
## Solution:
Substitute $\frac{1}{x}$ for $x$ in the original equation. Together with the original equation, we get a system of linear equations in terms of $f(x)$ and $f\left(\frac{1}{x}\right)$.
$$
\left\{\begin{array}{l}
(x-1) f(x)+f\left(\frac{1}{x}\right)=\frac{1}{x-1} \\
\left(\frac{1}{x}-1\right) f\left(\frac{1}{x}\right)+f(x)=\frac{x}{x-1}
\end{array}\right.
$$
Solving the obtained system, we find $f(x)=\frac{1}{1-x}$. Therefore, $f\left(\frac{2018}{2019}\right)=\frac{1}{1-\frac{2018}{2019}}=2019$.
|
2019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For any pair of numbers, a certain operation «*» is defined, satisfying the following properties: $a *(b * c)=(a * b) \cdot c$ and $a * a=1$, where the operation «$\cdot$» is the multiplication operation. Find the root $x$ of the equation: $\quad x * 2=2018$.
|
Answer: 4036.
## Solution:
Given the condition of the problem, we have $x * 1=x *(x * x)=(x * x) \cdot x=1 \cdot x=x$. Then
1) $(x * 2) \cdot 2=2018 \cdot 2=4036$,
2) $(x * 2) \cdot 2=x *(2 * 2)=x \cdot 1=x$.
Therefore, $x=4036$.
|
4036
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For any pair of numbers, a certain operation «*» is defined, satisfying the following properties: $\quad a *(b * c)=(a * b) \cdot c$ and $a * a=1$, where the operation «$\cdot$» is the multiplication operation. Find the root $x$ of the equation: $\quad x * 3=2019$.
|
Answer: 6057.
Solution: a similar solution to this problem is present in variant 1 under the same number.
|
6057
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. All passengers of the small cruise liner "Victory" can be accommodated in 7- and 11-seat lifeboats in case of emergency evacuation, with the number of 11-seat lifeboats being greater than the number of 7-seat lifeboats. If the number of 11-seat lifeboats is doubled, the total number of lifeboats will be more than 25, and if the number of 7-seat lifeboats is doubled, the total number of lifeboats will be less than 29. Determine the number of passengers on the cruise liner "Victory".
(7 points)
|
Answer: 60 possible options are given in the table below.
## Solution:
Let $x, y$ be the number of 7-seater and 11-seater boats, respectively, and $z$ be the total number of passengers.
Then $z=7 x+11 y$, where $x, y$ satisfy the system of inequalities: $\left\{\begin{array}{c}2 y+x>25, \\ 2 x+yx\end{array}\right.$ Let's consider the first two inequalities of the system in more detail.
1) Multiplying the first inequality by (-2), we get $\left\{\begin{array}{c}-4 y-2 x7\end{array}\right.$.
2) Multiplying the second inequality by (-2), we get $\left\{\begin{array}{c}2 y+x>25, \\ -4 x-2 y>-58\end{array}\right.$. Adding these two inequalities, we get $-3 x>-33$, hence, $\boldsymbol{x}<11$.
Next, we perform a selection that satisfies the system of inequalities and the obtained constraints, and then calculate $z=7 x+11 y$ - the total number of passengers (the values of $z$ are located in the cells at the intersection of rows and columns for the corresponding $x, y$ ).
| $\underline{x}$ | | $\sqrt{8}$ | 7 | 6 | 5 | 4 | $\sqrt{3}$ | $\sqrt{2}$ | $\\| 1$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathbf{8}_{8}$ | | | | | | | | | |
| | | $\|155\|$ | | | | | | | |
| 10 | 173 | 166 | \|159| | 152 | 156 | | | | |
| 11 | | 177[ | 170\| | 163 | 167 | \|149| | | | |
| 12 | | 188] | 181\| | 174 | 178 | \|160| | \|153| | 146 | |
| 13 | | 192\| | 185 | 189 | \|171| | \|164| | 157 | 150 |
| 14 | | | 203[ | 196 | 200 | \|182| | \|175| | 168 | 161 |
| 15 | | | 207 | 211 | \|193| | \|186| | 179 | 172 |
| 16 | | | | 218 | 222 | 204 | \|197| | 190 | 183 |
| $\overline{17}$ | | | | | 233 | 215\| | 208 | 201 | $\sqrt{192}$ |
| 18 | | | | | | 226 | \|219| | 212 | 205 |
| 19 | | | | | | 237 | 230 | 223 | 216 |
| 20 | | | | | | 248 | 241 | 234 | $\sqrt{227}$ |
| 21 | | | | | | | 2252 | 245 | 238 |
| 22 | | | | | | | \|263| | 256 | 249 |
| 23 | | | | | | | | 267 | 260 |
| 24 | | | | | | | | $[278$ | 271 |
| 25 | | | | | | | | | 282 |
| \|26 | | | | | | | | | 293 |
|
159
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Usually, Nikita leaves home at 8:00 AM, gets into Uncle Vanya's car, who drives him to school by a certain time. But on Friday, Nikita left home at 7:10 and ran in the opposite direction. Uncle Vanya waited for him and at $8: 10$ drove after him, caught up with Nikita, turned around, and delivered him to school 20 minutes late. How many times faster was Uncle Vanya's car speed compared to Nikita's running speed?
|
# Answer: 13 times.
Solution:
The car was on the road for 10 minutes longer than usual due to the 5 minutes spent catching up to Nikita and the 5 minutes spent returning home. The car caught up with Nikita at 8:15, and in 65 minutes (from 7:10 to 8:15), Nikita ran as far as the car traveled in 5 minutes, i.e., he spent $65: 5=13$ times more time.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In isosceles triangle $A B C$ with base $A B$, the angle bisectors $C L$ and $A K$ are drawn. Find $\angle A C B$ of triangle $A B C$, given that $A K = 2 C L$.
|
Answer: $108^{\circ}$
## Solution:
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For the quadratic trinomial $p(x)=(a+1) x^{2}-(a+1) x+2022$, it is known that $-2022 \leq p(x) \leq 2022$ for $x \in[0 ; 1]$. Find the greatest possible value of $a$.
|
# Answer: 16175.
Solution. Since $p(0)=p(1)=2022$, the graph of the quadratic trinomial is a parabola symmetric about the line $x=\frac{1}{2}$. From the conditions that $-2022 \leq$ $p(x) \leq 2022$ for $x \in[0 ; 1]$ and $p(0)=p(1)=2022$, it follows that the branches of the parabola are directed upwards. Then the minimum value of $p(x)$ is $p\left(\frac{1}{2}\right)=2022-\frac{(a+1)}{4}$. The maximum possible value of $a$ will be achieved when $p\left(\frac{1}{2}\right)=-2022$. Therefore,
$$
2022-\frac{(a+1)}{4}=-2022 \Rightarrow \frac{(a+1)}{4}=4044 \Rightarrow a+1=16176 \Rightarrow a=16175
$$
|
16175
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.