problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 2. $n$ mushroom pickers went to the forest and brought a total of 200 mushrooms (it is possible that some of them did not bring any mushrooms home). Boy Petya, upon learning this, said: "Some two of them must have brought the same number of mushrooms!" For what smallest $n$ will Petya definitely be right? Don't forget to justify your answer.
|
Answer: 21.
Solution. First, let's prove that when $n \leqslant 20$, Petya can be wrong. Suppose the first $n-1$ mushroom pickers collected $0,1, \ldots, n-2$ mushrooms, and the $n$-th collected all the rest. Since
$$
0+1+\ldots+(n-2) \leqslant 0+1+\ldots+18=171=200-29
$$
the last mushroom picker collected at least 29 mushrooms, i.e., more than each of the others. Thus, when $n \leqslant 20$, there exists an example where Petya could be wrong.
Let's show that when $n=21$, Petya will always be right. Suppose he is wrong and let the mushroom pickers have collected $a_{0}<a_{1}<\ldots<a_{20}$ mushrooms. It is easy to see that $a_{i} \geqslant i$, hence
$$
200=a_{0}+a_{1}+\ldots+a_{20} \geqslant 0+1+\ldots+20=210
$$
a contradiction.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A circle is inscribed in trapezoid $ABCD$, touching the lateral side $AD$ at point $K$. Find the area of the trapezoid if $AK=16, DK=4$ and $CD=6$.
|
Answer: 432.
Solution. Let $L, M, N$ be the points of tangency of the inscribed circle with the sides $BC, AB, CD$ respectively; let $I$ be the center of the inscribed circle. Denote the radius of the circle by $r$. Immediately note that $DN = DK = 4$ (the first equality follows from the equality of the segments of tangents), from which $CL = CN = CD - DN = 2$ (the first equality follows from the equality of the segments of tangents, the second is obvious).
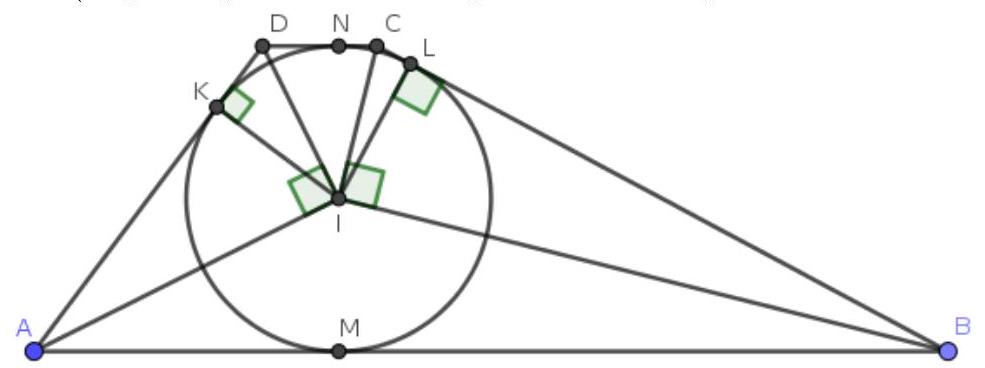
Since $I$ is the point of intersection of the bisectors of the internal angles of the trapezoid, then $\angle IAD + \angle IDA = (\angle DAB + \angle ADC) / 2 = 180^\circ / 2 = 90^\circ$, where the penultimate equality follows from the parallelism of the lines $AB$ and $CD$. Therefore, triangle $AID$ is a right triangle and $\angle AID = 90^\circ$. Similarly, triangle $BIC$ is also a right triangle.
Next, since $IK$ and $IL$ are radii drawn to the points of tangency, then $\angle IKD = 90^\circ$ and $\angle ILB = 90^\circ$. Therefore, $IK$ and $IL$ are altitudes in triangles $AID$ and $BIC$ respectively. Using the known fact that in a right triangle, the square of the altitude dropped to the hypotenuse equals the product of the segments into which it divides the hypotenuse. Then
$$
IK^2 = AK \cdot KD = 16 \cdot 4 = 64 = 8^2
$$
i.e., $r = IK = 8$, and also $8^2 = IL^2 = CL \cdot LB = 2 \cdot LB$, i.e., $LB = 32$.[^0]
Now we have everything to find the area. Note that $MN$ is the height of the trapezoid and $MN = 2r = 16, AB + CD = (AM + MB) + 6 = (AK + BL) + 6 = 16 + 32 + 6 = 54$, from which the answer $\frac{16 \cdot 54}{2} = 432$.
|
432
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
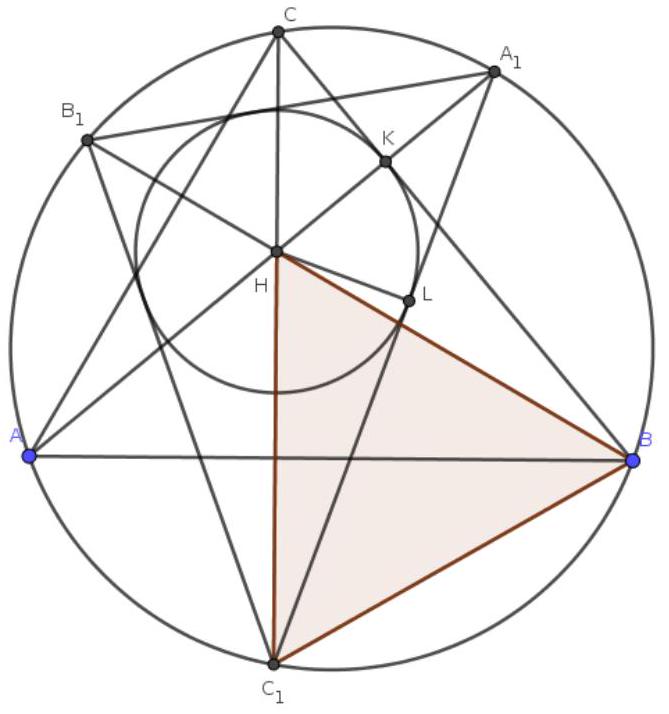
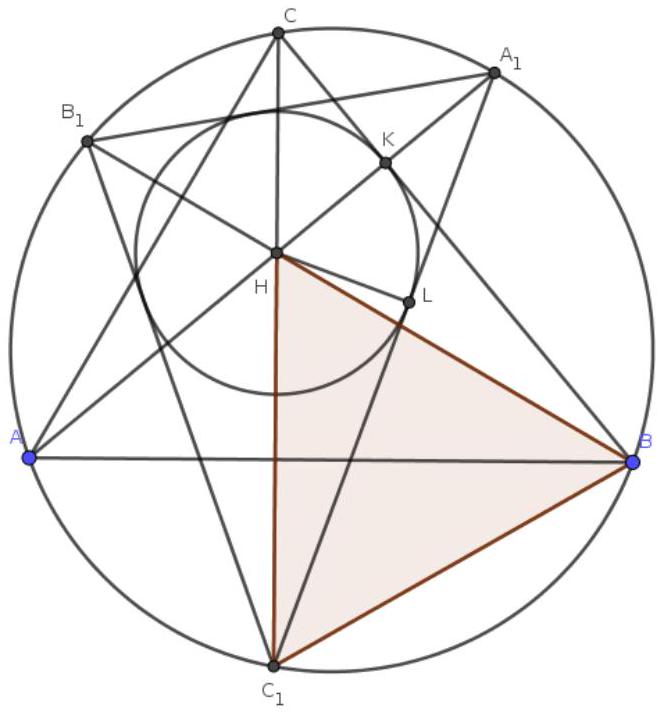
Problem 7. Points $A_{1}, B_{1}, C_{1}$ are the points of intersection of the extensions of the altitudes of an acute-angled triangle $A B C$ with the circumcircle of $A B C$. The incircle of triangle $A_{1} B_{1} C_{1}$ touches one of the sides of $A B C$, and one of the angles of triangle $A B C$ is $40^{\circ}$. Find the other two angles of triangle $A B C$.
|
Answer: $60^{\circ}$ and $80^{\circ}$.
Solution. Without loss of generality, let the circle $\omega$, inscribed in $A_{1} B_{1} C_{1}$, touch the side $B C$. Let $H$ be the orthocenter of triangle $A B C$, $K$ be the point of tangency of $\omega$ and $B C$, and $L$ be the point of tangency of $\omega$ and $A_{1} C_{1}$. We aim to prove that triangle $H B C_{1}$ is equilateral. Then $\angle B A C = \angle B C_{1} C = 60^{\circ}$, from which the answer follows given the condition.
First, note that $H$ is the intersection of the angle bisectors of triangle $A_{1} B_{1} C_{1}$. Indeed, for example, $\angle B_{1} C_{1} C = \angle B_{1} B C = 90^{\circ} - \angle C = \angle C A A_{1} = \angle C C_{1} A_{1}$, so $C_{1} H$ is the angle bisector of $\angle A_{1} C_{1} B_{1}$; similarly, it can be shown that $A_{1} H$ and $B_{1} H$ are also angle bisectors of the corresponding angles. Therefore, $H$ is the incenter of triangle $A_{1} B_{1} C_{1}$ and $H K = H L$. Moreover, it has been shown that $\angle H C_{1} L = \angle H B K$, so the right triangles $H C_{1} L$ and $H B K$ are congruent by a leg and an acute angle. Therefore, $H C_{1} = H B$.
It remains to note that $H B = B C_{1}$. This fact is well-known and can be proven in various ways. Here, we will present just one of them. Note that triangles $A H B$ and $A C_{1} B$ are congruent by a side (common side $A B$) and two angles ($\angle H A B = \angle A_{1} B_{1} B = \angle C_{1} B_{1} B = \angle C_{1} A B$; similarly, it can be shown that $\angle H B A = \angle C_{1} B A$).
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In the decimal representation of an even number $M$, only the digits $0, 2, 4, 5, 7$, and 9 are used, and digits can repeat. It is known that the sum of the digits of the number $2M$ is 35, and the sum of the digits of the number $M / 2$ is 29. What values can the sum of the digits of the number $M$ take? List all possible answers.
|
# Answer: 31.
Solution. Let's denote the sum of the digits of a natural number $n$ by $S(n)$. Notice the following facts, each of which is easy to verify if you add numbers in a column.
Lemma 1. Let $n$ be a natural number. Then the number of odd digits in the number $2n$ is equal to the number of carries when adding $n$ and $n$.
Lemma 2. Let $n$ be a natural number. Then the number of digits in the number $n$ that are greater than or equal to 5 is equal to the number of carries when adding $n$ and $n$.
Lemma 3. Let $n$ and $m$ be natural numbers. Then $S(n+m)=S(n)+S(m)-9k$, where $k$ is the number of carries when adding $n$ and $m$.
Let $N$ be the number of odd digits in the number $M$; according to the condition, $N$ is the number of digits in the number $M$ that are greater than or equal to 5. Notice that then, by Lemma 1, when adding $M/2$ and $M/2$, there were exactly $N$ carries, from which, by Lemma 3, we have $S(M)=2S(M/2)-9N=58-9N$. By Lemma 2, when adding $M$ and $M$, there were also $N$ carries, from which, again by Lemma 3, we have $35=S(2M)=2S(M)-9N$.
Thus, $S(M)=58-9N, 2S(M)=35+9N$, from which $3S(M)=93, S(M)=31$.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. $n$ mushroom pickers went to the forest and brought a total of 338 mushrooms (it is possible that some of them did not bring any mushrooms home). Boy Petya, upon learning this, said: "Some two of them must have brought the same number of mushrooms!" For what smallest $n$ will Petya definitely be right? Don't forget to justify your answer.
|
Answer: 27.
Solution. First, let's prove that when $n \leqslant 26$, Petya can be wrong. Suppose the first $n-1$ mushroom pickers collected $0,1, \ldots, n-2$ mushrooms, and the $n$-th collected all the rest. Since
$$
0+1+\ldots+(n-2) \leqslant 0+1+\ldots+24=300=338-38
$$
the last mushroom picker collected at least 38 mushrooms, i.e., more than each of the others. Thus, when $n \leqslant 26$, there exists an example where Petya could be wrong.
Let's show that when $n=27$, Petya will always be right. Suppose he is wrong and let the mushroom pickers have collected $a_{0}<a_{1}<\ldots<a_{26}$ mushrooms. It is easy to see that $a_{i} \geqslant i$, hence
$$
338=a_{0}+a_{1}+\ldots+a_{25} \geqslant 0+1+\ldots+25=351
$$
a contradiction
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A circle with radius 4 is inscribed in trapezoid $ABCD$, touching the base $AB$ at point $M$. Find the area of the trapezoid if $BM=16$ and $CD=3$.
|
Answer: 108.
Solution. Let $K, L, N$ be the points of tangency of the inscribed circle with the sides $AD, BC, CD$ respectively; let $I$ be the center of the inscribed circle. Immediately note that $BL = BM = 16$.
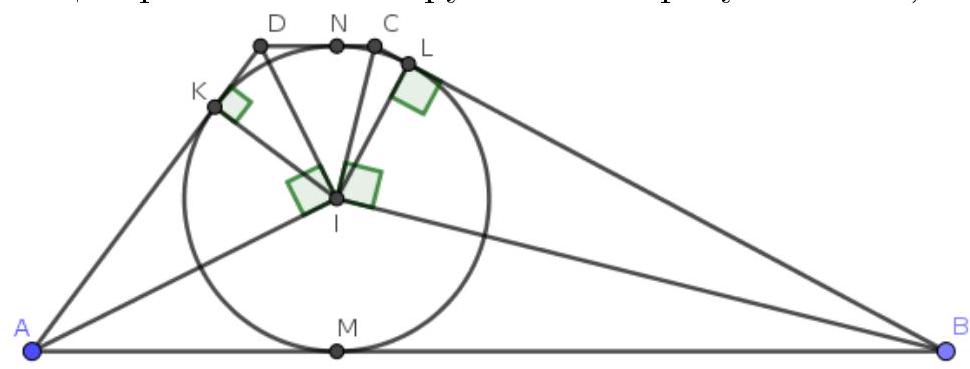
Since $I$ is the intersection point of the angle bisectors of the internal angles of the trapezoid, then $\angle IAD + \angle IDA = (\angle DAB + \angle ADC) / 2 = 180^\circ / 2 = 90^\circ$, where the penultimate equality follows from the parallelism of lines $AB$ and $CD$. Therefore, triangle $AID$ is a right triangle and $\angle AID = 90^\circ$. Similarly, triangle $BIC$ is also a right triangle.
Next, since $IK$ and $IL$ are radii drawn to the points of tangency, then $\angle IKD = 90^\circ$ and $\angle ILB = 90^\circ$. Therefore, $IK$ and $IL$ are altitudes in triangles $AID$ and $BIC$ respectively. Using the known fact that in a right triangle, the square of the altitude dropped to the hypotenuse equals the product of the segments into which it divides the hypotenuse. Then
$$
4^2 = IL^2 = CL \cdot LB = CL \cdot 16
$$
i.e., $CL = 1$. By the equality of tangent segments, we have $CN = CL = 1$, hence $DK = DN = CD - CN = 3 - 1 = 2$. In the right triangle $AID$, we get $4^2 = IK^2 = AK \cdot KD = AK \cdot 2$, i.e., $AK = 8$.
Now we have everything to find the area. Note that $LM$ is the height of the trapezoid and $LM = 2r = 8, AB + CD = AM + MB + CD = 8 + 16 + 3 = 27$, hence the answer $\frac{8 \cdot 27}{2} = 108$.
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
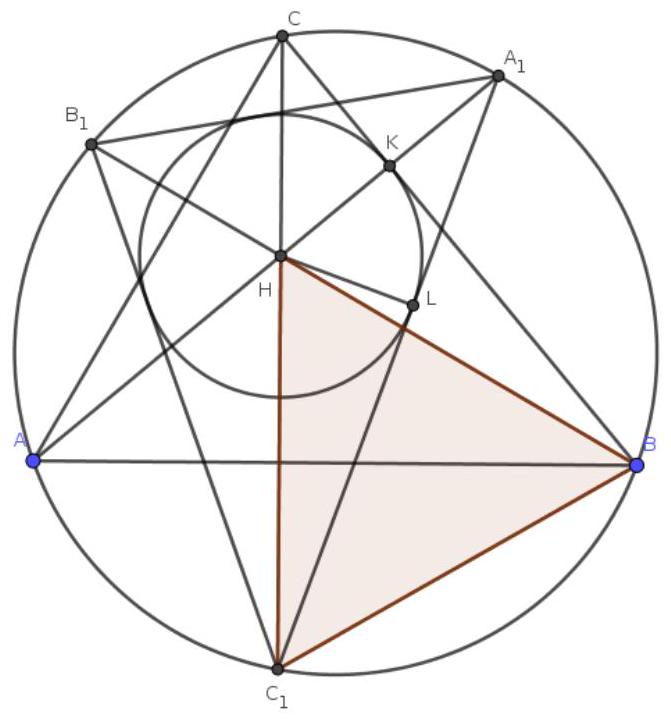
Problem 7. Points $A_{1}, B_{1}, C_{1}$ are the points of intersection of the extensions of the altitudes of an acute-angled triangle $A B C$ with the circumcircle of $A B C$. The incircle of triangle $A_{1} B_{1} C_{1}$ touches one of the sides of $A B C$, and one of the angles of triangle $A B C$ is $50^{\circ}$. Find the other two angles of triangle $A B C$.
|
Answer: $60^{\circ}$ and $70^{\circ}$.
Solution. Without loss of generality, let the circle $\omega$, inscribed in $A_{1} B_{1} C_{1}$, touch the side $B C$. Let $H$ be the orthocenter of triangle $A B C$, $K$ be the point of tangency of $\omega$ and $B C$, and $L$ be the point of tangency of $\omega$ and $A_{1} C_{1}$. We aim to prove that triangle $H B C_{1}$ is equilateral. Then $\angle B A C = \angle B C_{1} C = 60^{\circ}$, from which the answer follows given the condition.
First, note that $H$ is the intersection of the angle bisectors of triangle $A_{1} B_{1} C_{1}$. Indeed, for example, $\angle B_{1} C_{1} C = \angle B_{1} B C = 90^{\circ} - \angle C = \angle C A A_{1} = \angle C C_{1} A_{1}$, so $C_{1} H$ is the angle bisector of $\angle A_{1} C_{1} B_{1}$; similarly, it can be shown that $A_{1} H$ and $B_{1} H$ are also angle bisectors of the corresponding angles. Therefore, $H$ is the incenter of triangle $A_{1} B_{1} C_{1}$ and $H K = H L$. Moreover, it has been shown that $\angle H C_{1} L = \angle H B K$, so the right triangles $H C_{1} L$ and $H B K$ are congruent by a leg and an acute angle. Therefore, $H C_{1} = H B$.
It remains to note that $H B = B C_{1}$. This fact is well-known and can be proven in various ways. Here, we will present just one of them. Note that triangles $A H B$ and $A C_{1} B$ are congruent by a side (common side $A B$) and two angles ($\angle H A B = \angle A_{1} B_{1} B = \angle C_{1} B_{1} B = \angle C_{1} A B$; similarly, it can be shown that $\angle H B A = \angle C_{1} B A$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In the decimal representation of an even number $M$, only the digits $0, 2, 4, 5, 7$, and 9 are used, and digits may repeat. It is known that the sum of the digits of the number $2M$ is 31, and the sum of the digits of the number $M / 2$ is 28. What values can the sum of the digits of the number $M$ take? List all possible answers.
|
Answer: 29.
Solution. Let $S(n)$ denote the sum of the digits of a natural number $n$. Notice the following facts, each of which is easy to verify by adding numbers in a column.
Lemma 1. Let $n$ be a natural number. Then the number of odd digits in the number $2n$ is equal to the number of carries when adding $n$ and $n$.
Lemma 2. Let $n$ be a natural number. Then the number of digits in the number $n$ that are greater than or equal to 5 is equal to the number of carries when adding $n$ and $n$.
Lemma 3. Let $n$ and $m$ be natural numbers. Then $S(n+m)=S(n)+S(m)-9k$, where $k$ is the number of carries when adding $n$ and $m$.
Let $N$ be the number of odd digits in the number $M$; according to the condition, $N$ is the number of digits in the number $M$ that are greater than or equal to 5. Notice that then, by Lemma 1, when adding $M/2$ and $M/2$, there were exactly $N$ carries, from which, by Lemma 3, we have $S(M)=2S(M/2)-9N=56-9N$. By Lemma 2, when adding $M$ and $M$, there were also $N$ carries, from which, again by Lemma 3, we have $31=S(2M)=2S(M)-9N$.
Thus, $S(M)=56-9N, 2S(M)=31+9N$, from which $3S(M)=87, S(M)=29$.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. $n$ mushroom pickers went to the forest and brought a total of 450 mushrooms (each brought at least one mushroom home). Boy Petya, upon learning this, said: "Some two of them must have brought the same number of mushrooms!" For what smallest $n$ will Petya definitely be right? Don't forget to justify your answer.
|
Answer: 30.
Solution. First, let's prove that when $n \leqslant 29$, Petya can be wrong. Suppose the first $n-1$ mushroom pickers collected $1, \ldots, n-1$ mushrooms, and the $n$-th collected all the rest. Since
$$
1+\ldots+(n-1) \leqslant 1+\ldots+28=406=450-44
$$
the last mushroom picker collected at least 44 mushrooms, i.e., more than each of the others. Thus, when $n \leqslant 29$, there is an example where Petya could be wrong.
Let's show that when $n=30$, Petya will always be right. Suppose he is wrong and let the mushroom pickers have collected $a_{1}<\ldots<a_{30}$ mushrooms. It is easy to see that $a_{i} \geqslant i$, hence
$$
450=a_{1}+\ldots+a_{30} \geqslant 1+\ldots+30=465
$$
a contradiction
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. Points $A_{1}, B_{1}, C_{1}$ are the points of intersection of the extensions of the altitudes of an acute-angled triangle $A B C$ with the circumcircle of $A B C$. The incircle of triangle $A_{1} B_{1} C_{1}$ touches one of the sides of $A B C$, and one of the angles of triangle $A B C$ is $70^{\circ}$. Find the other two angles of triangle $A B C$.
|
Answer: $60^{\circ}$ and $50^{\circ}$.
Solution. Without loss of generality, let the circle $\omega$, inscribed in $A_{1} B_{1} C_{1}$, touch the side $B C$. Let $H$ be the orthocenter of triangle $A B C$, $K$ be the point of tangency of $\omega$ and $B C$, and $L$ be the point of tangency of $\omega$ and $A_{1} C_{1}$. We aim to prove that triangle $H B C_{1}$ is equilateral. Then $\angle B A C = \angle B C_{1} C = 60^{\circ}$, from which the answer follows given the condition.
First, note that $H$ is the intersection of the angle bisectors of triangle $A_{1} B_{1} C_{1}$. Indeed, for example, $\angle B_{1} C_{1} C = \angle B_{1} B C = 90^{\circ} - \angle C = \angle C A A_{1} = \angle C C_{1} A_{1}$, i.e., $C_{1} H$ is the angle bisector of $\angle A_{1} C_{1} B_{1}$; similarly, it can be shown that $A_{1} H$ and $B_{1} H$ are also angle bisectors of the corresponding angles. Therefore, $H$ is the incenter of triangle $A_{1} B_{1} C_{1}$ and $H K = H L$. Moreover, it has been shown that $\angle H C_{1} L = \angle H B K$, i.e., right triangles $H C_{1} L$ and $H B K$ are congruent by a leg and an acute angle. Therefore, $H C_{1} = H B$.
It remains to note that $H B = B C_{1}$. This fact is well-known and can be proven in various ways. Here, we will present just one of them. Note that triangles $A H B$ and $A C_{1} B$ are congruent by a side (common side $A B$) and two angles ($\angle H A B = \angle A_{1} B_{1} B = \angle C_{1} B_{1} B = \angle C_{1} A B$; similarly, it can be shown that $\angle H B A = \angle C_{1} B A$).
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In the decimal representation of an even number $M$, only the digits $0, 2, 4, 5, 7$, and 9 are used, and digits can repeat. It is known that the sum of the digits of the number $2M$ is 43, and the sum of the digits of the number $M / 2$ is 31. What values can the sum of the digits of the number $M$ take? List all possible answers.
|
# Answer: 35.
Solution. Let $S(n)$ denote the sum of the digits of a natural number $n$. Notice the following facts, each of which is easy to verify by adding numbers in a column.
Lemma 1. Let $n$ be a natural number. Then the number of odd digits in the number $2n$ is equal to the number of carries when adding $n$ and $n$.
Lemma 2. Let $n$ be a natural number. Then the number of digits in the number $n$ that are greater than or equal to 5 is equal to the number of carries when adding $n$ and $n$.
Lemma 3. Let $n$ and $m$ be natural numbers. Then $S(n+m) = S(n) + S(m) - 9k$, where $k$ is the number of carries when adding $n$ and $m$.
Let $N$ be the number of odd digits in the number $M$; according to the condition, $N$ is the number of digits in the number $M$ that are greater than or equal to 5. Notice that then, by Lemma 1, when adding $M/2$ and $M/2$, there were exactly $N$ carries, from which, by Lemma 3, we have $S(M) = 2S(M/2) - 9N = 62 - 9N$. By Lemma 2, when adding $M$ and $M$, there were also $N$ carries, from which, again by Lemma 3, we have $43 = S(2M) = 2S(M) - 9N$.
Thus, $S(M) = 62 - 9N, 2S(M) = 43 + 9N$, from which $3S(M) = 105, S(M) = 35$.
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. $n$ mushroom pickers went to the forest and brought a total of 162 mushrooms (each brought at least one mushroom home). Boy Petya, upon learning this, declared: "Some two of them must have brought the same number of mushrooms!" For what smallest $n$ will Petya definitely be right? Don't forget to justify your answer.
|
Answer: 18.
Solution. First, let's prove that when $n \leqslant 17$, Petya can be wrong. Suppose the first $n-1$ mushroom pickers collected $1, \ldots, n-1$ mushrooms, and the $n$-th collected all the rest. Since
$$
1+\ldots+(n-1) \leqslant 1+\ldots+16=136=162-26
$$
the last mushroom picker collected at least 26 mushrooms, i.e., more than each of the others. Thus, when $n \leqslant 17$, there is an example where Petya could be wrong.
Let's show that when $n=18$, Petya will always be right. Suppose he is wrong and let the mushroom pickers have collected $a_{1}<\ldots<a_{18}$ mushrooms. It is easy to see that $a_{i} \geqslant i$, hence
$$
162=a_{1}+\ldots+a_{18} \geqslant 1+\ldots+18=171
$$
a contradiction
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A circle with radius 2 is inscribed in trapezoid $ABCD$, touching the base $CD$ at point $N$. Find the area of the trapezoid if $DN=1$ and $AB=12$.
|
Answer: 27.
Solution. Let $K, L, M$ be the points of tangency of the inscribed circle with the sides $AD, BC, AB$ respectively; let $I$ be the center of the inscribed circle. Immediately note that $DK = DN = 1$.
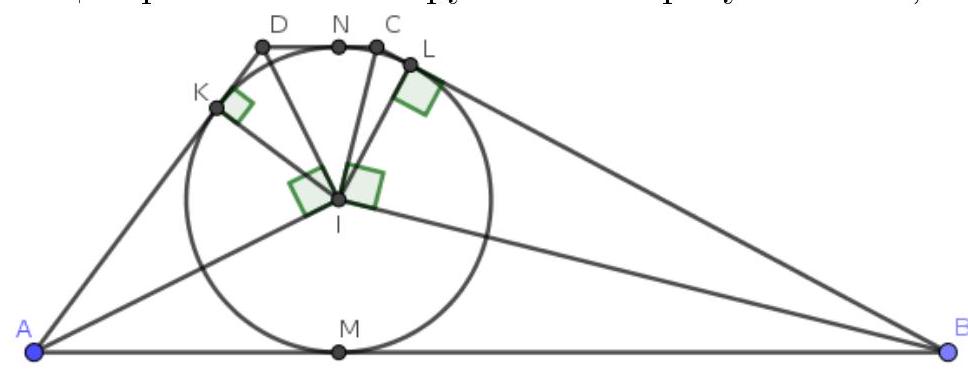
Since $I$ is the intersection of the angle bisectors of the internal angles of the trapezoid, $\angle IAD + \angle IDA = (\angle DAB + \angle ADC) / 2 = 180^\circ / 2 = 90^\circ$, where the penultimate equality follows from the parallelism of lines $AB$ and $CD$. Therefore, triangle $AID$ is a right triangle and $\angle AID = 90^\circ$. Similarly, triangle $BIC$ is also a right triangle.
Next, since $IK$ and $IL$ are radii drawn to the points of tangency, $\angle IKD = 90^\circ$ and $\angle ILB = 90^\circ$. Therefore, $IK$ and $IL$ are altitudes in triangles $AID$ and $BIC$ respectively. Using the known fact that in a right triangle, the square of the altitude dropped to the hypotenuse equals the product of the segments into which it divides the hypotenuse. Then
$$
4 = IK^2 = AK \cdot KD = 1 \cdot AK
$$
i.e., $AK = 4$. By the equality of tangent segments, we have $AM = AK = 4$, hence $BL = BM = AB - AM = 12 - 4 = 8$. In the right triangle $BIC$, we get $4 = IL^2 = CL \cdot LB = 8 \cdot CL$, i.e., $CL = 0.5$.
Now we have everything to find the area. Note that $LM$ is the height of the trapezoid and $LM = 2r = 4, AB + CD = AB + DN + CN = 12 + 1 + 0.5 = 13.5$, hence the answer $\frac{4 \cdot 13.5}{2} = 27$.
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
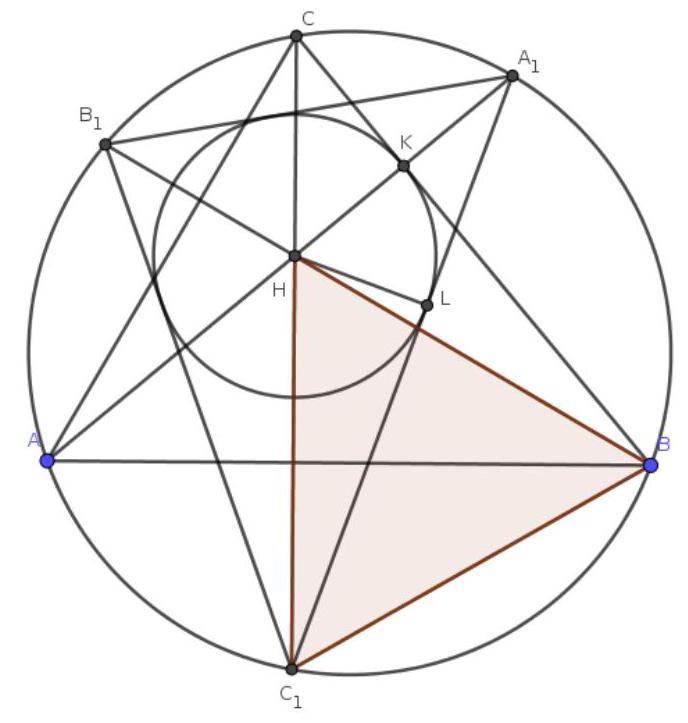
Problem 7. Points $A_{1}, B_{1}, C_{1}$ are the points of intersection of the extensions of the altitudes of an acute-angled triangle $A B C$ with the circumcircle of $A B C$. The incircle of triangle $A_{1} B_{1} C_{1}$ touches one of the sides of $A B C$, and one of the angles of triangle $A B C$ is $80^{\circ}$. Find the other two angles of triangle $A B C$.
|
Answer: $60^{\circ}$ and $40^{\circ}$.
Solution. Without loss of generality, let the circle $\omega$, inscribed in $A_{1} B_{1} C_{1}$, touch the side $B C$. Let $H$ be the orthocenter of triangle $A B C$, $K$ be the point of tangency of $\omega$ and $B C$, and $L$ be the point of tangency of $\omega$ and $A_{1} C_{1}$. We aim to prove that triangle $H B C_{1}$ is equilateral. Then $\angle B A C = \angle B C_{1} C = 60^{\circ}$, from which the answer follows given the condition.
First, note that $H$ is the intersection of the angle bisectors of triangle $A_{1} B_{1} C_{1}$. Indeed, for example, $\angle B_{1} C_{1} C = \angle B_{1} B C = 90^{\circ} - \angle C = \angle C A A_{1} = \angle C C_{1} A_{1}$, i.e., $C_{1} H$ is the angle bisector of $\angle A_{1} C_{1} B_{1}$; similarly, it can be shown that $A_{1} H$ and $B_{1} H$ are also angle bisectors of the corresponding angles. Therefore, $H$ is the incenter of triangle $A_{1} B_{1} C_{1}$ and $H K = H L$. Moreover, it has been shown that $\angle H C_{1} L = \angle H B K$, i.e., the right triangles $H C_{1} L$ and $H B K$ are congruent by a leg and an acute angle. Therefore, $H C_{1} = H B$.
It remains to note that $H B = B C_{1}$. This fact is well-known and can be proven in various ways. Here, we will present just one of them. Note that triangles $A H B$ and $A C_{1} B$ are congruent by a side (common side $A B$) and two angles ($\angle H A B = \angle A_{1} B_{1} B = \angle C_{1} B_{1} B = \angle C_{1} A B$; similarly, it can be shown that $\angle H B A = \angle C_{1} B A$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In the decimal representation of an even number $M$, only the digits $0, 2, 4, 5, 7$, and 9 are used, and digits may repeat. It is known that the sum of the digits of the number $2M$ is 39, and the sum of the digits of the number $M / 2$ is 30. What values can the sum of the digits of the number $M$ take? List all possible answers.
|
Answer: 33.
Solution. Let $S(n)$ denote the sum of the digits of a natural number $n$. Notice the following facts, each of which is easy to verify by adding numbers in a column.
Lemma 1. Let $n$ be a natural number. Then the number of odd digits in the number $2n$ is equal to the number of carries when adding $n$ and $n$.
Lemma 2. Let $n$ be a natural number. Then the number of digits in the number $n$ that are greater than or equal to 5 is equal to the number of carries when adding $n$ and $n$.
Lemma 3. Let $n$ and $m$ be natural numbers. Then $S(n+m) = S(n) + S(m) - 9k$, where $k$ is the number of carries when adding $n$ and $m$.
Let $N$ be the number of odd digits in the number $M$; according to the condition, $N$ is the number of digits in the number $M$ that are greater than or equal to 5. Notice that then, by Lemma 1, when adding $M/2$ and $M/2$, there were exactly $N$ carries, from which, by Lemma 3, we have $S(M) = 2S(M/2) - 9N = 60 - 9N$. By Lemma 2, when adding $M$ and $M$, there were also $N$ carries, from which, again by Lemma 3, we have $39 = S(2M) = 2S(M) - 9N$.
Thus, $S(M) = 60 - 9N, 2S(M) = 39 + 9N$, from which $3S(M) = 99, S(M) = 33$.
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In a football championship, 20 teams participate, each playing against each other once. What is the minimum number of games that must be played so that among any three teams, there are two that have already played against each other?
|
Answer: 90 games.
Solution. We will consider the games that have not been played. The condition means that the unplayed games do not form triangles. We will prove by induction on $k$ that for $2k$ teams, the maximum number of unplayed games is no more than $k^2$.
Base case: $k=1$ (the estimate is obvious).
Inductive step: Suppose it is proven for $k$, we will prove for $k+1$. If there are no unplayed games, then everything is proven. Otherwise, select any teams $A$ and $B$ that have not played against each other. Note that the number of unplayed games involving teams $A$ or $B$ is no more than $2k$ (not counting the game between $A$ and $B$), since for any team $C$, at least one of the games $AC$ and $BC$ has been played. Now consider all teams except $A$ and $B$ and apply the inductive hypothesis - among them, no more than $k^2$ games have not been played. Therefore, the total number of unplayed games is no more than $k^2 + (2k + 1) = (k+1)^2$, which is what we needed to prove.
Substituting $k=10$ gives that the number of unplayed games is no more than 100, and the total number of possible games is $\frac{20 \cdot 19}{2} = 190$, from which the number of played games is no less than $190 - 100 = 90$.
The estimate is achieved if the teams are divided into two equal groups, all matches are played within each group, and no matches are played between the groups.
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In a football championship, 16 teams participate, each playing against each other once. What is the minimum number of games that must be played so that among any three teams, there are two that have already played against each other?
#
|
# Answer: 56 games.
Solution. We will consider the games that have not been played. The condition means that there will be no three teams that have not played against each other at all. We will prove by induction on $k$ that for $2k$ teams, the maximum number of unplayed games is no more than $k^2$.
Base case: $k=1$ (the estimate is obvious).
Inductive step: Suppose it is proven for $k$, we will prove for $k+1$. If there are no unplayed games, then everything is proven. Otherwise, select any teams $A$ and $B$ that have not played against each other. Note that the number of unplayed games involving teams $A$ or $B$ is no more than $2k$ (not counting the game between $A$ and $B$), because for any team $C$, at least one of the games $AC$ or $BC$ has been played. Now consider all teams except $A$ and $B$ and apply the inductive hypothesis - among them, no more than $k^2$ games have not been played. Therefore, the total number of unplayed games is no more than $k^2 + (2k + 1) = (k+1)^2$, which is what we needed to prove.
Substituting $k=8$ gives that the number of unplayed games is no more than 64, and the total number of possible games is $\frac{16 \cdot 15}{2} = 120$, so the number of played games is no less than $120 - 64 = 56$.
The estimate is achieved if the teams are divided into two equal groups, all matches are played within each group, and no matches are played between the groups.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In a football championship, 16 teams participate, each playing against each other once. What is the minimum number of games that must be played so that among any three teams, there are two that have already played against each other?
|
Answer: 56 games.
Solution. We will consider the games that have not been played. The condition means that there will be no three teams that have not played with each other at all. We will prove by induction on $k$ that for $2k$ teams, the maximum number of unplayed games is no more than $k^2$.
Base case: $k=1$ (the estimate is obvious).
Inductive step: Suppose it is proven for $k$, we will prove for $k+1$. If there are no unplayed games, then everything is proven. Otherwise, select any teams $A$ and $B$ that have not played against each other. Note that the number of unplayed games involving teams $A$ or $B$ is no more than $2k$ (not counting the game between $A$ and $B$), because for any team $C$, at least one of the games $AC$ or $BC$ has been played. Now consider all teams except $A$ and $B$ and apply the inductive hypothesis - among them, no more than $k^2$ games have not been played. Therefore, the total number of unplayed games is no more than $k^2 + (2k + 1) = (k+1)^2$, which is what we needed to prove.
Substituting $k=8$ gives that the number of unplayed games is no more than 64, and the total number of possible games is $\frac{16 \cdot 15}{2} = 120$, so the number of played games is no less than $120 - 64 = 56$.
The estimate is achieved if the teams are divided into two equal groups, all matches are played within each group, and no matches are played between the groups.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. For what least $n$ do there exist $n$ numbers from the interval $(-1 ; 1)$ such that their sum is 0 and the sum of their squares is 30?
|
Answer: 32.
Solution. First, let's provide an example of 32 numbers whose sum is 0 and the sum of their squares is 30. For instance, the numbers $x_{1}=x_{2}=\ldots=x_{16}=\sqrt{\frac{15}{16}}, x_{17}=x_{18}=\ldots=x_{32}=-\sqrt{\frac{15}{16}}$ will work.
Now, we will prove that fewer than 32 numbers will not suffice. Suppose the contrary. Then, among all the numbers, either positive or negative, there are no more than 15. By multiplying all the numbers by -1 if necessary, we can assume that there are no more than 15 negative numbers.
Let $y_{1}, y_{2}, \ldots, y_{k}$ be all the negative numbers, and $y_{k+1}, \ldots, y_{n}$ be all the non-negative numbers. Then $y_{1}^{2}+y_{2}^{2}+\ldots+y_{k}^{2}<k \leqslant 15$, and
$$
y_{k+1}^{2}+y_{k+2}^{2}+\ldots+y_{n}^{2} \leqslant y_{k+1}+y_{k+2}+\ldots+y_{n}=-y_{1}-y_{2}-\ldots-y_{k}<k \leqslant 15
$$
Adding the obtained inequalities, we get, $30=y_{1}^{2}+y_{2}^{2}+\ldots+y_{n}^{2}<30$. Contradiction.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what values of the parameter $a$ does the equation $x^{3}-11 x^{2}+a x-8=0$ have three distinct real roots that form a geometric progression?
|
Answer: only 22.
Solution. Let the parameter $a$ be suitable. Then the polynomial $x^{3}-11 x^{2}+a x-8=0$ has three distinct roots $x_{1}, x_{2}, x_{3}$. We use Vieta's theorem for a polynomial of the third degree:
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=11 \\
x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a \\
x_{1} x_{2} x_{3}=8
\end{array}\right.
$$
Since $x_{1}, x_{2}, x_{3}$ form a geometric progression (let's assume in this order), there exist $b$ and $q$ such that $x_{1}=b, x_{2}=b q, x_{3}=b q^{2}$. Then from the equality $x_{1} x_{2} x_{3}=8$, we have $b^{3} q^{3}=8$, from which $x_{2}=b q=2, x_{1}=2 / q, x_{3}=2 q$.
Then $2\left(\frac{1}{q}+1+q\right)=11(*)$, after transformations $2 q^{2}-9 q+2=0$. The discriminant of this expression is $D=9^{2}-4 \cdot 2 \cdot 2>0$, so such $q$, and with it $x_{1}, x_{2}, x_{3}$, will exist. Then
$$
a=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=x_{1} x_{2} x_{3}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}\right)=8 \cdot\left(\frac{q}{2}+\frac{1}{2}+\frac{1}{2 q}\right)=4\left(q+1+\frac{1}{q}\right)=2 \cdot 11=22
$$
(In the penultimate transition, we used the equality $(*)$).
Comment. Naturally, $q, x_{1}, x_{2}, x_{3}$ can be calculated explicitly:
$$
q_{1,2}=\frac{9 \pm \sqrt{65}}{4}
$$
Choose $q$ with the “+” (if you choose with the “-”, then $x_{1}$ and $x_{3}$ will swap places, which will not affect the answer); then
$$
x_{1}=\frac{2 \cdot 4}{9+\sqrt{65}}=\frac{9-\sqrt{65}}{2}, x_{2}=2, x_{3}=\frac{9+\sqrt{65}}{2}
$$
$a$ could have been calculated by substituting the obtained numbers into the expression $x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}$.
|
22
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. For what least $n$ do there exist $n$ numbers from the interval $(-1 ; 1)$ such that their sum is 0 and the sum of their squares is 42?
|
Answer: 44.
Solution. First, let's provide an example of 44 numbers whose sum is 0 and the sum of their squares is 42. For instance, the numbers $x_{1}=x_{2}=\ldots=x_{22}=\sqrt{\frac{21}{22}}, x_{23}=x_{24}=\ldots=x_{44}=-\sqrt{\frac{21}{22}}$ will work.
Now, we will prove that it is impossible to achieve this with fewer than 44 numbers. Suppose the contrary. Then, among all the numbers, either the positive or the negative ones do not exceed 21. By multiplying all the numbers by -1 if necessary, we can assume that there are no more than 21 negative numbers.
Let $y_{1}, y_{2}, \ldots, y_{k}$ be all the negative numbers, and $y_{k+1}, \ldots, y_{n}$ be all the non-negative numbers. Then $y_{1}^{2}+y_{2}^{2}+\ldots+y_{k}^{2}<k \leqslant 21$, and
$$
y_{k+1}^{2}+y_{k+2}^{2}+\ldots+y_{n}^{2} \leqslant y_{k+1}+y_{k+2}+\ldots+y_{n}=-y_{1}-y_{2}-\ldots-y_{k}<k \leqslant 21
$$
Adding the obtained inequalities, we get, $42=y_{1}^{2}+y_{2}^{2}+\ldots+y_{n}^{2}<42$. Contradiction.
|
44
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what values of the parameter $a$ does the equation $x^{3}-14 x^{2}+a x-27=0$ have three distinct real roots that form a geometric progression?
|
Answer: only 42.
Solution. Let the parameter $a$ be suitable. Then the polynomial $x^{3}-14 x^{2}+a x-27=0$ has three distinct roots $x_{1}, x_{2}, x_{3}$. We use Vieta's theorem for a cubic polynomial:
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=14 \\
x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a \\
x_{1} x_{2} x_{3}=27
\end{array}\right.
$$
Since $x_{1}, x_{2}, x_{3}$ form a geometric progression (let's assume in this order), there exist $b$ and $q$ such that $x_{1}=b, x_{2}=b q, x_{3}=b q^{2}$. Then from the equality $x_{1} x_{2} x_{3}=27$, we have $b^{3} q^{3}=27$, hence $x_{2}=b q=3, x_{1}=3 / q, x_{3}=3 q$.
Then $3\left(\frac{1}{q}+1+q\right)=14(*)$, after transformations $3 q^{2}-11 q+3=0$. The discriminant of this expression is $D=11^{2}-4 \cdot 3 \cdot 3>0$, so such $q$, and with it $x_{1}, x_{2}, x_{3}$, exist. Then $a=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=x_{1} x_{2} x_{3}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}\right)=27 \cdot\left(\frac{q}{3}+\frac{1}{3}+\frac{1}{3 q}\right)=9\left(q+1+\frac{1}{q}\right)=3 \cdot 14=42$. (In the penultimate transition, we used the equality $(*)$ ).
Comment. Naturally, $q, x_{1}, x_{2}, x_{3}$ can be calculated explicitly:
$$
q_{1,2}=\frac{11 \pm \sqrt{85}}{6}
$$
Choose $q$ with the “+” (if you choose with the “-”, then $x_{1}$ and $x_{3}$ will swap places, which will not affect the answer); then
$$
x_{1}=\frac{3 \cdot 6}{11+\sqrt{85}}=\frac{11-\sqrt{85}}{2}, x_{2}=3, x_{3}=\frac{11+\sqrt{85}}{2} .
$$
$a$ could have been calculated by substituting the obtained numbers into the expression $x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}$.
|
42
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. For what least $n$ do there exist $n$ numbers from the interval $(-1 ; 1)$ such that their sum is 0 and the sum of their squares is 36?
#
|
# Answer: 38.
Solution. First, let's provide an example of 38 numbers whose sum is 0 and the sum of their squares is 36. For instance, the numbers $x_{1}=x_{2}=\ldots=x_{19}=\sqrt{\frac{18}{19}}, x_{20}=x_{21}=\ldots=x_{38}=-\sqrt{\frac{18}{19}}$ will work.
Now, we will prove that fewer than 38 numbers will not suffice. Suppose the contrary. Then, among all the numbers, either the positive or the negative ones do not exceed 18. By multiplying all the numbers by -1 if necessary, we can assume that there are no more than 18 negative numbers.
Let $y_{1}, y_{2}, \ldots, y_{k}$ be all the negative numbers, and $y_{k+1}, \ldots, y_{n}$ be all the non-negative numbers. Then $y_{1}^{2}+y_{2}^{2}+\ldots+y_{k}^{2}<k \leqslant 18$, and
$$
y_{k+1}^{2}+y_{k+2}^{2}+\ldots+y_{n}^{2} \leqslant y_{k+1}+y_{k+2}+\ldots+y_{n}=-y_{1}-y_{2}-\ldots-y_{k}<k \leqslant 18
$$
Adding the obtained inequalities, we get, $36=y_{1}^{2}+y_{2}^{2}+\ldots+y_{n}^{2}<36$. Contradiction.
|
38
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what values of the parameter $a$ does the equation $x^{3}-15 x^{2}+a x-64=0$ have three distinct real roots that form a geometric progression?
|
Answer: only 60.
Solution. Let the parameter $a$ be suitable. Then the polynomial $x^{3}-15 x^{2}+a x-64=0$ has three distinct roots $x_{1}, x_{2}, x_{3}$. We use Vieta's theorem for a polynomial of the third degree:
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=15 \\
x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a \\
x_{1} x_{2} x_{3}=64
\end{array}\right.
$$
Since $x_{1}, x_{2}, x_{3}$ form a geometric progression (let's assume in this order), there exist $b$ and $q$ such that $x_{1}=b, x_{2}=b q, x_{3}=b q^{2}$. Then from the equality $x_{1} x_{2} x_{3}=64$, we have $b^{3} q^{3}=64$, from which $x_{2}=b q=4, x_{1}=4 / q, x_{3}=4 q$.
Then $4\left(\frac{1}{q}+1+q\right)=15(*)$, after transformations $4 q^{2}-11 q+4=0$. The discriminant of this expression is $D=11^{2}-4 \cdot 4 \cdot 4>0$, so such $q$, and with it $x_{1}, x_{2}, x_{3}$, will exist. Then
$a=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=x_{1} x_{2} x_{3}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}\right)=64 \cdot\left(\frac{q}{4}+\frac{1}{4}+\frac{1}{4 q}\right)=16\left(q+1+\frac{1}{q}\right)=4 \cdot 15=60$. (In the penultimate transition, we used the equality $(*)$ ).
Comment. Naturally, $q, x_{1}, x_{2}, x_{3}$ can be calculated explicitly:
$$
q_{1,2}=\frac{11 \pm \sqrt{57}}{8}
$$
Choose $q$ with “+” (if you choose with “-”, then $x_{1}$ and $x_{3}$ will swap places, which will not affect the answer); then
$$
x_{1}=\frac{4 \cdot 8}{11+\sqrt{57}}=\frac{11-\sqrt{57}}{2}, x_{2}=4, x_{3}=\frac{11+\sqrt{57}}{2} .
$$
$a$ could have been calculated by substituting the obtained numbers into the expression $x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}$.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. For what least $n$ do there exist $n$ numbers from the interval $(-1 ; 1)$ such that their sum is 0 and the sum of their squares is 40?
|
Answer: 42.
Solution. First, let's provide an example of 42 numbers whose sum is 0 and the sum of their squares is 40. For instance, the numbers $x_{1}=x_{2}=\ldots=x_{21}=\sqrt{\frac{20}{21}}, x_{22}=x_{23}=\ldots=x_{42}=-\sqrt{\frac{20}{21}}$ will work.
Now, we will prove that fewer than 42 numbers will not suffice. Suppose the contrary. Then, among all the numbers, either the positive or the negative ones do not exceed 20. By multiplying all the numbers by -1 if necessary, we can assume that there are no more than 20 negative numbers.
Let $y_{1}, y_{2}, \ldots, y_{k}$ be all the negative numbers, and $y_{k+1}, \ldots, y_{n}$ be all the non-negative numbers. Then $y_{1}^{2}+y_{2}^{2}+\ldots+y_{k}^{2}<k \leqslant 20$, and
$$
y_{k+1}^{2}+y_{k+2}^{2}+\ldots+y_{n}^{2} \leqslant y_{k+1}+y_{k+2}+\ldots+y_{n}=-y_{1}-y_{2}-\ldots-y_{k}<k \leqslant 20
$$
Adding the obtained inequalities, we get, $40=y_{1}^{2}+y_{2}^{2}+\ldots+y_{n}^{2}<40$. Contradiction.
|
42
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. For what values of the parameter $a$ does the equation $x^{3}+16 x^{2}+a x+64=0$ have three distinct real roots that form a geometric progression?
|
Answer: only 64.
Solution. Let the parameter $a$ be suitable. Then the polynomial $x^{3}+16 x^{2}+a x+64=0$ has three distinct roots $x_{1}, x_{2}, x_{3}$. We use Vieta's theorem for a cubic polynomial:
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=-16 \\
x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a \\
x_{1} x_{2} x_{3}=-64
\end{array}\right.
$$
Since $x_{1}, x_{2}, x_{3}$ form a geometric progression (let's assume in this order), there exist $b$ and $q$ such that $x_{1}=b, x_{2}=b q, x_{3}=b q^{2}$. Then from the equality $x_{1} x_{2} x_{3}=-64$, we have $b^{3} q^{3}=-64$, from which $x_{2}=b q=-4, x_{1}=-4 / q, x_{3}=-4 q$.
Then $-4\left(\frac{1}{q}+1+q\right)=-16(*)$, after transformations $q^{2}-3 q+1=0$. The discriminant of this expression is $D=3^{2}-4 \cdot 1 \cdot 1>0$, so such a $q$, and with it $x_{1}, x_{2}, x_{3}$, will exist. Then
$a=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=x_{1} x_{2} x_{3}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}\right)=-64 \cdot\left(-\frac{q}{4}-\frac{1}{4}-\frac{1}{4 q}\right)=16\left(q+1+\frac{1}{q}\right)=4 \cdot 16=64$.
(In the penultimate transition, we used the equality $\left({ }^{*}\right)$ ).
Comment. Naturally, $q, x_{1}, x_{2}, x_{3}$ can be calculated explicitly:
$$
q_{1,2}=\frac{3 \pm \sqrt{5}}{2}
$$
Choose $q$ with the “+” (if you choose with the “-”, then $x_{1}$ and $x_{3}$ will swap places, which will not affect the answer); then
$$
x_{1}=\frac{-4 \cdot 2}{3+\sqrt{5}}=-2(3-\sqrt{5}), x_{2}=-4, x_{3}=-2(3+\sqrt{5})
$$
$a$ could have been calculated by substituting the obtained numbers into the expression $x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10. The sum of the surface areas of the polyhedra into which a parallelepiped is divided by sections is equal to the sum of the surface area of the parallelepiped and the areas of the internal surfaces. The sum of the areas of the internal surfaces is equal to twice the sum of the areas of the sections.
Let's find the maximum possible area of a section passing through the diagonal $XY$ of an arbitrary parallelepiped with edges $a \leq b \leq c$. The section is a parallelogram $ZXTY$, whose vertices lie on opposite edges of the parallelepiped. The area of the parallelogram is the product of the length of the diagonal $XY$ and the distance from point $Z$ to $XY$.
Consider the projection of the parallelepiped onto a plane perpendicular to the diagonal $XY$. From the diagram, it is clear that the distance from point $Z$ to the broken line $ABC$, and thus to the diagonal $XY$, is greatest if
$Z$ coincides with one of the vertices $A, B$, or $C$.
This means that the section passes through one of the edges of the parallelepiped. Therefore, the section with the largest area is one of the diagonal sections. All these sections are rectangles. Let's find the largest of their areas:
$$
S_{1}=a \sqrt{b^{2}+c^{2}}, \quad S_{2}=b \sqrt{a^{2}+c^{2}}, \quad \text{and} \quad S_{3}=c \sqrt{b^{2}+a^{2}}
$$
From the condition $a \leq b \leq c$, it follows that
$a^{2} b^{2}+a^{2} c^{2} \leq c^{2} b^{2}+a^{2} c^{2}$, and $a^{2} b^{2}+c^{2} b^{2} \leq c^{2} b^{2}+a^{2} c^{2}$. Therefore, $S_{1} \leq S_{3}$ and $S_{2} \leq S_{3}$. This means that the section with the largest area passes through the largest edge. According to the condition, the largest length is the edge $AA_{1}$, so the sections $AA_{1}C_{1}C$ and $BB_{1}D_{1}D$ have the largest area:
$5 \sqrt{4^{2}+3^{2}}=25$. The sum of the surface areas of the polyhedra into which the parallelepiped is divided by these sections (see the diagram) is
$$
2\left(A A_{1} \cdot A B + A A_{1} \cdot A D + A B \cdot A D\right) + 4 \cdot 25 = 194
$$
|
Answer: 194.
[^0]: ${ }^{1}$ This statement is a particular case of Cauchy's inequality.
|
194
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. A group of adventurers is showing off their loot. It is known that exactly 13 adventurers have rubies; exactly 9 have emeralds; exactly 15 have sapphires; exactly 6 have diamonds. In addition, it is known that
- if an adventurer has sapphires, then they have either emeralds or diamonds (but not both at the same time);
- if an adventurer has emeralds, then they have either rubies or sapphires (but not both at the same time).
What is the minimum number of adventurers that can be in such a group?
|
Answer: 22.
Solution. Note that the number of adventurers who have sapphires is equal to the total number of adventurers who have emeralds or diamonds. Then, from the first condition, it follows that 9 adventurers have sapphires and emeralds, and 6 have sapphires and diamonds. That is, every adventurer who has emeralds must also have sapphires. Then, from the second condition, there cannot be an adventurer who has both emeralds and rubies. Therefore, there must be at least $13+9=22$ adventurers.
This number of adventurers is indeed possible: let's say we have 9 adventurers who have sapphires and emeralds, 6 adventurers who have sapphires, diamonds, and rubies, and 7 adventurers who have only rubies. One can verify that this example meets all the conditions.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. In triangle $A B C$, side $A C=42$. The bisector $C L$ is divided by the point of intersection of the bisectors of the triangle in the ratio $2: 1$, counting from the vertex. Find the length of side $A B$, if the radius of the circle inscribed in triangle $A B C$ is 14.
|
Answer: 56.
Answer: Let $I$ be the center of the inscribed circle in triangle $ABC$ (i.e., the point of intersection of the angle bisectors). Noting that $AI$ is the angle bisector in triangle $ALC$, by the angle bisector theorem, we have: $AC: AL = CI: IL = 2: 1$, from which $AL = AC / 2 = 21$.
Next, $AC \cdot AL \cdot \sin \angle A = 2 S_{\triangle ALC} = 2 S_{\triangle AIC} + 2 S_{\triangle AIL} = AC \cdot r + AL \cdot r = (AC + AL) \cdot r$, where $r$ is the radius of the inscribed circle in triangle $ABC$. Thus, $42 \cdot 21 \cdot \sin \angle A = (42 + 21) \cdot 14$, i.e., $\sin \angle A = 1, \angle A = 90^{\circ}$.
By the angle bisector theorem for $BI$ in triangle $CLB$, we have $BC: BL = CI: IL = 2: 1$. Letting $BL = x$, we have $BC = 2x$. By the Pythagorean theorem: $AC^2 + AB^2 = BC^2$, i.e., $42^2 + (21 + x)^2 = (2x)^2$, from which $x = 35$, and $AB = x + 21 = 56$.
|
56
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. The function $F$ is defined on the set of triples of integers and takes real values. It is known that for any four integers $a, b, c$ and $n$ the equalities $F(n a, n b, n c)=n \cdot F(a, b, c)$, $F(a+n, b+n, c+n)=F(a, b, c)+n$, $F(a, b, c)=F(c, b, a)$ hold. Find $F(58,59,60)$.
|
Answer: 59.
Solution. Note that $F(-1,0,1)=F(1,0,-1)=(-1) \cdot F(-1,0,1)$, from which $F(-1,0,1)=0$. Then $F(58,59,60)=F(-1,0,1)+59=59$.
Comment. The function $F$ cannot be uniquely determined. For example, the functions $F(a, b, c)=(a+b+c) / 3$, $F(a, b, c)=b$, and $F(a, b, c)=$ median of the numbers $\{a, b, c\}$ all fit.
|
59
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. A group of adventurers is showing off their loot. It is known that exactly 5 adventurers have rubies; exactly 11 have emeralds; exactly 10 have sapphires; exactly 6 have diamonds. In addition, it is known that
- if an adventurer has diamonds, then they have either emeralds or sapphires (but not both at the same time);
- if an adventurer has emeralds, then they have either rubies or diamonds (but not both at the same time).
What is the minimum number of adventurers that can be in such a group?
|
Answer: 16.
Solution. Note that the number of adventurers who have emeralds is equal to the total number of adventurers who have rubies or diamonds. Then, from the second condition, it follows that 5 adventurers have rubies and emeralds, and 6 have emeralds and diamonds. That is, every adventurer who has diamonds must also have emeralds. Then, from the first condition, there cannot be an adventurer who has both sapphires and diamonds. Therefore, there are at least $10+6=16$ adventurers.
Indeed, there can be this many adventurers: let's say we have 6 adventurers who have emeralds and diamonds, 5 adventurers who have rubies, emeralds, and sapphires, and 5 adventurers who have only sapphires. One can verify that this example meets all the conditions.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. A landscaping team worked on a large and a small football field, with the area of the large field being twice the area of the small field. In the part of the team that worked on the large field, there were 6 more workers than in the part that worked on the small field. When the landscaping of the large field was completed, the part of the team that was on the small field was still working. What is the maximum number of workers that could have been in the team
|
Answer: 16.
Solution. Let the number of workers on the smaller field be $n$, then the number of workers on the larger field is $n+6$, and the total number of people in the team is $2n+6$. The problem "implicitly assumes" that the productivity of each worker is the same, denoted as $a$. Therefore, the productivities of each part of the team are $an$ and $a(n+6)$. If the area of the smaller field is $S$, then the area of the larger field is $2S$. The time spent on completing the entire work by each team is $\frac{S}{an}$ and $\frac{2S}{a(n+6)}$, respectively. According to the problem, $\frac{S}{an} > \frac{2S}{a(n+6)}$. Due to the positivity of all variables, this inequality is equivalent to the inequality $n+6 > 2n$, or $n < 6$. Therefore, $n \leqslant 5$, and $2n+6 \leqslant 16$. The equality situation is clearly possible: just take any positive $S$ and $a$.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. The function $f$ is defined on the set of triples of integers and takes real values. It is known that for any four integers $a, b, c$ and $n$ the equalities $f(n a, n b, n c)=n \cdot f(a, b, c)$, $f(a+n, b+n, c+n)=f(a, b, c)+n$, $f(a, b, c)=f(c, b, a)$ hold. Find $f(24,25,26)$.
|
Answer: 25.
Solution. Note that $f(-1,0,1)=f(1,0,-1)=(-1) \cdot f(-1,0,1)$, from which $f(-1,0,1)=0$. Then $f(24,25,26)=f(-1,0,1)+25=25$.
Comment. The function $f$ cannot be uniquely determined. For example, the functions $f(a, b, c)=(a+b+c) / 3$, $f(a, b, c)=b$, and $f(a, b, c)=$ median of the numbers $\{a, b, c\}$ all fit.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. A group of adventurers is showing off their loot. It is known that exactly 4 adventurers have rubies; exactly 10 have emeralds; exactly 6 have sapphires; exactly 14 have diamonds. Moreover, it is known that
- if an adventurer has rubies, then they have either emeralds or diamonds (but not both at the same time)
- if an adventurer has emeralds, then they have either rubies or sapphires (but not both at the same time).
What is the minimum number of adventurers that can be in such a group?
|
Answer: 18.
Solution. Note that the number of adventurers who have emeralds is equal to the total number of adventurers who have rubies or sapphires. Then, from the second condition, it follows that 4 adventurers have rubies and emeralds, and 6 have emeralds and sapphires. That is, every adventurer who has rubies must also have emeralds. Then, from the first condition, there cannot be an adventurer who has both rubies and diamonds. Therefore, there must be at least $4+14=18$ adventurers.
Indeed, there can be this many adventurers: suppose we have 4 adventurers who have emeralds and rubies, 6 adventurers who have diamonds, emeralds, and sapphires, and 10 adventurers who have only sapphires. One can verify that this example meets all the conditions.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. The function $G$ is defined on the set of triples of integers and takes real values. It is known that for any four integers $a, b, c$ and $n$, the equalities $G(n a, n b, n c)=n \cdot G(a, b, c)$, $G(a+n, b+n, c+n)=G(a, b, c)+n$, $G(a, b, c)=G(c, b, a)$ hold. Find $G(89,90,91)$.
|
Answer: 90.
Solution. Note that $G(-1,0,1)=G(1,0,-1)=(-1) \cdot G(-1,0,1)$, from which $G(-1,0,1)=0$. Then $G(89,90,91)=G(-1,0,1)+90=90$.
Comment. The function $G$ cannot be uniquely determined. For example, the functions $G(a, b, c)=(a+b+c) / 3, G(a, b, c)=b$ and $G(a, b, c)=$ median of the numbers $\{a, b, c\}$ are suitable.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. A group of adventurers is showing off their loot. It is known that exactly 9 adventurers have rubies; exactly 8 have emeralds; exactly 2 have sapphires; exactly 11 have diamonds. Moreover, it is known that
- if an adventurer has diamonds, then they have either rubies or sapphires (but not both at the same time);
- if an adventurer has rubies, then they have either emeralds or diamonds (but not both at the same time).
What is the smallest number of adventurers that can be in such a group?
|
Answer: 17.
Solution. Note that the number of adventurers who have diamonds is equal to the total number of adventurers who have rubies or sapphires. Then, from the first condition, it follows that 9 adventurers have rubies and diamonds, and 2 have sapphires and diamonds. That is, every adventurer who has rubies must also have diamonds. Then, from the second condition, there cannot be an adventurer who has both rubies and emeralds. Therefore, there must be at least $9+8=17$ adventurers.
Indeed, there can be this many adventurers: let's say we have 9 adventurers who have rubies and diamonds, 2 adventurers who have emeralds, sapphires, and diamonds, and 6 adventurers who have only emeralds. One can verify that this example meets all the conditions.
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A team of lumberjacks was cutting trees on a large and a small plot, with the area of the small plot being 3 times less than that of the large plot. In the part of the team that worked on the large plot, there were 8 more lumberjacks than in the part that worked on the small plot. When the tree harvesting on the large plot was completed, the part of the team that was on the small plot was still working. What is the maximum number of lumberjacks that could have been in the team?
|
Answer: 14.
Solution. Let the number of workers on the smaller plot be denoted as $n$, then the number of workers on the larger plot is $n+8$, and the total number of workers in the team is $2n+8$. The problem "implicitly assumes" that the productivity of each worker is the same, denoted as $a$. Therefore, the productivity of each part of the team is $an$ and $a(n+8)$. If the area of the smaller plot is $S$, then the area of the larger plot is $3S$. The time spent on completing the entire work by each part of the team is $\frac{S}{an}$ and $\frac{3S}{a(n+8)}$, respectively. According to the problem, $\frac{S}{an} > \frac{3S}{a(n+8)}$. Given the positivity of all variables, this inequality is equivalent to $n+8 > 3n$, or $n < 4$. Therefore, $n \leqslant 3$, and $2n+8 \leqslant 14$. The equality situation is clearly possible: just take any positive $S$ and $a$.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. In triangle $A B C$, side $B C=28$. The bisector $B L$ is divided by the point of intersection of the bisectors of the triangle in the ratio $4: 3$, counting from the vertex. Find the radius of the circumscribed circle around triangle $A B C$, if the radius of the inscribed circle in it is 12.
|
Answer: 50.
Solution. Let $I$ be the center of the inscribed circle in triangle $ABC$ (i.e., the point of intersection of the angle bisectors). Noting that $CI$ is the angle bisector in triangle $BLC$, by the angle bisector theorem, we have: $BC: CL = BI: IL = 4: 3$, from which $CL = 3BC / 4 = 21$.
Next, $BC \cdot CL \cdot \sin \angle C = 2 S_{\triangle BCL} = 2 S_{\triangle BIC} + 2 S_{\triangle CIL} = BC \cdot r + CL \cdot r = (BC + CL) \cdot r$, where $r$ is the radius of the inscribed circle in triangle $ABC$. Thus, $28 \cdot 21 \cdot \sin \angle C = (28 + 21) \cdot 12$, i.e., $\sin \angle C = 1, \angle C = 90^\circ$.
By the angle bisector theorem for $AI$ in triangle $ALB$, we have $BA: AL = BI: IL = 4: 3$. Letting $AL = 3x$, we have $AB = 4x$. By the Pythagorean theorem: $AC^2 + BC^2 = AB^2$, i.e., $28^2 + (21 + 3x)^2 = (4x)^2$, from which $x = 25$, and $R = AB / 2 = 4 \cdot 25 / 2 = 50$.
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. The function $g$ is defined on the set of triples of integers and takes real values. It is known that for any four integers $a, b, c$ and $n$ the equalities $g(n a, n b, n c)=$ $n \cdot g(a, b, c), g(a+n, b+n, c+n)=g(a, b, c)+n, g(a, b, c)=g(c, b, a)$ hold. Find $g(14,15,16)$.
|
Answer: 15.
Solution. Note that $g(-1,0,1)=g(1,0,-1)=(-1) \cdot g(-1,0,1)$, from which $g(-1,0,1)=0$. Then $g(14,15,16)=g(-1,0,1)+15=15$.
Comment. The function $g$ cannot be uniquely determined. For example, the functions $g(a, b, c)=(a+b+c) / 3$, $g(a, b, c)=b$, and $g(a, b, c)=$ median of the numbers $\{a, b, c\}$ all fit.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. In the $1^{\text{st}}$ grade class, each child was asked to write down two numbers: the number of their classmates and the number of their female classmates (in that exact order; the child does not count themselves). Each child wrote one number correctly, and the other number was off by exactly 2. Among the answers received were: $(13,11),(17,11),(14,14)$. How many boys and how many girls are in the class?
|
Answer: 15 boys and 12 girls.
Solution. First solution. Let's denote the children who gave the answers (13,11), (17,11), (14,14) as A, B, and C, respectively. Note that if there are $m$ boys in the class, then the first number in the answers of the girls has the same parity as $m$, and in the answers of the boys - the opposite. Therefore, children A and B are of the same gender, and C is of the other gender.
The first numbers in the answers of A and B differ by 4, so they are both incorrect. Thus, the number of classmates for A and B is 15, and the number of female classmates is 11.
If A and B are boys, then there are 16 boys and 11 girls in the class. In this case, girl C would have 16 classmates and 10 female classmates, and her answer (14,14) would contradict the condition. Therefore, A and B are girls, and there are 15 boys and 12 girls in the class.
Second solution. Suppose a child wrote the numbers $(m, d)$. If he wrote both numbers correctly, he would have written one of the four options: $(m-2, d),(m+2, d),(m, d-2),(m, d+2)$. Then, if this child is a boy, there are four possible options for the number of boys and girls in the class: $(m-1, d),(m+3, d),(m+1, d-2)$, and $(m+1, d+2)$. Similarly, if this child is a girl, the possible options in this case are: $(m-2, d+1),(m+2, d+1),(m, d-1),(m, d+3)$.
Thus, each answer gives us eight possible options for how many boys and girls could be in the class, one of which must be correct:
for $(13,11)$ these are $(12,11),(16,11),(14,9),(14,13),(11,12),(15,12),(13,10),(13,14)$;
for $(17,11)$ these are $(16,11),(20,11),(18,9),(18,13),(15,12),(19,12),(17,10),(17,14)$;
for $(14,14)$ these are $(13,14),(17,14),(15,12),(15,16),(12,15),(16,15),(14,13),(14,17)$.
It remains to note that only the option $(15,12)$ appears in all three rows.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In triangle $A B C$ with the ratio of sides $A B: A C=5: 4$, the bisector of angle $B A C$ intersects side $B C$ at point $L$. Find the length of segment $A L$, if the length of the vector $4 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C}$ is 2016.
|
Answer: 224.
Solution. Note that by the property of the angle bisector of a triangle $B L: L C=B A: A C=5: 4$, from which $\overrightarrow{B L}=5 / 9 \cdot \overrightarrow{B C}$. Now
$$
\overrightarrow{A L}=\overrightarrow{A B}+\overrightarrow{B L}=\overrightarrow{A B}+\frac{5}{9} \cdot \overrightarrow{B C}=\overrightarrow{A B}+\frac{5}{9}(\overrightarrow{A C}-\overrightarrow{A B})=\frac{4}{9} \cdot \overrightarrow{A B}+\frac{5}{9} \cdot \overrightarrow{A C}=\frac{1}{9}(4 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C})
$$
Therefore, $|A L|=1 / 9 \cdot|4 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C}|=1 / 9 \cdot 2016=224$.
|
224
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 9. The Federation of Wrestling has assigned each participant in the competition a qualification number. It is known that in matches between wrestlers whose qualification numbers differ by more than 2, the wrestler with the lower number always wins. The tournament for 256 wrestlers is held on an Olympic system: at the beginning of each day, the wrestlers are paired, the loser is eliminated from the competition (there are no draws). What is the highest qualification number that the winner can have?
|
Answer: 16
Solution. Note that a wrestler with number $k$ can only lose to a wrestler with number $k+1$ or $k+2$, so after each round, the smallest number cannot increase by more than 2 numbers. In a tournament with 256 participants, there are 8 rounds, so the number of the tournament winner does not exceed $1+2 \cdot 8=17$.
Suppose the wrestler with number 17 can win. Then in the first round, the wrestlers with numbers 1 and 2 must be eliminated. This is only possible if the wrestler with number 1 loses to the wrestler with number 3, and the wrestler with number 2 loses to the wrestler with number 4. Thus, after the first round, the wrestlers with numbers 3 and 4 will remain. Similarly, after the second round, the wrestlers with numbers 5 and 6 will remain, after the third round - 7 and $8, \ldots$, after the seventh round - 15 and 16. This means that in the final, decisive match, the wrestlers with numbers 15 and 16 will meet. Contradiction with the assumption that the wrestler with number 17 can win.
We will show that the wrestler with number 16 can win. Let's call the wrestlers with numbers greater than 16 weak. Suppose in the round with number $k \leqslant 7$ the wrestler with number $2 k-1$ loses to the wrestler with number $2 k+1$, the wrestler with number $2 k$ loses to the wrestler with number $2 k+2$, the wrestlers with numbers $2 k+3, \ldots, 16$ win against some weak wrestlers, and the remaining weak wrestlers play among themselves. Then after 7 rounds, the wrestlers with numbers 15 and 16 will remain, and in the final match, the wrestler with number 16 will win.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. In $1^{st}$ grade, each child was asked to write down two numbers: the number of their classmates and the number of their female classmates (in that exact order; the child does not count themselves). Each child wrote one number correctly, and the other number was off by exactly 4. Among the answers received were: $(15,18),(15,10),(12,13)$. How many boys and how many girls are in the class?
|
Answer: 16 boys and 14 girls.
Solution. First solution. Let's denote the children who gave the answers (15,18), (15,10), (12,13) as A, B, and C, respectively. Note that if there are $m$ boys in the class, then the first number in the answers of girls has the same parity as $m$, while in the answers of boys, it has the opposite parity. Therefore, children A and B are of the same gender, and C is of the opposite gender.
The second numbers in the answers of A and B differ by 8, which means they are both incorrect. Thus, the number of classmates for A and B is 15, and the number of female classmates is 14.
If A and B are girls, then there are 15 boys and 15 girls in the class. In this case, boy C would have 14 classmates and 15 female classmates, and his answer (12,13) would contradict the condition. Therefore, A and B are boys, and there are 16 boys and 14 girls in the class.
Second solution. Suppose a child wrote the numbers $(m, d)$. If he wrote both numbers correctly, he would have written one of the four options: $(m-4, d), (m+4, d), (m, d-4), (m, d+4)$. Then, if this child is a boy, there are four possible combinations of the number of boys and girls in the class: $(m-3, d), (m+5, d), (m+1, d-4)$, and $(m+1, d+4)$. Similarly, if this child is a girl, the possible combinations in this case are: $(m-4, d+1), (m+4, d+1), (m, d-3), (m, d+5)$.
Thus, each answer gives us eight possible combinations of the number of boys and girls in the class, one of which must be correct:
for $(15,18)$, these are $(12,18), (20,18), (16,14), (16,22), (11,19), (19,19), (15,15), (15,23)$;
for $(15,10)$, these are $(12,10), (20,12), (16,6), (16,14), (11,11), (19,11), (15,7), (15,15)$;
for (12,13), these are (9,13), (17,15), (13,9), (13,17), (8,14), (16,14), (12,10), (12,18).
It remains to note that only the option $(16,14)$ appears in all three rows.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In triangle $A B C$ with the ratio of sides $A B: A C=4: 3$, the bisector of angle $B A C$ intersects side $B C$ at point $L$. Find the length of segment $A L$, if the length of the vector $3 \cdot \overrightarrow{A B}+4 \cdot \overrightarrow{A C}$ is 2016.
|
Answer: 288.
Solution. Note that by the property of the angle bisector of a triangle $B L: L C=B A: A C=4: 3$, from which $\overrightarrow{B L}=4 / 7 \cdot \overrightarrow{B C}$. Now
$$
\overrightarrow{A L}=\overrightarrow{A B}+\overrightarrow{B L}=\overrightarrow{A B}+\frac{4}{7} \cdot \overrightarrow{B C}=\overrightarrow{A B}+\frac{4}{7}(\overrightarrow{A C}-\overrightarrow{A B})=\frac{3}{7} \cdot \overrightarrow{A B}+\frac{4}{7} \cdot \overrightarrow{A C}=\frac{1}{7}(3 \cdot \overrightarrow{A B}+4 \cdot \overrightarrow{A C})
$$
Therefore, $|A L|=1 / 7 \cdot|3 \cdot \overrightarrow{A B}+4 \cdot \overrightarrow{A C}|=1 / 7 \cdot 2016=288$.
|
288
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 9. The Federation of Wrestling has assigned each participant in the competition a qualification number. It is known that in matches between wrestlers whose qualification numbers differ by more than 2, the wrestler with the lower number always wins. The tournament for 512 wrestlers is held on an Olympic system: at the beginning of each day, the wrestlers are divided into pairs, the loser is eliminated from the competition (there are no draws). What is the highest qualification number that the winner can have?
|
Answer: 18.
Solution. Note that a wrestler with number $k$ can only lose to a wrestler with number $k+1$ or $k+2$, so after each round, the smallest number cannot increase by more than 2 numbers. In a tournament with 512 participants, there are 9 rounds, so the number of the tournament winner does not exceed $1+2 \cdot 9=19$.
Suppose the wrestler with number 19 can win. Then in the first round, the wrestlers with numbers 1 and 2 must be eliminated. This is only possible if the wrestler with number 1 loses to the wrestler with number 3, and the wrestler with number 2 loses to the wrestler with number 4. Thus, after the first round, the wrestlers with numbers 3 and 4 will remain. Similarly, after the second round, the wrestlers with numbers 5 and 6 will remain, after the third round - 7 and 8, ..., after the eighth round - 17 and 18. This means that in the final, decisive battle, the wrestlers with numbers 17 and 18 will meet. Contradiction with the assumption that the wrestler with number 19 can win.
We will show that the wrestler with number 18 can win. Let's call the wrestlers with numbers greater than 18 weak. Suppose in the round with number $k \leqslant 8$ the wrestler with number $2 k-1$ loses to the wrestler with number $2 k+1$, the wrestler with number $2 k$ loses to the wrestler with number $2 k+2$, the wrestlers with numbers $2 k+3, \ldots, 18$ win against some weak wrestlers, and the remaining weak wrestlers play among themselves. Then after 8 rounds, the wrestlers with numbers 17 and 18 will remain, and in the final battle, the wrestler with number 18 will win.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. In $1^{\text {st }}$ grade, each child was asked to write down two numbers: the number of their classmates and the number of their female classmates (in that exact order; the child does not count themselves). Each child wrote one number correctly, and the other number was off by exactly 2. Among the answers received were: $(12,18),(15,15),(11,15)$. How many boys and how many girls are in the class?
|
Answer: 13 boys and 16 girls.
Solution. First solution. Let's denote the children who gave the answers (12,18), (15,15), (11,15) as A, B, and C, respectively. Note that if there are $m$ boys in the class, then the first number in the girls' answers has the same parity as $m$, and in the boys' answers - the opposite. Therefore, children B and C are of the same gender, and A is of the other gender.
The first numbers in the answers of B and C differ by 4, so they are both incorrect. Thus, the number of classmates for B and C is 13, and the number of female classmates is 15.
If B and C are boys, then there are 14 boys and 15 girls in the class. In this case, girl A would have 14 classmates and 14 female classmates, and her answer (12,18) would contradict the condition. Therefore, B and C are girls, and there are 13 boys and 16 girls in the class.
Second solution. Suppose a child wrote the numbers $(m, d)$. If he wrote both numbers correctly, then he would have written one of the four options: $(m-2, d),(m+2, d),(m, d-2),(m, d+2)$. Then, if this child is a boy, there are four possible options for the number of boys and girls in the class: $(m-1, d),(m+3, d),(m+1, d-2)$, and $(m+1, d+2)$. Similarly, if this child is a girl, the possible options in this case are: $(m-2, d+1),(m+2, d+1),(m, d-1),(m, d+3)$.
Thus, each answer gives us eight options for how many boys and girls could be in the class, one of which must be correct:
for (12,18) these are (11,18),(15,18),(13,16),(13,20),(10,19),(14,19),(12,17),(12,21);
for (15,15) these are (14,15),(18,15),(16,13),(16,17),(13,16),(17,16),(15,14),(15,18);
for (11,15) these are (10,15),(14,15),(12,13),(12,17),(9,16),(13,16),(11,14),(11,18).
It remains to note that only the option (13,16) appears in all three rows.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In triangle $A B C$ with the ratio of sides $A B: A C=5: 2$, the bisector of angle $B A C$ intersects side $B C$ at point $L$. Find the length of segment $A L$, if the length of the vector $2 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C}$ is 2016.
|
Answer: 288.
Solution. Note that by the property of the angle bisector of a triangle $B L: L C=B A: A C=5: 2$, from which $\overrightarrow{B L}=5 / 7 \cdot \overrightarrow{B C}$. Now,
$$
\overrightarrow{A L}=\overrightarrow{A B}+\overrightarrow{B L}=\overrightarrow{A B}+\frac{4}{7} \cdot \overrightarrow{B C}=\overrightarrow{A B}+\frac{5}{7}(\overrightarrow{A C}-\overrightarrow{A B})=\frac{2}{7} \cdot \overrightarrow{A B}+\frac{5}{7} \cdot \overrightarrow{A C}=\frac{1}{7}(2 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C})
$$
Therefore, $|A L|=1 / 7 \cdot|2 \cdot \overrightarrow{A B}+5 \cdot \overrightarrow{A C}|=1 / 7 \cdot 2016=288$.
|
288
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. In the $1^{\text{st}}$ grade, each child was asked to write down two numbers: the number of their classmates and the number of their female classmates (in that exact order; the child does not count themselves). Each child wrote one number correctly, and the other number was off by exactly 4. Among the answers received were: $(10,14),(13,11),(13,19)$. How many boys and how many girls are in the class?
|
Answer: 14 boys and 15 girls.
Solution. First solution. Let's denote the children who gave the answers $(10,14),(13,11),(13,19)$ as A, B, and C, respectively. Note that if there are $m$ boys in the class, then the first number in the girls' answers has the same parity as $m$, and in the boys' answers - the opposite. Therefore, children B and C are of the same gender, and A is of the other gender.
The second numbers in the answers of B and C differ by 8, so they are both incorrect. Thus, the number of classmates for B and C is 13, and the number of female classmates is 15.
If B and C are girls, then there are 13 boys and 16 girls in the class. In this case, boy A would then have 12 classmates and 16 female classmates, and his answer $(10,14)$ would contradict the condition. Therefore, B and C are boys, and there are 14 boys and 15 girls in the class.
Second solution. Suppose a child wrote the numbers $(m, d)$. If he wrote both numbers correctly, he would have written one of the four options: $(m-4, d),(m+4, d),(m, d-4),(m, d+4)$. Then, if this child is a boy, there are four possible combinations of the number of boys and girls in the class: $(m-3, d),(m+5, d),(m+1, d-4)$, and $(m+1, d+4)$. Similarly, if this child is a girl, the possible combinations in this case are: $(m-4, d+1),(m+4, d+1),(m, d-3),(m, d+5)$.
Thus, each answer gives us eight possible combinations of the number of boys and girls in the class, one of which must be correct:
for $(10,14)$ these are $(7,14),(15,14),(11,10),(11,18),(6,15),(14,15),(10,11),(10,19)$;
for $(13,11)$ these are $(10,11),(18,11),(14,7),(14,15),(9,12),(17,12),(13,8),(13,16)$;
for $(13,19)$ these are $(10,19),(18,19),(14,15),(14,23),(9,20),(17,20),(13,16),(13,24)$.
It remains to note that only the variant $(14,15)$ appears in all three rows.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In triangle $A B C$ with the ratio of sides $A B: A C=7: 2$, the bisector of angle $B A C$ intersects side $B C$ at point $L$. Find the length of segment $A L$, if the length of the vector $2 \cdot \overrightarrow{A B}+7 \cdot \overrightarrow{A C}$ is 2016.
|
Answer: 224.
Solution. Note that by the property of the angle bisector of a triangle $B L: L C=B A: A C=7: 2$, from which $\overrightarrow{B L}=7 / 9 \cdot \overrightarrow{B C}$. Now,
$$
\overrightarrow{A L}=\overrightarrow{A B}+\overrightarrow{B L}=\overrightarrow{A B}+\frac{7}{9} \cdot \overrightarrow{B C}=\overrightarrow{A B}+\frac{7}{9}(\overrightarrow{A C}-\overrightarrow{A B})=\frac{2}{9} \cdot \overrightarrow{A B}+\frac{7}{9} \cdot \overrightarrow{A C}=\frac{1}{9}(2 \cdot \overrightarrow{A B}+7 \cdot \overrightarrow{A C})
$$
Therefore, $|A L|=1 / 9 \cdot|2 \cdot \overrightarrow{A B}+7 \cdot \overrightarrow{A C}|=1 / 9 \cdot 2016=224$.
|
224
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Egor borrowed 28 rubles from Nikita, and then returned them in four payments. It turned out that Egor always returned a whole number of rubles, and the amount of each payment increased and was divisible by the previous one. What was the last amount Egor paid?
|
Answer: 18 rubles
Solution:
1) If Egor paid $a$ rubles the first time, then the second time - not less than $2a$, the third - not less than $4a$, the fourth - not less than $8a$, and in total - not less than $15a$. Since $15a \leq 28$, we get that $a=1$.
2) The second time he paid 2 or 3 rubles (because if 4, then he paid at least $1+4+8+16=29>28$).
2.1) If he paid 2 rubles, then he had 25 rubles left to pay, and in this case, all subsequent payments would be even. This case is impossible.
2.2) Therefore, he paid 3 rubles, and for the last two times, he had 24 rubles left to pay. Let's say he paid $a$ times more the third time than the second, and $b$ times more the fourth time than the third. Then $3a + 3ab = 24$, which means $a + ab = a(b+1) = 8$. It follows that $a$ and $b+1$ are powers of two, and $b>1$, which is only possible with $a=2$ and $b=3$. Hence the answer.
## Criteria:
Only the answer $0-0$ points.
Only the answer with verification (all 4 sums are written out, showing that all conditions are met) - 1 point, it does not add up with anything.
Each of the points 1), 2), 2.1) is worth one point, these points are added up. A generally correct solution, but 2.2) is proven by incomplete enumeration - no more than 5 points.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. On a circular route, two buses operate with the same speed and a movement interval of 21 minutes. What will be the movement interval if 3 buses operate on this route at the same constant speed?
|
Answer: 14.
Solution: Since the interval of movement with two buses on the route is 21 minutes, the length of the route in "minutes" is 42 minutes. Therefore, the interval of movement with three buses on the route is $42: 3=14$ minutes.
Criteria: only answer, answer with verification - 3 points.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Natasha and Inna bought the same box of tea bags. It is known that one tea bag is enough for two or three cups of tea. Natasha's box was enough for only 41 cups of tea, while Inna's was enough for 58 cups. How many tea bags were in the box?
|
Answer: 20.
Solution: Let there be $n$ tea bags in the box. Then the number of brewings can vary from $2n$ to $3n$. Therefore, 58 is not greater than $3n$, which means $19<n$. Additionally, 41 is not less than $2n$, so $n<21$. Since the number of tea bags must be a natural number that is less than 21 but greater than 19, there are exactly 20 tea bags in the box.
Criteria: answer only - 0 points, answer with verification - 1 point. Correct system of inequalities without conclusions - 2 points, correct system of inequalities and correct answer - 4 points. Proof of one of the estimates for the number of packets in the pack (that there are not fewer than 20 or not more than 20) - 3 points regardless of whether the correct answer is given. These points DO NOT add up.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. On a line, one hundred points are marked: green, blue, and red. It is known that between any two red points there is a blue one, and between any two blue points there is a green one. In addition, there are no fewer red points than blue ones, and no fewer blue points than green ones. How many points are painted blue?
|
Answer: 33.
Solution: Let the number of red points be $n$, then the number of blue points is not less than $n-1$ (the number of intervals between "adjacent" red points), and since by condition the number of red points is not less than the number of blue points, the number of blue points is either $n$ or $n-1$. Similarly, if the number of blue points is $m$, then the number of green points is either $m$ or $m-1$. Thus, there are 4 possible cases.
| red | blue | green | total |
| :--: | :--: | :--: | :--: |
| $n$ | $n$ | $n$ | $3n$ |
| $n$ | $n$ | $n-1$ | $3n-1$ |
| $n$ | $n-1$ | $n-1$ | $3n-2$ |
| $n$ | $n-1$ | $n-2$ | $3n-3$ |
In each case, it is easy to find the total number of points (see table), which by condition is 100. Thus, we get 4 equations, only one of which has an integer solution $100=3n-2$. From this, the number of red points is 34, blue - 33, and green - 33.
Criteria: only answer, answer with verification - 0 points. Obtaining the estimate that the number of blue points is not less than the number of red points minus 1, and the number of green points is not less than the number of blue points minus 1 - 3 points (for both estimates together, not for each).
## Solutions to the tasks of the first stage of the All-Siberian Open Olympiad for schoolchildren in mathematics 2014-15, November 9, 2014
## 8th grade
Each task is worth 7 points.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. On a cubic planet, there live cubic mice, and they live only on the faces of the cube, not on the edges or vertices. It is known that different numbers of mice live on different faces, and the number on any two adjacent faces differs by at least 2. What is the minimum number of cubic mice that can live on this planet, given that there is at least one mouse on each face?
|
Solution: We will prove that no three consecutive numbers can be the number of mice on the faces. Indeed, if there were $x, x+1$, and $x+2$ mice on some three faces, then $x$ and $x+1$ would have to be on opposite faces. But then $x+2$ mice could not be anywhere.
Consider the first 8 natural numbers. Among the first three, there is at least one missing, and among the next three, there is at least one missing. Therefore, the minimum sum is $1+2+4+5+7+8=27$. It is possible to distribute 27 mice. For this, we will divide all the faces into pairs of opposite faces. On the first pair, there will be 1 and 2 mice, on the second pair - 4 and 5, on the third pair - 7 and 8. Thus, quantities differing by 1 are on opposite faces, and on adjacent faces, the difference is at least 2.
Criteria: Only the answer - 1 point.
Only an example (with or without justification) - 2 points.
Only the estimate - 5 points
Proved that no three consecutive numbers can be the number of mice on the faces - 2 points.
|
27
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Find the number of different ways to arrange all natural numbers from 1 to 9 inclusive in the cells of a 3 by 3 table, one number per cell, such that the sums of the numbers in each row and each column are equal. The table cannot be rotated or reflected.
|
Answer: 72 ways
Solution. Among the numbers from 1 to 9, there are 5 odd numbers. Since the sums in all rows and columns are $\frac{1}{3}(1+2+\ldots+9)=15$ - which are odd, there must be an odd number of odd numbers in each row and each column. This is only possible if one row contains three odd numbers, and the other rows contain one each, and one column contains three odd numbers, and the other columns contain one each. Therefore, all odd numbers must be in the union of a certain row and a certain column. At the intersection of these row and column, the number $15+15-(1+3+5+7+9)=5$ is written. Moreover, 7 and 9 cannot be in the same row or column. Therefore, we can write the number 5 in one of the nine cells, then write the number 9 in one of the four cells of the same row or column as 5, and then write the number 7 in two cells of the same row or column, not adjacent to 9. This gives us 9.4$\cdot$2=72 ways. Then we verify that at the intersection of the column and row containing 7 and 9, only 2 can be placed: 6 and 8 do not fit the sum, and 4 would give another 4 with 7. After this, it is clear that the remaining even numbers can be placed in the remaining cells of the table, and there is only one way to do this.
Grading Criteria. Noted that all odd numbers are in the union of a certain row and a certain column: 2 points.
Proved that the number 5 is written at the intersection of these row and column: 1 point.
Noted that 7 and 9 cannot be in the same row or column: 1 point.
Arrangements of the remaining odd digits in 72 ways: 2 points.
Lack of precise justification that the sums in rows and columns are 15: deduct 1 point. Arrangements differing by rotation or reflection are considered the same: deduct 2 points.
Loss of part of the solutions: deduct 2 points or more.
All required arrangements are constructed, but it is not proved that there are no others: no more than 3 points.
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Provide an example of a natural number that is a multiple of 2020, such that the sum of its digits is also a multiple of 2020.
|
Solution: For example, the number 20202020...2020, where the fragment 2020 repeats 505 times, fits. Such a number is obviously divisible by 2020, and the sum of its digits is $505 \times 4=2020$.
Criteria: Any correct answer with or without verification - 7 points.
Correctly conceived example, but with a calculation error (for example, 2020 repeats 500 times) - 3 points.
|
2020
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Vera Aleksandrovna urgently needed to cut out three 20-sided polygons (not necessarily identical) from one rectangular sheet of paper. She can take this sheet and cut it along a straight line into two parts. Then take one of the resulting parts and cut it along a straight line. Then take one of the available pieces, cut it, and so on. What is the minimum number of cuts Vera Aleksandrovna will have to make to ensure that among the resulting pieces there are the three 20-sided polygons she needs?
|
Answer: 50 cuts.
Solution: With each cut, the total number of paper pieces increases by 1 (one piece turns into two new pieces), so after $n$ cuts, there will be $(n+1)$ pieces of paper. Let's calculate how many vertices all the pieces together can have after $n$ cuts. With each cut, the total number of vertices increases by 2 (if cutting through two vertices), 3 (if cutting through a vertex and a side), or 4 (if cutting through sides). Since there were initially 4 vertices, after $n$ cuts, the total number of vertices in all pieces together will not exceed $4 n+4$.
Suppose that after $n$ cuts, we have found three 20-sided polygons. Since the total number of pieces obtained will be $n+1$, there will be $n+1-3$ pieces in addition to these 20-sided polygons. Each of these pieces has at least three vertices, so the total number of vertices is at least $20 \cdot 3+3(n-2)=3 n+54$.
Thus, $4 n+4 \geqslant 3 n+54$, from which $n \geqslant 50$.
Now let's show how to get three 20-sided polygons with 50 cuts. Here is one way: cut the original sheet into three rectangles (2 cuts) and convert each rectangle into a 20-sided polygon with 16 cuts by cutting off triangles from the corners $(3 \times 16=48$ cuts $)$. In total, exactly 50 cuts.
Criteria: Only the answer - 0 points.
Example of 50 cuts - 2 points.
Proof of the minimality of 50 - 5 points. These points are combined from proving the following statements:
- After $n$ cuts, the number of vertices is no more than $4 n+4$ - 2 points;
- After $n$ cuts, the number of vertices is no less than $3 n+54$ - 2 points;
- From the two previous estimates, $n \geqslant 50$ - 1 point.
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. On a 10 by 10 cell board, some 10 cells are marked. For what largest $n$ is it always possible, regardless of which cells are marked, to find a rectangle consisting of several cells, the perimeter of which will be at least $n$? The length or width of the rectangle can be equal to one cell.
|
Answer: $n=20$.
Solution. First, we prove that when $n=20$, it is always possible to find such a rectangle. Suppose 10 cells are colored. If there is a column or row without colored cells, then a rectangle of $1 \times 9$ with a perimeter of 20 (or even $1 \times 10$ with a perimeter of 22) can be cut from it. Now, let's assume that there is a colored cell in each column and each row. If the colored cell in the top row is in the column numbered $k$, then a rectangle of $1 \times 9$ with a perimeter of 20 can be cut from this column from the bottom.
When $n=22$, the required result is not always possible. For this, we color the cells along the diagonal. In this case, a rectangle can only be cut from the lower (or only from the upper part), but then the sum of the length and width cannot exceed 10, and the entire perimeter cannot exceed 20.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Let's call a four-digit number $\overline{a b c d}$ curious if the sum of the two-digit numbers $\overline{a b}$ and $\overline{c d}$ equals the two-digit number $\overline{b c}$. For example, the number 1978 is curious because 19+78=97. Find the number of curious numbers. Answer. 36.
|
Solution. Let's form the equation $\overline{a b}+\overline{c d}=10(a+c)+b+d=\overline{b c}=10 b+c$, from which we get $10 a+9 c+d=9 b$. The difference $9(b-c)$ is divisible by 9, so the sum $10 a+d=9(b-c)$ is also divisible by 9, which is equivalent to the divisibility by 9 of the sum $a+d=9(b-c-a)$. The sum of two different numbers from the interval from 0 to 9 is no less than 1 and no more than 17, so the latter is only possible when $a+d=9$. Substituting this into the previous equation, we get $b=a+c+1$, so the quadruple $(a, b, c, d)$ can be written in the form $(a, a+c+1, c, 9-a)$, where $a, c$ are any pair of digits satisfying the relations $a \geq 1, a+c \leq 8$. For each fixed $a=1,2, \ldots, 8$, the value of $c$ can be any from 0 to $8-a$, a total of $9-a$ options. Therefore, the total number of curious numbers is the sum $8+7+\ldots+1=36$.
Evaluation criteria. . ($\cdot$) It is proven that $a+d=9(b-c-a)$ is divisible by 9: 2 points. . ($\cdot$) It is proven that from this follows $a+d=9$: another 2 points. . ($\cdot$) The form of the quadruple of digits is written as $(a, a+c+1, c, 9-a)$: another 1 point. . ($\cdot$) The number of curious quadruples is found: 2 points.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Inside an isosceles triangle $\mathrm{ABC}$ with equal sides $\mathrm{AB}=\mathrm{BC}$ and an angle of 80 degrees at vertex $\mathrm{B}$, a point $\mathrm{M}$ is taken such that the angle
$\mathrm{MAC}$ is 10 degrees, and the angle $\mathrm{MCA}$ is 30 degrees. Find the measure of angle $\mathrm{AMB}$.
|
Answer: 70 degrees.
Solution. Draw a perpendicular from vertex B to side AC, and denote the points of its intersection with lines AC and CM as P and T, respectively. Since angle MAC is less than angle MCA, side CM of triangle MAC is shorter than side AM, so point M is closer to C than to A, and therefore T lies on the extension of segment CM. Point T lies on the perpendicular bisector AP of segment AC, so triangle ATC is isosceles, hence angle TAC is 30 degrees, and therefore angles BAT and MAT are 20 degrees each. The measures of angles $\mathrm{ABP}=\mathrm{ABC} / 2=80 / 2=40$ and $\mathrm{AMT}=\mathrm{MAC}+\mathrm{MCA}=10+30=40$ are equal, so triangles ABT and AMT are congruent by the common side AM and the adjacent angles. Therefore, the corresponding sides $\mathrm{AB}$ and $\mathrm{AM}$ are equal, and triangle $\mathrm{AMB}$ is isosceles. Consequently, its angle AMB at the base MB is $(180- BAM) / 2=(180-(50-10)) / 2=(180-40) / 2=70$ degrees.
Grading criteria. Proof that T lies on the extension of segment CM: 1 point. Proof of the isosceles nature of triangle ATC: 1 point. Proof of the isosceles nature of triangle AMB: 4 points. Finding the angle AMB: 1 point.
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. It is known that all krakozyabrs have horns or wings (possibly both). According to the results of the world census of krakozyabrs, it turned out that $20 \%$ of the krakozyabrs with horns also have wings, and $25 \%$ of the krakozyabrs with wings also have horns. How many krakozyabrs are left in the world, if it is known that their number is more than 25 but less than $35 ?$
|
Answer: 32.
Solution: Let $n$ be the number of krakozyabrs with both wings and horns. Then the number of horned krakozyabrs is $-5 n$, and the number of winged krakozyabrs is $-4 n$. Using the principle of inclusion-exclusion, the total number of krakozyabrs is $5 n + 4 n - n = 8 n$. There is only one integer between 25 and 35 that is divisible by 8.
Criterion: Answer, answer with verification - 1 point.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. At the school for slackers, a competition on cheating and giving hints was organized. It is known that $75 \%$ of the students did not show up for the competition at all, and all the rest participated in at least one of the competitions. When the results were announced, it turned out that $10 \%$ of all those who showed up participated in both competitions, and that those who participated in the hinting competition were one and a half times more than those who participated in the cheating competition. Find the smallest possible number of students in the school for slackers.
|
Answer: 200.
Solution. Let the number of students in our school be $n$ people. $\frac{n}{4}$ people attended the competitions. Taking into account $\frac{n}{40}$ people who participated in both competitions, the number of participants in the competition with hints was $\frac{3}{5}\left(\frac{n}{4}+\frac{n}{40}\right)=\frac{33 n}{200}$. For this number to be an integer, given the mutual simplicity of the numbers 33 and 200, $n$ must be divisible by 200. In the competition involving copying, $\frac{2}{5}\left(\frac{n}{4}+\frac{n}{40}\right)=\frac{11 n}{100}$ people participated, and it is sufficient for $n$ to be divisible by 100. Considering everything, it is necessary and sufficient for $n$ to be divisible by 200, in particular, to be no less than 200.
Example: 200 students: 50 people participated in the competitions, 33 people in the competition with hints, and 22 people in the copying competition, with 5 people participating in both.
Criterion. Answer with verification: 2 points.
Correct formulas: 3 points.
Correct conclusions about the divisibility of $n$ by 200: 2 points.
Lack of an example with 200: minus 1 point.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Ellie and Toto painted daisies in the field. On the first day, Ellie painted one fourteenth of the entire field. On the second day, she painted twice as much as on the first day, and on the third day, she painted twice as much as on the second day. Toto, in total, painted 7000 daisies. How many daisies were there in total on the field, given that all of them were painted? (Find all possible answers and prove that there are no others)
|
Solution. Let there be $n$ daisies in the field. Then Ellie painted $n / 14 + 2 n / 14 + 4 n / 14 = 7 n / 14 = n / 2$ daisies in total. This means Toto also painted half of the field, from which it follows that half of the field is 7000 daisies, and the entire field is 14000.
Criteria. Only the answer - 1 point.
The answer with a check that it is correct - 2 points.
|
14000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Anton from the village was given several zucchini, and he decided to give them to his friends. He gave half of the received zucchini to Arina, and a third (also from the received amount) to Vera. It turned out that after this, the number of zucchini Arina had became a square of some natural number, and the number of zucchini Vera had became a cube (they had no zucchini before). Find the smallest possible number of zucchini that Anton could have received from the village. (Find the answer and prove that it is minimal).
|
Solution. Let Anton receive $n$ zucchinis. Since both half and a third of $n$ are integers, $n$ is divisible by 6, that is, $n=6k$ for some natural number $k$. Then it is known that $3k$ is the square of a natural number, and $2k$ is a cube. Let $k=2^p 3^q m$. In other words, let $p$ and $q$ be the highest powers of two and three, respectively, by which $k$ is divisible. Then $3k=2^p 3^{q+1} m$, and since this is a square, $p$ and $q+1$ are even numbers. On the other hand, $2k=2^{p+1} 3^q m$ is a cube, so $p+1$ and $q$ are divisible by 3. Note that then $p$ is at least 2 (because $p+1$ is divisible by 3), and $q$ is at least 3 (because $q$ is divisible by 3 and $q \neq 0$ from the condition of the evenness of $q+1$). Then $k$ is divisible by at least 4 and 27, so $k$ is at least 108, and $n$ is at least 648. It is clear that $648=6 \times 4 \times 27$ fits the construction.
Criteria. Only the answer - 1 point.
Verification that the answer fits - 1 point (in this solution, this verification implicitly follows from the fact that we are looking for exactly the suitable numbers).
Proven that $n$ is divisible by 6 - 1 point.
Proof that $k$ must be divisible by 4 and 27 (or that $n$ is divisible by 8 and 81, which is the same) - 2 points for each fact.
All the above points are cumulative.
The answer can be left in the form of a product; no points are deducted for the lack of an explicit notation.
|
648
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. What two digits need to be appended to the right of the number 2013 so that the resulting six-digit number is divisible by 101? Find all possible solutions.
|
Answer: 94, the obtained number will be equal to 201394.
Solution: The remainder of dividing the number $\overline{2013 x y}$ by 101 is $\overline{x y}+7$ and this must be divisible by 101. This is greater than 0 but less than 202, so $\overline{x y}+7=101, \overline{x y}=94, x=9, y=4$.
Grading: Just the answer with verification: 1 point. Failure to justify $\overline{x y}+7=101$ minus points.
|
94
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. On the cells of an 8 by 8 board, chips are placed such that for each chip, the row or column of the board in which it lies contains only one chip. What is the maximum possible number of chips on the board?
|
Answer: 14.
Solution: Let's match each chip to the row or column of the board in which it is the only one. If it is the only one in both, we match it to the row. From the condition, it follows that different chips are matched to different rows and columns. If not all rows and columns are matched, then their total number does not exceed 14, in each of them there is no more than one chip, so the total number of chips does not exceed 14. If, however, all rows, say, are matched, then there is a chip in each row - a total of 8.
Example of placing 14 chips: all cells of the left column and the bottom row are filled, except for the bottom left corner cell.
Evaluation: 5 points. Example: 2 points. Any incorrect estimate with any reasoning - 0 points.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. At a diplomatic reception, there are 99 persons, each of whom has heard of no fewer than $n$ other attendees. If A has heard of B, it does not automatically mean that B has heard of A. For what minimum $n$ is it guaranteed that there will be two attendees who have heard of each other?
|
Answer. When $n=50$.
Solution. Let's call a situation where one of the guests has heard about another a half-acquaintance. If each guest has heard about at least 50 other participants at the reception, then there are at least $99 \cdot 50$ half-acquaintances, which is more than the total number of pairs of guests at the reception, equal to $\frac{\mathbf{9} \boldsymbol{9}}{\mathbf{2}} \underline{\underline{\mathbf{8}}} \boldsymbol{9 4}$: Therefore, in some pair, there are at least two half-acquaintances, and the guests in this pair have heard about each other.
Let's provide an example where each has heard about exactly 49 other guests, but there are no two guests who have heard about each other. Arranging the guests in a circle, we assume that each has heard only about the next 49 guests in the clockwise direction. In this case, each has been heard about only by the 49 guests located in front of them in the clockwise direction. These two sets do not intersect, so for each guest, there is no other guest who has heard about them and whom they have heard about.
Criteria. Proof that $n$ is not greater than $50: 4$ points. Example that $n$ is not less than 50: 3 points.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. What is the maximum number of 2 by 2 squares that can be placed on a 7 by 7 grid of squares so that any two placed squares share no more than one common cell? The 2 by 2 squares are placed along the grid lines such that each covers exactly 4 cells. The squares do not extend beyond the boundaries of the board.
|
Answer: 18 squares.
Solution: First, let's provide an example of laying out 18 squares of 2 by 2: 9 of them cover the left bottom square of size 6 by 6 of the board, and the other 9 cover the right top square of size 6 by 6 of the board.
We will prove that it is impossible to lay out 19 squares correctly. Note that if a cell of the board, adjacent to the edge, is covered by two squares, then they intersect in at least two cells, and if a cell of the board, not adjacent to the edge, is covered by three squares, then two of them intersect in at least two cells. Consequently, the edge cells of the board can be covered by squares no more than once, and the internal cells no more than twice. Therefore, the squares can contain no more than \(24 \cdot 1 + 25 \cdot 2 = 74\) cells in total, and the total number of squares cannot exceed \(74 / 4 = 18.5\) pieces.
Grading criteria: Any correct example: 2 points. Proof that the number of squares is no more than 18: 5 points.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. A bus with programmers left Novosibirsk for Pavlodar. When it had traveled 70 km, Pavel Viktorovich set off from Novosibirsk in a car along the same route, and caught up with the programmers in Karasuk. After that, Pavel drove another 40 km, while the bus traveled only 20 km in the same time. Find the distance from Novosibirsk to Karasuk, if both the car and the bus traveled at constant speeds. (Provide a complete solution, not just the answer.)
|
Solution. Since by the time the car has traveled 40 km, the bus has traveled half that distance, its speed is exactly half the speed of the car. However, when the bus has traveled 70 km after the car's departure, the car will have traveled 140 km and will just catch up with the bus. According to the problem, this happened in Karasuk, so 140 km is the answer.
Criteria. Only the answer -1 point.
Answer with verification (for example, for specific speeds) - 2 points. Proven that the car's speed is twice the speed of the bus - 3 points.
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Come up with at least one three-digit PAU number (all digits are different) such that $(П+\mathrm{A}+\mathrm{У}) \times \Pi \times \mathrm{A} \times \mathrm{Y}=300$ (it is sufficient to provide one example)
|
Solution: For example, PAU = 235 is suitable. There are other examples as well. Criteria: Any correct example - 7 points.
|
235
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Students in the seventh grade send each other New Year's stickers on Telegram. It is known that exactly 26 people received at least one sticker, exactly 25 - at least two stickers, ..., exactly 1 - at least 26 stickers. How many stickers did the students in this class receive in total, if it is known that no one received more than 26 stickers? (find all possible answers and prove that there are no others)
|
# Answer: 351
Solution: Note that exactly 1 sticker was received by one person, as it is precisely in this case that the difference between those who received at least 1 and those who received at least 2. Similarly, one person received exactly $2, 3, \ldots, 26$ stickers, so the total number of stickers is $1+\ldots+26=351$.
Criteria: Only the answer - 0 points.
Answer with verification that it is possible - 1 point.
Answer written in an open form (ellipsis left) or arithmetic error - minus 1 point.
|
351
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. In each of the four volleyball teams, there are six players, including a captain and a setter, and these are different people. In how many ways can a team of six players be formed from these four teams, such that there is at least one player from each team and there must be a pair of captain and setter from at least one team?
|
Answer: 9720.
Solution. Case 1. Three players, including the captain and the setter, are chosen from one of the teams, and one player is chosen from each of the remaining three teams. The team is chosen in four ways, the third player from it in another four ways, and the three players from the remaining teams in $6 \cdot 6 \cdot 6=216$ ways, resulting in $4 \cdot 4 \cdot 6 \cdot 6 \cdot 6=16 \cdot 216=3456$ possibilities for this case.
Case 2. Two players are chosen from two teams, with at least one team including the captain and the setter, and one player is chosen from each of the remaining two teams. The pair of teams can be chosen in $C_{4}^{2}=6$ ways, and choosing a pair of players from each can be done in $C_{6}^{2} \cdot C_{6}^{2}$ ways. However, we need to exclude $\left(C_{6}^{2}-1\right) \cdot\left(C_{6}^{2}-1\right)$ selections where neither of the two teams includes both the captain and the setter simultaneously, leaving us with $2 \cdot C_{6}^{2}-1=29$ ways. There are $6 \cdot 6=36$ ways to choose one player from each of the remaining two teams, resulting in a total of $6 \cdot 29 \cdot 36=6264$ ways in this case. In total, $6264+3456=9720-$ is the answer to the problem.
Grading criteria. Reducing the solution to cases 1 and 2: 1 point. Considering each of cases 1 and $2: 3$ points.
|
9720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Find the number of five-digit numbers containing two digits, one of which is divisible by the other.
|
Answer. $89760=9 \cdot 10^{4}-2 \cdot 5!$.
Solution. We will count the number of five-digit numbers in which no digit is divisible by any other digit, and then subtract this number from the total number of five-digit numbers, which is 90000, to get the answer to the problem.
Note that a number, none of whose digits are divisible by any other, does not contain the digit 0 (0 is divisible by any digit), 1 (any digit is divisible by 1), and does not contain identical digits (they always divide each other). Therefore, the smallest digit of such a five-digit number can be $2, 3, 4$ or 5. If it is 2, then the other four digits must be odd, specifically $3, 5, 7$ and 9, but 9 is divisible by 3. If it is 3, the other four digits can only be $4, 5, 7, 8$, but 8 is divisible by 4. The only numbers left are those composed of the digits $4, 5, 6, 7, 9$ or $5, 6, 7, 8, 9$. In each case, there are $5!=120$ possible permutations of these digits, totaling 240 numbers. Therefore, the number of numbers sought in the problem is 90000 $- 240 = 89760$.
Grading criteria. The idea of applying the principle of subtraction: 3 points. Correct calculation of the number of five-digit numbers: 1 point. Correct calculation of the number of five-digit numbers in which no digit is divisible by any other digit: 3 points. If the solution does not account for the divisibility of 0 by any digit or the divisibility of any digit by 1 or equal digits by each other: minus 3 points.
|
89760
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. There are 100 coins, 99 of which are genuine and weigh the same, and 1 is counterfeit and lighter than the others. Dmitry has a pair of balance scales without weights, which always show incorrect results (for example, if the left pan is heavier, they will show either balance or the right pan being heavier, but it is unknown which). Help Dmitry find 98 genuine coins.
|
# Solution:
Let's number the coins from 1 to 100. Weigh the first coin against the second. If the scales show equality, then one of them is fake, and all the other coins are genuine, and we have achieved the desired result. If the scales do not balance, assume the coin numbered 1 is heavier. Then the second coin is definitely genuine (otherwise, the scales would have shown the correct result). Set aside the second coin in the bag for genuine coins.
Re-number the remaining coins from 1 to 99, and repeat the process.
Either we will get one new genuine coin with each weighing, and after 98 weighings, we will have found 98 genuine coins, or at some point, the scales will show equality, and we will achieve the desired result.
Criteria: Algorithm only without justification - 1 point. Case of equality not considered in a similar solution, otherwise justified correctly - 5 points.
|
98
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. How much of a $5 \%$ and a $20 \%$ salt solution in water should be taken to obtain 90 kg of a $7 \%$ solution
|
Answer: 78 kg of 5% solution and 12 kg of 20% solution.
Solution. Let the mass of the 5% solution be $x$ kg, the mass of the 20% solution will be $90-x$ kg, and the total mass of salt in the 5% and 20% solutions is equal to the mass of salt in 90 kg of 7% solution: $\frac{5}{100} x+\frac{20}{100}(90-x)=\frac{7}{100} 90$, from which $1800-15 x=630$ and $x=78$.
Grading criteria. Answer found by guessing with verification: 1 point. Equations written but not solved: 2 points.
|
78
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Paramon set out from point A to point B. At $12^{00}$, when he had walked half the way to B, Agafon ran out from A to B, and at the same time, Solomon set out from B to A. At $13^{20}$, Agafon met Solomon, and at $14^{00}$, he caught up with Paramon. At what time did Paramon and Solomon meet?
|
Answer: At 13 o'clock.
Solution: Let the distance between A and B be $\mathrm{S}$ km, and the speeds of Paramon, Solomon, and Agafon be $x, y, z$ km per hour, respectively. Then from the condition, we get: $\frac{S / 2}{z-x}=2, \frac{S}{y+z}=\frac{4}{3}$, from which $x+y=\frac{1}{2} S$. Therefore, Paramon and Solomon will meet after $\frac{S / 2}{S / 2}=1$ hour past noon, that is, at 13 o'clock.
Instructions: Answer with verification: 1 point. Formulation of equations: 3 points.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. The median $A M$ of triangle $A B C$ divides the segment $P R$, parallel to side $A C$, with endpoints on sides $\mathrm{AB}$ and $\mathrm{BC}$, into segments of lengths 5 cm and 3 cm, starting from side $\mathrm{AB}$. What is the length of side AC?
|
Answer: 13 cm.
Solution. Let the ends of the segment be denoted as $\mathrm{P}$ and $\mathrm{R}$, and the point of intersection with the median $\mathrm{AM}$ as $\mathrm{Q}$, with $\mathrm{P}$ lying on side $\mathrm{AB}$ and $\mathrm{R}$ on side $\mathrm{BC}$. Draw the midline $\mathrm{MN}$ of the triangle, its length is half the length of $\mathrm{AC}$. Using the similarity of triangles $\mathrm{ANM}$ and $\mathrm{APQ}$, and $\mathrm{MAC}$ and $\mathrm{MRQ}$. The similarity ratio of the first pair is $\mathrm{k}=\mathrm{AM} / \mathrm{AQ}$, and of the second pair is $\mathrm{AM} / \mathrm{MQ}$, their sum equals one. Then $k \cdot N M=k \cdot \frac{A C}{2}=5,(1-k) \cdot A C=3$, from which $A C=13$.
Instructions. The midline is drawn and both similarities are noted: 2 points.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. In a row from left to right, there are $n$ coins. It is known that two of them are counterfeit, they lie next to each other, the left one weighs 9 grams, the right one 11 grams, and all the remaining ones are genuine and each weighs 10 grams. The coins are weighed on balance scales, which either show which of the two pans is heavier, or are in equilibrium, indicating that the weights on both pans are the same. For what maximum $n$ can the coin weighing 11 grams be found in three weighings?
|
Answer. $n=28$.
Solution. Let $n=28$. Divide all 28 coins into three piles: the first pile contains coins numbered $11,13,15,17,19,21,23,25,27$, the second pile contains coins numbered $12,14,16,18,20,22,24,26,28$, and the third pile contains coins numbered from 1 to 10. The first weighing compares the first and second piles. Note that if the scales are not in balance, the heavy coin is in the heavier pile. Indeed, if the numbers of both fake coins are greater than 10, then the light one will fall into one of the two weighed piles, and the heavy one will fall into the other, causing the heavier pile to tip. If the numbers of both fake coins are not greater than 10, then both will fall into the third pile, and the scales will remain in balance. If the numbers of the fake coins are 10 and 11, the heavy one will fall into the first pile, and the second will consist entirely of genuine coins, causing the first pile to tip. It is important to note that if a similar division is made from the beginning of the numbers rather than the end, it is incorrect when the fake coins are in the 18th and 19th positions. If the scales are in balance, then the heavy and light coins are in the third pile of 10 coins. In this "worst" case, we divide the third pile similarly into three: the first pile contains numbers $6,8,10$, the second pile contains numbers $5,7,9$, and the third pile contains numbers $1,2,3,4$. The second weighing compares the first and second piles to determine which of the three piles contains the heavy coin. If balance is again achieved and it is together with the light one in the third pile of 4 coins, we compare coins 3 and 4. If they are equal, the heavy one is the 2nd; if one is heavier, that one is the heavy one. The same applies if the heavy one is in the pile of 3 coins - we compare the second and third, the heavier one is the heavy one.
If the heavy coin is found, for example, in the first pile during the first weighing, we divide it into three groups of three: the first pile contains coins $19,23,27$, the second pile contains coins $17,21,25$, and the third pile contains coins $11,13,15$. We weigh the first and second piles to find the pile of three coins containing the heavy one. The final weighing of the second and third coins in this pile identifies the desired one. Similarly, if the heavy coin is found in the second pile during the first weighing. Note that the light coin participates in the third weighing if and only if the first two weighings result in balance.
If there are more than 28 coins, the number of possible positions for the heavy coin will be more than $27=3^3$, which is greater than the number of possible outcomes of three weighings, equal to 3.3.3. Therefore, it is impossible to uniquely associate the number of the heavy coin with a specific outcome of three weighings and find it.
Grading criteria. Algorithm for finding the heavy coin when $n=28$: 5 points ($\cdot$) If similar divisions as indicated in the author's solution are made but from the beginning of the numbers, and the rest is the same: deduct 2 points. ($\cdot$) If the correct division is made but there is no clear explanation that if the scales are not in balance during the first weighing, the heavy coin is in the heavier pile: deduct 1 point. ( $($ )
Proof that the heavy coin cannot be found with certainty in three weighings when $n>28$: 2 points.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. On the table, 28 coins of the same size but possibly different masses are arranged in a triangular shape (see figure). It is known that the total mass of any triplet of coins that touch each other pairwise is 10 g. Find the total mass of all 18 coins on the boundary of the triangle.
|
Answer: 60 g.
Solution 1: Take a rhombus made of 4 coins. As can be seen from the diagram, the masses of two non-touching coins in it are equal. Considering such rhombi, we get that if we color the coins in 3 colors, as shown in the diagram, then the coins of the same color will have the same mass.
Now it is easy to find the sum of the masses of the coins on the boundary: there are 6 coins of each color there, and the sum of the masses of three differently colored coins is 10 g; therefore, the total mass of the coins on the boundary is $6 \cdot 10=60$ g.
Solution 2: All coins except the central one can be divided into 9 triplets, and all internal coins except the central one can be divided into 3 triplets. This means that the coins on the boundary weigh as much as 9-3=6 triplets, i.e., 60 g.
Criteria: Only the answer - 0 points.
Rhombi are considered and it is shown that two coins in them have the same mass - 2 points.
In addition to this, it is proven that the weights in the entire triangle have the form shown in the diagram (coloring is done, but there is no further progress) - another 2 points.
|
60
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Represent the number 1000 as the sum of the maximum possible number of natural numbers, the sums of the digits of which are pairwise distinct.
|
Answer: 19.
Solution: Note that the smallest natural number with the sum of digits A is a99..99, where the first digit is the remainder, and the number of nines in the record is the incomplete quotient of the division of A by 9. From this, it follows that if A is less than B, then the smallest number with the sum of digits A is also less than the smallest number with the sum of digits B. Consider the smallest natural numbers with the sums of digits $1,2,3, \ldots, 19,20$, they are respectively $a_{1}=1, a_{2}=2, \ldots a_{9}=9, a_{10}=19, a_{11}=29, \ldots a_{18}=99, a_{19}=199, a_{20}=299$. The sum of the first 19 of them is 775, and the remainder of its division by 9 is 1, which is the same as the remainder of the division of 1000 by 9. Increase this sum by 225, taking 234 instead of 9, with the same sum of digits, and we get a representation of 1000 as the sum of 19 numbers $1,2,3,4,5,6,7,8,19,29,39,49,59,69,79,89,99,199,234$ with different sums of digits from 1 to 19.
Suppose that 1000 can be represented as the sum of $n \geq 20$ natural numbers $b_{1}, b_{2}, \ldots b_{n}$ with different sums of digits $s\left(b_{1}\right)<s\left(b_{2}\right)<\ldots<s\left(b_{n}\right)$. In this case, $s\left(b_{k}\right) \geq k, k=1,2, \ldots n,$ and, consequently, $b_{k} \geq a_{k}, k=1,2, \ldots n$. Therefore, $1000=b_{1}+b_{2}+\ldots+b_{n} \geq a_{1}+a_{2}+\ldots+a_{n} \geq a_{1}+a_{2}+\ldots+a_{20}=107$ - a contradiction.
Grading criteria: Finding a representation of 1000 as the sum of 19 numbers with different sums of digits: 3 points. Proof of the maximality of 19: 4 points.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In Nastya's room, 16 people gathered, each pair of whom either are friends or enemies. Upon entering the room, each of them wrote down the number of friends who had already arrived, and upon leaving - the number of enemies remaining in the room. What can the sum of all the numbers written down be, after everyone has first arrived and then left?
|
Answer: 120
Solution: Consider any pair of friends. Their "friendship" was counted exactly once, as it is included in the sum by the person who arrived later than their friend. Therefore, after everyone has arrived, the sum of the numbers on the door will be equal to the total number of friendships between people. Similarly, each "enmity" will be counted exactly once by the person who left earlier. Therefore, after everyone has left, the sum of the numbers on the door will be increased by the sum of all "enmities." In total, the overall sum of the numbers on the door will be equal to the sum of the total number of friendships and enmities, which is precisely the number of pairs of people who arrived, i.e., $16 * 15 / 2 = 120$.
Criteria: answer only - 0 points.
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Losharik is going to visit Sovunya along the river at a speed of 4 km/h. Every half hour, he launches paper boats that float to Sovunya at a speed of 10 km/h. With what time interval do the boats arrive at Sovunya? (Provide a complete solution, not just the answer.)
|
Solution: If Losyash launched the boats from one place, they would arrive every half hour. But since he is walking, the next boat has to travel a shorter distance than the previous one. In half an hour, the distance between Losyash and the last boat will be $(10-4) \cdot 0.5=3$. This means that the distance between adjacent boats is 3 km, and the next boat will have to travel exactly this distance when the previous one has already arrived at Sovunya. The speed of the boat is 10 km/h, which means 1 km in 6 minutes, so 3 km will be covered by the boat in 18 minutes, which is the answer.
Criteria: Correctly found the distance of 3 km - 3 points.
Only the answer or the answer with verification - 1 point.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Katya wrote a four-digit number on the board that was divisible by each of its digits without a remainder (there were no zeros in the number). Then she erased the first and last digits, and the number 89 remained on the board. What could have been written on the board initially? (Find all options and show that there are no others.)
|
Solution: The original number was divisible by 8. Therefore, the number formed by its last three digits is also divisible by 8. From the condition, this number has the form $\overline{89 x}$. Clearly, $x=6$ fits, and other numbers divisible by 8 do not fit into this decade. The entire number is divisible by 9, which means the sum of its digits is divisible by 9. Currently, it is $8+9+6=23$. It is 4 short of the nearest number divisible by 9, and 13 short of the next one. Therefore, this number is 4896. Since it is divisible by 8 and 9 by construction, it is also divisible by 4 (since 4 is a divisor of 8), and by 6 (due to divisibility by 8 and 9).
Criteria: Only the answer, answer with verification - 1 point.
One of the digits is found unambiguously - 3 points.
It is proven that it can only be 4896, but not verified that it fits - 7 points.
|
4896
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Vikentiy has two jars, a red one and a blue one, and a pile of 20 pebbles. Initially, both jars are empty. A move in Vikentiy's game consists of transferring a pebble from the pile to one of the jars or returning a pebble from one of the jars to the pile. The number of pebbles in the jars determines the game position. After each move, the number of pebbles in the red jar is always not less than the number of pebbles in the blue jar; and during the game, no position can be repeated. What is the maximum number of moves Vikentiy can make?
|
Answer: 110.
Solution: The position in Vikenty's game is uniquely defined by a pair of non-negative integers $(x, y)$, and $x+y \leq 20$, where $0 \leq y \leq x \leq 20$ are the numbers of pebbles in the blue and red jars, respectively. In total, there are $21+19+17 \ldots+1=121$ positions in Vikenty's game. We will call a position even if the sum of the numbers of pebbles in the jars is even, and odd otherwise. In total, there are $11+10+\ldots+1=66$ even positions and $121-66=55$ odd positions in the game. Each move in the game changes the parity of the position, so the game cannot contain more than 55 even and 56 odd positions (taking into account that it starts with an even position $(0,0)$), a total of 111 positions, and consist of no more than $111-1=110$ moves.
We will provide an example of a game where Vikenty can make 110 moves. In this case, he makes the only possible first move from $(0,0)$ to $(1,0)$, then he sequentially passes through all positions $(x, y)$ with odd $x=1,3,5, . ., 9$ from $(x, 0)$ to $(x, x)$, after which he moves to $(x+1, x)$, and all positions with even $x=2,4, . ., 10$ from $(x, x-1)$ to $(x, 0)$, after which he moves to $(x+1,0)$. After all of the above, he ends up in the position $(11,0)$, after which his strategy changes slightly. He sequentially passes through all positions $(x, y)$ with odd $x=11,13,15, .17$ from $(x, 0)$ to $(x, 19-x)$, after which he moves to $(x+1,19-x)$, and all positions with even $x=12,14, . ., 18$ from $(x, 20-x)$ to $(x, 0)$, after which he moves to $(x+1,0)$. In the end, he ends up in the position $(19,0)$ and makes the last move to $(20,0)$. The unvisited positions are $(2,2),(4,4), \ldots,(10,10),(11,9),(13,7), \ldots,(19,1)$ - exactly 10 of them, that is, exactly $121-10=111$ positions were visited. Exactly 110 moves were made.
Grading criteria. ($\cdot$) Proved that the number of moves is no more than 110: 3 points. ($\cdot$) Construction of an example with 110 moves with precise justification: 4 points. ($\cdot$) Lack of precise justification of the example: minus 2 points.
|
110
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. Find the number of different arrangements in a row of all natural numbers from 1 to 10 such that the sum of any three consecutive numbers is divisible by 3.
|
Answer: $4! \cdot 2 \cdot 3! \cdot 3! = 1728$
Solution. From the condition, it follows that the remainders of the numbers standing two apart when divided by 3 are equal. Therefore, the numbers standing at positions 1, 4, 7, and 10, as well as those at positions 2, 5, and 8, and at positions 3, 6, and 9, have equal remainders when divided by 3. Among the numbers from 1 to 10, four identical remainders of 1 are given only by 1, 4, 7, and 10, so any permutation of these numbers can be placed at positions 1, 4, 7, and 10, giving a total of 4! options. Similarly, at positions 2, 5, and 8, any arrangement of the numbers 2, 5, 8, or the numbers 3, 6, and 9 can be placed, and at positions 3, 6, and 9, the opposite. In total, we get $4! \cdot 3! \cdot 3! \cdot 2$ options.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. All natural numbers from 1 to 100 are written in some order in a circle. For each pair of adjacent numbers, the sum is calculated. Out of the hundred resulting numbers, what is the maximum number that can be divisible by 7?
|
Answer: 96.
Solution. For the sum of a pair of adjacent numbers to be divisible by 7, their remainders when divided by 7 must sum to 7: 0+0, 1+6, 2+5, and 3+4. Let's call such pairs of remainders suitable pairs. Among the numbers from 1 to 100, there are 14, 15, 15, 14, 14, 14, and 14 numbers with remainders 0, 1, 2, 3, 4, 5, and 6, respectively. A sequence of numbers with alternating suitable pairs of remainders will be called a correct series. If a correct series consists of \( x \) numbers, it will yield \( x-1 \) sums that are divisible by 7. If there are \( n \) such series, they will yield \( 15+14-n=29-n \) or \( 14+14-n=28-n \) such sums. Similarly, for other groups of remainders, we see that the total number of sums divisible by 7 is 100 minus the number of correct series into which all numbers from 1 to 100 are divided. For each pair of suitable remainders, there is at least one correct series, so the total number of sums divisible by 7 does not exceed \( 100-4=96 \).
An example for 96 can be constructed easily: first, all numbers divisible by 7 go in a row, then numbers with remainders 1 and 6 alternate, followed by numbers with remainders 2 and 5 alternating, and finally, all numbers with remainders 3 and 4 alternate. Since the quantities of numbers in groups with different remainders differ by no more than 1, this is possible.
|
96
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Lesha wrote down a number, and then replaced the same digits with the same letters, and different digits with different letters. He ended up with the word NOVOSIBIRSK. Could the original number be divisible by 3?
|
Answer: Yes, it could.
Solution: For example, 10203454638.
Criteria: Any correct example without verification - 7 points.
|
10203454638
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. The steamship "Raritet" after leaving the city moves at a constant speed for three hours, then drifts for an hour, moving with the current, then moves for three hours at the same speed, and so on. If the steamship starts its journey from city A and heads to city B, it takes 10 hours. If it starts from city B and heads to city A, it takes 15 hours. How long would it take to travel from city A to city B on a raft?
|
Answer: 60 hours.
Solution: Let the speed of the steamboat be $U$, and the speed of the river be $V$. When the steamboat travels from B to A, it arrives at the destination just before the fourth engine stop, meaning it travels 12 hours at a speed of $U-V$ towards A, and then 3 hours back at a speed of $V$ towards B. Therefore, the distance between the cities is $S=12(U-V)-3 V=12 U-15 V(1)$.
When the steamboat travels from A to B, it manages to break down twice and then continue for another two hours on its own. So, it travels 8 hours at a speed of $U+V$ towards B and 2 hours at a speed of $V$ with the current towards B. Thus, the distance is $S=8(U+V)+2 V=8 U+10 V(2)$. Equating the two, we get $12 U-15 V=8 U+10 V$ or $4 U=25 V$ or $(U / V)=(25 / 4)$. The time it will take to travel by raft is $S / V=12(U / V)-15(V / V)=12 *(25 / 4)$ - 15 $=60$ hours.
Criteria: Only the answer - 0 points. Correctly formulated equation (1) or (2) - 1 point (these points are cumulative).
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. A kilogram of meat with bones costs 165 rubles, a kilogram of meat without bones costs 240 rubles, and a kilogram of bones costs 40 rubles. How many grams of bones are there in a kilogram of meat with bones?
|
Answer: 375 grams.
Solution: Let $x$ kilos of bones be in a kilogram of meat with bones. Then $40 x + 240(1-x) = 165$, from which $x=0.375$.
|
375
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. From the highway, four roads sequentially lead to four villages A, B, C, D. It is known that the route by road/highway/road from A to B is 9 km, from A to C - 13 km, from B to C - 8 km, from B to D - 14 km. Find the length of the route by road/highway/road from A to D. Explain your answer.
|
Answer: 19 km.
Solution. Let's add the distances from $A$ to $C$ and from $B$ to $D$. Then the highway segment from the turn to $B$ to the turn to $C$ will be counted twice, while the highway segments from the turn to $A$ to the turn to $B$ and from the turn to $C$ to the turn to $D$, as well as the four roads from the highway to the villages, will be counted once. Therefore, if we now subtract the distance from $B$ to $C$ from the resulting sum, the difference will include each of the three highway segments and the access roads to $A$ and $D$ exactly once, which is precisely the path from $A$ to $D$. Thus, the length of this path is $13+14-8=19$ km.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. There are 100 boxes numbered from 1 to 100. One of the boxes contains a prize, and the host knows where it is. The audience can send the host a batch of notes with questions that require a "yes" or "no" answer. The host shuffles the notes in the batch and, without reading the questions aloud, honestly answers all of them. What is the minimum number of notes that need to be sent to definitely find out where the prize is?
|
Answer: 99.
Solution: To be able to definitively determine which of the 100 boxes contains the prize, it is necessary to have the possibility of receiving at least 100 different answers to one set of questions. Since the host's answers for different prize positions can only differ by the number of "yes" responses, it is necessary to have the possibility of receiving at least 100 different counts of "yes." Therefore, at least 99 questions are required (from 0 to 99 "yes").
Example with 99 questions. Let the $k$-th question be: "Is the number of the box containing the prize less than or equal to $k$?" Then, if the number of "yes" answers is zero, the prize is in the hundredth box; if one, it is in the 99th box, and so on.
Criteria: Only the evaluation -3 points, only the example -3 points. Only the answer -0 points.
|
99
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Find the number of all five-digit numbers $\overline{a b c d e}$, all digits of which are distinct and $ad>e$.
|
Answer: 1134.
Solution. For the correct notation of a number satisfying the condition of the problem, one needs to arbitrarily select a quintet of different digits from 10 possible ones, and then arrange two of them to the left of the maximum in ascending order and the two remaining to the right of the maximum in descending order. There are two different cases possible.
1) The selected quintet does not contain zero. Then it can be chosen in $C_{9}^{5}$ ways, then choose two non-maximum and non-zero digits from them in $C_{4}^{2}$ ways, and arrange them to the left of the largest in ascending order in a unique way, and write the two remaining to the right of the maximum in descending order. In total, we have $C_{9}^{5} \cdot C_{4}^{2}=126 \cdot 6=756$ such numbers.
2) The selected quintet contains zero. Then its non-zero digits can be chosen in $C_{9}^{4}$ ways, then choose two non-maximum digits from them in $C_{4}^{2}$ ways, and then arrange them to the left of the largest in ascending order in a unique way, and write one remaining and zero to the right of the maximum in descending order. In total, we have $C_{9}^{4} \cdot C_{3}^{2}=126 \cdot 3=378$ such numbers.
In total, we get $756+378=1134$ numbers.
Grading criteria. The idea of separately considering the cases when there is a 0 among the digits of the number and when there is not: 1 point. Correct consideration of each case: 3 points.
|
1134
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Prove that for any $0 \leq x, y \leq 1$ the inequality $\frac{x}{1+y}+\frac{y}{1+x} \leq 1$ holds.
Proof 1. Replace the ones in the denominators of the fractions on the left side of the inequality with $0 \leq x \leq 1$ and $0 \leq y \leq 1$ respectively. In this case, the denominators of the fractions will not increase and will remain positive, and the values of the fractions will not decrease: $\frac{x}{1+y}+\frac{y}{1+x} \leq \frac{x}{x+y}+\frac{y}{y+x}=\frac{x+y}{x+y}=1$ - which is what we needed to prove.
Proof 2. Eliminate the denominators and combine like terms, we get $x^{2}+y^{2} \leq 1+x y$. If $x \leq y$, then the required inequality is obtained by adding the inequalities $y^{2} \leq 1$ and $x^{2} \leq x y$. If $y \leq x$, then the required inequality is obtained by adding the inequalities $x^{2} \leq 1$ and $y^{2} \leq x y$.
10.4. Point $M$ is the midpoint of side $A B$ of triangle $A B C$. Points $P$ and $Q$ are chosen on segment $C M$ such that $P$ is closer to $M$, $Q$ is closer to $C$, and $C Q=2 P M$. It turns out that $B Q=A C$. Find the measure of angle $A P M$.
|
Answer. $A P M=90^{\circ}$.
Solution. Mark a point T on the extension of CM beyond M such that MT=MP. In this case, segments $\mathrm{AB}$ and TP are bisected by their intersection point M, so quadrilateral ATBP is a parallelogram. In particular, segments AP and BT are equal and parallel. Consider triangles $\mathrm{BQT}$ and $\mathrm{APC}$. In them, sides $\mathrm{BQ}$ and $\mathrm{AC}$ are equal by condition, QT and PC are equal by construction, and sides AP and BT are equal as proven above. Therefore, triangles BQT and APC are equal, meaning their corresponding angles BTQ and APC are equal. From the parallelism of AP and BT, it follows that the sum of these angles is $180^{\circ}$, so each of them is $90^{\circ}$. Then the angle APM, supplementary to APC, is also $90^{\circ}$.
Remark. Another solution can be obtained if a point E is marked on the extension of CM beyond M such that $\mathrm{ME}=\mathrm{MQ}$ and it is noticed that triangle $\mathrm{ACE}$ is isosceles, with $\mathrm{P}$ being the midpoint of its base.
Evaluation Criteria. An attempt is made to set $\mathrm{MT}=\mathrm{MP}$ or $\mathrm{ME}=\mathrm{MQ}$ without further progress: 1 point. It is noted in this case that triangle ACE is isosceles: another 1 point.
|
90
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In a trapezoid, one lateral side is twice as large as the other, and the sum of the angles at the larger base is 120 degrees. Find the angles of the trapezoid.
|
Answer: 90 and 30 degrees.
Solution: Let the vertices of the trapezoid be A, B, C, D, with the larger base AD, and assume CD is twice as long as AB. Choose a point E on AD such that BE is parallel (and equal) to CD, and let M be the midpoint of segment BE. Then triangle ABM is isosceles with a 60-degree angle at vertex B, so it is equilateral, and point M is equidistant from A, B, and E. Therefore, M is the center of the circle containing points A, B, and E, and BE is its diameter. Angle BAE is an inscribed angle subtending this diameter, so its measure is 90 degrees, which means the measure of angle BAD is also 90 degrees, and the measure of angle CDA is 30 degrees.
Criteria: The idea of constructing segment BE: 2 points.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. $N$ different natural numbers, not exceeding 1000, are written in a circle such that the sum of any two of them, standing one apart, is divisible by 3. Find the maximum possible value of $N$.
#
|
# Answer: 664.
Solution. Consider the remainders of the numbers when divided by 3. Divisibility by 3 means that in each pair of numbers standing one apart, either both numbers are divisible by 3, or one has a remainder of 1 and the other has a remainder of 2 when divided by 3. Among the numbers from 1 to 1000, 333 are divisible by 3, 334 give a remainder of 1, and 333 give a remainder of 2.
1) Suppose \( \mathrm{N} \) is odd. Then the remainders 1 and 2 cannot alternate throughout the circle, so all numbers in the circle will be divisible by 3, and there will be no more than 333 of them.
2) Suppose \( \mathrm{N} \) is even. The numbers are divided into two cycles of equal length \( \mathrm{N}/2 \): those in even positions and those in odd positions. In each of them, either all numbers are divisible by 3, or they alternate with remainders of 1 and 2.
A cycle of numbers divisible by 3 has a length of no more than 333. A cycle with alternating remainders has an even length, not exceeding 666.
If there are numbers divisible by 3 among the listed ones, then there is a cycle of such numbers with a length of no more than 333. The second cycle would then consist of no more than 333 even numbers with remainders of 1 and 2, i.e., no more than 332 numbers. Then the total number of numbers would be no more than 664. This number is achievable: one cycle contains numbers divisible by 3 from 3 to 996, and the second: all numbers from 1 to 498 that are not divisible by 3.
If there are no numbers divisible by 3, then the lengths of the cycles are equal and even, so the total number of numbers written should be no more than 667 and divisible by 4, i.e., no more than 664.
Criteria. Consider the case 1) \( \mathrm{N} \) is odd: 1 point. Consider the case 2) \( \mathrm{N} \) is even - the idea of two cycles: 1 point, estimating the length of each cycle: 1 and 2 points respectively. Constructing an example: 2 points.
|
664
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. For what smallest $n$ is the following condition satisfied: if $n$ crosses are placed in some cells of a $6 \times 6$ table in any order (no more than one per cell), then there will definitely be three cells forming a strip of length 3, either vertical or horizontal, each containing a cross?
|
Answer. $n=25$.
Solution. If there are no fewer than 25 crosses, then one of the rows of the table contains no fewer than 5 crosses, and no more than one empty cell. Then either the three left cells of this row, or the three right cells of it, all contain crosses and form the desired strip.
If there are fewer than 25 crosses, they can be arranged so that there are no three crosses forming a strip. For this, all cells of one main diagonal, and the cells of two parallel diagonals of length 3, should be left empty.
Grading criteria. Estimation (if more than 24, then a strip will always be found): 3 points. Example of arranging 24 or fewer crosses without three crosses in a row: 4 points.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Lesha wrote down a number, and then replaced the same digits with the same letters, and different digits with different letters. He ended up with the word NOVOSIBIRSK. Could the original number be divisible by 9?
|
Answer: Yes, it could.
Solution: For example, 10203454638.
Criteria: Any correct example without verification - 7 points.
|
10203454638
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. The steamship "Raritet" after leaving the city moves at a constant speed for three hours, then drifts for an hour, moving with the current, then moves for three hours at the same speed, and so on. If the steamship starts its journey from city A and heads to city B, it takes 10 hours. If it starts from city B and heads to city A, it takes 15 hours. How long would it take to travel from city A to city B on a raft?
|
Answer: 60 hours.
Solution: Let the speed of the steamboat be $U$, and the speed of the river be $V$. When the steamboat travels from B to A, it arrives at the destination just before the fourth engine stop, meaning it travels 12 hours at a speed of $U-V$ towards A, and then 3 hours back at a speed of $V$ towards B. Therefore, the distance between the cities is $S=12(U-V)-3 V=12 U-15 V(1)$.
When the steamboat travels from A to B, it manages to break down twice and then continue for another two hours on its own. So, it travels 8 hours at a speed of $U+V$ towards B and 2 hours at a speed of $V$ with the current towards B. Thus, the distance is $S=8(U+V)+2 V=8 U+10 V$ (2). Equating the two, we get $12 U-15 V=8 U+10 V$ or $4 U=25 V$ or $(U / V)=(25 / 4)$. The time it will take to travel by raft is $S / V=12(U / V)-15(V / V)=12 *(25 / 4)$ - 15 $=60$ hours.
Criteria: Only the answer - 0 points. Correctly formulated equation (1) or (2) - 1 point (these points are cumulative).
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find all four-digit numbers $\overline{x y z t}$, where all digits $x, y, z, t$ are distinct and not equal to 0, such that the sum of all four-digit numbers obtained from $\overline{x y z t}$ by all possible permutations of the digits is 10 times the number $\overline{x x x x}$.
|
Answer. The number 9123 and all numbers obtained from it by permuting the last three digits, a total of 6 answers.
Solution. The number of four-digit numbers obtained from $\overline{x y z t}$ by all possible permutations of the digits is 24, in each of which each of the digits $x, y, z, t$ appears exactly 6 times in each place. Therefore, the sum of all such numbers is $6(x+y+z+t)(1000+100+10+1)=6666(x+y+z+t)$, which, by condition, equals $11110 x$. From this, $3(y+z+t)=2 x$. According to the condition, all digits $x, y, z, t$ are distinct and not equal to 0, so the left side of the equation is no less than $3(1+2+3)=18$, from which we get the only possibility $x=9$ and $y, z, t$ are any permutation of the digits $1,2,3$.
Evaluation Criteria. If a complete correct answer with verification is provided: 1 point. Correct finding of the sum on the left side of the equation: 3 points.
|
9123
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Around a circle, 32 numbers $a_{1}, a_{2}, \ldots, a_{32}$ are written, each of which is either -1 or 1. In one operation, each number $a_{n}, n=1,2, \ldots, 32$ is replaced by the product $a_{n} a_{n+1}$ of it and the next number in the cycle, with indices considered cyclically, $a_{33}=a_{1}, a_{34}=a_{2}$, and so on. Prove that for any initial set of numbers $a_{1}, a_{2}, \ldots a_{32}$, after some finite number of operations, a set of 32 ones will always be obtained. Find the smallest number $\mathrm{N}$ of operations such that after applying $\mathrm{N}$ operations, a set of 32 ones will always be obtained from any initial set of numbers.
|
Answer: 32.
Solution: We will prove by induction on $n$ that if $2^n$ numbers are written in a circle, the answer to the problem is $2^n$. The base case $n=1$ is straightforward: either $\{1,-1\} \rightarrow\{-1,-1\} \rightarrow\{1,1\}$, or $\{-1,-1\} \rightarrow\{1,1\}$, in any case, two operations are always sufficient, but fewer are not always enough.
Inductive step. Suppose $2^{n+1}$ numbers are written in a circle and the statement is true for any $2^n$ plus-minus ones in a circle. Consider separately the set A, consisting of $2^n$ numbers in the positions with odd indices, and set B - consisting of $2^n$ numbers in the positions with even indices. Note that after performing two operations, each number $a_k, k=1,2, \ldots, 32$ will be replaced by the product $\left(a_k a_{k+1}\right)\left(a_{k+1} a_{k+2}\right)=a_k a_{k+2}$, since $a_{k+1}^2=1$. This means that, as a result of performing two operations on the initial set of $2^{n+1}$ numbers, sets A and B change as if one operation had been performed on each of them. By the inductive hypothesis, to get sets of all ones from sets A and B, $2^n$ operations are sufficient, so to get all ones from the initial set, twice as many operations are needed, i.e., $2 \cdot 2^n = 2^{n+1}$ operations. An example of a set of numbers for which exactly $2^{n+1}$ operations are needed is a set of 31 ones and one minus one. After two operations, it will give similar sets of numbers A and B, for which, by induction, exactly $2^n$ operations are needed, so for the initial set, exactly $2 \cdot 2^n = 2^{n+1}$ operations are needed.
For the number of numbers $32=2^5$, the number of necessary operations is 32.
Evaluation criteria. It is proven that 32 operations are sufficient: 4 points. It is proven that fewer than 32 operations may not be enough: 3 points.
|
32
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.