problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
8.1. A number is called good if any two adjacent digits in its notation differ by at least 4. Vera wrote some good number, and then replaced identical digits with identical letters, and different ones with different letters. Could she have ended up with the word NOVOSIBIRSK?
|
Answer: For example, the number 82729161593 could work ( $\mathrm{H}=8, \mathrm{O}=2, \mathrm{~B}=7, \mathrm{C}=9$, I = 1, B = 6, $\mathrm{P}=5, \mathrm{~K}=3$).
Criterion: any valid example without verification - 7 points.
|
82729161593
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Find the angle $D A C$, given that $A B=B C$ and $A C=C D$, and the lines on which points $A, B, C, D$ lie are parallel, with the distances between adjacent lines being equal. Point $A$ is to the left of $B$, $C$ is to the left of $B$, and $D$ is to the right of $C$ (see figure).
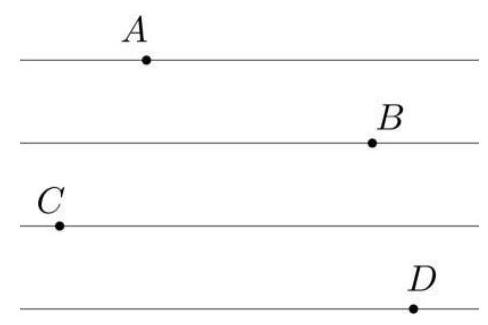
|
Answer: 30 degrees.
Solution: Let the line on which point $B$ lies be $b$, the line on which point $C$ lies be $c$, and the line on which point $D$ lies be $d$.
Suppose line $A C$ intersects line $b$ at point $M$. By Thales' theorem, $A M = M C$, since the distances between parallel lines are equal. Therefore, $B M$ is the median in the isosceles triangle $A B C$. Thus, $B M$ is also the altitude, meaning that angle $A M B$ is a right angle, as lines $b$ and $c$ are parallel, so $A C$ is perpendicular to line $c$. Let $A C = 2 x$, then the distance between the parallel lines is $x$. Extend $A C$ to intersect line $d$ at point $E$. Then $C E = x$, as the distance between the parallel lines, and $C D = 2 x$, since $A C = 2 x$. Additionally, in triangle $C E D$, angle $E$ is a right angle. Therefore, in the right triangle $C E D$, the hypotenuse is twice the length of one of the legs. This means that angle $E C D$ is 60 degrees, and the adjacent angle $A C D$ is 120 degrees. Then, in the isosceles triangle $A C D$, the two acute angles are each 30 degrees.
Criteria: It is proven that $A C$ is perpendicular to line $c-2$ points.
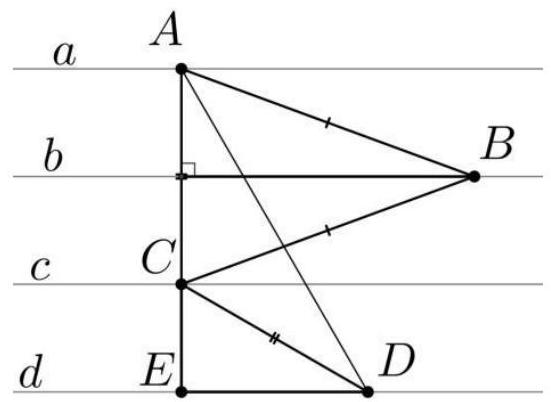
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Find the maximum odd natural number that cannot be represented as the sum of three distinct composite numbers.
|
Answer: 17.
Solution: An odd number gives a remainder of 1 or 3 when divided by 4. In the first case, the desired representation has the form \( n = 4k + 1 = 4(k-4) + 8 + 9, k \geq 5, n \geq 21 \), in the second case - \( n = 4k + 3 = 4(k-3) + 6 + 9, k \geq 4, n \geq 19 \). On the other hand, the three smallest composite numbers are 4, 6, 8, the sum of which is 18, so the number 17 cannot be represented in the required form. It is the answer to the problem.
Grading: Simply providing the answer with verification: 0 points. Failure to justify the non-representability of 17 in the desired form - minus 2 points.
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. In the cells of an 8 by 8 board, tokens are placed such that for each token, the row or column of the board in which it lies contains no more than three tokens. What is the maximum possible number of tokens on the board?
|
Answer: 30.
Solution: By swapping the verticals and horizontals, we assume that only the left $x$ verticals and the bottom $y$ horizontals contain more than 3 chips. From the condition, it follows that there are no chips at all in the lower left rectangle at the intersection of these verticals and horizontals. Each vertical passing through the chips in these horizontals contains no more than three chips, and each horizontal passing through the chips in these verticals contains no more than three chips. Then the total number of chips on the board does not exceed $3(8-x)+3(8-y)=48-3(x+y)$, which does not exceed 30 when $x+y \geq 6$.
Let $x+y \leq 5$ and $x \leq y$, then $x \leq 2$. We estimate the total number of chips on the board from above as $3(8-x)+x(8-y)=24+5x-xy$. For $x=2$, this is no more than 30, for $x=1, x=0$ - no more than 29 and 24, respectively.
Example of placing 30 chips: all cells of the three left verticals and the three bottom horizontals are filled, except for the lower left 3 by 3 square. Evaluation: 5 points for the estimate. 2 points for the example. Any incorrect estimate with any reasoning - 0 points.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Given the number 1836549, you can take two adjacent non-zero digits and swap their places, after which you subtract 1 from each of them. What is the smallest number that can result from these operations?
|
Answer: 1010101
Solution: The digits in the number alternate in parity: odd, even, etc. Note that with the described operation, even and odd numbers swap places, and then 1 is subtracted from them, thereby not disrupting the order of parity. Thus, it is impossible to obtain a number less than 1010101 (in each place, the smallest odd or even digit is placed, respectively).
Let's show how this result can be achieved (we perform the operation on the underlined digits, sometimes on two pairs simultaneously): $\underline{\underline{83}} 65 \underline{49}>12 \underline{7658} 3>125 \underline{6743}>12 \underline{56543}>12 \underline{54343}>1 \underline{23} 4343>1 \underline{214343}>$ 1014343
Next, each pair 43 is transformed into 23, then into 21, and then into 01, after which we get 1010101.
## Criteria for Determining Winners and Prize Winners of the All-Siberian Open Mathematics Olympiad for Schoolchildren (2015-2016 academic year)
According to the Regulations, the winners and prize winners of the Olympiad were determined based on the results of the Final Stage of the Olympiad. The total number of winners and prize winners was 380 out of 1578 participants, which is $24.08 \%$. The number of winners was 85, which is $5.38 \%$.
Based on the overall ranking of participants and taking into account the noticeable gaps in the scores of the groups of participants at the top of the ranking, the Olympiad jury developed the following criteria for determining winners and prize winners: The maximum possible score is 35 points.
## 11th Grade:
Winners:
Participants who scored more than $77 \%$ of the maximum possible points, i.e., from 27 to 35 points;
Prize winners:
2nd degree - more than $62 \%$ of the maximum possible points, i.e., from 22 to 26 points
3rd degree - more than $51 \%$ of the maximum possible points, i.e., from 18 to 21 points
10th Grade:
Winners:
Participants who scored more than $85 \%$ of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than $62 \%$ of the maximum possible points, i.e., from 22 to 29 points
3rd degree - more than $51 \%$ of the maximum possible points, i.e., from 18 to 21 points
9th Grade:
Winners:
Participants who scored more than $85 \%$ of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than $65 \%$ of the maximum possible points, i.e., from 24 to 29 points
3rd degree - more than $51 \%$ of the maximum possible points, i.e., from 18 to 23 points
8th Grade:
Winners:
Participants who scored more than $82 \%$ of the maximum possible points, i.e., from 29 to 35 points;
Prize winners:
2nd degree - more than $62 \%$ of the maximum possible points, i.e., from 22 to 28 points
3rd degree - more than $48 \%$ of the maximum possible points, i.e., from 17 to 21 points
7th Grade:
Winners:
Participants who scored more than $85 \%$ of the maximum possible points, i.e., from 30 to 35 points;
Prize winners:
2nd degree - more than $71 \%$ of the maximum possible points, i.e., from 24 to 29 points
3rd degree - more than $42 \%$ of the maximum possible points, i.e., from 15 to 21 points
Co-Chair of the Mathematics Jury

A.Yu. Avdyushenko
|
1010101
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. There is a steamship route between the cities of Dzerzhinsk and Lviv. Every midnight, a steamship departs from Dzerzhinsk, arriving exactly eight days later in Lviv. How many steamships will the steamship "Raritet" meet on its way to Dzerzhinsk if it departs from Lviv exactly at midnight and spends the same eight days on the journey?
|
Answer: 17.
Solution: As "Raritet" departs from Lviv, a steamer arrives there, which left Dzerzhinsk 8 days ago. By the time "Raritet" arrives at its final destination, 8 days have passed since the initial moment, and at this moment, the last steamer departs from Dzerzhinsk, which "Raritet" meets on its way. Thus, "Raritet" will meet all the steamers that departed from Dzerzhinsk, starting 8 days before the initial time and ending 8 days after the initial time - a total of 17 steamers (if it is considered that the ships meet when one departs and the other arrives at the same moment).
Criteria: only the answer, answer with verification - 0 points.
If it is considered that "Raritet" does not meet the first and/or last steamers - do not deduct points.
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Egor, Nikita, and Innokentiy took turns playing chess with each other (two play, one watches). After each game, the loser gave up their place at the board to the spectator (there were no draws). In the end, it turned out that Egor participated in 13 games, and Nikita in 27. How many games did Innokentiy play?
|
Answer: 14.
Solution: On the one hand, there were no fewer than 27 games. On the other hand, a player cannot skip two games in a row, meaning each player participates in at least every other game. Therefore, if there were at least 28 games, Egor would have participated in at least 14, which contradicts the condition. Thus, exactly 27 games were played, and Nikita participated in all of them. In 13 of these, his opponent was Egor, so in the remaining 14, it was Innokentiy, and this is the answer.
Criteria: Only the answer, answer with verification - 0 points.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Among all natural numbers from 1 to 20 inclusive, some 10 numbers were painted blue, and the other 10 - red, then all possible sums of pairs of numbers, one of which is blue and the other is red, were counted. What is the maximum number of different sums that can be among the hundred obtained numbers?
|
9.6. Answer. A maximum of 35 different numbers.
The sum of a blue and a red number can be a natural number from $1+2=3$ to $19+20=39$ inclusive, so there cannot be more than 37 different numbers. Moreover, note that one of the numbers $3,4, . ., 13$ must not be the sum of a blue and a red number. Otherwise, if the number 1 is blue, then 3 can only be represented as $1+2$, so 2 is red. The number 4 can only be represented as $1+3$, so 3 is also red. Next, $5=1+4=2+3$, but 2 and 3 are red, so only the first representation is valid, hence 4 is also red, and so on, we get that all 11 numbers $2,3, . ., 12$ are red, which is impossible. Similarly, we show that if all the numbers $29,30, \ldots, 39$ are sums of a blue and a red number, then 11 numbers $9, . ., 19$ are of the same color. Thus, there cannot be more than $37-2=35$ different numbers. One possible example where there are exactly 35 is as follows: $1,11,12, \ldots, 19$ are blue, and $2,3, \ldots, 10,20$ are red.
Grading remarks. Only the correct answer - 0 points. The correct answer and an example where it is achieved - 3 points. A correct proof of the maximum number 35 is worth 4 points. Attempts to solve where other estimates, different from 35, are proven, are graded 0 points.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In the bus, there are single and double seats. In the morning, 13 people were sitting in the bus, and there were 9 completely free seats. In the evening, 10 people were sitting in the bus, and 6 seats were completely free. How many seats are there in the bus?
|
Answer: 16.
Solution: If in the morning passengers sat on 6 double seats (i.e., as densely as possible), then they occupied 7 seats, with 9 seats still free. In total: 16 seats. If they did not sit as densely, then they would have occupied more seats. That is, there are no fewer than 16 seats in the bus, on the one hand.
On the other hand, if in the evening each passenger took a seat, then 10 seats were occupied, with 6 still free, a total of 16 seats. If some sat together, there would have been fewer seats. Therefore, there are no more than 16 seats.
Thus, there are no more, but also no fewer than 16 seats. Therefore, there are exactly 16 seats.
Criteria: only the answer, answer with verification - 1 point, estimation from only one side - 3 points, no points deducted for the lack of an example.
|
16
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In the country, there are 15 cities, some of which are connected by roads. Each city is assigned a number equal to the number of roads leading out of it. It turned out that there are no roads between cities with the same number. What is the maximum number of roads that can be in the country?
|
Answer: 85.
Solution: Let's order the city numbers in non-increasing order:
$$
a_{1} \geq a_{2} \geq \cdots \geq a_{15}
$$
Notice that the number of cities with number $15-i$ is no more than $i$. Indeed, if there are at least $i+1$ such cities, then they cannot be connected to each other, and thus can be connected to no more than $15-(i+1)=14-i$ cities, but they should be connected to $15-i$ cities, which is a contradiction.
Therefore, the maximum number is no more than 14, the next two are no more than 13, the next three are no more than 12, the next four are no more than 11, and the remaining five are no more than 10. The total sum of the numbers is no more than $14 + 2 \times 13 + 3 \times 12 + 4 \times 11 + 5 \times 10 = 170$. Since each road contributes to the numbers of exactly two cities, the total number of roads is no more than $170 \div 2 = 85$.
We will show that this can be achieved. Divide the country into 5 regions. In the first region, there is one city, in the second region, there are two, in the third region, there are three, and so on. Let the cities be connected if and only if they lie in different regions. Then the first city is connected to all others (has number 14), the cities in the second region are connected to all except each other (and have number 13), the cities in the third region are connected to $15-3=12$ cities, the cities in the fourth region are connected to $15-4=11$ cities, and the cities in the fifth region are connected to $15-5=10$ cities.
Criteria: evaluation - 4 points, example - 2 points
|
85
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. A square with a side of $100 \mathrm{~cm}$ was drawn on the board. Alexei crossed it with two lines parallel to one pair of sides of the square. Then Danil crossed the square with two lines parallel to the other pair of sides of the square. As a result, the square was divided into 9 rectangles, and it turned out that the lengths of the sides of the central section were 40 cm and 60 cm. Find the sum of the areas of the corner rectangles.
|
Answer: 2400.
Solution 1: Without loss of generality, we will assume that the central rectangle has a width of 60 cm and a height of 40 cm. Let $x$ and $y$ be the width and height, respectively, of the lower left rectangle. Then the upper left rectangle has sides $x$ and $(60-y)$, the upper right rectangle has sides $(40-x)$ and $(60-y)$, and the lower right rectangle has sides $(40-x)$ and $y$. The total area of the corner rectangles is
$$
x y + 60 x - x y + 40 y - x y + 2400 - 60 x - 40 y + x y = 2400.
$$
Solution 2: Suppose Alexei not only drew the lines but also cut out the entire central part bounded by these lines, and then Daniil did the same. Then, from the original square, only a rectangle of 60 by 40 remains on one side. On the other hand, everything that remains is the rectangles in question. Therefore, the area of the corner rectangles is equal to the area of the remaining rectangle and is 2400.
Criteria: Only the answer - 0 points. Answer with verification - 1 point.
In the solution, it is explicitly assumed that the cuts were made along the grid lines: if the solution relies on this (for example, by enumeration) - no more than 3 points; if the solution does not use this - do not deduct points.
|
2400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Egor, Nikita, and Innokentiy took turns playing chess with each other (two play, one watches). After each game, the loser would give up their place at the board to the spectator (there were no draws). In the end, it turned out that Egor participated in 13 games, and Nikita in 27. How many games did Innokentiy play?
|
Answer: 14.
Solution: On the one hand, there were no fewer than 27 games. On the other hand, a player cannot skip two games in a row, meaning each player participates in at least every other game. Therefore, if there were at least 28 games, Egor would have participated in at least 14, which contradicts the condition. Thus, exactly 27 games were played, and Nikita participated in all of them. In 13 of these, his opponent was Egor, so in the remaining 14, it was Innokentiy, and this is the answer.
Criteria: Only the answer, answer with verification - 0 points.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. On the table, 28 coins of the same size but possibly different masses are arranged in a triangular shape (see figure). It is known that the total mass of any triplet of coins that touch each other pairwise is 10 g. Find the total mass of all 18 coins on the boundary of the triangle.
|
Answer: 60 g.
Solution 1: Take a rhombus made of 4 coins. As can be seen from the diagram, the masses of two non-touching coins in it are equal. Considering such rhombi, we get that if we color the coins in 3 colors, as shown in the diagram, then the coins of the same color will have the same mass. Now it is easy to find the sum of the masses of the coins on the boundary: there are 6 coins of each color there, and the sum of the masses of three differently colored coins is 10 g; therefore, the total mass of the coins on the boundary is $6 \cdot 10=60$ g.
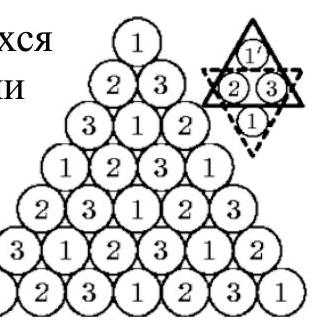
Solution 2: All coins except the central one can be divided into 9 triplets, and all internal coins except the central one can be divided into 3 triplets. Therefore, the coins on the boundary weigh as much as 9-3=6 triplets, i.e., 60 g.
Criteria: Only the answer - 0 points.
Rhombi are considered and it is shown that two coins in them have the same mass - 2 points. In addition to this, it is proven that the weights in the entire triangle are as shown in the diagram (coloring is done, but there is no further progress) - another 2 points.
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Find the smallest natural number divisible by 99, all digits of which are even.
|
Answer: 228888.
Solution. Let the sum of the digits of the desired number $X$, located in even-numbered positions (tens, thousands, etc.), be denoted by $A$, and the sum of the digits in odd-numbered positions (units, hundreds, etc.) be denoted by $B$. According to the divisibility rules for 9 and 11, $A+B$ is divisible by 9, and $A-B$ is divisible by 11. Given the evenness of the digits of the number, $A$ and $B$ are even, so $A+B$ is also divisible by 18, and $A-B$ is divisible by 22. If $A-B=0$, then $A$ and $B$ are equal and divisible by 9, and considering their evenness, $A$ and $B$ are divisible by 18. From this, it is easy to see that in this case, the desired number is not less than 228888, and the digits of the number 228888 are even and it is divisible by 9. Therefore, if there is such a number less than 228888, then for it $A \leq 18, B \leq 24$. Thus, if $A-B$ is not equal to 0, then $A-B=-22$, and either $A=0, B=22$, or $A=2, B=24$. In both cases, $A+B$ is not divisible by 9. Therefore, $X=228888$.
|
228888
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Find the smallest natural number ending in the digit 4 that quadruples when its last digit is moved to the beginning of the number.
|
# 7.4. Answer: 102564
If a number ending in 4 is multiplied by 4, the result is a number ending in 6, so the last digits of the desired number are 64. If such a number is multiplied by 4, the result is a number ending in 56, so the desired number ends in 564. Continuing to restore the number in this way, it turns out that the desired number should end in 102564. The smallest number ending with these digits is 102564. Comments on evaluation.
Answer only: 3 points. Answer and the observation that the number can be restored from the end: 4 points.
#
|
102564
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Find the maximum natural number $A$ such that for any arrangement of all natural numbers from 1 to 100 inclusive in a row in some order, there will always be ten consecutively placed numbers whose sum is not less than $A$.
|
Answer: 505.
Solution: The sum of all numbers from 1 to 100 is 5050. Let's divide the 100 numbers in a row into 10 segments, each containing 10 numbers. Clearly, the sum of the numbers in one of these segments is not less than 505, so A is not less than 505.
We will show that among the numbers arranged in the following order: $100,1,99,2,98,3, \ldots, 51,50$, there are no ten consecutive numbers whose sum is greater than 505. This will prove that A is not greater than 505, and considering the above, that $A=505$.
We will use the fact that in this arrangement, all numbers in odd positions decrease monotonically, while those in even positions increase monotonically, and the sum of a number in an odd position and the one following it is always 101. Therefore, the sum of any 10 consecutive numbers, the first of which is in an odd position, is always $505=5 * 101$. The sum of a segment of 10 consecutive numbers, the first of which is in an even position, is 505 minus the rightmost number among those to the left of this segment plus the last number of this segment. The two mentioned numbers are in odd positions, differing by 10, so the first is 5 greater than the second, and thus the entire sum is 500, which is less than 505.
Grading Criteria: Proof that A is not less than 505: 3 points. No justification for the lower bound $\mathrm{A}=505: -2$ points or -1 point.
Example proving that A is not greater than 505: 4 points.
Insufficient justification of the example: -2 points.
|
505
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. A merchant bought several bags of salt in Tver and sold them in Moscow with a profit of 100 rubles. With all the money earned, he again bought salt in Tver (at the Tver price) and sold it in Moscow (at the Moscow price). This time the profit was 120 rubles. How much money did he spend on the first purchase?
|
Answer: 500 rubles.
Solution: The additional 100 rubles spent the second time brought the merchant an additional 20 rubles in profit. Therefore, the first time, to earn $5 \cdot 20=100$ rubles in profit, the merchant must have paid $5 \cdot 100=500$ rubles.
Second solution: Let the amount of the first purchase be $x$, then for every ruble invested in Tver, he would receive $\frac{x+100}{x}$ rubles in Moscow. Consequently, after the second purchase-sale, he would receive $\frac{x+100}{x}(x+100)=x+100+120$ rubles. Solving this, we get $x=500$.
Grading criteria: Only the answer with verification: 2 points.
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Ten numbers are written around a circle, the sum of which is 100. It is known that the sum of any three consecutive numbers is not less than 29. Indicate the smallest number $A$ such that in any set of numbers satisfying the condition, each number does not exceed $A$.
|
Answer. $A=13$
Solution. Let $X$ be the largest of the listed numbers. The remaining numbers can be divided into 3 "neighbor" triplets. The sum of the numbers in each such triplet is no less than 29, therefore, $X \leq 100 - 3 \cdot 29 = 13$. An example of a set with the maximum number 13: $13,9,10,10,9,10,10,9,10,10$.
Grading criteria. Proven that the desired number is no less than 13: 4 points. Example for 13: 3 points
|
13
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Find the smallest natural number in which each digit occurs exactly once and which is divisible by 990.
|
Answer: 1234758690.
Solution. The number 990 is the product of coprime numbers 2, 5, 9, and 11. Any ten-digit number composed of different digits, each used once, is divisible by 9, since their sum, which is 45, is divisible by 9. According to the divisibility rule for 10, the desired number must end in 0. It remains to address the divisibility by 11.
The divisibility rule for 11 states: a number is divisible by 11 if and only if the difference between the sum of all its digits in odd positions from left to right and the sum of its digits in even positions is divisible by 11. Let's estimate the value of $\mathrm{S}$, the sum of the digits of the desired number in odd positions: it is no less than $1+2+3+4+5=15$ and no more than $5+6+7+8+9=35$. Therefore, the difference between the sum of all the digits in odd positions and the sum of the digits in even positions, equal to $2S-45$, is an odd number in the interval from -15 to 25, divisible by 11.
There are only two such numbers: -11 and 11, for which $\mathrm{S}$ is 17 and 28, respectively. It is easy to verify that for $S=17$ there are only two options: $S=1+2+3+4+7$ and $S=1+2+3+5+6$. Considering the minimality, this gives the number 1526384970.
For $\mathrm{S}=28$, we will list the smallest possible digits from left to right, as long as it is possible while maintaining the condition that the sum of the digits in odd positions can ultimately be 28, and the sum of the digits in even positions can be 17. This results in 1234, and the sum of the remaining 3 digits in the fifth, seventh, and ninth positions must equal 24, which is only possible if they are 7, 8, and 9, leading to the number in the answer. This number is smaller than the previously found 1526384970 for $S=17$. If a smaller number could be found, it would have $S=28$ and the fifth digit from the left would be less than 7, which, as we have seen, is impossible.
Grading criteria. If the answer is guessed and divisibility is verified: 1 point. Possible values of S are found: 2 points. The answer is written, and then the minimality is proven by full enumeration: 7 points.
|
1234758690
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In the list $1,2, \ldots, 2016$, two numbers $a<b$ were marked, dividing the sequence into 3 parts (some of these parts might not contain any numbers at all). After that, the list was shuffled in such a way that $a$ and $b$ remained in their places, and no other of the 2014 numbers remained in the same part where they were initially. In how many ways could $a$ and $b$ have been chosen?
|
Answer: $1+2+\ldots+1008=1009 * 504=508536$ ways.
## Solution:
Hypothesis. We will prove that the question is equivalent to counting the number of ways to split 2014 into three ordered non-negative addends $2014=x+y+z$, for which the non-strict triangle inequality holds, i.e., $x+y \geq z, x+z \geq y, y+z \geq x$.
Necessity. If we choose $a$ and $b$, then we have formed three numerical segments, in which there are 2014 numbers in total. It is clear that if the number of numbers in one of them is greater than the sum of the numbers in the other two, we will not be able to shuffle the numbers in the specified way.
Sufficiency. Choose $a=x+1, b=x+y+2$, that is, divide the sequence into parts with $x, y$ and $z$ numbers. We will prove that we can shuffle the numbers in the specified way. Assume $x \geq y \geq z$. It is known that $y+z \geq x$, and the other inequalities are automatically satisfied. Now we will swap numbers from $y$ and $z$ in pairs until the number of untouched numbers in $y$ and $z$ is exactly $x$. After that, we swap all numbers from $x$ with all untouched numbers from $y$ and $z$ and obtain the desired permutation.
Why is this possible? First, the number of numbers in $y$ and $z$ is at least $x$ by the triangle inequality, and each action reduces the number of untouched numbers by 2. But $x+y+z=$
2014, so $x$ and $(y+z)$ have the same parity, which means we will eventually get the required result.
Counting the ways: We will iterate over $x$. It changes from 0 to 1007, then $y+z \geq x$ is satisfied.
$x=0, y \geq z, z \geq y$, therefore, $z=y=1007$ - one way
$x=1,1+y \geq z, z+1 \geq y, y=2013-z$, therefore, $1007 \geq z ; z \geq 1006$ - two ways
$x=k . k+y \geq z, z+k \geq y, y=2014-k-z$. Therefore, $k+2014-k-z \geq z, z+k \geq 2014-k-z$, that is, $1007 \geq z ; z \geq 1007-k-(k+1)$ ways.
In total, $1+2+\ldots+1008=1009 * 504=508536$ ways.
Criteria:
Only the answer - 0 points
Only the hypothesis - 1 point.
Only the necessity - 1 point.
Only the sufficiency - 2 points.
Only the counting - 3 points.
These points are summed.
|
508536
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Let $A$ be a set of ten distinct positive numbers (not necessarily integers). Determine the maximum possible number of arithmetic progressions consisting of three distinct numbers from the set $A$.
|
Answer: 20.
Solution: Let the elements of set $A$ be denoted as $a_{1}<a_{2}<\ldots<a_{10}$. Three numbers $a_{k}<a_{l}<a_{m}$ form a three-term arithmetic progression if and only if $a_{l}-a_{k}=a_{m}-a_{l}$. Let's see how many times each element of $A$ can be the middle term $a_{l}$ of such a progression. It is easy to see that for an element $a_{l}, l=2,3,4,5$, the first element $a_{k}$ can be chosen in no more than $l-1$ different ways - it can only be $a_{1}, a_{2}, \ldots, a_{l-1}$. Therefore, the number of such progressions with the middle term $a_{l}, l=2,3,4,5$ cannot exceed $1+2+3+4=10$. Similarly, for an element $a_{l}, l=6,7,8,9$, the third element $a_{m}$ can be chosen in no more than $10-l$ different ways - it can only be $a_{l+1}, a_{l+2}, \ldots, a_{10}$. Therefore, the number of such progressions with the middle term $a_{l}, l=6,7,8,9$ cannot exceed $4+3+2+1=10$. Any sought three-term progression must be one of these two types, so the total number of such ways cannot exceed $1+2+3+4+4+3+2+1=20$.
As an example of a set $A$ with 10 elements where the value 20 is achieved, one can take the set of all natural numbers from 1 to 10 inclusive.
Grading criteria. ($\cdot$) Proven that the number of progressions is no more than 20: 5 points. ($\cdot$) Example with 20 progressions: 2 points.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. How many cells need to be marked on an 8 by 8 grid so that each cell on the board, including the marked ones, is adjacent by side to some marked cell? Find all possible answers. Note that a cell is not considered adjacent to itself.
|
Answer: 20.
Solution: First, let's gather our strength and mark twenty cells on an 8 by 8 board as required by the problem. For example, as shown in the figure. In this case, the board naturally divides into 10 parts, as indicated by the bold lines in the figure. Each part consists of cells adjacent to the given pair of marked cells.

Now, using the constructed example, we will prove that the only answer to the problem is indeed 20 cells. Consider the division of the board into 10 parts as shown in the example. From now on, we will call these parts figures, as in the example. We will call the central cells of each figure those that are marked in the example in the figure. Recall that the chessboard has a natural coloring of cells in a checkerboard pattern, and consider the black and white parts of each figure, consisting of black and white cells of this figure, respectively. Note that the white central cell of a figure is adjacent only to black cells of this figure, and only to all of them, and the black central cell of a figure is adjacent only to white cells of this figure, and only to all of them.
Now consider any marking of cells on the board that satisfies the problem's condition, and prove that each figure contains exactly two marked cells, from which the answer to the problem will follow. Indeed, if some figure contains at least three marked cells, then it contains at least two white marked cells or at least two black marked cells, then the central cell of the opposite color of this figure will be adjacent to at least two marked cells, which contradicts the condition. And if some figure contains no more than one marked cell, then it either has no white marked cells or no black marked cells, then the central cell of the opposite color of this figure will not be adjacent to any marked cell, which also contradicts the condition. Therefore, each figure contains exactly two marked cells, so any example contains exactly 20 marked cells.
Note that the example constructed in this solution is not unique, and we did not prove that the marked cells of any example coincide with those marked by us. The board can be rotated by 90 degrees, and a new example different from the one considered will result, but still, each figure contains exactly two marked cells from the new example.
Remark. The estimate for 20 can also be done differently, by first proving that the number of extreme marked cells is at least 9, etc. This is a long and risky path with case-by-case analysis. When evaluating such claimed solutions, each step must be very carefully assessed, and if such a solution contains unconsidered cases or errors in calculations, the estimation part of the solution is not rated higher than 1 point.
Evaluation Criteria: (•) An example with 20 cells is constructed: 3 points. (•) It is proven that the number of marked cells is always 20: 4 points. (•) The idea of considering figures from the board solution for estimation (without significant progress): 1 point.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Pasha and Sasha made three identical toy cars. Sasha did one-fifth of the total work. After selling the cars, they divided the proceeds in proportion to the work done. Pasha noticed that if he gave Sasha 400 rubles, and Sasha made another such car and sold it, they would have the same amount of money. How much does one car cost?
|
Answer: 1000 rubles.
Solution: Sasha did one-fifth of the entire work, which means he made 0.6 of one car, while Pasha did the remaining 2.4. That is, the difference is 1.8 cars. If Sasha makes another car, the difference will be 0.8 of one car. Pasha gave 400 of his rubles, thereby reducing the amount of money he had by 400 rubles and increasing the amount of money Pasha had by the same amount. That is, he changed the difference in the amount of money between one and the other by 800 rubles. Thus, 0.8 of a car corresponds to 800 rubles. Therefore, a whole car costs 1000 rubles.
Criteria: Only the answer - 0 points.
Answer with verification - 1 point.
Solution, in which 0.8 of a car corresponds to 400 rubles - no more than 2 points.
|
1000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. The company receives apple and grape juices in standard barrels and produces a cocktail (mixture) of these juices in standard cans. Last year, one barrel of apple juice was enough for 6 cans of cocktail, and one barrel of grape juice was enough for 10. This year, the proportion of juices in the cocktail (mixture) has changed, and now a standard barrel of apple juice is enough for 5 cans of cocktail. How many cans of cocktail will now be enough for a standard barrel of grape juice?
|
Answer: 15 cans.
Solution. Last year, one barrel of apple juice was enough for 6 cans of cocktail, which means each can contained $1 / 6$ of a barrel of apple juice. Similarly, one barrel of grape juice was enough for 10 cans, which means each can contained $1 / 10$ of a barrel of grape juice. Therefore, the capacity of a can is $1 / 6 + 1 / 10 = 4 / 15$ of a standard barrel. After the proportion change in the new year, each can now contains $1 / 5$ of a barrel of apple juice, which means the amount of grape juice in each can has become $4 / 15 - 1 / 5 = 1 / 15$ of a barrel. Therefore, a barrel of grape juice now suffices for 15 cans of cocktail.
Grading criteria. Clear explanation that the capacity of a can is 4/15 of a barrel: 3 points.
For not excluding an incorrect answer when the solution and answer are correct, minus 2 points.
For lack of explanation, from -2 to 0 points.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. For what minimum $\boldsymbol{n}$ in any set of $\boldsymbol{n}$ distinct natural numbers, not exceeding 100, will there be two numbers whose sum is a prime number?
|
Answer. $\boldsymbol{n}=51$.
Solution. The sum of two even natural numbers is always even and greater than two, hence it cannot be a prime number. Therefore, the example of a set of all fifty even numbers not exceeding 100 shows that the minimum $\boldsymbol{n}$ is not less than 51.
On the other hand, let's divide all natural numbers from 1 to 100 into 50 pairs, the sum of the numbers in each of which is the prime number 101: 1 and 100, 2 and 99, $\ldots, 50$ and 51. If the selected set contains no fewer than 51 numbers, then by the pigeonhole principle, at least two of them will fall into one pair, and their sum will be a prime number.
Grading criteria. Example showing that $\boldsymbol{n}$ is greater than 50: 2 points. Proof that in any set of 51 distinct natural numbers not exceeding 100, there will be two whose sum is a prime number: 5 points.
Idea of the example, but not explicitly provided +1 point.
|
51
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. In a set $X$ of 17 elements, a family of $N$ distinct non-empty subsets is selected such that each element of the set $X$ is contained in exactly two subsets from this family. What is the maximum value of $N$? Find the number of all possible different types of such families for the maximum $N$. Two families of subsets have different types if one cannot be obtained from the other by permuting the elements of $X$.
|
Answer. The maximum $N$ is 25, and there exist two different types of families of 25 subsets that satisfy the condition of the problem.
Solution. Consider an arbitrary family of $N$ distinct non-empty subsets such that each element of the set $X$ is contained in exactly two subsets of this family. If there are $x$ one-element subsets, then the total sum $\mathrm{S}$ of the cardinalities of the subsets in this family is at least $x + 2(N - x) = 2N - x$. On the other hand, each element of the set $X$ is contained in exactly two subsets of this family, so $\mathrm{S} = 34$, which means $\mathrm{N}$ does not exceed $(34 + x) / 2$. Finally, the number of one-element subsets $x$ does not exceed the number of elements in $X$, which is 17, so $N$ does not exceed 25. Note that for $N = 25$, the number of one-element subsets in the family can be 16 or 17.
1) If $x = 17$, then the remaining 8 "large" subsets must be two- or more-element subsets. If there are $y$ two-element subsets among them, then the total number of elements in the 8 large subsets is 17 and is at least $2y + 3(8 - y) = 24 - y$, so $y$ is at least 7. If it is greater than 7, then the three- and more-element subsets in total would contain one element, which is impossible. Therefore, the only possibility is 7 pairwise disjoint two-element subsets and one three-element subset. Together with the 17 one-element subsets, they form the first example of the family of subsets sought in the problem. An example of a family of this type: 17 one-element subsets $\{1\}, \{2\}, \ldots, \{17\}$, 7 two-element subsets $\{1, 2\}, \{3, 4\}, \ldots, \{13, 14\}$, and one three-element subset $\{15, 16, 17\}$.
2) If $x = 16$, then the remaining 9 subsets must be two- or more-element subsets. If there are $y$ two-element subsets among them, then the total number of elements in the 9 large subsets is 18 and is at least $2y + 3(9 - y) = 27 - y$, so $y$ is at least 9. Therefore, all large subsets are two-element subsets. In total, they contain 18 elements, so two of them intersect at one element (which does not lie in any one-element subset), while the rest are pairwise disjoint. Together with the 16 one-element subsets, they form the second, different from the first, example of the family of subsets sought in the problem. An example of a family of this type: 16 one-element subsets $\{1\}, \{2\}, \ldots, \{16\}$, 9 two-element subsets $\{1, 2\}$, $\{3, 4\}, \ldots, \{13, 14\}, \{15, 17\}, \{16, 17\}$.
In the course of the reasoning, we proved that there are no other families different from the ones found.
Grading criteria. For each found example of one of the two types of families: 1 point each. Proof of the maximality of $N = 25$: 3 points. Proof that there are exactly 2 types of maximal families: 2 points.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Given a triangle $\mathrm{ABC}$ with angle $\mathrm{BAC}$ equal to $30^{\circ}$. In this triangle, the median $\mathrm{BD}$ was drawn, and it turned out that angle $\mathrm{BDC}$ is $45^{\circ}$. Find angle $\mathrm{ABC}$.
|
Answer: $45^{\circ}$
Solution: Draw the height $C H$. Then $H D=A D=C D$ as the median to the hypotenuse. Moreover, $\angle H C D=\angle C H A-\angle H A C=60^{\circ}$, so triangle $C H D$ is equilateral, which means $\angle H D C=60^{\circ}$ (from which it follows, in particular, that $H$ lies between $A$ and $B$). Then $\angle H D B=\angle H D C-\angle B D C=15^{\circ}$. Furthermore, $\angle A B D=\angle B D C-\angle B A D=15^{\circ}$. Therefore, triangle $H B D$ is isosceles, and $H B=H D=H C$, which implies that $B H C$ is an isosceles right triangle, and thus $\angle A B C=45^{\circ}$.
Criteria: The height $C H$ is drawn - 1 point.
It is additionally proven that $\angle H D B=15^{\circ}$ - another 2 points.
No points are deducted for the lack of proof that $H$ lies between $A$ and $B$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In the city of Omsk, a metro has been built, represented by a straight line. On this same line is the house where Nikita and Egor live. Every morning they leave the house for classes at the same time, after which Egor runs to the nearest metro station at a speed of 12 km/h, while Nikita walks along the metro line to another station at a speed of 6 km/h. Despite this, every day Nikita manages to arrive on time for the first lesson, while Egor does not, even though he is not delayed anywhere. Find the greatest possible speed of the metro trains, given that it is constant and equal to an integer. (Assume that the school is located directly on a certain metro station, different from the given ones).
|
Answer: 23 km/h
Solution: Obviously, this is only possible if the subway train first arrives at the nearest station A, where Egor runs to, and then goes to station B, where Nikita is heading.
Let $v$ be the speed of the subway, $S$ be the distance between two adjacent stations, and $R$ be the distance between this subway train and the nearest station at the moment when Nikita and Egor leave home simultaneously.
Egor does not catch the subway, which means $R / v < (S / 2) / 6$
From this, we get: $S v / 12 - S1 / 10$ hours and does not make it.
The subway takes 4.75 km / 23 km/h = 4.75 / 23 hours to reach station B. Nikita walks to station B in $1.23 / 6$ hours < 4.75 / 23 and makes it!
Criteria: Only the answer - 3 points.
Only a complete example with full justification - 3 points
Deduct 2 points for a correct example without justification.
|
23
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. From points A and B towards each other with constant speeds, a motorcyclist and a cyclist started simultaneously from A and B, respectively. After 20 minutes from the start, the motorcyclist was 2 km closer to B than the midpoint of AB, and after 30 minutes, the cyclist was 3 km closer to B than the midpoint of AB. How many minutes after the start did the motorcyclist and the cyclist meet
|
Answer: In 24 minutes.
Solution: In 10 minutes, the motorcyclist travels $1 / 4$ of the distance from A to B plus 1 km, while the cyclist travels $1 / 6$ of the distance from A to B minus 1 km. Therefore, in 10 minutes, both of them, moving towards each other, cover $1 / 4 + 1 / 6 = 5 / 12$ of the distance from A to B. This means they will cover the distance from A to B, that is, meet, in $10 * 12 / 5 = 24$ minutes.
Grading Criteria. Correct answer with verification: 3 points. Correctly formulated system of equations: 3 points.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Several consecutive natural numbers are written on the board. It is known that $48 \%$ of them are even, and $36 \%$ of them are less than 30. Find the smallest of the written numbers.
|
Answer: 21.
Solution. $\frac{48}{100}=\frac{12}{25}, \frac{36}{100}=\frac{9}{25}$ - these are irreducible fractions, so the total number of numbers is divisible by 25. If there were 50 or more, then, by the condition, there would be at least 2 fewer even numbers than odd numbers, which is impossible for consecutive natural numbers. Therefore, there are 25, and exactly 9 of them are less than 30. Thus, the first one is 21.
|
21
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a family of 4 people. If Masha's scholarship is doubled, the total income of the entire family will increase by $5 \%$, if instead the mother's salary is doubled - by $15 \%$, if the father's salary is doubled - by $25 \%$. By what percentage will the family's total income increase if the grandfather's pension is doubled?
|
Answer: by $55 \%$.
Solution: When Masha's scholarship is doubled, the family's total income increases by the amount of this scholarship, so it constitutes $5 \%$ of the income. Similarly, the salaries of Masha's mother and father constitute $15 \%$ and $25 \%$. Therefore, the grandfather's pension constitutes $100-5-15-25=55 \%$, and if it is doubled, the family's income will increase by $55 \%$.
Criterion: Only the answer, answer with verification - 0 points.
|
55
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. There are 100 boxes numbered from 1 to 100. One of the boxes contains a prize, and the host knows where it is. The audience can send the host a batch of notes with questions that require a "yes" or "no" answer. The host shuffles the notes in the batch and, without reading the questions aloud, honestly answers all of them. What is the minimum number of notes that need to be sent to definitely find out where the prize is?
|
Answer: 99.
Solution: To be able to definitively determine which of the 100 boxes contains the prize, it is necessary to have the possibility of receiving at least 100 different answers to one set of questions. Since the host's answers for different prize positions can only differ by the number of "yes" responses, it is necessary to have the possibility of receiving at least 100 different counts of "yes." Therefore, at least 99 questions are required (from 0 to 99 "yes").
Example with 99 questions: Let the $k$-th question be: "Is the number of the box containing the prize less than or equal to $k$?" Then, if the number of "yes" answers is zero, the prize is in the hundredth box; if one, it is in the 99th box, and so on.
Criteria: Only the evaluation -3 points, only the example -3 points. Only the answer - 0 points.
|
99
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. On a certain island, only knights, who always tell the truth, and liars, who always lie, live. One day, 1001 inhabitants of this island stood in a circle, and each of them said: "All ten people following me in a clockwise direction are liars." How many knights could there be among those standing in the circle?
|
Answer: 91 knights.
Solution. Note that all people cannot be liars, because then it would mean that each of them is telling the truth. Therefore, among these people, there is at least one knight. Let's number all the people so that the knight is the 1001st in the sequence. Then the 10 people with numbers from 1 to 10 are liars (this follows from the knight's statement). Moreover, the 10 people with numbers 991-1000 are also liars, as they made an incorrect statement (there is a knight among the ten people standing after them). Therefore, since these 10 people stand in a row along our circle after person number 990, he told the truth and, consequently, is also a knight. Repeating the reasoning for him, we get that people with numbers 980-989 are liars, and so on. In the end, we get that the knights are people with numbers $1001, 990, 979, \ldots, 11$, that is, there are a total of $1001 / 11 = 91$ of them.
For completeness of the reasoning, note that we have proven that if the arrangement is possible, it looks exactly like this. It is not difficult to check that there are no contradictions, and the people could indeed stand this way.
Criteria. Only the answer - 0 points.
Only the answer with an example of the arrangement - 2 points.
The case where there are no knights is not considered - do not deduct points.
Not verified that the obtained arrangement fits - do not deduct points.
|
91
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. We will call a number remarkable if it can be decomposed into the sum of 2023 addends (not necessarily distinct), each of which is a natural composite number. Find the largest integer that is not remarkable.
|
Answer. $4 \times 2023+3=8095$.
Solution. Replace 2023 with $n$ and solve the problem in the general case for a sum of $n \geqslant 2$ composite addends. We will prove that the answer is $4 n+3$, from which we will obtain the answer to the original problem.
Claim 1. The number $4 n+3$ is not remarkable.
Proof of Claim 1. Note that $4 n+3$ is odd, so in its decomposition into a sum, there must be at least one odd addend. The smallest odd composite number is 9, and the smallest even composite number is 4. Therefore, the sum of $n$ addends is at least
$$
9+4(n-1)=4 n+5>4 n+3,
$$
from which it follows that $4 n+3$ cannot be decomposed into a sum of $n$ composite addends, that is, it is not remarkable.
Claim 2. Any natural number greater than $4 n+3$ is remarkable. Proof of Claim 2. Consider the number $a>4 n+3$. If it is even, then it can be written as
$$
a=(4 n-4)+b=b+\underbrace{4+4+\ldots+4}_{n-1},
$$
where $b \geqslant 8-$ is some even number that is composite. If $a$ is odd, then
$$
a=4 n+1+c=9+(4 n-8)+c=9+c+\underbrace{4+4+\ldots+4}_{n-2}
$$
where $c \geqslant 4-$ is some even number that is composite.
In total, the number $4 n+3$ is not remarkable, and all larger numbers are remarkable. From this, we obtain the answer to the question of the problem.
Criteria. Proof of Claim 1 or an equivalent statement - 3 points. Proof of Claim 2 or an equivalent statement - 2 points for the even and odd cases.
|
8095
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Let $n$ be a natural number not ending in 0, and $R(n)$ be the four-digit number obtained from $n$ by reversing the order of its digits, for example $R(3257)=7523$: Find all natural four-digit numbers $n$ such that $R(n)=4n+3$.
|
Answer: 1997.
Solution. Consider the decimal representation of the original four-digit number $n=\overline{a b c d}$, then $R(n)=\overline{d c b a}=4 n+3$ is also a four-digit number. Therefore, $4 a \leq 9$, so $a=1$ or $a=2$. Moreover, the number $R(n)=\overline{d c b a}=4 n+3$ is odd and ends in $a$, hence $a=1$. If the number $4 n+3$ ends in 1, then $n$ must end in 2 or 7, that is, $d=2$ or $d=7$. The first is impossible, since $d \geq 4 a \geq 4$, so $d=7$. Substituting the found values into the equation from the condition: $R(n)=4 \cdot \overline{a b c d}+3=4031+400 b+40 c=7001+100 c+10 b$, from which $13 b-2 c=99$. From this, $b \geq \frac{99}{13}=7 \frac{8}{13}$, that is, $b=8$ or $b=9$. When $b=8$, the left side of the equation $13 b-2 c=99$ is even, which is impossible, so $b=9$ and $c=9$.
Grading criteria. Answer: 2 points. Proof that there are no other answers: 5 points.
|
1997
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Losharik is going to visit Sovunya along the river at a speed of 4 km/h. Every half hour, he launches paper boats that float to Sovunya at a speed of 10 km/h. With what time interval do the boats arrive at Sovunya?
|
Solution: If Losyash launched the boats from one place, they would arrive every half hour. But since he is walking, the next boat has to travel a shorter distance than the previous one. In half an hour, the distance between Losyash and the last boat will be $(10-4) \cdot 0.5=3$. This means that the distance between adjacent boats is 3 km, and the next boat will have to travel exactly this distance when the previous one has already reached Sovunya. The speed of the boat is 10 km/h, which means 1 km in 6 minutes, so 3 km will be covered by the boat in 18 minutes, which is the answer.
Criteria: Correctly found the distance of 3 km - 3 points.
Only the answer or the answer with verification - 1 point.
|
18
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Find the largest four-digit number, all digits of which are different, and which is divisible by each of its digits. Of course, zero cannot be used.
|
Solution: Since the number of digits is fixed, the number will be larger the larger the digits in its higher places are. We will look for the number in the form $\overline{98 a}$. It must be divisible by 9. Therefore, the sum $a+b$ must give a remainder of 1 when divided by 9. At the same time, this sum does not exceed 13, as it consists of different single-digit addends, which are less than 8. Therefore, this sum is either 1 or 10. The largest variant that fits these conditions is 9873, but it does not work since it is not divisible by 8. The next highest in seniority, 9864, clearly works.
Solution: Only proven that the number 9864 works - 2 points. The idea to look for the answer in the form $\overline{98 a b}-1$ - 1 point.
|
9864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
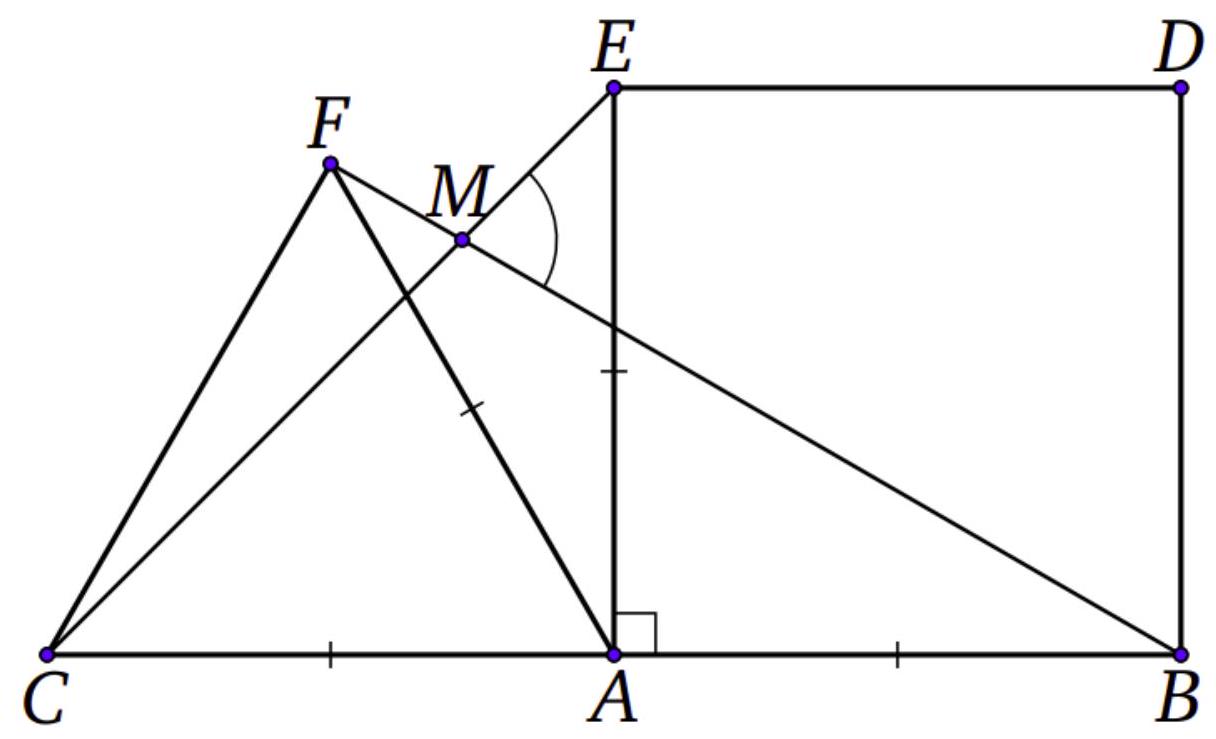
8.4. Point $A$ is located midway between points $B$ and $C$. The square $A B D E$ and the equilateral triangle $C F A$ are in the same half-plane relative to the line $B C$. Find the angle between the lines $C E$ and $B F$.
|
Solution: Let $M$ be the point of intersection of segments $B F$ and $C E$. Note that $\angle C F B = 90^{\circ}$, since $F A$ is a median equal to half the side to which it is drawn. From this, it follows that $\angle F B C = 180^{\circ} - 90^{\circ} - \angle F C B = 30^{\circ}$. From the isosceles right triangle $C A E$, it follows that $\angle E C A = 45^{\circ}$.
Then, in triangle $C M B$, the angle $\angle C M B = 180^{\circ} - \angle M B C - \angle M C B = 180^{\circ} - 30^{\circ} - 45^{\circ} = 105^{\circ}$, which is the answer.
Criteria: The angle $\angle C B F$ is found - 2 points.
The angle $\angle E C A$ is found - 1 point.
It doesn't matter whether the angle is found to be $105^{\circ}$ or $75^{\circ}$.
|
105
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. In each cell of a 10 by 10 table, a minus sign is written. In one operation, it is allowed to simultaneously change the signs to their opposites in all cells of some column and some row (plus to minus and vice versa). What is the minimum number of operations required to make all the signs in the table pluses?
|
Answer. In 100 operations.
Solution. There are 19 cells in total in the row and column passing through a given cell, so if we perform operations on all pairs of rows and columns of the table (a total of $10 \times 10=100$ operations), each sign in the table will change 19 times, turning from minus to plus, so 100 operations are sufficient.
We will call the operation of changing the signs in all cells of a certain column and a certain row an operation relative to the cell at the intersection of these row and column. Cells relative to which we performed operations will be called red, and the rest - blue. Rows and columns containing an even number of red cells will be called even, and those containing an odd number of red cells - odd. Suppose it is possible to change all the signs in the table in fewer than 100 operations, then consider some blue cell A in row X and column Y. For the sign in A to change, row X and column Y together must contain an odd number of red cells, we can assume row X is even, and column Y is odd. Note that at the intersection of rows and columns of the same parity, there should be a red cell, and at the intersection of rows and columns of different parity - a blue cell, otherwise the sign in this cell will not change after all operations. Therefore, the number of red cells in each even row is equal to the number of even columns, and the number of blue cells is equal to the number of odd columns in the table. There is at least one even row X, so there is an even number of odd columns in the table. But the number of red cells in each odd row (odd!) is equal to the number of odd columns, which is an even number - a contradiction with the fact that there is at least one odd column. Therefore, it is impossible to manage with fewer than 100 operations.
Instructions. Correct example for 100 operations with explanations: 2 points. Proof of the minimality of $100: 5$ points.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. In Nastya's room, 16 people gathered, each pair of whom either are friends or enemies. Upon entering the room, each of them wrote down the number of friends who had already arrived, and upon leaving - the number of enemies remaining in the room. What can the sum of all the numbers written down be, after everyone has first arrived and then left?
|
Answer: 120
Solution: Consider any pair of friends. Their "friendship" was counted exactly once, as it was included in the sum by the person who arrived later than their friend. Therefore, after everyone has arrived, the sum of the numbers on the door will be equal to the total number of friendships between people. Similarly, each "enmity" will be counted exactly once by the person who left earlier. Therefore, after everyone has left, the sum of the numbers on the door will be increased by the total number of "enmities." In total, the overall sum of the numbers on the door will be equal to the sum of the total number of friendships and enmities, which is precisely the number of pairs of people who arrived, i.e., $16 * 15 / 2 = 120$.
Criteria: only answer - 0 points.
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In a school, there are 1000 students and 35 classes. On the forehead of each student, the number of students in their class is written. What can the sum of the reciprocals of these numbers be? List all the options and prove that there are no others. Recall that the reciprocal of a number $a$ is the number $1 / a$.
|
Answer: 35.
Solution: Let there be a people in the class, then the sum of the fractions corresponding to the numbers from this class is 1 (a fractions, each equal to 1/a). There are 35 classes in total. Therefore, the total sum is 35.
Criteria:
Answer - 0 points.
Answer with examples - 0 points.
The idea of partitioning into classes and calculating sums separately for each class without further progress - 5 points.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a competition, there are 2018 Dota teams, all of different strengths. In a match between two teams, the stronger one always wins. All teams paired up and played one game. Then they paired up differently and played another game. It turned out that exactly one team won both games. How could this be
|
Solution: Let's number the teams in ascending order of strength from 1 to 2018. In the first round, we will have the matches 1 - 2, $3-4, \ldots, 2017$ - 2018, and in the second round - $2018-1, 2-3, 4$ - 5, ..., 2016 - 2017. It is obvious that only the team with the number 2018 will win in both rounds.
## Criteria:
Any correct example without explanation - 7 points.
|
2018
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Eleven of the best football teams each played one match against each other. It turned out that each team scored 1 goal in their first match, 2 goals in their second match, ..., 10 goals in their tenth match. What is the maximum number of matches that could have ended in a draw?
|
Solution: According to the condition, each team scored 1 goal in the first game. In the case of a draw, it also conceded 1 goal. Then for the other team, this match was also the first. Since the number of teams is odd, they cannot be paired. Therefore, at least one of the teams played a non-draw in their first match. The same is true for the second, third, ..., tenth matches. Since each match is counted twice, there were at least 5 non-draw matches, and then the number of draws was no more than $11 \cdot 10 / 2 - 5 = 50$.
Let's provide an example of a tournament with 50 draws. Number the teams from 1 to 11. Form 5 pairs of adjacent teams (leaving the 11th team without a pair). First, the teams in the pairs play against each other, and then the 11th team plays against the 1st (with a score of $1:2$). Again, we pair the teams, this time excluding the 1st, and let the teams in the pairs play again (resulting in 5 draws). Now arrange the teams in a circle with a step of 2, specifically in the order 1357911246810 (each team has two new neighbors). Applying the same match scheme, we get another 11 games, one of which is non-draw. Then apply this scheme for steps of 3, 4, and 5.
We can even write out a specific table:
| All play the first game, all draws | $12,34,56,78,910$ |
| :--- | :--- |
| 11 - first game, 1 - second game | 111 |
| All play the second game, all draws | $23,45,67,89,1011$ |
| All play the third game, all draws | $13,57,911,24,68$ |
| 10 - third game, 1 - fourth game | 101 |
| All play the fourth game, all draws | $35,79,112,46,810$ |
| All play the fifth game, all draws | $14,710,25,811,36$ |
| 9 - fifth game, 1 - sixth game | 91 |
| All play the sixth game, all draws | $47,102,58,113,69$ |
| All play the seventh game, all draws | $15,92,610,37,114$ |
| 8 - seventh game, 1 - eighth game | 81 |
| All play the eighth game, all draws | $59,26,103,711,48$ |
| All play the ninth game, all draws | $16,115,104,93,82$ |
| 7 - ninth game, 1 - tenth game | 71 |
| All play the tenth game, all draws | $611,510,49,38,27$ |
## Criteria:
Only the answer - 0 points.
Only the estimate that there are no more than $50-2$ points.
Only an example with 50 draws - 3 points.
There is an estimate and a correct idea for the example, but there are inaccuracies - 5 or 6 points depending on the size of the inaccuracies.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. In triangle $\mathrm{ABC}$, the bisectors of angles $\mathrm{BAC}$ and $\mathrm{BCA}$ intersect sides ВС and АВ at points К and Р, respectively. It is known that the length of side АС is equal to the sum of the lengths of segments АР and СК. Find the measure of angle $\mathrm{ABC}$.
|
Answer: $60^{\circ}$.
Solution 1. Let the angles of triangle ABC be denoted by the corresponding letters $\mathrm{A}, \mathrm{B}$, and $\mathrm{C}$, and the intersection point of the angle bisectors by I. Reflect points P and K with respect to the angle bisectors AK and CP, respectively; their images will be points $\mathrm{P}^{\prime}$ and $\mathrm{K}^{\prime}$ on side $\mathrm{AC}$ such that $\mathrm{AP}^{\prime}=\mathrm{AP}, \mathrm{CK}^{\prime}=C K$. Since $\mathrm{AP}^{\prime}+\mathrm{CK}^{\prime}=\mathrm{AP}+\mathrm{CK}=\mathrm{AC}$, points $\mathrm{P}^{\prime}$ and $\mathrm{K}^{\prime}$ coincide, and we denote this point as M. The measures of angles AMI=API=APC $=180^{\circ}-\mathrm{A}-$ C/2, CMI=CKI=CKA $=180^{\circ}-\mathrm{C}-\mathrm{A} / 2$. Their sum is $360^{\circ}-3(\mathrm{~A}+\mathrm{C}) / 2=360^{\circ}-$ $270^{\circ}+3 \mathrm{~B} / 2=90^{\circ}+3 \mathrm{~B} / 2=180^{\circ}$, from which $\mathrm{B}=60^{\circ}$. Therefore, the measure of angle $\mathrm{ABC}$ is 60.
Solution 2. Let the lengths of sides $\mathrm{AB}, \mathrm{BC}, \mathrm{AC}$ of the triangle be $c, a, b$ respectively, and find the lengths of all segments used in the problem using the property of the angle bisector. Then $A P=\frac{b c}{a+b}, C K=\frac{a b}{b+c}$, from which $A P+C K=\frac{b c}{a+b}+\frac{a b}{b+c}=\frac{b^{2} c+b c^{2}+a^{2} b+a b^{2}}{a b+a c+b c+b^{2}}=A C=b$. Simplify both sides by $b$, multiply by the denominator, combine like terms, and we get: $b^{2}=a^{2}+c^{2}-a c$. By the cosine rule, $b^{2}=a^{2}+c^{2}-2 a c \cdot \operatorname{Cos} B$, from which $\operatorname{Cos} B=\frac{1}{2}$ and $B=\angle A B C=60^{\circ}$.
Grading criteria. In the first solution ($\bullet$) The idea of reflecting points P and K with respect to the angle bisectors AK and CP is present: 1 point, ($\cdot$) It is shown that the images under such reflection will give a common point on side AC: another 1 point. In the second solution ($\cdot$) AP and CK are found: 3 points. ($\cdot$) The equality $b^{2}=a^{2}+c^{2}-a c$ is obtained: another 2 points. ($\cdot$) From this, $\operatorname{Cos} B=\frac{1}{2}$ is derived: 2 points.
($\cdot$) A special case with a certain arrangement of radii is considered: 2 points.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. On some cells of a rectangular board of size 101 by 99, there is one turtle each. Every minute, each of them simultaneously crawls to one of the cells adjacent to the one they are in, by side. In doing so, each subsequent move is made in a direction perpendicular to the previous one: if the previous move was horizontal - to the left or right, then the next one will be vertical - up or down, and vice versa. What is the maximum number of turtles that can move around the board indefinitely such that at each moment, no more than one turtle is in any cell?
|
Answer: 9800.
Solution. Examples of unlimited movement on the board of 9800 turtles.
Example 1. Place the reptiles in the cells of a rectangle consisting of cells at the intersection of the 98 lower horizontals and 100 leftmost verticals. They will all move in the same way: first all to the right, then all up, then all to the left, and then all down.
After 4 moves, the situation will coincide with the initial one, so the movement can continue in a permitted manner indefinitely.
Example 2. The initial placement of turtles is the same as in Example 1, but the movement is organized such that they are divided into 2x2 square cells, in each of which they simultaneously move clockwise.
We will prove that it is impossible to properly place more than 9800 turtles on a 101x99 board. Suppose the contrary, that the turtles are placed on the board in some way such that they have the possibility to move around the board indefinitely in the manner specified in the condition and not end up on the same cell in a quantity of two or more simultaneously. Color the cells of the board in a checkerboard pattern, with the lower left cell, as usual, being black. This will result in 5000 black and 4999 white cells. Among the black cells, we will call the cells with both vertical and horizontal coordinates being odd "odd" cells, and those with both coordinates being even "even" cells. Note that for white cells, one of these coordinates is even, and the other is odd. There will be $51 \cdot 50=2550$ odd black cells and $50 \cdot 49=2450$ even black cells. Clearly, at any moment, the number of turtles on even black cells should not exceed 2450.
Note that when two consecutive moves are performed, the parity of both coordinates of each turtle changes, so after two moves, all turtles from odd black cells will move to even black cells and vice versa, while turtles from white cells will move back to white cells. Consequently, at any time, the number of turtles on all black cells does not exceed $2 \cdot 2450=4900$.
Finally, when one move is performed, turtles from black cells move to white cells and vice versa, so the total number of turtles on the entire board cannot exceed $2 \cdot 4900=9800$.
Remark. In fact, we have proven that if there are more than 9800 turtles on the board, they will be able to make no more than two moves without ending up on the same cell in a quantity of two or more simultaneously.
Grading criteria. Proof of the maximality of the number 9800: 6 points. Construction of an example for 9800 turtles: 1 point. Attempt to prove any other estimate except 9800: 0 points.
|
9800
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. In each cell of a $5 \times 5$ table, one of the numbers $1,2,3,4,5$ is written in such a way that each row, each column, and each of the two diagonals of the table contains each of the numbers from 1 to 5. What is the maximum value that the sum of the five numbers written in the cells marked with dots on the diagram can take?
|
Answer: 22.
Solution. If all 4 numbers marked with a dot and not in the top right corner are different, then the sum of all numbers marked with a dot does not exceed $5+5+4+3+2=19$. Let's further assume that among these numbers there are two equal ones, and consider three possible arrangements of their positions. Denote the columns of the table from left to right by the letters $a, b, c, d, e$, and the rows by the numbers from 1 to 5. The diagonal from corner $a 1$ to corner $e 5$ will be called the main diagonal, and the diagonal from corner $a 5$ to corner $e 1$ will be called the secondary diagonal. The pair of equal numbers will be denoted by $a$.
1) The numbers in cells $a 4$ and $d 1$ are equal. The remaining numbers equal to $a$ cannot be placed in the 1st and 4th rows and in columns $a$ and $d$, so on the secondary diagonal, $a$ can only be in cell $c 3$. The two remaining numbers $a$ can only be in cells $b 5$ and $e 2$.
2) The numbers in cells $b 3$ and $c 2$ are equal. The remaining numbers equal to $a$ cannot be placed in the 2nd and 3rd rows and in columns $b$ and $c$, so on the diagonals, the number $a$ can only be in the corner cells and cell $d 4$.
The corner cells cannot contain two equal numbers, as any pair of corner cells lies either in the same row, column, or diagonal, so one $a$ is in cell $d 4$. It excludes cells on the main diagonal, row 4, and column $d 4$, so the two remaining numbers $a$ can only be in cells $a 5$ and $e 1$ on the secondary diagonal, which is impossible.
3) The numbers in cells $a 4$ and $c 2$ are equal. The remaining numbers equal to $a$ cannot be placed in the 2nd and 4th rows and in columns $a$ and $c$, so on the diagonals, the numbers $a$ can only be in the corner cells $e 1$ and $e 5$. These cells lie in the same column, which is impossible.
4) The numbers in cells $a 4$ and $b 3$ are equal. The remaining numbers equal to $a$ cannot be placed in the 3rd and 4th rows and in columns $a$ and $b$, and on the main diagonal, the number $a$ must be in cell $e 5$. Then on the secondary diagonal, it is in cell $d 2$, and on the first row, it is in cell $c 1$.
The conducted analysis shows that three identical numbers or two pairs of equal numbers among the 4 numbers marked with a dot and not in the top right corner cannot exist because the permissible configurations of cases 1) and 4) cannot occur simultaneously. Therefore, the sum of these four numbers does not exceed $5+5+4+3=17$, and the sum of the five numbers marked with dots does not exceed $17+5=22$. The upper bound has been obtained.
Example of number placement satisfying the condition with a sum of 22:
| 3 | 4 | 1 | 2 | 5 |
| :--- | :--- | :--- | :--- | :--- |
| 5 | 1 | 3 | 4 | 2 |
| 4 | 5 | 2 | 1 | 3 |
| 2 | 3 | 4 | 5 | 1 |
| 1 | 2 | 5 | 3 | 4 |
Grading criteria. Any attempt to prove an incorrect answer: 0 points. Correct answer with an example: 3 points. Proof of the maximum sum of 22: 4 points. If the enumeration in the proof is incomplete: points are reduced proportionally.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. A bus with programmers left Novosibirsk for Pavlodar. When it had traveled 70 km, Pavel Viktorovich set off from Novosibirsk in a car along the same route, and caught up with the programmers in Karasuk. After that, Pavel drove another 40 km, while the bus traveled only 20 km in the same time. Find the distance from Novosibirsk to Karasuk, given that both the car and the bus traveled at constant speeds.
|
Solution. Since by the time the car has traveled 40 km, the bus has traveled half that distance, its speed is exactly half the speed of the car. However, when the bus has traveled 70 km after the car's departure, the car will have traveled 140 km and will just catch up with the bus. According to the problem, this happened in Karasuk, so 140 km is the answer.
Criteria. Only the answer -1 point.
Answer with verification (for example, for specific speeds) - 2 points. Proven that the car's speed is twice the speed of the bus - 3 points.
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In triangle $A B C$, a point $D$ is marked on side $A C$ such that $B C = C D$. Find $A D$, given that $B D = 13$, and angle $C A B$ is three times smaller than angle $C B A$.
|
Solution. Let $\angle C A B=x$. Then $\angle C B A=3 x$ and $\angle A C B=180^{\circ}-4 x$. According to the problem, triangle $B C D$ is isosceles, so $\angle C D B=\angle C B D=\left(180^{\circ}-\angle B C D\right) / 2=2 x$. Therefore, $\angle D B A=\angle A B C-\angle D B C=3 x-2 x=x=\angle D A B$. Hence, triangle $A B D$ is isosceles, and $A D=B D=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 5 pieces of transparent glass of the same square shape and the same size. Each piece of glass is conditionally divided into 4 equal parts (right triangles) by its diagonals, and one of these triangles is painted with an opaque paint of its individual color, different from the colors of the painted parts of the other glasses. Then all these glasses are stacked on top of each other (with precise alignment of edges and vertices) with the painted parts facing up. How many different ways are there to stack the glasses so that the entire stack ends up completely opaque in the vertical direction.
(12 points)
|
Solution. First, consider some fixed vertical order of laying the glasses (from bottom to top). It is clear that by rotating the entire layout by some angle, we will not change the layout (we will not get a new layout). Therefore, we can assume that the bottom glass in the layout is always fixed (does not rotate). Then the layouts (with a fixed vertical order of glasses) will differ from each other by the rotation of each of the subsequent 4 upper glasses by $0^{\circ}, 90^{\circ}, 180^{\circ}$, and $270^{\circ}$ relative to the fixed bottom glass. Therefore, we will get a total of $4^{4}=256$ layout options with a fixed vertical order of glasses. Adding now all possible vertical permutations of the five glasses (5! = 120 options), we get the total number of possible glass layouts in a stack: $5!4^{4}=120 \cdot 256=30720$ pieces. But not all these layouts meet the condition of the problem. The condition of the problem is satisfied only by those layouts in which the entire stack turns out to be vertically opaque. Consider columns of triangles located above each of the four fixed triangles of the bottom glass. The condition of the problem will be met when each of these four columns is opaque. One of these columns is already opaque by default (the one standing on the bottom shaded triangle). Consider the ordered set (vector) of possible angles of rotation (for definiteness, clockwise) of the shaded triangles on each of the 4 upper glasses relative to the bottom shaded triangle: $\left(\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}\right)$, where $\alpha_{k} \in\left\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\right\}, k=1,2,3,4$.
All "columns" of glass triangles will be opaque if in this set of rotation angles there is at least one angle $90^{\circ}$, at least one angle $180^{\circ}$, and at least one angle $270^{\circ}$ (while the angle $0^{\circ}$ does not have to appear, although it will not hurt if it does appear). To count the total number of such sets (and thus the number of layouts with a fixed vertical order of glasses), we will divide them into four groups:
- sets in which all rotation angles are different, i.e., all $\alpha_{k}$ are pairwise different; there are 4! = 24 such sets (due to permutations);
- sets in which the rotation angles $180^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $90^{\circ}$ appears twice; there are $6 \cdot 2=12$ such sets (due to permutations) (here 6 is the number of positions in the vector for two $90^{\circ}$ angles, and 2 is the two permutations of the angles $180^{\circ}$ and $270^{\circ}$ in the remaining two positions);
- sets in which the rotation angles $90^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $180^{\circ}$ appears twice; similarly, there are $6 \cdot 2$ = 12 such sets (due to permutations);
- sets in which the rotation angles $90^{\circ}$ and $180^{\circ}$ appear once each, and the rotation angle $270^{\circ}$ appears twice; similarly, there are $6 \cdot 2=12$ such sets (due to permutations).
In the end, we get a total of $24+12+12+12=60$ ordered sets of rotation angles that meet the required condition. This is the total number of layouts with a fixed vertical order of glasses, in which the final stack turns out to be opaque. Finally, by permuting the glasses in $5!=120$ ways, we get the total number of $120 \cdot 60=7200$ layouts in which the final stack turns out to be opaque.
Answer: 7200 ways.
|
7200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find a natural number that has six natural divisors (including one and the number itself), two of which are prime, and the sum of all its natural divisors is 78.
|
Solution: The desired natural number $n$ can be represented as $n=p_{1}^{\alpha_{1}} \cdot p_{2}^{\alpha_{2}}, 12,1+p_{2}+p_{2}^{2}>7$, then no factorization of the number 78 into a product of two natural factors fits $78=1 \cdot 78,78=2 \cdot 39,78=3 \cdot 26,78=6 \cdot 13$ up to the order).
2) $\alpha_{1}=2, \alpha_{2}=1, n=p_{1}^{2} \cdot p_{2}$. Since the sum of all divisors is 78, then $\left(1+p_{1}+p_{1}^{2}\right)\left(1+p_{2}\right)=78$. Since $13,1+p_{1}+p_{1}^{2}>3$, we have
a) $1+p_{1}+p_{1}^{2}=6,1+p_{2}=13$, there are no natural solutions.
b) $1+p_{1}+p_{1}^{2}=13,1+p_{2}=6$, or $p_{1}=3, p_{2}=5, n=3^{2} \cdot 5=45$.
Answer: 45.
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The automatic line for processing body parts initially consisted of several identical machines. The line processed 38880 parts daily. After the production was modernized, all the machines on the line were replaced with more productive but also identical ones, and their number increased by 3. The automatic line began to process 44800 parts per day. How many parts did each machine process daily initially?
|
Solution: Let $x$ be the number of machines before modernization, $y$ be the productivity of each machine, i.e., the number of parts processed per day, and $z$ be the productivity of the new machines. Then we have $x y = 38880 = 2^{5} \cdot 3^{5} \cdot 5, (x+3) z = 44800 = 2^{8} \cdot 5^{2} \cdot 7, x > 1, y \frac{38880 \cdot 3}{5920} = \frac{2^{5} \cdot 3^{6} \cdot 5}{2^{5} \cdot 5 \cdot 37} = \frac{3^{6}}{37} = 19 \frac{26}{37}, \quad x \geq 20$. Since $(x+3) z = 2^{8} \cdot 5^{2} \cdot 7$, $x$ is not divisible by 3, and $x = 2^{\alpha} \cdot 5^{\beta}$, where $\alpha \in \{0,1,2,3,4,5\}, \beta \in \{0,1\}$.
1) $\beta=0, x=2^{\alpha}, \alpha \in \{5\}$. When $\alpha=5$ we have $x=32, x+3=35, y=3^{5} \cdot 5=1215, z=2^{8} \cdot 5=1280$
2) $\beta=1, x=2^{\alpha} \cdot 5, \alpha \in \{2,3,4,5\}$.
When $\alpha=2$ we have $x=20, x+3=23$, which is impossible.
When $\alpha=3$ we have $x=40, x+3=43$, which is impossible.
When $\alpha=4$ we have $x=80, x+3=83$, which is impossible.
When $\alpha=5$ we have $x=160, x+3=163$, which is impossible.
Answer: 1215.
|
1215
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numbers $u, v, w$ are roots of the equation $x^{3}-3 x-1=0$. Find $u^{9}+v^{9}+w^{9}$. (12 points)
|
Solution. $\quad$ According to Vieta's theorem, $u+v+w=0, uv+vw+uw=-3, uvw=1$. Consider the sequence $S_{n}=u^{n}+v^{n}+w^{n}$. We have $S_{0}=3, S_{1}=0$. Let's find $S_{2}$: $S_{2}=u^{2}+v^{2}+w^{2}=(u+v+w)^{2}-2(uv+vw+uw)=6. \quad$ Since $\quad u^{3}=3u+1, v^{3}=$ $3v+1, w^{3}=3w+1, \quad$ then $S_{3}=u^{3}+v^{3}+w^{3}=3S_{1}+S_{0}$. Further, $u^{n}=3u^{n-2}+u^{n-3}, v^{n}=$ $3v^{n-2}+v^{n-3}, w^{n}=3w^{n-2}+w^{n-3}$, then $S_{n}=3S_{n-2}+S_{n-3}$. We find $S_{3}=3, S_{4}=18, S_{5}=$ $15, S_{6}=57, S_{7}=63, S_{9}=246$
## Answer: 246
|
246
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the laboratory, there are flasks of two sizes (volume $V$ and volume $V / 3$) in a total of 100 pieces, with at least 2 flasks of each size. The lab assistant randomly selects two flasks in sequence, and fills the first one with a 70% salt solution, and the second one with a 40% salt solution. Then, he pours the contents of these two flasks into one dish and determines the percentage of salt in it. For what minimum number of large flasks $N$ will the event "the percentage of salt in the dish is between $50\%$ and $60\%$ inclusive" occur less frequently than the event "when two fair coins are tossed, one head and one tail appear (in any order)"? Justify your answer. (16 points)
|
Solution. Let $N$ be the number of large flasks in the laboratory, $N=2,3, \ldots, 98$, $n=100-N$ be the number of small flasks in the laboratory, $n=2,3, \ldots, 98$, and $\mathrm{P}(A)$ be the probability of the event $A=\{$ the salt content in the dish is between $50 \%$ and $60 \%$ inclusive\}. It is necessary to find the smallest $N$ such that $\mathrm{P}(A)45<N<55$. Therefore, $N_{\text {min }}=46$.
Answer: when $N=46$.
|
46
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The fraction $\frac{1}{5}$ is written as an infinite binary fraction. How many ones are there among the first 2022 digits after the decimal point in such a representation? (12 points)
|
Solution. The smallest number of the form $2^{n}-1$ divisible by 5 is 15. Then
$$
\frac{1}{5}=\frac{3}{15}=\frac{3}{16-1}=\frac{3}{2^{4}-1}=\frac{3}{16} \cdot \frac{1}{1-2^{-4}}=\left(\frac{1}{16}+\frac{1}{8}\right)\left(1+2^{-4}+2^{-8}+2^{-12}+\cdots\right)=
$$
$\left(2^{-3}+2^{-4}\right)\left(1+2^{-4}+2^{-8}+2^{-12}+\cdots\right)=0,001100110011 \ldots=0,(0011) \quad$ in $\quad$ binary. Since $2022=4 \cdot 505+2$, among the first 2022 digits after the decimal point, there will be 1010 ones.
## Answer: 1010.
|
1010
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There is a cube fixed on legs, and six different paints. In how many ways can all the faces of the cube be painted (each in one color, not all paints have to be used) so that adjacent faces (having a common edge) are of different colors? (16 points)
|
Solution. Let's consider 4 cases of coloring a cube.
1) The top and bottom faces are the same color, and the left and right faces are the same color. We choose the color for the top and bottom faces in 6 ways, then the color for the left and right faces in 5 ways, then the color for the front face in 4 ways, and the color for the back face in 4 ways. In total, $6 \cdot 5 \cdot 4 \cdot 4=480$ ways.
2) The top and bottom faces are the same color, and the left and right faces are different colors. We choose the color for the top and bottom faces in 6 ways, then the color for the left face in 5 ways, then the color for the right face in 4 ways, then the color for the front face in 3 ways, and the color for the back face in 3 ways.
In total, $6 \cdot 5 \cdot 4 \cdot 3 \cdot 3=1080$ ways.
3) The top and bottom faces are different colors, and the left and right faces are the same color. We choose the color for the left and right faces in 6 ways, then the color for the top face in 5 ways, then the color for the bottom face in 4 ways, then the color for the front face in 3 ways, and the color for the back face in 3 ways.
In total, $6 \cdot 5 \cdot 4 \cdot 3 \cdot 3=1080$ ways.
4) The top and bottom faces are different colors, and the left and right faces are different colors. We choose the color for the top face in 6 ways, then the color for the bottom face in 5 ways, then the color for the left face in 4 ways, then the color for the right face in 3 ways, then the color for the front face in 2 ways, and the color for the back face in 2 ways.
In total, $6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 2=1440$ ways.
Finally, we have $480+1080+1080+1440=4080$.
## Answer: 4080.
|
4080
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solution. First, consider some fixed vertical order of laying the glasses (from bottom to top). It is clear that by rotating the entire layout by some angle, we will not change the layout (we will not get a new layout). Therefore, we can assume that the bottom glass in the layout is always fixed (does not rotate). Then the layouts (with a fixed vertical order of glasses) will differ from each other by the rotation of each of the subsequent four upper glasses by $0^{\circ}, 90^{\circ}, 180^{\circ}$, and $270^{\circ}$ relative to the fixed bottom glass. Therefore, we will get a total of $4^{4}=256$ layout options with a fixed vertical order of glasses. Adding now all possible vertical permutations of the five glasses ($5!=120$ options), we get the total number of possible glass layouts in a stack: $5!4^{4}=120 \cdot 256=30720$ pieces. But not all these layouts meet the condition of the problem. The layouts that meet the condition of the problem are only those in which the entire stack turns out to be vertically opaque. Consider the columns of triangles located above each of the four fixed triangles of the bottom glass. The condition of the problem will be met when each of these four columns is opaque. One of these columns is already opaque by default (the one standing on the bottom shaded triangle). Consider the ordered set (vector) of possible angles of rotation (for definiteness, clockwise) of the shaded triangles on each of the 4 upper glasses relative to the bottom shaded triangle: $\left(\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}\right)$, where $\alpha_{k} \in\left\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\right\}, k=1,2,3,4$.
All "columns" of glass triangles will be opaque if in this set of rotation angles there is at least one angle $90^{\circ}$, at least one angle $180^{\circ}$, and at least one angle $270^{\circ}$ (while the angle $0^{\circ}$ does not have to appear, although it will not hurt if it does appear). To count the total number of such sets (and thus the number of layouts with a fixed vertical order of glasses), we will divide them into four groups:
- sets in which all rotation angles are different, i.e., all $\alpha_{k}$ are pairwise different; there are a total of $4!=24$ such sets (due to permutations);
- sets in which the rotation angles $180^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $90^{\circ}$ appears twice; there are a total of $6 \cdot 2=12$ such sets (here 6 is the number of positions in the vector for two angles of $90^{\circ}$, and 2 is the two permutations of the angles $180^{\circ}$ and $270^{\circ}$ in the remaining two positions);
- sets in which the rotation angles $90^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $180^{\circ}$ appears twice; similarly, there are a total of $6 \cdot 2=12$ such sets (due to permutations);
- sets in which the rotation angles $90^{\circ}$ and $180^{\circ}$ appear once each, and the rotation angle $270^{\circ}$ appears twice; similarly, there are a total of $6 \cdot 2=12$ such sets (due to permutations).
In the end, we get a total of $24+12+12+12=60$ ordered sets of rotation angles that meet the required condition. This is the total number of layouts with a fixed vertical order of glasses, in which the final stack turns out to be opaque. Finally, by permuting the glasses in $5!=120$ ways, we get the total number of $120 \cdot 60=7200$ layouts in which the final stack turns out to be opaque.
|
Answer: 7200 ways.
#
|
7200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solution. First, consider some fixed vertical order of laying the glasses (from bottom to top). It is clear that by rotating the entire layout by some angle, we will not change the layout (we will not get a new layout). Therefore, we can assume that the bottom glass in the layout is always fixed (does not rotate). Then different layouts (with a fixed vertical order of glasses) will differ from each other by the rotation of each of the subsequent 4 upper glasses by $0^{\circ}$, $120^{\circ}$, and $240^{\circ}$ relative to the fixed bottom glass. Therefore, we will get a total of $3^{4}=81$ layout options with a fixed vertical order of glasses. Taking into account all possible vertical permutations of the five glasses (5! = 120 options), we get the total number of possible glass layouts in a stack: 5! $3^{4}=120 \cdot 81=9720$ pieces. But not all these layouts meet the condition of the problem. The condition of the problem is satisfied by all layouts except those in which the entire stack turns out to be completely vertically opaque. Let's first find the number of such layouts.
For this, consider columns of isosceles triangles (parts located above each of the three fixed isosceles triangles of the bottom glass). Let's determine the number of such layouts in which each of these four columns is opaque. One of these columns is already opaque by default (the one standing on the bottom shaded isosceles triangle). Consider the ordered set (vector) of possible rotation angles (for definiteness, clockwise) of the shaded isosceles triangles on each of the 4 upper glasses relative to the bottom shaded equilateral triangle: $\left(\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}\right)$, where $\alpha_{k} \in\left\{0^{\circ}, 120^{\circ}, 240^{\circ}\right\}$, $k=1,2,3,4$.
All "columns" of glass isosceles triangles will be opaque if this set of rotation angles necessarily includes at least one $120^{\circ}$ and at least one $240^{\circ}$ (while the angle $0^{\circ}$ is not required to appear, although it will not hurt if it does appear). The other two places in the set can be occupied by any of the three possible values $\left\{0^{\circ}, 120^{\circ}, 240^{\circ}\right\}$, i.e., $0^{\circ}$ and $120^{\circ}$, or $0^{\circ}$ and $240^{\circ}$, or $120^{\circ}$ and $240^{\circ}$, as well as $0^{\circ}$ and $0^{\circ}$, or $120^{\circ}$ and $120^{\circ}$, or $240^{\circ}$ and $240^{\circ}$. Therefore, to count the total number of such sets (and thus the number of layouts with a fixed vertical order of glasses), we will divide them into the following six groups:
- If the two additional values are $0^{\circ}$ and $120^{\circ}$, then we get sets in which the rotation angles $0^{\circ}$ and $240^{\circ}$ appear once, and the angle $120^{\circ}$ appears twice. The total number of such sets (due to permutations) will be $6 \cdot 2=12$ (here 6 is the number of ways to choose places in the vector for two angles of $120^{\circ}$, and 2 is the number of ways to permute the angles $0^{\circ}$ and $240^{\circ}$ in the two remaining places);
- If the two additional values are $0^{\circ}$ and $240^{\circ}$, then we get sets in which the rotation angles $0^{\circ}$ and $120^{\circ}$ appear once, and the angle $240^{\circ}$ appears twice. Analogously to the previous case, the total number of such sets (due to permutations) will be $6 \cdot 2=12$;
- If the two additional values are $120^{\circ}$ and $240^{\circ}$, then we get sets in which the rotation angles $120^{\circ}$ and $240^{\circ}$ appear twice each. The total number of such sets (due to permutations) will be $6 \cdot 1=6$ (here 6 is the number of ways to choose two places out of four for placing two angles of $120^{\circ}$, and 1 is the only way to place two angles of $240^{\circ}$ in the two remaining places);
- If the two additional values are $0^{\circ}$ and $0^{\circ}$, then we get sets in which the rotation angles $120^{\circ}$ and $240^{\circ}$ appear once, and the angle $0^{\circ}$ appears twice. The total number of such sets (due to permutations) will be $6 \cdot 2=12$ (here 6 is the number of ways to choose two places out of four for placing two angles of $0^{\circ}$, and 2 is the number of ways to permute the angles $120^{\circ}$ and $240^{\circ}$ in the two remaining places);
- If the two additional values are $120^{\circ}$ and $120^{\circ}$, then we get sets in which the rotation angle $240^{\circ}$ appears once, and the angle $120^{\circ}$ appears three times. The total number of such sets will be $4 \cdot 1=4$ (here 4 is the number of ways to choose one place out of four for placing the angle $240^{\circ}$, and 1 is the only way to place the identical angles $120^{\circ}$ in the three remaining places);
- If the two additional values are $240^{\circ}$ and $240^{\circ}$, then we get sets in which the rotation angle $120^{\circ}$ appears once, and the angle $240^{\circ}$ appears three times. Analogously to the previous case, the total number of such sets will be $4 \cdot 1=4$.
In the end, we get a total of $12+12+6+12+4+4=50$ ordered sets of rotation angles that satisfy the required condition. This is the total number of layouts with a fixed vertical order of glasses in which the final stack turns out to be opaque. By permuting the glasses (in the vertical direction) in $5!=120$ ways, we get the total number of $120 \cdot 50=6000$ layouts in which the final stack turns out to be opaque. Finally, by subtracting the number of 6000 unwanted layouts from the total number of different layouts 9720, we finally get $9720-6000=3720$ ways to lay out a partially transparent stack of five glasses.
|
Answer: 3720 ways.
#
|
3720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the maximum value of the expression $x+y$, where $x, y-$ are integer solutions of the equation $3 x^{2}+5 y^{2}=345$
|
# Solution
Notice that 345 and $5 y^{2}$ are divisible by 5, so $3 x^{2}$ must also be divisible by 5. Therefore, $\quad x=5 t, t \in Z$. Similarly, $y=3 n, n \in Z$. After simplification, the equation becomes $5 t^{2}+3 n^{2}=23$. Therefore, $t^{2} \leq \frac{23}{5}$, $n^{2} \leq \frac{23}{3}$ or $|t| \leq 2,|n| \leq 2$. By trying the corresponding values of $t, n$, we get that $|t|=2,|n|=1$ or
$$
\left\{\begin{array}{c}
x_{1}=-10 \\
y_{1}=-3
\end{array},\left\{\begin{array}{c}
x_{2}=-10 \\
y_{2}=3
\end{array},\left\{\begin{array}{l}
x_{3}=10 \\
y_{3}=-3
\end{array},\left\{\begin{array}{c}
x_{4}=10 \\
y_{4}=3
\end{array}\right.\right.\right.\right.
$$
The maximum value of the expression $x+y$ is $10+3=13$.
Answer. 13.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The car traveled half of the distance at a speed of 60 km/h, then one third of the remaining distance at a speed of 120 km/h, and the remaining distance at a speed of 80 km/h.
Find the average speed of the car during this trip. Give your answer in km/h.
|
Solution: Let x hours be the time the car traveled at a speed of 60 km/h, then $60 x=\frac{s}{2}$. Let y hours be the time the car traveled at a speed of 120 km/h, then $120 y=\frac{s}{6}$. Let z hours be the time the car traveled at a speed of 80 km/h, then $80 z=\frac{s}{3}$. By definition $v_{cp}=\frac{s}{t_{\text{total}}}$. Then $v_{cp}=\frac{s}{x+y+z}=\frac{s}{\frac{s}{120}+\frac{s}{720}+\frac{s}{240}}=\frac{1}{\frac{1}{120}+\frac{1}{6 \cdot 120}+\frac{1}{2 \cdot 120}}=\frac{6 \cdot 120}{10}=72$.
Answer: 72.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.
On a coordinate line, 16 points are marked and numbered from left to right. The coordinate of any point, except for the extreme points, is equal to half the sum of the coordinates of the two adjacent points. Find the coordinate of the fifth point if the first point has a coordinate of 2 and the sixteenth point has a coordinate of 47.
#
|
# Solution
Solution. Let $a, b$ and $c$ be the coordinates of three consecutive points (from left to right). Then $b=\frac{a+c}{2}$, which means the second point is the midpoint of the segment with endpoints at the neighboring points. This condition holds for any triple of consecutive points, meaning the distances between any neighboring points are the same. The distance between the extreme points is 47-2=45, and there are 15 equal intervals between them, so the distance between neighboring points is $45: 15=3$. There are 4 equal intervals of length 3 between the fifth and the first point, so the coordinate of the fifth point is $2+3 \cdot$ $4=14$.
Answer: 14
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
In a 6-liter vessel, 4 liters of a 70% (by volume) sulfuric acid solution are poured, and in a second vessel of the same capacity, 3 liters of a 90% solution of sulfuric acid are poured. A certain amount of the solution is transferred from the second vessel to the first so that it becomes an $r-\%$ solution of sulfuric acid. Find the greatest integer value of $\mathrm{r}$ for which the problem has a solution.
|
# Solution.
Let $x$ liters of the solution be transferred from the second vessel to the first. Since it follows from the condition that $0 \leq x \leq 2$, to find the amount of pure acid in the new solution, we obtain the equation $2.8 + 0.9x = (4 + x) \frac{r}{100}$, from which $x = \frac{4r - 280}{90 - r}$. Now, considering that $x \in [0; 2]$, we conclude that the problem has a solution only when $r \in \left[70; \frac{230}{3}\right]$. Therefore, the largest integer $r$ for which the problem has a solution is 76.
Answer: 76
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.
In triangle $A B C$, the bisector $A L$ ( $L \in B C$ ) is drawn, and $M$ and $N$ are points on the other two bisectors (or their extensions) such that $M A=M L$ and $N A=N L, \angle B A C=50^{\circ}$.
Find the measure of $\angle M A N$ in degrees.
|
# Solution
We will use the auxiliary statements.
If the bisector $B K$ in triangle $A B C$ intersects the circumscribed circle at point $W$, then:
1) $A W=C W$ (since $\angle C A W=\angle C B W=\angle A B W=\angle A C W$, that is, triangle $A W C$ is isosceles and $A W=C W$).
2) Point $W$ lies on the perpendicular bisector of segment $A C$.
3) The bisector of the angle of a non-isosceles triangle and the perpendicular bisector of the opposite side intersect on the circumscribed circle.
Next, consider triangle $A B L (A B \neq B L)$, $M N$ is the perpendicular bisector of $A L$ and $B N$ is the bisector of angle $B$. Therefore, points $A, B, L, N$ lie on the same circle.
Similarly, points $A, C, L, M$ lie on the same circle.
Then:
$$
\begin{gathered}
\angle M A N=\angle L A M+\angle L A N=\angle L C M+\angle N B L= \\
=\frac{\angle C+\angle B}{2}=90^{\circ}-\frac{1}{2} \angle A=90^{\circ}-\frac{1}{2} \cdot 50^{\circ}=65^{\circ}
\end{gathered}
$$
Answer. 65.
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. We will call a ticket with a number from 0001 to 2014 excellent if the difference between some two adjacent digits of its number is 5. Find the number of excellent tickets.
|
Solution. The number of excellent tickets from 0001 to 2014 is equal to the number of excellent tickets from 0000 to 2014. First, let's calculate the number of non-excellent tickets from 0000 to 2014.
The number of non-excellent tickets from 0000 to 1999 can be found as follows. Let $a_{1} a_{2} a_{3} a_{4}$ be the number of a non-excellent ticket. Then, $a_{1}$ can be chosen as two digits: 0 and 1.
$a_{2}$ can be chosen as any digit except those forming pairs 0-5, 1-6, i.e., any of 9 digits.
$a_{3}, a_{4}$ can be chosen as any digit except those forming pairs 0-5, 1-6, 2-7, 3-8, 4-9, i.e., any of 9 digits.
In total, there will be $2 \cdot 9 \cdot 9 \cdot 9=1458$ tickets.
In tickets from 2000 to 2014, there are fourteen non-excellent tickets (all except 2005).
Thus, we get 1458+14=1472 - non-excellent, therefore, 2015-1472=543 excellent tickets from 0000 to 2014, which means there are also 543 excellent tickets from 0001 to 2014.
Answer: 543.
|
543
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (15 points) Pavel caught 32 crayfish and decided to sell them at the market. When part of his catch was bought, it turned out that the buyer paid 4.5 rubles less for each one than the number of crayfish that remained on the counter. At the same time, the boy earned the maximum amount of money possible. How much money did Pavel earn? How many crayfish did he sell?
|
Solution: Let $x$ be the number of crayfish left on the counter, then (32-x) crayfish were bought, ($x-4.5$) - the cost of one crayfish.
$(32-x)(x-4.5)$ - the cost of all crayfish.
$y=(32-x)(x-4.5)$
$x_{B}=18.25$.
$x_{1}=19, y_{1}=(32-19)(19-4.5)=13 * 14.5=188.5$.
$x_{2}=18, y_{2}=(32-18)(18-4.5)=14 * 13.5=189$. The maximum number is 14.
Answer: a) the maximum amount of money is 189 rubles;
b) sold 14 crayfish.
| Points | |
| :--- | :--- |
| 15 | The correct answer is obtained with justification. |
| 10 | An arithmetic error is made in an otherwise correct solution. |
| 5 | The problem is solved by trial and error, finding values of the variable that satisfy the condition. |
| 2 | There are some guesses. |
| 0 | The solution does not meet any of the criteria listed above. |
|
189
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) In an acute-angled triangle $\mathrm{ABC}$, a point $\mathrm{D}$ is chosen on side $\mathrm{BC}$ such that $\mathrm{CD}: \mathrm{DB}=2: 1$, and a point $\mathrm{K}$ is chosen on segment $\mathrm{AD}$ such that $\mathrm{AK}=\mathrm{CD}+\mathrm{DK}$. A line is drawn through point $\mathrm{K}$ and vertex $\mathrm{B}$, intersecting side $\mathrm{AC}$ at point $\mathrm{E}$. Triangle $\mathrm{AEK}$ is isosceles ($\mathrm{AE}=\mathrm{EK}$). Find the measure of angle $\mathrm{ADC}$ in degrees.
|
Solution: Extend SV beyond point V so that BN = BD. Draw NM || BE. NM intersects AD at point L. Draw segment $\mathrm{CH} \perp \mathrm{AD}$. Extend it to $\mathrm{P}$ such that $\mathrm{HP}=\mathrm{HC}, \mathrm{PN}|| \mathrm{AD}$.
In triangle DLN, segment $\mathrm{BK}$ is the midline, therefore, $\mathrm{DK}=\mathrm{KL}$ and thus $\mathrm{AL}=\mathrm{AK}-\mathrm{LK}=\mathrm{AK}-\mathrm{DK}=\mathrm{CD}$.
Triangle САР is isosceles (AH is the median and altitude), therefore $\angle \mathrm{PAD}=\angle \mathrm{DAC}$, but $\angle \mathrm{DAC}=\angle \mathrm{AKE}$ (by condition), $\angle \mathrm{AKE}=\angle \mathrm{ALM}$ (corresponding), $\angle \mathrm{ALM}=\angle \mathrm{NLD}$ (vertical), $\angle \mathrm{NLD}=\angle \mathrm{NLP}$ (alternate interior), hence, LN || AP, so ALNP is a parallelogram.
In the right triangle $\mathrm{CPN}$, the length $\mathrm{CN}=2 \mathrm{CD}=2 \mathrm{AL}=2 \mathrm{PN}$, i.e., $\angle \mathrm{PCN}=30^{\circ}$. Therefore, $\angle \mathrm{ADC}=60^{\circ}$.
Answer: $60^{0}$.
| Points | Grading Criteria |
| :---: | :---: |
| 20 | A well-reasoned and correctly executed solution to the problem. |
| 15 | The solution is correct and well-reasoned but contains an arithmetic error or is insufficiently justified. |
| 7 | The solution is correctly started, some intermediate results are obtained, but the further solution is incorrect or missing. |
| 0 | The solution does not meet the above requirements. |
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A farmer initially placed his produce in boxes with a capacity of 8 kg each, but one box was not fully loaded. Then the farmer repackaged all the produce into boxes with a capacity of 6 kg each, which required 8 more boxes, but in this case, one box was also not fully loaded. When all the produce was placed in boxes of 5 kg each, all the boxes were fully loaded, but it required an additional 5 boxes. How many kilograms did the farmer's produce weigh? Give your answer as a number without specifying the unit.
(5 points)
|
Solution. Let $x$ kg be the weight of the farmer's produce. Then $\quad 8(n-1)<x<8 n, \quad 6(n+7)<x<6(n+8)$, $5(n+13)=x, \Rightarrow 8(n-1)<5(n+13)<8 n, \quad 6(n+7)<5(n+13)<6(n+8)$,
$\Rightarrow 21 \frac{2}{3}<n<23, \quad n=22, \quad x=35 \cdot 5=175$.
Answer: 175.
|
175
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the country of Landia, which breeds an elite breed of horses, an annual festival is held to test their speed, in which only one-year-old, two-year-old, three-year-old, and four-year-old horses can participate. For each horse that meets the speed standard, the festival organizers pay a fixed amount of money to the stud farm where the horse was raised: 1 landric for a one-year-old, 2 landrics for a two-year-old, 3 landrics for a three-year-old, and 4 landrics for a four-year-old. Each stud farm participating in the festival annually presents four new horses (of any age combination as they wish) for testing, which have not previously participated in the tests, as well as personally all horses (not older than four years) that previously participated in the tests at a younger age and met the standard. What is the maximum amount of money a stud farm can earn in the first six years of its participation in the festival?
(12 points)
|
Solution. A four-year-old horse can earn a maximum of 4 landricks over its entire participation in festivals. If the horse starts participating in festivals at 1 year old, it can participate for another 3 years after that. In the case of winning every year, it will earn 1+2+3+4=10 landricks over 4 years. If the horse starts participating in festivals at 2 years old, it can earn a maximum of $2+3+4=9$ landricks over the 3 possible years of participation. If the horse starts participating in festivals at 3 years old, it can earn a maximum of $3+4=7$ landricks. Therefore, the most optimal strategy is as follows. In the first year, the stable enters 4 one-year-old horses. The maximum winnings amount to 4 landricks. In the second year, the stable enters 4 new one-year-old horses and 4 two-year-olds that participated and won in the first year. The maximum winnings amount to $4+4 \cdot 2=12$ landricks. In the third year, the stable enters 4 new one-year-old horses, 4 two-year-olds that participated in the second year, and 4 three-year-olds that participated in the previous 2 years. The maximum bonus is $4+4 \cdot 2+4 \cdot 3=24$ landricks. In the fourth year, there is no point in entering one-year-old horses, as they will only be able to participate for 2 more years. Therefore, it makes sense to enter 4 new two-year-old horses. The winnings will amount to $4 \cdot 2+4 \cdot 2+4 \cdot 3+4 \cdot 4=44$ landricks. Horses that start participating in the 5th year will only participate once after that, so it makes sense to enter new three-year-olds. The winnings will amount to $4 \cdot 3+4 \cdot 3+4 \cdot 3+4 \cdot 4=52$ landricks. In the sixth year, it makes sense to enter only four-year-olds. The winnings will amount to $4 \cdot 4+4 \cdot 4+4 \cdot 4+4 \cdot 4=64$ landricks. In total, over 6 years of participation in festivals, the stable can earn a maximum of $4+12+24+44+52+64=200$ landricks.
Answer: 200.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The number $N$ is written as the product of consecutive natural numbers from 2019 to 4036: $N=2019 \cdot 2020 \cdot 2021 \cdot \ldots \cdot 4034 \cdot 4035 \cdot 4036$. Determine the power of two in the prime factorization of the number $N$.
|
Solution. The number $N$ can be represented as
$$
\begin{aligned}
& N=\frac{(2 \cdot 2018)!}{2018!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 4034 \cdot 4035 \cdot 4036}{2018!}=\frac{(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot(2 \cdot 4 \cdot \ldots \cdot 4034 \cdot 4036)}{2018!}= \\
& =\frac{(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot 2 \cdot 2 \cdot \ldots \cdot 2 \cdot(1 \cdot 2 \cdot \ldots \cdot 2017 \cdot 2018)}{2018!}=(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot 2^{2018}
\end{aligned}
$$
We obtained the product of odd numbers and a power of two.
Answer: 2018.
|
2018
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many ways can a rectangular board of size $2 \times 18$ be covered with identical rectangular tiles of size $1 \times 2$? The tiles must be placed so that they fit entirely on the board and do not overlap.
(12 points)
|
Solution. Let there be a board of size $2 \times$ n. Denote the number of ways to tile it with tiles of size $1 \times 2$ by $P_{n}$. Then the following recurrence relation holds: $P_{n}=P_{n-1}+P_{n-2}$. Since $P_{1}=1, P_{2}=2$, performing sequential calculations using the recurrence relation, we arrive at the answer $P_{18}=4181$.
Answer: 4181.
|
4181
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine the smallest natural number $N$, among the divisors of which are all numbers of the form $x+y$, where $x$ and $y$ are natural solutions to the equation $6 x y-y^{2}-5 x^{2}=7$.
|
Solution. Transform the equation by factoring the right-hand side
$6 x y-y^{2}-5 x^{2}-x^{2}+x^{2}=7 \Rightarrow 6 x(y-x)-(y+x)(y-x)=7 \Rightarrow(y-x)(6 x-y-x)=7 \Rightarrow$ $(y-x)(5 x-y)=7$.
Considering that the variables are natural numbers, and 7 is a prime number, we get
$$
\left\{\begin{array} { l }
{ y - x = 7 , } \\
{ 5 x - y = 1 , \text { or } }
\end{array} \left\{\begin{array} { l }
{ y - x = - 7 , } \\
{ 5 x - y = - 1 , \text { or } }
\end{array} \left\{\begin{array} { l }
{ y - x = 1 , } \\
{ 5 x - y = 7 , \text { or } }
\end{array} \quad \left\{\begin{array}{l}
y-x=-1 \\
5 x-y=-7
\end{array}\right.\right.\right.\right.
$$
the second and fourth systems do not have natural solutions. The solution to the first system is the pair $(2 ; 9)$, and the third is $(2 ; 3)$. Therefore, $x+y=11$ or $x+y=5$. The smallest natural number that has 5 and 11 as divisors is 55.
Answer: 55.
|
55
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ of a circular track, a car and a motorcycle started simultaneously and in the same direction. The car drove two laps without stopping in one direction. At the moment when the car caught up with the motorcyclist, the motorcyclist turned around and increased his speed by $16 \mathrm{~km} / \mathrm{u}$, and after $3 / 8 \mathrm{~h}$ after the turn, arrived at point $A$ simultaneously with the car. Find the entire distance (in km) traveled by the motorcyclist, if this distance is 5.25 km shorter than the entire track. Provide the answer as a number without specifying the unit.
(5 points)
|
Solution. Let $x$ (km/h) be the speed of the motorcyclist, $y$ (km/h) be the speed of the car, and $S$ (km) be the distance the motorcyclist travels before turning around. Then the total length of the track is $2 S + 5.25$. We have $\frac{S}{x} = \frac{3 S + 5.25}{y}$, $\frac{3 x}{8} + 6 = S$, $\frac{3 y}{8} = S + 5.25$. This leads to the quadratic equation $4 S^2 - 36 S - 63 = 0$, whose positive solution is $S = 10.5$, and the entire distance traveled by the motorcyclist is $2 S = 21$.
Answer: 21.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the sum of all numbers of the form $x+y$, where $x$ and $y$ are natural number solutions to the equation $5 x+17 y=307$.
|
Solution. We solve the auxiliary equation $5 x+17 y=1$. For example, its solutions can be 7 and 2. Multiply them by 307, and consider linear combinations for integer $t$, we get values in natural numbers
$\left\{\begin{array}{l}x=7 \cdot 307-17 t, \\ y=-2 \cdot 307+5 t,\end{array} t \in Z, x>0, y>0 \Rightarrow t \in\{123,124,125,126\} \Rightarrow\right.$
$(58,1),(41,6),(24,11),(7,16)$
$59+47+35+23=164$
Answer: 164.
|
164
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) The creative competition at the institute consisted of four tasks. In total, there were 70 applicants. The first test was successfully passed by 35, the second by 48, the third by 64, and the fourth by 63 people, with no one failing all 4 tasks. Those who passed both the third and fourth tests were admitted to the institute. How many were admitted?
|
Solution. 1st and 2nd tasks were solved by at least $35+48-70=13$ people. 3rd and 4th - at least $64+63-70=57$ people. No one failed all tasks, so 1st and 2nd were solved by 13 people, 3rd and 4th - 57 people.
Answer: 57 people.
Criteria.
| Points | Conditions for awarding |
| :--- | :--- |
| 10 points | Justified solution |
| 5 points | An arithmetic error or insufficiently justified solution in an otherwise justified solution. |
| 0 points | Any other situation |
|
57
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) In one of the regions on the planet, seismic activity was studied. 80 percent of all days were quiet. The instrument predictions promised a calm situation in 64 out of 100 cases; moreover, in 70 percent of all cases when the day was quiet, the instrument predictions came true. What percentage of days with increased seismic activity are those in which the predictions did not match reality?
|
Solution. Let the total number of observed days be x. The number of actually quiet days was $0.8x$, and seismically active days were $0.2x$. The predictions of quiet days matched the actually quiet days: $0.7 \cdot 0.8x = 0.56x$. Then the number of active days that did not match the predictions was $0.64x - 0.56x = 0.08x$, and $\frac{0.08x}{0.2x} \cdot 100\% = 40\%$.
Answer: $40\%$
## Criteria
| Points | Conditions for Awarding |
| :---: | :--- |
| 10 points | Fully justified solution |
| 5 points | An arithmetic error was made with correct reasoning or insufficiently justified solution |
| 0 points | Incorrect reasoning or only the answer is written. |
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A car left point A for point B, and a second car left with some delay. When the first car had traveled half the distance, the second car had traveled $26 \frac{1}{4}$ km, and when the second car had traveled half the distance, the first car had traveled $31 \frac{1}{5}$ km. After overtaking the first car, the second car arrived at point B, immediately turned around, and after traveling 2 km, met the first car. Find the distance between points A and B. Provide the answer as a number without specifying the unit.
|
Solution. S - the distance between points A and B.
$$
\frac{S-2-S / 2}{S+2-26.25}=\frac{S-2-31.2}{S+2-S / 2}, \quad 5 S^{2}-383 S+5394=0, \quad \sqrt{D}=197, \quad S=58
$$
Answer: 58.
|
58
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given six socks, all of different colors and easily stretchable. You cannot turn them inside out. In how many ways can you put on 3 socks on each foot, considering which one to put on earlier and which one later?
|
Solution. There is a sequence of 6 sock puttings on: $\mathrm{C}_{6}^{3}=20$ ways to choose which puttings are for the right foot. For each such choice, there are $6!=720$ ways to choose which sock to take for each putting.
Answer: 14400.
|
14400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $x, y, z$ be the roots of the equation $t^{3}-2 t^{2}-9 t-1=0$. Find $\frac{y z}{x}+\frac{x z}{y}+\frac{x y}{z}$.
(12 points)
|
Solution. Let's bring the desired expression to a common denominator: $\frac{y^{2} z^{2}+x^{2} z^{2}+x^{2} y^{2}}{x y z}$. The polynomial has 3 different real roots, since $\mathrm{P}(-100)0, \mathrm{P}(0)0$. By Vieta's theorem $x+y+z=2, x y+x z+y z=-9, x y z=1$.
$$
\begin{aligned}
& x^{2} y^{2}+x^{2} z^{2}+y^{2} z^{2}=(x y+x z+y z)^{2}-2\left(x^{2} y z+y^{2} x z+z^{2} x y\right) \\
& =(x y+x z+y z)^{2}-2 x y z(x+y+z)=81-2 * 1 * 2=77
\end{aligned}
$$
Answer: 77.
|
77
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. The base of the pyramid $\mathrm{TABCD}$ is an isosceles trapezoid $\mathrm{ABCD}$, the midline of which is equal to $5 \sqrt{3}$. The ratio of the areas of the parts of the trapezoid $\mathrm{ABCD}$, into which it is divided by the midline, is $7: 13$. All lateral faces of the pyramid $\mathrm{TABCD}$ are inclined to the base plane at an angle of $30^{\circ}$. Find the volume of the pyramid TAKND, where points $\mathrm{K}$ and $\mathrm{N}$ are the midpoints of edges $\mathrm{TB}$ and $\mathrm{TC}$, respectively, and AD is the larger base of the trapezoid ABCD.
|
# Solution.
Let $TO$ be the height of the pyramid. Since all lateral faces are inclined to the base at the same angle, $O$ is the center of the circle inscribed in the base. Let $MP$ be the midline of the trapezoid, $\quad AD=a, BC=b. \quad$ According to the problem, we have $S_{MB CP}=7x, S_{\text{AMPD}}=13x, \quad \frac{7}{13}=\frac{b+5\sqrt{3}}{a+5\sqrt{3}}, a+b=10\sqrt{3}$, $a=8\sqrt{3}, b=2\sqrt{3}$. Since a circle can be inscribed in the trapezoid $ABCD$, then $AB+CD=a+b, \quad AB=CD=5\sqrt{3}$. We calculate the height of the trapezoid $h=\sqrt{AB^2-(a-b)^2/4}=4\sqrt{3}$. Draw a line through point $O$ perpendicular to the bases of the trapezoid and intersecting these bases at points $Q$ and $R, OR=h$. Since the lateral faces are inclined to the base plane at an angle of $30^\circ$, the height of the pyramid $TO=\frac{1}{2} QR \tan 30^\circ=2$.
Let $TF$ be the height of the pyramid TAKND, where $TF$ is the perpendicular dropped from point $T$ to the line $QS$, and $S$ is the midpoint of $KN$. We calculate the volume of the pyramid TAKND: $V_{\text{TAKND}}=\frac{1}{3} \cdot \frac{AD+KN}{2} \cdot QS \cdot TF$. The area of triangle $TQS$ can be calculated in two ways: $S_{\mathrm{TQS}}=\frac{QR \cdot TO}{4}, S_{\mathrm{TQS}}=\frac{QS \cdot TF}{2}, QS \cdot TF=\frac{QR \cdot TO}{2}$, $V_{\text{TAKND}}=\frac{1}{6} \cdot \frac{AD+KN}{2} \cdot QR \cdot TO$. From this, we get $V_{\text{TAKND}}=18$.
Answer: 18.
## First (online) stage of the academic competition "Step into the Future" for school students in the subject "Mathematics", autumn 2019, 11th grade
#
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A group of schoolchildren heading to a school camp was to be seated in buses so that each bus had the same number of passengers. Initially, 22 people were to be seated in each bus, but it turned out that three schoolchildren could not be seated. When one bus left empty, all the schoolchildren were able to sit evenly in the remaining buses. How many schoolchildren were in the group, given that no more than 18 buses were allocated for transporting the schoolchildren, and no more than 36 people can fit in each bus? Provide the answer as a number without specifying the unit.
$(2$ points)
|
Solution. Let $\mathrm{n}$ be the number of buses, $\mathrm{m}$ be the number of schoolchildren in each bus, and $\mathrm{S}$ be the total number of schoolchildren.
We have
$$
S=22 n+3, \quad S=(n-1) m, n \leq 10, m \leq 36, \quad 22 n+3=(n-1) m, \quad n=1+\frac{25}{m-22}
$$
Considering the constraints on $\mathrm{n}$ and $\mathrm{m}$, we get the only possible case: $m=27, \quad n=6, \quad S=135$.
Answer: 135.
|
135
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many ways can the line $x \sin \sqrt{16-x^{2}-y^{2}}=0$ be drawn without lifting the pencil and without retracing any part of the line? (12 points)
|
Solution. Since $\pi^{2}<16<(2 \pi)^{2}$, the given line consists of 2 circles with radii 4 and $\sqrt{16-\pi^{2}}$ and a vertical segment.

This line is unicursal, as it has only 2 odd points $\mathrm{A}(0 ; 4)$ and $\mathrm{B}(0 ;-4)$. You should start drawing the line from one of these points and finish at the other (2 options). Next, there are 3! ways to choose the order in which to pass the left arc, the right arc, and the diameter. When passing the diameter, there are also 3! ways to choose the order in which to pass the arcs and the diameter of the inner circle. In total, the number of ways is $2 * 3! * 3! = 72$.
Answer: 72.
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For how many two-digit natural numbers n are exactly two of these three statements true: (A) n is odd; (B) n is not divisible by $3 ;$ (C) n is divisible by 5?
|
Solution. We can consider the first 30 two-digit numbers (from 10 to 39), and then multiply the result by 3, since the remainders when dividing by 2, 3, and 5 do not change when shifted by 30 or 60. There are three mutually exclusive cases.
1) (A) and (B) are satisfied, and (C) is not. From (A) and (B), it follows that \( n \) is divisible by 6 with a remainder of 1 or 5, and \( n \) should not be divisible by 5. There are eight such numbers: 11, 13, 17, 19, 23, 29, 31, 37.
2) (A) is satisfied, (B) is not, and (C) is satisfied. Then \( n \) is divisible by 6 with a remainder of 3, and \( n \) is divisible by 5. There is one such number: 15.
3) (A) is not satisfied, (B) and (C) are satisfied. Then \( n \) is divisible by 6 with a remainder of 2 or 4, and \( n \) is divisible by 5. There are two such numbers: 10 and 20.
In total: \( 3 * (8 + 1 + 2) = 33 \) numbers.
Answer: 33.
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. The base of the pyramid $\mathrm{TABCD}$ is an isosceles trapezoid $\mathrm{ABCD}$, the length of the larger base $A D$ of which is $12 \sqrt{3}$. The ratio of the areas of the parts of the trapezoid $A B C D$, into which it is divided by the midline, is $5: 7$. All lateral faces of the pyramid TABCD are inclined to the base plane at an angle of $30^{\circ}$. Find the volume of the pyramid SAKND, where points $\mathrm{K}$ and $\mathrm{N}$ are the midpoints of edges ТВ and $\mathrm{TC}$ respectively, and point $\mathrm{S}$ lies on edge $\mathrm{TD}$, such that $\mathrm{TS}: \mathrm{SD}=1: 2$.
|
# Solution.
Let TO be the height of the pyramid. Since all lateral faces are inclined to the base at the same angle, O is the center of the circle inscribed in the base. Let MP be the midline of the trapezoid, $A D=a=12 \sqrt{3}, B C=b$.
According to the problem, we have
$S_{\text {MBCP }}=5 x, S_{\text {AMPD }}=7 x, \quad \frac{5}{7}=\frac{b+(a+b) / 2}{a+(a+b) / 2}=\frac{3 b+12 \sqrt{3}}{b+36 \sqrt{3}}, \quad b=6 \sqrt{3}$. Since a circle can be inscribed in trapezoid ABCD, then $A B+C D=a+b, \quad A B=C D=19 \sqrt{3}$. We calculate the height of the trapezoid $h=\sqrt{A B^{2}-(a-b)^{2} / 4}=6 \sqrt{6}$. Draw a line through point O perpendicular to the bases of the trapezoid, intersecting these bases at points $\mathrm{Q}$ and $\mathrm{R}, \mathrm{OR}=\mathrm{h}$. Since the lateral faces are inclined to the plane
of the base at an angle of $30^{\circ}$, the height of the pyramid $T O=\frac{1}{2} Q R \operatorname{tg} 30^{\circ}=3 \sqrt{2}$.
Let TF be the height of the pyramid TAKND, TF is the perpendicular dropped from point $\mathrm{T}$ to line $\mathrm{QL}$, where $\mathrm{L}$ is the midpoint of $\mathrm{KN}$. We calculate the volume of the pyramid
SAKND:
$$
V_{S A K N D}=\frac{1}{3} \cdot \frac{A D+K N}{2} \cdot Q S \cdot \frac{2}{3} T F
$$
we can
$S_{\mathrm{TQS}}=\frac{Q R \cdot T O}{4}, S_{\mathrm{TQS}}=\frac{Q S \cdot T F}{2}, \quad Q S \cdot T F=\frac{Q R \cdot T O}{2}$,
$V_{\text {and }} V_{S K N D}=\frac{1}{6} \cdot \frac{A D+K N}{2} \cdot \frac{2}{3} Q R \cdot T O$.
From this, we get $V_{\text {SAKND }}=90$.
Answer: 90.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. If a two-digit natural number is decreased by 54, the result is a two-digit number with the same digits but in reverse order. In the answer, specify the median of the sequence of all such numbers.
#
|
# Solution.
Let $\overline{x y}=10 x+y$ be the original two-digit number, then $\overline{y x}=10 y+x$ is the number written with the same digits but in reverse order. We get the equation $10 x+y=10 y+x+54$. From the equation, it is clear that the two-digit number is greater than 54. Let's start the investigation with the tens digit equal to 6.
| $\boldsymbol{X}$ | equation | $\boldsymbol{y}$ | number |
| :---: | :---: | :---: | :---: |
| 6 | $60+y=10 y+6+54$ | $y=0$ | 60 does not fit the condition |
| 7 | $70+y=10 y+7+54$ | $y=1$ | 71 |
| 8 | $80+y=10 y+8+54$ | $y=2$ | 82 |
| 9 | $90+y=10 y+9+54$ | $y=3$ | 93 |
These could be the numbers $71,82,93$. The median of the series is 82.
Answer: 82.
|
82
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The wolf saw a roe deer several meters away from him and chased after her along a straight forest path. The wolf's jump is $22\%$ shorter than the roe deer's jump. Both animals jump at a constant speed. All the roe deer's jumps are of the same length, and the wolf's jumps are also equal to each other. There is a period of time during which both the wolf and the roe deer make a certain whole number of jumps. Each time, it turns out that the wolf has made $t\%$ more jumps than the roe deer. Find the greatest integer value of $\mathrm{t}$, for which the wolf will not be able to catch the roe deer.
|
Solution: Let $x$ be the length of the roe deer's jump, then $0.78 x$ is the length of the wolf's jump; $y$ - the number of jumps the roe deer makes over the time interval specified in the condition, $y\left(1+\frac{t}{100}\right)$ - the number of jumps the wolf makes over the same time interval. The wolf will not be able to catch up with the roe deer if the distance covered by the roe deer over the specified time interval $x y$ - is not less than the distance covered by the wolf over the same time interval: $0.78 x y\left(1+\frac{t}{100}\right)$. We form the inequality: $0.78 x y\left(1+\frac{t}{100}\right) \leq x y$; $1+\frac{t}{100} \leq \frac{50}{39} ; t \leq \frac{1100}{39}$. The maximum value of $t$ that satisfies this inequality, $t=28 \%$. Answer: 28.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Ilya takes a triplet of numbers and transforms it according to the rule: at each step, each number is replaced by the sum of the other two. What is the difference between the largest and the smallest numbers in the triplet after 1989 applications of this rule, if the initial triplet of numbers was $\{70 ; 61; 20\}$? If the question allows multiple answers, write them without spaces in ascending order.
|
Solution. Let's denote the 3 numbers as $\{x ; x+a ; x+b\}$, where $0<a<b$. Then the difference between the largest and the smallest number at any step, starting from the zeroth step, will be an invariant, that is, unchanged and equal to $b$.
$B=70-20=50$.
Answer: 50.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given triangle $A B C$. Lines $O_{1} O_{2}, O_{1} O_{3}, O_{3} O_{2}$ are the bisectors of the external angles of triangle $A B C$, as shown in the figure. Point $O$ is the center of the inscribed circle of triangle $A B C$. Find the angle in degrees between the lines $O_{1} O_{2}$ and $O O_{3}$.
|
Solution. Point $O$ is the intersection point of the angle bisectors of triangle $ABC$, therefore, the bisector $BO$ is perpendicular to the line $O_{1} O_{2}$ (as the bisectors of adjacent angles of the triangle).

Point $O_{3}$, being equidistant from the lines $BA$ and $BC$, lies on $BO$. Therefore, the line $OO_{3}$, which coincides with $BO$, is perpendicular to the line $O_{1} O_{2}$.
Answer: 90 .
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given a rectangular trapezoid $\mathrm{ABCE}$, the bases of which $\mathrm{BC}$ and $\mathrm{AE}$ are equal to 3 and 4, respectively. The smaller lateral side $\mathrm{AB}$ is equal to $\mathrm{BC}$. On $\mathrm{AE}$, a point $\mathrm{D}$ is marked such that $\mathrm{AD}: \mathrm{DE}=3: 1$; on $\mathrm{AD}$, a point $\mathrm{F}$ is marked such that $\mathrm{AF}: \mathrm{FD}=2: 1$; on $\mathrm{BD}$, a point $\mathrm{G}$ is marked such that $\mathrm{BG}: \mathrm{GD}=1: 2$. Determine the degree measure of angle $\mathrm{CFG}$.
|
Solution. Construct the height $I H$ such that $G \in I H$ and connect points C and G.
1) $\triangle I G C = \triangle G F H$ - by two legs, since $I C = G H = 2, I G = H F = 1$, therefore $F G = G C$, $\angle I C G = \angle F G H = \alpha$, and $\angle H F G = \angle I G C = 90^{\circ} - \alpha$.
2) $\triangle F G C$ is a right isosceles triangle, since $F G = F D$,
$$
\begin{aligned}
& \angle H G F + \angle F G C + \angle I G C = 180^{\circ} \\
& \angle F G C = 180^{\circ} - \angle H G F - \angle I G C \\
& \angle F G C = 180^{\circ} - \alpha - 90^{\circ} + \alpha = 90^{\circ}
\end{aligned}
$$
Thus, $\angle C F G = 45^{\circ}$.
Answer: 45.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In triangle $A B C$ with angle $\angle B=120^{\circ}$, the angle bisectors $A A_{1}, B B_{1}, C C_{1}$ are drawn. Segment $A_{1} B_{1}$ intersects the angle bisector $C C_{1}$ at point M. Find the degree measure of angle $B_{1} M C_{1}$.
|
# Solution.
Extend side $A B$ beyond point $B$, then $B C$ is the bisector of angle $\angle B_{1} B K$, which means point $A_{1}$ is equidistant from sides $B_{1} B$ and $B K$. Considering that point $A_{1}$ lies on the bisector of $\angle B A C$, and thus is equidistant from its sides, we get that $A_{1}$ is equidistant from sides $B_{1} B$ and $B_{1} C$, and therefore lies on the bisector of $\angle B B_{1} C$. Similarly, we prove that $B_{1} C_{1}$ is the bisector of $\angle A B_{1} B$. Therefore, $\angle C_{1} B_{1} A_{1}=90^{\circ}$, as the angle between the bisectors of adjacent angles.
In triangle $B B_{1} C$, point $M$ is the intersection of the bisectors $B_{1} A_{1}$ and $C C_{1}$, and thus $B M$ is also the bisector of $\angle B_{1} B C$, so $\angle B_{1} B M=\angle M B C=30^{\circ}$. Further, $\angle A B M=\angle C_{1} B B_{1}+\angle B_{1} B M=60^{\circ}+30^{\circ}=90^{\circ}$, which means a circle can be circumscribed around quadrilateral $B M B_{1} C_{1}$. Therefore, $\angle B_{1} M C_{1}=\angle B_{1} B C_{1}=60^{\circ}$, as they subtend the same arc.
Answer: 60.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A chemistry student conducted an experiment: from a tank filled with syrup solution, he poured out several liters of liquid, refilled the tank with water, then poured out twice as much liquid and refilled the tank with water again. As a result, the amount of syrup in the tank decreased by $\frac{25}{3}$ times. Determine how many liters of liquid the student poured out the first time, if the tank's volume is 1000 liters.
#
|
# Solution.
1) Let the syrup content in the initial solution be $p \%$ and let $x$ liters of the solution were poured out the first time.
2) Then after pouring out the liquid, there remained $(1000-x)$ liters of the solution, and in it $(1000-x) \cdot \frac{p}{100}$ liters of syrup and $(1000-x) \cdot \frac{100-p}{100}$ water.
3) After adding $x$ liters of water, there became: 1000 liters of the solution, and in it $(1000-x) \cdot \frac{p}{100}$ liters of syrup and $(1000-x) \cdot \frac{100-p}{100}+x$ liters of water.
4) At the end of all the pouring, there became: 1000 liters of the solution with a syrup content of $\frac{3 p}{25} \%$,
$$
3 p
$$
that is, $1000 \cdot \frac{\overline{25}}{100}=\frac{30 p}{25}$ liters of syrup and $1000-\frac{30 p}{25}$ liters of water.
5) Then before the last addition of $2 x$ liters of water, there was $(1000-2 x)$ liters of the solution in the tank, and in it $\frac{30 p}{25}$ liters of syrup and $1000-\frac{30 p}{25}-2 x$ water. This is the same liquid as in point 3) of the solution, so the ratio of syrup to liquid in it is the same. We set up the equation:
$$
\frac{(1000-x) \cdot \frac{p}{100}}{1000}=\frac{\frac{30 p}{25}}{1000-2 x} \Leftrightarrow 2 x^{2}-3000 x+\frac{22}{25} \cdot 1000^{2}=0 \Leftrightarrow
$$
$\Leftrightarrow x \in\{1100 ; 400\}, 1100$ liters does not satisfy the condition of the problem.
Answer: 400.
## Solution variant № 2
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A warehouse has coffee packed in bags of 15 kg and 8 kg. How many bags of coffee in total does the warehouseman need to prepare to weigh out 1998 kg of coffee, with the number of 8 kg bags being the smallest possible?
|
Solution. Let $x$ be the number of bags weighing 15 kg, and $y$ be the number of bags weighing 8 kg. We get the equation $15 x + 8 y = 1998$. $8(x + y) + 7 x = 1998$, let $x + y = k$,
$8 k + 7 x = 1998$,
$7(k + x) + k = 1998$, let $k + x = t$,
$7 t + k = 1998$, $k = 1998 - 7 t$. Substitute into (2), $x = 8 t - 1998$.
Substitute into (1), $y = 2 \cdot 1998 - 15 t$.
Since $x > 0, y > 0$, then $250 \leq t \leq 266$. To have the smallest number of 8 kg coffee bags, then $t = 266$. Then accordingly $x = 130, y = 6$.
130 and 6 bags, a total of 136 bags.
Answer: 136.
|
136
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $A B C$ with angle $\angle B=120^{\circ}$, the angle bisectors $A A_{1}, B B_{1}, C C_{1}$ are drawn. Segment $A_{1} B_{1}$ intersects the angle bisector $C C_{1}$ at point M. Find the degree measure of angle $B_{1} B M$.
#
|
# Solution.
Extend side $A B$ beyond point $B$, then $B C$ is the bisector of angle $\angle B_{1} B K$, which means point $A_{1}$ is equidistant from sides $B_{1} B$ and $B K$. Considering that point $A_{1}$ lies on the bisector of $\angle B A C$, and thus is equidistant from its sides, we get that $A_{1}$ is equidistant from sides $B_{1} B$ and $B_{1} C$, and therefore lies on the bisector of $\angle B B_{1} C$. Thus, $B_{1} A_{1}$ is the bisector of $\angle B B_{1} C$.
In triangle $B B_{1} C$, point $M$ is the intersection of the bisectors $B_{1} A_{1}$ and $C C_{1}$, and therefore $B M$ is also the bisector of $\angle B_{1} B C$, so $\angle B_{1} B M = \angle M B C = 30^{\circ}$.
Answer: 30.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the sides $\mathrm{AB}$ and $\mathrm{AC}$ of the right triangle $\mathrm{ABC}\left(\angle B C A=90^{\circ}\right)$, right triangles АВТ and АСК are constructed externally such that $\angle A T B=\angle A K C=90^{\circ}$, $\angle A B T=\angle A C K=60^{\circ}$. On the side $\mathrm{BC}$, a point $\mathrm{M}$ is chosen such that $\mathrm{BM}=\mathrm{MC}$. Determine the degree measure of angle КМТ.
|
Solution. Mark points P and O at the midpoints of sides AB and AC, respectively. Connect point P with points M and T, and point O with points K and M.
Then: 1) $\Delta T P M = \Delta K O M$, by two sides and the angle between them, since
$$
\begin{gathered}
A O = \frac{1}{2} A C = K O = P M \\
A P = \frac{1}{2} A B = T P = O M \\
\angle T P M = \angle T P B + \angle B P M = \angle C O K + \angle C O M = \angle K O M
\end{gathered}
$$
Thus, TM = MK, $\angle P T M = \angle K M O$, and $\angle P M T = \angle M K O$.
2) Find the sum of angles $\angle P M T$ and $\angle K M O$:
$$
\angle P M T + \angle K M O = \angle M K O + \angle K M O = 180^{\circ} - \angle M O K
$$
In turn, $\angle M O K = \angle K O C + \angle M O C = 60^{\circ} + \angle B A C$.
3) $\angle K M T = \angle P M O + (\angle P M T + \angle K M O) = \angle B A C + (180^{\circ} - \angle M O K) = \angle K M T = \angle B A C + 180^{\circ} - 60^{\circ} - \angle B A C = 120^{\circ}$.
Answer: 120.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Right triangles $M D C$ and $A D K$ have a common right angle $D$. Point $K$ lies on $C D$ and divides it in the ratio $2: 3$, counting from point $C$. Point $M$ is the midpoint of side $A D$. Find the sum of the degree measures of angles $A K D$ and $M C D$, if $A D: C D=2: 5$.
|
Solution. Extend triangle $A D C$ to form a square $L J C D$.
Choose point $H$ on side $L J$ such that $L H: H J=2: 3$, point $N$ on side $C J$ such that $C N: N J=3: 2$, and point $B$ on side $C J$ such that $C B: B J=2: 3$. We obtain equal triangles: $\triangle A K D=\triangle A L H=\triangle H J N$.
Next, $\quad A H=H N, \angle A H N=90^{\circ}$, therefore, $\quad \angle H A N=45^{\circ} . \quad$ From the equality of triangles $M D C$ and $N A B$, we get $\angle N A B=\angle M C D$.
Next, $\angle L A B=\angle L A H+\angle H A N+\angle N A B=90^{\circ}$.
From this, finally, $\angle L A H+\angle N A B=\angle A K D+\angle M C D=45^{\circ}$.
Answer: 45.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number that has exactly 70 natural divisors (including 1 and the number itself).
(16 points)
|
Solution: Let $n$ be the required natural number, $n=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{m}^{k_{m}}$ - the prime factorization of the number $n$. Any natural divisor of this number has the form $d=p_{1}^{h_{1}} \cdot p_{2}^{l_{2}} \cdot \ldots \cdot p_{m}^{l_{m}^{m}}$, where $l_{i} \in\left\{0,1, \ldots, k_{i}\right\}, i=1, \ldots, m$. The number of divisors of the number $n$ is $\left(k_{1}+1\right)\left(k_{2}+1\right) \cdots\left(k_{m}+1\right)=70$. We decompose the number 70 into non-unit factors in all possible ways and choose the smallest number $n$. Since $70=2 \cdot 5 \cdot 7$, we have five cases:
1) $70=70$, the smallest number $n=2^{69}>40000$;
2) $70=35 \cdot 2$, the smallest number $n=2^{34} \cdot 3^{1}>40000$;
3) $70=14 \cdot 5$, the smallest number $n=2^{13} \cdot 3^{4}>40000$;
4) $70=10 \cdot 7$, the smallest number $n=2^{9} \cdot 3^{6}=512 \cdot 81>40000$;
5) $70=7 \cdot 5 \cdot 2$, the smallest number $n=2^{6} \cdot 3^{4} \cdot 5^{1}=25920$.
Answer: 25920.
|
25920
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A student wrote a program for recoloring a pixel into one of 128 different colors. These colors he numbered with natural numbers from 1 to 128, and the primary colors received the following numbers: white color - number 1, red - 5, orange - 13, yellow - 21, green - 45, blue - 75, dark blue - 87, purple - 91, black - 128. If the initial color of the pixel has a number \( n \leq 19 \), then the student's program recolors it to the color with the number \( n+4 \), and if the initial color of the pixel has a number \( n \geq 20 \), then the pixel is recolored to the color with the number \( |129-2n| \). Initially, the pixel was red. The student applied his program 2019 times sequentially. What color did the pixel end up as a result?
|
Solution. The final pixel color number is equal to $f^{[2019]}(5)$, where $f^{[k]}(n)=\underbrace{f(f(f(\ldots(f}_{k \text{ times}}(n) \ldots)-k$-fold composition of the function $f(n)$, which is equal to $n+4$ when $n \leq 19$, and equal to $|129-2 n|$ when $n \geq 20$. Let's compute and write down the first few values: $f(5)=9, f^{[2]}(5)=13, f^{[3]}(5)=17$, $f^{[4]}(5)=21, f^{[5]}(5)=87, f^{[6]}(5)=45, f^{[7]}(5)=39, f^{[8]}(5)=51, f^{[9]}(5)=27, f^{[10]}(5)=75$, $f^{[11]}(5)=21=f^{[4]}(5)$. We have obtained a cycle of length 7 operations. Therefore, for any natural value of $k$ and any $r=0,1, \ldots, 6$, we have $f^{[4+7 k+r]}(5)=f^{[r]}(21)$. Since $2019=4+287 \cdot 7+6$, then $r=6$, and $f^{[2019]}(5)=f^{[6]}(21)=75$. The pixel will be blue. Answer: blue.
|
75
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. (Option 2).
How to build a highway? (an old problem) From a riverside city A, goods need to be transported to point B, located $a$ kilometers downstream and $d$ kilometers from the riverbank. How should the highway be built from B to the river so that the transportation of goods from A to B is as cost-effective as possible, if the freight rate per ton-kilometer by river is half that of the highway?
|
Solution: Let the distance $AD$ be denoted by $x$ and the length of the highway $DB$ by $y$: by assumption, the length of $AC$ is $a$ and the length of $BC$ is $d$.
Since transportation along the highway is twice as expensive as along the river, the sum $x + 2y$ should be the smallest according to the problem's requirement. Let this smallest value be denoted by $m$.
We have the equation $x + 2y = m$. But $x = a - DC$, and $DC = \sqrt{y^2 - d^2}$; our equation becomes $a - \sqrt{y^2 - d^2} + 2y = m \quad \Rightarrow \quad 3y^2 - 4(m-a)y + (m-a)^2 + d^2 = 0$. $y = \frac{2}{3}(m-a) \pm \frac{\sqrt{(m-a)^2 - 3d^2}}{3}$
For $y$ to be real, $(m-a)^2$ must be at least $3d^2$.
The smallest value of $(m-a)^2$ is $3d^2$, and then $m - a = d\sqrt{3}$, $y = \frac{2(m-a) + 0}{3} = \frac{2d\sqrt{3}}{3} ; \sin \angle BDC = \frac{d}{y} = d : \frac{2d\sqrt{3}}{3} = \frac{\sqrt{3}}{2}$.
The angle whose sine is $\sqrt{3} / 2$ is $60^\circ$. Therefore, the highway should be built at an angle of $60^\circ$ to the river, regardless of the distance $AC$.
The solution only makes sense under certain conditions. If the point is located such that the highway, built at an angle of $60^\circ$ to the river, passes on the other side of city $A$, then the solution is invalid. In such a case, the point $B$ should be directly connected to city $A$ by a highway, without using the river for transportation at all.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. According to the inverse theorem of Vieta's theorem, we form a quadratic equation. We get $x^{2}-\sqrt{2019} x+248.75=0$.
Next, solving it, we find the roots $a$ and $b$: $a=\frac{\sqrt{2019}}{2}+\frac{32}{2}$ and $b=\frac{\sqrt{2019}}{2}-\frac{32}{2}$, and consequently, the distance between the points $a$ and $b$: $a-b=32$.
|
Answer: 32
| 15 points | The correct answer is obtained justifiably |
| :---: | :---: |
| 10 points | The quadratic equation is solved, but an arithmetic error is made or the distance between the points is not found |
| 5 points | The quadratic equation is correctly formulated according to the problem statement. |
| 0 points | The solution does not meet any of the criteria listed above |
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For a rectangle, the sum of two sides is 11, and the sum of three sides is 19.5. Find the product of all possible different values of the perimeter of such a rectangle.
|
Solution:
Let the sides of the rectangle be $a$ and $b$.
If the sum of adjacent sides is 11, then the system describing the condition of the problem is $\left\{\begin{array}{l}a+b=11 \\ 2 a+b=19.5\end{array}\right.$, its solution is $a=8.5, b=2.5$, the perimeter of the rectangle is $P_{1}=22$.
If, however, the number 11 is equal to the sum of opposite sides, then there are two possible cases $\left\{\begin{array}{l}2 a=11 \\ 2 a+b=19.5\end{array}\right.$ or $\left\{\begin{array}{l}2 a=11 \\ a+2 b=19.5\end{array}\right.$.
The solution to the first system is $a=5.5, b=8.5$, the perimeter of the rectangle is $P_{2}=28$.
The solution to the second system is $a=5.5, b=7$, the perimeter of the rectangle is
$P_{3}=25$. The product of the three possible perimeter values is $P_{1} \cdot P_{2} \cdot P_{3}=22 \cdot 28 \cdot 25=15400$.
Online (correspondence) stage of the "Step into the Future" School Students' Olympiad in the subject of Mathematics
Answer: 15400.
|
15400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) Find the area of a convex quadrilateral with equal diagonals, if the lengths of the segments connecting the midpoints of its opposite sides are 13 and 7.
|
Solution. Let $MK$ and $PH$ be segments connecting the midpoints of opposite sides of a convex quadrilateral $ABCD$, with $MK = PH$, $AC = 18$, and $BD = 7$.
We have: $MP \| AC$, $MP = \frac{1}{2} AC$ (as the midline of $\triangle ABC$); $HK \| AC$, $HK = \frac{1}{2} AC$ (as the midline of $\triangle ADC$). $\Rightarrow MP \| HK$, $MP = HK \Rightarrow MPKH$ is a parallelogram.

Since $MK = PH$, the quadrilateral $MPKH$ is a rectangle, with sides parallel to the diagonals $AC$ and $BD$ of the given quadrilateral $ABCD$, therefore $AC \perp BD$. This means that $S_{ABCD} = \frac{1}{2} AC \cdot BD = \frac{1}{2} \cdot 18 \cdot 7 = 63$ (sq.units).
Answer: 63.
| Criterion Description | Points |
| :--- | :---: |
| The correct answer is obtained with justification. | 15 |
| The solution contains a computational error, possibly leading to an incorrect answer, but the solution has a correct sequence of all steps. | 10 |
| In the solution, one or two formulas are correctly written, which could be the beginning of a possible solution. | 5 |
| The solution does not meet any of the criteria described above. | 0 |
| Maximum score | 15 |
|
63
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Four elevators of a skyscraper, differing in color (red, blue, green, and yellow), are moving in different directions and at different but constant speeds. Observing the elevators, someone started a stopwatch and, looking at its readings, began to record: 36th second - the red elevator caught up with the blue one (moving in the same direction). 42nd second - the red elevator passed the green one (moving in opposite directions), 48th second - the red elevator passed the yellow one, 51st second - the yellow elevator passed the blue one, 54th second - the yellow elevator caught up with the green elevator. At what second from the start of the count will the green elevator pass the blue one, if during the observation period the elevators did not stop and did not change their direction of movement?
(12 points)
|
Solution. Let's number the elevators: red - first, blue - second, green - third, yellow - fourth. The elevators move at constant speeds, so the distance traveled $S_{i}, i=1,2,3,4$, in some coordinate system depends on time according to the law $S_{i}=k_{i} t+b_{i}$. According to the problem, the red and blue elevators move in the same direction, and the red elevator is catching up with the blue one, so $k_{1} \cdot k_{2}>0, k_{1}>k_{2}$. For definiteness, let $k_{1}>0$, then $k_{2}>0$. The green and yellow elevators move in the opposite direction to the first two, and the yellow elevator is catching up with the green one, so $k_{3}<0, \quad k_{4}<0, \quad k_{3}<k_{4} \cdot$ Let's plot the graphs of the functions $S_{i}(t)$, according to the problem. We need to determine the abscissa of the point $M$ of intersection of the second graph with the third. Point $M$ is the point of intersection of the medians of triangle $A B C$. From this, we have $\frac{x-36}{51-x}=\frac{2}{1}, x=46$.
Answer: at 46 seconds.
|
46
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.