problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Example 1. Find $\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+6 x+5}-x\right)$.
|
Solution. When $x \rightarrow+\infty$, the given function represents the difference of two infinitely large quantities taking positive values (case $\infty-\infty$). By multiplying and dividing the given function by $\left(\sqrt{x^{2}+6 x+5}+x\right)$, we get
$$
\begin{gathered}
\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+6 x+5}-x\right)=\lim _{x \rightarrow+\infty} \frac{\left(\sqrt{x^{2}+6 x+5}-x\right)\left(\sqrt{x^{2}+6 x+5}+x\right)}{\sqrt{x^{2}+6 x+5}+x}= \\
=\lim _{x \rightarrow+\infty} \frac{\left(x^{2}+6 x+5\right)-x^{2}}{\sqrt{x^{2}+6 x+5+x}}=\lim _{x \rightarrow+\infty} \frac{6 x+5}{\sqrt{x^{2}+6 x+5+x}}=
\end{gathered}
$$
$$
=\lim _{x \rightarrow+\infty} \frac{6+\frac{5}{x}}{\sqrt{1+\frac{6}{x}+\frac{5}{x^{2}}}+1}=\frac{6}{1+1}=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find $\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{x}{3}$.
|
Solution. When $x \rightarrow 0$, we get an indeterminate form of $0 \cdot \infty$. Rewriting the given function in another form and applying formula (1.59), we find
$$
\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{x}{3}=\lim _{x \rightarrow 0} x \frac{\cos \frac{x}{3}}{\sin \frac{x}{3}}=\lim _{x \rightarrow 0} \frac{x}{\sin \frac{x}{3}} \cos \frac{x}{3}=
$$
$$
=\lim _{x \rightarrow 0} \frac{\frac{1}{3} x}{\frac{1}{3} \sin \frac{x}{3}} \cdot \cos \lim _{x \rightarrow 0} \frac{x}{3}=\frac{1}{\frac{1}{3}} \cdot 1=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow+\infty} x\left(\operatorname{arctg} x-\frac{\pi}{2}\right)$.
|
Solution. Let $\operatorname{arctg} x=\alpha$, then $x=\operatorname{tg} \alpha$, if $x \rightarrow+\infty$, then $\alpha \rightarrow \frac{\pi}{2}$.
Consequently,
$$
\begin{gathered}
\lim _{x \rightarrow+\infty} x\left(\operatorname{arctg} x-\frac{\pi}{2}\right)=\lim _{\alpha \rightarrow \frac{\pi}{2}} \operatorname{tg} \alpha\left(\alpha-\frac{\pi}{2}\right)= \\
=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \frac{\sin \alpha}{\cos \alpha}\left(\frac{\pi}{2}-\alpha\right)=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \sin \alpha \frac{\frac{\pi}{2}-\alpha}{\sin \left(\frac{\pi}{2}-\alpha\right)}= \\
=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \sin \alpha \cdot \lim _{\alpha \rightarrow \frac{\pi}{2}} \frac{\frac{\pi}{2}-\alpha}{\sin \left(\frac{\pi}{2}-\alpha\right)}=-1 \cdot 1=-1
\end{gathered}
$$
## Problems
Find the limits:
1. $\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+5 x+4}-\sqrt{x^{2}+x}\right)$.
2. $\lim _{x \rightarrow-4}\left(\frac{1}{x+4}-\frac{8}{16-x^{2}}\right)$.
3. $\lim _{x \rightarrow 0}\left(\frac{\cos x}{\sin ^{2} x}-\operatorname{ctg}^{2} x\right)$.
4. $\lim _{x \rightarrow 0}(\operatorname{ctg} x-\operatorname{cosec} x)$.
5. $\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{\pi}{2} x$.
6. $\lim _{x \rightarrow \frac{\pi}{2}}\left(x-\frac{\pi}{2}\right) \operatorname{tg} x$.
7. $\lim _{x \rightarrow 0} \frac{e^{-x}-1}{3 x}$.
8. $\lim _{m \rightarrow \infty} m[\ln (m+4)-\ln m]$.
9. $\lim _{x \rightarrow 0} \frac{\sqrt{x+9}-3}{\sin 6 x}$.
10. $\lim _{n \rightarrow \infty} \frac{5-2^{n}}{5+2^{n+1}}$.
11. $\lim _{x \rightarrow 0}(\cos 2 x)^{\operatorname{ctg}^{2} 2 x}$.
12. $\lim _{x \rightarrow 0} \frac{1+x^{2}-\cos x}{\sin ^{2} x}$.
## Answers
1.2.2. $-\frac{1}{8}$. 3. $\frac{1}{2}$. 4. 0. 5. $\frac{2}{\pi}$. 6. -1 . Hint. Let $x=\frac{\pi}{2}+\alpha$. 7. $-\frac{1}{3}$. 8.4.9. $\frac{1}{36} \cdot 10 .-\frac{1}{2} \cdot 11 \cdot \frac{1}{\sqrt{e}} \cdot$ 12. $\frac{3}{2}$.
## § 1.7. Comparison of Infinitesimals
1. Two infinitesimals $\alpha$ and $\beta$ are called infinitesimals of the same order if the limit of their ratio is not zero, i.e.
$$
\lim \frac{\alpha}{\beta}=a(a \neq 0)
$$
2. The quantity $\alpha$ is called an infinitesimal of higher order compared to $\beta$ if the limit of the ratio of $\alpha$ to $\beta$ is zero, i.e.
$$
\lim \frac{\alpha}{\beta}=0
$$
3. The quantity $\alpha$ is called an infinitesimal of lower order compared to $\beta$ if the ratio of $\alpha$ to $\beta$ is an infinitely large quantity, i.e.
$$
\lim \frac{\alpha}{\beta}=\infty
$$
4. Infinitesimals $\alpha$ and $\beta$ are called equivalent if the limit of their ratio is one, i.e.
$$
\lim \frac{\alpha}{\beta}=1
$$
Notation for equivalent infinitesimals $\alpha$ and $\beta$:
$$
\alpha \sim \beta
$$
Equivalent infinitesimals have the following properties:
1) the difference of two equivalent infinitesimals is an infinitesimal of higher order compared to each of them;
2) when finding the limit of the ratio of two infinitesimals, each of them (or only one) can be replaced by another infinitesimal equivalent to it, i.e., if $\alpha \sim \alpha_{1}$ and $\beta \sim \beta_{1}$, then
$$
\lim \frac{\alpha}{\beta}=\lim \frac{\alpha_{1}}{\beta}=\lim \frac{\alpha}{\beta_{1}}=\lim \frac{\alpha_{1}}{\beta_{1}}
$$
Remark 1. The product of two infinitesimals is an infinitesimal of higher order compared to each of them.
Remark 2. To compare infinitesimals, find the limit of their ratio. If this ratio does not have a limit, then the quantities are incomparable.
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow 3} \frac{\ln \left(x^{2}-5 x+7\right)}{x-3}$.
|
Solution. When $x \rightarrow 3$, we get an indeterminate form of $\frac{0}{0}$, since $x^{2}-5 x+7 \rightarrow 1$ and $\ln \left(x^{2}-5 x+7\right) \rightarrow 0$. The expression $x^{2}-5 x+7$ can be represented as:
$$
x^{2}-5 x+7=1+\left(x^{2}-5 x+6\right)=1+z
$$
where $\left(x^{2}-5 x+6\right)=z \rightarrow 0$ as $x \rightarrow 3$.
Since $\ln (1+z) \sim z$ as $z \rightarrow 0$ (see example 2), then
$$
\ln \left(x^{2}-5 x+7\right) \sim x^{2}-5 x+6
$$
Applying formula (1.74), we get
$$
\lim _{x \rightarrow 3} \frac{\ln \left(x^{2}-5 x+7\right)}{x-3}=\lim _{x \rightarrow 3} \frac{x^{2}-5 x+6}{x-3}=\lim _{x \rightarrow 3} \frac{(x-2)(x-3)}{x-3}=
$$
$$
=\lim _{x \rightarrow 3}(x-2)=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Calculate the value of the derivative of the implicit function $x y^{2}=4$ at the point $M(1,2)$.
|
Solution. First, let's find the derivative:
$$
x^{\prime} y^{2}+x 2 y y^{\prime}=0, y^{\prime}=-\frac{y}{2 x}
$$
Substituting the values \(x=1\), \(y=2\) into the right-hand side of the last equation, we get
$$
y^{\prime}=-\frac{2}{2 \cdot 1}=-1
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find the third-order derivative of the function $y=x^{2}+3 x+2$.
|
Solution. Differentiating successively, we obtain:
$$
\begin{gathered}
y^{\prime}=\left(x^{2}+3 x+2\right)^{\prime}=2 x+3 ; y^{\prime \prime}=(2 x+3)^{\prime}=2 \\
y^{\prime \prime \prime}=(2)^{\prime}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the derivative $y_{x}^{\prime}$ of the function $x=e^{t} \cos t$; $y=e^{t} \sin t$ at $t=0$.
|
Solution. The functions $x$ and $y$ have the following derivatives with respect to $t$:
$$
\begin{aligned}
& x_{i}^{\prime}=e^{t} \cos t-e^{t} \sin t=e^{t}(\cos t-\sin t) \\
& y_{t}^{\prime}=e^{t} \sin t+e^{t} \cos t=e^{t}(\sin t+\cos t)
\end{aligned}
$$
therefore
$$
y_{x}^{\prime}=\frac{\sin t+\cos t}{\cos t-\sin t}
$$
At $t=0$, we get $y_{x}^{\prime}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}$.
|
Solution. Using the L'Hôpital-Bernoulli rule, we get
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\frac{1}{\cos ^{2} x}}{\frac{3}{\cos ^{2} 3 x}}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos ^{2} 3 x}{3 \cos ^{2} x}
$$
The limit of the ratio of the first derivatives is an indeterminate form of $\frac{0}{0}$. We resolve this indeterminate form:
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos ^{2} 3 x}{3 \cos ^{2} x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{-6 \cos 3 x \sin 3 x}{-6 \cos x \sin x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin 6 x}{\sin 2 x}
$$
Again, we have an indeterminate form of $\frac{0}{0}$. Applying the L'Hôpital-Bernoulli rule once more, we find
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin 6 x}{\sin 2 x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{6 \cos 6 x}{2 \cos 2 x}=\frac{6}{2}=3
$$
Thus,
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{\sin x}\right)$.
|
Solution. When $x \rightarrow \mathbf{0}$, we get an indeterminate form of $\infty-\infty$. We will resolve this indeterminacy by converting it to an indeterminate form of $\frac{0}{0}$ and applying L'Hôpital-Bernoulli's rule,
$$
\begin{gathered}
\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{\sin x}\right)=\lim _{x \rightarrow 0} \frac{\sin x-x}{x \sin x}=\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin x+x \cos x}= \\
=\lim _{x \rightarrow 0} \frac{-\sin x}{\cos x+\cos x-x \sin x}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Find $\lim _{x \rightarrow 0}[(x-\sin x) \ln x]$.
|
Solution. Here we have an indeterminate form $0 \cdot \infty$. The given function can be represented as
$$
(x-\sin x) \ln x=\frac{\ln x}{\frac{1}{x-\sin x}}
$$
The resulting indeterminate form $\frac{\infty}{\infty}$ is resolved using L'Hôpital's rule:
$$
\lim _{x \rightarrow 0} \frac{\ln x}{\frac{1}{x-\sin x}}=\lim _{x \rightarrow 0} \frac{\frac{1}{x}}{\frac{-(1-\cos x)}{(x-\sin x)^{2}}}=\lim _{x \rightarrow 0} \frac{(x-\sin x)^{2}}{x(\cos x-1)}
$$
This is an indeterminate form of $\frac{0}{0}$, so
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{(x-\sin x)^{2}}{x(\cos x-1)}=\lim _{x \rightarrow 0} \frac{2(x-\sin x)(1-\cos x)}{\cos x-1-x \sin x}= \\
& =2 \lim _{x \rightarrow 0} \frac{(1-\cos x)^{2}+(x-\sin x) \sin x}{-\sin x-\sin x-x \cos x}= \\
& =2 \lim _{x \rightarrow 0} \frac{1-2 \cos x+\cos ^{2} x+x \sin x-\sin ^{2} x}{-2 \sin x-x \cos x}= \\
& \quad=2 \lim _{x \rightarrow 0} \frac{1-2 \cos x+x \sin x+\cos 2 x}{-2 \sin x-x \cos x}= \\
& =2 \lim _{x \rightarrow 0} \frac{2 \sin x+\sin x+x \cos x-2 \sin 2 x}{-3 \cos x+x \sin x}=0
\end{aligned}
$$
Thus,
$$
\lim _{x \rightarrow 0}(x-\sin x) \ln x=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Find $\lim _{x \rightarrow 1}(x-1)^{\ln x}$.
|
Solution. When $x \rightarrow 1$, we have the indeterminate form $0^{0}$. We will use the identity
$$
[f(x)]^{\varphi(x)}=e^{\varphi(x) \ln f(x)}
$$
which in this case will be
$$
(x-1)^{\ln x}=e^{\ln x \cdot \ln (x-1)}
$$
We have
$$
\lim _{x \rightarrow 1}(x-1)^{\ln x}=\lim _{x \rightarrow 1} e^{\ln x \cdot \ln (x-1)}=e^{\lim _{x \rightarrow 1}^{\ln x \cdot \lim _{x \rightarrow 1} \ln (x-1)}}
$$
Now we will find $\lim _{x \rightarrow 1}[\ln x \cdot \ln (x-1)]$. This is an indeterminate form of type $0 \cdot \infty$. Resolving this indeterminate form, we get
$$
\begin{gathered}
\lim _{x \rightarrow 1}[\ln x \cdot \ln (x-1)]=\lim _{x \rightarrow 1} \frac{\ln (x-1)}{\frac{1}{\ln x}}=\lim _{x \rightarrow 1} \frac{\frac{1}{1-x}}{-\frac{1}{x(\ln x)^{2}}}= \\
=-\lim _{x \rightarrow 1} \frac{x(\ln x)^{2}}{x-1}=-\lim _{x \rightarrow 1} \frac{(\ln x)^{2}+x 2 \ln x \cdot \frac{1}{x}}{1}= \\
=\lim _{x \rightarrow 1}\left[(\ln x)^{2}+2 \ln x\right]=0
\end{gathered}
$$
Therefore,
$$
\lim _{x \rightarrow 1}(x-1)^{\ln x}=e^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find $\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}$.
|
Solution. Since $\lim _{x \rightarrow 0} \frac{\sin x}{x}=1, \lim _{x \rightarrow 0} \frac{1}{x}=\infty$, we have an indeterminate form of $1^{\infty}$ here.
Taking into account identity (A) (see example 8), using L'Hôpital-Bernoulli's rule, we find
$$
\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}=\lim _{x \rightarrow 0} e^{\frac{1}{x} \ln \frac{\sin x}{x}}=e^{\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}}
$$
We need to find $\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}$, which is an indeterminate form of $\frac{0}{0}$:
$$
\begin{gathered}
\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}=\lim _{x \rightarrow 0} \frac{\frac{x}{\sin x} \cdot \frac{x \cos x-\sin x}{x^{2}}}{1}=\lim _{x \rightarrow 0} \frac{x \cos x-\sin x}{x \sin x}= \\
=\lim _{x \rightarrow 0} \frac{\cos x-x \sin x-\cos x}{\sin x+x \cos x}=-\lim _{x \rightarrow 0} \frac{x \sin x}{\sin x+x \cos x}= \\
=-\lim _{x \rightarrow 0} \frac{\sin x+x \cos x}{\cos x+\cos x-x \sin x}=0
\end{gathered}
$$
Thus, 104
$$
\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}=e^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find $\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}$.
|
Solution. Apply L'Hôpital's rule:
$$
\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}=\lim _{x \rightarrow \infty} \frac{1-\cos x}{1+\cos x}
$$
In the right-hand side of the last equality, the limit does not exist, so L'Hôpital's rule is not applicable here.
The specified limit can be found directly:
$$
\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}=\lim _{x \rightarrow \infty} \frac{1-\frac{\sin x}{x}}{1+\frac{\sin x}{x}}=1
$$
## Problems
Find the limits:
1. $\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x-\sin x}$.
2. $\lim _{x \rightarrow 0} \frac{\frac{\pi}{x}}{\cot \frac{\pi x}{2}}$.
3. $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 5 x}$.
4. $\lim _{x \rightarrow 0}(1-\cos x) \cot x$.
5. $\lim _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2}$.
6. $\lim _{x \rightarrow 1}\left(\frac{x}{x-1}-\frac{1}{\ln x}\right)$.
6. $\lim _{x \rightarrow 3}\left(\frac{1}{x-3}-\frac{5}{x^{2}-x-6}\right)$.
7. $\lim _{x \rightarrow 0} x^{x}$.
8. $\lim _{x \rightarrow 0}\left(\frac{1}{x}\right)^{\tan x}$.
9. $\lim _{x \rightarrow 0}(\cot x)^{\sin x}$.
10. $\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\frac{1}{1-\cos x}}$.
11. $\lim _{x \rightarrow+\infty}\left(\frac{\pi}{2}-\arctan x\right)^{\frac{1}{\ln x}}$.
## Answers
1.3. 2. $\frac{\pi^{2}}{2}$. 3.5. 4.0.5. $\frac{2}{\pi}$. 6. $\frac{1}{2}$. 7. $\frac{1}{5}$. 8.1. Hint. Let $x^{x}=y$, take the logarithm of this equation, and take the limit. 9.1. 10. 1. 11. $\frac{1}{\sqrt[3]{e}}$. 12. $\frac{1}{e}$.
## §3.2. Tangent and Normal to a Plane Curve. Angle Between Curves. Curvature of a Plane Curve. Velocity and Acceleration
The tangent to a curve $y=f(x)$ at its point $M_{0}\left(x_{0}, y_{0}\right)$ is the limiting position $M_{0} T$ of the secant $M M_{0}$, as the point $M$ approaches $M_{0}$ along the given curve (Fig. 3.1).
The equation of the tangent to the curve $y=f(x)$ at the point $M_{0}\left(x_{0}, y_{0}\right)$ is:
$$
y-y_{0}=f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)
$$
The normal to the curve at the point $M_{0}\left(x_{0}, y_{0}\right)$ is the line passing through $M_{0}$ and perpendicular to the tangent at that point.
The equation of the normal to the curve $y=f(x)$ at the point $M_{0}\left(x_{0}, y_{0}\right)$ is:
$$
y-y_{0}=-\frac{1}{f^{\prime}\left(x_{0}\right)}\left(x-x_{0}\right)
$$
The curvature of a curve at its point $M$ is the limit of the absolute value of the ratio of the angle $\Delta \alpha$ between the tangents at points $M$ and $N$ of the curve to the length of the arc $\breve{M N}=\Delta s$, as $N \rightarrow M$ (Fig. 3.2), i.e.,
$$
k=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \alpha}{\Delta s}\right|
$$
where the angle $\alpha$ is expressed in radians.

Fig. 3.1
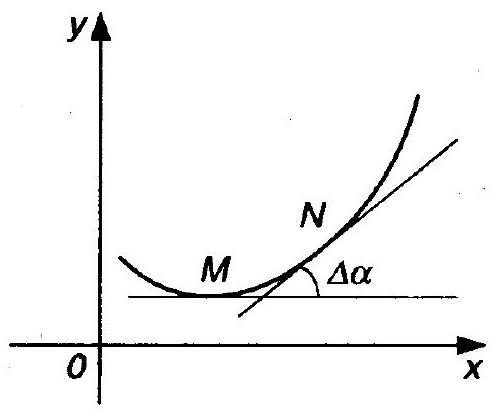
Fig. 3.2
The curvature of the curve $y=f(x)$ is calculated by the formula
$$
k=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}
$$
If the curve is given parametrically by $x=\varphi(t)$, $y=\varphi(t)$, then its curvature is determined by the formula
$$
k=\frac{\left|x^{\prime} y^{\prime \prime}-x^{\prime \prime} y^{\prime}\right|}{\left(x^{\prime 2}+y^{\prime 2}\right)^{\frac{3}{2}}}
$$
The radius of curvature of a curve at a point is the reciprocal of its curvature at that point. If the radius of curvature is denoted by $R$, then
$$
R=\frac{1}{k}
$$
The circle of curvature (osculating circle) of a curve at its point $M$ is the limiting position of the circle passing through the point $M$ and two other points $L$ and $N$ of the curve, as $L \rightarrow M$ and $N \rightarrow M$.
The radius of the circle of curvature is equal to the radius of curvature of the curve at the corresponding point.
The center of the circle of curvature is called the center of curvature of the curve at the given point $M$. The coordinates $X$ and $Y$ of the center of curvature of the curve $y=f(x)$ are calculated by the formulas:
$$
X=x-\frac{y^{\prime}\left(1+y^{\prime 2}\right)}{y^{\prime \prime}} ; Y=y+\frac{1+y^{\prime 2}}{y^{\prime \prime}}
$$
The evolute of a curve is the geometric locus of its centers of curvature.
Formulas (3.6) give the parametric equations of the evolute with parameter $x$ or $y$.
If the curve is given parametrically, then the equations of its evolute are:
$$
X=x-y^{\prime} \frac{x^{\prime 2}+y^{\prime 2}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}} ; Y=y+x^{\prime} \frac{x^{\prime 2}+y^{\prime 2}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}}
$$
The involute of a curve is a curve for which the given curve is the evolute.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Calculate the integral $\int_{0}^{\frac{\pi}{2}} \cos x d x$.
|
Solution.
$$
\int_{0}^{\frac{\pi}{2}} \cos x d x=\left.\sin x\right|_{0} ^{\frac{\pi}{2}}=\sin \frac{\pi}{2}-\sin 0=1-0=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Calculate $\int_{1}^{e} \ln x d x$.
|
Solution. We apply the integration by parts formula (5.5).
Letting $u=\ln x, d v=d x$, we determine $d u=\frac{1}{x} d x, v=x$.
Therefore,
$$
\begin{gathered}
\int_{1}^{e} \ln x d x=\left.x \ln x\right|_{1} ^{e}-\int_{1}^{e} \frac{1}{x} x d x=\left.x \ln x\right|_{1} ^{e}-\int_{1}^{e} d x=\left.x \ln x\right|_{1} ^{e}-\left.x\right|_{1} ^{e}= \\
=e \ln e-1 \cdot \ln 1-(e-1)=e-0-e+1=1
\end{gathered}
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Determine the area bounded by the arc of the cosine curve from $x=-\frac{\pi}{2}$ to $x=\frac{\pi}{2}$ and the $O x$ axis.
|
Solution. Based on the geometric meaning of the definite integral, we conclude that the desired area is expressed by the integral
$$
S=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x d x
$$
Evaluating this integral, we get
$$
S=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x d x=\left.\sin x\right|_{-\frac{\pi}{2}} ^{\frac{\pi}{2}}=\sin \frac{\pi}{2}-\sin \left(-\frac{\pi}{2}\right)=1-(-1)=2 \text { (sq. units) }
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Determine the area bounded by the lines $x y=6$, $x=1, x=e, y=0$ (Fig. 5.5).

Fig. 5.5
Fig. 5.6
|
Solution. Defining $y$ from the hyperbola equation $x y=6$, we get $y=\frac{6}{x}$. From the condition, it follows that $a=1, b=e$. Substituting the values of $a, b$ and $\frac{6}{x}$ (the expression for $y$) into formula (5.13), we find:
$$
S=\int_{1}^{e} \frac{6}{x} d x=6 \int_{1}^{e} \frac{d x}{x}=\left.6 \ln x\right|_{1} ^{e}=6(\ln e-\ln 1)=6(1-0)=6
$$
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the length of the arc of the astroid $x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$. What is the length of the astroid when $a=1, a=\frac{2}{3}?$
|
Solution. Since the astroid
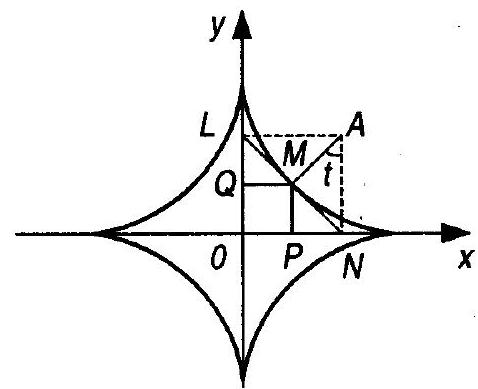
Fig. 5.13 is symmetric with respect to the coordinate axes (Fig. 5.13), it is sufficient to compute the length of the arc $AB$ and multiply the result by 4.
Differentiating the function $x^{\frac{2}{3}} + y^{\frac{2}{3}} = a^{\frac{2}{3}}$ implicitly, we get
$$
\frac{2}{3} x^{-\frac{1}{3}} + \frac{2}{3} y^{-\frac{1}{3}} y' = 0, \quad y' = -\frac{y^{\frac{1}{3}}}{x^{\frac{1}{3}}}
$$
We find the expression for the integrand in formula (2.18). We have
$$
\sqrt{1 + y'^2} = \sqrt{1 + \frac{y^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \sqrt{\frac{x^{\frac{2}{3}} + y^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \sqrt{\frac{a^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \frac{a^{\frac{1}{3}}}{x^{\frac{1}{3}}}
$$
Using formula (5.18), we find
$$
\begin{aligned}
\frac{1}{4} l & = \int_{0}^{a} \sqrt{1 + y'^2} \, dx = \int_{0}^{a} \frac{a^{\frac{1}{3}}}{x^{\frac{1}{3}}} \, dx = a^{\frac{1}{3}} \int_{0}^{a} x^{-\frac{1}{3}} \, dx = \\
& = \left. a^{\frac{1}{3}} \frac{x^{\frac{2}{3}}}{\frac{2}{3}} \right|_{0}^{a} = \left. \frac{3}{2} a^{\frac{1}{3}} x^{\frac{2}{3}} \right|_{0}^{a} = \frac{3}{2} a, \quad l = 6a
\end{aligned}
$$
For $a = 1$, we get $l = 6$, and for $a = \frac{2}{3}$, we get $l = 4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{y}$.
|
Solution. At the point $M(2,0)$, the function $z=\frac{\sin x y}{y}$ is undefined.
By multiplying and dividing the given function by $x \neq 0$, we get
$$
\frac{\sin x y}{y}=\frac{x \sin x y}{x y}=x \frac{\sin x y}{x y}
$$
Taking the limit in the last equality, we obtain
$$
\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{y}=\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} x \cdot \frac{\sin x y}{x y}=\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} x \cdot \lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{x y}=2 \cdot 1=2
$$
since $\lim _{\alpha \rightarrow 0} \frac{\sin \alpha}{\alpha}=1$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Given the function
$$
f(x, y)=x \sin \frac{1}{y}+y \sin \frac{1}{x} \quad\left(x^{2}+y^{2} \neq 0\right), \quad f(0, y)=0, \quad f(x, 0)=0
$$
find $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f(x, y)$.
|
Solution. Let $\varepsilon>0$, then for $|x|<\frac{\varepsilon}{2},|y|<\frac{\varepsilon}{2}$ we get $\rho=$
$$
=\sqrt{\left(\frac{\varepsilon}{2}\right)^{2}+\left(\frac{\varepsilon}{2}\right)^{2}}=\frac{\sqrt{2}}{2} \varepsilon . \text { We form the difference } f(x, y)-0 \text { and estimate it: }
$$
$$
|f(x, y)-0| \leq|x| \cdot\left|\sin \frac{1}{y}\right|+|y| \cdot\left|\sin \frac{1}{x}\right| \leq|x|+|y|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon
$$
Thus,
$$
|f(x, y)-0|<\varepsilon
$$
Based on formula (6.10), we conclude that
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f(x, y)=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2} y}{x^{2}+y^{2}}$.
|
Solution. The given function can be represented as:
$$
f(x, y)=\frac{x^{2} y}{x^{2}+y^{2}}=\frac{x y}{x^{2}+y^{2}} x .
$$
Since
$$
\left|\frac{x y}{x^{2}+y^{2}}\right| \leq \frac{1}{2}
$$
(this can be derived from the inequality $(x-y)^{2} \geq 0$ : $x^{2}-2 x y+y^{2} \geq 0$, $\left.x^{2}+y^{2} \geq 2 x y, \frac{1}{2} \geq \frac{x y}{x^{2}+y^{2}}\right)$, then
$$
|f(x, y)|=\left|\frac{x y}{x^{2}+y^{2}}\right| \cdot|x| \leq \frac{1}{2}|x|
$$
If given $\varepsilon>0$, then for $|x|<\delta$ and $\delta=2 \varepsilon$ we get
$$
|f(x, y)-0| \leq \frac{1}{2}|x|<\frac{1}{2} \cdot 2 \varepsilon=\varepsilon
$$
That is,
$$
|f(x, y)-0|<\varepsilon
$$
Therefore,
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2} y}{x^{2}+y^{2}}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Into how many parts should the interval of integration be divided to calculate $\int_{2}^{7} \frac{d x}{\sqrt{x+2}}$ with an accuracy of 0.1?
|
Solution. The absolute error in calculating a definite integral using the rectangle method is determined by inequality (13.4). In the problem, the condition $\left|R_{n}(f)\right| \leq \varepsilon$ is set, where $\varepsilon=0.1$. The inequality $\left|R_{n}(f)\right| \leq \varepsilon$ will be satisfied if $\frac{(b-a)^{2} M}{2 n} \leq \varepsilon$, from which
$$
n \geq \frac{(b-a)^{2} M}{2 \varepsilon}
$$
In this case, $a=2, b=7, \varepsilon=0.1$. Since $f(x)=\frac{1}{\sqrt{x+2}}$,
$$
\begin{aligned}
f^{\prime}(x)=-\frac{1}{2 \sqrt{(x+2)^{3}}}, M & =\max _{2 \leq x \leq 7}\left|f^{\prime}(x)\right|=\frac{1}{16}, \text { then } \\
n & \geq \frac{(7-2)^{2} \cdot \frac{1}{16}}{2 \cdot 0.1} \approx 7.8
\end{aligned}
$$
Since $n$ is an integer, we need to take $n=8$. (For convenience in calculations, $n=10$ can be taken).
## Problems
Using the rectangle formulas, with $n=10$, calculate the definite integrals:
1. $\int_{1}^{11} \frac{d x}{x+2}$.
2. $\int_{0}^{\frac{\pi}{6}} \sin 3 x d x$.
3. $\int_{0}^{10} \sqrt{x^{2}+2} d x$.
4. $\int_{0}^{1} \frac{\cos x}{1+x} d x$.
5. $\int_{0}^{0.9} \sin x^{2} d x$.
6. $\int_{0}^{1} \frac{d x}{\sqrt{x^{3}+1}}$.
How many parts should the integration interval be divided into to calculate the integrals with an accuracy of 0.1 using the rectangle formulas:
7. $\int_{1}^{2} \ln x d x$.
8. $\quad \int_{0}^{1} \frac{d x}{x+1}$.
9. $\int_{0}^{\frac{\pi}{8}} \cos 4 x d x$. \quad 10. $\int_{0}^{\frac{\pi}{8}} \sin \frac{x}{2} d x$.
## Answers
1. $J_{n}=1.603 ; J_{n}=1.348$. 2. $J_{n}=0.303 ; J_{n}=0.314$. 3. $J_{n}=48.891$. 4. $J_{n}=0.565 ; J_{n}=0.640$. 5. $J_{n}=0.266$. 6. $J_{n}=0.444$. 7.5. 8.5. 9.3.
## § 13.2. Trapezoidal Rule
The trapezoidal rule is given by
$$
\int_{a}^{b} f(x) d x \approx h\left(\frac{y_{0}}{2}+y_{1}+y_{2}+\ldots+y_{n-1}+\frac{y_{n}}{2}\right)
$$
where
$$
h=\frac{b-a}{n}, x_{k}=a+k h, y_{k}=f\left(x_{k}\right)(k=0,1,2, \ldots, n)
$$
The right-hand side of formula (13.5) represents the area of a figure consisting of trapezoids, each with height $h$ (Fig. 13.2). If $R_{n}$ is the remainder term of the approximate formula (13.5), then
$$
\left|R_{n}\right| \leq \frac{(b-a)^{3} M}{12 n^{2}}
$$
where $M=\max _{a \leq x \leq b}\left|f^{\prime \prime}(x)\right|$.
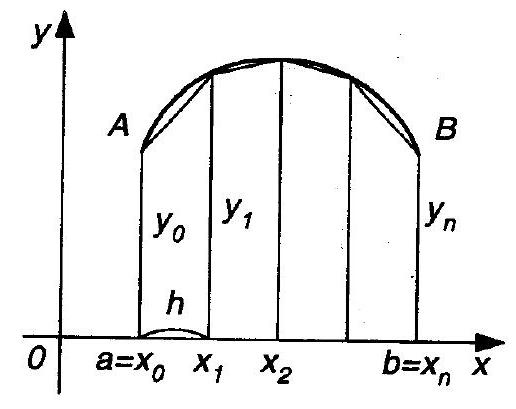
Fig. 13.2
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Construct a table of divided differences of various orders for the following values of $x$ and $y=f(x)$:
\[
\begin{gathered}
x_{0}=-3, x_{1}=-2, x_{2}=-1, x_{3}=1, x_{4}=2 \\
y_{0}=-9, y_{1}=-16, y_{2}=-3, y_{3}=11, y_{4}=36
\end{gathered}
\]
|
Solution. According to the definitions, we find the divided differences of the first order:
$$
\begin{gathered}
f\left(x_{1}, x_{0}\right)=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{-16-(-9)}{-2-(-3)}=-7 ; f\left(x_{2}, x_{1}\right)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-3-(-16)}{-1-(-2)}=13 \\
f\left(x_{3}, x_{2}\right)=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}=\frac{11-(-3)}{1-(-1)}=7 ; f\left(x_{4}, x_{3}\right)=\frac{y_{4}-y_{3}}{x_{4}-x_{3}}=\frac{36-11}{2-1}=25
\end{gathered}
$$
differences of the second order:
$$
\begin{aligned}
& f\left(x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{2}, x_{1}\right)-f\left(x_{1}, x_{0}\right)}{x_{2}-x_{0}}=\frac{13-(-7)}{-1-(-3)}=10 \\
& f\left(x_{3}, x_{2}, x_{1}\right)=\frac{f\left(x_{3}, x_{2}\right)-f\left(x_{2}, x_{1}\right)}{x_{3}-x_{1}}=\frac{7-13}{1-(-2)}=-2 \\
& f\left(x_{4}, x_{3}, x_{2}\right)=\frac{f\left(x_{4}, x_{3}\right)-f\left(x_{3}, x_{2}\right)}{x_{4}-x_{2}}=\frac{25-7}{2-(-1)}=6
\end{aligned}
$$
differences of the third order:
$$
\begin{aligned}
& f\left(x_{3}, x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{3}, x_{2}, x_{1}\right)-f\left(x_{2}, x_{1}, x_{0}\right)}{x_{3}-x_{0}}=\frac{-2-10}{1-(-3)}=-3 \\
& f\left(x_{4}, x_{3}, x_{2}, x_{1}\right)=\frac{f\left(x_{4}, x_{3}, x_{2}\right)-f\left(x_{3}, x_{2}, x_{1}\right)}{x_{4}-x_{1}}=\frac{6-(-2)}{2-(-2)}=2
\end{aligned}
$$
difference of the fourth order:
$$
f\left(x_{4}, x_{3}, x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{4}, x_{3}, x_{2}, x_{1}\right)-f\left(x_{3}, x_{2}, x_{1}, x_{0}\right)}{x_{4}-x_{0}}=\frac{2-(-3)}{2-(-3)}=1
$$
The obtained divided differences can be represented in the form of Table 15.3.
Table 15.3
| $x$ | $y$ | Divided differences | | | |
| :---: | ---: | ---: | ---: | ---: | ---: |
| -3 | -9 | -7 | 10 | | |
| -2 | -16 | 13 | 10 | -3 | 1 |
| -1 | -3 | 7 | -2 | 2 | |
| 1 | 11 | 25 | 6 | | |
| 2 | 36 | | | | |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. How many elementary outcomes favor the event "the same number of points fell on both dice" when two gaming dice are rolled?
|
Solution. This event is favored by 6 elementary outcomes (see Table 1.1$):(1 ; 1),(2 ; 2),(3 ; 3),(4 ; 4),(5 ; 5),(6 ; 6)$.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. The distribution law of a discrete random variable is given by the following table:
| $X$ | 0 | 1 | 2 | 3 |
| :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.2 | 0.4 | 0.3 | 0.1 |
Find the distribution function of this random variable.
|
Solution. To construct the distribution function $F(x)$ of a discrete random variable $X$, we use formula (2.2.11).
1. For $x \leq 0 \quad F(x)=\sum_{x_{k}3 \quad F(x)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=$
$$
=0.2+0.4+0.3+0.1=1
$$
The graph of the function $F(x)$ is shown in Fig. 2.7.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Two dice are rolled. The discrete random variable $X$ is the sum of the points that appear on both dice. Find the mathematical expectation of this random variable.
|
Solution. This random variable takes all integer values from 2 to 12. The distribution law can be given by the following table:
| $X$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ |
By formula (2.4.3) we find
$$
\begin{aligned}
& M(X)=2 \cdot \frac{1}{36}+3 \cdot \frac{2}{36}+4 \cdot \frac{3}{36}+5 \cdot \frac{4}{36}+6 \cdot \frac{5}{36}+ \\
& +7 \cdot \frac{6}{36}+8 \cdot \frac{5}{36}+9 \cdot \frac{4}{36}+10 \cdot \frac{3}{36}+11 \cdot \frac{2}{36}+12 \cdot \frac{1}{36}= \\
& =\frac{2+6+12+20+30+42+40+36+30+22+12}{36}=\frac{252}{36}=7
\end{aligned}
$$
Remark 1. This result can be obtained more easily. Let the random variable for the number of points that fall on one die be denoted by $X$, and on the other die by $Y$. These random variables have the same distribution laws (see Example 6). By formula (2.4.12) we get
$$
M(X+Y)=M(X)+M(Y)=3.5+3.5=7
$$
Remark 2. Since the variables $X$ and $Y$ are independent, we can also find the mathematical expectation of the random variable $Z=XY$ - the product of the number of points that fall when two dice are rolled simultaneously. By formula (2.4.15) we have:
$$
M(Z)=M(X \cdot Y)=M(X) \cdot M(Y)=3.5 \cdot 3.5=12.25
$$
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 13. Find the mathematical expectation of a random variable $X$, the distribution function of which is given by
$$
F(x)= \begin{cases}0 & \text { if } x \leq -a \\ \frac{(a+x)^{2}}{2 a^{2}} & \text { if } -a < x \leq a \\ 1 & \text { if } x > a\end{cases}
$$
|
Solution. First, let's find the probability density function of this random variable. Since \( p(x) = F'(x) \), we have:
\[
p(x)= \begin{cases}0 & \text{if } x \leq -a \\ \frac{1}{a}\left(1+\frac{x}{a}\right) & \text{if } -a < x \leq 0 \\ \frac{1}{a}\left(1-\frac{x}{a}\right) & \text{if } 0 < x \leq a \\ 0 & \text{if } x > a\end{cases}
\]
Using formula (2.4.7), we find the required expected value:
\[
\begin{aligned}
& M(X)=\int_{-a}^{a} x p(x) d x=\int_{-a}^{0} \frac{1}{a}\left(1+\frac{x}{a}\right) x d x+\int_{0}^{a} \frac{1}{a}\left(1-\frac{x}{a}\right) x d x= \\
& =\frac{1}{a} \int_{-a}^{0}\left(x+\frac{x^{2}}{a}\right) d x+\frac{1}{a} \int_{0}^{a}\left(x-\frac{x^{2}}{a}\right) d x=\left.\frac{1}{a}\left(\frac{x^{2}}{2}+\frac{x^{3}}{3 a}\right)\right|_{-a} ^{0}+ \\
& +\left.\frac{1}{a}\left(\frac{x^{2}}{2}-\frac{x^{3}}{3 a}\right)\right|_{0} ^{a}=\frac{1}{a}\left(-\frac{(-a)^{2}}{2}-\frac{(-a)^{3}}{3 a}\right)+\frac{1}{a}\left(\frac{(a)^{2}}{2}-\frac{(a)^{3}}{3 a}\right)=0
\end{aligned}
\]
## Problems
1. Find the expected value of a discrete random variable whose distribution is given by the table:
| $X$ | 1 | 2 | 3 | 4 | 5 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.15 | 0.25 | 0.3 | 0.2 | 0.1 |
2. The distribution of a discrete random variable is given by the table:
| $X$ | 3 | 6 | 9 | 12 |
| :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.1 | 0.2 | 0.3 | 0.4 |
Write the distribution laws for the random variables $2X$, $X/3$. Find the expected values of the random variables $X$, $2X$, $X/3$.
3. The expected values of two random variables $X$ and $Y$ are known: $M(X)=7$, $M(Y)=4$. Find the expected values of the sum and difference of these variables.
4. The expected values of two independent random variables $X$ and $Y$ are known: $M(X)=6$, $M(Y)=8$. Find the expected value of their product.
5. Find the expected value of the random variable $Y=8X+5$, if it is known that $M(X)=1.5$.
6. A discrete random variable $X$, which can take an infinite sequence of values, is given by the following distribution:
| $X$ | $1/4$ | $1/4^2$ | $1/4^3$ | $\ldots$ | $1/4^k$ | $\ldots$ |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | $1/2$ | $1/2^2$ | $1/2^3$ | $\ldots$ | $1/2^k$ | $\ldots$ |
\[
\sum_{k=1}^{\infty} \frac{1}{2^k}=1
\]
Find the expected value of this random variable.
7. The probability density function of a random variable $X$ is given by
\[
p(x)= \begin{cases}0 & \text{if } x \leq 0 \\ 3x^2 & \text{if } 0 < x \leq 1 \\ 0 & \text{if } x > 1\end{cases}
\]
Find the expected value of the random variable $X$.
8. Find the expected value of the random variable $X$, if the distribution function of this variable is given by
\[
F(x)= \begin{cases}0 & \text{if } x \leq 0 \\ x/3 & \text{if } 0 < x \leq 3 \\ 1 & \text{if } x > 3\end{cases}
\]
9. Find the expected value of the random variable $X$, if the distribution function is given by
\[
F(x)=\begin{cases}
0 & \text{if } x \leq 0 \\
1-e^{-\alpha x} & \text{if } x > 0
\end{cases} \quad (\alpha > 0)
\]
## Answers
1. 2.85. 2. 9, 18, 3. 11, 3. 4. 48. 5. 17. 6. 1/7. 7. 0.75. 8. 4.5. 9. 1/α.
## Questions
1. How is the expected value of a discrete random variable $X$ defined, which takes a finite set of values?
2. What other names are used for the expected value? What explains these names?
3. What is the expected value of a discrete random variable $X$ that takes a countable set of values?
4. How is the expected value of a continuous random variable defined, all values of which belong to the interval $[\alpha, \beta]$?
5. How is the expected value of a continuous random variable defined, all values of which belong to the infinite interval $(-\infty, +\infty)$?
6. What are the properties of the expected value of a random variable?
7. What conditions must random variables $X$ and $Y$ satisfy for equation (2.4.15) to hold?
8. Prove that the expected value of a non-negative discrete variable is non-negative.
## § 2.5. Variance of a Random Variable. Mean Square Deviation
The difference $X - M(X)$ is called the deviation of the random variable $X$ from its expected value $M(X)$. The expected value of the deviation is zero:
\[
M(X - M(X)) = 0
\]
The variance, or dispersion, of a random variable $X$ is the expected value of the square of its deviation:
\[
D(X) = M\left((X - M(X))^2\right)
\]
From the definition and properties of the expected value, it follows that the variance of any random variable is non-negative, i.e.,
\[
D(X) \geq 0
\]
For calculating the variance, the formula
\[
D(X) = M(X^2) - (M(X))^2
\]
is used.
The variance of a random variable has the following properties:
1. The variance of a constant is zero:
\[
D(C) = 0 \quad (C = \text{const})
\]
2. A constant factor can be factored out of the variance, squaring it:
\[
D(CX) = C^2 D(X) \quad (C = \text{const})
\]
4. The variance of the sum of two independent random variables is equal to the sum of their variances:
\[
D(X + Y) = D(X) + D(Y)
\]
5. The variance of the difference of two independent random variables is equal to the sum of their variances:
\[
D(X - Y) = D(X) + D(Y)
\]
Remark. Property 3 extends to $n$ independent random variables:
\[
D(X_1 + X_2 + \ldots + X_n) = D(X_1) + D(X_2) + \ldots + D(X_n)
\]
The variance of a discrete random variable with the distribution
\[
\begin{aligned}
& P(X = x_k) = p_k \quad (k = 1, 2, \ldots, n) \\
& \sum_{k=1}^{n} p_k = 1
\end{aligned}
\]
is defined by the formula
\[
D(X) = \sum_{k=1}^{n} (x_k - M(X))^2 p_k
\]
or the formula
\[
D(X) = \sum_{k=1}^{n} (x_k - a)^2 p_k
\]
where
\[
a = M(X)
\]
is another notation for the expected value. We will use this notation in the future, depending on the circumstances.
If a discrete random variable takes an infinite sequence of values with the distribution
\[
\begin{aligned}
& P(X = x_k) = p_k \quad (k = 1, 2, 3, \ldots) \\
& \sum
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Prove that
$$
\sum_{k=0}^{\infty} p_{k}=\sum_{k=0}^{\infty} \frac{a^{k} e^{-a}}{k!}=1
$$
|
Solution. Taking into account the power series expansion of the function $f(x)=e^{x}$
$$
e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots+\frac{x^{k}}{k!}+\ldots
$$
and the resulting equality
$$
e^{a}=1+\frac{a}{1!}+\frac{a^{2}}{2!}+\frac{a^{3}}{3!}+\ldots+\frac{a^{k}}{k!}+\ldots
$$
we obtain
$$
\sum_{k=0}^{\infty} \frac{a^{k} e^{-a}}{k!}=e^{-a} \sum_{k=0}^{\infty} \frac{a^{k}}{k!}=e^{-a}\left(1+\frac{a}{1!}+\frac{a^{2}}{2!}+\frac{a^{3}}{3!}+\ldots+\frac{a^{k}}{k!}+\ldots\right)=e^{-a} e^{a}=1
$$
Thus, the series of probabilities of the Poisson distribution converges and its sum is equal to one, i.e., condition (2.1.4) in the definition of the distribution law of a discrete random variable is satisfied.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. A factory sent 5000 good-quality items to a base. The probability that an item will be damaged during transportation is 0.0002. What is the probability that 3 defective items will arrive at the base?
$\mathrm{Pe} \mathrm{sh} \mathbf{e n i e . ~ F r o m ~ t h e ~ c o n d i t i o n ~ i t ~ f o l l o w s ~ t h a t ~} n=5000, p=0.0002, \text{ and } np=5000 \cdot 0.0002=1$. According to formula (3.3.1) we have
$$
P_{5000}(3)=\frac{1^{3}}{3!} e^{-1}=\frac{1}{6 e} \approx 0.0613
$$
Example 13. A radio apparatus consists of 1000 electrical elements. The probability of failure of one element in one year of operation is 0.001 and is independent of the state of other elements. What is the probability of the failure of two elements? What is the probability of the failure of at least two elements in a year?
|
Solution. Here it is required to find the probabilities: 1) $P_{1000}(2)$;
2) $P_{1000}(k \geq 2)$. According to the condition, $n=1000, p=0.001, a=n p=1000 \cdot 0.001=1$.
The probability of exactly two elements failing:
$$
P_{1000}(2)=\frac{a^{2}}{2!} e^{-a}=\frac{1}{2 e} \approx 0.1831
$$
The probability of at least two elements failing:
$$
P_{1000}(k \geq 2)=\sum_{k=2}^{\infty} p_{k}=1-p_{0}-p_{1}=1-e^{-a}(1+a)=1-\frac{2}{e} \approx 0.2642
$$
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find the mathematical expectation of a random variable $X$,
uniformly distributed on the interval $[2,8]$.
|
Solution. The mathematical expectation of a random variable $X$, uniformly distributed on the interval $[\alpha, \beta]$, is defined by formula (3.4.7). Since in this case $\alpha=2, \beta=8$, then
$$
M(X)=\frac{8+2}{2}=5
$$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Prove that the function (3.5.1), defining the density of the normal distribution, satisfies condition (2.3.6), i.e.
$$
\int_{-\infty}^{+\infty} p(x) d x=1
$$
|
Solution. In the integral
$$
\int_{-\infty}^{+\infty} p(x) d x=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x
$$
we will transition to a new variable \( t \) using the formula
$$
t=\frac{x-a}{\sigma}
$$
Then \( x=a+\sigma t, d x=\sigma d t \). Since the new limits of integration are the same as the old ones, we have
$$
\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-t^{2} / 2} \sigma d t=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-t^{2} / 2} d t=\frac{1}{\sqrt{2 \pi}} \cdot \sqrt{2 \pi}=1 .
$$
Here it is taken into account that
$$
\int_{-\infty}^{+\infty} e^{-t^{2} / 2} d t=\sqrt{2 \pi}
$$
Thus,
$$
\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x=1
$$
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Prove that the function (3.6.2) satisfies condition (2.3.6), i.e. $\int_{-\infty}^{+\infty} p(x) d x=1$.
|
Solution. Indeed,
$$
\int_{-\infty}^{+\infty} p(x) d x=\int_{-\infty}^{0} p(x) d x+\int_{0}^{+\infty} p(x) d x=\int_{-\infty}^{0} 0 \cdot d x+\int_{0}^{+\infty} \alpha e^{-\alpha x} d x=
$$
$$
=-\int_{0}^{+\infty} d\left(e^{-\alpha x}\right)=-\left.e^{-\alpha x}\right|_{0} ^{+\infty}=-\left(e^{-\infty}-e^{0}\right)=1
$$
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find the mathematical expectation of the random variable
$X$, the density of which is determined by the function $p(x)=0.2 e^{-0.2 x}$ for $x \geq 0$.
|
Solution. Since in this case $\alpha=0.2$ and $M(X)=\frac{1}{\alpha}$, then
$$
M(X)=\frac{1}{2 / 10}=\frac{10}{2}=5, \quad M(X)=5
$$
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the zeros of the function $f(z)=e^{z}-1-z$ and determine their order.
|
Solution.
1. Find the zeros of the function $f(z)$ by solving the equation $e^{z}-1-z=0$. We get $z=0$.
2. Determine the order of the obtained zero $z=0$. For this, we use the Taylor series expansion of the function $f(z)$ in powers of $z$:
$$
e^{z}-1-z=\left(1+z+\frac{z^{2}}{2!}+\frac{z^{3}}{3!}+\ldots\right)-1-z=\frac{z^{2}}{2!}+\frac{z^{3}}{3!}+\ldots
$$
Since in the obtained expansion the coefficients $c_{0}=c_{1}=0$, and $c_{2}=1 / 2 \neq 0$, the point $z=0$ is a zero of the 2nd order of the function $f(z)$.
Answer. $z=0$ is a zero of the 2nd order of the function $f(z)$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.13. Using the method of bordering minors, find the rank of the matrix
$$
A=\left(\begin{array}{ccccc}
2 & 1 & 2 & 1 & 2 \\
1 & 1 & 5 & -2 & 3 \\
-1 & 0 & -4 & 4 & 1 \\
3 & 3 & 8 & 1 & 9
\end{array}\right)
$$
|
Solution. The second-order minor
$$
M_{2}=\left|\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right|=2 \cdot 1-1 \cdot 1=1 \neq 0
$$
is non-zero and located in the upper left corner of matrix $A$. The third-order minor
$$
M_{3}=\left|\begin{array}{ccc}
2 & 1 & 2 \\
1 & 1 & 5 \\
-1 & 0 & 4
\end{array}\right|=\left|\begin{array}{ccc}
1 & 0 & -3 \\
1 & 1 & 5 \\
-1 & 0 & 4
\end{array}\right|=\left|\begin{array}{cc}
1 & -3 \\
-1 & 4
\end{array}\right|=4-3=1 \neq 0
$$
enclosing the minor $M_{2}$, is also non-zero. However, both fourth-order minors enclosing $M_{3}$,
$$
M_{4}=\left|\begin{array}{cccc}
2 & 1 & 2 & 1 \\
1 & 1 & 5 & -2 \\
-1 & 0 & -4 & 4 \\
3 & 3 & 8 & 1
\end{array}\right|, M_{4}=\left|\begin{array}{cccc}
2 & 1 & 2 & 2 \\
1 & 1 & 5 & 3 \\
-1 & 0 & -4 & 1 \\
3 & 3 & 8 & 9
\end{array}\right|
$$
are equal to zero. Therefore, the rank of matrix $A$ is 3, and a basis minor is, for example, the minor $M$ presented above.
The method of elementary transformations is based on the fact that elementary transformations of a matrix do not change its rank. Using these transformations, the matrix can be brought to a form where all its elements, except for $a_{11}, a_{22}, \ldots$, $a_{r r}(r \leqslant \min (m, n))$, are zero. This obviously means that rang $A=r$. Note that if an $n$-order matrix has the form of an upper triangular matrix, i.e., a matrix where all elements below the main diagonal are zero, then its determinant is equal to the product of the elements on the main diagonal. This property can be used when calculating the rank of a matrix using the method of elementary transformations: it is necessary to use them to bring the matrix to a triangular form, and then, by isolating the corresponding determinant, we find that the rank of the matrix is equal to the number of elements on the main diagonal that are non-zero.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.14. Using elementary transformations, find the rank of the matrix
$$
A=\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
9 & 16 & 24 & 98 & -31 \\
14 & 24 & 25 & 146 & -45 \\
11 & 12 & 24 & 94 & -25
\end{array}\right)
$$
|
Solution. Let's denote the $i$-th row of matrix $A$ by the symbol $\alpha_{i}$. In the first stage, we perform elementary transformations $\alpha_{2}^{\prime}=\alpha_{2}-\alpha_{3}+\alpha_{1}, \alpha_{3}^{\prime}=\alpha_{3}-\alpha_{2}-\alpha_{1} ; \alpha_{4}^{\prime}=\alpha_{4}-\alpha_{3}+\alpha_{1}$.
In the second stage, we perform the transformations
$$
\alpha_{3}^{n}=\alpha_{3}^{\prime}+\alpha_{2}^{\prime}, \alpha_{4}^{\prime \prime}=\alpha_{4}^{\prime}-\alpha_{2}^{\prime}
$$
As a result, we get
$$
\begin{aligned}
& \left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
9 & 16 & 24 & 98 & -31 \\
14 & 24 & 25 & 146 & -45 \\
11 & 12 & 24 & 94 & -25
\end{array}\right) \xrightarrow{1}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 1 & -11 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \xrightarrow{2} \\
& \xrightarrow{2}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & -4 & 6
\end{array}\right) \xrightarrow{3}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 0 & 0 & -4 & 6 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \xrightarrow{4} \\
& \xrightarrow{4}\left(\begin{array}{ccccc}
5 & 7 & 12 & 12 & -7 \\
0 & -1 & 0 & 2 & 0 \\
0 & 0 & -1 & 0 & 3 \\
0 & 0 & 0 & 0 & 0
\end{array}\right)
\end{aligned}
$$
In the third stage, we swapped the fourth row with the third row, and the third row with the fourth row. In the fourth stage, we divided the elements of the fourth and fifth columns by 4 and 2, respectively, and swapped the third and fourth columns. From the form of the matrix obtained after the fourth stage of transformation, it follows that
rank $A=3$. We could continue transforming matrix $A$, aiming to zero out the remaining elements of the matrix with different indices, but this is probably not advisable when finding the rank of the matrix. It is also worth noting that the resulting zero row from the elementary transformations could have been omitted in further transformations of the matrix, simply by deleting it, which, obviously, would not affect the rank of the original matrix.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.27. Given a linear transformation using a system of equations
$$
\left\{\begin{array}{l}
g_{1}=-x_{1}+0 \cdot x_{2}+0 \cdot x_{3} \\
g_{2}=0 \cdot x_{1}+1 \cdot x_{2}+0 \cdot x_{3} \\
g_{3}=0 \cdot x_{1}+0 \cdot x_{2}+1 \cdot x_{3}
\end{array}\right.
$$
Find the transformation matrix, will it be singular?
|
Solution. With the matrix representation of the transformation, we get:
$$
\left(\begin{array}{l}
g_{1} \\
g_{2} \\
g_{3}
\end{array}\right)=\left(\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right)
$$
Here, the transformation matrix
$$
A=\left(\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)
$$
has a non-zero determinant, equal to the product of all elements on the main diagonal \(\operatorname{det} A=(-1) \cdot 1 \cdot 1=-1 \neq 0\) (the mapping is also non-degenerate).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.13. Are the vectors coplanar
$$
\vec{a}, \vec{b}, \vec{c}: \vec{a}=\{1,-2,1\}, \vec{b}=\{3,1,-2\}, \vec{c}=\{7,14,-13\} ?
$$
|
Solution. To answer the given question, it is necessary to calculate the mixed product of these vectors, and if it turns out to be zero, this will indicate that the vectors $\ddot{a}, \vec{b}, \vec{c}$ are coplanar. We find the mixed product $\vec{a} \cdot \vec{b} \cdot \vec{c}$ using formula (2.40).
$$
\begin{aligned}
\vec{a} \times \vec{b} \cdot \vec{c} & =\left|\begin{array}{ccc}
1 & -2 & 1 \\
3 & 1 & -2 \\
7 & 14 & -13
\end{array}\right|=1\left|\begin{array}{cc}
1 & -2 \\
14 & -13
\end{array}\right|-(-2)\left|\begin{array}{cc}
3 & -2 \\
7 & -13
\end{array}\right|+1\left|\begin{array}{cc}
3 & 1 \\
7 & 14
\end{array}\right|= \\
& =-13+28+2(-39+14)+42-7=15-50+35=0
\end{aligned}
$$
Since the mixed product $\vec{a} \cdot \vec{b} \cdot \vec{c}$ turned out to be zero, the vectors $\vec{a}, \ddot{b}, \vec{c}$ are coplanar.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3. Obtain the equation of the line passing through two given points $P_{0}(1 ; 2)$ and $P_{1}(3 ; 2)$.
|
Solution.
1st step. Make a schematic drawing (Fig. 3.3).
2nd step. Write down the coordinates of the vectors defining the given geometric object - the line. This is the current vector lying on the line $\overrightarrow{P_{0} M}=\{x-1 ; y-2\}$ and the vector formed by two points on the line
$$
\overrightarrow{P_{0} P_{1}}=\{3-1 ; 2-2\}=\{1 ; 0\} .
$$
3rd step. Write down one of the conditions - orthogonality or collinearity, according to the problem. According to the problem, $\vec{P}_{0} M \| \bar{P}_{0} \vec{P}_{1}$, so we will use the condition of collinearity of two vectors in coordinate form $(x-1) / 2=(y-2) / 0$. We obtain the canonical equation of the line. Sometimes in the answer to the considered problem, it is mistakenly not written that part of the equation where zero appears in the denominator, referring to the fact that division by zero is not allowed. However, the equation $(x-1) / 2=(y-2) / 0$ does not describe division by zero; here only a symbolic notation is made that the current vector $\overrightarrow{P_{0} M}$ is collinear with the vector $\widetilde{P}_{0} \vec{P}_{1}$, one of whose components is zero.

Fig. 3.2
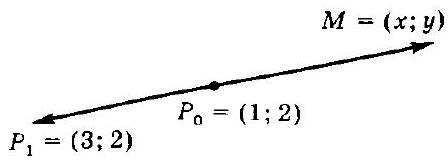
Fig. 3.3
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.23. Derive the polar equation of the ellipse $x^{2} / a^{2}+$ $+y^{2} / b^{2}=1$ under the condition that the direction of the polar axis coincides with the positive direction of the x-axis, and the pole is at the center of the ellipse.
|
Solution. Substitute into the ellipse equation the expressions for $x$ and $y$ in terms of the polar radius $\rho$ and the angle $\varphi$.
We have
$$
\frac{\rho^{2} \cos ^{2} \varphi}{a^{2}}+\frac{\rho^{2} \sin ^{2} \varphi}{b^{2}}=1, \rho^{2} \frac{b^{2} \cos ^{2} \varphi+a^{2} \sin ^{2} \varphi}{a^{2} b^{2}}=1
$$
Replace $b^{2}$ in the numerator with $a^{2}-c^{2}$ and use the fundamental trigonometric identity
$$
\begin{aligned}
& \cos ^{2} \varphi+\sin ^{2} \varphi=1, \quad \rho^{2} \frac{\left(a^{2}-c^{2}\right) \cos ^{2} \varphi+a^{2} \sin ^{2} \varphi}{a^{2} b^{2}}=1 \\
& \rho^{2} \frac{a^{2}-c^{2} \cos ^{2} \varphi}{a^{2} b^{2}}=1, \frac{\rho^{2}}{b^{2}}\left(1-\frac{c^{2}}{a^{2}} \cos ^{2} \varphi\right)=1
\end{aligned}
$$
Substitute $\varepsilon^{2}=c^{2} / a^{2}$, then we get $\rho^{2}=b^{2} /\left(1-\varepsilon^{2} \cos ^{2} \varphi\right)$. 3.24. At what point does the linear function $L(x, y)=\sqrt{2} x-y$ reach its maximum in the region described by the inequality $x^{2} / 9+y^{2} / 7 \leqslant 1 ?$
Solution. Applying Theorems 3.3 and 3.4, we get that the maximum of $L(x, y)$ is achieved at the point of tangency of the right tangent to the given ellipse, parallel to the line $\sqrt{2} x-y=0$. Using condition 3.39:
$$
k=\sqrt{2}=\sqrt{2} x-2 y, a=3, b=\sqrt{7} ; 2 \cdot 9+7=m^{2}
$$
From the two values $m= \pm 5$ we choose $m=-5$, since the function $L(x, y)=\sqrt{2} x-y$ will reach its maximum in the given region in the direction of the vector $\vec{n}=\{\sqrt{2} ;-1\}$ on the right tangent $y=\sqrt{2} x-5$. Determine the coordinates of the point of tangency by substituting $y$ with $\sqrt{2} x-5$ in the ellipse equation. Hence
$$
\begin{aligned}
& \frac{x^{2}}{9}+\frac{(\sqrt{2} x-5)^{2}}{7}=1 \\
& 25 x^{2}-90 \sqrt{2} x+162=0, \Rightarrow x_{1}=x_{2}=1.8 \sqrt{2}
\end{aligned}
$$
Substitute $x_{1}$ into the tangent equation and find $y_{1}=$ $=-1.4$. For these $x_{1}$ and $y_{1}$, the linear function reaches the following maximum value:
$$
L_{\max }(1.8 \sqrt{2},-1.4)=\sqrt{2} \cdot 1.8 \cdot \sqrt{2}-(-1.4)=5
$$
## 3.5 . PROBLEMS
## STRAIGHT LINE
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Find the limit of the sequence
$$
\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1}-\sqrt[3]{n^{3}+10}}{\sqrt{n^{2}+1}-\sqrt[4]{n+1}}
$$
|
Solution. Divide the numerator and the denominator of the fraction by $n$. After transformations and discarding infinitely small quantities, we obtain the required result:
$$
\begin{gathered}
\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1}-\sqrt[3]{n^{3}+10}}{\sqrt{n^{2}+1}-\sqrt[4]{n+1}}=\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1} / n-\sqrt[3]{n^{3}+10} / n}{\sqrt{n^{2}+1} / n-\sqrt[4]{n+1} / n}= \\
=\lim _{n \rightarrow \infty} \frac{\sqrt{2 / n-1 / n^{2}}-\sqrt[3]{1+10 / n^{3}}}{\sqrt{1+1 / n^{2}}-\sqrt[4]{1 / n^{3}+1 / n^{4}}}=-1
\end{gathered}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.9. Calculate the limit
$$
\lim _{x \rightarrow \pm \infty}\left(\sqrt{x^{2}+1}-\sqrt{x^{2}-1}\right)
$$
|
Solution. In this case, we have an indeterminate form of type «$\infty - \infty$». To resolve it, we multiply and divide the given expression by its conjugate. We get
$$
\begin{gathered}
\lim _{x \rightarrow \pm \infty}\left(\sqrt{x^{2}+1}-\sqrt{x^{2}-1}\right)=\lim _{x \rightarrow \pm \infty} \frac{x^{2}+1-x^{2}+1}{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}= \\
=\lim _{x \rightarrow \pm \infty} \frac{2}{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.10. Calculate the limit
$$
\lim _{x \rightarrow 0} \frac{\tan 6 x}{\sin 3 x}
$$
|
Solution. To calculate this limit, which represents an indeterminate form of the type "0/0", it is best to use the theorem on the replacement of infinitesimal functions with equivalent quantities.
According to this theorem, as $x \rightarrow 0, \operatorname{tg} 6 x \sim 6 x$, $\sin 3 x \sim 3 x$. Taking this into account, we have
$$
\lim _{x \rightarrow 0} \frac{\operatorname{tg} 6 x}{\sin 3 x}=\lim _{x \rightarrow 0} \frac{6 x}{3 x}=2
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.11. Compute the limit
$$
\lim _{x \rightarrow 0} \frac{1+\sin 2 x-\cos 2 x}{1-\sin 2 x-\cos 2 x}
$$
|
Solution. Under the limit sign, we have an indeterminate form of type "0/0". To resolve this, we will use the known trigonometric formulas:
$$
\sin 2 x=2 \sin x \cos x, \quad 1-\cos 2 x=2 \sin ^{2} x
$$
Taking this into account, we get
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{1+\sin 2 x-\cos 2 x}{1-\sin 2 x-\cos 2 x}=\lim _{x \rightarrow 0} \frac{2 \sin ^{2} x+2 \sin x \cos x}{2 \sin ^{2} x-2 \sin x \cos x}= \\
& =\lim _{x \rightarrow 0} \frac{2 \sin x(\sin x+\cos x)}{2 \sin x(\sin x-\cos x)}=\lim _{x \rightarrow 0} \frac{\sin x+\cos x}{\sin x-\cos x}=\frac{0+1}{0-1}=-1 .
\end{aligned}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.13. Calculate
$$
\lim _{x \rightarrow \pi}(\pi-x) \cot x
$$
|
Solution. The given limit represents an indeterminate form of type «0 $\cdot \infty »$. To resolve this, we introduce a new variable $\pi-x=t$. Then
$\lim _{x \rightarrow \pi}(\pi-x) \operatorname{ctg} x=\lim _{t \rightarrow 0} t \operatorname{ctg}(\pi-t)=-\lim _{t \rightarrow 0} t \operatorname{ctg} t=-\lim _{t \rightarrow 0} \frac{t}{\operatorname{tg} t}=-1$.
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.18. Calculate the limit
$$
\lim _{x \rightarrow \infty}\left(\frac{4 x^{2}-x+1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}
$$
|
Solution. This limit is not an indeterminate form, since when
$$
x \rightarrow \infty \frac{4 x^{2}-x+1}{2 x^{2}+x+1} \rightarrow 2, \text { and } \frac{x^{3}}{2-x} \sim -x^{2} \rightarrow -\infty
$$
Therefore:
$$
\begin{gathered}
\lim _{x \rightarrow \infty}\left(\frac{4 x^{2}-x+1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}=\lim _{x \rightarrow \infty}\left(2-\frac{3 x-1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}= \\
=\left(\lim _{x \rightarrow \infty}\left(2-\frac{3 x-1}{2 x^{2}+x+1}\right)\right)^{\lim _{x \rightarrow x} \frac{x^{3}}{2-x}}=2^{-\infty}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.22. Let
$$
f(x)=\left\{\begin{array}{l}
e^{3 x}, \text { if } x<0, \\
a+5 x, \text { if } x \geqslant 0
\end{array}\right.
$$
For which choice of the number $a$ will the function $f(x)$ be continuous?
|
The problem is solved. Let's write down the condition for the continuity of the function at the point \( x=0 \), where it is currently not continuous due to the arbitrariness of the number \( a \). We have
\[
\lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0+0} f(x)=f(0)
\]
In this case,
\[
\begin{aligned}
& \lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0-0} e^{3 x}=e^{0}=1 ; \\
& \lim _{x \rightarrow 0+0} f(x)=\lim _{x \rightarrow 0-0}(a+5 x)=a ; \\
& f(0)=\left.(a+5 x)\right|_{x=0}=a
\end{aligned}
\]
For the function to be continuous at the point \( x=0 \), the condition \( a=1 \) must be satisfied.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.24. Investigate the function
$$
f(x)=\frac{5^{1 / x}}{1+5^{1 / x}}
$$
for continuity and determine the nature of the points of discontinuity.
|
Solution. The function is defined everywhere except at the point $x=0$. Let's investigate the behavior of the function in the neighborhood of the point $x=0$. We will find the one-sided limits
$$
\lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0-0} \frac{5^{1 / x}}{1+5^{1 / x}}=0
$$
since as $x \rightarrow 0-0$, i.e., from the left of zero, $1 / x \rightarrow-\infty \Rightarrow$ $5^{1 / x} \rightarrow 0$.
$$
\lim _{x \rightarrow 0+0} f(x)=\lim _{x \rightarrow 0+0} \frac{5^{1 / x}}{1+5^{1 / x}}=\lim _{x \rightarrow 0+0} \frac{1}{5^{-1 / x}+1}=1
$$
since as $x \rightarrow 0+0$, $1 / x \rightarrow+\infty \Rightarrow 5^{-1 / x} \rightarrow 0$.
Thus, the one-sided limits of the function at the point $x=0$ exist but are not equal to each other. Therefore, the function $f(x)$ has a discontinuity of the first kind at the point $x=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.14. Find the derivative of the function
$$
f(x)=\left\{\begin{array}{l}
\operatorname{arctg}\left(x^{2} \cdot \sin (1 /(5 x))\right), \quad x \neq 0, \\
0, x=0
\end{array}\right.
$$
and compute its value at the point $x_{0}=0$.
|
Solution. Let's find the derivatives for $x \neq 0$. We have
$$
\begin{gathered}
f^{\prime}(x)=\frac{1}{1+\left(x^{2} \cdot \sin (1 / 5 x)\right)^{2}} \cdot\left(x^{2} \cdot \sin (1 /(5 x))\right)^{\prime}= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(\left(x^{2}\right)^{\prime} \cdot \sin (1 /(5 x))+x^{2} \cdot(\sin (1 /(5 x)))^{\prime}\right)= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(2 x \cdot \sin (1 /(5 x))+x^{2} \cdot \cos (1 /(5 x)) \cdot\left(-1 /\left(5 x^{2}\right)\right)\right)= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(2 x \cdot \sin (1 /(5 x))-\frac{\cos (1 /(5 x))}{5}\right), x \neq 0 .
\end{gathered}
$$
Since the one-sided limits
$$
\lim _{x \rightarrow 0 \pm 0} \sin (1 / 5 x)
$$
do not exist, the one-sided limits of $f^{\prime}(x)$ at $x_{0}=0$ do not exist either.
To find the derivative at the given point, we will use the definition of the derivative.
$$
f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{\operatorname{arctg}\left((0+\Delta x)^{2} \cdot \sin \left(\frac{1}{5(0+\Delta x)}\right)\right)-0}{\Delta x}
$$
Since the limit of the product of the bounded function $\sin (1 /(5 \Delta x))$ and the infinitesimal $\Delta x$ is zero, we get that $y^{\prime}(0)=0$.
Note that the original function $f(x)$ is continuous at the point $x_{0}=0$. Indeed, the function is defined both at the point $x_{0}=0$ and in some neighborhood of it, and
$$
\lim _{x \rightarrow 0} \operatorname{arctg}(x \cdot \sin (1 /(5 x)))=0=f(0)
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.28. Determine the angle at which the graph of the curve $f(x)=e^{x}-x$ intersects the y-axis.
|
Solution. $f_{x}^{\prime}(x)=e^{x}-1, f_{x}^{\prime}(0)=e^{0}-1=0$, hence the angle of intersection is $\alpha=0^{\circ}$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.31. Find the first differential of the function $y(x)=$ $=e^{3 x} \ln \left(1+x^{2}\right)$ and calculate its value at $x=0, d x=$ $=\Delta x=0.1$.
|
Solution. The first method is based on the direct application of the formula $d y(x)=y^{\prime}(x) d x$.
We have
$$
y^{\prime}(x)=3 e^{3 x} \cdot \ln \left(1+x^{2}\right)+\frac{e^{3 x} \cdot 2 x}{1+x^{2}}
$$
hence
$$
d y(x)=\left(3 e^{3 x} \cdot \ln \left(1+x^{2}\right)+\frac{e^{3 x} \cdot 2 x}{1+x^{2}}\right) \cdot d x
$$
The second method is based on the application of the rules for finding the differential of a product:
$$
\begin{aligned}
& d y(x)=d\left(e^{3 x}\right) \ln \left(1+x^{2}\right)+e^{3 x} d\left(\ln \left(1+x^{2}\right)\right)= \\
& \quad=3 e^{3 x} \ln \left(1+x^{2}\right) d x+\frac{e^{3 x} 2 x}{1+x^{2}} d x \\
& d y(0)=\left(3 e^{3 \cdot 0} \ln \left(1+0^{2}\right)+\frac{e^{3 \cdot 0} 2 \cdot 0}{1+0^{2}}\right) \cdot 0.1=0
\end{aligned}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.50. $\lim _{x \rightarrow 1} \frac{x^{4}-1}{\ln x}$.
|
Solution. Let's check the conditions for applying L'Hôpital's rule: 1) there is an indeterminate form
$$
\left.\frac{x^{4}-1}{\ln x}\right|_{x=1}=\frac{0}{0}
$$
2) the functions $x^{4}-1$ and $\ln x$ are differentiable in a neighborhood of the point $\left.x=1 ; 3)(\ln x)_{x=1}^{\prime} \neq 0 ; 4\right)$ the limit exists
$$
\lim _{x \rightarrow 1} \frac{\left(x^{4}-1\right)^{\prime}}{(\ln x)^{\prime}}=\lim _{x \rightarrow 1} \frac{4 x^{3}}{1 / x}=\lim _{x \rightarrow 1} 4 x^{4}=4
$$
Therefore, $\lim _{x \rightarrow 1} \frac{x^{4}-1}{\ln x}=\lim _{x \rightarrow 1} \frac{\left(x^{4}-1\right)^{\prime}}{(\ln x)^{\prime}}=4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.52. $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}$.
|
Solution.
$$
\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=(\infty / \infty)=\lim _{x \rightarrow+\infty} \frac{(\ln x)^{\prime}}{(x)^{\prime}}=\lim _{x \rightarrow+\infty} \frac{1 / x}{1}=\lim _{x \rightarrow+\infty} \frac{1}{x}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.53. $\lim _{x \rightarrow \infty} \frac{x}{e^{x}}$.
|
Solution.
$$
\lim _{x \rightarrow \infty} \frac{x}{e^{x}}=(\infty / \infty)=\lim _{x \rightarrow \infty} \frac{(x)^{\prime}}{\left(e^{x}\right)^{\prime}}=\lim _{x \rightarrow \infty} \frac{1}{e^{x}}=0
$$
## INDETERMINACY OF THE FORM «0 $\cdot$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.54. $\lim _{x \rightarrow \pi / 2}(x-\pi / 2) \cdot \tan x$.
|
Solution.
$$
\begin{aligned}
& \lim _{x \rightarrow \pi / 2}(x-\pi / 2) \cdot \tan x=(0 \cdot \infty)=\lim _{x \rightarrow \pi / 2} \frac{x-\pi / 2}{\cot x}= \\
& =(0 / 0)=\lim _{x \rightarrow \pi / 2} \frac{(x-\pi / 2)'}{(\cot x)'}=\lim _{x \rightarrow \pi / 2} \frac{1}{-\frac{1}{\sin ^{2} x}}=-1
\end{aligned}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.55. $\lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))$.
6.55. $\lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))$.
(No change needed as the text is already in English and contains mathematical notation which is universal.)
|
Solution.
$$
\begin{aligned}
& \lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))=(0 \cdot(-\infty))=\lim _{x \rightarrow 1+0} \frac{\ln (x-1)}{\frac{1}{\ln x}}=(-\infty /-\infty)= \\
& \quad=\lim _{x \rightarrow 1+0} \frac{(\ln (x-1))^{\prime}}{\left(\frac{1}{\ln x}\right)^{\prime}}=\lim _{x \rightarrow 1+0} \frac{\frac{1}{x-1}}{\frac{1}{x \ln ^2 x}}=\lim _{x \rightarrow 1+0} \frac{x \ln ^{2} x}{x-1}= \\
& \quad=\lim _{x \rightarrow 1+0} \frac{\ln ^{2} x}{1-\frac{1}{x}}=(0 / 0)=\lim _{x \rightarrow 1+0} \frac{\frac{\ln x}{x}}{\frac{1}{x^{2}}}=\lim _{x \rightarrow 1+0} 2 x \ln x=0 .
\end{aligned}
$$

|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.58. $\lim _{x \rightarrow+0} x^{x}$.
|
Solution.
$\lim _{x \rightarrow+0} x^{x}=e^{\lim _{x \rightarrow 0} x \ln x}=e^{\lim _{x \rightarrow 0 \rightarrow 0(1)}\left(\frac{(\ln x)'}{(1 / x)'}\right)}=e^{\lim _{x \rightarrow-0} \frac{1 / x}{-1 / x^{2}}}=e^{\lim _{x \rightarrow+0}(-x)}=e^{0}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.59. $\lim _{x \rightarrow 0}(1-\cos x)^{x}$.
|
Solution.
$$
\lim _{x \rightarrow 0}(1-\cos x)^{x}=\left(0^{0}\right)=e^{\lim _{x \rightarrow 0} x \ln (1-\cos x)}
$$
## Find separately
$$
\begin{aligned}
& \lim _{x \rightarrow 0} x \cdot \ln (1-\cos x)=(0 \cdot(-\infty))=\lim _{x \rightarrow 0} \frac{(\ln (1-\cos x))^{\prime}}{(1 / x)^{\prime}}=\lim _{x \rightarrow 0} \frac{\frac{\sin x}{1-\cos x}}{-\frac{1}{x^{2}}}= \\
& =-\lim _{x \rightarrow 0} \frac{x^{2} \cdot 2 \sin \frac{x}{2} \cos \frac{x}{2}}{2 \sin ^{2} \frac{x}{2}}=-\lim _{x \rightarrow 0} 2 x \cdot \lim _{x / 2 \rightarrow 0} \frac{x / 2}{\sin \frac{x}{2}} \cdot \lim _{x \rightarrow 0} \cos \frac{x}{2}=0
\end{aligned}
$$
Here, the first remarkable limit was used
$$
\lim _{\alpha \rightarrow 0} \frac{\alpha}{\sin \alpha}=1
$$
From here $e^{\lim _{x \rightarrow 0} x \ln (1-\cos x)}=e^{0}=1$.
## INDETERMINACY OF THE FORM « 1 *
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Let $X, Y$ be random variables, $\mathbf{E}|X|, \mathrm{E}|Y|<\infty$ and $\mathrm{E}(Y \mid X)=0$ a.s. Show that from the condition $\mathrm{E}(Y \mid X+Y)=0$ a.s. it follows that $Y=0$ with probability one.
|
Solution. Let $f(x)=|x|-\operatorname{arctg}|x|, x \in \mathbb{R}$. The function $f=f(x)$ is increasing on $\mathbb{R}_{+}$ and is an even, strictly convex function on $\mathbb{R}$, and $0 \leqslant f(x) \leqslant|x|$ for all $x \in \mathbb{R}$. By Jensen's inequality for conditional expectations, we have
$$
\begin{gathered}
\mathrm{E} f(X+Y)=\mathrm{E} f(\mathrm{E}[X+Y \mid X+Y])=\mathrm{E} f(\mathrm{E}[X \mid X+Y]) \leqslant \mathrm{E} f(X), \\
\mathrm{E} f(X)=\mathrm{E} f(\mathrm{E}[X+Y \mid X]) \leqslant \mathrm{E} f(X+Y),
\end{gathered}
$$
i.e., $\mathrm{E} f(X+Y)=\mathrm{E} f(\mathrm{E}[X+Y \mid X])$. The latter (in view of the remark to problem II.7.10) is possible only if $\mathrm{E}(X+Y \mid X)=X+Y$ a.s., which is equivalent to the equality $Y=\mathrm{E}(Y \mid X)=0$ a.s.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
232.
$$
\text { 1) }\left\{\begin{array}{l}
x=k \sin t+\sin k t \\
y=k \cos t+\cos k t ;\left(\frac{d y}{d x}\right)_{t=0} ?
\end{array}\right.
$$
What is the geometric meaning of the result?
2) $\left\{\begin{array}{l}x=\alpha^{2}+2 \alpha \\ y=\ln (\alpha+1) ; \frac{d^{2} y}{d x^{2}} ?\end{array}\right.$
3) $\left\{\begin{array}{l}x=1+e^{a \varphi} \\ y=a \varphi+e^{-a_{\varphi} \varphi} ; \frac{d^{3} y}{d x^{3}} ?\end{array}\right.$
|
Solution. 1) We find the derivatives of $x$ and $y$ with respect to the parameter $t$:
$$
\frac{d x}{d t}=k \cos t+k \cos k t ; \quad \frac{d y}{d t}=-k \sin t-k \sin k t
$$
The desired derivative of $y$ with respect to $x$ is found as the ratio of the derivatives of $y$ and $x$ with respect to $t$:
$\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=-\frac{k(\sin t+\sin k t)}{k(\cos t+\cos k t)}=-\frac{2 \sin \frac{t+k t}{2} \cos \frac{t-k t}{2}}{2 \cos \frac{t+k t}{2} \cos \frac{t-k t}{2}}=-\operatorname{tg} \frac{k+1}{2} t$.
At $t=0$, we get $\frac{d y}{d x}=0$. According to the geometric meaning of the derivative (§ 1), at the point $(0 ; k+1)$, where $t=0$, the tangent to the graph of the given function is parallel to the $O x$ axis.
2) We find the derivatives of $x$ and $y$ with respect to the parameter $\alpha$:
$$
\frac{d x}{d a}=2 \alpha+2 ; \frac{d y}{d \alpha}=\frac{1}{\alpha+1}
$$
and the desired derivative of $y$ with respect to $x$:
$$
y^{\prime}=\frac{d y}{d x}=\frac{d y}{d \alpha}: \frac{d x}{d \alpha}=\frac{1}{2(\alpha+1)^{2}}=\frac{1}{2}(\alpha+1)^{-2}
$$
Next, we find the derivative of $y^{\prime}$ with respect to $\alpha$, and then the desired second derivative of $y$ with respect to $x$ as the ratio of the derivatives of $y^{\prime}$ and $x$ with respect to $\alpha$:
$$
\frac{d y^{\prime}}{d \alpha}=-(\alpha+1)^{-3} ; \quad y^{\prime \prime}=\frac{d y^{\prime}}{d x}=\frac{d y^{\prime}}{d \alpha}: \frac{d x}{d \alpha}=\frac{-(\alpha+1)^{-3}}{2(\alpha+1)}=-\frac{1}{2(\alpha+1)^{4}}
$$
3) Using the general formulas (A) for the derivatives of a function given parametrically, we obtain
$$
\begin{aligned}
& y^{\prime}=\frac{d y}{d x}=\frac{d y}{d \varphi}: \frac{d x}{d \varphi}=\frac{a-a e^{-a \varphi}}{a e^{a \varphi}}=e^{-a \varphi}-e^{-2 \alpha \varphi} ; \\
& y^{\prime \prime}=\frac{d y^{\prime}}{d x}=\frac{d y^{\prime}}{d \varphi}: \frac{d x}{d \varphi}=\frac{2 a e^{-2 a \varphi}-a e^{-\alpha \varphi}}{a e^{a \varphi}}=2 e^{-3 a \varphi}-e^{-2 a \varphi} \\
& y^{\prime \prime \prime}=\frac{d y^{\prime \prime}}{d x}=\frac{d y^{\prime \prime}}{d \varphi}: \frac{d x}{d \varphi}=\frac{2 a e^{-2 a \varphi}-6 a e^{-3 a^{\prime} \varphi}}{a e^{a \varphi}}=2 e^{-3 a \varphi}-6 e^{-4 a \varphi} \\
& \text { 233. }\left\{\begin{array}{l}
x=t^{2} \\
y=t^{3} ; \frac{d y}{d x}
\end{array}\right. \\
& \text { 234. }\left\{\begin{array}{l}
x=\frac{3 a t}{1+t^{3}} \\
y=\frac{3 a t^{2}}{1+t^{3}} ; \frac{d y}{d x} ?
\end{array}\right. \\
& \text { 235. }\left\{\begin{array}{l}
x=a \cos t \\
y=a \sin t ; \frac{d^{2} y}{d x^{2}} ?
\end{array}\right. \\
& \text { 236. }\left\{\begin{array}{l}
p=\cos \alpha+\alpha \sin \alpha \\
q=\sin \alpha-\alpha \cos \alpha ; \frac{d^{2} q}{d p^{2}} ?
\end{array}\right. \\
& \text { 237. }\left\{\begin{array}{l}
x=z^{2} \\
y=z^{3}+z ;\left(\frac{d^{2} y}{d x^{2}}\right)_{z=1}
\end{array}\right\} \\
& \text { 238. }\left\{\begin{array}{l}
x=a \cos ^{3} t \\
y=a \sin ^{3} t
\end{array}\left(\frac{d^{2} y}{d x^{2}}\right)_{t=\frac{\pi}{6}} ?\right.
\end{aligned}
$$
## § 11. Tangent and Normal to a Plane Curve. Angle Between Two Curves
If a plane curve is referred to a rectangular coordinate system (Fig. 33), then the equations of the tangent and normal to it at the point $M\left(x_{0}, y_{0}\right)$ are:
$$
y-y_{0}=y_{0}^{\prime}\left(x-x_{0}\right) ; \quad y-y_{0}=-\frac{1}{y_{0}^{\prime}}\left(x-x_{0}\right)
$$
where $y_{0}^{\prime}$ is the value at the point $x_{0}$ of the derivative $\frac{d y}{d x}$ from the equation of the curve.
The direction of the curve at each of its points is determined by the direction of the tangent to it at that point. The angle between two intersecting curves is defined as the angle between two lines tangent to the curves at their point of intersection (Fig. 34) by the formula
$$
\operatorname{tg} \varphi=\frac{k_{1}-k_{2}}{1+k_{1} k_{2}}
$$
where $k_{1}$ and $k_{2}$ are the slopes of the tangents to the curves at their point of intersection $P\left(x_{0}, y_{0}\right)$, i.e., the particular values at the point $x_{0}$ of the derivatives of $y$ with respect to $x$ from the equations of these curves:
$$
k_{1}=\operatorname{tg} \alpha_{1}=\left(\frac{d y_{1}}{d x}\right)_{x=x_{0}} ; k_{2}=\operatorname{tg} \alpha_{2}=\left(\frac{d y_{2}}{d x}\right)_{x=x_{0}}
$$
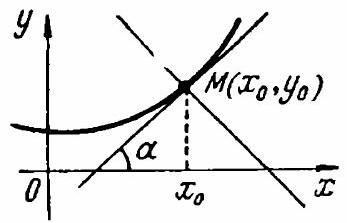
Fig. : 3

Fig. 34
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
315. Find the limits:
1) $\lim x \operatorname{ctg} 2 x$
2) $\lim _{x \rightarrow+0} \sqrt[3]{x} \ln x$
3) $\lim (\operatorname{tg} \varphi-\sec \varphi)$; $\varphi \rightarrow \frac{\pi}{2}$
4) $\lim _{x \rightarrow 1}\left(\frac{1}{\ln x}-\frac{x}{x-1}\right)$;
5) $\lim _{t \rightarrow 0}\left(\frac{1}{\sin t}-\frac{1}{t}\right)$
|
Solution. By establishing that the case is $0 \cdot \infty$ or $\infty - \infty$, we transform the function into a fraction where both the numerator and the denominator simultaneously tend to zero or infinity, then apply L'Hôpital's rule:
1) $\lim _{x \rightarrow 0} x \operatorname{ctg} 2 x=\lim \frac{x}{\operatorname{tg} 2 x}=\lim \frac{1}{2 \sec ^{2} 2 x}=\frac{1}{2}$;
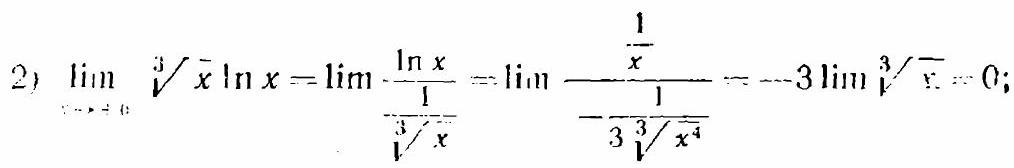
3) $\lim _{\varphi \rightarrow-\frac{\pi}{2}}(\operatorname{tg} \varphi-\sec \varphi)=\lim \frac{\sin \varphi-1}{\cos \varphi}=\lim \frac{\cos \varphi}{-\sin \varphi}=0$;
4) $\lim _{x \rightarrow 1}\left(\frac{1}{\ln x}-\frac{x}{x-1}\right)=\lim \frac{x-1-x \ln x}{(x-1) \ln x}=\lim \frac{-\ln x}{\ln x+\frac{x-1}{x}}=$
$$
:=-\lim \frac{x \ln x}{x \ln x+x-1}=-\lim \frac{1+\ln x}{2+\ln x}=\cdots \frac{1}{2}
$$
here L'Hôpital's rule is applied twice;
5) $\lim _{t \rightarrow 0}\left(-\frac{1}{\sin t}-\frac{1}{t}\right)=\lim \frac{t-\sin t}{t \sin t}=\lim \frac{1-\cos t}{\sin t+t \cos t}=$
$$
=\lim \frac{\sin t}{2 \cos t-t \sin t}=0
$$
here L'Hôpital's rule is applied twice.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
411. Find the curvature of the curve: 1) $x=t^{2}, y=2 t^{3}$ at the point where $t=1$; 2) $y=\cos 2 x$ at the point where $x=\frac{\pi}{2}$.
|
Solution. 1) We find the derivatives $\dot{x}=2 t, \ddot{x}=2, \dot{y}=6 t^{2}$, $\ddot{y}=12 t$, and compute their values at the point where $t=1$:
$$
\dot{x}=2, \ddot{x}=2, \dot{y}=6, \ddot{y}=12
$$
and, substituting into formula (1), we get
$$
K=\frac{|\ddot{x} \ddot{y}-\ddot{y} x|}{\left(\dot{x}^{2}+\dot{y}^{2}\right)^{\frac{3}{2}}}=\frac{2 \cdot 12-0.2}{\left(2^{2}+6^{2}\right)^{\frac{3}{2}}}=\frac{3}{20 \sqrt{10}}
$$
2) From the given equation, we find the first and second derivatives of $y$ with respect to $x$:
$$
y^{\prime}=-2 \sin 2 x, y^{\prime \prime}=-4 \cos 2 x
$$
we compute their values at the given point: $y^{\prime}\left(\frac{\pi}{2}\right)=0, y^{\prime \prime}\left(\frac{\pi}{2}\right)=4$ and, substituting into formula (1), we get $K=\frac{\left|y^{\prime \prime}\right|}{\left[1+\left(y^{\prime}\right)^{2}\right]^{\frac{3}{2}}}=4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
702. Using Simpson's formula, calculate the approximate value of the integral $\int_{0} \cos x d x$ with an accuracy of 0.00001.
|
Solution. First, we determine the number $n$ of parts into which the integration interval $\left[0, \frac{\pi}{2}\right]$ should be divided to achieve the required accuracy of the computation.
Assuming the error $\delta(n)$ of Simpson's formula is less than $10^{-5}$, we have
$$
\frac{(b-a)^{5}}{180 n^{4}} y_{H L}^{(4)}5 \pi \sqrt[4]{\frac{\pi}{36}}=8.5
$$
Next, assuming $n=10$ (the nearest even number greater than 8.5), we determine the division points $x_{i}$ and the corresponding values $y_{i}$ of the integrand function $y:=\cos x$ (with one extra decimal place, $\pi \approx 3.141592$):
$$
\begin{array}{ll}
x_{0}=0.000000 & y_{0}=1.000000 \\
x_{1}=0.157080 & y_{1}=0.987688 \\
x_{2}=0.314159 & y_{2}=0.951057 \\
x_{3}=0.471239 & y_{3}=0.891007 \\
x_{4}=0.628318 & y_{4}=0.809017 \\
x_{5}=0.785398 & y_{5}=0.707107 \\
x_{8}=0.942478 & y_{6}=0.587785 \\
x_{7}=1.099557 & y_{7}=0.453991 \\
x_{8}=1.256637 & y_{8}=0.309017 \\
x_{9}=1.413716 & y_{9}=0.156435 \\
x_{10}=1.570796 & y_{10}=0.000000
\end{array}
$$
Substituting into Simpson's formula, we obtain the desired value of the integral with an accuracy of $10^{-6}$:
$$
\int_{0}^{\frac{\pi}{2}} \cos x d x \approx 0.0523599(1+4 \cdot 3.196228+2 \cdot 2.656876) \approx 1.00000
$$
This solution demonstrates that for computing an integral with a given accuracy, when the analytical expression of the integrand function is known, one can determine in advance the necessary number of divisions of the integration interval, which would ensure the required accuracy, based on the specified inequalities for estimating the error of approximate formulas.
However, in many cases, the analytical expression of the integrand function is such that it is difficult to find the maximum value over the entire integration interval for the first, second, or fourth-order derivatives, which are contained in the inequalities determining the errors of the rectangle, trapezoidal, or Simpson's formulas. Therefore, in computational practice, other criteria are often used for estimating the error of approximate integration, which can be found in specialized manuals on approximate computations.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
714. Find the limits:
1) $\lim _{\substack{x \rightarrow 3 \\ y \rightarrow 0}} \frac{\tan(x y)}{y}$
2) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x}{x+y}$.
|
Solution. Having made sure that the function is not defined at the limit point, we perform transformations, guided by the instructions in § 7, Chapter I:
1) $\lim _{\substack{x \rightarrow 3 \\ y \rightarrow 0}} \frac{\tan(x y)}{y}=\lim x \cdot \lim \frac{\tan(x y)}{x y}=3 \cdot 1=3$, since $\lim _{a \rightarrow 0} \frac{\tan \alpha}{a}=1$.
2) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x}{x+y}=\lim \frac{1}{1+\frac{y}{x}}$ - does not exist, because the ratio $\frac{y}{x}$
does not have a limit as the point $M(x, y)$ approaches the point $M_{0}(0 ; 0)$ arbitrarily. Thus, if $M \rightarrow M_{0}$ along different lines $y=k x$, then $\frac{y}{x}=k$, i.e., it depends on the slope of the line along which the point $M$ moves.
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
875. Compute the line integrals:
1) $\oint_{-i} 2 x d x-(x+2 y) d y \quad$ and
2) $\oint_{+l} y \cos x d x+\sin x d y$
along the perimeter of the triangle with vertices $A(-1 ; 0), B(0 ; 2)$ and $C(2 ; 0)$.
|
Solution. 1) Here (Fig. 186) the integration line (closed) consists of three segments lying on different lines (with different equations). Accordingly, the line integral along the broken line $A B C A$ is calculated as the sum of integrals taken over the segments $A B, B C$, and $C A$.
By formulating the equation of the line $A B$,
Fig. 186 $y-2 x=2$, and based on this equation, we transform the line integral over the segment $A B$ into an ordinary integral with the variable $x$:
$$
\begin{gathered}
x=2 x+2, \quad d y=2 d x, \quad \int_{A B}=-8 \int_{x_{A}=-1}^{x_{B}=0}(x+1) d x= \\
=-\left.4(x+1)^{2}\right|_{-1} ^{0}=-4
\end{gathered}
$$
Similarly, calculating the line integral over the segments $B C$ and $C A$, we get
$$
\begin{aligned}
& x=2-y, d x=-d y, \quad \int_{B C}==\int_{u_{R}=2}^{4 / c^{=0}}(y-6) d y=\left.\frac{(y-6)^{2}}{2}\right|_{2} ^{0}=10 ; \\
& y=0, \quad d y=0, \int_{C A}=2 \int_{x_{C}=2}^{x_{A}=-1} x d x=\left.x^{2}\right|_{2} ^{-1}=-3
\end{aligned}
$$
Therefore,
$$
\oint_{A B C A}=\int_{A B}+\int_{B C}+\int_{C A}=-4+10-3=3
$$
2) Here the integrand is a complete differential of a function of two variables, since $(y \cos x)_{y}^{\prime}=(\sin x)_{x}^{\prime}=\cos x$. Therefore, this line integral, taken over the perimeter of the given triangle, is equal to zero. It will also be equal to zero over any other closed contour.
Calculate the line integrals:
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the singular solutions of the differential equation
$$
\left(y^{\prime}\right)^{2}=4 x^{2}
$$
|
Solution. Differentiating (23) with respect to $y_{1}$:
$$
2 y^{\prime}=0
$$
Excluding $y^{\prime}$ from (23) and (24), we get $x^{2}=0$. The discriminant curve is the y-axis. It is not an integral curve of equation (23), but according to scheme (16) it can be the geometric locus of points of tangency of integral curves.
The solutions of equation (23) are parabolas
$$
y=x^{2}+C, \quad y=-x^{2}+C
$$
and any smooth curves that can be composed from their parts (Fig. 21).
From the drawing, it is clear that the line $x=0$ is indeed the geometric locus of points of tangency of the integral curves of equation (23).
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Find the singular solutions of the differential equation
$$
\left(y^{\prime}\right)^{2}(2-3 y)^{2}=4(1-y)
$$
|
Solution. Let's find the PDK. Excluding $y^{\prime}$ from the system of equations
$$
\left\{\begin{aligned}
\left(y^{\prime}\right)^{2}(2-3 y)^{2}-4(1-y) & =0 \\
y^{\prime}(2-3 y)^{2} & =0
\end{aligned}\right.
$$
we obtain
$$
(2-3 y)^{2}(1-y)=0 .
$$
Transforming equation (25) to the form
$$
\frac{d x}{d y}= \pm \frac{2-3 y}{2 \sqrt{1-y}}
$$
we find its general integral
$$
y^{2}(1-y)=(x-C)^{2}
$$
Let's find the CDK. Excluding $C$ from the system of equations
$$
\left\{\begin{array}{r}
y^{2}(1-y)-(x-C)^{2}=0 \\
2(x-C)=0
\end{array}\right.
$$
we will have
$$
y^{2}(1-y)=0
$$
Thus, from (26) and (27) we have
$$
\begin{aligned}
& \text { PDK } \equiv(1-y)(2-3 y)^{2}=0 \\
& \text { CDK } \equiv(1-y) y^{2}=0
\end{aligned}
$$
The factor $1-y$ appears in the $p$-discriminant and in the $C$-discriminant to the first degree and gives the envelope, i.e., the function $y=1$ is a special solution of the differential equation (25). By direct substitution, we verify that $y=1$ indeed satisfies the equation.
The equation $2-3 y=0$, appearing in the $p$-discriminant to the second degree and not appearing in the $C$-discriminant at all, gives the place of tangency points ( $\Pi^{2}$ ).
Finally, the equation $y=0$, appearing in the $C$-discriminant to the second degree and not appearing in the $p$-discriminant at all, gives the place of nodal points $\left(P^{2}\right)$ (Fig. 22).
Fig. 22
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Find the Wronskian determinant for the functions: $y_{1}(x)=\sin x$,
$$
y_{2}(x)=\sin \left(x+\frac{\pi}{8}\right), y_{3}(x)=\sin \left(x-\frac{\pi}{8}\right)
$$
|
Solution. We have
$$
W\left[y_{1}, y_{2}, y_{3}\right]=\left|\begin{array}{rrr}
\sin x & \sin \left(x+\frac{\pi}{8}\right) & \sin \left(x-\frac{\pi}{8}\right) \\
\cos x & \cos \left(x+\frac{\pi}{8}\right) & \cos \left(x-\frac{\pi}{8}\right) \\
-\sin x & -\sin \left(x+\frac{\pi}{8}\right) & -\sin \left(x-\frac{\pi}{8}\right)
\end{array}\right|=0
$$
since the first and last rows of the determinant are proportional.
Theorem. If the system of functions $y_{1}(x), y_{2}(x), \ldots, y_{n}(x)$ is linearly dependent on the interval $[a, b]$, then its Wronskian determinant is identically zero on this interval.
For example, the system of functions $\sin x, \sin \left(x+\frac{\pi}{8}\right), \sin \left(x-\frac{\pi}{8}\right)$ is linearly dependent in the interval $(-\infty,+\infty)$, and the Wronskian determinant of these functions is zero everywhere in this interval (see examples 4 and 8).
This theorem provides a necessary condition for the linear dependence of a system of functions. The converse statement is false, i.e., the Wronskian determinant can be identically zero even when the given functions form a linearly independent system on some interval.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Investigate the stability of the solution of the degenerate equation for the equation
$$
\varepsilon \frac{d x}{d t}=x\left(e^{x}-2\right)
$$
|
Solution. The degenerate equation $x\left(e^{x}-2\right)=0$ has two solutions
$$
\text { 1) } x=0, \quad 2) x=\ln 2 \text {. }
$$
We have
$$
\left.\frac{\partial f(t, x)}{\partial x}\right|_{x=0}=\left.\left(e^{x}-2+x e^{x}\right)\right|_{x=0}=-1
$$
so the solution $x=0$ is stable;
$$
\left.\frac{\partial f(t, x)}{\partial x}\right|_{x=\ln 2}=\left.\left(e^{x}-2+x e^{x}\right)\right|_{x=\ln 2}=2 \ln 2>0,
$$
so the solution $x=\ln 2$ of the degenerate equation is unstable (Fig. 51).
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Calculate the sum:
$$
S=\frac{1}{(a-b)(a-c)}+\frac{1}{(b-a)(b-c)}+\frac{1}{(c-a)(c-b)}
$$
|
$$
\begin{aligned}
& S=\frac{1}{(a-b)(b-c)(c-a)}(-(b-c)-(c-a)-(a-b))= \\
& =\frac{-1}{(a-b)(b-c)(c-a)}(b-c+c-a+a-b)=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
114. Calculate the sum:
$$
x=\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}
$$
|
$$
\triangle$ Let's raise the equality to the third power, using the formula
$$
(a+b)^{3}=a^{3}+b^{3}+3 a b(a+b)
$$
We get:
$$
\begin{aligned}
& x^{3}=(9+4 \sqrt{5})+(9-4 \sqrt{5})+3 \sqrt[3]{81-80} \cdot(\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}) \\
& x^{3}=18+3 x, \quad x^{3}-3 x-18=0
\end{aligned}
$$
The last equation has an integer root $x=3$. It can be rewritten as
$$
(x-3)\left(x^{2}+3 x+6\right)=0
$$
The equation has no other real roots.
Answer: 3.
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
172. Prove that the numbers formed by the last two digits of the sequence $a_{n}=6^{n}$ form a periodic sequence. Find the period of such a sequence.
|
$\triangle$ That such a sequence is periodic is almost obvious: after all, the numbers formed by the last two digits of the power $6^{n}$ do not exceed 10: from 06 to 96. To find the period of the sequence, we will compute its first few terms:
$$
06,36,16,96,76,56,36,16
$$
It turned out that $a_{7}=a_{2}$, which means that for any natural $n \geq 2, a_{n+5}=a_{n}$. Therefore, the period of the sequence is 5.
Answer: 5.
|
5
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
390. Solve the equation:
$$
\sqrt[3]{x-1}+\sqrt[3]{2 x-1}=1
$$
|
$\triangle$ Let's raise both sides of the equation to the third power, using the formula
$$
(a+b)^{3}=a^{3}+b^{3}+3 a b(a+b)
$$
We will have:
$x-1+2 x-1+3 \sqrt[3]{(x-1)(2 x-1)} \cdot(\sqrt[3]{x-1}+\sqrt[3]{2 x-1})=1$,
$\sqrt[3]{(x-1)(2 x-1)} \cdot(\sqrt[3]{x-1}+\sqrt[3]{2 x-1})=1-x$.
But what now? Now let's use the original equation, according to which the sum in parentheses equals 1:
$$
\sqrt[3]{(x-1)(2 x-1)}=1-x
$$
We will also raise the last equation to the third power:
$(x-1)(2 x-1)=(1-x)^{3}, \quad(x-1)\left(2 x-1+(x-1)^{2}\right)=0$, $(x-1) x^{2}=0$.
From this
$$
x_{1}=1, \quad x_{2}=x_{3}=0
$$
It is interesting to check the original equation. It shows that the value $x=1$ satisfies it, while the value $x=0$ does not satisfy it.
Answer: 1.
A problem for reflection: Do you think at which step in the transition from the given original equation to the last one and for what reason did the extraneous root $x=0$ of the original equation appear? After all, it seems that we only used raising the equation to the third power, and as a result, we get an equation equivalent to the original one...
Note. The solution to problem 390 shows that when solving equations of the type
$$
\sqrt[3]{f_{1}(x)}+\sqrt[3]{f_{2}(x)}=\varphi(x)
$$
using this method, extraneous roots can appear. (When solving such equations by other methods, they may not appear.) Therefore, it is necessary to check the obtained roots by the original equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
394. Solve the equation:
$$
\sqrt[3]{x}+\sqrt[3]{x+19}=5
$$
|
$\triangle$ Equations of this type have already been encountered in section 11.1, with a different method of solution (see the solution to problem 390). Let's introduce two new variables:
$$
\sqrt[3]{x}=y, \quad \sqrt[3]{x+19}=z
$$
We obtain a system of rational equations:
$$
\left\{\begin{array}{l}
y+z=5 \\
y^{3}=x \\
z^{3}=x+19
\end{array}\right.
$$
Subtract the second equation from the third to eliminate $x$: $z^{3}-y^{3}=19$.
To solve the system of two equations
$$
y+z=5, \quad z^{3}-y^{3}=19
$$
express $z$ from the first equation and substitute this expression into the second equation:
$z=5-y, \quad(5-y)^{3}-y^{3}=19, \quad 125-75 y+15 y^{2}-2 y^{3}=19$, $2 y^{3}-15 y^{2}+75 y-106=0$.
Among the divisors of the free term, the last equation is satisfied by $y=2$. Then the equation reduces to:
$$
(y-2)\left(2 y^{2}-11 y+51\right)=0 .
$$
From this, it is clear that the equation has no other roots.
Therefore,
$$
x=y^{3}=2^{3}=8
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
403*. Solve the equation:
$$
\sqrt[4]{1-x^{2}}+\sqrt[4]{1-x}+\sqrt[4]{1+x}=3
$$
|
$\triangle$ The domain of the equation is the interval $[-1 ; 1]$. In this domain, we can apply the inequality between the geometric mean and the arithmetic mean of two non-negative numbers to each of the radicals in the left-hand side:
$\sqrt[4]{1-x^{2}}=\sqrt{\sqrt{1+x} \cdot \sqrt{1-x}} \leq \frac{\sqrt{1+x}+\sqrt{1-x}}{2}$,
$\sqrt[4]{1+x}=\sqrt{1 \cdot \sqrt{1+x}} \leq \frac{1+\sqrt{1+x}}{2}$,
$\sqrt[4]{1-x}=\sqrt{1 \cdot \sqrt{1-x}} \leq \frac{1+\sqrt{1-x}}{2}$.
We will add these three inequalities term by term, and apply the same inequality twice more to the expression in the right-hand side of the new inequality:
$$
\sqrt[4]{1-x^{2}}+\sqrt[4]{1+x}+4 \sqrt[4]{1-x} \leq 1+\sqrt{1+x}+\sqrt{1-x} \leq 1+\frac{1+(1+x)}{2}+\frac{1+(1-x)}{2}=3
$$
The obtained inequality must turn into an equality according to the condition. However, this is only possible if each of the inequalities used here turns into an equality. It is known that the geometric mean of two non-negative numbers equals their arithmetic mean only when these numbers are equal. In this case, we will have:
$$
1=1+x=1-x
$$
from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
447. A motorcyclist left point A at a speed of 45 km/h. After 40 minutes, a car left A in the same direction at a speed of 60 km/h. How much time after the car's departure will the distance between it and the motorcyclist be 36 km?
|
$\triangle$ Important question: at the moment when the car is 36 km away from the motorcycle, will it be ahead or behind the motorcycle?
In 40 minutes, the motorcycle will travel a distance of $45 \cdot \frac{2}{3}$ km $=30$ km, which is less than 36 km. Therefore, at the moment the car departs, it is 30 km behind the motorcycle, and the distance between them will continue to decrease until the car overtakes the motorcycle. This means that the car will be 36 km ahead of the motorcycle after the overtaking.
Fig. 1
In Fig. 1, points A and B denote the locations of the car and the motorcycle, respectively, at the moment the car departs, and points $\mathrm{A}_{1}$ and $\mathrm{B}_{1}$ denote their locations at the moment the car is 36 km ahead of the motorcycle. Then $\mathrm{AB}=30$ km, $\mathrm{B}_{1} \mathrm{~A}_{1}=36$ km.
Let the unknown be the distance $\mathrm{BB}_{1}: \mathrm{BB}_{1}=x$ km. If we find this distance, we will also find the time the car takes to travel the path $\mathrm{AA}_{1}$.
The verbal "equation" here is: the time the car takes to travel the path $\mathrm{AA}_{1}$ equals the time the motorcycle takes to travel the path $\mathrm{BB}_{1}$. Express both times in terms of $x$ and set the expressions equal:
$$
\frac{30+x+36}{60}=\frac{x}{45}
$$
Solve this equation:
$$
3(66+x)=4 x, \quad 198+3 x=4 x, \quad x=198
$$
From this, the time the car takes to travel the path $\mathrm{AA}_{1}$ is $\frac{198}{45}=\frac{22}{5}=4 \frac{2}{5}$ (hours), i.e., 4 hours 24 minutes. Answer: 4 hours 24 minutes.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
455*. From point A to point B, which is 40 km away from A, two tourists set off simultaneously: the first on foot at a speed of 6 km/h, and the second on a bicycle. When the second tourist overtook the first by 5 km, the first tourist got into a passing car traveling at a speed of 24 km/h. Two hours after leaving A, the first tourist caught up with the second and arrived in B before him. Find the speed of the tourist who was riding the bicycle.
|
$\triangle$ Let's make a drawing (Fig. 2). $\qquad$
Fig. 2
Let $\mathrm{A}_{1}$ and $\mathrm{B}_{1}$ be the points where the first and second tourists are, respectively, at the moment when the second tourist overtakes the first by $5 \mathrm{km}$, and let $\mathrm{K}$ be the point where the first tourist catches up with the second.
Denote the time the first tourist takes to travel $\mathrm{AA}_{1}$ (and simultaneously the second tourist to travel $\mathrm{AB}_{1}$) by $t_{1}$ hours, and the time the first tourist takes to travel $\mathrm{A}_{1} \mathrm{~K}$ (and the second to travel $\mathrm{B}_{1} \mathrm{~K}$) by $t_{2}$ hours. Let the speed of the cyclist be $v$ km/h.
Since each tourist traveled the distance $\mathrm{AK}$ in 2 hours, we have $t_{1}+t_{2}=2$.
Since in time $t_{1}$ the cyclist traveled 5 km more than the first tourist, we have $v t_{1}-6 t_{1}=5$.
Finally, express the distance $\mathrm{AK}$ in two ways - using quantities related to the first tourist and quantities related to the second, and equate the resulting expressions:
$$
6 t_{1}+24 t_{2}=v\left(t_{1}+t_{2}\right)
$$
We have the system of equations:
$$
\left\{\begin{array}{l}
t_{1}+t_{2}=2 \\
v t_{1}-6 t_{1}=5 \\
6 t_{1}+24 t_{2}=v\left(t_{1}+t_{2}\right)
\end{array}\right.
$$
From the first equation, $t_{2}=2-t_{1}$, and from the second, $-v=\frac{6 t_{1}+5}{t_{1}}$. Substitute these expressions for $t_{2}$ and $v$ into the third equation and solve the new equation with the unknown $t_{1}$:
$6 t_{1}+24\left(2-t_{1}\right)=\frac{2\left(6 t_{1}+5\right)}{t_{1}}, \quad 6 t_{1}^{2}+48 t_{1}-24 t_{1}^{2}=12 t_{1}+10$,
$18 t_{1}^{2}-36 t_{1}+10=0, \quad 9 t_{1}^{2}-18 t_{1}+5=0 ; \quad t_{1}=\frac{9 \pm 6}{9}$.
Thus, $t_{1}=\frac{5}{3}$ or $t_{1}=\frac{1}{3}$. Accordingly, $v=9$ or $v=21$.
Do both these values of $v$ fit? It turns out, no: if $v=21$ km/h, then the cyclist will travel a distance of 42 km in 2 hours, and this distance is greater than $A B=40$ km.
Answer: 9 km/h.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
489*. Three cyclists set off simultaneously: the first and second from point A, and the third towards them from point B. After 1.5 hours, the first cyclist was at an equal distance from the other two, and after 2 hours from the start, the third cyclist was at an equal distance from the first and second. How many hours after departure was the second cyclist at an equal distance from the first and third?
|
$\triangle$ Let's take the path AB as a unit. Denote the speeds of the first, second, and third cyclists as $v_{1}, v_{2}$, and $v_{3}$ (in fractions of this path per hour).
We will denote the positions of the first, second, and third cyclists in each of the three specified situations by the letters $\mathbf{M}_{1}, \mathbf{M}_{2}$, and $\mathbf{M}_{3}$, respectively.
After 1.5 hours from the start of the movement, the first cyclist was halfway between the second and the third (Fig. 4), and after 2 hours, the third cyclist was halfway between the first and the second (Fig. 5).
Fig. 4

Fig. 5
Since on Fig. $4 \mathrm{M}_{2} \mathrm{M}_{1}=\mathrm{M}_{1} \mathrm{M}_{3}$, where
$$
\mathbf{M}_{2} \mathbf{M}_{1}=1.5\left(v_{1}-v_{2}\right), \quad \mathbf{M}_{1} \mathbf{M}_{3}=1-1.5 v_{1}-1.5 v_{3},
$$
then
$$
1.5\left(v_{1}-v_{2}\right)=1-1.5\left(v_{1}+v_{3}\right)
$$
Since on Fig. $5 M_{2} M_{3}=M_{3} M_{1}$, where
$$
\mathbf{M}_{2} \mathbf{M}_{3}=1-2\left(v_{2}+v_{3}\right), \quad \mathbf{M}_{3} \mathbf{M}_{1}=2\left(v_{1}+v_{3}\right)-1
$$
then
$$
1-2\left(v_{2}+v_{3}\right)=2\left(v_{1}+v_{3}\right)-1
$$
We obtain the system of equations:
$$
\left\{\begin{array}{l}
1.5\left(v_{1}-v_{2}\right)=1-1.5\left(v_{1}+v_{3}\right) \\
1-2\left(v_{2}+v_{3}\right)=2\left(v_{1}+v_{3}\right)-1
\end{array}\right.
$$
From this, we find that
$$
v_{3}=\frac{1}{2}\left(1-v_{1}-v_{2}\right), \quad v_{1}-v_{2}=\frac{1}{9}
$$
(consider how to derive these equalities).
We are interested in the third position, when the second cyclist is halfway between the first and the third (Fig. 6).

Fig. 6
Let $t$ hours be the time from the start of the movement to this position. Since $\mathrm{M}_{3} \mathrm{M}_{2}=\mathrm{M}_{2} \mathrm{M}_{1}$, where
$$
\mathrm{M}_{3} \mathrm{M}_{2}=\left(v_{2}+v_{3}\right) t-1, \quad \mathbf{M}_{2} \mathbf{M}_{1}=\left(v_{1}-v_{2}\right) t
$$
then
$$
\left(v_{1}+v_{3}\right) t-1=\left(v_{1}-v_{2}\right) t .
$$
Solve for $t$, and then, using the obtained expressions for $v_{3}$ and $v_{1}-v_{2}$, calculate $t$:
$t=\frac{1}{2 v_{2}+v_{3}-v_{1}}=\frac{1}{2 v_{2}+\frac{1}{2}\left(1-v_{1}-v_{2}\right)-v_{1}}=\frac{2}{1-3 v_{1}+3 v_{2}}=2:\left(1-\frac{3}{9}\right)=3$.
Answer: after 3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
493. Four pumps of the same capacity, working together, filled the first tanker and a third of the second tanker (of a different volume) in 11 hours. If three pumps had filled the first tanker and then one of them filled a quarter of the second tanker, the work would have taken 18 hours. How many hours would it take for three pumps to fill the second tanker?
|
$\triangle$ Let one pump fill the first tanker in $x$ hours, and the second tanker in $y$ hours. Then four pumps, working together, will fill the first tanker in $\frac{x}{4}$ hours, and the second in $\frac{y}{4}$ hours.
We have the system of equations:
$$
\left\{\begin{array}{l}
\frac{x}{4}+\frac{y}{4 \cdot 3}=11 \\
\frac{x}{3}+\frac{y}{4}=18
\end{array}\right.
$$
From this, we find that $y=24$ hours. Therefore, three pumps can fill the second tanker in $\frac{24}{3}=8$ hours.
Answer: in 8 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
498. Three automatic lines produce the same product, but have different productivity. The combined productivity of all three lines working simultaneously is 1.5 times the productivity of the first and second lines working simultaneously. A shift assignment for the first line can be completed by the second and third lines working simultaneously 4 hours and 48 minutes faster than the first line. The same assignment is completed by the second line 2 hours faster than the first line. How many hours does the first line take to complete its shift assignment?
|
$\triangle$ Let's accept the shift task for the first line as a unit.
Let the first line complete its shift task in $x$ hours, and the third line the same task in $y$ hours. Then the second line completes the task of the first in $(x-2)$ hours.
Therefore, the productivity of the first, second, and third lines are respectively $\frac{1}{x}, \frac{1}{x-2}$, and $\frac{1}{y}$ (in fractions of the first line's task per hour).
Since the combined productivity of all three lines is 1.5 times greater than the combined productivity of the first and second lines, then
$$
\frac{1}{x}+\frac{1}{x-2}+\frac{1}{y}=1.5\left(\frac{1}{x}+\frac{1}{x-2}\right)
$$
Since the second and third lines, working simultaneously, can complete the shift task of the first line 4 hours and 48 minutes $=\frac{24}{5}$ hours faster than the first line, then
$$
x-\frac{24}{5}=1:\left(\frac{1}{x-2}+\frac{1}{y}\right)
$$
After simplifications, this equation reduces to the following form:
$$
1+\frac{x-2}{y}=\frac{5 x-10}{5 x-24}
$$
We obtain the system of equations:
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{1}{x-2}+\frac{1}{y}=1.5\left(\frac{1}{x}+\frac{1}{x-2}\right) \\
1+\frac{x-2}{y}=\frac{5 x-10}{5 x-24}
\end{array}\right.
$$
From the first equation of the system, express $y$ in terms of $x$:
$$
\frac{1}{y}=0.5\left(\frac{1}{x}+\frac{1}{x-2}\right), \quad \frac{1}{y}=\frac{1}{2} \cdot \frac{2 x-2}{x(x-2)}, \quad y=\frac{x(x-2)}{x-1}
$$
Substitute this expression into the second equation of the system:
$$
1+(x-2) \cdot \frac{x-1}{x(x-2)}=\frac{5 x-10}{5 x-24}, \quad 1+\frac{x-1}{x}=\frac{5 x-10}{5 x-24}
$$
The last equation reduces to the quadratic equation $5 x^{2}-43 x+24=0$. Its roots are $-x_{1}=8$ and $x_{2}=\frac{3}{5}$. Only the first root fits.
Answer: 8 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
507. Fresh mushrooms contain $90\%$ water, while dried ones contain $12\%$ water. How many kilograms of dried mushrooms can be obtained from 44 kg of fresh mushrooms?
|
$\triangle$ According to the condition, 44 kg of fresh mushrooms contain $44 \cdot 0.9 = 39.6$ kg of water, which means there is $44 - 39.6 = 4.4$ kg of dry matter.
Let's denote the mass of dried mushrooms that can be obtained from 44 kg of fresh mushrooms by $x$ kg. These $x$ kg consist of $0.12 x$ kg of water and $0.88 x$ kg of dry matter.
Since the mass of the dry matter is the same in both fresh and dried mushrooms,
$$
0.88 x = 4.4
$$
Therefore, $x = \frac{4.4}{0.88} = 5$.
This problem could also be solved without algebra - arithmetically.
Answer: 5 kg.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A mowing team had to mow two meadows, one twice as large as the other. For half a day, the team mowed the larger meadow. After that, they split in half: one half stayed on the large meadow and finished it by evening, while the other half mowed the smaller meadow but did not finish it. How many mowers were in the team, if it is known that the remaining work was completed by one mower on the following day?
|
7. If the whole brigade mowed a large meadow for half a day and half of the brigade mowed for another half a day, it is clear that the brigade mowed $\frac{2}{3}$ of the meadow in half a day, and half of the brigade mowed $\frac{1}{3}$ of the meadow in half a day. Since the second meadow is half the size of the first, after working on it with half of the brigade for half a day, the uncut area is $\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$. This area was mowed by one mower in one day. Therefore, one mower mows $\frac{1}{6}$ of the meadow in one day, and the whole brigade mows $\frac{4}{3}$. Answer: there were 8 mowers in the brigade.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. In the wallet, there are 71 kopecks in coins of 5, 2, and 1 kopeck. The number of 1 and 2 kopeck coins is the same. How many coins of each denomination are in the wallet if there are 31 of them in total?
|
25. 1 kopeck - 12 coins, 2 kopecks - 12 coins, and 5 kopecks - 7 coins.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find the remainder of the division of $67^{283}$ by 13.
|
12. $65=13 \cdot 5$, then $67^{283}=(65+2)^{283}=65^{283}+283 \cdot 65^{282} \cdot 2+\ldots+2^{283}$. Each term, except the last one, contains a factor of 65, and therefore, is divisible by 13.
$$
2^{283}=16^{70} \cdot 2^{3}=(13+3)^{70} \cdot 2^{3}=\left(13^{70}+70 \cdot 13^{69} \cdot 3+\ldots+3^{70}\right) \cdot 2^{3}
$$
Each term, except the last one, is divisible by 13.
Consider the last term:
$$
3^{70} \cdot 2^{3}=27^{23} \cdot 3 \cdot 2^{3}=(26+1)^{23} \cdot 3 \cdot 2^{3}=\left(26^{23}+23 \cdot 26^{22}+\ldots+1\right) \cdot 3 \cdot 2^{3}
$$
Each term, except the last one, is divisible by 13, as it contains a factor of 26. Consider the last term.
$$
1 \cdot 3 \cdot 2^{3}=24=13+11 \text{. Answer: the remainder is } 11.
$$
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. What digit does the number $777^{777}$ end with?
|
14. Let's determine the last digits of the powers of 777. \(777^1\) ends in 7. \(777^2\) ends in 9; \(777^3\) ends in 3; \(777^4\) ends in 1; \(777^5\) ends in 7; \(777^6\) ends in 9; \(777^7\) ends in 3; \(777^8\) ends in 1, and so on. We establish that 777776 ends in 1, therefore, \(777^{777}\) ends in 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. If the thought number is multiplied by 3, 2 is appended to the right, the resulting number is divided by 19, and 7 is added to the quotient, the result is three times the thought number. What is this number?
|
56. Let $x$ be the thought-of number. Then the condition of the problem can be written as: $(3 x \cdot 10 + 2) : 9 + 7 = 3 x$.
From which $x = 5$.
## $\S 3$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. The dividing circle of the dividing head is uniformly marked with 24 holes. What regular polygons can be marked using this instrument?
|
10. By connecting all 24 holes sequentially, we get a twenty-four-sided polygon, connecting every other hole - a twelve-sided polygon,
connecting every two holes - an eight-sided polygon, connecting every three holes - a six-sided polygon, and connecting every seven holes - a three-sided polygon. If $n$ is the number of vertices of the inscribed polygon, $3 \leqslant n \leqslant 24$, then $\frac{24-n}{n}=k-$ $5^{*}$
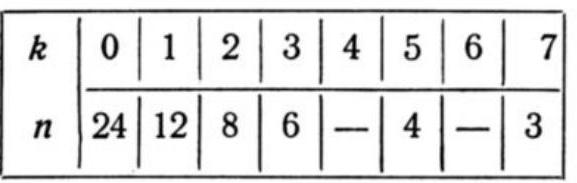
is an integer. Then $n=\frac{24}{k+1}$. Therefore, $0 \leqslant k \leqslant 7$.
Answer. Using a dividing circle with 24 holes, 6 different regular polygons can be marked.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. $\log _{\frac{\sqrt{3}}{3}}\left(\log _{8} \frac{\sqrt{2}}{2}-\log _{3} \frac{\sqrt{3}}{3}\right)$.
In № $15-27$ solve the equations:
|
14. We should switch to the logarithm with base $\frac{\sqrt{3}}{3}$.
Then replace $\frac{1}{3}$ with $\left(\frac{\sqrt{3}}{3}\right)^{2}$. Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. $\log _{4}\left\{2 \log _{3}\left[1+\log _{2}\left(1+3 \log _{2} x\right)\right]\right\}=\frac{1}{2}$.
|
16. Gradually potentiating, we arrive at the equation $1+3 \log _{2} x=4$. From which $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. $\log _{5} 120+(x-3)-2 \log _{5}\left(1-5^{x-3}\right)=-\log _{5}\left(0.2-5^{x-4}\right)$.
|
19. $1-5^{x-3} \neq 0, x \neq 3,0,2-5^{x-4}=\frac{1}{5}\left(1-5^{x-3}\right)$.
Raising the entire expression, we get
$$
\frac{120 \cdot 5^{x-3}}{\left(1-5^{x-3}\right)^{2}}=\frac{5}{1-5^{x-3}} ; \quad 5^{x-3}=5^{-2} . \quad \text { Hence } x=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Calculate the product $p=1 \cdot 2^{\frac{1}{2}} \cdot 4^{\frac{1}{4}} \cdot 8^{\frac{1}{8}} \cdot 16^{\frac{1}{16}} \cdot \ldots$
In № $15-20$ find the sums:
|
14. Let's write all powers as powers with base 2
$$
p=1 \cdot 2^{\frac{1}{2}} \cdot 2^{\frac{2}{4}} \cdot 2^{\frac{3}{8}} \cdot 2^{\frac{4}{16}} \ldots=2^{\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}+\cdots}
$$
The problem has been reduced to finding the sum $S=\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}+\ldots$
Divide each term of this equality by 2 and subtract the obtained result from the first equality
$$
\frac{1}{2} S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots ; \quad \frac{1}{2} S=1, \quad S=2, \quad p=4
$$
86
15, 16, 17. $S=\frac{n}{n+1}, \quad S=\frac{n}{3 n+1}, S=\frac{n}{2 n+1}$ respectively. The specified sums can be found by constructing sequences of partial sums or by decomposing the terms of these sums into simpler fractions.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Find the sum $\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+\ldots+\frac{n}{(n+1)!}$ and compute its limit as $n \rightarrow \infty$.
|
21. By forming the sequence of partial sums, we get
$$
S_{1}=\frac{2!-1}{2!}, \quad S_{2}=\frac{3!-1}{3!}, \ldots \quad \text { Hence } S_{n}=\frac{(n+1)!-1}{(n+1)!}, \quad S=\lim _{n \rightarrow \infty} S_{n}=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. $y=\frac{|x|-2}{|x|}$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
15. $y=\frac{|x|-2}{|x|}$.
|
15. (Fig. 15) The root of the submodular expression is 0.
For $x>0, \quad y=1-\frac{2}{x}$.
For $x<0, \quad y=1+\frac{2}{x}$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. How many planes of symmetry do the following have: a) a cube; b) a regular tetrahedron?
|
31. a) A cube has 9 planes of symmetry; b) a regular tetrahedron has 6 planes of symmetry.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. What is the maximum area that a triangle with sides \(a, b, c\) can have, given that the sides are within the following limits: \(0 \leqslant a \leqslant 1 \leqslant b \leqslant 2 \leqslant c \leqslant 3\) ?
|
21. $S=\frac{1}{2} a b \sin \alpha$. Takes the maximum value when $a=1, b=2, \sin \alpha=1$,
$S=\frac{1}{2} \cdot 1 \cdot 2 \cdot 1=1$. Under these conditions, $c=\sqrt{1+4}=\sqrt{5}$, which satisfies the problem's condition ( $2 \leqslant c \leqslant 3$).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Determine $a$ so that the sum of the squares of the roots of the equation $x^{2}+(2-a) x-a-3=0$ is the smallest.
|
33. $a=1$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Several families lived in one house. In total, there are more children in these families than adults: there are more adults than boys; more boys than girls; and more girls than families. There are no childless families, and no families have the same number of children. Each girl has at least one brother and at most one sister. In one of the families, there are more children than in all the others combined. How many families lived in the house? How many boys and how many girls are there in each of these families?
|
30. Three families lived in the house. In one of these families, there is a single child, a boy. In another family - two girls and a boy. In the third - two girls and three boys.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. During the lunch break, the members of the communist labor brigade started talking about how many newspapers each of them reads. It turned out that each member subscribes to and reads exactly two newspapers, each newspaper is read by five people, and any combination of two newspapers is read by one person. How many newspaper titles do the members of the brigade subscribe to? How many members are in the brigade?
|
32. 6 newspaper names, 15 members.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. There are three villages: $A, B$, and $C$. The inhabitants of $A$ always tell the truth, the inhabitants of $B$ always lie, and the inhabitants of $C$, depending on their mood, tell the truth or lie. Since the villages are located close to each other, the inhabitants visit each other. A tourist ended up in one of these villages. What is the minimum number of questions and what specific questions will he have to ask the first person he meets (who can only answer “yes” or “no”) to find out which village he is in and which village this person he met lives in?
|
51. Four questions: 1) Am I in one of the settlements $A$ and $B$? 2) Am I in settlement C? 3) Do you live in settlement C? 4) Am I in settlement $A^{*}$?
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. My friend has thought of an integer between 10 and 19. To guess which number he has in mind, I can ask him questions that he will answer with "yes" or "no": What is the smallest number of questions and which specific questions can I ask to determine which number he thought of?
|
52. The least number of questions is three. The first question: "Is the number you are thinking of among the first four numbers (11-14)?" If the answer is "Yes," then the second question can be: "Is the number you are thinking of among the numbers 11 and 12?" If the answer is "No," then the third question can be: "Is the number you are thinking of 13?" If the answer is "No," then the number you are thinking of is 14.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.