problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
78(1188). Check that the equality is correct:
a) $\sqrt{2 \frac{2}{3}}=2 \sqrt{\frac{2}{3}}$
b) $\sqrt{5 \frac{5}{24}}=5 \sqrt{\frac{5}{24}}$.
Specify the condition under which the observed pattern holds. Provide examples.
|
Solution. a) Method I. Transform the left side of the equation:
$$
\sqrt{2 \frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{\frac{4 \cdot 2}{3}}=2 \sqrt{\frac{2}{3}}
$$
Method II. Transform the right side of the equation:
$$
2 \sqrt{\frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{2 \frac{2}{3}}
$$
Method III. Square both sides of the equation:
$$
2 \frac{2}{3}=4 \cdot \frac{2}{3} ; 2 \frac{2}{3}=2 \frac{2}{3} .
$$
b) Method I. $\sqrt{5 \frac{5}{24}}=\sqrt{\frac{125}{24}}=\sqrt{\frac{25 \cdot 5}{24}}=5 \sqrt{\frac{5}{24}}$.
Method II. $5 \sqrt{\frac{5}{24}}=\sqrt{\frac{25 \cdot 5}{24}}=\sqrt{\frac{125}{24}}=\sqrt{5 \frac{5}{24}}$.
Method III. $5 \frac{5}{24}=25 \cdot \frac{5}{24} ; 5 \frac{5}{24}=5 \frac{5}{24}$.
Derive the condition under which
$$
\sqrt{k \frac{k}{n}}=k \sqrt{\frac{k}{n}}, \text { i.e., } \sqrt{\frac{k n+k}{n}}=k \sqrt{\frac{k}{n}}
$$
Method I. Square the obtained equation:
$$
\frac{k n+k}{n}=\frac{k^{3}}{n}
$$
from which $\frac{k(n+1)}{n}=\frac{k^{\prime}}{n}$, i.e., $n+1=k^{2}, k=\sqrt{n+1}$.
Thus, if $n+1=k^{2}$, then $\sqrt{k \frac{k}{n}}=k \sqrt{\frac{k}{n}}$. For example, if $n=15$, we get $k=4$ and $\sqrt{4 \frac{4}{15}}=4 \sqrt{\frac{4}{15}}$, if $n=80$, we get $k=9$ and $\sqrt{9 \frac{9}{80}}=9 \sqrt{\frac{9}{80}}$.
Method II. Let the integer part of the number $a$ be $x([a]=x)$, and the fractional part of the number $a$ be $y(\{a\}=y)$. Find the relationship between the integer and fractional parts of the number $a$, under which
$$
\sqrt{[a]+\{a\}}=[a] \cdot \sqrt{|a|} .
$$
## Square the equation (1):
$$
[a]+\{a\}=[a\}^{2} \cdot\{a\}
$$
from which $[a]=\{a\} \cdot\left([a]^{2}-1\right)$, i.e., $\{a\}=\frac{[a]}{[a]^{2}-1}$.
For example, if $[a]=6$, then $\{a\}=\frac{6}{36-1}=\frac{6}{35}$. We have $\sqrt{6 \frac{6}{35}}=$ $=6 \sqrt{\frac{6}{35}}$.
If $[a]=10$, then $\{a\}=\frac{10}{100-1}=\frac{10}{99}$. We have $\sqrt{10 \frac{10}{99}}=10 \sqrt{\frac{10}{99}}$.
$\triangle 79(1189)$. Find the value of the expression
$$
\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}}
$$
Solution. Method I.
$$
\begin{aligned}
& \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\ldots+\frac{1}{\sqrt{99+\sqrt{100}}}= \\
= & \frac{2-1}{\sqrt{2}+\sqrt{1}}+\frac{3-2}{\sqrt{3}+\sqrt{2}}+\frac{4-3}{\sqrt{4}+\sqrt{3}}+\ldots+\frac{100-99}{\sqrt{100}+\sqrt{99}}=
\end{aligned}
$$
$$
\begin{gathered}
=\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+\ldots+\sqrt{100}-\sqrt{99}= \\
=\sqrt{100}-\sqrt{1}=9
\end{gathered}
$$
Method II. By rationalizing the denominator of each fraction, we get that the denominator of each fraction will be equal to one, and the problem reduces to adding the numerators:
$$
\begin{gathered}
(\sqrt{2}-\sqrt{1})+(\sqrt{3}-\sqrt{2})+(\sqrt{4}-\sqrt{3})+\ldots+\sqrt{100}-\sqrt{99}= \\
=\sqrt{100}-\sqrt{1}=9
\end{gathered}
$$
$80(1190)$. From the first hundred natural numbers, 51 numbers are taken arbitrarily. Prove that among the taken numbers, there are definitely two such numbers, one of which is a multiple of the other.
Solution. Any natural number can be represented in the form $2^{n} \cdot p$, where $n$ is a non-negative integer, and $p$ is an odd number. Represent each of the first hundred natural numbers in the form $2^{n} \cdot p$, where $n$ is a non-negative integer, and $p$ is an odd number (for odd numbers, $n=0$). For example: $15=$ $=2^{0} \cdot 15 ; 8=2^{3} \cdot 1 ; 24=2^{3} \cdot 3 ; 98=2 \cdot 49$.
Obviously, from two numbers $2^{n} \cdot p$ and $2^{n} \cdot p$, having the same factor $p$, one is a multiple of the other. Indeed, since the first hundred contains 50 odd numbers, the factor $p$ in the expression $2^{n} \cdot p$ for the numbers of the first hundred can take only 50 different values. Therefore, if we take 51 numbers from the first hundred, at least two of them will have the same factor $p$, and thus one of them is a multiple of the other.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
101(1211). There are two arithmetic progressions $\left(a_{n}\right): 1 ; 5 ; 9 ; 13 ; 17 ; \ldots$ and $\left(b_{n}\right): 2 ; 5 ; 8 ; 11 ; 14 ; \ldots$. Prove that if you write down all the common terms of both progressions, the resulting sequence will also be an arithmetic progression. What is the common difference of this progression?
|
Solution. Method I. Let's find the $n$-th and $k$-th terms of the given arithmetic progressions. We have:
$$
\begin{aligned}
& a_{n}=a_{1}+d(n-1)=1+4(n-1)=4 n-3 \\
& b_{k}=b_{1}+d(k-1)=2+3(k-1)=3 k-1
\end{aligned}
$$
We need to find all such $n$ for which $a_{n}=b_{k}$, i.e., $4 n-3=3 k-1$, from which $k=\frac{4 n-2}{3}=n+\frac{n-2}{3}$.
We require that $n-2$ be divisible by three, i.e., $n-2=3 m$, where $m=0,1,2, \ldots$. Hence, $n=3 m+2$.
Thus, the common terms of both progressions are those terms of the progression $\left(a_{n}\right)$ that have numbers $n=3 m+2$, where $m=0,1,2, \ldots$, i.e., $a_{2}, a_{5}, a_{8}, a_{11}, \ldots$, or $5,17,29,41, \ldots$.
Clearly, the common terms of both progressions form an arithmetic progression, the first term of which is 5, and the common difference is 12.
Method II. We have:
$$
a_{n}=1+4(n-1), b_{n}=2+3(n-1)
$$
Then
$$
a_{n+1}=a_{n}+d=a_{n}+4=5+4(n-1)
$$
212
$$
\begin{gathered}
b_{n+1}=b_{n}+d=b_{n}+3=5+3(n-1) \\
c_{n}=a_{n+1}=b_{n+1}=5+4(n-1)=5+3(n-1)
\end{gathered}
$$
Therefore, $4(n-1)=3(n-1)$, from which we get that $n-1$ is divisible by 4 and by 3, i.e., $n-1$ is divisible by 12.
$$
n-1=12(k-1) ; c_{k}=5+12(k-1)
$$
|
12
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
109. In the equation $x^{2}-2 x+a=0$, the square of the difference of the roots is 20. Find $a$.
|
If $x_{1}$ and $x_{2}$ are the roots of the given quadratic equation, then we have the system of equations:
$$
\left\{\begin{array}{l}
\left(x_{1}-x_{2}\right)^{2}=20 \\
x_{1}+x_{2}=2
\end{array}\right.
$$
Squaring the second equation, we get:
$$
\left\{\begin{array}{c}
x_{1}^{2}-2 x_{1} x_{2}+x_{2}^{2}=20 \\
x_{1}^{2}+2 x_{1} x_{2}+x_{2}^{2}=4
\end{array}\right.
$$
from which $4 x_{1} x_{2}=-16 ; a=x_{1} x_{2}=-4$.
Answer: $a=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
140. Find the maximum value of the function
$$
y(x)=3 \sin x+4 \cos x
$$
|
Solution. $y(x)=5\left(\frac{3}{5} \sin x+\frac{4}{5} \cos x\right)$. Since $\left(\frac{3}{5}\right)^{2}+$ $+\left(\frac{4}{5}\right)^{2}=1$, there exists an angle $x_{0}$ such that $\frac{3}{5}=\cos x_{0}, \frac{4}{5}=\sin x_{0}$. Then $y(x)=5 \sin \left(x+x_{0}\right)$. It is obvious that the maximum value of $y(x)$ is 5.
Answer: 5.
$\square$ 141. Prove the identity $\cos 25^{\circ}+\cos 47^{\circ}=\cos 11^{\circ}+\cos 61^{\circ}+\sin 7^{\circ}$.
Solution. Method I. Multiply both sides of the identity by $2 \cos 18^{\circ}$. In the left part, we will have:
$2 \cos 18^{\circ}\left(\cos 25^{\circ}+\cos 47^{\circ}\right)=\cos 43^{\circ}+\cos 7^{\circ}+\cos 65^{\circ}+\cos 29^{\circ}$.
In the right part, we will get:
$$
\begin{aligned}
& 2 \cos 18^{\circ}\left(\cos 11^{\circ}+\cos 61^{\circ}+\sin 7^{\circ}\right)= \\
&= \cos 29^{\circ}+\cos 7^{\circ}+\cos 79^{\circ}+\cos 43^{\circ}+\sin 25^{\circ}-\sin 11^{\circ}
\end{aligned}
$$
Since $\cos 79^{\circ}=\sin 11^{\circ}$, and $\sin 25^{\circ}=\cos 65^{\circ}$, the identity is proven.
Method II. Apply the formula for the sum of cosines of two angles to the left part of the identity and to the sum $\cos 61^{\circ}+\cos 83^{\circ}\left(\sin 7^{\circ}=\right.$ $=\cos 83^{\circ}$ ) in the right part of the identity. We will have:
$$
2 \cos 36^{\circ} \cos 11^{\circ}=\cos 11^{\circ}+2 \cos 72^{\circ} \cos 11^{\circ}
$$
Move the product $2 \cos 72^{\circ} \cos 11^{\circ}$ to the left part and divide both sides of the obtained identity by $\cos 11^{\circ} \neq 0$. We will get the identity
$$
\begin{aligned}
& 2 \cos 36^{\circ}-2 \cos 72^{\circ}=1 \\
& 2 \cdot 2 \sin 54^{\circ} \sin 18^{\circ}=1
\end{aligned}
$$
To prove the obtained identity (1), multiply and divide its left part by $\cos 18^{\circ}$ (to use the formula for the sine of a double argument). We will have:
$$
\begin{gathered}
2 \cdot 2 \sin 54^{\circ} \sin 18^{\circ}=\frac{2 \cdot 2 \sin 54^{\circ} \sin 18^{\circ} \cos 18^{\circ}}{\cos 18^{\circ}}= \\
=\frac{2 \sin 54^{\circ} \sin 36^{\circ}}{\cos 18^{\circ}}=\frac{2 \cos 36^{\circ} \sin 36^{\circ}}{\cos 18^{\circ}}= \\
=\frac{\sin 72^{\circ}}{\cos 18^{\circ}}=1
\end{gathered}
$$
The identity (1), and thus the given identity, is proven.
Remark. It is advisable to solve this problem simultaneously with problems 1217 and 1223 from [3].
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
143. For which $n \in \boldsymbol{N}$ does the equality
$$
\sqrt[n]{17 \sqrt{5}+38}+\sqrt[n]{17 \sqrt{5}-38}=\sqrt{20} ?
$$
|
S o l u t i o n. Denoting the first term by $a$, we will have $a+\frac{1}{a}=\sqrt{20}$, from which $a=\sqrt{5}+2$. Since $(\sqrt{5}+2)^{3}=17 \sqrt{5}+$ $+38=(\sqrt{5}+2)^{n}$, then $n=3$.
A n s w e r: $n=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
168. Two pedestrians set out towards each other at the same time: the first from point $A$, the second from point $B$. The first pedestrian walked 1 km more before the meeting than the second. The first pedestrian arrived at point $B$ 45 minutes after the meeting. The second pedestrian arrived at point $A$ 1 hour and 20 minutes after the meeting. Find the distance from $A$ to $B$.
|
S o l u t i o n. Let the speed of the first pedestrian who left point $A$ be $v_{1}$ kilometers per hour, and the speed of the second pedestrian be $v_{2}$ kilometers per hour. Since after meeting, the first pedestrian walked $\frac{3}{4} v_{1}$ kilometers, and the second $-\frac{4}{3} v_{2}$ kilometers, and the first pedestrian walked 1 km less than the second, we have the equation
$$
\frac{4}{3} v_{2}-\frac{3}{4} v_{1}=1
$$
Since before the meeting, the pedestrians spent the same amount of time, we have
$$
\frac{\frac{4}{3} v_{2}}{v_{1}}=\frac{\frac{3}{4} v_{1}}{v_{2}}
$$
Thus, we have the system of equations:
$$
\left\{\begin{array} { l }
{ \frac { 4 } { 3 } v _ { 2 } - \frac { 3 } { 4 } v _ { 1 } = 1 , } \\
{ \frac { \frac { 4 } { 3 } v _ { 2 } } { v _ { 1 } } = \frac { \frac { 3 } { 4 } v _ { 1 } } { v _ { 2 } } , }
\end{array} \text { or } \quad \left\{\begin{array}{l}
v_{2}=\frac{12+9 v_{1}}{16}, \\
\frac{4}{3} v_{2}^{2}=\frac{3}{4} v_{1}^{2},
\end{array}\right.\right.
$$
from which $7 v_{1}^{2}-24 v_{1}-16=0, v_{1}=4$. Therefore, the distance from $A$ to $B$ is 7 km $\left(2 \cdot 4 \cdot \frac{3}{4}+1=7\right)$.
A n s w e r: 7 km.
## CONTENTS
Preface . . . . . . . . . . . . . . . . . 3
§1. Why do we solve problems in school (on the functions of problems in mathematics education) . . . . . . . . . . 5
§ 2. On the methodology of teaching students to solve non-standard algebraic problems . . . . . . . . . . 11
§3. On the role of observations and induction in finding ways to solve non-standard algebraic problems . . . . . . . . . 19
§4. On finding different ways to solve problems . . . . 24
§ 5. On constructing graphs of functions and dependencies containing the modulus sign . . . . . . . . . . 30
§6. Methodological recommendations for using challenging problems in the process of teaching algebra . . . . . . . . . 35
§ 7. Challenging problems in the algebra course for 7th grade . . . 40
§8. Challenging problems in the algebra course for 8th grade . . . 99
§9. Challenging problems in the algebra course for 9th grade . . . 157
## Educational Publication Kostrikina Nina Petrovna CHALLENGING PROBLEMS IN THE ALGEBRA COURSE $7-9$ grades
Editorial Board Chair $T$. A. Burmistrova Editor L. M. Kotoeva
Assistant Editor L. I. Zasedateleva Artists L. B. Nikolaev, V. V. Kostin Art Editor Yu. V. Pakhomov Technical Editor N. T. Rudnikova
Proofreader M. Yu. Sergeeva
IB № 12646
Submitted for typesetting 25. 12. 90. Signed for printing from transparencies 12. 08. 91. Format $60 \times 90^{1 / 16}$. Offset paper. Font. Offset printing. Usual printing sheets $15+0.25$ f. Usual printed sheets 15.75. Usual publication sheets $13.34+0.34$ f. Price 1 r. 90 k.
Order of the Red Banner of Labor publishing house "Prosveshchenie" of the Ministry of Printing and Mass Information of the RSFSR. 129846, Moscow, 3rd passage of Marinskaya Roshcha, 41.
Transparencies made by the Order of the Red Banner of Labor Saratov Polygraphic Combine of the Ministry of Printing and Mass Information of the RSFSR. 410004, Saratov, ul. Chernyshevskogo, 59.
Printed through V/O "Vneshpechat"
Printed by Graphischer Großbetrieb Pößneck GmbH - Ein Mohndruck-Betrieb
## SOME "REMARKABLE"
$$
\begin{aligned}
& (1+3+5+\ldots+(2 n-1))^{2}=n^{2} \\
& 1^{3}+2^{3}+3^{3}+\ldots+n^{3}=(1+2+3+\ldots+n)^{2} \\
& \frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\ldots+\frac{1}{(n-1) n}=\frac{n-1}{n} \\
& \frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}+\ldots+\frac{1}{(2 n-1)(2 n+1)}=\frac{n}{2 n+1}
\end{aligned}
$$
## EXAMPLES OF RULES
1) $\overline{a b} \cdot 11=100 a+10(a+b)+b$
$36 \cdot 11=100 \cdot 3+10(3+6)+b=391$
$\overline{a b c} \cdot 11=1000 a+100(a+b)+10(b+c)+c$
$243 \cdot 11=1000 \cdot 2+100(2+4)+10(4+3)+3=$
2) $\overline{a 5}^{2}=a(a+1) \cdot 100+25$
$65^{2}=6 \cdot 7 \cdot 100+25=4225$
3) If $b+c=10$, then $\overline{a b} \cdot \overline{a c}=100 a(a+1)+b c$ $38 \cdot 32=3 \cdot 4 \cdot 100+8 \cdot 2=1216$
## INEQUALITIES
$$
\begin{aligned}
& a+\frac{1}{a} \geqslant 2 \text { for } a>0 \\
& \frac{a+b}{2} \geqslant \sqrt{a b}, \frac{a+b+c}{3} \geqslant \sqrt{a b c} \text { for } a \geqslant 0, b \geqslant 0, c \geqslant 0 \\
& (a+b)(b+c)(c+a) \geqslant 8 a b c \quad \text { for } a>0, b>0, c>0 \\
& \sqrt{(a+c)(b+d)} \geqslant \sqrt{a b}+\sqrt{c d} \text { for } a \geqslant 0, b \geqslant 0, c \geqslant 0, d \geqslant 0
\end{aligned}
$$
## MENTAL CALCULATION
$$
\begin{aligned}
& \text { 4) }(a+b)(a-b)=a^{2}-b^{2} \\
& 71 \cdot 69=(70+1)(70-1)= \\
& =4900-1=4899 \\
& 111 \cdot 89=(100+11)(100-11)= \\
& =10000-121=9879 \\
& \text { 5) } a^{2}=a^{2}-b^{2}+b^{2}=(a+b)(a-b)+b^{2} \\
& 27^{2}=(27+3)(27-3)+3^{2}=729
\end{aligned}
$$
[^0]: ' Pólya G. Mathematical Discovery - M. Science, $1970-$ P. 16
[^1]: ' Problems $1-47$ in parentheses indicate the exercise numbers in the textbook $|4|$ 40
[^2]: ' Problems $48-79$ in parentheses indicate the exercise numbers in the textbook |I| 60
[^3]: ' Problems $80-120$ in parentheses indicate the exercise numbers in the textbook [7].
[^4]: ' Problems $1-64$ in parentheses indicate the exercise numbers in the textbook [6].
[^5]: ${ }^{1}$ Problems $65-107$ in parentheses indicate the exercise numbers in the textbook [3].
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A person has 12 pints of wine in a barrel (pint - an old French unit of volume, 1 pint ≈ 0.568 liters) and wants to give away half of the wine, but does not have a 6-pint container. However, there are two empty containers with capacities of 8 pints and 5 pints. How can one use them to measure out exactly 6 pints of wine?
This is the most famous problem of its kind; it is known as Poisson's problem. The famous French mathematician, mechanician, and physicist Siméon Denis Poisson (1781-1840) solved it in his youth and later said that it was precisely this problem that inspired him to become a mathematician.
|
$\triangle$ The solution to the problem can be written as follows:
| Vessel with a capacity of 8 pints | 0 | 8 | 3 | 3 | 0 | 8 | 6 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Vessel with a capacity of 5 pints | 0 | 0 | 5 | 0 | 3 | 3 | 5 | 0 |
This should be understood as follows. Initially, both vessels are empty (first column). We fill the vessel with a capacity of 8 pints (second column), then we fill the vessel with a capacity of 5 pints from it (third column), then we pour these 5 pints from the smaller vessel into a barrel that already contains 12 pints (fourth column), then we transfer 3 pints of wine from the vessel with a capacity of 8 pints to the vessel with a capacity of 5 pints (fifth column), and so on until the larger of the two vessels contains 6 pints of wine.
Try to solve the problem differently, by first filling the vessel with a capacity of 5 pints. Will the solution be shorter?
Another method for solving such problems - using graphs - is discussed in the reference [16].
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. There is no less than 10 liters of milk in the bucket. How can you pour exactly 6 liters of milk from it using an empty nine-liter bucket and a five-liter bucket?
|
$\triangle$ Let's denote the initial amount of milk in the first bucket as $a$ liters. Let's think about how to use the fact that the number $a$ is not less than 10. The difference $a-10$ can be used, but the difference $a-11$ cannot. The solution is written as follows:
| Bucket with volume $a$ l | $a$ | $a-5$ | $a-5$ | $a-10$ | $a-10$ | $a-1$ | $a-1$ | $a-6$ | $a-6$ |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Bucket with volume 9 l | 0 | 0 | 5 | 5 | 9 | 0 | 1 | 1 | 6 |
| Bucket with volume 5 l | 0 | 5 | 0 | 5 | 1 | 1 | 0 | 5 | 0 |
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. There are 9 coins, 8 of which are genuine and of the same weight, and one is counterfeit and heavier than the others. What is the minimum number of weighings on a balance scale without weights that are needed to find the counterfeit coin?
|
$\triangle$ Let's number the coins with natural numbers from 1 to 9. Here, it is better to weigh the coins by placing three on each pan of the balance. Place coins numbered $1,2,3$ on the left pan, and coins numbered $4,5,6$ on the right pan. There are two possible outcomes, as in problem 90.
Suppose the balance is in equilibrium (Fig. 30). Then the counterfeit coin is in the triplet with numbers $7,8,9$, and it can be found using one more weighing (see the solution to problem 90).
Suppose the balance is not in equilibrium. In this case, the counterfeit coin is in one of the first two triplets, which is heavier, and it can also be found using one more weighing.
Thus, two weighings were needed. Could the goal have been achieved in one? To answer this question, we need to change the weighing system, placing not three, but four, or two, or even one coin on each pan of the balance. But each of the mentioned options is less advantageous than the one we discussed.
Answer: two.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
93. There are 10 coins, 9 of which are genuine and of the same weight, and one is counterfeit and lighter than the others. What is the minimum number of weighings on a balance scale without weights that are needed to find the counterfeit coin?
|
$\triangle$ Let's number the coins. Place coins numbered $1,2,3$ on the left pan and coins numbered $4,5,6$ on the right pan. We can use Figure 30 for further steps.
If the scales balance, the counterfeit coin is among the remaining four. It takes two more weighings to determine the counterfeit coin from these four (see problem 91).
If the scales are unbalanced, the counterfeit coin is in the lighter of these two sets of three. One more weighing is needed to identify the counterfeit coin.
In general, three weighings are required. But could we have managed with two? Let's try placing four coins on each pan (other options are clearly worse). However, the counterfeit coin could be in one of these sets of four, which would still require two more weighings, totaling three.
Answer: three.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
97. There are 5 parts that are indistinguishable in appearance, 4 of which are standard and of the same mass, and one is defective, differing in mass from the others. What is the minimum number of weighings on a balance scale without weights that are needed to find the defective part?
|
$\triangle$ Let's number the parts. Now try to figure out the weighing scheme presented below (Fig. 32).
As can be seen from this, it took three weighings to find the defective part.
Answer: in three.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. There are 6 identical-looking coins, but 4 are genuine, of the same weight, while 2 are counterfeit, lighter, and also weigh the same. What is the minimum number of weighings on a balance scale without weights that are needed to find both counterfeit coins?
|
$\triangle$ As usual, let's number the coins. During the first weighing, we will place coins numbered $1,2,3$ on the left pan, and all the others on the right (Fig. 33).
The scales may balance. Then each of the triplets contains one counterfeit coin. To find them, we need two more weighings (see the solution to problem 90).
The scales may be unbalanced. In this case, both counterfeit coins are contained in one triplet - the lighter one (in this case - on the left pan). One more weighing will be required.
Answer: in three.

|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
111. How many five-digit natural numbers can be formed using the digits 1 and 0 if the digit 1 appears exactly three times in each number?
|
$\triangle$ We will search for the specified numbers by enumeration, ensuring that we do not miss any number. It is simpler to start by finding the positions for the two zeros, because if the positions for the zeros are determined, the three remaining positions will be filled with ones uniquely.
Let's fix one of the zeros in the second position; then the other zero can be placed in the third, fourth, or fifth positions. If we now fix one zero in the third position, the second zero can be placed in the fourth or fifth positions (the case where zeros are in the third and second positions has already been considered). Finally, if we fix one zero in the fourth position, the other zero can only be placed in the fifth position. This gives us the following 6 numbers:
$$
10011,10101,10110,11001,11010,11100 .
$$
## Answer: 6 .
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
215. The sequence $\left(x_{n}\right)$ is defined by the recurrence relations
$$
x_{1}=1, x_{2}=2, x_{n}=\left|x_{n-1}-x_{n-2}\right|(n>2) .
$$
Find $x_{1994}$.
|
$\triangle$ First, let's compute the first few terms of the sequence: $x_{1}=1, x_{2}=2, x_{3}=|2-1|=1, x_{4}=|1-2|=1, x_{5}=|1-1|=0, x_{6}=$ $=|0-1|=1, x_{7}=1, x_{8}=0, x_{9}=1, x_{10}=1, x_{11}=0$.
Starting from the third term, the terms of this sequence are either 1 or 0. Only the terms with indices
$$
5,8,11, \ldots, 5+3 k=2+(3+3 k)=2+3(k+1)
$$
are equal to 0, i.e., the terms whose indices, when divided by 3, give a remainder of 2. (The latter can be strictly proven by mathematical induction).
Let's check if the remainder of the division of the number 1994 by 3 is 2:
$$
1994=3 \cdot 664+2
$$
Therefore, $x_{1994}=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
234*. Once in a room, there were several inhabitants of an island where only truth-tellers and liars live. Three of them said the following.
- There are no more than three of us here. All of us are liars.
- There are no more than four of us here. Not all of us are liars.
- There are five of us. Three of us are liars.
How many people are in the room and how many of them are liars?
|
$\triangle$ Let's consider the first of the three speakers. Suppose he is a truth-teller. Then both of his statements, including the second one, "All of us are liars," would be true, which means he is a liar. We have reached a contradiction. Therefore, he can only be a liar.
In this case, both statements of the first person are false: in reality, there are more than three people in the room, and not all of them are liars.
Let's examine the statements of the second person. His statement "Not all of us are liars" is true, so he is a truth-teller. This means there are no more than four people in the room. Considering the previous conclusion, we get that there are exactly four people.
Since the statement of the third speaker, "There are five of us," is false, he is a liar. Therefore, there are not three liars in the room. Moreover, there are at least two liars in the room—the first and the third—and the number of liars is less than four, since there is a truth-teller among those present. In this case, there are exactly two liars.
Answer: 4 people, 2 liars.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
299. There are 8 balls: 2 red, 2 blue, 2 white, and 2 black. Players A and B take turns attaching one ball to one of the vertices of a cube. Player A aims to achieve a vertex such that this vertex and its three adjacent vertices each have a ball of a different color, while Player B aims to prevent this. Who will win with the correct strategy?
|
$\triangle$ The problem does not specify who starts the game - A or B. Therefore, let's consider two cases.
1) Suppose A starts the game.
If A, for example, attaches a red ball to one of the vertices of the cube, then B's best response is to attach a red ball to one of the adjacent vertices, and so on (Fig. 36). Consequently, in this case, B wins.
2) Suppose B makes the first move.
If B first attaches, say, a blue ball to one of the vertices, then A should attach a blue ball, but not to an adjacent vertex, rather to the opposite vertex, and so on (Fig. 37). Clearly, in this case, A wins.
Answer: The one who moves second wins.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
350. Among 18 coins, one is counterfeit. Genuine coins weigh the same, while the counterfeit coin differs in weight from the genuine ones. What is the minimum number of weighings on correct balance scales without weights needed to determine whether the counterfeit coin is lighter or heavier than the genuine ones? (There is no need to find the counterfeit coin.)
|
$\triangle$ Let's number the coins. Divide the set of coins into three piles, with 6 coins in each.
For the first weighing, place all the coins from the first pile on one scale pan, and all the coins from the second pile on the other. There are two possible cases.
1) Suppose the scales balance during this weighing. Then the counterfeit coin is in the third pile.
Now place the first pile of coins on one scale pan, and the third pile on the other. If, for example, the third pile tips the scales, then the counterfeit coin is heavier than the genuine ones.
2) Suppose the scales were unbalanced during the first weighing. Then the counterfeit coin is either in the first or the second pile. Therefore, all the coins in the third pile are genuine.
Place the first pile of coins on one scale pan, and the third pile on the other. If the scales are unbalanced, then the counterfeit coin is in the first pile, and the last weighing

will show whether it is lighter or heavier than the genuine ones. If the scales balance, then the counterfeit coin is in the second pile, and the first weighing will also determine whether it is lighter or heavier than the genuine ones.
Answer: in two.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
444. Eight hockey teams play against each other in a round-robin tournament to determine the final four. What is the minimum number of points that guarantees a team's advancement to the final four?
|
$\triangle$ All eight teams together will score $\frac{8 \cdot 7}{2} \cdot 2=56$ points. Therefore, 7, 8, and even 9 points do not guarantee a team's advancement to the final four.
What about 10 points? Imagine that there are five teams that played all their matches against each other to a draw, while the other three teams won all their matches. Then each of these teams will score $4+6=10$ points. However, 10 points still do not guarantee a team's advancement to the final, since there are five such teams, not four.
We will prove that if a team scores 11 points, it will advance to the final. Assume the opposite: there are five teams, each of which scores at least 11 points. In this case, they will score at least 55 points together, which means the remaining three teams will score no more than 1 point together. But this is impossible, since these three teams will score at least $\frac{3 \cdot 2}{2} \cdot 2=6$ points in matches against each other.
Answer: 11.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
454. Several identical boxes together weigh 10 tons, with each of them weighing no more than 1 ton. What is the minimum number of three-ton trucks needed to haul away all this cargo in one trip?
|
$\triangle$ Four trucks may not be enough. For example, if there are 13 identical boxes weighing $\frac{10}{13}$ tons each, then in one of the trucks, you cannot place more than three boxes, because with four boxes, the weight is $4 \cdot \frac{10}{13}$ tons, which is more than 3 tons. In this case, with four trucks, you can transport no more than 12 boxes out of 13.
Five trucks are sufficient in all cases. Indeed, we can load at least 2 tons of cargo into each truck: if less than 2 tons are loaded, then you can add another box (or boxes) since each box weighs no more than one ton by the condition. Therefore, with five trucks, you can load at least 10 tons of cargo.
Answer: 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 7.
The following very simple problem is one of many entertaining problems that have gained widespread popularity. In a dark room stands a wardrobe, in the drawer of which there are 24 red and 24 blue socks. How many socks should be taken from the drawer to ensure that at least one pair of socks of the same color can be formed? (In this and the next problem, the question is about the smallest number of socks.)
|
7. Usually, the question of the problem is given an incorrect answer: 25 socks. If the problem asked how many socks should be taken from the drawer to ensure that at least 2 socks of different colors are among them, then the correct answer would indeed be such: 25 socks. But in our problem, the question is about ensuring that at least 2 socks of the same color are among the taken socks, so the correct answer to the problem is different: 3 socks. If I take 3 socks from the drawer, then they will either all be of the same color (in which case I will certainly be able to choose at least 2 socks of the same color from them), or 2 socks will be of the same color, and the third sock will be of a different color, which will also allow me to form a pair of socks of the same color.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Alice returned the rattle to its rightful owner, but a few days later, another brother broke the rattle again. This time, the raven did not come to scare the brothers, and they began to beat each other with all their might. Alice grabbed the broken rattle and ran out of the forest.
After some time, Alice met the White King and told him in detail everything that had happened.
- All of this is very, very interesting, - the King assured her. - The most remarkable thing about the whole story is that, although you know to whom you returned the rattle, we still do not know who the owner is, Tralala or Trulala.
- You are quite right, your majesty, - agreed Alice. - But what are we to do with the broken rattle?
- Nonsense, - said the King. - It's nothing for me to fix it again.
And true to his word, the White King repaired the rattle so skillfully that it became as good as new, and a few days later he returned it to Alice. With trepidation, Alice set off for the forest, fearing that the brothers were still fighting. But by this time, Tralala and Trulala had declared a truce, and Alice found one of them resting under a tree. Alice approached him and asked:
- Which of you does the rattle belong to?
He answered enigmatically:
- The true owner of the rattle lies today.
What are the chances that he was the true owner of the rattle?
|
60. The chances are zero. Suppose the statement of the brother Alice met is true. Then the owner of the rattle should have been lying on the day of the meeting and, consequently, could not have been the brother Alice met. On the other hand, suppose the statement of the brother Alice met is false. Then the owner of the rattle should have been lying on the day of the meeting. Therefore, in this case, he also cannot be the owner of the rattle.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 107.
On another island of knights, liars, and normal people, the king held opposite views and gave his daughter different paternal advice: “My dear, I don’t want you to marry any knight or liar. I would like your husband to be a solid, reputable normal person. You should not marry a knight because all knights are hypocrites. You should not marry a liar either because all liars are treacherous. No, no matter what, a decent normal person would be just right for you!”
Suppose you are a resident of this island and a normal person. Your task is to convince the king that you are a normal person.
a) How many true statements will you need for this?
b) How many false statements will you need for the same purpose?
(In both cases, we are talking about the minimum number of statements.)
|
107. In both cases, a single statement would suffice. The King could be convinced by the true statement “I am not a knight” (such a statement could not belong to either a knight or a liar) and the false statement “I am a liar.”
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
132.
In one museum, I had the chance to see a pair of caskets adorned with the following inscriptions:
On the gold one
Both caskets in this set were made by members of the Cellini family
On the silver one
Neither of these caskets was made by either a son of Bellini or a son of Cellini
Whose work is each of the two caskets?
|
132. The statement engraved on the lid of the golden casket cannot be true, for otherwise we would have arrived at a contradiction. Therefore, the golden casket was made by someone from the Cellini family. Since the inscription on the golden casket is false, both caskets could not have been made by members of the Cellini family. Therefore, the silver casket was made by someone from the Bellini family. Thus, the statement engraved on the lid of the silver casket is true, so neither casket was made by either the son of Bellini or the son of Cellini. Therefore, the golden casket was made by Cellini, and the silver one by Bellini.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 28. How Many Favorites?
- "Here's a different kind of puzzle," said the Gryphon. "Once, the Queen of Hearts held a reception for thirty guests. She needed to distribute one hundred gingerbread cookies among the guests. Instead of cutting the cookies into pieces, the Queen preferred to give four cookies to each of her favorites, and three cookies to the rest of the guests.
How many favorites did the Queen of Hearts have?"
|
28. How many favorites? This problem, usually solved using algebra, is very simple if approached in the following way. First, let's distribute 3 pretzels to each of the 30 guests of the Queen. We will have 10 pretzels left. At this point, all non-favorites will have received all the pretzels they are entitled to, while each of the favorites still needs to receive 1 more pretzel.
Therefore, all the remaining pretzels are intended for the favorites—one pretzel each. This means there must be 10 favorites.
Verification. Each of the 10 favorites should receive 4 pretzels, which totals 40 pretzels for all the favorites. Each of the remaining 20 guests will receive 3 pretzels, which adds up to another 60 pretzels. \(40 + 60 = 100\). Therefore, our solution is correct.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 29. Pretzels and Pretzelkins
- Here's another problem,—began the Gryphon. One day, the Mock Turtle went to the store to buy pretzels for the next tea party.
- How much are your pretzels?—he asked the store owner.
- The price depends on the size: I can offer you small pretzelkins and large pretzels. One pretzel costs as much as three pretzelkins.
- How much do seven pretzels and four pretzelkins cost?—asked the Mock Turtle.
- Twelve cents more than four pretzels and seven pretzelkins,—came the mysterious answer.

How much does one pretzel cost?
|
29. Pretzels and pretzelkins. Since each pretzel costs as much as one pretzelkin, 7 pretzels cost as much as 21 pretzelkins, and 7 pretzels and 4 pretzelkins cost as much as 25 pretzelkins. On the other hand, 4 pretzels and 7 pretzelkins cost as much as 19 pretzelkins (since 4 pretzels cost as much as 12 pretzelkins). Thus, the difference in cost between 25 and 19 pretzelkins is 12 cents. Therefore, 6 pretzelkins (25-19=6) cost 12 cents, 1 pretzelkin costs 2 cents, and 1 pretzel costs 6 cents.
Verification. 4 pretzels and 7 pretzelkins cost $24+14=38$ cents, and 7 pretzels and 4 pretzelkins cost $42+8=50$ cents, which is indeed 12 cents more than in the first case.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. How many people got lost in the mountains?
Alice and the Griffin had to wait several minutes before the Tortoise Quasi gathered his strength and could continue.
- You see,一began the Tortoise Quasi.
- I don't see anything!- the Griffin cut in.
The Tortoise Quasi did not respond, only grabbing his head with his front paws again. After remaining silent for some time, he spoke again:
- Let's say... Nine people got lost in the mountains. They only had enough food for five days. Can you imagine, just five days!
Having reached this point in his story, the Tortoise Quasi was so moved by the tragedy that he could not continue from the overflow of emotions.
- Well, that's enough, there, there! - the Griffin tried to comfort him, patting his back.
- Can you imagine what will happen to them if they are not found! - the Tortoise Quasi sobbed. - But it happened (and this is the most beautiful part of the story!)... Yes, the most beautiful part of the story is that the next day the poor souls met another group of lost people in the mountains...
- What's so beautiful about that? - the Griffin asked.
- The most beautiful part is that the first group generously shared their supplies with the second - they divided the provisions equally among everyone, after which the food lasted for another three days.
How many people were in the second group?
|
33. How many people got lost in the mountains? Let's call one portion the amount of supplies one person consumes in a day. Initially, 9 people had 45 portions (a 5-day food supply). On the second day, they had only 36 portions left. On the same day, they met a second group, and the 36 remaining portions were enough for everyone for 3 days. Therefore, there should have been 12 people in total.
This means that the second group had 3 people.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Will the cyclist make it to the train?
- Wasn't the previous problem sad? the Turtle Quasi asked. - Just think! The poor frog spent so many days in a dark well! And to get out of there, she had to undertake a climb like a real mountaineer!
- Nonsense! - the Griffin interrupted him. - The saddest part of the whole story is that I kept hearing your voice and couldn't sleep for a minute! Tell us another problem!
- Alright, - the Turtle Quasi agreed. - A man set out on a bicycle for twelve miles to the railway station to catch a train. He reasoned as follows:
- I have one and a half hours to catch the train. Four miles of the road go uphill, and I will have to walk them. I think I can manage it in an hour. Then four miles of the road go downhill. On this section, I can reach a speed of twelve miles per hour. The last four miles of the road are on flat ground. On this section, I can reach a speed of eight miles per hour. On average, this is eight miles per hour, so I will get to the station on time.
Was the cyclist's reasoning correct?
|
37. Will the cyclist make it to the train? The cyclist reasoned incorrectly: he averaged distances, not time. If he had traveled at 4 miles per hour, 8 miles per hour, and 12 miles per hour for the same amount of time, his average speed would indeed have been 8 miles per hour. However, he spent more time climbing the hill (at 4 miles per hour) and less time descending the hill (at 12 miles per hour).
It is not difficult to calculate how long he was on the road. Climbing the hill took him 1 hour, he spent half an hour (or 30 minutes) traveling on the flat section of the road, and a third of an hour (or 20 minutes) descending the hill. In total, he was on the road for 1 hour and 50 minutes, missing the train by 20 minutes.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. How far is it to school?
All the time while Alice and the Griffin were solving the previous problem, the Tortoise Quasi was weeping inconsolably.
- Can you tell me what is sad about this problem? - the Griffin barked at him angrily. - After all, the passenger caught up with the train. Or did I misunderstand something?
- Everything is correct, - agreed the Tortoise Quasi, - but we don't know what happened afterward! After all, judging by everything, the train could have derailed!
- No, just think about it! - Alice got angry. - First, they come up with all sorts of nonsense, and then they make a sad story out of everything!
The Tortoise Quasi did not answer, only grabbing his head with his front paws.
- Alright, - he said finally. - I will tell you a sad story. One morning, a boy had to go to school...
- That's sad! - agreed the Griffin.
- No, no! That's not sad, - objected the Tortoise Quasi. - The saddest part is still to come.
Alice and the Griffin listened to the whole story attentively but found nothing sad in it.
- So, - continued the Tortoise Quasi, - the father said to the boy: "Hurry up, or you'll be late for school!" - "I won't be late, Dad! - the boy replied. - I have everything calculated precisely. If I walk at a speed of four miles per hour, I will be five minutes late for the start of classes, but if I walk at a speed of five miles per hour, I will arrive ten minutes before the start of classes."
How far is it to school?
|
39. How far is it to school? The difference in time between being 5 minutes late and arriving 10 minutes before the start of the lesson is 15 minutes. Therefore, if the boy walks to school at a speed of 5 miles per hour, he will save 15 minutes (compared to how long it would take him to walk if he went at a speed of 4 miles per hour). Five miles per hour is one mile in 12 minutes, and 4 miles per hour is one mile in 15 minutes. Therefore, by walking faster, the boy saves 3 minutes per mile, and 15 minutes over a distance of 5 miles.
Thus, the school is 5 miles from home.
Verification. Walking at a speed of 5 miles per hour, the boy spends one hour on the journey, and walking at a speed of 4 miles per hour, he spends one hour and fifteen minutes (in one hour he covers the first 4 miles, and in a quarter of an hour, the last mile), that is, 1 hour and 15 minutes. The time difference is indeed 15 minutes.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. Find the first 1963 digits after the decimal point in the decimal representation of the number $(\sqrt{26}+5)^{1963}$.
|
63.32. Since the sum $(\sqrt{26}+5)^{1963}+(5-\sqrt{26})^{1963}$ is an integer (this is verified using the binomial theorem), and the inequality $-0.1 < 5 - \sqrt{26} < 0$ holds, then $-10^{-1963} < (5 - \sqrt{26})^{1963} < 0 \quad$ and, consequently, the first 1963 digits of the number $(\sqrt{26}+5)^{1963}$ after the decimal point are zeros.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Solve the equation $x^{4}-2 y^{4}-4 z^{4}-8 t^{4}=$ $=0$ in integers.
|
63.37. Answer. $x=y=z=t=0$. Hint. Consider an integer solution with the smallest absolute value of $x$ and try to find another solution with $x_{1}=x / 2$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. For what values of $n$ is the expression $2^{n}+1$ a non-trivial power of a natural number?
|
63.40. Only for $n=3$. Indeed, if $2^{n}+1=A^{p}$, then $2^{n}=A^{p}-1=(A-1)\left(A^{p-1}+A^{p-2}+\ldots+A+1\right)$. Then $A^{p-1}+A^{p-2}+\ldots+A+1$ is a power of two, not equal to 1, and since $A$ is odd, and the given sum is even, there is an even number of terms in it. Let $p=2 q$. Then $2^{n}=A^{2 q}-1=$ $=\left(A^{q}-1\right)\left(A^{q}+1\right)$, i.e., both $A^{q}-1$ and $A^{q}+1$ are powers of two, differing by two. Therefore, these are two and four, i.e., $2^{n}=8$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the cells of a chessboard, natural numbers are placed such that each number is equal to the arithmetic mean of its neighbors. The sum of the numbers in the corners of the board is 16. Find the number standing on the field $e 2$.
|
64.3. Consider the largest number standing in one of the cells. Obviously, all adjacent numbers to it are equal to it. Those adjacent to them are also equal to them, and so on. Therefore, all numbers on the board are equal. Hence, the number written in the field $e 2$ is 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. Find the maximum of the expression
$$
\begin{aligned}
& x_{1}+x_{2}+x_{3}+x_{4}-x_{1} x_{2}-x_{1} x_{3}-x_{1} x_{4}-x_{2} x_{3}-x_{2} x_{4}-x_{3} x_{4}+ \\
& +x_{1} x_{2} x_{3}+x_{1} x_{2} x_{4}+x_{1} x_{3} x_{4}+x_{2} x_{3} x_{4}-x_{1} x_{2} x_{3} x_{4}
\end{aligned}
$$
|
74.27. The given expression can be rewritten as follows:
$$
1-\left(1-x_{1}\right)\left(1-x_{2}\right)\left(1-x_{3}\right)\left(1-x_{4}\right)
$$
Since $\left(1-x_{1}\right)\left(1-x_{2}\right)\left(1-x_{3}\right)\left(1-x_{4}\right)$ is a non-negative number that can be equal to zero, the maximum value of the expression is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. In seven consecutive vertices of a regular 100-gon, chips of seven colors are placed. In one move, it is allowed to move any chip 10 fields clockwise to the $11-\mathrm{th}$, if it is free. It is required to collect the chips in the seven vertices following the initial ones. How many different arrangements of chips in these seven vertices can result?
## 9th grade
|
75.18. Answer. There are seven possible arrangements.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. The angle $A$ at the vertex of the isosceles triangle $A B C$ is $100^{\circ}$. On the ray $A B$, a segment $A M$ is laid off, equal to the base $B C$. Find the measure of angle $B C M$.
|
83.40. Answer. $10^{\circ}$. Indeed, let's lay off on the ray $A M$ a segment $B N$, equal in length to $B C$. Then, in the isosceles triangle $B N C$, the line $C M$ is the bisector of angle $C$. This follows from the fact that $B M / B N = C B / C N$. Since $\angle B C N = 20^{\circ}$, then $\angle B C M = 10^{\circ}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. Compute the integral
$$
\int_{-1}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}
$$
|
86.58. The main idea of the solution is to use the "non-evenness" of the function \( 1 /\left(1+x^{3}+\sqrt{1+x^{6}}\right) \), specifically:
\[
\begin{aligned}
& \text { of the function } 1 /\left(1+x^{3}+\sqrt{1+x^{6}}\right) \text {, specifically: } \\
& \int_{-1}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}=\int_{-1}^{0} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}+\int_{0}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}= \\
& =\int_{0}^{1} \frac{d x}{1-x^{3}+\sqrt{1+x^{6}}}+\int_{0}^{1} \frac{d x}{1+x^{3}+\sqrt{1+x^{6}}}= \\
& =\int_{0}^{1}\left[\frac{1}{1-x^{3}+\sqrt{1+x^{6}}}+\frac{1}{1+x^{3}+\sqrt{1+x^{6}}}\right] d x= \\
& =\int_{0}^{1} \frac{\left(2+2 \sqrt{1+x^{6}}\right) d x}{\left(1+\sqrt{1+x^{6}}\right)^{2}-x^{6}}=\int_{0}^{1} 1 d x=1
\end{aligned}
\]
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Two players take turns placing crosses and noughts in the cells of a $9 \times 9$ square (the first player places crosses, and the opponent places noughts). At the end, the number of rows and columns where there are more crosses than noughts is counted - these are the points scored by the first player. The number of rows and columns where there are more noughts - the points scored by the second player. How can the first player win (score more points)?
## 6th grade
|
87.6. Hint. The first one needs to use central symmetry. The maximum guaranteed number of his points is 10, i.e., he can guarantee to win two points over the second one.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49*. On the board, there are 128 ones. In one move, you can replace a pair of numbers $a$ and $b$ with the number $a b + 1$. Let $A$ be the maximum number that can appear on the board after 127 such operations. What is its last digit?
## 11th grade
|
92.49. Hint. Prove that to obtain the maximum number, you can act according to the following scheme: at each moment, perform the operation on the two smallest numbers.
By now, carrying out the calculations in accordance with the derived algorithm, we get that the last digit of the maximum number is two.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the table, there are several boys and five girls, and on the table, on a plate, there are 30 buns. Each girl gave a bun (from the plate) to each boy she knew, and then each boy gave a bun (from the plate) to each girl he did not know. After this, it turned out that all the buns were given out. How many boys were there?
|
93.3. Let the number of boys be $n$. Then there are $5 n$ different boy-girl pairs. Each such pair corresponds to
one passed bun: if the boy and girl are acquainted, the bun was passed by the girl, and if they are not acquainted - by the boy. Hence $5 n=30$. Answer. $n=6$.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. What is the greatest value that the expression
$$
a e k-a f h+b f g-b d k+c d h-c e g
$$
can take if each of the numbers $a, \ldots, k$ is equal to 1 or -1?
|
93.11. Each of the six terms of the given sum is equal to 1 or -1, so this sum is even. It cannot take the value six, since in this case the terms $a e k, b f g, c d h$ must be equal to 1 and, therefore, their product is 1, and the terms $a f h, b d k, c e g$ must be equal to -1, and their product is -1. However, these products obviously coincide. The value 4 is achieved, for example, when $a=b=c=e=h=1, d=f=g=-1$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.
Find all natural numbers $n$ such that the sum $S(n)$ of the digits in the decimal representation of the number $2^{n}$ is 5.
|
Solution. To find the solution, we will construct a table of values for the expression $2^{n}$:
| $n$ | $2^{n}$ | $S(n)$ | $n$ | $2^{n}$ | $S(n)$ |
| :---: | ---: | ---: | :---: | ---: | :---: |
| 1 | 2 | 2 | 16 | 65536 | 25 |
| 2 | 4 | 4 | 17 | 131072 | 14 |
| 3 | 8 | 8 | 18 | 262144 | 19 |
| 4 | 16 | 7 | 19 | 524288 | 29 |
| 5 | 32 | 5 | 20 | 1048576 | 31 |
| 6 | 64 | 10 | 21 | 2097152 | 26 |
| 7 | 128 | 11 | 22 | +194304 | 25 |
| 8 | 256 | 13 | 23 | 8388608 | 41 |
| 9 | 512 | 8 | 24 | 16777216 | 37 |
| 10 | 1024 | 7 | 25 | 33554432 | 29 |
| 11 | 2048 | 14 | 26 | 67108864 | 40 |
| 12 | 4096 | 19 | 27 | 134217728 | 35 |
| 13 | 8192 | 20 | 28 | 268435456 | 43 |
| 14 | 16384 | 22 | 29 | 536870912 | 41 |
| 15 | 32768 | 26 | | | |
Careful examination of this table leads to the conjecture that
$$
S(k+6 n)=S(k)+9 m
$$
where $n, k$ are natural numbers; $m$ is a natural number or zero.
But why, when multiplying the number $2^{n}$ by $2^{6}$, do we get a number whose sum of digits is either equal to the sum of the digits of the number $2^{n}$, or differs from it by $9 m$? What property does the number $2^{6}$ and its sum of digits possess?
We notice that $S(6)=10$ and $2^{6}=64=63+1=9 \cdot 7+1$.
But what follows from this? Let's consider an example:
$2^{14} \cdot 2^{6}=16384(9 \cdot 7+1)=9 \cdot 7 \cdot 16384+16384$
The number $9 \cdot 7 \cdot 16384$ is divisible by 9. Therefore, the sum of its digits is also divisible by 9. Now it is clear why equation (1) is true.
So, $S(5)=5$. But why are there no other solutions?
By equation (1), they should be sought among $S(11), S(17), S(23), S(29), \ldots$. But $S(11), S(23), S(35), \ldots$ end in the digit 8. Therefore, we are only interested in $S(17), S(29), S(41), \ldots$, i.e., $S(5+12 k)$, where $k$ is a natural number.
It is easy to show that all $S(5+(2 k+1) 12)$ end in the digits 7 and 2, i.e., $S(5+(2 k+1) 12) \geqslant 9$. Therefore, we are only interested in $S(5+24 k)$, which end in the digits 1 and 2 for $k \geqslant 1$. But numbers of the form $2^{5}+24 k \quad(k \geqslant 1, \quad k$ - a natural number) are greater than 1000000012. The number 2000000012 (its sum of digits $S=5$) after division by $2^{2}$ becomes odd, but $2^{3}+24 k$ is even.
The numbers $1100000012, \quad 1010000012, \quad 1001000012$, $1000100012,1000010012,1000001012$ also give an odd number when divided by $2^{2}$. The number 1000000112 is not divisible by $2^{5}$.
Thus, we get the answer: $n=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 Task 1. For which natural $n(n \geqslant 2)$ is the equality
$$
-\sqrt[2]{17 \sqrt{5}+38}+\sqrt[2]{17 \sqrt{5}-38}=\sqrt{20} ?
$$
|
Solution. Using a calculator, we find:
$$
\begin{gathered}
17 \sqrt{5}+38 \approx 38.013154+38 \approx 76.013154>1 \\
17 \sqrt{5}-38 \approx 0.0131541$, and the function $\varphi(n)=\sqrt[n]{17 \sqrt{5}-38}$ is increasing, and $\varphi(n)<1$. To discover some properties of the function $\psi(n)=f(n)+\varphi(n)$, we will perform a mathematical experiment (construct a table of values of the function $\psi(n)$):
| $n$ | $f(n)$ | $\varphi(n)$ | $\varphi(n)$ |
| :---: | :---: | :---: | :---: |
| 2 | 8.7185522 | 0.1146908 | 8.8332422 |
| 3 | 4.2358226 | 0.2360586 | 4.4718813 |
| 4 | 2.952194 | 0.3386604 | 3.2913798 |
| 5 | 2.3777310 | 0.4205441 | 2.8002750 |
Now it is clear that equation (1) has a unique solution $n=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 17. The side of a regular triangle $ABC$ is 4. Point $D$ is the midpoint of side $BC$. A line passing through $B$ intersects side $AC$ at point $M$. Perpendiculars from points $D$ and $A$ to line $BM$ are $DH$ and $AK$. Calculate the length of segment $AM$, if
$$
AK^4 - DH^4 = 15
$$
|
Instruction. Equation (1) has a unique solution. Let $\angle A B M=x$. Then $D H=2 \sin \left(60^{\circ}-x\right)$, $A K=4 \sin x$. Equation (1) takes the form:
$$
256 \sin ^{4} x-16 \sin ^{4}\left(60^{\circ}-x\right)=15
$$
Solving equation (2) on a microcalculator, we get $x=30^{\circ}$, and therefore, $A M=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Find all values of $a$ for which the equation
$$
2 \lg (x+3)=\lg (a x)
$$
has a unique solution.
|
The first solution. Obviously, $x>-3, a x>0$, $x \neq 0$. From equation (1) we get:
$$
(x+3)^{2}=a x, a=\frac{(x+3)^{2}}{x}=\left(\sqrt{x}+\frac{3}{\sqrt{x}}\right)^{2}, \text { if } x>0
$$
Obviously,
$$
\left(\sqrt{x}+\frac{3}{\sqrt{x}}\right)=\left(\sqrt{x}-\frac{3}{\sqrt{x}}\right)^{2}+12
$$
From here it is clear that for positive $x$ the minimum value of the function
$$
a=\frac{(x+3)^{2}}{x}
$$
is 12. If $-3-3$. Now it is clear that for all $a>0$, the line $y=a x$ has a unique common point with the curve $y=(x+3)^{2}$ for $x>-3$ only when $y=a x$ is tangent to this curve. From this we get $a=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. How many solutions does the equation
$$
\arcsin 2x + \arcsin x = \frac{\pi}{3} ?
$$
|
Solution. The function $f(x)=\arcsin 2 x$ is defined on the interval $[-0.5 ; 0.5]$, and the function $\varphi(x)=\arcsin x$ is defined on the interval $[-1 ; 1]$. Therefore, the left side of equation (1) is defined on the interval $[-0.5 ; 0.5]$. The monotonic and continuous function $y=\arcsin 2 x+\arcsin x$ changes on the interval $[-0.5 ; 0.5]$ from $\left(-\frac{\pi}{2}-\frac{\pi}{6}\right)$ to $\left(\frac{\pi}{2}+\frac{\pi}{6}\right)$, i.e., from $-\frac{2}{3} \pi$ to $\frac{2}{3} \pi$. But $\frac{\pi}{3}<\frac{2}{3} \pi$. Therefore, equation (1) has a unique solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 13. Find the minimum value of the function
$$
\psi(x)=\sqrt{15-12 \cos x}+\sqrt{7-4 \sqrt{3} \sin x}
$$
on the interval $[0 ; 0.5 \pi]$.
|
Solution. Since $|\cos x| \leqslant 1$ and $|\sin x| \leqslant 1$, the function $\psi(x)$ is defined on the entire interval $[0 ; 0.5 \pi]$. To find the properties of the functions $f(x)=\sqrt{15-12 \cos x}$, $\varphi(x)=\sqrt{7-4 \sqrt{3} \sin x}, \quad \psi(x)=f(x)+\varphi(x) \quad$, we create a table of their values using a calculator:
| $x^{0}$ | $f(x)$ | $\varphi(x)$ | $\varphi(x)$ |
| ---: | :---: | :---: | :---: |
| 0 | 1.7320508 | 2.6457513 | 4.3778021 |
| 5 | 1.7451827 | 2.5290645 | 4.2742472 |
| 10 | 1.783921 | 2.407616 | 4.1915837 |
| 15 | 1.8463179 | 2.2818523 | 4.1281702 |
| 20 | 1.9296859 | 2.1518401 | 4.0815260 |
| 25 | 2.030887 | 2.017937 | 4.0487624 |
| 30 | 2.1465542 | 1.8803984 | 4.0269526 |
| 35 | 2.2738018 | 1.7395827 | 4.0133843 |
| 40 | 2.409884 | 1.5958185 | 4.0056669 |
| 45 | 2.5523945 | 1.4494896 | 4.0018841 |
| 50 | 2.6993608 | 1.3010333 | 4.0003941 |
| 55 | 2.8490493 | 1.1509769 | 4.0000262 |
| 60 | 3.000020 | 0.9999899 | 4.0000001 |
| 65 | 3.1509650 | 0.84906731 | 4.0000323 |
| 70 | 3.3008723 | 0.69972737 | 4.0003597 |
| 75 | 3.4487282 | 0.5548598 | 4.0036527 |
| 80 | 3.5939145 | 0.42077535 | 4.0146899 |
| 85 | 3.7355228 | 0.31330512 | 4.0488279 |
| 90 | 3.8729833 | 0.26794924 | 4.1409325 |
Based on the table, we can hypothesize that on the interval $[0 ; 0.5 \pi]$, the function $\psi(x) \geqslant 4$, and $\psi\left(\frac{\pi}{3}\right)=4$.
Thus, let's try to prove that
$$
\sqrt{15-12 \cos x}+\sqrt{7-4 \sqrt{3} \sin x} \geqslant 4
$$
Let $\sqrt{7-4 \sqrt{3} \sin x}=t$.
From this, $\sin x=\frac{7-t^{2}}{4 \sqrt{3}}, \cos x=\sqrt{1-\frac{\left(7-t^{2}\right)^{2}}{48}}$ and the inequality (2) takes the form:
$$
\sqrt{15-\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}}} \geqslant 4-t
$$
Both sides of the inequality (3) are non-negative, so after squaring both sides, we get an equivalent inequality:
$$
15-\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}} \geqslant(4-t)^{2}
$$
or
$$
\sqrt{3} \cdot \sqrt{48-\left(7-t^{2}\right)^{2}} \leqslant 8 t-1-t^{2}
$$
From here, $t^{4}-4 t^{3}+6 t^{2}-4 t+1 \geqslant 0$.
Applying the theorem of Bezout, we get $(t-1) \cdot\left(t^{3}-\right.$ $\left.-3 t^{2}+3 t-1\right) \geqslant 0$ or $(t-1)^{4} \geqslant 0$.
Thus, it is proven that the minimum value of the function $\psi(x)$ is 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 16. Solve the equation
$$
\lg \left(x^{2}+9\right)-3 \cdot 2^{x}+5=0
$$
|
Solution. The equation does not have negative roots because on $(-\infty ; 0)$ the function $P(x)=\lg \left(x^{2}+\right.$ $+9)+5$ is decreasing, the function $K(x)=3 \cdot 2^{x}$ is increasing, and $P(0)>K(0)$. To hypothesize about the number of roots of the given equation, we construct tables of the functions $P(x)$ and $K(x)$:
| $x$ | $P(x)$ | $K(x)$ | $x$ | $P(x)$ | $K(x)$ |
| :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | |
| 0 | 5.954 | 3 | 1.6 | 6.062 | 9.09 |
| 0.2 | 5.956 | 3.45 | 1.8 | 6.087 | 10.4 |
| 0.4 | 5.961 | 3.95 | 2 | 6.113 | 12 |
| 0.6 | 5.971 | 4.55 | 2.2 | 6.141 | 13.8 |
| 0.8 | 5.984 | 5.22 | 2.4 | 6.169 | 15.8 |
| 1 | 6 | 6 | 2.6 | 6.197 | 18.2 |
| 1.2 | 6.018 | 6.89 | 2.8 | 6.226 | 20.9 |
| 1.4 | 6.039 | 7.92 | 3 | 5.255 | 24 |
Now we can hypothesize that if $x>2$, then $\lg \left(x^{2}+9\right)<2^{x}$ (this inequality is easily proven using the derivative). After this, it becomes clear that all roots of the given equation belong to the interval $[0 ; 2]$. The number 1 is a root of the equation.
From the table, it is clear that the intervals $[0 ; 0.8]$ and $[1.2 ; 2]$ cannot contain roots of the equation (1).
To prove that 1 is the only root of the equation (1), we construct tables of the functions $P^{\prime}(x)$ and $K^{\prime}(x)$:
| $x$ | $P^{\prime}(x)$ | $K^{\prime}(x)$ | $x$ | $P^{\prime}(x)$ | $K^{\prime}(x)$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0.8 | 0.072 | 3.6 | 1.1 | 0.093 | 4.4 |
| 0.9 | 0.079 | 3.8 | 1.2 | 0.099 | 4.7 |
| 1 | 0.080 | 4.1 | | | |
Now it is clear that on the interval $(0.8 ; 1.2)$ the function $y=P(x)-K(x)$ is decreasing.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 a d a c h a 19. A circle with radius 1 and center at point $O$ is circumscribed around an equilateral triangle $A B C$. Prove that the sum of the squares of the distances from any point $M$ on the circle to the vertices of this triangle is equal to 6 (Fig. 9).
|
Solution. Obviously,
$\overline{C M}^{2}+\overline{M A}^{2}+\overline{M B}^{2}=(\overline{O M}-\overline{O C})^{2}+(\overline{O A}-\overline{O M})^{2}+$ $+(\overline{O B}-\overline{O M})^{2}=\overline{O M}^{2}+\overline{O C}^{2}-2 \overline{O M} \cdot \overline{O C}+\overline{O A}^{2}+$ $+\overline{O M}^{2}-2 \overline{O A} \cdot \overline{O M}+\overline{O B}^{2}+\overline{O M}^{2}-2 \overline{O B} \cdot \overline{O M}=6-$ $-2 \overline{O M}(\overline{O C}+\overline{O A}+\overline{O B})=6-2 \overline{O M} \cdot \bar{O}=6$.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. $DABC$ is a triangular pyramid (Fig. 5). $\overline{AK}=\overline{KD}, \overline{BP}=\overline{PC}, \overline{DM}=0.4 \overline{DC}$. Find the area $S$ of the section of the pyramid by the plane $KMP$, if the vertex $A$ is at a distance $h=1$ from the plane $KMP$ and the volume of the pyramid $DABC$ is 5.
|
Solution. We construct the section of the pyramid $DABC$ using the method of parallel projections. We choose the line $KP$ as the direction of projection. In this case, the pyramid $\dot{D}ABC$ is represented by the parallelogram $ABDC$ (Fig. 6), and the cutting plane is represented by the line $KM$, which intersects the edge $AB$ at point $E$. Point $K=P$ is the center of symmetry of the parallelogram $ABDC$, so $AE: EB = DM: MC = 2: 3$.
Thus, the section of the pyramid $DABC$ by the plane $KMP$ is the quadrilateral $KMPE$ (Fig. 5).
The quadrilateral pyramids $AEKMP$ and $DEKMP$ have the same base $KMPE$ and $AK = KD$. Therefore, their volumes are equal. The area of triangle $AMD$ is 0.4 of the area of triangle $ACD$, and the distance from point $P$ to the plane $ACD$ is half the distance from point $B$ to this plane. Therefore, the volumes of pyramids $PAMC$ and $DEPB$ constitute 0.6 of the volume of pyramid $DABC$. This means that the volume of pyramid $AKMPE$ is 0.2 of the volume of pyramid $DABC$, i.e., it is equal to 1.
Thus, $\frac{1}{3} S h = 1$. But $h = 1$, so $S = 3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. The base of the pyramid $HABCD$ is a square $ABCD$, and the edge $HA$ is perpendicular to the base plane. $AB=3, HA=4$. Prove that a sphere can be inscribed in the pyramid, and find its radius.
For comparison, we will provide two solutions to this problem.
|
The first solution. First, we find the radius of the sphere. Then we prove its existence. For this, we apply the formula $3 v = S r$. Clearly, $V = \frac{1}{3} \cdot 3 \cdot 3 \cdot 4 = 12$; $H B = 5$; $S(ABCD) = 9$; $S(BAH) = S(HAD) = 0.5 \cdot 3 \cdot 4 = 6$; $S(HBC) = S(HDC) = 0.5 \cdot 3 \cdot 5 = 7.5$. Therefore, $S = 9 + 2 \cdot 6 + 2 \cdot 7.5 = 36$. We get $r = 1$.
The planes $ABH$, $AHD$, and $ABD$ are mutually perpendicular. Therefore, the point $O$, which is 1 unit away from these planes, is the vertex of the cube $AB'C'D'A_1B_1OD_1$ (Fig. 8). We will prove that the point $O$ is 1 unit away from the planes $HBC$ and $HDC$.
Since the line $B_1O$ is parallel to the line $BC$, the distance from points $B_1$ and $O$ to the plane $HBC$ is the same. The planes $ABH$ and $BHC$ are perpendicular. Therefore, the distance from $B_1$ to the plane $HBC$ is equal to the distance from $B_1$ to the line $BH$.
Thus, the problem reduces to proving that the point $B_1$ is the center of the circle inscribed in the right triangle $HAB$. Since the area of the triangle $AHB$ and its semiperimeter are both 6, the radius of the inscribed circle is 1.
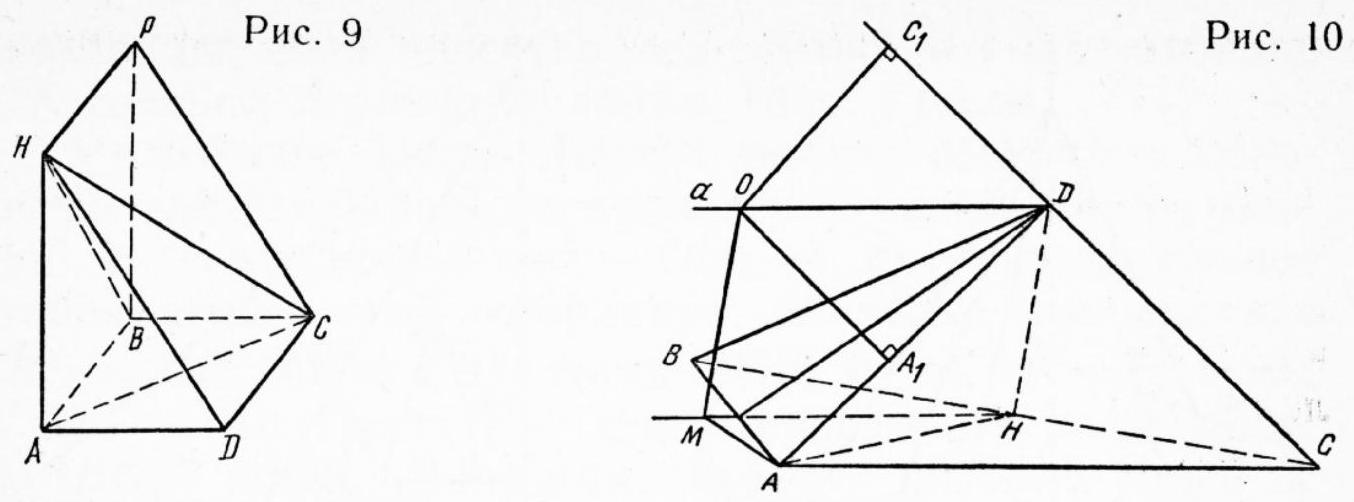
The second solution. We complete the given pyramid $HABCD$ to form a right triangular prism $HADPBC$ (Fig. 9). The right triangle $HAD$ is an orthogonal cross-section of this prism. Therefore, the radius of the sphere $\omega$, which touches the planes $HAB$, $ABD$, $HDC$, and $HAD$, is equal to the radius $r$ of the circle inscribed in the triangle $HAD$.
We already know that $r = 1$. Clearly, the center $O$ of the sphere $\omega$ is inside the pyramid $HABCD$. Therefore, the sphere $\omega$ touches the faces $ABCD$, $HAB$, $HAD$, and $HCD$ of this pyramid. The plane $HAC$ is a plane of symmetry of the pyramid $HABCD$. Therefore, the sphere $\omega$ also touches the face $HBC$, which is symmetric to the face $HDC$ relative to the plane $HAC$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
17. Two thirds in addition (to the unknown), $\frac{1}{3}$ in subtraction, 10 remains (i.e., two thirds of the unknown are added to it, and one third is subtracted from the resulting sum. The remainder is 10).
|
17. The equation will be:
$$
x+\frac{2}{3} x-\frac{1}{3}\left(x+\frac{2}{3} x\right)=10 ; x=9
$$
$\begin{array}{ll}\text { 18. } x=\frac{3}{10} ; x=\frac{15}{53} & \text { 19. } 4 \frac{1}{6} \text {. }\end{array}$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. In the Akhmim papyrus, the area of a circle, the circumference of which is the arithmetic mean of two given circumferences, is taken as the arithmetic mean of their areas. Show that this is incorrect, and find how large the error is in percentage, where the radii of the given circles \( r=5 \); \( R=10 \).

Problems attributed to Pythagoras.
|
28. For $r=5$ and $R=10$, the error is about $11\%$.
Greek mathematics reached its peak by the 3rd century BC (the Alexandrian period). From this time, a number of mathematical treatises (by Euclid, Archimedes, and Apollonius) have survived to the present day. Our knowledge of the preceding period is based primarily on reports from later authors, which are not always reliable. Following the period of prosperity, there was a decline in Greek mathematics, which was due to the decline of Greek culture as a whole. Although significant works in mathematics continued to appear until the 6th century AD, none of them could compare with the works of the Alexandrian period in terms of content or rigor of exposition.
Greek mathematicians brought the logical construction of mathematics, especially geometry, to a high level of perfection. It was not until the 19th century that this logical construction was raised to a higher level. The Greeks brought trigonometry (primarily spherical, the development of which was driven by the needs of astronomy) to a high level of perfection. Theoretical mechanics (particularly statics, hydrostatics, and the theory of machines) was developed using rigorous mathematical methods. The Greeks achieved significant success in solving problems that are now part of higher mathematics (integral calculus). Here, methods were created that were forgotten in later times and only re-emerged in the 17th century among Western European mathematicians.
We also find a well-developed theory of conic sections among the Greeks, which in terms of factual material is little different from the modern one.
The Greeks laid the foundations of algebraic methods; however, although they solved a number of difficult problems in this area, they did not develop a method as advanced as in the aforementioned fields.
The name of Pythagoras (6th century BC) is associated with a number of unreliable reports. In particular, the so-called "Pythagorean theorem" was undoubtedly known to the peoples of the ancient East, from whom the Greeks could have borrowed both the theorem and its proof.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Given a right triangle with sides 9, 12, 15. Find the diameter of the circle inscribed in this triangle.
## Problems of Marcus Junius Nipsus.
From the Erfurt Codex.
|
92. Solution: $A B=A E+R ; A E=A D$,
$$
B C=F C+R ; F C=D C
$$
therefore,
$$
A B+B C=2 R+A C
$$
from which
$$
2 R=A B+B C-A C
$$
in this case
$$
2 R=9+12-15=6
$$
Fig. 33.
The Erfurt Codex is a manuscript of later origin (possibly from the 11th century), representing a collection of excerpts, sometimes more complete than the Arzeryan Codex: it contains a series of stereometric problems that are almost absent in ancient lists.
Marcus Junius Nipsus (lived no later than the 2nd century). Roman writer - surveyor.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
98. In a cage, there is an unknown number of pheasants and rabbits. It is only known that the entire cage contains 35 heads and 94 feet. The task is to determine the number of pheasants and the number of rabbits.
|
98. If there were only pheasants in the cage, the number of legs would be 70, not 94. Therefore, the 24 extra legs belong to the rabbits, 2 per each. It is clear that there were 12 rabbits and, consequently, 23 pheasants.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
122. Find the number which, when multiplied by 3, then divided by 5, increased by 6, after which the square root is extracted, one is subtracted, and the result is squared, will give 4.
## Problem of Sridhara.
From the treatise "The Essence of Calculation."
|
122. The method of inverse actions involves approaching the unknown by performing actions on numbers in the reverse order of those specified in the problem, and, obviously, all actions are replaced by their inverses. Sometimes this technique is called the "method of inversion."
$$
\sqrt{4}=2 ; 2+1=3 ; 3^{2}=9 ; 9-6=3 ; 3 \cdot 5=15 ; \frac{15}{3}=5
$$
calculations. Bhaskara-Acharya refers to it and even borrows problems from it. The time of his life is not precisely known, but it was certainly in the period between the 6th and 10th centuries AD.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
156. What number, when added to nine, gives its own square root?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The last sentence is a note to the translator and should not be included in the translated text. Here is the final version:
156. What number, when added to nine, gives its own square root?
|
156. $x^{2}+9=6 x ; x=3$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
156. $x^{2}+9=6 x ; x=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
169. $x^{2}+10 x=39$.
169. $x^{2}+10 x=39$.
(Note: The equation is the same in both languages, so the translation is identical to the original text.)
|
169. Al-Karaji is looking for a number which, when added to $x^{2}+10 x$, would make a complete square. Such a number is 25. Then
$x^{2}+10 x+25=(x+5)^{2}=39+25=64 ; x+5=8$ and $x=3$.
He calls this method the "method of solving in the manner of Diophantus".
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
181. Find the area of a rectangle where the base is twice the height, and the area is numerically equal to the perimeter.
|
181. If the width is $x$, then the length is $2 x$. Thus, the area is $2 x^{2}$, and the perimeter is $6 x$. According to the condition, $2 x^{2}=6 x$, therefore, $x=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
192. If a number, when divided by 9, gives a remainder of 2 or 7, then the square of the number, when divided by 9, gives a remainder of 4.
|
192. Let $N=9 k+2, \quad$ then $N^{2}=81 k^{2}+18 k+4=$ $=$ multiple of 9 +4 ; let $N_{1}^{2}=9 k+7$, then $N_{1}^{2}=81 k^{2}+$ $+126 k+49=9\left(9 k^{2}+14 k+5\right)+4$.
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
203. $\frac{1}{x^{2}}+2 \frac{1}{x}=1 \frac{1}{4}$.
## Problems of Begh-Edin.
From the treatise "The Essence of the Art of Calculation".
|
203. Omar's Solution: $z=\frac{1}{x} ; \quad z^{2}+2 z=\frac{5}{4} ;$
$$
\begin{aligned}
& z^{2}+2 z+1=\frac{9}{4} ;(z+1)^{2}=\frac{9}{4} ; z+1=\frac{3}{2} ; z=\frac{1}{2} \\
& z^{2}=\frac{1}{4}, \text { therefore, } x^{2}=4 \text { and } x=2
\end{aligned}
$$
Bega Ed-Din (16th century), a Persian mathematician, author of the treatise "Kolasa-tal-Hisab" ("The Essence of the Art of Calculation"), which served as a guide for the study of mathematics in schools of Hindustan and Persia until the beginning of the 19th century.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
205. It is required to find a number which, when multiplied by itself, added to two, then doubled, added to three again, divided by 5, and finally multiplied by 10, results in 50.
|
205. $\frac{50}{10}=5 ; 5 \cdot 5=25 ; 25-3=22 ; 11-2=9 ; \sqrt{9}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
207. Zaimu is promised a reward in the form of the larger of two parts, which add up to 20, and the product of these parts is 96. How great is the reward?
|
207. The ordinary solution: Let the larger part be $x$. Then the smaller one is $20-x$. According to the condition, $x(20-x)=96$, or $x^{2}-20 x+96=0 ; x=10 \pm \sqrt{100-96}=10 \pm 2 ; x_{1}=12 ; x_{2}=8$. But Al-Baghdadi's solution is simpler: put one number as $10+x$, then the other is $10-x$. Their product is $100-x^{2}=96$, from which $x^{2}=4$ and $x=2$, therefore, $10+x=12$, $10-x=8$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
252. $\frac{x}{10-x}+\frac{10-x}{x}=25$.
|
252. $10 x=x^{2}+\frac{100}{27} ; x=5-\sqrt{21 \frac{8}{27}}$. But Regiomontanus also gives another solution, assuming $\frac{x}{10-x}=y$. Then $y+\frac{1}{y}=25 ; y=\frac{25}{2}-\sqrt{\frac{621}{4}}$. In both cases, Regiomontanus takes the roots with a minus sign.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
269. $3 x^{2}+12=12 x$
|
269. Two equal roots $(x=2)$.
270. $x=5 \pm \sqrt{21}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
309. 26 persons together spent 88 coins, with each man spending 6, each woman 4, and each girl 2 coins. How many were men, women, and girls?
|
309. 10 solutions; from $x+y+z=26$
and
$$
6 x+4 y+2 z=88
$$
we get:
$$
2 x+y=18
$$
from which
$$
y=18-2 x
$$
therefore,
$$
2 x \leqslant 18
$$
H
$$
x \leqslant 9
$$
T. e
$$
\begin{aligned}
& x=0, \quad 1, \quad 2, \quad 3, \quad 4, \quad 5, \quad 6, \quad 7, \quad 8, \quad 9 \\
& y=18,16,14,12,10, \quad 8, \quad 6, \quad 4, \quad 2, \quad 0 \\
& z=8, \quad 9,10,11,12,13,14,15,16,17
\end{aligned}
$$
If we exclude the cases $x=0, y=0$, then 8 solutions.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
314. Divide $\sqrt[3]{216}$ by $\sqrt[4]{16}$.
|
314. Rudolf's Solution:
$$
\begin{aligned}
& =\sqrt[12]{531441}=\sqrt[6]{729}=\sqrt[3]{27}=3
\end{aligned}
$$
Indeed: $\quad \sqrt[3]{216}: \sqrt[4]{16}=6: 2=3$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
340. Find the positive root of the equation by construction:
$$
x^{2}+6 x=91
$$
|
340. Cardano's Solution: Let the square $F D$ (Fig. 74) be $x^{2}$, hence its side $F H=x$. $D G=D B=3$ (half the coefficient of $x$). Construct the square $A F E C$. The rectangle $A D$ equals the rectangle $D E$, i.e., equals $3 x$. The sum of the square $F D$ and the two rectangles equals $x^{2}+6 x$, which, by the condition, is 91. The small square $B C G D=9$, hence the square $A F E C=100$. Therefore, $A C=10$; but $A C=x+3$, so $x=7$. The usual method:
$x^{2}+6 x-91=0 ; x=-3 \pm \sqrt{9+91}=$
Fig. 74.
$=-3 \pm 10 ; \quad x_{1}=7 ; \quad x_{2}=-13$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
351. Show that
$$
\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}=4
$$
|
351. $\sqrt[3]{2+v \overline{-121}}=\sqrt[3]{2+11 i}=\sqrt[3]{8+12 i-6-i}=$
$$
\begin{aligned}
& =\sqrt[3]{2^{3}+3 \cdot 2^{2} i+3 \cdot 2 \cdot i^{2}+i^{3}}=\sqrt[3]{(2+i)^{3}}=2+i \\
& \sqrt[3]{2-\sqrt{-121}}=\sqrt[3]{2-11 i}=\sqrt[3]{8-12 i-6+i}= \\
& =\sqrt[3]{2^{3}-3 \cdot 2^{2} \cdot i+3 \cdot 2 i^{2}-i^{3}}=\sqrt[3]{(2-i)^{3}}=2-i
\end{aligned}
$$
therefore,
$$
\begin{aligned}
& 13 \overline{2+11 i}+\sqrt[3]{2-11 i}=2+i+2-i=4 \\
& x^{3}-4 x^{2}+4 x^{2}-16 x+x-4=0 \\
& x^{2}(x-4)+4 x(x-4)+(x-4)=0 \\
& (x-4)\left(x^{2}+4 x+1\right)=0 \\
& x_{1}=4 ; x_{2,3}=-2 \pm \sqrt{3}
\end{aligned}
$$
156
## 17th century.
Thomas Harriot (1560-1621), English algebraist, author of the treatise "Artis analyticae Praxis," published posthumously in 1631. He was familiar with the relationships between the coefficients and roots of equations.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
382. What is the smallest number of weights and of what weight can be used to weigh any whole number of pounds from 1 to 40 on a balance scale, given that during weighing, weights can be placed on both pans of the scale.
|
382. The solution to the problem is based on the properties of the ternary system of numeration, which can express any numbers; since the number $40=27+9+3+1=3^{3}+3^{2}+3+1$, it is possible with four weights of $27, 9, 3$ and 1 pound, as is easy to verify by checking, to weigh any load up to forty pounds. It is sufficient to take any load and express it in the ternary system: for example,
$$
23=27-(3+1) ; 31=27+3+1
$$
and so on.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
393. Several people had dinner together and had to pay 175 shillings for the bill. It turned out that two of them had no money, so each of the rest had to pay 10 shillings more than their share. How many people had dinner?
|
393. Let $x$ be the number of people who had lunch. It is easy to form the equation
$$
\frac{175}{x-2}-\frac{175}{x}=10
$$
from which
$$
x^{2}-2 x=35
$$
Maclaurin would solve it as follows:
$$
\begin{gathered}
x^{2}-2 x+1=36 \\
(x-1)^{2}=36 ; x-1= \pm 6 ; x_{1}=7 \text { or } x_{2}=-5
\end{gathered}
$$
The second root is not valid.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
409. Several merchants contributed to a common fund 100 times as many rubles as there were merchants. They sent a trusted person to Venice, who received a number of rubles from each hundred rubles, twice the number of merchants. The question is: how many merchants were there, if the trusted person received 2662 rubles?
|
409. Let the number of merchants be $x$. Each contributed $100 x$, and the total capital is $100 x^{2}$. The profit on the capital is $2 x^{3}=2662$, from which $x^{3}=1331$, hence $x=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
426. A lazy worker was told that he would receive 24 su for each day he worked, with the condition of deducting 6 su for each day he skipped. After 30 days, it turned out that he did not receive anything. The question is: how many days did he work?
|
426. We form the equation $24 x=6(30-x)$, from which $x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
433. Several people have to pay 800 francs for the production of a lawsuit. But three of them have no money, so the rest have to add 60 francs to their share. How many participants are there in the payment of legal costs?
|
433. We form the equation $\frac{80}{x+3}=\frac{800}{x}-60$, where $x-$ is the number of participants in the payment. $x^{2}+3 x=40$, from which $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
471. Someone has twelve pints of wine and wants to give away half of it, but he does not have a six-pint container. He has two containers, one holds 8 pints and the other 5 pints; the question is: how can he pour six pints into the eight-pint container?
## Lebesgue's Problem.
|
471. Regarding this problem, Arago tells that it decided the fate of Poisson, as, by becoming interested in it, he thereby discovered his vocation and devoted his whole life to mathematics. We have already seen a similar problem (336). This one also has 2 solutions:
| 12 | 8 | 5 |
| ---: | ---: | ---: |
| 12 | 0 | 0 |
| 4 | 8 | 0 |
| 4 | 3 | 5 |
| 9 | 3 | 0 |
| 9 | 0 | 3 |
| 1 | 8 | 3 |
| 1 | 6 | 5 |
| 6 | 6 | 0 |
| 12 | 8 | 5 |
| ---: | ---: | ---: |
| 12 | 0 | 0 |
| 7 | 0 | 5 |
| 0 | 7 | 5 |
| 0 | 8 | 4 |
| 8 | 0 | 4 |
| 8 | 4 | 0 |
| 3 | 4 | 5 |
| 3 | 8 | 1 |
| 11 | 0 | 1 |
| 11 | 1 | 0 |
| 6 | 1 | 5 |
| 6 | 6 | 0 |
For more theoretical details, one can refer to the book by W. Ahrens "Mathematische Spiele".
Lebesgue, V. A., a French mathematician, professor at the Faculty of Sciences in Bordeaux. This problem is taken from his "Exercices d'analyse numérique," dedicated to indeterminate analysis and number theory (1859).
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
472. Solve the system in integers:
$$
\begin{aligned}
& 2 x+3 y+7 z=131 \\
& 2 x+3 y+8 z=140
\end{aligned}
$$
60
## Schläfli Problems.
|
472. Immediately find $z=9$ and $2 x+3 y=68$, from which in the usual way: $y=0,2,4, \ldots, 22$. In total, there are 12 solutions.
Schlömilch, Oscar (1823--1901), a well-known German mathematician, whose name is associated with the expression for the remainder term of a Taylor series. Author of the very useful course “Kompendium d. höheren Mathematik” (2 volumes).
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
475. Prove that
$$
\sqrt[3]{20+1+\sqrt{2}}+\sqrt[3]{20-14 \sqrt{ } 2}=4
$$
|
475. Cubing:
$$
\begin{gathered}
20+14 \sqrt{2}+20-14 \sqrt{2}+ \\
+3 \sqrt[3]{20+14 \sqrt{2}} \sqrt[3]{20-14 \sqrt{2}} \cdot 4=64 \\
40+12 \sqrt[3]{40-392}=40+24
\end{gathered}
$$
Another method:
$$
\begin{gathered}
\sqrt[3]{20+14 \sqrt{2}}=\sqrt[3]{8+12+12 \sqrt{2}+2 \sqrt{2}}= \\
=\sqrt[3]{2^{3}+3 \cdot 2} \cdot(\sqrt{2})^{2}+3 \cdot 2^{2} \cdot \sqrt{2}+(\sqrt{2})^{3}=2+\sqrt{2}
\end{gathered}
$$
Similarly:
$$
\sqrt[3]{20-14 \sqrt{2}}=2-\sqrt{2}
$$
The sum of (1) and (2) $=4$.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2.8. Let $n>1$ be a natural number. Find all positive solutions of the equation $x^{n}-n x+n-1=0$.
## 2.3. Equations with Radicals
In problems $2.9-2.15$, it is assumed that the values of square roots are non-negative. We are interested only in the real roots of the equations.
|
2.8. A n s w e r: $x=1$. It is clear that
$$
x^{n}-n x+n-1=\left(1+x+\ldots+x^{n-1}-n\right)(x-1)
$$
If $x>1$, then $1+x+\ldots+x^{n-1}-n>0$, and if $0<x<1$, then $1+x+\ldots$ $\cdots+x^{n-1}-n<0$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.9. Solve the equation $\sqrt{2 x-6}+\sqrt{x+4}=5$.
### 2.10. Solve the equation
$$
\sqrt[m]{(1+x)^{2}}-\sqrt[m]{(1-x)^{2}}=\sqrt[m]{1-x^{2}}
$$
|
2.9. Let $y=\sqrt{x+4}$. Then $x=y^{2}-4$, so $2 x-6=2 y^{2}-$ -14. Therefore, we get the equation $\sqrt{2 y^{2}-14}+y=5$. Move $y$ to the right side and square both sides. As a result, we get the equation $y^{2}+10 y-39=0$. Its roots are 3 and -13. But $y \geqslant 0$, so only the root $y=3$ remains, which corresponds to $x=5$. It is easy to verify that $x=5$ is indeed a root of the given equation.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.11. Solve the equation
$$
3 \sqrt{x^{2}-9}+4 \sqrt{x^{2}-16}+5 \sqrt{x^{2}-25}=\frac{120}{x}
$$
|
2.11. The expression on the left side increases as $x$ increases, while the expression on the right side decreases. Therefore, the equation has no more than one solution. It is easy to verify that $x=5$ is a solution.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.12. Solve the equation $x+\sqrt{3+\sqrt{x}}=3$.
|
2.12. If $x>1$, then $x+\sqrt{3+\sqrt{x}}>3$, and if $x<1$, then $x+$ $+\sqrt{3+\sqrt{x}}<3$. Only the root $x=1$ remains.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.13. $\left\{\begin{array}{l}\left(x_{3}+x_{4}+x_{5}\right)^{5}=3 x_{1}, \\ \left(x_{4}+x_{5}+x_{1}\right)^{5}=3 x_{2}, \\ \left(x_{5}+x_{1}+x_{2}\right)^{5}=3 x_{3}, \\ \left(x_{1}+x_{2}+x_{3}\right)^{5}=3 x_{4}, \\ \left(x_{2}+x_{3}+x_{4}\right)^{5}=3 x_{5} .\end{array}\right.$
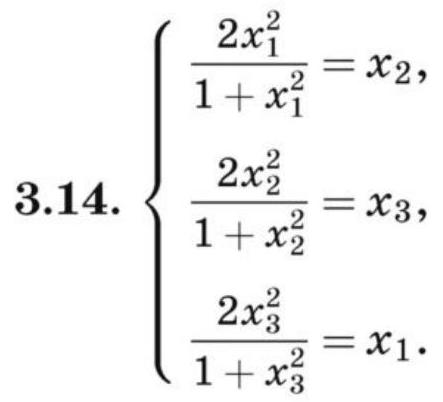
## 3.3. Positive solutions
|
3.13. After cyclic renumbering of the unknowns, we can assume that $x_{1} \geqslant x_{i}(i=2,3,4,5)$. The function $f(x)=x^{5}$ is monotonically increasing, so $3 x_{2}=\left(x_{4}+x_{5}+x_{1}\right)^{5} \geqslant\left(x_{3}+x_{4}+x_{5}\right)^{5}=3 x_{1}$. Therefore, $x_{1}=x_{2}$ and $x_{3}=x_{1}$. Moreover, $3 x_{4}=\left(x_{1}+x_{2}+x_{3}\right)^{5} \geqslant$ $\geqslant\left(x_{5}+x_{1}+x_{2}\right)^{5}=3 x_{3}$. Therefore, $x_{4}=x_{3}$ and $x_{5}=x_{3}$.
We have obtained that $x_{1}=x_{2}=x_{3}=x_{4}=x_{5}=x$. This number $x$ must satisfy the equation $(3 x)^{5}=3 x$. We get three solutions: $x=0$ or $\pm 1 / 3$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.48. Find the remainder when the number
$$
10^{10}+10^{\left(10^{2}\right)}+10^{\left(10^{3}\right)}+\ldots+10^{\left(10^{10}\right)}
$$
is divided by 7.
|
4.48. Answer: 5. Note that $10^{6} \equiv 1(\bmod 7)$, since $10^{3}+1$ is divisible by 7, and $10^{k} \equiv 4(\bmod 6)$ for $k \geqslant 1$, since the number $99 \ldots 96$ is even and divisible by 3. Therefore, $10^{10^{k}} \equiv 10^{4}(\bmod 7)$ for $k \geqslant 1$. Hence, the required remainder is the remainder of the division of the number $10 \cdot 10^{4}=10^{5}$ by 7. This remainder is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.12. Prove that the number $\sqrt[3]{20+14 \sqrt{2}}+\sqrt[3]{20-14 \sqrt{2}}$ is rational.
|
6.12. The identity $(2 \pm \sqrt{2})^{3}=20 \pm 14 \sqrt{2}$ shows that $\sqrt[3]{20 \pm 14 \sqrt{2}}=2 \pm \sqrt{2}$. Therefore, the considered number is 4.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.23. Find the first digit after the decimal point of the number $(2+\sqrt{3})^{1000}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
6.23. Answer: 9. Let $(2+\sqrt{3})^{n}=A_{n}+B_{n} \sqrt{3}$, where $A_{n}$ and $B_{n}$ are natural numbers. According to problem 6.22, $(2-\sqrt{3})^{n}=A_{n}-B_{n} \sqrt{3}$. Therefore, $(2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}$ is a natural number. But $2-\sqrt{3} \approx$ $\approx 0.2679 < 0.3$, so $(2-\sqrt{3})^{1000} \approx 0.0 \ldots$ (and then several more zeros follow).
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. A pedestrian left point $A$ for point $B$, which are 5 km apart. At the same time, a cyclist left point $B$ towards the pedestrian, with a speed twice that of the pedestrian. Upon meeting the pedestrian, he turned around and rode back to $B$. Upon reaching $B$, the cyclist turned again and rode towards the pedestrian, and so on. What distance will the cyclist have traveled by the time the pedestrian arrives at $B$?
## 7.2. Calculations
|
7.2. A n s w e r: 10 km. We can assume that the cyclist is always moving in one direction (the length of the path does not change from this).
His speed is twice the speed of the pedestrian, so in the time it takes the pedestrian to walk 5 km, the cyclist will travel 10 km.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.16. Ten workers need to assemble 50 items from parts. First, the parts of each item need to be painted; it takes one worker 10 minutes to do this. After painting, the parts dry for 5 minutes. Assembling an item takes one worker 20 minutes. How many workers should be assigned as painters and how many as assemblers to complete the work in the shortest time? (Two workers cannot paint or assemble the same item simultaneously.)
## 7.5. Correspondences
|
7.16. Answer: 3 painters and 6 assemblers (one worker is extra, i.e., you can assign 4 painters and 6 assemblers or 3 painters and 7 assemblers). It is easy to verify that 3 painters and 6 assemblers can complete the work in 195 minutes. Indeed, after 15 minutes from the start of the painters' work, 3 items are ready for assembly, and 3 assemblers will assemble them in 20 minutes. After that, 6 items will be ready for assembly, and the assemblers will never have to wait for the painters to finish painting the next item. After \(15 + 20 + 140 = 175\) minutes from the start of the work, \(3 + 7 \cdot 6 = 45\) items will be assembled. To assemble the remaining 5 items, another 20 minutes are needed (only 5 assemblers can work on this).
If there are fewer than three painters, painting will take no less than 250 minutes, and if there are fewer than six assemblers, assembly will take no less than 200 minutes.
|
3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.9. When dividing the polynomial $x^{1951}-1$ by $x^{4}+x^{3}+2 x^{2}+$ $+x+1$, a quotient and a remainder are obtained. Find the coefficient of $x^{14}$ in the quotient.
## 10.4. Vieta's Theorem
|
10.9. Answer: -1. The equalities $x^{4}+x^{3}+2 x^{2}+x+1=\left(x^{2}+1\right) \times$ $\times\left(x^{2}+x+1\right)$ and $x^{12}-1=(x-1)\left(x^{2}+x+1\right)\left(x^{3}+1\right)\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)$ show that
$$
\begin{aligned}
& x^{4}+x^{3}+2 x^{2}+x+1=\frac{x^{12}-1}{(x-1)\left(x^{3}+1\right)\left(x^{4}-x^{2}+1\right)}= \\
& =\frac{x^{12}-1}{x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1}
\end{aligned}
$$
Therefore, dividing the polynomial $x^{1951}-1$ by $x^{4}+x^{3}+2 x^{2}+x+1$ is the same as first dividing it by $x^{12}-1$, and then multiplying by $x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1$. But
$$
\frac{x^{1951}-1}{x^{12}-1}=x^{1939}+x^{1927}+x^{1915}+\ldots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}
$$
so the desired coefficient is the coefficient of $x^{14}$ in the product
$$
\left(x^{1939}+\ldots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}\right)\left(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\right)
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.31. What remainder does $x+x^{3}+x^{9}+x^{27}+x^{81}+x^{243}$ give when divided by $(x-1) ?$
|
10.31. Answer: 6. Let $x+x^{3}+x^{9}+x^{27}+x^{81}+x^{243}=P(x) \times$ $\times(x-1)+r$. By setting $x=1$, we get $r=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.6. Solve the equation $x+y=x y$ in natural numbers. 12.7. Solve the equation $2 x y+3 x+y=0$ in integers.
|
12.6. It is clear that $(x-1)(y-1)=x y-x-y+1=1$, therefore $x-1=y-1=1$, i.e., $x=y=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.15. Solve the equation in integers
$$
x^{3}-2 y^{3}-4 z^{3}=0
$$
|
12.15. Answer: $x=y=z=0$.
Let $x^{3}-2 y^{3}-4 z^{3}=0$, where $x, y, z$ are integers. Then the number $x$ is even. After substituting $x=2 x_{1}$, we get the equation $8 x_{1}^{3}-2 y^{3}-4 z^{3}=0$. Dividing by 2: $4 x_{1}^{3}-y^{3}-2 z^{3}=0$. Therefore, the number $y$ is even. After substituting $y=2 y_{1}$, we get the equation $4 x_{1}^{3}-8 y_{1}^{3}-2 z^{3}=0$. Dividing by 2 again: $2 x_{1}^{3}-4 y_{1}^{3}-z^{3}=0$. Therefore, the number $z$ is even. After substituting $z=2 z_{1}$, we get the equation $x_{1}^{3}-2 y_{1}^{3}-4 z_{1}^{3}=0$, which has the same form as the original equation. Therefore, we can again prove that the numbers $x_{1}, y_{1}, z_{1}$ are even, and so on. But this is only possible if $x=y=z=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.4. How many necklaces can be made from five white beads and two black ones?
|
14.4. Answer: 3. Black beads divide the white beads into two groups (one of these groups may contain 0 beads). The appearance of the necklace is completely determined by the number of beads in the smaller group. This number can be 0, 1, or 2.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.48. Which sum of the numbers rolled is more likely when throwing two dice: 9 or $10?$
|
14.48. A n s w e r: 9. The numbers 9 and 10 can be obtained in two different ways: $9=3+6=4+5$ and $10=4+6=5+5$. However, we need to consider the order in which the numbers fall on the dice. Therefore, the number 9 can be obtained in four different ways, while the number 10 can only be obtained in three: $9=3+6=6+3=4+5=5+4,10=4+6=6+4=5+5$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.51. In a drawer, there are red and black socks. If two socks are randomly pulled out of the drawer, the probability that both are red is $1 / 2$.
a) What is the smallest number of socks that can be in the drawer?
b) What is the smallest number of socks that can be in the drawer if it is known that the number of black socks is even?
|
14.51. a) Answer: 4. Let there be $m$ red socks and $n$ black socks in the box. The probability that the first selected sock is red is $\frac{m}{n+m}$. Given that the first selected sock is red, the probability that the second selected sock is also red is $\frac{m-1}{n+m-1}$. Therefore, the probability that both socks are red is $\frac{m}{n+m} \cdot \frac{m-1}{n+m-1}$. Thus, we need the equality
$$
\frac{m}{n+m} \cdot \frac{m-1}{n+m-1}=\frac{1}{2}
$$
For $n=1$, we get $m=3$. This set of socks suits us.
b) Answer: 21. Clearly, $n>0$. Then, as it is easy to check, $\frac{m}{n+m}>\frac{m-1}{n+m-1}$. Therefore, the inequalities must hold
$$
\left(\frac{m}{n+m}\right)^{2}>\frac{1}{2}>\left(\frac{m-1}{n+m-1}\right)^{2}
$$
i.e., $(\sqrt{2}+1) n<m<(\sqrt{2}+1) n+1$. By the condition, the number $n$ is even. For $n=2,4,6$ we get $m=5,10,15$. In the first two cases, the equality (1) does not hold, but in the third case, it does. In this case, $n+m=6+15=21$.
Remark. Let $x=m-n$ and $y=n$. Then the equality (1) can be rewritten as $(2 x-1)^{2}-2(2 y)^{2}=1$. Therefore, in the general case, we are dealing with a Pell's equation.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.13. a) There is a piece of chain consisting of 60 links, each weighing 1 g. What is the smallest number of links that need to be unbuckled so that from the resulting parts, all weights of 1 g, 2 g, 3 g, ..., 60 g can be formed (an unbuckled link also weighs 1 g)?
b) The same question for a chain consisting of 150 links.
|
16.13. a) Answer: 3 links. Let's determine the largest $n$ for which it is sufficient to break $k$ links of an $n$-link chain so that all integer weights from 1 to $n$ can be formed from the resulting parts. If $k$ links are broken, any number of links from 1 to $k$ can be formed from them. But we cannot form $k+1$ links if there is no part with $k+1$ or fewer links (we do not consider the broken links here). The most advantageous situation is to have a part with exactly $k+1$ links. Then we can form any number of links from 1 to $2k+1$. (Otherwise, we can form only the number of links from 1 to $l_1 + k$, where $l_1 \leq k$.) Next, the most advantageous situation is to have a part with $2(k+1)$ links, then with $4(k+1)$ links, and so on. Thus, if we break $k$ links, the most advantageous situation is when the $k+1$ parts obtained consist of $k+1$, $2(k+1)$, $4(k+1)$, $8(k+1)$, ..., $2^k(k+1)$ links (we do not consider the broken links here). In this case, any number of links from 1 to $n = 2^{k+1}(k+1) - 1$ can be formed. Therefore, if $2^k k \leq n \leq 2^{k+1}(k+1) - 1$, then $k$ breaks are sufficient and $k-1$ breaks are not sufficient. In particular, if $24 \leq n \leq 63$, the smallest number of broken links is 3. The four parts of the chain obtained after breaking should consist of 4, 8, 16, and 29 links.
b) Answer: 4 links. According to the solution of part a), for a chain consisting of $n$ links, where $64 \leq n \leq 159$, it is sufficient to break 4 links.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17.21. We took three numbers $x, y, z$ and computed the absolute values of their pairwise differences $x_{1}=|x-y|, y_{1}=|y-z|$, $z_{1}=|z-x|$. In the same way, from the numbers $x_{1}, y_{1}, z_{1}$ we constructed the numbers $x_{2}, y_{2}, z_{2}$ and so on. It turned out that for some $n$ we got $x_{n}=x, y_{n}=y, z_{n}=z$. Knowing that $x=1$, find $y$ and $z$.
|
17.21. Answer: $y=z=0$. The numbers $x_{n}, y_{n}, z_{n}$ are non-negative, so the numbers $x, y, z$ are also non-negative. If all the numbers $x$, $y, z$ were positive, then the largest of the numbers $x_{1}, y_{1}, z_{1}$ would be strictly less than the largest of the numbers $x, y, z$, and then the largest of the numbers $x_{n}, y_{n}, z_{n}$ would be strictly less than the largest of the numbers $x, y, z$. Therefore, among the numbers $x, y, z$ there is a 0. Similarly, it is proved that among the numbers $x_{1}, y_{1}, z_{1}$ there is a 0 (for $n=1$ there is nothing to prove, because then $x_{1}=x, y_{1}=y, z_{1}=z$). This means that two of the numbers $x, y, z$ are equal. In the end, we get that the unordered set of numbers $x, y, z$ can be either $0,0,1$ or $0,1,1$. It is easy to check that the second set does not have the required property.
228 Chapter 17. The Pigeonhole Principle. The Rule of the Extreme
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20.16. Some of the 20 metal cubes, identical in size and appearance, are aluminum, the rest* are duralumin (heavier). How can you determine the number of duralumin cubes using 11 weighings on a balance with two pans and no weights?
|
20.16. Let's put one cube on each pan of the balance. There are two possible cases.
Case 1. One of the cubes turned out to be heavier in the first weighing.
In this case, one of the selected cubes is aluminum, and the other is duralumin. Place the selected cubes on one pan and compare them with the remaining cubes. Specifically, divide the remaining 18 cubes into 9 pairs and place them on the other pan one by one. Each time, we can determine how many duralumin cubes are in the pair. Indeed, if the reference pair is lighter, then we placed two duralumin cubes; if the reference pair has the same weight, then we placed one aluminum and one duralumin cube; if the reference pair is heavier, then we placed two aluminum cubes. Thus, in the first case, 10 weighings are sufficient.
Case 2. The cubes turned out to be of equal weight in the first weighing.
In this case, either both selected cubes are aluminum or both are duralumin. Place the selected cubes on one pan and sequentially compare them with the remaining cubes. Suppose the first $k$ pairs have the same weight, and the $(k+1)$-th pair has a different weight. (If $k=9$, then all cubes have the same weight, so there are no duralumin cubes.) Let's assume for definiteness that the $(k+1)$-th pair is heavier. Then the first two cubes and the cubes of the first $k$ pairs are aluminum. Place one cube from the $(k+1)$-th pair on each pan of the balance. If these cubes have the same weight, then they are both duralumin. If the cubes have different weights, then one is aluminum and the other is duralumin. In both cases, we can form a pair of cubes, one of which is aluminum and the other is duralumin. We can compare the remaining pairs of cubes with this pair, as in the first case. The total number of weighings in the second case is 11.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21.3. The numbers $2^{n}$ and $5^{n}$ start with the digit $a$. What is $a$?
|
21.3. Answer: 3. By the condition $a \cdot 10^{p}<2^{n}<(a+1) 10^{p}$ and $a \cdot 10^{q}<5^{n}<$ $<(a+1) 10^{q}$. Therefore, $a^{2} 10^{p+q}<10^{n}<(a+1)^{2} 10^{p+q}$, i.e., $a^{2}<10^{n-p-q}<$ $<(a+1)^{2}$. At the same time, $(a+1)^{2} \leqslant 100$. Thus, $a^{2}<10<(a+1)^{2}$, i.e., $a=3$. The number 3 is the leading digit of the numbers $2^{5}$ and $5^{5}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21.16. All integers are written in a row, starting from one. What digit stands at the 206,788th place?
## 21.6. Periods of Decimal Fractions and Repunits
| Let $p$ be a prime number different from 2 and 5. The length of the period of the number $p$ is the number of digits in the period of the decimal representation of the fraction $1 / p$.
|
21.16. Answer: the digit 7. There are exactly 9 single-digit numbers, 99-9=90 two-digit numbers, 999-99-9=900 three-digit numbers, 9000 four-digit numbers, and so on. Single-digit numbers occupy the first 9 positions in the written sequence, two-digit numbers occupy $90 \cdot 2=180$ positions, three-digit numbers occupy $900 \cdot 3=2700$ positions, four-digit numbers occupy $9000 \cdot 4=36000$ positions, and five-digit numbers occupy $90000 \cdot 5=450000$ positions. Therefore, the digit we are interested in belongs to a five-digit number.
Digits belonging to numbers with no more than four digits have numbers from 1 to $9+180+2700+36000=38889$. The difference $206788-38889=167899$ needs to be divided by 5 with a remainder: $167899=5 \cdot 33579+4$. The digit we are interested in belongs to the 33580-th five-digit number, i.e., the number 43579 (the first five-digit number is 10000). In this number, the digit we are interested in is in the $4-th$ position.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21.33. If we consider digits in different positions as different, then in a $d$-ary numeral system, $n d$ digits allow us to write $d^{n}$ numbers (from 0 to $d^{n}-1$). Which numeral system is the most economical in this respect, i.e., allows recording the largest number of numbers using a given number of digits? (When comparing numeral systems with bases $d_{1}$ and $d_{2}$, we consider only sets of $m$ digits, where $m$ is divisible by $d_{1}$ and $d_{2}$.)
See also problems $20.15,20.17$.
### 21.10. Other representations of numbers
|
21.33. Answer: system with base 3. Using $m=d n$ digits, we can write $d^{m / d}$ numbers. Therefore, we need to prove that $3^{m / 3} \geqslant d^{m / d}$, i.e., $3^{d} \geqslant d^{3}$ for any natural $d$. This inequality is proven in the solution to problem 13.11.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23.21. For which natural numbers $n$ is the expression $a^{n}(b-c)+$ $+b^{n}(c-a)+c^{n}(a-b)$ divisible by $a^{2}+b^{2}+c^{2}+a b+b c+c a$?
|
23.21. Answer: only for $n=4$. It is easy to verify that for $n=4$ the result of the division is $(a-b)(b-c)(a-c)$. We will show that for all other natural $n$ the expression $a^{n}(b-c)+b^{n}(c-a)+c^{n}(a-b)$ does not divide $a^{2}+b^{2}+c^{2}+ab+bc+ca$. It is sufficient to check that the first expression does not divide the second when $b=2$ and $c=1$, i.e., $a^{n}-(2^{n}-1)a+(2^{n}-2)$ does not divide $a^{2}+3a+7$. For $n=2$ and 3, this is verified directly. Now let $n \geqslant 5$. The quadratic equation $a^{2}+3a+7=0$ has roots $\frac{-3 \pm i \sqrt{19}}{2}$; the modulus of each root is $\sqrt{7}$. Therefore, it is sufficient to check that if $z$ is a complex number and $|z|=\sqrt{7}$, then $z^{n}-(2^{n}-1)z+(2^{n}-2) \neq 0$. Clearly, $\left|z^{n}-(2^{n}-1)z+(2^{n}-2)\right| \geqslant \left|z^{n}\right|-(2^{n}-1)|z|-(2^{n}-2)=7^{n/2}-(2^{n}-1)\sqrt{7}-2^{n}+2>7^{n/2}-2^{n}(1+\sqrt{7})>7^{n/2}-4 \cdot 2^{n}$, since $\sqrt{7}>2$, it is sufficient to consider the case $n=5$. In this case, we need to check that $7^{5}>(4 \cdot 2^{5})^{2}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.