problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Ten men sit side by side at a long table, all facing the same direction. Each of them is either a knight (and always tells the truth) or a knave (and always lies). Each of the people announces: "There are more knaves on my left than knights on my right." How many knaves are in the line?
|
Number the people from 1 to 10, from left to right according to their own perspective.
Person 1 is certainly lying, since he has no one to his left, and hence is a knave.
Person 10 is therefore a knight, since he has no one to his right and at least one knave (person 1) to his left.
Person 2 has exactly one knave to his left and at least one knight to his right, so he is a knave.
Person 9 has exactly one knight to his right and at least two knaves to his left, so he is a knight.
Continuing in this way, we find that person 3 is a knave, 8 is a knight, 4 is a knave, 7 is a knight, 5 is a knave, and 6 is a knight. Thus there are five knaves in the line.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At a party with 100 people, everyone is either a knight, who always tells the truth, or a knave, who always lies. Each person says they shook hands with a different number of knights at the party, from 0 to 99 . Each pair of people shook hands at most once, and everyone knows whether each other person is a knight or knave. Determine how many knights were at the party.
|
Call the person who said they shook hands with $i$ people person $i$ for each $i$ from 0 to 99 . Now, if person 99 is telling the truth, person 99 must have shaken hands with everyone else, and all the other people must be knights. But then person 0 would be lying, since they said they shook hands with no knights but must have shaken hands with person 99 . This is a contradiction, so person 99 must be a knave.
Similarly, if person 98 is a knight, person 98 must have shaken hands with people 0 to 97 , and they must all be knights. This again means person 0 would be lying, a contradiction, so person 98 is also a knave. Continuing in this manner, we find that person 97 is a knave, as is person 96 , and so on down to person 1 . Thus, only person 0 is telling the truth, so there were 99 knaves and one knight at the party.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A castle has infinitely many rooms labeled $1,2,3, \ldots$, which are divided into several halls. Suppose room $n$ is on the same hall as rooms $3 n+1$ and $n+10$ for every $n$. Determine the maximum possible number of different halls in the castle.
|
There are at most three different halls in the castle. Because rooms $n$ and $n+10$ are on the same hall, any two rooms with the same units digit must be on the same hall.
Now, repeatedly using the rule that rooms $n$ and $3 n+1$ are on the same hall, we find that room 1 is on the same hall as rooms 4, 13, and 40, and 121, so all rooms with units digit $0,1,3$, or 4 are on the same hall. There need not be any other rooms on this hall, since whenever $n$ has units digit in this set, so does $3 n+1$, and so does $(n-1) / 3$, if it is a whole number.
Similarly, room 2 is on the same hall as rooms 7 and 22 , so all rooms with units digit 2 or 7 are on the same hall, and there need not be any other rooms on this hall. Finally, rooms 5, 16, 49, and 148 are on the same hall, so all rooms with units digit $5,6,8$ or 9 are on the same hall. Thus, we see that there are at most three different halls in the castle.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
You are out walking and see a group of rhinoceroses (which each have two horns and four legs) and triceratopses (which each have three horns and four legs). If you count 31 horns and 48 legs, how many triceratopses are there?
|
Since each animal has 4 legs, there must be $48 / 4=12$ animals. Each triceratops has 3 horns and each rhinoceros has 2, so if there are $t$ triceratopses and $r$ rhinoceroses we get $t+r=12$ and $3 t+2 r=31$. Subtracting twice the first equation from the second gives $t=7$.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that every positive real number $y$ satisfies
$$
2 y \geq 3-\frac{1}{y^{2}}
$$
When does equality occur?
|
(Problem source: Aops) Since $y$ is positive, we can multiply both sides by $y$ and rearrange to get the equivalent inequality
$$
2 y^{3}-3 y^{2}+1 \geq 0
$$
This factors as
$$
(2 y+1)(y-1)^{2} \geq 0 .
$$
The first factor is positive since $y>0$, and the second is nonnegative since it is a real number squared. Thus, the product must be nonnegative, and will be 0 iff $(y-1)^{2}=0$, which happens iff $y=1$.
Alternate solution: By AM-GM, we get
$$
\frac{\frac{1}{y^{2}}+y+y}{3} \geq \sqrt[3]{\frac{1}{y^{2}} \cdot y \cdot y}=1
$$
Multiplying by 3 and rearranging gives the desired inequality, and equality occurs iff $\frac{1}{y^{2}}=y$, which is true iff $y=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
It's a week before Thanksgiving, and a family is trying to find their turkey. There are 5 boxes in a row, and the turkey is hiding in one of the 5 boxes.
Every day, the family is allowed to check one box to try to find the turkey, and every night, the turkey moves to a box right next to the box it was in. For example, from box 3 it could move to box 2 or 4 , and from box 5 it must move to box 4 . Determine a strategy for the family to catch the turkey before Thanksgiving.
#
|
One strategy is as follows:
First assume the turkey starts in an even numbered box (box 2 or 4). On day 1, check box 2 . If the turkey is not there, he must have been in box 4 to begin with, so tomorrow he will be in box 3 or box 5 . On day 2 , check box 3 . If the turkey is not there, then he must currently be in box 5 (since he started in box 4), so tomorrow he will be in box 4 . Thus, on day 3 , check box 4 .
If he is not there, then the assumption that he began in an even numbered box must have been wrong. Thus, he started in an odd numbered box, which means on day 4 he will be in an even numbered box. Thus, we can repeat the same strategy of checking boxes 2,3 , and 4 on days 4,5 , and 6 , and we are guaranteed to find the turkey in at most 6 days.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that
$$
A=\sqrt{4-2 \sqrt{3}}-\frac{\sqrt{3}+1}{\sqrt{3}-1}
$$
is an integer.
|
$\sqrt{4-2 \sqrt{3}}=\sqrt{3^{2}-2 \sqrt{3}+\sqrt{1}^{2}}=\sqrt{(\sqrt{3}-1)^{2}}=|\sqrt{3}-1|=\sqrt{3}-1$. If multiply both numerator and the denominator of $\frac{\sqrt{3}+1}{\sqrt{3}-1}$ by $\sqrt{3}+1$ we get:
$$
\frac{\sqrt{3}+1}{\sqrt{3}-1}=\frac{(\sqrt{3}+1)^{2}}{\sqrt{3}^{2}-1^{2}}=\frac{4+2 \sqrt{3}}{2}=2+\sqrt{3}
$$
Thus $A=-1-2=-3$, which is an integer.
|
-3
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
A $2012 \times 2012$ table is to be filled with integers in such a way that each of the 4026 rows, columns, and main diagonals has a different sum. What is the smallest number of distinct values that must be used in the table?
|
Answer: 3.
If at most two numbers are used, say $x$ and $y$, the sum of every row and column is completely determined by the number of $y$ 's it has, which ranges from 0 to 2012 . Thus there are only 2013 possible sums, not enough for the 4026 rows, columns, and diagonals.
On the other hand, if $n$ is a large integer (say, 10000), then it is possible to fill the table using 0,1 , and $n$. Here is a $6 \times 6$ example that generalizes readily:
| 1 | 0 | 0 | 0 | 0 | 0 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 0 | 0 | 0 | $n$ |
| 1 | 1 | 1 | 0 | $n$ | $n$ |
| 1 | 1 | 0 | $n$ | $n$ | $n$ |
| 1 | 0 | 0 | 0 | $n$ | $n$ |
| 0 | 0 | 0 | 0 | 0 | $n$ |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5 married couples gather at a party. As they come in and greet each other, various people exchange handshakes - but, of course, people never shake hands with themselves or with their own respective spouses. At the end of the party, one woman goes around asking people how many hands they shook, and she gets nine different answers. How many hands did she herself shake?
|
Suppose that there were $n$ couples, and the woman asked all $2 n-1$ other attendees how many hands they shook and received $2 n-1$ different answers. We will show that she herself shook $n-1$ hands; hence, in our particular case, the answer is 4 .
We work by induction. When $n=1$, there is one couple, and no handshakes can occur, proving the base case. Now suppose the result holds for $n$ couples; we will prove it is valid for $n+1$ couples. With $n+1$ couples present, the woman receives $2 n+1$ different answers to her question. But no person $P$ can shake more than $2 n$ hands (for $2 n+2$ people, minus $P$ and $P$ 's spouse); hence, these $2 n+1$ numbers must be exactly $0,1,2, \ldots, 2 n$ in some order. In particular, one of these people, $A$, shook everyone else's hand except $A$ 's own spouse (that accounts for the " $2 n$ " answer), and another, $B$, shook no hands (the " 0 " answer). Because $B$ did not shake $A$ 's hand, $A$ and $B$ must be married to each other. The remaining $2 n$ people include the woman who asked the question, together with those who answered $1,2, \ldots, 2 n-1$ to her question. Now pretend that $A$ and $B$ had not attended the party, so we are left with $n$ couples. Each of these people shook hands with $A$ and not with $B$; therefore, when $A$ and $B$ are removed, their handshake counts become $0,1,2, \ldots, 2 n-2$. Hence, by the induction hypothesis, the questioner shook $n-1$ hands. But now, if we put $A$ and $B$ back in, we note that the woman shook $A$ 's hand as well (and not $B$ 's). So, altogether, she shook $n$ hands. This completes the induction step, and now the proof is done.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A circle is inscribed in a sector that is one sixth of a circle of radius 6 . (That is, the circle is tangent to both segments and the arc forming the sector.) Find, with proof, the radius of the small circle.
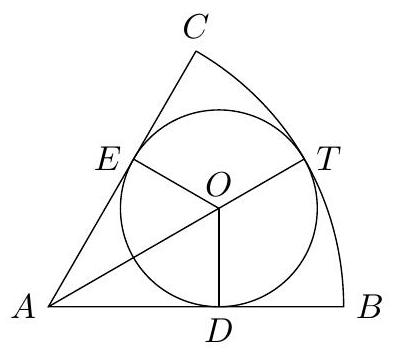
|
Because the circles are tangent, we can draw the line $A T$, which passes through the center $O$ of the other circle. Note that triangles $A D O$ and $A E O$ are symmetric (this is HL congruence: $A O$ is shared, radii $O D$ and $O E$ are equal, and angles $A D O$ and $A E O$ are right). Therefore, since $\angle B A C$ is $60^{\circ}$, angles $B A T$ and $T A C$ are each $30^{\circ}$. Now $A D O$ is a $30^{\circ}-60^{\circ}-90^{\circ}$ right triangle. If we let $r$ be the radius of the small circle, then $O D=r$ and $O A=2 r$, but $O T=r$ so $A T=3 r$. But $A T$ is the radius of the large circle, so $3 r=6$ and $r=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the hold of a pirate ship are ten treasure chests lying on pedestals in a circular arrangement. The captain would like to move each chest clockwise by one pedestal. However, the chests are so heavy that the captain and his assistant can only switch two chests at a time. What is the minimum number of switches needed to accomplish the task?
|
The answer is 9. It is easy to see that nine moves are sufficient; they can move a single chest counterclockwise one pedestal at a time, until after nine moves all of the other chests have been moved clockwise one pedestal.
Suppose that, at each stage of the game, we draw an arrow from each pedestal to the pedestal on which the chest which it now holds originally sat. Then every pedestal has one incoming and one outgoing arrow, and the overall graph can be decomposed into some number of disconnected cycles. Let $c$ be the number of cycles. We note that at the beginning of the process, $c=10$ (every arrow is its own cycle) while at the end, $c=1$ (all the pedestals are connected in a ring).
We now claim that at each move, $c$ cannot decrease by more than 1 . Each move affects only two pedestals, which may initially belong to one or two cycles; the performance of the move may fuse two cycles into one or break up cycles into more cycles, but it certainly cannot replace two cycles by zero cycles. Therefore, $c$ decreases by at most 1 at each move and hence cannot reach as low as 1 before the ninth move.
Remark. Math circlers with a penchant for enumerative combinatorics may wish to prove that there are precisely $100,000,000$ ways of accomplishing the task in nine moves.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Aerith repeatedly flips a fair coin.
a) Find the expected number of flips to get two heads in a row.
b) Find the expected number of flips to get heads followed by tails.
#
|
a) Let $x$ be the expected number of flips. There is a $\frac{1}{4}$ chance that she gets two heads right away. There is a $\frac{1}{2}$ chance the first flip is tails, in which case she is basically starting over after the first flip, so it will take an expected $x+1$ flips total. Finally, there is a $\frac{1}{4}$ chance the first flip is heads and the second tails, in
which case she is basically starting over after 2 flips, so it will take an expected $x+2$ flips total. Thus we get
$$
x=\frac{1}{4} \cdot 2+\frac{1}{2}(x+1)+\frac{1}{4}(x+2)=\frac{3}{2}+\frac{3}{4} x .
$$
Solving this gives $x=6$.
b) Let the expected number of flips be $y$. There is a $\frac{1}{2}$ chance you get tails on the first flip, in which case she is basically starting over, so it will take an expected $y+1$ flips total. If she gets heads on the first flip, then she is just waiting until she first gets tails. She has a $\frac{1}{2}$ chance of getting tails on each flip, so it will be an expected 2 flips before she first gets tails, for an expected 3 flips total. Thus we get
$$
y=\frac{1}{2}(y+1)+\frac{1}{2} \cdot 3=\frac{1}{2} y+2 .
$$
Solving this gives $y=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all composite positive integers $n$ such that all the divisors of $n$ can be written in the form $a^{r}+1$, where $a$ and $r$ are integers with $a \geq 0$ and $r \geq 2$.
|
The only such number is $n=10$. It is easy to see that $n=10$ indeed satisfies the conditions. Call $n$ "good" if every divisor of $n$ has the form $a^{r}+1, a \geq 0, r \geq 2$ (a good $n$ may be prime or composite).
First, it is easy to check that 4 is not good, and so 4 does not divide any good number.
Second, we show that a good integer is one more than a perfect square. Write $n=a^{r}+1$ with $r$ maximal. If $r$ is odd, $a+1$ divides $\mathrm{n}$, and so $a+1=a_{1}^{r_{1}}+1$. Hence $a=a_{1}^{r_{1}}$ and $n=a_{1}^{r r_{1}+1}$, violating the maximality assumption of $r$. Thus $r$ must be even. We conclude that $n=x^{2}+1$ for some positive integer $x$.
Third, we show that the product of two odd primes are not good. Assume on the contrary that $p q$ is good, where $p \leq q$ are odd primes. Then both $p$ and $q$ are good. We write $p=s^{2}+1, q=t^{2}+1$, and $p q=u^{2}+1$ (so $s \leq ts^{2}$ and $q$ is prime, $q$ must divide $u+t$. Note that both $t$ and $u$ are odd, so $u+t$ is even. Hence $2 q=2\left(t^{2}+1\right)$ divides $u+t$. It follows that $u+t \geq 2\left(t^{2}+1\right)=2 q$, and so $u-t \geq 2 t^{2}+2-2 t=t^{2}+1+(t-1)^{2}>s^{2}$, contradicting (5). Hence our assumption was wrong, and so no good number is divisible by a product of two odd primes.
It follows that any $n$ satisfying the conditions of the problem is of the form $n=2 p$, where $p$ is an odd prime. We can write $n=x^{2}+1$ and $p=y^{2}+1$. Hence $x^{2}+1=2 y^{2}+2$ or $p=y^{2}+1=x^{2}-y^{2}=(x-y)(x+y)$. This is true only if $x=y+1$, implying that $y=2, p=5$, and $n=10$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
With two properly chosen weights and a balance scale, it is possible to determine the weight of an unknown object known to weigh an integer number of pounds from 1 to $n$. Find the largest possible value of $n$.
Remark. The balance scale tells whether the weights placed on each side are equal and, if not, which side is heavier. It may be used an unlimited number of times.
|
Let $a$ and $b$ be the known weights. The balance scale allows one to compare the unknown weight with four known weights: $a, b, a+b$, and $a-b$ (the last of these is gotten by balancing $x+b$ on one side with $a$ on the other). After the comparisons are done, there are at most 4 values that $x$ can be known to equal and at most 5 gaps ( 3 between and 2 on the ends) for $x$ to lie in. Thus at most 9 values of $x$ can be distinguished.
To show $n=9$ is achievable, take the weights to be $a=6 \mathrm{lb}$ and $b=2 \mathrm{lb}$. Then the nine possibilities can be distinguished by
$$
1a+b
$$
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evaluate the sum
$$
\sum_{k=1}^{\infty}\left(\prod_{i=1}^{k} \frac{P_{i}-1}{P_{i+1}}\right)=\frac{1}{3}+\frac{1}{3} \cdot \frac{2}{5}+\frac{1}{3} \cdot \frac{2}{5} \cdot \frac{4}{7}+\frac{1}{3} \cdot \frac{2}{5} \cdot \frac{4}{7} \cdot \frac{6}{11}+\ldots
$$
where $P_{n}$ denotes the $n^{\text {th }}$ prime number.
|
Rewrite the given sum as
$$
\begin{gathered}
\frac{1}{3}+\frac{2}{3} \cdot \frac{1}{5}+\frac{2}{3} \cdot \frac{4}{5} \cdot \frac{1}{7}+\frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7}+\cdot \frac{1}{11}+\ldots \\
=\frac{1}{3}+\left(1-\frac{1}{3}\right) \frac{1}{5}+\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right) \frac{1}{7}+\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1-\frac{1}{7}\right) \frac{1}{11}+\ldots \\
=\frac{1}{3}+\frac{1}{5}-\frac{1}{3 \cdot 5}+\frac{1}{7}-\frac{1}{3 \cdot 7}-\frac{1}{5 \cdot 7}+\frac{1}{3 \cdot 5 \cdot 7}+\frac{1}{11}-\frac{1}{3 \cdot 11} \frac{1}{5 \cdot 11}-\frac{1}{7 \cdot 11}+\ldots
\end{gathered}
$$
Note that each term in this sum must have denominator of the form $p_{1} p_{2} \ldots p_{k}$, where the $p_{i}$ are distinct primes (WLOG $p_{1}<p_{2}<\cdots<p_{k}$ ). Further, each denominator
occurs exactly once, namely, in expanding the product whose last term is $\frac{1}{p_{k}}$, and its sign is $(-1)^{k-1}$, since it comes from the term
$$
\left(-\frac{1}{p_{1}}\right)\left(-\frac{1}{p_{2}}\right) \ldots\left(-\frac{1}{p_{k-1}}\right) \frac{1}{p_{k}}
$$
in the expansion of the product containing $\frac{1}{p_{k}}$. However, this lets us rewrite the left side as
$$
1-\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1-\frac{1}{7}\right) \ldots
$$
However, we can see that
$$
\begin{gathered}
\frac{1}{\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1-\frac{1}{7}\right)}=\frac{1}{1-\frac{1}{3}} \cdot \frac{1}{1-\frac{1}{5}} \cdot \frac{1}{1-\frac{1}{7}} \ldots \\
=\left(1+\frac{1}{3}+\frac{1}{3^{2}}+\ldots\right)\left(1+\frac{1}{5}+\frac{1}{5^{2}}+\ldots\right)\left(1+\frac{1}{7}+\frac{1}{7^{2}}+\ldots\right)=\sum_{n=1}^{\infty} \frac{1}{2 n+1} .
\end{gathered}
$$
Thus, since the Harmonic series diverges, the product
$$
\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\left(1-\frac{1}{7}\right) \ldots
$$
must equal 0 , so the desired sum is $1-0=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given a fixed triangle $\triangle A B C$ and a point $P$, find the maximum value of
$$
\frac{A B^{2}+B C^{2}+C A^{2}}{P A^{2}+P B^{2}+P C^{2}}
$$
|
We use the following lemma.
Lemma. Given $a, b, c, p \in \mathbb{R}$ such that not all of $a, b, c$ are equal,
$$
(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \leq 3\left((p-a)^{2}+(p-b)^{2}+(p-c)^{2}\right)
$$
with equality if and only if $p=(a+b+c) / 3$.
Proof. For fixed $a, b, c$, the right hand side is a quadratic in $p$, namely
$$
\begin{aligned}
3\left((p-a)^{2}+(p-b)^{2}+(p-c)^{2}\right) & =3\left(\left(p^{2}-2 a p+a^{2}\right)+\left(p^{2}-2 b p+b^{2}\right)+\left(p^{2}-2 c p+c^{2}\right)\right) \\
& =9 p^{2}-6(a+b+c) p+3\left(a^{2}+b^{2}+c^{2}\right) .
\end{aligned}
$$
and is thus minimized at $-\frac{-6(a+b+c)}{2 \cdot 9}=(a+b+c) / 3$. By plugging $p=(a+b+c) / 3$ into the original equation, we observe equality, as desired.
Using Cartesian coordinates, let $A=\left(a_{x}, a_{y}\right), B=\left(b_{x}, b_{y}\right), C=\left(c_{x}, c_{y}\right)$, and $P=$ $\left(p_{x}, p_{y}\right)$. By the Pythagorean theorem,
$$
\begin{gathered}
A B^{2}+B C^{2}+C A^{2}=\left[\left(a_{x}-b_{x}\right)^{2}+\left(a_{y}-b_{y}\right)^{2}\right]+\left[\left(b_{x}-c_{x}\right)^{2}+\left(b_{y}-c_{y}\right)^{2}\right] \\
+\left[\left(c_{x}-a_{x}\right)^{2}+\left(c_{y}-a_{y}\right)^{2}\right] \\
=\left[\left(a_{x}-b_{x}\right)^{2}+\left(b_{x}-c_{x}\right)^{2}+\left(c_{x}-a_{x}\right)^{2}\right] \\
+\left[\left(a_{y}-b_{y}\right)^{2}+\left(b_{y}-c_{y}\right)^{2}+\left(c_{y}-a_{y}\right)^{2}\right]
\end{gathered}
$$
so by the above,
$$
\begin{aligned}
A B^{2}+B C^{2}+C A^{2} \leq 3[ & \left.\left(p_{x}-a_{x}\right)^{2}+\left(p_{x}-b_{x}\right)^{2}+\left(p_{x}-c_{x}\right)^{2}\right] \\
& +3\left[\left(p_{y}-a_{y}\right)^{2}+\left(p_{y}-b_{y}\right)^{2}+\left(p_{y}-c_{y}\right)^{2}\right] \\
= & 3\left[\left(p_{x}-a_{x}\right)^{2}+\left(p_{y}-a_{y}\right)^{2}\right]+3\left[\left(p_{x}-b_{x}\right)^{2}+\left(p_{y}-b_{y}\right)^{2}\right] \\
& +3\left[\left(p_{x}-c_{x}\right)^{2}+\left(p_{y}-c_{y}\right)^{2}\right] \\
= & 3\left(P A^{2}+P B^{2}+P C^{2}\right) .
\end{aligned}
$$
This gives
$$
\frac{A B^{2}+B C^{2}+C A^{2}}{P A^{2}+P B^{2}+P C^{2}} \leq 3,
$$
with equality at
$$
P=\left(\frac{a_{x}+b_{x}+c_{x}}{3}, \frac{a_{y}+b_{y}+c_{y}}{3}\right),
$$
the centroid of $\triangle A B C$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive prime numbers $p$ such that $p+2$ and $p+4$ are prime as well.
Hint. Show that for most prime numbers $p$, either $p+2$ or $p+4$ is divisible by 3 .
|
For $p=3, p+2=5, p+4=7$ and these are obviously prime. For $p>3$, we know that $p$ is not divisible by 3 . The remainder of $p$ when divided by 3 can be either 1 or 2 . If it is one, then $p+2$ is divisible by 3 , if it is 2 , then $p+4$ is divisible by 3 . Hence $p=3$ is the only solution.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the units digit of $17^{2021}$.
|
The units digits of powers of 17 cycle: $7,9,3,1,7,9,3,1, \ldots$, so the units digit of $17^{n}$ is 1 whenever $n$ is a multiple of 4 . Since 2020 is a multiple of 4 , $17^{2020}$ has units digit 1 , so $17^{2021}$ has units digit 7 .
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Carl computes the number
$$
N=5^{555}+6^{666}+7^{777}
$$
and writes it in decimal notation. What is the last digit of $N$ that Carl writes?
|
We look at the last digit of each term.
- The last digit of $5^{\bullet}$ is always 5 .
- The last digit of $6^{\bullet}$ is always 6 .
- The last digit of $7^{\bullet}$ cycles $7,9,3,1,7,9,3, \ldots$.
So the last digits are $5,6,7$ in that order. Since $5+6+7=18$, the answer is 8 .
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If $a, b, c, d$ are positive real numbers such that $\frac{5 a+b}{5 c+d}=\frac{6 a+b}{6 c+d}$ and $\frac{7 a+b}{7 c+d}=9$, calculate $\frac{9 a+b}{9 c+d}$.
|
Let $\frac{5 a+b}{5 c+d}=\frac{6 a+b}{6 c+d}=k$. Then $5 a+b=k(5 c+d)$ and $6 a+b=k(6 c+d)$. Subtracting these two equations gives $a=k c$. Now we can easily get that $b=k d$. From $\frac{7 a+b}{7 c+d}=\frac{7 k c+k d}{7 c+d}=k=9$ we get $\frac{9 a+b}{9 c+d}=9$ as well.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle, two of whose sides are 3 and 4 , is inscribed in a circle. Find the minimal possible radius of the circle.
|
Since the circle has a chord of length 4 , its diameter is at least 4 and so its radius is at least 2 . To achieve equality, choose a right triangle with hypotenuse 4 and one leg 3 (the other leg will, by the Pythagorean theorem, have length $\sqrt{7}$ ). Then the midpoint of the hypotenuse is the center of a circle of radius 2 passing through all three vertices.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
There are three boxes of stones. Each hour, Sisyphus moves a stones from one box to another. For each transfer of a stone, he receives from Zeus a number of coins equal to the number of stones in the box from which the stone is drawn minus the number of stones in the recipient box, with the stone Sisyphus just carried not counted. If this number is negative, Sisyphus pays the corresponding amount (and can pay later if he is broke).
After 1000 years, all the stones lie in their initial boxes. What is the greatest possible earning of Sisyphus at that moment?
|
The myth of Sisyphus suggests the answer: 0 .
Let $x$ be the amount of money Sisyphus has and $a, b, c$ the sizes of the boxes. The key observation is that the quantity
$$
N=2 x+a^{2}+b^{2}+c^{2}
$$
does not change; for example, after one operation from the first box to the second the quantity becomes
$N^{\prime}=2(x+a-b-1)+(a-1)^{2}+(b+1)^{2}+c^{2}=2 x+2 a-2 b-2+a^{2}-2 a+1+b^{2}+2 b+1+c^{2}=2 x+a^{2}+b^{2}+c^{2}=$
Thus the quantity $N$ is an invariant.
Consequently, if Sisyphus has no money to begin with then he does not earn any money at the end, either.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A $23 \times 23$ square is divided into smaller squares of dimensions $1 \times 1,2 \times 2$, and $3 \times 3$. What is the minimum possible number of $1 \times 1$ squares?
|
Color the rows of the square black and white alternately, so the top and bottom rows are black. Then each $2 \times 2$ tile covers two cells of each color, and each $3 \times 3$ tile covers six of one color and three of the other. In particular, if only $2 \times 2$ and $3 \times 3$ tiles are used, the difference between the number of black and white cells covered is divisible by 3 . But the entire board has 23 more black than white cells (if the bottom row were removed, the colors would be equally represented). So there must

be at least one $1 \times 1$ tile.
To construct the required tiling with only one $1 \times 1$ tile, first use $3 \times 3$ tiles to build a $9 \times 12$ rectangle and $2 \times 2$ tiles to build a $2 \times 12$ rectangle. Join these two rectangles to form an $11 \times 12$ rectangle. Then use four copies of this $11 \times 12$ rectangle, together with the $1 \times 1$ square, to build a $23 \times 23$ square as shown in the diagram.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a_{1}=5$ and $a_{n+1}=a_{n}^{3}-2 a_{n}^{2}+2$ for all $n \geq 1$. Prove that if $p$ is a prime divisor of $a_{2014}+1$ and $p \equiv 3 \bmod 4$, then $p=3$.
|
Observe that $a_{n+1}-2=a_{n}^{2}\left(a_{n}-2\right)$ for all $n \geq 1$. By induction on $n$ we obtain
$$
a_{n+1}-2=3 a_{n}^{2} a_{n-1}^{2} \cdots a_{1}^{2}
$$
for all $n \geq 1$. Therefore
$$
a_{2014}+1=3\left(a_{2013}^{2} a_{2012}^{2} \cdots a_{1}^{2}+1\right)=3\left[\left(a_{2013} a_{2012} \cdots a_{1}\right)^{2}+1\right]
$$
It is well known that if $q$ is a prime divisor of $x^{2}+1(x \in \mathbb{Z})$ then $q \not \equiv 3 \bmod 4$. (This is a special case of a result known as quadratic reciprocity.) So the $p$ in the problem must be 3 .
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
a) One Sunday, Zvezda wrote 14 numbers in a circle, so that each number is equal to the sum of its two neighbors. Prove that the sum of all 14 numbers is 0 .
b) On the next Sunday, Zvezda wrote 21 numbers in a circle, and this time each number was equal to half the sum of its two neighbors. What is the sum of all 21 numbers, if one of the numbers is 3 ?
|
a) Denoting the numbers $a_{1}, a_{2}, \ldots, a_{14}$, and their sum as $S$ we have $a_{i}=$ $a_{i-1}+a_{i+1}$ for $i=1, \ldots, 14$ (we take $a_{15}=a_{1}, a_{0}=a_{14}$ ). Summing all these equalities we get $S=2 S$ (since each $a_{i}$ appears exactly once on the left and exactly twice on the right). Therefor $S=0$.
b) Again, let the numbers be $a_{1}, \ldots, a_{21}$. Let $a_{i}$ be maximal among the numbers. Then we have $a_{i} \geq a_{i-1}, a_{i} \geq a_{i+1}$ and so $a_{i} \geq \frac{a_{i-1}+a_{i+1}}{2}$. But $a_{i}=\frac{a_{i-1}+a_{i+1}}{2}$, so both inequalities are actually equalities. Next, considering now $a_{i-1}$ we conclude $a_{i+1}=a_{i+2}$. Proceeding in this way, we conclude that all the numbers are equal. As one of them is 3 , the sum of all numbers is $3 * 21=63$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which positive integers $n$ is $n^{4}+4$ equal to a prime number?
|
For $n=1$ we get $1^{4}+4=5$, which works.
For all other values of $n$, the key idea is that
$$
n^{4}+4=n^{4}+4 n^{2}+4-4 n^{2}=\left(n^{2}+2\right)^{2}-(2 n)^{2}=\left(n^{2}+2 n+2\right)\left(n^{2}-2 n+2\right)
$$
which is the product of two integers greater than 1, and hence cannot be prime.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A set $S$ of irrational real numbers has the property that among any subset of five numbers in $S$, one can find two with irrational sum. How large can $|S|$ be?
|
The answer is $|S| \leq 8$. An example is $S=\{n \pm \sqrt{2} \mid n=1,2,3,4\}$ (and any of its subsets).
In general, construct a graph with vertex set $S$ in which we join two numbers with rational sum. We claim this graph is bipartite; indeed if $a_{1}+a_{2}, a_{2}+a_{3}, \ldots, a_{n}+a_{1}$ are all rational for some odd $n$, solving the resulting system of equations gives $a_{1}$, $\ldots, a_{n}$ all rational numbers.
Accordingly we may 2-color $S$. If $|S| \geq 9$, then we may find a set of five numbers with rational sum, as desired.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given three squares of dimensions $2 \times 2,3 \times 3$, and $6 \times 6$, choose two of them and cut each into 2 figures, such that it is possible to make another square from the obtained 5 figures.
|
The solution is shown in the picture below
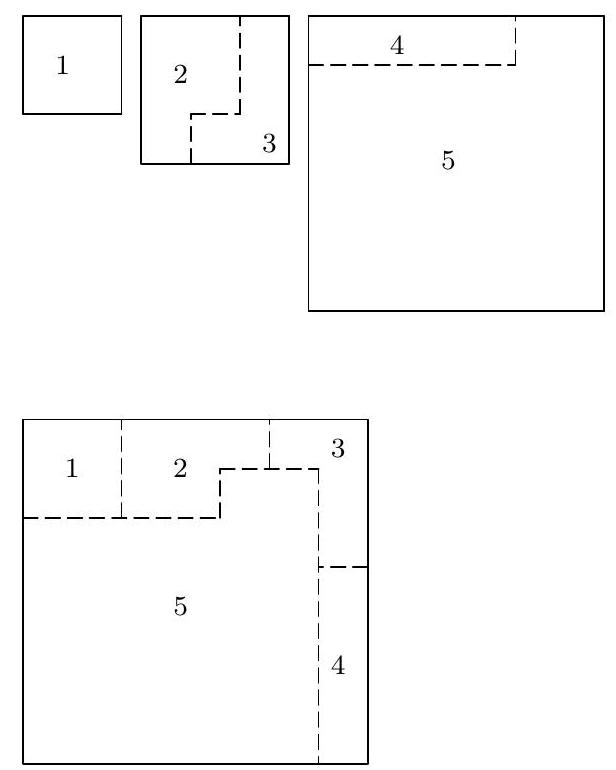
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $p$ such that $p, p+4$, and $p+8$ are all prime.
|
If $p=3$, then $p+4=7$ and $p+8=11$, both prime. If $p \neq 3$, then $p$ is not a multiple of 3 and is therefore of one of the forms $3 k+1,3 k+2(k \geq 0)$ If $p=3 k+1$, then $p+8=3 k+9=3(k+3)$, which is not prime since $k+3>1$. If $p=3 k+2$, then $p+4=3 k+6=3(k+2)$, which is not prime since $k+2>1$. Thus $p=3$ is the only solution with all three numbers prime.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The figure below consists of five congruent squares. If the area of the shaded triangle equals the area outside the shaded triangle, calculate the ratio $A B / B C$.
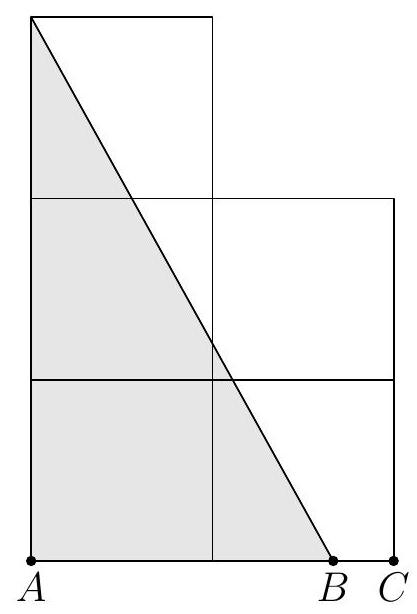
|
Let $s$ be the side length of the square. As the total area of the figure is $5 s^{2}$, the triangle should have area $5 s^{2} / 2$. Here $A B$ is a base of the triangle and the height is $3 s$, hence $A B=5 s / 3$. Since $A C=2 s$, we get $B C=s / 3$ and we obtain the final answer $A B: B C=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Simplify
$$
\frac{1}{1+a+a b}+\frac{1}{1+b+b c}+\frac{1}{1+c+c a} .
$$
|
We may let $a=y / x, b=z / y, c=x / z$ for some real numbers $x, y, z$. Then
$$
\begin{aligned}
\frac{1}{1+a+a b}+\frac{1}{1+b+b c}+\frac{1}{1+c+c a} & =\frac{1}{1+y / x+z / x}+\frac{1}{1+z / y+x / y}+\frac{1}{1+x / z+y / z} \\
& =\frac{x}{x+y+z}+\frac{y}{x+y+z}+\frac{z}{x+y+z} \\
& =1 .
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Lisa considers the number
$$
x=\frac{1}{1^{1}}+\frac{1}{2^{2}}+\cdots+\frac{1}{100^{100}} .
$$
Lisa wants to know what $x$ is when rounded to the nearest integer. Help her determine its value.
|
The answer is 1 . Indeed, note that
$$
x \leq 1+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\cdots+\frac{1}{2^{100}} .
$$
By the formula for the sum of a geometric series, we see that
$$
x \leq 1+\frac{1}{2}-\frac{1}{2^{101}} \text {. }
$$
Thus $x<3 / 2$, and the closest integer to $x$ is 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which prime numbers $p$ is $p^{2}+2$ also prime? Prove your answer.
|
The answer is $p=3$. This indeed works, since $3^{2}+2=11$.
Consider any other prime number $p \neq 3$. Then it follows that $p^{2} \equiv 1(\bmod 3)$; i.e. that $p$ leaves remainder 1 when divided by 3 . Consequently, $p^{2}+2$ is divisible by 3 . Since $p \geq 2$, we have $p^{2}+2 \geq 7$ as well, thus $p^{2}+2$ cannot be prime in this case.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find the minimal natural number $n$ with the following property: It is possible to tile the plane with squares whose side lengths belong to the set $\{1,2, \ldots, n\}$ so that no two squares with the same side length touch along a segment of an edge.
Remark. Squares with the same side length can touch at a vertex, however. Not all of the side lengths from 1 to $n$ need to be used in the tiling.
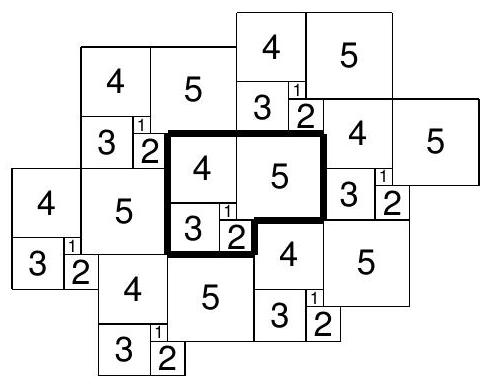
Figure 1
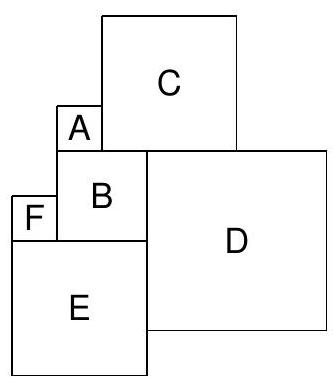
Figure 2
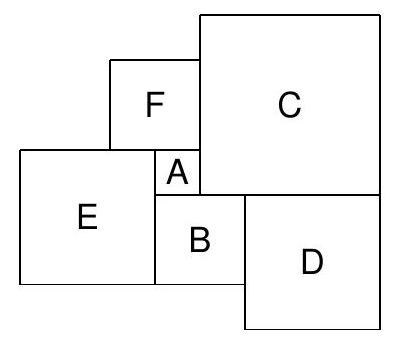
Figure 3
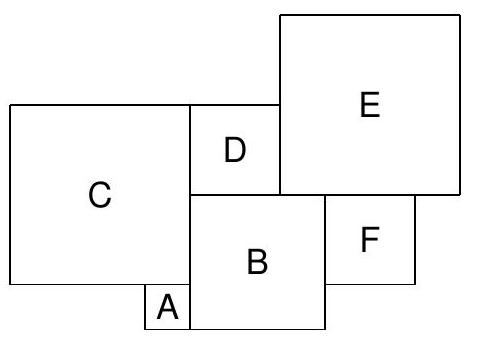
Figure 4
|
The answer is $n=5$. The desired tiling is shown in Figure 1. It is formed by translation from the L-shaped region in bold borders. Since none of the five squares in this region border on squares of like side length, neither does any square in the infinite tiling.
To show that $n \leq 4$ does not work, it is necessary to plow through many arrangements of the tiles until reaching a contradiction. We present one method of structuring the argument. Some square in the tiling must have minimal size. Its four sides must be covered by squares larger than itself. If one side is covered by squares that protrude on both ends (pictorially, $\square$ or $\square$ ), then it becomes impossible to cover the opposite side; consequently any minimal square must be covered by four squares in the pinwheel arrangement $\Vdash$.
Assume first that the smallest square is the $1 \times 1$ and it is surrounded by a $2 \times 2$ and a $3 \times 3$ in the manner of A, B, C in Figure 2. Now the upper left corner of $\mathrm{D}$ must be filled by a $4 \times 4$ (a $1 \times 1$ would lack the necessary pinwheel layout $)$ and likewise there is a $3 \times 3$ at $\mathrm{E}$. Now the corner $\mathrm{F}$ cannot be filled with a $4 \times 4$ square without wrecking the pinwheel at $\mathrm{A}$, so it must be a $1 \times 1$. The space above $\mathrm{F}$ is now calling for either a $3 \times 3$ or a $4 \times 4$, either of which disrupts the pinwheel at $\mathrm{A}$. Thus the arrangement $\mathrm{ABC}$ at Figure 2 is impossible.
So if a $2 \times 2$ borders on a $1 \times 1$, the resulting cavity must be filled by a $4 \times 4$ as in $\mathrm{ABC}$ of Figure 3 . The $3 \times 3$ at $\mathrm{D}$ is clear. The left side of the A-pinwheel must have a $3 \times 3$ (E) since a $4 \times 4$ would leave untilable space below B. The remaining spot on the pinwheel is necessarily occupied by a $2 \times 2$ (F). Now AFE of Figure 3 is the same configuration as ABC of Figure 2 . Hence this case is also impossible. So a $2 \times 2$ cannot touch a $1 \times 1$.
Thus any $1 \times 1$ must be covered alternately by $3 \times 3$ 's and $4 \times 4$ 's as at ABC of Figure 4 . The $2 \times 2$ at D follows immediately, and since a $1 \times 1$ cannot touch a $2 \times 2$, we must use a $4 \times 4$ at $\mathrm{E}$ and a $2 \times 2$ at $\mathrm{F}$. Now the space around $\mathrm{F}$ must be covered by a $3 \times 3$ and a $4 \times 4$ which is impossible.
We have left for last the case where there are no $1 \times 1$ 's. Since a tiling using only $3 \times 3$ 's and $4 \times 4$ 's is clearly impossible, the minimal square must be $2 \times 2$, covered alternately by $3 \times 3$ 's and $4 \times 4$ 's as at $\mathrm{D}$ and $\mathrm{CBE}$ of Figure 4 (ignore square A). We derive the $2 \times 2$ at $\mathrm{F}$ and the resulting contradiction in the same manner as the preceding case.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A point $P$ lies inside a regular hexagon $A B C D E F$. The distances from $P$ to the sides $A B, B C, C D, D E, E F$, and $F A$ are respectively $1,2,5,7,6$, and $x$. Find $x$.
|
Opposite sides of a regular hexagon are parallel. The sum of the distances from $P$ to $A B$ and to $D E$ is simply the distance between $A B$ and $D E$, which must therefore equal $1+7=8$. Because of the symmetry of the hexagon, the distance between any pair of opposite sides must be 8. Applying this to sides $C D$ and $F A$, we see that the distance from $P$ to $C D$ is 5 so the distance from $P$ to $F A$ must be $8-5=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two villages, $A$ and $B$, lie on opposite sides of a straight river in the positions shown. There will be a market in village $B$, and residents of village $A$ wish to attend. The people of village $A$ would like to build a bridge across and perpendicular to the river so that the total route walked by residents of $A$ to the bridge, across the bridge, and onward to $B$ is as short as possible. How can they find the exact location of the bridge, and how long will the route be?
|
For convenience, we label the point $X$, the foot of the perpendicular from $A$ to the river. We also label $Y$, the point where the perpendicular $B Y$ to the river through $B$ meets the parallel $A Y$ to the river through $A$. The key construction is to translate $B$ southward $1 \mathrm{~km}$ to point $E$. Let $A C D B$ be any route. Then segments $D C$ and $B E$ are congruent and parallel,
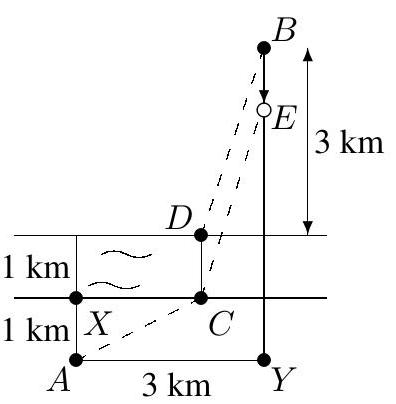
making a parallelogram $D C E B$. The total route is $A C+C D+D B=A C+C E+E B$. But by the triangle inequality, $A C+C E \geq A E$ so the total route cannot be shorter than $A E+E B=5+1=6 \mathrm{~km}$. (continued)
The residents of $A$ can ensure a 6 -kilometer route by putting the start $C$ of the bridge at the point where $A E$ crosses the lower bank of the river. In this situation, since $A, C$, and $E$ lie on a line, the triangle inequality is an equality, so the total route is $A C+C D+D B=A C+C E+E B=A E+E B=5+1=6$.
Remark. Using the fact that triangles $A C X$ and $E A Y$ are similar if $A, C$, and $E$ are collinear, it is possible to calculate that the optimal location of point $C$ is $0.75 \mathrm{~km}$ east of $X$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all prime numbers $p$ such that $p^{2}+8$ is prime number, as well.
Remark. A number $p$ is prime if it has exactly 2 divisors: 1 and $p$. Numbers $2,3,5,7,11,13, \ldots$ are prime, while 4 and 2007 are not.
Hint. Write down first several prime numbers (hint - you can copy them from the paragraph above), calculate $p^{2}+8$ for them, and look at those that happen to be composite. Notice further that they all have a common divisor.
|
For $p=3$ we have $p^{2}+8=17$, which is prime. If $p \neq 3$ then $p$ is not divisible by 3 . The remainder of $p$ when divided by 3 is either 1 or 2 . This means that $p=3 k+1$ for some integer $k$, or $p=3 l+1$ for some integer $l$. In the first case we get $p^{2}=9 k^{2}+6 k+1$ and in the second, $p^{2}=9 l^{2}-6 l+1$. In both cases $p^{2}$ gives a remainder 1 upon division by 3 . Hence $p^{2}+8$ is divisible by 3 for all prime numbers different than 3 .
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$p$ is a prime number such that the period of its decimal reciprocal is 200 . That is,
$$
\frac{1}{p}=0 . X X X X \ldots
$$
for some block of 200 digits $X$, but
$$
\frac{1}{p} \neq 0 . Y Y Y Y \ldots
$$
for all blocks $Y$ with less than 200 digits. Find the 101st digit, counting from the left, of $X$.
|
Let $X$ be a block of $n$ digits and let $a=0 . X \ldots$ Then $10^{n} a=X . X \ldots$. Subtracting the previous two equalities gives us $\left(10^{n}-1\right) a=X$, i.e. $a=\frac{X}{10^{n}-1}$.
Then the condition that $a=\frac{1}{p}$ reduces to $\frac{1}{p}=\frac{X}{10^{n}-1}$ or $p X=10^{n}-1$. For a given $p$ and $n$, such an $X$ exists if and only if $p$ divides $10^{n}-1$. Thus $p$ divides $10^{200}-1$ but not $10^{n}-1,1 \leq n \leq 199$. Note that $10^{200}-1$ can be factored in this way:
$$
\begin{aligned}
10^{200}-1 & =\left(10^{100}\right)^{2}-1 \\
& =\left(10^{100}-1\right)\left(10^{100}+1\right) .
\end{aligned}
$$
Since $p$ is prime and does not divide $10^{100}-1$, it must divide $10^{100}+1$, so that $10^{100}+1=k p$ for an integer $k$ and $X=\frac{\left(10^{100}-1\right)\left(10^{100}+1\right)}{p}=\left(10^{100}-1\right) k$.
If $p=2,3,5$, or 7 , the fraction $\frac{1}{p}$ either terminates or repeats less than 200 digits. Therefore $p>10$ and $k<\frac{10^{100}}{p}<10^{99}$. Now let us calculate the 101st digit of $X=10^{100} k-k$, i.e. the digit representing multiples of $10^{99}$. Since $10^{100} k$ is divisible by $10^{100}$, its $10^{99} \mathrm{~s}$ digit and all later digits are 0 . Since $k<10^{99}$, $k$ does not contribute a digit to the $10^{99} \mathrm{~s}$ place, but it generates a borrow to this place, changing it into a 9. Thus the 101st digit of $X$ is a 9 .
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The country of Squareland is shaped like a square and is divided into 64 congruent square cities. We want to divide Squareland into states and assign to each state a capital city so that the following rules are satisfied:
(a) Every city lies entirely within one state.
(b) Given any two states, the numbers of cities in them differ by at most 1 .
(c) Any city in a state shares at least one corner with the state's capital.
What is the smallest possible number of states?
|
In the diagram below, no city shares a corner with any two of the cities marked X. Therefore the nine X's are

in nine different states. The diagram at right shows that nine states are also sufficient ( $*$ denotes capital).

|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A palindrome is a positive integer that reads the same forward and backward, like 2552 or 1991. Find a positive integer greater than 1 that divides all four-digit palindromes.
|
We claim that 11 divides all four digit palindromes. Note that any four digit palindrome $a b b a$ is the sum
$$
a b b a=a 00 a+b b 0=a \times 1001+b \times 110 .
$$
Now, 110 is a multiple of 11 , since it is $11 \times 10$, and 1001 is a multiple of 11 , since it is $11 \times 91$. Thus, $a 00 a$ and $b b 0$ are multiples of 11 , so their sum is also a multiple of 11 .
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the following figure-not drawn to scale!- $E$ is the midpoint of $B C$, triangle $F E C$ has area 7, and quadrilateral $D B E G$ has area 27. Triangles $A D G$ and $G E F$ have the same area, $x$. Find $x$.

|
The answer is $x=8$.
Use the notation [.] to denote the area of a polygon. Draw $G B$; notice that triangles $G B E$ and $G E C$ have equal bases and altitudes, so $[G B E]=[G E C]=x+7$. Since $[A B E]=27+x$, we have $[G D B]=$ $20-x$.
Likewise, if we draw $A C$, we see that $[A B E]=[A E C]=27+x$, so $[A G C]=20$, which implies that $[C A D]=20+x$.
Now triangles $G A D$ and $G D B$ have the same altitude (from $G$ to $A B$ ), so their bases are proportional to their respective areas. In other words,
$$
\frac{A D}{D B}=\frac{[G A D]}{[G D B]}=\frac{x}{20-x}
$$
But $A D$ and $D B$ are also the bases of triangles $C A D$ and $C B D$, which have the same altitude (from $C$ to $A B)$. Hence
$$
\frac{A D}{D B}=\frac{[C A D]}{[C D B]}=\frac{20+x}{34+x}
$$
Equating these two fractions leads to the quadratic equation $34 x+x^{2}=400-x^{2}$; the only positive solution is $x=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a$ and $b$ be positive whole numbers such that $\frac{4.5}{11}<\frac{a}{b}<\frac{5}{11}$. Find the fraction $\frac{a}{b}$ for which the sum $a+b$ is as small as possible. Justify your answer.
#
|
By multiplying numerators and denominators by 7 , we can rewrite the inequalities as follows:
$$
\frac{7 \cdot 4.5}{7 \cdot 11}<\frac{a}{b}<\frac{7 \cdot 5}{7 \cdot 11} \Rightarrow \frac{31.5}{77}<\frac{a}{b}<\frac{35}{77}
$$
We now see that the fraction $\frac{a}{b}=\frac{33}{77}$ works: $\frac{31.5}{77}<\frac{33}{77}<\frac{35}{77}$. The fraction reduces to $\frac{a}{b}=\frac{3}{7}$, and its sum $a+b$ is $3+7=10$.
But is this the minimal possible sum $a+b$ ? To show that no other fraction with a smaller $a$ works, we multiply the inequalities by $11 b$ and solve for $b$ :
$$
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. In the $O-E$ game, a round starts with player $A$ paying $c$ cents to player $B$. Then $A$ secretly arranges the numbers $1,3,5,7,9,11,13$ in some order as a sequence $a_{1}, a_{2}, \ldots, a_{7}$, and $B$ secretly arranges $2,4,6,8,10,12,14$ as a sequence $b_{1}, b_{2}, \ldots, b_{7}$. Finally, the players show their sequences and $B$ pays $A$ one cent for each $i$ in $X=\{1,2,3,4,5,6,7\}$ such that $a_{i}<b_{i}$. This finishes the round. What number $c$ would make the game fair? (The game is fair if the total payments by $A$ to $B$ equals the total payments by $B$ to $A$ after all possible distinct rounds are played exactly once.)
|
I. Let $k$ be in $X$. There are $7 ! 6 !(8-k)$ choices of the sequences $a_{1}, a_{2}, \ldots, a_{7}$ and $b_{1}, b_{2}, \ldots, b_{7}$ for which $2 k-1$ is an $a_{j}$ with $a_{j}<b_{j}$. Indeed, the $a$ 's can be any of the 7 ! permutations of the 7 odd integers; then $j$ is the subscript such that $a_{j}=2 k-1$, and $b_{j}$ must be one of the $8-k$ numbers in $\{2 k, 2 k+2, \ldots, 14\}$; the remaining 6 even integers can be arranged in 6 ! ways.
The total of the payments by $B$ to $A$ for the $(7 !)^{2}$ possible rounds is then
$$
\sum_{k=1}^{7} 7 ! 6 !(8-k)=7 ! 6 !(7+6+\cdots+1)=7 ! 6 ! 28=(7 !)^{2} 4
$$
$A$ pays to $B$ a total of $(7 !)^{2} c$; so $c=4$ makes the game fair.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Prove that $1993^{1993}+1994^{1994}+1995^{1995}+1996^{1996}$ is divisible by 10 .
|
Since $5^{2}=25$ ends in 5 again, and $6^{2}=36$ ends in 6 again, no matter to what power we raise 5 or 6 , the resulting numbers will end in 5 or 6 , respectively. Thus, $1995^{1995}$ ends in 5 and $1996^{1996}$ ends in 6 . Further, $4^{1}=1,4^{2}=16,4^{3}=\ldots 4,4^{4}=\ldots 6$, etc, i.e. an odd power of 4 ends in 4, and an even power of 4 ends in 6 (why?) Hence, $1994^{1994}$ ends in 6 . So, the last digit of $1994^{1994}+1995^{1995}+1996^{1996}$ is the same as the last digit of $6+5+6=17$, i.e. it ends in 7 . It remains to show that $1993^{1993}$ ends in 3 (so that $3+7=10$.)
Indeed, $3^{1}=3,3^{2}=9,3^{3}=\ldots 7,3^{4}=\ldots 1,3^{5}=\ldots 3$, and the pattern will be $3,9,7,1,3,9,7,1, \ldots$, etc. So we need to figure out into which of these slots will the 1993-rd power of 3 fall. Equivalently, we need to find the remainder of 1993 when divided by 4 (the length of the pattern above is 4). Now, $1993=4 \cdot 498+1: 3^{1993}$ will complete 498 cycles of the pattern, and will end in 3 . This shows that $1993^{1993}$ ends in 3 . Therefore, the last digit of the total sum is the last digit of $3+6+5+6=20$, 0 , which makes the sum divisible by 10 .
|
0
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Determine all positive integers $n$ for which the equation
$$
x^{n}+(2+x)^{n}+(2-x)^{n}=0
$$
has an integer as a solution.
Answer: $n=1$.
#
|
If $n$ is even, $x^{n}+(2+x)^{n}+(2-x)^{n}>0$, so $n$ is odd.
For $n=1$, the equation reduces to $x+(2+x)+(2-x)=0$, which has the unique solution $x=-4$.
For $n>1$, notice that $x$ is even, because $x, 2-x$, and $2+x$ have all the same parity. Let $x=2 y$, so the equation reduces to
$$
y^{n}+(1+y)^{n}+(1-y)^{n}=0 \text {. }
$$
Looking at this equation modulo 2 yields that $y+(1+y)+(1-y)=y+2$ is even, so $y$ is even. Using the factorization
$$
a^{n}+b^{n}=(a+b)\left(a^{n-1}-a^{n-2} b+\cdots+b^{n-1}\right) \text { for } n \text { odd, }
$$
which has a sum of $n$ terms as the second factor, the equation is now equivalent to
$$
y^{n}+(1+y+1-y)\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right)=0
$$
or
$$
y^{n}=-2\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right) .
$$
Each of the $n$ terms in the second factor is odd, and $n$ is odd, so the second factor is odd. Therefore, $y^{n}$ has only one factor 2 , which is a contradiction to the fact that, $y$ being even, $y^{n}$ has at least $n>1$ factors 2 . Hence there are no solutions if $n>1$.
#
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given a permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ of the sequence $0,1, \ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \ldots, 3,2,0)$ regular?
Answer: $n=2$ and $n=2^{k}-1, k$ positive integer.
#
|
A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.
If $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.
Call a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is
$$
\begin{aligned}
& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\
& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\
& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\
& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\
& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\
& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\
& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\
& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)
\end{aligned}
$$
After exchanging 0 and 2 , the second pass is
$$
\begin{aligned}
& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\
& (1,2,14,15,12,13,10,11,8,9,0,7,4,5,6,3) \\
& (1,2,14,15,12,13,0,11,8,9,10,7,4,5,6,3) \\
& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)
\end{aligned}
$$
After exchanging 0 and 3 , the third pass is
$$
\begin{aligned}
& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\
& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\
& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\
& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)
\end{aligned}
$$
After exchanging 0 and 4 , the fourth pass is
$$
\begin{aligned}
& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\
& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)
\end{aligned}
$$
And then one can successively perform the operations to eventually find
$$
(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)
$$
after which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.
Case 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.
Case 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation
$$
[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \ldots,[2 R: 3 R-1],[R: 2 R-1]
$$
$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.
Then it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.
Starting from $P_{r}, r>0,0$ is successively transposed with $R, 3 R, \ldots, N-R$. The numbers $0, N-R, N-3 R, \ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become
$$
\begin{gathered}
{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \ldots} \\
{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}
\end{gathered}
$$
Note that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.
Now $0, N-R+1, N-3 R+1, \ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become
$$
\begin{gathered}
{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}
\end{gathered}
$$
The same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \ldots, R+u$ are shifted, $u=0,1,2, \ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with
$$
[1: 2 R-1],(0),[N-2 R: N-1], \ldots,[2 R: 4 R-1]
$$
which is precisely $P_{r+1}$.
Since $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.
Case 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \geq 1$, and define $P_{0}, \ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :
$$
\left[1: 2^{a}-1\right],(0),\left[N-2^{a}: N-1\right],\left[N-2^{a+1}: N-2^{a}-1\right], \ldots,\left[2^{a+1}: 3 \cdot 2^{a}-1\right],\left[2^{a}: 2^{a+1}-1\right]
$$
But then 0 is transposed with $2^{a}, 3 \cdot 2^{a}, \ldots,(2 b-1) \cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.
Comment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values
$$
1,2,5,14,47,189,891,4815,29547
$$
which is not catalogued at oeis.org.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. let $A, B, C$ and $D$ be four points lying in this order on a circle. Assume that there is a point $K$ on the line $A B$ such that $B D$ bisects the line $K C$ and $A C$ bisects the line $K D$. Determine the smallest possible value that $\left|\frac{A B}{C D}\right|$ can take.
|
Response: The minimum is 2.
Solution: We only use non-oriented (i.e., positive) distances.
We obtain a construction if $A B C D$ is an isosceles trapezoid with base $A B=2 C D$ and $K$ the midpoint of $A B$.
The condition on the midpoints implies that $[A D C]=[A K C]$ where the bracket notation denotes the area of the triangle. If we set $\alpha:=\angle C A D=\angle D B C$ and $\beta:=\angle B A C=\angle B D C$, we get
$$
\begin{aligned}
& {[A D C]=\frac{1}{2} \sin (\alpha) \cdot A C \cdot A D} \\
& {[A K C]=\frac{1}{2} \sin (\beta) \cdot A C \cdot A K}
\end{aligned}
$$
Thus, $A K / A D=\sin (\alpha) / \sin (\beta)$. Applying the Law of Sines to triangle $\triangle B C D$, we obtain
$$
\frac{\sin (\alpha)}{\sin (\beta)}=\frac{C D}{B C}
$$
and therefore $A K / C D=A D / B C$. By symmetry, $B C / C D=B C / A D$. Finally, using the AM-GM inequality:
$$
\frac{A B}{C D}=\frac{A K}{C D}+\frac{B K}{C D}=\frac{A D}{B C}+\frac{B C}{A D} \geq 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the smallest possible value of the expression
$$
\frac{a b+1}{a+b}+\frac{b c+1}{b+c}+\frac{c a+1}{c+a}
$$
where $a, b, c \in \mathbb{R}$ satisfy $a+b+c=-1$ and $a b c \leq-3$.
|
Solution: The minimum is 3 , which is obtained for $(a, b, c)=(1,1,-3)$ and permutations of this triple.
As $a b c$ is negative, the triple $(a, b, c)$ has either exactly one negative number or three negative numbers. Also, since $|a b c| \geq 3$, at least one of the three numbers has absolute value greater than 1 .
If all of $a, b, c$ were negative, the previous statement would contradict $a+b+c=-1$, hence exactly one of $a, b, c$ is negative.
Wlog let $c$ be the unique negative number. So $a, b>0>c$, as the value 0 isn't possible by $|a b c| \geq 3$. Let $S$ be the given sum of fractions. We then have
$$
\begin{aligned}
S+3 & =\sum_{c y c} \frac{a b+1+a+b}{a+b}=\sum_{c y c} \frac{(a+1)(b+1)}{a+b}=\sum_{c y c}-\frac{(a+1)(b+1)}{c+1} \\
& \geq \sum_{c y c}|a+1|=(a+1)+(b+1)-(c+1)=2 a+2 b+2
\end{aligned}
$$
using AM-GM on the three pairs of summands respectively for the inequality. We can do this since $a+1, b+1>0$ and $-(c+1)=a+b>0$, so every summand is positive.
So all we want to do now is show $a+b \geq 2$, to conclude $S \geq 3$. From the two given conditions we have $a b(1+a+b) \geq 3$. If $a+b<2$, then $a b \leq\left(\frac{a+b}{2}\right)^{2}<1$ and thereby $a b(1+a+b)<3$. So the implication $a b(1+a+b) \geq 3 \Rightarrow a+b \geq 2$ is indeed true.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Determine all integers $n \geq 3$ such that
$$
n!\mid \prod_{\substack{p<q \leq n \\ p, q \text { prime }}}(p+q)
$$
Remark: The expression on the right-hand side denotes the product over all sums of two distinct primes less than or equal to $n$. For $n=6$, this is equal to $(2+3)(2+5)(3+5)$.
|
Solution:For a fixed $n \geq 3$, let us denote the product on the right by $P(n)$ and let $r$ be the largest prime less than or equal to $n$. We now observe that
$$
r|n!| P(n)=P(r)
$$
and therefore there are primes $p<q \leq r$ with $r \mid p+q$. But $0<p+q<2 r$ implies $p+q=r$. Since $r \geq 3$ is an odd prime, we must have $p=2$ and $q=r-2$ is an odd prime. But now we also have
$$
r-2|n!| P(n)=P(r)=P(r-2) \prod_{\substack{s \leq r-2 \\ s \text { prime }}}(r+s)
$$
Hence either $r-2 \mid P(r-2)$ and similar to the above case we find that $r-4$ is prime, or there is a prime $s \leq r-2$ with $r-2 \mid r+s$. Since $r-2<r+s<3(r-2)$, we must have $r+s=2(r-2)$ and again $s=r-4$ is prime. We conclude that all of $r, r-2, r-4$ are prime and they have distinct residues modulo 3 , it follows that $r-4=3$ and thus $r=7$. It remains to check the values $n=7,8,9$ and 10 .
Observing that
$$
7!=2^{4} \cdot 3^{2} \cdot 5 \cdot 7 \mid 2^{6} \cdot 3^{3} \cdot 5^{2} \cdot 7=P(7)
$$
we find that $n=7$ is a solution. However, since $P(7)=P(8)=P(9)=P(10)$ and since all of $8!, 9$ !, 10 ! are divisible by $2^{7}$, we conclude that $n=7$ is the only solution.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Z1) Find all integer values that the expression
$$
\frac{p q+p^{p}+q^{q}}{p+q}
$$
where $p$ and $q$ are prime numbers.
Answer: The only integer value is 3 .
|
Solution: If $p$ and $q$ are both odd, then the numerator is odd and the denominator is even. Because an even number never divides an odd number, this does not yield an integer value, so we can assume that at least one of our primes is even, and therefore equal to 2. Because the expression is symmetric in $p$ and $q$, we can assume without restriction of generality that $q=2$.
So we enter $q=2$ and it is now sufficient to enter all integer values of the expression
$$
\frac{2 p+p^{p}+4}{p+2}=\frac{2(p+2)+p^{p}}{p+2}=2+\frac{p^{p}}{p+2}
$$
to find.
For this to be an integer, $p+2$ must be a divisor of $p^{p}$. But because $p$ is a prime number, all positive divisors of $p^{p}$ are the following: $1, p, p^{2}, \ldots, p^{p-1}$ and $p^{p}$. If $p>2$, then we have
$$
p2$ the number $p+2$ never divides $p^{p}$ and we do not get an integer value. The only case that remains is $p=q=2$, which results in a value of 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
N1) Find all integer values that the expression
$$
\frac{p q+p^{p}+q^{q}}{p+q}
$$
can take, where $p$ and $q$ are prime numbers.
|
Answer: The only attainable relative integer is 3. Solution: If $p$ and $q$ are odd, the numerator is odd but the denominator is even. Since an even number never divides an odd number, the expression is not a natural integer. Therefore, we can assume that at least one of the two primes is even. Since the expression is symmetric in $p$ and $q$, we can assume without loss of generality that $q=2$.
With $q=2$, it suffices to determine all the relative integers the following expression can take:
$$
\frac{2 p+p^{p}+4}{p+2}=\frac{2(p+2)+p^{p}}{p+2}=2+\frac{p^{p}}{p+2}
$$
For this expression to be an integer, it is necessary that $p+2$ is a divisor of $p^{p}$. But since $p$ is prime, the only positive divisors of $p^{p}$ are $1, p, p^{2}, \ldots, p^{p-1}$, and $p^{p}$. If $p>2$, we have
$$
p+2 > p \geq p^{1}
$$
Thus, for $p>2$, the expression $p+2$ never divides $p^{p}$, and we do not obtain any integer values. The only remaining case is when $p=q=2$, making the initial fraction equal to 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
N1) Determine all integer values that the expression
$$
\frac{p q+p^{p}+q^{q}}{p+q}
$$
can take, where $p$ and $q$ are both prime numbers.
Answer: The only possible integer value is 3 .
|
Solution: If both $p$ and $q$ are odd, then the numerator is odd while the denominator is even. Since an even number never divides an odd number, this does not lead to an integer value. Hence we can assume that one of our primes is even and therefore equal to 2 . Since the expression is symmetric in $p$ and $q$, we can assume without loss of generality that $q=2$.
Substituting $q=2$, it remains to determine all integer values taken by the expression
$$
\frac{2 p+p^{p}+4}{p+2}=\frac{2(p+2)+p^{p}}{p+2}=2+\frac{p^{p}}{p+2}
$$
In order for this to be an integer, we must have that $p+2$ is a divisor of $p^{p}$. But since $p$ is prime, the only positive divisors of $p^{p}$ are $1, p, p^{2}, \ldots, p^{p-1}$ and $p^{p}$. If $p>2$, then we have
$$
p2$ the expression $p+2$ never divides $p^{p}$ and we don't get integer values. The only case remaining is $p=q=2$, making the original expression equal to 3 .
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. the plane is divided into unit squares. Each square is to be colored with one of $n$ colors, so that the following applies: If four squares can be covered with an L-tetromino, then these squares have four different colors (the L-tetromino may be rotated and mirrored). Determine the smallest value of $n$ for which this is possible.
|
## Solution
Two of the seven fields within the figure on the left in Figure 1 can be covered simultaneously with an L-tetromino. These fields therefore have different colors, in particular $n \geq 7$. Assume that $n=7$ is possible and color the fields in the area as in Figure 1. The two fields to the right and left below the area must now have the colors 1 and 3, because otherwise two fields of the same color could be covered with an L-tetromino. The color of the two other fields on the right in Figure 1 is determined in the same way. Now there is no color left for the field with the marking, contradiction. An example for $n=8$ can be found in Figure 2 .

Figure 1: $n \geq 8$ applies.

Figure 2: $n=8$ is sufficient.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. let $a, b, c$ be positive real numbers with $a b c=1$. Determine all possible values that the expression
$$
\frac{1+a}{1+a+a b}+\frac{1+b}{1+b+b c}+\frac{1+c}{1+c+c a}
$$
can accept.
## Solution
|
Let $A$ be the given expression. The following applies because $a b c=1$
$$
\begin{aligned}
A & =\frac{1+a}{1+a+a b}+\frac{a(1+b)}{a(1+b+b c)}+\frac{a b(1+c)}{a b(1+c+c a)} \\
& =\frac{1+a}{1+a+a b}+\frac{a+a b}{1+a+a b}+\frac{a b+1}{1+a+a b} \\
& =\frac{2(1+a+a b)}{1+a+a b}=2
\end{aligned}
$$
The expression is therefore always equal to 2, regardless of $a, b, c$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The real numbers $a, b, c, d$ are positive and satisfy $(a+c)(b+d)=a c+b d$. Find the minimum of
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}
$$
Answer: 8.
|
Solution(Raphael):
After trying out some things one might suspect that the minimum is reached when $a=c$ and $b=d$. So we'll try to use an inequality with equality case $a=c$ and $b=d$. Going for the easiest such inequality one comes across:
$$
a c+b d=(a+c)(b+d) \geq 2 \sqrt{a c} \cdot 2 \sqrt{b d} \Leftrightarrow \sqrt{\frac{a c}{b d}}+\sqrt{\frac{b d}{a c}} \geq 4
$$
Where we just used AM-GM on the terms $(a+c)$ and $(b+d)$ and then divided everything by $\sqrt{a b c d}$, to get the second inequality.
Now if $a=c$ and $b=d$ then $\frac{a}{b}=\frac{c}{d}$ and $\frac{b}{c}=\frac{d}{a}$. So another inequality to try is:
$$
\frac{a}{b}+\frac{c}{d}+\frac{b}{c}+\frac{d}{a} \geq 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}
$$
which is once again AM-GM. So combining these two inequalities one gets:
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} \geq 2 \cdot\left(\sqrt{\frac{a c}{b d}}+\sqrt{\frac{b d}{a c}}\right) \geq 2 \cdot 4=8
$$
with equality only when $\frac{a}{b}=\frac{c}{d}$ and $\frac{b}{c}=\frac{d}{a}$.
Now we still have to show that numbers $a=c, b=d$ exist which fulfil the condition $a c+b d=$ $(a+c)(b+d)$ Plugging in $c=a$ and $d=b$ we get:
$$
a^{2}+b^{2}=4 a b \Leftrightarrow\left(\frac{a}{b}\right)^{2}-4 \frac{a}{b}+1=0
$$
which has the solutions $\frac{a}{b}=2 \pm \sqrt{3}$. so using $a=c=(2+\sqrt{3}) \cdot b=(2+\sqrt{3}) \cdot d$ fulfils the condition.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For which integers $n \geq 2$ can we arrange the numbers $1,2, \ldots, n$ in a row, such that for all integers $1 \leq k \leq n$ the sum of the first $k$ numbers in the row is divisible by $k$ ?
Answer: This is only possible for $n=3$.
|
Solution (Valentin): If we let $k=n$ we find that
$$
n \left\lvert\, \frac{n(n+1)}{2}\right.
$$
which implies that $n$ has to be odd. For $n=3$ the arrangement 1,3,2 satisfies the condition. From now on assume that $a_{1}, a_{2}, \ldots, a_{n}$ is a valid arrangement for an odd $n \geq 5$. If we now let $k=n-1$ we find that
$$
n-1 \left\lvert\, \frac{n(n+1)}{2}-a_{n} \Longrightarrow a_{n} \equiv n \cdot \frac{n+1}{2} \equiv \frac{n+1}{2} \quad \bmod n-1\right.
$$
But $1 \leq a_{n} \leq n$ and $n \geq 5$ implies that $a_{n}=\frac{n+1}{2}$ since $\frac{n+1}{2}+n-1$ would already exceed $n$. Now we let $k=n-2$ to find
$$
n-2 \left\lvert\, \frac{n(n+1)}{2}-\frac{n+1}{2}-a_{n-1} \Longrightarrow a_{n-1} \equiv \frac{n^{2}-1}{2}=(n-1) \cdot \frac{n+1}{2} \equiv \frac{n+1}{2} \quad \bmod n-2\right.
$$
But similarly to before since $1 \leq a_{n-1} \leq n$ and $n \geq 5$ this implies that $a_{n-1}=\frac{n+1}{2}$ as well, a contradiction. We conclude that $n=3$ is the only value for which this is possible.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. consider a $7 \times 7$ field that is divided into 49 unit squares. Into this field we want to place tiles in the shape of a Swiss cross, consisting of 5 unit squares. The edges of the crosses should lie on the lines of the field. Determine the smallest possible number of squares that must be marked on the field so that each cross, no matter where it is placed on the field, covers at least one marked square.
## Solution
|
Insert coordinates. It is easy to see that each cross represents one of the 7 squares
$$
(2,5),(3,2),(3,3),(4,6),(5,4),(6,2),(6,5)
$$
covered. This shows that 7 markings are sufficient. We now show that 7 marks are necessary. Assume not. The crosses with centers
$$
(2,2),(2,6),(3,4),(5,2),(5,6),(6,4)
$$
are disjoint, so each of these crosses must cover a marked field. Therefore, five markings are not enough. Assume that exactly 6 squares are marked. Then
each of the 6 crosses in (1) covers exactly one mark. Therefore, the squares $(1,1),(1,3),(1,4)$ and $(1,6)$ cannot be marked. By rotating and mirroring the cross arrangement (1) and analogous arguments, it follows that no square can be marked at the edge of the field. It also follows that the squares $(3,4),(4,3),(4,5)$ and $(6,4)$ cannot be marked. Consequently, $(4,4)$ is marked. The 5 crosses with center points
$$
(2,6),(3,3),(5,2),(5,6),(6,4)
$$
are disjoint and none contains the central square. Therefore, each covers a marked square and in particular the squares $(2,2),(2,4)$ and $(3,5)$ cannot be marked. If we replace the cross $(3,3)$ in (2) with $(2,3)$, we see analogously that the squares $(3,2)$ and $(3,4)$ cannot be marked. For reasons of symmetry, it now follows as before that not a single square other than $(4,4)$ can be marked, contradiction.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. A natural number $n \geq 2$ is called resistant if it is coprime with the sum of all its divisors (1 and $n$ included). What is the maximum length of a sequence of consecutive resistant numbers?
|
Response: The maximum length of such a sequence is 5.
Solution: (Louis) In this type of problem, it is important to try small values of $n$ in the hope that it will give us ideas to solve the problem. We see that among the numbers between 2 and 30, the most resistant numbers are $2,3,4,5,7,8,9,11,13$, $16,17,19,21,23,25,27,29$. On the one hand, we observe that among these numbers, the longest sequence of consecutive resistant numbers is the sequence $2,3,4,5$, of length 4. The length we are looking for is therefore at least 4, and we need to determine whether there is a longer sequence somewhere. On the other hand, it seems that there are only a few pairs of resistant pairs. It is therefore interesting to study the number of pairs to see what is actually happening.
For an even number $n$ to be resistant, it is necessary (but not sufficient) that the sum of its divisors be odd. Clearly, the sum of the divisors of $n$ is odd if and only if $n$ has an odd number of odd divisors. One can write $n=2^{k} m$ with $m$ odd, and then the odd divisors of $n$ are the divisors of $m$. Thus, $m$ must have an odd number of divisors, in other words, $m$ must be a perfect square. Since $2^{k}$ is either a perfect square or twice a perfect square, we find that for an even number to be resistant, it must be of the form $n=s^{2}$ or $n=2 s^{2}$.
Because perfect pairs are very rare among all numbers, it is expected that it will be difficult to find many pairs of successive numbers that are resistant. Let's try to formalize this intuition:
If $n$ and $n+2$ are two even resistant numbers, they must both be of the form $s^{2}$ or $2 s^{2}$.
- If $n=s^{2}$ and $n+2=t^{2}$, we have $2=t^{2}-s^{2}=(t-s)(t+s)$, but since the two factors have the same parity, it is impossible for their product to be 2.
- If $n=2 s^{2}$ and $n+2=2 t^{2}$, we get $2=2 t^{2}-2 s^{2}$, which simplifies to $1=t^{2}-s^{2}=(t-s)(t+s)$, the only solution in this case is $s=0$, which is impossible since $n \geq 2$.
For $n$ and $n+2$ to be two even resistant numbers, one of them must be of the form $s^{2}$ and the other must be of the form $2 t^{2}$. Is it possible that $n+4$ is also resistant? By the previous remark, for this to be the case, $n$ and $n+4$ must both be perfect squares or both be twice a perfect square.
- If they are both perfect squares, we get $4=t^{2}-s^{2}=(t-s)(t+s)$, and since the two factors have the same parity, we must necessarily have $(t-s)=(t+s)=2$ and thus $s=0$, which is impossible.
- If they are both twice a perfect square, we get $2=t^{2}-s^{2}$, and we have already proven above that this case is impossible.
We therefore observe that it is impossible to find three consecutive even numbers that are all resistant. One therefore concludes that there can be no sequence of length 6 or more.
We now find ourselves in a situation where we know that the answer is 4 or 5, without being able to say which is the right answer. From there, there are two ways to continue the problem: either you try to find a sequence of length 5, or you try to prove that there is no sequence of length 5. In the present case, as there is a very strict condition on the form that the two pairs of numbers in the sequence must have, it is interesting to look for a sequence of length 5 first, and if you don't succeed, you can try to find out what is preventing us from finding a set of length 5, so that you can either reaffirm the values studied or show that this will never be possible.
In order to find such a sequence, we first need to find two natural numbers $a$ and $b$ such that $\left|a^{2}-2 b^{2}\right|=2$. Those who know the Pell equation can use the formula that gives all the solutions to the equation written above, but it is also possible to proceed by brute force, just trying all the numbers to find the first pairs $(a, b)$ that are solutions. Before starting to search, one can also realize that in order to have a solution, $a$ must be even and close to $\sqrt{2} b$, which reduces the number of pairs to be tested. Whatever the method used, we find that the first solutions $(a, b)$ are
$$
(2,1),(4,3),(10,7),(24,17),(58,41)
$$
The last pair is already difficult to find if you don't know the Pell formula, but this is not important because by trying the first 4 pairs, we find that $(24,17)$ gives the sequence $575,576,577,578,579$ and a quick calculation shows that these 5 numbers are all resistant, which concludes the proof.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. let $q(n)$ be the sum of the digits of the natural number $n$. Determine the value of
$$
q\left(q\left(q\left(2000^{2000}\right)\right)\right)
$$
## Solution
|
It applies $q\left(2000^{2000}\right)=q\left(2^{2000}\right)$, because the two numbers only differ by appended zeros. We now estimate. The following applies $2^{2000}=4 \cdot 8^{666}<10^{667}$ and therefore
$$
q\left(2^{2000}\right) \leq 9 \cdot 667=6003
$$
Furthermore
$$
q\left(q\left(2^{2000}\right)\right) \leq 5+9+9+9=32 \quad \text { and } \quad q\left(q\left(q\left(2^{2000}\right)\right)\right) \leq 2+9=11
$$
On the other hand, $q(n) \equiv n(\bmod 9)$ applies to all natural numbers $n$. With $\varphi(9)=6$ this results in
$$
2000^{2000} \equiv 2^{333 \cdot 6+2}=\left(2^{6}\right)^{333} \cdot 4 \equiv 4 \quad(\bmod 9)
$$
The number you are looking for is therefore $\leq 11$ on the one hand and $\equiv 4(\bmod 9)$ on the other, i.e. equal to 4 .
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. let $m$ be a natural number greater than 1 . the sequence $x_{0}, x_{1}, x_{2}, \ldots$ is defined by
$$
x_{i}= \begin{cases}2^{i}, & \text { for } \quad 0 \leq i \leq m-1 \\ \sum_{j=1}^{m} x_{i-j} & \text { for } \quad i \geq m\end{cases}
$$
Find the largest $k$ such that there are $k$ consecutive sequential elements that are all divisible by $m$.
|
## Solution
Let $r_{i}$ be the remainder of $x_{i}$ when divided by $m$. Instead of the sequence $\left(x_{i}\right)$, we consider the sequence $\left(r_{i}\right)$. The recursion formula can be used to calculate the next, but also the previous one, from $m$ consecutive sequence members. Such $m$ consecutive links therefore determine the entire sequence. Because of $0 \leq r_{i} \leq m-1$ there are at most $m^{m}$ different $m$-tuples $\left(r_{i}, r_{i+1}, \ldots, r_{i+m-1}\right)$ of consecutive sequence members. According to the drawer principle, one of these $m$ tuples occurs several times in the sequence. This means that the sequence is periodic without a previous period (the elements can be calculated backwards).
Assume that $m$ consecutive $x_{i}$ are divisible by $m$. Then the sequence contains
( $\left.r_{i}\right) m$ consecutive zeros and from the recursion formula it follows that all sequence members are equal to zero, in contradiction to $x_{0}=r_{0}=1$.
On the other hand, the sequence $x_{i}$ can be continued backwards beyond $x_{0}$. The formula $x_{i}=x_{i+m}-\sum_{j=1}^{m-1} x_{i+j}$ now easily yields $x_{-1}=1$ and further $x_{-2}=x_{-3}=\ldots=x_{-m}=$ 0 . Due to the periodicity of $\left(r_{i}\right)$, there are therefore $m-1$ consecutive members in $\left(x_{i}\right)_{i \geq 0}$ that are divisible by $m$.
|
-1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. let $M$ be a finite set of real numbers with the following property: From every three different elements of $M$, two can always be selected whose sum lies in $M$. What is the maximum number of elements $M$ can have?
## Solution
|
Answer: 7 .
Assume that $M$ contains more than three positive elements and denote the four largest with $a>b>c>d>0$. According to the prerequisite, you can choose two of the three elements $a, b, c$ whose sum lies in $M$. Because of $a+b>a$ and $a+c>a$ and the maximality of $a$, these two sums are not in $M$. Consequently, $b+c must be \in M$ and because $b+c>b$, $a=b+c$. The same argument with the three elements $a, b, d$ shows that $a=b+d$ also applies. However, this implies $c=d$, contradiction. Consequently, $M$ contains at most three positive elements. Similarly, we show that $M$ also only contains at most three negative elements. Therefore, $|M| \leq 7$ applies (the zero can also still be in $M$).
On the other hand, for $a>0$ the following 7-element set has the required property:
$$
M=\{-3 a,-2 a,-a, 0, a, 2 a, 3 a\}
$$
The only sums of two different elements that are not in $M$ are $3 a+a, 3 a+2 a,(-3 a)+(-a)$ and $(-3 a)+(-2 a)$. The only problematic three-element subsets of $M$ are therefore $\{3 a, b,-3 a\}$, where $b= \pm a$ or $\pm 2 a$. In the case
$b>0$, however, $(-3 a)+b \in M$ applies, in case $b<0$ analogously $3 a+b \in M$. This shows everything.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. the polynomial $P(x)=x^{3}-2 x^{2}-x+1$ has the three real zeros $a>b>c$. Find the value of the expression
$$
a^{2} b+b^{2} c+c^{2} a
$$
## Solution
|
We set $A=a^{2} b+b^{2} c+c^{2} a$ and $B=a^{2} c+c^{2} b+b^{2} a$. Because $a>b>c$ applies
$$
A-B=(a-c)(c-b)(b-a)>0
$$
so $A$ is greater than $B$. In the following, we use the terms
$$
\begin{aligned}
u & =a+b+c \\
v & =a b+b c+c a \\
w & =a b c
\end{aligned}
$$
according to Vieta's theorem, $u=2, v=-1, w=-1$. Now applies
$$
\begin{aligned}
A+B & =a(a b+a c)+b(b c+b a)+c(c b+c a) \\
& =(a+b+c)(a b+b c+c a)-3 a b c=u v-3 w=1
\end{aligned}
$$
Using the identity $x^{3}+y^{3}+z^{3}-3 x y z=(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)$ further follows
$$
\begin{aligned}
A \cdot B & =\left(a^{3}+b^{3}+c^{3}-3 a b c\right) a b c+\left(a^{3} b^{3}+b^{3} c^{3}+c^{3} a^{3}-3 a^{2} b^{2} c^{2}\right)+9 a^{2} b^{2} c^{2} \\
& =u\left(u^{2}-3 v\right) w+v\left(v^{2}-3 u w\right)+9 w^{2}=-12
\end{aligned}
$$
Again according to Vieta, $A$ and $B$ are therefore the two zeros of the polynomial $Q(x)=x^{2}-x-12=(x+3)(x-4)$. Because $A>B$ this results in the value $A=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. find all natural numbers $k$ such that $3^{k}+5^{k}$ is a power of a natural number with exponent $\geq 2$.
## 1st solution
|
Assume that $3^{k}+5^{k}=n^{t}$ with $t \geq 2$. If $k$ is even, then $3^{k}+5^{k} \equiv 1+1=2$ $(\bmod 4)$, so the left side is even but not divisible by 4, a contradiction to $t \geq 2$. If $k$ is odd, then the following applies
$$
3^{k}+5^{k}=(3+5)\left(3^{k-1}-3^{k-2} \cdot 5+\ldots-3 \cdot 5^{k-2}+5^{k-1}\right)
$$
The second factor on the right is odd, because it consists of an odd number of summands, which are all odd. Consequently, $3^{k}+5^{k}$ is divisible by 8 but not by 16, so $t=3$ :
$$
3^{k}+5^{k}=n^{3}
$$
Obviously $k=1$ is a solution, we show that it is the only one. For $k \geq 2$ we consider the equation modulo 9. Since $k$ is odd, a quick calculation yields
$$
3^{k}+5^{k} \equiv 5^{k} \equiv\left\{\begin{array}{lll}
5, & k \equiv 1 & (\bmod 6) \\
8, & k \equiv 3 & (\bmod 6) \\
2, & k \equiv 5 & (\bmod 6)
\end{array} \quad(\bmod 9)\right.
$$
For the right-hand side, however, $n^{3} \equiv 0,1,8(\bmod 9)$. Consequently, $k \equiv 3(\bmod 6)$ must apply. We now look at the equation modulo 7. Since $k$ is odd, a quick calculation shows
$$
3^{k}+5^{k} \equiv\left\{\begin{array}{lll}
1, & k \equiv 1.5 & (\bmod 6) \\
5, & k \equiv 3 & (\bmod 6)
\end{array} \quad(\bmod 7)\right.
$$
For the right-hand side, however, $n^{3} \equiv 0,1,6(\bmod 7)$. Therefore, $k \equiv 1,5(\bmod 6)$ must apply, in contradiction to $k \equiv 3(\bmod 6)$.
## 2nd solution
You can also finish the proof as follows: The calculation modulo 9 shows that $k$ is divisible by 3, $k=3 l$. The equation now follows
$$
\left(3^{l}\right)^{3}+\left(5^{l}\right)^{3}=n^{3}
$$
which, according to Fermat's theorem, has no solution, contradiction.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. a regular 2008-vertical is somehow divided into many triangles with 2005 non-intersecting diagonals. Determine the smallest possible number of non-isosceles triangles that can occur in such a decomposition.
## 1st solution
|
We call an isosceles triangle good and a non-isosceles triangle bad. For a natural number $n$, let $n^{(2)}$ denote the number of ones in the binary representation of $n$. We will show more generally that in every triangulation of a regular $n$ vertex there are at least $n^{(2)}-2$ bad triangles. To do this, first consider the following:
Lemma 1: For any natural numbers $a, b$, $a^{(2)}+b^{(2)} \geq(a+b)^{(2)}$ with equality if and only if no carry occurs when adding $a+b$ in the binary system.
The main step consists of the following result:
Lemma 2: In every triangulation of a segment of the n-gon over an arc of $k \leq \frac{n}{2}$ sides at least $k^{(2)}-1$ bad triangles occur.
Proof. We use induction according to $k \geq 1$. For the degenerate case $k=1$ the assertion is trivial, we therefore assume $k>1$. The limiting diagonal of this segment is a side of a triangle $\Delta$ in the triangulation. The third vertex of $\Delta$ divides the arc into two partial arcs of lengths $a, b$ with $a+b=k$. According to the induction assumption, at least $a^{(2)}-1$ or $b^{(2)}-1$ bad triangles occur in the triangulation of these arcs. We distinguish between two cases:
(i) $\Delta$ is bad. Then a total of at least $\left(a^{(2)}-1\right)+\left(b^{(2)}-1\right)+1 \geq$ $(a+b)^{(2)}-1=k^{(2)}-1$ bad triangles occur.
(ii) $\Delta$ is good. Because of $k \leq \frac{n}{2}$ then $a=b=\frac{k}{2}$ must be. The number of bad triangles is therefore again at least $\left(a^{(2)}-1\right)+\left(b^{(2)}-1\right)=2\left(k^{(2)}-1\right) \geq k^{(2)}-1$.
We now come to the actual proof and again distinguish between two cases.
(a) One of the diagonals goes through the center of the $n$ vertex. In this case, $n=2 k$ is even and according to Lemma 2, the number of bad triangles is at least $2\left(k^{(2)}-1\right)=2\left(n^{(2)}-1\right)>n^{(2)}-2$.
(b) The center lies in the interior of a triangle $\Delta$ whose vertices divide the edge of the $n$-gon into three arcs of lengths $a, b, c$ with $a+b+c$. If $\Delta$ is bad, then the number of bad triangles is at least $\left(a^{(2)}-1\right)+\left(b^{(2)}-1\right)+\left(c^{(2)}-\right.$ 1) $+1 \geq(a+b+c)^{(2)}-2=n^{(2)}-2$. However, if $\Delta$ is good, then two of the three numbers $a, b, c$ are equal, oBdA let $a=b$. In this case, the number of bad triangles is at least $2 a^{(2)}+c^{(2)}-3 \geq\left((2 a)^{(2)}+1\right)+c^{(2)}-3 \geq n^{(2)}-2$.
Because $2008^{(2)}=7$, every triangulation contains at least 5 bad triangles. Finally, we construct another example with 5 bad triangles. Consider that every segment over an arc whose length is a power of two can be triangulated without bad triangles. If you do this for consecutive sectors of lengths 1024, 512, 256, 128, 64, 16 and 8, then the remaining 7-corner can of course be triangulated with 5 (bad) triangles. This shows everything.
## 2nd solution
We give a second argument that at least $n^{(2)}-2$ bad triangles exist.
Lemma 3 Let $k \leq \frac{n}{2}$ be a natural number.
(a) If a segment of the n-gon can be triangulated over an arc of $k$ sides without bad triangles, then $k$ is a power of two.
(b) If a segment of the n-corner can be triangulated over an arc of $k$ sides with s bad triangles, then so can every segment over an arc of $2 k$ sides.
Proof. For (a) we use induction on $k$, the case $k=1$ is trivial. The bounding diagonal of this segment is a side of an isosceles triangle $\Delta$ in the triangulation, and because of $k \leq \frac{n}{2}$ it must be the base of $\Delta$. The third vertex of $\Delta$ therefore divides the arc into two equally sized partial arcs whose length is a power of two according to the induction condition. Therefore, $k$ is also a power of two. For (b), "stretch" the sector together with its triangulation by a factor of 2 and add small isosceles triangles to the edge $k$.
We now consider a triangulation of the n-corner with the smallest possible number of bad triangles. If there is no bad triangle at all, then we choose a triangle that contains the center of the $n$-triangle in the interior or on the edge and apply (a) to the three segments that are bounded by its sides. The lengths of the corresponding arcs are therefore powers of two and two of them are equal. From this follows $n^{(2)} \leq 2$. We now assume that a bad triangle exists and denote the convex hull of all bad triangles by $H$, this is a convex polygon whose vertices are also vertices of the $n$ vertex. Let $\Delta$ be any good triangle. The two sides of equal size delimit segments of length $<\frac{n}{2}$, and we claim that there is no bad triangle in these segments. According to (b), the union $S$ of the two segments and $\Delta$ can be triangulated with the same number of bad triangles as one of the two segments. It therefore follows from the minimality that the other segment cannot contain any bad triangles. This shows that $H$ and $S$ have no common inner point and, in particular, that $\Delta$ is not contained in $H$. Since $\Delta$ was arbitrary, $H$ consists exclusively of bad triangles. The sides of $H$ therefore delimit segments that consist entirely of good triangles, whose length is therefore a power of two according to (a). The sum of these lengths is equal to $n$ and therefore $H$ has at least $n^{(2)}$ sides and the triangulation has at least $n^{(2)}-2$ bad triangles.
Note: The smallest possible number of bad triangles is actually $n^{(2)}-2$ (or 0 if $n$ is a power of two). The above construction for $n=2008$ immediately applies to the general case. The second solution also gives very precise information about the position of the bad triangles in an optimal triangulation.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. determine all odd natural numbers of the form
$$
\frac{p+q}{p-q}
$$
where $p>q$ are prime numbers.
## 1st solution
|
Let $n$ be this number. According to the prerequisite, $n(p-q)=p+q=(p-q)+2 q$, therefore $p-q$ is a divisor of $2 q$. Because $\operator name{ggT}(p-q, q)=1$, $p-q=1$ or $p-q=2$ therefore applies. In the first case, $p$ or $q$ is even, i.e. $p=3, q=2$ and $n=5$. In the second case, $p$ and $q$ are odd and therefore $n=\frac{p+q}{p-q}=\frac{2 q+2}{2}=q+1$ is even, contradiction. The only such number is therefore $n=5$.
## 2nd solution
Again, we consider the equation $n(p-q)=p+q$. We first assume that $p$ and $q$ are odd. $\operatorname{In}$ case $p \equiv q(\bmod 4)$ the left side of the equation is divisible by 4, but the right side is not. $\operatorname{In}$ case $p \not \equiv q(\bmod 4)$ the right side is divisible by 4, but the left side is not because $n$ is odd. This contradiction shows $q=2$. In this case, $n=\frac{p+2}{p-2}=1+\frac{4}{p-2}$, so $p-2$ is a divisor of 4 and therefore $p=3$ and $n=5$.
## 3rd solution
Transforming the equation from the second solution gives $p(n-1)=q(n+1)$. Since $p$ and $q$ are divisors, $n+1=a p$ and $n-1=b q$ for natural numbers $a, b$. Substitution shows $a=b$ and therefore $a(p-q)=(n+1)-(n-1)=2$. Again, $p-q=1$ or $=2$ and you can conclude as in the first solution.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Sei $A B C$ ein spitzwinkliges Dreieck mit $A B \neq B C$ und Umkreis $k$. Seien $P$ und $Q$ die Schnittpunkte von $k$ mit der Winkelhalbierenden beziehungsweise der Aussenwinkelhalbierenden von $\angle C B A$. Sei $D$ der Schnittpunkt von $A C$ und $P Q$. Bestimme das Verhältnis $A D: D C$.
## 1st solution:
|
By the inscribed angle theorem and the fact that $B P$ is the bisector of $\angle A B C, $\angle P C A=$ $\angle P B A=\angle P B C=\angle P A C$, so $\triangle A P C$ is isosceles. Similarly, let $R$ be a point on the line $A B$ such that $B$ lies between $A$ and $R$. Then $\angle Q A C=\angle Q B C=\angle Q B R=180^{\circ}-\angle Q B A=\angle Q C A$, where we've used the fact that $Q B$ is the exterior bisector of $\angle A B C$ and the fact that $A B Q C$ is an inscribed quadrilateral. So $\triangle A Q C$ is also an isosceles triangle. Since $P$ and $Q$ are both at equal distances from $A$ and $C$, $P Q$ is the perpendicular bisector of $A C$, which means that $D$ is the midpoint of the segment $A C$. We therefore obtain that $\frac{A D}{D C}=1$.
## 2nd solution:
As above, we demonstrate that $\triangle A Q C$ is isosceles at $Q$. Furthermore, $\angle C Q P=\angle C B P=$ $\angle A B P=\angle A Q P$, where we use the inscribed angle theorem and the fact that $B P$ is the interior bisector of $\angle A B C$. So $Q D$ is the bisector of $\angle A Q C$ and, since the triangle is isosceles, $Q D$ is the perpendicular bisector of $A B$. We therefore conclude that $\frac{A D}{D C}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. We have an $8 \times 8$ board. An inner edge is an edge between two $1 \times 1$ fields. We cut the board into $1 \times 2$ dominoes. For an inner edge $k$, $N(k)$ denotes the number of ways to cut the board such that the cut goes along the edge $k$. Calculate the last digit of the sum we get when we add all $N(k)$, where $k$ is an inner edge.
|
Solution: First, we calculate along how many inner edges a cut is made during a decomposition. In total, there are $7 \cdot 8$ horizontal and vertical inner edges each. During a decomposition, the board is cut along all inner edges except the 32 within a domino tile. Therefore, in each decomposition, cuts are made along $2 \cdot (7 \cdot 8) - 32 = 80$ inner edges. This means that each decomposition is counted 80 times. Therefore, we know that the sum of all $N(k)$ is divisible by 80. It follows that the last digit of the sum is zero.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Let $a, b, c$ be real numbers such that:
$$
\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=1
$$
Determine all values that the following expression can take:
$$
\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}
$$
|
## Solution:
$$
\begin{aligned}
& a+b+c=a+b+c \\\
& \overbrace{\left(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\right)}^{1} \cdot(a+b+c)=a+b+c \\
& \frac{a^{2}}{b+c}+\frac{a(b+c)}{b+c}+\frac{b^{2}}{a+c}+\frac{b(a+c)}{a+c}+\frac{c^{2}}{a+b}+\frac{c(a+b)}{a+b}=a+b+c \\
& \frac{a^{2}}{b+c}+\frac{b^{2}}{a+c}+\frac{c^{2}}{a+b}+a+b+c=a+b+c \\
& \frac{a^{2}}{b+c}+\frac{b^{2}}{a+c}+\frac{c^{2}}{a+b}=0
\end{aligned}
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The Brazilian IMO leader chooses two natural numbers $n$ and $k$ with $n>k$, and then tells these to his deputy and a participant. The leader then whispers a binary sequence of length $n$ into the deputy's ear. The deputy writes down all binary sequences of length $n$ that differ from the leader's sequence at exactly $k$ positions. (Example for $n=3$ and $k=1$: If the leader chooses 101, the deputy writes down 001, 100, 111.) The participant looks at the sequences written down by the deputy. Now the participant tries to guess the original sequence from the leader.
How many times does he need to guess at minimum (depending on $n$ and $k$) to ensure he guesses correctly at least once?
|
Remark: A binary sequence of length $n$ is a sequence of length $n$ that consists only of 0 and 1.
Solution: If we consider a fixed position in the solution sequence $L$, then $\binom{n-1}{k}$ of the listed sequences match $L$ at this position, and $\binom{n-1}{k-1}$ of the listed sequences differ from $L$ at this position. Since the participant knows $n$ and $k$, they can also calculate these values. Additionally, they can count how many of the listed sequences have a 0 or a 1 at this position and thus determine whether $L$ has a 0 or a 1 at this position, provided that $\binom{n-1}{k} \neq \binom{n-1}{k-1}$. They can do this for every position, so the solution sequence is unique for them, and they need only one guess.
If $\binom{n-1}{k} = \binom{n-1}{k-1}$, then $n-k = k$, so $k = \frac{n}{2}$. In this case, it is easy to see that the solution sequence generates the same list as its exact opposite $L^{-1}$ (if all 0s are replaced by 1s and vice versa): Every sequence on the list of $L$ differs from $L$ at half of the positions, so it differs from $L^{-1}$ at the other half of the positions and thus also appears on the list of $L^{-1}$. By symmetry, this also holds in reverse. Therefore, the lists of $L$ and $L^{-1}$ are indistinguishable, and the number of guesses required is at least 2. We now show that there can be no other sequence that generates the same list. Then the participant can eliminate all other possibilities by writing down all possible solutions and does not need to guess more than twice.
For this, the participant guesses the first number of the sequence, WLOG a 0 (since both $L$ and $L^{-1}$ are solutions, this will certainly lead to a possible solution). Then they strike out all $\left(\begin{array}{c}n-1 \\ k\end{array}\right)$ sequences that start with a 1 and strike out the 0 at the first position in all others. What remains (assuming the 0 was correct) are all sequences of length $n-1$ where $k$ entries have been changed. Since $k \neq \frac{n-1}{2}$, the solution is now unique for the participant according to the first case. The case with 1 works completely analogously. Therefore, there can be no other solutions.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. determine the largest natural number $k$ with the following property: The set of natural numbers can be divided into $k$ disjoint subsets $A_{1}, \ldots, A_{k}$ in such a way that every natural number $n \geq 15$ can be written as the sum of two different elements from $A_{i}$ for every $i \in\{1, \ldots, k\}$.
|
Solution For $k=3$ you can divide the natural numbers as follows:
$$
\begin{aligned}
& A_{1}=\{1,2,3\} \cup\{3 m \mid m \geq 4\} \\
& A_{2}=\{4,5,6\} \cup\{3 m-1 \mid m \geq 4\} \\
& A_{3}=\{7,8,9\} \cup\{3 m-2 \mid m \geq 4\}
\end{aligned}
$$
In $A_{1}$ all numbers $n \geq 12+1=13$ can be represented as a sum, in $A_{2}$ all $n \geq 11+4=15$ and in $A_{3}$ all $n \geq 10+7=17$. The numbers 15,16 are also sums of two elements from $A_{3}$ because $7+8=15$ and $7+9=16$.
Now assume $k \geq 4$. If $A_{1}, \ldots, A_{k}$ fulfill the condition, then surely $A_{1}, A_{2}, A_{3}, \bigcup_{4 \leq i \leq k} A_{i}$, so we can assume $k=4$. Set $B_{i}=A_{i} \cap\{1,2, \ldots, 23\}$. Then each of the numbers 15, 16, . . 23 must be written as a sum of two different elements from $B_{i}$, i.e. $\left|B_{i}\right| \geq 5$. On the other hand, $\left|B_{1}\right|+\left|B_{2}\right|+\left|B_{3}\right|+\left|B_{4}\right|=23$, so there is an $i$ with $\left|B_{i}\right|=5$, write $B_{i}=\left\{x_{1}, x_{2}, \ldots, x_{5}\right\}$. Now note that the 10 numbers $15,16, \ldots 24$ can all be written as the sum of two different elements from $B_{i}$, but with different elements from $B_{i}$ you can form at most 10 such sums. We therefore sum over all such sums and obtain
$$
4\left(x_{1}, \ldots, x_{5}\right)=15+16+\cdots+24=195
$$
is a contradiction, since 195 is not divisible by 4.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Z1) If $p \geq 5$ is a prime number, let $q$ be the smallest prime number such that $q>p$ and let $n$ be the number of positive divisors of $p+q$ ( 1 and $p+q$ included).
a) Show that no matter which prime number $p$ is chosen, the number $n$ is greater than or equal to 4.
b) Find the smallest possible value $m$ that $n$ can take among all possible choices of $p$. That is:
$b_{1}$ ) Give an example of a prime number $p$ so that the value $m$ is reached.
$\mathrm{b}_{2}$ ) Show that there is no prime number $p$ for which the value of $n$ is less than $m$.
|
Solution: Since $p \geq 5$, the two prime numbers $p, q$ are both odd and therefore $p+q$ even, so $p+q$ is divisible by $1,2, \frac{p+q}{2}$ and $p+q$. In addition, $p+q>4$ and therefore the divisors mentioned are all different. This proves part a).
for part $\mathrm{b}_{1}$ ) we can test small cases of $p$ and see that $n$ does not appear to be less than 6. We also see that $p+q$ has exactly 6 divisors when $p=5, q=7$ (These would be $1,2,3,4,6,12$.
For $\mathrm{b}_{2}$ ), the key idea is that $\frac{p+q}{2}$ is not a prime number because it lies between the consecutive primes $p$ and $q$ $\left(p8$ and therefore the only remaining case is that $p+q=16$. We see that $5+7=1216$. Because every $p>7$ results in an even higher sum, we conclude that $p+q=16$ is not possible.
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6 Given a real number $a$ such that there is only one real number $x$ satisfying the inequality $\left|x^{2}+2 a x+3 a\right| \leqslant 2$, then the number of all real numbers $a$ that satisfy the condition is ().
(A) 1
(B) 2
(C) 3
(D) infinitely many
|
6 Let $f(x)=x^{2}+2 a x+3 a$, from $f\left(-\frac{3}{2}\right)=\frac{9}{4}$ we know, the graph of function $f(x)$ passes through the point $\left(-\frac{3}{2}, \frac{9}{4}\right)$. To make the inequality $\left|x^{2}+2 a x+3 a\right| \leqslant 2$ have only one solution, the graph of the parabola $f(x)=x^{2}+2 a x+3 a$ must be tangent to the line $y=2$, that is, the discriminant of $x^{2}+2 a x+3 a-2=0$ is $\Delta=4 a^{2}-4(3 a-2)=0$. Solving for $a$ yields $a=1$, 2. Therefore, the answer is B.
|
2
|
Inequalities
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) Person A and Person B stand facing each other 30 meters apart. They play "Rock-Paper-Scissors," with the winner moving forward 8 meters, the loser moving back 5 meters, and in the case of a tie, both moving forward 1 meter. After 10 rounds, they are 7 meters apart. How many rounds did they tie?
|
【Answer】Solution: Assume all games end in a draw, then the distance between the two people should be: $30-10 \times 2=10$ (meters), $(10-7) \div(8-5-2)=3$ times (win)
Draws are: $10-3=7$ (times),
Answer: The number of draws is 7.
Therefore, the answer is: 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (10 points) On the clock tower of a railway station, there is an electronic clock. On the boundary of the circular clock face, there is a small colored light at each minute mark. At 9:35:20 PM, there are $\qquad$ small colored lights within the acute angle formed by the minute and hour hands.
|
【Analysis】First, find the angle between the hour hand and the minute hand at 9:35:20 PM; then, according to the clock face being divided into 60 small segments, with each large segment corresponding to an angle of $30^{\circ}$ and each small segment corresponding to an angle of $6^{\circ}$, we can find the minute marks between the hour hand and the minute hand at 9:35:20 PM, and thus determine the number of small lights inside the angle between the hour hand and the minute hand at 9:35:20 PM.
【Solution】At 9:35:20 PM, the angle between the hour hand and the minute hand is:
$$
\begin{array}{l}
9 \times 30^{\circ}+35 \times 0.5^{\circ}+20 \times 0.5^{\circ} \div 60-\left(7 \times 30^{\circ}+20 \times 6^{\circ} \div 60\right) \\
=270^{\circ}+17.5^{\circ}+10^{\circ} \div 60-210^{\circ}-2^{\circ} \\
=\left(75 \frac{2}{3}\right)^{\circ} \\
\left(75 \frac{2}{3}\right)^{\circ} \div 6 \approx 12 \text { (units). }
\end{array}
$$
Therefore, there are 12 small lights inside the acute angle between the minute hand and the hour hand.
The answer is: 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given $\mathbf{Z}$ is the set of integers, the set $A=\{x|| x-3 |<\pi, x \in \mathbf{Z}\}, B=\left\{x \mid x^{2}-11 x+5<0\right.$, $x \in \mathbf{Z}\}, C=\left\{x|| 2 x^{2}-11 x+10|\geqslant| 3 x-2 \mid, x \in \mathbf{Z}\right\}, \bar{C}$ is the complement of $C$ in $\mathbf{Z}$, then the number of proper subsets of $A \cap B \cap \bar{C}$ is
A. 7
B. 8
C. 15
D. 16
|
1. A Obviously, the sets are $A=\{0,1,2,3,4,5,6\} ; B=\{0,1,2,3,4,5,6,7,8,9,10\}$; for set $C$, $\left|2 x^{2}-11 x+10\right| \geqslant|3 x-2| \Leftrightarrow\left(2 x^{2}-11 x+10\right)^{2}-(3 x-2)^{2} \geqslant 0 \Leftrightarrow\left(2 x^{2}-8 x+8\right)\left(2 x^{2}-14 x+12\right)$ $\geqslant 0 \Leftrightarrow(x-2)^{2}(x-1)(x-6) \geqslant 0$, hence $C=\{x \mid x \leqslant 1$ or $x \geqslant 6$ or $x=2, x \in \mathbf{Z}\}$, thus $\bar{C}=\{3,4,5\}$, so $A \cap B \cap \bar{C}=\{3,4,5\}$, it has $2^{3}-1=7$ proper subsets.
|
7
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3.70 Can integers be written in each cell of an infinitely large grid paper so that in every rectangle consisting of $4 \times 6$ cells and bounded by grid lines, the sum of all numbers is equal to (1) $10, (2) 1$?
|
[Solution]The filling principle shown in the right figure is: select two sets of diagonal lines in different directions. The first set is to select a line every 4 cells moved, and fill in 1 and 0 alternately on the line; the second set is to select a line every 6 cells moved, and fill in -1 and 0 alternately on the line. It is easy to verify that in each $4 \times 6$ rectangle, there are 3 1s, 2 -1s, and 5 0s, and their sum is 1. The unfilled cells all represent 0.
If all the numbers already filled in the table are changed to 1, and the empty cells still represent 0, then the sum of the 24 numbers in each $4 \times 6$ rectangle is 10.
Of course, there are simpler ways to fill the numbers so that the sum is 10. See the figure below.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$33 \cdot 1$. The units digit of the number $2137^{753}$ is
(A) 1.
(B) 3.
(C) 5.
(D) 7.
(E) 9.
(12th American High School Mathematics Examination, 1961)
|
[Solution] Let $\langle a\rangle$ denote the unit digit of the integer $a$. Clearly, if the unit digit of $a$ is $b$, then $\langle a\rangle=\langle b\rangle$, and $\left\langle a^{n}\right\rangle=\left\langle b^{n}\right\rangle$ (where $n$ is a natural number).
Also, $\left\langle 7^{0}\right\rangle=1,\left\langle 7^{1}\right\rangle=7,\left\langle 7^{2}\right\rangle=9,\left\langle 7^{3}\right\rangle=3$.
It is easy to prove that $\left\langle 7^{4 n+r}\right\rangle=\left\langle 7^{r}\right\rangle$, meaning the unit digit of the powers of 7 cycles with a period of 4.
Thus, $\left\langle 2137^{753}\right\rangle=\left\langle 2137^{4 \times 188+1}\right\rangle=\left\langle 2137^{1}\right\rangle=7$.
Therefore, the answer is $(D)$.
Note: Regarding the unit digit (last digit) of $a^{n}$ for natural numbers, the following conclusions can be drawn:
(1) If the unit digit of $a$ is $b$, then $\left\langle a^{n}\right\rangle=\left\langle b^{n}\right\rangle$;
(2) The unit digit of any power of a natural number ending in $0,1,5,6$ remains $0,1,5,6$;
(3) The unit digit of the $n$-th power of $2,3,4,7,8,9$ is as follows:
Table of unit digits of $a$:
\begin{tabular}{c|c|c|c|c|c|c}
\hline$n-a$ & 2 & 3 & 4 & 7 & 8 & 9 \\
\hline $4 k+1$ & 2 & 3 & 4 & 7 & 8 & 9 \\
$4 k+2$ & 4 & 9 & 6 & 9 & 4 & 1 \\
$4 k+3$ & 8 & 7 & 4 & 3 & 2 & 9 \\
$4 k$ & 6 & 1 & 6 & 1 & 6 & 1 \\
\hline
\end{tabular}
|
7
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
5. Select some numbers without repetition from $1,2, \ldots 15$, such that the sum of any two numbers is not a perfect square of a natural number, then the maximum number of numbers that can be selected is ( ).
|
Answer: 8
Explanation: First, we argue that the first digit can just form the square number 16, with the groups being $(1,15) \quad(2,14) \ldots(7,9)$, (8)
There are 8 groups in total, and from each group, at most 1 number can be selected, so the maximum number of selections is 8.
Second, construction: if the maximum is 8, then there is no 1, there is 15, there is no 10, there is 6, there is no 3, there is 11, there is no 14, there is 2, there is no 7, there is 9, this is the only way to select 8 numbers.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (15 points) Insert 2 " $\div$ " and 2 "+" between the 9 "1"s below to make the calculation result an integer. The smallest integer is $\qquad$
\begin{tabular}{|lllllllllll|}
\hline 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & $=$ & $?$ \\
\hline
\end{tabular}
|
【Answer】Solution: According to the analysis, we have
$$
\begin{array}{l}
111 \div 111+1 \div 1+1 \\
=1+1+1 \\
=3
\end{array}
$$
Answer: The smallest integer is 3.
Therefore, the answer is: 1.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Let $[x]$ denote the greatest integer not exceeding the real number $x$. The sequence $\left\{a_{n}\right\}$ satisfies:
$$
x_{1}=1, x_{n+1}=4 x_{n}+\left[\sqrt{11} x_{n}\right] \text {. }
$$
Then the units digit of $x_{2021}$ is
|
8.9.
Given $x_{2}=7$.
Notice, for any $x_{n} \in \mathbf{Z}_{+}$,
$$
\begin{array}{l}
4 x_{n}+\sqrt{11} x_{n}-1<x_{n+1}<4 x_{n}+\sqrt{11} x_{n} \\
\Rightarrow 5 x_{n}-(4-\sqrt{11})<(4-\sqrt{11}) x_{n+1}<5 x_{n} \\
\Rightarrow\left\{\begin{array}{l}
4 x_{n+1}-5 x_{n}<\sqrt{11} x_{n+1}, \\
\sqrt{11} x_{n+1}+(4-\sqrt{11})<4 x_{n+1}-5 x_{n}
\end{array}\right. \\
\Rightarrow 4 x_{n+1}-5 x_{n}=\left[\sqrt{11} x_{n+1}\right] \\
\Rightarrow x_{n+2}=4 x_{n+1}+\left[\sqrt{11} x_{n+1}\right]=8 x_{n+1}-5 x_{n} \text {. } \\
\end{array}
$$
Clearly, $x_{n+2} \equiv x_{n}(\bmod 2)$,
$$
x_{n+2} \equiv 3 x_{n+1}(\bmod 5) \text {. }
$$
Given $x_{1}=1, x_{2}=7$, it is easy to prove by mathematical induction that for any $n \in \mathbf{Z}_{+}, x_{n} \equiv 1(\bmod 2)$.
Combining $x_{1}=1, x_{2}=7$, we get when $n \geqslant 2$,
$$
x_{n} \equiv 2 \times 3^{n-2}(\bmod 5) \text {. }
$$
Thus, $x_{2021} \equiv 2 \times 3^{2019} \equiv 2 \times 3^{3} \equiv 4(\bmod 5)$. Therefore, the required unit digit is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. As shown in the figure, $\angle A C B=90^{\circ}, A C=B C, A D \perp C E$, $B E \perp C E$, with the feet of the perpendiculars being $D, E$ respectively. Given $A D=8$, $B E=3$, then $D E=$ $\qquad$
|
In Rt $\triangle A C D$ and Rt $\triangle C B E$, $A C=B C, \angle C A D=\angle B C E$, then $\triangle A C D \cong \triangle C B E \Rightarrow C E=A D=8, C D=B E=3 \Rightarrow D E=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. Given the sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=1, a_{n+1}=\frac{1}{8} a_{n}^{2}+m\left(n \in \mathbf{N}^{*}\right)$, if for any positive integer $n$, we have $a_{n}<4$, find the maximum value of the real number $m$.
|
15. Given the sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=1, a_{n+1}=\frac{1}{8} a_{n}^{2}+m\left(n \in \mathbf{N}^{*}\right)$, if for any positive integer $n$, we have $a_{n}<4$, note that as $n \rightarrow+\infty$, $(m-2)(n-1) \rightarrow+\infty$,
Therefore, there exists a sufficiently large $n$ such that $1+(m-2)(n-1)>4$, i.e., $a_{n}>4$, which is a contradiction!
Thus, $m \leq 2$. $\qquad$
Furthermore, when $m=2$, it can be proven that for any positive integer $n$, we have $0<a_{n}<4$.
When $n=1, a_{1}=1<4$, the conclusion holds;
Assume that for $n=k(k \geq 1)$, the conclusion holds, i.e., $0<a_{k}<4$,
Then $0<a_{k+1}=2+\frac{1}{8} a_{k}^{2}<2+\frac{1}{8} \times 4^{2}=4$,
i.e., the conclusion holds for $n=k+1$.
By the principle of mathematical induction, for any positive integer $n$, we have $0<a_{n}<4$.
In summary, the maximum value of the real number $m$ is 2.
20 points
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given the complex numbers $z_{1}=\sin \alpha+2 \mathrm{i}, z_{2}=1+\mathrm{i} \cos \alpha$ (where $\alpha$ is a real number, $\mathrm{i}$ is the imaginary unit). Then the minimum value of $\frac{13-\left|z_{1}+\mathrm{i} z_{2}\right|^{2}}{\left|z_{1}-\mathrm{i} z_{2}\right|}$ is $\qquad$
|
4. 2 .
Let
$$
\left|z_{1}-\mathrm{i} z_{2}\right|=\sqrt{(\sin \alpha+\cos \alpha)^{2}+1^{2}}=\sqrt{2+\sin 2 \alpha}=t,
$$
then $t \in[1, \sqrt{3}]$, and at this time we have
$$
\left|z_{1}+\mathrm{i} z_{2}\right|=(\sin \alpha-\cos \alpha)^{2}+3^{2}=10-\sin 2 \alpha=12-t^{2},
$$
so
$$
\frac{13-\left|z_{1}+\mathrm{i} z_{2}\right|^{2}}{\left|z_{1}-\mathrm{i} z_{2}\right|}=\frac{1+t^{2}}{t} \geqslant 2 .
$$
When $t=1$, i.e., $\alpha=k \pi-\frac{\pi}{4}(k \in \mathbf{Z})$, the equality holds.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25-13 In the same Cartesian coordinate system, there are infinitely many lines with the expression $y=k x+b$ (where $k, b$ are real numbers, and $k \neq 0$). Among these lines, no matter how they are selected, it is necessary to ensure that there are two lines passing through exactly the same quadrants. What is the minimum number of lines that need to be selected?
(A) 4 lines.
(B) 5 lines.
(C) 6 lines.
(D) 7 lines.
(China Guangzhou, Wuhan, Fuzhou, and other five cities Junior High School Mathematics League, 1992)
|
[Solution] According to the quadrants in which the lines are located, the lines on the plane can be divided into the following six categories:
$$
k>0,\left\{\begin{array}{l}
b>0, \\
b=0, \\
b<0 ;
\end{array}\right.\right.
$$
$$
k<0,\left\{\begin{array}{l}
b>0, \\
b=0, \\
b<0 .
\end{array}\right.\right.
$$
To ensure that there are two lines passing through exactly the same quadrants, at least 7 lines need to be drawn. Therefore, the answer is (D).
|
7
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Example 3 Given that $\boldsymbol{a}$ and $\boldsymbol{b}$ are two mutually perpendicular unit vectors, and $|\boldsymbol{c}|=13, \boldsymbol{c} \cdot \boldsymbol{a}=3, \boldsymbol{c} \cdot \boldsymbol{b}=4$, then for any real numbers $t_{1}, t_{2},\left|\boldsymbol{c}-t_{1} \boldsymbol{a}-t_{2} \boldsymbol{b}\right|$ the minimum value is
A. 5
B. 7
C. 12
D. 13
|
Analyze According to the problem, we get $|\boldsymbol{a}|=|\boldsymbol{b}|=1$, and $\boldsymbol{a} \cdot \boldsymbol{b}=0$, thus $\left|\boldsymbol{c}-t_{1} \boldsymbol{a}-t_{2} \boldsymbol{b}\right|^{2}=c^{2}+t_{1}^{2} a^{2}+$ $t_{2}^{2} \boldsymbol{b}^{2}-2 t_{1} \boldsymbol{c} \cdot \boldsymbol{a}-2 t_{2} \boldsymbol{c} \cdot \boldsymbol{b}+2 t_{1} t_{2} \boldsymbol{a} \cdot \boldsymbol{b}=t_{1}^{2}+t_{2}^{2}-6 t_{1}-8 t_{2}+169=\left(t_{1}-3\right)^{2}+\left(t_{2}-4\right)^{2}+144 \geqslant 144$, so $\left|\boldsymbol{c}-t_{1} \boldsymbol{a}-t_{2} \boldsymbol{b}\right| \geqslant 12$, when and only when $t_{1}=3, t_{2}=4$, the above equation takes the equal sign, hence the minimum value sought is 12. Therefore, the answer is $\mathrm{C}$.
|
12
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
9. (10 points) Four black $1 \times 1 \times 1$ cubes and four white $1 \times 1 \times 1$ cubes can form $\qquad$ different $2 \times 2 \times 2$ cubes (considering the same cube after rotation as one situation).
|
【Analysis】First, analyze the case where a color is on the same face. Then, enumerate the cases where the white on the same face becomes 3 and then 2.
【Solution】Solution: According to the problem:
(1) White at the bottom positions 5, 6, 7, 8 is 1 case (same face).
(2) White at the bottom positions 5, 6, 7, the fourth block can be at positions $1,2,4$, a total of 3 cases.
(3) White at the bottom positions 5, 6, the top can be at positions 1,4 or 1,3, a total of 2 cases.
(4) White at the bottom positions 5, 7, the top can be at position 1,3, a total of 1 case.
$1+3+2+1=7$ (cases).
Therefore, the answer is: 7
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$12 \cdot 35$ If two sets are given as
$$
\begin{array}{l}
M=\left\{z \left\lvert\, z=\frac{t}{1+t}+i \frac{1+t}{t}\right., \quad t \in R, \quad t \neq-1, \quad t \neq 0\right\}, \\
N=\{z|z=\sqrt{2}[\cos (\arcsin t)+i \cos (\arccos t)], t \in R,| t \mid \leqslant 1\},
\end{array}
$$
then the number of elements in $M \cap N$ is
(A) 0 .
(B) 1 .
(C) 2 .
(D) 4 .
(China High School Mathematics League, 1989)
|
[Solution] In the Cartesian coordinate system, the elements of sets $M$ and $N$ are points on the curves
$M:\left\{\begin{array}{l}x=\frac{t}{1+t}, \\ y=\frac{1+t}{t} ;\end{array}\right.$
$(t \in R, \quad t \neq 0, \quad t \neq-1)$,
$N:\left\{\begin{array}{l}x=\sqrt{2\left(1-t^{2}\right)}, \\ y=\sqrt{2} t .\end{array}\right.$
$(t \in R, \quad|t| \leqslant 1)$
The parametric equations of $M$ and $N$ can be converted to the following ordinary equations:
$$
\begin{array}{l}
M: x y=1(x \neq 1, x \neq 0), \\
N: x^{2}+y^{2}=2 \quad(0 \leqslant x \leqslant \sqrt{2}) .
\end{array}
$$
Thus, the x-coordinates of the intersection points of curves $M$ and $N$ should satisfy the equation $x^{2}+\frac{1}{x^{2}}=2$, which yields
$$
x= \pm 1 .
$$
However, $\pm 1 \notin(0,1) \cup(1, \sqrt{2})$, meaning that $M \cap N=\varnothing$.
Therefore, the answer is $(A)$.
|
0
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Example 6 If there exists a permutation $a_{1}, a_{2}, \cdots, a_{n}$ of $1,2, \cdots, n$, such that $k+a_{k} (k=1,2, \cdots, n)$ are all perfect squares, then $n$ is called a "good number". Among the set $\{11,13,15,17,19\}$, which are "good numbers" and which are not "good numbers"? Explain your reasoning!
(2004 China Girls Mathematical Olympiad)
|
Analysis: Since $\{11,13,15,17,19\}$ is a finite set and contains only 5 elements, we can discuss these elements one by one.
Solution (1) 11 is not a "good number," because 4 can only be added to 5 to get $3^{2}$, and 11 can only be added to 5 to get $4^{2}$, thus there does not exist a permutation that meets the requirement.
(2) 13 is a "good number," because in the following permutation, $k+a_{k}(k=1,2, \cdots, 13)$ are all perfect squares.
$$
\begin{array}{llcccccccccccc}
k: & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\
a_{k}: & 8 & 2 & 13 & 12 & 11 & 10 & 9 & 1 & 7 & 6 & 5 & 4 & 3
\end{array}
$$
(3) 15 is a "good number," because in the following permutation, $k+a_{k}(k=1,2, \cdots, 15)$ are all perfect squares.
$$
\begin{array}{lccccccccccccccc}
k: & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \\
a_{k}: & 15 & 14 & 13 & 12 & 11 & 10 & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1
\end{array}
$$
(4) 17 is a "good number," because in the following permutation, $k+a_{k}(k=1,2, \cdots, 17)$ are all perfect squares.
$$
\begin{array}{llllllcccccccccccc}
k: & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 \\
a_{k}: & 3 & 7 & 6 & 5 & 4 & 10 & 2 & 17 & 16 & 15 & 14 & 13 & 12 & 11 & 1 & 9 & 8
\end{array}
$$
(5) 19 is a "good number," because in the following permutation, $k+a_{k}(k=1,2, \cdots, 19)$ are all perfect squares.
$$
\begin{array}{llllllllllllllllllll}
k: & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 \\
a_{k}: & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1 & 16 & 15 & 14 & 13 & 12 & 11 & 10 & 9 & 19 & 18 & 17
\end{array}
$$
In summary, in the set $\{11,13,15,17,19\}$, all elements except 11 are "good numbers".
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Let a set of three real numbers be represented both as $\left\{a, \frac{b}{a}, 1\right\}$ and as $\left\{a^{2}, a+b, 0\right\}$, then the value of $a^{2002}+b^{2003}$ is $\qquad$.
|
7. 1 .
$$
\left\{\begin{array} { l }
{ a + \frac { b } { a } + 1 = a ^ { 2 } + ( a + b ) + 0 } \\
{ a \cdot \frac { b } { a } \cdot 1 = a ^ { 2 } \cdot ( a + b ) \cdot 0 , }
\end{array} \text { thus } \left\{\begin{array}{l}
a=-1 \text { (discard } 1) \\
b=0,
\end{array} \text { hence } a^{2002}+b^{2003}=1\right.\right. \text {. }
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (5 points) A set of Go costs 24 yuan, and a set of Chinese chess costs 18 yuan. With 300 yuan, you can exactly buy a total of 14 sets of the two types of chess, among which there are $\qquad$ sets of Chinese chess.
|
【Analysis】Assuming all are Go boards, then there would be $24 \times 14=336$ yuan, which is $336-300$ $=36$ yuan more than the known 300 yuan. Since a Go board is $24-18=6$ yuan more expensive than a Chinese chess set, we can thus find the number of Chinese chess sets.
【Solution】Solution: Assuming all are Go boards, then the number of Chinese chess sets is:
$$
\begin{aligned}
& (24 \times 14-300) \div(24-18) \\
= & 36 \div 6 \\
= & 6 \text { (sets); }
\end{aligned}
$$
Answer: There are 6 sets of Chinese chess.
The answer is: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4 Let $x, y \in \mathbf{R}$, find the minimum value of the function $f(x, y)=x^{2}+$ $6 y^{2}-2 x y-14 x-6 y+72$.
|
Solution: $f(x, y)=(x-y-7)^{2}+5(y-2)^{2}+3$, so when $x=9, y=2$, $f_{\text {min }}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4 Given $f(x)=a \cos ^{2} x-b \sin x \cos x-\frac{a}{2}$ has a maximum value of $\frac{1}{2}$, and $f\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{4}$, then the value of $f\left(-\frac{\pi}{3}\right)$ is
A. $\frac{1}{2}$
B. $-\frac{\sqrt{3}}{4}$
C. $-\frac{1}{2}$ or $\frac{\sqrt{3}}{4}$
D. 0 or $-\frac{\sqrt{3}}{4}$
|
4 D.
$$
\begin{aligned}
f(x) & =\frac{a}{2}(1+\cos 2 x)-\frac{b}{2} \sin 2 x-\frac{a}{2} \\
& =\frac{1}{2}(a \cos 2 x-b \sin 2 x)
\end{aligned}
$$
The maximum value is $\frac{1}{2} \sqrt{a^{2}+b^{2}}$, so
$$
a^{2}+b^{2}=1
$$
From $f\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{4}$ we get
$$
a+\sqrt{3} b=-\sqrt{3}
$$
Solving (1) and (2) yields $a=0, b=-1$, or $a=-\frac{\sqrt{3}}{2}, b=-\frac{1}{2}$.
$$
f\left(-\frac{\pi}{3}\right)=\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{2} b=-\frac{\sqrt{3}}{4} \text { or } 0 .
$$
|
0
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
$7 n$ teams are to hold a double round-robin match (each pair of teams plays two matches, one home and one away match). Each team can play multiple matches within a week (from Sunday to Saturday). If a team has $1:1$ matches in a week, no away matches can be scheduled for this team in the same week. If all matches can be completed within 4 weeks, find the maximum value of $n$. (Proposed by Zonghu)
Note: The match held at the home venue of Team A and the away venue of Team B is called the home match of Team A and the away match of Team B.
|
(1) As shown in the table: The table has “*”, indicating that the team has a match in that week. It is easy to verify that, according to the schedule in the table, 6 teams can complete the matches in that week.
(2) The following proves that 7 teams cannot complete the matches in that week. Let $S_{i}(i=1, 2, 3, 4, 5, 6, 7)$ represent the set of weeks in which the $i$-th team plays home matches. Assuming 4 teams can complete the matches, then $S$ is the set of all matches of that team. Therefore, $S_{i}(i=1, 2, 3, 4, 5, 6, 7)$ are all non-empty sets.
Each set is a subset of the following sets:
$$
\begin{array}{l}
A=\{\{1\},\{1,2\},\{1,2,3\}\} \\
B=\{\{2\},\{2,3\},\{2,3,4\}\} \\
C=\{\{3\},\{1,3\},\{1,3,4\}\} \\
D=\{\{4\},\{1,4\},\{1,2,4\}\} \\
E=\{\{2,4\}\} \\
F=\{\{3,4\}\}
\end{array}
$$
Since $S_{i}$ is a subset of one of the sets $A$, $B$, $C$, $D$, $E$, or $F$, there must be $S_{i} \subseteq S$ or $S_{i} \neq S$.
In conclusion, the maximum value of $n$ is 6.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a constant $a \in(0,1)$, $|x|+|y| \leqslant 1$, the maximum value of the function $f(x, y)=a x+y$ is $\qquad$ .
|
6. 1 .
Solution: $f(x, y)=a x+y \leqslant|a x|+|y| \leqslant a|x|+(1$ $-|x|)=(a-1)|x|+1$ The first equality holds if $x \geqslant$ $0, y \geqslant 0$. When $0 \leqslant x \leqslant 1, 0<a<1$, $g(x)=(a-1) x+$ 1 is a decreasing function. When $x=0$, $g(x)_{\max }=1$, so $\left\{\begin{array}{l}x=0 \\ y=1\end{array}\right.$, $g(x)_{\max }=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. There are 2000 identical circular paper pieces on the table, some of which are externally tangent to each other. How many different colors are needed at minimum to color these paper pieces so that no two tangent pieces have the same color?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
23. As shown in the figure: If only 3 colors are used, assume there are 11 circular paper pieces, and let's say 6 of them are colored as indicated by the numbers in the figure. Thus, the three circular pieces $A$, $B$, and $C$ can only be colored with 2 or 3, and $A$ and $C$ must be the same color, but $A$ and $C$ must be different from $B$. Therefore, $D$ must be a different color from both $A$ and $B$, so $D$ is colored with color 1. Similarly, $E$ must be a different color from both $B$ and $C$, so $E$ is also colored with color 1, which contradicts the requirement that $D$ and $E$ must be different colors since they are adjacent.
Next, we prove that 4 colors are sufficient. We will prove this by induction on the number of circular paper pieces $n$. When $n \leqslant 4$, it is obviously true. Assume that for $k$ circular paper pieces, 4 colors are sufficient. When $n=k+1$, mark the centers of all the circular paper pieces, and take the convex hull of these $k+1$ centers, which must form a certain polygon. Choose one vertex $A$, which is the center of a certain circular paper piece. This paper piece can be adjacent to at most 3 other circular paper pieces. Remove this paper piece, and by the induction hypothesis, the remaining $k$ paper pieces can be colored with 4 colors such that any two adjacent paper pieces have different colors. When we put this paper piece back, it can be colored with the 4th color, which is different from the 3 adjacent paper pieces. Therefore, the conclusion also holds for $n=k+1$. Thus, for any $n$ circular paper pieces, 4 colors are sufficient to meet the requirement. In particular, for 2000 circular paper pieces, 4 colors are sufficient.
In summary, at least 4 colors are required.
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7. Five contestants $A, B, C, D, E$ participate in the "The Voice" competition, and the five of them stand in a row for a group appearance. They each have a contestant number on their chest, and the sum of the five numbers is 35. It is known that the sum of the numbers of the contestants standing to the right of $\mathrm{E}$ is 13; the sum of the numbers of the contestants standing to the right of $D$ is 31; the sum of the numbers of the contestants standing to the right of $A$ is 21; the sum of the numbers of the contestants standing to the right of $C$ is 7. What is the sum of the numbers of the contestants standing at the far left and the far right? $\qquad$
|
【Answer】 11
【Analysis】According to the problem, $D$ is on the far left, so $D=35-31=4, B$ is on the far right, so $B=7,7+4=11$.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Points $A, B, C, D$ lie on the circumference of a circle, and $B C=C D=4, E$ is the intersection of $A C$ and $B D$, and $A E=6$. The lengths of segments $B E$ and $D E$ are both integers. What is the length of $B D$?
(1988 National Junior High School League Question)
|
1. From $\triangle C D E \sim \triangle B A E$ and $\triangle C B E \sim \triangle D A E$, we have $A B=\frac{4 B E}{C E}, A D=\frac{4 D E}{C E}$. Applying Ptolemy's theorem to quadrilateral $A B C D$, we get $B D \cdot(A E+C E)=4(A B+A D)=16 \cdot \frac{B E+D E}{C E}$. Let $C E=x$, we obtain the equation $x^{2}+6 x-16=0$, solving which gives $x=2$ (discarding the negative value). Thus, $B E \cdot D E=C E \cdot A E=12$. Also, $B D<B C+D C=8$, yielding $B E=3, D E=4$ or $B E=4, D E=3$, in either case $B D=7$ is the desired result.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the Cartesian coordinate system, $A(1,2)$, $B(3,0)$, and $P$ is any point on the circle $(x-3)^{2}+(y-2)^{2}=1$. Let
$$
\overrightarrow{O P}=\lambda \overrightarrow{O A}+\mu \overrightarrow{O B}(\lambda, \mu \in \mathbf{R}) \text {. }
$$
Then the minimum value of $11 \lambda+9 \mu$ is
|
4. 12 .
Let $P(3+\cos \theta, 2+\sin \theta)(\theta \in[0,2 \pi))$.
Then by the given conditions,
$$
\lambda+3 \mu=3+\cos \theta, 2 \lambda=2+\sin \theta \text {. }
$$
Thus, $11 \lambda+9 \mu=3(\lambda+3 \mu)+4(2 \lambda)$
$$
\begin{array}{l}
=3(3+\cos \theta)+4(2+\sin \theta) \\
=17+3 \cos \theta+4 \sin \theta \\
=17+5 \sin (\theta+\varphi) \\
\geqslant 17-5=12 .
\end{array}
$$
Clearly, the equality in the above expression can be achieved.
Therefore, the minimum value of $11 \lambda+9 \mu$ is 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. For the cubic function $y=x^{3}+a x^{2}+b x+c$, its graph intersects the $x$-axis at points $A, T$, and $B$ in sequence. The lines $A P$ and $B Q$ are tangent to the cubic curve at points $P$ and $Q$ (where $P$ does not coincide with $A$, and $Q$ does not coincide with $B$). Then the ratio of the projections of $\overrightarrow{A B}$ and $\overrightarrow{P Q}$ on the $x$-axis is:
|
8. -2
Let the coordinates of $A, B, P$ be $(\alpha, 0), (\beta, 0), \left(x_{1}, y_{1}\right)$, and let $T(\gamma, 0)$, then
$$
y=(x-a)(x-\beta)(x-\gamma)
$$
For the line $y=m(x-\beta)$ passing through $A$ and intersecting (1) at two points, the x-coordinates of these two points are given by $(x-\beta)(x-\gamma)-m$. When these two points coincide, then $m=-(\beta-\gamma)^{2} / 4, x_{1}=(\beta+\gamma) / 2$, which means the projection of $P$ on the x-axis $\left(x_{1}, 0\right)$ is the midpoint of $B T$. Similarly, the projection of $Q$ on the x-axis is also the midpoint of $A T$. Therefore, the ratio of the projections of $\overrightarrow{A B}$ and $\overrightarrow{P Q}$ on the x-axis is -2 (since the projections of $\overrightarrow{A B}$ and $\overrightarrow{P Q}$ on the x-axis are in opposite directions).
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(1) If the circumcenter of $\triangle A B O$ lies on the ellipse, find the value of the real number $p$;
(2) If the circumcircle of $\triangle A B O$ passes through the point $N\left(0, \frac{13}{2}\right)$, find the value of the real number $p$.
11. (20 points) As shown in Figure 4, the ellipse $C_{1}: \frac{x^{2}}{4}+y^{2}=1$, the parabola $C_{2}: x^{2}=2 p y(p>0)$, let $C_{1}$ and $C_{2}$ intersect at points $A$ and $B$, and $O$ be the origin.
|
(1) From the symmetry of the parabola, ellipse, and circle, we know that the circumcenter of $\triangle A B O$ is the upper vertex $M(0,1)$ of the ellipse. Therefore,
$$
M A=M B=M O=1 \text {. }
$$
Let $B\left(x_{0}, y_{0}\right)\left(x_{0}>0\right)$. Hence,
$$
\left\{\begin{array} { l }
{ x _ { 0 } ^ { 2 } = 2 p y _ { 0 } , } \\
{ \frac { x _ { 0 } ^ { 2 } } { 4 } + y _ { 0 } ^ { 2 } = 1 , } \\
{ x _ { 0 } ^ { 2 } + ( y _ { 0 } - 1 ) ^ { 2 } = 1 }
\end{array} \Rightarrow \left\{\begin{array}{l}
x_{0}^{2}=\frac{4(2 \sqrt{13}-5)}{9}, \\
y_{0}=\frac{-1+\sqrt{13}}{3}, \\
p=\frac{7-\sqrt{13}}{6} .
\end{array}\right.\right.
$$
(2) It is easy to see that points $O, A, N, B$ are concyclic.
Let $A B$ intersect the $y$-axis at point $C\left(0, y_{0}\right)$.
By the intersecting chords theorem, we have
$$
\begin{array}{l}
A C \cdot C B=C N \cdot C O \\
\Rightarrow y_{0}\left(\frac{13}{2}-y_{0}\right)=x_{0} x_{0}=2 p y_{0} \\
\Rightarrow y_{0}=\frac{13}{2}-2 p .
\end{array}
$$
Substituting into $x_{0}^{2}=2 p y_{0}$, we get
$$
x_{0}^{2}=2 p\left(\frac{13}{2}-2 p\right) \text {. }
$$
Substituting equations (1) and (2) into the ellipse equation, we get
$$
\begin{array}{l}
\frac{13 p-4 p^{2}}{4}+\left(\frac{13}{2}-2 p\right)^{2}=1 \\
\Rightarrow p=3
\end{array}
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.