problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
## Task A-2.5.
Ivica made a large cube with a side length of $n$ from $n^3$ unit cubes and then painted some of the six faces of the large cube, while leaving others unpainted. When he disassembled the large cube, he found that exactly 1000 unit cubes had no painted faces. Show that this is indeed possible and determine the number of faces of the large cube that Ivica painted.
|
## Solution.
After painting some sides of a cube composed of $n^{3}$ smaller cubes, the number of unpainted smaller cubes is certainly less than $n^{3}$ and greater than $(n-2)^{3}$.
Thus, $(n-2)^{3}<1000<n^{3}$, so it must be that $(n-1)^{3}=10^{3}$, i.e., $n=11$.
Now let's count the unpainted smaller cubes in all cases, depending on the number of painted sides of the larger cube.
If 1 side of the larger cube is painted, the number of unpainted smaller cubes is $11 \cdot 10 \cdot 10=1210$.
If 2 sides of the larger cube are painted, the number of unpainted smaller cubes is $11 \cdot 10 \cdot 10=1100$ (if the painted sides are adjacent) or $11 \cdot 11 \cdot 9=1089$ (if the painted sides are not adjacent).
If 3 sides of the larger cube are painted, the number of unpainted smaller cubes can be $10 \cdot 10 \cdot 10=1000$ (if all three painted sides share a common vertex) or $11 \cdot 10 \cdot 9=990$ (if the three painted sides do not share a common vertex).
If 4 sides of the larger cube are painted, the number of unpainted smaller cubes is $10 \cdot 10 \cdot 9=900$ (if the two unpainted sides are adjacent) or $11 \cdot 9 \cdot 9=891$ (if the two unpainted sides are not adjacent).
If 5 sides of the larger cube are painted, the number of unpainted smaller cubes is $10 \cdot 9 \cdot 9=810$.
We see that only in the case where three sides of the larger cube are painted can the number of unpainted unit cubes be 1000, so we conclude that Ivica painted three sides of the larger cube.
Note: It is not necessary to calculate the exact number of painted cubes in each case, but to eliminate certain cases.
## COUNTY COMPETITION IN MATHEMATICS
## 3rd grade - high school - A variant
February 15, 2013.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.2.
Exactly three interior angles of a convex polygon are obtuse. What is the maximum number of sides that this polygon can have?
|
## First solution.
The sum of the exterior angles of a convex polygon is $360^{\circ}$.
Three exterior angles of the observed polygon are acute (opposite to the obtuse interior angles), while all other exterior angles must be obtuse or right.
2 points
At most three exterior angles can be obtuse or right, otherwise their sum would be $360^{\circ}$ or more, which is impossible.
This means that at most three interior angles are acute or right, so the observed polygon has at most six vertices.
We still need to check if there exists a hexagon with the described properties.
One such hexagon has angles of $90^{\circ}, 150^{\circ}, 90^{\circ}, 150^{\circ}, 90^{\circ}, 150^{\circ}$, and all sides are congruent.
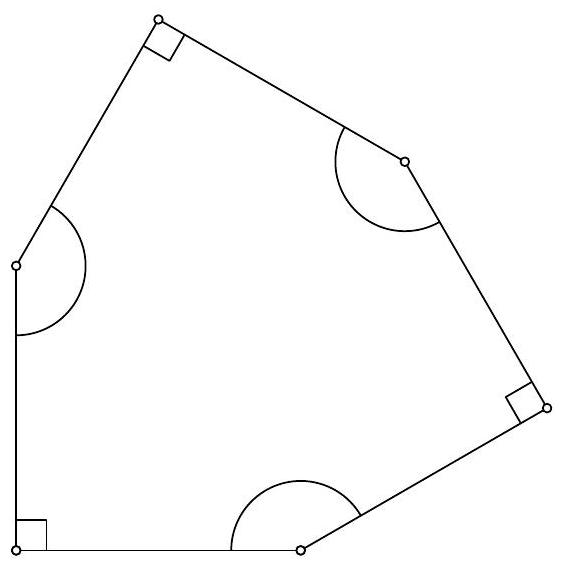
This shows that the maximum number of sides of a polygon with the given properties is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.3.
Solve the equation in the set of real numbers
$$
4^{2 x+\sqrt{-1+x^{2}}}-5 \cdot 2^{2 x-1+\sqrt{-1+x^{2}}}=6
$$
|
## Solution.
We solve the problem by substitution $2 x+\sqrt{-1+x^{2}}=y$ under the condition $x^{2}-1 \geq 0$.
(Or by substitution $2^{2 x+\sqrt{-1+x^{2}}}=t$.)
Then we have $2 \cdot\left(2^{y}\right)^{2}-5 \cdot 2^{y}-12=0$.
The solution is only $2^{y}=4$ since $2^{y}>0 \forall y \in \mathbb{R}$. Then $y=2$.
It follows that $2 x+\sqrt{-1+x^{2}}=2$, or
$$
\sqrt{-1+x^{2}}=2-2 x
$$
After squaring, under the condition $2-2 x \geq 0$, we get
$$
3 x^{2}-8 x+5=0, \quad x_{1}=1, x_{2}=\frac{5}{3}
$$
Only the solution $x=1$ satisfies the given conditions.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.5.
A bus left from place $A$ to place $B$. 50 minutes later, a car left from place $A$ and arrived at place $B$ 10 minutes before the bus. If they had left simultaneously, one from place $A$ and the other from place $B$ (one heading towards the other), they would have met after one hour and 12 minutes. If traveling the same route and at the same speed, how long will it take for the bus to return from place $B$ to place $A$?
|
## Solution.
The bus spent $x$ hours on the journey between locations $A$ and $B$, while the car spent $x-1$ hours, so it must be that $x>1$.
The speed of the bus is $\frac{s}{x}$ (where $s$ is the distance between locations $A$ and $B$).
The speed of the car is $\frac{s}{x-1}$.
Starting from location $A$, the bus traveled $\frac{6}{5} \cdot \frac{s}{x} \mathrm{~km}$ in 1 hour and 12 minutes (which is $\frac{6}{5}$ hours).
Starting from location $B$, the car traveled $\frac{6}{5} \cdot \frac{s}{x-1} \mathrm{~km}$ in 1 hour and 12 minutes. Therefore,
$$
\frac{6}{5} \cdot \frac{s}{x} + \frac{6}{5} \cdot \frac{s}{x-1} = s
$$
or
$$
\frac{1}{x} + \frac{1}{x-1} = \frac{5}{6}
$$
By simplifying, we get the equation $5 x^{2} - 17 x + 6 = 0$, whose solutions are 3 and $\frac{2}{5}$.
Since $x$ must be greater than 1, we conclude that the time required for the bus to travel the distance from $B$ to $A$ (or vice versa) is 3 hours.
## NATIONAL MATHEMATICS COMPETITION
## 3rd grade - high school - B variant Šibenik, April 29, 2010.
IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH IN AN APPROPRIATE MANNER.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.1.
Determine the value of the real parameter $p$ so that the solutions of the equation
$$
(p-3) x^{2}+\left(p^{2}+1\right) x-11 p+18=0
$$
are the lengths of the legs of a right triangle with a hypotenuse of length $\sqrt{17}$.
|
## Solution.
Let $x_{1}$ and $x_{2}$ be the solutions of the given equation. The condition given in the problem then states $x_{1}^{2}+x_{2}^{2}=17$. According to Viète's formulas, we have
$$
x_{1}+x_{2}=-\frac{p^{2}+1}{p-3} \quad \text { and } \quad x_{1} x_{2}=\frac{-11 p+18}{p-3}
$$
so
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=\left(\frac{p^{2}+1}{p-3}\right)^{2}-2 \cdot \frac{-11 p+18}{p-3}
$$
Therefore, we seek all real numbers $p$ such that
$$
\begin{gathered}
\left(\frac{p^{2}+1}{p-3}\right)^{2}-2 \cdot \frac{-11 p+18}{p-3}=17 \\
\Longleftrightarrow\left(p^{2}+1\right)^{2}-2(-11 p+18)(p-3)=17(p-3)^{2} \\
\Longleftrightarrow p^{4}+7 p^{2}-44=0
\end{gathered}
$$
By substituting $t=p^{2}$, we arrive at the quadratic equation
$$
t^{2}+7 t-44=0
$$
whose solutions are $t=4$ and $t=-11$.
Since the equation $p^{2}=-11$ has no solutions, we discard the second option. The first option leads to $p^{2}=4$, i.e., $p= \pm 2$.
Solving the initial equation for $p=-2$ yields the solutions $x_{1,2}=\frac{1-\sqrt{33}}{2}$, one of which is not a positive number, so we discard the option $p=-2$.
Solving the equation for $p=2$ yields $x_{1}=1$ and $x_{2}=4$, which are indeed positive real numbers. Therefore, the only solution is $p=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.5.
On a board of dimensions $8 \times 8$, kings and rooks are placed such that no figure is under attack. A king attacks the adjacent fields (eight of them, unless the king is on the edge of the board), and a rook attacks all the fields in the row and column it is in. What is the maximum number of figures on the board if the number of rooks is equal to the number of kings?
|
## Solution.
One rook covers its own square and attacks 7 additional squares in its row and column.
The second rook covers its own square and attacks 6 additional squares in its row and column (not counting those already attacked by the first rook).
Continuing this way, the sixth rook covers its own square and 2 additional squares in its row and column. In total, there are $15+13+11+9+7+5=60$ covered or attacked squares.
Thus, if we place six rooks, only 4 free squares remain, and we cannot place six kings on them.
In the figure, one valid arrangement of five kings (軑) and five rooks (單) is shown, so the answer is 10.

Note: In the proof that it is not possible to place six kings and six rooks, it is sufficient to comment that after placing six rooks, 6 rows and 6 columns are blocked; therefore, only 4 free squares remain.
## COUNTY COMPETITION IN MATHEMATICS
3rd grade - high school - A variant
## February 28, 2019.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.4.
Determine all triples $(x, y, z)$ of real numbers for which
$$
\begin{aligned}
& \left(x^{2}+1\right) y=z^{2}+1 \\
& \left(y^{2}+1\right) z=x^{2}+1 \\
& \left(z^{2}+1\right) x=y^{2}+1
\end{aligned}
$$
|
## First solution.
If we multiply all three given equations, we see that
$$
\left(x^{2}+1\right)\left(y^{2}+1\right)\left(z^{2}+1\right) y z x=\left(z^{2}+1\right)\left(x^{2}+1\right)\left(y^{2}+1\right)
$$
Notice that for all real numbers $t$, $t^{2}+1 \geqslant 1>0$, so from the above equation, we conclude that $x y z=1$.
Since $x^{2}+1>0$ and $z^{2}+1>0$, we conclude that $y>0$, and similarly $z>0$ and $x>0. \quad 1$ point
Without loss of generality, assume that $z=\min \{x, y, z\}$.
Assume that $z1>z^{2}$ (since $x y z=1$ ).
Consider the first equation
$$
z^{2}+1=\left(x^{2}+1\right) y \geqslant 2 x y=x y+x y>z^{2}+1
$$
where in the first inequality we use the fact that for any real number $x, x^{2}+1 \geqslant 2 x$, and in the second the fact that $x y>z^{2}$ and $x y>1$. Thus, the case where $z<1$ is impossible.
If $z \geqslant 1$, then the only possibility is $x=y=z=1$ (since $x y z=1$ ).
By substitution, we see that $x=y=z=1$ is indeed a solution, and the only solution to the given system.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For which real numbers $m$ does the equation $3 x+9=m(m-x)$ have a unique solution?
(8)
|
Solution. By rearranging we get $(m+3) x=m^{2}-9$.
For $m \neq-3$, $m+3 \neq 0$ so there is a unique solution $x=m-3$.
(for a complete solution 8 points)
(for the solution $x=m-3$ (always), 0 points)
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. If $a^{2}+b^{2}+c^{2}=a b+b c+c a$, what is $(a+2 b-3 c)^{2009}$?
|
Solution. If we multiply the given equation by 2 and move everything to the left side, we get
$$
2 a^{2}+2 b^{2}+2 c^{2}-2 a b-2 b c-2 c a=0
$$
If we rearrange the equation, we get
$$
a^{2}+b^{2}-2 a b+b^{2}+c^{2}-2 b c+c^{2}+a^{2}-2 c a=0
$$
or
$$
(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=0
$$
from which it follows that $a=b=c$
so the desired value is equal to zero.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Calculate the value of the expression $\log ^{2} 5+\log 2 \cdot \log 50$.
(8)
|
First solution. In order, we have:
$$
\begin{aligned}
\log ^{2} 5+\log 2 \cdot \log 50 & =\log ^{2} 5+\log 2 \cdot(\log 25+\log 2) \\
& =\log ^{2} 5+\log 2 \cdot(2 \log 5+\log 2) \\
& =\log ^{2} 5+2 \log 5 \cdot \log 2+\log ^{2} 2 \\
& =(\log 5+\log 2)^{2}=(\log 10)^{2}=1
\end{aligned}
$$
(full solution 8 points)
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Prove that for every natural number $n \geq 2$ the unit digit of the number $2^{2^{n}}$ is 6.
(8)
|
Solution. We prove the statement by mathematical induction.
Base of induction: For $n=2$ we have
$$
2^{2^{2}}=2^{4}=16
$$
so the statement holds.
Induction hypothesis: Assume that the statement holds for some natural number $n \geq 2$, i.e., the last digit of the number $2^{2^{n}}$ is 6.
Induction step: Prove that the statement holds for $n+1$:
$$
2^{2^{n+1}}=2^{2^{n} \cdot 2}=\left(2^{2^{n}}\right)^{2}=(\overline{* 6})^{2}=\overline{* * 6}
$$
Thus, the statement holds for $n+1$, and by the principle of mathematical induction, it holds for every natural number $n \geq 2$.
(full solution 8 points)
(for the correct base and induction hypothesis 4 points)
(8. In the expansion of $\left(x \sqrt{x}+\frac{1}{x^{4}}\right)^{n}$, the coefficient of the third term is 44 greater than the coefficient of the second term.
Determine the term that does not contain $x$.
Solution. The condition of the problem can be written in the form $\binom{n}{2}=\binom{n}{1}+44$.
From here, by simplifying we get
$$
\begin{aligned}
\frac{n(n-1)}{2} & =n+44 \\
n^{2}-3 n-88 & =0 \Rightarrow n_{1}=11, n_{2}=-8
\end{aligned}
$$
The only possibility is $n=11$. Let $A_{k}$ be the coefficient of the term that is equal to zero. Then we have
$$
A_{k}=\binom{11}{k}(x \sqrt{x})^{11-k}\left(\frac{1}{x^{4}}\right)^{k}=\binom{11}{k}\left(x^{\frac{3}{2}}\right)^{11-k} \cdot x^{-4 k}=\binom{11}{k} \cdot x^{\frac{3}{2}(11-k)-4 k}
$$
Since $A_{k}$ does not contain $x$, we have
$$
\frac{3}{2}(11-k)-4 k=0 \quad \Rightarrow \quad k=3
$$
The term that does not contain $x$ is $A_{3}=\binom{11}{3}=165$.
(full solution 8 points)
(for calculating $n=11,4$ points)
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.4. (20 points) If $a^{2}+b^{2}=1, c^{2}+d^{2}=1$ and $a c+b d=0$, what is $a b+c d ?$
|
First solution. Since $a^{2}+b^{2}=1$, $a$ and $b$ cannot both be 0 at the same time. Let $a \neq 0$.
From the third equality, we have $c=-\frac{b d}{a}$. Then,
$$
1=c^{2}+d^{2}=\frac{b^{2} d^{2}}{a^{2}}+d^{2}=\frac{d^{2}\left(a^{2}+b^{2}\right)}{a^{2}}=\frac{d^{2}}{a^{2}}
$$
from which we have $a^{2}=d^{2}$. Now,
$$
a b+c d=a b-\frac{b d^{2}}{a}=\frac{b}{a}\left(a^{2}-d^{2}\right)=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.1. (20 points) For complex numbers $z, w$ such that $|z|=|w|=|z-w|$, calculate $\left(\frac{z}{w}\right)^{99}$.
|
First solution. Let $u=\frac{z}{w}=x+y i$. Then $|u|=1,|u-1|=1$.
Then $x^{2}+y^{2}=1,(x-1)^{2}+y^{2}=1$.
By subtracting these equations, we get $x=\frac{1}{2}, y= \pm \frac{\sqrt{3}}{2}$, so $u=\frac{1}{2} \pm \frac{\sqrt{3}}{2} i$.
Now,
$$
\left(\frac{z}{w}\right)^{99}=u^{99}=\left[\left(\frac{1}{2} \pm \frac{\sqrt{3}}{2} i\right)^{3}\right]^{33}=\left(\frac{1}{8} \pm \frac{3 \sqrt{3}}{8} i-\frac{9}{8} \mp \frac{3 \sqrt{3}}{8} i\right)^{33}=(-1)^{33}=-1
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.1. (20 points) In an increasing arithmetic sequence, the product of the second and third term is 3, and the product of the third and fifth term is -3. How many of the first terms of the sequence need to be summed to achieve the minimum sum? What is that sum?
|
Solution. We will represent the members of the sequence using the first term $a_{1}$ and the difference of the sequence $d$.
According to the condition of the problem, we have these two equations:
\[
\begin{aligned}
\left(a_{1}+d\right)\left(a_{1}+2 d\right) & =3 \\
\left(a_{1}+2 d\right)\left(a_{1}+4 d\right) & =-3
\end{aligned}
\]
If we add these two equations, after rearranging, we get the homogeneous quadratic equation $2 a_{1}^{2}+9 a_{1} d+10 d^{2}=0$. Dividing by $d^{2}$, we get the quadratic equation
\[
2\left(\frac{a_{1}}{d}\right)^{2}+9 \cdot \frac{a_{1}}{d}+10=0
\]
Its solutions are $\frac{a_{1}}{d}=-2, \frac{a_{1}}{d}=-\frac{5}{2}$. This gives us $a_{1}=-2 d, a_{1}=-\frac{5}{2} d$.
The first solution $a_{1}=-2 d$ does not make sense because substituting it into the first equation gives $-d \cdot 0=3$!
For $a_{1}=-\frac{5}{2} d$, from the first equation we get $d= \pm 2$. However, $d=-2$ does not satisfy the condition because the sequence must be increasing. For $d=2$, we get $a_{1}=-5$.
The sum of the first $n$ terms of the sequence is
\[
S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)=\frac{n}{2}\left(a_{1}+a_{1}+(n-1) d\right)=n^{2}-6 n=(n-3)^{2}-9
\]
The minimum for $S_{n}$ is obtained for $n=3$ and it is $S_{\min }=-9$.
Note. If we divide the second equation by the first, we get $\frac{a_{1}+4 d}{a_{1}+d}=-1$, from which we obtain $a_{1}=-\frac{5}{2} d$, and then proceed as above.
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.2.
Prove that the value of the expression $\frac{\sqrt[3]{7+5 \sqrt{2}}(\sqrt{2}-1)}{\sqrt{4+2 \sqrt{3}}-\sqrt{3}}$ is a natural number.
|
## Solution.
In the numerator of the given fraction, we will place the expression in parentheses under the cube root, and in the denominator, we will recognize the square of a binomial under the first root:
$$
\begin{aligned}
& \frac{\sqrt[3]{7+5 \sqrt{2}}(\sqrt{2}-1)}{\sqrt{4+2 \sqrt{3}}-\sqrt{3}}=\frac{\sqrt[3]{(7+5 \sqrt{2})(\sqrt{2}-1)^{3}}}{\sqrt{1+2 \sqrt{3}+3}-\sqrt{3}} \\
& =\frac{\sqrt[3]{(7+5 \sqrt{2})(2 \sqrt{2}-6+3 \sqrt{2}-1)}}{\sqrt{(1+\sqrt{3})^{2}}-\sqrt{3}} \\
& =\frac{\sqrt[3]{(5 \sqrt{2}+7)(5 \sqrt{2}-7)}}{1+\sqrt{3}-\sqrt{3}} \\
& =\frac{\sqrt[3]{(5 \sqrt{2})^{2}-7^{2}}}{1} \\
& =\frac{\sqrt[3]{50-49}}{1}=1
\end{aligned}
$$
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.5.
In a kite where the lengths of the diagonals are $d_{1}=24 \mathrm{~cm}$ and $d_{2}=8 \mathrm{~cm}$, a rectangle is inscribed such that its sides are parallel to the diagonals of the kite. Determine the dimensions of the inscribed rectangle that has the maximum area.
|
## Solution.

Let $x$ and $y$ be the sides of the rectangle, and let $y \parallel d_{1}, x \parallel d_{2}$. Notice triangles $B C A$ and $B F E$. According to the K-K theorem,
$$
\triangle B C A \sim \triangle B F E
$$
Therefore, we have:
$$
\begin{aligned}
& d_{1}: y = \frac{d_{2}}{2} : \left(\frac{d_{2}}{2} - \frac{x}{2}\right) \\
& \Rightarrow 24: y = 4: \left(4 - \frac{x}{2}\right) \\
& \Rightarrow y = 24 - 3x .
\end{aligned}
$$
The area of the rectangle is a quadratic function of the side $x$:
$$
\begin{aligned}
& P = P(x) = x \cdot (24 - 3x) \\
& P(x) = 24x - 3x^2
\end{aligned}
$$
This quadratic function achieves its maximum value for
$$
x_{M} = -\frac{24}{2 \cdot (-3)} = 4 \text{ cm}
$$
It follows that $y_{M} = 24 - 3 \cdot 4 = 12 \text{ cm}$. 1 point
Thus, the rectangle with the largest possible area has sides of length $x = 4 \text{ cm}$ and $y = 12 \text{ cm}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.1.
In which number system does the equality $\sqrt{2521}-\sqrt{2400}=1$ hold?
|
## Solution.
Let the base of the sought number system be denoted by $b$. Clearly, $b>5$.
$$
\begin{aligned}
& \sqrt{2521}-\sqrt{2400}=1 \\
& \Rightarrow \sqrt{2521}=1+\sqrt{2400} /^{2} \\
& \Rightarrow 2521-1-2400=2 \sqrt{2400} \\
& \Rightarrow 120=2 \sqrt{2400}
\end{aligned}
$$
This equality, written in the system with base $b$, is
$$
\begin{array}{ll}
b^{2}+2 b=2 \sqrt{2 b^{3}+4 b^{2}} /^{2} & 2 \text { points } \\
\Rightarrow b^{4}-4 b^{3}-12 b^{2}=0 & \\
\Rightarrow b^{2} \cdot\left(b^{2}-4 b-12\right)=0 . & 2 \text { points }
\end{array}
$$
The solutions to this equation are $b_{1}=0, b_{2}=-2, b_{3}=6$.
The base of the sought number system is $b=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.1.
The perimeter of a right triangle is 18, and the area is 9. What is the length of the hypotenuse of this triangle?
|
## First Solution.
Let $a$ and $b$ be the lengths of the legs, and $c$ be the length of the hypotenuse of the given triangle.
Since $a+b+c=18$, we have
$$
(a+b)^{2}=(18-c)^{2}=18^{2}-36 c+c^{2}
$$
The given triangle is a right triangle, so by the Pythagorean theorem, $a^{2}+b^{2}=c^{2}$. 1 point It follows that
$$
(a+b)^{2}=a^{2}+2 a b+b^{2}=c^{2}+2 a b
$$
Since we have expressed $(a+b)^{2}$ in two ways, equating them gives
$$
2 a b=18^{2}-36 c
$$
Since the area of the triangle is 9, we have $a b=18$. 1 point
We conclude that $36=2 a b=18^{2}-36 c$. From this, $c=8$. 2 points
## Second Solution.
Let $a$ and $b$ be the lengths of the legs, and $c$ be the length of the hypotenuse of the given triangle.
The given triangle is a right triangle, so by the Pythagorean theorem, $a^{2}+b^{2}=c^{2}$. 1 point
Since $a+b+c=18$, we have
$$
a^{2}+b^{2}=c^{2}=(18-a-b)^{2}
$$
After squaring, we get
$$
a^{2}+b^{2}=18^{2}+a^{2}+b^{2}-36 a-36 b+2 a b
$$
or $18^{2}+2 a b=36(a+b)=36 \cdot(18-c)$. 2 points
Since the area of the triangle is 9, we have $a b=18$. 1 point
We conclude that $18^{2}+36=36 \cdot(18-c)$. From this, $c=8$. 2 points
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.2.
Let the complex numbers $a, b$ and $c$ be the solutions of the equation $x^{3}-2 x+2=0$. Determine
$$
\frac{a+1}{a-1}+\frac{b+1}{b-1}+\frac{c+1}{c-1}
$$
|
## Solution.
We use Viète's formulas. Since $a, b$, and $c$ are the solutions of the equation $x^{3}-2 x+2=0$, we have
$$
a+b+c=0, \quad a b+b c+c a=-2, \quad a b c=-2
$$
It remains to express the given expression in terms of $a+b+c, a b+b c+c a$, and $a b c$:
$$
\begin{aligned}
\frac{a+1}{a-1}+\frac{b+1}{b-1}+\frac{c+1}{c-1} & =1+\frac{2}{a-1}+1+\frac{2}{b-1}+1+\frac{2}{c-1} \\
& =3+2 \cdot \frac{(b-1)(c-1)+(a-1)(c-1)+(a-1)(b-1)}{(a-1)(b-1)(c-1)} \\
& =3+2 \cdot \frac{(a b+b c+c a)-2(a+b+c)+3}{a b c-(a b+b c+c a)+(a+b+c)-1} \\
& =3+2 \cdot \frac{-2-0+3}{-2-(-2)+0-1}=1
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine the largest natural number $n$ such that there exists a sequence of $n$ real numbers with the following properties:
(i) the sum of any three consecutive terms of the sequence is positive,
(ii) the sum of any five consecutive terms of the sequence is negative.
|
Solution.
For $n=6$ there exists a sequence with the desired property, for example,
$$
3,-5,3,3,-5,3
$$
(5 points)
Note. A student who finds only an example for $n=5$, (e.g., $-1-13-1-1$) gets 2 points.
Assume there exists a sequence of length $n \geqslant 7$ with the desired property. Choose any 7 consecutive terms
$$
a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}
$$
of such a sequence. Then, due to (i), we have
$$
\begin{aligned}
& \text { (1) }\left\{\begin{array}{l}
a_{1}+a_{2}+a_{3}>0 \\
a_{2}+a_{3}+a_{4}>0 \\
a_{3}+a_{4}+a_{5}>0 \\
a_{4}+a_{5}+a_{6}>0 \\
a_{5}+a_{6}+a_{7}>0
\end{array}\right. \\
& \text { (2) }\left\{\begin{array}{l}
a_{1}+a_{2}+a_{3}+a_{4}+a_{5}<0 \\
a_{2}+a_{3}+a_{4}+a_{5}+a_{6}<0 \\
a_{3}+a_{4}+a_{5}+a_{6}+a_{7}<0
\end{array}\right.
\end{aligned}
$$
By adding the inequalities (1),
$$
\left(a_{1}+a_{2}+a_{3}\right)+\left(a_{2}+a_{3}+a_{4}\right)+\left(a_{3}+a_{4}+a_{5}\right)+\left(a_{4}+a_{5}+a_{6}\right)+\left(a_{5}+a_{6}+a_{7}\right)>0
$$
By adding the inequalities (2),
$$
\left(a_{1}+a_{2}+a_{3}+a_{4}+a_{5}\right)+\left(a_{2}+a_{3}+a_{4}+a_{5}+a_{6}\right)+\left(a_{3}+a_{4}+a_{5}+a_{6}+a_{7}\right)<0
$$
The left sides of these inequalities are equal, leading to a contradiction.
(10 points) Therefore, $n<7$. The longest such sequence has 6 terms.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.2.
Ivo, Alen, Vanja, Marko, and Saša are chefs in a hotel. Alen and Marko are responsible for preparing breakfast and lunch, Ivo and Vanja work on preparing lunch and dinner, while Saša is available for all three meals. In how many ways can their daily cooking schedule be arranged if each meal is prepared by exactly two chefs, and a chef who works must be assigned to exactly two meals? Can each chef have at least one day off in the week with such a daily schedule? Explain.
|
## Solution.
Lunch can be cooked by all chefs, so we will first choose the person who will cook lunch. There are several cases:
1. If lunch is cooked by Alen or Marko, they must also cook breakfast, so for dinner, we would need to engage two new chefs who would work on only one meal. Therefore, Alen and Marko cannot cook lunch together. The same situation applies to Ivo and Vanja.
2. If lunch is cooked by Saša and Alen, then Alen must cook breakfast. However, if Marko were to cook breakfast with Alen, Marko would also have to cook lunch, but lunch is already being cooked by two chefs. The same situation would occur in any other combination where Saša cooks lunch, so Saša cannot cook lunch.
3. If lunch is cooked by Alen and Ivo, then breakfast is cooked by Alen and Saša, and in this case, Saša must cook dinner, and with him, Ivo must cook dinner. If Saša were not to cook breakfast, then in this case, Marko would have to cook breakfast, but then he would also have to cook lunch, which is already occupied. Therefore, Saša must cook breakfast and dinner every day.
4. Each schedule is defined by the pair that cooks lunch, and there are four such pairs, so there are 4 schedules in total. Since Saša must work every day, he will not be able to have a free day.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.4.
Fran decided to paint the fence with the help of his friends Tin and Luke. They estimated that it would take Tin 3 hours more than Fran to paint the fence alone, and Luke 2 hours less than Fran to paint the fence alone. Working together, each at their own pace, they would paint the fence in 4 hours. How many hours would it take each of them to paint the fence alone?
|
## First Solution.
Let's denote the number of hours needed for each of the three friends to paint the fence alone.
Fran: $x$ hours, Tin: $x+3$ hours, Luka: $x-2$ hours. Note that $x$ must be greater than 2.
Considering how much each of them paints in one hour, we get the equation
$$
\frac{1}{x}+\frac{1}{x+3}+\frac{1}{x-2}=\frac{1}{4}
$$
We can rewrite the equation as
$$
\frac{1}{x}+\frac{1}{x-2}=\frac{1}{4}-\frac{1}{x+3}
$$
Bringing both sides of the equation to a common denominator, we get
$$
\frac{2 x-2}{x(x-2)}=\frac{x-1}{4(x+3)}
$$
or
$$
\frac{2(x-1)}{x(x-2)}=\frac{x-1}{4(x+3)}
$$
Since $x>2$, after dividing by $(x-1)$, we get
$$
\frac{2}{x(x-2)}=\frac{1}{4(x+3)}
$$
Then the following equalities follow
$$
\begin{gathered}
8(x+3)=x(x-2) \\
8 x+24=x^{2}-2 x \\
x^{2}-10 x-24=0
\end{gathered}
$$
By writing the middle term as $-12 x+2 x$ and appropriate grouping, the last expression can be written in the form of a product
$$
(x-12)(x+2)=0
$$
Only the factor $x-12$ can be equal to zero, so the solution to the initial equation is $x=12$. Then Fran needs 12, Tin needs 15, and Luka needs 10 hours to paint the fence alone.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.1. Determine the remainder when the number $\left(7^{2012}\right)^{2014}-\left(3^{12}\right)^{14}$ is divided by 10.
|
Solution.
$$
7^{1}=7,7^{2}=49,7^{3}=343,7^{4}=2401,7^{5}=16807, \ldots
$$
Therefore, the powers of the number 7 end with the digits $7,9,3,1$.
$$
3^{1}=3,3^{2}=9,3^{3}=27,3^{4}=81,3^{5}=243, \ldots
$$
The powers of the number 3 end with the digits $3,9,7,1$.
The number 2012 is divisible by 4, so the number $7^{2012 \cdot 2014}$ has the last digit the same as $7^{4}$, which is the digit 1.
The number 12 is divisible by 4, so the number $3^{12 \cdot 14}$ has the last digit the same as $3^{4}$, which is the digit 1.
If we subtract the numbers $7^{2012 \cdot 2014}$ and $3^{12 \cdot 14}$, the last digit of the difference will be 0, so the given number is divisible by 10.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.2. Points $H$ and $N$ are the feet of the altitudes from vertex $A$ and vertex $B$ of an acute-angled triangle $ABC$. The length of the altitude from vertex $A$ is $5 \sqrt{3} \mathrm{~cm}$, the length of side $\overline{A B}$ is $14 \mathrm{~cm}$, and the measure of the angle between the altitudes $\overline{A H}$ and $\overline{B N}$ is $60^{\circ}$. Determine the lengths of the remaining sides of the triangle and the length of segment $\overline{H N}$.
|
## Solution.
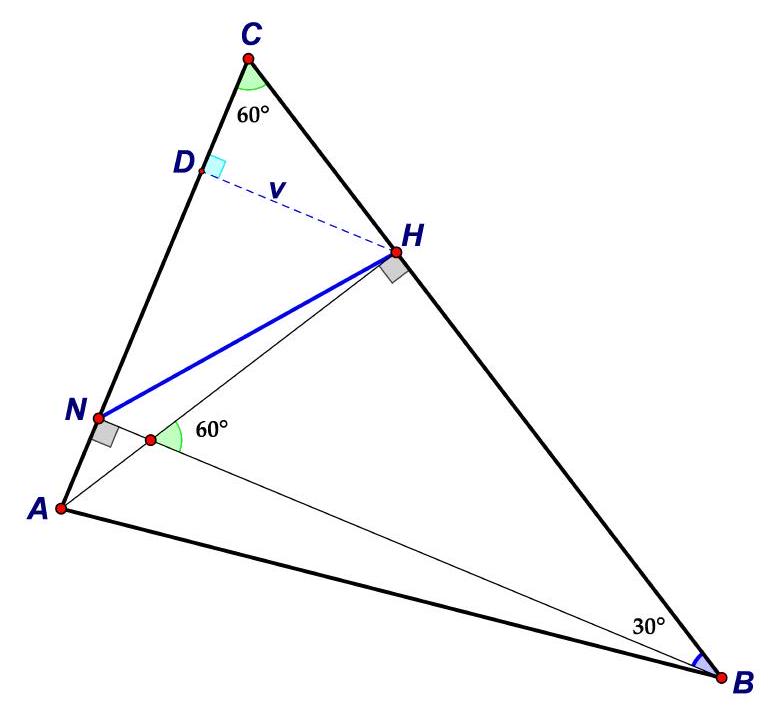
Since the given triangle is acute-angled, we conclude that the measure of angle $\angle B O H$ is $60^{\circ}$, so the measure of angle $\angle N B C = 90^{\circ} - 60^{\circ} = 30^{\circ}$, and the measure of angle $\angle A C B = 60^{\circ}$. From triangle $A H C$, we get $|A C| = \frac{|A H|}{\sin 60^{\circ}} = 10 \text{ cm}$.
Then, $|C H| = \frac{1}{2}|A C| = 5 \text{ cm}$.
From triangle $A B H$, we get
$$
|B H|^{2} = |A B|^{2} - |A H|^{2} = 196 - (5 \sqrt{3})^{2} = 121
$$
so $|B H| = 11 \text{ cm}$, and thus $|B C| = 11 + 5 = 16 \text{ cm}$.
It remains to determine the length of segment $\overline{H N}$.
From triangle $B N C$, we get $|N C| = |B C| \cos 60^{\circ} = 16 \cdot \frac{1}{2} = 8 \text{ cm}$. Triangles $A B C$ and $H N C$ are similar because they share an angle and the ratio of their sides is $\frac{|H C|}{|A C|} = \frac{|N C|}{|B C|}$, i.e., $\frac{5}{10} = \frac{8}{16} = \frac{1}{2}$.
We conclude that the ratio of the sides $\frac{|H N|}{|A B|} = \frac{1}{2}$, so the length of segment $\overline{H N}$ is $\frac{1}{2} \cdot 14 = 7 \text{ cm}$.
The desired length can also be calculated using the height $v$ from vertex $H$ in triangle $H N C$.
$$
\begin{aligned}
& v = |H C| \cdot \sin 60^{\circ} = 5 \frac{\sqrt{3}}{2} \text{ cm} \\
& |C D| = \frac{1}{2}|H C| = \frac{5}{2} \text{ cm} \\
& |D N| = |C N| - |C D| = 5.5 \text{ cm} \\
& |H N|^{2} = v^{2} + |D N|^{2} \Rightarrow |H N| = 7 \text{ cm}
\end{aligned}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.4. Determine all natural numbers $a$ for which the number $a^{3}+1$ is a power of 3.
|
## First solution.
If $a^{3}+1$ is divisible by 3, the number $a$ is of the form $a=3 p-1, p \in \mathbb{N}$. Then,
$$
a^{3}+1=(3 p-1)^{3}+1=27 p^{3}-27 p^{2}+9 p-1+1=9 p\left(3 p^{2}-3 p+1\right)
$$
The expression $3 p^{2}-3 p+1$ is not divisible by 3, and since $a^{3}+1$ is a power of 3, it can only be equal to $3^{0}$.
Then from
$$
3 p^{2}-3 p+1=1
$$
it follows that $p=1$, and $a^{3}+1=9$ so $a=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.4.
From the starting tram station, three trams depart at 5:00 AM. The first tram takes 1 hour and 30 minutes to return to the starting station, the second tram takes 1 hour, and the third tram takes 40 minutes. At what time will all three trams be at the starting station at the same time again? How many times will this happen on the same day if the trams operate from 5:00 AM to 24:00 (midnight), not counting the first departure at 5:00 AM?
|
## First solution.
The time required for all three trams to return to the starting station at the same time after a joint departure is the least common multiple of the times each tram individually needs to return to the starting station.
Thus, we are looking for the least common multiple of
1 hour and 30 minutes $=90$ minutes, 1 hour $=60$ minutes, and 40 minutes, which is the number:
$LCM(90,60,40)=10 \cdot 3 \cdot 3 \cdot 2 \cdot 2=360$.
The trams will meet at the starting station every 360 minutes, or every 6 hours.
They will first meet again at the starting station at 11:00.
They will meet at the starting station 3 times in the same day.
1 point
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.3.
The graphs of two linear functions have slopes of 3 and $\frac{1}{3}$, and intersect at the point $(3,3)$. Determine the area of the triangle bounded by these graphs and the $x$-axis.
|
## Solution.
The graphs of the given linear functions are lines with the equation $y=k x+l$.
The slope $k$ is given for both lines, as well as a point that belongs to these lines. Therefore, we can determine the equations of the given lines.
$p_{1} \ldots y=3 x+l$, or $3=9+l$ so $l=-6$, and the equation of the first line is $y=3 x-6$.
Similarly for the second line: $p_{2} \ldots y=\frac{1}{3} x+l$, or $3=1+l$ so $l=2$, and the equation of the second line is $y=\frac{1}{3} x+2$.
The sketch of the desired area is:

The intersection of the line $p_{1}$ with the $x$-axis is the point $B(2,0)$, and for the line $p_{2}$, the point $A(-6,0)$.
The area of the triangle $A B T$ is given by the expression:
$$
P=\frac{d(A, B) \cdot y_{T}}{2}=\frac{8 \cdot 3}{2}=12
$$
Note: The area of the triangle can also be calculated using the coordinate method.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.1.
Solve the equation $\binom{x+1}{x-2}+2\binom{x-1}{3}=7(x-1)$.
|
## First Solution.
Due to the definition of binomial coefficients, it must hold that $x-1 \geqslant 3$, i.e., $x \geqslant 4$.
Using the property of binomial coefficients $\binom{n}{k}=\binom{n}{n-k}$, we can rewrite the given equation as:
$\binom{x+1}{x+1-x+2}+2\binom{x-1}{3}=7(x-1)$, or
$\binom{x+1}{3}+2\binom{x-1}{3}=7(x-1)$.
1 point
By applying the rule for calculating binomial coefficients, we get
$\frac{(x+1) x(x-1)}{6}+2 \frac{(x-1)(x-2)(x-3)}{6}=7(x-1)$, and after dividing by $(x-1) \neq 0$, we have
$\frac{(x+1) x}{6}+2 \frac{(x-2)(x-3)}{6}=7$
This equation reduces to the quadratic equation $x^{2}-3 x-10=0$, 1 point
whose solutions are $x_{1}=5, x_{2}=-2$. 1 point
Due to the initial conditions, the solution to the given equation is $x=5$. 1 point
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.5.
Mate and Roko, while preparing for a competition, were challenging each other with "unsolvable" problems. So Roko asked Mate: Do you know what the sum of the digits of the number $3^{2018}$ is?
To this, Mate replied with a new question:
I don't know, but do you know what the 2018th number is if you continue the sequence where the first number is $3^{2018}$, the second number is the sum of its digits, the third number is the sum of the digits of the second number, and so on? Each subsequent number in this sequence is equal to the sum of the digits of the previous number!
Show that Mate's question is solvable and determine the 2018th number in this sequence.
|
## Solution.
Let's denote the first, second, third, ..., 2018th term of the given sequence of numbers as $a_{1}, a_{2}, a_{3}, \ldots, a_{2018}, \ldots$.
Notice that $a_{1}=3^{2018}=9 \cdot 3^{2016}$.
Since the first term of the sequence is divisible by 9, the sum of its digits is also divisible by 9. Therefore, the number $a_{2}$ is divisible by 9, and consequently, all subsequent terms of the sequence are also divisible by 9.
Since $a_{1}=3^{2018}=9^{1009}<10^{1009}$, the first term of the sequence cannot have more than 1009 digits, and each digit is at most 9. Therefore, $a_{2} \leqslant 9 \cdot 1009=9081$.
Thus, the second term of the sequence has at most 4 digits, so the third term of the sequence is at most $4 \cdot 9=36$.
Since the third term of the sequence is divisible by 9, it can only be $9, 18, 27$, or 36. In any case, the sum of its digits is 9, so each subsequent term of the sequence is equal to 9. Therefore, the 2018th term of the sequence is equal to 9.
## NATIONAL MATHEMATICS COMPETITION
## 4th grade - high school - B variant
Poreč, April 13, 2018.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.1.
In the equation $x^{2}+m-3 x=m x-2$, determine the positive real number $m$ so that the total sum of all solutions of the equation and their squares is 44.
|
## Solution.
Given the equation $x^{2}+m-3 x=m x-2$ we write it in the form $x^{2}-(m+3) x+m+2=0. \quad 1$ point The solutions of this quadratic equation must satisfy the condition $x_{1}+x_{2}+x_{1}^{2}+x_{2}^{2}=44$, or $x_{1}+x_{2}+\left(x_{1}+x_{2}\right)^{2}-2 x_{1} \cdot x_{2}=44$.
According to Vieta's formulas, we have
$$
\begin{array}{r}
x_{1}+x_{2}=m+3 \\
x_{1} x_{2}=m+2
\end{array}
$$
Substituting into the given condition $m+3+(m+3)^{2}-2(m+2)=44$ and after simplification, we get $m^{2}+5 m-36=0$.
This equation has solutions $m_{1}=-9, m_{2}=4$.
Since a positive number $m$ is sought, the solution is $m=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.6.
Students Marko and Luka worked on a part-time basis, Marko in a tourist office, and Luka in a hotel. Marko earned a total of 200 kn for his work. Luka worked 5 hours less than Marko and earned 125 kn. If Marko had worked as many hours as Luka, and Luka as many hours as Marko, then Luka would have earned 150 kn more than Marko. How many hours did Marko work, and how many did Luka, and what was the hourly wage for each of them?
|
## Solution.
$n=$ the number of hours Marko worked, $n>5$.
$x=$ Marko's hourly wage, $y=$ Luka's hourly wage
Then we have the following system of equations
$$
\begin{gathered}
n x=200 \\
(n-5) y=125 \\
n y-(n-5) x=150
\end{gathered}
$$
From the first and second equations, express $x, y$ :
$$
x=\frac{200}{n}, \quad y=\frac{125}{n-5}
$$
Substitute into the third equation:
$$
\begin{gathered}
n \cdot \frac{125}{n-5}-(n-5) \cdot \frac{200}{n}=150 \\
125 n^{2}-200(n-5)^{2}=150 n(n-5) \\
5 n^{2}-8(n-5)^{2}=6 n(n-5) \\
9 n^{2}-110 n+200=0
\end{gathered}
$$
from which we get $n=10$ or $n=\frac{20}{9}$.
The solution $n=\frac{20}{9}$ does not satisfy the condition $n>5$, so $n=10$.
Marko worked 10 hours, and Luka $n-5=5$ hours.
Marko earns $\frac{200}{10}=20 \mathrm{kn}$ per hour, and Luka $\frac{125}{5}=25 \mathrm{kn}$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.7.
The height $\overline{C D}$ divides the right triangle $A B C$ into two parts in which circles with centers $S_{1}, S_{2}$ are inscribed. Parallels to the height $\overline{C D}$ through the centers $S_{1}, S_{2}$ intersect the legs $\overline{A C}$ and $\overline{B C}$ at points $M$ and $N$, respectively. If the lengths are $|A C|=8,|B C|=6$, determine the lengths of the segments $\overline{C M}$ and $\overline{C N}$.
## Solution.

In triangle $A B C$, we calculate $c=10, \sin \alpha=\frac{6}{10}=\frac{3}{5}, \cos \alpha=\frac{4}{5}$.
From triangle $A C D$, we have $|A D|=8 \cos \alpha=\frac{32}{5},|C D|=8 \sin \alpha=\frac{24}{5}$,
$$
r_{1}=\frac{|C D| \cdot|A D|}{|C D|+|A D|+|A C|}=\frac{8}{5} \quad \text { by the formula } P=r s
$$
or
$$
r_{1}=\frac{1}{2}(|C D|+|A D|-|A C|)=\frac{8}{5} \quad \text { since } a+b=c+2 r \quad 2 \text { points }
$$
From triangle $B D C$, we have $|B D|=6 \cdot \sin \alpha=\frac{18}{5}$,
$$
r_{2}=\frac{|C D| \cdot|B D|}{|C D|+|B D|+|B C|}=\frac{6}{5} \quad \text { or } \quad r_{2}=\frac{1}{2}(|C D|+|B D|-|B C|)=\frac{6}{5} . \quad 2 \text { points }
$$
From triangle $C M E$, we get
$$
x=\frac{r_{1}}{\cos \alpha}=\frac{\frac{8}{5}}{\frac{4}{5}}=2
$$
Similarly, from triangle $C N E$, we obtain
$$
y=\frac{r_{2}}{\sin \alpha}=\frac{\frac{6}{5}}{\frac{3}{5}}=2
$$
Note: Students can calculate the required lengths using the similarity of triangles $A B C$, $A C D, C B D, M C E$ and $C N F$ (instead of trigonometry).
## COUNTY COMPETITION IN MATHEMATICS
## 3rd grade - high school - B variant
23rd February 2016.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
## Task B-3.1
Show that the value of the expression
$$
\sin ^{2}\left(x-\frac{2016 \pi}{3}\right)+\sin ^{2}\left(x-\frac{2017 \pi}{3}\right)+\sin ^{2}\left(x-\frac{2018 \pi}{3}\right)
$$
does not depend on $x$.
|
## Solution.
$$
\begin{aligned}
& \sin ^{2}\left(x-\frac{2016 \pi}{3}\right)+\sin ^{2}\left(x-\frac{2017 \pi}{3}\right)+\sin ^{2}\left(x-\frac{2018 \pi}{3}\right)= \\
& \sin ^{2}(x-672 \pi)+\sin ^{2}\left(x-\frac{\pi}{3}-672 \pi\right)+\sin ^{2}\left(x-\frac{2 \pi}{3}-672 \pi\right)= \\
& \sin ^{2}(x)+\sin ^{2}\left(x-\frac{\pi}{3}\right)+\sin ^{2}\left(x-\frac{2 \pi}{3}\right)= \\
& \sin ^{2}(x)+\left(\sin x \cos \frac{\pi}{3}-\cos x \sin \frac{\pi}{3}\right)^{2}+\left(\sin x \cos \frac{2 \pi}{3}-\cos x \sin \frac{2 \pi}{3}\right)^{2}= \\
& \sin ^{2}(x)+\left(\sin x \cdot \frac{1}{2}-\cos x \cdot \frac{\sqrt{3}}{2}\right)^{2}+\left(\sin x \cdot \frac{1}{2}+\cos x \cdot \frac{\sqrt{3}}{2}\right)^{2}= \\
& \sin ^{2} x+\frac{1}{4} \sin ^{2} x-\frac{\sqrt{3}}{2} \sin x \cos x+\frac{3}{4} \cos ^{2} x+\frac{1}{4} \sin ^{2} x+\frac{\sqrt{3}}{2} \sin x \cos x+\frac{3}{4} \cos ^{2} x= \\
& \frac{3}{2} \sin ^{2} x+\frac{3}{2} \cos ^{2} x=\frac{3}{2}
\end{aligned}
$$
Note: Alternatively, we can use the double-angle formula:
$$
\begin{gathered}
\sin ^{2}(x)+\sin ^{2}\left(x-\frac{\pi}{3}\right)+\sin ^{2}\left(x-\frac{2 \pi}{3}\right)= \\
\frac{1-\cos (2 x)}{2}+\frac{1-\cos \left(2 x-\frac{2 \pi}{3}\right)}{2}+\frac{1-\cos \left(2 x-\frac{4 \pi}{3}\right)}{2}
\end{gathered}
$$
It remains to prove the fact that $\cos (2 x)+\cos \left(2 x-\frac{2 \pi}{3}\right)+\cos \left(2 x-\frac{4 \pi}{3}\right)=0$.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5. (4 points)
In a bag, there is a sufficiently large number of red, white, and blue balls. Each student randomly takes three balls from the bag. How many students must there be at a minimum to ensure that at least one pair of them has the same combination of balls, i.e., the same number of balls of each color?
|
## Solution.
Let's denote the red ball with the letter $C$, the white ball with the letter $B$, and the blue ball with the letter $P$. The possible combinations of three balls are:
$C C C, B B B, P P P, C B B, C P P, B C C, B P P, P C C, P B B, C B P$.
There are a total of 10 possible combinations.
(2 points)
To ensure that there are at least two students with the same combination, it is sufficient to have at least 11 students.
(2 points)
Note. The conclusion that for $k$ combinations, $k+1$ students are needed is worth 2 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-1.6. (10 points)
If $a^{2}+2 b^{2}=3 c^{2}$, show that $\left(\frac{a+b}{b+c}+\frac{b-c}{b-a}\right) \cdot \frac{a+2 b+3 c}{a+c}$ is a natural number.
|
## First Solution.
First, we simplify the expression in parentheses:
$$
\begin{aligned}
& \frac{a+b}{b+c}+\frac{b-c}{b-a}=\frac{(a+b)(b-a)+(b-c)(b+c)}{(b+c)(b-a)} \\
& =\frac{b^{2}-a^{2}+b^{2}-c^{2}}{(b+c)(b-a)} \stackrel{(*)}{=} \frac{3 c^{2}-a^{2}-a^{2}-c^{2}}{(b+c)(b-a)} \\
& =\frac{2 c^{2}-2 a^{2}}{(b+c)(b-a)}=\frac{2(c-a)(c+a)}{(b+c)(b-a)}
\end{aligned}
$$
From this, it follows that
$$
\begin{aligned}
& \left(\frac{a+b}{b+c}+\frac{b-c}{b-a}\right) \cdot \frac{a+2 b+3 c}{a+c}=\frac{2(c-a)(c+a)}{(b+c)(b-a)} \cdot \frac{a+2 b+3 c}{a+c} \\
& =\frac{2(c-a)(a+2 b+3 c)}{(b+c)(b-a)}=2 \cdot \frac{a c+2 b c+3 c^{2}-a^{2}-2 a b-3 a c}{(b+c)(b-a)} \\
& \stackrel{(*)}{=} 2 \cdot \frac{a c+2 b c+2 b^{2}-2 a b-3 a c}{b^{2}-a b+b c-a c} \\
& =2 \cdot \frac{2\left(-a c+b c+b^{2}-a b\right)}{b^{2}-a b+b c-a c}=4
\end{aligned}
$$
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Task A-2.6. (10 points)
Let $z=\frac{1}{2}+i \frac{\sqrt{3}}{2}$. Calculate
$$
z+z^{2}+z^{3}+z^{4}+\ldots+z^{k}+\ldots+z^{2010}
$$
|
## Solution.
We calculate: $z^{2}=-\frac{1}{2}+i \frac{\sqrt{3}}{2}, z^{3}=-1, z^{4}=-\frac{1}{2}-i \frac{\sqrt{3}}{2}, z^{5}=\frac{1}{2}-i \frac{\sqrt{3}}{2}, z^{6}=1$. (5 points) By adding, we get $z+z^{2}+z^{3}+z^{4}+z^{5}+z^{6}=0$.
Since 2010 is divisible by 6, we have
$$
\begin{aligned}
& z+z^{2}+z^{3}+z^{4}+\ldots+z^{k}+\ldots+z^{2010} \\
& =\left(z+z^{2}+\cdots+z^{6}\right)+z^{6}\left(z+z^{2}+\cdots+z^{6}\right)+\cdots+z^{2004}\left(z+z^{2}+\cdots+z^{6}\right) \\
& =\left(z+z^{2}+z^{3}+z^{4}+z^{5}+z^{6}\right)\left(1+z^{6}+z^{12}+z^{18}+\cdots+z^{2004}\right)=0
\end{aligned}
$$
Note. Using the formula for the sum of a geometric series, we immediately get:
$$
z+z^{2}+z^{3}+z^{4}+\ldots+z^{k}+\ldots+z^{2010}=z \cdot \frac{z^{2010}-1}{z-1}=z \cdot \frac{\left(z^{3}\right)^{670}-1}{z-1}=0
$$
due to the fact that $z^{3}=-1$. Such a solution should also be scored with all 10 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.2. (4 points)
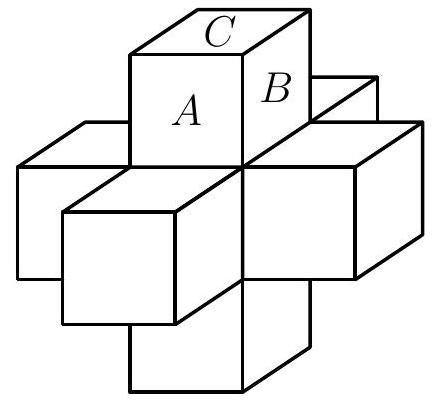
Legoplus is a body consisting of seven equal cubes joined in such a way that there is one cube that shares a common face with each of the remaining six cubes.
Each face of the legoplus must be painted with one color. How many colors are minimally needed to do this so that no two adjacent faces are painted the same color?
|
## Solution.
Obviously, there are three sides of the Lego brick for which it is true that any two are adjacent. For example, such sides are marked with the letters $A, B$ and $C$ in the image below. From this, we conclude that at least three colors are needed to color the Lego brick in the desired way.
(2 points)
If we color side $A$ and all sides parallel to it white, side $B$ and all sides parallel to it gray, and side $C$ and all sides parallel to it black, we will get a coloring with three colors that satisfies the conditions of the problem. This coloring is shown in the image below.
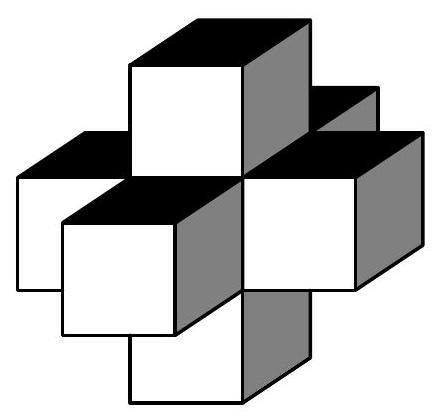
Therefore, the smallest number of colors needed to color the outer sides of the Lego brick so that no two adjacent sides are the same color is three.
(2 points)
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.3. (4 points)
What is the remainder when the number (ABCDE2010) ${ }_{15}$ is divided by 7?
Numbers in base 15 are written using the digits $0,1,2,3,4,5,6,7,8,9$, A, B, C, D, E whose values are respectively $0,1,2,3,4,5,6,7,8,9,10,11,12,13,14$.
|
## First Solution.
The number (ABCDE2010) ${ }_{15}$ can be written as
$$
a=10 \cdot 15^{8}+11 \cdot 15^{7}+12 \cdot 15^{6}+13 \cdot 15^{5}+14 \cdot 15^{4}+2 \cdot 15^{3}+1 \cdot 15^{1}
$$
Let $b=10+11+12+13+14+2+0+1+0=63$.
Notice that the number $15^{k}-1$ is divisible by 7 for any natural number $k$ because
$$
15^{k}-1=(15-1) \cdot\left(15^{k-1}+\ldots+1\right)
$$
Subtract the number $b$ from the number $a$:
$$
\begin{aligned}
& a-b= \\
& =10 \cdot 15^{8}+11 \cdot 15^{7}+12 \cdot 15^{6}+13 \cdot 15^{5}+14 \cdot 15^{4}+2 \cdot 15^{3}+1 \cdot 15^{1} \\
& \begin{array}{lllllll}
-10 & -11 & -12 & -13 & -14 & -2 & -1
\end{array} \\
& =10 \cdot\left(15^{8}-1\right)+11 \cdot\left(15^{7}-1\right)+12 \cdot\left(15^{6}-1\right)+13 \cdot\left(15^{5}-1\right)+14 \cdot\left(15^{4}-1\right)+ \\
& +2 \cdot\left(15^{3}-1\right)+1 \cdot(15-1)
\end{aligned}
$$
We conclude that this difference is divisible by 7 because each addend is divisible by 7.
(2 points)
On the other hand, we know that the number $b=63$ is divisible by 7, so it follows that the number $a$ is also divisible by 7.
Therefore, the remainder when divided by 7 is 0.
Note. The fact that when dividing $15^{k}$ by 7 we get a remainder of 1 (for $k=1, \ldots, 8$) can also be obtained using the binomial formula
$$
15^{k}=(14+1)^{k}=\sum_{i=0}^{k}\binom{k}{i} 14^{i}
$$
All terms in the sum are divisible by 7 except the first $\binom{k}{0} \cdot 1=1$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.1.
Determine all natural numbers $b$ for which the equality $11 \cdot 22 \cdot 33=13310$ holds in the number system with base $b$.
|
## First solution.
Let $b$ be the sought base of the number system.
The equality in the problem is equivalent to the equality
$$
(b+1)(2 b+2)(3 b+3)=b^{4}+3 b^{3}+3 b^{2}+b
$$
We can simplify the expression by factoring out a factor on the left side, and applying the binomial cube formula on the right side:
$$
6(b+1)^{3}=b(b+1)^{3}
$$
Since $b$ cannot be -1, it follows that $b=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.2.
Let $S=\{0,95\}$. In each step, Lucija expands the set $S$ by choosing some polynomial with coefficients from $S$, different from the zero polynomial, and adding all integer roots of that polynomial to the set $S$. The process continues by selecting another polynomial with coefficients from the thus expanded set $S$ as long as new roots can be obtained in this way.
Prove that Lucija can expand the set $S$ to a set that cannot be further expanded by a finite sequence of steps. How many elements will the set $S$ have then?
|
## Solution.
An integer root of a polynomial with integer coefficients must be a divisor of the free term. Since, without loss of generality, we can assume that the free term of the polynomial Lucija chooses is different from zero, we conclude that the set $S$ can only be extended by integer divisors of the number 95. Since the number of divisors of the number 95 is finite, Lucija will not be able to extend the set $S$ infinitely.
Let's prove that Lucija will add all integer divisors of 95 to the set $S$, i.e., that $S$ will eventually have 9 elements.
Since -1 is a root of the polynomial $95 x+95$, the number -1 can be added to $S$.
The number 1 is a root of the polynomial $-x^{95}-x^{94}-\cdots-x+95$, so 1 can be added to $S$.
Now the number -95 can be added because it is a root of the polynomial $x+95$.
The polynomial $-x^{3}+x^{2}+x+95$ with coefficients from $S$ has a root 5, so 5 can be added to $S$. Now we see that -5 can also be added to $S$ because -5 is a root of the polynomial $x+5$.
Similarly, at the end, $-19,19 \in S$ because they are roots of the polynomials $5 x+95$ and $5 x-95$.
Note: The polynomial for which 5 is a root can be obtained in a systematic way. Clearly, 5 cannot be obtained as a root of a linear polynomial with coefficients from the set $S=\{-95,-1,0,1,95\}$.
Assume that 5 is a root of the polynomial $a x^{2}+b x+c$, for $a, b, c \in S$. Then $5 \mid c$ and $c \neq 0$, so $c=95$ or $c=-95$. We have
$$
25 a+5 b= \pm 95
$$
or
$$
5 a+b= \pm 19
$$
which is impossible for $a, b \in S$. Therefore, if 5 is a root of a polynomial with coefficients from $S$, the polynomial must be of degree at least 3.
Assume that
$$
5^{3} a+5^{2} b+5 c+d=0
$$
for some $a, b, c, d \in S$. Then $5 \mid d$ and $d \neq 0$, so $d=95$ or $d=-95$.
If $d=95$, dividing the above equation by 5 gives
$$
25 a+5 b+c=-19
$$
so we see that $c \equiv 1(\bmod 5)$. Since $c \in S$, it must be $c=1$.
Now $5 a+b=-4$ from which it easily follows that $a=-1$ and $b=1$.
|
9
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.2.
A Gaussian integer is a complex number whose real and imaginary parts are integers. Determine the largest natural number $n$ for which there exists a set of $n$ Gaussian integers such that the squares of their absolute values are consecutive natural numbers.
|
## Solution.
If the complex number $z=x+y i$ is a Gaussian integer, then $|z|^{2}=x^{2}+y^{2}$ is the sum of the squares of two integers.
The square of an even integer is divisible by 4, while the square of an odd integer gives a remainder of 1 when divided by 4. Therefore, the sum of the squares of two integers can give remainders of 0, 1, or 2 when divided by 4.
If $n$ were greater than 3, then among any four consecutive natural numbers in the sequence
$$
\left|z_{1}\right|^{2},\left|z_{2}\right|^{2}, \ldots,\left|z_{n}\right|^{2}
$$
there would be a number that gives a remainder of 3 when divided by 4, which we have shown to be impossible. Therefore, $n$ is less than or equal to 3.
Notice that $2+2 i, 3, 3+i$ are Gaussian integers whose modulus squares sum to $8, 9, 10$ respectively. Thus, the largest natural number $n$ in the problem is equal to three.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.4.
For real numbers $a, b$ and $c$, it is given that $a+b+c=0$ and $abc=4$. Determine the value of the expression $a^{3}+b^{3}+c^{3}$.
|
## First Solution.
From the first equality, we have $a+b=-c$, or $(a+b)^{3}=-c^{3}$. 1 point
By applying the formula for the sum of cubes, we get
$$
\begin{array}{rlrl}
(a+b)^{3} & =a^{3}+3 a^{2} b+3 a b^{2}+b^{3}=-c^{3} & 1 \text { point } \\
a^{3} & +3 a b(a+b)+b^{3}=-c^{3} & 1 \text { point } \\
a^{3} & +b^{3}+c^{3}=-3 a b(a+b) . & 1 \text { point }
\end{array}
$$
From $a+b=-c$, we have $a b(a+b)=-a b c=-4$.
Therefore, we finally have $a^{3}+b^{3}+c^{3}=-3 a b(a+b)=(-3) \cdot(-4)=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.2.
Solve the equation $\sqrt{9-5 x}-\sqrt{3-x}=\frac{6}{\sqrt{3-x}}$ in the set of real numbers.
|
## Solution.
Let's group the expressions that include $\sqrt{3-x}$ on one side of the equation, then square it:
$$
\begin{array}{rlrl}
\sqrt{9-5 x} & =\sqrt{3-x}+\frac{6}{\sqrt{3-x}}, \quad /^{2} & \\
9-5 x & =3-x+12+\frac{36}{3-x}, & & 1 \text { point } \\
-6-4 x & =\frac{36}{3-x}, \quad / \cdot(3-x) & \\
(-6-4 x)(3-x)=36, & 1 \text { point } \\
4 x^{2}-6 x-54=0 . & 1 \text { point }
\end{array}
$$
The solutions to the resulting quadratic equation are $x=\frac{9}{2}$ and $x=-3$. 1 point
Substituting into the original equation, we see that for $x=\frac{9}{2}$ the equation is not defined, 1 point while $x=-3$ is a solution.
Thus, the only solution to the equation is $x=-3$.
Note: Instead of substituting the value $x=\frac{9}{2}$, it is possible to verify that the original equation is defined for values of $x$ that satisfy $9-5 x \geqslant 0$ and $3-x>0$, i.e., $x \leqslant \frac{9}{5}$. This analysis changes the second-to-last 1 point in the scoring scheme. The number $x=-3$ must be substituted regardless of this analysis.
The first steps of the solution can also be derived in a different order: it is possible to first multiply the equation by $\sqrt{3-x}$, and then square the rearranged equation. Each of these steps also carries 1 point.
Reducing the problem to a quadratic equation with the process totals 3 points. A different squaring method (such as squaring the original equation without prior rearrangement) can lead to a fourth-degree equation. In such a solution, the correct higher-degree equation is worth 2 points, while 1 point is awarded for justifying that finding the remaining roots of the polynomial and justifying that they are not solutions to the original equation. The last 3 points in the above scoring scheme are awarded in the same way.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.1.
For a natural number $n$, let $s(n)$ denote the sum of its positive divisors, and $d(n)$ the number of its positive divisors. Determine all natural numbers $n$ such that
$$
s(n)=n+d(n)+1
$$
|
## Solution.
Notice that $n=1$ is certainly not a solution, so $d(n) \geqslant 2$.
Furthermore, it is not possible for $d(n)=2$ because then the number $n$ would be prime and the given equation would read $1+n=n+2+1$, so $d(n) \geqslant 3$.
Let $1=D_{1}<D_{2}<\cdots<D_{d}=n$ be the divisors of the number $n$. The initial equation reads
$$
1+\sum_{i=2}^{d(n)-1} D_{i}+n=n+d(n)+1
$$
Since $D_{i} \geqslant 2$ for all $i \in\{2,3, \ldots, d(n)-1\}$, we have $d(n)=\sum_{i=2}^{d(n)-1} D_{i} \geqslant(d(n)-2) \cdot 2$, from which it follows that $d(n) \leqslant 4$, or $3 \leqslant d(n) \leqslant 4$.
For $d(n)=3$, the number $n$ is the square of some prime number $p$ and the initial equation reads
$$
1+p+p^{2}=p^{2}+3+1
$$
from which it follows that $p=3$ and $n=p^{2}=9$.
For $d(n)=4$ we have two possibilities.
a) If $n$ is the product of some prime numbers $q$ and $r(q<r)$, then the initial equation reads $1+q+r+q r=q r+4+1$, from which it follows that $q+r=4$. There are no such prime numbers $q$ and $r$.
b) If $n$ is the cube of some prime number $s$, then the initial equation reads $1+s+s^{2}+s^{3}=s^{3}+4+1$, from which it follows that $s^{2}+s-4=0$. There is no such natural number $s$.
Therefore, the only solution is $n=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.2.
With which digit does the number $2^{2022}+3^{2022}+7^{2022}$ end?
|
## Solution.
Powers of 2, starting from $2^{1}$, end with the digits $2,4,8,6$ and then repeat periodically.
Powers of 3, starting from $3^{1}$, end with the digits $3,9,7,1$ and then repeat periodically.
Powers of 7, starting from $7^{1}$, end with the digits $7,9,3,1$ and then repeat periodically.
To determine the last digit of the powers $2^{2022}$, $3^{2022}$, and $7^{2022}$, we will find the remainder when the exponent 2022 is divided by 4. Since 2022 : $4=505$ with a remainder of 2, it follows:
The number $2^{2022}$ ends with the same digit as the number $2^{2}$, which is the digit 4.
The number $3^{2022}$ ends with the same digit as the number $3^{2}$, which is the digit 9.
The number $7^{2022}$ ends with the same digit as the number $7^{2}$, which is the digit 9.
1 point
The sum $2^{2022}+3^{2022}+7^{2022}$ ends with the same digit as the number $4+9+9=22$, so the units digit of the number $2^{2022}+3^{2022}+7^{2022}$ is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.6.
The hotel owners at the beginning of the tourist season bought new blankets, towels, and pillowcases for 4000 kn. They paid 120 kn for each blanket, 50 kn for each towel, and 25 kn for each pillowcase. If they bought a total of 100 items, how many blankets, how many towels, and how many pillowcases were bought? They bought at least one item of each type.
|
## First solution.
Let $x$ be the number of duvets bought, $y$ be the number of blankets bought, and $z$ be the number of pillows bought, $x, y, z \in \mathbb{N}$.
According to the conditions of the problem, we have:
$x+y+z=100 \quad$ and $\quad 120 x+50 y+25 z=4000$.
1 point
Express one unknown from the first equation and substitute it into the second:
$z=100-x-y$
$120 x+50 y+25(100-x-y)=4000$
$19 x+5 y=300$
From the last equation, express one unknown in terms of the other again:
$x=\frac{300-5 y}{19}=\frac{5(60-y)}{19}$
Since $x$, $y$, and $z$ must be natural numbers, we conclude that the numerator must be divisible by the denominator, that is, the expression $60 - y$ must be a multiple of 19, and $y<60$ must hold.
Then $60-y=19$ or $60-y=19 \cdot 2=38$ or $60-y=19 \cdot 3=57$.
For each of these possibilities, we get one of the three solutions to the problem.
From $y=41$ it follows that $x=5$ and $z=54$, that is, 5 duvets, 41 blankets, and 54 pillows were bought.
From $y=22$ it follows that $x=10$ and $z=68$, that is, 10 duvets, 22 blankets, and 68 pillows were bought.
From $y=3$ it follows that $x=15$ and $z=82$, that is, 15 duvets, 3 blankets, and 82 pillows were bought.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.2.
Determine the zeros of the function $f: \mathbf{R} \rightarrow \mathbf{R}, f(x)=\log _{2}\left(18 \cdot 4^{x}-8 \cdot 2^{x}+1\right)-2 x-1$.
|
## Solution.
The zeros of the given function are the solutions of the equation $f(x)=0$.
Thus, we need to solve the equation $\log _{2}\left(18 \cdot 4^{x}-8 \cdot 2^{x}+1\right)-2 x-1=0$.
The equation can be written in the following form:
$$
\log _{2}\left(18 \cdot 4^{x}-8 \cdot 2^{x}+1\right)=2 x+1
$$
or
$$
\log _{2}\left(18 \cdot 4^{x}-8 \cdot 2^{x}+1\right)=\log _{2} 2^{2 x+1}
$$
Then we have
$$
\begin{gathered}
18 \cdot 4^{x}-8 \cdot 2^{x}+1=2^{2 x+1} \\
18 \cdot 4^{x}-8 \cdot 2^{x}+1=2 \cdot 4^{x} \\
16 \cdot 4^{x}-8 \cdot 2^{x}+1=0
\end{gathered}
$$
We can introduce the substitution $t=2^{x}$ and solve the corresponding quadratic equation, or notice that the last expression is equal to $\left(4 \cdot 2^{x}-1\right)^{2}=0$. From this, we conclude that
$$
\begin{aligned}
& 2^{x}=\frac{1}{4} \\
& x=-2
\end{aligned}
$$
Note: The expression $\log _{2}\left(18 \cdot 4^{x}-8 \cdot 2^{x}+1\right)=2 x+1$ could also be transformed into $18 \cdot 4^{x}-8 \cdot 2^{x}+1=2^{2 x+1}$ using the relation $\log _{a} b=c \Leftrightarrow a^{c}=b$, and this method should also be awarded one point.
Note: The domain of the function is given in the problem, so it is not necessary to determine its natural domain. For the same reason, it is not necessary to write down the condition that must be satisfied for the corresponding logarithmic equation to make sense.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-4.3.
Ako je $z+z^{-1}=2 \cos 5^{\circ}$, koliko je $\left(z^{2022}-z^{-2022}\right)^{2022}$ ?
|
## Rješenje.
Iz $z+z^{-1}=2 \cos 5^{\circ}$ nakon množenja brojem $z$ dobivamo kvadratnu jednadžbu:
$z^{2}-\left(2 \cos 5^{\circ}\right) z+1=0$.
1 bod
Njezina su rješenja:
$z_{1,2}=\frac{2 \cos 5^{\circ} \pm \sqrt{4 \cos ^{2} 5^{\circ}-4}}{2}=\frac{2 \cos 5^{\circ} \pm 2 \sqrt{\cos ^{2} 5^{\circ}-1}}{2}=\cos 5^{\circ} \pm i \sin 5^{\circ}$.
1 bod
Tada je:
$z^{2022}=\left(\cos 5^{\circ} \pm i \sin 5^{\circ}\right)^{2022}=\cos 10110^{\circ} \pm i \sin 10110^{\circ}=\cos 30^{\circ} \pm i \sin 30^{\circ}=\frac{\sqrt{3}}{2} \pm \frac{1}{2} i$.
2 boda
$z^{-2022}=\left(\cos 5^{\circ} \pm i \sin 5^{\circ}\right)^{-2022}=\cos \left(-30^{\circ}\right) \pm i \sin \left(-30^{\circ}\right)=\frac{\sqrt{3}}{2} \mp \frac{1}{2} i$.
1 bod
Konačno, vrijednost traženoga izraza jest:
$\left(z^{2022}-z^{-2022}\right)^{2022}=\left(\frac{\sqrt{3}}{2} \pm \frac{1}{2} i-\left(\frac{\sqrt{3}}{2} \mp \frac{1}{2} i\right)\right)^{2022}=( \pm i)^{2022}=i^{2022}=i^{2}=-1$.
1 bod
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.5.
Determine all natural numbers $y>1$ that satisfy the equation
$\log _{\sin x} y-3 \log _{y} \sqrt{\sin x}=\frac{1}{2}$, where $x \in\left[\frac{\pi}{6}, \frac{\pi}{3}\right]$.
|
## Solution.
Let's write the given equation in the following form:
$\log _{\sin x} y-\frac{3}{2} \cdot \frac{1}{\log _{\sin x} y}=\frac{1}{2}$.
Introduce the substitution $t=\log _{\sin x} y$ so that this equation becomes $t-\frac{3}{2} \cdot \frac{1}{t}=\frac{1}{2}$.
Note that $t=\log _{\sin x} y>0$ due to $y>1$, so the above equation is equivalent to $2 t^{2}-t-3=0$.
The solutions to this quadratic equation are $t_{1}=-1$ and $t_{2}=\frac{3}{2}$.
Thus, $\log _{\sin x} y=-1$ or $\log _{\sin x} y=\frac{3}{2}$, that is:
$y=\frac{1}{\sin x}$ or $y=(\sin x)^{\frac{3}{2}}$.
We discard the solution $y=(\sin x)^{\frac{3}{2}}$ because $y>1$, while $(\sin x)^{\frac{3}{2}} \leqslant 1$.
On the given interval $\left[\frac{\pi}{6}, \frac{\pi}{3}\right]$, we have $\frac{\pi}{6} \leqslant x \leqslant \frac{\pi}{3}$,
and since the sine function is increasing on this interval, it follows that:
$\sin \frac{\pi}{6} \leqslant \sin x \leqslant \sin \frac{\pi}{3}$, that is, $\frac{1}{2} \leqslant \sin x \leqslant \frac{\sqrt{3}}{2}$, so $\frac{2}{\sqrt{3}} \leqslant \frac{1}{\sin x} \leqslant 2$.
Thus, $y \in\left[\frac{2}{\sqrt{3}}, 2\right]$.
Since $y$ is a natural number and $y>1$, the only solution is $y=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.4. Ivo and Mate are clearing the road of snow. First, Ivo cleared $\frac{3}{5}$ of the road, and then Mate cleared the remaining part so that the entire road was cleared in 12 hours. How many hours would it take for them to clear the road together if it is known that it would take Mate 5 hours more to clear the road alone than it would take Ivo to clear it alone?
|
## Solution.
Let $x$ be the number of hours it would take Ivo to clear the road alone.
Then $x+5$ is the number of hours it would take Mate to clear the road alone.
(1 point)
For clearing $\frac{3}{5}$ of the road, Ivo needed $\frac{3 x}{5}$ hours, and for clearing the remaining $\frac{2}{5}$ of the road, Mate needed $\frac{2(x+5)}{5}$ hours.
(1 point)
Since the clearing was completed in 12 hours, we have
$$
\frac{3 x}{5}+\frac{2(x+5)}{5}=12
$$
From this, we get $x=10$,
Ivo can clear the road in 10 hours, and Mate in 15 hours.
(1 point)
Together, they would clear
$$
\frac{1}{10}+\frac{1}{15}=\frac{1}{6} \quad \text{of the road per hour}
$$
They would clear the entire road in 6 hours.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.2. The lengths of the sides of a triangle are three consecutive odd numbers, and the measure of one of the angles is $\frac{2 \pi}{3}$. Calculate the lengths of the sides of this triangle.
|
## Solution.
Let $a=2 n-1, b=2 n+1, c=2 n+3$.
Since $\frac{2 \pi}{3}$ is an obtuse angle, its opposite side is the longest, which is $c=2 n+3$.
From the cosine rule, we get
$$
\begin{aligned}
& \cos \frac{2 \pi}{3}=\frac{(2 n-1)^{2}+(2 n+1)^{2}-(2 n+3)^{2}}{2(2 n-1)(2 n+1)} \\
& \frac{-1}{2}=\frac{4 n^{2}-12 n-7}{2\left(4 n^{2}-1\right)} \\
& 8 n^{2}-12 n-8=0 \\
& n_{1,2}=\frac{3 \pm 5}{4}
\end{aligned}
$$
Since $n>0$, the solution to the equation is $n=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.4. Helena invited a certain number of children to her birthday party. The age of one child was one eighth of the sum of the ages of the remaining children. This age ratio did not change in later years. How many children were at the party?
|
## Solution.
Let $n$ be the number of children at the party, and $x$ be the age of the mentioned child.
Furthermore, let $x_{1}, x_{2}, \ldots, x_{n-1}$ be the ages of the remaining $n-1$ children. Then we have
$$
x=\frac{1}{8}\left(x_{1}+x_{2}+\cdots+x_{n-1}\right)
$$
(2 points)
If we add $t$ years to each child, the same ratio will hold, which we write as
$$
\begin{aligned}
x+t & =\frac{1}{8}\left(\left(x_{1}+t\right)+\left(x_{2}+t\right)+\cdots+\left(x_{n-1}+t\right)\right) \\
& =\frac{1}{8}\left(x_{1}+x_{2}+\cdots+x_{n-1}\right)+\frac{1}{8}(n-1) t
\end{aligned}
$$
From (1) and (2), we get $t=\frac{1}{8}(n-1) t$, and from this, $n=9$.
There were nine children at the party.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.5. Determine all natural numbers $n$ for which $2^{n}-1$ and $2^{n}+1$ are simultaneously prime numbers.
|
## Solution.
For $n=1$ we have $2^{n}-1=1$ and $2^{n}+1=3$, so $n=1$ is not a solution because 1 is not a prime number. (1 point)
For $n=2$ we have $2^{n}-1=3$ and $2^{n}+1=5$.
(1 point)
Let $n>2$. Then the numbers $2^{n}-1, 2^{n}, 2^{n}+1$ are three consecutive natural numbers, one of which is certainly divisible by 3.
(2 points)
Since the number $2^{n}$ is not divisible by 3, one of the numbers $2^{n}-1, 2^{n}+1$ must be divisible by 3, which means that they cannot both be prime.
(1 point)
Therefore, the only solution is $n=2$.
(1 point)
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.5.
Determine the minimum value of the expression $2 x^{2}+\frac{1}{2} y^{2}$ if $y+2 x=2$.
|
## Solution.
From the second equality, express $y=2-2 x$ and substitute into the first. Then we have
$$
\begin{aligned}
2 x^{2}+\frac{1}{2}(2-2 x)^{2} & =2 x^{2}+\frac{1}{2}\left(4-8 x+4 x^{2}\right) \\
& =4 x^{2}-4 x+2 \\
& =4 x^{2}-4 x+1+1 \\
& =(2 x-1)^{2}+1
\end{aligned}
$$
Since $(2 x-1)^{2} \geqslant 0$ for all $x \in \mathbb{R}$, the expression $(2 x-1)^{2}+1$ is greater than or equal to 1 for all real numbers $x$, so its minimum value is equal to 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.6.
Solve the equation $i z^{2}+2 \bar{z}=0$ in the set of complex numbers. Calculate the quotient of the sum of the cubes and the product of all solutions that are different from zero.
|
## Solution.
Let $z=x+i y, x, y \in \mathbb{R}$. Then we have
$$
\begin{array}{r}
i \cdot(x+i y)^{2}+2(x-i y)=0 \\
i\left(x^{2}+2 x y i-y^{2}\right)+2 x-2 y i=0 \\
i x^{2}-2 x y-i y^{2}+2 x-2 y i=0
\end{array}
$$
By equating the real and imaginary parts, we get the system of equations
$$
\begin{array}{r}
-2 x y+2 x=0 \\
x^{2}-y^{2}-2 y=0
\end{array}
$$
The left side of the first equation can be factored as $-2 x(y-1)=0$.
If $x=0$, from the second equation we get $y=0$ or $y=-2$.
Since $z \neq 0$, it must be $y=-2$, which means one solution of the system is $z_{1}=-2 i$.
If $x \neq 0$, then $y=1$, and from the second equation, we get
$$
x= \pm \sqrt{3}
$$
Finally, the solutions of the equation are $z_{1}=-2 i, z_{2}=\sqrt{3}+i, z_{3}=-\sqrt{3}+i$. Let's calculate the sum of the cubes and the product of these solutions.
$$
\begin{aligned}
& z_{1}^{3}=(-2 i)^{3}=8 i \\
& z_{2}^{3}=3 \sqrt{3}+9 i+3 \sqrt{3} i^{2}+i^{3}=8 i \\
& z_{3}^{3}=-3 \sqrt{3}+9 i-3 \sqrt{3} i^{2}+i^{3}=8 i
\end{aligned}
$$
Then we have
$$
\begin{gathered}
z_{1}^{3}+z_{2}^{3}+z_{3}^{3}=3 \cdot 8 i=24 i \\
z_{1} z_{2} z_{3}=-2 i(\sqrt{3}+i)(-\sqrt{3}+i)=-2 i(-3-1)=8 i
\end{gathered}
$$
The desired quotient is $\frac{24 i}{8 i}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.5.
The lengths of the sides of triangle $A B C$ are $|B C|=4 \mathrm{~cm}$ and $|A C|=5 \mathrm{~cm}$, and the length of the part of the angle bisector of $\varangle A C B$ that lies within the triangle is $s=\frac{10}{3} \mathrm{~cm}$. Calculate the length of side $\overline{A B}$.
|
## Solution.
The bisector of an angle in a triangle intersects the opposite side in the ratio of the remaining sides (The Angle Bisector Theorem of a Triangle), i.e., $\frac{x}{y}=\frac{5}{4}$, where $x=|A D|, y=|D B|$, and point $D$ is the intersection of the given bisector and side $\overline{A B}$. Then, $x=5 k, y=4 k$.
Apply the Law of Cosines to triangles $A D C$ and $C D B$.
$$
\cos \frac{\gamma}{2}=\frac{5^{2}+\left(\frac{10}{3}\right)^{2}-25 k^{2}}{2 \cdot 5 \cdot \frac{10}{3}}, \quad \cos \frac{\gamma}{2}=\frac{\left(\frac{10}{3}\right)^{2}+4^{2}-16 k^{2}}{2 \cdot 4 \cdot \frac{10}{3}}
$$
By equating the right-hand sides of these equations, we get
$$
\frac{5^{2}+\left(\frac{10}{3}\right)^{2}-25 k^{2}}{2 \cdot 5 \cdot \frac{10}{3}}=\frac{\left(\frac{10}{3}\right)^{2}+4^{2}-16 k^{2}}{2 \cdot 4 \cdot \frac{10}{3}}
$$
which simplifies to $k^{2}=\frac{4}{9}$,
so $k=\frac{2}{3}$.
Then, $|A B|=x+y=9 k=6 \text{ cm}$.
Note: A similar solution can be obtained by applying the Law of Cosines to triangles $A D C$ and $A B C$ to determine $\cos \alpha$.
If a student does not use the Angle Bisector Theorem of a Triangle, they can arrive at the ratio $\frac{x}{y}=\frac{5}{4}$ by applying the Law of Sines to triangles $A D C$ and $D B C$, which is worth 2 points:
$$
\frac{x}{\sin \frac{\gamma}{2}}=\frac{5}{\sin \varphi}, \quad \frac{y}{\sin \frac{\gamma}{2}}=\frac{4}{\sin \left(180^{\circ}-\varphi\right)}, \quad \text{where } \varphi=\angle A D C
$$
Since $\sin \left(180^{\circ}-\varphi\right)=\sin \varphi$, it follows that $\frac{x}{y}=\frac{5}{4}$, and we proceed as in the first solution.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-4.2.
Dane su beskonačne sume
$$
\begin{aligned}
& a=2020^{x+3}+2020^{x+2}+2020^{x+1}+2020^{x}+\ldots \\
& b=2019^{x+2}+2019^{x+1}+2019^{x}+2019^{x-1}+\ldots
\end{aligned}
$$
Odredite $x \in \mathbb{R}$ tako da vrijedi $\frac{a}{b}=2018$.
|
## Rješenje.
Uočimo da su beskonačne sume $a$ i $b$ geometrijski redovi. Njihovi kvocijenti su redom $\frac{1}{2020} \mathrm{i} \frac{1}{2019}$.
Kako su kvocijenti manji od 1 redovi su konvergentni, pa vrijedi
$$
\begin{aligned}
& a=2020^{x+3}+2020^{x+2}+2020^{x+1}+2020^{x}+\cdots=\frac{2020^{x+3}}{1-\frac{1}{2020}}=\frac{2020^{x+4}}{2019} \\
& b=2019^{x+2}+2019^{x+1}+2019^{x}+2019^{x-1}+\cdots=\frac{2019^{x+2}}{1-\frac{1}{2019}}=\frac{2019^{x+3}}{2018}
\end{aligned}
$$
Još treba riješiti jednadžbu
Slijedi $\frac{2020^{x+4}}{2019^{x+4}}=1$ odnosno $x+4=0, x=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
Spouses Ana and Tomislav came to a party where four other couples were also present. Upon arrival, a certain number of handshakes occurred. No one shook hands with their own spouse or with themselves. Later, when Tomislav asked everyone how many people they had shaken hands with, he received nine different answers. How many people did Ana shake hands with?
|
## Solution.
No one dealt with more than eight people, so the answers Tomislav received were: "0", "1", "2", "3", "4", "5", "6", "7", "8".
Ana definitely did not deal with eight people. If Ana had dealt with eight people, everyone else (except Tomislav) would have dealt with her, so no one would have answered "0".
Let's say person $A_{1}$ dealt with eight people. We can conclude that the only person who could have dealt with zero people is the spouse of $A_{1}$. Let's call this person $A_{2}$.
Now, if we assume that Ana dealt with seven people, then everyone except Tomislav and person $A_{2}$ would have dealt with Ana and person $A_{1}$, so no one would have answered "1".
Let's say person $B_{1}$ dealt with seven people. We conclude that the person who answered "1" is her spouse $B_{2}$, because all other people dealt with both Ana and person $A_{1}$.
By similar reasoning, we find that the couple $C_{1}$ and $C_{2}$ gave the answers "6" and "2", and the couple $D_{1}$ and $D_{2}$ gave the answers "5" and "3".
Finally, Ana is left, who gave the answer "4".
The following graph shows that this is indeed possible:
Therefore, Ana dealt with four people.
## NATIONAL MATHEMATICS COMPETITION
2nd grade - high school - A variant
April 3, 2011.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.3.
Determine all values of the parameter $a$ for which the system
$$
\begin{aligned}
2^{|x|}+|x| & =x^{2}+y+a \\
x^{2}+y^{2} & =1
\end{aligned}
$$
has exactly one solution $(x, y) \in \mathbb{R}^{2}$.
|
## Solution.
If the pair $(x, y)$ is a solution to the given system, then the pair $(-x, y)$ is also a solution.
We conclude that the unique solution of this system must be of the form $(0, y)$.
Substituting $x=0$ into the given system, we get
$$
\begin{aligned}
1 & =y+a \\
y^{2} & =1
\end{aligned}
$$
so $y=1$ or $y=-1$, and therefore $a=0$ or $a=2$.
Let's first consider the case $a=0$.
The initial system reduces to
$$
\begin{aligned}
2^{|x|}+|x| & =x^{2}+y \\
x^{2}+y^{2} & =1
\end{aligned}
$$
It is easy to see that $(0,1)$ is a solution. Let's show that there are no other solutions.
From the second equation, it follows that $|x| \leqslant 1$ and $|y| \leqslant 1$. Since $0 \leqslant|x| \leqslant 1$, we have $|x| \geqslant x^{2}$.
We also have
$$
2^{|x|} \geqslant 2^{0}=1 \geqslant|y| \geqslant y
$$
so
$$
2^{|x|}+|x| \geqslant x^{2}+y
$$
For equality to hold, we must have $|x|=0$ and $|y|=y$, i.e., $x=0$ and $y \geqslant 0$.
Due to the second equation, we then have $(x, y)=(0,1)$, so this system has no other solutions.
In the case $a=2$, we can observe that in addition to $(0,-1)$, the solutions of the system
$$
\begin{aligned}
2^{|x|}+|x| & =x^{2}+y+2 \\
x^{2}+y^{2} & =1
\end{aligned}
$$
are also the pairs $(1,0)$ and $(-1,0)$.
We conclude that the system has a unique solution if and only if $a=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-1.3.
Ako je $\frac{a}{b}=\frac{c}{d}, b \neq 0, d \neq 0$ koliko je
$$
\frac{(a+c)(b+d)}{a+b+c+d}-\frac{a b}{a+b}-\frac{c d}{c+d} ?
$$
|
## Prvo rješenje.
Ako je $\frac{a}{b}=\frac{c}{d}$, postoji neki $k \in \mathbb{R}, k \neq 0$, tako da je $a=k c$ i $b=k d$.
Tada je
$$
\begin{aligned}
\frac{(a+c)(b+d)}{a+b+c+d}-\frac{a b}{a+b}-\frac{c d}{c+d} & =\frac{c(1+k) d(1+k)}{c(1+k)+d(1+k)}-\frac{k c k d}{k(c+d)}-\frac{c d}{c+d} & & 1 \text { bod } \\
& =\frac{c d(1+k)}{c+d}-\frac{k c d}{c+d}-\frac{c d}{c+d} & & 2 \text { boda } \\
& =\frac{c d(1+k-k-1)}{c+d}=0 . & & 1 \text { bod }
\end{aligned}
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.4.
How many right triangles are there with the lengths of the legs being integers $a, b$, and the length of the hypotenuse $b+1$, where $b<100$?
|
## Solution.
For a right-angled triangle, we have $(b+1)^{2}=a^{2}+b^{2}$, which means $b^{2}+2 b+1=a^{2}+b^{2}$, from which it follows that $2 b=a^{2}-1, \text{i.e., } b=\frac{a^{2}-1}{2}$.
Since $b<100$, we have $\frac{a^{2}-1}{2}<100, a^{2}<201$.
The squares of integers less than 201 are 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196.
Since $b \in \mathbb{N}$, from $b=\frac{a^{2}-1}{2}$ it follows that $a^{2}$ is odd.
Then $a \in\{3,5,7,9,11,13\}$. It follows that $b \in\{4,12,24,40,60,84\}$.
Therefore, there are 6 triangles with sides $(a, b, b+1)$ and the given property.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.6.
Luka and Pero decided to visit a friend and set off from place $A$ to place $B$, which is $170 \mathrm{~km}$ away. Luka started walking, while Pero was driven by a motorcyclist. After some time, the motorcyclist returned to pick up Luka, and Pero continued on foot, so that both arrived at place $B$ at the same time. Both pedestrians walk at the same speed of $5 \mathrm{~km} / \mathrm{h}$, and the motorcyclist drives at a speed of $85 \mathrm{~km} / \mathrm{h}$. At what distance from place $B$ and after how much time did the motorcyclist stop and return to pick up Luka? How long did it take for Luka and Pero to travel from place $A$ to place $B$?
|
## Solution.
Since both arrived at the same time traveling at the same speed, it means they walked the same part of the path on foot and the same part on the motor.

Let's introduce some notations: $s=$ distance $|A B|$ (from place $A$ to place $B)$.
$|A D|=|C B|=x$ is the part of the path that Luka, respectively Pero, walked on foot.
Then $|A C|=|B D|=s-x,|C D|=s-2 x$.
While Luka was walking the distance $|A D|$, the motorcyclist was traveling the distance
$$
|A C|+|C D|=s-x+s-2 x=2 s-3 x
$$
From this, we have
$$
\frac{x}{5}=\frac{2 s-3 x}{85} \Rightarrow x=\frac{s}{10} \Rightarrow x=\frac{170}{10}=17 \mathrm{~km}
$$
From $|\overline{A D}|=17 \mathrm{~km}$ it follows that $|\overline{A C}|=s-x=153 \mathrm{~km}$.
The time the motorcyclist drove Pero is $t_{A C}=\frac{s-x}{85}=\frac{153}{85}=1 \mathrm{~h}$ and $48 \mathrm{~min}$.
The time Luka or Pero walked is $t_{C B}=t_{A D}=\frac{x}{5}=\frac{17}{5}=3 \mathrm{~h}$ and $24 \mathrm{~min}$. 1 point
The time of arrival from place $A$ to place $B$ is $t_{A C}+t_{C B}=\frac{153}{85}+\frac{17}{5}=5 \mathrm{~h}$ and $12 \mathrm{~min}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.2.
In a rectangular hall, there is a carpet in the shape of a rhombus. The area of the carpet is $54 \mathrm{~m}^{2}$, and the perimeter is $30 \mathrm{~m}$. The vertices of the rhombus are exactly at the midpoints of the sides of the rectangle. Determine the dimensions of the hall.
|
## Solution.
Notice that the dimensions of the hall (the sides of the rectangle $a$ and $b$) are also the diagonals of the rhombus.

If $P=\frac{a \cdot b}{2}=54$, and $o=4 d=30$, then the lengths of the sides are the solution to the following system of equations:
$$
\begin{aligned}
& a b=108 \\
& a^{2}+b^{2}=225
\end{aligned}
$$
If we multiply the first equation by -2 and add it to the second, we get $(a-b)^{2}=9$.
We can assume that $a>b$, so $a=b+3$ or $b^{2}+3 b-108=0$.
This gives $b=9$ and $a=12$.
Therefore, the dimensions of the hall are 12 and 9 meters.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.4.
Determine the last digit of the product of the first hundred natural numbers that give a remainder of 3 when divided by 5.
|
## Solution.
All natural numbers that give a remainder of 3 when divided by 5 can be written in the form $5k + 3, k \in \mathbb{N}_{0}$.
Let's write the product of the first hundred such numbers:
$$
\begin{aligned}
& 3 \cdot 8 \cdot 13 \cdot 18 \cdot 23 \cdot 28 \cdot 33 \cdots (5k + 3) \cdots 498 \\
& = (3 \cdot 8) \cdot (13 \cdot 18) \cdot (23 \cdot 28) \cdot (33 \cdot 38) \cdots ((5k - 2) \cdot (5k + 3)) \cdots (493 \cdot 498)
\end{aligned}
$$
Each of the 50 products in parentheses ends with the digit 4.
The last digit of our product is the last digit of the power $4^{50}$.
Since $4^{50} = 16^{25}$, and powers of 16 always end with the digit 6, the desired product ends with the digit 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.3.
Each of the 28 students visited at least one of the three countries. The number of students who visited only Italy and Spain is equal to the number of students who visited only Italy. No student visited only Spain or only Greece. Six students visited Greece and Italy, but not Spain. The number of students who visited only Greece and Spain is five times the number of students who visited all three countries. If the number of students who visited all three countries is even and different from zero, how many students visited only Italy?
|
## Solution.
We solve the problem using Venn diagrams. Let $x$ be the number of students who visited only Italy, and $y$ be the number of students who visited all three countries.
In set $I$ are all who visited Italy, in set $\check{S}$ all who visited Spain, and in set $G$ all who visited Greece. According to the conditions in the problem, we fill in the diagram. We have
$$
\begin{aligned}
& x+x+6+y+5 y=28 \\
& 2 x+6 y=22 \\
& x+3 y=11 \\
& x=11-3 y
\end{aligned}
$$
Since $y$ is even and different from 0, and $x \geqslant 0$, the only possibility is $y=2$.
Then $x=11-6=5$. Therefore, 5 students visited only Italy.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.5.
Ivo and Ana both drank lemonade at the cinema and watched a movie. Ivo took a medium size, and Ana a large one, which is $50\%$ larger than the medium. After both had drunk $\frac{3}{4}$ of their lemonade, Ana gave Ivo one third of what was left to her and an additional 0.5 dl. After the movie ended and they had finished all the lemonade, they found out that they had both drunk the same amount of lemonade. How many deciliters of lemonade did they drink in total?
|
## Solution.
Let $x$ be the average amount of lemonade Ivo took at the beginning. Ana took $1.5x$.
Ivo received from Ana $\frac{1}{3} \cdot \frac{1}{4} \cdot 1.5 x + 0.5 = \frac{1}{8} x + 0.5$,
which means he drank a total of $x + \frac{1}{8} x + 0.5 = \frac{9}{8} x + 0.5 \text{ dl}$ of lemonade.
Ana drank a total of $1.5 x - \left(\frac{1}{8} x + 0.5\right) = \frac{11}{8} x - 0.5$.
Then, $\frac{11}{8} x - 0.5 = \frac{9}{8} x + 0.5$, 1 point
$\frac{2}{8} x = 1, x = 4$.
The average amount of lemonade is $4 \text{ dl}$, and the total amount they drank is $x + 1.5 x = 2.5 x$, which is $10 \text{ dl}$ of lemonade.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.7.
Determine the value of the real parameter $m$ so that the solutions of the equation
$$
(m x-1) \cdot x=m x-2
$$
represent the lengths of the legs of a right triangle with a hypotenuse of length $\frac{5}{6}$.
|
## Solution.
The given equation can be written in the form $m x^{2}-(m+1) x+2=0$.
The solutions must be real, so the discriminant of the equation must be greater than or equal to zero,
$$
\begin{aligned}
& (m+1)^{2}-8 m \geqslant 0 \\
& m^{2}-6 m+1 \geqslant 0 \\
& m \in(-\infty, 3-2 \sqrt{2}] \cup[3+2 \sqrt{2}, \infty)
\end{aligned}
$$
If the solutions are the lengths of the legs of a right triangle, then the Pythagorean theorem applies:
$$
\begin{array}{ll}
x_{1}^{2}+x_{2}^{2}=\left(\frac{5}{6}\right)^{2}, & 1 \text { point } \\
\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=\frac{25}{36} . & 1 \text { point }
\end{array}
$$
According to Vieta's formulas, we have
$$
\begin{array}{ll}
x_{1}+x_{2}=-\frac{b}{a}=\frac{m+1}{m} & 1 \text { point } \\
x_{1} x_{2}=\frac{c}{a}=\frac{2}{m} & 1 \text { point }
\end{array}
$$
from which the quadratic equation follows
$$
11 m^{2}-72 m+36
$$
whose solutions are $m_{1}=6$ and $m_{2}=\frac{6}{11}$.
Since $m_{2}$ is not in the interval $(-\infty, 3-2 \sqrt{2}] \cup[3+2 \sqrt{2}, \infty)$, the solution to the problem is only $m_{1}=6$.
## SCHOOL/CITY COMPETITION IN MATHEMATICS
3rd grade - high school - B variant
January 4, 2015.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH IN AN APPROPRIATE MANNER.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.1.
Determine the value of the expression $A=1+\operatorname{tg} 35^{\circ}+\operatorname{tg} 10^{\circ}+\operatorname{tg} 35^{\circ} \cdot \operatorname{tg} 10^{\circ}$.
|
## Solution.
From $35^{\circ}+10^{\circ}=45^{\circ}$ it follows:
$$
\begin{aligned}
& 1=\tan 45^{\circ}=\tan\left(35^{\circ}+10^{\circ}\right)=\frac{\tan 35^{\circ}+\tan 10^{\circ}}{1-\tan 35^{\circ} \cdot \tan 10^{\circ}} \\
& \Rightarrow \tan 35^{\circ}+\tan 10^{\circ}=1-\tan 35^{\circ} \cdot \tan 10^{\circ} \\
& \Rightarrow A=1+\tan 35^{\circ}+\tan 10^{\circ}+\tan 35^{\circ} \cdot \tan 10^{\circ}=1+1-\tan 35^{\circ} \cdot \tan 10^{\circ}+\tan 35^{\circ} \cdot \tan 10^{\circ}=2 . \quad 2 \text { points }
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.1.
Solve the equation
$$
\binom{n}{n-2}+2\binom{n-1}{n-3}=\binom{n+1}{n-1}+\binom{n-2}{n-3}
$$
|
## Solution.
From the symmetry of binomial coefficients, it follows that
$$
\binom{n}{2}+2\binom{n-1}{2}=\binom{n+1}{2}+\binom{n-2}{1}
$$
The solution can be a natural number \( n \geqslant 3 \).
By expanding the binomial coefficients, we get:
$$
\begin{aligned}
& \frac{n(n-1)}{2}+2 \cdot \frac{(n-1)(n-2)}{2}=\frac{(n+1) n}{2}+(n-2) \quad / \cdot 2 \\
& n^{2}-n+2\left(n^{2}-2 n-n+2\right)=n^{2}+n+2 n-4 \\
& n^{2}-5 n+4=0
\end{aligned}
$$
The possible solutions to the equation are \( n_{1}=4 \) and \( n_{2}=1 \).
Given the condition, the only solution is \( n=4 \).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.2.
Determine the natural number $n$, so that the ratio of the seventh term counting from the beginning to the seventh term counting from the end, in the expansion of the binomial $\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^{n}$, is equal to $\frac{1}{6}$.
|
## Solution.
In the expansion of $\left(\sqrt[3]{2}+\frac{1}{\sqrt[3]{3}}\right)^{n}=\left(2^{\frac{1}{3}}+3^{-\frac{1}{3}}\right)^{n}$, the seventh term from the beginning is
$$
\binom{n}{6}\left(2^{\frac{1}{3}}\right)^{n-6}\left(3^{-\frac{1}{3}}\right)^{6}
$$
and the seventh term from the end is
$$
\binom{n}{6}\left(2^{\frac{1}{3}}\right)^{6}\left(3^{-\frac{1}{3}}\right)^{n-6}
$$
Then,
$$
\begin{aligned}
& \frac{\binom{n}{6}\left(2^{\frac{1}{3}}\right)^{n-6}\left(3^{-\frac{1}{3}}\right)^{6}}{\binom{n}{6}\left(2^{\frac{1}{3}}\right)^{6}\left(3^{-\frac{1}{3}}\right)^{n-6}}=\frac{1}{6} \\
& 2^{\frac{n-12}{3}} \cdot 3^{\frac{n-12}{3}}=\frac{1}{6} \\
& 6^{\frac{n-12}{3}}=6^{-1} \\
& n=9
\end{aligned}
$$
$$
1 \text { point }
$$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.3.
The lengths of the sides of a triangle are three consecutive natural numbers, not less than 3. Calculate the difference in the lengths of the segments that the height to the middle side divides on that side.
|
## Solution.
Let the lengths of the sides of the triangle be $|A C|=n-1,|A B|=n$ and $|B C|=n+1$, as shown in the figure.

$\overline{C N}$ is the altitude to the side $\overline{A B}$, the middle side in length, and $x$ and $y$ are the lengths of the segments into which point N divides the side $\overline{A B}$. Then, from the right triangles $A N C$ and $N B C$, by the Pythagorean theorem, we have
$$
(n-1)^{2}-x^{2}=v^{2}
$$
$$
(n+1)^{2}-y^{2}=v^{2} \text {. }
$$
If we equate the obtained expressions for the square of the altitude, we get:
$$
\begin{array}{cc}
(n-1)^{2}-x^{2}=(n+1)^{2}-y^{2} & 1 \text { point } \\
n^{2}-2 n+1-n^{2}-2 n-1=x^{2}-y^{2} & \\
y^{2}-x^{2}=4 n . & 1 \text { point }
\end{array}
$$
By applying the formula for the difference of squares, we get
$$
(y+x)(y-x)=4 n
$$
Since $y+x=n$, it follows that
$$
(y+x)(y-x)=4 n
$$
or
$$
y-x=4
$$
The desired difference of the segments is 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.6.
Determine the value of the real parameter $a$ for which each of the equations
$$
2 a-1=\frac{3-3 a}{x-1} \quad \text { and } \quad a^{2}(2 x-4)-1=a(4-5 x)-2 x
$$
has a unique solution and their solutions are equal.
|
## Solution.
First, let's solve the equation $2 a-1=\frac{3-3 a}{x-1}$. Note that $x \neq 1$ must hold. After multiplying the equation by $x-1$ and simplifying the resulting algebraic expressions, we get:
$$
\begin{gathered}
2 a x-2 a-x+1=3-3 a \\
x(2 a-1)=2-a \\
x=\frac{2-a}{2 a-1}, a \neq \frac{1}{2}
\end{gathered}
$$
Since $x \neq 1$, from $\frac{2-a}{2 a-1} \neq 1$ it follows that
$$
2-a \neq 2 a-1,
$$
which means $a \neq 1$.
Thus, for $a \in \mathbf{R}, a \neq \frac{1}{2}$ and $a \neq 1$, the equation has a unique solution $x=\frac{2-a}{2 a-1}$.
Now, let's solve the second equation.
$$
\begin{gathered}
a^{2}(2 x-4)-1=a(4-5 x)-2 x \\
2 x a^{2}-4 a^{2}-1=4 a-5 a x-2 x \\
x\left(2 a^{2}+5 a+2\right)=4 a^{2}+4 a+1 \\
x\left(2 a^{2}+4 a+a+2\right)=(2 a+1)^{2} \\
x[2 a(a+2)+a+2]=(2 a+1)^{2} \\
x(a+2)(2 a+1)=(2 a+1)^{2}
\end{gathered}
$$
From this equality, we conclude that for $a \in \mathbf{R}, a \neq-\frac{1}{2}$ and $a \neq-2$,
the equation has a unique solution
$$
x=\frac{2 a+1}{a+2} \text {. }
$$
Let's equate the solutions of the given equations.
$$
\frac{2-a}{2 a-1}=\frac{2 a+1}{a+2}
$$
This leads to $4-a^{2}=4 a^{2}-1$, so $a^{2}=1$, and
$$
a= \pm 1
$$
Since $a \neq 1$, it follows that the equations have the same solution only for $a=-1$.
Note: Instead of calculating the value of $a$ for which the condition $x \neq 1$ is satisfied, the student can check at the end whether the given equations have the same solution for the obtained real numbers $a= \pm 1$. In this case, the student can get all the expected points, but must have written the conditions for which these equations have a unique solution, i.e., $a \neq \frac{1}{2}$ for the first equation and $a \neq-\frac{1}{2}, a \neq-2$ for the second equation.
If the student has not written only these conditions, deduct 2 points. If the student has not written the condition $x \neq 1$, and has not discarded one solution and has not even checked the solutions, but has the previously mentioned conditions for the solutions of the equations individually, deduct 3 points.
If the student has none of the conditions, no checks, only the solution, they can get a maximum of 5 points.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.2.
Let $A=1202^{2}+2^{2021}$. Determine the units digit of the number $A^{2021}$.
|
## Solution.
The unit digit of the square of the number 1202 is 4.
1 point
Powers with a base of 2 have unit digits in the sequence $2,4,8$, 6, depending on the remainder when the exponent is divided by 4.
Therefore, the unit digit of the number $2^{2021}$ is 2.
Then the unit digit of the number $A$ is $4+2=6$.
The unit digit of any power with a base of 6 is always the number 6.
Therefore, the unit digit of the number $A^{2021}$ is also 6.
1 point
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.1.
Calculate $\left(\frac{6+4 \sqrt{2}}{\sqrt{2}+\sqrt{6+4 \sqrt{2}}}+\frac{6-4 \sqrt{2}}{\sqrt{2}-\sqrt{6-4 \sqrt{2}}}\right)^{2}$.
|
## Solution.
Notice that the following holds:
$$
\begin{aligned}
& \sqrt{6+4 \sqrt{2}}=\sqrt{4+4 \sqrt{2}+2}=\sqrt{(2+\sqrt{2})^{2}}=|2+\sqrt{2}|=2+\sqrt{2} \\
& \sqrt{6-4 \sqrt{2}}=\sqrt{4-4 \sqrt{2}+2}=\sqrt{(2-\sqrt{2})^{2}}=|2-\sqrt{2}|=2-\sqrt{2}
\end{aligned}
$$
By substituting the obtained equalities into the initial numerical expression, we determine its value.
$\left(\frac{6+4 \sqrt{2}}{\sqrt{2}+\sqrt{6+4 \sqrt{2}}}+\frac{6-4 \sqrt{2}}{\sqrt{2}-\sqrt{6-4 \sqrt{2}}}\right)^{2}=$
$\left(\frac{6+4 \sqrt{2}}{\sqrt{2}+2+\sqrt{2}}+\frac{6-4 \sqrt{2}}{\sqrt{2}-2+\sqrt{2}}\right)^{2}=$
$\left(\frac{6+4 \sqrt{2}}{2 \sqrt{2}+2} \cdot \frac{2 \sqrt{2}-2}{2 \sqrt{2}-2}+\frac{6-4 \sqrt{2}}{2 \sqrt{2}-2} \cdot \frac{2 \sqrt{2}+2}{2 \sqrt{2}+2}\right)^{2}=$
$\left(\frac{12 \sqrt{2}+16-12-8 \sqrt{2}}{(2 \sqrt{2})^{2}-2^{2}}+\frac{12 \sqrt{2}-16+12-8 \sqrt{2}}{(2 \sqrt{2})^{2}-2^{2}}\right)^{2}=$
$\left(\frac{4 \sqrt{2}+4}{4}+\frac{4 \sqrt{2}-4}{4}\right)^{2}=$
$(\sqrt{2}+1+\sqrt{2}-1)^{2}=$
$(2 \sqrt{2})^{2}=8$
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.6.
Solve the equation
$$
\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)\left(\frac{\sqrt{x}+1}{\sqrt{x}-1}+4 x-\frac{\sqrt{x}-1}{\sqrt{x}+1}\right)=112-4 \sqrt{x}
$$
|
## First Solution.
First, note that $x>0, x \neq 1$ must hold.
1 point
By simplifying the expression in parentheses, we get
$$
\begin{array}{cc}
\sqrt{x}-\frac{1}{\sqrt{x}}=\frac{x-1}{\sqrt{x}}, & 1 \text { point } \\
\frac{\sqrt{x}+1}{\sqrt{x}-1}+4 x-\frac{\sqrt{x}-1}{\sqrt{x}+1}=4 x+\frac{(\sqrt{x}+1)^{2}-(\sqrt{x}-1)^{2}}{x-1}=4 x+\frac{4 \sqrt{x}}{x-1} . & 2 \text { points }
\end{array}
$$
Therefore, the given equation is equivalent to
$$
\frac{x-1}{\sqrt{x}} \cdot\left(4 x+\frac{4 \sqrt{x}}{x-1}\right)=112-4 \sqrt{x}
$$
It follows that
$$
\begin{array}{cc}
4(x-1) \sqrt{x}+4=112-4 \sqrt{x} & 2 \text { points } \\
4 x \sqrt{x}=108 & \\
x \sqrt{x}=27 . & 1 \text { point }
\end{array}
$$
Thus, $\sqrt{x}=3, x=9$.
Note: If the student wrote the condition for the solution at the beginning but did not emphasize when multiplying the equation by $\sqrt{x}$ and $x-1$ (or $\sqrt{x}-1$) that the next step yields an equivalent equation under the condition $x>0$ or $x \neq 1$, do not deduct a point.
Conversely, if the student emphasized when multiplying the equation by $\sqrt{x}$ and $x-1$ (or $\sqrt{x}-1$) that the next step yields an equivalent equation under the condition $x>0$ or $x \neq 1$, it is not necessary to write the condition at the beginning.
If neither is done, deduct 1 point.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.1.
Let $a>1$. The points $(x, y)$ for which the coordinates satisfy $|x|+y=a, x^{2}+y=a|x|$ determine a figure in the coordinate plane with an area of 120 square units. Calculate the real number $a$.
|
## Solution.
From the first equation of the system, we have $y=-|x|+a$, which, when substituted into the second equation, gives
$$
x^{2}-|x|+a=a|x| \text {. }
$$
This leads to a series of equivalent equations
$$
\begin{aligned}
& x^{2}-|x|+a-a|x|=0 \\
\Longleftrightarrow & |x|^{2}-|x|+a-a|x|=0 \\
\Longleftrightarrow & |x|(|x|-1)-a(|x|-1)=0 \\
\Longleftrightarrow & (|x|-1)(|x|-a)=0
\end{aligned}
$$
We have two possibilities: $|x|=1$ or $|x|=a$. Both solutions are possible since $a>0$.
In the first case, $x=1$ or $x=-1$, and in the second case, $x=a$ or $x=-a$.
For $x=1, y=-1+a$, and for $x=-1, y=-1+a$.
For $x=a, y=0$ and for $x=-a, y=0$.
Then the vertices of the given figure are the following points:
$$
(-a, 0), \quad(a, 0), \quad(1, a-1), \quad(-1, a-1)
$$
These points in the coordinate system determine an isosceles trapezoid with the y-axis as its axis of symmetry, so its area is
$$
P=\frac{2 a+2}{2} \cdot(a-1)=(a+1)(a-1)=a^{2}-1
$$
From $120=a^{2}-1$, we get $a^{2}=121 \Rightarrow a=11(a>1)$.
Note: The problem can also be solved by distinguishing the cases $x \leqslant 0$ and $x>0$. In the first case, we get the equation $(x+1)(x+a)=0$, and in the second case, $(x-1)(x-a)=0$, whose solutions for $x$ are the numbers $-1,-a, 1, a$. We proceed as in the previous solution.
## Problem B-1.2
Solve the inequality
$\frac{x-8}{2012}+\frac{x-7}{2013}+\frac{x-6}{2014}+\frac{x-5}{2015}+\frac{x-4}{2016} \leqslant \frac{x-2012}{8}+\frac{x-2013}{7}+\frac{x-2014}{6}+\frac{x-2015}{5}+\frac{x-2016}{4}$.
## Solution.
$\frac{x-8}{2012}+\frac{x-7}{2013}+\frac{x-6}{2014}+\frac{x-5}{2015}+\frac{x-4}{2016} \leqslant \frac{x-2012}{8}+\frac{x-2013}{7}+\frac{x-2014}{6}+\frac{x-2015}{5}+\frac{x-2016}{4}$.
Add -1 five times to both sides
$$
\begin{aligned}
& \frac{x-8}{2012}-1+\frac{x-7}{2013}-1+\frac{x-6}{2014}-1+\frac{x-5}{2015}-1+\frac{x-4}{2016}-1 \leqslant \\
& \leqslant \frac{x-2012}{8}-1+\frac{x-2013}{7}-1+\frac{x-2014}{6}-1+\frac{x-2015}{5}-1+\frac{x-2016}{4}-1 \\
& \frac{x-2020}{2012}+\frac{x-2020}{2013}+\frac{x-2020}{2014}+\frac{x-2020}{2015}+\frac{x-2020}{2016} \leqslant \\
& \leqslant \frac{x-2020}{8}+\frac{x-2020}{7}+\frac{x-2020}{6}+\frac{x-2020}{5}+\frac{x-2020}{4} \\
& \quad(x-2020)\left(\frac{1}{2012}+\frac{1}{2013}+\frac{1}{2014}+\frac{1}{2015}+\frac{1}{2016}-\frac{1}{8}-\frac{1}{7}-\frac{1}{6}-\frac{1}{5}-\frac{1}{4}\right) \leqslant 0
\end{aligned}
$$
The expression in the second parenthesis is negative because each of the first 5 fractions is smaller than each of the other 5 fractions, making their difference negative. Therefore, the entire expression is less than or equal to zero only if $x-2020 \geqslant 0, x \geqslant 2020, x \in[2020,+\infty\rangle$.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.4.
For real numbers $x, y$ if the equality $|x+y|+|x-y|=2$ holds, determine the maximum value of the expression $x^{2}-6 x+y^{2}$.
|
## Solution.
We have the following cases:
1) $x+y \geqslant 0, x-y \geqslant 0$, that is, $y \geqslant-x, y \leqslant x$. Then we have
$$
x+y+x-y=2 \quad \Rightarrow \quad x=1, y \geqslant-1, y \leqslant 1 \quad \Rightarrow \quad x=1,|y| \leqslant 1
$$
In this case, the maximum value of the expression $x^{2}-6 x+y^{2}$ is the maximum value of the expression $y^{2}-5$ for $|y| \leqslant 1$, that is, on the interval $[-1,1]$. Since the quadratic function has a minimum at its vertex, the maximum can only be achieved at the endpoints of the interval $[-1,1]$. The maximum value for $y=1$ or -1 is -4.
2) $x+y \geqslant 0, x-y \leqslant 0$, that is, $x \geqslant-y, x \leqslant y$. Then we have
$$
x+y-x+y=2 \quad \Rightarrow \quad y=1,|x| \leqslant 1
$$
In this case, the maximum value of the expression $x^{2}-6 x+y^{2}$ is the maximum value of the expression $x^{2}-6 x+1$ on the interval $[-1,1]$. The maximum is achieved for $x=-1$ and is 8.
3) $x+y \leqslant 0, x-y \geqslant 0$, that is, $x \leqslant-y, x \geqslant y$. Then we have
$$
-x-y+x-y=2 \quad \Rightarrow \quad y=-1,|x| \leqslant 1
$$
In this case, the maximum value of the expression $x^{2}-6 x+y^{2}$ is the maximum value of the expression $x^{2}-6 x+1$ on the interval $[-1,1]$, which is the same as in the previous case, 8.
4) $x+y \leqslant 0, x-y \leqslant 0$, that is, $y \leqslant-x, y \geqslant x$. Then we have
$$
-x-y-x+y=2 \quad \Rightarrow \quad x=-1,|y| \leqslant 1
$$
In this case, the maximum value of the expression $x^{2}-6 x+y^{2}$ is the maximum value of the expression $7+y^{2}$ on the interval $[-1,1]$. Since the quadratic function has a minimum at its vertex, the maximum can only be achieved at the endpoints of the interval $[-1,1]$, so we conclude that the maximum value is achieved for $y=1$ or -1 and is 8.
We conclude that the maximum value of the given expression is 8, and it is achieved for
$$
(x, y)=(-1,1) \quad \mathrm{and} \quad(-1,-1)
$$
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.3.
If $f(x)=4 \sin ^{2} \frac{3 x}{2}-4 \cos ^{2} \frac{3 x}{2}$, determine $f\left(\frac{2020 \pi}{9}+2021 k \pi\right)$ depending on the integer $k$.
|
## Solution.
The function $f$ can be written in the following form:
$$
f(x)=4 \sin ^{2} \frac{3 x}{2}-4 \cos ^{2} \frac{3 x}{2}=-4\left(\cos ^{2} \frac{3 x}{2}-\sin ^{2} \frac{3 x}{2}\right)=-4 \cos 3 x
$$
Therefore,
$$
f\left(\frac{2020 \pi}{9}+2021 k \pi\right)=-4 \cos \left(3\left(\frac{2020 \pi}{9}+2021 k \pi\right)\right)=-4 \cos \left(\frac{2020 \pi}{3}+6063 k \pi\right)
$$
We have two cases.
$1^{\circ}$ if $k$ is even, the above expression is equal to
$$
-4 \cos \left(\frac{2020 \pi}{3}\right)=-4 \cos \left(\frac{4 \pi}{3}\right)=-4\left(-\frac{1}{2}\right)=2
$$
$2^{\circ}$ if $k$ is odd, the above expression is equal to
$$
-4 \cos \left(\frac{2020 \pi}{3}+\pi\right)=-4\left(-\cos \left(\frac{4 \pi}{3}\right)\right)=4 \cos \left(\frac{4 \pi}{3}\right)=4\left(-\frac{1}{2}\right)=-2
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.2.
Students wrote posts for Instagram in pairs to invite people to the "Math Evening." The pair that collects the most likes expects a reward. Maja collected 3731, Matko 2754, but they claim that together they have 6705, which makes other pairs suspicious of cheating.
If we allow the possibility that the numbers are not written in the decimal system, could Maja and Matko be right? Explain.
|
## Solution.
Let $b$ be the base of the number system used by Maja and Marko.
$$
\begin{array}{cc}
3731_{(b)}+2754_{(b)}=6705_{(b)} & 1 \text { point } \\
\left(3 b^{3}+7 b^{2}+3 b+1\right)+\left(2 b^{3}+7 b^{2}+5 b+4\right)=6 b^{3}+7 b^{2}+0 \cdot b+5 & 1 \text { point } \\
b^{3}-7 b^{2}-8 b & \\
b(b-8)(b+1)=0 & 2 \text { points }
\end{array}
$$
The solutions to this equation are $0, -1$, and 8, so the only possible base is 8.
Maja and Marko were adding likes in the octal system.
Note: A student who claims and verifies that the base $b=8$ satisfies the condition, but does not prove that there are no other solutions, gets 3 points.
A student who claims, without verification, that the only solution is $b=8$ gets 1 point.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.7.
Leda and Una are playing with clay in the shape of a cylinder whose height is 6 times greater than the diameter of its base. Leda took a part of that clay and made a larger ball, while Una made a smaller ball from the remainder. How many times greater is the volume of Leda's ball compared to the volume of Una's ball, if the sum of their radii is 3 times greater than the radius of the cylinder's base?
|
## Solution.
Let $r$ be the radius of the base of the cylinder. The height of the cylinder is 6 diameters, or 12 radii of the cylinder, so the volume of the cylinder is $V_{V}=r^{2} \pi v=r^{2} \pi 12 r=12 r^{3} \pi$.
Let $R_{L}$ be the radius of the sphere made by Leda, and $R_{U}$ be the radius of the sphere made by Una. The sum of the volumes of these spheres is equal to the volume of the cylinder.
$$
\frac{4}{3} R_{L}^{3} \pi+\frac{4}{3} R_{U}^{3} \pi=12 r^{3} \pi
$$
It follows that $R_{L}^{3}+R_{U}^{3}=9 r^{3}$, and from the condition in the problem, we also have $R_{L}+R_{U}=3 r$.
Let's solve this system of equations.
$$
\begin{aligned}
& \left(3 r-R_{U}\right)^{3}+R_{U}^{3}=9 r^{3} \\
& 27 r^{3}-27 r^{2} R_{U}+9 r R_{U}^{2}=9 r^{3} \\
& 3 r^{2}-3 r R_{U}+R_{U}^{2}=r^{2} \\
& R_{U}^{2}-3 r R_{U}+2 r^{2}=0
\end{aligned}
$$
From this, we get $R_{U}=2 r$ or $R_{U}=r$. 1 point
Since Leda's sphere has the larger radius, it follows that $R_{U}=r, R_{L}=3 r-r=2 r$.
Now we see that the ratio of the volumes is $\frac{V_{L}}{V_{U}}=\left(\frac{R_{L}}{R_{U}}\right)^{3}=\left(\frac{2 r}{r}\right)^{3}=8$.
The volume of Leda's sphere is 8 times greater than the volume of Una's sphere.
Note: In the equation $R_{L}^{3}+R_{U}^{3}=9 r^{3}$, we can recognize the sum of cubes and use $R_{L}+R_{U}=3 r$. After that, we also get a quadratic equation, either in terms of $R_{U}$ or $R_{L}$ or the ratio $\frac{R_{L}}{R_{U}}$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.2.
Let $a$ and $b$ be positive real numbers such that
$$
\frac{a}{b}+\frac{b}{a}=3 \quad \text { and } \quad \frac{a^{2}}{b}+\frac{b^{2}}{a}=10
$$
Determine $\frac{1}{a}+\frac{1}{b}$.
|
## Solution.
By multiplying each of the equalities by $a b$ we have
$$
a^{2}+b^{2}=3 a b \quad \text { and } \quad a^{3}+b^{3}=10 a b
$$
Notice, $a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)$.
Substituting the first equality into the second, we get $10 a b=(a+b)(3 a b-a b)=2 a b(a+b)$, from which dividing by $2 a b$ yields $a+b=5$.
From $(a+b)^{2}=a^{2}+2 a b+b^{2}$ and the first equality, we have $(a+b)^{2}=5 a b$.
Substituting, we get $5 a b=5^{2}$, or $a b=5$.
By bringing to a common denominator and adding, we have $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{a b}$.
Substituting the previously obtained values, we get $\frac{1}{a}+\frac{1}{b}=\frac{5}{5}=1$.
Note: The equality $a+b=5$ can be obtained in several ways. For example:
Multiplying the first equality by $a$ and by $b$ we have
$$
\frac{a^{2}}{b}+b=3 a \quad \text { and } \quad a+\frac{b^{2}}{a}=3 b
$$
Adding, we get $\frac{a^{2}}{b}+b+a+\frac{b^{2}}{a}=3(a+b)$.
Substituting the second equation, we have $a+b+10=3(a+b)$, or $a+b=5$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.6.
Borna wants to color each of the numbers $2,3, \ldots, 32$ with one of $k$ colors $(k \in \mathbb{N})$ such that no number is a multiple of another number of the same color. Determine the smallest natural number $k$ for which Borna can achieve this.
|
## Solution.
Notice that the numbers $2, 4, 8, 16,$ and 32$ must be colored with different colors according to the condition of the problem.
Therefore, at least 5 colors are needed.
It remains to prove that $k=5$ colors are sufficient. One possible coloring is:
- Color 1: numbers 2, 3
- Color 2: numbers $4, 5, 6, 7$
- Color 3: numbers $8, 9, \ldots, 15$
- Color 4: numbers $16, 17, \ldots, 31$
- Color 5: number 32.
Note: Various other colorings of the numbers in five colors are possible, and it is necessary to either explicitly state the color for each number as in the example or describe the coloring in words. For example, in color $k$, we can color all numbers that have exactly $k$ (not necessarily distinct) prime factors (the number 12 would be colored in color 3).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.5.
How many different bracelets can be made consisting of four black and four white beads arranged in a circle? Two bracelets are considered different if they cannot be rotated to have the same sequence of beads.
|
## Solution.
Let's consider how long the longest string consisting only of black balls is.
If it is 4 in length, then the remaining four balls are obviously white, and this is the only possibility in this case.

If it is 3 in length, then these three black balls are definitely surrounded by two whites, otherwise the string would be 4 in length. We need to place one more black ball in one of the three remaining positions. We have two different possibilities, as shown in the figure:

If it is 2 in length, then the remaining two black balls may or may not be adjacent.
If they are adjacent, we have two different possibilities, as shown in the figure:

If they are not adjacent, we have two possibilities, as shown in the figure:

If the longest described string is 1 in length, then we have only one bracelet, and that is the one where black and white balls alternate.

Therefore, there are a total of eight different bracelets.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.3.
Determine the last 2019 digits of the number $2^{2019} \cdot 5^{2018} \cdot 9^{2017}$.
|
## Solution.
Since
$$
2^{2019} \cdot 5^{2018} \cdot 9^{2017}=2 \cdot 9^{2017} \cdot(10)^{2018}
$$
and $2 \cdot 9^{2017}$ is not divisible by 10, we see that the decimal representation of the given number will end with 2018 zeros.
The last digit different from zero is equal to the last digit of the number 2 . $9^{2017}$.
Since
$$
9^{2017}+1=(9+1)\left(9^{2016}-9^{2015}+\cdots+1\right)
$$
the number $9^{2017}+1$ is divisible by 10.
Therefore, the last digit of the number $9^{2017}$ is 9, so the last digit of $2 \cdot 9^{2017}$ is 8.
Note: The last digit of the number $9^{2017}$ can be determined based on the fact that the remainders of the powers of $9^{n}$ when divided by 10 repeat periodically: $1,9,1,9, \ldots$ This fact does not need to be proven by students.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.7.
Marko places coins on some fields of a $3 \times 3$ board, and then records how many coins are in each individual row and column. How many coins at least must Marko place on the board if he wants these six numbers to be mutually distinct?
|
## Solution.
Let $Z$ be the sum of all six numbers (coins in rows and columns). 1 point
If all six numbers are different, the sum of these numbers $Z$ is at least $0+1+2+3+4+5=15. \quad 3$ points
Notice that $Z$ is an even number because it is equal to twice the number of coins on the board.
Due to its evenness, $Z \geqslant 16$, which means Marko must use at least eight coins.
An example shows that Marko can succeed with exactly eight coins:
| 0 | 0 | 0 |
| :--- | :--- | :--- |
| 0 | 0 | 2 |
| 1 | 3 | 2 |
In this example, the numbers in the rows are 0, 2, and 6, and the sums in the columns are 1, 3, and 4.
## SCHOOL/CITY COMPETITION IN MATHEMATICS
4th grade - high school - A variant
## January 28, 2019.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.1.
The product of the second and fourth terms of an arithmetic sequence with difference $d$ is $-d^{2}$. Determine the product of the third and fifth terms of this sequence.
|
## Solution.
Let's denote the first five terms of the given arithmetic sequence as $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$.
Since the common difference is $d$, we have $a_{2}=a_{1}+d, a_{3}=a_{1}+2 d, a_{4}=a_{1}+3 d, a_{5}=a_{1}+4 d$.
According to the condition of the problem, the product of the second and fourth terms is equal to $-d^{2}$ on one side, and on the other side,
$$
a_{2} \cdot a_{4}=\left(a_{1}+d\right)\left(a_{1}+3 d\right)=a_{1}^{2}+4 d a_{1}+3 d^{2}
$$
Equating the two expressions, we get:
$$
\begin{aligned}
a_{1}^{2}+4 d a_{1}+3 d^{2} & =-d^{2} \\
a_{1}^{2}+4 d a_{1}+4 d^{2} & =0 \\
\left(a_{1}+2 d\right)^{2} & =0 \\
a_{1}+2 d & =0
\end{aligned}
$$
Substituting the obtained result into the product $a_{3} \cdot a_{5}$, we get
$$
a_{3} \cdot a_{5}=\left(a_{1}+2 d\right)\left(a_{1}+4 d\right)=0
$$
since the first parenthesis is equal to zero.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.3.
For real numbers $x_{1}, x_{2}, \ldots, x_{30}$, the following holds:
$$
\begin{aligned}
& 20^{3} x_{1}+21^{3} x_{2}+\cdots+49^{3} x_{30}=13 \\
& 21^{3} x_{1}+22^{3} x_{2}+\cdots+50^{3} x_{30}=1 \\
& 22^{3} x_{1}+23^{3} x_{2}+\cdots+51^{3} x_{30}=19
\end{aligned}
$$
What is the value of $21 x_{1}+22 x_{2}+\cdots+50 x_{30}$?
|
## First solution.
It is known that for real numbers $a$ and $b$, $a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$.
If $a-b=1$, then $a^{3}-b^{3}=a^{2}+a b+b^{2}$. Therefore, by subtracting the first equation from the second, we get:
$\left(21^{2}+21 \cdot 20+20^{2}\right) x_{1}+\left(22^{2}+22 \cdot 21+21^{2}\right) x_{2}+\cdots+\left(50^{2}+50 \cdot 49+49^{2}\right) x_{30}=-12$.
Similarly, by subtracting the second equation from the third, we get:
$$
\left(22^{2}+22 \cdot 21+21^{2}\right) x_{1}+\left(23^{2}+23 \cdot 22+22^{2}\right) x_{2}+\cdots+\left(51^{2}+51 \cdot 50+50^{2}\right) x_{30}=18 . \quad 2 \text { points }
$$
Notice that for any real number $a$:
$$
\left((a+1)^{2}+(a+1) \cdot a+a^{2}\right)-\left(a^{2}+a \cdot(a-1)+(a-1)^{2}\right)=6 a
$$
Therefore, by subtracting the two previously obtained equations, we get:
$$
6 \cdot\left(21 x_{1}+22 x_{2}+\cdots+50 x_{30}\right)=30
$$
from which $21 x_{1}+22 x_{2}+\cdots+50 x_{30}=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
Martin assigns each of the 12 edges of a cube a number, either 1 or -1. Then he assigns to each of the six faces of the cube the product of the 4 numbers on the edges of that face. Finally, Martin sums all 18 numbers assigned to the edges and faces of the cube.
What is the smallest sum Martin can achieve?
|
## First Solution.
Consider the five numbers associated with one face and the four edges that bound it. Note that their sum can be at least -3.
Indeed, if all the numbers associated with the edges are -1, then their product is 1, so the sum is -3. If at least one of the numbers on the edges is not -1, then the sum is an odd number greater than -5, hence at least -3.
Let $s$ be the sum of all numbers on the faces of the cube, and $b$ be the sum of all numbers on the edges. We are interested in the minimum value of $s+b$.
Consider the six sums obtained by adding the five numbers associated with one face and the four edges that bound it.
In this sum, each number associated with the faces of the cube appears once, and each number associated with the edges of the cube appears twice.
Thus,
$$
s+2 b \geqslant 6 \cdot(-3)=-18
$$
Clearly, $s \geqslant-6$, so we conclude that $2 s+2 b \geqslant-24$, or that $s+b \geqslant-12$.
We will also show that it is indeed possible to achieve $s+b=-12$.
On the cube $A B C D E F G H$, assign the number -1 to the edges $\overline{A B}, \overline{G C}$, and $\overline{E H}$, and the number 1 to all other edges. This way, each face of the cube is assigned the number -1, so the total sum is indeed -12.

|
-12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.4.
Determine all natural numbers $m$ for which $2^{m}-63$ is the cube of some integer.
|
## Solution.
We seek all $m \in \mathbb{N}$ for which $2^{m} - 63 = n^{3}$ for some $n \in \mathbb{Z}$.
Consider the remainders that both sides of this equation give when divided by 7. 1 point
By listing all possible remainders for $n$ when divided by 7, we see that the cube of a natural number $n^{3}$ gives remainders 0, 1, or 6.
By listing all remainders that $2^{m}$ gives when divided by 7, we see that they are 2, 4, and 1.
Since 63 is divisible by 7, and both sides of the equation $2^{m} - 63 = n^{3}$ must give the same remainder when divided by 7, we conclude that the only possibility is that both $2^{m}$ and $n^{3}$ give a remainder of 1 when divided by 7. This is only achieved when $m$ is divisible by 3.
Let $k \in \mathbb{N}$ be such that $m = 3k$. Using the difference of cubes, we get
$$
63 = 2^{3k} - n^{3} = (2^{k} - n)(2^{2k} + 2^{k} \cdot n + n^{2})
$$
We check the possible factorizations of the number 63 into factors $a := 2^{k} - n$ and $b := 2^{2k} + 2^{k} \cdot n + n^{2}$. Since $b$ is a natural number, $a$ must also be a natural number.
We can conclude that $n$ must be a natural number. If $n \leq 0$, then from $2^{m} - 63 = n^{3} \leq 0$ we see that $m$ must be 0, which is not a natural number. From $2^{m} - 63 = n^{3} \leq 0$ we see that $m$ must be 0, which is not a natural number. Since $a b = 63$, we get $a^{3} < 63$, or $a \leq 3$. Therefore, the only possibilities for $(a, b)$ are the pairs $(1, 63)$ and $(3, 21)$.
We discard the possibility $(1, 63)$ because then the number $b - a^{2} = 62$ is not divisible by 3, and thus is not of the form $3 \cdot 2^{k} \cdot n$.
We are left to check the case $a = 2^{k} - n = 3$, $b = 2^{2k} + 2^{k} \cdot n + n^{2} = 21$. We also have $b - a^{2} = 3 \cdot 2^{k} \cdot n = 12$, or $2^{k} \cdot n = 4$. From this, we have two possibilities: $2^{k} = 2$, $n = 2$, or $2^{k} = 4$, $n = 1$.
By substituting into the remaining equations, only the second possibility gives a solution to the equation for $k = 2$, or $m = 6$. Therefore, $m = 6$ is the only natural number that satisfies the condition of the problem.
Note: The solution consists of proving that $m$ is divisible by 3 (4 points), factoring the equation using the difference of cubes (1 point), reducing the factorizations of the number 63 to only one case $3 \cdot 21$ (4 points), and finally finding the only such number $m$ (1 point). The reduction of the factorizations of the number 63 can be performed in multiple ways, including checking all possible factorizations. Such solutions should be graded according to the official solution.
The part of the solution that confirms $m = 6$ satisfies the condition of the problem (without proving it is the only such natural number) earns 1 point, corresponding to the last point in the grading scheme.
The part of the solution that directly verifies that no natural number $m$ less than 6 is a solution (or equivalently, that $n$ must be a natural number) earns 1 point, corresponding to the sixth point in the grading scheme.
The proof that $m$ is divisible by 3 can also be derived by looking at the remainders that both sides of the equation $2^{m} - 63$ give when divided by 9. The left side of the equation $2^{m} - 63 = n^{3}$ gives remainders 2, 4, 1, 7, 5, and 8, while the right side gives remainders 0, 1, and 8. The number $2^{m}$ gives remainders 1 and 8 only when $m$ is divisible by 3.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.2.
Determine the smallest value that the expression
$$
a^{2}+b^{2}+|a b-1|+|a b-4|
$$
can take for some real numbers $a$ and $b$.
|
## Solution.
Let $S:=a^{2}+b^{2}+|a b-1|+|a b-4|$. By considering the sign of the expressions $a b-1$ and $a b-4$, we distinguish three cases.
In the first case, let $a b \geqslant 4$. Then the expressions in both absolute value terms of the initial expression are non-negative, so the expression becomes
$$
S=a^{2}+b^{2}+a b-1+a b-4=(a-b)^{2}-5+4 a b
$$
The smallest value a square of a real number can achieve is 0 (which occurs when $a$ and $b$ are equal), and we necessarily have $a b \geqslant 4$. Therefore, the minimum value of the expression in this case is $0-5+4 \cdot 4=11$, and it is achieved when $a=b$ and $a b=4$, i.e., when $a=b=2$.
In the second case, we have $1 \leqslant a b \leqslant 4$. Then the initial expression similarly becomes
$$
S=a^{2}+b^{2}+a b-1-(a b-4)=a^{2}+b^{2}+3=(a-b)^{2}+3+2 a b \geqslant 0+3+2 \cdot 1=5
$$
The minimum is achieved when $a=b$ and $a b=1$, i.e., for $a=b=1$.
In the third case, we have $a b \leqslant 1$, and the initial expression becomes
$$
S=a^{2}+b^{2}-(a b-1)-(a b-4)=(a-b)^{2}+5 \geqslant 5
$$
The minimum is achieved for any two equal real numbers $a$ and $b$ whose product is less than or equal to 1.
Therefore, the smallest value that the expression $a^{2}+b^{2}+|a b-1|+|a b-4|$ can take is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.4.
Determine the smallest natural number $n$ for which there exist real numbers $x_{1}, \ldots, x_{n} \in [1,4]$ that satisfy the inequalities:
$$
\begin{aligned}
x_{1}+x_{2}+\ldots+x_{n} & \geqslant \frac{7}{3} n \\
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{n}} & \geqslant \frac{2}{3} n
\end{aligned}
$$
|
## First Solution.
Assume that for some natural number $n$ there exist real numbers $x_{1}, x_{2}, \ldots, x_{n}$ that satisfy the given conditions. Since $1 \leqslant x_{i} \leqslant 4$, the inequality holds:
$$
\left(4-x_{i}\right)\left(1-\frac{1}{x_{i}}\right) \geqslant 0
$$
where equality holds if and only if $x_{i}$ is equal to 1 or 4. Summing over all $i$, we get
$$
4 n-\left(x_{1}+x_{2}+\ldots+x_{n}\right)-4\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{n}}\right)+n \geqslant 0
$$
On the other hand, from the conditions of the problem, it follows that
$$
4 n-\left(x_{1}+x_{2}+\ldots+x_{n}\right)-4\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{n}}\right)+n \leqslant 4 n-\frac{7}{3} n-\frac{8}{3} n+n=0
$$
We conclude that equality must hold, which is possible only if all $x_{i}$ are in the set $\{1,4\}$.
Of the $n$ numbers $x_{1}, \ldots, x_{n}$, let $a \geqslant 0$ take the value 1, and $b \geqslant 0$ take the value 4. Then $a+b=n$, and we have
$$
\begin{array}{r}
a+4 b=x_{1}+x_{2}+\ldots+x_{n} \geqslant \frac{7}{3} n=\frac{7}{3} a+\frac{7}{3} b \\
a+\frac{1}{4} b=\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{n}} \geqslant \frac{2}{3} n=\frac{2}{3} a+\frac{2}{3} b
\end{array}
$$
From the first inequality, we get $4 a \geqslant 5 b$, and from the second, we get $5 a \geqslant 4 b$, from which we conclude that $4 a=5 b$. The smallest natural number $n$ for which such $a$ and $b$ exist is 9 (when $a=5, b=4$).
For $n=9$ and real numbers $x_{1}, \ldots, x_{n}$ such that five of them are equal to 1 and four are equal to 4, the conditions of the problem are satisfied, so this is indeed the smallest such natural number.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.2.
Let $S$ be the set of all natural numbers less than 1000 whose all digits in decimal notation are even. Let $\omega$ be a complex number such that $\omega^{2}+\omega+1=0$.
Calculate the sum $\sum_{k \in S} \omega^{k}$, i.e., the sum of the values $\omega^{k}$ for all $k$ in the set $S$.
|
## First Solution.
Let $Z$ be the desired sum. Multiplying the equation $\omega^{2}+\omega+1=0$ by $\omega-1$ we get $\omega^{3}=1$. In particular, the number $\omega^{n}$ is equal to the number $1, \omega$ or $\omega^{2}$ respectively if $n$ gives a remainder of 0, 1 or 2 when divided by 3.
Consider any three three-digit numbers of the form $\overline{4 a b}, \overline{6 a b}, \overline{8 a b}$, for some even digits $a$ and $b$. These three numbers give three different remainders when divided by 3, so we have
$$
\omega^{\overline{4 a b}}+\omega^{\overline{6 a b}}+\omega^{\overline{8 a b}}=1+\omega+\omega^{2}=0
$$
Using this identity for all such three-digit numbers, we conclude that in the desired sum, all terms with exponents $k$ whose hundreds digit is 4, 6, or 8 cancel out.
A similar argument shows that in the sum, all terms with $k$ whose tens digit is 4, 6, or 8 also cancel out, and then those whose units digit is 4, 6, or 8.
What remains is to calculate the sum of the numbers $\omega^{k}$ where $k$ are natural numbers less than 1000 whose digits are all 0 or 2. We have
$$
\begin{aligned}
Z & =\omega^{2}+\omega^{20}+\omega^{22}+\omega^{200}+\omega^{202}+\omega^{220}+\omega^{222} \\
& =1+3 \omega+3 \omega^{2}=1+3 \cdot(-1)=-2
\end{aligned}
$$
|
-2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.1. Calculate $\frac{1234321234321 \cdot 2468642468641-1234321234320}{1234321234320 \cdot 2468642468641+1234321234321}$.
|
Solution. Let $n=1234321234321$.
Then the given expression is equivalent to the expression
$$
\begin{aligned}
& \frac{n \cdot(2 n-1)-(n-1)}{(n-1) \cdot(2 n-1)+n}= \\
& \frac{2 n^{2}-n-n+1}{2 n^{2}-2 n-n+1+n}= \\
& \frac{2 n^{2}-2 n+1}{2 n^{2}-2 n+1}=1
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zadatak B-2.1. Izračunajte:
$$
\left[\frac{(1+\sqrt{3})+(1-\sqrt{3}) i}{\sqrt{6}+\sqrt{2} i}\right]^{2012}
$$
|
## Rješenje.
$$
\begin{aligned}
{\left[\frac{(1+\sqrt{3})+(1-\sqrt{3}) i}{\sqrt{6}+\sqrt{2} i}\right]^{2012} } & =\left[\frac{(1+\sqrt{3})+(1-\sqrt{3}) i}{\sqrt{6}+\sqrt{2} i} \cdot \frac{\sqrt{6}-\sqrt{2} i}{\sqrt{6}-\sqrt{2} i}\right]^{2012} \\
& =\left[\frac{4 \sqrt{2}-4 \sqrt{2} i}{6+2}\right]^{2012} \\
& =\left[\frac{(1-i)^{2}}{2}\right]^{1006}=\left(\frac{-2 i}{2}\right)^{1006}=(-i)^{1006} \\
& =-1
\end{aligned}
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.3. Calculate the area of the figure determined in the complex plane by the set of all complex numbers $z$ for which $|\operatorname{Re} z| \leq 1,|\operatorname{Im} z| \leq 1$.
翻译完成,但根据您的要求,最后一句是额外的,因此在翻译结果中未包含。如果需要任何进一步的修改或有其他要求,请告知。
|
Solution. Let $z=x+y i$. Then, according to the conditions of the problem, $|x| \leq 1$ and $|y| \leq 1$.
Sketch
(2 points)
The side of the square is 2, so its area is 4 square units.
(1 point)
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.4. Let $f(x)=x^{2}+b x+c, b, c \in \mathbb{R}$. If $f(0)+f(1)=\frac{1}{2}$, calculate $f\left(\frac{1}{2}\right)$.
|
## Solution.
$$
f(0)=c, \quad f(1)=1+b+c
$$
From $f(0)+f(1)=c+1+b+c=2 c+b+1=\frac{1}{2}$
it follows that $2 c+b=-\frac{1}{2}$,
or $c+\frac{1}{2} b=-\frac{1}{4}$. Then,
$$
f\left(\frac{1}{2}\right)=\frac{1}{4}+\frac{1}{2} b+c=\frac{1}{4}-\frac{1}{4}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.7. Today is Valentine's Day, and Valentino wants to go out with his girlfriend Lorna. With his 120 kuna, he can buy several roses and two lemonades. The price of one rose is equal to the price of one lemonade. Since they have a math test tomorrow, they will postpone the outing until Saturday. On Saturday, the price of one rose will decrease by 7 kuna. Valentino wants to buy the same number of roses, and instead of lemonades, he wants to buy a jumbo pizza and a Coca-Cola, which together cost 78 kuna. However, he would be short of 6 kuna. How many roses will Valentino buy for Lorna? At what price will he buy the roses on Saturday?
|
Solution. Let $x$ be the number of roses, and $y$ be the price of one rose on Valentine's Day. From the conditions of the problem, we have
$$
\begin{aligned}
x y+2 y & =120 \\
x(y-7)+78 & =126
\end{aligned}
$$
We solve the system
$$
\left\{\begin{array}{l}
x y+2 y=120 \\
x y-7 x=48
\end{array}\right.
$$
If we express $y=\frac{120}{x+2}$ from the first equation and substitute it into the second, we get
$$
x \cdot \frac{120}{x+2}-7 x=48
$$
which simplifies to the quadratic equation
$$
7 x^{2}-58 x+96=0
$$
Its integer solution is $x=6$.
Then $y=\frac{120}{6+2}=15$.
Valentino will buy 6 roses, and if he buys them on Saturday, he will pay 8 kn per piece.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.4. How many isosceles triangles have side lengths that are integers, and a perimeter of $30 \mathrm{~cm}$?
|
Solution. Let $a$ be the length of the base, and $b$ the length of the legs of the isosceles triangle. From $a+2 b=30$ it follows that $a$ must be an even number, and from the triangle inequality $a<b+b=2 b$.
(2 points)
Therefore, $a \leq 14$ and is an even number, so there are only these 7 cases:
$$
(a, b) \in\{(2,14),(4,13),(6,12),(8,11),(10,10),(12,9),(14,8)\}
$$
If the student does not have the possibility that $a=b=10 \mathrm{~cm}$, one point should be deducted.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.6. The area of a rectangle is $12 \mathrm{~cm}^{2}$, and if the acute angle between its diagonals is halved, the area is $7.5 \mathrm{~cm}^{2}$. What is the length of the diagonal of the rectangle?
|
## Solution.
If the angle between the diagonals is $\alpha$, the area is
$$
\begin{array}{r}
P=4 \cdot \frac{\frac{d}{2} \frac{d}{2} \sin \alpha}{2}=\frac{1}{2} d^{2} \sin \alpha=12 \\
d^{2} \sin \alpha=24
\end{array}
$$
If the angle between the diagonals is $\frac{\alpha}{2}$, the area is
$$
\begin{aligned}
P_{1}=\frac{1}{2} d^{2} \sin \frac{\alpha}{2} & =7.5 \\
d^{2} \sin \frac{\alpha}{2} & =15
\end{aligned}
$$
(1 point)
If we divide equations (1) and (2), we get
$$
\begin{aligned}
\frac{\sin \alpha}{\sin \frac{\alpha}{2}} & =\frac{8}{5} \\
\frac{2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}}{\sin \frac{\alpha}{2}} & =\frac{8}{5} \\
\cos \frac{\alpha}{2} & =\frac{4}{5}
\end{aligned}
$$
Then,
$$
\begin{aligned}
\sin \frac{\alpha}{2} & =\frac{3}{5} \\
d^{2}=\frac{15}{\sin \frac{\alpha}{2}}=\frac{15}{\frac{3}{5}} & =25 \\
d & =5 \text{ cm}
\end{aligned}
$$
Note: The area of the rectangle can also be calculated using the lengths of the sides of the rectangle $a, b$ :
$$
\begin{aligned}
& a=d \cos \frac{\alpha}{2}, \quad b=d \sin \frac{\alpha}{2} \\
& P=a \cdot b=d \cos \frac{\alpha}{2} \cdot d \sin \frac{\alpha}{2}=\frac{1}{2} d^{2} \sin \alpha
\end{aligned}
$$
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.1. Solve the equation
$$
\frac{1}{(2 n-4)!}=\frac{1}{(2 n-3)!}+\frac{8}{(2 n-2)!}
$$
|
Solution. The number $n$ must satisfy the condition $n \geq 2$.
If we multiply the equation
$$
\frac{1}{(2 n-4)!}=\frac{1}{(2 n-3)!}+\frac{8}{(2 n-2)!}
$$
by $(2 n-2)!$,
we get
$$
(2 n-2)(2 n-3)=2 n-2+8
$$
i.e., $n^{2}-3 n=0$.
The solutions to the last equation are $n=0$ and $n=3$.
However, only the solution $n=3$ satisfies the condition $n \geq 2$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.5. Let $z=-\cos \frac{9 \pi}{8}+i \sin \frac{7 \pi}{8}$ be a complex number. Determine the smallest natural number $n$ such that the real part of the number $z^{n}$ is 0.
|
Solution. Let's write the number $z=-\cos \frac{9 \pi}{8}+i \sin \frac{7 \pi}{8}$ in trigonometric form:
$$
z=\cos \frac{\pi}{8}+i \sin \frac{\pi}{8}
$$
Then $z^{n}=\cos \frac{n \pi}{8}+i \sin \frac{n \pi}{8}$.
Equate the real part to zero: $\cos \frac{n \pi}{8}=0$.
We get $\frac{n \pi}{8}=\frac{\pi}{2}+k \pi, k \in \mathbb{Z}$. The smallest natural number is $n=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.