title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Two Pointers | Python | BEATS 99.19%
|
assign-cookies
| 0
| 1
|
# Complexity\n- Time complexity:\n - After sorting, O(g).\n \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n\n g.sort()\n s.sort()\n\n a = len(g) - 1\n b = len(s) - 1\n maxs = 0\n\n while a >= 0 and b >= 0:\n if s[b] >= g[a]:\n maxs += 1\n a -= 1\n b -= 1\n else:\n a -= 1\n return maxs\n\n```
| 2
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
Python Solution Beats 94.98 %
|
assign-cookies
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findContentChildren(self, greed: List[int], size: List[int]) -> int:\n count =0\n i = 0\n greed = sorted(greed)\n size = sorted(size)\n\n for s in size :\n if i < len(greed) and greed[i] <= s :\n count+=1\n i+=1\n\n return count \n \n```
| 0
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
O(nlogn) python
|
assign-cookies
| 0
| 1
|
```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n g=sorted(g)\n s=sorted(s)\n i=0\n j=0\n c=0\n while i<len(g) and j<len(s):\n if g[i]<=s[j]:\n c+=1\n i+=1\n j+=1\n return c\n \n```
| 2
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
Python Solution - easy to understand
|
assign-cookies
| 0
| 1
|
```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int: \n if len(s)==0:\n return 0\n i=0\n j=0\n c=0\n g.sort()\n s.sort()\n while(i!=len(g) and len(s)!=j):\n if g[i]<=s[j]:\n c+=1\n i+=1\n j+=1\n else:\n j+=1\n return c\n```\n**Please upvote if you found it helpful**
| 2
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
LESS MEMORY | BEATS 95%
|
assign-cookies
| 0
| 1
|
Filling from the kid with highest requirement to the lowest. Simple Solution.\n# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n count = 0\n g.sort(reverse=True)\n s.sort(reverse=True)\n for i in g:\n for j in s:\n if i<=j:\n count+=1\n s.remove(j)\n break \n return count\n```
| 1
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
assign-cookies
|
assign-cookies
| 0
| 1
|
# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n g.sort()\n s.sort()\n l = len(g) - 1\n m = len(s) - 1\n count = 0\n while l>-1 and m>-1:\n if g[l]<=s[m]:\n l-=1\n m-=1\n count+=1\n else:\n l-=1\n print(count)\n return count\n\n\n\n \n\n\n \n\n \n```
| 0
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
python3 greedy solution
|
assign-cookies
| 0
| 1
|
# Code\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int:\n \n # step1: sort the array\n g.sort()\n s.sort()\n\n # create the index\n cookieIndex = len(s) - 1\n\n ret = 0\n # iterate the kids\n for i in range(len(g) - 1, -1, -1):\n if cookieIndex >= 0 and s[cookieIndex] >= g[i]:\n ret += 1\n cookieIndex -= 1\n\n return ret\n```\n\n```\nclass Solution:\n def findContentChildren(self, g: List[int], s: List[int]) -> int: \n s.sort()\n g.sort()\n\n kidIndex = 0\n\n ret = 0\n for i in range(len(s)):\n if kidIndex < len(g) and s[i] >= g[kidIndex]:\n ret += 1\n kidIndex += 1\n return ret\n```
| 0
|
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie.
Each child `i` has a greed factor `g[i]`, which is the minimum size of a cookie that the child will be content with; and each cookie `j` has a size `s[j]`. If `s[j] >= g[i]`, we can assign the cookie `j` to the child `i`, and the child `i` will be content. Your goal is to maximize the number of your content children and output the maximum number.
**Example 1:**
**Input:** g = \[1,2,3\], s = \[1,1\]
**Output:** 1
**Explanation:** You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
**Example 2:**
**Input:** g = \[1,2\], s = \[1,2,3\]
**Output:** 2
**Explanation:** You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
**Constraints:**
* `1 <= g.length <= 3 * 104`
* `0 <= s.length <= 3 * 104`
* `1 <= g[i], s[j] <= 231 - 1`
| null |
Easy Solution || Stack
|
132-pattern
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n stack<int> s;\n int max3 = INT_MIN;\n for (int i = nums.size() - 1; i >= 0; i--) {\n if (nums[i] < max3)\n return true;\n while (!s.empty() && s.top() < nums[i]) {\n max3 = s.top();\n s.pop();\n }\n s.push(nums[i]);\n }\n return false;\n }\n};\n```\n```Python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack = []\n max3 = float(\'-inf\')\n for i in range(len(nums) - 1, -1, -1):\n if nums[i] < max3:\n return True\n while stack and stack[-1] < nums[i]:\n max3 = stack[-1]\n stack.pop()\n stack.append(nums[i])\n return False\n\n```\n```Java []\nclass Solution {\n public boolean find132pattern(int[] nums) {\n Stack<Integer> stack = new Stack<>();\n int max3 = Integer.MIN_VALUE;\n for (int i = nums.length - 1; i >= 0; i--) {\n if (nums[i] < max3)\n return true;\n while (!stack.isEmpty() && stack.peek() < nums[i]) {\n max3 = stack.peek();\n stack.pop();\n }\n stack.push(nums[i]);\n }\n\n return false;\n }\n}\n\n```\n
| 8
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
🚀 99.01% || Stack Solution || Commented Code🚀
|
132-pattern
| 1
| 1
|
# Problem Description\n\nGiven an array of integers, `nums`, of length `n`. A **132 pattern** is a subsequence of three integers, `nums[i]`, `nums[j]`, and `nums[k]`, where `i < j < k` and `nums[i] < nums[k] < nums[j]`.\n\nDetermine whether the given array contains a **132 pattern**. Return **true** if a **132 pattern** exists; otherwise, return **false**.\n\n- **Constraints:**\n - `n == nums.length`\n - `1 <= n <= 2 * 10e5`\n - `-10e9 <= nums[i] <= 10e9`\n\n\n---\n\n\n# Intuition\nHi there, \uD83D\uDE00\n\nLet\'s take a look on our today\'s tough problem. \uD83D\uDCAA\nIn today\'s problem, we must determine if an array has **132 pattern** or not.\n\n**First solution** that would pop into mind is to use **Brute Force**.\uD83D\uDCAA\nUse **three for loop** to get what you want but unfortunately, it will throw `TLE` error. \uD83D\uDE22\neven if we lower them to **two for loops** it will also give us `TLE` error. \uD83D\uDE22\n\nSeems challenging problem. \uD83D\uDE20\nBut we can solve it. \uD83D\uDCAA\uD83D\uDE80\n\nlet\'s revise the **Brute Force** Solutions\nFor the **three loops** solution, We can loop on all the array elements to get the subsequence that satisfies the **132 pattern**.\n```\nfor (size_t i = 0; i < nums.size() - 2; i++) {\n for (size_t j = i + 1; j < nums.size() - 1; j++) {\n for (size_t k = j + 1; k < nums.size(); k++) {\n if (nums[k] > nums[i] and nums[j] > nums[k]) {\n return true;\n }\n }\n }\n }\n```\n\nFor the **two loops** solution, We can maintain the **minimum** number before our **current** number and simply add **second** loop to search for a number that is between the current number and minimum number.\n```\nfor (size_t j = 0; j < nums.size() - 1; j++) {\n min_i = min(min_i, nums[j]);\n for (size_t k = j + 1; k < nums.size(); k++) {\n if (nums[k] < nums[j] and min_i < nums[k]) {\n return true;\n }\n }\n }\n```\n\nTill now, everything looks great but how can we make the solution only **one** for loop? \uD83E\uDD14\nWe can realize here that our **problem** in the two for loop solution is the **third** number which is the **middle-value** in **132 pattern** and we need a way to find it without for loop. \uD83E\uDD29\n\nWhy not **reverse traversal** the array ? \uD83E\uDD14\nSince this number is always the **third** then simply **reverse traversal** and **cache** every number that you encounter in some way.\n\nwhat would be that way ?\uD83E\uDD14\nSoooooooo, in the **132 pattern** we need to find three numbers 1-valued call it `a`, 3-valued call it `b` and 2-valued call it `c`.\n\nwe can **cache** `c` element easy in some variable.\nwhat about `b` element ?\nHere comes the hero of the day **THE STACK** \uD83E\uDDB8\u200D\u2642\uFE0F.\n\n- We can use the stack for to things\n - Obviously to **store** all numbers from the end of the array\n - When you encouter number **bigger** than the **top** of the stack simply **pop** the top of the stack and put this number in the variable for `c`\n - push that **bigger** number into the stack\n\nWhy did we do the last two steps ? \uD83E\uDD14\nif the number we encoutered is **bigger** than the top of the stack then pop any number from the stack, **consider** the popped number as `c` the **encountered** number as `b`.\n- And we are sure from two values:\n - `b` which is in the top of the stack.\n - `c` which is in the cached variable.\n \nthe only remaining step is to find `a` and that what we will maintaining by continue the looping.\n \n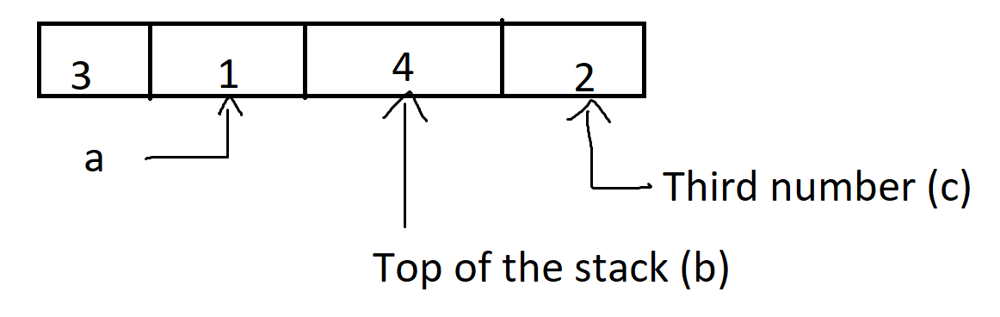\n\n\n---\n\n\n\n# Approach\n1. Create a stack `decreasingStack` to keep track of decreasing elements.\n2. Initialize `maxThirdElement` to the minimum possible value.\n3. **Traverse** the Array from Right to Left and for each element in the array:\n - If the **current** element is **less** than `maxThirdElement`, return **true** (found a 132 pattern).\n - While the **stack** is not empty and the top element of the stack is **less** than the current element:\n - **Update** `maxThirdElement` to the top element of the stack.\n - **Pop** the top element from the stack.\n - **Push** the Current Element onto the Stack.\n4. If no `132 pattern` is found after traversing the array, return **false**.\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating the array from right to left then it is **linear** time and all the operations inside the loop are `O(1)` then final complexity is `O(N)`.\n- **Space complexity:** $$O(N)$$\nSince we are maintaining a stack that at any point can have elements equal the elements of the array so complexity is `O(N)`.\n\n---\n\n# Code\n## Stack\n```C++ []\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n int length = nums.size();\n\n // Check if the array has less than 3 elements\n if (length < 3)\n return false;\n\n // Stack to keep track of decreasing elements.\n stack<int> decreasingStack;\n\n // Maximum value of the third element in the 132 pattern.\n int maxThirdElement = INT_MIN;\n\n // Traverse the array from right to left\n for (int i = length - 1; i >= 0; i--) {\n int currentNumber = nums[i];\n\n // Check for 132 pattern\n if (currentNumber < maxThirdElement)\n return true; // Found a 132 pattern.\n\n // Maintain the stack with decreasing elements\n while (!decreasingStack.empty() && decreasingStack.top() < currentNumber) {\n maxThirdElement = decreasingStack.top();\n decreasingStack.pop();\n }\n\n // Push the current element onto the stack.\n decreasingStack.push(currentNumber);\n }\n\n return false; // No 132 pattern found\n }\n};\n```\n```Java []\npublic class Solution {\n public boolean find132pattern(int[] nums) {\n int length = nums.length;\n \n // Check if the array has less than 3 elements\n if (length < 3)\n return false;\n\n // Stack to keep track of decreasing elements.\n Deque<Integer> decreasingStack = new ArrayDeque<>(length);\n\n // Maximum value of the third element in the 132 pattern.\n int maxThirdElement = Integer.MIN_VALUE;\n\n // Traverse the array from right to left\n for (int i = length - 1; i >= 0; i--) {\n int currentNumber = nums[i];\n\n // Check for 132 pattern\n if (currentNumber < maxThirdElement)\n return true; // Found a 132 pattern.\n\n // Maintain the stack with decreasing elements\n while (!decreasingStack.isEmpty() && decreasingStack.peek() < currentNumber) {\n maxThirdElement = decreasingStack.pop();\n }\n\n // Push the current element onto the stack.\n decreasingStack.push(currentNumber);\n }\n\n return false; // No 132 pattern found\n }\n}\n```\n```Python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n length = len(nums)\n\n # Check if the array has less than 3 elements\n if length < 3:\n return False\n\n # Stack to keep track of decreasing elements\n decreasing_stack = deque()\n\n # Maximum value of the third element in the 132 pattern\n max_third_element = float(\'-inf\')\n\n # Traverse the array from right to left\n for i in range(length - 1, -1, -1):\n current_number = nums[i]\n\n # Check for 132 pattern\n if current_number < max_third_element:\n return True # Found a 132 pattern\n\n # Maintain the stack with decreasing elements\n while decreasing_stack and decreasing_stack[0] < current_number:\n max_third_element = decreasing_stack.popleft()\n\n # Push the current element onto the stack\n decreasing_stack.appendleft(current_number)\n\n return False # No 132 pattern found\n```\n\n\n\n\n\n
| 64
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
O(n) Solution Using Stack with detailed Explanation Ever - Optimised Solution
|
132-pattern
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to find a "132" pattern in the given array nums. A "132" pattern consists of three elements, nums[i], nums[j], and nums[k], where i < j < k and nums[i] < nums[k] < nums[j]. The code aims to efficiently identify this pattern using two main steps: precomputing the minimum element to the left of each element and iterating through the array from right to left while maintaining a stack.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Check if the length of the input array nums is less than 3. If it is, return false because a "132" pattern requires at least three elements.\n\n2. Create a vector minLeft to store the minimum element to the left of each element in nums. Initialize the first element of minLeft as the first element of nums.\n\n3. Iterate through the nums array from left to right, updating minLeft[i] as the minimum between the previous minLeft[i-1] and nums[i].\n\n4. Initialize a stack st to keep track of potential candidates for the "2" element of the "132" pattern.\n\n5. Iterate through the nums array from right to left (starting from the last element):\n\n- If the current element nums[j] is greater than its corresponding minLeft[j], this element could potentially be the "2" element in a "132" pattern.\n- While the stack is not empty and the top element of the stack is less than or equal to minLeft[j], pop elements from the stack. This ensures that the top of the stack represents the maximum "2" element so far.\n- If the stack is not empty and the top element of the stack is less than nums[j], return true because a valid "132" pattern is found.\n- Push the current element nums[j] onto the stack as a potential "2" element.\n6. If no valid "132" pattern is found during the iteration, return false.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the nums array twice: once to compute minLeft, and once to check for the "132" pattern. Each iteration takes O(n) time, so the overall time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) because of the additional minLeft vector and the stack st, both of which can grow up to the size of the input nums.\n# Code\n```\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n int n = nums.size();\n if (n < 3) {\n return false;\n }\n\n vector<int> minLeft(n);\n minLeft[0] = nums[0];\n for (int i = 1; i < n; ++i) {\n minLeft[i] = min(minLeft[i - 1], nums[i]);\n }\n\n stack<int> st;\n for (int j = n - 1; j >= 0; --j) {\n if (nums[j] > minLeft[j]) {\n while (!st.empty() && st.top() <= minLeft[j]) {\n st.pop();\n }\n if (!st.empty() && st.top() < nums[j]) {\n return true;\n }\n st.push(nums[j]);\n }\n }\n\n return false;\n }\n};\n\n```
| 5
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
✅ 99.35% Stack & Left Approach & Binary Search
|
132-pattern
| 1
| 1
|
# Comprehensive Guide to Solving "132 Pattern": Detecting the Sneaky Subsequence\n\n## Introduction & Problem Statement\n\nHello, fellow code enthusiasts! Today, we\'re diving deep into the realm of number patterns. Specifically, we\'re tackling the "132 Pattern" problem. The task is to determine if there exists a subsequence of three integers in a given array such that the numbers follow the pattern: `nums[i] < nums[k] < nums[j]` with `i < j < k`. Sounds intriguing, right? Let\'s unwrap the intricacies of this problem and decode the solutions.\n\n## Key Concepts and Constraints\n\n### Why is This Problem Unique?\n\n1. **Subsequence Challenge**: \n Unlike other problems where you might need to find contiguous subsequences, here you\'re looking for any subsequence that matches the pattern.\n \n2. **Dual Approach**: \n We have two intriguing methods to solve this challenge, both with their unique mechanisms.\n\n3. **Constraints**: \n - The length of the array, `n`, is between $$1$$ and $$2 \\times 10^5$$.\n - Array elements are integers between $$-10^9$$ and $$10^9$$.\n\n### Strategies to Tackle the Problem\n\n1. **Stack-Based Approach**: \n Using a stack, we can traverse the array in reverse and efficiently check for the pattern.\n \n2. **Minimum from the Left (MinLeft) Approach**: \n By keeping track of the minimum value from the left for each element, we can employ another efficient method to detect the pattern.\n\n3. **Binary Search Approach**:\n While not the most optimal, this approach offers a unique perspective on the problem. Leveraging binary search, we maintain a sorted list of numbers encountered so far. This method systematically detects the 132 pattern and showcases the versatility of binary search in algorithmic challenges beyond traditional searching.\n\n---\n\n## Live Coding + Explenation of Stack-Based Approach\nhttps://youtu.be/PTn6ec9r5Jk?si=2y64rDvBTNYJUCiS\n\n## Stack-Based Approach Explained\n\n### The Mechanics of the Stack Approach\n\n1. **Initialize Stack and Third Variable**: \n Begin by initializing an empty stack and a variable `third` with a value of negative infinity. The `third` variable will store the value of our `nums[k]` when we find it.\n \n2. **Reverse Iteration**:\n Traverse the array in reverse. For each number:\n \n - If it\'s smaller than `third`, you\'ve found the pattern and can return `True`.\n - While the stack is not empty and the top of the stack is smaller than the current number, pop the stack and assign the popped value to `third`.\n - Push the current number onto the stack.\n \n3. **End of Iteration**:\n If the iteration completes without finding the pattern, return `False`.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n)$$, as we make a single pass through the array.\n- **Space Complexity**: $$O(n)$$, due to the use of the stack.\n\n\n# Code Stack\n``` Python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack, third = [], float(\'-inf\')\n \n for num in reversed(nums):\n if num < third:\n return True\n while stack and stack[-1] < num:\n third = stack.pop()\n stack.append(num)\n return False\n```\n``` C++ []\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n stack<int> s;\n int third = INT_MIN;\n\n for (int i = nums.size() - 1; i >= 0; i--) {\n if (nums[i] < third) return true;\n while (!s.empty() && s.top() < nums[i]) {\n third = s.top();\n s.pop();\n }\n s.push(nums[i]);\n }\n return false;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean find132pattern(int[] nums) {\n Stack<Integer> stack = new Stack<>();\n int third = Integer.MIN_VALUE;\n\n for (int i = nums.length - 1; i >= 0; i--) {\n if (nums[i] < third) return true;\n while (!stack.isEmpty() && stack.peek() < nums[i]) {\n third = stack.pop();\n }\n stack.push(nums[i]);\n }\n return false;\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find132pattern(nums: Vec<i32>) -> bool {\n let mut stack: Vec<i32> = Vec::new();\n let mut third = i32::MIN;\n\n for &num in nums.iter().rev() {\n if num < third {\n return true;\n }\n while let Some(&top) = stack.last() {\n if top < num {\n third = stack.pop().unwrap();\n } else {\n break;\n }\n }\n stack.push(num);\n }\n false\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @return {boolean}\n */\nvar find132pattern = function(nums) {\n let stack = [];\n let third = Number.MIN_SAFE_INTEGER;\n\n for (let i = nums.length - 1; i >= 0; i--) {\n if (nums[i] < third) return true;\n while (stack.length && stack[stack.length - 1] < nums[i]) {\n third = stack.pop();\n }\n stack.push(nums[i]);\n }\n return false;\n};\n```\n``` PHP []\nclass Solution {\n function find132pattern($nums) {\n $stack = [];\n $third = PHP_INT_MIN;\n\n for ($i = count($nums) - 1; $i >= 0; $i--) {\n if ($nums[$i] < $third) return true;\n while (count($stack) && end($stack) < $nums[$i]) {\n $third = array_pop($stack);\n }\n $stack[] = $nums[$i];\n }\n return false;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool Find132pattern(int[] nums) {\n Stack<int> stack = new Stack<int>();\n int third = int.MinValue;\n\n for (int i = nums.Length - 1; i >= 0; i--) {\n if (nums[i] < third) return true;\n while (stack.Count > 0 && stack.Peek() < nums[i]) {\n third = stack.Pop();\n }\n stack.Push(nums[i]);\n }\n return false;\n }\n}\n```\n``` Go []\nimport "math"\n\nfunc find132pattern(nums []int) bool {\n var stack []int\n third := math.MinInt32\n\n for i := len(nums) - 1; i >= 0; i-- {\n if nums[i] < third {\n return true\n }\n for len(stack) > 0 && stack[len(stack)-1] < nums[i] {\n third = stack[len(stack)-1]\n stack = stack[:len(stack)-1]\n }\n stack = append(stack, nums[i])\n }\n return false\n}\n```\n\n---\n\n## Minimum from the Left (MinLeft) Approach Explained\n\n### The Intricacies of the MinLeft Approach\n\n1. **Compute MinLeft Array**: \n Construct an array, `minFromLeft`, such that for every element in the original array, `minFromLeft[i]` represents the minimum value from index `0` to `i-1`.\n \n2. **Initialize a Stack**: \n This stack will assist in checking for the existence of the `132` pattern.\n \n3. **Reverse Iteration**:\n Traverse the array in reverse. For each number:\n \n - If the current number is greater than its corresponding value in `minFromLeft`, it means we have a potential `nums[i]` and `nums[j]` pair. Now, we aim to find a `nums[k]` such that `minFromLeft[j] < nums[k] < nums[j]`.\n - While the stack is not empty and the top of the stack is less than or equal to `minFromLeft[j]`, pop the stack.\n - If there\'s still a number in the stack and it\'s less than the current number, we\'ve found our pattern and can return `True`.\n - Push the current number onto the stack.\n \n4. **End of Iteration**:\n If the iteration completes without finding the pattern, return `False`.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n)$$, as we make a single pass through the array.\n- **Space Complexity**: $$O(n)$$, due to the use of the `minFromLeft` array and the stack.\n\n# Code MinLeft\n``` Python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n n = len(nums)\n \n minFromLeft = [nums[0]]\n for i in range(1, n):\n minFromLeft.append(min(minFromLeft[i-1], nums[i]))\n \n stack = [] \n \n for j in range(n-1, -1, -1):\n if nums[j] > minFromLeft[j]:\n while stack and stack[-1] <= minFromLeft[j]:\n stack.pop()\n if stack and stack[-1] < nums[j]:\n return True\n stack.append(nums[j])\n \n return False\n```\n\n---\n\n## Binary Search Approach Explained\n\n### The Mechanism of the Binary Search Approach\n\n1. **Pre-compute Running Minimum**:\n Create an array, `min_i`, where each entry `min_i[j]` denotes the minimum value in the array `nums` from index `0` to `j`. This helps us quickly identify the smallest value before our current index `j` in constant time.\n\n2. **Maintain a Sorted `afters` List**:\n As we traverse the array in reverse, this list keeps track of the numbers we\'ve seen so far in a sorted manner. This allows us to efficiently search for potential $$ \\text{nums}[k] $$ values for each $$ \\text{nums}[j] $$ using binary search.\n\n3. **Reverse Iteration**:\n Traverse the array from the end to the start:\n \n - If the current number $$ \\text{nums}[j] $$ is greater than the running minimum up to `j` , it indicates a potential increasing pattern.\n - We perform a binary search in the `afters` list to identify a potential $$ \\text{nums}[k] $$ that\'s less than $$ \\text{nums}[j] $$ but greater than the running minimum. If such a value exists, we\'ve found our 132 pattern.\n - Insert the current number $$ \\text{nums}[j] $$ into the `afters` list, ensuring it remains sorted.\n \n4. **Completion of Iteration**:\n If we traverse the entire array without detecting the 132 pattern, we return `False`.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(n \\log n)$$. While we do traverse the array in $$O(n)$$ time, the insertion into a sorted list takes $$O(\\log n)$$ time due to the binary search. Thus, the overall time complexity is $$O(n \\log n)$$.\n- **Space Complexity**: $$O(n)$$. We use additional space for the `min_i` array and the `afters` list. Both of these are of length $$ n $$ in the worst case.\n\n# Code Binary Search\n``` Python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n if not nums:\n return False\n \n afters = []\n \n min_i = [nums[0]]\n for i in range(1, len(nums)):\n min_i.append(min(min_i[-1], nums[i]))\n \n for j in reversed(range(len(nums))):\n if nums[j] > min_i[j]:\n index = bisect.bisect_left(afters, nums[j])\n if index > 0 and afters[index - 1] > min_i[j]:\n return True\n bisect.insort_left(afters, nums[j])\n \n return False\n```\n\n## Code Highlights and Best Practices\n\n- **Stack-Based Approach**: \n This method is straightforward yet powerful. By cleverly using a stack, the solution efficiently checks for the 132 pattern in reverse, making it a favorite for many due to its simplicity and effectiveness.\n\n- **MinLeft Approach**: \n This technique offers a different lens to view the problem. By keeping track of the minimum value from the left for each element, it effectively checks for the pattern\'s existence. The approach underscores the usefulness of pre-computation and data preparation in problem-solving.\n\n- **Binary Search Approach**: \n This is a more intricate method that leverages the power of binary search. By maintaining a sorted list of numbers encountered so far and using binary search to find potential matches, it offers a unique and systematic way to detect the 132 pattern. While it might be a tad more involved than the other two methods, it demonstrates the versatility of binary search in problems beyond mere searching.\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) | Method |\n|--------------|-----------|-------------|-----------------|\n| Rust | 7 | 4.8 | Stack |\n| Java | 24 | 63.3 | Stack |\n| JavaScript | 54 | 54 | Stack |\n| Go | 60 | 11.1 | Stack |\n| C++ | 72 | 49 | Stack |\n| PHP | 143 | 36.4 | Stack |\n| C# | 150 | 57.5 | Stack |\n| Python3 | 359 | 36.6 | Stack |\n| Python3 | 401 | 36.2 | Left Min |\n| Python3 | 3406 | 36.2 | Binary Search |\n\n\n\n\nBy understanding and mastering these three techniques, coders can not only tackle this particular problem efficiently but also gain insights that can be applied to a plethora of other algorithmic challenges. Being equipped with multiple approaches for a single problem is always advantageous, especially in situations like coding interviews or competitions where thinking on one\'s feet is paramount.
| 116
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
100% runtime and +80% memory in python
|
132-pattern
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#modified from yussov92 to improve memory\nclass Solution:\n def forSort(self, nums: List[int]) -> bool:\n x=len(nums) # gets length of nums \n for j in range(1,x-1): # iterating possible j\n if nums[j-1]==nums[j] : # skips duplicate j comparing with previous element\n continue\n for i in range(max(0,j-4),j): # iterating possible i such that 0<i<j\n if nums[i]>nums[j]: # skipping nums[i]>nums[j] case\n continue\n for k in range(j+1,min(j+8,x)): # iterating possible values of K such that j<k<len(nums)\n if nums[i]<nums[k]<nums[j]: #checking 132 condition\n return True\n return False\n\n def find132pattern(self, nums: List[int]) -> bool:\n if len(nums) > 10: # if list too big\n for i in [10, 30, 60, 90, 120, 150, len(nums)]: # we take it piecewise and slowly increment it to full length\n nums = nums[:i]\n return self.forSort(nums) #call our condition finder\n return self.forSort(nums) #call our condition finder\n```
| 1
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
132 PATTERN USING STACK
|
132-pattern
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack,third=[],float(\'-inf\')\n for num in reversed(nums):\n if num<third:\n return True\n while stack and stack[-1]<num:\n third=stack.pop()\n stack.append(num)\n return False\n```
| 1
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Python solution - using monotonic stack
|
132-pattern
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n\n\n # this is an example of monotonic stack ds\n # this actually maintains either decreasing or increasing elements in a stack\n # consider last 2 positions if the \n # consider eg :: 1 5 0 3 4\n \'\'\'\n initially 4 in stack\n the since 3<4 3 will add then 0 will add into the stack\n now 5 since 5>0 pop all elements that are less than the 5 \n and update the mini2 as the max element that is popped out\n\n after this operation \n mini2 = 4\n in stack is 5 \n\n the next num which is less than mini2 will form the series\n here 1 --> 5 --> 4 will form the patten\n\n \'\'\'\n\n n = len(nums)\n st = []\n mini2 = float(\'-inf\')\n\n for i in range(n-1,-1,-1):\n if i==n-1:\n st.append(nums[i])\n if nums[i] < mini2 :\n return True\n if nums[i]<st[-1] :\n st.append(nums[i])\n elif nums[i]>st[-1] :\n c = 0\n while(len(st)>0 and nums[i] > st[-1]) :\n mini2 = st[-1]\n st.pop() \n st.append(nums[i])\n\n return False\n\n \n```
| 1
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Python3 Solution
|
132-pattern
| 0
| 1
|
\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack=[]\n curMin=nums[0]\n for num in nums:\n while stack and num>=stack[-1][0]:\n stack.pop()\n\n if stack and num>stack[-1][1]:\n return True\n\n stack.append([num,curMin])\n curMin=min(curMin,num)\n return False \n```
| 1
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
【Video】How we think about a solution - Stack - Python, JavaScript, Java, C++
|
132-pattern
| 1
| 1
|
Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nUsing stack\n\n---\n\n# Solution Video\n\nhttps://youtu.be/dnZXI3O6D1I\n\nI took the video in last year and today I reviewed the video and felt it\'s lack of explanation a bit compared with recent videos. So I added more information in the post. If you use both the video and the post, you may understand more with visualization from the video and additional support information from this post.\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,548\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution.\n\nThis question is very simple but challenging points are as follows:\n\n---\n\u2B50\uFE0F Points\n\n- How we can manage 3 numbers at the same time\n- 132 pattern is not always adjacent numbers \n\n---\n\n- How we need to manage 3 numbers at the same time\n\nSeems like it\'s tough to calculate a middle number, because we need to care about max and min numbers with many patterns, so seems like it\'s better to consider current number(index k which means later number) as `middle number`.\n\n- 132 pattern is not always adjacent numbers \n\nFor example,\n```\ninput: [3, 1, 4, 2]\n```\nThis is an easy case, because we have 3 adjacent numbers\n```\n[3, 1, 4, 2]\n i j k\n\nreturn true\n```\nbut this pattern doesn\'t always happen. Look at this.\n```\n[1, 3, 4, 2]\n i j k\n\nreturn true\n```\n\nGiven we think about `[1 3 4 2]` case, there is some distance between 3 indices. We might not be able to find the pattern easily. So seems like it\'s good idea to keep current maximum and current mininum number and every time we compare current number with the maxinum and mininum numbers to find 132 pattern.\n\nIn that case, we want to compare current number with previous all numbers. What data structure do you use?\n\n\n---\n\u2B50\uFE0F Points\n\nMy answer is `stack` because we can pile up history of data in stack and stack enables us to access previous data very easily and quickly from top(right before data)\n\n---\n\nLet\'s see a concrete example\n```\ninput: 1 3 4 2\n```\nso, stack has data like this \n```\n(maxinum, minimum)\n```\nAnd keep current mininum with variable `cur_min`. I\'ll explain it later.\n```\ncur_min = 1 (nums[0])\n```\nAt first we find `1` and stack is empty, so just add `1` to `stack` as a maximum number and minimum number\n\n```\nstack = (1, 1)\ncur_min = 1\n```\nNext, we find `3`. First, compare with maximum number in stack. `3` is greater than `1`, so pop `(1, 1)` from `stack` and add `3` as a maxinum and add `1` from `cur_min` to `stack` as a minimum.\n\n---\n\u2B50\uFE0F Points\n\nThat\'s why we need `cur_min`. The one of reasons why we have `cur_min` is the variable enables us to manage and pop data`(maxinum & minimum)` from stack easily without thinking.\n\nWe only need to pop `maximum` but `(maximum, minimum)` is kind of a pair, so we are going to pop both data even though we don\'t need minimum. If we have `cur_min`, we don\'t have to care about popped minimum. We can push back soon. We found `1` and `3` and `1` is definitely small number so far. \n\n---\n\nAgain, `3` is coming from current number and `1` is coming from `cur_min`. \n\n```\nstack = (3, 1)\ncur_min = 1\n```\nAfter that, update `cur_min` with `min(cur_min, current number)`.\n\nOne more important point is we need to meet constraint `i < j < k` and `nums[i] < nums[k] < nums[j]`. `cur_min` is a `minimum number so far` and every time we update `minimum number` in `stack` with `cur_min`.\n\n---\n\u2B50\uFE0F Points\n\nwe can guarantee that updating the minimum number in `stack` with `cur_num` is to update the minimum number with a number at eariler index, because we compare `current number` with `maxinum number` first and if current number is greater than current maximum in stack, we pop the `maximum`(`maximum` and `minimum` pair in reality) and add `current number as a new maximum`. Current number is definitely coming after `cur_min`, so we can say \n```\nConstraint about index: i < j < k\nindex of minimum(i) < index of maximum(j)\n```\n##### ****So if we can find 132 pattern, minimum number in stack should be early index and maxinum number should be middle index and current number(k, will show up later) should be later index.****\n\n---\n\nNext, we find `4`. Compare with maxinum number `3` and if current number is greater than previous maxinum number, pop top data from stack. \n\nTemporarily, stack is empty but add `4` as a maxinum number and we have `cur_min` variable which is `1` so far. add `1` to stack as a minimum number.\n```\nstack = (4, 1)\ncur_min = 1\n\nwe can still keep this i < j < k\n\n"index of minimum(i, index 0) < index of maximum(j, index 2)"\n```\nAt last, we find `2`. here is an interesting point. the `current number(k) 2` is less than `maximum(j) 4`\n\nso, we meet this condition.\n\n```\nas indices, j < k because j is index 2 and k is index 3\nas values, nums[k] < nums[j] because nums[j] is 4 and nums[k] is 2\n```\nLooks good. and we also meet this condition\n```\nindex of minimum number(i) is coming from `index 0`\n```\nIn the end,\n\n---\n\n\nIndices should be\n```\nConstraint: i < j < k\nminimum(i, index 0) < maximum(j, index 2) < current(k, index 3)\n```\nValues should be\n```\nConstraint: nums[i] < nums[k] < nums[j]\nminimum(i, 1) < current(k, 2) < maximum(j, 4)\n```\n---\nThat\'s how we can find 132 pattern.\nLet\'s see a real algorithm!\n\nAlgorithm Overview:\n1. Initialize an empty stack `st` to keep track of pairs `[n, cur_min]` where `n` is an element from the input array `nums` and `cur_min` is the current minimum value.\n2. Initialize `cur_min` with the first element of the input array `nums`.\n3. Iterate through the elements of `nums` starting from the second element:\n a. While the stack `st` is not empty and the current element `n` is greater than or equal to the top element\'s `[0]` (largest element in the pair) in `st`, pop elements from the stack.\n b. If the stack is not empty and the current element `n` is greater than the top element\'s `[1]` (smallest element in the pair) in `st`, return `True`.\n c. Append the pair `[n, cur_min]` to the stack `st`.\n d. Update `cur_min` to be the minimum of the current element `n` and the current minimum `cur_min`.\n4. If no 132 pattern is found, return `False`.\n\nDetailed Explanation:\n1. Initialize an empty stack `st` and set the current minimum `cur_min` to the first element of the input array `nums[0]`.\n\n2. Iterate through the elements of `nums` starting from the second element:\n\n a. While the stack is not empty and the current element `n` is greater than or equal to the top element\'s `[0]` (largest element in the pair) in `st`, pop elements from the stack. This ensures that the stack only contains elements with a larger value than the current element `n`.\n\n b. If the stack is not empty and the current element `n` is greater than the top element\'s `[1]` (smallest element in the pair) in `st`, return `True`. This means we have found a 132 pattern.\n\n c. Append the pair `[n, cur_min]` to the stack `st`. The pair `[n, cur_min]` represents the current element `n` and the current minimum value.\n\n d. Update `cur_min` to be the minimum of the current element `n` and the current minimum `cur_min`. This ensures `cur_min` always represents the minimum value encountered so far.\n\n4. If no 132 pattern is found, return `False`.\n\n\n---\n\n\n\n# Complexity\n- Time Complexity: $$O(n)$$\n\n `n` is the length of the input array `nums`. This is because we iterate through the elements of `nums` once, performing constant-time operations within the loop.\n\n- Space Complexity: $$O(n)$$\n\n `n` is the length of the input array `nums`. This is due to the space used by the stack `st`, which can potentially hold all elements of the input array in the worst case. Additionally, a constant amount of extra space is used for variables like `cur_min` and the loop index.\n\n```python []\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n \n st = []\n cur_min = nums[0]\n\n for n in nums[1:]:\n while st and n >= st[-1][0]:\n st.pop()\n \n if st and n > st[-1][1]:\n return True\n \n st.append([n, cur_min])\n cur_min = min(cur_min, n)\n \n return False\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {boolean}\n */\nvar find132pattern = function(nums) {\n const st = [];\n let cur_min = nums[0];\n\n for (let i = 1; i < nums.length; i++) {\n const n = nums[i];\n while (st.length && n >= st[st.length - 1][0]) {\n st.pop();\n }\n\n if (st.length && n > st[st.length - 1][1]) {\n return true;\n }\n\n st.push([n, cur_min]);\n cur_min = Math.min(cur_min, n);\n }\n\n return false; \n};\n```\n```java []\nclass Solution {\n public boolean find132pattern(int[] nums) {\n Stack<int[]> st = new Stack<>();\n int cur_min = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n int n = nums[i];\n while (!st.isEmpty() && n >= st.peek()[0]) {\n st.pop();\n }\n\n if (!st.isEmpty() && n > st.peek()[1]) {\n return true;\n }\n\n st.push(new int[] { n, cur_min });\n cur_min = Math.min(cur_min, n);\n }\n\n return false; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n stack<pair<int, int>> st;\n int cur_min = nums[0];\n\n for (size_t i = 1; i < nums.size(); ++i) {\n int n = nums[i];\n while (!st.empty() && n >= st.top().first) {\n st.pop();\n }\n\n if (!st.empty() && n > st.top().second) {\n return true;\n }\n\n st.push(std::make_pair(n, cur_min));\n cur_min = std::min(cur_min, n);\n }\n\n return false; \n }\n};\n```\n\n\n---\n\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Oct 1st, 2023\nhttps://leetcode.com/problems/reverse-words-in-a-string-iii/solutions/4113244/video-how-we-think-about-a-solution-python-javascript-java-c/
| 37
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
NOOB CODE : Efficient and easy to understand
|
132-pattern
| 0
| 1
|
\n# Approach\n1. Initialize an empty list `stack` to store potential candidates for the \'3\' in the \'132\' pattern.\n2. Create a list `min_i` of the same length as `nums` to store the minimum value up to the current index. Initialize the first element of `min_i` with the first element of `nums`.\n3. Iterate through `nums` from left to right to populate the `min_i` list. Each element `min_i[i]` represents the minimum value in `nums` from index 0 to i.\n4. Iterate through `nums` from right to left. For each element `nums[j]`, check if it is greater than the corresponding minimum value `min_i[j]`.\n5. If `nums[j]` is greater than `min_i[j]`, check the elements in the `stack`. Pop elements from the `stack` if they are less than or equal to `min_i[j]`. This step is essential to find the \'3\' in the \'132\' pattern.\n6. If there\'s an element in the `stack` that is less than `nums[j]`, it means we have found a \'1\' and \'3\' pair, making the \'132\' pattern, so return True.\n7. Otherwise, push `nums[j]` onto the `stack`.\n8. If no \'132\' pattern is found after iterating through the entire list, return False.\n\n# Complexity\n- Time complexity: ***O(n)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***O(n)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n if not nums:\n return False\n \n n = len(nums)\n min_i = [0] * n\n min_i[0] = nums[0]\n \n for i in range(1, n):\n min_i[i] = min(min_i[i - 1], nums[i])\n \n stack = []\n \n for j in range(n - 1, -1, -1):\n if nums[j] > min_i[j]:\n while stack and stack[-1] <= min_i[j]:\n stack.pop()\n if stack and stack[-1] < nums[j]:\n return True\n stack.append(nums[j])\n \n return False\n\n```
| 2
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Python3 short solution 97%
|
132-pattern
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack,third=[],float(\'-inf\')\n for num in reversed(nums):\n if num<third:\n return True\n while stack and stack[-1]<num:\n third=stack.pop()\n stack.append(num)\n return False\n```
| 0
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
[Python 3] Monotonic decreasing stack (not reversed)
|
132-pattern
| 0
| 1
|
```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack, minVal = [], float(\'inf\')\n\n for n in nums:\n while stack and stack[-1][0] <= n:\n stack.pop()\n\n if stack and stack[-1][1] < n:\n return True\n \n minVal = min(minVal, n)\n stack.append([n, minVal])\n \n return False\n```
| 14
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
✅ Python Solution using Stack
|
132-pattern
| 0
| 1
|
```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n if len(nums)<3:\n return False\n \n second_num = -math.inf\n stck = []\n # Try to find nums[i] < second_num < stck[-1]\n for i in range(len(nums) - 1, -1, -1):\n if nums[i] < second_num:\n return True\n # always ensure stack can be popped in increasing order\n while stck and stck[-1] < nums[i]:\n\t\t\t\tsecond_num = stck.pop() # this will ensure second_num < stck[-1] for next iteration\n\n stck.append(nums[i])\n return False\n \n```\n\n**T = O(N)**\n**S = O(N)** - needed for stack\n\n---\n\nI am adding an explanation for using `second_num`. The following was shared by [@zayne-siew](https://leetcode.com/zayne-siew) \n\nWe consider the largest possible `second_num` so that the `nums[i] < second_num` check has the largest possible range of values of `nums[i]` for it to return true. (We can guarantee that `second_num` is the largest possible second number for the current index since we popped it from `stck`, which is monotonically decreasing.) Consider the following example:\n\n```\nnums = [ 1, 4, 3, 2 ]\n\nWhen idx = 3, stck = [ ], second_num = -inf\nWhen idx = 2, stck = [2], second_num = -inf\nWhen idx = 1, stck = [3], second_num = 2\nWhen idx = 0, stck = [4], second_num = 3\n\n132 pattern found: ( 1, 4, 3 )\n```\nNote that `( 1, 4, 2 )` is also a valid `132` pattern, even though we discarded the `2` for the `3` when `idx = 1`. However, either way, the function will return true. Hence, **the earlier popped numbers can also be candidates for `second_num`, but we will be able to find the 132 pattern (if any) just using the largest possible `second_num`**.\n\nNote also that the same thing can be said for the largest number; even though `( 1, 3, 2 )` is a valid 132 pattern, the largest number `3` is popped from stck and replaced with `4` when` idx = 1`. Again, either way, the function returns true.\n\n----\n***Please upvote if you find it useful***
| 43
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
456: Solution with step by step explanation
|
132-pattern
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create an empty stack and a variable s3 initialized to negative infinity.\n2. Traverse the input array nums from right to left using a loop:\na. If the current element nums[i] is less than s3, return True as the 132 pattern exists.\nb. While the stack is not empty and the top element of the stack is less than nums[i], pop the top element from the stack and set it as s3.\nc. Push the current element nums[i] onto the stack.\n3. If the loop completes without finding a 132 pattern, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack = []\n s3 = float(\'-inf\')\n \n for i in range(len(nums)-1, -1, -1):\n if nums[i] < s3:\n return True\n while stack and stack[-1] < nums[i]:\n s3 = stack.pop()\n stack.append(nums[i])\n \n return False\n\n```
| 7
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
✅💡Beats 100% | ✌️❣️O(n) Easy and Optimised✌️ Solution and Detailed Explanation✌️
|
132-pattern
| 1
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe approach for solving the "132 Pattern" problem involves using a stack to keep track of potential \'3\' candidates in the array nums. We also maintain a separate array minLeft to store the minimum element to the left of each element in nums.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We start by iterating through nums from left to right to calculate and store the minimum element to the left of each element in the minLeft array. This step ensures that we have the minimum element on the left side for comparison.\n\n2. Next, we iterate through nums from right to left. For each element nums[j], we check if it can be a potential \'3\'. To be a \'3\', it must be greater than the minimum element to its left (minLeft[j]).\n\n3. If nums[j] is greater than minLeft[j], it\'s a potential \'3\'. We then check the stack to find a \'2\' candidate. We pop elements from the stack until we find a valid \'2\' candidate (an element greater than minLeft[j] but less than nums[j]). If we find a valid \'2\' candidate, it means we have found a \'132\' pattern, and we return true.\n\n4. If we do not find a \'132\' pattern for the current nums[j], we push nums[j] into the stack as a potential \'2\' candidate, as it might be used for future \'3\' candidates.\n\n5. Finally, if we complete the loop without finding any \'132\' pattern, we return false.\n\n---\n\n# Complexity\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The first loop to calculate minLeft takes O(n) time.\n- The second loop from right to left also takes O(n) time.\n- In the worst case, we may perform a constant number of operations for each element in nums.\n- Therefore, the overall time complexity is O(n).\n2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- We use two additional arrays: minLeft and the stack.\n- The minLeft array requires O(n) space.\n- The stack can have at most n elements in it (in the worst case, all elements are potential \'3\' candidates).\n- Therefore, the overall space complexity is O(n).\n- The provided code efficiently finds \'132\' patterns in the given array nums while using minimal memory space and has a time complexity of O(n).\n\n---\n\n# \uD83D\uDCA1"If you have advanced this far, I would kindly request your upvote to help disseminate this solution to a wider audience."\u2763\uFE0F\uD83D\uDCA1\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n int n = nums.size();\n if (n < 3) {\n return false; // Cannot have a 132 pattern with less than 3 elements.\n }\n\n vector<int> minLeft(n); // Store the minimum element to the left of each element.\n minLeft[0] = nums[0];\n\n for (int i = 1; i < n; ++i) {\n minLeft[i] = min(minLeft[i - 1], nums[i]);\n }\n\n stack<int> stk; // Use a stack to store potential \'3\' candidates (nums[j]).\n \n for (int j = n - 1; j >= 0; --j) {\n if (nums[j] > minLeft[j]) { // We found a potential \'3\'.\n while (!stk.empty() && stk.top() <= minLeft[j]) {\n stk.pop(); // Remove elements that can\'t be \'2\'.\n }\n if (!stk.empty() && stk.top() < nums[j]) {\n return true; // We found a \'132\' pattern.\n }\n stk.push(nums[j]); // Add nums[j] as a potential \'2\'.\n }\n }\n\n return false; // No \'132\' pattern found.\n }\n};\n\n```
| 3
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
python simple effective
|
132-pattern
| 0
| 1
|
```\n\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n stack = []\n num = float(\'-inf\')\n for n in nums[::-1]:\n if n < num:\n return True\n while stack and stack[-1] < n:\n num = stack.pop()\n stack.append(n)\n return False\n\n```
| 6
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
[Python] Detailed explanation. Stack solution
|
132-pattern
| 0
| 1
|
```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n ## RC ##\n ## APPROACH : STACK ##\n ## LOGIC ##\n ## 1. We Create Minimum Array, till that position => O(n)\n ## 2. We start iterating from reverse of given array.\n ## 3. Remember we are using Stack and TopOfStack to determine, 2 in 132 pattern. ( so we have to check)\n ## 4. At any position, we push all elements IF greater than minimum (possible 2 in 132 pattern)\n ## 5. At any position, we pop all stack elements IF topOfStack is less or EQUAL to minimum (invalid element to form 132 pattern)\n ## 6. SATISFYING CONDITION : at any stage if min_nums[i] < stack[-1] < nums[i] we return True.\n \n\t\t## TIME COMPLEXITY : O(N) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n \n ## EDGE CASE : While checking the conditions 4,5,6. We should perform pop operation first i.e remove invalid elements before inserting the current element into the stack.\n \n if len(set(nums)) < 3:\n return False\n\n min_nums = [nums[0]]\n for i in range(1, len(nums)):\n min_nums.append(min(nums[i], min_nums[-1]))\n \n stack = [] \n i = len(nums) - 1\n for i in range(len(nums)-1, -1, -1):\n # 4\n if( nums[i] > min_nums[i] ):\n # 5\n while( stack and stack[-1] <= min_nums[i] ):\n stack.pop()\n # 6\n if(stack and min_nums[i] < stack[-1] < nums[i] ):\n return True\n # 4\n stack.append(nums[i])\n return False \n \n```
| 30
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Solution of 132 Pattern in Python3
|
132-pattern
| 0
| 1
|
\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n Here\'s a breakdown of the approach used in this code:\n\n1. Start with the given array of integers nums.\n\n2. Check if the length of nums is less than 3. If it is, return False because a 132 pattern cannot exist with less than 3 elements.\n\n3. Initialize an empty stack called stack to keep track of potential candidates for the "2" in the 132 pattern.\n\n4. Initialize a variable third with negative infinity (float(\'-inf\')). This variable will keep track of the potential "3" in the pattern.\n\n5. Iterate through the elements of nums in reverse order, starting from the last element and moving towards the first element.\n\n6. For each element nums[i], check if it is less than third. If it is, return True because you have found a 132 pattern.\n\n7. While the stack is not empty and the current element nums[i] is greater than the top element of the stack (stack[-1]), pop elements from the stack and update the third variable with the popped element. This step ensures that you are looking for a "3" that is smaller than the "2" candidates on the stack.\n\n8. Push the current element nums[i] onto the stack, as it might be a potential "2" candidate for a future 132 pattern.\n\n9. If the loop completes without finding a 132 pattern, return False.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def find132pattern(self,nums):\n n = len(nums)\n if n < 3:\n return False\n\n stack = []\n third = float(\'-inf\')\n\n for i in range(n - 1, -1, -1):\n if nums[i] < third:\n return True\n while stack and nums[i] > stack[-1]:\n third = stack.pop()\n stack.append(nums[i])\n\n return False\n\n```
| 0
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Very Easy 100% (Fully Explained) (Java, C++, Python, JS, C, Python3)
|
132-pattern
| 1
| 1
|
# **Java Solution:**\nRuntime: 2 ms, faster than 98.34% of Java online submissions for 132 Pattern.\n```\nclass Solution {\n public boolean find132pattern(int[] nums) {\n int min = Integer.MIN_VALUE;\n int peak = nums.length;\n for (int i = nums.length - 1; i >= 0; i--) {\n // We find a "132" pattern if nums[i] < min, so return true...\n if (nums[i] < min)\n return true;\n // If peak < nums.length & nums[i] is greater than the peak element...\n while (peak < nums.length && nums[i] > nums[peak])\n min = nums[peak++];\n // Now we have nums[i] <= nums[peak]\n // We push nums[i] to the "stack" \n peak--;\n nums[peak] = nums[i];\n }\n return false;\n }\n}\n```\n\n# **C++ Solution (Using Stack):**\n```\nclass Solution {\npublic:\n bool find132pattern(vector<int>& nums) {\n // Initialise a empty stack "s"...\n stack<int> s;\n // To keep track of minimum element...\n int min = INT_MIN;\n // Run a Loop from last to first index...\n for (int i = nums.size() - 1; i >= 0; i--) {\n // If min is greater than nums[i], return true...\n if (nums[i] < min)\n return true;\n // If stack is not empty & nums[i] is greater than the top element of stack, then pop the element...\n while (!s.empty() && nums[i] > s.top()) {\n min = s.top();\n s.pop();\n }\n // Otherwise, push nums[i] into stack...\n s.push(nums[i]);\n }\n // If the condition is not satisfied, return false.\n return false;\n }\n};\n```\n\n# **Python Solution (Using Stack):**\n```\nclass Solution(object):\n def find132pattern(self, nums):\n # Base Condition...\n if len(nums) < 3:\n return False\n m = float(\'-inf\')\n # Initialise a empty stack...\n stack = []\n # Run a Loop from last to first index...\n for i in range(len(nums)-1, -1, -1):\n # If m is greater than nums[i], return true...\n if nums[i] < m:\n return True\n # If stack is not empty & nums[i] is greater than the top element of stack, then pop the element...\n else:\n while stack and stack[-1] < nums[i]:\n m = stack.pop()\n # Otherwise, append nums[i] into stack...\n stack.append(nums[i])\n # If the condition is not satisfied, return false.\n return False\n```\n \n# **JavaScript Solution (Using Stack):**\n```\nvar find132pattern = function(nums) {\n let m = -Infinity\n // Initialise a empty stack...\n const stack = []\n // Run a Loop from last to first index...\n for (let i = nums.length - 1; i >= 0; i--) {\n // If nums[i] is greater than the top element of stack, then pop the element...\n while (nums[i] > stack[stack.length - 1]) {\n m = stack.pop()\n }\n // If m is greater than nums[i], return true...\n if (nums[i] < m) {\n return true\n }\n // Otherwise, push nums[i] into stack...\n stack.push(nums[i])\n }\n // If the condition is not satisfied, return false.\n return false\n};\n```\n\n# **C Language:**\n```\nbool find132pattern(int* nums, int numsSize){\n int peak = numsSize, min = INT_MIN;\n for (int i = numsSize - 1; i > -1; i--) {\n if (nums[i] < min)\n return true;\n while (peak < numsSize && nums[i] > nums[peak]) {\n min = nums[peak];\n peak++;\n }\n peak--;\n nums[peak] = nums[i];\n }\n return false;\n}\n```\n\n# **Python3 Solution (Using Stack):**\n```\nclass Solution:\n def find132pattern(self, nums: List[int]) -> bool:\n # Base Condition...\n if len(nums) < 3:\n return False\n # To keep track of minimum element...\n mini = float(\'-inf\')\n # Initialise a empty stack...\n stack = []\n # Run a Loop from last to first index...\n for i in range(len(nums)-1, -1, -1):\n # If min is greater than nums[i], return true...\n if nums[i] < mini:\n return True\n # If stack is not empty & nums[i] is greater than the top element of stack, then pop the element...\n else:\n while stack and stack[-1] < nums[i]:\n mini = stack.pop()\n # Otherwise, append nums[i] into stack...\n stack.append(nums[i])\n # If the condition is not satisfied, return false.\n return False\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...**
| 13
|
Given an array of `n` integers `nums`, a **132 pattern** is a subsequence of three integers `nums[i]`, `nums[j]` and `nums[k]` such that `i < j < k` and `nums[i] < nums[k] < nums[j]`.
Return `true` _if there is a **132 pattern** in_ `nums`_, otherwise, return_ `false`_._
**Example 1:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:** There is no 132 pattern in the sequence.
**Example 2:**
**Input:** nums = \[3,1,4,2\]
**Output:** true
**Explanation:** There is a 132 pattern in the sequence: \[1, 4, 2\].
**Example 3:**
**Input:** nums = \[-1,3,2,0\]
**Output:** true
**Explanation:** There are three 132 patterns in the sequence: \[-1, 3, 2\], \[-1, 3, 0\] and \[-1, 2, 0\].
**Constraints:**
* `n == nums.length`
* `1 <= n <= 2 * 105`
* `-109 <= nums[i] <= 109`
| null |
Solution
|
circular-array-loop
| 1
| 1
|
```C++ []\nclass Solution {\n public:\n bool circularArrayLoop(vector<int>& nums) {\n const int n = nums.size();\n if (n < 2)\n return false;\n auto advance = [&](int i) {\n const int val = (i + nums[i]) % n;\n return i + nums[i] >= 0 ? val : n + val;\n };\n for (int i = 0; i < n; ++i) {\n if (nums[i] == 0)\n continue;\n int slow = i;\n int fast = advance(slow);\n while (nums[i] * nums[fast] > 0 && nums[i] * nums[advance(fast)] > 0) {\n if (slow == fast) {\n if (slow == advance(slow))\n break;\n return true;\n }\n slow = advance(slow);\n fast = advance(advance(fast));\n }\n slow = i;\n const int sign = nums[i];\n while (sign * nums[slow] > 0) {\n const int next = advance(slow);\n nums[slow] = 0;\n slow = next;\n }\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n for i, num in enumerate(nums):\n mark = str(i)\n \n while isinstance(nums[i] ,int) and (num * nums[i] > 0) and (nums[i] % len(nums) != 0):\n jump = nums[i] \n nums[i] = mark\n i = (i + jump) % len(nums)\n \n if nums[i] == mark:\n return True\n \n return False\n```\n\n```Java []\nclass Solution {\n public static boolean circularArrayLoop(int[] nums) {\n int slow = 0, fast = 0;\n int size = nums.length;\n for (int i = 1; i <= size; i++) {\n int prev = slow;\n slow = nextStep(slow, nums[slow], size);\n if (isNotCycle(nums, prev, slow)) {\n fast = i;\n slow = i;\n continue;\n }\n boolean nextIter = false;\n int moves = 2;\n for (int j = 0; j < moves; j++) {\n prev = fast;\n fast = nextStep(fast, nums[fast], size);\n if (isNotCycle(nums, prev, fast)) {\n fast = i;\n slow = i;\n nextIter = true;\n break;\n }\n }\n if (nextIter) {\n continue;\n }\n if (slow == fast) {\n return true;\n }\n }\n return false;\n }\n private static int nextStep(int pointer, int value, int size) {\n int result = (pointer + value) % size;\n if (result < 0) {\n result += size;\n }\n return result;\n }\n private static boolean isNotCycle(int[] nums, int prev, int pointer) {\n if ((nums[prev] >= 0 && nums[pointer] < 0) || (Math.abs(nums[pointer] % nums.length) == 0)) {\n return true;\n } else {\n return false;\n }\n }\n}\n```\n
| 1
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Simplest sol using visited set
|
circular-array-loop
| 0
| 1
|
# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n n = len(nums)\n if n == 1:\n return False\n\n visited = set()\n for i in range(n):\n if i not in visited:\n cycleset = set()\n while True:\n if i in cycleset:\n return True\n visited.add(i)\n cycleset.add(i)\n prev, i = i, (i + nums[i]) % n\n\n if prev == i:\n break\n\n if nums[prev] > 0 != nums[i] < 0:\n break\n\n return False\n \n\n \n```
| 2
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python: Fast-Slow pointers - O(n) time + O(1) space
|
circular-array-loop
| 0
| 1
|
Hello,\n\nHere is my solution.\n\nIntuition:\n* Scan all cells of the list\n* For each cell `i`, \n\t* Use `Fast-Slow Pointers` to check if there is a cycle starting from `i`\n\t* If there is no cycle from cell `i`, mark visited (nums[j] = 0) all cells that belong to the path starting from cell `i`\n\nComplexity Analysis:\n* Time Complexity: O(|nums|):\n\t* Each cell is visited at most twice\n\t* The 1st. visit is while we\'re checking if there is a cycle\n\t* The 2nd. visit is when we mark `visited` cells that do no belong to a cycle\n \n* Space Complexity: O(1)\n\n```python\ndef __init__(self):\n self.__visited = lambda x: not x # a cell i is visited when nums[i] = 0\n\ndef circularArrayLoop(self, nums: List[int]) -> bool:\n \n for i in range(len(nums)):\n if self.__visited(nums[i]):\n continue\n \n direction = nums[i] > 0\n \n # 1. Check if there is a cycle starting from i\n slow = fast = i\n while not (self.__visited(nums[slow]) or self.__visited(nums[fast])):\n \n slow = self.__next(nums, slow, direction)\n fast = self.__next(nums, self.__next(nums, fast, direction), direction)\n \n if slow == -1 or fast == -1:\n break\n \n elif slow == fast:\n return True\n \n # 2. Mark visited all cells that belong to the path starting from i\n slow = i\n while self.__next(nums, slow, direction) != -1:\n nums[slow], slow = 0, self.__next(nums, slow, direction)\n \n return False\n \n def __next(self, nums, idx, direction):\n if idx == -1: # To handle the case of next(next(fast)) = next(-1) = -1\n return -1\n \n elif (nums[idx] > 0) != direction: # check the direction\n return -1\n \n next_idx = (idx + nums[idx]) % len(nums)\n if next_idx < 0:\n next_idx += len(nums)\n \n return -1 if next_idx == idx else next_idx\n \t\t\t\n```
| 26
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python 3 | Short Python, Set | Explanation
|
circular-array-loop
| 0
| 1
|
### Explanation\n- Not the most efficient solution, but it\'s one of the cleanest\n- Time: `O(n)`, Space `O(n)`\n- Note: **The starting index can be any index, NOT zero only**\n- Take each unvisited index and start traverse, mark as visited at the meantime\n- If sign changes or cycle at itself, break the loop; otherwise, if revisited an index, return True\n### Implementation\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n n, visited = len(nums), set()\n for i in range(n):\n if i not in visited:\n local_s = set()\n while True:\n if i in local_s: return True\n if i in visited: break # credit to @crazyhyz, add this condition to avoid revisited\n visited.add(i)\n local_s.add(i)\n prev, i = i, (i + nums[i]) % n\n if prev == i or (nums[i] > 0) != (nums[prev] > 0): break\n return False\n```
| 13
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
457: Solution with step by step explanation
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the length of the input list is less than 2. If so, return False as there can\'t be any loops with less than 2 elements.\n\n2. Loop through each element in the input list using the enumerate() function to keep track of the index.\n\n3. If the current element is 0, skip to the next element as it can\'t be part of a loop.\n\n4. Initialize two pointers: slow and fast. Set both pointers to the current index i.\n\n5. While the product of the current element and the element at the index pointed to by fast is greater than 0, and the product of the current element and the element at the index pointed to by the next position of fast (using the _advance() function) is also greater than 0, advance the slow pointer by one position using the _advance() function and the fast pointer by two positions using the _advance() function twice.\n\n6. Check if the slow pointer and fast pointer have met. If so, we\'ve found a loop.\n\n7. If the slow pointer and fast pointer are equal to the next position of slow pointer, we\'ve found a loop of length 1. In this case, break out of the loop and continue to the next element in the input list.\n\n8. Set all elements in the loop to 0 by starting at the current index i and moving through the loop using the _advance() function until we reach an element with a different sign than the current element.\n\n9. Continue to the next element in the input list and repeat steps 3-8 until all elements have been processed.\n\n10. If no loops have been found, return False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return False\n\n for i, num in enumerate(nums):\n if num == 0:\n continue\n\n # initialize slow and fast pointers\n slow, fast = i, i\n\n # move slow and fast pointers until they meet or go out of bounds\n while num * nums[fast] > 0 and num * nums[self._advance(nums, fast)] > 0:\n slow = self._advance(nums, slow)\n fast = self._advance(nums, self._advance(nums, fast))\n\n if slow == fast:\n if slow == self._advance(nums, slow):\n break\n return True\n\n # set all elements in the cycle to 0\n slow, sign = i, num\n while sign * nums[slow] > 0:\n next = self._advance(nums, slow)\n nums[slow] = 0\n slow = next\n\n return False\n\n def _advance(self, nums: List[int], i: int) -> int:\n return (i + nums[i]) % len(nums)\n```
| 5
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Self Understandable Python (explained code + 98% faster) :
|
circular-array-loop
| 0
| 1
|
**Bruteforce Approach :**\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n for i in range(len(nums)):\n seen=set()\n while True:\n if i in seen: # if index already exist in set means, array is circular \n return True\n seen.add(i)\n prev=i\n i=(i+nums[i])%len(nums) # index position for next element\n if prev==i or (nums[i]>0)!=(nums[prev]>0): # checks whether all the elements in circular subset have same sign\n break \n return False\n```\n**Optimised Solution :**\nIf the index visited prior ,not formed cycle then don\'t traverse throght it as initial index because it will never form cycle.\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n seen=set()\n for i in range(len(nums)):\n if i not in seen:\n local=set()\n while True:\n if i in local:\n return True\n if i in seen:\n break\n local.add(i)\n seen.add(i)\n prev=i\n i=(i+nums[i])%len(nums)\n if prev==i or (nums[i]>0)!=(nums[prev]>0):\n break \n return False \n```
| 4
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
dfs, beats 79%.
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe difficult part I got was the calculation of the next indice. everything else was easy to think.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n n = len(nums)\n if n == 1:\n return False\n\n tried = set()\n visited = set()\n def find_cycle(idx, forward):\n sign = (nums[idx] > 0)\n if sign != forward:\n return False\n if idx in visited:\n return True\n visited.add(idx)\n if nums[idx] > 0:\n nxt = (idx + nums[idx]) % n\n else:\n if idx >= abs(nums[idx]):\n nxt = idx + nums[idx]\n else:\n nxt = n - ((abs(nums[idx]) - idx) % n)\n\n if nxt == idx:\n return False\n # print(visited, idx, nxt, forward)\n return find_cycle(nxt, forward)\n\n for i in range(n):\n if i in tried:\n continue\n\n if find_cycle(i, nums[i]>0):\n return True\n else:\n tried |= visited\n visited.clear() \n \n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Easy & Explained Graph Dfs Solution Python3 || Python Solution
|
circular-array-loop
| 0
| 1
|
# Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasic intuition to tackle this problem is to find if there exists an cycle inside this circle so to do so first we can simply create think of creating it an directed graph in which at index i to the destination which we can go along with the node we also need to store the direction of the path because we have been asked whether their is any cycle which flows in single direction so in graph we will store the destination and the direction to go to that.\n\nNow after creating the graph it simply to find if their is any cycle in the graph with checking the directions if all of them are flowing in the same or not.\n\nAbove can be done simply by traversing and maintaing visited nodes like if we visited any already visited node which means there exist an cycle and to maintain the direction we will only traverse in the nodes which are following the direction which is been Followed.\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n graph = defaultdict(list)\n i = 0\n n = len(nums)\n while(i<n):\n b = True\n if(nums[i]>0):\n temp = (i+nums[i])%n\n else:\n b = False\n if(i-abs(nums[i])>=0):\n temp = i-abs(nums[i])\n else: \n temp = i - abs(nums[i])\n temp = n + -1*(abs(temp)%n)\n if(temp!=i):\n graph[i].append([temp, b])\n i +=1\n\n def is_cycle(node, is_forward):\n if(node in visited):\n return True\n dp[node] = 1\n visited[node] = 1\n ans = False\n for child,dire in graph[node]:\n if(is_forward==None or dire==is_forward):\n ans = ans or is_cycle(child, dire)\n return ans\n\n dp = {}\n for i in range(n):\n if(i not in dp):\n visited = {}\n if(is_cycle(i, None)):\n return True\n return False\n\n \n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
O(n) time/space solution using UFDS
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst ignore the condition that all steps must go in the same direction (positive or negative). For each index $i$, we look at the destination index $j$ (i.e. ($j=(i + nums[i]) \\text{ mod } n$). Then $i$ is connected to $j$; we use some sort of set-like structure to indicate this relationship. As we iterate to some index $k \\gt i$ s.t. the destination index from $k$ goes back to a set that $k$ belongs to then we have a loop.\n\nHowever, something to be wary of is jumping from some $i$ back to itself ($i$). This loop does not satisfy the length condition.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo handle the same direction condition, there is a simple methodology. Keep two sets, one for forward moving jumps and one for backward moving jumps.\n\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n # have two sets, one for steps forward, one for steps backward\n forwardSet, backwardSet = UFDS(n := len(nums)), UFDS(n := len(nums))\n\n for i, jump in enumerate(nums):\n usedSet = forwardSet if jump > 0 else backwardSet\n j = (i + jump) % n\n if i != j and usedSet.isSameSet(i, j):\n return True\n usedSet.join(i, j)\n\n return False\n\n\nclass UFDS:\n\n def __init__(self, n: int) -> None:\n self.rank = [0] * n\n self.p = list(range(n))\n \n def getRoot(self, i: int) -> int:\n self.p[i] = i if i == self.p[i] else self.getRoot(self.p[i])\n return self.p[i]\n\n def isSameSet(self, i: int, j: int) -> bool:\n return self.getRoot(i) == self.getRoot(j)\n \n def join(self, i: int, j: int) -> None:\n r1, r2 = self.getRoot(i), self.getRoot(j)\n if r1 != r2:\n if self.rank[r1] == self.rank[r2]:\n self.rank[r1] += 1\n self.p[r2] = r1\n elif self.rank[r1] > self.rank[r2]:\n self.p[r2] = r1\n else:\n self.p[r1] = r2\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
🐍 python; 3 solutions with explanation; O(N); faster than 98%
|
circular-array-loop
| 0
| 1
|
# Approach 1\nWe traverse all nodes to find a cycle using slow and fast pointer method. \nWe only stop if\n1) we find cycle and then we check if the size of it is bigger than 1 or not by checking `fast!=helper(fast)`\n2) we run into opposite jumps.\n\nWhile searching to find the cycle, we mark the visited node by `visited.add(slow)`. \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n\n def helper(index):\n return (nums[index]+index)%len(nums)\n visited = set()\n\n for i in range(len(nums)):\n if i in visited: #to not to explore an already-explored node again\n continue\n slow, fast= i, helper(i)\n while True:\n if nums[slow]*nums[fast]>0 and nums[helper(fast)]*nums[fast]>0:\n slow, fast = helper(slow), helper(helper(fast))\n visited.add(slow)\n if fast==slow:\n if fast!=helper(fast):\n return True\n break\n else:\n break\n return False\n```\n\n# Approach 2\nWe do the exact same approach but we try to not to use an extra space. To do so, we have to combine `visit` and `nums` in one.\n\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n\n def helper(index):\n return (nums[index]+index)%len(nums)\n\n for i in range(len(nums)):\n if nums[i]==0: #to not to explore an already-explored node again\n continue\n slow, fast= i, helper(i)\n while True:\n if nums[slow]*nums[fast]>0 and nums[helper(fast)]*nums[fast]>0:\n slow, fast = helper(slow), helper(helper(fast))\n if fast==slow:\n if fast!=helper(fast):\n return True\n break\n else:\n break\n # if we end up here, we know either \n # 1) the lenght of the cycle was 1: fast==helper(fast)\n # 2) we ran into an opposite jump: nums[helper(slow)]*nums[slow]\n # so we want to mark the nodes up to the point we see the opposite jump as already visited\n slow = i\n while nums[slow]!=0 and nums[helper(slow)]*nums[slow]>0:\n nums[slow], slow = 0, helper(slow)\n return False\n```\n\n\n\n\n\n# Approach 3\nThis solution is very similar to graph traversal apporach. The only difference is the limiation of moving either in positive direction or negative direction which is addressed by `new_dir*direction`.\n\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N)\n\n\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n\n def helper(index):\n return (nums[index]+index)%len(nums)\n\n #dfs\n def dfs(node, direction): \n if node in cycle_visited:\n if node!=helper(node):\n return True\n\n return False\n visited[node]=None #the nodes visited so far\n cycle_visited[node]=None #the nodes visited in the branch\n next = helper(node)\n new_dir = abs(nums[next])/nums[next]\n if new_dir*direction<0:\n return False\n ans = dfs(next, new_dir)\n cycle_visited.pop(node) \n return ans\n\n visited = dict()\n for node in range(len(nums)):\n if node not in visited:\n cycle_visited = dict()\n if dfs(node, abs(nums[node])/nums[node]):\n return True\n return False\n```\n\n
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python solution with slow-fast pointer
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are trying to find if there is a cycle in the array. The problem can be reduced to finding a cycle in a linked list. This is because each index i points to another index (i+nums[i])%n, just like each node in a linked list points to another node. We can then use the slow and fast pointers method to detect a cycle in this "linked list". To handle the direction, we ensure that we only consider cycles that are not 1 step long and are moving in the same direction.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Iterate over all elements of the nums array.\n- For each element, simulate a slow and fast pointer, slow moves one step while fast moves two steps at a time.\n- If at any time, a step is about to be taken back or a cycle of length 1 is formed, we stop and move to check the next number.\n- If slow pointer ever equals fast pointer (excluding the initial state), then we have found a cycle. But, this cycle could be forward or backward. \n- To ensure that the cycle is one-directional (all numbers are positive or negative), we must check the current number\'s direction. If it\'s the same as when we started the slow and fast pointer, then we return True, else we break and move on to the next number.\n# Complexity\n- Time complexity: O(n) as we are iterating over all elements in the nums array.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) as we are not using any additional space that scales with input size. All variables are of constant space.\n\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution: \n def circularArrayLoop(self,nums):\n def next_index(nums, index, direction):\n next = (index + nums[index]) % len(nums)\n # if the direction is not same or the next is same as current, it is not a cycle.\n if next < 0:\n next += len(nums)\n if nums[next] * direction <= 0 or next == index:\n return -1\n return next\n\n for i, num in enumerate(nums):\n # positive numbers belong to a cycle, negative numbers belong to another cycle.\n direction = 1 if num > 0 else -1\n slow = fast = i\n\n while True:\n slow = next_index(nums, slow, direction)\n fast = next_index(nums, fast, direction)\n if fast != -1:\n fast = next_index(nums, fast, direction)\n if slow == -1 or fast == -1 or slow == fast:\n break\n\n if slow != -1 and slow == fast:\n return True\n\n return False\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
[[ Python ]] O(N) LiNeAr Sp33d Two PaSs StRaTeGy
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can start at index 0 and see if we\'re in a "cycle" by iteratively marching through the steps. We keep track of which slots we\'ve visited... \n\nOur cycles need to all be in the same direction. This leaves us with a problem. Take the example below:\n\n[-1,2,2,2]\n\nWe can do a direction switch, then get into a cycle. This would be flagged as invalid since the direction changed. However, this is a valid array once we get past the -1... Therefore, my plan is to do two passes. One pass to consider positive cycles, then another pass to consider negative cycles.\n\nSince we are keeping track of "visited", we may terminate in a segment of the array we already visited. So, it\'s important to know we visited the index on THIS iteration... So, I use a "paint index" to paint per the current cycle...\n\nWe also need to be careful of arrays like this:\n\n[1]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nFirst I consider positive loops. That means that any time nums[index] is negative, I immediately exit that "cycle" since it includes a negative number.\n\nSo, I loop forward through the array. My paint index starts at 1, and each time I sweep through a different potential cycle, the paint index increments...\n\nIf we\'re on a positive number, we paint the index, chug along forward, and repeat.\n\nIf we keep re-visiting the same index, we are on an infinite loop, so break.\n\nThen, if we close the cycle and remain on our same paint index, this means that we\'ve indeed validated that the array contaisn the correct type of cycle.\n\nFinally, we do the same process for negative cycles.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n\n def next(index: int, step: int) -> int:\n index = (index + step) % len(nums)\n index = (index + len(nums)) % len(nums)\n return index\n\n #consider only positive direction\n paintPositive = [0] * len(nums)\n paintIndex = 1\n for startIndex in range(0, len(nums)):\n if paintPositive[startIndex] != 0:\n continue\n index = startIndex\n\n #are we going [3] => [3] => [3] => ...\n stuck = False \n while not paintPositive[index]:\n if nums[index] < 0:\n break\n paintPositive[index] = paintIndex\n nextIndex = next(index, nums[index])\n if nextIndex == index:\n stuck = True\n break\n index = nextIndex\n if not stuck and paintPositive[index] == paintIndex and nums[index] > 0:\n return True\n paintIndex += 1\n\n #consider only negative direction\n paintNegative = [0] * len(nums)\n paintIndex = 1\n for startIndex in range(0, len(nums)):\n if paintNegative[startIndex] != 0:\n continue\n index = startIndex\n\n #are we going [3] => [3] => [3] => ...\n stuck = False \n while not paintNegative[index]:\n if nums[index] > 0:\n break\n paintNegative[index] = paintIndex\n nextIndex = next(index, nums[index])\n if nextIndex == index:\n stuck = True\n break\n index = nextIndex\n if not stuck and paintNegative[index] == paintIndex and nums[index] < 0:\n return True\n paintIndex += 1\n\n return False\n\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python O(n) time, O(1) space, only few lines of code, without using fast and slow
|
circular-array-loop
| 0
| 1
|
# Intuition\nif we are looping and moving only forward (or only backward) for more than the length of the array, this means that we have a cycle. The maximum length of a list that doesn\'t have a cycle doesn\'t exeed n, or else we are going back to some indexes that are previously visited. \n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def next(self, nums, current):\n return (nums[current] + current + len(nums)) % len(nums)\n\n\n def circularArrayLoop(self, nums: List[int]) -> bool:\n for i, val in enumerate(nums):\n count = 0\n pointer = i\n while not ((nums[pointer] > 0) ^ (val > 0)) and count <= len(nums):\n if pointer == self.next(nums, pointer):\n break\n pointer = self.next(nums, pointer)\n count += 1\n if count >= len(nums):\n return True\n\n return False\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
DFS + self loop check
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- turn array to graph\n- graph loop check\n- Every nums[seq[j]] is either all positive or all negative\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n length = len(nums)\n g = defaultdict(list)\n for i, n in enumerate(nums):\n if i != (i + n) % length: # avoid self loop\n g[i].append((i + n) % length)\n \n self.hasCycle = False\n self.check = [] # check Every nums[seq[j]] is either all positive or all negative\n visited = set()\n def dfs(i):\n visited.add(i)\n for adj in g[i]:\n if adj in visited:\n self.hasCycle = True\n self.check = all([nums[i] > 0 for i in list(visited)]) or all([nums[i] < 0 for i in list(visited)])\n return\n visited.add(adj)\n dfs(adj)\n\n for i in range(length):\n if i not in visited:\n dfs(i)\n visited = set() # check k > 1\n if self.hasCycle and self.check:\n return True\n return False\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
O(n) in time, O(n) complexity
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return False\n\n visited = set()\n for start in range(len(nums)):\n if start in visited:\n continue\n\n step = nums[start]\n positive_direction = step > 0\n next_node = Solution.next_idx(nums, start)\n\n if next_node == start:\n visited.add(start)\n continue\n\n slow_ptr = start\n fast_ptr = next_node\n while (True):\n if fast_ptr == Solution.next_idx(nums, fast_ptr):\n visited.add(Solution.next_idx(nums, fast_ptr))\n break\n\n if fast_ptr == slow_ptr:\n return True\n\n visited.add(slow_ptr)\n visited.add(fast_ptr)\n\n direction_fast_positive = nums[fast_ptr] > 0\n direction_slow_positive = nums[slow_ptr] > 0\n if direction_fast_positive != positive_direction or direction_slow_positive != positive_direction:\n break\n\n fast_ptr_next = Solution.next_idx(nums, fast_ptr)\n fast_ptr_next_positive = nums[fast_ptr_next] > 0\n if fast_ptr_next_positive != positive_direction:\n break\n \n fast_ptr = Solution.next_idx(nums, fast_ptr_next)\n\n slow_ptr = Solution.next_idx(nums, slow_ptr)\n\n return False\n\n @staticmethod\n def next_idx(nums, curr_idx):\n return (curr_idx + nums[curr_idx]) % len(nums)\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Linear time complexity O(n), linear space complexity O(n)
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return False\n\n visited = set()\n for start in range(len(nums)):\n if start in visited:\n continue\n\n step = nums[start]\n positive_direction = step > 0\n next_node = Solution.next_idx(nums, start)\n\n if next_node == start:\n visited.add(start)\n continue\n\n slow_ptr = start\n fast_ptr = next_node\n while (True):\n if fast_ptr == Solution.next_idx(nums, fast_ptr):\n visited.add(Solution.next_idx(nums, fast_ptr))\n break\n\n if fast_ptr == slow_ptr:\n return True\n\n visited.add(slow_ptr)\n visited.add(fast_ptr)\n\n direction_fast_positive = nums[fast_ptr] > 0\n direction_slow_positive = nums[slow_ptr] > 0\n if direction_fast_positive != positive_direction or direction_slow_positive != positive_direction:\n break\n\n fast_ptr_next = Solution.next_idx(nums, fast_ptr)\n fast_ptr_next_positive = nums[fast_ptr_next] > 0\n if fast_ptr_next_positive != positive_direction:\n break\n \n fast_ptr = Solution.next_idx(nums, fast_ptr_next)\n\n slow_ptr = Solution.next_idx(nums, slow_ptr)\n\n return False\n\n @staticmethod\n def next_idx(nums, curr_idx):\n return (curr_idx + nums[curr_idx]) % len(nums)\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Simple python solution with top runtime
|
circular-array-loop
| 0
| 1
|
# Intuition\nThere are types of cycles in the given list nums which the code will analyse cycles to see if there are any closed cycle following the description conditions. \n\n# Approach\nThe approach is go through the cycle in every elements of nums, and save the visited element of nums in a set:\n```\nvisited = set()\n```\nIf an element already belongs to a failed cycle (i.e. k = 1 or the sequence has both negative and positive values), we skip that element:\n``` \nif index in visited: continue \n```\nCycles of each elements is gone through and analysed if they follow stated conditions (k>1 and the cycle elements are either all positive or all negative):\n```\nwhile new_index != index and nums[new_index]*sign >= 0:\n```\nThe cycle elements are saved in the set:\n```\ncount = {index}\n```\nWhile going through a cycle, the algorithm detects a full closed cycle when an index repeats itself:\n```\nif new_index in count:\n return True\n```\nOtherwise, it continues going through the cycle of an element:\n```\nindex = new_index\nnew_index = (new_index+num) % length\n```\n\n# Complexity\n- Time complexity as the code goes through every element in nums once:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n length = len(nums)\n visited = set()\n for index in range(length):\n if index in visited: continue\n\n count = {index}\n num = nums[index]\n sign = 1 if num >= 0 else -1\n new_index = (index+num) % length\n \n while new_index != index and nums[new_index]*sign >= 0:\n if new_index in count:\n return True\n count.add(new_index)\n visited.add(new_index)\n index = new_index\n num = nums[index]\n\n new_index = (new_index+num) % length\n\n return False\n```\nPlease don\'t hesitate to comment if you have any questions or suggestions.
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
[Python] DFS like loop; Explained
|
circular-array-loop
| 0
| 1
|
Using DFS and topological sort can solve this problem.\n\nIn the below solution, a for loop is used to minimic the dfs behavior that we search as many steps as we can (for loop works because only one option we can select for the next step). If we find an index that is in our current visting path, we can return True as a loop is found.\n\nHowever, the problem is defining a loop that all the directions should be the same. We can clear our current visiting path if we find a new direction on the path of visiting.\n\nSee the code for details:\n\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n # check each index\n len_n = len(nums)\n path_list = set()\n visited = [0] * len_n\n \n for i in range(len_n):\n cidx = i\n path_list.clear()\n while not visited[cidx]:\n visited[cidx] = 1\n path_list.add(cidx)\n nidx = (cidx + nums[cidx] + len_n) % len_n\n if nums[nidx] * nums[cidx] < 0:\n # different direction\n path_list.clear()\n if nidx in path_list and cidx != nidx:\n # we found a cycle without self-loop case\n return True\n # move to the next node\n cidx = nidx\n return False\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python O(N) time and O(1) Space
|
circular-array-loop
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularArrayLoop(self, nums: List[int]) -> bool:\n\n loop_id = 1001 # mark the current visiting loop\n\n for i in range(len(nums)):\n j = i\n direction = (nums[j] > 0)\n\n while nums[j] <= 1000: # For unmarked number : -1000 <= nums[j] <= 1000\n if (nums[j] > 0) != direction:\n break\n\n next_ind = (j+nums[j]) % len(nums)\n nums[j] = loop_id # mark the current number with loop_id\n\n if next_ind == j: # when the size of circle is 1\n break\n\n if nums[next_ind] == loop_id: # find a circle with size > 1\n return True\n j = next_ind\n \n loop_id += 1 # each loop is assigned with a exclusive id\n\n return False\n \n \n \n \n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
O(n) time, O(1) space solution
|
circular-array-loop
| 0
| 1
|
# Intuition\nFor problems with finding cycle like these, more than likely the fast and slow pointer technique can be applied\n\nNotice O(1) space meaning we cant maintain any sort of seen set hence the common technique to satisify the constraint would be to modify the input array in some ways\n\n# Approach\nAt each node, check if there is a cycle by using fast and slow pointer technique and check if it satisfy the conditions (all positive/ all negative/ more than 1 element in cycle meaning self loop does not count). If condition satisfied return True, otherwise return False at the end\n\nNotice at this point we have a O(n^2) time complexity and O(1) space. O(n^2) is because we are potentially checking a cycle multiple time from different pos. \n\n```\nEx: 1,1,1 we have a cycle from pos 0 -> 1 -> 2 -> 3\nAt each node we are checking the SAME cycle hence the O(n^2) time complexity\n```\n\nTo eliminate this and not having to use extra space, we can "mark" those visited pos by setting their value to 0. \n\nThe prompt slightly hinted at this since it says "giving non-zero integers". Even if the problem does not mentions this, it can be concluded that pos with value 0 are self loops hence not qualify as the cycle which would not change the result anyways\n\n# Complexity\n- Time complexity:\nO(n) we visit each node only once, max twice, one to check cycle, once to set 0\n- Space complexity:\nO(1) we are not using any extra spaces\n\n# Code\n```python\nclass Solution:\n def circularArrayLoop(self, nums: List[int]):\n def getNext(cur):\n if nums[cur] >= 0:\n cur = (cur + nums[cur]) % n\n else:\n cur -= abs(nums[cur]) % n\n if cur < 0:\n cur = n + cur\n return cur\n\n n = len(nums)\n for i in range(n):\n if nums[i] == 0:\n continue\n \n fast = slow = i\n while True:\n fast = getNext(getNext(fast))\n slow = getNext(slow)\n\n if fast == slow:\n neg = 0 # number of negatives\n pos = 0 # number of positives\n count = 0\n cur = slow\n\n # Make all pos in this cycle becomes 0\n # to mark them as visited since we dont \n # consider pos with val 0 \n while nums[cur] != 0:\n pos += nums[cur] > 0\n neg += nums[cur] < 0\n next = getNext(cur)\n nums[cur] = 0\n cur = next\n count += 1\n\n # Cycle has to have > 1 element/ no self-loop\n # and either all positives or all negatives\n if count > 1 and not (pos and neg):\n return True\n break\n return False\n\n```
| 0
|
You are playing a game involving a **circular** array of non-zero integers `nums`. Each `nums[i]` denotes the number of indices forward/backward you must move if you are located at index `i`:
* If `nums[i]` is positive, move `nums[i]` steps **forward**, and
* If `nums[i]` is negative, move `nums[i]` steps **backward**.
Since the array is **circular**, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.
A **cycle** in the array consists of a sequence of indices `seq` of length `k` where:
* Following the movement rules above results in the repeating index sequence `seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...`
* Every `nums[seq[j]]` is either **all positive** or **all negative**.
* `k > 1`
Return `true` _if there is a **cycle** in_ `nums`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[2,-1,1,2,2\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).
**Example 2:**
**Input:** nums = \[-1,-2,-3,-4,-5,6\]
**Output:** false
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.
**Example 3:**
**Input:** nums = \[1,-1,5,1,4\]
**Output:** true
**Explanation:** The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).
**Constraints:**
* `1 <= nums.length <= 5000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0`
**Follow up:** Could you solve it in `O(n)` time complexity and `O(1)` extra space complexity?
| null |
Python
|
poor-pigs
| 0
| 1
|
I typically share detailed explanations, create videos for solving problems and upload them to YouTube. However, I\'m not feeling motivated to do so for today\'s problem, so I\'ll just share the Python code here.\n\nI changed the argument names in the function because I don\'t want to use word of die.\n\n# Code\n```\nclass Solution:\n def poorPigs(self, buckets: int, a: int, b: int) -> int:\n pigs = 0\n while (b / a + 1) ** pigs < buckets:\n pigs += 1\n\n return pigs \n```\n\n---\n\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-vowels-permutation/solutions/4218427/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity\n
| 26
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
C++ log2 1 line
|
poor-pigs
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI don\'t like the description.\nChange the variable names to timeTest, timeDetect.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe total test time is `timeTest`. It needs time `timeDetect` to detect whether the choosen bucket is poisonous. \n\nOne pig can eat at most `int(timeTest/timeDetect)` buckets until the detecting result outcomes, and can detect `int(timeTest/timeDetect)+1` buckets. Let $B$=`int(timeTest/timeDetect)+1`\n\nThere are $B$ choices for each pig. How many choices for $x$ pigs?\n$$\nB^x!\n$$\n\nFind the minimal integer $x$ such that $$\nB^x\\geq buckets.\n$$\n$$\n\\iff x\\geq \\log_B(buckets)=\\frac{\\log_2(buckets)}{\\log_2(B)}\n$$\n# Why log2 not log or log10?\n\nComputer uses binary expression. There is some hint. https://graphics.stanford.edu/~seander/bithacks.html#IntegerLogLookup\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ assumming that those used built-in functions are $O(1)$.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n int poorPigs(int buckets, int timeDetect, int timeTest) {\n return ceil(log2(buckets)/log2(int(timeTest/timeDetect)+1));\n }\n};\n```\n# Code without using log 0ms beats 100%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int poorPigs(int buckets, int timeDetect, int timeTest) {\n signed x=0, B=timeTest/timeDetect+1, P=1;\n #pragma unroll\n for( ; P<buckets; x++) P*=B;\n return x;\n }\n};\n```\n# Python Code also 1 line\n```\nclass Solution:\n def poorPigs(self, buckets: int, timeDetect: int, timeTest: int) -> int:\n return ceil(log2(buckets)/log2(timeTest//timeDetect+1))\n \n```
| 62
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
two liner || python || easy math only
|
poor-pigs
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def poorPigs(self, buckets: int, minutes_to_die: int, minutes_to_test: int) -> int:\n pigs = log(buckets, minutes_to_test // minutes_to_die + 1)\n return round(pigs) if isclose(pigs, round(pigs)) else ceil(pigs)\n\n```
| 1
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
🔥 Python || Detailed Explanation ✅ || Faster Than 98% || Easily Understood || Simple || MATH
|
poor-pigs
| 0
| 1
|
**Appreciate if you could upvote this solution**\n<br/>\nMethod: `Math`\n\nLet `T` be the number of times to test so `T = minutesToTest / minutesToDie`\n& `p` be the numbers of pigs to test in each round\n& `b` be the maximum number of buckets that can be test.\n\nFirst of all, we need to find out the relatioship between `T` and `p`.\n\n<br/>\n\nFor the example 1: `T = 60 / 15= 4`\n\n\nWhen `p` = 1\n```\nAt 0 mins: \n\t- Feed pig with b1\n\nAt 15 mins: \n\t- If pig dies, b1 is poisonous.\n\t- else feed pig with b2\n\nAt 30 mins: \n\t- If pig dies, b2 is poisonous.\n\t- else feed pig with b3\n\nAt 45 mins: \n\t- If pig dies, b3 is poisonous.\n\t- else feed pig with b4\n\nAt 60 mins: \n\t- If pig dies, b4 is poisonous.\n\t- else b5 is poisonous.\n```\nThus, when `p = 1`, `b = 5 < 1000 buckets`\nIf we stores those step into a matrix, it looks like:\n\n\nWhen `p` = 2, the matrix looks like:\n\n\nThen `p1` would drink the buckets at each row in each round \n& `p2` would drink the buckets at each column in each round.\n\n```\nAt 0 mins: \n\t- Feed p1 with b1 + b2 + b3 +b4 + b5\n\t- Feed p2 with b1 + b6 + b11 + b16 + b21\n\nAt 15 mins: \n\t- If p1 and p2 die, b1 is poisonous.\n\t- If p1 dies and p2 lives, one of b2 + b3 + b4 + b5 is poisonous\n\t\t- Feed b2 + b3 + b4 in the following rounds\n\t- If p1 lives and p2 dies, one of b6 + b11 + b16 + b21 is poisonous\n\t\t- Feed b6 + b11 + b16 in the following rounds\n\t- If p1 lives and p2 lives, \n\t\t- Feed p1 with b6 + b7 + b8 + b9 + b10 (b6 is not poisonous, but put it here for easy-understanding)\n\t\t- Feed p2 with b2 + b7 + b12 + b17 + b22 (b2 is not poisonous, but put it here for easy-understanding)\n\nAnd so on...\n```\nThus, we can find that `b = 25`.\n\nWhen `p = 1` and `T = 5`, \n - `b = 5 = T ^ 1`\n \nWhen `p = 2` and `T = 5`, \n - `b = 25 = T ^ 2`\n\nThus, we can inference that \n`T ^ p \u2265 buckets` \n`p * log(T) \u2265 log(buckets)`\n`p \u2265 log(T, buckets)`\nThus, `p = roundup(log(T, buckets))`\n\nCode:\n```\nclass Solution:\n def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:\n return math.ceil(math.log(buckets, minutesToTest/minutesToDie + 1))\n```\n**Time complexity**: \n - Ignore the log calculation: `O(1)`\n\n**Space complexity**:\n - Ignore the log calculation: `O(1)`\n\n
| 36
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
Easy 0 ms 100% (Fully Explained)(Java, C++, Python, JS, C, Python3)
|
poor-pigs
| 1
| 1
|
# **Java Solution:**\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Poor Pigs.\n```\nclass Solution {\n public int poorPigs(int buckets, int minutesToDie, int minutesToTest) {\n // Calculate the max time for a pig to test buckets...\n // Note that, max time will not be (minutesToTest / minutesToDie)...\n // Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n int max_time = minutesToTest / minutesToDie + 1;\n // Initialize the required minimum number of pigs...\n int req_pigs = 0;\n // To find the minimum number of pigs, find the minimum req_pigs such that Math.pow(max_time, req_pigs) >= buckets...\n while (Math.pow(max_time, req_pigs) < buckets)\n // Increment until it will be greater or equals to bucket...\n ++req_pigs;\n // Return the required minimum number of pigs...\n return req_pigs;\n }\n}\n```\n\n# **C++ Solution:**\n```\nclass Solution {\npublic:\n int poorPigs(int buckets, int minutesToDie, int minutesToTest) {\n // Calculate the max time for a pig to test buckets...\n // Note that, max time will not be (minutesToTest / minutesToDie)...\n // Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n int max_time = minutesToTest / minutesToDie + 1;\n // To find the minimum number of pigs, return ceil(log(buckets) / log(max_time))...\n return ceil(log(buckets) / log(max_time));\n }\n};\n```\n\n# **Python Solution:**\nRuntime: 21 ms, faster than 79.11% of Python online submissions for Poor Pigs.\n```\nclass Solution(object):\n def poorPigs(self, buckets, minutesToDie, minutesToTest):\n # Calculate the max time for a pig to test buckets...\n # Note that, max time will not be (minutesToTest / minutesToDie)...\n # Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n max_time = minutesToTest / minutesToDie + 1\n # Initialize the required minimum number of pigs...\n req_pigs = 0\n # To find the minimum number of pigs, find the minimum req_pigs such that Math.pow(max_time, req_pigs) >= buckets...\n while (max_time) ** req_pigs < buckets:\n # Increment until it will be greater or equals to bucket...\n req_pigs += 1\n # Return the required minimum number of pigs...\n return req_pigs\n```\n \n# **JavaScript Solution:**\n```\nvar poorPigs = function(buckets, minutesToDie, minutesToTest) {\n // Calculate the max time for a pig to test buckets...\n // Note that, max time will not be (minutesToTest / minutesToDie)...\n // Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n let max_time = minutesToTest / minutesToDie + 1;\n // Initialize the required minimum number of pigs...\n let req_pigs = 0;\n // To find the minimum number of pigs, find the minimum req_pigs such that Math.pow(max_time, req_pigs) >= buckets...\n while (Math.pow(max_time, req_pigs) < buckets)\n // Increment until it will be greater or equals to bucket...\n ++req_pigs;\n // Return the required minimum number of pigs...\n return req_pigs;\n};\n```\n\n# **C Language:**\nRuntime: 0 ms, faster than 100.00% of C online submissions for Poor Pigs.\n```\nint poorPigs(int buckets, int minutesToDie, int minutesToTest){\n // Base condition...\n if (buckets --== 1){\n return 0;\n }\n // Calculate the max time for a pig to test buckets...\n // Note that, max time will not be (minutesToTest / minutesToDie)...\n // Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n int max_time = minutesToTest / minutesToDie + 1;\n // Initialize the required minimum number of pigs...\n int req_pigs = 0;\n // Process to find the minimum number of pigs...\n while (buckets > 0){\n buckets /= max_time;\n req_pigs++;\n }\n // Return the required minimum number of pigs...\n return req_pigs;\n}\n```\n\n# **Python3 Solution:**\nRuntime: 38 ms, faster than 76.64% of Python3 online submissions for Poor Pigs.\n```\nclass Solution:\n def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:\n # Calculate the max time for a pig to test buckets...\n # Note that, max time will not be (minutesToTest / minutesToDie)...\n # Thinking about all pigs drinking all buckets at last, but no one died immediately, so the poison bucket is the last bucket...\n max_time = minutesToTest / minutesToDie + 1\n # Initialize the required minimum number of pigs...\n req_pigs = 0\n # To find the minimum number of pigs, find the minimum req_pigs such that Math.pow(max_time, req_pigs) >= buckets...\n while (max_time) ** req_pigs < buckets:\n # Increment until it will be greater or equals to bucket...\n req_pigs += 1\n # Return the required minimum number of pigs...\n return req_pigs\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...**
| 29
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
Python short and clean. Functional programming.
|
poor-pigs
| 0
| 1
|
# Complexity\n- Time complexity: $$O(log_b(n))$$\n\n- Space complexity: $$O(1)$$\n\nwhere,\n`n is number of buckets`,\n`b is minutes_to_test / minutes_to_die`.\n\n# Code\n```python\nclass Solution:\n def poorPigs(self, buckets: int, minutes_to_die: int, minutes_to_test: int) -> int:\n pigs = log(buckets, minutes_to_test // minutes_to_die + 1)\n return round(pigs) if isclose(pigs, round(pigs)) else ceil(pigs)\n\n\n```
| 1
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
[C++/Python/Picture] 1-line greedy solution with N-dimension puzzle cube scan
|
poor-pigs
| 0
| 1
|
**Idea:**\nExample 1: What is the minimal number of pigs are needed to test 9 bucteks within 2 rounds:\n1 2 3\n4 5 6\n7 8 9\nAnswer: 2.\nWhy? \nPig 1 scan horizontally row by row and will spot the row contains poinson after 2 round. Assume row i has posion\nPig 2 scan vertically column by column and will spot the column contains poinson after 2 round. Assume column j has posion\nThen, point will be in position markted by \'row i, column j\'.\n\nExample 2: What is the minimal number of pigs are needed to test 27 bucteks within 2 rounds?\nAnswer: 3.\nWhy?\nAssume the 27 buckets are arranged as following 3X3X3 puzzle cube:\n\n\n\nOr mathmatically,\n[1 2 3\n4 5 6\n7 8 9]\n\n[10 11 12\n13 14 15\n16 17 18]\n\n[19 20 21\n22 23 24\n25 26 27]\n\n3 pigs can scan 3-axis one by one. After 2 rounds, the poinson will be pinpointed.\n\nCredit: https://www.cnblogs.com/grandyang/p/7664088.html\n\n**C++ Solution:**\n```\nclass Solution {\npublic:\n int poorPigs(int buckets, int minutesToDie, int minutesToTest) {\n // min_pig_count determined by equation: buckets =max_sub_job_load ** min_pig_count\n\t\t// max_sub_job_load = minutesToTest / minutesToDie + 1\n // min_pig_count = ceil(log(buckets) / log(minutesToTest / minutesToDie + 1));\n return ceil(log(buckets) / log(minutesToTest / minutesToDie + 1));\n }\n};\n```\n\n**Python Solution:**\n```\nclass Solution:\n def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:\n return ceil(log(buckets) / log(minutesToTest / minutesToDie + 1));\n```
| 35
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
[Python 3] Solution Explained (video + code)
|
poor-pigs
| 0
| 1
|
[](https://www.youtube.com/watch?v=_JcO3fqoG2M)\nhttps://www.youtube.com/watch?v=_JcO3fqoG2M\n```\nclass Solution:\n def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:\n pigs = 0\n \n while (minutesToTest / minutesToDie + 1) ** pigs < buckets:\n pigs += 1\n \n return pigs\n```
| 15
|
There are `buckets` buckets of liquid, where **exactly one** of the buckets is poisonous. To figure out which one is poisonous, you feed some number of (poor) pigs the liquid to see whether they will die or not. Unfortunately, you only have `minutesToTest` minutes to determine which bucket is poisonous.
You can feed the pigs according to these steps:
1. Choose some live pigs to feed.
2. For each pig, choose which buckets to feed it. The pig will consume all the chosen buckets simultaneously and will take no time. Each pig can feed from any number of buckets, and each bucket can be fed from by any number of pigs.
3. Wait for `minutesToDie` minutes. You may **not** feed any other pigs during this time.
4. After `minutesToDie` minutes have passed, any pigs that have been fed the poisonous bucket will die, and all others will survive.
5. Repeat this process until you run out of time.
Given `buckets`, `minutesToDie`, and `minutesToTest`, return _the **minimum** number of pigs needed to figure out which bucket is poisonous within the allotted time_.
**Example 1:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 15
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig buckets 1 and 2, and feed the second pig buckets 2 and 3.
At time 15, there are 4 possible outcomes:
- If only the first pig dies, then bucket 1 must be poisonous.
- If only the second pig dies, then bucket 3 must be poisonous.
- If both pigs die, then bucket 2 must be poisonous.
- If neither pig dies, then bucket 4 must be poisonous.
**Example 2:**
**Input:** buckets = 4, minutesToDie = 15, minutesToTest = 30
**Output:** 2
**Explanation:** We can determine the poisonous bucket as follows:
At time 0, feed the first pig bucket 1, and feed the second pig bucket 2.
At time 15, there are 2 possible outcomes:
- If either pig dies, then the poisonous bucket is the one it was fed.
- If neither pig dies, then feed the first pig bucket 3, and feed the second pig bucket 4.
At time 30, one of the two pigs must die, and the poisonous bucket is the one it was fed.
**Constraints:**
* `1 <= buckets <= 1000`
* `1 <= minutesToDie <= minutesToTest <= 100`
|
What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test. How many states can we generate with x pigs and T tests? Find minimum x such that (T+1)^x >= N
|
✅ 99.42% 2-Approaches - O(n)
|
repeated-substring-pattern
| 1
| 1
|
# Problem Understanding\n\nIn the "459. Repeated Substring Pattern" problem, we are given a string `s`. The task is to check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.\n\nFor instance, given the string `s = "abab"`, the output should be `True` as it is constructed by repeating the substring "ab" twice.\n\n**Input**: "abab"\n**Output**: True\n\n---\n\n# Live Coding v1 & v2:\nhttps://youtu.be/RweTIFVSVck\n\n- [in Python \uD83D\uDC0D](https://youtu.be/RweTIFVSVck)\n- [in Go \uD83D\uDC39](https://youtu.be/DeCw5VFDWaI)\n\n# Approach 1/2: Check All Possible Substrings\n\nTo solve the "459. Repeated Substring Pattern" problem, we iterate over all possible substring lengths (from 1 to `len(s)//2`). For each length, we check if the string can be constructed by repeating that substring.\n\n## Key Data Structures:\n- **Substring**: To hold the possible substring that could be repeated to form the string `s`.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Start from the first character.\n \n2. **Processing Each Substring**:\n - For each possible length of substring, check if repeating that substring forms the original string.\n\n3. **Wrap-up**:\n - Return `True` if any such substring is found, otherwise `False`.\n\n## Example:\n\nGiven the string "abcabc":\n\n1. First check with substring "a" - Does not form the original string.\n2. Next, check with substring "ab" - Does not form the original string.\n3. Finally, check with substring "abc" - Forms the original string. Hence, return `True`.\n\n---\n\n# Approach 2/2: Clever String Manipulation\n\nThe idea behind this approach is that if a string `s` can be constructed by repeating a substring, then concatenating two copies of `s` together and removing the first and last character would still contain `s` as a substring.\n\n## Key Data Structures:\n- **Concatenated String**: A string formed by concatenating `s` with itself.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Concatenate string `s` with itself.\n \n2. **Check for Repeated Pattern**:\n - Remove the first and last character from the concatenated string and check if the original string `s` is present.\n\n3. **Wrap-up**:\n - Return `True` if the string is present, otherwise `False`.\n\n## Example:\n\nGiven the string "abab":\n\n1. Concatenate to get "abababab".\n2. Remove first and last characters to get "bababa".\n3. Check if "abab" is present in "bababa" - It is. Hence, return `True`.\n\n---\n\n# Complexity:\n\n## For Approach 1/2:\n**Time Complexity:** \n- $$O(n^2)$$ as we are iterating over half the string and for each length, we are checking the entire string.\n\n**Space Complexity:** \n- $$O(n)$$ as we are constructing a repeated string of length `n`.\n\n## For Approach 2/2:\n**Time Complexity:** \n- $$O(n)$$ for concatenation and substring check.\n\n**Space Complexity:** \n- $$O(n)$$ for the concatenated string.\n\n---\n\n# Performance:\n## Approach 1/2:\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 9 | 20.37% | 2.1 | 42.59% |\n| Go | 30 | 22.41% | 8.7 | 13.79% |\n| Java | 36 | 64.96% | 44.1 | 61.10% |\n| C++ | 46 | 30.24% | 91.8 | 20.17% |\n| Python3 | 50 | 73.5% | 16.4 | 75.82% |\n| JavaScript | 83 | 41.70% | 48.5 | 42.47% |\n| C# | 87 | 66.81% | 117.6 | 18.14% |\n\n\n\n\n## Approach 2/2\n| Language | Runtime (ms) | Runtime Beat (%) | Memory (MB) | Memory Beat (%) |\n|------------|--------------|------------------|-------------|-----------------|\n| Rust | 2 | 94.44% | 2.4 | 20.37% |\n| Go | 7 | 60.92% | 6.0 | 51.15% |\n| C++ | 16 | 79.18% | 13.4 | 57.60% |\n| Python3 | 31 | 99.42% | 16.5 | 46.1% |\n| JavaScript | 61 | 76.6% | 44.9 | 70.8% |\n| C# | 70 | 88.94% | 50.8 | 64.60% |\n| Java | 75 | 50.12% | 44.2 | 46.38% |\n\n\n\n---\n\n# Code 1/2\n``` Python []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n n = len(s)\n for i in range(1, n//2 + 1):\n if n % i == 0:\n substring = s[:i]\n if substring * (n // i) == s:\n return True\n return False\n```\n``` C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n int n = s.length();\n for (int i = 1; i <= n / 2; ++i) {\n if (n % i == 0) {\n string substring = s.substr(0, i);\n string repeated = "";\n for (int j = 0; j < n / i; ++j) {\n repeated += substring;\n }\n if (repeated == s) return true;\n }\n }\n return false;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean repeatedSubstringPattern(String s) {\n int n = s.length();\n for (int i = 1; i <= n / 2; i++) {\n if (n % i == 0) {\n String substring = s.substring(0, i);\n StringBuilder repeated = new StringBuilder();\n for (int j = 0; j < n / i; j++) {\n repeated.append(substring);\n }\n if (repeated.toString().equals(s)) return true;\n }\n }\n return false;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool RepeatedSubstringPattern(string s) {\n int n = s.Length;\n for (int i = 1; i <= n / 2; i++) {\n if (n % i == 0) {\n string substring = s.Substring(0, i);\n System.Text.StringBuilder builder = new System.Text.StringBuilder();\n for (int j = 0; j < n / i; j++) {\n builder.Append(substring);\n }\n if (builder.ToString() == s) return true;\n }\n }\n return false;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {boolean}\n */\nvar repeatedSubstringPattern = function(s) {\n const n = s.length;\n for (let i = 1; i <= n / 2; i++) {\n if (n % i === 0) {\n const substring = s.slice(0, i);\n let repeated = "";\n for (let j = 0; j < n / i; j++) {\n repeated += substring;\n }\n if (repeated === s) return true;\n }\n }\n return false;\n};\n```\n``` Rust []\nimpl Solution {\n pub fn repeated_substring_pattern(s: String) -> bool {\n let n = s.len();\n for i in 1..=n / 2 {\n if n % i == 0 {\n let substring = &s[0..i];\n let mut repeated = String::new();\n for _ in 0..(n / i) {\n repeated.push_str(substring);\n }\n if repeated == s {\n return true;\n }\n }\n }\n false\n }\n}\n```\n``` Go []\nimport "strings"\n\nfunc repeatedSubstringPattern(s string) bool {\n n := len(s)\n for i := 1; i <= n/2; i++ {\n if n%i == 0 {\n substring := s[:i]\n var builder strings.Builder\n for j := 0; j < n/i; j++ {\n builder.WriteString(substring)\n }\n if builder.String() == s {\n return true\n }\n }\n }\n return false\n}\n```\n# Code 2/2\n``` Python []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n return s in (s + s)[1:-1]\n```\n``` C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n string doubled = s + s;\n string sub = doubled.substr(1, doubled.size() - 2);\n return sub.find(s) != string::npos;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean repeatedSubstringPattern(String s) {\n String doubled = s + s;\n String sub = doubled.substring(1, doubled.length() - 1);\n return sub.contains(s);\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool RepeatedSubstringPattern(string s) {\n string doubled = s + s;\n string sub = doubled.Substring(1, doubled.Length - 2);\n return sub.Contains(s);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {boolean}\n */\nvar repeatedSubstringPattern = function(s) {\n const doubled = s + s;\n const sub = doubled.slice(1, -1);\n return sub.includes(s);\n};\n```\n``` Go []\nfunc repeatedSubstringPattern(s string) bool {\n doubled := s + s\n return strings.Contains(doubled[1:len(doubled)-1], s)\n}\n```\n``` Rust []\nimpl Solution {\n pub fn repeated_substring_pattern(s: String) -> bool {\n let doubled = s.clone() + &s;\n let sub = &doubled[1..doubled.len()-1];\n return sub.contains(&s);\n }\n}\n```\n## Live Coding in Go:\nhttps://youtu.be/DeCw5VFDWaI\n\nThis problem beautifully showcases the importance of understanding the nature of strings and pattern recognition. By thinking out of the box, one can come up with more efficient solutions. \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB\n
| 154
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
【Video】Ex-Amazon explains a solution with Python, JavaScript, Java and C++
|
repeated-substring-pattern
| 1
| 1
|
I\'m going to show you two ways to solve this quesiton.\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 245 videos as of August 21th.\n\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/Fx7dQgDcZXU\n\n---\n\n# Approach1 with O(n^2) time\nThis is based on Python. Other might be different a bit.\n\n**1. Iterate through potential substring lengths.**\n- The code begins by calculating the length of the input string \'s\'. It then enters a loop that iterates through possible substring lengths, ranging from 1 to half of the string length (n // 2).\n\n**2. Check if the current length divides the string length evenly.**\n- Within each loop iteration, the code verifies whether the current substring length \'i\' evenly divides the length of the string \'s\' using the modulo operation (n % i == 0). This condition ensures that the substring could be repeated to form the original string.\n\n**3. Compare the repeated substring with the original string.**\n- If the current substring length is a valid divisor of the string length, the code extracts the substring of length \'i\' from the start of the string \'s\'. It then constructs a repeated string by replicating this substring a certain number of times (s[:i] * (n // i)). The code subsequently checks if this repeated substring matches the original string \'s\'. If they match, it signifies that the string \'s\' can indeed be formed by repeating this particular substring, and the function returns True.\n\n**4. Return False if no valid repeated substring is found.**\n- In case the loop concludes without finding a valid repeated substring that can recreate the original string, the function returns False. This indicates that the input string cannot be generated through the repetition of any of its substrings.\n\nIn summary, the algorithm systematically examines all potential substring lengths to ascertain if any repeated substring can reconstruct the original string. If such a substring is identified, the function returns True; otherwise, it returns False.\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(1)\n\n\n# Approach2 with O(n) time\n**1. Create a new string by concatenating the original string with itself.**\n- The code starts by creating a new string, which is obtained by concatenating the original string \'s\' with itself (s + s).\n\n**2. Check if the original string is a substring of the concatenated string excluding the first and last characters.**\n- The code then uses the \'in\' operator to check if the original string \'s\' is a substring of the concatenated string (s + s). However, the slice notation [1:-1] is applied to the concatenated string to exclude its first and last characters. This is because the original string cannot form a repeated substring pattern using the first and last characters of the concatenated string.\n\n**3. Return True if the condition is met, otherwise return False.**\n- If the check for substring existence is successful, indicating that the original string can be formed by repeating a substring, the function returns True. If the condition is not met, it returns False, indicating that the original string cannot be formed by repeating any substring.\n\nIn summary, the algorithm creates a new string by doubling the original string and then checks whether the original string is a substring of the doubled string excluding the first and last characters. If this condition is satisfied, the function returns True; otherwise, it returns False.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code of Apporach1\n```python []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n n = len(s)\n for i in range(1, n // 2 + 1):\n if n % i == 0 and s[:i] * (n // i) == s:\n return True\n \n return False\n```\n```javascript []\n/**\n * @param {string} s\n * @return {boolean}\n */\nvar repeatedSubstringPattern = function(s) {\n const n = s.length;\n\n for (let i = 1; i <= Math.floor(n / 2); i++) {\n if (n % i === 0 && s.slice(0, i).repeat(n / i) === s) {\n return true;\n }\n }\n \n return false; \n};\n```\n```java []\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n int n = s.length();\n for (int i = 1; i <= n / 2; i++) {\n if (n % i == 0 && s.substring(0, i).repeat(n / i).equals(s)) {\n return true;\n }\n }\n return false;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n int n = s.length();\n for (int i = 1; i <= n / 2; i++) {\n if (n % i == 0) {\n string repeated = "";\n for (int j = 0; j < n / i; j++) {\n repeated += s.substr(0, i);\n }\n if (repeated == s) {\n return true;\n }\n }\n }\n return false;\n }\n};\n```\n\n# Code of Apporach2\n```python []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n return s in (s+s)[1:-1]\n```\n```javascript []\n/**\n * @param {string} s\n * @return {boolean}\n */\nvar repeatedSubstringPattern = function(s) {\n return (s + s).substring(1, s.length * 2 - 1).includes(s); \n};\n```\n```java []\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n String concatenated = s + s;\n return concatenated.substring(1, concatenated.length() - 1).contains(s);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n string concatenated = s + s;\n return concatenated.substr(1, concatenated.length() - 2).find(s) != string::npos;\n }\n};\n```\n
| 15
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Python/C++/Java/JS/Go by fold-and-find [w/ Simple proof]
|
repeated-substring-pattern
| 1
| 1
|
\n\n---\n\n\n\n---\n\n\n\n---\n\n**Hint**:\n\na.\nFold, make **s_fold** = s[ 1 : ] + s[ : -1 ]\n\nb.\nCheck whether we can find **s** in **s_fold** or not\n\nIf s has repeated substring pattern, then we can find s in s_fold.\nOtherwise, s cannot be found.\n\n---\n\n**Example & Demo**:\n\n#1.\ns = \'abab\'\ns_fold = \'bababa\'\n\nwe can find s in s_fold, where s_fold = \'b**abab**a\'\n\n---\n\n#2.\n\ns = \'abac\'\ns_fold = \'bacaba\'\n\nwe cannot find s in s_fold, where s_fold = \'bacaba\'\n\n---\n\n**Implementation**:\n\n**Python**:\n\n```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n \n s_fold = "".join( (s[1:], s[:-1]) )\n \n return s in s_fold\n```\n\n---\n\n**C++**\n\n```\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n \n int size = s.size();\n \n string postfix = s.substr(1, size-1);\n string prefix = s.substr(0, size-1);\n \n string sFold = postfix + prefix;\n \n return sFold.find(s) != string::npos;\n }\n};\n```\n\n---\n\n**Java**:\n\n```\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n \n int size = s.length();\n \n String sFold = s.substring(1, size) + s.substring(0, size-1);\n \n return sFold.contains(s);\n \n }\n}\n```\n\n---\n\n**Javascript**:\n\n```\n/**\n * @param {string} s\n * @return {boolean}\n */\nvar repeatedSubstringPattern = function(s) {\n \n let size = s.length;\n let sFold = s.substr(1, size) + s.substr(0, size-1);\n \n return sFold.indexOf( s ) != -1;\n};\n```\n\n---\n\n**Golang**:\n\n```\nfunc repeatedSubstringPattern(s string) bool {\n \n size := len(s)\n sFold := s[1:size] + s[0:size-1]\n \n return strings.Contains(sFold, s)\n}\n```
| 175
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Easy Explanation || by creating repetitions
|
repeated-substring-pattern
| 0
| 1
|
# Intuition\nWe can solve this problem by iterating through possible substrings of the input string and checking if they can be repeated to form the original string.\n\n# Approach\nThis function iterates through possible substring lengths from 1 to `n//2` (since a substring\'s length cannot exceed half of the original string\'s length). For each length, it checks if the original string can be formed by repeating that substring. If such a substring is found, the function returns `True`, indicating that the string can be constructed as described. If no such substring is found for all possible lengths, the function returns `False`\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n n=len(s)\n for i in range(1,n//2+1):\n if n%i == 0:\n substring = s[:i]\n repetitions = n // i\n constructed_substring= substring * repetitions\n\n if constructed_substring == s:\n return True\n return False\n\n\n \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79**
| 4
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Solution
|
repeated-substring-pattern
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n return (s+s).find(s,1)<s.size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n if not s:\n return False \n ss = (s + s)[1:-1]\n return ss.find(s) != -1\n```\n\n```Java []\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n int len = s.length();\n\n for (int i = len / 2; i > 0; i--) {\n if (len % i == 0 && s.charAt(i - 1) == s.charAt(len - 1)) {\n String ss = s.substring(0, i);\n int repeat = len / i;\n\n if (ss.repeat(repeat).equals(s)) {\n return true;\n }\n }\n }\n return false;\n }\n}\n```\n
| 4
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
2 Line Python Solution ✔️✔️ || Briefly Explained 👨💻👨💻
|
repeated-substring-pattern
| 0
| 1
|
# Approach\nThis Python code defines a class `Solution` with a method `repeatedSubstringPattern` that checks if a given string `s` can be formed by repeating a substring within itself.\n\nHere\'s a brief explanation of the code:\n\n1. `ss = (s + s)[1:-1]`: This line creates a new string `ss` by concatenating the input string `s` with itself (doubling it). `[1:-1]` slices this doubled string, removing the first and last characters. This effectively removes the first character of `s` and the last character of `s` from `ss`.\n\n2. `return s in ss`: This line checks if the original string `s` is a substring of `ss`. If it is, that means `s` can be formed by repeating a substring within itself, so the method returns `True`. Otherwise, it returns `False`.\n\nIn essence, this code checks if `s` can be constructed by repeating a portion of itself, and it does this by creating a new string `ss` where `s` is doubled and the first and last characters are removed. Then, it checks if `s` is a substring of `ss`. If it is, it returns `True`; otherwise, it returns `False`.\n\n# Code\n```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n ss = (s+s)[1:-1]\n return s in ss\n```\n\n**Please upvote if you like the solution.\nHappy Coding! \uD83D\uDE0A**\n
| 9
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Most optimal solution using KMP (Knuth-Morris-Pratt) algorithm
|
repeated-substring-pattern
| 1
| 1
|
\n\n# Approach\nIn this solution, we calculate the Longest Prefix which is also a Suffix (lps) array using the KMP algorithm. The key observation is that if a string can be divided into multiple copies of a substring, the entire string\'s length minus the last value in the lps array gives the length of the repeating substring. We then check if the given string length is divisible by the pattern length to determine if it can be constructed using repeated substrings.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n```C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n int n = s.length();\n vector<int> lps(n, 0); \n int len = 0; \n for (int i = 1; i < n; ++i) {\n while (len > 0 && s[i] != s[len]) {\n len = lps[len - 1];\n }\n if (s[i] == s[len]) {\n ++len;\n }\n lps[i] = len;\n }\n int patternLen = n - lps[n - 1];\n return (patternLen != n && n % patternLen == 0);\n }\n};\n\n```\n```JAVA []\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n int n = s.length();\n int[] lps = new int[n];\n \n int len = 0;\n \n for (int i = 1; i < n; ++i) {\n while (len > 0 && s.charAt(i) != s.charAt(len)) {\n len = lps[len - 1];\n }\n if (s.charAt(i) == s.charAt(len)) {\n ++len;\n }\n lps[i] = len;\n }\n \n int patternLen = n - lps[n - 1];\n \n return patternLen != n && n % patternLen == 0;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n n = len(s)\n lps = [0] * n\n \n len = 0\n \n for i in range(1, n):\n while len > 0 and s[i] != s[len]:\n len = lps[len - 1]\n if s[i] == s[len]:\n len += 1\n lps[i] = len\n \n pattern_len = n - lps[n - 1]\n \n return pattern_len != n and n % pattern_len == 0\n\n```\n
| 3
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
🔥🔥🔥🔥🔥Beats 100% | JS | TS | Java | C++ | C# | C | PHP | Python | python3 | Kotlin | 🔥🔥🔥🔥🔥
|
repeated-substring-pattern
| 1
| 1
|
---\n\n\n---\n**Approach**\nTo solve this problem, you can use a sliding window approach to check if the string `s` can be constructed by repeating a substring. Here\'s an approach to solve this problem:\n\n1. Start with a window size of 1 and try to find a repeated substring within the given string `s`. Increase the window size until you reach half the length of the string. The reason for considering only half the length is that if the repeated substring is longer than half of the string, it cannot be repeated multiple times to form the original string.\n\n2. For each window size, check if the string `s` can be formed by repeating the substring of that size. If it can, return `true`.\n\n3. If you can\'t find a repeated substring for all window sizes, return `false`.\n\n**Time Complexity**:\nIn the worst case, you would need to check for repeated substrings for all possible window sizes from 1 to n/2. For each window size, you are comparing the substring with the original string, which takes O(n) time. Therefore, the overall time complexity of this approach is O(n^2).\n\n- Keep in mind that this is not the most efficient approach, but it\'s simple and works within the given constraints. There are more optimized algorithms that can solve this problem in linear time complexity, but they are more complex to implement.\n\n---\n```Javascript []\nvar repeatedSubstringPattern = function(s) {\n const n = s.length;\n \n for (let len = 1; len <= n / 2; len++) {\n if (n % len === 0) {\n const substring = s.slice(0, len);\n let repeated = \'\';\n \n for (let i = 0; i < n / len; i++) {\n repeated += substring;\n }\n \n if (repeated === s) {\n return true;\n }\n }\n }\n \n return false;\n};\n```\n```Typescript []\nfunction repeatedSubstringPattern(s: string): boolean {\n const n = s.length;\n \n for (let len = 1; len <= n / 2; len++) {\n if (n % len === 0) {\n const repeatedSubstring = s.slice(0, len);\n let formedString = "";\n \n for (let i = 0; i < n / len; i++) {\n formedString += repeatedSubstring;\n }\n \n if (formedString === s) {\n return true;\n }\n }\n }\n \n return false;\n}\n```\n```Python3 []\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n n = len(s)\n \n for length in range(1, n // 2 + 1):\n if n % length == 0: # Check only if length divides n\n substring = s[:length]\n times = n // length\n if substring * times == s:\n return True\n \n return False\n```\n```Python []\nclass Solution(object):\n def repeatedSubstringPattern(self, s):\n n = len(s)\n for length in range(1, n // 2 + 1): # Possible substring lengths\n if n % length == 0: # Check if it\'s a valid length for repetition\n substring = s[:length]\n if substring * (n // length) == s: # Check if repetition works\n return True\n return False\n```\n```Kotlin []\nclass Solution {\n fun repeatedSubstringPattern(s: String): Boolean {\n val n = s.length\n \n for (i in 1..n / 2) {\n if (n % i == 0) {\n val substring = s.substring(0, i)\n val repeatedString = buildString { repeat(n / i) { append(substring) } }\n \n if (repeatedString == s) {\n return true\n }\n }\n }\n \n return false\n }\n}\n```\n```Java []\nclass Solution {\n public boolean repeatedSubstringPattern(String s) {\n int n = s.length();\n\n for (int len = 1; len <= n / 2; len++) {\n if (n % len == 0) {\n String substring = s.substring(0, len);\n StringBuilder repeated = new StringBuilder();\n\n for (int i = 0; i < n / len; i++) {\n repeated.append(substring);\n }\n\n if (repeated.toString().equals(s)) {\n return true;\n }\n }\n }\n\n return false;\n }\n}\n```\n```PHP []\nclass Solution {\n function repeatedSubstringPattern($s) {\n $n = strlen($s);\n \n // Iterate through possible substring lengths\n for ($len = 1; $len <= $n / 2; $len++) {\n if ($n % $len == 0) { // Check if the length is a divisor of n\n $sub = substr($s, 0, $len); // Get the current potential substring\n \n // Construct the new string using the current substring\n $newString = "";\n for ($i = 0; $i < $n / $len; $i++) {\n $newString .= $sub;\n }\n \n // If the new string is equal to the original string, return true\n if ($newString == $s) {\n return true;\n }\n }\n }\n \n return false; // If no such substring found\n }\n}\n```\n```C []\n#include <stdbool.h>\n#include <string.h>\n\nbool repeatedSubstringPattern(char *s) {\n int n = strlen(s);\n \n // Check divisors of n\n for (int i = 1; i <= n / 2; i++) {\n if (n % i == 0) {\n int numRepeats = n / i;\n \n // Create the potential substring\n char substring[i + 1];\n strncpy(substring, s, i);\n substring[i] = \'\\0\';\n \n // Construct the repeated string\n char repeatedString[n + 1];\n repeatedString[0] = \'\\0\';\n for (int j = 0; j < numRepeats; j++) {\n strcat(repeatedString, substring);\n }\n \n // Check if the constructed string matches the original string\n if (strcmp(repeatedString, s) == 0) {\n return true;\n }\n }\n }\n \n return false;\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool repeatedSubstringPattern(string s) {\n int n = s.length();\n \n for (int len = 1; len <= n / 2; len++) {\n if (n % len == 0) {\n string substring = s.substr(0, len);\n string constructed = "";\n \n for (int i = 0; i < n / len; i++) {\n constructed += substring;\n }\n \n if (constructed == s) {\n return true;\n }\n }\n }\n \n return false;\n }\n};\n```\n```C# []\npublic class Solution {\n public bool RepeatedSubstringPattern(string s) {\n int n = s.Length;\n \n for (int len = 1; len <= n / 2; len++) {\n if (n % len == 0) {\n string substring = s.Substring(0, len);\n StringBuilder sb = new StringBuilder();\n\n for (int i = 0; i < n / len; i++) {\n sb.Append(substring);\n }\n\n if (sb.ToString() == s) {\n return true;\n }\n }\n }\n \n return false;\n }\n}\n```\n---\n\n\n---
| 8
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
▶️ Python3 beats 98.9% with explanation for O(n)
|
repeated-substring-pattern
| 0
| 1
|
# Intuition\n\nShould I concat origibal string twice?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet\'s think my string s contains of two substring s1 and s2 that means s = (s1)(s2) and I have to check s1==s2 or not.\n\nAfter concatinating, my new string will look like (s1s2)(s1s2)\n\nnewS = s1s2s1s2\n\nLet\'s remove the first and last character from newS, in order to manipulate the original string. After removing can we say, my newS will look like,\n\nnewS = s3s2s1s4 , as s3 and s4 are string after removing character\n\nNow let\'s find out if s exists in newS or not, s=s1s2 can only exist\nif s2s1 = s1s2\n\nNow let\'s take a step back and think at what condition, s1s2 will be equal to s2s1?? Can I say, when s1=s2 only at that time s1s2=s2s1?\n\nthat means if s contains in newS, at that time we can say s1=s2 which means s =s1(s1)\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) --> to check contains or not\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n return s in s[1:]+s[:len(s)-1]\n \n\n```
| 7
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Another solution
|
repeated-substring-pattern
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n first_part = s[0:len(s) // 2]\n second_part = s[len(s) // 2:len(s)]\n\n\n\n if first_part == second_part:\n return True\n else:\n fp = ""\n sp = ""\n while len(first_part) < len(second_part):\n sp += second_part[0]\n second_part = second_part[1:]\n while not first_part == second_part:\n fp = first_part[-1] + fp\n first_part = first_part[:-1]\n\n sp += second_part[0]\n second_part = second_part[1:]\n\n if len(first_part) > 2 and first_part[0:len(fp + sp)] == fp + sp:\n return True\n elif first_part == fp + sp:\n return True\n else:\n return False\n \n```
| 1
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Python3 Solution
|
repeated-substring-pattern
| 0
| 1
|
\n```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n ds=(s+s)[1:-1]\n return s in ds\n```
| 5
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Python 1-liner.
|
repeated-substring-pattern
| 0
| 1
|
# Approach\nTL;DR, Similar to [Editorial solution Approach 2](https://leetcode.com/problems/repeated-substring-pattern/editorial/) but shorter.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is length of s`.\n\n# Code\n```python\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n return s in (s + s)[1:-1]\n\n\n```
| 1
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
Python 3 -- One liner -- Beats 98.19%
|
repeated-substring-pattern
| 0
| 1
|
```\nclass Solution:\n def repeatedSubstringPattern(self, s: str) -> bool:\n return s in s[1:] + s[:-1]\n```
| 53
|
Given a string `s`, check if it can be constructed by taking a substring of it and appending multiple copies of the substring together.
**Example 1:**
**Input:** s = "abab "
**Output:** true
**Explanation:** It is the substring "ab " twice.
**Example 2:**
**Input:** s = "aba "
**Output:** false
**Example 3:**
**Input:** s = "abcabcabcabc "
**Output:** true
**Explanation:** It is the substring "abc " four times or the substring "abcabc " twice.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters.
| null |
python3 | OrderedDict and hashmap
|
lfu-cache
| 0
| 1
|
The following points help with the breakdown of logic. \n- get and put methods both increment the counter. \n- We need to keep track of frequencies of a key and the value associated with the key. \n- In order to drop the key with least frequency, we to know the minimum freq at all times. \n- Among minimum freq elements we need the least recently used item to drop. \n\nFor get and put, move the key from one freq (f) to f + 1 and keep track of minFreq. OrderedDict() of python helps with dropping the least recently used key.\n\nWe keep two data structures, values and frequencies.\nValues keep track of a key and its map to current number of get/put associated with it.\nFrequencies is a map from freq -> key dict {value}\n\nvalues -> {2: 7, 3: 4, 4: 7}\nThere are keys 2&4 and 3 with frequencies 7 and 4 respectively,\n\nFrequencies -> { 7: {2: 200, 4: 400 }, 4: { 3: 300} }\nThe keys with frequency 7 are 2 and 4 with values 200 and 400 repectively. \n\nLets say a put is done on 2 with 201. The data structures, change as below. \nFrequencies -> { 8: { 2:201 } ,7: { 4: 400 }, 4: { 3: 300} }\nvalues -> {2: 8, 3: 4, 4: 7}\n\n```\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.frequencies = defaultdict(lambda: OrderedDict())\n self.values = defaultdict(int)\n self.capacity = capacity\n self.minfreq = float(\'inf\')\n \n def get(self, key: int) -> int:\n f = self.values[key]\n\n if not f: \n del self.values[key]\n return -1\n \n self.frequencies[f+1][key] = self.frequencies[f][key]\n self.values[key] = f+1\n \n del self.frequencies[f][key]\n \n if self.minfreq == f and not len(self.frequencies[f]):\n self.minfreq = f+1\n \n return self.frequencies[f+1][key]\n\n def put(self, key: int, value: int) -> None:\n if not self.capacity: return \n \n if len(self.values) == self.capacity: \n if not self.values[key]:\n k = self.frequencies[self.minfreq].popitem(last=False)\n del self.values[k[0]] \n \n f = self.values[key]\n self.values[key] += 1\n \n if f != 0:\n self.frequencies[f+1][key] = value\n del self.frequencies[f][key]\n \n if self.minfreq == f and not len(self.frequencies[f]):\n self.minfreq = f+1\n else: \n self.frequencies[f+1][key] = value \n \n self.minfreq = min(self.values[key], self.minfreq)\n\n# Your LFUCache object will be instantiated and called as such:\n# obj = LFUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)
| 1
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python Solution: Two Dictionaries
|
lfu-cache
| 0
| 1
|
# Approach\n\nTwo dictionaries:\n1. `self.cache` - stores values and frequency count for a key\n2. `self.cache_counts` - ordered dictionary/set of keys for given frequency count\n\n# Code\n```\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.cache = dict() # key -> [value, count]\n self.cache_counts = dict() # count -> OrderedDict(key -> None)\n self.min_count = 0\n\n def get(self, key: int) -> int:\n if key not in self.cache: \n return -1\n \n value, old_count = self.cache[key]\n self.cache[key][1] += 1\n self.cache_counts[old_count].pop(key)\n self.update_cache_counts(key, old_count + 1)\n\n # if the old count was the previous minimum and there exists no more cache items\n # for that minimum then increment\n if old_count == self.min_count and len(self.cache_counts[old_count]) == 0:\n self.min_count = old_count + 1\n\n return value\n\n def put(self, key: int, value: int) -> None:\n if self.capacity <= 0: return\n\n # key exists,\n if key in self.cache:\n _ = self.get(key) # reuse get method to update count \n self.cache[key][0] = value # update value for the key\n return\n\n # need to make room in the cache\n if len(self.cache) == self.capacity:\n rm_key, _ = self.cache_counts[self.min_count].popitem(False)\n self.cache.pop(rm_key)\n \n # insert into cache\n self.cache[key] = [value, 1] \n self.update_cache_counts(key, 1)\n self.min_count = 1\n\n def update_cache_counts(self, key: int, count: int):\n # first occurence of frequency\n if count not in self.cache_counts: \n self.cache_counts[count] = collections.OrderedDict()\n\n # add to counts\n self.cache_counts[count][key] = None\n```
| 1
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
O(1) Time🔥🔥|| Full Explanation✅|| HashTable✅|| C++|| Java|| Python3
|
lfu-cache
| 1
| 1
|
# What is Cache & LFU Cache ?\n1. A cache is a data structure that stores a limited number of items and is used to quickly retrieve items that have been previously accessed.\n2. An LFU cache evicts the least frequently used item when it reaches capacity, as opposed to an LRU (Least Recently Used) cache, which evicts the least recently used item. \n# Explanation to Approach :\n- Here we are using three maps to store the key-value pairs, the key-frequency pairs and the frequency-key pairs. \n- The implementation uses a combination of a HashMap and a LinkedHashSet to keep track of the keys and their frequencies, and to maintain the order of the keys. \n- When the cache reaches its maximum capacity, the least frequently used item will be removed. \n- This is done by keeping track of the number of times each item is accessed and removing the one that has been accessed the least amount of times. \n- The get() method returns the value associated with the given key, and updates the key\'s frequency. \n- The put() method adds a new key-value pair to the cache, and evicts the least frequently used key if the cache is at capacity.\n\n# Complexity\n- Time complexity : O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ | Java] : with Comments\n```C++ []\nstruct Node {\n int key;\n int value;\n int freq;\n list<int>::const_iterator it;\n};\n\nclass LFUCache {\n public:\n LFUCache(int capacity) : capacity(capacity), minFreq(0) {}\n\n int get(int key) {\n if (!keyToNode.count(key))\n return -1;\n\n Node& node = keyToNode[key];\n touch(node);\n return node.value;\n }\n\n void put(int key, int value) {\n if (capacity == 0)\n return;\n if (keyToNode.count(key)) {\n Node& node = keyToNode[key];\n node.value = value;\n touch(node);\n return;\n }\n\n if (keyToNode.size() == capacity) {\n // Evict LRU key from the minFreq list\n const int keyToEvict = freqToList[minFreq].back();\n freqToList[minFreq].pop_back();\n keyToNode.erase(keyToEvict);\n }\n\n minFreq = 1;\n freqToList[1].push_front(key);\n keyToNode[key] = {key, value, 1, cbegin(freqToList[1])};\n }\n\n private:\n int capacity;\n int minFreq;\n unordered_map<int, Node> keyToNode;\n unordered_map<int, list<int>> freqToList;\n\n void touch(Node& node) {\n // Update the node\'s frequency\n const int prevFreq = node.freq;\n const int newFreq = ++node.freq;\n\n // Remove the iterator from prevFreq\'s list\n freqToList[prevFreq].erase(node.it);\n if (freqToList[prevFreq].empty()) {\n freqToList.erase(prevFreq);\n // Update minFreq if needed\n if (prevFreq == minFreq)\n ++minFreq;\n }\n\n // Insert the key to the front of newFreq\'s list\n freqToList[newFreq].push_front(node.key);\n node.it = cbegin(freqToList[newFreq]);\n }\n};\n```\n```Java []\nclass LFUCache {\n public LFUCache(int capacity) {\n this.capacity = capacity;\n }\n\n public int get(int key) {\n if (!keyToVal.containsKey(key))\n return -1;\n\n final int freq = keyToFreq.get(key);\n freqToLRUKeys.get(freq).remove(key);\n if (freq == minFreq && freqToLRUKeys.get(freq).isEmpty()) {\n freqToLRUKeys.remove(freq);\n ++minFreq;\n }\n\n // Increase key\'s freq by 1\n // Add this key to next freq\'s list\n putFreq(key, freq + 1);\n return keyToVal.get(key);\n }\n\n public void put(int key, int value) {\n if (capacity == 0)\n return;\n if (keyToVal.containsKey(key)) {\n keyToVal.put(key, value);\n get(key); // Update key\'s count\n return;\n }\n\n if (keyToVal.size() == capacity) {\n // Evict LRU key from the minFreq list\n final int keyToEvict = freqToLRUKeys.get(minFreq).iterator().next();\n freqToLRUKeys.get(minFreq).remove(keyToEvict);\n keyToVal.remove(keyToEvict);\n }\n\n minFreq = 1;\n putFreq(key, minFreq); // Add new key and freq\n keyToVal.put(key, value); // Add new key and value\n }\n\n private int capacity;\n private int minFreq = 0;\n private Map<Integer, Integer> keyToVal = new HashMap<>();\n private Map<Integer, Integer> keyToFreq = new HashMap<>();\n private Map<Integer, LinkedHashSet<Integer>> freqToLRUKeys = new HashMap<>();\n\n private void putFreq(int key, int freq) {\n keyToFreq.put(key, freq);\n freqToLRUKeys.putIfAbsent(freq, new LinkedHashSet<>());\n freqToLRUKeys.get(freq).add(key);\n }\n}\n```\n```Python3 []\nfrom collections import deque, defaultdict, OrderedDict\n\nclass Node:\n def __init__(self, key, value):\n self.key = key\n self.value = value\n self.freq = 1\n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.minFreq = 0\n self.keyToNode = dict()\n self.freqToList = defaultdict(deque)\n self.freqToKey = defaultdict(set)\n\n def get(self, key: int) -> int:\n if key not in self.keyToNode:\n return -1\n \n node = self.keyToNode[key]\n self.touch(node)\n return node.value\n\n def put(self, key: int, value: int) -> None:\n if self.capacity == 0:\n return\n \n if key in self.keyToNode:\n node = self.keyToNode[key]\n node.value = value\n self.touch(node)\n return\n \n if len(self.keyToNode) == self.capacity:\n keyToEvict = self.freqToList[self.minFreq].pop()\n self.freqToKey[self.minFreq].remove(keyToEvict)\n del self.keyToNode[keyToEvict]\n \n self.minFreq = 1\n self.freqToList[1].appendleft(key)\n self.freqToKey[1].add(key)\n self.keyToNode[key] = Node(key, value)\n \n\n def touch(self, node):\n prevFreq = node.freq\n newFreq = node.freq + 1\n self.freqToList[prevFreq].remove(node.key)\n self.freqToKey[prevFreq].remove(node.key)\n \n if len(self.freqToList[prevFreq]) == 0:\n del self.freqToList[prevFreq]\n if prevFreq == self.minFreq:\n self.minFreq += 1\n \n if newFreq not in self.freqToList:\n self.freqToList[newFreq] = deque()\n self.freqToKey[newFreq] = set()\n \n self.freqToList[newFreq].appendleft(node.key)\n self.freqToKey[newFreq].add(node.key)\n node.freq = newFreq\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n
| 78
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python ordereddict - few lines of code
|
lfu-cache
| 0
| 1
|
# My draft\n```text \n0 "LFUCache" [2] null\n1 "put" [1,1] null \n2 "put" [2,2] null \n3 "get" [1] 1\n4 "put" [3,3] null \n5 "get" [2] -1\n6 "get" [3] 3\n7 "put" [4,4] null \n8 "get" [1] -1\n9 "get" [3] 3\n10 "get" [4] 4\n\nstep1:\nfreq[1] = {1:1}\ncounter[1] = 1 # counter[key] saves how many times this key has been used, the value of counter[key] is the key of freq, so we can faster navigate to that OrderedDict\n\nstep2:\nfreq[1] = {1:1, 2:2}\ncounter[1] = 1\ncounter[2] = 1\n\nstep3:\nfreq[1] = {2:2}\nfreq[2] = {1:1}\ncounter[1] = 2\ncounter[2] = 1\n\nstep4:\nfreq[1] = {3:3} # we pop 2 since it\'s the least recent one\nfreq[2] = {1:1}\ncounter[1] = 2\ncounter[2] = 0\ncounter[3] = 1\n\nstep 6:\nfreq[1] = {}\nfreq[2] = {1:1, 3:3} \n# since OrderedDict always add new item to the most right, don\'t worry the order\ncounter[1] = 2\ncounter[2] = 0\ncounter[3] = 2\n\nstep 7:\nfreq[1] = {4:4}\nfreq[2] = {3:3} # we pop 1\ncounter[1] = 0\ncounter[2] = 0\ncounter[3] = 2\ncounter[4] = 1\n```\n\n# Code\n```python\nfrom collections import defaultdict, OrderedDict\n\nclass LFUCache:\n def __init__(self, capacity: int):\n self.cache = {}\n self.counter = defaultdict(int)\n self.freq = defaultdict(OrderedDict)\n self.min = 0\n self.cap = capacity\n\n def update(self, key):\n count = self.counter[key]\n self.counter[key] += 1\n if key in self.freq[count]:\n self.freq[count].move_to_end(key)\n self.freq[count].popitem()\n self.freq[count + 1][key] = key\n\n if count == self.min and len(self.freq[count]) == 0:\n self.min = count + 1\n\n def get(self, key: int) -> int:\n if key not in self.cache:\n return -1\n\n self.update(key)\n return self.cache[key]\n \n def put(self, key: int, value: int) -> None:\n if self.cap == 0:\n return\n\n if key not in self.cache and self.cap == len(self.cache):\n res, _ = self.freq[self.min].popitem(False)\n del self.cache[res]\n self.counter[res] = 0\n\n self.cache[key] = value\n self.update(key)\n self.min = min(self.min, self.counter[key])\n\n# Your LFUCache object will be instantiated and called as such:\n# obj = LFUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n```
| 1
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python solution using defaultdict and OrderedDict beats 70% time complexity :-)
|
lfu-cache
| 0
| 1
|
# Code\n```\nfrom collections import defaultdict\nfrom collections import OrderedDict\nclass Node:\n def __init__(self, key, val ,count):\n self.key = key\n self.val = val\n self.count = count\nclass LFUCache:\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.keyToNode = {}\n self.countToNode = defaultdict(OrderedDict)\n self.mini = None\n def get(self, key: int) -> int:\n if key not in self.keyToNode:\n return -1\n node = self.keyToNode[key]\n del self.countToNode[node.count][key]\n if not self.countToNode[node.count]:\n del self.countToNode[node.count]\n node.count += 1\n self.countToNode[node.count][key] = node\n if not self.countToNode[self.mini]:\n self.mini += 1\n return node.val\n def put(self, key: int, value: int) -> None:\n if not self.capacity:\n return\n if key in self.keyToNode:\n self.keyToNode[key].val = value\n self.get(key)\n return\n if len(self.keyToNode) == self.capacity:\n k, n = self.countToNode[self.mini].popitem(last = False)\n del self.keyToNode[k]\n self.countToNode[1][key] = self.keyToNode[key] = Node(key, value, 1)\n self.mini = 1\n return\n```
| 1
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Best Solution in Python
|
lfu-cache
| 0
| 1
|
\n# Code\n```\nclass ListNode:\n def __init__(self , key , value):\n self.key = key \n self.val = value \n self.freq = 1 \n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity \n self.cache = dict()\n self.usage = collections.defaultdict(collections.OrderedDict)\n self.LF = 0\n\n def get(self, key: int) -> int:\n if key not in self.cache:\n return -1 \n\n node = self.cache[key]\n\n self.update(node , node.val)\n return node.val\n \n\n def put(self, key: int, value: int) -> None:\n if self.capacity == 0:\n return \n if key not in self.cache:\n if len(self.cache) >= self.capacity:\n k,v = self.usage[self.LF].popitem(last = False)\n self.cache.pop(k)\n node = ListNode(key,value)\n self.cache[key] = node\n self.usage[1][key] = value\n self.LF = 1\n else:\n node = self.cache[key]\n node.val = value\n self.update(node,value)\n\n def update(self, node , newVal):\n k,f = node.key , node.freq\n self.usage[f].pop(k)\n if not self.usage[f] and self.LF == f:\n self.LF += 1\n self.usage[f+1][k] = newVal\n node.freq += 1\n
| 10
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
🚀Easy Solution🚀||🔥Fully Explained🔥|| C++ || Commented
|
lfu-cache
| 1
| 1
|
# Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful.\n```\n# Complexity\nTime Complexity : O(1)\n\nSpace Complexity : O(N)\n# Code\n```\nclass LFUCache {\n int maxSizeCache; // maximum capacity of the cache\n int size; // current number of elements in the cache\n int minFreq; // the minimum frequency of elements in the cache\n unordered_map<int, pair<int, int>> keyNode; // key to {value,freq}\n unordered_map<int, list<int>::iterator> keylist; // key to list iterator\n unordered_map<int, list<int>> freqKeyLt; // freq to key list\npublic:\n LFUCache(int capacity) {\n maxSizeCache = capacity; // setting the maximum capacity of the cache\n size = 0; // initially the size is zero\n }\n \n int get(int key) {\n // if the key is not in the cache, return -1\n if(keyNode.count(key)==0) return -1;\n \n // remove the key from its current frequency list\n freqKeyLt[keyNode[key].second].erase(keylist[key]);\n \n // increase the frequency of the key\n keyNode[key].second++;\n \n // add the key to the frequency list with its new frequency\n freqKeyLt[keyNode[key].second].push_back(key);\n \n // update the key\'s position in the keylist\n keylist[key]=--freqKeyLt[keyNode[key].second].end();\n \n // if the list of minimum frequency is empty, update the minimum frequency\n if(freqKeyLt[minFreq].size()==0 ) \n minFreq++;\n \n // return the value associated with the key\n return keyNode[key].first;\n }\n \n void put(int key, int value) {\n // if the cache has a maximum capacity of 0, return\n if(maxSizeCache<=0) return;\n \n // check if the key already exists in the cache\n int storedValue=get(key);\n if(storedValue!=-1)\n {\n // if the key already exists, update its value\n keyNode[key].first=value;\n return;\n }\n \n // if the cache is full, remove the least frequently used key\n if(size >= maxSizeCache)\n {\n keyNode.erase( freqKeyLt[minFreq].front() );\n keylist.erase( freqKeyLt[minFreq].front() );\n freqKeyLt[minFreq].pop_front();\n size--;\n }\n \n // add the new key to the cache\n keyNode[key]={value, 1};\n freqKeyLt[1].push_back(key);\n keylist[key]=--freqKeyLt[1].end();\n minFreq=1;\n size++;\n }\n};\n\n```\n```\n Give a \uD83D\uDC4D. It motivates me alot.\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/)
| 18
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python short and clean. DoublyLinkedList and HashMap.
|
lfu-cache
| 0
| 1
|
# Approach\nTLDR; Similar to [Editorial Solution](https://leetcode.com/problems/lfu-cache/solutions/2815229/lfu-cache/) but shorter and cleaner.\n\n# Complexity\n- Time complexity:\n `LFUCache.get`: $$O(1)$$\n `LFUCache.put`: $$O(1)$$\n\n- Space complexity:\n `LFUCache.get`: $$O(1)$$\n `LFUCache.put`: $$O(1)$$\n\n $$O(n)$$ after `n` calls to `LFUCache.put`\n\n# Code\n```python\nfrom dataclasses import dataclass\n\n\nclass DLLNode:\n\n def __init__(self, value=None, prev=None, next_=None):\n self.value = value\n self.prev = prev\n self.next = next_\n\n\nclass LFUCache:\n @dataclass\n class Data:\n key: int\n value: int\n freq: int\n node: DLLNode\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.cache: dict[int, LFUCache.Data] = {}\n self.freq_to_dll = defaultdict(DoublyLinkedList)\n self.min_freq = 1\n self.used = 0\n\n def get(self, key: int) -> int:\n if key not in self.cache: return -1\n\n d = self.cache[key]\n self.freq_to_dll[d.freq].remove(d.node)\n self.freq_to_dll[d.freq + 1].append(d.node)\n self.cache[key] = LFUCache.Data(key, d.value, d.freq + 1, d.node)\n self.min_freq += self.min_freq == d.freq and not self.freq_to_dll[d.freq]\n\n return d.value\n\n def put(self, key: int, value: int) -> None:\n if self.capacity == 0: return\n\n if key in self.cache:\n self.cache[key].value = value\n self.get(key)\n return\n\n if self.used == self.capacity:\n mf_dll = self.freq_to_dll[self.min_freq]\n mf_lru_key = mf_dll.popleft().value\n self.cache.pop(mf_lru_key)\n self.used -= 1\n\n d = LFUCache.Data(key, value, 1, DLLNode(key))\n self.freq_to_dll[d.freq].append(d.node)\n self.cache[key] = d\n self.used += 1\n self.min_freq = 1\n\n\nclass DoublyLinkedList:\n\n def __init__(self):\n self.head, self.tail = DLLNode(), DLLNode()\n self.head.next, self.tail.prev = self.tail, self.head\n\n def append(self, node: DLLNode) -> None:\n a, b, c = self.tail.prev, node, self.tail\n a.next, c.prev = b, b\n b.next, b.prev = c, a\n\n def appendleft(self, node: DLLNode) -> None: raise NotImplementedError()\n\n def pop(self) -> DLLNode: raise NotImplementedError()\n\n def popleft(self) -> DLLNode:\n node = self.head.next\n self.remove(node)\n return node\n\n def remove(self, node: DLLNode) -> None:\n a, b, c = node.prev, node, node.next\n a.next, c.prev = c, a\n b.next, b.prev = None, None\n\n def __bool__(self) -> bool:\n return self.head.next != self.tail\n\n def __iter__(self): raise NotImplementedError()\n\n```
| 5
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
[Python] Hashmap + Doubly Linked List - Daily Challenge Jan., Day 29
|
lfu-cache
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nconsider what kind of data structure do we need?\n1. we need to store key & value\n2. we need to know the relation between key & frequency\n3. if exceed capacity, we need to know the minimum frequency and least recently used node and remove it\n4. we need to be able to add/delete key-value pair efficiently.\n\nthink LRU cache, if we want to add/delete node with O(1) complexity, we can achieve by using hashmap with doubly linked list.\n\nthus, we can think each frequency owns a linked list and we store key-value as node in it.\n\nand for each frequency list:\n`head -> most recently used node -> ... -> least recently used node -> tail`\n\nbecause we need to remove least recently used node among all the frequency lists if capacity exceed limit, we maintain a `self.min` variable for us to find target list in O(1) operation.\n\n\n#### Summary\n```\nhashmap -> doubly linked-list\nfreq1 -> [key1, key2, key3...] -> min freq\nfreq2 -> [key1, key2, key3...]\nfreq3 -> [key1, key2, key3...]\n\nself.min -> for removing least recently used node\n```\n\n# Approach\n\njust remember to update these 4 varaible for `get` and `put` operation:\n\n- self.freq2node: store frequency lists\n- self.key2node: store each key-value pair in cache\n- self.key2freq: store frequency of each key-value pair\n- self.min: store current minimum frequency\n\n1. `get`\n 1. if not exists in cache, return `-1`\n 2. return value from cache and update its frequency\n 3. update self.min if needed\n\n2. `put`\n 1. check edge case: `capacity = 0`\n 2. if key already exists in cache, update value and its frequency. just like what we do in `get` operation\n 3. if it\'s a new key-value pair:\n 1. remove recenly used node if capacity is full\n 2. create a node to store key-value\n 2. set frequency to 1\n 3. insert to freqeuncy list\n 3. set self.min to 1\n\n# Complexity\n- Time complexity:\n$$O(1)$$\n\n- Space complexity:\n$$O(capacity)$$\n\n# Code\n```\nclass ListNode:\n def __init__(self, key, val):\n self.key = key\n self.val = val\n self.next = self.prev = None\n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.cap = capacity\n\n def initList():\n root = ListNode(-1, -1)\n root.next = root.prev = root\n return root\n self.freq2node = defaultdict(initList)\n self.key2node = {}\n self.key2freq = defaultdict(lambda: 1)\n self.min = 1\n\n def _insertAfter(self, target, node):\n node.prev = target\n node.next = target.next\n node.next.prev = node\n node.prev.next = node\n\n def _remove(self, node):\n node.prev.next = node.next\n node.next.prev = node.prev\n node.next = node.prev = None\n\n def get(self, key: int) -> int:\n if key not in self.key2node: return -1\n\n node = self.key2node[key]\n val = node.val\n \n freq = self.key2freq[key]\n self.key2freq[key] = freq + 1\n \n self._remove(node)\n self._insertAfter(self.freq2node[freq+1], node)\n \n if self.freq2node[self.min].next.key == -1:\n self.min = freq+1\n \n return val\n\n def put(self, key: int, value: int) -> None:\n if self.cap == 0: return\n if key in self.key2node:\n node = self.key2node[key]\n node.val = value\n \n freq = self.key2freq[key]\n self.key2freq[key] = freq+1\n self._remove(node)\n self._insertAfter(self.freq2node[freq+1], node)\n if self.freq2node[self.min].next.key == -1:\n self.min = freq+1\n return\n\n node = ListNode(key, value)\n if len(self.key2node) == self.cap:\n lru = self.freq2node[self.min].prev\n self._remove(lru)\n del self.key2node[lru.key]\n del self.key2freq[lru.key]\n\n self.key2node[key] = node\n self.key2freq[key] = 1\n self._insertAfter(self.freq2node[1], node)\n self.min = 1\n```
| 5
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
python3 Solution
|
lfu-cache
| 0
| 1
|
\n```\nclass ListNode:\n def __init__(self, key, value):\n self.key = key\n self.val = value\n self.freq = 1\n \nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.cache = dict() \n self.usage = collections.defaultdict(collections.OrderedDict)\n self.LF = 0\n\n def get(self, key: int) -> int:\n if key not in self.cache:return -1\n node = self.cache[key]\n\n self.update(node, node.val)\n return node.val\n \n def put(self, key: int, value: int) -> None:\n if self.capacity == 0: return\n if key not in self.cache: \n if len(self.cache) >= self.capacity:\n k, v = self.usage[self.LF].popitem(last=False)\n self.cache.pop(k)\n node = ListNode(key, value)\n self.cache[key] = node\n self.usage[1][key] = value\n self.LF = 1\n else: \n node = self.cache[key]\n node.val = value\n self.update(node, value)\n \n \n def update(self, node, newVal):\n k, f = node.key, node.freq\n self.usage[f].pop(k)\n if not self.usage[f] and self.LF == f:\n self.LF += 1\n self.usage[f+1][k] = newVal\n node.freq += 1\n```
| 3
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
460: Solution with step by step explanation
|
lfu-cache
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the Node class with attributes key, val, freq, prev, and next.\n2. Define the DoublyLinkedList class with attributes head and tail, and methods add_node_to_head, remove_node, is_empty, and remove_tail_node.\n3. Initialize the LFUCache class with attributes capacity, size, min_freq, node_dict, and freq_dict.\n4. Define the update_freq_dict method which takes a node as input and updates its frequency.\n5. Define the get method which takes a key as input and returns the value of the corresponding node if it exists in node_dict.\n6. Define the put method which takes a key and value as input and updates the cache.\na. If the cache is full, remove the least frequently used node.\nb. Create a new node with the given key and value, and add it to the head of the DoublyLinkedList with frequency 1.\nc. Update the node_dict and freq_dict accordingly.\n7. Return the value if get method is called.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Node:\n def __init__(self, key, val, freq):\n self.key = key\n self.val = val\n self.freq = freq\n self.prev = None\n self.next = None\n\nclass DoublyLinkedList:\n def __init__(self):\n self.head = Node(None, None, 0)\n self.tail = Node(None, None, 0)\n self.head.next = self.tail\n self.tail.prev = self.head\n \n def add_node_to_head(self, node):\n node.next = self.head.next\n node.prev = self.head\n self.head.next.prev = node\n self.head.next = node\n \n def remove_node(self, node):\n node.prev.next = node.next\n node.next.prev = node.prev\n \n def is_empty(self):\n return self.head.next == self.tail\n \n def remove_tail_node(self):\n if self.is_empty():\n return None\n tail_node = self.tail.prev\n self.remove_node(tail_node)\n return tail_node\n\nclass LFUCache:\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.size = 0\n self.min_freq = 0\n self.node_dict = {}\n self.freq_dict = {}\n \n def update_freq_dict(self, node):\n freq = node.freq\n self.freq_dict[freq].remove_node(node)\n if self.min_freq == freq and self.freq_dict[freq].is_empty():\n self.min_freq += 1\n node.freq += 1\n freq = node.freq\n if freq not in self.freq_dict:\n self.freq_dict[freq] = DoublyLinkedList()\n self.freq_dict[freq].add_node_to_head(node)\n \n def get(self, key: int) -> int:\n if key not in self.node_dict:\n return -1\n node = self.node_dict[key]\n self.update_freq_dict(node)\n return node.val\n \n def put(self, key: int, value: int) -> None:\n if self.capacity == 0:\n return\n \n if key in self.node_dict:\n node = self.node_dict[key]\n node.val = value\n self.update_freq_dict(node)\n else:\n if self.size == self.capacity:\n min_freq_list = self.freq_dict[self.min_freq]\n node_to_remove = min_freq_list.remove_tail_node()\n del self.node_dict[node_to_remove.key]\n self.size -= 1\n \n new_node = Node(key, value, 1)\n self.node_dict[key] = new_node\n if 1 not in self.freq_dict:\n self.freq_dict[1] = DoublyLinkedList()\n self.freq_dict[1].add_node_to_head(new_node)\n self.min_freq = 1\n self.size += 1\n```
| 4
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
[Python] Simple two hash maps; Explained
|
lfu-cache
| 0
| 1
|
We only need two hash maps to maintain the LFU cache:\n(1) the first hash map: maps key to (value, count) pair\n(2) the second hash map: maps count to an OrderedDict which maintains key, value pairs\n\nThe get method: we need to check the first hash map, and update the count in it. Based on the new count of the key, we update the second hash map: a) move the (key, value) pair from old_cnt to old_cnt + 1; b) move the (key, value) pair inside the OrderedDict to the tail.\n\nThe put method: we add one new key to the first hash map. If the cache is already full, we need to pop out the item with the least count. If there are multiple keys with the same least count, we just pop out the item from the head of the OrderedDict.\n\n```\nclass LFUCache:\n\n def __init__(self, capacity: int):\n # data structure 1: dictionary which maps key to count\n # data strcuture 2: dictionary which maps count to a orderedDict\n self.capacity = capacity\n self.used = 0\n self.cache_key = dict()\n self.cache_orderedCount = dict()\n self.min_cnt = 0\n \n\n def get(self, key: int) -> int:\n val = -1\n if key in self.cache_key:\n val = self.cache_key[key][0]\n old_cnt = self.cache_key[key][1]\n self.cache_key[key][1] += 1\n # update the count dictionary\n del self.cache_orderedCount[old_cnt][key]\n # insert the key into the new count dictionary\n new_cnt = self.cache_key[key][1]\n self._updateCacheCountDict(key, val, new_cnt)\n # update the min count\n if self.min_cnt == old_cnt and len(self.cache_orderedCount[old_cnt]) == 0:\n self.min_cnt = new_cnt\n return val\n \n\n def put(self, key: int, value: int) -> None:\n if self.capacity <= 0:\n return\n \n if key in self.cache_key:\n self.cache_key[key][0] = value\n old_cnt = self.cache_key[key][1]\n self.cache_key[key][1] += 1\n new_cnt = old_cnt + 1\n del self.cache_orderedCount[old_cnt][key]\n self._updateCacheCountDict(key, value, new_cnt)\n # update the min count\n if self.min_cnt == old_cnt and len(self.cache_orderedCount[old_cnt]) == 0:\n self.min_cnt = new_cnt\n else:\n # the key is not in cache yet\n if self.used < self.capacity:\n # the cache is not full, we can directly add the new key value pair\n self.cache_key[key] = [value, 1]\n self._updateCacheCountDict(key, value, 1)\n self.used += 1\n self.min_cnt = 1\n else:\n # the cache is full\n rm_key, rm_val = self.cache_orderedCount[self.min_cnt].popitem(0)\n del self.cache_key[rm_key]\n # add new key value\n self.cache_key[key] = [value, 1]\n self._updateCacheCountDict(key, value, 1)\n self.min_cnt = 1\n \n def _updateCacheCountDict(self, key, value, new_cnt):\n if new_cnt not in self.cache_orderedCount:\n self.cache_orderedCount[new_cnt] = OrderedDict()\n self.cache_orderedCount[new_cnt][key] = value\n self.cache_orderedCount[new_cnt].move_to_end(key)\n```
| 18
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python | Doubly Linked List and Hash Map | O(1) Get and Put operations
|
lfu-cache
| 0
| 1
|
# Approach\n1. Maintain a hash map for key to node mapping # {key: node}\n2. Maintain another hash map for frequency to DLL mapping # {freq: (head, tail)}\n3. For any get operation, return the value of key from corresponding node and increase the frequency by 1.\n4. For any put operation,\n a) If key value already exists, update the value in node and increase the frequency\n b) If key value does not exists and cache is not full, insert the new node in DLL of freq 1\n c) If key value does not exists and cache is full, then remove the key from least freq DLL and if multiple key exits with least freq then remove the LRU key\n\n# Complexity\n- Time complexity:\nO(1)\n\n\n# Code\n```\nclass Node:\n def __init__(self, key, value, next=None, prev=None):\n self.key = key\n self.value = value\n self.freq = 1\n self.next = next\n self.prev = prev\n\n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.key_node_hash = {} # {key: node}\n self.freq_dll_hash = {} # {freq: (head, tail)}\n self.min_freq = 1\n\n def __print_cache(self):\n """\n Method to print the content of cache\n """\n print("Cache")\n for freq, dll in self.freq_dll_hash.items():\n print("Freq: ", freq)\n curr_freq_node = dll[0]\n while curr_freq_node:\n print(curr_freq_node.key, curr_freq_node.value)\n curr_freq_node = curr_freq_node.next\n\n\n def __reset_min_freq(self):\n """\n Method to reset the min freq value\n """\n for freq, dll in sorted(self.freq_dll_hash.items()):\n head, tail = dll[0], dll[1]\n if head.next != tail:\n self.min_freq = freq\n return\n\n\n\n def __insert_node_next_to_head(self, node, head):\n """\n Method to insert the given node next to the given head\n """\n node.prev = head\n node.next = head.next\n head.next = node\n node.next.prev = node\n\n def __remove_the_given_node(self, node):\n """\n Method to remove the given node from DLL\n """\n node.prev.next = node.next\n node.next.prev = node.prev\n\n def __add_node_in_given_freq_dll(self, node, freq):\n """\n Method to add the node in the given freq DLL\n """\n if self.freq_dll_hash.get(freq):\n head, tail = self.freq_dll_hash[freq]\n else:\n head = Node("Head", "Head")\n tail = Node("Tail", "Tail")\n head.next = tail\n tail.prev = head\n self.freq_dll_hash[freq] = (head, tail)\n # Insert the node next to head of given freq\n self.__insert_node_next_to_head(node, head)\n\n def __increment_the_freq_of_node(self, node):\n """\n Method to increment the freq of given node and insert it in new freq DLL\n """\n # Increment the freq of node and move to the respective freq DLL\n old_freq = node.freq\n node.freq += 1\n\n # Move the node to the DLL of corresponding freq\n freq = node.freq\n # Remove the node from current freq DLL\n self.__remove_the_given_node(node)\n\n # Add the key to DLL of given freq\n self.__add_node_in_given_freq_dll(node, freq) \n\n # Update the min freq\n self.__reset_min_freq()\n\n\n def get(self, key: int) -> int:\n """\n Method to get the key value from cache\n """\n if self.key_node_hash.get(key):\n node = self.key_node_hash[key]\n self.__increment_the_freq_of_node(node)\n return node.value\n\n else:\n return -1\n\n\n def put(self, key: int, value: int) -> None:\n """\n Method to put the key value in cache\n """\n if self.key_node_hash.get(key):\n # Update the key value and frequency\n node = self.key_node_hash[key]\n node.value = value\n self.__increment_the_freq_of_node(node)\n else:\n if len(self.key_node_hash) == self.capacity:\n # Remove the key with least frequency, if two keys have same freq then\n # remove the LRU key\n head, tail = self.freq_dll_hash[self.min_freq]\n # Remove the node left to the tail of DLL\n node = tail.prev\n self.__remove_the_given_node(node)\n key_to_remove = node.key\n del self.key_node_hash[key_to_remove]\n del node\n\n # Add the new key to DLL of freq 1\n node = Node(key, value)\n self.key_node_hash[key] = node\n self.__add_node_in_given_freq_dll(node, 1) \n self.min_freq = 1\n else:\n # Add new key\n node = Node(key, value)\n self.key_node_hash[key] = node\n\n # Add the key to DLL of freq 1\n self.__add_node_in_given_freq_dll(node, 1) \n self.min_freq = 1\n \n\n \n\n\n# Your LFUCache object will be instantiated and called as such:\n# obj = LFUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n```
| 1
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
📌📌Python3 || ⚡859 ms, faster than 79.52% of Python3
|
lfu-cache
| 0
| 1
|
```\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.time = 0\n self.map = {} \n self.freq_time = {} \n self.priority_queue = [] \n self.update = set()\n\n def get(self, key: int) -> int:\n self.time += 1\n\n if key in self.map:\n freq, _ = self.freq_time[key]\n self.freq_time[key] = (freq + 1, self.time) \n self.update.add(key)\n return self.map[key]\n \n return -1\n\n def put(self, key: int, value: int) -> None:\n if self.capacity <= 0:\n return \n self.time += 1\n if not key in self.map:\n if len(self.map) >= self.capacity: \n while self.priority_queue and self.priority_queue[0][2] in self.update:\n _, _, k = heapq.heappop(self.priority_queue)\n f, t = self.freq_time[k]\n heapq.heappush(self.priority_queue, (f, t, k))\n self.update.remove(k)\n _, _, k = heapq.heappop(self.priority_queue)\n self.map.pop(k)\n self.freq_time.pop(k)\n self.freq_time[key] = (0, self.time)\n heapq.heappush(self.priority_queue, (0, self.time, key))\n else:\n freq, _ = self.freq_time[key]\n self.freq_time[key] = (freq + 1, self.time) \n self.update.add(key)\n\n self.map[key] = value\n\n\n```
| 5
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
[Python] O(1) using DLL and Dictionary
|
lfu-cache
| 0
| 1
|
**Approach:**\n\n*Data Structures:*\n1. Frequency Table: A dictionary to store the mapping of different frequency values with values as DLLs storing (key, value) pairs as nodes\n2. Cache Dicitionary: Nodes in the DLL are stored as values for each key pushed into the cache\n\n*Algorithm:*\n* get(key):\n\t* If key is not present in cache, return -1\n\t* Get the node from the cache\n\t* Update the node frequency\n\t* Remove the node from the DLL of node\'s previous frequency\n\t* Add the node to the DLL with the node\'s updated frequency\n\t* Update min frequency value\n\n* put(key, value):\n\t* If key is present in cache\n\t\t* Similar logic to that of get function\n\t\t* Only difference being that we need to update the value here\n\t* If key not present in cache\n\t\t* If the cache has already reached it\'s capacity, delete the tail node from the DLL with least frequency\n\t\t* Create the new node with the (key, value) pair passed as arguments\n\t\t* Add the node to the frequency table with frequency key = 1\n\t\t* Add the node to the cache \n\t\t* Update min frequency to be 1\n\n```\nclass ListNode:\n def __init__(self, key, val):\n self.key = key\n self.val = val\n self.freq = 1\n self.prev = None\n self.next = None\n \nclass DLL:\n def __init__(self):\n self.head = ListNode(0, 0)\n self.tail = ListNode(0, 0)\n self.head.next = self.tail\n self.tail.prev = self.head\n self.size = 0\n \n def insertHead(self, node):\n headNext = self.head.next\n headNext.prev = node\n self.head.next = node\n node.prev = self.head\n node.next = headNext\n self.size += 1\n \n def removeNode(self, node):\n node.next.prev = node.prev\n node.prev.next = node.next\n self.size -= 1\n \n def removeTail(self):\n tail = self.tail.prev\n self.removeNode(tail)\n return tail\n \n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.cache = {}\n self.freqTable = collections.defaultdict(DLL)\n self.capacity = capacity\n self.minFreq = 0\n \n \n def get(self, key: int) -> int:\n if key not in self.cache:\n return -1\n return self.updateCache(self.cache[key], key, self.cache[key].val)\n \n\n def put(self, key: int, value: int) -> None:\n if not self.capacity:\n return\n if key in self.cache:\n self.updateCache(self.cache[key], key, value)\n else:\n if len(self.cache) == self.capacity:\n prevTail = self.freqTable[self.minFreq].removeTail()\n del self.cache[prevTail.key]\n node = ListNode(key, value)\n self.freqTable[1].insertHead(node)\n self.cache[key] = node\n self.minFreq = 1\n \n \n def updateCache(self, node, key, value):\n node = self.cache[key]\n node.val = value\n prevFreq = node.freq\n node.freq += 1\n self.freqTable[prevFreq].removeNode(node)\n self.freqTable[node.freq].insertHead(node)\n if prevFreq == self.minFreq and self.freqTable[prevFreq].size == 0:\n self.minFreq += 1\n return node.val\n```
| 64
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python || Striver's Solution || HashMap + DLL
|
lfu-cache
| 0
| 1
|
```\nclass Node: \n def __init__(self, key, val):\n self.key=key\n self.val=val\n self.prev=None\n self.next=None\n self.cnt=1\n\nclass Doublell:\n def __init__(self):\n self.size=0\n self.head=Node(0,0)\n self.tail=Node(0,0)\n self.head.next=self.tail\n self.tail.prev=self.head \n\n def addNode(self, newnode):\n temp=self.head.next\n newnode.prev=self.head\n newnode.next=temp\n temp.prev=newnode\n self.head.next=newnode\n self.size+=1\n \n def deleteNode(self,delnode):\n prevv=delnode.prev\n nextt=delnode.next\n prevv.next=nextt\n nextt.prev=prevv\n self.size-=1\n \nclass LFUCache:\n def __init__(self, capacity: int):\n self.dic={}\n self.freqList={}\n self.capacity=capacity\n self.minFreq=1\n self.curSize=0\n \n def updateFreqList(self, node):\n del self.dic[node.key]\n self.freqList[node.cnt].deleteNode(node)\n if node.cnt==self.minFreq and self.freqList[node.cnt].size==0:\n self.minFreq+=1\n nextHigherFreqList=Doublell()\n if node.cnt + 1 in self.freqList:\n nextHigherFreqList=self.freqList[node.cnt+1]\n node.cnt+=1\n nextHigherFreqList.addNode(node)\n self.freqList[node.cnt]=nextHigherFreqList\n self.dic[node.key]=node\n \n def get(self, key: int) -> int:\n if key in self.dic:\n node=self.dic[key]\n value=node.val\n self.updateFreqList(node)\n return value\n return -1\n\n def put(self, key: int, value: int) -> None:\n if key in self.dic:\n node=self.dic[key]\n node.val=value\n self.updateFreqList(node)\n else:\n if self.curSize==self.capacity:\n dll=self.freqList[self.minFreq]\n del self.dic[dll.tail.prev.key]\n self.freqList[self.minFreq].deleteNode(dll.tail.prev)\n self.curSize-=1\n self.curSize+=1\n self.minFreq=1\n listFreq=Doublell()\n if self.minFreq in self.freqList:\n listFreq=self.freqList[self.minFreq]\n node=Node(key,value)\n listFreq.addNode(node)\n self.dic[key]=node\n self.freqList[self.minFreq]=listFreq\n```\n**An upvote will be encouraging**
| 2
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
[JAVA/C++/PYTHON] | EXPLAINED IN DETAIL | CONSTANT TIME | TWO HASHMAP'S
|
lfu-cache
| 1
| 1
|
# Intuition & Approach\n\nWe need to maintain all the keys, values and frequencies. Without invalidation (removing from the data structure when it reaches capacity), they can be maintained by a HashMap<Integer, Pair<Integer, Integer>>, keyed by the original key and valued by the frequency-value pair.\n\nWith the invalidation, we need to maintain the current minimum frequency and delete particular keys. Hence, we can group the keys with the same frequency together and maintain another HashMap<Integer, Set>, keyed by the frequency and valued by the set of keys that have the same frequency. This way, if we know the minimum frequency, we can access the potential keys to be deleted.\n\nAlso note that in the case of a tie, we\'re required to find the least recently used key and invalidate it, hence we need to keep the frequencies ordered in the Set. Instead of using a TreeSet which adds an extra O(log(N))O(log(N))O(log(N)) time complexity, we can maintain the keys using a LinkedList so that it supports finding both an arbitrary key and the least recently used key in constant time. Fortunately, LinkedHashSet can do the job. Once a key is inserted/updated, we put it to the end of the LinkedHashSet so that we can invalidate the first key in the LinkedHashSet corresponding to the minimum frequency.\n\nThe original operations can be transformed into operations on the 2 HashMaps, keeping them in sync and maintaining the minimum frequency.\n\nSince C++ lacks LinkedHashSet, we have to use a workaround like maintaining a list of key and value pairs instead of the LinkedHashSet and keeping the iterator with the frequency in another unordered_map to keep this connection. The idea is similar but a little bit complicated. Another workaround would be to implement your own LRU cache with a doubly linked list.\n\nAlgorithm\nTo make things simpler, assume we have 4 member variables:\n\nHashMap<Integer, Pair<Integer, Integer>> cache, keyed by the original key and valued by the frequency-value pair.\nHashMap<Integer, LinkedListHashSet<Integer>> frequencies, keyed by frequency and valued by the set of keys that have the same frequency.\nint minf, which is the minimum frequency at any given time.\nint capacity, which is the capacity given in the input.\nIt\'s also convenient to have a private utility function insert to insert a key-value pair with a given frequency.\n\nvoid insert(int key, int frequency, int value)\nInsert frequency-value pair into cache with the given key.\nGet the LinkedHashSet corresponding to the given frequency (default to empty Set) and insert the given key.\nint get(int key)\nIf the given key is not in the cache, return -1, otherwise go to step 2.\nGet the frequency and value from the cache.\nGet the LinkedHashSet associated with frequency from frequencies and remove the given key from it, since the usage of the current key is increased by this function call.\nIf minf == frequency and the above LinkedHashSet is empty, that means there are no more elements used minf times, so increase minf by 1.\nCall insert(key, frequency + 1, value), since the current key\'s usage has increased from this function call.\nReturn value\nvoid put(int key, int value)\nIf capacity <= 0, exit.\nIf the given key exists in cache, update the value in the original frequency-value (don\'t call insert here), and then increment the frequency by using get(key). Exit the function.\nIf cache.size() == capacity, get the first (least recently used) value in the LinkedHashSet corresponding to minf in frequencies, and remove it from cache and the LinkedHashSet.\nIf we didn\'t exit the function in step 2, it means that this element is a new one, so the minimum frequency cannot possibly be greater than one. Set minf to 1.\nCall insert(key, 1, value)\n\n\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Pair<K, V> {\n private K key;\n private V value;\n\n public Pair(K key, V value) {\n this.key = key;\n this.value = value;\n }\n\n public K getKey() {\n return this.key;\n }\n public V getValue() {\n return this.value;\n }\n }\n```\n```\n class LFUCache {\n // key: original key, value: frequency and original value.\n private Map<Integer, Pair<Integer, Integer>> cache;\n // key: frequency, value: All keys that have the same frequency.\n private Map<Integer, LinkedHashSet<Integer>> frequencies;\n private int minf;\n private int capacity;\n\n private void insert(int key, int frequency, int value) {\n cache.put(key, new Pair<>(frequency, value));\n frequencies.putIfAbsent(frequency, new LinkedHashSet<>());\n frequencies.get(frequency).add(key);\n }\n\n public LFUCache(int capacity) {\n cache = new HashMap<>();\n frequencies = new HashMap<>();\n minf = 0;\n this.capacity = capacity;\n }\n\n public int get(int key) {\n Pair<Integer, Integer> frequencyAndValue = cache.get(key);\n if (frequencyAndValue == null) {\n return -1;\n }\n final int frequency = frequencyAndValue.getKey();\n final Set<Integer> keys = frequencies.get(frequency);\n keys.remove(key);\n if (minf == frequency && keys.isEmpty()) {\n ++minf;\n }\n final int value = frequencyAndValue.getValue();\n insert(key, frequency + 1, value);\n return value;\n }\n\n public void put(int key, int value) {\n if (capacity <= 0) {\n return;\n }\n Pair<Integer, Integer> frequencyAndValue = cache.get(key);\n if (frequencyAndValue != null) {\n cache.put(key, new Pair<>(frequencyAndValue.getKey(), value));\n get(key);\n return;\n }\n if (capacity == cache.size()) {\n final Set<Integer> keys = frequencies.get(minf);\n final int keyToDelete = keys.iterator().next();\n cache.remove(keyToDelete);\n keys.remove(keyToDelete);\n }\n minf = 1;\n insert(key, 1, value);\n }\n }\n```\n# C++\n\n```\nclass LFUCache {\n // key: frequency, value: list of original key-value pairs that have the same frequency.\n unordered_map<int, list<pair<int, int>>> frequencies;\n // key: original key, value: pair of frequency and the iterator corresponding key int the\n // frequencies map\'s list.\n unordered_map<int, pair<int, list<pair<int, int>>::iterator>> cache;\n int capacity;\n int minf;\n\n void insert(int key, int frequency, int value) {\n frequencies[frequency].push_back({key, value});\n cache[key] = {frequency, --frequencies[frequency].end()};\n }\n\npublic:\n LFUCache(int capacity) : capacity(capacity), minf(0) {}\n\n int get(int key) {\n const auto it = cache.find(key);\n if (it == cache.end()) {\n return -1;\n }\n const int f = it->second.first;\n const auto iter = it->second.second;\n const pair<int, int> kv = *iter;\n frequencies[f].erase(iter);\n if (frequencies[f].empty() && minf == f) {\n ++minf;\n }\n insert(key, f + 1, kv.second);\n return kv.second;\n }\n\n void put(int key, int value) {\n if (capacity <= 0) {\n return;\n }\n const auto it = cache.find(key);\n if (it != cache.end()) {\n it->second.second->second = value;\n get(key);\n return;\n }\n if (capacity == cache.size()) {\n cache.erase(frequencies[minf].front().first);\n frequencies[minf].pop_front();\n }\n minf = 1;\n insert(key, 1, value);\n }\n};
| 2
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
O(1) - Two HashMap + DoubleLinkedList - Clean up Solution
|
lfu-cache
| 0
| 1
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nTwo HashMap + DoubleLinkedList approach:\n - HashMap to store (key, DoubleNode(key, value, freq, ...)) pairs\n - HashMap to store (freq, DoubleLinkedList for keys with this freq) pairs\n\nAlso, let\'s clean up empty DoubleLinkedLists and removed nodes.\n\n# Complexity\n\n## get method\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n## put method\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\n\n\nclass LFUCache:\n def __init__(self, capacity: int):\n """time: O(1), space: O(1)"""\n self.cache = {}\n self.freqs = defaultdict(DoubleLinkedList)\n self.capacity = capacity\n self.min_freq = 0\n\n def get(self, key: int) -> int:\n """time: O(1), space: O(1)"""\n if key not in self.cache:\n return -1\n value = self.cache[key].value\n self.update(key, value)\n return value\n\n def put(self, key: int, value: int) -> None:\n """time: O(1), space: O(1)"""\n if self.capacity == 0:\n return\n if key in self.cache:\n self.update(key, value)\n else:\n if len(self.cache) == self.capacity:\n removed_key = self.freqs[self.min_freq].pop_back()\n if self.freqs[self.min_freq].is_empty:\n del self.freqs[self.min_freq]\n del self.cache[removed_key]\n self.min_freq = 1\n self.freqs[self.min_freq].push_front(key, value, self.min_freq)\n self.cache[key] = self.freqs[self.min_freq].head\n\n def update(self, key: int, value: int) -> None:\n """time: O(1), space: O(1)"""\n node = self.cache[key]\n freq = node.freq\n self.freqs[freq + 1].push_front(key, value, freq + 1)\n self.cache[key] = self.freqs[freq + 1].head\n self.freqs[freq].remove_node(node)\n if (freq == self.min_freq) and self.freqs[freq].is_empty:\n self.min_freq += 1\n if self.freqs[freq].is_empty:\n del self.freqs[freq]\n\n\n\nclass DoubleNode:\n def __init__(self, key, value, freq=1, next=None, prev=None):\n self.key = key\n self.value = value\n self.freq = freq\n self.next = next\n self.prev = prev\n\n\nclass DoubleLinkedList:\n def __init__(self) -> None:\n """time: O(1), space: O(1)"""\n self.head = self.tail = None\n self.is_empty = True\n\n def __emptied__(self) -> None:\n """time: O(1), space: O(1)"""\n del self.head\n self.head = self.tail = None\n self.is_empty = True\n\n def push_front(self, key: int, value: int, freq: int) -> None:\n """time: O(1), space: O(1)"""\n if self.is_empty:\n self.head = self.tail = DoubleNode(key, value, freq)\n self.is_empty = False\n else:\n node = DoubleNode(key, value, freq, next=self.head)\n self.head.prev = node\n self.head = node\n\n def pop_front(self) -> int:\n """time: O(1), space: O(1)"""\n if self.is_empty:\n raise IndexError("LinkedList is empty!")\n key = self.head.key\n if self.head == self.tail:\n self.__emptied__()\n else:\n next = self.head.next\n self.head.next = next.prev = None\n del self.head\n self.head = next\n return key\n\n def pop_back(self) -> int:\n """time: O(1), space: O(1)"""\n if self.is_empty:\n raise IndexError("LinkedList is empty!")\n key = self.tail.key\n if self.head == self.tail:\n self.__emptied__()\n else:\n prev = self.tail.prev\n self.tail.prev = prev.next = None\n del self.tail\n self.tail = prev\n return key\n\n def remove_node(self, node: DoubleNode) -> None:\n """time: O(1), space: O(1)"""\n if self.is_empty or (node is None):\n raise IndexError("LinkedList is empty or node is None!")\n if node == self.head:\n self.pop_front()\n elif node == self.tail:\n self.pop_back()\n else:\n node.prev.next = node.next\n node.next.prev = node.prev\n node.prev = node.next = None\n del node\n\n\n# Your LFUCache object will be instantiated and called as such:\n# obj = LFUCache(capacity)\n# param_1 = obj.get(key)\n# obj.put(key,value)\n\n```
| 2
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
Python3 Solution Using Linked LIsts and HashMap
|
lfu-cache
| 0
| 1
|
# Approach\n\nThis is how it looks like. We have \'nested\' linked lists. One linked list is used for frequency levels holding. Inner one is for holding nodes sorted by updating time. Also we have map for quick getting values by key.\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n# Code\n```\nclass Node:\n\n def __init__(self, key, val, freq_node):\n self.key = key\n self.val = val\n self.left = None\n self.right = None\n self.freq_node = freq_node\n\n def __str__(self):\n res = \'\'\n if self.right:\n res += str(self.right) + \' => \'\n res += str(self.key)\n return res\n\n\nclass FreqNode:\n\n def __init__(self):\n self.upper = None\n self.lower = None\n self.first_val_node = None\n self.last_val_node = None\n\n def add_val(self, val_node):\n if self.first_val_node is None:\n self.first_val_node = val_node\n self.last_val_node = val_node\n else:\n self.first_val_node.left = val_node\n val_node.right = self.first_val_node\n self.first_val_node = val_node\n\n def pop_last(self):\n if self.empty():\n return None\n\n result = (self.last_val_node.key, self.last_val_node.val)\n if self.last_val_node.left is not None:\n self.last_val_node = self.last_val_node.left\n self.last_val_node.right = None\n return result\n else:\n self.last_val_node = None\n self.first_val_node = None\n return result\n\n def pop_first(self):\n if self.empty():\n return None\n\n result = (self.first_val_node.key, self.first_val_node.val)\n if self.first_val_node.right is not None:\n self.first_val_node = self.first_val_node.right\n self.first_val_node.left = None\n return result\n else:\n self.last_val_node = None\n self.first_val_node = None\n return result\n\n def del_node(self, node):\n if self.first_val_node == node:\n self.pop_first()\n elif self.last_val_node == node:\n self.pop_last()\n else:\n node.left.right = node.right\n node.right.left = node.left\n\n def empty(self):\n if self.first_val_node is None:\n return True\n return False\n\n def __str__(self):\n return str(self.first_val_node)\n\n\nclass LFUCache:\n\n def __init__(self, capacity: int):\n self.capacity = capacity\n self.map = {}\n self.lower_freq = FreqNode()\n self.higher_freq = self.lower_freq\n\n def get(self, key: int) -> int:\n if key not in self.map:\n return -1\n node = self.map[key]\n self._update_node(node)\n return node.val\n\n def put(self, key: int, value: int) -> None:\n if self.capacity == 0:\n return\n if key not in self.map:\n if len(self.map) == self.capacity:\n freq_node = self.lower_freq\n while freq_node.empty():\n freq_node = freq_node.upper\n del self.map[freq_node.pop_last()[0]]\n self.map[key] = Node(key, value, self.lower_freq)\n self.lower_freq.add_val(self.map[key])\n else:\n self.map[key].val = value\n self._update_node(self.map[key])\n\n def _update_node(self, node):\n if node.freq_node is self.higher_freq:\n self.higher_freq.upper = FreqNode()\n self.higher_freq = self.higher_freq.upper\n node.freq_node.del_node(node)\n node.left = None\n node.right = None\n node.freq_node.upper.add_val(node)\n node.freq_node = node.freq_node.upper\n\n def __str__(self):\n s = \' *\'\n freq = self.lower_freq\n rank = 0\n while freq:\n rank += 1\n s += \'\\n| | \\n[\' + str(rank) + \']\'\n if not freq.empty():\n s += \' => \' + str(freq)\n freq = freq.upper\n return s\n\n```
| 2
|
Design and implement a data structure for a [Least Frequently Used (LFU)](https://en.wikipedia.org/wiki/Least_frequently_used) cache.
Implement the `LFUCache` class:
* `LFUCache(int capacity)` Initializes the object with the `capacity` of the data structure.
* `int get(int key)` Gets the value of the `key` if the `key` exists in the cache. Otherwise, returns `-1`.
* `void put(int key, int value)` Update the value of the `key` if present, or inserts the `key` if not already present. When the cache reaches its `capacity`, it should invalidate and remove the **least frequently used** key before inserting a new item. For this problem, when there is a **tie** (i.e., two or more keys with the same frequency), the **least recently used** `key` would be invalidated.
To determine the least frequently used key, a **use counter** is maintained for each key in the cache. The key with the smallest **use counter** is the least frequently used key.
When a key is first inserted into the cache, its **use counter** is set to `1` (due to the `put` operation). The **use counter** for a key in the cache is incremented either a `get` or `put` operation is called on it.
The functions `get` and `put` must each run in `O(1)` average time complexity.
**Example 1:**
**Input**
\[ "LFUCache ", "put ", "put ", "get ", "put ", "get ", "get ", "put ", "get ", "get ", "get "\]
\[\[2\], \[1, 1\], \[2, 2\], \[1\], \[3, 3\], \[2\], \[3\], \[4, 4\], \[1\], \[3\], \[4\]\]
**Output**
\[null, null, null, 1, null, -1, 3, null, -1, 3, 4\]
**Explanation**
// cnt(x) = the use counter for key x
// cache=\[\] will show the last used order for tiebreakers (leftmost element is most recent)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=\[1,\_\], cnt(1)=1
lfu.put(2, 2); // cache=\[2,1\], cnt(2)=1, cnt(1)=1
lfu.get(1); // return 1
// cache=\[1,2\], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 2 is the LFU key because cnt(2)=1 is the smallest, invalidate 2.
// cache=\[3,1\], cnt(3)=1, cnt(1)=2
lfu.get(2); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,1\], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // Both 1 and 3 have the same cnt, but 1 is LRU, invalidate 1.
// cache=\[4,3\], cnt(4)=1, cnt(3)=2
lfu.get(1); // return -1 (not found)
lfu.get(3); // return 3
// cache=\[3,4\], cnt(4)=1, cnt(3)=3
lfu.get(4); // return 4
// cache=\[4,3\], cnt(4)=2, cnt(3)=3
**Constraints:**
* `1 <= capacity <= 104`
* `0 <= key <= 105`
* `0 <= value <= 109`
* At most `2 * 105` calls will be made to `get` and `put`.
| null |
easy to understand
|
hamming-distance
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe use the bigger number to determine the length of both the binary numbers.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n if x>=y:\n x1=bin(x).replace("0b","")\n p=len(x1)\n y1=bin(y).replace("0b","").zfill(p)\n else:\n y1=bin(y).replace("0b","")\n p=len(y1)\n x1=bin(x).replace("0b","").zfill(p)\n x1=list(x1)\n y1=list(y1)\n cnt=0\n for i in range(len(x1)):\n if x1[i]!=y1[i]:\n cnt+=1\n return cnt\n```
| 1
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Bitwise XOR and Divide-by-2 Method
|
hamming-distance
| 0
| 1
|
# Intuition and Approach\nThe XOR (Exclusive OR) operation in Python can be performed using the `^` operator. The XOR operation returns `True` if exactly one of the operands is `True`, and `False` otherwise. In other words, if the respective bits are different, it returns `1`. \n\nThen the divide-by-2 method is applied on the resulting integer. This involves dividing the number by 2 repeatedly until the quotient becomes 0. The remainders from each division are summed in reverse order to get the total count of 1s in the binary representation of that number.\n\n# Complexity\n- Time complexity: $$O(1))$$ due to constant bit size of the integer\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n z = x ^ y\n \n i = z\n count = 0\n while i > 0:\n count += i % 2\n i = i // 2\n \n return count\n```
| 1
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Python3 || One lined easy solution
|
hamming-distance
| 0
| 1
|
Please do upvote\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n return bin(x^y).count("1")\n```
| 1
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
easy python solution
|
hamming-distance
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n x = bin(x)[2:]\n y = bin(y)[2:]\n \n lx = len(x)\n ly = len(y)\n l = max(lx,ly)\n sm = 0\n x = \'0\'*(l-lx)+x\n y = \'0\'*(l-ly)+y\n\n for i in range(l-1,-1,-1):\n if x[i]!=y[i]:\n sm+=1\n\n return sm \n \n```
| 1
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Easy 1 line Python code using bitwise XOR operator
|
hamming-distance
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n return bin(x^y)[2:].count("1")\n\n\n\n```
| 2
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
[Python3] Solutions with explanation
|
hamming-distance
| 0
| 1
|
One way to compute Hamming distance between **x** and **y** is calculate XOR and count the number of \'1\'s in the binary representation.\n\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n return bin(x ^ y).count(\'1\')\n```\nAnother way to compute is calculate XOR, then iterate through all 32 bits and add the appropriate bit of the XOR result to the Hamming distance. In the first line of the for loop we get the least significant bit of xor and add it to the Hamming distance. In the second line we shift the bits of the variable xor to the right by 1 position, discarding the least significant bit and move on to the next most significant bit.\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n xor = x ^ y\n dist = 0\n \n for _ in range(32):\n dist += xor & 1\n xor >>= 1\n \n return dist\n```
| 1
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
461: Solution with step by step explanation
|
hamming-distance
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a variable "xor" with the XOR of the given integers "x" and "y".\n2. Initialize a variable "distance" with 0.\n3. While "xor" is not equal to 0, do the following:\na. Bitwise AND "xor" with "xor-1" to unset the rightmost set bit of "xor". This operation flips the rightmost set bit to 0 and all the bits to the right of it to 1. For example, if "xor" is 010110, "xor-1" is 010101, and "xor & (xor-1)" is 010100.\nb. Increment "distance" by 1.\n4. Return "distance" as the Hamming distance between "x" and "y".\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n # Calculate the XOR of the two numbers\n xor = x ^ y\n \n # Calculate the number of set bits in the XOR\n distance = 0\n while xor:\n xor &= xor - 1\n distance += 1\n \n return distance\n\n```
| 5
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
just cool one line solution
|
hamming-distance
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n return bin(x^y).count(\'1\')\n```
| 3
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Solution
|
hamming-distance
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int hammingDistance(int x, int y) {\n return __builtin_popcountll(x^y);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n binx,biny=bin(x).replace(\'0b\',\'0\'),bin(y).replace(\'0b\',\'0\')\n lx,ly=len(binx),len(biny)\n ans=0\n i,j=lx-1,ly-1\n while i>=0 and j>=0:\n ans+=binx[i]!=biny[j]\n i-=1\n j-=1\n while i>=0:\n ans+=binx[i]=="1"\n i-=1\n while j>=0:\n ans+=biny[j]=="1"\n j-=1\n return ans\n```\n\n```Java []\nclass Solution {\n public int hammingDistance(int x, int y) {\n int z = x ^ y;\n int res = 0;\n while (z > 0) {\n res++;\n z = z & (z-1);\n }\n return res;\n }\n}\n```\n
| 2
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Easy approach with bit manipulation with explanation
|
hamming-distance
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\nThe main idea is to use a XOR operator for these 2 numbers. If 2 bits are the same - we get \'0\' at this position and \'1\' otherwise. So our mission here is to calculate the number of \'1\'s. We can do so by comparing the last bit with number 1 via AND operator. After comparison we remove that checked bit and repeat the whole process till we have bits left.\n\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n diff = x^y\n res = 0\n while diff:\n res+= diff&1\n diff>>=1\n return res\n```
| 3
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Python 1-liner 32ms
|
hamming-distance
| 0
| 1
|
```\ndef hammingDistance(self, x, y):\n return bin(x^y).count(\'1\')\n```
| 9
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Beating 95% Single Line Easy Python Solution
|
hamming-distance
| 0
| 1
|
\n\n\n# Code\n```\nclass Solution(object):\n def hammingDistance(self, x, y):\n """\n :type x: int\n :type y: int\n :rtype: int\n """\n return str(bin(x^y)).count(\'1\')\n```
| 3
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Python3 || Two ways, string and bit manipulation (Commented)
|
hamming-distance
| 0
| 1
|
Any questions feel free to ask, if the comments helped, leave me a like :)\n```\nclass Solution:\n def hammingDistance(self, x: int, y: int) -> int:\n\n # String solution\n\t\t# TC O(n) SC O(1)\n longer = len(bin(y))-2 \n if x > y: longer = len(bin(x))-2\n\t\t # 2 lines above for padding 0\'s\n \n # turn both x and y to binary, keep count of mismatches with count variable\n x, y, count = format(x, \'0b\').zfill(longer), format(y, \'0b\').zfill(longer), 0 \n for i in range(len(x)):\n if x[i] != y[i]: count += 1\n return count\n\n # bit manipulation solution\n\t\t# TC O(n) SC O(1)\n xor = x ^ y # XOR your two integers\n ham = 0 # store number of 1\'s from the XOR operation\n while xor != 0: # while you have bits to check\n ham += xor % 2 # increase ham when a 1 is seen\n xor >>= 1 # right shift\n return ham\n```
| 2
|
The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given two integers `x` and `y`, return _the **Hamming distance** between them_.
**Example 1:**
**Input:** x = 1, y = 4
**Output:** 2
**Explanation:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The above arrows point to positions where the corresponding bits are different.
**Example 2:**
**Input:** x = 3, y = 1
**Output:** 1
**Constraints:**
* `0 <= x, y <= 231 - 1`
| null |
Solution
|
minimum-moves-to-equal-array-elements-ii
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int minMoves2(vector<int>& nums) {\n int result = 0, length = nums.size();\n sort(nums.begin(), nums.end());\n for (int i = 0; i < length; i++) {\n int median = length / 2;\n result += abs(nums[i] - nums[median]);\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n nums.sort()\n median = nums[len(nums)//2] \n count = 0 \n for n in nums:\n if n == median:\n continue\n count += abs(n - median)\n return count\n```\n\n```Java []\nclass Solution {\n public int minMoves2(int[] nums) {\n int length = nums.length;\n int result = 0;\n int median = helper(nums, 0, length - 1, (length - 1) / 2);\n for (int x : nums) {\n result += Math.abs(x - median);\n }\n return result;\n }\n private int helper(int[] q, int l, int r, int k) {\n if (l >= r) return q[r];\n int x = q[l + r >> 1], i = l - 1, j = r + 1;\n while (i < j) {\n while (q[++i] < x) ;\n while (q[--j] > x) ;\n if (i < j) {\n int t = q[i];\n q[i] = q[j];\n q[j] = t;\n }\n }\n if (k <= j) {\n return helper(q, l, j, k);\n }\n return helper(q, j + 1, r, k);\n }\n}\n```\n
| 1
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.