title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
📌 Python3 simple solution: Get the mid element from the sorted array
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
```\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n nums.sort()\n mid = nums[len(nums)//2]\n result = 0\n for i in nums:\n result+=abs(mid-i)\n return result\n```
| 6
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
462: Solution with step by step explanation
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Sort the input array nums.\n2. Calculate the median of nums by accessing the middle element of the sorted array. If n is odd, the median is nums[n // 2]. If n is even, the median is the average of nums[n // 2 - 1] and nums[n // 2].\n3. Initialize a variable moves to 0.\n4. Iterate over each element num in nums, and for each element, add the absolute difference between num and the median to moves. The absolute difference is calculated using the abs() function.\n5. Return moves as the output.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n # Calculate the median\n nums.sort()\n n = len(nums)\n median = nums[n // 2]\n # Calculate the sum of absolute differences from the median\n moves = 0\n for num in nums:\n moves += abs(num - median)\n \n return moves\n\n```
| 3
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Python easy approach || ✅Beats 92.72%
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
```\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n res = 0\n nums.sort()\n med = nums[len(nums)//2]\n for i in nums:\n res += abs(med-i)\n return res\n```\n**.\n.\n.\n.\n.**\n**Please Up-vote if you find this post helpful : )**
| 2
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Python || fastest || explanation
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
**Upvote if helpful**\n\nIt very basic that we need to sort the array and the elements are to be made equal to onr of the three measures of central tendency mean / median / mode. And we will need to increase values in left to specific value and decrease value at right of array to specific value. This central value is median in this case. \n\n```\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n nums.sort()\n middle_index= len(nums)//2\n mv= nums[middle_index] #median value\n \n ans=0\n for i in nums:\n ans+=abs(i-mv)\n \n return ans\n```
| 2
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Python Easy Greedy O(1) Space approach
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
```\n#First sort the array\n#then find the mid element\n#then loop through the nums array then see how much operation is need for each element of nums to change it into nums[n]\n#add the count of individual and return (it is the answer)\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n \n nums.sort()\n \n n= (len(nums)-1)//2\n \n ans = 0\n \n for i in range(len(nums)):\n if i!=n:\n\t\t\t#here is the greedy point we are checking how much operation is required to become \n\t\t\t#he middle element or equal to the middle element.\n ans+=(abs(nums[n]-nums[i]))\n \n \n return ans
| 1
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Python3 , 2 Line Solution , Median , Easy to Understand
|
minimum-moves-to-equal-array-elements-ii
| 0
| 1
|
# Upvote if useful \n```\nfrom statistics import median as m\nclass Solution:\n def minMoves2(self, nums: List[int]) -> int:\n x = int(m(nums))\n return sum([abs(i-x) for i in nums])\n```
| 4
|
Given an integer array `nums` of size `n`, return _the minimum number of moves required to make all array elements equal_.
In one move, you can increment or decrement an element of the array by `1`.
Test cases are designed so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:**
Only two moves are needed (remember each move increments or decrements one element):
\[1,2,3\] => \[2,2,3\] => \[2,2,2\]
**Example 2:**
**Input:** nums = \[1,10,2,9\]
**Output:** 16
**Constraints:**
* `n == nums.length`
* `1 <= nums.length <= 105`
* `-109 <= nums[i] <= 109`
| null |
Python solution Beats 100%
|
island-perimeter
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem was to iterate through the grid and for each cell with a value of 1, check the surrounding cells to see if they also have a value of 1. If they do, that means they are part of the same island and I can subtract from the perimeter count.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach to solving this problem is to iterate through the grid and for each cell with a value of 1, add 4 to the perimeter count. Then, check the surrounding cells to see if they also have a value of 1. If they do, that means they are part of the same island and I can subtract 2 from the perimeter count for each shared side.\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int:\n perimeter = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == 1:\n perimeter += 4\n if i > 0 and grid[i-1][j] == 1:\n perimeter -= 2\n if j > 0 and grid[i][j-1] == 1:\n perimeter -= 2\n return perimeter\n```
| 16
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
[python] Straight forward approach - beats 98.69% submissions
|
island-perimeter
| 0
| 1
|
Take the following single block as an example\n\nIt has four sides. So perimeter of one block is 4.\n\nNow take a look when two blocks intersect\n\nHere these blocks and they intersect at one edge. So perimeter(4+4=8) will be reduced by 2 (removing intersected edge at each square) upon each intersection. Each block in the land has four neighbours. We need to check whether the neighbour is land or not and decrement perimeter based on intersections.\n\nThe algorithm is simple as follows\n1. Traverse the grid block by block\n2. If the block is land increment perimeter by 4 and check it\'s top and left neighbours. If the neighbours are land blocks decrement perimeter by 2 per intersection.\n3. Repeat the process until the whole grid is traversed\n\nTime Complexity: O(n^2)\nSpace Complexity: O(1)\n\n```\ndef islandPerimeter(self, grid: List[List[int]]) -> int:\n\t R,C = len(grid), len(grid[0])\n perimeter = 0\n\t # Traverse the grid\n for i in range(R):\n for j in range(C):\n\t\t # If it is a land block increment perimeter by 4\n if grid[i][j] == 1:\n perimeter += 4\n\t\t\t# Check whether top neighbour is a land and decrement it by 2\n\t\t\t# as it intersects\n if i>0 and grid[i-1][j] == 1:\n perimeter -= 2\n\t\t\t# Check left neighbour is a land and decrement it by 2\n\t\t\t# as it intersects\n if j>0 and grid[i][j-1] == 1:\n perimeter -= 2\n return perimeter\n```\n\n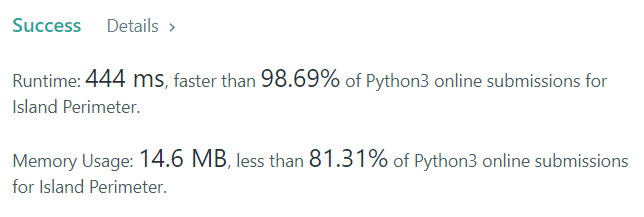\n\nThanks for reading. If this post had helped you kindly upvote :)
| 42
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
463: Solution with step by step explanation
|
island-perimeter
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named "islandPerimeter" that takes in a 2D list of integers called "grid" and returns an integer.\n2. Initialize a variable "perimeter" to 0.\n3. Loop through each cell in the grid using two nested for loops.\n4. Check if the current cell is a land cell (has a value of 1).\n5. If it is a land cell, check the cell\'s neighbors and add to the perimeter accordingly.\n6. Check the neighbor above the current cell. If it is a water cell or the current cell is on the top edge of the grid, add 1 to the perimeter.\n7. Check the neighbor to the left of the current cell. If it is a water cell or the current cell is on the left edge of the grid, add 1 to the perimeter.\n8. Check the neighbor below the current cell. If it is a water cell or the current cell is on the bottom edge of the grid, add 1 to the perimeter.\n9. Check the neighbor to the right of the current cell. If it is a water cell or the current cell is on the right edge of the grid, add 1 to the perimeter.\n10. After looping through all cells in the grid, return the final value of "perimeter".\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int:\n # Initialize perimeter to 0\n perimeter = 0\n \n # Loop through each cell in the grid\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n if grid[i][j] == 1:\n # Check the cell\'s neighbors and add to perimeter accordingly\n if i == 0 or grid[i-1][j] == 0:\n perimeter += 1\n if j == 0 or grid[i][j-1] == 0:\n perimeter += 1\n if i == len(grid)-1 or grid[i+1][j] == 0:\n perimeter += 1\n if j == len(grid[i])-1 or grid[i][j+1] == 0:\n perimeter += 1\n \n return perimeter\n\n```
| 6
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
Python Easy Solution | Fully Explained ✔
|
island-perimeter
| 0
| 1
|
\n\n\t# Time: O(mn)\n\tclass Solution:\n\t\t\tdef islandPerimeter(self, grid: List[List[int]]) -> int:\n\t\t\t\tisLands = 0\n\t\t\t\tnghbrs = 0\n\t\t\t\tgrd_len = len(grid)\n\t\t\t\tgrd0_len = len(grid[0])\n\t\t\t\tfor i in range(grd_len):\n\t\t\t\t\tfor j in range(grd0_len):\n\t\t\t\t\t\tif grid[i][j] == 1:\n\t\t\t\t\t\t\tisLands += 1\n\t\t\t\t\t\t\tif i < grd_len-1 and grid[i+1][j] == 1:\n\t\t\t\t\t\t\t\tnghbrs += 1 # Counting next Down Neighbour...\n\t\t\t\t\t\t\tif j < grd0_len-1 and grid[i][j+1] == 1:\n\t\t\t\t\t\t\t\tnghbrs += 1 # Counting next Right Neighbour...\n\t\t\t\treturn 4*isLands - 2*nghbrs\nIf you have any questions, please ask me, and if you like this approach, please **vote it up**!
| 24
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
Easy self explanatory solution - Python
|
island-perimeter
| 0
| 1
|
```python\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int: \n return sum(4 - sum(grid[i + dx][j + dy] if i + dx < len(grid) and j + dy < len(grid[0]) else 0 for dx, dy in [(0, 1), (1, 0)]) * 2 for i in range(len(grid)) for j in range(len(grid[0])) if grid[i][j] == 1)\n```
| 1
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
Python solution : beats 61.73% : with explanation
|
island-perimeter
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe need to find number of non land tiles(water or boundary)\n# Approach\n<!-- Describe your approach to solving the problem. -->\ntraverse the gienn grid to find a 1 and then check all four directions of the tile and check if there are water tiles or boundary of the grid\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int:\n r=len(grid)\n c=len(grid[0])\n per=0\n def walaco(i,j,grid):\n w=0\n r=len(grid)\n c=len(grid[0])\n if j==0 or grid[i][j-1]==0 :\n w+=1 \n if i==0 or grid[i-1][j]==0:\n w+=1\n if i==r-1 or grid[i+1][j]==0 :\n w+=1\n if j==c-1 or grid[i][j+1]==0:\n w+=1\n return w\n for i in range(r):\n for j in range(c):\n if grid[i][j]==1:\n per+=walaco(i,j,grid)\n return per\n\n \n\n\n\n```
| 2
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
Simple solution with 98% accuracy...
|
island-perimeter
| 0
| 1
|
# Intuition\nThe problem statement provides the following information:\n\n The grid represents a map where each cell can be either land (1) or water (0).\n The cells in the grid are connected horizontally or vertically, but not diagonally.\n The grid is completely surrounded by water.\n There is exactly one island, which means there is at least one land cell and all land cells are connected.\n The island doesn\'t have any "lakes," meaning there are no enclosed bodies of water within the island.\n Each cell represents a square with a side length of 1.\nThe dimensions of the grid (row and column) don\'t exceed 100.\n# Approach\nMY approach to solving the problem is correct. The code I provided implements the logic to calculate the perimeter of the island based on the given grid representation.\nThe code iterates over each cell in the grid and checks if it represents land (1). If a land cell is found, the perimeter is incremented by 4, representing the four sides of the square cell.\nThen, it checks if there is a neighboring land cell to the left or above the current cell. If such a neighbor exists, it means there is an adjacent land cell, and the perimeter is decremented by 2, as one side of the current cell is shared with the neighboring cell.\n\n\n# Complexity\n- Time complexity:\nO(n*m)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int:\n perimeter = 0\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == 1:\n perimeter += 4\n if i != 0 and grid[i-1][j] == 1:\n perimeter -= 2\n if j != 0 and grid[i][j-1] == 1:\n perimeter -= 2 \n \n return perimeter\n\n```
| 3
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
Solution in Python 3
|
island-perimeter
| 0
| 1
|
```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int: \n \tM, N, p = len(grid), len(grid[0]), 0\n \tfor m in range(M):\n \t\tfor n in range(N):\n \t\t\tif grid[m][n] == 1:\n \t\t\t\tif m == 0 or grid[m-1][n] == 0: p += 1\n \t\t\t\tif n == 0 or grid[m][n-1] == 0: p += 1\n \t\t\t\tif n == N-1 or grid[m][n+1] == 0: p += 1\n \t\t\t\tif m == M-1 or grid[m+1][n] == 0: p += 1\n \treturn p\n\t\t\n\t\t\t\n- Junaid Mansuri\n- Chicago, IL
| 40
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
✅✅✅ about 98.36% faster python solution
|
island-perimeter
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def islandPerimeter(self, grid: List[List[int]]) -> int:\n answer = 0\n n, m = len(grid), len(grid[0])\n for i in range(n):\n for j in range(m):\n if grid[i][j]:\n answer+=(i==0 or grid[i-1][j]==0)+(j==0 or grid[i][j-1]==0)+(i==n-1 or grid[i+1][j]==0)+(j==m-1 or grid[i][j+1]==0)\n return answer\n```
| 2
|
You are given `row x col` `grid` representing a map where `grid[i][j] = 1` represents land and `grid[i][j] = 0` represents water.
Grid cells are connected **horizontally/vertically** (not diagonally). The `grid` is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes ", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
**Example 1:**
**Input:** grid = \[\[0,1,0,0\],\[1,1,1,0\],\[0,1,0,0\],\[1,1,0,0\]\]
**Output:** 16
**Explanation:** The perimeter is the 16 yellow stripes in the image above.
**Example 2:**
**Input:** grid = \[\[1\]\]
**Output:** 4
**Example 3:**
**Input:** grid = \[\[1,0\]\]
**Output:** 4
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 100`
* `grid[i][j]` is `0` or `1`.
* There is exactly one island in `grid`.
| null |
464: Solution with step by step explanation
|
can-i-win
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function canIWin which takes in two integers, maxChoosableInteger and desiredTotal, and returns a boolean indicating whether the first player can win the game or not.\n\n2. Check if desiredTotal is less than or equal to zero. If it is, then the first player has already won and we return True.\n\n3. Check if the sum of all integers from 1 to maxChoosableInteger is less than desiredTotal. If it is, then it is not possible for the first player to win and we return False.\n\n4. Initialize a dictionary self.memo to store the sub-problems result.\n\n5. Call the can_win function which will traverse through all possible moves of player 1 and check if they can win the game.\n\n6. Define the can_win function which takes in choices - a tuple of integers representing the remaining integers that can be chosen, and target - the remaining total that needs to be reached, and returns a boolean indicating whether player 1 can win the game or not.\n\n7. If there is only one choice left and it\'s value is greater than or equal to target, then player 1 wins and we return True.\n\n8. If the sub-problem already exists in the self.memo dictionary, return its result.\n\n9. Traverse through all possible moves of player 1 by looping through the indices of choices.\n\n10. Remove the chosen integer from the choices tuple and subtract its value from the target.\n\n11. Recursively call the can_win function with the updated choices tuple and target value.\n\n12. If player 2 can\'t win with the current move of player 1, then player 1 can win and we return True.\n\n13. If no move of player 1 results in player 1 winning, then player 1 can\'t win and we return False.\n\n14. Finally, store the result in the self.memo dictionary for future reference.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n # If desiredTotal is less than or equal to zero, then player 1 wins\n if desiredTotal <= 0:\n return True\n # If the sum of all the integers is less than the desiredTotal, then player 1 can\'t win\n if (maxChoosableInteger * (maxChoosableInteger + 1)) // 2 < desiredTotal:\n return False\n \n # Store the sub-problems result\n self.memo = {}\n \n # Traverse through all possible moves of player 1\n return self.can_win(tuple(range(1, maxChoosableInteger+1)), desiredTotal)\n\n\n def can_win(self, choices, target):\n # If there is only one choice left and it\'s value is greater than or equal to target, then player 1 wins\n if choices[-1] >= target:\n return True\n \n # If the sub-problem already exists, return it\'s result\n if choices in self.memo:\n return self.memo[choices]\n \n # Traverse through all possible moves of player 1\n for i in range(len(choices)):\n # Player 1 chooses a number\n if not self.can_win(choices[:i]+choices[i+1:], target-choices[i]):\n # If player 2 can\'t win, then player 1 can win\n self.memo[choices] = True\n return True\n \n # If no move of player 1 results in player 1 winning, then player 1 can\'t win\n self.memo[choices] = False\n return False\n\n```
| 5
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Beats 99% Speed, 99% Memory, mathematical and bitwise approach
|
can-i-win
| 0
| 1
|
# Intuition\nI wanted to optimize average runtime even more because even memoized versions were not that great and I felt I solved this \ntoo fast and that there was more to this problem.\n\nSo I made a few additions quickly to the code and now\nit performs much better on typical benchmarks.\n\n> On average, beats over 98-100% of other solutions (Both memory and space). \n\n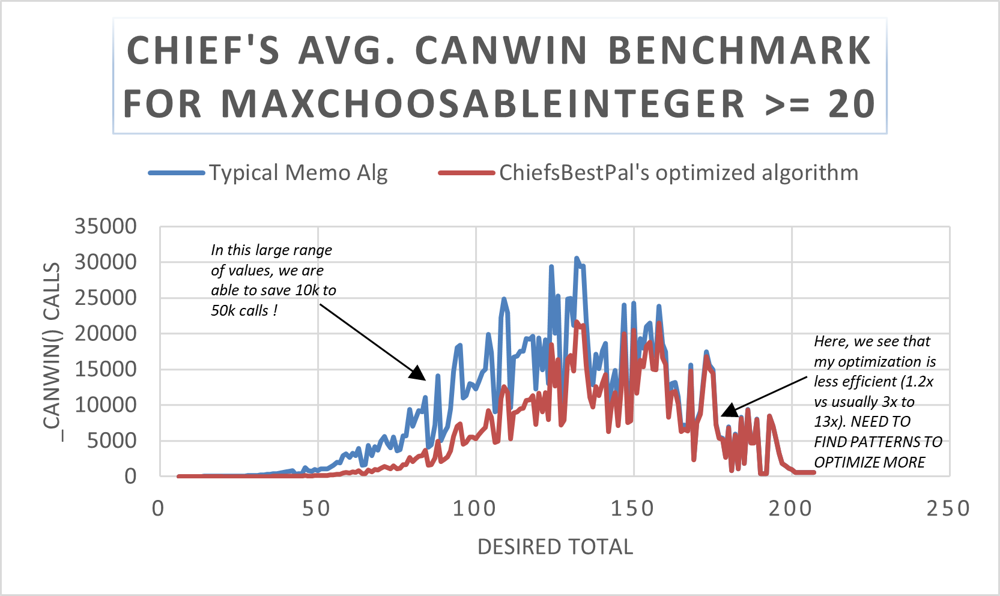\n\n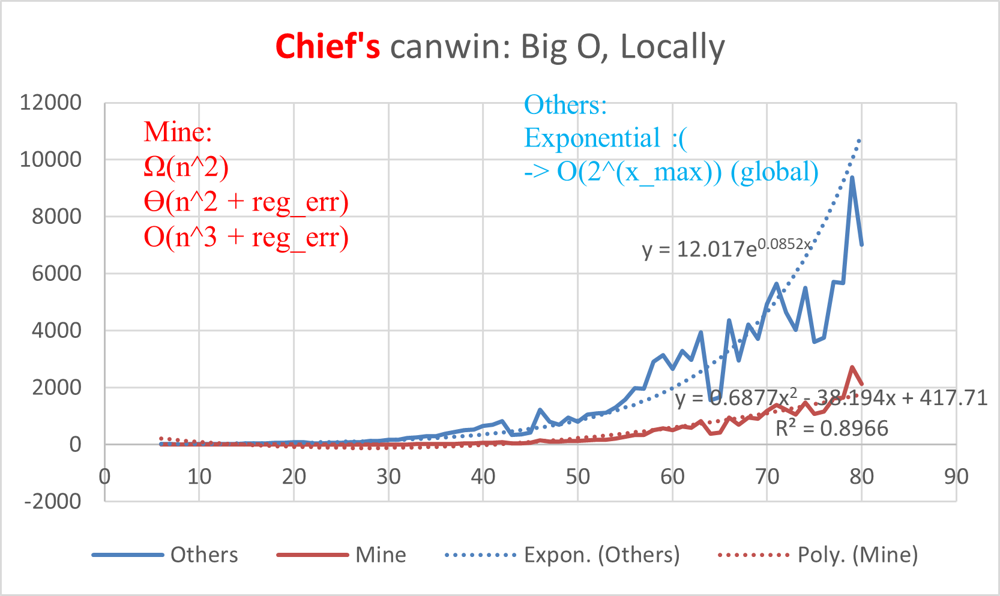\n\n\n# Approach\nX_MAX : maxChoosableInteger\nT: desiredTotal\n\nWith the addition of better edge case handling (see the canWin() method comments), I added a little filtering case that greatly reduced the number of recursive calls to _canWin() (like 2x - 15x on averages).\n\n```\n elif (clz_log2[1 << ((~x_pool & POOL_BITMASK).bit_length() - 1)] + 1 >= T):\n```\n**This basically selets the MSB as the current set bitmap index i.e. the largest x that has not yet been picked based on the state of the current turn. If player can now know he will win right now or on next turn, and avoids a lot of recursive calls by returning immiediately**\n\n\nNB: With builtins and compiler optimisations in C or C++, maybe this approach could even be improved ! e.g. __builtins_clz, etc... \n\nEdge case handling:\n\n``` # Natural number sum up to X_MAX is not greater than the total... \n elif (x_sum := (X_MAX * (X_MAX+1) >> 1)) <= T:\n \n # if sum == T, then there will be X_MAX turns ! Since player has the first turn (+1),\n # he has to have odd parity to also have the last turn, i.e. achieving sum of x used == T first !\n return (X_MAX & 1) == 1 if x_sum == T else False\n```\n\n# Complexity\n- Time complexity:\n$$O(2^{X_{MAX}} / LARGE\\_CONSTANT)$$\nBut if we consider the constraint only of the problem given by leetcode (locally), then it is closer to a higher order polynomial :D !$$ O(K* N^2) \\ or \\ O(K * N^3 )$$\n\n- Space complexity:\n$$O(2^{X_{MAX}})$$\n\nMy solution works very well with LeetCode test cases,\nbut it still extremely limited in terms of space complexity and eventually this will cause access overhead, and maybe even recursion stack overflow :( the same math logic I made could be used but one would have to memoize less generally or find better pattern and/or design for this because with X_MAX >= 20 and 100 <= T <= SUM(0 to X_MAX) - constant, there is signficant performance loss. \n\n# Author\nChiefsBestPal (ME :D )\n\n> **Feel free to leave your insight, this is my first post I never knew this feature existed lol**\nI know maybe some **deeper pattern analysis** could be done to optimize this maybe even more, the question is: Is it worth it for a problem of sort of small scale ?\n\n\n\n# Code\n```\nstate = None\nclz_log2 = {\n0x2 : 1,\n0x4 : 2,\n0x8 : 3,\n0x10 : 4,\n0x20 : 5,\n0x40 : 6,\n0x80 : 7,\n0x100 : 8,\n0x200 : 9,\n0x400 : 10,\n0x800 : 11,\n0x1000 : 12,\n0x2000 : 13,\n0x4000 : 14,\n0x8000 : 15,\n0x10000 : 16,\n0x20000 : 17,\n0x40000 : 18,\n0x80000 : 19\n}\n\nclass Solution:\n def canIWin(self,maxChoosableInteger: int, desiredTotal: int) -> bool:\n """\n Driver func for:\n Leetcode 464. Can I Win\n\n Solution by:\n ChiefsBestPal\n """\n global state\n X_MAX,T = maxChoosableInteger,desiredTotal\n #Shortcut win since player has first turn and one x is found to be larger than T needed !\n if X_MAX >= T: return True\n \n # Natural number sum up to X_MAX is not greater than the total... \n elif (x_sum := (X_MAX * (X_MAX+1) >> 1)) <= T:\n \n # if sum == T, then there will be X_MAX turns ! Since player has the first turn (+1),\n # he has to have odd parity to also have the last turn, i.e. achieving sum of x used == T first !\n return (X_MAX & 1) == 1 if x_sum == T else False\n \n #For Memoization. \n # The index will be the x_pool bitflag, which indicates which x are used (depending on if bitmap index is set or not)\n # The value will be the state: 0 undefined, +1 win, -1 loss\n state = [0]*(1 << X_MAX)\n \n return Solution._canIWin(X_MAX,(1 << X_MAX)-1,T,0)\n\n @staticmethod\n def _canIWin(X_MAX,POOL_BITMASK,T,x_pool):\n """\n Recur func for:\n Leetcode 464. Can I Win\n\n Solution by:\n ChiefsBestPal\n """\n global state \n \n # Bad Scenario \n if (T <= 0): return False\n \n # pool of number has already been memoized\n elif (state[x_pool]): return state[x_pool] == 1\n \n #Special check to see if current player can shortcut win with largest X remaining !\n #I made this and now _canIWin is called 13x less times just with the basic test cases ! :D \n elif (clz_log2[1 << ((~x_pool & POOL_BITMASK).bit_length() - 1)] + 1 >= T): \n \n return True\n\n for xi in range(X_MAX):\n #Skip already used Xs \n if (x_pool & (1 << xi)):\n continue\n \n #Test Next Player: remove x (i.e. bit index + 1) from total \n #and set x\'s used_flag so it is not used again.\n #if he loses, set current player state as winner\n elif (not Solution._canIWin(X_MAX,POOL_BITMASK, T - (xi + 1), x_pool | (1 << xi))):\n state[x_pool] = 1 \n return True\n \n #Current player at state lost.\n state[x_pool] = -1\n return False \n\n```
| 1
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
6 Lines Logical Python Solution
|
can-i-win
| 0
| 1
|
# Intuition\nConsider the cases where player A can win and lose\n\n# Approach\n- If the sum of all integers till maxInt is less than the required total then A can\'t win\n- If there exists a number which is greater than or equal to the total then A wins\n- If there exists any move that A can play so that B can\'t win in the next move\n\nJust code the above 3 conditions using recursion\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxInt: int, total: int) -> bool:\n #condition1\n if maxInt * (maxInt+1) / 2 < total: return False\n\n @cache\n def func(nums, total):\n #condition2\n if any(total <= x for x in nums): return True \n #condition3\n return any(not func(nums-{x}, total-x) for x in nums)\n\n return func(frozenset(range(1,maxInt+1)), total)\n\n \n```
| 1
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
4 lines Python with frozenset
|
can-i-win
| 0
| 1
|
```\n def canIWin(self, maxInt: int, total: int) -> bool:\n @functools.lru_cache(None)\n def dp(nums, left):\n return any(left - n <= 0 or not dp(frozenset(nums - {n}), left - n) for n in nums)\n \n return (1 + maxInt) * maxInt // 2 >= total and dp(frozenset(range(1, maxInt + 1)), total)\n```\n\n```(1 + maxInt) * maxInt // 2 >= total``` - this makes sure that first player can even win (sum of the +1 series)\n```frozenset(range(1, maxInt + 1)``` - creates hashable set possible numbers [1, 2, ..., maxInt]\nNow, in each recursive call, we check for all nums if it\'s possible to win drawing one of them:\n1. Either ```left - n <= 0``` which means that taking than number n will allow reaching the total or else..\n2. ```not dp(frozenset(nums - {n}), left - n)``` - which means that your opponent cannot win using numbers which left.\n\n```frozenset(nums - {n})``` - creates fresh new hashable set without n\n\nWe also cache by pair (nums, left) - every unique set of numbers is different.
| 8
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Bitmask DP/DFS solution
|
can-i-win
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n\n if maxChoosableInteger * (maxChoosableInteger + 1) // 2 < desiredTotal:\n return False\n\n if desiredTotal <= 0:\n return True\n \n dp = [-1] * (1 << maxChoosableInteger)\n \n def dfs(bitmask, value):\n if value >= desiredTotal:\n return False\n if dp[bitmask] != -1:\n return dp[bitmask] == 1\n for i in range(1, maxChoosableInteger + 1):\n if not (bitmask & (1 << (i - 1))):\n if not dfs(bitmask | (1 << (i - 1)), value + i):\n dp[bitmask] = 1\n return True\n dp[bitmask] = 0\n return False\n \n return dfs(0, 0)\n \n \n \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n \n \n \n\n\n\n \n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Recursion Python3
|
can-i-win
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n\n @cache\n def dfs(nums, total):\n return any(not dfs(nums[:i] + nums[i+1:], total + num) if total + num < desiredTotal else True for i, num in enumerate(nums))\n \n return False if sum(range(1,maxChoosableInteger+1)) < desiredTotal else dfs(tuple(range(1,maxChoosableInteger+1)), 0)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
MiniMax algo (gametree pruning) Python
|
can-i-win
| 0
| 1
|
# Intuition\nSince both players have complete information of game (which numbers have been chosen), play turnwise, minimax algorithm can be used.\n\n# Approach\n[Minimax algo.](https://www.youtube.com/watch?v=rMliVVTlLwY) See previous videos in the playlist for context on game theory.\n\nTraverse game tree, if you are player 2 node then try to choose False only, if False not present then choose True. But if you are player 1 node, then try to choose True only, if True not present then choose False.\nIn below code, you can see pruning of nodes for both player 1 and player 2 as if player 1 has found a true path, it can take it without harm so other children are pruned. Similarly, if player 2 has found a False path, it can take it without harm as it is trying to defeat us so other children are pruned.\n\n# Code\nTurn 1 means player 1 turn, turn -1 means player 2 turn\nLookout for comments\n```\nclass Solution:\n def f(self,available,turn,desired,csum,maxChoosableInteger,dp):\n if csum>=desired:\n return turn == -1 # Return True if turn is -1 i.e. player 1 made the winning move\n if dp.get((turn,tuple(available)),None) is not None:\n return dp[(turn,tuple(available))] # Taking memoized value\n if turn == -1:# Player 2 turn\n res = True\n for i in range(maxChoosableInteger):\n if available[i]:\n available[i] = False\n res = res and self.f(available,1,desired,csum+i+1,maxChoosableInteger,dp)\n available[i] = True # Backtracking \n if not res:# Pruning\n dp[(turn,tuple(available))] = False\n return res\n dp[(turn,tuple(available))] = res\n return res\n else:# Player 1 turn\n res = False\n for i in range(maxChoosableInteger):\n if available[i]:\n available[i] = False\n res = res or self.f(available,-1,desired,csum+i+1,maxChoosableInteger,dp)\n available[i] = True # Backtracking\n if res:# Pruning\n dp[(turn,tuple(available))] = True\n return res\n dp[(turn,tuple(available))] = res # Memoizing\n return res\n\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n available = [True]*maxChoosableInteger\n if desiredTotal> (maxChoosableInteger*(maxChoosableInteger+1))/2:\n return False\n dp = {}\n if desiredTotal == 0 or desiredTotal<=maxChoosableInteger:\n return True\n return self.f(available,1,desiredTotal,0,maxChoosableInteger,dp)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python Bitmask and 1D DP. Beats 70%
|
can-i-win
| 0
| 1
|
# Intuition\nUse Bitmask to store whether the numbers are used or not. We can use only 1D dp as the masks for p1 and p2 will never be same. This is because p1 will always have odd number of 1s and p2 will always have even number of 1s.\n\nIf desiredTotal is not achievable at all, that is its greater than 2 ** n or the natural sum of maxChoosableInteger (n) return False\n\nImagine the first step of search with 0, 0 being P2 turn. So the next turn we see if any of p1 can win and this is possible if currSum plus unused sum is grater than desiredTotal or the function call with the num chosen.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, n: int, desiredTotal: int) -> bool:\n memo = {}\n if desiredTotal >= 2 ** n:\n return False\n def search(mask, currSum):\n if mask in memo:\n return memo[mask]\n memo[mask] = True\n #Can I win at this step ? \n for i in range(n):\n if 1 << i & mask:\n continue\n if currSum + i + 1 >= desiredTotal or search(mask | 1 << i, currSum + i + 1):\n memo[mask] = False\n break\n return memo[mask]\n return not search(0, 0)\n \n\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python: concise dfs with memoization solution.
|
can-i-win
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n """\n dfs with backtracking, memoization.\n """\n @cache\n def dfs(tokens, total):\n if total + tokens[-1] >= desiredTotal: # can win now.\n return True\n if any(not dfs(tokens[:i]+tokens[i+1:], total+e)\\\n for i, e in enumerate(tokens)): # can win later.\n return True\n return False # can never win.\n\n if maxChoosableInteger*(maxChoosableInteger+1)//2 < desiredTotal:\n return False # neither can win.\n return dfs(tuple(i+1 for i in range(maxChoosableInteger)), 0)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python | top-down DP with bitmask. 20 lines clean code
|
can-i-win
| 0
| 1
|
# Intuition\nJust doing top-down DP to search if any move will make next player lose no matter what move that player to take. \nSo we can just apply top-down dfs to solve this problem\n\n# Approach\nSince we only have at most 20 choosable integers, we can use an integer as a bitmask to record which number has been used. e.g. `1001` means number `1` and `4` has been used. Note the value is equal to index + 1.\n \nWith `@Cache` annotation in python, we don\'t even need to manually implement a cache for the result. but the cache will still take at most O(2^maxChoosableInteger) space to cache all the combinations of the choosen integers.\n\n# Complexity\n- Time complexity: O(2^maxChoosableInteger)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^maxChoosableInteger)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n if sum([i + 1 for i in range(maxChoosableInteger)]) < desiredTotal:\n return False\n\n @cache\n def dfs(total: int, mask: int) -> bool:\n canWin = False;\n for i in range(maxChoosableInteger):\n if mask >> i & 1 == 0:\n if total + i + 1 >= desiredTotal:\n canWin = True\n break\n newMask = mask | 1 << i\n if not dfs(total + i + 1, newMask):\n canWin = True\n break\n return canWin\n \n return dfs(0, 0)\n \n \n \n \n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Explained !!
|
can-i-win
| 0
| 1
|
```\nGiven,\nn <= 20\n2 players A and B\nTarget <= 300\n\ninitially total = 0\n\nEach player can choose any value from pool alternatively\ni.e pool = [1 ... n]\n\nAnd increase the total by the picked value\ni.e new total = total + picked value\n\nevery value can be picked only once\n\nAssuming both players A and B plays optimally\nCan A win?\n```\n\n```\nAs target <= 300 ,\nand nothing but a possible sum of elements choosen from pool\n\nSo what are the possible values of pool?\n\nCASE 1 : sum(pool) < target\nCASE 2 : sum(pool) == target\nCASE 3 : sum(pool) > target\n\n--------------------------------------------------------\nCASE 1 : sum(pool) < target :\n i.e we cannot reach target A Lose // return False\n // if sum(pool) < target : return False\n---------------------------------------------------------\nCASE 2 : sum(pool) == target:\n i.e we have to choose every element to reach target\n\n We know player A will start\n And We want player A to end\n\n As we have to pick every element (i.e we have no choice to choose)\n it is only possible if number of elements is ODD.\n\n [ 1 2 3 4 5 ] tar = 15\n [ A B A B A ] -> A starts and A ends WIN\n\n [1 2 3 4 5 6 ] tar = 21\n [A B A B A B ] -> A starts and B ends LOSE\n\n // if sum(pool) == total: return n%2 != 0\n-----------------------------------------------------------\nCASE 3 : sum(pool)>target:\n we have choice to choose.\n```\n```\nCASE 3 : sum(pool)>target: we have choice to choose\nThe only way A can WIN is if A can force B to LOSE \n\nEx : if n = 7 target = 25\npool = [1,2,3,4,5,6,7]\n\nWhat can be A\'s first choice so B will LOSE ?\nif we can get any 1 of such case we can say A WILL win.\nA\'s first choice is what matters\n\nA wants B to Lose\n B wants A to Lose\n A wants B to Lose\n Ultimatelt the one who picks last Wins\n\n\n def f(pool,curr):\n //3. As pool is sorted\n // And if last element is >= curr. So target achieved\n // Who every reaches here first WINS(i.e last pick)\n if pool[-1]>=curr:\n return True\n\n //4. checking for remaining pool elements\n for i in range(len(pool)):\n //5. we decided to pick current Element the new total(curr) is updated and checked for new pool size with removed element\n // we want other player to LOSE\n // i.e if CURRENT pick this ith element and force the OTHER player to LOSE CURRENT player will WIN\n if not f(pool[:i]+pool[i+1:],curr-pool[i]):\n //6. if entered that means OTHER player LOST\n return True // CURRENT PLAYER WINS\n \n return False //7. CURRENT PLAYER LOST\n\n // 1 . initial pool\n pool = [(i+1) for i in range(n)]\n // 2 . check if for given pool can A force B to LOSE\n return f(pool,total)\n\nExplaining:\nA picks first\nAnd we can only have 2 scenario.\n\n !f() -> !f() -> !f() -> !f() -> arr[-1]>=tar\n T <- F <- T <- F <- return T\nTurn A B A B A WINS\n\n\n !f() -> !f() -> !f() -> !f() -> !f() -> arr[-1]>=tar\n F <- T <- F <- T <- F <- return T\nTurn A B A B A B WINS\n | | |\n \u25BC | |\n its A\'s turn| we want B not to WIN |\n \u25BC |\n its B\'s turn we want A not to WIN |\n |\n \'\'\'\' |\n \'\'\'\' \u25BC\n we reached end return True\n \n\n\nwhy We want B/A not to win or !f()?\nbecause on WINNING we are returning TRUE \n\nAnd we want B to LOSE i.e !f() = T for A\'s first choice\ni.e A picks and B LOST\n A picks and !f()=!(F)=T\n\nand ultimately everything comes down to A\'s first choice\nso, if A\'s first choice is pool[i] and !f() = T , then A will WIN.\n\n```\n\n### Optimizing Code\n```\nclass Solution:\n def canIWin(self, n: int, total: int) -> bool:\n\n canReach = n*(n+1) // 2\n if canReach<total:return False\n if canReach == total:return n%2\n dic = {}\n def f(arr,curr):\n if arr[-1]>=curr:\n return True\n if tuple(arr) in dic:\n return dic[tuple(arr)]\n for i in range(len(arr)):\n if not f(arr[:i]+arr[i+1:],curr-arr[i]):\n dic[tuple(arr)] = True\n return True\n dic[tuple(arr)] = False\n return False\n temp = [(i+1) for i in range(n)]\n return f(temp,total)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python Topdown DP with Bitmasking
|
can-i-win
| 0
| 1
|
# Intuition\nUse dp with memo to simulate the game.\n\n# Complexity\n\nAssume m = `maxChoosableInteger`, n = `desiredTotal`. We will have $$n * 2^m$$ combinations for dp.\n\n- Time complexity: $$O(n * 2^m)$$\n- Space complexity: $$O(n * 2^m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n # no one can win\n if sum(range(1, maxChoosableInteger + 1)) < desiredTotal:\n return False\n\n # dp choosable integers 1 to maxChoosableInteger, i - 1\n # bitmasking\n choosable = (1 << maxChoosableInteger) - 1\n\n @cache\n def dp(choosable, target):\n for i in range(maxChoosableInteger):\n if choosable >> i & 1:\n # let the first bit represent maxChoosableInteger\n item = maxChoosableInteger - i\n\n # win this turn\n if target - item <= 0:\n return True\n\n # opponent cannot win\n if not dp(choosable - (1 << i), target - item):\n return True\n\n # opponent can always win\n return False\n\n return dp(choosable, desiredTotal)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python3 - Memoization
|
can-i-win
| 0
| 1
|
# Intuition\nI didn\'t know how to do this, so I just tried it from the base case and recursed. It required a special test to see if the game were winnable at all, since the recursion is based on the assumption that the other playing forcing a win means you losing (as opposed to a draw)\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n if maxChoosableInteger * (maxChoosableInteger + 1) < desiredTotal + desiredTotal:\n return False\n @lru_cache(None)\n def r(tot, key):\n nonlocal maxChoosableInteger\n nonlocal desiredTotal\n for i in range(1, maxChoosableInteger+1):\n if ((1<<i) & key) == 0:\n if tot + i >= desiredTotal:\n return True\n elif not r(tot + i, key + (1<<i)):\n return True\n return False\n return r(0, 0)\n \n\n\n```\n\n# But ...\n\nSomething was bothering me though. tot was a function of key, so, a redundancy. So I tried combining them, but that slowed things down, even if just a little\n\n# Code\n\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n if maxChoosableInteger * (maxChoosableInteger + 1) < desiredTotal + desiredTotal:\n return False\n @lru_cache(None)\n def r(key):\n nonlocal maxChoosableInteger\n nonlocal desiredTotal\n tot = 0\n for i in range(1, maxChoosableInteger+1):\n if ((1<<i) & key):\n tot += i\n\n for i in range(1, maxChoosableInteger+1):\n if ((1<<i) & key) == 0:\n if tot + i >= desiredTotal:\n return True\n elif not r(key + (1<<i)):\n return True\n return False\n return r(0)\n\n```\n\n
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python | bitmask
|
can-i-win
| 0
| 1
|
# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n if (1+maxChoosableInteger)*maxChoosableInteger/2<desiredTotal:\n return False\n\n arr = [i for i in range(1, maxChoosableInteger+1)]\n\n @lru_cache(None)\n def dp(total, mask):\n if total <= 0:\n return True\n\n if total>0 and bin(mask)[2:] == "1"*maxChoosableInteger:\n return False\n\n for i in range(maxChoosableInteger):\n if arr[i]>=total and ((mask & (1<<i)) == 0):\n return True\n \n \n for i in range(maxChoosableInteger):\n if (mask & (1<<i)) == 0:\n if not dp(total-arr[i], mask | (1<<i)):\n return True\n\n return False\n \n\n return dp(desiredTotal, 0)\n \n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python DP Solution | Faster than 91% | Easy to Understand
|
can-i-win
| 0
| 1
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nJust choose one number out of the available list, update the available list and do a DFS from there\n\n# Code\n```python []\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n candidate = list(range(1, maxChoosableInteger + 1))\n if sum(candidate) < desiredTotal:\n return False\n \n @cache\n def dp(candidate: List[int], remainingTotal: int) -> bool:\n if candidate[-1] >= remainingTotal:\n return True\n for i in range(len(candidate)):\n if not dp(candidate[:i] + candidate[i + 1:], remainingTotal - candidate[i]):\n return True\n return False\n\n return dp(tuple(candidate), desiredTotal)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Top-down memo/python simple solution
|
can-i-win
| 0
| 1
|
# Intuition\nPlayer 1 can win if and only if Player 2 cannot win\n\n# Approach\nFor each number available, if one of them can lead to player 2\'s loss, then player 1 win\n\n# Complexity\n- Time complexity:\nO(N), N length of available candidate\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def canIWin(self, maxChoosableInteger: int, desiredTotal: int) -> bool:\n # 1,2,3,4,5 -> player 1\n # 2,3,4,5 -> player 2, choose any of them, cannot win\n # Then 1 win\n candidate = [i for i in range(1, maxChoosableInteger + 1)]\n\n if sum(candidate) < desiredTotal:\n return False\n \n memo = dict()\n def dfs(candidate, remain):\n if candidate[-1] >= remain:\n return True\n \n if tuple(candidate) in memo:\n return memo[tuple(candidate)]\n \n for i in range(len(candidate)):\n if not dfs(candidate[:i] + candidate[i + 1:], remain - candidate[i]):\n memo[tuple(candidate)] = True\n return True\n \n memo[tuple(candidate)] = False\n return False\n \n return dfs(candidate, desiredTotal)\n```
| 0
|
In the "100 game " two players take turns adding, to a running total, any integer from `1` to `10`. The player who first causes the running total to **reach or exceed** 100 wins.
What if we change the game so that players **cannot** re-use integers?
For example, two players might take turns drawing from a common pool of numbers from 1 to 15 without replacement until they reach a total >= 100.
Given two integers `maxChoosableInteger` and `desiredTotal`, return `true` if the first player to move can force a win, otherwise, return `false`. Assume both players play **optimally**.
**Example 1:**
**Input:** maxChoosableInteger = 10, desiredTotal = 11
**Output:** false
**Explanation:**
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
**Example 2:**
**Input:** maxChoosableInteger = 10, desiredTotal = 0
**Output:** true
**Example 3:**
**Input:** maxChoosableInteger = 10, desiredTotal = 1
**Output:** true
**Constraints:**
* `1 <= maxChoosableInteger <= 20`
* `0 <= desiredTotal <= 300`
| null |
Python 3 || Count The Repetitions || T/M: 34 ms / 13.9 MB 100% / 96%
|
count-the-repetitions
| 0
| 1
|
```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n\n rec, track = [0], defaultdict(int) \n ct = start = ptr1 = ptr2 = 0\n\n if not set(s2).issubset(set(s1)): return 0\n\n s1 = \'\'.join(char for char in s1 if char in set(s2))\n \n while True:\n for char in s2:\n ptr = s1.find(char, start)\n if ptr == -1:\n ct += 1\n ptr = s1.find(char)\n start = ptr+1\n rec.append(ct + 1)\n\n if rec[-1] > n1: return (len(rec)-2)//n2\n\n if ptr not in track: track[ptr] = len(rec)-1\n else: break\n \n cycleStart = rec[track[ptr]]\n cycle1, cycle2 = ct+1 - cycleStart, len(rec)-1 - track[ptr]\n rest = n1 - cycleStart\n \n rem = cycleStart + rest%cycle1\n\n while rec[ptr2] <= rem: ptr2+= 1\n\n return (cycle2 * (rest//cycle1) + ptr2-1)//n2\n```\n[https://leetcode.com/problems/count-the-repetitions/submissions/864907562/](http://)\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*).
| 3
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
Solution
|
count-the-repetitions
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int getMaxRepetitions(string s1, int n1, string s2, int n2) {\n vector<int> rapport(102,-1);\n vector<int> rest(102,-1);\n int b=-1;int posRest=0;int rap=0;\n int last=-1;\n rapport[0]=rest[0]=0;\n for(int i=1;i<=s2.size()+1;i++){\n int j;\n for(j=0;j<s1.size();j++){\n if(s2[posRest]==s1[j]){\n posRest++;\n if(posRest==s2.size()){\n rap++;\n posRest=0;\n }\n }\n }\n for(int k=0;k<i;k++){\n if(posRest==rest[k]){b=k;last=i;break;}\n }\n rapport[i]=rap;rest[i]=posRest;\n if(b>=0)break;\n }\n int interval=last-b;\n if(b>=n1)return rapport[n1]/n2;\n return ((n1-b)/interval*(rapport[last]-rapport[b])+rapport[(n1-b)%interval+b])/n2; }\n};\n```\n\n```Python3 []\nclass Solution(object):\n def getMaxRepetitions(self, s1, n1, s2, n2):\n start = {}\n s1_round, s2_round, s2_idx = 0, 0, 0\n while s1_round < n1:\n s1_round += 1\n for ch in s1:\n if ch == s2[s2_idx]:\n s2_idx += 1\n if s2_idx == len(s2):\n s2_round += 1\n s2_idx = 0\n if s2_idx in start:\n prev_s1_round, prev_s2_round = start[s2_idx]\n circle_s1_round, circle_s2_round = s1_round - prev_s1_round, s2_round - prev_s2_round\n res = (n1 - prev_s1_round)\n left_s1_round = (n1 - prev_s1_round) % circle_s1_round + prev_s1_round\n for key in start:\n val = start[key]\n if val[0] == left_s1_round:\n res += val[1]\n break\n return res \n else:\n start[s2_idx] = (s1_round, s2_round)\n return s2_round\n```\n\n```Java []\nclass Solution {\n public int getMaxRepetitions(String s1, int n1, String s2, int n2) {\n int l1 = s1.length(), l2 = s2.length();\n int[] next = new int[l2 + 1];\n int[] count = new int[l2 + 1];\n int cnt = 0, p = 0;\n for (int i = 0; i < n1; i++) {\n for (int j = 0; j < l1; j++) {\n if (s1.charAt(j) == s2.charAt(p)) {\n p++;\n }\n if (p == l2) {\n cnt++;\n p = 0;\n }\n }\n count[i] = cnt;\n next[i] = p;\n for (int j = 0; j < i; j++) {\n if (next[j] == p) {\n int prev_count = count[j];\n int pattern_count = (count[i] - count[j]) * ((n1 - j - 1) / (i - j));\n int remain_count = count[j + (n1 - j - 1) % (i - j)] - count[j];\n return (prev_count + pattern_count + remain_count) / n2;\n }\n }\n }\n return count[n1 - 1] / n2;\n }\n}\n```\n
| 200
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
java solution | 4ms runtime | with brief explanation
|
count-the-repetitions
| 1
| 1
|
# Explanation\n\n. For each repetition of s1, count the number of times we see s2\n. Store the seen count for each repetition of s1\n. Store the index of s2 where we stopped after each repetition of s1\n. For each repetition of s1, check if we\'ve seen this index of s2 before\n. If we have, then we\'ve found a repeating pattern\n. The number of times we see s2 in the pattern is (count[k] - count[start])\n. The number of times we see s2 outside the pattern is (count[start + (n1 - start) % (k - start)] - count[start])\n. The number of times we see s2 in total is (prefixCount + patternCount + suffixCount)\n. The number of times we see s2 in total divided by n2 is the answer\n\n# Code\n```\n// Count the repetitions\n// LeetCode: https://leetcode.com/problems/count-the-repetitions/\n\nclass Solution {\n public int getMaxRepetitions(String s1, int n1, String s2, int n2) {\n int[] next = new int[s2.length() + 1];\n int[] count = new int[s2.length() + 1];\n int j = 0, cnt = 0;\n for (int k = 1; k <= n1; k++) {\n for (int i = 0; i < s1.length(); i++) {\n if (s1.charAt(i) == s2.charAt(j)) {\n j++;\n if (j == s2.length()) {\n j = 0;\n cnt++;\n }\n }\n }\n count[k] = cnt;\n next[k] = j;\n for (int start = 0; start < k; start++) {\n if (next[start] == j) {\n int prefixCount = count[start];\n int patternCount = (count[k] - count[start]) * ((n1 - start) / (k - start));\n int suffixCount = count[start + (n1 - start) % (k - start)] - count[start];\n return (prefixCount + patternCount + suffixCount) / n2;\n }\n }\n }\n return count[n1] / n2;\n }\n}\n```\n```C++[]\nclass Solution {\npublic:\n int getMaxRepetitions(string s1, int n1, string s2, int n2) {\n vector<int> rapport(102,-1);\n vector<int> rest(102,-1);\n int b=-1;int posRest=0;int rap=0;\n int last=-1;\n rapport[0]=rest[0]=0;\n for(int i=1;i<=s2.size()+1;i++){\n int j;\n for(j=0;j<s1.size();j++){\n if(s2[posRest]==s1[j]){\n posRest++;\n if(posRest==s2.size()){\n rap++;\n posRest=0;\n }\n }\n }\n for(int k=0;k<i;k++){\n if(posRest==rest[k]){b=k;last=i;break;}\n }\n rapport[i]=rap;rest[i]=posRest;\n if(b>=0)break;\n }\n int interval=last-b;\n if(b>=n1)return rapport[n1]/n2;\n return ((n1-b)/interval*(rapport[last]-rapport[b])+rapport[(n1-b)%interval+b])/n2; }\n};\n```\n```python3 []\nclass Solution(object):\n def getMaxRepetitions(self, s1, n1, s2, n2):\n start = {}\n s1_round, s2_round, s2_idx = 0, 0, 0\n while s1_round < n1:\n s1_round += 1\n for ch in s1:\n if ch == s2[s2_idx]:\n s2_idx += 1\n if s2_idx == len(s2):\n s2_round += 1\n s2_idx = 0\n if s2_idx in start:\n prev_s1_round, prev_s2_round = start[s2_idx]\n circle_s1_round, circle_s2_round = s1_round - prev_s1_round, s2_round - prev_s2_round\n res = (n1 - prev_s1_round)\n left_s1_round = (n1 - prev_s1_round) % circle_s1_round + prev_s1_round\n for key in start:\n val = start[key]\n if val[0] == left_s1_round:\n res += val[1]\n break\n return res \n else:\n start[s2_idx] = (s1_round, s2_round)\n return s2_round\n```\n\n\n
| 0
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
Geez. Mad coz bad. /\
|
count-the-repetitions
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n if n1 == 0:\n return 0\n\n # Count the number of occurrences of s2 in each repetition of s1\n repeat_count = {} # Map of count2: (count1, next_index)\n count1, count2 = 0, 0\n next_index = 0\n\n while count1 < n1:\n for i in range(len(s1)):\n if s1[i] == s2[next_index]:\n next_index += 1\n if next_index == len(s2):\n next_index = 0\n count2 += 1\n\n count1 += 1\n\n if next_index in repeat_count:\n # Found a repeating pattern\n prev_count1, prev_count2 = repeat_count[next_index]\n pattern_count1 = count1 - prev_count1\n pattern_count2 = count2 - prev_count2\n pattern_repetitions = (n1 - prev_count1) // pattern_count1\n remaining_count1 = (n1 - prev_count1) % pattern_count1\n\n count2 = prev_count2 + pattern_count2 * pattern_repetitions\n count1 = prev_count1 + pattern_count1 * pattern_repetitions\n\n # Calculate remaining occurrences within the partial pattern\n for _ in range(remaining_count1):\n for char in s1:\n if char == s2[next_index]:\n next_index += 1\n if next_index == len(s2):\n next_index = 0\n count2 += 1\n\n break\n else:\n repeat_count[next_index] = (count1, count2)\n\n return count2 // n2\n\n```
| 0
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
Simple Python solution
|
count-the-repetitions
| 0
| 1
|
# Code\n```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n l1, l2 = len(s1), len(s2)\n visited = {}\n index = repeat_count = i = 0\n while i < n1:\n print(i)\n for j in range(l1):\n if s1[j] == s2[index]:\n index += 1\n if index == l2:\n index = 0\n repeat_count += 1\n if index in visited:\n prev_i, prev_repeat_count = visited[index]\n r = (n1-1-i) // (i-prev_i)\n i += (i-prev_i)*r\n repeat_count += (repeat_count-prev_repeat_count )*r\n visited = {}\n else:\n visited[index] = [i, repeat_count]\n i += 1\n return repeat_count // n2\n```
| 0
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
Python 3 -- Short Simple solution
|
count-the-repetitions
| 0
| 1
|
```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n dp = []\n for i in range(len(s2)):\n start = i\n cnt = 0\n for j in range(len(s1)):\n if s1[j] == s2[start]:\n start += 1\n if start == len(s2):\n start = 0\n cnt += 1\n dp.append((start,cnt))\n res = 0\n next = 0\n for _ in range(n1):\n res += dp[next][1]\n next = dp[next][0]\n return res // n2\n\t\t\n```
| 2
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
O(m*n) Python3 Solution
|
count-the-repetitions
| 0
| 1
|
\nIn my code, the first function defined what "contain" is and the second function is to find maximum m.\n\nWe know that, in the best case:\n S1 = s1*n1\n S2 = s2*n2\nWe compute the quotient of lengths of S1 and S2, which is M in the code and M is the best repetition we can get.\nAnd count down from M, return the repetition as long as S1 contains S2.\n\nFor example:\nif the length of S1 is 12, and S2\'s length is 3, the largest (best) m could be 4, or less, \nif 4*S2 can\'t meet the condition, then let m be 3, and check again.\nThis way, we only check 4 times at worst.\n\n```\ndef Contain(L1,L2):\n for i in range(len(L2)):\n if L2[i] in L1:\n L1 = L1[L1.index(L2[i]):]\n else:\n return False\n return True\n\ndef getMaxRepetitions(s1,n1,s2,n2):\n S1 = s1*n1\n S2 = s2*n2\n M = int(len(S1)//len(S2))\n for m in range(M,1,-1):\n if Contain(S1,S2*m):\n return m\n\n\n```\n\n ===================================================== 4/22/2019 Update =====================================================\n\nThanks to @luzi82 for pointing out my problem.\nIn this part, if the range is from M to 1, it\'ll exclude m=1\n```\nfor m in range(M,1,-1):\n if Contain(S1,S2*m):\n return m\n```\nI changed it into:\n```\nfor m in range(M,0,-1):\n if Contain(S1,S2*m):\n return m\n```\nAnd it worked for the cases of 1 repetition.\n\nAnd as for the case:\ns1="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"\nn1=1000000\nRunning time is up to 48s \nThe main part slowing things down is the calculation: S1 = s1n1\nWhen n1 is really large, this algorithm could be really slow.\n\nWhat\'s sarcastic is that I used the title \'fast solution\' when I first posted this answer.\nI\'ll keep updated on this section with better solution. \nAnd you\'re very welcome to give me some feedback and to let me know how to improve the algorithm. \n\n
| 1
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
[Python3] repeating patterns
|
count-the-repetitions
| 0
| 1
|
\n```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n cnt = idx = 0 \n count = []\n index = []\n for i in range(n1): \n for ch in s1: \n if ch == s2[idx]: \n idx += 1\n if idx == len(s2): \n cnt += 1\n idx = 0 \n count.append(cnt)\n index.append(idx)\n for ii in range(i): \n if index[ii] == idx: \n prev = count[ii]\n repeat = (cnt - prev) * ((n1-1-ii) // (i - ii))\n post = count[ii + (n1-1-ii) % (i-ii)] - count[ii]\n return (prev + repeat + post) // n2\n return count[-1]//n2\n```
| 0
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
python3 O(|S1|* |S2|) solution, with detailed explanation (beats 100%)
|
count-the-repetitions
| 0
| 1
|
\n\n\nThis is a quite tricky solution. It took me a day to understand the [discussion here](httphttps://leetcode.com/problems/count-the-repetitions/discuss/95397/C%2B%2B-0ms-O(str1.length*str2.length)://):\n\nThe basic idea is to detect the repeating pattern of S2 in multiple concated S1. After we find, say, `x1->x2` passes of S2 can be made from `y1->y2` passes of S1, then it means that n1 passes of S1 can make X passes of S2. And X is made from 2 parts:\n\n1. repeating part: `(n1 - y1)//(y2 - y1) * (x2-x1)`\n2. remaining part: `(n1 - y1)%(y2 - y1) + y1 *`\n\nNow the question is how to find out `x1, x2`, `y1, y2`:\n```\nclass Solution:\n def getMaxRepetitions(self, s1: str, n1: int, s2: str, n2: int) -> int:\n pass2s = [-1]*(len(s2) + 1) # pass2s[i]: i pass1 can make pass2s[i] passes of pass2\n index2s = [-1]*(len(s2) + 1) # index2s[i]: i pass1 match up to (not including) the pass2s[i] character of S2; all values in index2s should be different, otherwise we will catch the same value and return, as seen in the code below\n\t\t# initially without any pass S1:\n pass2s[0] = index2s[0] = 0\n index2 = 0\n pass2 = 0\n for pass1 in range(1, n1+1): # this outer loop will break within min(n1, n2) iterations\n for index1 in range(len(s1)): # use current pass of S1 to match as many characters in S2 as we can\n if s1[index1] == s2[index2]:\n index2 += 1\n if index2 == len(s2):\n index2 = 0\n pass2 += 1\n\t\t\t# now we know at pass1, how many pass2 we can make, and what the final stopping character\n index2s[pass1] = index2\n pass2s[pass1] = pass2\n\t\t\t\n # detect repeating pattern\n for i in range(pass1): # try fo find one prevous pass1 that can stop at the same character\n if index2s[i] == index2:\n\t\t\t\t\t# now we\'d like to match index^th character of S2, and we find that one previous pass1, i.e. the i^th pass, can already match that, then the repeating pattern is detected\n repeating_counts, remain = divmod(n1 - i, pass1 - i)\n ans = repeating_counts * (pass2s[pass1]-pass2s[i])\n ans += pass2s[i + remain]\n\t\t\t\t\t# ans here means that we can make ans passes of S2\n return ans // n2\n\t\t# if repeating pattern found, then just use all passes of S1, i.e. n1 to make S2\n return pass2s[n1] // n2\n \n```\n\nTotal compleity: \n- Outer Loop: O(min(n1, S2))\n- Innter Loop: O(S1)\n\nSo total complexity is O(|S1| * |S2|)
| 0
|
We define `str = [s, n]` as the string `str` which consists of the string `s` concatenated `n` times.
* For example, `str == [ "abc ", 3] == "abcabcabc "`.
We define that string `s1` can be obtained from string `s2` if we can remove some characters from `s2` such that it becomes `s1`.
* For example, `s1 = "abc "` can be obtained from `s2 = "ab**dbe**c "` based on our definition by removing the bolded underlined characters.
You are given two strings `s1` and `s2` and two integers `n1` and `n2`. You have the two strings `str1 = [s1, n1]` and `str2 = [s2, n2]`.
Return _the maximum integer_ `m` _such that_ `str = [str2, m]` _can be obtained from_ `str1`.
**Example 1:**
**Input:** s1 = "acb", n1 = 4, s2 = "ab", n2 = 2
**Output:** 2
**Example 2:**
**Input:** s1 = "acb", n1 = 1, s2 = "acb", n2 = 1
**Output:** 1
**Constraints:**
* `1 <= s1.length, s2.length <= 100`
* `s1` and `s2` consist of lowercase English letters.
* `1 <= n1, n2 <= 106`
| null |
Python3 - 100% Count unique start, length tuples
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Explanation\nIn this problem, a unique substring can be defined as a starting character and length. Also, this is my first 100% ever, so I\'m a little excited :) The proc() method was just so I didn\'t have to copy/paste the same handler code in two places (when I\'m done and when a run is broken)\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n \n ia = list(map(lambda x:ord(x) - ord(\'a\'), p))\n\n runs = {i: 0 for i in range(26)}\n st, r, la = ia[0], 1, ia[0]\n def proc():\n nonlocal st, r, la\n nonlocal runs\n for i in range(27):\n if runs[st]<r:\n runs[st]=r\n st, r = (st+1)%26, r - 1\n if r<=0:\n break\n\n\n for i in ia[1:]:\n if i == la + 1 or la == 25 and i == 0:\n st, r, la = st, r + 1, i\n else:\n proc()\n st, r, la = i, 1, i\n proc()\n\n ret = 0\n for i in runs.values():\n ret += i\n\n return ret\n\n\n\n```
| 1
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python solution with explanation
|
unique-substrings-in-wraparound-string
| 0
| 1
|
This is basically @fire4fly\'s solution but since there was no explanation I needed some time to figure out what exactly is being done and hopefully i\'ll help someone else with this post.\n\n**Solution**\n\nWe are doing a one pass on the string. On each step we compare if our current and previous character are one after the other in the alphabet - with wrapping over for \'z\' and \'a\' (the % 26 helps with that).\n\nThe goal is to count for each character in `p` what\'s the longest matching substring before that character. We store the longest substring before the character in our dict `d`, and at the end return sum of all values in dict. Our dict[x] for letter `x` is actually storing the ammount of unique combinations we found that end with that letter `x`.\n\n**Example**\nIf our string is `p = "abczbcde"`, our dict at the end will look something like this:\n`\'a\': 1, \'b\': 2, \'c\': 3, \'z\': 1, \'d\': 3, \'e\': 4}`\nThis means our final result is 14 unique strings.\nWhen we iterate through the first 4 characters(`abcz`) we will find 7 unique combinations:\n`a, b, ab, c, bc, abc, z` \nand our dict will look like:\n`\'a\': 1, \'b\': 2, \'c\': 3, \'z\': 1`\nOnce we get to the `bcde` part of the string, when we evaluate the `b` and `c`, they will have shorter streaks of matching characters before them, so we won\'t overwrite the values in our dict for those characters - because basically we already found the combinations `b, c, bc` before that, and the only remaining unique combinations are:\n`d, bcd, cd, e, de, bcde, cde`\n\n**Code**\n```class Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n from collections import defaultdict\n d = defaultdict(int)\n streak = 0 \n for i in range(len(p)):\n streak = streak + 1 if (ord(p[i - 1]) - 96) % 26 == (ord(p[i]) - 97) else 1\n d[p[i]] = max(d[p[i]], streak)\n return sum(d.values())```
| 15
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
467: Solution with step by step explanation
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. If s is empty, return 0.\n2. Create an empty dictionary called count to keep track of the maximum length of substring that ends with each character in s.\n3. Initialize curr_count and max_len to 0 and 1 respectively, and prev to the first character in s.\n4. Iterate over each character c in s.\n5. If the difference between the ASCII values of c and prev is 1 or 25 (the distance between \'a\' and \'z\' in a circular manner), increment max_len by 1. Otherwise, reset max_len to 1.\n6. If max_len is greater than or equal to curr_count, update curr_count to max_len. Otherwise, reset curr_count to 1.\n7. Set the value of count[c] to the maximum of its current value and curr_count.\n8. Update prev to c.\n9. Return the sum of the values in count.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n if not s:\n return 0\n \n count = {}\n curr_count = 0\n max_len = 1\n prev = s[0]\n \n for i in range(len(s)):\n if ord(s[i]) - ord(prev) == 1 or ord(prev) - ord(s[i]) == 25:\n max_len += 1\n else:\n max_len = 1\n \n if max_len >= curr_count:\n curr_count = max_len\n else:\n curr_count = 1\n \n count[s[i]] = max(count.get(s[i], 0), curr_count)\n \n prev = s[i]\n \n return sum(count.values())\n\n```
| 2
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python || dynamic programming || dictionaries || faster than 91%
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstoring the largest length of first character of substring in s which is also present in base\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n if len(s) == 1:return 1\n prev = ord(s[-1])\n j = len(s) - 1\n dp = [0] * 26\n dp[prev - 97] = 1\n for i in range(len(s) - 2, -1, -1):\n v = ord(s[i])\n l = 1\n n = 97 if s[i] == \'z\' else v + 1\n if prev == n:\n l = j - i + 1\n else:\n j = i\n if l > dp[v - 97]: dp[v - 97] = l\n prev = v\n return sum(dp)\n\n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
python3 solution for me bp
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n seen = {chr(97+i): 0 for i in range(26)}\n #print(seen)\n start = 0\n end = 0\n for end, ltr in enumerate(s):\n #print(ord(\'a\'),ord(s[end])-97, ord(s[start])-97, (ord(s[end])-97-ord(s[start])+97) , (end - start) % 26)\n if (ord(s[end])-97-ord(s[start])+97) % 26 == (end - start) % 26:\n \n continue\n while start < end:\n seen[s[start]] = max(seen[s[start]], end-start)\n start += 1\n while start <= end:\n seen[s[start]] = max(seen[s[start]], end-start+1)\n start += 1\n \n answer = 0\n for key in seen.keys():\n x = seen[key]\n answer += x\n #print(seen)\n\n\n return answer\n \n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Linear solution
|
unique-substrings-in-wraparound-string
| 0
| 1
|
## Approach \n\nWe have to find continuous or increasing substring where difference between consecutive elements is 1, and record no. of elements appeared before them against each of the elements. If we find a break in the subarray then reset the counter to 1, and then continue in same fashion. When encountered an element which has appeared before we have to record largest value for that element. See below example for more understanding. \n\n```\ncurrent , previous\n# Setting the counter \nif current - previous == 1 or current == \'a\' and previous == \'z\' : \n counter += 1 # increse the counter as our sequence continues \n else : counter = 1 # reset the counter as sequence breaks \n \n # Assigning the counter values \n if current exists already : \n count[current] = maximum(count[current], counter) \n else : # counter doesn\'t exist or is appearing for first time \n count[current] = counter \n```\n \n\n \n\n*Do this for all the elements except first and return sum of all the counts.*\n\n**Illustration**\n\n``` \nstring = abckdefxabcdxde\n\ncounter, current:count[current]\n\n1, a:1\n\n2, b:2 \n\n3, c:3\n\n1, k:1\n\n1, d:1\n\n2, e:2\n\n3, f:3\n\n1, x:1 \n\n1, a:1\n\n2, b:2\n\n3, c:3\n\n4, d:4\n\n1, x:1 \n\n1, d:4\n\n2, e:2\n```\n\nTime Complexity : O(N) \n\n \n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n count, n, so_far = {}, len(s), 1\n count[s[0]] = so_far \n for i in range(1,n):\n curr, prev = s[i], s[i-1]\n if (ord(curr) - ord(prev) == 1) or (curr == \'a\' and prev == \'z\'): so_far += 1 \n else : so_far = 1 \n if curr in count : count[curr] = max(count[curr], so_far) \n elif not (curr in count) : count[curr] = so_far \n\n # print(count)\n return sum(count.values())\n\n\n \n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
O(n) time one pass Python Solution
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n s += ","\n res = 0\n dp = [0] * 26\n count = 1\n for i in range(len(s)-1):\n if (s[i]==\'z\' and s[i+1]==\'a\') or (ord(s[i]) == ord(s[i+1])-1):\n count += 1\n else:\n count = 1\n res += max((count-dp[ord(s[i])-ord(\'a\')]),0)\n dp[ord(s[i])-ord(\'a\')] = max(dp[ord(s[i])-ord(\'a\')], count)\n return res\n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Solution
|
unique-substrings-in-wraparound-string
| 1
| 1
|
```C++ []\nclass Solution {\npublic:\n int findSubstringInWraproundString(string s) {\n vector<long long> mxAlpha(26);\n int n = s.length();\n long long ans = 0;\n for(int i=0;i<n;i++)\n {\n int st = i, len=0;\n char ch = s[i];\n while(i<n && s[i]==ch){\n i++;\n len++;\n if(ch==\'z\') ch = \'a\';\n else ch++;\n }\n st = s[st]-\'a\';\n bool flag = 1;\n for(int j = st;len-- && (flag || j!=st);j = (j+1)%26){\n \n flag = 0;\n if(len+1>mxAlpha[j]){\n ans+=len+1;\n ans -= mxAlpha[j];\n mxAlpha[j] = len+1;\n } \n } \n --i;\n }\n return ans; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n table = {c:value for c, value in zip("abcdefghijklmnopqrstuvwxyz", "bcdefghijklmnopqrstuvwxyza")}\n first, cnt = s[0], 1\n _next = table[first]\n record = []\n for c in s[1:]:\n if c==_next:\n cnt += 1\n else:\n record.append((cnt, first))\n first, cnt = c, 1\n _next = table[c]\n record.append((cnt, first))\n max_length = max(cnt for cnt, c in record)\n min_bound = max(max_length-26, 0)\n result = min_bound*26\n dp = {i:set() for i in range(max_length, min_bound, -1)}\n indics = "abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyz"\n for cnt, c in record:\n if cnt>min_bound:\n idx = ord(c)-97\n for l, i in enumerate(range(cnt, min_bound, -1), 1):\n dp[i].update(indics[idx:idx+l])\n return result+sum(len(values) for values in dp.values())\n```\n\n```Java []\nclass Solution {\n public int findSubstringInWraproundString(String s) {\n char[] str = s.toCharArray();\n int n = str.length;\n int ans = 0;\n int len = 1;\n int[] max = new int[256];\n max[str[0]] = 1;\n for(int i = 1; i < n; i++){\n char cur = str[i];\n char pre = str[i - 1];\n if((cur == \'a\' && pre == \'z\') || cur == pre + 1){\n len++;\n }else{\n len = 1;\n }\n max[cur] = Math.max(max[cur],len);\n }\n for(int i = 0; i < max.length; i++){\n ans += max[i];\n }\n return ans;\n}\n}\n```\n
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python concise sliding window solution
|
unique-substrings-in-wraparound-string
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s: str) -> int:\n\n\n left=0\n d=defaultdict(int)\n\n for right,ch in enumerate(s):\n if right==0:\n d[ch]=1\n prev=ch\n continue\n\n if not(ord(ch)-ord(prev)==1) and not(ord(prev)-ord(ch))==25:\n left=right\n \n\n d[ch]=max(d[ch],right-left+1)\n \n prev=ch\n \n return sum(d.values())\n \n \n \n \n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
python DP bottom-up solution
|
unique-substrings-in-wraparound-string
| 0
| 1
|
```\nclass Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n dp = [1] * len(p)\n res=0\n counter = {\'a\': 0, \'b\': 0, \'c\': 0, \'d\': 0, \'e\': 0, \'f\': 0, \'g\': 0, \'h\': 0, \'i\': 0, \'j\': 0, \'k\': 0, \'l\': 0\n , \'m\': 0, \'n\': 0, \'o\': 0, \'p\': 0, \'q\': 0, \'r\': 0, \'s\': 0, \'t\': 0, \'u\': 0, \'v\': 0, \'w\': 0, \'x\': 0, \'y\': 0, \'z\': 0}\n\n for i in range(1,len(p)):\n if ord(p[i]) - ord(p[i-1]) == 1 or p[i-1] == \'z\' and p[i] == \'a\':\n dp[i] += dp[i-1]\n\n for i in range(len(dp)):\n res += max(0,dp[i]-counter[p[i]])\n counter[p[i]] = max(counter[p[i]],dp[i])\n\n return res\n\n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python O(n)
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Intuition\n- We need to check consequtive characters to have sequential values (by module 26).\n- To maintain uniquiness we will be keeping track of longest substrings, that start at given value (first substring character defines the whole substring).\n\n# Approach\nWe can tackle that as a DP problem. \nLet\'s consider substring "abc" - this substring implies 6 wraparound string substrings - "abc", "ab", "a", "bc", "b", "c" - thus for each starting character we will be looking for a longest substring of the wraparound string which starts at this character. \nWe will also go backwards to get "suffices" subsrtings first - like in the example above - "c" and "bc".\n\n1. Initialize array ``dp`` of the length of the input string filled with ones - as long as every single character is a substring of the wraparound string.\n2. Initialize array ``starts`` which will contain longest substrings starting with the character ``chr(starts[i])`` in the input string.\n3. We will iterate characters of the input string backwards, and check if character at ``i`` has the previous value to the character at ``i+1``. At each iteration we update ``starts`` array with the information from the current character\n4. As long as ``starts`` array contain longest substrings starting with given character, and every prefix of this string is also wraparound string substring, each item of this array contains the number of substrings starting from the given character. So we sum it up and return as the result.\n\n# Complexity\n- Time complexity:\nWe iterate over string once - $$O(n)$$\n\n- Space complexity:\nWe have ``dp`` array of the string length, and starts array of the number of characters in the alphabet - 26, it\'s a constant in this problem.\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n n = len(p)\n dp = [1] * n\n starts = [0] * 26\n for i in range(n-1, -1, -1):\n if i < n-1 and ord(p[i+1])-ord(\'a\') == (ord(p[i])-ord(\'a\') + 1) % 26:\n dp[i] = dp[i+1] + 1\n starts[ord(p[i]) - ord(\'a\')] = max(starts[ord(p[i]) - ord(\'a\')], dp[i])\n return sum(starts)\n```\n\nMemory could be optimized to $$O(1)$$ as long as we only use previous step value.\n\n```\nclass Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n n = len(p)\n starts = [0] * 26\n dp = 1\n for i in range(n-1, -1, -1):\n if i < n-1 and ord(p[i+1])-ord(\'a\') == (ord(p[i])-ord(\'a\') + 1) % 26:\n dp += 1\n else:\n dp = 1\n starts[ord(p[i]) - ord(\'a\')] = max(starts[ord(p[i]) - ord(\'a\')], dp)\n return sum(starts)\n```\n\n\nShall you have questions or concerns - please comment, and upvote if you like it!
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python (Simple Maths)
|
unique-substrings-in-wraparound-string
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubstringInWraproundString(self, s):\n n, dict1, count = len(s), {i:1 for i in s}, 1\n\n for i in range(1,n):\n if (ord(s[i]) - ord(s[i-1]))%26 == 1:\n count += 1\n else:\n count = 1\n\n dict1[s[i]] = max(dict1[s[i]],count)\n\n return sum(dict1.values())\n\n \n\n\n\n\n \n```
| 0
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Python3 DP O(N) time O(1) space
|
unique-substrings-in-wraparound-string
| 0
| 1
|
Count the number of substrings ending at a letter. To do so, and to avoid counting duplicates, we only need to find the largest substring ending in the letter. The number of substrings ending at that letter is simply the length of that max substring.\n\ne.g.\nConsider p = abcdzabc\n\n**Consecutive Substrings ending in c**:\nabc\nbc\nc\nzabc\nabc\nbc\nc\n\nThe max length substring ending in c: zabc\nSo number of *unique* substrings ending in c is 4\n\nThe sum of the max lengths substring ending with each of the distinct letters in p will be the answer.\n```\nclass Solution:\n def findSubstringInWraproundString(self, p: str) -> int:\n consecutive = 1\n \n # stores the maximum length of a substring ending at a character \n maxSubstr = defaultdict(int)\n maxSubstr[p[0]] = 1\n \n ans = 0\n for x in range(1, len(p)):\n if ord(p[x]) - ord(p[x - 1]) == 1 or p[x] == \'a\' and p[x - 1] == \'z\':\n consecutive += 1\n else:\n consecutive = 1\n maxSubstr[p[x]] = max(maxSubstr[p[x]], consecutive)\n \n return sum(maxSubstr.values())\n```\nSince p only contains lowercase letters, maxSubstr will have at most 26 elements, and thus O(1) space
| 1
|
We define the string `base` to be the infinite wraparound string of `"abcdefghijklmnopqrstuvwxyz "`, so `base` will look like this:
* `"...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd.... "`.
Given a string `s`, return _the number of **unique non-empty substrings** of_ `s` _are present in_ `base`.
**Example 1:**
**Input:** s = "a "
**Output:** 1
**Explanation:** Only the substring "a " of s is in base.
**Example 2:**
**Input:** s = "cac "
**Output:** 2
**Explanation:** There are two substrings ( "a ", "c ") of s in base.
**Example 3:**
**Input:** s = "zab "
**Output:** 6
**Explanation:** There are six substrings ( "z ", "a ", "b ", "za ", "ab ", and "zab ") of s in base.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
|
One possible solution might be to consider allocating an array size of 26 for each character in the alphabet. (Credits to @r2ysxu)
|
Doubt: Inbuilt function answer not Accepted
|
validate-ip-address
| 0
| 1
|
Can anybody tell me why this Solution didn\'t work?\n```\nimport ipaddress\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n try:\n address = ipaddress.ip_address(queryIP)\n if address.version == 4:\n return "IPv4"\n elif address.version == 6:\n return "IPv6"\n else:\n return "Neither"\n except ValueError:\n return "Neither"\n```\n\nAlso,\n\n\nIs 2001:db8:85a3:0::8a2E:0370:7334 a valid IP address or not ?
| 2
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
Python3 | Beats 100% | Easy to understand
|
validate-ip-address
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n if self.validIPv4(queryIP):\n return "IPv4"\n elif self.validIPv6(queryIP):\n return "IPv6"\n else:\n return "Neither"\n \n def validIPv4(self, ip):\n ip_split = ip.split(\'.\')\n # check length\n if len(ip) < 7 or len(ip) > 15 or len(ip_split) != 4:\n return False\n # check octets value\n for s in ip_split:\n try:\n octet = int(s)\n except:\n return False\n if octet < 0 or octet > 255 or (octet < 10 and len(s) != 1) or \\\n (10 <= octet < 100 and len(s) != 2) or (octet >= 100 and len(s) != 3):\n return False\n # check characters\n for c in ip:\n if not (\'0\' <= c <= \'9\' or c == \'.\'):\n return False \n return True\n \n def validIPv6(self, ip):\n ip_split = ip.split(\':\')\n # check length\n if len(ip) < 15 or len(ip) > 39 or len(ip_split) != 8:\n return False\n # check hex\n for s in ip_split:\n if not (1 <= len(s) <= 4):\n return False\n for c in s:\n if not (\'0\' <= c <= \'9\' or \'A\' <= c <= \'F\' or \'a\' <= c <= \'f\'):\n return False\n return True\n\n```
| 1
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
468: Solution with step by step explanation
|
validate-ip-address
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function that takes in a string IP and returns a string "IPv4", "IPv6" or "Neither" based on whether IP is a valid IPv4 address, a valid IPv6 address, or not a correct IP of any type.\n\n2. Check if "." is in IP. If yes, split IP by "." into four segments.\n\n3. If the length of segments is not equal to 4, return "Neither".\n\n4. Iterate over the segments and check if each segment is a digit, has a value between 0 and 255 (inclusive), and does not contain leading zeros.\n\n5. If any of the conditions in step 4 are not satisfied, return "Neither".\n\n6. If all segments pass the checks in step 4, return "IPv4".\n\n7. Check if ":" is in IP. If yes, split IP by ":" into eight segments.\n\n8. If the length of segments is not equal to 8, return "Neither".\n\n9. Iterate over the segments and check if each segment is a hexadecimal string, has a length of at most 4, and contains only digits, lowercase English letters (\'a\' to \'f\') and upper-case English letters (\'A\' to \'F\').\n\n10. If any of the conditions in step 9 are not satisfied, return "Neither".\n\n11. If all segments pass the checks in step 9, return "IPv6".\n\n12. If "." or ":" is not in IP, return "Neither".\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, IP: str) -> str:\n if "." in IP:\n segments = IP.split(".")\n if len(segments) != 4:\n return "Neither"\n for segment in segments:\n if not segment.isdigit() or not 0 <= int(segment) <= 255 or (segment[0] == "0" and len(segment) > 1):\n return "Neither"\n return "IPv4"\n elif ":" in IP:\n segments = IP.split(":")\n if len(segments) != 8:\n return "Neither"\n for segment in segments:\n if not segment or len(segment) > 4 or not all(c in string.hexdigits for c in segment):\n return "Neither"\n return "IPv6"\n return "Neither"\n\n```
| 4
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
Check for both cases
|
validate-ip-address
| 0
| 1
|
# Intuition\nCheck for both ipv4 and ipv6. Whiever returns true first is the answer.\nIf neither is true then answer is neither\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n\n #check for ipv4\n def check_ipv4(string):\n \n #split\n array = queryIP.split(".")\n \n if len(array) != 4:\n return False\n \n #check for any trailing zero\n for num in array:\n \n #empty or not or trailing 0\n if len(num) <=0 or (len(num) > 1 and len(num) != len(num.lstrip("0"))):\n return False\n \n #check if not number\n for c in num:\n if not c.isnumeric():\n return False\n \n #now check if num is in range\n if not (0<=int(num) <= 255):\n return False\n return True\n\n #check for ipv6\n def check_ipv6(string):\n \n valid = {"a","b","c","d","e",\'f\',"A","B","C","D","E","F"}\n #split\n array = queryIP.split(":") \n\n if len(array) != 8:\n return False\n\n for num in array:\n if not(1<=len(num) <= 4):\n return False\n\n for c in num:\n\n if not c.isnumeric() and not c in valid:\n return False\n \n\n return True\n\n \n if check_ipv4(queryIP):\n return "IPv4"\n elif check_ipv6(queryIP):\n return "IPv6"\n \n return "Neither"\n \n```
| 1
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
Easy way, holds any case, brute-force
|
validate-ip-address
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n if \'.\' in queryIP:\n a=queryIP.split(\'.\')\n if len(a) != 4:\n return \'Neither\'\n for i in a:\n if i.isdigit() == False or len(i) != len(str(int(i))):\n return \'Neither\'\n for j in range(1,len(i)):\n try:\n if i[j].isdigit() and i[j] != \'0\' and int(i.split(i[j])[0]) == 0:\n return \'Neither\' \n except:\n return \'Neither\'\n l=list(map(int,a))\n if any(i > 255 or i < 0 for i in l):\n return \'Neither\'\n return \'IPv4\'\n elif \':\' in queryIP:\n v=[\'a\',\'b\',\'c\',\'d\',\'e\',\'f\',\'A\',\'B\',\'C\',\'D\',\'E\',\'F\',\'0\',\'1\',\'2\',\'3\',\'4\',\'5\',\'6\',\'7\',\'8\',\'9\']\n b=queryIP.split(\':\')\n if len(b) != 8:\n return \'Neither\'\n for i in b:\n if len(i) > 4 or len(i) < 1 or (i.isdigit() == False and any(j not in v for j in i)):\n return \'Neither\' \n return \'IPv6\'\n return \'Neither\'\n```
| 1
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
Brute Force Approach
|
validate-ip-address
| 0
| 1
|
\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n \n IPv4 = False\n IPv6 = False\n\n #IPv4\n if \'.\' in queryIP:\n splittedIP = queryIP.split(\'.\')\n if len(splittedIP) != 4:\n IPv4 = False\n else:\n IPv4 = True\n\n for num in splittedIP:\n if not num.isdigit() or not 0 <= int(num) <= 255:\n IPv4 = False\n break\n if len(num) > 1 and num[0] == \'0\': \n IPv4 = False\n break\n\n #IPv6\n allowed = set(\'abcdefABCDEF0123456789\')\n if \':\' in queryIP:\n splittedIP = queryIP.split(\':\')\n if len(splittedIP) == 8:\n IPv6 = True\n for segment in splittedIP:\n if len(segment) > 4 or len(segment) < 1:\n IPv6 = False\n break\n for char in segment:\n if char not in allowed:\n IPv6 = False\n break\n if not IPv6:\n break\n \n \n if IPv4:\n return \'IPv4\'\n elif IPv6:\n return \'IPv6\'\n else:\n return \'Neither\'\n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
check . : first, then check each parttern
|
validate-ip-address
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n def is_ipv4(pattern):\n subs = pattern.split(\'.\')\n if len(subs) != 4:\n return False\n \n for sub in subs:\n if len(sub) >= 2 and sub[0] == \'0\' or sub == \'\':\n return False\n\n cur_num = 0\n for ch in sub:\n if not ch.isdigit():\n return False\n cur_num = 10 * cur_num + int(ch)\n if cur_num > 255:\n return False\n return True\n\n def is_ipv6(pattern):\n subs = pattern.split(":")\n if len(subs) != 8:\n return False\n \n for sub in subs:\n if len(sub) > 4 or sub == \'\':\n return False\n \n sub = sub.lower()\n for ch in sub:\n if not ch.isdigit() and not ( ord(\'a\') <= ord(ch) <= ord(\'f\') ):\n return False\n return True\n\n if \'.\' in queryIP:\n return "IPv4" if is_ipv4(queryIP) else "Neither"\n elif \':\' in queryIP:\n return "IPv6" if is_ipv6(queryIP) else "Neither"\n else:\n return "Neither"\n\n\n# (1) contain . IPv4\n# (1) length >= 2 and first digit is not 0\n# (2) num <= 255\n# (2) contain : IPv6\n# (1) length 4\n# (2) digit good\n# (3) A -> F or a -> f good\n# (4) if leading 0 allowed, we only need to check length and char range\n# (4) otherwise false\n\n# 2**32 -> 4.2**9\n# 16**32 -> 3.4**38\n\n# edge case "1.0.1."\n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
💡💡 Neatly coded solution in python3
|
validate-ip-address
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIPv4 - has "." dividers, only numbers until 255 with no leading zeroes (total 4)\nIPv6 - uses ":" to divide, only hexadecimal with no leading zeroes (total 8)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n flag = 0\n if "." in queryIP:\n queryIP = queryIP.split(".")\n if len(queryIP) == 4:\n for i in queryIP:\n if (i.isnumeric() and 0 <= int(i) <= 255) and (len(i) == 1 or i[0] != "0"):\n continue\n else:\n flag = 1\n if flag == 0:\n return "IPv4"\n\n elif ":" in queryIP:\n queryIP = queryIP.split(":")\n if len(queryIP) == 8:\n for i in queryIP:\n if len(i) <= 4 and len(i) >= 1 and all(d in string.hexdigits for d in i):\n continue\n else:\n flag = 1\n if flag == 0:\n return "IPv6"\n\n return "Neither"\n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
i hate regexp
|
validate-ip-address
| 0
| 1
|
# Code\n```\nimport re\n\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n if queryIP == "":\n return "Neither"\n if \'.\' in queryIP:\n octets = queryIP.split(\'.\')\n if len(octets) != 4:\n return "Neither"\n for octet in octets:\n if octet == \'0\':\n continue\n if octet == \'\':\n return "Neither"\n if re.fullmatch(r\'[1-2][0-9]{,3}\', octet) is None:\n return "Neither"\n if not 1 <= int(octet) <= 255:\n return "Neither"\n return "IPv4"\n \n if \':\' in queryIP:\n _ipv6_pattern = re.compile("[0-9A-Fa-f]{,4}") \n octets = queryIP.split(":")\n if len(octets) != 8:\n return "Neither"\n for octet in octets:\n if octet == \'\':\n return "Neither"\n if len(octet) > 4:\n return "Neither"\n if re.fullmatch(r\'[0-9A-Fa-f]{,4}\', octet) is None:\n return "Neither"\n return "IPv6"\n \n \n\n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
Python
|
validate-ip-address
| 0
| 1
|
class Solution:\n def validIPAddress(self, queryIP: str) -> str:\n\n def validateIPv4(ip):\n parts = ip.split(\'.\')\n if len(parts) != 4:\n return False\n\n for part in parts:\n if not part.isdigit():\n return False\n\n num = int(part)\n if num < 0 or num > 255:\n return False\n\n if part[0] == \'0\' and len(part) > 1:\n return False\n\n return True\n\n def validateIPv6(ip):\n parts = ip.split(\':\')\n if len(parts) != 8:\n return False\n\n for part in parts:\n if len(part) < 1 or len(part) > 4:\n return False\n\n for char in part:\n if not (char.isdigit() or \'a\' <= char.lower() <= \'f\'):\n return False\n\n return True\n\n if \':\' in queryIP:\n return "IPv6" if validateIPv6(queryIP) else "Neither"\n else:\n return "IPv4" if validateIPv4(queryIP) else "Neither"\n\n\n\n
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
python using regex
|
validate-ip-address
| 0
| 1
|
```\nipv4 = re.compile(r\'^((25[0-5]|(2[0-4]|1\\d|[1-9]|)\\d)\\.?\\b){4}$\')\nipv6 = re.compile(r\'^([0-9a-fA-F]{0,4}:?\\b){8}$\')\n\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n \n if ipv4.fullmatch(queryIP):\n return \'IPv4\'\n elif ipv6.fullmatch(queryIP):\n return \'IPv6\'\n else:\n return \'Neither\'\n \n \n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
[Python3] Good enough
|
validate-ip-address
| 0
| 1
|
``` Python3 []\nclass Solution:\n def validIPAddress(self, queryIP: str) -> str:\n if queryIP.count(\'.\')==3:\n queryIP = queryIP.split(\'.\')\n for x in queryIP:\n if x.startswith(\'0\') and x!=\'0\':\n return \'Neither\'\n elif not x.isnumeric() or int(x)<0 or int(x)>255:\n return \'Neither\'\n return \'IPv4\'\n elif queryIP.count(\':\')==7:\n queryIP = queryIP.split(\':\')\n for x in queryIP:\n if not x or len(x)>4:\n return \'Neither\'\n for y in x:\n if y.lower() not in \'0123456789abcdef\':\n return \'Neither\'\n return \'IPv6\'\n else:\n return \'Neither\'\n```
| 0
|
Given a string `queryIP`, return `"IPv4 "` if IP is a valid IPv4 address, `"IPv6 "` if IP is a valid IPv6 address or `"Neither "` if IP is not a correct IP of any type.
**A valid IPv4** address is an IP in the form `"x1.x2.x3.x4 "` where `0 <= xi <= 255` and `xi` **cannot contain** leading zeros. For example, `"192.168.1.1 "` and `"192.168.1.0 "` are valid IPv4 addresses while `"192.168.01.1 "`, `"192.168.1.00 "`, and `"192.168@1.1 "` are invalid IPv4 addresses.
**A valid IPv6** address is an IP in the form `"x1:x2:x3:x4:x5:x6:x7:x8 "` where:
* `1 <= xi.length <= 4`
* `xi` is a **hexadecimal string** which may contain digits, lowercase English letter (`'a'` to `'f'`) and upper-case English letters (`'A'` to `'F'`).
* Leading zeros are allowed in `xi`.
For example, "`2001:0db8:85a3:0000:0000:8a2e:0370:7334 "` and "`2001:db8:85a3:0:0:8A2E:0370:7334 "` are valid IPv6 addresses, while "`2001:0db8:85a3::8A2E:037j:7334 "` and "`02001:0db8:85a3:0000:0000:8a2e:0370:7334 "` are invalid IPv6 addresses.
**Example 1:**
**Input:** queryIP = "172.16.254.1 "
**Output:** "IPv4 "
**Explanation:** This is a valid IPv4 address, return "IPv4 ".
**Example 2:**
**Input:** queryIP = "2001:0db8:85a3:0:0:8A2E:0370:7334 "
**Output:** "IPv6 "
**Explanation:** This is a valid IPv6 address, return "IPv6 ".
**Example 3:**
**Input:** queryIP = "256.256.256.256 "
**Output:** "Neither "
**Explanation:** This is neither a IPv4 address nor a IPv6 address.
**Constraints:**
* `queryIP` consists only of English letters, digits and the characters `'.'` and `':'`.
| null |
470: Solution with step by step explanation
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named rand10() that takes no arguments and returns an integer between 1 and 10.\n2. Use a while loop that runs indefinitely until a suitable random number is generated.\n3. Within the loop, use the rand7() function twice to generate a random number num in the range [1, 49].\n4. Check if num is within the range [1, 40]. If not, continue to the next iteration of the while loop.\n5. If num is within the range [1, 40], exit the while loop and return a value between 1 and 10.\n6. To obtain the random integer within the range [1, 10], use the modulus operator to find the remainder of dividing num by 10 and add 1 to the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n while True:\n # Generate a number in the range [1, 49] using rand7() twice\n num = (rand7() - 1) * 7 + rand7()\n \n # Reject numbers outside the range [1, 40]\n if num <= 40:\n break\n \n # Return a number in the range [1, 10] using modulus\n return num % 10 + 1\n\n```
| 8
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
470: Solution with step by step explanation
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named rand10() that takes no arguments and returns an integer between 1 and 10.\n2. Use a while loop that runs indefinitely until a suitable random number is generated.\n3. Within the loop, use the rand7() function twice to generate a random number num in the range [1, 49].\n4. Check if num is within the range [1, 40]. If not, continue to the next iteration of the while loop.\n5. If num is within the range [1, 40], exit the while loop and return a value between 1 and 10.\n6. To obtain the random integer within the range [1, 10], use the modulus operator to find the remainder of dividing num by 10 and add 1 to the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n while True:\n # Generate a number in the range [1, 49] using rand7() twice\n num = (rand7() - 1) * 7 + rand7()\n \n # Reject numbers outside the range [1, 40]\n if num <= 40:\n break\n \n # Return a number in the range [1, 10] using modulus\n return num % 10 + 1\n\n```
| 8
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Python generalised solution for RandM() using RandN()
|
implement-rand10-using-rand7
| 0
| 1
|
**Solution for creating rand10() using rand7()**\n\n```python\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n curr = 40\n while curr >= 40:\n curr = (rand7() - 1) * 7 + rand7() - 1\n return curr % 10 + 1\n```\n \n**Generalised solution for creating randM() using randN()**\n\n```python\n# The randN() API is already defined for you.\n# def randN():\n# @return a random integer in the range 1 to M\n\nclass Solution:\n def randM(self, N, M):\n """\n :rtype: int\n """\n # acceptable is the desired range which can generate required integer directly\n curr = acceptable = N * N - (N * N) % M \n # if current no is not in the acceptable range, discard it and repeat the process again\n while curr >= acceptable:\n curr = (randN() - 1) * N + randN() - 1\n return curr % M + 1\n\t\t\n```\n\n
| 12
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Python generalised solution for RandM() using RandN()
|
implement-rand10-using-rand7
| 0
| 1
|
**Solution for creating rand10() using rand7()**\n\n```python\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n curr = 40\n while curr >= 40:\n curr = (rand7() - 1) * 7 + rand7() - 1\n return curr % 10 + 1\n```\n \n**Generalised solution for creating randM() using randN()**\n\n```python\n# The randN() API is already defined for you.\n# def randN():\n# @return a random integer in the range 1 to M\n\nclass Solution:\n def randM(self, N, M):\n """\n :rtype: int\n """\n # acceptable is the desired range which can generate required integer directly\n curr = acceptable = N * N - (N * N) % M \n # if current no is not in the acceptable range, discard it and repeat the process again\n while curr >= acceptable:\n curr = (randN() - 1) * N + randN() - 1\n return curr % M + 1\n\t\t\n```\n\n
| 12
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Simple deterministic solution with 10 calls to rand7
|
implement-rand10-using-rand7
| 1
| 1
|
# Intuition\nIf could generate a set with `N` items with equal probability, where `N` was divisible by `10`, then we can easily partition the set into `10` equal groups, and then return `1` for the first group, `2` for the second group, etc... \n\n# Approach\nThe approach is simple. Our generator will just call `rand7()` `10` times. This produces a tuple $$(a_1,a_2,...,a_{10})$$, where each $$a_i$$ ranges from `1` to `7`. \n\nThis gives a total of `70` possible tuples that are produced. It should be straightforward to see that each tuple is produced with equal probability.\n\nWe now just need to partition this set into `10` equally sized and mutually disjoint groups. In my approach, I do this by adding up each $$a_i$$ and taking its remainder by dividing by `10`. \n\nWe add 1 to the remainder so that the result ranges from `1` to `10`.\n\n# Code\n```\nclass Solution {\npublic:\n int rand10() {\n int sum = 0;\n for (int i = 0; i < 10; ++i){\n sum += rand7();\n }\n return sum%10 + 1;\n }\n};\n```\n\n# Connect\nYou can connect with me on LinkedIn [here](https://www.linkedin.com/in/ammar-qadri-0/) to follow my progress.
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Simple deterministic solution with 10 calls to rand7
|
implement-rand10-using-rand7
| 1
| 1
|
# Intuition\nIf could generate a set with `N` items with equal probability, where `N` was divisible by `10`, then we can easily partition the set into `10` equal groups, and then return `1` for the first group, `2` for the second group, etc... \n\n# Approach\nThe approach is simple. Our generator will just call `rand7()` `10` times. This produces a tuple $$(a_1,a_2,...,a_{10})$$, where each $$a_i$$ ranges from `1` to `7`. \n\nThis gives a total of `70` possible tuples that are produced. It should be straightforward to see that each tuple is produced with equal probability.\n\nWe now just need to partition this set into `10` equally sized and mutually disjoint groups. In my approach, I do this by adding up each $$a_i$$ and taking its remainder by dividing by `10`. \n\nWe add 1 to the remainder so that the result ranges from `1` to `10`.\n\n# Code\n```\nclass Solution {\npublic:\n int rand10() {\n int sum = 0;\n for (int i = 0; i < 10; ++i){\n sum += rand7();\n }\n return sum%10 + 1;\n }\n};\n```\n\n# Connect\nYou can connect with me on LinkedIn [here](https://www.linkedin.com/in/ammar-qadri-0/) to follow my progress.
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Rejecting Sampling
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI used rejection sampling to get uniform random variables of [1,5]\nand [1,2], that way we can represent 10 different numbers (which i stored in the array arr, see the code)\nprobabilty to get one of [1,2,3,4,5] when rejecting 6 and 7 is 0.2\nprobability to get even or odd number number in [1,2,3,4,5,6] is 0.5\n(while rejecting 7)\nso in total we got 0.2 * 0.5 = 0.1 probability to get all numbers from [1,10]\n\nexpectency calculation.\nlet $$x$$ be random variable. as you know, if x ~ Geo(p) it means that x is the number of tries until first success, in our case probabily for success is $$5/7 $$ hence x ~ Geo(5/7), it is known that for geometry distributed random variables $$E(x) = 1/p = 7/5$$\n\nlet y be random variable, same as previously explained, y ~ Geo(6/7)\nso $$E(y) = 7/6$$\n\ntotal $$E(X + Y) = 7/5 + 7/6 = 2.56$$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n arr = [[1,2],[3,4],[5,6],[7,8],[9,10]]\n val1 = rand7()\n while val1 >= 6:\n val1 = rand7()\n val2 = rand7()\n while val2 >= 7:\n val2 = rand7()\n return arr[val1 - 1][val2 % 2]\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Rejecting Sampling
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI used rejection sampling to get uniform random variables of [1,5]\nand [1,2], that way we can represent 10 different numbers (which i stored in the array arr, see the code)\nprobabilty to get one of [1,2,3,4,5] when rejecting 6 and 7 is 0.2\nprobability to get even or odd number number in [1,2,3,4,5,6] is 0.5\n(while rejecting 7)\nso in total we got 0.2 * 0.5 = 0.1 probability to get all numbers from [1,10]\n\nexpectency calculation.\nlet $$x$$ be random variable. as you know, if x ~ Geo(p) it means that x is the number of tries until first success, in our case probabily for success is $$5/7 $$ hence x ~ Geo(5/7), it is known that for geometry distributed random variables $$E(x) = 1/p = 7/5$$\n\nlet y be random variable, same as previously explained, y ~ Geo(6/7)\nso $$E(y) = 7/6$$\n\ntotal $$E(X + Y) = 7/5 + 7/6 = 2.56$$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n arr = [[1,2],[3,4],[5,6],[7,8],[9,10]]\n val1 = rand7()\n while val1 >= 6:\n val1 = rand7()\n val2 = rand7()\n while val2 >= 7:\n val2 = rand7()\n return arr[val1 - 1][val2 % 2]\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
rejection sampling python3
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n val = 41\n while val > 40:\n idx1 = rand7()\n idx2 = rand7()\n val = (idx1-1)*7+idx2\n \n \n return val % 10 + 1\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
rejection sampling python3
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n val = 41\n while val > 40:\n idx1 = rand7()\n idx2 = rand7()\n val = (idx1-1)*7+idx2\n \n \n return val % 10 + 1\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
python3 solution
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\nUse two `rand7()` to get a two-digit 7-base number $X = Y_1 + 7 Y_2$. The number is at most 49. If the number is greater than 40, regenerate another sample. Conditioning on the condition $X \\le 40$, $X$ is uniformly distributed in $[1, \\cdots, 40]$. So, $\\mod(X, 10)$ is uniformly distributed.\n\n$$P(X \\le 40) = \\frac{40}{49}$$ so on average, one needs $49/40$ number of $X$ generations.\n\n\n# Complexity\n- Time complexity:\nSuppose `rand7()` costs $r$ numbers of operations. The total cost of `rand10()` is about $2.5 r$.\n\n- Space complexity:\n$O(1)$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n x = (rand7() - 1) * 7 + rand7() - 1\n while x >= 40:\n x = (rand7() - 1) * 7 + rand7() - 1\n return x % 10 + 1\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
python3 solution
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\nUse two `rand7()` to get a two-digit 7-base number $X = Y_1 + 7 Y_2$. The number is at most 49. If the number is greater than 40, regenerate another sample. Conditioning on the condition $X \\le 40$, $X$ is uniformly distributed in $[1, \\cdots, 40]$. So, $\\mod(X, 10)$ is uniformly distributed.\n\n$$P(X \\le 40) = \\frac{40}{49}$$ so on average, one needs $49/40$ number of $X$ generations.\n\n\n# Complexity\n- Time complexity:\nSuppose `rand7()` costs $r$ numbers of operations. The total cost of `rand10()` is about $2.5 r$.\n\n- Space complexity:\n$O(1)$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n x = (rand7() - 1) * 7 + rand7() - 1\n while x >= 40:\n x = (rand7() - 1) * 7 + rand7() - 1\n return x % 10 + 1\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Easy python solution with O(1) Time complexity
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n O(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n x = rand7()\n y = rand7()\n pos = (x-1)*7 + y\n if pos >= 41:\n return self.rand10()\n return pos%10 +1 \n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Easy python solution with O(1) Time complexity
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n O(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n x = rand7()\n y = rand7()\n pos = (x-1)*7 + y\n if pos >= 41:\n return self.rand10()\n return pos%10 +1 \n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
:(
|
implement-rand10-using-rand7
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def rand10(self):\n return sum(rand7() for _ in range(9)) % 10 + 1\n\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
:(
|
implement-rand10-using-rand7
| 0
| 1
|
\n# Code\n```\nclass Solution:\n def rand10(self):\n return sum(rand7() for _ in range(9)) % 10 + 1\n\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Python solution with Detailed explanation
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* We want to generate a random number between 1 and 10 using the rand7() function, which can only generate numbers between 1 and 7 with equal probability.\n\n* To do this, we generate a random number in a larger range, such as between 1 and 49, which has an equal probability of generating any number in that range.\n\n - When we generate a random number using rand7(), we have seven equally likely outcomes: 1, 2, 3, 4, 5, 6, or 7.\n - If we generate two independent random numbers using rand7(), we have 7*7=49 possible outcomes, each of which is equally likely to occur. \n - That\'s because the first number can be any of the seven values, and the second number can also be any of the seven values, resulting in 49 possible combinations.\n - Therefore, by generating two independent random numbers using rand7() and using them to create a number in the range [1, 49], we ensure that each number in that range has an equal probability of being generated.\n\n* We then reject any numbers outside the range [1, 40], which ensures that we have an equal probability of generating any number between 1 and 10.\n* The reason we use the range [1, 40] is that it is the largest multiple of 10 that is less than or equal to 49, which means that all numbers between 1 and 10 have an equal probability of being generated if we reject any numbers outside this range.\n* Finally, we use the modulo operator to map the remaining numbers to the range [1, 10], which gives us a uniform probability distribution for generating random numbers between 1 and 10 using the rand7() function.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the rand10() function is not constant because the number of calls to rand7() is not fixed, and it depends on how many times we need to generate a number between 1 and 40. \nHowever, the worst-case time complexity is `O(\u221E)` because there is a possibility that we will never generate a number between 1 and 40, and the loop will run forever.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is `O(1)` because we are not storing any data structures that grow with input size. \nWe are only using a constant amount of space to store the variables needed to generate the random numbers.\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n We want to generate a random number between 1 and 10 using the rand7() function, \n which can only generate numbers between 1 and 7 with equal probability.\n\n To do this, we generate a random number in a larger range, \n such as between 1 and 49, which has an equal probability of generating any number in that range.\n\n We then reject any numbers outside the range [1, 40], \n which ensures that we have an equal probability of generating any number between 1 and 10.\n\n The reason we use the range [1, 40] is that it is the largest multiple of 10 that is less \n than or equal to 49, \n\n which means that all numbers between 1 and 10 have an equal probability of being generated \n if we reject any numbers outside this range.\n\n Finally, we use the modulo operator to map the remaining numbers to the range [1, 10], \n which gives us a uniform probability distribution for generating random numbers between 1 and 10 \n using the rand7() function.\n """\n while True:\n # Generate a number in the range [1, 49] using rand7() twice because 7 * 7 = 49. We need 1 to 49 \n num = (rand7() - 1) * 7 + rand7()\n \n # Reject numbers outside the range [1, 40] because 40 % 10 = 0 and 40 / 10 = 4. We need 1 to 40 in order to get a number in the range [1, 10]\n if num <= 40:\n break\n \n # Return a number in the range [1, 10] using modulus.\n return num % 10 + 1\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Python solution with Detailed explanation
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* We want to generate a random number between 1 and 10 using the rand7() function, which can only generate numbers between 1 and 7 with equal probability.\n\n* To do this, we generate a random number in a larger range, such as between 1 and 49, which has an equal probability of generating any number in that range.\n\n - When we generate a random number using rand7(), we have seven equally likely outcomes: 1, 2, 3, 4, 5, 6, or 7.\n - If we generate two independent random numbers using rand7(), we have 7*7=49 possible outcomes, each of which is equally likely to occur. \n - That\'s because the first number can be any of the seven values, and the second number can also be any of the seven values, resulting in 49 possible combinations.\n - Therefore, by generating two independent random numbers using rand7() and using them to create a number in the range [1, 49], we ensure that each number in that range has an equal probability of being generated.\n\n* We then reject any numbers outside the range [1, 40], which ensures that we have an equal probability of generating any number between 1 and 10.\n* The reason we use the range [1, 40] is that it is the largest multiple of 10 that is less than or equal to 49, which means that all numbers between 1 and 10 have an equal probability of being generated if we reject any numbers outside this range.\n* Finally, we use the modulo operator to map the remaining numbers to the range [1, 10], which gives us a uniform probability distribution for generating random numbers between 1 and 10 using the rand7() function.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the rand10() function is not constant because the number of calls to rand7() is not fixed, and it depends on how many times we need to generate a number between 1 and 40. \nHowever, the worst-case time complexity is `O(\u221E)` because there is a possibility that we will never generate a number between 1 and 40, and the loop will run forever.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is `O(1)` because we are not storing any data structures that grow with input size. \nWe are only using a constant amount of space to store the variables needed to generate the random numbers.\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n We want to generate a random number between 1 and 10 using the rand7() function, \n which can only generate numbers between 1 and 7 with equal probability.\n\n To do this, we generate a random number in a larger range, \n such as between 1 and 49, which has an equal probability of generating any number in that range.\n\n We then reject any numbers outside the range [1, 40], \n which ensures that we have an equal probability of generating any number between 1 and 10.\n\n The reason we use the range [1, 40] is that it is the largest multiple of 10 that is less \n than or equal to 49, \n\n which means that all numbers between 1 and 10 have an equal probability of being generated \n if we reject any numbers outside this range.\n\n Finally, we use the modulo operator to map the remaining numbers to the range [1, 10], \n which gives us a uniform probability distribution for generating random numbers between 1 and 10 \n using the rand7() function.\n """\n while True:\n # Generate a number in the range [1, 49] using rand7() twice because 7 * 7 = 49. We need 1 to 49 \n num = (rand7() - 1) * 7 + rand7()\n \n # Reject numbers outside the range [1, 40] because 40 % 10 = 0 and 40 / 10 = 4. We need 1 to 40 in order to get a number in the range [1, 10]\n if num <= 40:\n break\n \n # Return a number in the range [1, 10] using modulus.\n return num % 10 + 1\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Python3 - [Made Simple] Inefficient but Easy
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n call = None\n\n while call is None:\n temp1 = rand7()\n temp2 = rand7()\n \n if temp1 == 1 and temp2 == 1:\n return 1\n elif temp1 == 1 and temp2 == 2:\n return 2\n elif temp1 == 1 and temp2 == 3:\n return 3\n elif temp1 == 1 and temp2 == 4:\n return 4\n elif temp1 == 1 and temp2 == 5:\n return 5\n elif temp1 == 1 and temp2 == 6:\n return 6\n elif temp1 == 1 and temp2 == 7:\n return 7\n elif temp1 == 2 and temp2 == 1:\n return 8\n elif temp1 == 2 and temp2 == 2:\n return 9\n elif temp1 == 2 and temp2 == 3:\n return 10\n\n \n \n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Python3 - [Made Simple] Inefficient but Easy
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n call = None\n\n while call is None:\n temp1 = rand7()\n temp2 = rand7()\n \n if temp1 == 1 and temp2 == 1:\n return 1\n elif temp1 == 1 and temp2 == 2:\n return 2\n elif temp1 == 1 and temp2 == 3:\n return 3\n elif temp1 == 1 and temp2 == 4:\n return 4\n elif temp1 == 1 and temp2 == 5:\n return 5\n elif temp1 == 1 and temp2 == 6:\n return 6\n elif temp1 == 1 and temp2 == 7:\n return 7\n elif temp1 == 2 and temp2 == 1:\n return 8\n elif temp1 == 2 and temp2 == 2:\n return 9\n elif temp1 == 2 and temp2 == 3:\n return 10\n\n \n \n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
[Python] | Simple | 2 rand7() calls per rand10()
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\nWe\'ll pick a random value from the matrix:\n```\n 1 2 3 4 5 6 7 8 9 10\n 2 3 4 5 6 7 8 9 10 1\n 3 4 5 6 7 8 9 10 1 2\ni-> 4 5 6 7 8 9 10 1 2 3\n 5 6 7 8 9 10 1 2 3 4\n 6 7 8 9 10 1 2 3 4 5\n 7 8 9 10 1 2 3 4 5 6\n 8 9 10 1 2 3 4 5 6 7\n ^\n |\n j\n```\nThe problem is that we can pick both `i` and `j` in the range [0, 6]. \n\nOne way to solve is to slide the window of possibilites by shifting the range for `j` by 1 to the right each time a number was picked. Meaning after 1st number the range for `j` will be [1, 7], after 2nd - [2, 8] and so on.\n\nThis way on avarage the distribution will be uniform in range [1, 10]\n\n# Complexity\n- Time complexity:\n$O(1)$\n\n- Space complexity:\n$O(1)$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n cnt = 0\n def rand10(self):\n """\n :rtype: int\n """\n i = rand7()\n j = (rand7() + self.cnt)%10\n self.cnt += 1\n return (i + j)%10 + 1\n \n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
[Python] | Simple | 2 rand7() calls per rand10()
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\nWe\'ll pick a random value from the matrix:\n```\n 1 2 3 4 5 6 7 8 9 10\n 2 3 4 5 6 7 8 9 10 1\n 3 4 5 6 7 8 9 10 1 2\ni-> 4 5 6 7 8 9 10 1 2 3\n 5 6 7 8 9 10 1 2 3 4\n 6 7 8 9 10 1 2 3 4 5\n 7 8 9 10 1 2 3 4 5 6\n 8 9 10 1 2 3 4 5 6 7\n ^\n |\n j\n```\nThe problem is that we can pick both `i` and `j` in the range [0, 6]. \n\nOne way to solve is to slide the window of possibilites by shifting the range for `j` by 1 to the right each time a number was picked. Meaning after 1st number the range for `j` will be [1, 7], after 2nd - [2, 8] and so on.\n\nThis way on avarage the distribution will be uniform in range [1, 10]\n\n# Complexity\n- Time complexity:\n$O(1)$\n\n- Space complexity:\n$O(1)$\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n cnt = 0\n def rand10(self):\n """\n :rtype: int\n """\n i = rand7()\n j = (rand7() + self.cnt)%10\n self.cnt += 1\n return (i + j)%10 + 1\n \n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
7 * (rand7() - 1) + rand7()
|
implement-rand10-using-rand7
| 0
| 1
|
```\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n while True:\n x = 7 * (rand7() - 1) \n y = rand7()\n if x + y <= 10:\n return x+y\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
7 * (rand7() - 1) + rand7()
|
implement-rand10-using-rand7
| 0
| 1
|
```\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n while True:\n x = 7 * (rand7() - 1) \n y = rand7()\n if x + y <= 10:\n return x+y\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Sample Solution Using Only Addition:
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n \n #Table of a+b, when a < 5 or b > 3\n # b 1 2 3 4 5 6 7\n #a --------------\n #1| 2 3 4 5 6 7 8\n #2| 3 4 5 6 7 8 9\n #3| 4 5 6 7 8 9 0\n #4| 5 6 7 8 9 0 1\n #5| x x x 9 0 1 2\n #6| x x x 0 1 2 3 \n #7| x x x 1 2 3 4\n \n a = rand7()\n b = rand7()\n\n return (a+b)%10+1 if a < 5 or b > 3 else self.rand10()\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Sample Solution Using Only Addition:
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n \n #Table of a+b, when a < 5 or b > 3\n # b 1 2 3 4 5 6 7\n #a --------------\n #1| 2 3 4 5 6 7 8\n #2| 3 4 5 6 7 8 9\n #3| 4 5 6 7 8 9 0\n #4| 5 6 7 8 9 0 1\n #5| x x x 9 0 1 2\n #6| x x x 0 1 2 3 \n #7| x x x 1 2 3 4\n \n a = rand7()\n b = rand7()\n\n return (a+b)%10+1 if a < 5 or b > 3 else self.rand10()\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Simple solution, Python3
|
implement-rand10-using-rand7
| 0
| 1
|
# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n sm = 0\n for _ in range(100):\n sm += rand7()\n res = sm % 10 + 1\n return res\n\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Simple solution, Python3
|
implement-rand10-using-rand7
| 0
| 1
|
# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n sm = 0\n for _ in range(100):\n sm += rand7()\n res = sm % 10 + 1\n return res\n\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Python3 - Same As Everyone Else's While Loop
|
implement-rand10-using-rand7
| 0
| 1
|
# Approach\nLooks like everyone pretty much did the same thing.\n\n# Code\n```\nclass Solution:\n def rand10(self):\n x = 50\n while x > 47:\n x = rand7() * 7 + rand7()\n return (x - 8) // 4 + 1\n \n \n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Python3 - Same As Everyone Else's While Loop
|
implement-rand10-using-rand7
| 0
| 1
|
# Approach\nLooks like everyone pretty much did the same thing.\n\n# Code\n```\nclass Solution:\n def rand10(self):\n x = 50\n while x > 47:\n x = rand7() * 7 + rand7()\n return (x - 8) // 4 + 1\n \n \n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Python easy solution
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- random first time to get 1-5 to get the bucket since i will split result to [1,2], [3,4] ..., [9,10]\n- assume I get [5,6] =>\nrandom one more time to get the first or last number [1,2,3] = left, [4,5,6] = right\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nExpected value = 7/5 + 7/6 = 2.333\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n mapping = {\n 1: [1, 2],\n 2: [3, 4],\n 3: [5, 6],\n 4: [7, 8],\n 5: [9, 10]\n }\n while True:\n random_val = rand7()\n if 1 <= random_val <= 5:\n break\n\n possible_vals = mapping[random_val]\n while True:\n random_val = rand7()\n if random_val != 7:\n break\n\n index = (random_val-1)//3\n return possible_vals[index]\n```
| 0
|
Given the **API** `rand7()` that generates a uniform random integer in the range `[1, 7]`, write a function `rand10()` that generates a uniform random integer in the range `[1, 10]`. You can only call the API `rand7()`, and you shouldn't call any other API. Please **do not** use a language's built-in random API.
Each test case will have one **internal** argument `n`, the number of times that your implemented function `rand10()` will be called while testing. Note that this is **not an argument** passed to `rand10()`.
**Example 1:**
**Input:** n = 1
**Output:** \[2\]
**Example 2:**
**Input:** n = 2
**Output:** \[2,8\]
**Example 3:**
**Input:** n = 3
**Output:** \[3,8,10\]
**Constraints:**
* `1 <= n <= 105`
**Follow up:**
* What is the [expected value](https://en.wikipedia.org/wiki/Expected_value) for the number of calls to `rand7()` function?
* Could you minimize the number of calls to `rand7()`?
| null |
Python easy solution
|
implement-rand10-using-rand7
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- random first time to get 1-5 to get the bucket since i will split result to [1,2], [3,4] ..., [9,10]\n- assume I get [5,6] =>\nrandom one more time to get the first or last number [1,2,3] = left, [4,5,6] = right\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nExpected value = 7/5 + 7/6 = 2.333\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# The rand7() API is already defined for you.\n# def rand7():\n# @return a random integer in the range 1 to 7\n\nclass Solution:\n def rand10(self):\n """\n :rtype: int\n """\n mapping = {\n 1: [1, 2],\n 2: [3, 4],\n 3: [5, 6],\n 4: [7, 8],\n 5: [9, 10]\n }\n while True:\n random_val = rand7()\n if 1 <= random_val <= 5:\n break\n\n possible_vals = mapping[random_val]\n while True:\n random_val = rand7()\n if random_val != 7:\n break\n\n index = (random_val-1)//3\n return possible_vals[index]\n```
| 0
|
You are given a string `s` of length `n` where `s[i]` is either:
* `'D'` means decreasing, or
* `'I'` means increasing.
A permutation `perm` of `n + 1` integers of all the integers in the range `[0, n]` is called a **valid permutation** if for all valid `i`:
* If `s[i] == 'D'`, then `perm[i] > perm[i + 1]`, and
* If `s[i] == 'I'`, then `perm[i] < perm[i + 1]`.
Return _the number of **valid permutations**_ `perm`. Since the answer may be large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** s = "DID "
**Output:** 5
**Explanation:** The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
**Example 2:**
**Input:** s = "D "
**Output:** 1
**Constraints:**
* `n == s.length`
* `1 <= n <= 200`
* `s[i]` is either `'I'` or `'D'`.
| null |
Simple Solution without Trie(Python)
|
concatenated-words
| 0
| 1
|
\n# Code\n```\ndef solve(string,s):\n for i in range(1,len(string)):\n left,right = string[0:i],string[i:len(string)]\n if left in s:\n if right in s or solve(right,s):\n return True\n return False\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n s = set(words)\n ans = []\n for i in words:\n if solve(i,s):\n ans.append(i)\n return ans\n\n \n```
| 1
|
Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105`
| null |
python - trie dfs
|
concatenated-words
| 0
| 1
|
\n# Code\n```\nfrom pprint import pprint\nfrom dataclasses import dataclass\n\n@dataclass\nclass Node:\n value: Optional[str]\n children: dict\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n root = Node(value=None, children={})\n \n # build trie\n for word in words:\n node = root\n for i, char in enumerate(word):\n value = word if (i == len(word) - 1) else None\n if char not in node.children:\n node.children[char] = Node(value=value, children={})\n node = node.children[char]\n node.value = node.value or value\n\n # dfs search generator\n def concat_count(word, pos, count, node):\n if pos == len(word):\n if not word:\n yield count\n return\n char = word[pos]\n if char not in node.children:\n return\n next_node = node.children[char]\n yield from concat_count(word, pos + 1, count, next_node)\n if next_node.value:\n new_word = word[word.find(next_node.value) + len(next_node.value):]\n yield from concat_count(new_word, 0, count + 1, root)\n\n\n result = []\n\n for word in words:\n for count in concat_count(word, 0, 0, root):\n if count > 1:\n result.append(word)\n break\n\n return result\n\n```
| 1
|
Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105`
| null |
Heavily Commented Trie
|
concatenated-words
| 0
| 1
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n def __init__(self, par = None):\n #words that can be made by adding given letters to this word\n self.children = {}\n #whether the given word exists in words\n self.exists = 0\n #keeps track of parent node. Used to prune the tree when \n self.par = par\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n\n #adds a word to the trie\n def add(self, word):\n node = self.root\n for c in word:\n if c not in node.children: node.children[c] = TrieNode(par=node)\n node = node.children[c]\n node.exists = 1\n \n #removes the word from the tree and removes the path to it\n #if the current letter is saved in each node, could optimize node removal\n def remove(self, node):\n node.exists = 0\n #Only prune the trie if there are no other words along that path.\n while (not node.exists) and (not node.children):# and node.par:\n par = node.par\n #O(1); 26 keys maximum in children\n for c in node.par.children:\n if node.par.children[c] == node:\n node.par.children.pop(c)\n break\n node = par\n return\n \n \n\n\n #given a word, returns whether it can be created using words in the array\n #\n def isConcat(self, word):\n #cached dfs using a node in the tree and an index in the word\n @lru_cache(maxsize=None)\n def dfs(i):\n node = self.root\n if i == len(word): return 1\n found = 0\n depth = 0\n while i+depth < len(word) and word[i+depth] in node.children:\n node = node.children[word[i+depth]]\n depth+=1 #depth increases by 1 when node goes to its child\n if node.exists:\n if depth == len(word):\n if found: self.remove(node)\n return found\n if not found:\n found |= dfs(i+depth)\n #^^doesn\'t break because we still want to remove the word\'s node\n return found\n return dfs(0)\n\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n trie = Trie()\n [trie.add(word) for word in words]\n words.sort(key=lambda x: len(x))\n return [word for word in words if trie.isConcat(word)]\n```
| 1
|
Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105`
| null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.