repo
stringclasses 900
values | file
stringclasses 754
values | content
stringlengths 4
215k
|
|---|---|---|
https://github.com/martynscn/Masters-Thesis-on-Quantum-Cryptography
|
martynscn
|
# This code has been adapted and modified from IBM Qiskit 2021 and also from https://github.com/ttlion/ShorAlgQiskit.
# It uses the implementation as contained in the work of Stephane Beauregard (https://arxiv.org/abs/quant-ph/0205095)
# Many thanks to IBM Qiskit team, Tiago Miguel (ttlion), Qubit by Qubit, Peter Shor and Stephane Beauregard.
from typing import Optional, Union, Tuple, List
import math
import array
import fractions
import logging
import numpy as np
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister, execute, IBMQ, transpile,BasicAer, Aer, assemble
from qiskit.circuit import Gate, Instruction, ParameterVector
from qiskit.circuit.library import QFT
from qiskit.providers import BaseBackend, Backend
from qiskit.quantum_info import partial_trace
from qiskit.utils import summarize_circuits
from qiskit.utils.arithmetic import is_power
from qiskit.utils.validation import validate_min
from qiskit.utils.quantum_instance import QuantumInstance
import qiskit.visualization
from qiskit.providers.aer import QasmSimulator
from datetime import datetime
import csv
# provider = IBMQ.enable_account("PUT TOKEN HERE")
backend = QasmSimulator()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all" #"last_expr" or "all"
# """ Function to check if N is of type q^p"""
def check_if_power(N):
# """ Check if N is a perfect power in O(n^3) time, n=ceil(logN) """
b=2
while (2**b) <= N:
a = 1
c = N
while (c-a) >= 2:
m = int( (a+c)/2 )
if (m**b) < (N+1):
p = int( (m**b) )
else:
p = int(N+1)
if int(p) == int(N):
print('N is {0}^{1}'.format(int(m),int(b)) )
return True
if p<N:
a = int(m)
else:
c = int(m)
b=b+1
return False
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def create_QFT(circuit,up_reg,n,with_swaps):
i=n-1
while i>=0:
circuit.h(up_reg[i])
j=i-1
while j>=0:
if (np.pi)/(pow(2,(i-j))) > 0:
circuit.cu1( (np.pi)/(pow(2,(i-j))) , up_reg[i] , up_reg[j] )
j=j-1
i=i-1
if with_swaps==1:
i=0
while i < ((n-1)/2):
circuit.swap(up_reg[i], up_reg[n-1-i])
i=i+1
def create_inverse_QFT(circuit,up_reg,n,with_swaps):
if with_swaps==1:
i=0
while i < ((n-1)/2):
circuit.swap(up_reg[i], up_reg[n-1-i])
i=i+1
i=0
while i<n:
circuit.h(up_reg[i])
if i != n-1:
j=i+1
y=i
while y>=0:
if (np.pi)/(pow(2,(j-y))) > 0:
circuit.cu1( - (np.pi)/(pow(2,(j-y))) , up_reg[j] , up_reg[y] )
y=y-1
i=i+1
def getAngle(a, N):
s=bin(int(a))[2:].zfill(N)
angle = 0
for i in range(0, N):
if s[N-1-i] == '1':
angle += math.pow(2, -(N-i))
angle *= np.pi
return angle
def getAngles(a,N):
s=bin(int(a))[2:].zfill(N)
angles=np.zeros([N])
for i in range(0, N):
for j in range(i,N):
if s[j]=='1':
angles[N-i-1]+=math.pow(2, -(j-i))
angles[N-i-1]*=np.pi
return angles
def ccphase(circuit, angle, ctl1, ctl2, tgt):
circuit.cu1(angle/2,ctl1,tgt)
circuit.cx(ctl2,ctl1)
circuit.cu1(-angle/2,ctl1,tgt)
circuit.cx(ctl2,ctl1)
circuit.cu1(angle/2,ctl2,tgt)
def phiADD(circuit, q, a, N, inv):
angle=getAngles(a,N)
for i in range(0,N):
if inv==0:
circuit.u1(angle[i],q[i])
else:
circuit.u1(-angle[i],q[i])
def cphiADD(circuit, q, ctl, a, n, inv):
angle=getAngles(a,n)
for i in range(0,n):
if inv==0:
circuit.cu1(angle[i],ctl,q[i])
else:
circuit.cu1(-angle[i],ctl,q[i])
def ccphiADD(circuit,q,ctl1,ctl2,a,n,inv):
angle=getAngles(a,n)
for i in range(0,n):
if inv==0:
ccphase(circuit,angle[i],ctl1,ctl2,q[i])
else:
ccphase(circuit,-angle[i],ctl1,ctl2,q[i])
def ccphiADDmodN(circuit, q, ctl1, ctl2, aux, a, N, n):
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
phiADD(circuit, q, N, n, 1)
# phiADD(circuit, q, a,N, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.cx(q[n-1],aux)
create_QFT(circuit,q,n,0)
cphiADD(circuit, q, aux, N, n, 0)
# cphiADD(circuit, q, aux, a, n, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.x(q[n-1])
circuit.cx(q[n-1], aux)
circuit.x(q[n-1])
create_QFT(circuit,q,n,0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
def ccphiADDmodN_inv(circuit, q, ctl1, ctl2, aux, a, N, n):
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.x(q[n-1])
circuit.cx(q[n-1],aux)
circuit.x(q[n-1])
create_QFT(circuit, q, n, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
cphiADD(circuit, q, aux, N, n, 1)
# cphiADD(circuit, q, aux, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.cx(q[n-1], aux)
create_QFT(circuit, q, n, 0)
phiADD(circuit, q, N, n, 0)
# phiADD(circuit, q, a, N, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
def cMULTmodN(circuit, ctl, q, aux, a, N, n):
# up_reg = QuantumRegister(1, name = "up_reg")
# down_reg = QuantumRegister(n, name = "down_reg")
# up_classic = ClassicalRegister(2*n, name="up_classic")
# c_aux = ClassicalRegister(1, name = "aux_classic")
# cMULTmodN_circuit = QuantumCircuit(
# up_reg ,down_reg , aux,up_classic, c_aux,
# name=r"${0}^{{{1}^{{{2}}}}} mod{3}$".format(2,2,int(math.log(math.log(a,2),2)), N)
# )
# create_QFT(cMULTmodN_circuit,aux,n+1,0)
# for i in range(0, n):
# ccphiADDmodN(cMULTmodN_circuit, aux, q[i], ctl, aux[n+1], (2**i)*a % N, N, n+1)
# create_inverse_QFT(cMULTmodN_circuit, aux, n+1, 0)
# for i in range(0, n):
# circuit.cswap(ctl,q[i],aux[i])
# cMULTmodN_circuit.cswap(ctl,q[i],aux[i])
# create_QFT(cMULTmodN_circuit, aux, n+1, 0)
# ccphiADDmodN_inv(cMULTmodN_circuit, aux, q[i], ctl, aux[n+1], math.pow(2,i)*a_inv % N, N, n+1)
# create_inverse_QFT(cMULTmodN_circuit, aux, n+1, 0)
# cMULTmodN_circuit_instruction = cMULTmodN_circuit.to_instruction()
# circuit.append(cMULTmodN_circuit_instruction, [ctl, *down_reg, *aux])
create_QFT(circuit,aux,n+1,0)
for i in range(0, n):
ccphiADDmodN(circuit, aux, q[i], ctl, aux[n+1], (2**i)*a % N, N, n+1)
create_inverse_QFT(circuit, aux, n+1, 0)
for i in range(0, n):
circuit.cswap(ctl,q[i],aux[i])
a_inv = modinv(a, N)
create_QFT(circuit, aux, n+1, 0)
i = n-1
while i >= 0:
ccphiADDmodN_inv(circuit, aux, q[i], ctl, aux[n+1], math.pow(2,i)*a_inv % N, N, n+1)
i -= 1
create_inverse_QFT(circuit, aux, n+1, 0)
def calculate_continued_fraction(b: array.array) -> int:
# """Calculate the continued fraction of x/T from the current terms of expansion b."""
x_over_T = 0
for i in reversed(range(len(b) - 1)):
x_over_T = 1 / (b[i + 1] + x_over_T)
x_over_T += b[0]
frac = fractions.Fraction(x_over_T).limit_denominator()
return frac.denominator
def get_factors(N: int, a: int, measurement: str) -> Optional[List[int]]:
# """Apply the continued fractions to find r and the gcd to find the desired factors."""
x_final = int(measurement, 2)
#print('In decimal, x_final value for this result is: {}.'.format(x_final))
if x_final <= 0:
fail_reason = 'x_final value is <= 0, there are no continued fractions.'
else:
fail_reason = None
#print('Running continued fractions for this case.')
# Calculate T and x/T
T_upper = len(measurement)
T = pow(2, T_upper)
x_over_T = x_final / T ## this is our theta
# Cycle in which each iteration corresponds to putting one more term in the
# calculation of the Continued Fraction (CF) of x/T
# Initialize the first values according to CF rule
i = 0
b = array.array('i')
t = array.array('f')
b.append(math.floor(x_over_T))
t.append(x_over_T - b[i])
exponential = 0.0
while i < N and fail_reason is None:
# From the 2nd iteration onwards, calculate the new terms of the CF based on the previous terms as the rule suggests
if i > 0:
try:
b_temp = math.floor(1 / t[i - 1])
except ZeroDivisionError as err:
b_temp = 0
b.append(b_temp)
try:
t_temp = (1 / t[i - 1]) - b[i]
except ZeroDivisionError as err:
t_temp = 0
t.append(t_temp) # type: ignore
# Calculate the denominator of the CF using the known terms
denominator = calculate_continued_fraction(b)
# Increment i for next iteration
i += 1
if denominator % 2 == 1:
#print('Odd denominator, will try next iteration of continued fractions.')
continue
# Denominator is even, try to get factors of N. Get the exponential a^(r/2)
if denominator < 1000:
try:
exponential = pow(a, denominator / 2)
except OverflowError as err:
exponential = 999999999
# Check if the value is too big or not
if exponential > 1000000:
if exponential == 999999999:
fail_reason = 'OverflowError'
else:
fail_reason = 'denominator of continued fraction is too big (> 10^3).'
else:
# The value is not too big, get the right values and do the proper gcd()
putting_plus = int(exponential + 1)
putting_minus = int(exponential - 1)
one_factor = math.gcd(putting_plus, N)
other_factor = math.gcd(putting_minus, N)
# Check if the factors found are trivial factors or are the desired factors
if any(factor in {1, N} for factor in (one_factor, other_factor)):
#print('Found just trivial factors, not good enough.')
# Check if the number has already been found, (use i - 1 because i was already incremented)
if t[i - 1] == 0:
fail_reason = 'the continued fractions found exactly x_final/(2^(2n)).'
else:
return sorted((one_factor, other_factor))
return None
def process_results(sim_result, circuit, shots, N, a, n):
counts_result = sim_result.get_counts(circuit)
total_counts = len(counts_result)
counts_result_sorted = sorted(counts_result.items(), key=lambda x: x[1], reverse=True)
counts_result_keys = list(counts_result.keys())
counts_result_values = list(counts_result.values())
prob_success=0
prob_failure=0
result_successful_counts = 0
result_failure_counts = 0
for initial_undesired_measurement, frequency in counts_result_sorted:
measurement = initial_undesired_measurement.split(" ")[1]
x_value = int(measurement, 2)
prob_this_result = 100 * frequency/shots
factors = get_factors(N, a, measurement)
if factors:
prob_success = prob_success + prob_this_result
result_successful_counts = result_successful_counts + 1
if factors not in result_factors:
result_factors.append(factors)
elif not factors:
prob_failure = prob_failure + prob_this_result
result_failure_counts = result_failure_counts + 1
return [result_factors, prob_success, prob_failure, total_counts, result_successful_counts,result_failure_counts]
def my_shor(a,N,shots):
start_time_number = datetime.now()
start_time = start_time_number.strftime("%H:%M:%S")
summary_result = dict()
validate_min('N', N, 3)
validate_min('a', a, 2)
if N < 1 or N % 2 == 0:
raise ValueError('The input needs to be an odd integer greater than 1.')
if a >= N or math.gcd(a, N) != 1:
raise ValueError('The integer a needs to satisfy a < N and gcd(a, N) = 1.')
n = math.ceil(math.log(N,2))
global result_factors
result_factors = []
tf, b, p = is_power(N, return_decomposition=True)
if tf:
print('The input integer is a power: {0}={1}^{2}.'.format(N, b, p))
result_factors.append(b)
# """auxilliary quantum register used in addition and multiplication"""
aux = QuantumRegister(size = n+2, name="aux_reg")
# """single qubit where the sequential QFT is performed"""
up_reg = QuantumRegister(1, name = "up_reg")
down_reg = QuantumRegister(n, name = "down_reg")
# """classical register where the measured values of the sequential QFT are stored"""
up_classic = ClassicalRegister(2*n, name="up_classic")
# """classical bit used to reset the state of the top qubit to 0 if the previous measurement was 1"""
c_aux = ClassicalRegister(1, name = "aux_classic")
# """ Create Quantum Circuit """
circuit = QuantumCircuit(up_reg ,down_reg , aux,up_classic, c_aux)
circuit.x(down_reg[0])
# circuit.draw(filename = "shor_semiclassical_QFT_initialization")
for i in range(0, 2*n):
circuit.x(up_reg).c_if(c_aux, 1)
circuit.h(up_reg)
cMULTmodN(circuit, up_reg[0], down_reg, aux, a**(2**(2*n-1-i)), N, n)
# later confirm if this should be up_reg[i] instead of up_reg[0]
for j in range(0, 2**i):
circuit.u1(getAngle(j, i), up_reg[0]).c_if(up_classic, j)
circuit.h(up_reg)
circuit.measure(up_reg[0], up_classic[i])
circuit.measure(up_reg[0], c_aux[0])
# circuit.draw(filename = "shor_semiclassical_QFT_final_circuit")
circuit.draw()
qc_compiled = transpile(circuit, backend, optimization_level = 3)
job_sim_1 = backend.run(qc_compiled, shots=shots)
sim_result=job_sim_1.result()
# counts_result = sim_result.get_counts(circuit)
# len(counts_result)
# measurement_plot = qiskit.visualization.plot_histogram(counts_result,figsize=(20, 12) ,number_to_keep = 30,bar_labels=True, title = "Measurement results from shor_standard_QFT circuit variant" )
# measurement_plot.savefig("shor_semiclassical_QFT_measurement_result")
# measurement_plot
processed_result = process_results(sim_result, circuit, shots, N, a, n)
end_time_number = datetime.now()
end_time = end_time_number.strftime("%H:%M:%S")
duration = end_time_number - start_time_number
print("Current Start Time =", start_time)
print(processed_result)
print("Current End Time =", end_time)
circuit_count_ops = circuit.count_ops()
circuit_decomposed = circuit.decompose()
circuit_decomposed_count_ops = circuit_decomposed.count_ops()
qc_compiled_count_ops = qc_compiled.count_ops()
summary_result["num_qubits"] = n
summary_result["Number(N)"] = N
summary_result["a"] = a
summary_result["start_time"] = start_time
summary_result["end_time"] = end_time
summary_result["duration"] = duration
summary_result["result_factors"] = processed_result[0]
summary_result["prob_success"] = processed_result[1]
summary_result["prob_failure"] = processed_result[2]
summary_result["total_counts"] = processed_result[3]
summary_result["result_successful_counts"] = processed_result[4]
summary_result["result_failure_counts"] = processed_result[5]
summary_result["circuit_width"] = circuit.width()
summary_result["circuit_depth"] = circuit.depth()
summary_result["circuit_size"] = circuit.size()
summary_result["circuit_num_nonlocal_gates"] = circuit.num_nonlocal_gates()
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_clbits"] = circuit.num_clbits
summary_result["circuit_num_qubits"] = circuit.num_qubits
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_of_count_ops"] = len(circuit_count_ops)
summary_result["circuit_num_of_x"] = circuit_count_ops.get('x')
summary_result["circuit_num_of_measure"] = circuit_count_ops.get('measure')
summary_result["circuit_num_of_h"] = circuit_count_ops.get('h')
summary_result["circuit_num_of_cswap"] = circuit_count_ops.get('cswap')
summary_result["circuit_num_of_swap"] = circuit_count_ops.get('swap')
summary_result["circuit_num_of_cx"] = circuit_count_ops.get('cx')
summary_result["circuit_num_of_toffoli"] = circuit_count_ops.get('toffoli')
summary_result["circuit_num_of_p"] = circuit_count_ops.get('p')
summary_result["circuit_num_of_t"] = circuit_count_ops.get('t')
summary_result["circuit_decomposed_width"] = circuit_decomposed.width()
summary_result["circuit_decomposed_depth"] = circuit_decomposed.depth()
summary_result["circuit_decomposed_size"] = circuit_decomposed.size()
summary_result["circuit_decomposed_num_nonlocal_gates"] = circuit_decomposed.num_nonlocal_gates()
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_clbits"] = circuit_decomposed.num_clbits
summary_result["circuit_decomposed_num_qubits"] = circuit_decomposed.num_qubits
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_of_count_ops"] = len(circuit_decomposed_count_ops)
summary_result["circuit_decomposed_num_of_x"] = circuit_decomposed_count_ops.get('x')
summary_result["circuit_decomposed_num_of_measure"] = circuit_decomposed_count_ops.get('measure')
summary_result["circuit_decomposed_num_of_h"] = circuit_decomposed_count_ops.get('h')
summary_result["circuit_decomposed_num_of_cswap"] = circuit_decomposed_count_ops.get('cswap')
summary_result["circuit_decomposed_num_of_swap"] = circuit_decomposed_count_ops.get('swap')
summary_result["circuit_decomposed_num_of_cx"] = circuit_decomposed_count_ops.get('cx')
summary_result["circuit_decomposed_num_of_toffoli"] = circuit_decomposed_count_ops.get('toffoli')
summary_result["circuit_decomposed_num_of_p"] = circuit_decomposed_count_ops.get('p')
summary_result["circuit_decomposed_num_of_t"] = circuit_decomposed_count_ops.get('t')
summary_result["qc_compiled_width"] = qc_compiled.width()
summary_result["qc_compiled_depth"] = qc_compiled.depth()
summary_result["qc_compiled_size"] = qc_compiled.size()
summary_result["qc_compiled_num_nonlocal_gates"] = qc_compiled.num_nonlocal_gates()
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_clbits"] = qc_compiled.num_clbits
summary_result["qc_compiled_num_qubits"] = qc_compiled.num_qubits
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_of_count_ops"] = len(qc_compiled_count_ops)
summary_result["qc_compiled_num_of_x"] = qc_compiled_count_ops.get('x')
summary_result["qc_compiled_num_of_measure"] = qc_compiled_count_ops.get('measure')
summary_result["qc_compiled_num_of_h"] = qc_compiled_count_ops.get('h')
summary_result["qc_compiled_num_of_cswap"] = qc_compiled_count_ops.get('cswap')
summary_result["qc_compiled_num_of_swap"] = qc_compiled_count_ops.get('swap')
summary_result["qc_compiled_num_of_cx"] = qc_compiled_count_ops.get('cx')
summary_result["qc_compiled_num_of_toffoli"] = qc_compiled_count_ops.get('toffoli')
summary_result["qc_compiled_num_of_p"] = qc_compiled_count_ops.get('p')
summary_result["qc_compiled_num_of_t"] = qc_compiled_count_ops.get('t')
return summary_result
# Run for just a single number N
%%time
N = 21
shots = 1024
global result_factors
all_summary_result_temp = []
for random_a in range(2, N):
if math.gcd(random_a,N) > 1:
continue
a = random_a
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n".format(a, N))
all_summary_result_temp.append(summary_result)
summary_result_list = []
for key, value in summary_result.items():
summary_result_list.append([key,value])
summary_result_list
with open("a({0})_N({1})_semiclassical.csv".format(a, N), 'a') as myfile:
write = csv.writer(myfile)
#write.writerow(fields)
write.writerows(summary_result_list)
all_summary_result_temp
# Run for many numbers N.
%%time
shots = 1024
global result_factors
all_summary_result = []
for N in [15, 21, 33, 35, 39, 51, 55, 57]:
for a in range(2, N):
if math.gcd(a,N) > 1:
continue
print("Beginning running for a = {} and N = {}".format(a, N))
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n\n".format(a, N))
all_summary_result.append(summary_result)
all_summary_result
%qiskit_copyright
|
https://github.com/martynscn/Masters-Thesis-on-Quantum-Cryptography
|
martynscn
|
# This code has been adapted and modified from IBM Qiskit 2021 and also from https://github.com/ttlion/ShorAlgQiskit.
# It uses the implementation as contained in the work of Stephane Beauregard (https://arxiv.org/abs/quant-ph/0205095)
# Many thanks to IBM Qiskit team, Tiago Miguel (ttlion), Qubit by Qubit, Peter Shor and Stephane Beauregard.
from typing import Optional, Union, Tuple, List
import math
import array
import fractions
import logging
import numpy as np
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister, execute, IBMQ, transpile,BasicAer, Aer, assemble
from qiskit.circuit import Gate, Instruction, ParameterVector
from qiskit.circuit.library import QFT
from qiskit.providers import BaseBackend, Backend
from qiskit.quantum_info import partial_trace
from qiskit.utils import summarize_circuits
from qiskit.utils.arithmetic import is_power
from qiskit.utils.validation import validate_min
from qiskit.utils.quantum_instance import QuantumInstance
import qiskit.visualization
from qiskit.providers.aer import QasmSimulator
from datetime import datetime
import csv
# provider = IBMQ.enable_account("PUT TOKEN HERE")
backend = QasmSimulator()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all" #"last_expr" or "all"
def get_angles(a: int, n) -> np.ndarray:
# """Calculates the array of angles to be used in the addition in Fourier Space."""
s = bin(int(a))[2:].zfill(n + 1)
angles = np.zeros([n + 1])
for i in range(0, n + 1):
for j in range(i, n + 1):
if s[j] == '1':
angles[n - i] += math.pow(2, -(j - i))
angles[n - i] *= np.pi
return angles[::-1]
# This returns the angles in the opposite order
def my_create_QFT(qft_num_qubits,approximation_degree: int = 0,do_swaps: bool = False,insert_barriers: bool = True, name: str = 'qft'):
# up_reg = QuantumRegister(size = qft_num_qubits, name="aux")
circuit_qft = QuantumCircuit(qft_num_qubits)
i=qft_num_qubits-1
while i>=0:
# circuit_qft.h(up_reg[i])
circuit_qft.h(i)
j=i-1
while j>=0:
if (np.pi)/(pow(2,(i-j))) > approximation_degree:
# circuit_qft.cu1( (np.pi)/(pow(2,(i-j))) , up_reg[i] , up_reg[j] )
circuit_qft.cu1( (np.pi)/(pow(2,(i-j))) , i , j )
j=j-1
if insert_barriers:
circuit_qft.barrier()
i=i-1
""" If specified, apply the Swaps at the end """
if do_swaps:
i=0
while i < ((qft_num_qubits-1)/2):
# circuit_qft.swap(up_reg[i], up_reg[qft_num_qubits-1-i])
circuit_qft.swap(i, qft_num_qubits-1-i)
i=i+1
circuit_qft.name = "QFT"
return circuit_qft
def my_create_inverse_QFT(qft_num_qubits,approximation_degree: int = 0,do_swaps: bool = False,insert_barriers: bool = True, name: str = 'iqft'):
my_create_QFT_circuit = my_create_QFT(qft_num_qubits,approximation_degree,do_swaps,insert_barriers, name)
my_create_inverse_QFT_circuit = my_create_QFT_circuit.inverse()
my_create_inverse_QFT_circuit.name = "QFT†"
return my_create_inverse_QFT_circuit
def phi_add_gate(size: int, angles: Union[np.ndarray, ParameterVector]) -> Gate:
# """Gate that performs addition by a in Fourier Space."""
circuit = QuantumCircuit(size, name="phi_add")
for i, angle in enumerate(angles):
circuit.p(angle, i)
return circuit.to_gate()
def double_controlled_phi_add_mod_N(num_qubits: int, angles: Union[np.ndarray, ParameterVector],reg_size, a, N, n) -> QuantumCircuit:
# """Creates a circuit which implements double-controlled modular addition by a."""
circuit = QuantumCircuit(num_qubits, name="ccphi_add_mod_N")
ctl_up = 0
ctl_down = 1
ctl_aux = 2
# get qubits from aux register, omitting the control qubit
qubits = range(3, num_qubits)
# store the gates representing addition/subtraction by a in Fourier Space
phi_add_a = phi_add_gate(len(qubits), angles)
iphi_add_a = phi_add_a.inverse()
phi_add_N = phi_add_gate(reg_size - 1, get_angles(N, n))
iphi_add_N = phi_add_N.inverse()
circuit.append(phi_add_a.control(2), [ctl_up, ctl_down, *qubits])
circuit.append(iphi_add_N, qubits)
qft = QFT(n + 1).to_instruction()
# qft = my_create_QFT(n + 1).to_instruction()
iqft = QFT(n + 1).inverse().to_instruction()
# iqft = my_create_inverse_QFT(n + 1).to_instruction()
circuit.append(iqft, qubits)
circuit.cx(qubits[0], ctl_aux)
circuit.append(qft, qubits)
circuit.append(phi_add_N, qubits)
circuit.append(iphi_add_a.control(2), [ctl_up, ctl_down, *qubits])
circuit.append(iqft, qubits)
circuit.x(qubits[0])
circuit.cx(qubits[0], ctl_aux)
circuit.x(qubits[0])
circuit.append(qft, qubits)
circuit.append(phi_add_a.control(2), [ctl_up, ctl_down, *qubits])
return circuit
# """Circuit that implements single controlled modular multiplication by a"""
def controlled_multiple_mod_N(num_qubits: int, N: int, a: int, n, aux_reg_size):
# """Implements modular multiplication by a as an instruction."""
circuit = QuantumCircuit(
num_qubits,
# name="multiply_by_{}_mod_{}".format(a % N, N),
name=r"${0}^{{{1}^{{{2}}}}} mod{3}$".format(2,2,int(math.log(math.log(a,2),2)), N)
)
# label = r"${0}^{{{1}^{{{2}}}}} mod{3}$".format("†","y")
down = circuit.qubits[1: n + 1]
aux = circuit.qubits[n + 1:]
qubits = [aux[i] for i in reversed(range(n + 1))]
ctl_up = 0
ctl_aux = aux[-1]
angle_params = ParameterVector("angles", length=len(aux) - 1)
double_controlled_phi_add = double_controlled_phi_add_mod_N(
len(aux) + 2, angle_params, aux_reg_size, a, N, n
)
idouble_controlled_phi_add = double_controlled_phi_add.inverse()
qft_circuit = QFT(n + 1).to_instruction()
# qft_circuit = my_create_QFT(n + 1).to_instruction()
iqft_circuit = QFT(n + 1).inverse().to_instruction()
# iqft_circuit = my_create_inverse_QFT(n + 1).to_instruction()
circuit.append(qft_circuit, qubits)
# perform controlled addition by a on the aux register in Fourier space
for i, ctl_down in enumerate(down):
a_exp = (2 ** i) * a % N
angles = get_angles(a_exp, n)
bound = double_controlled_phi_add.assign_parameters({angle_params: angles})
circuit.append(bound, [ctl_up, ctl_down, ctl_aux, *qubits])
circuit.append(iqft_circuit, qubits)
# perform controlled subtraction by a in Fourier space on both the aux and down register
for j in range(n):
circuit.cswap(ctl_up, down[j], aux[j])
circuit.append(qft_circuit, qubits)
a_inv = modinv(a, N)
for i in reversed(range(len(down))):
a_exp = (2 ** i) * a_inv % N
angles = get_angles(a_exp, n)
bound = idouble_controlled_phi_add.assign_parameters({angle_params: angles})
circuit.append(bound, [ctl_up, down[i], ctl_aux, *qubits])
circuit.append(iqft_circuit, qubits)
return circuit
def modinv(a: int, m: int) -> int:
# """Returns the modular multiplicative inverse of a with respect to the modulus m."""
def egcd(a: int, b: int) -> Tuple[int, int, int]:
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
g, x, _ = egcd(a, m)
if g != 1:
raise ValueError("The greatest common divisor of {} and {} is {}, so the "
"modular inverse does not exist.".format(a, m, g))
return x % m
def get_factors(N: int, a: int, measurement: str) -> Optional[List[int]]:
# """Apply the continued fractions to find r and the gcd to find the desired factors."""
x_final = int(measurement, 2)
#print('In decimal, x_final value for this result is: {}.'.format(x_final))
if x_final <= 0:
fail_reason = 'x_final value is <= 0, there are no continued fractions.'
else:
fail_reason = None
#print('Running continued fractions for this case.')
# Calculate T and x/T
T_upper = len(measurement)
T = pow(2, T_upper)
x_over_T = x_final / T ## this is our theta
# Cycle in which each iteration corresponds to putting one more term in the
# calculation of the Continued Fraction (CF) of x/T
# Initialize the first values according to CF rule
i = 0
b = array.array('i')
t = array.array('f')
b.append(math.floor(x_over_T))
t.append(x_over_T - b[i])
exponential = 0.0
while i < N and fail_reason is None:
# From the 2nd iteration onwards, calculate the new terms of the CF based on the previous terms as the rule suggests
if i > 0:
try:
b_temp = math.floor(1 / t[i - 1])
except ZeroDivisionError as err:
b_temp = 0
b.append(b_temp)
try:
t_temp = (1 / t[i - 1]) - b[i]
except ZeroDivisionError as err:
t_temp = 0
t.append(t_temp) # type: ignore
# Calculate the denominator of the CF using the known terms
denominator = calculate_continued_fraction(b)
# Increment i for next iteration
i += 1
if denominator % 2 == 1:
#print('Odd denominator, will try next iteration of continued fractions.')
continue
# Denominator is even, try to get factors of N. Get the exponential a^(r/2)
if denominator < 1000:
try:
exponential = pow(a, denominator / 2)
except OverflowError as err:
exponential = 999999999
# Check if the value is too big or not
if exponential > 1000000:
if exponential == 999999999:
fail_reason = 'OverflowError'
else:
fail_reason = 'denominator of continued fraction is too big (> 10^9).'
else:
# The value is not too big, get the right values and do the proper gcd()
putting_plus = int(exponential + 1)
putting_minus = int(exponential - 1)
one_factor = math.gcd(putting_plus, N)
other_factor = math.gcd(putting_minus, N)
# Check if the factors found are trivial factors or are the desired factors
if any(factor in {1, N} for factor in (one_factor, other_factor)):
#print('Found just trivial factors, not good enough.')
# Check if the number has already been found, (use i - 1 because i was already incremented)
if t[i - 1] == 0:
fail_reason = 'the continued fractions found exactly x_final/(2^(2n)).'
else:
return sorted((one_factor, other_factor))
# Search for factors failed, write the reason for failure to the debug logs
#print('Cannot find factors from measurement {0} because {1}'.format(measurement, fail_reason or 'it took too many attempts.'))
return None
def calculate_continued_fraction(b: array.array) -> int:
# """Calculate the continued fraction of x/T from the current terms of expansion b."""
x_over_T = 0
for i in reversed(range(len(b) - 1)):
x_over_T = 1 / (b[i + 1] + x_over_T)
x_over_T += b[0]
frac = fractions.Fraction(x_over_T).limit_denominator()
#print('Approximation number %s of continued fractions:'.format(len(b)))
#print("Numerator:{0} \t\t Denominator: {1}.".format(frac.numerator, frac.denominator))
return frac.denominator
def process_results(sim_result, circuit, shots, N, a, n):
counts_result = sim_result.get_counts(circuit)
total_counts = len(counts_result)
counts_result_sorted = sorted(counts_result.items(), key=lambda x: x[1], reverse=True)
# """ Print info to user from the simulation results """
# print('Printing the various results followed by how many times they happened (out of the {} cases):\n'.format(shots))
counts_result_keys = list(counts_result.keys())
counts_result_values = list(counts_result.values())
#i=0
#while i < len(counts_result):
#print('Result \"{0}\" happened {1} times out of {2}\n'.format(list(sim_result.get_counts().keys())[i],list(sim_result.get_counts().values())[i],shots))
#print('Result \"{0}\" happened {1} times out of {2}\n'.format(counts_result_keys[i],counts_result_values[i],shots))
#i=i+1
prob_success=0
prob_failure=0
result_successful_counts = 0
result_failure_counts = 0
# len(counts_result_sorted)
# For each simulation result, print proper info to user and try to calculate the factors of N
#for measurement in counts_result_keys:
for measurement, frequency in counts_result_sorted:
# Get the x_final value from the final state qubits
x_value = int(measurement, 2)
#prob_this_result = 100 * ( int(counts_result[measurement] ) ) / (shots)
prob_this_result = 100 * frequency/shots
# print("------> Analyzing result {0}. This result happened in {1:.4f} % of all cases\nIn decimal, x_final value for this result is: {2}".format(measurement,prob_this_result,x_value))
factors = get_factors(N, a, measurement)
if factors:
prob_success = prob_success + prob_this_result
# print('Found factors {0} from measurement {1} which is {2} in decimal.\n'.format(factors, measurement, x_value))
result_successful_counts = result_successful_counts + 1
if factors not in result_factors:
result_factors.append(factors)
elif not factors:
prob_failure = prob_failure + prob_this_result
result_failure_counts = result_failure_counts + 1
return [result_factors, prob_success, prob_failure, total_counts, result_successful_counts,result_failure_counts]
def my_shor(a,N,shots):
start_time_number = datetime.now()
start_time = start_time_number.strftime("%H:%M:%S")
summary_result = dict()
validate_min('N', N, 3)
validate_min('a', a, 2)
if N < 1 or N % 2 == 0:
raise ValueError('The input needs to be an odd integer greater than 1.')
if a >= N or math.gcd(a, N) != 1:
raise ValueError('The integer a needs to satisfy a < N and gcd(a, N) = 1.')
n = math.ceil(math.log(N,2))
global result_factors
result_factors = []
tf, b, p = is_power(N, return_decomposition=True)
if tf:
print('The input integer is a power: {0}={1}^{2}.'.format(N, b, p))
result_factors.append(b)
# """auxilliary quantum register used in addition and multiplication"""
aux_reg = QuantumRegister(size = n+2, name="aux_reg")
up_reg = QuantumRegister(2*n, name = "up_reg")
# """quantum register where the multiplications are made"""
down_reg = QuantumRegister(n, name = "down_reg")
# """classical register where the measured values of the QFT are stored"""
up_classic = ClassicalRegister(2*n, name="up_classic")
# """ Create Quantum Circuit """
circuit = QuantumCircuit(up_reg ,down_reg ,aux_reg, up_classic, name="Shor circuit(N={}, a={})".format(N, a))
# phi_add_N_gate = phiADD(circuit,q,a,N,inv)
phi_add_N_gate = phi_add_gate(aux_reg.size - 1, get_angles(N,n))
iphi_add_N_gate = phi_add_N_gate.inverse()
# """ Initialize down register to 1 and create maximal superposition in top register """
circuit.h(up_reg)
circuit.x(down_reg[0])
# circuit.draw(filename = "shor_standard_QFT")
# """ Apply the multiplication gates as showed in the report in order to create the exponentiation """
for i, ctl_up in enumerate(up_reg): # type: ignore
a_aux = int(pow(a, pow(2, i)))
controlled_multiple_mod_N_circuit = controlled_multiple_mod_N(
len(down_reg) + len(aux_reg) + 1, N, a_aux,n,aux_reg.size
)
controlled_multiple_mod_N_result = controlled_multiple_mod_N_circuit.to_instruction()
circuit.append(
controlled_multiple_mod_N_result, [ctl_up, *down_reg, *aux_reg]
)
# circuit.draw()
iqft = QFT(len(up_reg)).inverse().to_instruction()
# iqft = my_create_inverse_QFT(len(up_reg)).to_instruction()
# iqft = my_create_inverse_QFT(len(up_reg), insert_barriers = False).to_gate(label = r"$QFT^{{{0}}}$".format("†"))
circuit.append(iqft, up_reg)
circuit.measure(up_reg, up_classic)
# circuit.draw(filename = "shor_standard_QFT_final_circuit",fold = -1 )
# print(summarize_circuits(circuit))
# circuit.draw()
print('Running with N={0} and a={1} with number of qubits n={2}'.format(N, a, 4*n + 2))
qc_compiled = transpile(circuit, backend, optimization_level = 3)
job_sim_1 = backend.run(qc_compiled, shots=shots)
sim_result=job_sim_1.result()
# counts_result = sim_result.get_counts(circuit)
# len(counts_result)
# measurement_plot = qiskit.visualization.plot_histogram(counts_result,figsize=(20, 12) ,number_to_keep = 30,bar_labels=True, title = "Measurement results from shor_standard_QFT circuit variant" )
# measurement_plot.savefig("shor_standard_QFT_measurement")
# measurement_plot
processed_result = process_results(sim_result, circuit, shots, N, a, n)
end_time_number = datetime.now()
end_time = end_time_number.strftime("%H:%M:%S")
duration = end_time_number - start_time_number
print("Current Start Time =", start_time)
print(processed_result)
print("Current End Time =", end_time)
circuit_count_ops = circuit.count_ops()
circuit_decomposed = circuit.decompose()
circuit_decomposed_count_ops = circuit_decomposed.count_ops()
qc_compiled_count_ops = qc_compiled.count_ops()
summary_result["num_qubits"] = n
summary_result["Number(N)"] = N
summary_result["a"] = a
summary_result["start_time"] = start_time
summary_result["end_time"] = end_time
summary_result["duration"] = duration
summary_result["result_factors"] = processed_result[0]
summary_result["prob_success"] = processed_result[1]
summary_result["prob_failure"] = processed_result[2]
summary_result["total_counts"] = processed_result[3]
summary_result["result_successful_counts"] = processed_result[4]
summary_result["result_failure_counts"] = processed_result[5]
summary_result["circuit_width"] = circuit.width()
summary_result["circuit_depth"] = circuit.depth()
summary_result["circuit_size"] = circuit.size()
summary_result["circuit_num_nonlocal_gates"] = circuit.num_nonlocal_gates()
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_clbits"] = circuit.num_clbits
summary_result["circuit_num_qubits"] = circuit.num_qubits
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_of_count_ops"] = len(circuit_count_ops)
summary_result["circuit_num_of_x"] = circuit_count_ops.get('x')
summary_result["circuit_num_of_measure"] = circuit_count_ops.get('measure')
summary_result["circuit_num_of_h"] = circuit_count_ops.get('h')
summary_result["circuit_num_of_cswap"] = circuit_count_ops.get('cswap')
summary_result["circuit_num_of_swap"] = circuit_count_ops.get('swap')
summary_result["circuit_num_of_cx"] = circuit_count_ops.get('cx')
summary_result["circuit_num_of_toffoli"] = circuit_count_ops.get('toffoli')
summary_result["circuit_num_of_p"] = circuit_count_ops.get('p')
summary_result["circuit_num_of_t"] = circuit_count_ops.get('t')
summary_result["circuit_decomposed_width"] = circuit_decomposed.width()
summary_result["circuit_decomposed_depth"] = circuit_decomposed.depth()
summary_result["circuit_decomposed_size"] = circuit_decomposed.size()
summary_result["circuit_decomposed_num_nonlocal_gates"] = circuit_decomposed.num_nonlocal_gates()
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_clbits"] = circuit_decomposed.num_clbits
summary_result["circuit_decomposed_num_qubits"] = circuit_decomposed.num_qubits
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_of_count_ops"] = len(circuit_decomposed_count_ops)
summary_result["circuit_decomposed_num_of_x"] = circuit_decomposed_count_ops.get('x')
summary_result["circuit_decomposed_num_of_measure"] = circuit_decomposed_count_ops.get('measure')
summary_result["circuit_decomposed_num_of_h"] = circuit_decomposed_count_ops.get('h')
summary_result["circuit_decomposed_num_of_cswap"] = circuit_decomposed_count_ops.get('cswap')
summary_result["circuit_decomposed_num_of_swap"] = circuit_decomposed_count_ops.get('swap')
summary_result["circuit_decomposed_num_of_cx"] = circuit_decomposed_count_ops.get('cx')
summary_result["circuit_decomposed_num_of_toffoli"] = circuit_decomposed_count_ops.get('toffoli')
summary_result["circuit_decomposed_num_of_p"] = circuit_decomposed_count_ops.get('p')
summary_result["circuit_decomposed_num_of_t"] = circuit_decomposed_count_ops.get('t')
summary_result["qc_compiled_width"] = qc_compiled.width()
summary_result["qc_compiled_depth"] = qc_compiled.depth()
summary_result["qc_compiled_size"] = qc_compiled.size()
summary_result["qc_compiled_num_nonlocal_gates"] = qc_compiled.num_nonlocal_gates()
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_clbits"] = qc_compiled.num_clbits
summary_result["qc_compiled_num_qubits"] = qc_compiled.num_qubits
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_of_count_ops"] = len(qc_compiled_count_ops)
summary_result["qc_compiled_num_of_x"] = qc_compiled_count_ops.get('x')
summary_result["qc_compiled_num_of_measure"] = qc_compiled_count_ops.get('measure')
summary_result["qc_compiled_num_of_h"] = qc_compiled_count_ops.get('h')
summary_result["qc_compiled_num_of_cswap"] = qc_compiled_count_ops.get('cswap')
summary_result["qc_compiled_num_of_swap"] = qc_compiled_count_ops.get('swap')
summary_result["qc_compiled_num_of_cx"] = qc_compiled_count_ops.get('cx')
summary_result["qc_compiled_num_of_toffoli"] = qc_compiled_count_ops.get('toffoli')
summary_result["qc_compiled_num_of_p"] = qc_compiled_count_ops.get('p')
summary_result["qc_compiled_num_of_t"] = qc_compiled_count_ops.get('t')
return summary_result
# Run for just a single number N
%%time
N = 33
shots = 1024
global result_factors
all_summary_result_temp = []
for random_a in range(16, 17):
if math.gcd(random_a,N) > 1:
continue
a = random_a
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n".format(a, N))
all_summary_result_temp.append(summary_result)
summary_result_list = []
for key, value in summary_result.items():
summary_result_list.append([key,value])
summary_result_list
with open("a({0})_N({1})_standard.csv".format(a, N), 'a') as myfile:
write = csv.writer(myfile)
#write.writerow(fields)
write.writerows(summary_result_list)
all_summary_result_temp
# Run for many numbers N.
%%time
shots = 1024
global result_factors
all_summary_result = []
for N in [15, 21, 33, 35, 39, 51, 55, 57]:
for a in range(2, N):
if math.gcd(a,N) > 1:
continue
print("Beginning running for a = {} and N = {}".format(a, N))
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n\n".format(a, N))
all_summary_result.append(summary_result)
all_summary_result
%qiskit_copyright
|
https://github.com/AnkRaw/Quantum-Convolutional-Neural-Network
|
AnkRaw
|
# Importing Libraries
import torch
from torch import cat, no_grad, manual_seed
from torch.utils.data import DataLoader
from torchvision import transforms
import torch.optim as optim
from torch.nn import (
Module,
Conv2d,
Linear,
Dropout2d,
NLLLoss
)
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from qiskit_machine_learning.neural_networks import EstimatorQNN
from qiskit_machine_learning.connectors import TorchConnector
from qiskit.circuit.library import RealAmplitudes, ZZFeatureMap
from qiskit import QuantumCircuit
from qiskit.visualization import circuit_drawer
# Imports for CIFAR-10s
from torchvision.datasets import CIFAR10
from torchvision import transforms
def prepare_data(X, labels_to_keep, batch_size):
# Filtering out labels (originally 0-9), leaving only labels 0 and 1
filtered_indices = [i for i in range(len(X.targets)) if X.targets[i] in labels_to_keep]
X.data = X.data[filtered_indices]
X.targets = [X.targets[i] for i in filtered_indices]
# Defining dataloader with filtered data
loader = DataLoader(X, batch_size=batch_size, shuffle=True)
return loader
# Set seed for reproducibility
manual_seed(42)
# CIFAR-10 data transformation
transform = transforms.Compose([
transforms.ToTensor(), # convert the images to tensors
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # Normalization usign mean and std.
])
labels_to_keep = [0, 1]
batch_size = 1
# Preparing Train Data
X_train = CIFAR10(root="./data", train=True, download=True, transform=transform)
train_loader = prepare_data(X_train, labels_to_keep, batch_size)
# Preparing Test Data
X_test = CIFAR10(root="./data", train=False, download=True, transform=transform)
test_loader = prepare_data(X_test, labels_to_keep, batch_size)
print(f"Training dataset size: {len(train_loader.dataset)}")
print(f"Test dataset size: {len(test_loader.dataset)}")
# Defining and creating QNN
def create_qnn():
feature_map = ZZFeatureMap(2) # ZZFeatureMap with 2 bits, entanglement between qubits based on the pairwise product of input features.
ansatz = RealAmplitudes(2, reps=1) # parameters (angles, in the case of RealAmplitudes) that are adjusted during the training process to optimize the quantum model for a specific task.
qc = QuantumCircuit(2)
qc.compose(feature_map, inplace=True)
qc.compose(ansatz, inplace=True)
qnn = EstimatorQNN(
circuit=qc,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
input_gradients=True,
)
return qnn
qnn = create_qnn()
# Visualizing the QNN circuit
circuit_drawer(qnn.circuit, output='mpl')
# Defining torch NN module
class Net(Module):
def __init__(self, qnn):
super().__init__()
self.conv1 = Conv2d(3, 16, kernel_size=3, padding=1)
self.conv2 = Conv2d(16, 32, kernel_size=3, padding=1)
self.dropout = Dropout2d()
self.fc1 = Linear(32 * 8 * 8, 64)
self.fc2 = Linear(64, 2) # 2-dimensional input to QNN
self.qnn = TorchConnector(qnn)
self.fc3 = Linear(1, 1) # 1-dimensional output from QNN
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = self.dropout(x)
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
x = self.qnn(x)
x = self.fc3(x)
return cat((x, 1 - x), -1)
# Creating model
model = Net(qnn)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
# Defining model, optimizer, and loss function
optimizer = optim.Adam(model.parameters(), lr=0.001)
loss_func = NLLLoss()
# Starting training
epochs = 10
loss_list = []
model.train()
for epoch in range(epochs):
total_loss = []
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device) # Move data to GPU
optimizer.zero_grad(set_to_none=True)
output = model(data)
loss = loss_func(output, target)
loss.backward()
optimizer.step()
total_loss.append(loss.item())
loss_list.append(sum(total_loss) / len(total_loss))
print("Training [{:.0f}%]\tLoss: {:.4f}".format(100.0 * (epoch + 1) / epochs, loss_list[-1]))
# Plotting loss convergence
plt.plot(loss_list)
plt.title("Hybrid NN Training Convergence")
plt.xlabel("Training Iterations")
plt.ylabel("Neg. Log Likelihood Loss")
plt.show()
# Saving the model
torch.save( model.state_dict(), "model_cifar10_10EPOCHS.pt")
# Loading the model
qnn_cifar10 = create_qnn()
model_cifar10 = Net(qnn_cifar10)
model_cifar10.load_state_dict(torch.load("model_cifar10.pt"))
correct = 0
total = 0
model_cifar10.eval()
with torch.no_grad():
for data, target in test_loader:
output = model_cifar10(data)
_, predicted = torch.max(output.data, 1)
total += target.size(0)
correct += (predicted == target).sum().item()
# Calculating and print test accuracy
test_accuracy = correct / total * 100
print(f"Test Accuracy: {test_accuracy:.2f}%")
# Plotting predicted labels
n_samples_show = 6
count = 0
fig, axes = plt.subplots(nrows=1, ncols=n_samples_show, figsize=(10, 3))
model_cifar10.eval()
with no_grad():
for batch_idx, (data, target) in enumerate(test_loader):
if count == n_samples_show:
break
output = model_cifar10(data)
if len(output.shape) == 1:
output = output.reshape(1, *output.shape)
pred = output.argmax(dim=1, keepdim=True)
axes[count].imshow(np.transpose(data[0].numpy(), (1, 2, 0)))
axes[count].set_xticks([])
axes[count].set_yticks([])
axes[count].set_title("Predicted {0}\n Actual {1}".format(pred.item(), target.item()))
count += 1
plt.show()
|
https://github.com/EusseJhoan/DeutschJosza_algorithm
|
EusseJhoan
|
from qiskit import QuantumCircuit, transpile, Aer
from qiskit.visualization import plot_histogram
import numpy as np
sim = Aer.get_backend('aer_simulator')
def U_f1(qc):
return qc
def U_f2(qc):
qc.x(1) #Compuerta X al segundo qubit
return qc
def U_f3(qc):
qc.cx(0,1) #Compuerta CNOT entre primer y segundo quibit (el primero es el que controla)
return qc
def U_f4(qc):
qc.cx(0,1) #Compuerta CNOT entre primer y segundo quibit (el primero es el que controla)
qc.x(1) #Compuerta X al segundo qubit
return qc
def Deutsch(U_f):
qc=QuantumCircuit(2,1) #Se crea un circuito cuántico con 2 bits cuánticos y 1 canal clásico
qc.x(1) #Compuerta X al segundo qubit (inicializar estado |1>)
qc.h(0) #Compuerta H al primer qubit
qc.h(1) #Compuerta H al segundo qubit
qc.barrier() #Barrera (empieza oráculo)
qc = U_f(qc) #Agregamos el oráculo
qc.barrier() #Barrera (termina oráculo)
qc.h(0) #Compuerta H al primer qubit
qc.measure(0,0) #Medimos el primer qubit y enviamos señal al canal clásico
return qc
qc=Deutsch(U_f1) # definición circuito con oráculo usando f_1(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f2) #definición circuito con oráculo usando f_2(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas del simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f3) #definición circuito con oráculo usando f_3(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f4) #definición circuito con oráculo usando f_4(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
#oráculo para f(x) constante para un número n de bits en el registro
def constant(qc,n):
ran=np.random.randint(2) #selección aleatoria de 0 ó 1
if ran == 1:
qc.x(n) #si el número aleatorio es 1 se pone compuerta X en el objetivo (se induce fase global -1 al registro)
return qc
#oráculo para f(x) balanceado para un número n de bits en el registro
def balanced(qc,n):
for i in range(n):
qc.cx(i,n) #se crea una CNOT entre cada qubit del registro y el objetivo (los qubits del registro controlan)
ran=np.random.randint(2) #selección aleatoria de 0 ó 1
if ran == 1:
qc.x(n) #si el número aleatorio es 1 se pone compuerta X en el objetivo (se induce fase global -1 al registro)
return qc
def D_J(U_f,n):
qc=QuantumCircuit(n+1,n) #Se crea un circuito cuántico con n+1 quibits y n canales clásicos
qc.x(n) #Compuerta X al bit del registro
for i in range(n+1):
qc.h(i) #Compuerta H a todos los bits
qc.barrier() #Barrera (empieza oráculo)
qc = U_f(qc,n) #Agregamos el oráculo
qc.barrier() #Barrera (termina oráculo)
for i in range(n):
qc.h(i) #Compuerta H a los n bits del registro
qc.measure(i,i) #Medición los n bits del registro
return qc
qc=D_J(constant,3) #definición circuito con oráculo constante y 3 bits en registro
display(qc.draw()) #ver circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=D_J(balanced,3)
display(qc.draw())
counts = sim.run(qc).result().get_counts()
plot_histogram(counts)
|
https://github.com/strangequarkkk/BB84-Protocol-for-QKD
|
strangequarkkk
|
import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(assemble(qc))
plot_histogram(job.result().get_counts())
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(assemble(qc))
plot_histogram(job.result().get_counts())
n = 100
## Step 1
# Alice generates bits.
alice_bits = np.random.randint(0,2,n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = np.random.randint(0,2,n)
# Function to compare the bits & bases generated by alice, and then 'encode' the message. Basically determines the state of the qubit/photon to send.
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
# Alice computes the encoded message using the function defined above.
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = np.random.randint(0,2,n)
# Function to decode the message sent by alice by comparing qubit/photon states with Bob's generated bases.
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
qobj = assemble(message[q], shots=1, memory=True)
result = aer_sim.run(qobj).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
# Decode the message according to his bases
bob_results = measure_message(message, bob_bases)
## Step 4
# Function to perform sifting i.e. disregard the bits for which Bob's & A;ice's bases didnot match.
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
# Performing sifting for Alice's and Bob's bits.
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print("Alice's key after sifting (without interception)", alice_key)
print("Bob's key after sifting (without interception) ", bob_key)
# # Step 5
# # Function for parameter estimation i.e. determining the error rate by comparing subsets taen from both Alice's key & Bob's key.
# def sample_bits(bits, selection):
# sample = []
# for i in selection:
# # use np.mod to make sure the
# # bit we sample is always in
# # the list range
# i = np.mod(i, len(bits))
# # pop(i) removes the element of the
# # list at index 'i'
# sample.append(bits.pop(i))
# return sample
# # Performing parameter estimation & disregarding the bits used for comparison from Alice's & Bob's key.
# sample_size = 15
# bit_selection = np.random.randint(0,n,size=sample_size)
# bob_sample = sample_bits(bob_key, bit_selection)
# alice_sample = sample_bits(alice_key, bit_selection)
num = 0
for i in range(0,len(bob_key)):
if alice_key[i] == bob_key[i]:
num = num + 1
matching_bits = (num/len(bob_key))*100
print(matching_bits,"% of the bits match.")
## Step 1
alice_bits = np.random.randint(2, size=n)
## Step 2
alice_bases = np.random.randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = np.random.randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = np.random.randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print("Alice's key after sifting (with interception)", alice_key)
print("Bob's key after sifting (with interception) ", bob_key)
# ## Step 5
# sample_size = 15
# bit_selection = np.random.randint(n, size=sample_size)
# bob_sample = sample_bits(bob_key, bit_selection)
# alice_sample = sample_bits(alice_key, bit_selection)
num = 0
for i in range(0,len(bob_key)):
if alice_key[i] == bob_key[i]:
num = num + 1
matching_bits = (num/len(bob_key))*100
print(matching_bits,"% of the bits match.")
plt.rcParams['axes.linewidth'] = 2
mpl.rcParams['font.family'] = ['Georgia']
plt.figure(figsize=(10.5,6))
ax=plt.axes()
ax.set_title('')
ax.set_xlabel('$n$ (Number of bits drawn from the sifted keys for determining error rate)',fontsize = 18,labelpad=10)
ax.set_ylabel(r'$P(Eve\ detected)$',fontsize = 18,labelpad=10)
ax.xaxis.set_tick_params(which='major', size=8, width=2, direction='in', top='on')
ax.yaxis.set_tick_params(which='major', size=8, width=2, direction='in', top='on')
ax.tick_params(axis='x', labelsize=20)
ax.tick_params(axis='y', labelsize=20)
ax. xaxis. label. set_size(20)
ax. yaxis. label. set_size(20)
n = 30
x = np.arange(n+1)
y = 1 - 0.75**x
ax.plot(x,y,color = plt.cm.rainbow(np.linspace(0, 1, 5))[0], marker = "s", markerfacecolor='r')
|
https://github.com/luis6156/Shor-s-Quantum-Algorithm
|
luis6156
|
from qiskit import QuantumCircuit, Aer, execute, IBMQ
from qiskit.utils import QuantumInstance
import numpy as np
from qiskit.algorithms import Shor
IBMQ.enable_account('ENTER API TOKEN HERE') # Enter your API token here
provider = IBMQ.get_provider(hub='ibm-q')
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=1000)
my_shor = Shor(quantum_instance)
result_dict = my_shor.factor(15)
print(result_dict)
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
with open('in-exemplo.txt', 'r') as f:
print(f.read())
with open('out-exemplo.txt', 'r') as f:
print(f.read())
import time
import matplotlib.pyplot as plt
import pandas as pd
import os
import subprocess
%matplotlib inline
#Roda entradas
def roda_com_entrada(executavel, arquivo_in, envs = '1', deb = '0'):
with open(arquivo_in) as f:
start = time.perf_counter()
a = f.read()
proc = subprocess.run([executavel], input=a, text=True, capture_output=True, env=dict(OMP_NUM_THREADS=envs, DEBUG=deb, **os.environ))
end = time.perf_counter()
f.close()
ret = ''
for i in a:
if i == "\n":
break
ret += i
return (proc.stdout, end - start, int(ret))
v
#retorna tamanho do tour apartir do stdout
buf = ''
for i in out:
if i == " ":
return float(buf)
buf += i
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
resultados1 = []
resultados2 = []
resultados3 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca_local_antigo','busca-exaustiva/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt')
c = roda_com_entrada('./heuristico/heuristico','busca-exaustiva/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
resultados1.append(tamanho_tour(a[0]))
resultados2.append(tamanho_tour(b[0]))
resultados3.append(tamanho_tour(c[0]))
#Teste com entrada um pouco maior
print("Rodando entrada: 8")
tempos.append(roda_com_entrada('./busca_local_antigo','maior.txt')[1])
tempos_1.append(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[1])
tempos_2.append(roda_com_entrada('./heuristico/heuristico','maior.txt')[1])
tamanho_entradas.append(roda_com_entrada('./busca-local/busca-local','maior.txt')[2])
resultados1.append(tamanho_tour(roda_com_entrada('./busca_local_antigo','maior.txt')[0]))
resultados2.append(tamanho_tour(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[0]))
resultados3.append(tamanho_tour(roda_com_entrada('./heuristico/heuristico','maior.txt')[0]))
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-exaustiva", "busca-local","heuristico"])
plt.show()
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-local","heuristico"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-tempo"] = pd.Series(tempos)
df["busca-exaustiva-tempo"] = pd.Series(tempos_1)
df["heuristica-tempo"] = pd.Series(tempos_2)
df["busca-local-resultado"] = pd.Series(resultados1)
df["busca-exaustiva-resultado"] = pd.Series(resultados2)
df["heuristica-resultado"] = pd.Series(resultados3)
df
df.describe()
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
tempos_3 = []
tempos_4 = []
tempos_5 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','2')
c = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','3')
d = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','4')
e = roda_com_entrada('./busca_local_antigo','busca-local/in-'+str(i)+'.txt')
f = roda_com_entrada('./busca-local/busca-local-gpu','busca-local/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tempos_3.append(d[1])
tempos_4.append(e[1])
tempos_5.append(f[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.plot(tamanho_entradas, tempos_3)
plt.legend(["1 thread otimizado", "2 threads otimizado","3 threads otimizado", "4 threads otimizado", "Sem otimizações"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_3)
plt.plot(tamanho_entradas, tempos_5)
plt.legend(["4 thread otimizado", "GPU"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_4)
plt.legend(["1 thread otimizado", "Sem otimizações"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-1-thread"] = pd.Series(tempos)
df["busca-local-2-threads"] = pd.Series(tempos_1)
df["busca-local-3-threads"] = pd.Series(tempos_2)
df["busca-local-4-threads"] = pd.Series(tempos_3)
df["busca-local-gpu"] = pd.Series(tempos_5)
df["busca-local-semopt"] = pd.Series(tempos_4)
df
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
if i != 7:
a = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '1')
tempos.append(a[1])
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '8', '0')
c = roda_com_entrada('./busca-exaustiva-apenasbb','busca-exaustiva/in-'+str(i)+'.txt', '1', '0')
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas[:-1], tempos)
plt.plot(tamanho_entradas[:-1], tempos_2[:-1])
plt.legend(["Exaustivo Simples", "Exaustivo Branch and Bound"])
plt.show()
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["Branch and Bound Paralelo", "Branch and Bound Simples"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-exaustiva-simples"] = pd.Series(tempos)
df["busca-exaustiva-branchnbound"] = pd.Series(tempos_2)
df["busca-exaustiva-branchnbound-par"] = pd.Series(tempos_1)
df
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
with open('in-exemplo.txt', 'r') as f:
print(f.read())
with open('out-exemplo.txt', 'r') as f:
print(f.read())
import time
import matplotlib.pyplot as plt
import pandas as pd
import os
import subprocess
%matplotlib inline
#Roda entradas
def roda_com_entrada(executavel, arquivo_in, envs = '1', deb = '0'):
with open(arquivo_in) as f:
start = time.perf_counter()
a = f.read()
proc = subprocess.run([executavel], input=a, text=True, capture_output=True, env=dict(OMP_NUM_THREADS=envs, DEBUG=deb, **os.environ))
end = time.perf_counter()
f.close()
ret = ''
for i in a:
if i == "\n":
break
ret += i
return (proc.stdout, end - start, int(ret))
#retorna tamanho do tour apartir do stdout
def tamanho_tour(out):
buf = ''
for i in out:
if i == " ":
return float(buf)
buf += i
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
resultados1 = []
resultados2 = []
resultados3 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca_local_antigo','busca-exaustiva/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt')
c = roda_com_entrada('./heuristico/heuristico','busca-exaustiva/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
resultados1.append(tamanho_tour(a[0]))
resultados2.append(tamanho_tour(b[0]))
resultados3.append(tamanho_tour(c[0]))
#Teste com entrada um pouco maior
print("Rodando entrada: 8")
tempos.append(roda_com_entrada('./busca_local_antigo','maior.txt')[1])
tempos_1.append(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[1])
tempos_2.append(roda_com_entrada('./heuristico/heuristico','maior.txt')[1])
tamanho_entradas.append(roda_com_entrada('./busca-local/busca-local','maior.txt')[2])
resultados1.append(tamanho_tour(roda_com_entrada('./busca_local_antigo','maior.txt')[0]))
resultados2.append(tamanho_tour(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[0]))
resultados3.append(tamanho_tour(roda_com_entrada('./heuristico/heuristico','maior.txt')[0]))
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-exaustiva", "busca-local","heuristico"])
plt.show()
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-local","heuristico"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-tempo"] = pd.Series(tempos)
df["busca-exaustiva-tempo"] = pd.Series(tempos_1)
df["heuristica-tempo"] = pd.Series(tempos_2)
df["busca-local-resultado"] = pd.Series(resultados1)
df["busca-exaustiva-resultado"] = pd.Series(resultados2)
df["heuristica-resultado"] = pd.Series(resultados3)
df
df.describe()
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
tempos_3 = []
tempos_4 = []
tempos_5 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','2')
c = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','3')
d = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','4')
e = roda_com_entrada('./busca_local_antigo','busca-local/in-'+str(i)+'.txt')
f = roda_com_entrada('./busca-local/busca-local-gpu','busca-local/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tempos_3.append(d[1])
tempos_4.append(e[1])
tempos_5.append(f[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.plot(tamanho_entradas, tempos_3)
plt.legend(["1 thread otimizado", "2 threads otimizado","3 threads otimizado", "4 threads otimizado", "Sem otimizações"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_3)
plt.plot(tamanho_entradas, tempos_5)
plt.legend(["4 thread otimizado", "GPU"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_4)
plt.legend(["1 thread otimizado", "Sem otimizações"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-1-thread"] = pd.Series(tempos)
df["busca-local-2-threads"] = pd.Series(tempos_1)
df["busca-local-3-threads"] = pd.Series(tempos_2)
df["busca-local-4-threads"] = pd.Series(tempos_3)
df["busca-local-gpu"] = pd.Series(tempos_5)
df["busca-local-semopt"] = pd.Series(tempos_4)
df
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '1')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '0')
tempos.append(a[1])
tempos_1.append(b[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.legend(["Exaustivo Simples", "Exaustivo Branch and Bound"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-exaustiva-simples"] = pd.Series(tempos)
df["busca-exaustiva-branchnbound"] = pd.Series(tempos_1)
df
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
import math
import matplotlib.pyplot as plt
%matplotlib inline
class TSP:
def __init__(self):
self.flat_mat = flat_mat
self.n = 0
self.melhor_dist = 1e11
self.pontos = []
self.melhores_pontos = []
def busca_exaustiva(self, flat_mat, n, ite):
if ite == n:
dist = 0
for j in range(1, n):
dist += flat_mat[self.pontos[j-1] * n + self.pontos[j]]
dist += flat_mat[self.pontos[n-1] * n + self.pontos[0]]
if dist < self.melhor_dist:
self.melhor_dist = dist
self.melhores_pontos = self.pontos[:]
return
for i in range(n):
if self.pontos[i] == -1:
self.pontos[i] = ite
self.busca_exaustiva(flat_mat, n, ite + 1)
self.pontos[i] = -1
def dist_mat(self):
x = []
y = []
flat_mat = [] #matriz 1 dimensao contendo todas as distancias possiveis entre os pontos para facilitar cálculo.
while True:
try:
temp = input("Digite a coordenada x y: ").split()
x.append(float(temp[0]))
y.append(float(temp[1]))
except:
break
for i in range(len(x)):
for j in range(len(y)):
flat_mat.append(math.sqrt((x[i] - x[j])**2 + (y[i] - y[j])**2))
return flat_mat, x, y
def get_results(self):
self.flat_mat, x, _ = self.dist_mat()
self.n = len(x)
self.pontos = [-1]*self.n
self.pontos[0] = 0
self.busca_exaustiva(self.flat_mat, self.n, 1)
return self.melhor_dist, self.melhores_pontos
Tsp = TSP()
distancia, pontos = Tsp.get_results()
print("Melhor distancia encontrada: ", distancia)
print("Melhor caminho encontrado: ", pontos)
#plota gráfico
def connectpoints(x,y,p1,p2):
x1, x2 = x[p1], x[p2]
y1, y2 = y[p1], y[p2]
plt.plot([x1,x2],[y1,y2],'ro-')
for i in range(1, len(pontos)):
connectpoints(x,y,pontos[i-1],pontos[i])
connectpoints(x,y,pontos[len(x)-1],pontos[0])
plt.title("Percurso")
plt.show()
%%time
%%cmd
python TSP.py < in-1.txt
type out-1.txt
python TSP.py < in-2.txt
type out-2.txt
python TSP.py < in-3.txt
type out-3.txt
python TSP.py < in-4.txt
type out-4.txt
from qiskit import IBMQ
import numpy as np
#IBMQ.save_account('seu-tokenIBMQ-para-rodar-localmente')
IBMQ.load_account()
from qiskit import Aer
from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua import aqua_globals
from qiskit.aqua import QuantumInstance
from qiskit.optimization.applications.ising.common import sample_most_likely
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.problems import QuadraticProgram
import logging
from qiskit.aqua import set_qiskit_aqua_logging
#Preparando os dados segundo os imputs do usuario para serem resolvidos pelo qiskit max 4 pontos por limitação de qubits
coord = []
flat_mat, x, y = TSP().dist_mat()
dist_mat = np.array(flat_mat).reshape(len(x),len(x))
for i, j in zip(x, y):
coord.append([i,j])
ins = tsp.TspData('TSP_Q', dim=len(x), coord=np.array(coord), w=dist_mat)
qubitOp, offset = tsp.get_operator(ins)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
#Usando o numpyMinimumEigensolver como o solver do problema para resolver de forma quantica
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
print('energy:', result.eigenvalue.real)
print('tsp objective:', result.eigenvalue.real + offset)
x_Q = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
for i in range(1, len(z)):
connectpoints(x,y,z[i-1],z[i])
connectpoints(x,y,z[len(x)-1],z[0])
plt.title("Percurso")
plt.show()
#instanciando o simulador ou o computador real importante lembrar que nao ira funcionar para mais de 4 pontos pelo numero de qubits disponibilizados pela IBM que sao apenas 16 para o simulador qasm e 15 para a maquina quantica
provider = IBMQ.get_provider(hub = 'ibm-q')
device = provider.get_backend('ibmq_16_melbourne')
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('qasm_simulator')
#descomentar essa linha caso queira rodar na maquina real
#backend = device
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
#rodando no simulador quantico
spsa = SPSA(maxiter=10)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
result = vqe.run(quantum_instance)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
import math
import matplotlib.pyplot as plt
%matplotlib inline
class TSP:
def __init__(self):
self.flat_mat = flat_mat
self.n = 0
self.melhor_dist = 1e11
self.pontos = []
self.melhores_pontos = []
def busca_exaustiva(self, flat_mat, n, ite):
if ite == n:
dist = 0
for j in range(1, n):
dist += flat_mat[self.pontos[j-1] * n + self.pontos[j]]
dist += flat_mat[self.pontos[n-1] * n + self.pontos[0]]
if dist < self.melhor_dist:
self.melhor_dist = dist
self.melhores_pontos = self.pontos[:]
return
for i in range(n):
if self.pontos[i] == -1:
self.pontos[i] = ite
self.busca_exaustiva(flat_mat, n, ite + 1)
self.pontos[i] = -1
def dist_mat(self):
x = []
y = []
flat_mat = [] #matriz 1 dimensao contendo todas as distancias possiveis entre os pontos para facilitar cálculo.
while True:
try:
temp = input("Digite a coordenada x y: ").split()
x.append(float(temp[0]))
y.append(float(temp[1]))
except:
break
for i in range(len(x)):
for j in range(len(y)):
flat_mat.append(math.sqrt((x[i] - x[j])**2 + (y[i] - y[j])**2))
return flat_mat, x, y
def get_results(self):
self.flat_mat, x, _ = self.dist_mat()
self.n = len(x)
self.pontos = [-1]*self.n
self.pontos[0] = 0
self.busca_exaustiva(self.flat_mat, self.n, 1)
return self.melhor_dist, self.melhores_pontos
Tsp = TSP()
distancia, pontos = Tsp.get_results()
print("Melhor distancia encontrada: ", distancia)
print("Melhor caminho encontrado: ", pontos)
#plota gráfico
def connectpoints(x,y,p1,p2):
x1, x2 = x[p1], x[p2]
y1, y2 = y[p1], y[p2]
plt.plot([x1,x2],[y1,y2],'ro-')
for i in range(1, len(pontos)):
connectpoints(x,y,pontos[i-1],pontos[i])
connectpoints(x,y,pontos[len(x)-1],pontos[0])
plt.title("Percurso")
plt.show()
%%time
%%cmd
python TSP.py < in-1.txt
type out-1.txt
python TSP.py < in-2.txt
type out-2.txt
python TSP.py < in-3.txt
type out-3.txt
python TSP.py < in-4.txt
type out-4.txt
from qiskit import IBMQ
import numpy as np
#IBMQ.save_account('seu-tokenIBMQ-para-rodar-localmente')
IBMQ.load_account()
from qiskit import Aer
from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua import aqua_globals
from qiskit.aqua import QuantumInstance
from qiskit.optimization.applications.ising.common import sample_most_likely
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.problems import QuadraticProgram
import logging
from qiskit.aqua import set_qiskit_aqua_logging
#Preparando os dados segundo os imputs do usuario para serem resolvidos pelo qiskit max 4 pontos por limitação de qubits
coord = []
flat_mat, x, y = TSP().dist_mat()
dist_mat = np.array(flat_mat).reshape(len(x),len(x))
for i, j in zip(x, y):
coord.append([i,j])
ins = tsp.TspData('TSP_Q', dim=len(x), coord=np.array(coord), w=dist_mat)
qubitOp, offset = tsp.get_operator(ins)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
#Usando o numpyMinimumEigensolver como o solver do problema para resolver de forma quantica
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
print('energy:', result.eigenvalue.real)
print('tsp objective:', result.eigenvalue.real + offset)
x_Q = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
for i in range(1, len(z)):
connectpoints(x,y,z[i-1],z[i])
connectpoints(x,y,z[len(x)-1],z[0])
plt.title("Percurso")
plt.show()
#instanciando o simulador ou o computador real importante lembrar que nao ira funcionar para mais de 4 pontos pelo numero de qubits disponibilizados pela IBM que sao apenas 16 para o simulador qasm e 15 para a maquina quantica
provider = IBMQ.get_provider(hub = 'ibm-q')
device = provider.get_backend('ibmq_16_melbourne')
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('qasm_simulator')
#descomentar essa linha caso queira rodar na maquina real
#backend = device
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
#rodando no simulador quantico
spsa = SPSA(maxiter=10)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
result = vqe.run(quantum_instance)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
|
https://github.com/LeanderThiessen/antisymmetrization-circuit
|
LeanderThiessen
|
#General Imports
import numpy as np
import matplotlib.pyplot as plt
import time
from itertools import product,permutations
from string import ascii_lowercase as asc
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
#Qiskit Imports
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, transpile
from qiskit.circuit.library.standard_gates import MCXGate, CXGate, XGate, CSwapGate
from qiskit.circuit.library import Diagonal
from qiskit.quantum_info import partial_trace,purity
#############FUNCTIONS###########################################################################################################
#wrapper for measuring time taken by function 'func'
def timeis(func):
def wrap(*args,**kwargs):
start = time.time()
result = func(*args,**kwargs)
end = time.time()
if measure_time:
print("{} took {:.2f}s".format(func.__name__,end-start))
return result
return wrap
#check if inputs are valid
def check_inputs(n,m):
if n == 1:
print("Case n=1 currently not supported")
correct = 1
if m>2**n:
correct == 0
if correct == 1:
print("Inputs valid")
return 0
#initialize quantum circuit with electron register, swap_ancillas, record_ancillas, collision_ancillas
def initialize_circuit(n,m,L):
circuit = QuantumCircuit()
#add main electron register (seed/target)
for e in range(m):
r_q = QuantumRegister(n,'{}'.format(asc[e]))#asc[i]=ith letter of the alphabe
c = QuantumCircuit(r_q)
circuit = circuit.combine(c)
#add ancillas for comparator_swaps
for k in range(int(np.ceil(m/2))):
anc_q = QuantumRegister(n-1,'anc_{}'.format(k))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add 'record' register for storing outcomes of comparators
for l in range(L):
anc_q = QuantumRegister(1,'record_{}'.format(l))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add ancillas to store the occurence of collisions between pairs of electrons
for c in range(m-1):
anc_q = QuantumRegister(1,'coll_record_{}'.format(c))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add one ancilla to store if all other collision ancillas are '1'
anc_q = QuantumRegister(1,'collision_test')
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
return circuit
#returns x in binary format as string of length n, incl leading zeros
def binary_n(x,n):
return bin(x)[2:].zfill(n)
#initializes j-th electron register with number x
def binary_init(circuit,n,m,input):
for k,e in enumerate(input):
e_bin = binary_n(e,n)
for i in range(n):
if e_bin[i]=='1':
circuit.append(XGate(),[i+k*n])
return circuit
#Apply a Hadamard gate to each qubit in the electron register
def Hadamard(circuit,n,m):
for q in range(n*m):
circuit.h(q)
return circuit
#Compare bits at positions x and y, only output=(x<y) to position anc
def bit_compare(circuit,cbits,control,debug=True):
x = cbits[0]
y = cbits[1]
anc = cbits[2]
if debug:
circuit.barrier()
#control='01' for initial sorting and '10' for collision detection
circuit.append(MCXGate(2,ctrl_state=control),[x,y,anc])
if debug:
circuit.barrier()
return circuit
#split the array 'index' into array of pairs of adjacent indices; first entry is (e.g.) [0] if number of entries of index is odd
def get_subsets(index):
#index = [0,1,2,3] -> result = [[0,1],[2,3]]
#index = [0,1,2,3,4] -> result = [[0],[1,2],[3,4]]
M = len(index)
result = []
if M % 2 != 0:
result.append(np.array([0]))
n_split = int((M-1)/2)
for s in np.split(index[1:M],n_split):
result.append(s)
else:
result = np.split(index,M/2)
return result
#get position of first qubit in swap_control ancilla register
def get_first_swap_ctrl(n,m):
#n_comp_parallel is the number of comparators that are applied in each layer
#n*m = main register for storing electron registers;
#(n_comp_parallel)*(n-1) = fixed ancilla register needed for compare_n
n_comp_parallel = int(np.ceil(m/2))
ctrl_0 = n*m + (n-1)*n_comp_parallel
return ctrl_0
#get position of first qubit in collision_control ancilla register
def get_first_coll_ctrl(n,m,L):
coll_0 = get_first_swap_ctrl(n,m) + L
return coll_0
#return pairs of electron indices that need to be compared in collision-detection step
def get_coll_sets(m):
ind = np.arange(m)
if m == 2:
sets_a = [np.array([0,1])]
sets_b = []
return sets_a,sets_b
if m % 2 == 0:
sets_a = np.split(ind,m/2)
sets_b = np.split(ind[1:-1],(m-2)/2)
else:
sets_a = np.split(ind[:-1],(m-1)/2)
sets_b = np.split(ind[1:],(m-1)/2)
#all gates in sets_a can be applied in parallel
#all gates in sets_b can be applied in parallel
return sets_a,sets_b
#returns the first qubit position of the ancilla register used for swap of i and j (only really tested for m<6)
def get_anc(n,m,i,j):
if abs(j-i) == 1:
anc_reg = int( np.min([i,j])/2 )
elif abs(j-i) == 2:
anc_reg = int( np.ceil( np.min([i,j])/2 ))
else:
anc_reg = int( np.min([i,j]) )
anc = n*m + anc_reg*(n-1)
return anc
#Implement 'Compare2' function (Fig 3); input: two 2bit numbers, output: two 1bit numbers with same ordering
def compare_2(circuit,x_0,x_1,y_0,y_1,anc):
#Notation: x = 2^1*x_0 + x_1 (reverse from paper!!)
#compares numbers x,y and outputs two bits x',y' (at positions x_1 and y_1) with the same ordering
circuit.append(XGate(),[anc])
circuit.append(CXGate(),[y_0,x_0])
circuit.append(CXGate(),[y_1,x_1])
circuit.append(CSwapGate(),[x_0,x_1,anc])
circuit.append(CSwapGate(),[x_0,y_0,y_1])
circuit.append(CXGate(),[y_1,x_1])
return circuit
#Generalisation of 'compare2' two nbit numbers, output: two 1bit numbers with same ordering at positions x1,y1
def compare_n(circuit,n,m,i,j,l,L,debug):
index = np.arange(n)
subsets = get_subsets(index)
M = len(subsets)
anc = get_anc(n,m,i,j)
for s in subsets:
if len(s)==2:
if debug:
circuit.barrier()
x_0 = s[0] + i*n
x_1 = s[1] + i*n
y_0 = s[0] + j*n
y_1 = s[1] + j*n
circuit = compare_2(circuit,x_0,x_1,y_0,y_1,anc)
anc += 1
while (len(subsets)>1):
index = np.array([subsets[k][-1] for k in range(M)])
subsets = get_subsets(index)
M = len(subsets)
for s in subsets:
if len(s)==2:
if debug:
circuit.barrier()
x_0 = s[0] + i*n
x_1 = s[1] + i*n
y_0 = s[0] + j*n
y_1 = s[1] + j*n
circuit = compare_2(circuit,x_0,x_1,y_0,y_1,anc)
anc += 1
########################################################################################################################################
#at this point the bits x_1 and y_1 have the same ordering as numbers stored in registers i and j
#e(i)<e(j) -> x_1=0 and y_1=1
#e(i)>e(j) -> x_1=1 and y_1=0
#e(i)=e(j) -> x_1=0 y_1=0 if e(i) even or x_1=1 y_1=1 if e(i) odd
#prepare output for bit_compare function; anc iterates through the second ancilla register (+1 for each comparator)
#l = current swap; each new swap gets a new ancilla for storing the outcome
anc = get_first_swap_ctrl(n,m) + l
cbits = x_1,y_1,anc
return circuit,cbits
#apply diagonal phase shift to qubit i, conditioned on qubit 'ctrl'
def cphase_shift(circuit,ctrl,i):
target = i*n
CDiag = Diagonal([-1,-1]).control(1)
CDiag = CDiag.to_gate()
CDiag.label = "D" #doesn't work currently
circuit.append(CDiag,[ctrl,target])
return circuit
#performs swap of registers i and j conditioned on ancilla qubit 'ctrl'
def swap_registers(circuit,n,i,j,ctrl,debug):
for g in range(n):
circuit.append(CSwapGate(),[ctrl,i*n+g,j*n+g])
if debug:
circuit.barrier()
return circuit
#compare electron registers i and j; swap registers iff e(i)<(j); l=current swap (0 to L)
def comparator_swap(n,m,i,j,l,L,phase,debug):
#Perform comparison to generate output qubits "cbits"
circuit_compute = initialize_circuit(n,m,L)
circuit_compute,cbits = compare_n(circuit_compute,n,m,i,j,l,L,debug)
#Add bit_compare between the two output qubits and store in ancilla
circuit_bit_compare = initialize_circuit(n,m,L)
circuit_bit_compare = bit_compare(circuit_bit_compare,cbits,'10',debug)
#add uncomputing step only of the comparison circuit
circuit_uncompute = circuit_compute.inverse()
#Swap registers based on control ancilla
circuit_swap = initialize_circuit(n,m,L)
#apply a conditioned phase shift to the first qubit of the register pair; is only called when sn is applied backwards, that's why it's (phase,swap) and not (swap,phase)
if phase:
circuit_swap = cphase_shift(circuit_swap,cbits[2],i)
circuit_swap = swap_registers(circuit_swap,n,i,j,cbits[2],debug)
#Combine circuits
circuit_comparator = circuit_compute + circuit_bit_compare + circuit_uncompute + circuit_swap
return circuit_comparator
#Apply the sorting network sn, where each comparator stores the outcome in ctrl_register
def apply_sorting_network(circuit,n,m,sn,L,phase,debug):
for l,swap in enumerate(sn):
#swap = [i, j, direction]; dir = 0 : descending (from the top); dir = 1 : ascending (from the top)
if swap[2]==0:
i = swap[0]
j = swap[1]
if swap[2]==1:
i = swap[1]
j = swap[0]
circuit_comparator = comparator_swap(n,m,i,j,l,L,phase,debug)
circuit = circuit + circuit_comparator
return circuit
#Apply the reverse of the sorting networkl sn for antisymmetrizing the input state
def apply_reverse_sorting_network(circuit,n,m,sn,L,phase,debug):
circuit_sn = initialize_circuit(n,m,L)
circuit_sn = apply_sorting_network(circuit_sn,n,m,sn,L,phase,debug)
#reverse all gates in the circuit
circuit_reverse_sn = circuit_sn.inverse()
circuit = circuit + circuit_reverse_sn
return circuit
#reset first register to [|0>,|0>,|0>,...] (all zeros)
def reset_electrons(circuit,n,m):
circuit.barrier()
for g in range(m):
g_indices = np.arange(g*n,(g+1)*n) #classical register positions for electron g
for g_i in g_indices:
circuit.reset(g_i)
return circuit
#reset all registers except for the main electron register
def reset_ancillas(circuit,n,m,L):
circuit.barrier()
start = n*m
end = get_first_coll_ctrl(n,m,L) + m
for q in range(start,end):
circuit.reset(q)
return circuit
#Perform comparisons between all adjacent electron registers, with ctrl ancilla in the coll_register
def collision_compare(circuit,n,m,L,debug):
#all sets in sets_a can be applied simultaneously (same for sets_b); both for loops are otherwise identical and could be combined
sets_a,sets_b = get_coll_sets(m)
c = 0
for s in sets_a:
circuit_coll_test = initialize_circuit(n,m,L)
i = s[0]
j = s[1]
circuit_coll_test,cbits = compare_n(circuit_coll_test,n,m,i,j,0,L,debug)
x_1 = cbits[0]
y_1 = cbits[1]
coll_anc = get_first_coll_ctrl(n,m,L) + c
cbits = [x_1,y_1,coll_anc]
circuit_coll_test_reverse = circuit_coll_test.inverse()
circuit = circuit + circuit_coll_test
circuit = bit_compare(circuit,cbits,'01',debug)
circuit = circuit + circuit_coll_test_reverse
c+=1
for s in sets_b:
circuit_coll_test = initialize_circuit(n,m,L)
i = s[0]
j = s[1]
circuit_coll_test,cbits = compare_n(circuit_coll_test,n,m,i,j,0,L,debug)
x_1 = cbits[0]
y_1 = cbits[1]
coll_anc = get_first_coll_ctrl(n,m,L) + c
cbits = [x_1,y_1,coll_anc]
circuit_coll_test_reverse = circuit_coll_test.inverse()
circuit = circuit + circuit_coll_test
circuit = bit_compare(circuit,cbits,'01',debug)
circuit = circuit + circuit_coll_test_reverse
c+=1
return circuit
#apply X gate on last qubit, conditioned on all other coll_ancillas being 1 (which means that all elctron registers are different)
def collision_test(circuit,n,m,L,debug):
coll_ctrl_0 = get_first_coll_ctrl(n,m,L)
control = ''
qubits = []
for i in range(m-1):
control = control + '1'
qubits.append(coll_ctrl_0+i)
qubits.append(coll_ctrl_0+m-1)
circuit.append(MCXGate(m-1,ctrl_state=control),qubits)
return circuit
#not necessary
#returns True if output contains only unique elements; returns False otherwise (if two or more elements are the same)
def collision_check_old(output):
if len(output) == len(set(output)):
return True
else:
return False
#Perform measurement on last qubit in coll_register
def measure_collisions(circuit,n,m,L):
#add classical register to store measurement result
c_q = QuantumRegister(0)
c_reg = ClassicalRegister(1,'collision_check')
c = QuantumCircuit(c_q,c_reg)
circuit = circuit.combine(c)
#perform measurements on each electron register and store in separate memorey
circuit.measure(get_first_coll_ctrl(n,m,L) + m - 1, 0)
return circuit
#Add classical registers and apply measurements on the main electron register
def measure_electrons(circuit,n,m):
circuit.barrier()
for g in range(m):
#Add classicla register to store measurement outcomes
c_q = QuantumRegister(0)
c_reg = ClassicalRegister(n,'mem_{}'.format(asc[g]))
c = QuantumCircuit(c_q,c_reg)
circuit = circuit.combine(c)
#perform measurements on each electron register and store in separate memorey
circuit.measure(np.arange(g*n,(g+1)*n),np.arange(g*n + 1,(g+1)*n + 1))
return circuit
#Build the circuit with all gates and measurements
@timeis
def build_circuit(n,m,input,sn,L,debug=True):
#Initialize the circuit with the right number of qubits and ancillas
circuit = initialize_circuit(n,m,L)
#Apply Hadamard gates to each qubit in the first register
circuit = Hadamard(circuit,n,m)
#Apply the sorting network sn
phase = False
circuit = apply_sorting_network(circuit,n,m,sn,L,phase,debug)
#apply comparisons between all adjacent electron registers and store outcome in coll_register
circuit = collision_compare(circuit,n,m,L,debug)
#check if outcome of all comparisons is "not_equal"; flip last qubit in coll_register if this is the case
circuit = collision_test(circuit,n,m,L,debug)
#measure last qubit in coll_register, which stores (no collisions = 1) or (collisions = 0); result is kept until the end of the simulation and result accepted if (no collisions == True)
circuit = measure_collisions(circuit,n,m,L)
#Measurements: classical register 0 stores the random sorted array that can still include collisions
#circuit = measure_electrons(circuit,n,m)
#Reset main electron register
circuit = reset_electrons(circuit,n,m)
#Initialize main electron register in given input product state
circuit = binary_init(circuit,n,m,input)
#Apply the reverse of 'apply_sorting_network' and add a conditioned phase shift after each swap (this antisymmetrizes the input state)
phase = True
circuit = apply_reverse_sorting_network(circuit,n,m,sn,L,phase,debug)
#Reset all ancilla qubits and only keep the main electron register (disable for testing final state for antisymmetry)
#circuit = reset_ancillas(circuit,n,m,L)
#Measure electron register (for testing)
#circuit = measure_electrons(circuit,n,m)
return circuit
#Simulate circuit using specified backend and return simulation result
@timeis
def simulate(circuit,backend,shots):
simulator = Aer.get_backend(backend)
#transpile the circuit into the supported set of gates
circuit = transpile(circuit,backend=simulator)
result = simulator.run(circuit,shots=shots).result()
return result
#turns simulation result 'counts' into list of decimal numbers corresponding to the electron registers; only use if shots=1 or all outcomes are the same
def convert_output_to_decimal(counts,n,m):
output_list = list(counts.keys())[0][::-1]
coll_test = output_list[0]
output_list = output_list[2:]
output = []
offset = 0
for g in range(m):
start = g*n + offset
end = (g+1)*n + offset
g_out = int(output_list[start:end],2)
output.append(g_out)
offset += 1
output_0 = output[0:m]
return coll_test,output_0
#draw the circuit using size,name as input if plot==True
@timeis
def draw_circuit(circuit,plot_scale,fname):
circuit.draw(output='mpl',fold=-1,scale=plot_scale,plot_barriers=True)
plt.savefig(fname,dpi=700)
return 0
def plot_circuit(circuit,plot_scale,fname,plot=True):
if plot:
draw_circuit(circuit,plot_scale,fname)
plt.show()
return 0
print("Plot disabled")
return 0
#plot sorting network by itself, using cnot as directed comparator (only for visualizationo)
def plot_sorting_network(sn,m):
circuit_sn = QuantumCircuit(m)
for s in sn:
if s[2] == 0:
i,j = s[0],s[1]
else:
i,j = s[1],s[0]
circuit_sn.cz(i,j)
circuit_sn.draw(output='mpl')
plt.show()
return 0
#Generate a bitonic sorting network for m electrons; dir=0 (descending), dir=1 (ascending)
def sorting_network_bitonic(m,dir):
sn = []
def compAndSwap(i,j,dir):
sn.append([i,j,dir])
def bitonic_sort(low, cnt, dir):
if cnt>1:
k = cnt//2
dir_n = (dir + 1) % 2
bitonic_sort(low, k, dir_n)#n_dir
bitonic_sort(low + k, cnt-k, dir)#dir
bitonic_merge(low, cnt, dir)
def bitonic_merge(low, cnt, dir):
if cnt>1:
k = greatestPowerOfTwoLessThan(cnt)
i = low
while i < low+cnt-k:
compAndSwap(i, i+k, dir)
i+=1
bitonic_merge(low,k,dir)
bitonic_merge(low+k,cnt-k,dir)
def greatestPowerOfTwoLessThan(cnt):
i=1
while (2**i)<cnt:
i+=1
return 2**(i-1)
bitonic_sort(0,m,dir)
L = len(sn)
return sn,L
#Test if sorting network correctly sorts all possible inputs
def test_sn(sn,n,m):
all_inputs = list(product(range(2**n),repeat=m))
fail = 0
count = 0
for input in all_inputs:
input = np.array(input)
temp = np.copy(input)
for s in sn:
if s[2]==0:
i = s[0]
j = s[1]
if s[2]==1:
i = s[1]
j = s[0]
if input[i]<input[j]:
input[i],input[j] = input[j],input[i]
should_be = np.sort(temp)[::-1]
if (input == should_be).all():
fail += 0
else:
fail += 1
print(f"Testing sorting network {count}/{len(all_inputs)}",end="\r")
count+=1
print(" ", end = "\r")
if fail == 0:
print("Sorting network correct\n")
return 1
else:
print("Error in sorting network\n")
return 0
#Returns all steps of sorting network with corresponding ancilla registers (for testing)
def test_sn_anc(sn,n,m):
for s in sn:
i = s[0]
j = s[1]
anc = get_anc(n,m,i,j)
anc_reg = int((anc-n*m)/(n-1))
print(f"[{i},{j}] anc_reg={anc_reg}")
return 0
#Output density matrix of electron register (target) and compute purity, doesnt actually test antisymmetry yet!
def test_antisymmetry(result,n,m,L):
sv = result.get_statevector()
trace_out = list(np.arange(n*m,get_first_coll_ctrl(n,m,L)+m))
#print(f"Tracing out qubits: {trace_out}")
rho_e = partial_trace(sv,trace_out)
if rho_e.is_valid():
print("Target state is valid density matrix\n")
else:
print("Target state is not valid density matrix")
#print(rho_e)
p = purity(rho_e)
print(f"Purity of target state = {p}\n")
return p
###################MAINPART############################################################################################################
#Parameters
#n: number of qubits per electron; N = 2^n orbitals
n=3
#m: number of electrons
m=4
#input: list of orbitals the electrons are initialized in; needs to be in descending order, without repetitions
input = [5,4,3,2]
#dir: ordering descending (dir=0) or ascending (dir=1)
dir = 0
#plot and save the circuit
plot = True
#include barriers between comparators in the circuit for visualization
debug = False
#measure time of functions: {build_circuit, simulate, draw_circuit}
measure_time = True
#size of the plot
plot_scale = 0.2
#simulation method
backend = 'statevector_simulator'#'aer_simulator'
#number of circuit repetitions in 'simulate'
shots = 1
#check valid inputs
check_inputs(n,m)
#Generate sorting network
sn,L = sorting_network_bitonic(m,dir)
#Test sorting network
test_sn(sn,n,m)
#Plot sorting network
plot_sorting_network(sn,m)
#Build circuit
circuit = build_circuit(n,m,input,sn,L,debug)
#Simulate
result = simulate(circuit,backend,shots)
counts = result.get_counts(circuit)
print(f"Counts: {counts}\n")
#Test if final state is antisymmetric
test_antisymmetry(result,n,m,L)
output_list = list(counts.keys())[0][::-1]
coll_test = output_list[0]
if coll_test == '1':
print("No collisions detected - continue\n")
else:
print("Collisions detected - repeat\n")
#plot circuit
plot_circuit(circuit,plot_scale,f"Plots/Circuit_m{m}_n{n}_debug{debug}",plot)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-states-of-Li-and-Li-2-using-Variational-Quantum-EIgensolver
|
Bikramaditya0154
|
from qiskit import Aer
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver,
)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
molecule = Molecule(
geometry=[["Li", [0.0, 0.0, 0.0]]], charge=2, multiplicity=2
)
driver = ElectronicStructureMoleculeDriver(
molecule, basis="sto3g", driver_type=ElectronicStructureDriverType.PYSCF
)
es_problem = ElectronicStructureProblem(driver)
qubit_converter = QubitConverter(JordanWignerMapper())
from qiskit.providers.aer import StatevectorSimulator
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit_nature.algorithms import VQEUCCFactory
quantum_instance = QuantumInstance(backend=Aer.get_backend("aer_simulator_statevector"))
vqe_solver = VQEUCCFactory(quantum_instance=quantum_instance)
from qiskit.algorithms import VQE
from qiskit.circuit.library import TwoLocal
tl_circuit = TwoLocal(
rotation_blocks=["h", "rx"],
entanglement_blocks="cz",
entanglement="full",
reps=2,
parameter_prefix="y",
)
another_solver = VQE(
ansatz=tl_circuit,
quantum_instance=QuantumInstance(Aer.get_backend("aer_simulator_statevector")),
)
from qiskit_nature.algorithms import GroundStateEigensolver
calc = GroundStateEigensolver(qubit_converter, vqe_solver)
res = calc.solve(es_problem)
print(res)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-states-of-Li-and-Li-2-using-Variational-Quantum-EIgensolver
|
Bikramaditya0154
|
from qiskit import Aer
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver,
)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
molecule = Molecule(
geometry=[["Li", [0.0, 0.0, 0.0]]], charge=1, multiplicity=1
)
driver = ElectronicStructureMoleculeDriver(
molecule, basis="sto3g", driver_type=ElectronicStructureDriverType.PYSCF
)
es_problem = ElectronicStructureProblem(driver)
qubit_converter = QubitConverter(JordanWignerMapper())
from qiskit.providers.aer import StatevectorSimulator
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit_nature.algorithms import VQEUCCFactory
quantum_instance = QuantumInstance(backend=Aer.get_backend("aer_simulator_statevector"))
vqe_solver = VQEUCCFactory(quantum_instance=quantum_instance)
from qiskit.algorithms import VQE
from qiskit.circuit.library import TwoLocal
tl_circuit = TwoLocal(
rotation_blocks=["h", "rx"],
entanglement_blocks="cz",
entanglement="full",
reps=2,
parameter_prefix="y",
)
another_solver = VQE(
ansatz=tl_circuit,
quantum_instance=QuantumInstance(Aer.get_backend("aer_simulator_statevector")),
)
from qiskit_nature.algorithms import GroundStateEigensolver
calc = GroundStateEigensolver(qubit_converter, vqe_solver)
res = calc.solve(es_problem)
print(res)
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""Python implementation of Grovers algorithm through use of the Qiskit library to find the value 3 (|11>)
out of four possible values."""
#import numpy and plot library
import matplotlib.pyplot as plt
import numpy as np
# importing Qiskit
from qiskit import IBMQ, Aer, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.providers.ibmq import least_busy
from qiskit.quantum_info import Statevector
# import basic plot tools
from qiskit.visualization import plot_histogram
# define variables, 1) initialize qubits to zero
n = 2
grover_circuit = QuantumCircuit(n)
#define initialization function
def initialize_s(qc, qubits):
'''Apply a H-gate to 'qubits' in qc'''
for q in qubits:
qc.h(q)
return qc
### begin grovers circuit ###
#2) Put qubits in equal state of superposition
grover_circuit = initialize_s(grover_circuit, [0,1])
# 3) Apply oracle reflection to marked instance x_0 = 3, (|11>)
grover_circuit.cz(0,1)
statevec = job_sim.result().get_statevector()
from qiskit_textbook.tools import vector2latex
vector2latex(statevec, pretext="|\\psi\\rangle =")
# 4) apply additional reflection (diffusion operator)
grover_circuit.h([0,1])
grover_circuit.z([0,1])
grover_circuit.cz(0,1)
grover_circuit.h([0,1])
# 5) measure the qubits
grover_circuit.measure_all()
# Load IBM Q account and get the least busy backend device
provider = IBMQ.load_account()
device = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 3 and
not x.configuration().simulator and x.status().operational==True))
print("Running on current least busy device: ", device)
from qiskit.tools.monitor import job_monitor
job = execute(grover_circuit, backend=device, shots=1024, optimization_level=3)
job_monitor(job, interval = 2)
results = job.result()
answer = results.get_counts(grover_circuit)
plot_histogram(answer)
#highest amplitude should correspond with marked value x_0 (|11>)
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""The following is python code utilizing the qiskit library that can be run on extant quantum
hardware using 5 qubits for factoring the integer 15 into 3 and 5. Using period finding,
for a^r mod N = 1, where a = 11 and N = 15 (the integer to be factored) the problem is to find
r values for this identity such that one can find the prime factors of N. For 11^r mod(15) =1,
results (as shown in fig 1.) correspond with period r = 4 (|00100>) and r = 0 (|00000>).
To find the factor, use the equivalence a^r mod 15. From this:
(a^r -1) mod 15 = (a^(r/2) + 1)(a^(r/2) - 1) mod 15.In this case, a = 11. Plugging in the two r
values for this a value yields (11^(0/2) +1)(11^(4/2) - 1) mod 15 = 2*(11 +1)(11-1) mod 15
Thus, we find (24)(20) mod 15. By finding the greatest common factor between the two coefficients,
gcd(24,15) and gcd(20,15), yields 3 and 5 respectively. These are the prime factors of 15,
so the result of running shors algorithm to find the prime factors of an integer using quantum
hardware are demonstrated. Note, this is not the same as the technical implementation of shor's
algorithm described in this section for breaking the discrete log hardness assumption,
though the proof of concept remains."""
# Import libraries
from qiskit.compiler import transpile, assemble
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from numpy import pi
from qiskit import IBMQ, Aer, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.providers.ibmq import least_busy
from qiskit.visualization import plot_histogram
# Initialize qubit registers
qreg_q = QuantumRegister(5, 'q')
creg_c = ClassicalRegister(5, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.reset(qreg_q[0])
circuit.reset(qreg_q[1])
circuit.reset(qreg_q[2])
circuit.reset(qreg_q[3])
circuit.reset(qreg_q[4])
# Apply Hadamard transformations to qubit registers
circuit.h(qreg_q[0])
circuit.h(qreg_q[1])
circuit.h(qreg_q[2])
# Apply first QFT, modular exponentiation, and another QFT
circuit.h(qreg_q[1])
circuit.cx(qreg_q[2], qreg_q[3])
circuit.crx(pi/2, qreg_q[0], qreg_q[1])
circuit.ccx(qreg_q[2], qreg_q[3], qreg_q[4])
circuit.h(qreg_q[0])
circuit.rx(pi/2, qreg_q[2])
circuit.crx(pi/2, qreg_q[1], qreg_q[2])
circuit.crx(pi/2, qreg_q[1], qreg_q[2])
circuit.cx(qreg_q[0], qreg_q[1])
# Measure the qubit registers 0-2
circuit.measure(qreg_q[2], creg_c[2])
circuit.measure(qreg_q[1], creg_c[1])
circuit.measure(qreg_q[0], creg_c[0])
# Get least busy quantum hardware backend to run on
provider = IBMQ.load_account()
device = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 3 and
not x.configuration().simulator and x.status().operational==True))
print("Running on current least busy device: ", device)
# Run the circuit on available quantum hardware and plot histogram
from qiskit.tools.monitor import job_monitor
job = execute(circuit, backend=device, shots=1024, optimization_level=3)
job_monitor(job, interval = 2)
results = job.result()
answer = results.get_counts(circuit)
plot_histogram(answer)
#largest amplitude results correspond with r values used to find the prime factor of N.
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""Qiskit code for running Simon's algorithm on quantum hardware for 2 qubits and b = '11' """
# importing Qiskit
from qiskit import IBMQ, BasicAer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, execute
# import basic plot tools
from qiskit.visualization import plot_histogram
from qiskit_textbook.tools import simon_oracle
#set b equal to '11'
b = '11'
#1) initialize qubits
n = 2
simon_circuit_2 = QuantumCircuit(n*2, n)
#2) Apply Hadamard gates before querying the oracle
simon_circuit_2.h(range(n))
#3) Query oracle
simon_circuit_2 += simon_oracle(b)
#5) Apply Hadamard gates to the input register
simon_circuit_2.h(range(n))
#3) and 6) Measure qubits
simon_circuit_2.measure(range(n), range(n))
# Load saved IBMQ accounts and get the least busy backend device
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= n and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
# Execute and monitor the job
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(simon_circuit_2, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
# Get results and plot counts
device_counts = job.result().get_counts()
plot_histogram(device_counts)
#additionally, function for calculating dot product of results
def bdotz(b, z):
accum = 0
for i in range(len(b)):
accum += int(b[i]) * int(z[i])
return (accum % 2)
print('b = ' + b)
for z in device_counts:
print( '{}.{} = {} (mod 2) ({:.1f}%)'.format(b, z, bdotz(b,z), device_counts[z]*100/shots))
#the most significant results are those for which b dot z=0(mod 2).
'''b = 11
11.00 = 0 (mod 2) (45.0%)
11.01 = 1 (mod 2) (6.2%)
11.10 = 1 (mod 2) (6.4%)
11.11 = 0 (mod 2) (42.4%)'''
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""Python implementation of Grovers algorithm through use of the Qiskit library to find the value 3 (|11>)
out of four possible values."""
#import numpy and plot library
import matplotlib.pyplot as plt
import numpy as np
# importing Qiskit
from qiskit import IBMQ, Aer, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.providers.ibmq import least_busy
from qiskit.quantum_info import Statevector
# import basic plot tools
from qiskit.visualization import plot_histogram
# define variables, 1) initialize qubits to zero
n = 2
grover_circuit = QuantumCircuit(n)
#define initialization function
def initialize_s(qc, qubits):
'''Apply a H-gate to 'qubits' in qc'''
for q in qubits:
qc.h(q)
return qc
### begin grovers circuit ###
#2) Put qubits in equal state of superposition
grover_circuit = initialize_s(grover_circuit, [0,1])
# 3) Apply oracle reflection to marked instance x_0 = 3, (|11>)
grover_circuit.cz(0,1)
statevec = job_sim.result().get_statevector()
from qiskit_textbook.tools import vector2latex
vector2latex(statevec, pretext="|\\psi\\rangle =")
# 4) apply additional reflection (diffusion operator)
grover_circuit.h([0,1])
grover_circuit.z([0,1])
grover_circuit.cz(0,1)
grover_circuit.h([0,1])
# 5) measure the qubits
grover_circuit.measure_all()
# Load IBM Q account and get the least busy backend device
provider = IBMQ.load_account()
device = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 3 and
not x.configuration().simulator and x.status().operational==True))
print("Running on current least busy device: ", device)
from qiskit.tools.monitor import job_monitor
job = execute(grover_circuit, backend=device, shots=1024, optimization_level=3)
job_monitor(job, interval = 2)
results = job.result()
answer = results.get_counts(grover_circuit)
plot_histogram(answer)
#highest amplitude should correspond with marked value x_0 (|11>)
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""The following is python code utilizing the qiskit library that can be run on extant quantum
hardware using 5 qubits for factoring the integer 15 into 3 and 5. Using period finding,
for a^r mod N = 1, where a = 11 and N = 15 (the integer to be factored) the problem is to find
r values for this identity such that one can find the prime factors of N. For 11^r mod(15) =1,
results (as shown in fig 1.) correspond with period r = 4 (|00100>) and r = 0 (|00000>).
To find the factor, use the equivalence a^r mod 15. From this:
(a^r -1) mod 15 = (a^(r/2) + 1)(a^(r/2) - 1) mod 15.In this case, a = 11. Plugging in the two r
values for this a value yields (11^(0/2) +1)(11^(4/2) - 1) mod 15 = 2*(11 +1)(11-1) mod 15
Thus, we find (24)(20) mod 15. By finding the greatest common factor between the two coefficients,
gcd(24,15) and gcd(20,15), yields 3 and 5 respectively. These are the prime factors of 15,
so the result of running shors algorithm to find the prime factors of an integer using quantum
hardware are demonstrated. Note, this is not the same as the technical implementation of shor's
algorithm described in this section for breaking the discrete log hardness assumption,
though the proof of concept remains."""
# Import libraries
from qiskit.compiler import transpile, assemble
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from numpy import pi
from qiskit import IBMQ, Aer, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.providers.ibmq import least_busy
from qiskit.visualization import plot_histogram
# Initialize qubit registers
qreg_q = QuantumRegister(5, 'q')
creg_c = ClassicalRegister(5, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.reset(qreg_q[0])
circuit.reset(qreg_q[1])
circuit.reset(qreg_q[2])
circuit.reset(qreg_q[3])
circuit.reset(qreg_q[4])
# Apply Hadamard transformations to qubit registers
circuit.h(qreg_q[0])
circuit.h(qreg_q[1])
circuit.h(qreg_q[2])
# Apply first QFT, modular exponentiation, and another QFT
circuit.h(qreg_q[1])
circuit.cx(qreg_q[2], qreg_q[3])
circuit.crx(pi/2, qreg_q[0], qreg_q[1])
circuit.ccx(qreg_q[2], qreg_q[3], qreg_q[4])
circuit.h(qreg_q[0])
circuit.rx(pi/2, qreg_q[2])
circuit.crx(pi/2, qreg_q[1], qreg_q[2])
circuit.crx(pi/2, qreg_q[1], qreg_q[2])
circuit.cx(qreg_q[0], qreg_q[1])
# Measure the qubit registers 0-2
circuit.measure(qreg_q[2], creg_c[2])
circuit.measure(qreg_q[1], creg_c[1])
circuit.measure(qreg_q[0], creg_c[0])
# Get least busy quantum hardware backend to run on
provider = IBMQ.load_account()
device = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 3 and
not x.configuration().simulator and x.status().operational==True))
print("Running on current least busy device: ", device)
# Run the circuit on available quantum hardware and plot histogram
from qiskit.tools.monitor import job_monitor
job = execute(circuit, backend=device, shots=1024, optimization_level=3)
job_monitor(job, interval = 2)
results = job.result()
answer = results.get_counts(circuit)
plot_histogram(answer)
#largest amplitude results correspond with r values used to find the prime factor of N.
|
https://github.com/hamburgerguy/Quantum-Algorithm-Implementations
|
hamburgerguy
|
"""Qiskit code for running Simon's algorithm on quantum hardware for 2 qubits and b = '11' """
# importing Qiskit
from qiskit import IBMQ, BasicAer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, execute
# import basic plot tools
from qiskit.visualization import plot_histogram
from qiskit_textbook.tools import simon_oracle
#set b equal to '11'
b = '11'
#1) initialize qubits
n = 2
simon_circuit_2 = QuantumCircuit(n*2, n)
#2) Apply Hadamard gates before querying the oracle
simon_circuit_2.h(range(n))
#3) Query oracle
simon_circuit_2 += simon_oracle(b)
#5) Apply Hadamard gates to the input register
simon_circuit_2.h(range(n))
#3) and 6) Measure qubits
simon_circuit_2.measure(range(n), range(n))
# Load saved IBMQ accounts and get the least busy backend device
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= n and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
# Execute and monitor the job
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(simon_circuit_2, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
# Get results and plot counts
device_counts = job.result().get_counts()
plot_histogram(device_counts)
#additionally, function for calculating dot product of results
def bdotz(b, z):
accum = 0
for i in range(len(b)):
accum += int(b[i]) * int(z[i])
return (accum % 2)
print('b = ' + b)
for z in device_counts:
print( '{}.{} = {} (mod 2) ({:.1f}%)'.format(b, z, bdotz(b,z), device_counts[z]*100/shots))
#the most significant results are those for which b dot z=0(mod 2).
'''b = 11
11.00 = 0 (mod 2) (45.0%)
11.01 = 1 (mod 2) (6.2%)
11.10 = 1 (mod 2) (6.4%)
11.11 = 0 (mod 2) (42.4%)'''
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
header = ['instance', 'iteration', 'distance']
length_instances = 40
with open('qaoa_multiple_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
for instance in range(length_instances):
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution()
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
index = -1
for sample in UNIFORM_CONVERGENCE_SAMPLE:
mean = sample["mean"]
index += 1
distance_p_ground_state = np.max(np.abs(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - sample["probabilities"]))
UNIFORM_CONVERGENCE_SAMPLE[index]["distance_pgs"] = distance_p_ground_state
iteration = 0
for sample in UNIFORM_CONVERGENCE_SAMPLE:
iteration += 1
mean = sample["mean"]
distance = sample["distance_pgs"]
writer.writerow([instance,iteration, distance])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
header = ['p', 'state', 'probability', 'mean']
length_p = 10
with open('qaoa_multiple_p.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
first_p = False
for p in range(length_p):
p = p+1
if first_p == False:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
mean = UNIFORM_CONVERGENCE_SAMPLE[0]["mean"]
print(mean)
state = 0
for probability in UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"]:
state += 1
writer.writerow([p,state, probability,mean])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
import numpy as np
import networkx as nx
import qiskit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer, assemble
from qiskit.quantum_info import Statevector
from qiskit.aqua.algorithms import NumPyEigensolver
from qiskit.quantum_info import Pauli
from qiskit.aqua.operators import op_converter
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.visualization import plot_histogram
from qiskit.providers.aer.extensions.snapshot_statevector import *
from thirdParty.classical import rand_graph, classical, bitstring_to_path, calc_cost
from utils import mapeo_grafo
from collections import defaultdict
from operator import itemgetter
from scipy.optimize import minimize
import matplotlib.pyplot as plt
LAMBDA = 10
SEED = 10
SHOTS = 10000
# returns the bit index for an alpha and j
def bit(i_city, l_time, num_cities):
return i_city * num_cities + l_time
# e^(cZZ)
def append_zz_term(qc, q_i, q_j, gamma, constant_term):
qc.cx(q_i, q_j)
qc.rz(2*gamma*constant_term,q_j)
qc.cx(q_i, q_j)
# e^(cZ)
def append_z_term(qc, q_i, gamma, constant_term):
qc.rz(2*gamma*constant_term, q_i)
# e^(cX)
def append_x_term(qc,qi,beta):
qc.rx(-2*beta, qi)
def get_not_edge_in(G):
N = G.number_of_nodes()
not_edge = []
for i in range(N):
for j in range(N):
if i != j:
buffer_tupla = (i,j)
in_edges = False
for edge_i, edge_j in G.edges():
if ( buffer_tupla == (edge_i, edge_j) or buffer_tupla == (edge_j, edge_i)):
in_edges = True
if in_edges == False:
not_edge.append((i, j))
return not_edge
def get_classical_simplified_z_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# z term #
z_classic_term = [0] * N**2
# first term
for l in range(N):
for i in range(N):
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += -1 * _lambda
# second term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_jl
z_jl_index = bit(j, l, N)
z_classic_term[z_jl_index] += _lambda / 2
# third term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_ij
z_ij_index = bit(i, j, N)
z_classic_term[z_ij_index] += _lambda / 2
# fourth term
not_edge = get_not_edge_in(G) # include order tuples ej = (1,0), (0,1)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 4
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
z_classic_term[z_jlplus_index] += _lambda / 4
# fifthy term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
z_classic_term[z_il_index] += weight_ij / 4
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
z_classic_term[z_il_index] += weight_ji / 4
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ji / 4
return z_classic_term
def tsp_obj_2(x, G,_lambda):
# obtenemos el valor evaluado en f(x_1, x_2,... x_n)
not_edge = get_not_edge_in(G)
N = G.number_of_nodes()
tsp_cost=0
#Distancia
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# x_il
x_il_index = bit(edge_i, l, N)
# x_jlplus
l_plus = (l+1) % N
x_jlplus_index = bit(edge_j, l_plus, N)
tsp_cost+= int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ij
# add order term because G.edges() do not include order tuples #
# x_i'l
x_il_index = bit(edge_j, l, N)
# x_j'lplus
x_jlplus_index = bit(edge_i, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ji
#Constraint 1
for l in range(N):
penal1 = 1
for i in range(N):
x_il_index = bit(i, l, N)
penal1 -= int(x[x_il_index])
tsp_cost += _lambda * penal1**2
#Contstraint 2
for i in range(N):
penal2 = 1
for l in range(N):
x_il_index = bit(i, l, N)
penal2 -= int(x[x_il_index])
tsp_cost += _lambda*penal2**2
#Constraint 3
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# x_il
x_il_index = bit(i, l, N)
# x_j(l+1)
l_plus = (l+1) % N
x_jlplus_index = bit(j, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * _lambda
return tsp_cost
def get_classical_simplified_zz_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# zz term #
zz_classic_term = [[0] * N**2 for i in range(N**2) ]
# first term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
# z_jl
z_jl_index = bit(j, l, N)
zz_classic_term[z_il_index][z_jl_index] += _lambda / 2
# second term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
# z_ij
z_ij_index = bit(i, j, N)
zz_classic_term[z_il_index][z_ij_index] += _lambda / 2
# third term
not_edge = get_not_edge_in(G)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += _lambda / 4
# fourth term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ji / 4
return zz_classic_term
def get_classical_simplified_hamiltonian(G, _lambda):
# z term #
z_classic_term = get_classical_simplified_z_term(G, _lambda)
# zz term #
zz_classic_term = get_classical_simplified_zz_term(G, _lambda)
return z_classic_term, zz_classic_term
def get_cost_circuit(G, gamma, _lambda):
N = G.number_of_nodes()
N_square = N**2
qc = QuantumCircuit(N_square,N_square)
z_classic_term, zz_classic_term = get_classical_simplified_hamiltonian(G, _lambda)
# z term
for i in range(N_square):
if z_classic_term[i] != 0:
append_z_term(qc, i, gamma, z_classic_term[i])
# zz term
for i in range(N_square):
for j in range(N_square):
if zz_classic_term[i][j] != 0:
append_zz_term(qc, i, j, gamma, zz_classic_term[i][j])
return qc
def get_mixer_operator(G,beta):
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
for n in range(N**2):
append_x_term(qc, n, beta)
return qc
def get_QAOA_circuit(G, beta, gamma, _lambda):
assert(len(beta)==len(gamma))
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
# init min mix state
qc.h(range(N**2))
p = len(beta)
for i in range(p):
qc = qc.compose(get_cost_circuit(G, gamma[i], _lambda))
qc = qc.compose(get_mixer_operator(G, beta[i]))
qc.barrier(range(N**2))
qc.snapshot_statevector("final_state")
qc.measure(range(N**2),range(N**2))
return qc
def invert_counts(counts):
return {k[::-1] :v for k,v in counts.items()}
# Sample expectation value
def compute_tsp_energy_2(counts, G):
energy = 0
get_counts = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = tsp_obj_2(meas, G, LAMBDA)
energy += obj_for_meas*meas_count
total_counts += meas_count
mean = energy/total_counts
return mean
def get_black_box_objective_2(G,p):
backend = Aer.get_backend('qasm_simulator')
sim = Aer.get_backend('aer_simulator')
# function f costo
def f(theta):
beta = theta[:p]
gamma = theta[p:]
# Anzats
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
result = execute(qc, backend, seed_simulator=SEED, shots= SHOTS).result()
final_state_vector = result.data()["snapshots"]["statevector"]["final_state"][0]
state_vector = Statevector(final_state_vector)
probabilities = state_vector.probabilities()
probabilities_states = invert_counts(state_vector.probabilities_dict())
expected_value = 0
for state,probability in probabilities_states.items():
cost = tsp_obj_2(state, G, LAMBDA)
expected_value += cost*probability
counts = result.get_counts()
mean = compute_tsp_energy_2(invert_counts(counts),G)
return mean
return f
def crear_grafo(cantidad_ciudades):
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
return G, mejor_costo, mejor_camino
def run_QAOA(p,ciudades, grafo):
if grafo == None:
G, mejor_costo, mejor_camino = crear_grafo(ciudades)
print("Mejor Costo")
print(mejor_costo)
print("Mejor Camino")
print(mejor_camino)
print("Bordes del grafo")
print(G.edges())
print("Nodos")
print(G.nodes())
print("Pesos")
labels = nx.get_edge_attributes(G,'weight')
print(labels)
else:
G = grafo
intial_random = []
# beta, mixer Hammiltonian
for i in range(p):
intial_random.append(np.random.uniform(0,np.pi))
# gamma, cost Hammiltonian
for i in range(p):
intial_random.append(np.random.uniform(0,2*np.pi))
init_point = np.array(intial_random)
obj = get_black_box_objective_2(G,p)
res_sample = minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
print(res_sample)
if __name__ == '__main__':
# Run QAOA parametros: profundidad p, numero d ciudades,
run_QAOA(5, 3, None)
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
header = ['instance','p','distance', 'mean']
length_p = 3
length_instances = 2
with open('qaoa_multiple_p_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
instance_index = 0
for instance in range(length_instances):
instance_index += 1
first_p = False
UNIFORM_CONVERGENCE_P = []
UNIFORM_CONVERGENCE_SAMPLE = []
for p in range(length_p):
p = p+1
if first_p == False:
print("Vuelve a llamar a test_solution")
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
convergence_min = UNIFORM_CONVERGENCE_SAMPLE[0]
UNIFORM_CONVERGENCE_P.append({
"mean":convergence_min["mean"],
"probabilities": convergence_min["probabilities"]
})
cauchy_function_nk = UNIFORM_CONVERGENCE_P[len(UNIFORM_CONVERGENCE_P) - 1]
p_index = 0
for p_state in UNIFORM_CONVERGENCE_P:
p_index += 1
print(p_index)
mean = p_state["mean"]
print(p_state)
print(mean)
distance_p_cauchy_function_nk = np.max(np.abs(cauchy_function_nk["probabilities"] - p_state["probabilities"]))
writer.writerow([instance_index, p_index, distance_p_cauchy_function_nk, mean])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution()
plot_histogram(job_2.result().get_counts(), color='midnightblue', title="New Histogram", figsize=(30, 5))
plot_histogram(job_2.result().get_counts(), color='midnightblue', title="New Histogram", figsize=(30, 5))
G
labels = nx.get_edge_attributes(G,'weight')
labels
import json
# Array of JSON Objects
products = [{"name": "HDD", "brand": "Samsung", "price": "$100"},
{"name": "Monitor", "brand": "Dell", "price": "$120"},
{"name": "Mouse", "brand": "Logitech", "price": "$10"}]
# Print the original data
print("The original JSON data:\n{0}".format(products))
# Sort the JSON data based on the value of the brand key
products.sort(key=lambda x: x["price"])
# Print the sorted JSON data
print("The sorted JSON data based on the value of the brand:\n{0}".format(products))
_LAMBDA
UNIFORM_CONVERGENCE_SAMPLE
import json
# Array of JSON Objects
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
# Print the sorted JSON data
UNIFORM_CONVERGENCE_SAMPLE
np.max(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - UNIFORM_CONVERGENCE_SAMPLE[220]["probabilities"])
# generamos las distancias entre para la convergencia uniforme
index = -1
for sample in UNIFORM_CONVERGENCE_SAMPLE:
mean = sample["mean"]
index += 1
distance_p_ground_state = np.max(np.abs(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - sample["probabilities"]))
UNIFORM_CONVERGENCE_SAMPLE[index]["distance_pgs"] = distance_p_ground_state
UNIFORM_CONVERGENCE_SAMPLE
import csv
header = ['iteration', 'state', 'probability', 'mean']
header_q = ['iteration', 'distance']
with open('qaoa_cu.csv', 'w', encoding='UTF8') as f:
with open('qaoa_distance.csv', 'w', encoding='UTF8') as q:
writer = csv.writer(f)
writer_q = csv.writer(q)
# write the header
writer.writerow(header)
writer_q.writerow(header_q)
iteration = 0
for sample in UNIFORM_CONVERGENCE_SAMPLE:
iteration += 1
mean = sample["mean"]
distance = sample["distance_pgs"]
state = 0
for probability in sample["probabilities"]:
state += 1
# write the data
data = [iteration, state, probability, mean]
writer.writerow(data)
writer_q.writerow([iteration, distance])
#plot_histogram(job_2, color='midnightblue', title=str(mean), figsize=(30, 5)).savefig(str(contador) + "_2.png")
#print(sample["mean"])
plot_histogram(job_2, color='midnightblue', title="New Histogram", figsize=(30, 5)).savefig('out.png')
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from thirdParty.classical import rand_graph, classical, bitstring_to_path, calc_cost
from utils import mapeo_grafo
import qiskit
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
from operator import itemgetter
from scipy.optimize import minimize
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer, assemble
from qiskit.quantum_info import Statevector
from qiskit.aqua.algorithms import NumPyEigensolver
from qiskit.quantum_info import Pauli
from qiskit.aqua.operators import op_converter
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.visualization import plot_histogram
from qiskit.providers.aer.extensions.snapshot_statevector import *
import json
import csv
# Gloabal _lambda variable
_LAMBDA = 10
_SHOTS = 10000
_UNIFORM_CONVERGENCE_SAMPLE = []
# returns the bit index for an alpha and j
def bit(i_city, l_time, num_cities):
return i_city * num_cities + l_time
# e^(cZZ)
def append_zz_term(qc, q_i, q_j, gamma, constant_term):
qc.cx(q_i, q_j)
qc.rz(2*gamma*constant_term,q_j)
qc.cx(q_i, q_j)
# e^(cZ)
def append_z_term(qc, q_i, gamma, constant_term):
qc.rz(2*gamma*constant_term, q_i)
# e^(cX)
def append_x_term(qc,qi,beta):
qc.rx(-2*beta, qi)
def get_not_edge_in(G):
N = G.number_of_nodes()
not_edge = []
for i in range(N):
for j in range(N):
if i != j:
buffer_tupla = (i,j)
in_edges = False
for edge_i, edge_j in G.edges():
if ( buffer_tupla == (edge_i, edge_j) or buffer_tupla == (edge_j, edge_i)):
in_edges = True
if in_edges == False:
not_edge.append((i, j))
return not_edge
def get_classical_simplified_z_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# z term #
z_classic_term = [0] * N**2
# first term
for l in range(N):
for i in range(N):
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += -1 * _lambda
# second term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_jl
z_jl_index = bit(j, l, N)
z_classic_term[z_jl_index] += _lambda / 2
# third term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_ij
z_ij_index = bit(i, j, N)
z_classic_term[z_ij_index] += _lambda / 2
# fourth term
not_edge = get_not_edge_in(G) # include order tuples ej = (1,0), (0,1)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 4
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
z_classic_term[z_jlplus_index] += _lambda / 4
# fifthy term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
z_classic_term[z_il_index] += weight_ij / 4
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
z_classic_term[z_il_index] += weight_ji / 4
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ji / 4
return z_classic_term
def get_classical_simplified_zz_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# zz term #
zz_classic_term = [[0] * N**2 for i in range(N**2) ]
# first term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
# z_jl
z_jl_index = bit(j, l, N)
zz_classic_term[z_il_index][z_jl_index] += _lambda / 2
# second term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
# z_ij
z_ij_index = bit(i, j, N)
zz_classic_term[z_il_index][z_ij_index] += _lambda / 2
# third term
not_edge = get_not_edge_in(G)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += _lambda / 4
# fourth term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ji / 4
return zz_classic_term
def get_classical_simplified_hamiltonian(G, _lambda):
# z term #
z_classic_term = get_classical_simplified_z_term(G, _lambda)
# zz term #
zz_classic_term = get_classical_simplified_zz_term(G, _lambda)
return z_classic_term, zz_classic_term
def get_cost_circuit(G, gamma, _lambda):
N = G.number_of_nodes()
N_square = N**2
qc = QuantumCircuit(N_square,N_square)
z_classic_term, zz_classic_term = get_classical_simplified_hamiltonian(G, _lambda)
# z term
for i in range(N_square):
if z_classic_term[i] != 0:
append_z_term(qc, i, gamma, z_classic_term[i])
# zz term
for i in range(N_square):
for j in range(N_square):
if zz_classic_term[i][j] != 0:
append_zz_term(qc, i, j, gamma, zz_classic_term[i][j])
return qc
def get_mixer_operator(G,beta):
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
for n in range(N**2):
append_x_term(qc, n, beta)
return qc
def invert_counts(counts):
return {k[::-1] :v for k,v in counts.items()}
def get_QAOA_circuit(G, beta, gamma, _lambda):
assert(len(beta)==len(gamma))
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
# init min mix state
qc.h(range(N**2))
p = len(beta)
for i in range(p):
qc = qc.compose(get_cost_circuit(G, gamma[i], _lambda))
qc = qc.compose(get_mixer_operator(G, beta[i]))
qc.barrier(range(N**2))
qc.snapshot_statevector("final_state")
qc.measure(range(N**2),range(N**2))
return qc
def tsp_obj(x, G):
# obtenemos el valor evaluado en f(x_1, x_2,... x_n)
z_classic_term, zz_classic_term = get_classical_simplified_hamiltonian(G, _LAMBDA)
cost = 0
# z term
for index in range(len(x)):
z = (int(x[index]) * 2 ) -1
cost += z_classic_term[index] * z
## zz term
for i in range(len(x)):
z_1 = (int(x[i]) * 2 ) -1
for j in range(len(x)):
z_2 = (int(x[j]) * 2 ) -1
cost += zz_classic_term[i][j] * z_1 * z_1
return cost
# Sample expectation value
def compute_tsp_energy(counts, G):
energy = 0
get_counts = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = tsp_obj(meas, G)
energy += obj_for_meas*meas_count
total_counts += meas_count
return energy/total_counts
# Sample expectation value
def compute_tsp_energy_2(counts, G):
energy = 0
get_counts = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = tsp_obj_2(meas, G, _LAMBDA)
energy += obj_for_meas*meas_count
total_counts += meas_count
mean = energy/total_counts
return mean
def tsp_obj_2(x, G,_lambda):
# obtenemos el valor evaluado en f(x_1, x_2,... x_n)
not_edge = get_not_edge_in(G)
N = G.number_of_nodes()
tsp_cost=0
#Distancia
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# x_il
x_il_index = bit(edge_i, l, N)
# x_jlplus
l_plus = (l+1) % N
x_jlplus_index = bit(edge_j, l_plus, N)
tsp_cost+= int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ij
# add order term because G.edges() do not include order tuples #
# x_i'l
x_il_index = bit(edge_j, l, N)
# x_j'lplus
x_jlplus_index = bit(edge_i, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ji
#Constraint 1
for l in range(N):
penal1 = 1
for i in range(N):
x_il_index = bit(i, l, N)
penal1 -= int(x[x_il_index])
tsp_cost += _lambda * penal1**2
#Contstraint 2
for i in range(N):
penal2 = 1
for l in range(N):
x_il_index = bit(i, l, N)
penal2 -= int(x[x_il_index])
tsp_cost += _lambda*penal2**2
#Constraint 3
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# x_il
x_il_index = bit(i, l, N)
# x_j(l+1)
l_plus = (l+1) % N
x_jlplus_index = bit(j, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * _lambda
return tsp_cost
def get_black_box_objective(G,p):
backend = Aer.get_backend('qasm_simulator')
def f(theta):
beta = theta[:p]
gamma = theta[p:]
_lambda = _LAMBDA # get global _lambda
qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
counts = execute(qc, backend, seed_simulator=10, shots=_SHOTS).result().get_counts()
return compute_tsp_energy(invert_counts(counts),G)
return f
def get_black_box_objective_2(G,p):
backend = Aer.get_backend('qasm_simulator')
sim = Aer.get_backend('aer_simulator')
def f(theta):
beta = theta[:p]
gamma = theta[p:]
#print(beta)
_lambda = _LAMBDA # get global _lambda
qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
#print(beta)
result = execute(qc, backend, seed_simulator=10, shots=_SHOTS).result()
final_state_vector = result.data()["snapshots"]["statevector"]["final_state"][0]
state_vector = Statevector(final_state_vector)
probabilities = state_vector.probabilities()
# expected value
#print("prob-dict")
#print(state_vector.probabilities_dict())
probabilities_states = invert_counts(state_vector.probabilities_dict())
expected_value = 0
for state,probability in probabilities_states.items():
# get cost from state
cost = tsp_obj_2(state, G, _LAMBDA)
expected_value += cost*probability
#print(probabilities)
counts = result.get_counts()
#qc.save_statevector() # Tell simulator to save statevector
#qobj = assemble(qc) # Create a Qobj from the circuit for the simulator to run
#state_vector = sim.run(qobj).result().get_statevector()
#state_vector = Statevector(state_vector)
#probabilities = state_vector.probabilities()
mean = compute_tsp_energy_2(invert_counts(counts),G)
global _UNIFORM_CONVERGENCE_SAMPLE
_UNIFORM_CONVERGENCE_SAMPLE.append({
"beta" : beta,
"gamma" : gamma,
"counts" : counts,
"mean" : mean,
"probabilities" : probabilities,
"expected_value" : expected_value
})
return mean
return f
def compute_tsp_min_energy_2(counts, G):
energy = 0
get_counts = 0
total_counts = 0
min = 1000000000000000000000
index = 0
min_meas = ""
for meas, meas_count in counts.items():
index = index + 1
obj_for_meas = tsp_obj_2(meas, G, _LAMBDA)
if obj_for_meas < min:
min = obj_for_meas
min_meas = meas
return index, min, min_meas
def compute_tsp_min_energy_1(counts, G):
energy = 0
get_counts = 0
total_counts = 0
min = 1000000000000000000000
index = 0
min_meas = ""
for meas, meas_count in counts.items():
index = index + 1
obj_for_meas = tsp_obj(meas, G)
if obj_for_meas < min:
min = obj_for_meas
min_meas = meas
return index, min, min_meas
def test_counts_2(counts, G):
mean_energy2 = compute_tsp_energy_2(invert_counts(counts),G)
cantidad, min, min_meas = compute_tsp_min_energy_2(invert_counts(counts),G)
print("*************************")
print("En el algoritmo 2 (Marina) el valor esperado como resultado es " + str(mean_energy2))
print("El valor minimo de todos los evaluados es " + str(min) + " se evaluaron un total de " + str(cantidad))
print("El vector minimo es " + min_meas)
def test_counts_1(counts, G):
mean_energy1 = compute_tsp_energy(invert_counts(counts),G)
cantidad, min, min_meas = compute_tsp_min_energy_1(invert_counts(counts),G)
print("*************************")
print("En el algoritmo 1 (Pablo) el valor esperado como resultado es " + str(mean_energy1))
print("El valor minimo de todos los evaluados es " + str(min) + " se evaluaron un total de " + str(cantidad))
print("El vector minimo es " + min_meas)
def test_solution(grafo=None, p=7):
global _UNIFORM_CONVERGENCE_SAMPLE
_UNIFORM_CONVERGENCE_SAMPLE = []
if grafo == None:
cantidad_ciudades = 2
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
print(mejor_costo)
print(mejor_camino)
print(G.edges())
print(G.nodes())
else:
G = grafo
# beta [0,pi], gamma [0, 2pi]
# create bounds for beta [0,pi]
bounds = []
intial_random = []
for i in range(p):
bounds.append((0, np.pi))
intial_random.append(np.random.uniform(0,np.pi))
# create bounds for gamma [0,2*pi]
for i in range(p):
bounds.append((0, np.pi * 2))
intial_random.append(np.random.uniform(0,2*np.pi))
init_point = np.array(intial_random)
# Pablo Solutions
#obj = get_black_box_objective(G,p)
#res_sample_1 = minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
#print(res_sample_1)
# Marina Solutions
obj = get_black_box_objective_2(G,p)
res_sample_2 = minimize(obj, init_point, method="COBYLA", options={"maxiter":2500,"disp":True})
print(res_sample_2)
#theta_1 = res_sample_1.x
theta_2 = res_sample_2.x
#beta = theta_1[:p]
#gamma = theta_1[p:]
#_lambda = _LAMBDA # get global _lambda
#qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
#backend = Aer.get_backend('qasm_simulator')
#job_1 = execute(qc, backend, shots=_SHOTS)
#resutls_1 = job_1.result().get_counts()
#test_counts_1(resutls_1, G)
beta = theta_2[:p]
gamma = theta_2[p:]
_lambda = _LAMBDA # get global _lambda
qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job_2 = execute(qc, backend, shots=_SHOTS)
resutls_2 = job_2.result().get_counts()
test_counts_2(resutls_2, G)
#print( _UNIFORM_CONVERGENCE_SAMPLE)
return job_2, G, _UNIFORM_CONVERGENCE_SAMPLE
def create_multiple_p_mismo_grafo():
header = ['p', 'state', 'probability', 'mean']
length_p = 10
with open('qaoa_multiple_p.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
first_p = False
UNIFORM_CONVERGENCE_SAMPLE = []
for p in range(length_p):
p = p+1
if first_p == False:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
mean = UNIFORM_CONVERGENCE_SAMPLE[0]["mean"]
print(mean)
state = 0
for probability in UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"]:
state += 1
writer.writerow([p,state, probability,mean])
def create_multiple_p_mismo_grafo_multiples_instanncias():
header = ['instance','p','distance', 'mean']
length_p = 4
length_instances = 10
with open('qaoa_multiple_p_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
instance_index = 0
for instance in range(length_instances):
instance_index += 1
first_p = False
UNIFORM_CONVERGENCE_P = []
UNIFORM_CONVERGENCE_SAMPLE = []
for p in range(length_p):
p = p+1
print("p es igual " + str(p))
if first_p == False:
print("Vuelve a llamar a test_solution")
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["expected_value"])
convergence_min = UNIFORM_CONVERGENCE_SAMPLE[0]
UNIFORM_CONVERGENCE_P.append({
"mean":convergence_min["expected_value"],
"probabilities": convergence_min["probabilities"]
})
print("expected value min con p =" + str(p) + " : " + str(convergence_min["expected_value"]))
cauchy_function_nk = UNIFORM_CONVERGENCE_P[len(UNIFORM_CONVERGENCE_P) - 1]
p_index = 0
for p_state in UNIFORM_CONVERGENCE_P:
p_index += 1
print(p_index)
mean = p_state["mean"]
#print(p_state)
print("expected value min")
print(mean)
distance_p_cauchy_function_nk = np.max(np.abs(cauchy_function_nk["probabilities"] - p_state["probabilities"]))
writer.writerow([instance_index, p_index, distance_p_cauchy_function_nk, mean])
if __name__ == '__main__':
#create_multiple_p_mismo_grafo()
create_multiple_p_mismo_grafo_multiples_instanncias()
def defult_init():
cantidad_ciudades = 2
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
print(mejor_costo)
print(mejor_camino)
print(G.edges())
print(G.nodes())
print("labels")
labels = nx.get_edge_attributes(G,'weight')
#z_term, zz_term = get_classical_simplified_hamiltonian(G, 1)
#print("z term")
#print(z_term)
#print("*****************")
#print("zz term")
#print(zz_term)
#print(get_QAOA_circuit(G, beta = [2,3], gamma = [4,5], _lambda = 1))
p = 5
obj = get_black_box_objective(G,p)
init_point = np.array([0.8,2.2,0.83,2.15,0.37,2.4,6.1,2.2,3.8,6.1])
#res_sample = minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
#print(res_sample)
# Marina Solutions
obj = get_black_box_objective_2(G,p)
res_sample = minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
print(res_sample)
theta_2 = [0.72685401, 2.15678239, 0.86389827, 2.19403121, 0.26916675, 2.19832144, 7.06651453, 3.20333137, 3.81301611, 6.08893568]
theta_1 = [0.90644898, 2.15994212, 1.8609325 , 2.14042604, 1.49126214, 2.4127999, 6.10529434, 2.18238732, 3.84056674, 6.07097744]
beta = theta_1[:p]
gamma = theta_1[p:]
_lambda = _LAMBDA # get global _lambda
qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend)
print(plot_histogram(job.result().get_counts(), color='midnightblue', title="New Histogram"))
beta = theta_2[:p]
gamma = theta_2[p:]
_lambda = _LAMBDA # get global _lambda
qc = get_QAOA_circuit(G, beta, gamma, _LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend)
print(plot_histogram(job.result().get_counts(), color='midnightblue', title="New Histogram"))
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
import json
import csv
import numpy as np
import networkx as nx
import qiskit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer, assemble
from qiskit.quantum_info import Statevector
from qiskit.aqua.algorithms import NumPyEigensolver
from qiskit.quantum_info import Pauli
from qiskit.aqua.operators import op_converter
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.visualization import plot_histogram
from qiskit.providers.aer.extensions.snapshot_statevector import *
from thirdParty.classical import rand_graph, classical, bitstring_to_path, calc_cost
from utils import mapeo_grafo
from collections import defaultdict
from operator import itemgetter
from scipy.optimize import minimize
import matplotlib.pyplot as plt
LAMBDA = 10
SHOTS = 10000
UNIFORM_CONVERGENCE_SAMPLE = []
# returns the bit index for an alpha and j
def bit(i_city, l_time, num_cities):
return i_city * num_cities + l_time
# e^(cZZ)
def append_zz_term(qc, q_i, q_j, gamma, constant_term):
qc.cx(q_i, q_j)
qc.rz(2*gamma*constant_term,q_j)
qc.cx(q_i, q_j)
# e^(cZ)
def append_z_term(qc, q_i, gamma, constant_term):
qc.rz(2*gamma*constant_term, q_i)
# e^(cX)
def append_x_term(qc,qi,beta):
qc.rx(-2*beta, qi)
def get_not_edge_in(G):
N = G.number_of_nodes()
not_edge = []
for i in range(N):
for j in range(N):
if i != j:
buffer_tupla = (i,j)
in_edges = False
for edge_i, edge_j in G.edges():
if ( buffer_tupla == (edge_i, edge_j) or buffer_tupla == (edge_j, edge_i)):
in_edges = True
if in_edges == False:
not_edge.append((i, j))
return not_edge
def get_classical_simplified_z_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# z term #
z_classic_term = [0] * N**2
# first term
for l in range(N):
for i in range(N):
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += -1 * _lambda
# second term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_jl
z_jl_index = bit(j, l, N)
z_classic_term[z_jl_index] += _lambda / 2
# third term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 2
# z_ij
z_ij_index = bit(i, j, N)
z_classic_term[z_ij_index] += _lambda / 2
# fourth term
not_edge = get_not_edge_in(G) # include order tuples ej = (1,0), (0,1)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
z_classic_term[z_il_index] += _lambda / 4
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
z_classic_term[z_jlplus_index] += _lambda / 4
# fifthy term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
z_classic_term[z_il_index] += weight_ij / 4
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
z_classic_term[z_il_index] += weight_ji / 4
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
z_classic_term[z_jlplus_index] += weight_ji / 4
return z_classic_term
def get_classical_simplified_zz_term(G, _lambda):
# recorrer la formula Z con datos grafo se va guardando en diccionario que acumula si coinciden los terminos
N = G.number_of_nodes()
E = G.edges()
# zz term #
zz_classic_term = [[0] * N**2 for i in range(N**2) ]
# first term
for l in range(N):
for j in range(N):
for i in range(N):
if i < j:
# z_il
z_il_index = bit(i, l, N)
# z_jl
z_jl_index = bit(j, l, N)
zz_classic_term[z_il_index][z_jl_index] += _lambda / 2
# second term
for i in range(N):
for l in range(N):
for j in range(N):
if l < j:
# z_il
z_il_index = bit(i, l, N)
# z_ij
z_ij_index = bit(i, j, N)
zz_classic_term[z_il_index][z_ij_index] += _lambda / 2
# third term
not_edge = get_not_edge_in(G)
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# z_il
z_il_index = bit(i, l, N)
# z_j(l+1)
l_plus = (l+1) % N
z_jlplus_index = bit(j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += _lambda / 4
# fourth term
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# z_il
z_il_index = bit(edge_i, l, N)
# z_jlplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_j, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ij / 4
# add order term because G.edges() do not include order tuples #
# z_i'l
z_il_index = bit(edge_j, l, N)
# z_j'lplus
l_plus = (l+1) % N
z_jlplus_index = bit(edge_i, l_plus, N)
zz_classic_term[z_il_index][z_jlplus_index] += weight_ji / 4
return zz_classic_term
def get_classical_simplified_hamiltonian(G, _lambda):
# z term #
z_classic_term = get_classical_simplified_z_term(G, _lambda)
# zz term #
zz_classic_term = get_classical_simplified_zz_term(G, _lambda)
return z_classic_term, zz_classic_term
def get_cost_circuit(G, gamma, _lambda):
N = G.number_of_nodes()
N_square = N**2
qc = QuantumCircuit(N_square,N_square)
z_classic_term, zz_classic_term = get_classical_simplified_hamiltonian(G, _lambda)
# z term
for i in range(N_square):
if z_classic_term[i] != 0:
append_z_term(qc, i, gamma, z_classic_term[i])
# zz term
for i in range(N_square):
for j in range(N_square):
if zz_classic_term[i][j] != 0:
append_zz_term(qc, i, j, gamma, zz_classic_term[i][j])
return qc
def get_mixer_operator(G,beta):
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
for n in range(N**2):
append_x_term(qc, n, beta)
return qc
def invert_counts(counts):
return {k[::-1] :v for k,v in counts.items()}
def get_QAOA_circuit(G, beta, gamma, _lambda):
assert(len(beta)==len(gamma))
N = G.number_of_nodes()
qc = QuantumCircuit(N**2,N**2)
# init min mix state
qc.h(range(N**2))
p = len(beta)
for i in range(p):
qc = qc.compose(get_cost_circuit(G, gamma[i], _lambda))
qc = qc.compose(get_mixer_operator(G, beta[i]))
qc.barrier(range(N**2))
qc.snapshot_statevector("final_state")
qc.measure(range(N**2),range(N**2))
return qc
def tsp_obj(x, G):
# obtenemos el valor evaluado en f(x_1, x_2,... x_n)
z_classic_term, zz_classic_term = get_classical_simplified_hamiltonian(G, LAMBDA)
cost = 0
# z term
for index in range(len(x)):
z = (int(x[index]) * 2 ) -1
cost += z_classic_term[index] * z
## zz term
for i in range(len(x)):
z_1 = (int(x[i]) * 2 ) -1
for j in range(len(x)):
z_2 = (int(x[j]) * 2 ) -1
cost += zz_classic_term[i][j] * z_1 * z_1
return cost
# Sample expectation value
def compute_tsp_energy(counts, G):
energy = 0
get_counts = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = tsp_obj(meas, G)
energy += obj_for_meas*meas_count
total_counts += meas_count
return energy/total_counts
# Sample expectation value
def compute_tsp_energy_2(counts, G):
energy = 0
get_counts = 0
total_counts = 0
for meas, meas_count in counts.items():
obj_for_meas = tsp_obj_2(meas, G, LAMBDA)
energy += obj_for_meas*meas_count
total_counts += meas_count
mean = energy/total_counts
return mean
def tsp_obj_2(x, G,_lambda):
# obtenemos el valor evaluado en f(x_1, x_2,... x_n)
not_edge = get_not_edge_in(G)
N = G.number_of_nodes()
tsp_cost=0
#Distancia
weights = nx.get_edge_attributes(G,'weight')
for edge_i, edge_j in G.edges():
weight_ij = weights.get((edge_i,edge_j))
weight_ji = weight_ij
for l in range(N):
# x_il
x_il_index = bit(edge_i, l, N)
# x_jlplus
l_plus = (l+1) % N
x_jlplus_index = bit(edge_j, l_plus, N)
tsp_cost+= int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ij
# add order term because G.edges() do not include order tuples #
# x_i'l
x_il_index = bit(edge_j, l, N)
# x_j'lplus
x_jlplus_index = bit(edge_i, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * weight_ji
#Constraint 1
for l in range(N):
penal1 = 1
for i in range(N):
x_il_index = bit(i, l, N)
penal1 -= int(x[x_il_index])
tsp_cost += _lambda * penal1**2
#Contstraint 2
for i in range(N):
penal2 = 1
for l in range(N):
x_il_index = bit(i, l, N)
penal2 -= int(x[x_il_index])
tsp_cost += _lambda*penal2**2
#Constraint 3
for edge in not_edge:
for l in range(N):
i = edge[0]
j = edge[1]
# x_il
x_il_index = bit(i, l, N)
# x_j(l+1)
l_plus = (l+1) % N
x_jlplus_index = bit(j, l_plus, N)
tsp_cost += int(x[x_il_index]) * int(x[x_jlplus_index]) * _lambda
return tsp_cost
def get_black_box_objective(G,p):
backend = Aer.get_backend('qasm_simulator')
def f(theta):
beta = theta[:p]
gamma = theta[p:]
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
counts = execute(qc, backend, seed_simulator=10, shots=SHOTS).result().get_counts()
return compute_tsp_energy(invert_counts(counts),G)
return f
def get_black_box_objective_2(G,p):
backend = Aer.get_backend('qasm_simulator')
sim = Aer.get_backend('aer_simulator')
def f(theta):
beta = theta[:p]
gamma = theta[p:]
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
result = execute(qc, backend, seed_simulator=10, shots= SHOTS).result()
final_state_vector = result.data()["snapshots"]["statevector"]["final_state"][0]
state_vector = Statevector(final_state_vector)
probabilities = state_vector.probabilities()
probabilities_states = invert_counts(state_vector.probabilities_dict())
expected_value = 0
for state,probability in probabilities_states.items():
cost = tsp_obj_2(state, G, LAMBDA)
expected_value += cost*probability
counts = result.get_counts()
mean = compute_tsp_energy_2(invert_counts(counts),G)
global UNIFORM_CONVERGENCE_SAMPLE
UNIFORM_CONVERGENCE_SAMPLE.append({
"beta" : beta,
"gamma" : gamma,
"counts" : counts,
"mean" : mean,
"probabilities" : probabilities,
"expected_value" : expected_value
})
return mean
return f
def compute_tsp_min_energy_2(counts, G):
energy = 0
get_counts = 0
total_counts = 0
min = 1000000000000000000000
index = 0
min_meas = ""
for meas, meas_count in counts.items():
index = index + 1
obj_for_meas = tsp_obj_2(meas, G, LAMBDA)
if obj_for_meas < min:
min = obj_for_meas
min_meas = meas
return index, min, min_meas
def compute_tsp_min_energy_1(counts, G):
energy = 0
get_counts = 0
total_counts = 0
min = 1000000000000000000000
index = 0
min_meas = ""
for meas, meas_count in counts.items():
index = index + 1
obj_for_meas = tsp_obj(meas, G)
if obj_for_meas < min:
min = obj_for_meas
min_meas = meas
return index, min, min_meas
def test_counts_2(counts, G):
mean_energy2 = compute_tsp_energy_2(invert_counts(counts),G)
cantidad, min, min_meas = compute_tsp_min_energy_2(invert_counts(counts),G)
print("*************************")
print("En el algoritmo 2 (Marina) el valor esperado como resultado es " + str(mean_energy2))
print("El valor minimo de todos los evaluados es " + str(min) + " se evaluaron un total de " + str(cantidad))
print("El vector minimo es " + min_meas)
def test_counts_1(counts, G):
mean_energy1 = compute_tsp_energy(invert_counts(counts),G)
cantidad, min, min_meas = compute_tsp_min_energy_1(invert_counts(counts),G)
print("*************************")
print("En el algoritmo 1 (Pablo) el valor esperado como resultado es " + str(mean_energy1))
print("El valor minimo de todos los evaluados es " + str(min) + " se evaluaron un total de " + str(cantidad))
print("El vector minimo es " + min_meas)
def test_solution(grafo=None, p=7):
global UNIFORM_CONVERGENCE_SAMPLE
UNIFORM_CONVERGENCE_SAMPLE = []
if grafo == None:
cantidad_ciudades = 2
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
print(mejor_costo)
print(mejor_camino)
print(G.edges())
print(G.nodes())
else:
G = grafo
bounds = []
intial_random = []
for i in range(p):
bounds.append((0, np.pi))
intial_random.append(np.random.uniform(0,np.pi))
for i in range(p):
bounds.append((0, np.pi * 2))
intial_random.append(np.random.uniform(0,2*np.pi))
init_point = np.array(intial_random)
# Marina Solutions
obj = get_black_box_objective_2(G,p)
res_sample_2 = minimize(obj, init_point, method="COBYLA", options={"maxiter":2500,"disp":True})
theta_2 = res_sample_2.x
beta = theta_2[:p]
gamma = theta_2[p:]
_lambda = LAMBDA
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job_2 = execute(qc, backend, shots = SHOTS)
resutls_2 = job_2.result().get_counts()
test_counts_2(resutls_2, G)
return job_2, G, UNIFORM_CONVERGENCE_SAMPLE
def create_multiple_p_mismo_grafo():
header = ['p', 'state', 'probability', 'mean']
length_p = 10
with open('qaoa_multiple_p.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
writer.writerow(header)
first_p = False
uniform_convergence_sample = []
for p in range(length_p):
p = p+1
if first_p == False:
job_2, G, uniform_convergence_sample = test_solution(p=p)
first_p = True
else:
job_2, G, uniform_convergence_sample = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
uniform_convergence_sample.sort(key=lambda x: x["mean"])
mean = uniform_convergence_sample[0]["mean"]
print(mean)
state = 0
for probability in uniform_convergence_sample[0]["probabilities"]:
state += 1
writer.writerow([p,state, probability,mean])
def create_multiple_p_mismo_grafo_multiples_instanncias():
header = ['instance','p','distance', 'mean']
length_p = 4
length_instances = 10
with open('qaoa_multiple_p_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
writer.writerow(header)
instance_index = 0
for instance in range(length_instances):
instance_index += 1
first_p = False
UNIFORM_CONVERGENCE_P = []
uniform_convergence_sample = []
for p in range(length_p):
p = p+1
print("p es igual " + str(p))
if first_p == False:
print("Vuelve a llamar a test_solution")
job_2, G, uniform_convergence_sample = test_solution(p=p)
first_p = True
else:
job_2, G, uniform_convergence_sample = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
uniform_convergence_sample.sort(key=lambda x: x["expected_value"])
convergence_min = uniform_convergence_sample[0]
UNIFORM_CONVERGENCE_P.append({
"mean":convergence_min["expected_value"],
"probabilities": convergence_min["probabilities"]
})
cauchy_function_nk = UNIFORM_CONVERGENCE_P[len(UNIFORM_CONVERGENCE_P) - 1]
p_index = 0
for p_state in UNIFORM_CONVERGENCE_P:
p_index += 1
print(p_index)
mean = p_state["mean"]
distance_p_cauchy_function_nk = np.max(np.abs(cauchy_function_nk["probabilities"] - p_state["probabilities"]))
writer.writerow([instance_index, p_index, distance_p_cauchy_function_nk, mean])
if __name__ == '__main__':
create_multiple_p_mismo_grafo_multiples_instanncias()
def defult_init():
cantidad_ciudades = 2
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
print(mejor_costo)
print(mejor_camino)
print(G.edges())
print(G.nodes())
print("labels")
labels = nx.get_edge_attributes(G,'weight')
p = 5
obj = get_black_box_objective(G,p)
init_point = np.array([0.8,2.2,0.83,2.15,0.37,2.4,6.1,2.2,3.8,6.1])
# Marina Solutions
obj = get_black_box_objective_2(G,p)
res_sample = minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
print(res_sample)
theta_2 = [0.72685401, 2.15678239, 0.86389827, 2.19403121, 0.26916675, 2.19832144, 7.06651453, 3.20333137, 3.81301611, 6.08893568]
theta_1 = [0.90644898, 2.15994212, 1.8609325 , 2.14042604, 1.49126214, 2.4127999, 6.10529434, 2.18238732, 3.84056674, 6.07097744]
beta = theta_1[:p]
gamma = theta_1[p:]
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend)
beta = theta_2[:p]
gamma = theta_2[p:]
qc = get_QAOA_circuit(G, beta, gamma, LAMBDA)
backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend)
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
import qiskit
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
from operator import itemgetter
from scipy.optimize import minimize
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer
from qiskit.aqua.algorithms import NumPyEigensolver
from qiskit.quantum_info import Pauli
from qiskit.aqua.operators import op_converter
from qiskit.aqua.operators import WeightedPauliOperator
from tsp_qaoa import marina_solution
G=nx.Graph()
i=1
G.add_node(i,pos=(i,i))
G.add_node(2,pos=(2,2))
G.add_node(3,pos=(1,0))
G.add_edge(1,2,weight=20.5)
G.add_edge(1,3,weight=9.8)
pos=nx.get_node_attributes(G,'pos')
nx.draw(G,pos)
labels = nx.get_edge_attributes(G,'weight')
nx.draw_networkx_edge_labels(G,pos,edge_labels=labels)
def append_zz_term(qc,q1,q2,gamma):
qc.cx(q1,q2)
qc.rz(2*gamma,q2)
qc.cx(q1,q2)
def get_cost_circuit(G,gamma):
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
for i,j in G.edges():
append_zz_term(qc,i,j,gamma)
return qc
#print(get_cost_circuit(G,0.5))
def append_x_term(qc,q1,beta):
qc.rx(2*beta,q1)
def get_mixer_operator(G,beta):
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
for n in G.nodes():
append_x_term(qc,n,beta)
return qc
#print(get_mixer_operator(G,0.5))
def get_QAOA_circuit(G,beta,gamma):
assert(len(beta)==len(gamma))
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
qc.h(range(N))
p=len(beta)
#aplicamos las p rotaciones
for i in range(p):
qc=qc.compose(get_cost_circuit(G,gamma[i]))
qc=qc.compose(get_mixer_operator(G,beta[i]))
qc.barrier(range(N))
qc.measure(range(N),range(N))
return qc
print(get_QAOA_circuit(G,[0.5,0,6],[0.5,0,6]))
def invert_counts(counts):
return {k[::-1] :v for k,v in counts.items()}
qc=get_QAOA_circuit(G,[0.5,0,6],[0.5,0,6])
backend=Aer.get_backend('qasm_simulator')
job=execute(qc,backend)
result=job.result()
print(invert_counts(result.get_counts()))
def maxcut_obj(x,G):
cut=0
for i,j in G.edges():
if x[i]!=x[j]:
cut = cut-1
return cut
print(maxcut_obj("00011",G))
def compute_maxcut_energy(counts,G):
energy=0
get_counts=0
total_counts=0
for meas, meas_count in counts.items():
obj_for_meas=maxcut_obj(meas,G)
energy+=obj_for_meas*meas_count
total_counts+=meas_count
return energy/total_counts
def get_black_box_objective(G,p):
backend=Aer.get_backend('qasm_simulator')
def f(theta):
beta=theta[:p]
gamma=theta[p:]
qc=get_QAOA_circuit(G,beta,gamma)
counts=execute(qc,backend,seed_simulator=10).result().get_counts()
return compute_maxcut_energy(invert_counts(counts),G)
return f
p=5
obj=get_black_box_objective(G,p)
init_point=np.array([0.8,2.2,0.83,2.15,0.37,2.4,6.1,2.2,3.8,6.1])#([2,2,1,1,1,1,1,1,1,1])
res_sample=minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
res_sample
from thirdParty.classical import rand_graph, classical, bitstring_to_path, calc_cost
from utils import mapeo_grafo
cantidad_ciudades = 4
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
pos=nx.spring_layout(G)
nx.draw(G,pos)
labels = nx.get_edge_attributes(G,'weight')
nx.draw_networkx_edge_labels(G,pos,edge_labels=labels)
G
pos=nx.get_node_attributes(G,'weight')
pos
labels = nx.get_edge_attributes(G,'weight')
labels
def funcion_costo(multiplicador_lagrange, cantidad_ciudades, pesos, conexiones ):
N = G.number_of_nodes()
N_square = N^2
# restriccion 1
for i in range(cantidad_ciudades):
cur = sI(N_square)
for j in range(num_cities):
cur -= D(i, j)
ret += cur**2
# retorna el indice de qubit por conversion al problema
def quibit_indice(i, l, N):
return i * N + l
from qiskit.quantum_info.operators import Operator, Pauli
# Create an operator
XX = Operator(Pauli(label='XX'))
# Add to a circuit
circ = QuantumCircuit(2, 2)
circ.append(XX, [0, 1])
circ.measure([0,1], [0,1])
circ.draw('mpl')
# Add to a circuit
circ = QuantumCircuit(2, 2)
circ.append(a, [0])
#circ.measure([0,1], [0,1])
circ.draw('mpl')
a = I - ( 0.5*(I+ Z))**2
a = Operator(a)
a.is_unitary()
print(I @ Z)
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
# genera las distancias
index = -1
for sample in UNIFORM_CONVERGENCE_SAMPLE:
mean = sample["mean"]
index += 1
distance_p_ground_state = np.max(np.abs(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - sample["probabilities"]))
UNIFORM_CONVERGENCE_SAMPLE[index]["distance_pgs"] = distance_p_ground_state
header = ['instance', 'iteration', 'distance']
length_instances = 2
with open('qaoa_multiple_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
for i in range(length_instances):
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution()
iteration = 0
for sample in UNIFORM_CONVERGENCE_SAMPLE:
iteration += 1
mean = sample["mean"]
distance = sample["distance_pgs"]
state = 0
for probability in sample["probabilities"]:
state += 1
# write the data
data = [iteration, state, probability, mean]
writer.writerow(data)
writer_q.writerow([iteration, distance])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
header = ['p', 'state', 'probability', 'mean']
length_p = 10
with open('qaoa_multiple_p.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
first_p = False
for p in range(length_p):
p = p+1
if first_p == False:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
mean = UNIFORM_CONVERGENCE_SAMPLE[0]["mean"]
print(mean)
state = 0
for probability in UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"]:
state += 1
writer.writerow([p,state, probability,mean])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
import json
import csv
# Array of JSON Objects
header = ['instance','p','distance', 'mean']
length_p = 3
length_instances = 2
with open('qaoa_multiple_p_distance.csv', 'w', encoding='UTF8') as f:
writer = csv.writer(f)
# write the header
writer.writerow(header)
instance_index = 0
for instance in range(length_instances):
instance_index += 1
first_p = False
UNIFORM_CONVERGENCE_P = []
UNIFORM_CONVERGENCE_SAMPLE = []
for p in range(length_p):
p = p+1
if first_p == False:
print("Vuelve a llamar a test_solution")
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(p=p)
first_p = True
else:
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution(grafo=G, p=p)
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
convergence_min = UNIFORM_CONVERGENCE_SAMPLE[0]
UNIFORM_CONVERGENCE_P.append({
"mean":convergence_min["mean"],
"probabilities": convergence_min["probabilities"]
})
cauchy_function_nk = UNIFORM_CONVERGENCE_P[len(UNIFORM_CONVERGENCE_P) - 1]
p_index = 0
for p_state in UNIFORM_CONVERGENCE_P:
p_index += 1
print(p_index)
mean = p_state["mean"]
print(p_state)
print(mean)
distance_p_cauchy_function_nk = np.max(np.abs(cauchy_function_nk["probabilities"] - p_state["probabilities"]))
writer.writerow([instance_index, p_index, distance_p_cauchy_function_nk, mean])
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
from tsp_qaoa import test_solution
from qiskit.visualization import plot_histogram
import networkx as nx
import numpy as np
job_2, G, UNIFORM_CONVERGENCE_SAMPLE = test_solution()
plot_histogram(job_2.result().get_counts(), color='midnightblue', title="New Histogram", figsize=(30, 5))
plot_histogram(job_2.result().get_counts(), color='midnightblue', title="New Histogram", figsize=(30, 5))
G
labels = nx.get_edge_attributes(G,'weight')
labels
import json
# Array of JSON Objects
products = [{"name": "HDD", "brand": "Samsung", "price": "$100"},
{"name": "Monitor", "brand": "Dell", "price": "$120"},
{"name": "Mouse", "brand": "Logitech", "price": "$10"}]
# Print the original data
print("The original JSON data:\n{0}".format(products))
# Sort the JSON data based on the value of the brand key
products.sort(key=lambda x: x["price"])
# Print the sorted JSON data
print("The sorted JSON data based on the value of the brand:\n{0}".format(products))
_LAMBDA
UNIFORM_CONVERGENCE_SAMPLE
import json
# Array of JSON Objects
# Sort the JSON data based on the value of the brand key
UNIFORM_CONVERGENCE_SAMPLE.sort(key=lambda x: x["mean"])
# Print the sorted JSON data
UNIFORM_CONVERGENCE_SAMPLE
np.max(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - UNIFORM_CONVERGENCE_SAMPLE[220]["probabilities"])
# generamos las distancias entre para la convergencia uniforme
index = -1
for sample in UNIFORM_CONVERGENCE_SAMPLE:
mean = sample["mean"]
index += 1
distance_p_ground_state = np.max(np.abs(UNIFORM_CONVERGENCE_SAMPLE[0]["probabilities"] - sample["probabilities"]))
UNIFORM_CONVERGENCE_SAMPLE[index]["distance_pgs"] = distance_p_ground_state
UNIFORM_CONVERGENCE_SAMPLE
import csv
header = ['iteration', 'state', 'probability', 'mean']
header_q = ['iteration', 'distance']
with open('qaoa_cu.csv', 'w', encoding='UTF8') as f:
with open('qaoa_distance.csv', 'w', encoding='UTF8') as q:
writer = csv.writer(f)
writer_q = csv.writer(q)
# write the header
writer.writerow(header)
writer_q.writerow(header_q)
iteration = 0
for sample in UNIFORM_CONVERGENCE_SAMPLE:
iteration += 1
mean = sample["mean"]
distance = sample["distance_pgs"]
state = 0
for probability in sample["probabilities"]:
state += 1
# write the data
data = [iteration, state, probability, mean]
writer.writerow(data)
writer_q.writerow([iteration, distance])
#plot_histogram(job_2, color='midnightblue', title=str(mean), figsize=(30, 5)).savefig(str(contador) + "_2.png")
#print(sample["mean"])
plot_histogram(job_2, color='midnightblue', title="New Histogram", figsize=(30, 5)).savefig('out.png')
|
https://github.com/PabloMartinezAngerosa/QAOA-uniform-convergence
|
PabloMartinezAngerosa
|
import qiskit
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
from operator import itemgetter
from scipy.optimize import minimize
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer
from qiskit.aqua.algorithms import NumPyEigensolver
from qiskit.quantum_info import Pauli
from qiskit.aqua.operators import op_converter
from qiskit.aqua.operators import WeightedPauliOperator
from tsp_qaoa import marina_solution
G=nx.Graph()
i=1
G.add_node(i,pos=(i,i))
G.add_node(2,pos=(2,2))
G.add_node(3,pos=(1,0))
G.add_edge(1,2,weight=20.5)
G.add_edge(1,3,weight=9.8)
pos=nx.get_node_attributes(G,'pos')
nx.draw(G,pos)
labels = nx.get_edge_attributes(G,'weight')
nx.draw_networkx_edge_labels(G,pos,edge_labels=labels)
def append_zz_term(qc,q1,q2,gamma):
qc.cx(q1,q2)
qc.rz(2*gamma,q2)
qc.cx(q1,q2)
def get_cost_circuit(G,gamma):
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
for i,j in G.edges():
append_zz_term(qc,i,j,gamma)
return qc
#print(get_cost_circuit(G,0.5))
def append_x_term(qc,q1,beta):
qc.rx(2*beta,q1)
def get_mixer_operator(G,beta):
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
for n in G.nodes():
append_x_term(qc,n,beta)
return qc
#print(get_mixer_operator(G,0.5))
def get_QAOA_circuit(G,beta,gamma):
assert(len(beta)==len(gamma))
N=G.number_of_nodes()
qc=QuantumCircuit(N,N)
qc.h(range(N))
p=len(beta)
#aplicamos las p rotaciones
for i in range(p):
qc=qc.compose(get_cost_circuit(G,gamma[i]))
qc=qc.compose(get_mixer_operator(G,beta[i]))
qc.barrier(range(N))
qc.measure(range(N),range(N))
return qc
print(get_QAOA_circuit(G,[0.5,0,6],[0.5,0,6]))
def invert_counts(counts):
return {k[::-1] :v for k,v in counts.items()}
qc=get_QAOA_circuit(G,[0.5,0,6],[0.5,0,6])
backend=Aer.get_backend('qasm_simulator')
job=execute(qc,backend)
result=job.result()
print(invert_counts(result.get_counts()))
def maxcut_obj(x,G):
cut=0
for i,j in G.edges():
if x[i]!=x[j]:
cut = cut-1
return cut
print(maxcut_obj("00011",G))
def compute_maxcut_energy(counts,G):
energy=0
get_counts=0
total_counts=0
for meas, meas_count in counts.items():
obj_for_meas=maxcut_obj(meas,G)
energy+=obj_for_meas*meas_count
total_counts+=meas_count
return energy/total_counts
def get_black_box_objective(G,p):
backend=Aer.get_backend('qasm_simulator')
def f(theta):
beta=theta[:p]
gamma=theta[p:]
qc=get_QAOA_circuit(G,beta,gamma)
counts=execute(qc,backend,seed_simulator=10).result().get_counts()
return compute_maxcut_energy(invert_counts(counts),G)
return f
p=5
obj=get_black_box_objective(G,p)
init_point=np.array([0.8,2.2,0.83,2.15,0.37,2.4,6.1,2.2,3.8,6.1])#([2,2,1,1,1,1,1,1,1,1])
res_sample=minimize(obj, init_point,method="COBYLA",options={"maxiter":2500,"disp":True})
res_sample
from thirdParty.classical import rand_graph, classical, bitstring_to_path, calc_cost
from utils import mapeo_grafo
cantidad_ciudades = 4
pesos, conexiones = None, None
mejor_camino = None
while not mejor_camino:
pesos, conexiones = rand_graph(cantidad_ciudades)
mejor_costo, mejor_camino = classical(pesos, conexiones, loop=False)
G = mapeo_grafo(conexiones, pesos)
pos=nx.spring_layout(G)
nx.draw(G,pos)
labels = nx.get_edge_attributes(G,'weight')
nx.draw_networkx_edge_labels(G,pos,edge_labels=labels)
G
pos=nx.get_node_attributes(G,'weight')
pos
labels = nx.get_edge_attributes(G,'weight')
labels
def funcion_costo(multiplicador_lagrange, cantidad_ciudades, pesos, conexiones ):
N = G.number_of_nodes()
N_square = N^2
# restriccion 1
for i in range(cantidad_ciudades):
cur = sI(N_square)
for j in range(num_cities):
cur -= D(i, j)
ret += cur**2
# retorna el indice de qubit por conversion al problema
def quibit_indice(i, l, N):
return i * N + l
from qiskit.quantum_info.operators import Operator, Pauli
# Create an operator
XX = Operator(Pauli(label='XX'))
# Add to a circuit
circ = QuantumCircuit(2, 2)
circ.append(XX, [0, 1])
circ.measure([0,1], [0,1])
circ.draw('mpl')
# Add to a circuit
circ = QuantumCircuit(2, 2)
circ.append(a, [0])
#circ.measure([0,1], [0,1])
circ.draw('mpl')
a = I - ( 0.5*(I+ Z))**2
a = Operator(a)
a.is_unitary()
print(I @ Z)
|
https://github.com/jaykomarraju/Quantum-Optimization-for-Solar-Farm
|
jaykomarraju
|
import numpy as np
import networkx as nx
from qiskit import Aer
from qiskit.algorithms import QAOA, NumPyMinimumEigensolver
from qiskit.algorithms.optimizers import COBYLA
from qiskit.utils import QuantumInstance
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
num_time_slots = 24
# Define the QUBO problem
qubo = QuadraticProgram()
# Add binary variables for charging (c) and discharging (d) states
for t in range(num_time_slots):
qubo.binary_var(f'c_{t}')
qubo.binary_var(f'd_{t}')
# Define the objective function
# (In practice, you need to calculate Jij and hi based on the solar farm data)
Jij = np.random.rand(num_time_slots, num_time_slots) * 0.5
hi_c = -1 + np.random.rand(num_time_slots)
hi_d = 1 - np.random.rand(num_time_slots)
# Set linear and quadratic terms of the objective function
linear_terms = {}
quadratic_terms = {}
for t in range(num_time_slots):
linear_terms[f'c_{t}'] = hi_c[t]
linear_terms[f'd_{t}'] = hi_d[t]
for s in range(num_time_slots):
if t != s:
quadratic_terms[(f'c_{t}', f'c_{s}')] = Jij[t, s]
quadratic_terms[(f'd_{t}', f'd_{s}')] = Jij[t, s]
qubo.minimize(linear=linear_terms, quadratic=quadratic_terms)
# Set up the quantum instance
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, seed_simulator=42, seed_transpiler=42, shots=10000)
# Set up the QAOA algorithm and optimizer
optimizer = COBYLA(maxiter=500)
qaoa = QAOA(optimizer=optimizer, reps=5, quantum_instance=quantum_instance)
# Set up the minimum eigen optimizer
min_eig_optimizer = MinimumEigenOptimizer(qaoa)
# Solve the problem
result = min_eig_optimizer.solve(qubo)
print("QAOA result:", result)
# Solve the problem using a classical solver (NumPyMinimumEigensolver)
exact_solver = MinimumEigenOptimizer(NumPyMinimumEigensolver())
exact_result = exact_solver.solve(qubo)
print("Classical result:", exact_result)
|
https://github.com/jaykomarraju/Quantum-Optimization-for-Solar-Farm
|
jaykomarraju
|
import numpy as np
import networkx as nx
from qiskit import Aer
from qiskit.algorithms import QAOA, NumPyMinimumEigensolver
from qiskit.algorithms.optimizers import COBYLA
from qiskit.utils import QuantumInstance
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
num_time_slots = 24
# Define the QUBO problem
qubo = QuadraticProgram()
# Add binary variables for charging (c) and discharging (d) states
for t in range(num_time_slots):
qubo.binary_var(f'c_{t}')
qubo.binary_var(f'd_{t}')
# Define the objective function
# (In practice, you need to calculate Jij and hi based on the solar farm data)
Jij = np.random.rand(num_time_slots, num_time_slots) * 0.5
hi_c = -1 + np.random.rand(num_time_slots)
hi_d = 1 - np.random.rand(num_time_slots)
# Set linear and quadratic terms of the objective function
linear_terms = {}
quadratic_terms = {}
for t in range(num_time_slots):
linear_terms[f'c_{t}'] = hi_c[t]
linear_terms[f'd_{t}'] = hi_d[t]
for s in range(num_time_slots):
if t != s:
quadratic_terms[(f'c_{t}', f'c_{s}')] = Jij[t, s]
quadratic_terms[(f'd_{t}', f'd_{s}')] = Jij[t, s]
qubo.minimize(linear=linear_terms, quadratic=quadratic_terms)
# Set up the quantum instance
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, seed_simulator=42, seed_transpiler=42, shots=10000)
# Set up the QAOA algorithm and optimizer
optimizer = COBYLA(maxiter=500)
qaoa = QAOA(optimizer=optimizer, reps=5, quantum_instance=quantum_instance)
# Set up the minimum eigen optimizer
min_eig_optimizer = MinimumEigenOptimizer(qaoa)
# Solve the problem
result = min_eig_optimizer.solve(qubo)
print("QAOA result:", result)
# Solve the problem using a classical solver (NumPyMinimumEigensolver)
exact_solver = MinimumEigenOptimizer(NumPyMinimumEigensolver())
exact_result = exact_solver.solve(qubo)
print("Classical result:", exact_result)
|
https://github.com/ACDuriez/Ising-VQE
|
ACDuriez
|
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from tqdm import tqdm
from scipy.optimize import minimize
from dataclasses import dataclass
from qiskit.providers.fake_provider import FakeManila,FakeQuito,FakeLima,FakeKolkata,FakeNairobi
from qiskit.transpiler import CouplingMap
from qiskit.circuit import QuantumCircuit,ParameterVector,Parameter
from qiskit.circuit.library import EfficientSU2
from qiskit.quantum_info import SparsePauliOp
#from qiskit.opflow import PauliSumOp
from qiskit.primitives import Estimator,Sampler,BackendEstimator
from qiskit.algorithms.minimum_eigensolvers import VQE
from qiskit.algorithms.minimum_eigensolvers import NumPyMinimumEigensolver
from qiskit.algorithms.optimizers import SLSQP,COBYLA,L_BFGS_B,QNSPSA,SPSA
from qiskit_aer.noise import NoiseModel
from qiskit_ibm_runtime import Session,Options,QiskitRuntimeService
from qiskit_ibm_runtime import Estimator as IBM_Estimator
from qiskit_ibm_runtime import Sampler as IBM_Sampler
from qiskit_aer.primitives import Estimator as AerEstimator
J = 1
h = 0.5
n_qubits = 4
def get_line_graph(n_qubits):
"""This function creates a linear lattice with
open boundary conditions for a given number of qubits"""
graph_line = nx.Graph()
graph_line.add_nodes_from(range(n_qubits))
edge_list = []
for i in graph_line.nodes:
if i < n_qubits-1:
edge_list.append((i,i+1))
# Generate graph from the list of edges
graph_line.add_edges_from(edge_list)
return graph_line
graph = get_line_graph(n_qubits)
nx.draw_networkx(graph) #plotting the graph
def get_h_op(graph,J=1.,hx=0.5,hz=0.,ap=0.):
"""Creates a general Ising hamiltonian for
given values of the coupling, transverse field,
longitudinal field and antiparallel field
Args:
graph: networkx graph of the lattice
J: uniform coupling between first neighbors
hx: transverse field parameter
hz: longitudinal field parameter
ap: antiparallel field at the boundaries"""
num_qubits = len(graph.nodes())
sparse_list = []
# Uniform Z and X fields
for qubit in graph.nodes():
# X field
coeff = ('X',[qubit],-1*hx)
sparse_list.append(coeff)
# Z field
coeff = ('Z',[qubit],-1*hz)
sparse_list.append(coeff)
# Anti-paralel field at the borders
coeff = ('Z',[0],ap) #this is the positive field (order reversed)
sparse_list.append(coeff)
coeff = ('Z',[num_qubits-1],-1*ap)
sparse_list.append(coeff)
#Interaction field (ZZ)
for i,j in graph.edges():
coeff = ('ZZ',[i,j],-1*J)
sparse_list.append(coeff)
hamiltonian = SparsePauliOp.from_sparse_list(sparse_list,num_qubits=num_qubits).simplify()
return hamiltonian
def get_kk_op(graph):
"""Creates the number of kinks operator"""
sparse_list = []
for i,j in graph.edges():
coeff = ('II',[i,j],0.5)
sparse_list.append(coeff)
coeff = ('ZZ',[i,j],-0.5)
sparse_list.append(coeff)
kk_op = SparsePauliOp.from_sparse_list(sparse_list,num_qubits=len(graph.nodes))
return kk_op
# We show the Hamiltonian with the crittical boundary field as well as
# the number of kinks
print(get_h_op(graph,J,h,ap=np.sqrt(1-h)))
print(get_kk_op(graph))
exact_steps = 70
g_i = 0.
g_f = 1.6
exact_g_values = np.linspace(g_i,g_f,exact_steps)
def get_numpy_results(graph,J,h,g_values):
"""Returns the exact values of the energy and number of kinks
for a given lattice, coupling, transverse field and values of
the boundary field"""
n_qubits = len(graph.nodes())
numpy_solver = NumPyMinimumEigensolver()
E_values = []
kk_values = []
kk_op = get_kk_op(graph) #getting the (g-independent) number of kinks operator
for g in g_values:
h_op = get_h_op(graph,J,h,ap=g) #getting the hamiltonian operator for each g value
result = numpy_solver.compute_minimum_eigenvalue(operator=h_op,aux_operators=[kk_op])
E_values.append(result.eigenvalue)
kk_values.append(np.real(result.aux_operators_evaluated[0][0]))
return E_values,kk_values
exact_E,exact_kk = get_numpy_results(graph,J,h,exact_g_values) # getting the exact energy and number of kinks
#Plotting
f,ax = plt.subplots()
plt.plot(exact_g_values,exact_E)
plt.xlabel('boundary field')
plt.ylabel('groundstate energy')
inset_ax = f.add_axes([0.25, 0.3, 0.27, 0.27])# [left, bottom, width, height]
inset_ax.plot(exact_g_values,exact_kk)
inset_ax.set_ylabel('$<N_k>$')
inset_ax.set_xlabel('boundary field')
inset_ax.axvline(x=np.sqrt(1-h), color='red', linestyle='dashed') #indicating the critical boundary field
plt.show()
#Initialize runtime
service = QiskitRuntimeService(
channel='ibm_quantum',
instance='ibm-q/open/main',
token='your_token'
)
backend = service.backend("ibmq_qasm_simulator")
shots = 2**14 # shots for noisy simulations
def get_ansatz_hva(graph, theta_list):
"""Creates the hamiltonian variaitonal ansatz for a given
lattice graph and list of parameters. The parameters list must have a
lenght of 3*n_layers, and must have a form (coupling_i,transverse_i,boundary_i)
Args:
graph: lattice graph
theta_list: list of parameters
"""
n_qubits = len(graph.nodes())
n_layers = len(theta_list)//3
qc = QuantumCircuit(n_qubits)
even_edges = [edge for edge in graph.edges() if edge[0]%2==0]
odd_edges = [edge for edge in graph.edges() if edge[0]%2!=0]
# initial_state
qc.h(range(n_qubits))
for layer_index in range(n_layers):
# Coupling term
for pair in even_edges:
qc.rzz(2 * theta_list[3*layer_index],pair[0],pair[1])
for pair in odd_edges:
qc.rzz(2 * theta_list[3*layer_index],pair[0],pair[1])
# boundary field term
qc.rz(2 *theta_list[3*layer_index+2],0)
qc.rz(-2 * theta_list[3*layer_index+2], n_qubits-1)
# transverse field term
qc.rx(2 * theta_list[3*layer_index+1], range(n_qubits))
return qc
layers_hva = 4
theta_list_hva = ParameterVector('θ',3*layers_hva)
ansatz_hva = get_ansatz_hva(graph,theta_list_hva)
ansatz_hva.draw('mpl',style='iqx')
def get_ansatz_hea(graph,theta_list):
"""Creates the hardware efficient ansatz for a given
lattice graph and list of parameters. The parameters list must have a
lenght of 2*n_qubits_n_layers
Args:
graph: lattice graph
theta_list: list of parameters
"""
nqubits = len(graph.nodes())
n_layers = len(theta_list)//(2*nqubits)
assert len(theta_list)==2*n_qubits*n_layers, "The list of parameters does not have the correct size"
qc = QuantumCircuit(nqubits)
even_edges = [edge for edge in graph.edges() if edge[0]%2==0]
odd_edges = [edge for edge in graph.edges() if edge[0]%2!=0]
reversed_edges = [edge for edge in graph.edges()][::-1]
for layer_index in range(n_layers):
for qubit in range(nqubits):
qc.ry(theta_list[2*(nqubits)*layer_index+qubit], qubit)
# for pair in reversed_edges:
# qc.cnot(pair[0],pair[1])
for pair in even_edges:
qc.cnot(pair[0],pair[1])
for pair in odd_edges:
qc.cnot(pair[0],pair[1])
for qubit in range(nqubits):
qc.ry(theta_list[nqubits+2*(nqubits)*layer_index+qubit], qubit)
return qc
def get_ansatz_hea_ZNE(graph,theta_list):
"""Creates the folded version of hardware efficient ansatz for a given
lattice graph and list of parameters. The parameters list must have a
lenght of 2*n_qubits_n_layers. Used in the ZNE error mitigation protocol
Args:
graph: lattice graph
theta_list: list of parameters
"""
nqubits = len(graph.nodes())
n_layers = len(theta_list)//(2*nqubits)
assert len(theta_list)==2*n_qubits*n_layers, "The list of parameters does not have the correct size"
qc = QuantumCircuit(nqubits)
even_edges = [edge for edge in graph.edges() if edge[0]%2==0]
odd_edges = [edge for edge in graph.edges() if edge[0]%2!=0]
reversed_edges = [edge for edge in graph.edges()][::-1]
for layer_index in range(n_layers):
for qubit in range(nqubits):
qc.ry(theta_list[2*(nqubits)*layer_index+qubit], qubit)
# for pair in reversed_edges:
# qc.cnot(pair[0],pair[1])
#folding even edges
for pair in even_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
for pair in even_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
for pair in even_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
#folding odd edges
for pair in odd_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
for pair in odd_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
for pair in odd_edges:
qc.cnot(pair[0],pair[1])
qc.barrier()
for qubit in range(nqubits):
qc.ry(theta_list[nqubits+2*(nqubits)*layer_index+qubit], qubit)
return qc
# Here we define and show the circuit for the HEA
layers_hea = 1
theta_list = ParameterVector('t',2*n_qubits*layers_hea) # The list of parameters must
ansatz_hea = get_ansatz_hea(graph,theta_list)
ansatz_hea.draw('mpl', style="iqx")
# Here is the folded version of the HEA ansatz for the ZNE
ansatz_hea = get_ansatz_hea_ZNE(graph,theta_list)
ansatz_hea.draw('mpl', style="iqx")
def get_estimator(session,
server='qasm',
shots=2**14,
device=FakeKolkata(),
options_rtm=Options(),
seed=170):
"""Defines an estimator. Set 'qasm' for noiseless, 'noisy' for
backend estimator and 'rtm' for the runtime estimator"""
if server =='qasm':
estimator = Estimator(options={'shots':shots,'seed':seed})
elif server == 'noisy':
estimator = BackendEstimator(device,options={'shots':shots,'seed':seed})
elif server == 'rtm':
estimator = IBM_Estimator(session=session,options=options_rtm)
return estimator
def get_extrapolation(value_k1,value_k2,extrap='lin'):
"""Returns the exponential extrapolation given the
values for k=1 and k=2 noise factors"""
k_values = [1.,2.]
if extrap =='lin':
y_values = [value_k1,value_k2]
# Fit a linear regression model (polynomial of degree 1)
coefficients = np.polyfit(k_values, y_values, 1)
# The coefficients represent the slope (m) and y-intercept (b) of the line
slope, intercept = coefficients
extrapolation = intercept
if extrap == 'exp':
y_values = [np.abs(value_k1/value_k2),1.]
ln_y = np.log(y_values)
# Fit a linear regression model (polynomial of degree 1)
coefficients_exp = np.polyfit(k_values, ln_y, 1)
# The coefficients represent the slope (m) and y-intercept (b) of the line
slope_exp, intercept_exp = coefficients_exp
extrapolation = np.exp(intercept_exp)*value_k2
return extrapolation
def vqe_opt_scipy(graph,
service,
backend,
g=0.7071067811865476,
h=0.5,
ansatz_str='hea',
layers=1,
optimizer='SLSQP',
maxiter=50,
ftol=0.,
reps=1,
zne=False,
extrap='exp',
shots=None,
server='qasm',
device=FakeNairobi(),
options=Options()):
"""Runs the vqe for the Ising model with boundary fields for
a single value of the boundary field, using the scipy optimization function.
It gives data for the convergence of the optimization, which is the logs for
each sampling, the mean and standart deviation of these samplings, and also the
number of function evaluations
Args:
graph: networkx lattice graph
service: service for runtime
backend: backend for runtime (can include quantum backends)
g: value of the boundary field
h: value of the transverse field
ansatz_str: choice of ansatz, 'hea' for HEA and 'hva' for HVA
layers: number of layers for the ansatz
optimizer: optimization algorithm, as string for scipy
maxiter: maximum iterations for the optimization
ftol: tolerance for convergence, for scipy
reps: (int) number of initial parameters samplings
zne: (bool) zne option
extrap: type of extrapolation
shots: number of shots, set to None for statevector simulations
server: 'qasm' for noiseless, 'noisy' for aer, 'rtm' for runtime
device: noise model for noisy simulations
options: Options() class for runtime
"""
n_qubits = len(graph.nodes())
if ansatz_str == 'hea':
theta_list = ParameterVector('θ',2*n_qubits*layers)
ansatz = get_ansatz_hea(graph,theta_list)
ansatz_k2 = get_ansatz_hea_ZNE(graph,theta_list)
elif ansatz_str == 'hva':
theta_list = ParameterVector('θ',3*layers)
ansatz = get_ansatz_hva(graph,theta_list)
ansatz_k2 = get_ansatz_hva(graph,theta_list)
cost_operator = get_h_op(graph,hx=h,ap=g) #Defining Hamiltonian
# Now we set the cost function, with no mitigation, linear or exp extrapolation
if zne == False:
def cost_function_vqe(theta):
job = estimator.run(ansatz, cost_operator, theta)
values = job.result().values[0]
return values
if zne == True:
def cost_function_vqe(theta):
job = estimator.run([ansatz,ansatz_k2], 2*[cost_operator], 2*[theta])
value_k1 = job.result().values[0]
value_k2 = job.result().values[1]
extrapolation = get_extrapolation(value_k1=value_k1,value_k2=value_k2,extrap=extrap)
return extrapolation
log_list = []
nfev_list = []
with Session(service=service,backend=backend) as session:
estimator = get_estimator(server=server,
shots=shots,
device=device,
session=session,
options_rtm=options)
for i in tqdm(range(reps)):
random_point = np.random.random(ansatz.num_parameters)
iter_list = []
result_sample = minimize(cost_function_vqe,
x0=random_point,
method=optimizer,
callback=lambda xk: iter_list.append(list(xk)),
options={'maxiter':maxiter,'disp':False,'ftol':ftol})
iters = len(iter_list)
energy_list = estimator.run(iters*[ansatz],iters*[cost_operator],iter_list).result().values
nfev_list.append(int(result_sample.nfev))
log_list.append(list(energy_list))
session.close()
max_length = max(len(sublist) for sublist in log_list) # Finding the length of the largest list
for sublist in log_list:
if len(sublist) < max_length:
last_element = sublist[-1] # Extracting the last element
sublist.extend([last_element] * (max_length - len(sublist))) # Filling with the last element
mean_list = []
std_list = []
for i in range(len(log_list[0])):
values_list = [l[i] for l in log_list]
mean_list.append(np.mean(values_list))
std_list.append(np.std(values_list))
return log_list,mean_list,std_list,nfev_list
g_mag = 0.2
g_knk = 1.2
E_mag = NumPyMinimumEigensolver().compute_minimum_eigenvalue(get_h_op(graph,ap=g_mag)).eigenvalue
E_knk = NumPyMinimumEigensolver().compute_minimum_eigenvalue(get_h_op(graph,ap=g_knk)).eigenvalue
reps = 5 # we define the number of initial parameters samplings
logs_hva_mag,avgs_hva_mag,stds_hva_mag,nfevs_hva_mag = vqe_opt_scipy(graph=graph,
service=service,
backend=backend,
server='qasm',
g=g_mag,
layers=layers_hva,
ansatz_str='hva',
reps=reps,
maxiter=300,
shots=None,
ftol=1e-16)
avgs_list = avgs_hva_mag
stds_list = stds_hva_mag
g_value = g_mag
exact_energy = E_mag
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
plt.xlim((0,40))
x_lim = 60
# plt.xlim(0,60)
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -10, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
logs_hva_knk,avgs_hva_knk,stds_hva_knk,nfevs_hva_knk = vqe_opt_scipy(graph=graph,
service=service,
backend=backend,
server='qasm',
g=g_knk,
layers=layers_hva,
ansatz_str='hva',
reps=reps,
maxiter=300,
shots=None,
ftol=1e-16)
avgs_list = avgs_hva_knk
stds_list = stds_hva_knk
g_value = g_knk
exact_energy = E_knk
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
plt.xlim((0,40))
x_lim = 60
# plt.xlim(0,60)
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -10, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
# Here we define a different callback which is suited for the SPSA implementation of qiskit
intermediate_info = {
'nfev': [],
'parameters': [],
'energy': [],
'step_size': [],
'step_sucesss': []
}
def callback(nfev, parameters, energy, step_size,step_sucess):
intermediate_info['nfev'].append(nfev)
intermediate_info['parameters'].append(parameters)
intermediate_info['energy'].append(energy)
intermediate_info['step_size'].append(step_size)
intermediate_info['step_sucess'].append(step_sucess)
@dataclass
class VQELog:
values: list
parameters: list
def update(self, count, parameters, mean, step_size, step_sucess):
self.values.append(mean)
self.parameters.append(parameters)
print(f"Running circuit {count}", end="\r", flush=True)
# Here is the main function
def vqe_critical_spsa(graph,
service,
backend,
device=FakeKolkata(),
g=0.7071067811865476,
layers=1,
server='qasm',
learning_rate=0.07,
perturbation=0.1,
maxiter=200,
hx=0.5,
options=Options(),
zne=False,
extrap='exp',
reps=1,
shots=2**14,
ansatz_str='hea'):
"""Runs the vqe for the Ising model with boundary fields for
a single value of the boundary field, using the scipy optimization function.
It gives data for the convergence of the optimization, which is the logs for
each sampling, the mean and standart deviation of these samplings, and also the
number of function evaluations
Args:
graph: networkx lattice graph
service: service for runtime
backend: backend for runtime (can include quantum backends)
g: value of the boundary field
h: value of the transverse field
ansatz_str: choice of ansatz, 'hea' for HEA and 'hva' for HVA
layers: number of layers for the ansatz
maxiter: maximum iterations for the optimization
learning_rate: learning rate for the SPSA optimizer
perturbation: perturbation for the SPSA optimizer
reps: (int) number of initial parameters samplings
zne: (bool) zne option
extrap: type of extrapolation
shots: number of shots, set to None for statevector simulations
server: 'qasm' for noiseless, 'noisy' for aer, 'rtm' for runtime
device: noise model for noisy simulations
options: Options() class for runtime
"""
n_qubits = len(graph.nodes())
if ansatz_str == 'hea':
theta_list = ParameterVector('θ',2*n_qubits*layers)
ansatz = get_ansatz_hea(graph,theta_list)
ansatz_k2 = get_ansatz_hea_ZNE(graph,theta_list)
elif ansatz_str == 'hva':
theta_list = ParameterVector('θ',3*layers)
ansatz = get_ansatz_hva(graph,theta_list)
ansatz_k2 = get_ansatz_hva(graph,theta_list)
cost_operator = get_h_op(graph,hx=hx,ap=g) #Defining Hamiltonian
# Now we set the cost function, with no mitigation, linear or exp extrapolation
if zne == False:
def cost_function_vqe(theta):
job = estimator.run(ansatz, cost_operator, theta)
values = job.result().values[0]
return values
if zne == True:
def cost_function_vqe(theta):
job = estimator.run([ansatz,ansatz_k2], 2*[cost_operator], 2*[theta])
value_k1 = job.result().values[0]
value_k2 = job.result().values[1]
return get_extrapolation(value_k1=value_k1,value_k2=value_k2,extrap=extrap)
log_list = []
nfev_list = []
with Session(service=service,backend=backend) as session:
# estimator = BackendEstimator(FakeNairobiV2(),options={'shots':shots})
estimator = get_estimator(server=server,
shots=shots,
device=device,
session=session,
options_rtm=options)
for i in tqdm(range(reps)):
log = VQELog([], [])
spsa = SPSA(maxiter=maxiter,
trust_region=True,
learning_rate=learning_rate,
perturbation=perturbation,
callback=log.update)
random_point = np.random.random(ansatz.num_parameters)
result_sample = spsa.minimize(cost_function_vqe,x0=random_point)
log_list.append(log)
nfev_list.append(result_sample.nfev)
session.close()
max_length = max(len(sublist.values) for sublist in log_list) # Finding the length of the largest list
for sublist in log_list:
if len(sublist.values) < max_length:
last_element = sublist[-1] # Extracting the last element
sublist = list(sublist)[:].extend([last_element] * (max_length - len(sublist))) # Filling with the last element
mean_list = []
std_list = []
for i in range(len(log_list[0].values)):
values_list = [log.values[i] for log in log_list]
mean_list.append(np.mean(values_list))
std_list.append(np.std(values_list))
return log_list,mean_list,std_list,nfev_list
logs_hea_noisy_mag,avgs_hea_noisy_mag,stds_hea_noisy_mag,nfevs_hea_noisy_mag = vqe_critical_spsa(graph=graph,
service=service,
backend=backend,
device=FakeKolkata(),
g=g_mag,
server='noisy',
layers=1,
maxiter=170,
ansatz_str='hea',
reps=5,
zne=False,
shots = shots
)
avgs_list = avgs_hea_noisy_mag
stds_list = stds_hea_noisy_mag
g_value = g_mag
exact_energy = E_mag
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization noisy g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -3, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
reps = 3
logs_hea_zne_mag,avgs_hea_zne_mag,stds_hea_zne_mag,nfevs_hea_zne_mag = vqe_critical_spsa(graph=graph,
service=service,
backend=backend,
device=FakeKolkata(),
g=g_mag,
server='noisy',
layers=1,
maxiter=170,
ansatz_str='hea',
reps=reps,
zne=True,
extrap='exp',
shots=shots
)
avgs_list = avgs_hea_zne_mag
stds_list = stds_hea_zne_mag
g_value = g_mag
exact_energy = E_mag
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
x_lim = 60
# plt.xlim(0,60)
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization mitigated g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -3, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
logs_hea_noisy_knk,avgs_hea_noisy_knk,stds_hea_noisy_knk,nfevs_hea_noisy_knk = vqe_critical_spsa(graph=graph,
service=service,
backend=backend,
device=FakeKolkata(),
g=g_knk,
server='noisy',
layers=1,
maxiter=170,
ansatz_str='hea',
reps=reps,
zne=False,
shots=shots
)
avgs_list = avgs_hea_noisy_knk
stds_list = stds_hea_noisy_knk
g_value = g_knk
exact_energy = E_knk
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
x_lim = 60
# plt.xlim(0,60)
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization noisy g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -3, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
reps = 3
logs_hea_zne_knk,avgs_hea_zne_knk,stds_hea_zne_knk,nfevs_hea_zne_knk = vqe_critical_spsa(graph=graph,
service=service,
backend=backend,
device=FakeKolkata(),
g=g_knk,
server='noisy',
layers=1,
maxiter=170,
ansatz_str='hea',
reps=reps,
zne=True,
extrap='exp',
shots=shots
)
avgs_list = avgs_hea_zne_knk
stds_list = stds_hea_zne_knk
g_value = g_knk
exact_energy = E_knk
#Plots
x_values = np.arange(len(avgs_list))
f, ax = plt.subplots()
plt.plot(avgs_list)
# Calculating upper and lower bounds for the confidence interval
upper_bound = np.array(avgs_list) + 3 * np.array(stds_list) # 3 sigmas
lower_bound = np.array(avgs_list) - 3 * np.array(stds_list) # 3 sigmas
plt.fill_between(x_values, lower_bound, upper_bound, color='skyblue', alpha=0.4)
plt.axhline(y=exact_energy, color="tab:red", ls="--", label="exact")
# plt.xlim(0,60)
plt.xlabel("iteration")
plt.ylabel("cost function")
plt.title(f"VQE optimization mitigated g = {np.round(g_value,3)} {reps} samplings")
inset_ax = f.add_axes([0.6,0.6,0.25,0.25]) # [left, bottom, width, height]
inset_ax.plot([(exact_energy-avg)/exact_energy for avg in avgs_list])
inset_ax.set_yscale('log')
y_ticks = [10**i for i in range(-0, -3, -1)] # Change the range to suit your needs
inset_ax.set_yticks(y_ticks)
inset_ax.set_xlabel("iteration")
inset_ax.set_ylabel("relative error")
plt.show()
def vqe_phase_diagram(graph,
g_values,
optimizer,
init_optimizer,
service,
backend,
server='qasm',
device=FakeNairobi(),
angles_dict = {},
layers=1,
hx=0.5,
options=Options(),
zne=False,
extrap='exp',
init_reps=1,
shots=2**14,
ansatz_str='hea'):
"""Runs the vqe to simulate the antiparallel model in
the hardware efficient ansatz for different values of
the antiparallel field. Returns the list of energies as
well as a dictionary with the optimal angles for each
value of the boundary field.
Args:
graph: networkx lattice graph
g_values: list of values for the boundary field
angles_dict: dictionary of angles
optimizer: qiskit optimizer class
init_optimizer: optimizer for the first point
layers: layers for the ansatz
service: service for runtime
backend: backend for runtime (can include quantum backends)
h: value of the transverse field
ansatz_str: choice of ansatz, 'hea' for HEA and 'hva' for HVA
reps: number of initial parameters samplings for the first point
zne: (bool) zne option
extrap: type of extrapolation
shots: number of shots, set to None for statevector simulations
server: 'qasm' for noiseless, 'noisy' for aer, 'rtm' for runtime
device: noise model for noisy simulations
options: Options() class for runtime
"""
n_qubits = len(graph.nodes())
if ansatz_str == 'hea':
theta_list = ParameterVector('θ',2*n_qubits*layers)
ansatz = get_ansatz_hea(graph,theta_list)
ansatz_k2 = get_ansatz_hea_ZNE(graph,theta_list)
elif ansatz_str == 'hva':
theta_list = ParameterVector('θ',3*layers)
ansatz = get_ansatz_hva(graph,theta_list)
ansatz_k2 = get_ansatz_hva(graph,theta_list)
E_values = []
rev_g_values = g_values[::-1]
for i,g in enumerate(tqdm(rev_g_values)):
cost_operator = get_h_op(graph,hx=hx,ap=g) #Defining Hamiltonian
# Now we set the cost function, with no mitigation, linear or exp extrapolation
if zne == False:
def cost_function_vqe(theta):
job = estimator.run(ansatz, cost_operator, theta)
values = job.result().values[0]
return values
if zne == True:
def cost_function_vqe(theta):
job = estimator.run([ansatz,ansatz_k2], 2*[cost_operator], 2*[theta])
value_k1 = job.result().values[0]
value_k2 = job.result().values[1]
return get_extrapolation(value_k1=value_k1,value_k2=value_k2,extrap=extrap)
if i == 0:
sample = 0.
for j in range(init_reps): #Performs sampling of initial parameters for the first point
initial_point = np.random.uniform(0., 2*np.pi, size=ansatz.num_parameters)
with Session(service=service,backend=backend) as session:
estimator = get_estimator(server=server,
shots=shots,
device=device,
session=session,
options_rtm=options)
result_sample = init_optimizer.minimize(fun=cost_function_vqe,
x0=initial_point)
session.close()
if result_sample.fun < sample:
sample = result_sample.fun
result = result_sample
initial_point = result.x
else:
with Session(service=service,backend=backend) as session:
estimator = get_estimator(server=server,
shots=shots,
device=device,
session=session,
options_rtm=options)
result = optimizer.minimize(fun=cost_function_vqe,
x0=initial_point)
session.close()
E_values.append(result.fun)
#optimal angles storage
angles = list(result.x)
angles_dict[str(round(g,5))] = angles
return E_values,angles_dict
def vqe_optimal(graph,
service,
backend,
angles_opt,
server='qasm',
device=FakeNairobi(),
layers=1,
hx=0.5,
options=Options(),
zne=False,
extrap='lin',
shots=2**14,
ansatz_str='hea'):
""" Receives the optimal parameters for each value of
the boundary field and runs the circuits to compute the
energy as well as the number of kinks
Args:
graph: networkx lattice graph
g_values: list of values for the boundary field
angles_opt: dictionary of optimal angles
service: service for runtime
backend: backend for runtime (can include quantum backends)
h: value of the transverse field
ansatz_str: choice of ansatz, 'hea' for HEA and 'hva' for HVA
layers: layers for the ansatz
reps: number of initial parameters samplings for the first point
zne: (bool) zne option
extrap: type of extrapolation
shots: number of shots, set to None for statevector simulations
server: 'qasm' for noiseless, 'noisy' for aer, 'rtm' for runtime
device: noise model for noisy simulations
options: Options() class for runtime
Returns:
The values of the energy, number of kinks, and the associated values
of g to facilitate plotting
"""
n_qubits = len(graph.nodes())
g_values = [float(k) for k in angles_opt.keys()]
n_points = len(g_values)
# Setting the ansatz
if ansatz_str == 'hea':
theta_list = ParameterVector('θ',2*n_qubits*layers)
ansatz = get_ansatz_hea(graph,theta_list)
ansatz_k2 = get_ansatz_hea_ZNE(graph,theta_list)
elif ansatz_str == 'hva':
theta_list = ParameterVector('θ',3*layers)
ansatz = get_ansatz_hva(graph,theta_list)
ansatz_k2 = get_ansatz_hva(graph,theta_list)
# Getting the list of angles and hamiltonians
angles_list = []
h_list = []
g_list = []
kk_op = get_kk_op(graph)
E_values = []
kk_values = []
for g_str,angles in angles_opt.items():
g = float(g_str)
g_list.append(g)
h_list.append(get_h_op(graph,hx=hx,ap=g))
angles_list.append(angles)
with Session(service=service,backend=backend) as session:
estimator = get_estimator(server=server,
shots=shots,
device=device,
session=session,
options_rtm=options)
result_h = estimator.run(n_points*[ansatz],h_list,angles_list).result()
result_kk = estimator.run(n_points*[ansatz],n_points*[kk_op],angles_list).result()
if zne == False:
E_values = list(result_h.values)
kk_values = list(result_kk.values)
else:
result_h_k2 = estimator.run(n_points*[ansatz_k2],h_list,angles_list).result()
result_kk_k2 = estimator.run(n_points*[ansatz_k2],n_points*[kk_op],angles_list).result()
for i in range(n_points):
E_values.append(get_extrapolation(result_h.values[i],result_h_k2.values[i],extrap))
kk_values.append(get_extrapolation(result_kk.values[i],result_kk_k2.values[i],extrap))
session.close()
return E_values,kk_values,g_list
# We define the range of values of g used for the VQE implentation
g_values = np.linspace(g_i,g_f,25)
init_reps = 5
slsqp = SLSQP(150)
init_slsqp = SLSQP(150) # We consider more iterations for the first point
E_hva,angles_hva = vqe_phase_diagram(graph=graph,
g_values=g_values,
ansatz_str='hva',
backend=backend,
layers=layers_hva,
optimizer=slsqp,
init_optimizer=init_slsqp,
service=service,
server='qasm',
shots=None,
init_reps=init_reps)
# Now we run the circuits one last time with the optimal parameters
E_hva,kk_hva,g_hva = vqe_optimal(graph=graph,
service=service,
server='qasm',
angles_opt=angles_hva,
ansatz_str='hva',
layers=layers_hva,
backend=backend)
#Plotting
f,ax = plt.subplots()
#plt.plot(g_values,E_3,'ro')
plt.plot(exact_g_values,exact_E,label='exact')
plt.plot(g_hva,E_hva,'ro',label='VQE')
plt.xlabel('boundary field')
plt.ylabel('groundstate energy')
plt.legend()
inset_ax = f.add_axes([0.24, 0.22, 0.3, 0.3]) # [left, bottom, width, height]
plt.plot(exact_g_values,exact_kk)
plt.plot(g_hva,kk_hva,'ro',markersize=4)
inset_ax.set_xlabel('boundary field')
inset_ax.set_ylabel("$<N_k>$")
plt.show()
init_reps = 2
spsa = SPSA(maxiter=300,trust_region=True,learning_rate=0.07,perturbation=0.1)
init_spsa = SPSA(maxiter=300,trust_region=True,learning_rate=0.07,perturbation=0.1) # We consider more iterations for the first point
# To perform the whole optimization using ZNE, just set zne = True
# This step took 207 minutes to run on my machine
E_hea_noisy,angles_hea_noisy = vqe_phase_diagram(graph=graph,
g_values=g_values,
ansatz_str='hea',
backend=backend,
layers=layers_hea,
optimizer=spsa,
init_optimizer=init_spsa,
service=service,
server='noisy',
device=FakeKolkata(),
zne=False,
shots=shots,
init_reps=init_reps)
# Now we run the circuits one last time with the optimal parameters
E_opt_hea_noisy,kk_opt_hea_noisy,g_hea = vqe_optimal(graph=graph,
service=service,
server='noisy',
angles_opt=angles_hea_noisy,
device=FakeKolkata(),
ansatz_str='hea',
layers=layers_hea,
zne=False,
backend=backend,
shots=shots)
#Plotting
f,ax = plt.subplots()
#plt.plot(g_values,E_3,'ro')
plt.plot(exact_g_values,exact_E,label='exact')
plt.plot(g_hea,E_opt_hea_noisy,'o',label='noisy')
plt.xlabel('boundary field')
plt.ylabel('groundstate energy')
plt.legend()
inset_ax = f.add_axes([0.24, 0.22, 0.3, 0.3]) # [left, bottom, width, height]
plt.plot(exact_g_values,exact_kk)
plt.plot(g_hea,kk_opt_hea_noisy,'o',markersize=4)
inset_ax.set_xlabel('boundary field')
inset_ax.set_ylabel("$<N_k>$")
plt.show()
# Now we run the circuits now using ZNE
E_opt_hea_mitigated,kk_opt_hea_mitigated,g_hea = vqe_optimal(graph=graph,
service=service,
server='noisy',
angles_opt=angles_hea_noisy,
device=FakeKolkata(),
ansatz_str='hea',
layers=layers_hea,
zne=True,
extrap='exp',
backend=backend,
shots=shots)
#Plotting
f,ax = plt.subplots()
#plt.plot(g_values,E_3,'ro')
plt.plot(exact_g_values,exact_E,label='exact')
plt.plot(g_hea,E_opt_hea_noisy,'o',label='noisy')
plt.plot(g_hea,E_opt_hea_mitigated,'o',label='mitigated')
plt.xlabel('boundary field')
plt.ylabel('groundstate energy')
plt.legend()
inset_ax = f.add_axes([0.24, 0.22, 0.3, 0.3]) # [left, bottom, width, height]
plt.plot(exact_g_values,exact_kk)
plt.plot(g_hea,kk_opt_hea_noisy,'o',markersize=4)
plt.plot(g_hea,kk_opt_hea_mitigated,'o',markersize=4)
inset_ax.set_xlabel('boundary field')
inset_ax.set_ylabel("$<N_k>$")
plt.show()
# First we get the optimal parameters with statevector simulations
E_hea_noiseless,angles_hea_noiseless = vqe_phase_diagram(graph=graph,
g_values=g_values,
ansatz_str='hea',
backend=backend,
layers=layers_hea,
optimizer=spsa,
init_optimizer=init_spsa,
service=service,
server='qasm',
shots=None,
init_reps=init_reps)
# Setting options for runtime
# Noisy options
fake_device = FakeKolkata()
noise_model = NoiseModel.from_backend(fake_device)
options_noisy = Options()
options_noisy.execution.shots = shots
options_noisy.simulator = {
"noise_model": noise_model,
"basis_gates": fake_device.configuration().basis_gates,
"coupling_map": fake_device.configuration().coupling_map,
"seed_simulator": 42
}
options_noisy.optimization_level = 3 # no optimization
options_noisy.resilience_level = 0 # M3 for Sampler and T-REx for Estimator
# Mitigated options
options_mitigated = Options()
options_mitigated.execution.shots = shots
options_mitigated.simulator = {
"noise_model": noise_model,
"basis_gates": fake_device.configuration().basis_gates,
"coupling_map": fake_device.configuration().coupling_map
}
# Set number of shots, optimization_level and resilience_level
options_mitigated.optimization_level = 3
options_mitigated.resilience_level = 1 # setting T-REX
# Now we run the circuits in runtime with the optimal parameters
# To run on runtime we set server = 'rtm'
# First we run the unmitigated results
E_opt_hea_noisy_rtm,kk_opt_hea_noisy_rtm,g_hea = vqe_optimal(graph=graph,
service=service,
server='rtm',
options = options_noisy,
angles_opt=angles_hea_noiseless,
ansatz_str='hea',
layers=layers_hea,
zne=False,
extrap='exp',
backend=backend,
shots=shots)
# Now we run using ZNE and ZNE+T-REX
# ZNE
E_opt_hea_mitigated1_rtm,kk_opt_hea_mitigated1_rtm,g_hea = vqe_optimal(graph=graph,
service=service,
server='rtm',
options = options_noisy,
angles_opt=angles_hea_noiseless,
ansatz_str='hea',
layers=layers_hea,
zne=True,
extrap='exp',
backend=backend,
shots=shots)
# ZNE + T-REX
E_opt_hea_mitigated2_rtm,kk_opt_hea_mitigated2_rtm,g_hea = vqe_optimal(graph=graph,
service=service,
server='rtm',
options = options_mitigated,
angles_opt=angles_hea_noiseless,
ansatz_str='hea',
layers=layers_hea,
zne=True,
extrap='exp',
backend=backend,
shots=shots)
#Plotting
f,ax = plt.subplots()
#plt.plot(g_values,E_3,'ro')
plt.plot(exact_g_values,exact_E,label='exact')
plt.plot(g_hea,E_opt_hea_noisy_rtm,'o',label='noisy')
plt.plot(g_hea,E_opt_hea_mitigated1_rtm,'o',label='ZNE')
plt.plot(g_hea,E_opt_hea_mitigated2_rtm,'o',label='ZNE+T-REX')
plt.xlabel('boundary field')
plt.ylabel('groundstate energy')
plt.legend()
inset_ax = f.add_axes([0.24, 0.22, 0.3, 0.3]) # [left, bottom, width, height]
plt.plot(exact_g_values,exact_kk)
plt.plot(g_hea,kk_opt_hea_noisy_rtm,'o',markersize=4)
plt.plot(g_hea,kk_opt_hea_mitigated1_rtm,'o',markersize=4)
plt.plot(g_hea,kk_opt_hea_mitigated2_rtm,'o',markersize=4)
inset_ax.set_xlabel('boundary field')
inset_ax.set_ylabel("$<N_k>$")
plt.show()
|
https://github.com/unif2/Quantum-Computing-Mentorship-Task-4-Code
|
unif2
|
import numpy as np
from numpy import kron
import qiskit as qk
def decomposition(H):
"""Decompose any 4x4 Hermitian matrix into a sum of tensor products of two Pauli matrices
"""
identity = np.array([[1, 0],[ 0, 1]], dtype=np.complex128)
x = np.array([[0, 1], [ 1, 0]], dtype=np.complex128)
y = np.array([[0, -1j],[1j, 0]], dtype=np.complex128)
z = np.array([[1, 0], [0, -1]], dtype=np.complex128)
S = [identity, x, y, z]
labels = ['I', 'sigma_x', 'sigma_y', 'sigma_z']
d = {'00': 'I product I', '01': 'I product sigma_x', '02': 'I product sigma_y', '03': 'I product sigma_z',
'10': 'sigma_x product I', '11': 'sigma_x product sigma_x', '12': 'sigma_x product sigma_y',
'13': 'sigma_x product sigma_z', '20': 'sigma_y product I', '21': 'sigma_y product sigma_x',
'22': 'sigma_y product sigma_y', '23': 'sigma_y product sigma_z', '30': 'sigma_z product I',
'31': 'sigma_z product sigma_x', '32': 'sigma_z product sigma_y', '33': 'sigma_z product sigma_z'}
for i in range(4):
for j in range(4):
a_ij = 0.25 * np.dot(kron(S[i], S[j]), H).trace()
if a_ij != 0.0:
print(str(a_ij) + ' * ' + d[str(i)+str(j)])
H = np.array([[0,0,0,0],[0,-1,1,0],[0,1,-1,0],[0,0,0,0]])
decomposition(H)
def prepare_state(theta, n=3):
"""
Prepare three 2-qubit states with 3 associated quantum registers, 3 associated classical registers,
and 3 quantum circuits. We will prepare the state with the ansatz mentioned in the notes in which we act on
the first qubit with the Hadamard operator, then with the R_z operator, then we act on the 2-qubit state
with the CNOT gate, and then on the second qubit in each terms of the superposition with the sigma_x operator.
After that, we will take the first circuit and act on each qubit with the R_y(pi/2) operator, and take the second
circuit and act on each qubit with the R_x(-pi/2) operator as explained in the notes. We do this so that those
qubits will be in the basis of eigenvectors of sigma_x and sigma_y as explained in the notes. We can measure
the qubits in the other circuit as-is because we need the expectation value of sigma_z and the qubits are already
in the computational basis.
"""
qr0 = qk.QuantumRegister(2)
cr0 = qk.ClassicalRegister(2)
qc0 = qk.QuantumCircuit(qr0,cr0)
qr1 = qk.QuantumRegister(2)
cr1 = qk.ClassicalRegister(2)
qc1 = qk.QuantumCircuit(qr1,cr1)
qr2 = qk.QuantumRegister(2)
cr2 = qk.ClassicalRegister(2)
qc2 = qk.QuantumCircuit(qr2,cr2)
qregisters = [qr0,qr1,qr2]
cregisters = [cr0,cr1,cr2]
qcircuits = [qc0,qc1,qc2]
for i in range(n):
qcircuits[i].h(qregisters[i][0])
for i in range(n):
qcircuits[i].rz(theta, qregisters[i][0])
for i in range(n):
qcircuits[i].cx(qregisters[i][0], qregisters[i][1])
for i in range(n):
qcircuits[i].x(qregisters[i][1])
qcircuits[0].ry((np.pi)/2, qregisters[0][0])
qcircuits[0].ry((np.pi)/2, qregisters[0][1])
qcircuits[1].rx(-(np.pi)/2, qregisters[1][0])
qcircuits[1].rx(-(np.pi)/2, qregisters[1][1])
return qregisters, cregisters, qcircuits
qregisters, cregisters, qcircuits = prepare_state(np.pi, n=3)
qcircuits[0].draw(output='mpl')
qcircuits[1].draw(output='mpl')
qcircuits[2].draw(output='mpl')
def expectation(qcircuits, cregisters, qregisters, n_shots, n=3):
"""
For each circuit, execute and measure it using the classical simulator 5000 times as explained above. Multiply
each of the three expectation values by 0.5, add them up, and subtract -0.5. Return the result.
"""
expect = -0.5
for i in range(n):
qcircuits[i].measure(qregisters[i],cregisters[i])
qk.Aer.backends()
sim = qk.Aer.get_backend('qasm_simulator')
res = qk.execute(qcircuits[i], sim, shots=n_shots).result()
counts = res.get_counts()
sum = 0
for k,v in counts.items():
if k=='01' or k=='10':
sum += (-1)*v/n_shots
elif k=='00' or k=='11':
sum += v/n_shots
sum = 0.5*sum
expect += sum
return expect
# Consider 100 values of theta, between 0 and Pi. This theta is the one used in state preparation.
thetas = np.linspace(0, np.pi, 100)
# For each theta, store the resulting expectation value in results
results = []
# For each theta, find the expectation value
for theta in thetas:
qregisters, cregisters, qcircuits = prepare_state(theta, n=3)
expect = expectation(qcircuits, cregisters, qregisters, 5000, n=3)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
from qiskit import IBMQ
#IBMQ.delete_account()
IBMQ.save_account('my IBM token', overwrite=True)
IBMQ.load_account()
provider = IBMQ.get_provider()
procs=provider.backends(operational=True, simulator=False)
from qiskit.tools.jupyter import *
%qiskit_backend_overview
from qiskit.tools import monitor
backend = qk.providers.ibmq.least_busy([p for p in procs if len(p.properties().qubits) >= 2])
from qiskit.tools.monitor import backend_overview, backend_monitor
backend_monitor(backend)
def q_expectation(qcircuits, cregisters, qregisters, n_shots, n=3):
"""
For each circuit, execute and measure it using the classical simulator 5000 times as explained above. Multiply
each of the three expectation values by 0.5, add them up, and subtract -0.5. Return the result.
"""
expect = -0.5
for i in range(n):
qcircuits[i].measure(qregisters[i],cregisters[i])
qk.Aer.backends()
sim = qk.Aer.get_backend('qasm_simulator')
res = qk.execute(qcircuits[i], backend=backend, shots=n_shots).result()
#mon = monitor.job_monitor(res)
counts = res.get_counts()
sum = 0
for k,v in counts.items():
if k=='01' or k=='10':
sum += (-1)*v/n_shots
elif k=='00' or k=='11':
sum += v/n_shots
sum = 0.5*sum
expect += sum
return expect
# Consider 10 values of theta, between 0 and Pi. This theta is the one used in state preparation.
thetas = np.linspace(0, np.pi, 10)
# Use n_shots = 100
results = []
# For each theta, find the expectation value
for theta in thetas:
qregisters, cregisters, qcircuits = prepare_state(theta, n=3)
expect = q_expectation(qcircuits, cregisters, qregisters, 100, n=3)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
# Use n_shots = 1000
results = []
# For each theta, find the expectation value
for theta in thetas:
qregisters, cregisters, qcircuits = prepare_state(theta, n=3)
expect = q_expectation(qcircuits, cregisters, qregisters, 1000, n=3)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
# Use n_shots = 5000
results = []
# For each theta, find the expectation value
for theta in thetas:
qregisters, cregisters, qcircuits = prepare_state(theta, n=3)
expect = q_expectation(qcircuits, cregisters, qregisters, 5000, n=3)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
# Use n_shots = 8192 = max allowed
results = []
thetas = [np.pi]
# For each theta, find the expectation value
for theta in thetas:
qregisters, cregisters, qcircuits = prepare_state(theta, n=3)
expect = q_expectation(qcircuits, cregisters, qregisters, 8192, n=3)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
def decomposition(H):
"""Decompose any 4x4 Hermitian matrix into a sum of tensor products of two Pauli matrices
"""
A_ij = []
identity = np.array([[1, 0],[ 0, 1]], dtype=np.complex128)
x = np.array([[0, 1], [ 1, 0]], dtype=np.complex128)
y = np.array([[0, -1j],[1j, 0]], dtype=np.complex128)
z = np.array([[1, 0], [0, -1]], dtype=np.complex128)
S = [identity, x, y, z]
labels = ['I', 'sigma_x', 'sigma_y', 'sigma_z']
d = {'00': 'I product I', '01': 'I product sigma_x', '02': 'I product sigma_y', '03': 'I product sigma_z',
'10': 'sigma_x product I', '11': 'sigma_x product sigma_x', '12': 'sigma_x product sigma_y', '13': 'sigma_x product sigma_z',
'20': 'sigma_y product I', '21': 'sigma_y product sigma_x', '22': 'sigma_y product sigma_y', '23': 'sigma_y product sigma_z',
'30': 'sigma_z product I', '31': 'sigma_z product sigma_x', '32': 'sigma_z product sigma_y', '33': 'sigma_z product sigma_z'}
for i in range(4):
for j in range(4):
a_ij = 0.25 * np.dot(kron(S[i], S[j]), H).trace()
A_ij.append(a_ij)
if a_ij != 0.0:
print(str(a_ij) + ' * ' + d[str(i)+str(j)])
return np.asarray(A_ij).reshape(4,4)
def prepare_state2(A, theta):
qregisters = []
cregisters = []
qcircuits = []
identity = np.array([[1, 0],[ 0, 1]], dtype=np.complex128)
x = np.array([[0, 1], [ 1, 0]], dtype=np.complex128)
y = np.array([[0, -1j],[1j, 0]], dtype=np.complex128)
z = np.array([[1, 0], [0, -1]], dtype=np.complex128)
d = {}
for i in range(4):
for j in range(4):
if A[i,j] != 0:
if i !=0 and j!=0:
qr = qk.QuantumRegister(2)
cr = qk.ClassicalRegister(2)
qc = qk.QuantumCircuit(qr,cr)
qc.h(qr[0])
qc.rz(theta, qr[0])
qc.cx(qr[0], qr[1])
qc.x(qr[1])
if i==1:
qc.ry((np.pi)/2, qr[0])
if i==2:
qc.rx(-(np.pi)/2, qr[0])
if j==1:
qc.ry((np.pi)/2, qr[1])
if j==2:
qc.rx(-(np.pi)/2, qr[1])
qregisters.append(qr)
cregisters.append(cr)
qcircuits.append(qc)
d[(i,j)] = [qregisters, cregisters, qcircuits]
if i == 0 and j != 0:
qr = qk.QuantumRegister(2)
cr = qk.ClassicalRegister(2)
qc = qk.QuantumCircuit(qr,cr)
qc.h(qr[0])
qc.rz(theta, qr[0])
qc.cx(qr[0], qr[1])
qc.x(qr[1])
if j==1:
qc.ry((np.pi)/2, qr[1])
if j==2:
qc.rx(-(np.pi)/2, qr[1])
qregisters.append(qr)
cregisters.append(cr)
qcircuits.append(qc)
d[(i,j)] = [qregisters, cregisters, qcircuits]
if i != 0 and j == 0:
qr = qk.QuantumRegister(2)
cr = qk.ClassicalRegister(2)
qc = qk.QuantumCircuit(qr,cr)
qc.h(qr[0])
qc.rz(theta, qr[0])
qc.cx(qr[0], qr[1])
qc.x(qr[1])
if i==1:
qc.ry((np.pi)/2, qr[0])
if i==2:
qc.rx(-(np.pi)/2, qr[0])
qregisters.append(qr)
cregisters.append(cr)
qcircuits.append(qc)
d[(i,j)] = [qregisters, cregisters, qcircuits]
return d, A
def expectation2(d, A, n_shots):
"""
For each circuit, execute and measure it using the classical simulator 5000 times as explained above.
Return the result.
"""
expect = A[0,0]
qk.Aer.backends()
sim = qk.Aer.get_backend('qasm_simulator')
for k,v in d.items():
for i in range(len(v[2])):
v[2][i].measure(v[0][i],v[1][i])
res = qk.execute(v[2][i], sim, shots=n_shots).result()
counts = res.get_counts()
sum = 0
for m,n in counts.items():
if m=='01' or m=='10':
sum += (-1)*n/n_shots
elif m=='00' or m=='11':
sum += n/n_shots
sum = A[k[0],k[1]]*sum
expect += sum
return expect
thetas = np.linspace(0, np.pi, 100)
H = np.array([[0,0,0,0],[0,-1,1,0],[0,1,-1,0],[0,0,0,0]])
A = decomposition(H)
# For each theta, store the resulting expectation value in results
results = []
# For each theta, find the expectation value
for theta in thetas:
d, A = prepare_state2(A, theta)
expect = expectation2(d, A, 5000)
results.append(expect)
# Sort the results in ascending order. The first one is your minimum eigenvalue.
results.sort()
print("The minimum eigenvalue is: {}.".format(results[0]))
# -5??!! Maybe I missed something in my logic. Will continue to look into this. :-)
|
https://github.com/khaledalam/QuantumComputingAndPrimesAndOthers
|
khaledalam
|
# Author: Khaled Alam(khaledalam.net@gmail.com)
'''
Guess binary string (secret) of length N in 1 shot only using quantum computing circuit!
~ by using clasical computers we need at least N shots to guess string (secret) of length N
~ by using quantum computer we need 1 shot to guess string (secret) of ANY length ( cool isn't it! ^^ )
'''
secret = '01000001' # `01000001` = `A`
from qiskit import *
n = len(secret)
qCircuit = QuantumCircuit(n+1, n) # n+1 qubits and n classical bits
qCircuit.x(n)
qCircuit.barrier()
qCircuit.h(range(n+1))
qCircuit.barrier()
for ii, OZ in enumerate(reversed(secret)):
if OZ == '1':
qCircuit.cx(ii, n)
qCircuit.barrier()
qCircuit.h(range(n+1))
qCircuit.barrier()
qCircuit.measure(range(n), range(n))
%matplotlib inline
qCircuit.draw(output='mpl')
# run on simulator
simulator = Aer.get_backend('qasm_simulator')
result = execute(qCircuit, backend=simulator, shots=1).result() # only 1 shot
from qiskit.visualization import plot_histogram
plot_histogram(
result.get_counts(qCircuit)
)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
secret_number = '101001'
# here work is happen like buttom to up
for position,value in enumerate(reversed(secret_number)):
if value == '1':
print(position, value)
circuit = QuantumCircuit(6+1, 6)
circuit.h([0,1,2,3,4,5])
circuit.x(6)
circuit.h(6)
circuit.barrier()
circuit.draw(output='mpl')
circuit.cx(5, 6)
circuit.cx(3, 6)
circuit.cx(0, 6)
circuit.barrier()
circuit.draw(output='mpl')
circuit.h([0,1,2,3,4,5])
circuit.draw(output='mpl')
circuit.barrier()
circuit.measure([i for i in range(5)],[i for i in range(5)])
circuit.barrier()
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, backend=simulator, shots=1)
result = job.result()
counts = result.get_counts()
print(counts)
circuit = QuantumCircuit(len(secret_number)+1, len(secret_number))
circuit.h(range(len(secret_number)))
circuit.x(len(secret_number))
circuit.h(len(secret_number))
circuit.barrier()
for position,value in enumerate(reversed(secret_number)):
if value == '1':
circuit.cx(position, len(secret_number))
circuit.barrier()
circuit.h(range(len(secret_number)))
circuit.barrier()
circuit.measure(range(len(secret_number)), range(len(secret_number)))
circuit.barrier()
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, backend=simulator, shots=1)
result = job.result()
counts = result.get_counts()
print(counts)
def find_secret_number(secter_number):
secret_number = str(secter_number)
# Using Bernstein Vazirani Algorithm
circuit = QuantumCircuit(len(secret_number)+1, len(secret_number))
circuit.h(range(len(secret_number)))
circuit.x(len(secret_number))
circuit.h(len(secret_number))
circuit.barrier()
for position,value in enumerate(reversed(secret_number)):
if value == '1':
circuit.cx(position, len(secret_number))
circuit.barrier()
circuit.h(range(len(secret_number)))
circuit.barrier()
circuit.measure(range(len(secret_number)), range(len(secret_number)))
circuit.barrier()
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, backend=simulator, shots=1)
result = job.result()
counts = result.get_counts()
print(counts)
secret_number = int(input("enter number(digits should be 0 or 1): "))
find_secret_number(secret_number)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
from ibm_quantum_widgets import draw_circuit
# initialize two qubits in the zero state and
# two classical bits in the zero state in the quantum circuit
circuit = QuantumCircuit(3,3)
# C gate
# (2) => q2
circuit.x(2)
circuit.draw(output='mpl')
draw_circuit(circuit)
# Hadamard (H) gate
# (0) => (q0)
circuit.h(0)
circuit.draw(output='mpl')
draw_circuit(circuit)
# A controlled-NOT (CX NOT) gate, on control qubit 0
# and target qubit 1, putting the qubits in an entangled state.
# (2,1) = > q2(control bit)(quantum bit)(origin) --> q1(target bit)(quantum bit)(destination)
circuit.cx(2,1)
# (0,2) = > q0(control bit)(quantum bit)(origin) --> q2(target bit)(quantum bit)(destination)
circuit.cx(0,2)
circuit.draw(output='mpl')
draw_circuit(circuit)
# measurement between quantum state and classical state
# [1,1] => [q1,q1](quantum bit) and [2,0] => [c2,c0](classical bit)
circuit.measure([1,1],[2,0])
circuit.draw(output='mpl')
draw_circuit(circuit)
# The n qubit’s measurement result will be stored in the n classical bit
circuit.measure([1,1,2],[2,0,0])
circuit.draw(output='mpl')
draw_circuit(circuit)
simulator = Aer.get_backend("qasm_simulator")
job = execute(circuit, simulator, shots=2024)
result = job.result()
counts = result.get_counts(circuit)
print("Total count for 100 and 101 are: ", counts)
# 1.
plot_histogram(counts)
# 2.
from ibm_quantum_widgets import draw_circuit
draw_circuit(circuit)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
from ibm_quantum_widgets import draw_circuit
circuit = QuantumCircuit(2,2)
circuit
circuit.draw(output='mpl')
circuit.x(0)
circuit.draw(output='mpl')
circuit.h(0)
circuit.draw(output='mpl')
circuit.cx(0,1)
circuit.draw(output='mpl')
circuit.measure([0,1],[1,1])
circuit.draw(output='mpl')
draw_circuit(circuit)
simulator = Aer.get_backend('qasm_simulator')
simulator
job = execute(circuit, backend=simulator, shots=1024)
job
result = job.result()
result
counts = result.get_counts()
counts
plot_histogram(counts)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
from qiskit import *
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
circuit = QuantumCircuit(qr, cr)
%matplotlib inline
circuit.draw(output='mpl')
circuit.h(qr[0])
circuit.draw(output = 'mpl')
circuit.cx(qr[0], qr[1])
circuit.draw(output='mpl')
circuit.measure(qr, cr)
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
execute(circuit, backend=simulator)
result = execute(circuit, backend=simulator).result()
from qiskit.tools.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
from qiskit import IBMQ
MY_API_TOKEN = "b32678329f7f6dd426b8cf18f20bea23c2cd056b0bee2b4bcf49744b612e598f20f7170a8da4bfd99b009b6fa59d596edea7a6926fd388be158843d8e******"
IBMQ.save_account(MY_API_TOKEN, overwrite=True)
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
provider.backends()
backend = provider.get_backend('ibmq_santiago')
job =execute(circuit, backend= backend)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
# plot_histogram
plot_histogram(result.get_counts(circuit))
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
# Quantum Computation
import qiskit
print(qiskit.__version__)
import qiskit.quantum_info as qi
from qiskit.circuit.library import FourierChecking
from qiskit.visualization import plot_histogram
f = [1, -1, -1, -1]
g = [1, 1, -1, -1]
# How co-related fourier transform of function g to function f.
# we will check for probability '00', if p(f,g) >= 0.05, then,
# fourier transform of function g co-related to function f.
circ = FourierChecking(f=f,g=g)
circ.draw()
zero = qi.Statevector.from_label('00') # '00' or '01' or '10' or '11'
sv = zero.evolve(circ)
probs = sv.probabilities_dict()
plot_histogram(probs)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
from qiskit import *
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
circuit = QuantumCircuit(qr, cr)
%matplotlib inline
circuit.draw()
circuit.h(qr[0])
circuit.draw(output = 'mpl')
circuit.cx(qr[0], qr[1])
circuit.draw(output='mpl')
circuit.measure(qr, cr)
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
execute(circuit, backend=simulator)
result = execute(circuit, backend=simulator).result()
from qiskit.tools.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
# plot_histogram
provider = IBMQ.get_provider('ibm-q')
backend = provider.get_backend('ibmq_16_melbourne')
job =execute(circuit, backend= backend)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(circuit))
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
from qiskit import *
from qiskit.tools.visualization import plot_bloch_multivector
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('statevector_simulator')
result = execute(circuit, backend=simulator).result()
statevector = result.get_statevector()
print(statevector)
%matplotlib inline
circuit.draw(output='mpl')
# bloch sphere
plot_bloch_multivector(statevector)
# measurement
circuit.measure([0],[0])
backend = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=backend, shots=1024).result()
counts = result.get_counts()
from qiskit.tools.visualization import plot_histogram
plot_histogram(counts)
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('unitary_simulator')
result = execute(circuit, backend=simulator).result()
unitary = result.get_unitary()
print(unitary)
%matplotlib inline
circuit.draw(output='mpl')
# bloch sphere
plot_bloch_multivector(unitary)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
from qiskit.providers.aer import QasmSimulator
# use Aer's qasm_simulator
simulator = QasmSimulator()
# create quantum circute acting on the q register
circuit = QuantumCircuit(2,2)
# add a H gate on qubit 0
circuit.h(0)
# add a cx (CNOT) gate on control qubit 0 and target qubit 1
circuit.cx(0,1)
# map the quantum measurement to the classical bits
circuit.measure([0,1],[0,1])
# compile the circuit down to low-level QASM instructions
# supported by the backend (not needed for simple circuits)
compiled_circuit = transpile(circuit, simulator)
# execute the circuit on the qasm simulator
job = simulator.run(compiled_circuit, shots=1024)
# grad results from the job
result = job.result()
# return counts
counts = result.get_counts(compiled_circuit)
print('total count for 00 and 11 are: ',counts)
# draw circuit
circuit.draw(output='mpl')
# plot histogram
plot_histogram(counts)
from qiskit.circuit import QuantumCircuit, Parameter
from qiskit.providers.aer import AerSimulator
backend = AerSimulator()
circuit = QuantumCircuit(2)
theta = Parameter('theta')
circuit.rx(234, 0)
circuit.draw(output='mpl')
backend = AerSimulator()
circuit = QuantumCircuit(2)
# theta = Parameter('theta')
circuit.rx(20, 0)
circuit.x(0)
circuit.h(1)
result = execute(circuit, backend=backend, shots=1024).result()
# counts=result.get_counts()
# print(counts)
circuit.draw(output='mpl')
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
circuit = QuantumCircuit(3,3)
circuit
# qiskit.__dir__()
circuit.draw(output='mpl')
circuit.x(0)
circuit.barrier()
circuit.draw(output='mpl')
circuit.h(1)
circuit.cx(1,2)
circuit.draw(output='mpl')
circuit.barrier()
circuit.cx(0,1)
circuit.h(0)
circuit.draw(output='mpl')
circuit.barrier()
circuit.measure([0,1],[0,1])
circuit.draw(output='mpl')
circuit.barrier()
circuit.cx(1,2)
circuit.cx(0,2)
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, backend=simulator,shots=1024)
result = job.result()
counts=result.get_counts()
print(counts)
plot_histogram(counts)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
# import matplotlib.pyplot as plt
%matplotlib inline
print(qiskit.__version__)
circuit = QuantumCircuit(2,2)
circuit.h(0)
circuit.cx(0,1)
circuit.measure([0,1],[0,1])
# circuit.measure_all()
circuit.barrier()
# circuit.draw(output='mpl')
circuit.draw(output='mpl')
simulator = Aer.get_backend('aer_simulator')
result = execute(circuit, backend=simulator, shots=1024).result()
count = result.get_counts()
print(count)
from qiskit.tools.visualization import plot_histogram
plot_histogram(count)
from qiskit import IBMQ
IBMQ.save_account("b32678329f7f6dd426b8cf18f20bea23c2cd056b0bee2b4bcf49744b612e598f20f7170a8da4bfd99b009b6fa59d596edea7a6926fd388be158843d8ef******", overwrite=True)
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
provider.backends()
from qiskit.providers.ibmq import least_busy
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
print("least busy backend: ", backend)
job = execute(circuit, backend=backend, shots=1024)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
count = result.get_counts()
print(count)
from qiskit.tools.visualization import plot_histogram
plot_histogram(count)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
from qiskit import *
print(qiskit.__version__)
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
def find_secret_number(secter_number):
# Using Bernstein Vazirani Algorithm
secret_number = str(secter_number)
circuit = QuantumCircuit(len(secret_number)+1, len(secret_number))
circuit.h(range(len(secret_number)))
circuit.x(len(secret_number))
circuit.h(len(secret_number))
circuit.barrier()
for position,value in enumerate(reversed(secret_number)):
if value == '1':
circuit.cx(position, len(secret_number))
circuit.barrier()
circuit.h(range(len(secret_number)))
circuit.barrier()
circuit.measure(range(len(secret_number)), range(len(secret_number)))
circuit.barrier()
# circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
job = execute(circuit, backend=simulator, shots=1)
result = job.result()
counts = result.get_counts()
# print(counts)
return circuit, counts
secret_number = int(input("enter number: "))
circuit, number = find_secret_number(secret_number)
print('required number: ', number)
circuit.draw(output='mpl')
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
print(qiskit.__version__)
from qiskit.aqua.algorithms import Shor
from qiskit.aqua import QuantumInstance
import numpy as np
from qiskit import QuantumCircuit, Aer, execute
from qiskit.tools.visualization import plot_histogram
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend=backend, shots=1024)
my_shor = Shor(N=2189,a=4,quantum_instance=quantum_instance)
Shor.run(my_shor)
|
https://github.com/acfilok96/Quantum-Computation
|
acfilok96
|
import qiskit
print(qiskit.__version__)
from qiskit_machine_learning.datasets import ad_hoc_data
adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(training_size = 20, test_size = 5,
n = adhoc_dimension, gap=0.3,
plot_data =False, one_hot=False,
include_sample_total=True)
import numpy
print(numpy.array(adhoc_total).shape)
print("train data shape: ", train_features.shape,"\ttrain labels shape: ", train_labels.shape)
print("test data shape: ", test_features.shape,"\ttest labels shape: ", test_labels.shape)
print('train data:\n',train_features[:5])
print('\ntrain label:\n',train_labels[:5])
# plot_adhoc_dataset(train_features, train_labels, test_features, test_labels, adhoc_total)
from qiskit import Aer
from qiskit.utils import QuantumInstance
seed=20
quantum_instance = QuantumInstance(Aer.get_backend("qasm_simulator"), shots=1024,
seed_simulator=seed, seed_transpiler=seed)
from qiskit.circuit.library import ZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
z_feature_map = ZFeatureMap(feature_dimension=adhoc_dimension, reps=2)
z_kernel = QuantumKernel(feature_map = z_feature_map, quantum_instance=quantum_instance)
# z_feature_map.draw(output='mpl', scale=2)
z_feature_map.decompose().draw(output='mpl', scale=2)
from sklearn.svm import SVC
svc = SVC(kernel=z_kernel.evaluate)
svc.fit(train_features, train_labels)
score = svc.score(test_features, test_labels)
print('Callable kernel with ZFeatureMap classification test score: ', score)
prediction = svc.predict(test_features)
print(prediction)
from qiskit.circuit.library import ZZFeatureMap
zz_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement='linear')
zz_kernel = QuantumKernel(feature_map = zz_feature_map, quantum_instance=quantum_instance)
zz_feature_map.decompose().draw(output='mpl', scale=2)
from sklearn.svm import SVC
svc = SVC(kernel=zz_kernel.evaluate)
svc.fit(train_features, train_labels)
score = svc.score(test_features, test_labels)
print('Callable kernel with ZZFeatureMap classification test score: ', score)
prediction = svc.predict(test_features)
print(prediction)
from qiskit_machine_learning.algorithms import QSVC
qsvc = QSVC()
qsvc.quantum_kernel.quantum_instance = quantum_instance
qsvc.fit(train_features, train_labels)
score = qsvc.score(test_features, test_labels)
print('QSVC classification test score: ', score)
prediction = qsvc.predict(test_features)
print(prediction)
from qiskit.circuit.library import ZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
# here feature_dimension = 2 and reps = 1
adhoc_dimension = 2
z_feature_map = ZFeatureMap(feature_dimension=adhoc_dimension, reps=1)
z_kernel = QuantumKernel(feature_map = z_feature_map, quantum_instance=quantum_instance)
z_feature_map.decompose().draw(output='mpl', scale=2)
from qiskit.circuit.library import ZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
# here feature_dimension = 2 and reps = 2
adhoc_dimension = 2
z_feature_map = ZFeatureMap(feature_dimension=adhoc_dimension, reps=2)
z_kernel = QuantumKernel(feature_map = z_feature_map, quantum_instance=quantum_instance)
z_feature_map.decompose().draw(output='mpl', scale=2)
from qiskit.circuit.library import ZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
# here feature_dimension = 3 and reps = 4
adhoc_dimension = 3
z_feature_map = ZFeatureMap(feature_dimension=adhoc_dimension, reps=4)
z_kernel = QuantumKernel(feature_map = z_feature_map, quantum_instance=quantum_instance)
z_feature_map.decompose().draw(output='mpl', scale=2)
# same happens for ZZFeatureMap
from qiskit.circuit.library import ZZFeatureMap
adhoc_dimension=2
zz_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=1, entanglement='linear')
zz_kernel = QuantumKernel(feature_map = zz_feature_map, quantum_instance=quantum_instance)
zz_feature_map.decompose().draw(output='mpl', scale=2)
# same happens for ZZFeatureMap
from qiskit.circuit.library import ZZFeatureMap
adhoc_dimension=2
zz_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement='linear')
zz_kernel = QuantumKernel(feature_map = zz_feature_map, quantum_instance=quantum_instance)
zz_feature_map.decompose().draw(output='mpl', scale=2)
# same happens for ZZFeatureMap
from qiskit.circuit.library import ZZFeatureMap
adhoc_dimension=3
zz_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=1, entanglement='linear')
zz_kernel = QuantumKernel(feature_map = zz_feature_map, quantum_instance=quantum_instance)
zz_feature_map.decompose().draw(output='mpl', scale=2)
# same happens for ZZFeatureMap
from qiskit.circuit.library import ZZFeatureMap
adhoc_dimension=3
zz_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement='linear')
zz_kernel = QuantumKernel(feature_map = zz_feature_map, quantum_instance=quantum_instance)
zz_feature_map.decompose().draw(output='mpl', scale=2)
|
https://github.com/martynscn/Masters-Thesis-on-Quantum-Cryptography
|
martynscn
|
# This code has been adapted and modified from IBM Qiskit 2021 and
# uses the constant optimized modular exponentiation circuit for mod 15 as contained
# in https://arxiv.org/abs/1202.6614.
import numpy as np
import math
from decimal import *
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit.visualization import plot_histogram
from qiskit import Aer, transpile, assemble
import pandas as pd
from fractions import Fraction
#
# import math
# from math import gcd
# from numpy.random import randint
#
#
# from decimal import *
print("Imports Successful")
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
def my_mod(a,n):
getcontext().prec = 27
return round((Decimal(a)/Decimal(n) - Decimal(a)//Decimal(n) ) * n)
def constant_optimized_modular_exponentation_modulus15(a, power):
if a not in [2,7,8,11,13]:
raise ValueError("'a' must be 2,7,8,11 or 13")
U = QuantumCircuit(4)
for iteration in range(power):
if a in [2,13]:
U.swap(0,1)
U.swap(1,2)
U.swap(2,3)
if a in [7,8]:
U.swap(2,3)
U.swap(1,2)
U.swap(0,1)
if a == 11:
U.swap(1,3)
U.swap(0,2)
if a in [7,11,13]:
for q in range(4):
U.x(q)
U = U.to_gate()
U.name = "%i^%i mod 15" % (a, power)
control_U = U.control()
return control_U
def inverse_qft(n):
circuit = QuantumCircuit(n)
for i in range(n//2):
circuit.swap(i, n-1-i)
for j in range(n):
for m in range(j):
circuit.cp(-np.pi/float(2**(j-m)), m, j)
circuit.h(j)
circuit.name = "QFT†"
return circuit
N = 15
a = 7
n_count = 8
counting_register = QuantumRegister(size = n_count, name = "counting_register")
acting_register = QuantumRegister(size = 4, name="acting_register")
classic_register = ClassicalRegister(size = n_count, name="classic_register")
qc = QuantumCircuit(counting_register, acting_register ,classic_register)
initial_state = [1,0]
for q in range(8):
qc.initialize(initial_state, q)
qc.draw(output = 'mpl', filename = "Step0")
for q in range(n_count):
qc.h(q)
qc.draw(output = 'mpl', filename = "Step1")
qc.x(3+n_count)
qc.draw(output = 'mpl', filename = "Step1b")
for q in range(n_count):
qc.append(constant_optimized_modular_exponentation_modulus15(a, 2**q),
[q] + [i+n_count for i in range(4)])
qc.measure(range(n_count,n_count + 4), range(4))
qc.barrier()
qc.draw(output = 'mpl', filename = "Step2")
qc.append(inverse_qft(n_count), range(n_count))
qc.draw(output = 'mpl', filename = "Step3")
# Measure circuit
qc.measure(range(n_count), range(n_count))
qc.draw(output = 'mpl', filename = "Step4")
qasm_sim = Aer.get_backend('qasm_simulator')
t_qc = transpile(qc, qasm_sim)
qobj = assemble(t_qc)
results = qasm_sim.run(qobj).result()
counts = results.get_counts()
plot_histogram(counts)
rows, measured_phases = [], []
for output in counts:
decimal = int(output, 2)
phase = decimal/(2**n_count)
measured_phases.append(phase)
rows.append([f"{output}(bin) = {decimal:>3}(dec)",
f"{decimal}/{2**n_count} = {phase:.2f}"])
headers=["Register Output", "Phase"]
df = pd.DataFrame(rows, columns=headers)
df
rows = []
for phase in measured_phases:
frac = Fraction(phase).limit_denominator(15)
rows.append([phase, f"{frac.numerator}/{frac.denominator}", frac.denominator])
headers=["Phase", "Fraction", "Guess for r"]
df = pd.DataFrame(rows, columns=headers)
my_period_r = max(df["Guess for r"])
print("My period (r) is %i" % my_period_r)
# Confirm that the period is 4
xvals = np.arange(N)
xvals = [x.item() for x in xvals]
yvals = [my_mod(a**x, N) for x in xvals]
fig, ax = plt.subplots();
ax.plot(xvals, yvals, linewidth=1, linestyle='dotted', marker='x');
ax.set(xlabel='$x$', ylabel='$%i^x$ mod $%i$' % (a, N),
title="Example of Periodic Function in Shor's Algorithm");
try:
r = yvals[1:].index(1) +1
plt.annotate(s = '', xy=(0,1), xytext=(r,1), arrowprops=dict(arrowstyle='<->'));
plt.annotate(s = '$r=%i$' % r, xy=(r/3,1.5));
except ValueError:
print('Could not find a period')
first_shared_factor = math.gcd((7**(int(my_period_r/2)) + 1), 15)
first_shared_factor
second_shared_factor = math.gcd((7**(int(my_period_r/2)) - 1), 15)
second_shared_factor
%qiskit_copyright
|
https://github.com/martynscn/Masters-Thesis-on-Quantum-Cryptography
|
martynscn
|
# This code has been adapted and modified from IBM Qiskit 2021 and also from https://github.com/ttlion/ShorAlgQiskit.
# It uses the implementation as contained in the work of Stephane Beauregard (https://arxiv.org/abs/quant-ph/0205095)
# Many thanks to IBM Qiskit team, Tiago Miguel (ttlion), Qubit by Qubit, Peter Shor and Stephane Beauregard.
from typing import Optional, Union, Tuple, List
import math
import array
import fractions
import logging
import numpy as np
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister, execute, IBMQ, transpile,BasicAer, Aer, assemble
from qiskit.circuit import Gate, Instruction, ParameterVector
from qiskit.circuit.library import QFT
from qiskit.providers import BaseBackend, Backend
from qiskit.quantum_info import partial_trace
from qiskit.utils import summarize_circuits
from qiskit.utils.arithmetic import is_power
from qiskit.utils.validation import validate_min
from qiskit.utils.quantum_instance import QuantumInstance
import qiskit.visualization
from qiskit.providers.aer import QasmSimulator
from datetime import datetime
import csv
# provider = IBMQ.enable_account("PUT TOKEN HERE")
backend = QasmSimulator()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all" #"last_expr" or "all"
# """ Function to check if N is of type q^p"""
def check_if_power(N):
# """ Check if N is a perfect power in O(n^3) time, n=ceil(logN) """
b=2
while (2**b) <= N:
a = 1
c = N
while (c-a) >= 2:
m = int( (a+c)/2 )
if (m**b) < (N+1):
p = int( (m**b) )
else:
p = int(N+1)
if int(p) == int(N):
print('N is {0}^{1}'.format(int(m),int(b)) )
return True
if p<N:
a = int(m)
else:
c = int(m)
b=b+1
return False
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def create_QFT(circuit,up_reg,n,with_swaps):
i=n-1
while i>=0:
circuit.h(up_reg[i])
j=i-1
while j>=0:
if (np.pi)/(pow(2,(i-j))) > 0:
circuit.cu1( (np.pi)/(pow(2,(i-j))) , up_reg[i] , up_reg[j] )
j=j-1
i=i-1
if with_swaps==1:
i=0
while i < ((n-1)/2):
circuit.swap(up_reg[i], up_reg[n-1-i])
i=i+1
def create_inverse_QFT(circuit,up_reg,n,with_swaps):
if with_swaps==1:
i=0
while i < ((n-1)/2):
circuit.swap(up_reg[i], up_reg[n-1-i])
i=i+1
i=0
while i<n:
circuit.h(up_reg[i])
if i != n-1:
j=i+1
y=i
while y>=0:
if (np.pi)/(pow(2,(j-y))) > 0:
circuit.cu1( - (np.pi)/(pow(2,(j-y))) , up_reg[j] , up_reg[y] )
y=y-1
i=i+1
def getAngle(a, N):
s=bin(int(a))[2:].zfill(N)
angle = 0
for i in range(0, N):
if s[N-1-i] == '1':
angle += math.pow(2, -(N-i))
angle *= np.pi
return angle
def getAngles(a,N):
s=bin(int(a))[2:].zfill(N)
angles=np.zeros([N])
for i in range(0, N):
for j in range(i,N):
if s[j]=='1':
angles[N-i-1]+=math.pow(2, -(j-i))
angles[N-i-1]*=np.pi
return angles
def ccphase(circuit, angle, ctl1, ctl2, tgt):
circuit.cu1(angle/2,ctl1,tgt)
circuit.cx(ctl2,ctl1)
circuit.cu1(-angle/2,ctl1,tgt)
circuit.cx(ctl2,ctl1)
circuit.cu1(angle/2,ctl2,tgt)
def phiADD(circuit, q, a, N, inv):
angle=getAngles(a,N)
for i in range(0,N):
if inv==0:
circuit.u1(angle[i],q[i])
else:
circuit.u1(-angle[i],q[i])
def cphiADD(circuit, q, ctl, a, n, inv):
angle=getAngles(a,n)
for i in range(0,n):
if inv==0:
circuit.cu1(angle[i],ctl,q[i])
else:
circuit.cu1(-angle[i],ctl,q[i])
def ccphiADD(circuit,q,ctl1,ctl2,a,n,inv):
angle=getAngles(a,n)
for i in range(0,n):
if inv==0:
ccphase(circuit,angle[i],ctl1,ctl2,q[i])
else:
ccphase(circuit,-angle[i],ctl1,ctl2,q[i])
def ccphiADDmodN(circuit, q, ctl1, ctl2, aux, a, N, n):
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
phiADD(circuit, q, N, n, 1)
# phiADD(circuit, q, a,N, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.cx(q[n-1],aux)
create_QFT(circuit,q,n,0)
cphiADD(circuit, q, aux, N, n, 0)
# cphiADD(circuit, q, aux, a, n, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.x(q[n-1])
circuit.cx(q[n-1], aux)
circuit.x(q[n-1])
create_QFT(circuit,q,n,0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
def ccphiADDmodN_inv(circuit, q, ctl1, ctl2, aux, a, N, n):
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.x(q[n-1])
circuit.cx(q[n-1],aux)
circuit.x(q[n-1])
create_QFT(circuit, q, n, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 0)
cphiADD(circuit, q, aux, N, n, 1)
# cphiADD(circuit, q, aux, a, n, 1)
create_inverse_QFT(circuit, q, n, 0)
circuit.cx(q[n-1], aux)
create_QFT(circuit, q, n, 0)
phiADD(circuit, q, N, n, 0)
# phiADD(circuit, q, a, N, 0)
ccphiADD(circuit, q, ctl1, ctl2, a, n, 1)
def cMULTmodN(circuit, ctl, q, aux, a, N, n):
# up_reg = QuantumRegister(1, name = "up_reg")
# down_reg = QuantumRegister(n, name = "down_reg")
# up_classic = ClassicalRegister(2*n, name="up_classic")
# c_aux = ClassicalRegister(1, name = "aux_classic")
# cMULTmodN_circuit = QuantumCircuit(
# up_reg ,down_reg , aux,up_classic, c_aux,
# name=r"${0}^{{{1}^{{{2}}}}} mod{3}$".format(2,2,int(math.log(math.log(a,2),2)), N)
# )
# create_QFT(cMULTmodN_circuit,aux,n+1,0)
# for i in range(0, n):
# ccphiADDmodN(cMULTmodN_circuit, aux, q[i], ctl, aux[n+1], (2**i)*a % N, N, n+1)
# create_inverse_QFT(cMULTmodN_circuit, aux, n+1, 0)
# for i in range(0, n):
# circuit.cswap(ctl,q[i],aux[i])
# cMULTmodN_circuit.cswap(ctl,q[i],aux[i])
# create_QFT(cMULTmodN_circuit, aux, n+1, 0)
# ccphiADDmodN_inv(cMULTmodN_circuit, aux, q[i], ctl, aux[n+1], math.pow(2,i)*a_inv % N, N, n+1)
# create_inverse_QFT(cMULTmodN_circuit, aux, n+1, 0)
# cMULTmodN_circuit_instruction = cMULTmodN_circuit.to_instruction()
# circuit.append(cMULTmodN_circuit_instruction, [ctl, *down_reg, *aux])
create_QFT(circuit,aux,n+1,0)
for i in range(0, n):
ccphiADDmodN(circuit, aux, q[i], ctl, aux[n+1], (2**i)*a % N, N, n+1)
create_inverse_QFT(circuit, aux, n+1, 0)
for i in range(0, n):
circuit.cswap(ctl,q[i],aux[i])
a_inv = modinv(a, N)
create_QFT(circuit, aux, n+1, 0)
i = n-1
while i >= 0:
ccphiADDmodN_inv(circuit, aux, q[i], ctl, aux[n+1], math.pow(2,i)*a_inv % N, N, n+1)
i -= 1
create_inverse_QFT(circuit, aux, n+1, 0)
def calculate_continued_fraction(b: array.array) -> int:
# """Calculate the continued fraction of x/T from the current terms of expansion b."""
x_over_T = 0
for i in reversed(range(len(b) - 1)):
x_over_T = 1 / (b[i + 1] + x_over_T)
x_over_T += b[0]
frac = fractions.Fraction(x_over_T).limit_denominator()
return frac.denominator
def get_factors(N: int, a: int, measurement: str) -> Optional[List[int]]:
# """Apply the continued fractions to find r and the gcd to find the desired factors."""
x_final = int(measurement, 2)
#print('In decimal, x_final value for this result is: {}.'.format(x_final))
if x_final <= 0:
fail_reason = 'x_final value is <= 0, there are no continued fractions.'
else:
fail_reason = None
#print('Running continued fractions for this case.')
# Calculate T and x/T
T_upper = len(measurement)
T = pow(2, T_upper)
x_over_T = x_final / T ## this is our theta
# Cycle in which each iteration corresponds to putting one more term in the
# calculation of the Continued Fraction (CF) of x/T
# Initialize the first values according to CF rule
i = 0
b = array.array('i')
t = array.array('f')
b.append(math.floor(x_over_T))
t.append(x_over_T - b[i])
exponential = 0.0
while i < N and fail_reason is None:
# From the 2nd iteration onwards, calculate the new terms of the CF based on the previous terms as the rule suggests
if i > 0:
try:
b_temp = math.floor(1 / t[i - 1])
except ZeroDivisionError as err:
b_temp = 0
b.append(b_temp)
try:
t_temp = (1 / t[i - 1]) - b[i]
except ZeroDivisionError as err:
t_temp = 0
t.append(t_temp) # type: ignore
# Calculate the denominator of the CF using the known terms
denominator = calculate_continued_fraction(b)
# Increment i for next iteration
i += 1
if denominator % 2 == 1:
#print('Odd denominator, will try next iteration of continued fractions.')
continue
# Denominator is even, try to get factors of N. Get the exponential a^(r/2)
if denominator < 1000:
try:
exponential = pow(a, denominator / 2)
except OverflowError as err:
exponential = 999999999
# Check if the value is too big or not
if exponential > 1000000:
if exponential == 999999999:
fail_reason = 'OverflowError'
else:
fail_reason = 'denominator of continued fraction is too big (> 10^3).'
else:
# The value is not too big, get the right values and do the proper gcd()
putting_plus = int(exponential + 1)
putting_minus = int(exponential - 1)
one_factor = math.gcd(putting_plus, N)
other_factor = math.gcd(putting_minus, N)
# Check if the factors found are trivial factors or are the desired factors
if any(factor in {1, N} for factor in (one_factor, other_factor)):
#print('Found just trivial factors, not good enough.')
# Check if the number has already been found, (use i - 1 because i was already incremented)
if t[i - 1] == 0:
fail_reason = 'the continued fractions found exactly x_final/(2^(2n)).'
else:
return sorted((one_factor, other_factor))
return None
def process_results(sim_result, circuit, shots, N, a, n):
counts_result = sim_result.get_counts(circuit)
total_counts = len(counts_result)
counts_result_sorted = sorted(counts_result.items(), key=lambda x: x[1], reverse=True)
counts_result_keys = list(counts_result.keys())
counts_result_values = list(counts_result.values())
prob_success=0
prob_failure=0
result_successful_counts = 0
result_failure_counts = 0
for initial_undesired_measurement, frequency in counts_result_sorted:
measurement = initial_undesired_measurement.split(" ")[1]
x_value = int(measurement, 2)
prob_this_result = 100 * frequency/shots
factors = get_factors(N, a, measurement)
if factors:
prob_success = prob_success + prob_this_result
result_successful_counts = result_successful_counts + 1
if factors not in result_factors:
result_factors.append(factors)
elif not factors:
prob_failure = prob_failure + prob_this_result
result_failure_counts = result_failure_counts + 1
return [result_factors, prob_success, prob_failure, total_counts, result_successful_counts,result_failure_counts]
def my_shor(a,N,shots):
start_time_number = datetime.now()
start_time = start_time_number.strftime("%H:%M:%S")
summary_result = dict()
validate_min('N', N, 3)
validate_min('a', a, 2)
if N < 1 or N % 2 == 0:
raise ValueError('The input needs to be an odd integer greater than 1.')
if a >= N or math.gcd(a, N) != 1:
raise ValueError('The integer a needs to satisfy a < N and gcd(a, N) = 1.')
n = math.ceil(math.log(N,2))
global result_factors
result_factors = []
tf, b, p = is_power(N, return_decomposition=True)
if tf:
print('The input integer is a power: {0}={1}^{2}.'.format(N, b, p))
result_factors.append(b)
# """auxilliary quantum register used in addition and multiplication"""
aux = QuantumRegister(size = n+2, name="aux_reg")
# """single qubit where the sequential QFT is performed"""
up_reg = QuantumRegister(1, name = "up_reg")
down_reg = QuantumRegister(n, name = "down_reg")
# """classical register where the measured values of the sequential QFT are stored"""
up_classic = ClassicalRegister(2*n, name="up_classic")
# """classical bit used to reset the state of the top qubit to 0 if the previous measurement was 1"""
c_aux = ClassicalRegister(1, name = "aux_classic")
# """ Create Quantum Circuit """
circuit = QuantumCircuit(up_reg ,down_reg , aux,up_classic, c_aux)
circuit.x(down_reg[0])
# circuit.draw(filename = "shor_semiclassical_QFT_initialization")
for i in range(0, 2*n):
circuit.x(up_reg).c_if(c_aux, 1)
circuit.h(up_reg)
cMULTmodN(circuit, up_reg[0], down_reg, aux, a**(2**(2*n-1-i)), N, n)
# later confirm if this should be up_reg[i] instead of up_reg[0]
for j in range(0, 2**i):
circuit.u1(getAngle(j, i), up_reg[0]).c_if(up_classic, j)
circuit.h(up_reg)
circuit.measure(up_reg[0], up_classic[i])
circuit.measure(up_reg[0], c_aux[0])
# circuit.draw(filename = "shor_semiclassical_QFT_final_circuit")
circuit.draw()
qc_compiled = transpile(circuit, backend, optimization_level = 3)
job_sim_1 = backend.run(qc_compiled, shots=shots)
sim_result=job_sim_1.result()
# counts_result = sim_result.get_counts(circuit)
# len(counts_result)
# measurement_plot = qiskit.visualization.plot_histogram(counts_result,figsize=(20, 12) ,number_to_keep = 30,bar_labels=True, title = "Measurement results from shor_standard_QFT circuit variant" )
# measurement_plot.savefig("shor_semiclassical_QFT_measurement_result")
# measurement_plot
processed_result = process_results(sim_result, circuit, shots, N, a, n)
end_time_number = datetime.now()
end_time = end_time_number.strftime("%H:%M:%S")
duration = end_time_number - start_time_number
print("Current Start Time =", start_time)
print(processed_result)
print("Current End Time =", end_time)
circuit_count_ops = circuit.count_ops()
circuit_decomposed = circuit.decompose()
circuit_decomposed_count_ops = circuit_decomposed.count_ops()
qc_compiled_count_ops = qc_compiled.count_ops()
summary_result["num_qubits"] = n
summary_result["Number(N)"] = N
summary_result["a"] = a
summary_result["start_time"] = start_time
summary_result["end_time"] = end_time
summary_result["duration"] = duration
summary_result["result_factors"] = processed_result[0]
summary_result["prob_success"] = processed_result[1]
summary_result["prob_failure"] = processed_result[2]
summary_result["total_counts"] = processed_result[3]
summary_result["result_successful_counts"] = processed_result[4]
summary_result["result_failure_counts"] = processed_result[5]
summary_result["circuit_width"] = circuit.width()
summary_result["circuit_depth"] = circuit.depth()
summary_result["circuit_size"] = circuit.size()
summary_result["circuit_num_nonlocal_gates"] = circuit.num_nonlocal_gates()
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_clbits"] = circuit.num_clbits
summary_result["circuit_num_qubits"] = circuit.num_qubits
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_of_count_ops"] = len(circuit_count_ops)
summary_result["circuit_num_of_x"] = circuit_count_ops.get('x')
summary_result["circuit_num_of_measure"] = circuit_count_ops.get('measure')
summary_result["circuit_num_of_h"] = circuit_count_ops.get('h')
summary_result["circuit_num_of_cswap"] = circuit_count_ops.get('cswap')
summary_result["circuit_num_of_swap"] = circuit_count_ops.get('swap')
summary_result["circuit_num_of_cx"] = circuit_count_ops.get('cx')
summary_result["circuit_num_of_toffoli"] = circuit_count_ops.get('toffoli')
summary_result["circuit_num_of_p"] = circuit_count_ops.get('p')
summary_result["circuit_num_of_t"] = circuit_count_ops.get('t')
summary_result["circuit_decomposed_width"] = circuit_decomposed.width()
summary_result["circuit_decomposed_depth"] = circuit_decomposed.depth()
summary_result["circuit_decomposed_size"] = circuit_decomposed.size()
summary_result["circuit_decomposed_num_nonlocal_gates"] = circuit_decomposed.num_nonlocal_gates()
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_clbits"] = circuit_decomposed.num_clbits
summary_result["circuit_decomposed_num_qubits"] = circuit_decomposed.num_qubits
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_of_count_ops"] = len(circuit_decomposed_count_ops)
summary_result["circuit_decomposed_num_of_x"] = circuit_decomposed_count_ops.get('x')
summary_result["circuit_decomposed_num_of_measure"] = circuit_decomposed_count_ops.get('measure')
summary_result["circuit_decomposed_num_of_h"] = circuit_decomposed_count_ops.get('h')
summary_result["circuit_decomposed_num_of_cswap"] = circuit_decomposed_count_ops.get('cswap')
summary_result["circuit_decomposed_num_of_swap"] = circuit_decomposed_count_ops.get('swap')
summary_result["circuit_decomposed_num_of_cx"] = circuit_decomposed_count_ops.get('cx')
summary_result["circuit_decomposed_num_of_toffoli"] = circuit_decomposed_count_ops.get('toffoli')
summary_result["circuit_decomposed_num_of_p"] = circuit_decomposed_count_ops.get('p')
summary_result["circuit_decomposed_num_of_t"] = circuit_decomposed_count_ops.get('t')
summary_result["qc_compiled_width"] = qc_compiled.width()
summary_result["qc_compiled_depth"] = qc_compiled.depth()
summary_result["qc_compiled_size"] = qc_compiled.size()
summary_result["qc_compiled_num_nonlocal_gates"] = qc_compiled.num_nonlocal_gates()
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_clbits"] = qc_compiled.num_clbits
summary_result["qc_compiled_num_qubits"] = qc_compiled.num_qubits
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_of_count_ops"] = len(qc_compiled_count_ops)
summary_result["qc_compiled_num_of_x"] = qc_compiled_count_ops.get('x')
summary_result["qc_compiled_num_of_measure"] = qc_compiled_count_ops.get('measure')
summary_result["qc_compiled_num_of_h"] = qc_compiled_count_ops.get('h')
summary_result["qc_compiled_num_of_cswap"] = qc_compiled_count_ops.get('cswap')
summary_result["qc_compiled_num_of_swap"] = qc_compiled_count_ops.get('swap')
summary_result["qc_compiled_num_of_cx"] = qc_compiled_count_ops.get('cx')
summary_result["qc_compiled_num_of_toffoli"] = qc_compiled_count_ops.get('toffoli')
summary_result["qc_compiled_num_of_p"] = qc_compiled_count_ops.get('p')
summary_result["qc_compiled_num_of_t"] = qc_compiled_count_ops.get('t')
return summary_result
# Run for just a single number N
%%time
N = 21
shots = 1024
global result_factors
all_summary_result_temp = []
for random_a in range(2, N):
if math.gcd(random_a,N) > 1:
continue
a = random_a
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n".format(a, N))
all_summary_result_temp.append(summary_result)
summary_result_list = []
for key, value in summary_result.items():
summary_result_list.append([key,value])
summary_result_list
with open("a({0})_N({1})_semiclassical.csv".format(a, N), 'a') as myfile:
write = csv.writer(myfile)
#write.writerow(fields)
write.writerows(summary_result_list)
all_summary_result_temp
# Run for many numbers N.
%%time
shots = 1024
global result_factors
all_summary_result = []
for N in [15, 21, 33, 35, 39, 51, 55, 57]:
for a in range(2, N):
if math.gcd(a,N) > 1:
continue
print("Beginning running for a = {} and N = {}".format(a, N))
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n\n".format(a, N))
all_summary_result.append(summary_result)
all_summary_result
%qiskit_copyright
|
https://github.com/martynscn/Masters-Thesis-on-Quantum-Cryptography
|
martynscn
|
# This code has been adapted and modified from IBM Qiskit 2021 and also from https://github.com/ttlion/ShorAlgQiskit.
# It uses the implementation as contained in the work of Stephane Beauregard (https://arxiv.org/abs/quant-ph/0205095)
# Many thanks to IBM Qiskit team, Tiago Miguel (ttlion), Qubit by Qubit, Peter Shor and Stephane Beauregard.
from typing import Optional, Union, Tuple, List
import math
import array
import fractions
import logging
import numpy as np
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister, execute, IBMQ, transpile,BasicAer, Aer, assemble
from qiskit.circuit import Gate, Instruction, ParameterVector
from qiskit.circuit.library import QFT
from qiskit.providers import BaseBackend, Backend
from qiskit.quantum_info import partial_trace
from qiskit.utils import summarize_circuits
from qiskit.utils.arithmetic import is_power
from qiskit.utils.validation import validate_min
from qiskit.utils.quantum_instance import QuantumInstance
import qiskit.visualization
from qiskit.providers.aer import QasmSimulator
from datetime import datetime
import csv
# provider = IBMQ.enable_account("PUT TOKEN HERE")
backend = QasmSimulator()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all" #"last_expr" or "all"
def get_angles(a: int, n) -> np.ndarray:
# """Calculates the array of angles to be used in the addition in Fourier Space."""
s = bin(int(a))[2:].zfill(n + 1)
angles = np.zeros([n + 1])
for i in range(0, n + 1):
for j in range(i, n + 1):
if s[j] == '1':
angles[n - i] += math.pow(2, -(j - i))
angles[n - i] *= np.pi
return angles[::-1]
# This returns the angles in the opposite order
def my_create_QFT(qft_num_qubits,approximation_degree: int = 0,do_swaps: bool = False,insert_barriers: bool = True, name: str = 'qft'):
# up_reg = QuantumRegister(size = qft_num_qubits, name="aux")
circuit_qft = QuantumCircuit(qft_num_qubits)
i=qft_num_qubits-1
while i>=0:
# circuit_qft.h(up_reg[i])
circuit_qft.h(i)
j=i-1
while j>=0:
if (np.pi)/(pow(2,(i-j))) > approximation_degree:
# circuit_qft.cu1( (np.pi)/(pow(2,(i-j))) , up_reg[i] , up_reg[j] )
circuit_qft.cu1( (np.pi)/(pow(2,(i-j))) , i , j )
j=j-1
if insert_barriers:
circuit_qft.barrier()
i=i-1
""" If specified, apply the Swaps at the end """
if do_swaps:
i=0
while i < ((qft_num_qubits-1)/2):
# circuit_qft.swap(up_reg[i], up_reg[qft_num_qubits-1-i])
circuit_qft.swap(i, qft_num_qubits-1-i)
i=i+1
circuit_qft.name = "QFT"
return circuit_qft
def my_create_inverse_QFT(qft_num_qubits,approximation_degree: int = 0,do_swaps: bool = False,insert_barriers: bool = True, name: str = 'iqft'):
my_create_QFT_circuit = my_create_QFT(qft_num_qubits,approximation_degree,do_swaps,insert_barriers, name)
my_create_inverse_QFT_circuit = my_create_QFT_circuit.inverse()
my_create_inverse_QFT_circuit.name = "QFT†"
return my_create_inverse_QFT_circuit
def phi_add_gate(size: int, angles: Union[np.ndarray, ParameterVector]) -> Gate:
# """Gate that performs addition by a in Fourier Space."""
circuit = QuantumCircuit(size, name="phi_add")
for i, angle in enumerate(angles):
circuit.p(angle, i)
return circuit.to_gate()
def double_controlled_phi_add_mod_N(num_qubits: int, angles: Union[np.ndarray, ParameterVector],reg_size, a, N, n) -> QuantumCircuit:
# """Creates a circuit which implements double-controlled modular addition by a."""
circuit = QuantumCircuit(num_qubits, name="ccphi_add_mod_N")
ctl_up = 0
ctl_down = 1
ctl_aux = 2
# get qubits from aux register, omitting the control qubit
qubits = range(3, num_qubits)
# store the gates representing addition/subtraction by a in Fourier Space
phi_add_a = phi_add_gate(len(qubits), angles)
iphi_add_a = phi_add_a.inverse()
phi_add_N = phi_add_gate(reg_size - 1, get_angles(N, n))
iphi_add_N = phi_add_N.inverse()
circuit.append(phi_add_a.control(2), [ctl_up, ctl_down, *qubits])
circuit.append(iphi_add_N, qubits)
qft = QFT(n + 1).to_instruction()
# qft = my_create_QFT(n + 1).to_instruction()
iqft = QFT(n + 1).inverse().to_instruction()
# iqft = my_create_inverse_QFT(n + 1).to_instruction()
circuit.append(iqft, qubits)
circuit.cx(qubits[0], ctl_aux)
circuit.append(qft, qubits)
circuit.append(phi_add_N, qubits)
circuit.append(iphi_add_a.control(2), [ctl_up, ctl_down, *qubits])
circuit.append(iqft, qubits)
circuit.x(qubits[0])
circuit.cx(qubits[0], ctl_aux)
circuit.x(qubits[0])
circuit.append(qft, qubits)
circuit.append(phi_add_a.control(2), [ctl_up, ctl_down, *qubits])
return circuit
# """Circuit that implements single controlled modular multiplication by a"""
def controlled_multiple_mod_N(num_qubits: int, N: int, a: int, n, aux_reg_size):
# """Implements modular multiplication by a as an instruction."""
circuit = QuantumCircuit(
num_qubits,
# name="multiply_by_{}_mod_{}".format(a % N, N),
name=r"${0}^{{{1}^{{{2}}}}} mod{3}$".format(2,2,int(math.log(math.log(a,2),2)), N)
)
# label = r"${0}^{{{1}^{{{2}}}}} mod{3}$".format("†","y")
down = circuit.qubits[1: n + 1]
aux = circuit.qubits[n + 1:]
qubits = [aux[i] for i in reversed(range(n + 1))]
ctl_up = 0
ctl_aux = aux[-1]
angle_params = ParameterVector("angles", length=len(aux) - 1)
double_controlled_phi_add = double_controlled_phi_add_mod_N(
len(aux) + 2, angle_params, aux_reg_size, a, N, n
)
idouble_controlled_phi_add = double_controlled_phi_add.inverse()
qft_circuit = QFT(n + 1).to_instruction()
# qft_circuit = my_create_QFT(n + 1).to_instruction()
iqft_circuit = QFT(n + 1).inverse().to_instruction()
# iqft_circuit = my_create_inverse_QFT(n + 1).to_instruction()
circuit.append(qft_circuit, qubits)
# perform controlled addition by a on the aux register in Fourier space
for i, ctl_down in enumerate(down):
a_exp = (2 ** i) * a % N
angles = get_angles(a_exp, n)
bound = double_controlled_phi_add.assign_parameters({angle_params: angles})
circuit.append(bound, [ctl_up, ctl_down, ctl_aux, *qubits])
circuit.append(iqft_circuit, qubits)
# perform controlled subtraction by a in Fourier space on both the aux and down register
for j in range(n):
circuit.cswap(ctl_up, down[j], aux[j])
circuit.append(qft_circuit, qubits)
a_inv = modinv(a, N)
for i in reversed(range(len(down))):
a_exp = (2 ** i) * a_inv % N
angles = get_angles(a_exp, n)
bound = idouble_controlled_phi_add.assign_parameters({angle_params: angles})
circuit.append(bound, [ctl_up, down[i], ctl_aux, *qubits])
circuit.append(iqft_circuit, qubits)
return circuit
def modinv(a: int, m: int) -> int:
# """Returns the modular multiplicative inverse of a with respect to the modulus m."""
def egcd(a: int, b: int) -> Tuple[int, int, int]:
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
g, x, _ = egcd(a, m)
if g != 1:
raise ValueError("The greatest common divisor of {} and {} is {}, so the "
"modular inverse does not exist.".format(a, m, g))
return x % m
def get_factors(N: int, a: int, measurement: str) -> Optional[List[int]]:
# """Apply the continued fractions to find r and the gcd to find the desired factors."""
x_final = int(measurement, 2)
#print('In decimal, x_final value for this result is: {}.'.format(x_final))
if x_final <= 0:
fail_reason = 'x_final value is <= 0, there are no continued fractions.'
else:
fail_reason = None
#print('Running continued fractions for this case.')
# Calculate T and x/T
T_upper = len(measurement)
T = pow(2, T_upper)
x_over_T = x_final / T ## this is our theta
# Cycle in which each iteration corresponds to putting one more term in the
# calculation of the Continued Fraction (CF) of x/T
# Initialize the first values according to CF rule
i = 0
b = array.array('i')
t = array.array('f')
b.append(math.floor(x_over_T))
t.append(x_over_T - b[i])
exponential = 0.0
while i < N and fail_reason is None:
# From the 2nd iteration onwards, calculate the new terms of the CF based on the previous terms as the rule suggests
if i > 0:
try:
b_temp = math.floor(1 / t[i - 1])
except ZeroDivisionError as err:
b_temp = 0
b.append(b_temp)
try:
t_temp = (1 / t[i - 1]) - b[i]
except ZeroDivisionError as err:
t_temp = 0
t.append(t_temp) # type: ignore
# Calculate the denominator of the CF using the known terms
denominator = calculate_continued_fraction(b)
# Increment i for next iteration
i += 1
if denominator % 2 == 1:
#print('Odd denominator, will try next iteration of continued fractions.')
continue
# Denominator is even, try to get factors of N. Get the exponential a^(r/2)
if denominator < 1000:
try:
exponential = pow(a, denominator / 2)
except OverflowError as err:
exponential = 999999999
# Check if the value is too big or not
if exponential > 1000000:
if exponential == 999999999:
fail_reason = 'OverflowError'
else:
fail_reason = 'denominator of continued fraction is too big (> 10^9).'
else:
# The value is not too big, get the right values and do the proper gcd()
putting_plus = int(exponential + 1)
putting_minus = int(exponential - 1)
one_factor = math.gcd(putting_plus, N)
other_factor = math.gcd(putting_minus, N)
# Check if the factors found are trivial factors or are the desired factors
if any(factor in {1, N} for factor in (one_factor, other_factor)):
#print('Found just trivial factors, not good enough.')
# Check if the number has already been found, (use i - 1 because i was already incremented)
if t[i - 1] == 0:
fail_reason = 'the continued fractions found exactly x_final/(2^(2n)).'
else:
return sorted((one_factor, other_factor))
# Search for factors failed, write the reason for failure to the debug logs
#print('Cannot find factors from measurement {0} because {1}'.format(measurement, fail_reason or 'it took too many attempts.'))
return None
def calculate_continued_fraction(b: array.array) -> int:
# """Calculate the continued fraction of x/T from the current terms of expansion b."""
x_over_T = 0
for i in reversed(range(len(b) - 1)):
x_over_T = 1 / (b[i + 1] + x_over_T)
x_over_T += b[0]
frac = fractions.Fraction(x_over_T).limit_denominator()
#print('Approximation number %s of continued fractions:'.format(len(b)))
#print("Numerator:{0} \t\t Denominator: {1}.".format(frac.numerator, frac.denominator))
return frac.denominator
def process_results(sim_result, circuit, shots, N, a, n):
counts_result = sim_result.get_counts(circuit)
total_counts = len(counts_result)
counts_result_sorted = sorted(counts_result.items(), key=lambda x: x[1], reverse=True)
# """ Print info to user from the simulation results """
# print('Printing the various results followed by how many times they happened (out of the {} cases):\n'.format(shots))
counts_result_keys = list(counts_result.keys())
counts_result_values = list(counts_result.values())
#i=0
#while i < len(counts_result):
#print('Result \"{0}\" happened {1} times out of {2}\n'.format(list(sim_result.get_counts().keys())[i],list(sim_result.get_counts().values())[i],shots))
#print('Result \"{0}\" happened {1} times out of {2}\n'.format(counts_result_keys[i],counts_result_values[i],shots))
#i=i+1
prob_success=0
prob_failure=0
result_successful_counts = 0
result_failure_counts = 0
# len(counts_result_sorted)
# For each simulation result, print proper info to user and try to calculate the factors of N
#for measurement in counts_result_keys:
for measurement, frequency in counts_result_sorted:
# Get the x_final value from the final state qubits
x_value = int(measurement, 2)
#prob_this_result = 100 * ( int(counts_result[measurement] ) ) / (shots)
prob_this_result = 100 * frequency/shots
# print("------> Analyzing result {0}. This result happened in {1:.4f} % of all cases\nIn decimal, x_final value for this result is: {2}".format(measurement,prob_this_result,x_value))
factors = get_factors(N, a, measurement)
if factors:
prob_success = prob_success + prob_this_result
# print('Found factors {0} from measurement {1} which is {2} in decimal.\n'.format(factors, measurement, x_value))
result_successful_counts = result_successful_counts + 1
if factors not in result_factors:
result_factors.append(factors)
elif not factors:
prob_failure = prob_failure + prob_this_result
result_failure_counts = result_failure_counts + 1
return [result_factors, prob_success, prob_failure, total_counts, result_successful_counts,result_failure_counts]
def my_shor(a,N,shots):
start_time_number = datetime.now()
start_time = start_time_number.strftime("%H:%M:%S")
summary_result = dict()
validate_min('N', N, 3)
validate_min('a', a, 2)
if N < 1 or N % 2 == 0:
raise ValueError('The input needs to be an odd integer greater than 1.')
if a >= N or math.gcd(a, N) != 1:
raise ValueError('The integer a needs to satisfy a < N and gcd(a, N) = 1.')
n = math.ceil(math.log(N,2))
global result_factors
result_factors = []
tf, b, p = is_power(N, return_decomposition=True)
if tf:
print('The input integer is a power: {0}={1}^{2}.'.format(N, b, p))
result_factors.append(b)
# """auxilliary quantum register used in addition and multiplication"""
aux_reg = QuantumRegister(size = n+2, name="aux_reg")
up_reg = QuantumRegister(2*n, name = "up_reg")
# """quantum register where the multiplications are made"""
down_reg = QuantumRegister(n, name = "down_reg")
# """classical register where the measured values of the QFT are stored"""
up_classic = ClassicalRegister(2*n, name="up_classic")
# """ Create Quantum Circuit """
circuit = QuantumCircuit(up_reg ,down_reg ,aux_reg, up_classic, name="Shor circuit(N={}, a={})".format(N, a))
# phi_add_N_gate = phiADD(circuit,q,a,N,inv)
phi_add_N_gate = phi_add_gate(aux_reg.size - 1, get_angles(N,n))
iphi_add_N_gate = phi_add_N_gate.inverse()
# """ Initialize down register to 1 and create maximal superposition in top register """
circuit.h(up_reg)
circuit.x(down_reg[0])
# circuit.draw(filename = "shor_standard_QFT")
# """ Apply the multiplication gates as showed in the report in order to create the exponentiation """
for i, ctl_up in enumerate(up_reg): # type: ignore
a_aux = int(pow(a, pow(2, i)))
controlled_multiple_mod_N_circuit = controlled_multiple_mod_N(
len(down_reg) + len(aux_reg) + 1, N, a_aux,n,aux_reg.size
)
controlled_multiple_mod_N_result = controlled_multiple_mod_N_circuit.to_instruction()
circuit.append(
controlled_multiple_mod_N_result, [ctl_up, *down_reg, *aux_reg]
)
# circuit.draw()
iqft = QFT(len(up_reg)).inverse().to_instruction()
# iqft = my_create_inverse_QFT(len(up_reg)).to_instruction()
# iqft = my_create_inverse_QFT(len(up_reg), insert_barriers = False).to_gate(label = r"$QFT^{{{0}}}$".format("†"))
circuit.append(iqft, up_reg)
circuit.measure(up_reg, up_classic)
# circuit.draw(filename = "shor_standard_QFT_final_circuit",fold = -1 )
# print(summarize_circuits(circuit))
# circuit.draw()
print('Running with N={0} and a={1} with number of qubits n={2}'.format(N, a, 4*n + 2))
qc_compiled = transpile(circuit, backend, optimization_level = 3)
job_sim_1 = backend.run(qc_compiled, shots=shots)
sim_result=job_sim_1.result()
# counts_result = sim_result.get_counts(circuit)
# len(counts_result)
# measurement_plot = qiskit.visualization.plot_histogram(counts_result,figsize=(20, 12) ,number_to_keep = 30,bar_labels=True, title = "Measurement results from shor_standard_QFT circuit variant" )
# measurement_plot.savefig("shor_standard_QFT_measurement")
# measurement_plot
processed_result = process_results(sim_result, circuit, shots, N, a, n)
end_time_number = datetime.now()
end_time = end_time_number.strftime("%H:%M:%S")
duration = end_time_number - start_time_number
print("Current Start Time =", start_time)
print(processed_result)
print("Current End Time =", end_time)
circuit_count_ops = circuit.count_ops()
circuit_decomposed = circuit.decompose()
circuit_decomposed_count_ops = circuit_decomposed.count_ops()
qc_compiled_count_ops = qc_compiled.count_ops()
summary_result["num_qubits"] = n
summary_result["Number(N)"] = N
summary_result["a"] = a
summary_result["start_time"] = start_time
summary_result["end_time"] = end_time
summary_result["duration"] = duration
summary_result["result_factors"] = processed_result[0]
summary_result["prob_success"] = processed_result[1]
summary_result["prob_failure"] = processed_result[2]
summary_result["total_counts"] = processed_result[3]
summary_result["result_successful_counts"] = processed_result[4]
summary_result["result_failure_counts"] = processed_result[5]
summary_result["circuit_width"] = circuit.width()
summary_result["circuit_depth"] = circuit.depth()
summary_result["circuit_size"] = circuit.size()
summary_result["circuit_num_nonlocal_gates"] = circuit.num_nonlocal_gates()
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_clbits"] = circuit.num_clbits
summary_result["circuit_num_qubits"] = circuit.num_qubits
summary_result["circuit_num_ancillas"] = circuit.num_ancillas
summary_result["circuit_num_of_count_ops"] = len(circuit_count_ops)
summary_result["circuit_num_of_x"] = circuit_count_ops.get('x')
summary_result["circuit_num_of_measure"] = circuit_count_ops.get('measure')
summary_result["circuit_num_of_h"] = circuit_count_ops.get('h')
summary_result["circuit_num_of_cswap"] = circuit_count_ops.get('cswap')
summary_result["circuit_num_of_swap"] = circuit_count_ops.get('swap')
summary_result["circuit_num_of_cx"] = circuit_count_ops.get('cx')
summary_result["circuit_num_of_toffoli"] = circuit_count_ops.get('toffoli')
summary_result["circuit_num_of_p"] = circuit_count_ops.get('p')
summary_result["circuit_num_of_t"] = circuit_count_ops.get('t')
summary_result["circuit_decomposed_width"] = circuit_decomposed.width()
summary_result["circuit_decomposed_depth"] = circuit_decomposed.depth()
summary_result["circuit_decomposed_size"] = circuit_decomposed.size()
summary_result["circuit_decomposed_num_nonlocal_gates"] = circuit_decomposed.num_nonlocal_gates()
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_clbits"] = circuit_decomposed.num_clbits
summary_result["circuit_decomposed_num_qubits"] = circuit_decomposed.num_qubits
summary_result["circuit_decomposed_num_ancillas"] = circuit_decomposed.num_ancillas
summary_result["circuit_decomposed_num_of_count_ops"] = len(circuit_decomposed_count_ops)
summary_result["circuit_decomposed_num_of_x"] = circuit_decomposed_count_ops.get('x')
summary_result["circuit_decomposed_num_of_measure"] = circuit_decomposed_count_ops.get('measure')
summary_result["circuit_decomposed_num_of_h"] = circuit_decomposed_count_ops.get('h')
summary_result["circuit_decomposed_num_of_cswap"] = circuit_decomposed_count_ops.get('cswap')
summary_result["circuit_decomposed_num_of_swap"] = circuit_decomposed_count_ops.get('swap')
summary_result["circuit_decomposed_num_of_cx"] = circuit_decomposed_count_ops.get('cx')
summary_result["circuit_decomposed_num_of_toffoli"] = circuit_decomposed_count_ops.get('toffoli')
summary_result["circuit_decomposed_num_of_p"] = circuit_decomposed_count_ops.get('p')
summary_result["circuit_decomposed_num_of_t"] = circuit_decomposed_count_ops.get('t')
summary_result["qc_compiled_width"] = qc_compiled.width()
summary_result["qc_compiled_depth"] = qc_compiled.depth()
summary_result["qc_compiled_size"] = qc_compiled.size()
summary_result["qc_compiled_num_nonlocal_gates"] = qc_compiled.num_nonlocal_gates()
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_clbits"] = qc_compiled.num_clbits
summary_result["qc_compiled_num_qubits"] = qc_compiled.num_qubits
summary_result["qc_compiled_num_ancillas"] = qc_compiled.num_ancillas
summary_result["qc_compiled_num_of_count_ops"] = len(qc_compiled_count_ops)
summary_result["qc_compiled_num_of_x"] = qc_compiled_count_ops.get('x')
summary_result["qc_compiled_num_of_measure"] = qc_compiled_count_ops.get('measure')
summary_result["qc_compiled_num_of_h"] = qc_compiled_count_ops.get('h')
summary_result["qc_compiled_num_of_cswap"] = qc_compiled_count_ops.get('cswap')
summary_result["qc_compiled_num_of_swap"] = qc_compiled_count_ops.get('swap')
summary_result["qc_compiled_num_of_cx"] = qc_compiled_count_ops.get('cx')
summary_result["qc_compiled_num_of_toffoli"] = qc_compiled_count_ops.get('toffoli')
summary_result["qc_compiled_num_of_p"] = qc_compiled_count_ops.get('p')
summary_result["qc_compiled_num_of_t"] = qc_compiled_count_ops.get('t')
return summary_result
# Run for just a single number N
%%time
N = 33
shots = 1024
global result_factors
all_summary_result_temp = []
for random_a in range(16, 17):
if math.gcd(random_a,N) > 1:
continue
a = random_a
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n".format(a, N))
all_summary_result_temp.append(summary_result)
summary_result_list = []
for key, value in summary_result.items():
summary_result_list.append([key,value])
summary_result_list
with open("a({0})_N({1})_standard.csv".format(a, N), 'a') as myfile:
write = csv.writer(myfile)
#write.writerow(fields)
write.writerows(summary_result_list)
all_summary_result_temp
# Run for many numbers N.
%%time
shots = 1024
global result_factors
all_summary_result = []
for N in [15, 21, 33, 35, 39, 51, 55, 57]:
for a in range(2, N):
if math.gcd(a,N) > 1:
continue
print("Beginning running for a = {} and N = {}".format(a, N))
summary_result = my_shor(a,N,shots)
print("Finished running for a = {} and N = {}\n\n".format(a, N))
all_summary_result.append(summary_result)
all_summary_result
%qiskit_copyright
|
https://github.com/AnkRaw/Quantum-Convolutional-Neural-Network
|
AnkRaw
|
# Importing Libraries
import torch
from torch import cat, no_grad, manual_seed
from torch.utils.data import DataLoader
from torchvision import transforms
import torch.optim as optim
from torch.nn import (
Module,
Conv2d,
Linear,
Dropout2d,
NLLLoss
)
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from qiskit_machine_learning.neural_networks import EstimatorQNN
from qiskit_machine_learning.connectors import TorchConnector
from qiskit.circuit.library import RealAmplitudes, ZZFeatureMap
from qiskit import QuantumCircuit
from qiskit.visualization import circuit_drawer
# Imports for CIFAR-10s
from torchvision.datasets import CIFAR10
from torchvision import transforms
def prepare_data(X, labels_to_keep, batch_size):
# Filtering out labels (originally 0-9), leaving only labels 0 and 1
filtered_indices = [i for i in range(len(X.targets)) if X.targets[i] in labels_to_keep]
X.data = X.data[filtered_indices]
X.targets = [X.targets[i] for i in filtered_indices]
# Defining dataloader with filtered data
loader = DataLoader(X, batch_size=batch_size, shuffle=True)
return loader
# Set seed for reproducibility
manual_seed(42)
# CIFAR-10 data transformation
transform = transforms.Compose([
transforms.ToTensor(), # convert the images to tensors
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # Normalization usign mean and std.
])
labels_to_keep = [0, 1]
batch_size = 1
# Preparing Train Data
X_train = CIFAR10(root="./data", train=True, download=True, transform=transform)
train_loader = prepare_data(X_train, labels_to_keep, batch_size)
# Preparing Test Data
X_test = CIFAR10(root="./data", train=False, download=True, transform=transform)
test_loader = prepare_data(X_test, labels_to_keep, batch_size)
print(f"Training dataset size: {len(train_loader.dataset)}")
print(f"Test dataset size: {len(test_loader.dataset)}")
# Defining and creating QNN
def create_qnn():
feature_map = ZZFeatureMap(2) # ZZFeatureMap with 2 bits, entanglement between qubits based on the pairwise product of input features.
ansatz = RealAmplitudes(2, reps=1) # parameters (angles, in the case of RealAmplitudes) that are adjusted during the training process to optimize the quantum model for a specific task.
qc = QuantumCircuit(2)
qc.compose(feature_map, inplace=True)
qc.compose(ansatz, inplace=True)
qnn = EstimatorQNN(
circuit=qc,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
input_gradients=True,
)
return qnn
qnn = create_qnn()
# Visualizing the QNN circuit
circuit_drawer(qnn.circuit, output='mpl')
# Defining torch NN module
class Net(Module):
def __init__(self, qnn):
super().__init__()
self.conv1 = Conv2d(3, 16, kernel_size=3, padding=1)
self.conv2 = Conv2d(16, 32, kernel_size=3, padding=1)
self.dropout = Dropout2d()
self.fc1 = Linear(32 * 8 * 8, 64)
self.fc2 = Linear(64, 2) # 2-dimensional input to QNN
self.qnn = TorchConnector(qnn)
self.fc3 = Linear(1, 1) # 1-dimensional output from QNN
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = self.dropout(x)
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
x = self.qnn(x)
x = self.fc3(x)
return cat((x, 1 - x), -1)
# Creating model
model = Net(qnn)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
# Defining model, optimizer, and loss function
optimizer = optim.Adam(model.parameters(), lr=0.001)
loss_func = NLLLoss()
# Starting training
epochs = 10
loss_list = []
model.train()
for epoch in range(epochs):
total_loss = []
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device) # Move data to GPU
optimizer.zero_grad(set_to_none=True)
output = model(data)
loss = loss_func(output, target)
loss.backward()
optimizer.step()
total_loss.append(loss.item())
loss_list.append(sum(total_loss) / len(total_loss))
print("Training [{:.0f}%]\tLoss: {:.4f}".format(100.0 * (epoch + 1) / epochs, loss_list[-1]))
# Plotting loss convergence
plt.plot(loss_list)
plt.title("Hybrid NN Training Convergence")
plt.xlabel("Training Iterations")
plt.ylabel("Neg. Log Likelihood Loss")
plt.show()
# Saving the model
torch.save( model.state_dict(), "model_cifar10_10EPOCHS.pt")
# Loading the model
qnn_cifar10 = create_qnn()
model_cifar10 = Net(qnn_cifar10)
model_cifar10.load_state_dict(torch.load("model_cifar10.pt"))
correct = 0
total = 0
model_cifar10.eval()
with torch.no_grad():
for data, target in test_loader:
output = model_cifar10(data)
_, predicted = torch.max(output.data, 1)
total += target.size(0)
correct += (predicted == target).sum().item()
# Calculating and print test accuracy
test_accuracy = correct / total * 100
print(f"Test Accuracy: {test_accuracy:.2f}%")
# Plotting predicted labels
n_samples_show = 6
count = 0
fig, axes = plt.subplots(nrows=1, ncols=n_samples_show, figsize=(10, 3))
model_cifar10.eval()
with no_grad():
for batch_idx, (data, target) in enumerate(test_loader):
if count == n_samples_show:
break
output = model_cifar10(data)
if len(output.shape) == 1:
output = output.reshape(1, *output.shape)
pred = output.argmax(dim=1, keepdim=True)
axes[count].imshow(np.transpose(data[0].numpy(), (1, 2, 0)))
axes[count].set_xticks([])
axes[count].set_yticks([])
axes[count].set_title("Predicted {0}\n Actual {1}".format(pred.item(), target.item()))
count += 1
plt.show()
|
https://github.com/EusseJhoan/DeutschJosza_algorithm
|
EusseJhoan
|
from qiskit import QuantumCircuit, transpile, Aer
from qiskit.visualization import plot_histogram
import numpy as np
sim = Aer.get_backend('aer_simulator')
def U_f1(qc):
return qc
def U_f2(qc):
qc.x(1) #Compuerta X al segundo qubit
return qc
def U_f3(qc):
qc.cx(0,1) #Compuerta CNOT entre primer y segundo quibit (el primero es el que controla)
return qc
def U_f4(qc):
qc.cx(0,1) #Compuerta CNOT entre primer y segundo quibit (el primero es el que controla)
qc.x(1) #Compuerta X al segundo qubit
return qc
def Deutsch(U_f):
qc=QuantumCircuit(2,1) #Se crea un circuito cuántico con 2 bits cuánticos y 1 canal clásico
qc.x(1) #Compuerta X al segundo qubit (inicializar estado |1>)
qc.h(0) #Compuerta H al primer qubit
qc.h(1) #Compuerta H al segundo qubit
qc.barrier() #Barrera (empieza oráculo)
qc = U_f(qc) #Agregamos el oráculo
qc.barrier() #Barrera (termina oráculo)
qc.h(0) #Compuerta H al primer qubit
qc.measure(0,0) #Medimos el primer qubit y enviamos señal al canal clásico
return qc
qc=Deutsch(U_f1) # definición circuito con oráculo usando f_1(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f2) #definición circuito con oráculo usando f_2(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas del simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f3) #definición circuito con oráculo usando f_3(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=Deutsch(U_f4) #definición circuito con oráculo usando f_4(x)
display(qc.draw()) # visualización del circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
#oráculo para f(x) constante para un número n de bits en el registro
def constant(qc,n):
ran=np.random.randint(2) #selección aleatoria de 0 ó 1
if ran == 1:
qc.x(n) #si el número aleatorio es 1 se pone compuerta X en el objetivo (se induce fase global -1 al registro)
return qc
#oráculo para f(x) balanceado para un número n de bits en el registro
def balanced(qc,n):
for i in range(n):
qc.cx(i,n) #se crea una CNOT entre cada qubit del registro y el objetivo (los qubits del registro controlan)
ran=np.random.randint(2) #selección aleatoria de 0 ó 1
if ran == 1:
qc.x(n) #si el número aleatorio es 1 se pone compuerta X en el objetivo (se induce fase global -1 al registro)
return qc
def D_J(U_f,n):
qc=QuantumCircuit(n+1,n) #Se crea un circuito cuántico con n+1 quibits y n canales clásicos
qc.x(n) #Compuerta X al bit del registro
for i in range(n+1):
qc.h(i) #Compuerta H a todos los bits
qc.barrier() #Barrera (empieza oráculo)
qc = U_f(qc,n) #Agregamos el oráculo
qc.barrier() #Barrera (termina oráculo)
for i in range(n):
qc.h(i) #Compuerta H a los n bits del registro
qc.measure(i,i) #Medición los n bits del registro
return qc
qc=D_J(constant,3) #definición circuito con oráculo constante y 3 bits en registro
display(qc.draw()) #ver circuito
counts = sim.run(qc).result().get_counts() #contando las medidas de simulador cuántico
plot_histogram(counts) #histrograma de resultados
qc=D_J(balanced,3)
display(qc.draw())
counts = sim.run(qc).result().get_counts()
plot_histogram(counts)
|
https://github.com/strangequarkkk/BB84-Protocol-for-QKD
|
strangequarkkk
|
import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(assemble(qc))
plot_histogram(job.result().get_counts())
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(assemble(qc))
plot_histogram(job.result().get_counts())
n = 100
## Step 1
# Alice generates bits.
alice_bits = np.random.randint(0,2,n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = np.random.randint(0,2,n)
# Function to compare the bits & bases generated by alice, and then 'encode' the message. Basically determines the state of the qubit/photon to send.
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
# Alice computes the encoded message using the function defined above.
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = np.random.randint(0,2,n)
# Function to decode the message sent by alice by comparing qubit/photon states with Bob's generated bases.
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
qobj = assemble(message[q], shots=1, memory=True)
result = aer_sim.run(qobj).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
# Decode the message according to his bases
bob_results = measure_message(message, bob_bases)
## Step 4
# Function to perform sifting i.e. disregard the bits for which Bob's & A;ice's bases didnot match.
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
# Performing sifting for Alice's and Bob's bits.
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print("Alice's key after sifting (without interception)", alice_key)
print("Bob's key after sifting (without interception) ", bob_key)
# # Step 5
# # Function for parameter estimation i.e. determining the error rate by comparing subsets taen from both Alice's key & Bob's key.
# def sample_bits(bits, selection):
# sample = []
# for i in selection:
# # use np.mod to make sure the
# # bit we sample is always in
# # the list range
# i = np.mod(i, len(bits))
# # pop(i) removes the element of the
# # list at index 'i'
# sample.append(bits.pop(i))
# return sample
# # Performing parameter estimation & disregarding the bits used for comparison from Alice's & Bob's key.
# sample_size = 15
# bit_selection = np.random.randint(0,n,size=sample_size)
# bob_sample = sample_bits(bob_key, bit_selection)
# alice_sample = sample_bits(alice_key, bit_selection)
num = 0
for i in range(0,len(bob_key)):
if alice_key[i] == bob_key[i]:
num = num + 1
matching_bits = (num/len(bob_key))*100
print(matching_bits,"% of the bits match.")
## Step 1
alice_bits = np.random.randint(2, size=n)
## Step 2
alice_bases = np.random.randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = np.random.randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = np.random.randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print("Alice's key after sifting (with interception)", alice_key)
print("Bob's key after sifting (with interception) ", bob_key)
# ## Step 5
# sample_size = 15
# bit_selection = np.random.randint(n, size=sample_size)
# bob_sample = sample_bits(bob_key, bit_selection)
# alice_sample = sample_bits(alice_key, bit_selection)
num = 0
for i in range(0,len(bob_key)):
if alice_key[i] == bob_key[i]:
num = num + 1
matching_bits = (num/len(bob_key))*100
print(matching_bits,"% of the bits match.")
plt.rcParams['axes.linewidth'] = 2
mpl.rcParams['font.family'] = ['Georgia']
plt.figure(figsize=(10.5,6))
ax=plt.axes()
ax.set_title('')
ax.set_xlabel('$n$ (Number of bits drawn from the sifted keys for determining error rate)',fontsize = 18,labelpad=10)
ax.set_ylabel(r'$P(Eve\ detected)$',fontsize = 18,labelpad=10)
ax.xaxis.set_tick_params(which='major', size=8, width=2, direction='in', top='on')
ax.yaxis.set_tick_params(which='major', size=8, width=2, direction='in', top='on')
ax.tick_params(axis='x', labelsize=20)
ax.tick_params(axis='y', labelsize=20)
ax. xaxis. label. set_size(20)
ax. yaxis. label. set_size(20)
n = 30
x = np.arange(n+1)
y = 1 - 0.75**x
ax.plot(x,y,color = plt.cm.rainbow(np.linspace(0, 1, 5))[0], marker = "s", markerfacecolor='r')
|
https://github.com/luis6156/Shor-s-Quantum-Algorithm
|
luis6156
|
from qiskit import QuantumCircuit, Aer, execute, IBMQ
from qiskit.utils import QuantumInstance
import numpy as np
from qiskit.algorithms import Shor
IBMQ.enable_account('ENTER API TOKEN HERE') # Enter your API token here
provider = IBMQ.get_provider(hub='ibm-q')
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=1000)
my_shor = Shor(quantum_instance)
result_dict = my_shor.factor(15)
print(result_dict)
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
with open('in-exemplo.txt', 'r') as f:
print(f.read())
with open('out-exemplo.txt', 'r') as f:
print(f.read())
import time
import matplotlib.pyplot as plt
import pandas as pd
import os
import subprocess
%matplotlib inline
#Roda entradas
def roda_com_entrada(executavel, arquivo_in, envs = '1', deb = '0'):
with open(arquivo_in) as f:
start = time.perf_counter()
a = f.read()
proc = subprocess.run([executavel], input=a, text=True, capture_output=True, env=dict(OMP_NUM_THREADS=envs, DEBUG=deb, **os.environ))
end = time.perf_counter()
f.close()
ret = ''
for i in a:
if i == "\n":
break
ret += i
return (proc.stdout, end - start, int(ret))
v
#retorna tamanho do tour apartir do stdout
buf = ''
for i in out:
if i == " ":
return float(buf)
buf += i
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
resultados1 = []
resultados2 = []
resultados3 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca_local_antigo','busca-exaustiva/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt')
c = roda_com_entrada('./heuristico/heuristico','busca-exaustiva/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
resultados1.append(tamanho_tour(a[0]))
resultados2.append(tamanho_tour(b[0]))
resultados3.append(tamanho_tour(c[0]))
#Teste com entrada um pouco maior
print("Rodando entrada: 8")
tempos.append(roda_com_entrada('./busca_local_antigo','maior.txt')[1])
tempos_1.append(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[1])
tempos_2.append(roda_com_entrada('./heuristico/heuristico','maior.txt')[1])
tamanho_entradas.append(roda_com_entrada('./busca-local/busca-local','maior.txt')[2])
resultados1.append(tamanho_tour(roda_com_entrada('./busca_local_antigo','maior.txt')[0]))
resultados2.append(tamanho_tour(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[0]))
resultados3.append(tamanho_tour(roda_com_entrada('./heuristico/heuristico','maior.txt')[0]))
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-exaustiva", "busca-local","heuristico"])
plt.show()
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-local","heuristico"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-tempo"] = pd.Series(tempos)
df["busca-exaustiva-tempo"] = pd.Series(tempos_1)
df["heuristica-tempo"] = pd.Series(tempos_2)
df["busca-local-resultado"] = pd.Series(resultados1)
df["busca-exaustiva-resultado"] = pd.Series(resultados2)
df["heuristica-resultado"] = pd.Series(resultados3)
df
df.describe()
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
tempos_3 = []
tempos_4 = []
tempos_5 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','2')
c = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','3')
d = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','4')
e = roda_com_entrada('./busca_local_antigo','busca-local/in-'+str(i)+'.txt')
f = roda_com_entrada('./busca-local/busca-local-gpu','busca-local/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tempos_3.append(d[1])
tempos_4.append(e[1])
tempos_5.append(f[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.plot(tamanho_entradas, tempos_3)
plt.legend(["1 thread otimizado", "2 threads otimizado","3 threads otimizado", "4 threads otimizado", "Sem otimizações"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_3)
plt.plot(tamanho_entradas, tempos_5)
plt.legend(["4 thread otimizado", "GPU"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_4)
plt.legend(["1 thread otimizado", "Sem otimizações"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-1-thread"] = pd.Series(tempos)
df["busca-local-2-threads"] = pd.Series(tempos_1)
df["busca-local-3-threads"] = pd.Series(tempos_2)
df["busca-local-4-threads"] = pd.Series(tempos_3)
df["busca-local-gpu"] = pd.Series(tempos_5)
df["busca-local-semopt"] = pd.Series(tempos_4)
df
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
if i != 7:
a = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '1')
tempos.append(a[1])
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '8', '0')
c = roda_com_entrada('./busca-exaustiva-apenasbb','busca-exaustiva/in-'+str(i)+'.txt', '1', '0')
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas[:-1], tempos)
plt.plot(tamanho_entradas[:-1], tempos_2[:-1])
plt.legend(["Exaustivo Simples", "Exaustivo Branch and Bound"])
plt.show()
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["Branch and Bound Paralelo", "Branch and Bound Simples"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-exaustiva-simples"] = pd.Series(tempos)
df["busca-exaustiva-branchnbound"] = pd.Series(tempos_2)
df["busca-exaustiva-branchnbound-par"] = pd.Series(tempos_1)
df
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
with open('in-exemplo.txt', 'r') as f:
print(f.read())
with open('out-exemplo.txt', 'r') as f:
print(f.read())
import time
import matplotlib.pyplot as plt
import pandas as pd
import os
import subprocess
%matplotlib inline
#Roda entradas
def roda_com_entrada(executavel, arquivo_in, envs = '1', deb = '0'):
with open(arquivo_in) as f:
start = time.perf_counter()
a = f.read()
proc = subprocess.run([executavel], input=a, text=True, capture_output=True, env=dict(OMP_NUM_THREADS=envs, DEBUG=deb, **os.environ))
end = time.perf_counter()
f.close()
ret = ''
for i in a:
if i == "\n":
break
ret += i
return (proc.stdout, end - start, int(ret))
#retorna tamanho do tour apartir do stdout
def tamanho_tour(out):
buf = ''
for i in out:
if i == " ":
return float(buf)
buf += i
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
resultados1 = []
resultados2 = []
resultados3 = []
#Usando as mesmas entradas
for i in range(8):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca_local_antigo','busca-exaustiva/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt')
c = roda_com_entrada('./heuristico/heuristico','busca-exaustiva/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tamanho_entradas.append(a[2])
resultados1.append(tamanho_tour(a[0]))
resultados2.append(tamanho_tour(b[0]))
resultados3.append(tamanho_tour(c[0]))
#Teste com entrada um pouco maior
print("Rodando entrada: 8")
tempos.append(roda_com_entrada('./busca_local_antigo','maior.txt')[1])
tempos_1.append(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[1])
tempos_2.append(roda_com_entrada('./heuristico/heuristico','maior.txt')[1])
tamanho_entradas.append(roda_com_entrada('./busca-local/busca-local','maior.txt')[2])
resultados1.append(tamanho_tour(roda_com_entrada('./busca_local_antigo','maior.txt')[0]))
resultados2.append(tamanho_tour(roda_com_entrada('./busca-exaustiva/busca-exaustiva','maior.txt')[0]))
resultados3.append(tamanho_tour(roda_com_entrada('./heuristico/heuristico','maior.txt')[0]))
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-exaustiva", "busca-local","heuristico"])
plt.show()
plt.title("Comparacao Desempenho")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_2)
plt.legend(["busca-local","heuristico"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-tempo"] = pd.Series(tempos)
df["busca-exaustiva-tempo"] = pd.Series(tempos_1)
df["heuristica-tempo"] = pd.Series(tempos_2)
df["busca-local-resultado"] = pd.Series(resultados1)
df["busca-exaustiva-resultado"] = pd.Series(resultados2)
df["heuristica-resultado"] = pd.Series(resultados3)
df
df.describe()
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
tempos_2 = []
tempos_3 = []
tempos_4 = []
tempos_5 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt')
b = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','2')
c = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','3')
d = roda_com_entrada('./busca-local/busca-local-paralela','busca-local/in-'+str(i)+'.txt','4')
e = roda_com_entrada('./busca_local_antigo','busca-local/in-'+str(i)+'.txt')
f = roda_com_entrada('./busca-local/busca-local-gpu','busca-local/in-'+str(i)+'.txt')
tempos.append(a[1])
tempos_1.append(b[1])
tempos_2.append(c[1])
tempos_3.append(d[1])
tempos_4.append(e[1])
tempos_5.append(f[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.plot(tamanho_entradas, tempos_2)
plt.plot(tamanho_entradas, tempos_3)
plt.legend(["1 thread otimizado", "2 threads otimizado","3 threads otimizado", "4 threads otimizado", "Sem otimizações"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos_3)
plt.plot(tamanho_entradas, tempos_5)
plt.legend(["4 thread otimizado", "GPU"])
plt.show()
plt.title("Comparacao Desempenho Busca Local")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_4)
plt.legend(["1 thread otimizado", "Sem otimizações"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-local-1-thread"] = pd.Series(tempos)
df["busca-local-2-threads"] = pd.Series(tempos_1)
df["busca-local-3-threads"] = pd.Series(tempos_2)
df["busca-local-4-threads"] = pd.Series(tempos_3)
df["busca-local-gpu"] = pd.Series(tempos_5)
df["busca-local-semopt"] = pd.Series(tempos_4)
df
#Cria resultados
tamanho_entradas = []
tempos = []
tempos_1 = []
#Usando as mesmas entradas
for i in range(7):
print("Rodando entrada: "+str(i))
a = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '1')
b = roda_com_entrada('./busca-exaustiva/busca-exaustiva','busca-exaustiva/in-'+str(i)+'.txt', '1', '0')
tempos.append(a[1])
tempos_1.append(b[1])
tamanho_entradas.append(a[2])
plt.title("Comparacao Desempenho Busca Exaustiva")
plt.ylabel("Tempo (s)")
plt.xlabel("Tamanho entradas")
plt.plot(tamanho_entradas, tempos)
plt.plot(tamanho_entradas, tempos_1)
plt.legend(["Exaustivo Simples", "Exaustivo Branch and Bound"])
plt.show()
df = pd.DataFrame()
df["Tamanho Entrada"] = pd.Series(tamanho_entradas)
df["busca-exaustiva-simples"] = pd.Series(tempos)
df["busca-exaustiva-branchnbound"] = pd.Series(tempos_1)
df
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
import math
import matplotlib.pyplot as plt
%matplotlib inline
class TSP:
def __init__(self):
self.flat_mat = flat_mat
self.n = 0
self.melhor_dist = 1e11
self.pontos = []
self.melhores_pontos = []
def busca_exaustiva(self, flat_mat, n, ite):
if ite == n:
dist = 0
for j in range(1, n):
dist += flat_mat[self.pontos[j-1] * n + self.pontos[j]]
dist += flat_mat[self.pontos[n-1] * n + self.pontos[0]]
if dist < self.melhor_dist:
self.melhor_dist = dist
self.melhores_pontos = self.pontos[:]
return
for i in range(n):
if self.pontos[i] == -1:
self.pontos[i] = ite
self.busca_exaustiva(flat_mat, n, ite + 1)
self.pontos[i] = -1
def dist_mat(self):
x = []
y = []
flat_mat = [] #matriz 1 dimensao contendo todas as distancias possiveis entre os pontos para facilitar cálculo.
while True:
try:
temp = input("Digite a coordenada x y: ").split()
x.append(float(temp[0]))
y.append(float(temp[1]))
except:
break
for i in range(len(x)):
for j in range(len(y)):
flat_mat.append(math.sqrt((x[i] - x[j])**2 + (y[i] - y[j])**2))
return flat_mat, x, y
def get_results(self):
self.flat_mat, x, _ = self.dist_mat()
self.n = len(x)
self.pontos = [-1]*self.n
self.pontos[0] = 0
self.busca_exaustiva(self.flat_mat, self.n, 1)
return self.melhor_dist, self.melhores_pontos
Tsp = TSP()
distancia, pontos = Tsp.get_results()
print("Melhor distancia encontrada: ", distancia)
print("Melhor caminho encontrado: ", pontos)
#plota gráfico
def connectpoints(x,y,p1,p2):
x1, x2 = x[p1], x[p2]
y1, y2 = y[p1], y[p2]
plt.plot([x1,x2],[y1,y2],'ro-')
for i in range(1, len(pontos)):
connectpoints(x,y,pontos[i-1],pontos[i])
connectpoints(x,y,pontos[len(x)-1],pontos[0])
plt.title("Percurso")
plt.show()
%%time
%%cmd
python TSP.py < in-1.txt
type out-1.txt
python TSP.py < in-2.txt
type out-2.txt
python TSP.py < in-3.txt
type out-3.txt
python TSP.py < in-4.txt
type out-4.txt
from qiskit import IBMQ
import numpy as np
#IBMQ.save_account('seu-tokenIBMQ-para-rodar-localmente')
IBMQ.load_account()
from qiskit import Aer
from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua import aqua_globals
from qiskit.aqua import QuantumInstance
from qiskit.optimization.applications.ising.common import sample_most_likely
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.problems import QuadraticProgram
import logging
from qiskit.aqua import set_qiskit_aqua_logging
#Preparando os dados segundo os imputs do usuario para serem resolvidos pelo qiskit max 4 pontos por limitação de qubits
coord = []
flat_mat, x, y = TSP().dist_mat()
dist_mat = np.array(flat_mat).reshape(len(x),len(x))
for i, j in zip(x, y):
coord.append([i,j])
ins = tsp.TspData('TSP_Q', dim=len(x), coord=np.array(coord), w=dist_mat)
qubitOp, offset = tsp.get_operator(ins)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
#Usando o numpyMinimumEigensolver como o solver do problema para resolver de forma quantica
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
print('energy:', result.eigenvalue.real)
print('tsp objective:', result.eigenvalue.real + offset)
x_Q = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
for i in range(1, len(z)):
connectpoints(x,y,z[i-1],z[i])
connectpoints(x,y,z[len(x)-1],z[0])
plt.title("Percurso")
plt.show()
#instanciando o simulador ou o computador real importante lembrar que nao ira funcionar para mais de 4 pontos pelo numero de qubits disponibilizados pela IBM que sao apenas 16 para o simulador qasm e 15 para a maquina quantica
provider = IBMQ.get_provider(hub = 'ibm-q')
device = provider.get_backend('ibmq_16_melbourne')
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('qasm_simulator')
#descomentar essa linha caso queira rodar na maquina real
#backend = device
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
#rodando no simulador quantico
spsa = SPSA(maxiter=10)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
result = vqe.run(quantum_instance)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
|
https://github.com/hugoecarl/TSP-Problem-Study
|
hugoecarl
|
import math
import matplotlib.pyplot as plt
%matplotlib inline
class TSP:
def __init__(self):
self.flat_mat = flat_mat
self.n = 0
self.melhor_dist = 1e11
self.pontos = []
self.melhores_pontos = []
def busca_exaustiva(self, flat_mat, n, ite):
if ite == n:
dist = 0
for j in range(1, n):
dist += flat_mat[self.pontos[j-1] * n + self.pontos[j]]
dist += flat_mat[self.pontos[n-1] * n + self.pontos[0]]
if dist < self.melhor_dist:
self.melhor_dist = dist
self.melhores_pontos = self.pontos[:]
return
for i in range(n):
if self.pontos[i] == -1:
self.pontos[i] = ite
self.busca_exaustiva(flat_mat, n, ite + 1)
self.pontos[i] = -1
def dist_mat(self):
x = []
y = []
flat_mat = [] #matriz 1 dimensao contendo todas as distancias possiveis entre os pontos para facilitar cálculo.
while True:
try:
temp = input("Digite a coordenada x y: ").split()
x.append(float(temp[0]))
y.append(float(temp[1]))
except:
break
for i in range(len(x)):
for j in range(len(y)):
flat_mat.append(math.sqrt((x[i] - x[j])**2 + (y[i] - y[j])**2))
return flat_mat, x, y
def get_results(self):
self.flat_mat, x, _ = self.dist_mat()
self.n = len(x)
self.pontos = [-1]*self.n
self.pontos[0] = 0
self.busca_exaustiva(self.flat_mat, self.n, 1)
return self.melhor_dist, self.melhores_pontos
Tsp = TSP()
distancia, pontos = Tsp.get_results()
print("Melhor distancia encontrada: ", distancia)
print("Melhor caminho encontrado: ", pontos)
#plota gráfico
def connectpoints(x,y,p1,p2):
x1, x2 = x[p1], x[p2]
y1, y2 = y[p1], y[p2]
plt.plot([x1,x2],[y1,y2],'ro-')
for i in range(1, len(pontos)):
connectpoints(x,y,pontos[i-1],pontos[i])
connectpoints(x,y,pontos[len(x)-1],pontos[0])
plt.title("Percurso")
plt.show()
%%time
%%cmd
python TSP.py < in-1.txt
type out-1.txt
python TSP.py < in-2.txt
type out-2.txt
python TSP.py < in-3.txt
type out-3.txt
python TSP.py < in-4.txt
type out-4.txt
from qiskit import IBMQ
import numpy as np
#IBMQ.save_account('seu-tokenIBMQ-para-rodar-localmente')
IBMQ.load_account()
from qiskit import Aer
from qiskit.tools.visualization import plot_histogram
from qiskit.circuit.library import TwoLocal
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua import aqua_globals
from qiskit.aqua import QuantumInstance
from qiskit.optimization.applications.ising.common import sample_most_likely
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.problems import QuadraticProgram
import logging
from qiskit.aqua import set_qiskit_aqua_logging
#Preparando os dados segundo os imputs do usuario para serem resolvidos pelo qiskit max 4 pontos por limitação de qubits
coord = []
flat_mat, x, y = TSP().dist_mat()
dist_mat = np.array(flat_mat).reshape(len(x),len(x))
for i, j in zip(x, y):
coord.append([i,j])
ins = tsp.TspData('TSP_Q', dim=len(x), coord=np.array(coord), w=dist_mat)
qubitOp, offset = tsp.get_operator(ins)
print('Offset:', offset)
print('Ising Hamiltonian:')
print(qubitOp.print_details())
#Usando o numpyMinimumEigensolver como o solver do problema para resolver de forma quantica
ee = NumPyMinimumEigensolver(qubitOp)
result = ee.run()
print('energy:', result.eigenvalue.real)
print('tsp objective:', result.eigenvalue.real + offset)
x_Q = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
for i in range(1, len(z)):
connectpoints(x,y,z[i-1],z[i])
connectpoints(x,y,z[len(x)-1],z[0])
plt.title("Percurso")
plt.show()
#instanciando o simulador ou o computador real importante lembrar que nao ira funcionar para mais de 4 pontos pelo numero de qubits disponibilizados pela IBM que sao apenas 16 para o simulador qasm e 15 para a maquina quantica
provider = IBMQ.get_provider(hub = 'ibm-q')
device = provider.get_backend('ibmq_16_melbourne')
aqua_globals.random_seed = np.random.default_rng(123)
seed = 10598
backend = Aer.get_backend('qasm_simulator')
#descomentar essa linha caso queira rodar na maquina real
#backend = device
quantum_instance = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
#rodando no simulador quantico
spsa = SPSA(maxiter=10)
ry = TwoLocal(qubitOp.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubitOp, ry, spsa, quantum_instance=quantum_instance)
result = vqe.run(quantum_instance)
print('energy:', result.eigenvalue.real)
print('time:', result.optimizer_time)
x = sample_most_likely(result.eigenstate)
print('feasible:', tsp.tsp_feasible(x_Q))
z = tsp.get_tsp_solution(x_Q)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
|
https://github.com/LeanderThiessen/antisymmetrization-circuit
|
LeanderThiessen
|
#General Imports
import numpy as np
import matplotlib.pyplot as plt
import time
from itertools import product,permutations
from string import ascii_lowercase as asc
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
#Qiskit Imports
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, transpile
from qiskit.circuit.library.standard_gates import MCXGate, CXGate, XGate, CSwapGate
from qiskit.circuit.library import Diagonal
from qiskit.quantum_info import partial_trace,purity
#############FUNCTIONS###########################################################################################################
#wrapper for measuring time taken by function 'func'
def timeis(func):
def wrap(*args,**kwargs):
start = time.time()
result = func(*args,**kwargs)
end = time.time()
if measure_time:
print("{} took {:.2f}s".format(func.__name__,end-start))
return result
return wrap
#check if inputs are valid
def check_inputs(n,m):
if n == 1:
print("Case n=1 currently not supported")
correct = 1
if m>2**n:
correct == 0
if correct == 1:
print("Inputs valid")
return 0
#initialize quantum circuit with electron register, swap_ancillas, record_ancillas, collision_ancillas
def initialize_circuit(n,m,L):
circuit = QuantumCircuit()
#add main electron register (seed/target)
for e in range(m):
r_q = QuantumRegister(n,'{}'.format(asc[e]))#asc[i]=ith letter of the alphabe
c = QuantumCircuit(r_q)
circuit = circuit.combine(c)
#add ancillas for comparator_swaps
for k in range(int(np.ceil(m/2))):
anc_q = QuantumRegister(n-1,'anc_{}'.format(k))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add 'record' register for storing outcomes of comparators
for l in range(L):
anc_q = QuantumRegister(1,'record_{}'.format(l))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add ancillas to store the occurence of collisions between pairs of electrons
for c in range(m-1):
anc_q = QuantumRegister(1,'coll_record_{}'.format(c))
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
#add one ancilla to store if all other collision ancillas are '1'
anc_q = QuantumRegister(1,'collision_test')
c = QuantumCircuit(anc_q)
circuit = circuit.combine(c)
return circuit
#returns x in binary format as string of length n, incl leading zeros
def binary_n(x,n):
return bin(x)[2:].zfill(n)
#initializes j-th electron register with number x
def binary_init(circuit,n,m,input):
for k,e in enumerate(input):
e_bin = binary_n(e,n)
for i in range(n):
if e_bin[i]=='1':
circuit.append(XGate(),[i+k*n])
return circuit
#Apply a Hadamard gate to each qubit in the electron register
def Hadamard(circuit,n,m):
for q in range(n*m):
circuit.h(q)
return circuit
#Compare bits at positions x and y, only output=(x<y) to position anc
def bit_compare(circuit,cbits,control,debug=True):
x = cbits[0]
y = cbits[1]
anc = cbits[2]
if debug:
circuit.barrier()
#control='01' for initial sorting and '10' for collision detection
circuit.append(MCXGate(2,ctrl_state=control),[x,y,anc])
if debug:
circuit.barrier()
return circuit
#split the array 'index' into array of pairs of adjacent indices; first entry is (e.g.) [0] if number of entries of index is odd
def get_subsets(index):
#index = [0,1,2,3] -> result = [[0,1],[2,3]]
#index = [0,1,2,3,4] -> result = [[0],[1,2],[3,4]]
M = len(index)
result = []
if M % 2 != 0:
result.append(np.array([0]))
n_split = int((M-1)/2)
for s in np.split(index[1:M],n_split):
result.append(s)
else:
result = np.split(index,M/2)
return result
#get position of first qubit in swap_control ancilla register
def get_first_swap_ctrl(n,m):
#n_comp_parallel is the number of comparators that are applied in each layer
#n*m = main register for storing electron registers;
#(n_comp_parallel)*(n-1) = fixed ancilla register needed for compare_n
n_comp_parallel = int(np.ceil(m/2))
ctrl_0 = n*m + (n-1)*n_comp_parallel
return ctrl_0
#get position of first qubit in collision_control ancilla register
def get_first_coll_ctrl(n,m,L):
coll_0 = get_first_swap_ctrl(n,m) + L
return coll_0
#return pairs of electron indices that need to be compared in collision-detection step
def get_coll_sets(m):
ind = np.arange(m)
if m == 2:
sets_a = [np.array([0,1])]
sets_b = []
return sets_a,sets_b
if m % 2 == 0:
sets_a = np.split(ind,m/2)
sets_b = np.split(ind[1:-1],(m-2)/2)
else:
sets_a = np.split(ind[:-1],(m-1)/2)
sets_b = np.split(ind[1:],(m-1)/2)
#all gates in sets_a can be applied in parallel
#all gates in sets_b can be applied in parallel
return sets_a,sets_b
#returns the first qubit position of the ancilla register used for swap of i and j (only really tested for m<6)
def get_anc(n,m,i,j):
if abs(j-i) == 1:
anc_reg = int( np.min([i,j])/2 )
elif abs(j-i) == 2:
anc_reg = int( np.ceil( np.min([i,j])/2 ))
else:
anc_reg = int( np.min([i,j]) )
anc = n*m + anc_reg*(n-1)
return anc
#Implement 'Compare2' function (Fig 3); input: two 2bit numbers, output: two 1bit numbers with same ordering
def compare_2(circuit,x_0,x_1,y_0,y_1,anc):
#Notation: x = 2^1*x_0 + x_1 (reverse from paper!!)
#compares numbers x,y and outputs two bits x',y' (at positions x_1 and y_1) with the same ordering
circuit.append(XGate(),[anc])
circuit.append(CXGate(),[y_0,x_0])
circuit.append(CXGate(),[y_1,x_1])
circuit.append(CSwapGate(),[x_0,x_1,anc])
circuit.append(CSwapGate(),[x_0,y_0,y_1])
circuit.append(CXGate(),[y_1,x_1])
return circuit
#Generalisation of 'compare2' two nbit numbers, output: two 1bit numbers with same ordering at positions x1,y1
def compare_n(circuit,n,m,i,j,l,L,debug):
index = np.arange(n)
subsets = get_subsets(index)
M = len(subsets)
anc = get_anc(n,m,i,j)
for s in subsets:
if len(s)==2:
if debug:
circuit.barrier()
x_0 = s[0] + i*n
x_1 = s[1] + i*n
y_0 = s[0] + j*n
y_1 = s[1] + j*n
circuit = compare_2(circuit,x_0,x_1,y_0,y_1,anc)
anc += 1
while (len(subsets)>1):
index = np.array([subsets[k][-1] for k in range(M)])
subsets = get_subsets(index)
M = len(subsets)
for s in subsets:
if len(s)==2:
if debug:
circuit.barrier()
x_0 = s[0] + i*n
x_1 = s[1] + i*n
y_0 = s[0] + j*n
y_1 = s[1] + j*n
circuit = compare_2(circuit,x_0,x_1,y_0,y_1,anc)
anc += 1
########################################################################################################################################
#at this point the bits x_1 and y_1 have the same ordering as numbers stored in registers i and j
#e(i)<e(j) -> x_1=0 and y_1=1
#e(i)>e(j) -> x_1=1 and y_1=0
#e(i)=e(j) -> x_1=0 y_1=0 if e(i) even or x_1=1 y_1=1 if e(i) odd
#prepare output for bit_compare function; anc iterates through the second ancilla register (+1 for each comparator)
#l = current swap; each new swap gets a new ancilla for storing the outcome
anc = get_first_swap_ctrl(n,m) + l
cbits = x_1,y_1,anc
return circuit,cbits
#apply diagonal phase shift to qubit i, conditioned on qubit 'ctrl'
def cphase_shift(circuit,ctrl,i):
target = i*n
CDiag = Diagonal([-1,-1]).control(1)
CDiag = CDiag.to_gate()
CDiag.label = "D" #doesn't work currently
circuit.append(CDiag,[ctrl,target])
return circuit
#performs swap of registers i and j conditioned on ancilla qubit 'ctrl'
def swap_registers(circuit,n,i,j,ctrl,debug):
for g in range(n):
circuit.append(CSwapGate(),[ctrl,i*n+g,j*n+g])
if debug:
circuit.barrier()
return circuit
#compare electron registers i and j; swap registers iff e(i)<(j); l=current swap (0 to L)
def comparator_swap(n,m,i,j,l,L,phase,debug):
#Perform comparison to generate output qubits "cbits"
circuit_compute = initialize_circuit(n,m,L)
circuit_compute,cbits = compare_n(circuit_compute,n,m,i,j,l,L,debug)
#Add bit_compare between the two output qubits and store in ancilla
circuit_bit_compare = initialize_circuit(n,m,L)
circuit_bit_compare = bit_compare(circuit_bit_compare,cbits,'10',debug)
#add uncomputing step only of the comparison circuit
circuit_uncompute = circuit_compute.inverse()
#Swap registers based on control ancilla
circuit_swap = initialize_circuit(n,m,L)
#apply a conditioned phase shift to the first qubit of the register pair; is only called when sn is applied backwards, that's why it's (phase,swap) and not (swap,phase)
if phase:
circuit_swap = cphase_shift(circuit_swap,cbits[2],i)
circuit_swap = swap_registers(circuit_swap,n,i,j,cbits[2],debug)
#Combine circuits
circuit_comparator = circuit_compute + circuit_bit_compare + circuit_uncompute + circuit_swap
return circuit_comparator
#Apply the sorting network sn, where each comparator stores the outcome in ctrl_register
def apply_sorting_network(circuit,n,m,sn,L,phase,debug):
for l,swap in enumerate(sn):
#swap = [i, j, direction]; dir = 0 : descending (from the top); dir = 1 : ascending (from the top)
if swap[2]==0:
i = swap[0]
j = swap[1]
if swap[2]==1:
i = swap[1]
j = swap[0]
circuit_comparator = comparator_swap(n,m,i,j,l,L,phase,debug)
circuit = circuit + circuit_comparator
return circuit
#Apply the reverse of the sorting networkl sn for antisymmetrizing the input state
def apply_reverse_sorting_network(circuit,n,m,sn,L,phase,debug):
circuit_sn = initialize_circuit(n,m,L)
circuit_sn = apply_sorting_network(circuit_sn,n,m,sn,L,phase,debug)
#reverse all gates in the circuit
circuit_reverse_sn = circuit_sn.inverse()
circuit = circuit + circuit_reverse_sn
return circuit
#reset first register to [|0>,|0>,|0>,...] (all zeros)
def reset_electrons(circuit,n,m):
circuit.barrier()
for g in range(m):
g_indices = np.arange(g*n,(g+1)*n) #classical register positions for electron g
for g_i in g_indices:
circuit.reset(g_i)
return circuit
#reset all registers except for the main electron register
def reset_ancillas(circuit,n,m,L):
circuit.barrier()
start = n*m
end = get_first_coll_ctrl(n,m,L) + m
for q in range(start,end):
circuit.reset(q)
return circuit
#Perform comparisons between all adjacent electron registers, with ctrl ancilla in the coll_register
def collision_compare(circuit,n,m,L,debug):
#all sets in sets_a can be applied simultaneously (same for sets_b); both for loops are otherwise identical and could be combined
sets_a,sets_b = get_coll_sets(m)
c = 0
for s in sets_a:
circuit_coll_test = initialize_circuit(n,m,L)
i = s[0]
j = s[1]
circuit_coll_test,cbits = compare_n(circuit_coll_test,n,m,i,j,0,L,debug)
x_1 = cbits[0]
y_1 = cbits[1]
coll_anc = get_first_coll_ctrl(n,m,L) + c
cbits = [x_1,y_1,coll_anc]
circuit_coll_test_reverse = circuit_coll_test.inverse()
circuit = circuit + circuit_coll_test
circuit = bit_compare(circuit,cbits,'01',debug)
circuit = circuit + circuit_coll_test_reverse
c+=1
for s in sets_b:
circuit_coll_test = initialize_circuit(n,m,L)
i = s[0]
j = s[1]
circuit_coll_test,cbits = compare_n(circuit_coll_test,n,m,i,j,0,L,debug)
x_1 = cbits[0]
y_1 = cbits[1]
coll_anc = get_first_coll_ctrl(n,m,L) + c
cbits = [x_1,y_1,coll_anc]
circuit_coll_test_reverse = circuit_coll_test.inverse()
circuit = circuit + circuit_coll_test
circuit = bit_compare(circuit,cbits,'01',debug)
circuit = circuit + circuit_coll_test_reverse
c+=1
return circuit
#apply X gate on last qubit, conditioned on all other coll_ancillas being 1 (which means that all elctron registers are different)
def collision_test(circuit,n,m,L,debug):
coll_ctrl_0 = get_first_coll_ctrl(n,m,L)
control = ''
qubits = []
for i in range(m-1):
control = control + '1'
qubits.append(coll_ctrl_0+i)
qubits.append(coll_ctrl_0+m-1)
circuit.append(MCXGate(m-1,ctrl_state=control),qubits)
return circuit
#not necessary
#returns True if output contains only unique elements; returns False otherwise (if two or more elements are the same)
def collision_check_old(output):
if len(output) == len(set(output)):
return True
else:
return False
#Perform measurement on last qubit in coll_register
def measure_collisions(circuit,n,m,L):
#add classical register to store measurement result
c_q = QuantumRegister(0)
c_reg = ClassicalRegister(1,'collision_check')
c = QuantumCircuit(c_q,c_reg)
circuit = circuit.combine(c)
#perform measurements on each electron register and store in separate memorey
circuit.measure(get_first_coll_ctrl(n,m,L) + m - 1, 0)
return circuit
#Add classical registers and apply measurements on the main electron register
def measure_electrons(circuit,n,m):
circuit.barrier()
for g in range(m):
#Add classicla register to store measurement outcomes
c_q = QuantumRegister(0)
c_reg = ClassicalRegister(n,'mem_{}'.format(asc[g]))
c = QuantumCircuit(c_q,c_reg)
circuit = circuit.combine(c)
#perform measurements on each electron register and store in separate memorey
circuit.measure(np.arange(g*n,(g+1)*n),np.arange(g*n + 1,(g+1)*n + 1))
return circuit
#Build the circuit with all gates and measurements
@timeis
def build_circuit(n,m,input,sn,L,debug=True):
#Initialize the circuit with the right number of qubits and ancillas
circuit = initialize_circuit(n,m,L)
#Apply Hadamard gates to each qubit in the first register
circuit = Hadamard(circuit,n,m)
#Apply the sorting network sn
phase = False
circuit = apply_sorting_network(circuit,n,m,sn,L,phase,debug)
#apply comparisons between all adjacent electron registers and store outcome in coll_register
circuit = collision_compare(circuit,n,m,L,debug)
#check if outcome of all comparisons is "not_equal"; flip last qubit in coll_register if this is the case
circuit = collision_test(circuit,n,m,L,debug)
#measure last qubit in coll_register, which stores (no collisions = 1) or (collisions = 0); result is kept until the end of the simulation and result accepted if (no collisions == True)
circuit = measure_collisions(circuit,n,m,L)
#Measurements: classical register 0 stores the random sorted array that can still include collisions
#circuit = measure_electrons(circuit,n,m)
#Reset main electron register
circuit = reset_electrons(circuit,n,m)
#Initialize main electron register in given input product state
circuit = binary_init(circuit,n,m,input)
#Apply the reverse of 'apply_sorting_network' and add a conditioned phase shift after each swap (this antisymmetrizes the input state)
phase = True
circuit = apply_reverse_sorting_network(circuit,n,m,sn,L,phase,debug)
#Reset all ancilla qubits and only keep the main electron register (disable for testing final state for antisymmetry)
#circuit = reset_ancillas(circuit,n,m,L)
#Measure electron register (for testing)
#circuit = measure_electrons(circuit,n,m)
return circuit
#Simulate circuit using specified backend and return simulation result
@timeis
def simulate(circuit,backend,shots):
simulator = Aer.get_backend(backend)
#transpile the circuit into the supported set of gates
circuit = transpile(circuit,backend=simulator)
result = simulator.run(circuit,shots=shots).result()
return result
#turns simulation result 'counts' into list of decimal numbers corresponding to the electron registers; only use if shots=1 or all outcomes are the same
def convert_output_to_decimal(counts,n,m):
output_list = list(counts.keys())[0][::-1]
coll_test = output_list[0]
output_list = output_list[2:]
output = []
offset = 0
for g in range(m):
start = g*n + offset
end = (g+1)*n + offset
g_out = int(output_list[start:end],2)
output.append(g_out)
offset += 1
output_0 = output[0:m]
return coll_test,output_0
#draw the circuit using size,name as input if plot==True
@timeis
def draw_circuit(circuit,plot_scale,fname):
circuit.draw(output='mpl',fold=-1,scale=plot_scale,plot_barriers=True)
plt.savefig(fname,dpi=700)
return 0
def plot_circuit(circuit,plot_scale,fname,plot=True):
if plot:
draw_circuit(circuit,plot_scale,fname)
plt.show()
return 0
print("Plot disabled")
return 0
#plot sorting network by itself, using cnot as directed comparator (only for visualizationo)
def plot_sorting_network(sn,m):
circuit_sn = QuantumCircuit(m)
for s in sn:
if s[2] == 0:
i,j = s[0],s[1]
else:
i,j = s[1],s[0]
circuit_sn.cz(i,j)
circuit_sn.draw(output='mpl')
plt.show()
return 0
#Generate a bitonic sorting network for m electrons; dir=0 (descending), dir=1 (ascending)
def sorting_network_bitonic(m,dir):
sn = []
def compAndSwap(i,j,dir):
sn.append([i,j,dir])
def bitonic_sort(low, cnt, dir):
if cnt>1:
k = cnt//2
dir_n = (dir + 1) % 2
bitonic_sort(low, k, dir_n)#n_dir
bitonic_sort(low + k, cnt-k, dir)#dir
bitonic_merge(low, cnt, dir)
def bitonic_merge(low, cnt, dir):
if cnt>1:
k = greatestPowerOfTwoLessThan(cnt)
i = low
while i < low+cnt-k:
compAndSwap(i, i+k, dir)
i+=1
bitonic_merge(low,k,dir)
bitonic_merge(low+k,cnt-k,dir)
def greatestPowerOfTwoLessThan(cnt):
i=1
while (2**i)<cnt:
i+=1
return 2**(i-1)
bitonic_sort(0,m,dir)
L = len(sn)
return sn,L
#Test if sorting network correctly sorts all possible inputs
def test_sn(sn,n,m):
all_inputs = list(product(range(2**n),repeat=m))
fail = 0
count = 0
for input in all_inputs:
input = np.array(input)
temp = np.copy(input)
for s in sn:
if s[2]==0:
i = s[0]
j = s[1]
if s[2]==1:
i = s[1]
j = s[0]
if input[i]<input[j]:
input[i],input[j] = input[j],input[i]
should_be = np.sort(temp)[::-1]
if (input == should_be).all():
fail += 0
else:
fail += 1
print(f"Testing sorting network {count}/{len(all_inputs)}",end="\r")
count+=1
print(" ", end = "\r")
if fail == 0:
print("Sorting network correct\n")
return 1
else:
print("Error in sorting network\n")
return 0
#Returns all steps of sorting network with corresponding ancilla registers (for testing)
def test_sn_anc(sn,n,m):
for s in sn:
i = s[0]
j = s[1]
anc = get_anc(n,m,i,j)
anc_reg = int((anc-n*m)/(n-1))
print(f"[{i},{j}] anc_reg={anc_reg}")
return 0
#Output density matrix of electron register (target) and compute purity, doesnt actually test antisymmetry yet!
def test_antisymmetry(result,n,m,L):
sv = result.get_statevector()
trace_out = list(np.arange(n*m,get_first_coll_ctrl(n,m,L)+m))
#print(f"Tracing out qubits: {trace_out}")
rho_e = partial_trace(sv,trace_out)
if rho_e.is_valid():
print("Target state is valid density matrix\n")
else:
print("Target state is not valid density matrix")
#print(rho_e)
p = purity(rho_e)
print(f"Purity of target state = {p}\n")
return p
###################MAINPART############################################################################################################
#Parameters
#n: number of qubits per electron; N = 2^n orbitals
n=3
#m: number of electrons
m=4
#input: list of orbitals the electrons are initialized in; needs to be in descending order, without repetitions
input = [5,4,3,2]
#dir: ordering descending (dir=0) or ascending (dir=1)
dir = 0
#plot and save the circuit
plot = True
#include barriers between comparators in the circuit for visualization
debug = False
#measure time of functions: {build_circuit, simulate, draw_circuit}
measure_time = True
#size of the plot
plot_scale = 0.2
#simulation method
backend = 'statevector_simulator'#'aer_simulator'
#number of circuit repetitions in 'simulate'
shots = 1
#check valid inputs
check_inputs(n,m)
#Generate sorting network
sn,L = sorting_network_bitonic(m,dir)
#Test sorting network
test_sn(sn,n,m)
#Plot sorting network
plot_sorting_network(sn,m)
#Build circuit
circuit = build_circuit(n,m,input,sn,L,debug)
#Simulate
result = simulate(circuit,backend,shots)
counts = result.get_counts(circuit)
print(f"Counts: {counts}\n")
#Test if final state is antisymmetric
test_antisymmetry(result,n,m,L)
output_list = list(counts.keys())[0][::-1]
coll_test = output_list[0]
if coll_test == '1':
print("No collisions detected - continue\n")
else:
print("Collisions detected - repeat\n")
#plot circuit
plot_circuit(circuit,plot_scale,f"Plots/Circuit_m{m}_n{n}_debug{debug}",plot)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-states-of-Li-and-Li-2-using-Variational-Quantum-EIgensolver
|
Bikramaditya0154
|
from qiskit import Aer
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver,
)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
molecule = Molecule(
geometry=[["Li", [0.0, 0.0, 0.0]]], charge=2, multiplicity=2
)
driver = ElectronicStructureMoleculeDriver(
molecule, basis="sto3g", driver_type=ElectronicStructureDriverType.PYSCF
)
es_problem = ElectronicStructureProblem(driver)
qubit_converter = QubitConverter(JordanWignerMapper())
from qiskit.providers.aer import StatevectorSimulator
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit_nature.algorithms import VQEUCCFactory
quantum_instance = QuantumInstance(backend=Aer.get_backend("aer_simulator_statevector"))
vqe_solver = VQEUCCFactory(quantum_instance=quantum_instance)
from qiskit.algorithms import VQE
from qiskit.circuit.library import TwoLocal
tl_circuit = TwoLocal(
rotation_blocks=["h", "rx"],
entanglement_blocks="cz",
entanglement="full",
reps=2,
parameter_prefix="y",
)
another_solver = VQE(
ansatz=tl_circuit,
quantum_instance=QuantumInstance(Aer.get_backend("aer_simulator_statevector")),
)
from qiskit_nature.algorithms import GroundStateEigensolver
calc = GroundStateEigensolver(qubit_converter, vqe_solver)
res = calc.solve(es_problem)
print(res)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-states-of-Li-and-Li-2-using-Variational-Quantum-EIgensolver
|
Bikramaditya0154
|
from qiskit import Aer
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver,
)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
molecule = Molecule(
geometry=[["Li", [0.0, 0.0, 0.0]]], charge=1, multiplicity=1
)
driver = ElectronicStructureMoleculeDriver(
molecule, basis="sto3g", driver_type=ElectronicStructureDriverType.PYSCF
)
es_problem = ElectronicStructureProblem(driver)
qubit_converter = QubitConverter(JordanWignerMapper())
from qiskit.providers.aer import StatevectorSimulator
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit_nature.algorithms import VQEUCCFactory
quantum_instance = QuantumInstance(backend=Aer.get_backend("aer_simulator_statevector"))
vqe_solver = VQEUCCFactory(quantum_instance=quantum_instance)
from qiskit.algorithms import VQE
from qiskit.circuit.library import TwoLocal
tl_circuit = TwoLocal(
rotation_blocks=["h", "rx"],
entanglement_blocks="cz",
entanglement="full",
reps=2,
parameter_prefix="y",
)
another_solver = VQE(
ansatz=tl_circuit,
quantum_instance=QuantumInstance(Aer.get_backend("aer_simulator_statevector")),
)
from qiskit_nature.algorithms import GroundStateEigensolver
calc = GroundStateEigensolver(qubit_converter, vqe_solver)
res = calc.solve(es_problem)
print(res)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-state-of-LiH-molecule-using-Variational-Quantum-Eigensolver
|
Bikramaditya0154
|
from qiskit.algorithms import VQE
from qiskit_nature.algorithms import (GroundStateEigensolver,
NumPyMinimumEigensolverFactory)
from qiskit_nature.drivers import Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureMoleculeDriver, ElectronicStructureDriverType)
from qiskit_nature.transformers.second_quantization.electronic import FreezeCoreTransformer
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import ParityMapper
import matplotlib.pyplot as plt
import numpy as np
from qiskit_nature.circuit.library import UCCSD, HartreeFock
from qiskit.circuit.library import EfficientSU2
from qiskit.algorithms.optimizers import COBYLA, SPSA, SLSQP
from qiskit.opflow import TwoQubitReduction
from qiskit import BasicAer, Aer
from qiskit.utils import QuantumInstance
from qiskit.utils.mitigation import CompleteMeasFitter
from qiskit.providers.aer.noise import NoiseModel
def get_qubit_op(dist):
# Define Molecule
molecule = Molecule(
# Coordinates in Angstrom
geometry=[
["Li", [0.0, 0.0, 0.0] ],
["H", [dist, 0.0, 0.0] ]
],
multiplicity=1, # = 2*spin + 1
charge=0,
)
driver = ElectronicStructureMoleculeDriver(
molecule=molecule,
basis="sto3g",
driver_type=ElectronicStructureDriverType.PYSCF)
# Get properties
properties = driver.run()
num_particles = (properties
.get_property("ParticleNumber")
.num_particles)
num_spin_orbitals = int(properties
.get_property("ParticleNumber")
.num_spin_orbitals)
# Define Problem, Use freeze core approximation, remove orbitals.
problem = ElectronicStructureProblem(
driver,
[FreezeCoreTransformer(freeze_core=True,
remove_orbitals=[-3,-2])])
second_q_ops = problem.second_q_ops() # Get 2nd Quant OP
num_spin_orbitals = problem.num_spin_orbitals
num_particles = problem.num_particles
mapper = ParityMapper() # Set Mapper
hamiltonian = second_q_ops[0] # Set Hamiltonian
# Do two qubit reduction
converter = QubitConverter(mapper,two_qubit_reduction=True)
reducer = TwoQubitReduction(num_particles)
qubit_op = converter.convert(hamiltonian)
qubit_op = reducer.convert(qubit_op)
return qubit_op, num_particles, num_spin_orbitals, problem, converter
def exact_solver(problem, converter):
solver = NumPyMinimumEigensolverFactory()
calc = GroundStateEigensolver(converter, solver)
result = calc.solve(problem)
return result
backend = BasicAer.get_backend("statevector_simulator")
distances = np.arange(0.5, 4.0, 0.2)
exact_energies = []
vqe_energies = []
optimizer = SLSQP(maxiter=5)
for dist in distances:
(qubit_op, num_particles, num_spin_orbitals,
problem, converter) = get_qubit_op(dist)
result = exact_solver(problem,converter)
exact_energies.append(result.total_energies[0].real)
init_state = HartreeFock(num_spin_orbitals, num_particles, converter)
var_form = UCCSD(converter,
num_particles,
num_spin_orbitals,
initial_state=init_state)
vqe = VQE(var_form, optimizer, quantum_instance=backend)
vqe_calc = vqe.compute_minimum_eigenvalue(qubit_op)
vqe_result = problem.interpret(vqe_calc).total_energies[0].real
vqe_energies.append(vqe_result)
print(f"Interatomic Distance: {np.round(dist, 2)}",
f"VQE Result: {vqe_result:.5f}",
f"Exact Energy: {exact_energies[-1]:.5f}")
print("All energies have been calculated")
plt.plot(distances, exact_energies, label="Exact Energy")
plt.plot(distances, vqe_energies, label="VQE Energy")
plt.xlabel('Interatomic distance(Angstrom)')
plt.ylabel('Energy(Hartree)')
plt.legend()
plt.show()
|
https://github.com/MariosTsatsos/4qubitGrover
|
MariosTsatsos
|
#initialization
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'svg' # Makes the images look nice
import numpy as np
# importing Qiskit
from qiskit import IBMQ, BasicAer, Aer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
# import basic plot tools
from qiskit.visualization import plot_histogram
from qiskit.circuit import Parameter
from math import pi as pi
def n_controlled_Z(circuit, controls, target):
"""Implement a Z gate with multiple controls"""
if (len(controls) > 3):
raise ValueError('The controlled Z with more than 3 controls is not implemented')
elif (len(controls) == 1):
circuit.h(target)
circuit.cx(controls[0], target)
circuit.h(target)
elif (len(controls) == 2):
circuit.h(target)
circuit.ccx(controls[0], controls[1], target)
circuit.h(target)
elif (len(controls) == 3):
circuit.cu1(pi/4, controls[0], target)
circuit.cx(controls[0], controls[1])
circuit.cu1(-pi/4, controls[1],target)
circuit.cx(controls[0], controls[1])
circuit.cu1(pi/4, controls[1], target)
circuit.cx(controls[1], controls[2])
circuit.cu1(-pi/4, controls[2], target)
circuit.cx(controls[0], controls[2])
circuit.cu1(pi/4, controls[2], target)
circuit.cx(controls[1], controls[2])
circuit.cu1(-pi/4, controls[2], target)
circuit.cx(controls[0], controls[2])
circuit.cu1(pi/4, controls[2], target)
def grover_n(circuit, qr, N, barriers = True):
j = 0
while j < N:
#####################################
### Oracle for 0010
circuit.x(qr[0])
circuit.x(qr[2])
circuit.x(qr[3])
######### cccZ #####################
n_controlled_Z(circuit, [qr[i] for i in range(n-1)], qr[n-1])
if barriers:
circuit.barrier()
circuit.x(qr[0])
circuit.x(qr[2])
circuit.x(qr[3])
if barriers:
circuit.barrier()
######################################
#### Amplification
circuit.h(qr)
circuit.x(qr)
######## cccZ ###########
n_controlled_Z(circuit, [qr[i] for i in range(n-1)], qr[n-1])
if barriers:
circuit.barrier()
circuit.x(qr)
circuit.h(qr)
if barriers:
circuit.barrier()
j += 1
print("I implemented gate M.H.B.H",j,"time.")
barriers = True
theta = Parameter('θ')
n = 4
qr = QuantumRegister(n)
cr = ClassicalRegister(n)
groverCircuit = QuantumCircuit(qr,cr)
##########################
### Initialization
groverCircuit.h(qr)
if barriers:
groverCircuit.barrier()
#########################
### Grover gate - N times
grover_n(groverCircuit, qr, 3)
#########################
### measure
groverCircuit.measure(qr,cr)
groverCircuit.draw(output="mpl")
backend = BasicAer.get_backend('qasm_simulator')
shots = 2**12
results = execute(groverCircuit, backend=backend, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer)
# Load IBM Q account and get the least busy backend device
provider = IBMQ.load_account()
device = least_busy(provider.backends(simulator=False))
print("Running on current least busy device: ", device)
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 4 and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
# Run our circuit on the least busy backend. Monitor the execution of the job in the queue
from qiskit.tools.monitor import job_monitor
shots = 2**12
job = execute(groverCircuit, backend=backend, shots=shots)
job_monitor(job, interval = 2)
# Get the results from the computation
results = job.result()
answer = results.get_counts(groverCircuit)
plot_histogram(answer)
|
https://github.com/Bikramaditya0154/Quantum-Simulation-of-the-ground-state-of-Hydrogen-molecule-using-Variational-Quantum-Eigensolver-
|
Bikramaditya0154
|
from qiskit.algorithms import VQE
from qiskit_nature.algorithms import (GroundStateEigensolver,
NumPyMinimumEigensolverFactory)
from qiskit_nature.drivers import Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureMoleculeDriver, ElectronicStructureDriverType)
from qiskit_nature.transformers.second_quantization.electronic import FreezeCoreTransformer
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import ParityMapper
import matplotlib.pyplot as plt
import numpy as np
from qiskit_nature.circuit.library import UCCSD, HartreeFock
from qiskit.circuit.library import EfficientSU2
from qiskit.algorithms.optimizers import COBYLA, SPSA, SLSQP
from qiskit.opflow import TwoQubitReduction
from qiskit import BasicAer, Aer
from qiskit.utils import QuantumInstance
from qiskit.utils.mitigation import CompleteMeasFitter
from qiskit.providers.aer.noise import NoiseModel
def get_qubit_op(dist):
# Define Molecule
molecule = Molecule(
# Coordinates in Angstrom
geometry=[
["H", [0.0, 0.0, 0.0] ],
["H", [dist, 0.0, 0.0] ]
],
multiplicity=1, # = 2*spin + 1
charge=0,
)
driver = ElectronicStructureMoleculeDriver(
molecule=molecule,
basis="sto3g",
driver_type=ElectronicStructureDriverType.PYSCF)
# Get properties
properties = driver.run()
num_particles = (properties
.get_property("ParticleNumber")
.num_particles)
num_spin_orbitals = int(properties
.get_property("ParticleNumber")
.num_spin_orbitals)
# Define Problem, Use freeze core approximation, remove orbitals.
problem = ElectronicStructureProblem(
driver
)
second_q_ops = problem.second_q_ops() # Get 2nd Quant OP
num_spin_orbitals = problem.num_spin_orbitals
num_particles = problem.num_particles
mapper = ParityMapper() # Set Mapper
hamiltonian = second_q_ops[0] # Set Hamiltonian
# Do two qubit reduction
converter = QubitConverter(mapper,two_qubit_reduction=True)
reducer = TwoQubitReduction(num_particles)
qubit_op = converter.convert(hamiltonian)
qubit_op = reducer.convert(qubit_op)
return qubit_op, num_particles, num_spin_orbitals, problem, converter
def exact_solver(problem, converter):
solver = NumPyMinimumEigensolverFactory()
calc = GroundStateEigensolver(converter, solver)
result = calc.solve(problem)
return result
backend = BasicAer.get_backend("statevector_simulator")
distances = np.arange(0.5, 5.0, 0.1)
exact_energies = []
vqe_energies = []
optimizer = SLSQP(maxiter=5)
for dist in distances:
(qubit_op, num_particles, num_spin_orbitals,
problem, converter) = get_qubit_op(dist)
result = exact_solver(problem,converter)
exact_energies.append(result.total_energies[0].real)
init_state = HartreeFock(num_spin_orbitals, num_particles, converter)
var_form = UCCSD(converter,
num_particles,
num_spin_orbitals,
initial_state=init_state)
vqe = VQE(var_form, optimizer, quantum_instance=backend)
vqe_calc = vqe.compute_minimum_eigenvalue(qubit_op)
vqe_result = problem.interpret(vqe_calc).total_energies[0].real
vqe_energies.append(vqe_result)
print(f"Interatomic Distance: {np.round(dist, 2)}",
f"VQE Result: {vqe_result:.5f}",
f"Exact Energy: {exact_energies[-1]:.5f}")
print("All energies have been calculated.")
plt.plot(distances, exact_energies, label="Exact Energy")
plt.plot(distances, vqe_energies, label="VQE Energy")
plt.xlabel('Interatomic distance (Angstrom)')
plt.ylabel('Energy(Hartree)')
plt.legend()
plt.show()
|
https://github.com/AkshayPatil347/Grover-s-Code
|
AkshayPatil347
|
from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_histogram
from numpy import random
color_codes = [0,1,2,3,4,5,6,7]
random.shuffle(color_codes)
database = {}
for i in range(8):
database[i] = color_codes[i]
desired_color_code = 2
DB = QuantumCircuit(7)
def DB_function(QC, color_code):
if color_code == 7:
QC.mcx([0,1,2],3)
QC.mcx([0,1,2],4)
QC.mcx([0,1,2],5)
elif color_code == 6:
QC.mcx([0,1,2],3)
QC.mcx([0,1,2],4)
elif color_code == 5:
QC.mcx([0,1,2],3)
QC.mcx([0,1,2],5)
elif color_code == 4:
QC.mcx([0,1,2],3)
elif color_code == 3:
QC.mcx([0,1,2],4)
QC.mcx([0,1,2],5)
elif color_code == 2:
QC.mcx([0,1,2],4)
elif color_code == 1:
QC.mcx([0,1,2],5)
#for when index = 0 = 000
DB.x(0)
DB.x(1)
DB.x(2)
DB_function(DB, database[0])
DB.x(0)
DB.x(1)
DB.x(2)
#for when index = 1 = 001
DB.x(0)
DB.x(1)
DB_function(DB, database[1])
DB.x(0)
DB.x(1)
#for when index = 2 = 010
DB.x(0)
DB.x(2)
DB_function(DB, database[2])
DB.x(0)
DB.x(2)
#for when index = 3 = 011
DB.x(0)
DB_function(DB, database[3])
DB.x(0)
#for when index = 4 = 100
DB.x(1)
DB.x(2)
DB_function(DB, database[4])
DB.x(1)
DB.x(2)
#for when index = 5 = 101
DB.x(1)
DB_function(DB, database[5])
DB.x(1)
#for when index = 6 = 110
DB.x(2)
DB_function(DB, database[6])
DB.x(2)
#for when index = 7 = 111
DB_function(DB, database[7])
DB.draw()
MG = QuantumCircuit(7)
if desired_color_code == 0:
MG.x(3)
MG.x(4)
MG.x(5)
MG.mcx([3,4,5],6)
MG.x(3)
MG.x(4)
MG.x(5)
elif desired_color_code == 1:
MG.x(3)
MG.x(4)
MG.mcx([3,4,5],6)
MG.x(3)
MG.x(4)
elif desired_color_code == 2:
MG.x(3)
MG.x(5)
MG.mcx([3,4,5],6)
MG.x(3)
MG.x(5)
elif desired_color_code == 3:
MG.x(3)
MG.mcx([3,4,5],6)
MG.x(3)
elif desired_color_code == 4:
MG.x(4)
MG.x(5)
MG.mcx([3,4,5],6)
MG.x(4)
MG.x(5)
elif desired_color_code == 5:
MG.x(4)
MG.mcx([3,4,5],6)
MG.x(4)
elif desired_color_code == 6:
MG.x(4)
MG.mcx([3,4,5],6)
MG.x(4)
elif desired_color_code == 7:
MG.mcx([3,4,5],6)
MG.draw()
oracle = QuantumCircuit(7)
oracle = oracle + DB + MG + DB
oracle.draw()
phase = QuantumCircuit(7)
phase.x(0)
phase.x(1)
phase.x(2)
phase.h(2)
phase.ccx(0,1,2)
phase.h(2)
phase.x(0)
phase.x(1)
phase.x(2)
phase.draw()
Grover = QuantumCircuit(7)
Grover = Grover + oracle
Grover.h(0)
Grover.h(1)
Grover.h(2)
Grover = Grover + phase
Grover.h(0)
Grover.h(1)
Grover.h(2)
Grover = Grover + Grover
Grover.draw()
circuit = QuantumCircuit(7,3)
circuit.x(6)
circuit.h(0)
circuit.h(1)
circuit.h(2)
circuit.h(6)
circuit = circuit + Grover
circuit.measure(0,2)
circuit.measure(1,1)
circuit.measure(2,0)
sim = Aer.get_backend ('qasm_simulator')
results = execute(circuit,sim,shots = 1000)
counts = results.result().get_counts()
def mitigated_results(backend,circuit,results,results_sim):
# Import the required classes
from qiskit.providers.aer.noise import NoiseModel
from qiskit.ignis.mitigation.measurement import (complete_meas_cal,CompleteMeasFitter)
# Get noise model for backend
noise_model = NoiseModel.from_backend(backend)
# Create the measurement fitter
qr = QuantumRegister(circuit.num_qubits)
meas_calibs, state_labels = complete_meas_cal(qr=qr, circlabel='mcal')
job = execute(meas_calibs,
backend=Aer.get_backend('qasm_simulator'),
shots=1000, noise_model=noise_model)
cal_results = job.result()
meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal')
print(meas_fitter.cal_matrix)
# Get the filter object
meas_filter = meas_fitter.filter
# Results with mitigation
mitigated_results = meas_filter.apply(results)
mitigated_counts = mitigated_results.get_counts(0)
return(mitigated_counts)
plot_histogram( mitigated_counts)
plot_histogram(counts)
from qiskit import IBMQ, BasicAer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit,transpile,execute
from qiskit.tools.jupyter import *
import qiskit
# Qiskit quantum circuits libraries
# prepare your circuit to run
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-education', group='iisc-bangalore-1', project = 'm-tech-quantum-t')
device = provider.get_backend('ibmq_casablanca')
from qiskit.tools.monitor import job_monitor
from qiskit import transpile, assemble
def transpile_circuit(circuit,backend):
trans_circ = transpile(circuit, backend)
display(trans_circ.draw(output="mpl"))
transpiled_grover_circuit = transpile(circuit, device, optimization_level=3)
print("Circuit data\n\nDepth: ",transpiled_grover_circuit.depth(),"\
nWidth: ",transpiled_grover_circuit.width(),"\nSize: ",transpiled_grover_circuit.
size())
job = device.run(transpiled_grover_circuit)
job_monitor(job, interval=2)
results = job.result()
answer = results.get_counts(circuit)
plot_histogram(answer)
transpiled_grover_circuit.draw()
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
from qiskit import QuantumCircuit
# creating a quantum circuit
qc = QuantumCircuit(3)
qc.z(0)
qc.s(1)
qc.t(2)
qc.cx(0,1)
qc.h(2)
qc.ccx(0, 1, 2)
qc.draw()
# inverse of the quantum circuit
inverse_qc = qc.inverse()
# to draw the quantum circuit
inverse_qc.draw()
# If we measure the quantum circuit's each qubit's states
qc.measure()
# to draw the quantum circuit
qc.draw()
# inverse of the measured quantum circuit's qubit is not possible
inverse_qc = qc.inverse()
qc.measure()
# to draw the quantum circuit
inverse_qc.draw()
# creating a quantum circuit
m_circuit = QuantumCircuit(3)
m_circuit.h(2)
m_circuit.ccx(0, 1, 2)
m_circuit.cz(2, 1)
# draw the circuit
m_circuit.draw()
m_gate = m_circuit.to_gate()
type(m_gate)
new_circuit = QuantumCircuit(5)
new_circuit.append(m_gate, [1, 2, 4])
new_circuit.draw()
#decompose the circuit
new_circuit.decompose().draw()
from qiskit import QuantumCircuit, transpile, Aer
my_circuit = QuantumCircuit(3)
my_circuit.t(1)
my_circuit.h(0)
my_circuit.ccx(2,1,0)
my_circuit.s(2)
my_circuit.t(0)
my_circuit.draw()
my_gate = my_circuit.to_gate()
my_gate
my_inv_gate = my_gate.inverse()
my_inv_gate
my_inv_gate.name = 'My Inverse Gate'
new_circuit = QuantumCircuit(3)
new_circuit.append(my_inv_gate, [0,1,2])
new_circuit.draw()
new_circuit.decompose().draw()
my_circuit = QuantumCircuit(2)
my_circuit.cx(1,0)
my_circuit.cx(0,1)
my_circuit.cx(1,0)
my_circuit.draw()
my_gate = my_circuit.to_gate()
my_gate.name = "My Gate"
my_controlled_gate = my_gate.control()
new_circuit = QuantumCircuit(3)
new_circuit.append(my_controlled_gate, [0, 1, 2])
new_circuit.draw()
new_circuit.decompose().draw()
## What is the qsphere ?
## What is the unitary simulator ?
## How can i convert a Unitary Matrix to a set of One and Two Qubit gates ?
## How can i change qiskit's defoult behaviour ?
## How do i use parameterization circuit in Qiskit ?
## Why does qiskit order it's qubit the way it does ?
## How i combine two quantum circuits ?
## What is the difference between gates and instructions ?
## How can i use a specific version of qiskit ?
## How can i implement a multi controlled Toffoli Gate ?
## How can i monitor a job send to IBM Quantum ?
## How can i convert a quantum circuit to QASM ?
my_circuit = QuantumCircuit(3)
my_circuit.t(1)
my_circuit.h(0)
my_circuit.ccx(2,1,0)
my_circuit.s(2)
my_circuit.t(0)
my_circuit.draw('latex')
my_circuit.draw('latex_source')
print(my_circuit.draw('latex_source'))
## How can i bundle several circuit into a single job ?
## How can i save circuit Drawings to Different File Types ?
## How can i contruct a quantum volume circuit ?
## What trick can i do with draw methods ?
## How i can find reduced quantum states using qiskit ?
## In What different ways can i draw a quantum circuit ?
## How can i use a classical register for quantum compuation ?
## What is circuit depth and how can i calculate it ?
## How can i choose initial layout for the traspiler ?
## What are the Ancillary Qubits and how are they usefull ?
## What are registers ?
## How can i create a custom gate from matrix ?
## How can i find expectation value for an operator ?
## How can i measure the qubit midway through a quantum circuit ?
## How can i transpile a quantum circuit ?
## How can i make a noise model with qiskit ?
## How can i create a custome controlled gate ?
## How can i choose the best backend from a provider ?
## How can i perform state tomography ?
## How can i reset a qubit in a quantum circuit
## How do i perform a unitary projection in a quantum circuit ?
## How do i debuge an issue in transpiler ?
## How can i estimate Pi using a quantum computer ?
## How do i initialize a mixed states ?
## What is gate fidelity and how do i canculate it ?
## How do i check the state fedility with noisy simulator ?
## How do i change the fitter algorithm in a state tomography experiment ?
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit.quantum_info as qi
from qiskit.circuit.library import FourierChecking
from qiskit.visualization import plot_histogram
f = [1, -1, -1, -1]
g = [1, 1, -1, -1]
# FourierChecking() : How our Fourier Transform of F is correlated with G.
# if p(f,g) <= 0.01
# p(f, g) > 0.05 Fourier Exits between f and g
qc = FourierChecking(f=f, g=g)
qc.draw(output='mpl')
zero = qi.Statevector.from_label('00')
sv = zero.evolve(qc)
probs = sv.probabilities_dict()
plot_histogram(probs)
# We are only interested in 00 qubit thus our function f is correlated in 00 state to g with probabilites of 25%
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
from qiskit.visualization import plot_histogram
import numpy as np
def NOT(inp):
"""An NOT gate.
Parameters:
inp (str): Input, encoded in qubit 0.
Returns:
QuantumCircuit: Output NOT circuit.
str: Output value measured from qubit 0.
"""
qc = QuantumCircuit(1, 1) # A quantum circuit with a single qubit and a single classical bit
qc.reset(0)
# We encode '0' as the qubit state |0⟩, and '1' as |1⟩
# Since the qubit is initially |0⟩, we don't need to do anything for an input of '0'
# For an input of '1', we do an x to rotate the |0⟩ to |1⟩
if inp=='1':
qc.x(0)
# barrier between input state and gate operation
qc.barrier()
# Now we've encoded the input, we can do a NOT on it using x
qc.x(0)
#barrier between gate operation and measurement
qc.barrier()
# Finally, we extract the |0⟩/|1⟩ output of the qubit and encode it in the bit c[0]
qc.measure(0,0)
qc.draw()
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp in ['0', '1']:
qc, out = NOT(inp)
print('NOT with input',inp,'gives output',out)
display(qc.draw())
print('\n')
def XOR(inp1,inp2):
"""An XOR gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 1.
"""
qc = QuantumCircuit(2, 1)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
# barrier between input state and gate operation
qc.barrier()
# this is where your program for quantum XOR gate goes
qc.cx(0, 1)
# barrier between input state and gate operation
qc.barrier()
qc.measure(1,0) # output from qubit 1 is measured
#We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
#Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = XOR(inp1, inp2)
print('XOR with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def AND(inp1,inp2):
"""An AND gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum AND gate goes
qc.ccx(0,1,2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = AND(inp1, inp2)
print('AND with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def NAND(inp1,inp2):
"""An NAND gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output NAND circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum NAND gate goes
qc.ccx(0,1,2)
if inp=='1':
qc.x(2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('aer_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc,shots=1,memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = NAND(inp1, inp2)
print('NAND with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def OR(inp1,inp2):
"""An OR gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum OR gate goes
qc.cx(0, 2)
qc.cx(1, 2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('aer_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc,shots=1,memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = OR(inp1, inp2)
print('OR with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
from qiskit import IBMQ
#IBMQ.save_account("a68a35747d4eccd1d58f275e637909987c789ce5c0edd8a4f43014672bf0301b54b28b1b5f44ba8ff87500777429e1e4ceb79621a6ba248d6cca6bca0e233d23", overwrite=True)
IBMQ.load_account()
IBMQ.providers()
provider = IBMQ.get_provider('ibm-q')
provider.backends()
import qiskit.tools.jupyter
# run this cell
backend = provider.get_backend('ibmq_quito')
qc_and = QuantumCircuit(3)
qc_and.ccx(0,1,2)
print('AND gate')
display(qc_and.draw())
print('\n\nTranspiled AND gate with all the required connectivity')
qc_and.decompose().draw()
from qiskit.tools.monitor import job_monitor
# run the cell to define AND gate for real quantum system
def AND(inp1, inp2, backend, layout):
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
qc.ccx(0, 1, 2)
qc.barrier()
qc.measure(2, 0)
qc_trans = transpile(qc, backend, initial_layout=layout, optimization_level=3)
job = backend.run(qc_trans, shots=8192)
print(job.job_id())
job_monitor(job)
output = job.result().get_counts()
return qc_trans, output
backend
layout = [0, 1, 2]
output_all = []
qc_trans_all = []
prob_all = []
worst = 1
best = 0
for input1 in ['0','1']:
for input2 in ['0','1']:
qc_trans, output = AND(input1, input2, backend, layout)
output_all.append(output)
qc_trans_all.append(qc_trans)
prob = output[str(int( input1=='1' and input2=='1' ))]/8192
prob_all.append(prob)
print('\nProbability of correct answer for inputs',input1,input2)
print('{:.2f}'.format(prob) )
print('---------------------------------')
worst = min(worst,prob)
best = max(best, prob)
print('')
print('\nThe highest of these probabilities was {:.2f}'.format(best))
print('The lowest of these probabilities was {:.2f}'.format(worst))
print('Transpiled AND gate circuit for ibmq_vigo with input 0 0')
print('\nThe circuit depth : {}'.format (qc_trans_all[0].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[0].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[0]) )
qc_trans_all[0].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 0 1')
print('\nThe circuit depth : {}'.format (qc_trans_all[1].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[1].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[1]) )
qc_trans_all[1].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 1 0')
print('\nThe circuit depth : {}'.format (qc_trans_all[2].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[2].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[2]) )
qc_trans_all[2].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 1 1')
print('\nThe circuit depth : {}'.format (qc_trans_all[3].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[3].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[3]) )
qc_trans_all[3].draw()
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import QuantumCircuit
# Creating a quantum circuit with the 2 qubit and 2 bits to store
# the measurements of the qubits
3
qc = QuantumCircuit(2, 2)
# draw the quantum circuit
qc.draw()
# Measuring the qubits states and storing it into the classical bits
qc.measure([0,1], [0,1])
qc.draw()
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
my_list = [1,2,3 ,4,5, 6,8,8,3,23,7,75,54,3]
def my_oracle(my_input):
winner=7
if my_input is winner:
response = True
else:
response = False
return response
for index, trial_number in enumerate(my_list):
if my_oracle(trial_number) is True:
print('Winner found at index :%i'%index)
print('%i calls to the Oracle used'%(index+1))
break
from qiskit import *
from qiskit.qiskit_aer import Aer
from qiskit import QuantumCircuit
import matplotlib.pyplot as plt
import numpy as np
oracle = QuantumCircuit(2, name='oracle')
oracle.cz(0,1)
oracle.to_gate()
oracle.draw(output='mpl')
backend = Aer.get_backend('statevector_simulator')
grover_circ = QuantumCircuit(2,2)
grover_circ.h(0)
grover_circ.append(oracle,[0,1])
grover_circ.draw(output='mpl')
job = execute(grover_circ, backend)
result = job.result()
sv = result.get_statevector()
np.arount(sv, 2)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, execute
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from qiskit.providers.aer import QasmSimulator
backend = Aer.get_backend('statevector_simulator')
qc1 = QuantumCircuit(4)
# perform gate operations on individual qubits
qc1.x(0)
qc1.y(1)
qc1.z(2)
qc1.s(3)
# Draw circuit
qc1.draw()
# Plot blochshere
out1 = execute(qc1,backend).result().get_statevector()
plot_bloch_multivector(out1)
qc2 = QuantumCircuit(4)
# initialize qubits
qc2.x(range(4))
# perform gate operations on individual qubits
qc2.x(0)
qc2.y(1)
qc2.z(2)
qc2.s(3)
# Draw circuit
qc2.draw()
# Plot blochshere
out2 = execute(qc2,backend).result().get_statevector()
plot_bloch_multivector(out2)
qc3 = QuantumCircuit(4)
# initialize qubits
qc3.h(range(4))
# perform gate operations on individual qubits
qc3.x(0)
qc3.y(1)
qc3.z(2)
qc3.s(3)
# Draw circuit
qc3.draw()
# Plot blochshere
out3 = execute(qc3,backend).result().get_statevector()
plot_bloch_multivector(out3)
qc4 = QuantumCircuit(4)
# initialize qubits
qc4.x(range(4))
qc4.h(range(4))
# perform gate operations on individual qubits
qc4.x(0)
qc4.y(1)
qc4.z(2)
qc4.s(3)
# Draw circuit
qc4.draw()
# Plot blochshere
out4 = execute(qc4,backend).result().get_statevector()
plot_bloch_multivector(out4)
qc5 = QuantumCircuit(4)
# initialize qubits
qc5.h(range(4))
qc5.s(range(4))
# perform gate operations on individual qubits
qc5.x(0)
qc5.y(1)
qc5.z(2)
qc5.s(3)
# Draw circuit
qc5.draw()
# Plot blochshere
out5 = execute(qc5,backend).result().get_statevector()
plot_bloch_multivector(out5)
qc6 = QuantumCircuit(4)
# initialize qubits
qc6.x(range(4))
qc6.h(range(4))
qc6.s(range(4))
# perform gate operations on individual qubits
qc6.x(0)
qc6.y(1)
qc6.z(2)
qc6.s(3)
# Draw circuit
qc6.draw()
# Plot blochshere
out6 = execute(qc6,backend).result().get_statevector()
plot_bloch_multivector(out6)
import qiskit
qiskit.__qiskit_version__
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
import numpy as np
from numpy import linalg as la
from qiskit.tools.monitor import job_monitor
import qiskit.tools.jupyter
qc = QuantumCircuit(1)
#### your code goes here
# z measurement of qubit 0
measure_z = QuantumCircuit(1,1)
measure_z.measure(0,0)
# x measurement of qubit 0
measure_x = QuantumCircuit(1,1)
# your code goes here
# y measurement of qubit 0
measure_y = QuantumCircuit(1,1)
# your code goes here
shots = 2**14 # number of samples used for statistics
sim = Aer.get_backend('qasm_simulator')
bloch_vector_measure = []
for measure_circuit in [measure_x, measure_y, measure_z]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
counts = execute(qc+measure_circuit, sim, shots=shots).result().get_counts()
# calculate the probabilities for each bit value
probs = {}
for output in ['0','1']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
bloch_vector_measure.append( probs['0'] - probs['1'] )
# normalizing the bloch sphere vector
bloch_vector = bloch_vector_measure/la.norm(bloch_vector_measure)
print('The bloch sphere coordinates are [{0:4.3f}, {1:4.3f}, {2:4.3f}]'
.format(*bloch_vector))
from kaleidoscope.interactive import bloch_sphere
bloch_sphere(bloch_vector, vectors_annotation=True)
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector( bloch_vector )
# circuit for the state Tri1
Tri1 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri2
Tri2 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri3
Tri3 = QuantumCircuit(2)
# your code goes here
# circuit for the state Sing
Sing = QuantumCircuit(2)
# your code goes here
# <ZZ>
measure_ZZ = QuantumCircuit(2)
measure_ZZ.measure_all()
# <XX>
measure_XX = QuantumCircuit(2)
# your code goes here
# <YY>
measure_YY = QuantumCircuit(2)
# your code goes here
shots = 2**14 # number of samples used for statistics
A = 1.47e-6 #unit of A is eV
E_sim = []
for state_init in [Tri1,Tri2,Tri3,Sing]:
Energy_meas = []
for measure_circuit in [measure_XX, measure_YY, measure_ZZ]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
qc = state_init+measure_circuit
counts = execute(qc, sim, shots=shots).result().get_counts()
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E_sim.append(A * np.sum(np.array(Energy_meas)))
# Run this cell to print out your results
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_sim[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_sim[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_sim[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_sim[3]))
# reduced plank constant in (eV) and the speed of light(cgs units)
hbar, c = 4.1357e-15, 3e10
# energy difference between the triplets and singlet
E_del = abs(E_sim[0] - E_sim[3])
# frequency associated with the energy difference
f = E_del/hbar
# convert frequency to wavelength in (cm)
wavelength = c/f
print('The wavelength of the radiation from the transition\
in the hyperfine structure is : {:.1f} cm'.format(wavelength))
provider = IBMQ.load_account()
backend = provider.get_backend('ibmq_athens')
# run this cell to get the backend information through the widget
backend
# assign your choice for the initial layout to the list variable `initial_layout`.
initial_layout =
qc_all = [state_init+measure_circuit for state_init in [Tri1,Tri2,Tri3,Sing]
for measure_circuit in [measure_XX, measure_YY, measure_ZZ] ]
shots = 8192
job = execute(qc_all, backend, initial_layout=initial_layout, optimization_level=3, shots=shots)
print(job.job_id())
job_monitor(job)
# getting the results of your job
results = job.result()
## To access the results of the completed job
#results = backend.retrieve_job('job_id').result()
def Energy(results, shots):
"""Compute the energy levels of the hydrogen ground state.
Parameters:
results (obj): results, results from executing the circuits for measuring a hamiltonian.
shots (int): shots, number of shots used for the circuit execution.
Returns:
Energy (list): energy values of the four different hydrogen ground states
"""
E = []
A = 1.47e-6
for ind_state in range(4):
Energy_meas = []
for ind_comp in range(3):
counts = results.get_counts(ind_state*3+ind_comp)
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E.append(A * np.sum(np.array(Energy_meas)))
return E
E = Energy(results, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E[3]))
from qiskit.ignis.mitigation.measurement import *
# your code to create the circuits, meas_calibs, goes here
meas_calibs, state_labels =
# execute meas_calibs on your choice of the backend
job = execute(meas_calibs, backend, shots = shots)
print(job.job_id())
job_monitor(job)
cal_results = job.result()
## To access the results of the completed job
#cal_results = backend.retrieve_job('job_id').result()
# your code to obtain the measurement filter object, 'meas_filter', goes here
results_new = meas_filter.apply(results)
E_new = Energy(results_new, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_new[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_new[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_new[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_new[3]))
# results for the energy estimation from the simulation,
# execution on a quantum system without error mitigation and
# with error mitigation in numpy array format
Energy_exact, Energy_exp_orig, Energy_exp_new = np.array(E_sim), np.array(E), np.array(E_new)
# Calculate the relative errors of the energy values without error mitigation
# and assign to the numpy array variable `Err_rel_orig` of size 4
Err_rel_orig =
# Calculate the relative errors of the energy values with error mitigation
# and assign to the numpy array variable `Err_rel_new` of size 4
Err_rel_new =
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
without measurement error mitigation : {}'.format(Err_rel_orig))
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
with measurement error mitigation : {}'.format(Err_rel_new))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
# Importing standard Qiskit libraries
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import Aer, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector, plot_state_qsphere, plot_state_city, plot_state_paulivec, plot_state_hinton
# Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Define backend
sim = Aer.get_backend('aer_simulator')
def createBellStates(inp1, inp2):
qc = QuantumCircuit(2)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
qc, state, result = createBellStates(inp1, inp2)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp2 in ['0', '1']:
#for inp1 in ['0', '1']:
#qc, state, result = createBellStates(inp1, inp2)
#print('For inputs',inp2,inp1,'Representation of Entangled States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')'''
from qiskit import IBMQ, execute
from qiskit.providers.ibmq import least_busy
from qiskit.tools import job_monitor
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
def createBSRealDevice(inp1, inp2):
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr, cr)
qc.reset(range(2))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=100)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
print('For inputs',inp2,inp1,'Representation of Entangled States are,')
#first results
qc, first_result = createBSRealDevice(inp1, inp2)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = createBSRealDevice(inp1, inp2)
second_counts = second_result.get_counts()
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
def ghzCircuit(inp1, inp2, inp3):
qc = QuantumCircuit(3)
qc.reset(range(3))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
inp3 = 1
qc, state, result = ghzCircuit(inp1, inp2, inp3)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghzCircuit(inp1, inp2, inp3)
#print('For inputs',inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
def ghz5QCircuit(inp1, inp2, inp3, inp4, inp5):
qc = QuantumCircuit(5)
#qc.reset(range(5))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
if inp4 == 1:
qc.x(3)
if inp5 == 1:
qc.x(4)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
# Explore GHZ States for input 00010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 0
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 11001. Note: the input has been stated in little-endian format.
inp1 = 1
inp2 = 0
inp3 = 0
inp4 = 1
inp5 = 1
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 01010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 1
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Uncomment below code in order to explore other states
#for inp5 in ['0','1']:
#for inp4 in ['0','1']:
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
#print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 5
and not x.configuration().simulator
and x.status().operational==True))
def create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5):
qr = QuantumRegister(5)
cr = ClassicalRegister(5)
qc = QuantumCircuit(qr, cr)
qc.reset(range(5))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
if inp3=='1':
qc.x(1)
if inp4=='1':
qc.x(1)
if inp5=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=1000)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
inp3 = 0
inp4 = 0
inp5 = 0
#first results
qc, first_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
second_counts = second_result.get_counts()
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ circuit states are,')
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
import qiskit
qiskit.__qiskit_version__
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import SparsePauliOp
def heisenberg_hamiltonian(
length: int, jx: float = 1.0, jy: float = 0.0, jz: float = 0.0
) -> SparsePauliOp:
terms = []
for i in range(length - 1):
if jx:
terms.append(("XX", [i, i + 1], jx))
if jy:
terms.append(("YY", [i, i + 1], jy))
if jz:
terms.append(("ZZ", [i, i + 1], jz))
return SparsePauliOp.from_sparse_list(terms, num_qubits=length)
def state_prep_circuit(num_qubits: int, layers: int = 1) -> QuantumCircuit:
qubits = QuantumRegister(num_qubits, name="q")
circuit = QuantumCircuit(qubits)
circuit.h(qubits)
for _ in range(layers):
for i in range(0, num_qubits - 1, 2):
circuit.cx(qubits[i], qubits[i + 1])
circuit.ry(0.1, qubits)
for i in range(1, num_qubits - 1, 2):
circuit.cx(qubits[i], qubits[i + 1])
circuit.ry(0.1, qubits)
return circuit
length = 5
hamiltonian = heisenberg_hamiltonian(length, 1.0, 1.0)
circuit = state_prep_circuit(length, layers=2)
print(hamiltonian)
circuit.draw("mpl")
from qiskit_aer.primitives import Estimator
estimator = Estimator(approximation=True)
job = estimator.run(circuit, hamiltonian, shots=None)
result = job.result()
exact_value = result.values[0]
print(f"Exact energy: {exact_value}")
from qiskit_ibm_runtime import QiskitRuntimeService
hub = "ibm-q-internal"
group = "deployed"
project = "default"
service = QiskitRuntimeService(instance=f"{hub}/{group}/{project}")
from qiskit_ibm_runtime import Estimator, Options, Session
from qiskit.transpiler import CouplingMap
backend = service.get_backend("simulator_statevector")
# set simulation options
simulator = {
"basis_gates": ["id", "rz", "sx", "cx", "reset"],
"coupling_map": list(CouplingMap.from_line(length + 1)),
}
shots = 10000
import math
options = Options(
simulator=simulator,
resilience_level=0,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
from qiskit_aer.noise import NoiseModel, ReadoutError
noise_model = NoiseModel()
##### your code here #####
# P(A|B) = [P(A|0), P(A|1)] = [ 1 - q0_01, q0_01 ] = [ 0.8, 0.2 ]
q0_10 = 0.5
q0_01 = 0.2
qn_10 = 0.05
qn_01 = 0.02
re_l = [ReadoutError(
[
[1 - q0_01, q0_01],
[q0_10, 1 - q0_10],
]
)]
n_qubits = 6
for _ in range(n_qubits - 1):
re_l.append(ReadoutError(
[
[1 - qn_01, qn_01],
[qn_10, 1 - qn_10],
]
))
for q in range(n_qubits):
noise_model.add_readout_error(re_l[q], (q, ))
print(noise_model.to_dict())
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex1
grade_lab5_ex1(noise_model)
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=0,
transpilation=dict(initial_layout=list(range(length))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=0,
transpilation=dict(initial_layout=list(range(1, length + 1))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=1,
transpilation=dict(initial_layout=list(range(1, length + 1))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
new_shots: int
##### your code here #####
new_shots = 20000
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex2
grade_lab5_ex2(new_shots)
from qiskit_aer.noise import depolarizing_error
noise_model = NoiseModel()
##### your code here #####
error = depolarizing_error(0.01, 2)
noise_model.add_all_qubit_quantum_error(error, ['cx'])
print(noise_model)
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex3
grade_lab5_ex3(noise_model)
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=1,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=2,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variances = result.metadata[0]["zne"]["noise_amplification"]["variance"]
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variances: {variances}")
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit.quantum_info as qi
from qiskit.circuit.library import FourierChecking
from qiskit.visualization import plot_histogram
f = [1, -1, -1, -1]
g = [1, 1, -1, -1]
# FourierChecking() : How our Fourier Transform of F is correlated with G.
# if p(f,g) <= 0.01
# p(f, g) > 0.05 Fourier Exits between f and g
qc = FourierChecking(f=f, g=g)
qc.draw(output='mpl')
zero = qi.Statevector.from_label('00')
sv = zero.evolve(qc)
probs = sv.probabilities_dict()
plot_histogram(probs)
# We are only interested in 00 qubit thus our function f is correlated in 00 state to g with probabilites of 25%
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
my_list = [1,2,3 ,4,5, 6,8,8,3,23,7,75,54,3]
def my_oracle(my_input):
winner=7
if my_input is winner:
response = True
else:
response = False
return response
for index, trial_number in enumerate(my_list):
if my_oracle(trial_number) is True:
print('Winner found at index :%i'%index)
print('%i calls to the Oracle used'%(index+1))
break
from qiskit import *
from qiskit.qiskit_aer import Aer
from qiskit import QuantumCircuit
import matplotlib.pyplot as plt
import numpy as np
oracle = QuantumCircuit(2, name='oracle')
oracle.cz(0,1)
oracle.to_gate()
oracle.draw(output='mpl')
backend = Aer.get_backend('statevector_simulator')
grover_circ = QuantumCircuit(2,2)
grover_circ.h(0)
grover_circ.append(oracle,[0,1])
grover_circ.draw(output='mpl')
job = execute(grover_circ, backend)
result = job.result()
sv = result.get_statevector()
np.arount(sv, 2)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit.aqua.operators import WeightedPauliOperator
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
from qiskit.aqua.algorithms import NumPyMinimumEigensolver
ee = NumPyMinimumEigensolver(qubit_op)
result = ee.run()
print(result.eigenvalue.real)
from qiskit import BasicAer
from qiskit.aqua.algorithms import VQE
from qiskit.circuit.library import TwoLocal
from qiskit.aqua.components.optimizers import L_BFGS_B
var_form = TwoLocal(qubit_op.num_qubits, ['ry', 'rz'], 'cz', reps=3, entanglement='linear')
optimizer = L_BFGS_B(maxfun=1000)
vqe = VQE(qubit_op, var_form, optimizer)
backend = BasicAer.get_backend('statevector_simulator')
result = vqe.run(backend)
print(result.eigenvalue.real)
from qiskit.aqua import QuantumInstance
var_form = TwoLocal(qubit_op.num_qubits, ['ry', 'rz'], 'cz', reps=3, entanglement='linear')
optimizer = L_BFGS_B(maxfun=1000)
vqe = VQE(qubit_op, var_form, optimizer)
backend = BasicAer.get_backend('statevector_simulator')
qi = QuantumInstance(backend=backend)
result = vqe.run(qi)
print(result.eigenvalue.real)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
#initialization
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
# importing Qiskit
from qiskit import IBMQ, BasicAer
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.monitor import job_monitor
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# Load our saved IBMQ accounts.
IBMQ.load_account()
nQubits = 14 # number of physical qubits
a = 101 # the hidden integer whose bitstring is 1100101
# make sure that a can be represented with nQubits
a = a % 2**(nQubits)
# Creating registers
# qubits for querying the oracle and finding the hidden integer
qr = QuantumRegister(nQubits)
# for recording the measurement on qr
cr = ClassicalRegister(nQubits)
circuitName = "BernsteinVazirani"
bvCircuit = QuantumCircuit(qr, cr)
# Apply Hadamard gates before querying the oracle
for i in range(nQubits):
bvCircuit.h(qr[i])
# Apply barrier so that it is not optimized by the compiler
bvCircuit.barrier()
# Apply the inner-product oracle
for i in range(nQubits):
if (a & (1 << i)):
bvCircuit.z(qr[i])
else:
bvCircuit.iden(qr[i])
# Apply barrier
bvCircuit.barrier()
#Apply Hadamard gates after querying the oracle
for i in range(nQubits):
bvCircuit.h(qr[i])
# Measurement
bvCircuit.barrier(qr)
bvCircuit.measure(qr, cr)
bvCircuit.draw(output='mpl')
# use local simulator
backend = BasicAer.get_backend('qasm_simulator')
shots = 1000
results = execute(bvCircuit, backend=backend, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer)
backend = IBMQ.get_backend('ibmq_16_melbourne')
shots = 1000
bvCompiled = transpile(bvCircuit, backend=backend, optimization_level=1)
job_exp = execute(bvCircuit, backend=backend, shots=shots)
job_monitor(job_exp)
results = job_exp.result()
answer = results.get_counts(bvCircuit)
threshold = int(0.01 * shots) #the threshold of plotting significant measurements
filteredAnswer = {k: v for k,v in answer.items() if v >= threshold} #filter the answer for better view of plots
removedCounts = np.sum([ v for k,v in answer.items() if v < threshold ]) #number of counts removed
filteredAnswer['other_bitstrings'] = removedCounts #the removed counts is assigned to a new index
plot_histogram(filteredAnswer)
print(filteredAnswer)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
# useful additional packages
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# importing Qiskit
from qiskit import BasicAer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.monitor import job_monitor
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# Load our saved IBMQ accounts
IBMQ.load_account()
n = 13 # the length of the first register for querying the oracle
# Choose a type of oracle at random. With probability half it is constant,
# and with the same probability it is balanced
oracleType, oracleValue = np.random.randint(2), np.random.randint(2)
if oracleType == 0:
print("The oracle returns a constant value ", oracleValue)
else:
print("The oracle returns a balanced function")
a = np.random.randint(1,2**n) # this is a hidden parameter for balanced oracle.
# Creating registers
# n qubits for querying the oracle and one qubit for storing the answer
qr = QuantumRegister(n+1) #all qubits are initialized to zero
# for recording the measurement on the first register
cr = ClassicalRegister(n)
circuitName = "DeutschJozsa"
djCircuit = QuantumCircuit(qr, cr)
# Create the superposition of all input queries in the first register by applying the Hadamard gate to each qubit.
for i in range(n):
djCircuit.h(qr[i])
# Flip the second register and apply the Hadamard gate.
djCircuit.x(qr[n])
djCircuit.h(qr[n])
# Apply barrier to mark the beginning of the oracle
djCircuit.barrier()
if oracleType == 0:#If the oracleType is "0", the oracle returns oracleValue for all input.
if oracleValue == 1:
djCircuit.x(qr[n])
else:
djCircuit.iden(qr[n])
else: # Otherwise, it returns the inner product of the input with a (non-zero bitstring)
for i in range(n):
if (a & (1 << i)):
djCircuit.cx(qr[i], qr[n])
# Apply barrier to mark the end of the oracle
djCircuit.barrier()
# Apply Hadamard gates after querying the oracle
for i in range(n):
djCircuit.h(qr[i])
# Measurement
djCircuit.barrier()
for i in range(n):
djCircuit.measure(qr[i], cr[i])
#draw the circuit
djCircuit.draw(output='mpl',scale=0.5)
backend = BasicAer.get_backend('qasm_simulator')
shots = 1000
job = execute(djCircuit, backend=backend, shots=shots)
results = job.result()
answer = results.get_counts()
plot_histogram(answer)
backend = IBMQ.get_backend('ibmq_16_melbourne')
djCompiled = transpile(djCircuit, backend=backend, optimization_level=1)
djCompiled.draw(output='mpl',scale=0.5)
job = execute(djCompiled, backend=backend, shots=1024)
job_monitor(job)
results = job.result()
answer = results.get_counts()
threshold = int(0.01 * shots) # the threshold of plotting significant measurements
filteredAnswer = {k: v for k,v in answer.items() if v >= threshold} # filter the answer for better view of plots
removedCounts = np.sum([ v for k,v in answer.items() if v < threshold ]) # number of counts removed
filteredAnswer['other_bitstrings'] = removedCounts # the removed counts are assigned to a new index
plot_histogram(filteredAnswer)
print(filteredAnswer)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
from qiskit import BasicAer
from qiskit.transpiler import PassManager
from qiskit.aqua import QuantumInstance
from qiskit.aqua.operators import MatrixOperator, op_converter
from qiskit.aqua.algorithms import EOH
from qiskit.aqua.components.initial_states import Custom
num_qubits = 2
temp = np.random.random((2 ** num_qubits, 2 ** num_qubits))
qubit_op = op_converter.to_weighted_pauli_operator(MatrixOperator(matrix=temp + temp.T))
temp = np.random.random((2 ** num_qubits, 2 ** num_qubits))
evo_op = op_converter.to_weighted_pauli_operator(MatrixOperator(matrix=temp + temp.T))
evo_time = 1
num_time_slices = 1
state_in = Custom(qubit_op.num_qubits, state='uniform')
eoh = EOH(qubit_op, state_in, evo_op, evo_time=evo_time, num_time_slices=num_time_slices)
backend = BasicAer.get_backend('statevector_simulator')
quantum_instance = QuantumInstance(backend)
ret = eoh.run(quantum_instance)
print('The result is\n{}'.format(ret))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
from scipy.linalg import expm
from qiskit import BasicAer
from qiskit import execute as q_execute
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import state_fidelity
from qiskit.aqua.operators import MatrixOperator, op_converter
from qiskit.aqua.components.initial_states import Custom
num_qubits = 2
evo_time = 1
temp = np.random.random((2 ** num_qubits, 2 ** num_qubits))
h1 = temp + temp.T
qubitOp = MatrixOperator(matrix=h1)
state_in = Custom(num_qubits, state='random')
state_in_vec = state_in.construct_circuit('vector')
groundtruth = expm(-1.j * h1 * evo_time) @ state_in_vec
print('The directly computed groundtruth evolution result state is\n{}.'.format(groundtruth))
groundtruth_evolution = qubitOp.evolve(state_in_vec, evo_time, num_time_slices=0)
print('The groundtruth evolution result as computed by the Dynamics algorithm is\n{}.'.format(groundtruth_evolution))
np.testing.assert_allclose(groundtruth_evolution, groundtruth)
qubit_op = op_converter.to_weighted_pauli_operator(qubitOp)
quantum_registers = QuantumRegister(qubit_op.num_qubits)
circuit = state_in.construct_circuit('circuit', quantum_registers)
circuit += qubit_op.evolve(
None, evo_time, num_time_slices=1,
quantum_registers=quantum_registers,
expansion_mode='suzuki',
expansion_order=3
)
circuit.draw(output='mpl')
backend = BasicAer.get_backend('statevector_simulator')
job = q_execute(circuit, backend)
circuit_execution_result = np.asarray(job.result().get_statevector(circuit))
print('The evolution result state from executing the Dynamics circuit is\n{}.'.format(circuit_execution_result))
print('Fidelity between the groundtruth and the circuit result states is {}.'.format(
state_fidelity(groundtruth, circuit_execution_result)
))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import BasicAer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import Shor
N = 15
shor = Shor(N)
backend = BasicAer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=1024)
ret = shor.run(quantum_instance)
print("The list of factors of {} as computed by the Shor's algorithm is {}.".format(N, ret['factors'][0]))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
from qiskit import BasicAer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import Simon
from qiskit.aqua.components.oracles import TruthTableOracle
bitmaps = [
'01101001',
'10011001',
'01100110'
]
oracle = TruthTableOracle(bitmaps)
def compute_mask(input_bitmaps):
vals = list(zip(*input_bitmaps))[::-1]
def find_pair():
for i in range(len(vals)):
for j in range(i + 1, len(vals)):
if vals[i] == vals[j]:
return i, j
return 0, 0
k1, k2 = find_pair()
return np.binary_repr(k1 ^ k2, int(np.log2(len(input_bitmaps[0]))))
mask = compute_mask(bitmaps)
print(f'The groundtruth mask is {mask}.')
simon = Simon(oracle)
backend = BasicAer.get_backend('qasm_simulator')
result = simon.run(QuantumInstance(backend, shots=1024))
print('The mask computed using Simon is {}.'.format(result['result']))
assert(result['result'] == mask)
bitmaps = [
'00011110',
'01100110',
'10101010'
]
mask = compute_mask(bitmaps)
print(f'The groundtruth mask is {mask}.')
oracle = TruthTableOracle(bitmaps)
simon = Simon(oracle)
result = simon.run(QuantumInstance(backend, shots=1024))
print('The mask computed using Simon is {}.'.format(result['result']))
assert(result['result'] == mask)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
import pylab
from qiskit import Aer, IBMQ
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.circuit.library import TwoLocal
from qiskit.aqua.operators import WeightedPauliOperator
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
num_qubits = qubit_op.num_qubits
print('Number of qubits: {}'.format(num_qubits))
ee = NumPyMinimumEigensolver(qubit_op.copy())
result = ee.run()
ref = result.eigenvalue.real
print('Reference value: {}'.format(ref))
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend=backend, seed_simulator=167, seed_transpiler=167)
counts = []
values = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
aqua_globals.random_seed = 167
optimizer = SPSA(maxiter=200)
var_form = TwoLocal(num_qubits, 'ry', 'cz')
vqe = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result)
vqe_result = vqe.run(quantum_instance)
print('VQE on Aer qasm simulator (no noise): {}'.format(vqe_result.eigenvalue.real))
print('Delta from reference: {}'.format(vqe_result.eigenvalue.real-ref))
pylab.rcParams['figure.figsize'] = (12, 4)
pylab.plot(counts, values)
pylab.xlabel('Eval count')
pylab.ylabel('Energy')
pylab.title('Convergence with no noise')
import os
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.ibmq.exceptions import IBMQAccountCredentialsNotFound
backend = Aer.get_backend('qasm_simulator')
counts1 = []
values1 = []
noise_model = None
try:
os.environ['QISKIT_IN_PARALLEL'] = 'TRUE'
provider = IBMQ.load_account()
device = provider.get_backend('ibmqx2')
coupling_map = device.configuration().coupling_map
noise_model = NoiseModel.from_backend(device)
basis_gates = noise_model.basis_gates
print(noise_model)
quantum_instance = QuantumInstance(backend=backend, seed_simulator=167, seed_transpiler=167,
noise_model=noise_model,)
def store_intermediate_result1(eval_count, parameters, mean, std):
counts1.append(eval_count)
values1.append(mean)
aqua_globals.random_seed = 167
optimizer = SPSA(maxiter=200)
var_form = TwoLocal(num_qubits, 'ry', 'cz')
vqe = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result1)
vqe_result1 = vqe.run(quantum_instance)
print('VQE on Aer qasm simulator (with noise): {}'.format(vqe_result1.eigenvalue.real))
print('Delta from reference: {}'.format(vqe_result1.eigenvalue.real-ref))
except IBMQAccountCredentialsNotFound as ex:
print(str(ex))
if counts1 or values1:
pylab.rcParams['figure.figsize'] = (12, 4)
pylab.plot(counts1, values1)
pylab.xlabel('Eval count')
pylab.ylabel('Energy')
pylab.title('Convergence with noise')
from qiskit.ignis.mitigation.measurement import CompleteMeasFitter
counts1 = []
values1 = []
if noise_model is not None:
quantum_instance = QuantumInstance(backend=backend, seed_simulator=167, seed_transpiler=167,
noise_model=noise_model,
measurement_error_mitigation_cls=CompleteMeasFitter,
cals_matrix_refresh_period=30)
def store_intermediate_result1(eval_count, parameters, mean, std):
counts1.append(eval_count)
values1.append(mean)
aqua_globals.random_seed = 167
optimizer = SPSA(maxiter=200)
var_form = TwoLocal(num_qubits, 'ry', 'cz')
vqe = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result1)
vqe_result1 = vqe.run(quantum_instance)
print('VQE on Aer qasm simulator (with noise and measurement error mitigation): {}'.format(vqe_result1.eigenvalue))
print('Delta from reference: {}'.format(vqe_result1.eigenvalue.real-ref))
if counts1 or values1:
pylab.rcParams['figure.figsize'] = (12, 4)
pylab.plot(counts1, values1)
pylab.xlabel('Eval count')
pylab.ylabel('Energy')
pylab.title('Convergence with noise, enabling measurement error mitigation')
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
from qiskit import BasicAer
from qiskit.transpiler import PassManager
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver, IQPE
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.circuit.library import TwoLocal
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua.components.initial_states.var_form_based import VarFormBased
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
result_reference = NumPyMinimumEigensolver(qubit_op).run()
print('The reference ground energy level is {}.'.format(result_reference.eigenvalue.real))
random_seed = 0
np.random.seed(random_seed)
backend = BasicAer.get_backend('qasm_simulator')
var_form_depth = 3
var_form = TwoLocal(qubit_op.num_qubits, ['ry', 'rz'], 'cz', reps=var_form_depth)
spsa_max_trials=10
optimizer = SPSA(max_trials=spsa_max_trials)
vqe = VQE(qubit_op, var_form, optimizer)
quantum_instance = QuantumInstance(backend)
result_vqe = vqe.run(quantum_instance)
print('VQE estimated the ground energy to be {}.'.format(result_vqe.eigenvalue.real))
state_in = VarFormBased(var_form, result_vqe.optimal_point)
num_time_slices = 1
num_iterations = 6
iqpe = IQPE(qubit_op, state_in, num_time_slices, num_iterations,
expansion_mode='suzuki', expansion_order=2,
shallow_circuit_concat=True)
quantum_instance = QuantumInstance(backend, shots=100, seed_simulator=random_seed, seed_transpiler=random_seed)
result_iqpe = iqpe.run(quantum_instance)
print("Continuing with VQE's result, IQPE estimated the ground energy to be {}.".format(
result_iqpe.eigenvalue.real))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import numpy as np
import pylab
from qiskit import BasicAer
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms import VQE, NumPyMinimumEigensolver
from qiskit.aqua.components.initial_states import Zero
from qiskit.aqua.components.optimizers import COBYLA, L_BFGS_B, SLSQP
from qiskit.circuit.library import TwoLocal
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
optimizers = [COBYLA, L_BFGS_B, SLSQP]
converge_cnts = np.empty([len(optimizers)], dtype=object)
converge_vals = np.empty([len(optimizers)], dtype=object)
num_qubits = qubit_op.num_qubits
for i in range(len(optimizers)):
aqua_globals.random_seed = 250
optimizer = optimizers[i]()
print('\rOptimizer: {} '.format(type(optimizer).__name__), end='')
init_state = Zero(num_qubits)
var_form = TwoLocal(num_qubits, 'ry', 'cz', initial_state=init_state)
counts = []
values = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
algo = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result)
backend = BasicAer.get_backend('statevector_simulator')
quantum_instance = QuantumInstance(backend=backend)
algo_result = algo.run(quantum_instance)
converge_cnts[i] = np.asarray(counts)
converge_vals[i] = np.asarray(values)
print('\rOptimization complete ');
pylab.rcParams['figure.figsize'] = (12, 8)
for i in range(len(optimizers)):
pylab.plot(converge_cnts[i], converge_vals[i], label=optimizers[i].__name__)
pylab.xlabel('Eval count')
pylab.ylabel('Energy')
pylab.title('Energy convergence for various optimizers')
pylab.legend(loc='upper right')
ee = NumPyMinimumEigensolver(qubit_op)
result = ee.run()
ref = result.eigenvalue.real
print('Reference value: {}'.format(ref))
pylab.rcParams['figure.figsize'] = (12, 8)
for i in range(len(optimizers)):
pylab.plot(converge_cnts[i], abs(ref - converge_vals[i]), label=optimizers[i].__name__)
pylab.xlabel('Eval count')
pylab.ylabel('Energy difference from solution reference value')
pylab.title('Energy convergence for various optimizers')
pylab.yscale('log')
pylab.legend(loc='upper right')
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
#initialization
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
# importing Qiskit
from qiskit import IBMQ, BasicAer
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.monitor import job_monitor
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# Load our saved IBMQ accounts.
IBMQ.load_account()
nQubits = 14 # number of physical qubits
a = 101 # the hidden integer whose bitstring is 1100101
# make sure that a can be represented with nQubits
a = a % 2**(nQubits)
# Creating registers
# qubits for querying the oracle and finding the hidden integer
qr = QuantumRegister(nQubits)
# for recording the measurement on qr
cr = ClassicalRegister(nQubits)
circuitName = "BernsteinVazirani"
bvCircuit = QuantumCircuit(qr, cr)
# Apply Hadamard gates before querying the oracle
for i in range(nQubits):
bvCircuit.h(qr[i])
# Apply barrier so that it is not optimized by the compiler
bvCircuit.barrier()
# Apply the inner-product oracle
for i in range(nQubits):
if (a & (1 << i)):
bvCircuit.z(qr[i])
else:
bvCircuit.iden(qr[i])
# Apply barrier
bvCircuit.barrier()
#Apply Hadamard gates after querying the oracle
for i in range(nQubits):
bvCircuit.h(qr[i])
# Measurement
bvCircuit.barrier(qr)
bvCircuit.measure(qr, cr)
bvCircuit.draw(output='mpl')
# use local simulator
backend = BasicAer.get_backend('qasm_simulator')
shots = 1000
results = execute(bvCircuit, backend=backend, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer)
backend = IBMQ.get_backend('ibmq_16_melbourne')
shots = 1000
bvCompiled = transpile(bvCircuit, backend=backend, optimization_level=1)
job_exp = execute(bvCircuit, backend=backend, shots=shots)
job_monitor(job_exp)
results = job_exp.result()
answer = results.get_counts(bvCircuit)
threshold = int(0.01 * shots) #the threshold of plotting significant measurements
filteredAnswer = {k: v for k,v in answer.items() if v >= threshold} #filter the answer for better view of plots
removedCounts = np.sum([ v for k,v in answer.items() if v < threshold ]) #number of counts removed
filteredAnswer['other_bitstrings'] = removedCounts #the removed counts is assigned to a new index
plot_histogram(filteredAnswer)
print(filteredAnswer)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
# useful additional packages
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# importing Qiskit
from qiskit import BasicAer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.monitor import job_monitor
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# Load our saved IBMQ accounts
IBMQ.load_account()
n = 13 # the length of the first register for querying the oracle
# Choose a type of oracle at random. With probability half it is constant,
# and with the same probability it is balanced
oracleType, oracleValue = np.random.randint(2), np.random.randint(2)
if oracleType == 0:
print("The oracle returns a constant value ", oracleValue)
else:
print("The oracle returns a balanced function")
a = np.random.randint(1,2**n) # this is a hidden parameter for balanced oracle.
# Creating registers
# n qubits for querying the oracle and one qubit for storing the answer
qr = QuantumRegister(n+1) #all qubits are initialized to zero
# for recording the measurement on the first register
cr = ClassicalRegister(n)
circuitName = "DeutschJozsa"
djCircuit = QuantumCircuit(qr, cr)
# Create the superposition of all input queries in the first register by applying the Hadamard gate to each qubit.
for i in range(n):
djCircuit.h(qr[i])
# Flip the second register and apply the Hadamard gate.
djCircuit.x(qr[n])
djCircuit.h(qr[n])
# Apply barrier to mark the beginning of the oracle
djCircuit.barrier()
if oracleType == 0:#If the oracleType is "0", the oracle returns oracleValue for all input.
if oracleValue == 1:
djCircuit.x(qr[n])
else:
djCircuit.iden(qr[n])
else: # Otherwise, it returns the inner product of the input with a (non-zero bitstring)
for i in range(n):
if (a & (1 << i)):
djCircuit.cx(qr[i], qr[n])
# Apply barrier to mark the end of the oracle
djCircuit.barrier()
# Apply Hadamard gates after querying the oracle
for i in range(n):
djCircuit.h(qr[i])
# Measurement
djCircuit.barrier()
for i in range(n):
djCircuit.measure(qr[i], cr[i])
#draw the circuit
djCircuit.draw(output='mpl',scale=0.5)
backend = BasicAer.get_backend('qasm_simulator')
shots = 1000
job = execute(djCircuit, backend=backend, shots=shots)
results = job.result()
answer = results.get_counts()
plot_histogram(answer)
backend = IBMQ.get_backend('ibmq_16_melbourne')
djCompiled = transpile(djCircuit, backend=backend, optimization_level=1)
djCompiled.draw(output='mpl',scale=0.5)
job = execute(djCompiled, backend=backend, shots=1024)
job_monitor(job)
results = job.result()
answer = results.get_counts()
threshold = int(0.01 * shots) # the threshold of plotting significant measurements
filteredAnswer = {k: v for k,v in answer.items() if v >= threshold} # filter the answer for better view of plots
removedCounts = np.sum([ v for k,v in answer.items() if v < threshold ]) # number of counts removed
filteredAnswer['other_bitstrings'] = removedCounts # the removed counts are assigned to a new index
plot_histogram(filteredAnswer)
print(filteredAnswer)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# importing Qiskit
from qiskit import BasicAer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.visualization import plot_histogram
q = QuantumRegister(6)
qc = QuantumCircuit(q)
qc.x(q[2])
qc.cx(q[1], q[5])
qc.cx(q[2], q[5])
qc.cx(q[3], q[5])
qc.ccx(q[1], q[2], q[4])
qc.ccx(q[3], q[4], q[5])
qc.ccx(q[1], q[2], q[4])
qc.x(q[2])
qc.draw(output='mpl')
def black_box_u_f(circuit, f_in, f_out, aux, n, exactly_1_3_sat_formula):
"""Circuit that computes the black-box function from f_in to f_out.
Create a circuit that verifies whether a given exactly-1 3-SAT
formula is satisfied by the input. The exactly-1 version
requires exactly one literal out of every clause to be satisfied.
"""
num_clauses = len(exactly_1_3_sat_formula)
for (k, clause) in enumerate(exactly_1_3_sat_formula):
# This loop ensures aux[k] is 1 if an odd number of literals
# are true
for literal in clause:
if literal > 0:
circuit.cx(f_in[literal-1], aux[k])
else:
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
# Flip aux[k] if all literals are true, using auxiliary qubit
# (ancilla) aux[num_clauses]
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
# Flip back to reverse state of negative literals and ancilla
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
for literal in clause:
if literal < 0:
circuit.x(f_in[-literal-1])
# The formula is satisfied if and only if all auxiliary qubits
# except aux[num_clauses] are 1
if (num_clauses == 1):
circuit.cx(aux[0], f_out[0])
elif (num_clauses == 2):
circuit.ccx(aux[0], aux[1], f_out[0])
elif (num_clauses == 3):
circuit.ccx(aux[0], aux[1], aux[num_clauses])
circuit.ccx(aux[2], aux[num_clauses], f_out[0])
circuit.ccx(aux[0], aux[1], aux[num_clauses])
else:
raise ValueError('We only allow at most 3 clauses')
# Flip back any auxiliary qubits to make sure state is consistent
# for future executions of this routine; same loop as above.
for (k, clause) in enumerate(exactly_1_3_sat_formula):
for literal in clause:
if literal > 0:
circuit.cx(f_in[literal-1], aux[k])
else:
circuit.x(f_in[-literal-1])
circuit.cx(f_in[-literal-1], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
circuit.ccx(f_in[2], aux[num_clauses], aux[k])
circuit.ccx(f_in[0], f_in[1], aux[num_clauses])
for literal in clause:
if literal < 0:
circuit.x(f_in[-literal-1])
# -- end function
def n_controlled_Z(circuit, controls, target):
"""Implement a Z gate with multiple controls"""
if (len(controls) > 2):
raise ValueError('The controlled Z with more than 2 ' +
'controls is not implemented')
elif (len(controls) == 1):
circuit.h(target)
circuit.cx(controls[0], target)
circuit.h(target)
elif (len(controls) == 2):
circuit.h(target)
circuit.ccx(controls[0], controls[1], target)
circuit.h(target)
# -- end function
def inversion_about_average(circuit, f_in, n):
"""Apply inversion about the average step of Grover's algorithm."""
# Hadamards everywhere
for j in range(n):
circuit.h(f_in[j])
# D matrix: flips the sign of the state |000> only
for j in range(n):
circuit.x(f_in[j])
n_controlled_Z(circuit, [f_in[j] for j in range(n-1)], f_in[n-1])
for j in range(n):
circuit.x(f_in[j])
# Hadamards everywhere again
for j in range(n):
circuit.h(f_in[j])
# -- end function
qr = QuantumRegister(3)
qInvAvg = QuantumCircuit(qr)
inversion_about_average(qInvAvg, qr, 3)
qInvAvg.draw(output='mpl')
"""
Grover search implemented in Qiskit.
This module contains the code necessary to run Grover search on 3
qubits, both with a simulator and with a real quantum computing
device. This code is the companion for the paper
"An introduction to quantum computing, without the physics",
Giacomo Nannicini, https://arxiv.org/abs/1708.03684.
"""
def input_state(circuit, f_in, f_out, n):
"""(n+1)-qubit input state for Grover search."""
for j in range(n):
circuit.h(f_in[j])
circuit.x(f_out)
circuit.h(f_out)
# -- end function
# Make a quantum program for the n-bit Grover search.
n = 3
# Exactly-1 3-SAT formula to be satisfied, in conjunctive
# normal form. We represent literals with integers, positive or
# negative, to indicate a Boolean variable or its negation.
exactly_1_3_sat_formula = [[1, 2, -3], [-1, -2, -3], [-1, 2, 3]]
# Define three quantum registers: 'f_in' is the search space (input
# to the function f), 'f_out' is bit used for the output of function
# f, aux are the auxiliary bits used by f to perform its
# computation.
f_in = QuantumRegister(n)
f_out = QuantumRegister(1)
aux = QuantumRegister(len(exactly_1_3_sat_formula) + 1)
# Define classical register for algorithm result
ans = ClassicalRegister(n)
# Define quantum circuit with above registers
grover = QuantumCircuit()
grover.add_register(f_in)
grover.add_register(f_out)
grover.add_register(aux)
grover.add_register(ans)
input_state(grover, f_in, f_out, n)
T = 2
for t in range(T):
# Apply T full iterations
black_box_u_f(grover, f_in, f_out, aux, n, exactly_1_3_sat_formula)
inversion_about_average(grover, f_in, n)
# Measure the output register in the computational basis
for j in range(n):
grover.measure(f_in[j], ans[j])
# Execute circuit
backend = BasicAer.get_backend('qasm_simulator')
job = execute([grover], backend=backend, shots=1000)
result = job.result()
# Get counts and plot histogram
counts = result.get_counts(grover)
plot_histogram(counts)
IBMQ.load_account()
# get ibmq_16_melbourne configuration and coupling map
backend = IBMQ.get_backend('ibmq_16_melbourne')
# compile the circuit for ibmq_16_rueschlikon
grover_compiled = transpile(grover, backend=backend, seed_transpiler=1, optimization_level=3)
print('gates = ', grover_compiled.count_ops())
print('depth = ', grover_compiled.depth())
grover.draw(output='mpl', scale=0.5)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
from math import pi
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
%matplotlib inline
# importing Qiskit
from qiskit import BasicAer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
from qiskit.tools.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
# Load saved IBMQ accounts
IBMQ.load_account()
# We first define controlled gates used in the IPEA
def cu1fixed(qProg, c, t, a):
qProg.u1(-a, t)
qProg.cx(c, t)
qProg.u1(a, t)
qProg.cx(c, t)
def cu5pi8(qProg, c, t):
cu1fixed(qProg, c, t, -5.0*pi/8.0)
# We then prepare quantum and classical registers and the circuit
qr = QuantumRegister(2)
cr = ClassicalRegister(4)
circuitName="IPEAonSimulator"
ipeaCircuit = QuantumCircuit(qr, cr)
# Apply IPEA
ipeaCircuit.h(qr[0])
for i in range(8):
cu5pi8(ipeaCircuit, qr[0], qr[1])
ipeaCircuit.h(qr[0])
ipeaCircuit.measure(qr[0], cr[0])
ipeaCircuit.reset(qr[0])
ipeaCircuit.h(qr[0])
for i in range(4):
cu5pi8(ipeaCircuit, qr[0], qr[1])
ipeaCircuit.u1(-pi/2, qr[0]).c_if(cr, 1)
ipeaCircuit.h(qr[0])
ipeaCircuit.measure(qr[0], cr[1])
ipeaCircuit.reset(qr[0])
ipeaCircuit.h(qr[0])
for i in range(2):
cu5pi8(ipeaCircuit, qr[0], qr[1])
ipeaCircuit.u1(-pi/4, qr[0]).c_if(cr, 1)
ipeaCircuit.u1(-pi/2, qr[0]).c_if(cr, 2)
ipeaCircuit.u1(-3*pi/4, qr[0]).c_if(cr, 3)
ipeaCircuit.h(qr[0])
ipeaCircuit.measure(qr[0], cr[2])
ipeaCircuit.reset(qr[0])
ipeaCircuit.h(qr[0])
cu5pi8(ipeaCircuit, qr[0], qr[1])
ipeaCircuit.u1(-pi/8, qr[0]).c_if(cr, 1)
ipeaCircuit.u1(-2*pi/8, qr[0]).c_if(cr, 2)
ipeaCircuit.u1(-3*pi/8, qr[0]).c_if(cr, 3)
ipeaCircuit.u1(-4*pi/8, qr[0]).c_if(cr, 4)
ipeaCircuit.u1(-5*pi/8, qr[0]).c_if(cr, 5)
ipeaCircuit.u1(-6*pi/8, qr[0]).c_if(cr, 6)
ipeaCircuit.u1(-7*pi/8, qr[0]).c_if(cr, 7)
ipeaCircuit.h(qr[0])
ipeaCircuit.measure(qr[0], cr[3])
backend = BasicAer.get_backend('qasm_simulator')
shots = 1000
results = execute(ipeaCircuit, backend=backend, shots=shots).result()
plot_histogram(results.get_counts())
# We then prepare quantum and classical registers and the circuit
qr = QuantumRegister(5)
cr = ClassicalRegister(5)
realStep1Circuit = QuantumCircuit(qr, cr)
# Apply IPEA
realStep1Circuit.h(qr[0])
for i in range(8):
cu5pi8(realStep1Circuit, qr[0], qr[1])
realStep1Circuit.h(qr[0])
realStep1Circuit.measure(qr[0], cr[0])
#connect to remote API to be able to use remote simulators and real devices
print("Available backends:", [BasicAer.backends(), IBMQ.backends()])
backend = IBMQ.get_backend("ibmq_5_yorktown")
shots = 1000
job_exp1 = execute(realStep1Circuit, backend=backend, shots=shots)
job_monitor(job_exp1)
results1 = job_exp1.result()
plot_histogram(results1.get_counts())
realStep2Circuit = QuantumCircuit(qr, cr)
# Apply IPEA
realStep2Circuit.h(qr[0])
for i in range(4):
cu5pi8(realStep2Circuit, qr[0], qr[1])
realStep2Circuit.u1(-pi/2, qr[0]) # Assuming the value of the measurement on Step 1
realStep2Circuit.h(qr[0])
realStep2Circuit.measure(qr[0], cr[0])
job_exp2 = execute(realStep2Circuit, backend=backend, shots=shots)
job_monitor(job_exp1)
results2 = job_exp2.result()
plot_histogram(results2.get_counts())
realStep3Circuit = QuantumCircuit(qr, cr)
# Apply IPEA
realStep3Circuit.h(qr[0])
for i in range(2):
cu5pi8(realStep3Circuit, qr[0], qr[1])
realStep3Circuit.u1(-3*pi/4, qr[0]) # Assuming the value of the measurement on Step 1 and Step 2
realStep3Circuit.h(qr[0])
realStep3Circuit.measure(qr[0], cr[0])
job_exp3 = execute(realStep3Circuit, backend=backend, shots=shots)
job_monitor(job_exp3)
results3 = job_exp3.result()
plot_histogram(results3.get_counts())
realStep4Circuit = QuantumCircuit(qr, cr)
# Apply IPEA
realStep4Circuit.h(qr[0])
cu5pi8(realStep4Circuit, qr[0], qr[1])
realStep4Circuit.u1(-3*pi/8, qr[0]) # Assuming the value of the measurement on Step 1, 2, and 3
realStep4Circuit.h(qr[0])
realStep4Circuit.measure(qr[0], cr[0])
job_exp4 = execute(realStep4Circuit, backend=backend, shots=shots)
job_monitor(job_exp4)
results4 = job_exp4.result()
plot_histogram(results4.get_counts())
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import YouTubeVideo
YouTubeVideo('BYKc2RnQMqo', width=858, height=540)
!pip install qiskit --quiet
!pip install qiskit-aer --quiet
!pip install pylatexenc --quiet
# @markdown ### **1. Import `Qiskit` and essential packages** { display-mode: "form" }
from qiskit import QuantumCircuit, transpile, assemble
from qiskit.circuit.library import QFT
from qiskit_aer import AerSimulator
from fractions import Fraction
import random
import sympy
import math
# @markdown ### **2. Controlled Modular Multiplication for $U(x) = a^x mod N$** { display-mode: "form" }
class CtrlMultCircuit(QuantumCircuit):
def __init__(self, a, binary_power, N):
super().__init__(N.bit_length())
self.a = a
self.power = 2 ** binary_power # Convert binary to decimal
self.N = N
self.name = f'{self.a}^{self.power} mod {self.N}'
self._create_circuit()
def _create_circuit(self):
for dec_power in range(self.power):
a_exp = self.a ** dec_power % self.N
for i in range(self.num_qubits):
if a_exp >> i & 1: self.x(i)
for j in range(i + 1, self.num_qubits):
if a_exp >> j & 1: self.swap(i, j)
# @markdown ### **3. Quantum Phase Estimation with `Modular Exponentiation` and `Quantum Fourier Transform` to find period $r$** { display-mode: "form" }
# @markdown 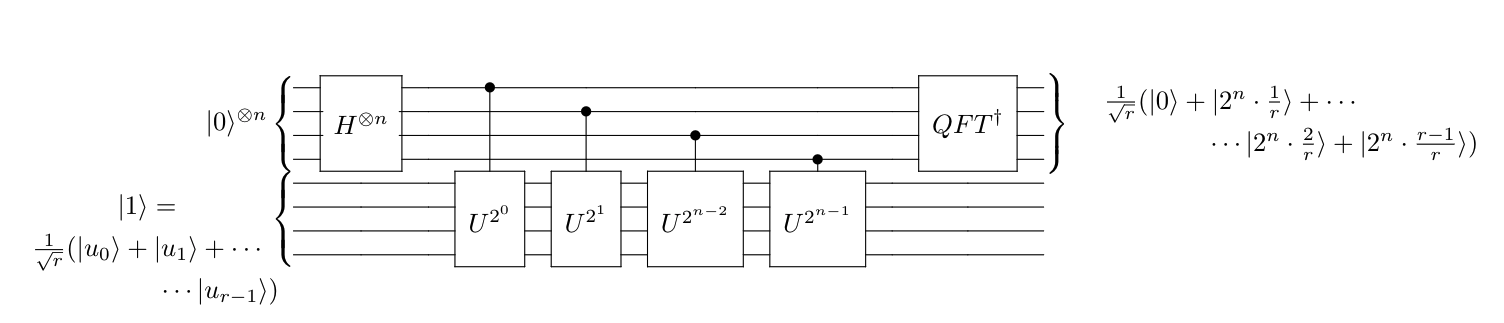
class QPECircuit(QuantumCircuit):
def __init__(self, a, N):
super().__init__(2 * N.bit_length(), N.bit_length())
self.a = a
self.N = N
self._create_circuit()
def _modular_exponentiation(self):
for qbit_idx in range(self.num_qubits // 2):
self.append(
CtrlMultCircuit(self.a, qbit_idx, self.N).to_gate().control(),
[qbit_idx] + list(range(self.num_qubits // 2, 2 * self.num_qubits // 2))
)
def _create_circuit(self):
self.h(range(self.num_qubits // 2)) # Apply Hadamard gates to the first n qubits
self.x(self.num_qubits - 1)
self.barrier()
self._modular_exponentiation() # Apply controlled modular exponentiation
self.barrier()
self.append(
QFT(self.num_qubits // 2, inverse=True),
range(self.num_qubits // 2) # Apply inverse QFT to the first n qubits
)
def collapse(self, simulator):
self.measure(range(self.num_qubits // 2), range(self.num_qubits // 2))
transpiled_circuit = transpile(self, simulator)
self.collapse_result = simulator.run(transpiled_circuit, memory=True).result()
return self.collapse_result
# @markdown ### **4. Completed Shor's Algorithm for Integer Factorization** { display-mode: "form" }
class ShorAlgorithm:
def __init__(self, N, max_attempts=-1, random_coprime_only=False, simulator=None):
self.N = N
self.simulator = simulator
self.max_attempts = max_attempts # -1 for all possible values of a
self.random_coprime_only = random_coprime_only # True to select only coprime values of a and N
def execute(self):
is_N_invalid = self._is_N_invalid()
if is_N_invalid: return is_N_invalid
# Only coprime values remain if random_coprime_only is enabled,
# Otherwise select a random integer in [2, N) as initial guess
a_values = [a for a in range(2, self.N) if not self.random_coprime_only or (math.gcd(a, self.N) == 1)]
print(f'[INFO] {len(a_values)} possible values of a: {a_values}')
self.max_attempts = len(a_values) if self.max_attempts <= -1 else min(self.max_attempts, len(a_values))
attempts_count = 0
while attempts_count < self.max_attempts:
print(f'\n===== Attempt {attempts_count + 1}/{self.max_attempts} =====')
attempts_count += 1
self.chosen_a = random.choice(a_values)
self.r = 1
print(f'[START] Chosen base a: {self.chosen_a}')
if not self.random_coprime_only:
gcd = math.gcd(self.chosen_a, self.N)
if gcd != 1:
print(f'=> {self.chosen_a} and {self.N} share common factor: {self.N} = {gcd} * {self.N // gcd}')
return gcd, self.N // gcd
print(f'>>> {self.chosen_a} and {self.N} are coprime => Perform Quantum Phase Estimation to find {self.chosen_a}^r - 1 = 0 (MOD {self.N})')
if not self._quantum_period_finding():
a_values.remove(self.chosen_a)
self.r = self.chosen_a = self.qpe_circuit = None
continue
factors = self._classical_postprocess()
if factors: return factors
a_values.remove(self.chosen_a)
self.r = self.chosen_a = self.qpe_circuit = None
print(f'[FAIL] No non-trivial factors found after {self.max_attempts} attempts.')
def _is_N_invalid(self):
if self.N <= 3:
print('[ERR] N must be > 3')
return 1, self.N
if self.N % 2 == 0:
print(f'=> {self.N} is an even number: {self.N} = 2 * {self.N // 2}')
return 2, self.N // 2
if sympy.isprime(self.N):
print(f'=> {self.N} is a prime number: {self.N} = 1 * {self.N}')
return 1, self.N
max_exponent = int(math.log2(self.N)) # Start with a large exponent and reduce
for k in range(max_exponent, 1, -1):
p = round(self.N ** (1 / k))
if p ** k == self.N:
print(f'=> {self.N} is a power of prime: {self.N} = {p}^{k}')
return p, k
return False
def _quantum_period_finding(self):
while self.chosen_a ** self.r % self.N != 1: # QPE + continued fractions may find wrong r
self.qpe_circuit = QPECircuit(self.chosen_a, self.N) # Find phase s/r
result = self.qpe_circuit.collapse(self.simulator)
state_bin = result.get_memory()[0]
state_dec = int(state_bin, 2) # Convert to decimal
bits_count = 2 ** (self.N.bit_length() - 1)
phase = state_dec / bits_count
# Continued fraction to find r
self.r = Fraction(phase).limit_denominator(self.N).denominator # Get fraction that most closely approximates phase
if self.r > self.N or self.r == 1: # Safety check to avoid infinite loops
print(f'[ERR] Invalid period found: r = {self.r} => Retry with different a.')
return False
print(f'>>> Output State: |{state_bin}⟩ = {state_dec} (dec) => Phase = {state_dec} / {bits_count} = {phase:.3f}')
return True
def _classical_postprocess(self):
# Classical postprocessing to find factors from the period
print(f'>>> Found r = {self.r} => a^{{r/2}} ± 1 = {self.chosen_a:.0f}^{self.r/2:.0f} ± 1')
if self.r % 2 != 0:
print(f'[ERR] r = {self.r} is odd => Retry with different a.')
return None
int1, int2 = self.chosen_a ** (self.r // 2) - 1, self.chosen_a ** (self.r // 2) + 1
if int1 % self.N == 0 or int2 % self.N == 0:
print(f'[ERR] {self.chosen_a}^{self.r/2:.0f} ± 1 is a multiple of {self.N} => Retry with different a.')
return None
factor1, factor2 = math.gcd(int1, self.N), math.gcd(int2, self.N)
if factor1 not in [1, self.N] and factor2 not in [1, self.N]: # Check to see if factor is non-trivial
print(f'[DONE] Successfully found non-trivial factors: {self.N} = {factor1} * {factor2}')
return factor1, factor2
print(f'[FAIL] Trivial factors found: [1, {self.N}] => Retry with different a.')
return None
# @markdown ### **5. Run the Factorization** { display-mode: "form" }
number_to_factor = 21 # @param {type:"slider", min: 15, max: 55, step: 1}
max_attempts = -1 # @param {type:"slider", min:-1, max:100, step:10}
random_coprime_only = False # @param {type:"boolean"}
# @markdown ***Note**: `max_attempts` will be limited to number of available values.
shor = ShorAlgorithm(number_to_factor, max_attempts, random_coprime_only, AerSimulator())
factors = shor.execute()
try: display(shor.qpe_circuit.draw(output='mpl', fold=-1))
except Exception: pass
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
qiskit.__qiskit_version__
#initialization
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# importing Qiskit
from qiskit import BasicAer, IBMQ
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.compiler import transpile
from qiskit.tools.monitor import job_monitor
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
# Load the saved IBMQ accounts
IBMQ.load_account()
s = "010101" # the hidden bitstring
assert 1 < len(s) < 20, "The length of s must be between 2 and 19"
for c in s:
assert c == "0" or c == "1", "s must be a bitstring of '0' and '1'"
n = len(s) #the length of the bitstring
# Step 1
# Creating registers
# qubits for querying the oracle and recording its output
qr = QuantumRegister(2*n)
# for recording the measurement on the first register of qr
cr = ClassicalRegister(n)
circuitName = "Simon"
simonCircuit = QuantumCircuit(qr, cr)
# Step 2
# Apply Hadamard gates before querying the oracle
for i in range(n):
simonCircuit.h(qr[i])
# Apply barrier to mark the beginning of the blackbox function
simonCircuit.barrier()
# Step 3 query the blackbox function
# copy the content of the first register to the second register
for i in range(n):
simonCircuit.cx(qr[i], qr[n+i])
# get the least index j such that s_j is "1"
j = -1
for i, c in enumerate(s):
if c == "1":
j = i
break
# Creating 1-to-1 or 2-to-1 mapping with the j-th qubit of x as control to XOR the second register with s
for i, c in enumerate(s):
if c == "1" and j >= 0:
simonCircuit.cx(qr[j], qr[n+i]) #the i-th qubit is flipped if s_i is 1
# get random permutation of n qubits
perm = list(np.random.permutation(n))
#initial position
init = list(range(n))
i = 0
while i < n:
if init[i] != perm[i]:
k = perm.index(init[i])
simonCircuit.swap(qr[n+i], qr[n+k]) #swap qubits
init[i], init[k] = init[k], init[i] #marked swapped qubits
else:
i += 1
# randomly flip the qubit
for i in range(n):
if np.random.random() > 0.5:
simonCircuit.x(qr[n+i])
# Apply the barrier to mark the end of the blackbox function
simonCircuit.barrier()
# Step 4 apply Hadamard gates to the first register
for i in range(n):
simonCircuit.h(qr[i])
# Step 5 perform measurement on the first register
for i in range(n):
simonCircuit.measure(qr[i], cr[i])
#draw the circuit
simonCircuit.draw(output='mpl')
# use local simulator
backend = BasicAer.get_backend("qasm_simulator")
# the number of shots is twice the length of the bitstring
shots = 2*n
job = execute(simonCircuit, backend=backend, shots=shots)
answer = job.result().get_counts()
plot_histogram(answer)
# Post-processing step
# Constructing the system of linear equations Y s = 0
# By k[::-1], we reverse the order of the bitstring
lAnswer = [ (k[::-1],v) for k,v in answer.items() if k != "0"*n ] #excluding the trivial all-zero
#Sort the basis by their probabilities
lAnswer.sort(key = lambda x: x[1], reverse=True)
Y = []
for k, v in lAnswer:
Y.append( [ int(c) for c in k ] )
#import tools from sympy
from sympy import Matrix, pprint, MatrixSymbol, expand, mod_inverse
Y = Matrix(Y)
#pprint(Y)
#Perform Gaussian elimination on Y
Y_transformed = Y.rref(iszerofunc=lambda x: x % 2==0) # linear algebra on GF(2)
#to convert rational and negatives in rref of linear algebra on GF(2)
def mod(x,modulus):
numer, denom = x.as_numer_denom()
return numer*mod_inverse(denom,modulus) % modulus
Y_new = Y_transformed[0].applyfunc(lambda x: mod(x,2)) #must takecare of negatives and fractional values
#pprint(Y_new)
print("The hidden bistring s[ 0 ], s[ 1 ]....s[",n-1,"] is the one satisfying the following system of linear equations:")
rows, cols = Y_new.shape
for r in range(rows):
Yr = [ "s[ "+str(i)+" ]" for i, v in enumerate(list(Y_new[r,:])) if v == 1 ]
if len(Yr) > 0:
tStr = " + ".join(Yr)
print(tStr, "= 0")
#Use one of the available backends
backend = IBMQ.get_backend("ibmq_16_melbourne")
# show the status of the backend
print("Status of", backend, "is", backend.status())
shots = 10*n #run more experiments to be certain
max_credits = 3 # Maximum number of credits to spend on executions.
simonCompiled = transpile(simonCircuit, backend=backend, optimization_level=1)
job_exp = execute(simonCompiled, backend=backend, shots=shots, max_credits=max_credits)
job_monitor(job_exp)
results = job_exp.result()
answer = results.get_counts(simonCircuit)
plot_histogram(answer)
# Post-processing step
# Constructing the system of linear equations Y s = 0
# By k[::-1], we reverse the order of the bitstring
lAnswer = [ (k[::-1][:n],v) for k,v in answer.items() ] #excluding the qubits that are not part of the inputs
#Sort the basis by their probabilities
lAnswer.sort(key = lambda x: x[1], reverse=True)
Y = []
for k, v in lAnswer:
Y.append( [ int(c) for c in k ] )
Y = Matrix(Y)
#Perform Gaussian elimination on Y
Y_transformed = Y.rref(iszerofunc=lambda x: x % 2==0) # linear algebra on GF(2)
Y_new = Y_transformed[0].applyfunc(lambda x: mod(x,2)) #must takecare of negatives and fractional values
#pprint(Y_new)
print("The hidden bistring s[ 0 ], s[ 1 ]....s[",n-1,"] is the one satisfying the following system of linear equations:")
rows, cols = Y_new.shape
for r in range(rows):
Yr = [ "s[ "+str(i)+" ]" for i, v in enumerate(list(Y_new[r,:])) if v == 1 ]
if len(Yr) > 0:
tStr = " + ".join(Yr)
print(tStr, "= 0")
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import math
b_max = math.pi / 5 # upper limit of integral
nbit = 3 # change this value to get discretized result closer to analytical results
analyticResult = (b_max / 2.0 - math.sin(2 * b_max) / 4.0 ) / b_max # the target integral can be analytically solved
print("Analytical Result:", analyticResult)
ndiv = 2**nbit #number of discretization
discretizedResult = 0.0
for i in range(ndiv):
discretizedResult += math.sin(b_max / ndiv * (i + 0.5))**2
discretizedResult = discretizedResult / ndiv
print("Discretized Result:", discretizedResult)
def P(qc, qx, nbit):
"""
Generating uniform probability distribution
qc: quantum circuit
qx: quantum register
nbit: number of qubits
The inverse of P = P
"""
qc.h(qx)
def R(qc, qx, qx_measure, nbit, b_max):
"""
Computing the integral function f()
qc: quantum circuit
qx: quantum register
qx_measure: quantum register for measurement
nbit: number of qubits
b_max: upper limit of integral
"""
qc.ry(b_max / 2**nbit * 2 * 0.5, qx_measure)
for i in range(nbit):
qc.cu3(2**i * b_max / 2**nbit * 2, 0, 0, qx[i], qx_measure[0])
def Rinv(qc, qx, qx_measure, nbit, b_max):
"""
The inverse of R
qc: quantum circuit
qx: quantum register
qx_measure : quantum register for measurement
nbit: number of qubits
b_max: upper limit of integral
"""
for i in range(nbit)[::-1]:
qc.cu3(-2**i * b_max / 2**nbit * 2, 0, 0, qx[i], qx_measure[0])
qc.ry(-b_max / 2**nbit * 2 * 0.5, qx_measure)
#Preparing qiskit environment
from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit
from qiskit import execute
from qiskit import IBMQ
from qiskit import Aer
from scipy import optimize
import sys, time
import mpmath as mp
import numpy as np
import matplotlib.pyplot as plt
# Functions to construct circuits for Grover operators
def multi_control_NOT(qc, qx, qx_measure, qx_ancilla, nbit, b_max):
"""
Computing multi controlled NOT gate
qc: quantum circuit
qx: quantum register
qx_measure: quantum register for measurement
qx_ancilla: temporal quantum register for decomposing multi controlled NOT gate
nbit: number of qubits
b_max: upper limit of integral
"""
if nbit == 1:
qc.cz(qx[0], qx_measure[0])
elif nbit == 2:
qc.h(qx_measure[0])
qc.ccx(qx[0], qx[1], qx_measure[0])
qc.h(qx_measure[0])
elif nbit > 2.0:
qc.ccx(qx[0], qx[1], qx_ancilla[0])
for i in range(nbit - 3):
qc.ccx(qx[i + 2], qx_ancilla[i], qx_ancilla[i + 1])
qc.h(qx_measure[0])
qc.ccx(qx[nbit - 1], qx_ancilla[nbit - 3], qx_measure[0])
qc.h(qx_measure[0])
for i in range(nbit - 3)[::-1]:
qc.ccx(qx[i + 2], qx_ancilla[i], qx_ancilla[i + 1])
qc.ccx(qx[0], qx[1], qx_ancilla[0])
def reflect(qc, qx, qx_measure, qx_ancilla, nbit, b_max):
"""
Computing reflection operator (I - 2|0><0|)
qc: quantum circuit
qx: quantum register
qx_measure: quantum register for measurement
qx_ancilla: temporal quantum register for decomposing multi controlled NOT gate
nbit: number of qubits
b_max: upper limit of integral
"""
for i in range(nbit):
qc.x(qx[i])
qc.x(qx_measure[0])
qc.barrier() #format the circuits visualization
multi_control_NOT(qc, qx, qx_measure, qx_ancilla, nbit, b_max)
qc.barrier() #format the circuits visualization
qc.x(qx_measure[0])
for i in range(nbit):
qc.x(qx[i])
# This is to implement Grover Operator
def Q_grover(qc, qx, qx_measure, qx_ancilla, nbit, b_max):
"""
The Grover operator: R P (I - 2|0><0|) P^+ R^+ U_psi_0
qc: quantum circuit
qx: quantum register
qx_measure: quantum register for measurement
qx_ancilla: temporal quantum register for decomposing multi controlled NOT gate
nbit: number of qubits
b_max: upper limit of integral
"""
qc.z(qx_measure[0])
Rinv(qc, qx, qx_measure, nbit, b_max)
qc.barrier() #format the circuits visualization
P(qc, qx, nbit)
reflect(qc, qx, qx_measure, qx_ancilla, nbit, b_max)
P(qc, qx, nbit)
qc.barrier() #format the circuits visualization
R(qc, qx, qx_measure, nbit, b_max)
def create_grover_circuit(numebr_grover_list, nbit, b_max):
"""
To generate quantum circuits running Grover operators with number of iterations in number_grover_list
numebr_grover_list: list of number of Grover operators
nbit: number of qubits (2**nbit = ndiv is the number of discretization in the Monte Carlo integration)
b_max: upper limit of integral
Return:
qc_list: quantum circuits with Grover operators as in number_grover_list
"""
qc_list = []
for igrover in range(len(numebr_grover_list)):
qx = QuantumRegister(nbit)
qx_measure = QuantumRegister(1)
cr = ClassicalRegister(1)
if (nbit > 2):
qx_ancilla = QuantumRegister(nbit - 2)
qc = QuantumCircuit(qx, qx_ancilla, qx_measure, cr)
else:
qx_ancilla = 0
qc = QuantumCircuit(qx, qx_measure, cr)
P(qc, qx, nbit)
R(qc, qx, qx_measure, nbit, b_max)
for ikAA in range(numebr_grover_list[igrover]):
Q_grover(qc, qx, qx_measure, qx_ancilla, nbit, b_max)
qc.measure(qx_measure[0], cr[0])
qc_list.append(qc)
return qc_list
qc_list = create_grover_circuit([2], nbit, b_max)
my_style = {'usepiformat': True, 'cregbundle': True,'compress': True }
qc_list[0].draw(output="mpl", style=my_style, plot_barriers=False )
def run_grover(qc_list, number_grover_list, shots_list, backend):
"""
Run the quantum circuits returned by create_grover_circuit()
qc_list: list of quantum circuits
numebr_grover_list: list of number of Grover operators
shots_list: list of number of shots
backend: name of backends
Return:
hit_list: list of count of obserbving "1" for qc_list
"""
hit_list = []
for k in range(len(number_grover_list)):
job = execute(qc_list[k], backend=backend, shots=shots_list[k])
lapse = 0
interval = 0.00001
time.sleep(interval)
while job.status().name != 'DONE':
time.sleep(interval)
lapse += 1
counts = job.result().get_counts(qc_list[k]).get("1", 0)
hit_list.append(counts)
return hit_list
def calculate_theta(hit_list, number_grover_list, shots_list):
"""
calculate optimal theta values
hit_list: list of count of obserbving "1" for qc_list
numebr_grover_list: list of number of Grover operators
shots_list: list of number of shots
Return:
thetaCandidate_list: list of optimal theta
"""
small = 1.e-15 # small valued parameter to avoid zero division
confidenceLevel = 5 # confidence level to determine the search range
thetaCandidate_list = []
rangeMin = 0.0 + small
rangeMax = 1.0 - small
for igrover in range(len(number_grover_list)):
def loglikelihood(p):
ret = np.zeros_like(p)
theta = np.arcsin(np.sqrt(p))
for n in range(igrover + 1):
ihit = hit_list[n]
arg = (2 * number_grover_list[n] + 1) * theta
ret = ret + 2 * ihit * np.log(np.abs(np.sin(arg))) + 2 * (
shots_list[n] - ihit) * np.log(np.abs(np.cos(arg)))
return -ret
searchRange = (rangeMin, rangeMax)
searchResult = optimize.brute(loglikelihood, [searchRange])
pCandidate = searchResult[0]
thetaCandidate_list.append(np.arcsin(np.sqrt(pCandidate)))
perror = CalcErrorCramérRao(igrover, shots_list, pCandidate, number_grover_list)
rangeMax = min(pCandidate+confidenceLevel*perror,1.0 - small)
rangeMin = max(pCandidate-confidenceLevel*perror,0.0 + small)
return thetaCandidate_list
#setting the number of shots and Grover operators.
shots_list = [100, 100, 100, 100, 100, 100, 100] # list of number of shots
number_grover_list = [0, 1, 2, 4, 8, 16, 32] # list of number of Grover operators
if len(shots_list) != len(number_grover_list):
raise Exception(
'The length of shots_list should be equal to the length of number_grover_list.'
)
backend = Aer.get_backend('qasm_simulator')
def CalcErrorCramérRao(M, shot_list, p0, number_grover_list):
"""
calculate Cramér-Rao lower bound
M: upper limit of the sum in Fisher information
shots_list: list of number of shots
p0: the true parameter value to be estimated
numebr_grover_list: list of number of Grover operators
Return:
square root of Cramér-Rao lower bound: lower bound on the standard deviation of unbiased estimators
"""
FisherInfo = 0
for k in range(M + 1):
Nk = shot_list[k]
mk = number_grover_list[k]
FisherInfo += Nk / (p0 * (1 - p0)) * (2 * mk + 1)**2
return np.sqrt(1 / FisherInfo)
def CalcNumberOracleCalls(M, shot_list, number_grover_list):
"""
calculate the total number of oracle calls
M: upper limit of the sum in Fisher information
shots_list: list of number of shots
numebr_grover_list: list of number of Grover operators
Return:
Norac: the total number of oracle calls
"""
Norac = 0
for k in range(M + 1):
Nk = shots_list[k]
mk = number_grover_list[k]
Norac += Nk * (2 * mk + 1)
return Norac
qc_list = create_grover_circuit(number_grover_list, nbit,
b_max) # list of Grover circuits
hit_list = run_grover(qc_list, number_grover_list, shots_list,
backend) # list of number of grover operators
thetaCandidate_list = calculate_theta(
hit_list, number_grover_list, shots_list) # list of estimated theta values
error_list = np.abs(np.sin(thetaCandidate_list)**2 - discretizedResult) # list of estimation errors
OracleCall_list = [] # list of number of oracle calls
ErrorCramérRao_list = [] # list of Cramér-Rao lower bound
for i in range(len(number_grover_list)):
OracleCall_list.append(
CalcNumberOracleCalls(i, shots_list, number_grover_list))
ErrorCramérRao_list.append(
CalcErrorCramérRao(i, shots_list, discretizedResult, number_grover_list))
p1 = plt.plot(OracleCall_list, error_list, 'o')
p2 = plt.plot( OracleCall_list, ErrorCramérRao_list)
plt.xscale('log')
plt.xlabel("Number of oracle calls")
plt.yscale('log')
plt.ylabel("Estimation Error")
plt.legend((p1[0], p2[0]), ("Estimated Value", "Cramér-Rao"))
plt.show()
n_trial = 100
error_list= np.zeros_like(number_grover_list,dtype=float)
qc_list = create_grover_circuit(number_grover_list, nbit, b_max)
for i in range(n_trial):
sys.stdout.write("n_trial=(%d/%d)\r" % ((i + 1), n_trial))
sys.stdout.flush()
hit_list = run_grover(qc_list, number_grover_list, shots_list, backend)
thetaCandidate_list = calculate_theta(hit_list, number_grover_list, shots_list)
error_list += (np.sin(thetaCandidate_list)**2 - discretizedResult)**2 # list of estimation errors
error_list = (error_list / (n_trial-1))**(1/2)
p1 = plt.plot(OracleCall_list, error_list, 'o')
p2 = plt.plot(OracleCall_list, ErrorCramérRao_list)
plt.xscale('log')
plt.xlabel("Number of oracle calls")
plt.yscale('log')
plt.ylabel("Estimation Error")
plt.legend((p1[0], p2[0]), ("Estimated Value", "Cramér-Rao"))
plt.show()
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
from qiskit.circuit.library import *
from qiskit.providers.aer import *
sim = AerSimulator(method='statevector', device='GPU')
qubits = 15
depth=10
shots = 10
circuit = QuantumVolume(qubits, depth, seed=0)
circuit.measure_all()
result = execute(circuit,sim,shots=shots,seed_simulator=12345).result()
print("{0} qubits Quantum Volume, Simulation Time = {1} sec".format(qubits,result.to_dict()['results'][0]['time_taken']))
counts = result.get_counts()
print(counts)
from qiskit import *
from qiskit.circuit.library import *
from qiskit.providers.aer import *
sim = AerSimulator(method='statevector', device='GPU', cuStateVec_enable=True)
qubits = 15
depth=10
shots = 10
circuit = QuantumVolume(qubits, depth, seed=0)
circuit.measure_all()
result = execute(circuit,sim,shots=shots,seed_simulator=12345).result()
if result.to_dict()['results'][0]['metadata']['cuStateVec_enable'] == True:
print("cuStateVector is used for the simulation")
print("{0} qubits, Time = {1} sec".format(qubits,result.to_dict()['results'][0]['time_taken']))
counts = result.get_counts()
print(counts)
from qiskit import *
from qiskit.circuit.library import *
from qiskit.providers.aer import *
import matplotlib.pyplot as plt
sim = AerSimulator(method='statevector', device='GPU')
shots = 100
depth=10
time_thrust= []
time_cuStateVec= []
qubits_list = []
for qubits in range (15, 26):
qubits_list.append(qubits)
circuit = QuantumVolume(qubits, depth, seed=0)
circuit.measure_all()
result = execute(circuit,sim,shots=shots,seed_simulator=12345,fusion_threshold=20,cuStateVec_enable=False).result()
time_thrust.append(float(result.to_dict()['results'][0]['time_taken']))
result_cuStateVec = execute(circuit,sim,shots=shots,seed_simulator=12345,fusion_threshold=20,cuStateVec_enable=True).result()
time_cuStateVec.append(float(result_cuStateVec.to_dict()['results'][0]['time_taken']))
plt.yscale("log")
plt.plot(qubits_list, time_thrust, marker="o", label='ThrustGPU')
plt.plot(qubits_list, time_cuStateVec, 'g', marker="x", label='cuStateVec')
plt.legend()
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
# create qubit using quantum registers
qr = QuantumRegister(2)
# create classical register to take measurement of `qr`
cr = ClassicalRegister(2)
# build a circuit
qc = QuantumCircuit(qr, cr)
# visualize the circuit to know how it's looks like or there any modification init ?
qc.draw()
# to add gates into the circuit so that
# to build entanglement in circuit we uses hadamard gate : H
qc.h(0)
qc.draw(output='mpl')
# two qubit controlled operation gate : CNOT gate
# cx(c_1, t) it controls the c_1 qubit and target the t qubit
qc.cx(0, 1)
#qc.cx(qr[0],qr[1])
qc.draw(output='mpl')
# to measure the qubits and store into classical bits
qc.measure(qr, cr)
qc.draw(output='mpl')
# How to run this quantum circuit on classical computer or quantum simulator
# used qiskit's Aer Simulator
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator).result()
plot_histogram(result.get_counts(qc))
# How to run this qunatum circuit on the Quantum computer
# IBM's Quantum Computer
# We access it from cloud using an api call with our account on the ibm experieance
#loading our ibm account
IBMQ.load_account('API_Key')
#
provider = IBMQ.get_provider('ibm-q')
qcomp = provider.get_backend('ibmqx2')
job = execute(qc, backend=qcomp)
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(qc))
"""
Question : Why there is a difference in output in executing quantum circuit on simulator and on actual quantum device ?
Question : What is the difference b/w the Quantum Simulator and a Quantum Computer ?
"""
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
from qiskit.tools.visualization import plot_bloch_multivector, plot_histogram
qc = QuantumCircuit(1, 1)
qc.x(0)
qc.draw(output='mpl')
simulator = Aer.get_backend('statevector_simulator')
result = execute(qc, backend=simulator).result()
statevector = result.get_statevector()
print(statevector)
plot_bloch_multivector(statevector)
qc.measure([0],[0])
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1024).result()
counts = result.get_counts()
print(counts)
plot_histogram(counts)
qc = QuantumCircuit(1, 1)
qc.x(0)
simulator = Aer.get_backend('unitary_simulator')
result = execute(qc, backend=simulator).result()
unitary = result.get_unitary()
print(unitary)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
qc = QuantumCircuit(3, 3)
qc.draw(output='mpl')
# we will teleport the state q_0 to q_2 with using q_1
qc.x(0)
qc.barrier()
qc.draw(output='mpl')
# barrier decide that after barrier q_0 has state |1> than of |0>
qc.h(1)
qc.cx(1, 2)
qc.draw(output='mpl')
# It created an entangled state means same qubit exits on q_1 and q_2 at the same time also
qc.cx(0, 1)
qc.h(0)
qc.draw(output='mpl')
qc.barrier()
qc.measure([0,1],[0,1])
qc.draw(output='mpl')
# before measure all the states are entangled but to complete the teleportation process
qc.barrier()
qc.cx(1,2)
qc.cz(0,2)
qc.draw(output='mpl')
# the qubit at q_0 teleported to the state q_2
# let's measure q_2 states
qc.measure(2,2)
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1024).result()
counts = result.get_counts()
plot_histogram(counts)
print(counts)
# It is used to transfer quantum information over long distances
"""
Question : Build a Quantum Teleportation circuit to teleport the qubit |+> or |->
"""
qc = QuantumCircuit(3, 3)
qc.h(0)
qc.barrier()
qc.draw(output='mpl')
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.