repo
stringclasses 900
values | file
stringclasses 754
values | content
stringlengths 4
215k
|
|---|---|---|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
secret_number = '101001'
qc = QuantumCircuit(6+1, 6)
qc.h([0, 1, 2, 3, 4, 5])
qc.x(6)
qc.h(6)
qc.barrier()
qc.draw(output='mpl')
# building box of secret number
qc.cx(5, 6)
qc.cx(3, 6)
qc.cx(0, 6)
qc.draw(output='mpl')
qc.barrier()
qc.h([0, 1, 2, 3, 4, 5])
qc.barrier()
qc.measure([0, 1, 2, 3, 4, 5], [0, 1, 2, 3, 4, 5])
qc.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1).result()
counts = result.get_counts()
print(counts)
secret_number = '1000100110010101001'
qc = QuantumCircuit(len(secret_number)+1, len(secret_number))
qc.h(range(len(secret_number)))
qc.x(len(secret_number))
qc.h(len(secret_number))
qc.barrier()
for ii, yesno in enumerate(reversed(secret_number)):
if yesno == '1':
qc.cx(ii, len(secret_number))
qc.barrier()
qc.h(range(len(secret_number)))
qc.barrier()
qc.measure(range(len(secret_number)), range(len(secret_number)))
qc.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1).result()
counts = result.get_counts()
print(counts)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="https://www.youtube.com/embed/yuDxHJOKsVA", width=1920/2, height=1080/2)
from qiskit import *
from qiskit.tools.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
from qiskit.ignis.mitigation.measurement import complete_meas_cal, CompleteMeasFitter
# let's create a circuit
n_qubits = 3
n_bits = 3
qc = QuantumCircuit(n_qubits, n_bits)
qc.h(0)
qc.cx(0, 1)
qc.cx(1, 2)
qc.measure([0,1,2], [0,1,2])
qc.draw('mpl')
# let's try to find what we have measured by simulating our circuit
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1024).result()
plot_histogram(result.get_counts(qc))
## let's run this circuit on the real ibm quantum computer
IBMQ.load_account()
provider = IBMQ.get_provider('ibm-q')
qcomp = provider.get_backend('ibmqx2')
job = execute(qc, backend=qcomp, shots=1024)
job_monitor(job)
job_result = qcomp.result()
plot_histogram(qcomp.get_counts(qc))
# lets calibrate the measurement error using ignis
cal_circuits, state_labels = complete_meas_cal(qr=qc.qregs[0],
circlabel='measurement_calibration')
cal_circuits[7].draw(output='mpl')
cal_job = execute(cal_circuits,
backend=qcomp,
shots=8192,
optimization_level=0)
#print(cal_job.job_id())
job_monitor(cal_job)
cal_results = cal_job.result()
plot_histogram(cal_results.get_counts(cal_circuits[3]))
# Creating the Measurement Fitter Object in Ignis
meas_fitter = CompleteMeasFitter(cal_results, state_labels)
meas_fitter.plot_calibration()
# Mitigating the measurement errors in our previous device run
meas_filter = meas_fitter.filter
mitigated_result = meas_filter.apply(device_result)
device_counts = device_result.get_counts(qc)
mitigated_counts = mitigated_result.get_counts(qc)
plot_histogram([device_counts, mitigated_counts],
legend=['device, noisy', 'device, mitigated'])
# Running error mitigation on a second circuit
circuit2 = QuantumCircuit(3,3)
circuit2.x(1)
circuit2.h(0)
circuit2.cx(0,1)
circuit2.cx(1,2)
circuit2.measure([0,1,2], [0,1,2])
circuit2.draw(output='mpl')
plot_histogram(
execute(circuit2, backend=simulator, shots=1024).result().get_counts(circuit2)
)
device_counts_2 = execute(circuit2, backend=qcomp, shots=1024).result().get_counts(circuit2)
plot_histogram(device_counts_2)
mitigated_counts_2 = meas_filter.apply(device_counts_2)
plot_histogram([device_counts_2, mitigated_counts_2], legend=['device, noisy','device, mitigated'])
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
# create qubit using quantum registers
qr = QuantumRegister(2)
# create classical register to take measurement of `qr`
cr = ClassicalRegister(2)
# build a circuit
qc = QuantumCircuit(qr, cr)
# visualize the circuit to know how it's looks like or there any modification init ?
qc.draw()
# to add gates into the circuit so that
# to build entanglement in circuit we uses hadamard gate : H
qc.h(0)
qc.draw(output='mpl')
# two qubit controlled operation gate : CNOT gate
# cx(c_1, t) it controls the c_1 qubit and target the t qubit
qc.cx(0, 1)
#qc.cx(qr[0],qr[1])
qc.draw(output='mpl')
# to measure the qubits and store into classical bits
qc.measure(qr, cr)
qc.draw(output='mpl')
# How to run this quantum circuit on classical computer or quantum simulator
# used qiskit's Aer Simulator
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator).result()
plot_histogram(result.get_counts(qc))
# How to run this qunatum circuit on the Quantum computer
# IBM's Quantum Computer
# We access it from cloud using an api call with our account on the ibm experieance
#loading our ibm account
IBMQ.load_account('API_Key')
#
provider = IBMQ.get_provider('ibm-q')
qcomp = provider.get_backend('ibmqx2')
job = execute(qc, backend=qcomp)
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(qc))
"""
Question : Why there is a difference in output in executing quantum circuit on simulator and on actual quantum device ?
Question : What is the difference b/w the Quantum Simulator and a Quantum Computer ?
"""
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
from qiskit.tools.visualization import plot_bloch_multivector, plot_histogram
qc = QuantumCircuit(1, 1)
qc.x(0)
qc.draw(output='mpl')
simulator = Aer.get_backend('statevector_simulator')
result = execute(qc, backend=simulator).result()
statevector = result.get_statevector()
print(statevector)
plot_bloch_multivector(statevector)
qc.measure([0],[0])
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=simulator, shots=1024).result()
counts = result.get_counts()
print(counts)
plot_histogram(counts)
qc = QuantumCircuit(1, 1)
qc.x(0)
simulator = Aer.get_backend('unitary_simulator')
result = execute(qc, backend=simulator).result()
unitary = result.get_unitary()
print(unitary)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="http://www.youtube.com/embed/RrUTwq5jKM4", width=1920/2, height=1080/2)
from qiskit import *
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
circuit = QuantumCircuit(qr, cr)
circuit = QuantumCircuit(2,2)
circuit.draw()
%matplotlib inline
circuit.draw(output='mpl')
# the quantum circuit has two qubits. they are indexed as qubits 0 and 1
circuit.h(0)
circuit.cx(0,1) # order is control, target
circuit.measure([0,1], [0,1]) # qubits [0,1] are measured and results are stored in classical bits [0,1] in order
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator).result()
from qiskit.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
IBMQ.load_account()
provider = IBMQ.get_provider(hub = 'ibm-q')
qcomp = provider.get_backend('ibmq_16_melbourne')
num_qubits = 2
from qiskit.providers.ibmq import least_busy
possible_devices = provider.backends(filters=lambda x:
x.configuration().n_qubits >= num_qubits
and
x.configuration().simulator == False)
qcomp = least_busy(possible_devices)
print(qcomp)
import qiskit.tools.jupyter
%qiskit_job_watcher
job = execute(circuit, backend=qcomp)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(circuit))
%qiskit_disable_job_watcher
qiskit.__qiskit_version__
%qiskit_copyright
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="http://www.youtube.com/embed/tBnWG_95F9c", width=1920/2, height=1080/2)
from qiskit import *
circuit = QuantumCircuit(1,1)
circuit.x(0)
%matplotlib inline
circuit.draw(output='mpl')
simulator = Aer.get_backend('unitary_simulator')
result = execute(circuit, backend=simulator).result()
unitary = result.get_unitary()
print(unitary)
from qiskit import *
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('statevector_simulator')
result = execute(circuit, backend=simulator).result()
statevector = result.get_statevector()
print(statevector)
# in the video, we imported from qiskit.tools.visualization.
# this part of Qiskit has been moved to qiskit.visualization, and we recommend using qiskit.visualization instead
from qiskit.visualization import plot_bloch_multivector
plot_bloch_multivector(statevector)
circuit = QuantumCircuit(1,1)
circuit.x(0)
circuit.measure([0], [0])
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1024).result()
counts = result.get_counts()
from qiskit.visualization import plot_histogram
plot_histogram(counts)
qiskit.__qiskit_version__
import qiskit.tools.jupyter
%qiskit_copyright
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="http://www.youtube.com/embed/mMwovHK2NrE", width=1920/2, height=1080/2)
from qiskit import *
circuit = QuantumCircuit(3,3)
# QUBIT ORDERING
# q0 = State |psi> that we want to teleport
# q1 = Alice's half of the Bell pair
# q2 = Bob's half of the Bell pair, the destination of the teleportation
# ========================
# Step 0: Create the state to be teleported in qubit 0
circuit.x(0) # qubit 0 is now in state |1>, and this is the state that we want to teleport
circuit.barrier() # just a visual aid
# ========================
# Step 1: create an entangled Bell pair between Alice and Bob (qubits 1 and 2)
circuit.h(1)
circuit.cx(1,2)
circuit.barrier() # just a visual aid
# ========================
# Step 2: Alice applies a series of operations
# between the state to teleport (qubit 0) and her half of the Bell pair (qubit 1)
circuit.cx(0,1)
circuit.h(0)
circuit.barrier() # just a visual aid
# ========================
# Step 3: Alice measures both qubits 0 and 1
circuit.measure([0, 1], [0, 1]) # results stored in classical bits 0 and 1, respectively
circuit.barrier() # just a visual aid
# ========================
# Step 4: Now that Alice has measured the two qubits, their states have collapsed to 0 and 1.
# Bob can do operations conditioned on these qubits to his half of the Bell pair
# Note that while we're conditioning Bob's operation on the collapsed qubits 0 and 1, we can
# do teleportation over long distances by transmitting the classical information in classical bits 0 and 1
circuit.cx(1, 2)
circuit.cz(0, 2)
# Step 5: Done! Measure Bob's qubit to find out what state it is in
circuit.measure([2], [2])
%matplotlib inline
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1024).result()
from qiskit.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
def create_state_psi(theta):
# Create a state along the x axis on the x-y plane and then rotate it by angle theta around the z-axis
# theta = 0 => state is exactly along x
# theta = pi/2 => state is exactly along y
create_circuit = QuantumCircuit(1, name='create_state_psi')
create_circuit.h(0)
create_circuit.rz(theta, 0)
return create_circuit
def create_Bell_pair():
create_Bell_circuit = QuantumCircuit(2, name='create_Bell_pair')
create_Bell_circuit.h(0)
create_Bell_circuit.cx(0,1)
return create_Bell_circuit
def teleportation_Alice():
teleportation_Alice_circuit = QuantumCircuit(2, name='teleportation_Alice')
teleportation_Alice_circuit.cx(0,1)
teleportation_Alice_circuit.h(0)
return teleportation_Alice_circuit
def Alice_measure():
Alice_measure_circuit = QuantumCircuit(2, 2, name='Alice_measure')
Alice_measure_circuit.measure([0,1], [0,1])
return Alice_measure_circuit
def teleportation_Bob():
teleportation_Bob_circuit = QuantumCircuit(3, name='teleportation_Bob')
teleportation_Bob_circuit.cx(1,2)
teleportation_Bob_circuit.cz(0,2)
return teleportation_Bob_circuit
def build_circuit(theta):
circuit = QuantumCircuit(3, 3)
# Step 0: create the state to teleport
circuit.append(create_state_psi(theta).to_instruction(), [0])
circuit.barrier()
# Step 1: create the Bell pair between Alice and Bob's qubits
circuit.append(create_Bell_pair().to_instruction(), [1,2])
circuit.barrier()
# Step 2: Alice applies a series of operations
circuit.append(teleportation_Alice().to_instruction(), [0,1])
circuit.barrier()
# Step 3: Alice measures her two qubits
circuit.append(Alice_measure().to_instruction(), [0,1], [0,1])
circuit.barrier()
# Step 4: Bob applies operations to his qubit depending on Alice's measurement outcomes
circuit.append(teleportation_Bob().to_instruction(), [0,1,2])
circuit.barrier()
# Step 5: Done. Now measure Bob's qubit to be sure that teleportation was successful
circuit.h(2) # note that the Hadamard gate here ensures that we measure in the Hadamard basis instead of z basis
circuit.measure([0,1,2], [0,1,2])
return circuit
circuit = build_circuit(0.01)
circuit.draw(output='mpl')
circuit.decompose().draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1024).result()
counts = result.get_counts(circuit)
print(counts)
num_c2_zero = sum(counts[c2c1c0] for c2c1c0 in counts if c2c1c0[0] == '0')
import numpy as np
thetas = np.arange(0, 4*np.pi, np.pi/16)
simulator = Aer.get_backend('qasm_simulator')
percent_ones = []
for theta in thetas:
circuit = build_circuit(theta)
result = execute(circuit, backend=simulator, shots=1024).result()
counts = result.get_counts(circuit)
num_c2_ones = sum(counts[c2c1c0] for c2c1c0 in counts if c2c1c0[0] == '1')
percent_ones.append(num_c2_ones*100./1024)
import matplotlib.pyplot as plotter
plotter.plot(thetas, percent_ones)
plotter.xlabel('Initial angle, theta (radians)')
plotter.ylabel('Percentage of 1 counts')
plotter.show()
# build circuits
thetas = np.arange(0, 4*np.pi, np.pi/16)
circuits = []
for theta in thetas:
circuit = build_circuit(theta)
circuits.append(circuit)
# load account
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
qcomp = provider.get_backend('ibmq_16_melbourne')
# run the job on the backend qcomp
job = execute(circuits, backend=qcomp, shots=512, initial_layout=[6,8,7])
print(job.job_id())
from qiskit.tools.monitor import job_monitor
job_monitor(job)
simresult = execute(circuits, backend=simulator, shots=512).result()
result = job.result()
percent_ones = []
for circuit in circuits:
thiscircuit_counts = result.get_counts(circuit)
num_c2_ones = sum(thiscircuit_counts[c2c1c0] for c2c1c0 in thiscircuit_counts if c2c1c0[0] == '1')
percent_ones.append(num_c2_ones*100./512)
percent_ones_sim = []
for circuit in circuits:
thiscircuit_counts = simresult.get_counts(circuit)
num_c2_ones = sum(thiscircuit_counts[c2c1c0] for c2c1c0 in thiscircuit_counts if c2c1c0[0] == '1')
percent_ones_sim.append(num_c2_ones*100./512)
plotter.plot(thetas, percent_ones, 'r.', label='Real device')
plotter.plot(thetas, percent_ones_sim, 'k', label='Simulator')
plotter.xlabel('Initial angle, theta (radians)')
plotter.ylabel('Percentage of 1 counts')
plotter.legend()
plotter.show()
thetas = np.arange(0, 4*np.pi, np.pi/16)
circuits_classicalcontrol = []
for theta in thetas:
cr1 = ClassicalRegister(1)
cr2 = ClassicalRegister(1)
cr3 = ClassicalRegister(1)
qr = QuantumRegister(3)
circuit = QuantumCircuit(qr, cr1, cr2, cr3)
# ========================
# Step 0: Create the state to be teleported in qubit 0
circuit.h(0)
circuit.rz(theta, 0)
circuit.barrier()
# ========================
# Step 1: create an entangled Bell pair between Alice and Bob (qubits 1 and 2)
circuit.h(1)
circuit.cx(1,2)
circuit.barrier()
# ========================
# Step 2: Alice applies a series of operations
# between the state to teleport (qubit 0) and her half of the Bell pair (qubit 1)
circuit.cx(0,1)
circuit.h(0)
circuit.barrier()
# ========================
# Step 3: Alice measures both qubits 0 and 1
circuit.measure([0, 1], [0, 1]) # results stored in classical bits 0 and 1, respectively
circuit.barrier()
# ========================
# Step 4: Now that Alice has measured the two qubits, their states have collapsed to 0 and 1.
# Use the classical bits from Alice's measurements to do operations on Bob's half of the Bell pair
circuit.x(2).c_if(cr2, 1)
circuit.z(2).c_if(cr1, 1)
circuit.barrier()
# Step 5: Done! Measure Bob's qubit in the Hadamard basis to find out what state it is in
circuit.h(2)
circuit.measure([2], [2])
circuits_classicalcontrol.append(circuit)
circuits_classicalcontrol[0].draw()
simulator = Aer.get_backend('qasm_simulator')
simresult_classicalcontrol = execute(circuits_classicalcontrol, backend=simulator, shots=512).result()
percent_ones_sim = []
for ii in range(len((circuits))):
thiscircuit_counts = simresult_classicalcontrol.get_counts(ii)
num_c2_ones = sum(thiscircuit_counts[c2c1c0] for c2c1c0 in thiscircuit_counts if c2c1c0[0] == '1')
percent_ones_sim.append(num_c2_ones*100./512)
plotter.plot(thetas, percent_ones_sim, 'k', label='Simulator')
plotter.xlabel('Initial angle, theta (radians)')
plotter.ylabel('Percentage of 1 counts')
plotter.legend()
plotter.show()
qiskit.__qiskit_version__
import qiskit.tools.jupyter
%qiskit_copyright
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="http://www.youtube.com/embed/sqJIpHYl7oo", width=1920/2, height=1080/2)
s = '110101'
from qiskit import *
n = len(s)
circuit = QuantumCircuit(n+1,n)
# Step 0
circuit.x(n) # the n+1 qubits are indexed 0...n, so the last qubit is index n
circuit.barrier() # just a visual aid for now
# Step 1
circuit.h(range(n+1)) # range(n+1) returns [0,1,2,...,n] in Python. This covers all the qubits
circuit.barrier() # just a visual aid for now
# Step 2
for ii, yesno in enumerate(reversed(s)):
if yesno == '1':
circuit.cx(ii, n)
circuit.barrier() # just a visual aid for now
# Step 3
circuit.h(range(n+1)) # range(n+1) returns [0,1,2,...,n] in Python. This covers all the qubits
circuit.barrier() # just a visual aid for now
circuit.measure(range(n), range(n)) # measure the qubits indexed from 0 to n-1 and store them into the classical bits indexed 0 to n-1
%matplotlib inline
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1).result()
from qiskit.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1000).result()
from qiskit.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
qiskit.__qiskit_version__
import qiskit.tools.jupyter
%qiskit_copyright
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from IPython.display import IFrame
IFrame(src="http://www.youtube.com/embed/yuDxHJOKsVA", width=1920/2, height=1080/2)
from qiskit import *
nqubits = 3
circuit = QuantumCircuit(nqubits, nqubits)
circuit.h(0)
circuit.cx(0,1)
circuit.cx(1,2)
circuit.measure([0,1,2], [0,1,2])
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
sim_result = execute(circuit, backend=simulator, shots=1024).result()
from qiskit.visualization import plot_histogram
plot_histogram(sim_result.get_counts(circuit))
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
device = provider.get_backend('ibmqx2')
job = execute(circuit, backend=device, shots=1024)
#print(job.job_id())
from qiskit.tools.monitor import job_monitor
job_monitor(job)
device_result = job.result()
plot_histogram(device_result.get_counts(circuit))
from qiskit.ignis.mitigation.measurement import (complete_meas_cal, CompleteMeasFitter)
cal_circuits, state_labels = complete_meas_cal(qr=circuit.qregs[0],
circlabel='measurement_calibration')
cal_circuits[7].draw(output='mpl')
len(cal_circuits)
cal_job = execute(cal_circuits,
backend=device,
shots=8192,
optimization_level=0)
#print(cal_job.job_id())
job_monitor(cal_job)
cal_results = cal_job.result()
plot_histogram(cal_results.get_counts(cal_circuits[3]))
meas_fitter = CompleteMeasFitter(cal_results, state_labels)
meas_fitter.plot_calibration()
meas_filter = meas_fitter.filter
mitigated_result = meas_filter.apply(device_result)
device_counts = device_result.get_counts(circuit)
mitigated_counts = mitigated_result.get_counts(circuit)
plot_histogram([device_counts, mitigated_counts],
legend=['device, noisy', 'device, mitigated'])
circuit2 = QuantumCircuit(3,3)
circuit2.x(1)
circuit2.h(0)
circuit2.cx(0,1)
circuit2.cx(1,2)
circuit2.measure([0,1,2], [0,1,2])
circuit2.draw(output='mpl')
plot_histogram(
execute(circuit2, backend=simulator, shots=1024).result().get_counts(circuit2)
)
device_counts_2 = execute(circuit2, backend=device, shots=1024).result().get_counts(circuit2)
plot_histogram(device_counts_2)
mitigated_counts_2 = meas_filter.apply(device_counts_2)
plot_histogram([device_counts_2, mitigated_counts_2], legend=['device, noisy','device, mitigated'])
import qiskit
qiskit.__qiskit_version__
import qiskit.tools.jupyter
%qiskit_copyright
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
import qiskit
from qiskit import QuantumCircuit
# creating a quantum circuit
qc = QuantumCircuit(3)
qc.z(0)
qc.s(1)
qc.t(2)
qc.cx(0,1)
qc.h(2)
qc.ccx(0, 1, 2)
qc.draw(output='mpl')
# inverse of the quantum circuit
inverse_qc = qc.inverse()
# to draw the quantum circuit
inverse_qc.draw(output='mpl')
# If we measure the quantum circuit's each qubit's states
qc.measure()
# to draw the quantum circuit
qc.draw(output='mpl')
# inverse of the measured quantum circuit's qubit is not possible
inverse_qc = qc.inverse()
qc.measure()
# to draw the quantum circuit
inverse_qc.draw(output='mpl')
# creating a quantum circuit
m_circuit = QuantumCircuit(3)
m_circuit.h(2)
m_circuit.ccx(0, 1, 2)
m_circuit.cz(2, 1)
# draw the circuit
m_circuit.draw(output='mpl')
m_gate = m_circuit.to_gate()
type(m_gate)
new_circuit = QuantumCircuit(5)
new_circuit.append(m_gate, [1, 2, 4])
new_circuit.draw(output='mpl')
#decompose the circuit
new_circuit.decompose().draw(output='mpl')
from qiskit import QuantumCircuit, transpile, Aer
my_circuit = QuantumCircuit(3)
my_circuit.t(1)
my_circuit.h(0)
my_circuit.ccx(2,1,0)
my_circuit.s(2)
my_circuit.t(0)
my_circuit.draw()
my_gate = my_circuit.to_gate()
my_gate
my_inv_gate = my_gate.inverse()
my_inv_gate
my_inv_gate.name = 'My Inverse Gate'
new_circuit = QuantumCircuit(3)
new_circuit.append(my_inv_gate, [0,1,2])
new_circuit.draw()
new_circuit.decompose().draw()
my_circuit = QuantumCircuit(2)
my_circuit.cx(1,0)
my_circuit.cx(0,1)
my_circuit.cx(1,0)
my_circuit.draw()
my_gate = my_circuit.to_gate()
my_gate.name = "My Gate"
my_controlled_gate = my_gate.control()
new_circuit = QuantumCircuit(3)
new_circuit.append(my_controlled_gate, [0, 1, 2])
new_circuit.draw()
new_circuit.decompose().draw()
from qiskit import Aer, IBMQ, QuantumCircuit, execute, transpile, assemble
from qiskit.providers.aer.noise import NoiseModel
from qiskit.visualization import histogram
my_qc = QuantumCircuit(5)
my_qc.h(0)
for q in range(4):
my_qc.cx(0, q+1)
my_qc.measure_all()
my_qc.draw()
## What is the qsphere ?
## What is the unitary simulator ?
## How can i convert a Unitary Matrix to a set of One and Two Qubit gates ?
## How can i change qiskit's defoult behaviour ?
## How do i use parameterization circuit in Qiskit ?
## Why does qiskit order it's qubit the way it does ?
## How i combine two quantum circuits ?
## What is the difference between gates and instructions ?
## How can i use a specific version of qiskit ?
## How can i implement a multi controlled Toffoli Gate ?
## How can i monitor a job send to IBM Quantum ?
## How can i convert a quantum circuit to QASM ?
my_circuit = QuantumCircuit(3)
my_circuit.t(1)
my_circuit.h(0)
my_circuit.ccx(2,1,0)
my_circuit.s(2)
my_circuit.t(0)
my_circuit.draw('latex')
my_circuit.draw('latex_source')
print(my_circuit.draw('latex_source'))
## How can i bundle several circuit into a single job ?
## How can i save circuit Drawings to Different File Types ?
## How can i contruct a quantum volume circuit ?
## What trick can i do with draw methods ?
## How i can find reduced quantum states using qiskit ?
## In What different ways can i draw a quantum circuit ?
## How can i use a classical register for quantum compuation ?
## What is circuit depth and how can i calculate it ?
## How can i choose initial layout for the traspiler ?
## What are the Ancillary Qubits and how are they usefull ?
## What are registers ?
## How can i create a custom gate from matrix ?
## How can i find expectation value for an operator ?
## How can i measure the qubit midway through a quantum circuit ?
## How can i transpile a quantum circuit ?
## How can i make a noise model with qiskit ?
## How can i create a custome controlled gate ?
## How can i choose the best backend from a provider ?
## How can i perform state tomography ?
## How can i reset a qubit in a quantum circuit
## How do i perform a unitary projection in a quantum circuit ?
## How do i debuge an issue in transpiler ?
## How can i estimate Pi using a quantum computer ?
## How do i initialize a mixed states ?
## What is gate fidelity and how do i canculate it ?
## How do i check the state fedility with noisy simulator ?
## How do i change the fitter algorithm in a state tomography experiment ?
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
# required imports:
from qiskit.visualization import array_to_latex
from qiskit.quantum_info import Statevector, random_statevector
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit import QuantumCircuit
from qiskit.circuit.library import HGate, CXGate
import numpy as np
ket0 = [[1],[0]]
array_to_latex(ket0)
bra0 = [1,0]
array_to_latex(bra0)
ket1 = [[0],[1]]# put your answer answer here for |1⟩
bra1 = [0,1]# put answer here for ⟨1|
from qc_grader.challenges.qgss_2023 import grade_lab1_ex1
grade_lab1_ex1([ket1, bra1])
sv_bra0 = Statevector(bra0)
sv_bra0
sv_bra0.draw('latex')
sv_eq = Statevector([1/2, 3/4, 4/5, 6/8])
sv_eq.draw('latex')
sv_eq.is_valid()
from math import sqrt
sv_valid = Statevector([1/sqrt(2),1/sqrt(2)])
sv_valid.is_valid()# create your statevector here
from qc_grader.challenges.qgss_2023 import grade_lab1_ex2
grade_lab1_ex2(sv_valid)
op_bra0 = Operator(bra0)
op_bra0
op_ket0 = Operator(ket0)
op_bra0.tensor(op_ket0)
braket = np.dot(op_bra0,op_ket0)
array_to_latex(braket)
ketbra = np.outer(ket0,bra0)
array_to_latex(ketbra)
braket = np.dot(op_bra0,op_ket0)
array_to_latex(braket)
bra1ket0 = np.dot(bra1, ket0)# put your answer for ⟨1|0⟩ here
bra0ket1 = np.dot(bra0, ket1) # put your answer for ⟨0|1⟩ here
bra1ket1 = np.dot(bra1, ket1)# put your answer for ⟨1|1⟩ here
ket1bra0 = np.outer(ket1, bra0)# put your answer for |1⟩⟨0| here
ket0bra1 = np.outer(ket0, bra1)# put your answer for |0⟩⟨1| here
ket1bra1 = np.outer(ket1, bra1)# put your answer for |1⟩⟨1| here
from qc_grader.challenges.qgss_2023 import grade_lab1_ex3
grade_lab1_ex3([bra1ket0, bra0ket1, bra1ket1, ket1bra0, ket0bra1, ket1bra1])
np.dot(bra1, ket0)
# add or remove your answer from this list
answer = ['a']
from qc_grader.challenges.qgss_2023 import grade_lab1_ex4
grade_lab1_ex4(answer)
m1 = Operator([[1,1],[0,0]])
array_to_latex(m1)
m3 = Operator([[0,1],[1,0]])
array_to_latex(m3)
array_to_latex(m1@ket0)
m2 = Operator([[1, 0],
[0, 1]])
# create an operator for m2 here
m4 = Operator([[0, 0],
[1, 1]])# create and operator for m4 here
from qc_grader.challenges.qgss_2023 import grade_lab1_ex5
grade_lab1_ex5([m2, m4])
cnot = CXGate()
array_to_latex(cnot)
m3.is_unitary()
random = Operator(np.array([[ 0.50778085-0.44607116j, -0.1523741 +0.14128434j, 0.44607116+0.50778085j,
-0.14128434-0.1523741j ],
[ 0.16855994+0.12151822j, 0.55868196+0.38038841j, -0.12151822+0.16855994j,
-0.38038841+0.55868196j],
[ 0.50778085-0.44607116j, -0.1523741 +0.14128434j, -0.44607116-0.50778085j,
0.14128434+0.1523741j ],
[ 0.16855994+0.12151822j, 0.55868196+0.38038841j, 0.12151822-0.16855994j,
0.38038841-0.55868196j]]))
random.is_unitary()
non_unitary_op = Operator(np.array([[1/2,9],[9/5,2]]))# create your operator here
non_unitary_op.is_unitary()
from qc_grader.challenges.qgss_2023 import grade_lab1_ex6
grade_lab1_ex6(non_unitary_op)
pauli_x = Pauli('X')
array_to_latex(pauli_x)
pauli_y = Pauli('Y')
array_to_latex(pauli_y)
pauli_z = Pauli('Z')
array_to_latex(pauli_z)
op_x = Operator(pauli_x)
op_x
op_new = np.dot(op_x,ket0)
array_to_latex(op_new)
result = np.dot(Operator(pauli_z), ket1)# do your operations here
from qc_grader.challenges.qgss_2023 import grade_lab1_ex7
grade_lab1_ex7(result)
hadamard = HGate()
array_to_latex(hadamard)
hop = Operator(hadamard)
hop.is_unitary()
bell = QuantumCircuit(2)
bell.h(0) # apply an H gate to the circuit
bell.cx(0,1) # apply a CNOT gate to the circuit
bell.draw(output="mpl")
bell_op = Operator(bell)
array_to_latex(bell_op)
ghz = QuantumCircuit(3)
##############################
# add gates to your circuit here
ghz.h(0)
ghz.cx(0,1)
ghz.cx(1,2)
##############################
ghz.draw(output='mpl')
from qc_grader.challenges.qgss_2023 import grade_lab1_ex8
grade_lab1_ex8(ghz)
plus_state = Statevector.from_label("+")
plus_state.draw('latex')
plus_state
plus_state.probabilities_dict()
# run this cell multiple times to show collapsing into one state or the other
res = plus_state.measure()
res
qc = QuantumCircuit(1,1)
qc.h(0)
qc.measure(0, 0)
qc.draw(output="mpl")
sv_bell = Statevector([np.sqrt(1/2), 0, 0, np.sqrt(1/2)])
sv_bell.draw('latex')
sv_bell.probabilities_dict()
sv_bell = Statevector([np.sqrt(1/2), 0, 0, - np.sqrt(1/2)])
sv_psi_plus = Statevector([1 / 2**0.5, 0, 0, 1 / 2**0.5])# create a statevector for |𝜓+⟩ here
prob_psi_plus = sv_psi_plus.probabilities_dict() # find the measurement probabilities for |𝜓+⟩ here
sv_psi_minus = Statevector([1 / 2**0.5, 0, 0, -1 / 2**0.5]) # create a statevector for |𝜓−⟩ here
prob_psi_minus = sv_psi_minus.probabilities_dict()# find the measurement probabilities for |𝜓−⟩ here
sv_phi_minus = Statevector([0, 1 / 2**0.5, -1 / 2**0.5, 0])# create a statevector for |𝜙−⟩ here
prob_phi_minus = sv_phi_minus.probabilities_dict()# find the measurement probabilities for |𝜙−⟩ here
from qc_grader.challenges.qgss_2023 import grade_lab1_ex9
grade_lab1_ex9([prob_psi_plus, prob_psi_minus, prob_phi_minus])
qft = QuantumCircuit(2)
##############################
# add gates to your circuit here
qft.h(1)
qft.cp(np.pi/2, 0, 1)
qft.h(0)
qft.swap(0, 1)
##############################
qft.draw(output='mpl')
from qc_grader.challenges.qgss_2023 import grade_lab1_ex10
grade_lab1_ex10(qft)
U = Operator(qft)
array_to_latex(U)
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit.circuit import QuantumCircuit
from qiskit.primitives import Estimator, Sampler
from qiskit.quantum_info import SparsePauliOp
from qiskit.visualization import plot_histogram
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('dark_background') # optional
# create excited |1> state
qc_1 = QuantumCircuit(1)
qc_1.x(0)
qc_1.draw('mpl')
# create superposition |+> state
qc_plus = QuantumCircuit(1)
qc_plus.h(0)
qc_plus.draw('mpl')
qc_1.measure_all()
qc_plus.measure_all()
sampler = Sampler()
job_1 = sampler.run(qc_1)
job_plus = sampler.run(qc_plus)
job_1.result().quasi_dists
job_plus.result().quasi_dists
legend = ["Excited State", "Plus State"] # TODO: Excited State does not appear
plot_histogram([job_1.result().quasi_dists[0], job_plus.result().quasi_dists[0]], legend=legend)
qc_1.remove_final_measurements()
qc_plus.remove_final_measurements()
# rotate into the X-basis
qc_1.h(0)
qc_plus.h(0)
qc_1.measure_all()
qc_plus.measure_all()
sampler = Sampler()
job_1 = sampler.run(qc_1)
job_plus = sampler.run(qc_plus)
plot_histogram([job_1.result().quasi_dists[0], job_plus.result().quasi_dists[0]], legend=legend)
qc2_1 = QuantumCircuit(1)
qc2_1.x(0)
qc2_plus = QuantumCircuit(1)
qc2_plus.h(0)
obsvs = list(SparsePauliOp(['Z', 'X']))
estimator = Estimator()
job2_1 = estimator.run([qc2_1]*len(obsvs), observables=obsvs)
job2_plus = estimator.run([qc2_plus]*len(obsvs), observables=obsvs)
job2_1.result()
# TODO: make this into module that outputs a nice table
print(f' | <Z> | <X> ')
print(f'----|------------------')
print(f'|1> | {job2_1.result().values[0]} | {job2_1.result().values[1]}')
print(f'|+> | {job2_plus.result().values[0]} | {job2_plus.result().values[1]}')
A, a, B, b = SparsePauliOp(["Z", "X", "Z", "X"])
obsv = A.tensor(B) - A.tensor(b)+ a.tensor(B) + a.tensor(b) # create operator for chsh witness
from qc_grader.challenges.qgss_2023 import grade_lab2_ex1
grade_lab2_ex1(obsv)
from qiskit.circuit import Parameter
theta = Parameter('θ')
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
qc.ry(theta, 0)
qc.draw('mpl')
angles = [[float(v)] for v in np.linspace(0, 2*np.pi, 10).astype(np.float32)]
# create a parameterization of angles that will violate the inequality
estimator = Estimator()
job = estimator.run([qc]*len(angles), observables=[obsv]*len(angles), parameter_values=angles)
exps = job.result().values
plt.plot(angles, exps, marker='x', ls='-', color='green')
plt.plot(angles, [2]*len(angles), ls='--', color='red', label='Classical Bound')
plt.plot(angles, [-2]*len(angles), ls='--', color='red')
plt.xlabel('angle (rad)')
plt.ylabel('CHSH Witness')
plt.legend(loc=4)
from qc_grader.challenges.qgss_2023 import grade_lab2_ex2
grade_lab2_ex2(obsv, angles)
from qiskit.circuit import ClassicalRegister, QuantumRegister
theta = Parameter('θ')
qr = QuantumRegister(1, 'q')
qc = QuantumCircuit(qr)
qc.ry(theta, 0)
qc.draw('mpl')
tele_qc = qc.copy()
bell = QuantumRegister(2, 'Bell')
alice = ClassicalRegister(2, 'Alice')
bob = ClassicalRegister(1, 'Bob')
tele_qc.add_register(bell, alice, bob)
tele_qc.draw('mpl')
# create Bell state with other two qubits
tele_qc.barrier()
tele_qc.h(1)
tele_qc.cx(1, 2)
tele_qc.barrier()
tele_qc.draw('mpl')
# alice operates on her qubits
tele_qc.cx(0, 1)
tele_qc.h(0)
tele_qc.barrier()
tele_qc.draw('mpl')
tele_qc.measure([qr[0], bell[0]], alice)
tele_qc.draw('mpl')
graded_qc = tele_qc.copy()
##############################
# add gates to graded_qc here
with graded_qc.if_test((alice[1], 1)) as _:
graded_qc.x(2)
with graded_qc.if_test((alice[0], 1)) as _:
graded_qc.z(2)
##############################
graded_qc.draw('mpl')
graded_qc.barrier()
graded_qc.measure(bell[1], bob)
graded_qc.draw('mpl')
from qc_grader.challenges.qgss_2023 import grade_lab2_ex3
grade_lab2_ex3(graded_qc, theta, 5*np.pi/7)
from qiskit_aer.primitives import Sampler
angle = 5*np.pi/7
sampler = Sampler()
qc.measure_all()
job_static = sampler.run(qc.bind_parameters({theta: angle}))
job_dynamic = sampler.run(graded_qc.bind_parameters({theta: angle}))
print(f"Original Dists: {job_static.result().quasi_dists[0].binary_probabilities()}")
print(f"Teleported Dists: {job_dynamic.result().quasi_dists[0].binary_probabilities()}")
from qiskit.result import marginal_counts
tele_counts = marginal_counts(
job_dynamic.result().quasi_dists[0].binary_probabilities(),
indices=[2],
) # marginalize counts
legend = ['Original State', 'Teleported State']
plot_histogram([job_static.result().quasi_dists[0].binary_probabilities(), tele_counts], legend=legend)
from qc_grader.challenges.qgss_2023 import grade_lab2_ex4
grade_lab2_ex4(tele_counts, job_dynamic.result())
import qiskit.tools.jupyter
%qiskit_version_table
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import *
import numpy as np
from numpy import linalg as la
from qiskit.tools.monitor import job_monitor
import qiskit.tools.jupyter
qc = QuantumCircuit(1)
#### your code goes here
# z measurement of qubit 0
measure_z = QuantumCircuit(1,1)
measure_z.measure(0,0)
# x measurement of qubit 0
measure_x = QuantumCircuit(1,1)
# your code goes here
# y measurement of qubit 0
measure_y = QuantumCircuit(1,1)
# your code goes here
shots = 2**14 # number of samples used for statistics
sim = Aer.get_backend('qasm_simulator')
bloch_vector_measure = []
for measure_circuit in [measure_x, measure_y, measure_z]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
counts = execute(qc+measure_circuit, sim, shots=shots).result().get_counts()
# calculate the probabilities for each bit value
probs = {}
for output in ['0','1']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
bloch_vector_measure.append( probs['0'] - probs['1'] )
# normalizing the bloch sphere vector
bloch_vector = bloch_vector_measure/la.norm(bloch_vector_measure)
print('The bloch sphere coordinates are [{0:4.3f}, {1:4.3f}, {2:4.3f}]'
.format(*bloch_vector))
from kaleidoscope.interactive import bloch_sphere
bloch_sphere(bloch_vector, vectors_annotation=True)
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector( bloch_vector )
# circuit for the state Tri1
Tri1 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri2
Tri2 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri3
Tri3 = QuantumCircuit(2)
# your code goes here
# circuit for the state Sing
Sing = QuantumCircuit(2)
# your code goes here
# <ZZ>
measure_ZZ = QuantumCircuit(2)
measure_ZZ.measure_all()
# <XX>
measure_XX = QuantumCircuit(2)
# your code goes here
# <YY>
measure_YY = QuantumCircuit(2)
# your code goes here
shots = 2**14 # number of samples used for statistics
A = 1.47e-6 #unit of A is eV
E_sim = []
for state_init in [Tri1,Tri2,Tri3,Sing]:
Energy_meas = []
for measure_circuit in [measure_XX, measure_YY, measure_ZZ]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
qc = state_init+measure_circuit
counts = execute(qc, sim, shots=shots).result().get_counts()
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E_sim.append(A * np.sum(np.array(Energy_meas)))
# Run this cell to print out your results
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_sim[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_sim[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_sim[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_sim[3]))
# reduced plank constant in (eV) and the speed of light(cgs units)
hbar, c = 4.1357e-15, 3e10
# energy difference between the triplets and singlet
E_del = abs(E_sim[0] - E_sim[3])
# frequency associated with the energy difference
f = E_del/hbar
# convert frequency to wavelength in (cm)
wavelength = c/f
print('The wavelength of the radiation from the transition\
in the hyperfine structure is : {:.1f} cm'.format(wavelength))
provider = IBMQ.load_account()
backend = provider.get_backend('ibmq_athens')
# run this cell to get the backend information through the widget
backend
# assign your choice for the initial layout to the list variable `initial_layout`.
initial_layout =
qc_all = [state_init+measure_circuit for state_init in [Tri1,Tri2,Tri3,Sing]
for measure_circuit in [measure_XX, measure_YY, measure_ZZ] ]
shots = 8192
job = execute(qc_all, backend, initial_layout=initial_layout, optimization_level=3, shots=shots)
print(job.job_id())
job_monitor(job)
# getting the results of your job
results = job.result()
## To access the results of the completed job
#results = backend.retrieve_job('job_id').result()
def Energy(results, shots):
"""Compute the energy levels of the hydrogen ground state.
Parameters:
results (obj): results, results from executing the circuits for measuring a hamiltonian.
shots (int): shots, number of shots used for the circuit execution.
Returns:
Energy (list): energy values of the four different hydrogen ground states
"""
E = []
A = 1.47e-6
for ind_state in range(4):
Energy_meas = []
for ind_comp in range(3):
counts = results.get_counts(ind_state*3+ind_comp)
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E.append(A * np.sum(np.array(Energy_meas)))
return E
E = Energy(results, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E[3]))
from qiskit.ignis.mitigation.measurement import *
# your code to create the circuits, meas_calibs, goes here
meas_calibs, state_labels =
# execute meas_calibs on your choice of the backend
job = execute(meas_calibs, backend, shots = shots)
print(job.job_id())
job_monitor(job)
cal_results = job.result()
## To access the results of the completed job
#cal_results = backend.retrieve_job('job_id').result()
# your code to obtain the measurement filter object, 'meas_filter', goes here
results_new = meas_filter.apply(results)
E_new = Energy(results_new, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_new[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_new[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_new[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_new[3]))
# results for the energy estimation from the simulation,
# execution on a quantum system without error mitigation and
# with error mitigation in numpy array format
Energy_exact, Energy_exp_orig, Energy_exp_new = np.array(E_sim), np.array(E), np.array(E_new)
# Calculate the relative errors of the energy values without error mitigation
# and assign to the numpy array variable `Err_rel_orig` of size 4
Err_rel_orig =
# Calculate the relative errors of the energy values with error mitigation
# and assign to the numpy array variable `Err_rel_new` of size 4
Err_rel_new =
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
without measurement error mitigation : {}'.format(Err_rel_orig))
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
with measurement error mitigation : {}'.format(Err_rel_new))
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
# Importing standard Qiskit libraries
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import Aer, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector, plot_state_qsphere, plot_state_city, plot_state_paulivec, plot_state_hinton
# Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Define backend
sim = Aer.get_backend('aer_simulator')
def createBellStates(inp1, inp2):
qc = QuantumCircuit(2)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
qc, state, result = createBellStates(inp1, inp2)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp2 in ['0', '1']:
#for inp1 in ['0', '1']:
#qc, state, result = createBellStates(inp1, inp2)
#print('For inputs',inp2,inp1,'Representation of Entangled States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')'''
from qiskit import IBMQ, execute
from qiskit.providers.ibmq import least_busy
from qiskit.tools import job_monitor
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
def createBSRealDevice(inp1, inp2):
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr, cr)
qc.reset(range(2))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=100)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
print('For inputs',inp2,inp1,'Representation of Entangled States are,')
#first results
qc, first_result = createBSRealDevice(inp1, inp2)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = createBSRealDevice(inp1, inp2)
second_counts = second_result.get_counts()
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
def ghzCircuit(inp1, inp2, inp3):
qc = QuantumCircuit(3)
qc.reset(range(3))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
inp3 = 1
qc, state, result = ghzCircuit(inp1, inp2, inp3)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghzCircuit(inp1, inp2, inp3)
#print('For inputs',inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
def ghz5QCircuit(inp1, inp2, inp3, inp4, inp5):
qc = QuantumCircuit(5)
#qc.reset(range(5))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
if inp4 == 1:
qc.x(3)
if inp5 == 1:
qc.x(4)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
# Explore GHZ States for input 00010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 0
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 11001. Note: the input has been stated in little-endian format.
inp1 = 1
inp2 = 0
inp3 = 0
inp4 = 1
inp5 = 1
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 01010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 1
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Uncomment below code in order to explore other states
#for inp5 in ['0','1']:
#for inp4 in ['0','1']:
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
#print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 5
and not x.configuration().simulator
and x.status().operational==True))
def create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5):
qr = QuantumRegister(5)
cr = ClassicalRegister(5)
qc = QuantumCircuit(qr, cr)
qc.reset(range(5))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
if inp3=='1':
qc.x(1)
if inp4=='1':
qc.x(1)
if inp5=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=1000)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
inp3 = 0
inp4 = 0
inp5 = 0
#first results
qc, first_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
second_counts = second_result.get_counts()
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ circuit states are,')
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
import qiskit
qiskit.__qiskit_version__
|
https://github.com/mathelatics/QGSS-2023-From-Theory-to-Implementations
|
mathelatics
|
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import SparsePauliOp
def heisenberg_hamiltonian(
length: int, jx: float = 1.0, jy: float = 0.0, jz: float = 0.0
) -> SparsePauliOp:
terms = []
for i in range(length - 1):
if jx:
terms.append(("XX", [i, i + 1], jx))
if jy:
terms.append(("YY", [i, i + 1], jy))
if jz:
terms.append(("ZZ", [i, i + 1], jz))
return SparsePauliOp.from_sparse_list(terms, num_qubits=length)
def state_prep_circuit(num_qubits: int, layers: int = 1) -> QuantumCircuit:
qubits = QuantumRegister(num_qubits, name="q")
circuit = QuantumCircuit(qubits)
circuit.h(qubits)
for _ in range(layers):
for i in range(0, num_qubits - 1, 2):
circuit.cx(qubits[i], qubits[i + 1])
circuit.ry(0.1, qubits)
for i in range(1, num_qubits - 1, 2):
circuit.cx(qubits[i], qubits[i + 1])
circuit.ry(0.1, qubits)
return circuit
length = 5
hamiltonian = heisenberg_hamiltonian(length, 1.0, 1.0)
circuit = state_prep_circuit(length, layers=2)
print(hamiltonian)
circuit.draw("mpl")
from qiskit_aer.primitives import Estimator
estimator = Estimator(approximation=True)
job = estimator.run(circuit, hamiltonian, shots=None)
result = job.result()
exact_value = result.values[0]
print(f"Exact energy: {exact_value}")
from qiskit_ibm_runtime import QiskitRuntimeService
hub = "ibm-q-internal"
group = "deployed"
project = "default"
service = QiskitRuntimeService(instance=f"{hub}/{group}/{project}")
from qiskit_ibm_runtime import Estimator, Options, Session
from qiskit.transpiler import CouplingMap
backend = service.get_backend("simulator_statevector")
# set simulation options
simulator = {
"basis_gates": ["id", "rz", "sx", "cx", "reset"],
"coupling_map": list(CouplingMap.from_line(length + 1)),
}
shots = 10000
import math
options = Options(
simulator=simulator,
resilience_level=0,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
from qiskit_aer.noise import NoiseModel, ReadoutError
noise_model = NoiseModel()
##### your code here #####
# P(A|B) = [P(A|0), P(A|1)] = [ 1 - q0_01, q0_01 ] = [ 0.8, 0.2 ]
q0_10 = 0.5
q0_01 = 0.2
qn_10 = 0.05
qn_01 = 0.02
re_l = [ReadoutError(
[
[1 - q0_01, q0_01],
[q0_10, 1 - q0_10],
]
)]
n_qubits = 6
for _ in range(n_qubits - 1):
re_l.append(ReadoutError(
[
[1 - qn_01, qn_01],
[qn_10, 1 - qn_10],
]
))
for q in range(n_qubits):
noise_model.add_readout_error(re_l[q], (q, ))
print(noise_model.to_dict())
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex1
grade_lab5_ex1(noise_model)
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=0,
transpilation=dict(initial_layout=list(range(length))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=0,
transpilation=dict(initial_layout=list(range(1, length + 1))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=1,
transpilation=dict(initial_layout=list(range(1, length + 1))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
new_shots: int
##### your code here #####
new_shots = 20000
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex2
grade_lab5_ex2(new_shots)
from qiskit_aer.noise import depolarizing_error
noise_model = NoiseModel()
##### your code here #####
error = depolarizing_error(0.01, 2)
noise_model.add_all_qubit_quantum_error(error, ['cx'])
print(noise_model)
# Submit your answer
from qc_grader.challenges.qgss_2023 import grade_lab5_ex3
grade_lab5_ex3(noise_model)
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=1,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variance = result.metadata[0]["variance"]
std = math.sqrt(variance / shots)
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variance: {variance}")
print(f"Standard error: {std}")
options = Options(
simulator=dict(noise_model=noise_model, **simulator),
resilience_level=2,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0]
error = abs(experiment_value - exact_value)
variances = result.metadata[0]["zne"]["noise_amplification"]["variance"]
print(f"Estimated energy: {experiment_value}")
print(f"Energy error: {error}")
print(f"Variances: {variances}")
|
https://github.com/oracleagent/qSHA256
|
oracleagent
|
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer
from qiskit.circuit.library import XGate, RZGate, CXGate, CCXGate, U2Gate
def quantum_xor(circuit, a, b, output):
"""Quantum XOR gate using CNOTs."""
circuit.cx(a, output)
circuit.cx(b, output)
def quantum_and(circuit, a, b, output, ancilla):
"""Quantum AND gate using Toffoli gate."""
circuit.ccx(a, b, ancilla)
circuit.cx(ancilla, output)
circuit.reset(ancilla)
def right_rotate(circuit, qubits, rotation):
"""Performs a right rotation on a register."""
for _ in range(rotation):
circuit.swap(qubits[0], qubits[-1])
qubits.insert(0, qubits.pop())
def quantum_adder(circuit, a, b, output, carry):
"""Quantum full-adder for bitwise addition."""
for i in range(len(a)):
quantum_xor(circuit, a[i], b[i], output[i])
# Implementing carry is a complex process and would involve more auxiliary qubits
def initialize_constants(circuit, qubits):
"""Initializes SHA-256 constants into the first part of a quantum register."""
# SHA-256 constants, first 32 bits of the fractional parts of the square roots of the first 8 primes
constants = [
0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a,
0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19
]
for idx, const in enumerate(constants):
for bit_pos in range(32):
if const & (1 << bit_pos):
circuit.x(qubits[idx*32 + bit_pos])
def main_compression_loop(circuit, message_schedule, working_vars):
# Implements the main loop of SHA-256 with quantum gates.
for i in range(64):
# Ch, Maj, sum0, sum1 are functions that need quantum implementations
# These are placeholders and would be implemented similarly to the example functions above
pass
def sha256_quantum():
"""Constructs a full SHA-256 quantum circuit."""
# For simplicity, assume a single 512-bit message block
num_qubits = 8 * 32 + 512 # 8x32 for initial hash values, 512 for message schedule
qr = QuantumRegister(num_qubits, 'qr')
cr = ClassicalRegister(256, 'cr') # Output is 256 bits
circuit = QuantumCircuit(qr, cr)
# Initialize constants and hash values
initialize_constants(circuit, qr[:8*32]) # Initial hash values
# Message schedule would be loaded here
# Main compression loop
main_compression_loop(circuit, qr[8*32:], qr[:8*32])
# Measure the output hash into classical bits
circuit.measure(qr[:256], cr)
return circuit
circuit = sha256_quantum()
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1).result()
counts = result.get_counts()
print(counts)
|
https://github.com/18520339/uts-quantum-computing
|
18520339
|
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from termcolor import colored
class Board:
def __init__(self, size=3, simulator=None):
# Initialize the quantum circuit with one qubit and classical bit for each cell
self.size = size
self.simulator = simulator
self.superposition_count = 0
self.cells = [[' ' for _ in range(size)] for _ in range(size)] # Initialize the board representation
self.qubits = QuantumRegister(size**2, 'q')
self.bits = ClassicalRegister(size**2, 'c')
self.circuit = QuantumCircuit(self.qubits, self.bits)
''' For a 3x3 board, the winning lines are:
- Horizontal lines: (0, 1, 2), (3, 4, 5), (6, 7, 8)
- Vertical lines: (0, 3, 6), (1, 4, 7), (2, 5, 8)
- Diagonal lines: (0, 4, 8), (2, 4, 6)
'''
self.winning_lines = [tuple(range(i, size**2, size)) for i in range(size)] + \
[tuple(range(i * size, (i + 1) * size)) for i in range(size)] + \
[tuple(range(0, size**2, size + 1)), tuple(range(size - 1, size**2 - 1, size - 1))]
def __str__(self):
# Create a colorful string representation of the board
board_str = ''
for i, row in enumerate(self.cells):
for cell in row:
if '?' in cell: cell_color = 'cyan' # Quantum move
elif cell == 'X': cell_color = 'red'
elif cell == 'O': cell_color = 'green'
else: cell_color = 'yellow'
board_str += f' {colored(cell, cell_color)} '
board_str += '|' if '?' in cell else ' |'
board_str = board_str[:-1] + '\n' # Remove last separator
if i < self.size - 1: # Add horizontal separator
board_str += '-' * (5 * self.size - 1) + '\n'
return board_str
def make_classical_move(self, row, col, player_mark, is_collapsed=False):
if self.cells[row][col] == ' ' or is_collapsed: # Check if the cell is occupied
self.cells[row][col] = player_mark
index = row * self.size + col
if player_mark == 'X': self.circuit.x(self.qubits[index])
else: self.circuit.id(self.qubits[index])
return True
return False
def make_swap_move(self, row1, col1, row2, col2, **kwargs):
if self.cells[row1][col1] != ' ' and self.cells[row2][col2] != ' ':
indices = [row1 * self.size + col1, row2 * self.size + col2]
self.circuit.swap(self.qubits[indices[0]], self.qubits[indices[1]])
self.cells[row1][col1], self.cells[row2][col2] = self.cells[row2][col2], self.cells[row1][col1]
return True
return False
def make_superposition_move(self, row, col, player_mark, **kwargs):
if self.cells[row][col] == ' ':
index = row * self.size + col
self.circuit.h(self.qubits[index])
self.cells[row][col] = player_mark + '?'
self.superposition_count += 1
return True
return False
def make_entangled_move(self, *positions, risk_level, player_mark, **kwargs):
# Entangle the quantum states of 2 or 3 cells based on the risk level
pos_count = len(positions)
if pos_count not in [2, 3] or risk_level not in [1, 2, 3, 4] or len(set(positions)) != pos_count or \
(pos_count == 2 and risk_level not in [1, 3]) or (pos_count == 3 and risk_level not in [2, 4]) or \
any(self.cells[row][col] != ' ' for row, col in positions): return False
indices = [row * self.size + col for row, col in positions]
self.circuit.h(self.qubits[indices[0]])
if pos_count == 2:
# Pairwise Entanglement with Bell state for 2 qubits:
# Lv1. |Ψ+⟩ = (∣01⟩ + ∣10⟩)/√2 | Lv3. |Φ+⟩ = (∣00⟩ + ∣11⟩)/√2
if risk_level == 1: self.circuit.x(self.qubits[indices[1]])
self.circuit.cx(self.qubits[indices[0]], self.qubits[indices[1]])
else:
# Triple Entanglement with GHZ state for 3 qubits:
# Lv2. (∣010⟩ + ∣101⟩)/√2 | Lv4. (∣000⟩ + ∣111⟩)/√2
if risk_level == 2:
self.circuit.x(self.qubits[indices[1]])
self.circuit.x(self.qubits[indices[2]])
# Apply CNOT chain to entangle all 3 qubits
self.circuit.cx(self.qubits[indices[0]], self.qubits[indices[1]])
self.circuit.cx(self.qubits[indices[1]], self.qubits[indices[2]])
for row, col in positions: self.cells[row][col] = player_mark + '?'
self.superposition_count += pos_count
return True
def can_be_collapsed(self):
# If superpositions/entanglement cells form a potential winning line => collapse
for line in self.winning_lines:
if all(self.cells[i // self.size][i % self.size].endswith('?') for i in line):
return True
return False
def collapse_board(self):
# Update the board based on the measurement results and apply the corresponding classical moves
self.circuit.barrier()
self.circuit.measure(self.qubits, self.bits) # Measure all qubits to collapse them to classical states
transpiled_circuit = transpile(self.circuit, self.simulator)
job = self.simulator.run(transpiled_circuit, memory=True)
counts = job.result().get_counts()
max_state = max(counts, key=counts.get)[::-1] # Get the state with the highest probability
for i in range(self.size ** 2):
row, col = divmod(i, self.size)
if self.cells[row][col].endswith('?'):
self.circuit.reset(self.qubits[i])
self.make_classical_move(row, col, 'X' if max_state[i] == '1' else 'O', is_collapsed=True)
self.superposition_count = 0
return counts
def check_win(self):
# Dynamic implementation for above logic with dynamic winning lines
for line in self.winning_lines:
# Check if all cells in the line are the same and not empty
first_cell = self.cells[line[0] // self.size][line[0] % self.size]
if first_cell not in [' ', 'X?', 'O?']:
is_same = all(self.cells[i // self.size][i % self.size] == first_cell for i in line)
if is_same: return line
# If no spaces and no superpositions left => 'Draw'
# If all cells are filled but some are still in superpositions => collapse_board
if all(self.cells[i // self.size][i % self.size] not in [' '] for i in range(self.size**2)):
if self.superposition_count <= 0: return 'Draw'
return self.superposition_count
return None
|
https://github.com/18520339/uts-quantum-computing
|
18520339
|
from IPython.display import YouTubeVideo
YouTubeVideo('U6_wSh_-EQc', width=960, height=490)
!pip install qiskit --quiet
!pip install qiskit-aer --quiet
!pip install pylatexenc --quiet
# @markdown ### **1. Import `Qiskit` and essential packages for UI demonstration** { display-mode: "form" }
from abc import abstractmethod, ABCMeta # For define pure virtual functions
from IPython.display import clear_output
from ipywidgets import Output, Button, HBox, VBox, HTML, Dropdown
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile
from qiskit.visualization import plot_bloch_multivector, plot_histogram
from qiskit_aer import AerSimulator
# @markdown ### **2. `Board` class for essential quantum operations** { display-mode: "form" }
class Board:
def __init__(self, size=3, simulator=None):
# Initialize the quantum circuit with one qubit and classical bit for each cell
self.size = size
self.simulator = simulator
self.superposition_count = 0
self.cells = [[' ' for _ in range(size)] for _ in range(size)] # Initialize the board representation
self.qubits = QuantumRegister(size**2, 'q')
self.bits = ClassicalRegister(size**2, 'c')
self.circuit = QuantumCircuit(self.qubits, self.bits)
''' For a 3x3 board, the winning lines are:
- Horizontal lines: (0, 1, 2), (3, 4, 5), (6, 7, 8)
- Vertical lines: (0, 3, 6), (1, 4, 7), (2, 5, 8)
- Diagonal lines: (0, 4, 8), (2, 4, 6)
'''
self.winning_lines = [tuple(range(i, size**2, size)) for i in range(size)] + \
[tuple(range(i * size, (i + 1) * size)) for i in range(size)] + \
[tuple(range(0, size**2, size + 1)), tuple(range(size - 1, size**2 - 1, size - 1))]
def make_classical_move(self, row, col, player_mark, is_collapsed=False):
if self.cells[row][col] == ' ' or is_collapsed: # Check if the cell is occupied
self.cells[row][col] = player_mark
index = row * self.size + col
if player_mark == 'X': self.circuit.x(self.qubits[index])
else: self.circuit.id(self.qubits[index])
return True
return False
def make_swap_move(self, row1, col1, row2, col2, **kwargs):
if self.cells[row1][col1] != ' ' and self.cells[row2][col2] != ' ':
indices = [row1 * self.size + col1, row2 * self.size + col2]
self.circuit.swap(self.qubits[indices[0]], self.qubits[indices[1]])
self.cells[row1][col1], self.cells[row2][col2] = self.cells[row2][col2], self.cells[row1][col1]
return True
return False
def make_superposition_move(self, row, col, player_mark, **kwargs):
if self.cells[row][col] == ' ':
index = row * self.size + col
self.circuit.h(self.qubits[index])
self.cells[row][col] = player_mark + '?'
self.superposition_count += 1
return True
return False
def make_entangled_move(self, *positions, risk_level, player_mark, **kwargs):
# Entangle the quantum states of 2 or 3 cells based on the risk level
pos_count = len(positions)
if pos_count not in [2, 3] or risk_level not in [1, 2, 3, 4] or len(set(positions)) != pos_count or \
(pos_count == 2 and risk_level not in [1, 3]) or (pos_count == 3 and risk_level not in [2, 4]) or \
any(self.cells[row][col] != ' ' for row, col in positions): return False
indices = [row * self.size + col for row, col in positions]
self.circuit.h(self.qubits[indices[0]])
if pos_count == 2:
# Pairwise Entanglement with Bell state for 2 qubits:
# Lv1. |Ψ+⟩ = (∣01⟩ + ∣10⟩)/√2 | Lv3. |Φ+⟩ = (∣00⟩ + ∣11⟩)/√2
if risk_level == 1: self.circuit.x(self.qubits[indices[1]])
self.circuit.cx(self.qubits[indices[0]], self.qubits[indices[1]])
else:
# Triple Entanglement with GHZ state for 3 qubits:
# Lv2. (∣010⟩ + ∣101⟩)/√2 | Lv4. (∣000⟩ + ∣111⟩)/√2
if risk_level == 2:
self.circuit.x(self.qubits[indices[1]])
self.circuit.x(self.qubits[indices[2]])
# Apply CNOT chain to entangle all 3 qubits
self.circuit.cx(self.qubits[indices[0]], self.qubits[indices[1]])
self.circuit.cx(self.qubits[indices[1]], self.qubits[indices[2]])
for row, col in positions: self.cells[row][col] = player_mark + '?'
self.superposition_count += pos_count
return True
def can_be_collapsed(self):
# If superpositions/entanglement cells form a potential winning line => collapse
for line in self.winning_lines:
if all(self.cells[i // self.size][i % self.size].endswith('?') for i in line):
return True
return False
def collapse_board(self):
# Update the board based on the measurement results and apply the corresponding classical moves
self.circuit.barrier()
self.circuit.measure(self.qubits, self.bits) # Measure all qubits to collapse them to classical states
transpiled_circuit = transpile(self.circuit, self.simulator)
job = self.simulator.run(transpiled_circuit, memory=True)
counts = job.result().get_counts()
max_state = max(counts, key=counts.get)[::-1] # Get the state with the highest probability
for i in range(self.size ** 2):
row, col = divmod(i, self.size)
if self.cells[row][col].endswith('?'):
self.circuit.reset(self.qubits[i])
self.make_classical_move(row, col, 'X' if max_state[i] == '1' else 'O', is_collapsed=True)
self.superposition_count = 0
return counts
def check_win(self):
# Dynamic implementation for above logic with dynamic winning lines
for line in self.winning_lines:
# Check if all cells in the line are the same and not empty
first_cell = self.cells[line[0] // self.size][line[0] % self.size]
if first_cell not in [' ', 'X?', 'O?']:
is_same = all(self.cells[i // self.size][i % self.size] == first_cell for i in line)
if is_same: return line
# If no spaces and no superpositions left => 'Draw'
# If all cells are filled but some are still in superpositions => collapse_board
if all(self.cells[i // self.size][i % self.size] not in [' '] for i in range(self.size**2)):
if self.superposition_count <= 0: return 'Draw'
return self.superposition_count
return None
# @markdown ### **3. `QuantumT3Widgets` class for game interface**
class QuantumT3Widgets(metaclass=ABCMeta):
def __init__(self, board, current_player, quantum_move_mode):
self.board = board
self.current_player = current_player
self.quantum_move_mode = quantum_move_mode
self.log = Output(layout={'margin': '10px 0 0 0'})
self.histogram_output = Output(layout={'margin': '0 0 10px 10px'})
self.circuit_output = Output()
self.create_widgets()
def create_widgets(self):
# Create widgets for each cell and controls for game actions
self.buttons = []
for row in range(self.board.size):
self.buttons.append([])
for col in range(self.board.size):
button = Button(
description = ' ',
layout = {'width': '100px', 'height': '100px', 'border': '1px solid black'},
style = {'button_color': 'lightgray', 'font_weight': 'bold', 'text_color': 'white'}
)
button.on_click(self.create_on_cell_clicked(row, col))
self.buttons[row].append(button)
self.create_action_buttons()
self.game_info = HTML(f'<b>Current Player: {self.current_player} / Quantum Mode: {self.quantum_move_mode}</b>')
self.board_histogram_widget = HBox(
[VBox([VBox([HBox(row) for row in self.buttons]), self.game_info]), self.histogram_output],
layout = {'display': 'flex', 'justify_content': 'center', 'align_items': 'flex-end'}
)
display(VBox([self.board_histogram_widget, self.action_buttons, self.log, self.circuit_output]))
def create_action_buttons(self):
self.reset_btn = Button(description='Reset', button_style='danger')
self.collapse_btn = Button(description='Collapse', button_style='warning')
self.classical_btn = Button(description='Classical Move', button_style='primary')
self.swap_btn = Button(description='SWAP Move', button_style='info')
self.superposition_btn = Button(description='Superposition', button_style='success')
self.entangled_btn = Button(description='Entanglement', button_style='success')
self.entangled_options = Dropdown(options=[
('', 0), # Qubits collapse to opposite states (not consecutive)
('Lv1. PAIRWAISE: ∣Ψ+⟩ = (∣01⟩ + ∣10⟩) / √2', 1), # Qubits collapse to opposite states (not consecutive)
('Lv2. TRIPLE: GHZ_Xs = (∣010⟩ + ∣101⟩) / √2', 2),
('Lv3. PAIRWAISE: ∣Φ+⟩ = (∣00⟩ + ∣11⟩) / √2', 3), # Can form consecutive winning cells or accidentally help the opponent
('Lv4. TRIPLE: GHZ = (∣000⟩ + ∣111⟩) / √2', 4),
], value=0, disabled=True)
self.entangled_options.observe(self.update_entangled_options, names='value')
self.reset_btn.on_click(self.on_reset_btn_clicked)
self.collapse_btn.on_click(self.on_collapse_btn_clicked)
self.classical_btn.on_click(self.create_on_move_clicked('CLASSICAL'))
self.swap_btn.on_click(self.create_on_move_clicked('SWAP', 'Select 2 cells to swap their states.'))
self.superposition_btn.on_click(self.create_on_move_clicked('SUPERPOSITION', 'Select a cell to put in superposition.'))
self.entangled_btn.on_click(self.create_on_move_clicked('ENTANGLED', 'Select 2/3 cells based on risk level to entangle.'))
self.action_buttons = HBox([
self.reset_btn, self.collapse_btn, self.classical_btn, self.swap_btn,
self.superposition_btn, self.entangled_btn, self.entangled_options
])
@abstractmethod # Pure virtual functions => Must be overridden in the derived classes
def on_reset_btn_clicked(self, btn=None):
raise NotImplementedError('on_reset_btn_clicked method is not implemented.')
@abstractmethod # Pure virtual functions => Must be overridden in the derived classes
def on_collapse_btn_clicked(self, btn=None):
raise NotImplementedError('on_collapse_btn_clicked method is not implemented.')
@abstractmethod # Pure virtual functions => Must be overridden in the derived classes
def on_move_clicked(self, mode, message=''):
raise NotImplementedError('on_move_clicked method is not implemented.')
@abstractmethod # Pure virtual functions => Must be overridden in the derived classes
def on_cell_clicked(self, btn, row, col):
raise NotImplementedError('on_cell_clicked method is not implemented.')
def update_entangled_options(self, change):
with self.log:
self.entangled_options.disabled = change.new != 0
for row in self.buttons:
for button in row: button.disabled = change.new == 0
# Check if there are enough empty cells for the selected operation
empty_count = sum(cell == ' ' for row in self.board.cells for cell in row)
total_empty_required = {1: 2, 2: 3, 3: 2, 4: 3} # Total empty cells required for each risk level
if change.new == 0: return
elif empty_count < total_empty_required[change.new]:
print(f'Not enough empty cells to perform entanglement with risk level {change.new}. Please select another.')
self.entangled_options.value = 0
else:
print(f'Risk Level {change.new} ACTIVATED =>', end=' ')
if change.new in [1, 3]: print(f'Select 2 cells (qubits) for this PAIRWAISE entanglement.')
else: print(f'Select 3 cells (qubits) for this TRIPLE entanglement.')
def create_on_move_clicked(self, mode, message=''):
def on_move_clicked(btn):
with self.log:
try: self.on_move_clicked(mode, message)
except Exception as e: print(f'ERROR: {e}')
return on_move_clicked
def create_on_cell_clicked(self, row, col):
def on_cell_clicked(btn):
with self.log:
try: self.on_cell_clicked(btn, row, col)
except Exception as e: print(f'ERROR: {e}')
return on_cell_clicked
def display_circuit(self):
with self.circuit_output:
clear_output(wait=True)
display(self.board.circuit.draw('mpl', fold=-1, initial_state=True))
def display_histogram(self, counts):
with self.histogram_output:
clear_output(wait=True)
display(plot_histogram(counts, figsize=(9, 4)))
# @markdown ### **4. `QuantumT3GUI` class for game flow and interaction between players and `Board`**
class QuantumT3GUI(QuantumT3Widgets):
def __init__(self, size=3, simulator=None):
super().__init__(Board(size, simulator), 'X', 'CLASSICAL')
self.quantum_moves_selected = [] # Selected cells for operation on multi-qubit gates
self.game_over = False
def buttons_disabled(self, is_disabled=True):
for btn in self.action_buttons.children[1:]: btn.disabled = is_disabled
for row in self.buttons:
for btn in row: btn.disabled = is_disabled
def update_entire_board(self):
for row in range(self.board.size):
for col in range(self.board.size):
cell = self.board.cells[row][col]
color_map = {'X': 'dodgerblue', 'O': 'purple', '?': 'green', ' ': 'lightgray'}
self.buttons[row][col].description = cell if cell != ' ' else ' '
self.buttons[row][col].style.button_color = color_map[cell[-1]]
def clean_incompleted_quantum_moves(self):
for row, col in self.quantum_moves_selected:
if self.board.cells[row][col] == ' ':
self.buttons[row][col].description = ' '
self.buttons[row][col].style.button_color = 'lightgray'
self.quantum_moves_selected = []
def on_reset_btn_clicked(self, btn=None):
with self.log:
clear_output(wait=True)
self.board = Board(self.board.size, self.board.simulator)
self.current_player = 'X'
self.quantum_move_mode = 'CLASSICAL'
self.quantum_moves_selected = []
self.game_info.value = f'<b>Current Player: {self.current_player} / Quantum Mode: {self.quantum_move_mode}</b>'
self.game_over = False
self.update_entire_board()
self.buttons_disabled(False)
self.entangled_options.disabled = True
with self.histogram_output: clear_output()
with self.circuit_output: clear_output()
print('Game reset. New game started.')
def on_collapse_btn_clicked(self, btn=None):
with self.log:
if self.quantum_moves_selected:
print('Please complete the current quantum operation before measuring the board.')
return
clear_output(wait=True)
counts = self.board.collapse_board()
self.display_histogram(counts)
self.update_entire_board() # Update the board cells with the collapsed states
self.check_win()
print('Board measured and quantum states collapsed.')
def on_move_clicked(self, mode, message=''):
clear_output(wait=True)
self.quantum_move_mode = mode
self.game_info.value = f'<b>Current Player: {self.current_player} / Quantum Mode: {self.quantum_move_mode}</b>'
self.clean_incompleted_quantum_moves()
for row in self.buttons:
for button in row: button.disabled = mode == 'ENTANGLED'
if mode == 'ENTANGLED': self.entangled_options.value = 0
self.entangled_options.disabled = mode != 'ENTANGLED'
print(f'{mode} mode ACTIVATED' + (f': {message}' if message else ''))
def on_cell_clicked(self, btn, row, col):
if self.quantum_move_mode == 'CLASSICAL':
if self.board.make_classical_move(row, col, self.current_player):
btn.description = self.board.cells[row][col]
btn.style.button_color = 'dodgerblue' if self.current_player == 'X' else 'purple'
self.check_win()
else: print('That position is already occupied. Please choose another.')
elif self.quantum_move_mode == 'SUPERPOSITION':
if self.board.cells[row][col] == ' ':
btn.description = self.current_player + '?'
btn.style.button_color = 'green'
self.make_quantum_move_wrapper(
pos=(row, col), board_func=self.board.make_superposition_move,
success_msg='Cell is now in superposition state.')
else: print('Invalid SUPERPOSITION move. Cell must be empty.')
elif len(self.quantum_moves_selected) < 3: # Multi-qubit gates operation
self.quantum_moves_selected.append((row, col)) # Store the selected cell of operation
print(f'Cell ({row + 1}, {col + 1}) selected for {self.quantum_move_mode} move.')
if self.quantum_move_mode == 'SWAP' and len(self.quantum_moves_selected) == 2:
flat_pos = sum(self.quantum_moves_selected, ()) # Flatten the tuple to match 4 arguments in Board.make_swap_move
pos1, pos2 = self.quantum_moves_selected
self.make_quantum_move_wrapper(
pos=flat_pos, board_func=self.board.make_swap_move,
success_msg=f'SWAPPED Cell {pos1} to {pos2}', success_func=self.swap_on_board,
failure_msg='Invalid SWAP move. Both cells must be non-empty.')
elif self.quantum_move_mode == 'ENTANGLED':
if self.board.cells[row][col] == ' ':
btn.description = self.current_player + '?'
btn.style.button_color = 'green'
total_empty_required = {1: 2, 2: 3, 3: 2, 4: 3} # Total empty cells required for each risk level
if len(self.quantum_moves_selected) == total_empty_required[self.entangled_options.value]:
self.make_quantum_move_wrapper(
pos=self.quantum_moves_selected, board_func=self.board.make_entangled_move,
success_msg='These positions are now entangled and in a superposition state.',
failure_msg='Invalid ENTANGLEMENT move. Duplicated cell selection.')
else:
clear_output(wait=True)
print('Invalid ENTANGLEMENT move. A position is already occupied.')
self.quantum_moves_selected.pop() # Remove the invalid cell from the selected list
def swap_on_board(self):
row1, col1 = self.quantum_moves_selected[0][0], self.quantum_moves_selected[0][1]
row2, col2 = self.quantum_moves_selected[1][0], self.quantum_moves_selected[1][1]
# Swap the description and color of the selected cells
self.buttons[row1][col1].description, self.buttons[row2][col2].description = \
self.buttons[row2][col2].description, self.buttons[row1][col1].description
self.buttons[row1][col1].style.button_color, self.buttons[row2][col2].style.button_color = \
self.buttons[row2][col2].style.button_color, self.buttons[row1][col1].style.button_color
def make_quantum_move_wrapper(self, pos, board_func, success_msg='', success_func=None, failure_msg=''):
if board_func(*pos, risk_level=self.entangled_options.value, player_mark=self.current_player):
if success_msg: print(success_msg)
if success_func: success_func()
if self.board.can_be_collapsed():
print('Perform automatic board measurement and collapse the states.')
self.quantum_moves_selected = []
self.on_collapse_btn_clicked()
else: self.check_win()
else:
clear_output(wait=True)
if failure_msg: print(failure_msg)
self.clean_incompleted_quantum_moves()
def check_win(self):
self.quantum_moves_selected = []
while not self.game_over: # Check if the game is over after each move
self.display_circuit()
result = self.board.check_win()
if result == 'Draw': # All cells are filled but no winner yet
self.game_over = True
print("Game Over. It's a draw!")
elif type(result) == tuple: # A player wins
self.game_over = True
for cell_index in result:
row, col = divmod(cell_index, self.board.size)
self.buttons[row][col].style.button_color = 'orangered'
print(f'Game Over. {self.board.cells[row][col]} wins!')
elif type(result) == int: # All cells are filled but some are still in superpositions
print(f'All cells are filled but {result} of them still in superpositions => Keep Collapsing...')
self.quantum_moves_selected = []
self.on_collapse_btn_clicked() # Automatically collapse the board
break
else: # Switch players if no winner yet then continue the game
self.current_player = 'O' if self.current_player == 'X' else 'X' # Switch players
self.game_info.value = f'<b>Current Player: {self.current_player} / Quantum Mode: {self.quantum_move_mode}</b>'
break
if self.game_over: self.buttons_disabled(True)
game = QuantumT3GUI(size=3, simulator=AerSimulator())
|
https://github.com/18520339/uts-quantum-computing
|
18520339
|
from qiskit import QuantumCircuit, transpile, assemble
from qiskit.circuit.library import QFT
class CtrlMultCircuit(QuantumCircuit):
def __init__(self, a, binary_power, N):
super().__init__(N.bit_length())
self.a = a
self.power = 2 ** binary_power # Convert binary to decimal
self.N = N
self.name = f'{self.a}^{self.power} mod {self.N}'
self._create_circuit()
def _create_circuit(self):
for dec_power in range(self.power):
a_exp = self.a ** dec_power % self.N
for i in range(self.num_qubits):
if a_exp >> i & 1: self.x(i)
for j in range(i + 1, self.num_qubits):
if a_exp >> j & 1: self.swap(i, j)
class QPECircuit(QuantumCircuit):
def __init__(self, a, N):
super().__init__(2 * N.bit_length(), N.bit_length())
self.a = a
self.N = N
self._create_circuit()
def _modular_exponentiation(self):
for qbit_idx in range(self.num_qubits // 2):
self.append(
CtrlMultCircuit(self.a, qbit_idx, self.N).to_gate().control(),
[qbit_idx] + list(range(self.num_qubits // 2, 2 * self.num_qubits // 2))
)
def _create_circuit(self):
self.h(range(self.num_qubits // 2)) # Apply Hadamard gates to the first n qubits
self.x(self.num_qubits - 1)
self.barrier()
self._modular_exponentiation() # Apply controlled modular exponentiation
self.barrier()
self.append(
QFT(self.num_qubits // 2, inverse=True),
range(self.num_qubits // 2) # Apply inverse QFT to the first n qubits
)
def collapse(self, simulator):
self.measure(range(self.num_qubits // 2), range(self.num_qubits // 2))
transpiled_circuit = transpile(self, simulator)
self.collapse_result = simulator.run(transpiled_circuit, memory=True).result()
return self.collapse_result
|
https://github.com/18520339/uts-quantum-computing
|
18520339
|
from IPython.display import YouTubeVideo
YouTubeVideo('BYKc2RnQMqo', width=858, height=540)
!pip install qiskit --quiet
!pip install qiskit-aer --quiet
!pip install pylatexenc --quiet
# @markdown ### **1. Import `Qiskit` and essential packages** { display-mode: "form" }
from qiskit import QuantumCircuit, transpile, assemble
from qiskit.circuit.library import QFT
from qiskit_aer import AerSimulator
from fractions import Fraction
import random
import sympy
import math
# @markdown ### **2. Controlled Modular Multiplication for $U(x) = a^x mod N$** { display-mode: "form" }
class CtrlMultCircuit(QuantumCircuit):
def __init__(self, a, binary_power, N):
super().__init__(N.bit_length())
self.a = a
self.power = 2 ** binary_power # Convert binary to decimal
self.N = N
self.name = f'{self.a}^{self.power} mod {self.N}'
self._create_circuit()
def _create_circuit(self):
for dec_power in range(self.power):
a_exp = self.a ** dec_power % self.N
for i in range(self.num_qubits):
if a_exp >> i & 1: self.x(i)
for j in range(i + 1, self.num_qubits):
if a_exp >> j & 1: self.swap(i, j)
# @markdown ### **3. Quantum Phase Estimation with `Modular Exponentiation` and `Quantum Fourier Transform` to find period $r$** { display-mode: "form" }
# @markdown 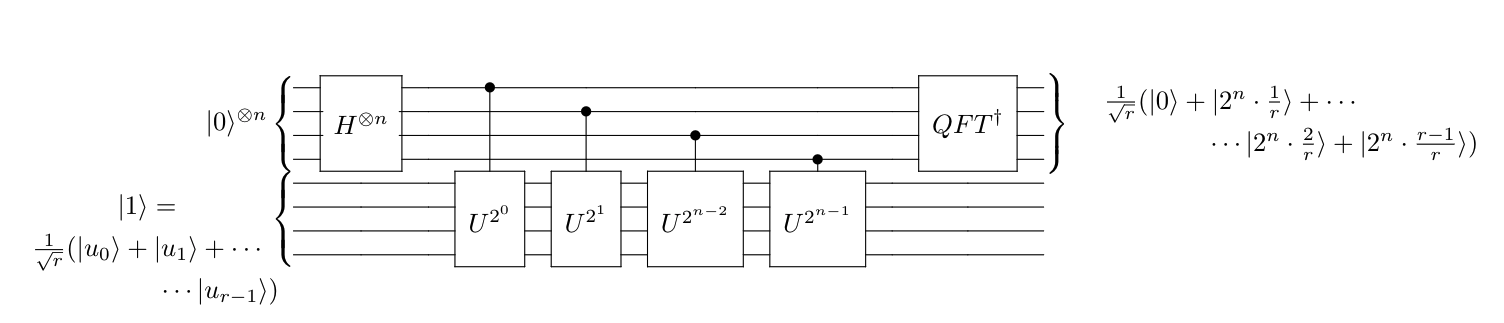
class QPECircuit(QuantumCircuit):
def __init__(self, a, N):
super().__init__(2 * N.bit_length(), N.bit_length())
self.a = a
self.N = N
self._create_circuit()
def _modular_exponentiation(self):
for qbit_idx in range(self.num_qubits // 2):
self.append(
CtrlMultCircuit(self.a, qbit_idx, self.N).to_gate().control(),
[qbit_idx] + list(range(self.num_qubits // 2, 2 * self.num_qubits // 2))
)
def _create_circuit(self):
self.h(range(self.num_qubits // 2)) # Apply Hadamard gates to the first n qubits
self.x(self.num_qubits - 1)
self.barrier()
self._modular_exponentiation() # Apply controlled modular exponentiation
self.barrier()
self.append(
QFT(self.num_qubits // 2, inverse=True),
range(self.num_qubits // 2) # Apply inverse QFT to the first n qubits
)
def collapse(self, simulator):
self.measure(range(self.num_qubits // 2), range(self.num_qubits // 2))
transpiled_circuit = transpile(self, simulator)
self.collapse_result = simulator.run(transpiled_circuit, memory=True).result()
return self.collapse_result
# @markdown ### **4. Completed Shor's Algorithm for Integer Factorization** { display-mode: "form" }
class ShorAlgorithm:
def __init__(self, N, max_attempts=-1, random_coprime_only=False, simulator=None):
self.N = N
self.simulator = simulator
self.max_attempts = max_attempts # -1 for all possible values of a
self.random_coprime_only = random_coprime_only # True to select only coprime values of a and N
def execute(self):
is_N_invalid = self._is_N_invalid()
if is_N_invalid: return is_N_invalid
# Only coprime values remain if random_coprime_only is enabled,
# Otherwise select a random integer in [2, N) as initial guess
a_values = [a for a in range(2, self.N) if not self.random_coprime_only or (math.gcd(a, self.N) == 1)]
print(f'[INFO] {len(a_values)} possible values of a: {a_values}')
self.max_attempts = len(a_values) if self.max_attempts <= -1 else min(self.max_attempts, len(a_values))
attempts_count = 0
while attempts_count < self.max_attempts:
print(f'\n===== Attempt {attempts_count + 1}/{self.max_attempts} =====')
attempts_count += 1
self.chosen_a = random.choice(a_values)
self.r = 1
print(f'[START] Chosen base a: {self.chosen_a}')
if not self.random_coprime_only:
gcd = math.gcd(self.chosen_a, self.N)
if gcd != 1:
print(f'=> {self.chosen_a} and {self.N} share common factor: {self.N} = {gcd} * {self.N // gcd}')
return gcd, self.N // gcd
print(f'>>> {self.chosen_a} and {self.N} are coprime => Perform Quantum Phase Estimation to find {self.chosen_a}^r - 1 = 0 (MOD {self.N})')
if not self._quantum_period_finding():
a_values.remove(self.chosen_a)
self.r = self.chosen_a = self.qpe_circuit = None
continue
factors = self._classical_postprocess()
if factors: return factors
a_values.remove(self.chosen_a)
self.r = self.chosen_a = self.qpe_circuit = None
print(f'[FAIL] No non-trivial factors found after {self.max_attempts} attempts.')
def _is_N_invalid(self):
if self.N <= 3:
print('[ERR] N must be > 3')
return 1, self.N
if self.N % 2 == 0:
print(f'=> {self.N} is an even number: {self.N} = 2 * {self.N // 2}')
return 2, self.N // 2
if sympy.isprime(self.N):
print(f'=> {self.N} is a prime number: {self.N} = 1 * {self.N}')
return 1, self.N
max_exponent = int(math.log2(self.N)) # Start with a large exponent and reduce
for k in range(max_exponent, 1, -1):
p = round(self.N ** (1 / k))
if p ** k == self.N:
print(f'=> {self.N} is a power of prime: {self.N} = {p}^{k}')
return p, k
return False
def _quantum_period_finding(self):
while self.chosen_a ** self.r % self.N != 1: # QPE + continued fractions may find wrong r
self.qpe_circuit = QPECircuit(self.chosen_a, self.N) # Find phase s/r
result = self.qpe_circuit.collapse(self.simulator)
state_bin = result.get_memory()[0]
state_dec = int(state_bin, 2) # Convert to decimal
bits_count = 2 ** (self.N.bit_length() - 1)
phase = state_dec / bits_count
# Continued fraction to find r
self.r = Fraction(phase).limit_denominator(self.N).denominator # Get fraction that most closely approximates phase
if self.r > self.N or self.r == 1: # Safety check to avoid infinite loops
print(f'[ERR] Invalid period found: r = {self.r} => Retry with different a.')
return False
print(f'>>> Output State: |{state_bin}⟩ = {state_dec} (dec) => Phase = {state_dec} / {bits_count} = {phase:.3f}')
return True
def _classical_postprocess(self):
# Classical postprocessing to find factors from the period
print(f'>>> Found r = {self.r} => a^{{r/2}} ± 1 = {self.chosen_a:.0f}^{self.r/2:.0f} ± 1')
if self.r % 2 != 0:
print(f'[ERR] r = {self.r} is odd => Retry with different a.')
return None
int1, int2 = self.chosen_a ** (self.r // 2) - 1, self.chosen_a ** (self.r // 2) + 1
if int1 % self.N == 0 or int2 % self.N == 0:
print(f'[ERR] {self.chosen_a}^{self.r/2:.0f} ± 1 is a multiple of {self.N} => Retry with different a.')
return None
factor1, factor2 = math.gcd(int1, self.N), math.gcd(int2, self.N)
if factor1 not in [1, self.N] and factor2 not in [1, self.N]: # Check to see if factor is non-trivial
print(f'[DONE] Successfully found non-trivial factors: {self.N} = {factor1} * {factor2}')
return factor1, factor2
print(f'[FAIL] Trivial factors found: [1, {self.N}] => Retry with different a.')
return None
# @markdown ### **5. Run the Factorization** { display-mode: "form" }
number_to_factor = 21 # @param {type:"slider", min: 15, max: 55, step: 1}
max_attempts = -1 # @param {type:"slider", min:-1, max:100, step:10}
random_coprime_only = False # @param {type:"boolean"}
# @markdown ***Note**: `max_attempts` will be limited to number of available values.
shor = ShorAlgorithm(number_to_factor, max_attempts, random_coprime_only, AerSimulator())
factors = shor.execute()
try: display(shor.qpe_circuit.draw(output='mpl', fold=-1))
except Exception: pass
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.aqua.components.initial_states import Zero
from qiskit.aqua.components.variational_forms import RY
from qiskit import BasicAer
from qiskit.aqua.algorithms.classical import ExactEigensolver
import matplotlib.pyplot as plt
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
num_qubits = qubit_op.num_qubits
print('Number of qubits: {}'.format(num_qubits))
init_state = Zero(num_qubits)
var_form = RY(num_qubits, initial_state=init_state)
backend = BasicAer.get_backend('statevector_simulator')
from qiskit.aqua.components.optimizers import COBYLA, L_BFGS_B, SLSQP
import numpy as np
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms.adaptive import VQE
optimizers = [COBYLA, L_BFGS_B, SLSQP]
converge_cnts = np.empty([len(optimizers)], dtype=object)
converge_vals = np.empty([len(optimizers)], dtype=object)
param_vals = np.empty([len(optimizers)], dtype=object)
num_qubits = qubit_op.num_qubits
for i in range(len(optimizers)):
aqua_globals.random_seed = 250
optimizer = optimizers[i]()
print('\rOptimizer: {} '.format(type(optimizer).__name__), end='')
counts = []
values = []
params = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
params.append(parameters)
algo = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result)
quantum_instance = QuantumInstance(backend=backend)
algo_result = algo.run(quantum_instance)
converge_cnts[i] = np.asarray(counts)
converge_vals[i] = np.asarray(values)
param_vals[i] = np.asarray(params)
print('\rOptimization complete ');
ee = ExactEigensolver(qubit_op)
result = ee.run()
ref = result['energy']
print('Reference value: {}'.format(ref))
plt.figure(figsize=(10,5))
for i in range(len(optimizers)):
plt.plot(converge_cnts[i], abs(ref - converge_vals[i]), label=optimizers[i].__name__)
plt.xlabel('Eval count')
plt.ylabel('Energy difference from solution reference value')
plt.title('Energy convergence for various optimizers')
plt.yscale('log')
plt.legend(loc='upper right')
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
from qiskit.chemistry.drivers import PySCFDriver, UnitsType
from qiskit.aqua.components.optimizers.cobyla import COBYLA
from qiskit.chemistry.components.variational_forms import UCCSD
from qiskit.chemistry.core import Hamiltonian, TransformationType, QubitMappingType
from qiskit.aqua.algorithms.adaptive.vqe.vqe import VQE
from qiskit.chemistry import FermionicOperator
from qiskit import Aer, IBMQ
from qiskit.chemistry.components.initial_states import HartreeFock
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit import execute
from qiskit.aqua import QuantumInstance
from qiskit.chemistry.algorithms.q_equation_of_motion.q_equation_of_motion import QEquationOfMotion
from qiskit.providers.aer import noise
from qiskit.aqua.algorithms import ExactEigensolver
from qiskit.quantum_info import Pauli
import numpy as np
import os
import logging
import copy
qasm_simulator = Aer.get_backend('qasm_simulator')
sv_simulator = Aer.get_backend('statevector_simulator')
def spin_operator(num_qubits):
pauli_list = []
for i in range(num_qubits):
if i < num_qubits:
c = 1/2
else:
c = -1/2
a_z = np.asarray([0] * i + [1] + [0] * (num_qubits - i - 1), dtype=np.bool)
a_x = np.asarray([0] * i + [0] + [0] * (num_qubits - i - 1), dtype=np.bool)
pauli_list.append([c, Pauli(a_z, a_x)])
op = WeightedPauliOperator(pauli_list)
return op
def number_operator(num_qubits):
h1 = np.identity(num_qubits)
op = FermionicOperator(h1)
num_op = op.mapping('jordan_wigner')
return num_op
def exact_eigenstates(hamiltonian, num_particles, num_spin):
num_qubits = hamiltonian.num_qubits
exact_eigensolver = ExactEigensolver(hamiltonian, k=1<<num_qubits)
exact_results = exact_eigensolver.run()
results = [[],[]]
number_op = number_operator(num_qubits)
spin_op = spin_operator(num_qubits)
for i in range(len(exact_results['eigvals'])):
particle = round(number_op.evaluate_with_statevector(exact_results['eigvecs'][i])[0],1)
spin = round(spin_op.evaluate_with_statevector(exact_results['eigvecs'][i])[0],1)
if particle != num_particles or spin != num_spin:
continue
results[0].append(exact_results['eigvals'][i])
results[1].append(exact_results['eigvecs'][i])
return results
two_qubit_reduction = False
qubit_mapping = 'jordan_wigner'
distance = 0.75
pyscf_driver = PySCFDriver(atom='H .0 .0 {}; H .0 .0 .0'.format(distance),
unit=UnitsType.ANGSTROM, charge=0, spin=0, basis='sto3g')
molecule = pyscf_driver.run()
core = Hamiltonian(transformation=TransformationType.FULL,
qubit_mapping=QubitMappingType.JORDAN_WIGNER,
two_qubit_reduction=two_qubit_reduction,
freeze_core=False,
orbital_reduction=[])
algo_input = core.run(molecule)
hamiltonian = algo_input[0]
num_orbitals = core.molecule_info['num_orbitals']
num_particles = core.molecule_info['num_particles']
init_state = HartreeFock(hamiltonian.num_qubits, num_orbitals, num_particles,
qubit_mapping=qubit_mapping, two_qubit_reduction=two_qubit_reduction)
depth = 1
var_form = UCCSD(hamiltonian.num_qubits, depth, num_orbitals, num_particles, initial_state=init_state,
qubit_mapping=qubit_mapping, two_qubit_reduction=two_qubit_reduction)
optimizer = COBYLA(maxiter = 5000)
algo = VQE(hamiltonian, var_form, optimizer)
results = algo.run(sv_simulator)
print(results)
energy = results['energy']
opt_params = results['opt_params']
ground_state = results['min_vector']
eom = QEquationOfMotion(hamiltonian, num_orbitals, num_particles, qubit_mapping=qubit_mapping,
two_qubit_reduction=two_qubit_reduction)
excitation_energies, eom_matrices = eom.calculate_excited_states(ground_state)
print(excitation_energies)
qeom_energies = [energy]
for gap_i in excitation_energies:
qeom_energies.append(energy+gap_i)
reference = exact_eigenstates(hamiltonian, 2, 0) #returns only the states with 2 electrons and singlet spin state.
exact_energies = []
tmp = 1000
for i in range(len(reference[0])):
if np.abs(reference[0][i]-tmp)>1e-5:
exact_energies.append(np.real(reference[0][i]))
tmp = reference[0][i]
for i in range(4):
print('State {} -> exact energy={} , qeom energy={}'.format(i, exact_energies[i], qeom_energies[i]))
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-internal',group='dev-qiskit')
provider.backends()
device = provider.get_backend('ibmq_boeblingen')
properties = device.properties()
coupling_map = device.configuration().coupling_map
noise_model = noise.device.basic_device_noise_model(properties)
basis_gates = noise_model.basis_gates
shots = 10000
quantum_instance = QuantumInstance(qasm_simulator, shots=shots, basis_gates=basis_gates,
coupling_map=coupling_map, noise_model=noise_model)
wave_function = var_form.construct_circuit(opt_params)
excitation_energies, eom_matrices = eom.calculate_excited_states(wave_function, quantum_instance = quantum_instance)
qeom_energies_noisy = [energy]
for gap_i in excitation_energies:
qeom_energies_noisy.append(energy+gap_i)
for i in range(4):
print('State {} -> exact energy={} , qeom energy={}'.format(i, exact_energies[i], qeom_energies_noisy[i]))
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import numpy as np
from qiskit import Aer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import VQE, ExactEigensolver
from qiskit.aqua.operators import Z2Symmetries
from qiskit.aqua.components.optimizers import COBYLA
from qiskit.chemistry import FermionicOperator
from qiskit.chemistry.drivers import PySCFDriver, UnitsType
from qiskit.chemistry.components.variational_forms import UCCSD
from qiskit.chemistry.components.initial_states import HartreeFock
driver = PySCFDriver(atom='Li .0 .0 .0; H .0 .0 1.6', unit=UnitsType.ANGSTROM,
charge=0, spin=0, basis='sto3g')
molecule = driver.run()
map_type = 'parity'
# please be aware that the idx here with respective to original idx
freeze_list = [0]
remove_list = [-3, -2] # negative number denotes the reverse order
h1 = molecule.one_body_integrals
h2 = molecule.two_body_integrals
nuclear_repulsion_energy = molecule.nuclear_repulsion_energy
num_particles = molecule.num_alpha + molecule.num_beta
num_spin_orbitals = molecule.num_orbitals * 2
print("HF energy: {}".format(molecule.hf_energy - molecule.nuclear_repulsion_energy))
print("# of electrons: {}".format(num_particles))
print("# of spin orbitals: {}".format(num_spin_orbitals))
# prepare full idx of freeze_list and remove_list
# convert all negative idx to positive
remove_list = [x % molecule.num_orbitals for x in remove_list]
freeze_list = [x % molecule.num_orbitals for x in freeze_list]
# update the idx in remove_list of the idx after frozen, since the idx of orbitals are changed after freezing
remove_list = [x - len(freeze_list) for x in remove_list]
remove_list += [x + molecule.num_orbitals - len(freeze_list) for x in remove_list]
freeze_list += [x + molecule.num_orbitals for x in freeze_list]
# prepare fermionic hamiltonian with orbital freezing and eliminating, and then map to qubit hamiltonian
# and if PARITY mapping is selected, reduction qubits
energy_shift = 0.0
qubit_reduction = True if map_type == 'parity' else False
ferOp = FermionicOperator(h1=h1, h2=h2)
if len(freeze_list) > 0:
ferOp, energy_shift = ferOp.fermion_mode_freezing(freeze_list)
num_spin_orbitals -= len(freeze_list)
num_particles -= len(freeze_list)
if len(remove_list) > 0:
ferOp = ferOp.fermion_mode_elimination(remove_list)
num_spin_orbitals -= len(remove_list)
qubitOp = ferOp.mapping(map_type=map_type, threshold=0.00000001)
qubitOp = Z2Symmetries.two_qubit_reduction(qubitOp, num_particles) if qubit_reduction else qubitOp
qubitOp.chop(10**-10)
print(qubitOp)
print(qubitOp.print_details())
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import warnings
from qiskit.tools.jupyter import *
from qiskit import IBMQ
from qiskit import assemble
from qiskit import pulse
from qiskit.pulse import pulse_lib
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-internal',group='dev-qiskit')
backend = provider.get_backend('ibmq_johannesburg')
backend_config = backend.configuration()
assert backend_config.open_pulse, "Backend doesn't support OpenPulse"
backend_defaults = backend.defaults()
dt = backend_config.dt
print(f"Sampling time: {dt} ns") # The configuration returns dt in seconds
cmd_def = pulse.CmdDef.from_defaults(backend.defaults().cmd_def, backend.defaults().pulse_library)
qubit = 0
x_gate = cmd_def.get('u3', [qubit], P0=np.pi, P1=0.0, P2=np.pi)
measure_gate = cmd_def.get('measure', qubits=backend_config.meas_map[qubit])
drive_chan = pulse.DriveChannel(qubit)
meas_chan = pulse.MeasureChannel(qubit)
acq_chan = pulse.AcquireChannel(qubit)
measure_time = 40
schedule = pulse.Schedule(name='Distribution Comparisons')
schedule += x_gate
schedule += measure_gate << measure_time
schedule.draw(plot_range=[0,150],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=10.0)
meas_schedule = pulse.Schedule(name='Distribution Comparisons')
meas_schedule += cmd_def.get('measure', qubits=backend_config.meas_map[qubit]) << measure_time
meas_schedule.draw(plot_range=[0,150],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 8192
readout_cal = assemble([schedule,meas_schedule],
backend=backend,
meas_level=1,
meas_return='single',
shots=num_shots_per_frequency)
job = backend.run(readout_cal)
print (job.job_id())
distribution_compare = backend.retrieve_job('5e2f6ca31663de0019d01c3a')
distribution_compare_result = distribution_compare.result(timeout=3600)
ground = [shot[0] for shot in distribution_compare_result.get_memory(1)]
excited = [shot[0] for shot in distribution_compare_result.get_memory(0)]
plt.figure(figsize=(10,10))
plt.scatter(np.real(ground)/1e15, np.imag(ground)/1e15,s=5, cmap='viridis', c='grey',alpha=1.0, label='state_0_mean')
plt.scatter(np.real(excited)/1e15, np.imag(excited)/1e15,s=5, cmap='viridis', c='blue',alpha=1.0, label='state_1_mean')
plt.ylabel('I [a.u.]', fontsize=15)
plt.xlabel('Q [a.u.]', fontsize=15)
plt.legend(["|0>","|1>"],fontsize=25)
plt.show()
mean_gnd = np.mean(ground) # takes mean of both real and imaginary parts
mean_exc = np.mean(excited)
import math
def classify(point: complex):
"""Classify the given state as |0> or |1>."""
def distance(a, b):
return math.sqrt((np.real(a) - np.real(b))**2 + (np.imag(a) - np.imag(b))**2)
return int(distance(point, mean_exc) < distance(point, mean_gnd))
fidelity_g = []
fidelity_e = []
for i in range(len(excited)):
fidelity_g.append(classify(ground[i]))
fidelity_e.append(classify(excited[i]))
def get_closest_multiple_of_16(num):
return (int(num) - (int(num)%16))
# Find out which group of qubits need to be acquired with this qubit
meas_map_idx = None
for i, measure_group in enumerate(backend_config.meas_map):
if qubit in measure_group:
meas_map_idx = i
break
assert meas_map_idx is not None, f"Couldn't find qubit {qubit} in the meas_map!"
meas_samples_us = 4.0
meas_sigma_us = 1.0 # The width of the gaussian part of the rise and fall
meas_risefall_us = 0.1 # and the truncating parameter: how many samples to dedicate to the risefall
meas_samples = get_closest_multiple_of_16(meas_samples_us * 1e-6/dt)
meas_sigma = get_closest_multiple_of_16(meas_sigma_us * 1e-6/dt) # The width of the gaussian part of the rise and fall
meas_risefall = get_closest_multiple_of_16(meas_risefall_us * 1e-6/dt)
meas_amp = 0.2
acq_cmd = pulse.Acquire(duration=meas_samples)
meas_pulse = pulse_lib.gaussian_square(duration=meas_samples,
sigma=meas_sigma,
amp=meas_amp,
risefall=meas_risefall,
name='measurement_pulse')
measure_schedule = meas_pulse(meas_chan)<<measure_time
measure_schedule += acq_cmd([pulse.AcquireChannel(i) for i in backend_config.meas_map[meas_map_idx]],
[pulse.MemorySlot(i) for i in backend_config.meas_map[meas_map_idx]])
measure_schedule.draw(plot_range=[0,1250],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
schedule = pulse.Schedule(name='Readout_Discrim')
schedule += x_gate
schedule += measure_schedule << measure_time
schedule.draw(plot_range=[0,1250],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 8192
readout_cal = assemble([schedule,measure_schedule],
backend=backend,
meas_level=1,
meas_return='single',
shots=num_shots_per_frequency)
job = backend.run(readout_cal)
print (job.job_id())
readout_tune = backend.retrieve_job('5e2f6d496d9b6d001c2cd56b') #amp is 0.2 4us pulse
readout_tune_result = readout_tune.result(timeout=3600)
ground = [shot[0] for shot in readout_tune_result.get_memory(1)]
excited = [shot[0] for shot in readout_tune_result.get_memory(0)]
plt.figure(figsize=(10,10))
plt.scatter(np.real(ground)/1e15, np.imag(ground)/1e15,s=5, cmap='viridis', c='grey',alpha=1.0, label='state_0_mean')
plt.scatter(np.real(excited)/1e15, np.imag(excited)/1e15,s=5, cmap='viridis', c='blue',alpha=1.0, label='state_1_mean')
plt.ylabel('I [a.u.]', fontsize=15)
plt.xlabel('Q [a.u.]', fontsize=15)
plt.legend(["|0>","|1>"],fontsize=25)
plt.show()
mean_gnd = np.mean(ground) # takes mean of both real and imaginary parts
mean_exc = np.mean(excited)
fidelity_g = []
fidelity_e = []
for i in range(len(excited)):
fidelity_g.append(classify(ground[i]))
fidelity_e.append(classify(excited[i]))
print (np.sum(fidelity_g)/len(fidelity_g))
print (np.sum(fidelity_e)/len(fidelity_e))
GHz = 1.0e9
MHz = 1.0e6
# We will find the qubit frequency for the following qubit.
qubit = 0
# The sweep will be centered around the estimated qubit frequency.
center_frequency_Hz = backend_defaults.meas_freq_est[qubit] # The default frequency is given in Hz
# warning: this will change in a future release
print(f"Qubit {qubit} has an estimated frequency of {center_frequency_Hz / GHz} GHz.")
# We will sweep 40 MHz around the estimated frequency
frequency_span_Hz = 2 * MHz
# in steps of 1 MHz.
frequency_step_Hz = 0.1 * MHz
# We will sweep 20 MHz above and 20 MHz below the estimated frequency
frequency_min = center_frequency_Hz - frequency_span_Hz / 2
frequency_max = center_frequency_Hz + frequency_span_Hz / 2
# Construct an np array of the frequencies for our experiment
frequencies_GHz = np.arange(frequency_min,
frequency_max,
frequency_step_Hz)
print(f"The sweep will go from {frequency_min / GHz} GHz to {frequency_max / GHz} GHz \
in steps of {frequency_step_Hz / MHz} MHz.")
qubit = 0
x_gate = cmd_def.get('u3', [qubit], P0=np.pi, P1=0.0, P2=np.pi)
measure_gate = cmd_def.get('measure', qubits=backend_config.meas_map[qubit])
schedule0 = pulse.Schedule(name='Readout Frequency sweep')
schedule0 += measure_gate <<measure_time
schedule1 = pulse.Schedule(name='Readout Frequency sweep')
schedule1 += x_gate
schedule1 += measure_gate <<measure_time
schedule_frequencies = [{meas_chan: freq} for freq in frequencies_GHz]
schedule1.draw(plot_range=[0,100],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 8192
ground_resonator_freq_sweep = assemble(schedule0,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency,
schedule_los=schedule_frequencies)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
num_shots_per_frequency = 8192
excited_resonator_freq_sweep = assemble(schedule1,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency,
schedule_los=schedule_frequencies)
job = backend.run(excited_resonator_freq_sweep)
print (job.job_id())
# chi_test_codes = ["5e2f1fbf3648b10018931256","5e2f1fc56840bc0018a436f6"] #codes for singapore backend
# chi_test_codes = ["5e2f2cd851c04c0018c7d86d","5e2f2cdaf5a50800187c237d"] #codes for johannesburg backend
# chi_test_codes = ["5e2f2d8df5a50800187c2380","5e2f2d9051c04c0018c7d877"] #codes for johannesburg backend
# chi_test_codes = ["5e2f302f6840bc0018a437a0","5e2f30323648b10018931300"] #codes for johannesburg backend
chi_test_codes = ["5e2f3e9151c04c0018c7d91a","5e2f3e94c4ffc4001882be47"] #codes for johannesburg backend
qubit=0
all_vals = []
for i in range(len(chi_test_codes)):
sweep_values = []
job = backend.retrieve_job(chi_test_codes[i])
frequency_sweep_results = job.result(timeout=120)
for j in range(len(frequency_sweep_results.results)):
res = frequency_sweep_results.get_memory(j)
sweep_values.append(res[qubit])
all_vals.append(sweep_values)
plt.figure(figsize=(10,5))
for i in range(len(chi_test_codes)):
plt.plot(frequencies_GHz, all_vals[i],"*--")
plt.axvline(center_frequency_Hz)
plt.legend(["|0>","|1>"],fontsize=15)
plt.show()
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import numpy as np
from qiskit import execute, QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.quantum_info.operators import Kraus, SuperOp
from qiskit.providers.aer import QasmSimulator
from qiskit.tools.visualization import plot_histogram
# Qiskit Aer noise module imports
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.aer.noise.errors import QuantumError, ReadoutError
from qiskit.providers.aer.noise.errors import pauli_error
from qiskit.providers.aer.noise.errors import depolarizing_error
from qiskit.providers.aer.noise.errors import thermal_relaxation_error
# Construct a 1-qubit bit-flip and phase-flip errors
p_error = 0.05
bit_flip = pauli_error([('X', p_error), ('I', 1 - p_error)])
phase_flip = pauli_error([('Z', p_error), ('I', 1 - p_error)])
print(bit_flip)
print(phase_flip)
# Compose two bit-flip and phase-flip errors
bitphase_flip = bit_flip.compose(phase_flip)
print(bitphase_flip)
# Tensor product two bit-flip and phase-flip errors with
# bit-flip on qubit-0, phase-flip on qubit-1
error2 = phase_flip.tensor(bit_flip)
print(error2)
# Convert to Kraus operator
bit_flip_kraus = Kraus(bit_flip)
print(bit_flip_kraus)
# Convert to Superoperator
phase_flip_sop = SuperOp(phase_flip)
print(phase_flip_sop)
# Convert back to a quantum error
print(QuantumError(bit_flip_kraus))
# Check conversion is equivalent to original error
QuantumError(bit_flip_kraus) == bit_flip
# Measurement miss-assignement probabilities
p0given1 = 0.1
p1given0 = 0.05
ReadoutError([[1 - p1given0, p1given0], [p0given1, 1 - p0given1]])
# Create an empty noise model
noise_model = NoiseModel()
# Add depolarizing error to all single qubit u1, u2, u3 gates
error = depolarizing_error(0.05, 1)
noise_model.add_all_qubit_quantum_error(error, ['u1', 'u2', 'u3'])
# Print noise model info
print(noise_model)
# Create an empty noise model
noise_model = NoiseModel()
# Add depolarizing error to all single qubit u1, u2, u3 gates on qubit 0 only
error = depolarizing_error(0.05, 1)
noise_model.add_quantum_error(error, ['u1', 'u2', 'u3'], [0])
# Print noise model info
print(noise_model)
# Create an empty noise model
noise_model = NoiseModel()
# Add depolarizing error on qubit 2 forall single qubit u1, u2, u3 gates on qubit 0
error = depolarizing_error(0.05, 1)
noise_model.add_nonlocal_quantum_error(error, ['u1', 'u2', 'u3'], [0], [2])
# Print noise model info
print(noise_model)
# Simulator
simulator = QasmSimulator()
# System Specification
n_qubits = 4
circ = QuantumCircuit(n_qubits, n_qubits)
# Test Circuit
circ.h(0)
for qubit in range(n_qubits - 1):
circ.cx(qubit, qubit + 1)
circ.measure(range(4), range(4))
print(circ)
# Ideal execution
job = execute(circ, simulator)
result_ideal = job.result()
plot_histogram(result_ideal.get_counts(0))
# Example error probabilities
p_reset = 0.03
p_meas = 0.1
p_gate1 = 0.05
# QuantumError objects
error_reset = pauli_error([('X', p_reset), ('I', 1 - p_reset)])
error_meas = pauli_error([('X',p_meas), ('I', 1 - p_meas)])
error_gate1 = pauli_error([('X',p_gate1), ('I', 1 - p_gate1)])
error_gate2 = error_gate1.tensor(error_gate1)
# Add errors to noise model
noise_bit_flip = NoiseModel()
noise_bit_flip.add_all_qubit_quantum_error(error_reset, "reset")
noise_bit_flip.add_all_qubit_quantum_error(error_meas, "measure")
noise_bit_flip.add_all_qubit_quantum_error(error_gate1, ["u1", "u2", "u3"])
noise_bit_flip.add_all_qubit_quantum_error(error_gate2, ["cx"])
print(noise_bit_flip)
# Run the noisy simulation
job = execute(circ, simulator,
basis_gates=noise_bit_flip.basis_gates,
noise_model=noise_bit_flip)
result_bit_flip = job.result()
counts_bit_flip = result_bit_flip.get_counts(0)
# Plot noisy output
plot_histogram(counts_bit_flip)
# T1 and T2 values for qubits 0-3
T1s = np.random.normal(50e3, 10e3, 4) # Sampled from normal distribution mean 50 microsec
T2s = np.random.normal(70e3, 10e3, 4) # Sampled from normal distribution mean 50 microsec
# Truncate random T2s <= T1s
T2s = np.array([min(T2s[j], 2 * T1s[j]) for j in range(4)])
# Instruction times (in nanoseconds)
time_u1 = 0 # virtual gate
time_u2 = 50 # (single X90 pulse)
time_u3 = 100 # (two X90 pulses)
time_cx = 300
time_reset = 1000 # 1 microsecond
time_measure = 1000 # 1 microsecond
# QuantumError objects
errors_reset = [thermal_relaxation_error(t1, t2, time_reset)
for t1, t2 in zip(T1s, T2s)]
errors_measure = [thermal_relaxation_error(t1, t2, time_measure)
for t1, t2 in zip(T1s, T2s)]
errors_u1 = [thermal_relaxation_error(t1, t2, time_u1)
for t1, t2 in zip(T1s, T2s)]
errors_u2 = [thermal_relaxation_error(t1, t2, time_u2)
for t1, t2 in zip(T1s, T2s)]
errors_u3 = [thermal_relaxation_error(t1, t2, time_u3)
for t1, t2 in zip(T1s, T2s)]
errors_cx = [[thermal_relaxation_error(t1a, t2a, time_cx).expand(
thermal_relaxation_error(t1b, t2b, time_cx))
for t1a, t2a in zip(T1s, T2s)]
for t1b, t2b in zip(T1s, T2s)]
# Add errors to noise model
noise_thermal = NoiseModel()
for j in range(4):
noise_thermal.add_quantum_error(errors_reset[j], "reset", [j])
noise_thermal.add_quantum_error(errors_measure[j], "measure", [j])
noise_thermal.add_quantum_error(errors_u1[j], "u1", [j])
noise_thermal.add_quantum_error(errors_u2[j], "u2", [j])
noise_thermal.add_quantum_error(errors_u3[j], "u3", [j])
for k in range(4):
noise_thermal.add_quantum_error(errors_cx[j][k], "cx", [j, k])
print(noise_thermal)
# Run the noisy simulation
job = execute(circ, simulator,
basis_gates=noise_thermal.basis_gates,
noise_model=noise_thermal)
result_thermal = job.result()
counts_thermal = result_thermal.get_counts(0)
# Plot noisy output
plot_histogram(counts_thermal)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
# Import general libraries (needed for functions)
import numpy as np
import time
# Import Qiskit classes
import qiskit
from qiskit import QuantumRegister, QuantumCircuit, ClassicalRegister, Aer
from qiskit.providers.aer import noise
from qiskit.tools.visualization import plot_histogram
# Import measurement calibration functions
from qiskit.ignis.mitigation.measurement import (complete_meas_cal, tensored_meas_cal,
CompleteMeasFitter, TensoredMeasFitter)
from qiskit import IBMQ
IBMQ.load_account()
# Generate the calibration circuits
qr = qiskit.QuantumRegister(5)
qubit_list = [2,3,4]
meas_calibs, state_labels = complete_meas_cal(qubit_list=qubit_list, qr=qr, circlabel='mcal')
state_labels
provider = IBMQ.get_provider(hub='ibm-q-internal',group='dev-qiskit')
backend = provider.get_backend('ibmq_johannesburg')
backend_config = backend.configuration()
assert backend_config.open_pulse, "Backend doesn't support OpenPulse"
backend_defaults = backend.defaults()
dt = backend_config.dt
print(f"Sampling time: {dt} ns") # The configuration returns dt in seconds
# Execute the calibration circuits without noise
job = qiskit.execute(meas_calibs, backend=backend, shots=1000)
cal_results = job.result()
# The calibration matrix without noise is the identity matrix
meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal')
print(meas_fitter.cal_matrix)
# Generate a noise model for the 5 qubits
noise_model = noise.NoiseModel()
for qi in range(5):
read_err = noise.errors.readout_error.ReadoutError([[0.9, 0.1],[0.25,0.75]])
noise_model.add_readout_error(read_err, [qi])
# Execute the calibration circuits
backend = qiskit.Aer.get_backend('qasm_simulator')
job = qiskit.execute(meas_calibs, backend=backend, shots=1000, noise_model=noise_model)
cal_results = job.result()
# Calculate the calibration matrix with the noise model
meas_fitter = CompleteMeasFitter(cal_results, state_labels, qubit_list=qubit_list, circlabel='mcal')
print(meas_fitter.cal_matrix)
# Plot the calibration matrix
meas_fitter.plot_calibration()
# What is the measurement fidelity?
print("Average Measurement Fidelity: %f" % meas_fitter.readout_fidelity())
# What is the measurement fidelity of Q0?
print("Average Measurement Fidelity of Q0: %f" % meas_fitter.readout_fidelity(
label_list = [['000','001','010','011'],['100','101','110','111']]))
# Make a 3Q GHZ state
cr = ClassicalRegister(3)
ghz = QuantumCircuit(qr, cr)
ghz.h(qr[2])
ghz.cx(qr[2], qr[3])
ghz.cx(qr[3], qr[4])
ghz.measure(qr[2],cr[0])
ghz.measure(qr[3],cr[1])
ghz.measure(qr[4],cr[2])
job = qiskit.execute([ghz], backend=backend, shots=5000, noise_model=noise_model)
results = job.result()
# Results without mitigation
raw_counts = results.get_counts()
# Get the filter object
meas_filter = meas_fitter.filter
# Results with mitigation
mitigated_results = meas_filter.apply(results)
mitigated_counts = mitigated_results.get_counts(0)
from qiskit.tools.visualization import *
plot_histogram([raw_counts, mitigated_counts], legend=['raw', 'mitigated'])
# Make a 2Q Bell state between Q2 and Q4
cr = ClassicalRegister(2)
bell = QuantumCircuit(qr, cr)
bell.h(qr[2])
bell.cx(qr[2], qr[4])
bell.measure(qr[2],cr[0])
bell.measure(qr[4],cr[1])
job = qiskit.execute([bell], backend=backend, shots=5000, noise_model=noise_model)
results = job.result()
#build a fitter from the subset
meas_fitter_sub = meas_fitter.subset_fitter(qubit_sublist=[2,4])
#The calibration matrix is now in the space Q2/Q4
meas_fitter_sub.cal_matrix
# Results without mitigation
raw_counts = results.get_counts()
# Get the filter object
meas_filter_sub = meas_fitter_sub.filter
# Results with mitigation
mitigated_results = meas_filter_sub.apply(results)
mitigated_counts = mitigated_results.get_counts(0)
from qiskit.tools.visualization import *
plot_histogram([raw_counts, mitigated_counts], legend=['raw', 'mitigated'])
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.chemistry import FermionicOperator
from qiskit.chemistry.drivers import PySCFDriver, UnitsType
from qiskit.aqua.components.initial_states import Zero
from qiskit.chemistry.components.initial_states import HartreeFock
from qiskit.chemistry.components.variational_forms import UCCSD
from qiskit.aqua.operators import Z2Symmetries
from qiskit.aqua.components.variational_forms import RY, RYRZ, swaprz
from qiskit import BasicAer
from qiskit.aqua.components.optimizers import COBYLA, L_BFGS_B, SLSQP
import numpy as np
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms.adaptive import VQE
from qiskit.aqua.algorithms.classical import ExactEigensolver
import pylab
import matplotlib.pyplot as plt
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
num_qubits = qubit_op.num_qubits
print('Number of qubits: {}'.format(num_qubits))
# using driver to get fermionic Hamiltonian
# PySCF example
driver = PySCFDriver(atom='Li .0 .0 .0; H .0 .0 1.6', unit=UnitsType.ANGSTROM,
charge=0, spin=0, basis='sto3g')
molecule = driver.run()
# please be aware that the idx here with respective to original idx
freeze_list = [0]
remove_list = [-3, -2] # negative number denotes the reverse order
map_type = 'parity'
h1 = molecule.one_body_integrals
h2 = molecule.two_body_integrals
nuclear_repulsion_energy = molecule.nuclear_repulsion_energy
num_particles = molecule.num_alpha + molecule.num_beta
num_spin_orbitals = molecule.num_orbitals * 2
print("HF energy: {}".format(molecule.hf_energy - molecule.nuclear_repulsion_energy))
print("# of electrons: {}".format(num_particles))
print("# of spin orbitals: {}".format(num_spin_orbitals))
# prepare full idx of freeze_list and remove_list
# convert all negative idx to positive
remove_list = [x % molecule.num_orbitals for x in remove_list]
freeze_list = [x % molecule.num_orbitals for x in freeze_list]
# update the idx in remove_list of the idx after frozen, since the idx of orbitals are changed after freezing
remove_list = [x - len(freeze_list) for x in remove_list]
remove_list += [x + molecule.num_orbitals - len(freeze_list) for x in remove_list]
freeze_list += [x + molecule.num_orbitals for x in freeze_list]
# prepare fermionic hamiltonian with orbital freezing and eliminating, and then map to qubit hamiltonian
# and if PARITY mapping is selected, reduction qubits
energy_shift = 0.0
qubit_reduction = True if map_type == 'parity' else False
ferOp = FermionicOperator(h1=h1, h2=h2)
if len(freeze_list) > 0:
ferOp, energy_shift = ferOp.fermion_mode_freezing(freeze_list)
num_spin_orbitals -= len(freeze_list)
num_particles -= len(freeze_list)
if len(remove_list) > 0:
ferOp = ferOp.fermion_mode_elimination(remove_list)
num_spin_orbitals -= len(remove_list)
qubit_op = ferOp.mapping(map_type=map_type)
qubit_op = Z2Symmetries.two_qubit_reduction(qubit_op, num_particles) if qubit_reduction else qubitOp
qubit_op.chop(10**-10)
# print(qubit_op.print_operators())
print(qubit_op)
print(qubit_op.num_qubits)
num_qubits = qubit_op.num_qubits
init_state_UCCSD = HartreeFock(qubit_op.num_qubits, num_spin_orbitals, num_particles, map_type,
qubit_reduction)
init_state_Zero = Zero(num_qubits)
UCCSD_var_form = UCCSD(num_qubits,depth=1, num_orbitals=num_spin_orbitals,num_particles=num_particles, initial_state=init_state_UCCSD)
## Some code that extract the variational form. Ideally it will draw it out as well.
init_state = Zero(num_qubits)
var_form = RY(num_qubits, initial_state=init_state_Zero)
backend = BasicAer.get_backend('statevector_simulator')
optimizers = [COBYLA, SLSQP]
converge_cnts = np.empty([len(optimizers)], dtype=object)
converge_vals = np.empty([len(optimizers)], dtype=object)
param_vals = np.empty([len(optimizers)], dtype=object)
num_qubits = qubit_op.num_qubits
for i in range(len(optimizers)):
aqua_globals.random_seed = 250
optimizer = optimizers[i]()
print('\rOptimizer: {} '.format(type(optimizer).__name__), end='')
counts = []
values = []
params = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
params.append(parameters)
algo = VQE(qubit_op, UCCSD_var_form, optimizer, callback=store_intermediate_result)
quantum_instance = QuantumInstance(backend=backend)
algo_result = algo.run(quantum_instance)
converge_cnts[i] = np.asarray(counts)
converge_vals[i] = np.asarray(values)
param_vals[i] = np.asarray(params)
print('\rOptimization complete ');
ee = ExactEigensolver(qubit_op)
result = ee.run()
ref = result['energy']
print('Reference value: {}'.format(ref))
plt.figure(figsize=(10,5))
for i in range(len(optimizers)):
plt.plot(converge_cnts[i], abs(ref - converge_vals[i]), label=optimizers[i].__name__)
plt.xlabel('Eval count')
plt.ylabel('Energy difference from solution reference value')
plt.title('Energy convergence for various optimizers')
plt.yscale('log')
plt.legend(loc='upper right')
optimizers = [COBYLA, SLSQP]
converge_cnts = np.empty([len(optimizers)], dtype=object)
converge_vals = np.empty([len(optimizers)], dtype=object)
param_vals = np.empty([len(optimizers)], dtype=object)
num_qubits = qubit_op.num_qubits
for i in range(len(optimizers)):
aqua_globals.random_seed = 250
optimizer = optimizers[i]()
print('\rOptimizer: {} '.format(type(optimizer).__name__), end='')
counts = []
values = []
params = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
params.append(parameters)
algo = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result)
quantum_instance = QuantumInstance(backend=backend)
algo_result = algo.run(quantum_instance)
converge_cnts[i] = np.asarray(counts)
converge_vals[i] = np.asarray(values)
param_vals[i] = np.asarray(params)
print('\rOptimization complete ');
test = 0
interesting_pt = param_vals[1][test]
circuit = algo.construct_circuit(interesting_pt)
circuit[0].draw()
ee = ExactEigensolver(qubit_op)
result = ee.run()
ref = result['energy']
print('Reference value: {}'.format(ref))
plt.figure(figsize=(10,5))
for i in range(len(optimizers)):
plt.plot(converge_cnts[i], abs(ref - converge_vals[i]), label=optimizers[i].__name__)
plt.xlabel('Eval count')
plt.ylabel('Energy difference from solution reference value')
plt.title('Energy convergence for various optimizers')
plt.yscale('log')
plt.legend(loc='upper right')
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import warnings
from qiskit.tools.jupyter import *
from qiskit import IBMQ
from qiskit import assemble
from qiskit import pulse
from qiskit.pulse import pulse_lib
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-internal',group='dev-qiskit')
backend = provider.get_backend('ibmq_johannesburg')
backend_config = backend.configuration()
assert backend_config.open_pulse, "Backend doesn't support OpenPulse"
backend_defaults = backend.defaults()
dt = backend_config.dt
print(f"Sampling time: {dt} ns") # The configuration returns dt in seconds
cmd_def = pulse.CmdDef.from_defaults(backend.defaults().cmd_def, backend.defaults().pulse_library)
qubit = 0
x_gate = cmd_def.get('u3', [qubit], P0=np.pi, P1=0.0, P2=np.pi)
measure_gate = cmd_def.get('measure', qubits=backend_config.meas_map[qubit])
drive_chan = pulse.DriveChannel(qubit)
meas_chan = pulse.MeasureChannel(qubit)
acq_chan = pulse.AcquireChannel(qubit)
measure_time = 40
# drive pulse parameters
drive_power = 0.4
drive_samples = 128
drive_sigma = 16
powers = np.linspace(0.01,0.5,60)
# creating drive pulse
schedules = []
for ii,drive_power in enumerate(powers):
schedule = pulse.Schedule(name='Qubit Rabi')
drive_pulse = pulse_lib.gaussian(duration=drive_samples, amp=drive_power,
sigma=drive_sigma, name='mydrivepulse')
drive_pulse_qubit = drive_pulse(drive_chan)
schedule += drive_pulse_qubit
schedule += measure_gate << schedule.duration
schedules.append(schedule)
schedules[-1].draw(plot_range=[0,400],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency =4096
rabi_sweep = assemble(schedules,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
qubit_spec_codes = ["5e31bf1730629b0011ab3e16"] #codes for johannesburg backend
job = backend.retrieve_job("5e31bf1730629b0011ab3e16")
qubit=0
rabi_result = job.result()
rabi_data = np.ones(len(powers), dtype=np.complex_)
for i in range(len(powers)):
rabi_data[i] = rabi_result.get_memory(i)[qubit]
plt.figure(figsize=(10,5))
plt.plot(powers,rabi_data,"*--")
plt.show()
# auto-phase the output measurement signal
def get_amplitude(vec):
i_signal = np.imag(vec)
r_signal = np.real(vec)
mvec = [np.mean(r_signal), np.mean(i_signal)]
src_mat = np.vstack((r_signal - mvec[0], i_signal - mvec[1])).T
(_, _, v_mat) = np.linalg.svd(src_mat)
dvec = v_mat[0, 0:2]
if dvec.dot(mvec) < 0:
dvec = -dvec
return src_mat.dot(dvec)
from scipy.optimize import curve_fit
scale_factor = 1e-14
rabi_amp_data = get_amplitude(rabi_data)*scale_factor
fit_func = lambda x,A,B,T,phi: (A*np.cos(2*np.pi*x/T+phi)+B)
#Fit the data
fitparams, conv = curve_fit(fit_func, powers, rabi_amp_data, [2.0,0.0,0.08,0])
#get the pi amplitude
pi_amp = (np.pi-fitparams[3])*fitparams[2]/4/np.pi
plt.plot(powers, fit_func(powers, *fitparams), color='red')
plt.scatter(powers, rabi_amp_data, label='target qubit')
plt.xlim(0, 0.2)
plt.ylim(-5, 5)
plt.legend()
plt.xlabel('CR pulse amplitude, a.u.', fontsize=20)
plt.ylabel('Signal, a.u.', fontsize=20)
plt.title('CR Rabi oscillation', fontsize=20)
print(pi_amp)
# drive pulse parameters
drive_power = 0.4
drive_samples = 128
drive_sigma = 16
powers_lin = [pi_amp,pi_amp*3,pi_amp*5,pi_amp*7,pi_amp*9,pi_amp*11,pi_amp*13,pi_amp*15,pi_amp*17,pi_amp*19,pi_amp*21,pi_amp*23,pi_amp*25,pi_amp*27,pi_amp*29,pi_amp*31,pi_amp*33,pi_amp*35,pi_amp*37,pi_amp*39,pi_amp*41,pi_amp*43]
# creating drive pulse
schedules = []
for ii,drive_power in enumerate(powers_lin):
schedule = pulse.Schedule(name='Qubit Rabi')
drive_pulse = pulse_lib.gaussian(duration=drive_samples, amp=drive_power,
sigma=drive_sigma, name='mydrivepulse')
drive_pulse_qubit = drive_pulse(drive_chan)
schedule += drive_pulse_qubit
schedule += measure_gate << schedule.duration
schedules.append(schedule)
schedules[-1].draw(plot_range=[0,400],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency =4096
rabi_sweep = assemble(schedules,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
job = backend.retrieve_job("5e31c52c7eba0a00115e1ca0")
qubit=0
rabi_result = job.result()
rabi_linear_data = np.ones(len(powers), dtype=np.complex_)
for i in range(len(powers)):
rabi_linear_data[i] = rabi_result.get_memory(i)[qubit]
plt.figure(figsize=(10,5))
plt.plot(powers,rabi_data,"*--")
plt.plot(powers_lin,rabi_linear_data,".")
plt.show()
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import numpy as np
import matplotlib.pyplot as plt
from qiskit import IBMQ
import qiskit.pulse as pulse
import qiskit.pulse.pulse_lib as pulse_lib
from qiskit.compiler import assemble
from qiskit.qobj.utils import MeasLevel, MeasReturnType
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-internal', group='deployed', project='default')
backend = provider.get_backend('ibmq_johannesburg')
backend_config = backend.configuration()
config = backend.configuration()
defaults = backend.defaults()
# qubit to use for exeperiment
control_qubit = 1
target_qubit = 0
control_channel_index = 1
# exp configuration
exps = 30
shots = 512
# Rabi pulse
cr_amps = np.linspace(0, 0.2, exps)
cr_samples = 200
cr_sigma = 4
cr_rise_fall = 16
# scaling factor for data returned by backend
# note: You may have to adjust this for the backend you use
scale_factor= 1e-14
[control_qubit, target_qubit] in config.coupling_map
defaults.qubit_freq_est[control_qubit] > defaults.qubit_freq_est[target_qubit]
config.u_channel_lo[control_channel_index]
# Create schedule
schedules = []
for ii, cr_amp in enumerate(cr_amps):
# drive pulse
cr_rabi_pulse_p = pulse_lib.gaussian_square(duration=cr_samples,
amp=cr_amp,
sigma=cr_sigma,
risefall=cr_rise_fall,
name='cr_rabi_pulse_p%d' % ii)
cr_rabi_pulse_m = pulse_lib.gaussian_square(duration=cr_samples,
amp=-cr_amp,
sigma=cr_sigma,
risefall=cr_rise_fall,
name='cr_rabi_pulse_m%d' % ii)
control_channel = pulse.ControlChannel(control_channel_index)
# We get the state preparation and measurement pulses we need from the
# defaults `circuit_instruction_map`
pi_pulse_q0 = defaults.circuit_instruction_map.get('u3', (control_qubit,), np.pi, 0, np.pi)
measure = defaults.circuit_instruction_map.get('measure', config.meas_map[0])
# add commands to schedule
schedule = pulse.Schedule(name='CR Rabi Experiment at drive amp = %s' % cr_amp)
schedule |= cr_rabi_pulse_p(control_channel)
schedule |= pi_pulse_q0 << schedule.duration
schedule |= cr_rabi_pulse_m(control_channel) << schedule.duration
schedule |= measure << schedule.duration
schedules.append(schedule)
schedules[1].draw(channels_to_plot=[pulse.DriveChannel(control_qubit),
pulse.DriveChannel(target_qubit),
control_channel,
pulse.MeasureChannel(control_qubit),
pulse.MeasureChannel(target_qubit)],
scaling=10.0, label=False, plot_range=(0, 700))
cr_rabi_qobj = assemble(schedules, backend, meas_level=MeasLevel.KERNELED,
meas_return=MeasReturnType.AVERAGE, shots=shots)
job = backend.run(cr_rabi_qobj)
job.job_id()
job.status()
cr_rabi_result = job.result(timeout=3600)
job = backend.retrieve_job('5e31bf8e0520030011cbdb08')
cr_rabi_results = job.result(timeout=120)
target_qubit_rabi_data = np.ones(exps, dtype=np.complex_)
control_qubit_rabi_data = np.ones(exps, dtype=np.complex_)
for i in range(exps):
target_qubit_rabi_data[i] = cr_rabi_result.get_memory(i)[target_qubit]
control_qubit_rabi_data[i] = cr_rabi_result.get_memory(i)[control_qubit]
# auto-phase the output measurement signal
def get_amplitude(vec):
i_signal = np.imag(vec)
r_signal = np.real(vec)
mvec = [np.mean(r_signal), np.mean(i_signal)]
src_mat = np.vstack((r_signal - mvec[0], i_signal - mvec[1])).T
(_, _, v_mat) = np.linalg.svd(src_mat)
dvec = v_mat[0, 0:2]
if dvec.dot(mvec) < 0:
dvec = -dvec
return src_mat.dot(dvec)
target_rabi_amp_data = get_amplitude(target_qubit_rabi_data)*scale_factor
control_rabi_amp_data = get_amplitude(control_qubit_rabi_data)*scale_factor
fit_func = lambda x,A,B,T,phi: (A*np.cos(2*np.pi*x/T+phi)+B)
#Fit the data
fitparams, conv = curve_fit(fit_func, cr_amps, target_rabi_amp_data, [3.0,0.0,0.1,0])
#get the pi amplitude
cr_pi_2_amp = (np.pi-fitparams[3])*fitparams[2]/4/np.pi
plt.plot(cr_amps, fit_func(cr_amps, *fitparams), color='red')
plt.axvline(cr_pi_2_amp, color='black', linestyle='dashed')
plt.scatter(cr_amps, target_rabi_amp_data, label='target qubit')
plt.scatter(cr_amps, control_rabi_amp_data, label='control qubit')
plt.xlim(0, 0.2)
plt.ylim(-5, 5)
plt.legend()
plt.xlabel('CR pulse amplitude, a.u.', fontsize=20)
plt.ylabel('Signal, a.u.', fontsize=20)
plt.title('CR Rabi oscillation', fontsize=20)
print(cr_pi_2_amp)
defaults.circuit_instruction_map.get('cx', (control_qubit, target_qubit)).draw(show_framechange_channels=False)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import warnings
from qiskit.tools.jupyter import *
from qiskit import IBMQ
from qiskit import assemble
from qiskit import pulse
from qiskit.pulse import pulse_lib
import numpy as np
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q-internal',group='dev-qiskit')
backend = provider.get_backend('ibmq_johannesburg')
backend_config = backend.configuration()
assert backend_config.open_pulse, "Backend doesn't support OpenPulse"
backend_defaults = backend.defaults()
dt = backend_config.dt
print(f"Sampling time: {dt} ns") # The configuration returns dt in seconds
cmd_def = pulse.CmdDef.from_defaults(backend.defaults().cmd_def, backend.defaults().pulse_library)
qubit = 0
x_gate = cmd_def.get('u3', [qubit], P0=np.pi, P1=0.0, P2=np.pi)
measure_gate = cmd_def.get('measure', qubits=backend_config.meas_map[qubit])
drive_chan = pulse.DriveChannel(qubit)
meas_chan = pulse.MeasureChannel(qubit)
acq_chan = pulse.AcquireChannel(qubit)
measure_time = 40
GHz = 1.0e9
MHz = 1.0e6
# We will find the qubit frequency for the following qubit.
qubit = 0
# The sweep will be centered around the estimated qubit frequency.
center_frequency_Hz = backend_defaults.qubit_freq_est[qubit] # The default frequency is given in Hz
# warning: this will change in a future release
print(f"Qubit {qubit} has an estimated frequency of {center_frequency_Hz / GHz} GHz.")
# We will sweep 40 MHz around the estimated frequency
frequency_span_Hz = 40 * MHz
# in steps of 1 MHz.
frequency_step_Hz = 2 * MHz
# We will sweep 20 MHz above and 20 MHz below the estimated frequency
frequency_min = center_frequency_Hz - frequency_span_Hz / 2
frequency_max = center_frequency_Hz + frequency_span_Hz / 2
# Construct an np array of the frequencies for our experiment
frequencies_GHz = np.arange(frequency_min,
frequency_max,
frequency_step_Hz)
print(f"The sweep will go from {frequency_min / GHz} GHz to {frequency_max / GHz} GHz \
in steps of {frequency_step_Hz / MHz} MHz.")
schedule = pulse.Schedule(name='Qubit Frequency sweep')
schedule += x_gate
schedule += measure_gate <<measure_time
schedule_frequencies = [{drive_chan: freq} for freq in frequencies_GHz]
schedule.draw(plot_range=[0,100],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 1024
ground_resonator_freq_sweep = assemble(schedule,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency,
schedule_los=schedule_frequencies)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
# qubit_spec_codes = ["5e308314edc73f0018347bc9"] #codes for johannesburg backend
qubit_spec_codes = ["5e3084545b1d1100124c0fff"] #codes for johannesburg backend
qubit=0
all_vals = []
for i in range(len(qubit_spec_codes)):
sweep_values = []
job = backend.retrieve_job(qubit_spec_codes[i])
frequency_sweep_results = job.result(timeout=120)
for j in range(len(frequency_sweep_results.results)):
res = frequency_sweep_results.get_memory(j)
sweep_values.append(res[qubit])
all_vals.append(sweep_values)
plt.figure(figsize=(10,5))
for i in range(len(qubit_spec_codes)):
plt.plot(frequencies_GHz, all_vals[i],"*--")
plt.axvline(center_frequency_Hz)
plt.show()
anharmonicity = 312.0e6
GHz = 1.0e9
MHz = 1.0e6
# We will find the qubit frequency for the following qubit.
qubit = 0
# The sweep will be centered around the estimated qubit frequency.
center_frequency_Hz = backend_defaults.qubit_freq_est[qubit] - anharmonicity/2.0 # The default frequency is given in Hz
# warning: this will change in a future release
print(f"Qubit {qubit} has an estimated frequency of {center_frequency_Hz / GHz} GHz.")
# We will sweep 40 MHz around the estimated frequency
frequency_span_Hz = 10 * MHz
# in steps of 1 MHz.
frequency_step_Hz = 0.5 * MHz
# We will sweep 20 MHz above and 20 MHz below the estimated frequency
frequency_min = center_frequency_Hz - frequency_span_Hz / 2
frequency_max = center_frequency_Hz + frequency_span_Hz / 2
# Construct an np array of the frequencies for our experiment
frequencies_GHz = np.arange(frequency_min,
frequency_max,
frequency_step_Hz)
print(f"The sweep will go from {frequency_min / GHz} GHz to {frequency_max / GHz} GHz \
in steps of {frequency_step_Hz / MHz} MHz.")
schedule = pulse.Schedule(name='Qubit Frequency sweep')
schedule += x_gate
schedule += measure_gate <<measure_time
schedule_frequencies = [{drive_chan: freq} for freq in frequencies_GHz]
schedule.draw(plot_range=[0,100],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 8192
ground_resonator_freq_sweep = assemble(schedule,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency,
schedule_los=schedule_frequencies)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
qubit_spec_codes = ["5e30e0845b1d1100124c11ea"] #codes for johannesburg backend
qubit=0
all_vals = []
for i in range(len(qubit_spec_codes)):
sweep_values = []
job = backend.retrieve_job(qubit_spec_codes[i])
frequency_sweep_results = job.result(timeout=120)
for j in range(len(frequency_sweep_results.results)):
res = frequency_sweep_results.get_memory(j)
sweep_values.append(res[qubit])
all_vals.append(sweep_values)
plt.figure(figsize=(10,5))
for i in range(len(qubit_spec_codes)):
plt.plot(frequencies_GHz, all_vals[i],"*--")
plt.axvline(center_frequency_Hz)
plt.show()
schedule = pulse.Schedule(name='Qubit Frequency sweep')
# drive pulse parameters
drive_power = 0.4
drive_samples = 128
drive_sigma = 16
# creating drive pulse
drive_pulse = pulse_lib.gaussian(duration=drive_samples, amp=drive_power,
sigma=drive_sigma, name='mydrivepulse')
drive_pulse_qubit = drive_pulse(drive_chan)
schedule += drive_pulse_qubit
schedule += measure_gate <<schedule.duration
schedule_frequencies = [{drive_chan: freq} for freq in frequencies_GHz]
schedule.draw(plot_range=[0,400],channels_to_plot=[drive_chan, meas_chan], label=True, scaling=1.0)
num_shots_per_frequency = 8192
ground_resonator_freq_sweep = assemble(schedule,
backend=backend,
meas_level=1,
meas_return='avg',
shots=num_shots_per_frequency,
schedule_los=schedule_frequencies)
job = backend.run(ground_resonator_freq_sweep)
print (job.job_id())
# qubit_spec_codes = ["5e30c8589706bd001221a2b3"] #codes for johannesburg backend
qubit_spec_codes = ["5e30e0a69706bd001221a2c2"] #codes for johannesburg backend
qubit=0
all_vals = []
for i in range(len(qubit_spec_codes)):
sweep_values = []
job = backend.retrieve_job(qubit_spec_codes[i])
frequency_sweep_results = job.result(timeout=120)
for j in range(len(frequency_sweep_results.results)):
res = frequency_sweep_results.get_memory(j)
sweep_values.append(res[qubit])
all_vals.append(sweep_values)
plt.figure(figsize=(10,5))
for i in range(len(qubit_spec_codes)):
plt.plot(frequencies_GHz, all_vals[i],"*--")
plt.axvline(center_frequency_Hz)
plt.show()
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
import numpy as np
import pylab
from qiskit import Aer, IBMQ
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.algorithms.adaptive import VQE
from qiskit.aqua.algorithms.classical import ExactEigensolver
from qiskit.aqua.components.optimizers import SPSA
from qiskit.aqua.components.variational_forms import RY
from qiskit.aqua.operators import WeightedPauliOperator
import matplotlib.pyplot as plt
import numpy as np
from qiskit import execute, QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit.quantum_info.operators import Kraus, SuperOp
from qiskit.providers.aer import QasmSimulator
from qiskit.tools.visualization import plot_histogram
# Qiskit Aer noise module imports
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.aer.noise.errors import QuantumError, ReadoutError
from qiskit.providers.aer.noise.errors import pauli_error
from qiskit.providers.aer.noise.errors import depolarizing_error
from qiskit.providers.aer.noise.errors import thermal_relaxation_error
from qiskit.providers.aer import noise
provider = IBMQ.load_account()
pauli_dict = {
'paulis': [{"coeff": {"imag": 0.0, "real": -1.052373245772859}, "label": "II"},
{"coeff": {"imag": 0.0, "real": 0.39793742484318045}, "label": "ZI"},
{"coeff": {"imag": 0.0, "real": -0.39793742484318045}, "label": "IZ"},
{"coeff": {"imag": 0.0, "real": -0.01128010425623538}, "label": "ZZ"},
{"coeff": {"imag": 0.0, "real": 0.18093119978423156}, "label": "XX"}
]
}
qubit_op = WeightedPauliOperator.from_dict(pauli_dict)
num_qubits = qubit_op.num_qubits
print('Number of qubits: {}'.format(num_qubits))
ee = ExactEigensolver(qubit_op.copy())
result = ee.run()
ref = result['energy']
print('Reference value: {}'.format(ref))
# T1 and T2 values for qubits 0-3
T1s = np.random.normal(50e3, 10e3, 4) # Sampled from normal distribution mean 50 microsec
T2s = np.random.normal(70e3, 10e3, 4) # Sampled from normal distribution mean 50 microsec
# Truncate random T2s <= T1s
T2s = np.array([min(T2s[j], 2 * T1s[j]) for j in range(4)])
# Instruction times (in nanoseconds)
time_u1 = 0 # virtual gate
time_u2 = 50 # (single X90 pulse)
time_u3 = 100 # (two X90 pulses)
time_cx = 300
time_reset = 1000 # 1 microsecond
time_measure = 1000 # 1 microsecond
# QuantumError objects
errors_reset = [thermal_relaxation_error(t1, t2, time_reset)
for t1, t2 in zip(T1s, T2s)]
errors_measure = [thermal_relaxation_error(t1, t2, time_measure)
for t1, t2 in zip(T1s, T2s)]
errors_u1 = [thermal_relaxation_error(t1, t2, time_u1)
for t1, t2 in zip(T1s, T2s)]
errors_u2 = [thermal_relaxation_error(t1, t2, time_u2)
for t1, t2 in zip(T1s, T2s)]
errors_u3 = [thermal_relaxation_error(t1, t2, time_u3)
for t1, t2 in zip(T1s, T2s)]
errors_cx = [[thermal_relaxation_error(t1a, t2a, time_cx).expand(
thermal_relaxation_error(t1b, t2b, time_cx))
for t1a, t2a in zip(T1s, T2s)]
for t1b, t2b in zip(T1s, T2s)]
# Add errors to noise model
noise_thermal = NoiseModel()
for j in range(4):
noise_thermal.add_quantum_error(errors_reset[j], "reset", [j])
noise_thermal.add_quantum_error(errors_measure[j], "measure", [j])
noise_thermal.add_quantum_error(errors_u1[j], "u1", [j])
noise_thermal.add_quantum_error(errors_u2[j], "u2", [j])
noise_thermal.add_quantum_error(errors_u3[j], "u3", [j])
for k in range(4):
noise_thermal.add_quantum_error(errors_cx[j][k], "cx", [j, k])
print(noise_thermal)
device = provider.get_backend('ibmq_essex')
coupling_map = device.configuration().coupling_map
noise_model = noise.device.basic_device_noise_model(device.properties())
basis_gates = noise_model.basis_gates
print(noise_model)
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend=backend, seed_simulator=167, seed_transpiler=167,
noise_model=noise_thermal)
counts1 = []
values1 = []
def store_intermediate_result1(eval_count, parameters, mean, std):
counts1.append(eval_count)
values1.append(mean)
aqua_globals.random_seed = 167
optimizer = SPSA(max_trials=200)
var_form = RY(num_qubits)
vqe = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result1)
vqe_result1 = vqe.run(quantum_instance)
print('VQE on Aer qasm simulator (with noise): {}'.format(vqe_result1['energy']))
print('Delta from reference: {}'.format(vqe_result1['energy']-ref))
plt.figure(figsize=[10,5])
plt.plot(counts1, values1)
plt.xlabel('Eval count')
plt.ylabel('Energy')
plt.title('Convergence with noise');
plt.axhline(ref)
# T1 and T2 values for qubits 0-3
T1s = np.random.normal(5e3, 1e3, 4) # Sampled from normal distribution mean 50 microsec
T2s = np.random.normal(7e3, 1e3, 4) # Sampled from normal distribution mean 50 microsec
# Truncate random T2s <= T1s
T2s = np.array([min(T2s[j], 2 * T1s[j]) for j in range(4)])
# Instruction times (in nanoseconds)
time_u1 = 0 # virtual gate
time_u2 = 50 # (single X90 pulse)
time_u3 = 100 # (two X90 pulses)
time_cx = 300
time_reset = 1000 # 1 microsecond
time_measure = 1000 # 1 microsecond
# QuantumError objects
errors_reset = [thermal_relaxation_error(t1, t2, time_reset)
for t1, t2 in zip(T1s, T2s)]
errors_measure = [thermal_relaxation_error(t1, t2, time_measure)
for t1, t2 in zip(T1s, T2s)]
errors_u1 = [thermal_relaxation_error(t1, t2, time_u1)
for t1, t2 in zip(T1s, T2s)]
errors_u2 = [thermal_relaxation_error(t1, t2, time_u2)
for t1, t2 in zip(T1s, T2s)]
errors_u3 = [thermal_relaxation_error(t1, t2, time_u3)
for t1, t2 in zip(T1s, T2s)]
errors_cx = [[thermal_relaxation_error(t1a, t2a, time_cx).expand(
thermal_relaxation_error(t1b, t2b, time_cx))
for t1a, t2a in zip(T1s, T2s)]
for t1b, t2b in zip(T1s, T2s)]
# Add errors to noise model
noise_thermal = NoiseModel()
for j in range(4):
noise_thermal.add_quantum_error(errors_reset[j], "reset", [j])
noise_thermal.add_quantum_error(errors_measure[j], "measure", [j])
noise_thermal.add_quantum_error(errors_u1[j], "u1", [j])
noise_thermal.add_quantum_error(errors_u2[j], "u2", [j])
noise_thermal.add_quantum_error(errors_u3[j], "u3", [j])
for k in range(4):
noise_thermal.add_quantum_error(errors_cx[j][k], "cx", [j, k])
print(noise_thermal)
device = provider.get_backend('ibmq_essex')
coupling_map = device.configuration().coupling_map
noise_model = noise.device.basic_device_noise_model(device.properties())
basis_gates = noise_model.basis_gates
print(noise_model)
backend = Aer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend=backend, seed_simulator=167, seed_transpiler=167,
noise_model=noise_thermal)
counts = []
values = []
def store_intermediate_result1(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
aqua_globals.random_seed = 167
optimizer = SPSA(max_trials=200)
var_form = RY(num_qubits)
vqe = VQE(qubit_op, var_form, optimizer, callback=store_intermediate_result1)
vqe_result1 = vqe.run(quantum_instance)
print('VQE on Aer qasm simulator (with noise): {}'.format(vqe_result1['energy']))
print('Delta from reference: {}'.format(vqe_result1['energy']-ref))
plt.figure(figsize=[10,5])
plt.plot(counts, values)
plt.xlabel('Eval count')
plt.ylabel('Energy')
plt.title('Convergence with noise');
plt.axhline(ref)
qiskit.__qiskit_version__
import qiskit
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
# Import useful packages
import os
import sys
import time
import pickle
import numpy as np
import pandas as pd
import seaborn as sns
from datetime import datetime
from tabulate import tabulate
import matplotlib.pyplot as plt
# Import QISKit
from qiskit import Aer, execute, BasicAer
from qiskit.aqua.components.initial_states import Zero
from qiskit.aqua.algorithms.adaptive import VQE
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.aqua.algorithms import ExactEigensolver
from qiskit.aqua.components.initial_states import Custom
from qiskit.aqua.components.variational_forms import RY, RYRZ
from qiskit.aqua.operators.op_converter import to_weighted_pauli_operator
from qiskit.aqua.components.optimizers import COBYLA, SPSA, L_BFGS_B, SLSQP
from qiskit.aqua.operators import (TPBGroupedWeightedPauliOperator,
WeightedPauliOperator,
MatrixOperator)
# For IBMQ
from qiskit import IBMQ
from qiskit.providers.ibmq import least_busy
from qiskit.tools.monitor import job_monitor, backend_monitor, backend_overview
class RunVQE:
"""Runs VQE via IBM's QISKit
Attributes:
file_path (str): File path to text file representation of Hamiltonian
file_name (str): File name of text file representation of Hamiltonian
init_state_name (QISKit object): Initial state
vf_name (QISKit object): Variational Form
depth (int): Quantum depth for circuit
shots (int): Number of shots
n_qubits (int): Number of qubits used
n_paulis (int): Number of pauli terms generated
ref (float): Exact energy of Hamiltonian
optimizers (list of strs): List of optimzers used in VQE run
The following dictionaries all have the optimzers used in VQE run as keys:
algos (dict of VQE objects): QISKit VQE objects
algo_results (dict): Dictionary of algorithm results from each VQE run
result_df (DataFrame): Contains all convergence values from each
optimizer used in the run. The index represents the convergence counts
"""
def __init__(self, kwargs, use_ibmq=False):
"""Constructor method
Args:
kwargs (dict): Key word argument dictionary containing parameters
for VQE run
save_figs (bool): If True will save figures generated in current
directory if the plt_state_vector(), plt_opt_convergence(), or
plt_energy_convergence() methods are called
use_ibmq (bool): If True will activate IBMQ account and run on an
IBMQ backend (default is least busy, see get_least_busy_device()
method below for more details)
"""
self.file_path = kwargs['file_path']
self.file_name = self.file_path.split("/")[-1].replace('.txt', '')
self.init_state_name = kwargs['init_state_name']
self.vf_name = kwargs['vf_name']
self.depth = kwargs['depth']
self.shots = kwargs['shots']
self.add_k_count = 0
if use_ibmq:
self.activate_ibmq()
self.device = self.get_least_busy_device()
self.backend = self.provider.get_backend(self.device)
else:
self.device = kwargs['simulator']
self.backend = BasicAer.get_backend(self.device)
self.run_VQE()
if 'nonzero' in self.file_name:
self._add_k(25)
print(self.result_table())
def construct_wpo_operator(self):
"""Returns Weighted Pauli Operator (WPO) constructed from Hamiltonian
text file.
Args:
None
Returns:
qubit_op (QISKit WPO object): Weighted Pauli Operator
"""
# Loading matrix representation of Hamiltonian txt file
H = np.loadtxt(self.file_path)
# Converting Hamiltonian to Matrix Operator
qubit_op = MatrixOperator(matrix=H)
# Converting to Pauli Operator
qubit_op = to_weighted_pauli_operator(qubit_op)
self.num_qubits = qubit_op.num_qubits
self.num_paulis = len(qubit_op.paulis)
return qubit_op
def exact_eigensolver(self, qubit_op):
"""Returns exact solution of eigen value problem
Args:
qubit_op (object): Weighted Pauli Operator
Returns:
exact_energy (float): Exact energy of Hamiltonian
"""
# Solving system exactly for reference value
ee = ExactEigensolver(qubit_op)
result = ee.run()
exact_energy = result['energy']
return exact_energy
def run_VQE(self):
"""Runs the Variational Quantum Eigensolver (VQE)"""
qubit_op = self.construct_wpo_operator()
self.ref = self.exact_eigensolver(qubit_op)
# Setting initial state, variational form, and backend
init_state = self.init_state_name(self.num_qubits)
var_form = self.vf_name(self.num_qubits,
depth=self.depth,
entanglement='linear',
initial_state=init_state)
# Don't use SPSA if using a noiseless simulator
if self.device == 'statevector_simulator':
optimizers = [COBYLA, L_BFGS_B, SLSQP]
else:
optimizers = [COBYLA, SPSA]
print(self.param_table())
# Initializing empty lists & dicts for storage
df = pd.DataFrame()
algos = {}
algo_results = {}
for optimizer in optimizers:
# For reproducibility
aqua_globals.random_seed = 250
print(f'\rOptimizer: {optimizer.__name__} ', end='')
counts = []
values = []
params = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
params.append(parameters)
# Running VQE
algo = VQE(qubit_op,
var_form,
optimizer(),
callback=store_intermediate_result)
quantum_instance = QuantumInstance(backend=self.backend, shots=self.shots)
algo_result = algo.run(quantum_instance)
df[optimizer.__name__] = pd.Series(data=values, index=counts)
algos[optimizer.__name__] = algo
algo_results[optimizer.__name__] = algo_result
print('\rOptimization complete')
self.algos = algos
self.result_df = df
self.algo_results = algo_results
self.optimizers = algo_results.keys()
self.results_to_save = {
'file_path': self.file_path,
'ref': self.ref,
'n_qubits': self.num_qubits,
'n_paulis': self.num_paulis,
'depth': self.depth,
'n_shots': self.shots,
'algo_results': self.algo_results,
'result_df': self.result_df
}
def _add_k(self, k):
"""Adds a constant k to energy to get around optimizer error when
optimizing near zero
Args:
k (int or float): constant to add
Returns:
None
"""
if self.add_k_count != 0:
return 'Method already called, to prevent adding k too many times no operation has been carried out.'
else:
self.ref += k
self.result_df = self.result_df.apply(lambda x: x + k)
for opt in self.optimizers:
self.algo_results[opt]['energy'] += 25
print('\n**WARNING** Outside operation has been performed on algorithm results')
self.add_k_count += 1
def save_data_to_pkl(self, out_name):
"""Saves results_to_save dict to pickle file
Args:
out_name (str): File name/path for data to be written to
Returns:
None
"""
with open(out_name, 'xb') as file:
pickle.dump(self.results_to_save, file)
print(f'Data wiitten to {out_name}')
def save_output(self, out_name):
"""Saves out put from param_table and result_table to text file
Args:
out_name (str): File name/path for data to be written to
Returns:
None
"""
with open(out_name, 'x') as file:
file.write(self.param_table())
file.write('\n')
file.write(self.result_table())
print(f'Output wiitten to {out_name}')
def load_data(self, data_file):
"""Loads data from pickle file
Args:
data_file (str): pickle file containing data to load
Returns:
None
"""
with open(data_file, 'rb') as file:
data = pickle.load(file)
return data
def find_total_time(self):
"""Finds total simulation time in seconds"""
eval_times = []
for opt in self.optimizers:
eval_times.append(self.algo_results[opt]['eval_time'])
return round(sum(eval_times))
def get_state(self):
"""Returns State of Hamiltonian based on state mapping"""
hamiltonian_info = self.file_name.split('_')
state_mapping = {
'E0':'Ground State',
'E1':'1st Excited',
'E2':'2nd Excited',
'E3':'3rd Excited',
'E4':'4th Excited'
}
for key in state_mapping:
if key in hamiltonian_info:
state = state_mapping[key]
else:
pass
return state
def get_basis(self):
"""Returns basis of Hamiltonian based on basis mapping"""
hamiltonian_info = self.file_name.split('_')
basis_mapping = {
'pos': 'Position',
'osc': 'Oscillator',
'finite': 'Finite Difference'
}
for key in basis_mapping:
if key in hamiltonian_info:
basis = basis_mapping[key]
else:
pass
return basis
def param_table(self):
"""Returns string outlining parameters for current VQE run"""
run_settings = [['State', self.get_state()],
['Basis', self.get_basis()],
['Backend', self.device],
['InitState', self.init_state_name.__name__],
['VarForm', self.vf_name.__name__],
['Depth', self.depth],
['# Shots', self.shots],
['# Qubits', self.num_qubits],
['# Paulis', self.num_paulis]
]
out_str = f"""{datetime.utcnow()}\nRunning: {self.file_path}\n{tabulate(run_settings, tablefmt="fancy_grid", stralign='right')}"""
return out_str
def result_table(self):
"""Returns string outlining results of VQE simulation for each optimizer"""
ref_str = f'Reference Value: {self.ref}'
t_str = f'\n{self.find_total_time()} s to complete'
vals = []
for opt in self.optimizers:
if 'nonzero' in self.file_name:
vals.append([opt,
self.algo_results[opt]['energy'],
abs((self.algo_results[opt]['energy'] - self.ref)/self.ref)*100])
sorted_vals = sorted(vals, key=lambda x: x[2])
headers = ['Optimizer', 'VQE Energy', '% Error']
out_str = f"""{t_str}\n{ref_str}\n{tabulate(sorted_vals,tablefmt="fancy_grid",headers=headers,numalign="right")}"""
return out_str
def plt_energy_convergence(self, save_figs=True):
"""Graphs optimizer energy convergence and convergence of most
effective optimizer.
"""
plt.figure(figsize=(10, 5))
for opt in self.optimizers:
self.result_df[opt].apply(lambda x: abs(x - self.ref)).plot(logy=True, label=opt)
plt.title('Optimizer Energy Convergence', size=24)
plt.xlabel('Evaluation Count', size=18)
plt.ylabel('Energy Difference', size=18)
plt.legend(fontsize='x-large')
sns.despine()
if save_figs:
if os.path.exists(fr'{self.file_name}_energy_convergence.png'):
plt.savefig(fr'{self.file_name}_energy_convergence(1).png');
else:
plt.savefig(fr'{self.file_name}_energy_convergence.png');
else:
plt.show()
def find_most_precise(self):
"""Returns name of most precise optimizer"""
p_err_mins = {}
for opt in self.optimizers:
p_err = self.result_df[opt].apply(lambda x: abs((x - self.ref)/self.ref)*100)
p_err_mins[opt] = p_err.min()
most_precise = sorted(p_err_mins.items(), key=lambda x: x[1])[0][0]
return most_precise
def plt_opt_convergence(self, save_figs=True):
"""Plots most effective optimizer"""
most_precise = self.find_most_precise()
fig, ax = plt.subplots(figsize=(10, 5))
self.result_df[most_precise].plot(label=f"{most_precise} = {self.algo_results[most_precise]['energy']:.6f}")
ax.hlines(y=self.ref,
xmin=0,
xmax=len(self.result_df[most_precise]),
colors='r',
label=f'Exact = {self.ref:.6f}')
plt.title('Convergence', size=24)
plt.xlabel('Optimization Steps', size=18)
plt.ylabel('Energy', size=18)
plt.legend(fontsize='x-large')
sns.despine()
if save_figs:
if os.path.exists(fr'{self.file_name}_opt_convergence.png'):
plt.savefig(fr'{self.file_name}_opt_convergence(1).png');
else:
plt.savefig(fr'{self.file_name}_opt_convergence.png');
else:
plt.show()
def plt_state_vector(self, save_figs=True):
"""Plots state vector for each optimizer"""
plt.figure(figsize=(10, 5))
for optimizer in self.optimizers:
circ = self.algos[optimizer].construct_circuit(self.algo_results[optimizer]['opt_params'])
e0wf = execute(circ[0],
Aer.get_backend(self.device),
shots=1).result().get_statevector(circ[0])
plt.plot(np.flip(e0wf.real), label=f'{optimizer}')
plt.title('State Vectors', size=24)
plt.legend(fontsize='x-large')
sns.despine()
if save_figs:
if os.path.exists(fr'{self.file_name}_st_vecs.png'):
plt.savefig(fr'{self.file_name}_st_vecs(1).png');
else:
plt.savefig(fr'{self.file_name}_st_vecs.png');
else:
plt.show()
def activate_ibmq(self):
"""Activates IBMQ account and gets IBMQ provider Note: you will get an
import error if you do not have a python scipt named my_secrets.py
with your IBMQ API token in the same directory as this file
"""
from my_secrets import pw
key = pw
try:
IBMQ.enable_account(key)
except:
print('IBMQAccountError: Account already activated')
finally:
self.provider = IBMQ.get_provider('ibm-q')
def get_least_busy_device(self):
"""Returns name (str) of least busy IBMQ backend that is not a
simulator and has more than one qubit.
"""
lb_backend = least_busy(self.provider.backends(filters=lambda x: not x.configuration().simulator and x.configuration().n_qubits > 1))
return lb_backend.name()
# Uncomment and run with valid Hamiltonian file
def main():
params = {
'file_path':fr'Morse_pos/Morse_pos_E0_16x16.txt',
'init_state_name':Zero,
'vf_name':RY,
'depth':1,
'shots':1,
'simulator': 'statevector_simulator'
}
v_q_e = RunVQE(params)
v_q_e.save_data_to_pkl(f'{v_q_e.file_name}_data.pkl')
v_q_e.save_output(f'{v_q_e.file_name}_output.txt')
v_q_e.plt_energy_convergence()
v_q_e.plt_opt_convergence()
v_q_e.plt_state_vector()
if __name__ == "__main__":
main()
|
https://github.com/Juan-Varela11/BNL_2020_Summer_Internship
|
Juan-Varela11
|
# Importing useful packages
import sys
import time
import numpy as np
import pandas as pd
import seaborn as sns
from tabulate import tabulate
import matplotlib.pyplot as plt
# Importing QISKit
from qiskit import Aer, execute, BasicAer
from qiskit.aqua.components.initial_states import Zero
from qiskit.aqua.algorithms.adaptive import VQE
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.aqua.operators import WeightedPauliOperator
from qiskit.aqua.algorithms import ExactEigensolver
from qiskit.aqua.components.initial_states import Custom
from qiskit.aqua.components.variational_forms import RY, RYRZ
from qiskit.aqua.operators.op_converter import to_weighted_pauli_operator
from qiskit.aqua.components.optimizers import COBYLA, SPSA, L_BFGS_B, SLSQP
from qiskit.aqua.operators import (TPBGroupedWeightedPauliOperator, WeightedPauliOperator, MatrixOperator)
import qiskit.tools.jupyter
%qiskit_version_table
def run_VQE(**kwargs):
"""Runs the Variational Quantum Eigensolver (VQE)
Args:
file_path (str): path to txt file containing Hamiltonian
simulator (str): [statevector_simulator, qasm_simulator] The type of simulator
you wish to use (statevector is noiseless, while qasm contains a noise model)
Returns:
return_dict (dict): Dictionary with the following Keys:
file_name (str): Name of file used for simulation
result_df (DataFrame): Pandas DataFrame containing the
convergence count (df index), convergence_vals, and percent_error
reference_val (float): GS Energy found using the Exact Eigen Solver
algos (QISKit VQE Object): Object returned by the VQE algorithm class
algo_results (dict): Results from VQE run (one algorithim result dict
for each optimizer)
"""
file_path = kwargs['file_path']
init_state_name = kwargs['init_state_name']
vf_name = kwargs['vf_name']
depth = kwargs['depth']
shots = kwargs['shots']
simulator = kwargs['simulator']
# Loading matrix representation of Hamiltonian txt file
H = np.loadtxt(file_path)
# Converting Hamiltonian to Matrix Operator
qubit_op = MatrixOperator(matrix=H)
# Converting to Pauli Operator
qubit_op = to_weighted_pauli_operator(qubit_op)
start = time.time()
num_qubits = qubit_op.num_qubits
num_paulis = len(qubit_op.paulis)
num_qubits = qubit_op.num_qubits
print(f"""{num_paulis} Pauli factors \n{round(time.time()-start)} s to process""")
# Solving system exactly for reference value
ee = ExactEigensolver(qubit_op)
result = ee.run()
ref = result['energy']
# Setting initial state, variational form, and backend
init_state = init_state_name(num_qubits)
var_form = vf_name(num_qubits,
depth=depth,
entanglement='linear',
initial_state=init_state)
backend = BasicAer.get_backend(simulator)
# Don't use SPSA if using a noiseless simulator
if simulator == 'statevector_simulator':
optimizers = [COBYLA, L_BFGS_B, SLSQP]
else:
optimizers = [SPSA]
# Initializing empty lists & dicts for storage
dfs = []
algos = {}
algo_results = {}
for optimizer in optimizers:
# For reproducibility
aqua_globals.random_seed = 250
print(f'\rOptimizer: {optimizer.__name__} ', end='')
counts = []
values = []
params = []
def store_intermediate_result(eval_count, parameters, mean, std):
counts.append(eval_count)
values.append(mean)
params.append(parameters)
# Running VQE
algo = VQE(qubit_op, var_form, optimizer(), callback=store_intermediate_result)
quantum_instance = QuantumInstance(backend=backend, shots=shots)
algo_result = algo.run(quantum_instance)
# Appending each optimizer data frame to one list
dfs.append(pd.DataFrame(values, columns=['convergence_vals'], index=counts))
algos[optimizer.__name__] = algo
algo_results[optimizer.__name__] = algo_result
print('\rOptimization complete')
# Formatting return data frame
results = pd.concat([df for df in dfs], keys=[optimizer.__name__ for optimizer in optimizers])
results['energy_diff'] = results['convergence_vals'].apply(lambda x: abs(x - ref))
results['percent_error'] = results['convergence_vals'].apply(lambda x: (abs(x - ref)/ref)*100)
return_dict = {}
return_dict['file_name'] = file_path
return_dict['result_df'] = results
return_dict['reference_val'] = ref
return_dict['algos'] = algos
return_dict['algo_results'] = algo_results
return return_dict
def print_table(**result_dict):
"""Prints results of VQE simulation for each optimizer
Args:
result_dict (dict): Dictionary returned from run_VQE function
Returns: None
"""
algo_results = result_dict['algo_results']
ref_val = result_dict['reference_val']
file_name = result_dict['file_name']
fn = file_name.split('/')[-1].replace(".txt", "")
print(f'\nHamiltonian: {fn}')
print(f'Reference Value: {ref_val}')
optimizers = algo_results.keys()
vals = []
for opt in optimizers:
vals.append([opt,
algo_results[opt]['energy'],
abs((algo_results[opt]['energy'] - ref_val)/ref_val)*100])
sorted_vals = sorted(vals, key=lambda x: x[2])
print(tabulate(sorted_vals,
tablefmt="fancy_grid",
headers=['Optimizer', 'VQE Energy', '% Error'],
numalign="right"))
def visualize_results(**result_dict):
"""Graphs optimizer energy convergence and convergence of most effective
optimizer.
Args:
result_dict (dict): Dictionary returned from run_VQE function
Returns: None
"""
result_df = result_dict['result_df']
algo_results = result_dict['algo_results']
ref_val = result_dict['reference_val']
# Optimizer Convergence
plt.figure(figsize=(10, 5))
for opt in result_df.index.unique(0):
result_df['energy_diff'][opt].plot(logy=True, label=opt)
plt.title('Optimizer Energy Convergence')
plt.xlabel('Eval count')
plt.ylabel('Energy difference from solution reference value')
plt.legend()
sns.despine()
plt.show();
# Most effective optimizer
most_eff = sorted([(opt,
result_df['percent_error'][opt].iloc[-1]) for opt in result_df.index.unique(0)],
key=lambda x: x[1])
fig, ax = plt.subplots(figsize=(10, 5))
result_df['convergence_vals'][most_eff[0][0]].plot(label=f"{most_eff[0][0]} = {algo_results[most_eff[0][0]]['energy']:.6f}")
ax.hlines(y=ref_val,
xmin=0,
xmax=len(result_df['convergence_vals'][most_eff[0][0]]),
colors='r',
label=f'Exact = {ref_val:.6f}')
plt.title('Convergence', size=24)
plt.xlabel('Optimization Steps', size=18)
plt.ylabel('Energy', size=18)
plt.legend()
sns.despine()
plt.show();
def plt_state_vector(**result_dict):
"""Plots state vector for each optimizer
Args:
result_dict (dict): Dictionary returned from run_VQE function
Returns: None
"""
algos = result_dict['algos']
algo_results = result_dict['algo_results']
optimizers = result_dict['algos'].keys()
for optimizer in optimizers:
circ = algos[optimizer].construct_circuit(algo_results[optimizer]['opt_params'])
e0wf = execute(circ[0],
Aer.get_backend('statevector_simulator'),
shots=1).result().get_statevector(circ[0])
plt.figure(figsize=(10,5))
plt.plot(np.flip(e0wf.real))
plt.title(f'({optimizer}) State Vector', size=24)
sns.despine()
plt.show();
h_osc_params = {
'file_path': r'JA_harmonic_oscillator_q=4.txt',
'init_state_name': Zero,
'vf_name': RY,
'depth': 3,
'shots': 1000,
'simulator': 'statevector_simulator'
}
harmonic_osc = run_VQE(**h_osc_params)
print_table(**harmonic_osc)
for key in harmonic_osc.keys():
print(f'{key}: {harmonic_osc[key]}')
print('\n')
visualize_results(**harmonic_osc)
plt_state_vector(**harmonic_osc)
anh_gs = (3/8) * (6 / (1/2)**2) ** (1/3)
print(f'Upper bound for the ground state energy of the anharmonic oscillator: {anh_gs:.2f} eV')
print(f'Percent error: {abs((anh_gs-1.06)/1.06)*100:.2f}%')
anh_osc_params = {
'file_path': r'JA_adapted_anharmonic_oscillator_q=4.txt',
'init_state_name': Zero,
'vf_name': RY,
'depth': 5,
'shots': 5000,
'simulator': 'statevector_simulator'
}
anharmonic_osc = run_VQE(**anh_osc_params)
print_table(**anharmonic_osc)
visualize_results(**anharmonic_osc)
plt_state_vector(**anharmonic_osc)
%qiskit_copyright
|
https://github.com/Quantum-Simulation-Group-2/Session-2
|
Quantum-Simulation-Group-2
|
import numpy as np
from qiskit import *
%matplotlib inline
circ = QuantumCircuit(2)
circ.h(0)
circ.x(1)
circ.h(1)
circ.cx(0,1) #oracle here for f(x)=x
circ.h(0)
circ.draw('mpl')
meas = QuantumCircuit(2, 2)
meas.barrier(range(2))
meas.measure(range(2), range(2)) # map the quantum measurement to the classical bits
qc = circ + meas
qc.draw()
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator. We've set the number of repeats of the circuit to be 1024, which is the default.
job_sim = execute(qc, backend_sim, shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(qc)
print("Counts for QASM:", counts)
from qiskit.visualization import plot_histogram
plot_histogram(counts)
from qiskit.providers.ibmq import least_busy
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= (3) and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(qc, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
from qiskit.visualization import plot_histogram
results = job.result()
answer = results.get_counts()
print("Counts for IBM machine:", answer)
plot_histogram((counts, answer), legend=['QASM simulation','IBM machine']) # ibm machine
n = 2
grover = QuantumCircuit(n)
grover.h([0,1])
grover.cz(0,1) # Oracle
# Diffusion operator (U_s)
grover.h([0,1])
grover.z([0,1])
grover.cz(0,1)
grover.h([0,1])
grover.draw()
meas = QuantumCircuit(2, 2)
meas.barrier(range(2))
meas.measure(range(2), range(2)) # map the quantum measurement to the classical bits
qc3 = grover + meas
qc3.draw()
#Simulator
from qiskit.visualization import plot_histogram
backend = Aer.get_backend('statevector_simulator')
shots = 1024
results = execute(qc3, backend=backend, shots=shots).result()
counts = results.get_counts()
plot_histogram(counts)
from qiskit.providers.ibmq import least_busy
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= (3) and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(qc3, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
from qiskit.visualization import plot_histogram
results = job.result()
answer = results.get_counts()
print("Counts for IBM machine:", answer)
plot_histogram((counts, answer), legend=['QASM simulation','IBM machine']) # ibm machine
circ2 = QuantumCircuit(3)
for i in range(2):
circ2.h(i)
circ2.x(i)
circ2.h(2)
circ2.x(2)
circ2.h(2)
# Toffoli gate = oracle
circ2.ccx(0,1,2)
for i in range(2):
circ2.h(i)
circ2.x(i)
circ2.h(2)
circ2.x(2)
circ2.h(2)
circ2.draw('mpl')
meas2 = QuantumCircuit(3, 3)
meas2.barrier(range(3))
meas2.measure(range(3), range(3)) # map the quantum measurement to the classical bits
qc2 = circ2 + meas2
qc2.draw()
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator. We've set the number of repeats of the circuit to be 1024, which is the default.
job_sim = execute(qc2, backend_sim, shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(qc2)
print("Counts for QASM:", counts)
from qiskit.visualization import plot_histogram
plot_histogram(counts)
from qiskit.providers.ibmq import least_busy
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= (3) and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(qc2, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
from qiskit.visualization import plot_histogram
results = job.result()
answer = results.get_counts()
print("Counts for IBM machine:", answer)
plot_histogram((counts, answer), legend=['QASM simulation','IBM machine']) # ibm machine
# The groover algorithm needs 3 work qubits to execute the algorithm, therefore 8 qubits needed here
circ2 = QuantumCircuit(8)
for i in range(4):
circ2.h(i)
circ2.x(i)
circ2.h(7)
circ2.x(7)
circ2.h(7)
# Toffoli gate = oracle
circ2.ccx(0,1,4)
circ2.ccx(4,2,5)
circ2.ccx(5,3,6)
circ2.cx(6,7)
circ2.ccx(5,3,6)
circ2.ccx(4,2,5)
circ2.ccx(0,1,4)
for i in range(4):
circ2.h(i)
circ2.x(i)
circ2.h(7)
circ2.x(7)
circ2.h(7)
circ2.draw('mpl')
meas2 = QuantumCircuit(8, 8)
meas2.barrier([0,1,2,3,7])
meas2.measure([0,1,2,3,7], [0,1,2,3,7]) # map the quantum measurement to the classical bits
qc2 = circ2 + meas2
qc2.draw()
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator. We've set the number of repeats of the circuit to be 1024, which is the default.
job_sim = execute(qc2, backend_sim, shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(qc2)
print("Counts for QASM:", counts)
from qiskit.visualization import plot_histogram
plot_histogram(counts)
from qiskit.providers.ibmq import least_busy
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= (3) and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
from qiskit.tools.monitor import job_monitor
shots = 1024
job = execute(qc2, backend=backend, shots=shots, optimization_level=3)
job_monitor(job, interval = 2)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import numpy as np
import cirq
def main():
circuit = make_bell_test_circuit()
print("Circuit:")
print(circuit)
#Run Simulation
sim = cirq.Simulator()
repetitions = 1000
print("Simulating {} repetitions".format(repetitions))
result = sim.run(program=circuit, repetitions=repetitions)
## Collect Results
a = np.array(result.measurements['a'] [:, 0])
b = np.array(result.measurements['b'] [:, 0])
x = np.array(result.measurements['x'] [:, 0])
y = np.array(result.measurements['y'] [:, 0])
outcomes = a ^ b == x & y
win_percent = len([e for e in outcomes if e]) * 100/repetitions
print()
print('Results')
print('a:', bitstring(a))
print('b:', bitstring(b))
print('x:', bitstring(x))
print('y:', bitstring(y))
print('(a XOR b) == (x AND y): \n', bitstring(outcomes))
print('Win rate: {}%' .format(win_percent))
def make_bell_test_circuit():
alice = cirq.GridQubit(0, 0)
bob = cirq.GridQubit(1, 0)
alice_referee = cirq.GridQubit(0, 1)
bob_referee = cirq.GridQubit(1,1)
circuit = cirq.Circuit()
## Prepare shared entanglement
circuit.append([cirq.H(alice),
cirq.CNOT(alice, bob),
cirq.X(alice)**-0.25,])
## Referee flip coins
circuit.append([cirq.H(alice_referee),
cirq.H(bob_referee),
])
## Players do oa sqrt based on their referee coin
circuit.append([cirq.CNOT(alice_referee, alice)**0.5,
cirq.CNOT(bob_referee, bob)**0.5,
])
circuit.append([
cirq.measure(alice, key = 'a'),
cirq.measure(bob, key = 'b'),
cirq.measure(alice_referee, key = 'x'),
cirq.measure(bob_referee, key = 'y'),
])
return circuit
def bitstring(bits):
return ''.join('1' if e else '_' for e in bits)
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
import random
def make_quantum_teleportation_circuit(ranX, ranY):
circuit = cirq.Circuit()
msg, alice, bob = cirq.LineQubit.range(3)
## Bell State
circuit.append([cirq.H(alice), cirq.CNOT(alice, bob)])
## Adding random message in message qubit
circuit.append([cirq.X(msg)**ranX, cirq.Y(msg)**ranY])
## Entangling msg and Alice qubits
circuit.append([cirq.CNOT(msg, alice), cirq.H(msg)])
## Measurements
circuit.append([cirq.measure(alice, msg)])
## We use two classical bit from the bell measurement to recover the state of qubit
circuit.append([cirq.CNOT(alice, bob), cirq.CZ(msg, bob)])
return msg, circuit
def main():
## Creating random variable
ranX = random.random()
ranY = random.random()
msg, circuit = make_quantum_teleportation_circuit(ranX, ranY)
## Simulating the circuit
sim = cirq.Simulator()
message = sim.simulate(cirq.Circuit.from_ops([cirq.X(msg)**ranX, cirq.Y(msg)**ranY]))
print("Block Spehere of Alice Qubit")
b0x, b0y, b0z = cirq.bloch_vector_from_state_vector(message.final_state, 0)
print("X: ", round(b0x, 4),
"Y: ", round(b0y, 4),
"Z: ", round(b0z, 4))
print("\n Circuit:")
print(circuit)
final_results = sim.simulate(circuit)
print("\n Block Spehere of Bob's Qubits:")
b2x, b2y, b2z = cirq.bloch_vector_from_state_vector(final_results.final_state, 2)
print("X: ", round(b2x, 4),
"Y: ", round(b2y, 4),
"Z: ", round(b2z, 4))
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
## Function for visualizing output
def bitstring(bits):
return ''.join('1' if e else '0' for e in bits)
## Create two quantum and classical registers
qreg = [cirq.LineQubit(x) for x in range(2)]
circuit = cirq.Circuit()
message = {"00" : [],
"10" : [cirq.X(qreg[0])],
"01" : [cirq.Z(qreg[0])],
"11" : [cirq.X(qreg[0]), cirq.Z(qreg[0])]}
## Creating a bell pair
circuit.append(cirq.H(qreg[0]))
circuit.append(cirq.CNOT(qreg[0], qreg[1]))
m = "10"
print("Alice sent a message")
## Encodding the message in qubits
circuit.append(message[m])
## Bob is trying to decode
circuit.append(cirq.CNOT(qreg[0], qreg[1]))
circuit.append(cirq.H(qreg[0]))
circuit.append([cirq.measure(qreg[0]), cirq.measure(qreg[1])])
print("\n Circuit is :")
print(circuit)
sim = cirq.Simulator()
res = sim.run(circuit, repetitions = 1)
print("BOB recieved message: ",bitstring(res.measurements.values()))
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
import random
def main(qubit_count = 8):
circuit_sample_count = 3
# Choose qubits to use.
input_qubits = [cirq.GridQubit(i, 0) for i in range(qubit_count)]
output_qubit = cirq.GridQubit(qubit_count, 0)
# Pick coefficients for the oracle and create a circuit to query it.
secret_bias_bit = random.randint(0, 1)
secret_factor_bits = [random.randint(0, 1) for _ in range(qubit_count)]
oracle = make_oracle(input_qubits,
output_qubit,
secret_factor_bits,
secret_bias_bit)
print('Secret function:\nf(a) = a·<{}> + {} (mod 2)'.format(
', '.join(str(e) for e in secret_factor_bits),
secret_bias_bit))
# Embed the oracle into a special quantum circuit querying it exactly once.
circuit = make_bernstein_vazirani_circuit(
input_qubits, output_qubit, oracle)
print('Circuit:')
print(circuit)
# Sample from the circuit a couple times.
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=circuit_sample_count)
frequencies = result.histogram(key='result', fold_func=bitstring)
print('Sampled results:\n{}'.format(frequencies))
# Check if we actually found the secret value.
most_common_bitstring = frequencies.most_common(1)[0][0]
print('Most common matches secret factors:\n{}'.format(
most_common_bitstring == bitstring(secret_factor_bits)))
def make_oracle(input_qubits,
output_qubit,
secret_factor_bits,
secret_bias_bit):
"""Gates implementing the function f(a) = a·factors + bias (mod 2)."""
if secret_bias_bit:
yield cirq.X(output_qubit)
for qubit, bit in zip(input_qubits, secret_factor_bits):
if bit:
yield cirq.CNOT(qubit, output_qubit)
def make_bernstein_vazirani_circuit(input_qubits, output_qubit, oracle):
"""Solves for factors in f(a) = a·factors + bias (mod 2) with one query."""
c = cirq.Circuit()
# Initialize qubits.
c.append([
cirq.X(output_qubit),
cirq.H(output_qubit),
cirq.H.on_each(*input_qubits),
])
# Query oracle.
c.append(oracle)
# Measure in X basis.
c.append([
cirq.H.on_each(*input_qubits),
cirq.measure(*input_qubits, key='result')
])
return c
def bitstring(bits):
return ''.join(str(int(b)) for b in bits)
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
## Data qubit and target qubit
q0, q1 = cirq.LineQubit.range(2)
## Dictionary of oracles
oracles = {'0' : [], '1' : [cirq.X(q1)], 'x' : [cirq.CNOT(q0, q1)], 'notx' : [cirq.CNOT(q0, q1), cirq.X(q1)]}
def deutsch_algorithm(oracle):
## Yield a circuit for Deustch algorithm given operations implementing
yield cirq.X(q1)
yield cirq.H(q0), cirq.H(q1)
yield oracle
yield cirq.H(q0)
yield cirq.measure(q0)
for key, oracle in oracles.items():
print('Circuit for {} :'. format(key))
print(cirq.Circuit.from_ops(deutsch_algorithm(oracle)), end = "\n\n")
simulator = cirq.Simulator()
for key, oracle in oracles.items():
result = simulator.run(cirq.Circuit.from_ops(deutsch_algorithm(oracle)), repetitions=20)
print('Oracle : {:<4} results: {}'. format(key, result))
import cirq
q0, q1, q2 = cirq.LineQubit.range(3)
## Oracles for constant functions
constant = ([], [cirq.X(q2)])
## Oracles for balanced functions
balanced = ([cirq.CNOT(q0, q2)],
[cirq.CNOT(q1, q2)],
[cirq.CNOT(q0, q2), cirq.CNOT(q1, q2)],
[cirq.CNOT(q0, q2), cirq.X(q2)],
[cirq.CNOT(q1, q2), cirq.X(q2)],
[cirq.CNOT(q0, q2), cirq.CNOT(q1, q2), cirq.X(q2)]
)
def your_circuit(oracle):
## Phase kickback trick
yield cirq.X(q2), cirq.H(q2)
## Equal Superposition over input bits
yield cirq.H(q0), cirq.H(q1)
## Query the function
yield oracle
## interface to get result, put last qubit into |1>
yield cirq.H(q0), cirq.H(q1), cirq.H(q2)
## a final OR gate to put result in final qubit
yield cirq.X(q0), cirq.X(q1), cirq.CCX(q0, q1, q2)
yield cirq.measure(q2)
simulator = cirq.Simulator()
print("your result on constant functions:")
for oracle in constant:
result = simulator.run(cirq.Circuit.from_ops(your_circuit(oracle)), repetitions=10)
print(result)
print("your result on balanced functions:")
for oracle in balanced:
result = simulator.run(cirq.Circuit.from_ops(your_circuit(oracle)), repetitions=10)
print(result)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
pip install cirq
import cirq
circuit = cirq.Circuit()
(q0,q1) = cirq.LineQubit.range(2)
circuit.append([cirq.H(q0), cirq.CNOT(q0, q1)])
circuit.append([cirq.measure(q0), cirq.measure(q1)])
print(circuit)
sim = cirq.Simulator()
results = sim.run(circuit, repetitions=10)
print(results)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
%config InlineBackend.figure_format = 'svg' # Makes the images look nice
qc = QuantumCircuit(1)
initial_state = [0,1]
qc.initialize(initial_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc,backend).result()
state_vector = result.get_statevector()
print(state_vector)
qc.measure_all()
qc.draw()
result = execute(qc, backend).result()
counts = result.get_counts()
plot_histogram(counts)
initial_state = [1/sqrt(2), complex(0,1/sqrt(2))]
qc = QuantumCircuit(1)
qc.initialize(initial_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
statevector = result.get_statevector()
print(statevector)
counts = result.get_counts()
plot_histogram(counts)
initialize_state = [1/sqrt(3), sqrt(2/3)]
qc = QuantumCircuit(1)
qc.initialize(initialize_state, 0)
qc.draw()
result = execute(qc, backend).result()
counts = result.get_counts()
plot_histogram(counts)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import qiskit
qiskit.__qiskit_version__
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()
counts = execute(qc_ha, Aer.get_backend('qasm_simulator')).result().get_counts()
plot_histogram(counts)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import *
from math import pi
import numpy as np
from qiskit.visualization import plot_bloch_multivector, plot_histogram
qc = QuantumCircuit(3)
for qubit in range(3):
qc.h(qubit)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc, backend).result().get_statevector()
print(final_state)
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.draw()
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
qiskit.__qiskit_version__
qc = QuantumCircuit(3)
qc.x(0)
qc.z(1)
qc.h(2)
qc.draw()
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,backend).result().get_statevector()
print(final_state)
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
# Apply a CNOT:
qc.cx(0,1)
qc.draw()
final_state = Aer.get_backend('statevector_simulator')
final_state = execute(qc, backend).result().get_statevector()
print(final_state)
results = execute(qc,backend).result().get_counts()
plot_histogram(results)
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.cx(0,1)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result().get_statevector()
print(result)
result = execute(qc, backend).result().get_counts()
plot_histogram(result)
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
%config InlineBackend.figure_format = 'svg'
qc = QuantumCircuit(1)
initialize_state = [1,0]
qc.initialize(initialize_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
out_state = result.get_statevector()
print(out_state)
qc.measure_all()
qc.draw()
counts = execute(qc, backend).result().get_counts()
plot_histogram(counts)
initial_state = [1/sqrt(3), complex(0, sqrt(2)/sqrt(3))]
qc = QuantumCircuit(1)
qc.initialize(initial_state, 0)
state = execute(qc, backend).result().get_statevector()
print(state)
count = execute(qc, backend).result().get_counts()
plot_histogram(count)
qc = QuantumCircuit(1) # Redefine qc
initial_state = [0.+1.j/sqrt(2),1/sqrt(2)+0.j]
qc.initialize(initial_state, [0])
qc.draw()
qc.measure_all()
qc.draw()
state = execute(qc,backend).result().get_statevector()
print("State of Measured Qubit = " + str(state))
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import numpy as np
import cirq
def main():
circuit = make_bell_test_circuit()
print("Circuit:")
print(circuit)
#Run Simulation
sim = cirq.Simulator()
repetitions = 1000
print("Simulating {} repetitions".format(repetitions))
result = sim.run(program=circuit, repetitions=repetitions)
## Collect Results
a = np.array(result.measurements['a'] [:, 0])
b = np.array(result.measurements['b'] [:, 0])
x = np.array(result.measurements['x'] [:, 0])
y = np.array(result.measurements['y'] [:, 0])
outcomes = a ^ b == x & y
win_percent = len([e for e in outcomes if e]) * 100/repetitions
print()
print('Results')
print('a:', bitstring(a))
print('b:', bitstring(b))
print('x:', bitstring(x))
print('y:', bitstring(y))
print('(a XOR b) == (x AND y): \n', bitstring(outcomes))
print('Win rate: {}%' .format(win_percent))
def make_bell_test_circuit():
alice = cirq.GridQubit(0, 0)
bob = cirq.GridQubit(1, 0)
alice_referee = cirq.GridQubit(0, 1)
bob_referee = cirq.GridQubit(1,1)
circuit = cirq.Circuit()
## Prepare shared entanglement
circuit.append([cirq.H(alice),
cirq.CNOT(alice, bob),
cirq.X(alice)**-0.25,])
## Referee flip coins
circuit.append([cirq.H(alice_referee),
cirq.H(bob_referee),
])
## Players do oa sqrt based on their referee coin
circuit.append([cirq.CNOT(alice_referee, alice)**0.5,
cirq.CNOT(bob_referee, bob)**0.5,
])
circuit.append([
cirq.measure(alice, key = 'a'),
cirq.measure(bob, key = 'b'),
cirq.measure(alice_referee, key = 'x'),
cirq.measure(bob_referee, key = 'y'),
])
return circuit
def bitstring(bits):
return ''.join('1' if e else '_' for e in bits)
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
import random
def make_quantum_teleportation_circuit(ranX, ranY):
circuit = cirq.Circuit()
msg, alice, bob = cirq.LineQubit.range(3)
## Bell State
circuit.append([cirq.H(alice), cirq.CNOT(alice, bob)])
## Adding random message in message qubit
circuit.append([cirq.X(msg)**ranX, cirq.Y(msg)**ranY])
## Entangling msg and Alice qubits
circuit.append([cirq.CNOT(msg, alice), cirq.H(msg)])
## Measurements
circuit.append([cirq.measure(alice, msg)])
## We use two classical bit from the bell measurement to recover the state of qubit
circuit.append([cirq.CNOT(alice, bob), cirq.CZ(msg, bob)])
return msg, circuit
def main():
## Creating random variable
ranX = random.random()
ranY = random.random()
msg, circuit = make_quantum_teleportation_circuit(ranX, ranY)
## Simulating the circuit
sim = cirq.Simulator()
message = sim.simulate(cirq.Circuit.from_ops([cirq.X(msg)**ranX, cirq.Y(msg)**ranY]))
print("Block Spehere of Alice Qubit")
b0x, b0y, b0z = cirq.bloch_vector_from_state_vector(message.final_state, 0)
print("X: ", round(b0x, 4),
"Y: ", round(b0y, 4),
"Z: ", round(b0z, 4))
print("\n Circuit:")
print(circuit)
final_results = sim.simulate(circuit)
print("\n Block Spehere of Bob's Qubits:")
b2x, b2y, b2z = cirq.bloch_vector_from_state_vector(final_results.final_state, 2)
print("X: ", round(b2x, 4),
"Y: ", round(b2y, 4),
"Z: ", round(b2z, 4))
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
## Function for visualizing output
def bitstring(bits):
return ''.join('1' if e else '0' for e in bits)
## Create two quantum and classical registers
qreg = [cirq.LineQubit(x) for x in range(2)]
circuit = cirq.Circuit()
message = {"00" : [],
"10" : [cirq.X(qreg[0])],
"01" : [cirq.Z(qreg[0])],
"11" : [cirq.X(qreg[0]), cirq.Z(qreg[0])]}
## Creating a bell pair
circuit.append(cirq.H(qreg[0]))
circuit.append(cirq.CNOT(qreg[0], qreg[1]))
m = "10"
print("Alice sent a message")
## Encodding the message in qubits
circuit.append(message[m])
## Bob is trying to decode
circuit.append(cirq.CNOT(qreg[0], qreg[1]))
circuit.append(cirq.H(qreg[0]))
circuit.append([cirq.measure(qreg[0]), cirq.measure(qreg[1])])
print("\n Circuit is :")
print(circuit)
sim = cirq.Simulator()
res = sim.run(circuit, repetitions = 1)
print("BOB recieved message: ",bitstring(res.measurements.values()))
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
import random
def main(qubit_count = 8):
circuit_sample_count = 3
# Choose qubits to use.
input_qubits = [cirq.GridQubit(i, 0) for i in range(qubit_count)]
output_qubit = cirq.GridQubit(qubit_count, 0)
# Pick coefficients for the oracle and create a circuit to query it.
secret_bias_bit = random.randint(0, 1)
secret_factor_bits = [random.randint(0, 1) for _ in range(qubit_count)]
oracle = make_oracle(input_qubits,
output_qubit,
secret_factor_bits,
secret_bias_bit)
print('Secret function:\nf(a) = a·<{}> + {} (mod 2)'.format(
', '.join(str(e) for e in secret_factor_bits),
secret_bias_bit))
# Embed the oracle into a special quantum circuit querying it exactly once.
circuit = make_bernstein_vazirani_circuit(
input_qubits, output_qubit, oracle)
print('Circuit:')
print(circuit)
# Sample from the circuit a couple times.
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=circuit_sample_count)
frequencies = result.histogram(key='result', fold_func=bitstring)
print('Sampled results:\n{}'.format(frequencies))
# Check if we actually found the secret value.
most_common_bitstring = frequencies.most_common(1)[0][0]
print('Most common matches secret factors:\n{}'.format(
most_common_bitstring == bitstring(secret_factor_bits)))
def make_oracle(input_qubits,
output_qubit,
secret_factor_bits,
secret_bias_bit):
"""Gates implementing the function f(a) = a·factors + bias (mod 2)."""
if secret_bias_bit:
yield cirq.X(output_qubit)
for qubit, bit in zip(input_qubits, secret_factor_bits):
if bit:
yield cirq.CNOT(qubit, output_qubit)
def make_bernstein_vazirani_circuit(input_qubits, output_qubit, oracle):
"""Solves for factors in f(a) = a·factors + bias (mod 2) with one query."""
c = cirq.Circuit()
# Initialize qubits.
c.append([
cirq.X(output_qubit),
cirq.H(output_qubit),
cirq.H.on_each(*input_qubits),
])
# Query oracle.
c.append(oracle)
# Measure in X basis.
c.append([
cirq.H.on_each(*input_qubits),
cirq.measure(*input_qubits, key='result')
])
return c
def bitstring(bits):
return ''.join(str(int(b)) for b in bits)
if __name__ == '__main__':
main()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import cirq
## Data qubit and target qubit
q0, q1 = cirq.LineQubit.range(2)
## Dictionary of oracles
oracles = {'0' : [], '1' : [cirq.X(q1)], 'x' : [cirq.CNOT(q0, q1)], 'notx' : [cirq.CNOT(q0, q1), cirq.X(q1)]}
def deutsch_algorithm(oracle):
## Yield a circuit for Deustch algorithm given operations implementing
yield cirq.X(q1)
yield cirq.H(q0), cirq.H(q1)
yield oracle
yield cirq.H(q0)
yield cirq.measure(q0)
for key, oracle in oracles.items():
print('Circuit for {} :'. format(key))
print(cirq.Circuit.from_ops(deutsch_algorithm(oracle)), end = "\n\n")
simulator = cirq.Simulator()
for key, oracle in oracles.items():
result = simulator.run(cirq.Circuit.from_ops(deutsch_algorithm(oracle)), repetitions=20)
print('Oracle : {:<4} results: {}'. format(key, result))
import cirq
q0, q1, q2 = cirq.LineQubit.range(3)
## Oracles for constant functions
constant = ([], [cirq.X(q2)])
## Oracles for balanced functions
balanced = ([cirq.CNOT(q0, q2)],
[cirq.CNOT(q1, q2)],
[cirq.CNOT(q0, q2), cirq.CNOT(q1, q2)],
[cirq.CNOT(q0, q2), cirq.X(q2)],
[cirq.CNOT(q1, q2), cirq.X(q2)],
[cirq.CNOT(q0, q2), cirq.CNOT(q1, q2), cirq.X(q2)]
)
def your_circuit(oracle):
## Phase kickback trick
yield cirq.X(q2), cirq.H(q2)
## Equal Superposition over input bits
yield cirq.H(q0), cirq.H(q1)
## Query the function
yield oracle
## interface to get result, put last qubit into |1>
yield cirq.H(q0), cirq.H(q1), cirq.H(q2)
## a final OR gate to put result in final qubit
yield cirq.X(q0), cirq.X(q1), cirq.CCX(q0, q1, q2)
yield cirq.measure(q2)
simulator = cirq.Simulator()
print("your result on constant functions:")
for oracle in constant:
result = simulator.run(cirq.Circuit.from_ops(your_circuit(oracle)), repetitions=10)
print(result)
print("your result on balanced functions:")
for oracle in balanced:
result = simulator.run(cirq.Circuit.from_ops(your_circuit(oracle)), repetitions=10)
print(result)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
pip install cirq
import cirq
circuit = cirq.Circuit()
(q0,q1) = cirq.LineQubit.range(2)
circuit.append([cirq.H(q0), cirq.CNOT(q0, q1)])
circuit.append([cirq.measure(q0), cirq.measure(q1)])
print(circuit)
sim = cirq.Simulator()
results = sim.run(circuit, repetitions=10)
print(results)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
# Cell 1
import numpy as np
from qiskit import Aer, QuantumCircuit, execute
from qiskit.visualization import plot_histogram
from IPython.display import display, Math, Latex
from may4_challenge import plot_state_qsphere
from may4_challenge.ex1 import minicomposer
from may4_challenge.ex1 import check1, check2, check3, check4, check5, check6, check7, check8
from may4_challenge.ex1 import return_state, vec_in_braket, statevec
# Cell 2
# press shift + return to run this code cell
# then, click on the gate that you want to apply to your qubit
# next, you have to choos
# the qubit that you want to apply it to (choose '0' here)
# click on clear to restart
minicomposer(1, dirac=True, qsphere=True)
# Cell 3
def create_circuit():
qc = QuantumCircuit(1)
qc.x(0)
return qc
# check solution
qc = create_circuit()
state = statevec(qc)
check1(state)
plot_state_qsphere(state.data, show_state_labels=True, show_state_angles=True)
# Cell 4
def create_circuit2():
qc = QuantumCircuit(1)
qc.h(0)
return qc
qc = create_circuit2()
state = statevec(qc)
check2(state)
plot_state_qsphere(state.data, show_state_labels=True, show_state_angles=True)
# Cell 5
def create_circuit3():
qc = QuantumCircuit(1)
qc.x(0)
qc.h(0)
return qc
qc = create_circuit3()
state = statevec(qc)
check3(state)
plot_state_qsphere(state.data, show_state_labels=True, show_state_angles=True)
# Cell 6
def create_circuit4():
qc = QuantumCircuit(1)
qc.x(0)
qc.h(0)
qc.s(0)
return qc
qc = create_circuit4()
state = statevec(qc)
check4(state)
plot_state_qsphere(state.data, show_state_labels=True, show_state_angles=True)
# Cell 7
# press shift + return to run this code cell
# then, click on the gate that you want to apply followed by the qubit(s) that you want it to apply to
# for controlled gates, the first qubit you choose is the control qubit and the second one the target qubit
# click on clear to restart
minicomposer(2, dirac = True, qsphere = True)
# Cell 8
def create_circuit():
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0,1)
return qc
qc = create_circuit()
state = statevec(qc) # determine final state after running the circuit
display(Math(vec_in_braket(state.data)))
check5(state)
qc.draw(output='mpl') # we draw the circuit
# Cell 9
def create_circuit6():
qc = QuantumCircuit(2,2) # this time, we not only want two qubits, but also
# two classical bits for the measurement later
qc.h(0)
qc.cx(0,1)
qc.y(1)
return qc
qc = create_circuit6()
state = statevec(qc) # determine final state after running the circuit
display(Math(vec_in_braket(state.data)))
check6(state)
qc.measure(0, 0) # we perform a measurement on qubit q_0 and store the information on the classical bit c_0
qc.measure(1, 1) # we perform a measurement on qubit q_1 and store the information on the classical bit c_1
qc.draw(output='mpl') # we draw the circuit
# Cell 10
def run_circuit(qc):
backend = Aer.get_backend('qasm_simulator') # we choose the simulator as our backend
result = execute(qc, backend, shots = 1000).result() # we run the simulation
counts = result.get_counts() # we get the counts
return counts
counts = run_circuit(qc)
print(counts)
plot_histogram(counts) # let us plot a histogram to see the possible outcomes and corresponding probabilities
def run_circuit(qc):
backend = Aer.get_backend('qasm_simulator') # we choose the simulator as our backend
result = execute(qc, backend, shots = 1000).result() # we run the simulation
counts = result.get_counts() # we get the counts
return counts
counts = run_circuit(qc)
print(counts)
check
plot_histogram(counts) # let us plot a histogram to see the possible outcomes and corresponding probabilities
def create_circuit6():
qc = QuantumCircuit(3,3) # this time, we not only want two qubits, but also
# two classical bits for the measurement later
qc.h(0)
qc.cx(0,1)
qc.cx(1,2)
return qc
qc = create_circuit6()
state = statevec(qc)
display(Math(vec_in_braket(state.data)))
qc.measure(0, 0) # we perform a measurement on qubit q_0 and store the information on the classical bit c_0
qc.measure(1, 1)
qc.measure(2,2)# we perform a measurement on qubit q_1 and store the information on the classical bit c_1
qc.draw(output='mpl') # we draw the circuit
def run_circuit(qc):
backend = Aer.get_backend('qasm_simulator') # we choose the simulator as our backend
result = execute(qc, backend, shots = 2000).result() # we run the simulation
counts = result.get_counts() # we get the counts
return counts
counts = run_circuit(qc)
print(counts)
check8(counts)
plot_histogram(counts)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
#initialization
%matplotlib inline
# Importing standard Qiskit libraries and configuring account
from qiskit import IBMQ
from qiskit.compiler import transpile, assemble
from qiskit.providers.ibmq import least_busy
from qiskit.tools.jupyter import *
from qiskit.tools.monitor import job_monitor
from qiskit.visualization import *
from qiskit.ignis.mitigation.measurement import complete_meas_cal, CompleteMeasFitter
provider = IBMQ.load_account() # load your IBM Quantum Experience account
# If you are a member of the IBM Q Network, fill your hub, group, and project information to
# get access to your premium devices.
# provider = IBMQ.get_provider(hub='', group='', project='')
from may4_challenge.ex2 import get_counts, show_final_answer
num_qubits = 5
meas_calibs, state_labels = complete_meas_cal(range(num_qubits), circlabel='mcal')
# find the least busy device that has at least 5 qubits
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= num_qubits and
not x.configuration().simulator and x.status().operational==True))
backend
# run experiments on a real device
shots = 8192
experiments = transpile(meas_calibs, backend=backend, optimization_level=3)
job = backend.run(assemble(experiments, shots=shots))
print(job.job_id())
%qiskit_job_watcher
# get measurement filter
cal_results = job.result()
meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal')
meas_filter = meas_fitter.filter
#print(meas_fitter.cal_matrix)
meas_fitter.plot_calibration()
# get noisy counts
noisy_counts = get_counts(backend)
plot_histogram(noisy_counts[0])
# apply measurement error mitigation and plot the mitigated counts
mitigated_counts_0 = meas_filter.apply(noisy_counts[0])
plot_histogram([mitigated_counts_0, noisy_counts[0]])
# uncomment whatever answer you think is correct
# answer1 = 'a'
# answer1 = 'b'
answer1 = 'c'
# answer1 = 'd'
# plot noisy counts
plot_histogram(noisy_counts[1])
# apply measurement error mitigation
# insert your code here to do measurement error mitigation on noisy_counts[1]
mitigated_counts_1 = meas_filter.apply(noisy_counts[1])
plot_histogram([mitigated_counts_1, noisy_counts[1]])
# uncomment whatever answer you think is correct
# answer2 = 'a'
#answer2 = 'b'
#answer2 = 'c'
answer2 = 'd'
# plot noisy counts
plot_histogram(noisy_counts[2])
# apply measurement error mitigation
# insert your code here to do measurement error mitigation on noisy_counts[2]
mitigated_counts_2 = meas_filter.apply(noisy_counts[2])
plot_histogram([mitigated_counts_2, noisy_counts[2]])
# uncomment whatever answer you think is correct
# answer3 = 'a'
answer3 = 'b'
#answer3 = 'c'
# answer3 = 'd'
# plot noisy counts
plot_histogram(noisy_counts[3])
# apply measurement error mitigation
# insert your code here to do measurement error mitigation on noisy_counts[3]
mitigated_counts_3 = meas_filter.apply(noisy_counts[3])
plot_histogram([mitigated_counts_3, noisy_counts[3]])
# uncomment whatever answer you think is correct
#answer4 = 'a'
answer4 = 'b'
#answer4 = 'c'
#answer4 = 'd'
# answer string
show_final_answer(answer1, answer2, answer3, answer4)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
%config InlineBackend.figure_format = 'svg' # Makes the images look nice
qc = QuantumCircuit(1)
initial_state = [0,1]
qc.initialize(initial_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc,backend).result()
state_vector = result.get_statevector()
print(state_vector)
qc.measure_all()
qc.draw()
result = execute(qc, backend).result()
counts = result.get_counts()
plot_histogram(counts)
initial_state = [1/sqrt(2), complex(0,1/sqrt(2))]
qc = QuantumCircuit(1)
qc.initialize(initial_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
statevector = result.get_statevector()
print(statevector)
counts = result.get_counts()
plot_histogram(counts)
initialize_state = [1/sqrt(3), sqrt(2/3)]
qc = QuantumCircuit(1)
qc.initialize(initialize_state, 0)
qc.draw()
result = execute(qc, backend).result()
counts = result.get_counts()
plot_histogram(counts)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
n = 8
n_q = n
n_b = n
qc_output = QuantumCircuit(n_q,n_b)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import qiskit
qiskit.__qiskit_version__
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()
counts = execute(qc_ha, Aer.get_backend('qasm_simulator')).result().get_counts()
plot_histogram(counts)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit
from qiskit.circuit import Gate
from math import pi
qc = QuantumCircuit(2)
c = 0
t = 1
qc = QuantumCircuit(2)
# a controlled-Y
qc.sdg(t)
qc.cx(c,t)
qc.s(t)
qc.draw()
qc = QuantumCircuit(2)
# also a controlled-Z
qc.h(t)
qc.cx(c,t)
qc.h(t)
qc.draw()
qc = QuantumCircuit(2)
# a controlled-H
qc.ry(pi/4,t)
qc.cx(c,t)
qc.ry(-pi/4,t)
qc.draw()
#Controlled Rotations
qc = QuantumCircuit(2)
theta = pi # theta can be anything (pi chosen arbitrarily)
qc.ry(theta/2,t)
qc.cx(c,t)
qc.ry(-theta/2,t)
qc.cx(c,t)
qc.draw()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import *
from math import pi
import numpy as np
from qiskit.visualization import plot_bloch_multivector, plot_histogram
qc = QuantumCircuit(3)
for qubit in range(3):
qc.h(qubit)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc, backend).result().get_statevector()
print(final_state)
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.draw()
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
qiskit.__qiskit_version__
qc = QuantumCircuit(3)
qc.x(0)
qc.z(1)
qc.h(2)
qc.draw()
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,backend).result().get_statevector()
print(final_state)
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
# Apply a CNOT:
qc.cx(0,1)
qc.draw()
final_state = Aer.get_backend('statevector_simulator')
final_state = execute(qc, backend).result().get_statevector()
print(final_state)
results = execute(qc,backend).result().get_counts()
plot_histogram(results)
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.cx(0,1)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result().get_statevector()
print(result)
result = execute(qc, backend).result().get_counts()
plot_histogram(result)
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc, backend).result().get_unitary()
print(unitary)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, Aer, execute
from math import pi
import numpy as np
from qiskit.visualization import plot_bloch_multivector, plot_histogram
qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.draw()
statevector_backend = Aer.get_backend('statevector_simulator')
final_state = execute(qc,statevector_backend).result().get_statevector()
print(final_state)
plot_bloch_multivector(final_state)
qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.z(1)
qc.draw()
final_state = execute(qc,statevector_backend).result().get_statevector()
print(final_state)
plot_bloch_multivector(final_state)
qc.cx(0,1)
qc.draw()
final_state = execute(qc,statevector_backend).result().get_statevector()
print(final_state)
plot_bloch_multivector(final_state)
qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.h(0)
qc.h(1)
display(qc.draw())
# `display` is an IPython tool, remove if it cases an error
unitary_backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,unitary_backend).result().get_unitary()
print(unitary)
qc = QuantumCircuit(2)
qc.cx(1,0)
display(qc.draw())
unitary_backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,unitary_backend).result().get_unitary()
print(unitary)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
import qiskit
qiskit.__qiskit_version__
from qiskit import IBMQ
IBMQ.save_account('Type in the id you get from your IBM account')
IBMQ.load_account()
from qiskit import *
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
circuit = QuantumCircuit(qr,cr)
%matplotlib inline
circuit.draw()
circuit.h(qr[0])
circuit.draw(output='mpl')
circuit.cx(qr[0], qr[1])
circuit.draw(output='mpl')
circuit.measure(qr,cr)
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit,backend=simulator).result()
from qiskit.tools.visualization import plot_histogram
plot_histogram(result.get_counts(circuit))
IBMQ.load_account()
provider = IBMQ.get_provider('ibm-q')
qcomp = provider.get_backend('ibmq_16_melbourne')
job = execute(circuit, backend=qcomp)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(circuit))
from qiskit import *
from qiskit.tools.visualization import plot_bloch_multivector
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('statevector_simulator')
result = execute(circuit, backend=simulator).result()
statevector = result.get_statevector()
print(statevector)
%matplotlib inline
circuit.draw(output = 'mpl')
plot_bloch_multivector(statevector)
circuit.measure([0],[0])
backend = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend = backend, shots = 1024).result()
counts = result.get_counts()
from qiskit.tools.visualization import plot_histogram
plot_histogram(counts)
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('unitary_simulator')
result = execute(circuit, backend=simulator).result()
unitary = result.get_unitary()
print(unitary)
%matplotlib inline
circuit.draw(output = 'mpl')
from qiskit import *
%matplotlib inline
circuit = QuantumCircuit(3,3)
circuit.draw(output='mpl')
circuit.x(0)
circuit.barrier()
circuit.draw(output='mpl')
circuit.h(1)
circuit.cx(1,2)
circuit.draw(output='mpl')
circuit.cx(0,1)
circuit.h(0)
circuit.draw(output='mpl')
circuit.barrier()
circuit.measure([0,1], [0,1])
circuit.draw(output='mpl')
circuit.barrier()
circuit.cx(1,2)
circuit.cz(0,2)
circuit.draw(output='mpl')
circuit.measure(2,2)
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit,backend=simulator, shots=1024).result()
counts = result.get_counts()
plot_histogram(counts)
print(counts)
from qiskit import *
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
secretnumber = '10000001'
circuit = QuantumCircuit(len(secretnumber)+1, len(secretnumber))
circuit.h(range(len(secretnumber)))
circuit.x(len(secretnumber))
circuit.h(len(secretnumber))
circuit.barrier()
circuit.draw(output='mpl')
for ii, yesno in enumerate(secretnumber):
if yesno == '1':
circuit.cx(ii,len(secretnumber))
# circuit.cx(5,6)
# circuit.cx(3,6)
# circuit.cx(0,6)
circuit.barrier()
# circuit.h([0,1,2,3,4,5])
circuit.h(range(len(secretnumber)))
circuit.draw(output='mpl')
circuit.barrier()
# circuit.measure([0,1,2,3,4,5],[0,1,2,3,4,5])
circuit.measure(range(len(secretnumber)), range(len(secretnumber)))
circuit.barrier()
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend = simulator, shots = 1).result()
counts = result.get_counts()
plot_histogram(counts)
IBMQ.load_account()
provider = IBMQ.get_provider('ibm-q')
qcomp = provider.get_backend('ibmq_16_melbourne')
job = execute(circuit, backend=qcomp)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(circuit))
import qiskit
from qiskit import *
nqubits = 3
circuit = QuantumCircuit(nqubits, nqubits)
circuit.h(0)
circuit.cx(0,1)
circuit.cx(1,2)
circuit.measure([0,1,2], [0,1,2])
%matplotlib inline
from qiskit.tools.visualization import plot_histogram
circuit.draw(output='mpl')
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=simulator, shots=1024).result()
plot_histogram(result.get_counts(circuit))
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
%config InlineBackend.figure_format = 'svg'
qc = QuantumCircuit(1)
initialize_state = [1,0]
qc.initialize(initialize_state, 0)
qc.draw()
backend = Aer.get_backend('statevector_simulator')
result = execute(qc, backend).result()
out_state = result.get_statevector()
print(out_state)
qc.measure_all()
qc.draw()
counts = execute(qc, backend).result().get_counts()
plot_histogram(counts)
initial_state = [1/sqrt(3), complex(0, sqrt(2)/sqrt(3))]
qc = QuantumCircuit(1)
qc.initialize(initial_state, 0)
state = execute(qc, backend).result().get_statevector()
print(state)
count = execute(qc, backend).result().get_counts()
plot_histogram(count)
qc = QuantumCircuit(1) # Redefine qc
initial_state = [0.+1.j/sqrt(2),1/sqrt(2)+0.j]
qc.initialize(initial_state, [0])
qc.draw()
qc.measure_all()
qc.draw()
state = execute(qc,backend).result().get_statevector()
print("State of Measured Qubit = " + str(state))
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import *
from math import pi
from qiskit.visualization import plot_bloch_multivector
%config InlineBackend.figure_format = 'svg' # For Jupyter Notebooks
qc = QuantumCircuit(1)
qc.x(0)
qc.draw('mpl')
backend = Aer.get_backend('statevector_simulator')
out = execute(qc,backend).result().get_statevector()
plot_bloch_multivector(out)
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
from qiskit import QuantumCircuit
from qiskit.circuit import Gate
from math import pi
qc = QuantumCircuit(2)
c = 0
t = 1
qc = QuantumCircuit(2)
# a controlled-Y
qc.sdg(t)
qc.cx(c,t)
qc.s(t)
qc.draw()
qc = QuantumCircuit(2)
# also a controlled-Z
qc.h(t)
qc.cx(c,t)
qc.h(t)
qc.draw()
qc = QuantumCircuit(2)
# a controlled-H
qc.ry(pi/4,t)
qc.cx(c,t)
qc.ry(-pi/4,t)
qc.draw()
#Controlled Rotations
qc = QuantumCircuit(2)
theta = pi # theta can be anything (pi chosen arbitrarily)
qc.ry(theta/2,t)
qc.cx(c,t)
qc.ry(-theta/2,t)
qc.cx(c,t)
qc.draw()
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
# Do the necessary imports
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, BasicAer, IBMQ
from qiskit.visualization import plot_histogram, plot_bloch_multivector
### Creating 3 qubit and 2 classical bits in each separate register
qr = QuantumRegister(3)
crz = ClassicalRegister(1)
crx = ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
### A third party eve helps to create an entangled state
def create_bell_pair(qc, a, b):
qc.h(a)
qc.cx(a, b)
create_bell_pair(teleportation_circuit, 1, 2)
teleportation_circuit.draw()
def alice_gates(qc, a, b):
qc.cx(a, b)
qc.h(a)
teleportation_circuit.barrier()
alice_gates(teleportation_circuit, 0, 1)
teleportation_circuit.draw()
def measure_and_send(qc, a, b):
qc.barrier()
qc.measure(a,0)
qc.measure(b,1)
teleportation_circuit.barrier()
measure_and_send(teleportation_circuit, 0, 1)
teleportation_circuit.draw()
def bob_gates(qc, qubit, crz, crx):
qc.x(qubit).c_if(crx, 1)
qc.z(qubit).c_if(crz, 1)
teleportation_circuit.barrier()
bob_gates(teleportation_circuit, 2, crz, crx)
teleportation_circuit.draw()
from qiskit.extensions import Initialize
import math
qc = QuantumCircuit(1)
initial_state = [0,1]
init_gate = Initialize(initial_state)
# qc.append(initialize_qubit, [0])
qr = QuantumRegister(3) # Protocol uses 3 qubits
crz = ClassicalRegister(1) # and 2 classical registers
crx = ClassicalRegister(1)
qc = QuantumCircuit(qr, crz, crx)
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
# Alice then sends her classical bits to Bob
measure_and_send(qc, 0, 1)
# Bob decodes qubits
bob_gates(qc, 2, crz, crx)
qc.draw()
backend = BasicAer.get_backend('statevector_simulator')
out_vector = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out_vector)
inverse_init_gate = init_gate.gates_to_uncompute()
qc.append(inverse_init_gate, [2])
qc.draw()
cr_result = ClassicalRegister(1)
qc.add_register(cr_result)
qc.measure(2,2)
qc.draw()
backend = BasicAer.get_backend('qasm_simulator')
counts = execute(qc, backend, shots=1024).result().get_counts()
plot_histogram(counts)
def bob_gates(qc, a, b, c):
qc.cz(a, c)
qc.cx(b, c)
qc = QuantumCircuit(3,1)
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
qc.barrier()
# Alice sends classical bits to Bob
bob_gates(qc, 0, 1, 2)
# We undo the initialisation process
qc.append(inverse_init_gate, [2])
# See the results, we only care about the state of qubit 2
qc.measure(2,0)
# View the results:
qc.draw()
from qiskit import IBMQ
IBMQ.save_account('### IMB TOKEN ')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
from qiskit.providers.ibmq import least_busy
backend = least_busy(provider.backends(filters=lambda b: b.configuration().n_qubits >= 3 and
not b.configuration().simulator and b.status().operational==True))
job_exp = execute(qc, backend=backend, shots=8192)
exp_result = job_exp.result()
exp_measurement_result = exp_result.get_counts(qc)
print(exp_measurement_result)
plot_histogram(exp_measurement_result)
error_rate_percent = sum([exp_measurement_result[result] for result in exp_measurement_result.keys() if result[0]=='1']) \
* 100./ sum(list(exp_measurement_result.values()))
print("The experimental error rate : ", error_rate_percent, "%")
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
# Importing everything
from qiskit import *
from qiskit.visualization import plot_histogram
# For Jupyter Notebooks, change the settings to get nicer images
%config InlineBackend.figure_format = 'svg'
def create_bell_pair(qc, a, b):
qc.h(a)
qc.cx(a, b)
def encode_message(qc, qubit, message):
if message == "00":
pass
elif message == "01":
qc.z(qubit)
elif message == "10":
qc.x(qubit)
elif message == "11":
qc.z(qubit)
qz.x(qubit)
else:
print("Enter Valid message please")
def decode_message(qc, a, b):
qc.cx(a, b)
qc.h(a)
# Create the quantum circuit with 2 qubits
qc = QuantumCircuit(2)
# First, Eve creates the entangled pair between Alice and Bob
create_bell_pair(qc, 0, 1)
qc.barrier() # This adds a barrier to our circuit. A barrier
# separates the gates in our diagram and makes it
# clear which part of the circuit is which
# At this point, qubit 0 goes to Alice and qubit 1 goes to Bob
# Next, Alice encodes her message onto qubit 0. In this case,
# we want to send the message '10'. You can try changing this
# value and see how it affects the circuit
message = "10"
encode_message(qc, 0, message)
qc.barrier()
# Alice then sends her qubit to Bob.
# After recieving qubit 0, Bob applies the recovery protocol:
decode_message(qc, 0, 1)
# Finally, Bob measures his qubits to read Alice's message
qc.measure_all()
# Draw our output
qc.draw(output = "mpl")
backend = Aer.get_backend('qasm_simulator')
job_sim = execute(qc, backend, shots=1024)
sim_result = job_sim.result()
measurement_result = sim_result.get_counts(qc)
print(measurement_result)
plot_histogram(measurement_result)
from qiskit import IBMQ
from qiskit.providers.ibmq import least_busy
shots = 256
# Load local account information
IBMQ.load_account()
# Get the least busy backend
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
print("least busy backend: ", backend)
# Run our circuit
job = execute(qc, backend=backend, shots=shots)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(qc))
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
# Do the necessary imports
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, BasicAer, IBMQ
from qiskit.visualization import plot_histogram, plot_bloch_multivector
### Creating 3 qubit and 2 classical bits in each separate register
qr = QuantumRegister(3)
crz = ClassicalRegister(1)
crx = ClassicalRegister(1)
teleportation_circuit = QuantumCircuit(qr, crz, crx)
### A third party eve helps to create an entangled state
def create_bell_pair(qc, a, b):
qc.h(a)
qc.cx(a, b)
create_bell_pair(teleportation_circuit, 1, 2)
teleportation_circuit.draw()
def alice_gates(qc, a, b):
qc.cx(a, b)
qc.h(a)
teleportation_circuit.barrier()
alice_gates(teleportation_circuit, 0, 1)
teleportation_circuit.draw()
def measure_and_send(qc, a, b):
qc.barrier()
qc.measure(a,0)
qc.measure(b,1)
teleportation_circuit.barrier()
measure_and_send(teleportation_circuit, 0, 1)
teleportation_circuit.draw()
def bob_gates(qc, qubit, crz, crx):
qc.x(qubit).c_if(crx, 1)
qc.z(qubit).c_if(crz, 1)
teleportation_circuit.barrier()
bob_gates(teleportation_circuit, 2, crz, crx)
teleportation_circuit.draw()
from qiskit.extensions import Initialize
import math
qc = QuantumCircuit(1)
initial_state = [0,1]
init_gate = Initialize(initial_state)
# qc.append(initialize_qubit, [0])
qr = QuantumRegister(3) # Protocol uses 3 qubits
crz = ClassicalRegister(1) # and 2 classical registers
crx = ClassicalRegister(1)
qc = QuantumCircuit(qr, crz, crx)
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
# Alice then sends her classical bits to Bob
measure_and_send(qc, 0, 1)
# Bob decodes qubits
bob_gates(qc, 2, crz, crx)
qc.draw()
backend = BasicAer.get_backend('statevector_simulator')
out_vector = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out_vector)
inverse_init_gate = init_gate.gates_to_uncompute()
qc.append(inverse_init_gate, [2])
qc.draw()
cr_result = ClassicalRegister(1)
qc.add_register(cr_result)
qc.measure(2,2)
qc.draw()
backend = BasicAer.get_backend('qasm_simulator')
counts = execute(qc, backend, shots=1024).result().get_counts()
plot_histogram(counts)
def bob_gates(qc, a, b, c):
qc.cz(a, c)
qc.cx(b, c)
qc = QuantumCircuit(3,1)
# First, let's initialise Alice's q0
qc.append(init_gate, [0])
qc.barrier()
# Now begins the teleportation protocol
create_bell_pair(qc, 1, 2)
qc.barrier()
# Send q1 to Alice and q2 to Bob
alice_gates(qc, 0, 1)
qc.barrier()
# Alice sends classical bits to Bob
bob_gates(qc, 0, 1, 2)
# We undo the initialisation process
qc.append(inverse_init_gate, [2])
# See the results, we only care about the state of qubit 2
qc.measure(2,0)
# View the results:
qc.draw()
from qiskit import IBMQ
IBMQ.save_account('### IMB TOKEN ')
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
provider.backends()
from qiskit.providers.ibmq import least_busy
backend = least_busy(provider.backends(filters=lambda b: b.configuration().n_qubits >= 3 and
not b.configuration().simulator and b.status().operational==True))
job_exp = execute(qc, backend=backend, shots=8192)
exp_result = job_exp.result()
exp_measurement_result = exp_result.get_counts(qc)
print(exp_measurement_result)
plot_histogram(exp_measurement_result)
error_rate_percent = sum([exp_measurement_result[result] for result in exp_measurement_result.keys() if result[0]=='1']) \
* 100./ sum(list(exp_measurement_result.values()))
print("The experimental error rate : ", error_rate_percent, "%")
|
https://github.com/hephaex/Quantum-Computing-Awesome-List
|
hephaex
|
# Importing everything
from qiskit import *
from qiskit.visualization import plot_histogram
# For Jupyter Notebooks, change the settings to get nicer images
%config InlineBackend.figure_format = 'svg'
def create_bell_pair(qc, a, b):
qc.h(a)
qc.cx(a, b)
def encode_message(qc, qubit, message):
if message == "00":
pass
elif message == "01":
qc.z(qubit)
elif message == "10":
qc.x(qubit)
elif message == "11":
qc.z(qubit)
qz.x(qubit)
else:
print("Enter Valid message please")
def decode_message(qc, a, b):
qc.cx(a, b)
qc.h(a)
# Create the quantum circuit with 2 qubits
qc = QuantumCircuit(2)
# First, Eve creates the entangled pair between Alice and Bob
create_bell_pair(qc, 0, 1)
qc.barrier() # This adds a barrier to our circuit. A barrier
# separates the gates in our diagram and makes it
# clear which part of the circuit is which
# At this point, qubit 0 goes to Alice and qubit 1 goes to Bob
# Next, Alice encodes her message onto qubit 0. In this case,
# we want to send the message '10'. You can try changing this
# value and see how it affects the circuit
message = "10"
encode_message(qc, 0, message)
qc.barrier()
# Alice then sends her qubit to Bob.
# After recieving qubit 0, Bob applies the recovery protocol:
decode_message(qc, 0, 1)
# Finally, Bob measures his qubits to read Alice's message
qc.measure_all()
# Draw our output
qc.draw(output = "mpl")
backend = Aer.get_backend('qasm_simulator')
job_sim = execute(qc, backend, shots=1024)
sim_result = job_sim.result()
measurement_result = sim_result.get_counts(qc)
print(measurement_result)
plot_histogram(measurement_result)
from qiskit import IBMQ
from qiskit.providers.ibmq import least_busy
shots = 256
# Load local account information
IBMQ.load_account()
# Get the least busy backend
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
print("least busy backend: ", backend)
# Run our circuit
job = execute(qc, backend=backend, shots=shots)
from qiskit.tools.monitor import job_monitor
job_monitor(job)
result = job.result()
plot_histogram(result.get_counts(qc))
|
https://github.com/RakhshandaMujib/Grover-Search-Algorithm
|
RakhshandaMujib
|
import numpy as np
# Importing standard Qiskit libraries:
from qiskit import QuantumCircuit, transpile, Aer, IBMQ, execute
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from qiskit.providers.ibmq import least_busy
def phase_oracle(n, indices_to_mark, name = 'Oracle'):
'''
Brief:
Generates the orcale matrix to flip the phase of the marked elements.
Transforms the matrix to the corresponding unitary gate. In practicality,
the phase of the winning state(s) get(s) flipped.
Parameters:
n = Integer. Number of qubits.
indices_to_mark = List of intergs representing the indices of winning
elements to search for.
name = Name of the QuantumCircuit object returned.
Returns:
qc = QuantumCircuit object. Has the oracle gate as an element of a circuit.
'''
qc = QuantumCircuit(n, name = name) #Initialize a quantum circuit with n qubits.
oracle_matrix = np.identity(2**n) #Get an identity matrix of n^2 dimension.
for index_to_mark in indices_to_mark: #For each key in the list of keys...
oracle_matrix[index_to_mark, index_to_mark] = -1 #flip the sign of the key.
qc.unitary(oracle_matrix, range(n)) #Apply the matrix to the circuit as a unitary gate
#with range of qubits being [0, ..., n-1].
return qc
def diffuser(n, name = 'Diffuser'):
'''
Brief:
Prepares the diffuser circuit and generates the matrix to flip the state 0.
Physically, the diffuser amplifies the amplitudes of the winning states.
Parameters:
n = Integer. Number of qubits.
Returns:
qc = QuantumCircuit object. Diffuser circuit.
'''
all_num = lsit(range(2 ** n)) #[0, ..., (2**n) -1]
except_zero = all_num[1:] #[1, ..., (2**n) -1]
qc = QuantumCircuit(n, name = name) #Initialize a quantum circuit with n qubits.
qc.h(range(n)) #Prepare the state |s> = H|0>.
diffuser_matrix = phase_oracle(n, except_zero) #Generate the diffuser matrix.
qc.append(diffuser_matrix, range(n)) #Apply the diffuser matrix=> V|s>.
qc.h(range(n)) #Apply the H gate to the cicuit=> HV|s>.
return qc
def groverSearch(n, marked):
'''
Brief:
Prpares the entire circuit for the Grover's search algorithm. Searches for
the marked elements in the range (0, ..., 2^(n-1)).
Parameters:
n = Integer. Number of qubits.
marked = List of keys.
Returns:
qc = QuantumCircuit object. Final Grover's search circuit.
'''
qc = QuantumCircuit(n, n) #Initialize a quantum circuit with n qubits and classical bits.
M = len(marked) #Say, we have M marked element.
N = 2 ** n #Total number of elements that can be represented with n qubits.
theta = 2 * np.arcsin(np.sqrt(M/N)) #Get the angle of rotation.
rounds = int(np.ceil(np.pi / (2 * theta))- (1 / 2)) #Get the number of rounds needed.
#Print the information:
print(f"Number of qubits: {n}")
print(f"Key(s) to search: {marked}")
print(f"Number of rounds needed: {rounds}")
qc.h(range(n)) #Step 1: Prepare the superposition states of each qubit.
for _ in range(rounds): #For all the rounds...
qc.append(phase_oracle(n, marked), range(n)) #Step 2: Apply the phase oracle.
qc.append(diffuser(n), range(n)) #Step 3: Apply the diffuser.
qc.measure(range(n), range(n)) #Final step: Measure the qubits.
return qc
n = int(input("Enter the number of qubits:"))
marked = list(map(int, input('Enter the elements:\n').split()))
qc = groverSearch(n, marked)
qc.draw()
#Run it in the simulator:
backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend, shots = 8192).result()
counts = result.get_counts(qc)
#Print the results:
print(counts)
plot_histogram(counts)
|
https://github.com/gaurav-iiser/qosf_task1
|
gaurav-iiser
|
import numpy as np
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute,Aer
from qiskit import quantum_info as qi
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_histogram
import sys
class Task_1:
"""
Class for creating a quantum state which is a superposition of the indices of the numbers from a given list such that
these number's binary representation alternates in 0 and 1.
Valid input: List of integers.
Output: 1. A histogram indicating the states of superpostion and their coefficient in the superposed state.
2. The state vector of the final quantum state.
Variables and functions in this class:
self.integer_list: List of input integers
self.binary : List of binary representation of the above integers
self.index_binary: List of binary representation of the indices of the above integers
self.qc : List of quantum circuits. Each element is a quantum circuit pertaining to the preparation of a state
which is a tensor product of the state formed from the index and the state formed from the binary
representation of the number at that index
self.q and self.c: List of quantum registers and classical registers used for the above Quantum Circuits
Basic idea of the algorithm (step-wise):
1. self.construct_state() : prepares a list of quantum states which encode the index along with the respective integer
from the provided list.
2. self.construct_superposition() : prepares a state which is an equal superposition of the states prepared above.
This is stored in self.superposed_vec. This is an object of Statevector class.
3. self.construct_proj() : Constructs the projection operator pertaining to the desired result. The result is stored in
self.proj
4. self.apply_proj() : This function applies the above projection operator to the state prepared in step 2. The resultant
state is an equal superposition of the desired states
5. self.evol() : This function further processes the resultant vector obtained from step 4. First this function gets rid
of all the qubits (except one) which contain the information of the binary representation of the special
numbers. We are now left with an entangled state whose first part is the index of the desired number and]
the second part is |0> or |1>. Then, this function projects the second part of this system onto the
maximally coherent state or the |+> state and traces it away. We are now left with the desired superposed
state.
Other functions that I have added (although, the idea was to enhance the code even further by adding more such helper
functions, but due to the deadline and other time constraints, I will submit the code as is for now leaving scope for
adding more functions later):
get_integers() : Prints the list of integers
get_binary() : Prints the binary representation of integers
get_index_binary(): Prints the indices of the integers.
"""
def __init__(self, integer_list=[0,1]):
if any(not isinstance(x, int) for x in integer_list):
sys.exit("Numbers in the list are not all integers.")
self.integer_list = integer_list
self.binary = self.convert_to_bin(self.integer_list)
self.index_binary = self.convert_to_bin(len(self.integer_list))
self.qc = []
self.q = []
self.c = []
self.construct_state()
self.superposed_vec = self.construct_superposition()
self.proj = self.construct_proj()
self.vec_after_proj = self.apply_proj()
self.evolved_vec = self.evol()
print(self.evolved_vec)
def convert_to_bin(self, list_or_num):
binary_list=[]
if isinstance(list_or_num, list):
max_elem = max(list_or_num)
self.total_dig = np.log2(max_elem)
if abs(self.total_dig - int(self.total_dig))<1e-12:
self.total_dig += 1
else:
self.total_dig = np.ceil(self.total_dig)
self.total_dig = int(self.total_dig)
for integer in list_or_num:
if isinstance(integer,int):
binary_list.append(self.binary_(integer,self.total_dig))
else:
sys.exit("the input list has elements which are not integers")
return binary_list
elif isinstance(list_or_num, int):
self.index_total_dig = np.log2(list_or_num-1)
if abs(self.index_total_dig - int(self.index_total_dig))<1e-12:
self.index_total_dig += 1
else:
self.index_total_dig = np.ceil(self.index_total_dig)
self.index_total_dig = int(self.index_total_dig)
for integer_index in range(list_or_num):
binary_list.append(self.binary_(integer_index, self.index_total_dig))
return binary_list
else:
sys.exit("the input is not a list")
def binary_(self, number, total_digits):
return np.binary_repr(number, width=total_digits)
def construct_state(self):
num_qbits = self.index_total_dig + self.total_dig
self.total_qubit_registers = num_qbits
for i in range(len(self.integer_list)):
self.q.append(QuantumRegister(num_qbits,"qreg"))
self.qc.append(QuantumCircuit(self.q[i]))
new_string = self.index_binary[i] + self.binary[i]
for j in range(num_qbits):
if new_string[j] == '1':
self.qc[i].x(self.q[i][j])
def construct_superposition(self):
new_qc = QuantumCircuit(self.total_qubit_registers, 1)
for i in range(self.total_qubit_registers):
new_qc.h(i)
superposed_state = Statevector(new_qc)
proj_ = []
index_proj = []
for i in range(len(self.qc)):
proj_.append(Statevector(self.qc[i]))
proj_[i] = proj_[i].to_operator()
for i in range(self.total_qubit_registers):
index_proj.append(i)
projector = proj_[0]
if len(self.qc)>1:
for i in range(1,len(self.qc)):
projector += proj_[i]
superposed_state = superposed_state.evolve(projector,index_proj)
tr = superposed_state.trace()
superposed_state = superposed_state/np.sqrt(tr)
return superposed_state
def construct_proj(self):
n = self.total_dig
qc1 = QuantumCircuit(n)
qc2 = QuantumCircuit(n)
for i in range(n):
if i%2 == 0:
qc1.x(i)
else:
qc2.x(i)
proj_1 = qi.Statevector(qc1)
proj_2 = qi.Statevector(qc2)
proj_1 = proj_1.to_operator()
proj_2 = proj_2.to_operator()
proj = proj_1+proj_2
return proj
def apply_proj(self):
index_proj_list = []
for i in range(self.total_qubit_registers-1,self.index_total_dig-1, -1):
index_proj_list.append(i)
new_qc_statevec = self.superposed_vec.evolve(self.proj,index_proj_list)
temp_op = qi.DensityMatrix(new_qc_statevec)
tr = temp_op.trace()
if tr <= 1e-12:
sys.exit("No number in the input whose binary structure is alternate")
return
temp_op = temp_op/tr
new_qc_statevec = temp_op.to_statevector()
return new_qc_statevec
def evol(self):
### Create a quantum circuit and initialize it with the vector obtained after projection.
qc_evol = QuantumCircuit(self.total_qubit_registers)
qc_evol.initialize(self.vec_after_proj)
###############################################################################################################
### Apply CNOT to the qubits that contain the binary representation of selected integers and ####
### leave the index part as it is. The control qubit can be chosen to any qubit. For simplicity, we have ####
### chosen the first qubit of the state containing the binary rep of selected integer from the list. ####
### See step 7 of algorithm given above. ####
###############################################################################################################
for i in range(self.index_total_dig+1, self.total_qubit_registers):
qc_evol.cnot(self.index_total_dig, i)
new_statevec = qi.Statevector(qc_evol)
#####################################################
### Project the control qubit to the plus state. ###
### See step 9 of algorithm ###
#####################################################
qc2 = QuantumCircuit(1)
qc2.h(0)
plus_St = Statevector(qc2)
plus_St = plus_St.to_operator()
new_statevec = new_statevec.evolve(plus_St,[self.index_total_dig])
partial_trace_index = []
for j in range(self.index_total_dig, self.total_qubit_registers):
partial_trace_index.append(j)
if len(partial_trace_index)!=0:
new_statevec = qi.partial_trace(new_statevec, partial_trace_index)
tr = new_statevec.trace()
new_statevec = (1/tr)*new_statevec
new_statevec = new_statevec.to_statevector()
qc_fin = QuantumCircuit(self.index_total_dig, self.index_total_dig)
qc_fin.initialize(new_statevec)
for i in range(int(np.floor(self.index_total_dig/2))):
if i!=self.index_total_dig-1 -i:
qc_fin.swap(i,self.index_total_dig-1 -i)
qc_fin_ = qc_fin
new_statevec = Statevector(qc_fin)
#########################################################
######### Measurements to represent the counts ##########
#########################################################
for i in range(self.index_total_dig):
qc_fin_.measure(i,i)
job = execute(qc_fin_,Aer.get_backend('qasm_simulator'),shots=10000)
counts = job.result().get_counts(qc_fin_)
print(counts) # print the outcomes
display(plot_histogram(counts))
return new_statevec
#######################################################################################
############################## Helper Functions #######################################
#######################################################################################
def get_integers(self):
return self.integer_list
def get_binary(self):
#self.binary = self.convert_to_bin(self.integer_list)
return self.binary
def get_index_binary(self):
#self.index_binary = self.convert_to_bin(len(self.integer_list))
return self.index_binary
c = Task_1([1,5,7,10])
d = Task_1([3,5,8,10,11,12])
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer,assemble, transpile
from qiskit import BasicAer
from random import randrange
from qiskit.tools.visualization import plot_histogram, plot_state_city
import numpy as np
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit.quantum_info import Operator, Statevector
q = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c = ClassicalRegister(6)
Q = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q.u(np.pi/2,0,np.pi,q[0])
Q.u(np.pi/2,0,np.pi,q[1])
#S operator
Q.x(q[0])
Q.x(q[1])
Q.mct([q[0],q[1]],q[3])
Q.mct([q[0],q[1]],q[5])
Q.x(q[0])
Q.x(q[1])
Q.barrier()
Q.x(q[0])
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[3])
Q.x(q[0])
Q.barrier()
Q.x(q[1])
Q.mct([q[0],q[1]],q[4])
Q.mct([q[0],q[1]],q[5])
Q.x(q[1])
Q.barrier()
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[4])
Q.measure_all()
Q.draw(output='mpl')
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = execute(Q, backend_sim, shots=1000)
# Grab the results from the job.
result_sim = job_sim.result()
counts = result_sim.get_counts(Q)
print(counts)
plot_histogram(counts, color='midnightblue', title="Decision Histogram")
q_o = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c_o = ClassicalRegister(6)
Q_o = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q_o.u(2*np.pi/3,0,np.pi,q[0])
Q_o.u(np.pi/2,0,np.pi,q[1])
#S operator
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[3])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.barrier()
Q_o.x(q[0])
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[3])
Q_o.x(q[0])
Q_o.barrier()
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[4])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[1])
Q_o.barrier()
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[4])
Q_o.measure_all()
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim_o = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim_o = execute(Q_o, backend_sim, shots=1000)
# Grab the results from the job.
result_sim_o = job_sim_o.result()
counts_o = result_sim_o.get_counts(Q_o)
print(counts_o)
plot_histogram(counts_o, color='midnightblue', title="Decision Histogram")
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
from qiskit.visualization import plot_state_city
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import networkx as nx
import random
import math
from qiskit.tools.monitor import job_monitor
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
#discrete time quantum random walk with a hadamard coin
n=2
steps=1
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=2
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=3
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit.quantum_info import DensityMatrix
from qiskit.visualization import plot_state_city
#discrete time quantum random walk with a hadamard coin
n=3
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
state = DensityMatrix.from_instruction(QC)
plot_state_city(state,figsize=(15, 8), color=['midnightblue', 'midnightblue'],
title="New State City")
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
# Import Aer
from qiskit import Aer
# Run the quantum circuit on a statevector simulator backend
backend = Aer.get_backend('statevector_simulator')
# Create a Quantum Program for execution
job = execute(QC, backend)
result = job.result()
outputstate = result.get_statevector(QC, decimals=3)
print(outputstate)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |0>
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |1>
QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit import *
%matplotlib inline
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
pi=math.pi
#initialized coin Ugate
QC.u(pi/2, 3*pi/2, 0, qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer,assemble, transpile
from qiskit import BasicAer
from random import randrange
from qiskit.tools.visualization import plot_histogram, plot_state_city
import numpy as np
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit.quantum_info import Operator, Statevector
q = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c = ClassicalRegister(6)
Q = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q.u(np.pi/2,0,np.pi,q[0])
Q.u(np.pi/2,0,np.pi,q[1])
#S operator
Q.x(q[0])
Q.x(q[1])
Q.mct([q[0],q[1]],q[3])
Q.mct([q[0],q[1]],q[5])
Q.x(q[0])
Q.x(q[1])
Q.barrier()
Q.x(q[0])
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[3])
Q.x(q[0])
Q.barrier()
Q.x(q[1])
Q.mct([q[0],q[1]],q[4])
Q.mct([q[0],q[1]],q[5])
Q.x(q[1])
Q.barrier()
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[4])
Q.measure_all()
Q.draw(output='mpl')
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = execute(Q, backend_sim, shots=1000)
# Grab the results from the job.
result_sim = job_sim.result()
counts = result_sim.get_counts(Q)
print(counts)
plot_histogram(counts, color='midnightblue', title="Decision Histogram")
q_o = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c_o = ClassicalRegister(6)
Q_o = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q_o.u(2*np.pi/3,0,np.pi,q[0])
Q_o.u(np.pi/2,0,np.pi,q[1])
#S operator
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[3])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.barrier()
Q_o.x(q[0])
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[3])
Q_o.x(q[0])
Q_o.barrier()
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[4])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[1])
Q_o.barrier()
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[4])
Q_o.measure_all()
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim_o = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim_o = execute(Q_o, backend_sim, shots=1000)
# Grab the results from the job.
result_sim_o = job_sim_o.result()
counts_o = result_sim_o.get_counts(Q_o)
print(counts_o)
plot_histogram(counts_o, color='midnightblue', title="Decision Histogram")
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
from qiskit.visualization import plot_state_city
from random import randrange
from qiskit.tools.monitor import job_monitor
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import random
import math
#discrete time quantum random walk with a hadamard coin
n=2
steps=1
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=2
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=3
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit.quantum_info import DensityMatrix
from qiskit.visualization import plot_state_city
#discrete time quantum random walk with a hadamard coin
n=3
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
state = DensityMatrix.from_instruction(QC)
plot_state_city(state,figsize=(15, 8), color=['midnightblue', 'midnightblue'],
title="New State City")
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
# Import Aer
from qiskit import Aer
# Run the quantum circuit on a statevector simulator backend
backend = Aer.get_backend('statevector_simulator')
# Create a Quantum Program for execution
job = execute(QC, backend)
result = job.result()
outputstate = result.get_statevector(QC, decimals=3)
print(outputstate)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |0>
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |1>
QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit import *
%matplotlib inline
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
pi=math.pi
#initialized coin Ugate
QC.u(pi/2, 3*pi/2, 0, qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
from qiskit.visualization import plot_state_city
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import networkx as nx
import random
import math
from qiskit.tools.monitor import job_monitor
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
class quantom_walk:
def __init__(self):
self.__n=2
self.__steps=1
self.__theta=0
self.__phi=0
self.__qtype=1
self.__shot=5000
def main_qw(self,n,steps,qtype,theta,phi):
self.__qpos = QuantumRegister(n,'qpos')
self.__qcoin = QuantumRegister(1,'qcoin')
self.__cpos = ClassicalRegister(n,'cr')
self.__QC = QuantumCircuit(self.__qpos, self.__qcoin)
if qtype==2: self.__QC.x(self.__qcoin[0])
if qtype==3: self.__QC.u(theta, phi, 0, self.__qcoin[0])
for i in range(steps):
self.__QC.h(self.__qcoin[0])
self.__QC.barrier()
for i in range(n):
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
self.__QC.barrier()
self.__QC.x(self.__qcoin[0])
for i in range(n):
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.barrier()
a=n/2
p=math.floor(a)
for k in range(n):
if(k<p):
self.__QC.swap(self.__qpos[n-1-k],self.__qpos[k])
def displayh(self):
display(self.__QC.draw(output="mpl"))
def histagramh(self,shot):
self.__QC.measure_all()
job = execute(self.__QC,Aer.get_backend('aer_simulator'),shots=5000)
counts = job.result().get_counts(self.__QC)
return counts
def spacevectorh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
print(outputstate)
def plotcityh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
from qiskit.visualization import plot_state_city
plot_state_city(outputstate)
return outputstate
def unitaryh(self):
backend = Aer.get_backend('unitary_simulator')
job = execute(self.__QC, backend)
result = job.result()
yy=result.get_unitary(self.__QC, decimals=3)
print(yy)
def IBMQh(self):
from qiskit import IBMQ
IBMQ.save_account('d1441affe8622903745ae099f50bce72c21036f85b14600d18195c977b9efcdee621dd4a981b92d8028c03c4dc1860c82d70f501d345023471402f4f8dad0181',overwrite=True)
provider = IBMQ.load_account()
device = provider.get_backend('ibmq_quito') #we use ibmq_16_melbourne quantum device
job = execute(self.__QC, backend = device) #we pass our circuit and backend as usual
from qiskit.tools.monitor import job_monitor
job_monitor(job) #to see our status in queue
result = job.result()
counts= result.get_counts(self.__QC)
return counts
def instructionset(self):
print(self.__QC.qasm())
qw = quantom_walk()
qw.main_qw(4,4,1,1.5,4)
#qw.instructionset()
#qw.displayh()
#plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#qw.histagramh(3000)
#qw.spacevectorh()
#qw.unitaryh()
#qw.plotcityh()
#plot_state_city(qw.plotcityh(), figsize=(20, 10))
#plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#qw.IBMQh()
qw = quantom_walk()
qw.main_qw(2,2,1,1.5,4)
qw.displayh()
qw.main_qw(6,25,1,1.5,4)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
qw.main_qw(3,4,1,1.5,4)
qw.spacevectorh()
qw.main_qw(3,15,1,1.5,4)
plot_state_city(qw.plotcityh(), figsize=(20, 10))
qw.main_qw(2,3,1,1.5,4)
qw.unitaryh()
qw.main_qw(3,2,1,1.5,4)
qw.instructionset()
qw.main_qw(2,1,1,1.5,4)
plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#hadamrad...qtype=1
qw = quantom_walk()
qw.main_qw(3,32,1,0,0)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#optimized ugate applied...qtype=3
qw = quantom_walk()
qw.main_qw(3,32,3,1.57,1.57)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
from qiskit.visualization import plot_state_city
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import networkx as nx
import random
import math
from qiskit.tools.monitor import job_monitor
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
class quantom_walk:
def __init__(self):
self.__n=2
self.__steps=1
self.__theta=0
self.__phi=0
self.__qtype=1
self.__shot=5000
def main_qw(self,n,steps,qtype,theta,phi):
self.__qpos = QuantumRegister(n,'qpos')
self.__qcoin = QuantumRegister(1,'qcoin')
self.__cpos = ClassicalRegister(n,'cr')
self.__QC = QuantumCircuit(self.__qpos, self.__qcoin)
if qtype==2: self.__QC.x(self.__qcoin[0])
if qtype==3: self.__QC.u(theta, phi, 0, self.__qcoin[0])
for i in range(steps):
self.__QC.h(self.__qcoin[0])
self.__QC.barrier()
for i in range(n):
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
self.__QC.barrier()
self.__QC.x(self.__qcoin[0])
for i in range(n):
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.barrier()
a=n/2
p=math.floor(a)
for k in range(n):
if(k<p):
self.__QC.swap(self.__qpos[n-1-k],self.__qpos[k])
def displayh(self):
display(self.__QC.draw(output="mpl"))
def histagramh(self,shot):
self.__QC.measure_all()
job = execute(self.__QC,Aer.get_backend('aer_simulator'),shots=5000)
counts = job.result().get_counts(self.__QC)
return counts
def spacevectorh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
print(outputstate)
def plotcityh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
from qiskit.visualization import plot_state_city
plot_state_city(outputstate)
return outputstate
def unitaryh(self):
backend = Aer.get_backend('unitary_simulator')
job = execute(self.__QC, backend)
result = job.result()
yy=result.get_unitary(self.__QC, decimals=3)
print(yy)
def IBMQh(self):
from qiskit import IBMQ
IBMQ.save_account('d1441affe8622903745ae099f50bce72c21036f85b14600d18195c977b9efcdee621dd4a981b92d8028c03c4dc1860c82d70f501d345023471402f4f8dad0181',overwrite=True)
provider = IBMQ.load_account()
device = provider.get_backend('ibmq_quito') #we use ibmq_16_melbourne quantum device
job = execute(self.__QC, backend = device) #we pass our circuit and backend as usual
from qiskit.tools.monitor import job_monitor
job_monitor(job) #to see our status in queue
result = job.result()
counts= result.get_counts(self.__QC)
return counts
def instructionset(self):
print(self.__QC.qasm())
qw = quantom_walk()
qw.main_qw(4,4,1,1.5,4)
#qw.instructionset()
#qw.displayh()
#plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#qw.histagramh(3000)
#qw.spacevectorh()
#qw.unitaryh()
#qw.plotcityh()
#plot_state_city(qw.plotcityh(), figsize=(20, 10))
#plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#qw.IBMQh()
qw = quantom_walk()
qw.main_qw(2,2,1,1.5,4)
qw.displayh()
qw.main_qw(6,25,1,1.5,4)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
qw.main_qw(3,4,1,1.5,4)
qw.spacevectorh()
qw.main_qw(3,15,1,1.5,4)
plot_state_city(qw.plotcityh(), figsize=(20, 10))
qw.main_qw(2,3,1,1.5,4)
qw.unitaryh()
qw.main_qw(3,2,1,1.5,4)
qw.instructionset()
qw.main_qw(2,1,1,1.5,4)
plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#hadamrad...qtype=1
qw = quantom_walk()
qw.main_qw(3,13,1,0,0)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#optimized ugate applied...qtype=3
qw = quantom_walk()
qw.main_qw(3,13,3,1.57,1.57)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import matplotlib.pyplot as plt
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer,assemble, transpile
from qiskit import BasicAer
from random import randrange
from qiskit.tools.visualization import plot_histogram, plot_state_city
import numpy as np
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit.quantum_info import Operator, Statevector
q = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c = ClassicalRegister(6)
Q = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q.u(np.pi/2,0,np.pi,q[0])
Q.u(np.pi/2,0,np.pi,q[1])
#S operator
Q.x(q[0])
Q.x(q[1])
Q.mct([q[0],q[1]],q[3])
Q.mct([q[0],q[1]],q[5])
Q.x(q[0])
Q.x(q[1])
Q.barrier()
Q.x(q[0])
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[3])
Q.x(q[0])
Q.barrier()
Q.x(q[1])
Q.mct([q[0],q[1]],q[4])
Q.mct([q[0],q[1]],q[5])
Q.x(q[1])
Q.barrier()
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[4])
Q.measure_all()
Q.draw(output='mpl')
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = execute(Q, backend_sim, shots=1000)
# Grab the results from the job.
result_sim = job_sim.result()
counts = result_sim.get_counts(Q)
print(counts)
plot_histogram(counts, color='midnightblue', title="Decision Histogram")
q_o = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c_o = ClassicalRegister(6)
Q_o = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q_o.u(2*np.pi/3,0,np.pi,q[0])
Q_o.u(np.pi/2,0,np.pi,q[1])
#S operator
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[3])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.barrier()
Q_o.x(q[0])
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[3])
Q_o.x(q[0])
Q_o.barrier()
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[4])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[1])
Q_o.barrier()
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[4])
Q_o.measure_all()
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim_o = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim_o = execute(Q_o, backend_sim, shots=1000)
# Grab the results from the job.
result_sim_o = job_sim_o.result()
counts_o = result_sim_o.get_counts(Q_o)
print(counts_o)
plot_histogram(counts_o, color='midnightblue', title="Decision Histogram")
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
from qiskit.visualization import plot_state_city
from random import randrange
from qiskit.tools.monitor import job_monitor
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import random
import math
#discrete time quantum random walk with a hadamard coin
n=2
steps=1
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=2
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=3
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit.quantum_info import DensityMatrix
from qiskit.visualization import plot_state_city
#discrete time quantum random walk with a hadamard coin
n=3
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
state = DensityMatrix.from_instruction(QC)
plot_state_city(state,figsize=(15, 8), color=['midnightblue', 'midnightblue'],
title="New State City")
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
# Import Aer
from qiskit import Aer
# Run the quantum circuit on a statevector simulator backend
backend = Aer.get_backend('statevector_simulator')
# Create a Quantum Program for execution
job = execute(QC, backend)
result = job.result()
outputstate = result.get_statevector(QC, decimals=3)
print(outputstate)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |0>
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |1>
QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit import *
%matplotlib inline
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
pi=math.pi
#initialized coin Ugate
QC.u(pi/2, 3*pi/2, 0, qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
from qiskit.visualization import plot_state_city
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import networkx as nx
import random
import math
from qiskit.tools.monitor import job_monitor
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
class quantom_walk:
def __init__(self):
self.__n=2
self.__steps=1
self.__theta=0
self.__phi=0
self.__qtype=1
self.__shot=5000
def main_qw(self,n,steps,qtype,theta,phi):
self.__qpos = QuantumRegister(n,'qpos')
self.__qcoin = QuantumRegister(1,'qcoin')
self.__cpos = ClassicalRegister(n,'cr')
self.__QC = QuantumCircuit(self.__qpos, self.__qcoin)
if qtype==2: self.__QC.x(self.__qcoin[0])
if qtype==3: self.__QC.u(theta, phi, 0, self.__qcoin[0])
for i in range(steps):
self.__QC.h(self.__qcoin[0])
self.__QC.barrier()
for i in range(n):
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
self.__QC.barrier()
self.__QC.x(self.__qcoin[0])
for i in range(n):
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.barrier()
a=n/2
p=math.floor(a)
for k in range(n):
if(k<p):
self.__QC.swap(self.__qpos[n-1-k],self.__qpos[k])
def displayh(self):
display(self.__QC.draw(output="mpl"))
def histagramh(self,shot):
self.__QC.measure_all()
job = execute(self.__QC,Aer.get_backend('aer_simulator'),shots=5000)
counts = job.result().get_counts(self.__QC)
return counts
def spacevectorh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
print(outputstate)
def plotcityh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
from qiskit.visualization import plot_state_city
plot_state_city(outputstate)
return outputstate
def unitaryh(self):
backend = Aer.get_backend('unitary_simulator')
job = execute(self.__QC, backend)
result = job.result()
yy=result.get_unitary(self.__QC, decimals=3)
print(yy)
def IBMQh(self):
from qiskit import IBMQ
IBMQ.save_account('d1441affe8622903745ae099f50bce72c21036f85b14600d18195c977b9efcdee621dd4a981b92d8028c03c4dc1860c82d70f501d345023471402f4f8dad0181',overwrite=True)
provider = IBMQ.load_account()
device = provider.get_backend('ibmq_quito') #we use ibmq_16_melbourne quantum device
job = execute(self.__QC, backend = device) #we pass our circuit and backend as usual
from qiskit.tools.monitor import job_monitor
job_monitor(job) #to see our status in queue
result = job.result()
counts= result.get_counts(self.__QC)
return counts
def instructionset(self):
print(self.__QC.qasm())
qw = quantom_walk()
qw.main_qw(4,4,1,1.5,4)
#qw.instructionset()
#qw.displayh()
#plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#qw.histagramh(3000)
#qw.spacevectorh()
#qw.unitaryh()
#qw.plotcityh()
#plot_state_city(qw.plotcityh(), figsize=(20, 10))
#plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#qw.IBMQh()
qw = quantom_walk()
qw.main_qw(2,2,3,1.5,1.5)
qw.displayh()
qw.main_qw(6,25,1,1.5,4)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
qw.main_qw(3,4,1,1.5,4)
qw.spacevectorh()
qw.main_qw(3,15,1,1.5,4)
plot_state_city(qw.plotcityh(), figsize=(20, 10))
qw.main_qw(2,3,1,1.5,4)
qw.unitaryh()
qw.main_qw(3,2,1,1.5,4)
qw.instructionset()
qw.main_qw(2,1,1,1.5,4)
plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#hadamrad...qtype=1
qw = quantom_walk()
qw.main_qw(3,32,1,0,0)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#optimized ugate applied...qtype=3
qw = quantom_walk()
qw.main_qw(3,32,3,1.57,1.57)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import matplotlib.pyplot as plt
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer,assemble, transpile
from qiskit import BasicAer
from random import randrange
from qiskit.tools.visualization import plot_histogram, plot_state_city
import numpy as np
from qiskit.quantum_info.operators import Operator, Pauli
from qiskit.quantum_info import Operator, Statevector
q = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c = ClassicalRegister(6)
Q = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q.u(np.pi/2,0,np.pi,q[0])
Q.u(np.pi/2,0,np.pi,q[1])
#S operator
Q.x(q[0])
Q.x(q[1])
Q.mct([q[0],q[1]],q[3])
Q.mct([q[0],q[1]],q[5])
Q.x(q[0])
Q.x(q[1])
Q.barrier()
Q.x(q[0])
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[3])
Q.x(q[0])
Q.barrier()
Q.x(q[1])
Q.mct([q[0],q[1]],q[4])
Q.mct([q[0],q[1]],q[5])
Q.x(q[1])
Q.barrier()
Q.mct([q[0],q[1]],q[2])
Q.mct([q[0],q[1]],q[4])
Q.measure_all()
Q.draw(output='mpl')
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = execute(Q, backend_sim, shots=1000)
# Grab the results from the job.
result_sim = job_sim.result()
counts = result_sim.get_counts(Q)
print(counts)
plot_histogram(counts, color='midnightblue', title="Decision Histogram")
q_o = QuantumRegister(6) # "Qubits q[0] and q[1] for coin 1 and 2", "q[2] and q[3] for player 1" and q[4] and q[5] for player 2"
c_o = ClassicalRegister(6)
Q_o = QuantumCircuit(q,c)
#Coin Operators
# Apply u gate as Hadamard gate to each coin
Q_o.u(2*np.pi/3,0,np.pi,q[0])
Q_o.u(np.pi/2,0,np.pi,q[1])
#S operator
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[3])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[0])
Q_o.x(q[1])
Q_o.barrier()
Q_o.x(q[0])
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[3])
Q_o.x(q[0])
Q_o.barrier()
Q_o.x(q[1])
Q_o.mct([q[0],q[1]],q[4])
Q_o.mct([q[0],q[1]],q[5])
Q_o.x(q[1])
Q_o.barrier()
Q_o.mct([q[0],q[1]],q[2])
Q_o.mct([q[0],q[1]],q[4])
Q_o.measure_all()
# Execute the circuit on the qasm simulator
# Use Aer's qasm_simulator
backend_sim_o = Aer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim_o = execute(Q_o, backend_sim, shots=1000)
# Grab the results from the job.
result_sim_o = job_sim_o.result()
counts_o = result_sim_o.get_counts(Q_o)
print(counts_o)
plot_histogram(counts_o, color='midnightblue', title="Decision Histogram")
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
from qiskit.visualization import plot_state_city
from random import randrange
from qiskit.tools.monitor import job_monitor
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import random
import math
#discrete time quantum random walk with a hadamard coin
n=2
steps=1
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=2
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=2
steps=3
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit.quantum_info import DensityMatrix
from qiskit.visualization import plot_state_city
#discrete time quantum random walk with a hadamard coin
n=3
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
state = DensityMatrix.from_instruction(QC)
plot_state_city(state,figsize=(15, 8), color=['midnightblue', 'midnightblue'],
title="New State City")
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
# Import Aer
from qiskit import Aer
# Run the quantum circuit on a statevector simulator backend
backend = Aer.get_backend('statevector_simulator')
# Create a Quantum Program for execution
job = execute(QC, backend)
result = job.result()
outputstate = result.get_statevector(QC, decimals=3)
print(outputstate)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |0>
#QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
#initialized coin |1>
QC.x(qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
from qiskit import *
%matplotlib inline
#discrete time quantum random walk with a hadamard coin
n=6
steps=11
qpos = QuantumRegister(n,'qpos')
qcoin = QuantumRegister(1,'qcoin')
cpos = ClassicalRegister(n,'cr')
QC = QuantumCircuit(qpos, qcoin)
pi=math.pi
#initialized coin Ugate
QC.u(pi/2, 3*pi/2, 0, qcoin[0])
for i in range(steps):
#coin
QC.h(qcoin[0])
QC.barrier()
#increment gate operator
for i in range(n):
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
QC.barrier()
#decrement gate operator
QC.x(qcoin[0])
for i in range(n):
if i+1 < n: QC.x(qpos[i+1:])
QC.mct([qcoin[0]]+qpos[i+1:], qpos[i], None, mode='noancilla')
if i+1 < n: QC.x(qpos[i+1:])
QC.barrier()
a=n/2
p=math.floor(a)
#print(p)
for k in range(n):
if(k<p):
QC.swap(qpos[n-1-k],qpos[k])
#print(a)
display(QC.draw(output="mpl"))
QC.measure_all()
# # Execute the circuit on the qasm simulator
job = execute(QC,Aer.get_backend('aer_simulator'),shots=10000)
counts = job.result().get_counts(QC)
print(counts)
plot_histogram(counts, figsize=(10, 2), color='midnightblue', title="New Histogram")
#aer_sim = Aer.get_backend('aer_simulator')
#qobj = assemble(had)
#result = aer_sim.run(qobj).result()
#counts = result.get_counts()
#plot_histogram(counts)
|
https://github.com/Spintronic6889/Introduction-of-Quantum-walk-its-application-on-search-and-decision-making
|
Spintronic6889
|
!python --version
!pip install qiskit
!pip install pylatexenc
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt
from qiskit.visualization import plot_state_city
%matplotlib inline
import matplotlib as mpl
from random import randrange
import numpy as np
import networkx as nx
import random
import math
from qiskit.tools.monitor import job_monitor
from random import randrange
pose=[]
for i in range(400):
pose.append([])
#print(pose)
#pose[-1]=1
#print(pose[-1])
pose[0]=200
for k in range(200):
rand = randrange(0,2)
if rand==0:
#print(rand)
pose[k+1]=pose[k]+1
if rand==1:
pose[k+1]=pose[k]-1
#print(pose)
yc=[]
for e in range(400):
yc.append([])
for q in range(400):
yc[q]=0
for h in range(400):
if pose[h]==q:
yc[q]=yc[q]+1
#print((yc))
#print(len(yc))
xc = np.arange(0, 400, 1)
plt.plot(yc)
plt.xlim(150, 250)
class quantom_walk:
def __init__(self):
self.__n=2
self.__steps=1
self.__theta=0
self.__phi=0
self.__qtype=1
self.__shot=5000
def main_qw(self,n,steps,qtype,theta,phi):
self.__qpos = QuantumRegister(n,'qpos')
self.__qcoin = QuantumRegister(1,'qcoin')
self.__cpos = ClassicalRegister(n,'cr')
self.__QC = QuantumCircuit(self.__qpos, self.__qcoin)
if qtype==2: self.__QC.x(self.__qcoin[0])
if qtype==3: self.__QC.u(theta, phi, 0, self.__qcoin[0])
for i in range(steps):
self.__QC.h(self.__qcoin[0])
self.__QC.barrier()
for i in range(n):
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
self.__QC.barrier()
self.__QC.x(self.__qcoin[0])
for i in range(n):
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.mct([self.__qcoin[0]]+self.__qpos[i+1:], self.__qpos[i], None, mode='noancilla')
if i+1 < n: self.__QC.x(self.__qpos[i+1:])
self.__QC.barrier()
a=n/2
p=math.floor(a)
for k in range(n):
if(k<p):
self.__QC.swap(self.__qpos[n-1-k],self.__qpos[k])
def displayh(self):
display(self.__QC.draw(output="mpl"))
def histagramh(self,shot):
self.__QC.measure_all()
job = execute(self.__QC,Aer.get_backend('aer_simulator'),shots=5000)
counts = job.result().get_counts(self.__QC)
return counts
def spacevectorh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
print(outputstate)
def plotcityh(self):
backend = Aer.get_backend('statevector_simulator')
job = execute(self.__QC, backend)
result = job.result()
outputstate = result.get_statevector(self.__QC, decimals=3)
from qiskit.visualization import plot_state_city
plot_state_city(outputstate)
return outputstate
def unitaryh(self):
backend = Aer.get_backend('unitary_simulator')
job = execute(self.__QC, backend)
result = job.result()
yy=result.get_unitary(self.__QC, decimals=3)
print(yy)
def IBMQh(self):
from qiskit import IBMQ
IBMQ.save_account('d1441affe8622903745ae099f50bce72c21036f85b14600d18195c977b9efcdee621dd4a981b92d8028c03c4dc1860c82d70f501d345023471402f4f8dad0181',overwrite=True)
provider = IBMQ.load_account()
device = provider.get_backend('ibmq_quito') #we use ibmq_16_melbourne quantum device
job = execute(self.__QC, backend = device) #we pass our circuit and backend as usual
from qiskit.tools.monitor import job_monitor
job_monitor(job) #to see our status in queue
result = job.result()
counts= result.get_counts(self.__QC)
return counts
def instructionset(self):
print(self.__QC.qasm())
qw = quantom_walk()
qw.main_qw(4,4,1,1.5,4)
#qw.instructionset()
#qw.displayh()
#plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#qw.histagramh(3000)
#qw.spacevectorh()
#qw.unitaryh()
#qw.plotcityh()
#plot_state_city(qw.plotcityh(), figsize=(20, 10))
#plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#qw.IBMQh()
qw = quantom_walk()
qw.main_qw(2,2,1,1.5,4)
qw.displayh()
qw.main_qw(6,25,1,1.5,4)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
qw.main_qw(3,4,1,1.5,4)
qw.spacevectorh()
qw.main_qw(3,15,1,1.5,4)
plot_state_city(qw.plotcityh(), figsize=(20, 10))
qw.main_qw(2,3,1,1.5,4)
qw.unitaryh()
qw.main_qw(3,2,1,1.5,4)
qw.instructionset()
qw.main_qw(2,1,1,1.5,4)
plot_histogram(qw.IBMQh(), figsize=(5, 2), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None, filename=None)
#hadamrad...qtype=1
qw = quantom_walk()
qw.main_qw(3,32,1,0,0)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
#optimized ugate applied...qtype=3
qw = quantom_walk()
qw.main_qw(3,32,3,1.57,1.57)
plot_histogram(qw.histagramh(3000), figsize=(20, 5), color=None, number_to_keep=None, sort='asc', target_string=None, legend=None, bar_labels=True, title=None, ax=None)
|
https://github.com/krish-baner/quantum-information-security
|
krish-baner
|
%matplotlib inline
# Importing standard Qiskit libraries and configuring account
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer, IBMQ
from qiskit.compiler import transpile, assemble
from qiskit.tools.jupyter import *
from qiskit.visualization import *
# Loading your IBM Q account(s)
provider = IBMQ.load_account()
# Setup the circuit function
def dense_coding_circuit(bitstring, # bit string to be sent
backend='qasm_simulator', # backend to be used, default is set to 'qasm_simulator'
eve=False # if Eve's malware is activated, the quantum malware attack takes place
):
# Get backend
if backend == 'qasm_simulator':
device = Aer.get_backend(backend) # use Aer if the backend is the 'qasm_simulator' (default)
else:
device = provider.get_backend(backend) # use the provider otherwise
# Quantum circuit to simulate the communication process
Alice = QuantumRegister(1,'alice') # Alice's Quantum Register
Bob = QuantumRegister(1,'bob') # Bob's Quantum Register
cr = ClassicalRegister(2,'c') # classical registers (we need two of them, and they belong to Bob)
circuit = QuantumCircuit() # quantum circuit (initially empty)
circuit.add_register(Alice) # add Alice's quantum register to the quantum circuit
circuit.add_register(Bob) # add Bob's quantum register to the quantum circuit
circuit.add_register(cr) # add the two classical registers for measurement
# Initial circuit preparation stage: Alice and Bob initially share an entangled pair
circuit.h(Alice) # apply a Haddamard transform to Alice's qubit
circuit.cx(Alice,Bob) # apply a CNOT gate that effectively leads to the entangled pair
circuit.barrier([Alice,Bob]) # barrier is setup to separate the preparation stage
# Now the quantum dense coding protocol is simulated
# If the bit string is 00:
if bitstring == '00':
# If Eve is on then the quantum malware attack simulation is run
if eve == True:
circuit.z(Alice) # Eve's quantum malware transforms Alice's qubit without Alice realizing it
circuit.barrier([Alice,Bob]) # we use a barrier to separate Bob's stage
# Alice's device sends her qubit to Bob whose automated device applies the following operations:
circuit.cx(Alice,Bob) # CNOT using Alice's qubit for control
circuit.h(Alice) # Haddamard transform on Alice's qubit
# If the bit string is 10:
elif bitstring == '10':
# Alice's system applies an X gate to her qubit
circuit.x(Alice)
# If Eve is on then the quantum malware attack simulation is run
if eve == True:
circuit.z(Alice) # Eve's quantum malware transforms Alice's qubit without Alice realizing it
circuit.barrier([Alice,Bob]) # we use a barrier to separate Alice's stage from Bob
# Alice's device sends her qubit to Bob whose automated device applies the following operations:
circuit.cx(Alice,Bob) # CNOT using Alice's qubit for control
circuit.h(Alice) # Haddamard transform on Alice's qubit
elif bitstring == '01':
# Alice applies a Z gate to her qubit
circuit.z(Alice)
# If Eve is on then the quantum malware attack simulation is run
if eve == True:
circuit.z(Alice) # Eve's quantum malware transforms Alice's qubit without Alice realizing it
circuit.barrier([Alice,Bob])
# Alice's device sends her qubit to Bob whose automated device applies the following operations:
circuit.cx(Alice,Bob) # CNOT using Alice's qubit for control
circuit.h(Alice) # Haddamard transform on Alice's qubit
else:
# Alice applies an X gate followed by a Z gate to her qubit
circuit.x(Alice)
circuit.z(Alice)
# If Eve is on then the quantum malware attack simulation is run
if eve == True:
circuit.z(Alice) # Eve's quantum malware transforms Alice's qubit without Alice realizing it
circuit.barrier([Alice,Bob])
# Alice's device sends her qubit to Bob whose automated device applies the following operations:
circuit.cx(Alice,Bob) # CNOT using Alice's qubit for control
circuit.h(Alice) # Haddamard transform on Alice's qubit
# Bob's system measures the qubit he received from Alice and his own qubit
circuit.barrier([Alice,Bob])
circuit.measure(Alice, cr[0])
circuit.measure(Bob, cr[1])
# The Python function returns the circuit and the device for simulation
return circuit, device
def run_circuit(circuit,device,num_shots=1000):
# Execute the circuit on the device for the number of shots defined
job = execute(circuit, device, shots=num_shots)
# Get the simulation results for the repeated experiments
result = job.result()
# Extract the counts, print them and return them for further processing
counts = result.get_counts(circuit)
print(counts)
return counts
circuit, device = dense_coding_circuit(bitstring='00')
circuit.draw()
counts = run_circuit(circuit,device)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='00',backend='ibmq_london')
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='00',eve=True)
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='00',eve=True)
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='00',backend='ibmq_london',eve=True)
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='10',backend='ibmq_london')
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='10',backend='ibmq_london',eve=True)
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='01',backend='ibmq_london')
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='01',backend='ibmq_london',eve=True)
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='11',backend='ibmq_london')
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='11',backend='ibmq_london',eve=True)
counts = run_circuit(circuit,device,num_shots=8192)
plot_histogram(counts)
circuit, device = dense_coding_circuit(bitstring='10')
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='01')
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='11')
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='10',eve=True)
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='01',eve=True)
circuit.draw()
circuit, device = dense_coding_circuit(bitstring='11',eve=True)
circuit.draw()
|
https://github.com/christopherporter1/VQE_with_Runtime
|
christopherporter1
|
from qiskit_nature.drivers import Molecule
from qiskit_nature.drivers.second_quantization import (
ElectronicStructureDriverType,
ElectronicStructureMoleculeDriver)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.transformers.second_quantization.electronic import FreezeCoreTransformer
molecule = Molecule([["O",[0.0,0.0,0.0]],["H", [0.757,0.586,0.0]], ["H", [-0.757,0.586,0.0]]], charge = 0, multiplicity = 1)
driver = ElectronicStructureMoleculeDriver(molecule, basis = "sto3g", driver_type = ElectronicStructureDriverType.PYSCF)
es_problem = ElectronicStructureProblem(driver, transformers=[FreezeCoreTransformer(freeze_core=True,
remove_orbitals=[])])
second_q_ops = es_problem.second_q_ops()
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper, ParityMapper
mapper = ParityMapper()
converter = QubitConverter(mapper = mapper, two_qubit_reduction = True)
qubit_op = converter.convert(second_q_ops["ElectronicEnergy"],num_particles = es_problem.num_particles)
print(qubit_op)
from qiskit.circuit.library import PauliTwoDesign, TwoLocal, EfficientSU2
from qiskit_nature.circuit.library import HartreeFock
init_state = HartreeFock(es_problem.num_spin_orbitals, es_problem.num_particles, converter)
#init_state = None
rotation_blocks = ['ry','rx']
entanglement_blocks = ['crx']
ansatz = TwoLocal(qubit_op.num_qubits, rotation_blocks, entanglement_blocks, 'sca', insert_barriers = False,initial_state = init_state)
from qiskit.algorithms.optimizers import COBYLA, SPSA, SLSQP, NELDER_MEAD
optimizer = COBYLA(maxiter=50)
from qiskit_ibm_runtime import Estimator, QiskitRuntimeService, Session, Options
service = QiskitRuntimeService(channel = "ibm_quantum")
options = Options()
options.execution.shots = 2000
options.resilience_level = 0
options.optimization_level = 0
estimator = Estimator(session=Session(service, backend = "ibmq_qasm_simulator"), options=options)
print(Options._DEFAULT_RESILIENCE_LEVEL,Options._DEFAULT_OPTIMIZATION_LEVEL)
counts = []
values = []
def store_intermediate_result(eval_counts, parameters, mean, std):
counts.append(eval_counts)
values.append(mean)
from qiskit.algorithms.minimum_eigensolvers import VQE
vqe = VQE(estimator, ansatz, optimizer,callback=store_intermediate_result)
result = vqe.compute_minimum_eigenvalue(qubit_op)
print(result)
from qiskit.algorithms import NumPyEigensolver
exact = NumPyEigensolver()
exact_run = exact.compute_eigenvalues(qubit_op)
print(exact_run)
print(es_problem.grouped_property_transformed._properties["ElectronicEnergy"])
result_freeze=result
values_freeze = values
for i in range(len(values)):
values_freeze[i] = values[i]-60.66177520599246
counts_freeze = counts
import matplotlib.pyplot as plt
plt.rcParams["font.size"] = 14
# Plot energy and reference value
plt.figure(figsize=(12, 6))
plt.plot(counts_freeze, values_freeze, label='spsa')
plt.axhline(y=-84.206, color="tab:red", ls="--", label="Target")
plt.legend(loc="best")
plt.xlabel("Iteration")
plt.ylabel("Energy [H]")
plt.title("VQE energy")
plt.show()
#Not to be shown in code walkthrough; just for me to have.
import numpy
f = open("qasm_spsa_H2O", "w+")
f.write("# optimization_step Energy\n") # column names
numpy.savetxt(f, numpy.array([counts_freeze, values_freeze]).T)
#x, y = numpy.loadtxt("trialdata", unpack=True)
from qiskit import IBMQ
provider = IBMQ.load_account()
from qiskit_ibm_runtime import Estimator, QiskitRuntimeService, Session, Options
optimizer = SPSA(maxiter = 50)
counts = []
values = []
#def store_intermediate_result(eval_counts, parameters, mean, std):
# counts.append(eval_counts)
# values.append(mean)
service = QiskitRuntimeService()
backend = "ibm_washington"
with Session(service=service, backend=backend) as session:
options = Options()
options.execution.shots = 2000
options.resilience_level = 1
options.optimization_level = 3
vqe = VQE(Estimator(session=session, options=options),
ansatz, optimizer, callback=store_intermediate_result)
result = vqe.compute_minimum_eigenvalue(qubit_op)
print(result)
session.close()
result_real=result
counts_real=counts
values_real=values
#Not to be shown in code walkthrough. Just for me to have.
f = open("wash_spsa_H2O", "w+")
f.write("# optimization_step Energy\n") # column names
numpy.savetxt(f, numpy.array([counts_real, values_real]).T)
#x, y = numpy.loadtxt("trialdata", unpack=True)
for i in range(len(values)):
values_real[i] = values[i]-60.66177520599246
plt.rcParams["font.size"] = 14
# Plot energy and reference value
plt.figure(figsize=(12, 6))
plt.plot(counts_real, values_real, label='spsa on ibm_washington')
plt.axhline(y=-84.206, color="tab:red", ls="--", label="Target")
plt.legend(loc="best")
plt.xlabel("Iteration")
plt.ylabel("Energy [H]")
plt.title("VQE energy")
plt.show()
counts = []
values = []
with Session(service=service, backend=backend) as session:
options = Options()
options.execution.shots = 2000
options.resilience_level = 0
options.optimization_level = 0
vqe = VQE(Estimator(session=session, options=options),
ansatz, optimizer, callback=store_intermediate_result)
result = vqe.compute_minimum_eigenvalue(qubit_op)
print(result)
session.close()
result_zero=result
values_zero = values
for i in range(len(values)):
values_zero[i] = values[i]-60.66177520599246
counts_zero = counts
#Not to be shown in walkthrough. Just for me to have.
f = open("qasm_spsa_H2O", "w+")
f.write("# optimization_step Energy\n") # column names
numpy.savetxt(f, numpy.array([counts_zero, values_zero]).T)
plt.rcParams["font.size"] = 14
# Plot energy and reference value
plt.figure(figsize=(12, 6))
plt.plot(counts_real, values_real, label='Default')
plt.plot(counts_zero, values_zero, label='Res=0,Opt=0')
plt.axhline(y=-84.206, color="tab:red", ls="--", label="Target")
plt.legend(loc="best")
plt.xlabel("Iteration")
plt.ylabel("Energy [H]")
plt.title("VQE energy")
plt.show()
|
https://github.com/esquivelgor/Quantum-Route-Minimizer
|
esquivelgor
|
# To clean enviroment variables
%reset
import numpy as np
import pandas as pd
import folium
import matplotlib.pyplot as plt
try:
import cplex
from cplex.exceptions import CplexError
except:
print("Warning: Cplex not found.")
import math
from qiskit.utils import algorithm_globals
from qiskit_algorithms import SamplingVQE
from qiskit_algorithms.optimizers import SPSA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Sampler
df = pd.read_csv("uscities.csv")
columnsNeeded = ["city", "lat", "lng"]
# Inicialization of variables
locationsNumber = 15 # OJO que en local me crashea si sobrepaso 5
coordenatesDf = df[columnsNeeded].iloc[:locationsNumber]
n = coordenatesDf.shape[0] # number of nodes + depot (n+1)
K = 3 # number of vehicles
print(coordenatesDf)
# Initialize instance values by calculate the squared Euclidean distances between a set of coordinates
# represented in the dataframe.
def generate_instance(coordenatesDf):
n = coordenatesDf.shape[0]
xc = coordenatesDf["lat"]
yc = coordenatesDf["lng"]
loc = coordenatesDf["city"]
instance = np.zeros([n, n])
for ii in range(0, n):
for jj in range(ii + 1, n):
instance[ii, jj] = (xc[ii] - xc[jj]) ** 2 + (yc[ii] - yc[jj]) ** 2
instance[jj, ii] = instance[ii, jj]
return xc, yc, instance, loc
# Initialize the problem by randomly generating the instance
lat, lng, instance, loc = generate_instance(coordenatesDf)
print(lat, lng, loc, instance)
#print(instance)
class ClassicalOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n # number of nodes
self.K = K # number of vehicles
def compute_allowed_combinations(self):
f = math.factorial
return f(self.n) / f(self.K) / f(self.n - self.K)
def cplex_solution(self):
# refactoring
instance = self.instance
n = self.n
K = self.K
my_obj = list(instance.reshape(1, n**2)[0]) + [0.0 for x in range(0, n - 1)]
my_ub = [1 for x in range(0, n**2 + n - 1)]
my_lb = [0 for x in range(0, n**2)] + [0.1 for x in range(0, n - 1)]
my_ctype = "".join(["I" for x in range(0, n**2)]) + "".join(
["C" for x in range(0, n - 1)]
)
my_rhs = (
2 * ([K] + [1 for x in range(0, n - 1)])
+ [1 - 0.1 for x in range(0, (n - 1) ** 2 - (n - 1))]
+ [0 for x in range(0, n)]
)
my_sense = (
"".join(["E" for x in range(0, 2 * n)])
+ "".join(["L" for x in range(0, (n - 1) ** 2 - (n - 1))])
+ "".join(["E" for x in range(0, n)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + ii, n**2, n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
# Sub-tour elimination constraints:
for ii in range(0, n):
for jj in range(0, n):
if (ii != jj) and (ii * jj > 0):
col = [ii + (jj * n), n**2 + ii - 1, n**2 + jj - 1]
coef = [1, 1, -1]
rows.append([col, coef])
for ii in range(0, n):
col = [(ii) * (n + 1)]
coef = [1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(instance, n, K)
# Print number of feasible solutions
print("Number of feasible solutions = " + str(classical_optimizer.compute_allowed_combinations()))
# Solve the problem in a classical fashion via CPLEX
x = None
z = None
try:
x, classical_cost = classical_optimizer.cplex_solution()
# Put the solution in the z variable
z = [x[ii] for ii in range(n**2) if ii // n != ii % n]
# Print the solution
print(z)
except:
print("CPLEX may be missing.")
m = folium.Map(location=[39.487660, -97.594333], zoom_start=0)
marker_icon1 = folium.Icon(color = "red")
for i in range(len(lat)):
if (i == 0):
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}", icon=marker_icon1).add_to(m)
else:
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}").add_to(m)
for ii in range(0, n**2):
if x[ii] > 0:
ix = ii // n
iy = ii % n
folium.PolyLine([(lat[ix], lng[ix]), (lat[iy], lng[iy])], color="blue").add_to(m)
m
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit.algorithms.minimum_eigensolvers import QAOA, NumPyMinimumEigensolver
class QuantumOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n
self.K = K
def binary_representation(self, x_sol=0):
instance = self.instance
n = self.n
K = self.K
A = np.max(instance) * 100 # A parameter of cost function
# Determine the weights w
instance_vec = instance.reshape(n**2)
w_list = [instance_vec[x] for x in range(n**2) if instance_vec[x] > 0]
w = np.zeros(n * (n - 1))
for ii in range(len(w_list)):
w[ii] = w_list[ii]
# Some variables I will use
Id_n = np.eye(n)
Im_n_1 = np.ones([n - 1, n - 1])
Iv_n_1 = np.ones(n)
Iv_n_1[0] = 0
Iv_n = np.ones(n - 1)
neg_Iv_n_1 = np.ones(n) - Iv_n_1
v = np.zeros([n, n * (n - 1)])
for ii in range(n):
count = ii - 1
for jj in range(n * (n - 1)):
if jj // (n - 1) == ii:
count = ii
if jj // (n - 1) != ii and jj % (n - 1) == count:
v[ii][jj] = 1.0
vn = np.sum(v[1:], axis=0)
# Q defines the interactions between variables
Q = A * (np.kron(Id_n, Im_n_1) + np.dot(v.T, v))
# g defines the contribution from the individual variables
g = (
w
- 2 * A * (np.kron(Iv_n_1, Iv_n) + vn.T)
- 2 * A * K * (np.kron(neg_Iv_n_1, Iv_n) + v[0].T)
)
# c is the constant offset
c = 2 * A * (n - 1) + 2 * A * (K**2)
try:
max(x_sol)
# Evaluates the cost distance from a binary representation of a path
fun = (
lambda x: np.dot(np.around(x), np.dot(Q, np.around(x)))
+ np.dot(g, np.around(x))
+ c
)
cost = fun(x_sol)
except:
cost = 0
return Q, g, c, cost
def construct_problem(self, Q, g, c) -> QuadraticProgram:
qp = QuadraticProgram()
for i in range(n * (n - 1)):
qp.binary_var(str(i))
qp.objective.quadratic = Q
qp.objective.linear = g
qp.objective.constant = c
return qp
def solve_problem(self, qp):
algorithm_globals.random_seed = 10598
#vqe = SamplingVQE(sampler=Sampler(), optimizer=SPSA(), ansatz=RealAmplitudes())
#optimizer = MinimumEigenOptimizer(min_eigen_solver=vqe)
meo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver())
result = meo.solve(qp)
# compute cost of the obtained result
_, _, _, level = self.binary_representation(x_sol=result.x)
return result.x, level
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(instance, n, K)
# Check if the binary representation is correct
try:
if z is not None:
Q, g, c, binary_cost = quantum_optimizer.binary_representation(x_sol=z)
print("Binary cost:", binary_cost, "classical cost:", classical_cost)
if np.abs(binary_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the binary formulation")
else:
print("Could not verify the correctness, due to CPLEX solution being unavailable.")
Q, g, c, binary_cost = quantum_optimizer.binary_representation()
print("Binary cost:", binary_cost)
except NameError as e:
print("Warning: Please run the cells above first.")
print(e)
qp = quantum_optimizer.construct_problem(Q, g, c)
print(qp)
#quantum_solution, quantum_cost = quantum_optimizer.solve_problem(qp)
quantum_solution, quantum_cost = quantum_optimizer.solve_problem(qp)
print(quantum_solution, quantum_cost)
print(classical_cost)
m = folium.Map(location=[39.487660, -97.594333], zoom_start=0)
marker_icon1 = folium.Icon(color = "red")
for i in range(len(lat)):
if (i == 0):
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}", icon=marker_icon1).add_to(m)
else:
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}").add_to(m)
for ii in range(0, n**2):
if x[ii] > 0:
ix = ii // n
iy = ii % n
folium.PolyLine([(lat[ix], lng[ix]), (lat[iy], lng[iy])], color="blue").add_to(m)
m
print(quantum_cost)
x_quantum = np.zeros(n**2)
kk = 0
for ii in range(n**2):
if ii // n != ii % n:
x_quantum[ii] = quantum_solution[kk]
kk += 1
m = folium.Map(location=[39.487660, -97.594333], zoom_start=0)
marker_icon1 = folium.Icon(color = "red")
for i in range(len(lat)):
if (i == 0):
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}", icon=marker_icon1).add_to(m)
else:
folium.Marker(location=[lat[i], lng[i]], tooltip=f"Location: {loc[i]}, Order: {i}").add_to(m)
for ii in range(0, n**2):
if x_quantum[ii] > 0:
ix = ii // n
iy = ii % n
folium.PolyLine([(lat[ix], lng[ix]), (lat[iy], lng[iy])], color="blue").add_to(m)
m
algorithms = ("Classic", "Quantum")
data = {
'K = 1': (2249.2068134000006, 1706.2245994000696),
'k = 2': (2771.940853740001, 1845.127222779207),
'K = 3': (3981.1556002800016, 3981.155600280501),
}
x = np.arange(len(algorithms)) # the label locations
width = 0.25 # the width of the bars
multiplier = 0
fig, ax = plt.subplots(layout='constrained')
for attribute, measurement in data.items():
offset = width * multiplier
rects = ax.bar(x + offset, measurement, width, label=attribute)
ax.bar_label(rects, padding=3)
multiplier += 1
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Length (mm)')
ax.set_title('Comparision of Quantum and Classical Cost')
ax.set_xticks(x + width, algorithms)
ax.legend(loc='upper left', ncols=3)
ax.set_ylim(0, 5000)
plt.show()
|
https://github.com/esquivelgor/Quantum-Route-Minimizer
|
esquivelgor
|
from qiskit import *
from qiskit.visualization import plot_histogram
import numpy as np
def NOT(inp):
"""An NOT gate.
Parameters:
inp (str): Input, encoded in qubit 0.
Returns:
QuantumCircuit: Output NOT circuit.
str: Output value measured from qubit 0.
"""
qc = QuantumCircuit(1, 1) # A quantum circuit with a single qubit and a single classical bit
qc.reset(0)
# We encode '0' as the qubit state |0⟩, and '1' as |1⟩
# Since the qubit is initially |0⟩, we don't need to do anything for an input of '0'
# For an input of '1', we do an x to rotate the |0⟩ to |1⟩
if inp=='1':
qc.x(0)
# barrier between input state and gate operation
qc.barrier()
# Now we've encoded the input, we can do a NOT on it using x
qc.x(0)
#barrier between gate operation and measurement
qc.barrier()
# Finally, we extract the |0⟩/|1⟩ output of the qubit and encode it in the bit c[0]
qc.measure(0,0)
qc.draw()
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp in ['0', '1']:
qc, out = NOT(inp)
print('NOT with input',inp,'gives output',out)
display(qc.draw())
print('\n')
def XOR(inp1,inp2):
"""An XOR gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 1.
"""
qc = QuantumCircuit(2, 1)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
# barrier between input state and gate operation
qc.barrier()
# this is where your program for quantum XOR gate goes
qc.cx(0, 1)
# barrier between input state and gate operation
qc.barrier()
qc.measure(1,0) # output from qubit 1 is measured
#We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
#Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = XOR(inp1, inp2)
print('XOR with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def AND(inp1,inp2):
"""An AND gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum AND gate goes
qc.ccx(0,1,2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('qasm_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc, shots=1, memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = AND(inp1, inp2)
print('AND with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def NAND(inp1,inp2):
"""An NAND gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output NAND circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum NAND gate goes
qc.ccx(0,1,2)
if inp=='1':
qc.x(2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('aer_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc,shots=1,memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = NAND(inp1, inp2)
print('NAND with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
def OR(inp1,inp2):
"""An OR gate.
Parameters:
inpt1 (str): Input 1, encoded in qubit 0.
inpt2 (str): Input 2, encoded in qubit 1.
Returns:
QuantumCircuit: Output XOR circuit.
str: Output value measured from qubit 2.
"""
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
# this is where your program for quantum OR gate goes
qc.cx(0, 2)
qc.cx(1, 2)
qc.barrier()
qc.measure(2, 0) # output from qubit 2 is measured
# We'll run the program on a simulator
backend = Aer.get_backend('aer_simulator')
# Since the output will be deterministic, we can use just a single shot to get it
job = backend.run(qc,shots=1,memory=True)
output = job.result().get_memory()[0]
return qc, output
## Test the function
for inp1 in ['0', '1']:
for inp2 in ['0', '1']:
qc, output = OR(inp1, inp2)
print('OR with inputs',inp1,inp2,'gives output',output)
display(qc.draw())
print('\n')
from qiskit import IBMQ
#IBMQ.save_account("a68a35747d4eccd1d58f275e637909987c789ce5c0edd8a4f43014672bf0301b54b28b1b5f44ba8ff87500777429e1e4ceb79621a6ba248d6cca6bca0e233d23", overwrite=True)
IBMQ.load_account()
IBMQ.providers()
provider = IBMQ.get_provider('ibm-q')
provider.backends()
import qiskit.tools.jupyter
# run this cell
backend = provider.get_backend('ibmq_quito')
qc_and = QuantumCircuit(3)
qc_and.ccx(0,1,2)
print('AND gate')
display(qc_and.draw())
print('\n\nTranspiled AND gate with all the required connectivity')
qc_and.decompose().draw()
from qiskit.tools.monitor import job_monitor
# run the cell to define AND gate for real quantum system
def AND(inp1, inp2, backend, layout):
qc = QuantumCircuit(3, 1)
qc.reset(range(3))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
qc.ccx(0, 1, 2)
qc.barrier()
qc.measure(2, 0)
qc_trans = transpile(qc, backend, initial_layout=layout, optimization_level=3)
job = backend.run(qc_trans, shots=8192)
print(job.job_id())
job_monitor(job)
output = job.result().get_counts()
return qc_trans, output
backend
layout = [0, 1, 2]
output_all = []
qc_trans_all = []
prob_all = []
worst = 1
best = 0
for input1 in ['0','1']:
for input2 in ['0','1']:
qc_trans, output = AND(input1, input2, backend, layout)
output_all.append(output)
qc_trans_all.append(qc_trans)
prob = output[str(int( input1=='1' and input2=='1' ))]/8192
prob_all.append(prob)
print('\nProbability of correct answer for inputs',input1,input2)
print('{:.2f}'.format(prob) )
print('---------------------------------')
worst = min(worst,prob)
best = max(best, prob)
print('')
print('\nThe highest of these probabilities was {:.2f}'.format(best))
print('The lowest of these probabilities was {:.2f}'.format(worst))
print('Transpiled AND gate circuit for ibmq_vigo with input 0 0')
print('\nThe circuit depth : {}'.format (qc_trans_all[0].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[0].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[0]) )
qc_trans_all[0].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 0 1')
print('\nThe circuit depth : {}'.format (qc_trans_all[1].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[1].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[1]) )
qc_trans_all[1].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 1 0')
print('\nThe circuit depth : {}'.format (qc_trans_all[2].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[2].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[2]) )
qc_trans_all[2].draw()
print('Transpiled AND gate circuit for ibmq_vigo with input 1 1')
print('\nThe circuit depth : {}'.format (qc_trans_all[3].depth()))
print('# of nonlocal gates : {}'.format (qc_trans_all[3].num_nonlocal_gates()))
print('Probability of correct answer : {:.2f}'.format(prob_all[3]) )
qc_trans_all[3].draw()
|
https://github.com/esquivelgor/Quantum-Route-Minimizer
|
esquivelgor
|
import numpy as np
# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, execute
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from qiskit.providers.aer import QasmSimulator
backend = Aer.get_backend('statevector_simulator')
qc1 = QuantumCircuit(4)
# perform gate operations on individual qubits
qc1.x(0)
qc1.y(1)
qc1.z(2)
qc1.s(3)
# Draw circuit
qc1.draw()
# Plot blochshere
out1 = execute(qc1,backend).result().get_statevector()
plot_bloch_multivector(out1)
qc2 = QuantumCircuit(4)
# initialize qubits
qc2.x(range(4))
# perform gate operations on individual qubits
qc2.x(0)
qc2.y(1)
qc2.z(2)
qc2.s(3)
# Draw circuit
qc2.draw()
# Plot blochshere
out2 = execute(qc2,backend).result().get_statevector()
plot_bloch_multivector(out2)
qc3 = QuantumCircuit(4)
# initialize qubits
qc3.h(range(4))
# perform gate operations on individual qubits
qc3.x(0)
qc3.y(1)
qc3.z(2)
qc3.s(3)
# Draw circuit
qc3.draw()
# Plot blochshere
out3 = execute(qc3,backend).result().get_statevector()
plot_bloch_multivector(out3)
qc4 = QuantumCircuit(4)
# initialize qubits
qc4.x(range(4))
qc4.h(range(4))
# perform gate operations on individual qubits
qc4.x(0)
qc4.y(1)
qc4.z(2)
qc4.s(3)
# Draw circuit
qc4.draw()
# Plot blochshere
out4 = execute(qc4,backend).result().get_statevector()
plot_bloch_multivector(out4)
qc5 = QuantumCircuit(4)
# initialize qubits
qc5.h(range(4))
qc5.s(range(4))
# perform gate operations on individual qubits
qc5.x(0)
qc5.y(1)
qc5.z(2)
qc5.s(3)
# Draw circuit
qc5.draw()
# Plot blochshere
out5 = execute(qc5,backend).result().get_statevector()
plot_bloch_multivector(out5)
qc6 = QuantumCircuit(4)
# initialize qubits
qc6.x(range(4))
qc6.h(range(4))
qc6.s(range(4))
# perform gate operations on individual qubits
qc6.x(0)
qc6.y(1)
qc6.z(2)
qc6.s(3)
# Draw circuit
qc6.draw()
# Plot blochshere
out6 = execute(qc6,backend).result().get_statevector()
plot_bloch_multivector(out6)
import qiskit
qiskit.__qiskit_version__
|
https://github.com/esquivelgor/Quantum-Route-Minimizer
|
esquivelgor
|
from qiskit import *
import numpy as np
from numpy import linalg as la
from qiskit.tools.monitor import job_monitor
import qiskit.tools.jupyter
qc = QuantumCircuit(1)
#### your code goes here
# z measurement of qubit 0
measure_z = QuantumCircuit(1,1)
measure_z.measure(0,0)
# x measurement of qubit 0
measure_x = QuantumCircuit(1,1)
# your code goes here
# y measurement of qubit 0
measure_y = QuantumCircuit(1,1)
# your code goes here
shots = 2**14 # number of samples used for statistics
sim = Aer.get_backend('qasm_simulator')
bloch_vector_measure = []
for measure_circuit in [measure_x, measure_y, measure_z]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
counts = execute(qc+measure_circuit, sim, shots=shots).result().get_counts()
# calculate the probabilities for each bit value
probs = {}
for output in ['0','1']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
bloch_vector_measure.append( probs['0'] - probs['1'] )
# normalizing the bloch sphere vector
bloch_vector = bloch_vector_measure/la.norm(bloch_vector_measure)
print('The bloch sphere coordinates are [{0:4.3f}, {1:4.3f}, {2:4.3f}]'
.format(*bloch_vector))
from kaleidoscope.interactive import bloch_sphere
bloch_sphere(bloch_vector, vectors_annotation=True)
from qiskit.visualization import plot_bloch_vector
plot_bloch_vector( bloch_vector )
# circuit for the state Tri1
Tri1 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri2
Tri2 = QuantumCircuit(2)
# your code goes here
# circuit for the state Tri3
Tri3 = QuantumCircuit(2)
# your code goes here
# circuit for the state Sing
Sing = QuantumCircuit(2)
# your code goes here
# <ZZ>
measure_ZZ = QuantumCircuit(2)
measure_ZZ.measure_all()
# <XX>
measure_XX = QuantumCircuit(2)
# your code goes here
# <YY>
measure_YY = QuantumCircuit(2)
# your code goes here
shots = 2**14 # number of samples used for statistics
A = 1.47e-6 #unit of A is eV
E_sim = []
for state_init in [Tri1,Tri2,Tri3,Sing]:
Energy_meas = []
for measure_circuit in [measure_XX, measure_YY, measure_ZZ]:
# run the circuit with a the selected measurement and get the number of samples that output each bit value
qc = state_init+measure_circuit
counts = execute(qc, sim, shots=shots).result().get_counts()
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E_sim.append(A * np.sum(np.array(Energy_meas)))
# Run this cell to print out your results
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_sim[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_sim[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_sim[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_sim[3]))
# reduced plank constant in (eV) and the speed of light(cgs units)
hbar, c = 4.1357e-15, 3e10
# energy difference between the triplets and singlet
E_del = abs(E_sim[0] - E_sim[3])
# frequency associated with the energy difference
f = E_del/hbar
# convert frequency to wavelength in (cm)
wavelength = c/f
print('The wavelength of the radiation from the transition\
in the hyperfine structure is : {:.1f} cm'.format(wavelength))
provider = IBMQ.load_account()
backend = provider.get_backend('ibmq_athens')
# run this cell to get the backend information through the widget
backend
# assign your choice for the initial layout to the list variable `initial_layout`.
initial_layout =
qc_all = [state_init+measure_circuit for state_init in [Tri1,Tri2,Tri3,Sing]
for measure_circuit in [measure_XX, measure_YY, measure_ZZ] ]
shots = 8192
job = execute(qc_all, backend, initial_layout=initial_layout, optimization_level=3, shots=shots)
print(job.job_id())
job_monitor(job)
# getting the results of your job
results = job.result()
## To access the results of the completed job
#results = backend.retrieve_job('job_id').result()
def Energy(results, shots):
"""Compute the energy levels of the hydrogen ground state.
Parameters:
results (obj): results, results from executing the circuits for measuring a hamiltonian.
shots (int): shots, number of shots used for the circuit execution.
Returns:
Energy (list): energy values of the four different hydrogen ground states
"""
E = []
A = 1.47e-6
for ind_state in range(4):
Energy_meas = []
for ind_comp in range(3):
counts = results.get_counts(ind_state*3+ind_comp)
# calculate the probabilities for each computational basis
probs = {}
for output in ['00','01', '10', '11']:
if output in counts:
probs[output] = counts[output]/shots
else:
probs[output] = 0
Energy_meas.append( probs['00'] - probs['01'] - probs['10'] + probs['11'] )
E.append(A * np.sum(np.array(Energy_meas)))
return E
E = Energy(results, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E[3]))
from qiskit.ignis.mitigation.measurement import *
# your code to create the circuits, meas_calibs, goes here
meas_calibs, state_labels =
# execute meas_calibs on your choice of the backend
job = execute(meas_calibs, backend, shots = shots)
print(job.job_id())
job_monitor(job)
cal_results = job.result()
## To access the results of the completed job
#cal_results = backend.retrieve_job('job_id').result()
# your code to obtain the measurement filter object, 'meas_filter', goes here
results_new = meas_filter.apply(results)
E_new = Energy(results_new, shots)
print('Energy expection value of the state Tri1 : {:.3e} eV'.format(E_new[0]))
print('Energy expection value of the state Tri2 : {:.3e} eV'.format(E_new[1]))
print('Energy expection value of the state Tri3 : {:.3e} eV'.format(E_new[2]))
print('Energy expection value of the state Sing : {:.3e} eV'.format(E_new[3]))
# results for the energy estimation from the simulation,
# execution on a quantum system without error mitigation and
# with error mitigation in numpy array format
Energy_exact, Energy_exp_orig, Energy_exp_new = np.array(E_sim), np.array(E), np.array(E_new)
# Calculate the relative errors of the energy values without error mitigation
# and assign to the numpy array variable `Err_rel_orig` of size 4
Err_rel_orig =
# Calculate the relative errors of the energy values with error mitigation
# and assign to the numpy array variable `Err_rel_new` of size 4
Err_rel_new =
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
without measurement error mitigation : {}'.format(Err_rel_orig))
np.set_printoptions(precision=3)
print('The relative errors of the energy values for four bell basis\
with measurement error mitigation : {}'.format(Err_rel_new))
|
https://github.com/esquivelgor/Quantum-Route-Minimizer
|
esquivelgor
|
# Importing standard Qiskit libraries
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import Aer, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector, plot_state_qsphere, plot_state_city, plot_state_paulivec, plot_state_hinton
# Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Define backend
sim = Aer.get_backend('aer_simulator')
def createBellStates(inp1, inp2):
qc = QuantumCircuit(2)
qc.reset(range(2))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
qc, state, result = createBellStates(inp1, inp2)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp2 in ['0', '1']:
#for inp1 in ['0', '1']:
#qc, state, result = createBellStates(inp1, inp2)
#print('For inputs',inp2,inp1,'Representation of Entangled States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')'''
from qiskit import IBMQ, execute
from qiskit.providers.ibmq import least_busy
from qiskit.tools import job_monitor
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 2
and not x.configuration().simulator
and x.status().operational==True))
def createBSRealDevice(inp1, inp2):
qr = QuantumRegister(2)
cr = ClassicalRegister(2)
qc = QuantumCircuit(qr, cr)
qc.reset(range(2))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=100)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
print('For inputs',inp2,inp1,'Representation of Entangled States are,')
#first results
qc, first_result = createBSRealDevice(inp1, inp2)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = createBSRealDevice(inp1, inp2)
second_counts = second_result.get_counts()
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
def ghzCircuit(inp1, inp2, inp3):
qc = QuantumCircuit(3)
qc.reset(range(3))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
print('Note: Since these qubits are in entangled state, their state cannot be written as two separate qubit states. This also means that we lose information when we try to plot our state on separate Bloch spheres as seen below.\n')
inp1 = 0
inp2 = 1
inp3 = 1
qc, state, result = ghzCircuit(inp1, inp2, inp3)
display(plot_bloch_multivector(state))
# Uncomment below code in order to explore other states
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghzCircuit(inp1, inp2, inp3)
#print('For inputs',inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
def ghz5QCircuit(inp1, inp2, inp3, inp4, inp5):
qc = QuantumCircuit(5)
#qc.reset(range(5))
if inp1 == 1:
qc.x(0)
if inp2 == 1:
qc.x(1)
if inp3 == 1:
qc.x(2)
if inp4 == 1:
qc.x(3)
if inp5 == 1:
qc.x(4)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.save_statevector()
qobj = assemble(qc)
result = sim.run(qobj).result()
state = result.get_statevector()
return qc, state, result
# Explore GHZ States for input 00010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 0
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 11001. Note: the input has been stated in little-endian format.
inp1 = 1
inp2 = 0
inp3 = 0
inp4 = 1
inp5 = 1
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Explore GHZ States for input 01010. Note: the input has been stated in little-endian format.
inp1 = 0
inp2 = 1
inp3 = 0
inp4 = 1
inp5 = 0
qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
display(plot_state_qsphere(state))
print('\n')
# Uncomment below code in order to explore other states
#for inp5 in ['0','1']:
#for inp4 in ['0','1']:
#for inp3 in ['0','1']:
#for inp2 in ['0','1']:
#for inp1 in ['0','1']:
#qc, state, result = ghz5QCircuit(inp1, inp2, inp3, inp4, inp5)
#print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ States are:')
# Uncomment any of the below functions to visualize the resulting quantum states
# Draw the quantum circuit
#display(qc.draw())
# Plot states on QSphere
#display(plot_state_qsphere(state))
# Plot states on Bloch Multivector
#display(plot_bloch_multivector(state))
# Plot histogram
#display(plot_histogram(result.get_counts()))
# Plot state matrix like a city
#display(plot_state_city(state))
# Represent state matix using Pauli operators as the basis
#display(plot_state_paulivec(state))
# Plot state matrix as Hinton representation
#display(plot_state_hinton(state))
#print('\n')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 5
and not x.configuration().simulator
and x.status().operational==True))
def create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5):
qr = QuantumRegister(5)
cr = ClassicalRegister(5)
qc = QuantumCircuit(qr, cr)
qc.reset(range(5))
if inp1=='1':
qc.x(0)
if inp2=='1':
qc.x(1)
if inp3=='1':
qc.x(1)
if inp4=='1':
qc.x(1)
if inp5=='1':
qc.x(1)
qc.barrier()
qc.h(0)
qc.cx(0,1)
qc.cx(0,2)
qc.cx(0,3)
qc.cx(0,4)
qc.measure(qr, cr)
job = execute(qc, backend=backend, shots=1000)
job_monitor(job)
result = job.result()
return qc, result
inp1 = 0
inp2 = 0
inp3 = 0
inp4 = 0
inp5 = 0
#first results
qc, first_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
first_counts = first_result.get_counts()
# Draw the quantum circuit
display(qc.draw())
#second results
qc, second_result = create5QGHZRealDevice(inp1, inp2, inp3, inp4, inp5)
second_counts = second_result.get_counts()
print('For inputs',inp5,inp4,inp3,inp2,inp1,'Representation of GHZ circuit states are,')
# Plot results on histogram with legend
legend = ['First execution', 'Second execution']
plot_histogram([first_counts, second_counts], legend=legend)
import qiskit
qiskit.__qiskit_version__
|
https://github.com/dukeskardashian/encryptedConnQ
|
dukeskardashian
|
from qiskit import QuantumCircuit, Aer, execute
# Erstellen eines Quanten-Schaltkreises
qc = QuantumCircuit(2, 2)
qc.h(0)
qc.cx(0, 1)
# Simulation der Quantenverschlüsselung
simulator = Aer.get_backend('qasm_simulator')
job = execute(qc, simulator, shots=1)
result = job.result()
counts = result.get_counts(qc)
# Ausgabe der verschlüsselten Bits
print('Ergebnis:', counts)
#Allgemeines Beispiel für den Aufbau einer verschlüsselten Verbindung mit einer
#simulierten Quantenverschlüsselung unter Verwendung des Qiskit-Frameworks von IBM Quantum.
|
https://github.com/danielzoch/QPEHashing
|
danielzoch
|
!pip install qiskit_ibm_provider
!pip install pylatexenc
!pip install qiskit
!pip install qiskit-ibmq-provider
from qiskit import QuantumCircuit, transpile, assemble
from qiskit.visualization import plot_histogram
from qiskit.providers.ibmq import least_busy, IBMQ
import numpy as np
# Function to create controlled addition gate
def cadd(a, N):
U = QuantumCircuit(3, name=f'cadd_{a}')
for _ in range(a):
U.x(0)
U.mcx([0, 1], 2)
U.x(0)
return U
# Function to create inverse Quantum Fourier Transform gate
def qft_dagger(n):
qc = QuantumCircuit(n)
for qubit in range(n//2):
qc.swap(qubit, n-qubit-1)
for j in range(n):
for m in range(j):
qc.cp(-np.pi/float(2**(j-m)), m, j)
qc.h(j)
qc.name = "QFT†"
return qc
def qpe_circuit(a, exponent, N, precision):
# Quantum registers
n_count = len(bin(N)[2:]) # Number of bits to represent N in binary
qr = QuantumCircuit(n_count + precision + 1, precision)
# Apply Hadamard gate to counting qubits
qr.h(range(n_count + precision))
# Prepare counting qubits in state |1>
qr.x(n_count + precision)
# Controlled-U operations
for q in range(precision):
cu_gate = cadd(2**(n_count - 1), N)
qr.append(cu_gate, [i for i in range(3)]) # Use only the first 3 qubits
# Inverse QFT
qr.append(qft_dagger(n_count + precision),
[i for i in range(n_count + precision)]) # Do inverse QFT
# Measure counting qubits
qr.measure(range(n_count, n_count + precision), range(precision))
# Run on IBM Quantum device
backend = get_backend()
result = run_on_ibmq(qr, backend)
# Extract counts of the first register
first_register_counts = {key[:n_count]: val for key, val in result.items()}
return first_register_counts, result
# Function to get the least busy IBM Quantum device
def get_backend():
IBMQ.save_account("ENTER_API_KEY_HERE", overwrite=True)
# Load IBM Quantum account
IBMQ.load_account()
# Get the least busy IBM Quantum device
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 3
and not x.configuration().simulator
and x.status().operational==True))
return backend
# Function to run the circuit on an IBM Quantum device
def run_on_ibmq(qc, backend):
t_qpe = transpile(qc, backend, optimization_level=3)
qpe_circuit_instance = assemble(t_qpe)
result = backend.run(qpe_circuit_instance, shots=1).result()
counts = result.get_counts()
return counts
a = 2
exponent = 3
N = 15
precision = 6 # Precision for Quantum Phase Estimation
# Run the quantum circuit
results = {}
first_register_counts, all_counts = qpe_circuit(a, exponent, N, precision)
# Plot histogram for the first register counts
plot_histogram(first_register_counts, title='Measurement Histogram - ibmq', bar_labels=True, figsize=(10, 6), color='skyblue')
# Print out the results of the first register
sorted_dict = dict(sorted(first_register_counts.items()))
print("Results of the First Register:")
for key, value in sorted_dict.items():
print(f"{key}: {value}")
import hashlib
def quantum_hash(qpe_results):
# Combine quantum results into a classical hash
hash_value = 0
for result in qpe_results:
# Assuming qpe_results are 0 or 1, XOR them into the hash_value
hash_value ^= result
return hash_value
def sha2_hash(message):
# Use SHA-256 from Python's hashlib library
sha2 = hashlib.sha256()
sha2.update(message.encode())
return sha2.hexdigest()
def hybrid_hash(qpe_results, message):
# Combine quantum and classical hashes
quantum_part = quantum_hash(qpe_results)
classical_part = sha2_hash(message)
# XOR the quantum and classical hashes
hybrid_result = quantum_part ^ int(classical_part, 16)
# Convert the result to hexadecimal for representation
hex_result = hex(hybrid_result)[2:]
return hex_result
# Example QPE results (replace this with your actual QPE results)
qpe_results = [int(bit) for bit in list(first_register_counts.keys())[0]]
# Example message to hash
message = "Hello, Quantum World!"
# Generate hybrid hash
hybrid_result = hybrid_hash(qpe_results, message)
# Output the hybrid hash result
print("Hybrid Hash Value: " + hybrid_result)
|
https://github.com/allanwing-qc/DTQW_General_Coin
|
allanwing-qc
|
#pip install qiskit
#pip install qiskit[visualization]
import qiskit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, Aer
from qiskit.circuit.library import MCMT
from qiskit.circuit.library import MCMTVChain
from qiskit.circuit.library import SXdgGate
from qiskit.quantum_info.operators import Operator, Pauli
import qiskit.quantum_info as qi
import numpy as np
import math as m
from qiskit import *
from qiskit import Aer
qreg = qiskit.QuantumRegister(4)
creg = qiskit.ClassicalRegister(2)
circuit = qiskit.QuantumCircuit(qreg,creg)
n_steps=1
for i in range(n_steps):
circuit.h(2)
circuit.h(3)
circuit.cx(3,1)
circuit.cx(2,0)
circuit.measure(0,0)
circuit.measure(1,1)
circuit.draw('mpl')
#Changing the simulator
sim = qiskit.Aer.get_backend('qasm_simulator')
#job execution and getting the result as an object
job = execute(circuit, sim,shots=100000)
result = job.result()
counts = job.result().get_counts()
factor=1.0/sum(counts.values())
probabilities1 = {k: v*factor for k, v in counts.items()}
qiskit.visualization.plot_histogram(probabilities1)
q = QuantumRegister(4)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)
csxdg_gate = SXdgGate().control(2)
for i in range(n_steps):
qc.x(0)
qc.x(1)
qc.append(csxdg_gate, [0,1,2])
qc.append(csxdg_gate, [0,1,3])
qc.x(0)
qc.x(1)
qc.x(0)
qc.append(MCMT('h',2,2), list(range(4)))
qc.x(0)
qc.x(1)
qc.append(csxdg_gate, [0,1,2])
qc.append(csxdg_gate, [0,1,3])
qc.x(1)
qc.append(MCMT('h',2,2), list(range(4)))
qc.cx(3,1)
qc.cx(2,0)
qc.measure(q[0],c[0])
qc.measure(q[1],c[1])
qc.draw('mpl')
#Changing the simulator
sim = qiskit.Aer.get_backend('qasm_simulator')
#job execution and getting the result as an object
job = execute(qc, sim,shots=100000)
result = job.result()
counts = job.result().get_counts()
factor=1.0/sum(counts.values())
probabilities2 = {k: v*factor for k, v in counts.items()}
qiskit.visualization.plot_histogram(probabilities2)
legend = ['Hadamard coin', 'General coin']
qiskit.visualization.plot_histogram([probabilities1, probabilities2], color=['midnightblue','crimson'],
title="Step 6")
|
https://github.com/ALI3Nass/X-Circuit-with-Statevector-and-Unitary-Gate
|
ALI3Nass
|
# Qiskit Example: Basic Quantum Circuit Simulation
## Importing Required Libraries
from qiskit import QuantumCircuit, Aer, execute
from qiskit.tools.visualization import plot_bloch_multivector, plot_histogram
from qiskit.quantum_info import Operator
# Create a quantum circuit with 1 qubit and 1 classical bit
circuit = QuantumCircuit(1, 1)
# Apply X gate to the qubit
circuit.x(0)
# Draw the circuit
circuit.draw('mpl')
# Simulate the circuit and obtain the statevector
simulator = Aer.get_backend('statevector_simulator')
result = execute(circuit, backend=simulator).result()
statevector = result.get_statevector()
# Print the statevector
print(statevector)
# Plot the Bloch vector
plot_bloch_multivector(statevector)
# Measure the qubit and obtain the counts
circuit.measure([0], [0])
backend = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend=backend, shots=1024).result()
counts = result.get_counts()
# Plot the histogram of counts
plot_histogram(counts)
circuit = QuantumCircuit(1,1)
circuit.x(0)
simulator = Aer.get_backend('unitary_simulator')
result = execute(circuit, backend = simulator).result()
unitary = result.get_unitary()
print(unitary)
circuit.draw()
|
https://github.com/rubenandrebarreiro/fct-nova-introduction-to-operations-research-labs
|
rubenandrebarreiro
|
# Import Scipy Python's Library and,
# its Optimisation Module and Linear Programming Sub-Module
from scipy.optimize import linprog
# Import the NumPy Python's Library, with the alias 'np'
import numpy as np
# Import the matplotlib Python's Library, with the alias 'plt'
import matplotlib.pyplot as plt
%matplotlib inline
# Construct Graphic Lines
# Steps for Implementation in Python:
# - 1) Set the Lines for the Bounds, as equalities:
# - The variable x is set indenpendindependently;
# - The variable y is set as one of yi's, in this case the y0;
# - 2) Set the Lines for the Constraints, as equalities:
# - All the equations always are solvable, in order to yi;
# - 3) Build the Graphic and Plot the Lines;
# - 4) Fill the Feasible Region:
# - Set the Maximum and Minimum of the Feasible Region,
# where, usually the inequations with '>=' are the maximums
# and the inequations with '<=' are the minimums;
# - Then, fill the Feasible Region;
# 1) Set the Lines for the Bounds, as equalities:
# a) x >= 0
x = np.linspace(0, 20, 2000)
# b) y >= 0
y0 = (x*0)
# 2) Set the Lines for the Constraints, as equalities:
# a) x + y <= 3 (=) y <= 3 - x
y1 = ( 3 - x )
# b) x + 4y >= 4 (=) 4y >= 4 - x (=) y >= (4 - x) / 4
y2 = ( 4 - x ) / 4
# c) -x + y <= 0 (=) y <= x
y3 = x
# 3) Build the Graphic and Plot the Lines:
plt.plot(x, y0, label=r'$ y \geq 0 $')
plt.plot(x, y1, label=r'$ x + y \leq 3 $')
plt.plot(x, y2, label=r'$ x + 4y \geq 4 $')
plt.plot(x, y3, label=r'$ -x + y \leq 0 $')
plt.xlim((0, 4.5))
plt.ylim((0, 4.5))
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
# 4) Fill the Feasible Region:
y4 = np.minimum(y1, y3)
y5 = np.maximum(y0, y2)
plt.fill_between(x, y4, y5, where=y4>y5, color='grey', alpha=0.5)
# Extras:
# - Add a Title to the Graphic Plot:
plt.title('Feasible Region for Exercise 1')
# - Add a Legend to the Graphic Plot:
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.0)
# - Adjust the size of the Graphic Plot:
plt.figure(figsize=(80,80))
# - Save the Graphic Plot, in PNG format:
#plt.savefig('exercise-1.png')
##### Extra: Building the Linear Programming Model
objective_function = [-1, -2]
# ─┬ ─┬
# │ └┤ Coefficient for y
# └────┤ Coefficient for x
constraints_inequalities = [ [ 1 , 1 ], # Constraint #1
[ 1 , 4 ], # Constraint #2
[ -1 , 1 ] ] # Constraint #3
constraints_function_values = [ 3, # Function Value for Constraint #1
4, # Function Value for Constraint #2
0 ] # Function Value for Constraint #3
variable_bounds = [ (0, float("inf")), # Bounds of x
(0, float("inf")) ] # Bounds of y
optimization_problem = linprog(c=objective_function,
A_ub=constraints_inequalities,
b_ub = constraints_function_values,
bounds=variable_bounds,
method="revised simplex")
optimization_problem
optimization_problem.fun
optimization_problem.success
optimization_problem.x
|
https://github.com/moaz-aljohani/HelloQuantum
|
moaz-aljohani
|
#---------------------1-------------------------
from qiskit import QuantumCircuit as qubit # Import QuantumCircuit class from qiskit library as qubit
qc = qubit(2) # Create a quantum circuit with 2 qubits
qc.h(0) # Apply a Hadamard gate to the first qubit (qubit 0), putting it in a superposition state
qc.cx(0, 1) # Apply a CNOT gate with the first qubit (qubit 0) as control and the second qubit (qubit 1) as target, entangling them
qc.draw(output="mpl") # Draw the circuit diagram using matplotlib (mpl)
#---------------------2-------------------------
from qiskit.quantum_info import Pauli # Import Pauli class from qiskit library for Pauli operators
from qiskit_aer.primitives import Estimator # Import Estimator class from qiskit library for estimating expectation values
ZZ = Pauli("ZZ") # Define a Pauli operator ZZ
ZI = Pauli("ZI") # Define a Pauli operator ZI
IZ = Pauli("IZ") # Define a Pauli operator IZ
XX = Pauli("XX") # Define a Pauli operator XX
XI = Pauli("XI") # Define a Pauli operator XI
IX = Pauli("IX") # Define a Pauli operator IX
observable = [ZZ, ZI, IZ, XX, XI, IX] # List of observables (tensor products of Pauli operators)
estimator = Estimator() # Initialize an Estimator to calculate expectation values
job = estimator.run([qc] * len(observable), observable) # Run the estimator on the quantum circuit for each observable
print(job.result()) # Print the result of the estimation
#---------------------3-------------------------
import matplotlib.pyplot as plt # Import pyplot class from matplotlib library for plotting
data = ["ZZ", "ZI", "IZ", "XX", "XI", "IX"] # List of observables as strings
values = job.result().values # Get the expectation values from the job result
plt.plot(data, values, '-o') # Plot the data with expectation values
plt.xlabel("Observables") # Set the label for the x-axis
plt.ylabel("Expectation value") # Set the label for the y-axis
plt.show() # Show the plot
#---------------------4-------------------------
def QcforNQubits(n: int): # Define a function that creates a quantum circuit with n qubits
qc = qubit(n) # Initialize a quantum circuit with n qubits
qc.h(0) # Apply a Hadamard gate to the first qubit (qubit 0)
for i in range(n - 1): # Loop through qubits from 0 to n-1
qc.cx(i, i + 1) # Apply a CNOT gate between each qubit and the next one
return qc # Return the created quantum circuit
n = 10 # Number of qubits for the new circuit
qc = QcforNQubits(n) # Create a quantum circuit with 10 qubits
qc.draw(output="mpl") # Draw the circuit diagram using matplotlib (mpl)
#---------------------5-------------------------
from qiskit.quantum_info import SparsePauliOp # Import SparsePauliOp class from qiskit library for sparse Pauli operators
operatorStrings = ["Z" + "I" * i + "Z" + "I" * (n - 2 - i) for i in range(n - 1)] # Create operator strings for ZZ measurements at different distances
operators = [SparsePauliOp(operatorString) for operatorString in operatorStrings] # Convert operator strings to SparsePauliOp objects
print(operatorStrings)
#---------------------6-------------------------
from qiskit_ibm_runtime import QiskitRuntimeService # Import QiskitRuntimeService class for accessing IBM's quantum services
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager # Import function to generate preset pass managers
from qiskit_ibm_runtime import EstimatorV2 # Import EstimatorV2 class for estimating expectation values using IBM runtime
from qiskit_ibm_runtime import EstimatorOptions # Import EstimatorOptions class for configuring the EstimatorV2
backendName = "ibm_brisbane" # Define the name of the backend to use
# Initialize the IBM Quantum service with the provided API token and channel
backend = QiskitRuntimeService(token="API_TOKEN", channel="ibm_quantum").backend(backendName)
# Generate a preset pass manager for circuit optimization
passManager = generate_preset_pass_manager(optimization_level=1, backend=backend)
qcTranspiled = passManager.run(qc) # Transpile the quantum circuit for the backend
operatorsTranspiledList = [op.apply_layout(qcTranspiled.layout) for op in operators] # Apply the layout to each operator
options = EstimatorOptions() # Initialize Estimator options
options.resilience_level = 1 # Set resilience level to 1
options.optimization_level = 0 # Set optimization level to 0
options.dynamical_decoupling.enable = True # Enable dynamical decoupling
options.dynamical_decoupling.sequence_type = "XY4" # Set dynamical decoupling sequence type to XY4
estimatorv2 = EstimatorV2(backend, options=options) # Initialize EstimatorV2 with the backend and options
job = estimatorv2.run([(qcTranspiled, operatorsTranspiledList)]) # Run the estimator job with the transpiled circuit and operators
|
https://github.com/udayapeddirajub/Grovers-Algorithm-Implementation-on-3-qubit-database
|
udayapeddirajub
|
import numpy as np
# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, IBMQ
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from ibm_quantum_widgets import *
from qiskit.providers.aer import QasmSimulator
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
from qiskit.circuit.library.standard_gates import XGate, HGate
from operator import *
n = 3
N = 8 #2**n
index_colour_table = {}
colour_hash_map = {}
index_colour_table = {'000':"yellow", '001':"red", '010':"blue", '011':"red", '100':"green", '101':"blue", '110':"orange", '111':"red"}
colour_hash_map = {"yellow":'100', "red":'011', "blue":'000', "green":'001', "orange":'010'}
def database_oracle(index_colour_table, colour_hash_map):
circ_database = QuantumCircuit(n + n)
for i in range(N):
circ_data = QuantumCircuit(n)
idx = bin(i)[2:].zfill(n) # removing the "0b" prefix appended by the bin() funtion
colour = index_colour_table[idx]
colour_hash = colour_hash_map[colour][::-1]
for j in range(n):
if colour_hash[j] == '1':
circ_data.x(j)
# qiskit maps the rightmost bit as the 0th qubit -> qn, ..., q0
# we therefore reverse the index string -> q0, ..., qn
data_gate = circ_data.to_gate(label=colour).control(num_ctrl_qubits=n, ctrl_state=idx, label="index-"+colour)
circ_database.append(data_gate, list(range(n+n)))
return circ_database
# drawing the database oracle circuit
print("Database Encoding")
database_oracle(index_colour_table, colour_hash_map).draw()
circ_data = QuantumCircuit(n)
m = 4
idx = bin(m)[2:].zfill(n) # removing the "0b" prefix appended by the bin() funtion
colour = index_colour_table[idx]
colour_hash = colour_hash_map[colour][::-1]
for j in range(n):
if colour_hash[j] == '1':
circ_data.x(j)
print("Internal colour encoding for the colour green (as an example)");
circ_data.draw()
def oracle_grover(database, data_entry):
circ_grover = QuantumCircuit(n + n + 1)
circ_grover.append(database, list(range(n+n)))
target_reflection_gate = XGate().control(num_ctrl_qubits=n, ctrl_state=colour_hash_map[data_entry], label="Reflection of " + "\"" + data_entry + "\" Target")
# control() missing 1 required positional argument: 'self' .... if only 'XGate' used instead of 'XGate()'
# The “missing 1 required positional argument: 'self'” error is raised when you do not instantiate an object of a class before calling a class method. This error is also raised when you incorrectly instantiate a class.
circ_grover.append(target_reflection_gate, list(range(n, n+n+1)))
circ_grover.append(database, list(range(n+n)))
return circ_grover
print("Grover Oracle (target example: orange)")
oracle_grover(database_oracle(index_colour_table, colour_hash_map).to_gate(label="Database Encoding"), "orange").decompose().draw()
def mcz_gate(num_qubits):
num_controls = num_qubits - 1
mcz_gate = QuantumCircuit(num_qubits)
target_mcz = QuantumCircuit(1)
target_mcz.z(0)
target_mcz = target_mcz.to_gate(label="Z_Gate").control(num_ctrl_qubits=num_controls, ctrl_state=None, label="MCZ")
mcz_gate.append(target_mcz, list(range(num_qubits)))
return mcz_gate.reverse_bits()
print("Multi-controlled Z (MCZ) Gate")
mcz_gate(n).decompose().draw()
def diffusion_operator(num_qubits):
circ_diffusion = QuantumCircuit(num_qubits)
qubits_list = list(range(num_qubits))
# Layer of H^n gates
circ_diffusion.h(qubits_list)
# Layer of X^n gates
circ_diffusion.x(qubits_list)
# Layer of Multi-controlled Z (MCZ) Gate
circ_diffusion = circ_diffusion.compose(mcz_gate(num_qubits), qubits_list)
# Layer of X^n gates
circ_diffusion.x(qubits_list)
# Layer of H^n gates
circ_diffusion.h(qubits_list)
return circ_diffusion
print("Diffusion Circuit")
diffusion_operator(n).draw()
# Putting it all together ... !!!
item = "green"
print("Searching for the index of the colour", item)
circuit = QuantumCircuit(n + n + 1, n)
circuit.x(n + n)
circuit.barrier()
circuit.h(list(range(n)))
circuit.h(n+n)
circuit.barrier()
unitary_oracle = oracle_grover(database_oracle(index_colour_table, colour_hash_map).to_gate(label="Database Encoding"), item).to_gate(label="Oracle Operator")
unitary_diffuser = diffusion_operator(n).to_gate(label="Diffusion Operator")
M = countOf(index_colour_table.values(), item)
Q = int(np.pi * np.sqrt(N/M) / 4)
for i in range(Q):
circuit.append(unitary_oracle, list(range(n + n + 1)))
circuit.append(unitary_diffuser, list(range(n)))
circuit.barrier()
circuit.measure(list(range(n)), list(range(n)))
circuit.draw()
backend_sim = Aer.get_backend('qasm_simulator')
job_sim = backend_sim.run(transpile(circuit, backend_sim), shots=1024)
result_sim = job_sim.result()
counts = result_sim.get_counts(circuit)
if M==1:
print("Index of the colour", item, "is the index with most probable outcome")
else:
print("Indices of the colour", item, "are the indices the most probable outcomes")
from qiskit.visualization import plot_histogram
plot_histogram(counts)
|
https://github.com/alexandrepdumont/Quantum-Random-Number-Generator
|
alexandrepdumont
|
#!/usr/bin/env python
# coding: utf-8
import numpy as np
from qiskit import *
get_ipython().run_line_magic('matplotlib', 'inline')
num_of_bits = 64
recorded_response = np.zeros(num_of_bits)
for i in range(num_of_bits):
q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.h(q[0])
qc.measure(q, c)
backend = BasicAer.get_backend('statevector_simulator')
job_sim = execute(qc, backend, shots=1)
sim_result = job_sim.result()
outputstate = sim_result.get_statevector(qc)
recorded_response[i] = int(outputstate[0].real)
print((recorded_response))
res = int("".join(str(int(x)) for x in recorded_response), 2)
print(res)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.