problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $N$ be a strictly positive integer. Suppose there exist four subsets $A_{1}, A_{2}, A_{3}$ and $\boldsymbol{A}_{4}$ of $\{1, \ldots, \boldsymbol{N}\}$, each of cardinality 500, and suppose that for all $x, y$ in $\{1, \ldots, N\}$, there exists an index $i$ such that $x$ and $y$ are in $A_{i}$. Determine the largest possible value of $N$.
|
Answer: 833.
We will tackle this problem using graph theory. The problem's modeling leads us to consider a graph where the vertices are the elements of $S$, and they are connected by an edge of color $i$ if the two vertices belong to the set $A_i$.
In the following, we will also say that a graph $G_1$ covers a graph $G_2$ if every edge of $G_2$ is an edge of $G_1$.
We denote $K_m$ as the graph consisting of $m$ vertices where all vertices are connected. Such a graph is called complete.
We denote $K_{m, m}$ as the graph consisting of two sets of vertices $S_1$ and $S_2$, both of cardinality $m$, and in which each vertex of $S_1$ is connected to all vertices of $S_2$. Such a graph is commonly called a complete bipartite graph, and we will call $S_1$ and $S_2$ the teams of $K_{m, m}$.
Lemma: Let $K_{m, m}$ be a complete bipartite graph and $S_1$ and $S_2$ its teams. Suppose it is possible to cover $K_{m, m}$ with complete graphs $K_k$ and $K_\ell$ of sizes $k, \ell < 2m$. Then $m < \frac{k + \ell}{3}$.
Proof of the lemma: Let's start by showing that $K_k$ and $K_\ell$ each contain either $S_1$ or $S_2$. Indeed, let $v \in S_1$ not belonging to $K_\ell$. For any vertex $w$ of $S_2$, the edge $vw$ therefore belongs to $K_k$, but then $w$ belongs to $K_k$, so $K_k$ contains all the vertices of $S_2$. But then, by reasoning on a vertex of $S_1$ not belonging to $K_k$, we obtain that $K_\ell$ also contains all the elements of $S_2$. Thus, each vertex of $S_2$ belongs to $K_k$ and $K_\ell$ and each vertex of $S_1$ belongs to $K_k$ or $K_\ell$, so that $k + \ell \geq |S_1| + 2|S_2| = 3m$.
Let's return to the problem. Suppose, for the sake of contradiction, that $N \geq 834$. Note that if we could have $N$ even larger, we could reduce to the case $N = 834$ by arbitrarily adding elements of $\{1, \ldots, 834\}$ that were not yet in the sets.
We partition our set of points as follows:
- $Z$ the set of points in $A_1$ and $A_2$.
- $X$ the set of points in $A_1$ but not in $A_2$.
- $Y$ the set of points in $A_2$ but not in $A_1$.
- $W$ the rest (neither in $A_1$ nor in $A_2$).
We then have $|X| + |Y| + |Z| + |W| = 834$ and $|X| + |Z| = |Y| + |Z| = 500$, which gives us $|W| - |Z| = -166$.
Case 1: $|W| = 0$. It follows that $|Z| = 166$, $|X| = |Y| = 334$. This contradicts our lemma because it implies that we can cover $K_{334,334}$ with two cliques of size 500.
Case 2: $|W| > 0$. Then $Z \subset K_2 \cap K_3$ (i.e., each of its elements is in $A_3$ or $A_4$) so that each of its vertices is connected to the elements of $|W|$, thus $|K_3 \cap Z| + |K_4 \cap Z| \geq |Z|$. Thus, we can see that if $|W| > 0$: (Using that $W \subset K_3 \cap K_4$)
$$
|K_3 \cap (X \cup Y)| + |K_4 \cap (X \cup Y)| \leq 1000 - 2|W| - |Z|
$$
Then, we must cover $K_{500-|Z|, 500-|Z|}$ (the graph formed using the sets $X$ and $Y$) with two cliques of sizes $|K_3 \cap (X \cup Y)|, |K_4 \cap (X \cup Y)|$. By our lemma, $3(500 - |Z|) \leq 1000 - 2|W| - |Z|$, and since $|Z| = |W| + 166$, we obtain a contradiction!
Moreover, for $N = 833$, we have an explicit construction: Using our notations $X, Y, Z$. With $|Z| = 167$ and $|X| = |Y| = 333$. We place all the elements of $X$ in $A_3$ and $A_4$ and one element of $Y$ in both, half of the remaining elements of $Y$ in $A_3$ and the other half in $A_4$.
Comment from the graders: The problem was little addressed and solved by only one student.
## Senior Exercises
|
833
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $N$ un entier strictement positif. On suppose qu'il existe quatre sous-ensembles $A_{1}, A_{2}, A_{3}$ et $\boldsymbol{A}_{4}$ de $\{1, \ldots, \boldsymbol{N}\}$, chacun de cardinal 500 et on suppose que, pour tous $x, y$ dans $\{1, \ldots, N\}$, il existe un indice $i$ tel que $x$ et $y$ sont dans $A_{i}$. Déterminer la plus grande valeur de $N$ possible.
|
Réponse : 833.
Nous allons traiter ce problème avec le langage des graphes. La modélisation du problème pousse à considérer le graphe dont les sommets sont les éléments de $S$, qui sont reliés par une arête de couleur $i$ si les deux sommets apprtiennent à l'ensemble $A_{i}$.
Dans la suite, on dira également qu'un graphe $G_{1}$ recouvre un graphe $G_{2}$ si toute arête de $G_{2}$ est une arête de $\mathrm{G}_{1}$.
On note $\mathrm{K}_{\mathrm{m}}$ le graphe constitué de m sommets et dont tous les sommets sont réliés. Un tel graphe est dit complet.
On note $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ le graphe constitué de 2 ensembles de sommets $S_{1}$ et $S_{2}$, tous les deux de cardinal m et dans lequel chaque sommet de $S_{1}$ est relié à tous les sommets de $S_{2}$. Un tel graphe est communément appelé bipartite complet, et on appellera $\mathrm{S}_{1}$ et $\mathrm{S}_{2}$ les équipes de $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$.
Lemme : Soit $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ un graphe bipartite complet et $S_{1}$ et $S_{2}$ ses équipes. Supposons qu'il est possible de recouvrir $K_{m, m}$ avec de graphes complets $K_{k}$ et $K_{\ell}$ de taille respective $k, \ell<2 \mathrm{~m}$. Alors $\mathrm{m}<\frac{\mathrm{k}+\ell}{3}$.
Preuve du lemme: Commençons par montrer que $\mathrm{K}_{\mathrm{k}}$ et $\mathrm{K}_{\ell}$ contiennent chacun soit $S_{1}$ soit $S_{2}$. En effet, soit $v \in S_{1}$ n' appartenant pas à $K_{\ell}$. Pour tout sommet $w$ de $S_{2}$, l'arête $v w$ appartient donc à $K_{k}$, mais alors $w$ appartient à $K_{k}$, donc $K_{k}$ contient tous les sommets de $S_{2}$. Mais alors, en raisonnant sur un sommet de $S_{1}$ n'appartenant pas à $K_{k}$, on obtient que $K_{\ell}$ contient aussi tous les éléments de $S_{2}$. Ainsi, chaque sommet de $S_{2}$ appartient à $K_{k}$ et à $K_{\ell}$ et chaque sommet de $S_{1}$ appartient à $K_{k}$ ou à $K_{\ell}$, de sorte que $k+\ell \geqslant\left|S_{1}\right|+2\left|S_{2}\right|=3 \mathrm{~m}$
Revenons au problème. On suppose par l'absurde que $\mathrm{N} \geqslant 834$. Remarquons que si on pouvait avoir N encore plus grand, on pourrait se ramener au cas $\mathrm{N}=834$ en ajoutant arbitrairement des éléments de $\{1, . .834\}$ qui n'y étaient pas encore aux ensembles.
Nous partitionnons notre ensemble de points comme suit:
- Z l'ensemble des points dans $A_{1}$ et $A_{2}$.
- Xl'ensemble des points dans $A_{1}$ mais pas $A_{2}$.
- Yl'ensemble des points dans $A_{2}$ mais pas $A_{1}$.
- $W$ le reste (ni dans $A_{1}$, ni dans $A_{2}$ ).
On a alors $|\mathrm{X}|+|\mathrm{Y}|+|\mathrm{Z}|+|\mathrm{W}|=834$ et $|\mathrm{X}|+|\mathrm{Z}|=|\mathrm{Y}|+|\mathrm{Z}|=500$ ce qui nous donne $|\mathrm{W}|-|\mathrm{Z}|=-166$.
Cas 1: $|W|=0$. Il vient $|Z|=166,|X|=|Y|=334$. Ceci contredit notre lemme car cela implique que nous pouvons couvrir $\mathrm{K}_{334,334}$ avec deux cliques de taille 500 .
Cas 2: $|W|>O$. Alors $Z \subset K_{2} \cap K_{3}$ (c'est-à-dire que chacun de ses éléments est dans $A_{3}$ ou $A_{4}$ ) pour que chacun de ses sommets soit connecté aux éléments de $|W|$ donc $\left|K_{3} \cap Z\right|+\left|K_{4} \cap Z\right| \geqslant|Z|$. Ainsi, nous pouvons voir que si $|W|>0$ : (En utilisant que $W \subset K_{3} \cap K_{4}$ )
$$
\left|K_{3} \cap(X \cup Y)\right|+\left|K_{4} \cap(X \cup Y)\right| \leqslant 1000-2|W|-|Z|
$$
Alors, nous devons couvrir $K_{500-|Z|, 500-|Z|}$ (graphe formé à l'aide des ensembles $X$ et $Y$ ) avec deux cliques de tailles $\left|K_{3} \cap(X \cup Y)\right|, \mid K_{4} \cap(X \cup Y)$. Par notre lemme, $3(500-|Z|) \leqslant 1000-2|W|-|Z|$ or comme $|Z|=|W|+166$, on obtient une contradiction!
Par ailleurs, pour $\mathrm{N}=833$, on dispose d'une construction explicite : En reprenant nos notations $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$. Avec $|Z|=167$ et $|\mathrm{X}|=|\mathrm{Y}|=333$. On place tous les éléments de X dans $A_{3}$ et $A_{4}$ et un élément de $|\mathrm{Y}|$ dans les deux, la moitié des éléments de Y qu'il reste dans $A_{3}$ et l'autre dans $A_{4}$.
Commentaire des correcteurs : L'exercice a été peu traité, et résolu par un seul élève.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution de l'exercice 9"
}
|
84d8c6fe-6085-51a7-be68-193cfb479dc9
| 607,225
|
Let $k$ be a strictly positive integer and $P$ a point in the plane. Determine the smallest integer $n$ having the following property: one can draw $n$ lines not passing through $P$ such that every ray originating from the point $P$ intersects at least $k$ lines.
|
Answer: $\mathrm{n}=2 \mathrm{k}+1$
The statement asks to determine the smallest integer $n$ possessing a certain property, it necessarily contains two parts. On the one hand, we show that if $n$ is less than $2 k$, it does not satisfy the property, on the other hand we show that $2 \mathrm{k}+1$ satisfies the property.
Let $n$ be an integer less than or equal to $2 k$. Consider a set of $n$ lines not passing through $P$. Take $d$ a line passing through $P$ and parallel to one of the $n$ lines. The line $d$ intersects at most $n-1 \leqslant 2 k-1$ of the other lines. We can distribute these points of intersection into two groups of points, such that the points of each group are located on the same side of $d$ relative to $P$. One of the groups is of size less than $k-1$, so there exists a ray emanating from $P$ that intersects at most $k-1$ lines.
Construction for $n=2 k+1$: Consider a regular polygon $A_{1} \ldots, A_{2 k+1}$ with $2 k+1$ sides and whose circumcircle is centered at $P$ and whose sides are extended. We obtain a set of $2 k+1$ lines. Consider a ray emanating from the vertex $P$, and say it intersects the segment $\left[A_{1} A_{2}\right]$ (possibly at one of its endpoints) by forming an angle of $\theta \leqslant \frac{360}{2 \mathrm{n}}$ with its perpendicular bisector, and such that the intersection point between $d$ and $\left[A_{1} A_{2}\right]$ is closer to $A_{2}$ than to $A_{1}$. Then the ray intersects the line $\left(A_{r} \mathcal{A}_{r+1}\right)$ if and only if it forms an angle less than $\pi / 2$ with the perpendicular bisector of the segment $\left[A_{r} A_{r+1}\right]$. This condition induces the following inequality on $r$
$$
\frac{r}{n} 360^{\circ}-\theta \leqslant 90^{\circ} .
$$
This inequality is valid for the $r \leqslant\left\lfloor\frac{k+1}{2}\right\rfloor$.
Similarly, the ray $d$ intersects the line $\left(A_{2 k+2-r} A_{2 k+1-r}\right)$ for the $r$ satisfying $r \leqslant\left\lfloor\frac{k}{2}\right\rfloor-1$. It follows that the line $d$ intersects the segment $\left[A 1 A_{2}\right]$ and at least $\left.\left\lfloor\frac{k+1}{2}\right\rfloor+\frac{k}{2}\right\rfloor-1=k-1$ lines, which is at least $k$ lines.
Comment from the graders: A rather mixed review for this problem. Most students find the correct bound of $2 \mathrm{k}+1$ and the proof that it cannot be less, but many have difficulty finding a construction or proving its proper functioning. The main point here was to understand under what condition a given line intersects our ray emanating from $P$.
|
2k+1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Soit $k$ un entier strictement positif et $P$ un point du plan. Déterminer le plus petit entier $n$ ayant la propriété suivante : on peut tracer $n$ droites ne passant pas par $P$ de sorte que toute demi-droite d'origine le point $P$ coupe au moins $k$ droites.
|
Réponse : $\mathrm{n}=2 \mathrm{k}+1$
L'énoncé demande de déterminer le plus petit entier n possédant une certaine propriété, il contient nécessairement deux parties. D'une part, on montre que si $n$ est inférieur à $2 k$, il ne vérifie pas la propriété, d'autre part on montre que $2 \mathrm{k}+1$ vérifie la propriété.
Soit $n$ un entier inférieur ou égal à $2 k$. Considérons un ensemble de $n$ droites ne passant pas par $P$. Prenons $d$ une droite passant par $P$ et parallèle à l'une des $n$ droites. La droite $d$ coupe au plus $n-1 \leqslant 2 k-1$ des autres droites. On peut répartir ces points d'intersection en deux groupes de points, de sorte que les points de chaque groupe sont situés du même côté sur d par rapport à $P$. L'un des groupes est de taille inférieure à $k-1$, de sorte qu'il existe une demi-droite issue de P coupent au plus $k-1$ droites.
Construction pour $n=2 k+1$ : Considérons un polygone régulier $A_{1} \ldots, A_{2 k+1}$ à $2 k+1$ côtés et dont le cercle circonscrit est de centre $P$ et dont on prolonge les côtés. On obtient un ensemble de $2 k+1$ droites. Considérons une demi-droite dissue du sommet $P$, et disons qu'elle intersecte le segment $\left[A_{1} A_{2}\right]$ (éventuellement en l'une de ses extrémités) en effectuant un angle de $\theta \leqslant \frac{360}{2 \mathrm{n}}$ avec sa médiatrice, et de sorte que le point d'intersection entre d et $\left[A_{1} A_{2}\right]$ soit plus proche de $A_{2}$ que de $A_{1}$. Alors la demi-droit coupe la droite $\left(A_{r} \mathcal{A}_{r+1}\right)$ si et seulement si elle forme un angle inférieur à $\pi / 2$ avec la médiatrice du segment $\left[A_{r} A_{r+1}\right]$. Cette condition induit l'inégalité suivante sur $r$
$$
\frac{r}{n} 360^{\circ}-\theta \leqslant 90^{\circ} .
$$
Cette inégalité est valable pour les $r \leqslant\left\lfloor\frac{k+1}{2}\right\rfloor$.
De la même façon, la demi-droite d coupe la droite $\left(A_{2 k+2-r} A_{2 k+1-r}\right)$ pour les $r$ satisfaisant $r \leqslant\left\lfloor\frac{k}{2}\right\rfloor-1$. Il vient que la droite $d$ coupe le segment $\left[A 1 A_{2}\right]$ et au moins $\left.\left\lfloor\frac{k+1}{2}\right\rfloor+\frac{k}{2}\right\rfloor-1=k-1$ droites, soit au moins $k$ droites.
Commentaire des correcteurs : Un bilan assez mitigé pour cet exercice. La plupart des élèves trouvent la bonne borne de $2 \mathrm{k}+1$ et la preuve qu'on ne peut pas faire moins, mais beaucoup ont du mal à trouver une construction ou bien à donner preuve de son bon fonctionnement. Il s'agissait ici surtout de bien comprendre sous quelle condition une droite donnée intersecte notre demi-droite partant de P .
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution de l'exercice 12"
}
|
cf62fdc0-d371-57ba-b012-eeb4a8334eca
| 607,226
|
Consider a regular 2022-gon with side length 1. The points are numbered $A_{1}, \ldots, A_{2022}$ in a certain order. Initially, Elie starts from point $A_{1}$, then jumps from point to point to $A_{2}$, then from $A_{2}$ to $A_{3}$, and so on, each time taking the shortest arc. When he reaches $A_{2022}$, he finally returns to $A_{1}$. Determine the maximum value of the sum of the lengths of the arcs that Elie has traveled, among all possible numberings of the points.
|
Response: $\mathrm{If} N=1011$, The maximum value is $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$.
The problem asks to find the maximum value of a sum of lengths, which necessarily involves two parts. First, we show that the path traveled by Elie is necessarily of length less than $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$, this part is called the analysis. Second, we provide an example of a numbering for which the path traveled is exactly of length $2\left(N^{2}-N+1\right)$, this step is called the construction.
Analysis: In the following, we keep the notation $N=1011$. We also denote $\underline{P Q}$ as the length of the shortest arc connecting P and Q, and $\overline{\mathrm{PQ}}$ as the length of the longest arc. Consider a numbering $A_{1}, \ldots, A_{2 N}$ in any order. We also set $A_{2 N+1}=A_{1}$.
Since estimating each segment $A_{i} A_{i+1}$ by its minimum length is too rough, we will instead lower-bound the sum $A_{1} \overline{A_{2}+\ldots}+A_{2 N} A_{1}$ by upper-bounding groups of terms. More precisely, we will look at the path traveled between two consecutive odd vertices.
Let $1 \leqslant i \leqslant N$. We want to show that $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$, in other words, that passing through $A_{2 i}$ is less costly than taking the large arc $A_{2 i-1} \mathcal{A}_{2 i+1}$. The desire to prove such an inequality can come from attempts on small cases.
If $A_{2 i}$ is on the small arc $A_{2 i-1} A_{2 i+1}$, then $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\underline{A_{2 i-1} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$. Suppose now that $A_{2 i}$ is on the large arc $A_{2 i-1} A_{2 i+1}$. If the small arc $A_{2 i} A_{2 i+1}$ does not contain $A_{2 i-1}$ or if the small arc $A_{2 i-1} A_{2 i}$ does not contain $A_{2 i+1}$, then $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. If now $A_{2 i-1}$ is on the small arc $A_{2 i} A_{2 i+1}$, then $A_{2 i+1}$ is on the large arc $A_{2 i-1} A_{2 i}$ and $A_{2 i-1} A_{2 i}+$ $\underline{A_{2 i} A_{2 i+1}} \leqslant \underline{A_{2 i-1} A_{2 i}}+\overline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. The case where $A_{2 i-1}$ is on the small arc $A_{2 i} A_{2 i+1}$ is treated similarly.
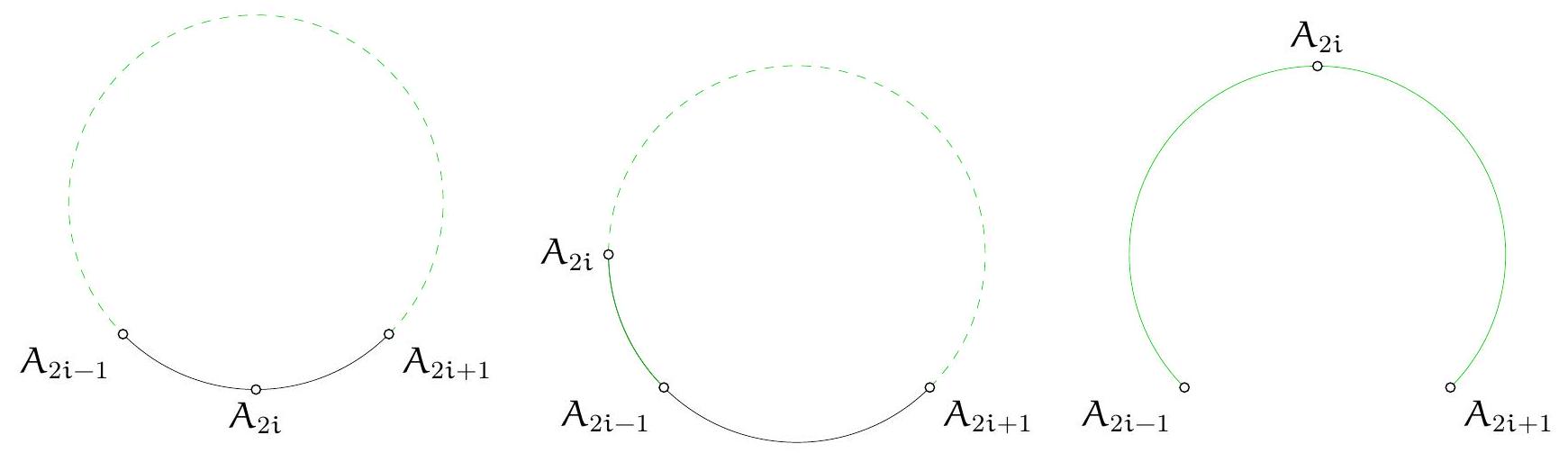
We therefore have
$$
\begin{aligned}
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} & \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \\
& =\left(2 \mathrm{~N}-\underline{A_{1} A_{3}}\right)+\ldots+\left(2 N-\underline{A_{2 N-1} A_{1}}\right) \\
& \left.=2 N^{2}-\underline{\left(A_{1} A_{3}\right.}+\ldots+\underline{A_{2 N-1}} \overline{A_{1}}\right) .
\end{aligned}
$$
It is therefore sufficient to minimize the sum $\underline{A_{1} A_{3}}+\ldots+\underline{A_{2 N-1} A_{1}}$. For this, note that there exist two odd-numbered vertices $A$ and B at a distance of at least $\mathrm{N}-1$ (since there are N odd vertices). As the sum is cyclic, we can assume that $A=A_{1}$ (by renumbering the vertices if necessary). But then the path $A_{1} \ldots A_{2 N-1} A_{1}$ requires traveling an arc $\underline{A_{1} B}$ to go from $A_{1}$ to $B$ and then an arc $B A_{1}$ to go from $B$ to $A_{1}$. Such a path is therefore at least twice the length of the small arc $A B$, which is $2(N-1)$.
It follows that
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \geqslant 2 N^{2}-2(N-1)=2\left(N^{2}-N+1\right)
$$
Construction: Conversely, number the vertices in the order $A_{1} A_{3} \ldots A_{2 N-1} A_{2} \ldots A_{2 N}$. The path of Elie is then of length
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}}=\underbrace{N+N-1+\ldots+N+N-1}_{N-1 \text { times }}+N+1=2 N^{2}-2 N+2
$$
Graders' Comments: The problem was not solved by many students. Many students found a construction that achieves the correct bound, but among those who attempted the problem, too many students still try to justify that one cannot do better by one of the two arguments:
- Either by saying that at each step, the point $A_{k}$ is placed in the "optimal" position. But performing the "best" operation at each step is not a guarantee of arriving at the best configuration. Here, placing the point $A_{k}$ diametrically opposite to the point $A_{k+1}$ forces, at the end, to have $A_{2022}$ and $A_{1}$ adjacent. Who says that not systematically placing the points $A_{k}$ and $A_{k+1}$ as far apart as possible does not allow increasing the distance between $A_{1}$ and $A_{2022}$ to have a greater total distance?
- Or by saying that if points are swapped on the found configuration, the distance is not increased. This reasoning also does not prove that the configuration is a global maximum, but only proves that the configuration is a local maximum.
We hope that upon reading this comment, students will no longer make these two common reasoning errors.
|
2(N^2 - N + 1)
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
On considère un 2022-gone régulier de côté 1 . Les points sont numérotés $A_{1}, \ldots, A_{2022}$ dans un certain ordre. Au départ, Elie part du point $A_{1}$, puis saute de point en point vers le point $A_{2}$, puis de $A_{2}$ vers $A_{3}$ etc... chaque fois en prenant l'arc le plus court. Lorsqu'il atteint $A_{2022}$, il rejoint finalement $A_{1}$. Déterminer la valeur maximale de la somme des longueurs des arcs qu'a parcouru Elie, parmi toutes les numérotations de points possibles.
|
Réponse: $\mathrm{Si} N=1011$, La valeur maximale est $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$.
Le problème demande de trouver la valeur maximale d'une somme de longueurs, il contient nécessairement deux parties. Dans un premier temps, on montre que le chemin parcouru par Elie est forcément de longueur inférieure à $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$, cette partie s'appelle l'analyse. Dans un second temps, on donne l'exemple d'une numérotation pour laquelle le chemin parcouru est exactement de longueur $2\left(N^{2}-N+1\right)$, cette étape s'appelle la construction.
Analyse : Dans la suite, on garde la notation $N=1011$. On note également $\underline{P Q}$ la longueur de l'arc le plus court reliant P et Q et $\overline{\mathrm{PQ}}$ la longueur de l'arc le plus long. Considérons une numérotation $A_{1}, \ldots, A_{2 N}$ dans un ordre quelconque. On pose aussi $A_{2 N+1}=A_{1}$.
Puisque majorer chaque portion $A_{i} A_{i+1}$ par sa longueur minimale est une estimation trop grossière, on va plutôt minorer la somme $A_{1} \overline{A_{2}+\ldots}+A_{2 N} A_{1}$ en majorant des paquets de terme. Plus précisément, nous allons regarder le chemin parcouru entre deux sommets impairs consécutifs.
Soit $1 \leqslant i \leqslant N$. On désire montrer que $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$, autrement dit, que passer par $A_{2 i}$ est moins coûteux que prendre le grand arc $A_{2 i-1} \mathcal{A}_{2 i+1}$. La volonté de démontrer une telle inégalité peut venir de tentatives sur des petits cas.
Si $A_{2 i}$ est sur le petit arc $A_{2 i-1} A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\underline{A_{2 i-1} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$. Supposons désormais que $A_{2 i}$ est sur le grand arc $A_{2 i-1} A_{2 i+1}$. Si le petit arc $A_{2 i} A_{2 i+1}$ ne contient pas $A_{2 i-1}$ ou si le petit arc $A_{2 i-1} A_{2 i}$ ne contient pas $A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Si maintenant $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$, alors $A_{2 i+1}$ est sur le grand arc $A_{2 i-1} A_{2 i}$ et $A_{2 i-1} A_{2 i}+$ $\underline{A_{2 i} A_{2 i+1}} \leqslant \underline{A_{2 i-1} A_{2 i}}+\overline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Le cas où $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$ se traite de façon similaire.

On a donc
$$
\begin{aligned}
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} & \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \\
& =\left(2 \mathrm{~N}-\underline{A_{1} A_{3}}\right)+\ldots+\left(2 N-\underline{A_{2 N-1} A_{1}}\right) \\
& \left.=2 N^{2}-\underline{\left(A_{1} A_{3}\right.}+\ldots+\underline{A_{2 N-1}} \overline{A_{1}}\right) .
\end{aligned}
$$
Il suffit donc de minimiser la somme $\underline{A_{1} A_{3}}+\ldots+\underline{A_{2 N-1} A_{1}}$. Pour cela, notons qu'il existe deux sommets $A$ et B de numéro impair à distance au moins $\mathrm{N}-1$ (car il y a N sommets impairs). Comme la somme
est cyclique, on peut supposer que $A=A_{1}$ (quitte à renuméroter les sommets). Mais alors le chemin $A_{1} \ldots A_{2 N-1} A_{1}$ nécessite de parcourir un arc $\underline{A_{1} B}$ pour aller de $A_{1}$ vers $B$ puis un arc $B A_{1}$ pour aller de $B$ vers $A_{1}$. Un tel chemin est donc de longueur au moins le double du petit arc $A B$, soit $2(N-1)$.
Il vient
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \geqslant 2 N^{2}-2(N-1)=2\left(N^{2}-N+1\right)
$$
Construction : Réciproquement, numérotons les sommets dans l'ordre $A_{1} A_{3} \ldots A_{2 N-1} A_{2} \ldots A_{2 N}$. Le chemin d'Elie est alors de longueur
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}}=\underbrace{N+N-1+\ldots+N+N-1}_{N-1 \text { fois }}+N+1=2 N^{2}-2 N+2
$$
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu. Beaucoup d'élèves ont trouvé une construction réalisant la bonne borne, mais parmi ceux qui ont cherché l'exercice, trop d'élèves encore tentent de justifier qu'on ne peut pas faire mieux par l'un des deux arguments :
- Soit en disant qu'à chaque étape on place le point $A_{k}$ à l'endroit "optimal". Mais effectuer la "meilleure" opération à chaque fois n'est pas gage d'arriver à la meilleure configuration. Ici, placer le point $A_{k}$ diamétralement opposé au point $A_{k+1}$ impose à la fin d'avoir $A_{2022}$ et $A_{1}$ adjacents. Qui nous dit que ne pas systématiquement placer les points $A_{k}$ et $A_{k+1}$ le plus éloigné possible ne permet pas d'augmenter la distance entre $A_{1}$ et $A_{2022}$ pour avoir une plus grande distance totale?
- Soit en disant que si l'on échange des points sur la configuration trouvée, on n'augmente pas la distance. Là aussi, ce raisonnement ne permet pas de prouver que la configuration est un maximum global, mais seulement de prouver que la configuration est un maximum local.
Nous espérons qu'à la lecture de ce commentaire, les élèves ne commettront plus ces deux erreurs communes de raisonnement.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "\nSolution de l'exercice 16"
}
|
1d1c0f74-757a-5c13-a985-ec536bb1cd45
| 607,230
|
2024 students, all of different heights, need to line up in a single file. However, each student does not want to have both a shorter student in front of them and a shorter student behind them. How many ways are there to form such a line?
|
Let's look at the tallest student: if they are not placed at the very beginning or the very end of the line, they are between two students who are shorter than them. Thus, the tallest student must be placed at the end or at the beginning.
By this reasoning, and by looking at small cases, we can conjecture that if we need to place $n \geqslant 1$ students all of different heights with the constraint given in the statement, there are $2^{\text {n-1 }}$ possibilities. Let's prove this by induction on $n$.
Initialization: for $\mathrm{n}=1$ student, there is only one possible line and $1=2^{\mathrm{n}-1}$.
Hereditary: suppose the hypothesis is true at rank $n$ for a $n \geqslant 1$, let's show that it is true at rank $n+1$. The tallest student is necessarily placed either at the very beginning or at the very end. If we remove this student from the line, the line of $n$ people still satisfies the statement: there are therefore potentially $2^{n-1}$ possibilities for the line without the tallest person. If we add the tallest person at the front or the back of the line, the line still satisfies the statement (since the person next to the tallest will not be between two people who are shorter), as there are two choices for placing the tallest person, there are $2^{\mathfrak{n}}=2^{\mathfrak{n + 1 - 1}}$ possibilities to form the line, which concludes the induction.
Thus, by applying the property for $\mathrm{n}=2024$, there are $2^{2023}$ possibilities.
Comment from the graders: The exercise was very well done overall, with few errors. Two main methods of proof were used: the first is similar to what the statement suggests, and involves seeing how to place the students, one by one. The second involves understanding what the "shape" of the distribution of students will be, in a V shape, and counting these configurations using various arguments.
|
2^{2023}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
2024 élèves, tous de taille différente, doivent se placer en file indienne. Cependant, chaque élève ne souhaite pas avoir à la fois devant lui et derrière lui un élève plus petit que lui. Combien y a-t-il de façons de former une telle file indienne?
|
Regardons l'élève de plus grande taille : s'il n'est pas placé au tout début ou à la toute fin de la file, il est entre deux élèves plus petits que lui. Ainsi l'élève le plus grand doit être placé à la fin ou au début.
Via ce raisonnement, et en regardant les petits cas on peut conjecturer que si on doit placer $n \geqslant 1$ élèves tous de taille différente avec la contrainte de l'énoncé, il y a $2^{\text {n-1 }}$ possibilités. Montrons cela par récurrence sur n .
Initialisation : pour $\mathrm{n}=1$ élèves, il n'y a qu'une file possible et $1=2^{\mathrm{n}-1}$.
Hérédité : supposons l'hypothèse vraie au rang $n$ pour un $n \geqslant 1$, montrons qu'elle l'est au rang $n+1$. L'élève le plus grand est frocément placé soit au tout début, soit à la toute fin. Si on l'enlève de la file, la file de $n$ personnes vérifie toujours l'énoncé : il y a donc potentiellement $2^{n-1}$ possibilité pour la file sans la personne la plus grande. Si on rajoute la personne la plus grande devant ou derrière la file vérifie toujours l'énoncé (car la personne à côté du plus grand ne sera pas entre deux personnes plus petites), comme il y a deux choix de placements du plus grand, il y a $2^{\mathfrak{n}}=2^{\mathfrak{n + 1 - 1}}$ possibilités pour former la file, ce qui conclut la récurrence.
Ainsi en appliquant la propriété pour $\mathrm{n}=2024$, il y a $2^{2023}$ possibilités.
Commentaire des correcteurs: Exercice très bien réussi dans l'ensemble, avec peu d'erreurs. Deux méthodes de preuve principales ont été employées : la première est semblable à ce que fait l'énoncé, et consiste à voir comment placer les élèves, un par un. La seconde consiste à comprendre quelle va être la "forme" de la répartition des élèves, en V , et à compter ces configurations par divers arguments.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
2753c623-2f7c-50d8-8a4d-65333b8f29d5
| 607,236
|
It is said that an integer $k>1$ is superb if there exist $\mathrm{m}, \mathrm{n}, \mathrm{a}$ three strictly positive integers such that
$$
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
$$
Determine the smallest superb integer.
|
Suppose $k=2$ is superb: there exist three strictly positive integers $\mathrm{m}, \mathrm{n}, \mathrm{a}$ such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{2}$. By looking modulo 3, $5^{\mathrm{m}}+1 \equiv 2^{\mathrm{m}}+1 \equiv \mathrm{a}^{2}(\bmod 3)$. The powers of 2 modulo 9 alternate between 2 if m is odd, and 1 if m is even, so $2^{\mathrm{m}}+1$ is either 2 or 0 modulo 3. Since squares modulo 3 are 0 and 1, we deduce that $2^{\mathrm{m}}+1$ is 0 modulo 3, hence $m$ is odd. By looking modulo 7, we get $5^{\mathrm{m}} \equiv \boldsymbol{a}^{2}(\bmod 7)$. The squares modulo 7 are $0,1,2,4$, and the powers of 5 alternate between $1,5,4,6,2,3$. Thus $5^{\mathrm{m}}$ is 0, 1, 2, or 4 if and only if $m$ is 0, 2, or 4 modulo 6, which is impossible since $m$ is odd. Thus $k \neq 2$.
Suppose $k=3$ is superb: there exist three strictly positive integers $\mathrm{m}, \mathrm{n}$, a such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{3}$. By looking modulo 7, $5^{\mathrm{m}} \equiv \mathrm{a}^{3}$. The cubes modulo 7 are $0,1,6$. The powers of 5 modulo 7 alternate between $1,5,4,6,2,3$. Thus we get that $m \equiv 0(\bmod 6)$ or $m \equiv 3(\bmod 6)$: in all cases, 3 divides m. We then look modulo 9: we have $5^{\mathrm{m}}+4 \equiv \mathrm{a}^{3}$. Since m is divisible by 3, $5^{m}$ and $a^{3}$ are cubes. The cubes modulo 9 are $0,1,8$. Thus $5^{m}-a^{3}$ can be 0, 1, 2, 7, 8 modulo 9, but not 4, which is contradictory. Thus $k \neq 3$.
Suppose $k=3$ is superb: there exist three strictly positive integers $\mathbf{m}, \mathrm{n}$, a such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{4}=\left(a^{2}\right)^{2}$. In particular, 2 is superb, which is contradictory.
Note that 5 is superb: by taking $\mathbf{a}=3$, we have $\mathbf{a}^{\mathrm{k}}=3^{5}=243=5^{1}+63 \times 3+49$ so 5 is superb. Thus 5 is the smallest superb integer.
Comment from the graders: The problem was solved by few students, who did it well.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un entier $k>1$ est superbe s'il existe $\mathrm{m}, \mathrm{n}, \mathrm{a}$ trois entiers strictement positifs tels que
$$
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
$$
Déterminer le plus petit entier superbe.
|
Supposons que $k=2$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}, \mathrm{a}$ tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{2}$. En regardant modulo $3,5^{\mathrm{m}}+1 \equiv 2^{\mathrm{m}}+1 \equiv \mathrm{a}^{2}(\bmod 3)$. Or les puissances de 2 modulo 9 valent alternativement 2 si m est impair, puis 1 si m est pair, donc $2^{\mathrm{m}}+1$ vaut soit 2 soit 0 modulo 3 . Comme les carrés modulo 3 sont 0 et 1 , on en déduit que $2^{\mathrm{m}}+1$ vaut 0 modulo 3 , donc que $m$ est impair. En regardant modulo 7 , on obtient que $5^{\mathrm{m}} \equiv \boldsymbol{a}^{2}(\bmod 7)$. Or les carrés modulo 7 sont $0,1,2,4$, et les puissances de 5 alternent entre $1,5,4,6,2,3$. Ainsi $5^{\mathrm{m}}$ vaut $0,1,2$ ou 4 si et seulement si $m$ vaut 0,2 ou 4 modulo 6 , ce qui est impossible car $m$ est pair. Ainsi $k \neq 2$.
Supposons que $\mathrm{k}=3$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{3}$. En regardant modulo $7,5^{\mathrm{m}} \equiv \mathrm{a}^{3}$. Or les cubes modulo 7 sont $0,1,6$. Et les puissances de 5 modulo 7 alternent entre $1,5,4,6,2,3$. Ainsi on obtient que $m \equiv 0(\bmod 6)$ ou $m \equiv 3(\bmod 6)$ : dans tous les cas 3 divise m . On regarde alors modulo 9 : on a $5^{\mathrm{m}}+4 \equiv \mathrm{a}^{3}$. Or comme m est divisible par 3 , $5^{m}$ et $a^{3}$ sont des cubes. Les cubes modulo 9 sont $0,1,8$. Ainsi $5^{m}-a^{3}$ peut valoir $0,1,2,7,8$ modulo 9 , mais pas 4 ce qui est contradictoire. Ainsi $k \neq 3$.
Supposons que $k=3$ est superbe : il existe trois entiers strictement positifs $\mathbf{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{4}=\left(a^{2}\right)^{2}$. En particulier, 2 est superbe ce qui est contradictoire.
Notons que 5 est superbe : en prenant $\mathbf{a}=3$, on a $\mathbf{a}^{\mathrm{k}}=3^{5}=243=5^{1}+63 \times 3+49$ donc 5 est superbe. Ainsi 5 est le plus petit entier superbe.
Commentaire des correcteurs : L'exercice a été traité par peu d'élèves, qui l'ont bien résolu.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution de l'exercice 7"
}
|
f846ce5e-1c3f-5def-8885-912f9aac77fc
| 607,239
|
Let $x, y, z$ be three real numbers satisfying $x+y+z=2$ and $xy+yz+zx=1$. Determine the maximum value that $x-y$ can take.
|
Let $(x, y, z)$ be a triplet satisfying the statement. By swapping $x$ and the maximum of the triplet, and then $z$ and the minimum of the triplet, we can assume $x \geqslant z \geqslant y$, while increasing $x-y$.
Since $x+y+z=2$, we have $4=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z)=x^{2}+y^{2}+z^{2}+2$, thus $x^{2}+y^{2}+z^{2}=2$.
In particular, $(x-y)^{2}+(y-z)^{2}+(x-z)^{2}=2\left(x^{2}+y^{2}+z^{2}\right)-2(x y+y z+x z)=2$. By the arithmetic-quadratic inequality, $(x-z)^{2}+(z-y)^{2} \geqslant \frac{(x-z+z-y)^{2}}{2}=\frac{(x-y)^{2}}{2}$, so $2 \geqslant(x-y)^{2}+\frac{(x-y)^{2}}{2}=\frac{3(x-y)^{2}}{2}$, thus $(x-y) \leqslant \frac{2}{\sqrt{3}}$.
Let's try to show that this value is attainable. If we have $x-y=\frac{2}{\sqrt{3}}$, then we have equality in the arithmetic-quadratic inequality: thus $x-z=z-y$, so since their sum is $x-y$, $x-z=z-y=\frac{1}{\sqrt{3}}$. In particular, since $x+y+z=3 z+(z-x)+(z-y)=3 z$, we have $z=\frac{2}{3}, x=\frac{2}{3}+\frac{1}{\sqrt{3}}$ and $y=\frac{2}{3}-\frac{1}{\sqrt{3}}$. Conversely, for these values of $x, y, z$, we indeed have:
$-x+y+z=3 \times \frac{2}{3}=2$
$-x y+y z+z x=x y+(x+y) z=\left(\frac{2}{3}+\frac{1}{\sqrt{3}}\right)\left(\frac{2}{3}-\frac{1}{\sqrt{3}}+\frac{4}{3} \times \frac{2}{3}=\frac{4}{9}-\frac{1}{3}+\frac{8}{9}=\frac{9}{9}=1\right)$
$-x-y=2 \times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
Thus $(x, y, z)$ satisfies the conditions of the statement, and $x-y=\frac{2}{\sqrt{3}}$, so the maximum value that $x-y$ can take is $\frac{2}{\sqrt{3}}$.
Graders' comment: The exercise was not approached much. The main mistake is forgetting to find $x, y, z$ for which equality holds.
|
\frac{2}{\sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y, z$ trois nombres réels vérifiant $x+y+z=2$ et $x y+y z+z x=1$. Déterminer la valeur maximale que peut prendre $x-y$.
|
Soit ( $x, y, z$ ) un triplet vérifiant l'énoncé. Quitte à échanger $x$ et le maximum du triplet, puis $z$ et le minimum du triplet, on peut supposer $x \geqslant z \geqslant y$, tout en augmentant $x-y$.
Comme $x+y+z=2$, on a $4=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z)=x^{2}+y^{2}+z^{2}+2$, donc $x^{2}+y^{2}+z^{2}=2$.
En particulier $(x-y)^{2}+(y-z)^{2}+(x-z)^{2}=2\left(x^{2}+y^{2}+z^{2}\right)-2(x y+y z+x z)=2$. Or par inégalité arithmético quadratique, $(x-z)^{2}+(z-y)^{2} \geqslant \frac{(x-z+z-y)^{2}}{2}=\frac{(x-y)^{2}}{2}$, donc $2 \geqslant(x-y)^{2}+\frac{(x-y)^{2}}{2}=$ $\frac{3(x-y)^{2}}{2}$, donc $(x-y) \leqslant \frac{2}{\sqrt{3}}$.
Essayons de montrer que cette valeur est atteignable. Si on a $x-y=\frac{2}{\sqrt{3}}$, alors on a égalité dans l'inégalité arithmético quadratique : ainsi $x-z=z-y$, donc comme leur somme vaut $x-y, x-z=z-y=\frac{1}{\sqrt{3}}$. En particulier, comme $x+y+z=3 z+(z-x)+(z-y)=3 z$, on a $z=\frac{2}{3}, x=\frac{2}{3}+\frac{1}{\sqrt{3}}$ et $y=\frac{2}{3}-\frac{1}{\sqrt{3}}$. Réciproquement, pour ces valeurs de $x, y, z$, on a bien :
$-x+y+z=3 \times \frac{2}{3}=2$
$-x y+y z+z x=x y+(x+y) z=\left(\frac{2}{3}+\frac{1}{\sqrt{3}}\right)\left(\frac{2}{3}-\frac{1}{\sqrt{3}}+\frac{4}{3} \times \frac{2}{3}=\frac{4}{9}-\frac{1}{3}+\frac{8}{9}=\frac{9}{9}=1\right.$
$-x-y=2 \times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
Ainsi $(x, y, z)$ vérifie les conditions de l'énoncé, et $x-y=\frac{2}{\sqrt{3}}$, donc la valeur maximale que peut prendre $x-y$ est $\frac{2}{\sqrt{3}}$.
Commentaire des correcteurs : L'exercice a été assez peu abordé. La principale erreur est d'oublier de trouver des $x, y, z$ pour lesquels on a égalité.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
303aaa58-4016-57bd-8fb0-4c18a2ccefee
| 607,240
|
Félix wants to color the integers from 1 to 2023 such that if $a, b$ are two distinct integers between 1 and 2023 and $a$ divides $\mathbf{b}$, then $a$ and $b$ are of different colors. What is the minimum number of colors Félix needs?
|
We can try to color the numbers greedily: 1 can be colored with a color we denote as $a$, 2 and 3 with the same color $b$ (but not color $a$), then 4 and 6 with color $c$ (we can also color 5 and 7 with color $c$), etc. It seems that an efficient coloring is to color all numbers $n$ such that $2^{k} \leqslant n<2^{k+1}$ with color $k+1$, as long as $n \leqslant 2023$. Thus, we color $[1,2[$ with color $1$, $[2,4[$ with color $2$, ..., $[1024,2023]$ with color $11$. If $a \neq b$ are of the same color $k \in \{1, \ldots, 11\}$, then $0<\frac{a}{b}<\frac{2^{k+1}}{2^{k}}=2$, so if $b$ divides $a$, then $\frac{a}{b}$ is an integer and must be 1. Thus, $a=b$, which is a contradiction. Therefore, our coloring satisfies the condition of the problem and requires 11 colors.
Conversely, if a coloring satisfies the problem statement, the numbers $2^{0}=1, 2^{1}, \ldots, 2^{10}$ are between 1 and 2023, and if we take $a \neq b$ among these 11 numbers, either $a$ divides $b$ or $b$ divides $a$. Thus, these 11 numbers must be of different colors. Therefore, at least 11 colors are needed.
Thus, the minimum number of colors required is 11.
Comment from the graders: The exercise is very well done. As in any problem where we need to find the minimum number such that, it is important to split the proof into two parts: why $n=11$ colors are sufficient, and why if $n \leqslant 10$, $n$ colors are not sufficient.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Félix souhaite colorier les entiers de 1 à 2023 tels que si $a, b$ sont deux entiers distincts entre 1 et 2023 et a divise $\mathbf{b}$, alors a et $b$ sont de couleur différentes. Quel est le nombre minimal de couleur dont Félix a besoin?
|
On peut essayer de colorier de manière gloutonne les nombres : 1 peut être colorié d'une couleur qu'on note $a$, 2 et 3 de la même couleur $b$ (mais pas de la couleur $a$ ), puis 4,6 de la couleur $c$ (on peut aussi colorier 5 et 7 de la couleur c), etc. Il semble donc qu'une coloriation performante soit pour tout $k$ de colorier les nombres $n$ vérifiant $2^{k} \leqslant n<2^{k+1}$ de la couleur $k+1$, tant que $n \leqslant 2023$. Ainsi on colorie $[1,2[$ de couleur $1,[2,4[$ de couleur $2, \ldots,[1024,2023]$ de couleur 11 . Si $a \neq b$ sont de la même couleur $\mathrm{k} \in\{1, \ldots, 11\}$ alors $0<\frac{\mathrm{a}}{\mathrm{b}}<\frac{2^{k+1}}{2^{k}}=2$, donc si b divise a , alors $\frac{\mathrm{a}}{\mathrm{b}}$ est entier donc vaut 1 . On a alors $\mathrm{a}=\mathrm{b}$ ce qui est contradictoire. Ainsi notre coloriage vérifie bien la condition de l'énoncé, et nécessite 11 couleurs.
Réciproquement si un coloriage vérifie l'énoncé, les nombres $2^{0}=1,2^{1}, \ldots, 2^{10}$ sont entre 1 et 2023 , et si on prend $a \neq b$ parmi ces 11 nombres, soit $a$ divise $b$, soit $b$ divise $a$. Ainsi ces 11 nombres sont de couleurs différentes. Il faut donc au moins 11 couleurs.
Ainsi le nombre minimal de couleurs requises est 11.
Commentaire des correcteurs : L'exercice est très bien réussi. Comme dans tout exercice où on demande de trouver le nombre minimal tel que, il est important de découper la preuve en deux parties : pourquoi $n=11$ couleurs suffisent, et pourquoi si $n \leqslant 10, n$ couleurs ne suffisent pas.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"problem_match": "\nExercice 11.",
"solution_match": "## Solution de l'exercice 11"
}
|
d25a7782-76af-50e2-a9f2-06be58fdaae0
| 607,242
|
It is said that a polynomial $P$ is fantastic if there exist real numbers $\mathrm{a}_{0}, \ldots, \mathrm{a}_{2022}$ such that
$$
P(X)=X^{2023}+a_{2022} X^{2022}+\cdots+a_{1} X+a_{0}
$$
if it has 2023 roots $r_{1}, \ldots, r_{2023}$ (not necessarily distinct) in $[0,1]$, and if $P(0)+P(1)=0$. Determine the maximum value that $\mathrm{r}_{1} \cdot \mathrm{r}_{2} \cdots \mathrm{r}_{2023}$ can take for a fantastic polynomial.
|
The answer is $2^{-2023}$, we will show this in two steps: first, we will show that we cannot find a polynomial with a larger value, and second, we will exhibit a polynomial that satisfies the conditions of the problem and whose product of roots is indeed equal to $2^{-2023}$.
By hypothesis, we can rewrite $P(X)=\prod_{k=1}^{2023}\left(X-r_{k}\right)$. In particular, $P(0)=-\prod_{k=1}^{2023} r_{k}$ and $P(1)=\prod_{k=1}^{2023}\left(1-r_{k}\right)$. The hypothesis $P(0)+P(1)=0$ becomes:
$$
\prod_{k=1}^{2023}\left(1-r_{k}\right)=\prod_{k=1}^{2023} r_{k}=r_{1} \cdot r_{2} \cdots r_{2023}
$$
Thus, since for all $k, r_{k} \geqslant 0$ and $1-r_{k} \geqslant 0$, by the arithmetic-geometric mean inequality,
$$
\left(r_{1} \cdot r_{2} \cdots r_{2023}\right)^{2}=\prod_{k=1}^{2023}\left(1-r_{k}\right) r_{k} \leqslant \prod_{k=1}^{2023}\left(\frac{\left(1-r_{k}\right)+r_{k}}{2}\right)^{2}=\frac{1}{4^{2023}}
$$
Thus, $r_{1} \cdot r_{2} \cdots r_{2023} \leqslant 2^{-2023}$.
Furthermore, if $P(X)=\left(X-\frac{1}{2}\right)^{2023}$, then $P$ is a monic polynomial of degree 2023, has 2023 roots in $[0,1]$, and satisfies $P(0)+P(1)=\left(-\frac{1}{2}\right)^{2023}+\left(\frac{1}{2}\right)^{2023}=0$, so $P$ is fantastic. The product of its roots is $2^{-2023}$. Therefore, the maximum value that $r_{1} \cdot r_{2} \cdots r_{2023}$ can take for a fantastic polynomial is $2^{-2023}$.
Graders' comments: The exercise required finding the maximum value that the product of roots could take for a particular class of polynomials. Almost all students found the case achieving the maximum (and thus its value), and a satisfactory proportion of these students completed the proof, generally by applying the AM-GM inequality. Vieta's formulas seem to be well mastered but were absolutely not necessary for solving the problem. A key takeaway: the AM-GM inequality is often a judicious inequality to show that a product of positive reals is maximal when all its terms are equal.
|
2^{-2023}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On dit qu'un polynôme $P$ est fantabuleux s'il existe des réels $\mathrm{a}_{0}, \ldots, \mathrm{a}_{2022}$ tel que
$$
P(X)=X^{2023}+a_{2022} X^{2022}+\cdots+a_{1} X+a_{0}
$$
s'il a 2023 racines $r_{1}, \ldots, r_{2023}$ (non nécessairement distinctes) dans $[0,1]$, et si $P(0)+P(1)=0$. Déterminer la valeur maximale que peut prendre $\mathrm{r}_{1} \cdot \mathrm{r}_{2} \cdots \mathrm{r}_{2023}$ pour un polynôme fantabuleux.
|
La réponse est $2^{-2023}$, on va montrer cela en deux temps, dans un premier temps on va montrer que l'on ne peut pas trouver de polynôme avec une valeur plus grand et dans un second temps exhiber un polynôme qui vérifie les conditions de l'énoncé et dont le produit de racine est bien égal à $2^{-2023}$.
Notons que par hypothèse, on peut réécrire $P(X)=\prod_{k=1}^{2023}\left(X-r_{k}\right)$. En particulier, $P(0)=-\prod_{k=1}^{2023} r_{k}$ et $\mathrm{P}(1)=\prod_{\mathrm{k}=1}^{2023}\left(1-\mathrm{r}_{\mathrm{k}}\right)$. L'hypothèse $\mathrm{P}(0)+\mathrm{P}(1)=0$ devient :
$$
\prod_{k=1}^{2023}\left(1-r_{k}\right)=\prod_{k=1}^{2023} r_{k}=r_{1} \cdot r_{2} \cdots r_{2023}
$$
Ainsi comme pour tout $k, r_{k} \geqslant 0$ et $1-\mathrm{r}_{\mathrm{k}} \geqslant 0$, par inégalité arithmético-géométrique,
$$
\left(r_{1} \cdot r_{2} \cdots r_{2023}\right)^{2}=\prod_{k=1}^{2023}\left(1-r_{k}\right) r_{k} \leqslant \prod_{k=1}^{2023}\left(\frac{\left(1-r_{k}\right)+r_{k}}{2}\right)^{2}=\frac{1}{4^{2023}}
$$
Ainsi $r_{1} \cdot r_{2} \cdots r_{2023} \leqslant 2^{-2023}$.
Notons de plus que si $\mathrm{P}(\mathrm{X})=\left(\mathrm{X}-\frac{1}{2}\right)^{2023}$, P est bien unitaire de degré 2023, a 2023 racines dans $[0,1]$, vérifie $\mathrm{P}(0)+\mathrm{P}(1)=\left(-\frac{1}{2}\right)^{2023}+\left(\frac{1}{2}\right)^{2023}=0$ donc P est fantabuleux. Le produit de ses racines vaut $2^{-2023}$. Ainsi la valeur maximale que peut prendre $r_{1} \cdot r_{2} \cdots r_{2023}$ pour un polynôme fantabuleux est $2^{-2023}$.
Commentaire des correcteurs: L'exercice demandait de trouver la valeur maximale que pouvait prendre un produit de racines pour une classe de polynômes particuliers. Presque tous les élèves ont trouvé le cas réalisant le maximum (et donc sa valeur), et une proportion satisfaisante de ces élèves ont mené la preuve jusqu'au bout, généralement en appliquant l'IAG. Les relations de Viète semblent bien maitrisées mais n'étaient absolument pas nécessaires à la résolution du problème. Une idée à retenir : l'IAG est souvent une inégalité judicieuse pour montrer qu'un produit de réels positifs est maximal lorsque tous ses termes sont égaux.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "## Solution de l'exercice 13"
}
|
d491094a-94cc-5d75-aaab-867945aba6ca
| 607,244
|
Find all integers $p$ such that $p, p+2$ and $p+4$ are all three prime?
A prime number is an integer $\geqslant 2$ that is divisible only by 1 and itself.
|
First, we can expect there to be very few. We wish to obtain information about these prime numbers.
Note that a prime number divisible by 3 is a fortiori equal to 3. We consider 3 cases based on the remainder of the division of $p$ by 3 (modulo 3):
$-p=3k: p$ is divisible by 3, so $p=3$. $\{3,5,7\}$ is indeed a triplet of prime numbers.
$-p=3k+1: p+2$ is divisible by 3 and prime, so $p=1$ (impossible).
$-p=3k+2: p+4$ is divisible by 3 and prime, so $p=-1$ (impossible).
Hence $\mathrm{p}=3$.
Comment from the markers The exercise is generally very well handled, apart from some attempts modulo 10, the argument modulo 3 was well understood. Be careful not to forget the case $\mathrm{p}=2$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $p$ tels que $p, p+2$ et $p+4$ soient tous les 3 premiers?
Un nombre premier est un entier $\geqslant 2$ qui n'est divisible que par 1 et lui-même.
|
Tout d'abord, on peut s'attendre à ce qu'il n'y en ait que très peu. On souhaite obtenir des informations sur ces nombres premiers.
Notons qu'un nombre premier divisible par 3 est a fortiori égal à 3 . On considère 3 cas en fonction du reste de la division de $p$ par 3 (modulo 3 ):
$-p=3 k: p$ est divisible par 3 donc $p=3 .\{3,5,7\}$ est bien un triplet de nombres premiers.
$-p=3 k+1: p+2$ est divisible par 3 et premier donc $p=1$ (impossible).
$-p=3 k+2: p+4$ est divisible par 3 et premier donc $p=-1$ (impossible).
D'où $\mathrm{p}=3$.
Commentaire des correcteurs L'exercice est globalement très bien traité, à part quelques tentatives modulo 10 , l'argument modulo 3 a bien été compris. Attention à ne pas oublier le cas $\mathrm{p}=2$.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
c7b17c37-ee82-5e5d-8a7b-b1c7b57f9a72
| 607,284
|
Let $p \geqslant 3$ be a prime number. For $k \in \mathbb{N}$ satisfying $1 \leqslant k \leqslant p-1$, the number of divisors of $\mathrm{kp}+1$ that are strictly between $k$ and $p$ is denoted by $a_{k}$.
What is the value of $a_{1}+a_{2}+\ldots+a_{p-1}$?
|
The answer is $p-2$.
We will show that each of $\{2, \ldots, \boldsymbol{p}-1\}$ contributes exactly once to the count represented by $a_{1}+a_{2}+\ldots+a_{p-1}$.
Let $2 \leqslant \mathrm{~m} \leqslant \mathrm{p}-1$ be an integer, we aim to show two things:
1. $m$ is counted at most once
2. $m$ is indeed counted
$m$ is counted at most once:
By contradiction, suppose there exist $1 \leqslant i<j \leqslant p-1$ two integers satisfying:
- $m \mid i p+1$ and $m>i$
- $m \mid j p+1$ and $m>j$
We then have $m \mid p(j-i)$, but $\operatorname{gcd}(m, p)=1$, so $m \mid j-i$. However, this is impossible because $0<j-i<$ $j<m$: $m$ is counted at most once.
$m$ is indeed counted:
Consider the $m-1$ integers $\{p+1,2 p+1, \ldots,(m-1) p+1\}$.
Just as before, we see that they are distinct modulo $m$. Moreover, none of them is $\equiv 1(\bmod m)$ because if we remove the +1, no integer is divisible by $m$.
Thus, $m$ is counted exactly once, and this concludes the proof.
Comment from the graders
The approach was generally understood, but the formalization of this reasoning was not always rigorous.
|
p-2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $p \geqslant 3$ un nombre premier. Pour $k \in \mathbb{N}$ vérifiant $1 \leqslant k \leqslant p-1$, le nombre de diviseurs de $\mathrm{kp}+1$ qui sont compris strictement entre $k$ et $p$ est noté $a_{k}$.
Que vaut $a_{1}+a_{2}+\ldots+a_{p-1}$ ?
|
La réponse est $p-2$.
Nous allons montrer que chacun de $\{2, \ldots, \boldsymbol{p}-1\}$ contribue exactement une fois au comptage représenté $\operatorname{par} a_{1}+a_{2}+\ldots+a_{p-1}$.
Soit $2 \leqslant \mathrm{~m} \leqslant \mathrm{p}-1$ un entier, on se propose de montrer deux choses :
1. $m$ est compté au plus une fois
2. m est bien compté
m est compté au plus une fois :
Par l'absurde, on suppose qu'il existe $1 \leqslant i<j \leqslant p-1$ deux entiers vérifiant:
- $m \mid i p+1$ et $m>i$
- $m \mid j p+1$ et $m>j$
On a donc $m \mid p(j-i)$ or $\operatorname{pgcd}(m, p)=1$ donc $m \mid j-i$. Cependant, c'est impossible car $0<j-i<$ $j<m$ : m est compté au plus une fois
m est bien compté :
On considère les $m-1$ entiers $\{p+1,2 p+1, \ldots,(m-1) p+1\}$.
Exactement comme précédemment, on voit qu'ils sont 2 à 2 distincts modulo m. De plus, aucun d'entre eux n'est $\equiv 1(\bmod m)$ car si on retire les +1 aucun entier n'est divisible par $m$.
D'où $m$ est compté une et une fois et cela conclut.
Commentaire des correcteurs
Le chemin à suivre a été globalement compris, mais la formalisation de ce raisonnement n'était pas toujours rigoureuse.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
de1046cb-ba4b-57fc-af91-2c2817cfe10b
| 607,290
|
In how many ways can 7 rooks be placed on a $7 \times 7$ chessboard such that no rook can attack another?
A rook can attack another rook if it is on the same row or the same column.
|
If we place 7 towers so that no two towers are in the same column, knowing that there are 7 columns, then there will be exactly one tower on each column (and the same for each row).
There are 7 possible positions to place a tower in the first column. There are then 6 possible positions to place a tower in the second column without it being in the same row as the first tower. And so on, on the $k$-th column there are $8-k$ ways to place a tower without it being in the same row as a tower already placed.
Thus, there are 7! $=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040$ ways to arrange the towers in this manner.
If we denote $\sigma(i)$ as the row number of the tower present on the i-th column in one of the configurations satisfying the statement, then $\sigma$ is what is called a permutation.
Comment from the graders
The problem was very well done.
|
5040
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
De combien de façons peut-on placer 7 tours sur un échiquier $7 \times 7$ telle qu'aucune tour ne puisse en attaquer une autre?
Une tour peut attaquer une autre tour si elle se situe sur la même ligne ou la même colonne.
|
Si on place 7 tours de sorte que deux tours ne soient pas sur la même colonne, sachant qu'il y a 7 colonne, alors il y aura exactement une tour sur chaque colonne (et de même sur chaque ligne).
Il y a 7 positions possibles pour placer une tour sur la première colonne. Il y a ensuite 6 positions possibles pour placer une tour sur la seconde colonne sans qu'elle soit sur la même ligne que la première tour. Ainsi de suite, sur la $k$-ième colonne il y a $8-k$ manières de placer une tour sans qu'elle soit sur la même ligne qu'une tour déjà placée.
Ainsi il y a 7 ! $=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040$ manières de disposer les tours de cette manière.
Si on note $\sigma(i)$ le numéro de ligne de la tour présente sur la i-ième colonne dans une des configurations satisfaisant l'énoncé, alors $\sigma$ est ce que l'on appelle une permutation.
Commentaire des correcteurs
Le problème a été très bien réussi.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
caac369c-da33-5074-89e8-7f1ebd610bf3
| 607,302
|
The integers from 1 to 2020 are written on the board. Jacques has the right to erase two of them and write their difference or their sum in their place, and to repeat this until only one integer remains. Is it possible for the integer obtained at the end to be 321?
|
The statement presents a finite sequence of operations, and the problem asks whether it is possible to go from the initial situation to a certain final situation. A first idea to try in this case is to look for an invariant.
A second idea is to test the problem with smaller values. For example, one can test the statement for integers written from 1 to 4 and see what values can be reached at the end of the process described in the statement. It is observed that starting from a fixed value \( n \), all possible results have the same parity, that of the sum of the numbers from 1 to \( n \). After testing this conjecture for integers written from 1 to 5, one then tries to show that the parity of the sum of the integers written on the board is invariant under the described operation.
If at a given moment, the sum of the integers written on the board is \( S \) and Jacques chooses the integers \( x \) and \( y \), then these integers will be replaced by \( x+y \) or by \( x-y \), and then \( S \) will be replaced by \((S-x-y)+y-x = S-2x\) or by \((S-y-x)+(x-y) = S-2y\). These two integers have the same parity, so the sum of the integers written on the board retains the same parity throughout the process. Since in the initial situation, the sum of the integers written on the board is
\[
1+2+3+\cdots+2020 = \frac{2020 \cdot 2021}{2} = 1010 \cdot 2021
\]
and is even, the number written on the board in the final situation will also be even and it cannot therefore be the number 321.
Comment from the graders
It was necessary in this problem to invoke the notion of invariant. Explanations from students who did not explicitly mention the parity invariant were not always very convincing. Be careful not to give a reasoning that is too "hands-on."
|
321
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Les entiers de 1 à 2020 sont écris au tableau. Jacques a le droit d'en effacer deux et d'écrire à la place leur différence ou leur somme, et de recommencer jusqu'à ce qu'il ne reste plus qu'un entier. Est-il possible que l'entier obtenu à la fin soit 321 ?
|
L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée à essayer dans ce cas est de chercher un invariant.
Une seconde idée est de tester le problème avec des plus petites valeurs. Par exemple, on peut tester l'énoncé pour les entiers écrits de 1 à 4 et regarder à quelles valeurs ont peut aboutir à la fin du processus décrit dans l'énoncé. On remarque que partant d'une valeur fixée n , les résultats possibles ont tous la même parité, celle de la somme des nombres de 1 à $n$. Après avoir testé cette conjecture pour les entiers écrits de 1 à 5 , on essaye donc de montrer que la parité de la somme des entiers écrits au tableau est invariante sous l'opération décrite.
Si un instant donné, la somme des entiers écrits au tableau vaut $S$ et que Jacques choisit les entiers $x$ et $y$, alors ces entiers seront remplacés par $x+y$ ou par $x-y$ et alors $S$ sera remplacé par $(S-x-y)+y-x=$ $S-2 x$ ou par $(S-y-x)+(x-y)=S-2 y$. Ces deux entiers ont la même parité, donc la somme des entiers écrits au tableau garde la même parité tout au long du processus. Puisque dans la situation initiale, la somme des entiers écrits au tableau est
$$
1+2+3+\cdots+2020=\frac{2020 \cdot 2021}{2}=1010 \cdot 2021
$$
et est paire, le nombre écrit au tableau dans la situation finale sera également pair et il ne peut donc pas s'agir du nombre 321.
Commentaire des correcteurs
Il était nécessaire dans ce problème d'évoquer la notion d'invariant. Les explications des élèves qui n'évoquaient pas explicitement l'invariant de parité n'étaient pas toujours très convaincantes. Attention à ne pas faire un raisonnement qui soit trop "avec les mains".
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
a3c0a7ba-eeb3-5699-b7e2-9092e3a3674f
| 607,303
|
Martin is trying to fill each cell of a rectangular grid with 8 rows and n columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and M such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer n for which this is possible?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that $c$ is indeed the largest integer, we will on the one hand show that if an integer $n$ satisfies the property, then $n \leqslant \mathrm{c}$, and on the other hand, we will show that we can find a table with exactly c columns. The statement provides an assumption about the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are $\binom{8}{2}=28$ pairs of rows.
We then look at the information we have about the columns of the table. Since the statement's hypothesis mentions identical letters within the same column, we will count how many pairs of identical letters belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column, there are 8 letters, so a letter appears at least 2 times.
- If each letter appears at most 2 times, then each letter appears exactly 2 times since there are 8 cells in the column and 4 possible letters. We thus have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter $P$, then we can form 3 pairs of letters $P$. Among the 5 remaining letters, at least one of the letters $O, F$, and $M$ appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter $P$, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the statement's hypothesis, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most $4 \times n$ pairs of rows. So $4 \mathrm{n} \leqslant 28$ and $n \leqslant 7$.
Conversely, there exists a configuration with the following 7 columns:
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
The largest integer n of columns is therefore $\mathrm{n}=7$.
Graders' Comments
The exercise is generally well done; students have understood that the constraint is that each column adds 4 pairs of identical letters, but few have provided a fully rigorous proof of this fact. Some have given a set of 7 columns and justified that 7 is optimal because it was not possible to add a column to what they had done. However, this justification is not sufficient. Indeed, just because the construction cannot be enlarged does not mean that its size is maximal: one can imagine a larger, very different construction from the one given.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et n colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que $c$ est bien le plus grand entier, on va d'une part montrer que si un entier $n$ satisfait la propriété, alors $n \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes. L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
- Si chaque lettre apparaît au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
- Si une lettre apparait exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $n \leqslant 7$.
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
Commentaire des correcteurs
L'exercice est globalement bien réussi, les élèves ont bien compris que la contrainte était que chaque colonne rajoutait 4 paires de lettres identiques, mais peu ont fait une preuve totalement rigoureuse de ce fait. Certains ont donné un ensemble de 7 colonnes et justifié le fait que 7 était optimal car il n'était pas possible de rajouter une colonne à ce qu'ils avaient faits. Mais cette justification n'est pas suffisante. En
effet, ce n'est pas parce que la construction ne peut être agrandie que pour autant sa taille est maximale : on peut imaginer qu'il existe une construction plus grande très différente de celle donnée.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
884853a1-ce91-58c9-9e48-3d2e6109a7c0
| 607,306
|
In 5 boxes, there are respectively 402, 403, 404, 405, and 406 stones. The only allowed operation is to take 4 stones from a pile that has at least 4 stones and put one stone in each of the other piles. What is the maximum number of stones that can be in a single pile?
|
The statement presents a sequence of operations and describes a certain initial situation. A first idea to try in this case is to look for an invariant.
A second idea is to test the statement for smaller values, for example, for piles of size $0,1,2,3$ and 4. After several trials, one notices that the piles always have, up to permutation, the sizes $0,1,2,3$ and 4. After testing on piles of size $1,2,3,4$ and 5, one realizes that the piles always have distinct values modulo 5. One hastens to prove this conjecture.
Removing 4 stones from a pile is equivalent, modulo 5, to adding 1. Since one adds one to each of the other piles, the values of the piles all increase by 1 modulo 5. Thus, if before the operation these values were distinct modulo 5, after the operation they will remain distinct modulo 5. We have thus determined our invariant.
Thus, the sum of the sizes of any 4 piles will never exceed $0+1+2+3=6$, and therefore no pile will ever contain more than $2020-6=2014$ stones.
Conversely, we must now prove that it is always possible to ensure that a pile contains 2014 stones after a finite number of operations. For this, it suffices to never touch the pile containing 404 stones, and to perform the operation on the other piles until it is no longer possible to perform a single operation. Thus, the remaining piles will have $0,1,2,3$ stones at the end of the process, so there will indeed be $2020-(0+1+2+3)=2014$ stones in the same pile.
## Comment from the Examiners
Many students are content with constructing the bound without showing that it is indeed optimal. In rarer cases, some students prove only the minimality without the attainability. Most proofs of optimality are based on work modulo 5, but some more original proofs avoid this, with work on the last operations (rarely perfectly executed).
|
2014
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Dans 5 boites se trouvent respectivement 402,403, 404, 405 et 406 pierres. La seule opération autorisée est de prendre 4 pierres dans un tas ayant au moins 4 pierres et d'en mettre une dans chacun des autres tas. Quel est le plus grand nombre de pierre qu'il est possible d'avoir dans un seul tas?
|
L'énoncé présente une suite d'opérations et décrit une certaine situation initiale. Une première idée à essayer dans ce cas est de chercher un invariant.
Une deuxième idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour des tas de taille $0,1,2,3$ et 4 . Après plusieurs essais, on remarque que les tas ont toujours, à permutation près, les tailles $0,1,2,3$ et 4 . Après avoir testé sur des tas de taille $1,2,3,4$ et 5 , on s'aperçoit que les tas ont toujours des valeurs distinctes deux à deux modulo 5 . On s'empresse de démontrer cette conjecture.
Enlever 4 pierres d'un tas revient, modulo 5, à en ajouter 1. Comme on en ajoute une dans chacun des autres tas, les valeurs des tas augmentent toutes de 1 modulo 5 . Ainsi, si avant l'opération ces valeurs étaient distinctes deux à deux modulo 5 , après l'opération elles resteront distinctes deux à deux modulo 5 . On a donc déterminé notre invariant.
Ainsi la somme des tailles de 4 tas quelconques ne pourra jamais dépasser $0+1+2+3=6$ et donc un tas quelconque ne pourra jamais contenir plus que $2020-6=2014$ pierres.
Réciproquement, nous devons désormais démontrer que l'on peut toujours faire en sorte qu'un tas contienne 2014 pierres au bout d'un nombre fini d'opérations. Pour cela, il suffit de ne jamais toucher au tas contenant 404 pierres, et de faire l'opération sur les autres tas jusqu'à ce que ce ne soit plus possible de faire une seule opération. Ainsi les tas restants auront $0,1,2,3$ pierres à la fin du procédé, donc il y aura bien $2020-(0+1+2+3)=2014$ pierres sur le même tas.
## Commentaire des correcteurs
Un grand nombre d'élèves se contente de la construction de la borne sans montrer qu'elle est effectivement optimale. Dans de plus rares cas, certains élèves ne prouvent que la minimalité sans l'atteignabilité. La majorité des preuves d'optimalité se basent sur un travail modulo 5 , mais certaines preuves plus originales s'en passent, avec un travail sur les dernières opérations (travail rarement parfaitement exécuté).
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
7c8e7d73-7e88-5d7c-8ef9-328a62675ead
| 607,307
|
A coloring of the integers $\{1,2, \cdots, 2020\}$ in blue and red is said to be pleasant if there do not exist two distinct integers in $\{1,2, \cdots, 2020\}$ of the same color whose sum is a power of 2. How many such colorings exist?
|
A first idea is to test the statement for smaller values, for example for a coloring of the integers from 1 to 7.
Let's color the numbers in order: to color 1, there is no apparent constraint, the same for coloring 2. However, since $3+1=4$, the color of 3 is imposed. To color 4, there is no apparent constraint because $4+3=7$, $4+2=6$, and $4+1=5$ are not powers of two. However, since $5+3=6+2=7+1=8$, the color of 5, 6, and 7 is imposed. By testing all possible colorings, we see that regardless of the colors chosen to color 1, 2, and 4, the resulting coloring is pleasant. We can therefore assume that a pleasant coloring is fixed once the colors of the powers of 2 are chosen and that any coloring of the powers of 2 can be extended to a pleasant coloring.
We will show that for any coloring of the powers of 2 between 1 and 2020, there exists a unique way to color the other numbers to obtain a pleasant coloring.
To do this, we will proceed by induction. Let's show that if we color the powers of 2 from 1 to N, then there is a unique pleasant way to color the other integers from 1 to N.
The result is clear for $N=1$.
Let N be such that the result is true for $N-1$. We color the powers of 2 from 1 to N. By the induction hypothesis, there is a unique pleasant way to color the other integers from 1 to $N-1$.
If $N=2^k$ for some integer k, then N is already colored and the coloring is pleasant: indeed, if $1 \leq \ell < 2^k$, then $2^k + \ell$ is not a power of 2 because $2^k < 2^k + \ell < 2^{k+1}$. Thus, in this case, there is a unique way to complete the coloring.
If N is not a power of 2, then $N=2^k + n$ with $1 \leq n < 2^k$ and k an integer. Then N cannot be colored the same color as $2^k - n$ because $N + 2^k - n = 2^{k+1}$. We therefore color N with the other color, and this is indeed the unique way to complete the coloring in a pleasant manner. The resulting coloring is pleasant: indeed, let t be an integer such that $1 \leq t < N$ and $t + N$ is a power of 2, we have $2^k < N \leq t + N < 2N = 2^{k+1} + 2n < 2^{k+1} + 2^{k+1} = 2^{k+2}$, so $t + N = 2^{k+1}$. Therefore, $t = 2^{k+1} - 2^k - n = 2^k - n$. Since we have colored N and $2^k - n$ with different colors, the coloring is pleasant.
There are 11 powers of 2 between 1 and 2020, which are $1=2^0, 2=2^1, \cdots, 1024=2^{10}$, and there are $2^{11}$ ways to color them in blue and red. Thus, there are $2^{11}$ pleasant colorings.
Comment from the graders
Most students recognized the importance of the powers of 2. Some proposed alternatively to look at elements congruent to $2^n$ modulo $2^{n+1}$, which also worked. Many proved that there were at most 2048 colorings, but very few verified that the colorings thus produced were suitable, which was, however, an important part of the exercise. It is important to detail the arguments used: for example, making an induction is a good idea when you want to generalize something.
|
2^{11}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Un coloriage des entiers $\{1,2, \cdots, 2020\}$ en bleu et rouge est dit agréable s'il n'existe pas deux entiers distincts dans $\{1,2, \cdots, 2020\}$ de même couleur dont la somme est une puissance de 2 . Combien de tels coloriage existent-ils?
|
Une première idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour un coloriage des entiers de 1 à 7 .
Colorions dans l'ordre les nombres : pour colorier 1, on n'a pas de contrainte apparente, idem pour colorier 2 . Par contre comme $3+1=4$, la couleur de 3 est imposée. Pour colorier 4 , il n'y a pas de contrainte apparente car $4+3=7,4+2=6$ et $4+1=5$ ne sont pas des puissances de deux. Par contre comme $5+3=6+2=7+1=8$, la couleur de 5,6 et 7 est imposée. En testant tous les coloriages possibles, on voit que peu importe les couleurs choisies pour colorier 1, 2 et 4 , le coloriage obtenu est agréable. On peut donc supposer qu'un coloriage agréable est fixé une fois la couleur des puissances de 2 est choisie et que tout coloriage des puissances de 2 peut être prolonger en un coloriage agréable.
Nous allons montrer que pour tout coloriage des puissances de 2 entre 1 et 2020, il existe une unique manière de colorier les autres nombres de sorte à obtenir un coloriage agréable.
Pour cela nous allons procéder par récurrence. Montrons que si on colorie les puissances de 2 de 1 à N , alors il existe une unique manière agréable de colorier les autres entiers de 1 à N .
Le résultat est clair pour $N=1$.
Soit N tel que le résultat soit vrai pour $\mathrm{N}-1$. On colorie les puissances de 2 de 1 à N . Par hypothèse de récurrence, il existe une unique manière agréable de colorier les autres entiers de 1 à $\mathrm{N}-1$.
Si $\mathrm{N}=2^{\mathrm{k}}$ pour un certain entier k , alors N est déjà colorié et le coloriage est agréable : en effet si $1 \leqslant \ell<2^{k}$, alors $2^{k}+\ell$ n'est pas une puissance de 2 car $2^{k}<2^{k}+\ell<2^{k+1}$. Ainsi dans ce cas il y a une unique manière de compléter le coloriage.
Si $N$ n'est pas une puissance de 2 , alors $N=2^{k}+n$ avec $1 \leqslant n<2^{k}$ et $k$ un entier. Alors $N$ ne peut pas être colorié de la même couleur que $2^{k}-n$ car $N+2^{k}-n=2^{k+1}$. On colorie donc N de l'autre couleur, et c'est bien l'unique manière de compléter le coloriage de manière agréable. Le coloriage obtenu est agréable : en effet soit $t$ entier tel que $1 \leqslant t<N$ et $t+N$ est une puissance de 2 , on a $2^{k}<\mathrm{N} \leqslant \mathrm{t}+\mathrm{N}<2 \mathrm{~N}=2^{\mathrm{k}+1}+2 \mathrm{n}<2^{\mathrm{k}+1}+2^{\mathrm{k}+1}=2^{\mathrm{k}+2}$, donc $\mathrm{t}+\mathrm{N}=2^{\mathrm{k}+1}$. On a donc $\mathrm{t}=2^{\mathrm{k}+1}-2^{k}-\mathrm{n}=2^{k}-\mathrm{n}$. Comme on a colorié N et $2^{k}-\mathrm{n}$ de deux couleurs différentes, le coloriage est agréable.
Il y a 11 puissances de 2 entre 1 et 2020 qui sont $1=2^{0}, 2=2^{2}, \cdots, 1024=2^{10}$, et il y a $2^{11}$ manières de les colorier en bleu et rouge. Ainsi il y a $2^{11}$ coloriages agréables.
Commentaire des correcteurs
La majorité des élèves a vu l'importance des puissances de 2 . Certains ont proposé alternativement de regarder les éléments congrus à $2^{n}$ modulo $2^{n+1}$ ce qui fonctionnait aussi. Nombreux sont ceux qui ont prouvé qu'il y avait au plus 2048 coloriages, mais très peu ont vérifié que les coloriages ainsi produit convenaient, alors que c'était pourtant une partie importante de l'exercice. Il faut penser à détailler les arguments utilisés : par exemple faire une récurrence est une bonne idée quand on veut généraliser quelque chose.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
9b252410-7ff9-50f7-993d-a81a97f0a605
| 607,309
|
Martin is trying to fill each cell of a rectangular grid with 8 rows and $n$ columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and M such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer $n$ for which this is possible?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will on the one hand show that if an integer n satisfies the property, then $n \leqslant c$, and on the other hand, we will show that we can find a table with exactly c columns.
The statement presents a hypothesis about the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are $\binom{8}{2}=28$ pairs of rows.
We then look at the information we have about the columns of the table. Since the hypothesis in the statement mentions identical letters within the same column, we will count how many pairs of identical letters belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column, there are 8 letters, so a letter appears at least twice.
- If each letter appears at most twice, then each letter appears exactly twice since there are 8 cells in the column and 4 possible letters. We therefore have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter $P$, then we can form 3 pairs of letters $P$. Among the 5 remaining letters, at least one of the letters $O, F$, and $M$ appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter $P$, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the hypothesis of the statement, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most $4 \times n$ pairs of rows. So $4 \mathrm{n} \leqslant 28$ and $\mathrm{n} \leqslant 7$.
Conversely, there exists a configuration with the following 7 columns:
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
The largest integer n of columns is therefore $\mathrm{n}=7$.
Examiner's Comment
Many students managed to find the answer $\mathrm{n}=7$ and provided an example. Most propose a correct argument to show that it is optimal, but sometimes this reasoning is written in a somewhat unclear manner.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et $n$ colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \leqslant c$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes.
L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
- Si chaque lettre apparait au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
- Si une lettre apparaît exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $\mathrm{n} \leqslant 7$.
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
Commentaire des correcteurs
De nombreux élèves ont réussi à trouver la réponse $\mathrm{n}=7$ et ont exhibé un exemple. La plupart proposent un argument correct pour montrer que c'est optimal, mais parfois ce raisonnement est rédigé de façon peu claire.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution de l'exercice 12"
}
|
fd6ef02c-af03-5f9f-8d77-d0bd3f952da2
| 607,313
|
Consider a grid of size $2019 \times 2019$. On this grid, pebbles are placed. A configuration is said to be beautiful if there does not exist a parallelogram formed by four pebbles $A B C D$, such that $A, B, C$, and $D$ are not all aligned.
What is the maximum number of pebbles that can be placed on the grid?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will first show that if an integer n satisfies the property, then $\mathrm{n} \leqslant \mathrm{c}$, and secondly, we will show that we can find a grid with exactly c pebbles satisfying the property.
We quickly test the statement for smaller values, for example, for a grid of size $3 \times 3$, $4 \times 4$, or even $5 \times 5$, in order to guess the value. We find in these small cases that the largest integers are 5, 7, and 9, respectively. We can conjecture that the value sought will therefore be $2 \times 2019-1=4037$. By testing these small values, we have noticed that the presence of pebbles in a column forces certain positions to be empty. We will therefore try to formalize this reasoning.
We consider pairs of pebbles that are in the same column. If there are two such pairs whose pebbles are at the same distance on different columns, then we obtain a parallelogram, which we want to avoid.
Let $n_{i}$ be the number of pebbles in the $i$-th column. Consequently, there are at least $n_{i}-1$ pairs with distinct distances on column $i$. Since for two fixed columns, the distance between any two pebbles in the first column must be different from the distance between any two pebbles in the second column, all the distances between pairs of pebbles in the same column must be distinct. This gives a total of $\left(n_{1}-1\right)+\left(n_{2}-1\right)+\cdots+\left(n_{2019}-1\right)=n-2019$ distinct distances with n being the total number of pebbles. However, there are at most 2018 possible distances, since there are 2019 positions for a pebble in a column. This shows that $\mathrm{n} \leqslant 2018+2019=4037$.
Conversely, if we fill each cell in the first row with a pebble and each cell in the first column with a pebble and leave the other cells empty, we then place $2 \times 2019-1=4037$ pebbles without creating any parallelograms.
The largest integer sought is therefore 4037.
Grader's Comments
Many students had the right idea to solve the problem, but many had difficulty formalizing the result correctly. If one attempts to solve this problem by induction, one must explicitly state the grids being manipulated and be careful that a sub-grid of a "maximal" grid is not necessarily maximal.
|
4037
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère une grille de taille $2019 \times 2019$. Sur cette grille sont posés des cailloux. Une configuration est dite belle s'il n'existe pas de parallélogramme formé par quatre cailloux $A B C D$, tels que $A, B, C$, et $D$ ne soient pas tous alignés.
Quel est le plus grand nombre de cailloux qu'il est possible de mettre dans une grille?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $\mathrm{n} \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver une grille possédant exactement c cailloux satisfaisant la propriété.
On s'empresse de tester l'énoncé pour des valeurs plus petites, par exemple pour une grille de taille $3 \times 3$, $4 \times 4$ ou même $5 \times 5$, afin de deviner la valeur. On trouve dans ces petits cas que les plus grands entiers sont respectivement 5, 7 et 9 . On peut conjecturer que la valeur recherchée sera donc $2 \times 2019-1=4037$. En testant ces petites valeurs, on a pu remarquer que la présence de cailloux sur une colonne forçait que certains emplacements soient vides. Nous allons donc essayer de formaliser ce raisonnement.
On considère les paires de cailloux qui sont sur la même colonne. S'il y a deux telles paires dont les cailloux sont à même distance sur des colonnes différentes alors on obtient un parallélogramme, ce que l'on veut éviter.
Soit $n_{i}$ le nombre de cailloux dans la $i$-ième colonne. Sur la colonne $i$ il y a par conséquent au moins $n_{i}-1$ paires à distances distinctes. Puisque pour deux colonnes fixées, la distance entre deux quelconques cailloux de la première colonne doit être différente de la distance entre deux quelconques cailloux de la deuxième colonne, toutes les distances entre deux paires de cailloux appartenant à la même colonne doivent être distinctes. Cela fait en tout $\left(n_{1}-1\right)+\left(n_{2}-1\right)+\cdots+\left(n_{2019}-1\right)=n-2019$ distances distinctes avec n le nombre total de cailloux. Or il y a au plus 2018 distances possibles, puisqu'il y a 2019 emplacements pour un cailloux dans une colonne. Ceci montre que $\mathrm{n} \leqslant 2018+2019=4037$.
Réciproquement, si on remplit chaque case de la première ligne par un caillou et chaque case de la première colonne par un caillou et on laisse les autres cases vides, on a alors placé $2 \times 2019-1=4037$ cailloux sans créer de parallélogrammes.
Le plus grand entier recherché est donc 4037.
Commentaire des correcteurs
Une grande partie des élèves a eu la bonne idée pour résoudre l'exercice, mais beaucoup ont eu du mal à formaliser le résultat correctement. Si on tente de résoudre cet exercice par récurrence, il faut expliciter les grilles que l'on manipule et faire attention au fait qu'une sous-grille d'une grille "maximale" n'est pas forcément maximale.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "\nSolution de l'exercice 14"
}
|
c6515434-9ddd-59d5-975f-0fd69fac6b74
| 607,315
|
Determine the smallest integer $\mathrm{n} \geqslant 2$ such that there exist strictly positive integers $a_{1}, \ldots, a_{n}$ such that
$$
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
|
Let's analyze the problem. In this problem, we are looking for the smallest integer \( n \) satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer \( c \). To show that \( c \) is indeed the smallest integer, we must on the one hand show that if an integer \( n \) satisfies the property, then \( n \geqslant c \), and on the other hand, we must show that we can find \( c \) integers satisfying the divisibility relation.
Since there is a divisibility relation, we can expect to use various ideas:
- If \( a \mid b \) then \( a \) divides the linear combinations of \( a \) and \( b \)
- If \( a \mid b \) and \( a \) and \( b \) are strictly positive, then \( a \mid b \)
- If \( a \mid b \), the divisors of \( a \) also divide \( b \)
Once this initial analysis is done, we can start by looking for integers \( a_{i} \) satisfying the property for small values of \( n \), for example, for \( n=2,3 \) or even 4 if we are brave, before realizing that this method will not allow us to determine \( n \).
However, having searched for \( a_{i} \) for small values of \( n \) allows us to find potential properties that the \( a_{i} \) must satisfy. For example, we may have noticed that the integers \( a_{i} \) cannot all be even, since in that case the sum of the \( a_{i}^{2} \) would be even but \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is odd. We then realize that what matters in this argument is not the parity of the \( a_{i} \) but the parity of the sum.
We obtain that \( a_{1}+a_{2}+\ldots+a_{n} \) is odd. Otherwise, since \( a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv a_{1}+a_{2}+\ldots+a_{n} \bmod 2 \), \( a_{1}+\ldots+a_{n} \) is also even, but then \( a_{1}^{2}+\ldots+a_{n}^{2} \) is even and divides \( \left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1 \) which is odd, which is absurd.
We deduce that \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is even. The previous parity argument invites us to refine this study. We will therefore look to see if \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is divisible by 4, 8, etc. The presence of multiple squares invites us to look at each term with well-chosen moduli.
For example, modulo 4, \( \left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1 \) so 4 divides \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \). Let's not stop here; we also know that the squares of odd numbers can only be 1 modulo 8. Thus, \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is divisible by 8. Since 8 is coprime with \( a_{1}^{2}+\ldots+a_{n}^{2} \) which is odd, we deduce that
\[
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid \left(a_{1}+\ldots+a_{n}\right)^{2}-1
\]
Another remark that we can make about the statement is that it involves the sum of squares of numbers on one side and the square of the sum of numbers on the other side. This suggests the Cauchy-Schwarz inequality or the inequality of arithmetic and quadratic means. We can therefore try to compare the quantities \( 8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \) and \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \).
This idea of comparing the terms is consistent with what we are trying to show. The divisibility obtained gives that \( 8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \). In the inequality of arithmetic and quadratic means, the square of the sum is smaller than the sum of the squares of the elements multiplied by the number of variables. We suspect that the inequality obtained will be false for \( n \) too small, which will provide the desired bound. More precisely,
\[
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-1 < n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)
\]
where the middle inequality corresponds to the inequality of arithmetic and quadratic means. We finally obtain that \( n > 8 \) so \( n \geqslant 9 \).
Conversely, we seek 9 integers satisfying the property. We can expect that small integers will work. We can therefore look for \( a_{i} \) equal to 1 or 2. Finally, we find that by taking \( a_{1}=\cdots=a_{7}=1 \) and \( a_{8}=a_{9}=2 \), we have 15 which divides \( 11^{2}-1=120=15 \times 8 \).
The expected answer is therefore \( n=9 \).
Comment from the graders: The problem was solved by only one student. This is an instructive and very complete exercise, involving both arithmetic arguments and inequalities.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer le plus petit entier $\mathrm{n} \geqslant 2$ tel qu'il existe des entiers strictement positifs $a_{1}, \ldots, a_{n}$ tels que
$$
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
|
Analysons le problème. Dans ce problème, on cherche le plus petit entier n satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c'est bien le plus petit entier, on doit d'une part montrer que si un entier n satisfait la propriété, alors $n \geqslant c$ et on doit montrer d'autre part que l'on peut trouver $c$ entiers satisfaisant la relation de divisibilité.
Pusiqu'il y a une relation de divisibilité, on peut s'attendre à utiliser divers idées :
- Si $a \mid b$ alors $a$ divise les combinaisons linéaires de $a$ et $b$
- Si $a \mid b$ et que $a$ et $b$ sont strictement positifs, alors $a \mid b$
- Si $a \mid b$, les diviseurs de $a$ divisent également $b$
Une fois cette première analyse effectuée, on peut commencer par regarder si on trouve des entiers $a_{i}$ satisfaisant la propriété pour des petites valeurs de $n$, par exemple pour $n=2,3$ ou même 4 si on est courageux, avant de se convaincre que cette méthode ne permettra pas de déterminer n .
Néanmoins, avoir cherché des $a_{i}$ pour des petites valeurs de $n$ nous permet de trouver d'éventuelles propriétés que doivent satisfaire les $a_{i}$. Par exemple, on a pu remarquer que les entiers $a_{i}$ ne peuvent pas tous être pairs, puisque dans ce cas la somme des $a_{i}^{2}$ serait paire mais $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est impair. On se rend alors compte que ce qui importe dans cet argument, ce n'est pas la parité des $a_{i}$ qui entre en jeu mais la parité de la somme.
On obtient que $a_{1}+a_{2}+\ldots+a_{n}$ est impair. Dans le cas contraire, puisque $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv$ $a_{1}+a_{2}+\ldots+a_{n} \bmod 2, a_{1}+\ldots+a_{n}$ est pair également mais alors $a_{1}^{2}+\ldots+a_{n}^{2}$ est pair et divise $\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1$ qui est impair, ce qui est absurde.
On déduit que $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est pair. L'argument de parité précédent nous invite à préciser cette étude. On va donc chercher si $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par $4,8 \ldots$. La présence des multiples carré nous invite à regarder chaque terme avec des modulos bien choisis.
Par exemple, modulo $4,\left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1$ donc 4 divise $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Ne nous arrêtons pas en si bon chemin, nous savons également que les carrés des nombres impairs ne peuvent que valoir 1 modulo 8. Ainsi, $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par 8 . Or 8 est premier avec $a_{1}^{2}+\ldots+a_{n}^{2}$ qui est impair. On déduit de tout cela que
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
Enfin, une autre remarque que l'on peut formuler sur l'énoncé est qu'il implique la somme des carrés de nombres d'un côté et le carré de la somme des nombres de l'autre côté. Ceci fait penser à l'inégalité de Cauchy-Schwarz, ou à l'inégalité des moyennes arithmétiques et quadratiques. On peut donc essayer de comparer les quantités $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)$ et $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$.
Cette idée de comparer les termes est cohérente avec ce que l'on cherche à montrer. La divisibilité obtenue donne que $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Or, dans l'inégalité des moyennes arithmétique et quadratique, le carré de la somme est plus petit que la somme des carrés des éléments multipliée par le
nombre de variables. On se doute donc que l'inégalité obtenue va être fausse pour n trop petit, ce qui va nous fournir la borne souhaitée. Plus précisement,
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-1<n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)
$$
où l'inégalité au milieu correspond à l'inégalité des moyennes arithmétiques et quadratiques. On obtient finalement que $\mathrm{n}>8$ donc $\mathrm{n} \geqslant 9$.
Réciproquement, on cherche 9 entiers satisfaisant la propriété. On peut s'attendre à ce que de petits entiers fonctionnent. On peut donc chercher des $a_{i}$ valant 1 ou 2 . Finalement, on trouve qu'en prenant $a_{1}=\cdots=a_{7}=1$ et $a_{8}=a_{9}=2$, on a bien 15 qui divise $11^{2}-1=120=15 \times 8$.
La réponse attendue est donc $\mathrm{n}=9$.
Commentaire des correcteurs: L'exercice n'a été résolu que par un élève. C'est un exercice instructif et très complet, faisant appel à des arguments arithmétiques et des inégalités.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
eebbe023-687f-58cd-8ff5-20d19d479fc6
| 607,328
|
Let $(a_n)$ be a sequence of real numbers. Suppose that $a_0 = 1$ and for all $n \geqslant 1, a_n$ is the smallest positive solution of
$$
\left(a_n - a_{n-1}\right)\left(a_n + a_{n-1} - 2 \sqrt{n}\right) = 2.
$$
Find the smallest integer $n$ such that $a_n \geqslant 2022$.
|
To get an idea of the problem, we calculate the first values of $a_{n}$: for $a_{1}$, the equation is
$$
\left(a_{1}-1\right)\left(a_{1}-1\right)=2
$$
so $a_{1}-1=\sqrt{2}$ or $-\sqrt{2}$. Only the first case gives a positive solution $a_{1}=1+\sqrt{2}$. Now let's calculate $a_{2}$: the equation becomes
$$
\left(a_{2}-1-\sqrt{2}\right)\left(a_{2}+1-\sqrt{2}\right)=2
$$
which can be expanded to
$$
\left(a_{2}-\sqrt{2}\right)^{2}-1^{2}=2
$$
or $a_{2}-\sqrt{2}= \pm \sqrt{3}$. Only one sign gives a positive solution $a_{2}=\sqrt{2}+\sqrt{3}$.
From these first values, we hypothesize that the sequence $a_{n}$ is given by $a_{n}=\sqrt{n}+\sqrt{n+1}$ and we prove this by induction. It is true for $n=0$. Suppose it is true for $n-1$ and show it for $n$: the equation giving $a_{n}$ is
$$
\left(a_{n}-\sqrt{n-1}-\sqrt{n}\right)\left(a_{n}+\sqrt{n-1}-\sqrt{n}\right)=2
$$
which can be expanded to
$$
\left(a_{n}-\sqrt{n}\right)^{2}-(\sqrt{n-1})^{2}=2
$$
and thus
$$
\left(a_{n}-\sqrt{n}\right)^{2}=n+1
$$
so $a_{n}-\sqrt{n}= \pm \sqrt{n+1}$. Only the positive sign gives a positive solution, so we have $a_{n}=\sqrt{n}+$ $\sqrt{n+1}$, which concludes the induction.
We immediately notice that the sequence $(a_{n})$ is increasing, and consequently, if we find an $n$ such that $a_{n-1}<2022 \leqslant a_{n}$, it is the $n$ we are looking for. Indeed, if we have $0 \leqslant m<n$, then $m \leqslant n-1$ and thus $a_{m} \leqslant a_{n-1}<2022$ as required: $n$ is indeed the smallest index such that $a_{n} \geqslant 2022$.
But now we have
$$
\mathrm{a}_{1011^{2}-1}=\sqrt{1011^{2}-1}+1011<2 \cdot 1011=2022<1011+\sqrt{1011^{2}+1}=a_{1011^{2}}
$$
so the sought $n$ is $\mathrm{n}=1011^{2}$.
Comment from the graders: The problem was well solved by the students who submitted a paper. A vast majority perfectly conjectured $a_{n}=\sqrt{n}+\sqrt{n+1}$ and then proved it by induction. It is worth noting that calculating the first terms to guess an expression is a very good initiative to take in the rough draft as it can be the first step in solving a problem (as was the case here). From there, one could quickly conclude, but it was important to avoid calculation errors and to justify properly (arguments of increasing were relevant). These points were missing in some papers. It is also worth noting that in a test or competition, there is no calculator, so one must get used to looking for efficient calculations by hand.
|
1011^2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit ( $a_{n}$ ) une suite de réels. On suppose que $a_{0}=1$ et que pour tout $n \geqslant 1, a_{n}$ est la plus petite solution strictement positive de
$$
\left(a_{n}-a_{n-1}\right)\left(a_{n}+a_{n-1}-2 \sqrt{n}\right)=2 .
$$
Trouver le plus petit entier $n$ tel que $a_{n} \geqslant 2022$.
|
Pour se donner une idée du problème, on calcule les premières valeurs de $a_{n}$ : pour $a_{1}$, l'équation s'écrit
$$
\left(a_{1}-1\right)\left(a_{1}-1\right)=2
$$
donc $a_{1}-1=\sqrt{2}$ ou $-\sqrt{2}$. Seul le premier cas donne une solution positive $a_{1}=1+\sqrt{2}$. Cherchons maintenant à calculer $a_{2}: 1$ 'équation devient
$$
\left(a_{2}-1-\sqrt{2}\right)\left(a_{2}+1-\sqrt{2}\right)=2
$$
ce que l'on peut développer en
$$
\left(a_{2}-\sqrt{2}\right)^{2}-1^{2}=2
$$
ou encore $a_{2}-\sqrt{2}= \pm \sqrt{3}$. Un seul signe donne une solution positive $a_{2}=\sqrt{2}+\sqrt{3}$.
A partir de ces premières valeurs, on fait l'hypothèse que la suite $a_{n}$ est donnée par $a_{n}=\sqrt{n}+\sqrt{n+1}$ et on montre ceci par récurrence. C'est vrai pour $n=0$. Supposons que ceci soit vrai pour $n-1$ et montrons le au rang $n$ : l'équation donnant $a_{n}$ est
$$
\left(a_{n}-\sqrt{n-1}-\sqrt{n}\right)\left(a_{n}+\sqrt{n-1}-\sqrt{n}\right)=2
$$
ce que l'on développe en
$$
\left(a_{n}-\sqrt{n}\right)^{2}-(\sqrt{n-1})^{2}=2
$$
et donc
$$
\left(a_{n}-\sqrt{n}\right)^{2}=n+1
$$
donc $a_{n}-\sqrt{n}= \pm \sqrt{n+1}$. Seul le signe + donne une solution positive, donc on a bien $a_{n}=\sqrt{n}+$ $\sqrt{n+1}$ ce qui conclut la récurrence.
On remarque immédiatement que la suite ( $a_{n}$ ) est croissante, et par conséquent si on trouve un $n$ tel que $a_{n-1}<2022 \leqslant a_{n}$, il s'agit du $n$ cherché. En effet, si on a $0 \leqslant m<n$, on a alors $m \leqslant n-1$ donc $a_{m} \leqslant a_{n-1}<2022$ comme voulu : $n$ est bien le plus petit indice tel que $a_{n} \geqslant 2022$.
Mais maintenant on a
$$
\mathrm{a}_{1011^{2}-1}=\sqrt{1011^{2}-1}+1011<2 \cdot 1011=2022<1011+\sqrt{1011^{2}+1}=a_{1011^{2}}
$$
donc le n cherché est $\mathrm{n}=1011^{2}$.
Commentaire des correcteurs : Le problème a été bien réussi par les élèves qui ont rendu une copie. Une très grande majorité a parfaitement conjecturé $a_{n}=\sqrt{n}+\sqrt{n+1}$ puis l'a montré par récurrence. On rappelle que calculer les premiers termes pour deviner une expression est une très bonne initiative à prendre au brouillon car ça peut être la première étape dans la résolution d'un problème (comme c'était le cas ici). À partir de là on pouvait rapidement conclure, mais il fallait faire attention à ne pas faire d'erreurs de calculs, et à bien justifier (notamment des arguments de croissance étaient pertinents). Ces points là manquaient dans certaines copies. On notera aussi qu'en test ou en compétition, il n'y a pas de calculatrice, il faut donc prendre l'habitude de chercher à faire des calculs efficaces à la main.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution de l'exercice 12"
}
|
62bf6b51-fba7-58f1-a191-f32d5eaf28b0
| 607,365
|
A East-West maritime line sees 10 ships departing every morning at distinct times, 5 ships depart from the West side and 5 from the East side. We assume that they all sail at the same speed and that as soon as two ships meet, they turn around and head back in the direction they came from, always at the same speed. What is the possible number of encounters between ships?
|
The number of crossings does not change if we say that the boats continue straight ahead instead of turning around when they meet. Each boat that leaves from one side crosses all the other boats that leave from the other side. Therefore, there are $5 \times 5=25$ encounters.
Comment from the graders: The poorly worded statement of this exercise clearly confused the students, perhaps because it was not precise enough. Indeed, it was considered that all the boats were already in the water and had set off before the first encounter. It was then necessary to determine how many encounters there could be between the boats (not just the maximum number, but all possible numbers of encounters).
While many students gave the correct number (there are always 25), very few seemed to understand (or at least explain) that it did not actually depend on the gaps between the boats. Some students recognized that the changes in direction of the boats followed certain "phases" (the first two boats meet, head off in opposite directions, "transmit" this to the outermost boats, which head off in the opposite direction and "retransmit" the correct direction to the central boats, one by one) and tried to use this to arrive at 25. But none justified the existence of these phases, nor why they could be treated separately, even though they do not really occur successively! To convince oneself of this, one can consider the case where the three boats coming from the west and the five boats coming from the east are very close to each other, but the last two boats coming from the west are much farther away. Other approaches were attempted, with generally insufficient justifications. It is recalled that assertions, in an olympic exercise, are insufficient: they must be demonstrated. If one does not know how to demonstrate them, it is an even surer sign that a proof is necessary. A better approach (which a few rare papers found, in various forms) was to note, as in the solution, that from the point of view of the number of encounters, the statement produces the same results as if the two boats continued on their way after a crossing. In this case, a crossing must involve two boats heading in opposite directions, each boat coming from the west must cross each boat coming from the east, hence $5 \cdot 5=25$ crossings.
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une ligne maritime Est-Ouest voit partir chaque matin 10 bateaux à des moments tous distincts, 5 bateaux partent du côté Ouest et 5 du côté Est. On suppose qu'ils naviguent tous à la même vitesse et que dès que deux bateaux se rencontrent ils se retournent et repartent chacun de leur côté, toujours à la même vitesse. Quel est le nombre possible de rencontres entre bateaux?
|
Le nombre de croisements ne change pas si on dit que les bateaux continuent tout droit au lieu de faire demi-tour lors d'une rencontre. Chaque bateau qui part d'un côté croise tous les autres bateaux qui partent de l'autre côté. Il y a donc $5 \times 5=25$ rencontres.
Commentaire des correcteurs: L'énoncé de cet exercice mal réussi a manifestement troublé les élèves, peut-être parce qu'il n'était pas assez précis. On considérait en effet que tous les bateaux étaient déjà à l'eau et partis avant la première rencontre. Il fallait alors déterminer combien il pouvait y avoir de rencontres entre bateaux (pas simplement le nombre maximal, mais bien tous les nombres de rencontres possibles).
Si beaucoup d'élèves ont donné le nombre correct (il y en a toujours 25), très peu semblent avoir compris (ou du moins expliqué) que cela ne dépendait effectivement pas des écarts entre les bateaux. Un certain nombre d'élèves ont reconnu que les changements de sens des bateaux suivaient des sortes de "phases", (les deux premiers bateaux se rencontrent, repartent dans des directions opposés, "transmettent" cela vers les bateaux extrêmes, qui repartent en sens opposé et "retransmettent" de proche en proche vers les bateaux centraux la bonne direction) et ont tenté de s'en servir pour aboutir au 25. Mais aucun n'a justifié l'existence de ces phases, ni pourquoi on pouvait les traiter séparément, alors que celles-ci ne se déroulent pas vraiment successivement! Pour s'en convaincre, on pourra considérer le cas où les trois bateaux venant de l'ouest et les cinq bateaux venant de l'est sont très proches les uns des autres, mais les deux derniers bateaux venant de l'ouest sont bien plus lointains. D'autres approches ont été tentées, avec des justifications en général insuffisantes. On rappelle que les affirmations, dans un exercice olympique, sont insuffisantes : celles-ci doivent être démontrées. Si l'on ne sait pas les démontrer, c'est un signe d'autant plus sûr qu'une preuve est nécessaire. Une meilleure approche (que quelques rares copies ont trouvée, sous diverses formes) consistait à remarquer, comme dans le corrigé, que du point de vue du nombre de rencontres, l'énoncé produit les mêmes résultats que si les deux bateaux poursuivaient leur chemin après un croisement. Dans ce cas, un croisement doit impliquer deux bateaux de directions opposées, chaque bateau venant de l'ouest doit croiser chaque bateau venant de l'est, d'où $5 \cdot 5=25$ croisements.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
7c6b3636-d5cc-5b0d-9a32-5461021dd1bf
| 607,389
|
In a tournament organized between 6 teams, each team plays against each other team exactly once. When a team wins, it gets 3 points, and the losing team receives 0 points. If the game is a draw, both teams receive 1 point. Determine the values of \( a \) for which it is possible that the final scores of the teams can be the six consecutive numbers \( a, a+1, \ldots, a+5 \)?
|
In each match, between two and three points are awarded in total. Given that there are 15 matches in total, there must have been between 30 and 45 points distributed among the teams. Therefore, we must have:
$$
\begin{aligned}
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
& 30 \leqslant 6 a+15 \leqslant 45
\end{aligned}
$$
This means that $a$ can only be 3, 4, or 5.
If $a=5$, no match could have ended in a draw, so all scores are multiples of 3. It is therefore not possible to have 6 consecutive numbers for the scores, and this case is not possible.
If $a=3$, the scores are $3,4,5,6,7,8$. The teams with 6 and 7 points have each won at least one match, and the team with 8 points has won at least 2 matches, so at least 4 matches did not end in a draw. Thus, the total number of points distributed among the teams is at least 34, but $3+4+5+6+7+8=33$, so this case is not possible.
The case $a=4$ is possible. The scores are $4,5,6,7,8,9$. Here is a table that works:
| X | 3 | 1 | 0 | 0 | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | X | 1 | 0 | 3 | 1 |
| 1 | 1 | X | 3 | 0 | 1 |
| 3 | 3 | 0 | X | 1 | 0 |
| 3 | 0 | 3 | 1 | X | 1 |
| 3 | 1 | 1 | 3 | 1 | X |
The number written in the j-th column of the i-th row is the score obtained by team i in its match against team $j$.
Comment from the graders: The exercise was very well done by the students who attempted it.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dans un tournoi organisé entre 6 équipes, chaque équipe joue contre chaque autre équipe exactement une fois. Lorsqu'une équipe gagne, elle obtient 3 points, et l'équipe perdante reçoit 0 point. Si la partie est nulle, les deux équipes reçoivent un point. Déterminez les a pour lesquels il est possible que les scores finaux des équipes puissent être les six nombres consécutifs $a, a+1, \ldots, a+5$ ?
|
Lors de chaque match, entre deux et trois points sont attribués au total. Étant donné qu'il y a 15 matchs au total, il y a donc eu entre 30 et 45 points de répartis entre les équipes. On doit donc avoir:
$$
\begin{aligned}
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
& 30 \leqslant 6 a+15 \leqslant 45
\end{aligned}
$$
Ce qui signifie que a peut seulement être 3,4 ou 5 .
Si $a=5$, aucun match n'a pu être nul donc tous les scores sont des multiples de 3. Il n'est donc pas possible d'avoir 6 nombres consécutifs pour les scores, et ce cas n'est pas possible.
Si $a=3$, les scores sont $3,4,5,6,7,8$. Les équipes qui ont 6 et 7 points ont chacune gagné au moins un match, et l'équipe qui a 8 points a gagné au moins 2 matchs, donc au moins 4 matchs n'ont pas fini par une partie nulle. Ainsi, le nombre total de points répartis entre les équipe vaut au moins 34 , or $3+4+5+6+7+8=33$, ce cas n'est donc pas possible.
Le cas $a=4$ est possible. Les scores sont $4,5,6,7,8,9$. Voici un tableau qui fonctionne :
| X | 3 | 1 | 0 | 0 | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | X | 1 | 0 | 3 | 1 |
| 1 | 1 | X | 3 | 0 | 1 |
| 3 | 3 | 0 | X | 1 | 0 |
| 3 | 0 | 3 | 1 | X | 1 |
| 3 | 1 | 1 | 3 | 1 | X |
Le nombre écrit sur la j-ème colonne de la i-ème ligne est le score obtenu par l'équipe i lors de son match contre l'équipe $j$.
Commentaire des correcteurs: L'exercice est très bien réussi par les élèves l'ayant traité.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
72ab25a5-c358-5be3-ad90-567350e84faa
| 607,395
|
Count the number of rearrangements $\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \ldots, \boldsymbol{a}_{2023}$ of the sequence $1,2, \ldots, 2023$ such that $\mathrm{a}_{\mathrm{k}}>\mathrm{k}$ for exactly one value of $k$.
|
To a valid rearrangement, one can associate a subset of 1, ..., 2023 of cardinality at least 2: the set of $k$ such that $a_{k} \neq k$.
It can be shown that to a subset of cardinality at least 2 of $1, \ldots, 2023$, one can associate a unique valid rearrangement that corresponds to it. If the set is $\mathrm{E}=\left\{e_{1}, \ldots, e_{n}\right\}$ with $e_{1}<e_{2}<\cdots<e_{n}$, the unique rearrangement that has $E$ as its associated set satisfies: $a_{e_{1}}=e_{n}, a_{e_{2}}=e_{1}, a_{e_{3}}=e_{2}, \ldots, a_{e_{n}}=e_{n-1}$ and for all $k \notin E, a_{k}=k$.
Thus, the number of valid rearrangements is equal to the number of subsets of $1, \ldots, 2023$ of cardinality at least 2. The answer is therefore:
$$
2^{2023}-2024
$$
Graders' comments: Most of the submitted solutions are correct. Only two reasoned as in the solution. The others either reasoned by induction by replacing 2023 with n, or proceeded by summation (two submissions presented the correct sum but did not know how to compute it: perhaps they do not know the sum of a geometric series)
|
2^{2023}-2024
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Comptez le nombre de réarrangements $\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \ldots, \boldsymbol{a}_{2023}$ de la séquence $1,2, \ldots, 2023$ telle que $\mathrm{a}_{\mathrm{k}}>\mathrm{k}$ pour exactement une valeur de $k$.
|
À un réarrangement valide, on peut lui associer un sous-ensemble de 1, ..., 2023 de cardinal au moins $2: l$ 'ensemble des $k$ tels que $a_{k} \neq k$.
On peut montrer qu'à un sous-ensemble de cardinal au moins 2 de $1, \ldots, 2023$, on peut associer un unique réarrangement valide qui lui correspond. Si l'ensemble est $\mathrm{E}=\left\{e_{1}, \ldots, e_{n}\right\}$ avec $e_{1}<e_{2}<\cdots<e_{n}$, l'unique réarrangement qui a pour ensemble associé $E$ vérifie : $a_{e_{1}}=e_{n}, a_{e_{2}}=e_{1}, a_{e_{3}}=e_{2}, \ldots, a_{e_{n}}=$ $e_{n-1}$ et pour tout $k \notin E, a_{k}=k$.
Ainsi, le nombre de réarrangements valides est égal au nombre de sous-ensembles de $1, \ldots, 2023$ de cardinal au moins 2 . La réponse est donc :
$$
2^{2023}-2024
$$
Commentaire des correcteurs: La plupart des copies rendues donnent une solution correcte. Seulement deux ont raisonné comme dans le corrigé. Les autres ont soit raisonné par récurrence en remplaçant 2023 par n, soit omt procédé par sommation (deux copies ont présenté la somme correcte mais n'ont pas su la calculer : peut-être qu'il ne connaissent pas la somme d'une suite géométrique)
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
f3b5f913-04b9-5feb-a2ab-c5b102a31341
| 607,397
|
Let $k \geqslant 1$ be an integer. What is the smallest integer $n$ such that, no matter how $n$ points are placed in the plane, it is possible to choose a subset $S$ consisting of $k$ of these points that satisfies "for every pair $P, Q$ of points in $S$, the distance between $P$ and $Q$ is less than or equal to 2" or "for every pair $P, Q$ of points in $S$, the distance between $P$ and $Q$ is strictly greater than 1."
|
Let's start by showing that $\mathrm{n}=(k-1)^{2}+1$ is possible. For this, consider the disk of radius 1 centered at a point $P_{1}$ of the set. If there are at least $k$ points in this disk, we can take for $S$ these $k$ points (the distances between them are less than or equal to 2). Therefore, we can assume that there are at most $(k-1)$ points in the disk.
Now consider a disk of radius 1 centered at a $P_{2}$ of the set that is not in the previous disk. By the same argument, we can assume that there are at most $(k-1)$ points in this disk.
Continuing to choose points outside the previous disks, and since we exclude at most $(k-1)$ points at each step, we can construct $S=\left\{P_{1}, \ldots, P_{k}\right\}$ such that the distances between these points are all strictly greater than 1.
To show that $\mathrm{n}=(\mathrm{k}-1)^{2}$ is not possible, we place at a very large distance from each other $k-1$ groups, where each group consists of $\mathrm{k}-1$ points at a very small distance from each other.
Comment from the graders: This exercise was very well done by those who tackled it, with very varied methods: some used the same technique as the solution, others resorted to graph theory, for example.
|
(k-1)^2 + 1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k \geqslant 1$ un entier. Quel est le plus petit entier $n$ tel que, quelque soit la manière de placer n points dans le plan, il est possible de choisir un sous-ensemble $S$ constitué de $k$ de ces points qui vérifie "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est inférieure ou égale à 2 " ou "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est strictement plus grande que 1."
|
Commençons par montrer que $\mathrm{n}=(k-1)^{2}+1$ est possible. Pour cela, considérons le disque de rayon 1 centré sur un point $P_{1}$ de l'ensemble. S'il y a au moins $k$ points dans ce disque, on peut prendre pour $S$ ces $k$ points (les distances entre eux sont inférieures ou égales à 2 ). On peut donc supposer qu'il y a au plus $(k-1)$ points dans le disque.
Considérons alors un disque de rayon 1 centré sur un $P_{2}$ de l'ensemble qui n'est pas dans le disque précédent. Par le même argument, on peut supposer qu'il y a au plus $(k-1)$ points dans ce disque.
En continuant à choisir des points en dehors des disques précédents, et comme on exclut au plus ( $k-1)$ points à chaque étape, on arrive à construire $S=\left\{P_{1}, \ldots, P_{k}\right\}$ de telle manière à ce que les distances entre ces points soient toutes strictement supérieures à 1 .
Pour montrer que $\mathrm{n}=(\mathrm{k}-1)^{2}$ n'est pas possible, on place à distance très grande les uns des autres $k-1$ groupes, ou chaque groupe est constitué de $\mathrm{k}-1$ points à distance très petite.
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont traité, avec des méthodes très variées : certains ont utilisé la même technique que la correction, d'autres ont recouru à la théorie des graphes par exemples.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "\nSolution de l'exercice 16"
}
|
8794478b-9ac3-5dd3-86b9-7e35af2d6576
| 607,403
|
Let $k, n \geqslant 1$ be two fixed integers. Thanima had 2 n candies of each color. She gave two candies of different colors to each of the children in her family. Knowing that no matter how $k+1$ children are chosen, there are two among them who received a candy of the same color, find the maximum possible number of children.
|
We can model the problem with a graph: each vertex of this graph is a color. If Thanima gave a candy of color $\mathrm{c}_{1}$ and a candy of color $\mathrm{c}_{2}$ to a child in her family, we add an edge between $\mathrm{c}_{1}$ and $\mathrm{c}_{2}$.
Since Thanima has only 2 n candies of each color, the maximum degree of each vertex is 2 n. We also know that it is impossible to choose $k+1$ disjoint edges. We are looking for the maximum number of edges.
We see that it is possible to obtain 3 kn edges. For this, we create a graph in which we put $k$ times the following structure: we create three vertices, and between each pair of these three vertices, we add n edges. Let's show that it is not possible to do more than 3 kn. For this, we consider a set C of disjoint edges of maximum cardinality. According to the statement, we have $|\mathrm{C}| \leqslant \mathrm{k}$. Thus, each edge of the graph must intersect one of the edges of C, otherwise it would contradict the maximality of C. Let $\mathrm{V}_{\mathrm{C}}$ be the set of vertices that appear in one of the edges of C. The number of edges in the graph is:
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2}
$$
where $\mathrm{d}_{\text {ext }}(v)$ is the number of edges that connect $v$ to vertices that are not in $V_{C}$, and $\mathrm{d}_{\text {int }}(v)$ is the number of edges that connect $v$ to vertices of $\mathrm{V}_{\mathrm{C}}$. Let $(\mathrm{a}, \mathrm{b})$ be an edge of C, and let $x, y$ be two different vertices that are not in $\mathrm{V}_{\mathrm{C}}$, we cannot have both edges between a and $x$ and between $b$ and $y$, otherwise replacing $(a, b)$ with $(a, x)$ and $(b, y)$ in $C$ would give a larger set of disjoint edges. Two cases can occur:
- Both $a$ and $b$ have edges to the complement of $\mathrm{V}_{\mathrm{C}}$, in this case, all these edges go to the same vertex, and the degree bound on this vertex gives $d_{\text {ext }}(a)+d_{\text {ext }}(b) \leqslant 2 n$.
- Or there is at most one vertex among $a$ and $b$ that has edges to the complement of $\mathrm{V}_{\mathrm{C}}$, in this case we also have $\mathrm{d}_{\text {ext }}(a)+\mathrm{d}_{\text {ext }}(b) \leqslant 2 \mathrm{n}$.
Since $\mathrm{d}_{\mathrm{int}}(v) \leqslant 2 \mathrm{n}-\mathrm{d}_{\text {ext }}(v)$ for all vertices $v$, we have:
$$
\begin{aligned}
\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \leqslant d_{e x t}(a)+d_{e x t}(b)+\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\
& =2 n+\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\
& \leqslant 3 n
\end{aligned}
$$
Thus, by grouping the terms two by two, we obtain that the number of edges in the graph is:
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2} \leqslant 3 \mathrm{kn}
$$
Comment from the graders: The exercise was very little addressed.
|
3kn
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k, n \geqslant 1$ deux entiers fixés. Thanima possédait 2 n bonbons de chaque couleur. Elle a donné deux bonbons de couleurs différentes à chacun des enfants de sa famille. Sachant que quelque soit la manière de choisir $k+1$ enfants, il y en a deux parmi eux qui ont reçu une couleur de bonbon en commun, trouvez le nombre maximum possible d'enfants.
|
On peut modéliser le problème par un graphe : chaque sommet de ce graphe est une couleur. Si Thanima a donné un bonbon d'une couleur $\mathrm{c}_{1}$ et un bonbon d'une couleur $\mathrm{c}_{2}$ à un enfant de sa famille, on ajoute une arête entre $\mathrm{c}_{1}$ et $\mathrm{c}_{2}$.
Comme Thanima n'a que 2 n bonbons de chaque couleur, le degré maximal de chaque sommet est 2 n . On sait de plus qu'il est impossible de choisir $k+1$ arêtes disjointes. On cherche le nombre maximal d'arêtes.
On voit qu'il est possible d'obtenir 3 kn arêtes. Pour cela, on crée un graphe dans lequel on met $k$ fois la structure suivante : on crée trois sommets, et entre chaque paire de ces trois sommets, on ajoute n arêtes. Montrons qu'il n'est pas possible de faire plus que 3 kn . Pour cela, on considère un ensemble C d'arêtes disjointes de plus grand cardinal. D'après l'énoncé, on a $|\mathrm{C}| \leqslant \mathrm{k}$. Ainsi, chaque arête du graphe doit intersecter l'une des arêtes de C , sinon cela contredirait la maximalité de C . Notons $\mathrm{V}_{\mathrm{C}}$ l'ensemble des sommets qui apparaissent dans l'une des arêtes de C. Le nombre d'arêtes du graphe vaut :
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2}
$$
où $\mathrm{d}_{\text {ext }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets qui ne sont pas dans $V_{C}$, et $\mathrm{d}_{\text {int }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets de $\mathrm{V}_{\mathrm{C}}$. Soit $(\mathrm{a}, \mathrm{b}$ ) une arête de C , et soient $x, y$ deux sommets différents qui ne sont pas dans $\mathrm{V}_{\mathrm{C}}$, on ne peut pas à la fois avoir d'arêtes entre a et $x$ et entre $b$ et $y$, sinon remplacer $(a, b)$ par $(a, x)$ et $(b, y)$ dans $C$ donnerait un ensemble d'arêtes disjointes plus grand. Deux cas peuvent arriver :
- À la fois $a$ et $b$ ont des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas, toutes ces arêtes vont vers le même sommet, et la borne de degré sur ce sommet donnent $d_{\text {ext }}(a)+d_{\text {ext }}(b) \leqslant 2 n$.
- Soit il y a au plus un sommet parmi $a$ et $b$ qui a des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas on a aussi $\mathrm{d}_{\text {ext }}(a)+\mathrm{d}_{\text {ext }}(b) \leqslant 2 \mathrm{n}$.
Comme $\mathrm{d}_{\mathrm{int}}(v) \leqslant 2 \mathrm{n}-\mathrm{d}_{\text {ext }}(v)$ pour tout sommet $v$, on a :
$$
\begin{aligned}
\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \leqslant d_{e x t}(a)+d_{e x t}(b)+\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\
& =2 n+\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\
& \leqslant 3 n
\end{aligned}
$$
Ainsi, en groupant les termes deux à deux, on obtient que le nombre d'arête dans le graphe est :
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2} \leqslant 3 \mathrm{kn}
$$
Commentaire des correcteurs : L'exercice a été très peu abordé.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "\nSolution de l'exercice 17"
}
|
22a278f5-b7fb-50df-a671-422e5a5102d9
| 607,404
|
Let $x, y, z$ be strictly positive real numbers such that
$$
x+\frac{y}{z}=y+\frac{z}{x}=z+\frac{x}{y}=2
$$
Determine all possible values that the number $x+y+z$ can take.
|
In such a problem, one must seek to examine each equation separately but also to relate them. In practice, this involves looking at the equation obtained when performing the sum or product of two or more equations. Another idea is to apply known inequalities on one side or the other of the equation. Indeed, often the equalities present in the problems are only possible when the variables satisfy the equality case of a well-known inequality.
Let's start with a separate examination. We consider the first equation $x+\frac{y}{z}=2$. According to the inequality of means, we have
$$
2=x+\frac{y}{z} \geqslant 2 \sqrt{x \cdot \frac{y}{z}}
$$
which gives $\sqrt{\frac{x y}{z}} \leqslant 1$. Similarly, the second equation $y+\frac{z}{x}=2$ gives $\sqrt{\frac{y z}{x}} \leqslant 1$. By multiplying these two inequalities, we obtain
$$
1 \geqslant \sqrt{\frac{x y}{z}} \cdot \sqrt{\frac{y z}{x}}=y
$$
Thus $y \leqslant 1$, and similarly we find that $x \leqslant 1$ and $z \leqslant 1$. We now seek to apply these estimates or to prove inverse estimates (for example, $y \geqslant 1$, which would imply that $y=1$).
Note that the relation $x+\frac{y}{z}=2$ can be rewritten as $x z+y=2 z$. Similarly, we obtain $y x+z=2 x$ and $y z+x=2 y$. By summing these three relations, we find that $x z+y x+y z+x+y+z=2(x+y+z)$, or equivalently $x y+y z+z x=x+y+z$. But then
$$
x+y+z=x y+y z+z x \leqslant x \cdot 1+y \cdot 1+z \cdot 1=x+y+z
$$
Our inequality is in fact an equality. And since $x, y$, and $z$ are non-zero, each of the inequalities used in the line above is in fact an equality. Therefore, we have $x=y=z=1$ and $x+y+z=3$. This value is indeed attainable since the triplet $(1,1,1)$ satisfies the system given in the problem, which completes our problem.
## Comments from the graders:
A well-executed exercise. The methods of resolution are extremely varied. Some students made the mistake of considering the problem symmetric, whereas it is only cyclic.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soient $x, y, z$ des réels strictement positifs tels que
$$
x+\frac{y}{z}=y+\frac{z}{x}=z+\frac{x}{y}=2
$$
Déterminer toutes les valeurs possibles que peut prendre le nombre $x+y+z$.
|
Dans un tel problème, il faut chercher à examiner chaque équation séparément mais aussi à les mettre en relation. En pratique, cela consiste à regarder l'équation obtenue lorsque l'on effectue la somme ou le produit de deux ou plusieurs équations. Une autre idée est d'appliquer des inégalités connues d'un côté ou de l'autre de l'équation. En effet, souvent les égalités présentes dans les problèmes ne sont possibles que lorsque les variables vérifient le cas d'égalité d'une inégalité bien connue.
Commençons par un examen séparé. On considère la première équation $x+\frac{y}{z}=2$. D'après l'inégalité des moyennes, on a
$$
2=x+\frac{y}{z} \geqslant 2 \sqrt{x \cdot \frac{y}{z}}
$$
soit $\sqrt{\frac{x y}{z}} \leqslant 1$. De même, la deuxième équation $y+\frac{z}{x}=2$ donne $\sqrt{\frac{y z}{x}} \leqslant 1$. En multipliant ces deux inégalités, on obtient
$$
1 \geqslant \sqrt{\frac{x y}{z}} \cdot \sqrt{\frac{y z}{x}}=y
$$
Ainsi $y \leqslant 1$, et de même on trouve que $x \leqslant 1$ et $z \leqslant 1$. On cherche désormais à appliquer ces estimations ou à prouver des estimations inverses (par exemple $y \geqslant 1$, ce qui imposerait que $y=1$ ).
Notons que la relation $x+\frac{y}{z}=2$ se réécrit $x z+y=2 z$. On obtient de même que $y x+z=2 x$ et $y z+x=2 y$. En sommant ces trois relations, on trouve que $x z+y x+y z+x+y+z=2(x+y+z)$, ou encore $x y+y z+z x=x+y+z$. Mais alors
$$
x+y+z=x y+y z+z x \leqslant x \cdot 1+y \cdot 1+z \cdot 1=x+y+z
$$
Notre inégalité est en fait une égalité. Et puisque $x, y$ et $z$ sont non nuls, chacune des inégalités utilisées dans la ligne ci-dessus est en fait une égalité. On a donc $x=y=z=1$ et $x+y+z=3$. Cette valeur est bien atteignable puisque le triplet $(1,1,1)$ vérifie bien le système de l'énoncé, ce qui termine notre problème.
## Commentaires des correcteurs:
Exercice plutôt bien réussi. Les méthodes de résolution sont extrêmement variées. Certains élèves ont commis l'erreur de considérer que le problème est symétrique, alors qu'il n'est que cyclique.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
003fa970-1edf-5f1a-afb9-77e784a15b71
| 607,410
|
A digicode opens as soon as the correct unique combination of 4 digits (which may possibly contain repetitions) is entered. For example, if the sequence of digits 000125 is entered, the digicode will open if the code is either 0001, 0012, or 0125. Little Pierre does not know the code. How many digits at a minimum must he enter to be sure to open the digicode?
|
It is clear that at least 10003 digits are needed, because all 10000 combinations must be tried. Let's show that this number is also sufficient.
Draw 1000 points corresponding to all sequences of 3 digits. Draw an arrow between two points if the last two digits of the first combination match the first two digits of the second combination (and in the same order). For example, there will be an arrow from the point 200 to the point 009 and another from the point 201 to the point 017; between the points 303 and 030 there will be two arrows in both directions; on the point 777 there will be a loop arrow that returns to its starting point. Thus, each arrow corresponds to a unique possible code.
It is easy to see that there are 10 incoming arrows and 10 outgoing arrows at each point. Indeed, to get an outgoing arrow, for example, one must choose a digit from 0 to 9 to add to the last two digits of the point's number, which gives exactly 10 choices.
It is also easy to see that the graph formed by the points and arrows is connected. Indeed, one can go from a point \(abc\) to the point def in three arrows \(abc \rightarrow bcd \rightarrow cde \rightarrow\) def.
The well-known Euler's theorem (see, for example, "Eulerian Graph" on Wikipedia) then ensures that it is possible to traverse all the arrows of the graph without passing through the same arrow twice. This traversal will give the desired sequence of 10003 digits: one will need to type the 3 digits of the starting point and then just the last digit of each point in the traversal. The fact that each arrow of the graph is passed exactly once means that each possible 4-digit code will be tried exactly once.

|
10003
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Un digicode s'ouvre dès qu'on fait l'unique combinaison correcte de 4 chiffres (qui peut éventuellement contenir des répétitions). Par exemple, si l'on tape la suite des chiffres 000125 le digicode s'ouvrira si le code est soit 0001, soit 0012, soit 0125. Petit Pierre ne connaît pas le code. Combien de chiffres au minimum doit-il taper pour ouvrir le digicode à coup sûr?
|
Il est clair qu'il faut au moins 10003 chiffres, car il faut essayer toutes les 10000 combinaisons. Montrons que ce nombre est aussi suffisant.
Dessinons 1000 points correspondant à toutes les suites de 3 chiffres. Dessinons une flèche entre deux points si les deux derniers chiffres de la première combinaison coincident avec les deux premiers chiffres de la deuxième combinaison (et vont dans le même ordre). Par exemple, il y aura une flèche allant du point 200 vers le point 009 et une autre allant du point 201 vers le point 017 ; entre les points 303 et 030 il y aura deux flèches allant dans les deux sens; sur le point 777 il y aura une flèche en forme de boucle qui revient vers son point de départ. Ainsi, chaque flèche correspond à un unique code possible.
On voit facilement qu'il y a 10 flèches entrantes et 10 flèches sortantes dans chaque point. En effet, pour obtenir une flèche sortante, par exemple, il faut choisir un chiffre de 0 à 9 à rajouter aux derniers chiffres du numéro du point, ce qui fait exactement 10 choix.
Il est facile à voir également que le graphe formé par les points et les flèches est connexe. En effet, on passe d'un point $a b c$ au point def en trois flèches $a b c \rightarrow b c d \rightarrow c d e \rightarrow$ def.
Le théorème d'Euler bien connu (voir, par exemple, "Graphe Eulérien" dans wikipédia) assure alors qu'on peut parcourir toutes les flèches du graphe sans passer deux fois par la même flèche. Ce parcours donnera la suite de 10003 chiffres recherchée : il faudra taper les 3 chiffres du point de départ et ensuite juste le dernier chiffre de chaque point du parcours. Le fait qu'on passe une et une seule fois par chaque flèche du graphe signifie exactement que chaque code possible de 4 chiffres sera essayé une et une seule fois.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi2-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution."
}
|
62cfa2c7-8144-5f33-801e-06ec833b38e0
| 607,455
|
Let $E$ be a finite set of strictly positive real numbers such that, for any strictly positive real number $x$, $E$ contains as many elements strictly greater than $x$ as elements strictly less than $\frac{1}{x}$. Determine the product of all elements of $E$.
|
Let $x_{0} \in E$ such that $x_{0}>1$. Then, by hypothesis,
- the sets $\mathrm{E} \cap$ ] - $\infty, \frac{1}{x_{0}}$ [ and $\left.\mathrm{E} \cap\right] \mathrm{x}_{0},+\infty[$ have cardinals of the same parity,
- the sets $\mathrm{E} \cap]-\infty, \mathrm{x}_{0}\left[\right.$ and $\mathrm{E} \cap \frac{1}{\mathrm{x}_{0}},+\infty[$ have cardinals of the same parity.
Consequently, the two sets
$$
\begin{aligned}
\left.\mathrm{E} \cap] \frac{1}{x_{0}}, x_{0}\right] & =(\mathrm{E} \cap] \frac{1}{x_{0}},+\infty[) \backslash(\mathrm{E} \cap] \mathrm{x}_{0},+\infty[) \\
\mathrm{E} \cap\left[\frac{1}{x_{0}}, x_{0}[ \right. & =(\mathrm{E} \cap]-\infty, \mathrm{x}_{0}[) \backslash(\mathrm{E} \cap]-\infty, \frac{1}{x_{0}}[)
\end{aligned}
$$
have cardinals of the same parity. These sets are composed of the same elements, except possibly $x_{0}$ and $\frac{1}{x_{0}}$: the first set contains $x_{0}$ but not $\frac{1}{x_{0}}$; thus, the second set contains one and only one element of $\left\{\frac{1}{x_{0}}, x_{0}\right\}$ but cannot contain $x_{0}$: it therefore contains $\frac{1}{x_{0}}$.
We have thus established that if $x_{0} \in E$, then $\frac{1}{x_{0}} \in E$. The product of all elements of $E$ is therefore 1.

## Common Exercises
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $E$ un ensemble fini de réels strictement positifs tels que, pour tout réel $x$ strictement positif, E contient autant d'éléments strictement supérieurs à $x$ que d'éléments strictement inférieurs à $\frac{1}{x}$. Déterminer le produit de tous les éléments de E.
|
Soit $x_{0} \in E$ tel que $x_{0}>1$. Alors, par hypothèse,
- les ensembles $\mathrm{E} \cap$ ] - $\infty, \frac{1}{x_{0}}$ [et $\left.\mathrm{E} \cap\right] \mathrm{x}_{0},+\infty[$ ont des cardinaux de même parité,
- les ensembles $\mathrm{E} \cap]-\infty, \mathrm{x}_{0}\left[\right.$ et $\mathrm{E} \cap \frac{1}{\mathrm{x}_{0}},+\infty[$ ont des cardinaux de même parité.
Par conséquent, les deux ensembles
$$
\begin{aligned}
\left.\mathrm{E} \cap] \frac{1}{x_{0}}, x_{0}\right] & =(\mathrm{E} \cap] \frac{1}{x_{0}},+\infty[) \backslash(\mathrm{E} \cap] \mathrm{x}_{0},+\infty[) \\
\mathrm{E} \cap\left[\frac{1}{x_{0}}, x_{0}[ \right. & =(\mathrm{E} \cap]-\infty, \mathrm{x}_{0}[) \backslash(\mathrm{E} \cap]-\infty, \frac{1}{x_{0}}[)
\end{aligned}
$$
ont des cardinaux de même parité. Or, ils sont composés des mêmes éléments, sauf éventuellement $x_{0}$ et $\frac{1}{x_{0}}$, le premier ensemble contient $\chi_{0}$ mais pas $\frac{1}{x_{0}}$ : ainsi, le second ensemble contient un et un seul élément de $\left\{\frac{1}{x_{0}}, x_{0}\right\}$ mais ne peut contenir $x_{0}:$ il contient donc $\frac{1}{x_{0}}$.
On a ainsi établi que si $x_{0} \in E$, alors $\frac{1}{x_{0}} \in E$. Le produit de tous les éléments de $E$ donne donc 1 .

## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi4-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
53ec30a7-33fd-5df4-9cac-e26b448f20f5
| 607,469
|
Let $A B C D E F$ be a regular hexagon and $M \in[A, C], N \in[C, E]$. Suppose that $\frac{A M}{A C}$ and $\frac{C N}{C E}$ are equal to a number $r>0$, and that $B, M, N$ are collinear. Determine the value of $r$.
|
We can assume that the hexagon is inscribed in a circle of radius 1. We place ourselves in a coordinate system such that the coordinates of $A, B, C$ are respectively $A=(0,1), B=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ and $C=\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$.
Since $C E=\sqrt{3}$, we have $C N=r \sqrt{3}$, so $\overrightarrow{C N}=(-r \sqrt{3}, 0)$. We deduce that
$$
N=\left(\frac{\sqrt{3}}{2}-r \sqrt{3},-\frac{1}{2}\right)
$$
Since $\overrightarrow{A C}=\left(\frac{\sqrt{3}}{2},-\frac{3}{2}\right)$, we have $\overrightarrow{A M}=\left(\frac{\sqrt{3}}{2} r,-\frac{3 r}{2}\right)$, so
$$
M=\left(\frac{\sqrt{3}}{2} r, 1-\frac{3 r}{2}\right)
$$
We can easily calculate that
$$
\overrightarrow{B M}=\left(\frac{\sqrt{3}}{2}(r-1), \frac{1}{2}-\frac{3 r}{2}\right), \quad \overrightarrow{B N}=(-r \sqrt{3},-1)
$$
The fact that $B, M, N$ are collinear means that these two vectors are collinear, which is equivalent to
$$
\frac{\sqrt{3}}{2}(1-r)+r \sqrt{3}\left(\frac{1}{2}-\frac{3 r}{2}\right)=0
$$
which simplifies to $r=\frac{1}{\sqrt{3}}$.
|
\frac{1}{\sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Soit $A B C D E F$ un hexagone régulier et $M \in[A, C], N \in[C, E]$. On suppose que $\frac{A M}{A C}$ et $\frac{C N}{C E}$ sont égaux à un nombre $r>0$, et que $B, M, N$ sont colinéaires. Déterminer la valeur de $r$.

|
On peut supposer que l'hexagone est inscrit dans un cercle de rayon 1. On se place dans un repère tel que les coordonnées de $A, B, C$ sont respectivement $A=(0,1), B=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$ et $C=\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)$.
Comme $C E=\sqrt{3}$, on a $C N=r \sqrt{3}$ donc $\overrightarrow{C N}=(-r \sqrt{3}, 0)$. On en déduit que
$$
N=\left(\frac{\sqrt{3}}{2}-r \sqrt{3},-\frac{1}{2}\right)
$$
Comme $\overrightarrow{A C}=\left(\frac{\sqrt{3}}{2},-\frac{3}{2}\right)$, on a $\overrightarrow{A M}=\left(\frac{\sqrt{3}}{2} r,-\frac{3 r}{2}\right)$ donc
$$
M=\left(\frac{\sqrt{3}}{2} r, 1-\frac{3 r}{2}\right)
$$
On calcule aisément que
$$
\overrightarrow{B M}=\left(\frac{\sqrt{3}}{2}(r-1), \frac{1}{2}-\frac{3 r}{2}\right), \quad \overrightarrow{B N}=(-r \sqrt{3},-1)
$$
Le fait que $B, M, N$ sont alignés signifie que ces deux vecteurs sont colinéaires, ce qui équivaut à
$$
\frac{\sqrt{3}}{2}(1-r)+r \sqrt{3}\left(\frac{1}{2}-\frac{3 r}{2}\right)=0
$$
ce qui se simplifie en $r=\frac{1}{\sqrt{3}}$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution."
}
|
f51bb446-2903-5f1b-92fc-bfcd0e76d44c
| 607,489
|
It is said that a 9-digit number is interesting if each digit from 1 to 9 appears exactly once, the digits from 1 to 5 appear in order but the digits from 1 to 6 do not, for example 189236457.
How many interesting numbers are there?
|
To build an interesting number, we can first place the digits from 1 to 5, then intercalate the 6 somewhere, then the 7, the 8, and the 9. The order of the digits from 1 to 5 is fixed. Then, the 6 can be placed anywhere except after the 5 because the digits from 1 to 6 would not be in order. Therefore, there are 5 ways to place the 6. Next, the 7 can be placed anywhere, so there are 7 ways to place it, and similarly, 8 ways to place the 8 and 9 ways to place the 9.
Thus, there are $5 * 7 * 8 * 9=2520$ interesting numbers.
|
2520
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On dit qu'un nombre à 9 chiffres est intéressant si chaque chiffre de 1 à 9 y apparaît une unique fois, que les chiffres de 1 à 5 y apparaissent dans l'ordre mais pas les chiffres de 1 à 6 , par exemple 189236457 .
Combien y a-t-il de nombres intéressants?
|
Pour construire un nombre intéressant, on peut placer d'abord les chiffres de 1 à 5 , puis intercaler le 6 quelque part, puis le 7 , le 8 et le 9 . L'ordre des chiffres de 1 à 5 est imposé. Ensuite, le 6 peut être placé n'importe où sauf après le 5 car les chiffres de 1 à 6 ne sont pas dans l'ordre. Il y a donc 5 manières de placer le 6 . Ensuite, on peut placer le 7 n'importe où, donc il y a 7 manières de le placer, et de même 8 manières de placer le 8 et 9 pour le 9.
Il y a donc $5 * 7 * 8 * 9=2520$ nombres intéressants.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 1",
"solution_match": "\nSolution de l'exercice 1"
}
|
d08f3ea9-9f6e-54c4-9fd6-af1b9a0a2099
| 607,501
|
Scientists participate in a conference, each scientist being either a mathematician or a physicist. Of course, physicists always lie, and mathematicians always tell the truth, except when they make a mistake. During the final dinner, all are seated in a circle around a table, and each one claims to be sitting between a mathematician and a physicist. It turns out that exactly one distracted mathematician made a mistake. How many physicists are at the conference?
|
If 2 physicists are sitting side by side, since they lied, they are not between a physicist and a mathematician, so each is between two physicists, and so on, so the conference only hosts physicists, which is absurd because there is at least one mathematician (the one who was wrong...). Each physicist is therefore between two mathematicians.
On the other hand, each mathematician is between a mathematician and a physicist, except the one who was wrong. Let's call him Thomas: if Thomas is between two physicists, then everywhere else there is an alternation of two mathematicians, one physicist... But then, if there are $k$ pairs of mathematicians side by side, there are $2 k+1$ mathematicians and $k+1$ physicists, so $3 k+2$ scientists, which is absurd because $3 k+2 \neq 2014$.
Thomas is therefore between two mathematicians, so we have three mathematicians side by side, and the others in pairs. If there are $k$ pairs, then we have $2 k+3$ mathematicians and $k+1$ physicists, so $3 k+4=2014$ so $k=670$ and there are 671 physicists.
## Common Exercises
|
671
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
scientifiques participent à un congrès, chaque scientifique étant soit un mathématicien, soit un physicien. Bien sûr, les physiciens mentent toujours et les mathématiciens disent toujours la vérité, sauf quand ils se trompent. Lors du dîner final, tous sont assis en rond autour d'une table, et chacun prétend se trouver entre un mathématicien et un physicien. Il se trouve qu'exactement un mathématicien distrait s'est trompé. Combien y a-t-il de physiciens au congrès?
|
Si 2 physiciens sont assis côté à côté, comme ils ont menti, ils ne sont pas entre un physicien et un mathématicien, donc chacun est entre deux physiciens, et ainsi de suite, donc le congrès n'accueille que des physiciens, ce qui est absurde car il y a au moins un mathématicien (celui qui s'est trompé...). Chaque physicien est donc entre deux mathématiciens.
D'autre part, chaque mathématicien est entre un mathématicien et un physicien, sauf celui qui s'est trompé. Appelons-le Thomas : si Thomas est entre deux physiciens, alors on a partout ailleurs une alternance de deux mathématiciens, un physicien... Mais alors, si il y a k paires de mathématiciens côte à côte, il y a $2 k+1$ mathématiciens et $k+1$ physiciens, donc $3 k+2$ scientifiques, ce qui est absurde car $3 k+2 \neq 2014$.
Thomas est donc entre deux mathématiciens, donc on a trois mathématiciens côté à côte, et les autres par paires. Si il y a $k$ paires, alors on a $2 k+3$ mathématiciens et $k+1$ physiciens donc $3 k+4=2014$ donc $k=670$ et il y a 671 physiciens.
## Exercices communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 32014",
"solution_match": "\nSolution de l'exercice 3"
}
|
520c5c54-e89b-5b46-a520-0b732c6c174f
| 607,503
|
We are given $n$ points in the plane, such that no three of them are ever collinear. Each point is colored either red or blue. We assume that there is exactly one blue point inside each triangle whose vertices are red, and one red point inside each triangle whose vertices are blue.
What is the largest possible value of $n$?
## Exercise Group A
|
First, we show that the blue points form a convex polygon: if this were not the case, we could find a blue point inside a blue polygon, and by cutting this polygon into triangles, we could find a blue point inside a blue triangle. The large blue triangle must contain a single red point, but we can cut it into three triangles, each containing a single red point, which is absurd.
The blue points therefore form a convex polygon, as do the red points. Moreover, there can be at most 2 red points inside the blue polygon, because if there were 3, they would form a triangle with no blue point inside.
Finally, if $k$ is the number of blue points, we can cut the blue polygon into $k-2$ triangles, each of which must contain a red point, so $k-2 \leqslant 2$ and $k \leqslant 4$. Similarly, there can be at most 4 red points, so $\mathrm{n} \leqslant 8$. We can then verify that the following configuration with 8 points works:
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On se donne $n$ points du plan, tels que trois quelconques d'entre eux ne sont jamais alignés. Chacun est colorié en rouge ou en bleu. On suppose qu'il y a exactement un point bleu à l'intérieur de chaque triangle dont les sommets sont rouges, et un point rouge à l'intérieur de chaque triangle dont les sommets sont bleus.
Quelle est la plus grande valeur possible de n?
## Exercices groupe A
|
On montre d'abord que les points bleus forment un polygone convexe: si ce n'était pas le cas, on pourrait trouver un point bleu à l'intérieur d'un polygone bleu, donc on en découpant ce polygone en triangles, on pourrait trouver un point bleu à l'intérieur d'un triangle bleu. Le grand triangle bleu doit contenir un unique point rouge, mais on peut le découper en trois triangles qui contiennent chacun un unique point rouge, ce qui est absurde.
Les points bleus forment donc un polygone convexe, de même que les rouges. De plus, il y a au maximum 2 points rouges à l'intérieur du polygone bleu, car s'il y en avait 3 ils formeraient un triangle sans point bleu à l'intérieur.
Enfin, si $k$ est le nombre de points bleus, on peut découper le polygone bleu en $k-2$ triangles, qui chacun doivent contenir un point rouge, donc $k-2 \leqslant 2$ et $k \leqslant 4$. De même, il y a au plus 4 points rouges donc $\mathrm{n} \leqslant 8$. On peut alors vérifier que la configuration à 8 points suivante convient:

|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 7",
"solution_match": "\nSolution de l'exercice 7"
}
|
0be97fae-6367-55fa-bac3-8e369d86951f
| 607,506
|
How many pairs of strictly positive integers ( $a, b$ ) are there such that
$$
\frac{1}{a}+\frac{1}{b}=\frac{1}{2014} ?
$$
|
Let $a, b$ be two strictly positive integers such that $1 / a + 1 / b = 1 / 2014$. In particular, $a, b > 2014$. Therefore, we can multiply the equation by $ab$: we are actually looking for integers $a, b > 2014$ such that $ab - 2014a - 2014b = 0$ or, equivalently, such that $(a - 2014)(b - 2014) = 2014^2$. We deduce that the number we are looking for is the number of pairs of strictly positive integers $(u, v)$ such that $uv = 2014^2$, i.e., the number of positive divisors of $2014^2$. Since $2014^2 = 2^2 \cdot 19^2 \cdot 53^2$, $2014^2$ has $(2+1) \cdot (2+1) \cdot (2+1) = 27$ positive divisors.
The answer is therefore 27.
|
27
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Combien existe-t-il de couples d'entiers strictement positifs ( $a, b$ ) tels que
$$
\frac{1}{a}+\frac{1}{b}=\frac{1}{2014} ?
$$
|
Soient $a, b$ deux entiers strictement positifs tels que $1 / a+1 / b=1 / 2014$. On a en particulier $\mathrm{a}, \mathrm{b}>2014$. On peut donc multiplier l'équation $\mathrm{ab}:$ on cherche en fait les entiers $\mathrm{a}, \mathrm{b}>2014$ tels que $\mathrm{ab}-2014 \mathrm{a}-2014 \mathrm{~b}=0$ ou encore, de manière équivalente, tels que ( $a-$ $2014)(b-2014)=2014^{2}$. On en déduit que le nombre recherché est le nombre de couples d'entiers strictement positifs $(u, v)$ tels que $u v=2014^{2}$, autrement dit le nombre de diviseurs positifs de $2014^{2}$. Comme $2014^{2}=2^{2} \cdot 19^{2} \cdot 53^{2}, 2014^{2}$ possède $(2+1) \cdot(2+1) \cdot(2+1)=27$ diviseurs positifs.
La réponse est donc 27 .
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
1d9bd8c5-1308-58ce-8afd-6702b29c70c6
| 607,517
|
Find the number of sequences $\left(u_{n}\right)_{n \geqslant 1}$ of integers such that $u_{n} \neq-1$ for all integers $n \geqslant 1$ and such that
$$
u_{n+2}=\frac{2014+u_{n}}{1+u_{n+1}}
$$
for all integers $\mathrm{n} \geqslant 1$.
|
The relation in the statement imposes that $\left(u_{n+1}-u_{n-1}\right)\left(u_{n}+1\right)=u_{n}-u_{n-2}$ for $\mathrm{n} \geqslant 3$. By induction, it follows that
$$
\mathbf{u}_{3}-\mathbf{u}_{1}=\prod_{i=3}^{n}\left(u_{i}+1\right)\left(u_{n+1}-u_{n-1}\right)
$$
Suppose by contradiction that $u_{3} \neq u_{1}$. Thus $u_{n+1} \neq u_{n-1}$ for all $n \geqslant 2$. By increasing $n$, we see that there cannot be an infinite number of terms $u_{i}$ such that $u_{i} \neq 0, -2$. Thus, $u_{i}=0$ or -2 from a certain rank (since $\mathfrak{u}_{3}-\mathfrak{u}_{1}$ has a finite number of divisors). It is easily verified from the recurrence relation in the statement that this is not possible. Therefore, $u_{3}=u_{1}$, and by (1) we deduce that $u_{n+2}=u_{n}$ for all integers $n \geqslant 1$.
Under this assumption, the relation to verify becomes $\left(1+u_{n+1}\right) u_{n}=2014+u_{n}$, or equivalently $u_{n} u_{n+1}=2014$, which is equivalent to $u_{1} \mathfrak{u}_{2}=2014$. Thus, the number of sequences $\left(u_{n}\right)_{n \geqslant 1}$ that fit is the number of pairs of integers $(a, b)$ such that $a b=2014$, with $a \neq-1$ and $b \neq-1$: this is exactly the number of divisors (positive or negative) of 2014, minus 2. Since $2014=2 \cdot 19 \cdot 53$, it has $2 \cdot(1+1) \cdot(1+1) \cdot(1+1)=16$ divisors (positive or negative), so 14 sequences fit.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver le nombre de suites $\left(u_{n}\right)_{n \geqslant 1}$ d'entiers relatifs telles que $u_{n} \neq-1$ pour tout entier $n \geqslant 1$ et telles que
$$
u_{n+2}=\frac{2014+u_{n}}{1+u_{n+1}}
$$
pour tout entier $\mathrm{n} \geqslant 1$.
|
La relation de l'énoncé impose que $\left(u_{n+1}-u_{n-1}\right)\left(u_{n}+1\right)=u_{n}-u_{n-2}$ pour $\mathrm{n} \geqslant 3$. Par récurrence, il vient
$$
\mathbf{u}_{3}-\mathbf{u}_{1}=\prod_{i=3}^{n}\left(u_{i}+1\right)\left(u_{n+1}-u_{n-1}\right)
$$
Supposons par l'absurde que $u_{3} \neq u_{1}$. Ainsi $u_{n+1} \neq u_{n-1}$ pour tout $n \geqslant 2$. En faisant croitre $n$, on voit qu'il ne peut pas y avoir une infinité de termes $u_{i}$ tels que $u_{i} \neq 0,-2$. Ainsi, $u_{i}=0$ ou -2 à partir d'un certain rang (car $\mathfrak{u}_{3}-\mathfrak{u}_{1}$ a un nombre fini de diviseurs). On vérifie aisément à partir de la relation de récurence de l'énoncé que ceci n'est pas possible. Donc $u_{3}=u_{1}$, et par (1) on en déduit que $u_{n+2}=u_{n}$ pour tout entier $n \geqslant 1$.
Sous cette hypothèse, la relation à vérifier devient $\left(1+u_{n+1}\right) u_{n}=2014+u_{n}$, ou encore $u_{n} u_{n+1}=$ 2014, ce qui est équivalent à $u_{1} \mathfrak{u}_{2}=2014$. Ainsi, le nombre de suites $\left(u_{n}\right)_{n \geqslant 1}$ qui conviennent est le nombre paires d'entiers $(a, b)$ telles que $a b=2014$, avec $a \neq-1$ et $b \neq-1$ : c'est exactement le nombre de diviseurs (positifs ou négatifs) de 2014, moins 2. Comme $2014=2 \cdot 19 \cdot 53$, celui-ci a $2 \cdot(1+1) \cdot(1+1) \cdot(1+1)=16$ diviseurs (positifs ou négatifs), donc 14 suites conviennent.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
a678e475-312a-59c0-8f53-771a8c6deee2
| 607,525
|
Let $K$ be the maximum value of
$$
\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right|
$$
where $x_{1}, x_{2}, x_{3}, x_{4} \in[0 ; 1]$.
a) Prove that $\frac{4}{243}<K<\frac{1}{27}$.
b) Determine $K$.
|
a) Let $x_{1}, x_{2}, x_{3}, x_{4} \in [0 ; 1]$.
We define
$$
f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right| .
$$
If two of the numbers $x_{1}, x_{2}, x_{3}, x_{4}$ are equal, we have $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=0$, which is clearly not the maximum value of $f$. Without loss of generality, we can therefore assume that $x_{1}>x_{2}>x_{3}>x_{4}$. According to the arithmetic-geometric mean inequality, we have
$$
\sqrt[3]{\left(x_{1}-x_{2}\right)\left(x_{2}-x_{3}\right)\left(x_{3}-x_{4}\right)} \leqslant \frac{\left(x_{1}-x_{2}\right)+\left(x_{2}-x_{3}\right)+\left(x_{3}-x_{4}\right)}{3}=\frac{x_{1}-x_{4}}{3} \leqslant \frac{1}{3}
$$
and thus $\left|x_{1}-x_{2}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{3}-x_{4}\right| \leqslant \frac{1}{27}$.
On the other hand, we have $\left|x_{1}-x_{3}\right|<1,\left|x_{1}-x_{4}\right| \leqslant 1$ and $\left|x_{2}-x_{4}\right|<1$, so $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)<\frac{1}{27}$.
Thus, we have $K<\frac{1}{27}$.
On the other hand, it is easy to verify that $f\left(1, \frac{3}{4}, \frac{1}{4}, 0\right)=\frac{9}{512}>\frac{4}{243}$, so $K>\frac{4}{243}$.
b) Without loss of generality, we still assume that $x_{1}>x_{2}>x_{3}>x_{4}$. However, it is easy to see that $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \leqslant f\left(1, x_{2}, x_{3}, 0\right)$. Thus, by setting $x_{2}=y$ and $x_{3}=z$, we seek the maximum value of
$$
g(x, y)=(1-y)(1-z)(y-z) y z
$$
under the constraint $0<z<y<1$.
Let $s$ be a real number.
We recall that if $a, b$ are two real numbers such that $a+b=s$ then $a b=\frac{1}{4} s^{2}-\left(a-\frac{s}{2}\right)^{2} \leqslant \frac{1}{4} s^{2}$, with equality if and only if $a=b=\frac{1}{2} s$.
Now let $t \in (0,1)$, and consider the pairs $(y, z)$ for which $y-z=t$.
In these conditions, the values $(1-y)+z=1-t$ and $(1-z)+y=1+t$ are fixed. According to the recall, the product $(1-y) z$ is therefore maximal for $y+z=1$, and the same is true for the product $(1-z) y$. Given $y-z=t$, this corresponds to $y=\frac{1+t}{2}$ and $z=\frac{1-t}{2}$, and in these conditions, we have $g(y, z)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$.
Thus, we need to find the maximum value of $P(t)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$, when $t \in (0,1)$.
It is easy to verify that, for all $t \in (0,1)$, we have $P^{\prime}(t)=\frac{1}{16}\left(1-t^{2}\right)\left(1-5 t^{2}\right)$. This ensures that the sought maximum value is $P\left(\frac{1}{\sqrt{5}}\right)=\frac{\sqrt{5}}{125}$.
Thus, we have $K=\frac{\sqrt{5}}{125}$.
## Exercises of Group A
|
\frac{\sqrt{5}}{125}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On désigne par $K$ la valeur maximale de
$$
\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right|
$$
où $x_{1}, x_{2}, x_{3}, x_{4} \in[0 ; 1]$.
a) Prouver que $\frac{4}{243}<K<\frac{1}{27}$.
b) Déterminer $K$.
|
a) Soit $x_{1}, x_{2}, x_{3}, x_{4} \in[0 ; 1]$.
On pose
$$
f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=\left|x_{1}-x_{2}\right| \cdot\left|x_{1}-x_{3}\right| \cdot\left|x_{1}-x_{4}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{2}-x_{4}\right| \cdot\left|x_{3}-x_{4}\right| .
$$
Si deux des nombres $x_{1}, x_{2}, x_{3}, x_{4}$ sont égaux, on a $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=0$, qui n'est clairement pas la valeur maximale de $f$. Sans perte de généralité, on peut donc supposer que $x_{1}>x_{2}>x_{3}>x_{4}$. D'après l'inégalité arithmético-géométrique, on a
$$
\sqrt[3]{\left(x_{1}-x_{2}\right)\left(x_{2}-x_{3}\right)\left(x_{3}-x_{4}\right)} \leqslant \frac{\left(x_{1}-x_{2}\right)+\left(x_{2}-x_{3}\right)+\left(x_{3}-x_{4}\right)}{3}=\frac{x_{1}-x_{4}}{3} \leqslant \frac{1}{3}
$$
et donc $\left|x_{1}-x_{2}\right| \cdot\left|x_{2}-x_{3}\right| \cdot\left|x_{3}-x_{4}\right| \leqslant \frac{1}{27}$.
D'autre part, on a $\left|x_{1}-x_{3}\right|<1,\left|x_{1}-x_{4}\right| \leqslant 1$ et $\left|x_{2}-x_{4}\right|<1$, d'où $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)<\frac{1}{27}$.
Et ainsi, on a $K<\frac{1}{27}$.
D'autre part, on vérifie facilement que $f\left(1, \frac{3}{4}, \frac{1}{4}, 0\right)=\frac{9}{512}>\frac{4}{243}$, d'où $K>\frac{4}{243}$.
b) Sans perte de généralité, on suppose toujours que $x_{1}>x_{2}>x_{3}>x_{4}$. Mais, il est facile de constater que $f\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \leqslant f\left(1, x_{2}, x_{3}, 0\right)$. Ainsi, en posant $x_{2}=y$ et $x_{3}=z$, on cherche la valeur maximale de
$$
g(x, y)=(1-y)(1-z)(y-z) y z
$$
sous la contrainte $0<z<y<1$.
Soit $s$ un réel.
On rappelle que si $a, b$ sont deux réels tels que $a+b=s$ alors $a b=\frac{1}{4} s^{2}-\left(a-\frac{s}{2}\right)^{2} \leqslant \frac{1}{4} s^{2}$, avec égalité si et seulement si $a=b=\frac{1}{2} s$.
Soit alors $t \in] 0,1[$, et considérons les couples $(y, z)$ pour lesquels $y-z=t$.
Dans ces conditions, les valeurs $(1-y)+z=1-t$ et $(1-z)+y=1+t$ sont fixées. D'après le rappel, le produit $(1-y) z$ est donc maximal pour $y+z=1$, et il en est de même pour le produit $(1-z) y$. Compte-tenu de $y-z=t$, cela correspond à $y=\frac{1+t}{2}$ et $z=\frac{1-t}{2}$ et, dans ces conditions, on a $g(y, z)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$.
Il s'agit donc de chercher la valeur maximale de $P(t)=\frac{1}{16} t\left(1-t^{2}\right)^{2}$, lorsque $\left.t \in\right] 0,1[$.
Il est facile de vérifier que, pour tout $t \in] 0,1\left[\right.$, on a $P^{\prime}(t)=\frac{1}{16}\left(1-t^{2}\right)\left(1-5 t^{2}\right)$. Cela assure que la valeur maximale cherchée est $P\left(\frac{1}{\sqrt{5}}\right)=\frac{\sqrt{5}}{125}$.
Ainsi, on a $K=\frac{\sqrt{5}}{125}$.
## Exercices du groupe A
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-6-solutions.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
37c2f161-5503-5d42-ae9a-4e8e047affe5
| 607,540
|
Consider a standard $8 \times 8$ chessboard. A zigzag is a path on the white squares, starting from any square on the bottom row and moving up row by row until reaching the top row (on any square): at each step, one moves up one square diagonally. How many zigzags are there?
|
We write a 1 in each of the four white squares at the bottom. Then in the second row, we write the sum of the white squares that lead to them: this is the number of ways to reach these squares. We repeat this in the third row, etc., up to the eighth row: on each of the four squares, we have the number of zigzags that reach this square. The total number of zigzags is therefore $69+103+35+89=296$.

|
296
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère un échiquier classique $8 \times 8$. Un zigzag est un chemin sur les cases blanches, qui part d'une case (quelconque) de la ligne du bas, et monte de ligne en ligne jusqu'à atteindre celle du haut (sur n'importe quelle case) : à chaque étape, on monte d'une case en diagonale. Combien y a-t-il de zigzags?
|
On écrit un 1 dans chacune des quatre cases blanches du bas. Puis dans la deuxième ligne, on écrit la somme des cases blanches qui y mènent : c'est le nombre de manières d'atteindre ces cases. On recommence dans la troisième ligne, etc. jusqu'à la huitième ligne : sur chacune des quatre cases, on a le nombre de zigzags qui arrivent à cette case. Le nombre total de zigzags est donc $69+103+35+89=296$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 1",
"solution_match": "\nSolution "
}
|
ceaa78ca-c455-5bad-9157-411c03a65ae0
| 607,544
|
How many six-digit numbers have four even digits, two odd digits, and are multiples of 5? Note: a number does not start with 0.
|
Such a number ends with 0 or 5. We will count separately the numbers that end with 0 and those that end with 5.
Numbers whose last digit is 0:
- If the first digit is even, we have 4 possibilities to choose it (2,4,6,8, but not 0). It remains to choose the 4 middle digits. There are 6 ways to position the odd digits:
$$
(p, p, i, i),(p, i, p, i),(p, i, i, p),(i, p, i, p),(i, i, p, p),(i, p, p, i)
$$
(where $p$ represents an even digit and $i$ an odd digit). Then there are 5 possibilities for the choice of each digit. So $6 \times 4 \times 5^{4}$ possibilities.
- If the first digit is odd, we have 5 possibilities to choose it. There are 4 ways to position the odd digit in the middle. And again 5 choices for each middle digit. So $4 \times 5^{5}$ possible numbers.
Numbers whose last digit is 5:
- If the first digit is even, we have 4 possibilities to choose it. There are 4 possibilities for the position of the odd digit in the middle, 5 choices for each middle digit, so $16 \times 5^{4}$ possibilities.
- If the first digit is odd, there are 5 possibilities to choose it. It then remains to determine the even digits in the middle: 5 choices each time, so $5^{5}$ choices in total.
In total, there are $24 \times 5^{4}+4 \times 5^{5}+16 \times 5^{4}+5^{5}=13 \times 5^{5}=40625$ possibilities.
|
40625
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Combien y a-t-il de nombres à six chiffres qui ont quatre chiffres pairs, deux chiffres impairs et qui sont multiples de 5 ? Note: un nombre ne commence pas par un 0 .
|
Un tel nombre termine par 0 ou 5 . Nous allons compter séparément les nombres qui se terminent par 0 et ceux qui se terminent par 5 .
Nombres dont le dernier chiffre est 0 :
- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir (2,4,6,8, mais pas 0 ). Il reste à choisir les 4 chiffres du milieu. On a 6 manières de positionner les impairs :
$$
(p, p, i, i),(p, i, p, i),(p, i, i, p),(i, p, i, p),(i, i, p, p),(i, p, p, i)
$$
(où $p$ représente un chiffre pair et $i$ un chiffre impair). Ensuite, il y a 5 possibilités pour le choix de chaque chiffre. Donc $6 \times 4 \times 5^{4}$ possibilités.
- Si le premier chiffre est impair, nous avons 5 possibilités pour le choisir . Il reste 4 manières de positionner l'impair du milieu. Et de nouveau 5 choix pour chaque chiffre du milieu. Donc $4 \times 5^{5}$ nombres possibles.
Nombres dont le dernier chiffre est 5 :
- Si le premier chiffre est pair, nous avons 4 possibilités pour le choisir. Il y a 4 possibilités pour la place de l'impair du milieu, 5 choix pour chacun des chiffres du milieu, donc $16 \times 5^{4}$ possibilités.
- Si le premier chiffre est impair il y a 5 possibilités pour le choisir. Il reste alors simplement à déterminer les pairs du milieu : 5 choix à chaque fois, donc $5^{5}$ choix en tout.
Au total, il y a $24 \times 5^{4}+4 \times 5^{5}+16 \times 5^{4}+5^{5}=13 \times 5^{5}=40625$ possibilités.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 3",
"solution_match": "\nSolution "
}
|
5b555056-26bc-5fb0-a2e5-bfe0c94c6a95
| 607,546
|
In a circus, there are several clowns. Each one uses at least 5 colors, among 12 possible, to paint themselves. The same color is used by at most 20 clowns. Two clowns never have exactly the same colors. What is the maximum number of clowns?
|
Let $n$ be the number of clowns and $N$ be the number of pairs $(L, c)$ where $L$ is a clown and $c$ is a color he wears. On the one hand, since each clown has at least 5 colors, $N \geq 5 \times n$. On the other hand, each of the 12 colors can appear in at most 20 pairs. Therefore, $N \leq 20 \times 12$. We deduce that $5 n \leq 240$, so $n \leq 48$.
Now, consider the quintuples: $A=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}\right), B=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{6}\right), C=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{7}\right), D=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{8}\right)$. Imagine that the 12 colors are arranged in order on a circle (like the numbers on a clock, for example), and let $A_{i}$ be the quintuple obtained by shifting the colors of $A$ by $i$ positions in the increasing direction $\left(A_{0}=A, A_{1}=\left(c_{1+1}, c_{2+1}, c_{3+1}, c_{4+1}, c_{5+1}\right)=\left(c_{2}, c_{3}, c_{4}, c_{5}, c_{6}\right)\right.$, $A_{9}=\left(c_{10}, c_{11}, c_{12}, c_{1}, c_{2}\right.$, etc.). We do the same for $B, C, D$. Concretely, each such quintuple of colors consists of four consecutive colors on the circle, then makes a "jump" for the number of the last color, which is 1 for the $A_{i}$, 2 for the $B_{i}$, 3 for the $C_{i}$, and 4 for the $D_{i}$.
Consider the set of $K_{i}$ with $K=A, B, C$ or $D$ and $0 \leq i \leq 11$. This gives 48 sets of 5 colors. And we can easily verify that two sets cannot be identical: if for some $i$ and $j$ and some $K$ and $K^{\prime}$ we had $K_{i}=K_{j}^{\prime}$, then $K=K^{\prime}$ to have the same "jump" between the "set" of four consecutive colors and the fifth (1 for $A$, 2 for $B$, 3 for $C$, 4 for $D$), so $K_{i}=K_{j}$, and we see that $i=j$, so that the two sets of four consecutive colors are the same.
Finally, each color is used exactly 20 times. Indeed, we can note that all the colors play the same role here (since we have "cyclically shifted" the sets $A, B, C, D$), so each will be represented as much as the others. We have a total of $5 \times 48=240$ uses of color, so each of the 12 colors is used $240 / 12=20$ times. To be more convinced, we can fix a color: it appears once and only once as the "first" color of a set of type $A_{i}$, then as "second", etc., so 5 sets $A_{i}$ use this color, and the same for $B, C$, and $D$. It is therefore used 20 times. Conclusion: we can indeed have $n=48$ clowns, by giving each clown one of the 48 sets of colors we have just constructed.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dans un cirque, il y a plusieurs clowns. Chacun utilise au moins 5 couleurs, parmi 12 possibles, pour se peindre. Une même couleur est utilisée par au plus 20 clowns. Deux clowns n'ont jamais exactement les mêmes couleurs. Combien y a-t-il de clowns au maximum?
|
Soit $n$ le nombre de clowns et $N$ le nombre de paires $(L, c)$ où $L$ est un cLown et $c$ une couleur qu'il porte. D'une part, chaque clown ayant au moins 5 couleurs, $N \geq 5 \times n$. D'autre part, chacune des 12 couleurs peut apparaître dans au plus 20 paires. Donc $N \leq 20 \times 12$. On en déduit que $5 n \leq 240$, donc $n \leq 48$.
Maintenant, on considère les quintuplets : $A=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}\right), B=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{6}\right), C=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{7}\right)$, $D=\left(c_{1}, c_{2}, c_{3}, c_{4}, c_{8}\right)$. On imagine que les 12 couleurs sont disposées dans l'ordre sur un cercle (comme les nombres sur une pendule par exemple), et on note $A_{i}$ le quintuplet obtenu en décalant les couleurs de $A$ de $i$ rangs dans le sens croissant $\left(A_{0}=A, A_{1}=\left(c_{1+1}, c_{2+1}, c_{3+1}, c_{4+1}, c_{5+1}\right)=\left(c_{2}, c_{3}, c_{4}, c_{5}, c_{6}\right)\right.$, $A_{9}=\left(c_{10}, c_{11}, c_{12}, c_{1}, c_{2}\right.$, etc. $)$, et on fait de même pour $B, C, D$. Concrètement, chaque tel quintuplet de couleurs consiste donc de quatre couleurs consécutives sur le cercle, puis fait un "saut" pour le numéro de la dernière couleur qui est de taille 1 pour les $A_{i}$, de 2 pour les $B_{i}$, de 3 pour les $C_{i}$ et de 4 pour les $C_{i}$.
Considérons l'ensemble des $K_{i}$ avec $K=A, B, C$ ou $D$ et $0 \leq i \leq 11$. Cela donne 48 paquets de 5 couleurs. Et on vérifie aisément que deux paquets ne peuvent être identiques : si pour certains $i$ et $j$ et certains $K$ et $K^{\prime}$ on avait $K_{i}=K_{j}^{\prime}$, alors $K=K^{\prime}$ pour avoir le même "saut" entre le "paquet" des quatre couleurs consécutives et la cinquième ( 1 pour $A, 2$ pour $B, 3$ pour $C, 4$ pour $D$ ), donc $K_{i}=K_{j}$, et on voit bien que $i=j$, pour que les deux paquets de quatre couleurs consécutives soient les mêmes.
Enfin, chaque couleur est utilisée exactement 20 fois. En effet, on peut remarquer que toutes les couleurs jouent ici le même rôle(puisqu'on a "décalé" cycliquement les ensembles $A, B, C, D$ ), donc chacune sera représentée autant que les autres. On a au total $5 \times 48=240$ utilisations de couleur, donc chacune des 12 couleurs est utilisée $240 / 12=20$ fois. Pour s'en convaincre plus concrètement, on peut fixer une couleur : elle apparaît une et une seule fois comme "première" couleur d'un paquet de type $A_{i}$, puis comme "deuxième", etc., donc 5 paquets $A_{i}$ utilisent cette couleur, et de même pour $B, C$ et $D$. Elle est donc utilisée 20 fois. Conclusion : on peut bien avoir $n=48$ clowns, en donnant à chaque clown un des 48 paquets de couleurs qu'on vient de construire.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 6",
"solution_match": "\nSolution "
}
|
2cea4157-4979-5c9e-a12f-667c82742c6e
| 607,549
|
Jules and Jim, two roommates, receive 10 other pairs of roommates at their place. Jules conducts a small survey during the evening and interviews the 21 other people. Among them, no one has shaken hands with their roommate, and no two people have shaken the same number of hands. How many hands has Jim shaken?
|
During the evening, among the 21, each person shakes between 0 and 20 hands. Since they all shake a different number of hands, for every n between 0 and 20, there is one and only one person $A_{n}$ among the 21 who has shaken exactly n hands.
Since $A_{20}$ has shaken 20 hands, $A_{20}$ has shaken hands with everyone except himself and his roommate. However, $A_{0}$ has not shaken hands with anyone, so $A_{0}$ is the roommate of $A_{20}$.
Since $A_{19}$ has shaken 19 hands, $A_{19}$ has shaken hands with everyone except himself, his roommate, and $A_{0}$. However, $A_{1}$ has shaken hands with $A_{20}$ and no one else, so $A_{1}$ has not shaken hands with $A_{19}$. We deduce that $A_{1}$ is the roommate of $A_{19}$.
Continuing this reasoning, we show that $A_{n}$ is the roommate of $A_{20-n}$ for all $\boldsymbol{n}=0,1, \ldots, 9$, so $A_{10}$ is the roommate of Jules. Finally, Jules has shaken 10 hands.
## Common Exercises
|
10
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Jules et Jim, deux colocataires, reçoivent 10 autres paires de colocataires chez eux. Jules fait un petit sondage au cours de la soirée et interroge les 21 autres personnes. Parmi elles, aucune n'a serré la main de son colocataire, et il n'y en a pas deux qui ont serré le même nombre de mains. Combien de mains a serré Jim?
|
Au cours de la soirée, parmi les 21 , chaque personne serre entre 0 et 20 mains. Comme elles serrent toutes un nombre différent de mains, pour tout n compris entre 0 et 20 il existe une et une seule personne $A_{n}$ parmi les 21 qui a serré exactement n mains.
Comme $A_{20}$ a serré 20 mains, $A_{20}$ a serré la main à tout le monde sauf lui même et son colocataire. Or, $A_{0}$ n'a serré la main à personne, donc $A_{0}$ est le colocataire de $A_{20}$.
Comme $\AA_{19}$ a serré 19 mains, $\AA_{19}$ a serré la main à tout le monde sauf lui-même, son colocataire et $A_{0}$. Or, $A_{1}$ a serré la main à $A_{20}$ et à personne d'autre, donc n'a pas serré la main à $A_{19}$. On en déduit que $A_{1}$ est le colocataire de $A_{19}$.
En continuant le raisonnement, on montre que $A_{n}$ est le colocataire de $A_{20-n}$ pour tout $\boldsymbol{n}=0,1, \ldots, 9$, donc $A_{10}$ est le colocataire de Jules. Finalement, Jules a serré 10 mains.
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
cfaed2dd-d687-5c94-b62e-cb77925cc843
| 607,585
|
Calculate
$$
\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}+\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}+\cdots+\sqrt{1+\frac{1}{2014^{2}}+\frac{1}{2015^{2}}}
$$
|
We reduce to a common denominator
$$
\begin{aligned}
1+\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}} & =\frac{n^{2}(n+1)^{2}+(n+1)^{2}+n^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{n^{4}+n^{2}(2 n+1)+n^{2}+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{n^{4}+2 n^{2}(n+1)+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{\left(n^{2}+(n+1)\right)^{2}}{n^{2}(n+1)^{2}}
\end{aligned}
$$
We deduce that the desired sum is
$$
\begin{aligned}
\sum_{n=1}^{2014} \frac{n^{2}+n+1}{n(n+1)} & =\sum_{n=1}^{2014} 1+\frac{1}{n(n+1)} \\
& =2014+\sum_{n=1}^{2014} \frac{1}{n(n+1)} \\
& =2014+\sum_{n=1}^{2014} \frac{1}{n}-\frac{1}{n+1} \\
& =2014+\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2014}-\frac{1}{2015}\right)
\end{aligned}
$$
We recognize a telescoping sum. The terms cancel out pairwise, except for 1 and $\frac{1}{2015}$, so the sum is
$$
2014+1-\frac{1}{2015}=2015-\frac{1}{2015}
$$
|
2015-\frac{1}{2015}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Calculer
$$
\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}+\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}+\cdots+\sqrt{1+\frac{1}{2014^{2}}+\frac{1}{2015^{2}}}
$$
|
On réduit au même dénominateur
$$
\begin{aligned}
1+\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}} & =\frac{n^{2}(n+1)^{2}+(n+1)^{2}+n^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{n^{4}+n^{2}(2 n+1)+n^{2}+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{n^{4}+2 n^{2}(n+1)+(n+1)^{2}}{n^{2}(n+1)^{2}} \\
& =\frac{\left(n^{2}+(n+1)\right)^{2}}{n^{2}(n+1)^{2}}
\end{aligned}
$$
On en déduit que la somme recherchée vaut
$$
\begin{aligned}
\sum_{n=1}^{2014} \frac{n^{2}+n+1}{n(n+1)} & =\sum_{n=1}^{2014} 1+\frac{1}{n(n+1)} \\
& =2014+\sum_{n=1}^{2014} \frac{1}{n(n+1)} \\
& =2014+\sum_{n=1}^{2014} \frac{1}{n}-\frac{1}{n+1} \\
& =2014+\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2014}-\frac{1}{2015}\right)
\end{aligned}
$$
On reconnaît une somme télescopique. Les termes se simplifient deux à deux, sauf 1 et $\frac{1}{2015}$, donc la somme vaut
$$
2014+1-\frac{1}{2015}=2015-\frac{1}{2015}
$$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
fd2fbce3-d1ee-5789-aaa8-6c57665ed7b5
| 607,592
|
Let $p$ and $q$ be two prime numbers greater than or equal to 7. Let $x=\frac{p^{2012}+q^{2016}}{120}$. Calculate $x-[x]$, where $[x]$ denotes the integer part of $x$, that is, the greatest integer less than or equal to $x$.
|
If \( a \) is an integer not divisible by 2, 3, and 5, it is easy to verify that \( a^4 \) is congruent to 1 modulo 3, 5, and 8. In other words, \( a^4 - 1 \) is divisible by 3, 5, and 8, and thus by \( 3 \times 5 \times 8 = 120 \). We can deduce that \( p^4 \) and \( q^4 \) are congruent to 1 modulo 120, so \( p^{2012} + q^{2016} \equiv 1 + 1 \equiv 2 \pmod{120} \).
We can deduce that \( x - [x] = \frac{2}{120} = \frac{1}{60} \).
|
\frac{1}{60}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soient $p$ et $q$ deux nombres premiers supérieurs ou égaux à 7 . Soit $x=\frac{p^{2012}+q^{2016}}{120}$. Calculer $x-[x]$, où $[x]$ désigne la partie entière de $x$, c'est-à-dire le plus grand entier inférieur ou égal à $x$.
|
Si a est un entier non divisible par 2,3 et 5 , on vérifie facilement que a ${ }^{4}$ est congru à 1 modulo 3,5 et 8 . Autrement dit, a ${ }^{4}-1$ est divisible par 3,5 et 8 , donc par $3 \times 5 \times 8=$ 120 . On en déduit que $p^{4}$ et $q^{4}$ sont congrus à 1 modulo 120 , donc $p^{2012}+q^{2016} \equiv 1+1 \equiv 2$ $(\bmod 120)$.
On en déduit que $x-[x]=\frac{2}{120}=\frac{1}{60}$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
96c75c0e-d960-5fba-9080-f1d8f4a754cd
| 607,593
|
Find the smallest positive integer that cannot be written in the form $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ for $a, b, c, d \in \mathbb{N}$.
|
Let $E$ be the set of strictly positive integers that can be written in this form. Let's start by noting that
$$
\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \frac{2^{a-b}-1}{2^{c-d}-1}
$$
Thus, if $x>0$ is written as $x=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, then $b-d=v_{2}(x)$ and if we call $y$ the odd integer such that $x=2^{v_{2}(x)} y$, then $y$ can be written in the form $\frac{2^{n}-1}{2^{m}-1}$. In particular, the integer we are looking for is necessarily odd. On the other hand, we can immediately exclude integers of the form $2^{n}-1$, which are reached with $m=1$.
It is classical that if $2^{m}-1$ divides $2^{n}-1$, then $m$ divides $n$. Thus, by writing $n=m d, y$ is of the form
$$
y=\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\ldots+2^{m}+1
$$
In other words, denoting $u=\underbrace{0 \ldots 0}_{m-1 \text { zeros }} 1$, the binary representation of $y$ is of the form $\overline{1 u \ldots u}^{2}$, with $u$ appearing $d-1$ times. The odd integers belonging to $E$ are exactly those having such a binary representation for well-chosen $m$ and $d$. The binary representations of the first odd integers that are not of the form $2^{n}-1$ are
$$
5=\overline{101}^{2}, 9={\overline{1001}^{2}}^{2}, 11={\overline{1011}^{2}}^{2}
$$
According to the criterion above, the smallest integer sought is 11.
Remark: This exercise can also be done by finding ways to write the integers 1 to 10 in this form, then showing that 11 cannot be written in this form: indeed, since 11 is odd, we can assume $b=d=1$. Then
$$
\left(2^{a}-1\right)=11\left(2^{c}-1\right)
$$
rewrites as
$$
10=2^{c} \times 11-2^{a}
$$
Since $10=2 \times 5$, we have $a=1$ or $c=1$. If $a=1$, we get $2^{c} \times 11=12$, which has no solution, and if $c=1$, we get $2^{a}=12$, which has no solution either. Therefore, 11 is the integer sought.
## 2 Common Exercises
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \in \mathbb{N}$.
|
: Soit E l'ensemble des entiers strictement positifs s'écrivant sous cette forme. Commençons par remarquer que
$$
\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \frac{2^{a-b}-1}{2^{c-d}-1}
$$
Ainsi, si $x>0$ s'écrit $x=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, alors $b-d=v_{2}(x)$ et si on appelle $y$ l'entier impair tel que $x=2^{v_{2}(x)} y$, alors $y$ s'écrit sous la forme $\frac{2^{n}-1}{2^{m}-1}$. En particulier, l'entier que nous cherchons est nécessairement impair. D'autre part, on peut tout de suite exclure les entiers de la forme $2^{n}-1$, atteints avec $m=1$.
Il est classique que si $2^{m}-1$ divise $2^{n}-1$, alors $m$ divise $n$. Ainsi, en écrivant $n=m d, y$ est de la forme
$$
y=\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\ldots+2^{m}+1
$$
Autrement dit, en notant $u=\underbrace{0 \ldots 0}_{m-1 \text { zéros }} 1$, l'écriture en base 2 de $y$ est de la forme $\overline{1 u \ldots u}^{2}$, avec $u$ apparaissant $d-1$ fois. Les entiers impairs appartenant à $E$ sont exactement ceux ayant une telle écriture binaire pour $m$ et $d$ bien choisis. Les écritures binaires des premiers entiers impairs qui ne sont pas de la forme $2^{n}-1$ sont
$$
5=\overline{101}^{2}, 9={\overline{1001}^{2}}^{2}, 11={\overline{1011}^{2}}^{2}
$$
D'après le critère ci-dessus, le plus petit entier cherché est 11.
Remarque : cet exercice peut aussi se faire en trouvant des manières d'écrire les entiers 1 à 10 sous cette forme, puis en montrant que 11 ne s'écrit pas sous cette forme : en effet, vu que 11 est impair, on peut supposer $b=d=1$. Ensuite
$$
\left(2^{a}-1\right)=11\left(2^{c}-1\right)
$$
se réécrit
$$
10=2^{c} \times 11-2^{a}
$$
Puisque $10=2 \times 5$, nous avons $a=1$ ou $c=1$. Si $a=1$, on trouve $2^{c} \times 11=12$, qui n'a pas de solution, et si $c=1$, on trouve $2^{a}=12$, qui n'a pas de solution non plus. Donc 11 est l'entier cherché.
## 2 Exercices communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 3",
"solution_match": "\nSolution de l'exercice 3"
}
|
8f3a3904-2cf5-5591-8086-3e23212fe99f
| 607,606
|
Find all strictly positive integers $n$ such that $2^{n-1} n+1$ is a perfect square.
|
We want to solve $2^{n-1} n+1=m^{2}$, that is, $2^{n-1} n=(m-1)(m+1)$. Since $n=1$ is not a solution, we have $n \geq 2$, and therefore $m$ must be odd, and $m-1$ and $m+1$ are even (in particular, $n \geq 3$). We set $k=\frac{m-1}{2}$. It then suffices to solve $2^{n-3} n=k(k+1)$. Among the integers $k$ and $k+1$, exactly one is even, and thus they are of the form $2^{n-3} d$ and $\frac{n}{d}$ with $d$ a divisor of $n$. A divisor of $n$ cannot be at a distance of 1 from an integer greater than $2^{n-3}$ if $n$ is too large. More precisely, we have $2^{n-3} d \geq 2^{n-3} \geq n+2$ if $n \geq 6$, so we must have $n \leq 5$. For $n=5$, we find $2^{4} \times 5+1=9^{2}$, so 5 is a solution. We verify that $2,3,4$ are not solutions. Therefore, $n=5$ is the only solution.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.
|
: On veut résoudre $2^{n-1} n+1=m^{2}$, c'est-à-dire $2^{n-1} n=(m-1)(m+1)$. Puisque $n=1$ n'est pas solution, on a $n \geq 2$, et donc $m$ est nécessairement impair, et $m-1$ et $m+1$ sont pairs (en particulier $n \geq 3$ ). On pose $k=\frac{m-1}{2}$. Il suffit alors de résoudre $2^{n-3} n=k(k+1)$. Parmi les entiers $k$ et $k+1$ exactement un est pair, et donc ils sont de la forme $2^{n-3} d$ et $\frac{n}{d}$ avec $d$ un diviseur de $n$. Or un diviseur de $n$ ne peut pas être à distance 1 d'un entier supérieur à $2^{n-3}$ si $n$ est trop grand. Plus précisément, on a $2^{n-3} d \geq 2^{n-3} \geq n+2$ si $n \geq 6$, donc on a nécessairement $n \leq 5$. Pour $n=5$, on trouve $2^{4} \times 5+1=9^{2}$, donc 5 est solution. On vérifie que $2,3,4$ ne sont pas solutions. Donc $n=5$ est la seule solution.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 5",
"solution_match": "\nSolution de l'exercice 5"
}
|
43de005f-5839-5f0f-b9ea-914704399f20
| 607,608
|
Let $n \geqslant 2$. We place a coin on each square of an $n \times n$ chessboard. A move consists of moving each coin to a square that touches the starting square exactly by a corner (multiple coins can end up on the same square).
What is the smallest integer $k$ such that it is possible that after a certain number of moves, only $k$ squares contain at least one coin?
|
The answer is 4.
We denote $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and D as the four cells that form the $2 \times 2$ square in the top right:
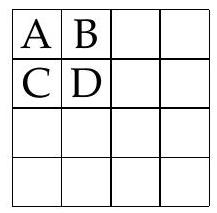
Each piece can be moved to one of the cells $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and D, and then oscillate between $A$ and $D$ or between $B$ and $C$ at each move. Therefore, it is possible that after a certain number of moves, all pieces are on one of the four cells $A, B, C$, and $D$.
It remains to show that it is not possible to do better than 4. We consider the following coloring of the chessboard (here for $\mathrm{n}=4$):
Since $n \geqslant 2$, there is at least one piece on a cell of each color at the beginning. But at each move, the pieces that are on blue cells move to red cells, those on red cells move to blue cells, those on yellow cells move to green cells, and those on green cells move to yellow cells. At each step, there are therefore always pieces on at least one cell of each color, so there are always at least 4 cells that contain at least one piece.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geqslant 2$. On place une pièce sur chaque case d'un échiquier $n \times n$. Un mouvement consiste à déplacer chaque pièce sur une case qui touche la case de départ par un coin exactement (plusieurs pièces peuvent se retrouver sur la même case).
Quel est le plus petit entier $k$ tel qu'il est possible qu'après un certain nombre de mouvements, seules $k$ cases contiennent au moins une pièce?
|
La réponse est 4.
On note $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D les quatre cases quif forment le carré $2 \times 2$ en haut à droite :

Chaque pièce peut être amenée sur une des cases $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D , puis osciller à chaque mouvement entre $A$ et $D$ ou entre $B$ et $C$. Il est donc possible qu'après un certain nombre de mouvements, toutes les pièces soient sur une des quatre cases $A, B, C$ et $D$.
Il reste à montrer qu'on ne peut pas faire mieux que 4 . On considère le coloriage suivant de l'échiquier (ici pour $\mathrm{n}=4$ ) :

Comme $n \geqslant 2$, il y a au début au moins une pièce sur une case de chaque couleur. Mais à chaque mouvement, les pièces qui se trouvent sur des cases bleues passent sur des cases rouges, celles sur des cases rouges passent sur des bleues, celles sur des jaunes passent sur des vertes et celles sur des vertes passent sur des jaunes. A chaque étape, il y a donc des pièces sur au moins une case de chaque couleur, donc il y a toujours au moins 4 cases qui contiennent au moins une pièce.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
2e64c46b-d800-5c1a-a996-12cdf3cf11ee
| 607,630
|
The seven dwarfs have distinct heights. They go to the mine in a column in a certain order, such that the dwarf at the front is taller than the second, who is shorter than the third, who is taller than the fourth, and so on...
How many such ways are there to arrange the dwarfs?
|
We denote $u_{3}$ as the number of ways to arrange 3 dwarfs such that the first is taller than the second, who is taller than the third, $\mathfrak{u}_{5}$ as the number of similar ways to arrange 5 dwarfs, and $u_{7}$ as the solution to the problem.
With 3 dwarfs, we are forced to place the shortest dwarf in the middle, and we can then place the other two as we wish.
With 5 dwarfs, the shortest dwarf can be in the second or fourth position:
- If he is in position 2, any dwarf can be first, so we have 4 choices for the first dwarf. It then remains to order the last three: there are $\mathfrak{u}_{3}$ ways to do this, so we get $4 \mathfrak{u}_{3}$ arrangements.
- If he is in position 4, we similarly have $4 u_{3}$ arrangements (by first choosing the fifth).
We therefore have $\mathfrak{u}_{5}=4 u_{3}+4 u_{3}=8 \times 2=16$.
With 7 dwarfs, the shortest dwarf can be in position 2, 4, or 6:
- If he is in position 2, any dwarf can be first (6 choices), and there are $u_{5}$ ways to order the last five, giving $6 \mathbf{u}_{5}$ possible orders.
- If he is in position 6, any dwarf can be last (6 choices), and there are $u_{5}$ ways to order the first five, giving $6 \mathfrak{u}_{5}$ possible orders.
- If he is in position 4, we can first sort the dwarfs who will be in front of him from those who will be behind. There are $\binom{6}{3}=20$ ways to do this sorting. Then there are $u_{3}$ ways to order the three in front and $u_{3}$ ways to order the three behind, giving $20 u_{3}^{2}$ possible orders.
We therefore have $\mathfrak{u}_{7}=6 \mathfrak{u}_{5}+6 \mathfrak{u}_{5}+20 \mathfrak{u}_{3}^{2}=6 \times 16+6 \times 16+20 \times 2^{2}=272$.
|
272
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Les sept nains ont des tailles deux à deux distinctes. Ils se rendent à la mine en colonne dans un certain ordre, de telle manière que le nain en tête est plus grand que le deuxième, qui est plus petit que le troisième, qui est plus grand que le quatrième et ainsi de suite...
Combien y a-t-il de telles manières d'arranger les nains?
|
On note $u_{3}$ le nombre de manières d'arranger 3 nains de manière à ce que le premier est plus grand que le second, qui est plus grand que le troisième, $\mathfrak{u}_{5}$ le nombre de manières similaires d'arranger 5 nains et $u_{7}$ la solution de l'exercice.
Avec 3 nains, on est obligé de mettre le nain le plus petit au milieu et on peut ensuite placer comme on veut les deux autres.
Avec 5 nains, le nain le plus petit peut être en deuxième ou quatrième position :
- S'il est en position 2, n'importe quel nain peut être en premier, donc on a 4 choix pour le premier nain. Il reste à ordonner les trois derniers : il y a $\mathfrak{u}_{3}$ manières de le faire, donc on obtient $4 \mathfrak{u}_{3}$ arrangements.
- S'il est en position 4 , on a de même $4 u_{3}$ arrangements (en choisissant d'abord le cinquième).
On a donc $\mathfrak{u}_{5}=4 u_{3}+4 u_{3}=8 \times 2=16$.
Avec 7 nains, le nain le plus petit peut être en position 2, 4 ou 6 :
- S'il est en position 2 , n'importe quel nain peut être en premier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq derniers, soit $6 \mathbf{u}_{5}$ ordres possibles.
- S'il est en position 6 , n'importe quel nain peut être en dernier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq premiers, soit $6 \mathfrak{u}_{5}$ ordres possibles.
- S'il est en position 4, on peut d'abord trier les nains qui seront devant lui de ceux qui seront derrière. Il y a $\binom{6}{3}=20$ manières de faire ce tri. Puis il y a $u_{3}$ manières d'ordonner les trois nains de devant et $u_{3}$ manières d'ordonner les trois de derrière, soit $20 u_{3}^{2}$ ordres popssibles.
On a donc $\mathfrak{u}_{7}=6 \mathfrak{u}_{5}+6 \mathfrak{u}_{5}+20 \mathfrak{u}_{3}^{2}=6 \times 16+6 \times 16+20 \times 2^{2}=272$.
## Exercices communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
86046a5b-f210-5729-85c4-6057df5080b2
| 607,632
|
Let $S$ be the set of integers from 1 to 2016. How many ways are there to partition $S$ into two subsets $A$ and $B$ such that neither $A$ nor $B$ contains two integers whose sum is a power of 2?
Note. We say that $A$ and $B$ form a partition of $S$ if neither $A$ nor $B$ is empty, $A$ and $B$ are disjoint, and their union is equal to $S$.
|
The answer is $2^{11}=2048$. More precisely, we will show that it is possible to distribute the numbers $1,2,4,8, \ldots, 1024=2^{10}$ as we wish between $A$ and $B$, and that once these numbers are placed, there is a unique way to distribute the others. We can then conclude because there are $2^{11}=2048$ ways to distribute these 11 numbers between $A$ and $B$.
The fact that the distribution of $1,2,4,8, \ldots, 1024$ determines the position of $k$ can be shown by strong induction on $k$: the positions of 1 and 2 have already been fixed, and 3 must be in the set that does not contain $1$ because $3+1=2^{2}$. Suppose now that the positions of all numbers from 1 to $k-1$ are fixed: if $k$ is a power of 2, then the position of $k$ is fixed by hypothesis. Otherwise, there exists $a$ such that $2^{a-1}<k<2^{a}$. But then $0<2^{a}-k<k$, so $2^{a}-k$ is in $A$ or $B$, and its position has already been fixed. Therefore, $k$ must be in the other set. Thus, there is at most one partition that works once the distribution of the powers of 2 is fixed.
It remains to show that such a distribution exists. However, the previous proof provides an algorithm that allows distributing the integers that are not powers of 2 between $\mathcal{A}$ and $B$ in such a way that for all $k$ and $a$ such that $2^{a-1}<k<2^{a}$, the numbers $k$ and $2^{a}-k$ are not in the same set. If two numbers $x \neq y$ have a sum that is a power of 2, denoted by $2^{a}$, we can assume $x>y$. Then $x>\frac{x+y}{2}=2^{a-1}$, so $2^{a-1}<x<2^{a}$ and $y=2^{a}-x$, so $x$ and $y$ are not in the same set, hence there is always a distribution that works.
|
2048
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On note $S$ l'ensemble des entiers de 1 à 2016. Combien y a-t-il de manières de partitionner $S$ en deux sous-ensembles $A$ et $B$ de telle manière que ni $A$ ni $B$ ne contient deux entiers dont la somme est une puissance de 2 ?
Remarque. On dit que $A$ et $B$ forment une partition de $S$ si ni $A$ ni $B$ n'est vide, $A$ et $B$ sont d'intersection vide et si leur union est égale à $S$.
|
La réponse est $2^{11}=2048$. Plus précisément, on va montrer qu'il est possible de répartir comme on veut les nombres $1,2,4,8, \ldots, 1024=2^{10}$ comme on veut entre $A$ et $B$ et qu'une fois ces nombres placés il existe une unique manière de répartir les autres. On peut alors conclure car il y a $2^{11}=2048$ manières de répartir ces 11 nombres entre $A$ et $B$.
Le fait que la répartition de $1,2,4,8, \ldots, 1024$ impose la position de $k$ se montre par récurrence forte sur k : la position de 1 et 2 a déjà été fixée, et 3 doit être dans l'ensemble qui ne contient pas $1 \mathrm{car} 3+1=2^{2}$. Supposons maintenant que toutes les positions de nombres de 1 à $k-1$ soient fixées : si $k$ est une puissance de 2, alors la position de $k$ est fixée par hypothèse. Sinon, il existe a tel que $2^{a-1}<k<2^{a}$. Mais alors $0<2^{a}-k<k$ donc $2^{a}-k$ est dans $A$ ou $B$, et sa position a déjà été fixée. $k$ est donc nécessairement dans l'autre ensemble. Il existe donc au plus une partition qui convient une fois fixée la répartition des puissances de 2 .
Il reste à montrer qu'une telle répartition existe bien. Mais la preuve précédente fournit un algorithme qui permet de répartir les entiers qui ne sont pas des puissances de 2 entre $\mathcal{A}$ et $B$ de telle manière que pour tous $k$ et $a$ tel que $2^{a-1}<k<2^{a}$, les nombres $k$ et $2^{a}-k$ ne sont pas dans le même ensemble. Or, si deux nombres $x \neq y$ ont pour somme une puissance de 2 notée $2^{a}$, on peut supposer $x>y$. On a alors $x>\frac{x+y}{2}=2^{a-1}$, donc $2^{a-1}<x<2^{a}$ et $y=2^{a}-x$, donc $x$ et $y$ ne sont pas dans le même ensemble, donc il existe bien toujours une répartition qui convient.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
6a4a5883-a07e-5449-b68b-9df1346106c9
| 607,634
|
Let $n \in \mathbb{N}^{*}$. We place $1 \times n$ and $n \times 1$ rectangles on a $2 n \times 2 n$ chessboard, in such a way that no two rectangles intersect and each rectangle covers exactly $n$ squares. A set of such rectangles is said to be saturated if it is impossible to add another rectangle without intersecting a rectangle already in place.
Find the smallest $k$ such that there exists a saturated set of $k$ rectangles.
|
Let's start with the case $n \geqslant 3$: the answer is $k=2n+1$. The following set (in the case $n=5$, the construction generalizes easily) works:
It remains to show that with 2n rectangles, it is always possible to add one that does not intersect them. If the 2n rectangles are oriented in the same direction, for example, all horizontal, then there must be exactly one on each row (otherwise there would be an empty row), and it cannot be at the end of the row (if it were all the way to the left, one could add a rectangle to its right). Consequently, the first and last columns are empty, and it is possible to add a vertical rectangle.
If there are rectangles in both directions, we can assume there are at most n vertical rectangles. Suppose the configuration is saturated. Let $1 \leqslant k \leqslant n$ such that column $k$ contains a vertical rectangle denoted $r$. By shifting $r$ one cell to the left, it must intersect an already placed rectangle, denoted $r'$ (otherwise one could add a rectangle). However, if $r'$ were horizontal, it would have to intersect $r$ because there is not enough space for a horizontal rectangle to the left of $r$. The rectangle $r'$ is therefore vertical, and thus column $k-1$ contains a vertical rectangle, and similarly for columns $k-2, \ldots, 2,1$.
Similarly, if $n+1 \leqslant k \leqslant 2n$ is such that column $k$ contains a vertical rectangle, then all columns to its right contain a vertical rectangle. The set of columns not containing a vertical rectangle is therefore a set of at least $n$ consecutive columns. There is thus an $n \times 2n$ rectangle that does not intersect any of the vertical rectangles. If the configuration is saturated, it therefore requires 2n horizontal rectangles to "block" each row within this $n \times 2n$ rectangle. Since we have assumed there is at least one vertical rectangle, there are therefore at least $2n+1$ rectangles, which is absurd.
Let's move on to the cases $n=1$ and $n=2$: the case $n=1$ is trivial and the answer is 4 (one must cover everything, otherwise one could add a 1x1 square). For $n=2$, there is no saturated set of 5 rectangles.
To show this, one can either perform a somewhat tedious case disjunction, or adapt the previous proof: if all rectangles have the same direction, it is not possible (one row contains 2 rectangles, so only one rectangle can intersect the first column, leaving room for a vertical domino in the first column). Otherwise, we can assume there are at most 2 vertical dominos. The proof for $n \geqslant 3$ shows that there are two consecutive free columns, so at least 4 horizontal dominos, so only one vertical. Moreover, the columns without a vertical domino are consecutive, so we can assume the vertical domino is in column 1. It must be in the middle of the column to avoid leaving space, and it is then easy to see that it is impossible to "plug all the holes" with 4 horizontal dominos.
Finally, the following configuration works with $k=6$:
|
2n+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \in \mathbb{N}^{*}$. On place des rectangles $1 \times n$ et $n \times 1$ sur un échiquier $2 n \times 2 n$, de telle manière que deux rectangles ne s'intersectent jamais et que chaque rectangle recouvre exactement n cases. Un ensemble de tels rectangles est dit saturé s'il est impossible d'ajouter un rectangle sans intersecter un rectangle déjà en place.
Trouver le plus petit $k$ tel qu'il existe un ensemble saturé de $k$ rectangles.
|
Commençons par le cas $n \geqslant 3$ : la réponse est $k=2 n+1$. L'ensemble suivant (dans le cas $\mathrm{n}=5$, la construction se généralisant facilement) convient :

Il reste à montrer qu'avec 2 n rectangles il est toujours possible d'en ajouter un qui ne les intersecte pas. Si les 2 n rectangles sont orientés dans le même sens, par exemple tous horizontaux, alors il doit y en avoir exactement un sur chaque ligne (sinon il y aurait une ligne vide), et il ne peut pas être tout au bout de la ligne (s'il était tout à gauche, on pourrait ajouter un rectangle à sa droite). Par conséquent, la première et la dernière colonne sont vides, et il est possible d'ajouter un rectangle vertical.
S'il y a des rectangles dans les deux sens, on peut supposer qu'il y a au plus n rectangles verticaux. Supposons que la configuration soit saturée. Soit $1 \leqslant k \leqslant n$ tel que la colonne $k$ contient un rectangle vertical noté $r$. En décalant $r$ d'une case vers la gauche, on doit intersecter un rectangle déjà en place, noté $r^{\prime}$ (sinon on pourrait ajouter un rectangle). Cependant, si $r^{\prime}$ était horizontal, il devrait intersecter $r$ car il n'y a pas assez de place pour un rectangle horizontal à gauche de $r$. Le rectangle $r^{\prime}$ est donc vertical, donc la colonne $k-1$ contient un rectangle vertical et de même pour les colonnes $k-2, \ldots, 2,1$.
De même, si $\mathrm{n}+1 \leqslant \mathrm{k} \leqslant 2 \mathrm{n}$ est tel que la colonne k contient un rectangle vertical, alors toutes les colonnes à sa droite contiennent un rectangle vertical. L'ensemble des colonnes ne contenant pas de rectangle vertical est donc un ensemble d'au moins n colonnes consécutives. Il y a donc un rectangle $\mathrm{n} \times 2 \mathrm{n}$ qui ne rencontre aucun des rectangles verticaux. Si la configuration est saturée, il faut donc 2 n rectangles horizontaux pour "bloquer" chaque ligne dans ce rectangle $\mathrm{n} \times 2 \mathrm{n}$. Comme on a supposé qu'il y avait au moins un rectangle vertical, il y a donc au moins $2 \mathrm{n}+1$ rectangles, ce qui est absurde.
Passons aux cas $n=1$ et $n=2$ : le cas $n=1$ est trivial et la réponse est 4 (il faut tout couvrir, sinon on pourrait ajouter un carré 1 . Pour $n=2$, il n'y a pas d'ensemble saturé de 5 rectangles.
Pour le montrer, on peut soit effectuer une disjonction de cas un peu fastidieuse, soit adapter la preuve précédente : si tous les rectangles ont la même direction, ce n'est pas possible (une seule ligne contient 2 rectangles donc un seul rectangle peut intersecter la première colonne donc il reste la place pour un domino vertical dans la première colonne). Sinon, on peut supposer qu'il y a au plus 2 dominos verticaux. La preuve pour $n \geqslant 3$ montre qu'il y a deux colonnes consécutives libres, donc au moins 4 dominos horizontaux, donc un seul vertical. De plus, les colonnes sans domino vertical sont consécutives donc on peut supposer que le domino vertical est dans la colonne 1. Il doit être au milieu de la colonne pour ne pas laisser une place, et il est alors facile de voir qu'il est impossible de "boucher tous les trous" avec 4 dominos horizontaux.
Enfin, la configuration suivante marche avec $\mathrm{k}=6$ :

|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
56704cbd-a784-5be0-8be5-40c76c93af08
| 607,637
|
Determine all natural numbers \( a \) for which there exist prime numbers \(\mathbf{p}, \mathbf{q}, \mathrm{r}\), not necessarily distinct, such that
\[
a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}
\]
|
First, if $p=q=r$, then we get $\mathrm{a}=6$, which is indeed a solution. Let's show that this is the only solution, and suppose there exists a solution $a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}$ with $p, q, r$ being primes and not all equal.
- If two of the numbers $p, q, r$ are equal, say $p=q \neq r$, then:
$$
\mathrm{a}=2\left(\frac{\mathrm{p}}{\mathrm{r}}+\frac{\mathrm{r}}{\mathrm{p}}\right)+2=\frac{2\left(\mathrm{p}^{2}+\mathrm{r}^{2}\right)}{\mathrm{pr}}+2
$$
Thus, $\frac{2\left(\mathfrak{p}^{2}+r^{2}\right)}{p r}$ is an integer. We deduce that the prime number $p$ divides $2 r^{2}$ while being coprime with $r$, and therefore that $p=2$. The same reasoning applies to show that $r=2$, which contradicts that $r \neq p$. Therefore, there is no solution in this case.
- If $p, q, r$ are pairwise distinct, then, without loss of generality, we can assume that $p>q>r$ (noting that then $p$ and $q$ are odd), and then
$$
\operatorname{apqr}=\mathrm{pq}(\mathrm{p}+\mathrm{q})+\mathrm{qr}(\mathbf{q}+\mathrm{r})+\mathrm{rp}(\mathrm{r}+\mathrm{p})
$$
Thus, $p$ divides $q r(q+r)$. Since $p$ is coprime with $q r$, it must divide $q+r$. But $0<q+r<2 p$ so $p=q+r$. This implies that $r$ is even, and therefore that $r=2$. We then have $p=q+2$ and $a=(q+1)+1+\frac{q+4}{q}=q+3+\frac{4}{q}$. In particular, $\frac{4}{q}$ must be an integer, which is impossible for $\mathrm{q}>1$ odd. Thus, there is no solution in this case, which concludes.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\mathbf{p}, \mathbf{q}, \mathrm{r}$, pas forcément distincts, tels que
$$
a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}
$$
|
Tout d'abord, si $p=q=r$, alors on obtient $\mathrm{a}=6$, qui est bien une solution. Montrons qu'il s'agit de la seule solution, et supposons qu'il existe une solution $a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}$ avec $p, q, r$ premiers et non tous égaux.
- Si deux des nombres $p, q, r$ sont égaux, disons $p=q \neq r$, alors:
$$
\mathrm{a}=2\left(\frac{\mathrm{p}}{\mathrm{r}}+\frac{\mathrm{r}}{\mathrm{p}}\right)+2=\frac{2\left(\mathrm{p}^{2}+\mathrm{r}^{2}\right)}{\mathrm{pr}}+2
$$
Ainsi, $\frac{2\left(\mathfrak{p}^{2}+r^{2}\right)}{p r}$ est un entier. On en déduit que le nombre premier $p$ divise $2 r^{2}$ tout en étant premier avec $r$, et donc que $p=2$. Le raisonnement $s^{\prime}$ adapte mot pour mot pour prouver que $r=2$, ce qui contredit que $r \neq p$. Il n'y a donc pas de solution dans ce cas.
- Si $p, q, r$ sont deux à deux distincts alors, sans perte de généralité, on peut supposer que $p>q>$ $r$ (on note qu'alors $p$ et $q$ sont impairs), et alors
$$
\operatorname{apqr}=\mathrm{pq}(\mathrm{p}+\mathrm{q})+\mathrm{qr}(\mathbf{q}+\mathrm{r})+\mathrm{rp}(\mathrm{r}+\mathrm{p})
$$
Ainsi, $p$ divise $q r(q+r)$. Puisque $p$ est premier avec $q r$, il divise donc $q+r$. Mais $0<q+r<2 p$ donc $p=q+r$. Cela implique que $r$ est pair, et donc que $r=2$. On a alors $p=q+2$ et $a=(q+1)+1+\frac{q+4}{q}=q+3+\frac{4}{q}$. En particulier, $\frac{4}{q}$ soit être un entier, ce qui est impossible pour $\mathrm{q}>1$ impair. Il n'y a ainsi pas de solution dans ce cas, ce qui conclut.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
2f7abe22-5b5e-58c5-bd69-0cb41194da82
| 607,639
|
A finite and non-empty set E of strictly positive real numbers is said to be powerful when, for all $a, b \in E$ distinct, at least one of the numbers $a^{b}$ and $b^{a}$ also belongs to E. Determine the maximum number of elements that a powerful set can contain.
|
First, the set
$$
\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{16}\right\}
$$
is a powerful set containing four elements. Let $S$ be a powerful set, and $n$ its cardinality: we will show that $\mathrm{n} \leqslant 4$.
First, let's prove the following lemma: there do not exist elements $a$ and $b$ in $S$ such that $\mathrm{a}<1<\mathrm{b}$. Indeed, if we had $a<1<b$, then $a^{b}<a<1<b^{a}<b$; by taking $a=\min S$ and $b=\min \{s \in S: 1<s\}$, we would ensure that neither $a^{b}$ nor $b^{a}$ belongs to $S$, contradicting the fact that $S$ is powerful.
On the other hand, if $S$ is a powerful set, then $S \cup\{1\}$ is also powerful. Our search for a powerful set of maximum cardinality leads us to consider two cases.
1. If $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, with $n \geqslant 5$ and $1=a_{1}<a_{2}<\cdots<a_{n}$, then we observe that
$$
a_{n}<a_{n}^{a_{2}}<a_{n}^{a_{3}}<\ldots<a_{n}^{a_{n-1}}
$$
thus, $S$ contains the elements
$$
a_{2}<a_{2}^{a_{n}}<a_{3}^{a_{n}}<\ldots<a_{n-1}^{a_{n}} .
$$
This shows that $a_{i+1}=a_{i}^{a_{n}}$ for all $i \in\{2, \ldots, \mathfrak{n}-1\}$. However, we note that
$$
\mathrm{a}_{2}<\mathrm{a}_{2}^{\mathrm{a}_{3}}<\mathrm{a}_{2}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{3}<\mathrm{a}_{3}^{\mathrm{a}_{2}}<\mathrm{a}_{3}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{4}
$$
which shows that neither $a_{2}^{a_{3}}$ nor $a_{3}^{a_{2}}$ belongs to $S$, which therefore cannot be powerful.
2. If $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, with $n \geqslant 5$ and $a_{1}<a_{2}<\cdots<a_{n}=1$, then we observe that
$$
a_{n-1}<a_{n-1}^{a_{n-2}}<a_{n-1}^{a_{n-3}}<\ldots<a_{n-1}^{a_{1}}<a_{n}
$$
thus, $S$ contains the elements
$$
a_{1}<a_{1}^{a_{n-1}}<a_{2}^{a_{n-1}}<\ldots<a_{n-2}^{a_{n-1}}<a_{n}=1
$$
This shows that $a_{i+1}=a_{i}^{a_{n-1}}$ for all $i \in\{1, \ldots, n-2\}$. Similarly, we observe that
$$
a_{n-1}=a_{n-2}^{a_{n-1}}<a_{n-2}^{a_{n-3}}<\ldots<a_{n-2}^{a_{1}}<a_{n}=1
$$
thus, $S$ contains the elements
$$
a_{2}=a_{1}^{a_{n-1}}<a_{1}^{a_{n-2}}<a_{2}^{a_{n-2}}<\ldots<a_{n-3}^{a_{n-2}}<a_{n}=1 .
$$
This also shows that $a_{i+2}=a_{i}^{a_{n-2}}=a_{i}^{a_{n-1}^{2}}$ for all $i \in\{1, \ldots, n-3\}$.
We deduce that $a_{n-1}=a_{n-2}^{a_{n-1}}=a_{n-1}^{2 a_{n-1}}$ and then that $1=2 a_{n-1}$, so $a_{n-i}=2^{-2^{i}}$ for $i \in\{1, \ldots, n-1\}$. However, since $n \geqslant 5$, then $a_{n-4}^{a_{n-3}}=2^{-2^{-4}}$ and $a_{n-3}^{a_{n-4}}=2^{-2^{-13}}$, so $S$ does not contain either $a_{n-4}^{a_{n-3}}$ or $a_{n-3}^{a_{n-4}}$ and cannot be powerful.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Un ensemble E fini et non vide de réels strictement positifs est dit puissant lorsque, pour tous $a, b \in E$ distincts, l'un au moins des nombres $a^{b}$ et $b^{a}$ appartient aussi à $E$. Déterminer le nombre maximal d'éléments que peut contenir un ensemble puissant.
|
Tout d'abord, l'ensemble
$$
\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{16}\right\}
$$
est un ensemble puissant qui contient quatre éléments. Soit S un ensemble puissant, et n son cardinal : nous allons montrer que $\mathrm{n} \leqslant 4$.
Démontrons d'abord le lemme suivant : il n'existe pas d'éléments a et b de $S$ tels que $\mathrm{a}<1<\mathrm{b}$. En effet, si l'on avait $a<1<b$, alors $a^{b}<a<1<b^{a}<b$; en prenant $a=\min S$ et $b=\min \{s \in S: 1<s\}$, on s'assurerait donc que ni $a^{b}$ ni $b^{a}$ n'appartient à $S$, contredisant le fait que $S$ est puissant.
D'autre part, si $S$ est un ensemble puissant, alors $S \cup\{1\}$ l'est aussi. Notre recherche d'un ensemble puissant de cardinal maximal nous amène donc à considérer deux cas.
1. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $1=a_{1}<a_{2}<\cdots<a_{n}$, alors on observe que
$$
a_{n}<a_{n}^{a_{2}}<a_{n}^{a_{3}}<\ldots<a_{n}^{a_{n-1}}
$$
donc que $S$ contient les éléments
$$
a_{2}<a_{2}^{a_{n}}<a_{3}^{a_{n}}<\ldots<a_{n-1}^{a_{n}} .
$$
Cela montre que $a_{i+1}=a_{i}^{a_{n}}$ pour tout $i \in\{2, \ldots, \mathfrak{n}-1\}$. On remarque cependant que
$$
\mathrm{a}_{2}<\mathrm{a}_{2}^{\mathrm{a}_{3}}<\mathrm{a}_{2}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{3}<\mathrm{a}_{3}^{\mathrm{a}_{2}}<\mathrm{a}_{3}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{4}
$$
ce qui montre que ni $a_{2}^{a_{3}} n i a_{3}^{a_{2}} n$ 'appartient à $S$, qui ne peut donc pas être puissant.
2. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $a_{1}<a_{2}<\cdots<a_{n}=1$, alors on observe que
$$
a_{n-1}<a_{n-1}^{a_{n-2}}<a_{n-1}^{a_{n-3}}<\ldots<a_{n-1}^{a_{1}}<a_{n}
$$
donc que $S$ contient les éléments
$$
a_{1}<a_{1}^{a_{n-1}}<a_{2}^{a_{n-1}}<\ldots<a_{n-2}^{a_{n-1}}<a_{n}=1
$$
Cela montre que $a_{i+1}=a_{i}^{a_{n-1}}$ pour tout $i \in\{1, \ldots, n-2\}$. De même, on observe que
$$
a_{n-1}=a_{n-2}^{a_{n-1}}<a_{n-2}^{a_{n-3}}<\ldots<a_{n-2}^{a_{1}}<a_{n}=1
$$
donc que $S$ contient les éléments
$$
a_{2}=a_{1}^{a_{n-1}}<a_{1}^{a_{n-2}}<a_{2}^{a_{n-2}}<\ldots<a_{n-3}^{a_{n-2}}<a_{n}=1 .
$$
Cela montre aussi que $a_{i+2}=a_{i}^{a_{n-2}}=a_{i}^{a_{n-1}^{2}}$ pour tout $i \in\{1, \ldots, n-3\}$.
On en déduit que $a_{n-1}=a_{n-2}^{a_{n-1}}=a_{n-1}^{2 a_{n-1}}$ puis que $1=2 a_{n-1}$, donc que $a_{n-i}=2^{-2^{i}}$ pour $i \in\{1, \ldots, n-1\}$. Cependant, puisque $n \geqslant 5$, alors $a_{n-4}^{a_{n-3}}=2^{-2^{-4}}$ et $a_{n-3}^{a_{n-4}}=2^{-2^{-13}}$, donc $S$ ne contient ni $a_{n-4}^{a_{n-3}}$ et $a_{n-3}^{a_{n-4}}$ et ne peut pas être puissant.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
bcb35558-b104-52ec-aa09-b01c7f4d940b
| 607,646
|
We define a sequence as follows:
$$
\left\{\begin{array}{l}
u_{0}=15, u_{1}=57 \\
u_{n}=u_{n-1}+u_{n-2} \text { for all } n \geq 2
\end{array}\right.
$$
Find the largest integer $k$ such that $3^{k} \mid u_{2017}$.
|
Let $k$ be the integer sought. The first terms of the sequence are 15, 57, 72, 129, 201, 330, 541,... apparently all divisible by 3. Indeed, $u_{0}$ and $u_{1}$ are multiples of 3, so $u_{2}=u_{0}+u_{1}$ is also. Similarly, $u_{3}$ is divisible by 3. More generally, if $u_{n-1}$ and $u_{n-2}$ are multiples of 3, then $u_{n}$ is as well. Thus, we prove step by step (by induction, in fact) that for all integers $n$, $u_{n}$ is divisible by 3, so $3 \mid u_{2017}$ and $k \geq 1$.
Now let's reason modulo 9 to see if $k \geq 2$. We find:
$u_{0} \equiv 6(\bmod 9)$
$u_{1} \equiv 3(\bmod 9)$
$u_{2} \equiv 0(\bmod 9)$
$u_{3} \equiv 3(\bmod 9)$
$u_{4} \equiv 3(\bmod 9)$
$u_{5} \equiv 6(\bmod 9)$
$u_{6} \equiv 0(\bmod 9)$
$u_{7} \equiv 6(\bmod 9)$
$u_{8} \equiv 6(\bmod 9)$
$u_{9} \equiv 3(\bmod 9)$
We observe that $u_{8} \equiv u_{0}(\bmod 9)$ and $u_{9} \equiv u_{1}(\bmod 9)$, so $u_{10} \equiv u_{2}(\bmod 9)$, since the modulos add up. More generally, we establish as before that $u_{n+8} \equiv u_{n}(\bmod 9)$ for all $n \in \mathbb{N}$. Thus, the sequence $\left(u_{n}(\bmod 9)\right)$ is periodic with period 8. Since $2017=252 \times 8+1$, we have $u_{2017} \equiv u_{1} \equiv 3(\bmod 9)$. Therefore, $k<2$. Conclusion: $k=1$.
Remark. If $l$ is any natural number, then the sequence $\left(v_{n}\right)$ defined by $v_{n}=u_{n}(\bmod l)$ is periodic from a certain rank. Indeed, there are $l \times l=l^{2}$ possibilities for the pair $\left(v_{n}, v_{n+1}\right)$. Therefore, if we look at $\left(v_{0}, v_{1}\right),\left(v_{1}, v_{2}\right), \cdots,\left(v_{l^{2}}, v_{l^{2}+1}\right)$, this makes $l^{2}+1$ pairs. According to the pigeonhole principle (i.e., if we put $c+1$ socks into $c$ drawers, one drawer will contain at least 2 socks), two pairs are equal, so there exist $0 \leqslant i<j \leqslant l^{2}$ such that $\left(v_{i}, v_{i+1}\right)=$ $\left(v_{j}, v_{j+1}\right)$. In other words, $u_{i} \equiv u_{j}(\bmod l)$ and $u_{i+1} \equiv u_{j+1}(\bmod l)$. Therefore, $u_{i+2} \equiv u_{j+2}(\bmod l)$, or $\left(v_{i+1}, v_{i+2}\right)=\left(v_{j+1}, v_{j+2}\right)$. We deduce similarly that $v_{i+3}=v_{j+3}, v_{i+4}=v_{j+4}$, etc. Thus, $\left(v_{n}\right)$ is periodic from rank $i$ (at the latest), with period $i-j$.
However, it may have a smaller period (exercise: show that the minimal period divides $i-j$).
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On définit une suite ainsi:
$$
\left\{\begin{array}{l}
u_{0}=15, u_{1}=57 \\
u_{n}=u_{n-1}+u_{n-2} \text { pour tout } n \geq 2
\end{array}\right.
$$
Trouver le plus grand entier $k$ tel que $3^{k} \mid u_{2017}$.
|
Soit $k$ l'entier cherché. Les premiers termes de la suite sont 15, 57, 72, 129, 201, 330, 541,... apparemment tous divisibles par 3 . En effet, $u_{0}$ et $u_{1}$ sont multiples de 3 , donc $u_{2}=u_{0}+u_{1}$ aussi. De même, $u_{3}$ est divisible par 3. Plus généralement, si $u_{n-1}$ et $u_{n-2}$ sont multiples de 3, alors $u_{n}$ aussi. On prouve ainsi de proche en proche (par récurrence, en fait) que pour tout entier $n$, $u_{n}$ est divisible par 3, donc $3 \mid u_{2017}$ et $k \geq 1$.
Raisonnons maintenant modulo 9 pour voir si $k \geq 2$. On trouve :
$u_{0} \equiv 6(\bmod 9)$
$u_{1} \equiv 3(\bmod 9)$
$u_{2} \equiv 0(\bmod 9)$
$u_{3} \equiv 3(\bmod 9)$
$u_{4} \equiv 3(\bmod 9)$
$u_{5} \equiv 6(\bmod 9)$
$u_{6} \equiv 0(\bmod 9)$
$u_{7} \equiv 6(\bmod 9)$
$u_{8} \equiv 6(\bmod 9)$
$u_{9} \equiv 3(\bmod 9)$
On constate que $u_{8} \equiv u_{0}(\bmod 9)$ et $u_{9} \equiv u_{1}(\bmod 9)$, donc $u_{10} \equiv u_{2}(\bmod 9)$, car les modulos s'additionnent. Plus généralement, on établit comme précédemment que $u_{n+8} \equiv u_{n}(\bmod 9)$ pour tout $n \in \mathbb{N}$. Ainsi, la suite $\left(u_{n}(\bmod 9)\right)$ est périodique de période 8 . Or $2017=252 \times 8+1$, donc $u_{2017} \equiv u_{1} \equiv 3(\bmod 9)$. Donc $k<2$. Conclusion : $k=1$.
Remarque. Si $l$ est un entier naturel quelconque, alors la suite $\left(v_{n}\right)$ définie par $v_{n}=u_{n}(\bmod l)$ est périodique artir d'un certain rang. En effet, il y a $l \times l=l^{2}$ possibilités pour le couple $\left(v_{n}, v_{n+1}\right)$. Donc, si on regarde $\left(v_{0}, v_{1}\right),\left(v_{1}, v_{2}\right), \cdots,\left(v_{l^{2}}, v_{l^{2}+1}\right)$, cela fait $l^{2}+1$ couples. D'après le principe des tiroirs (ie si on range $c+1$ chaussettes dans $c$ tiroirs, un tiroir contiendra au moins 2 chaussettes), deux couples sont égaux, il existe donc $0 \leqslant i<j \leqslant l^{2}$ tels que $\left(v_{i}, v_{i+1}\right)=$ $\left(v_{j}, v_{j+1}\right)$. Autrement dit, $u_{i} \equiv u_{j}(\bmod l)$ et $u_{i+1} \equiv u_{j+1}(\bmod l)$. Donc $u_{i+2} \equiv u_{j+2}(\bmod l)$, soit $\left(v_{i+1}, v_{i+2}\right)=\left(v_{j+1}, v_{j+2}\right)$. On en déduit de même que $v_{i+3}=v_{j+3}, v_{i+4}=v_{j+4}$, etc. Ainsi, $\left(v_{n}\right)$ est périodique artir du rang $i$ (au plus tard), de période $i-j$.
Elle peut toutefois avoir une période plus petite (exercice : montrer que la période minimale divise $i-j$ ).
|
{
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
6efff13c-320a-5872-9d7b-44ef2fc4c4ae
| 607,647
|
Determine the minimum value of
$$
\left\lfloor\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{~d}}\right\rfloor+\left\lfloor\frac{\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{a}}\right\rfloor+\left\lfloor\frac{\mathrm{c}+\mathrm{d}+\mathrm{a}}{\mathrm{~b}}\right\rfloor+\left\lfloor\frac{\mathrm{d}+\mathrm{a}+\mathrm{b}}{\mathrm{c}}\right\rfloor
$$
when $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ range over $\mathbb{N}^{*}$.
|
The minimum sought is 9.
Indeed, if a, b, c, d are non-zero natural numbers, we define
$$
f(a, b, c, d)=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor .
$$
We recall that for any real number $x$, we have $\lfloor x\rfloor>x-1$. Thus, for all integers $a, b, c, d>0$, we have
$$
\begin{aligned}
f(a, b, c, d)+4 & >\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c} \\
& >\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right) \\
& >6 \times 2 \text{ since } t+\frac{1}{t} \geqslant 2 \text{ for all real } t>0 .
\end{aligned}
$$
Thus, $f(a, b, c, d)>8$. Since $f(a, b, c, d)$ is clearly an integer, it follows that $f(a, b, c, d) \geqslant$ 9. It remains to verify that $f(5,5,5,4)=9$ to conclude.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer la valeur minimale de
$$
\left\lfloor\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{~d}}\right\rfloor+\left\lfloor\frac{\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{a}}\right\rfloor+\left\lfloor\frac{\mathrm{c}+\mathrm{d}+\mathrm{a}}{\mathrm{~b}}\right\rfloor+\left\lfloor\frac{\mathrm{d}+\mathrm{a}+\mathrm{b}}{\mathrm{c}}\right\rfloor
$$
lorsque $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ décrivent $\mathbb{N}^{*}$.
|
Le minimum cherché est 9.
En effet, si a, b, c, d sont des entiers naturels non nuls, on pose
$$
f(a, b, c, d)=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor .
$$
On rappelle que, pour tout réel $x$, on a $\lfloor x\rfloor>x-1$. Ainsi, pour tous entiers $a, b, c, d>0$, on a
$$
\begin{aligned}
f(a, b, c, d)+4 & >\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c} \\
& >\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right) \\
& >6 \times 2 \text { car } t+\frac{1}{t} \geqslant 2 \text { pour tout réel } t>0 .
\end{aligned}
$$
Ainsi, $f(a, b, c, d)>8$. Or, $f(a, b, c, d)$ étant clairement un entier, $c^{\prime}$ est donc que $f(a, b, c, d) \geqslant$ 9. Il reste à vérifier que $f(5,5,5,4)=9$ pour conclure.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"problem_match": "## Exercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
a110a2cf-52e5-5799-95e8-514ccde3204c
| 607,655
|
How many $3 \times 3$ tables can be constructed by filling them with the numbers from 1 to 3 such that no number appears twice in the same row or column? And how many $4 \times 4$ tables with the numbers from 1 to 4?
|
We present below a complete proof of the exercise. It was not necessary to be so precise to get all the points, but it is good, when counting objects, to have an idea of the proof to show that we have not forgotten anything or counted anything twice.
We have six ways to fill the first row (three ways to place the 1, then two to place the 2, and one way to place the 3). Then, we have two ways to fill the column already containing a 1 (which makes twelve in total). We end up with, for example, the table
$$
\left[\begin{array}{lll}
2 & 1 & 3 \\
& 2 & A \\
& 3 &
\end{array}\right] .
$$
We realize that there is only one way to fill the cell $A$, that is, the one in the row containing a 2 and the column containing a 3. Then we complete the table in the only possible way.
Therefore, there are twelve ways to fill a $3 \times 3$ table as described in the statement.
For $4 \times 4$ tables, it is roughly the same idea. We have twenty-four ways to fill the first row and six ways to fill the column containing a 1. We obtain a table similar to
$$
\left[\begin{array}{cccc}
2 & 1 & 4 & 3 \\
& 4 & & \\
A_{3,2} & 3 & & \\
& 2 & &
\end{array}\right] .
$$
Now, let $A_{k, l}, k, l \in\{2,3,4\}$, be the cell in the row containing $k$ and the column containing $l$. We see that there are two possibilities for filling $A_{3,2}$:
- if we fill $A_{3,2}$ with 1, we will have only one possibility for $A_{4,2}$, and then, in order, $A_{2,2}, A_{3,4}, A_{3,3}, A_{4,4}, A_{4,3}, A_{2,4}$, and $A_{2,3}$. We obtain the unique table
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & 1 & 2 \\
1 & 3 & 2 & 4 \\
4 & 2 & 3 & 1
\end{array}\right]
$$
- if we fill $A_{3,2}$ with 4, we have two possibilities again:
* we fill $A_{4,2}$ with 1 and then fill the other cells in the only possible way.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
1 & 4 & 3 & 2 \\
4 & 3 & 2 & 1 \\
3 & 2 & 1 & 4
\end{array}\right] .
$$
* we fill $A_{4,2}$ with 3 and then fill $A_{2,2}, A_{2,4}$, and $A_{2,3}$ in the only possible way. There remain two ways to fill the obtained table.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & & \\
4 & 3 & & \\
1 & 2 & 3 & 4
\end{array}\right] .
$$
Note that all the statements are always true, not just in the example. Therefore, no matter how we fill the first row and the column containing a 1, there are always four ways to fill the table. There are thus $24 \cdot 6 \cdot 4=576$ ways to fill a $4 \times 4$ table according to the statement.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Combien de tableaux $3 \times 3$ peut-on construire en les remplissant avec les nombres de 1 à 3 tels qu'il n'y ait pas deux fois le même nombre dans une ligne ni dans une colonne. Et de tableaux $4 \times 4$ avec les nombres de 1 à 4 ?
|
Nous présentons ci-dessous une preuve complète de l'exercice. Il n'était pas nécessaire d'être aussi précis pour avoir tous les points mais il est bon, lorsque que l'on compte des objets, d'avoir une idée de la preuve pour démontrer que nous n'avons rien oublié ni compté en double.
Nous avons six façons de remplir la première rangée (trois façons de placer le 1 puis deux de placer le 2 puis une seule possibilité pour placer le 3). Ensuite, il nous reste deux façons de remplir la colonne contenant déjà un 1 (ce qui fait douze en tout). On se retrouve avec, par exemple, le tableau
$$
\left[\begin{array}{lll}
2 & 1 & 3 \\
& 2 & A \\
& 3 &
\end{array}\right] .
$$
On se rend compte qu'il n'y a qu'une seule façon de remplir la case $A$, c'est-à-dire celle qui est dans la rangée contenant un 2 et dans la colonne contenant un 3 . Puis on complète le tableau de la seule manière possible.
On a donc douze façons de remplir un tableau $3 \times 3$ comme dans l'énoncé.
Pour les tableaux $4 \times 4$, c'est à peu près la même idée. Nous avons vingt-quatre façons de remplir la première rangée et six façons de remplir la colonne contenant un 1 . Nous obtenons un tableau ressemblant à
$$
\left[\begin{array}{cccc}
2 & 1 & 4 & 3 \\
& 4 & & \\
A_{3,2} & 3 & & \\
& 2 & &
\end{array}\right] .
$$
Maintenant, notons $A_{k, l}, k, l \in\{2,3,4\}$, la case dans la rangée contenant $k$ et la colonne contenant l. Nous voyons qu'il y a deux possibilités pour remplir $A_{3,2}$ :
- si l'on remplit $A_{3,2}$ avec 1 , nous n'aurons plus qu'une seule possibilité pour $A_{4,2}$ puis, dans l'ordre, $A_{2,2}, A_{3,4}, A_{3,3}, A_{4,4}, A_{4,3}, A_{2,4}$ et $A_{2,3}$. On obtient l'unique tableau
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & 1 & 2 \\
1 & 3 & 2 & 4 \\
4 & 2 & 3 & 1
\end{array}\right]
$$
- si l'on remplit $A_{3,2}$ avec 4 nous avons de nouveau deux possibilités:
* on remplit $A_{4,2}$ avec 1 puis on remplit les autres cases de la seule façon possible.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
1 & 4 & 3 & 2 \\
4 & 3 & 2 & 1 \\
3 & 2 & 1 & 4
\end{array}\right] .
$$
* on remplit $A_{4,2}$ avec 3 puis on remplit $A_{2,2}, A_{2,4}$ et $A_{2,3}$ de la seule façon possible. Il reste deux façons de remplir le tableau obtenu.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & & \\
4 & 3 & & \\
1 & 2 & 3 & 4
\end{array}\right] .
$$
Remarque que toutes les affirmations sont toujours vraies, pas seulement dans l'exemple. Donc, quelque soit la façon de remplir la première rangée et la colonne contenant un 1, il reste toujours quatre façons de remplir le tableau. Il y a donc en tout $24 \cdot 6 \cdot 4=576$ façons de remplir un tableau $4 \times 4$ selon l'énoncé.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"problem_match": "## Exercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
5eb53561-e24a-549f-a7e1-a73f8f87cd83
| 607,676
|
A cell can divide into 42 or 44 smaller cells. How many divisions are needed to obtain exactly 2017 cells from one cell?
|
A division increases the number of cells by 41 or 43. Let $a$ be the number of divisions into 42 cells, and $b$ the number of divisions into 44 cells. We want to find $a+b$, given that
$$
2017=1+41 a+43 b=1+41(a+b)+2 b=1+43(a+b)-2 b
$$
We see that $41(a+b) \leq 2016$, so $a+b<50$.
Similarly, $43(a+b) \geq 2016$, so $a+b>46$.
Now, $2017=1+41 \times 49+7=1+41 \times 48+48=1+41 \times 47+89$. Since $2 b$ is even, the only solution is $a+b=48$ (with $2 b=48$ thus $a=b=24$).
|
48
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une cellule peut se diviser en 42 ou en 44 petites cellules. Combien de divisions faut-il pour obtenir, à partir d'une cellule, exactement 2017 cellules?
|
Une division augmente de 41 ou 43 le nombre de cellules. Soit $a$ le nombre de divisions en 42 cellules, et $b$ le nombre de divisions en 44 cellules. On veut trouver $a+b$, sachant que
$$
2017=1+41 a+43 b=1+41(a+b)+2 b=1+43(a+b)-2 b
$$
On voit que $41(a+b) \leq 2016$, donc $a+b<50$.
De même, $43(a+b) \geq 2016$, donc $a+b>46$.
Or $2017=1+41 \times 49+7=1+41 \times 48+48=1+41 \times 47+89$. Comme $2 b$ est pair, la seule solution est $a+b=48$ (avec $2 b=48$ donc $a=b=24$ ).
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi1-corrige.jsonl",
"problem_match": "\nExercice 1",
"solution_match": "\nSolution "
}
|
d5bc0377-bd01-55a2-bf61-80e9b052e2d5
| 607,691
|
We place the integers from 1 to 9 in each of the cells of a $3 \times 3$ grid. For $i=1$, 2 and 3, we denote $\ell_{i}$ as the largest integer present in the $i^{\text {th }}$ row and $c_{i}$ as the smallest integer present in the $i^{\text {th }}$ column.
How many grids are there such that $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\}=\max \left\{\mathbf{c}_{1}, \mathbf{c}_{2}, \mathbf{c}_{3}\right\}=4$?
|
Let $G$ be any grid, and let $i$ and $j$ be the integers such that the integer 4 is located at the $i^{\text{th}}$ row and the $j^{\text{th}}$ column. We say that the grid $G$ is good if $\ell_{i} = c_{j} = 4$.
First, $\operatorname{simin}\left\{\ell_{1}, \ell_{2}, \ell_{3}\right\} = \max \left\{c_{1}, c_{2}, c_{3}\right\} = 4$, then $4 = \ell_{i} = c_{j}$, so $G$ is a good grid. Conversely, if $G$ is a good grid, then for any integer $j'$, the column $j'$ contains one of the integers from the row $i$. This integer is therefore at most 4, which shows that $c_{j'} \leq 4$. Similarly, for any integer $i'$, we have $\ell_{i'} \geq 4$. Therefore, we have $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\} = \max \left\{c_{1}, c_{2}, c_{3}\right\} = 4$.
Consequently, we are actually trying to count how many good grids there are. To construct a good grid, it suffices to choose successively:
$\triangleright$ the integers $i$ and $j$, i.e., the position of the 4: there are 9 possible choices;
$\triangleright$ each of the two other integers that are on the row $i$. Since $\ell_{i} = 4$, these two integers must be smaller than 4, so they must be chosen from $\{1,2,3\}$. There are 3 ways to choose the first (say the leftmost), and 2 ways to choose the second;
$\triangleright$ each of the two other integers that are on the column $j$. Since $c_{j} = 4$, the two other integers must be greater than 4, so they must be chosen from $\{5,6,7,8,9\}$. There are 5 ways to choose the first, and 4 ways to choose the second;
$\triangleright$ each of the four remaining integers to be placed: there are 4! ways to proceed.
Therefore, there are $9 \times 3 \times 2 \times 5 \times 4 \times 4! = 25920$ grids such that $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\} = \max \left\{c_{1}, c_{2}, c_{3}\right\} = 4$.
Remark: In general, regardless of the size of the grid, the smallest of the integers $\ell_{i}$ is necessarily equal to the largest of the integers $c_{i}$. This is known as the Minimax Theorem. More information on this topic is available at:
en.wikipedia.org/wiki/Minimax_theorem
|
25920
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On place les entiers de 1 à 9 dans chacune des cases d'une grille $3 \times 3$. Pour $i=1$, 2 et 3 , on note $\ell_{i}$ le plus grand entier présent dans la $i^{\text {ème }}$ ligne et $c_{i}$ le plus petit entier présent dans la $i^{\text {ème }}$ colonne.
Combien existe-t-il de grilles telles que $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\}=\max \left\{\mathbf{c}_{1}, \mathbf{c}_{2}, \mathbf{c}_{3}\right\}=4$ ?
|
Soit $G$ une grille quelconque, et soit $i$ et $j$ les entiers tels que l'entier 4 se trouve sur la ${ }^{\text {ème }}$ ligne et la $j^{\text {ème }}$ colonne. On dit que la grille $G$ est bonne si $\ell_{i}=\mathrm{c}_{j}=4$.
Tout d'abord, $\operatorname{simin}\left\{\ell_{1}, \ell_{2}, \ell_{3}\right\}=\max \left\{\mathbf{c}_{1}, \mathrm{c}_{2}, \mathrm{c}_{3}\right\}=4$, alors $4=\ell_{i}=\mathrm{c}_{\mathrm{j}}$, donc G est une bonne grille. Réciproquement, si $G$ est une bonne grille, alors, pour tout entier $j^{\prime}$, la colonne $j^{\prime}$ comporte un des entiers de la ligne $i$. Cet entier vaut donc au plus 4 , ce qui montre que $c_{j^{\prime}} \leqslant 4$. De même, pour tout entier $i^{\prime}$, on a $\ell_{i^{\prime}} \geqslant 4$. On a donc bien $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\}=\max \left\{\mathrm{c}_{1}, \mathrm{c}_{2}, \mathrm{c}_{3}\right\}=4$.
Par conséquent, on cherche en fait à compter combien il existe de bonnes grilles. Pour construire une bonne grille, il suffit de choisir successivement :
$\triangleright$ les entiers $i$ et j, c'est-à-dire l'emplacement du 4 : on a 9 choix possibles;
$\triangleright$ chacun des deux autres entiers qui se trouvent sur la ligne $i$. Comme $l_{i}=4$, ces deux entiers doivent être plus petits que 4 , donc être choisis dans $\{1,2,3\}$. On a 3 manières de choisir le premier (disons le plus à gauche), puis 2 manières de choisir le second;
$\triangleright$ chacun des deux autres entiers qui se trouvent sur la colonne $j$. Comme $c_{j}=4$, les deux autres entiers doivent être plus grands que 4 , donc être choisis dans $\{5,6,7,8,9\}$. On a 5 manières de choisir le premier, puis 4 manières de choisir le second;
$\triangleright$ chacun des quatre autres entiers qui restent à placer : on a 4 ! manières de procéder.
Il existe donc $9 \times 3 \times 2 \times 5 \times 4 \times 4!=25920$ grilles telles que $\min \left\{\ell_{1}, \ell_{2}, \ell_{3}\right\}=\max \left\{\mathbf{c}_{1}, \mathrm{c}_{2}, \mathrm{c}_{3}\right\}=4$.
Remarque : De manière générale, quelle que soit la taille de la grille, le plus petit des entiers $\ell_{i}$ est nécessairement égal au plus grand des entiers $c_{i}$. C'est ce que l'on appelle Théorème du minimax. Plus d'informations à ce propos sont disponibles sur :
fr.wikipedia.org/wiki/Théorème_du_minimax_de_von_Neumann
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
7b0baa74-3682-58ed-8739-1bf179d296d4
| 607,717
|
Let G be an infinite directed graph, where every vertex has finite degree. We assume that, for each vertex $s$, the in-degree of $s$ is strictly less than the out-degree of $s$. Let $v$ be a vertex of G. For any integer $n \geqslant 1$, we denote $V_{n}$ as the number of vertices that can be reached from $v$ by passing through at most n edges, including $v$.
What is the smallest possible value of $\mathrm{V}_{\mathrm{n}}$?
|
For any integer $n \geqslant 0$, we denote by $E_{n}$ the set of vertices reached by passing through $n$ edges of $G$ or fewer, and by $F_{n}$ the set $E_{n} \backslash E_{n-1}$, i.e., the set of vertices reached by passing through $n$ edges of $G$ at a minimum. Furthermore, we denote by $a_{n}$ the number of edges $(x, y)$ such that $x, y \in E_{n}$, and by $b_{n}$ the number of edges $(x, y)$ such that $x \in E_{n}$ and $y \notin E_{n}$. Note that these are exactly the edges $(x, y)$ such that $x \in F_{n}$ and $y \in F_{n+1}$.
By construction, we know that $a_{n}$ is less than or equal to the sum of the in-degrees of the vertices in $E_{n}$, while $a_{n}+b_{n}$ is equal to the sum of the out-degrees of the vertices in $E_{n}$. Consequently, we have $a_{n}+b_{n} \geqslant a_{n}+\left|E_{n}\right|$, so $b_{n} \geqslant\left|E_{n}\right|$. The pigeonhole principle then indicates that at least one of the vertices in $F_{n}$ has an out-degree of $b_{n} /\left|F_{n}\right|$ or more, so $\left|\mathrm{F}_{\mathrm{n}+1}\right| \geqslant \mathrm{b}_{\mathrm{n}} /\left|\mathrm{F}_{\mathrm{n}}\right| \geqslant\left|\mathrm{E}_{\mathrm{n}}\right| /\left|\mathrm{F}_{\mathrm{n}}\right|$. This shows in particular that
$$
\left|E_{n+2}\right|=\left|E_{n+1}\right|+\left|F_{n+2}\right| \geqslant\left|E_{n+1}\right|+\left|E_{n+1}\right| /\left|F_{n+1}\right|=\left|E_{n}\right|+\left|F_{n+1}\right|+\left(\left|E_{n}\right|+\left|F_{n+1}\right|\right) /\left|F_{n+1}\right| .
$$
The arithmetic-geometric mean inequality shows that $\left|\mathrm{F}_{\mathrm{n}+1}\right|+\left|\mathrm{E}_{\boldsymbol{n}}\right| /\left|\mathrm{F}_{\mathrm{n}+1}\right| \geqslant 2 \sqrt{\mid \mathrm{E}_{\mathbf{n}}} \mid$, from which we deduce that $\left|E_{n+2}\right| \geqslant\left|E_{n}\right|+2 \sqrt{\left|E_{n}\right|}+1$.
We note that $\mathrm{E}_{0}=\mathrm{F}_{0}=\{v\}$, so $\left|\mathrm{E}_{0}\right|=\left|\mathrm{F}_{0}\right|=1$, and thus $\left|\mathrm{E}_{1}\right|=\left|\mathrm{E}_{0}\right|+\left|\mathrm{F}_{1}\right| \geqslant$ $1+\left|\mathrm{E}_{0}\right| /\left|\mathrm{F}_{0}\right|=2$. We then prove by induction on $n$ that $\left|\mathrm{E}_{2 n}\right| \geqslant(n+1)^{2}$ and that $\left|\mathrm{E}_{2 n+1}\right| \geqslant$ $(n+1)(n+2)$. First, this is true for $n=0$. Moreover, if these two equalities are true for an integer $n \geqslant 0$, then:
$$
\begin{aligned}
& \triangleright\left|E_{2 n+2}\right| \geqslant\left|E_{2 n}\right|+2 \sqrt{\left|E_{2 n}\right|}+1 \geqslant(n+1)^{2}+2(n+1)+1=(n+2)^{2} ; \\
& \triangleright\left|E_{2 n+3}\right| \geqslant\left|E_{2 n+1}\right|+2 \sqrt{\left|E_{2 n+1}\right|}+1>(n+1)(n+2)+2(n+1)+1=(n+2)(n+3)-1, \\
& \quad \text { so }\left|E_{2 n+3}\right| \geqslant(n+2)(n+3) .
\end{aligned}
$$
This concludes our induction.
Conversely, suppose that the vertices of the graph $G$ are the pairs $(a, b)$ such that $0 \leqslant$ $2 b \leqslant a$, and that the edges are the pairs $\left((a, b),\left(a+1, b^{\prime}\right)\right)$. Then each vertex $(a, b)$ has an in-degree of $\lceil a / 2\rceil$ and an out-degree of $\lceil a / 2\rceil+1$. Moreover, if $v$ is the vertex $(0,0)$, then $E_{n}$ is the set of vertices $(a, b)$ such that $a \leqslant n$, which shows that $\left|E_{2 n}\right|=\sum_{k=0}^{n-1} 2(k+1)+$ $(n+1)=(n+1)^{2}$ and that $\left|E_{2 n+1}\right|=\left|E_{2 n}\right|+(n+1)=(n+1)(n+2)$.
Consequently, we can assert that the smallest possible value of $V_{n}=\left|E_{n}\right|$ is $(n+2)^{2} / 4$ if $n$ is even, or $(n+1)(n+3) / 4$ if $n$ is odd, i.e., $\left\lfloor(n+2)^{2} / 4\right\rfloor$ in all cases.
|
\left\lfloor(n+2)^{2} / 4\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit G un graphe orienté infini, dont tout sommet est de degré fini. On suppose que, pour chaque sommet $s$, le degré entrant de $s$ est strictement inférieur au degré sortant de s. Soit $v$ un sommet de G. Pour tout entier $n \geqslant 1$, on note $V_{n}$ le nombre de sommets que l'on peut atteindre à partir de $v$ en passant par au plus n arêtes, $v$ compris.
Quelle est la plus petite valeur possible de $\mathrm{V}_{\mathrm{n}}$ ?
|
Pour tout entier $n \geqslant 0$, on note $E_{n}$ l'ensemble des sommets atteints en passant par $n$ arêtes de $G$ ou moins, et $F_{n}$ l'ensemble $E_{n} \backslash E_{n-1}$, c'est-à-dire l'ensemble des sommets atteints en passant par $n$ arêtes de $G$ au minimum. En outre, on note $a_{n}$ le nombre d'arêtes $(x, y)$ telles que $x, y \in E_{n}$, et $b_{n}$ le nombre d'arêtes $(x, y)$ telles que $x \in E_{n}$ et $y \notin E_{n}$. Remarquons qu'il s'agit exactement des arêtes $(x, y)$ telles que $x \in F_{n}$ et $y \in F_{n+1}$.
Par construction, on sait que $a_{n}$ est inférieur ou égal à la somme des degrés entrants des sommets de $E_{n}$, tandis que $a_{n}+b_{n}$ est égal à la somme des degrés sortants des sommets de $E_{n}$. Par conséquent, on a $a_{n}+b_{n} \geqslant a_{n}+\left|E_{n}\right|$, donc $b_{n} \geqslant\left|E_{n}\right|$. Le principe des tiroirs indique alors que l'un des sommets de $F_{n}$ au moins est de degré sortant $b_{n} /\left|F_{n}\right|$ ou plus, donc que $\left|\mathrm{F}_{\mathrm{n}+1}\right| \geqslant \mathrm{b}_{\mathrm{n}} /\left|\mathrm{F}_{\mathrm{n}}\right| \geqslant\left|\mathrm{E}_{\mathrm{n}}\right| /\left|\mathrm{F}_{\mathrm{n}}\right|$. Cela montre en particulier que
$$
\left|E_{n+2}\right|=\left|E_{n+1}\right|+\left|F_{n+2}\right| \geqslant\left|E_{n+1}\right|+\left|E_{n+1}\right| /\left|F_{n+1}\right|=\left|E_{n}\right|+\left|F_{n+1}\right|+\left(\left|E_{n}\right|+\left|F_{n+1}\right|\right) /\left|F_{n+1}\right| .
$$
L'inégalité arithmético-géométrique montre que $\left|\mathrm{F}_{\mathrm{n}+1}\right|+\left|\mathrm{E}_{\boldsymbol{n}}\right| /\left|\mathrm{F}_{\mathrm{n}+1}\right| \geqslant 2 \sqrt{\mid \mathrm{E}_{\mathbf{n}}} \mid$, d'où l'on déduit en fait que $\left|E_{n+2}\right| \geqslant\left|E_{n}\right|+2 \sqrt{\left|E_{n}\right|}+1$.
On remarque alors que $\mathrm{E}_{0}=\mathrm{F}_{0}=\{v\}$, donc que $\left|\mathrm{E}_{0}\right|=\left|\mathrm{F}_{0}\right|=1$, et donc que $\left|\mathrm{E}_{1}\right|=\left|\mathrm{E}_{0}\right|+\left|\mathrm{F}_{1}\right| \geqslant$ $1+\left|\mathrm{E}_{0}\right| /\left|\mathrm{F}_{0}\right|=2$. On montre alors par récurrence sur $n$ que $\left|\mathrm{E}_{2 n}\right| \geqslant(n+1)^{2}$ et que $\left|\mathrm{E}_{2 n+1}\right| \geqslant$ $(n+1)(n+2)$. Tout d'abord, c'est vrai pour $n=0$. Par ailleurs, si ces deux égalités sont vraies pour un entier $n \geqslant 0$, alors:
$$
\begin{aligned}
& \triangleright\left|E_{2 n+2}\right| \geqslant\left|E_{2 n}\right|+2 \sqrt{\left|E_{2 n}\right|}+1 \geqslant(n+1)^{2}+2(n+1)+1=(n+2)^{2} ; \\
& \triangleright\left|E_{2 n+3}\right| \geqslant\left|E_{2 n+1}\right|+2 \sqrt{\left|E_{2 n+1}\right|}+1>(n+1)(n+2)+2(n+1)+1=(n+2)(n+3)-1, \\
& \quad \text { donc }\left|E_{2 n+3}\right| \geqslant(n+2)(n+3) .
\end{aligned}
$$
Ceci conclut notre récurrence.
Réciproquement, supposons que les sommets du graphe $G$ sont les paires $(a, b)$ telles que $0 \leqslant$ $2 b \leqslant a$, et dont les arêtes sont les paires $\left((a, b),\left(a+1, b^{\prime}\right)\right)$. Alors chaque sommet $(a, b)$ est de degré entrant $\lceil a / 2\rceil$ et de degré sortant $\lceil a / 2\rceil+1$. Par ailleurs, si $v$ est le sommet $(0,0)$, alors $E_{n}$ est l'ensemble des sommets $(a, b)$ tels que $a \leqslant n$, ce qui montre que $\left|E_{2 n}\right|=\sum_{k=0}^{n-1} 2(k+1)+$ $(n+1)=(n+1)^{2}$ et que $\left|E_{2 n+1}\right|=\left|E_{2 n}\right|+(n+1)=(n+1)(n+2)$.
Par conséquent, on peut affimer que la plus petite valeur possible de $V_{n}=\left|E_{n}\right|$ est $(n+2)^{2} / 4$ si $n$ est pair, ou bien $(n+1)(n+3) / 4$ si $n$ est impair, c'est-à-dire $\left\lfloor(n+2)^{2} / 4\right\rfloor$ dans tous les cas.

|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
ce5d8365-b2cb-5fa6-949c-ecc54c390cec
| 607,722
|
Patricia placed 2018 points in the plane, such that the distances between any two points are all distinct. She then colors each of her 2018 points, making sure that for each point $P$, the points $Q$ and $R$ placed closest and farthest from $P$ are the same color as $P$.
How many colors, at most, could Patricia have used?
|
We will show that Patricia could have used a maximum of 504 colors. First, as soon as a color is used to color a vertex $v$, it is also used to color the closest and farthest vertices from $v$, i.e., at least 3 vertices.
Now suppose that at least two colors have been used to color only 3 vertices each. We call these vertices $A_{1}, A_{2}, A_{3}$ and $B_{1}, B_{2}, B_{3}$, respectively. Without loss of generality, we assume that $A_{1} A_{2} < A_{2} A_{3} < A_{3} A_{1}$ and that $B_{1} B_{2} < B_{2} B_{3} < B_{3} B_{1}$. Then $A_{2}$ is the vertex closest to $A_{3}$ and $B_{3}$ is the vertex farthest from $B_{2}$, so $A_{2} A_{3} < B_{2} A_{3} < B_{2} B_{3}$. We would similarly show that $B_{2} B_{3} < A_{2} A_{3}$, leading to a contradiction. Therefore, our assumption was false, and at most one color has been used to color only 3 vertices.
If Patricia used $k$ colors, she has therefore colored at least $4k - 1$ vertices. This shows that $4k - 1 \leq 2018$, hence
$$
k \leq \left\lfloor \frac{2018 + 1}{4} \right\rfloor = 504.
$$
Conversely, here is a possible construction for 14 instead of 2018. We detail the construction for 2018 below.
Patricia constructs a regular 1008-gon. She numbers its vertices clockwise from $A_{1}$ to $A_{1008}$, then slightly moves them so that the distances between points $A_{i}$ are all distinct: such perturbations can be chosen to be arbitrarily small. Next, near each point $A_{i}$, and still ensuring that the distances between points are all distinct, she places a point $B_{i}$. Finally, she places two points $C_{1}$ and $C_{2}$ near $A_{1}$ and $A_{2}$.
Then, for each vertex $X_{i}$, where $X \in \{A, B, C\}$, the closest vertex is one of the other vertices $X_{i}$, and the farthest vertex is one of the vertices $X_{504+i}$ (if $1 \leq i \leq 504$) or $X_{i-504}$ (if $505 \leq i \leq 1008$). Patricia thus uses colors numbered from 1 to 504, and paints the vertices $X_{k}$ and $X_{k+504}$ with color $k$. The first sentence of the paragraph shows that this coloring respects the conditions of the problem, and Patricia has therefore indeed used 504 colors, which concludes the exercise.
Remark: As in Exercise 2, the argument used to show that at most 504 colors were available makes use of the minimax theorem: the largest of the minimal distances from a point to the other points is equal to the smallest of the maximal distances from a point to the other points. Here, this result was applied to the points $A_{2}, A_{3}, B_{2}$, and $B_{3}$.
|
504
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Patricia a placé 2018 points dans le plan, de sorte que les distances entre 2 points quelconques soient deux à deux distinctes. Elle colorie alors chacun de ses 2018 points, en faisant attention à ce que ; pour chaque point $P$, les points $Q$ et $R$ placés le plus près et le plus loin de $P$ sont de la même couleur que $P$.
Combien de couleurs, au plus, Patricia a-t-elle pu utiliser?
|
On va montrer que Patricia a pu utiliser un maximum de 504 couleurs. Tout d'abord, dès qu'une couleur sert à colorier un sommet $v$, elle sert aussi à colorier les sommets le plus proche et le plus éloigné de $v$, c'est-à-dire 3 sommets au moins.
Supposons maintenant que deux couleurs, au moins, n'ont servi à colorier que 3 sommets chacune. On appelle ces sommets respectivement $A_{1}, A_{2}, A_{3}$ et $B_{1}, B_{2}, B_{3}$. Sans perte de généralité, on suppose que $A_{1} A_{2}<A_{2} A_{3}<A_{3} A_{1}$ et que $B_{1} B_{2}<B_{2} B_{3}<B_{3} B_{1}$. Alors $A_{2}$ est le sommet le plus proche de $A_{3}$ et $B_{3}$ est le sommet le plus éloigné de $B_{2}$, donc $A_{2} A_{3}<B_{2} A_{3}<B_{2} B_{3}$. On montrerait de même que $B_{2} B_{3}<A_{2} A_{3}$, aboutissant à une contradiction. Notre supposition était donc fausse, et au plus une couleur n'a servi à colorier que 3 sommets.
Si Patricia a utilisé $k$ couleurs, elle a donc colorié au moins $4 k-1$ sommets. Cela montre que $4 \mathrm{k}-1 \leqslant 2018$, donc que
$$
k \leqslant\left\lfloor\frac{2018+1}{4}\right\rfloor=504 .
$$
Réciproquement, voici une figure d'une construction possible pour 14 au lieu de 2018. Nous détaillons ci-dessous la construction pour 2018.

Patricia construit un 1008-gone régulier. Elle numérote ses sommets dans le sens des aiguilles d'une montre, de $A_{1}$ à $A_{1008}$, puis elle les bouge très légèrement, de manière à ce que les distances entre points $A_{i}$ soient deux à deux distinctes: de telles perturbations peuvent être choisies de manière à être arbitrairement petites. Ensuite, à proximité immédiate de chaque point $A_{i}$, et toujours en faisant en sorte que les distances entre points soient deux à deux distinctes, elle place un point $B_{i}$. Enfin, elle place à proximité de $A_{1}$ et de $A_{2}$ deux points $C_{1}$ et $C_{2}$.
Alors, pour chaque sommet $X_{i}$, où $X \in\{A, B, C\}$, le sommet le plus proche est l'un des autres sommets $X_{i}$, et le sommet le plus éloigné est l'un des sommets $X_{504+i}$ (si $1 \leqslant i \leqslant 504$ ) ou $X_{i-504}$ (si $505 \leqslant \mathfrak{i} \leqslant 1008$ ). Patricia utilise donc des couleurs numérotées de 1 à 504 , et peint de la couleur $k$ les sommets $X_{k}$ et $X_{k+504}$. La première phrase du paragraphe montre que ce coloriage respecte bien les conditions de l'énoncé, et Patricia a donc bien pu utliser 504 couleurs, ce qui conclut l'exercice.
Remarque: Comme à l'exercice 2, l'argument utilisé pour montrer que 504 couleurs au plus étaient disponibles fait appel au théorème du minimax : la plus grande des distances minimales d'un point aux autres points est égale à la plus petite des distances maximales d'un point aux autres points. Ici, on a utilisé ce résultat sur les points $A_{2}, A_{3}, B_{2}$ et $B_{3}$.
|
{
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi4-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
5e0b1fbe-0b57-5e2b-b133-c218c83edd02
| 607,723
|
Is it possible to arrange 601 disks of radius 1 in a rectangular box of size $4 \times 600$ without any two disks overlapping (they can, however, touch each other)?
|
The answer is yes! To show this, we consider the triangular arrangement in the figure below.
Let's calculate $d$. We denote $\left(x_{A}, y_{A}\right)$ as the coordinates of the center of disk $A$, and so on. We have directly
$$
x_{A}=1, \quad x_{B}=2, \quad x_{C}=3, \quad \text { and } \quad y_{A}=1, \quad y_{B}=?, \quad y_{C}=1
$$
To determine $y_{B}$, we write that $\left(x_{A}-x_{B}\right)^{2}+\left(y_{A}-y_{B}\right)^{2}=4$, from which $y_{B}=1+\sqrt{3}$. Next, we determine the position of the center of disk $D$. We know that $y_{D}=3$, and then we must have $\left(x_{D}-x_{B}\right)^{2}+\left(y_{D}-y_{B}\right)^{2}=4$, from which $x_{D}=2+\sqrt{4 \sqrt{3}-3}$. We find that the coordinates of the center of $E$ are
$$
x_{E}=x_{D}+1=3+\sqrt{4 \sqrt{3}-3} \quad \text { and } \quad y_{E}=4-y_{B}=3-\sqrt{3}
$$
We verify that disks $E$ and $C$ are tangent, as $\left(x_{E}-x_{C}\right)^{2}+\left(y_{E}-y_{C}\right)^{2}=4$. Therefore, our figure is valid (no overlaps). In the end, we find $\mathrm{d}=\mathrm{x}_{\mathrm{E}}+1=4+\sqrt{4 \sqrt{3}-3}$.
We can then repeat our arrangement starting from the abscissa $d$. In other words, we can fit 6 disks in an interval of length $d$, and thus $6 k$ disks in an interval of length $d k$. By taking $k=100$, we find that we can fit 600 disks in an interval of length $100 \mathrm{~d} \approx 596.4$. There is still plenty of room to fit the last disk in the bottom right corner.
|
601
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Est-il possible de ranger 601 disques de rayon 1 dans une boîte rectangulaire de taille $4 \times 600$ sans que deux disques ne se chevauchent (ils peuvent toutefois se toucher)?
|
La réponse est oui! Pour le montrer, on considère la disposition en triangle sur la figure ci-dessous.
Calculons $d$. On note $\left(x_{A}, y_{A}\right)$ les coordonnées du centre du disque $A$, et ainsi de suite. On a donc directement
$$
x_{A}=1, \quad x_{B}=2, \quad x_{C}=3, \quad \text { et } \quad y_{A}=1, \quad y_{B}=?, \quad y_{C}=1
$$
Pour déterminer $y_{B}$, on écrit que $\left(x_{A}-x_{B}\right)^{2}+\left(y_{A}-y_{B}\right)^{2}=4$, d'où $y_{B}=1+\sqrt{3}$. On détermine ensuite la position du centre du disque $D$. On sait que $y_{D}=3$, puis on doit avoir $\left(x_{D}-x_{B}\right)^{2}+\left(y_{D}-y_{B}\right)^{2}=4$, d'où $x_{D}=2+\sqrt{4 \sqrt{3}-3}$. On obtient que les coordonnées du centre de $E$ sont
$$
x_{E}=x_{D}+1=3+\sqrt{4 \sqrt{3}-3} \quad \text { et } \quad y_{E}=4-y_{B}=3-\sqrt{3}
$$

On vérifie que les disques $E$ et $C$ sont tangents, car $\left(x_{E}-x_{C}\right)^{2}+\left(y_{E}-y_{C}\right)^{2}=4$. Donc notre figure est valide (pas de recouvrements). Au final, on trouve $\mathrm{d}=\mathrm{x}_{\mathrm{E}}+1=4+\sqrt{4 \sqrt{3}-3}$.
On peut alors recommencer notre disposition à partir de l'abscisse d. Autrement dit, on peut mettre 6 disques dans un intervalle $d$, et donc $6 k$ disques dans un intervalle $d k$. En prenant $k=100$, on trouve qu'on peut mettre 600 disques dans un intervalle de taille $100 \mathrm{~d} \approx 596.4$. Il reste donc plein de place pour mettre le dernier disque dans le coin en bas à droite.
|
{
"resource_path": "French/segmented/envois/fr-pofm_2017-2018-envoi5-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
a55f79cf-3d01-5f27-82ae-529714890c38
| 607,728
|
In the plane, we are given 2011 distinct points, each colored either blue or red.
(i) We assume that for every blue point, the disk centered at this point with radius 1 contains exactly two red points. What is the maximum number of blue points possible?
(ii) We assume that for every blue point, the circle centered at this point with radius 1 contains exactly two red points. What is the maximum number of blue points possible?
|
(i) If there is a blue point, there must be at least two red points, so there cannot be more than 2009 blue points.
Conversely, if we consider 2009 disks of radius 1 having a common interior that is non-empty, it suffices to mark two red points in this common part and to mark the centers of these 2009 disks in blue to obtain a configuration with 2009 blue points that satisfies the conditions of the statement.
The maximum sought is therefore 2009.
(ii) Consider a configuration of $r$ red points and $b$ blue points satisfying the conditions of the statement, with $r+b=2011$. As above, we have $r \geq 2$.
If $R_{1}$ and $R_{2}$ are two distinct red points, we denote by $n\left(R_{1}, R_{2}\right)$ the number of blue points that are centers of circles of radius 1 passing through $R_{1}$ and $R_{2}$.
Since every circle of radius 1 centered at a blue point passes through exactly two red points, this ensures that:
- every blue point is counted at least once in some $n\left(R_{1}, R_{2}\right)$,
- if $\left\{R_{1}, R_{2}\right\}$ and $\left\{R_{1}^{\prime}, R_{2}^{\prime}\right\}$ are two distinct pairs of red points, then the blue points counted in $n\left(R_{1}, R_{2}\right)$ are distinct from the blue points counted in $n\left(R_{1}^{\prime}, R_{2}^{\prime}\right)$.
Thus, each blue point is counted exactly once in some $n\left(R_{1}, R_{2}\right)$. Summing over the pairs of red points, we get
$$
\sum_{\left\{R_{1}, R_{2}\right\}} n\left(R_{1}, R_{2}\right)=b
$$
On the other hand, for any pair of points in the plane, there are at most two circles of radius 1 that pass through these two points, so we have $n\left(R_{1}, R_{2}\right) \leq 2$ for any pair $R_{1}, R_{2}$ of red points. Since there are $r(r-1) / 2$ pairs of red points, we then have:
$$
b=\sum_{\left\{R_{1}, R_{2}\right\}} n\left(R_{1}, R_{2}\right) \leq \sum_{\left\{R_{1}, R_{2}\right\}} 2=r(r-1),
$$
and thus $r(r-1) \geq 2011-r$, or equivalently $r^{2} \geq 2011$. It is easy to deduce that $r \geq 45$, and therefore that $b \leq 1966$.
Conversely, consider 45 red points, all located on the same segment of length 1. Any two of these red points always belong to two circles of radius 1. We draw only 1966 of these circles (we could draw $1980=45 \times 44$), and we mark in blue the centers of these circles. It is easy to verify that we thus obtain a configuration of 2011 colored points that satisfies the conditions of the statement.
The maximum sought is therefore 1966.
|
2009
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Dans le plan on se donne 2011 points deux à deux distincts colorés soit en bleu, soit en rouge.
(i) On suppose que pour tout point bleu le disque de centre ce point et de rayon 1 contienne exactement deux points rouges. Quel est le plus grand nombre possible de points bleus?
(ii) On suppose que pour tout point bleu le cercle de centre ce point et de rayon 1 contienne exactement deux points rouges. Quel est le plus grand nombre possible de points bleus?
|
(i) S'il existe un point bleu, il doit exister au moins deux points rouges donc il ne peut y avoir plus de 2009 points bleus.
Réciproquement, si l'on considère 2009 disques de rayon 1 ayant un intérieur commun à tous qui soit non vide, il suffit de marquer deux points rouges dans cette partie commune et de marquer en bleu les centres de ces 2009 disques pour obtenir une configuration à 2009 points bleus qui vérifie les conditions de l'énoncé.
Le maximum cherché est donc 2009.
(ii) Considérons une configuration de $r$ points rouges et $b$ points bleus vérifiant les conditions de l'énoncé, avec $r+b=2011$. Comme ci-dessus, on a $r \geq 2$.
Si $R_{1}$ et $R_{2}$ sont deux points rouges distincts, on note $n\left(R_{1}, R_{2}\right)$ le nombre de points bleus qui sont centres de cercles de rayon 1 passant par $R_{1}$ et $R_{2}$.
Puisque tout cercle de rayon 1 et centré en un point bleu passe par exactement deux points rouges, cela assure que:
- tout point bleu est compté au moins une fois dans un certain $n\left(R_{1}, R_{2}\right)$,
- si $\left\{R_{1}, R_{2}\right\}$ et $\left\{R_{1}^{\prime}, R_{2}^{\prime}\right\}$ sont deux paires distinctes de points rouges, alors les points bleus comptés dans $n\left(R_{1}, R_{2}\right)$ sont deux à deux distincts des points bleus comptés dans $n\left(R_{1}^{\prime}, R_{2}^{\prime}\right)$.
Ainsi, chaque point bleu est compté une et une seule fois dans un certain $n\left(R_{1}, R_{2}\right)$. En sommant sur les paires de points rouges, il vient
$$
\sum_{\left\{R_{1}, R_{2}\right\}} n\left(R_{1}, R_{2}\right)=b
$$
D'autre part, pour toute paire de points du plan, il n'existe qu'au plus deux cercles de rayon 1 qui passent par ces deux points, on a donc $n\left(R_{1}, R_{2}\right) \leq 2$ pour toute paire $R_{1}, R_{2}$ de points rouges. Comme il y a $r(r-1) / 2$ paires de points rouges, on a alors :
$$
b=\sum_{\left\{R_{1}, R_{2}\right\}} n\left(R_{1}, R_{2}\right) \leq \sum_{\left\{R_{1}, R_{2}\right\}} 2=r(r-1),
$$
et donc $r(r-1) \geq 2011-r$, ou encore $r^{2} \geq 2011$. On en déduit facilement que $r \geq 45$, et donc que $b \leq 1966$.
Réciproquement, considérons 45 points rouges, tous situés sur un même segment de longueur 1. Deux quelconques de ces points rouges appartiennent alors toujours à deux cercles de rayon 1. On trace seulement 1966 de ces cercles (on pourrait en tracer $1980=$ $45 \times 44$ ), et on marque en bleu les centres de ces cercles. Il est facile de vérifier que l'on obtient ainsi une configuration à 2011 points colorés qui vérifie les conditions de l'énoncé.
Le maximum cherché est donc 1966.
|
{
"resource_path": "French/segmented/tests/fr-2011-2012-ofm-2011-2012-test-janvier-corrige.jsonl",
"problem_match": "## Exercice 1\n",
"solution_match": "## Solution."
}
|
dac21aa8-ee0c-56a5-a7f3-e9fa72c11f7e
| 606,289
|
Find the largest integer $\mathrm{n} \geqslant 3$, satisfying:
"for all integers $k \in\{2,3, \cdots, \mathfrak{n}\}$ if $k$ and $\boldsymbol{n}$ are coprime then $k$ is a prime number."
|
First, we notice that $\mathrm{n}=30$ satisfies the property. Indeed, if $\mathrm{k}>1$ is coprime with $n$, then it is coprime with $2,3,5$. If, in addition, $k$ is not prime, then it admits a non-trivial factorization $\mathrm{k}=\mathrm{lm}$ with $\ell, \mathrm{m}>1$. Since $\ell$, $m$ are coprime with $n$, they are coprime with $2,3,5$, so $\ell$, $\mathrm{m} \geqslant 7$, which implies that $k \geqslant 7 \times 7=49>n$.
Conversely, let's show that if $n$ satisfies the property, then $n \leqslant 30$. Suppose, for the sake of contradiction, that $n>30$. Let $p$ be the smallest prime number that does not divide $n$. Since $p^{2} n$ is not prime but is coprime with $n$, we have $p^{2}>n>30>5^{2}$, so $p \geqslant 7$. In particular, 2, 3, and 5 divide $n$, so 30 divides $n$. Since $\mathrm{n}>30$, we deduce that $\mathrm{p}^{2}>\mathrm{n} \geqslant 60>7^{2}$, so $\mathrm{p}>7$, hence $\mathrm{p} \geqslant 11$.
Let $p_{1}<p_{2}<p_{3}<\cdots$ be the list of prime numbers ($p_{1}=2$, $p_{2}=3$, etc.). The above shows that $p=p_{k+1}$ where $k \geqslant 4$. Moreover, $p_{1}, \ldots, p_{k}$ divide $n$, so $p_{k+1}^{2}>n \geqslant p_{1} \cdots p_{k}$, which contradicts Bonse's inequality.
Remark: if one does not know Bonse's inequality, it can be easily derived from Bertrand's postulate, which states that $\boldsymbol{p}_{j+1}<2 p_{j}$ for all $\boldsymbol{j}$. Indeed,
$$
\mathrm{p}_{\mathrm{k}+1}^{2}<4 \mathrm{p}_{\mathrm{k}}^{2}<8 \mathrm{p}_{\mathrm{k}-1} \mathrm{p}_{\mathrm{k}}<2 \times 3 \times 5 \times \mathrm{p}_{\mathrm{k}-1} \mathrm{p}_{\mathrm{k}} \leqslant \mathrm{p}_{1} \mathrm{p}_{2} \cdots \mathrm{p}_{\mathrm{k}}
$$
if $k \geqslant 5$. Moreover, if $k=4$, we can verify directly that $p_{k+1}^{2}=121<210=2 \times 3 \times 5 \times 7=p_{1} \cdots p_{k}$.
Remark: there is an elementary proof of Bonse's inequality that does not use Bertrand's postulate. First, we verify by hand that if $4 \leqslant n \leqslant 7$ then $p_{1} p_{2} \cdots p_{n}>p_{n+1}^{2}$.
Suppose, for the sake of contradiction, that there exists $n \geqslant 8$ such that $p_{1} p_{2} \cdots p_{n} \leqslant p_{n+1}^{2}$. Let $m=\left[\frac{n}{2}\right]$. We have
$$
\left(p_{1} p_{2} \cdots p_{m}\right)^{2}<p_{1} p_{2} \cdots p_{n} \leqslant p_{n+1}^{2}
$$
so $\mathrm{p}_{1} \mathrm{p}_{2} \cdots \mathrm{p}_{\mathrm{m}}<\mathrm{p}_{\mathrm{n}+1}$.
Consider the integers $N_{j}=j p_{1} p_{2} \cdots p_{m-1}-1\left(1 \leqslant j \leqslant p_{m}\right)$. For all $j$, we have $N_{j}<p_{1} p_{2} \cdots p_{m}<$ $p_{n+1}$ and $N_{j}$ is coprime with $p_{1}, p_{2}, \ldots, p_{m-1}$. Therefore, if $q_{j}$ is the smallest prime number dividing $N_{j}$, we have $p_{m} \leqslant q_{j} \leqslant p_{n}$.
The $q_{j}$ are distinct because if $j<\ell$ and $q_{j}=q_{\ell}$, then $q_{j}$ divides $N_{\ell}-N_{j}=(\ell-j) p_{1} p_{2} \cdots p_{m}$, so $q_{j}$ divides $\ell-\mathfrak{j}$, which is impossible since $1 \leqslant \ell-\mathfrak{j}<p_{m} \leqslant q_{j}$.
Therefore, there are at least $p_{m}$ distinct prime numbers between $p_{m}$ and $p_{n}$: in other words, $p_{m} \leqslant n-m+1$. Since $n \leqslant 2 m+1$, we have $p_{m} \leqslant m+2$.
Since $p_{m} \geqslant 2 m-1$ for all $m \geqslant 1$, this implies $2 m-1 \leqslant m+2$, so $m \leqslant 3$, and thus $n \leqslant 7$.

|
30
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver le plus grand entier $\mathrm{n} \geqslant 3$, vérifiant:
"pour tout entier $k \in\{2,3, \cdots, \mathfrak{n}\}$ si $k$ et $\boldsymbol{n}$ sont premiers entre eux alors $k$ est un nombre premier."
|
On remarque d'abord que $\mathrm{n}=30$ vérifie la propriété. En effet, si $\mathrm{k}>1$ est premier avec n , alors il est premier avec $2,3,5$. Si de plus k n'est pas premier, alors il admet une factorisation non triviale $\mathrm{k}=\mathrm{lm}$ avec $\ell, \mathrm{m}>1$. Comme $\ell$, m sont premiers avec n , ils sont premiers avec $2,3,5$, donc $\ell$, $\mathrm{m} \geqslant 7$, ce qui entraîne que $k \geqslant 7 \times 7=49>n$.
Réciproquement, montrons que si $n$ vérifie la propriété alors $n \leqslant 30$. Supposons par l'absurde que $n>30$. Soit $p$ le plus petit entier premier ne divisant pas $n$. Comme $p^{2} n$ 'est pas premier mais est premier avec $n$, on a $p^{2}>n>30>5^{2}$ donc $p \geqslant 7$. En particulier, 2,3 et 5 divisent $n$ donc 30 divise $n$. Comme $\mathrm{n}>30$, on en déduit que $\mathrm{p}^{2}>\mathrm{n} \geqslant 60>7^{2}$ donc $\mathrm{p}>7$, par conséquent $\mathrm{p} \geqslant 11$.
Notons $p_{1}<p_{2}<p_{3}<\cdots$ la liste des nombres premiers ( $p_{1}=2$, $p_{2}=3$, etc.). Ce qui précède montre que $p=p_{k+1}$ où $k \geqslant 4$. De plus, $p_{1}, \ldots, p_{k}$ divisent $n$ donc $p_{k+1}^{2}>n \geqslant p_{1} \cdots p_{k}$, ce qui contredit l'inégalité de Bonse.
Remarque: si on ne connaît pas l'inégalité de Bonse, on la retrouve facilement à partir du postulat de Bertrand qui dit que $\boldsymbol{p}_{j+1}<2 p_{j}$ pour tout $\boldsymbol{j}$. En effet,
$$
\mathrm{p}_{\mathrm{k}+1}^{2}<4 \mathrm{p}_{\mathrm{k}}^{2}<8 \mathrm{p}_{\mathrm{k}-1} \mathrm{p}_{\mathrm{k}}<2 \times 3 \times 5 \times \mathrm{p}_{\mathrm{k}-1} \mathrm{p}_{\mathrm{k}} \leqslant \mathrm{p}_{1} \mathrm{p}_{2} \cdots \mathrm{p}_{\mathrm{k}}
$$
si $k \geqslant 5$. De plus, si $k=4$ on vérifie directement que $p_{k+1}^{2}=121<210=2 \times 3 \times 5 \times 7=p_{1} \cdots p_{k}$.
Remarque : il existe une démonstration élémentaire de l'inégalité de Bonse n'utilisant pas le postulat de Bertrand. On vérifie d'abord à la main que si $4 \leqslant n \leqslant 7$ alors $p_{1} p_{2} \cdots p_{n}>p_{n+1}^{2}$.
Supposons par l'absurde qu'il existe $n \geqslant 8$ tel que $p_{1} p_{2} \cdots p_{n} \leqslant p_{n+1}^{2}$. Soit $m=\left[\frac{n}{2}\right]$. On a
$$
\left(p_{1} p_{2} \cdots p_{m}\right)^{2}<p_{1} p_{2} \cdots p_{n} \leqslant p_{n+1}^{2}
$$
donc $\mathrm{p}_{1} \mathrm{p}_{2} \cdots \mathrm{p}_{\mathrm{m}}<\mathrm{p}_{\mathrm{n}+1}$.
Considérons les entiers $N_{j}=j p_{1} p_{2} \cdots p_{m-1}-1\left(1 \leqslant j \leqslant p_{m}\right)$. Pour tout $j$, on a $N_{j}<p_{1} p_{2} \cdots p_{m}<$ $p_{n+1}$ et $N_{j}$ est premier avec $p_{1}, p_{2}, \ldots, p_{m-1}$. Donc si $q_{j}$ est le plus petit entier premier divisant $N_{j}$, on a $p_{m} \leqslant q_{j} \leqslant p_{n}$.
Les $q_{j}$ sont distincts car si $j<\ell$ et $q_{j}=q_{\ell}$, alors $q_{j}$ divise $N_{\ell}-N_{j}=(\ell-j) p_{1} p_{2} \cdots p_{m}$, donc $q_{j}$ divise $\ell-\mathfrak{j}$, ce qui est impossible puisque $1 \leqslant \ell-\mathfrak{j}<p_{m} \leqslant q_{j}$.
Par conséquent, il y a au moins $p_{m}$ nombres premiers distincts compris entre $p_{m}$ et $p_{n}$ : autrement dit, $p_{m} \leqslant n-m+1$. Or, $n \leqslant 2 m+1$ donc $p_{m} \leqslant m+2$.
Comme $p_{m} \geqslant 2 m-1$ pour tout $m \geqslant 1$, cela entraîne $2 m-1 \leqslant m+2$, donc $m \leqslant 3$, et donc $n \leqslant 7$.

|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution."
}
|
e4816d1e-b5b9-5fc0-9d49-6ed9fdae7504
| 604,366
|
In the plane, consider the set $S$ of points with coordinates $(x, y)$, where $x, y \in$ $\{1,2, \ldots, 2013\}$. Two points in $S$ are called neighbors if they are at a distance of 1 from each other. Every second, a fly and some spiders move on the points of $S$ as follows: first, the fly either stays still or moves to a neighboring point of the one it is on. Then, each spider either stays still or moves to a neighboring point of the one it is on. Several spiders can be on the same point at the same time, and the fly as well as the spiders know each other's positions.
a) Determine the smallest integer $k$ for which $k$ spiders can always catch the fly in a finite time, regardless of the initial positions of the fly and the spiders on the points of $S$.
b) Answer the same question if we assume this time that we are in the usual space and that $S$ is the set of points with coordinates $(x, y, z)$ where $x, y, z \in\{1,2, \ldots, 2013\}$.
|
A single spider cannot catch the fly: indeed, the fly can wait until the spider is at a neighboring point to where it is located. From that moment on, it moves to a diagonally opposite point to the one the spider is on if the spider is at a neighboring point, and otherwise stays where it is.
We will now prove that, in the plane as in space, two spiders are sufficient to catch the fly.
For this, we denote $M$ as the fly, and we designate by $P$ and $Q$ the two spiders. For each animal $A$, we respectively denote $A_{x}, A_{y}$, and $A_{z}$ its abscissa, ordinate, and height.
a) The spiders $P$ and $Q$ first position themselves at the point with coordinates $(1,1)$. Since $M$ cannot indefinitely escape to the right, $P$ can then, in a finite time and by moving only horizontally, position itself at a point such that $P_{x}=M_{x}$ and $P_{y}=1$. Similarly, $Q$ positions itself at a point such that $Q_{x}=1$ and $Q_{y}=M_{y}$ (it is clear that if, for example, $P$ reaches this first goal before $Q$, it can follow the movements of $M$ by maintaining $P_{x}=M_{x}$ and $P_{y}=1$ and wait for the appropriate positioning of $Q$).
From these positions, reached at time $t_{0}$:
- if $M$ moves horizontally (i.e., such that $M_{x}$ changes), then $P$ does the same to maintain $P_{x}=M_{x}$.
- otherwise, $P$ moves vertically, towards $M$.
The spider $Q$ proceeds in the same way, but by swapping the roles of the abscissas and ordinates.
Using this strategy and from $t_{0}$, the quantity $\left|P_{y}-M_{y}\right|+\left|Q_{x}-M_{x}\right|$ never increases. However, this quantity remains constant only during a move of $M$ to the right or upwards, which can only happen a finite number of times. Consequently, after a finite time, at least one of the two terms of the sum will be equal to 0, indicating the loss of the fly.
b) The two spiders first position themselves at the point $(1,1,1)$. Then, by staying in the plane $\pi$ with the equation $z=1$ and by using the strategy from a), one of them will catch the shadow of $M$ in $\pi$ (i.e., the orthogonal projection of $M$ onto $\pi$). Without loss of generality, we can assume it is $P$, and we have $P_{x}=M_{x}$ and $P_{y}=M_{y}$. Once this is achieved, $P$ mimics its movements on those of $M$ to maintain these two equalities. However, if $M$ moves parallel to the height axis or remains stationary, then $P$ moves parallel to the height axis, but towards $M$ (and we note that $P_{z} \leqslant M_{z}$). Since $M_{z}$ cannot increase indefinitely, $M$ cannot escape from $P$ except by making a finite number of movements parallel to the height axis and by remaining stationary a finite number of times. Consequently, from a time $t_{1}$, the fly $M$ will no longer move in a single plane $\pi^{\prime}$ with the equation $z=$ constant, and without remaining stationary.
The spider $Q$ then positions itself in the plane $\pi^{\prime}$. By remaining stationary if necessary, it can make the quantity $f=\left|Q_{x}-M_{x}\right|+\left|Q_{y}-M_{y}\right|$ even. From this moment, noted $t_{2}$, $Q$ follows the following procedure:
- If $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$, then $Q$ moves parallel to the abscissa axis, so that $\left|Q_{x}-M_{x}\right|$ does not increase ($Q$ moves horizontally, along a line $d$, towards the projection of $M$ on the line $d$).
- Otherwise, $Q$ moves parallel to the ordinate axis, under similar conditions.
To fix ideas, we can assume that for all $t \in \mathbb{N}$, the fly moves at time $t+\frac{1}{3}$ and the spider at time $t+\frac{2}{3}$. Since neither $M$ nor $Q$ remains stationary, the movement of $M$ increases or decreases $f$ by one unit and the movement of $Q$ decreases $f$ by one unit, so for all $t \in \mathbb{N}$, $f(t)$ is even (in particular, $Q$ will never position itself on a neighboring point of $M$) and furthermore $f(t+1) \leqslant f(t)$.
Let $g=\max \left(\left|Q_{x}-M_{x}\right|,\left|Q_{y}-M_{y}\right|\right)$. We observe that the movement of $Q$ can only decrease $g$. Moreover,
- If the movement of $M$ at time $t+\frac{1}{3}$ decreases $g$, then $g(t+1) \leqslant g(t)$.
- Suppose that the movement of $M$ at time $t+\frac{1}{3}$ increases $g$. If, for example, $M$ has moved in the direction of the $x$-axis, necessarily $\left|Q_{x}(t)-M_{x}(t)\right| \geqslant\left|Q_{y}(t)-M_{y}(t)\right|$ and $M$ has moved away from $Q$, so after the movement of $M$ we have $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$. Consequently, the spider moves in the same direction as the fly, and we have $g(t+1)=g(t)$.
In all cases, we see that $g(t+1) \leqslant g(t)$ for all $t \in \mathbb{N}$, so there exists $t_{2} \in \mathbb{N}$ such that $g(t)=g\left(t_{2}\right)$ and $f(t)=f\left(t_{2}\right)$ for all $t \geqslant t_{2}$. Suppose by contradiction that $g\left(t_{2}\right)>0$.
By changing the orientation of the axes if necessary, we can assume that $Q_{x}\left(t_{2}\right) \leqslant M_{x}\left(t_{2}\right)$ and $Q_{y}\left(t_{2}\right) \leqslant M_{y}\left(t_{2}\right)$. - First case: $Q_{y}\left(t_{2}\right)=M_{y}\left(t_{2}\right)$. Since $f\left(t_{2}\right)$ is even, we have $M_{x}\left(t_{2}\right) \geqslant Q_{x}\left(t_{2}\right)+2$. If between times $t_{2}$ and $t_{2}+1$ the fly moves in the direction of the $y$-axis, then the spider moves to the right, and $g\left(t_{2}+1\right)=g\left(t_{2}\right)-1$. Impossible. If the fly moves to the left, then its movement decreases $f$ by one unit, so $f\left(t_{2}+1\right)=f\left(t_{2}\right)-2$. Impossible. We deduce that the fly moves to the right, and consequently the spider as well. By immediate induction, we get that $M_{x}\left(t_{2}+k\right)=M_{x}\left(t_{2}\right)+k$ for all $k \in \mathbb{N}$, which is impossible.
- Second case: $Q_{x}\left(t_{2}\right)=M_{x}\left(t_{2}\right)$. Analogous.
- Third case: $Q_{x}\left(t_{2}\right)<M_{x}\left(t_{2}\right)$ and $Q_{y}\left(t_{2}\right)<M_{y}\left(t_{2}\right)$. Since the movement of $Q$ strictly decreases the quantity $f$, the movement of $M$ must increase $f$ by one unit. Consequently, between times $t_{2}$ and $t_{2}+1$, the fly must move to the right or upwards. We easily deduce that $Q_{x}\left(t_{2}+1\right)<M_{x}\left(t_{2}+1\right)$ and $Q_{y}\left(t_{2}+1\right)<M_{y}\left(t_{2}+1\right)$. By immediate induction, the sequence $\left(M_{x}\left(t_{2}+k\right)+M_{y}\left(t_{2}+k\right)\right)_{k \in \mathbb{N}}$ is strictly increasing, which is impossible since it is bounded and takes integer values.
In all cases, we have reached a contradiction, which proves that $g\left(t_{2}\right)=0$ and that the spider has caught the fly at time $t_{2}$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dans le plan, on considère l'ensemble $S$ des points de coordonnées $(x, y)$, où $x, y \in$ $\{1,2, \ldots, 2013\}$. Deux points de $S$ sont dits voisins s'ils sont à une distance 1 l'un de l'autre. A chaque seconde, une mouche et des araignées se déplacent sur les points de $S$ de la façon suivante : tout d'abord, la mouche soit ne bouge pas, soit va sur un point voisin de celui sur lequel elle se trouve. Puis, chaque araignée soit ne bouge pas, soit va sur un point voisin de celui sur lequel elle se trouve. Plusieurs araignées peuvent se trouver simultanément sur un même point, et la mouche ainsi que les araignées connaissent les positions respectives des unes et des autres.
a) Déterminer le plus petit entier $k$ pour lequel $k$ araignées pourront toujours finir par attraper la mouche en un temps fini, et ce quelles que soient les positions initiales de la mouche et des araignées sur les points de $S$.
b) Répondre à la même question si l'on suppose cette fois que l'on est dans l'espace usuel et que $S$ est l'ensemble des points de coordonnéees $(x, y, z)$ où $x, y, z \in\{1,2, \ldots, 2013\}$.
|
Une seule araignée ne peut attraper la mouche : en effet, la mouche peut attendre jusqu'à ce que l'araignée soit sur un point voisin de celui sur lequel elle se trouve. A partir de ce moment, elle se déplace à chaque fois sur un point diagonalement opposé à celui sur lequel est l'araignée si celle-ci est sur un point voisin, et sinon attend où elle est.
On va prouver maintenant que, dans le plan comme dans l'espace, deux araignées suffisent pour attraper la mouche.
Pour cela, on note $M$ la mouche, et on désigne par $P$ et $Q$ les deux araignées. Pour chaque animal $A$, on note respectivement $A_{x}, A_{y}$ et $A_{z}$ son abscisse, son ordonnée et sa cote.
a) Les araignées $P$ et $Q$ se placent tout d'abord sur le point de coordonnées $(1,1)$. Puisque $M$ ne peut s'enfuir indéfiniment vers la droite, $P$ peut alors en un temps fini, et en ne se déplaçant qu'horizontalement, se trouver en un point tel que $P_{x}=M_{x}$ et $P_{y}=1$. De même, $Q$ se place en un point tel que $Q_{x}=1$ et $Q_{y}=M_{y}$ (il est clair que si $P$, par exemple, atteint ce premier objectif avant $Q$, elle peut suivre les déplacements de $M$ en conservant $P_{x}=M_{x}$ et $P_{y}=1$ et attendre le positionnement adéquat de Q).
A partir de ces positions, atteintes au temps $t_{0}$ :
- si $M$ se déplace horizontalement (c'est-à-dire de sorte que $M_{x}$ change) alors $P$ fait de même afin de conserver $\mathrm{P}_{\mathrm{x}}=\mathrm{M}_{\mathrm{x}}$.
- sinon, $P$ se déplace verticalement, en allant vers $M$.
L'araignée $Q$ procède de la même façon, mais en échangeant les rôles des abscisses et ordonnées.
En utilisant cette stratégie et à partir de $t_{0}$, la quantité $\left|P_{y}-M_{y}\right|+\left|Q_{x}-M_{x}\right|$ n'augmente jamais. Mais, cette quantité ne reste constante que lors d'un déplacement de $M$ vers la droite ou vers le haut, ce qui ne peut arriver qu'un nombre fini de fois. Par suite, après un temps fini, au moins l'un des deux termes de la somme va être égal à 0 , signifiant ainsi la perte de la mouche.
b) Les deux araignées se placent tout d'abord sur le point $(1,1,1)$. Puis, en restant dans le plan $\pi$ d'équation $z=1$ et par utilisation de la stratégie du a), l'une d'elles va attraper l'ombre de $M$ dans $\pi$ (i.e. la projection orthogonale de $M$ sur $\pi$ ). Sans perte de généralité, on peut supposer qu'il s'agit de $P$, et on a donc $P_{x}=M_{x}$ et $P_{y}=M_{y}$. Une fois ceci réalisé, $P$ calque ses déplacements sur ceux de $M$ de façon à conserver ces deux égalités. Toutefois, si $M$ se déplace parallèlement à l'axe des cotes ou reste immobile, alors $P$ se déplace parallèlement à l'axe des cotes, mais en allant vers $M$ (et on note qu'on a toujours $P_{z} \leqslant M_{z}$ ). Puisque $M_{z}$ ne peut augmenter indéfiniment, $M$ ne peut échapper à $P$ qu'en ne faisant qu'un nombre fini de déplacements parallèlement à l'axe des cotes et en ne restant immobile
qu'un nombre fini de fois. Par conséquent, à partir d'un instant $t_{1}$, la mouche $M$ ne se déplacera plus que dans un même plan $\pi^{\prime}$ d'équation $z=$ constante, et sans rester immobile.
L'araignée Q vient alors se placer dans le plan $\pi^{\prime}$. Quitte à rester immobile, elle peut rendre la quantité $f=\left|Q_{x}-M_{x}\right|+\left|Q_{y}-M_{y}\right|$ paire. A partir de cet instant, noté $t_{2}, Q$ suit la procédure suivante :
- Si $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$ alors $Q$ se déplace parallèlement à l'axe des abscisses, de sorte que $\left|Q_{x}-M_{x}\right|$ n'augmente pas ( $Q$ se déplace horizontalement, le long d'une droite $d$, en allant vers la projection de $M$ sur la droite $d$ ).
- Sinon, $Q$ se déplace parallèlement à l'axe des ordonnées, dans des conditions analogues.
Pour se fixer les idées, on peut supposer que pour tout $t \in \mathbb{N}$, la mouche se déplace à l'instant $t+\frac{1}{3}$ et l'araignée à l'instant $t+\frac{2}{3}$. Puisque ni $M$ ni $Q$ ne reste immobile, le mouvement de $M$ fait augmenter ou diminuer $f$ d'une unité et le mouvement de $Q$ fait diminuer $f$ d'une unité, donc pour tout $t \in \mathbb{N}, f(t)$ est pair (en particulier, $Q$ ne se placera jamais sur un point voisin de $M$ ) et de plus $f(t+1) \leqslant f(t)$.
Soit $g=\max \left(\left|Q_{x}-M_{x}\right|,\left|Q_{y}-M_{y}\right|\right)$. On observe que le mouvement de $Q$ ne peut que faire décroître g. De plus,
- Si le mouvement de $M$ à l'instant $t+\frac{1}{3}$ fait décroître $g$, alors $g(t+1) \leqslant g(t)$.
- Supposons que le mouvement de $M$ à l'instant $t+\frac{1}{3}$ fait croître $g$. Si par exemple $M$ s'est déplacée dans la direction des $x$, nécessairement $\left|Q_{x}(t)-M_{x}(t)\right| \geqslant\left|Q_{y}(t)-M_{y}(t)\right|$ et $M$ s'est éloignée de $Q$, donc après le mouvement de $M$ on a $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$. Par conséquent l'araignée se déplace dans le même sens que la mouche et on a $g(t+1)=g(t)$.
Dans tous les cas, on voit que $g(t+1) \leqslant g(t)$ pour tout $t \in \mathbb{N}$, donc il existe $t_{2} \in \mathbb{N}$ tel que $g(t)=g\left(t_{2}\right)$ et $f(t)=f\left(t_{2}\right)$ pour tout $t \geqslant t_{2}$. Supposons par l'absurde que $g\left(t_{2}\right)>0$.
Quitte changer l'orientation des axes, on peut supposer que $Q_{x}\left(t_{2}\right) \leqslant M_{x}\left(t_{2}\right)$ et $Q_{y}\left(t_{2}\right) \leqslant M_{y}\left(t_{2}\right)$. - Premier cas: $Q_{y}\left(t_{2}\right)=M_{y}\left(t_{2}\right)$. Comme $f\left(t_{2}\right)$ est pair, on a $M_{x}\left(t_{2}\right) \geqslant Q_{x}\left(t_{2}\right)+2$. Si entre les instants $t_{2}$ et $t_{2}+1$ la mouche se déplace dans la direction des $y$, alors l'araignée se déplace vers la droite, et $g\left(t_{2}+1\right)=g\left(t_{2}\right)-1$. Impossible. Si la mouche se déplace vers la gauche, alors son déplacement fait diminuer f d'une unité, donc $\mathrm{f}\left(\mathrm{t}_{2}+1\right)=\mathrm{f}\left(\mathrm{t}_{2}\right)-2$. Impossible. On en déduit que la mouche se déplace vers la droite, et du coup l'araignée également. Par une récurrence immédiate, on obtient que $M_{x}\left(t_{2}+k\right)=M_{x}\left(t_{2}\right)+k$ pour tout $k \in \mathbb{N}$, ce qui est impossible.
- Deuxième cas: $Q_{x}\left(t_{2}\right)=M_{x}\left(t_{2}\right)$. Analogue.
- Troisième cas: $\mathrm{Q}_{\mathrm{x}}\left(\mathrm{t}_{2}\right)<\mathrm{M}_{\mathrm{x}}\left(\mathrm{t}_{2}\right)$ et $\mathrm{Q}_{\mathrm{y}}\left(\mathrm{t}_{2}\right)<\mathrm{M}_{\mathrm{y}}\left(\mathrm{t}_{2}\right)$. Comme le déplacement de Q fait diminuer strictement la quantité f , le déplacement de $M$ doit faire augmenter f d'une unité. Par conséquent, entre les instants $t_{2}$ et $t_{2}+1$, la mouche doit se déplacer vers la droite ou vers le haut. On en déduit facilement que $Q_{x}\left(t_{2}+1\right)<M_{x}\left(t_{2}+1\right)$ et $Q_{y}\left(t_{2}+1\right)<M_{y}\left(t_{2}+1\right)$. Par une récurrence immédiate, la suite $\left(M_{x}\left(t_{2}+k\right)+M_{y}\left(t_{2}+k\right)\right)_{k \in \mathbb{N}}$ est strictement croissante, ce qui est impossible puisqu'elle est bornée et à valeurs entières.
Dans tous les cas on a abouti à une contradiction, ce qui prouve que $\mathrm{g}\left(\mathrm{t}_{2}\right)=0$ et que l'araignée a rattrapé la mouche à l'instant $t_{2}$.
|
{
"resource_path": "French/segmented/tests/fr-2012-2013-ofm-2012-2013-test-mars-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
721d4425-c3af-55a7-84da-ea0d60500539
| 604,433
|
Let $n$ be a strictly positive integer. Find the smallest integer $k$ having the following property: for all real numbers $a_{1}, \ldots, a_{d}$ satisfying $a_{1}+a_{2}+\cdots+a_{d}=n$ and $0 \leqslant a_{i} \leqslant 1$ for $i=1,2, \ldots, d$, it is possible to group the numbers into $k$ packets (possibly empty) such that the sum of the numbers in each packet is $\leqslant 1$.
|
$\triangleright$ The reals $a_{1}=\ldots=a_{2 n-1}=\frac{n}{2 n-1}$ belong to the interval $\left.] \frac{1}{2}, 1\right]$ and their sum is $n$. Since each real is strictly greater than $\frac{1}{2}$, each package contains at most one of these $2 n-1$ reals (because the sum of two of them is strictly greater than 1): therefore, at least $2 n-1$ packages are needed.
$\triangleright$ Suppose we have partitioned our set of reals $a_{1}, \ldots, a_{d}$ into $k \geq 2 n$ packages and let $\alpha_{1} \leq \ldots \leq \alpha_{k}$ be the sums associated with these packages, arranged in ascending order. Then, by grouping these numbers two by two, we get
$$
\begin{aligned}
n & =\alpha_{1}+\alpha_{2}+\ldots+\alpha_{k} \\
& =\left(\alpha_{1}+\alpha_{2}\right)+\left(\alpha_{3}+\alpha_{4}\right)+\ldots \\
& \geq\left\lfloor\frac{k}{2}\right\rfloor\left(\alpha_{1}+\alpha_{2}\right) \geq n\left(\alpha_{1}+\alpha_{2}\right)
\end{aligned}
$$
Thus, $\alpha_{1}+\alpha_{2} \leq 1$ and we can group the two corresponding packages into a new package with a total sum less than or equal to 1, and we are reduced to $k-1$ packages.
$\triangleright$ In conclusion, it is necessary to have $2 n-1$ packages, and if we have partitioned into more than $2 n$ packages, we can proceed with a grouping and reduce the number of necessary packages. The value sought is therefore $2 n-1$.
|
2n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n$ un entier strictement positif. Trouver le plus petit entier $k$ ayant la propriété suivante : pour tous réels $a_{1}, \ldots, a_{d}$ vérifiant $a_{1}+a_{2}+\cdots+a_{d}=n$ et $0 \leqslant a_{i} \leqslant 1$ pour $i=1,2, \ldots, d$, il est possible de regrouper les nombres en $k$ paquets (éventuellement vides) de sorte que la somme des nombres de chaque paquet soit $\leqslant 1$.
|
$\triangleright$ Les réels $a_{1}=\ldots=a_{2 n-1}=\frac{n}{2 n-1}$ appartiennent à l'intervalle $\left.] \frac{1}{2}, 1\right]$ et leur somme vaut $n$. Comme chaque réel est strictement plus grand que $\frac{1}{2}$, chaque paquet contient au plus un de ces $2 n-1$ réels (car la somme de deux d'entre eux est strictement supérieure à 1 ) : il faut donc au moins $2 n-1$ paquets.
$\triangleright$ Supposons que l'on ait partitionné notre ensemble de réels $a_{1}, \ldots, a_{d}$ en $k \geq 2 n$ paquets et notons $\alpha_{1} \leq \ldots \leq \alpha_{k}$ les sommes associées à ces paquets classées par ordre croissant. Alors, en regroupant ces nombres deux par deux, on obtient
$$
\begin{aligned}
n & =\alpha_{1}+\alpha_{2}+\ldots+\alpha_{k} \\
& =\left(\alpha_{1}+\alpha_{2}\right)+\left(\alpha_{3}+\alpha_{4}\right)+\ldots \\
& \geq\left\lfloor\frac{k}{2}\right\rfloor\left(\alpha_{1}+\alpha_{2}\right) \geq n\left(\alpha_{1}+\alpha_{2}\right)
\end{aligned}
$$
Ainsi, $\alpha_{1}+\alpha_{2} \leq 1$ et on peut regrouper les deux paquets correspondants en un nouveau paquet de somme totale inférieure ou égale à 1 et on est ramené à $k-1$ paquets.
$\triangleright$ En conclusion, il est nécessaire d'avoir $2 n-1$ paquets et, si l'on a partitionné en plus de $2 n$ paquets, on peut procéder à un regroupement et faire diminuer le nombre de paquets nécessaires. La valeur recherchée est donc $2 n-1$.
|
{
"resource_path": "French/segmented/tests/fr-2013-2014-ofm-2013-2014-test-mai-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
6f2a1bc2-743e-5b87-bdf8-7f9c98cfd1b4
| 604,748
|
It is said that a strictly positive integer $n$ is amusing if for every strictly positive divisor $d$ of $n$, the integer $d+2$ is prime. Determine all the amusing integers that have the maximum number of divisors.
|
Let $n$ be an amusing integer and $p$ a prime divisor of $n$. Then $p$ is odd, since $p+2$ is prime.
Suppose that $p \geqslant 5$. Then $p+2$ is prime, and $p+2>3$, so $p+2$ is not divisible by 3. We deduce that $p$ is not congruent to 1 modulo 3. It is clear that $p$ is not congruent to 0 modulo 3, so $p \equiv 2(\bmod 3)$. Suppose that $p^{2} \mid n$. Then $p^{2} \equiv 1(\bmod 3)$, so $p^{2}+2 \equiv 0$ $(\bmod 3)$. Furthermore, $p^{2}+2$ is prime, so $p^{2}+2=3$, which is impossible.
We deduce from the above that if $p \geqslant 5$ is a prime divisor of $n$, then $p^{2}$ does not divide $n$.
Similarly, if $p_{1}$ and $p_{2}$ are distinct prime divisors $\geqslant 5$ of $n$, then $p_{1} p_{2}$ divides $n$, so $p_{1} p_{2}+2$ is divisible by 3, which is impossible.
Therefore, every amusing integer $n$ is of the form $n=3^{k}$ or $3^{k} p$ where $p$ is prime.
We check that $3+2, 3^{2}+2, 3^{3}+2$, and $3^{4}+2$ are prime, but $3^{5}+2$ is not, so $k \leqslant 4$. The amusing integers of the form $3^{k}$ therefore have at most 5 divisors.
If $n=3^{4} \times 5=405$, then $n+2$ is not prime, so $n$ is not amusing.
If $n=3^{k} p$ with $p \geqslant 7$ prime, and $k \geqslant 3$, then the numbers $p, 3 p, 9 p, 27 p$ are divisors of $n$ congruent to $p, 3 p, 4 p, 2 p$ modulo 5. None is congruent to 0 modulo 5, and the congruences of these four numbers modulo 5 are distinct, so in some order they are $1, 2, 3, 4$. We deduce that there is a divisor $d \geqslant 7$ of $n$ such that $d \equiv 3(\bmod 5)$. We have $d+2>5$ and $5 \mid d$, which implies that $d$ is not prime.
We deduce from the above that the amusing integers of the form $3^{k} p$ satisfy $k \leqslant 2$ or $(k \leqslant 3$ and $p=5$), so have at most 8 divisors, with equality only when $k=3$ and $p=5$. Conversely, we check that $3^{3} \times 5$ is amusing, so the unique amusing integer having a maximum number of divisors is $3^{3} \times 5=135$.
|
135
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un entier strictement positif $n$ est amusant si pour tout diviseur strictement positif $d$ de $n$, l'entier $d+2$ est premier. Déterminer tous les entiers amusants dont le nombre de diviseurs est maximum.
|
Soit $n$ un entier amusant et $p$ un diviseur premier de $n$. Alors $p$ est impair, puisque $p+2$ est premier.
Supposons que $p \geqslant 5$. Alors $p+2$ est premier, et $p+2>3$, donc $p+2$ n'est pas divisible par 3. On en déduit que $p$ n'est pas congru à 1 modulo 3 . Il est clair que $p \mathrm{n}^{\prime}$ est pas congru à 0 modulo 3 , donc $p \equiv 2(\bmod 3)$. Supposons que $p^{2} \mid n$. Alors $p^{2} \equiv 1(\bmod 3)$, donc $p^{2}+2 \equiv 0$ $(\bmod 3)$. De plus, $p^{2}+2$ est premier, donc $p^{2}+2=3$, ce qui est impossible.
On déduit de ce qui précède que si $p \geqslant 5$ est un diviseur premier de $n$, alors $p^{2}$ ne divise pas $n$.
De même, si $p_{1}$ et $p_{2}$ sont des diviseurs premiers distincts $\geqslant 5$ de $n$, alors $p_{1} p_{2}$ divise $n$, donc $p_{1} p_{2}+2$ est divisible par 3 , ce qui est impossible.
Par conséquent, tout entier amusant $n$ est de la forme $n=3^{k}$ ou bien $3^{k} p$ où $p$ est premier.
On vérifie que $3+2,3^{2}+2,3^{3}+2$ et $3^{4}+2$ sont premiers mais $3^{5}+2$ ne l'est pas, donc $k \leqslant 4$. Les entiers amusants de la forme $3^{k}$ ont donc au plus 5 diviseurs.
Si $n=3^{4} \times 5=405$, alors $n+2$ n'est pas premier donc $n$ n'est pas amusant.
Si $n=3^{k} p$ avec $p \geqslant 7$ premier, et $k \geqslant 3$, alors les nombres $p, 3 p, 9 p, 27 p$ sont des diviseurs de $n$ congrus à $p, 3 p, 4 p, 2 p$ modulo 5 . Aucun n'est congru à 0 modulo 5 , et les congruences de ces quatre nombres modulo 5 sont deux à deux distinctes, donc à l'ordre près valent $1,2,3,4$. On en déduit qu'il existe un diviseur $d \geqslant 7$ de $n$ tel que $d \equiv 3(\bmod 5)$. On a donc $d+2>5$ et $5 \mid d$, ce qui entraîne que $d$ n'est pas premier.
On déduit de ce qui précède que les entiers amusants de la forme $3^{k} p$ vérifient $k \leqslant 2$ ou bien $(k \leqslant 3$ et $p=5$ ), donc ont au plus 8 diviseurs, avec égalité seulement lorsque $k=3$ et $p=5$. Réciproquement, on vérifie que $3^{3} \times 5$ est amusant, donc l'unique entier ammusant ayant un nombre maximal de diviseurs est $3^{3} \times 5=135$.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
a5479f02-956b-59bf-99b0-6a4c89637da7
| 604,895
|
We want to color the three-element parts of $\{1,2,3,4,5,6,7\}$, such that if two of these parts have no element in common, then they must be of different colors. What is the minimum number of colors needed to achieve this goal?
|
Consider the sequence of sets $\{1,2,3\},\{4,5,6\},\{1,2,7\},\{3,4,6\},\{1,5,7\},\{2,3,6\},\{4,5,7\}$, $\{1,2,3\}$.
Each set must have a different color from the next, so there must be at least two colors. If there were exactly two colors, then the colors would have to alternate, which is impossible because the last set is the same as the first and should be of the opposite color.
Conversely, let's show that three colors suffice:
- We color blue the sets that contain at least two elements among 1, 2, 3.
- We color green the sets not colored blue and that contain at least two elements among 4, 5, 6.
- We color red the sets not colored blue or green.
It is clear that two blue sets have an element in common among 1, 2, 3; similarly, two green sets have an element in common among 4, 5, 6. Finally, any red set contains three elements, which necessarily includes the element 7: two red sets therefore also have an element in common.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On veut colorier les parties à trois éléments de $\{1,2,3,4,5,6,7\}$, de sorte que si deux de ces parties n'ont pas d'élément en commun alors elles soient de couleurs différentes. Quel est le nombre minimum de couleurs pour réaliser cet objectif?
|
Considérons la suite de parties $\{1,2,3\},\{4,5,6\},\{1,2,7\},\{3,4,6\},\{1,5,7\},\{2,3,6\},\{4,5,7\}$, $\{1,2,3\}$.
Chaque partie doit avoir une couleur différente de la suivante, donc déjà il y a au moins deux couleurs. S'il n'y avait qu'exactement deux couleurs, alors les couleurs devraient alterner, ce qui est impossible car la dernière partie est la même que la première et devrait être de couleur opposée.
Réciproquement, montrons que trois couleurs suffisent:
- On colorie en bleu les parties qui contiennent au moins deux éléments parmi 1, 2, 3.
- On colorie en vert les parties non coloriées en bleu et qui contiennent au moins deux éléments parmi 4, 5, 6 .
- On colorie en rouge les parties non coloriées en bleu ou en vert.
Il est évident que deux parties bleues ont un élément en commun parmi 1, 2, 3 ; de même, deux parties vertes ont un élément en commun parmi $4,5,6$. Enfin, toute partie rouge contient trois éléments, dont contient nécessairement l'élément 7 : deux parties rouges ont donc également un élément en commun.
|
{
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
7385a734-6555-5566-bb0d-ffb44a73924c
| 604,954
|
Consider 7 islands $A_{1}, \ldots, A_{7}$. We are allowed to build bridges, either between an island $A_{i}$ and the next island $A_{i+1}$ (for $i \in\{1,2, \ldots, 6\}$), or between an island $A_{i}$ and the last one $A_{7}$ (for $i \in\{1,2, \ldots, 6\}$). In how many ways can these constructions be carried out with the minimum number of bridges so that one can travel from any island to any other?
Example for 3 islands instead of 7: the three possible constructions using two bridges are
1) a bridge between $A_{1}$ and $A_{2}$, and a bridge between $A_{1}$ and $A_{3}$
2) a bridge between $A_{1}$ and $A_{2}$, and a bridge between $A_{2}$ and $A_{3}$
3) a bridge between $A_{1}$ and $A_{3}$, and a bridge between $A_{2}$ and $A_{3}$.
|
A configuration will be considered good if it satisfies the conditions of the statement.
Let $a_{n}$ be the number of good configurations with $n$ islands. We have $a_{1}=a_{2}=1$ and $a_{3}=3$.
Starting from a good configuration with $n$ islands such that $A_{n-1}$ and $A_{n}$ are not connected, then $A_{n-1}$ and $A_{n-2}$ are necessarily connected, so if we remove the island $A_{n-1}$, we obtain a good configuration with $n-1$ islands. Conversely, any good configuration with $n-1$ islands comes from one and only one good configuration with $n$ islands where the last two are not connected: it is indeed sufficient to interpose an island between the last two and to place a bridge between it and the $n$ - 2-nd.
We deduce that there are $a_{n-1}$ good configurations with $n$ islands such that $A_{n-1}$ and $A_{n}$ are not connected.
On the other hand, starting from a good configuration with bridges between $A_{n}$ and $A_{n-1}, A_{n-1}$ and $A_{n-2}, \ldots$, $A_{n-k+1}$ and $A_{n-k}(k \geqslant 1)$ but not between $A_{n-k}$ and $A_{n_{k}-1}$, if we remove the islands $A_{n-1}, \ldots, A_{n-k}$, then we obtain a good configuration with $n-k$ islands. We deduce as above that there are $a_{n-1}+a_{n-2}+\cdots+a_{1}$ good configurations with a bridge between $A_{n}$ and $A_{n-1}$.
We see, therefore, that $a_{n}=2 a_{n-1}+a_{n-2}+\cdots+a_{1}$.
We deduce step by step that $a_{4}=8, a_{5}=21, a_{6}=55$ and $a_{7}=144$.
|
144
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère 7 îles $A_{1}, \ldots, A_{7}$. On est autorisé à construire des ponts, soit entre une île $A_{i}$ et l'île suivante $A_{i+1}$ (pour $i \in\{1,2, \ldots, 6\}$ ), soit entre une île $A_{i}$ et la dernière $A_{7}$ (pour $i \in\{1,2, \ldots, 6\}$ ). De combien de manières peut-on réaliser ces constructions avec le moins de ponts possibles de sorte que l'on puisse se rendre d'une île vers n'importe quelle autre ?
Exemple pour 3 îles au lieu de 7 : les trois constructions possibles utilisant deux ponts sont 1) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{1}$ et $A_{3}$
2) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{2}$ et $A_{3}$
3) un pont entre $A_{1}$ et $A_{3}$, et un pont entre $A_{2}$ et $A_{3}$.
|
On dira qu'une configuration est bonne si elle satisfait les conditions de l'énoncé.
Notons $a_{n}$ le nombre de bonnes configurations avec $n$ îles. On a $a_{1}=a_{2}=1$ et $a_{3}=3$.
Partant d'une bonne configuration avec $n$ îles telle que $A_{n-1}$ et $A_{n}$ ne soient pas reliées, alors $A_{n-1}$ et $A_{n-2}$ sont nécessairement reliées, donc si on supprime l'île $A_{n-1}$ on obtient une bonne configuration avec $n-1$ îles. Réciproquement, toute bonne configuration avec $n-1$ îles provient d'une et une seule bonne configuration avec $n$ îles dont les deux dernières ne sont pas reliées : il suffit en effet d'intercaler une île entre les deux dernières et de mettre un pont entre celle-ci et la $n$ - 2-ième.
On en déduit qu'il y a $a_{n-1}$ bonnes configurations avec $n$ îles telles que $A_{n-1}$ et $A_{n}$ ne soient pas reliées.
D'autre part, partant d'une bonne configuration avec des ponts entre $A_{n}$ et $A_{n-1}, A_{n-1}$ et $A_{n-2}, \ldots$, $A_{n-k+1}$ et $A_{n-k}(k \geqslant 1)$ mais pas entre $A_{n-k}$ et $A_{n_{k}-1}$, si on supprime les îles $A_{n-1}, \ldots, A_{n-k}$ alors on obtient une bonne configuration avec $n-k$ îles. On en déduit comme ci-dessus qu'il y a $a_{n-1}+a_{n-2}+\cdots+a_{1}$ bonnes configurations comportant un pont entre $A_{n}$ et $A_{n-1}$.
On voit donc que $a_{n}=2 a_{n-1}+a_{n-2}+\cdots+a_{1}$.
On en déduit de proche en proche que $a_{4}=8, a_{5}=21, a_{6}=55$ et $a_{7}=144$.
|
{
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
334728fc-4452-5182-bd32-9f4eb07fa5a6
| 605,141
|
Consider 2017 lines in the plane, which intersect pairwise at distinct points. Let $E$ be the set of these intersection points.
We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors.
What is the minimum number of colors needed to achieve such a coloring?
|
The sought minimum $m$ is $m=3$, and with what follows, it will be quite evident that the result remains true for $n \geq 3$ lines.
First, we note that, in the obtained configuration, there is at least one non-subdivided region that is a triangle. Indeed, three non-concurrent lines and two never parallel lines form a triangle. Now, any line that crosses a triangle divides it into two polygons, at least one of which is a triangle. Therefore, starting from three of the given lines and "adding" the other 2014 one by one, we are assured of the existence of such a triangular region in the final configuration. The three vertices of such a triangle must be of different colors, which implies that $m \geq 3$.
To conclude, we will construct an appropriate three-coloring. We start by noting that, since there are only a finite number of intersection points, we can choose an orthogonal coordinate system in which these points have distinct x-coordinates. We then number the points $M_{1}, M_{2}, \ldots, M_{k}$ according to increasing x-coordinates (where $k=\frac{2017 \times 2016}{2}$). For any $i$, the point $M_{i}$ has at most four neighbors, and if it belongs to a segment joining two of its neighbors, only one of these two neighbors has an x-coordinate less than that of $M_{i}$. This ensures that, for any $i \leq k$, among the neighbors of $M_{i}$, at most two have indices less than $i$. We can then color the $M_{i}$ in the order of the numbering according to the following procedure: we color $M_{1}$ green and $M_{2}$ red. And, for any $i$ such that $2 \leq i \leq k-1$, if we assume that the points $M_{1}, M_{2}, \ldots, M_{i}$ have been colored either green, red, or blue so that no two adjacent points are (yet) the same color, then, according to the previous remark, at most two neighbors of $M_{i+1}$ have already been colored, leaving one color free for $M_{i+1}$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère 2017 droites du plan, qui se rencontrent deux à deux en des points distincts. On appelle $E$ l'ensemble de ces points d'intersection.
On veut attribuer une couleur à chacun des points de $E$ de sorte que deux quelconques de ces points qui appartiennent à une même droite et dont le segment qui les relient ne contient aucun autre point de $E$, soient de couleurs différentes.
Combien faut-il au minimum de couleurs pour pouvoir réaliser une telle coloration?
|
Le minimum $m$ cherché est $m=3$ et, avec ce qui suit, il sera assez évident que le résultat reste vrai pour $n \geq 3$ droites.
Tout d'abord, on note que, dans la configuration obtenue, il y a au moins une région non subdivisée qui est un triangle. En effet, trois droites non concourantes et deux jamais parallèles forment un triangle. Or, toute droite qui traverse un triangle, le partage en deux polygones dont
au moins un est un triangle et donc, en partant de trois des droites données et en "ajoutant" une par une les 2014 autres, on est assuré de l'existence d'une telle région triangulaire dans la configuration finale. Les trois sommets d'un tel triangle doivent être de couleurs distinctes, ce qui implique que $m \geq 3$.
Pour conclure, nous allons construire une coloration adéquate à trois couleurs. On commence par remarquer que, puisqu'il n'y a qu'un nombre fini de points d'intersection, on peut choisir un repère orthogonal dans lequel ces points ont des abscisses deux à deux distinctes. On numérote alors les points $M_{1}, M_{2} \ldots, M_{k}$ selon les abscisses croissantes (et où $k=\frac{2017 \times 2016}{2}$ ). Pour tout $i$, le point $M_{i}$ possède au plus quatre voisins et, s'il appartient à un segment qui joint deux de ses voisins, un seul de ces deux voisins a une abscisse inférieure à celle de $M_{i}$. Cela assure que, pour tout $i \leq k$, parmi les voisins de $M_{i}$, il y en a au plus deux qui ont des indices inférieurs à $i$. On peut alors colorier les $M_{i}$ dans l'ordre de la numérotation selon la procédure suivante : on colorie $M_{1}$ en vert et $M_{2}$ en rouge. Et, pour tout $i$ tel que $2 \leq i \leq k-1$, si l'on suppose que les points $M_{1}, M_{2} \ldots, M_{i}$ ont été colorés chacun soit en vert, soit en rouge, soit en bleu de sorte que deux points voisins ne soient pas (encore) de la même couleur alors, d'après la remarque précédente, au plus deux voisins de $M_{i+1}$ ont déjà été colorés, ce qui laisse une couleur libre pour $M_{i+1}$.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
00418346-ab3a-5158-b607-639aecdd2f18
| 605,212
|
Let $S$ be the set of two-digit numbers that do not contain the digit 0. Two numbers in $S$ are called friends if their largest digits are equal, and if the difference between their smallest digits is equal to 1. For example, 68 and 85 are friends, 78 and 88 are friends, but 58 and 75 are not friends.
Determine the largest integer $m$ such that there exists a subset $T$ of $S$ with $m$ elements, such that any two elements of $T$ are not friends.
|
Answer: 45. We can take for $T$ the set of numbers whose smallest digit is odd.
Conversely, if $x=\overline{a b}$ with $1 \leqslant b<a \leqslant 9$ then $x$ and $x+1$ are friends. If $x=\overline{a b}$ with $2 \leqslant a<b \leqslant 9$ and $a$ even, then $x$ and $x+10$ are friends. We have thus found 36 disjoint pairs of friends. Consequently, among the 72 numbers $\geqslant 21, T$ can contain at most 36 numbers, so $|T| \leqslant 9+36=45$.
|
45
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $S$ l'ensemble des nombres à deux chiffres qui ne contiennent pas le chiffre 0. Deux nombres de $S$ sont dits amis si leurs plus grands chiffres sont égaux, et si la différence entre leurs plus petits chiffres est égale à 1 . Par exemple, 68 et 85 sont amis, 78 et 88 sont amis, mais 58 et 75 ne sont pas amis.
Déterminer le plus grand entier $m$ tel qu'il existe une partie $T$ de $S$ possédant $m$ éléments, telle que deux éléments quelconques de $T$ ne soient pas amis.
|
Réponse : 45 . On peut prendre pour $T$ l'ensemble des nombres dont le plus petit chiffre est impair.
Réciproquement, si $x=\overline{a b}$ avec $1 \leqslant b<a \leqslant 9$ alors $x$ et $x+1$ sont amis. Si $x=\overline{a b}$ avec $2 \leqslant a<b \leqslant 9$ et $a$ pair, alors $x$ et $x+10$ sont amis. On a ainsi trouvé 36 paires d'amis disjointes. Par conséquent, parmi les 72 nombres $\geqslant 21, T$ ne peut contenir qu'au plus 36 nombres, donc $|T| \leqslant 9+36=45$.
|
{
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
b7cfe7cb-9967-57af-91e6-68a3e7890f47
| 605,269
|
The integers $1,2, \ldots, 2018$ are written on the board. Then 2017 operations are performed as follows: choose two numbers $a$ and $b$, erase them, and write $a+b+2 a b$ in their place. At the end, only one integer remains on the board.
What are the possible values that its units digit can take?
|
Since there are 1009 odd numbers between 1 and 2018, we know that the sum of the integers initially written on the board is odd. Furthermore, one of these integers is congruent to $2(\bmod 5)$. An immediate induction then shows that, after each operation, the sum of the integers written on the board remains odd, and one of these integers is congruent to 2 $(\bmod 5)$. Consequently, the last integer written on the board is congruent to $1(\bmod 2)$ and to 2 $(\bmod 5)$, that is, to $7(\bmod 10)$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Les entiers $1,2, \ldots, 2018$ sont écrits au tableau. On effectue alors 2017 opérations comme suit : choisir deux nombres $a$ et $b$, les effacer, et écrire $a+b+2 a b$ à la place. À la fin, il ne reste qu'un seul entier sur le tableau.
Quelles sont les valeurs que son chiffre des unités peut prendre?
|
Puisqu'il y a 1009 nombres impairs entre 1 et 2018, on sait que la somme des entiers initialement inscrits au tableau est impaire. En outre, l'un de ces entiers est congru à $2(\bmod 5)$. Une récurrence immédiate permet alors de montrer que, après chaque opération, la somme des entiers écrits sur le tableau reste impaire, et l'un de ces entiers est congru à 2 $(\bmod 5)$. Par conséquent, le dernier entier écrit sur le tableau est congru à $1(\bmod 2)$ et à 2 $(\bmod 5)$, c'est-à-dire à $7(\bmod 10)$.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
7c3df6e0-a879-5208-b93b-d64ade721275
| 605,345
|
Let $n \geq 3$ be an integer and consider $n$ lines in general position (i.e., no three lines are concurrent and no two lines are parallel). How many triangles are formed by these lines?
N.B. For example, in the figure below, there are 4 triangles.
|
If we number the $n$ lines from 1 to $n$, we notice that each triangle is encoded by a subset of $\{1,2, \ldots, n\}$ with three elements. Therefore, there are $\binom{n}{3}=$ $\frac{n(n-1)(n-2)}{6}$ triangles.
|
\frac{n(n-1)(n-2)}{6}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geq 3$ un entier et considérons $n$ droites en position générale (c'est-à-dire que trois droites ne sont jamais concourantes et deux droites jamais parallèles). Combien de triangles sont formés par ces droites?
N.B. Par exemple, dans la figure ci-dessous, il y a 4 triangles.

|
Si on numérote de 1 à $n$ les $n$ droites, on remarque que chaque triangle est codé par la donnée d'un sous-ensemble de $\{1,2, \ldots, n\}$ à trois éléments. Il y a donc $\binom{n}{3}=$ $\frac{n(n-1)(n-2)}{6}$ triangles.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
c5ac9715-0551-5b7f-83ae-f2859ac073a5
| 605,415
|
Let $n \geqslant 1$ be an integer. For any non-empty subset $A$ of $\{1,2, \ldots, n\}$, we denote $P(A)$ as the product of all elements of $A$. For example, for $A=\{2,4,7\}$, we have $P(A)=$ 56. Determine the sum of $\frac{1}{P(A)}$ as $A$ ranges over all non-empty subsets of $\{1,2, \ldots, n\}$.
|
We have the identity $\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sum x_{i}+\sum_{i<j} x_{i} x_{j}+\cdots$. By taking $x_{i}=\frac{1}{a_{i}}$, we obtain
$$
\sum_{k \geqslant 0} \sum_{a_{1}<\cdots<a_{k}} \frac{1}{a_{1} a_{2} \cdots a_{k}}=\left(1+\frac{1}{1}\right) \cdots\left(1+\frac{1}{n}\right)=\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \cdots \times \frac{n+1}{n}=n+1
$$
Thus, $1+\sum_{A} \frac{1}{P(A)}=n+1$ and therefore $\sum_{A} \frac{1}{P(A)}=n$.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geqslant 1$ un entier. Pour tout sous-ensemble non vide $A$ de $\{1,2, \ldots, n\}$, on note $P(A)$ le produit de tous les éléments de $A$. Par exemple, pour $A=\{2,4,7\}$, on a $P(A)=$ 56. Déterminer la somme des $\frac{1}{P(A)}$ lorsque $A$ parcourt tous les sous-ensembles non vides de $\{1,2, \ldots, n\}$.
|
On a l'identité $\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sum x_{i}+\sum_{i<j} x_{i} x_{j}+\cdots$. En prenant $x_{i}=\frac{1}{a_{i}}$, on obtient
$$
\sum_{k \geqslant 0} \sum_{a_{1}<\cdots<a_{k}} \frac{1}{a_{1} a_{2} \cdots a_{k}}=\left(1+\frac{1}{1}\right) \cdots\left(1+\frac{1}{n}\right)=\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \cdots \times \frac{n+1}{n}=n+1
$$
On a donc $1+\sum_{A} \frac{1}{P(A)}=n+1$ donc $\sum_{A} \frac{1}{P(A)}=n$.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
eea7997f-033a-5c8e-8bc9-ce096f6a5ea7
| 605,441
|
Determine the maximum value of $\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}$ when $x, y, z$ are strictly positive real numbers satisfying $x+y+z=3$.
|
According to the Cauchy-Schwarz inequality, we have
$$
\sqrt{x} \sqrt{1}+\sqrt{y+1} \sqrt{2}+\sqrt{z+2} \sqrt{3} \leqslant \sqrt{x+y+1+z+2} \sqrt{1+2+3}=6
$$
Equality is achieved when $x=y=z=1$. Therefore, the maximum value is 6.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Déterminer la valeur maximale de $\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}$ lorsque $x, y, z$ sont des nombres réels strictement positifs vérifiant $x+y+z=3$.
|
D'après l'inégalité de Cauchy-Schwarz, on a
$$
\sqrt{x} \sqrt{1}+\sqrt{y+1} \sqrt{2}+\sqrt{z+2} \sqrt{3} \leqslant \sqrt{x+y+1+z+2} \sqrt{1+2+3}=6
$$
L'égalité est atteinte lorsque $x=y=z=1$. Donc la valeur maximale est 6 .
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
b3331776-a505-5e7b-9bba-fd2a233a60a1
| 605,450
|
Find all possible values for $f(2018)$ where $f$ is a function from $\mathbb{Q}$ to $\mathbb{R}_{+}$ satisfying the following three conditions:
- $f(2)=1 / 2$;
- for any rational $x$, if $f(x) \leqslant 1$, then $f(x+1) \leqslant 1$;
- $f(x y)=f(x) f(y)$ for all rational $x$ and $y$.
|
First, the equality $1 / 2=f(2)=f(1 \times 2)=f(1) f(2)=f(1) / 2$ shows that $f(1)=1$, and thus that $f(n) \leqslant 1$ for any non-zero natural number $n$.
Furthermore, for all $x, y$ with $y \neq 0$ we have $f(y) \neq 0$, and $f(x / y)=f(x) / f(y)$ since $f(x / y) f(y)=f((x / y) y)=f(x)$. In particular, $f(1 / 2)=2$. Finally, for any rational $x$, we have $f(x)^{2}=f\left(x^{2}\right)=f(-x)^{2}$, so $f$ is even.
Let then $k$ be an odd natural number, of the form $k=2 n+1$: we necessarily have $f(k) \leqslant 1$. We also know that $f(-k / 2)>1$, since $1 / 2=-k / 2+(n+1)$, so $f(-2 / k)=1 / f(-k / 2) \leqslant 1$, which implies that $f\left(\frac{k-2}{k}\right)=f\left(-\frac{2}{k}+1\right) \leqslant 1$, consequently $f(k-2) \leqslant f(k)$.
This allows us to show by induction that for any $k \geqslant 1$ odd we have $f(k) \geqslant 1$, and thus $f(k)=1$.
We deduce from all this that $f(2018)=f(2) f(1009)=1 / 2$.
Conversely, it remains to verify that a function $f$ as described in the statement does indeed exist. It suffices for this to observe that the function $f$ defined by
$$
f: p / q \mapsto \begin{cases}0 & \text { if } p=0 \\ 2^{v_{2}(q)-v_{2}(p)} & \text { if } p \neq 0\end{cases}
$$
where $v_{2}(n)$ denotes the 2-adic valuation of the integer $n$, satisfies the conditions of the statement.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les valeurs possibles pour $f(2018)$ où $f$ est une fonction de $\mathbb{Q}$ dans $\mathbb{R}_{+}$vérifiant les trois conditions suivantes:
- $f(2)=1 / 2$ ;
- pour tout rationnel $x$, si $f(x) \leqslant 1$, alors $f(x+1) \leqslant 1$;
- $f(x y)=f(x) f(y)$ pour tous rationnels $x$ et $y$.
|
Tout d'abord, l'égalité $1 / 2=f(2)=f(1 \times 2)=f(1) f(2)=f(1) / 2$ montre que $f(1)=1$, et donc que $f(n) \leqslant 1$ pour tout entier naturel non nul $n$.
Notons de plus que pour tous $x, y$ avec $y \neq 0$ on a $f(y) \neq 0$, et $f(x / y)=f(x) / f(y)$ puisque $f(x / y) f(y)=f((x / y) y)=f(x)$. En particulier, $f(1 / 2)=2$. Enfin, pour tout rationnel $x$, on a $f(x)^{2}=f\left(x^{2}\right)=f(-x)^{2}$, donc $f$ est paire.
Soit alors $k$ un entier naturel impair, de la forme $k=2 n+1$ : on a nécessairement $f(k) \leqslant 1$. On sait également que $f(-k / 2)>1$, puisque $1 / 2=-k / 2+(n+1)$, donc $f(-2 / k)=1 / f(-k / 2) \leqslant 1$, ce qui implique que $f\left(\frac{k-2}{k}\right)=f\left(-\frac{2}{k}+1\right) \leqslant 1$, par conséquent $f(k-2) \leqslant f(k)$.
Ceci permet de montrer par récurrence que pour tout $k \geqslant 1$ impair on a $f(k) \geqslant 1$, et donc $f(k)=1$.
On déduit de tout ceci que $f(2018)=f(2) f(1009)=1 / 2$.
Réciproquement, il reste à vérifier qu'une fonction $f$ telle que décrite dans l'énoncé existe bien. Il suffit pour ce faire de constater que la fonction $f$ définie par
$$
f: p / q \mapsto \begin{cases}0 & \text { si } p=0 \\ 2^{v_{2}(q)-v_{2}(p)} & \text { si } p \neq 0\end{cases}
$$
où $v_{2}(n)$ désigne la valuation 2-adique de l'entier $n$, satisfait bien les conditions de l'énoncé.
|
{
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
af519c75-f168-538b-bbce-b7b7822f6443
| 605,467
|
Each cell of an $8 \times 8$ table can be colored white or black, such that each rectangle of size $2 \times 3$ or $3 \times 2$ contains two black cells that share a side. Determine the minimum number of black cells that can be on the table.
|
As usual in this kind of problem, we start by searching for upper (by exhibiting a configuration) and lower bounds (by double counting and/or tiling arguments) on the minimum number of black squares the board must contain.
For example, the configuration below (on the left) ensures that 28 black squares are sufficient; indeed, any vertical rectangle (of size $3 \times 2$) contains two squares on one of the rows 3 or 6, and any horizontal rectangle (of size $2 \times 3$) contains two squares on one of the columns 3 or 6. On the other hand, each of the 10 rectangles in the partial tiling below (on the right) must contain at least 2 black squares, so 20 black squares are necessary.
Unfortunately, these two bounds are not equal. We need to improve both of them until they are equal.
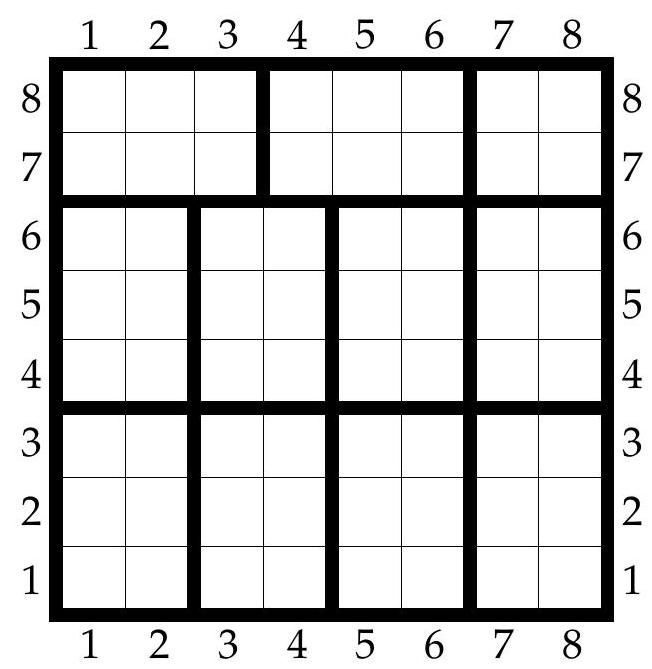
By trial and error, we eventually find a new configuration that satisfies the conditions of the problem but contains only 24 black squares. It is the configuration below.
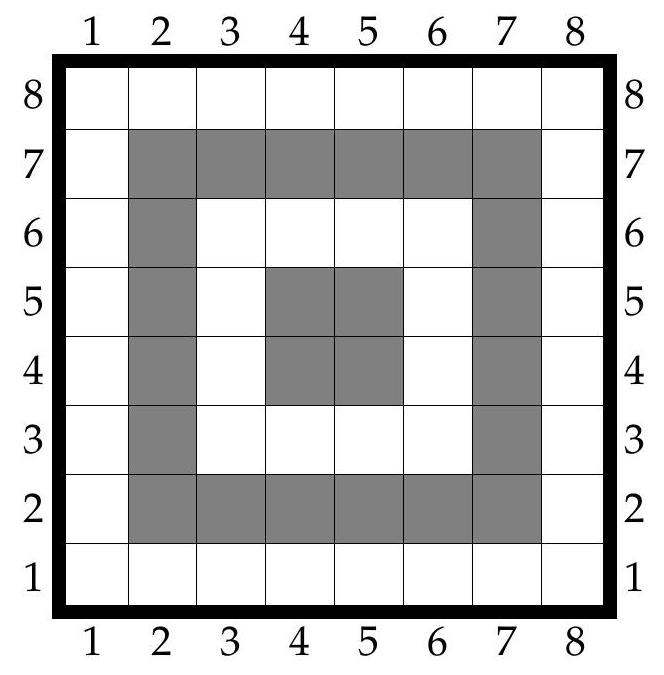
On the other hand, using a simple tiling by rectangles seems a bit too brutal to indicate the best possible lower bound on the number of black squares needed. We study a given rectangle:
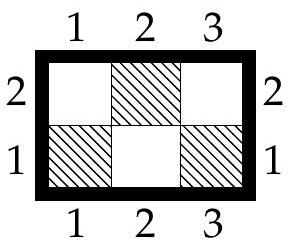
Here we observe that, among the 3 hatched squares, at least one must be a black square, otherwise our rectangle will never contain two adjacent black squares. In particular, the square in row 1, column 2 must have a black neighbor within this rectangle. Similarly, the square in row 2, column 2 must also have a black neighbor within our rectangle.
Armed with this observation, we focus on the minimum number of black neighbors that each square $c$ on the chessboard has:
$\triangleright$ if $c$ is one of the four corners, it could a priori have no black neighbors (which is indeed the case in our previous configuration);
$\triangleright$ if $c$ is one of the $2 \times 6=12$ squares on the top or bottom edge, it belongs to the central column of a horizontal rectangle, so it has at least one black neighbor;
$\triangleright$ similarly, if $c$ is one of the $2 \times 6=12$ squares on the left or right edge, it belongs to the central row of a vertical rectangle, so it has at least one black neighbor;
$\triangleright$ finally, if $c$ is one of the $6 \times 6=36$ squares in the center of the chessboard, it already has one black neighbor (say $d$); but then $c$ also belongs to the column (respectively, the row) of another horizontal (resp., vertical) rectangle that does not contain $d$, so $c$ has a second black neighbor.
In conclusion, we actually have at least $12+12+36 \times 2=96$ pairs $(c, d)$ of adjacent squares such that $d$ is a black square. Since each black square has at most four neighbors, it belongs to at most four such pairs. Therefore, we have at least $96 / 4=24$ black squares on our chessboard, which matches the upper bound found previously, and thus concludes the problem.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Chaque case d'un tableau de taille $8 \times 8$ peut être coloriée en blanc ou en noir, de telle sorte que chaque rectangle de taille $2 \times 3$ ou $3 \times 2$ contient deux cases noires ayant un côté en commun. Déterminer le nombre minimal de cases noires qu'il peut y avoir sur le tableau.
|
Comme d'habitude dans ce genre de problèmes, on commence par rechercher des bornes supérieures (en exhibant une configuration) et inférieures (par des arguments de double comptage et/ou de pavage) sur le nombre minimal de cases noires que doit contenir le tableau.
Par exemple, la configuration ci-dessous (à gauche) nous assure que 28 cases noires sont suffisantes; en effet, tout rectangle vertical (de taille $3 \times 2$ ) contient deux cases sur l'une des lignes 3 ou 6 , et tout rectangle horizontal (de taille $2 \times 3$ ) contient deux cases sur l'une des colonnes 3 ou 6. D'autre part, chacun des 10 rectangles du pavage partiel ci-dessous (à droite) doit contenir au moins 2 cases noires, de sorte que 20 cases noires ont nécessaires.
Malheureusement, ces deux bornes ne sont pas égales l'une à l'autre. Il nous faut donc chercher à les améliorer toutes les deux jusqu'à les rendre égales.


En tâtonnant, on finit par trouver une nouvelle configuration satisfaisant les conditions de l'énoncé, mais qui ne contient que 24 cases noires. Il s'agit de la configuration ci-dessous.

D'autre part, utiliser un simple pavage par des rectangles semble un peu trop brutal pour nous indiquer la meilleure borne inférieure possible sur le nombre de cases noires nécessaires. On étudie un rectangle quelconque donné :

On constate ici que, parmi les 3 cases hachurées, au moins une doit être une case noire, ce sans quoi notre rectangle ne contiendra jamais deux cases noires adjacentes. En particulier, la case en ligne 1 , colonne 2 a nécessairement une voisine noire au sein de ce rectangle. De même, la case en ligne 2, colonne 2 , a aussi une voisine noire au sein de notre rectangle.
Forts de ce constat, on s'intéresse, pour chaque case $c$ de l'échiquier, au nombre minimal de voisines noires que possède la case $c$ :
$\triangleright$ si $c$ est un des quatre coins, a priori, elle pourrait n'avoir aucune voisine noire (c'est d'ailleurs le cas dans notre configuration précédente);
$\triangleright$ si $c$ est une des $2 \times 6=12$ cases situées sur le côté haut ou bas, elle appartient à la colonne centrale d'un rectangle horizontal, donc elle a au moins une voisine noire;
$\triangleright$ de même, si $c$ est une des $2 \times 6=12$ cases situées sur le côté gauche ou droit, elle appartient à la ligne centrale d'un rectangle vertical, donc elle a au moins une voisine noire;
$\triangleright$ enfin, si $c$ est une des $6 \times 6=36$ cases situées au centre de l'échiquier, elle a déjà une voisine noire au minimum (disons $d$ ) ; mais alors $c$ appartient également à la colonne (respectivement, à la ligne) d'un autre rectangle horizontal (resp., vertical) ne contenant pas $d$, donc $c$ a une deuxième voisine noire.
En conclusion, on dispose en fait d'au moins $12+12+36 \times 2=96$ paires $(c, d)$ de cases adjacentes telles que $d$ est une case noire. Or, chaque case noire a au plus quatre voisines, donc appartient à au plus quatre telles paires. On a donc au moins $96 / 4=24$ cases noires sur notre échiquier, ce qui rejoint la borne supérieure trouvée précédemment, et conclut donc.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
4fbb497b-e527-589e-8737-86a067160a65
| 606,222
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
Suppose $n \geqslant 7$ and that the circle $\omega_{A, B}$ contains $k \geqslant 2$ points of $\mathcal{S}$. Lemmas 1 and 2 respectively ensure that $\ell_{A, B}$ contains at most two points of $\mathcal{S}$, and that $A$ is the only point of $\mathcal{S}$ belonging to $\omega_{B, A}$. We deduce that $k \geqslant n-3$, with equality if and only if $\ell_{A, B}$ contains exactly two points of $\mathcal{S}$, none of which belong to $\omega_{A, B}$. If $k=n-3$, let $C$ be another point on $\omega_{A, B}$. For the same reasons as before, the line $\ell_{A, C}$ contains two points of $\mathcal{S}$, none of which belong to $\omega_{A, C}=\omega_{A, B}$. Since $\ell_{A, B}$ and $\ell_{A, C}$ have at most one point in common, they therefore contain at least, between the two of them, three points of $\mathcal{S}$. If we add the point $A$ and the $k$ points of $\mathcal{S}$ belonging to $\omega_{A, B}$, this gives us a total of $k+4=n+1$ points in $\mathcal{S}$. Our initial assumption was therefore invalid, which proves the lemma.
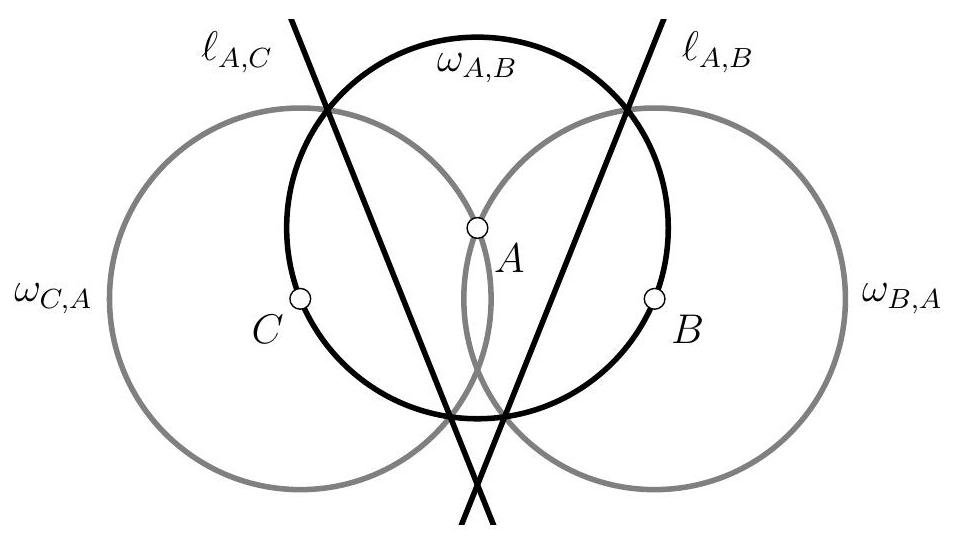
In conclusion, let's return to the statement itself. We will assume that $n \geqslant 7$ and arrive at a contradiction. Let $A, B$, and $C$ be three points of $\mathcal{S}$. The line $\ell_{A, B}$ contains at most two points of $\mathcal{S}$, so one of the circles $\omega_{A, B}$ and $\omega_{B, A}$ (say $\omega_{A, B}$) contains at least two points. Lemma 3 then ensures that $\omega_{A, B}$ contains at least $n-2$ points of $\mathcal{S}$. Similarly, one of the circles $\omega_{B, C}$ and $\omega_{C, B}$ (say $\omega_{X, Y}$) contains at least $n-2$ points of $\mathcal{S}$. We then have two circles, with centers $A$ and $X$, each containing $n-2$ points of $\mathcal{S}$. They therefore have at least $n-4 \geqslant 3$ points in common, which is absurd since their centers are distinct. We have thus reached the desired contradiction, which concludes our solution.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
Supposons que $n \geqslant 7$ et que le cercle $\omega_{A, B}$ contient $k \geqslant 2$ points de $\mathcal{S}$. Les lemmes 1 et 2 nous assurent respectivement que $\ell_{A, B}$ contient au plus deux points de $\mathcal{S}$, et que $A$ est le seul point de $\mathcal{S}$ appartenant à $\omega_{B, A}$. On en déduit que $k \geqslant n-3$, avec égalité si et seulement si $\ell_{A, B}$ contient exactement deux points de $\mathcal{S}$, dont aucun n'appartient à $\omega_{A, B}$. Si $k=n-3$, soit $C$ un autre point de $\omega_{A, B}$. Pour les mêmes raisons que précédemment, la droite $\ell_{A, C}$ contient deux points de $\mathcal{S}$, dont aucun n'appartient à $\omega_{A, C}=\omega_{A, B}$. Or, puisque $\ell_{A, B}$ et $\ell_{A, C}$ ont au plus un point commun, elles contiennent donc au moins, à elles deux, trois points de $\mathcal{S}$. Si l'on ajoute le point $A$ et les $k$ points de $\mathcal{S}$ appartenant à $\omega_{A, B}$, cela nous fait un total de $k+4=n+1$ points dans $\mathcal{S}$. Notre supposition initiale était donc invalide, ce qui démontre le lemme.

En conclusion, revenons à l'énoncé lui-même. Nous allons supposer que $n \geqslant 7$ et aboutir à une absurdité. Soit $A, B$ et $C$ trois points de $\mathcal{S}$. La droite $\ell_{A, B}$ contient au plus deux points de $\mathcal{S}$, donc l'un des cercles $\omega_{A, B}$ et $\omega_{B, A}$ (disons $\omega_{A, B}$ ) en contient au moins deux. Le lemme 3 nous assure alors que $\omega_{A, B}$ contient au moins $n-2$ points de $\mathcal{S}$.
De même, l'un des cercles $\omega_{B, C}$ et $\omega_{C, B}$ (disons $\omega_{X, Y}$ ) contient au moins $n-2$ points de $\mathcal{S}$. On dispose alors de deux cercles, de centres $A$ et $X$, qui contiennent chacun $n-2$ points de $\mathcal{S}$. Ils ont donc au moins $n-4 \geqslant 3$ points communs, ce qui est absurde puisque leurs centres sont distincts. On tient donc ici l'absurdité tant désirée, qui conclut notre solution.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nDémonstration:"
}
|
db815651-861c-5951-9c68-674706a9a8b7
| 604,505
|
We denote by $\mathbb{R}_{>0}$ the set of strictly positive real numbers. Find all functions $f: \mathbb{R}_{>0} \mapsto \mathbb{R}_{>0}$ such that
$$
f(x+f(x y))+y=f(x) f(y)+1
$$
for all strictly positive real numbers $x$ and $y$.
|
Let $f$ be a potential solution to the problem. In the following, we will denote $\mathbf{E}_{x, y}$ the given equality. Let $a$ and $b$ be two strictly positive real numbers such that $f(a)=f(b)$. The equalities $\mathbf{E}_{1, a}$ and $\mathbf{E}_{1, b}$ indicate that
$$
a=f(1) f(a)+1-f(1+f(a))=f(1) f(b)+1-f(1+f(b))=b
$$
which means that $f$ is injective.
Next, let $c$ and $d$ be two real numbers such that $0<c<d$, and let $t$ be a strictly positive real number. Since $f$ is injective, the equalities $\mathbf{E}_{c / t, t}$ and $\mathbf{E}_{d / t, t}$ indicate that
$$
f(c / t+f(c))=f(c / t) f(t)+1-t \neq f(d / t) f(t)+1-t=f(d / t+f(d))
$$
so that $c / t+f(c) \neq d / t+f(d)$, or equivalently that $f(d)-f(c) \neq (c-d) / t$. Since this inequality holds for all $t>0$, we deduce that $f(d) \geqslant f(c)$, which means that $f$ is increasing.
We then set $p=\inf \{f(x): x>0\}$ and $q=\inf \{f(x): x>p\}$. Since $f$ is increasing, we know that $f(x) \rightarrow p$ as $x \rightarrow 0$ and $x>0$, and that $f(y) \rightarrow q$ as $y \rightarrow p$ and $y>p$. For a fixed positive real number $y$, if we let $x$ tend to 0, we deduce that $f(x) \rightarrow p$ and that $f(x y) \rightarrow p$, so that $x+f(x y) \rightarrow p$ and that $f(x+f(x y)) \rightarrow q$. Consequently, the equality $\mathbf{E}_{x, y}$ indicates that
$$
y-1=f(x) f(y)-f(x+f(x y)) \rightarrow p f(y)-q,
$$
which means that $f(y)=y+(q-1) / p$.
The function $f$ is therefore an affine function, of the form $f: t \mapsto u t+v$. Conversely, once the coefficients $u$ and $v$ are fixed, the equality $\mathbf{E}_{x, y}$ indicates that
$$
u^{2} x y+u x+u v+v+y=f(x+f(x y))+y=f(x) f(y)+1=u^{2} x y+u v x+u v y+v^{2}+1
$$
or equivalently that $u(v-1) x+(u v-1) y=u v+v-v^{2}-1$. This means that
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
We deduce that $u-1=(u v-1)-(u v-u)=0$, that is, $u=1$, and then that $v-1=u v-u=0$, that is, $v=1$. But then the triple equality
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
is indeed satisfied.
In conclusion, the function $f: t \mapsto t+1$ is the unique solution to the problem.
Comment from the graders This problem was extremely difficult, and no student (nor any mentor from the POFM) managed to pass the crucial step of proving that $f$ is increasing. Several students had excellent reflexes: looking for a particular solution (the function $f: t \mapsto t+1$), examining specific values of $x$ and $y$ (here, $x=1$), investigating the injectivity of $f$, conjecturing that $f$ is increasing (by identifying an infinity of values $x<y$ such that $f(x)<f(y)$), and then using this conjecture. These excellent initiatives almost always earned their authors some points.
However, the graders noted a few avoidable errors or missteps, in the hope that students will avoid them in other situations:
$\triangleright$ Several students looked at what happened when $x=0$ or $y=0$. This often allowed them to identify the function $f: t \mapsto t+1$, which was very positive. However, of course, one could not base any proof on the equalities obtained when $x=0$ or $y=0$, since the function $f$ was only defined on $\mathbb{R}_{>0}$.
$\triangleright$ Many students looked at what happened when $y=1$, but not when $x=1$. Others looked at the case where $x=1$, but did not think to deduce the injectivity of $f$, even though they had the equality $f(1+f(x))+x=1+f(1) f(x)$, which made the injectivity of $f$ immediate.
$\triangleright$ Several students checked if the identity or constant functions could be solutions. It is a pity that they did not directly treat the case of affine functions, which was just as easy to handle, and which would have allowed them to identify the only solution to the problem.
|
f: t \mapsto t+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On note $\mathbb{R}_{>0}$ l'ensemble des réels strictement positifs. Trouver toutes les fonctions $f: \mathbb{R}_{>0} \mapsto \mathbb{R}_{>0}$ telles que
$$
f(x+f(x y))+y=f(x) f(y)+1
$$
pour tous les réels strictement positifs $x$ et $y$.
|
Soit $f$ une solution éventuelle du problème. Dans la suite, on notera $\mathbf{E}_{x, y}$ l'égalité de l'énoncé. Soit $a$ et $b$ deux réels strictement positifs tels que $f(a)=f(b)$. Les égalités $\mathbf{E}_{1, a}$ et $\mathbf{E}_{1, b}$ indiquent que
$$
a=f(1) f(a)+1-f(1+f(a))=f(1) f(b)+1-f(1+f(b))=b
$$
ce qui signifie que $f$ est injective.
Soit ensuite $c$ et $d$ deux réels tels que $0<c<d$, puis soit $t$ un réel strictement positif. Puisque $f$ est injective, les égalités $\mathbf{E}_{c / t, t}$ et $\mathbf{E}_{d / t, t}$ indiquent que
$$
f(c / t+f(c))=f(c / t) f(t)+1-t \neq f(d / t) f(t)+1-t=f(d / t+f(d))
$$
de sorte que $c / t+f(c) \neq d / t+f(d)$, ou encore que $f(d)-f(c) \neq(c-d) / t$. Cette dernière inégalité étant valide pour tout $t>0$, on en déduit que $f(d) \geqslant f(c)$, ce qui signifie que $f$ est croissante.
On pose alors $p=\inf \{f(x): x>0\}$ et $q=\inf \{f(x): x>p\}$. Puisque $f$ est croissante, on sait que $f(x) \rightarrow p$ lorsque $x \rightarrow 0$ et que $x>0$, et que $f(y) \rightarrow q$ lorsque $y \rightarrow p$ et que $y>p$. Un réel $y>0$ étant fixé, si on fait tendre $x$ vers 0 , on en déduit que $f(x) \rightarrow p$ et que $f(x y) \rightarrow p$, de sorte que $x+f(x y) \rightarrow p$ et que $f(x+f(x y)) \rightarrow q$. Par conséquent, l'égalité $\mathbf{E}_{x, y}$ indique que
$$
y-1=f(x) f(y)-f(x+f(x y)) \rightarrow p f(y)-q,
$$
ce qui signifie que $f(y)=y+(q-1) / p$.
La fonction $f$ est donc une fonction affine, de la forme $f: t \mapsto u t+v$. Réciproquement, une fois les coefficients $u$ et $v$ fixés, l'égalité $\mathbf{E}_{x, y}$ indique que
$$
u^{2} x y+u x+u v+v+y=f(x+f(x y))+y=f(x) f(y)+1=u^{2} x y+u v x+u v y+v^{2}+1
$$
ou encore que $u(v-1) x+(u v-1) y=u v+v-v^{2}-1$. Cela signifie que
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
On en déduit que $u-1=(u v-1)-(u v-u)=0$, c'est-à-dire que $u=1$, puis que $v-1=$ $u v-u=0$, c'est-à-dire que $v=1$. Mais alors la triple égalité
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
est bien respectée.
En conclusion, la fonction $f: t \mapsto t+1$ est l'unique solution du problème.
Commentaire des correcteurs Cet exercice était extrêmement difficile, et aucun élève (ni encadrant de la POFM) n'est parvenu à passer l'étape cruciale qui consistait à démontrer que $f$ était croissante. Plusieurs élèves ont eu d'excellents réflexes : rechercher une solution particulière (la fonction $f: t \mapsto t+1$ ), regarder des valeurs particulières de $x$ et $y$ (ici, $x=1$ ), s'intéresser à l'injectivité de $f$, conjecturer que $f$ était croissante (en repérant une infinité de valeurs $x<y$ telles que $f(x)<f(y)$ ), puis utiliser cette conjecture. Ces excellentes initiatives ont à peu près toutes permis à leur auteur d'obtenir quelques points.
Mentionnons cependant quelques erreurs ou maladresses évitables que les correcteurs ont repérées, dans l'espoir que les élèves les éviteront en d'autres occasions:
$\triangleright$ Plusieurs élèves ont regardé ce qui se passait lorsque $x=0$ ou $y=0$. Cela leur a souvent permis de repérer la fonction $f: t \mapsto t+1$, ce qui était très positif. Cependant, on ne pouvait bien sûr pas se baser sur les égalités obtenues lorsque $x=0$ ou $y=0$ pour démontrer quoi que ce soit, puisque la fonction $f$ n'était définie que sur $\mathbb{R}_{>0}$.
$\triangleright$ De nombreux élèves ont regardé ce qui se passait lorsque $y=1$, mais pas lorsque $x=1$. D'autres ont regardé le cas où $x=1$, mais n'ont pas pensé à en déduire l'injectivité de $f$, alors même qu'ils disposaient de l'égalité $f(1+f(x))+x=1+f(1) f(x)$, ce qui rendait l'injectivité de $f$ immédiate.
$\triangleright$ Plusieurs élèves ont regardé si l'identité ou les fonctions constantes pouvaient être solutions. Il est dommage de ne pas avoir traité directement le cas des fonctions affines, qui était aussi facile à traiter, et qui leur aurait permis d'identifier la seule solution du problème.
## Problèmes EGMO
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
c074fa2a-8652-5e42-a7a8-5a071ac96914
| 604,565
|
Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
can take.
|
The quantity we wish to maximize can be rewritten as
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\
& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\
& =(x y+y z+z x-1)^{2}-8 x y z .
\end{aligned}
$$
Since $0 \leqslant x y+y z+z x \leqslant(x+y+z)^{2} / 2=1 / 2$, we deduce that $\mathcal{S} \leqslant 1$. Conversely, if $x=y=0$ and $z=1$, we have $\mathcal{S}=1$, which concludes the proof.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y$ et $z$ trois nombres réels tels que $0 \leqslant x \leqslant y \leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
|
La quantité que l'on souhaite maximiser peut se récrire comme
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\
& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\
& =(x y+y z+z x-1)^{2}-8 x y z .
\end{aligned}
$$
Puisque $0 \leqslant x y+y z+z x \leqslant(x+y+z)^{2} / 2=1 / 2$, on en déduit que $\mathcal{S} \leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\mathcal{S}=1$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
13a00691-6cb4-56ae-a28f-6136795340eb
| 604,692
|
We denote by $\mathbb{Z}[x, y, z]$ the set of polynomials with integer coefficients in the three variables $x, y$, and $z$. We then say that a polynomial $P \in \mathbb{Z}[x, y, z]$ is Olympic if $\mathbb{Z}[x, y, z]$ contains polynomials $A, B$, and $C$ such that
$$
P(x, y, z)=(x+y+z) A(x, y, z)+(x y+y z+z x) B(x, y, z)+x y z C(x, y, z).
$$
Find the largest integer $n$ for which there exist natural numbers $i, j$, and $k$ with sum $i+j+k=n$ and such that the polynomial $x^{i} y^{j} z^{k}$ is not Olympic.
Note: A polynomial with integer coefficients in the variables $x, y$, and $z$ is a function that can be written as a sum of terms of the form $\lambda x^{i} y^{j} z^{k}$, where $\lambda$ is an integer and $i, j$, and $k$ are natural numbers. For example, $x-y+1$ and $x y+y z+z x$ are such polynomials, but $\pi x y z, \exp (x), x /\left(y^{2}+1\right)$, and $\sqrt{x y+z}$ are not.
|
Let $s_{1}=x+y+z, s_{2}=x y+y z+z x$ and $s_{3}=x y z$. We observe that
$$
\begin{cases}x^{3} \equiv-x^{2}(y+z) \equiv-x(x y+x z) \equiv x y z \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right) \\ x^{2} y^{2} \equiv x y(-x z-y z) \equiv-x y z(x+y) \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right)\end{cases}
$$
which means that $x^{3}$ and $x^{2} y^{2}$ are Olympic. Moreover, the set of Olympic polynomials is stable under multiplication by any polynomial and permutation of the variables.
Therefore, consider a polynomial $x^{i} y^{j} z^{k}$, which is not Olympic. Without loss of generality, we assume that $i \geqslant j \geqslant k$. If $i \geqslant 3, j \geqslant 2$ or $k \geqslant 1$, our polynomial is a multiple of $x^{3}$, $x^{2} y^{2}$, or $x y z$, so it is Olympic. We deduce that $i \leqslant 2, j \leqslant 1$ and $k \leqslant 0$, so that $i+j+k \leqslant 3$. This already ensures that $n \leqslant 3$.
Conversely, let us consider the set $\mathcal{E}$ of Olympic polynomials whose monomials all have a total degree of 3, i.e., polynomials $x^{i} y^{j} z^{k}$ such that $i+j+k=3$. By restricting $A, B$ and $C$ to their monomials of total degrees 2, 1, and 0 respectively, each polynomial in $\mathcal{E}$ can be written in the form
$$
\begin{aligned}
P= & (x+y+z)\left(a x^{2}+b y^{2}+c z^{2}+d x y+e x z+f y z\right)+(x y+y z+z x)(g x+h y+i z)+j x y z \\
= & a x^{3}+b y^{2}+c z^{3}+(a+d+g) x^{2} y+(a+e+g) x^{2} z+(b+d+h) y^{2} x+(b+f+h) y^{2} z \\
& \quad+(c+e+i) z^{2} x+(c+f+i) z^{2} y+(d+e+f+g+h+i+j) x y z .
\end{aligned}
$$
If $x^{2} y$ is Olympic, we then have
$$
1=(a+d+g)+(b+f+h)+(c+e+i)-(a+e+g)-(b+d+h)-(c+f+i)=0,
$$
which is absurd. Thus, the polynomial $x^{2} y$ is not Olympic, and the largest integer sought is $n=3$.
**Comment from the graders** The problem was difficult, but many students made significant progress by showing that several polynomials were Olympic. However, be careful of calculation errors!
Some tried to show that $x^{2} y$ was not Olympic by doing arithmetic on polynomials in several variables. This approach was risky and, like any complicated path to the solution, led to many errors.
Here, the key was to look at the terms of degree 3 but in two variables, i.e., $x^{2} y, x^{2} z, z^{2} x, z^{2} y, y^{2} x$ and $y^{2} z$. However, be careful: some students proceeded by contradiction and, from polynomials $(A, B, C)$ that allowed obtaining $x^{2} y$, exhibited new $\left(A^{\prime}, B^{\prime}, C^{\prime}\right)$ that allowed obtaining $\pm y^{2} x$, and then concluded directly that since they reduced to the same case (up to symmetry) it was impossible. There is no a priori reason for this to be the case: there could be many triplets $(A, B, C)$ that allow obtaining that $x^{2} y$ is Olympic!
Finally, after restricting to terms of degree 3, some forgot the terms in $x^{2}, y^{2}$ and $z^{2}$ in $A$, which is a pity.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On note $\mathbb{Z}[x, y, z]$ l'ensemble des polynômes à coefficients entiers en les trois variables $x, y$ et $z$. On dit ensuite qu'un polynôme $P \in \mathbb{Z}[x, y, z]$ est olympique si $\mathbb{Z}[x, y, z]$ contient des polynômes $A, B$ et $C$ tels que
$$
P(x, y, z)=(x+y+z) A(x, y, z)+(x y+y z+z x) B(x, y, z)+x y z C(x, y, z) .
$$
Trouver le plus grand entier $n$ pour lequel il existe des entiers naturels $i, j$ et $k$ de somme $i+j+k=n$ et tels que le polynôme $x^{i} y^{j} z^{k}$ ne soit pas olympique.
Note : Un polynôme à coefficients entiers en les variables $x, y$ et $z$ est une fonction que l'on peut écrire comme une somme de termes de la forme $\lambda x^{i} y^{j} z^{k}$, où $\lambda$ est un entier relatif et $i, j$ et $k$ sont des entiers naturels. Par exemple, $x-y+1$ et $x y+y z+z x$ sont de tels polynômes, mais $\pi x y z, \exp (x), x /\left(y^{2}+1\right)$ et $\sqrt{x y+z}$ n'en sont pas.
|
Posons $s_{1}=x+y+z, s_{2}=x y+y z+z x$ et $s_{3}=x y z$. On constate que
$$
\begin{cases}x^{3} \equiv-x^{2}(y+z) \equiv-x(x y+x z) \equiv x y z \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right) \\ x^{2} y^{2} \equiv x y(-x z-y z) \equiv-x y z(x+y) \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right)\end{cases}
$$
ce qui signifie que $x^{3}$ et $x^{2} y^{2}$ sont olympiques. Or, l'ensemble des polynômes olympiques est stable par multiplication par tout polynôme et par permutation des variables.
Par conséquent, considérons un polynôme $x^{i} y^{j} z^{k}$, non olympique. Sans perte de généralité, on suppose que $i \geqslant j \geqslant k$. Si $i \geqslant 3, j \geqslant 2$ ou $k \geqslant 1$, notre polynôme est un multiple de $x^{3}$, de $x^{2} y^{2}$ ou de $x y z$, donc il est olympique. On en déduit que $i \leqslant 2, j \leqslant 1$ et $k \leqslant 0$, de sorte que $i+j+k \leqslant 3$. Cela nous assure déjà que $n \leqslant 3$.
Réciproquement, intéressons-nous à l'ensemble $\mathcal{E}$ des polynômes olympiques dont tous les monômes sont de degré total 3, c'est-à-dire sont des polynômes $x^{i} y^{j} z^{k}$ tels que $i+j+k=3$. Quitte à restreindre respectivement $A, B$ et $C$ à leurs monômes de degrés totaux 2,1 et 0 , chaque polynôme de $\mathcal{E}$ s'écrit sous la forme
$$
\begin{aligned}
P= & (x+y+z)\left(a x^{2}+b y^{2}+c z^{2}+d x y+e x z+f y z\right)+(x y+y z+z x)(g x+h y+i z)+j x y z \\
= & a x^{3}+b y^{2}+c z^{3}+(a+d+g) x^{2} y+(a+e+g) x^{2} z+(b+d+h) y^{2} x+(b+f+h) y^{2} z \\
& \quad+(c+e+i) z^{2} x+(c+f+i) z^{2} y+(d+e+f+g+h+i+j) x y z .
\end{aligned}
$$
Si $x^{2} y$ est olympique, on a alors
$$
1=(a+d+g)+(b+f+h)+(c+e+i)-(a+e+g)-(b+d+h)-(c+f+i)=0,
$$
ce qui est absurde. Ainsi, le polynôme $x^{2} y$ n'est pas olympique, et le plus grand entier recherché est $n=3$.
Commentaire des correcteurs L'exercice était difficile, mais de nombreux élèves ont bien avancé sur le problème, en montrant que plusieurs polynômes étaient olympiques. Attention néanmoins aux erreurs de calcul!
Certains ont essayé de montrer que $x^{2} y$ n'était pas olympique en faisant de l'arithmétique sur les polynômes à plusieurs variables. Cette approche était risquée et, comme toute voie compliquée pour obtenir la solution, elle a mené à de nombreuses erreurs.
Ici, la la clé était de regarder les termes de degré 3 mais en deux variables, c'est-à-dire en $x^{2} y, x^{2} z, z^{2} x, z^{2} y, y^{2} x$ et $y^{2} z$. Attention, toutefois: certains élèves ont procédé par l'absurde
et, à partir de polynômes $(A, B, C)$ qui permettaient d'obtenir $x^{2} y$, ont exhibé de nouveaux $\left(A^{\prime}, B^{\prime}, C^{\prime}\right)$ qui permettaient d'obtenir $\pm y^{2} x$, puis en ont conclu directement que comme on se ramenait au même cas (à symétrie près) c'était impossible. Il n'y a à priori pas de raison que ce soit le cas : il pourrait y avoir de nombreux triplets $(A, B, C)$ permettant d'obtenir que $x^{2} y$ est olympique!
Enfin, après s'être restreints aux termes de degré 3 , certains oublient les termes en $x^{2}, y^{2}$ et $z^{2}$ dans $A$, ce qui est dommage.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
846d4bd6-f837-55a0-a8ac-798ce32839ed
| 604,750
|
A permutation of the set $\{1, \ldots, 2021\}$ is a sequence $\sigma=\left(\sigma_{1}, \ldots, \sigma_{2021}\right)$ such that each element of the set $\{1, \ldots, 2021\}$ is equal to exactly one term $\sigma_{i}$. We define the weight of such a permutation $\sigma$ as the sum
$$
\sum_{i=1}^{2020}\left|\sigma_{i+1}-\sigma_{i}\right|
$$
What is the greatest possible weight of permutations of $\{1, \ldots, 2021\}$?
|
Let $n=2021$, and let $\sigma$ be a permutation of $\{1,2, \ldots, n\}$ and let $\mathbf{W}(\sigma)$ be its weight. For all integers $k \leqslant n$, we define
$$
\alpha_{k}=\left\{\begin{array}{ll}
1 & \text { if } k \neq n \text { and } \sigma(k)>\sigma(k+1) \\
0 & \text { if } k=n \\
-1 & \text { if } k \neq n \text { and } \sigma(k)<\sigma(k+1)
\end{array} \text { and } \beta_{k}= \begin{cases}1 & \text { if } k \neq 1 \text { and } \sigma(k)>\sigma(k-1) \\
0 & \text { if } k=1 \\
-1 & \text { if } k \neq 1 \text { and } \sigma(k)<\sigma(k-1)\end{cases}\right.
$$
Finally, we set $\varepsilon_{k}=\alpha_{\sigma^{-1}(k)}+\beta_{\sigma^{-1}(k)}$. We then observe that
$$
\mathbf{W}(\sigma)=\sum_{k=1}^{n}\left(\alpha_{k}+\beta_{k}\right) \sigma(k)=\sum_{k=1}^{n} k \varepsilon_{k} .
$$
We now denote by $\mathcal{X}$ the set of $n$-tuples $\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ such that
$\triangleright x_{1}+x_{2}+\ldots+x_{n}=0$ and
$\triangleright$ there exist two indices $i$ and $j$ for which $x_{i}, x_{j} \in\{-1,+1\}$, and $x_{k} \in\{-2,0,2\}$ whenever $k \notin\{i, j\}$.
By construction, the $n$-tuple $\left(\varepsilon_{1}, \ldots, \varepsilon_{n}\right)$ belongs to $\mathcal{X}$.
More generally, we set $\mathbf{W}(\mathbf{x})=\sum_{k=1}^{n} k x_{k}$ for any $n$-tuple $\mathbf{x} \in \mathcal{X}$, and we consider an $n$-tuple $\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right) \in \mathcal{X}$ for which $\mathbf{W}(y)$ is maximal.
The rearrangement inequality indicates that $y_{1} \leqslant y_{2} \leqslant \ldots \leqslant y_{n}$. Suppose further that there exists an index $i$ for which $y_{i}=0$. If $i \geqslant 2$ and $y_{i-1}=-1$, replacing $y_{i}$ and $y_{i+1}$ by -2 and 1 increases $\mathbf{W}(\mathbf{y})$ by 2. Similarly, if $i \leqslant n-1$ and $y_{i+1}=1$, replacing $y_{i}$ and $y_{i+1}$ by -1 and 2 increases $\mathbf{W}(\mathbf{y})$ by 2. Since the $n$-tuple $\mathbf{y}$ must contain coordinates equal to $\pm 1$, all its coordinates are therefore non-zero.
Finally, let $a$ be the number of indices $i$ for which $y_{i}=-2$, and $b$ the number of indices $i$ for which $y_{i}=2$. We know that $y_{1}=\ldots=y_{a}=-2, y_{a+1}= \pm 1, y_{a+2}= \pm 1$ and $y_{a+3}=\ldots=y_{n}=2$, so that $a+b+2=n$ and that $-2 a+y_{a+1}+y_{a+2}+2 b=0$. Thus,
$$
a=\frac{2 n+y_{a+1}+y_{a+2}}{4}-1 \text { and } b=\frac{2 n-y_{a+1}-y_{a+2}}{4}-1 .
$$
We then distinguish three cases, depending on the values of $y_{a+1}$ and $y_{a+2}$:
1. If $y_{a+1}=y_{a+2}=-1$, then $a=(n-3) / 2, b=(n-1) / 2$, so
$$
\mathbf{W}(\mathbf{y})=-2 \sum_{k=1}^{a} k-(a+1)-(a+2)+2 \sum_{k=a+3}^{n} k=\left(n^{2}-3\right) / 2
$$
2. If $y_{a+1}=y_{a+2}=1$, then $a=(n-1) / 2, b=(n-3) / 2$, so
$$
\mathbf{W}(\mathbf{y})=-2 \sum_{k=1}^{a} k+(a+1)+(a+2)+2 \sum_{k=a+3}^{n} k=\left(n^{2}-3\right) / 2
$$
3. If $y_{a+1}=-1$ and $y_{a+2}=1$, then $a=b=(n-2) / 2$, which is impossible since $n$ is odd.
Consequently, $\mathbf{W}(\sigma) \leqslant\left(n^{2}-3\right) / 2$.
Conversely, we set $\ell=(n-1) / 2$, and we denote by $\sigma$ the permutation of $\{1,2, \ldots, n\}$ defined by
$$
\begin{cases}\sigma(2 k-1)=\ell+1+k & \text { if } 1 \leqslant k \leqslant \ell \\ \sigma(2 k)=k & \text { if } 1 \leqslant k \leqslant \ell \\ \sigma(n)=\ell+1 & \end{cases}
$$
This permutation is associated with the $n$-tuple $(-2, \ldots,-2,1,1,2, \ldots, 2)$ with $\ell$ coordinates equal to -2 and $\ell$ coordinates equal to 2, so its weight is $\left(n^{2}-3\right) / 2$, as shown in case 2 above.
In conclusion, the maximum weight sought is $\left(n^{2}-3\right) / 2$, which is 2042219.
$\underline{\text { Alternative Solution } n^{\circ} 1}$ Let $n=2021$, and let $\sigma$ be a permutation of $\{1,2, \ldots, n\}$ of maximum weight. Below, we set $k=(n-1) / 2=1010$.
Suppose there exists an integer $i$ such that $2 \leqslant i \leqslant n-1$ and $\sigma_{i-1}<\sigma_{i}<\sigma_{i+1}$ or $\sigma_{i-1}>\sigma_{i}>\sigma_{i+1}$. We then denote by $\sigma^{\prime}$ the permutation of $\{1,2, \ldots, n\}$ defined by:
$$
\begin{aligned}
& \triangleright \sigma_{j}^{\prime}=\sigma_{j} \text { when } 1 \leqslant j \leqslant i-1 ; \\
& \triangleright \sigma_{j}^{\prime}=\sigma_{j+1} \text { when } i \leqslant j \leqslant n-1 ; \\
& \triangleright \sigma_{n}^{\prime}=\sigma_{i} .
\end{aligned}
$$
Since $\left|\sigma_{i}-\sigma_{i+1}\right|+\left|\sigma_{i+1}-\sigma_{i+2}\right|=\left|\sigma_{i}-\sigma_{i+2}\right|$, the weight of $\sigma^{\prime}$ is that of $\sigma$ plus $\left|\sigma_{n}-\sigma_{1}\right|$, which contradicts the maximality of the weight of $\sigma$.
Furthermore, and by replacing $\sigma$ with its "horizontal mirror" permutation, i.e., by replacing each term $\sigma_{j}$ with $n+1-\sigma_{j}$, which does not change the weight of $\sigma$, we assume without loss of generality that $\sigma_{1}<\sigma_{2}$. The absence of an integer $i$ as described in the previous paragraph ensures that $\sigma_{2 j-1}<\sigma_{2 j}>\sigma_{2 j+1}$ for all integers $j$ such that $1 \leqslant j \leqslant k$.
The weight of $\sigma$ is then
$$
\sum_{j=1}^{k} 2 \sigma_{2 j}-\sigma_{1}-\sigma_{n}-\sum_{j=1}^{k-1} 2 \sigma_{2 j+1}
$$
Since $\sigma$ does not take the same value twice, we have
$$
\begin{aligned}
& \sum_{j=1}^{k} 2 \sigma_{2 j} \leqslant \sum_{j=n+1-k}^{n} 2 j=n(n+1)-(n-k)(n+1-k)=3 k^{2}+3 k \text { and } \\
& \sum_{j=1}^{k-1} 2 \sigma_{2 j+1}+\sigma_{1}+\sigma_{n} \geqslant \sum_{j=1}^{k-1} 2 j+k+(k+1)=k(k-1)+(2 k+1)=k^{2}+k+1
\end{aligned}
$$
Consequently, the weight of $\sigma$ cannot exceed $2 k^{2}+2 k-1=2042219$.
Conversely, the permutation indicated at the end of the
|
2042219
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une permutation de l'ensemble $\{1, \ldots, 2021\}$ est une suite $\sigma=\left(\sigma_{1}, \ldots, \sigma_{2021}\right)$ telle que chaque élément de l'ensemble $\{1, \ldots, 2021\}$ soit égal à exactement un terme $\sigma_{i}$. On définit le poids d'une telle permutation $\sigma$ comme la somme
$$
\sum_{i=1}^{2020}\left|\sigma_{i+1}-\sigma_{i}\right|
$$
Quelle est le plus grand poids possible des permutations de $\{1, \ldots, 2021\}$ ?
|
Soit $n=2021$, et soit $\sigma$ une permutation de $\{1,2, \ldots, n\}$ et soit $\mathbf{W}(\sigma)$ son poids. Pour tout entier $k \leqslant n$, on pose
$$
\alpha_{k}=\left\{\begin{array}{ll}
1 & \text { si } k \neq n \text { et } \sigma(k)>\sigma(k+1) \\
0 & \text { si } k=n \\
-1 & \text { si } k \neq n \text { et } \sigma(k)<\sigma(k+1)
\end{array} \text { et } \beta_{k}= \begin{cases}1 & \text { si } k \neq 1 \text { et } \sigma(k)>\sigma(k-1) \\
0 & \text { si } k=1 \\
-1 & \text { si } k \neq 1 \text { et } \sigma(k)<\sigma(k-1)\end{cases}\right.
$$
Enfin, on pose $\varepsilon_{k}=\alpha_{\sigma^{-1}(k)}+\beta_{\sigma^{-1}(k)}$. On constate alors que
$$
\mathbf{W}(\sigma)=\sum_{k=1}^{n}\left(\alpha_{k}+\beta_{k}\right) \sigma(k)=\sum_{k=1}^{n} k \varepsilon_{k} .
$$
On note maintenant $\mathcal{X}$ l'ensemble des $n$-uplets $\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ tels que
$\triangleright x_{1}+x_{2}+\ldots+x_{n}=0$ et
$\triangleright$ il existe deux indices $i$ et $j$ pour lesquels $x_{i}, x_{j} \in\{-1,+1\}$, et $x_{k} \in\{-2,0,2\}$ dès lors que $k \notin\{i, j\}$.
Par construction, le $n$-uplet $\left(\varepsilon_{1}, \ldots, \varepsilon_{n}\right)$ appartient à $\mathcal{X}$.
Plus généralement, on pose donc $\mathbf{W}(\mathbf{x})=\sum_{k=1}^{n} k x_{k}$ pour tout $n$-uplet $\mathbf{x} \in \mathcal{X}$, et on considère alors un $n$-tuplet $\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right) \in \mathcal{X}$ pour lequel $\mathbf{W}(y)$ est maximal.
L'inégalité du réordonnement indique que $y_{1} \leqslant y_{2} \leqslant \ldots \leqslant y_{n}$. Supposons en outre qu'il existe un indice $i$ pour lequel $y_{i}=0$. Si $i \geqslant 2$ et $y_{i-1}=-1$, remplacer $y_{i}$ et $y_{i+1}$ par -2 et 1 augmente $\mathbf{W}(\mathbf{y})$ de 2 . De même, si $i \leqslant n-1$ et $y_{i+1}=1$, remplacer $y_{i}$ et $y_{i+1}$ par -1 et 2 augmente $\mathbf{W}(\mathbf{y})$ de 2. Puisque le $n$-uplet y contient nécessairement des coordonnées égales à $\pm 1$, ses coordonnées sont donc toutes non nulles.
Enfin, soit $a$ le nombre d'indices $i$ pour lesquels $y_{i}=-2$, et $b$ le nombre d'indices $i$ pour lesquels $y_{i}=2$. On sait que $y_{1}=\ldots=y_{a}=-2, y_{a+1}= \pm 1, y_{a+2}= \pm 1$ et $y_{a+3}=\ldots=y_{n}=2$, de sorte que $a+b+2=n$ et que $-2 a+y_{a+1}+y_{a+2}+2 b=0$. Ainsi,
$$
a=\frac{2 n+y_{a+1}+y_{a+2}}{4}-1 \text { et } b=\frac{2 n-y_{a+1}-y_{a+2}}{4}-1 .
$$
On distingue alors trois cas, en fonction de valeurs de $y_{a+1}$ et $y_{a+2}$ :
1. Si $y_{a+1}=y_{a+2}=-1$, alors $a=(n-3) / 2, b=(n-1) / 2$, donc
$$
\mathbf{W}(\mathbf{y})=-2 \sum_{k=1}^{a} k-(a+1)-(a+2)+2 \sum_{k=a+3}^{n} k=\left(n^{2}-3\right) / 2
$$
2. Si $y_{a+1}=y_{a+2}=1$, alors $a=(n-1) / 2, b=(n-3) / 2$, donc
$$
\mathbf{W}(\mathbf{y})=-2 \sum_{k=1}^{a} k+(a+1)+(a+2)+2 \sum_{k=a+3}^{n} k=\left(n^{2}-3\right) / 2
$$
3. Si $y_{a+1}=-1$ et $y_{a+2}=1$, alors $a=b=(n-2) / 2$, ce qui est impossible puisque $n$ est impair.
Par conséquent, $\mathbf{W}(\sigma) \leqslant\left(n^{2}-3\right) / 2$.
Réciproquement, on pose $\ell=(n-1) / 2$, puis on note $\sigma$ la permutation de $\{1,2, \ldots, n\}$ définie par
$$
\begin{cases}\sigma(2 k-1)=\ell+1+k & \text { si } 1 \leqslant k \leqslant \ell \\ \sigma(2 k)=k & \text { si } 1 \leqslant k \leqslant \ell \\ \sigma(n)=\ell+1 & \end{cases}
$$

Cette permutation est associée au $n$-uplet $(-2, \ldots,-2,1,1,2, \ldots, 2)$ avec $\ell$ coordonnées égales à -2 et $\ell$ coordonnées égales à 2 , donc son poids vaut $\left(n^{2}-3\right) / 2$, comme montré dans le cas 2 ci-dessus.
En conclusion, le poids maximum recherché est $\left(n^{2}-3\right) / 2$, c'est-à-dire 2042219.
$\underline{\text { Solution alternative } n^{\circ} 1}$ Soit $n=2021$, et soit $\sigma$ une permutation de $\{1,2, \ldots, n\}$ de poids maximal. Ci-dessous, on pose $k=(n-1) / 2=1010$.
Supposons qu'il existe un entier $i$ tel que $2 \leqslant i \leqslant n-1$ et $\sigma_{i-1}<\sigma_{i}<\sigma_{i+1}$ ou $\sigma_{i-1}>\sigma_{i}>\sigma_{i+1}$. On note alors $\sigma^{\prime}$ la permutation de $\{1,2, \ldots, n\}$ définie par :
$$
\begin{aligned}
& \triangleright \sigma_{j}^{\prime}=\sigma_{j} \text { lorsque } 1 \leqslant j \leqslant i-1 ; \\
& \triangleright \sigma_{j}^{\prime}=\sigma_{j+1} \text { lorsque } i \leqslant j \leqslant n-1 ; \\
& \triangleright \sigma_{n}^{\prime}=\sigma_{i} .
\end{aligned}
$$
Comme $\left|\sigma_{i}-\sigma_{i+1}\right|+\left|\sigma_{i+1}-\sigma_{i+2}\right|=\left|\sigma_{i}-\sigma_{i+2}\right|$, le poids de $\sigma^{\prime}$ vaut celui de $\sigma$ auquel on ajoute $\left|\sigma_{n}-\sigma_{1}\right|$, ce qui contredit la maximalité du poids de $\sigma$.
En outre, et quitte à remplacer $\sigma$ par sa permutation « miroir horizontal », c'est-à-dire à remplacer chaque terme $\sigma_{j}$ par $n+1-\sigma_{j}$, ce qui ne changera rien au poids de $\sigma$, on suppose sans perte de généralité que $\sigma_{1}<\sigma_{2}$. L'absence d'un entier $i$ tel que décrit au paragraphe précédent nous assure alors que $\sigma_{2 j-1}<\sigma_{2 j}>\sigma_{2 j+1}$ pour tout entier $j$ tel que $1 \leqslant j \leqslant k$.
Le poids de $\sigma$ vaut alors
$$
\sum_{j=1}^{k} 2 \sigma_{2 j}-\sigma_{1}-\sigma_{n}-\sum_{j=1}^{k-1} 2 \sigma_{2 j+1}
$$
Comme $\sigma$ ne prend pas deux fois la même valeur, on a
$$
\begin{aligned}
& \sum_{j=1}^{k} 2 \sigma_{2 j} \leqslant \sum_{j=n+1-k}^{n} 2 j=n(n+1)-(n-k)(n+1-k)=3 k^{2}+3 k \text { et } \\
& \sum_{j=1}^{k-1} 2 \sigma_{2 j+1}+\sigma_{1}+\sigma_{n} \geqslant \sum_{j=1}^{k-1} 2 j+k+(k+1)=k(k-1)+(2 k+1)=k^{2}+k+1
\end{aligned}
$$
Par conséquent, le poids de $\sigma$ ne peut pas dépasser $2 k^{2}+2 k-1=2042219$.
Réciproquement, la permutation indiquée à la fin de la solution précédente est bien de poids 2042219, et il s'agit donc bien là du poids maximal.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
cb098472-18ba-5a8f-9bea-511d89e6a847
| 604,942
|
Maena and Théodore are playing a game. They play on a square grid consisting of $99 \times 99$ cells. Two cells are considered adjacent if they share a vertex or a side.
Initially, Maéna numbers the cells of the grid from 1 to $99^{2}$, in an arbitrary manner. Théodore then places a token on one of the cells of the square, and he allows himself moves of the following form: he can move the token from one cell to another only if these cells are adjacent and if the new cell on which the token lands has a strictly greater number than the old cell.
What is the minimum number of moves Théodore can guarantee, regardless of how Maena placed her integers?
|
First, Théodore can always manage to make at least three moves. To do this, he just needs to select a $2 \times 2$ square within the $99 \times 99$ square, then traverse its four cells, which are necessarily adjacent since they share a vertex.
Conversely, here is how Maena can proceed to prevent Théodore from making more than three moves. She numbers the rows and columns from 1 to 99, then groups the $99 \times 99$ cells of the square into four categories:
$\triangleright$ Category 1 contains the cells located in an odd row and an odd column;
$\triangleright$ Category 2 contains the cells located in an odd row and an even column;
$\triangleright$ Category 3 contains the cells located in an even row and an odd column;
$\triangleright$ Category 4 contains the cells located in an even row and an even column.
Two cells of the same category are never adjacent.
Next, Maena places her integers, in ascending order, in cells of category 1, then category 2, then category 3, and finally category 4. Thus, Théodore can never move between two cells of the same category, and even less so to a lower category. Any move therefore increases the category of the cell in which Théodore's token is located, thus limiting him to a maximum of three moves.
Comment from the graders In a problem like this, there are two things to do:
1. Propose a strategy that Maena can use to prevent Théodore from making too many moves;
2. Propose a strategy that Théodore can use to make at least $k$ moves (with $k$ to be chosen) regardless of Maena's strategy.
Among the students who looked for a strategy for Maena, many concluded that she could prevent Théodore from making more than three moves. Among those who looked for a strategy for Théodore, many concluded that he could always make at least three moves.
Unfortunately, few students thought to look for strategies for both Maena and Théodore. In particular, proving that Théodore can always make at least three moves when Maena follows the strategy she chose is almost useless, since Maena still has $\left(99^{2}\right)!-1 \approx 10^{34864}$ alternative ways to number the grid, and it remains to prove that Théodore can also make at least three moves in each of these $\left(99^{2}\right)!-1$ cases.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Maena et Théodore jouent à un jeu. Ils jouent sur une grille carrée formée de $99 \times 99$ cases. On considère que deux cases sont adjacentes si elles ont un sommet ou un côté en commun.
Initialement, Maéna numérote les cases de la grille de 1 à $99^{2}$, de façon arbitraire. Théodore place alors un jeton sur l'une des cases du carré, puis il s'autorise des mouvements de la forme suivante : il peut déplacer le jeton d'une case vers une autre uniquement si ces cases sont adjacentes et si la nouvelle case sur laquelle se retrouve le jeton a un numéro strictement plus grand que l'ancienne case.
Combien de mouvements au minimum Théodore peut-il garantir, quelle que soit la manière avec laquelle Maena a placé ses entiers?
|
Tout d'abord, Théodore peut toujours se débrouiller pour effectuer au moins trois mouvements. Pour ce faire, il lui suffit de sélectionner un carré de taille $2 \times 2$ à l'intérieur du carré de taille $99 \times 99$, puis d'en parcourir les quatre cases, qui sont nécessairement adjacentes puisqu'elles ont un sommet en commun.
Réciproquement, voici comment peut procéder Maena pour empêcher Théodore d'effecuter plus de trois mouvements. Elle numérote lignes et colonnes de 1 à 99 , puis regroupe les $99 \times 99$ cases du carré en quatre catégories :
$\triangleright$ la catégorie 1 contient les cases situées en une ligne et une colonne impaires;
$\triangleright$ la catégorie 2 contient les cases situées en une ligne impaire et une colonne paire;
$\triangleright$ la catégorie 3 contient les cases situées en une ligne paire et une colonne impaire;
$\triangleright$ la catégorie 4 contient les cases situées en une ligne et une colonne paires.
Deux cases de la même catégorie ne sont jamais adjacentes.
Ensuite, Maena place ses entiers, dans l'ordre croissant, dans des cases de catégorie 1, puis de catégorie 2, puis de catégorie 3, et enfin de catégorie 4. Ainsi, Théodore ne peut jamais se déplacer entre deux cases de même catégorie, et encore moins baisser de catégorie. Tout mouvement augmente donc la catégorie de la case dans laquelle se trouve le jeton de Théodore, qui se voit ainsi limité à effectuer au plus trois mouvements.
Commentaire des correcteurs Dans un problème tel que celui-ci, il y a deux choses à faire:
1. proposer une stratégie que pourra utiliser Maena pour empêcher Théodore de faire trop de mouvements;
2. proposer une stratégie que pourra utiliser Théodore pour faire au moins $k$ mouvements (avec $k$ à choisir) quelle que soit la stratégie de Maena.
Parmi les élèves qui ont recherché une stratégie pour Maena, nombreux sont ceux qui ont conclu qu'elle pouvait empêcher Théodore de faire plus de trois mouvements. Parmi ceux qui ont recherché une stratégie pour Théodore, nombreux sont ceux qui ont conclu qu'il pouvait toujours faire au moins trois mouvements.
Malheureusement, peu nombreux sont les élèves qui ont pensé à rechercher des stratégies pour Maena et pour Théodore. En particulier, démontrer que Théodore peut toujours faire au moins trois mouvements quand Maena suit la stratégie qu'elle a choisi est à peu près inutile, puisque Maena a encore $\left(99^{2}\right)!-1 \approx 10^{34864}$ manières alternatives de numéroter la grille, et qu'il reste alors à démontrer que Théodore peut aussi faire au moins trois mouvements dans chacun de ces $\left(99^{2}\right)!-1$ cas.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
9e0a5148-bf33-55c8-8dab-fe3a2ef05425
| 605,171
|
A permutation of the integers 1 to 2022 is a sequence $\sigma=\left(\sigma_{1}, \ldots, \sigma_{2022}\right)$ such that each element of the set $\{1, \ldots, 2022\}$ is equal to exactly one term $\sigma_{i}$. What is the smallest possible value that the sum
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{2022}}{2022}\right\rfloor
$$
can take when the integers $a_{1}, a_{2}, \ldots, a_{2022}$ form a permutation of the integers from 1 to 2022?
|
In general, let $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ denote the sum
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{n}}{n}\right\rfloor,
$$
and let $\mathcal{S}_{n}$ be the smallest value that $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ can take when the integers $a_{1}, a_{2}, \ldots, a_{n}$ form a permutation of the integers from 1 to $n$.
Given such a permutation, let $k$ be the integer such that $a_{k}=n$. Then, for every integer $i \leqslant k$, let $b_{i}$ be the rank of the integer $a_{i}$ within the set $\left\{a_{1}, \ldots, a_{k-1}\right\}$, i.e., the number of indices $j \leqslant k-1$ for which $a_{j} \leqslant a_{i}$. Since $a_{i} \geqslant b_{i}$, we observe that
$$
\begin{aligned}
\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right) & \geqslant\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{k}}{k}\right\rfloor \\
& \geqslant\left\lfloor\frac{b_{1}}{1}\right\rfloor+\left\lfloor\frac{b_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{b_{k-1}}{k-1}\right\rfloor+\left\lfloor\frac{n}{k}\right\rfloor \\
& \geqslant \mathcal{S}_{k-1}+\left\lfloor\frac{n}{k}\right\rfloor,
\end{aligned}
$$
with the convention that $\mathcal{S}_{0}=0$.
Furthermore, if $a_{1}, a_{2}, \ldots, a_{k-1}$ is a permutation of the integers from 1 to $k-1$ for which $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{k-1}\right)=\mathcal{S}_{k-1}$ and if we set $a_{i}=i-1$ for all $i \geqslant k+1$, we have
$$
\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)=\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{k-1}}{k-1}\right\rfloor+\left\lfloor\frac{n}{k}\right\rfloor=\mathcal{S}_{k-1}+\left\lfloor\frac{n}{k}\right\rfloor .
$$
We deduce that $\mathcal{S}_{n}=\min \left\{\mathcal{S}_{k-1}+\lfloor n / k\rfloor: 1 \leqslant k \leqslant n\right\}$.
We will now prove by induction on $n$ that $\mathcal{S}_{n}=\left\lceil\log _{2}(n+1)\right\rceil$ for all integers $n \geqslant 0$, which will allow us to assert that $\mathcal{S}_{2022}=\left\lceil\log _{2}(2023)\right\rceil=11$.
Indeed, this is true for $n=0$. Now let $n$ be a non-zero natural number, and let $k$ be an integer such that $1 \leqslant k \leqslant n$ and $\mathcal{S}_{n}=\mathcal{S}_{k-1}+\lfloor n / k\rfloor$. If we set $\lambda=\lfloor n / k\rfloor$, we observe that $k>n /(\lambda+1)$ and that
$$
2^{\lambda}=\sum_{i=0}^{\lambda}\binom{\lambda}{i} \geqslant\binom{\lambda}{0}+\binom{\lambda}{1}=1+\lambda
$$
so that
$$
\mathcal{S}_{n}=\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right) \geqslant \mathcal{S}_{k-1}+\lfloor n / k\rfloor \geqslant \log _{2}(k)+\lambda>\log _{2}\left(2^{\lambda} n /(\lambda+1)\right) \geqslant \log _{2}(n)
$$
This means that $2^{\mathcal{S}_{n}}>n$, or equivalently, $2^{\mathcal{S}_{n}} \geqslant n+1$, hence $\mathcal{S}_{n} \geqslant\left\lceil\log _{2}(n+1)\right\rceil$.
Conversely, let $k=\lceil(n+1) / 2\rceil$ and $\ell=\left\lceil\log _{2}((n+1) / 2)\right\rceil$. Since $(n+1) / 2 \leqslant 2^{\ell}$, we also know that $k \leqslant 2^{\ell}$, so
$$
\mathcal{S}_{n} \leqslant \mathcal{S}_{k-1}+\lfloor n / k\rfloor=\left\lceil\log _{2}(k)\right\rceil+1 \leqslant \ell+1=\left\lceil\log _{2}(n+1)\right\rceil,
$$
which concludes the induction.
Comment from the graders: The problem was difficult, and many students claimed to have a complete solution incorrectly. Many candidates only treated specific cases, or did not prove their claims, which can result in losing many points.
Be sure to justify all your claims: it is better to spend a little more time on a problem and solve it completely, rather than trying to get points on a more difficult problem (which clearly was not successful on problem 7).
|
11
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une permutation des entiers 1 à 2022 est une suite $\sigma=\left(\sigma_{1}, \ldots, \sigma_{2022}\right)$ telle que chaque élément de l'ensemble $\{1, \ldots, 2022\}$ soit égal à exactement un terme $\sigma_{i}$. Quelle est la plus petite valeur possible que peut prendre la somme
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{2022}}{2022}\right\rfloor
$$
lorsque les entiers $a_{1}, a_{2}, \ldots, a_{2022}$ forment une permutation des entiers de 1 à 2022 ?
|
De manière générale, notons $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ la somme
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{n}}{n}\right\rfloor,
$$
et $\mathcal{S}_{n}$ la plus petite valeur que peut prendre $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ lorsque les entiers $a_{1}, a_{2}, \ldots, a_{n}$ forment une permutation des entiers de 1 à $n$.
Étant donnée une telle permutation, soit $k$ l'entier tel que $a_{k}=n$. Puis, pour tout entier $i \leqslant k$, soit $b_{i}$ le rang de l'entier $a_{i}$ au sein de l'ensemble $\left\{a_{1}, \ldots, a_{k-1}\right\}$, c'est-à-dire le nombre d'indices $j \leqslant k-1$ pour lesquels $a_{j} \leqslant a_{i}$. Puisque $a_{i} \geqslant b_{i}$, on constate alors que
$$
\begin{aligned}
\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right) & \geqslant\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{k}}{k}\right\rfloor \\
& \geqslant\left\lfloor\frac{b_{1}}{1}\right\rfloor+\left\lfloor\frac{b_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{b_{k-1}}{k-1}\right\rfloor+\left\lfloor\frac{n}{k}\right\rfloor \\
& \geqslant \mathcal{S}_{k-1}+\left\lfloor\frac{n}{k}\right\rfloor,
\end{aligned}
$$
avec la convention selon laquelle $\mathcal{S}_{0}=0$.
En outre, si $a_{1}, a_{2}, \ldots, a_{k-1}$ est une permutation des entiers de 1 à $k-1$ pour laquelle $\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{k-1}\right)=\mathcal{S}_{k-1}$ et si l'on pose $a_{i}=i-1$ pour tout $i \geqslant k+1$, on a bien
$$
\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right)=\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\ldots+\left\lfloor\frac{a_{k-1}}{k-1}\right\rfloor+\left\lfloor\frac{n}{k}\right\rfloor=\mathcal{S}_{k-1}+\left\lfloor\frac{n}{k}\right\rfloor .
$$
On en déduit que $\mathcal{S}_{n}=\min \left\{\mathcal{S}_{k-1}+\lfloor n / k\rfloor: 1 \leqslant k \leqslant n\right\}$.
Nous allons maintenant démontrer par récurrence sur $n$ que $\mathcal{S}_{n}=\left\lceil\log _{2}(n+1)\right\rceil$ pour tout entier $n \geqslant 0$, ce qui nous permettra d'affirmer que $\mathcal{S}_{2022}=\left\lceil\log _{2}(2023)\right\rceil=11$.
En effet, c'est bien le cas pour $n=0$. Soit maintenant $n$ un entier naturel non nul, puis $k$ un entier tel que $1 \leqslant k \leqslant n$ et $\mathcal{S}_{n}=\mathcal{S}_{k-1}+\lfloor n / k\rfloor$. Si l'on pose $\lambda=\lfloor n / k\rfloor$, on constate que $k>n /(\lambda+1)$ et que
$$
2^{\lambda}=\sum_{i=0}^{\lambda}\binom{\lambda}{i} \geqslant\binom{\lambda}{0}+\binom{\lambda}{1}=1+\lambda
$$
de sorte que
$$
\mathcal{S}_{n}=\mathcal{S}\left(a_{1}, a_{2}, \ldots, a_{n}\right) \geqslant \mathcal{S}_{k-1}+\lfloor n / k\rfloor \geqslant \log _{2}(k)+\lambda>\log _{2}\left(2^{\lambda} n /(\lambda+1)\right) \geqslant \log _{2}(n)
$$
Cela signifie que $2^{\mathcal{S}_{n}}>n$, ou encore que $2^{\mathcal{S}_{n}} \geqslant n+1$, donc que $\mathcal{S}_{n} \geqslant\left\lceil\log _{2}(n+1)\right\rceil$.
Réciproquement, soit $k=\lceil(n+1) / 2\rceil$ et $\ell=\left\lceil\log _{2}((n+1) / 2)\right\rceil$. Pusique $(n+1) / 2 \leqslant 2^{\ell}$, on sait aussi que $k \leqslant 2^{\ell}$, de sorte que
$$
\mathcal{S}_{n} \leqslant \mathcal{S}_{k-1}+\lfloor n / k\rfloor=\left\lceil\log _{2}(k)\right\rceil+1 \leqslant \ell+1=\left\lceil\log _{2}(n+1)\right\rceil,
$$
ce qui conclut la récurrence.
Commentaire des correcteurs Le problème était difficile, et nombreux sont les élèves qui ont prétendu à tort avoir une solution complète. Beaucoup de candidats ont traité uniquement des cas particuliers, ou ne prouvent pas leurs affirmations, ce qui peut faire perdre beaucoup de points.
Attention à bien justifier toutes ses affirmations : il vaut mieux passer un peu plus de temps sur un problème et le réussir totalement, que de tenter d'avoir des points sur un problème plus difficile (ce qui manifestement n'a pas été réussi sur le problème 7).
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-4.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
878ac4fb-62a4-59ca-898c-ed8f63909356
| 605,335
|
The government of Bosnia and Herzegovina has decided to implement a new system of license plates. Each license plate must contain 8 digits, each of which can be $0,1,2,3,4,5,6,7,8$ or 9. Furthermore, two distinct license plates must always have at least two different digits. For example, if it puts the license plate 00000000 into circulation, the government cannot put the license plate 00010000 into circulation.
Find the maximum number of license plates that the government can put into circulation.
|
We will show that the maximum number of available plates is equal to $10^{7}$.
First, we say that two plates belong to the same family if their first seven digits are different. Each family contains ten plates, so there are $10^{7}$ distinct families. However, the government cannot put more than one plate from each family into circulation. Therefore, it can put at most $10^{7}$ plates into circulation.
Conversely, the government can manage to create $10^{7}$ plates as follows: the last digit of each plate is equal to the negative of the sum, modulo 10, of the first seven digits of the plate. Thus, it creates one plate per family.
Moreover, the sum of the digits of each plate is divisible by 10. But if two plates differ in exactly one digit, the sums of their digits cannot be equal to each other (modulo 10). Therefore, two distinct plates always differ in at least two digits, which concludes the proof.
Graders' Comments This difficult exercise was fully solved by only one student. Several students found interesting constructions or lower bounds, allowing them, for example, to assert that at least $10^{4}$ or $8!=40320$ license plates could be put into place.
However, very few students managed to obtain the appropriate construction to reach $10^{7}$ plates. The most reliable way to achieve such a construction was to look at what would happen with 1 digit, then 2 digits, then 3 digits, and to identify regular patterns that appeared in all relevant copies: an integer was equal to the sum of the others.
Furthermore, and independently, very few students attempted to find an upper bound on the number of possible plates, even though a simple application of the pigeonhole principle would have sufficed here, and many students seemed to have an intuition about it. It is always a pity not to seek upper and lower bounds when trying to estimate a quantity, and even if these bounds are not necessarily easy to find.
|
10^7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Le gouvernement de Bosnie-Herzégovine a décidé de mettre en place un nouveau système de plaques d'immatriculations. Chaque plaque d'immatriculation devra contenir 8 chiffres, chacun pouvant valoir $0,1,2,3,4,5,6,7,8$ ou 9 . En outre, deux plaques d'immatriculation distinctes devront toujours avoir au moins deux chiffres différents. Par exemple, s'il met en circulation la plaque 00000000 , le gouvernement ne pourra pas mettre en circulation la plaque 00010000 .
Trouver le nombre maximum de plaques d'immatriculation que le gouvernement peut mettre en circulation.
|
Nous allons montrer que le nombre maximal de plaques disponibles est égal à $10^{7}$.
Tout d'abord, on dit que deux plaques font partie de la même famille si leur sept premiers chiffres sont différents. Chaque famille contient dix plaques, donc il y a $10^{7}$ familles distinctes. Or, le gouvernement ne peut pas mettre en circulation plus d'une plaque par famille. Il met donc en circulation au plus $10^{7}$ plaques.
Réciproquement, il peut se débrouiller pour créer $10^{7}$ plaques en procédant comme suit : le dernier chiffre de chaque plaque est égal à l'opposé de la somme, modulo 10, des sept premiers chiffres de la plaque. Ainsi, il crée bien une plaque par famille.
En outre, la somme des chiffres de chaque plaque est divisible par 10. Mais si deux plaques ont exactement un chiffre de différence, les sommes de leurs chiffres ne peuvent être égales l'une à l'autre (modulo 10). Ainsi, deux plaques distinctes ont toujours au moins deux chiffres de différence, ce qui conclut.
Commentaire des correcteurs Cet exercice difficile n'a été résolu intégralement que par un seul élève. Plusieurs élèves ont trouvé des constructions ou bornes inférieures intéressantes, leur permettant par exemple d'affirmer que l'on pourrait mettre en place au moins $10^{4}$ ou $8!=40320$ plaques d'immatriculation.
Cependant, très peu d'élèves ont réussi à obtenir la construction adéquate permettant d'atteindre $10^{7}$ plaques. Le moyen le plus sûr d'obtenir une telle construction consistait à regarder ce qui se passait si on avait droit à 1 chiffre, puis 2 chiffres, puis 3 chiffres, et à repérer des motifs réguliers qui apparaissaient dans toutes les copies concernées : un entier était égal à la somme des autres.
Par ailleurs, et indépendamment, très peu d'élèves ont entrepris de trouver une borne supérieure sur le nombre de plaques possibles, alors même qu'une simple application du principe des tiroirs suffisait ici et que de nombreux élèves semblaient en avoir l'intuition. Il est toujours dommage de ne pas chercher des bornes supérieures et inférieures quand on cherche à évaluer une quantité, et même si ces bornes ne sont pas nécessairement faciles à trouver.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
160bfca7-09b3-5fc1-98b3-15347e5cf9b6
| 605,372
|
Anna and Baptiste are playing the following game. At the beginning of the game, 2022 white squares are placed in front of them, numbered from 1 to 2022. Then, each in turn, starting with Anna, they choose a white square and color it in the color of their choice: either red or blue. The game ends after 2022 turns, that is, when the last white square is colored.
Anna's score is then equal to the number of integers $a \leqslant 2019$ such that the two squares numbered $a$ and $a+3$ are of the same color. Anna wants to have the highest score possible; Baptiste wants Anna's score to be as low as possible. What is the highest score Anna can ensure, regardless of the moves Baptiste chooses to play?
|
For simplicity, we will say that two integers $a$ and $b$ are friends if $a = b \pm 3$. We will say that $a$ is pretty if $a = b - 3$ and if $a$ and $b$ are colored the same color, and that $a$ is ugly if $a = b - 3$ and if $a$ and $b$ are colored different colors: Anna therefore wants to maximize the number of pretty integers at the end of the game. If $a$ or $b$ is not yet colored, $a$ is neither pretty nor ugly.
Furthermore, for each integer $k = 0, 1,$ and $2$, we will denote by $\mathcal{E}_{k}$ the set of integers $n$ such that $1 \leq n \leq 2022$ and $n \equiv k \pmod{3}$. We say that a set $\mathcal{E}_{k}$ is started as soon as at least one cell whose number is in $\mathcal{E}_{k}$ has been colored.
We will first prove that Anna can ensure a score of at least 1008 points. To do this, the strategy Anna adopts is as follows.
1. If there exists an integer $a$ that is not yet colored, and a friend, say $b$, is colored, then Anna chooses such an integer $a$ and colors it the same color as $b$; if several integers $a$ and/or $b$ were available, any of these integers $a$ and $b$ will do.
2. If, on the contrary, no such integer $a$ exists, Anna colors a random white cell.
In case 1, the integer $\min \{a, b\}$ becomes pretty, which increases Anna's score by at least 1. In case 2, if a set $\mathcal{E}_{k}$ was already started when Anna is about to play, it means that all its elements were already colored; consequently, with her move, Anna starts a new set $\mathcal{E}_{k}$.
In particular, case 2 occurs at most 3 times in the game, and since Anna plays 1011 moves, case 1 occurs at least 1008 times in the game. As expected, Anna thus ensures a final score of at least 1008 points.
Conversely, we will now prove that Baptiste can prevent Anna from scoring more than 1008 points, regardless of the moves she decides to make. To do this, the strategy Baptiste adopts is as follows.
1. If there exists an integer $a$ that is not yet colored, and a friend, say $b$, is colored, then Baptiste chooses such an integer $a$ and colors it the opposite color to that of $b$; if several integers $a$ and/or $b$ were available, any of these integers $a$ and $b$ will do.
2. If, on the contrary, no such integer $a$ exists, Baptiste colors a random white cell. In case 1, the integer $\min \{a, b\}$ becomes ugly. In case 2, any set $\mathcal{E}_{k}$ already started when Baptiste is about to play was already colored; if $n$ sets were started at that moment, it means that $2022n / 3 = 674n$ moves had already been played, and thus it was actually Anna's turn to play.
Consequently, case 2 never occurs, and since Baptiste plays 1011 moves, there are at least 1011 ugly integers at the end of the game. Moreover, the three integers 2020, 2021, and 2022 will be neither pretty nor ugly. Among our 2022 integers, there are therefore at least $1011 + 3$ that will never be pretty, and Anna's score will thus never exceed $2022 - (1011 + 3) = 1008$.
Comment from the graders: This problem was solved unevenly, with students falling into two main categories: on the one hand, those, quite numerous, who managed to solve the problem; on the other hand, those, equally numerous, who, although they had a reasonable intuition of what could happen, failed to correctly define strategies for Anna and Baptiste.
Students in this second category simply described how, move by move, Anna and Baptiste were supposed to play if they wanted to play optimally. However, this could in no way constitute a proof: in general, when giving a strategy for a player, it is necessary to indicate what moves this player should make even if their opponent plays in an apparently random manner. Incidentally, doing so generally results in much simpler proofs.
Furthermore, the description these students gave was almost systematically incorrect, as Baptiste is not required to directly counter Anna to prevent her from scoring more than 1008 points. For example, if Anna colors the integer 1 red, a relevant strategy for Baptiste could be to color the integer 7 blue.
It is therefore unfortunate that many students end up with very few points, thinking they had solved the problem. For these students, it will be very important to remember the proper way to define a strategy for a player, as described above.
|
1008
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Anna et Baptiste joue au jeu suivant. Au début du jeu sont placées devant eux 2022 cases blanches, numérotées de 1 à 2022. Puis, chacun son tour, en commençant par Anna, ils choisissent une case blanche et la colorient de la couleur de leur choix : soit en rouge, soit en bleu. La partie s'arrête au bout de 2022 tours de jeu, c'est-à-dire au moment où la dernière case blanche est coloriée.
Le score d'Anna est alors égal au nombre d'entiers $a \leqslant 2019$ tels que les deux cases de numéros $a$ et $a+3$ sont de la même couleur. Anna souhaite avoir le score le plus élevé possible; Baptiste souhaite que le score d'Anna soit le plus faible possible. Quel est le score maximal qu'Anna peut s'assurer d'obtenir quels que soient les coups que Baptiste choisira de jouer?
|
Pour plus de simplicité, on dira que deux entiers $a$ et $b$ sont amis si $a=b \pm 3$. On dira que $a$ est joli si $a=b-3$ et si $a$ et $b$ sont coloriés de la même couleur, et que $a$ est laid si $a=b-3$ et si $a$ et $b$ s'ils sont coloriés de couleurs différentes : Anna souhaite donc maximiser le nombre d'entiers jolis à la fin de la partie. Si $a$ ou $b$ n'est pas encore colorié, $a$ n'est ni joli, ni laid.
En outre, pour chacun des entiers $k=0,1$ et 2 , nous noterons $\mathcal{E}_{k}$ l'ensemble des entiers $n$ tels que $1 \leqslant n \leqslant 2022$ et $n \equiv k(\bmod 3)$. On dit qu'un ensemble $\mathcal{E}_{k}$ est entamé dès lors qu'au moins une case dont le numéro est dans $\mathcal{E}_{k}$ a été coloriée.
Nous allons tout d'abord démontrer qu'Anna peut s'assurer de gagner au moins 1008 points. Pour ce faire, la stratégie qu'adopte Anna est la suivante.
1. S'il existe un entier $a$ qui n'est pas encore colorié, et dont un ami, disons $b$, est colorié, alors Anna choisit un tel entier $a$ et le colorie de la même couleur que $b$; si plusieurs entiers $a$ et/ou $b$ étaient disponibles, n'importe lesquels de ces entiers $a$ et $b$ feront l'affaire.
2. Si, au contraire, aucun tel entier $a$ n'existe, Anna colorie au hasard une case blanche.
Dans le cas 1, l'entier $\min \{a, b\}$ devient joli, ce qui augmente le score d'Anna d'au moins 1. Dans le cas 2 , si un ensemble $\mathcal{E}_{k}$ était déjà entamé au moment où Anna s'apprête à jouer, c'est que tous ses éléments étaient déjà coloriés; par conséquent, avec son coup, Anna entame un nouvel ensemble $\mathcal{E}_{k}$.
En particulier, le cas 2 survient au plus 3 fois dans la partie, et comme Anna joue 1011 coups, le cas 1 survient au moins 1008 fois dans la partie. Comme prévu, Anna s'assure donc un score final d'au moins 1008 points.
Réciproquement, nous allons maintenant démontrer que Baptiste peut empêcher Anna de gagner strictement plus de 1008 points, et ce quels que soient les coups qu'elle décidera de jouer. Pour ce faire, la stratégie qu'adopte Baptiste est la suivante.
1. S'il existe un entier $a$ qui n'est pas encore colorié, et dont un ami, disons $b$, est colorié, alors Baptiste choisit un tel entier $a$ et le colorie de la couleur opposée à celle $b$; si plusieurs entiers $a$ et/ou $b$ étaient disponibles, n'importe lesquels de ces entiers $a$ et $b$ feront l'affaire.
2. Si, au contraire, aucun tel entier $a$ n'existe, Baptiste colorie au hasard une case blanche. Dans le cas 1, l'entier $\min \{a, b\}$ devient laid. Dans le cas 2 , tout ensemble $\mathcal{E}_{k}$ déjà entamé au moment où Baptiste s'apprête à jouer était déjà colorié; si $n$ ensembles étaient entamés à ce moment-là, cela signifie que $2022 n / 3=674 n$ coups avaient déjà été joués, et donc que c'était en fait à Anna de jouer.
Par conséquent, le cas 2 ne survient jamais, et comme Baptiste joue 1011 coups, il y a au moins 1011 entiers laids à la fin de la partie. Par ailleurs, les trois entiers 2020, 2021 et 2022 ne seront ni jolis, ni laids. Parmi nos 2022 entiers, il y en a donc au moins $1011+3$ qui ne seront jamais jolis, et le score d'Anna ne pourra ainsi jamais dépasser $2022-(1011+3)=1008$.
Commentaire des correcteurs Ce problème a été résolu de manière inégale, les élèves se départageant en deux catégories principales : d'une part ceux, assez nombreux, qui ont réussi le problème; d'autre part ceux, tout aussi nombreux, qui, bien qu'ayant une intuition raisonnable de ce qui pouvait se passer, n'ont pas réussi à définir correctement des stratégies pour Anna et Baptiste.
Les élèves de cette deuxième catégorie ont simplement raconté comment, coup après coup, Anna et Baptiste étaient selon eux censés jouer s'ils voulaient jouer de façon optimale. Cependant, cela ne pouvait en aucun cas constituer une preuve: de manière générale, quand on donne une stratégie pour un joueur, il faut donc indiquer quels coups ce joueur doit jouer y compris si son adversaire joue de manière apparemment anarchique. Accessoirement, s'y prendre ainsi permet en général d'avoir des preuve beaucoup plus simples.
En outre, la description que ces élèves donnaient était à peu près systématiquement fausse, car Baptiste n'est pas obligé de contrer directement Anna pour l'empêcher d'avoir plus de 1008 points. Par exemple, si Anna colorie l'entier 1 en rouge, une stratégie pertinente pour Baptiste peut consister à colorier l'entier 7 en bleu.
Il est donc dommage que de nombreux élèves finissent par n'obtenir que très peu de points alors qu'ils pensaient avoir résolu le problème. Pour ces élèves, il sera très important de retenir la manière adéquate de définir une stratégie pour un joueur, manière décrite cidessus.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-5.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
99e1af5d-b061-55b1-b714-6050f3d2bf6c
| 605,653
|
An Olympic sequence is a sequence $s_{1}, s_{2}, \ldots, s_{2023}$ where each of the 2023 terms is equal to 1 or -1. A slowly increasing sequence is a sequence of integers $t_{1}, t_{2}, \ldots, t_{n}$ such that $1 \leqslant t_{1}<t_{2}<\cdots<t_{n} \leqslant 2023$, and each of the $n-1$ differences $t_{i+1}-t_{i}$ is 1 or 2.
Find the largest integer $C$ such that, for any Olympic sequence $s_{1}, s_{2}, \ldots, s_{2023}$, there exists an integer $n \geqslant 1$ and a slowly increasing sequence $t_{1}, t_{2}, \ldots, t_{n}$ of length $n$ such that
$$
\left|s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}\right| \geqslant C
$$
|
A study of small cases leads us to consider the sequence $\left(s_{i}\right)$ whose terms are $+1,+1,-1,-1,+1,+1,-1,-1, \ldots$, and which seems to be a "worst" case. It is divided into 1011 blocks of length 2, denoted $B_{1}, B_{2}, \ldots, B_{1011}$, and a block $B_{1012}$ of length 1: the sequence is $(-1)^{i+1}$ on each block $B_{i}$.
We now consider a sum of the form $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}$. Its terms $s_{t_{i}}$ have been chosen from consecutive blocks $B_{u}, B_{u+1}, \ldots, B_{u+v-1}$. At most $(v+1) / 2$ of these 1 blocks contain terms +1; the others contain terms -1. Among the numbers $s_{t_{1}}, s_{t_{2}}, \ldots, s_{t_{n}}$, there are therefore at most $v+1$ that are +1 and at least $(v-1) / 2$ that are -1. Since $v \leqslant 1012$, we deduce that $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}} \leqslant(v+1)-(v-1) / 2=(v+3) / 2<508$. We show similarly that $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}>-508$, so that $C \leqslant 507$.
Conversely, let $(s_{i})$ be any Olympic sequence. By replacing each term with its opposite if necessary, we assume that $(s_{i})$ contains at least 1012 terms equal to +1. As before, we subdivide this sequence into maximal blocks on which $(s_{i})$ is constant; these blocks are denoted $B_{1}, B_{2}, \ldots, B_{k}$, and their lengths are denoted $b_{1}, b_{2}, \ldots, b_{k}$. Assuming $B_{1}$ is empty if necessary, we assume that $s_{j}=(-1)^{i}$ when $j$ belongs to a block $B_{i}$. Thus, $b_{2}+b_{4}+b_{6}+\cdots \geqslant 1012$ and $1011 \geqslant b_{1}+b_{3}+b_{5}+\cdots$
We then choose $\left(t_{i}\right)$ as the non-increasing sequence that takes all values $j$ belonging to a block $B_{2}, B_{4}, B_{6}, \ldots$ or located in an even position of a block $B_{1}, B_{3}, B_{5}, \ldots$ In this way, among the numbers $s_{t_{1}}, s_{t_{2}}, \ldots$, there are $b_{2}+b_{4}+b_{6}+\cdots$ that are +1; each of $\left\lfloor b_{1} / 2\right\rfloor+\left\lfloor b_{3} / 2\right\rfloor+\left\lfloor b_{5} / 2\right\rfloor+\cdots$ other terms is -1. We conclude that
$$
\begin{aligned}
s_{t_{1}}+s_{t_{2}}+\cdots & =\left(b_{2}+b_{4}+b_{6}+\cdots\right)-\left(\left\lfloor b_{1} / 2\right\rfloor+\left\lfloor b_{3} / 2\right\rfloor+\left\lfloor b_{5} / 2\right\rfloor+\cdots\right) \\
& \geqslant\left(b_{2}+b_{4}+b_{6}+\cdots\right)-\left(b_{1}+b_{3}+b_{5}+\cdots\right) / 2 \\
& \geqslant 1012-1011 / 2>506
\end{aligned}
$$
so that $s_{t_{1}}+s_{t_{2}}+\cdots \geqslant 507$.
In conclusion, the integer $C$ sought is $C=507$.
Examiner's Comment This problem was generally well done. However, many students rushed into things, neglecting to rigorously prove why, in the case of a sequence $1,1,-1,-1,1,1,-1,-1, \ldots$, it was impossible to have a sum greater than 507 (in absolute value). Generally, any use of a phrase such as "it is clear that" immediately suggests to the examiner that, contrary to what the student claims, "he does not see at all how to prove that."
Moreover, many students rushed into things in their handling of edge cases, thus proposing answers equal to 506 or 508 rather than 507. It is a pity to lose a point in this way when one has essentially finished the problem.
|
507
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une suite olympique est une suite $s_{1}, s_{2}, \ldots, s_{2023}$ dont chacun des 2023 termes est égal à 1 ou à -1 . Une suite peu croissante est une suite d'entiers $t_{1}, t_{2}, \ldots, t_{n}$ telle que $1 \leqslant t_{1}<t_{2}<\cdots<t_{n} \leqslant 2023$, et dont chacune des $n-1$ différences $t_{i+1}-t_{i}$ vaut 1 ou 2 .
Trouver le plus grand entier $C$ tel que, pour toute suite olympique $s_{1}, s_{2}, \ldots, s_{2023}$, il existe un entier $n \geqslant 1$ et une suite peu croissante $t_{1}, t_{2}, \ldots, t_{n}$ de longueur $n$ tels que
$$
\left|s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}\right| \geqslant C
$$
|
Une étude des petits cas nous pousse à nous intéresser à la suite $\left(s_{i}\right)$ dont les termes valent $+1,+1,-1,-1,+1,+1,-1,-1, \ldots$, et qui semble être un «pire» cas. On la subdivise en 1011 blocs de longueur 2 , notés $B_{1}, B_{2}, \ldots, B_{1011}$, et un bloc $B_{1012}$ de longueur 1 : la suite vaut $(-1)^{i+1}$ sur chaque bloc $B_{i}$.
On considère maintenant une somme de la forme $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}$. Ses termes $s_{t_{i}}$ ont été choisis parmi des blocs consécutifs $B_{u}, B_{u+1}, \ldots, B_{u+v-1}$. Au plus $(v+1) / 2$ de ces 1 blocs contiennent des termes +1 ; les autres contiennent des termes -1 . Parmi les nombres $s_{t_{1}}, s_{t_{2}}, \ldots, s_{t_{n}}$, il y en a donc au plus $v+1$ qui valent +1 et au moins $(v-1) / 2$ qui valent -1 . Puisque $v \leqslant 1012$, on en déduit que $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}} \leqslant(v+1)-(v-1) / 2=(v+3) / 2<508$. On montre de même que $s_{t_{1}}+s_{t_{2}}+\cdots+s_{t_{n}}>-508$, de sorte que $C \leqslant 507$.
Réciproquement, soit ( $s_{i}$ ) une suite olympique quelconque. Quitte à remplacer chaque terme par son opposé, on suppose que $\left(s_{i}\right)$ compte au moins 1012 termes égaux à +1 . Comme précédemment, on subdivise cette suite en blocs maximaux sur lesquels ( $s_{i}$ ) est constante; ces blocs sont notés $B_{1}, B_{2}, \ldots, B_{k}$, et leurs longueurs sont notés $b_{1}, b_{2}, \ldots, b_{k}$. Quitte à supposer que $B_{1}$ est vide, on suppose que $s_{j}=(-1)^{i}$ lorsque $j$ appartient à un bloc $B_{i}$. Ainsi, $b_{2}+b_{4}+b_{6}+\cdots \geqslant 1012$ et $1011 \geqslant b_{1}+b_{3}+b_{5}+\cdots$
On choisit ensuite $\left(t_{i}\right)$ comme la suite peu croissante qui prend toutes les valeurs $j$ appartenant à un bloc $B_{2}, B_{4}, B_{6}, \ldots$ ou bien situées en position paire d'un bloc $B_{1}, B_{3}, B_{5}, \ldots$ De la sorte, parmi les nombres $s_{t_{1}}, s_{t_{2}}, \ldots$, il y en a $b_{2}+b_{4}+b_{6}+\cdots$ qui valent +1 ; chacun $\operatorname{des}\left\lfloor b_{1} / 2\right\rfloor+\left\lfloor b_{3} / 2\right\rfloor+\left\lfloor b_{5} / 2\right\rfloor+\cdots$ autres termes vaut -1 . On en conclut que
$$
\begin{aligned}
s_{t_{1}}+s_{t_{2}}+\cdots & =\left(b_{2}+b_{4}+b_{6}+\cdots\right)-\left(\left\lfloor b_{1} / 2\right\rfloor+\left\lfloor b_{3} / 2\right\rfloor+\left\lfloor b_{5} / 2\right\rfloor+\cdots\right) \\
& \geqslant\left(b_{2}+b_{4}+b_{6}+\cdots\right)-\left(b_{1}+b_{3}+b_{5}+\cdots\right) / 2 \\
& \geqslant 1012-1011 / 2>506
\end{aligned}
$$
de sorte que $s_{t_{1}}+s_{t_{2}}+\cdots \geqslant 507$.
En conclusion, l'entier $C$ recherché vaut $C=507$.
Commentaire des correcteurs Ce problème a été très bien réussi dans l'ensemble. Cependant, de nombreux élèves sont allés trop vite en besogne, négligeant de démontrer rigoureusement pourquoi, dans le cas d'une suite $1,1,-1,-1,1,1,-1,-1, \ldots$, il était impossible d'avoir de somme supérieure à 507 (en valeur absolue). De manière générale, toute utilisation d'un vocable tel que « on voit bien que » suggère immédiatement au correcteur que, au contraire de ce que l'élève affirme, « il ne voit pas du tout comment démontrer que».
Par ailleurs, de nombreux élèves sont allés trop vite en besogne dans leur gestion des cas de bords, proposant ainsi des réponses égales à 506 ou à 508 plutôt que 507. Il est dommage de perdre ainsi un point alors que l'on a essentiellement fini le problème.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-5.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
b7091557-a136-5be0-9350-aeb494038655
| 605,688
|
It is said that an integer $n \geqslant 1$ is Japanese if it admits three divisors $d_{1}, d_{2}$, and $d_{3}$ such that $1 \leqslant d_{1}<d_{2}<d_{3}$ and $d_{1}+d_{2}+d_{3}=2022$.
What is the smallest Japanese integer?
|
First, we notice that $2 \times 2019$ is Japanese, since the integers 1, 2, and 2019 are among its divisors.
Let $n$ be the smallest Japanese integer: it is the LCM of the integers $d_{1}, d_{2}$, and $d_{3}$. We then set $a_{k}=n / d_{k}$, so that $1 \leqslant a_{3}<a_{2}<a_{1}$, that $\operatorname{GCD}\left(a_{1}, a_{2}, a_{3}\right)=1$ and that
$$
n\left(\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}\right)=2022=2 \times 3 \times 337.
$$
To minimize $n$, we want to maximize the sum of the fractions $1 / a_{i}$, so we seek to minimize the integers $a_{i}$ themselves. We start by looking at the small values of $a_{2}$ and $a_{3}$.
For example, if $a_{3}=1$ and $a_{2}=2$, our equation becomes
$$
\left(3 a_{1}+2\right) d_{1}=2^{2} \times 3 \times 337
$$
Thus, $3 a_{1}+2$ is a factor of $2^{2} \times 3 \times 337$ congruent to 2 modulo 3, that is, 2 or $2 \times 337=674$. The first case is impossible because $3 a_{1}+2 \geqslant 3 \times 3+2>2$. We deduce that $a_{1}=672 / 3=224$, and then that $d_{1}=2 \times 3=6$, so $n=6 \times 224=1344$. In particular, 1344 is a multiple of 1 and 2, so it is a Japanese integer, with $d_{1}=6, d_{2}=672$, and $d_{3}=1344$.
We are therefore looking for a possible Japanese integer $n<1344$. In such a case, if we write the sum $1 / a_{1}+1 / a_{2}+1 / a_{3}$ as an irreducible fraction $p / q$, our equality becomes
$$
n \times p=2 \times 3 \times 337 \times q,
$$
and $p$ is coprime with $q$, so it divides $2 \times 3 \times 337$. Furthermore, since we can no longer have $a_{3}=1$ and $a_{2}=2$, we necessarily have $a_{2} \geqslant 3$. Thus,
$$
1+\frac{1}{3}+\frac{1}{a_{3}} \geqslant \frac{p}{q}=\frac{2022}{n}>\frac{2022}{1344}>1+\frac{1}{2}=1+\frac{1}{3}+\frac{1}{6}
$$
so $a_{1} \leqslant 5$.
We are left to study the triplets $\left(a_{1}, a_{2}, a_{3}\right)=(4,3,1),(5,3,1),(5,4,1),(4,3,2),(5,3,2)$, $(5,4,2)$, and $(5,4,3)$, which lead us respectively to the fractions $p / q=19 / 12,23 / 15,29 / 20$, $13 / 12,31 / 30,19 / 20$, and $47 / 60$. The numerator $p$ never divides $2 \times 3 \times 337$, so none of these cases is possible.
In conclusion, the smallest Japanese integer is $n=1344$.
|
1344
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un entier $n \geqslant 1$ est nippon s'il admet trois diviseurs $d_{1}, d_{2}$ et $d_{3}$ tels que $1 \leqslant d_{1}<d_{2}<d_{3}$ et $d_{1}+d_{2}+d_{3}=2022$.
Quel est le plus petit entier nippon?
|
Tout d'abord, on remarque que $2 \times 2019$ est nippon, puisque les entiers 1, 2 et 2019 figurent parmi ses diviseurs.
Soit $n$ l'entier nippon minimal : il s'agit du PPCM des entiers $d_{1}, d_{2}$ et $d_{3}$. On pose alors $a_{k}=n / d_{k}$, de sorte que $1 \leqslant a_{3}<a_{2}<a_{1}$, que $\operatorname{PGCD}\left(a_{1}, a_{2}, a_{3}\right)=1$ et que
$$
n\left(\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}\right)=2022=2 \times 3 \times 337 .
$$
Pour minimiser $n$, on souhaite maximiser la somme des fractions $1 / a_{i}$, donc on cherche à minimiser les entiers $a_{i}$ eux-mêmes. On commence donc par regarder les petites valeurs de $a_{2}$ et de $a_{3}$.
Par exemple, si $a_{3}=1$ et $a_{2}=2$, notre équation devient
$$
\left(3 a_{1}+2\right) d_{1}=2^{2} \times 3 \times 337
$$
Ainsi, $3 a_{1}+2$ est un facteur de $2^{2} \times 3 \times 337$ congru à 2 modulo 3 , c'est-à-dire 2 ou $2 \times 337=674$. Le premier cas est impossible car $3 a_{1}+2 \geqslant 3 \times 3+2>2$. On en déduit que $a_{1}=672 / 3=224$, puis que $d_{1}=2 \times 3=6$, de sorte que $n=6 \times 224=1344$. En particulier, 1344 est un multiple de 1 et de 2, donc il s'agit d'un entier nippon, avec $d_{1}=6, d_{2}=672$ et $d_{3}=1344$.
On recherche donc un éventuel entier nippon $n<1344$. Dans un tel cas, si on écrit la somme $1 / a_{1}+1 / a_{2}+1 / a_{3}$ sous forme d'une fraction irréductible $p / q$, notre égalité devient
$$
n \times p=2 \times 3 \times 337 \times q,
$$
et $p$ est premier avec $q$, donc divise $2 \times 3 \times 337$. En outre, puisque l'on ne peut plus avoir $a_{3}=1$ et $a_{2}=2$, on a nécessairement $a_{2} \geqslant 3$. Ainsi,
$$
1+\frac{1}{3}+\frac{1}{a_{3}} \geqslant \frac{p}{q}=\frac{2022}{n}>\frac{2022}{1344}>1+\frac{1}{2}=1+\frac{1}{3}+\frac{1}{6}
$$
donc $a_{1} \leqslant 5$.
Il nous reste donc à étudier les triplets $\left(a_{1}, a_{2}, a_{3}\right)=(4,3,1),(5,3,1),(5,4,1),(4,3,2),(5,3,2)$, $(5,4,2)$ et $(5,4,3)$, qui nous amènent respectivement aux fractions $p / q=19 / 12,23 / 15,29 / 20$, $13 / 12,31 / 30,19 / 20$ et $47 / 60$. Le numérateur $p$ ne divise jamais $2 \times 3 \times 337$, donc aucun de ces cas n'est possible.
En conclusion, le plus petit entier nippon est $n=1344$.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
ba3f6019-3149-52b8-bad1-bf322052cfde
| 605,742
|
Let $n \geqslant 3$ be an integer. For each pair of prime numbers $p$ and $q$ such that $p<q \leqslant n$, Morgane writes the sum $p+q$ on the board. She then notes $\mathcal{P}(n)$ as the product of all these sums. For example, $\mathcal{P}(5)=(2+3) \times(2+5) \times(3+5)=280$.
Find all values of $n \geqslant 3$ for which $n$ ! divides $\mathcal{P}(n)$.
Note: If two sums $p+q$ formed from two different pairs are equal to each other, Morgane writes them both. For example, if $n=13$, she writes both sums $3+13$ and $5+11$.
|
Let $n$ be a potential solution, and let $r$ be the largest prime number such that $r \leqslant n$. Since $r$ divides $n$!, it divides $\mathcal{P}(n)$, so there exist two prime numbers $p$ and $q$ such that $p<q \leqslant n$ and $r$ divides $p+q$. By the maximality of $r$, we know that $p+q<2 r$, so $p+q=r$. Since $q$ and $r$ are odd, $p$ is therefore even, and $p=2$.
Similarly, there exist two prime numbers $s$ and $t$ such that $s<t \leqslant n$ and $q$ divides $s+t$. We will prove that $q-2$ is prime. Indeed, if $t \leqslant q$, then $s+t=q$, so $s=2$ and $t=q-2$. Otherwise, $t=r=q+2$, so $q<t+s<2 q+2<3 q$, which means $t+s=2 q$ and $s=q-2$.
In particular, 3 divides one of the three prime numbers $q-2, q$ and $q+2$; it must necessarily be $q-2$, which means that $q-2=3$ and that $q+2=r=7$. Thus, $n \geqslant 7$, and $n$! divides
$$
\mathcal{P}(n)=(2+3) \times(2+5) \times(2+7) \times(3+5) \times(3+7) \times(5+7)=2^{6} \times 3^{3} \times 5^{2} \times 7
$$
Since $2 \times 4 \times 6 \times 8=2^{7} \times 3$ does not divide $\mathcal{P}(n)$, we must have $n=7$.
Conversely, $n=7$ is indeed a solution, as $7!=2^{4} \times 3^{2} \times 5 \times 7$.
Comment from the graders: The problem was rarely attempted; it's a pity, as a number of students had good ideas. However, as mentioned in the comment on problem 5, the writing was problematic: do not hesitate to look at the comment on problem 5 to see various recurring errors.
## Senior Problems
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $n \geqslant 3$ un entier. Pour chaque couple de nombres premiers $p$ et $q$ tels que $p<q \leqslant n$, Morgane a écrit la somme $p+q$ au tableau. Elle note ensuite $\mathcal{P}(n)$ le produit de toutes ces sommes. Par exemple, $\mathcal{P}(5)=(2+3) \times(2+5) \times(3+5)=280$.
Trouver toutes les valeurs de $n \geqslant 3$ pour lesquelles $n$ ! divise $\mathcal{P}(n)$.
Note : Si deux sommes $p+q$ formées à partir de deux couples différents sont égales l'une à l'autre, Morgane les écrit toutes deux. Par exemple, si $n=13$, elle écrit bien les deux sommes $3+13$ et $5+11$.
|
Soit $n$ une solution éventuelle, et soit $r$ le plus grand nombre premier tel que $r \leqslant n$. Puisque $r$ divise $n$ !, il divise $\mathcal{P}(n)$, donc il existe deux nombres premiers $p$ et $q$ tels que $p<q \leqslant n$ et $r$ divise $p+q$. Par maximalité de $r$, on sait que $p+q<2 r$, de sorte que $p+q=r$. Puisque $q$ et $r$ sont impairs, $p$ est donc pair, et $p=2$.
De même, il existe deux nombres premiers $s$ et $t$ tels que $s<t \leqslant n$ et $q$ divise $s+t$. Nous allons démontrer que $q-2$ est premier. En effet, si $t \leqslant q$, alors $s+t=q$, donc $s=2$ et $t=q-2$. Sinon, $t=r=q+2$, donc $q<t+s<2 q+2<3 q$, de sorte que $t+s=2 q$ et $s=q-2$.
En particulier, 3 divise l'un des trois nombres premiers $q-2, q$ et $q+2$;il s'agit nécessairement de $q-2$, ce qui signifie que $q-2=3$ et que $q+2=r=7$. Ainsi, $n \geqslant 7$, et $n$ ! divise
$$
\mathcal{P}(n)=(2+3) \times(2+5) \times(2+7) \times(3+5) \times(3+7) \times(5+7)=2^{6} \times 3^{3} \times 5^{2} \times 7
$$
Puisque $2 \times 4 \times 6 \times 8=2^{7} \times 3$ ne divise pas $\mathcal{P}(n)$, on a nécessairement $n=7$.
Réciproquement, $n=7$ est bien une solution, car $7!=2^{4} \times 3^{2} \times 5 \times 7$.
Commentaire des correcteurs L'exercice a été très peu abordé; c'est dommage, puisqu'un certain nombre d'élèves ont eu de bonnes idées. Néanmoins, comme dit dans le commentaire du problème 5 , la rédaction a posé problème : n'hésitez pas à regarder le commentaire du problème 5 pour voir différentes erreurs récurrentes.
## Problèmes Senior
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
8f5c194a-a30a-5cf3-8698-ac36c77f4ab4
| 605,828
|
We denote by $\mathcal{F}$ the set of functions $f: \mathbb{R} \mapsto \mathbb{R}$ such that
$$
f(x+f(y))=f(x)+f(y)
$$
for all real numbers $x$ and $y$. Find all rational numbers $q$ such that, for every function $f \in \mathcal{F}$, there exists a real number $z$ such that $f(z)=q z$.
|
Let $f$ be a function belonging to $\mathcal{F}$. For all real numbers $x$ and $y$, it is immediately shown by induction that $f(x+k f(y))=f(x)+k f(y)$ for any integer $k \geqslant 0$. We denote this equality by $E_{k}(x, y)$.
If we set $x^{\prime}=x-k f(y)$, we also observe that $f\left(x^{\prime}\right)=f\left(x^{\prime}+k f(y)\right)-k f(y)=f(x)-k f(y)$. Thus, the equality $E_{k}(x, y)$ is valid even when $k \leqslant 0$.
In particular, if $k \neq 0$ and $z=k f(0)$, the equality $E_{k}(0,0)$ indicates that $f(z)=(k+1) z / k$. This means that all rational numbers of the form $q=1+1 / k$, where $k$ is a non-zero integer, are solutions to the problem.
Conversely, let $a / b$ be an irreducible fraction such that $a / b-1$ is not the reciprocal of an integer, i.e., such that $a \neq b \pm 1$. We then consider the function $f$ defined as follows: for any real number $x$ such that $0 \leqslant x<1$ and any integer $k$, we set
$$
f(k+x)= \begin{cases}k+1 & \text { if } a x \text { is an integer that divides } b-a ; \\ k & \text { otherwise. }\end{cases}
$$
Since $f$ takes integer values, we verify that
$$
f(k+x+f(\ell+y))=f(k+\ell+f(y)+x)=k+\ell+f(y)+f(x)=f(k+x)+f(\ell+x),
$$
which means that $f \in \mathcal{F}$.
Suppose there exists an integer $k$ and a real number $z$ such that $0 \leqslant z<1$ and $f(k+z)=a(k+z) / b$. If $a z$ is not an integer that divides $b-a$, then
$$
a k+a z \equiv b f(k+z) \equiv b k \equiv a k \quad(\bmod b-a),
$$
which is absurd. Thus, $a z$ is an integer that divides $b-a$, and
$$
a k \equiv a(k+z) \equiv b f(k+z) \equiv b(k+1) \equiv a(k+1) \quad(\bmod b-a) .
$$
But then $b-a$ divides $a$, and thus also divides $b$, and even $\operatorname{PGCD}(a, b)=1$, which contradicts the fact that $a-b \neq \pm 1$. Therefore, the fraction $a / b$ is not a solution to the problem.
In conclusion, the solutions to the problem are the fractions of the form $1+1 / k$, where $k$ is a non-zero integer.
Comment from the graders: The problem was difficult and divided into two parts. The first part was to identify the rational solutions by iterating the equation to obtain a formula of the form $f(x+k f(y))=f(x)+k f(y)$ for any integer $k$, which uses elementary reasoning on functional equations. The second part, showing that the rationals found are indeed the only ones, required significantly more ideas, notably constructing somewhat pathological functions that are solutions. This second part was barely touched upon by the students.
We should also note frequent and crossed errors that should no longer be found in a selection test copy:
$\triangleright$ Many students misread the statement. Whether they thought that $q$ had to satisfy the equality $f(z)=q z$ for all $z$ (instead of a single $z$) or that $q$ had to satisfy $f(z)=q z$ for a function $f$ (instead of all functions $f$), students should have realized their mistake by seeing the (very quick, or even too quick) conclusion they reached.
$\triangleright$ Many students claim that the only solutions are the functions $x \mapsto x+c$ with $c$ real. Once again, it was possible to avoid this pitfall by critically examining the final solution obtained (which did not use the rationality of $q$, for example). The sources of errors are often that students, after obtaining that $f(f(y))=f(y)+f(0)$, set $x=f(y)$, obtain $f(x)=x+c$, and conclude, forgetting that the variable $x$ does not necessarily cover $\mathbb{R}$, but only the image of $f$, which is not necessarily surjective. More daring students tried to differentiate the functional equation, which should be avoided when there are no regularity assumptions on $f$.
|
1+1/k
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On note $\mathcal{F}$ l'ensemble des fonctions $f: \mathbb{R} \mapsto \mathbb{R}$ telles que
$$
f(x+f(y))=f(x)+f(y)
$$
pour tous les réels $x$ et $y$. Trouver tous les nombres rationnels $q$ tels que, pour toute fonction $f \in \mathcal{F}$, il existe un réel $z$ tel que $f(z)=q z$.
|
Soit $f$ une fonction appartenant à $\mathcal{F}$. Pour tous réels $x$ et $y$, on montre par récurrence immédiate que $f(x+k f(y))=f(x)+k f(y)$ pour tout entier $k \geqslant 0$. On note $E_{k}(x, y)$ cette égalité.
Si l'on pose $x^{\prime}=x-k f(y)$, on constate aussi que $f\left(x^{\prime}\right)=f\left(x^{\prime}+k f(y)\right)-k f(y)=f(x)-k f(y)$. Ainsi, l'égalité $E_{k}(x, y)$ est valide même lorsque $k \leqslant 0$.
En particulier, si $k \neq 0$ et $z=k f(0)$, l'égalité $E_{k}(0,0)$ indique que $f(z)=(k+1) z / k$. Cela signifie que tous les nombres rationnels de la forme $q=1+1 / k$, lorsque $k$ est un entier non nul, sont des solutions du problème.
Réciproquement, soit $a / b$ une fraction irréductible telle que $a / b-1$ n'est pas l'inverse d'un entier, c'est-à-dire telle que $a \neq b \pm 1$. On considère alors la fonction $f$ définie comme suit : pour tout réel $x$ tel que $0 \leqslant x<1$ et tout entier $k$, on pose
$$
f(k+x)= \begin{cases}k+1 & \text { si } a x \text { et un entier que divise } b-a ; \\ k & \text { sinon. }\end{cases}
$$
Puisque $f$ est à valeurs entières, on vérifie bien que
$$
f(k+x+f(\ell+y))=f(k+\ell+f(y)+x)=k+\ell+f(y)+f(x)=f(k+x)+f(\ell+x),
$$
ce qui signifie que $f \in \mathcal{F}$.
Supposons qu'il existe un entier $k$ et un réel $z$ tels que $0 \leqslant z<1$ et $f(k+z)=a(k+z) / b$. Si $a z$ n'est pas un entier que divise $b-a$, alors
$$
a k+a z \equiv b f(k+z) \equiv b k \equiv a k \quad(\bmod b-a),
$$
ce qui est absurde. Ainsi, $a z$ est un entier que divise $b-a$, et
$$
a k \equiv a(k+z) \equiv b f(k+z) \equiv b(k+1) \equiv a(k+1) \quad(\bmod b-a) .
$$
Mais alors $b-a$ divise $a$, donc divise aussi $b$, et même $\operatorname{PGCD}(a, b)=1$, ce qui contredit le fait que $a-b \neq \pm 1$. Par conséquent, la fraction $a / b$ n'est pas une solution du problème.
En conclusion, les solutions du problème sont les fractions de la forme $1+1 / k$, où $k$ est un entier relatif non nul.
Commentaire des correcteurs Le problème était difficile et se divisait en deux parties. La première partie était d'identifier les rationnels solutions en itérant l'équation pour avoir une formule de la forme $f(x+k f(y))=f(x)+k f(y)$ pour tout entier $k$, ce qui utilise des raisonnements élémentaires sur les équations fonctionnelles. La deuxième partie, consistant à montrer que les rationnels trouvés sont bien les seuls, demandait nettement plus d'idées et notamment de construire des fonctions solutions un peu pathologiques. Cette deuxième partie a été très peu effleurée par les élèves.
Signalons tout de même des erreurs croisées fréquemment et qu'il ne faudrait plus trouver dans une copie de test de sélection :
$\triangleright$ Beaucoup d'élèves ont mal lu l'énoncé. Que ce soit parce qu'ils pensaient que $q$ devait satisfaire l'égalité $f(z)=q z$ pour tout $z$ (au lieu d'un seul $z$ ) ou bien parce qu'ils pensaient que $q$ devait satisfaire $f(z)=q z$ pour une fonction $f$ (au lieu de toutes les fonctions $f$ ), les élèves auraient dû se rendre compte de leur méprise en voyant la conclusion (très rapide, voire trop rapide) à laquelle ils aboutissaient.
$\triangleright$ Beaucoup d'élèves prétendent que les seules fonctions solutions sont les $x \mapsto x+c$ avec $c$ réel. Une fois encore, il était possible d'éviter cet écueil en ayant un regard critique sur la solution finale obtenue (qui n'utilisait pas le caractère rationnel de $q$, par exemple). Les sources d'erreurs sont bien souvent que les élèves, après avoir obtenu que $f(f(y))=f(y)+f(0)$, posent $x=f(y)$, obtiennent $f(x)=x+c$ et concluent, en oubliant que la variable $x$ ne parcourt pas forcément $\mathbb{R}$, mais seulement l'image de $f$, qui n'est pas nécessairement surjective. D'autres élèves plus téméraires ont voulu dériver l'équation fonctionnelle, ce dont il faut se garder quand on n'a aucune hypothèse de régularité sur $f$.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
b61d5dec-73c8-5e84-bb1e-422b22428921
| 605,846
|
In chess, the winner receives 1 point and the loser 0 points. In the event of a draw (remis), each player receives $1 / 2$ point.
Fourteen chess players, no two of whom were the same age, participated in a tournament where each played against every other. After the tournament, a ranking list was created. In the case of two players with the same number of points, the younger one received a better ranking.
After the tournament, Jan noticed that the top three players had a total number of points exactly equal to the total number of points of the last nine players. Jörg added that the number of games that ended in a draw was maximized. Determine the number of drawn games.
|
The total number of points of the last nine players is at least (9*8):2 = 36 points (because if each of the nine played only against another of the nine, then there would already be 36 points in total, as one point is awarded in each match). The total number of points of the top three, however, is at most $13+12+11=36$ points, if they win all their games against the remaining 13 players.
It follows that the last nine players do not win any of their games against the others, and the top three win all their games, although they can play to a draw against each other.
The number of drawn matches (which, according to Jörg, is maximized!) must therefore be $3+1+36=40$.
|
40
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Beim Schachspiel erhält der Sieger 1 Punkt und der Besiegte 0 Punkte. Bei Unentschieden (Remis) erhält jeder der Spieler $1 / 2$ Punkt.
Vierzehn Schachspieler, von denen keine zwei gleich alt waren, trugen einen Wettbewerb aus, in dem jeder gegen jeden spielte. Nach Abschluss des Wettbewerbs wurde eine Rangliste erstellt. Von zwei Spielern mit gleicher Punktezahl, erhält der Jüngere eine bessere Platzierung.
Nach dem Wettbewerb stellte Jan fest, dass die drei Bestplatzierten insgesamt genau so viele Punkte erhielten wie die Gesamtzahl der Punkte der letzten neun Spieler. Jörg bemerkte dazu, dass dabei die Zahl der unentschieden ausgegangenen Spiele maximal war. Man ermittle die Anzahl der unentschiedenen Spiele.
|
Die Gesamtzahl der Punkte der letzten neun Spieler beträgt mindestens (9.8):2 = 36 Punkte (denn wenn nur jeder der neun gegen einen anderen der neun spielen würde, dann wären es, da in jeder Partie ein Punkt vergeben wird, insgesamt schon 36 Punkte). Die Gesamtzahl der drei Erstplatzierten ist aber höchstens $13+12+11=36$ Punkte, falls sie alle Spiele gegen die restlichen 13 Spieler gewinnen würden.
Es folgt also, dass die letzten neun Spieler keines der Spiele mit den anderen gewinnen und die drei ersten, alle, wobei sie untereinander durchaus unentschieden spielen können.
Die Anzahl der unentschieden gespielten Partien (die ja gemäß Jörg maximal ist!) muss also $3+1+36=40$ sein.
|
{
"resource_path": "Germany_TST/segmented/de-2003-loes_awkl1_03.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Lösung\n"
}
|
0cf5fd74-bc08-5e5b-9e7b-3acde2ca7a5f
| 606,030
|
A function $f$ is given by $f(x)+f\left(1-\frac{1}{x}\right)=1+x$ for $x \in \mathbb{R} \backslash\{0,1\}$.
Determine a formula for $f$.
|
Let $x \in \mathbb{R} \backslash\{0,1\}$ and $y=1-\frac{1}{x}$ and $z=\frac{1}{1-x}$. It is easy to see that together with $x$, $y$ and thus also $z$ belong to $\mathbb{R} \backslash\{0,1\}$. Substituting $y$ and $z$ into the original equation leads to:
$$
f\left(1-\frac{1}{x}\right)+f\left(\frac{1}{1-x}\right)=2-\frac{1}{x} \text { and } f\left(\frac{1}{1-x}\right)+f(x)=1+\frac{1}{1-x}
$$
Subtracting the last two relations gives:
$$
f(x)-f\left(1-\frac{1}{x}\right)=\frac{1}{1-x}+\frac{1}{x}-1
$$
and adding this to the original equation finally results in
$$
f(x)=\frac{1}{2}\left(\frac{1}{1-x}+\frac{1}{x}+x\right)=\frac{-x^{3}+x^{2}+1}{2 x(1-x)}
$$
|
\frac{-x^{3}+x^{2}+1}{2 x(1-x)}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Eine Funktion $f$ ist gegeben durch $f(x)+f\left(1-\frac{1}{x}\right)=1+x$ für $x \in \mathbb{R} \backslash\{0,1\}$.
Man ermittle eine Formel für $f$.
|
Sei $x \in \mathbb{R} \backslash\{0,1\}$ und $y=1-\frac{1}{x}$ und $z=\frac{1}{1-x}$. Es ist leicht einzusehen, dass zusammen mit $x$ auch $y$ und damit auch $z$ zu $\mathbb{R} \backslash\{0,1\}$ gehören. Einsetzen von $y$ und $z$ in die Ausgangsgleichung führt zu:
$$
f\left(1-\frac{1}{x}\right)+f\left(\frac{1}{1-x}\right)=2-\frac{1}{x} \text { und } f\left(\frac{1}{1-x}\right)+f(x)=1+\frac{1}{1-x}
$$
Durch Subtraktion der beiden letzten Beziehungen erhält man:
$$
f(x)-f\left(1-\frac{1}{x}\right)=\frac{1}{1-x}+\frac{1}{x}-1
$$
und nach Addition zur Ausgangsgleichung führt das schließlich zu
$$
f(x)=\frac{1}{2}\left(\frac{1}{1-x}+\frac{1}{x}+x\right)=\frac{-x^{3}+x^{2}+1}{2 x(1-x)}
$$
|
{
"resource_path": "Germany_TST/segmented/de-2004-loes_awkl1_04.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Lösung\n"
}
|
4a8cb5e0-dfc1-5d5e-81af-8f50a6091e79
| 606,074
|
Gegeben sind die positiven reellen Zahle $a$ und $b$ und die natürliche Zahl $n$.
Man ermittle in Abhängigkeit von $a, b$ und $n$ das größte der $n+1$ Glieder in der Entwicklung von $(a+b)^{n}$.
|
Das $k$-te Glied $\mathrm{G}(\mathrm{k})$ in der Entwicklung von $(\mathrm{a}+\mathrm{b})^{\mathrm{n}}$ ist gegeben durch die Formel: $G(k)=\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1}$, wobei $\binom{n}{0}=1$ und $1 \leq \mathrm{k} \leq \mathrm{n}+1$.
Da es endlich viele Glieder gibt und jede endliche Zahlenmenge (mindestens) ein maximales Element enthält, wird untersucht unter welchen Bedingungen das k-te Element maximal ist. Dafür müssen die folgenden Beziehungen gleichzeitig erfüllt sein: $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k} \cdot a^{n-k} \cdot b^{k}$ und $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k-2} \cdot a^{n-k+2} \cdot b^{k-2}$, wobei im letzten Fall $k \geq 2$ sein muss und eine dieser Ungleichungen streng ist (einfacher Nachweis!).
Das führt einerseits $\mathrm{zu} \frac{1}{n-k+1} \cdot a \geq \frac{1}{k} \cdot b$ und andererseits $\mathrm{zu} \frac{1}{k-1} \cdot b \geq \frac{1}{n-k+2} \cdot a$, woraus sowohl $\mathrm{n}+1 \geq \mathrm{k} \geq \frac{n b+b}{a+b}$, als auch $1 \leq \mathrm{k} \leq \frac{n b+2 b+a}{a+b}=\frac{n b+b}{a+b}+1$ folgt.
Falls $\mathrm{i}=\frac{n b+b}{a+b}$ nicht ganzzahlig ist, ist $\mathrm{G}(\mathrm{i})$ das größte Glied, andernfalls sind $\mathrm{G}(\mathrm{i})$ und $\mathrm{G}(\mathrm{i}+1)$ maximal.
Weitere maximale Glieder kann es nicht geben.
|
\frac{n b+b}{a+b}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Gegeben sind die positiven reellen Zahle $a$ und $b$ und die natürliche Zahl $n$.
Man ermittle in Abhängigkeit von $a, b$ und $n$ das größte der $n+1$ Glieder in der Entwicklung von $(a+b)^{n}$.
|
Das $k$-te Glied $\mathrm{G}(\mathrm{k})$ in der Entwicklung von $(\mathrm{a}+\mathrm{b})^{\mathrm{n}}$ ist gegeben durch die Formel: $G(k)=\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1}$, wobei $\binom{n}{0}=1$ und $1 \leq \mathrm{k} \leq \mathrm{n}+1$.
Da es endlich viele Glieder gibt und jede endliche Zahlenmenge (mindestens) ein maximales Element enthält, wird untersucht unter welchen Bedingungen das k-te Element maximal ist. Dafür müssen die folgenden Beziehungen gleichzeitig erfüllt sein: $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k} \cdot a^{n-k} \cdot b^{k}$ und $\binom{n}{k-1} \cdot a^{n-k+1} \cdot b^{k-1} \geq\binom{ n}{k-2} \cdot a^{n-k+2} \cdot b^{k-2}$, wobei im letzten Fall $k \geq 2$ sein muss und eine dieser Ungleichungen streng ist (einfacher Nachweis!).
Das führt einerseits $\mathrm{zu} \frac{1}{n-k+1} \cdot a \geq \frac{1}{k} \cdot b$ und andererseits $\mathrm{zu} \frac{1}{k-1} \cdot b \geq \frac{1}{n-k+2} \cdot a$, woraus sowohl $\mathrm{n}+1 \geq \mathrm{k} \geq \frac{n b+b}{a+b}$, als auch $1 \leq \mathrm{k} \leq \frac{n b+2 b+a}{a+b}=\frac{n b+b}{a+b}+1$ folgt.
Falls $\mathrm{i}=\frac{n b+b}{a+b}$ nicht ganzzahlig ist, ist $\mathrm{G}(\mathrm{i})$ das größte Glied, andernfalls sind $\mathrm{G}(\mathrm{i})$ und $\mathrm{G}(\mathrm{i}+1)$ maximal.
Weitere maximale Glieder kann es nicht geben.
|
{
"resource_path": "Germany_TST/segmented/de-2005-loes_awkl1_05.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Lösung\n"
}
|
9d5813f3-101a-5435-8968-8bc73a0727a1
| 606,139
|
Let $E=\{-1,0,1\}$ and $M$ be a set of lattice points in the plane. The points in $M$ are connected by a network of line segments (S) such that one can travel from any point in $M$ to any other point in $M$ without leaving (S). The line segments of the network can have endpoints other than the lattice points.
Determine the shortest total length of the network of line segments, if:
a) $M=\{(i, j) \mid i, j \in E$ and $i \cdot j=0\}$
b) $M=\{(i, j) \mid i, j \in E\}$
|
Part a): Due to symmetry, it initially suffices to find the optimal network of segments for the points \(O(0,0)\), \(A(1,0)\), and \(C(0,1)\). By reflecting at \(O\), one then obtains the desired network for the points in \(M\). By rotating the plane \(x O y\) around \(O\) by an angle of \(60^\circ\) (Fig. 1), the triangle \(\triangle O A C\) is transformed into the triangle \(\triangle O A' C'\), where the segment \(P'C'\) is the image of \(PC\). The shortest system of segments that connects the points \(O\), \(A\), and \(C\) as required has a total length equal to that of the segment \(A C'\).
Fig. 1
In the triangle \(\triangle OAC'\), however, \(AC' = \sqrt{2 - 2 \cos 150^\circ} = \sqrt{2 + \sqrt{3}}\) (by the Law of Cosines). By reflecting at the origin \(O\), one obtains a shortest system of segments for part a) with a total length of \(2 \sqrt{2 + \sqrt{3}} = \sqrt{2} + \sqrt{6}\).
Part b): Similarly, due to symmetry, it initially suffices to find the shortest system of segments for the points \(D(-1 \mid 1)\), \(O(0 \mid 0)\), \(A(1 \mid 0)\), \(B(1 \mid 1)\), and \(C(0 \mid 1)\). Since the distance from \(D\) to the other four points is at least 1, such a system has a total length of \(1 + \frac{\sqrt{2} + \sqrt{6}}{\sqrt{2}} = 1 + 1 + \sqrt{3} = 2 + \sqrt{3}\) (see Fig. 2).
Fig. 2
Thus,
(after reflecting at \(0\)) for part b) a total length of \(2(2 + \sqrt{3}) = 4 + 2 \sqrt{3}\) is obtained.
Remark: The point \(P\) from part a) is the Fermat point of the triangle \(\triangle OAC\); the sum of its distances to the vertices \(O\), \(A\), and \(C\) is minimal. Every triangle in which no angle is greater than or equal to \(120^\circ\) contains such a point in its interior. However, if, for example, in a triangle \(\triangle ABC\), \(\alpha \geq 120^\circ\), then \(AB + AC\) is minimal. These properties were likely first discovered by Evangelista Torricelli (1608 - 1647) and further investigated by Pierre Fermat (1601 - 1665).
|
4 + 2 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Sei $E=\{-1,0,1\}$ und $M$ eine Menge von Gitterpunkten der Ebene. Die Punkte aus $M$ sind so durch ein Streckennetz (S) miteinander verbunden, dass man von jedem Punkt aus M zu jedem anderen Punkt aus M gelangen kann ohne ( S ) zu verlassen. Dabei können die Strecken des Streckennetzes außer den Gitterpunkten auch andere Endpunkte enthalten.
Man ermittle die kürzeste Gesamtlänge des Streckennetzes, falls:
a) $M=\{(i, j) \mid i, j \in E$ und $i \cdot j=0\}$
b) $M=\{(i, j) \mid i, j \in E\}$
|
Teil a): Aus Symmetriegründen reicht es zunächst das günstigste Streckennetz für die Punkte $O(0,0)$, $A(1,0)$ und $C(0,1)$ zu finden. Durch Spiegelung an O erhält man dann das gewünschte Netz für die Punkte aus M. Durch eine Drehung der Ebene $x O y$ um O mit Drehwinkel $60^{\circ}$ (Fig. 1) wird das Dreieck $\triangle O A C$ in das Dreieck $\triangle O A^{\prime} C^{\prime}$ überführt, wobei die Strecke P'C' das Bild von PC ist. Das kürzeste Streckensystem, das die Punkte O, A und $C$ wie gefordert verbindet, hat also eine Gesamtlänge, die gleich jener der Strecke $A C^{\prime}$ ist.

Fig. 1
Im Dreieck $\triangle \mathrm{OAC}^{\prime}$ ist aber $\mathrm{AC}^{\prime}=\sqrt{2-2 \cos 150^{\circ}}=\sqrt{2+\sqrt{3}}$ (Kosinussatz). Durch Spiegelung am Ursprung O erhält man ein für Teil a) kürzestes Streckensystem mit einer Gesamtlänge von $2 \sqrt{2+\sqrt{3}}=\sqrt{2}+\sqrt{6}$.
Teil b): Ebenfalls aus Symmetriegründen reicht es zunächst das kürzeste Streckensystem für die Punkte $D(-1 \mid 1), O(0 \mid 0), A(1 \mid 0), B(1 \mid 1)$ und $C(0 \mid 1)$ zu finden. Da die Entfernung von D zu den restlichen vier Punkten mindestens 1 beträgt, hat ein solches System eine Gesamtlänge von $1+\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2}}=1+1+\sqrt{3}=2+\sqrt{3}$ (siehe Fig. 2).

Fig. 2
Damit ergibt
(nach Spiegelung an 0 ) für b) eine Gesamtlänge von $2(2+\sqrt{3})=4+2 \sqrt{3}$.
Bemerkung: Der Punkt $P$ aus Teil a) ist der Fermat-Punkt des Dreiecks $\triangle \mathrm{OAC}$; die Summe seiner Abstände zu den Eckpunkten O, A und C ist minimal. Jedes Dreieck, in dem kein Winkel größer-gleich $120^{\circ}$ ist, enthält im Inneren einen solchen Punkt. Ist aber z.B. in einem Dreieck $\triangle A B C \alpha \geq 120^{\circ}$, dann ist dort $A B+A C$ minimal. Diese Eigenschaften wurden wohl zum ersten Mal von Evangelista Torricelli (1608 - 1647) entdeckt und von Pierre Fermat (1601 - 1665) weiter untersucht.
|
{
"resource_path": "Germany_TST/segmented/de-2005-loes_awkl1_05.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
deb74947-24d2-5d9e-ae17-70eb66fafac6
| 606,149
|
Let $n$ be a positive integer greater than one and $B=\left\{1,2, \ldots, 2^{n}\right\}$. A subset $A$ of $B$ is called quirky if for any two distinct elements $x, y$ of $B$, whose sum is a power of two, it contains exactly one of them. How many quirky subsets does $B$ have?
|
The number is $2^{n+1}$. We argue by complete induction on $n$ and set $B_{n}=\left\{1,2, \ldots, 2^{n}\right\}$. Induction base, $n=1$. This case is clear: all four subsets of $B_{1}=\{1,2\}$ are quirky. Induction step, $n \longrightarrow n+1$. It is already known that $B_{n}$ has exactly $2^{n+1}$ quirky subsets. For each quirky set $A$ of $B_{n}$, construct the sets $C_{n}(A)=\left\{2^{n+1}-m \mid\right.$ $\left.m \in B_{n} \backslash A, m<2^{n}\right\}, M_{n}(A)=A \cup C_{n}(A)$ and $N_{n}(A)=M_{n}(A) \cup\left\{2^{n+1}\right\}$. Clearly, $A, C_{n}(A)$ and $\left\{2^{n+1}\right\}$ are pairwise disjoint. The sets $M_{n}(A)$ and $N_{n}(A)$ are quirky: For this, let $x, y$ be different elements of $B_{n+1}$, whose sum is a power of two; without loss of generality, assume $x<y$. In the case $1 \leq x<y \leq 2^{n}$, i.e., $x, y \in B_{n}$, exactly one of the two is contained in $M_{n}(A)$ or $N_{n}(A)$, since $A$ is quirky. In the case $1 \leq x \leq 2^{n}<y \leq 2^{n+1}$, we have $2^{n}<x+y<2^{n+2}$, so $x+y=2^{n+1}$; since $x \geq 1$, $y \neq 2^{n+1}$. By the choice of $C_{n}(A)$, either $x$ is in $A$ or $y$ is in $C_{n}(A)$. The case $2^{n}<x<y \leq 2^{n+1}$ cannot occur, as then $2^{n+1}<x+y<2^{n+2}$. - On the other hand, if $M$ is a quirky subset of $B_{n+1}$, then $A:=M \cap B_{n}$ is a quirky subset of $B_{n}$. The element $y=2^{n+1}-x$ of $B_{n+1}$ with $1 \leq x<2^{n}$ is contained in $M$ if and only if $x \in B_{n}$ is not contained in $A$, since $x+y=2^{n+1}$ is a power of two. The quirkiness of $M$ thus determines for all elements $y$ of $B_{n+1}$ with $2^{n}<y<2^{n+1}$ whether they are contained in $M$; only whether $2^{n+1}$ is an element is still free. Thus, $M$ equals either $M_{n}(A)$ or $N_{n}(A)$, and exactly two quirky subsets of $B_{n+1}$ can be assigned to each quirky subset of $B_{n}$. This completes the proof.
Remark. Often it was mistakenly assumed that the numbers $2^{n-1}$ and $2^{n}$ could not be elements of a quirky subset of $B_{n}$, since for no $x \in B_{n}$ with $x \neq 2^{n-1}$ the number $2^{n-1}+x$ is a power of two and the same phenomenon occurs with $2^{n}$. However, this situation only shows that for every $X \subseteq B_{n}-\left\{2^{n-1}, 2^{n}\right\}$ the four sets $X, X \cup\left\{2^{n-1}\right\}, X \cup\left\{2^{n}\right\}, X \cup\left\{2^{n-1}, 2^{n}\right\}$ are either all quirky or all unquirky subsets of $B_{n}$.
|
2^{n+1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Es seien $n$ eine positive ganze Zahl größer als Eins und $B=\left\{1,2, \ldots, 2^{n}\right\}$. Eine Teilmenge $A$ von $B$ heiße ulkig, wenn sie von je zwei verschiedenen Elementen $x, y$ von $B$, deren Summe eine Zweierpotenz ist, genau eines enthält. Wie viele ulkige Teilmengen hat $B$ ?
|
Die Anzahl ist $2^{n+1}$. Wir argumentieren mit vollständiger Induktion nach $n$ und setzen hierzu $B_{n}=\left\{1,2, \ldots, 2^{n}\right\}$. Induktionsanfang, $n=1$. Dieser Fall ist klar: alle vier Teilmengen von $B_{1}=\{1,2\}$ sind ulkig. Induktionsschritt, $n \longrightarrow n+1$. Es sei also bereits bekannt, daß $B_{n}$ genau $2^{n+1}$ viele ulkige Teilmengen hat. Für jede ulkige Menge $A$ von $B_{n}$ konstruiere die Mengen $C_{n}(A)=\left\{2^{n+1}-m \mid\right.$ $\left.m \in B_{n} \backslash A, m<2^{n}\right\}, M_{n}(A)=A \cup C_{n}(A)$ und $N_{n}(A)=M_{n}(A) \cup\left\{2^{n+1}\right\}$. Offenbar sind $A, C_{n}(A)$ und $\left\{2^{n+1}\right\}$ paarweise elementfremd. Die Mengen $M_{n}(A)$ und $N_{n}(A)$ sind ulkig: Hierzu seien $x, y$ verschiedene Elemente von $B_{n+1}$, deren Summe eine Zweierpotenz ist; ohne Einschränkung gelte $x<y$. $\operatorname{Im}$ Fall $1 \leq x<y \leq 2^{n}$, also $x, y \in B_{n}$, ist genau eines von beiden in $M_{n}(A)$ bzw. $N_{n}(A)$ enthalten, da $A$ ulkig ist. Im Fall $1 \leq x \leq 2^{n}<y \leq 2^{n+1}$ ist $2^{n}<x+y<2^{n+2}$, also $x+y=2^{n+1}$; wegen $x \geq 1$ ist $y \neq 2^{n+1}$. Nach Wahl von $C_{n}(A)$ liegt entweder $x$ in $A$ oder $y$ in $C_{n}(A)$. Der Fall $2^{n}<x<y \leq 2^{n+1}$ kann nicht auftreten, da dann $2^{n+1}<x+y<2^{n+2}$. - Ist andererseits $M$ ulkige Teilmenge von $B_{n+1}$, so ist offenbar $A:=M \cap B_{n}$ ulkige Teilmenge von $B_{n}$. Das Element $y=2^{n+1}-x$ von $B_{n+1}$ mit $1 \leq x<2^{n}$ ist genau dann in $M$ enthalten, wenn $x \in B_{n}$ nicht in $A$ enthalten ist, da $x+y=2^{n+1}$ Zweierpotenz ist. Die Ulkigkeit von $M$ legt also bei Kenntnis von $M \cap B_{n}$ für alle Elemente $y$ von $B_{n+1}$ mit $2^{n}<y<2^{n+1}$ fest, ob sie in $M$ enthalten sind; es steht nur noch frei, ob $2^{n+1}$ Element ist. Damit gleicht $M$ entweder $M_{n}(A)$ oder $N_{n}(A)$, und es lassen sich jeder ulkigen Teilmenge von $B_{n}$ genau zwei ulkige Teilmengen von $B_{n+1}$ zuordnen. Das beendet den Beweis.
Bemerkung. Oft wurde irrtümlich angenommen, die Zahlen $2^{n-1}$ und $2^{n}$ könnten gar nicht Elemente einer ulkigen Teilmenge von $B_{n}$ sein, da für kein $x \in B_{n}$ mit $x \neq 2^{n-1}$ die Zahl $2^{n-1}+x$ eine Zweierpotenz ist und das gleiche Phänomen bei $2^{n}$ auftritt. Diese Sachlage zeigt allerdings nur, daß für jedes $X \subseteq B_{n}-\left\{2^{n-1}, 2^{n}\right\}$ die vier Mengen $X, X \cup\left\{2^{n-1}\right\}, X \cup\left\{2^{n}\right\}, X \cup\left\{2^{n-1}, 2^{n}\right\}$ entweder gleichzeitig ulkige oder gleichzeitig unulkige Teilmengen von $B_{n}$ sind.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "1. Aufgabe\n",
"solution_match": "\nLösung."
}
|
46abbedd-1a74-5870-b3d3-ee37f53df14d
| 604,219
|
On a table, 2009 cards are laid out in a row. Initially, all cards have their white side up and their black side down. The cards are numbered from 1 to 2009.
Two players $A$ and $B$ take turns making a move, with $A$ starting first. Each move consists of the player selecting a card with number $k (k < 1969)$, whose white side is up, and then flipping the cards with numbers $k, k+1, k+2, \ldots, k+40$ in their positions. The last player who can make a valid move wins the game.
a) Determine whether this game necessarily ends.
b) For which of the two players does a winning strategy exist?
|
a) If the game does not end, then due to the at most $2^{2008}$ different possible game states, there must exist a periodically repeating sequence of states. Let $k$ be the smallest number of the cards that are flipped within this period. To flip the card with the number $k$ from black to white, however, a card with a smaller number than $k$ must be chosen - contradiction to the minimality! Therefore, the game must end after a finite number of moves.
b) We consider the cards with the numbers $41k$, where $1 \leq k \leq 48$. The highest of these cards with the number 1968 is the last one that can be selected. With each move, exactly one of these cards is flipped. Since the game ends when all cards up to the number 1968 are black, and because these cards are all white at the beginning, after each double move by $A$ and $B$, an even number of them are white again; $B$ thus always finds an odd number of white cards from this set and can always make a move. Therefore, $B$ necessarily wins the game, regardless of how he plays.
Hints: The finiteness can also be shown by translating the game states into a monotonically changing binary number. If the card with the number 1969 were also allowed to be selected in the problem statement, then $A$ would have a winning strategy. For part a), 4 points were awarded, and for part b), 6 points were awarded.
|
B
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Auf einem Tisch liegen nebeneinander 2009 Karten in einer Reihe. Zunächst ist bei allen Karten die Oberseite weiß und die Unterseite schwarz. Die Karten seien von 1 bis 2009 nummeriert.
Zwei Spieler $A$ und $B$ führend abwechselnd einen Spielzug aus, wobei $A$ beginnt. Jeder Spielzug besteht darin, dass der Spieler eine Karte mit der Nummer $k(k<1969)$ wählt, deren weiße Seite oben liegt, und anschließend die Karten mit den Nummern $k, k+1, k+2, \ldots, k+40$ auf ihren Plätzen umdreht. Der letzte Spieler, der einen gültigen Spielzug machen konnte, gewinnt das Spiel.
a) Man entscheide, ob dieses Spiel notwendigerweise endet.
b) Für welchen der beiden Spieler existiert eine Gewinnstrategie?
|
a) Wenn das Spiel nicht endet, dann muss wegen der höchstens $2^{2008}$ verschiedenen möglichen Spielzustände eine sich periodisch wiederholende Folge von Zuständen existieren. Dabei sei $k$ die kleinste Nummer der Karten, die innerhalb dieser Periode umgedreht werden. Um die Karte mit der Nummer $k$ von schwarz auf weiß umzudrehen, ist jedoch eine Karte mit einer kleineren Nummer als $k$ auszuwählen - Widerspruch zur Minimalität! Also muss das Spiel nach endlich vielen Zügen enden.
b) Wir betrachten die Karten mit den Nummern $41 k$, wobei $1 \leq k \leq 48$. Die höchste dieser Karten mit der Nummer 1968 ist die letzte, die ausgewählt werden kann. Bei jedem Spielzug wird genau eine dieser Karten umgedreht. Weil das Spiel endet, wenn alle Karten bis zur Nummer 1968 schwarz sind, und weil diese Karten zu Beginn alle weiß sind, ist nach jedem Doppelzug von $A$ und $B$ wieder eine gerade Anzahl von ihnen weiß; $B$ findet also stets eine ungerade Anzahl weißer Karten aus dieser Menge vor und kann stets ziehen. Daher gewinnt $B$ zwangsläufig das Spiel, egal wie er zieht.
Hinweise: Die Endlichkeit kann auch mit der Übersetzung der Spielzustände in eine monoton sich verändernde Binärzahl gezeigt werden. Würde in der Aufgabenstellung die Karte mit der Nummer 1969 auch zur Auswahl zugelassen, so hätte $A$ eine Gewinnstrategie. Für Teil a) wurden 4 P. und für Teil b) 6 P. vergeben.
|
{
"resource_path": "Germany_TST/segmented/de-2010-loes_awkl2_10.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
76ad36bd-bceb-5b53-9bdd-34d1f6698331
| 604,615
|
Determine the smallest positive number $k$ for which the following is true: If Cain writes integers into the cells of a $2011 \times 2011$ chessboard in such a way that the 4022 sums obtained by adding all the numbers in a row or column are pairwise equal, then it is possible for Abel to achieve that these 4022 sums are pairwise distinct by altering the entries in only $k$ of the cells.
|
$k=2681$. Proof of $k \geq 2681$: Abel must change at least 4021 of the sums, w.l.o.g. all column sums and all but at most one row sum. To change the column sums, Abel must alter at least one entry in each column. This Abel does w.l.o.g. first and then pauses. At the time of this pause, let $n$ rows be unaltered. Thus, Abel must alter an entry in $n-1$ of these rows so that the row sums can differ. This Abel does w.l.o.g. subsequently and pauses again. For $n \geq 671$, at least 2681 entries have already been altered. Now let $n \leq 670$. A cell is called insufficient if Abel has changed its entry but no further entry in the same row or column. Since the row and column sums of an insufficient cell are the same, no cell can be insufficient at the end. There are at least 2011 - $2 n$ insufficient cells during Abel's first pause. With each change up to the second pause, Abel can eliminate at most one of these insufficient cells (by changing an entry in the same column), and with each change after the second pause, at most two insufficient cells. Therefore, after the second pause, at least $\frac{1}{2}(2011-2 n-(n-1))$ entries must be altered, so in total at least $2011+(n-1)+\frac{1}{2}(2011-2 n-(n-1))=3016-\frac{n}{2} \geq 2681$.
Proof idea for $k \leq 2681$: For $1 \leq m, n \leq 2011$, let the cell in row $m$ and column $n$ be denoted by $\langle m ; n\rangle$. Abel increases the entry of 2681 cells $\langle m ; n\rangle$ each by $2(m+n)+1$, specifically from $\langle 2 ; 1\rangle$ and for $l=1, \ldots, 670$ from $\langle 3 l-1 ; 3 l-1\rangle,\langle 3 l ; 3 l-1\rangle,\langle 3 l+1 ; 3 l\rangle$ and $\langle 3 l+1 ; 3 l+1\rangle$.
Remarks: Sometimes it was argued that by changing two entries in the same row (or column), Abel can change three sums and this is optimal, and from this $k \geq 2681$ was concluded. However, it was implicitly assumed that an arrangement of cells with altered entries as in the proof of $k \leq 2681$ is already optimal.
|
2681
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Man bestimme die kleinste positive Zahl $k$, für die folgendes der Fall ist: Wenn Kain in solcher Weise ganze Zahlen in die Zellen eines $2011 \times 2011$-Schachbrettes schreibt, dass die 4022 Summen, die man durch Addition aller Zahlen einer Zeile oder Spalte erhalten kann, paarweise übereinstimmen, so ist es für Abel möglich, durch Abänderung der Einträge aus nur $k$ der Zellen zu erreichen, dass diese 4022 Summen paarweise verschieden werden.
|
$k=2681$. Beweis von $k \geq 2681$ : Abel muss mindestens 4021 der Summen ändern, o. B. d. A. alle Spaltensummen und alle bis auf höchstens eine Zeilensumme. Um die Spaltensummen zu ändern, muss Abel in jeder Spalte mindestens einen Eintrag abändern. Dies erledige Abel o. B. d. A. zuerst und pausiere dann. Zum Zeitpunkt dieser Pause seien $n$ Zeilen unverändert. Somit muss Abel in $n-1$ dieser Zeilen einen Eintrag abändern, damit sich die Zeilensummen unterscheiden können. Dies erledige Abel o. B. d. A. im Anschluss und pausiere wieder. Für $n \geq 671$ sind nun bereits mindestens 2681 Einträge abgeändert. Nun sei $n \leq 670$. Eine Zelle heiße unzureichend, wenn Abel ihren Eintrag geändert hat, aber keinen weiteren Eintrag einer Zelle in derselben Zeile oder Spalte. Da die Zeilen- und Spaltensumme einer unzureichenden Zelle gleich sind, darf am Ende keine Zelle unzureichend sein. Es gibt während Abels erster Pause mindestens 2011 - $2 n$ unzureichende Zellen. Durch jede Änderung bis zur zweiten Pause kann Abel höchstens eine dieser unzureichenden Zellen (durch Ändern eines Eintrags in derselben Spalte) eliminieren, durch jede Änderung nach der zweiten Pause höchstens zwei unzureichende Zellen. Daher sind nach der zweiten Pause mindestens $\frac{1}{2}(2011-2 n-(n-1))$ Einträge abzuändern, also zusammen mindestens $2011+(n-1)+\frac{1}{2}(2011-2 n-(n-1))=3016-\frac{n}{2} \geq 2681$.
Beweisidee zu $k \leq 2681$ : Für $1 \leq m, n \leq 2011$ sei die Zelle in Zeile $m$ und Spalte $n$ mit $\langle m ; n\rangle$ bezeichnet. Abel erhöht den Eintrag von 2681 Zellen $\langle m ; n\rangle$ jeweils um $2(m+n)+1$, und zwar von $\langle 2 ; 1\rangle$ sowie für $l=1, \ldots, 670$ von $\langle 3 l-1 ; 3 l-1\rangle,\langle 3 l ; 3 l-1\rangle,\langle 3 l+1 ; 3 l\rangle$ und $\langle 3 l+1 ; 3 l+1\rangle$.
Bemerkungen: Manchmal wurde argumentiert, dass mit Abändern zweier Einträge in derselben Zeile (oder Spalte) Abel drei Summen ändern könne und dies optimal sei, und daraus $k \geq 2681$ gefolgert. Dabei wurde aber implizit angenommen, dass eine Anordnung der Zellen mit geänderten Einträgen nach der Art wie der im Beweis von $k \leq 2681$ bereits optimal ist.
|
{
"resource_path": "Germany_TST/segmented/de-2012-loes_awkl1_12.jsonl",
"problem_match": "\nAufgabe 1 ",
"solution_match": "\nLösung:"
}
|
0dcd3478-3dfd-5685-8bb2-c505b499bc28
| 604,730
|
In the plane, there are two concentric circles with radii $r_{1}=13$ and $r_{2}=8$.
Let $A B$ be a diameter of the larger circle and $B C$ one of its chords, which touches the smaller circle at point $D$.
Calculate the length of the segment $A D$.
|
The two possible positions of $D$ are symmetric with respect to the line $(A B)$, so it suffices to consider the case where the triangle $A B D$ is oriented counterclockwise (see figure). The common center of the two circles is denoted by $M$. Since the radius $MD$ is perpendicular to the tangent $B C$, the triangle $M B D$ is right-angled, so from the Pythagorean theorem
$|B D|^{2}=|M B|^{2}-|M D|^{2}=r_{1}^{2}-r_{2}^{2}=169-64=105$ follows.
By the Thales' theorem, $\angle A C B=90^{\circ}$. Since $\angle A C B=\angle M D B=90^{\circ}$ and the common angle $\angle D B M=\angle C B A$, the triangles $A B C$ and $M B D$ are similar, and since $|M B|=r_{1}=|M A|$, it also follows that $|D C|=|B D|=\sqrt{105}$ and $|C A|=2 \cdot|D M|=16$. Thus, the lengths of the legs in the right-angled triangle $A D C$ are known, and it follows that $|A D|=\sqrt{105+16^{2}}=\sqrt{361}=19$. Therefore, the side $A D$ has a length of 19.
Hints: Numerous other solution methods are possible. Because the problem is relatively simple, points were also deducted for errors in the final calculation step (examples: $\sqrt{360}, \sqrt{461}$, or even $\sqrt{361} \approx 18.5$).
|
19
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In der Ebene liegen zwei konzentrische Kreise mit den Radien $r_{1}=13$ und $r_{2}=8$.
Es sei $A B$ ein Durchmesser des größeren Kreises und $B C$ eine seiner Sehnen, die den kleineren Kreis im Punkt $D$ berührt.
Man berechne die Länge der Strecke $A D$.
|
Die beiden möglichen Lagen von $D$ sind symmetrisch zur Geraden $(A B)$, so dass es ausreicht, den Fall zu betrachten, bei dem das Dreieck $A B D$ gegen den Uhrzeigersinn orientiert ist (siehe Figur). Der gemeinsame Mittelpunkt der beiden Kreise sei mit $M$ bezeichnet. Weil der Berührradius MD auf der Tangente $B C$ senkrecht steht, ist $M B D$ rechtwinklig, so dass aus dem Satz des Pythagoras

$|B D|^{2}=|M B|^{2}-|M D|^{2}=r_{1}^{2}-r_{2}^{2}=169-64=105$ folgt.
Nach dem Satz des Thales ist $\Varangle A C B=90^{\circ}$. Da wegen $\Varangle A C B=\Varangle M D B=90^{\circ}$ und des gemeinsamen Winkels $\Varangle D B M=\Varangle C B A$ die Dreiecke $A B C$ und $M B D$ ähnlich sind, und da $|M B|=r_{1}=|M A|$ gilt, ist auch $|D C|=|B D|=\sqrt{105}$ sowie $|C A|=2 \cdot|D M|=16$. Damit sind die Längen der Katheten im rechtwinkligen Dreieck $A D C$ bekannt und es folgt $|A D|=\sqrt{105+16^{2}}=\sqrt{361}=19$. Die Seite $A D$ hat also die Länge 19.
Hinweise: Zahlreiche andere Lösungswege sind möglich. Weil die Aufgabe recht einfach ist, mussten auch für Fehler im letzten Rechenschritt (Beispiele: $\sqrt{360}, \sqrt{461}$ oder sogar $\sqrt{361} \approx 18,5$ ) Punkte abgezogen werden.
|
{
"resource_path": "Germany_TST/segmented/de-2013-loes_awkl_13.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
93b58bf1-e6ca-50a5-8dee-a941cc2a7a50
| 604,846
|
A natural number $n$ has the following property:
For arbitrary real numbers $a_{1}, a_{2}, \ldots, a_{d}$, which both satisfy $a_{1}+a_{2}+\ldots+a_{d}=2013$ and $0 \leq a_{i} \leq 1$ for $i=1,2, \ldots, d$, there exists a partition of the set of these real numbers into $n$ pairwise disjoint subsets (some of which may be empty), such that the sum of the numbers in each subset is at most 1.
Determine the smallest number $n$ with this property.
|
The smallest number $n$ with this property is 4025.
We first show $n \geq 4025$. For this, we choose $d=4025$ and $a_{1}=\ldots=a_{4025}=\frac{2013}{4025}>\frac{1}{2}$. Then $a_{1}+\ldots+a_{4025}=2013$ and since $a_{i}+a_{j}=\frac{4026}{4025}>1$ for all $1 \leq i \neq j \leq 4025$, 4025 subsets are required.
Now we show $n \leq 4025$. For this, we perform a case distinction based on $d$.
For $d \leq 4025$, each $a_{i}$ gets its own subset. Thus, all subsets, some of which may be empty, are disjoint and have sums of at most 1.
For $d>4025$, there must exist two numbers $a_{x}$ and $a_{y}$ such that $a_{x}+a_{y} \leq 1$. Otherwise, in the sum $\left(a_{1}+a_{2}\right)+\left(a_{3}+a_{4}\right)+\ldots+\left(a_{4025}+a_{4026}\right)$, each parenthesis would be greater than 1, and the sum of all $a_{i}$ would be greater than 2013, a contradiction! Therefore, we can replace $a_{x}$ and $a_{y}$ with $a_{z}=a_{x}+a_{y}$ and obtain a set with $d-1$ elements that satisfies all conditions. This step can be repeated until the replacement yields a set with 4025 elements. For this set, and thus also for the original set, the desired partition exists. This completes the proof.
Note: Some of the $a_{i}$ may indeed be equal; two subsets are then disjoint if they do not contain the same element (with respect to the numbering). The problem statement allowed for many solution paths.
|
4025
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Eine natürliche Zahl $n$ habe die folgende Eigenschaft:
Für beliebige reelle Zahlen $a_{1}, a_{2}, \ldots, a_{d}$, die sowohl $a_{1}+a_{2}+\ldots+a_{d}=2013$ als auch $0 \leq a_{i} \leq 1$ für $i=1,2, \ldots, d$ erfüllen, existiert eine Zerlegung der Menge dieser reeller Zahlen in $n$ paarweise disjunkte Teilmengen (von denen einige leer sein dürfen), so dass die Summe der Zahlen in jeder Teilmenge höchstens 1 beträgt.
Man bestimme die kleinste Zahl $n$ mit dieser Eigenschaft.
|
Die kleinste Zahl $n$ mit dieser Eigenschaft ist 4025.
Wir zeigen zunächst $n \geq 4025$. Dazu wählen wir $d=4025$ sowie $a_{1}=\ldots=a_{4025}=\frac{2013}{4025}>\frac{1}{2}$. Dann ist $a_{1}+\ldots+a_{4025}=2013$ und wegen $a_{i}+a_{j}=\frac{4026}{4025}>1$ für alle $1 \leq i \neq j \leq 4025$ werden hier 4025 Teilmengen benötigt.
Nun zeigen wir $n \leq 4025$. Dazu führen wir eine Fallunterscheidung nach $d$ durch.
Für $d \leq 4025$ erhält jedes $a_{i}$ seine eigene Teilmenge. Damit sind alle Teilmengen, von denen einige leer sein dürfen, disjunkt und haben Elementsummen von höchstens 1.
Für $d>4025$ müssen zwei Zahlen $a_{x}$ und $a_{y}$ existieren mit $a_{x}+a_{y} \leq 1$. Andernfalls wäre schon in der Summe $\left(a_{1}+a_{2}\right)+\left(a_{3}+a_{4}\right)+\ldots+\left(a_{4025}+a_{4026}\right)$ jede Klammer größer als 1 und die Summe aller $a_{i}$ größer als 2013, Widerspruch! Somit können wir $a_{x}$ und $a_{y}$ durch $a_{z}=a_{x}+a_{y}$ ersetzen und erhalten eine Menge mit $d-1$ Elementen, die alle Bedingungen erfüllt. Dieser Schritt kann wiederholt werden, bis die Ersetzung eine Menge mit 4025 Elementen liefert. Für diese und damit auch für die Ausgangsmenge existiert die gewünschte Aufteilung. Damit ist alles gezeigt.
Hinweis: Einige der $a_{i}$ dürfen durchaus gleich sein; zwei Teilmengen sind dann disjunkt, wenn sie nicht dasselbe Element (bezogen auf die Nummerierung) enthalten. Die Aufgabenstellung ließ viele Lösungswege zu.
|
{
"resource_path": "Germany_TST/segmented/de-2014-loes_awkl_14.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
6f12f835-6049-5b8f-b45f-343458182f6b
| 604,921
|
Determine the smallest positive integer $n$ for which there exists a polynomial
$$
P(X)=a_{2 n} X^{2 n}+a_{2 n-1} X^{2 n-1}+\ldots+a_{1} X+a_{0}
$$
with real coefficients that satisfies the following two properties:
- For $i=0,1, \ldots, 2 n$, we have $2014 \leq a_{i} \leq 2015$.
- There exists a real number $\xi$ such that $P(\xi)=0$.
|
It is $n=2014$. First, define for a specific choice of coefficients $a_{k}$, namely 2014 for even $k$ and 2015 for odd $k$, the polynomial $Q_{n}(X)=2014 X^{2 n}+2015 X^{2 n-1}+2014 X^{2 n-2}+\ldots+2015 X+2014$. It is $Q_{2014}(-1)=0$, so the desired number is at most 2014. It remains to show that $P(X)$ has no real roots for $n \leq 2013$. For $x \geq 0$, $P(x) \geq a_{0}>0$, since the coefficients are positive; for $x<0$, $P(x) \geq Q_{n}(x)$, since $x^{k}$ is positive for even $k$, so $a_{k} x^{k} \geq 2014 x^{k}$, and $x^{k}$ is negative for odd $k$, so $a_{k} x^{k} \geq 2015 x^{k}$. It remains to show that $Q_{m}(x)>0$ for $m \leq 2013$.
1. Proof: It can be verified that for real $x$,
$$
Q_{m}(x)=1007\left(\sum_{\nu=0}^{m-1}\left(x^{\nu}+x^{\nu+1}\right)^{2}\right)+\frac{1}{2}\left(\sum_{\nu=0}^{m-1}\left(x^{2 \nu+1}+1\right)\left(x^{2 m-2 \nu-1}+1\right)\right)+\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)
$$
The terms of the first sum are non-negative as squares. Since $x^{2 k+1}+1$ is positive, zero, or negative for all $k \geq 0$ for $x>-1$, $x=-1$, or $x<-1$, the terms in the second sum are non-negative. Therefore, for $x<0$ and $m \leq 2013$:
$$
P(x) \geq Q_{m}(x) \geq\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)>\frac{1}{2}
$$
2. Proof (using calculus): Define for $x<0$ the real function $f_{m}(x)=\left(x^{2}-1\right) Q_{m}(x)=2014\left(x^{2 m+2}-1\right)+2015 x\left(x^{2 m}-1\right)$. The second derivative $f_{m}^{\prime \prime}(x)=2(2 m+1)\left(2014(m+1) x^{2 m}+2015 m x^{2 m-1}\right)$ has the only negative root $x_{m}=-\frac{2015 m}{2014(m+1)}>-1$ for $m \leq 2013$, and it is
$$
\begin{aligned}
f_{m}^{\prime}\left(x_{m}\right) & =2014(2 m+2) x_{m}^{2 m+1}+2015(2 m+1) x_{m}^{2 m}-2015= \\
& =\left(2014(2 m+2) x_{m}+2015(2 m+1)\right) x_{m}^{2 m}-2015=2015 \cdot x_{m}^{2 m}-2015<0
\end{aligned}
$$
For $x<x_{m}$ or $x_{m}<x<0$, $f_{m}^{\prime}$ increases or decreases strictly, since the derivative $f_{m}^{\prime \prime}$ is positive or negative; hence $f_{m}^{\prime}$ has a global maximum at $x=x_{m}$ for $x<0$ and is negative for all $x<0$. Therefore, $f_{m}$ decreases strictly, and is positive for $x>-1$ and negative for $x<-1$. Thus, $Q_{m}(x)$ is positive for $x \neq-1$; for $x=-1$, it directly follows that $Q_{m}(-1)=2014-m>0$.
## Remarks:
1. The polynomial function $P(x)$ can have no real roots outside the interval ] $-\frac{2015}{2014},-\frac{2014}{2015}$ [.
2. Often, terms $g_{k}(x)=2014 x^{2 k}+2015 x^{2 k-1}$ of $Q_{m}(x)$ for individual $k$ were considered in isolation and incorrectly estimated against $g_{k}(-1)$. As shown by differentiation, $g_{k}$ increases or decreases strictly for $0>x>-\frac{2015(2 k-1)}{2014 \cdot 2 k}$ or $x<-\frac{2015(2 k-1)}{2014 \cdot 2 k}$. This implies $g_{k}(x)>g_{k}(-1)$ for $k \leq 1007$ and $x<-1$ or for $k>1007$ and $-1>x>0$. Thus, one can only show $Q_{m}(x) \geq Q_{m}(-1)$ for $x<-1$ and $m \leq 1007$ in this way.
## » BILDUNG \& BEGABUNG GEMEINNÜTZIGE GMBH
Kortrijker Straße 1, 53177 Bonn | Postfach 2002 01, 53132 Bonn | Tel.: (02 28) 9 59 15-0, Fax: (02 28) 959 15-19 info@bildung-und-begabung.de, www.bildung-und-begabung.de I Registergericht: Amtsgericht Essen, HRB 22445 Tax No.: 206/5887/1089 | VAT ID No.: DE217481695 | Bank details: IBAN: DE27 370501980029002250 BIC: COLSDE33XXX, Sparkasse KölnBonn I Management: Dr. Elke Völmicke, Prof. Dr. Andreas Schlüter
|
2014
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Man bestimme die kleinste positive ganze Zahl $n$, für die es ein Polynom
$$
P(X)=a_{2 n} X^{2 n}+a_{2 n-1} X^{2 n-1}+\ldots+a_{1} X+a_{0}
$$
mit reellen Koeffizienten gibt, das die beiden folgenden Eigenschaften aufweist:
- Für $i=0,1, \ldots, 2 n$ gilt $2014 \leq a_{i} \leq 2015$.
- Es gibt eine reelle Zahl $\xi$ mit $P(\xi)=0$.
|
Es ist $n=2014$. Zunächst definiere für eine spezielle Wahl der Koeffizienten $a_{k}$, nämlich 2014 für gerades $k$ und 2015 für ungerades $k$, das Polynom $Q_{n}(X)=2014 X^{2 n}+2015 X^{2 n-1}+2014 X^{2 n-2}+\ldots+2015 X+2014$. Es ist $Q_{2014}(-1)=0$, die gesuchte Zahl ist also höchstens 2014. Es bleibt zu zeigen, dass $P(X)$ für $n \leq 2013$ keine reelle Nullstelle hat. Für $x \geq 0$ ist $P(x) \geq a_{0}>0$, da die Koeffizienten positiv sind; für $x<0$ ist $P(x) \geq Q_{n}(x)$, da $x^{k}$ für gerades $k$ positiv ist, also $a_{k} x^{k} \geq 2014 x^{k}$, und $x^{k}$ für ungerades $k$ negativ ist, also $a_{k} x^{k} \geq 2015 x^{k}$. Es bleibt zu zeigen, dass $Q_{m}(x)>0$ für $m \leq 2013$.
1. Beweis: Man rechnet nach, dass für reelles $x$ gilt
$$
Q_{m}(x)=1007\left(\sum_{\nu=0}^{m-1}\left(x^{\nu}+x^{\nu+1}\right)^{2}\right)+\frac{1}{2}\left(\sum_{\nu=0}^{m-1}\left(x^{2 \nu+1}+1\right)\left(x^{2 m-2 \nu-1}+1\right)\right)+\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)
$$
Die Summanden der ersten Summe sind als Quadrate nicht negativ. Da $x^{2 k+1}+1$ für alle $k \geq 0$ positiv bzw. 0 bzw. negativ ist für $x>-1$ bzw. $x=-1$ bzw. $x<-1$, sind die Summanden in der zweiten Summe nicht negativ. Damit ist für $x<0$ und $m \leq 2013$ :
$$
P(x) \geq Q_{m}(x) \geq\left(1007-\frac{m}{2}\right)\left(x^{2 m}+1\right)>\frac{1}{2}
$$
2. Beweis (mit Analysis): Definiere für $x<0$ die reelle Funktion $f_{m}(x)=\left(x^{2}-1\right) Q_{m}(x)=2014\left(x^{2 m+2}-\right.$ $1)+2015 x\left(x^{2 m}-1\right)$. Die zweite Ableitung $f_{m}^{\prime \prime}(x)=2(2 m+1)\left(2014(m+1) x^{2 m}+2015 m x^{2 m-1}\right)$ hat die einzige negative Nullstelle $x_{m}=-\frac{2015 m}{2014(m+1)}>-1$ für $m \leq 2013$, und es ist
$$
\begin{aligned}
f_{m}^{\prime}\left(x_{m}\right) & =2014(2 m+2) x_{m}^{2 m+1}+2015(2 m+1) x_{m}^{2 m}-2015= \\
& =\left(2014(2 m+2) x_{m}+2015(2 m+1)\right) x_{m}^{2 m}-2015=2015 \cdot x_{m}^{2 m}-2015<0
\end{aligned}
$$
Für $x<x_{m}$ bzw. $x_{m}<x<0$ wächst bzw. fällt $f_{m}^{\prime}$ streng monoton, da die Ableitung $f_{m}^{\prime \prime}$ positiv bzw. negativ ist; daher hat $f_{m}^{\prime}$ für $x<0$ ein globales Maximum bei $x=x_{m}$ und ist negativ für alle $x<0$. Daher fällt $f_{m}$ streng monoton, ist also wegen $f_{m}(-1)=0$ positiv für $x>-1$ und negativ für $x<-1$. Somit ist $Q_{m}(x)$ positiv für $x \neq-1$; für $x=-1$ ergibt sich direkt $Q_{m}(-1)=2014-m>0$.
## Bemerkungen:
1. Die Polynomfunktion $P(x)$ kann keine reellen Nullstellen außerhalb des Intervalls ] $-\frac{2015}{2014},-\frac{2014}{2015}$ [haben.
2. Oftmals wurden Summanden $g_{k}(x)=2014 x^{2 k}+2015 x^{2 k-1}$ von $Q_{m}(x)$ für einzelne $k$ isoliert betrachtet und fehlerhaft gegen $g_{k}(-1)$ abgeschätzt. Wie man durch Ableiten zeigt, wächst bzw. fällt $g_{k}$ streng monoton für $0>x>-\frac{2015(2 k-1)}{2014 \cdot 2 k}$ bzw. $x<-\frac{2015(2 k-1)}{2014 \cdot 2 k}$. Daraus folgt $g_{k}(x)>g_{k}(-1)$ für $k \leq 1007$ und $x<-1$ oder für $k>1007$ und $-1>x>0$. Damit kann man auf diese Weise $Q_{m}(x) \geq Q_{m}(-1)$ nur für $x<-1$ und $m \leq 1007$ nachweisen.
## » BILDUNG \& BEGABUNG GEMEINNÜTZIGE GMBH
Kortrijker Straße 1, 53177 Bonn | Postfach 2002 01, 53132 Bonn | Tel.: (02 28) 9 59 15-0, Fax: (02 28) 959 15-19 info@bildung-und-begabung.de, www.bildung-und-begabung.de I Registergericht: Amtsgericht Essen, HRB 22445 Steuer-Nr.: 206/5887/1089 | USt.-IDNr.: DE217481695 | Bankverbindung: IBAN: DE27 370501980029002250 BIC: COLSDE33XXX, Sparkasse KölnBonn I Geschäftsführung: Dr. Elke Völmicke, Prof. Dr. Andreas Schlüter
|
{
"resource_path": "Germany_TST/segmented/de-2015-loes_awkl_15.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
44d213ee-4a92-54b8-9424-37f882c37b6a
| 604,957
|
Determine the smallest real constant $C$ with the following property:
For any five arbitrary positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$, which do not necessarily have to be distinct, there always exist pairwise different indices $i, j, k, l$ such that
$\left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leq C$ holds.
|
The desired value is $C=\frac{1}{2}$.
First, we prove that $C \leq \frac{1}{2}$. To do this, we assume without loss of generality (oBdA) that $a_{1} \leq a_{2} \leq a_{3} \leq a_{4} \leq a_{5}$ and consider the five fractions $\frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}}$. By the pigeonhole principle, at least three of these fractions lie in one of the intervals ]0, $\frac{1}{2}$ ] or $\left.] \frac{1}{2}, 1\right]$. Among these, two fractions are consecutive in the list or the first and the last fraction are included. In any case, the positive difference between these two fractions is less than $\frac{1}{2}$, and the four involved indices are pairwise distinct.
Now we show that $C \geq \frac{1}{2}$. For this, consider the example 1, 2, 2, 2, $r$, where $r$ is a very large number. With these numbers, we can form the fractions $\frac{1}{r}, \frac{2}{r}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{r}{2}, \frac{r}{1}$, ordered by size. According to the problem statement, $\frac{1}{r}$ and $\frac{2}{r}$ cannot both be chosen. Therefore, the smallest positive difference is $\frac{1}{2}-\frac{2}{r}$, which approaches the value $\frac{1}{2}$ from below as $r \rightarrow \infty$. $\square$
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Man bestimme die kleinste reelle Konstante $C$ mit folgender Eigenschaft:
Für fünf beliebige positive reelle Zahlen $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$, die nicht unbedingt verschieden sein müssen, lassen sich stets paarweise verschiedene Indizes $i, j, k, l$ finden, so dass
$\left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leq C$ gilt.
|
Der gesuchte Wert ist $C=\frac{1}{2}$.
Zunächst beweisen wir, dass $C \leq \frac{1}{2}$ gilt. Dazu nehmen wir oBdA $a_{1} \leq a_{2} \leq a_{3} \leq a_{4} \leq a_{5}$ an und betrachten die fünf Brüche $\frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}}$. Nach dem Schubfachprinzip liegen in einem der Intervalle ]0, $\frac{1}{2}$ ] bzw. $\left.] \frac{1}{2}, 1\right]$ drei verschiedene dieser Brüche, wobei zwei von diesen in der Aufzählung direkt aufeinanderfolgen oder der erste und der letzte Bruch dabei sind. Jedenfalls ist die positive Differenz dieser beiden Brüche kleiner als $\frac{1}{2}$ und die vier beteiligten Indizes sind paarweise verschieden.
Nun zeigen wir, dass $C \geq \frac{1}{2}$ gilt. Dazu betrachten das Beispiel 1, 2, 2, 2 , $r$, wobei $r$ eine Riesenzahl sein soll. Mit diesen Zahlen lassen sich - der Größe nach geordnet - die Brüche $\frac{1}{r}, \frac{2}{r}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{r}{2}, \frac{r}{1}$ bilden, wobei nach der Aufgabenstellung $\frac{1}{r}$ und $\frac{2}{r}$ nicht gleichzeitig gewählt werden dürfen. Daher ist die kleinste positive Differenz gleich $\frac{1}{2}-\frac{2}{r}$, und dies nähert sich für $r \rightarrow \infty$ dem Wert $\frac{1}{2}$ von unten beliebig gut an. $\square$
|
{
"resource_path": "Germany_TST/segmented/de-2017-loes_awkl_17.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
6d76a62b-e400-5fe9-a009-19a3cee90dd9
| 605,100
|
We consider all positive real numbers $a, b, c, d$ for which $(a+c)(b+d)=a c+b d$ holds.
Determine the smallest value that $S=\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ can take.
|
The smallest possible value for $S$ is 8.
To show that $S \geq 8$ always holds, we apply the AM-GM inequality twice:
$\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geq 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geq 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8$.
Equality holds at the points of the inequalities when $a=c$ and $b=d$. This allows us to rewrite $(a+c)(b+d)=a c+b d$ as $4 a b=a^{2}+b^{2}$. Solving for $a$ yields $a=b(2 \pm \sqrt{3})$, and thus a possible solution $S=8$ for $b=d=1$ and $a=c=2+\sqrt{3}$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Wir betrachten alle positiven reellen Zahlen $a, b, c, d$, für die $(a+c)(b+d)=a c+b d$ gilt.
Bestimmen Sie den kleinsten Wert, den $S=\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ annehmen kann.
|
Der kleinste mögliche Wert für $S$ ist 8 .
Um zu zeigen, dass stets $S \geq 8$ gilt, wenden wir zweimal die AM-GM-Ungleichung an:
$\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geq 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geq 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8$.
An den Stellen der Ungleichungen gilt Gleichheit, wenn $a=c$ und $b=d$ ist. Damit lässt sich $(a+c)(b+d)=a c+b d$ umschreiben als $4 a b=a^{2}+b^{2}$. Auflösen nach $a$ liefert $a=b(2 \pm \sqrt{3})$ und damit eine mögliche Lösung $S=8$ für $b=d=1$ und $a=c=2+\sqrt{3}$.
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "# Erste Lösung:"
}
|
8f8f82a1-17d5-5e0f-852d-3dd03276b089
| 605,431
|
Determine ${ }^{1}$ the smallest value that the expression
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2022}}{2022}\right\rfloor
$$
can take, where $a_{1}, a_{2}, \ldots, a_{2022} \geq 1$ are real numbers such that $\left|a_{i}-a_{j}\right| \geq 1$ for all $1 \leq i<j \leq 2022$.
Note: For a real number $x$, $\lfloor x\rfloor$, called the floor of $x$, denotes the greatest integer not greater than $x$.
|
From the premise, it follows that the smallest of the numbers $a_{1}, a_{2}, \ldots, a_{2022}$ is at least 1, the second smallest is at least 2, and so on, up to the 2022nd, which must be at least 2022. If we now replace the numbers $a_{1}, \ldots, a_{2022}$ successively by $1,2, \ldots, 2022$ in order of size, the sum from the problem statement will not increase. We thus see that we may restrict ourselves to the case where $\left(a_{1}, a_{1}, \ldots, a_{2022}\right)$ are pairwise distinct positive integers. Now we replace 2022 with an arbitrary positive integer $k$ and claim that the smallest value $s(k)$ that the sum
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor
$$
can take, when $a_{1}, a_{1}, \ldots, a_{k}$ are pairwise distinct positive integers, is exactly $\left\lfloor\log _{2}(k)\right\rfloor$.
- Lower Bound: Since $m$ is evidently monotonically increasing, it suffices to show that $m\left(2^{t}\right) \geq t$ holds. The case $t=0$ is clear, for $t>0$ we use induction and assume $m\left(2^{t-1}\right) \geq t-1$ as known. Let $a_{1}, a_{1}, \ldots, a_{2}$ be arbitrary pairwise distinct positive integers. Then the maximum $a_{i}$ of these numbers is at least $2^{t}$. If $i>2^{t-1}$, then
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\left\lfloor\frac{a_{i}}{i}\right\rfloor \geq m\left(2^{t-1}\right)+1=t-1+1=t$
If, however, $i \leq 2^{t-1}$, then the set $X=\left\{1,2, \ldots, 2^{t-1}\right\} \backslash\left\{a_{1}, a_{2}, \ldots, a_{2^{t-1}}\right\}$ is not empty. Let $b \in X$ be arbitrary. Then $a_{i} \geq 2^{t}=2^{t-1}+2^{t-1} \geq b+i$, so
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\cdots+\left\lfloor\frac{b+i}{i}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\geq m\left(2^{t-1}\right)+1=t-1+1=t$
- Upper Bound: We set
$$
a_{i}=\left\{\begin{array}{l}
i-1, \text { if } i \text { is not a power of two, } \\
2^{s+1}-1, \text { if } i=2^{s} .
\end{array}\right.
$$
Then $a_{1}, a_{2}, \ldots, a_{k}$ are pairwise distinct positive integers and it holds that
$$
\left\lfloor\frac{a_{i}}{i}\right\rfloor=\left\{\begin{array}{l}
0, \text { if } i \text { is not a power of two, } \\
1 \text { otherwise. }
\end{array}\right.
$$
Thus, $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor=\left\lfloor\log _{2}(k)\right\rfloor$.
Applied to the specific situation of the problem statement, we obtain that the smallest value that the given sum can take is $\left\lfloor\log _{2}(2022)\right\rfloor=11$.
[^0]
## NATIONAL
MATHEMATICS COMPETITIONS
Education & Talent
# Selection Competition for the International Mathematical Olympiad 2022
## Example Solutions and Hints for the 2nd Selection Test
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bestimmen Sie ${ }^{1}$ den kleinsten Wert, den der Ausdruck
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2022}}{2022}\right\rfloor
$$
annehmen kann, wobei $a_{1}, a_{2}, \ldots, a_{2022} \geq 1$ reelle Zahlen sind, sodass $\left|a_{i}-a_{j}\right| \geq 1$ für alle $1 \leq i<j \leq 2022$ gilt.
Anmerkung: Für eine reelle Zahl $x$ bezeichnet $\lfloor x\rfloor$, genannt Gauß-Klammer von $x$, die größte ganze Zahl, die nicht größer als $x$ ist.
|
Aus der Voraussetzung folgt, dass die kleinste der Zahlen $a_{1}, a_{2}, \ldots, a_{2022}$ mindestens 1, die zweitkleinste mindestens 2 ist, usw. bis zur 2022-ten, die mindestens 2022 sein muss. Wenn wir nun die Zahlen $a_{1}, \ldots, a_{2022}$ sukzessive der Größe nach durch $1,2, \ldots, 2022$ ersetzen, so wird die Summe aus dem Aufgabentext nicht größer. Wir sehen also, dass wir uns auf den Fall einschränken dürfen, dass $\left(a_{1}, a_{1}, \ldots, a_{2022}\right)$ paarweise verschiedene positive ganze Zahlen sind. Nun ersetzen wir 2022 durch eine beliebige positive ganze Zahl $k$ und behaupten, dass der kleinste Wert $s(k)$, den die Summe
$$
\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor
$$
annehmen kann, wenn $a_{1}, a_{1}, \ldots, a_{k}$ paarweise verschiedene positive ganze Zahlen sind, genau $\left\lfloor\log _{2}(k)\right\rfloor$ beträgt.
- Untere Schranke: Da $m$ offenbar monoton steigend ist, genügt es zu zeigen, dass $m\left(2^{t}\right) \geq t$ gilt. Der Fall $t=0$ ist klar, für $t>0$ verwenden wir vollständige Induktion und setzen daher $m\left(2^{t-1}\right) \geq t-1$ als bekannt voraus. Es seien $a_{1}, a_{1}, \ldots, a_{2}$ beliebige paarweise verschiedene positive ganze Zahlen. Dann ist das Maximum $a_{i}$ dieser Zahlen mindestens $2^{t}$. Falls $i>2^{t-1}$, so gilt nun
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\left\lfloor\frac{a_{i}}{i}\right\rfloor \geq m\left(2^{t-1}\right)+1=t-1+1=t$
Falls jedoch $i \leq 2^{t-1}$, so ist die Menge $X=\left\{1,2, \ldots, 2^{t-1}\right\} \backslash\left\{a_{1}, a_{2}, \ldots, a_{2^{t-1}}\right\}$ nicht leer. Sei $b \in X$ beliebig. Dann gilt $a_{i} \geq 2^{t}=2^{t-1}+2^{t-1} \geq b+i$, also gilt
$\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t}}}{2^{t}}\right\rfloor \geq\left\lfloor\frac{a_{1}}{1}\right\rfloor+\cdots+\left\lfloor\frac{b+i}{i}\right\rfloor+\cdots+\left\lfloor\frac{a_{2^{t-1}}}{2^{t-1}}\right\rfloor+\geq m\left(2^{t-1}\right)+1=t-1+1=t$
- Obere Schranke: Wir setzen
$$
a_{i}=\left\{\begin{array}{l}
i-1, \text { falls } i \text { keine Zweierpotenz ist, } \\
2^{s+1}-1, \text { falls } i=2^{s} .
\end{array}\right.
$$
Dann sind $a_{1}, a_{2}, \ldots, a_{k}$ paarweise verschiedene positive ganze Zahlen und es gilt
$$
\left\lfloor\frac{a_{i}}{i}\right\rfloor=\left\{\begin{array}{l}
0, \text { falls } i \text { keine Zweierpotenz ist, } \\
1 \text { andernfalls. }
\end{array}\right.
$$
also folgt $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{k}}{k}\right\rfloor=\left\lfloor\log _{2}(k)\right\rfloor$.
Angewandt auf die konkrete Situation der Aufgabenstellung erhalten wir, dass der kleinste Wert, den die angegebene Summe annehmen kann, gleich $\left\lfloor\log _{2}(2022)\right\rfloor=11$ ist.
[^0]
## BUNDESWEITE
MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2022
## Beispiellösungen und Hinweise zur 2. Auswahlklausur
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
35c7d508-b02b-51b6-953b-8e2cea0b4709
| 605,489
|
Determine all integers $n \geq 1$ for which there exists a pair $(a, b)$ of positive integers with the following properties:
i) No third power of a prime divides $a^{2}+b+3$.
ii) It holds that $\frac{a b+3 b+8}{a^{2}+b+3}=n$.
|
Let $p$ be any prime factor of $a^{2}+b+3$ (such a prime exists because $a^{2}+b+3 \geq 5$). Then $b \equiv -a^{2}-3 \bmod p$. Due to the integrality of $n$, $p$ must also be a prime factor of $a b+3 b+8$. Therefore, $0 \equiv a b+3 b+8 \equiv a\left(-a^{2}-3\right)+3\left(-a^{2}-3\right)+8 \equiv -a^{3}-3 a^{2}-3 a-1 \equiv -(a+1)^{3} \bmod p$, so $p$ must also be a prime factor of $a+1$. Because of $i$), $p$ can occur in $a^{2}+b+3$ at most quadratically, i.e., at most twice as often as in $a+1$. Since this holds for every prime factor, we get $a^{2}+b+3 \leq (a+1)^{2}$. If a prime factor $p$ occurred in $a^{2}+b+3$ at most simply, we would have $a^{2}+b+3 \leq \frac{(a+1)^{2}}{p} \leq \frac{(a+1)^{2}}{2}$, in contradiction to $\frac{(a+1)^{2}}{2} \leq a^{2}+1 < a^{2}+4 \leq a^{2}+b+3$.
Therefore, $a^{2}+b+3 = (a+1)^{2}$ must hold. Consequently, $b = 2a - 2$ and thus $a b + 3 b + 8 = a(2a - 2) + 3(2a - 2) + 8 = 2a^{2} + 4a + 2 = 2(a+1)^{2}$.
Hence, $n = 2$ is the only possible solution. The example $(a, b) = (2, 2)$ with $a^{2} + b + 3 = 9$ shows that $n = 2$ is indeed a solution. ㅁ
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bestimmen Sie alle ganzen Zahlen $n \geq 1$, für die es ein Paar $(a, b)$ von positiven ganzen Zahlen mit folgenden Eigenschaften gibt:
i) Keine dritte Potenz einer Primzahl teilt $a^{2}+b+3$.
ii) Es gilt $\frac{a b+3 b+8}{a^{2}+b+3}=n$.
Antwort: Die einzige ganze Zahl mit diesen Eigenschaften ist $n=2$.
|
Es sei $p$ ein beliebiger Primfaktor von $a^{2}+b+3$ (ein solcher existiert, weil $a^{2}+b+3 \geq 5$ gilt). Dann ist $b \equiv-a^{2}-3 \bmod p$. Wegen der Ganzzahligkeit von $n$ muss $p$ aber auch ein Primfaktor von $a b+3 b+8$ sein. Somit gilt $0 \equiv a b+3 b+8 \equiv a\left(-a^{2}-3\right)+3\left(-a^{2}-3\right)+8 \equiv-a^{3}-3 a^{2}-3 a-1 \equiv-(a+1)^{3} \bmod p$, also muss $p$ auch ein Primfaktor von $a+1$ sein. Wegen $i$ ) kann $p$ in $a^{2}+b+3$ höchstens quadratisch vorkommen, also höchstens doppelt so oft wie in $a+1$. Weil das für jeden Primfaktor gilt, erhalten wir $a^{2}+b+3 \leq(a+1)^{2}$. Würde ein Primfaktor $p$ in $a^{2}+b+3$ dagegen höchstens einfach vorkommen, so hätten wir $a^{2}+b+3 \leq \frac{(a+1)^{2}}{p} \leq \frac{(a+1)^{2}}{2}$, im Widerspruch zu $\frac{(a+1)^{2}}{2} \leq a^{2}+1<a^{2}+4 \leq a^{2}+b+3$.
Also muss $a^{2}+b+3=(a+1)^{2}$ gelten. Folglich ist $b=2 a-2$ und damit $a b+3 b+8=a(2 a-2)+3(2 a-2)+8=2 a^{2}+4 a+2=2(a+1)^{2}$.
Somit ist $n=2$ die einzige mögliche Lösung. Das Beispiel $(a, b)=(2,2)$ mit $a^{2}+b+3=9$ zeigt, dass $n=2$ tatsächlich eine Lösung ist. ㅁ
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Erste Lösung:"
}
|
721a034b-d10b-5ba5-8e4a-5d79ab5a2f9b
| 605,526
|
For a fixed positive integer $k$, let $K$ be the set of all lattice points $(x, y)$ in the plane, both of whose coordinates $x$ and $y$ are nonnegative integers less than $2k$. Thus, $|K|=4k^2$.
A set $V$ consists of $k^2$ non-degenerate quadrilaterals with the following properties:
i) The vertices of all these quadrilaterals are elements of $K$.
ii) Each point in $K$ is a vertex of exactly one of the quadrilaterals in $V$.
Determine the maximum possible value that the sum of the areas of all $k^2$ quadrilaterals in $V$ can take.
|
Every point in $K$ is the vertex of a uniquely defined central square. Therefore, the set $Q$ of all central squares is acceptable. We show $S(V) \leq S(Q)=S(k)$, from which the answer follows.
We use the following
Lemma 1. For every quadrilateral $V=A_{1} A_{2} A_{3} A_{4}$ and any point $O$ in the plane, we have
$[V] \leq \frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$
where equality holds if and only if $V$ is a square with center $O$.
Proof: For $i=1, \ldots, 4$ and $A_{5}=A_{1}$, we have $\left[O A_{i} A_{i+1}\right] \leq \frac{O A_{i} \cdot O A_{i+1}}{2} \leq \frac{O A_{i}^{2}+O A_{i+1}^{2}}{4}$. Therefore, $[V] \leq \sum_{i=1}^{4}\left[O A_{i} A_{i+1}\right] \leq \frac{1}{4} \sum_{i=1}^{4}\left(O A_{i}^{2}+O A_{i+1}^{2}\right)=\frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$, which proves (2). Indeed, equality holds in each case if $V$ is a square with center $O$. Now consider any acceptable set $V$. Applying Lemma 1 to each element of $V$ and each element of $Q$ yields $S(V) \leq \frac{1}{2} \sum_{A<K} O A^{2}=S(Q)$, which proves the left side of (1).
Now we calculate $S(Q)=\frac{1}{2} \sum_{A c K} O A^{2}=\frac{1}{2} \sum_{i=0}^{2 k-1} \sum_{j=0}^{2 k-1}\left(\left(k-\frac{1}{2}-i\right)^{2}+\left(k-\frac{1}{2}-j\right)^{2}\right)$
$=\frac{1}{8} \cdot 4 \cdot 2 k \sum_{i=0}^{k-1}(2 k-2 i-1)^{2}=k \sum_{j=0}^{k-1}(2 j+1)^{2}=k\left(\sum_{j=1}^{2 k} j^{2}-\sum_{j=1}^{k}(2 j)^{2}\right)$
$=k\left(\frac{2 k(2 k+1)(4 k+1)}{6}-4 \cdot \frac{k(k+1)(2 k+1)}{6}\right)=\frac{k^{2}(2 k+1)(2 k-1)}{3}=S(k)$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
\frac{1}{3} k^2 (2k+1)(2k-1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Für eine feste positive ganze Zahl $k$ sei $K$ die Menge aller Gitterpunkte $(x, y)$ in der Ebene, deren beide Koordinaten $x$ und $y$ nichtnegative ganze Zahlen kleiner als $2 k$ sind. Es gilt also $|K|=4 k^{2}$.
Eine Menge $V$ bestehe nun aus $k^{2}$ nicht-ausgearteten Vierecken mit folgenden Eigenschaften:
i) Die Ecken aller dieser Vierecke sind Elemente von $K$.
ii) Jeder Punkt in $K$ ist Eckpunkt von genau einem der Vierecke in $V$.
Bestimmen Sie den größtmöglichen Wert, den die Summe der Flächeninhalte aller $k^{2}$ Vierecke in $V$ annehmen kann.
Antwort: Der gröBtmögliche Wert der Flächensumme beträgt $S(k):=\frac{1}{3} k^{2}(2 k+1)(2 k-1)$.
Bezeichnungen: Der Flächeninhalt eines Polygons $X$ sei mit $[X]$ bezeichnet. Ein Viereck heiße legal, wenn alle seine Eckpunkte zu $K$ gehören. Weiter sei $O=\left(k-\frac{1}{2}, k-\frac{1}{2}\right)$ der Mittelpunkt von $K$. Ein legales Viereck heiße zentral, wenn es punktsymmetrisch mit $O$ als Mittelpunkt ist. Jede Menge $V$ von Vierecken, die die Bedingungen der Aufgabenstellung erfüllt, heiße akzeptabel. Für jede akzeptable Menge $V$ sei die Flächensumme ihrer Vierecke mit $S(V)$ bezeichnet.
|
Jeder Punkt aus $K$ ist Eckpunkt eines eindeutig definierten zentralen Quadrats. Daher ist die Menge $Q$ aller zentralen Quadrate akzeptabel. Wir zeigen $S(V) \leq S(Q)=S(k)$
woraus die Antwort folgt.
Wir benutzen das folgende
Lemma 1. Für jedes Viereck $V=A_{1} A_{2} A_{3} A_{4}$ und jeden beliebigen Punkt $O$ in der Ebene gilt
$[V] \leq \frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$
wobei Gleichheit genau dann gilt, wenn $V$ ein Quadrat mit Mittelpunkt $O$ ist.
Beweis: Für $i=1, \ldots, 4$ und $A_{5}=A_{1}$ gilt $\left[O A_{i} A_{i+1}\right] \leq \frac{O A_{i} \cdot O A_{i+1}}{2} \leq \frac{O A_{i}^{2}+O A_{i+1}^{2}}{4}$. Daher gilt $[V] \leq \sum_{i=1}^{4}\left[O A_{i} A_{i+1}\right] \leq \frac{1}{4} \sum_{i=1}^{4}\left(O A_{i}^{2}+O A_{i+1}^{2}\right)=\frac{1}{2} \sum_{i=1}^{4} O A_{i}^{2}$, womit (2) bewiesen ist. In der Tat herrscht jeweils Gleichheit, wenn $V$ ein Quadrat mit Mittelpunkt $O$ ist. Nun betrachten wir eine beliebige akzeptable Menge $V$. Lemma 1 auf jedes Element von $V$ und jedes Element von $Q$ angewendet liefert $S(V) \leq \frac{1}{2} \sum_{A<K} O A^{2}=S(Q)$, womit die linke Seite von (1) bewiesen ist.
Nun berechnen wir $S(Q)=\frac{1}{2} \sum_{A c K} O A^{2}=\frac{1}{2} \sum_{i=0}^{2 k-1} \sum_{j=0}^{2 k-1}\left(\left(k-\frac{1}{2}-i\right)^{2}+\left(k-\frac{1}{2}-j\right)^{2}\right)$
$=\frac{1}{8} \cdot 4 \cdot 2 k \sum_{i=0}^{k-1}(2 k-2 i-1)^{2}=k \sum_{j=0}^{k-1}(2 j+1)^{2}=k\left(\sum_{j=1}^{2 k} j^{2}-\sum_{j=1}^{k}(2 j)^{2}\right)$
$=k\left(\frac{2 k(2 k+1)(4 k+1)}{6}-4 \cdot \frac{k(k+1)(2 k+1)}{6}\right)=\frac{k^{2}(2 k+1)(2 k-1)}{3}=S(k)$.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "# Erste Lösung:"
}
|
812da5bc-7657-5c40-86cd-f6376f6f0913
| 605,544
|
Compute
$$
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor
$$
(Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
2006. We have
$$
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor=\left\lfloor\frac{\left(2007 \cdot 2006+\frac{1}{2005}\right) \cdot 2005!}{(2006+1) \cdot 2005!}\right\rfloor=\left\lfloor\frac{2007 \cdot 2006+\frac{1}{2005}}{2007}\right\rfloor=\left\lfloor 2006+\frac{1}{2005 \cdot 2007}\right\rfloor
$$
|
2006
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute
$$
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor
$$
(Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
2006. We have
$$
\left\lfloor\frac{2007!+2004!}{2006!+2005!}\right\rfloor=\left\lfloor\frac{\left(2007 \cdot 2006+\frac{1}{2005}\right) \cdot 2005!}{(2006+1) \cdot 2005!}\right\rfloor=\left\lfloor\frac{2007 \cdot 2006+\frac{1}{2005}}{2007}\right\rfloor=\left\lfloor 2006+\frac{1}{2005 \cdot 2007}\right\rfloor
$$
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-alg-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
cf7e0dbd-5c58-53b8-a12f-8ca7487d40d7
| 608,132
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.