problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
In how many ways can the number 2000 be written as a sum of three positive, not necessarily different integers? (Sums like $1+2+3$ and $3+1+2$ etc. are the same.)
|
Since 3 is not a factor of 2000 , there has to be at least two different numbers among any three summing up to 2000 . Denote by $x$ the number of such sums with three different summands and by $y$ the number of sums with two different summands. Consider 3999 boxes consequtively numbered fron 1 to 3999 such that all boxes labelled by an odd number contain a red ball. Every way to put two blue balls in the even-numbered boxes produces a partition of 2000 in three summands. There are $\binom{1999}{2}=999 \cdot 1999$ ways to place the blue balls. But htere are $3!=6$ different placements, which produce the same partition of 2000 into three different summands, and $\frac{3!}{2}=3$ different placements, which produce the same partition of 2000 into summands two which are equal. Thus $6 x+3 y=$ 1999.999. But $y=999$, because the number appering twice in the partition can be any of the numbers $1,2, \ldots, 999$. This leads to $x=998 \cdot 333$, so $x+y=1001 \cdot 333=333333$.
|
333333
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can the number 2000 be written as a sum of three positive, not necessarily different integers? (Sums like $1+2+3$ and $3+1+2$ etc. are the same.)
|
Since 3 is not a factor of 2000 , there has to be at least two different numbers among any three summing up to 2000 . Denote by $x$ the number of such sums with three different summands and by $y$ the number of sums with two different summands. Consider 3999 boxes consequtively numbered fron 1 to 3999 such that all boxes labelled by an odd number contain a red ball. Every way to put two blue balls in the even-numbered boxes produces a partition of 2000 in three summands. There are $\binom{1999}{2}=999 \cdot 1999$ ways to place the blue balls. But htere are $3!=6$ different placements, which produce the same partition of 2000 into three different summands, and $\frac{3!}{2}=3$ different placements, which produce the same partition of 2000 into summands two which are equal. Thus $6 x+3 y=$ 1999.999. But $y=999$, because the number appering twice in the partition can be any of the numbers $1,2, \ldots, 999$. This leads to $x=998 \cdot 333$, so $x+y=1001 \cdot 333=333333$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n00.1. ",
"solution_match": "\nSolution. "
}
|
285efc37-926d-5175-8b04-d9a79366810d
| 607,968
|
The persons $P_{1}, P_{1}, \ldots, P_{n-1}, P_{n}$ sit around a table, in this order, and each one of them has a number of coins. In the start, $P_{1}$ has one coin more than $P_{2}, P_{2}$ has one coin more than $P_{3}$, etc., up to $P_{n-1}$ who has one coin more than $P_{n}$. Now $P_{1}$ gives one coin to $P_{2}$, who in turn gives two coins to $P_{3}$ etc., up to $P_{n}$ who gives $n$ coins to $P_{1}$. Now the process continues in the same way: $P_{1}$ gives $n+1$ coins to $P_{2}, P_{2}$ gives $n+2$ coins to $P_{3}$; in this way the transactions go on until someone has not enough coins, i.e. a person no more can give away one coin more than he just received. At the moment when the process comes to an end in this manner, it turns out that there are to neighbours at the table such that one of them has exactly five times as many coins as the other. Determine the number of persons and the number of coins circulating around the table.
|
Assume that $P_{n}$ has $m$ coins in the start. Then $P_{n-1}$ has $m+1$ coins, ... and $P_{1}$ has $m+n-1$ coins. In every move a player receives $k$ coins and gives $k+1$ coins away, so her net loss is one coin. After the first round, when $P_{n}$ has given $n$ coins to $P_{1}$, $P_{n}$ has $m-1$ coins, $P_{n-1}$ has $m$ coins etc., after two rounds $P_{n}$ has $m-2$ coins, $P_{n-1}$ has $m-1$ coins etc. This can go on during $m$ rounds, after which $P_{n}$ has no money, $P_{n-1}$ has one coin etc. On round $m+1$ each player still in possession of money can receive and give away coins as before. The penniless $P_{n}$ can no more give away coins according to the rule. She receives $n(m+1)-1$ coins from $P_{n-1}$, but is unable to give $n(m+1)$ coins to $P_{1}$. So when the game ends, $P_{n-1}$ has no coins and $P_{1}$ has $n-2$ coins. The only pair of neighbours such that one has 5 times as many coins as the other can be $\left(P_{1}, P_{n}\right)$. Because $n-2<n(m+1)-1$, this would mean $5(n-2)=n(m+1)-1$ or $n(4-m)=9$. Since $n>1$, the possibilities are $n=3, m=1$ or $n=9, m=3$. Both are indeed possible. In the first case the number of coins is $3+2+1=6$, in the second $11+10+\cdots+3=63$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The persons $P_{1}, P_{1}, \ldots, P_{n-1}, P_{n}$ sit around a table, in this order, and each one of them has a number of coins. In the start, $P_{1}$ has one coin more than $P_{2}, P_{2}$ has one coin more than $P_{3}$, etc., up to $P_{n-1}$ who has one coin more than $P_{n}$. Now $P_{1}$ gives one coin to $P_{2}$, who in turn gives two coins to $P_{3}$ etc., up to $P_{n}$ who gives $n$ coins to $P_{1}$. Now the process continues in the same way: $P_{1}$ gives $n+1$ coins to $P_{2}, P_{2}$ gives $n+2$ coins to $P_{3}$; in this way the transactions go on until someone has not enough coins, i.e. a person no more can give away one coin more than he just received. At the moment when the process comes to an end in this manner, it turns out that there are to neighbours at the table such that one of them has exactly five times as many coins as the other. Determine the number of persons and the number of coins circulating around the table.
|
Assume that $P_{n}$ has $m$ coins in the start. Then $P_{n-1}$ has $m+1$ coins, ... and $P_{1}$ has $m+n-1$ coins. In every move a player receives $k$ coins and gives $k+1$ coins away, so her net loss is one coin. After the first round, when $P_{n}$ has given $n$ coins to $P_{1}$, $P_{n}$ has $m-1$ coins, $P_{n-1}$ has $m$ coins etc., after two rounds $P_{n}$ has $m-2$ coins, $P_{n-1}$ has $m-1$ coins etc. This can go on during $m$ rounds, after which $P_{n}$ has no money, $P_{n-1}$ has one coin etc. On round $m+1$ each player still in possession of money can receive and give away coins as before. The penniless $P_{n}$ can no more give away coins according to the rule. She receives $n(m+1)-1$ coins from $P_{n-1}$, but is unable to give $n(m+1)$ coins to $P_{1}$. So when the game ends, $P_{n-1}$ has no coins and $P_{1}$ has $n-2$ coins. The only pair of neighbours such that one has 5 times as many coins as the other can be $\left(P_{1}, P_{n}\right)$. Because $n-2<n(m+1)-1$, this would mean $5(n-2)=n(m+1)-1$ or $n(4-m)=9$. Since $n>1$, the possibilities are $n=3, m=1$ or $n=9, m=3$. Both are indeed possible. In the first case the number of coins is $3+2+1=6$, in the second $11+10+\cdots+3=63$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n00.2. ",
"solution_match": "\nSolution. "
}
|
a4f148d5-f0b7-5964-933a-67c4ac664faf
| 607,969
|
Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0<x<1$, then $0>x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0<x<1$, then $0>x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n01.3. ",
"solution_match": "\nSolution. "
}
|
c41a8ca9-da84-5a28-b2ba-3fa6a86d7bee
| 607,974
|
In two bowls there are in total $N$ balls, numbered from 1 to $N$. One ball is moved from one of the bowls to the other. The average of the numbers in the bowls is increased in both of the bowls by the same amount, $x$. Determine the largest possible value of $x$.
|
Consider the situation before the ball is moved from urn one to urn two. Let the number of balls in urn one be $n$, and let the sum of numbers in the balls in that urn be $a$. The number of balls in urn two is $m$ and the sum of numbers $b$. If $q$ is the number written in the ball which was moved, the conditions of the problem imply
$$
\left\{\begin{array}{l}
\frac{a-q}{n-1}=\frac{a}{n}+x \\
\frac{b+q}{m+1}=\frac{b}{m}+x
\end{array}\right.
$$
or
$$
\left\{\begin{array}{l}
a=n q+n(n-1) x \\
b=m q-m(m+1) x
\end{array}\right.
$$
Because $n+m=N$ and $a+b=\frac{1}{2} N(N+1)$, we obtain
$$
\frac{1}{2} N(N+1)=N q+x\left(n^{2}-m^{2}-N\right)=N q+x N(n-m-1)
$$
and $q=\frac{1}{2}(N+1)-x(n-m-1), b=\frac{1}{2} m(N+1)-x m n$. But $b \geq 1+2+\cdots+m=\frac{1}{2} m(m+1)$. So $\frac{1}{2}(N+1)-x n=\frac{1}{2}(m+n+1)-x n \geq \frac{1}{2}(m+1)$ or $\frac{n}{2}-x n \geq 0$. Hence $x \leq \frac{1}{2}$. The inequality is sharp or $x=\frac{1}{2}$, when the nubers in the balls in urn one are $m+1, m+2$, $\ldots, N$, the numbers in urn two are $1,2, \ldots, m$, and $q=m+1$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
In two bowls there are in total $N$ balls, numbered from 1 to $N$. One ball is moved from one of the bowls to the other. The average of the numbers in the bowls is increased in both of the bowls by the same amount, $x$. Determine the largest possible value of $x$.
|
Consider the situation before the ball is moved from urn one to urn two. Let the number of balls in urn one be $n$, and let the sum of numbers in the balls in that urn be $a$. The number of balls in urn two is $m$ and the sum of numbers $b$. If $q$ is the number written in the ball which was moved, the conditions of the problem imply
$$
\left\{\begin{array}{l}
\frac{a-q}{n-1}=\frac{a}{n}+x \\
\frac{b+q}{m+1}=\frac{b}{m}+x
\end{array}\right.
$$
or
$$
\left\{\begin{array}{l}
a=n q+n(n-1) x \\
b=m q-m(m+1) x
\end{array}\right.
$$
Because $n+m=N$ and $a+b=\frac{1}{2} N(N+1)$, we obtain
$$
\frac{1}{2} N(N+1)=N q+x\left(n^{2}-m^{2}-N\right)=N q+x N(n-m-1)
$$
and $q=\frac{1}{2}(N+1)-x(n-m-1), b=\frac{1}{2} m(N+1)-x m n$. But $b \geq 1+2+\cdots+m=\frac{1}{2} m(m+1)$. So $\frac{1}{2}(N+1)-x n=\frac{1}{2}(m+n+1)-x n \geq \frac{1}{2}(m+1)$ or $\frac{n}{2}-x n \geq 0$. Hence $x \leq \frac{1}{2}$. The inequality is sharp or $x=\frac{1}{2}$, when the nubers in the balls in urn one are $m+1, m+2$, $\ldots, N$, the numbers in urn two are $1,2, \ldots, m$, and $q=m+1$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n02.2. ",
"solution_match": "\nSolution. "
}
|
d9ba3c6d-d8f6-5dcc-9f42-fd16cdea0cae
| 607,977
|
A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
Consider the expression $x^{5}+487$ modulo 4. Clearly $x \equiv 0 \Rightarrow x^{5}+487 \equiv 3$, $x \equiv 1 \Rightarrow x^{5}+487 \equiv 0 ; x \equiv 2 \Rightarrow x^{5}+487 \equiv 3$, and $x \equiv 3 \Rightarrow x^{5}+487 \equiv 2$. Square numbers are always $\equiv 0$ or $\equiv 1 \bmod 4$. If there is an even square in the sequence, then all subsequent numbers of the sequence are either $\equiv 2$ or $\equiv 3 \bmod 4$, and hence not squares. If there is an odd square in the sequence, then the following number in the sequence can be an even square, but then none of the other numbers are squares. So the maximal number of squares in the sequence is two. In this case the first number of the sequence has to be the first square, since no number of the sequence following another one satisfies $x \equiv 1 \bmod 4$. We have to find numbers $k^{2}$ such that $k^{10}+487=n^{2}$. We factorize $n^{2}-k^{10}$. Because 487 is a prime, $n-k^{5}=1$ and $n+k^{5}=487$ or $n=244$ and $k=3$. The only solution of the problem thus is $m=3^{2}=9$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
Consider the expression $x^{5}+487$ modulo 4. Clearly $x \equiv 0 \Rightarrow x^{5}+487 \equiv 3$, $x \equiv 1 \Rightarrow x^{5}+487 \equiv 0 ; x \equiv 2 \Rightarrow x^{5}+487 \equiv 3$, and $x \equiv 3 \Rightarrow x^{5}+487 \equiv 2$. Square numbers are always $\equiv 0$ or $\equiv 1 \bmod 4$. If there is an even square in the sequence, then all subsequent numbers of the sequence are either $\equiv 2$ or $\equiv 3 \bmod 4$, and hence not squares. If there is an odd square in the sequence, then the following number in the sequence can be an even square, but then none of the other numbers are squares. So the maximal number of squares in the sequence is two. In this case the first number of the sequence has to be the first square, since no number of the sequence following another one satisfies $x \equiv 1 \bmod 4$. We have to find numbers $k^{2}$ such that $k^{10}+487=n^{2}$. We factorize $n^{2}-k^{10}$. Because 487 is a prime, $n-k^{5}=1$ and $n+k^{5}=487$ or $n=244$ and $k=3$. The only solution of the problem thus is $m=3^{2}=9$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n06.3. ",
"solution_match": "\nSolution. "
}
|
ed520dd4-594e-5634-9890-399249838de1
| 607,992
|
Assume that $n \geq 3$ people with different names sit around a round table. We call any unordered pair of them, say $M$ and $N$, dominating, if
(i) $M$ and $N$ do not sit on adjacent seats, and
(ii) on one (or both) of the arcs connecting $M$ and $N$ along the table edge, all people have names that come alphabetically after the names of $M$ and $N$.
Determine the minimal number of dominating pairs.
|
We will show by induction that the number of dominating pairs (hence also the minimal number of dominating pairs) is $n-3$ for $n \geq 3$. If $n=3$, all pairs of people sit on adjacent seats, so there are no dominating pairs. Assume that the number of dominating pairs is $n-3$ for some $n>3$. If there are $n+1$ people around the table, let the person whose name is alphabetically last leave the table. The two people sitting next to that person, who formed a dominating pair, no longer do. On the other hand, any other dominating pair remains a dominating pair in the new configuration of $n$ people, and any dominating pair in the new configuration was also a dominating pair in the old. The number of dominating pairs in the new configuration is $n-3$, so the number in the old was $(n+1)-3$.
|
n-3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Assume that $n \geq 3$ people with different names sit around a round table. We call any unordered pair of them, say $M$ and $N$, dominating, if
(i) $M$ and $N$ do not sit on adjacent seats, and
(ii) on one (or both) of the arcs connecting $M$ and $N$ along the table edge, all people have names that come alphabetically after the names of $M$ and $N$.
Determine the minimal number of dominating pairs.
|
We will show by induction that the number of dominating pairs (hence also the minimal number of dominating pairs) is $n-3$ for $n \geq 3$. If $n=3$, all pairs of people sit on adjacent seats, so there are no dominating pairs. Assume that the number of dominating pairs is $n-3$ for some $n>3$. If there are $n+1$ people around the table, let the person whose name is alphabetically last leave the table. The two people sitting next to that person, who formed a dominating pair, no longer do. On the other hand, any other dominating pair remains a dominating pair in the new configuration of $n$ people, and any dominating pair in the new configuration was also a dominating pair in the old. The number of dominating pairs in the new configuration is $n-3$, so the number in the old was $(n+1)-3$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n08.2. ",
"solution_match": "\nSolution. "
}
|
7dd4e882-3472-504a-b4e9-4fb95feac3d5
| 607,999
|
On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
We denote the polynomial $x^{2}+x+a$ by $P_{a}(x)$, the polynomial forming the other factor of the left side by $Q(x)$ and the polynomial on the right side by $R(x)$. The polynomials are integer valued for every integer $x$. For $x=0$ we get $P_{a}(0)=a$ and $R(0)=-90$, so $a$ is a divisor of $90=2 \cdot 3 \cdot 3 \cdot 5$. For $x=-1$ we get $P_{a}(-1)=-184$, so $a$ is also a divisor of $184=2 \cdot 2 \cdot 2 \cdot 23$. But the only prime factor in common is 2 . So the only possibilities for $a$ are $\pm 2$ and $\pm 1$. If $a=1$, we get for $x=1$ that $P_{1}(1)=3$, while $R(1)=4-180=-176$, which cannot be divided by 3 . If $a=-2$ we get for $x=1$ that $P_{2}(1)=0$, i.e. the left side is equal to 0 , while the right side is equal to $R(1)=-176$, which is different from 0 . Neither $a=1$ nor $a=-2$ will thus work. It remains to check $a=2$ and $a=-1$. Before we use the procedure above again, we need a factorization of $R(x)$. We observe that $x^{4}+1$ is a divisor of $R(x)$, since the right side may be written as $\left(x^{4}+1\right)\left(x^{13}+x-90\right)$. If $a=-1$ we get for $x=2$ that $P_{1}(2)=5$, while $x^{4}+1=17$ and $x^{13}+x-90=8104$. So the right hand side is not divisible by 5 . Now, the only remaining possibility is $a=2$, i.e. $x^{2}+x+2$ is a divisor of $R(x)$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
We denote the polynomial $x^{2}+x+a$ by $P_{a}(x)$, the polynomial forming the other factor of the left side by $Q(x)$ and the polynomial on the right side by $R(x)$. The polynomials are integer valued for every integer $x$. For $x=0$ we get $P_{a}(0)=a$ and $R(0)=-90$, so $a$ is a divisor of $90=2 \cdot 3 \cdot 3 \cdot 5$. For $x=-1$ we get $P_{a}(-1)=-184$, so $a$ is also a divisor of $184=2 \cdot 2 \cdot 2 \cdot 23$. But the only prime factor in common is 2 . So the only possibilities for $a$ are $\pm 2$ and $\pm 1$. If $a=1$, we get for $x=1$ that $P_{1}(1)=3$, while $R(1)=4-180=-176$, which cannot be divided by 3 . If $a=-2$ we get for $x=1$ that $P_{2}(1)=0$, i.e. the left side is equal to 0 , while the right side is equal to $R(1)=-176$, which is different from 0 . Neither $a=1$ nor $a=-2$ will thus work. It remains to check $a=2$ and $a=-1$. Before we use the procedure above again, we need a factorization of $R(x)$. We observe that $x^{4}+1$ is a divisor of $R(x)$, since the right side may be written as $\left(x^{4}+1\right)\left(x^{13}+x-90\right)$. If $a=-1$ we get for $x=2$ that $P_{1}(2)=5$, while $x^{4}+1=17$ and $x^{13}+x-90=8104$. So the right hand side is not divisible by 5 . Now, the only remaining possibility is $a=2$, i.e. $x^{2}+x+2$ is a divisor of $R(x)$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n09.2. ",
"solution_match": "\nSolution. "
}
|
a7eca4c9-218d-5280-9192-739e1dee29a4
| 608,003
|
Laura has 2010 lamps connected with 2010 buttons in front of her. For each button, she wants to know the corresponding lamp. In order to do this, she observes which lamps are lit when Richard presses a selection of buttons. (Not pressing anything is also a possible selection.) Richard always presses the buttons simultaneously, so the lamps are lit simultaneously, too.
a) If Richard chooses the buttons to be pressed, what is the maximum number of different combinations of buttons he can press until Laura can assign the buttons to the lamps correctly?
b) Supposing that Laura will choose the combinations of buttons to be pressed, what is the minimum number of attempts she has to do until she is able to associate the buttons with the lamps in a correct way?
|
a) Let us say that two lamps are separated, if one of the lamps is turned on while the other lamp remains off. Laura can find out which lamps belong to the buttons if every two lamps are separated. Let Richard choose two arbitrary lamps. To begin with, he turns both lamps on and then varies all the other lamps in all possible ways. There are $2^{2008}$ different combinations for the remaining $2010-2=2008$ lamps. Then Richard turns
the two chosen lamps off. Also, at this time there are $2^{2008}$ combinations for the remaining lamps. Consequently, for the $2^{2009}$ combinations in all, it is not possible to separate the two lamps of the first pair. However, we cannot avoid the separation if we add one more combination. Indeed, for every pair of lamps, we see that if we turn on a combination of lamps $2^{2009}+1$ times, there must be at least one setup where exactly one of the lamps is turned on and the other is turned off. Thus, the answer is $2^{2009}+1$.
b) For every new step with a combination of lamps turned on, we get a partition of the set of lamps into smaller and smaller subsets where elements belonging to the same subset cannot be separated. In each step every subset is either unchanged or divided into two smaller parts, i.e. the total number of subsets after $\mathrm{k}$ steps will be at most $2^{k}$. We are finished when the number of subsets is equal to 2010 , so the answer is at least $\left\lceil\log _{2} 2010\right\rceil=11$. But it is easy to see that Laura certainly can choose buttons in every step in such a way that there are at most $2^{11-k}$ lamps in every part of the partition after $k$ steps. Thus, the answer is 11 .
|
2^{2009}+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Laura has 2010 lamps connected with 2010 buttons in front of her. For each button, she wants to know the corresponding lamp. In order to do this, she observes which lamps are lit when Richard presses a selection of buttons. (Not pressing anything is also a possible selection.) Richard always presses the buttons simultaneously, so the lamps are lit simultaneously, too.
a) If Richard chooses the buttons to be pressed, what is the maximum number of different combinations of buttons he can press until Laura can assign the buttons to the lamps correctly?
b) Supposing that Laura will choose the combinations of buttons to be pressed, what is the minimum number of attempts she has to do until she is able to associate the buttons with the lamps in a correct way?
|
a) Let us say that two lamps are separated, if one of the lamps is turned on while the other lamp remains off. Laura can find out which lamps belong to the buttons if every two lamps are separated. Let Richard choose two arbitrary lamps. To begin with, he turns both lamps on and then varies all the other lamps in all possible ways. There are $2^{2008}$ different combinations for the remaining $2010-2=2008$ lamps. Then Richard turns
the two chosen lamps off. Also, at this time there are $2^{2008}$ combinations for the remaining lamps. Consequently, for the $2^{2009}$ combinations in all, it is not possible to separate the two lamps of the first pair. However, we cannot avoid the separation if we add one more combination. Indeed, for every pair of lamps, we see that if we turn on a combination of lamps $2^{2009}+1$ times, there must be at least one setup where exactly one of the lamps is turned on and the other is turned off. Thus, the answer is $2^{2009}+1$.
b) For every new step with a combination of lamps turned on, we get a partition of the set of lamps into smaller and smaller subsets where elements belonging to the same subset cannot be separated. In each step every subset is either unchanged or divided into two smaller parts, i.e. the total number of subsets after $\mathrm{k}$ steps will be at most $2^{k}$. We are finished when the number of subsets is equal to 2010 , so the answer is at least $\left\lceil\log _{2} 2010\right\rceil=11$. But it is easy to see that Laura certainly can choose buttons in every step in such a way that there are at most $2^{11-k}$ lamps in every part of the partition after $k$ steps. Thus, the answer is 11 .
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n10.3. ",
"solution_match": "\nSolution. "
}
|
e0ac19a0-3ebb-5fee-8bd2-61fbbfe9de70
| 608,008
|
A positive integer is called simple if its ordinary decimal representation consists entirely of zeroes and ones. Find the least positive integer $k$ such that each positive integer $n$ can be written as $n=a_{1} \pm a_{2} \pm a_{3} \pm \cdots \pm a_{k}$, where $a_{1}, \ldots, a_{k}$ are simple.
|
We can always write $n=a_{l}+a_{2}+\cdots+a_{9}$ where $a_{j}$ has 1 's in the places where $n$ has digits greater or equal to $j$ and 0 's in the other places. So $k \leq 9$. To show that $k \geq 9$, consider $n=10203040506070809$. Suppose $n=a_{l}+a_{2}+\cdots+a_{j}-a_{j+l}-a_{j+2}-\cdots-a_{k}$, where $a_{l}, \ldots, a_{k}$ are simple, and $k<9$. Then all digits of $b_{l}=a_{l}+\cdots+a_{j}$ are not greater than $j$ and all digits of $b_{2}=a_{j+l}+\cdots+a_{k}$ are not greater than $k-j$. We have $n+b_{2}=b_{l}$. We perform column addition of $n$ and $b_{2}$ and consider digit $j+1$ in the number $n$. There will be no carry digit coming from lower decimal places, since the sum there is less that $10 \ldots 0+88 \ldots 8=98 \ldots 8$. So in the column of $j+1$ we get the sum of $j+1$ and the corresponding digit in $b_{2}$. The resulting digit should be less than $j+1$. Thus in the corresponding place in $b_{2}$ we have at least $9-j$. But $9-j \leq k-j$, implying $k \geq 9$. Hence, we have proved that the maximal $k$ is 9 .
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is called simple if its ordinary decimal representation consists entirely of zeroes and ones. Find the least positive integer $k$ such that each positive integer $n$ can be written as $n=a_{1} \pm a_{2} \pm a_{3} \pm \cdots \pm a_{k}$, where $a_{1}, \ldots, a_{k}$ are simple.
|
We can always write $n=a_{l}+a_{2}+\cdots+a_{9}$ where $a_{j}$ has 1 's in the places where $n$ has digits greater or equal to $j$ and 0 's in the other places. So $k \leq 9$. To show that $k \geq 9$, consider $n=10203040506070809$. Suppose $n=a_{l}+a_{2}+\cdots+a_{j}-a_{j+l}-a_{j+2}-\cdots-a_{k}$, where $a_{l}, \ldots, a_{k}$ are simple, and $k<9$. Then all digits of $b_{l}=a_{l}+\cdots+a_{j}$ are not greater than $j$ and all digits of $b_{2}=a_{j+l}+\cdots+a_{k}$ are not greater than $k-j$. We have $n+b_{2}=b_{l}$. We perform column addition of $n$ and $b_{2}$ and consider digit $j+1$ in the number $n$. There will be no carry digit coming from lower decimal places, since the sum there is less that $10 \ldots 0+88 \ldots 8=98 \ldots 8$. So in the column of $j+1$ we get the sum of $j+1$ and the corresponding digit in $b_{2}$. The resulting digit should be less than $j+1$. Thus in the corresponding place in $b_{2}$ we have at least $9-j$. But $9-j \leq k-j$, implying $k \geq 9$. Hence, we have proved that the maximal $k$ is 9 .
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n10.4. ",
"solution_match": "\nSolution. "
}
|
750ddac5-1257-5a4a-97c6-777c2468296d
| 608,009
|
Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
$$
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
$$
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \ldots, x_{k}$ as for $n=k$, and
let $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.
For $n=9$ we have $8+6+3=9+4+4$, and $8 \cdot 6 \cdot 3=9 \cdot 4 \cdot 4$, so that a set of numbers as required will exist for all $n \geq 9$. It remains to eliminate $n=8$.
Assume $x_{1}, \ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \cdot 5>8$ and $2 \cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \cdots x_{8}=2^{7} \cdot 3^{2}$, and $x_{3}+x_{4}+\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .
Case 1. $x_{3}=x_{4}=3$
We then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.
Case 2. $x_{3}=3, x_{4}=6$
We have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\left\{x_{1}, x_{2}, \ldots, x_{8}\right\}=\{1,2, \ldots, 8\}$.
Case 3. $x_{3}=x_{4}=6$
Now we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.
Thus the smallest positive integer with the required property is 9 .
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
$$
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
$$
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \ldots, x_{k}$ as for $n=k$, and
let $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.
For $n=9$ we have $8+6+3=9+4+4$, and $8 \cdot 6 \cdot 3=9 \cdot 4 \cdot 4$, so that a set of numbers as required will exist for all $n \geq 9$. It remains to eliminate $n=8$.
Assume $x_{1}, \ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \cdot 5>8$ and $2 \cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \cdots x_{8}=2^{7} \cdot 3^{2}$, and $x_{3}+x_{4}+\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .
Case 1. $x_{3}=x_{4}=3$
We then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.
Case 2. $x_{3}=3, x_{4}=6$
We have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\left\{x_{1}, x_{2}, \ldots, x_{8}\right\}=\{1,2, \ldots, 8\}$.
Case 3. $x_{3}=x_{4}=6$
Now we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.
Thus the smallest positive integer with the required property is 9 .
|
{
"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl",
"problem_match": "\n\nProblem 3.",
"solution_match": "\n\nSolution."
}
|
9eed5b3d-a3e7-5f1e-b444-b3a0eedb1984
| 608,016
|
In a football tournament there are $n$ teams, with $n \geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).
|
Note that the total number of games equals the number of different pairings, that is, $n(n-1) / 2$. Suppose the lowest scoring team ends with $k$ points. Then the total score for all teams is
$$
k+(k+1)+\cdots+(k+n-1)=n k+\frac{(n-1) n}{2}
$$
Some games must end in a tie, for otherwise, all team scores would be a multiple of 3 and cannot be 1 point apart. Since the total score of a tie is only 2 points compared to 3 points if one of the teams wins, we therefore know that
$$
n k+\frac{(n-1) n}{2}<3 \cdot \frac{n(n-1)}{2}
$$
so $n k<n(n-1)$, and hence $k<n-1$. It follows that the lowest scoring team can score no more than $n-2$ points.
We now show by induction that it is indeed possible for the lowest scoring team to score $n-2$ points.
The following scoreboard shows this is possible for $n=4$ :
| - | 3 | 1 | 1 | 5 |
| :---: | :---: | :---: | :---: | :---: |
| 0 | - | 1 | 3 | 4 |
| 1 | 1 | - | 1 | 3 |
| 1 | 0 | 1 | - | 2 |
Now suppose we have a scoreboard for $n$ teams labelled $T_{n-2}, \ldots, T_{2 n-3}$, where team $T_{i}$ scores $i$ points. Keep the results among these teams unchanged while adding one more team.
Write $n=3 q+r$ with $r \in\{1,-1,0\}$, and let the new team tie with just one of the original teams, lose against $q$ teams, and win against the rest of them. The new team thus wins $n-1-q$ games, and gets $1+3(n-1-q)=3 n-2-3 q=2 n-2+r$ points.
Moreover, we arrange for the $q$ teams which win against the new team to form an arithmetic sequence $T_{j}, T_{j+3}, \ldots, T_{j+3(q-1)}=T_{j+n-r-3}$, so that each of them, itself having gained three points, fills the slot vacated by the next one.
(i) If $r=1$, then let the new team tie with team $T_{n-2}$ and lose to each of the teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-5}$.
Team $T_{n-2}$ now has $n-1$ points and takes the place vacated by $T_{n-1}$. At the other end, $T_{2 n-5}$ now has $2 n-2$ points, just one more than the previous top team $T_{2 n-3}$. And the new team has $2 n-2+r=2 n-1$ points, becoming the new top team. The teams now have all scores from $n-1$ up to $2 n-1$.
(ii) If $r=-1$, then let the new team tie with team $T_{2 n-3}$ and lose to each of the teams $T_{n-2}, T_{n+1}, \ldots, T_{n-2+n-r-3}=T_{2 n-4}$.
The old top team $T_{2 n-3}$ now has $2 n-2$ points, and its former place is filled by the new team, which gets $2 n-2+r=2 n-3$ points. $T_{2 n-4}$ now has $2 n-1$ points and is the new top team. So again we have all scores ranging from $n-1$ up to $2 n-1$.
(iii) If $r=0$, then let the new team tie with team $T_{n-2}$ and lose to teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-4}$.
Team $T_{n-2}$ now has $n-1$ points and fills the slot vacated by $T_{n-1}$. At the top end, $T_{2 n-4}$ now has $2 n-1$ points, while the new team has $2 n-2+r=2 n-2$ points, and yet again we have all scores from $n-1$ to $2 n-1$.
This concludes the proof.
|
n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a football tournament there are $n$ teams, with $n \geq 4$, and each pair of teams meets exactly once. Suppose that, at the end of the tournament, the final scores form an arithmetic sequence where each team scores 1 more point than the following team on the scoreboard. Determine the maximum possible score of the lowest scoring team, assuming usual scoring for football games (where the winner of a game gets 3 points, the loser 0 points, and if there is a tie both teams get 1 point).
|
Note that the total number of games equals the number of different pairings, that is, $n(n-1) / 2$. Suppose the lowest scoring team ends with $k$ points. Then the total score for all teams is
$$
k+(k+1)+\cdots+(k+n-1)=n k+\frac{(n-1) n}{2}
$$
Some games must end in a tie, for otherwise, all team scores would be a multiple of 3 and cannot be 1 point apart. Since the total score of a tie is only 2 points compared to 3 points if one of the teams wins, we therefore know that
$$
n k+\frac{(n-1) n}{2}<3 \cdot \frac{n(n-1)}{2}
$$
so $n k<n(n-1)$, and hence $k<n-1$. It follows that the lowest scoring team can score no more than $n-2$ points.
We now show by induction that it is indeed possible for the lowest scoring team to score $n-2$ points.
The following scoreboard shows this is possible for $n=4$ :
| - | 3 | 1 | 1 | 5 |
| :---: | :---: | :---: | :---: | :---: |
| 0 | - | 1 | 3 | 4 |
| 1 | 1 | - | 1 | 3 |
| 1 | 0 | 1 | - | 2 |
Now suppose we have a scoreboard for $n$ teams labelled $T_{n-2}, \ldots, T_{2 n-3}$, where team $T_{i}$ scores $i$ points. Keep the results among these teams unchanged while adding one more team.
Write $n=3 q+r$ with $r \in\{1,-1,0\}$, and let the new team tie with just one of the original teams, lose against $q$ teams, and win against the rest of them. The new team thus wins $n-1-q$ games, and gets $1+3(n-1-q)=3 n-2-3 q=2 n-2+r$ points.
Moreover, we arrange for the $q$ teams which win against the new team to form an arithmetic sequence $T_{j}, T_{j+3}, \ldots, T_{j+3(q-1)}=T_{j+n-r-3}$, so that each of them, itself having gained three points, fills the slot vacated by the next one.
(i) If $r=1$, then let the new team tie with team $T_{n-2}$ and lose to each of the teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-5}$.
Team $T_{n-2}$ now has $n-1$ points and takes the place vacated by $T_{n-1}$. At the other end, $T_{2 n-5}$ now has $2 n-2$ points, just one more than the previous top team $T_{2 n-3}$. And the new team has $2 n-2+r=2 n-1$ points, becoming the new top team. The teams now have all scores from $n-1$ up to $2 n-1$.
(ii) If $r=-1$, then let the new team tie with team $T_{2 n-3}$ and lose to each of the teams $T_{n-2}, T_{n+1}, \ldots, T_{n-2+n-r-3}=T_{2 n-4}$.
The old top team $T_{2 n-3}$ now has $2 n-2$ points, and its former place is filled by the new team, which gets $2 n-2+r=2 n-3$ points. $T_{2 n-4}$ now has $2 n-1$ points and is the new top team. So again we have all scores ranging from $n-1$ up to $2 n-1$.
(iii) If $r=0$, then let the new team tie with team $T_{n-2}$ and lose to teams $T_{n-1}, T_{n+2}, \ldots, T_{n-1+n-r-3}=T_{2 n-4}$.
Team $T_{n-2}$ now has $n-1$ points and fills the slot vacated by $T_{n-1}$. At the top end, $T_{2 n-4}$ now has $2 n-1$ points, while the new team has $2 n-2+r=2 n-2$ points, and yet again we have all scores from $n-1$ to $2 n-1$.
This concludes the proof.
|
{
"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl",
"problem_match": "\n\nProblem 2.",
"solution_match": "\n\nSolution."
}
|
91851e2a-218d-5b57-a912-121c826b9fa3
| 608,019
|
An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:
(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.
(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.
How many different permutations of the volumes can be obtained by using these two operations repeatedly?
|
(By the proposer.) Let the positions of the books in the stack be $1,2,3, \ldots, 2000$ from the top (and consider them modulo 2000). Notice that both operations fix the parity of the number of the book at a any given position. Operation (i) subtracts an even integer from the number of the book at each position. If $A$ is an operation of type (i), and $B$ is an operation of type (ii), then the operation $A^{-1} B A$ changes the order of the books in the positions $n+1$ to $n+m$ where $n$ is even and $m$ is odd. This is called turning the interval.
Now we prove that all the volumes in odd positions can be placed in the odd positions in every way we like: If the volume we want in position 1 is in position $m_{1}$, we turn the interval 1 to $m_{1}$. Now if the volume we want in position 3 is in position $m_{3}$, we turn the interval 3 to $m_{3}$, and so on. In this way we can permute the volumes in odd positions exactly as we want to.
Now we prove that we can permute the volumes in even positions exactly as we want without changing the positions of the volumes in the odd positions: We can make a transposition of the two volumes in position $2 n$ and $2 n+2 m$ by turning the interval $2 n+1$ to $2 n+2 m-1$, then turning the interval $2 n+2 m+1$ to $2 n-1$, then turning the interval $2 n+1$ to $2 n-1$, and finally adding $2 m$ to the number of the volume in each position.
Since there are 1000! permutations of the volumes in the odd positions, and 1000! permutations of the volumes in the even positions, altogether we have (1000!) ${ }^{2}$ different permutations.
|
(1000!)^2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An encyclopedia consists of 2000 numbered volumes. The volumes are stacked in order with number 1 on top and 2000 in the bottom. One may perform two operations with the stack:
(i) For $n$ even, one may take the top $n$ volumes and put them in the bottom of the stack without changing the order.
(ii) For $n$ odd, one may take the top $n$ volumes, turn the order around and put them on top of the stack again.
How many different permutations of the volumes can be obtained by using these two operations repeatedly?
|
(By the proposer.) Let the positions of the books in the stack be $1,2,3, \ldots, 2000$ from the top (and consider them modulo 2000). Notice that both operations fix the parity of the number of the book at a any given position. Operation (i) subtracts an even integer from the number of the book at each position. If $A$ is an operation of type (i), and $B$ is an operation of type (ii), then the operation $A^{-1} B A$ changes the order of the books in the positions $n+1$ to $n+m$ where $n$ is even and $m$ is odd. This is called turning the interval.
Now we prove that all the volumes in odd positions can be placed in the odd positions in every way we like: If the volume we want in position 1 is in position $m_{1}$, we turn the interval 1 to $m_{1}$. Now if the volume we want in position 3 is in position $m_{3}$, we turn the interval 3 to $m_{3}$, and so on. In this way we can permute the volumes in odd positions exactly as we want to.
Now we prove that we can permute the volumes in even positions exactly as we want without changing the positions of the volumes in the odd positions: We can make a transposition of the two volumes in position $2 n$ and $2 n+2 m$ by turning the interval $2 n+1$ to $2 n+2 m-1$, then turning the interval $2 n+2 m+1$ to $2 n-1$, then turning the interval $2 n+1$ to $2 n-1$, and finally adding $2 m$ to the number of the volume in each position.
Since there are 1000! permutations of the volumes in the odd positions, and 1000! permutations of the volumes in the even positions, altogether we have (1000!) ${ }^{2}$ different permutations.
|
{
"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl",
"problem_match": "\n## Problem 4.",
"solution_match": "\n\nSolution 1."
}
|
99d32c28-deac-5c13-8cbd-661f55abfa47
| 608,029
|
King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.
What is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?
|
Answer: 2016
An island cannot be connected with just one bridge, since this bridge could be destroyed. Consider the case of two islands, each with only two bridges, connected by a bridge. (It is not possible that they are connected with two bridges, since then they would be isolated from the other islands no matter what.) If they are also connected to two separate islands, then they would be isolated if the rebel movement destroys the two bridges from these islands not connecting the two. So the two bridges not connecting them must go to the same island. That third island must have at least two other bridges, otherwise the rebel movement could cut off these three islands.
Suppose there is a pair of islands with exactly two bridges that are connected to each other. From the above it is easy to see that removing the pair (and the three bridges connected to them) must leave a set of islands with the same properties. Continue removing such pairs, until there are none left. (Note that the reduced set of islands could have a new such pair and that also needs to be removed.) Suppose we are left with $n$ islands and since two islands are removed at a time, $n$ must be an even number. And from the argument above it is clear that $n \geq 4$.
Consider the remaining set of islands and let $x$ be the number of islands with exactly two bridges (which now are not connected to each other). Then $n-x$ islands have at least three bridges each. Let $B^{\prime}$ be the number of bridges in the reduced set. Now $B^{\prime} \geq 2 x$ and $2 B^{\prime} \geq 2 x+3(n-x)=3 n-x$. Hence $2 B^{\prime} \geq \max (4 x, 3 n-x) \geq 4 \cdot \frac{3 n}{5}$, and thus $B^{\prime} \geq \frac{6 n}{5}$. Now let $B$ be the number of bridges in the original set. Then
$$
B=B^{\prime}+3 \cdot \frac{1680-n}{2} \geq \frac{6 n}{5}+\frac{6(1680-n)}{4} \geq \frac{6 \cdot 1680}{5}=2016
$$
It is possible to construct an example with exactly 2016 bridges: Take 672 of the islands and number them $0,1,2, \ldots 671$. Connect island number $i$ with the islands numbered $i-1$, $i+1$ and $i+336$ (modulo 672). This gives 1008 bridges. We now have a circular path of 672 bridges: $0-1-2-\cdots-671-0$. If one of these 672 bridges are destroyed, the 672 islands are still connected. If two of these bridges are destroyed, the path is broken into two parts. Let $i$ be an island on the shortest path (if they have the same length, just pick a random one). Then island $i+336$ (modulo 672) must be on the other part of the path, and the bridge connecting these two islands will connect the two paths. Hence no matter which two bridges the rebel movement destroys, it is possible to travel between any of the 672 islands.
Now for every of the 1008 bridges above, replace it with two bridges with a new island between the two. This increases the number of bridges to 2016 and the number of islands to $672+1008=1680$ completing the construction. Since the rebel movement does not destroy two bridges from the same island, the same argument as above shows that with this construction it is possible to travel between any of the 1680 islands after the destruction of the two bridges.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
King George has decided to connect the 1680 islands in his kingdom by bridges. Unfortunately the rebel movement will destroy two bridges after all the bridges have been built, but not two bridges from the same island.
What is the minimal number of bridges the King has to build in order to make sure that it is still possible to travel by bridges between any two of the 1680 islands after the rebel movement has destroyed two bridges?
|
Answer: 2016
An island cannot be connected with just one bridge, since this bridge could be destroyed. Consider the case of two islands, each with only two bridges, connected by a bridge. (It is not possible that they are connected with two bridges, since then they would be isolated from the other islands no matter what.) If they are also connected to two separate islands, then they would be isolated if the rebel movement destroys the two bridges from these islands not connecting the two. So the two bridges not connecting them must go to the same island. That third island must have at least two other bridges, otherwise the rebel movement could cut off these three islands.
Suppose there is a pair of islands with exactly two bridges that are connected to each other. From the above it is easy to see that removing the pair (and the three bridges connected to them) must leave a set of islands with the same properties. Continue removing such pairs, until there are none left. (Note that the reduced set of islands could have a new such pair and that also needs to be removed.) Suppose we are left with $n$ islands and since two islands are removed at a time, $n$ must be an even number. And from the argument above it is clear that $n \geq 4$.
Consider the remaining set of islands and let $x$ be the number of islands with exactly two bridges (which now are not connected to each other). Then $n-x$ islands have at least three bridges each. Let $B^{\prime}$ be the number of bridges in the reduced set. Now $B^{\prime} \geq 2 x$ and $2 B^{\prime} \geq 2 x+3(n-x)=3 n-x$. Hence $2 B^{\prime} \geq \max (4 x, 3 n-x) \geq 4 \cdot \frac{3 n}{5}$, and thus $B^{\prime} \geq \frac{6 n}{5}$. Now let $B$ be the number of bridges in the original set. Then
$$
B=B^{\prime}+3 \cdot \frac{1680-n}{2} \geq \frac{6 n}{5}+\frac{6(1680-n)}{4} \geq \frac{6 \cdot 1680}{5}=2016
$$
It is possible to construct an example with exactly 2016 bridges: Take 672 of the islands and number them $0,1,2, \ldots 671$. Connect island number $i$ with the islands numbered $i-1$, $i+1$ and $i+336$ (modulo 672). This gives 1008 bridges. We now have a circular path of 672 bridges: $0-1-2-\cdots-671-0$. If one of these 672 bridges are destroyed, the 672 islands are still connected. If two of these bridges are destroyed, the path is broken into two parts. Let $i$ be an island on the shortest path (if they have the same length, just pick a random one). Then island $i+336$ (modulo 672) must be on the other part of the path, and the bridge connecting these two islands will connect the two paths. Hence no matter which two bridges the rebel movement destroys, it is possible to travel between any of the 672 islands.
Now for every of the 1008 bridges above, replace it with two bridges with a new island between the two. This increases the number of bridges to 2016 and the number of islands to $672+1008=1680$ completing the construction. Since the rebel movement does not destroy two bridges from the same island, the same argument as above shows that with this construction it is possible to travel between any of the 1680 islands after the destruction of the two bridges.
|
{
"resource_path": "Nordic_MO/segmented/en-2016-sol.jsonl",
"problem_match": "\n## Problem 4",
"solution_match": "\n\nSolution 4"
}
|
6a3a6451-9b25-5935-ae78-c2176ebb2804
| 608,033
|
In Wonderland, the towns are connected by roads, and whenever there is a direct road between two towns there is also a route between these two towns that does not use that road. (There is at most one direct road between any two towns.) The Queen
of Hearts ordered the Spades to provide a list of all "even" subsystems of the system of roads, that is, systems formed by subsets of the set of roads, where each town is connected to an even number of roads (possibly none). For each such subsystem they should list its roads. If there are totally $n$ roads in Wonderland and $x$ subsystems on the Spades' list, what is the number of roads on their list when each road is counted as many times as it is listed?
|
The answer is $\frac{1}{2} n x$.
Proof: We reformulate the problem in terms of graph theory with the towns being vertices and the roads being edges of a graph $G=(V, E)$. The given information implies that every edge $e \in E$ is part of a cycle. The subgraphs to be counted are those with every valence even, briefly the even subgraphs. Let $N$ be the sum of the numbers of edges in those subgraphs. We can calculate this number by counting for each edge $e \in E$ the even subgraphs of $G$ containing $e$. If $S(e)$ is the set of these graphs, then $N=\sum_{e \in E}|S(e)|$. Now consider for a given $e \in E$ some cycle $c(e)$ containing $e$. For every even subgraph $H$ of $G$ one can define the graph $H^{\prime}$ obtained from $H$ by replacing the set of edges in $H$ that are also edges in $c(e)$ by the set of edges in $c(e)$ that are not edges in $H$. For a given vertex $v \in V$ the following possibilities exist. (i) $c(e)$ does not pass through $v$. (ii) Both edges in $c(e)$ adjacent to $v$ are in $H$. They are then absent from $H^{\prime}$. (iii) None of the edges in $c(e)$ adjacent to $v$ are in $H$. They are then both in $H^{\prime}$. (iv) Exactly one of the edges in $c(e)$ adjacent to $v$ are in $H$. It is then not in $H^{\prime}$ while the other one belongs to $H^{\prime}$. In every case any edge adjacent to $v$ that is not in $c(e)$ is in either none or both of $H$ and $H^{\prime}$. It follows that $H^{\prime}$ is an even subgraph of $G$. Since evidently $H^{\prime \prime}=H$, the total set of even subgraphs of $G$ is thus the union of disjoint pairs $\left\{H, H^{\prime}\right\}$. Exactly one member of each pair belongs to $S(e)$, so $|S(e)|=x / 2$, and $N=\frac{1}{2} n x$.
|
\frac{1}{2} n x
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In Wonderland, the towns are connected by roads, and whenever there is a direct road between two towns there is also a route between these two towns that does not use that road. (There is at most one direct road between any two towns.) The Queen
of Hearts ordered the Spades to provide a list of all "even" subsystems of the system of roads, that is, systems formed by subsets of the set of roads, where each town is connected to an even number of roads (possibly none). For each such subsystem they should list its roads. If there are totally $n$ roads in Wonderland and $x$ subsystems on the Spades' list, what is the number of roads on their list when each road is counted as many times as it is listed?
|
The answer is $\frac{1}{2} n x$.
Proof: We reformulate the problem in terms of graph theory with the towns being vertices and the roads being edges of a graph $G=(V, E)$. The given information implies that every edge $e \in E$ is part of a cycle. The subgraphs to be counted are those with every valence even, briefly the even subgraphs. Let $N$ be the sum of the numbers of edges in those subgraphs. We can calculate this number by counting for each edge $e \in E$ the even subgraphs of $G$ containing $e$. If $S(e)$ is the set of these graphs, then $N=\sum_{e \in E}|S(e)|$. Now consider for a given $e \in E$ some cycle $c(e)$ containing $e$. For every even subgraph $H$ of $G$ one can define the graph $H^{\prime}$ obtained from $H$ by replacing the set of edges in $H$ that are also edges in $c(e)$ by the set of edges in $c(e)$ that are not edges in $H$. For a given vertex $v \in V$ the following possibilities exist. (i) $c(e)$ does not pass through $v$. (ii) Both edges in $c(e)$ adjacent to $v$ are in $H$. They are then absent from $H^{\prime}$. (iii) None of the edges in $c(e)$ adjacent to $v$ are in $H$. They are then both in $H^{\prime}$. (iv) Exactly one of the edges in $c(e)$ adjacent to $v$ are in $H$. It is then not in $H^{\prime}$ while the other one belongs to $H^{\prime}$. In every case any edge adjacent to $v$ that is not in $c(e)$ is in either none or both of $H$ and $H^{\prime}$. It follows that $H^{\prime}$ is an even subgraph of $G$. Since evidently $H^{\prime \prime}=H$, the total set of even subgraphs of $G$ is thus the union of disjoint pairs $\left\{H, H^{\prime}\right\}$. Exactly one member of each pair belongs to $S(e)$, so $|S(e)|=x / 2$, and $N=\frac{1}{2} n x$.
|
{
"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl",
"problem_match": "\n## Problem 2",
"solution_match": "\n\nSolution."
}
|
435d659d-cf73-5329-a945-1bbd9a82f8ad
| 608,041
|
For a positive integer $a$, define a sequence of integers $x_{1}, x_{2}, \ldots$ by letting $x_{1}=a$ and $x_{n+1}=2 x_{n}+1$ for $n \geq 1$. Let $y_{n}=2^{x_{n}}-1$. Determine the largest possible $k$ such that, for some positive integer $a$, the numbers $y_{1}, \ldots, y_{k}$ are all prime.
(Russia) Valery Senderov
|
The largest such is $k=2$. Notice first that if $y_{i}$ is prime, then $x_{i}$ is prime as well. Actually, if $x_{i}=1$ then $y_{i}=1$ which is not prime, and if $x_{i}=m n$ for integer $m, n>1$ then $2^{m}-1 \mid 2^{x_{i}}-1=y_{i}$, so $y_{i}$ is composite. In particular, if $y_{1}, y_{2}, \ldots, y_{k}$ are primes for some $k \geq 1$ then $a=x_{1}$ is also prime.
Now we claim that for every odd prime $a$ at least one of the numbers $y_{1}, y_{2}, y_{3}$ is composite (and thus $k<3$ ). Assume, to the contrary, that $y_{1}, y_{2}$, and $y_{3}$ are primes; then $x_{1}, x_{2}, x_{3}$ are primes as well. Since $x_{1} \geq 3$ is odd, we have $x_{2}>3$ and $x_{2} \equiv 3(\bmod 4)$; consequently, $x_{3} \equiv 7$ $(\bmod 8)$. This implies that 2 is a quadratic residue modulo $p=x_{3}$, so $2 \equiv s^{2}(\bmod p)$ for some integer $s$, and hence $2^{x_{2}}=2^{(p-1) / 2} \equiv s^{p-1} \equiv 1(\bmod p)$. This means that $p \mid y_{2}$, thus $2^{x_{2}}-1=x_{3}=2 x_{2}+1$. But it is easy to show that $2^{t}-1>2 t+1$ for all integer $t>3$. A contradiction.
Finally, if $a=2$, then the numbers $y_{1}=3$ and $y_{2}=31$ are primes, while $y_{3}=2^{11}-1$ is divisible by 23 ; in this case we may choose $k=2$ but not $k=3$.
Remark. The fact that $23 \mid 2^{11}-1$ can be shown along the lines in the solution, since 2 is a quadratic residue modulo $x_{4}=23$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer $a$, define a sequence of integers $x_{1}, x_{2}, \ldots$ by letting $x_{1}=a$ and $x_{n+1}=2 x_{n}+1$ for $n \geq 1$. Let $y_{n}=2^{x_{n}}-1$. Determine the largest possible $k$ such that, for some positive integer $a$, the numbers $y_{1}, \ldots, y_{k}$ are all prime.
(Russia) Valery Senderov
|
The largest such is $k=2$. Notice first that if $y_{i}$ is prime, then $x_{i}$ is prime as well. Actually, if $x_{i}=1$ then $y_{i}=1$ which is not prime, and if $x_{i}=m n$ for integer $m, n>1$ then $2^{m}-1 \mid 2^{x_{i}}-1=y_{i}$, so $y_{i}$ is composite. In particular, if $y_{1}, y_{2}, \ldots, y_{k}$ are primes for some $k \geq 1$ then $a=x_{1}$ is also prime.
Now we claim that for every odd prime $a$ at least one of the numbers $y_{1}, y_{2}, y_{3}$ is composite (and thus $k<3$ ). Assume, to the contrary, that $y_{1}, y_{2}$, and $y_{3}$ are primes; then $x_{1}, x_{2}, x_{3}$ are primes as well. Since $x_{1} \geq 3$ is odd, we have $x_{2}>3$ and $x_{2} \equiv 3(\bmod 4)$; consequently, $x_{3} \equiv 7$ $(\bmod 8)$. This implies that 2 is a quadratic residue modulo $p=x_{3}$, so $2 \equiv s^{2}(\bmod p)$ for some integer $s$, and hence $2^{x_{2}}=2^{(p-1) / 2} \equiv s^{p-1} \equiv 1(\bmod p)$. This means that $p \mid y_{2}$, thus $2^{x_{2}}-1=x_{3}=2 x_{2}+1$. But it is easy to show that $2^{t}-1>2 t+1$ for all integer $t>3$. A contradiction.
Finally, if $a=2$, then the numbers $y_{1}=3$ and $y_{2}=31$ are primes, while $y_{3}=2^{11}-1$ is divisible by 23 ; in this case we may choose $k=2$ but not $k=3$.
Remark. The fact that $23 \mid 2^{11}-1$ can be shown along the lines in the solution, since 2 is a quadratic residue modulo $x_{4}=23$.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
956e4393-91e4-5b03-b9fe-9a1f32f8f0c7
| 605,569
|
Let $n$ be an integer greater than 1 and let $X$ be an $n$-element set. A non-empty collection of subsets $A_{1}, \ldots, A_{k}$ of $X$ is tight if the union $A_{1} \cup \cdots \cup A_{k}$ is a proper subset of $X$ and no element of $X$ lies in exactly one of the $A_{i}$ s. Find the largest cardinality of a collection of proper non-empty subsets of $X$, no non-empty subcollection of which is tight.
Note. A subset $A$ of $X$ is proper if $A \neq X$. The sets in a collection are assumed to be distinct. The whole collection is assumed to be a subcollection.
## Alexander Polyansky, Russia
|
. (Ilya Bogdanov) The required maximum is $2 n-2$. To describe a ( $2 n-2$ )-element collection satisfying the required conditions, write $X=\{1,2, \ldots, n\}$ and set $B_{k}=\{1,2, \ldots, k\}$, $k=1,2, \ldots, n-1$, and $B_{k}=\{k-n+2, k-n+3, \ldots, n\}, k=n, n+1, \ldots, 2 n-2$. To show that no subcollection of the $B_{k}$ is tight, consider a subcollection $\mathcal{C}$ whose union $U$ is a proper subset of $X$, let $m$ be an element in $X \backslash U$, and notice that $\mathcal{C}$ is a subcollection of $\left\{B_{1}, \ldots, B_{m-1}, B_{m+n-1}, \ldots, B_{2 n-2}\right\}$, since the other $B$ 's are precisely those containing $m$. If $U$ contains elements less than $m$, let $k$ be the greatest such and notice that $B_{k}$ is the only member of $\mathcal{C}$ containing $k$; and if $U$ contains elements greater than $m$, let $k$ be the least such and notice that $B_{k+n-2}$ is the only member of $\mathcal{C}$ containing $k$. Consequently, $\mathcal{C}$ is not tight.
We now proceed to show by induction on $n \geq 2$ that the cardinality of a collection of proper non-empty subsets of $X$, no subcollection of which is tight, does not exceed $2 n-2$. The base case $n=2$ is clear, so let $n>2$ and suppose, if possible, that $\mathcal{B}$ is a collection of $2 n-1$ proper non-empty subsets of $X$ containing no tight subcollection.
To begin, notice that $\mathcal{B}$ has an empty intersection: if the members of $\mathcal{B}$ shared an element $x$, then $\mathcal{B}^{\prime}=\{B \backslash\{x\}: B \in \mathcal{B}, B \neq\{x\}\}$ would be a collection of at least $2 n-2$ proper non-empty subsets of $X \backslash\{x\}$ containing no tight subcollection, and the induction hypothesis would be contradicted.
Now, for every $x$ in $X$, let $\mathcal{B}_{x}$ be the (non-empty) collection of all members of $\mathcal{B}$ not containing $x$. Since no subcollection of $\mathcal{B}$ is tight, $\mathcal{B}_{x}$ is not tight, and since the union of $\mathcal{B}_{x}$ does not contain $x$, some $x^{\prime}$ in $X$ is covered by a single member of $\mathcal{B}_{x}$. In other words, there is a single set in $\mathcal{B}$ covering $x^{\prime}$ but not $x$. In this case, draw an arrow from $x$ to $x^{\prime}$. Since there is at least one arrow from each $x$ in $X$, some of these arrows form a (minimal) cycle $x_{1} \rightarrow x_{2} \rightarrow \cdots \rightarrow x_{k} \rightarrow x_{k+1}=x_{1}$ for some suitable integer $k \geq 2$. Let $A_{i}$ be the unique member of $\mathcal{B}$ containing $x_{i+1}$ but not $x_{i}$, and let $X^{\prime}=\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$.
Remove $A_{1}, A_{2}, \ldots, A_{k}$ from $\mathcal{B}$ to obtain a collection $\mathcal{B}^{\prime}$ each member of which either contains or is disjoint from $X^{\prime}$ : for if a member $B$ of $\mathcal{B}^{\prime}$ contained some but not all elements of $X^{\prime}$, then $B$ should contain $x_{i+1}$ but not $x_{i}$ for some $i$, and $B=A_{i}$, a contradiction. This rules out the case $k=n$, for otherwise $\mathcal{B}=\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}$, so $|\mathcal{B}|<2 n-1$.
To rule out the case $k<n$, consider an extra element $x^{*}$ outside $X$ and let
$$
\mathcal{B}^{*}=\left\{B: B \in \mathcal{B}^{\prime}, B \cap X^{\prime}=\varnothing\right\} \cup\left\{\left(B \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}: B \in \mathcal{B}^{\prime}, X^{\prime} \subseteq B\right\} ;
$$
thus, in each member of $\mathcal{B}^{\prime}$ containing $X^{\prime}$, the latter is collapsed to singleton $x^{*}$. Notice that $\mathcal{B}^{*}$ is a collection of proper non-empty subsets of $X^{*}=\left(X \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}$, no subcollection of which is tight. By the induction hypothesis, $\left|\mathcal{B}^{\prime}\right|=\left|\mathcal{B}^{*}\right| \leq 2\left|X^{*}\right|-2=2(n-k)$, so $|\mathcal{B}| \leq 2(n-k)+k=$ $2 n-k<2 n-1$, a final contradiction.
|
2n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be an integer greater than 1 and let $X$ be an $n$-element set. A non-empty collection of subsets $A_{1}, \ldots, A_{k}$ of $X$ is tight if the union $A_{1} \cup \cdots \cup A_{k}$ is a proper subset of $X$ and no element of $X$ lies in exactly one of the $A_{i}$ s. Find the largest cardinality of a collection of proper non-empty subsets of $X$, no non-empty subcollection of which is tight.
Note. A subset $A$ of $X$ is proper if $A \neq X$. The sets in a collection are assumed to be distinct. The whole collection is assumed to be a subcollection.
## Alexander Polyansky, Russia
|
. (Ilya Bogdanov) The required maximum is $2 n-2$. To describe a ( $2 n-2$ )-element collection satisfying the required conditions, write $X=\{1,2, \ldots, n\}$ and set $B_{k}=\{1,2, \ldots, k\}$, $k=1,2, \ldots, n-1$, and $B_{k}=\{k-n+2, k-n+3, \ldots, n\}, k=n, n+1, \ldots, 2 n-2$. To show that no subcollection of the $B_{k}$ is tight, consider a subcollection $\mathcal{C}$ whose union $U$ is a proper subset of $X$, let $m$ be an element in $X \backslash U$, and notice that $\mathcal{C}$ is a subcollection of $\left\{B_{1}, \ldots, B_{m-1}, B_{m+n-1}, \ldots, B_{2 n-2}\right\}$, since the other $B$ 's are precisely those containing $m$. If $U$ contains elements less than $m$, let $k$ be the greatest such and notice that $B_{k}$ is the only member of $\mathcal{C}$ containing $k$; and if $U$ contains elements greater than $m$, let $k$ be the least such and notice that $B_{k+n-2}$ is the only member of $\mathcal{C}$ containing $k$. Consequently, $\mathcal{C}$ is not tight.
We now proceed to show by induction on $n \geq 2$ that the cardinality of a collection of proper non-empty subsets of $X$, no subcollection of which is tight, does not exceed $2 n-2$. The base case $n=2$ is clear, so let $n>2$ and suppose, if possible, that $\mathcal{B}$ is a collection of $2 n-1$ proper non-empty subsets of $X$ containing no tight subcollection.
To begin, notice that $\mathcal{B}$ has an empty intersection: if the members of $\mathcal{B}$ shared an element $x$, then $\mathcal{B}^{\prime}=\{B \backslash\{x\}: B \in \mathcal{B}, B \neq\{x\}\}$ would be a collection of at least $2 n-2$ proper non-empty subsets of $X \backslash\{x\}$ containing no tight subcollection, and the induction hypothesis would be contradicted.
Now, for every $x$ in $X$, let $\mathcal{B}_{x}$ be the (non-empty) collection of all members of $\mathcal{B}$ not containing $x$. Since no subcollection of $\mathcal{B}$ is tight, $\mathcal{B}_{x}$ is not tight, and since the union of $\mathcal{B}_{x}$ does not contain $x$, some $x^{\prime}$ in $X$ is covered by a single member of $\mathcal{B}_{x}$. In other words, there is a single set in $\mathcal{B}$ covering $x^{\prime}$ but not $x$. In this case, draw an arrow from $x$ to $x^{\prime}$. Since there is at least one arrow from each $x$ in $X$, some of these arrows form a (minimal) cycle $x_{1} \rightarrow x_{2} \rightarrow \cdots \rightarrow x_{k} \rightarrow x_{k+1}=x_{1}$ for some suitable integer $k \geq 2$. Let $A_{i}$ be the unique member of $\mathcal{B}$ containing $x_{i+1}$ but not $x_{i}$, and let $X^{\prime}=\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$.
Remove $A_{1}, A_{2}, \ldots, A_{k}$ from $\mathcal{B}$ to obtain a collection $\mathcal{B}^{\prime}$ each member of which either contains or is disjoint from $X^{\prime}$ : for if a member $B$ of $\mathcal{B}^{\prime}$ contained some but not all elements of $X^{\prime}$, then $B$ should contain $x_{i+1}$ but not $x_{i}$ for some $i$, and $B=A_{i}$, a contradiction. This rules out the case $k=n$, for otherwise $\mathcal{B}=\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}$, so $|\mathcal{B}|<2 n-1$.
To rule out the case $k<n$, consider an extra element $x^{*}$ outside $X$ and let
$$
\mathcal{B}^{*}=\left\{B: B \in \mathcal{B}^{\prime}, B \cap X^{\prime}=\varnothing\right\} \cup\left\{\left(B \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}: B \in \mathcal{B}^{\prime}, X^{\prime} \subseteq B\right\} ;
$$
thus, in each member of $\mathcal{B}^{\prime}$ containing $X^{\prime}$, the latter is collapsed to singleton $x^{*}$. Notice that $\mathcal{B}^{*}$ is a collection of proper non-empty subsets of $X^{*}=\left(X \backslash X^{\prime}\right) \cup\left\{x^{*}\right\}$, no subcollection of which is tight. By the induction hypothesis, $\left|\mathcal{B}^{\prime}\right|=\left|\mathcal{B}^{*}\right| \leq 2\left|X^{*}\right|-2=2(n-k)$, so $|\mathcal{B}| \leq 2(n-k)+k=$ $2 n-k<2 n-1$, a final contradiction.
|
{
"resource_path": "RMM/segmented/en-2017-Solutions_RMM2017-1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 1"
}
|
6fcd80fd-12e4-5bfd-a862-601fdf01101f
| 605,834
|
Fix an integer $n \geq 2$. An $n \times n$ sieve is an $n \times n$ array with $n$ cells removed so that exactly one cell is removed from every row and every column. A stick is a $1 \times k$ or $k \times 1$ array for any positive integer $k$. For any sieve $A$, let $m(A)$ be the minimal number of sticks required to partition $A$. Find all possible values of $m(A)$, as $A$ varies over all possible $n \times n$ sieves.
Palmer Mebane and Nikolai Beluhov
|
. Given $A, m(A)=2 n-2$, and it is achieved, for instance, by dissecting $A$ along all horizontal (or vertical) grid lines. It remains to prove that $m(A) \geq 2 n-2$ for every $A$.
By holes we mean the cells which are cut out from the board. The cross of a hole in $A$ is the union of the row and the column through that hole.
Arguing indirectly, consider a dissection of $A$ into $2 n-3$ or fewer sticks. Horizontal sticks are all labelled $h$, and vertical sticks are labelled $v ; 1 \times 1$ sticks are both horizontal and vertical, and labelled arbitrarily. Each cell of $A$ inherits the label of the unique containing stick.
Assign each stick in the dissection to the cross of the unique hole on its row, if the stick is horizontal; on its column, if the stick is vertical.
Since there are at most $2 n-3$ sticks and exactly $n$ crosses, there are two crosses each of which is assigned to at most one stick in the dissection. Let the crosses be $c$ and $d$, centred at $a=\left(x_{a}, y_{a}\right)$ and $b=\left(x_{b}, y_{b}\right)$, respectively, and assume, without loss of generality, $x_{a}<x_{b}$ and $y_{a}<y_{b}$. The sticks covering the cells $\left(x_{a}, y_{b}\right)$ and $\left(x_{b}, y_{a}\right)$ have like labels, for otherwise one of the two crosses would be assigned to at least two sticks. Say the common label is $v$, so each of $c$ and $d$ contains a stick covering one of those two cells. It follows that the lower (respectively, upper) arm of $c$ (respectively, $d$ ) is all- $h$, and the horizontal arms of both crosses are all- $v$, as illustrated below.
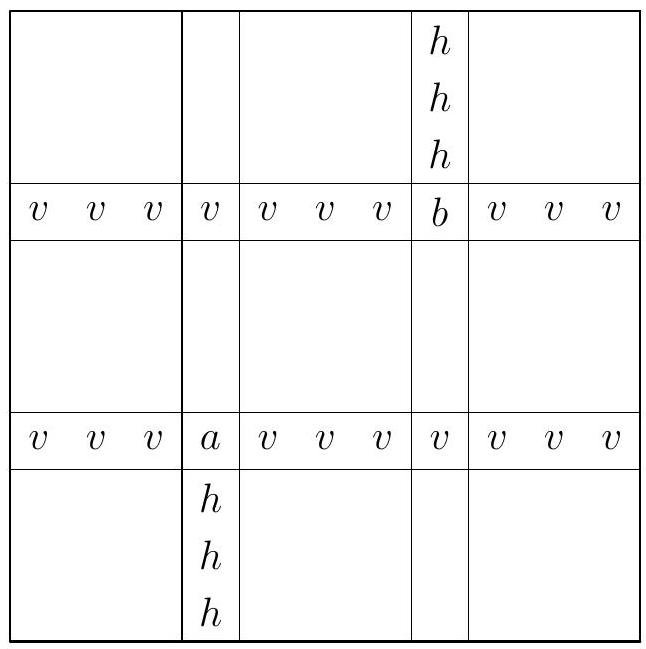
Each of the rows between the rows of $a$ and $b$, that is, rows $y_{a}+1, y_{a}+2, \ldots, y_{b}-1$, contains a hole. The column of each such hole contains at least two $v$-sticks. All other columns contain at least one $v$-stick each. In addition, all rows below $a$ and all rows above $b$ contain at least one $h$-stick each. This amounts to a total of at least $2\left(y_{b}-y_{a}-1\right)+\left(n-y_{b}+y_{a}+1\right)+\left(n-y_{b}\right)+\left(y_{a}-1\right)=2 n-2$ sticks. A contradiction.
Remark. One may find a different argument finishing the solution. Since $c$ and $d$ are proven to contain one stick each, there is a third cross $e$ centred at $\left(x_{*}, y_{*}\right)$ also containing at most one stick. It meets the horizontal arms of $c$ and $d$ at two $v$-cells, so all the cells where two of the three crosses meet are labelled with $v$. Now, assuming (without loss of generality) that $y_{a}<y_{*}<y_{b}$, we obtain that both vertical arms of $e$ contain $v$-cells, so $e$ is assigned to two different $v$-sticks. A contradiction.
|
2n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Fix an integer $n \geq 2$. An $n \times n$ sieve is an $n \times n$ array with $n$ cells removed so that exactly one cell is removed from every row and every column. A stick is a $1 \times k$ or $k \times 1$ array for any positive integer $k$. For any sieve $A$, let $m(A)$ be the minimal number of sticks required to partition $A$. Find all possible values of $m(A)$, as $A$ varies over all possible $n \times n$ sieves.
Palmer Mebane and Nikolai Beluhov
|
. Given $A, m(A)=2 n-2$, and it is achieved, for instance, by dissecting $A$ along all horizontal (or vertical) grid lines. It remains to prove that $m(A) \geq 2 n-2$ for every $A$.
By holes we mean the cells which are cut out from the board. The cross of a hole in $A$ is the union of the row and the column through that hole.
Arguing indirectly, consider a dissection of $A$ into $2 n-3$ or fewer sticks. Horizontal sticks are all labelled $h$, and vertical sticks are labelled $v ; 1 \times 1$ sticks are both horizontal and vertical, and labelled arbitrarily. Each cell of $A$ inherits the label of the unique containing stick.
Assign each stick in the dissection to the cross of the unique hole on its row, if the stick is horizontal; on its column, if the stick is vertical.
Since there are at most $2 n-3$ sticks and exactly $n$ crosses, there are two crosses each of which is assigned to at most one stick in the dissection. Let the crosses be $c$ and $d$, centred at $a=\left(x_{a}, y_{a}\right)$ and $b=\left(x_{b}, y_{b}\right)$, respectively, and assume, without loss of generality, $x_{a}<x_{b}$ and $y_{a}<y_{b}$. The sticks covering the cells $\left(x_{a}, y_{b}\right)$ and $\left(x_{b}, y_{a}\right)$ have like labels, for otherwise one of the two crosses would be assigned to at least two sticks. Say the common label is $v$, so each of $c$ and $d$ contains a stick covering one of those two cells. It follows that the lower (respectively, upper) arm of $c$ (respectively, $d$ ) is all- $h$, and the horizontal arms of both crosses are all- $v$, as illustrated below.

Each of the rows between the rows of $a$ and $b$, that is, rows $y_{a}+1, y_{a}+2, \ldots, y_{b}-1$, contains a hole. The column of each such hole contains at least two $v$-sticks. All other columns contain at least one $v$-stick each. In addition, all rows below $a$ and all rows above $b$ contain at least one $h$-stick each. This amounts to a total of at least $2\left(y_{b}-y_{a}-1\right)+\left(n-y_{b}+y_{a}+1\right)+\left(n-y_{b}\right)+\left(y_{a}-1\right)=2 n-2$ sticks. A contradiction.
Remark. One may find a different argument finishing the solution. Since $c$ and $d$ are proven to contain one stick each, there is a third cross $e$ centred at $\left(x_{*}, y_{*}\right)$ also containing at most one stick. It meets the horizontal arms of $c$ and $d$ at two $v$-cells, so all the cells where two of the three crosses meet are labelled with $v$. Now, assuming (without loss of generality) that $y_{a}<y_{*}<y_{b}$, we obtain that both vertical arms of $e$ contain $v$-cells, so $e$ is assigned to two different $v$-sticks. A contradiction.
|
{
"resource_path": "RMM/segmented/en-2017-Solutions_RMM2017-2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1"
}
|
eacfe7f3-f09d-5f5a-b6d3-c1e645a30766
| 605,891
|
Xenia and Sergey play the following game. Xenia thinks of a positive integer $N$ not exceeding 5000. Then she fixes 20 distinct positive integers $a_{1}, a_{2}, \ldots, a_{20}$ such that, for each $k=1,2, \ldots, 20$, the numbers $N$ and $a_{k}$ are congruent modulo $k$. By a move, Sergey tells Xenia a set $S$ of positive integers not exceeding 20, and she tells him back the set $\left\{a_{k}: k \in S\right\}$ without spelling out which number corresponds to which index. How many moves does Sergey need to determine for sure the number Xenia thought of?
Russia, Sergey Kudrya
|
Sergey can determine Xenia's number in 2 but not fewer moves.
We first show that 2 moves are sufficient. Let Sergey provide the set $\{17,18\}$ on his first move, and the set $\{18,19\}$ on the second move. In Xenia's two responses, exactly one number occurs twice, namely, $a_{18}$. Thus, Sergey is able to identify $a_{17}, a_{18}$, and $a_{19}$, and thence the residue of $N$ modulo $17 \cdot 18 \cdot 19=5814>5000$, by the Chinese Remainder Theorem. This means that the given range contains a single number satisfying all congruences, and Sergey achieves his goal.
To show that 1 move is not sufficient, let $M=\operatorname{lcm}(1,2, \ldots, 10)=2^{3} \cdot 3^{2} \cdot 5 \cdot 7=2520$. Notice that $M$ is divisible by the greatest common divisor of every pair of distinct positive integers not exceeding 20. Let Sergey provide the set $S=\left\{s_{1}, s_{2}, \ldots, s_{k}\right\}$. We show that there exist pairwise distinct positive integers $b_{1}, b_{2}, \ldots, b_{k}$ such that $1 \equiv b_{i}\left(\bmod s_{i}\right)$ and $M+1 \equiv b_{i-1}\left(\bmod s_{i}\right)$ (indices are reduced modulo $k$ ). Thus, if in response Xenia provides the set $\left\{b_{1}, b_{2}, \ldots, b_{k}\right\}$, then Sergey will be unable to distinguish 1 from $M+1$, as desired.
To this end, notice that, for each $i$, the numbers of the form $1+m s_{i}, m \in \mathbb{Z}$, cover all residues modulo $s_{i+1}$ which are congruent to $1(\equiv M+1)$ modulo $\operatorname{gcd}\left(s_{i}, s_{i+1}\right) \mid M$. Xenia can therefore choose a positive integer $b_{i}$ such that $b_{i} \equiv 1\left(\bmod s_{i}\right)$ and $b_{i} \equiv M+1\left(\bmod s_{i+1}\right)$. Clearly, such choices can be performed so as to make the $b_{i}$ pairwise distinct, as required.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Xenia and Sergey play the following game. Xenia thinks of a positive integer $N$ not exceeding 5000. Then she fixes 20 distinct positive integers $a_{1}, a_{2}, \ldots, a_{20}$ such that, for each $k=1,2, \ldots, 20$, the numbers $N$ and $a_{k}$ are congruent modulo $k$. By a move, Sergey tells Xenia a set $S$ of positive integers not exceeding 20, and she tells him back the set $\left\{a_{k}: k \in S\right\}$ without spelling out which number corresponds to which index. How many moves does Sergey need to determine for sure the number Xenia thought of?
Russia, Sergey Kudrya
|
Sergey can determine Xenia's number in 2 but not fewer moves.
We first show that 2 moves are sufficient. Let Sergey provide the set $\{17,18\}$ on his first move, and the set $\{18,19\}$ on the second move. In Xenia's two responses, exactly one number occurs twice, namely, $a_{18}$. Thus, Sergey is able to identify $a_{17}, a_{18}$, and $a_{19}$, and thence the residue of $N$ modulo $17 \cdot 18 \cdot 19=5814>5000$, by the Chinese Remainder Theorem. This means that the given range contains a single number satisfying all congruences, and Sergey achieves his goal.
To show that 1 move is not sufficient, let $M=\operatorname{lcm}(1,2, \ldots, 10)=2^{3} \cdot 3^{2} \cdot 5 \cdot 7=2520$. Notice that $M$ is divisible by the greatest common divisor of every pair of distinct positive integers not exceeding 20. Let Sergey provide the set $S=\left\{s_{1}, s_{2}, \ldots, s_{k}\right\}$. We show that there exist pairwise distinct positive integers $b_{1}, b_{2}, \ldots, b_{k}$ such that $1 \equiv b_{i}\left(\bmod s_{i}\right)$ and $M+1 \equiv b_{i-1}\left(\bmod s_{i}\right)$ (indices are reduced modulo $k$ ). Thus, if in response Xenia provides the set $\left\{b_{1}, b_{2}, \ldots, b_{k}\right\}$, then Sergey will be unable to distinguish 1 from $M+1$, as desired.
To this end, notice that, for each $i$, the numbers of the form $1+m s_{i}, m \in \mathbb{Z}$, cover all residues modulo $s_{i+1}$ which are congruent to $1(\equiv M+1)$ modulo $\operatorname{gcd}\left(s_{i}, s_{i+1}\right) \mid M$. Xenia can therefore choose a positive integer $b_{i}$ such that $b_{i} \equiv 1\left(\bmod s_{i}\right)$ and $b_{i} \equiv M+1\left(\bmod s_{i+1}\right)$. Clearly, such choices can be performed so as to make the $b_{i}$ pairwise distinct, as required.
|
{
"resource_path": "RMM/segmented/en-2021-RMM2021-Day1-English_Solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
d729436f-eb73-5f7b-9c07-394dedcc29cc
| 606,130
|
Determine the smallest natural number that is divisible by 2009 and whose sum of digits equals 2009.
|
Since $2009=223 \cdot 9+2$, the sought number has at least 224 digits. We will consider 224-digit numbers $x=\overline{c_{223} c_{222} \ldots c_{1} c_{0}}$. Clearly, $c_{223} \geq 2$. Furthermore, if $c_{223}=2$ then $c_{222}=\cdots=c_{0}=9$ and $x=3 \cdot 10^{223}-1 \equiv 3 \cdot 10-1$, which is not divisible by $2009=7^{2} \cdot 41$ since $x \equiv 1(\bmod 7)$.
Now let $c_{223}=3$. Then the number $x$ has the form $399 \ldots 9899 \ldots 9=4 \cdot 10^{223}-10^{i}-1$ for some $i$. Since $10^{5} \equiv 1(\bmod 41)$, we have $10^{i} \equiv 1,10,18,16$ or 37 $(\bmod 41)$ for $i=0,1,2,3,4(\bmod 5)$ respectively, and thus $x \equiv 4 \cdot 10^{3}-10^{i}-1 \equiv 22-10^{i}$ $(\bmod 41)$ is never divisible by 41.
Let $c_{223}=4$. Among the digits $c_{222}, \ldots, c_{0}$ there are two eights or one seven, while all others are nines; in any case, $x=5 \cdot 10^{223}-10^{i}10^{j}-1 \equiv 38-\left(10^{i}+10^{j}\right)(\bmod 41)$, where $i$ and $j$ are not necessarily distinct. From the previous, $10^{i}+10^{j} \equiv 38(\bmod 41)$ if and only if $(i, j) \equiv(0,4)$ or $(4,0)(\bmod 5)$. Among other things, $i \neq j$ and $i, j \leq 220$.
Let's try to set $j=220$ and $i \equiv 4(\bmod 5)$. We need to choose $i$, if it exists, such that $7^{2} \mid x=5 \cdot 10^{223}-10^{220}-10^{i}-1 \equiv 5 \cdot 10^{13}-10^{10}-10^{i}-1 \equiv 31-10^{i}$ $(\bmod 49)$. It is easy to find that $10^{i} \equiv 31(\bmod 49)$ if and only if $i \equiv 7$ $(\bmod 42)$, which together with $i \equiv 4(\bmod 5)$ gives the only possibility $i=49$. Therefore, the sought number is
$$
4998 \underbrace{9 \ldots 99}_{170} 8 \underbrace{99 \ldots 9}_{49} .
$$
|
4998 \underbrace{9 \ldots 99}_{170} 8 \underbrace{99 \ldots 9}_{49}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Одредити најмањи природан број који је дељив са 2009 и коме је збир цифара једнак 2009.
|
Пошто је $2009=223 \cdot 9+2$, тражени број има бар 224 цифре. Посматраћемо 224 -цифрене бројеве $x=\overline{c_{223} c_{222} \ldots c_{1} c_{0}}$. Јасно је да је $c_{223} \geq 2$. Притом, ако је $c_{223}=2$ онда је $c_{222}=\cdots=c_{0}=9$ и $x=3 \cdot 10^{223}-1 \equiv 3 \cdot 10-1$, а то није дељиво са $2009=7^{2} \cdot 41$ јер је $x \equiv 1(\bmod 7)$.
Нека је сада $c_{223}=3$. Тада број $x$ има облик $399 \ldots 9899 \ldots 9=4 \cdot 10^{223}-$ $10^{i}-1$ за неко $i$. Како је $10^{5} \equiv 1(\bmod 41)$, имамо $10^{i} \equiv 1,10,18,16$ или 37 $(\bmod 41)$ за $i=0,1,2,3,4(\bmod 5)$ редом, и одатле $x \equiv 4 \cdot 10^{3}-10^{i}-1 \equiv 22-10^{i}$ $(\bmod 41)$ никад није дељиво са 41.
Нека је $c_{223}=4$. Међу цифрама $c_{222}, \ldots, c_{0}$ налазе се две осмице или једна седмица, док су све остале деветке; у сваком случају, $x=5 \cdot 10^{223}-10^{i}$ $10^{j}-1 \equiv 38-\left(10^{i}+10^{j}\right)(\bmod 41)$, где $i$ и $j$ нису обавезно различити. По претходном је $10^{i}+10^{j} \equiv 38(\bmod 41)$ ако и само ако је $(i, j) \equiv(0,4)$ или $(4,0)(\bmod 5)$. Између осталог, $i \neq j$ и $i, j \leq 220$.
Пробајмо да ставимо $j=220$ и $i \equiv 4(\bmod 5)$. Треба одабрати $i$, ако постоји, тако да $7^{2} \mid x=5 \cdot 10^{223}-10^{220}-10^{i}-1 \equiv 5 \cdot 10^{13}-10^{10}-10^{i}-1 \equiv 31-10^{i}$ $(\bmod 49)$. Лако налазимо да је $10^{i} \equiv 31(\bmod 49)$ ако и само ако је $i \equiv 7$ $(\bmod 42)$, што заједно са $i \equiv 4(\bmod 5)$ даје као једину могућност $i=49$. Према томе, тражени број је
$$
4998 \underbrace{9 \ldots 99}_{170} 8 \underbrace{99 \ldots 9}_{49} .
$$
|
{
"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
907cc421-5685-531e-a3d6-daa99f4dbfd8
| 608,061
|
Determine the largest natural number $n$ for which there exist distinct sets $S_{1}, S_{2}, \ldots, S_{n}$ such that:
$1^{\circ}\left|S_{i} \cup S_{j}\right| \leqslant 2004$ for any two integers $1 \leqslant i, j \leqslant n$, and
$2^{\circ} S_{i} \cup S_{j} \cup S_{k}=\{1,2, \ldots, 2008\}$ for any three integers $1 \leqslant i<j<k \leqslant n$.
(Ivan Matic)
## SERBIAN MATHEMATICAL OLYMPIAD
competition of high school students in mathematics
Novi Sad, 14.04.2009.
## Second day
|
Each set $S_{i}$ has at most 2003 elements. Indeed, if $|S_{i}|=2004$, then from condition $1^{\circ}$ it follows that $S_{j} \subset S_{i}$ for all $j$, contradicting condition $2^{\circ}$. Consider the sets
$$
G_{\{i, j\}}=\{1,2, \ldots, 2008\} \backslash\left(S_{i} \cup S_{j}\right) \quad \text { for } 1 \leq i, j \leq n
$$
Then $|G_{\{i, j\}}| \geqslant 4$ and all $\binom{n}{2}$ sets $G_{\{i, j\}}$ are mutually disjoint (otherwise, if $x \in G_{\{i, j\}} \cap G_{\{k, l\}}$, then $x \notin S_{i} \cup S_{j} \cup S_{k} \cup S_{l}$, which is impossible if at least three of $i, j, k, l$ are distinct). It follows that $4\binom{n}{2} \leqslant 2008$, from which $n \leqslant 32$.
We will construct 32 sets that satisfy $1^{\circ}$ and $2^{\circ}$. Decompose the set $\{1,2, \ldots, 2008\}$ arbitrarily into $\binom{32}{2}=496$ (disjoint) sets $G_{\{i, j\}}$, where $|G_{\{i, j\}}| \geqslant 4$ for $1 \leqslant i, j \leqslant 32$, and define
$$
S_{i}=\{1,2, \ldots, 2008\} \backslash \bigcup_{j \neq i} G_{\{i, j\}} \quad \text { for } i=1, \ldots, 32
$$
Condition $1^{\circ}$ is automatically satisfied. Moreover, each $s \in\{1,2, \ldots, 2008\}$ belongs to at most one of the sets $G_{\{p, q\}}$, meaning that there are at most two sets $S_{i}$ that do not contain it (these are $S_{p}$ and $S_{q}$), so condition $2^{\circ}$ is also satisfied. Therefore, the answer is $n=32$.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Одредити највећи природан број $n$ за који постоје различити скупови $S_{1}, S_{2}, \ldots, S_{n}$ такви да је:
$1^{\circ}\left|S_{i} \cup S_{j}\right| \leqslant 2004$ за свака два цела броја $1 \leqslant i, j \leqslant n$, и
$2^{\circ} S_{i} \cup S_{j} \cup S_{k}=\{1,2, \ldots, 2008\}$ за свака три цела броја $1 \leqslant i<j<k \leqslant n$.
(Иван Матић)
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
такмичење ученика средњих школа из математике
Нови Сад, 14.04.2009.
## Други дан
|
Сваки скуп $S_{i}$ има највише 2003 елемената. Заиста, ако је $\left|S_{i}\right|=2004$, из услова $1^{\circ}$ следи да је $S_{j} \subset S_{i}$ за све $j$, противно услову $2^{\circ}$. Посматрајмо скупове
$$
G_{\{i, j\}}=\{1,2, \ldots, 2008\} \backslash\left(S_{i} \cup S_{j}\right) \quad \text { за } 1 \leq i, j \leq n
$$
Тада је $\left|G_{\{i, j\}}\right| \geqslant 4$ и свих $\binom{n}{2}$ скупова $G_{\{i, j\}}$ су међусобно дисјунктни (у супротном, ако $x \in G_{\{i, j\}} \cap G_{\{k, l\}}$, онда $x \notin S_{i} \cup S_{j} \cup S_{k} \cup S_{l}$, што је немогуће ако су бар три међу $i, j, k, l$ различита). Следи да је $4\binom{n}{2} \leqslant 2008$, одакле je $n \leqslant 32$.
Конструисаћемо 32 скупа који задовољавају $1^{\circ}$ и $2^{\circ}$. Разложимо скуп $\{1,2, \ldots, 2008\}$ произвољно на $\binom{32}{2}=496$ (дисјунктних) скупова $G_{\{i, j\}}$, при чему је $\left|G_{\{i, j\}}\right| \geqslant 4$ за $1 \leqslant i, j \leqslant 32$, и дефинишимо
$$
S_{i}=\{1,2, \ldots, 2008\} \backslash \bigcup_{j \neq i} G_{\{i, j\}} \quad \text { за } i=1, \ldots, 32
$$
Услов $1^{\circ}$ је аутоматски задовољен. Осим тога, свако $s \in\{1,2, \ldots, 2008\}$ припада највише једном од скупова $G_{\{p, q\}}$, што значи да постоје највише два скупа $S_{i}$ који га не садрже (то су $S_{p}$ и $S_{q}$ ), па је и услов $2^{\circ}$ задовољен. Према томе, одговор је $n=32$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
629e3ef1-b808-537a-9e3d-f29f8318bdad
| 608,062
|
Let $n \in \mathbb{N}$ and $A_{n}$ be the set of all permutations $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the set $\{1,2, \ldots, n\}$ such that
$$
k \mid 2\left(a_{1}+a_{2}+\cdots+a_{k}\right) \quad \text { for every } 1 \leqslant k \leqslant n
$$
Determine the number of elements in the set $A_{n}$.
(Vidan Govedarija)
|
Let $F_{n}$ denote the number of elements in the set $A_{n}$. We have $F_{1}=1, F_{2}=2$ and $F_{3}=6$. For $n>3$, consider any permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ in $A_{n}$. Since $n-1$ divides $2\left(a_{1}+\cdots+a_{n-1}\right)=n(n+1)-2 a_{n} \equiv 2-2 a_{n}(\bmod n-1)$, it follows that $a_{n}$ is equal to $1, \frac{n+1}{2}$ or $n$.
Assume that $a_{n}=\frac{n+1}{2}$. Then $n-2$ divides $2\left(a_{1}+\cdots+a_{n-2}\right)=n^{2}-$ $1-2 a_{n-1} \equiv 3-2 a_{n-1}(\bmod n-2)$. Therefore, it must be that $2 a_{n-1}-3=n-2$, but then $a_{n-1}=\frac{n+1}{2}=a_{n}$, a contradiction.
If $a_{n}=n$, then $\left(a_{1}, \ldots, a_{n}\right) \rightarrow\left(a_{1}, \ldots, a_{n-1}\right)$ is a bijective mapping to the set $A_{n-1}$, so there are $F_{n-1}$ such permutations.
If $a_{n}=1$, then $\left(a_{1}-1, \ldots, a_{n-1}-1\right)$ is a permutation on $\{1, \ldots, n-1\}$ that belongs to the set $A_{n-1}$ since $2\left(\left(a_{1}-1\right)+\cdots+\left(a_{k}-1\right)\right)=2\left(a_{1}+\cdots+a_{k}\right)-2 k$ is divisible by $k$ for $1 \leqslant k \leqslant n-1$. As in the previous case, there are $F_{n-1}$ such permutations.
We conclude that $F_{n}=2 F_{n-1}$ for $n>3$, which together with $F_{3}=6$ gives $F_{n}=$ $3 \cdot 2^{n-2}$ for $n \geqslant 3$.
|
3 \cdot 2^{n-2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Нека је $n \in \mathbb{N}$ и $A_{n}$ скуп свих пермутација $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ скупа $\{1,2, \ldots, n\}$ таквих да важи
$$
k \mid 2\left(a_{1}+a_{2}+\cdots+a_{k}\right) \quad \text { за свако } 1 \leqslant k \leqslant n
$$
Одредити број елемената скупа $A_{n}$.
(Видан Говедарииа)
|
Означимо са $F_{n}$ број елемената скупа $A_{n}$. Имамо $F_{1}=1, F_{2}=2$ и $F_{3}=6$. За $n>3$, посматрајмо било коју пермутацију $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ у $A_{n}$. Како $n-1$ дели $2\left(a_{1}+\cdots+a_{n-1}\right)=n(n+1)-2 a_{n} \equiv 2-2 a_{n}(\bmod n-1)$, следи да је $a_{n}$ једнако $1, \frac{n+1}{2}$ или $n$.
Претпоставимо да је $a_{n}=\frac{n+1}{2}$. Тада $n-2$ дели $2\left(a_{1}+\cdots+a_{n-2}\right)=n^{2}-$ $1-2 a_{n-1} \equiv 3-2 a_{n-1}(\bmod n-2)$. Зато мора бити $2 a_{n-1}-3=n-2$, али тада је $a_{n-1}=\frac{n+1}{2}=a_{n}$, контрадикција.
Ако је $a_{n}=n$, онда је $\left(a_{1}, \ldots, a_{n}\right) \rightarrow\left(a_{1}, \ldots, a_{n-1}\right)$ бијективно пресликавање у скуп $A_{n-1}$, па оваквих пермутација има $F_{n-1}$.
Ако је $a_{n}=1$, онда је $\left(a_{1}-1, \ldots, a_{n-1}-1\right)$ пермутација на $\{1, \ldots, n-1\}$ која припада скупу $A_{n-1}$ јер је $2\left(\left(a_{1}-1\right)+\cdots+\left(a_{k}-1\right)\right)=2\left(a_{1}+\cdots+a_{k}\right)-2 k$ дељиво са $k$ за $1 \leqslant k \leqslant n-1$. Као и у претходном случају, оваквих пермутација има $F_{n-1}$.
Закључујемо да је $F_{n}=2 F_{n-1}$ за $n>3$, што заједно са $F_{3}=6$ даје $F_{n}=$ $3 \cdot 2^{n-2}$ за $n \geqslant 3$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
3499804d-0ceb-5e68-b0c1-f8ee450c827b
| 608,063
|
On a $2012 \times 2012$ square grid, a fly and $k$ spiders are located. A move consists of the following: the fly moves to an adjacent vertex or stays in the same place, and then each of the $k$ spiders moves to an adjacent vertex or stays in the same place (multiple spiders can be in the same vertex). At any time, each spider and the fly can see the positions of the others.
a) Find the smallest $k$ such that the spiders can catch the fly in a finite number of moves, regardless of the initial positions of the fly and the spiders.
b) Answer the same question for a cubic grid $2012 \times 2012 \times 2012$.
(Vertices are adjacent if they differ in exactly one coordinate by 1. A spider catches the fly if they are in the same vertex.)
(Nikola Milosavljević)
Time for work: 270 minutes.
Each problem is worth 7 points.
# SERBIAN MATHEMATICAL OLYMPIAD
for high school students
Belgrade, 01.04.2012.
## Second day
|
A single spider cannot catch a fly. It is enough for the fly to remain stationary if the spider is not on an adjacent field, or to move to the diagonally opposite field if it is.
We will prove that two spiders are sufficient for both parts of the problem - let's denote them as $P$ and $Q$, the fly as $M$, and the $x$- and $y$-coordinates of point $A$ as $A_{x}$ and $A_{y}$.
(a) Place the coordinate origin at the bottom left corner of the grid. Initially, moving along the $x$-axis, $P$ achieves $P_{x} = M_{x}$ in a finite number of moves. Similarly, $Q$ achieves $Q_{y} = M_{y}$. Then the spiders move as follows: whenever the fly changes its $x$-coordinate, $P$ does the same to maintain $P_{x} = M_{x}$, otherwise it moves one step closer to the fly along the $y$-axis; the movement of $Q$ is analogous. In this way, the quantity $\left|P_{y} - M_{y}\right| + \left|Q_{x} - M_{x}\right|$ either decreases or remains the same, and it can remain the same for at most $2 \cdot 2010$ moves (when the fly retreats). Therefore, after a finite number of moves, at least one of the terms will become zero, i.e., the fly will be caught.
(b) Ignoring the $z$-axis, based on part (a), one of the spiders, say $P$, can achieve $P_{x} = M_{x}$ and $P_{y} = M_{y}$. Furthermore, whenever the fly takes a step along the $z$-axis, spider $P$ moves towards it, and otherwise moves so that it is always directly below the fly. It is clear that the fly can only take a finite number of steps along the $z$-axis or remain in place without being caught by spider $P$. Therefore, from some point onward, the fly must move exclusively within its $xy$-plane without stopping.
Now spider $Q$ reaches the $xy$-plane in which the fly is moving in a finite number of moves. Also, by staying in place when necessary, $Q$ achieves that $f = \left|Q_{x} - M_{x}\right| + \left|Q_{y} - M_{y}\right|$ is even. In each subsequent move, spider $Q$ moves closer to the fly along the $x$-axis if $\left|Q_{x} - M_{x}\right| > \left|Q_{y} - M_{y}\right|$, and along the $y$-axis otherwise. After each move, the value of $f$ does not increase and does not change its parity, and it can remain the same only a finite number of times (when the fly runs away from the spider towards the edge of the grid). Therefore, at some point, $f$ will be $0$, and the fly will be caught.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
У неким чворовима квадратне решетке $2012 \times 2012$ налази се мува и $k$ паукова. Један потез састоји се у следећем: мува се помера на суседан чвор или остаје на истом месту, а након тога се сваки од $k$ паукова помера на неки суседан чвор или остаје на истом месту (у једном чвору може бити више паукова). У сваком тренутку сваки паук и мува имају увид у позиције осталих.
a) Наћи најмање $k$ тако да пауци могу ухватити муву у коначном броју потеза, без обзира на почетну позицију муве и паукова.
б) Одговорити на исто питање за кубну решетку $2012 \times 2012 \times 2012$.
(Чворови су суседни ако се разликују на тачно једној координати, и то за 1. Паук хвата муву уколико се налазе у истом чвору.)
(Никола Милосављевић)
Време за рад 270 минута.
Сваки задатак вреди 7 поена.
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
ученика средњих школа
Београд, 01.04.2012.
## Други дан
|
Један паук не може да ухвати муву. Довољно је да мува не мрда ако паук није на суседном пољу, односно да се помери на поље дијагонално супротно пауковом ако јесте.
Доказаћемо да су два паука довољна у оба дела задатка - означимо их са $P$ и $Q$, муву са $M$, а $x$ - и $y$-координату тачке $A$ са $A_{x}$ и $A_{y}$.
(a) Поставимо координатни почетак у доњи леви угао мреже. На почетку, крећући се дуж $x$-осе, $P$ у коначном броју потеза постиже да буде $P_{x}=$ $M_{x}$. Аналогно, $Q$ постиже да буде $Q_{y}=M_{y}$. Потом се пауци крећу на следећи начин: кад год мува промени $x$-координату, $P$ учини исто тако да остане $P_{x}=M_{x}$, у супротном приђе муви један корак дуж $y$-осе; кретање $Q$ је аналогно. На овај начин величина $\left|P_{y}-M_{y}\right|+\left|Q_{x}-M_{x}\right|$ се или смањује или остаје иста, при чему може остати иста кроз највише $2 \cdot 2010$ потеза (када се мува повлачи). Према томе, после коначног броја потеза бар један сабирак ће постати нула, тј. мува ће бити ухваћена.
(б) Занемарујући $z$-осу, на основу дела под (a), један од паукова, рецимо $P$, може постићи да буде $P_{x}=M_{x}$ и $P_{y}=M_{y}$. Надаље, кад год мува направи корак дуж $z$-осе, паук $P$ иде ка њој, а супротном се креће тако да увек буде тачно испод муве. Јасно је да мува може само коначно много пута да направи корак дуж $z$-осе или остане у месту, а да је паук $P$ не ухвати. Према томе, почев од неког момента, мува мора да се креће искључиво по својој $x y$-равни, без стајања у месту.
Сада паук $Q$ у коначно много потеза долази до $x y$-равни по којој се креће мува. Такође, стајањем у месту по потреби, $Q$ постиже да $f=\left|Q_{x}-M_{x}\right|+$ $\left|Q_{y}-M_{y}\right|$ буде парно. У сваком следећем потезу, паук $Q$ се приближава муви дуж $x$-осе ако је $\left|Q_{x}-M_{x}\right|>\left|Q_{y}-M_{y}\right|$, а дуж $y$-осе у супротном. После сваког потеза, величина $f$ се не повећава и не мења парност, при чему само коначно много пута може да остане иста (када мува бежи од паука према крају решетке). Према томе, у неком тренутку ће бити $f=0$, и мува ће бити ухваћена.
|
{
"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
8d0960f2-8c43-59d1-8f8a-94b49a3553b8
| 608,080
|
Let a composition contain $n>1$ wagons with gold coins. There are two types of visually identical gold coins: genuine and fake. In each wagon, there are only coins of one type. Coins of the same type have the same mass, while coins of different types do not have the same mass. The mass of a genuine gold coin is known.
Determine the minimum number of measurements on a digital scale that can determine which wagons contain fake gold coins, as well as what is the mass of a fake gold coin.
(It is assumed that any number of coins can be taken from each wagon.)
(Miloš Milosavljević)
## SOLUTIONS
|
We will prove that the minimum number of measurements is equal to 2. Let the weights of the genuine and counterfeit gold coins be denoted by $x$ and $y$ respectively, and let $a_{i}=1$ if the gold coins in the $i$-th wagon are counterfeit, and $a_{i}=0$ otherwise.
In the first measurement, take one gold coin from each wagon. Then we have $a_{1} + a_{2} + \cdots + a_{n} = \frac{n x - m_{1}}{x - y}$, where $m_{1}$ is the obtained weight. Assume that $m_{1} \neq n x$, otherwise there are no counterfeit coins. In the second measurement, for some $q \in \mathbb{N}$, take $q^{i-1}$ gold coins from the $i$-th wagon. If the obtained weight is $m_{2}$, we have $a_{1} + q a_{2} + \cdots + q^{n-1} a_{n-1} = \frac{\left(1 + q + \cdots + q^{n-1}\right) x - m_{2}}{x - y}$. From this, we get
$$
f\left(a_{1}, a_{2}, \ldots, a_{n}\right) = \frac{a_{1} + q a_{2} + \cdots + q^{n-1} a_{n-1}}{a_{1} + a_{2} + \cdots + a_{n}} = \frac{\left(1 + q + \cdots + q^{n-1}\right) x - m_{2}}{n x - m_{1}}
$$
We want the value of $f$ to uniquely determine $a_{1}, \ldots, a_{n}$. Therefore, it is sufficient to show that there exists a natural number $q$ such that the function $f: \{0,1\}^{n} \backslash \{(0,0, \ldots, 0)\} \rightarrow \mathbb{R}$ is injective.
For fixed $\mathfrak{a} = \left(a_{1}, a_{2}, \ldots, a_{n}\right)$ and $\mathfrak{b} = \left(b_{1}, b_{2}, \ldots, b_{n}\right)$, the equality $f(\mathfrak{a}) = f(\mathfrak{b})$ is equivalent to $P_{\mathfrak{a}, \mathfrak{b}}(q) = \left(a_{n} b - b_{n} a\right) q^{n-1} + \cdots + \left(a_{2} b - b_{2} a\right) q + \left(a_{1} b - b_{1} a\right) = 0$, where $a = a_{1} + a_{2} + \ldots + a_{n} \neq 0 \neq b_{1} + b_{2} + \ldots + b_{n} = b$. Therefore, if the function $f$ is not injective, then $q$ is a root of the polynomial
$$
P(q) = \prod_{\mathfrak{a}, \mathfrak{b}} P_{\mathfrak{a}, \mathfrak{b}}(q)
$$
Since none of the polynomials $P_{\mathfrak{a}, \mathfrak{b}}$ are identically zero, there are only finitely many numbers $q$ for which $P(q) = 0$, so it is possible to choose $q$ such that $f$ is an injective function.
Thus, in two measurements, we can determine $a_{1}, \ldots, a_{n}$, i.e., the wagons with counterfeit gold coins. Finally, $y$ is determined from the equality $y = x - \frac{n x - m_{1}}{a_{1} + a_{2} + \cdots + a_{n}}$.
On the other hand, one measurement is not sufficient, because by taking $k_{i}$ gold coins from the $i$-th wagon, we get the equation $k_{1} a_{1} + \cdots + k_{n} a_{n} = \frac{k x - m}{x - y}$ (where $k = k_{1} + \cdots + k_{n}$), which in general has multiple solutions. For example, two possible solutions for $\left(a_{1}, a_{2}, \ldots, a_{n}, y\right)$ are $\left(1, 0, \ldots, 0, x - \frac{k x - m}{k_{1}}\right)$ and $\left(0, 0, \ldots, 1, x - \frac{k x - m}{k_{n}}\right)$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Нека композиција садржи $n>1$ вагона са златницима. Постоје две врсте наизглед истих златника: прави и лажни. У сваком вагону се налазе златници само једне врсте. Златници исте врсте су исте масе, док златници различитих врста немају исту масу. Маса правог златника је позната.
Одредити минималан број мерења на дигиталној ваги којима је могуће утврдити који све вагони садрже лажне златнике, као и која је маса лажног златника.
(Претпоставља се да се из сваког вагона може узети било који број златника.)
(Милош Милосављевић)
## РЕШЕЊА
|
Доказаћемо да је минималан број мерења једнак 2. Означимо тежине правог и лажног златника са $x$ и $y$ редом, и нека је $a_{i}=1$ ако су златници у $i$-том вагону лажни, а $a_{i}=0$ у супротном.
Узмимо у првом мерењу по један златник из сваког вагона. Тада је $a_{1}+$ $a_{2}+\cdots+a_{n}=\frac{n x-m_{1}}{x-y}$, где је $m_{1}$ добијена маса. Претпостављамо да је $m_{1} \neq n x$, јер у супротном нема лажних златника. У другом мерењу, за неко $q \in \mathbb{N}$, узимамо из $i$-тог вагона $q^{i-1}$ златника. Ако је добијена маса
$m_{2}$, имамо $a_{1}+q a_{2}+\cdots+q^{n-1} a_{n-1}=\frac{\left(1+q+\cdots+q^{n-1}\right) x-m_{2}}{x-y}$. Одавде добијамо
$$
f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=\frac{a_{1}+q a_{2}+\cdots+q^{n-1} a_{n-1}}{a_{1}+a_{2}+\cdots+a_{n}}=\frac{\left(1+q+\cdots+q^{n-1}\right) x-m_{2}}{n x-m_{1}}
$$
Желимо да нам вредност $f$ једнозначно одреди $a_{1}, \ldots, a_{n}$. Дакле, довољно је показати да постоји природан број $q$ такав да је функција $f:\{0,1\}^{n} \backslash$ $\{(0,0, \ldots, 0)\} \rightarrow \mathbb{R}$ инјективна.
За фиксиране $\mathfrak{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ и $\mathfrak{a}=\left(b_{1}, b_{2}, \ldots, b_{n}\right)$, једнакост $f(\mathfrak{a})=f(\mathfrak{b})$ је еквивалентна са $P_{\mathfrak{a}, \mathfrak{b}}(q)=\left(a_{n} b-b_{n} a\right) q^{n-1}+\cdots+\left(a_{2} b-b_{2} a\right) q+\left(a_{1} b-b_{1} a\right)=0$, где је $a=a_{1}+a_{2}+\ldots+a_{n} \neq 0 \neq b_{1}+b_{2}+\ldots b_{n}=b$. Према томе, ако функција $f$ није инјективна, онда је $q$ нула полинома
$$
P(q)=\prod_{\mathfrak{a}, \mathfrak{b}} P_{\mathfrak{a}, \mathfrak{b}}(q)
$$
Како ниједан од полинома $P_{\mathfrak{a}, \mathfrak{b}}$ није идентички једнак 0 , постоји само коначно много бројева $q$ за које је $P(q)=0$, па је могуће одабрати $q$ за које је $f$ инјективна функција.
Овако у два мерења можемо да одредимо $a_{1}, \ldots, a_{n}$, тј. вагоне са лажним златницима. Најзад, $y$ одређујемо из једнакости $y=x-\frac{n x-m_{1}}{a_{1}+a_{2}+\cdots+a_{n}}$.
С друге стране, једно мерење није довољно, јер узимањем $k_{i}$ златника из $i$-тог вагона добијамо једначину $k_{1} a_{1}+\cdots+k_{n} a_{n}=\frac{k x-m}{x-y}$ (где је $k=k_{1}+$ $\cdots+k_{n}$ ) која у општем случају има више решења. На пример, два могућа решења за $\left(a_{1}, a_{2}, \ldots, a_{n}, y\right)$ су $\left(1,0, \ldots, 0, x-\frac{k x-m}{k_{1}}\right)$ и $\left(0,0, \ldots, 1, x-\frac{k x-m}{k_{n}}\right)$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
74bd4107-ce47-5d3f-99dc-9c2ce05465cd
| 608,083
|
Find the largest constant $K \in \mathbb{R}$ with the following property: if $a_{1}, a_{2}, a_{3}, a_{4}>0$ are such that for all $i, j, k \in \mathbb{N}, 1 \leqslant i<j<k \leqslant 4$, we have $a_{i}^{2}+a_{j}^{2}+a_{k}^{2} \geqslant 2\left(a_{i} a_{j}+a_{j} a_{k}+a_{k} a_{i}\right)$, then
$$
a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2} \geqslant K\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
$$
(Dusan Dukic)
## SOLUTIONS
|
Let $\max \left\{a_{1}, a_{2}\right\} \leqslant a_{3} \leqslant a_{4}$. Denote $a_{2}=\beta^{2}$ and $a_{3}=\gamma^{2}, \beta, \gamma \geqslant 0$. From the condition of the problem, it follows that $a_{1} \leqslant(\gamma-\beta)^{2}$ and $a_{4} \geqslant(\gamma+\beta)^{2}$.
Assume that both these inequalities are actually equalities. Then we have $a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}=3\left(\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}\right)$ and $a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}=3\left(\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}\right)$. Given that $\gamma \leqslant 2 \beta$, we have $\frac{\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3 \beta^{2} \gamma^{2}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3}{1+\frac{\beta^{2}}{\gamma^{2}}+\frac{\gamma^{2}}{\beta^{2}}} \geqslant \frac{11}{7}$, with equality for $\gamma=2 \beta$. Therefore, in this case, $K \geqslant \frac{11}{7}$, and equality is achieved for $a_{1}: a_{2}: a_{3}: a_{4}=1: 1: 4: 9$.
Let's show that we can take $a_{1}=(\gamma-\beta)^{2}$ and $a_{4}=(\gamma+\beta)^{2}$. Consider the expression
$$
F=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}-\frac{11}{7}\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
$$
For fixed $a_{2}, a_{3}, a_{4}, F$ is a decreasing function of $a_{1}$ for $a_{1}<$ $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right)$, and $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right) \geqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\beta+\gamma)^{2}\right)$ $\geqslant(\gamma-\beta)^{2} \geqslant a_{1}$, so $F$ does not increase if $a_{1}$ is replaced by $(\gamma-\beta)^{2}$. Now we can assume without loss of generality that $a_{1} \leqslant a_{2}$, i.e., $\beta \leqslant \gamma \leqslant 2 \beta$. Similarly, for fixed $a_{1}, a_{2}, a_{3}, F$ is an increasing function of $a_{4}$ for $a_{4}>\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$, and $\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$ $\leqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\gamma-\beta)^{2}\right) \leqslant(\gamma+\beta)^{2} \leqslant a_{4}$, so $F$ does not increase if $a_{4}$ is replaced by $(\gamma+\beta)^{2}$.
|
\frac{11}{7}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Наћи највећу константу $K \in \mathbb{R}$ са следећим својством: ако су $a_{1}, a_{2}, a_{3}, a_{4}>0$ такви да за све $i, j, k \in \mathbb{N}, 1 \leqslant i<j<k \leqslant 4$, важи $a_{i}^{2}+a_{j}^{2}+a_{k}^{2} \geqslant 2\left(a_{i} a_{j}+a_{j} a_{k}+a_{k} a_{i}\right)$, онда је
$$
a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2} \geqslant K\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
$$
(Душан Ђукић)
## РЕШЕЊА
|
Нека је $\max \left\{a_{1}, a_{2}\right\} \leqslant a_{3} \leqslant a_{4}$. Означимо $a_{2}=\beta^{2}$ и $a_{3}=\gamma^{2}, \beta, \gamma \geqslant 0$. Из услова задатка следи $a_{1} \leqslant(\gamma-\beta)^{2}$ и $a_{4} \geqslant(\gamma+\beta)^{2}$.
Претпоставимо да су обе ове неједнакости заправо једнакости. Тада имамо $a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}=3\left(\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}\right)$ и $a_{1} a_{2}+a_{1} a_{3}+$ $a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}=3\left(\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}\right)$. При том је $\gamma \leqslant 2 \beta$, па је $\frac{\beta^{4}+4 \beta^{2} \gamma^{2}+\gamma^{4}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3 \beta^{2} \gamma^{2}}{\beta^{4}+\beta^{2} \gamma^{2}+\gamma^{4}}=1+\frac{3}{1+\frac{\beta^{2}}{\gamma^{2}}+\frac{\gamma^{2}}{\beta^{2}}} \geqslant \frac{11}{7}$, уз једнакост за $\gamma=2 \beta$. Према томе, у овом случају је $K \geqslant \frac{11}{7}$, а једнакост се достиже за $a_{1}: a_{2}: a_{3}: a_{4}=1: 1: 4: 9$.
Покажимо још да можемо да узмемо $a_{1}=(\gamma-\beta)^{2}$ и $a_{4}=(\gamma+\beta)^{2}$. Посматрајмо израз
$$
F=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}-\frac{11}{7}\left(a_{1} a_{2}+a_{1} a_{3}+a_{1} a_{4}+a_{2} a_{3}+a_{2} a_{4}+a_{3} a_{4}\right)
$$
За фиксирано $a_{2}, a_{3}, a_{4}, F$ је опадајућа функција по $a_{1}$ за $a_{1}<$ $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right)$, при чему је $\frac{11}{14}\left(a_{2}+a_{3}+a_{4}\right) \geqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\beta+\gamma)^{2}\right)$ $\geqslant(\gamma-\beta)^{2} \geqslant a_{1}$, па се $F$ не повећава ако $a_{1}$ заменимо са $(\gamma-\beta)^{2}$. Сада можемо да ставимо без смањења општости да је $a_{1} \leqslant a_{2}$, тј. $\beta \leqslant \gamma \leqslant 2 \beta$. Слично као горе, за фиксирано $a_{1}, a_{2}, a_{3}, F$ је растућа функција по $a_{4}$ за $a_{4}>\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$, и при том је $\frac{11}{14}\left(a_{1}+a_{2}+a_{3}\right)$ $\leqslant \frac{11}{14}\left(\beta^{2}+\gamma^{2}+(\gamma-\beta)^{2}\right) \leqslant(\gamma+\beta)^{2} \leqslant a_{4}$, дакле $F$ се не повећава ако $a_{4}$ заменимо са $(\gamma+\beta)^{2}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
8980fd93-6d02-5678-aab1-40354ec944b5
| 608,089
|
A regular $n$-gon is divided into triangles using $n-3$ diagonals, none of which have any common interior points. What is the maximum number of these triangles that can be mutually non-congruent?
(Dusan Dukic)
|
The answer is $\left[\frac{3 n-7}{4}\right]$ for $n>3$, and 1 for $n=3$.
Triangles with two, one, or no sides that are also sides of the $n$-gon ($n>3$) are called, respectively, thin, medium, and thick triangles. Let there be $a$ thick triangles, $b$ medium, and $c$ thin ones in the partition. The number of sides of the $n$-gon they occupy is $b+2 c=n$. On the other hand, the total number of triangles is $a+b+c=n-2$. From these two relations, we get $c=a+2$.
Since the number of triangles that are not thick is at most $\left[\frac{n-1}{2}\right]$ different, the total number $N$ of non-congruent triangles in the partition is not greater than $\frac{n-1}{2}+a$. On the other hand, in such a partition, there are $a+2$ thin triangles, and all thin triangles are congruent, so $N \leqslant n-2-(a+1)=n-a-3$. By adding these, we get $2 N \leqslant\left(\frac{n-1}{2}+a\right)+(n-a-3)=\frac{3 n-7}{2}$, i.e., $N \leqslant\left[\frac{3 n-7}{4}\right]$.
Finally, by drawing diagonals $A_{0} A_{2 i}$ and $A_{2 i-2} A_{2 i}\left(1 \leqslant i \leqslant\left[\frac{n}{4}\right]\right)$ and $A_{0} A_{j}$ $\left(2\left[\frac{n}{4}\right]<j \leqslant n-2\right)$, we obtain an example with exactly $\left[\frac{n-1}{2}\right]+\left[\frac{n}{4}\right]-1=\left[\frac{3 n-7}{4}\right]$ non-congruent triangles.
|
\left[\frac{3 n-7}{4}\right]
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Правилан $n$-тоугао подељен је на троуглове помоћу $n-3$ дијагонале од којих никоје две немају заједничких унутрашњих тачака. Колико највише међу овим троугловима може бити међусобно неподударних?
(Душан Ђукић)
|
Одговор је $\left[\frac{3 n-7}{4}\right]$ за $n>3$, односно 1 за $n=3$.
Троуглове са по две, једном или ниједном страницом која је уједно страница $n$-тоугла ( $n>3$ ) зовемо редом уиима, танким и дебелим троугловима. Нека у подели има $a$ дебелих троуглова, $b$ танких и c ушију. Број страница $n$-тоугла које они заузимају је $b+2 c=n$. С друге стране, укупан број троуглова је $a+b+c=n-2$. Из ове две релације добијамо $c=a+2$.
Како троуглова који нису дебели има највише $\left[\frac{n-1}{2}\right]$ различитих, укупан број $N$ неподударних троуглова у подели није већи од $\frac{n-1}{2}+a$. С друге стране, у таквој подели има $a+2$ ушију, а све уши су подударне, па је $N \leqslant n-2-(a+1)=n-a-3$. Сабирањем добијамо $2 N \leqslant\left(\frac{n-1}{2}+a\right)+(n-a-3)=\frac{3 n-7}{2}$, тј. $N \leqslant\left[\frac{3 n-7}{4}\right]$.
Најзад, повлачењем дијагонала $A_{0} A_{2 i}$ и $A_{2 i-2} A_{2 i}\left(1 \leqslant i \leqslant\left[\frac{n}{4}\right]\right)$ и $A_{0} A_{j}$ $\left(2\left[\frac{n}{4}\right]<j \leqslant n-2\right)$ добијамо пример са тачно $\left[\frac{n-1}{2}\right]+\left[\frac{n}{4}\right]-1=\left[\frac{3 n-7}{4}\right]$ неподударних троуглова.
|
{
"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
367593bb-8cc6-5a62-9c0a-c30152ebdee9
| 608,094
|
The guard suggests the following game to the prisoners. All of them will be led to the courtyard, where each of them will be placed a hat of one of 5 possible colors on their head. The guard will then line them up so that each prisoner can see all the hats except their own, and ask the first prisoner in the line whether they know the color of their hat. The prisoner answers "yes" or "no" out loud. If they answer "no," they will be immediately locked in solitary confinement. If they answer "yes," the guard will ask them what color their hat is, to which the prisoner must respond in such a way that the other prisoners do not hear the answer. If the answer is incorrect, that prisoner will be immediately locked in solitary confinement in front of everyone, and if the answer is correct, that prisoner will be immediately released in front of everyone. The guard then approaches the next prisoner in line and repeats the same procedure, and so on until the last prisoner. The prisoners have the opportunity to devise a strategy before the game begins, but once the game starts, no communication between prisoners is allowed. If there are 2015 prisoners in the prison, what is the maximum number of prisoners who will be guaranteed to be released if the prisoners apply the optimal strategy?
(Bojan Bašić)
Time for work 270 minutes.
Solutions to the problems should be explained in detail.
Each problem is worth 7 points.
## Ministry of Education, Science and Technological Development Mathematical Society of Serbia
## 9th SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
## Second day
|
Assign values $0,1,2,3,4$ to the colors and let $B$ be the color of the second prisoner's hat, and $S$ be the sum of the colors of the hats from the third to the last prisoner modulo 5. We will describe a strategy for the first two prisoners after which all the others will know $S$, and thus, knowing the colors of the other hats, they will be able to determine their own. This way, freedom will be guaranteed for at least 2013 prisoners. The first prisoner answers "no" if $S \in\{0, B, B+1\}$ or $(B, S)=(4,1)$. Then the second answers "no" if $S=0$, and otherwise says "yes" and gives the answer $S$ to the guard. In this way, if two "no" answers are heard, the others know that $S=0$. If the second says "yes" and is freed, the others know that $S=B$, while otherwise they know that $S=B+1$ if $B \neq 4$, or $S=1$ if $B=4$.
In all other cases, the first prisoner says "yes" (it doesn't matter what will happen to him). Then the second says "yes" if $S \in\{2,4\}$ and gives the answer $S-2$ to the guard. If $B=0$, then $S \notin\{0,1\}$, so the others know that $S=2$ if the second is freed, $S=3$ if he says "no", and $S=4$ if he says "yes" and misses. Finally, if $B \neq 0$, given the affirmative answer from the first, $S \equiv B+2$ or $S \equiv B+3(\bmod 4)$, and the answer of the second determines the parity of $S$, which allows the others to determine $S$.
It remains to prove that no strategy guarantees the freedom of 2014 prisoners. Suppose such a strategy exists and consider a set of five arrangements that differ only in the color of the second prisoner's hat. In at most one of these arrangements, the strategy dictates that the first says "no" (otherwise the second would not be able to determine the color of his hat with certainty). In at least three of the remaining four arrangements, the first would have to miss, so the second would not be able to determine the color of his hat. This completes the proof.
|
2013
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Стражар предлаже затвореницима следећу игру. Сви ће бити изведени у двориште, где ће свакоме од њих бити стављен на главу шешир у једној од 5 могућих боја. Стражар ће их потом поређати у врсту тако да сваки затвореник види све шешире осим сопственог и питати првог затвореника у врсти да ли зна боју свог шешира. Затвореник гласно одговара “да" или "не". Ако одговори "не", биће одмах закључан у самицу. Ако одговори “да", стражар ће га питати које је боје његов шешир, на шта затвореник треба да одговори на такав начин да остали затвореници не чују одговор. Уколико је одговор погрешан, тај затвореник биће одмах закључан у самицу пред свима, а ако је одговор тачан, тај затвореник биће одмах ослобођен пред свима. Стражар потом прилази следећем затворенику у реду и понавља исти поступак, и тако све до последњег затвореника. Затвореници имају могућност да осмисле стратегију пре почетка игре, али кад игра почне, никаква комуникација међу затвореницима није дозвољена. Ако у затвору има 2015 затвореника, који је максималан број затвореника који ће загарантовано бити ослобођени уколико затвореници примењују оптималну стратегију?
(Бојан Башић)
Време за рад 270 минута.
Решења задатака детаљно образложити.
Сваки задатак вреди 7 бодова.
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије
## 9. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
## Други дан
|
Доделимо бојама вредности $0,1,2,3,4$ и означимо са $B$ боју шешира другог затвореника, а са $S$ збир боја шешира од трећег до последњег затвореника по модулу 5. Описаћемо стратегију прва два затвореника након које ће сви остали затвореници знати $S$, те ће, знајући боје осталих шешира, моћи да одреде своју. Овако ће за бар 2013 затвореника бити обезбеђена слобода. Први затвореник одговара "не" ако је $S \in\{0, B, B+1\}$ или $(B, S)=(4,1)$. На то други одговара "не" ако је $S=0$, а у супротном каже "да" и стражару даје одговор $S$. На овај начин, ако чују два одговора "не", остали знају да је $S=0$. Ако други каже "да" и буде ослобођен, остали знају да је $S=B$, док у супротном знају да је $S=B+1$ ако $B \neq 4$, односно $S=1$ ако $B=4$.
У осталим случајевима први затвореник каже “да" (небитно је шта ће бити с њим). На то други каже "да" ако $S \in\{2,4\}$ и стражару даје одговор $S-2$. Ако је $B=0$, онда $S \notin\{0,1\}$, па остали знају да је $S=2$ ако други буде ослобођен, $S=3$ ако каже "не", и $S=4$ ако каже "да" и промаши. Најзад, ако је $B \neq 0$, с обзиром на потврдан одговор првог важи $S \equiv B+2$ или $S \equiv B+3(\bmod 4)$, а одговор другог одређује парност $S$, што осталима омогућује да одреде $S$.
Остаје да докажемо да ниједна стратегија не гарантује слободу 2014 затвореника. Претпоставимо да таква стратегија постоји и посматрајмо скуп од
пет распореда који се разликују само у боји шешира другог затвореника. У највише једном од ових распореда стратегија предвиђа да први каже "не" (у супротном други не би могао да са сигурношћу одреди боју свог шешира). У бар три од преостала четири распореда први би морао да промаши, па други не би могао да одреди боју свог шешира. Овим је доказ завршен.
|
{
"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
440777a6-83bb-5f98-b87a-2bf0d108aa00
| 608,098
|
For an integer $a, a \neq 0$, denote by $v_{2}(a)$ the largest non-negative integer $k$ such that $2^{k} \mid a$. For a given $n \in \mathbb{N}$, determine the largest possible cardinality of a subset $A$ of the set $\left\{1,2,3, \ldots, 2^{n}\right\}$ with the following property:
$$
\text { for all } x, y \in A, x \neq y, \text { the number } v_{2}(x-y) \text { is even. }
$$
(Dušan Đukić)
|
We will prove by induction on $k$ that the set $A$ contains at most $2^k$ distinct elements modulo $2^{2k}$. This trivially holds for $k=0$. Let $k>0$. By the induction hypothesis, the elements of the set $A$ give at most $2^{k-1}$ remainders modulo $2^{2k-2}$. Assume that the elements of $A$ give more than $2^k$ remainders modulo $2^{2k}$. By the Dirichlet principle, at least three of these remainders are equal modulo $2^{2k-2}$. But among these three remainders, two differ by $2^{2k-1} \pmod{2^{2k}}$, contradicting the condition of the problem.
It follows that $|A| \leqslant 2^{\left[\frac{n+1}{2}\right]}$. An example of a set $A$ with $2^{\left[\frac{n+1}{2}\right]}$ elements is obtained by including numbers of the form $\sum_{i \in B} 4^i$ for all subsets $B$ of the set $\left\{0,1, \ldots,\left[\frac{n-1}{2}\right]\right\}$.
Second solution. We say that a set $X$ is lucky if $v_2(x-y)$ is even for all $x, y \in X (x \neq y)$, and unlucky if $v_2(x-y)$ is odd for all $x, y \in X (x \neq y)$. Let $a_n$ and $b_n$ be the maximum cardinality of a lucky and an unlucky subset of the set $T_n = \left\{1, 2, \ldots, 2^n\right\}$, respectively.
Consider a lucky set $A \subset T_n, n \geqslant 1$. Since $v_2(2x - 2y) = v_2(x - y) + 1$, the sets $A_0 = \left\{\frac{x}{2} \mid x \in A, 2 \mid x\right\}$ and $A_1 = \left\{\left.\frac{x-1}{2} \right\rvert\, x \in A, 2 \nmid x\right\}$ are unlucky subsets of the set $T_{n-1}$ and have at most $b_{n-1}$ elements each. On the other hand, if $A_0 \subset T_{n-1}$ is an unlucky set, the set $\left\{2x, 2x+1 \mid x \in A_0\right\} \subset T_n$ is lucky and has $2|A_0|$ elements. It follows that $a_n = 2b_{n-1}$.
Similarly, if $B \subset T_n$ is an odd set, all its elements have the same parity, and the set $B' = \left\{\left.\left\lceil\frac{x}{2}\right\rceil \right\rvert\, x \in B\right\} \subset T_{n-1}$ is lucky. On the other hand, if $B' \subset T_{n-1}$ is lucky, the set $B = \left\{2x-1 \mid x \in B'\right\} \subset T_n$ is unlucky. Hence, $b_n = a_{n-1}$.
The obtained relations give $a_n = 2a_{n-2}$ for $n \geqslant 2$, and from $a_0 = 1$ and $a_1 = 2$, simple induction yields $a_n = 2^{\left[\frac{n+1}{2}\right]}$.
|
2^{\left[\frac{n+1}{2}\right]}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
За цео број $a, a \neq 0$, означимо са $v_{2}(a)$ највећи ненегативан цео број $k$ такав да $2^{k} \mid a$. За дато $n \in \mathbb{N}$ одредити највећу могућу кардиналност подскупа $A$ скупа $\left\{1,2,3, \ldots, 2^{n}\right\}$ са следећим својством:
$$
\text { за све } x, y \in A, x \neq y, \text { број } v_{2}(x-y) \text { је паран. }
$$
(Дуиан Ђукић)
|
Доказаћемо индукцијом по $k$ да скуп $A$ садржи највише $2^{k}$ различитих елемената по модулу $2^{2 k}$. То тривијално важи за $k=0$. Нека је $k>0$. По индуктивној претпоставци, елементи скупа $A$ дају највише $2^{k-1}$ остатака по модулу $2^{2 k-2}$. Претпоставимо да елементи $A$ дају више од $2^{k}$ остатака по модулу $2^{2 k}$. На основу Дирихлеовог принципа, бар три од ових остатака су једнаки по модулу $2^{2 k-2}$. Али међу ова три остатка, два се разликују за $2^{2 k-1}\left(\bmod 2^{2 k}\right)$, противно услову задатка.
Следи да је $|A| \leqslant 2^{\left[\frac{n+1}{2}\right]}$. Пример скупа $A$ са $2^{\left[\frac{n+1}{2}\right]}$ елемената добијамо укључивањем бројева облика $\sum_{i \in B} 4^{i}$ за све подскупове $B$ скупа $\left\{0,1, \ldots,\left[\frac{n-1}{2}\right]\right\}$.
Друго решеъе. Кажемо да је скуп $X$ срећан ако је $v_{2}(x-y)$ парно за све $x, y \in X(x \neq y)$, а несрећан ако је $v_{2}(x-y)$ непарно за све $x, y \in X(x \neq y)$. Означимо са $a_{n}$ и $b_{n}$ редом максималне кардиналности срећног и несрећног подскупа скупа $T_{n}=\left\{1,2, \ldots, 2^{n}\right\}$.
Посматрајмо срећан скуп $A \subset T_{n}, n \geqslant 1$. Како је $v_{2}(2 x-2 y)=v_{2}(x-y)+1$, скупови $A_{0}=\left\{\frac{x}{2}|x \in A, 2| x\right\}$ и $A_{1}=\left\{\left.\frac{x-1}{2} \right\rvert\, x \in A, 2 \nmid x\right\}$ су несрећни подскупови скупа $T_{n-1}$ и имају највише по $b_{n-1}$ елемената. С друге стране, ако је $A_{0} \subset T_{n-1}$ несрећан скуп, скуп $\left\{2 x, 2 x+1 \mid x \in A_{0}\right\} \subset T_{n}$ је срећан и има $2\left|A_{0}\right|$ елемената. Следи да је $a_{n}=2 b_{n-1}$.
Слично, ако је $B \subset T_{n}$ непаран скуп, сви његови елементи су исте парности, а скуп $B^{\prime}=\left\{\left.\left\lceil\frac{x}{2}\right\rceil \right\rvert\, x \in B\right\} \subset T_{n-1}$ је срећан. С друге стране, ако је $B^{\prime} \subset T_{n-1}$ срећан, скуп $B=\left\{2 x-1 \mid x \in B^{\prime}\right\} \subset T_{n}$ је несрећан. Одавде је $b_{n}=a_{n-1}$.
Добијене релације дају $a_{n}=2 a_{n-2}$ за $n \geqslant 2$, па из $a_{0}=1$ и $a_{1}=2$ једноставном индукцијом добијамо $a_{n}=2^{\left[\frac{n+1}{2}\right]}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
2863ac19-6108-5cb8-8264-a32efe75950e
| 608,099
|
Let $n$ be a natural number. We define $f(0, j)=f(i, 0)=0, f(1,1)=n$ and
$$
f(i, j)=\left\lfloor\frac{f(i-1, j)}{2}\right\rfloor+\left\lfloor\frac{f(i, j-1)}{2}\right\rfloor
$$
for all natural numbers $i$ and $j, (i, j) \neq(1,1)$. How many ordered pairs of natural numbers $(i, j)$ are there for which $f(i, j)$ is an odd number? (Dusan Dukic)
|
The answer is $n$.
For $m \geqslant 2$ let $s_{m}=\sum_{i+j=m} f(i, j)$. Since the remainder of $f(i, j)$ when divided by 2 is $f(i, j)-2\left[\frac{f(i, j)}{2}\right]$, the number of odd numbers among $f(i, j)$ for $i, j \geqslant 0$ and $i+j=m$ is
\[
\begin{aligned}
\sum_{i+j=m}\left(f(i, j)-2\left[\frac{f(i, j)}{2}\right]\right) & =s_{m}-\sum_{i+j=m}\left(\left[\frac{f(i-1, j+1)}{2}\right]+\left[\frac{f(i, j)}{2}\right]\right) \\
& =s_{m}-s_{m+1}
\end{aligned}
\]
It follows that the number of pairs $(i, j)$ for which $f(i, j)$ is odd and $i+j<m$ is equal to $s_{2}-s_{m}=n-s_{m}$.
It remains to show that $s_{m}=0$ for all sufficiently large $m$. Clearly, the sequence $s_{m}$ is non-negative and non-increasing, so there exist $N$ and $k$ such that $s_{m}=k$ for all $m \geqslant N$. This means that $f(i, j)$ is even whenever $i+j \geqslant m$. Suppose $k>0$ and consider the smallest $i$ such that $f(i, m-i)>0$. By simple induction, we get $f(i, m+r-i)=\left[\frac{f(i, m-i)}{2^{r}}\right]$ for $r \geqslant 1$. However, if $2^{r} \leqslant f(i, m-i)<2^{r+1}$, then $f(i, m+r-i)=1$, contradicting the assumption.
Second solution (U. Dinić). Place $n$ tokens at the point $(1,1)$ in the coordinate plane. In each step, from each point $(i, j)$, we will move the integer part of half of its tokens to the points $(i+1, j)$ and $(i, j+1)$. Note that if a row or column is non-empty at some point, it will always remain non-empty. Thus, no token can leave the square $[1, n] \times[1, n]$, so the game ends in a finite number of steps.
It is not hard to see that after $i+j-2$ steps, there are exactly $f(i, j)$ tokens at the point $(i, j)$. Moreover, the number $f(i, j)$ is odd if after the next step, one token remains at the point $(i, j)$. Since there are exactly $n$ tokens in the final position, it follows that among the members of the sequence $f(i, j)$, there are $n$ odd numbers.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Дат је природан број $n$. Дефинишимо $f(0, j)=f(i, 0)=0, f(1,1)=n$ и
$$
f(i, j)=\left\lfloor\frac{f(i-1, j)}{2}\right\rfloor+\left\lfloor\frac{f(i, j-1)}{2}\right\rfloor
$$
за све природне бројеве $i$ и $j,(i, j) \neq(1,1)$. Колико има уређених парова природних бројева $(i, j)$ за које је $f(i, j)$ непаран број? (Душан Ђукић)
|
Одговор је $n$.
За $m \geqslant 2$ означимо $s_{m}=\sum_{i+j=m} f(i, j)$. Како је остатак $f(i, j)$ при дељењу са 2 једнак $f(i, j)-2\left[\frac{f(i, j)}{2}\right]$, број непарних међу бројевима $f(i, j)$ за $i, j \geqslant 0$ и $i+j=m$ једнак је
$$
\begin{aligned}
\sum_{i+j=m}\left(f(i, j)-2\left[\frac{f(i, j)}{2}\right]\right) & =s_{m}-\sum_{i+j=m}\left(\left[\frac{f(i-1, j+1)}{2}\right]+\left[\frac{f(i, j)}{2}\right]\right) \\
& =s_{m}-s_{m+1}
\end{aligned}
$$
Следи да је број парова $(i, j)$ за које је $f(i, j)$ непарно и $i+j<m$ једнак $s_{2}-s_{m}=n-s_{m}$.
Остаје да покажемо да је $s_{m}=0$ за све довољно велике $m$. Јасно је да је низ $s_{m}$ ненегативан и нерастући, па постоје $N$ и $k$ такви да је $s_{m}=k$ за све $m \geqslant N$. То значи да је $f(i, j)$ парно кад год је $i+j \geqslant m$. Претпоставимо да је $k>0$ и посматрајмо најмање $i$ такво да је $f(i, m-i)>0$. Једноставном индукцијом добијамо $f(i, m+r-i)=\left[\frac{f(i, m-i)}{2^{r}}\right]$ за $r \geqslant 1$. Међутим, ако је $2^{r} \leqslant f(i, m-i)<2^{r+1}$, одавде је $f(i, m+r-i)=1$, противно претпоставци.
Друго решење (У. Динић). Поставимо $n$ жетона у тачку $(1,1)$ у координатној равни. У сваком кораку, из сваке тачке $(i, j)$ ћемо пребацити по цео део половине њених жетона у тачке $(i+1, j)$ и $(i, j+1)$. Приметимо да, ако је нека врста или колона у неком тренутку непразна, она ће увек остати непразна. Тако ниједан жетон не може изаћи из квадрата $[1, n] \times[1, n]$, па се игра завршава у коначном броју корака.
Није тешко видети да се након $i+j-2$ корака у тачки $(i, j)$ налази тачно $f(i, j)$ жетона. Шта више, број $f(i, j)$ је непаран ако након следећег корака
у тачки $(i, j)$ остане један жетон. Како у завршној позицији има тачно $n$ жетона, следи да међу члановима низа $f(i, j)$ има $n$ непарних бројева.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
fb1dd20c-7570-53af-af03-a6436f78ea8d
| 608,103
|
There are $2 n-1$ light bulbs in a row. Initially, the middle ($n$-th) one is on, and all the others are off. In one step, it is allowed to choose two non-adjacent off bulbs between which all bulbs are on, and change the state of those two bulbs, as well as all the bulbs between them (for example, from the configuration $\cdot$ооо $\cdot$ we get о $\cdot$ $\cdot$). What is the maximum number of steps that can be performed?
(Dusan Dukic)
## Ministry of Education, Science and Technological Development Mathematical Society of Serbia <br> 11th SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
## April 1, 2017.
## Second day
|
The answer is $\left[\frac{2^{n+1}-5}{3}\right]$.
We associate the number $2^{|i-n|}$ with the $i$-th light and define the value of a configuration as the sum of the numbers on the lit lights. The value of the initial configuration is 1, and at each step, it increases by a natural multiple of the number 3. A step increases the value by exactly 3 if the $n$-th light changes state; such a step is called good.
Since the value cannot exceed $2^{n+1}-4$ (since all lights cannot be lit), it is not possible to perform more than $\left[\frac{2^{n+1}-5}{3}\right]$ steps. This number can be achieved: it is sufficient to show that it is possible to perform at least $\frac{2^{n+1}-7}{3}$ steps.
We will prove by induction on $n$ that, starting from a configuration of value at most 3, we can obtain a configuration of value at least $2^{n+1}-6$ by a sequence of good steps. This can be directly verified for $n \leqslant 2$. Let $n \geqslant 3$. By the inductive hypothesis for $n-1$, it is possible to reach a configuration of value at least $2^{n}-6$ with the first and last light off. In such a configuration, apart from the first and last light, the following can be off: (1) only the $n$-th, (2) only the $n$-th and one of its neighbors, or (3) only one of the two neighbors. In each of these three cases, in at most three good steps, we achieve that the first and last lights are on and that the value of the rest of the configuration (excluding these two lights) is at most 3.
(1)
(2)
(3)
Reapplying the inductive hypothesis for $n-1$ completes the induction.
|
\left[\frac{2^{n+1}-5}{3}\right]
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
У врсти се налази $2 n-1$ сијалица. У почетку је средња ( $n$-та) упаљена, а све остале су угашене. У једном кораку је дозвољено одабрати две несуседне угашене сијалице између којих су све сијалице упаљене, и променити стање тим двема сијалицама, као и свим сијалицама између њих (на пример, од конфигурације $\cdot$ооо $\cdot$ добија се о $\cdot$ $\cdot$ ). Колико највише корака је могуће извршити?
(Душан Ђукић)
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 11. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
## 1. април 2017 .
## Други дан
|
Одговор је $\left[\frac{2^{n+1}-5}{3}\right]$.
Придружимо $i$-тој сијалици број $2^{|i-n|}$ и дефинишимо вредност конфигурације као збир бројева на упаљеним сијалицама. Вредност полазне конфигурације је 1, а при сваком кораку она се повећава за природан умножак броја 3. Корак повећава вредност за тачно 3 ако $n$-та сијалица мења стање; овакав корак зовемо добрим.
Пошто вредност не може да премаши $2^{n+1}-4$ (jep cе не могу упалити све сијалице), није могуће извршити више од $\left[\frac{2^{n+1}-5}{3}\right]$ корака. Овај број се може достићи: довољно је показати да је могуће извршити бар $\frac{2^{n+1}-7}{3}$ корака.
Доказаћемо индукцијом по $n$ да, почевши од конфигурације вредности највише 3 , можемо да низом добрих корака добијемо конфигурацију вредности бар $2^{n+1}-6$. Ово се директно проверава за $n \leqslant 2$. Нека је $n \geqslant 3$. По индуктивној претпоставци за $n-1$, могуће је доћи до конфигурације вредности бар $2^{n}-6$ са првом и последњом сијалицом угашеном. У таквој конфигурацији, осим прве и последње сијалице, могу бити угашене ( $1^{\circ}$ ) само $n$-та, $\left(2^{\circ}\right)$ само $n$-та и једна од њој суседних, или (3) само једна од две суседне. У сваком од ова три случаја, у највише три добра корака постижемо да прва и последња сијалица буду упаљене и да вредност остатка конфигурације (без ове две сијалице) буде највише 3.

$\left(1^{\circ}\right)$

$\left(2^{\circ}\right)$

$\left(3^{\circ}\right)$
Поновна примена индуктивне претпоставке за $n$ - 1 завршава индукцију.
|
{
"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
1bbceecb-e014-5f92-9557-72f64893b65e
| 608,110
|
Determine the maximum number of queens that can be placed on a $2017 \times 2017$ board, such that each queen can attack at most one of the remaining.
(Bojan Bašić and the committee)
|
Let $n=2017$. Suppose $m>n$ queens are placed. No row contains more than two queens, so in at least $m-n$ rows, there are two queens, meaning there are at most $m-2(m-n)=2n-m$ queens that are alone in their row. Similarly, at most $2n-m$ queens are alone in their column. On the other hand, each queen is alone in its row or column, so $m \leqslant 2(2n-m)$, from which $m \leqslant\left[\frac{4n}{3}\right]=2689$.
In Figure A, a placement of 8 queens on a $6 \times 6$ board is shown, in accordance with the problem's requirements. Before constructing an example on the $2017 \times 2017$ board, let's consider the following arrangement of queens:
- On a $335 \times 335$ board, it is possible to place 335 queens that do not attack each other, even if the diagonals are extended modulo 335. Indeed, it is sufficient to place the queens on all squares $(x, y), 1 \leqslant x, y \leqslant 335$, for which $y \equiv 2x (\bmod 335)$, as shown in Figure B. Indeed, then all sums $x+y$ are distinct modulo 335, and all differences $x-y$ are also distinct, so no two queens are in the same row, column, or diagonal.
Divide the $2017 \times 2017$ board into rectangles and squares with side lengths of 335, 6, and 1, as shown in Figure C. The squares marked B and A will be filled in the order shown in Figures B and A, and one more queen will be placed in the top right cell of the board. This way, we have placed a total of $8 \cdot 335 + 8 + 1 = 2689$ queens. It is easy to verify that this placement satisfies the conditions of the problem.
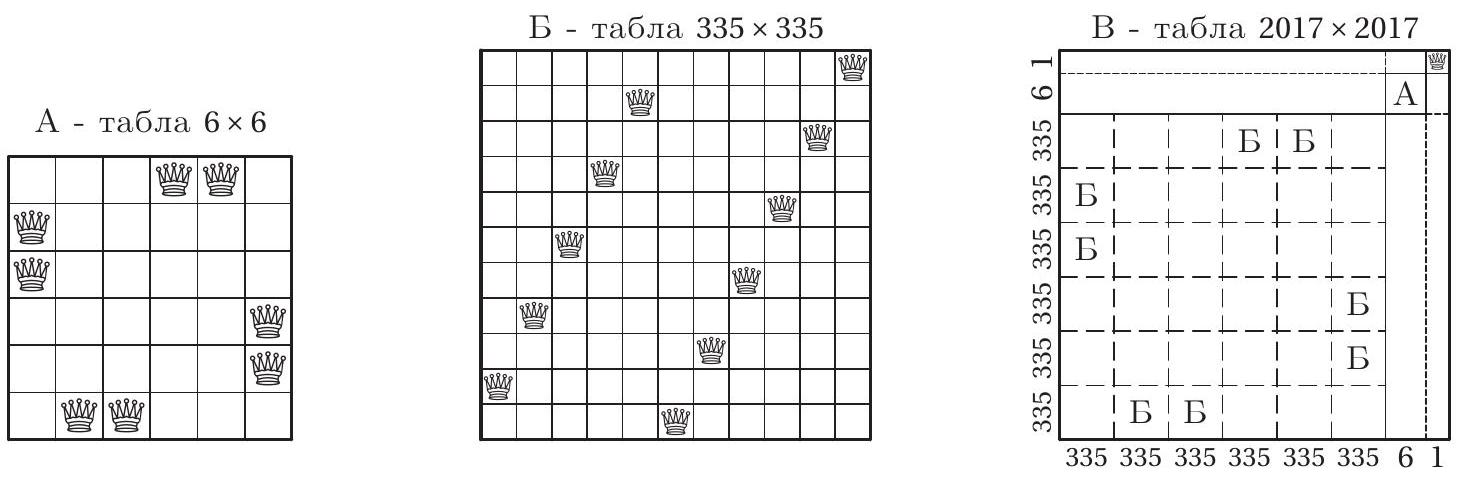
Note. A $n \times n$ board whose diagonals are extended modulo $n$ is called a toroidal board. On a toroidal $n \times n$ board, it is possible to place $n$ queens that do not attack each other if and only if $n \equiv \pm 1 (\bmod 6)$. This has been proven in problem 4 of SMO 2012.
|
2689
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Одредити колико се највише краљица може поставити на таблу $2017 \times 2017$, при чему свака краљица сме да напада највише једну од преосталих.
(Бојан Башић и комисија)
|
Означимо $n=2017$. Претпоставимо да је постављено $m>n$ краљица. Ни у једној врсти нема више од две краљице, па се у бар $m-n$ врста налазе по две краљице, тако да има највише $m-2(m-n)=2 n-m$ краљица које су саме у својој врсти. Слично, највише $2 n-m$ краљица су саме у својој колони. С друге стране, свака краљица је сама у својој врсти или у својој колони, па је $m \leqslant 2(2 n-m)$, одакле је $m \leqslant\left[\frac{4 n}{3}\right]=2689$.
На слици А је приказано постављање 8 краљица на таблу $6 \times 6$ у складу са захтевом задатка. Пре конструкције примера на табли $2017 \times 2017$ размотрићемо следећи распоред краљица:
- На таблу $335 \times 335$ могуће је поставити 335 краљица које се међусобно не нападају чак ни ако се дијагонале продуже по модулу 335. Заиста, довољно је поставити краљице на сва поља $(x, y), 1 \leqslant x, y \leqslant 335$, за која је $y \equiv 2 x(\bmod 335)$, као на слици Б. Заиста, тада су сви збирови $x+y$ међусобно различити по модулу 335 , све разлике $x-y$ такође, па никоје две краљице нису у истој врсти, колони или дијагонали.
Поделимо таблу $2017 \times 2017$ на правоугаонике и квадрате страница 335, 6 и 1 , као на слици В. Квадрате обележене са Б и А попунићемо редом као на сликама Б и А, а у горње десно поље табле поставићемо још једну краљицу. Овако смо укупно поставили $8 \cdot 335+8+1=2689$ краљица. Лако се проверава да овакво постављање задовољава услове задатка.

Напомена. Табла $n \times n$ чије су дијагонале продужене по модулу $n$ зове се торусна табла. На торусну таблу $n \times n$ могуће је поставити $n$ краљица које се међусобно не нападају ако и само ако је $n \equiv \pm 1(\bmod 6)$. Ово је доказано у 4. задатку са СMO 2012.
|
{
"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
a448ba24-e6de-5e60-98f0-afff0a696b06
| 608,112
|
Let $P(n)$ be the number of permutations $\left(a_{1}, \ldots, a_{n}\right)$ of the numbers $(1,2, \ldots, n)$ for which $k a_{k}$ is a perfect square for all $1 \leq k \leq n$. Find with proof the smallest $n$ such that $P(n)$ is a multiple of 2010 .
|
The answer is $n=4489$. We begin by giving a complete description of $P(n)$ : Claim - We have $$ P(n)=\prod_{c \text { squarefree }}\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor! $$ $$ S_{c}=\left\{c \cdot 1^{2}, c \cdot 2^{2}, c \cdot 3^{2}, \ldots\right\} \cap\{1,2, \ldots, n\} $$ and each integer from 1 through $n$ will be in exactly one $S_{c}$. Note also that $$ \left|S_{c}\right|=\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor . $$ Then, the permutations in the problem are exactly those which send elements of $S_{c}$ to elements of $S_{c}$. In other words, $$ P(n)=\prod_{c \text { squarefree }}\left|S_{c}\right|!=\prod_{c \text { squarefree }}\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor! $$ We want the smallest $n$ such that 2010 divides $P(n)$. - Note that $P\left(67^{2}\right)$ contains 67 ! as a term, which is divisible by 2010 , so $67^{2}$ is a candidate. - On the other hand, if $n<67^{2}$, then no term in the product for $P(n)$ is divisible by the prime 67 . So $n=67^{2}=4489$ is indeed the minimum.
|
4489
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $P(n)$ be the number of permutations $\left(a_{1}, \ldots, a_{n}\right)$ of the numbers $(1,2, \ldots, n)$ for which $k a_{k}$ is a perfect square for all $1 \leq k \leq n$. Find with proof the smallest $n$ such that $P(n)$ is a multiple of 2010 .
|
The answer is $n=4489$. We begin by giving a complete description of $P(n)$ : Claim - We have $$ P(n)=\prod_{c \text { squarefree }}\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor! $$ $$ S_{c}=\left\{c \cdot 1^{2}, c \cdot 2^{2}, c \cdot 3^{2}, \ldots\right\} \cap\{1,2, \ldots, n\} $$ and each integer from 1 through $n$ will be in exactly one $S_{c}$. Note also that $$ \left|S_{c}\right|=\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor . $$ Then, the permutations in the problem are exactly those which send elements of $S_{c}$ to elements of $S_{c}$. In other words, $$ P(n)=\prod_{c \text { squarefree }}\left|S_{c}\right|!=\prod_{c \text { squarefree }}\left\lfloor\sqrt{\frac{n}{c}}\right\rfloor! $$ We want the smallest $n$ such that 2010 divides $P(n)$. - Note that $P\left(67^{2}\right)$ contains 67 ! as a term, which is divisible by 2010 , so $67^{2}$ is a candidate. - On the other hand, if $n<67^{2}$, then no term in the product for $P(n)$ is divisible by the prime 67 . So $n=67^{2}=4489$ is indeed the minimum.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f48c618b-75f2-58b8-aed5-8922d7828b44
| 604,198
|
For distinct positive integers $a, b<2012$, define $f(a, b)$ to be the number of integers $k$ with $1 \leq k<2012$ such that the remainder when $a k$ divided by 2012 is greater than that of $b k$ divided by 2012 . Let $S$ be the minimum value of $f(a, b)$, where $a$ and $b$ range over all pairs of distinct positive integers less than 2012. Determine $S$.
|
The answer is $S=502$ (not 503 !). Claim - If $\operatorname{gcd}(k, 2012)=1$, then necessarily either $k$ or $2012-k$ will counts towards $S$. So if $r_{a}$ is the remainder of $a k(\bmod 2012)$, then $2012-r_{a}$ is the remainder of $a(2012-k)$ $(\bmod 2012)$ Similarly we can consider $r_{b}$ and $2012-r_{b}$. As mentioned already, we have $r_{a} \neq r_{b}$. So either $r_{a}>r_{b}$ or $2012-r_{a}>2012-r_{b}$. This implies $S \geq \frac{1}{2} \varphi(2012)=502$. But this can actually be achieved by taking $a=4$ and $b=1010$, since - If $k$ is even, then $a k \equiv b k(\bmod 2012)$ so no even $k$ counts towards $S$; and - If $k \equiv 0(\bmod 503)$, then $a k \equiv 0(\bmod 2012)$ so no such $k$ counts towards $S$. This gives the final answer $S \geq 502$.
|
502
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For distinct positive integers $a, b<2012$, define $f(a, b)$ to be the number of integers $k$ with $1 \leq k<2012$ such that the remainder when $a k$ divided by 2012 is greater than that of $b k$ divided by 2012 . Let $S$ be the minimum value of $f(a, b)$, where $a$ and $b$ range over all pairs of distinct positive integers less than 2012. Determine $S$.
|
The answer is $S=502$ (not 503 !). Claim - If $\operatorname{gcd}(k, 2012)=1$, then necessarily either $k$ or $2012-k$ will counts towards $S$. So if $r_{a}$ is the remainder of $a k(\bmod 2012)$, then $2012-r_{a}$ is the remainder of $a(2012-k)$ $(\bmod 2012)$ Similarly we can consider $r_{b}$ and $2012-r_{b}$. As mentioned already, we have $r_{a} \neq r_{b}$. So either $r_{a}>r_{b}$ or $2012-r_{a}>2012-r_{b}$. This implies $S \geq \frac{1}{2} \varphi(2012)=502$. But this can actually be achieved by taking $a=4$ and $b=1010$, since - If $k$ is even, then $a k \equiv b k(\bmod 2012)$ so no even $k$ counts towards $S$; and - If $k \equiv 0(\bmod 503)$, then $a k \equiv 0(\bmod 2012)$ so no such $k$ counts towards $S$. This gives the final answer $S \geq 502$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
57c4775b-6eb9-52eb-b636-246d48aeaea6
| 245,696
|
Each cell of an $m \times n$ board is filled with some nonnegative integer. Two numbers in the filling are said to be adjacent if their cells share a common side. The filling is called a garden if it satisfies the following two conditions: (i) The difference between any two adjacent numbers is either 0 or 1 . (ii) If a number is less than or equal to all of its adjacent numbers, then it is equal to 0. Determine the number of distinct gardens in terms of $m$ and $n$.
|
The numerical answer is $2^{m n}-1$. But we claim much more, by giving an explicit description of all gardens: Let $S$ be any nonempty subset of the $m n$ cells. Suppose we fill each cell $\theta$ with the minimum (taxicab) distance from $\theta$ to some cell in $S$ (in particular, we write 0 if $\theta \in S$ ). Then - This gives a garden, and - All gardens are of this form. Since there are $2^{m n}-1$ such nonempty subsets $S$, this would finish the problem. An example of a garden with $|S|=3$ is shown below. $$ \left[\begin{array}{llllll} 2 & 1 & 2 & 1 & 0 & 1 \\ 1 & 0 & 1 & 2 & 1 & 2 \\ 1 & 1 & 2 & 3 & 2 & 3 \\ 0 & 1 & 2 & 3 & 3 & 4 \end{array}\right] $$ It is actually fairly easy to see that this procedure always gives a garden; so we focus our attention on showing that every garden is of this form. Given a garden, note first that it has at least one cell with a zero in it - by considering the minimum number across the entire garden. Now let $S$ be the (thus nonempty) set of cells with a zero written in them. We contend that this works, i.e. the following sentence holds: Claim - If a cell $\theta$ is labeled $d$, then the minimum distance from that cell to a cell in $S$ is $d$.
|
2^{m n}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Each cell of an $m \times n$ board is filled with some nonnegative integer. Two numbers in the filling are said to be adjacent if their cells share a common side. The filling is called a garden if it satisfies the following two conditions: (i) The difference between any two adjacent numbers is either 0 or 1 . (ii) If a number is less than or equal to all of its adjacent numbers, then it is equal to 0. Determine the number of distinct gardens in terms of $m$ and $n$.
|
The numerical answer is $2^{m n}-1$. But we claim much more, by giving an explicit description of all gardens: Let $S$ be any nonempty subset of the $m n$ cells. Suppose we fill each cell $\theta$ with the minimum (taxicab) distance from $\theta$ to some cell in $S$ (in particular, we write 0 if $\theta \in S$ ). Then - This gives a garden, and - All gardens are of this form. Since there are $2^{m n}-1$ such nonempty subsets $S$, this would finish the problem. An example of a garden with $|S|=3$ is shown below. $$ \left[\begin{array}{llllll} 2 & 1 & 2 & 1 & 0 & 1 \\ 1 & 0 & 1 & 2 & 1 & 2 \\ 1 & 1 & 2 & 3 & 2 & 3 \\ 0 & 1 & 2 & 3 & 3 & 4 \end{array}\right] $$ It is actually fairly easy to see that this procedure always gives a garden; so we focus our attention on showing that every garden is of this form. Given a garden, note first that it has at least one cell with a zero in it - by considering the minimum number across the entire garden. Now let $S$ be the (thus nonempty) set of cells with a zero written in them. We contend that this works, i.e. the following sentence holds: Claim - If a cell $\theta$ is labeled $d$, then the minimum distance from that cell to a cell in $S$ is $d$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
127ad4df-63f3-5952-984e-4b6c291ce014
| 604,569
|
Let $f(n)$ be the number of ways to write $n$ as a sum of powers of 2 , where we keep track of the order of the summation. For example, $f(4)=6$ because 4 can be written as $4,2+2,2+1+1,1+2+1,1+1+2$, and $1+1+1+1$. Find the smallest $n$ greater than 2013 for which $f(n)$ is odd.
|
The answer is 2047. For convenience, we agree that $f(0)=1$. Then by considering cases on the first number in the representation, we derive the recurrence $$ f(n)=\sum_{k=0}^{\left\lfloor\log _{2} n\right\rfloor} f\left(n-2^{k}\right) $$ We wish to understand the parity of $f$. The first few values are $$ \begin{aligned} & f(0)=1 \\ & f(1)=1 \\ & f(2)=2 \\ & f(3)=3 \\ & f(4)=6 \\ & f(5)=10 \\ & f(6)=18 \\ & f(7)=31 . \end{aligned} $$ Inspired by the data we make the key claim that Claim - $f(n)$ is odd if and only if $n+1$ is a power of 2. This only takes a few cases: - If $n=2^{k}$, then $(\odot)$ has exactly two repetitive terms on the right-hand side, namely 0 and $2^{k}-1$. - If $n=2^{k}+2^{\ell}-1$, then $(\odot)$ has exactly two repetitive terms on the right-hand side, namely $2^{\ell+1}-1$ and $2^{\ell}-1$. - If $n=2^{k}-1$, then $(\bigcirc)$ has exactly one repetitive terms on the right-hand side, namely $2^{k-1}-1$. - For other $n$, there are no repetitive terms at all on the right-hand side of $(\Omega)$. Thus the induction checks out. So the final answer to the problem is 2047.
|
2047
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $f(n)$ be the number of ways to write $n$ as a sum of powers of 2 , where we keep track of the order of the summation. For example, $f(4)=6$ because 4 can be written as $4,2+2,2+1+1,1+2+1,1+1+2$, and $1+1+1+1$. Find the smallest $n$ greater than 2013 for which $f(n)$ is odd.
|
The answer is 2047. For convenience, we agree that $f(0)=1$. Then by considering cases on the first number in the representation, we derive the recurrence $$ f(n)=\sum_{k=0}^{\left\lfloor\log _{2} n\right\rfloor} f\left(n-2^{k}\right) $$ We wish to understand the parity of $f$. The first few values are $$ \begin{aligned} & f(0)=1 \\ & f(1)=1 \\ & f(2)=2 \\ & f(3)=3 \\ & f(4)=6 \\ & f(5)=10 \\ & f(6)=18 \\ & f(7)=31 . \end{aligned} $$ Inspired by the data we make the key claim that Claim - $f(n)$ is odd if and only if $n+1$ is a power of 2. This only takes a few cases: - If $n=2^{k}$, then $(\odot)$ has exactly two repetitive terms on the right-hand side, namely 0 and $2^{k}-1$. - If $n=2^{k}+2^{\ell}-1$, then $(\odot)$ has exactly two repetitive terms on the right-hand side, namely $2^{\ell+1}-1$ and $2^{\ell}-1$. - If $n=2^{k}-1$, then $(\bigcirc)$ has exactly one repetitive terms on the right-hand side, namely $2^{k-1}-1$. - For other $n$, there are no repetitive terms at all on the right-hand side of $(\Omega)$. Thus the induction checks out. So the final answer to the problem is 2047.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9a58ba03-8487-5a6e-923e-1b2ae453a05c
| 604,593
|
Let $X_{1}, X_{2}, \ldots, X_{100}$ be a sequence of mutually distinct nonempty subsets of a set $S$. Any two sets $X_{i}$ and $X_{i+1}$ are disjoint and their union is not the whole set $S$, that is, $X_{i} \cap X_{i+1}=\emptyset$ and $X_{i} \cup X_{i+1} \neq S$, for all $i \in\{1, \ldots, 99\}$. Find the smallest possible number of elements in $S$.
|
Solution with Danielle Wang: the answer is that $|S| \geq 8$. To see that $|S|=8$ is the minimum possible size, consider a chain on the set $S=$ $\{1,2, \ldots, 7\}$ satisfying $X_{i} \cap X_{i+1}=\emptyset$ and $X_{i} \cup X_{i+1} \neq S$. Because of these requirements any subset of size 4 or more can only be neighbored by sets of size 2 or less, of which there are $\binom{7}{1}+\binom{7}{2}=28$ available. Thus, the chain can contain no more than 29 sets of size 4 or more and no more than 28 sets of size 2 or less. Finally, since there are only $\binom{7}{3}=35$ sets of size 3 available, the total number of sets in such a chain can be at most $29+28+35=92<100$, contradiction. ब Construction. We will provide an inductive construction for a chain of subsets $X_{1}, X_{2}, \ldots, X_{2^{n-1}+1}$ of $S=\{1, \ldots, n\}$ satisfying $X_{i} \cap X_{i+1}=\varnothing$ and $X_{i} \cup X_{i+1} \neq S$ for each $n \geq 4$. For $S=\{1,2,3,4\}$, the following chain of length $2^{3}+1=9$ will work: $$ \begin{array}{lllllllll} 34 & 1 & 23 & 4 & 12 & 3 & 14 & 2 & 13 . \end{array} $$ Now, given a chain of subsets of $\{1,2, \ldots, n\}$ the following procedure produces a chain of subsets of $\{1,2, \ldots, n+1\}$ : 1. take the original chain, delete any element, and make two copies of this chain, which now has even length; 2. glue the two copies together, joined by $\varnothing$ in between; and then 3. insert the element $n+1$ into the sets in alternating positions of the chain starting with the first. For example, the first iteration of this construction gives: $$ \begin{array}{ccccccccc} 345 & 1 & 235 & 4 & 125 & 3 & 145 & 2 & 5 \\ 34 & 15 & 23 & 45 & 12 & 35 & 14 & 25 & \end{array} $$ It can be easily checked that if the original chain satisfies the requirements, then so does the new chain, and if the original chain has length $2^{n-1}+1$, then the new chain has length $2^{n}+1$, as desired. This construction yields a chain of length 129 when $S=\{1,2, \ldots, 8\}$. Remark. Here is the construction for $n=8$ in its full glory. | 345678 | 1 | 235678 | 4 | 125678 | 3 | 145678 | 2 | 5678 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 34 | 15678 | 23 | 45678 | 12 | 35678 | 14 | 678 | | | 345 | 1678 | 235 | 4678 | 125 | 3678 | 145 | 2678 | 5 | | 34678 | 15 | 23678 | 45 | 12678 | 35 | 78 | | | | 3456 | 178 | 2356 | 478 | 1256 | 378 | 1456 | 278 | 56 | | 3478 | 156 | 2378 | 456 | 1278 | 356 | 1478 | 6 | | | 34578 | 16 | 23578 | 46 | 12578 | 36 | 14578 | 26 | 578 | | 346 | 1578 | 236 | 4578 | 126 | 8 | | | | | 34567 | 18 | 23567 | 48 | 12567 | 38 | 14567 | 28 | 567 | | 348 | 1567 | 238 | 4567 | 128 | 3567 | 148 | 67 | | | 3458 | 167 | 2358 | 467 | 1258 | 367 | 1458 | 267 | 58 | | 3467 | 158 | 2367 | 458 | 1267 | 358 | 7 | | | | 34568 | 17 | 23568 | 47 | 12568 | 37 | 14568 | 27 | 568 | | 347 | 1568 | 237 | 4568 | 127 | 3568 | 147 | 68 | | | 3457 | 168 | 2357 | 468 | 1257 | 368 | 1457 | 268 | 57 | | 3468 | 157 | 2368 | 457 | 1268 | | | | |
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $X_{1}, X_{2}, \ldots, X_{100}$ be a sequence of mutually distinct nonempty subsets of a set $S$. Any two sets $X_{i}$ and $X_{i+1}$ are disjoint and their union is not the whole set $S$, that is, $X_{i} \cap X_{i+1}=\emptyset$ and $X_{i} \cup X_{i+1} \neq S$, for all $i \in\{1, \ldots, 99\}$. Find the smallest possible number of elements in $S$.
|
Solution with Danielle Wang: the answer is that $|S| \geq 8$. To see that $|S|=8$ is the minimum possible size, consider a chain on the set $S=$ $\{1,2, \ldots, 7\}$ satisfying $X_{i} \cap X_{i+1}=\emptyset$ and $X_{i} \cup X_{i+1} \neq S$. Because of these requirements any subset of size 4 or more can only be neighbored by sets of size 2 or less, of which there are $\binom{7}{1}+\binom{7}{2}=28$ available. Thus, the chain can contain no more than 29 sets of size 4 or more and no more than 28 sets of size 2 or less. Finally, since there are only $\binom{7}{3}=35$ sets of size 3 available, the total number of sets in such a chain can be at most $29+28+35=92<100$, contradiction. ब Construction. We will provide an inductive construction for a chain of subsets $X_{1}, X_{2}, \ldots, X_{2^{n-1}+1}$ of $S=\{1, \ldots, n\}$ satisfying $X_{i} \cap X_{i+1}=\varnothing$ and $X_{i} \cup X_{i+1} \neq S$ for each $n \geq 4$. For $S=\{1,2,3,4\}$, the following chain of length $2^{3}+1=9$ will work: $$ \begin{array}{lllllllll} 34 & 1 & 23 & 4 & 12 & 3 & 14 & 2 & 13 . \end{array} $$ Now, given a chain of subsets of $\{1,2, \ldots, n\}$ the following procedure produces a chain of subsets of $\{1,2, \ldots, n+1\}$ : 1. take the original chain, delete any element, and make two copies of this chain, which now has even length; 2. glue the two copies together, joined by $\varnothing$ in between; and then 3. insert the element $n+1$ into the sets in alternating positions of the chain starting with the first. For example, the first iteration of this construction gives: $$ \begin{array}{ccccccccc} 345 & 1 & 235 & 4 & 125 & 3 & 145 & 2 & 5 \\ 34 & 15 & 23 & 45 & 12 & 35 & 14 & 25 & \end{array} $$ It can be easily checked that if the original chain satisfies the requirements, then so does the new chain, and if the original chain has length $2^{n-1}+1$, then the new chain has length $2^{n}+1$, as desired. This construction yields a chain of length 129 when $S=\{1,2, \ldots, 8\}$. Remark. Here is the construction for $n=8$ in its full glory. | 345678 | 1 | 235678 | 4 | 125678 | 3 | 145678 | 2 | 5678 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | 34 | 15678 | 23 | 45678 | 12 | 35678 | 14 | 678 | | | 345 | 1678 | 235 | 4678 | 125 | 3678 | 145 | 2678 | 5 | | 34678 | 15 | 23678 | 45 | 12678 | 35 | 78 | | | | 3456 | 178 | 2356 | 478 | 1256 | 378 | 1456 | 278 | 56 | | 3478 | 156 | 2378 | 456 | 1278 | 356 | 1478 | 6 | | | 34578 | 16 | 23578 | 46 | 12578 | 36 | 14578 | 26 | 578 | | 346 | 1578 | 236 | 4578 | 126 | 8 | | | | | 34567 | 18 | 23567 | 48 | 12567 | 38 | 14567 | 28 | 567 | | 348 | 1567 | 238 | 4567 | 128 | 3567 | 148 | 67 | | | 3458 | 167 | 2358 | 467 | 1258 | 367 | 1458 | 267 | 58 | | 3467 | 158 | 2367 | 458 | 1267 | 358 | 7 | | | | 34568 | 17 | 23568 | 47 | 12568 | 37 | 14568 | 27 | 568 | | 347 | 1568 | 237 | 4568 | 127 | 3568 | 147 | 68 | | | 3457 | 168 | 2357 | 468 | 1257 | 368 | 1457 | 268 | 57 | | 3468 | 157 | 2368 | 457 | 1268 | | | | |
|
{
"resource_path": "USAJMO/segmented/en-JMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
11a263e2-acc3-5bad-b9ac-17f83bf0b47b
| 245,916
|
For each positive integer $n$, find the number of $n$-digit positive integers for which no two consecutive digits are equal, and the last digit is a prime.
|
Almost trivial. Let $a_{n}$ be the desired answer. We have $$ a_{n}+a_{n-1}=4 \cdot 9^{n-1} $$ for all $n$, by padding the $(n-1)$ digit numbers with a leading zero. Since $a_{0}=0, a_{1}=4$, solving the recursion gives $$ a_{n}=\frac{2}{5}\left(9^{n}-(-1)^{n}\right) $$ The end. Remark. For concreteness, the first few terms are $0,4,32,292, \ldots$.
|
\frac{2}{5}\left(9^{n}-(-1)^{n}\right)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For each positive integer $n$, find the number of $n$-digit positive integers for which no two consecutive digits are equal, and the last digit is a prime.
|
Almost trivial. Let $a_{n}$ be the desired answer. We have $$ a_{n}+a_{n-1}=4 \cdot 9^{n-1} $$ for all $n$, by padding the $(n-1)$ digit numbers with a leading zero. Since $a_{0}=0, a_{1}=4$, solving the recursion gives $$ a_{n}=\frac{2}{5}\left(9^{n}-(-1)^{n}\right) $$ The end. Remark. For concreteness, the first few terms are $0,4,32,292, \ldots$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e498cb4-4257-5956-82a3-999e61a42f59
| 245,998
|
Let $n$ be a nonnegative integer. Determine the number of ways to choose sets $S_{i j} \subseteq\{1,2, \ldots, 2 n\}$, for all $0 \leq i \leq n$ and $0 \leq j \leq n$ (not necessarily distinct), such that - $\left|S_{i j}\right|=i+j$, and - $S_{i j} \subseteq S_{k l}$ if $0 \leq i \leq k \leq n$ and $0 \leq j \leq l \leq n$.
|
The answer is $(2 n)!\cdot 2^{n^{2}}$. First, we note that $\varnothing=S_{00} \subsetneq S_{01} \subsetneq \cdots \subsetneq S_{n n}=\{1, \ldots, 2 n\}$ and thus multiplying by (2n)! we may as well assume $S_{0 i}=\{1, \ldots, i\}$ and $S_{i n}=\{1, \ldots, n+i\}$. We illustrate this situation by placing the sets in a grid, as below for $n=4$; our goal is to fill in the rest of the grid. $\left[\begin{array}{ccccc}1234 & 12345 & 123456 & 1234567 & 12345678 \\ 123 & & & & \\ 12 & & & & \\ 1 & & & & \\ \varnothing & & & & \end{array}\right]$ We claim the number of ways to do so is $2^{n^{2}}$. In fact, more strongly even the partial fillings are given exactly by powers of 2 . Claim - Fix a choice $T$ of cells we wish to fill in, such that whenever a cell is in $T$, so are all the cells above and left of it. (In other words, $T$ is a Young tableau.) The number of ways to fill in these cells with sets satisfying the inclusion conditions is $2^{|T|}$. An example is shown below, with an indeterminate set marked in red (and the rest of $T$ marked in blue). $\left[\begin{array}{ccccc}1234 & 12345 & 123456 & 1234567 & 12345678 \\ 123 & 1234 & 12346 & 123467 & \\ 12 & 124 & 1234 \text { or } 1246 & & \\ 1 & 12 & & & \\ \varnothing & 2 & & & \end{array}\right]$ Now suppose we have a corner $\left[\begin{array}{cc}B & C \\ A & S\end{array}\right]$ where $A, B, C$ are fixed and $S$ is to be chosen. Then we may write $B=A \cup\{x\}$ and $C=A \cup\{x, y\}$ for $x, y \notin A$. Then the two choices of $S$ are $A \cup\{x\}$ (i.e. $B$ ) and $A \cup\{y\}$, and both of them are seen to be valid. In this way, we gain a factor of 2 any time we add one cell as above to $T$. Since we can achieve any Young tableau in this way, the induction is complete.
|
(2 n)!\cdot 2^{n^{2}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a nonnegative integer. Determine the number of ways to choose sets $S_{i j} \subseteq\{1,2, \ldots, 2 n\}$, for all $0 \leq i \leq n$ and $0 \leq j \leq n$ (not necessarily distinct), such that - $\left|S_{i j}\right|=i+j$, and - $S_{i j} \subseteq S_{k l}$ if $0 \leq i \leq k \leq n$ and $0 \leq j \leq l \leq n$.
|
The answer is $(2 n)!\cdot 2^{n^{2}}$. First, we note that $\varnothing=S_{00} \subsetneq S_{01} \subsetneq \cdots \subsetneq S_{n n}=\{1, \ldots, 2 n\}$ and thus multiplying by (2n)! we may as well assume $S_{0 i}=\{1, \ldots, i\}$ and $S_{i n}=\{1, \ldots, n+i\}$. We illustrate this situation by placing the sets in a grid, as below for $n=4$; our goal is to fill in the rest of the grid. $\left[\begin{array}{ccccc}1234 & 12345 & 123456 & 1234567 & 12345678 \\ 123 & & & & \\ 12 & & & & \\ 1 & & & & \\ \varnothing & & & & \end{array}\right]$ We claim the number of ways to do so is $2^{n^{2}}$. In fact, more strongly even the partial fillings are given exactly by powers of 2 . Claim - Fix a choice $T$ of cells we wish to fill in, such that whenever a cell is in $T$, so are all the cells above and left of it. (In other words, $T$ is a Young tableau.) The number of ways to fill in these cells with sets satisfying the inclusion conditions is $2^{|T|}$. An example is shown below, with an indeterminate set marked in red (and the rest of $T$ marked in blue). $\left[\begin{array}{ccccc}1234 & 12345 & 123456 & 1234567 & 12345678 \\ 123 & 1234 & 12346 & 123467 & \\ 12 & 124 & 1234 \text { or } 1246 & & \\ 1 & 12 & & & \\ \varnothing & 2 & & & \end{array}\right]$ Now suppose we have a corner $\left[\begin{array}{cc}B & C \\ A & S\end{array}\right]$ where $A, B, C$ are fixed and $S$ is to be chosen. Then we may write $B=A \cup\{x\}$ and $C=A \cup\{x, y\}$ for $x, y \notin A$. Then the two choices of $S$ are $A \cup\{x\}$ (i.e. $B$ ) and $A \cup\{y\}$, and both of them are seen to be valid. In this way, we gain a factor of 2 any time we add one cell as above to $T$. Since we can achieve any Young tableau in this way, the induction is complete.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a4433a6-9ab9-5a63-b16e-f546ce4f432d
| 246,085
|
An empty $2020 \times 2020 \times 2020$ cube is given, and a $2020 \times 2020$ grid of square unit cells is drawn on each of its six faces. A beam is a $1 \times 1 \times 2020$ rectangular prism. Several beams are placed inside the cube subject to the following conditions: - The two $1 \times 1$ faces of each beam coincide with unit cells lying on opposite faces of the cube. (Hence, there are $3 \cdot 2020^{2}$ possible positions for a beam.) - No two beams have intersecting interiors. - The interiors of each of the four $1 \times 2020$ faces of each beam touch either a face of the cube or the interior of the face of another beam. What is the smallest positive number of beams that can be placed to satisfy these conditions?
|
\I Answer. 3030 beams. 【 Construction. We first give a construction with $3 n / 2$ beams for any $n \times n \times n$ box, where $n$ is an even integer. Shown below is the construction for $n=6$, which generalizes. (The left figure shows the cube in 3 d ; the right figure shows a direct view of the three visible faces.) 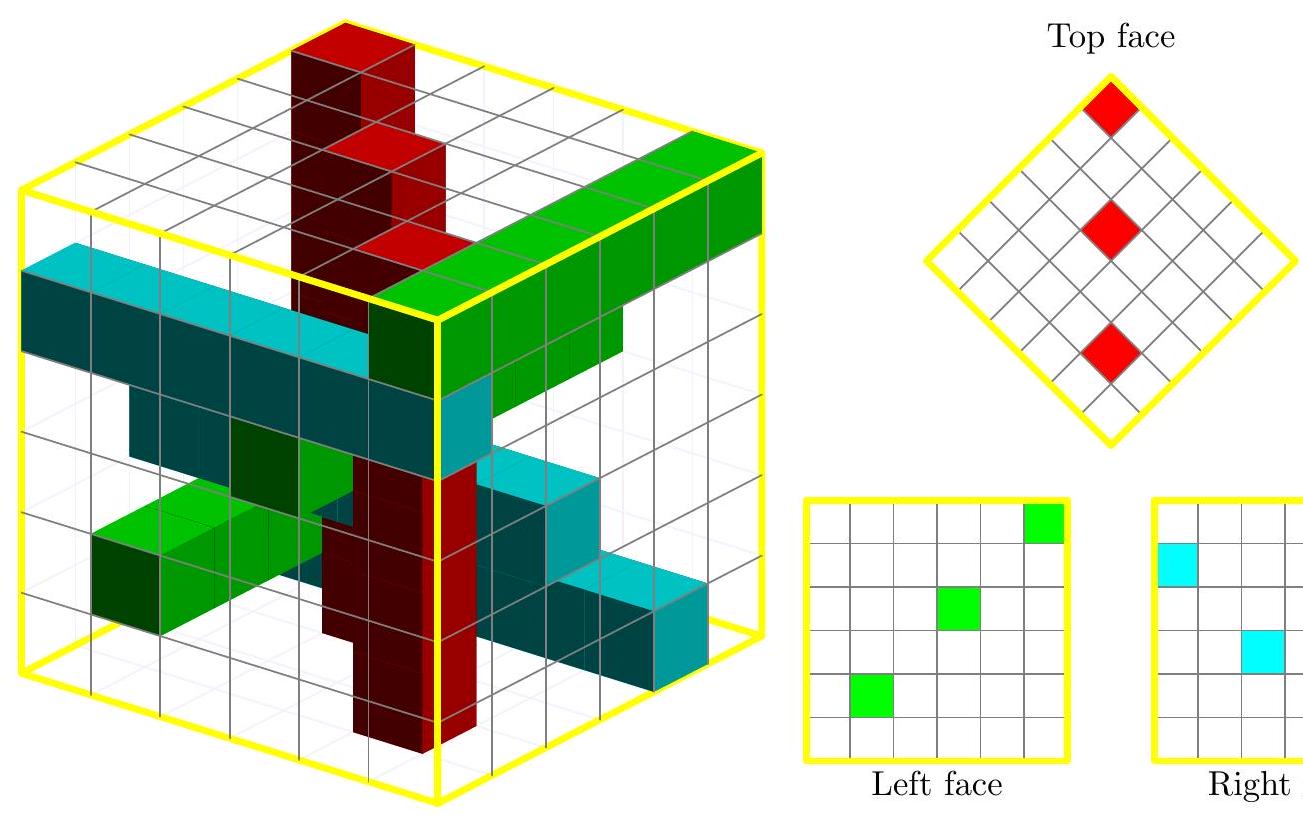  Left face  Right face To be explicit, impose coordinate axes such that one corner of the cube is the origin. We specify a beam by two opposite corners. The $3 n / 2$ beams come in three directions, $n / 2$ in each direction: - $(0,0,0) \rightarrow(1,1, n),(2,2,0) \rightarrow(3,3, n),(4,4,0) \rightarrow(5,5, n)$, and so on; - $(1,0,0) \rightarrow(2, n, 1),(3,0,2) \rightarrow(4, n, 3),(5,0,4) \rightarrow(6, n, 5)$, and so on; - $(0,1,1) \rightarrow(n, 2,2),(0,3,3) \rightarrow(n, 4,4),(0,5,5) \rightarrow(n, 6,6)$, and so on. This gives the figure we drew earlier and shows 3030 beams is possible. Necessity. We now show at least $3 n / 2$ beams are necessary. Maintain coordinates, and call the beams $x$-beams, $y$-beams, $z$-beams according to which plane their long edges are perpendicular too. Let $N_{x}, N_{y}, N_{z}$ be the number of these. Claim - If $\min \left(N_{x}, N_{y}, N_{z}\right)=0$, then at least $n^{2}$ beams are needed. We henceforth assume $\min \left(N_{x}, N_{y}, N_{z}\right)>0$. Claim - If $N_{z}>0$, then we have $N_{x}+N_{y} \geq n$. Proceeding in a similar fashion, we arrive at the three relations $$ \begin{aligned} & N_{x}+N_{y} \geq n \\ & N_{y}+N_{z} \geq n \\ & N_{z}+N_{x} \geq n \end{aligned} $$ Summing gives $N_{x}+N_{y}+N_{z} \geq 3 n / 2$ too. Remark. The problem condition has the following "physics" interpretation. Imagine the cube is a metal box which is sturdy enough that all beams must remain orthogonal to the faces of the box (i.e. the beams cannot spin). Then the condition of the problem is exactly what is needed so that, if the box is shaken or rotated, the beams will not move. Remark. Walter Stromquist points out that the number of constructions with 3030 beams is actually enormous: not dividing out by isometries, the number is $(2 \cdot 1010!)^{3}$.
|
3030
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An empty $2020 \times 2020 \times 2020$ cube is given, and a $2020 \times 2020$ grid of square unit cells is drawn on each of its six faces. A beam is a $1 \times 1 \times 2020$ rectangular prism. Several beams are placed inside the cube subject to the following conditions: - The two $1 \times 1$ faces of each beam coincide with unit cells lying on opposite faces of the cube. (Hence, there are $3 \cdot 2020^{2}$ possible positions for a beam.) - No two beams have intersecting interiors. - The interiors of each of the four $1 \times 2020$ faces of each beam touch either a face of the cube or the interior of the face of another beam. What is the smallest positive number of beams that can be placed to satisfy these conditions?
|
\I Answer. 3030 beams. 【 Construction. We first give a construction with $3 n / 2$ beams for any $n \times n \times n$ box, where $n$ is an even integer. Shown below is the construction for $n=6$, which generalizes. (The left figure shows the cube in 3 d ; the right figure shows a direct view of the three visible faces.)   Left face  Right face To be explicit, impose coordinate axes such that one corner of the cube is the origin. We specify a beam by two opposite corners. The $3 n / 2$ beams come in three directions, $n / 2$ in each direction: - $(0,0,0) \rightarrow(1,1, n),(2,2,0) \rightarrow(3,3, n),(4,4,0) \rightarrow(5,5, n)$, and so on; - $(1,0,0) \rightarrow(2, n, 1),(3,0,2) \rightarrow(4, n, 3),(5,0,4) \rightarrow(6, n, 5)$, and so on; - $(0,1,1) \rightarrow(n, 2,2),(0,3,3) \rightarrow(n, 4,4),(0,5,5) \rightarrow(n, 6,6)$, and so on. This gives the figure we drew earlier and shows 3030 beams is possible. Necessity. We now show at least $3 n / 2$ beams are necessary. Maintain coordinates, and call the beams $x$-beams, $y$-beams, $z$-beams according to which plane their long edges are perpendicular too. Let $N_{x}, N_{y}, N_{z}$ be the number of these. Claim - If $\min \left(N_{x}, N_{y}, N_{z}\right)=0$, then at least $n^{2}$ beams are needed. We henceforth assume $\min \left(N_{x}, N_{y}, N_{z}\right)>0$. Claim - If $N_{z}>0$, then we have $N_{x}+N_{y} \geq n$. Proceeding in a similar fashion, we arrive at the three relations $$ \begin{aligned} & N_{x}+N_{y} \geq n \\ & N_{y}+N_{z} \geq n \\ & N_{z}+N_{x} \geq n \end{aligned} $$ Summing gives $N_{x}+N_{y}+N_{z} \geq 3 n / 2$ too. Remark. The problem condition has the following "physics" interpretation. Imagine the cube is a metal box which is sturdy enough that all beams must remain orthogonal to the faces of the box (i.e. the beams cannot spin). Then the condition of the problem is exactly what is needed so that, if the box is shaken or rotated, the beams will not move. Remark. Walter Stromquist points out that the number of constructions with 3030 beams is actually enormous: not dividing out by isometries, the number is $(2 \cdot 1010!)^{3}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e4f89dc-cfce-5992-89ae-bd6955e55da7
| 605,411
|
Suppose that $\left(a_{1}, b_{1}\right),\left(a_{2}, b_{2}\right), \ldots,\left(a_{100}, b_{100}\right)$ are distinct ordered pairs of nonnegative integers. Let $N$ denote the number of pairs of integers $(i, j)$ satisfying $1 \leq i<j \leq 100$ and $\left|a_{i} b_{j}-a_{j} b_{i}\right|=1$. Determine the largest possible value of $N$ over all possible choices of the 100 ordered pairs.
|
The answer is 197 . In general, if 100 is replaced by $n \geq 2$ the answer is $2 n-3$. The idea is that if we let $P_{i}=\left(a_{i}, b_{i}\right)$ be a point in the coordinate plane, and let $O=(0,0)$ then we wish to maximize the number of triangles $\triangle O P_{i} P_{j}$ which have area $1 / 2$. Call such a triangle good. 【 Construction of 197 points. It suffices to use the points $(1,0),(1,1),(2,1),(3,1)$, ..., $(99,1)$ as shown. Notice that: - There are 98 good triangles with vertices $(0,0),(k, 1)$ and $(k+1,1)$ for $k=1, \ldots, 98$. - There are 99 good triangles with vertices $(0,0),(1,0)$ and $(k, 1)$ for $k=1, \ldots, 99$. This is a total of $98+99=197$ triangles.  For the inductive step, suppose (without loss of generality) that the point $P=P_{n}=$ $(a, b)$ is the farthest away from the point $O$ among all points. Claim - This farthest point $P=P_{n}$ is part of at most two good triangles.  Since $\operatorname{gcd}(a, b)=1$, see that only two lattice points on this locus actually lie inside the quarter-circle centered at $O$ with radius $O P$. Indeed if one of the points is $(u, v)$ then the others on the line are $(u \pm a, v \pm b)$ where the signs match. This proves the claim. This claim allows us to complete the induction by simply deleting $P_{n}$.
|
197
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Suppose that $\left(a_{1}, b_{1}\right),\left(a_{2}, b_{2}\right), \ldots,\left(a_{100}, b_{100}\right)$ are distinct ordered pairs of nonnegative integers. Let $N$ denote the number of pairs of integers $(i, j)$ satisfying $1 \leq i<j \leq 100$ and $\left|a_{i} b_{j}-a_{j} b_{i}\right|=1$. Determine the largest possible value of $N$ over all possible choices of the 100 ordered pairs.
|
The answer is 197 . In general, if 100 is replaced by $n \geq 2$ the answer is $2 n-3$. The idea is that if we let $P_{i}=\left(a_{i}, b_{i}\right)$ be a point in the coordinate plane, and let $O=(0,0)$ then we wish to maximize the number of triangles $\triangle O P_{i} P_{j}$ which have area $1 / 2$. Call such a triangle good. 【 Construction of 197 points. It suffices to use the points $(1,0),(1,1),(2,1),(3,1)$, ..., $(99,1)$ as shown. Notice that: - There are 98 good triangles with vertices $(0,0),(k, 1)$ and $(k+1,1)$ for $k=1, \ldots, 98$. - There are 99 good triangles with vertices $(0,0),(1,0)$ and $(k, 1)$ for $k=1, \ldots, 99$. This is a total of $98+99=197$ triangles.  For the inductive step, suppose (without loss of generality) that the point $P=P_{n}=$ $(a, b)$ is the farthest away from the point $O$ among all points. Claim - This farthest point $P=P_{n}$ is part of at most two good triangles.  Since $\operatorname{gcd}(a, b)=1$, see that only two lattice points on this locus actually lie inside the quarter-circle centered at $O$ with radius $O P$. Indeed if one of the points is $(u, v)$ then the others on the line are $(u \pm a, v \pm b)$ where the signs match. This proves the claim. This claim allows us to complete the induction by simply deleting $P_{n}$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
efe860a6-647e-5844-999e-d4b4cb0b2601
| 605,444
|
Carina has three pins, labeled $A, B$, and $C$, respectively, located at the origin of the coordinate plane. In a move, Carina may move a pin to an adjacent lattice point at distance 1 away. What is the least number of moves that Carina can make in order for triangle $A B C$ to have area 2021?
|
The answer is 128 . Define the bounding box of triangle $A B C$ to be the smallest axis-parallel rectangle which contains all three of the vertices $A, B, C$.  ## Lemma The area of a triangle $A B C$ is at most half the area of the bounding box. So, suppose the bounding box is $A X Y Z$. Imagine fixing $C$ and varying $B$ along the perimeter entire rectangle. The area is a linear function of $B$, so the maximal area should be achieved when $B$ coincides with one of the vertices $\{A, X, Y, Z\}$. But obviously the area of $\triangle A B C$ is - exactly 0 if $B=A$, - at most half the bounding box if $B \in\{X, Z\}$ by one-half-base-height, - at most half the bounding box if $B=Y$, since $\triangle A B C$ is contained inside either $\triangle A Y Z$ or $\triangle A X Z$. Claim - If $n$ moves are made, the bounding box has area at most $(n / 2)^{2}$. (In other words, a bounding box of area $A$ requires at least $\lceil 2 \sqrt{A}\rceil$ moves.) This immediately implies $n \geq 128$, since the bounding box needs to have area at least $4042>63.5^{2}$. On the other hand, if we start all the pins at the point $(3,18)$ then we can reach the following three points in 128 moves: $$ \begin{aligned} & A=(0,0) \\ & B=(64,18) \\ & C=(3,64) \end{aligned} $$ and indeed triangle $A B C$ has area exactly 2021. Remark. In fact, it can be shown that to obtain an area of $n / 2$, the bounding-box bound of $\lceil 2 \sqrt{n}\rceil$ moves is best possible, i.e. there will in fact exist a triangle with area $n / 2$. However, since this was supposed to be a JMO4 problem, the committee made a choice to choose $n=4042$ so that contestants only needed to give a single concrete triangle rather than a general construction for all integers $n$.
|
128
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Carina has three pins, labeled $A, B$, and $C$, respectively, located at the origin of the coordinate plane. In a move, Carina may move a pin to an adjacent lattice point at distance 1 away. What is the least number of moves that Carina can make in order for triangle $A B C$ to have area 2021?
|
The answer is 128 . Define the bounding box of triangle $A B C$ to be the smallest axis-parallel rectangle which contains all three of the vertices $A, B, C$.  ## Lemma The area of a triangle $A B C$ is at most half the area of the bounding box. So, suppose the bounding box is $A X Y Z$. Imagine fixing $C$ and varying $B$ along the perimeter entire rectangle. The area is a linear function of $B$, so the maximal area should be achieved when $B$ coincides with one of the vertices $\{A, X, Y, Z\}$. But obviously the area of $\triangle A B C$ is - exactly 0 if $B=A$, - at most half the bounding box if $B \in\{X, Z\}$ by one-half-base-height, - at most half the bounding box if $B=Y$, since $\triangle A B C$ is contained inside either $\triangle A Y Z$ or $\triangle A X Z$. Claim - If $n$ moves are made, the bounding box has area at most $(n / 2)^{2}$. (In other words, a bounding box of area $A$ requires at least $\lceil 2 \sqrt{A}\rceil$ moves.) This immediately implies $n \geq 128$, since the bounding box needs to have area at least $4042>63.5^{2}$. On the other hand, if we start all the pins at the point $(3,18)$ then we can reach the following three points in 128 moves: $$ \begin{aligned} & A=(0,0) \\ & B=(64,18) \\ & C=(3,64) \end{aligned} $$ and indeed triangle $A B C$ has area exactly 2021. Remark. In fact, it can be shown that to obtain an area of $n / 2$, the bounding-box bound of $\lceil 2 \sqrt{n}\rceil$ moves is best possible, i.e. there will in fact exist a triangle with area $n / 2$. However, since this was supposed to be a JMO4 problem, the committee made a choice to choose $n=4042$ so that contestants only needed to give a single concrete triangle rather than a general construction for all integers $n$.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
625c503b-340f-52c8-9dac-0effc03701e5
| 605,527
|
A finite set $S$ of positive integers has the property that, for each $s \in S$, and each positive integer divisor $d$ of $s$, there exists a unique element $t \in S$ satisfying $\operatorname{gcd}(s, t)=d$. (The elements $s$ and $t$ could be equal.) Given this information, find all possible values for the number of elements of $S$.
|
The answer is that $|S|$ must be a power of 2 (including 1 ), or $|S|=0$ (a trivial case we do not discuss further). Construction. For any nonnegative integer $k$, a construction for $|S|=2^{k}$ is given by $$ S=\left\{\left(p_{1} \text { or } q_{1}\right) \times\left(p_{2} \text { or } q_{2}\right) \times \cdots \times\left(p_{k} \text { or } q_{k}\right)\right\} $$ for $2 k$ distinct primes $p_{1}, \ldots, p_{k}, q_{1}, \ldots, q_{k}$. 【 Converse. The main claim is as follows. Claim - In any valid set $S$, for any prime $p$ and $x \in S, \nu_{p}(x) \leq 1$. - On the one hand, by taking $x$ in the statement, we see $\frac{e}{e+1}$ of the elements of $S$ are divisible by $p$. - On the other hand, consider a $y \in S$ such that $\nu_{p}(y)=1$ which must exist (say if $\operatorname{gcd}(x, y)=p)$. Taking $y$ in the statement, we see $\frac{1}{2}$ of the elements of $S$ are divisible by $p$. So $e=1$, contradiction. Now since $|S|$ equals the number of divisors of any element of $S$, we are done.
|
2^k
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A finite set $S$ of positive integers has the property that, for each $s \in S$, and each positive integer divisor $d$ of $s$, there exists a unique element $t \in S$ satisfying $\operatorname{gcd}(s, t)=d$. (The elements $s$ and $t$ could be equal.) Given this information, find all possible values for the number of elements of $S$.
|
The answer is that $|S|$ must be a power of 2 (including 1 ), or $|S|=0$ (a trivial case we do not discuss further). Construction. For any nonnegative integer $k$, a construction for $|S|=2^{k}$ is given by $$ S=\left\{\left(p_{1} \text { or } q_{1}\right) \times\left(p_{2} \text { or } q_{2}\right) \times \cdots \times\left(p_{k} \text { or } q_{k}\right)\right\} $$ for $2 k$ distinct primes $p_{1}, \ldots, p_{k}, q_{1}, \ldots, q_{k}$. 【 Converse. The main claim is as follows. Claim - In any valid set $S$, for any prime $p$ and $x \in S, \nu_{p}(x) \leq 1$. - On the one hand, by taking $x$ in the statement, we see $\frac{e}{e+1}$ of the elements of $S$ are divisible by $p$. - On the other hand, consider a $y \in S$ such that $\nu_{p}(y)=1$ which must exist (say if $\operatorname{gcd}(x, y)=p)$. Taking $y$ in the statement, we see $\frac{1}{2}$ of the elements of $S$ are divisible by $p$. So $e=1$, contradiction. Now since $|S|$ equals the number of divisors of any element of $S$, we are done.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5ec4b7b3-bbd7-5e67-8c5c-e76080335e45
| 605,537
|
Consider an $n$-by- $n$ board of unit squares for some odd positive integer $n$. We say that a collection $C$ of identical dominoes is a maximal grid-aligned configuration on the board if $C$ consists of $\left(n^{2}-1\right) / 2$ dominoes where each domino covers exactly two neighboring squares and the dominoes don't overlap: $C$ then covers all but one square on the board. We are allowed to slide (but not rotate) a domino on the board to cover the uncovered square, resulting in a new maximal gridaligned configuration with another square uncovered. Let $k(C)$ be the number of distinct maximal grid-aligned configurations obtainable from $C$ by repeatedly sliding dominoes. Find the maximum possible value of $k(C)$ as a function of $n$.
|
The answer is that $$ k(C) \leq\left(\frac{n+1}{2}\right)^{2} $$ Remark (Comparison with USAMO version). In the USAMO version of the problem, students instead are asked to find all possible values of $k(C)$. The answer is $k(C) \in$ $\left\{1,2, \ldots,\left(\frac{n-1}{2}\right)^{2}\right\} \cup\left\{\left(\frac{n+1}{2}\right)^{2}\right\}$. Index the squares by coordinates $(x, y) \in\{1,2, \ldots, n\}^{2}$. We say a square is special if it is empty or it has the same parity in both coordinates as the empty square. Construct a directed graph $G=G(C)$ whose vertices are special squares as follows: for each domino on a special square $s$, we draw a directed edge from $s$ to the special square that domino points to, if any. (If the special square has both odd coordinates, all special squares have an outgoing edge except the empty cell. In the even-even case, some arrows may point "off the board" and not be drawn.)  Now focus specifically on the weakly connected component $T$ of $G$ (i.e. the connected component of the undirected version of $G$ ) containing the empty square. Claim - The graph $T$ has no cycles, even undirected. Hence, the undirected version of $T$ is tree. Notice that all the arrows along $T$ point towards the empty cell, and moving a domino corresponds to flipping an arrow. Therefore: Claim - $k(C)$ is exactly the number of vertices of $T$. This implies that $k(C) \leq\left(\frac{n+1}{2}\right)^{2}$, the total number of vertices of $G$ (this could only occur if the special squares are odd-odd, not even-even). Equality is achieved as long as $T$ is a spanning tree; one example of a way to achieve this is using the snake configuration below. 
|
\left(\frac{n+1}{2}\right)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider an $n$-by- $n$ board of unit squares for some odd positive integer $n$. We say that a collection $C$ of identical dominoes is a maximal grid-aligned configuration on the board if $C$ consists of $\left(n^{2}-1\right) / 2$ dominoes where each domino covers exactly two neighboring squares and the dominoes don't overlap: $C$ then covers all but one square on the board. We are allowed to slide (but not rotate) a domino on the board to cover the uncovered square, resulting in a new maximal gridaligned configuration with another square uncovered. Let $k(C)$ be the number of distinct maximal grid-aligned configurations obtainable from $C$ by repeatedly sliding dominoes. Find the maximum possible value of $k(C)$ as a function of $n$.
|
The answer is that $$ k(C) \leq\left(\frac{n+1}{2}\right)^{2} $$ Remark (Comparison with USAMO version). In the USAMO version of the problem, students instead are asked to find all possible values of $k(C)$. The answer is $k(C) \in$ $\left\{1,2, \ldots,\left(\frac{n-1}{2}\right)^{2}\right\} \cup\left\{\left(\frac{n+1}{2}\right)^{2}\right\}$. Index the squares by coordinates $(x, y) \in\{1,2, \ldots, n\}^{2}$. We say a square is special if it is empty or it has the same parity in both coordinates as the empty square. Construct a directed graph $G=G(C)$ whose vertices are special squares as follows: for each domino on a special square $s$, we draw a directed edge from $s$ to the special square that domino points to, if any. (If the special square has both odd coordinates, all special squares have an outgoing edge except the empty cell. In the even-even case, some arrows may point "off the board" and not be drawn.)  Now focus specifically on the weakly connected component $T$ of $G$ (i.e. the connected component of the undirected version of $G$ ) containing the empty square. Claim - The graph $T$ has no cycles, even undirected. Hence, the undirected version of $T$ is tree. Notice that all the arrows along $T$ point towards the empty cell, and moving a domino corresponds to flipping an arrow. Therefore: Claim - $k(C)$ is exactly the number of vertices of $T$. This implies that $k(C) \leq\left(\frac{n+1}{2}\right)^{2}$, the total number of vertices of $G$ (this could only occur if the special squares are odd-odd, not even-even). Equality is achieved as long as $T$ is a spanning tree; one example of a way to achieve this is using the snake configuration below. 
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
7ff9911c-94e5-561d-90ce-192b47f1015c
| 605,758
|
Two players, Blake and Ruby, play the following game on an infinite grid of unit squares, all initially colored white. The players take turns starting with Blake. On Blake's turn, Blake selects one white unit square and colors it blue. On Ruby's turn, Ruby selects two white unit squares and colors them red. The players alternate until Blake decides to end the game. At this point, Blake gets a score, given by the number of unit squares in the largest (in terms of area) simple polygon containing only blue unit squares. What is the largest score Blake can guarantee?
|
The answer is 4 squares. ब Algorithm for Blake to obtain at least 4 squares. We simply let Blake start with any cell blue, then always draw adjacent to a previously drawn blue cell until this is no longer possible. Note that for $n \leq 3$, any connected region of $n$ blue cells has more than $2 n$ liberties (non-blue cells adjacent to a blue cell); up to translation, rotation, and reflection, all the cases are shown in the figure below with liberties being denoted by circles.  So as long as $n \leq 3$, it's impossible that Ruby has blocked every liberty, since Ruby has colored exactly $2 n$ cells red. Therefore, this algorithm could only terminate once $n \geq 4$. \ Algorithm for Ruby to prevent more than 4 squares. Divide the entire grid into $2 \times 2$ squares, which we call windows. Any time Blake makes a move in a cell $c$, let Ruby mark any orthogonal neighbors of $c$ in its window; then place any leftover red cells arbitrarily. Claim - It's impossible for any window to contain two orthogonally adjacent blue cells. We show this gives the upper bound of 4 squares. Consider a blue cell $w$, and assume WLOG it is in the southeast corner of a window. Label squares $x, y, z$ as shown below.  Note that by construction, the blue polygon cannot leave the square $\{w, x, y, z\}$, since whenever one of these four cells is blue, its neighbours outside that square are guaranteed to be red. This implies the bound. Remark (For Tetris fans). Here is a comedic alternative finish after proving the claim. Consider the possible tetrominoes (using the notation of https://en.wikipedia.org/wiki/ Tetromino\#One-sided_tetrominoes). We claim that only the square (0) is obtainable; as - T, J/L, and I all have three cells in a row, so they can't occur; - S and Z can't occur either; if the bottom row of an S crossed a window boundary, then the top row doesn't for example. Moreover, the only way a blue 0 could be obtained is if each of it cells is in a different window. In that case, no additional blue cells can be added: it's fully surrounded by red. Finally, for any $k$-omino with $k>4$, one can find a tetromino as a subset. (Proof: take the orthogonal adjacency graph of the $k$-omino, choose a spanning tree, and delete leaves from the tree until there are only four vertices left.) As written, this strategy does not work. The reason is that one can end up in the following situation (imagine the blue square in the center is played first; moves for Ruby are drawn as red X's):  In order to prevent Blake from winning, Ruby would need to begin playing moves not adjacent to Blake's most recent move. It is even more difficult to come up with a solution involving playing on just "some" two neighbors of recently added blue squares without the "prefer north and west" idea.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Two players, Blake and Ruby, play the following game on an infinite grid of unit squares, all initially colored white. The players take turns starting with Blake. On Blake's turn, Blake selects one white unit square and colors it blue. On Ruby's turn, Ruby selects two white unit squares and colors them red. The players alternate until Blake decides to end the game. At this point, Blake gets a score, given by the number of unit squares in the largest (in terms of area) simple polygon containing only blue unit squares. What is the largest score Blake can guarantee?
|
The answer is 4 squares. ब Algorithm for Blake to obtain at least 4 squares. We simply let Blake start with any cell blue, then always draw adjacent to a previously drawn blue cell until this is no longer possible. Note that for $n \leq 3$, any connected region of $n$ blue cells has more than $2 n$ liberties (non-blue cells adjacent to a blue cell); up to translation, rotation, and reflection, all the cases are shown in the figure below with liberties being denoted by circles.  So as long as $n \leq 3$, it's impossible that Ruby has blocked every liberty, since Ruby has colored exactly $2 n$ cells red. Therefore, this algorithm could only terminate once $n \geq 4$. \ Algorithm for Ruby to prevent more than 4 squares. Divide the entire grid into $2 \times 2$ squares, which we call windows. Any time Blake makes a move in a cell $c$, let Ruby mark any orthogonal neighbors of $c$ in its window; then place any leftover red cells arbitrarily. Claim - It's impossible for any window to contain two orthogonally adjacent blue cells. We show this gives the upper bound of 4 squares. Consider a blue cell $w$, and assume WLOG it is in the southeast corner of a window. Label squares $x, y, z$ as shown below.  Note that by construction, the blue polygon cannot leave the square $\{w, x, y, z\}$, since whenever one of these four cells is blue, its neighbours outside that square are guaranteed to be red. This implies the bound. Remark (For Tetris fans). Here is a comedic alternative finish after proving the claim. Consider the possible tetrominoes (using the notation of https://en.wikipedia.org/wiki/ Tetromino\#One-sided_tetrominoes). We claim that only the square (0) is obtainable; as - T, J/L, and I all have three cells in a row, so they can't occur; - S and Z can't occur either; if the bottom row of an S crossed a window boundary, then the top row doesn't for example. Moreover, the only way a blue 0 could be obtained is if each of it cells is in a different window. In that case, no additional blue cells can be added: it's fully surrounded by red. Finally, for any $k$-omino with $k>4$, one can find a tetromino as a subset. (Proof: take the orthogonal adjacency graph of the $k$-omino, choose a spanning tree, and delete leaves from the tree until there are only four vertices left.) As written, this strategy does not work. The reason is that one can end up in the following situation (imagine the blue square in the center is played first; moves for Ruby are drawn as red X's):  In order to prevent Blake from winning, Ruby would need to begin playing moves not adjacent to Blake's most recent move. It is even more difficult to come up with a solution involving playing on just "some" two neighbors of recently added blue squares without the "prefer north and west" idea.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2023-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9677edbe-d110-5ea8-bffe-3033691af18a
| 605,767
|
Let $n \geq 3$ be an integer. Rowan and Colin play a game on an $n \times n$ grid of squares, where each square is colored either red or blue. Rowan is allowed to permute the rows of the grid and Colin is allowed to permute the columns. A grid coloring is orderly if: - no matter how Rowan permutes the rows of the coloring, Colin can then permute the columns to restore the original grid coloring; and - no matter how Colin permutes the columns of the coloring, Rowan can then permute the rows to restore the original grid coloring. In terms of $n$, how many orderly colorings are there?
|
The answer is $2 n!+2$. In fact, we can describe all the orderly colorings as follows: - The all-blue coloring. - The all-red coloring. - Each of the $n$ ! colorings where every row/column has exactly one red cell. - Each of the $n$ ! colorings where every row/column has exactly one blue cell. These obviously work; we turn our attention to proving these are the only ones. For the other direction, fix a orderly coloring $\mathcal{A}$. Consider any particular column $C$ in $\mathcal{A}$ and let $m$ denote the number of red cells that $C$ has. Any row permutation (say $\sigma$ ) that Rowan chooses will transform $C$ into some column $\sigma(C)$, and our assumption requires $\sigma(C)$ has to appear somewhere in the original assignment $\mathcal{A}$. An example for $n=7, m=2$, and a random $\sigma$ is shown below.  On the other hand, the number of possible patterns of $\sigma(C)$ is easily seen to be exactly ( $\binom{n}{m}$ - and they must all appear. In particular, if $m \notin\{0,1, n-1, n\}$, then we immediately get a contradiction because $\mathcal{A}$ would need too many columns (there are only $n$ columns in $\mathcal{A}$, which is fewer than $\binom{n}{m}$ ). Moreover, if either $m=1$ or $m=n-1$, these columns are all the columns of $\mathcal{A}$; these lead to the $2 n$ ! main cases we found before. The only remaining case is when $m \in\{0, n\}$ for every column, i.e. every column is monochromatic. It's easy to see in that case the columns must all be the same color.
|
2 n! + 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geq 3$ be an integer. Rowan and Colin play a game on an $n \times n$ grid of squares, where each square is colored either red or blue. Rowan is allowed to permute the rows of the grid and Colin is allowed to permute the columns. A grid coloring is orderly if: - no matter how Rowan permutes the rows of the coloring, Colin can then permute the columns to restore the original grid coloring; and - no matter how Colin permutes the columns of the coloring, Rowan can then permute the rows to restore the original grid coloring. In terms of $n$, how many orderly colorings are there?
|
The answer is $2 n!+2$. In fact, we can describe all the orderly colorings as follows: - The all-blue coloring. - The all-red coloring. - Each of the $n$ ! colorings where every row/column has exactly one red cell. - Each of the $n$ ! colorings where every row/column has exactly one blue cell. These obviously work; we turn our attention to proving these are the only ones. For the other direction, fix a orderly coloring $\mathcal{A}$. Consider any particular column $C$ in $\mathcal{A}$ and let $m$ denote the number of red cells that $C$ has. Any row permutation (say $\sigma$ ) that Rowan chooses will transform $C$ into some column $\sigma(C)$, and our assumption requires $\sigma(C)$ has to appear somewhere in the original assignment $\mathcal{A}$. An example for $n=7, m=2$, and a random $\sigma$ is shown below.  On the other hand, the number of possible patterns of $\sigma(C)$ is easily seen to be exactly ( $\binom{n}{m}$ - and they must all appear. In particular, if $m \notin\{0,1, n-1, n\}$, then we immediately get a contradiction because $\mathcal{A}$ would need too many columns (there are only $n$ columns in $\mathcal{A}$, which is fewer than $\binom{n}{m}$ ). Moreover, if either $m=1$ or $m=n-1$, these columns are all the columns of $\mathcal{A}$; these lead to the $2 n$ ! main cases we found before. The only remaining case is when $m \in\{0, n\}$ for every column, i.e. every column is monochromatic. It's easy to see in that case the columns must all be the same color.
|
{
"resource_path": "USAJMO/segmented/en-JMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c2b44838-1e7d-5288-862a-3718a9fc4fb7
| 605,883
|
Find the smallest positive integer $n$ such that if $n$ squares of a $1000 \times 1000$ chessboard are colored, then there will exist three colored squares whose centers form a right triangle with sides parallel to the edges of the board.
|
The answer is $n=1999$. For a construction with $n=1998$, take a punctured L as illustrated below (with 1000 replaced by 4): $$ \left[\begin{array}{llll} 1 & & & \\ 1 & & & \\ 1 & & & \\ & 1 & 1 & 1 \end{array}\right] . $$ We now show that if there is no right triangle, there are at most 1998 tokens (colored squares). In every column with more than two tokens, we have token emit a bidirectional horizontal death ray (laser) covering its entire row: the hypothesis is that the death ray won't hit any other tokens.  Assume there are $n$ tokens and that $n>1000$. Then obviously some column has more than two tokens, so at most 999 tokens don't emit a death ray (namely, any token in its own column). Thus there are at least $n-999$ death rays. On the other hand, we can have at most 999 death rays total (since it would not be okay for the whole board to have death rays, as some row should have more than two tokens). Therefore, $n \leq 999+999=1998$ as desired.
|
1999
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the smallest positive integer $n$ such that if $n$ squares of a $1000 \times 1000$ chessboard are colored, then there will exist three colored squares whose centers form a right triangle with sides parallel to the edges of the board.
|
The answer is $n=1999$. For a construction with $n=1998$, take a punctured L as illustrated below (with 1000 replaced by 4): $$ \left[\begin{array}{llll} 1 & & & \\ 1 & & & \\ 1 & & & \\ & 1 & 1 & 1 \end{array}\right] . $$ We now show that if there is no right triangle, there are at most 1998 tokens (colored squares). In every column with more than two tokens, we have token emit a bidirectional horizontal death ray (laser) covering its entire row: the hypothesis is that the death ray won't hit any other tokens.  Assume there are $n$ tokens and that $n>1000$. Then obviously some column has more than two tokens, so at most 999 tokens don't emit a death ray (namely, any token in its own column). Thus there are at least $n-999$ death rays. On the other hand, we can have at most 999 death rays total (since it would not be okay for the whole board to have death rays, as some row should have more than two tokens). Therefore, $n \leq 999+999=1998$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
fd6f3e48-0662-5d4c-bcdb-0434dcbc44ad
| 46,117
|
Legs $L_{1}, L_{2}, L_{3}, L_{4}$ of a square table each have length $n$, where $n$ is a positive integer. For how many ordered 4 -tuples ( $k_{1}, k_{2}, k_{3}, k_{4}$ ) of nonnegative integers can we cut a piece of length $k_{i}$ from the end of leg $L_{i}$ and still have a stable table? (The table is stable if it can be placed so that all four of the leg ends touch the floor. Note that a cut leg of length 0 is permitted.)
|
Flip the table upside-down so that that the table's surface rests on the floor. Then, we see that we want the truncated legs to have endpoints $A, B, C, D$ which are coplanar (say). Claim - This occurs if and only if $A B C D$ is a parallelogram. In still other words, we are counting the number of solutions to $$ \left(n-k_{1}\right)+\left(n-k_{3}\right)=\left(n-k_{2}\right)+\left(n-k_{4}\right) \Longleftrightarrow k_{1}+k_{3}=k_{2}+k_{4} . $$ Define $$ a_{r}=\#\{(a, b) \mid a+b=r, 0 \leq a, b \leq n\} $$ $$ \begin{aligned} \sum_{r=0}^{2 n} a_{r}^{2} & =1^{2}+2^{2}+\cdots+n^{2}+(n+1)^{2}+n^{2}+\cdots+1^{2} \\ & =\frac{1}{3}(n+1)\left(2 n^{2}+4 n+3\right) \end{aligned} $$
|
\frac{1}{3}(n+1)\left(2 n^{2}+4 n+3\right)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Legs $L_{1}, L_{2}, L_{3}, L_{4}$ of a square table each have length $n$, where $n$ is a positive integer. For how many ordered 4 -tuples ( $k_{1}, k_{2}, k_{3}, k_{4}$ ) of nonnegative integers can we cut a piece of length $k_{i}$ from the end of leg $L_{i}$ and still have a stable table? (The table is stable if it can be placed so that all four of the leg ends touch the floor. Note that a cut leg of length 0 is permitted.)
|
Flip the table upside-down so that that the table's surface rests on the floor. Then, we see that we want the truncated legs to have endpoints $A, B, C, D$ which are coplanar (say). Claim - This occurs if and only if $A B C D$ is a parallelogram. In still other words, we are counting the number of solutions to $$ \left(n-k_{1}\right)+\left(n-k_{3}\right)=\left(n-k_{2}\right)+\left(n-k_{4}\right) \Longleftrightarrow k_{1}+k_{3}=k_{2}+k_{4} . $$ Define $$ a_{r}=\#\{(a, b) \mid a+b=r, 0 \leq a, b \leq n\} $$ $$ \begin{aligned} \sum_{r=0}^{2 n} a_{r}^{2} & =1^{2}+2^{2}+\cdots+n^{2}+(n+1)^{2}+n^{2}+\cdots+1^{2} \\ & =\frac{1}{3}(n+1)\left(2 n^{2}+4 n+3\right) \end{aligned} $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2005-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6ca03ab9-9693-538c-bae2-b86c66024285
| 606,398
|
There are 68 ordered pairs (not necessarily distinct) of nonzero integers on a blackboard. It's known that for no integer $k$ does both $(k, k)$ and $(-k,-k)$ appear. A student erases some of the 136 integers such that no two erased integers have sum zero, and scores one point for each ordered pair with at least one erased integer. What is the maximum possible score the student can guarantee?
|
The answer is 43. The structure of this problem is better understood as follows: we construct a multigraph whose vertices are the entries, and the edges are the 68 ordered pairs on the blackboard. To be precise, construct a multigraph $G$ with vertices $a_{1}, b_{1}, \ldots, a_{n}, b_{n}$, with $a_{i}=-b_{i}$ for each $i$. The ordered pairs then correspond to 68 edges in $G$, with self-loops allowed (WLOG) only for vertices $a_{i}$. The student may then choose one of $\left\{a_{i}, b_{i}\right\}$ for each $i$ and wishes to maximize the number of edges adjacent to the set of chosen vertices.  First we use the probabilistic method to show $N \geq 43$. We select the real number $p=\frac{\sqrt{5}-1}{2} \approx 0.618$ satisfying $p=1-p^{2}$. For each $i$ we then select $a_{i}$ with probability $p$ and $b_{i}$ with probability $1-p$. Then - Every self-loop $\left(a_{i}, a_{i}\right)$ is chosen with probability $p$. - Any edge $\left(b_{i}, b_{j}\right)$ is chosen with probability $1-p^{2}$. All other edges are selected with probability at least $p$, so in expectation we have $68 p \approx 42.024$ edges scored. Hence $N \geq 43$. For a construction showing 43 is optimal, we let $n=8$, and put five self-loops on each $a_{i}$, while taking a single $K_{8}$ on the $b_{i}$ 's. The score achieved for selecting $m$ of the $a_{i}$ 's and $8-m$ of the $b_{i}$ 's is $$ 5 m+\left(\binom{8}{2}-\binom{m}{2}\right) \leq 43 $$ with equality when either $m=5$ and $m=6$. Remark (Colin Tang). Here is one possible motivation for finding the construction. In equality case we probably want all the edges to either be $a_{i}$ loops or $b_{i} b_{j}$ edges. Now if $b_{i}$ and $b_{j}$ are not joined by an edge, one can "merge them together", also combining the corresponding $a_{i}$ 's, to get another multigraph with 68 edges whose optimal score is at most the original ones. So by using this smoothing algorithm, we can reduce to a situation where the $b_{i}$ and $b_{j}$ are all connected to each other. It's not unnatural to assume it's a clique then, at which point fiddling with parameters gives the construction. Also, there is a construction for $\lceil 2 / 3 n\rceil$ which is not too difficult to find, and applying this smoothing operation to this construction could suggest a clique of at least 8 vertices too. Remark (David Lee). One could consider changing the probability $p(n)$ to be a function of the number $n$ of non-loops (hence there are $68-n$ loops); we would then have $$ \mathbb{E}[\text { points }] \geq(68-n) p(n)+n\left(1-p(n)^{2}\right) $$ The optimal value of $p(n)$ is then $$ p(n)= \begin{cases}\frac{68-n}{2 n}=\frac{34}{n}-\frac{1}{2} & n \geq 23 \\ 1 & n<22\end{cases} $$ For $n>23$ we then have $$ \begin{aligned} E(n)= & (68-n)\left(\frac{34}{n}-\frac{1}{2}\right)+n\left(1-\left(\frac{34}{n}-\frac{1}{2}\right)^{2}\right) \\ & =\frac{5 n}{4}+\frac{34^{2}}{n}-34 \end{aligned} $$ which has its worst case at around $5 n^{2}=68^{2}$, so at $n=30$ and $n=31$. Indeed, one can find $$ \begin{aligned} & E(30)=42.033 \\ & E(31)=42.040 \end{aligned} $$ This gives another way to get the lower bound 43, and gives a hint about approximately how many non-loops one would want in order to achieve such a bound.
|
43
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 68 ordered pairs (not necessarily distinct) of nonzero integers on a blackboard. It's known that for no integer $k$ does both $(k, k)$ and $(-k,-k)$ appear. A student erases some of the 136 integers such that no two erased integers have sum zero, and scores one point for each ordered pair with at least one erased integer. What is the maximum possible score the student can guarantee?
|
The answer is 43. The structure of this problem is better understood as follows: we construct a multigraph whose vertices are the entries, and the edges are the 68 ordered pairs on the blackboard. To be precise, construct a multigraph $G$ with vertices $a_{1}, b_{1}, \ldots, a_{n}, b_{n}$, with $a_{i}=-b_{i}$ for each $i$. The ordered pairs then correspond to 68 edges in $G$, with self-loops allowed (WLOG) only for vertices $a_{i}$. The student may then choose one of $\left\{a_{i}, b_{i}\right\}$ for each $i$ and wishes to maximize the number of edges adjacent to the set of chosen vertices.  First we use the probabilistic method to show $N \geq 43$. We select the real number $p=\frac{\sqrt{5}-1}{2} \approx 0.618$ satisfying $p=1-p^{2}$. For each $i$ we then select $a_{i}$ with probability $p$ and $b_{i}$ with probability $1-p$. Then - Every self-loop $\left(a_{i}, a_{i}\right)$ is chosen with probability $p$. - Any edge $\left(b_{i}, b_{j}\right)$ is chosen with probability $1-p^{2}$. All other edges are selected with probability at least $p$, so in expectation we have $68 p \approx 42.024$ edges scored. Hence $N \geq 43$. For a construction showing 43 is optimal, we let $n=8$, and put five self-loops on each $a_{i}$, while taking a single $K_{8}$ on the $b_{i}$ 's. The score achieved for selecting $m$ of the $a_{i}$ 's and $8-m$ of the $b_{i}$ 's is $$ 5 m+\left(\binom{8}{2}-\binom{m}{2}\right) \leq 43 $$ with equality when either $m=5$ and $m=6$. Remark (Colin Tang). Here is one possible motivation for finding the construction. In equality case we probably want all the edges to either be $a_{i}$ loops or $b_{i} b_{j}$ edges. Now if $b_{i}$ and $b_{j}$ are not joined by an edge, one can "merge them together", also combining the corresponding $a_{i}$ 's, to get another multigraph with 68 edges whose optimal score is at most the original ones. So by using this smoothing algorithm, we can reduce to a situation where the $b_{i}$ and $b_{j}$ are all connected to each other. It's not unnatural to assume it's a clique then, at which point fiddling with parameters gives the construction. Also, there is a construction for $\lceil 2 / 3 n\rceil$ which is not too difficult to find, and applying this smoothing operation to this construction could suggest a clique of at least 8 vertices too. Remark (David Lee). One could consider changing the probability $p(n)$ to be a function of the number $n$ of non-loops (hence there are $68-n$ loops); we would then have $$ \mathbb{E}[\text { points }] \geq(68-n) p(n)+n\left(1-p(n)^{2}\right) $$ The optimal value of $p(n)$ is then $$ p(n)= \begin{cases}\frac{68-n}{2 n}=\frac{34}{n}-\frac{1}{2} & n \geq 23 \\ 1 & n<22\end{cases} $$ For $n>23$ we then have $$ \begin{aligned} E(n)= & (68-n)\left(\frac{34}{n}-\frac{1}{2}\right)+n\left(1-\left(\frac{34}{n}-\frac{1}{2}\right)^{2}\right) \\ & =\frac{5 n}{4}+\frac{34^{2}}{n}-34 \end{aligned} $$ which has its worst case at around $5 n^{2}=68^{2}$, so at $n=30$ and $n=31$. Indeed, one can find $$ \begin{aligned} & E(30)=42.033 \\ & E(31)=42.040 \end{aligned} $$ This gives another way to get the lower bound 43, and gives a hint about approximately how many non-loops one would want in order to achieve such a bound.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5b086146-565c-5a13-a069-abe62ffbb729
| 248,609
|
Let $a, b, c, d$ be real numbers such that $b-d \geq 5$ and all zeros $x_{1}, x_{2}, x_{3}$, and $x_{4}$ of the polynomial $P(x)=x^{4}+a x^{3}+b x^{2}+c x+d$ are real. Find the smallest value the product $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)\left(x_{3}^{2}+1\right)\left(x_{4}^{2}+1\right)$ can take.
|
The answer is 16 . This can be achieved by taking $x_{1}=x_{2}=x_{3}=x_{4}=1$, whence the product is $2^{4}=16$, and $b-d=5$. We now show the quantity is always at least 16. We prove: Claim - We always have $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)\left(x_{3}^{2}+1\right)\left(x_{4}^{2}+1\right)=(b-d-1)^{2}+(a-c)^{2}$. $$ \prod_{j=1}^{4}\left(x_{j}^{2}+1\right)=\prod_{j=1}^{4}\left(x_{j}-i\right)\left(x_{j}+i\right)=P(i) P(-i)=|P(i)|^{2} $$ Since $P(i)=(-1+b-d)+(c-a) i$, the claim follows. Since $b-d-1 \geq 4$, we get the desired lower bound of $4^{2}+0^{2}=16$.
|
16
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d$ be real numbers such that $b-d \geq 5$ and all zeros $x_{1}, x_{2}, x_{3}$, and $x_{4}$ of the polynomial $P(x)=x^{4}+a x^{3}+b x^{2}+c x+d$ are real. Find the smallest value the product $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)\left(x_{3}^{2}+1\right)\left(x_{4}^{2}+1\right)$ can take.
|
The answer is 16 . This can be achieved by taking $x_{1}=x_{2}=x_{3}=x_{4}=1$, whence the product is $2^{4}=16$, and $b-d=5$. We now show the quantity is always at least 16. We prove: Claim - We always have $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)\left(x_{3}^{2}+1\right)\left(x_{4}^{2}+1\right)=(b-d-1)^{2}+(a-c)^{2}$. $$ \prod_{j=1}^{4}\left(x_{j}^{2}+1\right)=\prod_{j=1}^{4}\left(x_{j}-i\right)\left(x_{j}+i\right)=P(i) P(-i)=|P(i)|^{2} $$ Since $P(i)=(-1+b-d)+(c-a) i$, the claim follows. Since $b-d-1 \geq 4$, we get the desired lower bound of $4^{2}+0^{2}=16$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
dad93604-3591-5292-9035-00a0af49bd14
| 248,758
|
Let $S=\{1,2, \ldots, n\}$, where $n \geq 1$. Each of the $2^{n}$ subsets of $S$ is to be colored red or blue. (The subset itself is assigned a color and not its individual elements.) For any set $T \subseteq S$, we then write $f(T)$ for the number of subsets of $T$ that are blue. Determine the number of colorings that satisfy the following condition: for any subsets $T_{1}$ and $T_{2}$ of $S$, $$ f\left(T_{1}\right) f\left(T_{2}\right)=f\left(T_{1} \cup T_{2}\right) f\left(T_{1} \cap T_{2}\right) $$
|
For an $n$-coloring $\mathcal{C}$ (by which we mean a coloring of the subsets of $\{1, \ldots, n\}$ ), define the support of $\mathcal{C}$ as $$ \operatorname{supp}(\mathcal{C})=\{T \mid f(T) \neq 0\} $$ Call a coloring nontrivial if $\operatorname{supp}(\mathcal{C}) \neq \varnothing$ (equivalently, the coloring is not all red). In that case, notice that - the support is closed under unions and intersections: since if $f\left(T_{1}\right) f\left(T_{2}\right) \neq 0$ then necessarily both $f\left(T_{1} \cap T_{2}\right)$ and $f\left(T_{1} \cup T_{2}\right)$ are nonzero; and - the support is obviously upwards closed. Thus, the support must take the form $$ \operatorname{supp}(\mathcal{C})=[X, S] \stackrel{\text { def }}{=}\{T \mid X \subseteq T \subseteq S\} $$ for some set $X$ (for example by letting $X$ be the minimal (by size) element of the support). Say $\mathcal{C}$ has full support if $X=\varnothing$ (equivalently, $\varnothing$ is blue). ## Lemma For a given $n$ and $B \subseteq\{1, \ldots, n\}$, there is exactly one $n$-coloring with full support in which the singletons colored blue are exactly those in $B$. Therefore there are exactly $2^{n} n$-colorings with full support. $$ f(T)=2^{|T \cap B|} $$ which satisfies the condition by Inclusion-Exclusion. To see this extension is unique, note that $f(\{b\})$ is determined for each $b$ and we can then determine $f(T)$ inductively on $|T|$; hence there is at most one way to complete a coloring of the singletons, which completes the proof. For a general nontrivial $n$-coloring $\mathcal{C}$, note that if $\operatorname{supp}(\mathcal{C})=[X, S]$, then we can think of it as an $(n-|X|)$-coloring with full support. For $|X|=k$, there are $\binom{n}{k}$ possible choices of $X \subseteq S$. Adding back in the trivial coloring, the final answer is $$ 1+\sum_{k=0}^{n}\binom{n}{k} 2^{k}=1+3^{n} $$ Remark. To be more explicit, the possible nontrivial colorings are exactly described by specifying two sets $X$ and $Y$ with $X \subseteq Y$, and coloring blue only the sets $T$ with $X \subseteq T \subseteq Y$. In particular, one deduces that in a working coloring, $f(T)$ is always either zero or a power of two. If one manages to notice this while working on the problem, it is quite helpful for motivating the solution, as it leads one to suspect that the working colorings have good structure.
|
1+3^{n}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S=\{1,2, \ldots, n\}$, where $n \geq 1$. Each of the $2^{n}$ subsets of $S$ is to be colored red or blue. (The subset itself is assigned a color and not its individual elements.) For any set $T \subseteq S$, we then write $f(T)$ for the number of subsets of $T$ that are blue. Determine the number of colorings that satisfy the following condition: for any subsets $T_{1}$ and $T_{2}$ of $S$, $$ f\left(T_{1}\right) f\left(T_{2}\right)=f\left(T_{1} \cup T_{2}\right) f\left(T_{1} \cap T_{2}\right) $$
|
For an $n$-coloring $\mathcal{C}$ (by which we mean a coloring of the subsets of $\{1, \ldots, n\}$ ), define the support of $\mathcal{C}$ as $$ \operatorname{supp}(\mathcal{C})=\{T \mid f(T) \neq 0\} $$ Call a coloring nontrivial if $\operatorname{supp}(\mathcal{C}) \neq \varnothing$ (equivalently, the coloring is not all red). In that case, notice that - the support is closed under unions and intersections: since if $f\left(T_{1}\right) f\left(T_{2}\right) \neq 0$ then necessarily both $f\left(T_{1} \cap T_{2}\right)$ and $f\left(T_{1} \cup T_{2}\right)$ are nonzero; and - the support is obviously upwards closed. Thus, the support must take the form $$ \operatorname{supp}(\mathcal{C})=[X, S] \stackrel{\text { def }}{=}\{T \mid X \subseteq T \subseteq S\} $$ for some set $X$ (for example by letting $X$ be the minimal (by size) element of the support). Say $\mathcal{C}$ has full support if $X=\varnothing$ (equivalently, $\varnothing$ is blue). ## Lemma For a given $n$ and $B \subseteq\{1, \ldots, n\}$, there is exactly one $n$-coloring with full support in which the singletons colored blue are exactly those in $B$. Therefore there are exactly $2^{n} n$-colorings with full support. $$ f(T)=2^{|T \cap B|} $$ which satisfies the condition by Inclusion-Exclusion. To see this extension is unique, note that $f(\{b\})$ is determined for each $b$ and we can then determine $f(T)$ inductively on $|T|$; hence there is at most one way to complete a coloring of the singletons, which completes the proof. For a general nontrivial $n$-coloring $\mathcal{C}$, note that if $\operatorname{supp}(\mathcal{C})=[X, S]$, then we can think of it as an $(n-|X|)$-coloring with full support. For $|X|=k$, there are $\binom{n}{k}$ possible choices of $X \subseteq S$. Adding back in the trivial coloring, the final answer is $$ 1+\sum_{k=0}^{n}\binom{n}{k} 2^{k}=1+3^{n} $$ Remark. To be more explicit, the possible nontrivial colorings are exactly described by specifying two sets $X$ and $Y$ with $X \subseteq Y$, and coloring blue only the sets $T$ with $X \subseteq T \subseteq Y$. In particular, one deduces that in a working coloring, $f(T)$ is always either zero or a power of two. If one manages to notice this while working on the problem, it is quite helpful for motivating the solution, as it leads one to suspect that the working colorings have good structure.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
b3b8d6a0-fc50-5f96-9aed-719e2e1592e4
| 605,239
|
Find the minimum possible value of $$ \frac{a}{b^{3}+4}+\frac{b}{c^{3}+4}+\frac{c}{d^{3}+4}+\frac{d}{a^{3}+4} $$ given that $a, b, c, d$ are nonnegative real numbers such that $a+b+c+d=4$.
|
The minimum $\frac{2}{3}$ is achieved at $(a, b, c, d)=(2,2,0,0)$ and cyclic permutations. The problem is an application of the tangent line trick: we observe the miraculous identity $$ \frac{1}{b^{3}+4} \geq \frac{1}{4}-\frac{b}{12} $$ since $12-(3-b)\left(b^{3}+4\right)=b(b+1)(b-2)^{2} \geq 0$. Moreover, $$ a b+b c+c d+d a=(a+c)(b+d) \leq\left(\frac{(a+c)+(b+d)}{2}\right)^{2}=4 $$ Thus $$ \sum_{\mathrm{cyc}} \frac{a}{b^{3}+4} \geq \frac{a+b+c+d}{4}-\frac{a b+b c+c d+d a}{12} \geq 1-\frac{1}{3}=\frac{2}{3} $$ Remark. The main interesting bit is the equality at $(a, b, c, d)=(2,2,0,0)$. This is the main motivation for trying tangent line trick, since a lower bound of the form $\sum a(1-\lambda b)$ preserves the unusual equality case above. Thus one takes the tangent at $b=2$ which miraculously passes through the point $(0,1 / 4)$ as well.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the minimum possible value of $$ \frac{a}{b^{3}+4}+\frac{b}{c^{3}+4}+\frac{c}{d^{3}+4}+\frac{d}{a^{3}+4} $$ given that $a, b, c, d$ are nonnegative real numbers such that $a+b+c+d=4$.
|
The minimum $\frac{2}{3}$ is achieved at $(a, b, c, d)=(2,2,0,0)$ and cyclic permutations. The problem is an application of the tangent line trick: we observe the miraculous identity $$ \frac{1}{b^{3}+4} \geq \frac{1}{4}-\frac{b}{12} $$ since $12-(3-b)\left(b^{3}+4\right)=b(b+1)(b-2)^{2} \geq 0$. Moreover, $$ a b+b c+c d+d a=(a+c)(b+d) \leq\left(\frac{(a+c)+(b+d)}{2}\right)^{2}=4 $$ Thus $$ \sum_{\mathrm{cyc}} \frac{a}{b^{3}+4} \geq \frac{a+b+c+d}{4}-\frac{a b+b c+c d+d a}{12} \geq 1-\frac{1}{3}=\frac{2}{3} $$ Remark. The main interesting bit is the equality at $(a, b, c, d)=(2,2,0,0)$. This is the main motivation for trying tangent line trick, since a lower bound of the form $\sum a(1-\lambda b)$ preserves the unusual equality case above. Thus one takes the tangent at $b=2$ which miraculously passes through the point $(0,1 / 4)$ as well.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ab2ed31-25d7-5e89-8c9e-abcd9274e053
| 605,465
|
An empty $2020 \times 2020 \times 2020$ cube is given, and a $2020 \times 2020$ grid of square unit cells is drawn on each of its six faces. A beam is a $1 \times 1 \times 2020$ rectangular prism. Several beams are placed inside the cube subject to the following conditions: - The two $1 \times 1$ faces of each beam coincide with unit cells lying on opposite faces of the cube. (Hence, there are $3 \cdot 2020^{2}$ possible positions for a beam.) - No two beams have intersecting interiors. - The interiors of each of the four $1 \times 2020$ faces of each beam touch either a face of the cube or the interior of the face of another beam. What is the smallest positive number of beams that can be placed to satisfy these conditions?
|
【 A Answer. 3030 beams. 【 Construction. We first give a construction with $3 n / 2$ beams for any $n \times n \times n$ box, where $n$ is an even integer. Shown below is the construction for $n=6$, which generalizes. (The left figure shows the cube in 3 d ; the right figure shows a direct view of the three visible faces.)   Left face 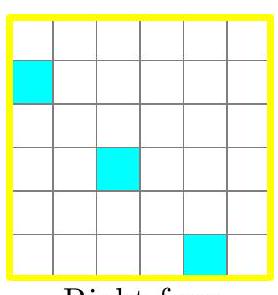 Right face To be explicit, impose coordinate axes such that one corner of the cube is the origin. We specify a beam by two opposite corners. The $3 n / 2$ beams come in three directions, $n / 2$ in each direction: - $(0,0,0) \rightarrow(1,1, n),(2,2,0) \rightarrow(3,3, n),(4,4,0) \rightarrow(5,5, n)$, and so on; - $(1,0,0) \rightarrow(2, n, 1),(3,0,2) \rightarrow(4, n, 3),(5,0,4) \rightarrow(6, n, 5)$, and so on; - $(0,1,1) \rightarrow(n, 2,2),(0,3,3) \rightarrow(n, 4,4),(0,5,5) \rightarrow(n, 6,6)$, and so on. This gives the figure we drew earlier and shows 3030 beams is possible. Necessity. We now show at least $3 n / 2$ beams are necessary. Maintain coordinates, and call the beams $x$-beams, $y$-beams, $z$-beams according to which plane their long edges are perpendicular too. Let $N_{x}, N_{y}, N_{z}$ be the number of these. Claim - If $\min \left(N_{x}, N_{y}, N_{z}\right)=0$, then at least $n^{2}$ beams are needed. We henceforth assume $\min \left(N_{x}, N_{y}, N_{z}\right)>0$. Claim - If $N_{z}>0$, then we have $N_{x}+N_{y} \geq n$. Proceeding in a similar fashion, we arrive at the three relations $$ \begin{aligned} & N_{x}+N_{y} \geq n \\ & N_{y}+N_{z} \geq n \\ & N_{z}+N_{x} \geq n \end{aligned} $$ Summing gives $N_{x}+N_{y}+N_{z} \geq 3 n / 2$ too. Remark. The problem condition has the following "physics" interpretation. Imagine the cube is a metal box which is sturdy enough that all beams must remain orthogonal to the faces of the box (i.e. the beams cannot spin). Then the condition of the problem is exactly what is needed so that, if the box is shaken or rotated, the beams will not move. Remark. Walter Stromquist points out that the number of constructions with 3030 beams is actually enormous: not dividing out by isometries, the number is $(2 \cdot 1010!)^{3}$.
|
3030
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An empty $2020 \times 2020 \times 2020$ cube is given, and a $2020 \times 2020$ grid of square unit cells is drawn on each of its six faces. A beam is a $1 \times 1 \times 2020$ rectangular prism. Several beams are placed inside the cube subject to the following conditions: - The two $1 \times 1$ faces of each beam coincide with unit cells lying on opposite faces of the cube. (Hence, there are $3 \cdot 2020^{2}$ possible positions for a beam.) - No two beams have intersecting interiors. - The interiors of each of the four $1 \times 2020$ faces of each beam touch either a face of the cube or the interior of the face of another beam. What is the smallest positive number of beams that can be placed to satisfy these conditions?
|
【 A Answer. 3030 beams. 【 Construction. We first give a construction with $3 n / 2$ beams for any $n \times n \times n$ box, where $n$ is an even integer. Shown below is the construction for $n=6$, which generalizes. (The left figure shows the cube in 3 d ; the right figure shows a direct view of the three visible faces.)   Left face  Right face To be explicit, impose coordinate axes such that one corner of the cube is the origin. We specify a beam by two opposite corners. The $3 n / 2$ beams come in three directions, $n / 2$ in each direction: - $(0,0,0) \rightarrow(1,1, n),(2,2,0) \rightarrow(3,3, n),(4,4,0) \rightarrow(5,5, n)$, and so on; - $(1,0,0) \rightarrow(2, n, 1),(3,0,2) \rightarrow(4, n, 3),(5,0,4) \rightarrow(6, n, 5)$, and so on; - $(0,1,1) \rightarrow(n, 2,2),(0,3,3) \rightarrow(n, 4,4),(0,5,5) \rightarrow(n, 6,6)$, and so on. This gives the figure we drew earlier and shows 3030 beams is possible. Necessity. We now show at least $3 n / 2$ beams are necessary. Maintain coordinates, and call the beams $x$-beams, $y$-beams, $z$-beams according to which plane their long edges are perpendicular too. Let $N_{x}, N_{y}, N_{z}$ be the number of these. Claim - If $\min \left(N_{x}, N_{y}, N_{z}\right)=0$, then at least $n^{2}$ beams are needed. We henceforth assume $\min \left(N_{x}, N_{y}, N_{z}\right)>0$. Claim - If $N_{z}>0$, then we have $N_{x}+N_{y} \geq n$. Proceeding in a similar fashion, we arrive at the three relations $$ \begin{aligned} & N_{x}+N_{y} \geq n \\ & N_{y}+N_{z} \geq n \\ & N_{z}+N_{x} \geq n \end{aligned} $$ Summing gives $N_{x}+N_{y}+N_{z} \geq 3 n / 2$ too. Remark. The problem condition has the following "physics" interpretation. Imagine the cube is a metal box which is sturdy enough that all beams must remain orthogonal to the faces of the box (i.e. the beams cannot spin). Then the condition of the problem is exactly what is needed so that, if the box is shaken or rotated, the beams will not move. Remark. Walter Stromquist points out that the number of constructions with 3030 beams is actually enormous: not dividing out by isometries, the number is $(2 \cdot 1010!)^{3}$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e4f89dc-cfce-5992-89ae-bd6955e55da7
| 605,411
|
Let $p$ be an odd prime. An integer $x$ is called a quadratic non-residue if $p$ does not divide $x-t^{2}$ for any integer $t$. Denote by $A$ the set of all integers $a$ such that $1 \leq a<p$, and both $a$ and $4-a$ are quadratic non-residues. Calculate the remainder when the product of the elements of $A$ is divided by $p$.
|
The answer is that $\prod_{a \in A} a \equiv 2(\bmod p)$ regardless of the value of $p$. In the following solution, we work in $\mathbb{F}_{p}$ always and abbreviate "quadratic residue" and "non-quadratic residue" to "QR" and "non-QR", respectively. We define $$ \begin{aligned} & A=\left\{a \in \mathbb{F}_{p} \mid a, 4-a \text { non-QR }\right\} \\ & B=\left\{b \in \mathbb{F}_{p} \mid b, 4-b \mathrm{QR}, b \neq 0, b \neq 4\right\} . \end{aligned} $$ Notice that $$ A \cup B=\left\{n \in \mathbb{F}_{p} \mid n(4-n) \text { is } \mathrm{QR} n \neq 0,4\right\} . $$ 【 First approach (based on Holden Mui's presentation in Mathematics Magazine). The idea behind this approach is that $n(4-n)$ is itself an element of $B$ for $n \in A \cup B$, because $4-n(4-n)=(n-2)^{2}$. This motivates the following claim. Claim - The map $$ A \cup B \backslash\{2\} \rightarrow B \quad \text { by } \quad n \mapsto n(4-n) $$ is a well-defined two-to-one map, i.e. every $b \in B$ has exactly two pre-images. Choose $b \in B$. The quadratic equation $n(4-n)=b$ in $n$ rewrites as $n^{2}-4 n+b=0$, and has discriminant $4(4-b)$, which is a nonzero QR. Hence there are exactly two values of $n$, as desired. Therefore, it follows that $$ \prod_{n \in A B[\{2]} n=\prod_{\ell \in B} $$ by pairing $n$ with $4-n$ on the left-hand side. So, $\prod_{a \in A} a=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be an odd prime. An integer $x$ is called a quadratic non-residue if $p$ does not divide $x-t^{2}$ for any integer $t$. Denote by $A$ the set of all integers $a$ such that $1 \leq a<p$, and both $a$ and $4-a$ are quadratic non-residues. Calculate the remainder when the product of the elements of $A$ is divided by $p$.
|
The answer is that $\prod_{a \in A} a \equiv 2(\bmod p)$ regardless of the value of $p$. In the following solution, we work in $\mathbb{F}_{p}$ always and abbreviate "quadratic residue" and "non-quadratic residue" to "QR" and "non-QR", respectively. We define $$ \begin{aligned} & A=\left\{a \in \mathbb{F}_{p} \mid a, 4-a \text { non-QR }\right\} \\ & B=\left\{b \in \mathbb{F}_{p} \mid b, 4-b \mathrm{QR}, b \neq 0, b \neq 4\right\} . \end{aligned} $$ Notice that $$ A \cup B=\left\{n \in \mathbb{F}_{p} \mid n(4-n) \text { is } \mathrm{QR} n \neq 0,4\right\} . $$ 【 First approach (based on Holden Mui's presentation in Mathematics Magazine). The idea behind this approach is that $n(4-n)$ is itself an element of $B$ for $n \in A \cup B$, because $4-n(4-n)=(n-2)^{2}$. This motivates the following claim. Claim - The map $$ A \cup B \backslash\{2\} \rightarrow B \quad \text { by } \quad n \mapsto n(4-n) $$ is a well-defined two-to-one map, i.e. every $b \in B$ has exactly two pre-images. Choose $b \in B$. The quadratic equation $n(4-n)=b$ in $n$ rewrites as $n^{2}-4 n+b=0$, and has discriminant $4(4-b)$, which is a nonzero QR. Hence there are exactly two values of $n$, as desired. Therefore, it follows that $$ \prod_{n \in A B[\{2]} n=\prod_{\ell \in B} $$ by pairing $n$ with $4-n$ on the left-hand side. So, $\prod_{a \in A} a=2$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
967dca13-a364-5f1d-851c-7bb16d40b74a
| 605,744
|
A finite set $S$ of points in the coordinate plane is called overdetermined if $|S| \geq 2$ and there exists a nonzero polynomial $P(t)$, with real coefficients and of degree at most $|S|-2$, satisfying $P(x)=y$ for every point $(x, y) \in S$. For each integer $n \geq 2$, find the largest integer $k$ (in terms of $n$ ) such that there exists a set of $n$ distinct points that is not overdetermined, but has $k$ overdetermined subsets.
|
We claim the answer is $k=2^{n-1}-n$. We denote the $n$ points by $A$. ## Lemma If $S$ is a finite set of points in the plane there is at most one polynomial with real coefficients and of degree at most $|S|-1$ whose graph passes through all points of $S$. Otherwise, suppose $f$ and $g$ are two such polynomials. Then $f-g$ has degree at most $|S|-1$, but it has $|S|$ roots, so is the zero polynomial. Remark. Actually Lagrange interpolation implies that such a polynomial exists as long as all the $x$-coordinates are different! Construction: Consider the set $A=\{(1, a),(2, b),(3, b),(4, b), \ldots,(n, b)\}$, where $a$ and $b$ are two distinct nonzero real numbers. Any subset of the latter $n-1$ points with at least one element is overdetermined, and there are $2^{n-1}-n$ such sets. Bound: Say a subset $S$ of $A$ is flooded if it is not overdetermined. For brevity, an $m$-set refers simply to a subset of $A$ with $m$ elements. Claim - If $S$ is an flooded $m$-set for $m \geq 3$, then at most one ( $m-1$ )-subset of $S$ is not flooded. Since $f$ and $g$ agree on $S-\left\{p_{i}, p_{j}\right\}$, which has $m-2$ elements, by the lemma we have $f=g$. Thus this common polynomial (actually of degree at most $m-3$ ) witnesses that $S$ is overdetermined, which is a contradiction. Claim - For all $m=2,3, \ldots, n$ there are at least $\binom{n-1}{m-1}$ flooded $m$-sets of $A$. $$ \frac{m-1}{n-(m-1)}\binom{n-1}{m-1}=\binom{n-1}{m-2} $$ as desired. $$ \sum_{m=2}^{n}\left(\binom{n}{m}-\binom{n-1}{m-1}\right)=2^{n-1}-n $$ overdetermined sets, as desired. Remark (On repeated $x$-coordinates). Suppose $A$ has two points $p$ and $q$ with repeated $x$ coordinates. We can argue directly that $A$ satisfies the bound. Indeed, any overdetermined set contains at most one of $p$ and $q$. Moreover, given $S \subseteq A-\{p, q\}$, if $S \cup\{p\}$ is overdetermined then $S \cup\{q\}$ is not, and vice-versa. (Recall that overdetermined sets always have distinct $x$-coordinates.) This gives a bound $\left[2^{n-2}-(n-2)-1\right]+\left[2^{n-2}-1\right]=2^{n-1}-n$ already.
|
2^{n-1}-n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A finite set $S$ of points in the coordinate plane is called overdetermined if $|S| \geq 2$ and there exists a nonzero polynomial $P(t)$, with real coefficients and of degree at most $|S|-2$, satisfying $P(x)=y$ for every point $(x, y) \in S$. For each integer $n \geq 2$, find the largest integer $k$ (in terms of $n$ ) such that there exists a set of $n$ distinct points that is not overdetermined, but has $k$ overdetermined subsets.
|
We claim the answer is $k=2^{n-1}-n$. We denote the $n$ points by $A$. ## Lemma If $S$ is a finite set of points in the plane there is at most one polynomial with real coefficients and of degree at most $|S|-1$ whose graph passes through all points of $S$. Otherwise, suppose $f$ and $g$ are two such polynomials. Then $f-g$ has degree at most $|S|-1$, but it has $|S|$ roots, so is the zero polynomial. Remark. Actually Lagrange interpolation implies that such a polynomial exists as long as all the $x$-coordinates are different! Construction: Consider the set $A=\{(1, a),(2, b),(3, b),(4, b), \ldots,(n, b)\}$, where $a$ and $b$ are two distinct nonzero real numbers. Any subset of the latter $n-1$ points with at least one element is overdetermined, and there are $2^{n-1}-n$ such sets. Bound: Say a subset $S$ of $A$ is flooded if it is not overdetermined. For brevity, an $m$-set refers simply to a subset of $A$ with $m$ elements. Claim - If $S$ is an flooded $m$-set for $m \geq 3$, then at most one ( $m-1$ )-subset of $S$ is not flooded. Since $f$ and $g$ agree on $S-\left\{p_{i}, p_{j}\right\}$, which has $m-2$ elements, by the lemma we have $f=g$. Thus this common polynomial (actually of degree at most $m-3$ ) witnesses that $S$ is overdetermined, which is a contradiction. Claim - For all $m=2,3, \ldots, n$ there are at least $\binom{n-1}{m-1}$ flooded $m$-sets of $A$. $$ \frac{m-1}{n-(m-1)}\binom{n-1}{m-1}=\binom{n-1}{m-2} $$ as desired. $$ \sum_{m=2}^{n}\left(\binom{n}{m}-\binom{n-1}{m-1}\right)=2^{n-1}-n $$ overdetermined sets, as desired. Remark (On repeated $x$-coordinates). Suppose $A$ has two points $p$ and $q$ with repeated $x$ coordinates. We can argue directly that $A$ satisfies the bound. Indeed, any overdetermined set contains at most one of $p$ and $q$. Moreover, given $S \subseteq A-\{p, q\}$, if $S \cup\{p\}$ is overdetermined then $S \cup\{q\}$ is not, and vice-versa. (Recall that overdetermined sets always have distinct $x$-coordinates.) This gives a bound $\left[2^{n-2}-(n-2)-1\right]+\left[2^{n-2}-1\right]=2^{n-1}-n$ already.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ed2ac6df-3f71-5e38-b984-f7dad1083c33
| 605,780
|
The Planar National Park is a undirected 3-regular planar graph (i.e. all vertices have degree 3). A visitor walks through the park as follows: she begins at a vertex and starts walking along an edge. When she reaches the other endpoint, she turns left. On the next vertex she turns right, and so on, alternating left and right turns at each vertex. She does this until she gets back to the vertex where she started. What is the largest possible number of times she could have entered any vertex during her walk, over all possible layouts of the park?
|
The answer is 3. We consider the trajectory of the visitor as an ordered sequence of turns. A turn is defined by specifying a vertex, the incoming edge, and the outgoing edge. Hence there are six possible turns for each vertex. Claim - Given one turn in the sequence, one can reconstruct the entire sequence of turns. This implies already that the trajectory of the visitor, when extended to an infinite sequence, is totally periodic (not just eventually periodic), because there are finitely many possible turns, so some turn must be repeated. So, any turn appears at most once in the period of the sequence, giving a naïve bound of 6 for the original problem. However, the following claim improves the bound to 3 . Claim - It is impossible for both of the turns $a \rightarrow b \rightarrow c$ and $c \rightarrow b \rightarrow a$ to occur in the same trajectory.  However, we assumed for contradiction the red and blue paths were part of the same trajectory, yet they clearly never meet. It remains to give a construction showing 3 can be achieved. There are many, many valid constructions. One construction due to Danielle Wang is given here, who provided the following motivation: "I was lying in bed and drew the first thing I could think of". The path is CAHIFGDBAHEFGJBAC which visits $A$ three times.  Remark. As the above example shows it is possible to transverse an edge more than once even in the same direction, as in edge $A H$ above.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Planar National Park is a undirected 3-regular planar graph (i.e. all vertices have degree 3). A visitor walks through the park as follows: she begins at a vertex and starts walking along an edge. When she reaches the other endpoint, she turns left. On the next vertex she turns right, and so on, alternating left and right turns at each vertex. She does this until she gets back to the vertex where she started. What is the largest possible number of times she could have entered any vertex during her walk, over all possible layouts of the park?
|
The answer is 3. We consider the trajectory of the visitor as an ordered sequence of turns. A turn is defined by specifying a vertex, the incoming edge, and the outgoing edge. Hence there are six possible turns for each vertex. Claim - Given one turn in the sequence, one can reconstruct the entire sequence of turns. This implies already that the trajectory of the visitor, when extended to an infinite sequence, is totally periodic (not just eventually periodic), because there are finitely many possible turns, so some turn must be repeated. So, any turn appears at most once in the period of the sequence, giving a naïve bound of 6 for the original problem. However, the following claim improves the bound to 3 . Claim - It is impossible for both of the turns $a \rightarrow b \rightarrow c$ and $c \rightarrow b \rightarrow a$ to occur in the same trajectory.  However, we assumed for contradiction the red and blue paths were part of the same trajectory, yet they clearly never meet. It remains to give a construction showing 3 can be achieved. There are many, many valid constructions. One construction due to Danielle Wang is given here, who provided the following motivation: "I was lying in bed and drew the first thing I could think of". The path is CAHIFGDBAHEFGJBAC which visits $A$ three times.  Remark. As the above example shows it is possible to transverse an edge more than once even in the same direction, as in edge $A H$ above.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
801830b1-6f8a-5746-9e62-bd51ee658b6a
| 605,831
|
A finite set $S$ of positive integers has the property that, for each $s \in S$, and each positive integer divisor $d$ of $s$, there exists a unique element $t \in S$ satisfying $\operatorname{gcd}(s, t)=d$. (The elements $s$ and $t$ could be equal.) Given this information, find all possible values for the number of elements of $S$.
|
The answer is that $|S|$ must be a power of 2 (including 1 ), or $|S|=0$ (a trivial case we do not discuss further). 【 Construction. For any nonnegative integer $k$, a construction for $|S|=2^{k}$ is given by $$ S=\left\{\left(p_{1} \text { or } q_{1}\right) \times\left(p_{2} \text { or } q_{2}\right) \times \cdots \times\left(p_{k} \text { or } q_{k}\right)\right\} $$ for $2 k$ distinct primes $p_{1}, \ldots, p_{k}, q_{1}, \ldots, q_{k}$. ■ Converse. The main claim is as follows. Claim - In any valid set $S$, for any prime $p$ and $x \in S, \nu_{p}(x) \leq 1$. - On the one hand, by taking $x$ in the statement, we see $\frac{e}{e+1}$ of the elements of $S$ are divisible by $p$. - On the other hand, consider a $y \in S$ such that $\nu_{p}(y)=1$ which must exist (say if $\operatorname{gcd}(x, y)=p$ ). Taking $y$ in the statement, we see $\frac{1}{2}$ of the elements of $S$ are divisible by $p$. So $e=1$, contradiction. Now since $|S|$ equals the number of divisors of any element of $S$, we are done.
|
2^k
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A finite set $S$ of positive integers has the property that, for each $s \in S$, and each positive integer divisor $d$ of $s$, there exists a unique element $t \in S$ satisfying $\operatorname{gcd}(s, t)=d$. (The elements $s$ and $t$ could be equal.) Given this information, find all possible values for the number of elements of $S$.
|
The answer is that $|S|$ must be a power of 2 (including 1 ), or $|S|=0$ (a trivial case we do not discuss further). 【 Construction. For any nonnegative integer $k$, a construction for $|S|=2^{k}$ is given by $$ S=\left\{\left(p_{1} \text { or } q_{1}\right) \times\left(p_{2} \text { or } q_{2}\right) \times \cdots \times\left(p_{k} \text { or } q_{k}\right)\right\} $$ for $2 k$ distinct primes $p_{1}, \ldots, p_{k}, q_{1}, \ldots, q_{k}$. ■ Converse. The main claim is as follows. Claim - In any valid set $S$, for any prime $p$ and $x \in S, \nu_{p}(x) \leq 1$. - On the one hand, by taking $x$ in the statement, we see $\frac{e}{e+1}$ of the elements of $S$ are divisible by $p$. - On the other hand, consider a $y \in S$ such that $\nu_{p}(y)=1$ which must exist (say if $\operatorname{gcd}(x, y)=p$ ). Taking $y$ in the statement, we see $\frac{1}{2}$ of the elements of $S$ are divisible by $p$. So $e=1$, contradiction. Now since $|S|$ equals the number of divisors of any element of $S$, we are done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a493f2a0-435e-5b2e-bca5-838a8ad770e9
| 605,851
|
A function $f: \mathbb{R} \rightarrow \mathbb{R}$ is essentially increasing if $f(s) \leq f(t)$ holds whenever $s \leq t$ are real numbers such that $f(s) \neq 0$ and $f(t) \neq 0$. Find the smallest integer $k$ such that for any 2022 real numbers $x_{1}, x_{2}, \ldots, x_{2022}$, there exist $k$ essentially increasing functions $f_{1}, \ldots, f_{k}$ such that $$ f_{1}(n)+f_{2}(n)+\cdots+f_{k}(n)=x_{n} \quad \text { for every } n=1,2, \ldots, 2022 $$
|
The answer is 11 and, more generally, if 2022 is replaced by $N$ then the answer is $\left\lfloor\log _{2} N\right\rfloor+1$. 『 Bound. Suppose for contradiction that $2^{k}-1>N$ and choose $x_{n}=-n$ for each $n=1, \ldots, N$. Now for each index $1 \leq n \leq N$, define $$ S(n)=\left\{\text { indices } i \text { for which } f_{i}(n) \neq 0\right\} \subseteq\{1, \ldots, k\} $$ As each $S(n t)$ is nonempty, by pigeonhole, two $S(n)$ 's coincide, say $S(n)=S\left(n^{\prime}\right)$ for $n<n^{\prime}$. But it's plainly impossible that $x_{n}>x_{n^{\prime}}$ in that case due to the essentially increasing condition. 【 Construction. It suffices to do $N=2^{k}-1$. Rather than drown the reader in notation, we'll just illustrate an example of the (inductive) construction for $k=4$. Empty cells are zero. | | $f_{1}$ | $f_{2}$ | $f_{3}$ | $f_{4}$ | | ---: | ---: | ---: | ---: | ---: | | $x_{1}=3$ | 3 | | | | | $x_{2}=1$ | 10 | -9 | | | | $x_{3}=4$ | | 4 | | | | $x_{4}=1$ | 100 | 200 | $-\mathbf{2 9 9}$ | | | $x_{5}=5$ | | 200 | -195 | | | $x_{6}=9$ | 100 | | -91 | | | $x_{7}=2$ | | | 2 | | | $x_{8}=6$ | 1000 | 2000 | 4000 | $-\mathbf{6 9 9 4}$ | | $x_{9}=5$ | | 2000 | 4000 | -5995 | | $x_{10}=3$ | 1000 | | 4000 | -4997 | | $x_{11}=5$ | | | 4000 | -3995 | | $x_{12}=8$ | 1000 | 2000 | | -2992 | | $x_{13}=9$ | | 2000 | | -1991 | | $x_{14}=7$ | 1000 | | | -993 | | $x_{15}=9$ | | | | 9 | The general case is handled in the same way with powers of 10 replaced by powers of $B$, for a sufficiently large number $B$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A function $f: \mathbb{R} \rightarrow \mathbb{R}$ is essentially increasing if $f(s) \leq f(t)$ holds whenever $s \leq t$ are real numbers such that $f(s) \neq 0$ and $f(t) \neq 0$. Find the smallest integer $k$ such that for any 2022 real numbers $x_{1}, x_{2}, \ldots, x_{2022}$, there exist $k$ essentially increasing functions $f_{1}, \ldots, f_{k}$ such that $$ f_{1}(n)+f_{2}(n)+\cdots+f_{k}(n)=x_{n} \quad \text { for every } n=1,2, \ldots, 2022 $$
|
The answer is 11 and, more generally, if 2022 is replaced by $N$ then the answer is $\left\lfloor\log _{2} N\right\rfloor+1$. 『 Bound. Suppose for contradiction that $2^{k}-1>N$ and choose $x_{n}=-n$ for each $n=1, \ldots, N$. Now for each index $1 \leq n \leq N$, define $$ S(n)=\left\{\text { indices } i \text { for which } f_{i}(n) \neq 0\right\} \subseteq\{1, \ldots, k\} $$ As each $S(n t)$ is nonempty, by pigeonhole, two $S(n)$ 's coincide, say $S(n)=S\left(n^{\prime}\right)$ for $n<n^{\prime}$. But it's plainly impossible that $x_{n}>x_{n^{\prime}}$ in that case due to the essentially increasing condition. 【 Construction. It suffices to do $N=2^{k}-1$. Rather than drown the reader in notation, we'll just illustrate an example of the (inductive) construction for $k=4$. Empty cells are zero. | | $f_{1}$ | $f_{2}$ | $f_{3}$ | $f_{4}$ | | ---: | ---: | ---: | ---: | ---: | | $x_{1}=3$ | 3 | | | | | $x_{2}=1$ | 10 | -9 | | | | $x_{3}=4$ | | 4 | | | | $x_{4}=1$ | 100 | 200 | $-\mathbf{2 9 9}$ | | | $x_{5}=5$ | | 200 | -195 | | | $x_{6}=9$ | 100 | | -91 | | | $x_{7}=2$ | | | 2 | | | $x_{8}=6$ | 1000 | 2000 | 4000 | $-\mathbf{6 9 9 4}$ | | $x_{9}=5$ | | 2000 | 4000 | -5995 | | $x_{10}=3$ | 1000 | | 4000 | -4997 | | $x_{11}=5$ | | | 4000 | -3995 | | $x_{12}=8$ | 1000 | 2000 | | -2992 | | $x_{13}=9$ | | 2000 | | -1991 | | $x_{14}=7$ | 1000 | | | -993 | | $x_{15}=9$ | | | | 9 | The general case is handled in the same way with powers of 10 replaced by powers of $B$, for a sufficiently large number $B$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2022-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
45ee22c5-d23e-5803-a34a-0e2a63c482a4
| 605,943
|
Let $n>2$ be an integer and let $\ell \in\{1,2, \ldots, n\}$. A collection $A_{1}, \ldots, A_{k}$ of (not necessarily distinct) subsets of $\{1,2, \ldots, n\}$ is called $\ell$-large if $\left|A_{i}\right| \geq \ell$ for all $1 \leq i \leq k$. Find, in terms of $n$ and $\ell$, the largest real number $c$ such that the inequality $$ \sum_{i=1}^{k} \sum_{j=1}^{k} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right| \cdot\left|A_{j}\right|} \geq c\left(\sum_{i=1}^{k} x_{i}\right)^{2} $$ holds for all positive integer $k$, all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{k}$, and all $\ell$-large collections $A_{1}, A_{2}, \ldots, A_{k}$ of subsets of $\{1,2, \ldots, n\}$.
|
The answer turns out to be $$ c=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ 【 Rewriting as a dot product. For $i=1, \ldots, n$ define $\mathbf{v}_{i}$ by $$ \mathbf{v}_{i}[p, q]:=\left\{\begin{array}{ll} \frac{1}{\left|A_{i}\right|} & p \in A_{i} \text { and } q \in A_{i} \\ 0 & \text { otherwise; } \end{array} \quad \mathbf{v}:=\sum_{i} x_{i} \mathbf{v}_{i}\right. $$ Then $$ \begin{aligned} \sum_{i} \sum_{j} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right|\left|A_{j}\right|} & =\sum_{i} \sum_{j} x_{i} x_{j}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle \\ & =\left\langle\sum_{i} x_{i} \mathbf{v}_{i}, \sum_{j} x_{i} \mathbf{v}_{i}\right\rangle=\left\|\sum_{i} x_{i} \mathbf{v}_{i}\right\|^{2}=\|\mathbf{v}\|^{2} . \end{aligned} $$ $$ \begin{aligned} & \langle\mathbf{e}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{e}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i} \\ & \langle\mathbf{1}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{1}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i}\left|A_{i}\right| . \end{aligned} $$ That means for any positive real constants $\alpha$ and $\beta$, by Cauchy-Schwarz for vectors, we should have $$ \begin{aligned} \|\alpha \mathbf{e}+\beta \mathbf{1}\|\|\mathbf{v}\| & \geq\langle\alpha \mathbf{e}+\beta \mathbf{1}, \mathbf{v}\rangle=\alpha\langle\mathbf{e}, \mathbf{v}\rangle+\beta\langle\mathbf{1}, \mathbf{v}\rangle \\ & =\alpha \cdot \sum x_{i}+\beta \cdot \sum x_{i}\left|A_{i}\right| \\ & \geq(\alpha+\ell \beta) \sum x_{i} . \end{aligned} $$ Set $\mathbf{w}:=\alpha \mathbf{e}+\beta \mathbf{1}$ for brevity. Then $$ \mathbf{w}[p, q]= \begin{cases}\alpha+\beta & \text { if } p=q \\ \beta & \text { if } p \neq q\end{cases} $$ SO $$ \|\mathbf{w}\|=\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}} $$ Therefore, we get an lower bound $$ \frac{\|\mathbf{v}\|}{\sum x_{i}} \geq \frac{\alpha+\ell \beta}{\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}}} $$ Letting $\alpha=n-\ell$ and $\beta=\ell-1$ gives a proof that the constant $$ c=\frac{((n-\ell)+\ell(\ell-1))^{2}}{n \cdot(n-1)^{2}+\left(n^{2}-n\right) \cdot(\ell-1)^{2}}=\frac{\left(n+\ell^{2}-2 \ell\right)^{2}}{n(n-1)\left(n+\ell^{2}-2 \ell\right)}=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ makes the original inequality always true. (The choice of $\alpha: \beta$ is suggested by the example below.) 【 Example showing this $c$ is best possible. Let $k=\binom{n}{\ell}$, let $A_{i}$ run over all $\binom{n}{\ell}$ subsets of $\{1, \ldots, n\}$ of size $\ell$, and let $x_{i}=1$ for all $i$. We claim this construction works. To verify this, it would be sufficient to show that $\mathbf{w}$ and $\mathbf{v}$ are scalar multiples, so that the above Cauchy-Schwarz is equality. However, we can compute $$ \mathbf{w}[p, q]=\left\{\begin{array}{ll} n-1 & \text { if } p=q \\ \ell-1 & \text { if } p \neq q \end{array}, \quad \mathbf{v}[p, q]= \begin{cases}\binom{n-1}{\ell-1} \cdot \frac{1}{\ell} & \text { if } p=q \\ \binom{n-2}{\ell-2} \cdot \frac{1}{\ell} & \text { if } p \neq q\end{cases}\right. $$ which are indeed scalar multiples, finishing the proof.
|
\frac{n+\ell^{2}-2 \ell}{n(n-1)}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $n>2$ be an integer and let $\ell \in\{1,2, \ldots, n\}$. A collection $A_{1}, \ldots, A_{k}$ of (not necessarily distinct) subsets of $\{1,2, \ldots, n\}$ is called $\ell$-large if $\left|A_{i}\right| \geq \ell$ for all $1 \leq i \leq k$. Find, in terms of $n$ and $\ell$, the largest real number $c$ such that the inequality $$ \sum_{i=1}^{k} \sum_{j=1}^{k} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right| \cdot\left|A_{j}\right|} \geq c\left(\sum_{i=1}^{k} x_{i}\right)^{2} $$ holds for all positive integer $k$, all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{k}$, and all $\ell$-large collections $A_{1}, A_{2}, \ldots, A_{k}$ of subsets of $\{1,2, \ldots, n\}$.
|
The answer turns out to be $$ c=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ 【 Rewriting as a dot product. For $i=1, \ldots, n$ define $\mathbf{v}_{i}$ by $$ \mathbf{v}_{i}[p, q]:=\left\{\begin{array}{ll} \frac{1}{\left|A_{i}\right|} & p \in A_{i} \text { and } q \in A_{i} \\ 0 & \text { otherwise; } \end{array} \quad \mathbf{v}:=\sum_{i} x_{i} \mathbf{v}_{i}\right. $$ Then $$ \begin{aligned} \sum_{i} \sum_{j} x_{i} x_{j} \frac{\left|A_{i} \cap A_{j}\right|^{2}}{\left|A_{i}\right|\left|A_{j}\right|} & =\sum_{i} \sum_{j} x_{i} x_{j}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle \\ & =\left\langle\sum_{i} x_{i} \mathbf{v}_{i}, \sum_{j} x_{i} \mathbf{v}_{i}\right\rangle=\left\|\sum_{i} x_{i} \mathbf{v}_{i}\right\|^{2}=\|\mathbf{v}\|^{2} . \end{aligned} $$ $$ \begin{aligned} & \langle\mathbf{e}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{e}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i} \\ & \langle\mathbf{1}, \mathbf{v}\rangle=\sum_{i} x_{i}\left\langle\mathbf{1}, \mathbf{v}_{i}\right\rangle=\sum_{i} x_{i}\left|A_{i}\right| . \end{aligned} $$ That means for any positive real constants $\alpha$ and $\beta$, by Cauchy-Schwarz for vectors, we should have $$ \begin{aligned} \|\alpha \mathbf{e}+\beta \mathbf{1}\|\|\mathbf{v}\| & \geq\langle\alpha \mathbf{e}+\beta \mathbf{1}, \mathbf{v}\rangle=\alpha\langle\mathbf{e}, \mathbf{v}\rangle+\beta\langle\mathbf{1}, \mathbf{v}\rangle \\ & =\alpha \cdot \sum x_{i}+\beta \cdot \sum x_{i}\left|A_{i}\right| \\ & \geq(\alpha+\ell \beta) \sum x_{i} . \end{aligned} $$ Set $\mathbf{w}:=\alpha \mathbf{e}+\beta \mathbf{1}$ for brevity. Then $$ \mathbf{w}[p, q]= \begin{cases}\alpha+\beta & \text { if } p=q \\ \beta & \text { if } p \neq q\end{cases} $$ SO $$ \|\mathbf{w}\|=\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}} $$ Therefore, we get an lower bound $$ \frac{\|\mathbf{v}\|}{\sum x_{i}} \geq \frac{\alpha+\ell \beta}{\sqrt{n \cdot(\alpha+\beta)^{2}+\left(n^{2}-n\right) \cdot \beta^{2}}} $$ Letting $\alpha=n-\ell$ and $\beta=\ell-1$ gives a proof that the constant $$ c=\frac{((n-\ell)+\ell(\ell-1))^{2}}{n \cdot(n-1)^{2}+\left(n^{2}-n\right) \cdot(\ell-1)^{2}}=\frac{\left(n+\ell^{2}-2 \ell\right)^{2}}{n(n-1)\left(n+\ell^{2}-2 \ell\right)}=\frac{n+\ell^{2}-2 \ell}{n(n-1)} $$ makes the original inequality always true. (The choice of $\alpha: \beta$ is suggested by the example below.) 【 Example showing this $c$ is best possible. Let $k=\binom{n}{\ell}$, let $A_{i}$ run over all $\binom{n}{\ell}$ subsets of $\{1, \ldots, n\}$ of size $\ell$, and let $x_{i}=1$ for all $i$. We claim this construction works. To verify this, it would be sufficient to show that $\mathbf{w}$ and $\mathbf{v}$ are scalar multiples, so that the above Cauchy-Schwarz is equality. However, we can compute $$ \mathbf{w}[p, q]=\left\{\begin{array}{ll} n-1 & \text { if } p=q \\ \ell-1 & \text { if } p \neq q \end{array}, \quad \mathbf{v}[p, q]= \begin{cases}\binom{n-1}{\ell-1} \cdot \frac{1}{\ell} & \text { if } p=q \\ \binom{n-2}{\ell-2} \cdot \frac{1}{\ell} & \text { if } p \neq q\end{cases}\right. $$ which are indeed scalar multiples, finishing the proof.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2024-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
40d1a6cb-fd7d-57d7-8016-c450754e1085
| 606,156
|
Fix a positive integer $n$. A tournament on $n$ vertices has all its edges colored by $\chi$ colors, so that any two directed edges $u \rightarrow v$ and $v \rightarrow w$ have different colors. Over all possible tournaments on $n$ vertices, determine the minimum possible value of $\chi$.
|
The answer is $$ \chi=\left\lceil\log _{2} n\right\rceil $$ First, we prove by induction on $n$ that $\chi \geq \log _{2} n$ for any coloring and any tournament. The base case $n=1$ is obvious. Now given any tournament, consider any used color $c$. Then it should be possible to divide the tournament into two subsets $A$ and $B$ such that all $c$-colored edges point from $A$ to $B$ (for example by letting $A$ be all vertices which are the starting point of a $c$-edge).  One of $A$ and $B$ has size at least $n / 2$, say $A$. Since $A$ has no $c$ edges, and uses at least $\log _{2}|A|$ colors other than $c$, we get $$ \chi \geq 1+\log _{2}(n / 2)=\log _{2} n $$ completing the induction. One can read the construction off from the argument above, but here is a concrete description. For each integer $n$, consider the tournament whose vertices are the binary representations of $S=\{0, \ldots, n-1\}$. Instantiate colors $c_{1}, c_{2}, \ldots$. Then for $v, w \in S$, we look at the smallest order bit for which they differ; say the $k$ th one. If $v$ has a zero in the $k$ th bit, and $w$ has a one in the $k$ th bit, we draw $v \rightarrow w$. Moreover we color the edge with color $c_{k}$. This works and uses at most $\left\lceil\log _{2} n\right\rceil$ colors. Remark (Motivation). The philosophy "combinatorial optimization" applies here. The idea is given any color $c$, we can find sets $A$ and $B$ such that all $c$-edges point $A$ to $B$. Once you realize this, the next insight is to realize that you may as well color all the edges from $A$ to $B$ by $c$; after all, this doesn't hurt the condition and makes your life easier. Hence, if $f$ is the answer, we have already a proof that $f(n)=1+\max (f(|A|), f(|B|))$ and we choose $|A| \approx|B|$. This optimization also gives the inductive construction.
|
\left\lceil\log _{2} n\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Fix a positive integer $n$. A tournament on $n$ vertices has all its edges colored by $\chi$ colors, so that any two directed edges $u \rightarrow v$ and $v \rightarrow w$ have different colors. Over all possible tournaments on $n$ vertices, determine the minimum possible value of $\chi$.
|
The answer is $$ \chi=\left\lceil\log _{2} n\right\rceil $$ First, we prove by induction on $n$ that $\chi \geq \log _{2} n$ for any coloring and any tournament. The base case $n=1$ is obvious. Now given any tournament, consider any used color $c$. Then it should be possible to divide the tournament into two subsets $A$ and $B$ such that all $c$-colored edges point from $A$ to $B$ (for example by letting $A$ be all vertices which are the starting point of a $c$-edge).  One of $A$ and $B$ has size at least $n / 2$, say $A$. Since $A$ has no $c$ edges, and uses at least $\log _{2}|A|$ colors other than $c$, we get $$ \chi \geq 1+\log _{2}(n / 2)=\log _{2} n $$ completing the induction. One can read the construction off from the argument above, but here is a concrete description. For each integer $n$, consider the tournament whose vertices are the binary representations of $S=\{0, \ldots, n-1\}$. Instantiate colors $c_{1}, c_{2}, \ldots$. Then for $v, w \in S$, we look at the smallest order bit for which they differ; say the $k$ th one. If $v$ has a zero in the $k$ th bit, and $w$ has a one in the $k$ th bit, we draw $v \rightarrow w$. Moreover we color the edge with color $c_{k}$. This works and uses at most $\left\lceil\log _{2} n\right\rceil$ colors. Remark (Motivation). The philosophy "combinatorial optimization" applies here. The idea is given any color $c$, we can find sets $A$ and $B$ such that all $c$-edges point $A$ to $B$. Once you realize this, the next insight is to realize that you may as well color all the edges from $A$ to $B$ by $c$; after all, this doesn't hurt the condition and makes your life easier. Hence, if $f$ is the answer, we have already a proof that $f(n)=1+\max (f(|A|), f(|B|))$ and we choose $|A| \approx|B|$. This optimization also gives the inductive construction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2015.jsonl",
"problem_match": null,
"solution_match": null
}
|
74d9ae4f-cfe6-5f19-9094-4a100cd80830
| 246,479
|
In a sports league, each team uses a set of at most $t$ signature colors. A set $S$ of teams is color-identifiable if one can assign each team in $S$ one of their signature colors, such that no team in $S$ is assigned any signature color of a different team in $S$. For all positive integers $n$ and $t$, determine the maximum integer $g(n, t)$ such that: In any sports league with exactly $n$ distinct colors present over all teams, one can always find a color-identifiable set of size at least $g(n, t)$.
|
Answer: $\lceil n / t\rceil$. To see this is an upper bound, note that one can easily construct a sports league with that many teams anyways. A quick warning: Remark (Misreading the problem). It is common to misread the problem by ignoring the word "any". Here is an illustration. Suppose we have two teams, MIT and Harvard; the colors of MIT are red/grey/black, and the colors of Harvard are red/white. (Thus $n=4$ and $t=3$.) The assignment of MIT to grey and Harvard to red is not acceptable because red is a signature color of MIT, even though not the one assigned. 【 Approach by deleting teams (Gopal Goel). Initially, place all teams in a set $S$. Then we repeat the following algorithm: If there is a team all of whose signature colors are shared by some other team in $S$ already, then we delete that team. (If there is more than one such team, we pick arbitrarily.) At the end of the process, all $n$ colors are still present at least once, so at least $\lceil n / t\rceil$ teams remain. Moreover, since the algorithm is no longer possible, the remaining set $S$ is already color-identifiable. Remark (Gopal Goel). It might seem counter-intuitive that we are deleting teams from the full set when the original problem is trying to get a large set $S$. This is less strange when one thinks of it instead as "safely deleting useless teams". Basically, if one deletes such a team, the problem statement implies that the task must still be possible, since $g(n, t)$ does not depend on the number of teams: $n$ is the number of colors present, and deleting a useless team does not change this. It turns out that this optimization is already enough to solve the problem.
|
\lceil n / t\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a sports league, each team uses a set of at most $t$ signature colors. A set $S$ of teams is color-identifiable if one can assign each team in $S$ one of their signature colors, such that no team in $S$ is assigned any signature color of a different team in $S$. For all positive integers $n$ and $t$, determine the maximum integer $g(n, t)$ such that: In any sports league with exactly $n$ distinct colors present over all teams, one can always find a color-identifiable set of size at least $g(n, t)$.
|
Answer: $\lceil n / t\rceil$. To see this is an upper bound, note that one can easily construct a sports league with that many teams anyways. A quick warning: Remark (Misreading the problem). It is common to misread the problem by ignoring the word "any". Here is an illustration. Suppose we have two teams, MIT and Harvard; the colors of MIT are red/grey/black, and the colors of Harvard are red/white. (Thus $n=4$ and $t=3$.) The assignment of MIT to grey and Harvard to red is not acceptable because red is a signature color of MIT, even though not the one assigned. 【 Approach by deleting teams (Gopal Goel). Initially, place all teams in a set $S$. Then we repeat the following algorithm: If there is a team all of whose signature colors are shared by some other team in $S$ already, then we delete that team. (If there is more than one such team, we pick arbitrarily.) At the end of the process, all $n$ colors are still present at least once, so at least $\lceil n / t\rceil$ teams remain. Moreover, since the algorithm is no longer possible, the remaining set $S$ is already color-identifiable. Remark (Gopal Goel). It might seem counter-intuitive that we are deleting teams from the full set when the original problem is trying to get a large set $S$. This is less strange when one thinks of it instead as "safely deleting useless teams". Basically, if one deletes such a team, the problem statement implies that the task must still be possible, since $g(n, t)$ does not depend on the number of teams: $n$ is the number of colors present, and deleting a useless team does not change this. It turns out that this optimization is already enough to solve the problem.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2017.jsonl",
"problem_match": null,
"solution_match": null
}
|
157234af-7ccf-5fec-900c-5f52db36f874
| 246,556
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. 【 A third remixed solution. We use Lemma I and Lemma II' from before. As before, assume $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ is valiant, and $n$ has a prime divisor $p \leq 101$. Also, let $e=\nu_{p}(n)$. Then $(p-1)!\sum_{x} x^{p-1} \equiv 0(\bmod n)$ by Lemma I, and now $$ \begin{aligned} 0 & \equiv \sum_{x} x^{p-1} \quad\left(\bmod p^{e}\right) \\ & \equiv \frac{n}{p^{e}} \sum_{x=1}^{p^{e}-1} x^{p-1} \not \equiv 0 \quad\left(\bmod p^{e}\right) \end{aligned} $$ by Lemma II', contradiction.
|
all numbers relatively prime to 101!
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\mathbb{Z} / n \mathbb{Z}$ denote the set of integers considered modulo $n$ (hence $\mathbb{Z} / n \mathbb{Z}$ has $n$ elements). Find all positive integers $n$ for which there exists a bijective function $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$, such that the 101 functions $$ g(x), \quad g(x)+x, \quad g(x)+2 x, \quad \ldots, \quad g(x)+100 x $$ are all bijections on $\mathbb{Z} / n \mathbb{Z}$.
|
Call a function $g$ valiant if it obeys this condition. We claim the answer is all numbers relatively prime to 101 !. The construction is to just let $g$ be the identity function. Remark (Motivation for both parts). The following solution is dense, and it is easier to think about some small cases first, to motivate the ideas. We consider the result where 101 is replaced by 2 or 3 . - If we replaced 101 with 2 , you can show $2 \nmid n$ easily: write $$ \sum_{x} x \equiv \sum_{x} g(x) \equiv \sum_{x}(g(x)+x) \quad(\bmod n) $$ which implies $$ 0 \equiv \sum_{x} x=\frac{1}{2} n(n+1) \quad(\bmod n) $$ which means $\frac{1}{2} n(n+1) \equiv 0(\bmod n)$, hence $n$ odd. - If we replaced 101 with 3 , then you can try a similar approach using squares, since $$ \begin{aligned} 0 & \equiv \sum_{x}\left[(g(x)+2 x)^{2}-2(g(x)+x)^{2}+g(x)^{2}\right] \quad(\bmod n) \\ & =\sum_{x} 2 x^{2}=2 \cdot \frac{n(n+1)(2 n+1)}{6} \end{aligned} $$ which is enough to force $3 \nmid n$. 【 A third remixed solution. We use Lemma I and Lemma II' from before. As before, assume $g: \mathbb{Z} / n \mathbb{Z} \rightarrow \mathbb{Z} / n \mathbb{Z}$ is valiant, and $n$ has a prime divisor $p \leq 101$. Also, let $e=\nu_{p}(n)$. Then $(p-1)!\sum_{x} x^{p-1} \equiv 0(\bmod n)$ by Lemma I, and now $$ \begin{aligned} 0 & \equiv \sum_{x} x^{p-1} \quad\left(\bmod p^{e}\right) \\ & \equiv \frac{n}{p^{e}} \sum_{x=1}^{p^{e}-1} x^{p-1} \not \equiv 0 \quad\left(\bmod p^{e}\right) \end{aligned} $$ by Lemma II', contradiction.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
900d2e37-91bc-5367-8c62-439ce24a69e7
| 606,410
|
There are 2022 equally spaced points on a circular track $\gamma$ of circumference 2022. The points are labeled $A_{1}, A_{2}, \ldots, A_{2022}$ in some order, each label used once. Initially, Bunbun the Bunny begins at $A_{1}$. She hops along $\gamma$ from $A_{1}$ to $A_{2}$, then from $A_{2}$ to $A_{3}$, until she reaches $A_{2022}$, after which she hops back to $A_{1}$. When hopping from $P$ to $Q$, she always hops along the shorter of the two $\operatorname{arcs} \overparen{P Q}$ of $\gamma$; if $\overline{P Q}$ is a diameter of $\gamma$, she moves along either semicircle. Determine the maximal possible sum of the lengths of the 2022 arcs which Bunbun traveled, over all possible labellings of the 2022 points.
|
Replacing 2022 with $2 n$, the answer is $2 n^{2}-2 n+2$. (When $n=1011$, the number is 2042222.)  【 Construction. The construction for $n=5$ shown on the left half of the figure easily generalizes for all $n$. Remark. The validity of this construction can also be seen from the below proof. ब First proof of bound. Let $d_{i}$ be the shorter distance from $A_{2 i-1}$ to $A_{2 i+1}$. Claim - The distance of the leg of the journey $A_{2 i-1} \rightarrow A_{2 i} \rightarrow A_{2 i+1}$ is at most $2 n-d_{i}$. That means the total distance is at most $$ \sum_{i=1}^{n}\left(2 n-d_{i}\right)=2 n^{2}-\left(d_{1}+d_{2}+\cdots+d_{n}\right) $$ Claim - We have $$ d_{1}+d_{2}+\cdots+d_{n} \geq 2 n-2 $$
|
2 n^{2}-2 n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 2022 equally spaced points on a circular track $\gamma$ of circumference 2022. The points are labeled $A_{1}, A_{2}, \ldots, A_{2022}$ in some order, each label used once. Initially, Bunbun the Bunny begins at $A_{1}$. She hops along $\gamma$ from $A_{1}$ to $A_{2}$, then from $A_{2}$ to $A_{3}$, until she reaches $A_{2022}$, after which she hops back to $A_{1}$. When hopping from $P$ to $Q$, she always hops along the shorter of the two $\operatorname{arcs} \overparen{P Q}$ of $\gamma$; if $\overline{P Q}$ is a diameter of $\gamma$, she moves along either semicircle. Determine the maximal possible sum of the lengths of the 2022 arcs which Bunbun traveled, over all possible labellings of the 2022 points.
|
Replacing 2022 with $2 n$, the answer is $2 n^{2}-2 n+2$. (When $n=1011$, the number is 2042222.)  【 Construction. The construction for $n=5$ shown on the left half of the figure easily generalizes for all $n$. Remark. The validity of this construction can also be seen from the below proof. ब First proof of bound. Let $d_{i}$ be the shorter distance from $A_{2 i-1}$ to $A_{2 i+1}$. Claim - The distance of the leg of the journey $A_{2 i-1} \rightarrow A_{2 i} \rightarrow A_{2 i+1}$ is at most $2 n-d_{i}$. That means the total distance is at most $$ \sum_{i=1}^{n}\left(2 n-d_{i}\right)=2 n^{2}-\left(d_{1}+d_{2}+\cdots+d_{n}\right) $$ Claim - We have $$ d_{1}+d_{2}+\cdots+d_{n} \geq 2 n-2 $$
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7a86ff7-693c-5864-bd27-99e520e890e5
| 604,377
|
Consider pairs $(f, g)$ of functions from the set of nonnegative integers to itself such that - $f(0) \geq f(1) \geq f(2) \geq \cdots \geq f(300) \geq 0 ;$ - $f(0)+f(1)+f(2)+\cdots+f(300) \leq 300$; - for any 20 nonnegative integers $n_{1}, n_{2}, \ldots, n_{20}$, not necessarily distinct, we have $$ g\left(n_{1}+n_{2}+\cdots+n_{20}\right) \leq f\left(n_{1}\right)+f\left(n_{2}\right)+\cdots+f\left(n_{20}\right) . $$ Determine the maximum possible value of $g(0)+g(1)+\cdots+g(6000)$ over all such pairs of functions.
|
Replace $300=\frac{24 \cdot 25}{2}$ with $\frac{s(s+1)}{2}$ where $s=24$, and 20 with $k$. The answer is $115440=$ $\frac{k s(k s+1)}{2}$. Equality is achieved at $f(n)=\max (s-n, 0)$ and $g(n)=\max (k s-n, 0)$. To prove $$ g\left(n_{1}+\cdots+n_{k}\right) \leq f\left(n_{1}\right)+\cdots+f\left(n_{k}\right) $$ write it as $$ \max \left(x_{1}+\cdots+x_{k}, 0\right) \leq \max \left(x_{1}, 0\right)+\cdots+\max \left(x_{k}, 0\right) $$ with $x_{i}=s-n_{i}$. This can be proven from the $k=2$ case and induction. It remains to show the upper bound. For this problem, define a partition to be a nonincreasing function $p: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}_{\geq 0}$ such that $p(n)=0$ for some $n$. The sum of $p$ is defined to be $\sum_{n=0}^{\infty} p(n)$, which is finite under the previous assumption. Let $L=\mathbb{Z}_{\geq 0}^{2}$. The Young diagram of the partition is the set of points $$ \mathcal{P}:=\{(x, y) \in L: y<p(x)\} . $$ The number of points in $\mathcal{P}$ is equal to the sum of $p$. The conjugate of a partition defined as $$ p_{*}(n)=\text { the number of } i \text { for which } p(i)>n \text {. } $$ This is a partition with the same sum as $p$. Geometrically, the Young diagrams of $p$ and $p_{*}$ are reflections about $x=y$. Since each $g(n)$ is independent, we may maximize each one separately for all $n$ and assume that $$ g(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f\left(n_{1}\right)+\cdots+f\left(n_{k}\right)\right) . $$ The conditions of the problem statement imply that $f\left(\frac{s(s+1)}{2}\right)=0$. Then, for any $n \leq k \frac{s(s+1)}{2}$, there exists an optimal combination $\left(n_{1}, \ldots, n_{k}\right)$ in $\left(^{*}\right)$ where all $n_{i}$ are at most $\frac{s(s+1)}{2}$, by replacing any term in an optimum greater than $\frac{s(s+1)}{2}$ by $\frac{s(s+1)}{2}$ and shifting the excess to smaller terms (because $f$ is nonincreasing). Therefore we may extend $f$ to a partition by letting $f(n)=0$ for $n>\frac{s(s+1)}{2}$ without affecting the relevant values of $g$. Then $\left(^{*}\right)$ implies that $g$ is a partition as well. The problem can be restated as follows: $f$ is a partition with sum $\frac{s(s+1)}{2}$, and $g$ is a partition defined by $\left(^{*}\right)$. Find the maximum possible sum of $g$. The key claim is that the problem is the same under conjugation. Claim - Under these conditions, we have $$ g_{*}(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f_{*}\left(n_{1}\right)+\cdots+f_{*}\left(n_{k}\right)\right) . $$ $$ \overline{\mathcal{G}}=\underbrace{\overline{\mathcal{F}}+\cdots+\overline{\mathcal{F}}}_{k \overline{\mathcal{F}}^{\prime} \mathrm{s}} $$ where + denotes set addition. This definition remains invariant under reflection about $x=y$, which swaps $f$ and $g$ with their conjugates. Let $A$ be the sum of $g$. We now derive different bounds on $A$. First, by Hermite's identity $$ n=\sum_{i=0}^{k-1}\left\lfloor\frac{n+i}{k}\right\rfloor $$ we have $$ \begin{aligned} A & =\sum_{n=0}^{\infty} g(n) \\ & \leq \sum_{n=0}^{\infty} \sum_{i=0}^{k-1} f\left(\left\lfloor\frac{n+i}{k}\right\rfloor\right) \\ & =k^{2} \sum_{n=0}^{\infty} f(n)-\frac{k(k-1)}{2} f(0) \\ & =k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) . \end{aligned} $$ By the claim, we also get the second bound $A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0)$. For the third bound, note that $f\left(f_{*}(0)\right)=0$ and thus $g\left(k f_{*}(0)\right)=0$. Moreover, $$ g\left(q f_{*}(0)+r\right) \leq q \cdot f\left(f_{*}(0)\right)+(k-q-1) f(0)+f(r)=(k-q-1) f(0)+f(r), $$ so we have $$ \begin{aligned} A & =\sum_{\substack{0 \leq q<k \\ 0 \leq r<f_{*}(0)}} g\left(q f_{*}(0)+r\right) \\ & \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \sum_{0 \leq r<f_{*}(0)} f(r) \\ & =\frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} . \end{aligned} $$ Now we have three cases: - If $f(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) \leq \frac{k s(k s+1)}{2} $$ - If $f_{*}(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0) \leq \frac{k s(k s+1)}{2} $$ - Otherwise, $f(0) f_{*}(0) \leq s^{2}$ and $$ A \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} \leq \frac{k s(k s+1)}{2} $$ In all cases, $A \leq \frac{k s(k s+1)}{2}$, as desired. Remark. One can estimate the answer to be around $k^{2} \frac{s(s+1)}{2}$ by observing the set addition operation "dilates" $\mathcal{F}$ by a factor of $k$, but significant care is needed to sharpen the bound.
|
115440
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider pairs $(f, g)$ of functions from the set of nonnegative integers to itself such that - $f(0) \geq f(1) \geq f(2) \geq \cdots \geq f(300) \geq 0 ;$ - $f(0)+f(1)+f(2)+\cdots+f(300) \leq 300$; - for any 20 nonnegative integers $n_{1}, n_{2}, \ldots, n_{20}$, not necessarily distinct, we have $$ g\left(n_{1}+n_{2}+\cdots+n_{20}\right) \leq f\left(n_{1}\right)+f\left(n_{2}\right)+\cdots+f\left(n_{20}\right) . $$ Determine the maximum possible value of $g(0)+g(1)+\cdots+g(6000)$ over all such pairs of functions.
|
Replace $300=\frac{24 \cdot 25}{2}$ with $\frac{s(s+1)}{2}$ where $s=24$, and 20 with $k$. The answer is $115440=$ $\frac{k s(k s+1)}{2}$. Equality is achieved at $f(n)=\max (s-n, 0)$ and $g(n)=\max (k s-n, 0)$. To prove $$ g\left(n_{1}+\cdots+n_{k}\right) \leq f\left(n_{1}\right)+\cdots+f\left(n_{k}\right) $$ write it as $$ \max \left(x_{1}+\cdots+x_{k}, 0\right) \leq \max \left(x_{1}, 0\right)+\cdots+\max \left(x_{k}, 0\right) $$ with $x_{i}=s-n_{i}$. This can be proven from the $k=2$ case and induction. It remains to show the upper bound. For this problem, define a partition to be a nonincreasing function $p: \mathbb{Z}_{\geq 0} \rightarrow \mathbb{Z}_{\geq 0}$ such that $p(n)=0$ for some $n$. The sum of $p$ is defined to be $\sum_{n=0}^{\infty} p(n)$, which is finite under the previous assumption. Let $L=\mathbb{Z}_{\geq 0}^{2}$. The Young diagram of the partition is the set of points $$ \mathcal{P}:=\{(x, y) \in L: y<p(x)\} . $$ The number of points in $\mathcal{P}$ is equal to the sum of $p$. The conjugate of a partition defined as $$ p_{*}(n)=\text { the number of } i \text { for which } p(i)>n \text {. } $$ This is a partition with the same sum as $p$. Geometrically, the Young diagrams of $p$ and $p_{*}$ are reflections about $x=y$. Since each $g(n)$ is independent, we may maximize each one separately for all $n$ and assume that $$ g(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f\left(n_{1}\right)+\cdots+f\left(n_{k}\right)\right) . $$ The conditions of the problem statement imply that $f\left(\frac{s(s+1)}{2}\right)=0$. Then, for any $n \leq k \frac{s(s+1)}{2}$, there exists an optimal combination $\left(n_{1}, \ldots, n_{k}\right)$ in $\left(^{*}\right)$ where all $n_{i}$ are at most $\frac{s(s+1)}{2}$, by replacing any term in an optimum greater than $\frac{s(s+1)}{2}$ by $\frac{s(s+1)}{2}$ and shifting the excess to smaller terms (because $f$ is nonincreasing). Therefore we may extend $f$ to a partition by letting $f(n)=0$ for $n>\frac{s(s+1)}{2}$ without affecting the relevant values of $g$. Then $\left(^{*}\right)$ implies that $g$ is a partition as well. The problem can be restated as follows: $f$ is a partition with sum $\frac{s(s+1)}{2}$, and $g$ is a partition defined by $\left(^{*}\right)$. Find the maximum possible sum of $g$. The key claim is that the problem is the same under conjugation. Claim - Under these conditions, we have $$ g_{*}(n)=\min _{n_{1}+\cdots+n_{k}=n}\left(f_{*}\left(n_{1}\right)+\cdots+f_{*}\left(n_{k}\right)\right) . $$ $$ \overline{\mathcal{G}}=\underbrace{\overline{\mathcal{F}}+\cdots+\overline{\mathcal{F}}}_{k \overline{\mathcal{F}}^{\prime} \mathrm{s}} $$ where + denotes set addition. This definition remains invariant under reflection about $x=y$, which swaps $f$ and $g$ with their conjugates. Let $A$ be the sum of $g$. We now derive different bounds on $A$. First, by Hermite's identity $$ n=\sum_{i=0}^{k-1}\left\lfloor\frac{n+i}{k}\right\rfloor $$ we have $$ \begin{aligned} A & =\sum_{n=0}^{\infty} g(n) \\ & \leq \sum_{n=0}^{\infty} \sum_{i=0}^{k-1} f\left(\left\lfloor\frac{n+i}{k}\right\rfloor\right) \\ & =k^{2} \sum_{n=0}^{\infty} f(n)-\frac{k(k-1)}{2} f(0) \\ & =k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) . \end{aligned} $$ By the claim, we also get the second bound $A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0)$. For the third bound, note that $f\left(f_{*}(0)\right)=0$ and thus $g\left(k f_{*}(0)\right)=0$. Moreover, $$ g\left(q f_{*}(0)+r\right) \leq q \cdot f\left(f_{*}(0)\right)+(k-q-1) f(0)+f(r)=(k-q-1) f(0)+f(r), $$ so we have $$ \begin{aligned} A & =\sum_{\substack{0 \leq q<k \\ 0 \leq r<f_{*}(0)}} g\left(q f_{*}(0)+r\right) \\ & \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \sum_{0 \leq r<f_{*}(0)} f(r) \\ & =\frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} . \end{aligned} $$ Now we have three cases: - If $f(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f(0) \leq \frac{k s(k s+1)}{2} $$ - If $f_{*}(0) \geq s$ then $$ A \leq k^{2} \frac{s(s+1)}{2}-\frac{k(k-1)}{2} f_{*}(0) \leq \frac{k s(k s+1)}{2} $$ - Otherwise, $f(0) f_{*}(0) \leq s^{2}$ and $$ A \leq \frac{k(k-1)}{2} f_{*}(0) f(0)+k \frac{s(s+1)}{2} \leq \frac{k s(k s+1)}{2} $$ In all cases, $A \leq \frac{k s(k s+1)}{2}$, as desired. Remark. One can estimate the answer to be around $k^{2} \frac{s(s+1)}{2}$ by observing the set addition operation "dilates" $\mathcal{F}$ by a factor of $k$, but significant care is needed to sharpen the bound.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
ba51ab8e-b968-5987-a105-7f4a6d229baf
| 604,472
|
Let $m$ and $n$ be fixed positive integers. Tsvety and Freyja play a game on an infinite grid of unit square cells. Tsvety has secretly written a real number inside of each cell so that the sum of the numbers within every rectangle of size either $m \times n$ or $n \times m$ is zero. Freyja wants to learn all of these numbers. One by one, Freyja asks Tsvety about some cell in the grid, and Tsvety truthfully reveals what number is written in it. Freyja wins if, at any point, Freyja can simultaneously deduce the number written in every cell of the entire infinite grid. (If this never occurs, Freyja has lost the game and Tsvety wins.) In terms of $m$ and $n$, find the smallest number of questions that Freyja must ask to win, or show that no finite number of questions can suffice.
|
The answer is the following: - If $\operatorname{gcd}(m, n)>1$, then Freyja cannot win. - If $\operatorname{gcd}(m, n)=1$, then Freyja can win in a minimum of $(m-1)^{2}+(n-1)^{2}$ questions. First, we dispose of the case where $\operatorname{gcd}(m, n)>1$. Write $d=\operatorname{gcd}(m, n)$. The idea is that any labeling where each $1 \times d$ rectangle has sum zero is valid. Thus, to learn the labeling, Freyja must ask at least one question in every row, which is clearly not possible in a finite number of questions. Now suppose $\operatorname{gcd}(m, n)=1$. We split the proof into two halves. 【 Lower bound. Clearly, any labeling where each $m \times 1$ and $1 \times m$ rectangle has sum zero is valid. These labelings form a vector space with dimension $(m-1)^{2}$, by inspection. (Set the values in an $(m-1) \times(m-1)$ square arbitrarily and every other value is uniquely determined.) Similarly, labelings where each $n \times 1$ and $1 \times n$ rectangle have sum zero are also valid, and have dimension $(n-1)^{2}$. It is also easy to see that no labeling other than the all-zero labeling belongs to both categories; labelings in the first space are periodic in both directions with period $m$, while labelings in the second space are periodic in both directions with period $n$; and hence any labeling in both categories must be constant, ergo all-zero. Taking sums of these labelings gives a space of valid labelings of dimension $(m-1)^{2}+$ $(n-1)^{2}$. Thus, Freyja needs at least $(m-1)^{2}+(n-1)^{2}$ questions to win. Claim (Periodicity) - Any valid labeling is doubly periodic with period $m n$. Then both $m n \times N$ and $m n \times(N+1)$ rectangles have zero sum, so $m n \times 1$ rectangles have zero sum. This implies that any two cells with a vertical displacement of $m n$ are equal; similarly for horizontal displacements. With that in mind, consider a valid labeling. It naturally corresponds to a generating function $$ f(x, y)=\sum_{a=0}^{m n-1} \sum_{b=0}^{m n-1} c_{a, b} x^{a} y^{b} $$ where $c_{a, b}$ is the number in $(a, b)$. The generating function corresponding to sums over $n \times m$ rectangles is $$ f(x, y)\left(1+x+\cdots+x^{m-1}\right)\left(1+y+\cdots+y^{n-1}\right)=f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} . $$ Similarly, the one for $m \times n$ rectangles is $$ f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} . $$ Thus, the constraints for $f$ to be valid are equivalent to $$ f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} \quad \text { and } \quad f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} $$ being zero when reduced modulo $x^{m n}-1$ and $y^{m n}-1$, or, letting $\omega=\exp (2 \pi i / m n)$, both terms being zero when powers of $\omega$ are plugged in. To restate the constraints one final time, we need $$ f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 $$ for all $a, b \in\{0, \ldots, m n-1\}$. Claim - This implies that $f\left(\omega^{a}, \omega^{b}\right)=0$ for all but at most $(m-1)^{2}+(n-1)^{2}$ values of $(a, b) \in\{0, \ldots, m n-1\}^{2}$. $$ \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=\frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 . $$ This happens when (at least) one fraction in either product is zero. - If the first fraction is zero, then either $n \mid a$ and $a>0$, or $m \mid b$ and $b>0$. - If the second fraction is zero, then either $m \mid a$ and $a>0$, or $n \mid b$ and $b>0$. If the first condition holds in both cases, then $m n \mid a$, but $0<a<m n$, a contradiction. Thus if $n \mid a$, then we must have $n \mid b$, and similarly if $m \mid a$ then $m \mid b$. The former case happens $(m-1)^{2}$ times, and the latter case happens $(n-1)^{2}$ times. Thus, at most $(m-1)^{2}+(n-1)^{2}$ values of $f\left(\omega^{a}, \omega^{b}\right)$ are nonzero. Claim - The $(m n)^{2}$ equations $f\left(\omega^{a}, \omega^{b}\right)=0$ are linearly independent when viewed as linear equations in $(m n)^{2}$ variables $c_{a, b}$. Hence, any subset of these equations is also linearly independent. It follows that the dimension of the space of valid labelings is at most $(m-1)^{2}+(n-1)^{2}$, as desired. T Explicit version of winning algorithm by Freyja, from author. Suppose that $\operatorname{gcd}(m, n)=1$ and $m \leq n$. Let $[a, b]$ denote the set of integers between $a$ and $b$ inclusive. Let Freyja ask about all cells $(x, y)$ in the two squares $$ \begin{aligned} & S_{1}=[1, m-1] \times[1, m-1] \\ & S_{2}=[m, m+n-2] \times[1, n-1] . \end{aligned} $$ In the beginning, one by one, Freyja determines all values inside of the rectangle $Q:=$ $[1, m-1] \times[m, n-1]$. To that end, on each step she considers some rectangle with $m$ rows and $n$ columns such that its top left corner is in $Q$ and all of the other values in it have been determined already. In this way, Freyja uncovers all of $Q$, starting with its lower right corner and then proceeding upwards and to the left. Thus Freyja can learn all numbers inside of the rectangle $$ R:=[1, m+n-2] \times[1, n-1]=Q \cup S_{1} \cup S_{2} . $$ See the figure below for an illustration for $(m, n)=(5,8)$. The first cell of $Q$ is uncovered using the dotted green rectangle.  We need one lemma: ## Lemma Let $m$ and $n$ be positive integers with $\operatorname{gcd}(m, n)=1$. Consider an unknown sequence of real numbers $z_{1}, z_{2}, \ldots, z_{s}$ with $s \geq m+n-2$. Suppose that we know the sums of all contiguous blocks of size either $m$ or $n$ in this sequence. Then we can determine all individual entries in the sequence as well. Let $T$ be the rectangle $[1, m+n-2] \times\{n\}$. By looking at appropriate rectangles of sizes $m \times n$ and $n \times m$ such that their top row is contained within $T$ and all of their other rows are contained within $R$, Freyja can learn the sums of all contiguous blocks of values of sizes $m$ and $n$ within $T$. By the Lemma, it follows that Freyja can uncover all of $T$. In this way, with the help of the Lemma, Freyja can extend her rectangular area of knowledge both upwards and downwards. Once its height reaches $m+n-2$, by the same method she will be able to extend it to the left and right as well. This allows Freyja to determine all values in the grid. Therefore, $(m-1)^{2}+(n-1)^{2}$ questions are indeed sufficient. Let $m$ and $n$ be relatively prime positive integers. Consider an infinite grid of unit square cells coloured in such a way that every rectangle of size either $m \times n$ or $n \times m$ contains the same multiset of colours. Then the colouring is either doubly periodic with period length $m$ or doubly periodic with period length $n$. (Here, "doubly periodic with period length $s$ " means "both horizontally and vertically periodic with period length $s$ ".) $$ f_{i j}(x, y):=\left\{\begin{array}{rll} +1 & \text { when }(x, y) \equiv(0,0) \text { or }(i, j) & (\bmod m) ; \\ -1 & \text { when }(x, y) \equiv(0, j) \text { or }(i, 0) & (\bmod m) ; \text { and } \\ 0 & \text { otherwise. } \end{array}\right. $$ Define $g_{i, j}$ similarly, but with $1 \leq i, j \leq n-1$ and " $\bmod m$ " everywhere replaced by " $\bmod$ $n$ ". First we show that if a linear combination $h:=\sum \alpha_{i, j} f_{i, j}+\sum \beta_{i, j} g_{i, j}$ of the $f_{i, j}$ and $g_{i, j}$ contains only two distinct values, then either all of the $\alpha_{i, j}$ vanish or all of the $\beta_{i, j}$ do. It follows that each colour, considered in isolation, is either doubly periodic with period length $m$ or doubly periodic with period length $n$. Finally, we check that different period lengths cannot mix. On the other hand, if $m$ and $n$ are not relatively prime, then there exist infinitely many non-isomorphic valid colourings. Furthermore, when $\operatorname{gcd}(m, n)=2$, there exist valid colourings which are not horizontally periodic; and, when $\operatorname{gcd}(m, n) \geq 3$, there exist valid colourings which are neither horizontally nor vertically periodic.
|
(m-1)^{2}+(n-1)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ and $n$ be fixed positive integers. Tsvety and Freyja play a game on an infinite grid of unit square cells. Tsvety has secretly written a real number inside of each cell so that the sum of the numbers within every rectangle of size either $m \times n$ or $n \times m$ is zero. Freyja wants to learn all of these numbers. One by one, Freyja asks Tsvety about some cell in the grid, and Tsvety truthfully reveals what number is written in it. Freyja wins if, at any point, Freyja can simultaneously deduce the number written in every cell of the entire infinite grid. (If this never occurs, Freyja has lost the game and Tsvety wins.) In terms of $m$ and $n$, find the smallest number of questions that Freyja must ask to win, or show that no finite number of questions can suffice.
|
The answer is the following: - If $\operatorname{gcd}(m, n)>1$, then Freyja cannot win. - If $\operatorname{gcd}(m, n)=1$, then Freyja can win in a minimum of $(m-1)^{2}+(n-1)^{2}$ questions. First, we dispose of the case where $\operatorname{gcd}(m, n)>1$. Write $d=\operatorname{gcd}(m, n)$. The idea is that any labeling where each $1 \times d$ rectangle has sum zero is valid. Thus, to learn the labeling, Freyja must ask at least one question in every row, which is clearly not possible in a finite number of questions. Now suppose $\operatorname{gcd}(m, n)=1$. We split the proof into two halves. 【 Lower bound. Clearly, any labeling where each $m \times 1$ and $1 \times m$ rectangle has sum zero is valid. These labelings form a vector space with dimension $(m-1)^{2}$, by inspection. (Set the values in an $(m-1) \times(m-1)$ square arbitrarily and every other value is uniquely determined.) Similarly, labelings where each $n \times 1$ and $1 \times n$ rectangle have sum zero are also valid, and have dimension $(n-1)^{2}$. It is also easy to see that no labeling other than the all-zero labeling belongs to both categories; labelings in the first space are periodic in both directions with period $m$, while labelings in the second space are periodic in both directions with period $n$; and hence any labeling in both categories must be constant, ergo all-zero. Taking sums of these labelings gives a space of valid labelings of dimension $(m-1)^{2}+$ $(n-1)^{2}$. Thus, Freyja needs at least $(m-1)^{2}+(n-1)^{2}$ questions to win. Claim (Periodicity) - Any valid labeling is doubly periodic with period $m n$. Then both $m n \times N$ and $m n \times(N+1)$ rectangles have zero sum, so $m n \times 1$ rectangles have zero sum. This implies that any two cells with a vertical displacement of $m n$ are equal; similarly for horizontal displacements. With that in mind, consider a valid labeling. It naturally corresponds to a generating function $$ f(x, y)=\sum_{a=0}^{m n-1} \sum_{b=0}^{m n-1} c_{a, b} x^{a} y^{b} $$ where $c_{a, b}$ is the number in $(a, b)$. The generating function corresponding to sums over $n \times m$ rectangles is $$ f(x, y)\left(1+x+\cdots+x^{m-1}\right)\left(1+y+\cdots+y^{n-1}\right)=f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} . $$ Similarly, the one for $m \times n$ rectangles is $$ f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} . $$ Thus, the constraints for $f$ to be valid are equivalent to $$ f(x, y) \cdot \frac{x^{m}-1}{x-1} \cdot \frac{y^{n}-1}{y-1} \quad \text { and } \quad f(x, y) \cdot \frac{x^{n}-1}{x-1} \cdot \frac{y^{m}-1}{y-1} $$ being zero when reduced modulo $x^{m n}-1$ and $y^{m n}-1$, or, letting $\omega=\exp (2 \pi i / m n)$, both terms being zero when powers of $\omega$ are plugged in. To restate the constraints one final time, we need $$ f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=f\left(\omega^{a}, \omega^{b}\right) \cdot \frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 $$ for all $a, b \in\{0, \ldots, m n-1\}$. Claim - This implies that $f\left(\omega^{a}, \omega^{b}\right)=0$ for all but at most $(m-1)^{2}+(n-1)^{2}$ values of $(a, b) \in\{0, \ldots, m n-1\}^{2}$. $$ \frac{\omega^{a m}-1}{\omega^{a}-1} \cdot \frac{\omega^{b n}-1}{\omega^{b}-1}=\frac{\omega^{a n}-1}{\omega^{a}-1} \cdot \frac{\omega^{b m}-1}{\omega^{b}-1}=0 . $$ This happens when (at least) one fraction in either product is zero. - If the first fraction is zero, then either $n \mid a$ and $a>0$, or $m \mid b$ and $b>0$. - If the second fraction is zero, then either $m \mid a$ and $a>0$, or $n \mid b$ and $b>0$. If the first condition holds in both cases, then $m n \mid a$, but $0<a<m n$, a contradiction. Thus if $n \mid a$, then we must have $n \mid b$, and similarly if $m \mid a$ then $m \mid b$. The former case happens $(m-1)^{2}$ times, and the latter case happens $(n-1)^{2}$ times. Thus, at most $(m-1)^{2}+(n-1)^{2}$ values of $f\left(\omega^{a}, \omega^{b}\right)$ are nonzero. Claim - The $(m n)^{2}$ equations $f\left(\omega^{a}, \omega^{b}\right)=0$ are linearly independent when viewed as linear equations in $(m n)^{2}$ variables $c_{a, b}$. Hence, any subset of these equations is also linearly independent. It follows that the dimension of the space of valid labelings is at most $(m-1)^{2}+(n-1)^{2}$, as desired. T Explicit version of winning algorithm by Freyja, from author. Suppose that $\operatorname{gcd}(m, n)=1$ and $m \leq n$. Let $[a, b]$ denote the set of integers between $a$ and $b$ inclusive. Let Freyja ask about all cells $(x, y)$ in the two squares $$ \begin{aligned} & S_{1}=[1, m-1] \times[1, m-1] \\ & S_{2}=[m, m+n-2] \times[1, n-1] . \end{aligned} $$ In the beginning, one by one, Freyja determines all values inside of the rectangle $Q:=$ $[1, m-1] \times[m, n-1]$. To that end, on each step she considers some rectangle with $m$ rows and $n$ columns such that its top left corner is in $Q$ and all of the other values in it have been determined already. In this way, Freyja uncovers all of $Q$, starting with its lower right corner and then proceeding upwards and to the left. Thus Freyja can learn all numbers inside of the rectangle $$ R:=[1, m+n-2] \times[1, n-1]=Q \cup S_{1} \cup S_{2} . $$ See the figure below for an illustration for $(m, n)=(5,8)$. The first cell of $Q$ is uncovered using the dotted green rectangle.  We need one lemma: ## Lemma Let $m$ and $n$ be positive integers with $\operatorname{gcd}(m, n)=1$. Consider an unknown sequence of real numbers $z_{1}, z_{2}, \ldots, z_{s}$ with $s \geq m+n-2$. Suppose that we know the sums of all contiguous blocks of size either $m$ or $n$ in this sequence. Then we can determine all individual entries in the sequence as well. Let $T$ be the rectangle $[1, m+n-2] \times\{n\}$. By looking at appropriate rectangles of sizes $m \times n$ and $n \times m$ such that their top row is contained within $T$ and all of their other rows are contained within $R$, Freyja can learn the sums of all contiguous blocks of values of sizes $m$ and $n$ within $T$. By the Lemma, it follows that Freyja can uncover all of $T$. In this way, with the help of the Lemma, Freyja can extend her rectangular area of knowledge both upwards and downwards. Once its height reaches $m+n-2$, by the same method she will be able to extend it to the left and right as well. This allows Freyja to determine all values in the grid. Therefore, $(m-1)^{2}+(n-1)^{2}$ questions are indeed sufficient. Let $m$ and $n$ be relatively prime positive integers. Consider an infinite grid of unit square cells coloured in such a way that every rectangle of size either $m \times n$ or $n \times m$ contains the same multiset of colours. Then the colouring is either doubly periodic with period length $m$ or doubly periodic with period length $n$. (Here, "doubly periodic with period length $s$ " means "both horizontally and vertically periodic with period length $s$ ".) $$ f_{i j}(x, y):=\left\{\begin{array}{rll} +1 & \text { when }(x, y) \equiv(0,0) \text { or }(i, j) & (\bmod m) ; \\ -1 & \text { when }(x, y) \equiv(0, j) \text { or }(i, 0) & (\bmod m) ; \text { and } \\ 0 & \text { otherwise. } \end{array}\right. $$ Define $g_{i, j}$ similarly, but with $1 \leq i, j \leq n-1$ and " $\bmod m$ " everywhere replaced by " $\bmod$ $n$ ". First we show that if a linear combination $h:=\sum \alpha_{i, j} f_{i, j}+\sum \beta_{i, j} g_{i, j}$ of the $f_{i, j}$ and $g_{i, j}$ contains only two distinct values, then either all of the $\alpha_{i, j}$ vanish or all of the $\beta_{i, j}$ do. It follows that each colour, considered in isolation, is either doubly periodic with period length $m$ or doubly periodic with period length $n$. Finally, we check that different period lengths cannot mix. On the other hand, if $m$ and $n$ are not relatively prime, then there exist infinitely many non-isomorphic valid colourings. Furthermore, when $\operatorname{gcd}(m, n)=2$, there exist valid colourings which are not horizontally periodic; and, when $\operatorname{gcd}(m, n) \geq 3$, there exist valid colourings which are neither horizontally nor vertically periodic.
|
{
"resource_path": "USA_TST/segmented/en-sols-TST-IMO-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
5c33b434-b4c0-5b8c-9a6b-09443ecefcde
| 604,500
|
Given a set $S$ of $n$ variables, a binary operation $\times$ on $S$ is called simple if it satisfies $(x \times y) \times z=x \times(y \times z)$ for all $x, y, z \in S$ and $x \times y \in\{x, y\}$ for all $x, y \in S$. Given a simple operation $\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \rightarrow x \times(y \times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.
|
The answer is $(n!)^{2}$. In fact it is possible to essentially find all $x$ : one assigns a real number to each variable in $S$. Then $x \times y$ takes the larger of $\{x, y\}$, and in the event of a tie picks either "left" or "right", where the choice of side is fixed among elements of each size. 【 First solution (Steven Hao). The main trick is the two lemmas, which are not hard to show (and are motivated by our conjecture). $$ \begin{aligned} x x & =x \\ x y x z x & =x y z x . \end{aligned} $$ Consequently, define a double rainbow to be the concatenation of two full strings of length $n$, of which there are $(n!)^{2}$. We claim that these form equivalence classes for $T$. To see that any string $s$ is equivalent to a double rainbow, note that $s=s s$, and hence using the second identity above repeatedly lets us reduce ss to a double rainbow. To see two distinct double rainbows $R_{1}$ and $R_{2}$ aren't equivalent, one can use the construction mentioned in the beginning. Specifically, take two variables $a$ and $b$ which do not appear in the same order in $R_{1}$ and $R_{2}$. Then it's not hard to see that $a b a b, a b b a$, $b a a b, b a b a$ are pairwise non-equivalent by choosing "left" or "right" appropriately. Now construct $\times$ on the whole set by having $a$ and $b$ be the largest variables, so the rest of the variables don't matter in the evaluation of the string.
|
(n!)^2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given a set $S$ of $n$ variables, a binary operation $\times$ on $S$ is called simple if it satisfies $(x \times y) \times z=x \times(y \times z)$ for all $x, y, z \in S$ and $x \times y \in\{x, y\}$ for all $x, y \in S$. Given a simple operation $\times$ on $S$, any string of elements in $S$ can be reduced to a single element, such as $x y z \rightarrow x \times(y \times z)$. A string of variables in $S$ is called full if it contains each variable in $S$ at least once, and two strings are equivalent if they evaluate to the same variable regardless of which simple $\times$ is chosen. For example $x x x, x x$, and $x$ are equivalent, but these are only full if $n=1$. Suppose $T$ is a set of full strings such that any full string is equivalent to exactly one element of $T$. Determine the number of elements of $T$.
|
The answer is $(n!)^{2}$. In fact it is possible to essentially find all $x$ : one assigns a real number to each variable in $S$. Then $x \times y$ takes the larger of $\{x, y\}$, and in the event of a tie picks either "left" or "right", where the choice of side is fixed among elements of each size. 【 First solution (Steven Hao). The main trick is the two lemmas, which are not hard to show (and are motivated by our conjecture). $$ \begin{aligned} x x & =x \\ x y x z x & =x y z x . \end{aligned} $$ Consequently, define a double rainbow to be the concatenation of two full strings of length $n$, of which there are $(n!)^{2}$. We claim that these form equivalence classes for $T$. To see that any string $s$ is equivalent to a double rainbow, note that $s=s s$, and hence using the second identity above repeatedly lets us reduce ss to a double rainbow. To see two distinct double rainbows $R_{1}$ and $R_{2}$ aren't equivalent, one can use the construction mentioned in the beginning. Specifically, take two variables $a$ and $b$ which do not appear in the same order in $R_{1}$ and $R_{2}$. Then it's not hard to see that $a b a b, a b b a$, $b a a b, b a b a$ are pairwise non-equivalent by choosing "left" or "right" appropriately. Now construct $\times$ on the whole set by having $a$ and $b$ be the largest variables, so the rest of the variables don't matter in the evaluation of the string.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2012.jsonl",
"problem_match": null,
"solution_match": null
}
|
70867c63-6170-5efd-b6dd-c3a6bc9cd3c1
| 247,013
|
A finite sequence of integers $a_{1}, a_{2}, \ldots, a_{n}$ is called regular if there exists a real number $x$ satisfying $$ \lfloor k x\rfloor=a_{k} \quad \text { for } 1 \leq k \leq n $$ Given a regular sequence $a_{1}, a_{2}, \ldots, a_{n}$, for $1 \leq k \leq n$ we say that the term $a_{k}$ is forced if the following condition is satisfied: the sequence $$ a_{1}, a_{2}, \ldots, a_{k-1}, b $$ is regular if and only if $b=a_{k}$. Find the maximum possible number of forced terms in a regular sequence with 1000 terms.
|
The answer is 985 . WLOG, by shifting $a_{1}=0$ (clearly $a_{1}$ isn't forced). Now, we construct regular sequences inductively using the following procedure. Start with the inequality $$ \frac{0}{1} \leq x<\frac{1}{1} $$ Then for each $k=2,3, \ldots, 1000$ we perform the following procedure. If there is no fraction of the form $F=\frac{m}{k}$ in the interval $A \leq x<B$, then $a_{k}$ is forced, and the interval of possible $x$ values does not change. Otherwise, $a_{k}$ is not forced, and we pick a value of $a_{k}$ and update the interval accordingly. The theory of Farey sequences tells us that when we have a stage $\frac{a}{b} \leq x<\frac{c}{d}$ then the next time we will find a fraction in that interval is exactly $\frac{a+c}{b+d}$ (at time $k=b+d$ ), and it will be the only such fraction. So essentially, starting with $\frac{0}{1} \leq x<\frac{1}{1}$ we repeatedly replace one of the endpoints of the intervals with the mediant, until one of the denominators exceeds 1000; we are trying to minimize the number of non-forced terms, which is the number of denominators that appear in this process. It is not hard to see that this optimum occurs by always replacing the smaller of the denominators, so that the sequence is $\frac{0}{1} \leq x<\frac{1}{1}$ $\frac{0}{1} \leq x<\frac{1}{2}$ $\frac{1}{3} \leq x<\frac{1}{2}$ $\frac{1}{3} \leq x<\frac{2}{5}$ $\frac{3}{8} \leq x<\frac{2}{5}$ $\frac{3}{8} \leq x<\frac{5}{13}$ and so on; we see that the non-forced terms in this optimal configuration are exactly the Fibonacci numbers. There are 15 Fibonacci numbers less than 1000, hence the answer $1000-15=985$.
|
985
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A finite sequence of integers $a_{1}, a_{2}, \ldots, a_{n}$ is called regular if there exists a real number $x$ satisfying $$ \lfloor k x\rfloor=a_{k} \quad \text { for } 1 \leq k \leq n $$ Given a regular sequence $a_{1}, a_{2}, \ldots, a_{n}$, for $1 \leq k \leq n$ we say that the term $a_{k}$ is forced if the following condition is satisfied: the sequence $$ a_{1}, a_{2}, \ldots, a_{k-1}, b $$ is regular if and only if $b=a_{k}$. Find the maximum possible number of forced terms in a regular sequence with 1000 terms.
|
The answer is 985 . WLOG, by shifting $a_{1}=0$ (clearly $a_{1}$ isn't forced). Now, we construct regular sequences inductively using the following procedure. Start with the inequality $$ \frac{0}{1} \leq x<\frac{1}{1} $$ Then for each $k=2,3, \ldots, 1000$ we perform the following procedure. If there is no fraction of the form $F=\frac{m}{k}$ in the interval $A \leq x<B$, then $a_{k}$ is forced, and the interval of possible $x$ values does not change. Otherwise, $a_{k}$ is not forced, and we pick a value of $a_{k}$ and update the interval accordingly. The theory of Farey sequences tells us that when we have a stage $\frac{a}{b} \leq x<\frac{c}{d}$ then the next time we will find a fraction in that interval is exactly $\frac{a+c}{b+d}$ (at time $k=b+d$ ), and it will be the only such fraction. So essentially, starting with $\frac{0}{1} \leq x<\frac{1}{1}$ we repeatedly replace one of the endpoints of the intervals with the mediant, until one of the denominators exceeds 1000; we are trying to minimize the number of non-forced terms, which is the number of denominators that appear in this process. It is not hard to see that this optimum occurs by always replacing the smaller of the denominators, so that the sequence is $\frac{0}{1} \leq x<\frac{1}{1}$ $\frac{0}{1} \leq x<\frac{1}{2}$ $\frac{1}{3} \leq x<\frac{1}{2}$ $\frac{1}{3} \leq x<\frac{2}{5}$ $\frac{3}{8} \leq x<\frac{2}{5}$ $\frac{3}{8} \leq x<\frac{5}{13}$ and so on; we see that the non-forced terms in this optimal configuration are exactly the Fibonacci numbers. There are 15 Fibonacci numbers less than 1000, hence the answer $1000-15=985$.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2013.jsonl",
"problem_match": null,
"solution_match": null
}
|
00caefd7-0a1a-5fa6-8c61-9a5245469bd5
| 604,860
|
Find the maximum number $E$ such that the following holds: there is an edge-colored graph with 60 vertices and $E$ edges, with each edge colored either red or blue, such that in that coloring, there is no monochromatic cycles of length 3 and no monochromatic cycles of length 5 .
|
The answer is $E=30^{2}+2 \cdot 15^{2}=6 \cdot 15^{2}=1350$. First, we prove $E \leq 1350$. Observe that: Claim - $G$ contains no $K_{5}$. Hence by Turán theorem we have $E \leq\binom{ 4}{2} \cdot 15^{2}=1350$. To show this is achievable, take a red $K_{30,30}$, and on each side draw a blue $K_{15,15}$. This graph has no monochromatic odd cycles at all as desired.
|
1350
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the maximum number $E$ such that the following holds: there is an edge-colored graph with 60 vertices and $E$ edges, with each edge colored either red or blue, such that in that coloring, there is no monochromatic cycles of length 3 and no monochromatic cycles of length 5 .
|
The answer is $E=30^{2}+2 \cdot 15^{2}=6 \cdot 15^{2}=1350$. First, we prove $E \leq 1350$. Observe that: Claim - $G$ contains no $K_{5}$. Hence by Turán theorem we have $E \leq\binom{ 4}{2} \cdot 15^{2}=1350$. To show this is achievable, take a red $K_{30,30}$, and on each side draw a blue $K_{15,15}$. This graph has no monochromatic odd cycles at all as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2014.jsonl",
"problem_match": null,
"solution_match": null
}
|
0209c696-7fed-541b-b3be-b22ce3fbdd29
| 85,389
|
Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions: - The frog visits only points in $\left\{1,2, \ldots, 2^{n}-1\right\}$, each at most once. - The length of each hop is in $\left\{2^{0}, 2^{1}, 2^{2}, \ldots\right\}$. (The hops may be either direction, left or right.) Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?
|
We claim the answer is $\frac{4^{n}-1}{3}$. We first prove the bound. First notice that the hop sizes are in $\left\{2^{0}, 2^{1}, \ldots, 2^{n-1}\right\}$, since the frog must stay within bounds the whole time. Let $a_{i}$ be the number of hops of size $2^{i}$ the frog makes, for $0 \leq i \leq n-1$. Claim - For any $k=1, \ldots, n$ we have $$ a_{n-1}+\cdots+a_{n-k} \leq 2^{n}-2^{n-k} $$ Within each fixed residue modulo $2^{m}$, the frog can make at most $\frac{2^{n}}{2^{m}}-1$ large jumps. So the total number of large jumps is at most $2^{m}\left(\frac{2^{n}}{2^{m}}-1\right)=2^{n}-2^{m}$. (As an example, when $n=3$ this means there are at most four hops of length 4 , at most six hops of length 2 or 4 , and at most seven hops total. Of course, if we want to max the length of the hops, we see that we want $a_{2}=4, a_{1}=2, a_{0}=1$, and in general equality is achieved when $a_{m}=2^{m}$ for any $m$.) Now, the total distance the frog travels is $$ S=a_{0}+2 a_{1}+4 a_{2}+\cdots+2^{n-1} a_{n-1} $$ We rewrite using the so-called "summation by parts": $$ \begin{array}{rrrr} S & =a_{0}+a_{1}+a_{2}+ & a_{3}+\ldots+ & a_{n-1} \\ & + & a_{1}+a_{2}+a_{3}+\ldots+ & a_{n-1} \\ & + & 2 a_{2}+2 a_{3}+\ldots+ & 2 a_{n-1} \\ & + & 4 a_{3}+\ldots+ & 4 a_{n-1} \\ & \vdots & \ddots & \vdots \\ & & & \\ + & & & 2^{n-2} a_{n-1} \end{array} $$ Hence $$ \begin{aligned} S & \leq\left(2^{n}-2^{0}\right)+\left(2^{n}-2^{1}\right)+2\left(2^{n}-2^{2}\right)+\cdots+2^{n-2}\left(2^{n}-2^{n-1}\right) \\ & =\frac{4^{n}-1}{3} . \end{aligned} $$ It remains to show that equality can hold. There are many such constructions but most are inductive. Here is one approach. We will construct two family of paths such that there are $2^{k}$ hops of size $2^{k}$, for every $0 \leq k \leq n-1$, and we visit each of $\left\{0, \ldots, 2^{n}-1\right\}$ once, starting on 0 and ending on $x$, for the two values $x \in\left\{1,2^{n}-1\right\}$. The base case $n=1$ is clear. To take a path from 0 to $2^{n+1}-1$. - Take a path on $\left\{0,2,4, \ldots, 2^{n+1}-2\right\}$ starting from 0 and ending on 2 (by inductive hypothesis). - Take a path on $\left\{1,3,5, \ldots, 2^{n+1}-1\right\}$ starting from 1 and ending on $2^{n+1}-1$ (by inductive hypothesis). - Link them together by adding a single jump $2 \rightarrow 1$. The other case is similar, but we route $0 \rightarrow\left(2^{n+1}-2\right) \rightarrow\left(2^{n+1}-1\right) \rightarrow 1$ instead. (This can also be visualized as hopping along a hypercube of binary strings; each inductive step takes two copies of the hypercube and links them together by a single edge.) Remark (Ashwin Sah). The problem can also be altered to ask for the minimum value of the sum of the reciprocals of the hop sizes, where further we stipulate that the frog must hit every point precisely once (to avoid triviality). With a nearly identical proof that also exploits the added condition $a_{0}+\cdots+a_{n-1}=2^{n}-1$, the answer is $n$. This yields a nicer form for the generalization. The natural generalization changes the above problem by replacing $2^{k}$ with $a_{k}$ where $a_{k} \mid a_{k+1}$, so that the interval covered by hops is of size $a_{n}$ and the hop sizes are restricted to the $a_{i}$, where $a_{0}=1$. In this case, similar bounding yields $$ \sum_{i=1}^{2^{n}-1} \frac{1}{b_{k}} \geq \sum_{i=0}^{n-1}\left(\frac{a_{k+1}}{a_{k}}-1\right) $$ Bounds for the total distance traveled happen in the same way as the solution above, and equality for both can be constructed in an analogous fashion.
|
\frac{4^{n}-1}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions: - The frog visits only points in $\left\{1,2, \ldots, 2^{n}-1\right\}$, each at most once. - The length of each hop is in $\left\{2^{0}, 2^{1}, 2^{2}, \ldots\right\}$. (The hops may be either direction, left or right.) Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?
|
We claim the answer is $\frac{4^{n}-1}{3}$. We first prove the bound. First notice that the hop sizes are in $\left\{2^{0}, 2^{1}, \ldots, 2^{n-1}\right\}$, since the frog must stay within bounds the whole time. Let $a_{i}$ be the number of hops of size $2^{i}$ the frog makes, for $0 \leq i \leq n-1$. Claim - For any $k=1, \ldots, n$ we have $$ a_{n-1}+\cdots+a_{n-k} \leq 2^{n}-2^{n-k} $$ Within each fixed residue modulo $2^{m}$, the frog can make at most $\frac{2^{n}}{2^{m}}-1$ large jumps. So the total number of large jumps is at most $2^{m}\left(\frac{2^{n}}{2^{m}}-1\right)=2^{n}-2^{m}$. (As an example, when $n=3$ this means there are at most four hops of length 4 , at most six hops of length 2 or 4 , and at most seven hops total. Of course, if we want to max the length of the hops, we see that we want $a_{2}=4, a_{1}=2, a_{0}=1$, and in general equality is achieved when $a_{m}=2^{m}$ for any $m$.) Now, the total distance the frog travels is $$ S=a_{0}+2 a_{1}+4 a_{2}+\cdots+2^{n-1} a_{n-1} $$ We rewrite using the so-called "summation by parts": $$ \begin{array}{rrrr} S & =a_{0}+a_{1}+a_{2}+ & a_{3}+\ldots+ & a_{n-1} \\ & + & a_{1}+a_{2}+a_{3}+\ldots+ & a_{n-1} \\ & + & 2 a_{2}+2 a_{3}+\ldots+ & 2 a_{n-1} \\ & + & 4 a_{3}+\ldots+ & 4 a_{n-1} \\ & \vdots & \ddots & \vdots \\ & & & \\ + & & & 2^{n-2} a_{n-1} \end{array} $$ Hence $$ \begin{aligned} S & \leq\left(2^{n}-2^{0}\right)+\left(2^{n}-2^{1}\right)+2\left(2^{n}-2^{2}\right)+\cdots+2^{n-2}\left(2^{n}-2^{n-1}\right) \\ & =\frac{4^{n}-1}{3} . \end{aligned} $$ It remains to show that equality can hold. There are many such constructions but most are inductive. Here is one approach. We will construct two family of paths such that there are $2^{k}$ hops of size $2^{k}$, for every $0 \leq k \leq n-1$, and we visit each of $\left\{0, \ldots, 2^{n}-1\right\}$ once, starting on 0 and ending on $x$, for the two values $x \in\left\{1,2^{n}-1\right\}$. The base case $n=1$ is clear. To take a path from 0 to $2^{n+1}-1$. - Take a path on $\left\{0,2,4, \ldots, 2^{n+1}-2\right\}$ starting from 0 and ending on 2 (by inductive hypothesis). - Take a path on $\left\{1,3,5, \ldots, 2^{n+1}-1\right\}$ starting from 1 and ending on $2^{n+1}-1$ (by inductive hypothesis). - Link them together by adding a single jump $2 \rightarrow 1$. The other case is similar, but we route $0 \rightarrow\left(2^{n+1}-2\right) \rightarrow\left(2^{n+1}-1\right) \rightarrow 1$ instead. (This can also be visualized as hopping along a hypercube of binary strings; each inductive step takes two copies of the hypercube and links them together by a single edge.) Remark (Ashwin Sah). The problem can also be altered to ask for the minimum value of the sum of the reciprocals of the hop sizes, where further we stipulate that the frog must hit every point precisely once (to avoid triviality). With a nearly identical proof that also exploits the added condition $a_{0}+\cdots+a_{n-1}=2^{n}-1$, the answer is $n$. This yields a nicer form for the generalization. The natural generalization changes the above problem by replacing $2^{k}$ with $a_{k}$ where $a_{k} \mid a_{k+1}$, so that the interval covered by hops is of size $a_{n}$ and the hop sizes are restricted to the $a_{i}$, where $a_{0}=1$. In this case, similar bounding yields $$ \sum_{i=1}^{2^{n}-1} \frac{1}{b_{k}} \geq \sum_{i=0}^{n-1}\left(\frac{a_{k+1}}{a_{k}}-1\right) $$ Bounds for the total distance traveled happen in the same way as the solution above, and equality for both can be constructed in an analogous fashion.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2018.jsonl",
"problem_match": null,
"solution_match": null
}
|
9005f0b6-2151-5ec9-9d54-cc4beecaa27b
| 605,603
|
Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.
|
The answer is $C=\frac{50}{51}$. The lower bound is obtained if we have 51 coins of value $\frac{1}{51}$ and 49 coins of value 1. (Alternatively, 51 coins of value $1-\frac{\varepsilon}{51}$ and 49 coins of value $\frac{\varepsilon}{49}$ works fine for $\varepsilon>0$.) We now present two (similar) proofs that this $C=\frac{50}{51}$ suffices. 【 First proof (original). Let $a_{1} \leq \cdots \leq a_{100}$ denote the values of the coins in ascending order. Since the 51 coins $a_{50}, \ldots, a_{100}$ are worth at least $51 a_{50}$, it follows that $a_{50} \leq \frac{50}{51}$; likewise $a_{51} \geq \frac{1}{51}$. We claim that choosing the stacks with coin values $$ a_{1}, a_{3}, \ldots, a_{49}, \quad a_{52}, a_{54}, \ldots, a_{100} $$ and $$ a_{2}, a_{4}, \ldots, a_{50}, \quad a_{51}, a_{53}, \ldots, a_{99} $$ works. Let $D$ denote the (possibly negative) difference between the two total values. Then $$ \begin{aligned} D & =\left(a_{1}-a_{2}\right)+\cdots+\left(a_{49}-a_{50}\right)-a_{51}+\left(a_{52}-a_{53}\right)+\cdots+\left(a_{98}-a_{99}\right)+a_{100} \\ & \leq 25 \cdot 0-\frac{1}{51}+24 \cdot 0+1=\frac{50}{51} \end{aligned} $$ Similarly, we have $$ \begin{aligned} D & =a_{1}+\left(a_{3}-a_{2}\right)+\cdots+\left(a_{49}-a_{48}\right)-a_{50}+\left(a_{52}-a_{51}\right)+\cdots+\left(a_{100}-a_{99}\right) \\ & \geq 0+24 \cdot 0-\frac{50}{51}+25 \cdot 0=-\frac{50}{51} \end{aligned} $$ It follows that $|D| \leq \frac{50}{51}$, as required.
|
\frac{50}{51}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider coins with positive real denominations not exceeding 1. Find the smallest $C>0$ such that the following holds: if we are given any 100 such coins with total value 50 , then we can always split them into two stacks of 50 coins each such that the absolute difference between the total values of the two stacks is at most $C$.
|
The answer is $C=\frac{50}{51}$. The lower bound is obtained if we have 51 coins of value $\frac{1}{51}$ and 49 coins of value 1. (Alternatively, 51 coins of value $1-\frac{\varepsilon}{51}$ and 49 coins of value $\frac{\varepsilon}{49}$ works fine for $\varepsilon>0$.) We now present two (similar) proofs that this $C=\frac{50}{51}$ suffices. 【 First proof (original). Let $a_{1} \leq \cdots \leq a_{100}$ denote the values of the coins in ascending order. Since the 51 coins $a_{50}, \ldots, a_{100}$ are worth at least $51 a_{50}$, it follows that $a_{50} \leq \frac{50}{51}$; likewise $a_{51} \geq \frac{1}{51}$. We claim that choosing the stacks with coin values $$ a_{1}, a_{3}, \ldots, a_{49}, \quad a_{52}, a_{54}, \ldots, a_{100} $$ and $$ a_{2}, a_{4}, \ldots, a_{50}, \quad a_{51}, a_{53}, \ldots, a_{99} $$ works. Let $D$ denote the (possibly negative) difference between the two total values. Then $$ \begin{aligned} D & =\left(a_{1}-a_{2}\right)+\cdots+\left(a_{49}-a_{50}\right)-a_{51}+\left(a_{52}-a_{53}\right)+\cdots+\left(a_{98}-a_{99}\right)+a_{100} \\ & \leq 25 \cdot 0-\frac{1}{51}+24 \cdot 0+1=\frac{50}{51} \end{aligned} $$ Similarly, we have $$ \begin{aligned} D & =a_{1}+\left(a_{3}-a_{2}\right)+\cdots+\left(a_{49}-a_{48}\right)-a_{50}+\left(a_{52}-a_{51}\right)+\cdots+\left(a_{100}-a_{99}\right) \\ & \geq 0+24 \cdot 0-\frac{50}{51}+25 \cdot 0=-\frac{50}{51} \end{aligned} $$ It follows that $|D| \leq \frac{50}{51}$, as required.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
7bfbb735-76fb-584d-a156-f603e32ef3a4
| 605,678
|
Let $\mathcal{S}$ be a set of 16 points in the plane, no three collinear. Let $\chi(\mathcal{S})$ denote the number of ways to draw 8 line segments with endpoints in $\mathcal{S}$, such that no two drawn segments intersect, even at endpoints. Find the smallest possible value of $\chi(\mathcal{S})$ across all such $\mathcal{S}$.
|
The answer is 1430 . In general, we prove that with $2 n$ points the answer is the $n^{\text {th }}$ Catalan number $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$. First of all, it is well-known that if $\mathcal{S}$ is a convex $2 n$-gon, then $\chi(\mathcal{S})=C_{n}$. It remains to prove the lower bound. We proceed by (strong) induction on $n$, with the base case $n=0$ and $n=1$ clear. Suppose the statement is proven for $0,1, \ldots, n$ and consider a set $\mathcal{S}$ with $2(n+1)$ points. Let $P$ be a point on the convex hull of $\mathcal{S}$, and label the other $2 n+1$ points $A_{1}, \ldots, A_{2 n+1}$ in order of angle from $P$. Consider drawing a segment $\overline{P A_{2 k+1}}$. This splits the $2 n$ remaining points into two halves $\mathcal{U}$ and $\mathcal{V}$, with $2 k$ and $2(n-k)$ points respectively.  Note that by choice of $P$, no segment in $\mathcal{U}$ can intersect a segment in $\mathcal{V}$. By the inductive hypothesis, $$ \chi(\mathcal{U}) \geq C_{k} \quad \text { and } \quad \chi(\mathcal{V}) \geq C_{n-k} $$ Thus, drawing $\overline{P A_{2 k+1}}$, we have at least $C_{k} C_{n-k}$ ways to complete the drawing. Over all choices of $k$, we obtain $$ \chi(\mathcal{S}) \geq C_{0} C_{n}+\cdots+C_{n} C_{0}=C_{n+1} $$ as desired. Remark. It is possible to show directly from the lower bound proof that convex $2 n$-gons achieve the minimum: indeed, every inequality is sharp, and no segment $\overline{P A_{2 k}}$ can be drawn (since this splits the rest of the points into two halves with an odd number of points, and no crossing segment can be drawn). Bobby Shen points out that in the case of 6 points, a regular pentagon with its center also achieves equality, so this is not the only equality case. Remark. The result that $\chi(S) \geq 1$ for all $S$ is known (consider the choice of 8 segments with smallest sum), and appeared on Putnam 1979. However, it does not seem that knowing this gives an advantage for this problem, since the answer is much larger than 1.
|
1430
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $\mathcal{S}$ be a set of 16 points in the plane, no three collinear. Let $\chi(\mathcal{S})$ denote the number of ways to draw 8 line segments with endpoints in $\mathcal{S}$, such that no two drawn segments intersect, even at endpoints. Find the smallest possible value of $\chi(\mathcal{S})$ across all such $\mathcal{S}$.
|
The answer is 1430 . In general, we prove that with $2 n$ points the answer is the $n^{\text {th }}$ Catalan number $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$. First of all, it is well-known that if $\mathcal{S}$ is a convex $2 n$-gon, then $\chi(\mathcal{S})=C_{n}$. It remains to prove the lower bound. We proceed by (strong) induction on $n$, with the base case $n=0$ and $n=1$ clear. Suppose the statement is proven for $0,1, \ldots, n$ and consider a set $\mathcal{S}$ with $2(n+1)$ points. Let $P$ be a point on the convex hull of $\mathcal{S}$, and label the other $2 n+1$ points $A_{1}, \ldots, A_{2 n+1}$ in order of angle from $P$. Consider drawing a segment $\overline{P A_{2 k+1}}$. This splits the $2 n$ remaining points into two halves $\mathcal{U}$ and $\mathcal{V}$, with $2 k$ and $2(n-k)$ points respectively.  Note that by choice of $P$, no segment in $\mathcal{U}$ can intersect a segment in $\mathcal{V}$. By the inductive hypothesis, $$ \chi(\mathcal{U}) \geq C_{k} \quad \text { and } \quad \chi(\mathcal{V}) \geq C_{n-k} $$ Thus, drawing $\overline{P A_{2 k+1}}$, we have at least $C_{k} C_{n-k}$ ways to complete the drawing. Over all choices of $k$, we obtain $$ \chi(\mathcal{S}) \geq C_{0} C_{n}+\cdots+C_{n} C_{0}=C_{n+1} $$ as desired. Remark. It is possible to show directly from the lower bound proof that convex $2 n$-gons achieve the minimum: indeed, every inequality is sharp, and no segment $\overline{P A_{2 k}}$ can be drawn (since this splits the rest of the points into two halves with an odd number of points, and no crossing segment can be drawn). Bobby Shen points out that in the case of 6 points, a regular pentagon with its center also achieves equality, so this is not the only equality case. Remark. The result that $\chi(S) \geq 1$ for all $S$ is known (consider the choice of 8 segments with smallest sum), and appeared on Putnam 1979. However, it does not seem that knowing this gives an advantage for this problem, since the answer is much larger than 1.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2019.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f0ce004-6324-5c3d-9ee1-14f10a373353
| 247,445
|
Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold: - The sides of each rectangle are parallel to the sides of the unit square. - Each point in $S$ is not in the interior of any rectangle. - Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles. (The interior of a polygon does not contain its boundary.)
|
We claim the answer is $k=2 n+2$. The lower bound is given by picking $$ S=\left\{\left(s_{1}, s_{1}\right),\left(s_{2}, s_{2}\right), \ldots,\left(s_{n}, s_{n}\right)\right\} $$ for some real numbers $0<s_{1}<s_{2}<\cdots<s_{n}<1$. Consider the $4 n$ points $$ S^{\prime}=S+\{(\varepsilon, 0),(0, \varepsilon),(-\varepsilon, 0),(0,-\varepsilon)\} \subset(0,1)^{2} $$ for some sufficiently small $\varepsilon>0$. The four rectangles covering each of $$ \left(s_{1}-\varepsilon, s_{1}\right),\left(s_{1}, s_{1}-\varepsilon\right),\left(s_{n}+\varepsilon, s_{n}\right),\left(s_{n}, s_{n}+\varepsilon\right) $$ cannot cover any other points in $S^{\prime}$; all other rectangles can only cover at most 2 points in $S^{\prime}$, giving a bound of $$ k \geq 4+\frac{\left|S^{\prime}\right|-4}{2}=2 n+2 $$  To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let $$ 0=x_{0}<x_{1}<\cdots<x_{m}<x_{m+1}=1 $$ where $x_{1}, \ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \leq i \leq m$, include the $\left|Y_{i}\right|+1$ rectangles $$ \left(x_{i-1}, x_{i+1}\right) \times\left((0,1) \backslash Y_{i}\right) $$ in the union, and also include $\left(0, x_{1}\right) \times(0,1)$ and $\left(x_{m}, 1\right) \times(0,1)$; this uses $m+n+2$ rectangles.  All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\left\{x_{i}, x_{i+1}\right\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with $$ \left(x_{i}, x_{i+1}\right) \times(y-\varepsilon, y+\varepsilon) $$ for some sufficiently small $\varepsilon>0$ gives a total of $$ (m+n+2)+(n-m)=2 n+2 $$ rectangles.
|
2n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the smallest positive integer $k$ such that for any set $S$ of $n$ points in the interior of the unit square, there exists a set of $k$ rectangles such that the following hold: - The sides of each rectangle are parallel to the sides of the unit square. - Each point in $S$ is not in the interior of any rectangle. - Each point in the interior of the unit square but not in $S$ is in the interior of at least one of the $k$ rectangles. (The interior of a polygon does not contain its boundary.)
|
We claim the answer is $k=2 n+2$. The lower bound is given by picking $$ S=\left\{\left(s_{1}, s_{1}\right),\left(s_{2}, s_{2}\right), \ldots,\left(s_{n}, s_{n}\right)\right\} $$ for some real numbers $0<s_{1}<s_{2}<\cdots<s_{n}<1$. Consider the $4 n$ points $$ S^{\prime}=S+\{(\varepsilon, 0),(0, \varepsilon),(-\varepsilon, 0),(0,-\varepsilon)\} \subset(0,1)^{2} $$ for some sufficiently small $\varepsilon>0$. The four rectangles covering each of $$ \left(s_{1}-\varepsilon, s_{1}\right),\left(s_{1}, s_{1}-\varepsilon\right),\left(s_{n}+\varepsilon, s_{n}\right),\left(s_{n}, s_{n}+\varepsilon\right) $$ cannot cover any other points in $S^{\prime}$; all other rectangles can only cover at most 2 points in $S^{\prime}$, giving a bound of $$ k \geq 4+\frac{\left|S^{\prime}\right|-4}{2}=2 n+2 $$  To prove that $2 n+2$ rectangles are sufficient, assume that the number of distinct $y$-coordinates is at least the number of distinct $x$-coordinates. Let $$ 0=x_{0}<x_{1}<\cdots<x_{m}<x_{m+1}=1 $$ where $x_{1}, \ldots, x_{m}$ are the distinct $x$-coordinates of points in $S$, and let $Y_{i}$ be the set of $y$-coordinates of points with $x$-coordinate $x_{i}$. For each $1 \leq i \leq m$, include the $\left|Y_{i}\right|+1$ rectangles $$ \left(x_{i-1}, x_{i+1}\right) \times\left((0,1) \backslash Y_{i}\right) $$ in the union, and also include $\left(0, x_{1}\right) \times(0,1)$ and $\left(x_{m}, 1\right) \times(0,1)$; this uses $m+n+2$ rectangles.  All remaining uncovered points are between pairs of points with the same $y$-coordinate and adjacent $x$-coordinates $\left\{x_{i}, x_{i+1}\right\}$. There are at most $n-m$ such pairs by the initial assumption, so covering the points between each pair with $$ \left(x_{i}, x_{i+1}\right) \times(y-\varepsilon, y+\varepsilon) $$ for some sufficiently small $\varepsilon>0$ gives a total of $$ (m+n+2)+(n-m)=2 n+2 $$ rectangles.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
4ae66bf6-7b6f-507c-b781-800aefa2e411
| 606,232
|
Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.) In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $\left.A_{2022}\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
The answer is 22 . To prove the lower bound, note that there are $2022 \cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring. Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\ldots, B_{k}$ in $\left\lceil\log _{2} k\right\rceil$ queries. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\lceil k / 2\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \ldots, B_{\lceil k / 2\rceil}$ are red or all of $B_{\lceil k / 2\rceil}, \ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds. Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\leq 2^{k}-1$ points $A_{i}, \ldots, A_{j}$ with $j-i+1 \leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\lceil(j-i+1) / 2\rceil}$. If it is blue, he finishes in $2 \log _{2}\lceil(j-i+1) / 2\rceil \leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\leq 2^{k-1}-1$ points in two queries, at which point we induct.
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $A_{1}, \ldots, A_{2022}$ be the vertices of a regular 2022 -gon in the plane. Alice and Bob play a game. Alice secretly chooses a line and colors all points in the plane on one side of the line blue, and all points on the other side of the line red. Points on the line are colored blue, so every point in the plane is either red or blue. (Bob cannot see the colors of the points.) In each round, Bob chooses a point in the plane (not necessarily among $A_{1}, \ldots$, $\left.A_{2022}\right)$ and Alice responds truthfully with the color of that point. What is the smallest number $Q$ for which Bob has a strategy to always determine the colors of points $A_{1}, \ldots, A_{2022}$ in $Q$ rounds?
|
The answer is 22 . To prove the lower bound, note that there are $2022 \cdot 2021+2>2^{21}$ possible colorings. If Bob makes less than 22 queries, then he can only output $2^{21}$ possible colorings, which means he is wrong on some coloring. Now we show Bob can always win in 22 queries. A key observation is that the set of red points is convex, as is the set of blue points, so if a set of points is all the same color, then their convex hull is all the same color. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}$ and $B_{k+1}$ differ and are known. Then it is possible to determine the colors of $B_{1}$, $\ldots, B_{k}$ in $\left\lceil\log _{2} k\right\rceil$ queries. ## Lemma Let $B_{0}, \ldots, B_{k+1}$ be equally spaced points on a circular arc such that colors of $B_{0}, B_{\lceil k / 2\rceil}, B_{k+1}$ are both red and are known. Then at least one of the following holds: all of $B_{1}, \ldots, B_{\lceil k / 2\rceil}$ are red or all of $B_{\lceil k / 2\rceil}, \ldots, B_{k}$ are red. Furthermore, in one query we can determine which one of the cases holds. Now the strategy is: Bob picks $A_{1}$. WLOG it is red. Now suppose Bob does not know the colors of $\leq 2^{k}-1$ points $A_{i}, \ldots, A_{j}$ with $j-i+1 \leq 2^{k}-1$ and knows the rest are red. I claim Bob can win in $2 k-1$ queries. First, if $k=1$, there is one point and he wins by querying the point, so the base case holds, so assume $k>1$. Bob queries $A_{i+\lceil(j-i+1) / 2\rceil}$. If it is blue, he finishes in $2 \log _{2}\lceil(j-i+1) / 2\rceil \leq 2(k-1)$ queries by the first lemma, for a total of $2 k-1$ queries. If it is red, he can query one more point and learn some half of $A_{i}, \ldots, A_{j}$ that are red by the second lemma, and then he has reduced it to the case with $\leq 2^{k-1}-1$ points in two queries, at which point we induct.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2022.jsonl",
"problem_match": null,
"solution_match": null
}
|
692daa50-d7d5-512c-86a2-10a8b9c7f00f
| 606,278
|
The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up. In a move, Vera may flip over one of the coins in the row, subject to the following rules: - On the first move, Vera may flip over any of the 2023 coins. - On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.) Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$. Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times. The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all. 【 Construction. For $k=0,1, \ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.  It is easy to check this works, and there are 4044 flips, as desired.
|
4044
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Bank of Pittsburgh issues coins that have a heads side and a tails side. Vera has a row of 2023 such coins alternately tails-up and heads-up, with the leftmost coin tails-up. In a move, Vera may flip over one of the coins in the row, subject to the following rules: - On the first move, Vera may flip over any of the 2023 coins. - On all subsequent moves, Vera may only flip over a coin adjacent to the coin she flipped on the previous move. (We do not consider a coin to be adjacent to itself.) Determine the smallest possible number of moves Vera can make to reach a state in which every coin is heads-up.
|
The answer is 4044 . In general, replacing 2023 with $4 n+3$, the answer is $8 n+4$. Bound. Observe that the first and last coins must be flipped, and so every coin is flipped at least once. Then, the $2 n+1$ even-indexed coins must be flipped at least twice, so they are flipped at least $4 n+2$ times. The $2 n+2$ odd-indexed coins must then be flipped at least $4 n+1$ times. Since there are an even number of these coins, the total flip count must be even, so they are actually flipped a total of at least $4 n+2$ times, for a total of at least $8 n+4$ flips in all. 【 Construction. For $k=0,1, \ldots, n-1$, flip $(4 k+1,4 k+2,4 k+3,4 k+2,4 k+3,4 k+$ $4,4 k+3,4 k+4)$ in that order; then at the end, flip $4 n+1,4 n+2,4 n+3,4 n+2$. This is illustrated below for $4 n+3=15$.  It is easy to check this works, and there are 4044 flips, as desired.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
b5821934-eea4-5dd4-b035-8be780ea3df0
| 606,355
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 【 Synthetic approach (from author). We prove the converse of the problem first: Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}$, and $\overline{A_{1} B_{2}}$ are concurrent.  Hence the result follows by Brianchon's theorem. Now suppose $p \neq 1$. Let $\overline{B_{2}^{\prime} C_{1}^{\prime}}$ be the dilation of $\overline{B_{2} C_{1}}$ with ratio $\frac{1}{p}$ at center $A$, and define $C_{2}^{\prime}, A_{1}^{\prime}, A_{2}^{\prime}, B_{1}^{\prime}$ similarly. The following diagram showcases the situation $p<1$.  By the reasoning in the $p=1$ case, note that $\overline{B_{1}^{\prime} C_{2}^{\prime}}, \overline{C_{1}^{\prime} A_{2}^{\prime}}$, and $\overline{A_{1}^{\prime} B_{2}^{\prime}}$ are concurrent. However, $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}, \overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\prime} C_{2}^{\prime}, C A C_{1}^{\prime} A_{2}^{\prime}$, and $A B A_{1}^{\prime} B_{2}^{\prime}$, and these quadrilaterals do not share an interior point, a contradiction. Thus $p \geq 1$. Similarly, we can show $p \leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).
|
1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle with side length 1. Points $A_{1}$ and $A_{2}$ are chosen on side $B C$, points $B_{1}$ and $B_{2}$ are chosen on side $C A$, and points $C_{1}$ and $C_{2}$ are chosen on side $A B$ such that $B A_{1}<B A_{2}, C B_{1}<C B_{2}$, and $A C_{1}<A C_{2}$. Suppose that the three line segments $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent, and the perimeters of triangles $A B_{2} C_{1}, B C_{2} A_{1}$, and $C A_{2} B_{1}$ are all equal. Find all possible values of this common perimeter.
|
The only possible value of the common perimeter, denoted $p$, is 1 . 【 Synthetic approach (from author). We prove the converse of the problem first: Claim ( $p=1$ implies concurrence) - Suppose the six points are chosen so that triangles $A B_{2} C_{1}, B C_{2} A_{1}, C A_{2} B_{1}$ all have perimeter 1. Then lines $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}$, and $\overline{A_{1} B_{2}}$ are concurrent.  Hence the result follows by Brianchon's theorem. Now suppose $p \neq 1$. Let $\overline{B_{2}^{\prime} C_{1}^{\prime}}$ be the dilation of $\overline{B_{2} C_{1}}$ with ratio $\frac{1}{p}$ at center $A$, and define $C_{2}^{\prime}, A_{1}^{\prime}, A_{2}^{\prime}, B_{1}^{\prime}$ similarly. The following diagram showcases the situation $p<1$.  By the reasoning in the $p=1$ case, note that $\overline{B_{1}^{\prime} C_{2}^{\prime}}, \overline{C_{1}^{\prime} A_{2}^{\prime}}$, and $\overline{A_{1}^{\prime} B_{2}^{\prime}}$ are concurrent. However, $\overline{B_{1} C_{2}}, \overline{C_{1} A_{2}}, \overline{A_{1} B_{2}}$ lie in the interior of quadrilaterals $B C B_{1}^{\prime} C_{2}^{\prime}, C A C_{1}^{\prime} A_{2}^{\prime}$, and $A B A_{1}^{\prime} B_{2}^{\prime}$, and these quadrilaterals do not share an interior point, a contradiction. Thus $p \geq 1$. Similarly, we can show $p \leq 1$, and so $p=1$ is forced (and achieved if, for example, the three triangles are equilateral with side length $1 / 3$ ).
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
e2b11d98-03f6-5594-9d1c-5a27657d59d7
| 606,357
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ 【 First solution by author. For convenience in what follows, set $d=\nu_{p}(a)$, let $a=p^{d} \cdot b$, and let a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be essential if it equals one of its iterated finite differences. The key claim is the following. Claim (Characterization of essential functions) - A function $f$ is essential if and only if $$ f(x)+f\left(x+p^{d}\right)+\cdots+f\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. ## Lemma Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \equiv 0 \quad(\bmod p) $$ for all $x$. $$ h(x)=\Delta^{p^{d}} g(x)=\sum_{k=0}^{p^{d}}(-1)^{k}\binom{p^{d}}{k} g\left(x+p^{d}-k\right) $$ However, it is known that $\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \leq k \leq p^{d}-1$, so $$ h(x) \equiv g\left(x+p^{d}\right)+(-1)^{p^{d}} g(x) \quad(\bmod p) . $$ Using this, we easily obtain $$ \begin{aligned} & h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \\ \equiv & \begin{cases}0 & p>2 \\ 2\left(g(x)+g\left(x+p^{d}\right)+\cdots+g\left(x+(b-1) p^{d}\right)\right) & p=2\end{cases} \\ \equiv & 0 \quad(\bmod p) \end{aligned} $$ as desired. ## Corollary Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{e p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. $$ h_{1}(x)=\frac{h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)}{p} . $$ Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$. This immediately settles this direction, since $f$ is in the image of $\Delta^{e p^{d}}$. We will show that $\Delta$ is injective on $\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\mathcal{S}$ with $\Delta f=\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\lambda$. However, then $$ \begin{aligned} & g(0)+g\left(p^{e}\right)+\cdots+g\left((b-1) p^{e}\right) \\ = & (f(0)+\lambda)+\left(f\left(p^{e}\right)+\lambda\right)+\cdots+\left(f\left((b-1) p^{e}\right)+\lambda\right) \\ = & b \lambda \end{aligned} $$ This should also be zero. Since $p \nmid b$, we obtain $\lambda=0$, as desired. Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of $$ \left(p^{e}\right)^{a-p^{d}}=p^{e\left(a-p^{\nu_{p}(a)}\right)}, $$ as promised.
|
p^{e\left(a-p^{\nu_{p}(a)}\right)}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$ 。
|
Let $p$ be a fixed prime and let $a \geq 2$ and $e \geq 1$ be fixed integers. Given a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ and an integer $k \geq 0$, the $k$ th finite difference, denoted $\Delta^{k} f$, is the function from $\mathbb{Z} / a \mathbb{Z}$ to $\mathbb{Z} / p^{e} \mathbb{Z}$ defined recursively by $$ \begin{aligned} & \Delta^{0} f(n)=f(n) \\ & \Delta^{k} f(n)=\Delta^{k-1} f(n+1)-\Delta^{k-1} f(n) \quad \text { for } k=1,2, \ldots \end{aligned} $$ Determine the number of functions $f$ such that there exists some $k \geq 1$ for which $\Delta^{k} f=f$. The answer is $$ \left(p^{e}\right)^{a} \cdot p^{-e p^{\nu} p(a)}=p^{e\left(a-p^{\nu_{p}(a)}\right)} $$ 【 First solution by author. For convenience in what follows, set $d=\nu_{p}(a)$, let $a=p^{d} \cdot b$, and let a function $f: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be essential if it equals one of its iterated finite differences. The key claim is the following. Claim (Characterization of essential functions) - A function $f$ is essential if and only if $$ f(x)+f\left(x+p^{d}\right)+\cdots+f\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. ## Lemma Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \equiv 0 \quad(\bmod p) $$ for all $x$. $$ h(x)=\Delta^{p^{d}} g(x)=\sum_{k=0}^{p^{d}}(-1)^{k}\binom{p^{d}}{k} g\left(x+p^{d}-k\right) $$ However, it is known that $\binom{p^{d}}{k}$ is a multiple of $p$ if $1 \leq k \leq p^{d}-1$, so $$ h(x) \equiv g\left(x+p^{d}\right)+(-1)^{p^{d}} g(x) \quad(\bmod p) . $$ Using this, we easily obtain $$ \begin{aligned} & h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right) \\ \equiv & \begin{cases}0 & p>2 \\ 2\left(g(x)+g\left(x+p^{d}\right)+\cdots+g\left(x+(b-1) p^{d}\right)\right) & p=2\end{cases} \\ \equiv & 0 \quad(\bmod p) \end{aligned} $$ as desired. ## Corollary Let $g: \mathbb{Z} / a \mathbb{Z} \rightarrow \mathbb{Z} / p^{e} \mathbb{Z}$ be any function, and let $h=\Delta^{e p^{d}} g$. Then $$ h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)=0 $$ for all $x$. $$ h_{1}(x)=\frac{h(x)+h\left(x+p^{d}\right)+\cdots+h\left(x+(b-1) p^{d}\right)}{p} . $$ Applying the lemma to $h_{1}$ shows the corollary for $e=2$, since $h_{1}(x)$ is divisible by $p$, hence the numerator is divisible by $p^{2}$. Continue in this manner to get the result for general $e>2$. This immediately settles this direction, since $f$ is in the image of $\Delta^{e p^{d}}$. We will show that $\Delta$ is injective on $\mathcal{S}$. Suppose otherwise, and consider two functions $f$, $g$ in $\mathcal{S}$ with $\Delta f=\Delta g$. Then, we obtain that $f$ and $g$ differ by a constant; say $g=f+\lambda$. However, then $$ \begin{aligned} & g(0)+g\left(p^{e}\right)+\cdots+g\left((b-1) p^{e}\right) \\ = & (f(0)+\lambda)+\left(f\left(p^{e}\right)+\lambda\right)+\cdots+\left(f\left((b-1) p^{e}\right)+\lambda\right) \\ = & b \lambda \end{aligned} $$ This should also be zero. Since $p \nmid b$, we obtain $\lambda=0$, as desired. Counting Finally, we can count the essential functions: all but the last $p^{d}$ entries can be chosen arbitrarily, and then each remaining entry has exactly one possible choice. This leads to a count of $$ \left(p^{e}\right)^{a-p^{d}}=p^{e\left(a-p^{\nu_{p}(a)}\right)}, $$ as promised.
|
{
"resource_path": "USA_TSTST/segmented/en-sols-TSTST-2023.jsonl",
"problem_match": null,
"solution_match": null
}
|
2f2e90a9-8552-51bd-8408-439b8523f7d5
| 606,361
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.