problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Four people are playing rock-paper-scissors. They each play one of the three options (rock, paper, or scissors) independently at random, with equal probability of each choice. Compute the probability that someone beats everyone else.
(In rock-paper-scissors, a player that plays rock beats a player that plays scissors, a player that plays paper beats a player that plays rock, and a player that plays scissors beats a player that plays paper.)
|
As the four players and three events are symmetric, the probability a particular player makes a particular move and beats everyone else is the same regardless of the choice of player or move. So, focusing on one such scenario, the desired probability is 12 times the probability that player 1 plays rock and beats everyone else.
In this case, player 1 plays rock and all other players must play scissors. All four of these events have probability $\frac{1}{3}$, so this scenario has probability $\frac{1}{3^{4}}=\frac{1}{81}$. Thus,
$$
\mathbb{P}(\text { one beats all })=12 \cdot \frac{1}{81}=\frac{4}{27}
$$
|
\frac{4}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Four people are playing rock-paper-scissors. They each play one of the three options (rock, paper, or scissors) independently at random, with equal probability of each choice. Compute the probability that someone beats everyone else.
(In rock-paper-scissors, a player that plays rock beats a player that plays scissors, a player that plays paper beats a player that plays rock, and a player that plays scissors beats a player that plays paper.)
|
As the four players and three events are symmetric, the probability a particular player makes a particular move and beats everyone else is the same regardless of the choice of player or move. So, focusing on one such scenario, the desired probability is 12 times the probability that player 1 plays rock and beats everyone else.
In this case, player 1 plays rock and all other players must play scissors. All four of these events have probability $\frac{1}{3}$, so this scenario has probability $\frac{1}{3^{4}}=\frac{1}{81}$. Thus,
$$
\mathbb{P}(\text { one beats all })=12 \cdot \frac{1}{81}=\frac{4}{27}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
0833dae8-d46b-5d67-9610-be3e6c552f95
| 78,080
|
A regular $n$-gon $P_{1} P_{2} \ldots P_{n}$ satisfies $\angle P_{1} P_{7} P_{8}=178^{\circ}$. Compute $n$.
|
Let $O$ be the center of the $n$-gon. Then
$$
\angle P_{1} O P_{8}=2\left(180^{\circ}-\angle P_{1} P_{7} P_{8}\right)=4^{\circ}=\frac{360^{\circ}}{90}
$$
which means the arc $\widehat{P_{1} P_{8}}$ that spans 7 sides of the $n$-gon also spans $1 / 90$ of its circumcircle. Thus $n=7 \cdot 90=630$.
|
630
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular $n$-gon $P_{1} P_{2} \ldots P_{n}$ satisfies $\angle P_{1} P_{7} P_{8}=178^{\circ}$. Compute $n$.
|
Let $O$ be the center of the $n$-gon. Then
$$
\angle P_{1} O P_{8}=2\left(180^{\circ}-\angle P_{1} P_{7} P_{8}\right)=4^{\circ}=\frac{360^{\circ}}{90}
$$
which means the arc $\widehat{P_{1} P_{8}}$ that spans 7 sides of the $n$-gon also spans $1 / 90$ of its circumcircle. Thus $n=7 \cdot 90=630$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
e9a792b7-6107-593e-b79a-d86bf95bb3a5
| 610,627
|
Compute the number of positive four-digit multiples of 11 whose sum of digits (in base ten) is divisible by 11 .
|
Answer: 72
|
72
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the number of positive four-digit multiples of 11 whose sum of digits (in base ten) is divisible by 11 .
|
Answer: 72
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nProposed by: Ankit Bisain, Eric Shen, Pitchayut Saengrungkongka, Sean Li\n"
}
|
4951a1e1-4053-5c3c-84c9-aaceb71e812b
| 610,628
|
Suppose that $a$ and $b$ are real numbers such that the line $y=a x+b$ intersects the graph of $y=x^{2}$ at two distinct points $A$ and $B$. If the coordinates of the midpoint of $A B$ are $(5,101)$, compute $a+b$.
|
Let $A=\left(r, r^{2}\right)$ and $B=\left(s, s^{2}\right)$. Since $r$ and $s$ are roots of $x^{2}-a x-b$ with midpoint 5 , $r+s=10=a$ (where the last equality follows by Vieta's formula).
Now, as $-r s=b$ (Vieta's formula), observe that
$$
202=r^{2}+s^{2}=(r+s)^{2}-2 r s=100+2 b .
$$
This means $b=51$, so the answer is $10+51=61$.
|
61
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $a$ and $b$ are real numbers such that the line $y=a x+b$ intersects the graph of $y=x^{2}$ at two distinct points $A$ and $B$. If the coordinates of the midpoint of $A B$ are $(5,101)$, compute $a+b$.
|
Let $A=\left(r, r^{2}\right)$ and $B=\left(s, s^{2}\right)$. Since $r$ and $s$ are roots of $x^{2}-a x-b$ with midpoint 5 , $r+s=10=a$ (where the last equality follows by Vieta's formula).
Now, as $-r s=b$ (Vieta's formula), observe that
$$
202=r^{2}+s^{2}=(r+s)^{2}-2 r s=100+2 b .
$$
This means $b=51$, so the answer is $10+51=61$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution 1: "
}
|
1cb6cbd7-7fbc-5c09-8d40-f9f5bb331837
| 610,629
|
On an $8 \times 8$ chessboard, 6 black rooks and $k$ white rooks are placed on different cells so that each rook only attacks rooks of the opposite color. Compute the maximum possible value of $k$.
(Two rooks attack each other if they are in the same row or column and no rooks are between them.)
|
The answer is $k=14$. For a valid construction, place the black rooks on cells $(a, a)$ for $2 \leq a \leq 7$ and the white rooks on cells $(a, a+1)$ and $(a+1, a)$ for $1 \leq a \leq 7$.
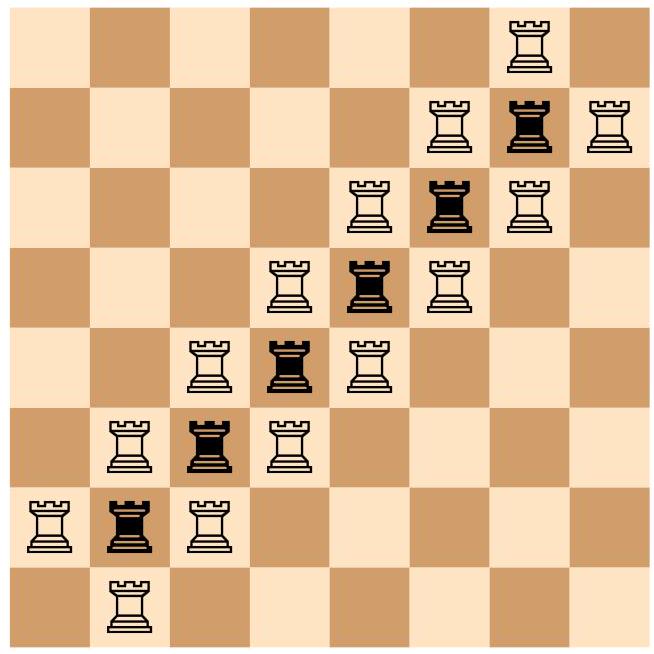
Now, we prove the optimality. As rooks can only attack opposite color rooks, the color of rooks in each row is alternating. The difference between the number of black and white rooks is thus at most the number of rooks. Thus, $k \leq 6+8=14$.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On an $8 \times 8$ chessboard, 6 black rooks and $k$ white rooks are placed on different cells so that each rook only attacks rooks of the opposite color. Compute the maximum possible value of $k$.
(Two rooks attack each other if they are in the same row or column and no rooks are between them.)
|
The answer is $k=14$. For a valid construction, place the black rooks on cells $(a, a)$ for $2 \leq a \leq 7$ and the white rooks on cells $(a, a+1)$ and $(a+1, a)$ for $1 \leq a \leq 7$.

Now, we prove the optimality. As rooks can only attack opposite color rooks, the color of rooks in each row is alternating. The difference between the number of black and white rooks is thus at most the number of rooks. Thus, $k \leq 6+8=14$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
d07f1b26-e668-501d-9739-e76778d9ed93
| 610,630
|
Let $A B C D$ be a square of side length 5. A circle passing through $A$ is tangent to segment $C D$ at $T$ and meets $A B$ and $A D$ again at $X \neq A$ and $Y \neq A$, respectively. Given that $X Y=6$, compute $A T$.
|
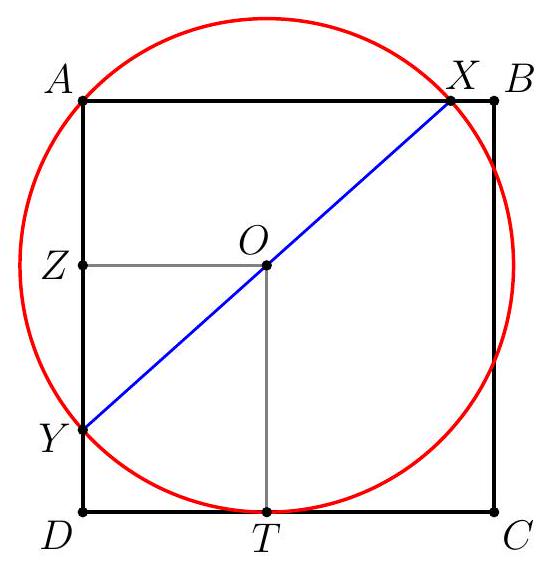
Let $O$ be the center of the circle, and let $Z$ be the foot from $O$ to $A D$. Since $X Y$ is a diameter, $O T=Z D=3$, so $A Z=2$. Then $O Z=\sqrt{5}$ and $A T=\sqrt{O Z^{2}+25}=\sqrt{30}$.
|
\sqrt{30}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a square of side length 5. A circle passing through $A$ is tangent to segment $C D$ at $T$ and meets $A B$ and $A D$ again at $X \neq A$ and $Y \neq A$, respectively. Given that $X Y=6$, compute $A T$.
|

Let $O$ be the center of the circle, and let $Z$ be the foot from $O$ to $A D$. Since $X Y$ is a diameter, $O T=Z D=3$, so $A Z=2$. Then $O Z=\sqrt{5}$ and $A T=\sqrt{O Z^{2}+25}=\sqrt{30}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution:\n\n"
}
|
aa00ebd8-adc5-50cd-8d30-18b51dd14040
| 610,631
|
Mark writes the expression $\sqrt{d}$ for each positive divisor $d$ of 8 ! on the board. Seeing that these expressions might not be worth points on HMMT, Rishabh simplifies each expression to the form $a \sqrt{b}$, where $a$ and $b$ are integers such that $b$ is not divisible by the square of a prime number. (For example, $\sqrt{20}, \sqrt{16}$, and $\sqrt{6}$ simplify to $2 \sqrt{5}, 4 \sqrt{1}$, and $1 \sqrt{6}$, respectively.) Compute the sum of $a+b$ across all expressions that Rishabh writes.
|
Let $\sqrt{n}$ simplify to $a_{n} \sqrt{b_{n}}$. Notice that both $a_{n}$ and $b_{n}$ are multiplicative. Thus, $\sum_{d \mid n} a_{d}$ and $\sum_{d \mid n} b_{d}$ are multiplicative.
We consider the sum $\sum_{d \mid p^{k}} a_{d}$ and $\sum_{d \mid p^{k}} b_{d}$. Notice that for $d=p^{l}, a_{d}=p^{\lfloor l / 2\rfloor}$ and $b_{d}=p^{2\{l / 2\}}$, so
$$
\sum_{d \mid p^{k}} a_{d}=2\left(\frac{p^{(k+1) / 2}-1}{p-1}\right) \quad \text { and } \quad \sum_{d \mid p^{k}} b_{d}=\frac{(p+1)(k+1)}{2}
$$
for odd $k$, while
$$
\sum_{d \mid p^{k}} a_{d}=\left(\frac{p^{(k+2) / 2}+p^{k / 2}-2}{p-1}\right) \quad \text { and } \quad \sum_{d \mid p^{k}} b_{d}=\frac{(p+1) k}{2}+1
$$
for even $k$.
Notice $8!=2^{7} \cdot 3^{2} \cdot 5 \cdot 7$, so
$$
\sum_{d \mid 8!} a_{d}=\left(\frac{2(16-1)}{2-1}\right)\left(\frac{9+3-2}{3-1}\right)(1+1)(1+1)=30 \cdot 5 \cdot 2 \cdot 2=600
$$
and
$$
\sum_{d \mid 8!} b_{d}=\left(\frac{3 \cdot 8}{2}\right)\left(1+\frac{4 \cdot 2}{2}\right)(1+5)(1+7)=12 \cdot 5 \cdot 6 \cdot 8=2880
$$
so the sum of $a_{d}+b_{d}$ would be $600+2880=3480$.
|
3480
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Mark writes the expression $\sqrt{d}$ for each positive divisor $d$ of 8 ! on the board. Seeing that these expressions might not be worth points on HMMT, Rishabh simplifies each expression to the form $a \sqrt{b}$, where $a$ and $b$ are integers such that $b$ is not divisible by the square of a prime number. (For example, $\sqrt{20}, \sqrt{16}$, and $\sqrt{6}$ simplify to $2 \sqrt{5}, 4 \sqrt{1}$, and $1 \sqrt{6}$, respectively.) Compute the sum of $a+b$ across all expressions that Rishabh writes.
|
Let $\sqrt{n}$ simplify to $a_{n} \sqrt{b_{n}}$. Notice that both $a_{n}$ and $b_{n}$ are multiplicative. Thus, $\sum_{d \mid n} a_{d}$ and $\sum_{d \mid n} b_{d}$ are multiplicative.
We consider the sum $\sum_{d \mid p^{k}} a_{d}$ and $\sum_{d \mid p^{k}} b_{d}$. Notice that for $d=p^{l}, a_{d}=p^{\lfloor l / 2\rfloor}$ and $b_{d}=p^{2\{l / 2\}}$, so
$$
\sum_{d \mid p^{k}} a_{d}=2\left(\frac{p^{(k+1) / 2}-1}{p-1}\right) \quad \text { and } \quad \sum_{d \mid p^{k}} b_{d}=\frac{(p+1)(k+1)}{2}
$$
for odd $k$, while
$$
\sum_{d \mid p^{k}} a_{d}=\left(\frac{p^{(k+2) / 2}+p^{k / 2}-2}{p-1}\right) \quad \text { and } \quad \sum_{d \mid p^{k}} b_{d}=\frac{(p+1) k}{2}+1
$$
for even $k$.
Notice $8!=2^{7} \cdot 3^{2} \cdot 5 \cdot 7$, so
$$
\sum_{d \mid 8!} a_{d}=\left(\frac{2(16-1)}{2-1}\right)\left(\frac{9+3-2}{3-1}\right)(1+1)(1+1)=30 \cdot 5 \cdot 2 \cdot 2=600
$$
and
$$
\sum_{d \mid 8!} b_{d}=\left(\frac{3 \cdot 8}{2}\right)\left(1+\frac{4 \cdot 2}{2}\right)(1+5)(1+7)=12 \cdot 5 \cdot 6 \cdot 8=2880
$$
so the sum of $a_{d}+b_{d}$ would be $600+2880=3480$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
d76ac685-1b8a-5eaf-b06d-cf252511a4c5
| 610,633
|
An entry in a grid is called a saddle point if it is the largest number in its row and the smallest number in its column. Suppose that each cell in a $3 \times 3$ grid is filled with a real number, each chosen independently and uniformly at random from the interval $[0,1]$. Compute the probability that this grid has at least one saddle point.
|
With probability 1, all entries of the matrix are unique. If this is the case, we claim there can only be one saddle point. To see this, suppose $A_{i j}$ and $A_{k l}$ are both saddle points. They cannot be in the same row, since they cannot both be the greatest number in the same row, and similarly they cannot be in the same column, since they cannot both be the least number in the same column. If they are in different rows and different columns, then $A_{i j}<A_{i l}$ and $A_{k l}>A_{i l}$, so $A_{i j}<A_{k l}$. However, we also have $A_{i j}>A_{k j}$ and $A_{k l}<A_{k j}$, so $A_{i j}>A_{k l}$. This is a contradiction, so there is only one saddle point.
Each entry of the matrix is equally likely to be a saddle point by symmetry, so we can just multiply the probability that $A_{11}$ is a saddle point by 9 to find the answer. For $A_{11}$ to be a saddle point, it must be greater than $A_{21}$ and $A_{31}$, but less than $A_{12}$ and $A_{13}$. There are $5!=120$ equally likely ways that the numbers $A_{11}, A_{12}, A_{13}, A_{21}, A_{31}$ could be arranged in increasing order, and 4 of them work, so the probability that $A_{11}$ is a saddle point is $\frac{1}{30}$. Therefore, the probability that $A$ has a saddle point is $9 \cdot \frac{1}{30}=\frac{3}{10}$.
|
\frac{3}{10}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An entry in a grid is called a saddle point if it is the largest number in its row and the smallest number in its column. Suppose that each cell in a $3 \times 3$ grid is filled with a real number, each chosen independently and uniformly at random from the interval $[0,1]$. Compute the probability that this grid has at least one saddle point.
|
With probability 1, all entries of the matrix are unique. If this is the case, we claim there can only be one saddle point. To see this, suppose $A_{i j}$ and $A_{k l}$ are both saddle points. They cannot be in the same row, since they cannot both be the greatest number in the same row, and similarly they cannot be in the same column, since they cannot both be the least number in the same column. If they are in different rows and different columns, then $A_{i j}<A_{i l}$ and $A_{k l}>A_{i l}$, so $A_{i j}<A_{k l}$. However, we also have $A_{i j}>A_{k j}$ and $A_{k l}<A_{k j}$, so $A_{i j}>A_{k l}$. This is a contradiction, so there is only one saddle point.
Each entry of the matrix is equally likely to be a saddle point by symmetry, so we can just multiply the probability that $A_{11}$ is a saddle point by 9 to find the answer. For $A_{11}$ to be a saddle point, it must be greater than $A_{21}$ and $A_{31}$, but less than $A_{12}$ and $A_{13}$. There are $5!=120$ equally likely ways that the numbers $A_{11}, A_{12}, A_{13}, A_{21}, A_{31}$ could be arranged in increasing order, and 4 of them work, so the probability that $A_{11}$ is a saddle point is $\frac{1}{30}$. Therefore, the probability that $A$ has a saddle point is $9 \cdot \frac{1}{30}=\frac{3}{10}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
f1f2249c-2fac-586c-a677-d103f9675765
| 610,634
|
Let $A B C D$ be a convex trapezoid such that $\angle A B C=\angle B C D=90^{\circ}, A B=3, B C=6$, and $C D=12$. Among all points $X$ inside the trapezoid satisfying $\angle X B C=\angle X D A$, compute the minimum possible value of $C X$.
|

Let $P=A D \cap B C$. Then, the given angle condition $\angle X B C=\angle X A D$ implies that $\angle X B D+\angle X P D=$ $180^{\circ}$, so $X$ always lies on circle $\odot(P B D)$, which is fixed. Thus, we see that the locus if $X$ is the arc $\widehat{B D}$ of $\odot(P B D)$. Let $O$ and $R$ be the center and the radius of $\odot(P B D)$. Then, by triangle inequality, we get that
$$
C X \geq C O-O X=C O-R
$$
and the equality occurs when $X$ is the intersection of segment $C O$ and $\odot(P B D)$, as shown in the diagram above. Hence, the maximum value is $C O-R$.
To compute $C O$ and $R$, we let $T$ be the second intersection of $\odot(P B D)$ and $C D$. We can compute $B P=2$, so by Power of Point, $C T \cdot C D=C P \cdot C B=48$, so $C T=4$, which means that $D T=8$. The projections of $O$ onto $C D$ and $C B$ are midpoints of $B P$ and $D T$. Let those midpoints be $M$ and $N$, respectively. Then, we get by Pythagorean theorem that
$$
\begin{aligned}
C O & =\sqrt{C N^{2}+O N^{2}}=\sqrt{\left(4+\frac{8}{2}\right)^{2}+\left(6+\frac{2}{2}\right)^{2}}=\sqrt{8^{2}+7^{2}}=\sqrt{113} \\
R & =\sqrt{B M^{2}+M O^{2}}=\sqrt{1^{2}+\left(4+\frac{8}{2}\right)^{2}}=\sqrt{1^{2}+8^{2}}=\sqrt{65},
\end{aligned}
$$
so the answer is $\sqrt{113}-\sqrt{65}$.
|
\sqrt{113}-\sqrt{65}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex trapezoid such that $\angle A B C=\angle B C D=90^{\circ}, A B=3, B C=6$, and $C D=12$. Among all points $X$ inside the trapezoid satisfying $\angle X B C=\angle X D A$, compute the minimum possible value of $C X$.
|

Let $P=A D \cap B C$. Then, the given angle condition $\angle X B C=\angle X A D$ implies that $\angle X B D+\angle X P D=$ $180^{\circ}$, so $X$ always lies on circle $\odot(P B D)$, which is fixed. Thus, we see that the locus if $X$ is the arc $\widehat{B D}$ of $\odot(P B D)$. Let $O$ and $R$ be the center and the radius of $\odot(P B D)$. Then, by triangle inequality, we get that
$$
C X \geq C O-O X=C O-R
$$
and the equality occurs when $X$ is the intersection of segment $C O$ and $\odot(P B D)$, as shown in the diagram above. Hence, the maximum value is $C O-R$.
To compute $C O$ and $R$, we let $T$ be the second intersection of $\odot(P B D)$ and $C D$. We can compute $B P=2$, so by Power of Point, $C T \cdot C D=C P \cdot C B=48$, so $C T=4$, which means that $D T=8$. The projections of $O$ onto $C D$ and $C B$ are midpoints of $B P$ and $D T$. Let those midpoints be $M$ and $N$, respectively. Then, we get by Pythagorean theorem that
$$
\begin{aligned}
C O & =\sqrt{C N^{2}+O N^{2}}=\sqrt{\left(4+\frac{8}{2}\right)^{2}+\left(6+\frac{2}{2}\right)^{2}}=\sqrt{8^{2}+7^{2}}=\sqrt{113} \\
R & =\sqrt{B M^{2}+M O^{2}}=\sqrt{1^{2}+\left(4+\frac{8}{2}\right)^{2}}=\sqrt{1^{2}+8^{2}}=\sqrt{65},
\end{aligned}
$$
so the answer is $\sqrt{113}-\sqrt{65}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-gen-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution:\n\n"
}
|
b64706c8-0e6c-5a48-9437-8af0497214c3
| 610,635
|
The formula to convert Celsius to Fahrenheit is
$$
F^{\circ}=1.8 \cdot C^{\circ}+32
$$
In Celsius, it is $10^{\circ}$ warmer in New York right now than in Boston. In Fahrenheit, how much warmer is it in New York than in Boston?
|
Let $x$ and $y$ be the temperatures in New York and Boston, respectively, in Fahrenheit. Then $x-y=10$, so we compute
$$
(1.8 \cdot x+32)-(1.8 \cdot y+32)=1.8 \cdot(x-y)=18
$$
|
18
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The formula to convert Celsius to Fahrenheit is
$$
F^{\circ}=1.8 \cdot C^{\circ}+32
$$
In Celsius, it is $10^{\circ}$ warmer in New York right now than in Boston. In Fahrenheit, how much warmer is it in New York than in Boston?
|
Let $x$ and $y$ be the temperatures in New York and Boston, respectively, in Fahrenheit. Then $x-y=10$, so we compute
$$
(1.8 \cdot x+32)-(1.8 \cdot y+32)=1.8 \cdot(x-y)=18
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nSolution: "
}
|
20da7b4c-36e5-5756-a920-437a98f290e4
| 610,636
|
Compute the number of dates in the year 2023 such that when put in MM/DD/YY form, the three numbers are in strictly increasing order.
For example, $06 / 18 / 23$ is such a date since $6<18<23$, while today, $11 / 11 / 23$, is not.
|
Answer: 186
|
186
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of dates in the year 2023 such that when put in MM/DD/YY form, the three numbers are in strictly increasing order.
For example, $06 / 18 / 23$ is such a date since $6<18<23$, while today, $11 / 11 / 23$, is not.
|
Answer: 186
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nProposed by: William Hu\n"
}
|
919e44b2-3fec-5f69-85d4-aa2f5c58f3a8
| 610,637
|
Let $A B C D$ be a rectangle with $A B=20$ and $A D=23$. Let $M$ be the midpoint of $C D$, and let $X$ be the reflection of $M$ across point $A$. Compute the area of triangle $X B D$.
|
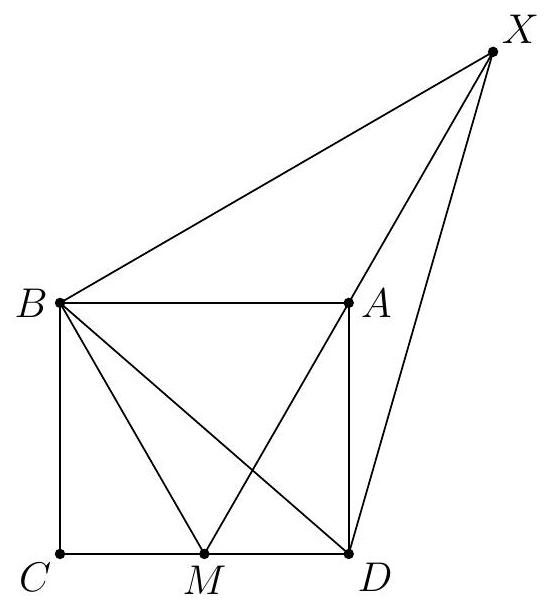
Observe that $[X B D]=[B A D]+[B A X]+[D A X]$. We will find the area of each of these triangles individually.
- We have $[A B D]=\frac{1}{2}[A B C D]$.
- Because $A M=A X,[B A X]=[B A M]$ as the triangles have the same base and height. Thus, as $[B A M]$ have the same base and height as $A B C D,[B A X]=[B A M]=\frac{1}{2}[A B C D]$.
- From similar reasoning, we know that $[D A X]=[D A M]$. We have that $D A M$ has the same base and half the height of the rectangle. Thus, $[D A X]=[D A M]=\frac{1}{4}[A B C D]$.
Hence, we have
$$
\begin{aligned}
{[X B D] } & =[B A D]+[B A X]+[D A X] \\
& =\frac{1}{2}[A B C D]+\frac{1}{2}[A B C D]+\frac{1}{4}[A B C D] \\
& =\frac{5}{4}[A B C D]
\end{aligned}
$$
Thus, our answer is $\frac{5}{4}[A B C D]=\frac{5}{4}(20 \cdot 23)=575$.
|
575
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a rectangle with $A B=20$ and $A D=23$. Let $M$ be the midpoint of $C D$, and let $X$ be the reflection of $M$ across point $A$. Compute the area of triangle $X B D$.
|

Observe that $[X B D]=[B A D]+[B A X]+[D A X]$. We will find the area of each of these triangles individually.
- We have $[A B D]=\frac{1}{2}[A B C D]$.
- Because $A M=A X,[B A X]=[B A M]$ as the triangles have the same base and height. Thus, as $[B A M]$ have the same base and height as $A B C D,[B A X]=[B A M]=\frac{1}{2}[A B C D]$.
- From similar reasoning, we know that $[D A X]=[D A M]$. We have that $D A M$ has the same base and half the height of the rectangle. Thus, $[D A X]=[D A M]=\frac{1}{4}[A B C D]$.
Hence, we have
$$
\begin{aligned}
{[X B D] } & =[B A D]+[B A X]+[D A X] \\
& =\frac{1}{2}[A B C D]+\frac{1}{2}[A B C D]+\frac{1}{4}[A B C D] \\
& =\frac{5}{4}[A B C D]
\end{aligned}
$$
Thus, our answer is $\frac{5}{4}[A B C D]=\frac{5}{4}(20 \cdot 23)=575$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nSolution:\n"
}
|
91cfe02e-5dee-53f0-907f-e5b71d7fa9c4
| 610,638
|
The number 5.6 may be expressed uniquely (ignoring order) as a product $\underline{a} \cdot \underline{b} \times \underline{c} . \underline{d}$ for digits $a, b, c, d$ all nonzero. Compute $\underline{a} \cdot \underline{b}+\underline{c} \cdot \underline{d}$.
|
We want $\overline{a b} \times \overline{c d}=560=2^{4} \times 5 \times 7$. To avoid a zero digit, we need to group the 5 with the 7 to get 3.5 and 1.6 , and our answer is $3.5+1.6=5.1$.
|
5.1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The number 5.6 may be expressed uniquely (ignoring order) as a product $\underline{a} \cdot \underline{b} \times \underline{c} . \underline{d}$ for digits $a, b, c, d$ all nonzero. Compute $\underline{a} \cdot \underline{b}+\underline{c} \cdot \underline{d}$.
|
We want $\overline{a b} \times \overline{c d}=560=2^{4} \times 5 \times 7$. To avoid a zero digit, we need to group the 5 with the 7 to get 3.5 and 1.6 , and our answer is $3.5+1.6=5.1$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n4. [6]",
"solution_match": "\nSolution: "
}
|
835b8b0b-ac3c-582a-b960-30665c6746b3
| 610,639
|
Let $A B C D E$ be a convex pentagon such that
$$
\begin{aligned}
& A B+B C+C D+D E+E A=64 \text { and } \\
& A C+C E+E B+B D+D A=72 .
\end{aligned}
$$
Compute the perimeter of the convex pentagon whose vertices are the midpoints of the sides of $A B C D E$.
|
Answer: 36
|
36
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that
$$
\begin{aligned}
& A B+B C+C D+D E+E A=64 \text { and } \\
& A C+C E+E B+B D+D A=72 .
\end{aligned}
$$
Compute the perimeter of the convex pentagon whose vertices are the midpoints of the sides of $A B C D E$.
|
Answer: 36
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n5. [6]",
"solution_match": "\nProposed by: Arul Kolla\n"
}
|
11248387-623f-5770-93e3-eed8542d2552
| 610,640
|
There are five people in a room. They each simultaneously pick two of the other people in the room independently and uniformly at random and point at them. Compute the probability that there exists a group of three people such that each of them is pointing at the other two in the group.
|
The desired probability is the number of ways to pick the two isolated people times the probability that the remaining three point at each other. So,
$$
P=\binom{5}{2} \cdot\left(\frac{\binom{2}{2}}{\binom{4}{2}}\right)^{3}=10 \cdot\left(\frac{1}{6}\right)^{3}=\frac{5}{108}
$$
is the desired probability.
|
\frac{5}{108}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are five people in a room. They each simultaneously pick two of the other people in the room independently and uniformly at random and point at them. Compute the probability that there exists a group of three people such that each of them is pointing at the other two in the group.
|
The desired probability is the number of ways to pick the two isolated people times the probability that the remaining three point at each other. So,
$$
P=\binom{5}{2} \cdot\left(\frac{\binom{2}{2}}{\binom{4}{2}}\right)^{3}=10 \cdot\left(\frac{1}{6}\right)^{3}=\frac{5}{108}
$$
is the desired probability.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n6. [6]",
"solution_match": "\nSolution: "
}
|
afb6d1fb-7031-57d6-a3d4-bb1d1e5ff385
| 610,641
|
Suppose $a$ and $b$ be positive integers not exceeding 100 such that
$$
a b=\left(\frac{\operatorname{lcm}(a, b)}{\operatorname{gcd}(a, b)}\right)^{2}
$$
Compute the largest possible value of $a+b$.
|
For any prime $p$ and a positive integer $n$, let $\nu_{p}(n)$ be the largest nonnegative integer $k$ for which $p^{k}$ divides $n$. Taking $\nu_{p}$ on both sides of the given equation, we get
$$
\nu_{p}(a)+\nu_{p}(b)=2 \cdot\left|\nu_{p}(a)-\nu_{p}(b)\right|
$$
which means $\frac{\nu_{p}(a)}{\nu_{p}(b)} \in\left\{3, \frac{1}{3}\right\}$ for all primes $p$. Using this with $a, b \leq 100$, we get that
- We must have $\left(\nu_{2}(a), \nu_{2}(b)\right) \in\{(0,0),(1,3),(3,1),(2,6),(6,2)\}$ because $a$ and $b$ cannot be divisible by $2^{7}$.
- We must have $\left(\nu_{3}(a), \nu_{3}(b)\right) \in\{(0,0),(1,3),(3,1)\}$ because $a$ and $b$ cannot be divisible by $3^{6}>100$.
- $a$ and $b$ cannot be divisible by any prime $p \geq 5$, because if not, then one of $a$ and $b$ must be divisible by $p^{3} \geq 5^{3}>100$.
If $\left(\nu_{2}(a), \nu_{2}(b)\right)=(2,6)$ (and similarly with $(6,2)$ ), then we must have $(a, b)=(4,64)$, so the sum is 68.
If $\left(\nu_{3}(a), \nu_{3}(b)\right)=(1,3)$ (and similarly with $(3,1)$ ), then we must have $\nu_{2}(b) \leq 1$ (otherwise, $b \geq$ $\left.2^{2} \cdot 3^{3}>100\right)$. Hence, the optimal pair is $(a, b)=\left(2^{3} \cdot 3^{1}, 2^{1} \cdot 3^{3}\right)=(24,54)$, so the sum is $24+54=78$.
If neither of the above happens, then $a+b \leq 2^{1}+2^{3} \leq 10$, which is clearly not optimal.
Hence, the optimal pair is $(24,54)$, and the answer is 78 .
|
78
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Suppose $a$ and $b$ be positive integers not exceeding 100 such that
$$
a b=\left(\frac{\operatorname{lcm}(a, b)}{\operatorname{gcd}(a, b)}\right)^{2}
$$
Compute the largest possible value of $a+b$.
|
For any prime $p$ and a positive integer $n$, let $\nu_{p}(n)$ be the largest nonnegative integer $k$ for which $p^{k}$ divides $n$. Taking $\nu_{p}$ on both sides of the given equation, we get
$$
\nu_{p}(a)+\nu_{p}(b)=2 \cdot\left|\nu_{p}(a)-\nu_{p}(b)\right|
$$
which means $\frac{\nu_{p}(a)}{\nu_{p}(b)} \in\left\{3, \frac{1}{3}\right\}$ for all primes $p$. Using this with $a, b \leq 100$, we get that
- We must have $\left(\nu_{2}(a), \nu_{2}(b)\right) \in\{(0,0),(1,3),(3,1),(2,6),(6,2)\}$ because $a$ and $b$ cannot be divisible by $2^{7}$.
- We must have $\left(\nu_{3}(a), \nu_{3}(b)\right) \in\{(0,0),(1,3),(3,1)\}$ because $a$ and $b$ cannot be divisible by $3^{6}>100$.
- $a$ and $b$ cannot be divisible by any prime $p \geq 5$, because if not, then one of $a$ and $b$ must be divisible by $p^{3} \geq 5^{3}>100$.
If $\left(\nu_{2}(a), \nu_{2}(b)\right)=(2,6)$ (and similarly with $(6,2)$ ), then we must have $(a, b)=(4,64)$, so the sum is 68.
If $\left(\nu_{3}(a), \nu_{3}(b)\right)=(1,3)$ (and similarly with $(3,1)$ ), then we must have $\nu_{2}(b) \leq 1$ (otherwise, $b \geq$ $\left.2^{2} \cdot 3^{3}>100\right)$. Hence, the optimal pair is $(a, b)=\left(2^{3} \cdot 3^{1}, 2^{1} \cdot 3^{3}\right)=(24,54)$, so the sum is $24+54=78$.
If neither of the above happens, then $a+b \leq 2^{1}+2^{3} \leq 10$, which is clearly not optimal.
Hence, the optimal pair is $(24,54)$, and the answer is 78 .
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n7. [7]",
"solution_match": "\nSolution: "
}
|
9c992521-f1e9-58aa-bebd-a3dfc24ea777
| 610,642
|
Six standard fair six-sided dice are rolled and arranged in a row at random. Compute the expected number of dice showing the same number as the sixth die in the row.
|
For each $i=1,2, \ldots, 6$, let $X_{i}$ denote the indicator variable of whether the $i$-th die shows the same number as the sixth die. Clearly, $X_{6}=1$ always. For all other $i, X_{i}$ is 1 with probability $\frac{1}{6}$ and 0 otherwise, so $\mathbb{E}\left[X_{i}\right]=\frac{1}{6}$. By linearity of expectation, the answer is
$$
\mathbb{E}\left[X_{1}+\cdots+X_{6}\right]=\mathbb{E}\left[X_{1}\right]+\cdots+\mathbb{E}\left[X_{6}\right]=5 \cdot \frac{1}{6}+1=\frac{11}{6}
$$
|
\frac{11}{6}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Six standard fair six-sided dice are rolled and arranged in a row at random. Compute the expected number of dice showing the same number as the sixth die in the row.
|
For each $i=1,2, \ldots, 6$, let $X_{i}$ denote the indicator variable of whether the $i$-th die shows the same number as the sixth die. Clearly, $X_{6}=1$ always. For all other $i, X_{i}$ is 1 with probability $\frac{1}{6}$ and 0 otherwise, so $\mathbb{E}\left[X_{i}\right]=\frac{1}{6}$. By linearity of expectation, the answer is
$$
\mathbb{E}\left[X_{1}+\cdots+X_{6}\right]=\mathbb{E}\left[X_{1}\right]+\cdots+\mathbb{E}\left[X_{6}\right]=5 \cdot \frac{1}{6}+1=\frac{11}{6}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n8. [7]",
"solution_match": "\nSolution: "
}
|
06ad57ff-83ed-5b63-8565-b2bbc84f85d1
| 610,643
|
The largest prime factor of 101101101101 is a four-digit number $N$. Compute $N$.
|
Note that
$$
\begin{aligned}
101101101101 & =101 \cdot 1001001001 \\
& =101 \cdot 1001 \cdot 1000001 \\
& =101 \cdot 1001 \cdot\left(100^{3}+1\right) \\
& =101 \cdot 1001 \cdot(100+1)\left(100^{2}-100+1\right) \\
& =101 \cdot 1001 \cdot 101 \cdot 9901 \\
& =101^{2} \cdot 1001 \cdot 9901 \\
& =(7 \cdot 11 \cdot 13) \cdot 101^{2} \cdot 9901,
\end{aligned}
$$
and since we are given that the largest prime factor must be four-digit, it must be 9901 . One can also check manually that it is prime.
|
9901
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The largest prime factor of 101101101101 is a four-digit number $N$. Compute $N$.
|
Note that
$$
\begin{aligned}
101101101101 & =101 \cdot 1001001001 \\
& =101 \cdot 1001 \cdot 1000001 \\
& =101 \cdot 1001 \cdot\left(100^{3}+1\right) \\
& =101 \cdot 1001 \cdot(100+1)\left(100^{2}-100+1\right) \\
& =101 \cdot 1001 \cdot 101 \cdot 9901 \\
& =101^{2} \cdot 1001 \cdot 9901 \\
& =(7 \cdot 11 \cdot 13) \cdot 101^{2} \cdot 9901,
\end{aligned}
$$
and since we are given that the largest prime factor must be four-digit, it must be 9901 . One can also check manually that it is prime.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nSolution: "
}
|
ee703249-df19-56e8-b4fc-d74ccdc42268
| 610,644
|
A real number $x$ is chosen uniformly at random from the interval $(0,10)$. Compute the probability that $\sqrt{x}, \sqrt{x+7}$, and $\sqrt{10-x}$ are the side lengths of a non-degenerate triangle.
|
For any positive reals $a, b, c$, numbers $a, b, c$ is a side length of a triangle if and only if
$$
(a+b+c)(-a+b+c)(a-b+c)(a+b-c)>0 \Longleftrightarrow \sum_{\mathrm{cyc}}\left(2 a^{2} b^{2}-a^{4}\right)>0
$$
(to see why, just note that if $a \geq b+c$, then only the factor $-a+b+c$ is negative). Therefore, $x$ works if and only if
$$
\begin{aligned}
2(x+7)(10-x)+2 x(x+7)+2 x(10-x) & >x^{2}+(x+7)^{2}+(10-x)^{2} \\
-5 x^{2}+46 x-9 & >0 \\
x & \in\left(\frac{1}{5}, 9\right)
\end{aligned}
$$
giving the answer $\frac{22}{25}$.
|
\frac{22}{25}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A real number $x$ is chosen uniformly at random from the interval $(0,10)$. Compute the probability that $\sqrt{x}, \sqrt{x+7}$, and $\sqrt{10-x}$ are the side lengths of a non-degenerate triangle.
|
For any positive reals $a, b, c$, numbers $a, b, c$ is a side length of a triangle if and only if
$$
(a+b+c)(-a+b+c)(a-b+c)(a+b-c)>0 \Longleftrightarrow \sum_{\mathrm{cyc}}\left(2 a^{2} b^{2}-a^{4}\right)>0
$$
(to see why, just note that if $a \geq b+c$, then only the factor $-a+b+c$ is negative). Therefore, $x$ works if and only if
$$
\begin{aligned}
2(x+7)(10-x)+2 x(x+7)+2 x(10-x) & >x^{2}+(x+7)^{2}+(10-x)^{2} \\
-5 x^{2}+46 x-9 & >0 \\
x & \in\left(\frac{1}{5}, 9\right)
\end{aligned}
$$
giving the answer $\frac{22}{25}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nSolution 1: "
}
|
022fb098-0c50-53e3-b41e-5d1edcc59727
| 610,645
|
Let $A B C D$ and $W X Y Z$ be two squares that share the same center such that $W X \| A B$ and $W X<A B$. Lines $C X$ and $A B$ intersect at $P$, and lines $C Z$ and $A D$ intersect at $Q$. If points $P, W$, and $Q$ are collinear, compute the ratio $A B / W X$.
|
Answer: $\sqrt{2}+1$
|
\sqrt{2}+1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ and $W X Y Z$ be two squares that share the same center such that $W X \| A B$ and $W X<A B$. Lines $C X$ and $A B$ intersect at $P$, and lines $C Z$ and $A D$ intersect at $Q$. If points $P, W$, and $Q$ are collinear, compute the ratio $A B / W X$.
|
Answer: $\sqrt{2}+1$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n11. [8]",
"solution_match": "\nProposed by: Edward Yu\n"
}
|
4527b4db-25b4-5927-bbc6-77b71d1a5970
| 610,646
|
A jar contains 97 marbles that are either red, green, or blue. Neil draws two marbles from the jar without replacement and notes that the probability that they would be the same color is $\frac{5}{12}$. After Neil puts his marbles back, Jerry draws two marbles from the jar with replacement. Compute the probability that the marbles that Jerry draws are the same color.
|
Note that $\frac{5}{12}=\frac{40.97}{97 \cdot 96}$. Of all of the original ways we could've drawn marbles, we are adding 97 ways, namely drawing the same marble twice, all of which work. Thus, the answer is
$$
\frac{40 \cdot 97+97}{97 \cdot 96+97}=\frac{41}{97}
$$
|
\frac{41}{97}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A jar contains 97 marbles that are either red, green, or blue. Neil draws two marbles from the jar without replacement and notes that the probability that they would be the same color is $\frac{5}{12}$. After Neil puts his marbles back, Jerry draws two marbles from the jar with replacement. Compute the probability that the marbles that Jerry draws are the same color.
|
Note that $\frac{5}{12}=\frac{40.97}{97 \cdot 96}$. Of all of the original ways we could've drawn marbles, we are adding 97 ways, namely drawing the same marble twice, all of which work. Thus, the answer is
$$
\frac{40 \cdot 97+97}{97 \cdot 96+97}=\frac{41}{97}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n12. [8]",
"solution_match": "\nSolution 1: "
}
|
00165436-0a07-5008-9a38-f6298765b200
| 610,647
|
Suppose that point $D$ lies on side $B C$ of triangle $A B C$ such that $A D$ bisects $\angle B A C$, and let $\ell$ denote the line through $A$ perpendicular to $A D$. If the distances from $B$ and $C$ to $\ell$ are 5 and 6 , respectively, compute $A D$.
|
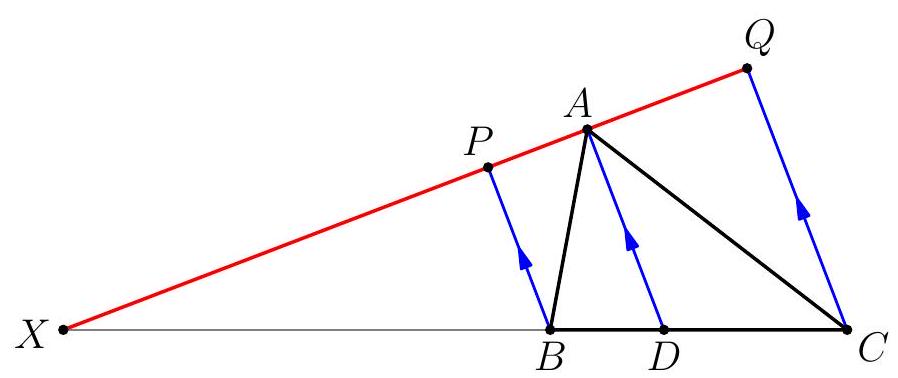
Let $\ell$, the external angle bisector, intersect $B C$ at $X$. By the external angle bisector theorem, $A B$ : $A C=X B: X C=5: 6$, so $B D: D C=5: 6$ by the angle bisector theorem. Then $A D$ is a weighted average of the distances from $B$ and $C$ to $\ell$, namely
$$
\frac{6}{11} \cdot 5+\frac{5}{11} \cdot 6=\frac{60}{11}
$$
|
\frac{60}{11}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose that point $D$ lies on side $B C$ of triangle $A B C$ such that $A D$ bisects $\angle B A C$, and let $\ell$ denote the line through $A$ perpendicular to $A D$. If the distances from $B$ and $C$ to $\ell$ are 5 and 6 , respectively, compute $A D$.
|

Let $\ell$, the external angle bisector, intersect $B C$ at $X$. By the external angle bisector theorem, $A B$ : $A C=X B: X C=5: 6$, so $B D: D C=5: 6$ by the angle bisector theorem. Then $A D$ is a weighted average of the distances from $B$ and $C$ to $\ell$, namely
$$
\frac{6}{11} \cdot 5+\frac{5}{11} \cdot 6=\frac{60}{11}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n14. [9]",
"solution_match": "\nSolution:\n"
}
|
465e7321-71ae-5bb2-9f88-ddd8a7ea0757
| 610,649
|
Lucas writes two distinct positive integers on a whiteboard. He decreases the smaller number by 20 and increases the larger number by 23 , only to discover the product of the two original numbers is equal to the product of the two altered numbers. Compute the minimum possible sum of the original two numbers on the board.
|
Let the original numbers be $m<n$. We know
$$
m n=(m-20)(n+23)=m n-20 n+23 m-460 \Longrightarrow 23 m-20 n=460
$$
Furthermore, $23 m<23 n$ hence $460<3 n \Longrightarrow n \geq 154$. Furthermore, we must have $23 \mid n$ hence the least possible value of $n$ is 161 which corresponds $m=160$.
This yields a minimum sum of $161+160=321$.
|
321
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Lucas writes two distinct positive integers on a whiteboard. He decreases the smaller number by 20 and increases the larger number by 23 , only to discover the product of the two original numbers is equal to the product of the two altered numbers. Compute the minimum possible sum of the original two numbers on the board.
|
Let the original numbers be $m<n$. We know
$$
m n=(m-20)(n+23)=m n-20 n+23 m-460 \Longrightarrow 23 m-20 n=460
$$
Furthermore, $23 m<23 n$ hence $460<3 n \Longrightarrow n \geq 154$. Furthermore, we must have $23 \mid n$ hence the least possible value of $n$ is 161 which corresponds $m=160$.
This yields a minimum sum of $161+160=321$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n15. [9]",
"solution_match": "\nSolution: "
}
|
f28120a2-992b-583b-9d32-85ba9ce03e57
| 610,650
|
Compute the number of tuples $\left(a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ of (not necessarily positive) integers such that $a_{i} \leq i$ for all $0 \leq i \leq 5$ and
$$
a_{0}+a_{1}+\cdots+a_{5}=6
$$
|
Answer: 2002
|
2002
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of tuples $\left(a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ of (not necessarily positive) integers such that $a_{i} \leq i$ for all $0 \leq i \leq 5$ and
$$
a_{0}+a_{1}+\cdots+a_{5}=6
$$
|
Answer: 2002
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n16. [10]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
9da6df61-2303-5fda-8c21-bb682472d5d4
| 610,651
|
Let $A B C$ be an equilateral triangle of side length 15 . Let $A_{b}$ and $B_{a}$ be points on side $A B, A_{c}$ and $C_{a}$ be points on side $A C$, and $B_{c}$ and $C_{b}$ be points on side $B C$ such that $\triangle A A_{b} A_{c}, \triangle B B_{c} B_{a}$, and $\triangle C C_{a} C_{b}$ are equilateral triangles with side lengths 3, 4 , and 5 , respectively. Compute the radius of the circle tangent to segments $\overline{A_{b} A_{c}}, \overline{B_{a} B_{c}}$, and $\overline{C_{a} C_{b}}$.
|
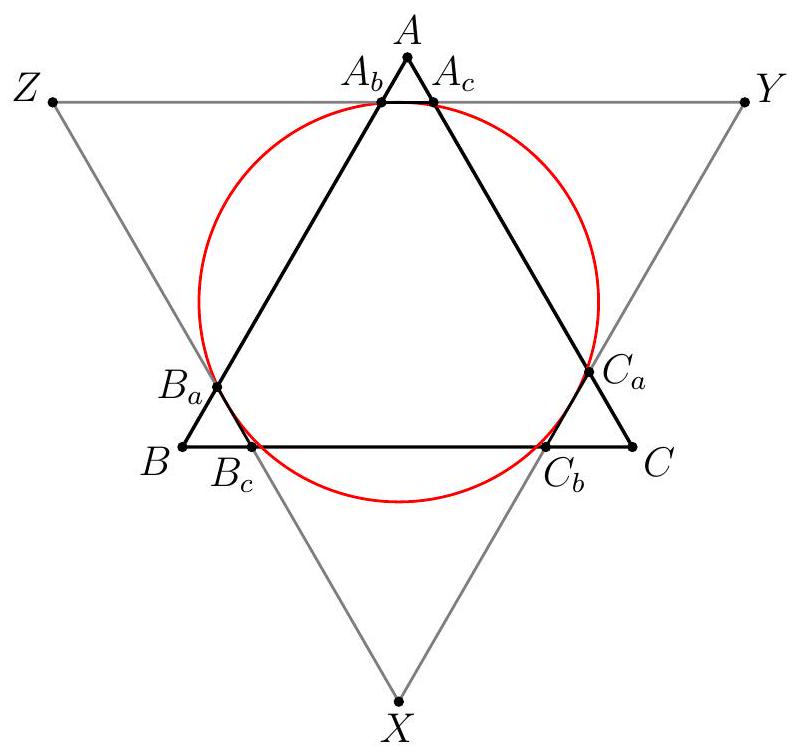
Let $\triangle X Y Z$ be the triangle formed by lines $A_{b} A_{c}, B_{a} B_{c}$, and $C_{a} C_{b}$. Then, the desired circle is the incircle of $\triangle X Y Z$, which is equilateral. We have
$$
\begin{aligned}
Y Z & =Y A_{c}+A_{c} A_{b}+A_{b} Z \\
& =A_{c} C_{a}+A_{c} A_{b}+A_{b} B_{a} \\
& =(15-3-5)+3+(15-3-4) \\
& =18,
\end{aligned}
$$
and so the inradius is $\frac{1}{2 \sqrt{3}} \cdot 18=3 \sqrt{3}$.
|
3 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle of side length 15 . Let $A_{b}$ and $B_{a}$ be points on side $A B, A_{c}$ and $C_{a}$ be points on side $A C$, and $B_{c}$ and $C_{b}$ be points on side $B C$ such that $\triangle A A_{b} A_{c}, \triangle B B_{c} B_{a}$, and $\triangle C C_{a} C_{b}$ are equilateral triangles with side lengths 3, 4 , and 5 , respectively. Compute the radius of the circle tangent to segments $\overline{A_{b} A_{c}}, \overline{B_{a} B_{c}}$, and $\overline{C_{a} C_{b}}$.
|

Let $\triangle X Y Z$ be the triangle formed by lines $A_{b} A_{c}, B_{a} B_{c}$, and $C_{a} C_{b}$. Then, the desired circle is the incircle of $\triangle X Y Z$, which is equilateral. We have
$$
\begin{aligned}
Y Z & =Y A_{c}+A_{c} A_{b}+A_{b} Z \\
& =A_{c} C_{a}+A_{c} A_{b}+A_{b} B_{a} \\
& =(15-3-5)+3+(15-3-4) \\
& =18,
\end{aligned}
$$
and so the inradius is $\frac{1}{2 \sqrt{3}} \cdot 18=3 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n17. [10]",
"solution_match": "\nSolution:\n"
}
|
5b02d716-d0bc-57de-ae69-378d91e8f664
| 610,652
|
Over all real numbers $x$ and $y$ such that
$$
x^{3}=3 x+y \quad \text { and } \quad y^{3}=3 y+x
$$
compute the sum of all possible values of $x^{2}+y^{2}$.
|
First, we eliminate easy cases.
- if $x=-y$, then $x^{3}=3 x-x=2 x$, so $x \in\{0, \sqrt{2},-\sqrt{2}\}$. Therefore, we get $(\sqrt{2},-\sqrt{2}),(-\sqrt{2}, \sqrt{2})$, and $(0,0)$.
- if $x=y \neq 0$, then $x^{3}=3 x+x=4 x$, so $x \in\{2,-2\}$. Therefore, we get $(2,2)$ and $(-2,-2)$.
Otherwise, adding two equations gives
$$
\begin{aligned}
x^{3}+y^{3} & =4 x+4 y \\
(x+y)\left(x^{2}-x y+y^{2}\right) & =4(x+y) \\
x^{2}-x y+y^{2} & =4
\end{aligned}
$$
and subtracting the two equations gives
$$
\begin{aligned}
x^{3}-y^{3} & =2 x-2 y \\
(x-y)\left(x^{2}+x y+y^{2}\right) & =2(x-y) \\
x^{2}+x y+y^{2} & =2
\end{aligned}
$$
We have $x^{2}-x y+y^{2}=4$ and $x^{2}+x y+y^{2}=2$, so adding these gives $x^{2}+y^{2}=3$. One can also see that $x y=-1$, so the solution obtained will be real.
The final answer is $4+8+0+3=15$.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Over all real numbers $x$ and $y$ such that
$$
x^{3}=3 x+y \quad \text { and } \quad y^{3}=3 y+x
$$
compute the sum of all possible values of $x^{2}+y^{2}$.
|
First, we eliminate easy cases.
- if $x=-y$, then $x^{3}=3 x-x=2 x$, so $x \in\{0, \sqrt{2},-\sqrt{2}\}$. Therefore, we get $(\sqrt{2},-\sqrt{2}),(-\sqrt{2}, \sqrt{2})$, and $(0,0)$.
- if $x=y \neq 0$, then $x^{3}=3 x+x=4 x$, so $x \in\{2,-2\}$. Therefore, we get $(2,2)$ and $(-2,-2)$.
Otherwise, adding two equations gives
$$
\begin{aligned}
x^{3}+y^{3} & =4 x+4 y \\
(x+y)\left(x^{2}-x y+y^{2}\right) & =4(x+y) \\
x^{2}-x y+y^{2} & =4
\end{aligned}
$$
and subtracting the two equations gives
$$
\begin{aligned}
x^{3}-y^{3} & =2 x-2 y \\
(x-y)\left(x^{2}+x y+y^{2}\right) & =2(x-y) \\
x^{2}+x y+y^{2} & =2
\end{aligned}
$$
We have $x^{2}-x y+y^{2}=4$ and $x^{2}+x y+y^{2}=2$, so adding these gives $x^{2}+y^{2}=3$. One can also see that $x y=-1$, so the solution obtained will be real.
The final answer is $4+8+0+3=15$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n18. [10]",
"solution_match": "\nSolution 1: "
}
|
e5d39799-3d11-52ef-a218-b45a836827bb
| 610,653
|
Let $A B C D$ be a square of side length 10 . Point $E$ is on ray $\overrightarrow{A B}$ such that $A E=17$, and point $F$ is on ray $\overrightarrow{A D}$ such that $A F=14$. The line through $B$ parallel to $C E$ and the line through $D$ parallel to $C F$ meet at $P$. Compute the area of quadrilateral $A E P F$.
|
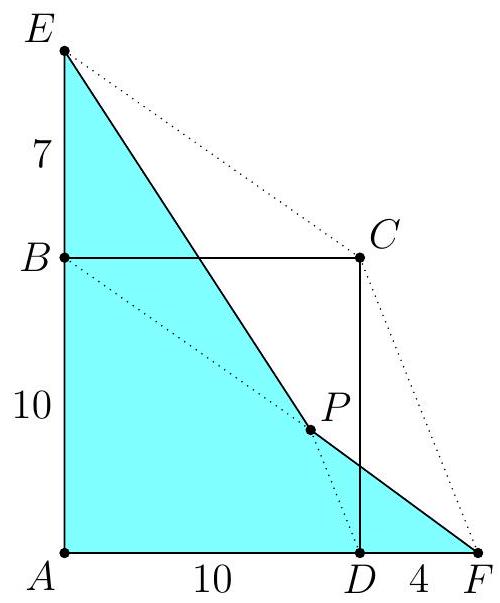
From $B P \| C E$, we get that $[B P E]=[B P C]$. From $D P \| C F$, we get that $[D P F]=[D P C]$. Thus,
$$
\begin{aligned}
{[A E P F] } & =[B A C P]+[B P E]+[D P F] \\
& =[B A C P]+[B P C]+[D P C] \\
& =[A B C D] \\
& =10^{2}=100 .
\end{aligned}
$$
|
100
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a square of side length 10 . Point $E$ is on ray $\overrightarrow{A B}$ such that $A E=17$, and point $F$ is on ray $\overrightarrow{A D}$ such that $A F=14$. The line through $B$ parallel to $C E$ and the line through $D$ parallel to $C F$ meet at $P$. Compute the area of quadrilateral $A E P F$.
|

From $B P \| C E$, we get that $[B P E]=[B P C]$. From $D P \| C F$, we get that $[D P F]=[D P C]$. Thus,
$$
\begin{aligned}
{[A E P F] } & =[B A C P]+[B P E]+[D P F] \\
& =[B A C P]+[B P C]+[D P C] \\
& =[A B C D] \\
& =10^{2}=100 .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n20. [11]",
"solution_match": "\n## Solution:\n\n"
}
|
1df7b346-f903-541d-8b49-6f5c4339677a
| 610,655
|
An integer $n$ is chosen uniformly at random from the set $\{1,2,3, \ldots, 2023!\}$. Compute the probability that
$$
\operatorname{gcd}\left(n^{n}+50, n+1\right)=1
$$
|
Answer: $\square$
$\frac{265}{357}$.
|
\frac{265}{357}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
An integer $n$ is chosen uniformly at random from the set $\{1,2,3, \ldots, 2023!\}$. Compute the probability that
$$
\operatorname{gcd}\left(n^{n}+50, n+1\right)=1
$$
|
Answer: $\square$
$\frac{265}{357}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n21. [11]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
761a82b4-b227-5810-9847-8720b1bba43c
| 610,656
|
There is a $6 \times 6$ grid of lights. There is a switch at the top of each column and on the left of each row. A light will only turn on if the switches corresponding to both its column and its row are in the "on" position. Compute the number of different configurations of lights.
|
Take any configuration of switches such that there exists at least one row and one column which are switched on. There are $\left(2^{6}-1\right)^{2}=3969$ such configurations.
We prove that any two such configurations $A$ and $B$ lead to a different set of lights. Without loss of generality assume $A$ has row $r$ switched on and $B$ doesn't have row $r$ switched on. Thus, configuration $A$ will contain at least one light turned on in row $r$ (since there exists at least one column switch which is turned on), while configuration $B$ contains zero such lights turned on. Thus configuration $A$ and $B$ lead to different sets of lights.
All configurations where all columns or all rows are turned off lead to all lights being turned off. We add 1 extra option to account for this case, getting $3969+1=3970$ total possibilities.
|
3970
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There is a $6 \times 6$ grid of lights. There is a switch at the top of each column and on the left of each row. A light will only turn on if the switches corresponding to both its column and its row are in the "on" position. Compute the number of different configurations of lights.
|
Take any configuration of switches such that there exists at least one row and one column which are switched on. There are $\left(2^{6}-1\right)^{2}=3969$ such configurations.
We prove that any two such configurations $A$ and $B$ lead to a different set of lights. Without loss of generality assume $A$ has row $r$ switched on and $B$ doesn't have row $r$ switched on. Thus, configuration $A$ will contain at least one light turned on in row $r$ (since there exists at least one column switch which is turned on), while configuration $B$ contains zero such lights turned on. Thus configuration $A$ and $B$ lead to different sets of lights.
All configurations where all columns or all rows are turned off lead to all lights being turned off. We add 1 extra option to account for this case, getting $3969+1=3970$ total possibilities.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nSolution: "
}
|
17f071d7-163e-541d-a1e5-15c4c0cc5e5a
| 610,657
|
Compute the smallest positive integer $k$ such that 49 divides $\binom{2 k}{k}$.
|
The largest $a$ such that $7^{a} \left\lvert\,\binom{ 2 k}{k}\right.$ is equal to the number of carries when you add $k+k$ in base 7, by Kummer's Theorem. Thus, we need two carries, so $2 k$ must have at least 3 digits in base 7 . Hence, $2 k \geq 49$, so $k \geq 25$. We know $k=25$ works because $25+25=34_{7}+34_{7}=101_{7}$ has two carries.
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the smallest positive integer $k$ such that 49 divides $\binom{2 k}{k}$.
|
The largest $a$ such that $7^{a} \left\lvert\,\binom{ 2 k}{k}\right.$ is equal to the number of carries when you add $k+k$ in base 7, by Kummer's Theorem. Thus, we need two carries, so $2 k$ must have at least 3 digits in base 7 . Hence, $2 k \geq 49$, so $k \geq 25$. We know $k=25$ works because $25+25=34_{7}+34_{7}=101_{7}$ has two carries.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nSolution: "
}
|
69317d54-2e52-57a8-a8d2-e40ad7042d2b
| 610,659
|
A right triangle and a circle are drawn such that the circle is tangent to the legs of the right triangle. The circle cuts the hypotenuse into three segments of lengths 1,24 , and 3 , and the segment of length 24 is a chord of the circle. Compute the area of the triangle.
|
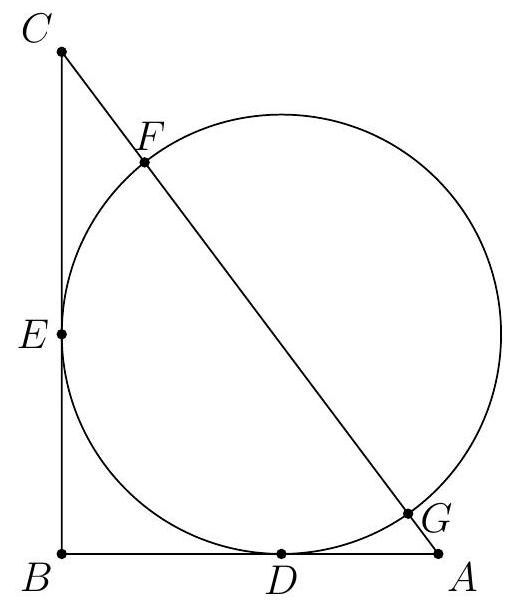
Let the triangle be $\triangle A B C$, with $A C$ as the hypotenuse, and let $D, E, F, G$ be on sides $A B, B C, A C$, $A C$, respectively, such that they all lie on the circle. We have $A G=1, G F=24$, and $F C=3$.
By power of a point, we have
$$
\begin{aligned}
& A D=\sqrt{A G \cdot A F}=\sqrt{1(1+24)}=5 \\
& C E=\sqrt{C F \cdot C G}=\sqrt{3(3+24)}=9
\end{aligned}
$$
Now, let $B D=B E=x$. By the Pythagorean Theorem, we get that
$$
\begin{aligned}
(x+5)^{2}+(x+9)^{2} & =28^{2} \\
(x+5)^{2}+(x+9)^{2}-((x+9)-(x+5))^{2} & =28^{2}-4^{2} \\
2(x+5)(x+9) & =768 \\
(x+5)(x+9) & =384 .
\end{aligned}
$$
The area of $\triangle A B C$ is $\frac{1}{2}(x+5)(x+9)=\frac{1}{2} \cdot 384=192$.
|
192
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A right triangle and a circle are drawn such that the circle is tangent to the legs of the right triangle. The circle cuts the hypotenuse into three segments of lengths 1,24 , and 3 , and the segment of length 24 is a chord of the circle. Compute the area of the triangle.
|

Let the triangle be $\triangle A B C$, with $A C$ as the hypotenuse, and let $D, E, F, G$ be on sides $A B, B C, A C$, $A C$, respectively, such that they all lie on the circle. We have $A G=1, G F=24$, and $F C=3$.
By power of a point, we have
$$
\begin{aligned}
& A D=\sqrt{A G \cdot A F}=\sqrt{1(1+24)}=5 \\
& C E=\sqrt{C F \cdot C G}=\sqrt{3(3+24)}=9
\end{aligned}
$$
Now, let $B D=B E=x$. By the Pythagorean Theorem, we get that
$$
\begin{aligned}
(x+5)^{2}+(x+9)^{2} & =28^{2} \\
(x+5)^{2}+(x+9)^{2}-((x+9)-(x+5))^{2} & =28^{2}-4^{2} \\
2(x+5)(x+9) & =768 \\
(x+5)(x+9) & =384 .
\end{aligned}
$$
The area of $\triangle A B C$ is $\frac{1}{2}(x+5)(x+9)=\frac{1}{2} \cdot 384=192$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n25. [13]",
"solution_match": "\n## Solution 1:\n\n"
}
|
a24048e1-27dc-564d-b00b-785fe9e9e2d0
| 610,660
|
Compute the smallest multiple of 63 with an odd number of ones in its base two representation.
|
Notice that $63=2^{6}-1$, so for any $a$ we know
$$
63 a=64 a-a=2^{6}(a-1)+(64-a)
$$
As long as $a \leq 64$, we know $a-1$ and $64-a$ are both integers between 0 and 63 , so the binary representation of $63 a$ is just $a-1$ followed by $64-a$ in binary (where we append leading 0 s to make the latter 6 digits).
Furthermore, $a-1$ and $64-a$ sum to $63=111111_{2}$, so $a-1$ has 1 s in binary where $64-a$ has 0 s, and vice versa. Thus, together, they have six 1 s, so $63 a$ will always have six 1 s in binary when $a \leq 64$. We can also check $63 \cdot 65=2^{12}-1$ has twelve 1s, while $63 \cdot 66=2(63 \cdot 33)$ has the same binary representation with an extra 0 at the end, so it also has six 1s. Finally,
$$
63 \cdot 67=2^{12}+125=1000001111101_{2}
$$
has seven 1 s, so the answer is $63 \cdot 67=4221$.
|
4221
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the smallest multiple of 63 with an odd number of ones in its base two representation.
|
Notice that $63=2^{6}-1$, so for any $a$ we know
$$
63 a=64 a-a=2^{6}(a-1)+(64-a)
$$
As long as $a \leq 64$, we know $a-1$ and $64-a$ are both integers between 0 and 63 , so the binary representation of $63 a$ is just $a-1$ followed by $64-a$ in binary (where we append leading 0 s to make the latter 6 digits).
Furthermore, $a-1$ and $64-a$ sum to $63=111111_{2}$, so $a-1$ has 1 s in binary where $64-a$ has 0 s, and vice versa. Thus, together, they have six 1 s, so $63 a$ will always have six 1 s in binary when $a \leq 64$. We can also check $63 \cdot 65=2^{12}-1$ has twelve 1s, while $63 \cdot 66=2(63 \cdot 33)$ has the same binary representation with an extra 0 at the end, so it also has six 1s. Finally,
$$
63 \cdot 67=2^{12}+125=1000001111101_{2}
$$
has seven 1 s, so the answer is $63 \cdot 67=4221$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n26. [13]",
"solution_match": "\nSolution: "
}
|
87ba057a-7289-5e66-be70-0b90d991b738
| 610,661
|
Compute the number of ways to color the vertices of a regular heptagon red, green, or blue (with rotations and reflections distinct) such that no isosceles triangle whose vertices are vertices of the heptagon has all three vertices the same color.
|
Number the vertices 1 through 7 in order. Then, the only way to have three vertices of a regular heptagon that do not form an isosceles triangle is if they are vertices $1,2,4$, rotated or reflected. Thus, it is impossible for have four vertices in the heptagon of one color because it is impossible for all subsets of three vertices to form a valid scalene triangle. We then split into two cases:
Case 1: Two colors with three vertices each, one color with one vertex. There is only one way to do this up to permutations of color and rotations and reflections; if vertices $1,2,4$ are the same color, of the remaining 4 vertices, only $3,5,6$ form a scalene triangle. Thus, we have 7 possible locations for the vertex with unique color, 3 ways to pick a color for that vertex, and 2 ways to assign the remaining two colors to the two triangles, for a total of 42 ways.
Case 2: Two colors with two vertices each, one color with three vertices. There are 3 choices of color for the set of three vertices, 14 possible orientations of the set of three vertices, and $\binom{4}{2}$ choices of which pair of the remaining four vertices is of a particular remaining color; as there are only two of each color, any such assignment is valid. This is a total of total of $3 \cdot 14 \cdot 6=252$ ways.
Thus, the final total is $42+252=294$.
|
294
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of ways to color the vertices of a regular heptagon red, green, or blue (with rotations and reflections distinct) such that no isosceles triangle whose vertices are vertices of the heptagon has all three vertices the same color.
|
Number the vertices 1 through 7 in order. Then, the only way to have three vertices of a regular heptagon that do not form an isosceles triangle is if they are vertices $1,2,4$, rotated or reflected. Thus, it is impossible for have four vertices in the heptagon of one color because it is impossible for all subsets of three vertices to form a valid scalene triangle. We then split into two cases:
Case 1: Two colors with three vertices each, one color with one vertex. There is only one way to do this up to permutations of color and rotations and reflections; if vertices $1,2,4$ are the same color, of the remaining 4 vertices, only $3,5,6$ form a scalene triangle. Thus, we have 7 possible locations for the vertex with unique color, 3 ways to pick a color for that vertex, and 2 ways to assign the remaining two colors to the two triangles, for a total of 42 ways.
Case 2: Two colors with two vertices each, one color with three vertices. There are 3 choices of color for the set of three vertices, 14 possible orientations of the set of three vertices, and $\binom{4}{2}$ choices of which pair of the remaining four vertices is of a particular remaining color; as there are only two of each color, any such assignment is valid. This is a total of total of $3 \cdot 14 \cdot 6=252$ ways.
Thus, the final total is $42+252=294$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n27. [13]",
"solution_match": "\nSolution: "
}
|
5e2f19e3-fef8-52ae-a139-e896bf78c61b
| 610,662
|
There is a unique quadruple of positive integers $(a, b, c, k)$ such that $c$ is not a perfect square and $a+\sqrt{b+\sqrt{c}}$ is a root of the polynomial $x^{4}-20 x^{3}+108 x^{2}-k x+9$. Compute $c$.
|
There are many ways to do this, including bashing it out directly.
The four roots are $a \pm \sqrt{b \pm \sqrt{c}}$, so the sum of roots is 20 , so $a=5$. Next, we compute the sum of squares of roots:
$$
(a+\sqrt{b \pm \sqrt{c}})^{2}+(a-\sqrt{b \pm \sqrt{c}})^{2}=2 a^{2}+2 b \pm 2 \sqrt{c}
$$
so the sum of squares of roots is $4 a^{2}+4 b$. However, from Vieta, it is $20^{2}-2 \cdot 108=184$, so $100+4 b=$ $184 \Longrightarrow b=21$. Finally, the product of roots is
$$
\left(a^{2}-(b+\sqrt{c})\right)\left(a^{2}-(b-\sqrt{c})\right)=\left(a^{2}-b\right)^{2}-c=16-c,
$$
so we have $c=7$.
Remark. Here we provide a justification that there is a unique quadruple. Let $P(x)=x^{4}-20 x^{3}+$ $108 x^{2}-k x+9$ and $r=a+\sqrt{b+\sqrt{c}}$. Then, note that
- $r$ cannot be an integer because if not, then $b+\sqrt{c}$ must be an integer, so $c$ must be a perfect square.
- $r$ cannot be a root of an irreducible cubic. One can check this directly because the remaining factor must be linear, so it must be $x \pm 1, x \pm 3$, or $x \pm 9$. We can also argue using the theory of field extensions: $[\mathbb{Q}(r): \mathbb{Q}]=3$. However, we have the tower,
$$
\mathbb{Q}(r) \supset \mathbb{Q}(b+\sqrt{c}) \stackrel{\operatorname{deg} 2}{\supset} \mathbb{Q},
$$
and by multiplicativity of degree of field extensions, this forces $[\mathbb{Q}(r): \mathbb{Q}(b+\sqrt{c})]$ to not be an integer.
- $r$ cannot be a root of quadratic. If not, then $P$ factors into two quadratic polynomials $\left(x^{2}-m x+\right.$ $p)\left(x^{2}-n x+q\right)$. We then have $m+n=20, p q=9$, and $m n+p+q=108$. By AM-GM, we have $m n \leq 100$, so $p+q \geq 8$, which forces $(p, q)=(1,9)$, but this makes $m n=98$, which is impossible.
Thus, the minimal polynomial of $r$ must be the quartic $P(x)$. This means that all roots of $P$ are $a \pm \sqrt{b \pm c}$, and we can proceed as in the solution.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
There is a unique quadruple of positive integers $(a, b, c, k)$ such that $c$ is not a perfect square and $a+\sqrt{b+\sqrt{c}}$ is a root of the polynomial $x^{4}-20 x^{3}+108 x^{2}-k x+9$. Compute $c$.
|
There are many ways to do this, including bashing it out directly.
The four roots are $a \pm \sqrt{b \pm \sqrt{c}}$, so the sum of roots is 20 , so $a=5$. Next, we compute the sum of squares of roots:
$$
(a+\sqrt{b \pm \sqrt{c}})^{2}+(a-\sqrt{b \pm \sqrt{c}})^{2}=2 a^{2}+2 b \pm 2 \sqrt{c}
$$
so the sum of squares of roots is $4 a^{2}+4 b$. However, from Vieta, it is $20^{2}-2 \cdot 108=184$, so $100+4 b=$ $184 \Longrightarrow b=21$. Finally, the product of roots is
$$
\left(a^{2}-(b+\sqrt{c})\right)\left(a^{2}-(b-\sqrt{c})\right)=\left(a^{2}-b\right)^{2}-c=16-c,
$$
so we have $c=7$.
Remark. Here we provide a justification that there is a unique quadruple. Let $P(x)=x^{4}-20 x^{3}+$ $108 x^{2}-k x+9$ and $r=a+\sqrt{b+\sqrt{c}}$. Then, note that
- $r$ cannot be an integer because if not, then $b+\sqrt{c}$ must be an integer, so $c$ must be a perfect square.
- $r$ cannot be a root of an irreducible cubic. One can check this directly because the remaining factor must be linear, so it must be $x \pm 1, x \pm 3$, or $x \pm 9$. We can also argue using the theory of field extensions: $[\mathbb{Q}(r): \mathbb{Q}]=3$. However, we have the tower,
$$
\mathbb{Q}(r) \supset \mathbb{Q}(b+\sqrt{c}) \stackrel{\operatorname{deg} 2}{\supset} \mathbb{Q},
$$
and by multiplicativity of degree of field extensions, this forces $[\mathbb{Q}(r): \mathbb{Q}(b+\sqrt{c})]$ to not be an integer.
- $r$ cannot be a root of quadratic. If not, then $P$ factors into two quadratic polynomials $\left(x^{2}-m x+\right.$ $p)\left(x^{2}-n x+q\right)$. We then have $m+n=20, p q=9$, and $m n+p+q=108$. By AM-GM, we have $m n \leq 100$, so $p+q \geq 8$, which forces $(p, q)=(1,9)$, but this makes $m n=98$, which is impossible.
Thus, the minimal polynomial of $r$ must be the quartic $P(x)$. This means that all roots of $P$ are $a \pm \sqrt{b \pm c}$, and we can proceed as in the solution.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nSolution: "
}
|
edb8313a-5d57-564c-9938-d5cfdfd151e9
| 610,663
|
Let $A_{1} A_{2} \ldots A_{6}$ be a regular hexagon with side length $11 \sqrt{3}$, and let $B_{1} B_{2} \ldots B_{6}$ be another regular hexagon completely inside $A_{1} A_{2} \ldots A_{6}$ such that for all $i \in\{1,2, \ldots, 5\}, A_{i} A_{i+1}$ is parallel to $B_{i} B_{i+1}$. Suppose that the distance between lines $A_{1} A_{2}$ and $B_{1} B_{2}$ is 7 , the distance between lines $A_{2} A_{3}$ and $B_{2} B_{3}$ is 3 , and the distance between lines $A_{3} A_{4}$ and $B_{3} B_{4}$ is 8 . Compute the side length of $B_{1} B_{2} \ldots B_{6}$.
|
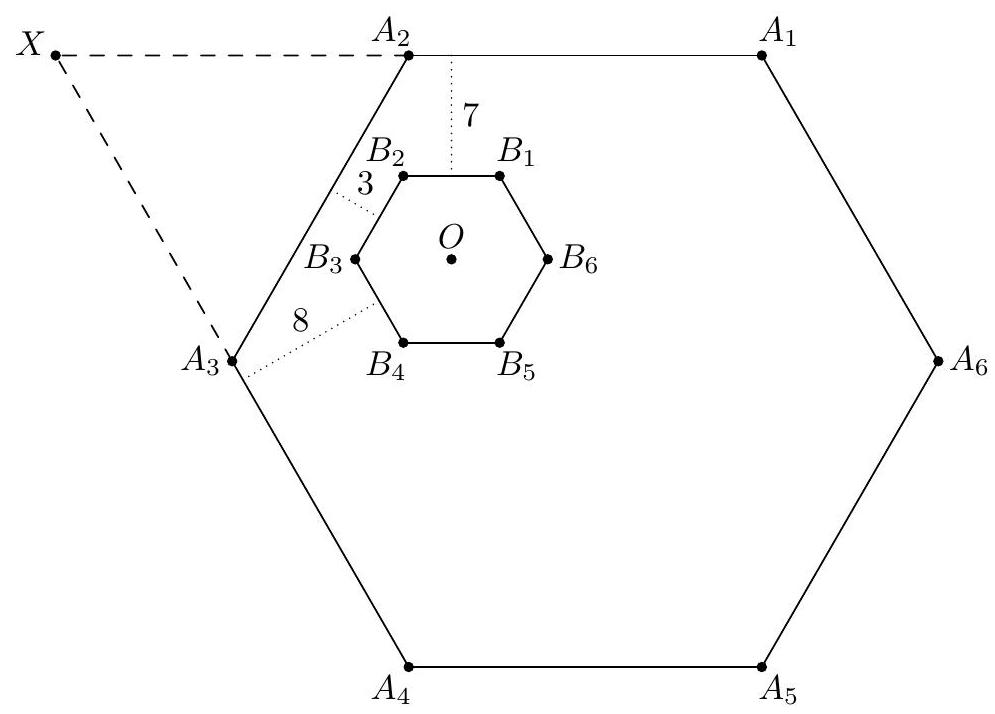
Let $X=A_{1} A_{2} \cap A_{3} A_{4}$, and let $O$ be the center of $B_{1} B_{2} \ldots B_{6}$. Let $p$ be the apothem of hexagon $B$. Since $O A_{2} X A_{3}$ is a convex quadrilateral, we have
$$
\begin{aligned}
{\left[A_{2} A_{3} X\right] } & =\left[A_{2} X O\right]+\left[A_{3} X O\right]-\left[A_{2} A_{3} O\right] \\
& =\frac{11 \sqrt{3}(7+p)}{2}+\frac{11 \sqrt{3}(8+p)}{2}-\frac{11 \sqrt{3}(3+p)}{2} \\
& =\frac{11 \sqrt{3}(12+p)}{2} .
\end{aligned}
$$
Since $\left[A_{2} A_{3} X\right]=(11 \sqrt{3})^{2} \frac{\sqrt{3}}{4}$, we get that
$$
\frac{12+p}{2}=(11 \sqrt{3}) \frac{\sqrt{3}}{4}=\frac{33}{4} \Longrightarrow p=\frac{9}{2}
$$
Thus, the side length of hexagon $B$ is $p \cdot \frac{2}{\sqrt{3}}=3 \sqrt{3}$.
|
3 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A_{1} A_{2} \ldots A_{6}$ be a regular hexagon with side length $11 \sqrt{3}$, and let $B_{1} B_{2} \ldots B_{6}$ be another regular hexagon completely inside $A_{1} A_{2} \ldots A_{6}$ such that for all $i \in\{1,2, \ldots, 5\}, A_{i} A_{i+1}$ is parallel to $B_{i} B_{i+1}$. Suppose that the distance between lines $A_{1} A_{2}$ and $B_{1} B_{2}$ is 7 , the distance between lines $A_{2} A_{3}$ and $B_{2} B_{3}$ is 3 , and the distance between lines $A_{3} A_{4}$ and $B_{3} B_{4}$ is 8 . Compute the side length of $B_{1} B_{2} \ldots B_{6}$.
|

Let $X=A_{1} A_{2} \cap A_{3} A_{4}$, and let $O$ be the center of $B_{1} B_{2} \ldots B_{6}$. Let $p$ be the apothem of hexagon $B$. Since $O A_{2} X A_{3}$ is a convex quadrilateral, we have
$$
\begin{aligned}
{\left[A_{2} A_{3} X\right] } & =\left[A_{2} X O\right]+\left[A_{3} X O\right]-\left[A_{2} A_{3} O\right] \\
& =\frac{11 \sqrt{3}(7+p)}{2}+\frac{11 \sqrt{3}(8+p)}{2}-\frac{11 \sqrt{3}(3+p)}{2} \\
& =\frac{11 \sqrt{3}(12+p)}{2} .
\end{aligned}
$$
Since $\left[A_{2} A_{3} X\right]=(11 \sqrt{3})^{2} \frac{\sqrt{3}}{4}$, we get that
$$
\frac{12+p}{2}=(11 \sqrt{3}) \frac{\sqrt{3}}{4}=\frac{33}{4} \Longrightarrow p=\frac{9}{2}
$$
Thus, the side length of hexagon $B$ is $p \cdot \frac{2}{\sqrt{3}}=3 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n29. [15]",
"solution_match": "\nSolution:\n"
}
|
cd419edc-5c9a-5b98-9a14-92239d5bf0d7
| 610,664
|
An HMMT party has $m$ MIT students and $h$ Harvard students for some positive integers $m$ and $h$, For every pair of people at the party, they are either friends or enemies. If every MIT student has 16 MIT friends and 8 Harvard friends, and every Harvard student has 7 MIT enemies and 10 Harvard enemies, compute how many pairs of friends there are at the party.
|
We count the number of MIT-Harvard friendships. Each of the $m$ MIT students has 8 Harvard friends, for a total of $8 m$ friendships. Each of the $h$ Harvard students has $m-7$ MIT friends, for a total of $h(m-7)$ friendships. So, $8 m=h(m-7) \Longrightarrow m h-8 m-7 h=0 \Longrightarrow(m-7)(h-8)=56$.
Each MIT student has 16 MIT friends, so $m \geq 17$. Each Harvard student has 10 Harvard enemies, so $h \geq 11$. This means $m-7 \geq 10$ and $h-8 \geq 3$. The only such pair ( $m-7, h-8$ ) that multiplies to 56 is $(14,4)$, so there are 21 MIT students and 12 Harvard students.
We can calculate the number of friendships as $\frac{16 m}{2}+8 m+\frac{(h-1-10) h}{2}=168+168+6=342$.
|
342
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An HMMT party has $m$ MIT students and $h$ Harvard students for some positive integers $m$ and $h$, For every pair of people at the party, they are either friends or enemies. If every MIT student has 16 MIT friends and 8 Harvard friends, and every Harvard student has 7 MIT enemies and 10 Harvard enemies, compute how many pairs of friends there are at the party.
|
We count the number of MIT-Harvard friendships. Each of the $m$ MIT students has 8 Harvard friends, for a total of $8 m$ friendships. Each of the $h$ Harvard students has $m-7$ MIT friends, for a total of $h(m-7)$ friendships. So, $8 m=h(m-7) \Longrightarrow m h-8 m-7 h=0 \Longrightarrow(m-7)(h-8)=56$.
Each MIT student has 16 MIT friends, so $m \geq 17$. Each Harvard student has 10 Harvard enemies, so $h \geq 11$. This means $m-7 \geq 10$ and $h-8 \geq 3$. The only such pair ( $m-7, h-8$ ) that multiplies to 56 is $(14,4)$, so there are 21 MIT students and 12 Harvard students.
We can calculate the number of friendships as $\frac{16 m}{2}+8 m+\frac{(h-1-10) h}{2}=168+168+6=342$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n30. [15]",
"solution_match": "\nSolution: "
}
|
ea8fbecf-7268-5f07-baa8-2e485c45f4f0
| 610,665
|
Let $s(n)$ denote the sum of the digits (in base ten) of a positive integer $n$. Compute the number of positive integers $n$ at most $10^{4}$ that satisfy
$$
s(11 n)=2 s(n)
$$
|
Answer: 2530
|
2530
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $s(n)$ denote the sum of the digits (in base ten) of a positive integer $n$. Compute the number of positive integers $n$ at most $10^{4}$ that satisfy
$$
s(11 n)=2 s(n)
$$
|
Answer: 2530
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n31. [17]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
a03cb6e4-62a6-5c15-b729-6beb3c569a4a
| 610,666
|
Compute
$$
\sum_{\substack{a+b+c=12 \\ a \geq 6, b, c \geq 0}} \frac{a!}{b!c!(a-b-c)!}
$$
where the sum runs over all triples of nonnegative integers $(a, b, c)$ such that $a+b+c=12$ and $a \geq 6$.
|
We tile a $1 \times 12$ board with red $1 \times 1$ pieces, blue $1 \times 2$ pieces, and green $1 \times 2$ pieces. Suppose we use $a$ total pieces, $b$ blue pieces, and $c$ green pieces. Then we must have $a+b+c=12$, and the number of ways to order the pieces is
$$
\binom{a}{b, c, a-b-c} .
$$
Thus, the desired sum is the number of ways to do this.
Let $a_{n}$ be the number of ways to do this on a $1 \times n$ board. Then we have the recursion $a_{n}=a_{n-1}+2 a_{n-2}$ by casework on the first piece: if it is $1 \times 1$, we are left with a $1 \times n-1$ board, and otherwise we are left with a $1 \times n-2$ board. We also know $a_{1}=1$ and $a_{2}=3$, so the characteristic polynomial for this recursion is $t^{2}-t-2=0$, which has roots 2 and -1 . Thus,
$$
a_{n}=A \cdot(-1)^{n}+B \cdot 2^{n}
$$
Then plugging in $n=1$ and $n=2$ gives $A=-\frac{1}{3}$ and $B=\frac{2}{3}$, so
$$
a_{n}=\frac{2^{n+1}+(-1)^{n}}{3}
$$
With $n=12$, this evaluates to our answer of 2731 .
|
2731
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute
$$
\sum_{\substack{a+b+c=12 \\ a \geq 6, b, c \geq 0}} \frac{a!}{b!c!(a-b-c)!}
$$
where the sum runs over all triples of nonnegative integers $(a, b, c)$ such that $a+b+c=12$ and $a \geq 6$.
|
We tile a $1 \times 12$ board with red $1 \times 1$ pieces, blue $1 \times 2$ pieces, and green $1 \times 2$ pieces. Suppose we use $a$ total pieces, $b$ blue pieces, and $c$ green pieces. Then we must have $a+b+c=12$, and the number of ways to order the pieces is
$$
\binom{a}{b, c, a-b-c} .
$$
Thus, the desired sum is the number of ways to do this.
Let $a_{n}$ be the number of ways to do this on a $1 \times n$ board. Then we have the recursion $a_{n}=a_{n-1}+2 a_{n-2}$ by casework on the first piece: if it is $1 \times 1$, we are left with a $1 \times n-1$ board, and otherwise we are left with a $1 \times n-2$ board. We also know $a_{1}=1$ and $a_{2}=3$, so the characteristic polynomial for this recursion is $t^{2}-t-2=0$, which has roots 2 and -1 . Thus,
$$
a_{n}=A \cdot(-1)^{n}+B \cdot 2^{n}
$$
Then plugging in $n=1$ and $n=2$ gives $A=-\frac{1}{3}$ and $B=\frac{2}{3}$, so
$$
a_{n}=\frac{2^{n+1}+(-1)^{n}}{3}
$$
With $n=12$, this evaluates to our answer of 2731 .
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n32. [17]",
"solution_match": "\nSolution: "
}
|
af0ebc19-99b1-55cb-83ac-93aecef3306f
| 610,667
|
Compute the smallest positive integer that does not appear in any problem statement on any round at HMMT November 2023.
Submit a positive integer $A$. If the correct answer is $C$, you will receive $\max (0,20-5|A-C|)$ points.
|
Answer: 22
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the smallest positive integer that does not appear in any problem statement on any round at HMMT November 2023.
Submit a positive integer $A$. If the correct answer is $C$, you will receive $\max (0,20-5|A-C|)$ points.
|
Answer: 22
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n34. [20]",
"solution_match": "\nProposed by: Arul Kolla\n"
}
|
02af9064-0066-5e7e-a9d0-e35e4096d880
| 610,669
|
Dorothea has a $3 \times 4$ grid of dots. She colors each dot red, blue, or dark gray. Compute the number of ways Dorothea can color the grid such that there is no rectangle whose sides are parallel to the grid lines and whose vertices all have the same color.
Submit a positive integer $A$. If the correct answer is $C$ and your answer is $A$, you will receive $\left\lfloor 20\left(\min \left(\frac{A}{C}, \frac{C}{A}\right)\right)^{2}\right\rfloor$ points.
|
Answer: 284688
|
284688
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dorothea has a $3 \times 4$ grid of dots. She colors each dot red, blue, or dark gray. Compute the number of ways Dorothea can color the grid such that there is no rectangle whose sides are parallel to the grid lines and whose vertices all have the same color.
Submit a positive integer $A$. If the correct answer is $C$ and your answer is $A$, you will receive $\left\lfloor 20\left(\min \left(\frac{A}{C}, \frac{C}{A}\right)\right)^{2}\right\rfloor$ points.
|
Answer: 284688
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-guts-solutions.jsonl",
"problem_match": "\n35. [20]",
"solution_match": "\nProposed by: Amy Feng, Isabella Quan, Pitchayut Saengrungkongka, Rishabh Das, Vidur Jasuja\n"
}
|
7cb4c005-d2ea-5c84-899d-47ace470709e
| 610,670
|
Let $A B C$ be an equilateral triangle with side length 2 that is inscribed in a circle $\omega$. A chord of $\omega$ passes through the midpoints of sides $A B$ and $A C$. Compute the length of this chord.
|
Answer: $\sqrt{5}$
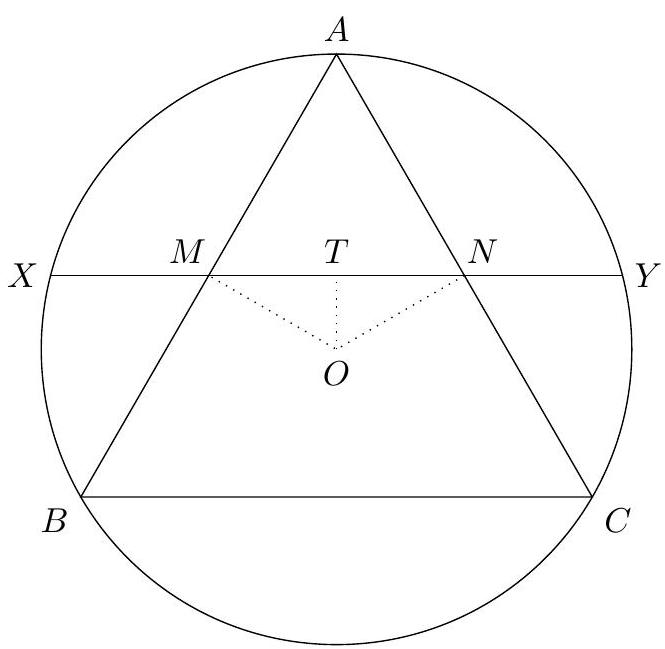
|
\sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle with side length 2 that is inscribed in a circle $\omega$. A chord of $\omega$ passes through the midpoints of sides $A B$ and $A C$. Compute the length of this chord.
|
Answer: $\sqrt{5}$

|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
5342c0ec-4ec7-53b3-a329-fe81be0a0920
| 610,672
|
A real number $x$ satisfies $9^{x}+3^{x}=6$. Compute the value of $16^{1 / x}+4^{1 / x}$.
|
Setting $y=3^{x}$ in the given equation yields
$$
y^{2}+y=6 \Longrightarrow y^{2}+y-6=0 \Longrightarrow y=-3,2
$$
Since $y>0$ we must have
$$
3^{x}=2 \Longrightarrow x=\log _{3}(2) \Longrightarrow 1 / x=\log _{2}(3)
$$
This means that
$$
16^{1 / x}+4^{1 / x}=\left(2^{1 / x}\right)^{4}+\left(2^{1 / x}\right)^{2}=3^{4}+3^{2}=90 .
$$
|
90
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A real number $x$ satisfies $9^{x}+3^{x}=6$. Compute the value of $16^{1 / x}+4^{1 / x}$.
|
Setting $y=3^{x}$ in the given equation yields
$$
y^{2}+y=6 \Longrightarrow y^{2}+y-6=0 \Longrightarrow y=-3,2
$$
Since $y>0$ we must have
$$
3^{x}=2 \Longrightarrow x=\log _{3}(2) \Longrightarrow 1 / x=\log _{2}(3)
$$
This means that
$$
16^{1 / x}+4^{1 / x}=\left(2^{1 / x}\right)^{4}+\left(2^{1 / x}\right)^{2}=3^{4}+3^{2}=90 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n2. [20]",
"solution_match": "\nSolution: "
}
|
f9b51228-4769-59df-b697-c30f04778fac
| 610,673
|
Two distinct similar rhombi share a diagonal. The smaller rhombus has area 1 , and the larger rhombus has area 9 . Compute the side length of the larger rhombus.
|
Let $d$ be the length of the smaller diagonal of the smaller rhombus. Since the ratio of the areas is $9: 1$, the ratio of the lengths is $3: 1$. This means that the smaller diagonal of the larger rhombus (which is also the longer diagonal of the smaller rhombus) has length $3 d$.
(Diagram not to scale.)
Therefore, the smaller rhombus has diagonal lengths $d$ and $3 d$, so since it has area 1 , we have
$$
\frac{1}{2} d(3 d)=1 \Longrightarrow d=\sqrt{\frac{2}{3}}
$$
By the Pythagorean Theorem, the side length of the smaller rhombus is
$$
\sqrt{\left(\frac{d}{2}\right)^{2}+\left(\frac{3 d}{2}\right)^{2}}=\sqrt{\frac{5 d^{2}}{2}}=\sqrt{\frac{5}{3}}
$$
The side length of the larger rhombus is three times this, i.e. $\sqrt{15}$.
|
\sqrt{15}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two distinct similar rhombi share a diagonal. The smaller rhombus has area 1 , and the larger rhombus has area 9 . Compute the side length of the larger rhombus.
|
Let $d$ be the length of the smaller diagonal of the smaller rhombus. Since the ratio of the areas is $9: 1$, the ratio of the lengths is $3: 1$. This means that the smaller diagonal of the larger rhombus (which is also the longer diagonal of the smaller rhombus) has length $3 d$.

(Diagram not to scale.)
Therefore, the smaller rhombus has diagonal lengths $d$ and $3 d$, so since it has area 1 , we have
$$
\frac{1}{2} d(3 d)=1 \Longrightarrow d=\sqrt{\frac{2}{3}}
$$
By the Pythagorean Theorem, the side length of the smaller rhombus is
$$
\sqrt{\left(\frac{d}{2}\right)^{2}+\left(\frac{3 d}{2}\right)^{2}}=\sqrt{\frac{5 d^{2}}{2}}=\sqrt{\frac{5}{3}}
$$
The side length of the larger rhombus is three times this, i.e. $\sqrt{15}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nSolution: "
}
|
a24bd852-a6c8-54c0-aea7-875d4975c637
| 610,674
|
There are six empty slots corresponding to the digits of a six-digit number. Claire and William take turns rolling a standard six-sided die, with Claire going first. They alternate with each roll until they have each rolled three times. After a player rolls, they place the number from their die roll into a remaining empty slot of their choice. Claire wins if the resulting six-digit number is divisible by 6 , and William wins otherwise. If both players play optimally, compute the probability that Claire wins.
|
A number being divisible by 6 is equivalent to the following two conditions:
- the sum of the digits is divisible by 3
- the last digit is even
Regardless of Claire and William's strategies, the first condition is satisfied with probability $\frac{1}{3}$. So Claire simply plays to maximize the chance of the last digit being even, while William plays to minimize this chance. In particular, clearly Claire's strategy is to place an even digit in the last position if she ever rolls one (as long as the last slot is still empty), and to try to place odd digits anywhere else. William's strategy is to place an odd digit in the last position if he ever rolls one (as long as the last slot is still empty), and to try to place even digits anywhere else.
To compute the probability that last digit ends up even, we split the game into the following three cases:
- If Claire rolls an even number before William rolls an odd number, then Claire immediately puts the even number in the last digit.
- If William rolls an odd number before Claire rolls an even number, then William immediately puts the odd number in the last digit.
- If William never rolls an odd number and Claire never rolls an even number, then since William goes last, he's forced to place his even number in the last slot.
The last digit ends up even in the first and third cases. The probability of the first case happening is $\frac{1}{2}+\frac{1}{2^{3}}+\frac{1}{2^{5}}$, depending on which turn Claire rolls her even number. The probability of the third case is $\frac{1}{2^{6}}$. So the probability the last digit is even is
$$
\frac{1}{2}+\frac{1}{2^{3}}+\frac{1}{2^{5}}+\frac{1}{2^{6}}=\frac{43}{64}
$$
Finally we multiply by the $\frac{1}{3}$ chance that the sum of all the digits is divisible by 3 (this is independent from the last-digit-even condition by e.g. Chinese Remainder Theorem), making our final answer
$$
\frac{1}{3} \cdot \frac{43}{64}=\frac{43}{192}
$$
|
\frac{43}{192}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are six empty slots corresponding to the digits of a six-digit number. Claire and William take turns rolling a standard six-sided die, with Claire going first. They alternate with each roll until they have each rolled three times. After a player rolls, they place the number from their die roll into a remaining empty slot of their choice. Claire wins if the resulting six-digit number is divisible by 6 , and William wins otherwise. If both players play optimally, compute the probability that Claire wins.
|
A number being divisible by 6 is equivalent to the following two conditions:
- the sum of the digits is divisible by 3
- the last digit is even
Regardless of Claire and William's strategies, the first condition is satisfied with probability $\frac{1}{3}$. So Claire simply plays to maximize the chance of the last digit being even, while William plays to minimize this chance. In particular, clearly Claire's strategy is to place an even digit in the last position if she ever rolls one (as long as the last slot is still empty), and to try to place odd digits anywhere else. William's strategy is to place an odd digit in the last position if he ever rolls one (as long as the last slot is still empty), and to try to place even digits anywhere else.
To compute the probability that last digit ends up even, we split the game into the following three cases:
- If Claire rolls an even number before William rolls an odd number, then Claire immediately puts the even number in the last digit.
- If William rolls an odd number before Claire rolls an even number, then William immediately puts the odd number in the last digit.
- If William never rolls an odd number and Claire never rolls an even number, then since William goes last, he's forced to place his even number in the last slot.
The last digit ends up even in the first and third cases. The probability of the first case happening is $\frac{1}{2}+\frac{1}{2^{3}}+\frac{1}{2^{5}}$, depending on which turn Claire rolls her even number. The probability of the third case is $\frac{1}{2^{6}}$. So the probability the last digit is even is
$$
\frac{1}{2}+\frac{1}{2^{3}}+\frac{1}{2^{5}}+\frac{1}{2^{6}}=\frac{43}{64}
$$
Finally we multiply by the $\frac{1}{3}$ chance that the sum of all the digits is divisible by 3 (this is independent from the last-digit-even condition by e.g. Chinese Remainder Theorem), making our final answer
$$
\frac{1}{3} \cdot \frac{43}{64}=\frac{43}{192}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nSolution: "
}
|
072b2abb-10de-56f5-b0bb-c814dcead9b3
| 610,675
|
A complex quartic polynomial $Q$ is quirky if it has four distinct roots, one of which is the sum of the other three. There are four complex values of $k$ for which the polynomial $Q(x)=x^{4}-k x^{3}-x^{2}-x-45$ is quirky. Compute the product of these four values of $k$.
|
Answer: 720
|
720
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A complex quartic polynomial $Q$ is quirky if it has four distinct roots, one of which is the sum of the other three. There are four complex values of $k$ for which the polynomial $Q(x)=x^{4}-k x^{3}-x^{2}-x-45$ is quirky. Compute the product of these four values of $k$.
|
Answer: 720
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n5. [35]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
afc62040-0e6c-5ace-bcc3-205c2e421980
| 610,676
|
The pairwise greatest common divisors of five positive integers are
$$
2,3,4,5,6,7,8, p, q, r
$$
in some order, for some positive integers $p, q, r$. Compute the minimum possible value of $p+q+r$.
|
To see that 9 can be achieved, take the set $\{6,12,40,56,105\}$, which gives
$$
\{p, q, r\}=\{2,3,4\}
$$
Now we show it's impossible to get lower.
Notice that if $m$ of the five numbers are even, then exactly $\binom{m}{2}$ of the gcd's will be even. Since we're shown four even gcd's and three odd gcd's, the only possibility is $m=4$. Hence exactly two of $p, q, r$ are even.
Similarly, if $n$ of the five numbers are divisible by 3 , then exactly $\binom{n}{2}$ of the gcd's will be divisible by 3. Since we're shown two gcd's that are multiples of 3 and five gcd's that aren't, the only possibility is $n=3$. Hence exactly one of $p, q, r$ is divisible by 3 .
Similarly, if $k$ of the five numbers are divisible by 4, then exactly $\binom{k}{2}$ of the gcd's will be divisible by 4. Since we're shown two gcd's that are multiples of 4 and five gcd's that aren't, the only possibility is $k=3$. Hence exactly one of $p, q, r$ is divisible by 4 .
So two of $p, q, r$ are even, one of them is divisible by 4 , and one of them is divisible by 3 . It's easy to see by inspection there are no possibilities where $p+q+r<9$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The pairwise greatest common divisors of five positive integers are
$$
2,3,4,5,6,7,8, p, q, r
$$
in some order, for some positive integers $p, q, r$. Compute the minimum possible value of $p+q+r$.
|
To see that 9 can be achieved, take the set $\{6,12,40,56,105\}$, which gives
$$
\{p, q, r\}=\{2,3,4\}
$$
Now we show it's impossible to get lower.
Notice that if $m$ of the five numbers are even, then exactly $\binom{m}{2}$ of the gcd's will be even. Since we're shown four even gcd's and three odd gcd's, the only possibility is $m=4$. Hence exactly two of $p, q, r$ are even.
Similarly, if $n$ of the five numbers are divisible by 3 , then exactly $\binom{n}{2}$ of the gcd's will be divisible by 3. Since we're shown two gcd's that are multiples of 3 and five gcd's that aren't, the only possibility is $n=3$. Hence exactly one of $p, q, r$ is divisible by 3 .
Similarly, if $k$ of the five numbers are divisible by 4, then exactly $\binom{k}{2}$ of the gcd's will be divisible by 4. Since we're shown two gcd's that are multiples of 4 and five gcd's that aren't, the only possibility is $k=3$. Hence exactly one of $p, q, r$ is divisible by 4 .
So two of $p, q, r$ are even, one of them is divisible by 4 , and one of them is divisible by 3 . It's easy to see by inspection there are no possibilities where $p+q+r<9$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n6. [45]",
"solution_match": "\nSolution: "
}
|
dd535fca-d3cd-57fd-84fb-919f7d8d6527
| 610,677
|
Let $A B C D$ be a convex trapezoid such that $\angle B A D=\angle A D C=90^{\circ}, A B=20, A D=21$, and $C D=28$. Point $P \neq A$ is chosen on segment $A C$ such that $\angle B P D=90^{\circ}$. Compute $A P$.
|
Answer: $\frac{143}{5}$
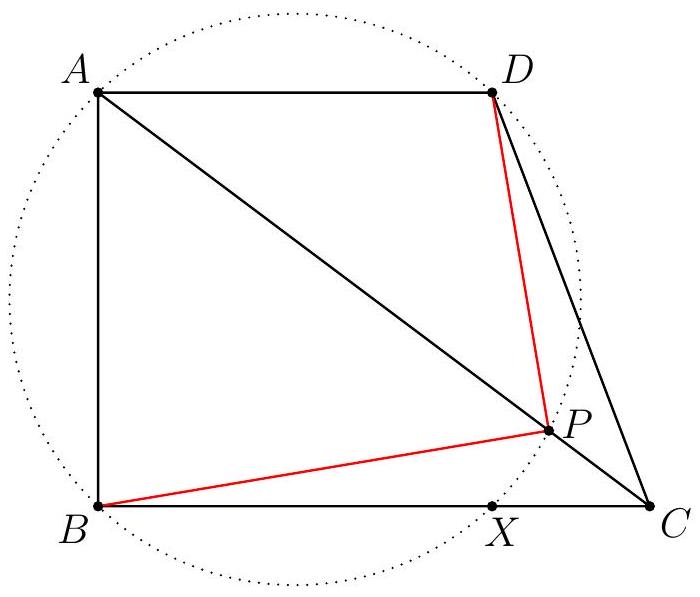
|
\frac{143}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex trapezoid such that $\angle B A D=\angle A D C=90^{\circ}, A B=20, A D=21$, and $C D=28$. Point $P \neq A$ is chosen on segment $A C$ such that $\angle B P D=90^{\circ}$. Compute $A P$.
|
Answer: $\frac{143}{5}$

|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n7. [45]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
58c2bfbb-8543-5eb9-b232-d1f7dca391c5
| 610,678
|
There are $n \geq 2$ coins, each with a different positive integer value. Call an integer $m$ sticky if some subset of these $n$ coins have total value $m$. We call the entire set of coins a stick if all the sticky numbers form a consecutive range of integers. Compute the minimum total value of a stick across all sticks containing a coin of value 100.
|
Sort a stick by increasing value. Note that all sticks must contain 1 by necessity, or the largest and second largest sticky values would not be consecutive. So, let's say a stick's highest coin value is $a$, and all the other terms have a value of $S$. If $a \geq S+2$, we cannot build $S+1$, but we can produce $S$ and $S+2$, meaning that this cannot happen. So, $a \leq S+1$, and therefore $100 \leq S+1 \rightarrow S \geq 99$ giving a lower bound on the answer of 199 . This is easily achievable by picking any stick with $S=99$. For instance, $\{1,2,3,7,12,24,50,100\}$ is a construction.
|
199
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are $n \geq 2$ coins, each with a different positive integer value. Call an integer $m$ sticky if some subset of these $n$ coins have total value $m$. We call the entire set of coins a stick if all the sticky numbers form a consecutive range of integers. Compute the minimum total value of a stick across all sticks containing a coin of value 100.
|
Sort a stick by increasing value. Note that all sticks must contain 1 by necessity, or the largest and second largest sticky values would not be consecutive. So, let's say a stick's highest coin value is $a$, and all the other terms have a value of $S$. If $a \geq S+2$, we cannot build $S+1$, but we can produce $S$ and $S+2$, meaning that this cannot happen. So, $a \leq S+1$, and therefore $100 \leq S+1 \rightarrow S \geq 99$ giving a lower bound on the answer of 199 . This is easily achievable by picking any stick with $S=99$. For instance, $\{1,2,3,7,12,24,50,100\}$ is a construction.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n8. [55]",
"solution_match": "\nSolution: "
}
|
a16ad4c6-6149-5296-86a8-25bfca0250d8
| 610,679
|
Let $r_{k}$ denote the remainder when $\binom{127}{k}$ is divided by 8 . Compute $r_{1}+2 r_{2}+3 r_{3}+\cdots+63 r_{63}$. Proposed by: Rishabh Das
|
Let $p_{k}=\frac{128-k}{k}$, so
$$
\binom{127}{k}=p_{1} p_{2} \cdots p_{k}
$$
Now, for $k \leq 63$, unless $32 \mid \operatorname{gcd}(k, 128-k)=\operatorname{gcd}(k, 128), p_{k} \equiv-1(\bmod 8)$. We have $p_{32}=\frac{96}{32}=3$. Thus, we have the following characterization:
$$
r_{k}= \begin{cases}1 & \text { if } k \text { is even and } k \leq 31 \\ 7 & \text { if } k \text { is odd and } k \leq 31 \\ 5 & \text { if } k \text { is even and } k \geq 32 \\ 3 & \text { if } k \text { is odd and } k \geq 32\end{cases}
$$
We can evaluate this sum as
$$
\begin{aligned}
4 \cdot & (0+1+2+3+\cdots+63) \\
& +3 \cdot(-0+1-2+3-\cdots-30+31) \\
& +(32-33+34-35+\cdots+62-63) \\
= & 4 \cdot 2016+3 \cdot 16+(-16)=8064+32=8096 .
\end{aligned}
$$
|
8096
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $r_{k}$ denote the remainder when $\binom{127}{k}$ is divided by 8 . Compute $r_{1}+2 r_{2}+3 r_{3}+\cdots+63 r_{63}$. Proposed by: Rishabh Das
|
Let $p_{k}=\frac{128-k}{k}$, so
$$
\binom{127}{k}=p_{1} p_{2} \cdots p_{k}
$$
Now, for $k \leq 63$, unless $32 \mid \operatorname{gcd}(k, 128-k)=\operatorname{gcd}(k, 128), p_{k} \equiv-1(\bmod 8)$. We have $p_{32}=\frac{96}{32}=3$. Thus, we have the following characterization:
$$
r_{k}= \begin{cases}1 & \text { if } k \text { is even and } k \leq 31 \\ 7 & \text { if } k \text { is odd and } k \leq 31 \\ 5 & \text { if } k \text { is even and } k \geq 32 \\ 3 & \text { if } k \text { is odd and } k \geq 32\end{cases}
$$
We can evaluate this sum as
$$
\begin{aligned}
4 \cdot & (0+1+2+3+\cdots+63) \\
& +3 \cdot(-0+1-2+3-\cdots-30+31) \\
& +(32-33+34-35+\cdots+62-63) \\
= & 4 \cdot 2016+3 \cdot 16+(-16)=8064+32=8096 .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n9. [60]",
"solution_match": "\nSolution: "
}
|
cf6577b5-050e-5b34-8f2e-c7df979a3473
| 610,680
|
Compute the number of ways a non-self-intersecting concave quadrilateral can be drawn in the plane such that two of its vertices are $(0,0)$ and $(1,0)$, and the other two vertices are two distinct lattice points $(a, b),(c, d)$ with $0 \leq a, c \leq 59$ and $1 \leq b, d \leq 5$.
(A concave quadrilateral is a quadrilateral with an angle strictly larger than $180^{\circ}$. A lattice point is a point with both coordinates integers.)
|
We instead choose points $(0,0),(1,0),(a, b),(c, d)$ with $0 \leq a, c \leq 59$ and $0 \leq b, d \leq 5$ with $(c, d)$ in the interior of the triangle formed by the other three points. Any selection of these four points may be connected to form a concave quadrilateral in precisely three ways.
Apply Pick's theorem to this triangle. If $I$ is the count of interior points, and $B$ is the number of boundary lattice points, we have that the triangle's area is equal to
$$
\frac{b}{2}=I+\frac{B}{2}-1
$$
Let's first compute the number of boundary lattice points on the segment from $(0,0)$ to $(a, b)$, not counting $(0,0)$. This is just $\operatorname{gcd}(a, b)$. Similarly, there are $\operatorname{gcd}(a-1, b)$ boundary lattice points from $(1,0)$ to $(a, b)$. Adjusting for the overcounting at $(a, b)$, we have
$$
B=\operatorname{gcd}(a, b)+\operatorname{gcd}(a-1, b)-1
$$
and thus
$$
I=\frac{b-\operatorname{gcd}(a, b)-\operatorname{gcd}(a-1, b)+1}{2}
$$
which we notice is periodic in $a$ with period $b$. That is, the count of boundary points does not change between choices $(a, b)$ and $(a+b, b)$.
We wanted to find the sum across all $(a, b)$ of $I$, the number of interior points $(c, d)$. Using casework on $b$, the periodicity allows us to just check $I$ across points with $0 \leq a<b$, and then multiply the count by $\frac{60}{b}$ to get the sum of $I$ across the entire row of points.
For $b=1,2$, we always have $I=0$.
For $b=3$, we have $I=0$ at $(0,3),(1,3)$ and $I=1$ for $(2,3)$. Using periodicity, this $y$-coordinate has a total a total of
$$
(0+0+1) \cdot \frac{60}{3}=20
$$
For $b=4$, we have $I=0$ at $(0,4)$ and $(1,4)$, and $I=1$ at both $(2,4)$ and $(3,4)$. Using periodicity, this $y$-coordinate has a total of
$$
(0+0+1+1) \cdot \frac{60}{4}=30
$$
For $b=5$, we have $I=0$ at $(0,5),(1,5)$ and $I=2$ at $(2,5),(3,5),(4,5)$. Using periodicity, this $y$-coordinate has a total of
$$
(0+0+2+2+2) \cdot \frac{60}{5}=72
$$
Adding our cases, we have $20+30+72=122$ ways to choose the four points. Multiplying back by the number of ways to connect the quadrilateral gives an answer of $122 \cdot 3=366$.
|
366
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of ways a non-self-intersecting concave quadrilateral can be drawn in the plane such that two of its vertices are $(0,0)$ and $(1,0)$, and the other two vertices are two distinct lattice points $(a, b),(c, d)$ with $0 \leq a, c \leq 59$ and $1 \leq b, d \leq 5$.
(A concave quadrilateral is a quadrilateral with an angle strictly larger than $180^{\circ}$. A lattice point is a point with both coordinates integers.)
|
We instead choose points $(0,0),(1,0),(a, b),(c, d)$ with $0 \leq a, c \leq 59$ and $0 \leq b, d \leq 5$ with $(c, d)$ in the interior of the triangle formed by the other three points. Any selection of these four points may be connected to form a concave quadrilateral in precisely three ways.
Apply Pick's theorem to this triangle. If $I$ is the count of interior points, and $B$ is the number of boundary lattice points, we have that the triangle's area is equal to
$$
\frac{b}{2}=I+\frac{B}{2}-1
$$
Let's first compute the number of boundary lattice points on the segment from $(0,0)$ to $(a, b)$, not counting $(0,0)$. This is just $\operatorname{gcd}(a, b)$. Similarly, there are $\operatorname{gcd}(a-1, b)$ boundary lattice points from $(1,0)$ to $(a, b)$. Adjusting for the overcounting at $(a, b)$, we have
$$
B=\operatorname{gcd}(a, b)+\operatorname{gcd}(a-1, b)-1
$$
and thus
$$
I=\frac{b-\operatorname{gcd}(a, b)-\operatorname{gcd}(a-1, b)+1}{2}
$$
which we notice is periodic in $a$ with period $b$. That is, the count of boundary points does not change between choices $(a, b)$ and $(a+b, b)$.
We wanted to find the sum across all $(a, b)$ of $I$, the number of interior points $(c, d)$. Using casework on $b$, the periodicity allows us to just check $I$ across points with $0 \leq a<b$, and then multiply the count by $\frac{60}{b}$ to get the sum of $I$ across the entire row of points.
For $b=1,2$, we always have $I=0$.
For $b=3$, we have $I=0$ at $(0,3),(1,3)$ and $I=1$ for $(2,3)$. Using periodicity, this $y$-coordinate has a total a total of
$$
(0+0+1) \cdot \frac{60}{3}=20
$$
For $b=4$, we have $I=0$ at $(0,4)$ and $(1,4)$, and $I=1$ at both $(2,4)$ and $(3,4)$. Using periodicity, this $y$-coordinate has a total of
$$
(0+0+1+1) \cdot \frac{60}{4}=30
$$
For $b=5$, we have $I=0$ at $(0,5),(1,5)$ and $I=2$ at $(2,5),(3,5),(4,5)$. Using periodicity, this $y$-coordinate has a total of
$$
(0+0+2+2+2) \cdot \frac{60}{5}=72
$$
Adding our cases, we have $20+30+72=122$ ways to choose the four points. Multiplying back by the number of ways to connect the quadrilateral gives an answer of $122 \cdot 3=366$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-team-solutions.jsonl",
"problem_match": "\n10. [65]",
"solution_match": "\nSolution: "
}
|
950a8025-550f-5e1e-afa0-e37c5d54ac38
| 610,681
|
Tyler has an infinite geometric series with sum 10 . He increases the first term of his sequence by 4 and swiftly changes the subsequent terms so that the common ratio remains the same, creating a new geometric series with sum 15. Compute the common ratio of Tyler's series.
|
Let $a$ and $r$ be the first term and common ratio of the original series, respectively. Then $\frac{a}{1-r}=10$ and $\frac{a+4}{1-r}=15$. Dividing these equations, we get that
$$
\frac{a+4}{a}=\frac{15}{10} \Longrightarrow a=8
$$
Solving for $r$ with $\frac{a}{1-r}=\frac{8}{1-r}=10$ gives $r=\frac{1}{5}$.
|
\frac{1}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Tyler has an infinite geometric series with sum 10 . He increases the first term of his sequence by 4 and swiftly changes the subsequent terms so that the common ratio remains the same, creating a new geometric series with sum 15. Compute the common ratio of Tyler's series.
|
Let $a$ and $r$ be the first term and common ratio of the original series, respectively. Then $\frac{a}{1-r}=10$ and $\frac{a+4}{1-r}=15$. Dividing these equations, we get that
$$
\frac{a+4}{a}=\frac{15}{10} \Longrightarrow a=8
$$
Solving for $r$ with $\frac{a}{1-r}=\frac{8}{1-r}=10$ gives $r=\frac{1}{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
1887e0f0-368b-53e5-94d7-2dbdb9552a2a
| 610,682
|
Suppose rectangle $F O L K$ and square $L O R E$ are on the plane such that $R L=12$ and $R K=11$. Compute the product of all possible areas of triangle $R K L$.
|
There are two possible configurations, as shown below.
If $R L=12$, the side length of the square is $6 \sqrt{2}$. Now
$$
121=R K^{2}=R E^{2}+E K^{2}=(6 \sqrt{2})^{2}+E K^{2}
$$
so $E K=7$. Then the possible values of $L K$ are $6 \sqrt{2} \pm 7$. Note that the area of $\triangle R L K$ is
$$
\frac{L K \cdot R E}{2}=L K \cdot 3 \sqrt{2},
$$
and so the product of all possible areas are
$$
\begin{aligned}
3 \sqrt{2}(6 \sqrt{2}+7) \cdot 3 \sqrt{2}(6 \sqrt{2}-7) & =(6 \sqrt{2}+7)(6 \sqrt{2}-7) \cdot(3 \sqrt{2})^{2} \\
& =(72-49) \cdot 18=414
\end{aligned}
$$
|
414
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose rectangle $F O L K$ and square $L O R E$ are on the plane such that $R L=12$ and $R K=11$. Compute the product of all possible areas of triangle $R K L$.
|
There are two possible configurations, as shown below.

If $R L=12$, the side length of the square is $6 \sqrt{2}$. Now
$$
121=R K^{2}=R E^{2}+E K^{2}=(6 \sqrt{2})^{2}+E K^{2}
$$
so $E K=7$. Then the possible values of $L K$ are $6 \sqrt{2} \pm 7$. Note that the area of $\triangle R L K$ is
$$
\frac{L K \cdot R E}{2}=L K \cdot 3 \sqrt{2},
$$
and so the product of all possible areas are
$$
\begin{aligned}
3 \sqrt{2}(6 \sqrt{2}+7) \cdot 3 \sqrt{2}(6 \sqrt{2}-7) & =(6 \sqrt{2}+7)(6 \sqrt{2}-7) \cdot(3 \sqrt{2})^{2} \\
& =(72-49) \cdot 18=414
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
ed4732d0-d6a6-5626-b20c-9efe0d0b9e9e
| 610,683
|
There are 17 people at a party, and each has a reputation that is either $1,2,3,4$, or 5 . Some of them split into pairs under the condition that within each pair, the two people's reputations differ by at most 1. Compute the largest value of $k$ such that no matter what the reputations of these people are, they are able to form $k$ pairs.
|
First, note that $k=8$ fails when there are $15,0,1,0,1$ people of reputation $1,2,3,4$, 5 , respectively. This is because the two people with reputation 3 and 5 cannot pair with anyone, and there can only be at maximum $\left\lfloor\frac{15}{2}\right\rfloor=7$ pairs of people with reputation 1 .
Now, we show that $k=7$ works. Suppose that we keep pairing people until we cannot make a pair anymore. Consider that moment. If there are two people with the same reputation, then these two people can pair up. Thus, there is at most one person for each reputation. Furthermore, if there are at least 4 people, then there must exist two people of consecutive reputations, so they can pair up. Thus, there are at most 3 people left, so we have formed at least $\frac{17-3}{2}=7$ pairs.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 17 people at a party, and each has a reputation that is either $1,2,3,4$, or 5 . Some of them split into pairs under the condition that within each pair, the two people's reputations differ by at most 1. Compute the largest value of $k$ such that no matter what the reputations of these people are, they are able to form $k$ pairs.
|
First, note that $k=8$ fails when there are $15,0,1,0,1$ people of reputation $1,2,3,4$, 5 , respectively. This is because the two people with reputation 3 and 5 cannot pair with anyone, and there can only be at maximum $\left\lfloor\frac{15}{2}\right\rfloor=7$ pairs of people with reputation 1 .
Now, we show that $k=7$ works. Suppose that we keep pairing people until we cannot make a pair anymore. Consider that moment. If there are two people with the same reputation, then these two people can pair up. Thus, there is at most one person for each reputation. Furthermore, if there are at least 4 people, then there must exist two people of consecutive reputations, so they can pair up. Thus, there are at most 3 people left, so we have formed at least $\frac{17-3}{2}=7$ pairs.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
677045bf-d532-5e1e-81c5-c06b55a645e5
| 610,684
|
Let $L O V E R$ be a convex pentagon such that $L O V E$ is a rectangle. Given that $O V=20$ and $L O=$ $V E=R E=R L=23$, compute the radius of the circle passing through $R, O$, and $V$.
|
Let $X$ be the point such that $R X O L$ is a rhombus. Note that line $R X$ defines a line of symmetry on the pentagon $L O V E R$. Then by symmetry $R X V E$ is also a rhombus, so $R X=O X=V X=23$. This makes $X$ the center of the circle, and the radius is 23 .
|
23
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $L O V E R$ be a convex pentagon such that $L O V E$ is a rectangle. Given that $O V=20$ and $L O=$ $V E=R E=R L=23$, compute the radius of the circle passing through $R, O$, and $V$.
|

Let $X$ be the point such that $R X O L$ is a rhombus. Note that line $R X$ defines a line of symmetry on the pentagon $L O V E R$. Then by symmetry $R X V E$ is also a rhombus, so $R X=O X=V X=23$. This makes $X$ the center of the circle, and the radius is 23 .
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution:\n"
}
|
6f4b8270-8cfa-5414-8cc3-16a8999a8817
| 610,685
|
Compute the unique positive integer $n$ such that $\frac{n^{3}-1989}{n}$ is a perfect square.
|
We need $n^{2}-\frac{1989}{n}$ to be a perfect square, so $n \mid 1989$. Also, this perfect square would be less than $n^{2}$, so it would be at most $(n-1)^{2}=n^{2}-2 n+1$. Thus,
$$
\frac{1989}{n} \geq 2 n-1 \Longrightarrow 1989 \geq 2 n^{2}-n
$$
so $n \leq 31$. Moreover, we need
$$
n^{2} \geq \frac{1989}{n} \Longrightarrow n^{3} \geq 1989
$$
so $n \geq 13$. Factoring gives $1989=3^{2} \cdot 13 \cdot 17$, which means the only possible values of $n$ are 13 and 17 . Checking both gives that only $n=13$ works. (In fact, $\frac{13^{3}-1989}{13}=4^{2}$.)
|
13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the unique positive integer $n$ such that $\frac{n^{3}-1989}{n}$ is a perfect square.
|
We need $n^{2}-\frac{1989}{n}$ to be a perfect square, so $n \mid 1989$. Also, this perfect square would be less than $n^{2}$, so it would be at most $(n-1)^{2}=n^{2}-2 n+1$. Thus,
$$
\frac{1989}{n} \geq 2 n-1 \Longrightarrow 1989 \geq 2 n^{2}-n
$$
so $n \leq 31$. Moreover, we need
$$
n^{2} \geq \frac{1989}{n} \Longrightarrow n^{3} \geq 1989
$$
so $n \geq 13$. Factoring gives $1989=3^{2} \cdot 13 \cdot 17$, which means the only possible values of $n$ are 13 and 17 . Checking both gives that only $n=13$ works. (In fact, $\frac{13^{3}-1989}{13}=4^{2}$.)
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution 1: "
}
|
5b4c6879-dc67-5a46-a434-b14ad0f6053c
| 610,686
|
A function $g$ is ever more than a function $h$ if, for all real numbers $x$, we have $g(x) \geq h(x)$. Consider all quadratic functions $f(x)$ such that $f(1)=16$ and $f(x)$ is ever more than both $(x+3)^{2}$ and $x^{2}+9$. Across all such quadratic functions $f$, compute the minimum value of $f(0)$.
|
Let $g(x)=(x+3)^{2}$ and $h(x)=x^{2}+9$. Then $f(1)=g(1)=16$. Thus, $f(x)-g(x)$ has a root at $x=1$. Since $f$ is ever more than $g$, this means that in fact
$$
f(x)-g(x)=c(x-1)^{2}
$$
for some constant $c$.
Now
$$
f(x)-h(x)=\left((f(x)-g(x))+(g(x)-h(x))=c(x-1)^{2}+6 x=c x^{2}-(2 c-6) x+c\right.
$$
is always nonnegative. The discriminant is
$$
(2 c-6)^{2}-4 c^{2}=24 c-36 \geq 0
$$
so the smallest possible value of $c$ is $\frac{3}{2}$. Then
$$
f(0)=g(0)+c(x-1)^{2}=9+c \geq \frac{21}{2}
$$
with equality at $c=\frac{3}{2}$.
|
\frac{21}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A function $g$ is ever more than a function $h$ if, for all real numbers $x$, we have $g(x) \geq h(x)$. Consider all quadratic functions $f(x)$ such that $f(1)=16$ and $f(x)$ is ever more than both $(x+3)^{2}$ and $x^{2}+9$. Across all such quadratic functions $f$, compute the minimum value of $f(0)$.
|
Let $g(x)=(x+3)^{2}$ and $h(x)=x^{2}+9$. Then $f(1)=g(1)=16$. Thus, $f(x)-g(x)$ has a root at $x=1$. Since $f$ is ever more than $g$, this means that in fact
$$
f(x)-g(x)=c(x-1)^{2}
$$
for some constant $c$.
Now
$$
f(x)-h(x)=\left((f(x)-g(x))+(g(x)-h(x))=c(x-1)^{2}+6 x=c x^{2}-(2 c-6) x+c\right.
$$
is always nonnegative. The discriminant is
$$
(2 c-6)^{2}-4 c^{2}=24 c-36 \geq 0
$$
so the smallest possible value of $c$ is $\frac{3}{2}$. Then
$$
f(0)=g(0)+c(x-1)^{2}=9+c \geq \frac{21}{2}
$$
with equality at $c=\frac{3}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
7e0af33f-7fb6-503c-96fd-b4710280e206
| 610,687
|
Betty has a $3 \times 4$ grid of dots. She colors each dot either red or maroon. Compute the number of ways Betty can color the grid such that there is no rectangle whose sides are parallel to the grid lines and whose vertices all have the same color.
|
First suppose no 3 by 1 row is all red or all blue. Then each row is either two red and one blue, or two blue and one red. There are 6 possible configurations of such a row, and as long as no row is repeated, there's no monochromatic rectangle This gives $6 \cdot 5 \cdot 4 \cdot 3=360$ possibilities.
Now suppose we have a 3 by 1 row that's all red. Then the remaining rows must be two blue and one red, and all 3 such configurations must appear. This gives $4!=24$, and having an all blue row is also $4!=24$.
The final answer is $360+24+24=408$.
|
408
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Betty has a $3 \times 4$ grid of dots. She colors each dot either red or maroon. Compute the number of ways Betty can color the grid such that there is no rectangle whose sides are parallel to the grid lines and whose vertices all have the same color.
|
First suppose no 3 by 1 row is all red or all blue. Then each row is either two red and one blue, or two blue and one red. There are 6 possible configurations of such a row, and as long as no row is repeated, there's no monochromatic rectangle This gives $6 \cdot 5 \cdot 4 \cdot 3=360$ possibilities.
Now suppose we have a 3 by 1 row that's all red. Then the remaining rows must be two blue and one red, and all 3 such configurations must appear. This gives $4!=24$, and having an all blue row is also $4!=24$.
The final answer is $360+24+24=408$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
5725bc8a-d614-542e-87f7-fa75e80aa127
| 610,688
|
Call a number feared if it contains the digits 13 as a contiguous substring and fearless otherwise. (For example, 132 is feared, while 123 is fearless.) Compute the smallest positive integer $n$ such that there exists a positive integer $a<100$ such that $n$ and $n+10 a$ are fearless while $n+a, n+2 a, \ldots, n+9 a$ are all feared.
|
Answer: 1287
|
1287
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Call a number feared if it contains the digits 13 as a contiguous substring and fearless otherwise. (For example, 132 is feared, while 123 is fearless.) Compute the smallest positive integer $n$ such that there exists a positive integer $a<100$ such that $n$ and $n+10 a$ are fearless while $n+a, n+2 a, \ldots, n+9 a$ are all feared.
|
Answer: 1287
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
a64623dc-18cc-5ea9-b504-317aa929689a
| 610,689
|
Pentagon $S P E A K$ is inscribed in triangle $N O W$ such that $S$ and $P$ lie on segment $N O, K$ and $A$ lie on segment $N W$, and $E$ lies on segment $O W$. Suppose that $N S=S P=P O$ and $N K=K A=A W$. Given that $E P=E K=5$ and $E A=E S=6$, compute $O W$.
|
Answer: $\frac{3 \sqrt{610}}{5}=3 \sqrt{\frac{122}{5}}$
|
\frac{3 \sqrt{610}}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Pentagon $S P E A K$ is inscribed in triangle $N O W$ such that $S$ and $P$ lie on segment $N O, K$ and $A$ lie on segment $N W$, and $E$ lies on segment $O W$. Suppose that $N S=S P=P O$ and $N K=K A=A W$. Given that $E P=E K=5$ and $E A=E S=6$, compute $O W$.
|
Answer: $\frac{3 \sqrt{610}}{5}=3 \sqrt{\frac{122}{5}}$
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
0d4d7e25-c6ae-553b-b2f8-6bc5085893aa
| 610,690
|
It is midnight on April 29th, and Abigail is listening to a song by her favorite artist while staring at her clock, which has an hour, minute, and second hand. These hands move continuously. Between two consecutive midnights, compute the number of times the hour, minute, and second hands form two equal angles and no two hands overlap.
|
Let $t \in[0,2]$ represent the position of the hour hand, i.e., how many full revolutions it has made. Then, the position of the minute hand is $12 t$ (it makes 12 full revolutions per 1 revolution of the hour hand), and the position of the second hand is $720 t$ (it makes 60 full revolutions per 1 revolution of the minute hand). Then, in order for equal angles to be formed, we need $(a-b)-(b-c)=a-2 b+c \equiv 0$ $(\bmod 1)$, where $a, b, c$ is a permutation of $t, 12 t, 720 t$. (Here, $b$ would correspond to the hand that's the angle bisector.) Checking all three possibilities,
$$
\begin{aligned}
12 t-2(t)+720 t \equiv 697 t & \equiv 0 \quad(\bmod 1) \\
t-2(12 t)+720 t \equiv 730 t \equiv 0 & (\bmod 1), \\
t-2(720 t)+12 t \equiv-1427 t & \equiv 0 \quad(\bmod 1)
\end{aligned}
$$
Then we require $t$ to be a multiple of $\frac{1}{697}, \frac{1}{730}$, or $\frac{1}{1427}$. Since 697,730 , and 1427 are pairwise relatively prime, the possible values of $t$ are
$$
\begin{array}{r}
\frac{1}{697}, \frac{2}{697}, \ldots, \frac{696}{697}, \frac{698}{697}, \ldots, \frac{2 \cdot 697-1}{697}, \\
\frac{1}{730}, \frac{2}{730}, \ldots, \frac{729}{730}, \frac{731}{730}, \ldots, \frac{2 \cdot 730-1}{730}, \\
\frac{1}{1427}, \frac{2}{1427}, \ldots, \frac{1426}{1427}, \frac{1428}{1427}, \ldots, \frac{2 \cdot 1427-1}{1427}
\end{array}
$$
since $t \in[0,2]$. This gives a count of $2((697-1)+(730-1)+(1427-1))=5702$.
Note that in the above count we don't count $t=0,1,2$ since then all three hands would overlap. If two hands overlap, then one of $11 t, 708 t, 719 t \equiv 0(\bmod 1)$, and the only way one of these can happen and $t$ being a multiple of $\frac{1}{697}, \frac{1}{730}$, or $\frac{1}{1427}$ is if $t=\frac{1}{2}$ and $t=\frac{3}{2}$ (which correspond to 6:00 AM and $\mathrm{PM})$. This is because the only pair of numbers that are not relatively prime among 11, 708, 719, 697, 730,1427 is 708 and 730 . The only common divisor of these two numbers is 2 , hence $t=\frac{1}{2}, \frac{3}{2}$. Thus the final answer is $5702-2=5700$.
|
5700
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
It is midnight on April 29th, and Abigail is listening to a song by her favorite artist while staring at her clock, which has an hour, minute, and second hand. These hands move continuously. Between two consecutive midnights, compute the number of times the hour, minute, and second hands form two equal angles and no two hands overlap.
|
Let $t \in[0,2]$ represent the position of the hour hand, i.e., how many full revolutions it has made. Then, the position of the minute hand is $12 t$ (it makes 12 full revolutions per 1 revolution of the hour hand), and the position of the second hand is $720 t$ (it makes 60 full revolutions per 1 revolution of the minute hand). Then, in order for equal angles to be formed, we need $(a-b)-(b-c)=a-2 b+c \equiv 0$ $(\bmod 1)$, where $a, b, c$ is a permutation of $t, 12 t, 720 t$. (Here, $b$ would correspond to the hand that's the angle bisector.) Checking all three possibilities,
$$
\begin{aligned}
12 t-2(t)+720 t \equiv 697 t & \equiv 0 \quad(\bmod 1) \\
t-2(12 t)+720 t \equiv 730 t \equiv 0 & (\bmod 1), \\
t-2(720 t)+12 t \equiv-1427 t & \equiv 0 \quad(\bmod 1)
\end{aligned}
$$
Then we require $t$ to be a multiple of $\frac{1}{697}, \frac{1}{730}$, or $\frac{1}{1427}$. Since 697,730 , and 1427 are pairwise relatively prime, the possible values of $t$ are
$$
\begin{array}{r}
\frac{1}{697}, \frac{2}{697}, \ldots, \frac{696}{697}, \frac{698}{697}, \ldots, \frac{2 \cdot 697-1}{697}, \\
\frac{1}{730}, \frac{2}{730}, \ldots, \frac{729}{730}, \frac{731}{730}, \ldots, \frac{2 \cdot 730-1}{730}, \\
\frac{1}{1427}, \frac{2}{1427}, \ldots, \frac{1426}{1427}, \frac{1428}{1427}, \ldots, \frac{2 \cdot 1427-1}{1427}
\end{array}
$$
since $t \in[0,2]$. This gives a count of $2((697-1)+(730-1)+(1427-1))=5702$.
Note that in the above count we don't count $t=0,1,2$ since then all three hands would overlap. If two hands overlap, then one of $11 t, 708 t, 719 t \equiv 0(\bmod 1)$, and the only way one of these can happen and $t$ being a multiple of $\frac{1}{697}, \frac{1}{730}$, or $\frac{1}{1427}$ is if $t=\frac{1}{2}$ and $t=\frac{3}{2}$ (which correspond to 6:00 AM and $\mathrm{PM})$. This is because the only pair of numbers that are not relatively prime among 11, 708, 719, 697, 730,1427 is 708 and 730 . The only common divisor of these two numbers is 2 , hence $t=\frac{1}{2}, \frac{3}{2}$. Thus the final answer is $5702-2=5700$.
|
{
"resource_path": "HarvardMIT/segmented/en-271-2023-nov-thm-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
8fdbe785-f300-59a1-8def-09bb1ee21128
| 610,691
|
Suppose $a$ and $b$ are positive integers. Isabella and Vidur both fill up an $a \times b$ table. Isabella fills it up with numbers $1,2, \ldots, a b$, putting the numbers $1,2, \ldots, b$ in the first row, $b+1, b+2, \ldots, 2 b$ in the second row, and so on. Vidur fills it up like a multiplication table, putting $i j$ in the cell in row $i$ and column $j$. (Examples are shown for a $3 \times 4$ table below.)
| 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
Isabella's Grid
| 1 | 2 | 3 | 4 | |
| :---: | :---: | :---: | :---: | :---: |
| 2 | 4 | 6 | 8 | |
| 3 | 6 | 9 | 12 | |
| Vidur's Grid | | | | |
Isabella sums up the numbers in her grid, and Vidur sums up the numbers in his grid; the difference between these two quantities is 1200 . Compute $a+b$.
|
Using the formula $1+2+\cdots+n=\frac{n(n+1)}{2}$, we get
$$
\begin{aligned}
\frac{a b(a b+1)}{2}-\frac{a(a+1)}{2} \cdot \frac{b(b+1)}{2} & =\frac{a b(2(a b+1)-(a+1)(b+1))}{4} \\
& =\frac{a b(a b-a-b+1)}{4} \\
& =\frac{a b(a-1)(b-1)}{4} \\
& =\frac{a(a-1)}{2} \cdot \frac{b(b-1)}{2}
\end{aligned}
$$
This means we can write the desired equation as
$$
a(a-1) \cdot b(b-1)=4800
$$
Assume $b \leq a$, so we know $b(b-1) \leq a(a-1)$, so $b(b-1)<70$. Thus, $b \leq 8$.
If $b=7$ or $b=8$, then $b(b-1)$ has a factor of 7 , which 4800 does not, so $b \leq 6$.
If $b=6$ then $b(b-1)=30$, so $a(a-1)=160$, which can be seen to have no solutions.
If $b=5$ then $b(b-1)=20$, so $a(a-1)=240$, which has the solution $a=16$, giving $5+16=21$.
We need not continue since we are guaranteed only one solution, but we check the remaining cases for completeness. If $b=4$ then $a(a-1)=\frac{4800}{12}=400$, which has no solutions. If $b=3$ then $a(a-1)=\frac{4800}{6}=800$ which has no solutions. Finally, if $b=2$ then $a(a-1)=\frac{4800}{2}=2400$, which has no solutions.
The factorization of the left side may come as a surprise; here's a way to see it should factor without doing the algebra. If either $a=1$ or $b=1$, then the left side simplifies to 0 . As a result, both $a-1$ and $b-1$ should be a factor of the left side.
|
21
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $a$ and $b$ are positive integers. Isabella and Vidur both fill up an $a \times b$ table. Isabella fills it up with numbers $1,2, \ldots, a b$, putting the numbers $1,2, \ldots, b$ in the first row, $b+1, b+2, \ldots, 2 b$ in the second row, and so on. Vidur fills it up like a multiplication table, putting $i j$ in the cell in row $i$ and column $j$. (Examples are shown for a $3 \times 4$ table below.)
| 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
Isabella's Grid
| 1 | 2 | 3 | 4 | |
| :---: | :---: | :---: | :---: | :---: |
| 2 | 4 | 6 | 8 | |
| 3 | 6 | 9 | 12 | |
| Vidur's Grid | | | | |
Isabella sums up the numbers in her grid, and Vidur sums up the numbers in his grid; the difference between these two quantities is 1200 . Compute $a+b$.
|
Using the formula $1+2+\cdots+n=\frac{n(n+1)}{2}$, we get
$$
\begin{aligned}
\frac{a b(a b+1)}{2}-\frac{a(a+1)}{2} \cdot \frac{b(b+1)}{2} & =\frac{a b(2(a b+1)-(a+1)(b+1))}{4} \\
& =\frac{a b(a b-a-b+1)}{4} \\
& =\frac{a b(a-1)(b-1)}{4} \\
& =\frac{a(a-1)}{2} \cdot \frac{b(b-1)}{2}
\end{aligned}
$$
This means we can write the desired equation as
$$
a(a-1) \cdot b(b-1)=4800
$$
Assume $b \leq a$, so we know $b(b-1) \leq a(a-1)$, so $b(b-1)<70$. Thus, $b \leq 8$.
If $b=7$ or $b=8$, then $b(b-1)$ has a factor of 7 , which 4800 does not, so $b \leq 6$.
If $b=6$ then $b(b-1)=30$, so $a(a-1)=160$, which can be seen to have no solutions.
If $b=5$ then $b(b-1)=20$, so $a(a-1)=240$, which has the solution $a=16$, giving $5+16=21$.
We need not continue since we are guaranteed only one solution, but we check the remaining cases for completeness. If $b=4$ then $a(a-1)=\frac{4800}{12}=400$, which has no solutions. If $b=3$ then $a(a-1)=\frac{4800}{6}=800$ which has no solutions. Finally, if $b=2$ then $a(a-1)=\frac{4800}{2}=2400$, which has no solutions.
The factorization of the left side may come as a surprise; here's a way to see it should factor without doing the algebra. If either $a=1$ or $b=1$, then the left side simplifies to 0 . As a result, both $a-1$ and $b-1$ should be a factor of the left side.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
e1b2d676-cba9-593e-96e8-c97c36fec251
| 610,693
|
Compute the sum of all two-digit positive integers $x$ such that for all three-digit (base 10) positive integers $\underline{a} \underline{b} \underline{c}$, if $\underline{a} \underline{b} \underline{c}$ is a multiple of $x$, then the three-digit (base 10) number $\underline{b} \underline{c} \underline{a}$ is also a multiple of $x$.
|
Note that $\overline{a b c 0}-\overline{b c a}=a\left(10^{4}-1\right)$ must also be a multiple of $x$. Choosing $a=1$ means that $x$ divides $10^{3}-1$, and this is clearly a necessary and sufficient condition. The only two-digit factors of $10^{3}-1$ are 27 and 37 , so our answer is $27+37=64$.
|
64
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all two-digit positive integers $x$ such that for all three-digit (base 10) positive integers $\underline{a} \underline{b} \underline{c}$, if $\underline{a} \underline{b} \underline{c}$ is a multiple of $x$, then the three-digit (base 10) number $\underline{b} \underline{c} \underline{a}$ is also a multiple of $x$.
|
Note that $\overline{a b c 0}-\overline{b c a}=a\left(10^{4}-1\right)$ must also be a multiple of $x$. Choosing $a=1$ means that $x$ divides $10^{3}-1$, and this is clearly a necessary and sufficient condition. The only two-digit factors of $10^{3}-1$ are 27 and 37 , so our answer is $27+37=64$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
ba472fae-5ef5-5c03-8123-b4e6baa9b01a
| 610,694
|
Let $f(x)$ be a quotient of two quadratic polynomials. Given that $f(n)=n^{3}$ for all $n \in\{1,2,3,4,5\}$, compute $f(0)$.
|
Let $f(x)=p(x) / q(x)$. Then, $x^{3} q(x)-p(x)$ has $1,2,3,4,5$ as roots. Therefore, WLOG, let
$$
x^{3} q(x)-p(x)=(x-1)(x-2)(x-3)(x-4)(x-5)=x^{5}-15 x^{4}+85 x^{3}-\ldots
$$
Thus, $q(x)=x^{2}-15 x+85$, so $q(0)=85$. Plugging $x=0$ in the above equation also gives $-p(0)=-120$. Hence, the answer is $\frac{120}{85}=\frac{24}{17}$.
Remark. From the solution above, it is not hard to see that the unique $f$ that satisfies the problem is
$$
f(x)=\frac{225 x^{2}-274 x+120}{x^{2}-15 x+85}
$$
|
\frac{24}{17}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)$ be a quotient of two quadratic polynomials. Given that $f(n)=n^{3}$ for all $n \in\{1,2,3,4,5\}$, compute $f(0)$.
|
Let $f(x)=p(x) / q(x)$. Then, $x^{3} q(x)-p(x)$ has $1,2,3,4,5$ as roots. Therefore, WLOG, let
$$
x^{3} q(x)-p(x)=(x-1)(x-2)(x-3)(x-4)(x-5)=x^{5}-15 x^{4}+85 x^{3}-\ldots
$$
Thus, $q(x)=x^{2}-15 x+85$, so $q(0)=85$. Plugging $x=0$ in the above equation also gives $-p(0)=-120$. Hence, the answer is $\frac{120}{85}=\frac{24}{17}$.
Remark. From the solution above, it is not hard to see that the unique $f$ that satisfies the problem is
$$
f(x)=\frac{225 x^{2}-274 x+120}{x^{2}-15 x+85}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
fb312c06-36ad-55dc-8360-7f9551fce40d
| 610,695
|
Compute the sum of all positive integers $n$ such that $50 \leq n \leq 100$ and $2 n+3$ does not divide $2^{n!}-1$.
|
Answer: 222
|
222
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all positive integers $n$ such that $50 \leq n \leq 100$ and $2 n+3$ does not divide $2^{n!}-1$.
|
Answer: 222
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
3fb256ae-1a14-5e8b-bc7a-c8ecc9ac7410
| 610,697
|
Let $P(n)=\left(n-1^{3}\right)\left(n-2^{3}\right) \ldots\left(n-40^{3}\right)$ for positive integers $n$. Suppose that $d$ is the largest positive integer that divides $P(n)$ for every integer $n>2023$. If $d$ is a product of $m$ (not necessarily distinct) prime numbers, compute $m$.
|
Answer: 48
|
48
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $P(n)=\left(n-1^{3}\right)\left(n-2^{3}\right) \ldots\left(n-40^{3}\right)$ for positive integers $n$. Suppose that $d$ is the largest positive integer that divides $P(n)$ for every integer $n>2023$. If $d$ is a product of $m$ (not necessarily distinct) prime numbers, compute $m$.
|
Answer: 48
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nProposed by: Nithid Anchaleenukoon\n"
}
|
6770852d-eb62-5ea1-a459-11087b2ad92c
| 610,698
|
Let $\zeta=\cos \frac{2 \pi}{13}+i \sin \frac{2 \pi}{13}$. Suppose $a>b>c>d$ are positive integers satisfying
$$
\left|\zeta^{a}+\zeta^{b}+\zeta^{c}+\zeta^{d}\right|=\sqrt{3}
$$
Compute the smallest possible value of $1000 a+100 b+10 c+d$.
|
Answer: 7521
|
7521
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\zeta=\cos \frac{2 \pi}{13}+i \sin \frac{2 \pi}{13}$. Suppose $a>b>c>d$ are positive integers satisfying
$$
\left|\zeta^{a}+\zeta^{b}+\zeta^{c}+\zeta^{d}\right|=\sqrt{3}
$$
Compute the smallest possible value of $1000 a+100 b+10 c+d$.
|
Answer: 7521
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
50bfab78-6a4b-52bf-a6e8-336f627722ef
| 610,699
|
A polynomial $f \in \mathbb{Z}[x]$ is called splitty if and only if for every prime $p$, there exist polynomials $g_{p}, h_{p} \in \mathbb{Z}[x]$ with $\operatorname{deg} g_{p}, \operatorname{deg} h_{p}<\operatorname{deg} f$ and all coefficients of $f-g_{p} h_{p}$ are divisible by $p$. Compute the sum of all positive integers $n \leq 100$ such that the polynomial $x^{4}+16 x^{2}+n$ is splitty.
|
We claim that $x^{4}+a x^{2}+b$ is splitty if and only if either $b$ or $a^{2}-4 b$ is a perfect square. (The latter means that the polynomial splits into $\left(x^{2}-r\right)\left(x^{2}-s\right)$ ).
Assuming the characterization, one can easily extract the answer. For $a=16$ and $b=n$, one of $n$ and $64-n$ has to be a perfect square. The solutions to this that are at most 64 form 8 pairs that sum to 64 (if we include 0 ), and then we additionally have 81 and 100 . This means the sum is $64 \cdot 8+81+100=693$.
Now, we move on to prove the characterization.
## Necessity.
Take a prime $p$ such that neither $a^{2}-4 b$ nor $b$ is a quadratic residue modulo $p$ (exists by Dirichlet + CRT +QR ). Work in $\mathbb{F}_{p}$. Now, suppose that
$$
x^{4}+a x^{2}+b=\left(x^{2}+m x+n\right)\left(x^{2}+s x+t\right)
$$
Then, looking at the $x^{3}$-coefficient gives $m+s=0$ or $s=-m$. Looking at the $x$-coefficient gives $m(n-t)=0$.
- If $m=0$, then $s=0$, so $x^{4}+a x^{2}+b=\left(x^{2}+n\right)\left(x^{2}+t\right)$, which means $a^{2}-4 b=(n+t)^{2}-4 n t=(n-t)^{2}$, a quadratic residue modulo $p$, contradiction.
- If $n=t$, then $b=n t$ is a square modulo $p$, a contradiction. (The major surprise of this problem is that this suffices, which will be shown below.)
## Sufficiency.
Clearly, the polynomial splits in $p=2$ because in $\mathbb{F}_{2}[x]$, we have $x^{4}+a x^{2}+b=\left(x^{2}+a x+b\right)^{2}$. Now, assume $p$ is odd.
If $a^{2}-4 b$ is a perfect square, then $x^{4}+a x^{2}+b$ splits into $\left(x^{2}-r\right)\left(x^{2}-s\right)$ even in $\mathbb{Z}[x]$.
If $b$ is a perfect square, then let $b=k^{2}$. We then note that
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}-r\right)\left(x^{2}-s\right)$ if $\left(\frac{a^{2}-4 k^{2}}{p}\right)=1$.
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}+r x+k\right)\left(x^{2}-r x+k\right)$ if $a=2 k-r^{2}$, or $\left(\frac{2 k-a}{p}\right)=1$.
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}+r x-k\right)\left(x^{2}-r x-k\right)$ if $a=-2 k-r^{2}$, or $\left(\frac{-2 k-a}{p}\right)=1$.
Since $(2 k-a)(-2 k-a)=a^{2}-4 k^{2}$, it follows that at least one of these must happen.
|
693
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A polynomial $f \in \mathbb{Z}[x]$ is called splitty if and only if for every prime $p$, there exist polynomials $g_{p}, h_{p} \in \mathbb{Z}[x]$ with $\operatorname{deg} g_{p}, \operatorname{deg} h_{p}<\operatorname{deg} f$ and all coefficients of $f-g_{p} h_{p}$ are divisible by $p$. Compute the sum of all positive integers $n \leq 100$ such that the polynomial $x^{4}+16 x^{2}+n$ is splitty.
|
We claim that $x^{4}+a x^{2}+b$ is splitty if and only if either $b$ or $a^{2}-4 b$ is a perfect square. (The latter means that the polynomial splits into $\left(x^{2}-r\right)\left(x^{2}-s\right)$ ).
Assuming the characterization, one can easily extract the answer. For $a=16$ and $b=n$, one of $n$ and $64-n$ has to be a perfect square. The solutions to this that are at most 64 form 8 pairs that sum to 64 (if we include 0 ), and then we additionally have 81 and 100 . This means the sum is $64 \cdot 8+81+100=693$.
Now, we move on to prove the characterization.
## Necessity.
Take a prime $p$ such that neither $a^{2}-4 b$ nor $b$ is a quadratic residue modulo $p$ (exists by Dirichlet + CRT +QR ). Work in $\mathbb{F}_{p}$. Now, suppose that
$$
x^{4}+a x^{2}+b=\left(x^{2}+m x+n\right)\left(x^{2}+s x+t\right)
$$
Then, looking at the $x^{3}$-coefficient gives $m+s=0$ or $s=-m$. Looking at the $x$-coefficient gives $m(n-t)=0$.
- If $m=0$, then $s=0$, so $x^{4}+a x^{2}+b=\left(x^{2}+n\right)\left(x^{2}+t\right)$, which means $a^{2}-4 b=(n+t)^{2}-4 n t=(n-t)^{2}$, a quadratic residue modulo $p$, contradiction.
- If $n=t$, then $b=n t$ is a square modulo $p$, a contradiction. (The major surprise of this problem is that this suffices, which will be shown below.)
## Sufficiency.
Clearly, the polynomial splits in $p=2$ because in $\mathbb{F}_{2}[x]$, we have $x^{4}+a x^{2}+b=\left(x^{2}+a x+b\right)^{2}$. Now, assume $p$ is odd.
If $a^{2}-4 b$ is a perfect square, then $x^{4}+a x^{2}+b$ splits into $\left(x^{2}-r\right)\left(x^{2}-s\right)$ even in $\mathbb{Z}[x]$.
If $b$ is a perfect square, then let $b=k^{2}$. We then note that
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}-r\right)\left(x^{2}-s\right)$ if $\left(\frac{a^{2}-4 k^{2}}{p}\right)=1$.
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}+r x+k\right)\left(x^{2}-r x+k\right)$ if $a=2 k-r^{2}$, or $\left(\frac{2 k-a}{p}\right)=1$.
- $x^{4}+a x^{2}+b$ splits in form $\left(x^{2}+r x-k\right)\left(x^{2}-r x-k\right)$ if $a=-2 k-r^{2}$, or $\left(\frac{-2 k-a}{p}\right)=1$.
Since $(2 k-a)(-2 k-a)=a^{2}-4 k^{2}$, it follows that at least one of these must happen.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-algnt-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
d59f6dfa-5bb0-5209-8201-fb01b7cc73da
| 610,701
|
Compute the number of ways to divide a $20 \times 24$ rectangle into $4 \times 5$ rectangles. (Rotations and reflections are considered distinct.)
|
For convenience, say the edge of length 20 is vertical.
Consider some vertical line inside the rectangle. It must pass through rectangles of some heights adding to 20. In particular, these heights correspond to ways to add up to 20 with fours and fives, which is either $4+4+4+4+4$ or $5+5+5+5$. These options correspond to columns of rectangles with width 5 or 4 , respectively. In particular, we need to span the width of the original $20 \times 24$ rectangle using these columns, meaning that we can just count the number of ways to add to 24 with fours and fives.
There are two ways to do this: either $4+4+4+4+4+4$ or $4+5+5+5+5$. Considering the orders in which the second sum can be written, we get an answer of $1+5=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of ways to divide a $20 \times 24$ rectangle into $4 \times 5$ rectangles. (Rotations and reflections are considered distinct.)
|
For convenience, say the edge of length 20 is vertical.
Consider some vertical line inside the rectangle. It must pass through rectangles of some heights adding to 20. In particular, these heights correspond to ways to add up to 20 with fours and fives, which is either $4+4+4+4+4$ or $5+5+5+5$. These options correspond to columns of rectangles with width 5 or 4 , respectively. In particular, we need to span the width of the original $20 \times 24$ rectangle using these columns, meaning that we can just count the number of ways to add to 24 with fours and fives.

There are two ways to do this: either $4+4+4+4+4+4$ or $4+5+5+5+5$. Considering the orders in which the second sum can be written, we get an answer of $1+5=6$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
02a7f7e3-93a5-5f2f-8498-d4faf7315ece
| 610,702
|
A lame king is a chess piece that can move from a cell to any cell that shares at least one vertex with it, except for the cells in the same column as the current cell.
A lame king is placed in the top-left cell of a $7 \times 7$ grid. Compute the maximum number of cells it can visit without visiting the same cell twice (including its starting cell).
|
Color the columns all-black and all-white, alternating by column. Each move the lame king takes will switch the color it's on. Assuming the king starts on a black cell, there are 28 black and 21 white cells, so it can visit at most $22+21=43$ cells in total, which is easily achievable:

|
43
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A lame king is a chess piece that can move from a cell to any cell that shares at least one vertex with it, except for the cells in the same column as the current cell.
A lame king is placed in the top-left cell of a $7 \times 7$ grid. Compute the maximum number of cells it can visit without visiting the same cell twice (including its starting cell).
|
Color the columns all-black and all-white, alternating by column. Each move the lame king takes will switch the color it's on. Assuming the king starts on a black cell, there are 28 black and 21 white cells, so it can visit at most $22+21=43$ cells in total, which is easily achievable:

|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
5e576a8a-eb13-55db-a097-c82b2955619d
| 610,703
|
Compute the number of ways there are to assemble 2 red unit cubes and 25 white unit cubes into a $3 \times 3 \times 3$ cube such that red is visible on exactly 4 faces of the larger cube. (Rotations and reflections are considered distinct.)
|
We do casework on the two red unit cubes; they can either be in a corner, an edge, or the center of the face.
- If they are both in a corner, they must be adjacent - for each configuration, this corresponds to an edge, of which there are 12.
- If one is in the corner and the other is at an edge, we have 8 choices to place the corner. For the edge, the red edge square has to go on the boundary of the faces touching the red corner square, and there are six places here. Thus, we get $8 \cdot 6=48$ configurations.

- If one is a corner and the other is in the center of a face, we again have 8 choices for the corner and 3 choices for the center face (the faces not touching the red corner). This gives $8 \cdot 3=8+8+8=24$ options.

- We have now completed the cases with a red corner square! Now suppose we have two edges: If we chose in order, we have 12 choices for the first cube. For the second cube, we must place the edge so it covers two new faces, and thus we have five choices. Since we could have picked these edges in either order, we divide by two to avoid overcounting, and we have $12 \cdot 5 / 2=30$ in this case.
Now, since edges and faces only cover at most 2 and 1 face respectively, no other configuration works. Thus we have all the cases, and we add: $12+48+24+30=114$.
|
114
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of ways there are to assemble 2 red unit cubes and 25 white unit cubes into a $3 \times 3 \times 3$ cube such that red is visible on exactly 4 faces of the larger cube. (Rotations and reflections are considered distinct.)
|
We do casework on the two red unit cubes; they can either be in a corner, an edge, or the center of the face.
- If they are both in a corner, they must be adjacent - for each configuration, this corresponds to an edge, of which there are 12.

- If one is in the corner and the other is at an edge, we have 8 choices to place the corner. For the edge, the red edge square has to go on the boundary of the faces touching the red corner square, and there are six places here. Thus, we get $8 \cdot 6=48$ configurations.

- If one is a corner and the other is in the center of a face, we again have 8 choices for the corner and 3 choices for the center face (the faces not touching the red corner). This gives $8 \cdot 3=8+8+8=24$ options.

- We have now completed the cases with a red corner square! Now suppose we have two edges: If we chose in order, we have 12 choices for the first cube. For the second cube, we must place the edge so it covers two new faces, and thus we have five choices. Since we could have picked these edges in either order, we divide by two to avoid overcounting, and we have $12 \cdot 5 / 2=30$ in this case.

Now, since edges and faces only cover at most 2 and 1 face respectively, no other configuration works. Thus we have all the cases, and we add: $12+48+24+30=114$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution:\n\n"
}
|
ab7e7a92-97c6-5b65-8232-f60c5988f534
| 610,704
|
Sally the snail sits on the $3 \times 24$ lattice of points $(i, j)$ for all $1 \leq i \leq 3$ and $1 \leq j \leq 24$. She wants to visit every point in the lattice exactly once. In a move, Sally can move to a point in the lattice exactly one unit away. Given that Sally starts at $(2,1)$, compute the number of possible paths Sally can take.
|
On her first turn, Sally cannot continue moving down the middle row. She must turn either to the bottom row or the top row. WLOG, she turns to the top row, and enters the cell $(3,1)$ and we will multiply by 2 later. Then, we can see that the path must finish in $(1,1)$. So, we will follow these two branches of the path, one for the start and one for the end. These branches must both move one unit up, and then one of the paths must move into the center row. Both branches move up one unit, and then the path in the middle row must go back to fill the corner. After this, we have exactly the same scenario as before, albeit with two fewer rows. So, for each additional two rows, we have a factor of two and thus there are $2^{12}=4096$ paths.
|
4096
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sally the snail sits on the $3 \times 24$ lattice of points $(i, j)$ for all $1 \leq i \leq 3$ and $1 \leq j \leq 24$. She wants to visit every point in the lattice exactly once. In a move, Sally can move to a point in the lattice exactly one unit away. Given that Sally starts at $(2,1)$, compute the number of possible paths Sally can take.
|
On her first turn, Sally cannot continue moving down the middle row. She must turn either to the bottom row or the top row. WLOG, she turns to the top row, and enters the cell $(3,1)$ and we will multiply by 2 later. Then, we can see that the path must finish in $(1,1)$. So, we will follow these two branches of the path, one for the start and one for the end. These branches must both move one unit up, and then one of the paths must move into the center row. Both branches move up one unit, and then the path in the middle row must go back to fill the corner. After this, we have exactly the same scenario as before, albeit with two fewer rows. So, for each additional two rows, we have a factor of two and thus there are $2^{12}=4096$ paths.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution 1:\n\n"
}
|
4a6df480-216c-5d5b-8cd8-1a82423242f3
| 610,705
|
The country of HMMTLand has 8 cities. Its government decides to construct several two-way roads between pairs of distinct cities. After they finish construction, it turns out that each city can reach exactly 3 other cities via a single road, and from any pair of distinct cities, either exactly 0 or 2 other cities can be reached from both cities by a single road. Compute the number of ways HMMTLand could have constructed the roads.
|
Let the cities be numbered $1,2,3,4,5,6,7,8$. WLOG, 1 is connected to 2,3 , and 4 . First suppose 2 and 3 are connected; then 3 and 1 share a second common neighbor, which must be 4 (as 1 is not connected to anything else). Likewise 2 and 4 are connected, and so 5, 6, 7, 8 are pairwise connected as well, so the graph consists of two disjoint copies of $K_{4}$ :
There are $\frac{1}{2}\binom{8}{4}=35$ ways to partition the 8 vertices into two groups of 4 , so there are 35 such graphs.
Otherwise, none of $2,3,4$ are connected to each other. Then 2 and 3 must share a common neighbor, as must 3 and 4 , and 2 and 4 . If these are the same neighbor, this vertex would share all three neighbors with 1, so they must be pairwise distinct. The last vertex must then be connected to these three, creating a cube graph.
A cube has 48 symmetries, so the number of such graphs is $\frac{8!}{48}=840$.
The total is $35+840=875$.
|
875
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The country of HMMTLand has 8 cities. Its government decides to construct several two-way roads between pairs of distinct cities. After they finish construction, it turns out that each city can reach exactly 3 other cities via a single road, and from any pair of distinct cities, either exactly 0 or 2 other cities can be reached from both cities by a single road. Compute the number of ways HMMTLand could have constructed the roads.
|
Let the cities be numbered $1,2,3,4,5,6,7,8$. WLOG, 1 is connected to 2,3 , and 4 . First suppose 2 and 3 are connected; then 3 and 1 share a second common neighbor, which must be 4 (as 1 is not connected to anything else). Likewise 2 and 4 are connected, and so 5, 6, 7, 8 are pairwise connected as well, so the graph consists of two disjoint copies of $K_{4}$ :

There are $\frac{1}{2}\binom{8}{4}=35$ ways to partition the 8 vertices into two groups of 4 , so there are 35 such graphs.
Otherwise, none of $2,3,4$ are connected to each other. Then 2 and 3 must share a common neighbor, as must 3 and 4 , and 2 and 4 . If these are the same neighbor, this vertex would share all three neighbors with 1, so they must be pairwise distinct. The last vertex must then be connected to these three, creating a cube graph.

A cube has 48 symmetries, so the number of such graphs is $\frac{8!}{48}=840$.
The total is $35+840=875$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
98d4208f-592a-58e0-95a7-219481fac189
| 610,706
|
In each cell of a $4 \times 4$ grid, one of the two diagonals is drawn uniformly at random. Compute the probability that the resulting 32 triangular regions can be colored red and blue so that any two regions sharing an edge have different colors.
|
Give each cell coordinates from $(1,1)$ to $(4,4)$.
Claim. The grid has a desired coloring if and only if every vertex not on the boundary meets an even number of edges and diagonals.
Proof. If this were not the case, the odd number of regions around the vertex would have to alternate between the two colors, which is clearly impossible. In the event that every vertex has an even number of incident edges, it is not hard to show that the grid is always colorable.
We claim the diagonals drawn in the cells of form $(1, a)$ and $(a, 1)$ for $1 \leq a \leq 4$ uniquely determine the rest (for a valid coloring to exist). Indeed, given the diagonals for any three cells around a vertex, we can uniquely determine the fourth one using the parity in the claim above. If $(1,1),(1,2),(2,1)$ are fixed, so is $(2,2)$; likewise so are $(2,3)$ and $(2,4)$, etc. until the whole grid is fixed.
The solid lines force the dotted lines as described above.
Thus, once the seven cells along the top row and leftmost column are determined, the remaining nine have a $\frac{1}{2^{9}}=\frac{1}{512}$ chance of being selected in a way that admits a coloring.
|
\frac{1}{512}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In each cell of a $4 \times 4$ grid, one of the two diagonals is drawn uniformly at random. Compute the probability that the resulting 32 triangular regions can be colored red and blue so that any two regions sharing an edge have different colors.
|
Give each cell coordinates from $(1,1)$ to $(4,4)$.
Claim. The grid has a desired coloring if and only if every vertex not on the boundary meets an even number of edges and diagonals.
Proof. If this were not the case, the odd number of regions around the vertex would have to alternate between the two colors, which is clearly impossible. In the event that every vertex has an even number of incident edges, it is not hard to show that the grid is always colorable.
We claim the diagonals drawn in the cells of form $(1, a)$ and $(a, 1)$ for $1 \leq a \leq 4$ uniquely determine the rest (for a valid coloring to exist). Indeed, given the diagonals for any three cells around a vertex, we can uniquely determine the fourth one using the parity in the claim above. If $(1,1),(1,2),(2,1)$ are fixed, so is $(2,2)$; likewise so are $(2,3)$ and $(2,4)$, etc. until the whole grid is fixed.

The solid lines force the dotted lines as described above.
Thus, once the seven cells along the top row and leftmost column are determined, the remaining nine have a $\frac{1}{2^{9}}=\frac{1}{512}$ chance of being selected in a way that admits a coloring.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
11570fd4-3fe6-5ed7-b3ba-8c481ea609e1
| 610,707
|
There is a grid of height 2 stretching infinitely in one direction. Between any two edge-adjacent cells of the grid, there is a door that is locked with probability $\frac{1}{2}$ independent of all other doors. Philip starts in a corner of the grid (in the starred cell). Compute the expected number of cells that Philip can reach, assuming he can only travel between cells if the door between them is unlocked.
|
For clarity, we will number our grid, with $(0,0)$ being the corner that Philip starts in, and the grid stretching in the positive $x$ direction, i.e. all elements of the grid are of the form $(x, y)$, with $y \in\{0,1\}$ and $x \in \mathbb{N}$.
We will use recursion and casework. Let $A$ be the expected number of reachable cells given that the door between $(0,0)$ and $(0,1)$ is unlocked, and $B$ be the expected number of cells given that door is closed. Since that door is locked $\frac{1}{2}$ of the time, our answer is $\frac{A+B}{2}$.
We can write recurrence relations by considering the different configurations of the doors in the first 4 cells.
For the sake of writing, let $W$ be the $(0,0)-(0,1)$ door, $X$ be the $(0,0)-(1,0)$ door, $Y$ be the $(0,1)-(1,1)$ door, and $Z$ be the $(1,0)-(1,1)$ door.
Let's start with the case where $W$ is unlocked and compute $A$ :

Case 1: W is unlocked. Shaded cells represent inaccessible cells, and the arrows show Philip's movements between cells.
- If $X, Y$ are both locked, then Philip can reach exactly 2 rooms. This occurs with probability $\frac{1}{4}$.
- If both of $X, Y$ are unlocked, then we have exactly the same case of $A$, except with the ability to reach two extra cells. This occurs with probability $\frac{1}{4}$.
- If exactly one of $X, Y$ are unlocked, we have back to the original case, except with the ability to access two more cells, which occurs with probability $\frac{1}{2}$.
So, we get the equation:
$$
A=\frac{1}{4}(2)+\frac{1}{4}(A+2)+\frac{1}{2}\left(\frac{A+B}{2}+2\right)
$$
Now, let's consider when $W$ is locked.
Case 2: W is locked.
- If $X$ is locked, Philip can only reach one cell. This occurs with probability $\frac{1}{2}$.
- If $X$ is unlocked and $Y$ is locked, we have exactly the original problem, except with the ability to reach one more cell. This occurs with probability $\frac{1}{4}$.
- In the case where $X$ is unlocked and $Y$ is unlocked, this is the same as the original configuration, except with the ability to reach one extra cell (the start) and possibly the cell at ( 0,1 ).
Now, let's compute the probability that Philip can reach $(0,1)$ in this case. This is the probability that Philip can reach $(1,1)$ since $Y$ is unlocked. We can compute that the probability that Philip can reach $(1,1)$ from $(1,0)$ is equal to
$$
\sum_{n=0}^{\infty} \frac{1}{2^{3 n+1}}
$$
by looking at the minimum distance Philip has to go to the right before getting back to $(1,1)$. This is a geometric series with sum $\frac{4}{7}$. So, in this case, on average Philip can reach $1+\frac{4}{7}$ more cells than the original case. This case occurs with probability $\frac{1}{4}$.
So, we can write the equation:
$$
B=\frac{1}{2}(1)+\frac{1}{4}\left(\frac{A+B}{2}+1\right)+\frac{1}{4}\left(\frac{A+B}{2}+1+\frac{4}{7}\right)
$$
Solving the system of these two linear equations, we get $A=\frac{40}{7}, B=\frac{24}{7}$ and $\frac{A+B}{2}=\frac{32}{7}$.
|
\frac{32}{7}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There is a grid of height 2 stretching infinitely in one direction. Between any two edge-adjacent cells of the grid, there is a door that is locked with probability $\frac{1}{2}$ independent of all other doors. Philip starts in a corner of the grid (in the starred cell). Compute the expected number of cells that Philip can reach, assuming he can only travel between cells if the door between them is unlocked.

|
For clarity, we will number our grid, with $(0,0)$ being the corner that Philip starts in, and the grid stretching in the positive $x$ direction, i.e. all elements of the grid are of the form $(x, y)$, with $y \in\{0,1\}$ and $x \in \mathbb{N}$.
We will use recursion and casework. Let $A$ be the expected number of reachable cells given that the door between $(0,0)$ and $(0,1)$ is unlocked, and $B$ be the expected number of cells given that door is closed. Since that door is locked $\frac{1}{2}$ of the time, our answer is $\frac{A+B}{2}$.
We can write recurrence relations by considering the different configurations of the doors in the first 4 cells.
For the sake of writing, let $W$ be the $(0,0)-(0,1)$ door, $X$ be the $(0,0)-(1,0)$ door, $Y$ be the $(0,1)-(1,1)$ door, and $Z$ be the $(1,0)-(1,1)$ door.
Let's start with the case where $W$ is unlocked and compute $A$ :

Case 1: W is unlocked. Shaded cells represent inaccessible cells, and the arrows show Philip's movements between cells.
- If $X, Y$ are both locked, then Philip can reach exactly 2 rooms. This occurs with probability $\frac{1}{4}$.
- If both of $X, Y$ are unlocked, then we have exactly the same case of $A$, except with the ability to reach two extra cells. This occurs with probability $\frac{1}{4}$.
- If exactly one of $X, Y$ are unlocked, we have back to the original case, except with the ability to access two more cells, which occurs with probability $\frac{1}{2}$.
So, we get the equation:
$$
A=\frac{1}{4}(2)+\frac{1}{4}(A+2)+\frac{1}{2}\left(\frac{A+B}{2}+2\right)
$$
Now, let's consider when $W$ is locked.

Case 2: W is locked.
- If $X$ is locked, Philip can only reach one cell. This occurs with probability $\frac{1}{2}$.
- If $X$ is unlocked and $Y$ is locked, we have exactly the original problem, except with the ability to reach one more cell. This occurs with probability $\frac{1}{4}$.
- In the case where $X$ is unlocked and $Y$ is unlocked, this is the same as the original configuration, except with the ability to reach one extra cell (the start) and possibly the cell at ( 0,1 ).
Now, let's compute the probability that Philip can reach $(0,1)$ in this case. This is the probability that Philip can reach $(1,1)$ since $Y$ is unlocked. We can compute that the probability that Philip can reach $(1,1)$ from $(1,0)$ is equal to
$$
\sum_{n=0}^{\infty} \frac{1}{2^{3 n+1}}
$$
by looking at the minimum distance Philip has to go to the right before getting back to $(1,1)$. This is a geometric series with sum $\frac{4}{7}$. So, in this case, on average Philip can reach $1+\frac{4}{7}$ more cells than the original case. This case occurs with probability $\frac{1}{4}$.
So, we can write the equation:
$$
B=\frac{1}{2}(1)+\frac{1}{4}\left(\frac{A+B}{2}+1\right)+\frac{1}{4}\left(\frac{A+B}{2}+1+\frac{4}{7}\right)
$$
Solving the system of these two linear equations, we get $A=\frac{40}{7}, B=\frac{24}{7}$ and $\frac{A+B}{2}=\frac{32}{7}$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
d44d8830-b157-5616-8ff2-596d5997abda
| 610,708
|
Compute the number of triples $(f, g, h)$ of permutations on $\{1,2,3,4,5\}$ such that
$$
\begin{aligned}
& f(g(h(x)))=h(g(f(x)))=g(x), \\
& g(h(f(x)))=f(h(g(x)))=h(x), \text { and } \\
& h(f(g(x)))=g(f(h(x)))=f(x)
\end{aligned}
$$
for all $x \in\{1,2,3,4,5\}$.
|
Let $f g$ represent the composition of permutations $f$ and $g$, where $(f g)(x)=f(g(x))$ for all $x \in\{1,2,3,4,5\}$.
Evaluating $f g h f h$ in two ways, we get
$$
f=g f h=(f g h) f h=f g h f h=f(g h f) h=f h h,
$$
so $h h=1$. Similarly, we get $f, g$, and $h$ are all involutions. Then
$$
f g h=g \Longrightarrow f g=g h,
$$
so $f g=g h=h f$. Let $x:=f g=g h=h f$. Then
$$
x^{3}=(f g)(g h)(h f)=1
$$
We can also show that $f g=g h=h f$ along with $f, g, h$ being involutions is enough to recover the initial conditions, so we focus on satisfying these new conditions.
If $x=1$, then $f=g=h$ is an involution. There are $1+\binom{5}{2}+\frac{1}{2}\binom{5}{2,2,1}=26$ involutions, so this case gives 26 solutions.
Suppose $x \neq 1$. Then since $x^{3}=1, x$ is composed of a 3 -cycle and two fixed points, of which there are 20 choices. WLOG $x=(123)$. It can be checked that $\{1,2,3\}$ must map to itself for all of $f, g, h$ and also $\{4,5\}$. We can either have all of $f, g, h$ map 4 and 5 to themselves or each other. Restricted to $\{1,2,3\}$, they are some rotation of (12), (23), (13). Each of the 20 cases thus gives $2 \cdot 3=6$ triples, so overall we get $20 \cdot 6=120$.
The final answer is $26+120=146$.
|
146
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of triples $(f, g, h)$ of permutations on $\{1,2,3,4,5\}$ such that
$$
\begin{aligned}
& f(g(h(x)))=h(g(f(x)))=g(x), \\
& g(h(f(x)))=f(h(g(x)))=h(x), \text { and } \\
& h(f(g(x)))=g(f(h(x)))=f(x)
\end{aligned}
$$
for all $x \in\{1,2,3,4,5\}$.
|
Let $f g$ represent the composition of permutations $f$ and $g$, where $(f g)(x)=f(g(x))$ for all $x \in\{1,2,3,4,5\}$.
Evaluating $f g h f h$ in two ways, we get
$$
f=g f h=(f g h) f h=f g h f h=f(g h f) h=f h h,
$$
so $h h=1$. Similarly, we get $f, g$, and $h$ are all involutions. Then
$$
f g h=g \Longrightarrow f g=g h,
$$
so $f g=g h=h f$. Let $x:=f g=g h=h f$. Then
$$
x^{3}=(f g)(g h)(h f)=1
$$
We can also show that $f g=g h=h f$ along with $f, g, h$ being involutions is enough to recover the initial conditions, so we focus on satisfying these new conditions.
If $x=1$, then $f=g=h$ is an involution. There are $1+\binom{5}{2}+\frac{1}{2}\binom{5}{2,2,1}=26$ involutions, so this case gives 26 solutions.
Suppose $x \neq 1$. Then since $x^{3}=1, x$ is composed of a 3 -cycle and two fixed points, of which there are 20 choices. WLOG $x=(123)$. It can be checked that $\{1,2,3\}$ must map to itself for all of $f, g, h$ and also $\{4,5\}$. We can either have all of $f, g, h$ map 4 and 5 to themselves or each other. Restricted to $\{1,2,3\}$, they are some rotation of (12), (23), (13). Each of the 20 cases thus gives $2 \cdot 3=6$ triples, so overall we get $20 \cdot 6=120$.
The final answer is $26+120=146$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
d476929b-36ae-53e3-8be1-47f330599bd4
| 610,710
|
A peacock is a ten-digit positive integer that uses each digit exactly once. Compute the number of peacocks that are exactly twice another peacock.
|
We begin with the following observation:
Claim 1. Let $x$ be a peacock. Then, $2 x$ is a peacock if and only if:
- the multiplication $x \cdot 2$ uses five carries,
- each of the pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ receives exactly one carry.
- The leading digit is not $5,6,7,8,9$.
Proof. After the multiplication of $x \cdot 2$, we will have a ten digit number. Let's first consider the output without carrying. It consists of the digits $0,2,4,6,8$ twice each, occupying positions where pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ were in $x$. However, we guaranteed that one digit from each pair received a carry, meaning all ten digits are present after adding in the carries.
We will now biject all peacocks to the following combination of objects:
- a queue of low digits $0,1,2,3,4$, in any order with the constraint that 0 is not first,
- a queue of high digits $5,6,7,8,9$, in any order, and
- of each of the pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ mark one of them to receive a carry, except we are not allowed to mark the final digit in the high queue.
We construct a correspondence from these objects to peacocks by accumulating digits to an initially empty string. We'll say that we poll a queue by popping its front entry and appending it to the end of this string. First, poll the low queue. Then, if we have just polled a marked digit, poll the high queue; otherwise, poll the low queue. We repeat this until all queues are emptied.
As an example of this process, let our low queue be $1,4,0,2,3$, our high queue be $8,5,9,6,7$, and mark the digits $0,1,2,3,9$ marked to receive a carry. Our steps are as follows:
- Poll the low queue, so that our string is now 1.
- Since 1 was marked to receive a carry, we poll the high queue, making our string 18.
- Since 8 was not marked, we poll the low queue to reach 184.
- Since 4 was not marked, we poll the low queue to reach 1840 .
- Since 0 was marked, we poll the high queue to reach 18405.
- etc.
In the end, we will construct the peacock 1840529637, which is the one shown earlier to work.
Claim 2. Any string of digits $x$ constructed through this process will be a peacock that satisfies the constraints outlined in Claim 1.
The order in which digits get polled to construct 1840529637; note the 4 connected components in the high queue. The circled digits are those that have been marked for carrying.
Proof. We first argue that all digits end up being polled. In particular, if a high digit is marked, let's connect it by an edge to the digit on its right (using the requirement that the last digit is not marked). If $h$ of the high digits are marked, then we will have $5-h$ connected components among these high digits. However, we then have $5-h$ marked digits in the low queue, and every time we poll a marked low digit we will end up polling all digits from the next connected component in the high queue.
So, all digits end up being polled. Notice that our marked digits will always be followed immediately by a high digit, satisfying the first and second conditions of the claim. As we do not start with a high
digit, the third constraint is satisfied. Therefore any peacock $x$ output by this process will also have $2 x$ a peacock.
Since we always use all the digits, this process is evidently injective. To map from peacocks back to these sequences of digits, we can just let the queues be the order of appearances of the low and high digits in the peacock, and mark the carried digits accordingly. Indeed, we notice that this mapping is also injective.
Using this bijection, we just need to find the number of initial settings of the queues and marked digits. There are $4 \cdot 4$ ! ways to order the low number queue. There are then 5 ! ways to order the high number queue. Finally, of each of the four pairs of digits not inluding the final high digit, there are $2^{4}$ ways to mark them. This gives an answer of
$$
4 \cdot 4!\cdot 5!\cdot 2^{4}=184320
$$
|
184320
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A peacock is a ten-digit positive integer that uses each digit exactly once. Compute the number of peacocks that are exactly twice another peacock.
|
We begin with the following observation:
Claim 1. Let $x$ be a peacock. Then, $2 x$ is a peacock if and only if:
- the multiplication $x \cdot 2$ uses five carries,
- each of the pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ receives exactly one carry.
- The leading digit is not $5,6,7,8,9$.
Proof. After the multiplication of $x \cdot 2$, we will have a ten digit number. Let's first consider the output without carrying. It consists of the digits $0,2,4,6,8$ twice each, occupying positions where pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ were in $x$. However, we guaranteed that one digit from each pair received a carry, meaning all ten digits are present after adding in the carries.
We will now biject all peacocks to the following combination of objects:
- a queue of low digits $0,1,2,3,4$, in any order with the constraint that 0 is not first,
- a queue of high digits $5,6,7,8,9$, in any order, and
- of each of the pairs of digits $(0,5),(1,6),(2,7),(3,8),(4,9)$ mark one of them to receive a carry, except we are not allowed to mark the final digit in the high queue.
We construct a correspondence from these objects to peacocks by accumulating digits to an initially empty string. We'll say that we poll a queue by popping its front entry and appending it to the end of this string. First, poll the low queue. Then, if we have just polled a marked digit, poll the high queue; otherwise, poll the low queue. We repeat this until all queues are emptied.
As an example of this process, let our low queue be $1,4,0,2,3$, our high queue be $8,5,9,6,7$, and mark the digits $0,1,2,3,9$ marked to receive a carry. Our steps are as follows:
- Poll the low queue, so that our string is now 1.
- Since 1 was marked to receive a carry, we poll the high queue, making our string 18.
- Since 8 was not marked, we poll the low queue to reach 184.
- Since 4 was not marked, we poll the low queue to reach 1840 .
- Since 0 was marked, we poll the high queue to reach 18405.
- etc.
In the end, we will construct the peacock 1840529637, which is the one shown earlier to work.
Claim 2. Any string of digits $x$ constructed through this process will be a peacock that satisfies the constraints outlined in Claim 1.

The order in which digits get polled to construct 1840529637; note the 4 connected components in the high queue. The circled digits are those that have been marked for carrying.
Proof. We first argue that all digits end up being polled. In particular, if a high digit is marked, let's connect it by an edge to the digit on its right (using the requirement that the last digit is not marked). If $h$ of the high digits are marked, then we will have $5-h$ connected components among these high digits. However, we then have $5-h$ marked digits in the low queue, and every time we poll a marked low digit we will end up polling all digits from the next connected component in the high queue.
So, all digits end up being polled. Notice that our marked digits will always be followed immediately by a high digit, satisfying the first and second conditions of the claim. As we do not start with a high
digit, the third constraint is satisfied. Therefore any peacock $x$ output by this process will also have $2 x$ a peacock.
Since we always use all the digits, this process is evidently injective. To map from peacocks back to these sequences of digits, we can just let the queues be the order of appearances of the low and high digits in the peacock, and mark the carried digits accordingly. Indeed, we notice that this mapping is also injective.
Using this bijection, we just need to find the number of initial settings of the queues and marked digits. There are $4 \cdot 4$ ! ways to order the low number queue. There are then 5 ! ways to order the high number queue. Finally, of each of the four pairs of digits not inluding the final high digit, there are $2^{4}$ ways to mark them. This gives an answer of
$$
4 \cdot 4!\cdot 5!\cdot 2^{4}=184320
$$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-comb-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution:\n\n"
}
|
f4afd570-d98b-5452-8246-2d2d052823e1
| 610,711
|
Inside an equilateral triangle of side length 6 , three congruent equilateral triangles of side length $x$ with sides parallel to the original equilateral triangle are arranged so that each has a vertex on a side of the larger triangle, and a vertex on another one of the three equilateral triangles, as shown below.
A smaller equilateral triangle formed between the three congruent equilateral triangles has side length 1. Compute $x$.
|
Let $x$ be the side length of the shaded triangles. Note that the centers of the triangles with side lengths 1 and 6 coincide; call this common center $O$.
The distance from $O$ to a side of the equilateral triangle with side length 1 is $\sqrt{3} / 6$. Similarly the distance from $O$ to a side of the equilateral triangle with side length 6 is $\sqrt{3}$. Notice the difference of these two distances is exactly the length of the altitude of one of shaded triangles. So
$$
\sqrt{3}-\frac{\sqrt{3}}{6}=\frac{\sqrt{3}}{2} x \Longrightarrow x=\begin{array}{|c}
\frac{5}{3} \\
\hline
\end{array}
$$
|
\frac{5}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Inside an equilateral triangle of side length 6 , three congruent equilateral triangles of side length $x$ with sides parallel to the original equilateral triangle are arranged so that each has a vertex on a side of the larger triangle, and a vertex on another one of the three equilateral triangles, as shown below.

A smaller equilateral triangle formed between the three congruent equilateral triangles has side length 1. Compute $x$.
|

Let $x$ be the side length of the shaded triangles. Note that the centers of the triangles with side lengths 1 and 6 coincide; call this common center $O$.
The distance from $O$ to a side of the equilateral triangle with side length 1 is $\sqrt{3} / 6$. Similarly the distance from $O$ to a side of the equilateral triangle with side length 6 is $\sqrt{3}$. Notice the difference of these two distances is exactly the length of the altitude of one of shaded triangles. So
$$
\sqrt{3}-\frac{\sqrt{3}}{6}=\frac{\sqrt{3}}{2} x \Longrightarrow x=\begin{array}{|c}
\frac{5}{3} \\
\hline
\end{array}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution:\n\n"
}
|
21752934-d7de-5aba-b5eb-31ddaa774226
| 610,712
|
Let $A B C$ be a triangle with $\angle B A C=90^{\circ}$. Let $D, E$, and $F$ be the feet of altitude, angle bisector, and median from $A$ to $B C$, respectively. If $D E=3$ and $E F=5$, compute the length of $B C$.
|
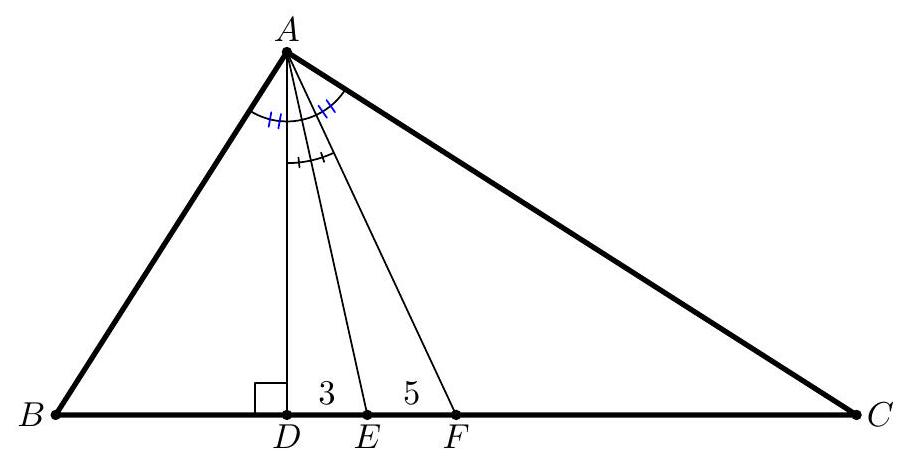
Since $F$ is the circumcenter of $\triangle A B C$, we have that $A E$ bisects $\angle D A F$. So by the angle bisector theorem, we can set $A D=3 x$ and $A F=5 x$. Applying Pythagorean theorem to $\triangle A D E$ then gives
$$
(3 x)^{2}+(5+3)^{2}=(5 x)^{2} \Longrightarrow x=2
$$
So $A F=5 x=10$ and $B C=2 A F=20$.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $\angle B A C=90^{\circ}$. Let $D, E$, and $F$ be the feet of altitude, angle bisector, and median from $A$ to $B C$, respectively. If $D E=3$ and $E F=5$, compute the length of $B C$.
|

Since $F$ is the circumcenter of $\triangle A B C$, we have that $A E$ bisects $\angle D A F$. So by the angle bisector theorem, we can set $A D=3 x$ and $A F=5 x$. Applying Pythagorean theorem to $\triangle A D E$ then gives
$$
(3 x)^{2}+(5+3)^{2}=(5 x)^{2} \Longrightarrow x=2
$$
So $A F=5 x=10$ and $B C=2 A F=20$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution 1:\n\n"
}
|
a045cb0f-0a42-507e-b0d7-38fd13ec1448
| 610,713
|
Let $\Omega$ and $\omega$ be circles with radii 123 and 61 , respectively, such that the center of $\Omega$ lies on $\omega$. A chord of $\Omega$ is cut by $\omega$ into three segments, whose lengths are in the ratio $1: 2: 3$ in that order. Given that this chord is not a diameter of $\Omega$, compute the length of this chord.
|
Denote the center of $\Omega$ as $O$. Let the chord intersect the circles at $W, X, Y, Z$ so that $W X=t, X Y=2 t$, and $Y Z=3 t$. Notice that $Y$ is the midpoint of $W Z$; hence $\overline{O Y} \perp \overline{W X Y Z}$.
The fact that $\angle O Y X=90^{\circ}$ means $X$ is the antipode of $O$ on $\omega$, so $O X=122$. Now applying power of point to $X$ with respect to $\Omega$ gives
$$
245=123^{2}-O X^{2}=W X \cdot X Z=5 t^{2} \Longrightarrow t=7
$$
Hence the answer is $6 t=42$.
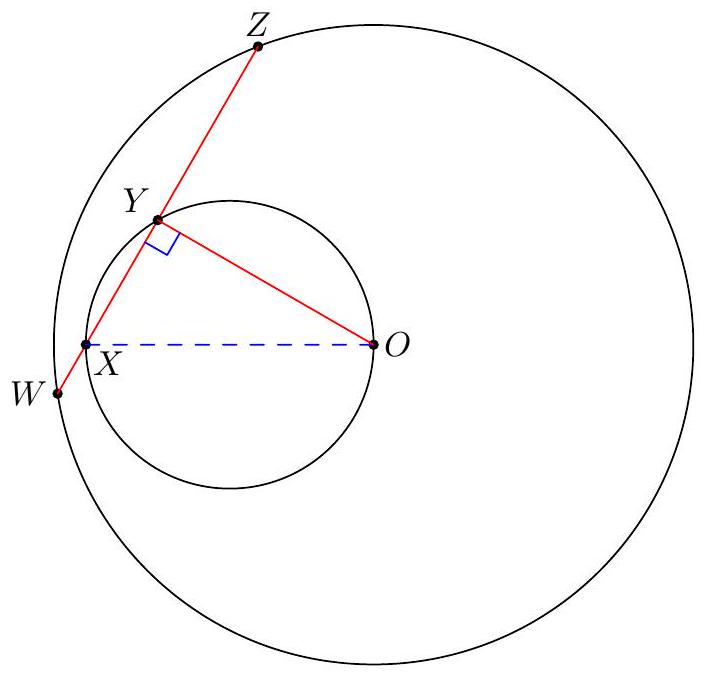
|
42
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Omega$ and $\omega$ be circles with radii 123 and 61 , respectively, such that the center of $\Omega$ lies on $\omega$. A chord of $\Omega$ is cut by $\omega$ into three segments, whose lengths are in the ratio $1: 2: 3$ in that order. Given that this chord is not a diameter of $\Omega$, compute the length of this chord.
|
Denote the center of $\Omega$ as $O$. Let the chord intersect the circles at $W, X, Y, Z$ so that $W X=t, X Y=2 t$, and $Y Z=3 t$. Notice that $Y$ is the midpoint of $W Z$; hence $\overline{O Y} \perp \overline{W X Y Z}$.
The fact that $\angle O Y X=90^{\circ}$ means $X$ is the antipode of $O$ on $\omega$, so $O X=122$. Now applying power of point to $X$ with respect to $\Omega$ gives
$$
245=123^{2}-O X^{2}=W X \cdot X Z=5 t^{2} \Longrightarrow t=7
$$
Hence the answer is $6 t=42$.

|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
a22d6fae-ed66-57d6-9347-01e86bc0cf49
| 610,714
|
Let $A B C D$ be a square, and let $\ell$ be a line passing through the midpoint of segment $\overline{A B}$ that intersects segment $\overline{B C}$. Given that the distances from $A$ and $C$ to $\ell$ are 4 and 7 , respectively, compute the area of $A B C D$.
|
Consider the line $\ell^{\prime}$ through $B$ parallel to $\ell$, and drop perpendiculars from $A$ to $\ell^{\prime}$ and $C$ to $\ell^{\prime}$. Note that because $\ell$ passes through the midpoint of segment $A B$, the distance from $B$ to $\ell$ is 4 . Thus, the distances from $A$ to $\ell^{\prime}$ and from $C$ to $\ell^{\prime}$ are $4+4=8$ and $4+7=11$, respectively. Let $P$ be the foot from $A$ to $\ell^{\prime}$. Rotating the square $90^{\circ}$ from $B$ to $A$ sends the altitude from $C$ to $\ell^{\prime}$ to the segment along $\ell^{\prime}$ between $B$ and the foot from $A$ to $\ell^{\prime}$; hence $B P=11$. So the side length of the square is $\sqrt{A P^{2}+B P^{2}}=\sqrt{8^{2}+11^{2}}$, which means the area of the square is $8^{2}+11^{2}=185$.
|
185
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a square, and let $\ell$ be a line passing through the midpoint of segment $\overline{A B}$ that intersects segment $\overline{B C}$. Given that the distances from $A$ and $C$ to $\ell$ are 4 and 7 , respectively, compute the area of $A B C D$.
|

Consider the line $\ell^{\prime}$ through $B$ parallel to $\ell$, and drop perpendiculars from $A$ to $\ell^{\prime}$ and $C$ to $\ell^{\prime}$. Note that because $\ell$ passes through the midpoint of segment $A B$, the distance from $B$ to $\ell$ is 4 . Thus, the distances from $A$ to $\ell^{\prime}$ and from $C$ to $\ell^{\prime}$ are $4+4=8$ and $4+7=11$, respectively. Let $P$ be the foot from $A$ to $\ell^{\prime}$. Rotating the square $90^{\circ}$ from $B$ to $A$ sends the altitude from $C$ to $\ell^{\prime}$ to the segment along $\ell^{\prime}$ between $B$ and the foot from $A$ to $\ell^{\prime}$; hence $B P=11$. So the side length of the square is $\sqrt{A P^{2}+B P^{2}}=\sqrt{8^{2}+11^{2}}$, which means the area of the square is $8^{2}+11^{2}=185$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution:\n\n"
}
|
f1888752-7db9-5772-8837-c77f6e444c06
| 610,715
|
Let $A B C D$ be a convex trapezoid such that $\angle D A B=\angle A B C=90^{\circ}, D A=2, A B=3$, and $B C=8$. Let $\omega$ be a circle passing through $A$ and tangent to segment $\overline{C D}$ at point $T$. Suppose that the center of $\omega$ lies on line $B C$. Compute $C T$.
|
Let $A^{\prime}$ be the reflection of $A$ across $B C$, and let $P=A B \cap C D$. Then since the center of $\omega$ lies on $B C$, we have that $\omega$ passes through $A^{\prime}$. Thus, by power of a point, $P T^{2}=P A \cdot P A^{\prime}$. By similar triangles, we have
$$
\frac{P A}{A D}=\frac{P B}{B C} \Longrightarrow \frac{P A}{2}=\frac{P A+3}{8} \Longrightarrow P A=1
$$
and $A^{\prime} P=1+2 \cdot 3=7$, so $P T=\sqrt{7}$. But by the Pythagorean Theorem, $P C=\sqrt{P B^{2}+B C^{2}}=4 \sqrt{5}$, and since $T$ lies on segment $C D$, it lies between $C$ and $P$, so $C T=4 \sqrt{5}-\sqrt{7}$.
|
4 \sqrt{5}-\sqrt{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex trapezoid such that $\angle D A B=\angle A B C=90^{\circ}, D A=2, A B=3$, and $B C=8$. Let $\omega$ be a circle passing through $A$ and tangent to segment $\overline{C D}$ at point $T$. Suppose that the center of $\omega$ lies on line $B C$. Compute $C T$.
|

Let $A^{\prime}$ be the reflection of $A$ across $B C$, and let $P=A B \cap C D$. Then since the center of $\omega$ lies on $B C$, we have that $\omega$ passes through $A^{\prime}$. Thus, by power of a point, $P T^{2}=P A \cdot P A^{\prime}$. By similar triangles, we have
$$
\frac{P A}{A D}=\frac{P B}{B C} \Longrightarrow \frac{P A}{2}=\frac{P A+3}{8} \Longrightarrow P A=1
$$
and $A^{\prime} P=1+2 \cdot 3=7$, so $P T=\sqrt{7}$. But by the Pythagorean Theorem, $P C=\sqrt{P B^{2}+B C^{2}}=4 \sqrt{5}$, and since $T$ lies on segment $C D$, it lies between $C$ and $P$, so $C T=4 \sqrt{5}-\sqrt{7}$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution:\n"
}
|
c9bd07ce-ba55-555e-9c8d-fcbe81135152
| 610,716
|
In triangle $A B C$, a circle $\omega$ with center $O$ passes through $B$ and $C$ and intersects segments $\overline{A B}$ and $\overline{A C}$ again at $B^{\prime}$ and $C^{\prime}$, respectively. Suppose that the circles with diameters $B B^{\prime}$ and $C C^{\prime}$ are externally tangent to each other at $T$. If $A B=18, A C=36$, and $A T=12$, compute $A O$.
|
By Radical Axis Theorem, we know that $A T$ is tangent to both circles. Moreove, consider power of a point $A$ with respect to these three circles, we have $A B \cdot A B^{\prime}=A T^{2}=A C \cdot A C^{\prime}$. Thus $A B^{\prime}=\frac{12^{2}}{18}=8$, and $A C^{\prime}=\frac{12^{2}}{36}=4$. Consider the midpoints $M_{B}, M_{C}$ of segments $\overline{B B^{\prime}}, \overline{C C^{\prime}}$, respectively. We have $\angle O M_{B} A=\angle O M_{C} A=90^{\circ}$, so $O$ is the antipode of $A$ in $\left(A M_{B} M_{C}\right)$. Notice that $\triangle A M_{B} T \sim \triangle A O M_{C}$, so $\frac{A O}{A M_{C}}=\frac{A M_{B}}{A T}$. Now, we can do the computations as follow:
$$
\begin{aligned}
A O & =\frac{A M_{B} \cdot A M_{C}}{A T} \\
& =\left(\frac{A B+A B^{\prime}}{2}\right)\left(\frac{A C+A C^{\prime}}{2}\right) \frac{1}{A T} \\
& =\left(\frac{8+18}{2}\right)\left(\frac{36+4}{2}\right) \frac{1}{12}=\frac{65}{3}
\end{aligned}
$$
|
\frac{65}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C$, a circle $\omega$ with center $O$ passes through $B$ and $C$ and intersects segments $\overline{A B}$ and $\overline{A C}$ again at $B^{\prime}$ and $C^{\prime}$, respectively. Suppose that the circles with diameters $B B^{\prime}$ and $C C^{\prime}$ are externally tangent to each other at $T$. If $A B=18, A C=36$, and $A T=12$, compute $A O$.
|

By Radical Axis Theorem, we know that $A T$ is tangent to both circles. Moreove, consider power of a point $A$ with respect to these three circles, we have $A B \cdot A B^{\prime}=A T^{2}=A C \cdot A C^{\prime}$. Thus $A B^{\prime}=\frac{12^{2}}{18}=8$, and $A C^{\prime}=\frac{12^{2}}{36}=4$. Consider the midpoints $M_{B}, M_{C}$ of segments $\overline{B B^{\prime}}, \overline{C C^{\prime}}$, respectively. We have $\angle O M_{B} A=\angle O M_{C} A=90^{\circ}$, so $O$ is the antipode of $A$ in $\left(A M_{B} M_{C}\right)$. Notice that $\triangle A M_{B} T \sim \triangle A O M_{C}$, so $\frac{A O}{A M_{C}}=\frac{A M_{B}}{A T}$. Now, we can do the computations as follow:
$$
\begin{aligned}
A O & =\frac{A M_{B} \cdot A M_{C}}{A T} \\
& =\left(\frac{A B+A B^{\prime}}{2}\right)\left(\frac{A C+A C^{\prime}}{2}\right) \frac{1}{A T} \\
& =\left(\frac{8+18}{2}\right)\left(\frac{36+4}{2}\right) \frac{1}{12}=\frac{65}{3}
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution 1:\n"
}
|
b55f1657-5926-5a9e-b82e-e288b187a30c
| 610,717
|
Let $A B C$ be an acute triangle. Let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $\overline{B C}$, $\overline{C A}$, and $\overline{A B}$, respectively, and let $Q$ be the foot of altitude from $A$ to line $E F$. Given that $A Q=20$, $B C=15$, and $A D=24$, compute the perimeter of triangle $D E F$.
|
Note that $A$ is the excenter of $\triangle D E F$ and $A Q$ is the length of the exradius. Let $T$ be the tangency point of the $A$-excircle to line $D F$. We have $A Q=A T=20$. It is well known that the length of $D T$ is the semiperimeter of $D E F$. Note that $\triangle A D T$ is a right triangle, so
$$
A T^{2}+D T^{2}=A D^{2}
$$
which implies
$$
D T=\sqrt{24^{2}-20^{2}}=4 \sqrt{11}
$$
Thus, the perimeter of $\triangle D E F$ is $2 \cdot 4 \sqrt{11}=8 \sqrt{11}$.
|
8 \sqrt{11}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute triangle. Let $D, E$, and $F$ be the feet of altitudes from $A, B$, and $C$ to sides $\overline{B C}$, $\overline{C A}$, and $\overline{A B}$, respectively, and let $Q$ be the foot of altitude from $A$ to line $E F$. Given that $A Q=20$, $B C=15$, and $A D=24$, compute the perimeter of triangle $D E F$.
|

Note that $A$ is the excenter of $\triangle D E F$ and $A Q$ is the length of the exradius. Let $T$ be the tangency point of the $A$-excircle to line $D F$. We have $A Q=A T=20$. It is well known that the length of $D T$ is the semiperimeter of $D E F$. Note that $\triangle A D T$ is a right triangle, so
$$
A T^{2}+D T^{2}=A D^{2}
$$
which implies
$$
D T=\sqrt{24^{2}-20^{2}}=4 \sqrt{11}
$$
Thus, the perimeter of $\triangle D E F$ is $2 \cdot 4 \sqrt{11}=8 \sqrt{11}$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\n## Solution:\n\n"
}
|
6c89f80b-ff1f-5a20-b146-a49baa7b4478
| 610,718
|
Let $A B T C D$ be a convex pentagon with area 22 such that $A B=C D$ and the circumcircles of triangles $T A B$ and $T C D$ are internally tangent. Given that $\angle A T D=90^{\circ}, \angle B T C=120^{\circ}, B T=4$, and $C T=5$, compute the area of triangle $T A D$.
|
Paste $\triangle T C D$ outside the pentagon to get $\triangle A B X \cong \triangle D C T$. From the tangent circles condition, we get
$$
\begin{aligned}
\angle X B T & =360^{\circ}-\angle X B A-\angle A B T \\
& =360^{\circ}-\angle D C T-\angle A B T \\
& =360^{\circ}-270^{\circ}=90^{\circ} \\
\angle X A T & =90^{\circ}-\angle B X A-\angle A T B \\
& =90^{\circ}-\angle C T D-\angle A T B \\
& =90^{\circ}-\left(120^{\circ}-90^{\circ}\right)=60^{\circ} .
\end{aligned}
$$
Moreover, if $x=A T$ and $y=T D$, then notice that
$$
\begin{aligned}
{[A B T C D] } & =[A B T]+[C D T]+[A T D] \\
& =[X A T]-[X B T]+[A T D] \\
& =\frac{1}{2} x y \sin 60^{\circ}-\frac{1}{2} \cdot 4 \cdot 5+\frac{1}{2} x y \\
& =\frac{2+\sqrt{3}}{4} x y-10
\end{aligned}
$$
so we have
$$
x y=32 \cdot \frac{4}{2+\sqrt{3}}=128(2-\sqrt{3}) \Longrightarrow[A T D]=\frac{1}{2} x y=64(2-\sqrt{3}) .
$$
|
64(2-\sqrt{3})
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B T C D$ be a convex pentagon with area 22 such that $A B=C D$ and the circumcircles of triangles $T A B$ and $T C D$ are internally tangent. Given that $\angle A T D=90^{\circ}, \angle B T C=120^{\circ}, B T=4$, and $C T=5$, compute the area of triangle $T A D$.
|
Paste $\triangle T C D$ outside the pentagon to get $\triangle A B X \cong \triangle D C T$. From the tangent circles condition, we get
$$
\begin{aligned}
\angle X B T & =360^{\circ}-\angle X B A-\angle A B T \\
& =360^{\circ}-\angle D C T-\angle A B T \\
& =360^{\circ}-270^{\circ}=90^{\circ} \\
\angle X A T & =90^{\circ}-\angle B X A-\angle A T B \\
& =90^{\circ}-\angle C T D-\angle A T B \\
& =90^{\circ}-\left(120^{\circ}-90^{\circ}\right)=60^{\circ} .
\end{aligned}
$$
Moreover, if $x=A T$ and $y=T D$, then notice that
$$
\begin{aligned}
{[A B T C D] } & =[A B T]+[C D T]+[A T D] \\
& =[X A T]-[X B T]+[A T D] \\
& =\frac{1}{2} x y \sin 60^{\circ}-\frac{1}{2} \cdot 4 \cdot 5+\frac{1}{2} x y \\
& =\frac{2+\sqrt{3}}{4} x y-10
\end{aligned}
$$
so we have
$$
x y=32 \cdot \frac{4}{2+\sqrt{3}}=128(2-\sqrt{3}) \Longrightarrow[A T D]=\frac{1}{2} x y=64(2-\sqrt{3}) .
$$

|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
f8e50ad6-6af0-5aa7-924e-b827ff0cbc10
| 610,719
|
Let $A B C$ be a triangle. Let $X$ be the point on side $\overline{A B}$ such that $\angle B X C=60^{\circ}$. Let $P$ be the point on segment $\overline{C X}$ such that $B P \perp A C$. Given that $A B=6, A C=7$, and $B P=4$, compute $C P$.
|
Answer: $\sqrt{38}-3$
|
\sqrt{38}-3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle. Let $X$ be the point on side $\overline{A B}$ such that $\angle B X C=60^{\circ}$. Let $P$ be the point on segment $\overline{C X}$ such that $B P \perp A C$. Given that $A B=6, A C=7$, and $B P=4$, compute $C P$.
|
Answer: $\sqrt{38}-3$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
b4a8ffcc-5ce2-5622-b2d3-ee98e8ada956
| 610,720
|
Suppose point $P$ is inside quadrilateral $A B C D$ such that
$$
\begin{aligned}
& \angle P A B=\angle P D A \\
& \angle P A D=\angle P D C, \\
& \angle P B A=\angle P C B, \text { and } \\
& \angle P B C=\angle P C D
\end{aligned}
$$
If $P A=4, P B=5$, and $P C=10$, compute the perimeter of $A B C D$.
|
Answer: $\frac{9 \sqrt{410}}{5}$
|
\frac{9 \sqrt{410}}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose point $P$ is inside quadrilateral $A B C D$ such that
$$
\begin{aligned}
& \angle P A B=\angle P D A \\
& \angle P A D=\angle P D C, \\
& \angle P B A=\angle P C B, \text { and } \\
& \angle P B C=\angle P C D
\end{aligned}
$$
If $P A=4, P B=5$, and $P C=10$, compute the perimeter of $A B C D$.
|
Answer: $\frac{9 \sqrt{410}}{5}$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
7f7487e1-46c2-5352-8d15-3e34a6d83597
| 610,721
|
Compute the sum of all integers $n$ such that $n^{2}-3000$ is a perfect square.
|
If $n^{2}-3000$ is a square, then $(-n)^{2}-3000$ is also a square, so the sum is 0 .
|
0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all integers $n$ such that $n^{2}-3000$ is a perfect square.
|
If $n^{2}-3000$ is a square, then $(-n)^{2}-3000$ is also a square, so the sum is 0 .
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nSolution: "
}
|
0055d5af-15f5-5bff-bbb9-df0d6a032dcf
| 610,722
|
Jerry and Neil have a 3 -sided die that rolls the numbers 1,2 , and 3 , each with probability $\frac{1}{3}$. Jerry rolls first, then Neil rolls the die repeatedly until his number is at least as large as Jerry's. Compute the probability that Neil's final number is 3 .
|
Answer: $\frac{11}{18}$
|
\frac{11}{18}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jerry and Neil have a 3 -sided die that rolls the numbers 1,2 , and 3 , each with probability $\frac{1}{3}$. Jerry rolls first, then Neil rolls the die repeatedly until his number is at least as large as Jerry's. Compute the probability that Neil's final number is 3 .
|
Answer: $\frac{11}{18}$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
fdff5744-1e47-5138-b67a-a46f8359e56a
| 610,723
|
Compute the number of even positive integers $n \leq 2024$ such that $1,2, \ldots, n$ can be split into $\frac{n}{2}$ pairs, and the sum of the numbers in each pair is a multiple of 3.
|
There have to be an even number of multiples of 3 at most $n$, so this means that $n \equiv 0,2$ $(\bmod 6)$. (We can also say that there should be an equal number of $1(\bmod 3)$ and $2(\bmod 3)$ numbers, which gives the same restriction.)
We claim that all these work. We know there are an even number of multiples of 3, so we can pair them; then we can pair $3 k+1$ and $3 k+2$ for all $k$.
This means the answer is $\frac{2022}{3}+1=675$.
|
675
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of even positive integers $n \leq 2024$ such that $1,2, \ldots, n$ can be split into $\frac{n}{2}$ pairs, and the sum of the numbers in each pair is a multiple of 3.
|
There have to be an even number of multiples of 3 at most $n$, so this means that $n \equiv 0,2$ $(\bmod 6)$. (We can also say that there should be an equal number of $1(\bmod 3)$ and $2(\bmod 3)$ numbers, which gives the same restriction.)
We claim that all these work. We know there are an even number of multiples of 3, so we can pair them; then we can pair $3 k+1$ and $3 k+2$ for all $k$.
This means the answer is $\frac{2022}{3}+1=675$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nSolution: "
}
|
81e52037-b41c-5d96-888e-532d3da91ac3
| 610,724
|
In triangle $A B C$, points $M$ and $N$ are the midpoints of $A B$ and $A C$, respectively, and points $P$ and $Q$ trisect $B C$. Given that $A, M, N, P$, and $Q$ lie on a circle and $B C=1$, compute the area of triangle $A B C$.
|
Note that $M P \| A Q$, so $A M P Q$ is an isosceles trapezoid. In particular, we have $A M=$ $M B=B P=P Q=\frac{1}{3}$, so $A B=\frac{2}{3}$. Thus $A B C$ is isoceles with base 1 and legs $\frac{2}{3}$, and the height from $A$ to $B C$ is $\frac{\sqrt{7}}{6}$, so the area is $\frac{\sqrt{7}}{12}$.
|
\frac{\sqrt{7}}{12}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C$, points $M$ and $N$ are the midpoints of $A B$ and $A C$, respectively, and points $P$ and $Q$ trisect $B C$. Given that $A, M, N, P$, and $Q$ lie on a circle and $B C=1$, compute the area of triangle $A B C$.
|
Note that $M P \| A Q$, so $A M P Q$ is an isosceles trapezoid. In particular, we have $A M=$ $M B=B P=P Q=\frac{1}{3}$, so $A B=\frac{2}{3}$. Thus $A B C$ is isoceles with base 1 and legs $\frac{2}{3}$, and the height from $A$ to $B C$ is $\frac{\sqrt{7}}{6}$, so the area is $\frac{\sqrt{7}}{12}$.

|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n6. [6]",
"solution_match": "\nSolution: "
}
|
72fb0676-db8f-54a3-95f1-9d6ca4f1096b
| 610,727
|
Positive integers $a, b$, and $c$ have the property that $a^{b}, b^{c}$, and $c^{a}$ end in 4,2 , and 9 , respectively. Compute the minimum possible value of $a+b+c$.
|
This minimum is attained when $(a, b, c)=(2,2,13)$. To show that we cannot do better, observe that $a$ must be even, so $c$ ends in 3 or 7 . If $c \geq 13$, since $a$ and $b$ are even, it's clear $(2,2,13)$ is optimal. Otherwise, $c=3$ or $c=7$, in which case $b^{c}$ can end in 2 only when $b$ ends in 8 . However, no eighth power ends in 4 , so we would need $b \geq 18$ (and $a \geq 2$ ), which makes the sum $2+18+3=23$ larger than 17 .
|
17
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Positive integers $a, b$, and $c$ have the property that $a^{b}, b^{c}$, and $c^{a}$ end in 4,2 , and 9 , respectively. Compute the minimum possible value of $a+b+c$.
|
This minimum is attained when $(a, b, c)=(2,2,13)$. To show that we cannot do better, observe that $a$ must be even, so $c$ ends in 3 or 7 . If $c \geq 13$, since $a$ and $b$ are even, it's clear $(2,2,13)$ is optimal. Otherwise, $c=3$ or $c=7$, in which case $b^{c}$ can end in 2 only when $b$ ends in 8 . However, no eighth power ends in 4 , so we would need $b \geq 18$ (and $a \geq 2$ ), which makes the sum $2+18+3=23$ larger than 17 .
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nSolution: "
}
|
bce73de8-854b-5a1b-9e43-b0084460e563
| 610,728
|
Compute the sum of all positive integers $n$ such that $n^{2}-3000$ is a perfect square.
|
Suppose $n^{2}-3000=x^{2}$, so $n^{2}-x^{2}=3000$. This factors as $(n-x)(n+x)=3000$. Thus, we have $n-x=2 a$ and $n+x=2 b$ for some positive integers $a, b$ such that $a b=750$ and $a<b$. Therefore, we have $n=a+b$, so the sum will be just sum of divisors of $750=2 \cdot 3 \cdot 5^{3}$, which is
$$
(1+2)(1+3)(1+5+25+125)=1872 .
$$
Remark. Problem 1 and 9 have slightly different statements.
|
1872
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all positive integers $n$ such that $n^{2}-3000$ is a perfect square.
|
Suppose $n^{2}-3000=x^{2}$, so $n^{2}-x^{2}=3000$. This factors as $(n-x)(n+x)=3000$. Thus, we have $n-x=2 a$ and $n+x=2 b$ for some positive integers $a, b$ such that $a b=750$ and $a<b$. Therefore, we have $n=a+b$, so the sum will be just sum of divisors of $750=2 \cdot 3 \cdot 5^{3}$, which is
$$
(1+2)(1+3)(1+5+25+125)=1872 .
$$
Remark. Problem 1 and 9 have slightly different statements.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nSolution: "
}
|
b7cde79a-83ba-5708-85ac-fad392416179
| 610,730
|
Alice, Bob, and Charlie are playing a game with 6 cards numbered 1 through 6 . Each player is dealt 2 cards uniformly at random. On each player's turn, they play one of their cards, and the winner is the person who plays the median of the three cards played. Charlie goes last, so Alice and Bob decide to tell their cards to each other, trying to prevent him from winning whenever possible. Compute the probability that Charlie wins regardless.
|
Answer: $\frac{2}{15}$
|
\frac{2}{15}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice, Bob, and Charlie are playing a game with 6 cards numbered 1 through 6 . Each player is dealt 2 cards uniformly at random. On each player's turn, they play one of their cards, and the winner is the person who plays the median of the three cards played. Charlie goes last, so Alice and Bob decide to tell their cards to each other, trying to prevent him from winning whenever possible. Compute the probability that Charlie wins regardless.
|
Answer: $\frac{2}{15}$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nProposed by: Ethan Liu\n"
}
|
f9895aff-7a44-5c60-be12-20a7f264c977
| 610,731
|
Compute the number of quadruples $(a, b, c, d)$ of positive integers satisfying
$$
12 a+21 b+28 c+84 d=2024
$$
|
Looking at the equation mod 7 gives $a \equiv 3(\bmod 7)$, so let $a=7 a^{\prime}+3$. Then mod 4 gives $b \equiv 0(\bmod 4)$, so let $b=4 b^{\prime}$. Finally, $\bmod 3$ gives $c \equiv 2(\bmod 3)$, so let $c=3 c^{\prime}+2$.
Now our equation yields
$$
84 a^{\prime}+84 b^{\prime}+84 c^{\prime}+84 d=2024-3 \cdot 12-2 \cdot 28=1932 \Longrightarrow a^{\prime}+b^{\prime}+c^{\prime}+d=23
$$
Since $a, b, c, d$ are positive integers, we have $a^{\prime}$ and $c^{\prime}$ are nonnegative and $b^{\prime}$ and $d$ are positive. Thus, let $b^{\prime \prime}=b^{\prime}+1$ and $d^{\prime}=d+1$, so $a^{\prime}, b^{\prime \prime}, c^{\prime}, d^{\prime}$ are nonnegative integers summing to 21 . By stars and bars, there are $\binom{24}{3}=2024$ such solutions.
|
2024
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the number of quadruples $(a, b, c, d)$ of positive integers satisfying
$$
12 a+21 b+28 c+84 d=2024
$$
|
Looking at the equation mod 7 gives $a \equiv 3(\bmod 7)$, so let $a=7 a^{\prime}+3$. Then mod 4 gives $b \equiv 0(\bmod 4)$, so let $b=4 b^{\prime}$. Finally, $\bmod 3$ gives $c \equiv 2(\bmod 3)$, so let $c=3 c^{\prime}+2$.
Now our equation yields
$$
84 a^{\prime}+84 b^{\prime}+84 c^{\prime}+84 d=2024-3 \cdot 12-2 \cdot 28=1932 \Longrightarrow a^{\prime}+b^{\prime}+c^{\prime}+d=23
$$
Since $a, b, c, d$ are positive integers, we have $a^{\prime}$ and $c^{\prime}$ are nonnegative and $b^{\prime}$ and $d$ are positive. Thus, let $b^{\prime \prime}=b^{\prime}+1$ and $d^{\prime}=d+1$, so $a^{\prime}, b^{\prime \prime}, c^{\prime}, d^{\prime}$ are nonnegative integers summing to 21 . By stars and bars, there are $\binom{24}{3}=2024$ such solutions.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n12. [7]",
"solution_match": "\nSolution: "
}
|
6df32a81-a0fe-5ee2-92f6-913b99f6f9a5
| 610,733
|
Mark has a cursed six-sided die that never rolls the same number twice in a row, and all other outcomes are equally likely. Compute the expected number of rolls it takes for Mark to roll every number at least once.
|
Suppose Mark has already rolled $n$ unique numbers, where $1 \leq n \leq 5$. On the next roll, there are 5 possible numbers he could get, with $6-n$ of them being new. Therefore, the probability of getting another unique number is $\frac{6-n}{5}$, so the expected number of rolls before getting another unique number is $\frac{5}{6-n}$. Since it always takes 1 roll to get the first number, the expected total number of rolls
is $1+\frac{5}{5}+\frac{5}{4}+\frac{5}{3}+\frac{5}{2}+\frac{5}{1}=\frac{149}{12}$.
|
\frac{149}{12}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Mark has a cursed six-sided die that never rolls the same number twice in a row, and all other outcomes are equally likely. Compute the expected number of rolls it takes for Mark to roll every number at least once.
|
Suppose Mark has already rolled $n$ unique numbers, where $1 \leq n \leq 5$. On the next roll, there are 5 possible numbers he could get, with $6-n$ of them being new. Therefore, the probability of getting another unique number is $\frac{6-n}{5}$, so the expected number of rolls before getting another unique number is $\frac{5}{6-n}$. Since it always takes 1 roll to get the first number, the expected total number of rolls
is $1+\frac{5}{5}+\frac{5}{4}+\frac{5}{3}+\frac{5}{2}+\frac{5}{1}=\frac{149}{12}$.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n13. [9]",
"solution_match": "\nSolution: "
}
|
c2c3be4e-0d7a-5d4f-9a29-c5d901108b3a
| 610,734
|
Compute the smallest positive integer such that, no matter how you rearrange its digits (in base ten), the resulting number is a multiple of 63 .
|
First, the number must be a multiple of 9 and 7. The first is easy to check and holds for all permutations. Note that when two adjacent digits $a$ and $b$ are swapped, the number changes by $9(a-b) \cdot 10^{k}$ (we disregard sign), so $9(a-b)$ must also be a multiple of 63 for all digits $a$ and $b$. In particular, this is sufficient, since a permutation can be represented as a series of transpositions.
This means that $a-b$ must be a multiple of 7 for all digits $a$ and $b$, so either all digits are equal or they are in $\{0,7\},\{1,8\}$, or $\{2,9\}$. We find the minimum for each case separately.
We first provide the following useful fact: the first repunit (numbers $1,11,111, \ldots$ ) that is a multiple of 7 is 111111 . This is because $10 \bmod 7=3$, and 3 is a generator modulo 7 (of course, you can just compute the powers of 3 by hand, and it will not take much longer).
If a number $k \cdot 1 \ldots 1$ is a multiple of 63 , then either $k$ or $1 \ldots 1$ is a multiple of 7 ; if it is $k$, then it's clear that we need 777777777 to make the sum a multiple of 9 . If $1 \ldots 1$ is a multiple of 7 , then it is at least 111111 , then to make a multiple of 9 , we need 333333 .
If the only digits are 7 and 0 , then we need at least nine sevens to make the digit sum a multiple of nine, which has more digits than 333333 .
If the only digits are 8 and 1 , then we can note that since 8 and 1 are both $1(\bmod 7)$, these numbers are equivalent to the repunits modulo 7 , so such numbers have at least six digits. The best such six-digit number with digits summing to a multiple of 9 is 111888 , which is our new candidate.
If the only digits are 9 and 2 , then by analogous logic such numbers have at least six digits. But the smallest such number is 999 999, which is not better.
So our best answer is 111888 . It works.
|
111888
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the smallest positive integer such that, no matter how you rearrange its digits (in base ten), the resulting number is a multiple of 63 .
|
First, the number must be a multiple of 9 and 7. The first is easy to check and holds for all permutations. Note that when two adjacent digits $a$ and $b$ are swapped, the number changes by $9(a-b) \cdot 10^{k}$ (we disregard sign), so $9(a-b)$ must also be a multiple of 63 for all digits $a$ and $b$. In particular, this is sufficient, since a permutation can be represented as a series of transpositions.
This means that $a-b$ must be a multiple of 7 for all digits $a$ and $b$, so either all digits are equal or they are in $\{0,7\},\{1,8\}$, or $\{2,9\}$. We find the minimum for each case separately.
We first provide the following useful fact: the first repunit (numbers $1,11,111, \ldots$ ) that is a multiple of 7 is 111111 . This is because $10 \bmod 7=3$, and 3 is a generator modulo 7 (of course, you can just compute the powers of 3 by hand, and it will not take much longer).
If a number $k \cdot 1 \ldots 1$ is a multiple of 63 , then either $k$ or $1 \ldots 1$ is a multiple of 7 ; if it is $k$, then it's clear that we need 777777777 to make the sum a multiple of 9 . If $1 \ldots 1$ is a multiple of 7 , then it is at least 111111 , then to make a multiple of 9 , we need 333333 .
If the only digits are 7 and 0 , then we need at least nine sevens to make the digit sum a multiple of nine, which has more digits than 333333 .
If the only digits are 8 and 1 , then we can note that since 8 and 1 are both $1(\bmod 7)$, these numbers are equivalent to the repunits modulo 7 , so such numbers have at least six digits. The best such six-digit number with digits summing to a multiple of 9 is 111888 , which is our new candidate.
If the only digits are 9 and 2 , then by analogous logic such numbers have at least six digits. But the smallest such number is 999 999, which is not better.
So our best answer is 111888 . It works.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n14. [9]",
"solution_match": "\nSolution: "
}
|
32463e7d-1840-5a26-8fe2-9bfad3aed1a3
| 610,735
|
Let $a \star b=a b-2$. Compute the remainder when $(((579 \star 569) \star 559) \star \cdots \star 19) \star 9$ is divided by 100 . Proposed by: Rishabh Das
|
Note that
$$
(10 a+9) \star(10 b+9)=(100 a b+90 a+90 b+81)-2 \equiv 90(a+b)+79 \quad(\bmod 100)
$$
so throughout our process all numbers will end in 9 , so we will just track the tens digit. Then the "new operation" is
$$
a \dagger b \equiv-(a+b)+7 \bmod 10
$$
where $a$ and $b$ track the tens digits. Now
$$
(a \dagger b) \dagger c \equiv(-(a+b)+7) \dagger c \equiv a+b-c \quad \bmod 10 .
$$
Thus, our expression has tens digit congruent to
$$
-0+1-2+3-\cdots-54+55-56-57+7 \equiv-28-57+7 \equiv 2 \bmod 10
$$
making the answer 29 .
|
29
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a \star b=a b-2$. Compute the remainder when $(((579 \star 569) \star 559) \star \cdots \star 19) \star 9$ is divided by 100 . Proposed by: Rishabh Das
|
Note that
$$
(10 a+9) \star(10 b+9)=(100 a b+90 a+90 b+81)-2 \equiv 90(a+b)+79 \quad(\bmod 100)
$$
so throughout our process all numbers will end in 9 , so we will just track the tens digit. Then the "new operation" is
$$
a \dagger b \equiv-(a+b)+7 \bmod 10
$$
where $a$ and $b$ track the tens digits. Now
$$
(a \dagger b) \dagger c \equiv(-(a+b)+7) \dagger c \equiv a+b-c \quad \bmod 10 .
$$
Thus, our expression has tens digit congruent to
$$
-0+1-2+3-\cdots-54+55-56-57+7 \equiv-28-57+7 \equiv 2 \bmod 10
$$
making the answer 29 .
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n15. [9]",
"solution_match": "\nSolution: "
}
|
4f5d974e-9add-5b0b-8116-8b84f00bb46a
| 610,736
|
Let $A B C$ be an acute isosceles triangle with orthocenter $H$. Let $M$ and $N$ be the midpoints of sides $\overline{A B}$ and $\overline{A C}$, respectively. The circumcircle of triangle $M H N$ intersects line $B C$ at two points $X$ and $Y$. Given $X Y=A B=A C=2$, compute $B C^{2}$.
|
Let $D$ be the foot from $A$ to $B C$, also the midpoint of $B C$. Note that $D X=D Y=M A=M B=$ $M D=N A=N C=N D=1$. Thus, $M N X Y$ is cyclic with circumcenter $D$ and circumradius 1. $H$ lies on this circle too, hence $D H=1$.
If we let $D B=D C=x$, then since $\triangle H B D \sim \triangle B D A$,
$$
B D^{2}=H D \cdot A D \Longrightarrow x^{2}=\sqrt{4-x^{2}} \Longrightarrow x^{4}=4-x^{2} \Longrightarrow x^{2}=\frac{\sqrt{17}-1}{2}
$$
Our answer is $B C^{2}=(2 x)^{2}=4 x^{2}=2(\sqrt{17}-1)$
|
2(\sqrt{17}-1)
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute isosceles triangle with orthocenter $H$. Let $M$ and $N$ be the midpoints of sides $\overline{A B}$ and $\overline{A C}$, respectively. The circumcircle of triangle $M H N$ intersects line $B C$ at two points $X$ and $Y$. Given $X Y=A B=A C=2$, compute $B C^{2}$.
|

Let $D$ be the foot from $A$ to $B C$, also the midpoint of $B C$. Note that $D X=D Y=M A=M B=$ $M D=N A=N C=N D=1$. Thus, $M N X Y$ is cyclic with circumcenter $D$ and circumradius 1. $H$ lies on this circle too, hence $D H=1$.
If we let $D B=D C=x$, then since $\triangle H B D \sim \triangle B D A$,
$$
B D^{2}=H D \cdot A D \Longrightarrow x^{2}=\sqrt{4-x^{2}} \Longrightarrow x^{4}=4-x^{2} \Longrightarrow x^{2}=\frac{\sqrt{17}-1}{2}
$$
Our answer is $B C^{2}=(2 x)^{2}=4 x^{2}=2(\sqrt{17}-1)$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n16. [9]",
"solution_match": "\n## Solution:\n\n"
}
|
f9315e77-60a2-5b8b-81c8-cf62e7c5a5d3
| 610,737
|
The numbers $1,2, \ldots, 20$ are put into a hat. Claire draws two numbers from the hat uniformly at random, $a<b$, and then puts them back into the hat. Then, William draws two numbers from the hat uniformly at random, $c<d$.
Let $N$ denote the number of integers $n$ that satisfy exactly one of $a \leq n \leq b$ and $c \leq n \leq d$. Compute the probability $N$ is even.
|
Answer: $\frac{181}{361}$
|
\frac{181}{361}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The numbers $1,2, \ldots, 20$ are put into a hat. Claire draws two numbers from the hat uniformly at random, $a<b$, and then puts them back into the hat. Then, William draws two numbers from the hat uniformly at random, $c<d$.
Let $N$ denote the number of integers $n$ that satisfy exactly one of $a \leq n \leq b$ and $c \leq n \leq d$. Compute the probability $N$ is even.
|
Answer: $\frac{181}{361}$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n17. [11]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
7dd7d633-ec7e-5829-915b-4328c3d8bb53
| 610,738
|
An ordered pair $(a, b)$ of positive integers is called spicy if $\operatorname{gcd}(a+b, a b+1)=1$. Compute the probability that both $(99, n)$ and $(101, n)$ are spicy when $n$ is chosen from $\{1,2, \ldots, 2024$ ! $\}$ uniformly at random.
|
Answer:
$\frac{96}{595}$
|
\frac{96}{595}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
An ordered pair $(a, b)$ of positive integers is called spicy if $\operatorname{gcd}(a+b, a b+1)=1$. Compute the probability that both $(99, n)$ and $(101, n)$ are spicy when $n$ is chosen from $\{1,2, \ldots, 2024$ ! $\}$ uniformly at random.
|
Answer:
$\frac{96}{595}$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-guts-solutions.jsonl",
"problem_match": "\n18. [11]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n"
}
|
e78533d0-c2f1-5caf-ba2e-8bc1377c2ebf
| 610,739
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.