problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
3. (CZS 3) ${ }^{\mathrm{IMO} 1}$ In a convex quadrangle with area $32 \mathrm{~cm}^{2}$, the sum of the lengths of two nonadjacent edges and of the length of one diagonal is equal to 16 cm . (a) What is the length of the other diagonal? (b) What are the lengths of the edges of the quadrangle if the perimeter is a minimum? (c) Is it possible to choose the edges in such a way that the perimeter is a maximum?
|
3. (a) Let $A B C D$ be a quadrangle with $16=d=A B+C D+A C$, and let $S$ be its area. Then $S \leq(A C \cdot A B+A C \cdot C D) / 2=A C(d-A C) / 2 \leq$ $d^{2} / 8=32$, where equality occurs if and only if $A B \perp A C \perp C D$ and $A C=A B+C D=8$. In this case $B D=8 \sqrt{2}$. (b) Let $A^{\prime}$ be the point with $\overrightarrow{D A^{\prime}}=\overrightarrow{A C}$. The triangular inequality implies $A D+B C \geq A A^{\prime}=8 \sqrt{5}$. Thus the perimeter attains its minimum for $A B=C D=4$. (c) Let us assume w.l.o.g. that $C D \leq A B$. Then $C$ lies inside $\triangle B D A^{\prime}$ and hence $B C+A D=B C+C A^{\prime}<B D+D A^{\prime}$. The maximal value $B D+D A^{\prime}$ of $B C+A D$ is attained when $C$ approaches $D$, making a degenerate quadrangle.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
3. (CZS 3) ${ }^{\mathrm{IMO} 1}$ In a convex quadrangle with area $32 \mathrm{~cm}^{2}$, the sum of the lengths of two nonadjacent edges and of the length of one diagonal is equal to 16 cm . (a) What is the length of the other diagonal? (b) What are the lengths of the edges of the quadrangle if the perimeter is a minimum? (c) Is it possible to choose the edges in such a way that the perimeter is a maximum?
|
3. (a) Let $A B C D$ be a quadrangle with $16=d=A B+C D+A C$, and let $S$ be its area. Then $S \leq(A C \cdot A B+A C \cdot C D) / 2=A C(d-A C) / 2 \leq$ $d^{2} / 8=32$, where equality occurs if and only if $A B \perp A C \perp C D$ and $A C=A B+C D=8$. In this case $B D=8 \sqrt{2}$. (b) Let $A^{\prime}$ be the point with $\overrightarrow{D A^{\prime}}=\overrightarrow{A C}$. The triangular inequality implies $A D+B C \geq A A^{\prime}=8 \sqrt{5}$. Thus the perimeter attains its minimum for $A B=C D=4$. (c) Let us assume w.l.o.g. that $C D \leq A B$. Then $C$ lies inside $\triangle B D A^{\prime}$ and hence $B C+A D=B C+C A^{\prime}<B D+D A^{\prime}$. The maximal value $B D+D A^{\prime}$ of $B C+A D$ is attained when $C$ approaches $D$, making a degenerate quadrangle.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b0fea919-a4fd-5103-af66-cd77b9d02fb3
| 25,089
|
43. (FIN 1) Evaluate $$ S=\sum_{k=1}^{n} k(k+1) \cdots(k+p), $$ where $n$ and $p$ are positive integers.
|
43. Since $\left.k(k+1) \cdots(k+p)=(p+1)!\binom{k+p}{p+1}=(p+1)!\left[\begin{array}{c}k+p+1 \\ p+2\end{array}\right)-\binom{k+p}{p+2}\right]$, it follows that $\sum_{k=1}^{n} k(k+1) \cdots(k+p)=(p+1)!\binom{n+p+1}{p+2}=\frac{n(n+1) \cdots(n+p+1)}{p+2}$.
|
\frac{n(n+1) \cdots(n+p+1)}{p+2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
43. (FIN 1) Evaluate $$ S=\sum_{k=1}^{n} k(k+1) \cdots(k+p), $$ where $n$ and $p$ are positive integers.
|
43. Since $\left.k(k+1) \cdots(k+p)=(p+1)!\binom{k+p}{p+1}=(p+1)!\left[\begin{array}{c}k+p+1 \\ p+2\end{array}\right)-\binom{k+p}{p+2}\right]$, it follows that $\sum_{k=1}^{n} k(k+1) \cdots(k+p)=(p+1)!\binom{n+p+1}{p+2}=\frac{n(n+1) \cdots(n+p+1)}{p+2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
89bf2a16-e493-57dd-b94a-102185ee35ac
| 23,602
|
8. (GBR 4) Let $S$ be the set of all the odd positive integers that are not multiples of 5 and that are less than $30 \mathrm{~m}, \mathrm{~m}$ being an arbitrary positive integer. What is the smallest integer $k$ such that in any subset of $k$ integers from $S$ there must be two different integers, one of which divides the other?
|
8. Take the subset $\left\{a_{i}\right\}=\{1,7,11,13,17,19,23,29, \ldots, 30 m-1\}$ of $S$ containing all the elements of $S$ that are not multiples of 3 . There are 8 m such elements. Every element in $S$ can be uniquely expressed as $3^{t} a_{i}$ for some $i$ and $t \geq 0$. In a subset of $S$ with $8 m+1$ elements, two of them will have the same $a_{i}$, hance one will divide the other. On the other hand, for each $i=1,2, \ldots, 8 m$ choose $t \geq 0$ such that $10 \mathrm{~m}<$ $b_{i}=3^{t} a_{i}<30 \mathrm{~m}$. Then there are $8 \mathrm{~m} b_{i}$ 's in the interval $(10 \mathrm{~m}, 30 \mathrm{~m})$, and the quotient of any two of them is less than 3 , so none of them can divide any other. Thus the answer is 8 m .
|
8m
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
8. (GBR 4) Let $S$ be the set of all the odd positive integers that are not multiples of 5 and that are less than $30 \mathrm{~m}, \mathrm{~m}$ being an arbitrary positive integer. What is the smallest integer $k$ such that in any subset of $k$ integers from $S$ there must be two different integers, one of which divides the other?
|
8. Take the subset $\left\{a_{i}\right\}=\{1,7,11,13,17,19,23,29, \ldots, 30 m-1\}$ of $S$ containing all the elements of $S$ that are not multiples of 3 . There are 8 m such elements. Every element in $S$ can be uniquely expressed as $3^{t} a_{i}$ for some $i$ and $t \geq 0$. In a subset of $S$ with $8 m+1$ elements, two of them will have the same $a_{i}$, hance one will divide the other. On the other hand, for each $i=1,2, \ldots, 8 m$ choose $t \geq 0$ such that $10 \mathrm{~m}<$ $b_{i}=3^{t} a_{i}<30 \mathrm{~m}$. Then there are $8 \mathrm{~m} b_{i}$ 's in the interval $(10 \mathrm{~m}, 30 \mathrm{~m})$, and the quotient of any two of them is less than 3 , so none of them can divide any other. Thus the answer is 8 m .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ffd7ffe5-ad9b-5e57-b625-e2766915be08
| 23,694
|
9. $\mathbf{( G B R} \mathbf{5})^{\mathrm{IMO} 3}$ Let $\{f(n)\}$ be a strictly increasing sequence of positive integers: $0<f(1)<f(2)<f(3)<\cdots$. Of the positive integers not belonging to the sequence, the $n$th in order of magnitude is $f(f(n))+1$. Determine $f(240)$.
|
9. Since the $n$th missing number (gap) is $f(f(n))+1$ and $f(f(n))$ is a member of the sequence, there are exactly $n-1$ gaps less than $f(f(n))$. This leads to $$ f(f(n))=f(n)+n-1 $$ Since 1 is not a gap, we have $f(1)=1$. The first gap is $f(f(1))+1=2$. Two consecutive integers cannot both be gaps (the predecessor of a gap is of the form $f(f(m))$ ). Now we deduce $f(2)=3$; a repeated application of the formula above gives $f(3)=3+1=4, f(4)=4+2=6, f(6)=9$, $f(9)=14, f(14)=22, f(22)=35, f(35)=56, f(56)=90, f(90)=145$, $f(145)=234, f(234)=378$. Also, $f(f(35))+1=91$ is a gap, so $f(57)=92$. Then by $(1), f(92)=148$, $f(148)=239, f(239)=386$. Finally, here $f(f(148))+1=387$ is a gap, so $f(240)=388$. Second solution. As above, we arrive at formula (1). Then by simple induction it follows that $f\left(F_{n}+1\right)=F_{n+1}+1$, where $F_{k}$ is the Fibonacci sequence ( $F_{1}=F_{2}=1$ ). We now prove by induction (on $n$ ) that $f\left(F_{n}+x\right)=F_{n+1}+f(x)$ for all $x$ with $1 \leq x \leq F_{n-1}$. This is trivially true for $n=0,1$. Supposing that it holds for $n-1$, we shall prove it for $n$ : (i) If $x=f(y)$ for some $y$, then by the inductive assumption and (1) $$ \begin{aligned} f\left(F_{n}+x\right) & =f\left(F_{n}+f(y)\right)=f\left(f\left(F_{n-1}+y\right)\right) \\ & =F_{n}+f(y)+F_{n-1}+y-1=F_{n+1}+f(x) \end{aligned} $$ (ii) If $x=f(f(y))+1$ is a gap, then $f\left(F_{n}+x-1\right)+1=F_{n+1}+f(x-1)+1$ is a gap also: $$ \begin{aligned} F_{n+1}+f(x)+1 & =F_{n+1}+f(f(f(y)))+1 \\ & =f\left(F_{n}+f(f(y))\right)+1=f\left(f\left(F_{n-1}+f(y)\right)\right)+1 \end{aligned} $$ It follows that $f\left(F_{n}+x\right)=F_{n+1}+f(x-1)+2=F_{n+1}+f(x)$. Now, since we know that each positive integer $x$ is expressible as $x=$ $F_{k_{1}}+F_{k_{2}}+\cdots+F_{k_{r}}$, where $0<k_{r} \neq 2, k_{i} \geq k_{i+1}+2$, we obtain $f(x)=F_{k_{1}+1}+F_{k_{2}+1}+\cdots+F_{k_{r}+1}$. Particularly, $240=233+5+2$, so $f(240)=377+8+3=388$. Remark. It can be shown that $f(x)=[\alpha x]$, where $\alpha=(1+\sqrt{5}) / 2$.
|
388
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
9. $\mathbf{( G B R} \mathbf{5})^{\mathrm{IMO} 3}$ Let $\{f(n)\}$ be a strictly increasing sequence of positive integers: $0<f(1)<f(2)<f(3)<\cdots$. Of the positive integers not belonging to the sequence, the $n$th in order of magnitude is $f(f(n))+1$. Determine $f(240)$.
|
9. Since the $n$th missing number (gap) is $f(f(n))+1$ and $f(f(n))$ is a member of the sequence, there are exactly $n-1$ gaps less than $f(f(n))$. This leads to $$ f(f(n))=f(n)+n-1 $$ Since 1 is not a gap, we have $f(1)=1$. The first gap is $f(f(1))+1=2$. Two consecutive integers cannot both be gaps (the predecessor of a gap is of the form $f(f(m))$ ). Now we deduce $f(2)=3$; a repeated application of the formula above gives $f(3)=3+1=4, f(4)=4+2=6, f(6)=9$, $f(9)=14, f(14)=22, f(22)=35, f(35)=56, f(56)=90, f(90)=145$, $f(145)=234, f(234)=378$. Also, $f(f(35))+1=91$ is a gap, so $f(57)=92$. Then by $(1), f(92)=148$, $f(148)=239, f(239)=386$. Finally, here $f(f(148))+1=387$ is a gap, so $f(240)=388$. Second solution. As above, we arrive at formula (1). Then by simple induction it follows that $f\left(F_{n}+1\right)=F_{n+1}+1$, where $F_{k}$ is the Fibonacci sequence ( $F_{1}=F_{2}=1$ ). We now prove by induction (on $n$ ) that $f\left(F_{n}+x\right)=F_{n+1}+f(x)$ for all $x$ with $1 \leq x \leq F_{n-1}$. This is trivially true for $n=0,1$. Supposing that it holds for $n-1$, we shall prove it for $n$ : (i) If $x=f(y)$ for some $y$, then by the inductive assumption and (1) $$ \begin{aligned} f\left(F_{n}+x\right) & =f\left(F_{n}+f(y)\right)=f\left(f\left(F_{n-1}+y\right)\right) \\ & =F_{n}+f(y)+F_{n-1}+y-1=F_{n+1}+f(x) \end{aligned} $$ (ii) If $x=f(f(y))+1$ is a gap, then $f\left(F_{n}+x-1\right)+1=F_{n+1}+f(x-1)+1$ is a gap also: $$ \begin{aligned} F_{n+1}+f(x)+1 & =F_{n+1}+f(f(f(y)))+1 \\ & =f\left(F_{n}+f(f(y))\right)+1=f\left(f\left(F_{n-1}+f(y)\right)\right)+1 \end{aligned} $$ It follows that $f\left(F_{n}+x\right)=F_{n+1}+f(x-1)+2=F_{n+1}+f(x)$. Now, since we know that each positive integer $x$ is expressible as $x=$ $F_{k_{1}}+F_{k_{2}}+\cdots+F_{k_{r}}$, where $0<k_{r} \neq 2, k_{i} \geq k_{i+1}+2$, we obtain $f(x)=F_{k_{1}+1}+F_{k_{2}+1}+\cdots+F_{k_{r}+1}$. Particularly, $240=233+5+2$, so $f(240)=377+8+3=388$. Remark. It can be shown that $f(x)=[\alpha x]$, where $\alpha=(1+\sqrt{5}) / 2$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ed5997af-8874-5e66-ae34-c6d2d5618e3a
| 23,697
|
12. (GDR 3) Let $R$ be a set of exactly 6 elements. A set $F$ of subsets of $R$ is called an $S$-family over $R$ if and only if it satisfies the following three conditions: (i) For no two sets $X, Y$ in $F$ is $X \subseteq Y$; (ii) For any three sets $X, Y, Z$ in $F, X \cup Y \cup Z \neq R$, (iii) $\bigcup_{X \in F} X=R$. We define $|F|$ to be the number of elements of $F$ (i.e., the number of subsets of $R$ belonging to $F$ ). Determine, if it exists, $h=\max |F|$, the maximum being taken over all S-families over $R$.
|
12. The first criterion ensures that all sets in an $S$-family are distinct. Since the number of different families of subsets is finite, $h$ has to exist. In fact, we will show that $h=11$. First of all, if there exists $X \in F$ such that $|X| \geq 5$, then by (3) there exists $Y \in F$ such that $X \cup Y=R$. In this case $|F|$ is at most 2. Similarly, for $|X|=4$, for the remaining two elements either there exists a subset in $F$ that contains both, in which case we obtain the previous case, or there exist different $Y$ and $Z$ containing them, in which case $X \cup Y \cup Z=R$, which must not happen. Hence we can assume $|X| \leq 4$ for all $X \in F$. Assume $|X|=1$ for some $X$. In that case other sets must not contain that subset and hence must be contained in the remaining 5 -element subset. These elements must not be subsets of each other. From elementary combinatorics, the largest number of subsets of a 5 -element set of which none is subset of another is $\binom{5}{2}=10$. This occurs when we take all 2-element subsets. These subsets also satisfy (2). Hence $|F|_{\max }=11$ in this case. Otherwise, let us assume $|X|=3$ for some $X$. Let us define the following families of subsets: $G=\{Z=Y \backslash X \mid Y \in F\}$ and $H=\{Z=Y \cap X \mid Y \in$ $F\}$. Then no two sets in $G$ must complement each other in $R \backslash X$, and $G$ must cover this set. Hence $G$ contains exactly the sets of each of the remaining 3 elements. For each element of $G$ no two sets in $H$ of which one is a subset of another may be paired with it. There can be only 3 such subsets selected within a 3 -element set $X$. Hence the number of remaining sets is smaller than $3 \cdot 3=9$. Hence in this case $|F|_{\max }=10$. In the remaining case all subsets have two elements. There are $\binom{6}{2}=15$ of them. But for every three that complement each other one must be discarded; hence the maximal number for $F$ in this case is $2 \cdot 15 / 3=10$. It follows that $h=11$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
12. (GDR 3) Let $R$ be a set of exactly 6 elements. A set $F$ of subsets of $R$ is called an $S$-family over $R$ if and only if it satisfies the following three conditions: (i) For no two sets $X, Y$ in $F$ is $X \subseteq Y$; (ii) For any three sets $X, Y, Z$ in $F, X \cup Y \cup Z \neq R$, (iii) $\bigcup_{X \in F} X=R$. We define $|F|$ to be the number of elements of $F$ (i.e., the number of subsets of $R$ belonging to $F$ ). Determine, if it exists, $h=\max |F|$, the maximum being taken over all S-families over $R$.
|
12. The first criterion ensures that all sets in an $S$-family are distinct. Since the number of different families of subsets is finite, $h$ has to exist. In fact, we will show that $h=11$. First of all, if there exists $X \in F$ such that $|X| \geq 5$, then by (3) there exists $Y \in F$ such that $X \cup Y=R$. In this case $|F|$ is at most 2. Similarly, for $|X|=4$, for the remaining two elements either there exists a subset in $F$ that contains both, in which case we obtain the previous case, or there exist different $Y$ and $Z$ containing them, in which case $X \cup Y \cup Z=R$, which must not happen. Hence we can assume $|X| \leq 4$ for all $X \in F$. Assume $|X|=1$ for some $X$. In that case other sets must not contain that subset and hence must be contained in the remaining 5 -element subset. These elements must not be subsets of each other. From elementary combinatorics, the largest number of subsets of a 5 -element set of which none is subset of another is $\binom{5}{2}=10$. This occurs when we take all 2-element subsets. These subsets also satisfy (2). Hence $|F|_{\max }=11$ in this case. Otherwise, let us assume $|X|=3$ for some $X$. Let us define the following families of subsets: $G=\{Z=Y \backslash X \mid Y \in F\}$ and $H=\{Z=Y \cap X \mid Y \in$ $F\}$. Then no two sets in $G$ must complement each other in $R \backslash X$, and $G$ must cover this set. Hence $G$ contains exactly the sets of each of the remaining 3 elements. For each element of $G$ no two sets in $H$ of which one is a subset of another may be paired with it. There can be only 3 such subsets selected within a 3 -element set $X$. Hence the number of remaining sets is smaller than $3 \cdot 3=9$. Hence in this case $|F|_{\max }=10$. In the remaining case all subsets have two elements. There are $\binom{6}{2}=15$ of them. But for every three that complement each other one must be discarded; hence the maximal number for $F$ in this case is $2 \cdot 15 / 3=10$. It follows that $h=11$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3b0fd09e-0a0e-5214-b427-14aafea48ce9
| 23,706
|
19. (ROM 1) Consider the sequences $\left(a_{n}\right),\left(b_{n}\right)$ defined by $$ a_{1}=3, \quad b_{1}=100, \quad a_{n+1}=3^{a_{n}}, \quad b_{n+1}=100^{b_{n}} . $$ Find the smallest integer $m$ for which $b_{m}>a_{100}$.
|
19. Let us define $i_{j}$ for two positive integers $i$ and $j$ in the following way: $i_{1}=i$ and $i_{j+1}=i^{i_{j}}$ for all positive integers $j$. Thus we must find the smallest $m$ such that $100_{m}>3_{100}$. Since $100_{1}=100>27=3_{2}$, we inductively have $100_{j}=10^{100_{j-1}}>3^{100_{j-1}}>3^{3_{j}}=3_{j+1}$ and hence $m \leq 99$. We now prove that $m=99$ by proving $100_{98}<3_{100}$. We note that $\left(100_{1}\right)^{2}=10^{4}<27^{4}=3^{12}<3^{27}=3_{3}$. We also note for $d>12$ (which trivially holds for all $d=100_{i}$ ) that if $c>d^{2}$, then we have $$ 3^{c}>3^{d^{2}}>3^{12 d}=\left(3^{12}\right)^{d}>10000^{d}=\left(100^{d}\right)^{2} $$ Hence from $3_{3}>\left(100_{1}\right)^{2}$ it inductively follows that $3_{j}>\left(100_{j-2}\right)^{2}>$ $100_{j-2}$ and hence that $100_{99}>3_{100}>100_{98}$. Hence $m=99$.
|
99
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
19. (ROM 1) Consider the sequences $\left(a_{n}\right),\left(b_{n}\right)$ defined by $$ a_{1}=3, \quad b_{1}=100, \quad a_{n+1}=3^{a_{n}}, \quad b_{n+1}=100^{b_{n}} . $$ Find the smallest integer $m$ for which $b_{m}>a_{100}$.
|
19. Let us define $i_{j}$ for two positive integers $i$ and $j$ in the following way: $i_{1}=i$ and $i_{j+1}=i^{i_{j}}$ for all positive integers $j$. Thus we must find the smallest $m$ such that $100_{m}>3_{100}$. Since $100_{1}=100>27=3_{2}$, we inductively have $100_{j}=10^{100_{j-1}}>3^{100_{j-1}}>3^{3_{j}}=3_{j+1}$ and hence $m \leq 99$. We now prove that $m=99$ by proving $100_{98}<3_{100}$. We note that $\left(100_{1}\right)^{2}=10^{4}<27^{4}=3^{12}<3^{27}=3_{3}$. We also note for $d>12$ (which trivially holds for all $d=100_{i}$ ) that if $c>d^{2}$, then we have $$ 3^{c}>3^{d^{2}}>3^{12 d}=\left(3^{12}\right)^{d}>10000^{d}=\left(100^{d}\right)^{2} $$ Hence from $3_{3}>\left(100_{1}\right)^{2}$ it inductively follows that $3_{j}>\left(100_{j-2}\right)^{2}>$ $100_{j-2}$ and hence that $100_{99}>3_{100}>100_{98}$. Hence $m=99$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b72628d0-5a7f-5cf4-a140-d0873cf73e91
| 23,725
|
2. (BEL 4) From a bag containing 5 pairs of socks, each pair a different color, a random sample of 4 single socks is drawn. Any complete pairs in the sample are discarded and replaced by a new pair draw from the bag. The process continues until the bag is empty or there are 4 socks of different colors held outside the bag. What is the probability of the latter alternative?
|
2. The only way to arrive at the latter alternative is to draw four different socks in the first drawing or to draw only one pair in the first drawing and then draw two different socks in the last drawing. We will call these probabilities respectively $p_{1}, p_{2}, p_{3}$. We calculate them as follows: $$ p_{1}=\frac{\binom{5}{4} 2^{4}}{\binom{10}{4}}=\frac{8}{21}, \quad p_{2}=\frac{5\binom{4}{2} 2^{2}}{\binom{10}{4}}=\frac{4}{7}, \quad p_{3}=\frac{4}{\binom{6}{2}}=\frac{4}{15} . $$ We finally calculate the desired probability: $P=p_{1}+p_{2} p_{3}=\frac{8}{15}$.
|
\frac{8}{15}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
2. (BEL 4) From a bag containing 5 pairs of socks, each pair a different color, a random sample of 4 single socks is drawn. Any complete pairs in the sample are discarded and replaced by a new pair draw from the bag. The process continues until the bag is empty or there are 4 socks of different colors held outside the bag. What is the probability of the latter alternative?
|
2. The only way to arrive at the latter alternative is to draw four different socks in the first drawing or to draw only one pair in the first drawing and then draw two different socks in the last drawing. We will call these probabilities respectively $p_{1}, p_{2}, p_{3}$. We calculate them as follows: $$ p_{1}=\frac{\binom{5}{4} 2^{4}}{\binom{10}{4}}=\frac{8}{21}, \quad p_{2}=\frac{5\binom{4}{2} 2^{2}}{\binom{10}{4}}=\frac{4}{7}, \quad p_{3}=\frac{4}{\binom{6}{2}}=\frac{4}{15} . $$ We finally calculate the desired probability: $P=p_{1}+p_{2} p_{3}=\frac{8}{15}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
619ed4e7-aff4-585a-81f6-a29e4175d43c
| 23,727
|
20. (SWE 2) Given the integer $n>1$ and the real number $a>0$ determine the maximum of $\sum_{i=1}^{n-1} x_{i} x_{i+1}$ taken over all nonnegative numbers $x_{i}$ with sum $a$.
|
20. Let $x_{k}=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$. Then $x_{i} x_{i+1} \leq x_{i} x_{k}$ for $i=1,2, \ldots, k-1$ and $x_{i} x_{i+1} \leq x_{k} x_{i+1}$ for $i=k, \ldots, n-1$. Summing up these inequalities for $i=1,2, \ldots, n-1$ we obtain $$ \sum_{i=1}^{n-1} \leq x_{k}\left(x_{1}+\cdots+x_{k-1}+x_{k+1}+\cdots+x_{n}\right)=x_{k}\left(a-x_{k}\right) \leq \frac{a^{2}}{4} $$ We note that the value $a^{2} / 4$ is attained for $x_{1}=x_{2}=a / 2$ and $x_{3}=\cdots=$ $x_{n}=0$. Hence $a^{2} / 4$ is the required maximum.
|
\frac{a^2}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
20. (SWE 2) Given the integer $n>1$ and the real number $a>0$ determine the maximum of $\sum_{i=1}^{n-1} x_{i} x_{i+1}$ taken over all nonnegative numbers $x_{i}$ with sum $a$.
|
20. Let $x_{k}=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$. Then $x_{i} x_{i+1} \leq x_{i} x_{k}$ for $i=1,2, \ldots, k-1$ and $x_{i} x_{i+1} \leq x_{k} x_{i+1}$ for $i=k, \ldots, n-1$. Summing up these inequalities for $i=1,2, \ldots, n-1$ we obtain $$ \sum_{i=1}^{n-1} \leq x_{k}\left(x_{1}+\cdots+x_{k-1}+x_{k+1}+\cdots+x_{n}\right)=x_{k}\left(a-x_{k}\right) \leq \frac{a^{2}}{4} $$ We note that the value $a^{2} / 4$ is attained for $x_{1}=x_{2}=a / 2$ and $x_{3}=\cdots=$ $x_{n}=0$. Hence $a^{2} / 4$ is the required maximum.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3c4940d3-d6b6-5d4f-ad42-8d65d9094e77
| 23,729
|
23. (USA 4) Find all natural numbers $n$ for which $2^{8}+2^{11}+2^{n}$ is a perfect square.
|
23. It is easily verified that no solutions exist for $n \leq 8$. Let us now assume that $n>8$. We note that $2^{8}+2^{11}+2^{n}=2^{8} \cdot\left(9+2^{n-8}\right)$. Hence $9+2^{n-8}$ must also be a square, say $9+2^{n-8}=x^{2}, x \in \mathbb{N}$, i.e., $2^{n-8}=x^{2}-9=$ $(x-3)(x+3)$. Thus $x-3$ and $x+3$ are both powers of 2 , which is possible only for $x=5$ and $n=12$. Hence, $n=12$ is the only solution.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
23. (USA 4) Find all natural numbers $n$ for which $2^{8}+2^{11}+2^{n}$ is a perfect square.
|
23. It is easily verified that no solutions exist for $n \leq 8$. Let us now assume that $n>8$. We note that $2^{8}+2^{11}+2^{n}=2^{8} \cdot\left(9+2^{n-8}\right)$. Hence $9+2^{n-8}$ must also be a square, say $9+2^{n-8}=x^{2}, x \in \mathbb{N}$, i.e., $2^{n-8}=x^{2}-9=$ $(x-3)(x+3)$. Thus $x-3$ and $x+3$ are both powers of 2 , which is possible only for $x=5$ and $n=12$. Hence, $n=12$ is the only solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
08d01b2c-62cf-5283-88cb-6999acb9a137
| 23,736
|
5. (CZS 2) Let $n \geq 2$ be an integer. Find the maximal cardinality of a set $M$ of pairs $(j, k)$ of integers, $1 \leq j<k \leq n$, with the following property: If $(j, k) \in M$, then $(k, m) \notin M$ for any $m$.
|
5. Let $A=\{x \mid(x, y) \in M\}$ and $B=\{y \mid(x, y) \in M$. Then $A$ and $B$ are disjoint and hence $$ |M| \leq|A| \cdot|B| \leq \frac{(|A|+|B|)^{2}}{4} \leq\left[\frac{n^{2}}{4}\right] $$ These cardinalities can be achieved for $M=\{(a, b) \mid a=1,2, \ldots,[n / 2]$, $b=[n / 2]+1, \ldots, n\}$.
|
\left[\frac{n^{2}}{4}\right]
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
5. (CZS 2) Let $n \geq 2$ be an integer. Find the maximal cardinality of a set $M$ of pairs $(j, k)$ of integers, $1 \leq j<k \leq n$, with the following property: If $(j, k) \in M$, then $(k, m) \notin M$ for any $m$.
|
5. Let $A=\{x \mid(x, y) \in M\}$ and $B=\{y \mid(x, y) \in M$. Then $A$ and $B$ are disjoint and hence $$ |M| \leq|A| \cdot|B| \leq \frac{(|A|+|B|)^{2}}{4} \leq\left[\frac{n^{2}}{4}\right] $$ These cardinalities can be achieved for $M=\{(a, b) \mid a=1,2, \ldots,[n / 2]$, $b=[n / 2]+1, \ldots, n\}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e04129c1-bef2-5495-a339-7dfd6aa344d1
| 23,751
|
10. (FRA) Determine the smallest natural number $n$ having the following property: For every integer $p, p \geq n$, it is possible to subdivide (partition) a given square into $p$ squares (not necessarily equal).
|
10. It is easy to see that partitioning into $p=2 k$ squares is possible for $k \geq 2$ (Fig. 1). Furthermore, whenever it is possible to partition the square into $p$ squares, there is a partition of the square into $p+3$ squares: namely, in the partition into $p$ squares, divide one of them into four new squares.  Fig. 1  Fig. 2 This implies that both $p=2 k$ and $p=2 k+3$ are possible if $k \geq 2$, and therefore all $p \geq 6$ are possible. On the other hand, partitioning the square into 5 squares is not possible. Assuming it is possible, one of its sides would be covered by exactly two squares, which cannot be of the same size (Fig. 2). The rest of the big square cannot be partitioned into three squares. Hence, the answer is $n=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
10. (FRA) Determine the smallest natural number $n$ having the following property: For every integer $p, p \geq n$, it is possible to subdivide (partition) a given square into $p$ squares (not necessarily equal).
|
10. It is easy to see that partitioning into $p=2 k$ squares is possible for $k \geq 2$ (Fig. 1). Furthermore, whenever it is possible to partition the square into $p$ squares, there is a partition of the square into $p+3$ squares: namely, in the partition into $p$ squares, divide one of them into four new squares.  Fig. 1  Fig. 2 This implies that both $p=2 k$ and $p=2 k+3$ are possible if $k \geq 2$, and therefore all $p \geq 6$ are possible. On the other hand, partitioning the square into 5 squares is not possible. Assuming it is possible, one of its sides would be covered by exactly two squares, which cannot be of the same size (Fig. 2). The rest of the big square cannot be partitioned into three squares. Hence, the answer is $n=6$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8276f84d-bcd7-5ba9-bd85-a78ffc9f257a
| 23,764
|
12. (NET) ${ }^{\mathrm{IMO} 3}$ Determine the maximum value of $m^{2}+n^{2}$ where $m$ and $n$ are integers satisfying $$ m, n \in\{1,2, \ldots, 100\} \quad \text { and } \quad\left(n^{2}-m n-m^{2}\right)^{2}=1 $$
|
12. We will solve the contest problem (in which $m, n \in\{1,2, \ldots, 1981\}$ ). For $m=1, n$ can be either 1 or 2 . If $m>1$, then $n(n-m)=m^{2} \pm 1>0$; hence $n-m>0$. Set $p=n-m$. Since $m^{2}-m p-p^{2}=m^{2}-p(m+p)=$ $-\left(n^{2}-n m-m^{2}\right)$, we see that $(m, n)$ is a solution of the equation if and only if $(p, m)$ is a solution too. Therefore, all the solutions of the equation are given as two consecutive members of the Fibonacci sequence $$ 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584, \ldots $$ So the required maximum is $987^{2}+1597^{2}$.
|
987^{2}+1597^{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
12. (NET) ${ }^{\mathrm{IMO} 3}$ Determine the maximum value of $m^{2}+n^{2}$ where $m$ and $n$ are integers satisfying $$ m, n \in\{1,2, \ldots, 100\} \quad \text { and } \quad\left(n^{2}-m n-m^{2}\right)^{2}=1 $$
|
12. We will solve the contest problem (in which $m, n \in\{1,2, \ldots, 1981\}$ ). For $m=1, n$ can be either 1 or 2 . If $m>1$, then $n(n-m)=m^{2} \pm 1>0$; hence $n-m>0$. Set $p=n-m$. Since $m^{2}-m p-p^{2}=m^{2}-p(m+p)=$ $-\left(n^{2}-n m-m^{2}\right)$, we see that $(m, n)$ is a solution of the equation if and only if $(p, m)$ is a solution too. Therefore, all the solutions of the equation are given as two consecutive members of the Fibonacci sequence $$ 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584, \ldots $$ So the required maximum is $987^{2}+1597^{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ae24c4fa-60b6-57b1-a6ac-b18e3c74e74a
| 23,769
|
15. (GBR) ${ }^{\mathrm{IMO} 1}$ Find the point $P$ inside the triangle $A B C$ for which $$ \frac{B C}{P D}+\frac{C A}{P E}+\frac{A B}{P F} $$ is minimal, where $P D, P E, P F$ are the perpendiculars from $P$ to $B C, C A$, $A B$ respectively.
|
15. Set $B C=a, C A=b, A B=c$, and denote the area of $\triangle A B C$ by $P$, and $a / P D+b / P E+c / P F$ by $S$. Since $a \cdot P D+b \cdot P E+c \cdot P F=2 P$, by the Cauchy-Schwarz inequality we have $$ 2 P S=(a \cdot P D+b \cdot P E+c \cdot P F)\left(\frac{a}{P D}+\frac{b}{P E}+\frac{c}{P F}\right) \geq(a+b+c)^{2} $$ with equality if and only if $P D=P E=P F$, i.e., $P$ is the incenter of $\triangle A B C$. In that case, $S$ attains its minimum: $$ S_{\min }=\frac{(a+b+c)^{2}}{2 P} $$
|
\frac{(a+b+c)^{2}}{2 P}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
15. (GBR) ${ }^{\mathrm{IMO} 1}$ Find the point $P$ inside the triangle $A B C$ for which $$ \frac{B C}{P D}+\frac{C A}{P E}+\frac{A B}{P F} $$ is minimal, where $P D, P E, P F$ are the perpendiculars from $P$ to $B C, C A$, $A B$ respectively.
|
15. Set $B C=a, C A=b, A B=c$, and denote the area of $\triangle A B C$ by $P$, and $a / P D+b / P E+c / P F$ by $S$. Since $a \cdot P D+b \cdot P E+c \cdot P F=2 P$, by the Cauchy-Schwarz inequality we have $$ 2 P S=(a \cdot P D+b \cdot P E+c \cdot P F)\left(\frac{a}{P D}+\frac{b}{P E}+\frac{c}{P F}\right) \geq(a+b+c)^{2} $$ with equality if and only if $P D=P E=P F$, i.e., $P$ is the incenter of $\triangle A B C$. In that case, $S$ attains its minimum: $$ S_{\min }=\frac{(a+b+c)^{2}}{2 P} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9eafe655-1701-5804-9eb3-7201706d9fca
| 23,776
|
3. (CAN) Find the minimum value of $$ \max (a+b+c, b+c+d, c+d+e, d+e+f, e+f+g) $$ subject to the constraints (i) $a, b, c, d, e, f, g \geq 0$, (ii) $a+b+c+d+e+f+g=1$.
|
3. Denote $\max (a+b+c, b+c+d, c+d+e, d+e+f, e+f+g)$ by $p$. We have $$ (a+b+c)+(c+d+e)+(e+f+g)=1+c+e \leq 3 p $$ which implies that $p \geq 1 / 3$. However, $p=1 / 3$ is achieved by taking $(a, b, c, d, e, f, g)=(1 / 3,0,0,1 / 3,0,0,1 / 3)$. Therefore the answer is $1 / 3$. Remark. In fact, one can prove a more general statement in the same way. Given positive integers $n, k, n \geq k$, if $a_{1}, a_{2}, \ldots, a_{n}$ are nonnegative real numbers with sum 1 , then the minimum value of $\max _{i=1, \ldots, n-k+1}\left\{a_{i}+\right.$ $\left.a_{i+1}+\cdots+a_{i+k-1}\right\}$ is $1 / r$, where $r$ is the integer with $k(r-1)<n \leq k r$.
|
\frac{1}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
3. (CAN) Find the minimum value of $$ \max (a+b+c, b+c+d, c+d+e, d+e+f, e+f+g) $$ subject to the constraints (i) $a, b, c, d, e, f, g \geq 0$, (ii) $a+b+c+d+e+f+g=1$.
|
3. Denote $\max (a+b+c, b+c+d, c+d+e, d+e+f, e+f+g)$ by $p$. We have $$ (a+b+c)+(c+d+e)+(e+f+g)=1+c+e \leq 3 p $$ which implies that $p \geq 1 / 3$. However, $p=1 / 3$ is achieved by taking $(a, b, c, d, e, f, g)=(1 / 3,0,0,1 / 3,0,0,1 / 3)$. Therefore the answer is $1 / 3$. Remark. In fact, one can prove a more general statement in the same way. Given positive integers $n, k, n \geq k$, if $a_{1}, a_{2}, \ldots, a_{n}$ are nonnegative real numbers with sum 1 , then the minimum value of $\max _{i=1, \ldots, n-k+1}\left\{a_{i}+\right.$ $\left.a_{i+1}+\cdots+a_{i+k-1}\right\}$ is $1 / r$, where $r$ is the integer with $k(r-1)<n \leq k r$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
10e275b0-4ce1-5851-b184-8dec8ad693c3
| 23,789
|
5. (COL) A cube is assembled with 27 white cubes. The larger cube is then painted black on the outside and disassembled. A blind man reassembles it. What is the probability that the cube is now completely black on the outside? Give an approximation of the size of your answer.
|
5. There are four types of small cubes upon disassembling: (1) 8 cubes with three faces, painted black, at one corner; (2) 12 cubes with two black faces, both at one edge; (3) 6 cubes with one black face; (4) 1 completely white cube. All cubes of type (1) must go to corners, and be placed in a correct way (one of three): for this step we have $3^{8} \cdot 8$ ! possibilities. Further, all cubes of type (2) must go in a correct way (one of two) to edges, admitting $2^{12} \cdot 12$ ! possibilities; similarly, there are $4^{6} \cdot 6$ ! ways for cubes of type (3), and 24 ways for the cube of type (4). Thus the total number of good reassemblings is $3^{8} 8!\cdot 2^{12} 12!\cdot 4^{6} 6!\cdot 24$, while the number of all possible reassemblings is $24^{27} \cdot 27!$. The desired probability is $\frac{3^{8} 8!\cdot 2^{12} 12!\cdot 4^{6} 6!\cdot 24}{24^{27} \cdot 27!}$. It is not necessary to calculate these numbers to find out that the blind man practically has no chance to reassemble the cube in a right way: in fact, the probability is of order $1.8 \cdot 10^{-37}$.
|
1.8 \cdot 10^{-37}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
5. (COL) A cube is assembled with 27 white cubes. The larger cube is then painted black on the outside and disassembled. A blind man reassembles it. What is the probability that the cube is now completely black on the outside? Give an approximation of the size of your answer.
|
5. There are four types of small cubes upon disassembling: (1) 8 cubes with three faces, painted black, at one corner; (2) 12 cubes with two black faces, both at one edge; (3) 6 cubes with one black face; (4) 1 completely white cube. All cubes of type (1) must go to corners, and be placed in a correct way (one of three): for this step we have $3^{8} \cdot 8$ ! possibilities. Further, all cubes of type (2) must go in a correct way (one of two) to edges, admitting $2^{12} \cdot 12$ ! possibilities; similarly, there are $4^{6} \cdot 6$ ! ways for cubes of type (3), and 24 ways for the cube of type (4). Thus the total number of good reassemblings is $3^{8} 8!\cdot 2^{12} 12!\cdot 4^{6} 6!\cdot 24$, while the number of all possible reassemblings is $24^{27} \cdot 27!$. The desired probability is $\frac{3^{8} 8!\cdot 2^{12} 12!\cdot 4^{6} 6!\cdot 24}{24^{27} \cdot 27!}$. It is not necessary to calculate these numbers to find out that the blind man practically has no chance to reassemble the cube in a right way: in fact, the probability is of order $1.8 \cdot 10^{-37}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4080e64a-93c7-5d3e-93db-fd861c6a7700
| 23,793
|
1. A1 (GBR 3) ${ }^{\mathrm{IMO}}$ The function $f(n)$ is defined for all positive integers $n$ and takes on nonnegative integer values. Also, for all $m, n$, $$ \begin{gathered} f(m+n)-f(m)-f(n)=0 \text { or } 1 \\ f(2)=0, \quad f(3)>0, \quad \text { and } \quad f(9999)=3333 \end{gathered} $$ Determine $f(1982)$.
|
1. From $f(1)+f(1) \leq f(2)=0$ we obtain $f(1)=0$. Since $0<f(3) \leq$ $f(1)+f(2)+1$, it follows that $f(3)=1$. Note that if $f(3 n) \geq n$, then $f(3 n+3) \geq f(3 n)+f(3) \geq n+1$. Hence by induction $f(3 n) \geq n$ holds for all $n \in \mathbb{N}$. Moreover, if the inequality is strict for some $n$, then it is so for all integers greater than $n$ as well. Since $f(9999)=3333$, we deduce that $f(3 n)=n$ for all $n \leq 3333$. By the given condition, we have $3 f(n) \leq f(3 n) \leq 3 f(n)+2$. Therefore $f(n)=[f(3 n) / 3]=[n / 3]$ for $n \leq 3333$. In particular, $f(1982)=$ $[1982 / 3]=660$.
|
660
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
1. A1 (GBR 3) ${ }^{\mathrm{IMO}}$ The function $f(n)$ is defined for all positive integers $n$ and takes on nonnegative integer values. Also, for all $m, n$, $$ \begin{gathered} f(m+n)-f(m)-f(n)=0 \text { or } 1 \\ f(2)=0, \quad f(3)>0, \quad \text { and } \quad f(9999)=3333 \end{gathered} $$ Determine $f(1982)$.
|
1. From $f(1)+f(1) \leq f(2)=0$ we obtain $f(1)=0$. Since $0<f(3) \leq$ $f(1)+f(2)+1$, it follows that $f(3)=1$. Note that if $f(3 n) \geq n$, then $f(3 n+3) \geq f(3 n)+f(3) \geq n+1$. Hence by induction $f(3 n) \geq n$ holds for all $n \in \mathbb{N}$. Moreover, if the inequality is strict for some $n$, then it is so for all integers greater than $n$ as well. Since $f(9999)=3333$, we deduce that $f(3 n)=n$ for all $n \leq 3333$. By the given condition, we have $3 f(n) \leq f(3 n) \leq 3 f(n)+2$. Therefore $f(n)=[f(3 n) / 3]=[n / 3]$ for $n \leq 3333$. In particular, $f(1982)=$ $[1982 / 3]=660$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7f207038-b679-5978-ae20-2d7cad568980
| 23,806
|
12. B6 (FIN 3) Four distinct circles $C, C_{1}, C_{2}, C_{3}$ and a line $L$ are given in the plane such that $C$ and $L$ are disjoint and each of the circles $C_{1}, C_{2}, C_{3}$ touches the other two, as well as $C$ and $L$. Assuming the radius of $C$ to be 1 , determine the distance between its center and $L$.
|
12. Let $y$ be the line perpendicular to $L$ passing through the center of $C$. It can be shown by a continuity argument that there exists a point $Y \in y$ such that an inversion $\Psi$ centered at $Y$ maps $C$ and $L$ onto two concentric circles $\widehat{C}$ and $\widehat{L}$. Let $\widehat{X}$ denote the image of an object $X$ under $\Psi$. Then the circles $\widehat{C_{i}}$ touch $\widehat{C}$ externally and $\widehat{L}$ internally, and all have the same radius. Let us now rotate the picture around the common center $Z$ of $\widehat{C}$ and $\widehat{L}$ so that $\widehat{C_{3}}$ passes through $Y$. Applying the inversion $\Psi$ again on the picture thus obtained, $\widehat{C}$ and $\widehat{L}$ go back to $C$ and $L$, but $\widehat{C_{3}}$ goes to a line $C_{3}^{\prime}$ parallel to $L$, while the images of $\widehat{C_{1}}$ and $\widehat{C_{2}}$ go to two equal circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$ touching $L, C_{3}^{\prime}$, and $C$. This way we have achieved that $C_{3}$ becomes a line. Denote by $O_{1}, O_{2}, O$ respectively the centers of the circles $C_{1}^{\prime}, C_{2}^{\prime}, C$ and by $T$ the point of tangency of the circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$. If $x$ is the common radius of the circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$, then from $\triangle O_{1} T O$ we obtain 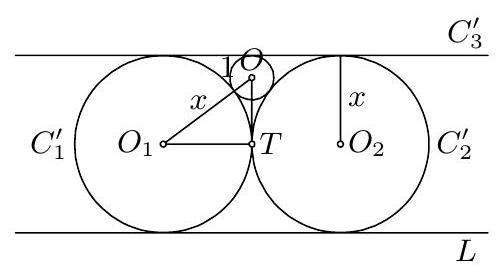 that $(x-1)^{2}+x^{2}=(x+1)^{2}$, and thus $x=4$. Hence the distance of $O$ from $L$ equals $2 x-1=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
12. B6 (FIN 3) Four distinct circles $C, C_{1}, C_{2}, C_{3}$ and a line $L$ are given in the plane such that $C$ and $L$ are disjoint and each of the circles $C_{1}, C_{2}, C_{3}$ touches the other two, as well as $C$ and $L$. Assuming the radius of $C$ to be 1 , determine the distance between its center and $L$.
|
12. Let $y$ be the line perpendicular to $L$ passing through the center of $C$. It can be shown by a continuity argument that there exists a point $Y \in y$ such that an inversion $\Psi$ centered at $Y$ maps $C$ and $L$ onto two concentric circles $\widehat{C}$ and $\widehat{L}$. Let $\widehat{X}$ denote the image of an object $X$ under $\Psi$. Then the circles $\widehat{C_{i}}$ touch $\widehat{C}$ externally and $\widehat{L}$ internally, and all have the same radius. Let us now rotate the picture around the common center $Z$ of $\widehat{C}$ and $\widehat{L}$ so that $\widehat{C_{3}}$ passes through $Y$. Applying the inversion $\Psi$ again on the picture thus obtained, $\widehat{C}$ and $\widehat{L}$ go back to $C$ and $L$, but $\widehat{C_{3}}$ goes to a line $C_{3}^{\prime}$ parallel to $L$, while the images of $\widehat{C_{1}}$ and $\widehat{C_{2}}$ go to two equal circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$ touching $L, C_{3}^{\prime}$, and $C$. This way we have achieved that $C_{3}$ becomes a line. Denote by $O_{1}, O_{2}, O$ respectively the centers of the circles $C_{1}^{\prime}, C_{2}^{\prime}, C$ and by $T$ the point of tangency of the circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$. If $x$ is the common radius of the circles $C_{1}^{\prime}$ and $C_{2}^{\prime}$, then from $\triangle O_{1} T O$ we obtain  that $(x-1)^{2}+x^{2}=(x+1)^{2}$, and thus $x=4$. Hence the distance of $O$ from $L$ equals $2 x-1=7$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4683e15f-b194-594d-ba0c-0c8a1976277d
| 23,812
|
18. C6 (FRA 2) Let $O$ be a point of three-dimensional space and let $l_{1}, l_{2}, l_{3}$ be mutually perpendicular straight lines passing through $O$. Let $S$ denote the sphere with center $O$ and radius $R$, and for every point $M$ of $S$, let $S_{M}$ denote the sphere with center $M$ and radius $R$. We denote by $P_{1}, P_{2}, P_{3}$ the intersection of $S_{M}$ with the straight lines $l_{1}, l_{2}, l_{3}$, respectively, where we put $P_{i} \neq O$ if $l_{i}$ meets $S_{M}$ at two distinct points and $P_{i}=O$ otherwise ( $i=$ $1,2,3)$. What is the set of centers of gravity of the (possibly degenerate) triangles $P_{1} P_{2} P_{3}$ as $M$ runs through the points of $S$ ?
|
18. Set the coordinate system with the axes $x, y, z$ along the lines $l_{1}, l_{2}, l_{3}$ respectively. The coordinates $(a, b, c)$ of $M$ satisfy $a^{2}+b^{2}+c^{2}=R^{2}$, and so $S_{M}$ is given by the equation $(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=R^{2}$. Hence the coordinates of $P_{1}$ are $(x, 0,0)$ with $(x-a)^{2}+b^{2}+c^{2}=R^{2}$, implying that either $x=2 a$ or $x=0$. Thus by the definition we obtain $x=2 a$. Similarly, the coordinates of $P_{2}$ and $P_{3}$ are $(0,2 b, 0)$ and $(0,0,2 c)$ respectively. Now, the centroid of $\triangle P_{1} P_{2} P_{3}$ has the coordinates $(2 a / 3,2 b / 3,2 c / 3)$. Therefore the required locus of points is the sphere with center $O$ and radius $2 R / 3$.
|
\frac{2R}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
18. C6 (FRA 2) Let $O$ be a point of three-dimensional space and let $l_{1}, l_{2}, l_{3}$ be mutually perpendicular straight lines passing through $O$. Let $S$ denote the sphere with center $O$ and radius $R$, and for every point $M$ of $S$, let $S_{M}$ denote the sphere with center $M$ and radius $R$. We denote by $P_{1}, P_{2}, P_{3}$ the intersection of $S_{M}$ with the straight lines $l_{1}, l_{2}, l_{3}$, respectively, where we put $P_{i} \neq O$ if $l_{i}$ meets $S_{M}$ at two distinct points and $P_{i}=O$ otherwise ( $i=$ $1,2,3)$. What is the set of centers of gravity of the (possibly degenerate) triangles $P_{1} P_{2} P_{3}$ as $M$ runs through the points of $S$ ?
|
18. Set the coordinate system with the axes $x, y, z$ along the lines $l_{1}, l_{2}, l_{3}$ respectively. The coordinates $(a, b, c)$ of $M$ satisfy $a^{2}+b^{2}+c^{2}=R^{2}$, and so $S_{M}$ is given by the equation $(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=R^{2}$. Hence the coordinates of $P_{1}$ are $(x, 0,0)$ with $(x-a)^{2}+b^{2}+c^{2}=R^{2}$, implying that either $x=2 a$ or $x=0$. Thus by the definition we obtain $x=2 a$. Similarly, the coordinates of $P_{2}$ and $P_{3}$ are $(0,2 b, 0)$ and $(0,0,2 c)$ respectively. Now, the centroid of $\triangle P_{1} P_{2} P_{3}$ has the coordinates $(2 a / 3,2 b / 3,2 c / 3)$. Therefore the required locus of points is the sphere with center $O$ and radius $2 R / 3$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f58f9343-2f67-5e59-a101-9f77d75618ac
| 23,827
|
4. A4 (BUL 2) Determine all real values of the parameter $a$ for which the equation $$ 16 x^{4}-a x^{3}+(2 a+17) x^{2}-a x+16=0 $$ has exactly four distinct real roots that form a geometric progression.
|
4. Suppose that $a$ satisfies the requirements of the problem and that $x, q x$, $q^{2} x, q^{3} x$ are the roots of the given equation. Then $x \neq 0$ and we may assume that $|q|>1$, so that $|x|<|q x|<\left|q^{2} x\right|<\left|q^{3} x\right|$. Since the equation is symmetric, $1 / x$ is also a root and therefore $1 / x=q^{3} x$, i.e., $q=x^{-2 / 3}$. It follows that the roots are $x, x^{1 / 3}, x^{-1 / 3}, x^{-1}$. Now by Vieta's formula we have $x+x^{1 / 3}+x^{-1 / 3}+x^{-1}=a / 16$ and $x^{4 / 3}+x^{2 / 3}+2+x^{-2 / 3}+x^{-4 / 3}=$ $(2 a+17) / 16$. On setting $z=x^{1 / 3}+x^{-1 / 3}$ these equations become $$ \begin{aligned} z^{3}-2 z & =a / 16 \\ \left(z^{2}-2\right)^{2}+z^{2}-2 & =(2 a+17) / 16 \end{aligned} $$ Substituting $a=16\left(z^{3}-2 z\right)$ in the second equation leads to $z^{4}-2 z^{3}-$ $3 z^{2}+4 z+15 / 16=0$. We observe that this polynomial factors as $(z+$ $3 / 2)(z-5 / 2)\left(z^{2}-z-1 / 4\right)$. Since $|z|=\left|x^{1 / 3}+x^{-1 / 3}\right| \geq 2$, the only viable value is $z=5 / 2$. Consequently $a=170$ and the roots are $1 / 8,1 / 2,2,8$.
|
170
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
4. A4 (BUL 2) Determine all real values of the parameter $a$ for which the equation $$ 16 x^{4}-a x^{3}+(2 a+17) x^{2}-a x+16=0 $$ has exactly four distinct real roots that form a geometric progression.
|
4. Suppose that $a$ satisfies the requirements of the problem and that $x, q x$, $q^{2} x, q^{3} x$ are the roots of the given equation. Then $x \neq 0$ and we may assume that $|q|>1$, so that $|x|<|q x|<\left|q^{2} x\right|<\left|q^{3} x\right|$. Since the equation is symmetric, $1 / x$ is also a root and therefore $1 / x=q^{3} x$, i.e., $q=x^{-2 / 3}$. It follows that the roots are $x, x^{1 / 3}, x^{-1 / 3}, x^{-1}$. Now by Vieta's formula we have $x+x^{1 / 3}+x^{-1 / 3}+x^{-1}=a / 16$ and $x^{4 / 3}+x^{2 / 3}+2+x^{-2 / 3}+x^{-4 / 3}=$ $(2 a+17) / 16$. On setting $z=x^{1 / 3}+x^{-1 / 3}$ these equations become $$ \begin{aligned} z^{3}-2 z & =a / 16 \\ \left(z^{2}-2\right)^{2}+z^{2}-2 & =(2 a+17) / 16 \end{aligned} $$ Substituting $a=16\left(z^{3}-2 z\right)$ in the second equation leads to $z^{4}-2 z^{3}-$ $3 z^{2}+4 z+15 / 16=0$. We observe that this polynomial factors as $(z+$ $3 / 2)(z-5 / 2)\left(z^{2}-z-1 / 4\right)$. Since $|z|=\left|x^{1 / 3}+x^{-1 / 3}\right| \geq 2$, the only viable value is $z=5 / 2$. Consequently $a=170$ and the roots are $1 / 8,1 / 2,2,8$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
bb97f102-f391-596a-b98b-63b31e2d5daf
| 23,839
|
5. A5 (NET 2) ${ }^{\mathrm{IMO}}$ Let $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}$ be a regular hexagon. Each of its diagonals $A_{i-1} A_{i+1}$ is divided into the same ratio $\frac{\lambda}{1-\lambda}$, where $0<\lambda<1$, by a point $B_{i}$ in such a way that $A_{i}, B_{i}$, and $B_{i+2}$ are collinear ( $i \equiv$ $1, \ldots, 6(\bmod 6))$. Compute $\lambda$.
|
5. We first observe that $\triangle A_{5} B_{4} A_{4} \cong$ $\triangle A_{3} B_{2} A_{2}$. Since $\angle A_{5} A_{3} A_{2}=90^{\circ}$, we have $\angle A_{2} B_{4} A_{4}=\angle A_{2} B_{4} A_{3}+$ $\angle A_{3} B_{4} A_{4}=\left(90^{\circ}-\angle B_{2} A_{2} A_{3}\right)+$ $\left(\angle B_{4} A_{5} A_{4}+\angle A_{5} A_{4} B_{4}\right)=90^{\circ}+$ $\angle B_{4} A_{5} A_{4}=120^{\circ}$. Hence $B_{4}$ belongs to the circle with center $A_{3}$ and radius $A_{3} A_{4}$, so $A_{3} A_{4}=A_{3} B_{4}$. 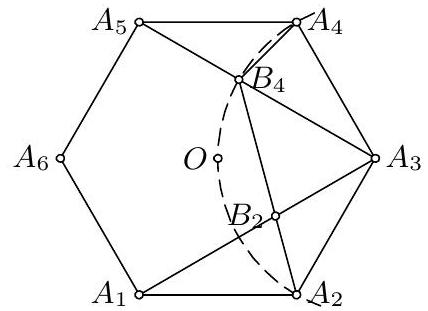 Thus $\lambda=A_{3} B_{4} / A_{3} A_{5}=A_{3} A_{4} / A_{3} A_{5}=1 / \sqrt{3}$.
|
\frac{1}{\sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
5. A5 (NET 2) ${ }^{\mathrm{IMO}}$ Let $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}$ be a regular hexagon. Each of its diagonals $A_{i-1} A_{i+1}$ is divided into the same ratio $\frac{\lambda}{1-\lambda}$, where $0<\lambda<1$, by a point $B_{i}$ in such a way that $A_{i}, B_{i}$, and $B_{i+2}$ are collinear ( $i \equiv$ $1, \ldots, 6(\bmod 6))$. Compute $\lambda$.
|
5. We first observe that $\triangle A_{5} B_{4} A_{4} \cong$ $\triangle A_{3} B_{2} A_{2}$. Since $\angle A_{5} A_{3} A_{2}=90^{\circ}$, we have $\angle A_{2} B_{4} A_{4}=\angle A_{2} B_{4} A_{3}+$ $\angle A_{3} B_{4} A_{4}=\left(90^{\circ}-\angle B_{2} A_{2} A_{3}\right)+$ $\left(\angle B_{4} A_{5} A_{4}+\angle A_{5} A_{4} B_{4}\right)=90^{\circ}+$ $\angle B_{4} A_{5} A_{4}=120^{\circ}$. Hence $B_{4}$ belongs to the circle with center $A_{3}$ and radius $A_{3} A_{4}$, so $A_{3} A_{4}=A_{3} B_{4}$.  Thus $\lambda=A_{3} B_{4} / A_{3} A_{5}=A_{3} A_{4} / A_{3} A_{5}=1 / \sqrt{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1b9cb988-d2e5-5d1e-8645-997cb0999caa
| 23,842
|
13. (LUX 2) Let $E$ be the set of $1983^{3}$ points of the space $\mathbb{R}^{3}$ all three of whose coordinates are integers between 0 and 1982 (including 0 and 1982). A coloring of $E$ is a map from $E$ to the set $\{$ red, blue $\}$. How many colorings of $E$ are there satisfying the following property: The number of red vertices among the 8 vertices of any right-angled parallelepiped is a multiple of 4 ?
|
13. Given any coloring of the $3 \times 1983-2$ points of the axes, we prove that there is a unique coloring of $E$ having the given property and extending this coloring. The first thing to notice is that given any rectangle $R_{1}$ parallel to a coordinate plane and whose edges are parallel to the axes, there is an even number $r_{1}$ of red vertices on $R_{1}$. Indeed, let $R_{2}$ and $R_{3}$ be two other rectangles that are translated from $R_{1}$ orthogonally to $R_{1}$ and let $r_{2}, r_{3}$ be the numbers of red vertices on $R_{2}$ and $R_{3}$ respectively. Then $r_{1}+r_{2}$, $r_{1}+r_{3}$, and $r_{2}+r_{3}$ are multiples of 4 , so $r_{1}=\left(r_{1}+r_{2}+r_{1}+r_{3}-r_{2}-r_{3}\right) / 2$ is even. Since any point of a coordinate plane is a vertex of a rectangle whose remaining three vertices lie on the corresponding axes, this determines uniquely the coloring of the coordinate planes. Similarly, the coloring of the inner points of the parallelepiped is completely determined. The solution is hence $2^{3 \times 1983-2}=2^{5947}$.
|
2^{5947}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
13. (LUX 2) Let $E$ be the set of $1983^{3}$ points of the space $\mathbb{R}^{3}$ all three of whose coordinates are integers between 0 and 1982 (including 0 and 1982). A coloring of $E$ is a map from $E$ to the set $\{$ red, blue $\}$. How many colorings of $E$ are there satisfying the following property: The number of red vertices among the 8 vertices of any right-angled parallelepiped is a multiple of 4 ?
|
13. Given any coloring of the $3 \times 1983-2$ points of the axes, we prove that there is a unique coloring of $E$ having the given property and extending this coloring. The first thing to notice is that given any rectangle $R_{1}$ parallel to a coordinate plane and whose edges are parallel to the axes, there is an even number $r_{1}$ of red vertices on $R_{1}$. Indeed, let $R_{2}$ and $R_{3}$ be two other rectangles that are translated from $R_{1}$ orthogonally to $R_{1}$ and let $r_{2}, r_{3}$ be the numbers of red vertices on $R_{2}$ and $R_{3}$ respectively. Then $r_{1}+r_{2}$, $r_{1}+r_{3}$, and $r_{2}+r_{3}$ are multiples of 4 , so $r_{1}=\left(r_{1}+r_{2}+r_{1}+r_{3}-r_{2}-r_{3}\right) / 2$ is even. Since any point of a coordinate plane is a vertex of a rectangle whose remaining three vertices lie on the corresponding axes, this determines uniquely the coloring of the coordinate planes. Similarly, the coloring of the inner points of the parallelepiped is completely determined. The solution is hence $2^{3 \times 1983-2}=2^{5947}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
385f09a6-be94-5298-af44-5e2b17465336
| 23,861
|
21. (SWE 1) Find the greatest integer less than or equal to $\sum_{k=1}^{2^{1983}} k^{1 / 1983-1}$.
|
21. Using the identity $$ a^{n}-b^{n}=(a-b) \sum_{m=0}^{n-1} a^{n-m-1} b^{m} $$ with $a=k^{1 / n}$ and $b=(k-1)^{1 / n}$ one obtains $$ 1<\left(k^{1 / n}-(k-1)^{1 / n}\right) n k^{1-1 / n} \text { for all integers } n>1 \text { and } k \geq 1 $$ This gives us the inequality $k^{1 / n-1}<n\left(k^{1 / n}-(k-1)^{1 / n}\right)$ if $n>1$ and $k \geq 1$. In a similar way one proves that $n\left((k+1)^{1 / n}-k^{1 / n}\right)<k^{1 / n-1}$ if $n>1$ and $k \geq 1$. Hence for $n>1$ and $m>1$ it holds that $$ \begin{aligned} n \sum_{k=1}^{m}\left((k+1)^{1 / n}-k^{1 / n}\right) & <\sum_{k=1}^{m} k^{1 / n-1} \\ & <n \sum_{k=2}^{m}\left(k^{1 / n}-(k-1)^{1 / n}\right)+1, \end{aligned} $$ or equivalently, $$ n\left((m+1)^{1 / n}-1\right)<\sum_{k=1}^{m} k^{1 / n-1}<n\left(m^{1 / n}-1\right)+1 $$ The choice $n=1983$ and $m=2^{1983}$ then gives $$ 1983<\sum_{k=1}^{2^{1983}} k^{1 / 1983-1}<1984 $$ Therefore the greatest integer less than or equal to the given sum is 1983.
|
1983
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
21. (SWE 1) Find the greatest integer less than or equal to $\sum_{k=1}^{2^{1983}} k^{1 / 1983-1}$.
|
21. Using the identity $$ a^{n}-b^{n}=(a-b) \sum_{m=0}^{n-1} a^{n-m-1} b^{m} $$ with $a=k^{1 / n}$ and $b=(k-1)^{1 / n}$ one obtains $$ 1<\left(k^{1 / n}-(k-1)^{1 / n}\right) n k^{1-1 / n} \text { for all integers } n>1 \text { and } k \geq 1 $$ This gives us the inequality $k^{1 / n-1}<n\left(k^{1 / n}-(k-1)^{1 / n}\right)$ if $n>1$ and $k \geq 1$. In a similar way one proves that $n\left((k+1)^{1 / n}-k^{1 / n}\right)<k^{1 / n-1}$ if $n>1$ and $k \geq 1$. Hence for $n>1$ and $m>1$ it holds that $$ \begin{aligned} n \sum_{k=1}^{m}\left((k+1)^{1 / n}-k^{1 / n}\right) & <\sum_{k=1}^{m} k^{1 / n-1} \\ & <n \sum_{k=2}^{m}\left(k^{1 / n}-(k-1)^{1 / n}\right)+1, \end{aligned} $$ or equivalently, $$ n\left((m+1)^{1 / n}-1\right)<\sum_{k=1}^{m} k^{1 / n-1}<n\left(m^{1 / n}-1\right)+1 $$ The choice $n=1983$ and $m=2^{1983}$ then gives $$ 1983<\sum_{k=1}^{2^{1983}} k^{1 / 1983-1}<1984 $$ Therefore the greatest integer less than or equal to the given sum is 1983.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
99270d30-c458-5bbe-aa29-fd18ab45bed8
| 23,881
|
8. (SPA 2) In a test, $3 n$ students participate, who are located in three rows of $n$ students in each. The students leave the test room one by one. If $N_{1}(t), N_{2}(t), N_{3}(t)$ denote the numbers of students in the first, second, and third row respectively at time $t$, find the probability that for each $t$ during the test, $$ \left|N_{i}(t)-N_{j}(t)\right|<2, \quad i \neq j, \quad i, j=1,2, \ldots $$
|
8. Situations in which the condition of the statement is fulfilled are the following: $S_{1}: N_{1}(t)=N_{2}(t)=N_{3}(t)$ $S_{2}: N_{i}(t)=N_{j}(t)=h, N_{k}(t)=h+1$, where $(i, j, k)$ is a permutation of the set $\{1,2,3\}$. In this case the first student to leave must be from row $k$. This leads to the situation $S_{1}$. $S_{3}: N_{i}(t)=h, N_{j}(t)=N_{k}(t)=h+1,((i, j, k)$ is a permutation of the set $\{1,2,3\})$. In this situation the first student leaving the room belongs to row $j$ (or $k$ ) and the second to row $k$ (or $j$ ). After this we arrive at the situation $S_{1}$. Hence, the initial situation is $S_{1}$ and after each triple of students leaving the room the situation $S_{1}$ must recur. We shall compute the probability $P_{h}$ that from a situation $S_{1}$ with $3 h$ students in the room $(h \leq n)$ one arrives at a situation $S_{1}$ with $3(h-1)$ students in the room: $$ P_{h}=\frac{(3 h) \cdot(2 h) \cdot h}{(3 h) \cdot(3 h-1) \cdot(3 h-2)}=\frac{3!h^{3}}{3 h(3 h-1)(3 h-2)} $$ Since the room becomes empty after the repetition of $n$ such processes, which are independent, we obtain for the probability sought $$ P=\prod_{h=1}^{n} P_{h}=\frac{(3!)^{n}(n!)^{3}}{(3 n)!} $$
|
\frac{(3!)^{n}(n!)^{3}}{(3 n)!}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
8. (SPA 2) In a test, $3 n$ students participate, who are located in three rows of $n$ students in each. The students leave the test room one by one. If $N_{1}(t), N_{2}(t), N_{3}(t)$ denote the numbers of students in the first, second, and third row respectively at time $t$, find the probability that for each $t$ during the test, $$ \left|N_{i}(t)-N_{j}(t)\right|<2, \quad i \neq j, \quad i, j=1,2, \ldots $$
|
8. Situations in which the condition of the statement is fulfilled are the following: $S_{1}: N_{1}(t)=N_{2}(t)=N_{3}(t)$ $S_{2}: N_{i}(t)=N_{j}(t)=h, N_{k}(t)=h+1$, where $(i, j, k)$ is a permutation of the set $\{1,2,3\}$. In this case the first student to leave must be from row $k$. This leads to the situation $S_{1}$. $S_{3}: N_{i}(t)=h, N_{j}(t)=N_{k}(t)=h+1,((i, j, k)$ is a permutation of the set $\{1,2,3\})$. In this situation the first student leaving the room belongs to row $j$ (or $k$ ) and the second to row $k$ (or $j$ ). After this we arrive at the situation $S_{1}$. Hence, the initial situation is $S_{1}$ and after each triple of students leaving the room the situation $S_{1}$ must recur. We shall compute the probability $P_{h}$ that from a situation $S_{1}$ with $3 h$ students in the room $(h \leq n)$ one arrives at a situation $S_{1}$ with $3(h-1)$ students in the room: $$ P_{h}=\frac{(3 h) \cdot(2 h) \cdot h}{(3 h) \cdot(3 h-1) \cdot(3 h-2)}=\frac{3!h^{3}}{3 h(3 h-1)(3 h-2)} $$ Since the room becomes empty after the repetition of $n$ such processes, which are independent, we obtain for the probability sought $$ P=\prod_{h=1}^{n} P_{h}=\frac{(3!)^{n}(n!)^{3}}{(3 n)!} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e1b5aa22-e59f-5961-835f-00af905d35ea
| 23,901
|
18. (USA 5) Inside triangle $A B C$ there are three circles $k_{1}, k_{2}, k_{3}$ each of which is tangent to two sides of the triangle and to its incircle $k$. The radii of $k_{1}, k_{2}, k_{3}$ are 1, 4, and 9 . Determine the radius of $k$.
|
18. Suppose that circles $k_{1}\left(O_{1}, r_{1}\right), k_{2}\left(O_{2}, r_{2}\right)$, and $k_{3}\left(O_{3}, r_{3}\right)$ touch the edges of the angles $\angle B A C, \angle A B C$, and $\angle A C B$, respectively. Denote also by $O$ and $r$ the center and radius of the incircle. Let $P$ be the point of tangency of the incircle with $A B$ and let $F$ be the foot of the perpendicular from $O_{1}$ to $O P$. From $\triangle O_{1} F O$ we obtain $\cot (\alpha / 2)=2 \sqrt{r r_{1}} /\left(r-r_{1}\right)$ and analogously $\cot (\beta / 2)=2 \sqrt{r r_{2}} /\left(r-r_{2}\right), \cot (\gamma / 2)=2 \sqrt{r r_{3}} /\left(r-r_{3}\right)$. We will now use a well-known trigonometric identity for the angles of a triangle: $$ \cot \frac{\alpha}{2}+\cot \frac{\beta}{2}+\cot \frac{\gamma}{2}=\cot \frac{\alpha}{2} \cdot \cot \frac{\beta}{2} \cdot \cot \frac{\gamma}{2} . $$ (This identity follows from $\tan (\gamma / 2)=\cot (\alpha / 2+\beta / 2)$ and the formula for the cotangent of a sum.) Plugging in the obtained cotangents, we get $$ \begin{aligned} \frac{2 \sqrt{r r_{1}}}{r-r_{1}}+\frac{2 \sqrt{r r_{2}}}{r-r_{2}}+\frac{2 \sqrt{r r_{3}}}{r-r_{3}}= & \frac{2 \sqrt{r r_{1}}}{r-r_{1}} \cdot \frac{2 \sqrt{r r_{2}}}{r-r_{2}} \cdot \frac{2 \sqrt{r r_{3}}}{r-r_{3}} \Rightarrow \\ & \sqrt{r_{1}}\left(r-r_{2}\right)\left(r-r_{3}\right)+\sqrt{r_{2}}\left(r-r_{1}\right)\left(r-r_{3}\right) \\ & +\sqrt{r_{3}}\left(r-r_{1}\right)\left(r-r_{2}\right)=4 r \sqrt{r_{1} r_{2} r_{3}} . \end{aligned} $$ For $r_{1}=1, r_{2}=4$, and $r_{3}=9$ we get $(r-4)(r-9)+2(r-1)(r-9)+3(r-1)(r-4)=24 r \Rightarrow 6(r-1)(r-11)=0$. Clearly, $r=11$ is the only viable value for $r$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
18. (USA 5) Inside triangle $A B C$ there are three circles $k_{1}, k_{2}, k_{3}$ each of which is tangent to two sides of the triangle and to its incircle $k$. The radii of $k_{1}, k_{2}, k_{3}$ are 1, 4, and 9 . Determine the radius of $k$.
|
18. Suppose that circles $k_{1}\left(O_{1}, r_{1}\right), k_{2}\left(O_{2}, r_{2}\right)$, and $k_{3}\left(O_{3}, r_{3}\right)$ touch the edges of the angles $\angle B A C, \angle A B C$, and $\angle A C B$, respectively. Denote also by $O$ and $r$ the center and radius of the incircle. Let $P$ be the point of tangency of the incircle with $A B$ and let $F$ be the foot of the perpendicular from $O_{1}$ to $O P$. From $\triangle O_{1} F O$ we obtain $\cot (\alpha / 2)=2 \sqrt{r r_{1}} /\left(r-r_{1}\right)$ and analogously $\cot (\beta / 2)=2 \sqrt{r r_{2}} /\left(r-r_{2}\right), \cot (\gamma / 2)=2 \sqrt{r r_{3}} /\left(r-r_{3}\right)$. We will now use a well-known trigonometric identity for the angles of a triangle: $$ \cot \frac{\alpha}{2}+\cot \frac{\beta}{2}+\cot \frac{\gamma}{2}=\cot \frac{\alpha}{2} \cdot \cot \frac{\beta}{2} \cdot \cot \frac{\gamma}{2} . $$ (This identity follows from $\tan (\gamma / 2)=\cot (\alpha / 2+\beta / 2)$ and the formula for the cotangent of a sum.) Plugging in the obtained cotangents, we get $$ \begin{aligned} \frac{2 \sqrt{r r_{1}}}{r-r_{1}}+\frac{2 \sqrt{r r_{2}}}{r-r_{2}}+\frac{2 \sqrt{r r_{3}}}{r-r_{3}}= & \frac{2 \sqrt{r r_{1}}}{r-r_{1}} \cdot \frac{2 \sqrt{r r_{2}}}{r-r_{2}} \cdot \frac{2 \sqrt{r r_{3}}}{r-r_{3}} \Rightarrow \\ & \sqrt{r_{1}}\left(r-r_{2}\right)\left(r-r_{3}\right)+\sqrt{r_{2}}\left(r-r_{1}\right)\left(r-r_{3}\right) \\ & +\sqrt{r_{3}}\left(r-r_{1}\right)\left(r-r_{2}\right)=4 r \sqrt{r_{1} r_{2} r_{3}} . \end{aligned} $$ For $r_{1}=1, r_{2}=4$, and $r_{3}=9$ we get $(r-4)(r-9)+2(r-1)(r-9)+3(r-1)(r-4)=24 r \Rightarrow 6(r-1)(r-11)=0$. Clearly, $r=11$ is the only viable value for $r$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b4462430-4504-55a2-90cc-98d619cc9b8e
| 23,924
|
19. (ISR 3) For which integers $n \geq 3$ does there exist a regular $n$-gon in the plane such that all its vertices have integer coordinates in a rectangular coordinate system?
|
19. Suppose that for some $n>6$ there is a regular $n$-gon with vertices having integer coordinates, and that $A_{1} A_{2} \ldots A_{n}$ is the smallest such $n$-gon, of side length $a$. If $O$ is the origin and $B_{i}$ the point such that $\overrightarrow{O B_{i}}=\overrightarrow{A_{i-1} A_{i}}$, $i=1,2, \ldots, n$ (where $A_{0}=A_{n}$ ), then $B_{i}$ has integer coordinates and $B_{1} B_{2} \ldots B_{n}$ is a regular polygon of side length $2 a \sin (\pi / n)<a$, which is impossible. It remains to analyze the cases $n \leq 6$. If $\mathcal{P}$ is a regular $n$-gon with $n=$ $3,5,6$, then its center $C$ has rational coordinates. We may suppose that $C$ also has integer coordinates and then rotate $\mathcal{P}$ around $C$ thrice through $90^{\circ}$, thus obtaining a regular 12 -gon or 20 -gon, which is impossible. Hence we must have $n=4$ which is indeed a solution.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
19. (ISR 3) For which integers $n \geq 3$ does there exist a regular $n$-gon in the plane such that all its vertices have integer coordinates in a rectangular coordinate system?
|
19. Suppose that for some $n>6$ there is a regular $n$-gon with vertices having integer coordinates, and that $A_{1} A_{2} \ldots A_{n}$ is the smallest such $n$-gon, of side length $a$. If $O$ is the origin and $B_{i}$ the point such that $\overrightarrow{O B_{i}}=\overrightarrow{A_{i-1} A_{i}}$, $i=1,2, \ldots, n$ (where $A_{0}=A_{n}$ ), then $B_{i}$ has integer coordinates and $B_{1} B_{2} \ldots B_{n}$ is a regular polygon of side length $2 a \sin (\pi / n)<a$, which is impossible. It remains to analyze the cases $n \leq 6$. If $\mathcal{P}$ is a regular $n$-gon with $n=$ $3,5,6$, then its center $C$ has rational coordinates. We may suppose that $C$ also has integer coordinates and then rotate $\mathcal{P}$ around $C$ thrice through $90^{\circ}$, thus obtaining a regular 12 -gon or 20 -gon, which is impossible. Hence we must have $n=4$ which is indeed a solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c87d0c0-7634-5dae-aa64-6cac2bf12750
| 23,971
|
2. (BRA 3) A polyhedron has 12 faces and is such that: (i) all faces are isosceles triangles, (ii) all edges have length either $x$ or $y$, (iii) at each vertex either 3 or 6 edges meet, and (iv) all dihedral angles are equal. Find the ratio $x / y$.
|
2. The polyhedron has $3 \cdot 12 / 2=18$ edges, and by Euler's formula, 8 vertices. Let $v_{1}$ and $v_{2}$ be the numbers of vertices at which respectively 3 and 6 edges meet. Then $v_{1}+v_{2}=8$ and $3 v_{1}+6 v_{2}=2 \cdot 18$, implying that $v_{1}=4$. Let $A, B, C, D$ be the vertices at which three edges meet. Since the dihedral angles are equal, all the edges meeting at $A$, say $A E, A F, A G$, must have equal length, say $x$. (If $x=A E=A F \neq A G=y$, and $A E F$, $A F G$, and $A G E$ are isosceles, $\angle E A F \neq \angle F A G$, in contradiction to the equality of the dihedral angles.) It is easy to see that at $E, F$, and $G$ six edges meet. One proceeds to conclude that if $H$ is the fourth vertex of this kind, $E F G H$ must be a regular tetrahedron of edge length $y$, and the other vertices $A, B, C$, and $D$ are tops of isosceles pyramids based on $E F G, E F H, F G H$, and $G E H$. Let the plane through $A, B, C$ meet $E F$, $H F$, and $G F$, at $E^{\prime}, H^{\prime}$, and $G^{\prime}$. Then $A E^{\prime} B H^{\prime} C G^{\prime}$ is a regular hexagon, and since $x=F A=F E^{\prime}$, we have $E^{\prime} G^{\prime}=x$ and $A E^{\prime}=x / \sqrt{3}$. From the isosceles triangles $A E F$ and $F A E^{\prime}$ we obtain finally, with $\measuredangle E F A=\alpha$, $\frac{y}{2 x}=\cos \alpha=1-2 \sin ^{2}(\alpha / 2), x /(2 x \sqrt{3})=\sin (\alpha / 2)$, and $y / x=5 / 3$.
|
\frac{5}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
2. (BRA 3) A polyhedron has 12 faces and is such that: (i) all faces are isosceles triangles, (ii) all edges have length either $x$ or $y$, (iii) at each vertex either 3 or 6 edges meet, and (iv) all dihedral angles are equal. Find the ratio $x / y$.
|
2. The polyhedron has $3 \cdot 12 / 2=18$ edges, and by Euler's formula, 8 vertices. Let $v_{1}$ and $v_{2}$ be the numbers of vertices at which respectively 3 and 6 edges meet. Then $v_{1}+v_{2}=8$ and $3 v_{1}+6 v_{2}=2 \cdot 18$, implying that $v_{1}=4$. Let $A, B, C, D$ be the vertices at which three edges meet. Since the dihedral angles are equal, all the edges meeting at $A$, say $A E, A F, A G$, must have equal length, say $x$. (If $x=A E=A F \neq A G=y$, and $A E F$, $A F G$, and $A G E$ are isosceles, $\angle E A F \neq \angle F A G$, in contradiction to the equality of the dihedral angles.) It is easy to see that at $E, F$, and $G$ six edges meet. One proceeds to conclude that if $H$ is the fourth vertex of this kind, $E F G H$ must be a regular tetrahedron of edge length $y$, and the other vertices $A, B, C$, and $D$ are tops of isosceles pyramids based on $E F G, E F H, F G H$, and $G E H$. Let the plane through $A, B, C$ meet $E F$, $H F$, and $G F$, at $E^{\prime}, H^{\prime}$, and $G^{\prime}$. Then $A E^{\prime} B H^{\prime} C G^{\prime}$ is a regular hexagon, and since $x=F A=F E^{\prime}$, we have $E^{\prime} G^{\prime}=x$ and $A E^{\prime}=x / \sqrt{3}$. From the isosceles triangles $A E F$ and $F A E^{\prime}$ we obtain finally, with $\measuredangle E F A=\alpha$, $\frac{y}{2 x}=\cos \alpha=1-2 \sin ^{2}(\alpha / 2), x /(2 x \sqrt{3})=\sin (\alpha / 2)$, and $y / x=5 / 3$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6e125fb3-396f-5993-aca6-a9706e0ff6c6
| 23,974
|
8. 1b.(TUR 5) Find the smallest positive integer $n$ such that (i) $n$ has exactly 144 distinct positive divisors, and (ii) there are ten consecutive integers among the positive divisors of $n$.
|
8. Among ten consecutive integers that divide $n$, there must exist numbers divisible by $2^{3}, 3^{2}, 5$, and 7 . Thus the desired number has the form $n=$ $2^{\alpha_{1}} 3^{\alpha_{2}} 5^{\alpha_{3}} 7^{\alpha_{4}} 11^{\alpha_{5}} \cdots$, where $\alpha_{1} \geq 3, \alpha_{2} \geq 2, \alpha_{3} \geq 1, \alpha_{4} \geq 1$. Since $n$ has $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+1\right) \cdots$ distinct factors, and $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+\right.$ $1)\left(\alpha_{4}+1\right) \geq 48$, we must have $\left(\alpha_{5}+1\right) \cdots \leq 3$. Hence at most one $\alpha_{j}$, $j>4$, is positive, and in the minimal $n$ this must be $\alpha_{5}$. Checking through the possible combinations satisfying $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \cdots\left(\alpha_{5}+1\right)=144$ one finds that the minimal $n$ is $2^{5} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 11=110880$.
|
110880
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
8. 1b.(TUR 5) Find the smallest positive integer $n$ such that (i) $n$ has exactly 144 distinct positive divisors, and (ii) there are ten consecutive integers among the positive divisors of $n$.
|
8. Among ten consecutive integers that divide $n$, there must exist numbers divisible by $2^{3}, 3^{2}, 5$, and 7 . Thus the desired number has the form $n=$ $2^{\alpha_{1}} 3^{\alpha_{2}} 5^{\alpha_{3}} 7^{\alpha_{4}} 11^{\alpha_{5}} \cdots$, where $\alpha_{1} \geq 3, \alpha_{2} \geq 2, \alpha_{3} \geq 1, \alpha_{4} \geq 1$. Since $n$ has $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+1\right) \cdots$ distinct factors, and $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)\left(\alpha_{3}+\right.$ $1)\left(\alpha_{4}+1\right) \geq 48$, we must have $\left(\alpha_{5}+1\right) \cdots \leq 3$. Hence at most one $\alpha_{j}$, $j>4$, is positive, and in the minimal $n$ this must be $\alpha_{5}$. Checking through the possible combinations satisfying $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \cdots\left(\alpha_{5}+1\right)=144$ one finds that the minimal $n$ is $2^{5} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 11=110880$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
11994b38-14cb-5209-a412-c1cb8dcd3b44
| 23,998
|
9. 2a.(USA 3) Determine the radius of a sphere $S$ that passes through the centroids of each face of a given tetrahedron $T$ inscribed in a unit sphere with center $O$. Also, determine the distance from $O$ to the center of $S$ as a function of the edges of $T$.
|
9. Let $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ denote the vectors $\overrightarrow{O A}, \overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O D}$ respectively. Then $|\vec{a}|=|\vec{b}|=|\vec{c}|=|\vec{d}|=1$. The centroids of the faces are $(\vec{b}+\vec{c}+\vec{d}) / 3$, $(\vec{a}+\vec{c}+\vec{d}) / 3$, etc., and each of these is at distance $1 / 3$ from $P=$ $(\vec{a}+\vec{b}+\vec{c}+\vec{d}) / 3$; hence the required radius is $1 / 3$. To compute $|P|$ as a function of the edges of $A B C D$, observe that $A B^{2}=(\vec{b}-\vec{a})^{2}=$ $2-2 \vec{a} \cdot \vec{b}$ etc. Now $$ \begin{aligned} P^{2} & =\frac{|\vec{a}+\vec{b}+\vec{c}+\vec{d}|^{2}}{9} \\ & =\frac{16-2\left(A B^{2}+B C^{2}+A C^{2}+A D^{2}+B D^{2}+C D^{2}\right)}{9} \end{aligned} $$
|
\frac{16-2\left(A B^{2}+B C^{2}+A C^{2}+A D^{2}+B D^{2}+C D^{2}\right)}{9}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
9. 2a.(USA 3) Determine the radius of a sphere $S$ that passes through the centroids of each face of a given tetrahedron $T$ inscribed in a unit sphere with center $O$. Also, determine the distance from $O$ to the center of $S$ as a function of the edges of $T$.
|
9. Let $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ denote the vectors $\overrightarrow{O A}, \overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O D}$ respectively. Then $|\vec{a}|=|\vec{b}|=|\vec{c}|=|\vec{d}|=1$. The centroids of the faces are $(\vec{b}+\vec{c}+\vec{d}) / 3$, $(\vec{a}+\vec{c}+\vec{d}) / 3$, etc., and each of these is at distance $1 / 3$ from $P=$ $(\vec{a}+\vec{b}+\vec{c}+\vec{d}) / 3$; hence the required radius is $1 / 3$. To compute $|P|$ as a function of the edges of $A B C D$, observe that $A B^{2}=(\vec{b}-\vec{a})^{2}=$ $2-2 \vec{a} \cdot \vec{b}$ etc. Now $$ \begin{aligned} P^{2} & =\frac{|\vec{a}+\vec{b}+\vec{c}+\vec{d}|^{2}}{9} \\ & =\frac{16-2\left(A B^{2}+B C^{2}+A C^{2}+A D^{2}+B D^{2}+C D^{2}\right)}{9} \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7b1b51b1-a387-541d-8111-ad66d203ae2a
| 24,001
|
19. (BUL 2) A tetrahedron $A B C D$ is given such that $A D=B C=a$; $A C=B D=b ; A B \cdot C D=c^{2}$. Let $f(P)=A P+B P+C P+D P$, where $P$ is an arbitrary point in space. Compute the least value of $f(P)$.
|
19. Let $M$ and $N$ be the midpoints of segments $A B$ and $C D$, respectively. The given conditions imply that $\triangle A B D \cong \triangle B A C$ and $\triangle C D A \cong \triangle D C B$; hence $M C=M D$ and $N A=N B$. It follows that $M$ and $N$ both lie on the perpendicular bisectors of $A B$ and $C D$, and consequently $M N$ is the common perpendicular bisector of $A B$ and $C D$. Points $B$ and $C$ are symmetric to $A$ and $D$ with respect to $M N$. Now if $P$ is a point in space and $P^{\prime}$ the point symmetric to $P$ with respect to $M N$, we have $B P=A P^{\prime}, C P=D P^{\prime}$, and thus $f(P)=A P+A P^{\prime}+D P+D P^{\prime}$. Let $P P^{\prime}$ intersect $M N$ in $Q$. Then $A P+A P^{\prime} \geq 2 A Q$ and $D P+D P^{\prime} \geq 2 D Q$, from which it follows that $f(P) \geq 2(A Q+D Q)=f(Q)$. It remains to minimize $f(Q)$ with $Q$ moving along the line $M N$. Let us rotate point $D$ around $M N$ to a point $D^{\prime}$ that belongs to the plane $A M N$, on the side of $M N$ opposite to $A$. Then $f(Q)=2\left(A Q+D^{\prime} Q\right) \geq$ $A D^{\prime}$, and equality occurs when $Q$ is the intersection of $A D^{\prime}$ and $M N$. Thus $\min f(Q)=A D^{\prime}$. We note that $4 M D^{2}=2 A D^{2}+2 B D^{2}-A B^{2}=$ $2 a^{2}+2 b^{2}-A B^{2}$ and $4 M N^{2}=4 M D^{2}-C D^{2}=2 a^{2}+2 b^{2}-A B^{2}-C D^{2}$. Now, $A D^{\prime 2}=\left(A M+D^{\prime} N\right)^{2}+M N^{2}$, which together with $A M+D^{\prime} N=$ $(a+b) / 2$ gives us $$ A D^{\prime 2}=\frac{a^{2}+b^{2}+A B \cdot C D}{2}=\frac{a^{2}+b^{2}+c^{2}}{2} $$ We conclude that $\min f(Q)=\sqrt{\left(a^{2}+b^{2}+c^{2}\right) / 2}$.
|
\sqrt{\frac{a^2 + b^2 + c^2}{2}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
19. (BUL 2) A tetrahedron $A B C D$ is given such that $A D=B C=a$; $A C=B D=b ; A B \cdot C D=c^{2}$. Let $f(P)=A P+B P+C P+D P$, where $P$ is an arbitrary point in space. Compute the least value of $f(P)$.
|
19. Let $M$ and $N$ be the midpoints of segments $A B$ and $C D$, respectively. The given conditions imply that $\triangle A B D \cong \triangle B A C$ and $\triangle C D A \cong \triangle D C B$; hence $M C=M D$ and $N A=N B$. It follows that $M$ and $N$ both lie on the perpendicular bisectors of $A B$ and $C D$, and consequently $M N$ is the common perpendicular bisector of $A B$ and $C D$. Points $B$ and $C$ are symmetric to $A$ and $D$ with respect to $M N$. Now if $P$ is a point in space and $P^{\prime}$ the point symmetric to $P$ with respect to $M N$, we have $B P=A P^{\prime}, C P=D P^{\prime}$, and thus $f(P)=A P+A P^{\prime}+D P+D P^{\prime}$. Let $P P^{\prime}$ intersect $M N$ in $Q$. Then $A P+A P^{\prime} \geq 2 A Q$ and $D P+D P^{\prime} \geq 2 D Q$, from which it follows that $f(P) \geq 2(A Q+D Q)=f(Q)$. It remains to minimize $f(Q)$ with $Q$ moving along the line $M N$. Let us rotate point $D$ around $M N$ to a point $D^{\prime}$ that belongs to the plane $A M N$, on the side of $M N$ opposite to $A$. Then $f(Q)=2\left(A Q+D^{\prime} Q\right) \geq$ $A D^{\prime}$, and equality occurs when $Q$ is the intersection of $A D^{\prime}$ and $M N$. Thus $\min f(Q)=A D^{\prime}$. We note that $4 M D^{2}=2 A D^{2}+2 B D^{2}-A B^{2}=$ $2 a^{2}+2 b^{2}-A B^{2}$ and $4 M N^{2}=4 M D^{2}-C D^{2}=2 a^{2}+2 b^{2}-A B^{2}-C D^{2}$. Now, $A D^{\prime 2}=\left(A M+D^{\prime} N\right)^{2}+M N^{2}$, which together with $A M+D^{\prime} N=$ $(a+b) / 2$ gives us $$ A D^{\prime 2}=\frac{a^{2}+b^{2}+A B \cdot C D}{2}=\frac{a^{2}+b^{2}+c^{2}}{2} $$ We conclude that $\min f(Q)=\sqrt{\left(a^{2}+b^{2}+c^{2}\right) / 2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
dcdabf55-3f44-5d20-98e7-7a1dccaf9c1f
| 24,029
|
3. (USA 3) Let $A, B$, and $C$ be three points on the edge of a circular chord such that $B$ is due west of $C$ and $A B C$ is an equilateral triangle whose side is 86 meters long. A boy swam from $A$ directly toward $B$. After covering a distance of $x$ meters, he turned and swam westward, reaching the shore after covering a distance of $y$ meters. If $x$ and $y$ are both positive integers, determine $y$.
|
3. Let $E$ be the point where the boy turned westward, reaching the shore at $D$. Let the ray $D E$ cut $A C$ at $F$ and the shore again at $G$. Then $E F=$ $A E=x$ (because $A E F$ is an equilateral triangle) and $F G=D E=y$. From $A E \cdot E B=D E \cdot E G$ we obtain $x(86-x)=y(x+y)$. If $x$ is odd, then $x(86-x)$ is odd, while $y(x+y)$ is even. Hence $x$ is even, and so $y$ must also be even. Let $y=2 y_{1}$. The above equation can be rewritten as $$ \left(x+y_{1}-43\right)^{2}+\left(2 y_{1}\right)^{2}=\left(43-y_{1}\right)^{2} \text {. } $$ Since $y_{1}<43$, we have $\left(2 y_{1}, 43-y_{1}\right)=1$, and thus $\left(\left|x+y_{1}-43\right|, 2 y_{1}, 43-\right.$ $\left.y_{1}\right)$ is a primitive Pythagorean triple. Consequently there exist integers $a>b>0$ such that $y_{1}=a b$ and $43-y_{1}=a^{2}+b^{2}$. We obtain that $a^{2}+b^{2}+a b=43$, which has the unique solution $a=6, b=1$. Hence $y=12$ and $x=2$ or $x=72$. Remark. The Diophantine equation $x(86-x)=y(x+y)$ can be also solved directly. Namely, we have that $x(344-3 x)=(2 y+x)^{2}$ is a square, and since $x$ is even, we have $(x, 344-3 x)=2$ or 4 . Consequently $x, 344-3 x$ are either both squares or both two times squares. The rest is easy.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
3. (USA 3) Let $A, B$, and $C$ be three points on the edge of a circular chord such that $B$ is due west of $C$ and $A B C$ is an equilateral triangle whose side is 86 meters long. A boy swam from $A$ directly toward $B$. After covering a distance of $x$ meters, he turned and swam westward, reaching the shore after covering a distance of $y$ meters. If $x$ and $y$ are both positive integers, determine $y$.
|
3. Let $E$ be the point where the boy turned westward, reaching the shore at $D$. Let the ray $D E$ cut $A C$ at $F$ and the shore again at $G$. Then $E F=$ $A E=x$ (because $A E F$ is an equilateral triangle) and $F G=D E=y$. From $A E \cdot E B=D E \cdot E G$ we obtain $x(86-x)=y(x+y)$. If $x$ is odd, then $x(86-x)$ is odd, while $y(x+y)$ is even. Hence $x$ is even, and so $y$ must also be even. Let $y=2 y_{1}$. The above equation can be rewritten as $$ \left(x+y_{1}-43\right)^{2}+\left(2 y_{1}\right)^{2}=\left(43-y_{1}\right)^{2} \text {. } $$ Since $y_{1}<43$, we have $\left(2 y_{1}, 43-y_{1}\right)=1$, and thus $\left(\left|x+y_{1}-43\right|, 2 y_{1}, 43-\right.$ $\left.y_{1}\right)$ is a primitive Pythagorean triple. Consequently there exist integers $a>b>0$ such that $y_{1}=a b$ and $43-y_{1}=a^{2}+b^{2}$. We obtain that $a^{2}+b^{2}+a b=43$, which has the unique solution $a=6, b=1$. Hence $y=12$ and $x=2$ or $x=72$. Remark. The Diophantine equation $x(86-x)=y(x+y)$ can be also solved directly. Namely, we have that $x(344-3 x)=(2 y+x)^{2}$ is a square, and since $x$ is even, we have $(x, 344-3 x)=2$ or 4 . Consequently $x, 344-3 x$ are either both squares or both two times squares. The rest is easy.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3a69804f-3a85-5c9d-bff7-551b4f3c3caa
| 24,038
|
4. (CZS 3) Let $n$ be a positive integer and let $p$ be a prime number, $p>3$. Find at least $3(n+1)$ [easier version: $2(n+1)]$ sequences of positive integers $x, y, z$ satisfying $$ x y z=p^{n}(x+y+z) $$ that do not differ only by permutation.
|
4. Let $x=p^{\alpha} x^{\prime}, y=p^{\beta} y^{\prime}, z=p^{\gamma} z^{\prime}$ with $p \nmid x^{\prime} y^{\prime} z^{\prime}$ and $\alpha \geq \beta \geq \gamma$. From the given equation it follows that $p^{n}(x+y)=z\left(x y-p^{n}\right)$ and consequently $z^{\prime} \mid x+y$. Since also $p^{\gamma} \mid x+y$, we have $z \mid x+y$, i.e., $x+y=q z$. The given equation together with the last condition gives us $$ x y=p^{n}(q+1) \quad \text { and } \quad x+y=q z . $$ Conversely, every solution of (1) gives a solution of the given equation. For $q=1$ and $q=2$ we obtain the following classes of $n+1$ solutions each: $$ \begin{array}{ll} q=1:(x, y, z)=\left(2 p^{i}, p^{n-i}, 2 p^{i}+p^{n-i}\right) & \text { for } i=0,1,2, \ldots, n \\ q=2:(x, y, z)=\left(3 p^{j}, p^{n-j}, \frac{3 p^{j}+p^{n-j}}{2}\right) & \text { for } j=0,1,2, \ldots, n \end{array} $$ For $n=2 k$ these two classes have a common solution $\left(2 p^{k}, p^{k}, 3 p^{k}\right)$; otherwise, all these solutions are distinct. One further solution is given by $(x, y, z)=\left(1, p^{n}\left(p^{n}+3\right) / 2, p^{2}+2\right)$, not included in the above classes for $p>3$. Thus we have found $2(n+1)$ solutions. Another type of solution is obtained if we put $q=p^{k}+p^{n-k}$. This yields the solutions $$ (x, y, z)=\left(p^{k}, p^{n}+p^{n-k}+p^{2 n-2 k}, p^{n-k}+1\right) \quad \text { for } k=0,1, \ldots, n $$ For $k<n$ these are indeed new solutions. So far, we have found $3(n+1)-1$ or $3(n+1)$ solutions. One more solution is given by $(x, y, z)=\left(p, p^{n}+\right.$ $\left.p^{n-1}, p^{n-1}+p^{n-2}+1\right)$.
|
3(n+1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
4. (CZS 3) Let $n$ be a positive integer and let $p$ be a prime number, $p>3$. Find at least $3(n+1)$ [easier version: $2(n+1)]$ sequences of positive integers $x, y, z$ satisfying $$ x y z=p^{n}(x+y+z) $$ that do not differ only by permutation.
|
4. Let $x=p^{\alpha} x^{\prime}, y=p^{\beta} y^{\prime}, z=p^{\gamma} z^{\prime}$ with $p \nmid x^{\prime} y^{\prime} z^{\prime}$ and $\alpha \geq \beta \geq \gamma$. From the given equation it follows that $p^{n}(x+y)=z\left(x y-p^{n}\right)$ and consequently $z^{\prime} \mid x+y$. Since also $p^{\gamma} \mid x+y$, we have $z \mid x+y$, i.e., $x+y=q z$. The given equation together with the last condition gives us $$ x y=p^{n}(q+1) \quad \text { and } \quad x+y=q z . $$ Conversely, every solution of (1) gives a solution of the given equation. For $q=1$ and $q=2$ we obtain the following classes of $n+1$ solutions each: $$ \begin{array}{ll} q=1:(x, y, z)=\left(2 p^{i}, p^{n-i}, 2 p^{i}+p^{n-i}\right) & \text { for } i=0,1,2, \ldots, n \\ q=2:(x, y, z)=\left(3 p^{j}, p^{n-j}, \frac{3 p^{j}+p^{n-j}}{2}\right) & \text { for } j=0,1,2, \ldots, n \end{array} $$ For $n=2 k$ these two classes have a common solution $\left(2 p^{k}, p^{k}, 3 p^{k}\right)$; otherwise, all these solutions are distinct. One further solution is given by $(x, y, z)=\left(1, p^{n}\left(p^{n}+3\right) / 2, p^{2}+2\right)$, not included in the above classes for $p>3$. Thus we have found $2(n+1)$ solutions. Another type of solution is obtained if we put $q=p^{k}+p^{n-k}$. This yields the solutions $$ (x, y, z)=\left(p^{k}, p^{n}+p^{n-k}+p^{2 n-2 k}, p^{n-k}+1\right) \quad \text { for } k=0,1, \ldots, n $$ For $k<n$ these are indeed new solutions. So far, we have found $3(n+1)-1$ or $3(n+1)$ solutions. One more solution is given by $(x, y, z)=\left(p, p^{n}+\right.$ $\left.p^{n-1}, p^{n-1}+p^{n-2}+1\right)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c7e05a25-f810-58bf-8e70-ff63d64006f9
| 24,040
|
1. (AUS 6) Let $f$ be a function that satisfies the following conditions: (i) If $x>y$ and $f(y)-y \geq v \geq f(x)-x$, then $f(z)=v+z$, for some number $z$ between $x$ and $y$. (ii) The equation $f(x)=0$ has at least one solution, and among the solutions of this equation, there is one that is not smaller than all the other solutions; (iii) $f(0)=1$. (iv) $f(1987) \leq 1988$. (v) $f(x) f(y)=f(x f(y)+y f(x)-x y)$. Find $f(1987)$.
|
1. By (ii), $f(x)=0$ has at least one solution, and there is the greatest among them, say $x_{0}$. Then by (v), for any $x$, $$ 0=f(x) f\left(x_{0}\right)=f\left(x f\left(x_{0}\right)+x_{0} f(x)-x_{0} x\right)=f\left(x_{0}(f(x)-x)\right) $$ It follows that $x_{0} \geq x_{0}(f(x)-x)$. Suppose $x_{0}>0$. By (i) and (iii), since $f\left(x_{0}\right)-x_{0}<0<f(0)-0$, there is a number $z$ between 0 and $x_{0}$ such that $f(z)=z$. By (1), $0=f\left(x_{0}(f(z)-\right.$ $z))=f(0)=1$, a contradiction. Hence, $x_{0}<0$. Now the inequality $x_{0} \geq x_{0}(f(x)-x)$ gives $f(x)-x \geq 1$ for all $x$; so, $f(1987) \geq 1988$. Therefore $f(1987)=1988$.
|
1988
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
1. (AUS 6) Let $f$ be a function that satisfies the following conditions: (i) If $x>y$ and $f(y)-y \geq v \geq f(x)-x$, then $f(z)=v+z$, for some number $z$ between $x$ and $y$. (ii) The equation $f(x)=0$ has at least one solution, and among the solutions of this equation, there is one that is not smaller than all the other solutions; (iii) $f(0)=1$. (iv) $f(1987) \leq 1988$. (v) $f(x) f(y)=f(x f(y)+y f(x)-x y)$. Find $f(1987)$.
|
1. By (ii), $f(x)=0$ has at least one solution, and there is the greatest among them, say $x_{0}$. Then by (v), for any $x$, $$ 0=f(x) f\left(x_{0}\right)=f\left(x f\left(x_{0}\right)+x_{0} f(x)-x_{0} x\right)=f\left(x_{0}(f(x)-x)\right) $$ It follows that $x_{0} \geq x_{0}(f(x)-x)$. Suppose $x_{0}>0$. By (i) and (iii), since $f\left(x_{0}\right)-x_{0}<0<f(0)-0$, there is a number $z$ between 0 and $x_{0}$ such that $f(z)=z$. By (1), $0=f\left(x_{0}(f(z)-\right.$ $z))=f(0)=1$, a contradiction. Hence, $x_{0}<0$. Now the inequality $x_{0} \geq x_{0}(f(x)-x)$ gives $f(x)-x \geq 1$ for all $x$; so, $f(1987) \geq 1988$. Therefore $f(1987)=1988$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
bb26df36-57e8-56c7-99a1-489c48a2793b
| 24,054
|
11. (POL 1) Find the number of partitions of the set $\{1,2, \ldots, n\}$ into three subsets $A_{1}, A_{2}, A_{3}$, some of which may be empty, such that the following conditions are satisfied: (i) After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity. (ii) If $A_{1}, A_{2}, A_{3}$ are all nonempty, then in exactly one of them the minimal number is even.
|
11. Let $A_{1}$ be the set that contains 1 , and let the minimal element of $A_{2}$ be less than that of $A_{3}$. We shall construct the partitions with required properties by allocating successively numbers to the subsets that always obey the rules. The number 1 must go to $A_{1}$; we show that for every subsequent number we have exactly two possibilities. Actually, while $A_{2}$ and $A_{3}$ are both empty, every successive number can enter either $A_{1}$ or $A_{2}$. Further, when $A_{2}$ is no longer empty, we use induction on the number to be placed, denote it by $m$ : if $m$ can enter $A_{i}$ or $A_{j}$ but not $A_{k}$, and it enters $A_{i}$, then $m+1$ can be placed in $A_{i}$ or $A_{k}$, but not in $A_{j}$. The induction step is finished. This immediately gives us that the final answer is $2^{n-1}$.
|
2^{n-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
11. (POL 1) Find the number of partitions of the set $\{1,2, \ldots, n\}$ into three subsets $A_{1}, A_{2}, A_{3}$, some of which may be empty, such that the following conditions are satisfied: (i) After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity. (ii) If $A_{1}, A_{2}, A_{3}$ are all nonempty, then in exactly one of them the minimal number is even.
|
11. Let $A_{1}$ be the set that contains 1 , and let the minimal element of $A_{2}$ be less than that of $A_{3}$. We shall construct the partitions with required properties by allocating successively numbers to the subsets that always obey the rules. The number 1 must go to $A_{1}$; we show that for every subsequent number we have exactly two possibilities. Actually, while $A_{2}$ and $A_{3}$ are both empty, every successive number can enter either $A_{1}$ or $A_{2}$. Further, when $A_{2}$ is no longer empty, we use induction on the number to be placed, denote it by $m$ : if $m$ can enter $A_{i}$ or $A_{j}$ but not $A_{k}$, and it enters $A_{i}$, then $m+1$ can be placed in $A_{i}$ or $A_{k}$, but not in $A_{j}$. The induction step is finished. This immediately gives us that the final answer is $2^{n-1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5406a88a-9e23-53c0-bd71-db324d8c784b
| 24,060
|
12. (POL 5) Given a nonequilateral triangle $A B C$, the vertices listed counterclockwise, find the locus of the centroids of the equilateral triangles $A^{\prime} B^{\prime} C^{\prime}$ (the vertices listed counterclockwise) for which the triples of points $A, B^{\prime}, C^{\prime} ; A^{\prime}, B, C^{\prime}$; and $A^{\prime}, B^{\prime}, C$ are collinear.
|
12. Here all angles will be oriented and measured counterclockwise. Note that $\measuredangle C A^{\prime} B=\measuredangle A B^{\prime} C=$ $\measuredangle B C^{\prime} A=\pi / 3$. Let $a^{\prime}, b^{\prime}, c^{\prime}$ denote respectively the inner bisectors of angles $A^{\prime}, B^{\prime}, C^{\prime}$ in triangle $A^{\prime} B^{\prime} C^{\prime}$. The lines $a^{\prime}, b^{\prime}, c^{\prime}$ meet at the centroid $X$ of $A^{\prime} B^{\prime} C^{\prime}$, and $\measuredangle\left(a^{\prime}, b^{\prime}\right)=$ $\measuredangle\left(b^{\prime}, c^{\prime}\right)=\measuredangle\left(c^{\prime}, a^{\prime}\right)=2 \pi / 3$. Now let $K, L, M$ be the points such that $K B=K C, L C=L A, M A=M B$, and $\measuredangle B K C=\measuredangle C L A=\measuredangle A M B=$ $2 \pi / 3$, and let $C_{1}, C_{2}, C_{3}$ be the circles circumscribed about triangles 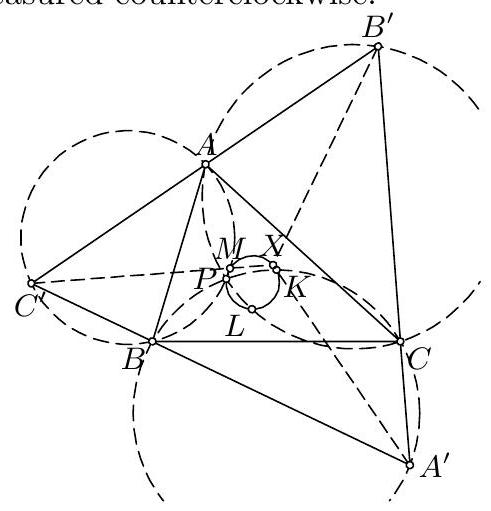 $B K C, C L A$, and $A M B$ respectively. These circles are characterized by $C_{1}=\{Z \mid \measuredangle B Z C=2 \pi / 3\}$, etc.; hence we deduce that they meet at a point $P$ such that $\measuredangle B P C=\measuredangle C P A=\measuredangle A P B=2 \pi / 3$ (Torricelli's point). Points $A^{\prime}, B^{\prime}, C^{\prime}$ run over $C_{1} \backslash\{P\}, C_{2} \backslash\{P\}, C_{3} \backslash\{P\}$ respectively. As for $a^{\prime}, b^{\prime}, c^{\prime}$, we see that $K \in a^{\prime}, L \in b^{\prime}, M \in c^{\prime}$, and also that they can take all possible directions except $K P, L P, M P$ respectively (if $K=P, K P$ is assumed to be the corresponding tangent at $K$ ). Then, since $\measuredangle K X L=$ $2 \pi / 3, X$ runs over the circle defined by $\{Z \mid \measuredangle K Z L=2 \pi / 3\}$, without $P$. But analogously, $X$ runs over the circle $\{Z \mid \measuredangle L Z M=2 \pi / 3\}$, from which we can conclude that these two circles are the same, both equal to the circumcircle of $K L M$, and consequently also that triangle $K L M$ is equilateral (which is, anyway, a well-known fact). Therefore, the locus of the points $X$ is the circumcircle of $K L M$ minus point $P$.
|
\
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
12. (POL 5) Given a nonequilateral triangle $A B C$, the vertices listed counterclockwise, find the locus of the centroids of the equilateral triangles $A^{\prime} B^{\prime} C^{\prime}$ (the vertices listed counterclockwise) for which the triples of points $A, B^{\prime}, C^{\prime} ; A^{\prime}, B, C^{\prime}$; and $A^{\prime}, B^{\prime}, C$ are collinear.
|
12. Here all angles will be oriented and measured counterclockwise. Note that $\measuredangle C A^{\prime} B=\measuredangle A B^{\prime} C=$ $\measuredangle B C^{\prime} A=\pi / 3$. Let $a^{\prime}, b^{\prime}, c^{\prime}$ denote respectively the inner bisectors of angles $A^{\prime}, B^{\prime}, C^{\prime}$ in triangle $A^{\prime} B^{\prime} C^{\prime}$. The lines $a^{\prime}, b^{\prime}, c^{\prime}$ meet at the centroid $X$ of $A^{\prime} B^{\prime} C^{\prime}$, and $\measuredangle\left(a^{\prime}, b^{\prime}\right)=$ $\measuredangle\left(b^{\prime}, c^{\prime}\right)=\measuredangle\left(c^{\prime}, a^{\prime}\right)=2 \pi / 3$. Now let $K, L, M$ be the points such that $K B=K C, L C=L A, M A=M B$, and $\measuredangle B K C=\measuredangle C L A=\measuredangle A M B=$ $2 \pi / 3$, and let $C_{1}, C_{2}, C_{3}$ be the circles circumscribed about triangles  $B K C, C L A$, and $A M B$ respectively. These circles are characterized by $C_{1}=\{Z \mid \measuredangle B Z C=2 \pi / 3\}$, etc.; hence we deduce that they meet at a point $P$ such that $\measuredangle B P C=\measuredangle C P A=\measuredangle A P B=2 \pi / 3$ (Torricelli's point). Points $A^{\prime}, B^{\prime}, C^{\prime}$ run over $C_{1} \backslash\{P\}, C_{2} \backslash\{P\}, C_{3} \backslash\{P\}$ respectively. As for $a^{\prime}, b^{\prime}, c^{\prime}$, we see that $K \in a^{\prime}, L \in b^{\prime}, M \in c^{\prime}$, and also that they can take all possible directions except $K P, L P, M P$ respectively (if $K=P, K P$ is assumed to be the corresponding tangent at $K$ ). Then, since $\measuredangle K X L=$ $2 \pi / 3, X$ runs over the circle defined by $\{Z \mid \measuredangle K Z L=2 \pi / 3\}$, without $P$. But analogously, $X$ runs over the circle $\{Z \mid \measuredangle L Z M=2 \pi / 3\}$, from which we can conclude that these two circles are the same, both equal to the circumcircle of $K L M$, and consequently also that triangle $K L M$ is equilateral (which is, anyway, a well-known fact). Therefore, the locus of the points $X$ is the circumcircle of $K L M$ minus point $P$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
652ee2b9-173b-50b9-872c-c19f935c0515
| 24,061
|
18. (ROM 4) For any integer $r \geq 1$, determine the smallest integer $h(r) \geq 1$ such that for any partition of the set $\{1,2, \ldots, h(r)\}$ into $r$ classes, there are integers $a \geq 0,1 \leq x \leq y$, such that $a+x, a+y, a+x+y$ belong to the same class.
|
18. Note first that the statement that some $a+x, a+y, a+x+y$ belong to a class $C$ is equivalent to the following statement: (1) There are positive integers $p, q \in C$ such that $p<q \leq 2 p$. Indeed, given $p, q$, take simply $x=y=q-p, a=2 p-q$; conversely, if $a, x, y(x \leq y)$ exist such that $a+x, a+y, a+x+y \in C$, take $p=a+y$, $q=a+x+y$ : clearly, $p<q \leq 2 p$. We will show that $h(r)=2 r$. Let $\{1,2, \ldots, 2 r\}=C_{1} \cup C_{2} \cup \cdots \cup C_{r}$ be an arbitrary partition into $r$ classes. By the pigeonhole principle, two among the $r+1$ numbers $r, r+1, \ldots, 2 r$ belong to the same class, say $i, j \in C_{k}$. If w.l.o.g. $i<j$, then obviously $i<j \leq 2 i$, and so by (1) this $C_{k}$ has the required property. On the other hand, we consider the partition $$ \{1,2, \ldots, 2 r-t\}=\bigcup_{k=1}^{r-t}\{k, k+r\} \cup\{r-t+1\} \cup \cdots \cup\{r\} $$ and prove that (1), and thus also the required property, does not hold. In fact, none of the classes in the partition contains $p$ and $q$ with $p<q \leq 2 p$, because $k+r>2 k$.
|
2r
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
18. (ROM 4) For any integer $r \geq 1$, determine the smallest integer $h(r) \geq 1$ such that for any partition of the set $\{1,2, \ldots, h(r)\}$ into $r$ classes, there are integers $a \geq 0,1 \leq x \leq y$, such that $a+x, a+y, a+x+y$ belong to the same class.
|
18. Note first that the statement that some $a+x, a+y, a+x+y$ belong to a class $C$ is equivalent to the following statement: (1) There are positive integers $p, q \in C$ such that $p<q \leq 2 p$. Indeed, given $p, q$, take simply $x=y=q-p, a=2 p-q$; conversely, if $a, x, y(x \leq y)$ exist such that $a+x, a+y, a+x+y \in C$, take $p=a+y$, $q=a+x+y$ : clearly, $p<q \leq 2 p$. We will show that $h(r)=2 r$. Let $\{1,2, \ldots, 2 r\}=C_{1} \cup C_{2} \cup \cdots \cup C_{r}$ be an arbitrary partition into $r$ classes. By the pigeonhole principle, two among the $r+1$ numbers $r, r+1, \ldots, 2 r$ belong to the same class, say $i, j \in C_{k}$. If w.l.o.g. $i<j$, then obviously $i<j \leq 2 i$, and so by (1) this $C_{k}$ has the required property. On the other hand, we consider the partition $$ \{1,2, \ldots, 2 r-t\}=\bigcup_{k=1}^{r-t}\{k, k+r\} \cup\{r-t+1\} \cup \cdots \cup\{r\} $$ and prove that (1), and thus also the required property, does not hold. In fact, none of the classes in the partition contains $p$ and $q$ with $p<q \leq 2 p$, because $k+r>2 k$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5e90d13a-5b45-53a4-a233-9fdecea00670
| 24,075
|
11. (GDR 3) The lock on a safe consists of three wheels, each of which may be set in eight different positions. Due to a defect in the safe mechanism the door will open if any two of the three wheels are in the correct position. What is the smallest number of combinations that must be tried if one is to guarantee being able to open the safe (assuming that the "right combination" is not known)?
|
11. The answer is 32 . Write the combinations as triples $k=(x, y, z), 0 \leq$ $x, y, z \leq 7$. Define the sets $K_{1}=\{(1,0,0),(0,1,0),(0,0,1),(1,1,1)\}$, $K_{2}=\{(2,0,0),(0,2,0),(0,0,2),(2,2,2)\}, K_{3}=\{(0,0,0),(4,4,4)\}$, and $K=\left\{k=k_{1}+k_{2}+k_{3} \mid k_{i} \in K_{i}, i=1,2,3\right\}$. There are 32 combinations in $K$. We shall prove that these combinations will open the safe in every case. Let $t=(a, b, c)$ be the right combination. Set $k_{3}=(0,0,0)$ if at least two of $a, b, c$ are less than 4 , and $k_{3}=(4,4,4)$ otherwise. In either case, the difference $t-k_{3}$ contains two nonnegative elements not greater than 3 . Choosing a suitable $k_{2}$ we can achieve that $t-k_{3}-k_{2}$ contains two elements that are 0,1 . So, there exists $k_{1}$ such that $t-k_{3}-k_{2}-k_{1}=t-k$ contains two zeros, for $k \in K$. This proves that 32 is sufficient. Suppose that $K$ is a set of at most 31 combinations. We say that $k \in K$ covers the combination $k_{1}$ if $k$ and $k_{1}$ differ in at most one position. One of the eight sets $M_{i}=\{(i, y, z) \mid 0 \leq y, z \leq 7\}, i=0,1, \ldots, 7$, contains at most three elements of $K$. Suppose w.l.o.g. that this is $M_{0}$. Further, among the eight sets $N_{j}=\{(0, j, z) \mid 0 \leq z \leq 7\}, j=0, \ldots, 7$, there are at least five, say w.l.o.g. $N_{0}, \ldots, N_{4}$, not containing any of the combinations from $K$. Of the 40 elements of the set $N=\{(0, y, z) \mid 0 \leq y \leq 4,0 \leq z \leq 7\}$, at most $5 \cdot 3=15$ are covered by $K \cap M_{0}$, and at least 25 aren't. Consequently, the intersection of $K$ with $L=\{(x, y, z) \mid 1 \leq x \leq 7,0 \leq y \leq 4,0 \leq z \leq 7\}$ contains at least 25 elements. So $K$ has at most $31-25=6$ elements in the set $P=\{(x, y, z) \mid 0 \leq x \leq 7,5 \leq y \leq 7,0 \leq z \leq 7\}$. This implies that for some $j \in\{5,6,7\}$, say w.l.o.g. $j=7, K$ contains at most two elements in $Q_{j}=\{(x, y, z) \mid 0 \leq x, z \leq 7, y=j\}$; denote them by $l_{1}, l_{2}$. Of the 64 elements of $Q_{7}$, at most 30 are covered by $l_{1}$ and $l_{2}$. But then there remain 34 uncovered elements, which must be covered by different elements of $K \backslash Q_{7}$, having itself less at most 29 elements. Contradiction.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
11. (GDR 3) The lock on a safe consists of three wheels, each of which may be set in eight different positions. Due to a defect in the safe mechanism the door will open if any two of the three wheels are in the correct position. What is the smallest number of combinations that must be tried if one is to guarantee being able to open the safe (assuming that the "right combination" is not known)?
|
11. The answer is 32 . Write the combinations as triples $k=(x, y, z), 0 \leq$ $x, y, z \leq 7$. Define the sets $K_{1}=\{(1,0,0),(0,1,0),(0,0,1),(1,1,1)\}$, $K_{2}=\{(2,0,0),(0,2,0),(0,0,2),(2,2,2)\}, K_{3}=\{(0,0,0),(4,4,4)\}$, and $K=\left\{k=k_{1}+k_{2}+k_{3} \mid k_{i} \in K_{i}, i=1,2,3\right\}$. There are 32 combinations in $K$. We shall prove that these combinations will open the safe in every case. Let $t=(a, b, c)$ be the right combination. Set $k_{3}=(0,0,0)$ if at least two of $a, b, c$ are less than 4 , and $k_{3}=(4,4,4)$ otherwise. In either case, the difference $t-k_{3}$ contains two nonnegative elements not greater than 3 . Choosing a suitable $k_{2}$ we can achieve that $t-k_{3}-k_{2}$ contains two elements that are 0,1 . So, there exists $k_{1}$ such that $t-k_{3}-k_{2}-k_{1}=t-k$ contains two zeros, for $k \in K$. This proves that 32 is sufficient. Suppose that $K$ is a set of at most 31 combinations. We say that $k \in K$ covers the combination $k_{1}$ if $k$ and $k_{1}$ differ in at most one position. One of the eight sets $M_{i}=\{(i, y, z) \mid 0 \leq y, z \leq 7\}, i=0,1, \ldots, 7$, contains at most three elements of $K$. Suppose w.l.o.g. that this is $M_{0}$. Further, among the eight sets $N_{j}=\{(0, j, z) \mid 0 \leq z \leq 7\}, j=0, \ldots, 7$, there are at least five, say w.l.o.g. $N_{0}, \ldots, N_{4}$, not containing any of the combinations from $K$. Of the 40 elements of the set $N=\{(0, y, z) \mid 0 \leq y \leq 4,0 \leq z \leq 7\}$, at most $5 \cdot 3=15$ are covered by $K \cap M_{0}$, and at least 25 aren't. Consequently, the intersection of $K$ with $L=\{(x, y, z) \mid 1 \leq x \leq 7,0 \leq y \leq 4,0 \leq z \leq 7\}$ contains at least 25 elements. So $K$ has at most $31-25=6$ elements in the set $P=\{(x, y, z) \mid 0 \leq x \leq 7,5 \leq y \leq 7,0 \leq z \leq 7\}$. This implies that for some $j \in\{5,6,7\}$, say w.l.o.g. $j=7, K$ contains at most two elements in $Q_{j}=\{(x, y, z) \mid 0 \leq x, z \leq 7, y=j\}$; denote them by $l_{1}, l_{2}$. Of the 64 elements of $Q_{7}$, at most 30 are covered by $l_{1}$ and $l_{2}$. But then there remain 34 uncovered elements, which must be covered by different elements of $K \backslash Q_{7}$, having itself less at most 29 elements. Contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a123995d-5027-5dd2-b0a4-c64a515f3136
| 24,113
|
18. (LUX 1) ${ }^{\mathrm{IMO}}$ Consider two concentric circles of radii $R$ and $r(R>r)$ with center $O$. Fix $P$ on the small circle and consider the variable chord $P A$ of the small circle. Points $B$ and $C$ lie on the large circle; $B, P, C$ are collinear and $B C$ is perpendicular to $A P$. (a) For what value(s) of $\angle O P A$ is the sum $B C^{2}+C A^{2}+A B^{2}$ extremal? (b) What are the possible positions of the midpoints $U$ of $B A$ and $V$ of $A C$ as $\angle O P A$ varies?
|
18. (i) Define $\angle A P O=\phi$ and $S=A B^{2}+A C^{2}+B C^{2}$. We calculate $P A=$ $2 r \cos \phi$ and $P B, P C=\sqrt{R^{2}-r^{2} \cos ^{2} \phi} \pm r \sin \phi$. We also have $A B^{2}=$ $P A^{2}+P B^{2}, A C^{2}=P A^{2}+P C^{2}$ and $B C=B P+P C$. Combining all these we obtain $$ \begin{aligned} S & =A B^{2}+A C^{2}+B C^{2}=2\left(P A^{2}+P B^{2}+P C^{2}+P B \cdot P C\right) \\ & =2\left(4 r^{2} \cos ^{2} \phi+2\left(R^{2}-r^{2} \cos ^{2} \phi+r^{2} \sin ^{2} \phi\right)+R^{2}-r^{2}\right) \\ & =6 R^{2}+2 r^{2} . \end{aligned} $$ Hence it follows that $S$ is constant; i.e., it does not depend on $\phi$. (ii) Let $B_{1}$ and $C_{1}$ respectively be points such that $A P B B_{1}$ and $A P C C_{1}$ are rectangles. It is evident that $B_{1}$ and $C_{1}$ lie on the larger circle and that $\overrightarrow{P U}=\frac{1}{2} \overrightarrow{P B_{1}}$ and $\overrightarrow{P V}=\frac{1}{2} \overrightarrow{P C_{1}}$. It is evident that we can arrange for an arbitrary point on the larger circle to be $B_{1}$ or $C_{1}$. Hence, the locus of $U$ and $V$ is equal to the circle obtained when the larger circle is shrunk by a factor of $1 / 2$ with respect to point $P$.
|
6 R^{2}+2 r^{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
18. (LUX 1) ${ }^{\mathrm{IMO}}$ Consider two concentric circles of radii $R$ and $r(R>r)$ with center $O$. Fix $P$ on the small circle and consider the variable chord $P A$ of the small circle. Points $B$ and $C$ lie on the large circle; $B, P, C$ are collinear and $B C$ is perpendicular to $A P$. (a) For what value(s) of $\angle O P A$ is the sum $B C^{2}+C A^{2}+A B^{2}$ extremal? (b) What are the possible positions of the midpoints $U$ of $B A$ and $V$ of $A C$ as $\angle O P A$ varies?
|
18. (i) Define $\angle A P O=\phi$ and $S=A B^{2}+A C^{2}+B C^{2}$. We calculate $P A=$ $2 r \cos \phi$ and $P B, P C=\sqrt{R^{2}-r^{2} \cos ^{2} \phi} \pm r \sin \phi$. We also have $A B^{2}=$ $P A^{2}+P B^{2}, A C^{2}=P A^{2}+P C^{2}$ and $B C=B P+P C$. Combining all these we obtain $$ \begin{aligned} S & =A B^{2}+A C^{2}+B C^{2}=2\left(P A^{2}+P B^{2}+P C^{2}+P B \cdot P C\right) \\ & =2\left(4 r^{2} \cos ^{2} \phi+2\left(R^{2}-r^{2} \cos ^{2} \phi+r^{2} \sin ^{2} \phi\right)+R^{2}-r^{2}\right) \\ & =6 R^{2}+2 r^{2} . \end{aligned} $$ Hence it follows that $S$ is constant; i.e., it does not depend on $\phi$. (ii) Let $B_{1}$ and $C_{1}$ respectively be points such that $A P B B_{1}$ and $A P C C_{1}$ are rectangles. It is evident that $B_{1}$ and $C_{1}$ lie on the larger circle and that $\overrightarrow{P U}=\frac{1}{2} \overrightarrow{P B_{1}}$ and $\overrightarrow{P V}=\frac{1}{2} \overrightarrow{P C_{1}}$. It is evident that we can arrange for an arbitrary point on the larger circle to be $B_{1}$ or $C_{1}$. Hence, the locus of $U$ and $V$ is equal to the circle obtained when the larger circle is shrunk by a factor of $1 / 2$ with respect to point $P$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5071a2d4-fe8a-5497-83c2-771fe20ef2da
| 24,129
|
19. (MEX 1) Let $f(n)$ be a function defined on the set of all positive integers and having its values in the same set. Suppose that $f(f(m)+f(n))=m+n$ for all positive integers $n, m$. Find all possible values for $f(1988)$.
|
19. We will show that $f(n)=n$ for every $n$ (thus also $f(1988)=1988$ ). Let $f(1)=r$ and $f(2)=s$. We obtain respectively the following equalities: $f(2 r)=f(r+r)=2 ; f(2 s)=f(s+s)=4 ; f(4)=f(2+2)=4 r ; f(8)=$ $f(4+4)=4 s ; f(5 r)=f(4 r+r)=5 ; f(r+s)=3 ; f(8)=f(5+3)=6 r+s$. Then $4 s=6 r+s$, which means that $s=2 r$. Now we prove by induction that $f(n r)=n$ and $f(n)=n r$ for every $n \geq 4$. First we have that $f(5)=f(2+3)=3 r+s=5 r$, so that the statement is true for $n=4$ and $n=5$. Suppose that it holds for $n-1$ and $n$. Then $f(n+1)=f(n-1+2)=(n-1) r+2 r=(n+1) r$, and $f((n+1) r)=f((n-1) r+2 r)=(n-1)+2=n+1$. This completes the induction. Since $4 r \geq 4$, we have that $f(4 r)=4 r^{2}$, and also $f(4 r)=4$. Then $r=1$, and consequently $f(n)=n$ for every natural number $n$. Second solution. $f(f(1)+n+m)=f(f(1)+f(f(n)+f(m)))=1+f(n)+$ $f(m)$, so $f(n)+f(m)$ is a function of $n+m$. Hence $f(n+1)+f(1)=$ $f(n)+f(2)$ and $f(n+1)-f(n)=f(2)-f(1)$, implying that $f(n)=A n+B$ for some constants $A, B$. It is easy to check that $A=1, B=0$ is the only possibility.
|
1988
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
19. (MEX 1) Let $f(n)$ be a function defined on the set of all positive integers and having its values in the same set. Suppose that $f(f(m)+f(n))=m+n$ for all positive integers $n, m$. Find all possible values for $f(1988)$.
|
19. We will show that $f(n)=n$ for every $n$ (thus also $f(1988)=1988$ ). Let $f(1)=r$ and $f(2)=s$. We obtain respectively the following equalities: $f(2 r)=f(r+r)=2 ; f(2 s)=f(s+s)=4 ; f(4)=f(2+2)=4 r ; f(8)=$ $f(4+4)=4 s ; f(5 r)=f(4 r+r)=5 ; f(r+s)=3 ; f(8)=f(5+3)=6 r+s$. Then $4 s=6 r+s$, which means that $s=2 r$. Now we prove by induction that $f(n r)=n$ and $f(n)=n r$ for every $n \geq 4$. First we have that $f(5)=f(2+3)=3 r+s=5 r$, so that the statement is true for $n=4$ and $n=5$. Suppose that it holds for $n-1$ and $n$. Then $f(n+1)=f(n-1+2)=(n-1) r+2 r=(n+1) r$, and $f((n+1) r)=f((n-1) r+2 r)=(n-1)+2=n+1$. This completes the induction. Since $4 r \geq 4$, we have that $f(4 r)=4 r^{2}$, and also $f(4 r)=4$. Then $r=1$, and consequently $f(n)=n$ for every natural number $n$. Second solution. $f(f(1)+n+m)=f(f(1)+f(f(n)+f(m)))=1+f(n)+$ $f(m)$, so $f(n)+f(m)$ is a function of $n+m$. Hence $f(n+1)+f(1)=$ $f(n)+f(2)$ and $f(n+1)-f(n)=f(2)-f(1)$, implying that $f(n)=A n+B$ for some constants $A, B$. It is easy to check that $A=1, B=0$ is the only possibility.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4c6580b8-7ba6-51f8-85ea-dea911de4eb5
| 24,132
|
20. (MON 4) Find the least natural number $n$ such that if the set $\{1,2, \ldots, n\}$ is arbitrarily divided into two nonintersecting subsets, then one of the subsets contains three distinct numbers such that the product of two of them equals the third.
|
20. Suppose that $A_{n}=\{1,2, \ldots, n\}$ is partitioned into $B_{n}$ and $C_{n}$, and that neither $B_{n}$ nor $C_{n}$ contains 3 distinct numbers one of which is equal to the product of the other two. If $n \geq 96$, then the divisors of 96 must be split up. Let w.l.o.g. $2 \in B_{n}$. There are four cases. (i) $3 \in B_{n}, 4 \in B_{n}$. Then $6,8,12 \in C_{n} \Rightarrow 48,96 \in B_{n}$. A contradiction for $96=2 \cdot 48$. (ii) $3 \in B_{n}, 4 \in C_{n}$. Then $6 \in C_{n}, 24 \in B_{n}, 8,12,48 \in C_{n}$. A contradiction for $48=6 \cdot 8$. (iii) $3 \in C_{n}, 4 \in B_{n}$. Then $8 \in C_{n}, 24 \in B_{n}, 6,48 \in C_{n}$. A contradiction for $48=6 \cdot 8$. (iv) $3 \in C_{n}, 4 \in C_{n}$. Then $12 \in B_{n}, 6,24 \in C_{n}$. A contradiction for $24=4 \cdot 6$. If $n=95$, there is a very large number of ways of partitioning $A_{n}$. For example, $B_{n}=\left\{1, p, p^{2}, p^{3} q^{2}, p^{4} q, p^{2} q r \mid p, q, r=\operatorname{distinct}\right.$ primes $\}$, $C_{n}=\left\{p^{3}, p^{4}, p^{5}, p^{6}, p q, p^{2} q, p^{3} q, p^{2} q^{2}, p q r \mid p, q, r=\right.$ distinct primes $\}$. Then $B_{95}=\{1,2,3,4,5,7,9,11,13,17,19,23,25,29,31,37,41$, $43,47,48,49,53,59,60,61,67,71,72,73,79,80,83,84,89,90\}$.
|
96
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
20. (MON 4) Find the least natural number $n$ such that if the set $\{1,2, \ldots, n\}$ is arbitrarily divided into two nonintersecting subsets, then one of the subsets contains three distinct numbers such that the product of two of them equals the third.
|
20. Suppose that $A_{n}=\{1,2, \ldots, n\}$ is partitioned into $B_{n}$ and $C_{n}$, and that neither $B_{n}$ nor $C_{n}$ contains 3 distinct numbers one of which is equal to the product of the other two. If $n \geq 96$, then the divisors of 96 must be split up. Let w.l.o.g. $2 \in B_{n}$. There are four cases. (i) $3 \in B_{n}, 4 \in B_{n}$. Then $6,8,12 \in C_{n} \Rightarrow 48,96 \in B_{n}$. A contradiction for $96=2 \cdot 48$. (ii) $3 \in B_{n}, 4 \in C_{n}$. Then $6 \in C_{n}, 24 \in B_{n}, 8,12,48 \in C_{n}$. A contradiction for $48=6 \cdot 8$. (iii) $3 \in C_{n}, 4 \in B_{n}$. Then $8 \in C_{n}, 24 \in B_{n}, 6,48 \in C_{n}$. A contradiction for $48=6 \cdot 8$. (iv) $3 \in C_{n}, 4 \in C_{n}$. Then $12 \in B_{n}, 6,24 \in C_{n}$. A contradiction for $24=4 \cdot 6$. If $n=95$, there is a very large number of ways of partitioning $A_{n}$. For example, $B_{n}=\left\{1, p, p^{2}, p^{3} q^{2}, p^{4} q, p^{2} q r \mid p, q, r=\operatorname{distinct}\right.$ primes $\}$, $C_{n}=\left\{p^{3}, p^{4}, p^{5}, p^{6}, p q, p^{2} q, p^{3} q, p^{2} q^{2}, p q r \mid p, q, r=\right.$ distinct primes $\}$. Then $B_{95}=\{1,2,3,4,5,7,9,11,13,17,19,23,25,29,31,37,41$, $43,47,48,49,53,59,60,61,67,71,72,73,79,80,83,84,89,90\}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
db51ed1a-0425-5f81-9fda-47bf01751d68
| 24,136
|
26. (GBR 2) ${ }^{\mathrm{IMO} 3} \mathrm{~A}$ function $f$ defined on the positive integers (and taking positive integer values) is given by $$ \begin{aligned} f(1) & =1, \quad f(3)=3 \\ f(2 n) & =f(n) \\ f(4 n+1) & =2 f(2 n+1)-f(n) \\ f(4 n+3) & =3 f(2 n+1)-2 f(n) \end{aligned} $$ for all positive integers $n$. Determine with proof the number of positive integers less than or equal to 1988 for which $f(n)=n$.
|
26. The overline in this problem will exclusively denote binary representation. We will show by induction that if $n=\overline{c_{k} c_{k-1} \ldots c_{0}}=\sum_{i=0}^{k} c_{i} 2^{i}$ is the binary representation of $n\left(c_{i} \in\{0,1\}\right)$, then $f(n)=\overline{c_{0} c_{1} \ldots c_{k}}=$ $\sum_{i=0}^{k} c_{i} 2^{k-i}$ is the number whose binary representation is the palindrome of the binary representation of $n$. This evidently holds for $n \in\{1,2,3\}$. Let us assume that the claim holds for all numbers up to $n-1$ and show it holds for $n=\overline{c_{k} c_{k-1} \ldots c_{0}}$. We observe three cases: (i) $c_{0}=0 \Rightarrow n=2 m \Rightarrow f(n)=f(m)=\overline{0 c_{1} \ldots c_{k}}=\overline{c_{0} c_{1} \ldots c_{k}}$. (ii) $c_{0}=1, c_{1}=0 \Rightarrow n=4 m+1 \Rightarrow f(n)=2 f(2 m+1)-f(m)=$ $2 \cdot \overline{1 c_{2} \ldots c_{k}}-\overline{c_{2} \ldots c_{k}}=2^{k}+2 \cdot \overline{c_{2} \ldots c_{k}}-\overline{c_{2} \ldots c_{k}}=\overline{10 c_{2} \ldots c_{k}}=$ $\overline{c_{0} c_{1} \ldots c_{k}}$. (iii) $c_{0}=1, c_{1}=1 \Rightarrow n=4 m+3 \Rightarrow f(n)=3 f(2 m+1)-2 f(m)=$ $3 \cdot \overline{1 c_{2} \ldots c_{k}}-2 \cdot \overline{c_{2} \ldots c_{k}}=2^{k}+2^{k-1}+3 \cdot \overline{c_{2} \ldots c_{k}}-2 \cdot \overline{c_{2} \ldots c_{k}}=$ $\overline{11 c_{2} \ldots c_{k}}=\overline{c_{0} c_{1} \ldots c_{k}}$. We thus have to find the number of palindromes in binary representation smaller than $1998=\overline{11111000100}$. We note that for all $m \in \mathbb{N}$ the numbers of $2 m$ - and $(2 m-1)$-digit binary palindromes are both equal to $2^{m-1}$. We also note that $\overline{11111011111}$ and $\overline{11111111111}$ are the only 11-digit palindromes larger than 1998. Hence we count all palindromes of up to 11 digits and exclude the largest two. The number of $n \leq 1998$ such that $f(n)=n$ is thus equal to $1+1+2+2+4+4+8+8+16+16+32-2=92$.
|
92
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
26. (GBR 2) ${ }^{\mathrm{IMO} 3} \mathrm{~A}$ function $f$ defined on the positive integers (and taking positive integer values) is given by $$ \begin{aligned} f(1) & =1, \quad f(3)=3 \\ f(2 n) & =f(n) \\ f(4 n+1) & =2 f(2 n+1)-f(n) \\ f(4 n+3) & =3 f(2 n+1)-2 f(n) \end{aligned} $$ for all positive integers $n$. Determine with proof the number of positive integers less than or equal to 1988 for which $f(n)=n$.
|
26. The overline in this problem will exclusively denote binary representation. We will show by induction that if $n=\overline{c_{k} c_{k-1} \ldots c_{0}}=\sum_{i=0}^{k} c_{i} 2^{i}$ is the binary representation of $n\left(c_{i} \in\{0,1\}\right)$, then $f(n)=\overline{c_{0} c_{1} \ldots c_{k}}=$ $\sum_{i=0}^{k} c_{i} 2^{k-i}$ is the number whose binary representation is the palindrome of the binary representation of $n$. This evidently holds for $n \in\{1,2,3\}$. Let us assume that the claim holds for all numbers up to $n-1$ and show it holds for $n=\overline{c_{k} c_{k-1} \ldots c_{0}}$. We observe three cases: (i) $c_{0}=0 \Rightarrow n=2 m \Rightarrow f(n)=f(m)=\overline{0 c_{1} \ldots c_{k}}=\overline{c_{0} c_{1} \ldots c_{k}}$. (ii) $c_{0}=1, c_{1}=0 \Rightarrow n=4 m+1 \Rightarrow f(n)=2 f(2 m+1)-f(m)=$ $2 \cdot \overline{1 c_{2} \ldots c_{k}}-\overline{c_{2} \ldots c_{k}}=2^{k}+2 \cdot \overline{c_{2} \ldots c_{k}}-\overline{c_{2} \ldots c_{k}}=\overline{10 c_{2} \ldots c_{k}}=$ $\overline{c_{0} c_{1} \ldots c_{k}}$. (iii) $c_{0}=1, c_{1}=1 \Rightarrow n=4 m+3 \Rightarrow f(n)=3 f(2 m+1)-2 f(m)=$ $3 \cdot \overline{1 c_{2} \ldots c_{k}}-2 \cdot \overline{c_{2} \ldots c_{k}}=2^{k}+2^{k-1}+3 \cdot \overline{c_{2} \ldots c_{k}}-2 \cdot \overline{c_{2} \ldots c_{k}}=$ $\overline{11 c_{2} \ldots c_{k}}=\overline{c_{0} c_{1} \ldots c_{k}}$. We thus have to find the number of palindromes in binary representation smaller than $1998=\overline{11111000100}$. We note that for all $m \in \mathbb{N}$ the numbers of $2 m$ - and $(2 m-1)$-digit binary palindromes are both equal to $2^{m-1}$. We also note that $\overline{11111011111}$ and $\overline{11111111111}$ are the only 11-digit palindromes larger than 1998. Hence we count all palindromes of up to 11 digits and exclude the largest two. The number of $n \leq 1998$ such that $f(n)=n$ is thus equal to $1+1+2+2+4+4+8+8+16+16+32-2=92$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c499ff3c-975e-52e4-8c21-b117e909833d
| 24,150
|
17. (MON 1) Given seven points in the plane, some of them are connected by segments so that: (i) among any three of the given points, two are connected by a segment; (i) the number of segments is minimal. How many segments does a figure satisfying (i) and (ii) contain? Give an example of such a figure.
|
17. A figure consisting of 9 lines is shown below. 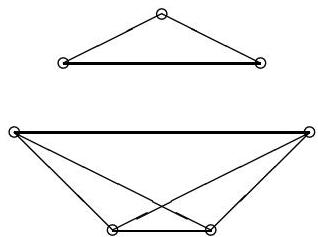 Now we show that 8 lines are not sufficient. Assume the opposite. By the pigeonhole principle, there is a vertex, say $A$, that is joined to at most 2 other vertices. Let $B, C, D, E$ denote the vertices to which $A$ is not joined, and $F, G$ the other two vertices. Then any two vertices of $B, C, D, E$ must be mutually joined for an edge to exist within the triangle these two points form with A. This accounts for 6 segments. Since only two segments remain, among $A, F$, and $G$ at least two are not joined. Taking these two and one of $B, C, D, E$ that is not joined to any of them (it obviously exists), we get a triple of points, no two of which are joined; a contradiction. Second solution. Since (a) is equivalent to the fact that no three points make a "blank triangle," by Turan's theorem the number of "blank edges" cannot exceed $\left[7^{2} / 4\right]=12$, leaving at least $7 \cdot 6 / 2-12=9$ segments. For general $n$, the answer is $[(n-1) / 2]^{2}$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
17. (MON 1) Given seven points in the plane, some of them are connected by segments so that: (i) among any three of the given points, two are connected by a segment; (i) the number of segments is minimal. How many segments does a figure satisfying (i) and (ii) contain? Give an example of such a figure.
|
17. A figure consisting of 9 lines is shown below.  Now we show that 8 lines are not sufficient. Assume the opposite. By the pigeonhole principle, there is a vertex, say $A$, that is joined to at most 2 other vertices. Let $B, C, D, E$ denote the vertices to which $A$ is not joined, and $F, G$ the other two vertices. Then any two vertices of $B, C, D, E$ must be mutually joined for an edge to exist within the triangle these two points form with A. This accounts for 6 segments. Since only two segments remain, among $A, F$, and $G$ at least two are not joined. Taking these two and one of $B, C, D, E$ that is not joined to any of them (it obviously exists), we get a triple of points, no two of which are joined; a contradiction. Second solution. Since (a) is equivalent to the fact that no three points make a "blank triangle," by Turan's theorem the number of "blank edges" cannot exceed $\left[7^{2} / 4\right]=12$, leaving at least $7 \cdot 6 / 2-12=9$ segments. For general $n$, the answer is $[(n-1) / 2]^{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
81cba49e-f97d-57a7-b4c2-d908eb0efb42
| 24,206
|
18. (MON 4) Given a convex polygon $A_{1} A_{2} \ldots A_{n}$ with area $S$, and a point $M$ in the same plane, determine the area of polygon $M_{1} M_{2} \ldots M_{n}$, where $M_{i}$ is the image of $M$ under rotation $\mathcal{R}_{A_{i}}^{\alpha}$ around $A_{i}$ by $\alpha, i=1,2, \ldots, n$.
|
18. Consider the triangle $M A_{i} M_{i}$. Obviously, the point $M_{i}$ is the image of $A_{i}$ under the composition $C$ of rotation $R_{M}^{\alpha / 2-90^{\circ}}$ and homothety $H_{M}^{2 \sin (\alpha / 2)}$. Therefore, the polygon $M_{1} M_{2} \ldots M_{n}$ is obtained as the image of $A_{1} A_{2} \ldots A_{n}$ under the rotational homothety $C$ with coefficient $2 \sin (\alpha / 2)$. Therefore $S_{M_{1} M_{2} \ldots M_{n}}=4 \sin ^{2}(\alpha / 2) \cdot S$.
|
4 \sin ^{2}(\alpha / 2) \cdot S
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
18. (MON 4) Given a convex polygon $A_{1} A_{2} \ldots A_{n}$ with area $S$, and a point $M$ in the same plane, determine the area of polygon $M_{1} M_{2} \ldots M_{n}$, where $M_{i}$ is the image of $M$ under rotation $\mathcal{R}_{A_{i}}^{\alpha}$ around $A_{i}$ by $\alpha, i=1,2, \ldots, n$.
|
18. Consider the triangle $M A_{i} M_{i}$. Obviously, the point $M_{i}$ is the image of $A_{i}$ under the composition $C$ of rotation $R_{M}^{\alpha / 2-90^{\circ}}$ and homothety $H_{M}^{2 \sin (\alpha / 2)}$. Therefore, the polygon $M_{1} M_{2} \ldots M_{n}$ is obtained as the image of $A_{1} A_{2} \ldots A_{n}$ under the rotational homothety $C$ with coefficient $2 \sin (\alpha / 2)$. Therefore $S_{M_{1} M_{2} \ldots M_{n}}=4 \sin ^{2}(\alpha / 2) \cdot S$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
49d873ff-db9f-5679-bc7a-f0e28eab902d
| 24,209
|
24. (POL 5) For points $A_{1}, \ldots, A_{5}$ on the sphere of radius 1 , what is the maximum value that $\min _{1 \leq i, j \leq 5} A_{i} A_{j}$ can take? Determine all configurations for which this maximum is attained. (Or: determine the diameter of any set $\left\{A_{1}, \ldots, A_{5}\right\}$ for which this maximum is attained.)
|
24. Instead of Euclidean distance, we will use the angles $\angle A_{i} O A_{j}, O$ denoting the center of the sphere. Let $\left\{A_{1}, \ldots, A_{5}\right\}$ be any set for which $\min _{i \neq j} \angle A_{i} O A_{j} \geq \pi / 2$ (such a set exists: take for example five vertices of an octagon). We claim that two of the $A_{i}$ 's must be antipodes, thus implying that $\min _{i \neq j} \angle A_{i} O A_{j}$ is exactly equal to $\pi / 2$, and consequently that $\min _{i \neq j} A_{i} A_{j}=\sqrt{2}$. Suppose no two of the five points are antipodes. Visualize $A_{5}$ as the south pole. Then $A_{1}, \ldots, A_{4}$ lie in the northern hemisphere, including the equator (but excluding the north pole). No two of $A_{1}, \ldots, A_{4}$ can lie in the interior of a quarter of this hemisphere, which means that any two of them differ in longitude by at least $\pi / 2$. Hence, they are situated on four meridians that partition the sphere into quarters. Finally, if one of them does not lie on the equator, its two neighbors must. Hence, in any case there will exist an antipodal pair, giving us a contradiction.
|
\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
24. (POL 5) For points $A_{1}, \ldots, A_{5}$ on the sphere of radius 1 , what is the maximum value that $\min _{1 \leq i, j \leq 5} A_{i} A_{j}$ can take? Determine all configurations for which this maximum is attained. (Or: determine the diameter of any set $\left\{A_{1}, \ldots, A_{5}\right\}$ for which this maximum is attained.)
|
24. Instead of Euclidean distance, we will use the angles $\angle A_{i} O A_{j}, O$ denoting the center of the sphere. Let $\left\{A_{1}, \ldots, A_{5}\right\}$ be any set for which $\min _{i \neq j} \angle A_{i} O A_{j} \geq \pi / 2$ (such a set exists: take for example five vertices of an octagon). We claim that two of the $A_{i}$ 's must be antipodes, thus implying that $\min _{i \neq j} \angle A_{i} O A_{j}$ is exactly equal to $\pi / 2$, and consequently that $\min _{i \neq j} A_{i} A_{j}=\sqrt{2}$. Suppose no two of the five points are antipodes. Visualize $A_{5}$ as the south pole. Then $A_{1}, \ldots, A_{4}$ lie in the northern hemisphere, including the equator (but excluding the north pole). No two of $A_{1}, \ldots, A_{4}$ can lie in the interior of a quarter of this hemisphere, which means that any two of them differ in longitude by at least $\pi / 2$. Hence, they are situated on four meridians that partition the sphere into quarters. Finally, if one of them does not lie on the equator, its two neighbors must. Hence, in any case there will exist an antipodal pair, giving us a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a5bf8851-9646-50b5-b509-f3605726d665
| 24,230
|
29. (ROM 4) A flock of 155 birds sit down on a circle $C$. Two birds $P_{i}, P_{j}$ are mutually visible if $m\left(P_{i} P_{j}\right) \leq 10^{\circ}$. Find the smallest number of mutually visible pairs of birds. (One assumes that a position (point) on $C$ can be occupied simultaneously by several birds.)
|
29. Let $P_{i}$, sitting at the place $A$, and $P_{j}$ sitting at $B$, be two birds that can see each other. Let $k$ and $l$ respectively be the number of birds visible from $B$ but not from $A$, and the number of those visible from $A$ but not from $B$. Assume that $k \geq l$. Then if all birds from $B$ fly to $A$, each of them will see $l$ new birds, but won't see $k$ birds anymore. Hence the total number of mutually visible pairs does not increase, while the number of distinct positions occupied by at least one bird decreases by one. Repeating this operation as many times as possible one can arrive at a situation in which two birds see each other if and only if they are in the same position. The number of such distinct positions is at most 35 , while the total number of mutually visible pairs is not greater than at the beginning. Thus the problem is equivalent to the following one: (1) If $x_{i} \geq 0$ are integers with $\sum_{j=1}^{35} x_{j}=155$, find the least possible value of $\sum_{j=1}^{35}\left(x_{j}^{2}-x_{j}\right) / 2$. If $x_{j} \geq x_{i}+2$ for some $i, j$, then the sum of $\left(x_{j}^{2}-x_{j}\right) / 2$ decreases (for $x_{j}-x_{i}-2$ ) if $x_{i}, x_{j}$ are replaced with $x_{i}+1, x_{j}-1$. Consequently, our sum attains its minimum when the $x_{i}$ 's differ from each other by at most 1 . In this case, all the $x_{i}$ 's are equal to either $[155 / 35]=4$ or $[155 / 35]+1=5$, where $155=20 \cdot 4+15 \cdot 5$. It follows that the (minimum possible) number of mutually visible pairs is $20 \cdot \frac{4 \cdot 3}{2}+15 \cdot \frac{5 \cdot 4}{2}=270$. Second solution for (1). Considering the graph consisting of birds as vertices and pairs of mutually nonvisible birds as edges, we see that there is no complete 36 -subgraph. Turan's theorem gives the answer immediately. (See problem (SL89-17).)
|
270
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
29. (ROM 4) A flock of 155 birds sit down on a circle $C$. Two birds $P_{i}, P_{j}$ are mutually visible if $m\left(P_{i} P_{j}\right) \leq 10^{\circ}$. Find the smallest number of mutually visible pairs of birds. (One assumes that a position (point) on $C$ can be occupied simultaneously by several birds.)
|
29. Let $P_{i}$, sitting at the place $A$, and $P_{j}$ sitting at $B$, be two birds that can see each other. Let $k$ and $l$ respectively be the number of birds visible from $B$ but not from $A$, and the number of those visible from $A$ but not from $B$. Assume that $k \geq l$. Then if all birds from $B$ fly to $A$, each of them will see $l$ new birds, but won't see $k$ birds anymore. Hence the total number of mutually visible pairs does not increase, while the number of distinct positions occupied by at least one bird decreases by one. Repeating this operation as many times as possible one can arrive at a situation in which two birds see each other if and only if they are in the same position. The number of such distinct positions is at most 35 , while the total number of mutually visible pairs is not greater than at the beginning. Thus the problem is equivalent to the following one: (1) If $x_{i} \geq 0$ are integers with $\sum_{j=1}^{35} x_{j}=155$, find the least possible value of $\sum_{j=1}^{35}\left(x_{j}^{2}-x_{j}\right) / 2$. If $x_{j} \geq x_{i}+2$ for some $i, j$, then the sum of $\left(x_{j}^{2}-x_{j}\right) / 2$ decreases (for $x_{j}-x_{i}-2$ ) if $x_{i}, x_{j}$ are replaced with $x_{i}+1, x_{j}-1$. Consequently, our sum attains its minimum when the $x_{i}$ 's differ from each other by at most 1 . In this case, all the $x_{i}$ 's are equal to either $[155 / 35]=4$ or $[155 / 35]+1=5$, where $155=20 \cdot 4+15 \cdot 5$. It follows that the (minimum possible) number of mutually visible pairs is $20 \cdot \frac{4 \cdot 3}{2}+15 \cdot \frac{5 \cdot 4}{2}=270$. Second solution for (1). Considering the graph consisting of birds as vertices and pairs of mutually nonvisible birds as edges, we see that there is no complete 36 -subgraph. Turan's theorem gives the answer immediately. (See problem (SL89-17).)
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5d52ad93-f1f7-5592-bf50-bd8cda8f0354
| 24,241
|
10. (ICE 2) A plane cuts a right circular cone into two parts. The plane is tangent to the circumference of the base of the cone and passes through the midpoint of the altitude. Find the ratio of the volume of the smaller part to the volume of the whole cone.
|
10. Let $r$ be the radius of the base and $h$ the height of the cone. We may assume w.l.o.g. that $r=1$. Let $A$ be the top of the cone, $B C$ the diameter of the circumference of the base such that the plane touches the circumference at $B, O$ the center of the base, and $H$ the midpoint of $O A$ (also belonging to the plane). Let $B H$ cut the sheet of the cone at $D$. By applying Menelaus's theorem to $\triangle A O C$ and $\triangle B H O$, we conclude that $\frac{A D}{D C}=\frac{C B}{B O} \cdot \frac{O H}{H A}=\frac{1}{2}$ and $\frac{H D}{D B}=\frac{H A}{A O} \cdot \frac{O C}{C B}=\frac{1}{4}$. The plane cuts the cone in an ellipse whose major axis is $B D$. Let $E$ be the center of this ellipse and $F G$ its minor axis. We have $\frac{B E}{E D}=\frac{1}{2}$. Let $E^{\prime}, F^{\prime}, G^{\prime}$ be radial projections of $E, F, G$ from $A$ onto the base of the cone. Then $E$ sits on $B C$. Let $h(X)$ denote the height of a point $X$ with respect to the base of the cone. We have $h(E)=h(D) / 2=h / 3$. Hence $E F=2 E^{\prime} F^{\prime} / 3$. Applying Menelaus's theorem to $\triangle B H O$ we get $\frac{O E^{\prime}}{E^{\prime} B}=\frac{B E}{E H} \cdot \frac{H A}{A O}=1$. Hence $E F=\frac{2}{3} \frac{\sqrt{3}}{2}=\frac{1}{\sqrt{3}}$. Let $d$ denote the distance from $A$ to the plane. Let $V_{1}$ and $V$ denote the volume of the cone above the plane (on the same side of the plane as $A$ ) and the total volume of the cone. We have $$ \begin{aligned} \frac{V_{1}}{V} & =\frac{B E \cdot E F \cdot d}{h}=\frac{(2 B H / 3)(1 / \sqrt{3})\left(2 S_{A H B} / B H\right)}{h} \\ & =\frac{(2 / 3)(1 / \sqrt{3})(h / 2)}{h}=\frac{1}{3 \sqrt{3}} . \end{aligned} $$ Since this ratio is smaller than $1 / 2$, we have indeed selected the correct volume for our ratio.
|
\frac{1}{3 \sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
10. (ICE 2) A plane cuts a right circular cone into two parts. The plane is tangent to the circumference of the base of the cone and passes through the midpoint of the altitude. Find the ratio of the volume of the smaller part to the volume of the whole cone.
|
10. Let $r$ be the radius of the base and $h$ the height of the cone. We may assume w.l.o.g. that $r=1$. Let $A$ be the top of the cone, $B C$ the diameter of the circumference of the base such that the plane touches the circumference at $B, O$ the center of the base, and $H$ the midpoint of $O A$ (also belonging to the plane). Let $B H$ cut the sheet of the cone at $D$. By applying Menelaus's theorem to $\triangle A O C$ and $\triangle B H O$, we conclude that $\frac{A D}{D C}=\frac{C B}{B O} \cdot \frac{O H}{H A}=\frac{1}{2}$ and $\frac{H D}{D B}=\frac{H A}{A O} \cdot \frac{O C}{C B}=\frac{1}{4}$. The plane cuts the cone in an ellipse whose major axis is $B D$. Let $E$ be the center of this ellipse and $F G$ its minor axis. We have $\frac{B E}{E D}=\frac{1}{2}$. Let $E^{\prime}, F^{\prime}, G^{\prime}$ be radial projections of $E, F, G$ from $A$ onto the base of the cone. Then $E$ sits on $B C$. Let $h(X)$ denote the height of a point $X$ with respect to the base of the cone. We have $h(E)=h(D) / 2=h / 3$. Hence $E F=2 E^{\prime} F^{\prime} / 3$. Applying Menelaus's theorem to $\triangle B H O$ we get $\frac{O E^{\prime}}{E^{\prime} B}=\frac{B E}{E H} \cdot \frac{H A}{A O}=1$. Hence $E F=\frac{2}{3} \frac{\sqrt{3}}{2}=\frac{1}{\sqrt{3}}$. Let $d$ denote the distance from $A$ to the plane. Let $V_{1}$ and $V$ denote the volume of the cone above the plane (on the same side of the plane as $A$ ) and the total volume of the cone. We have $$ \begin{aligned} \frac{V_{1}}{V} & =\frac{B E \cdot E F \cdot d}{h}=\frac{(2 B H / 3)(1 / \sqrt{3})\left(2 S_{A H B} / B H\right)}{h} \\ & =\frac{(2 / 3)(1 / \sqrt{3})(h / 2)}{h}=\frac{1}{3 \sqrt{3}} . \end{aligned} $$ Since this ratio is smaller than $1 / 2$, we have indeed selected the correct volume for our ratio.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2b4fa711-bc65-590d-a54c-e9386f70db8f
| 24,269
|
11. (IND $\left.3^{\prime}\right)^{\mathrm{IMO}}$ Given a circle with two chords $A B, C D$ that meet at $E$, let $M$ be a point of chord $A B$ other than $E$. Draw the circle through $D, E$, and $M$. The tangent line to the circle $D E M$ at $E$ meets the lines $B C, A C$ at $F, G$, respectively. Given $\frac{A M}{A B}=\lambda$, find $\frac{G E}{E F}$.
|
11. Assume $\mathcal{B}(A, E, M, B)$. Since $A, B, C, D$ lie on a circle, we have $\angle G C E=$ $\angle M B D$ and $\angle M A D=\angle F C E$. Since $F D$ is tangent to the circle around $\triangle E M D$ at $E$, we have $\angle M D E=\angle F E B=\angle A E G$. Consequently, $\angle C E F=180^{\circ}-\angle C E A-\angle F E B=180^{\circ}-\angle M E D-\angle M D E=\angle E M D$ and $\angle C E G=180^{\circ}-\angle C E F=180^{\circ}-\angle E M D=\angle D M B$. It follows that $\triangle C E F \sim \triangle A M D$ and $\triangle C E G \sim$ $\triangle B M D$. From the first similarity we obtain $C E \cdot M D=A M \cdot E F$, and from the second we obtain $C E$. $M D=B M \cdot E G$. Hence $$ \begin{gathered} A M \cdot E F=B M \cdot E G \Longrightarrow \\ \frac{G E}{E F}=\frac{A M}{B M}=\frac{\lambda}{1-\lambda} . \end{gathered} $$  If $\mathcal{B}(A, M, E, B)$, interchanging the roles of $A$ and $B$ we similarly obtain $\frac{G E}{E F}=\frac{\lambda}{1-\lambda}$.
|
\frac{\lambda}{1-\lambda}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
11. (IND $\left.3^{\prime}\right)^{\mathrm{IMO}}$ Given a circle with two chords $A B, C D$ that meet at $E$, let $M$ be a point of chord $A B$ other than $E$. Draw the circle through $D, E$, and $M$. The tangent line to the circle $D E M$ at $E$ meets the lines $B C, A C$ at $F, G$, respectively. Given $\frac{A M}{A B}=\lambda$, find $\frac{G E}{E F}$.
|
11. Assume $\mathcal{B}(A, E, M, B)$. Since $A, B, C, D$ lie on a circle, we have $\angle G C E=$ $\angle M B D$ and $\angle M A D=\angle F C E$. Since $F D$ is tangent to the circle around $\triangle E M D$ at $E$, we have $\angle M D E=\angle F E B=\angle A E G$. Consequently, $\angle C E F=180^{\circ}-\angle C E A-\angle F E B=180^{\circ}-\angle M E D-\angle M D E=\angle E M D$ and $\angle C E G=180^{\circ}-\angle C E F=180^{\circ}-\angle E M D=\angle D M B$. It follows that $\triangle C E F \sim \triangle A M D$ and $\triangle C E G \sim$ $\triangle B M D$. From the first similarity we obtain $C E \cdot M D=A M \cdot E F$, and from the second we obtain $C E$. $M D=B M \cdot E G$. Hence $$ \begin{gathered} A M \cdot E F=B M \cdot E G \Longrightarrow \\ \frac{G E}{E F}=\frac{A M}{B M}=\frac{\lambda}{1-\lambda} . \end{gathered} $$  If $\mathcal{B}(A, M, E, B)$, interchanging the roles of $A$ and $B$ we similarly obtain $\frac{G E}{E F}=\frac{\lambda}{1-\lambda}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
51931521-3c2f-5772-9b61-7e7aa2e153a1
| 24,271
|
8. (HUN 1) For a given positive integer $k$ denote the square of the sum of its digits by $f_{1}(k)$ and let $f_{n+1}(k)=f_{1}\left(f_{n}(k)\right)$. Determine the value of $f_{1991}\left(2^{1990}\right)$.
|
8. Since $2^{1990}<8^{700}<10^{700}$, we have $f_{1}\left(2^{1990}\right)<(9 \cdot 700)^{2}<4 \cdot 10^{7}$. We then have $f_{2}\left(2^{1990}\right)<(3+9 \cdot 7)^{2}<4900$ and finally $f_{3}\left(2^{1990}\right)<(3+9 \cdot 3)^{2}=30^{2}$. It is easily shown that $f_{k}(n) \equiv f_{k-1}(n)^{2}(\bmod 9)$. Since $2^{6} \equiv 1(\bmod 9)$, we have $2^{1990} \equiv 2^{4} \equiv 7$ (all congruences in this problem will be $\bmod 9$ ). It follows that $f_{1}\left(2^{1990}\right) \equiv 7^{2} \equiv 4$ and $f_{2}\left(2^{1990}\right) \equiv 4^{2} \equiv 7$. Indeed, it follows that $f_{2 k}\left(2^{1990}\right) \equiv 7$ and $f_{2 k+1}\left(2^{1990}\right) \equiv 4$ for all integer $k>0$. Thus $f_{3}\left(2^{1990}\right)=r^{2}$ where $r<30$ is an integer and $r \equiv f_{2}\left(2^{1990}\right) \equiv 7$. It follows that $r \in\{7,16,25\}$ and hence $f_{3}\left(2^{1990}\right) \in\{49,256,625\}$. It follows that $f_{4}\left(2^{1990}\right)=169, f_{5}\left(2^{1990}\right)=256$, and inductively $f_{2 k}\left(2^{1990}\right)=169$ and $f_{2 k+1}\left(2^{1990}\right)=256$ for all integer $k>1$. Hence $f_{1991}\left(2^{1990}\right)=256$.
|
256
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
8. (HUN 1) For a given positive integer $k$ denote the square of the sum of its digits by $f_{1}(k)$ and let $f_{n+1}(k)=f_{1}\left(f_{n}(k)\right)$. Determine the value of $f_{1991}\left(2^{1990}\right)$.
|
8. Since $2^{1990}<8^{700}<10^{700}$, we have $f_{1}\left(2^{1990}\right)<(9 \cdot 700)^{2}<4 \cdot 10^{7}$. We then have $f_{2}\left(2^{1990}\right)<(3+9 \cdot 7)^{2}<4900$ and finally $f_{3}\left(2^{1990}\right)<(3+9 \cdot 3)^{2}=30^{2}$. It is easily shown that $f_{k}(n) \equiv f_{k-1}(n)^{2}(\bmod 9)$. Since $2^{6} \equiv 1(\bmod 9)$, we have $2^{1990} \equiv 2^{4} \equiv 7$ (all congruences in this problem will be $\bmod 9$ ). It follows that $f_{1}\left(2^{1990}\right) \equiv 7^{2} \equiv 4$ and $f_{2}\left(2^{1990}\right) \equiv 4^{2} \equiv 7$. Indeed, it follows that $f_{2 k}\left(2^{1990}\right) \equiv 7$ and $f_{2 k+1}\left(2^{1990}\right) \equiv 4$ for all integer $k>0$. Thus $f_{3}\left(2^{1990}\right)=r^{2}$ where $r<30$ is an integer and $r \equiv f_{2}\left(2^{1990}\right) \equiv 7$. It follows that $r \in\{7,16,25\}$ and hence $f_{3}\left(2^{1990}\right) \in\{49,256,625\}$. It follows that $f_{4}\left(2^{1990}\right)=169, f_{5}\left(2^{1990}\right)=256$, and inductively $f_{2 k}\left(2^{1990}\right)=169$ and $f_{2 k+1}\left(2^{1990}\right)=256$ for all integer $k>1$. Hence $f_{1991}\left(2^{1990}\right)=256$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
77d4ef2c-faf5-5268-820a-081e0084dfb6
| 24,328
|
12. $(\mathbf{C H N} 3)^{\mathrm{IMO} 3}$ Let $S=\{1,2,3, \ldots, 280\}$. Find the minimal natural number $n$ such that in any $n$-element subset of $S$ there are five numbers that are pairwise relatively prime.
|
12. Let $A_{m}$ be the set of those elements of $S$ which are divisible by $m$. By the inclusion-exclusion principle, the number of elements divisible by $2,3,5$ or 7 equals $$ \begin{aligned} & \left|A_{2} \cup A_{3} \cup A_{5} \cup A_{7}\right| \\ & =\left|A_{2}\right|+\left|A_{3}\right|+\left|A_{5}\right|+\left|A_{7}\right|-\left|A_{6}\right|-\left|A_{10}\right|-\left|A_{14}\right|-\left|A_{15}\right| \\ & \quad-\left|A_{21}\right|-\left|A_{35}\right|+\left|A_{30}\right|+\left|A_{42}\right|+\left|A_{70}\right|+\left|A_{105}\right|-\left|A_{210}\right| \\ & =140+93+56+40-46-28-20-18 \\ & \quad-13-8+9+6+4+2-1=216 . \end{aligned} $$ Among any five elements of the set $A_{2} \cup A_{3} \cup A_{5} \cup A_{7}$, one of the sets $A_{2}, A_{3}, A_{5}, A_{7}$ contains at least two, and those two are not relatively prime. Therefore $n>216$. We claim that the answer is $n=217$. First notice that the set $A_{2} \cup A_{3} \cup$ $A_{5} \cup A_{7}$ consists of four prime $(2,3,5,7)$ and 212 composite numbers. The set $S \backslash A$ contains exactly 8 composite numbers: namely, $11^{2}, 11 \cdot 13,11$. $17,11 \cdot 19,11 \cdot 23,13^{2}, 13 \cdot 17,13 \cdot 19$. Thus $S$ consists of the unity, 220 composite numbers and 59 primes. Let $A$ be a 217 -element subset of $S$, and suppose that there are no five pairwise relatively prime numbers in $A$. Then $A$ can contain at most 4 primes (or unity and three primes) and at least 213 composite numbers. Hence the set $S \backslash A$ contains at most 7 composite numbers. Consequently, at least one of the following 8 five-element sets is disjoint with $S \backslash A$, and is thus entirely contained in $A$ : $$ \begin{array}{ll} \{2 \cdot 23,3 \cdot 19,5 \cdot 17,7 \cdot 13,11 \cdot 11\}, & \{2 \cdot 29,3 \cdot 23,5 \cdot 19,7 \cdot 17,11 \cdot 13\}, \\ \{2 \cdot 31,3 \cdot 29,5 \cdot 23,7 \cdot 19,11 \cdot 17\}, & \{2 \cdot 37,3 \cdot 31,5 \cdot 29,7 \cdot 23,11 \cdot 19\}, \\ \{2 \cdot 41,3 \cdot 37,5 \cdot 31,7 \cdot 29,11 \cdot 23\}, & \{2 \cdot 43,3 \cdot 41,5 \cdot 37,7 \cdot 31,13 \cdot 17\}, \\ \{2 \cdot 47,3 \cdot 43,5 \cdot 41,7 \cdot 37,13 \cdot 19\}, & \{2 \cdot 2,3 \cdot 3,5 \cdot 5,7 \cdot 7,13 \cdot 13\} . \end{array} $$ As each of these sets consists of five numbers relatively prime in pairs, the claim is proved.
|
217
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
12. $(\mathbf{C H N} 3)^{\mathrm{IMO} 3}$ Let $S=\{1,2,3, \ldots, 280\}$. Find the minimal natural number $n$ such that in any $n$-element subset of $S$ there are five numbers that are pairwise relatively prime.
|
12. Let $A_{m}$ be the set of those elements of $S$ which are divisible by $m$. By the inclusion-exclusion principle, the number of elements divisible by $2,3,5$ or 7 equals $$ \begin{aligned} & \left|A_{2} \cup A_{3} \cup A_{5} \cup A_{7}\right| \\ & =\left|A_{2}\right|+\left|A_{3}\right|+\left|A_{5}\right|+\left|A_{7}\right|-\left|A_{6}\right|-\left|A_{10}\right|-\left|A_{14}\right|-\left|A_{15}\right| \\ & \quad-\left|A_{21}\right|-\left|A_{35}\right|+\left|A_{30}\right|+\left|A_{42}\right|+\left|A_{70}\right|+\left|A_{105}\right|-\left|A_{210}\right| \\ & =140+93+56+40-46-28-20-18 \\ & \quad-13-8+9+6+4+2-1=216 . \end{aligned} $$ Among any five elements of the set $A_{2} \cup A_{3} \cup A_{5} \cup A_{7}$, one of the sets $A_{2}, A_{3}, A_{5}, A_{7}$ contains at least two, and those two are not relatively prime. Therefore $n>216$. We claim that the answer is $n=217$. First notice that the set $A_{2} \cup A_{3} \cup$ $A_{5} \cup A_{7}$ consists of four prime $(2,3,5,7)$ and 212 composite numbers. The set $S \backslash A$ contains exactly 8 composite numbers: namely, $11^{2}, 11 \cdot 13,11$. $17,11 \cdot 19,11 \cdot 23,13^{2}, 13 \cdot 17,13 \cdot 19$. Thus $S$ consists of the unity, 220 composite numbers and 59 primes. Let $A$ be a 217 -element subset of $S$, and suppose that there are no five pairwise relatively prime numbers in $A$. Then $A$ can contain at most 4 primes (or unity and three primes) and at least 213 composite numbers. Hence the set $S \backslash A$ contains at most 7 composite numbers. Consequently, at least one of the following 8 five-element sets is disjoint with $S \backslash A$, and is thus entirely contained in $A$ : $$ \begin{array}{ll} \{2 \cdot 23,3 \cdot 19,5 \cdot 17,7 \cdot 13,11 \cdot 11\}, & \{2 \cdot 29,3 \cdot 23,5 \cdot 19,7 \cdot 17,11 \cdot 13\}, \\ \{2 \cdot 31,3 \cdot 29,5 \cdot 23,7 \cdot 19,11 \cdot 17\}, & \{2 \cdot 37,3 \cdot 31,5 \cdot 29,7 \cdot 23,11 \cdot 19\}, \\ \{2 \cdot 41,3 \cdot 37,5 \cdot 31,7 \cdot 29,11 \cdot 23\}, & \{2 \cdot 43,3 \cdot 41,5 \cdot 37,7 \cdot 31,13 \cdot 17\}, \\ \{2 \cdot 47,3 \cdot 43,5 \cdot 41,7 \cdot 37,13 \cdot 19\}, & \{2 \cdot 2,3 \cdot 3,5 \cdot 5,7 \cdot 7,13 \cdot 13\} . \end{array} $$ As each of these sets consists of five numbers relatively prime in pairs, the claim is proved.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2d6ee48c-ac95-548f-9976-e7d7dec482b9
| 24,340
|
18. (BUL 1) Find the highest degree $k$ of 1991 for which $1991^{k}$ divides the number $$ 1990^{1991^{1992}}+1992^{1991^{1990}} $$
|
18. For integers $a>0, n>0$ and $\alpha \geq 0$, we shall write $a^{\alpha} \| n$ when $a^{\alpha} \mid n$ and $a^{\alpha+1} \nmid n$. Lemma. For every odd number $a \geq 3$ and an integer $n \geq 0$ it holds that $$ a^{n+1} \|(a+1)^{a^{n}}-1 \quad \text { and } \quad a^{n+1} \|(a-1)^{a^{n}}+1 $$ Proof. We shall prove the first relation by induction (the second is analogous). For $n=0$ the statement is obvious. Suppose that it holds for some $n$, i.e. that $(1+a)^{a^{n}}=1+N a^{n+1}, a \nmid N$. Then $$ (1+a)^{a^{n+1}}=\left(1+N a^{n+1}\right)^{a}=1+a \cdot N a^{n+1}+\binom{a}{2} N^{2} a^{2 n+2}+M a^{3 n+3} $$ for some integer $M$. Since $\binom{a}{2}$ is divisible by $a$ for $a$ odd, we deduce that the part of the above sum behind $1+a \cdot N a^{n+1}$ is divisible by $a^{n+3}$. Hence $(1+a)^{a^{n+1}}=1+N^{\prime} a^{n+2}$, where $a \nmid N^{\prime}$. It follows immediately from Lemma that $$ 1991^{1993} \| 1990^{1991^{1992}}+1 \quad \text { and } \quad 1991^{1991} \| 1992^{1991^{1990}}-1 $$ Adding these two relations we obtain immediately that $k=1991$ is the desired value.
|
1991
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
18. (BUL 1) Find the highest degree $k$ of 1991 for which $1991^{k}$ divides the number $$ 1990^{1991^{1992}}+1992^{1991^{1990}} $$
|
18. For integers $a>0, n>0$ and $\alpha \geq 0$, we shall write $a^{\alpha} \| n$ when $a^{\alpha} \mid n$ and $a^{\alpha+1} \nmid n$. Lemma. For every odd number $a \geq 3$ and an integer $n \geq 0$ it holds that $$ a^{n+1} \|(a+1)^{a^{n}}-1 \quad \text { and } \quad a^{n+1} \|(a-1)^{a^{n}}+1 $$ Proof. We shall prove the first relation by induction (the second is analogous). For $n=0$ the statement is obvious. Suppose that it holds for some $n$, i.e. that $(1+a)^{a^{n}}=1+N a^{n+1}, a \nmid N$. Then $$ (1+a)^{a^{n+1}}=\left(1+N a^{n+1}\right)^{a}=1+a \cdot N a^{n+1}+\binom{a}{2} N^{2} a^{2 n+2}+M a^{3 n+3} $$ for some integer $M$. Since $\binom{a}{2}$ is divisible by $a$ for $a$ odd, we deduce that the part of the above sum behind $1+a \cdot N a^{n+1}$ is divisible by $a^{n+3}$. Hence $(1+a)^{a^{n+1}}=1+N^{\prime} a^{n+2}$, where $a \nmid N^{\prime}$. It follows immediately from Lemma that $$ 1991^{1993} \| 1990^{1991^{1992}}+1 \quad \text { and } \quad 1991^{1991} \| 1992^{1991^{1990}}-1 $$ Adding these two relations we obtain immediately that $k=1991$ is the desired value.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7898e1a8-df15-5484-96c7-beff4fa16bbe
| 24,354
|
27. (POL 2) Determine the maximum value of the sum $$ \sum_{i<j} x_{i} x_{j}\left(x_{i}+x_{j}\right) $$ over all $n$-tuples $\left(x_{1}, \ldots, x_{n}\right)$, satisfying $x_{i} \geq 0$ and $\sum_{i=1}^{n} x_{i}=1$.
|
27. Write $F\left(x_{1}, \ldots, x_{n}\right)=\sum_{i<j} x_{i} x_{j}\left(x_{i}+x_{j}\right)$. Choose an $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$, $\sum_{i=1}^{n} x_{i}=1, x_{i} \geq 0$ with at least three nonzero components, and assume w.l.o.g. that $x_{1} \geq \cdots \geq x_{k-1} \geq x_{k} \geq x_{k+1}=\cdots=x_{n}=0$. We claim that replacing $x_{k-1}, x_{k}$ with $x_{k-1}+x_{k}, 0$ the value of $F$ increases. Write for brevity $x_{k-1}=a, x_{k}=b$. Then $$ \begin{gathered} F(\ldots, a+b, 0,0, \ldots)-F(\ldots, a, b, 0, \ldots) \\ =\sum_{i=1}^{k-2} x_{i}(a+b)\left(x_{i}+a+b\right)-\sum_{i=1}^{k-2}\left[x_{i} a\left(x_{i}+a\right)+x_{i} b\left(x_{i}+b\right)\right]-a b(a+b) \end{gathered} $$ $$ =a b\left(2 \sum_{i=1}^{k-2} x_{i}-a-b\right)=a b(2-3(a+b))>0 $$ because $x_{k-1}+x_{k} \leq \frac{2}{3}\left(x_{1}+x_{k-1}+x_{k-2}\right) \leq \frac{2}{3}$. Repeating this procedure we can reduce the number of nonzero $x_{i}$ 's to two, increasing the value of $F$ in each step. It remains to maximize $F$ over $n$-tuples $\left(x_{1}, x_{2}, 0, \ldots, 0\right)$ with $x_{1}, x_{2} \geq 0, x_{1}+x_{2}=1$ : in this case $F$ equals $x_{1} x_{2}$ and attains its maximum value $\frac{1}{4}$ when $x_{1}=x_{2}=\frac{1}{2}, x_{3}=\ldots, x_{n}=0$.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
27. (POL 2) Determine the maximum value of the sum $$ \sum_{i<j} x_{i} x_{j}\left(x_{i}+x_{j}\right) $$ over all $n$-tuples $\left(x_{1}, \ldots, x_{n}\right)$, satisfying $x_{i} \geq 0$ and $\sum_{i=1}^{n} x_{i}=1$.
|
27. Write $F\left(x_{1}, \ldots, x_{n}\right)=\sum_{i<j} x_{i} x_{j}\left(x_{i}+x_{j}\right)$. Choose an $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$, $\sum_{i=1}^{n} x_{i}=1, x_{i} \geq 0$ with at least three nonzero components, and assume w.l.o.g. that $x_{1} \geq \cdots \geq x_{k-1} \geq x_{k} \geq x_{k+1}=\cdots=x_{n}=0$. We claim that replacing $x_{k-1}, x_{k}$ with $x_{k-1}+x_{k}, 0$ the value of $F$ increases. Write for brevity $x_{k-1}=a, x_{k}=b$. Then $$ \begin{gathered} F(\ldots, a+b, 0,0, \ldots)-F(\ldots, a, b, 0, \ldots) \\ =\sum_{i=1}^{k-2} x_{i}(a+b)\left(x_{i}+a+b\right)-\sum_{i=1}^{k-2}\left[x_{i} a\left(x_{i}+a\right)+x_{i} b\left(x_{i}+b\right)\right]-a b(a+b) \end{gathered} $$ $$ =a b\left(2 \sum_{i=1}^{k-2} x_{i}-a-b\right)=a b(2-3(a+b))>0 $$ because $x_{k-1}+x_{k} \leq \frac{2}{3}\left(x_{1}+x_{k-1}+x_{k-2}\right) \leq \frac{2}{3}$. Repeating this procedure we can reduce the number of nonzero $x_{i}$ 's to two, increasing the value of $F$ in each step. It remains to maximize $F$ over $n$-tuples $\left(x_{1}, x_{2}, 0, \ldots, 0\right)$ with $x_{1}, x_{2} \geq 0, x_{1}+x_{2}=1$ : in this case $F$ equals $x_{1} x_{2}$ and attains its maximum value $\frac{1}{4}$ when $x_{1}=x_{2}=\frac{1}{2}, x_{3}=\ldots, x_{n}=0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9fec8e6-876b-5ab9-8643-13b33cb54c4a
| 24,376
|
14. (POL 2) For any positive integer $x$ define $$ \begin{aligned} g(x) & =\text { greatest odd divisor of } x, \\ f(x) & =\left\{\begin{array}{l} x / 2+x / g(x), \text { if } x \text { is even; } \\ 2^{(x+1) / 2}, \text { if } x \text { is odd. } \end{array}\right. \end{aligned} $$ Construct the sequence $x_{1}=1, x_{n+1}=f\left(x_{n}\right)$. Show that the number 1992 appears in this sequence, determine the least $n$ such that $x_{n}=1992$, and determine whether $n$ is unique.
|
14. We see that $x_{1}=2^{0}$. Suppose that for some $m, r \in \mathbb{N}$ we have $x_{m}=2^{r}$. Then inductively $x_{m+i}=2^{r-i}(2 i+1)$ for $i=1,2, \ldots, r$ and $x_{m+r+1}=$ $2^{r+1}$. Since every natural number can be uniquely represented as the product of an odd number and a power of two, we conclude that every natural number occurs in our sequence exactly once. Moreover, it follows that $2 k-1=x_{k(k+1) / 2}$. Thus $x_{n}=1992=2^{3} \cdot 249$ implies that $x_{n+3}=255=2 \cdot 128-1=x_{128 \cdot 129 / 2}=x_{8256}$. Hence $n=8253$.
|
8253
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
14. (POL 2) For any positive integer $x$ define $$ \begin{aligned} g(x) & =\text { greatest odd divisor of } x, \\ f(x) & =\left\{\begin{array}{l} x / 2+x / g(x), \text { if } x \text { is even; } \\ 2^{(x+1) / 2}, \text { if } x \text { is odd. } \end{array}\right. \end{aligned} $$ Construct the sequence $x_{1}=1, x_{n+1}=f\left(x_{n}\right)$. Show that the number 1992 appears in this sequence, determine the least $n$ such that $x_{n}=1992$, and determine whether $n$ is unique.
|
14. We see that $x_{1}=2^{0}$. Suppose that for some $m, r \in \mathbb{N}$ we have $x_{m}=2^{r}$. Then inductively $x_{m+i}=2^{r-i}(2 i+1)$ for $i=1,2, \ldots, r$ and $x_{m+r+1}=$ $2^{r+1}$. Since every natural number can be uniquely represented as the product of an odd number and a power of two, we conclude that every natural number occurs in our sequence exactly once. Moreover, it follows that $2 k-1=x_{k(k+1) / 2}$. Thus $x_{n}=1992=2^{3} \cdot 249$ implies that $x_{n+3}=255=2 \cdot 128-1=x_{128 \cdot 129 / 2}=x_{8256}$. Hence $n=8253$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
127e4a61-89f2-5293-955b-a724db32322d
| 24,415
|
4. $(\mathbf{C H N} 3)^{\mathrm{IMO}}$ Given nine points in space, no four of which are coplanar, find the minimal natural number $n$ such that for any coloring with red or blue of $n$ edges drawn between these nine points there always exists a triangle having all edges of the same color.
|
4. There are 36 possible edges in total. If not more than 3 edges are left undrawn, then we can choose 6 of the given 9 points no two of which are connected by an undrawn edge. These 6 points together with the edges between them form a two-colored complete graph, and thus by a wellknown result there exists at least one monochromatic triangle. It follows that $n \leq 33$. In order to show that $n=33$, we shall give an example of a graph with 32 edges that does not contain a monochromatic triangle. Let us start with a complete graph $C_{5}$ with 5 vertices. Its edges can be colored in two colors so that there is no monochromatic triangle (Fig. 1). Furthermore, given a graph $\mathcal{H}$ with $k$ vertices without monochromatic triangles, we can add to it a new vertex, join it to all vertices of $\mathcal{H}$ except $A$, and color each edge $B X$ in the same way as $A X$. The obtained graph obviously contains no monochromatic triangles. Applying this construction four times to the graph $C_{5}$ we get an example like that of Fig. 2.  Fig. 1  Fig. 2 Second solution. For simplicity, we call the colors red and blue. Let $r(k, l)$ be the least positive integer $r$ such that each complete $r$-graph whose edges are colored in red and blue contains either a complete red $k$-graph or a complete blue $l$-graph. Also, let $t(n, k)$ be the greatest possible number of edges in a graph with $n$ vertices that does not contain a complete $k$-graph. These numbers exist by the theorems of Ramsey and Turán. Let us assume that $r(k, l)<n$. Every graph with $n$ vertices and $t(n, r(k, l))$ +1 edges contains a complete subgraph with $r(k, l)$ vertices, and this subgraph contains either a red complete $k$-graph or a blue complete $l$ graph. We claim that $t(n, r(k, l))+1$ is the smallest number of edges with the above property. By the definition of $r(k, l)$ there exists a coloring of the complete graph $H$ with $r(k, l)-1$ vertices in two colors such that no red complete $k$-graph or blue complete $l$-graph exists. Let $c_{i j}$ be the color in which the edge $(i, j)$ of $H$ is colored, $1 \leq i<j \leq r(k, l)-1$. Consider a complete $r(k, l)$-1-partite graph $G$ with $n$ vertices and exactly $t(n, r(k, l))$ edges and denote its partitions by $P_{i}, i=1, \ldots, r(k, l)-1$. If we color each edge of $H$ between $P_{i}$ and $P_{j}(j<i)$ in the color $c_{i j}$, we obviously obtain a graph with $n$ vertices and $t(n, r(k, l))$ edges in two colors that contains neither a red complete $k$-graph nor a blue complete $l$-graph. Therefore the answer to our problem is $t(9, r(3,3))+1=t(9,6)+1=33$.
|
33
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
4. $(\mathbf{C H N} 3)^{\mathrm{IMO}}$ Given nine points in space, no four of which are coplanar, find the minimal natural number $n$ such that for any coloring with red or blue of $n$ edges drawn between these nine points there always exists a triangle having all edges of the same color.
|
4. There are 36 possible edges in total. If not more than 3 edges are left undrawn, then we can choose 6 of the given 9 points no two of which are connected by an undrawn edge. These 6 points together with the edges between them form a two-colored complete graph, and thus by a wellknown result there exists at least one monochromatic triangle. It follows that $n \leq 33$. In order to show that $n=33$, we shall give an example of a graph with 32 edges that does not contain a monochromatic triangle. Let us start with a complete graph $C_{5}$ with 5 vertices. Its edges can be colored in two colors so that there is no monochromatic triangle (Fig. 1). Furthermore, given a graph $\mathcal{H}$ with $k$ vertices without monochromatic triangles, we can add to it a new vertex, join it to all vertices of $\mathcal{H}$ except $A$, and color each edge $B X$ in the same way as $A X$. The obtained graph obviously contains no monochromatic triangles. Applying this construction four times to the graph $C_{5}$ we get an example like that of Fig. 2.  Fig. 1  Fig. 2 Second solution. For simplicity, we call the colors red and blue. Let $r(k, l)$ be the least positive integer $r$ such that each complete $r$-graph whose edges are colored in red and blue contains either a complete red $k$-graph or a complete blue $l$-graph. Also, let $t(n, k)$ be the greatest possible number of edges in a graph with $n$ vertices that does not contain a complete $k$-graph. These numbers exist by the theorems of Ramsey and Turán. Let us assume that $r(k, l)<n$. Every graph with $n$ vertices and $t(n, r(k, l))$ +1 edges contains a complete subgraph with $r(k, l)$ vertices, and this subgraph contains either a red complete $k$-graph or a blue complete $l$ graph. We claim that $t(n, r(k, l))+1$ is the smallest number of edges with the above property. By the definition of $r(k, l)$ there exists a coloring of the complete graph $H$ with $r(k, l)-1$ vertices in two colors such that no red complete $k$-graph or blue complete $l$-graph exists. Let $c_{i j}$ be the color in which the edge $(i, j)$ of $H$ is colored, $1 \leq i<j \leq r(k, l)-1$. Consider a complete $r(k, l)$-1-partite graph $G$ with $n$ vertices and exactly $t(n, r(k, l))$ edges and denote its partitions by $P_{i}, i=1, \ldots, r(k, l)-1$. If we color each edge of $H$ between $P_{i}$ and $P_{j}(j<i)$ in the color $c_{i j}$, we obviously obtain a graph with $n$ vertices and $t(n, r(k, l))$ edges in two colors that contains neither a red complete $k$-graph nor a blue complete $l$-graph. Therefore the answer to our problem is $t(9, r(3,3))+1=t(9,6)+1=33$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2ae10712-5281-5c69-89c3-7537dbaff98a
| 24,440
|
18. N1 (BUL) $M$ is a subset of $\{1,2,3, \ldots, 15\}$ such that the product of any three distinct elements of $M$ is not a square. Determine the maximum number of elements in $M$.
|
18. Since for each of the subsets $\{1,4,9\},\{2,6,12\},\{3,5,15\}$ and $\{7,8,14\}$ the product of its elements is a square and these subsets are disjoint, we have $|M| \leq 11$. Suppose that $|M|=11$. Then $10 \in M$ and none of the disjoint subsets $\{1,4,9\},\{2,5\},\{6,15\},\{7,8,14\}$ is a subset of $M$. Consequently $\{3,12\} \subset M$, so none of $\{1\},\{4\},\{9\},\{2,6\},\{5,15\}$, and $\{7,8,14\}$ is a subset of $M$ : thus $|M| \leq 9$, a contradiction. It follows that $|M| \leq 10$, and this number is attained in the case $M=\{1,4,5,6,7,10,11,12,13,14\}$.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
18. N1 (BUL) $M$ is a subset of $\{1,2,3, \ldots, 15\}$ such that the product of any three distinct elements of $M$ is not a square. Determine the maximum number of elements in $M$.
|
18. Since for each of the subsets $\{1,4,9\},\{2,6,12\},\{3,5,15\}$ and $\{7,8,14\}$ the product of its elements is a square and these subsets are disjoint, we have $|M| \leq 11$. Suppose that $|M|=11$. Then $10 \in M$ and none of the disjoint subsets $\{1,4,9\},\{2,5\},\{6,15\},\{7,8,14\}$ is a subset of $M$. Consequently $\{3,12\} \subset M$, so none of $\{1\},\{4\},\{9\},\{2,6\},\{5,15\}$, and $\{7,8,14\}$ is a subset of $M$ : thus $|M| \leq 9$, a contradiction. It follows that $|M| \leq 10$, and this number is attained in the case $M=\{1,4,5,6,7,10,11,12,13,14\}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
936a6fdc-a932-5d05-8f85-c23c0b2ed3c6
| 24,547
|
21. N4 (FRA) For any positive integer $x_{0}$, three sequences $\left\{x_{n}\right\},\left\{y_{n}\right\}$, and $\left\{z_{n}\right\}$ are defined as follows: (i) $y_{0}=4$ and $z_{0}=1$; (ii) if $x_{n}$ is even for $n \geq 0, x_{n+1}=\frac{x_{n}}{2}, y_{n+1}=2 y_{n}$, and $z_{n+1}=z_{n}$; (iii) if $x_{n}$ is odd for $n \geq 0, x_{n+1}=x_{n}-\frac{y_{n}}{2}-z_{n}, y_{n+1}=y_{n}$, and $z_{n+1}=$ $y_{n}+z_{n}$. The integer $x_{0}$ is said to be good if $x_{n}=0$ for some $n \geq 1$. Find the number of good integers less than or equal to 1994.
|
21. Note first that $y_{n}=2^{k}(k \geq 2)$ and $z_{k} \equiv 1(\bmod 4)$ for all $n$, so if $x_{n}$ is odd, $x_{n+1}$ will be even. Further, it is shown by induction on $n$ that $y_{n}>z_{n}$ when $x_{n-1}$ is even and $2 y_{n}>z_{n}>y_{n}$ when $x_{n-1}$ is odd. In fact, $n=1$ is the trivial case, while if it holds for $n \geq 1$, then $y_{n+1}=2 y_{n}>z_{n}=z_{n+1}$ if $x_{n}$ is even, and $2 y_{n+1}=2 y_{n}>y_{n}+z_{n}=z_{n+1}$ if $x_{n}$ is odd (since then $x_{n-1}$ is even). If $x_{1}=0$, then $x_{0}=3$ is good. Suppose $x_{n}=0$ for some $n \geq 2$. Then $x_{n-1}$ is odd and $x_{n-2}$ is even, so that $y_{n-1}>z_{n-1}$. We claim that a pair $\left(y_{n-1}, z_{n-1}\right)$, where $2^{k}=y_{n-1}>z_{n-1}>0$ and $z_{n-1} \equiv 1$ $(\bmod 4)$, uniquely determines $x_{0}=f\left(y_{n-1}, z_{n-1}\right)$. We see that $x_{n-1}=$ $\frac{1}{2} y_{n-1}+z_{n-1}$, and define $\left(x_{k}, y_{k}, z_{k}\right)$ backwards as follows, until we get $\left(y_{k}, z_{k}\right)=(4,1)$. If $y_{k}>z_{k}$, then $x_{k-1}$ must have been even, so we define $\left(x_{k-1}, y_{k-1}, z_{k-1}\right)=\left(2 x_{k}, y_{k} / 2, z_{k}\right)$; otherwise $x_{k-1}$ must have been odd, so we put $\left(x_{k-1}, y_{k-1}, z_{k-1}\right)=\left(x_{k}-y_{k} / 2+z_{k}, y_{k}, z_{k}-y_{k}\right)$. We eventually arrive at $\left(y_{0}, z_{0}\right)=(4,1)$ and a good integer $x_{0}=f\left(y_{n-1}, z_{n-1}\right)$, as claimed. Thus for example $\left(y_{n-1}, z_{n-1}\right)=(64,61)$ implies $x_{n-1}=93$, $\left(x_{n-2}, y_{n-2}, z_{n-2}\right)=(186,32,61)$ etc., and $x_{0}=1953$, while in the case of $\left(y_{n-1}, z_{n-1}\right)=(128,1)$ we get $x_{0}=2080$. Note that $y^{\prime}>y \Rightarrow f\left(y^{\prime}, z^{\prime}\right)>f(y, z)$ and $z^{\prime}>z \Rightarrow f\left(y, z^{\prime}\right)>f(y, z)$. Therefore there are no $y, z$ for which $1953<f(y, z)<2080$. Hence all good integers less than or equal to 1994 are given as $f(y, z), y=2^{k} \leq 64$ and $0<z \equiv 1(\bmod 4)$, and the number of $\operatorname{such}(y, z)$ equals $1+2+4+8+16=$ 31. So the answer is 31 .
|
31
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
21. N4 (FRA) For any positive integer $x_{0}$, three sequences $\left\{x_{n}\right\},\left\{y_{n}\right\}$, and $\left\{z_{n}\right\}$ are defined as follows: (i) $y_{0}=4$ and $z_{0}=1$; (ii) if $x_{n}$ is even for $n \geq 0, x_{n+1}=\frac{x_{n}}{2}, y_{n+1}=2 y_{n}$, and $z_{n+1}=z_{n}$; (iii) if $x_{n}$ is odd for $n \geq 0, x_{n+1}=x_{n}-\frac{y_{n}}{2}-z_{n}, y_{n+1}=y_{n}$, and $z_{n+1}=$ $y_{n}+z_{n}$. The integer $x_{0}$ is said to be good if $x_{n}=0$ for some $n \geq 1$. Find the number of good integers less than or equal to 1994.
|
21. Note first that $y_{n}=2^{k}(k \geq 2)$ and $z_{k} \equiv 1(\bmod 4)$ for all $n$, so if $x_{n}$ is odd, $x_{n+1}$ will be even. Further, it is shown by induction on $n$ that $y_{n}>z_{n}$ when $x_{n-1}$ is even and $2 y_{n}>z_{n}>y_{n}$ when $x_{n-1}$ is odd. In fact, $n=1$ is the trivial case, while if it holds for $n \geq 1$, then $y_{n+1}=2 y_{n}>z_{n}=z_{n+1}$ if $x_{n}$ is even, and $2 y_{n+1}=2 y_{n}>y_{n}+z_{n}=z_{n+1}$ if $x_{n}$ is odd (since then $x_{n-1}$ is even). If $x_{1}=0$, then $x_{0}=3$ is good. Suppose $x_{n}=0$ for some $n \geq 2$. Then $x_{n-1}$ is odd and $x_{n-2}$ is even, so that $y_{n-1}>z_{n-1}$. We claim that a pair $\left(y_{n-1}, z_{n-1}\right)$, where $2^{k}=y_{n-1}>z_{n-1}>0$ and $z_{n-1} \equiv 1$ $(\bmod 4)$, uniquely determines $x_{0}=f\left(y_{n-1}, z_{n-1}\right)$. We see that $x_{n-1}=$ $\frac{1}{2} y_{n-1}+z_{n-1}$, and define $\left(x_{k}, y_{k}, z_{k}\right)$ backwards as follows, until we get $\left(y_{k}, z_{k}\right)=(4,1)$. If $y_{k}>z_{k}$, then $x_{k-1}$ must have been even, so we define $\left(x_{k-1}, y_{k-1}, z_{k-1}\right)=\left(2 x_{k}, y_{k} / 2, z_{k}\right)$; otherwise $x_{k-1}$ must have been odd, so we put $\left(x_{k-1}, y_{k-1}, z_{k-1}\right)=\left(x_{k}-y_{k} / 2+z_{k}, y_{k}, z_{k}-y_{k}\right)$. We eventually arrive at $\left(y_{0}, z_{0}\right)=(4,1)$ and a good integer $x_{0}=f\left(y_{n-1}, z_{n-1}\right)$, as claimed. Thus for example $\left(y_{n-1}, z_{n-1}\right)=(64,61)$ implies $x_{n-1}=93$, $\left(x_{n-2}, y_{n-2}, z_{n-2}\right)=(186,32,61)$ etc., and $x_{0}=1953$, while in the case of $\left(y_{n-1}, z_{n-1}\right)=(128,1)$ we get $x_{0}=2080$. Note that $y^{\prime}>y \Rightarrow f\left(y^{\prime}, z^{\prime}\right)>f(y, z)$ and $z^{\prime}>z \Rightarrow f\left(y, z^{\prime}\right)>f(y, z)$. Therefore there are no $y, z$ for which $1953<f(y, z)<2080$. Hence all good integers less than or equal to 1994 are given as $f(y, z), y=2^{k} \leq 64$ and $0<z \equiv 1(\bmod 4)$, and the number of $\operatorname{such}(y, z)$ equals $1+2+4+8+16=$ 31. So the answer is 31 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
538c4cbf-b450-55d2-babf-e618c5ad19e6
| 24,557
|
6. C1 (UKR) On a $5 \times 5$ board, two players alternately mark numbers on empty cells. The first player always marks 1's, the second 0's. One number is marked per turn, until the board is filled. For each of the nine $3 \times 3$ squares the sum of the nine numbers on its cells is computed. Denote by $A$ the maximum of these sums. How large can the first player make $A$, regardless of the responses of the second player?
|
6. Call the first and second player $M$ and $N$ respectively. $N$ can keep $A \leq 6$. Indeed, let 10 dominoes be placed as shown in the picture, and whenever $M$ marks a 1 in a cell of some domino, let $N$ mark 0 in the other cell of that domino if it is still empty. Since any $3 \times 3$ square contains at least three complete domi-  noes, there are at least three 0 's inside. Hence $A \leq 6$. We now show that $M$ can make $A=6$. Let him start by marking 1 in $c 3$. By symmetry, we may assume that $N$ 's response is made in row 4 or 5 . Then $M$ marks 1 in $c 2$. If $N$ puts 0 in $c 1$, then $M$ can always mark two 1's in $b \times\{1,2,3\}$ as well as three 1's in $\{a, d\} \times\{1,2,3\}$. Thus either $\{a, b, c\} \times\{1,2,3\}$ or $\{b, c, d\} \times\{1,2,3\}$ will contain six 1's. However, if $N$ does not play his second move in $c 1$, then $M$ plays there, and thus he can easily achieve to have six 1's either in $\{a, b, c\} \times\{1,2,3\}$ or $\{c, d, e\} \times\{1,2,3\}$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
6. C1 (UKR) On a $5 \times 5$ board, two players alternately mark numbers on empty cells. The first player always marks 1's, the second 0's. One number is marked per turn, until the board is filled. For each of the nine $3 \times 3$ squares the sum of the nine numbers on its cells is computed. Denote by $A$ the maximum of these sums. How large can the first player make $A$, regardless of the responses of the second player?
|
6. Call the first and second player $M$ and $N$ respectively. $N$ can keep $A \leq 6$. Indeed, let 10 dominoes be placed as shown in the picture, and whenever $M$ marks a 1 in a cell of some domino, let $N$ mark 0 in the other cell of that domino if it is still empty. Since any $3 \times 3$ square contains at least three complete domi-  noes, there are at least three 0 's inside. Hence $A \leq 6$. We now show that $M$ can make $A=6$. Let him start by marking 1 in $c 3$. By symmetry, we may assume that $N$ 's response is made in row 4 or 5 . Then $M$ marks 1 in $c 2$. If $N$ puts 0 in $c 1$, then $M$ can always mark two 1's in $b \times\{1,2,3\}$ as well as three 1's in $\{a, d\} \times\{1,2,3\}$. Thus either $\{a, b, c\} \times\{1,2,3\}$ or $\{b, c, d\} \times\{1,2,3\}$ will contain six 1's. However, if $N$ does not play his second move in $c 1$, then $M$ plays there, and thus he can easily achieve to have six 1's either in $\{a, b, c\} \times\{1,2,3\}$ or $\{c, d, e\} \times\{1,2,3\}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef4c80c1-4491-5501-8c08-03b3faaf1277
| 24,576
|
19. N5 (IRE) At a meeting of $12 k$ people, each person exchanges greetings with exactly $3 k+6$ others. For any two people, the number who exchange greetings with both is the same. How many people are at the meeting?
|
19. For each two people let $n$ be the number of people exchanging greetings with both of them. To determine $n$ in terms of $k$, we shall count in two ways the number of triples $(A, B, C)$ of people such that $A$ exchanged greetings with both $B$ and $C$, but $B$ and $C$ mutually did not. There are $12 k$ possibilities for $A$, and for each $A$ there are $(3 k+6)$ possibilities for $B$. Since there are $n$ people who exchanged greetings with both $A$ and $B$, there are $3 k+5-n$ who did so with $A$ but not with $B$. Thus the number of triples $(A, B, C)$ is $12 k(3 k+6)(3 k+5-n)$. On the other hand, there are $12 k$ possible choices of $B$, and $12 k-1-(3 k+6)=9 k-7$ possible choices of $C$; for every $B, C, A$ can be chosen in $n$ ways, so the number of considered triples equals $12 k n(9 k-7)$. Hence $(3 k+6)(3 k+5-n)=n(9 k-7)$, i.e., $n=\frac{3(k+2)(3 k+5)}{12 k-1}$. This gives us that $\frac{4 n}{3}=\frac{12 k^{2}+44 k+40}{12 k-1}=k+4-\frac{3 k-44}{12 k-1}$ is an integer too. It is directly verified that only $k=3$ gives an integer value for $n$, namely $n=6$. Remark. The solution is complete under the assumption that such a $k$ exists. We give an example of such a party with 36 persons, $k=3$. Let the people sit in a $6 \times 6$ array $\left[P_{i j}\right]_{i, j=1}^{6}$, and suppose that two persons $P_{i j}, P_{k l}$ exchanged greetings if and only if $i=k$ or $j=l$ or $i-j \equiv k-l$ (mod 6). Thus each person exchanged greetings with exactly 15 others, and it is easily verified that this party satisfies the conditions.
|
36
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
19. N5 (IRE) At a meeting of $12 k$ people, each person exchanges greetings with exactly $3 k+6$ others. For any two people, the number who exchange greetings with both is the same. How many people are at the meeting?
|
19. For each two people let $n$ be the number of people exchanging greetings with both of them. To determine $n$ in terms of $k$, we shall count in two ways the number of triples $(A, B, C)$ of people such that $A$ exchanged greetings with both $B$ and $C$, but $B$ and $C$ mutually did not. There are $12 k$ possibilities for $A$, and for each $A$ there are $(3 k+6)$ possibilities for $B$. Since there are $n$ people who exchanged greetings with both $A$ and $B$, there are $3 k+5-n$ who did so with $A$ but not with $B$. Thus the number of triples $(A, B, C)$ is $12 k(3 k+6)(3 k+5-n)$. On the other hand, there are $12 k$ possible choices of $B$, and $12 k-1-(3 k+6)=9 k-7$ possible choices of $C$; for every $B, C, A$ can be chosen in $n$ ways, so the number of considered triples equals $12 k n(9 k-7)$. Hence $(3 k+6)(3 k+5-n)=n(9 k-7)$, i.e., $n=\frac{3(k+2)(3 k+5)}{12 k-1}$. This gives us that $\frac{4 n}{3}=\frac{12 k^{2}+44 k+40}{12 k-1}=k+4-\frac{3 k-44}{12 k-1}$ is an integer too. It is directly verified that only $k=3$ gives an integer value for $n$, namely $n=6$. Remark. The solution is complete under the assumption that such a $k$ exists. We give an example of such a party with 36 persons, $k=3$. Let the people sit in a $6 \times 6$ array $\left[P_{i j}\right]_{i, j=1}^{6}$, and suppose that two persons $P_{i j}, P_{k l}$ exchanged greetings if and only if $i=k$ or $j=l$ or $i-j \equiv k-l$ (mod 6). Thus each person exchanged greetings with exactly 15 others, and it is easily verified that this party satisfies the conditions.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
43e6870a-160c-586d-bae7-fc4a465fa992
| 24,613
|
24. S2 (POL) ${ }^{\text {IMO4 }}$ The positive real numbers $x_{0}, x_{1}, \ldots, x_{1995}$ satisfy $x_{0}=$ $x_{1995}$ and $$ x_{i-1}+\frac{2}{x_{i-1}}=2 x_{i}+\frac{1}{x_{i}} $$ for $i=1,2, \ldots, 1995$. Find the maximum value that $x_{0}$ can have.
|
24. The given condition is equivalent to $\left(2 x_{i}-x_{i-1}\right)\left(x_{i} x_{i-1}-1\right)=0$, so either $x_{i}=\frac{1}{2} x_{i-1}$ or $x_{i}=\frac{1}{x_{i-1}}$. We shall show by induction on $n$ that for any $n \geq 0, x_{n}=2^{k_{n}} x_{0}^{e_{n}}$ for some integer $k_{n}$, where $\left|k_{n}\right| \leq n$ and $e_{n}=(-1)^{n-k_{n}}$. Indeed, this is true for $n=0$. If it holds for some $n$, then $x_{n+1}=\frac{1}{2} x_{n}=2^{k_{n}-1} x_{0}^{e_{n}}$ (hence $k_{n+1}=k_{n}-1$ and $e_{n+1}=e_{n}$ ) or $x_{n+1}=\frac{1}{x_{n}}=2^{-k_{n}} x_{0}^{-e_{n}}$ (hence $k_{n+1}=-k_{n}$ and $e_{n+1}=-e_{n}$ ). Thus $x_{0}=x_{1995}=2^{k_{1995}} x_{0}^{e_{1995}}$. Note that $e_{1995}=1$ is impossible, since in that case $k_{1995}$ would be odd, although it should equal 0 . Therefore $e^{1995}=-1$, which gives $x_{0}^{2}=2^{k_{1995}} \leq 2^{1994}$, so the maximal value that $x_{0}$ can have is $2^{997}$. This value is attained in the case $x_{i}=2^{997-i}$ for $i=0, \ldots, 997$ and $x_{i}=2^{i-998}$ for $i=998, \ldots, 1995$. Second solution. First we show that there is an $n, 0 \leq n \leq 1995$, such that $x_{n}=1$. Suppose the contrary. Then each of $x_{n}$ belongs to one of the intervals $I_{-i-1}=\left[2^{-i-1}, 2^{-i}\right)$ or $I_{i}=\left(2^{i}, 2^{i+1}\right]$, where $i=0,1,2, \ldots$ Let $x_{n} \in I_{i_{n}}$. Note that by the formula for $x_{n}, i_{n}$ and $i_{n-1}$ are of different parity. Hence $i_{0}$ and $i_{1995}$ are also of different parity, contradicting $x_{0}=$ $x_{1995}$. It follows that for some $n, x_{n}=1$. Now if $n \leq 997$, then $x_{0} \leq 2^{997}$, while if $n \geq 998$, we also have $x_{0}=x_{1995} \leq 2^{997}$.
|
2^{997}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
24. S2 (POL) ${ }^{\text {IMO4 }}$ The positive real numbers $x_{0}, x_{1}, \ldots, x_{1995}$ satisfy $x_{0}=$ $x_{1995}$ and $$ x_{i-1}+\frac{2}{x_{i-1}}=2 x_{i}+\frac{1}{x_{i}} $$ for $i=1,2, \ldots, 1995$. Find the maximum value that $x_{0}$ can have.
|
24. The given condition is equivalent to $\left(2 x_{i}-x_{i-1}\right)\left(x_{i} x_{i-1}-1\right)=0$, so either $x_{i}=\frac{1}{2} x_{i-1}$ or $x_{i}=\frac{1}{x_{i-1}}$. We shall show by induction on $n$ that for any $n \geq 0, x_{n}=2^{k_{n}} x_{0}^{e_{n}}$ for some integer $k_{n}$, where $\left|k_{n}\right| \leq n$ and $e_{n}=(-1)^{n-k_{n}}$. Indeed, this is true for $n=0$. If it holds for some $n$, then $x_{n+1}=\frac{1}{2} x_{n}=2^{k_{n}-1} x_{0}^{e_{n}}$ (hence $k_{n+1}=k_{n}-1$ and $e_{n+1}=e_{n}$ ) or $x_{n+1}=\frac{1}{x_{n}}=2^{-k_{n}} x_{0}^{-e_{n}}$ (hence $k_{n+1}=-k_{n}$ and $e_{n+1}=-e_{n}$ ). Thus $x_{0}=x_{1995}=2^{k_{1995}} x_{0}^{e_{1995}}$. Note that $e_{1995}=1$ is impossible, since in that case $k_{1995}$ would be odd, although it should equal 0 . Therefore $e^{1995}=-1$, which gives $x_{0}^{2}=2^{k_{1995}} \leq 2^{1994}$, so the maximal value that $x_{0}$ can have is $2^{997}$. This value is attained in the case $x_{i}=2^{997-i}$ for $i=0, \ldots, 997$ and $x_{i}=2^{i-998}$ for $i=998, \ldots, 1995$. Second solution. First we show that there is an $n, 0 \leq n \leq 1995$, such that $x_{n}=1$. Suppose the contrary. Then each of $x_{n}$ belongs to one of the intervals $I_{-i-1}=\left[2^{-i-1}, 2^{-i}\right)$ or $I_{i}=\left(2^{i}, 2^{i+1}\right]$, where $i=0,1,2, \ldots$ Let $x_{n} \in I_{i_{n}}$. Note that by the formula for $x_{n}, i_{n}$ and $i_{n-1}$ are of different parity. Hence $i_{0}$ and $i_{1995}$ are also of different parity, contradicting $x_{0}=$ $x_{1995}$. It follows that for some $n, x_{n}=1$. Now if $n \leq 997$, then $x_{0} \leq 2^{997}$, while if $n \geq 998$, we also have $x_{0}=x_{1995} \leq 2^{997}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
207bc5bd-c447-500d-a47e-3210d9460377
| 24,629
|
25. S3 (POL) For an integer $x \geq 1$, let $p(x)$ be the least prime that does not divide $x$, and define $q(x)$ to be the product of all primes less than $p(x)$. In particular, $p(1)=2$. For $x$ such that $p(x)=2$, define $q(x)=1$. Consider the sequence $x_{0}, x_{1}, x_{2}, \ldots$ defined by $x_{0}=1$ and $$ x_{n+1}=\frac{x_{n} p\left(x_{n}\right)}{q\left(x_{n}\right)} $$ for $n \geq 0$. Find all $n$ such that $x_{n}=1995$.
|
25. By the definition of $q(x)$, it divides $x$ for all integers $x>0$, so $f(x)=$ $x p(x) / q(x)$ is a positive integer too. Let $\left\{p_{0}, p_{1}, p_{2}, \ldots\right\}$ be all prime numbers in increasing order. Since it easily follows by induction that all $x_{n}$ 's are square-free, we can assign to each of them a unique code according to which primes divide it: if $p_{m}$ is the largest prime dividing $x_{n}$, the code corresponding to $x_{n}$ will be $\ldots 0 s_{m} s_{m-1} \ldots s_{0}$, with $s_{i}=1$ if $p_{i} \mid x_{n}$ and $s_{i}=0$ otherwise. Let us investigate how $f$ acts on these codes. If the code of $x_{n}$ ends with 0 , then $x_{n}$ is odd, so the code of $f\left(x_{n}\right)=x_{n+1}$ is obtained from that of $x_{n}$ by replacing $s_{0}=0$ by $s_{0}=1$. Furthermore, if the code of $x_{n}$ ends with $011 \ldots 1$, then the code of $x_{n+1}$ ends with $100 \ldots 0$ instead. Thus if we consider the codes as binary numbers, $f$ acts on them as an addition of 1 . Hence the code of $x_{n}$ is the binary representation of $n$ and thus $x_{n}$ uniquely determines $n$. Specifically, if $x_{n}=1995=3 \cdot 5 \cdot 7 \cdot 19$, then its code is 10001110 and corresponds to $n=142$.
|
142
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
25. S3 (POL) For an integer $x \geq 1$, let $p(x)$ be the least prime that does not divide $x$, and define $q(x)$ to be the product of all primes less than $p(x)$. In particular, $p(1)=2$. For $x$ such that $p(x)=2$, define $q(x)=1$. Consider the sequence $x_{0}, x_{1}, x_{2}, \ldots$ defined by $x_{0}=1$ and $$ x_{n+1}=\frac{x_{n} p\left(x_{n}\right)}{q\left(x_{n}\right)} $$ for $n \geq 0$. Find all $n$ such that $x_{n}=1995$.
|
25. By the definition of $q(x)$, it divides $x$ for all integers $x>0$, so $f(x)=$ $x p(x) / q(x)$ is a positive integer too. Let $\left\{p_{0}, p_{1}, p_{2}, \ldots\right\}$ be all prime numbers in increasing order. Since it easily follows by induction that all $x_{n}$ 's are square-free, we can assign to each of them a unique code according to which primes divide it: if $p_{m}$ is the largest prime dividing $x_{n}$, the code corresponding to $x_{n}$ will be $\ldots 0 s_{m} s_{m-1} \ldots s_{0}$, with $s_{i}=1$ if $p_{i} \mid x_{n}$ and $s_{i}=0$ otherwise. Let us investigate how $f$ acts on these codes. If the code of $x_{n}$ ends with 0 , then $x_{n}$ is odd, so the code of $f\left(x_{n}\right)=x_{n+1}$ is obtained from that of $x_{n}$ by replacing $s_{0}=0$ by $s_{0}=1$. Furthermore, if the code of $x_{n}$ ends with $011 \ldots 1$, then the code of $x_{n+1}$ ends with $100 \ldots 0$ instead. Thus if we consider the codes as binary numbers, $f$ acts on them as an addition of 1 . Hence the code of $x_{n}$ is the binary representation of $n$ and thus $x_{n}$ uniquely determines $n$. Specifically, if $x_{n}=1995=3 \cdot 5 \cdot 7 \cdot 19$, then its code is 10001110 and corresponds to $n=142$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0cca6204-5b89-5b9b-aa13-9542d8778e5f
| 24,631
|
19. N1 (UKR) Four integers are marked on a circle. At each step we simultaneously replace each number by the difference between this number and the next number on the circle, in a given direction (that is, the numbers $a, b, c, d$ are replaced by $a-b, b-c, c-d, d-a)$. Is it possible after 1996 such steps to have numbers $a, b, c, d$ such that the numbers $|b c-a d|,|a c-b d|,|a b-c d|$ are primes?
|
19. It is easy to check that after 4 steps we will have all $a, b, c, d$ even. Thus $|a b-c d|,|a c-b d|,|a d-b c|$ remain divisible by 4 , and clearly are not prime. The answer is no. Second solution. After one step we have $a+b+c+d=0$. Then $a c-b d=$ $a c+b(a+b+c)=(a+b)(b+c)$ etc., so $$ |a b-c d| \cdot|a c-b d| \cdot|a d-b c|=(a+b)^{2}(a+c)^{2}(b+c)^{2} $$ However, the product of three primes cannot be a square, hence the answer is $n o$.
|
no
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
19. N1 (UKR) Four integers are marked on a circle. At each step we simultaneously replace each number by the difference between this number and the next number on the circle, in a given direction (that is, the numbers $a, b, c, d$ are replaced by $a-b, b-c, c-d, d-a)$. Is it possible after 1996 such steps to have numbers $a, b, c, d$ such that the numbers $|b c-a d|,|a c-b d|,|a b-c d|$ are primes?
|
19. It is easy to check that after 4 steps we will have all $a, b, c, d$ even. Thus $|a b-c d|,|a c-b d|,|a d-b c|$ remain divisible by 4 , and clearly are not prime. The answer is no. Second solution. After one step we have $a+b+c+d=0$. Then $a c-b d=$ $a c+b(a+b+c)=(a+b)(b+c)$ etc., so $$ |a b-c d| \cdot|a c-b d| \cdot|a d-b c|=(a+b)^{2}(a+c)^{2}(b+c)^{2} $$ However, the product of three primes cannot be a square, hence the answer is $n o$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f15452cf-188e-5c9e-ab05-e26c3da359d3
| 24,687
|
20. N2 (RUS) ${ }^{\mathrm{IMO} 4}$ The positive integers $a$ and $b$ are such that the numbers $15 a+16 b$ and $16 a-15 b$ are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?
|
20. Let $15 a+16 b=x^{2}$ and $16 a-15 b=y^{2}$, where $x, y \in \mathbb{N}$. Then we obtain $x^{4}+y^{4}=(15 a+16 b)^{2}+(16 a-15 b)^{2}=\left(15^{2}+16^{2}\right)\left(a^{2}+b^{2}\right)=481\left(a^{2}+b^{2}\right)$. In particular, $481=13 \cdot 37 \mid x^{4}+y^{4}$. We have the following lemma. Lemma. Suppose that $p \mid x^{4}+y^{4}$, where $x, y \in \mathbb{Z}$ and $p$ is an odd prime, where $p \not \equiv 1(\bmod 8)$. Then $p \mid x$ and $p \mid y$. Proof. Since $p \mid x^{8}-y^{8}$ and by Fermat's theorem $p \mid x^{p-1}-y^{p-1}$, we deduce that $p \mid x^{d}-y^{d}$, where $d=(p-1,8)$. But $d \neq 8$, so $d \mid 4$. Thus $p \mid x^{4}-y^{4}$, which implies that $p \mid 2 y^{4}$, i.e., $p \mid y$ and $p \mid x$. In particular, we can conclude that $13 \mid x, y$ and $37 \mid x, y$. Hence $x$ and $y$ are divisible by 481 . Thus each of them is at least 481. On the other hand, $x=y=481$ is possible. It is sufficient to take $a=$ $31 \cdot 481$ and $b=481$. Second solution. Note that $15 x^{2}+16 y^{2}=481 a^{2}$. It can be directly verified that the divisibility of $15 x^{2}+16 y^{2}$ by 13 and by 37 implies that both $x$ and $y$ are divisible by both primes. Thus $481 \mid x, y$.
|
481
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
20. N2 (RUS) ${ }^{\mathrm{IMO} 4}$ The positive integers $a$ and $b$ are such that the numbers $15 a+16 b$ and $16 a-15 b$ are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?
|
20. Let $15 a+16 b=x^{2}$ and $16 a-15 b=y^{2}$, where $x, y \in \mathbb{N}$. Then we obtain $x^{4}+y^{4}=(15 a+16 b)^{2}+(16 a-15 b)^{2}=\left(15^{2}+16^{2}\right)\left(a^{2}+b^{2}\right)=481\left(a^{2}+b^{2}\right)$. In particular, $481=13 \cdot 37 \mid x^{4}+y^{4}$. We have the following lemma. Lemma. Suppose that $p \mid x^{4}+y^{4}$, where $x, y \in \mathbb{Z}$ and $p$ is an odd prime, where $p \not \equiv 1(\bmod 8)$. Then $p \mid x$ and $p \mid y$. Proof. Since $p \mid x^{8}-y^{8}$ and by Fermat's theorem $p \mid x^{p-1}-y^{p-1}$, we deduce that $p \mid x^{d}-y^{d}$, where $d=(p-1,8)$. But $d \neq 8$, so $d \mid 4$. Thus $p \mid x^{4}-y^{4}$, which implies that $p \mid 2 y^{4}$, i.e., $p \mid y$ and $p \mid x$. In particular, we can conclude that $13 \mid x, y$ and $37 \mid x, y$. Hence $x$ and $y$ are divisible by 481 . Thus each of them is at least 481. On the other hand, $x=y=481$ is possible. It is sufficient to take $a=$ $31 \cdot 481$ and $b=481$. Second solution. Note that $15 x^{2}+16 y^{2}=481 a^{2}$. It can be directly verified that the divisibility of $15 x^{2}+16 y^{2}$ by 13 and by 37 implies that both $x$ and $y$ are divisible by both primes. Thus $481 \mid x, y$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d5d6474a-ca90-511f-bb42-f8b478303b0f
| 24,693
|
25. C2 (UKR) An $(n-1) \times(n-1)$ square is divided into $(n-1)^{2}$ unit squares in the usual manner. Each of the $n^{2}$ vertices of these squares is to be colored red or blue. Find the number of different colorings such that each unit square has exactly two red vertices. (Two coloring schemes are regarded as different if at least one vertex is colored differently in the two schemes.)
|
25. Let the vertices in the bottom row be assigned an arbitrary coloring, and suppose that some two adjacent vertices receive the same color. The number of such colorings equals $2^{n}-2$. It is easy to see that then the colors of the remaining vertices get fixed uniquely in order to satisfy the requirement. So in this case there are $2^{n}-2$ possible colorings. Next, suppose that the vertices in the bottom row are colored alternately red and blue. There are two such colorings. In this case, the same must hold for every row, and thus we get $2^{n}$ possible colorings. It follows that the total number of considered colorings is $\left(2^{n}-2\right)+2^{n}=$ $2^{n+1}-2$.
|
2^{n+1}-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
25. C2 (UKR) An $(n-1) \times(n-1)$ square is divided into $(n-1)^{2}$ unit squares in the usual manner. Each of the $n^{2}$ vertices of these squares is to be colored red or blue. Find the number of different colorings such that each unit square has exactly two red vertices. (Two coloring schemes are regarded as different if at least one vertex is colored differently in the two schemes.)
|
25. Let the vertices in the bottom row be assigned an arbitrary coloring, and suppose that some two adjacent vertices receive the same color. The number of such colorings equals $2^{n}-2$. It is easy to see that then the colors of the remaining vertices get fixed uniquely in order to satisfy the requirement. So in this case there are $2^{n}-2$ possible colorings. Next, suppose that the vertices in the bottom row are colored alternately red and blue. There are two such colorings. In this case, the same must hold for every row, and thus we get $2^{n}$ possible colorings. It follows that the total number of considered colorings is $\left(2^{n}-2\right)+2^{n}=$ $2^{n+1}-2$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0eb609e1-ccf9-5e8a-a4f7-294836622c92
| 24,707
|
9. A9 (POL) Let the sequence $a(n), n=1,2,3, \ldots$, be generated as follows: $a(1)=0$, and for $n>1$, $$ a(n)=a([n / 2])+(-1)^{\frac{n(n+1)}{2}} . \quad(\text { Here }[t]=\text { the greatest integer } \leq t .) $$ (a) Determine the maximum and minimum value of $a(n)$ over $n \leq 1996$ and find all $n \leq 1996$ for which these extreme values are attained. (b) How many terms $a(n), n \leq 1996$, are equal to 0 ?
|
9. From the definition of $a(n)$ we obtain $$ a(n)-a([n / 2])=\left\{\begin{array}{r} 1 \text { if } n \equiv 0 \text { or } n \equiv 3(\bmod 4) \\ -1 \text { if } n \equiv 1 \text { or } n \equiv 2(\bmod 4) . \end{array}\right. $$ Let $n=\overline{b_{k} b_{k-1} \ldots b_{1} b_{0}}$ be the binary representation of $n$, where we assume $b_{k}=1$. If we define $p(n)$ and $q(n)$ to be the number of indices $i=0,1, \ldots, k-1$ with $b_{i}=b_{i+1}$ and the number of $i=0,1, \ldots, k-1$ with $b_{i} \neq b_{i+1}$ respectively, we get $$ a(n)=p(n)-q(n) $$ (a) The maximum value of $a(n)$ for $n \leq 1996$ is 9 when $p(n)=9$ and $q(n)=0$, i.e., in the case $n=\overline{1111111111}_{2}=1023$. The minimum value is -10 and is attained when $p(n)=0$ and $q(n)=$ 10, i.e., only for $n=\overline{10101010101}_{2}=1365$. (b) From (1) we have that $a(n)=0$ is equivalent to $p(n)=q(n)=k / 2$. Hence $k$ must be even, and the $k / 2$ indices $i$ for which $b_{i}=b_{i+1}$ can be chosen in exactly $\binom{k}{k / 2}$ ways. Thus the number of positive integers $n<2^{11}=2048$ with $a(n)=0$ is equal to $$ \binom{0}{0}+\binom{2}{1}+\binom{4}{2}+\binom{6}{3}+\binom{8}{4}+\binom{10}{5}=351 $$ But five of these numbers exceed 1996: these are $2002=\overline{11111010010}_{2}$, $2004=\overline{11111010100}_{2}, 2006=\overline{11111010110}_{2}, 2010=\overline{11111011010}_{2}$, $2026=\overline{11111101010}_{2}$. Therefore there are 346 numbers $n \leq 1996$ for which $a(n)=0$.
|
346
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
9. A9 (POL) Let the sequence $a(n), n=1,2,3, \ldots$, be generated as follows: $a(1)=0$, and for $n>1$, $$ a(n)=a([n / 2])+(-1)^{\frac{n(n+1)}{2}} . \quad(\text { Here }[t]=\text { the greatest integer } \leq t .) $$ (a) Determine the maximum and minimum value of $a(n)$ over $n \leq 1996$ and find all $n \leq 1996$ for which these extreme values are attained. (b) How many terms $a(n), n \leq 1996$, are equal to 0 ?
|
9. From the definition of $a(n)$ we obtain $$ a(n)-a([n / 2])=\left\{\begin{array}{r} 1 \text { if } n \equiv 0 \text { or } n \equiv 3(\bmod 4) \\ -1 \text { if } n \equiv 1 \text { or } n \equiv 2(\bmod 4) . \end{array}\right. $$ Let $n=\overline{b_{k} b_{k-1} \ldots b_{1} b_{0}}$ be the binary representation of $n$, where we assume $b_{k}=1$. If we define $p(n)$ and $q(n)$ to be the number of indices $i=0,1, \ldots, k-1$ with $b_{i}=b_{i+1}$ and the number of $i=0,1, \ldots, k-1$ with $b_{i} \neq b_{i+1}$ respectively, we get $$ a(n)=p(n)-q(n) $$ (a) The maximum value of $a(n)$ for $n \leq 1996$ is 9 when $p(n)=9$ and $q(n)=0$, i.e., in the case $n=\overline{1111111111}_{2}=1023$. The minimum value is -10 and is attained when $p(n)=0$ and $q(n)=$ 10, i.e., only for $n=\overline{10101010101}_{2}=1365$. (b) From (1) we have that $a(n)=0$ is equivalent to $p(n)=q(n)=k / 2$. Hence $k$ must be even, and the $k / 2$ indices $i$ for which $b_{i}=b_{i+1}$ can be chosen in exactly $\binom{k}{k / 2}$ ways. Thus the number of positive integers $n<2^{11}=2048$ with $a(n)=0$ is equal to $$ \binom{0}{0}+\binom{2}{1}+\binom{4}{2}+\binom{6}{3}+\binom{8}{4}+\binom{10}{5}=351 $$ But five of these numbers exceed 1996: these are $2002=\overline{11111010010}_{2}$, $2004=\overline{11111010100}_{2}, 2006=\overline{11111010110}_{2}, 2010=\overline{11111011010}_{2}$, $2026=\overline{11111101010}_{2}$. Therefore there are 346 numbers $n \leq 1996$ for which $a(n)=0$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
06cfaf09-1b6b-5d8a-be54-03e8608eed0b
| 24,738
|
26. (ITA) For every integer $n \geq 2$ determine the minimum value that the sum $a_{0}+a_{1}+\cdots+a_{n}$ can take for nonnegative numbers $a_{0}, a_{1}, \ldots, a_{n}$ satisfying the condition $$ a_{0}=1, \quad a_{i} \leq a_{i+1}+a_{i+2} \quad \text { for } i=0, \ldots, n-2 $$ ### 3.39 The Thirty-Ninth IMO
|
26. Let us first examine the case that all the inequalities in the problem are actually equalities. Then $a_{n-2}=a_{n-1}+a_{n}, a_{n-3}=2 a_{n-1}+a_{n}, \ldots, a_{0}=$ $F_{n} a_{n-1}+F_{n-1} a_{n}=1$, where $F_{n}$ is the $n$th Fibonacci number. Then it is easy to see (from $F_{1}+F_{2}+\cdots+F_{k}=F_{k+2}$ ) that $a_{0}+\cdots+a_{n}=$ $\left(F_{n+2}-1\right) a_{n-1}+F_{n+1} a_{n}=\frac{F_{n+2}-1}{F_{n}}+\left(F_{n+1}-\frac{F_{n-1}\left(F_{n+2}-1\right)}{F_{n}}\right) a_{n}$. Since $\frac{F_{n-1}\left(F_{n+2}-1\right)}{F_{n}} \leq F_{n+1}$, it follows that $a_{0}+a_{1}+\cdots+a_{n} \geq \frac{F_{n+2}-1}{F_{n}}$, with equality holding if and only if $a_{n}=0$ and $a_{n-1}=\frac{1}{F_{n}}$. We denote by $M_{n}$ the required minimum in the general case. We shall prove by induction that $M_{n}=\frac{F_{n+2}-1}{F_{n}}$. For $M_{1}=1$ and $M_{2}=2$ it is easy to show that the formula holds; hence the inductive basis is true. Suppose that $n>2$. The sequences $1, \frac{a_{2}}{a_{1}}, \ldots, \frac{a_{n}}{a_{1}}$ and $1, \frac{a_{3}}{a_{2}}, \ldots, \frac{a_{n}}{a_{2}}$ also satisfy the conditions of the problem. Hence we have $$ a_{0}+\cdots+a_{n}=a_{0}+a_{1}\left(1+\frac{a_{2}}{a_{1}}+\cdots+\frac{a_{n}}{a_{1}}\right) \geq 1+a_{1} M_{n-1} $$ and $$ a_{0}+\cdots+a_{n}=a_{0}+a_{1}+a_{2}\left(1+\frac{a_{3}}{a_{2}}+\cdots+\frac{a_{n}}{a_{2}}\right) \geq 1+a_{1}+a_{2} M_{n-2} $$ Multiplying the first inequality by $M_{n-2}-1$ and the second one by $M_{n-1}$, adding the inequalities and using that $a_{1}+a_{2} \geq 1$, we obtain ( $M_{n-1}+$ $\left.M_{n-2}+1\right)\left(a_{0}+\cdots+a_{n}\right) \geq M_{n-1} M_{n-2}+M_{n-1}+M_{n-2}+1$, so $$ M_{n} \geq \frac{M_{n-1} M_{n-2}+M_{n-1}+M_{n-2}+1}{M_{n-1}+M_{n-2}+1} $$ Since $M_{n-1}=\frac{F_{n+1}-1}{F_{n-1}}$ and $M_{n-2}=\frac{F_{n}-1}{F_{n-2}}$, the above inequality easily yields $M_{n} \geq \frac{F_{n+2}-1}{F_{n}}$. However, we have shown above that equality can occur; hence $\frac{F_{n+2}-1}{F_{n}}$ is indeed the required minimum.
|
\frac{F_{n+2}-1}{F_{n}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
26. (ITA) For every integer $n \geq 2$ determine the minimum value that the sum $a_{0}+a_{1}+\cdots+a_{n}$ can take for nonnegative numbers $a_{0}, a_{1}, \ldots, a_{n}$ satisfying the condition $$ a_{0}=1, \quad a_{i} \leq a_{i+1}+a_{i+2} \quad \text { for } i=0, \ldots, n-2 $$ ### 3.39 The Thirty-Ninth IMO
|
26. Let us first examine the case that all the inequalities in the problem are actually equalities. Then $a_{n-2}=a_{n-1}+a_{n}, a_{n-3}=2 a_{n-1}+a_{n}, \ldots, a_{0}=$ $F_{n} a_{n-1}+F_{n-1} a_{n}=1$, where $F_{n}$ is the $n$th Fibonacci number. Then it is easy to see (from $F_{1}+F_{2}+\cdots+F_{k}=F_{k+2}$ ) that $a_{0}+\cdots+a_{n}=$ $\left(F_{n+2}-1\right) a_{n-1}+F_{n+1} a_{n}=\frac{F_{n+2}-1}{F_{n}}+\left(F_{n+1}-\frac{F_{n-1}\left(F_{n+2}-1\right)}{F_{n}}\right) a_{n}$. Since $\frac{F_{n-1}\left(F_{n+2}-1\right)}{F_{n}} \leq F_{n+1}$, it follows that $a_{0}+a_{1}+\cdots+a_{n} \geq \frac{F_{n+2}-1}{F_{n}}$, with equality holding if and only if $a_{n}=0$ and $a_{n-1}=\frac{1}{F_{n}}$. We denote by $M_{n}$ the required minimum in the general case. We shall prove by induction that $M_{n}=\frac{F_{n+2}-1}{F_{n}}$. For $M_{1}=1$ and $M_{2}=2$ it is easy to show that the formula holds; hence the inductive basis is true. Suppose that $n>2$. The sequences $1, \frac{a_{2}}{a_{1}}, \ldots, \frac{a_{n}}{a_{1}}$ and $1, \frac{a_{3}}{a_{2}}, \ldots, \frac{a_{n}}{a_{2}}$ also satisfy the conditions of the problem. Hence we have $$ a_{0}+\cdots+a_{n}=a_{0}+a_{1}\left(1+\frac{a_{2}}{a_{1}}+\cdots+\frac{a_{n}}{a_{1}}\right) \geq 1+a_{1} M_{n-1} $$ and $$ a_{0}+\cdots+a_{n}=a_{0}+a_{1}+a_{2}\left(1+\frac{a_{3}}{a_{2}}+\cdots+\frac{a_{n}}{a_{2}}\right) \geq 1+a_{1}+a_{2} M_{n-2} $$ Multiplying the first inequality by $M_{n-2}-1$ and the second one by $M_{n-1}$, adding the inequalities and using that $a_{1}+a_{2} \geq 1$, we obtain ( $M_{n-1}+$ $\left.M_{n-2}+1\right)\left(a_{0}+\cdots+a_{n}\right) \geq M_{n-1} M_{n-2}+M_{n-1}+M_{n-2}+1$, so $$ M_{n} \geq \frac{M_{n-1} M_{n-2}+M_{n-1}+M_{n-2}+1}{M_{n-1}+M_{n-2}+1} $$ Since $M_{n-1}=\frac{F_{n+1}-1}{F_{n-1}}$ and $M_{n-2}=\frac{F_{n}-1}{F_{n-2}}$, the above inequality easily yields $M_{n} \geq \frac{F_{n+2}-1}{F_{n}}$. However, we have shown above that equality can occur; hence $\frac{F_{n+2}-1}{F_{n}}$ is indeed the required minimum.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3b5052f2-9ff5-5e06-a2d0-5f9d73f5fbad
| 24,790
|
13. (BUL) ${ }^{\mathrm{IMO} 6}$ Determine the least possible value of $f(1998)$, where $f$ is a function from the set $\mathbb{N}$ of positive integers into itself such that for all $m, n \in \mathbb{N}$, $$ f\left(n^{2} f(m)\right)=m[f(n)]^{2} $$
|
13. Denote by $\mathcal{F}$ the set of functions considered. Let $f \in \mathcal{F}$, and let $f(1)=a$. Putting $n=1$ and $m=1$ we obtain $f(f(z))=a^{2} z$ and $f\left(a z^{2}\right)=f(z)^{2}$ for all $z \in \mathbb{N}$. These equations, together with the original one, imply $f(x)^{2} f(y)^{2}=f(x)^{2} f\left(a y^{2}\right)=f\left(x^{2} f\left(f\left(a y^{2}\right)\right)\right)=f\left(x^{2} a^{3} y^{2}\right)=$ $f\left(a(a x y)^{2}\right)=f(a x y)^{2}$, or $f(a x y)=f(x) f(y)$ for all $x, y \in \mathbb{N}$. Thus $f(a x)=a f(x)$, and we conclude that $$ a f(x y)=f(x) f(y) \quad \text { for all } x, y \in \mathbb{N} $$ We now prove that $f(x)$ is divisible by $a$ for each $x \in \mathbb{N}$. In fact, we inductively get that $f(x)^{k}=a^{k-1} f\left(x^{k}\right)$ is divisible by $a^{k-1}$ for every $k$. If $p^{\alpha}$ and $p^{\beta}$ are the exact powers of a prime $p$ that divide $f(x)$ and $a$ respectively, we deduce that $k \alpha \geq(k-1) \beta$ for all $k$, so we must have $\alpha \geq \beta$ for any $p$. Therefore $a \mid f(x)$. Now we consider the function on natural numbers $g(x)=f(x) / a$. The above relations imply $$ g(1)=1, \quad g(x y)=g(x) g(y), \quad g(g(x))=x \quad \text { for all } x, y \in \mathbb{N} $$ Since $g \in \mathcal{F}$ and $g(x) \leq f(x)$ for all $x$, we may restrict attention to the functions $g$ only. Clearly $g$ is bijective. We observe that $g$ maps a prime to a prime. Assume to the contrary that $g(p)=u v, u, v>1$. Then $g(u v)=p$, so either $g(u)=1$ and $g(v)=1$. Thus either $g(1)=u$ or $g(1)=v$, which is impossible. We return to the problem of determining the least possible value of $g(1998)$. Since $g(1998)=g\left(2 \cdot 3^{3} \cdot 37\right)=g(2) \cdot g(3)^{3} \cdot g(37)$, and $g(2)$, $g(3), g(37)$ are distinct primes, $g(1998)$ is not smaller than $2^{3} \cdot 3 \cdot 5=120$. On the other hand, the value of 120 is attained for any function $g$ satisfying (2) and $g(2)=3, g(3)=2, g(5)=37, g(37)=5$. Hence the answer is 120 .
|
120
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
13. (BUL) ${ }^{\mathrm{IMO} 6}$ Determine the least possible value of $f(1998)$, where $f$ is a function from the set $\mathbb{N}$ of positive integers into itself such that for all $m, n \in \mathbb{N}$, $$ f\left(n^{2} f(m)\right)=m[f(n)]^{2} $$
|
13. Denote by $\mathcal{F}$ the set of functions considered. Let $f \in \mathcal{F}$, and let $f(1)=a$. Putting $n=1$ and $m=1$ we obtain $f(f(z))=a^{2} z$ and $f\left(a z^{2}\right)=f(z)^{2}$ for all $z \in \mathbb{N}$. These equations, together with the original one, imply $f(x)^{2} f(y)^{2}=f(x)^{2} f\left(a y^{2}\right)=f\left(x^{2} f\left(f\left(a y^{2}\right)\right)\right)=f\left(x^{2} a^{3} y^{2}\right)=$ $f\left(a(a x y)^{2}\right)=f(a x y)^{2}$, or $f(a x y)=f(x) f(y)$ for all $x, y \in \mathbb{N}$. Thus $f(a x)=a f(x)$, and we conclude that $$ a f(x y)=f(x) f(y) \quad \text { for all } x, y \in \mathbb{N} $$ We now prove that $f(x)$ is divisible by $a$ for each $x \in \mathbb{N}$. In fact, we inductively get that $f(x)^{k}=a^{k-1} f\left(x^{k}\right)$ is divisible by $a^{k-1}$ for every $k$. If $p^{\alpha}$ and $p^{\beta}$ are the exact powers of a prime $p$ that divide $f(x)$ and $a$ respectively, we deduce that $k \alpha \geq(k-1) \beta$ for all $k$, so we must have $\alpha \geq \beta$ for any $p$. Therefore $a \mid f(x)$. Now we consider the function on natural numbers $g(x)=f(x) / a$. The above relations imply $$ g(1)=1, \quad g(x y)=g(x) g(y), \quad g(g(x))=x \quad \text { for all } x, y \in \mathbb{N} $$ Since $g \in \mathcal{F}$ and $g(x) \leq f(x)$ for all $x$, we may restrict attention to the functions $g$ only. Clearly $g$ is bijective. We observe that $g$ maps a prime to a prime. Assume to the contrary that $g(p)=u v, u, v>1$. Then $g(u v)=p$, so either $g(u)=1$ and $g(v)=1$. Thus either $g(1)=u$ or $g(1)=v$, which is impossible. We return to the problem of determining the least possible value of $g(1998)$. Since $g(1998)=g\left(2 \cdot 3^{3} \cdot 37\right)=g(2) \cdot g(3)^{3} \cdot g(37)$, and $g(2)$, $g(3), g(37)$ are distinct primes, $g(1998)$ is not smaller than $2^{3} \cdot 3 \cdot 5=120$. On the other hand, the value of 120 is attained for any function $g$ satisfying (2) and $g(2)=3, g(3)=2, g(5)=37, g(37)=5$. Hence the answer is 120 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6483eaf9-bfcc-541a-9fc1-b611f3af2cbb
| 24,820
|
16. (UKR) Determine the smallest integer $n \geq 4$ for which one can choose four different numbers $a, b, c$, and $d$ from any $n$ distinct integers such that $a+b-c-d$ is divisible by 20 .
|
16. Let $S$ be a set of integers such that for no four distinct elements $a, b, c, d \in$ $S$, it holds that $20 \mid a+b-c-d$. It is easily seen that there cannot exist distinct elements $a, b, c, d$ with $a \equiv b$ and $c \equiv d(\bmod 20)$. Consequently, if the elements of $S$ give $k$ different residues modulo 20, then $S$ itself has at most $k+2$ elements. Next, consider these $k$ elements of $S$ with different residues modulo 20. They give $\frac{k(k-1)}{2}$ different sums of two elements. For $k \geq 7$ there are at least 21 such sums, and two of them, say $a+b$ and $c+d$, are equal modulo 20 ; it is easy to see that $a, b, c, d$ are discinct. It follows that $k$ cannot exceed 6 , and consequently $S$ has at most 8 elements. An example of a set $S$ with 8 elements is $\{0,20,40,1,2,4,7,12\}$. Hence the answer is $n=9$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
16. (UKR) Determine the smallest integer $n \geq 4$ for which one can choose four different numbers $a, b, c$, and $d$ from any $n$ distinct integers such that $a+b-c-d$ is divisible by 20 .
|
16. Let $S$ be a set of integers such that for no four distinct elements $a, b, c, d \in$ $S$, it holds that $20 \mid a+b-c-d$. It is easily seen that there cannot exist distinct elements $a, b, c, d$ with $a \equiv b$ and $c \equiv d(\bmod 20)$. Consequently, if the elements of $S$ give $k$ different residues modulo 20, then $S$ itself has at most $k+2$ elements. Next, consider these $k$ elements of $S$ with different residues modulo 20. They give $\frac{k(k-1)}{2}$ different sums of two elements. For $k \geq 7$ there are at least 21 such sums, and two of them, say $a+b$ and $c+d$, are equal modulo 20 ; it is easy to see that $a, b, c, d$ are discinct. It follows that $k$ cannot exceed 6 , and consequently $S$ has at most 8 elements. An example of a set $S$ with 8 elements is $\{0,20,40,1,2,4,7,12\}$. Hence the answer is $n=9$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8423a0d-79b9-5076-8959-c78d72128c47
| 24,829
|
17. (GBR) A sequence of integers $a_{1}, a_{2}, a_{3}, \ldots$ is defined as follows: $a_{1}=1$, and for $n \geq 1, a_{n+1}$ is the smallest integer greater than $a_{n}$ such that $a_{i}+a_{j} \neq 3 a_{k}$ for any $i, j, k$ in $\{1,2, \ldots, n+1\}$, not necessarily distinct. Determine $a_{1998}$.
|
17. Initially, we determine that the first few values for $a_{n}$ are $1,3,4,7,10$, $12,13,16,19,21,22,25$. Since these are exactly the numbers of the forms $3 k+1$ and $9 k+3$, we conjecture that this is the general pattern. In fact, it is easy to see that the equation $x+y=3 z$ has no solution in the set $K=\{3 k+1,9 k+3 \mid k \in \mathbb{N}\}$. We shall prove that the sequence $\left\{a_{n}\right\}$ is actually this set ordered increasingly. Suppose $a_{n}>25$ is the first member of the sequence not belonging to $K$. We have several cases: (i) $a_{n}=3 r+2, r \in \mathbb{N}$. By the assumption, one of $r+1, r+2, r+3$ is of the form $3 k+1$ (and smaller than $a_{n}$ ), and therefore is a member $a_{i}$ of the sequence. Then $3 a_{i}$ equals $a_{n}+1$, $a_{n}+4$, or $a_{n}+7$, which is a contradiction because $1,4,7$ are in the sequence. (ii) $a_{n}=9 r, r \in \mathbb{N}$. Then $a_{n}+a_{2}=3(3 r+1)$, although $3 r+1$ is in the sequence, a contradiction. (iii) $a_{n}=9 r+6, r \in \mathbb{N}$. Then one of the numbers $3 r+3,3 r+6,3 r+9$ is a member $a_{j}$ of the sequence, and thus $3 a_{j}$ is equal to $a_{n}+3$, $a_{n}+12$, or $a_{n}+21$, where $3,12,21$ are members of the sequence, again a contradiction. Once we have revealed the structure of the sequence, it is easy to compute $a_{1998}$. We have $1998=4 \cdot 499+2$, which implies $a_{1998}=9 \cdot 499+a_{2}=4494$.
|
4494
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
17. (GBR) A sequence of integers $a_{1}, a_{2}, a_{3}, \ldots$ is defined as follows: $a_{1}=1$, and for $n \geq 1, a_{n+1}$ is the smallest integer greater than $a_{n}$ such that $a_{i}+a_{j} \neq 3 a_{k}$ for any $i, j, k$ in $\{1,2, \ldots, n+1\}$, not necessarily distinct. Determine $a_{1998}$.
|
17. Initially, we determine that the first few values for $a_{n}$ are $1,3,4,7,10$, $12,13,16,19,21,22,25$. Since these are exactly the numbers of the forms $3 k+1$ and $9 k+3$, we conjecture that this is the general pattern. In fact, it is easy to see that the equation $x+y=3 z$ has no solution in the set $K=\{3 k+1,9 k+3 \mid k \in \mathbb{N}\}$. We shall prove that the sequence $\left\{a_{n}\right\}$ is actually this set ordered increasingly. Suppose $a_{n}>25$ is the first member of the sequence not belonging to $K$. We have several cases: (i) $a_{n}=3 r+2, r \in \mathbb{N}$. By the assumption, one of $r+1, r+2, r+3$ is of the form $3 k+1$ (and smaller than $a_{n}$ ), and therefore is a member $a_{i}$ of the sequence. Then $3 a_{i}$ equals $a_{n}+1$, $a_{n}+4$, or $a_{n}+7$, which is a contradiction because $1,4,7$ are in the sequence. (ii) $a_{n}=9 r, r \in \mathbb{N}$. Then $a_{n}+a_{2}=3(3 r+1)$, although $3 r+1$ is in the sequence, a contradiction. (iii) $a_{n}=9 r+6, r \in \mathbb{N}$. Then one of the numbers $3 r+3,3 r+6,3 r+9$ is a member $a_{j}$ of the sequence, and thus $3 a_{j}$ is equal to $a_{n}+3$, $a_{n}+12$, or $a_{n}+21$, where $3,12,21$ are members of the sequence, again a contradiction. Once we have revealed the structure of the sequence, it is easy to compute $a_{1998}$. We have $1998=4 \cdot 499+2$, which implies $a_{1998}=9 \cdot 499+a_{2}=4494$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e6c5d587-87bb-5304-88ba-a648e1f8a598
| 24,832
|
21. (CAN) Let $a_{0}, a_{1}, a_{2}, \ldots$ be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form $a_{i}+2 a_{j}+4 a_{k}$, where $i, j, k$ are not necessarily distinct. Determine $a_{1998}$.
|
21. Such a sequence is obviously strictly increasing. We note that it must be unique. Indeed, given $a_{0}, a_{1}, \ldots, a_{n-1}$, then $a_{n}$ is the least positive integer not of the form $a_{i}+2 a_{j}+4 a_{k}, i, j, k<n$. We easily get that the first few $a_{n}$ 's are $0,1,8,9,64,65,72,73, \ldots$ Let $\left\{c_{n}\right\}$ be the increasing sequence of all positive integers that consist of zeros and ones in base 8 , i.e., those of the form $t_{0}+2^{3} t_{1}+\cdots+2^{3 q} t_{q}$ where $t_{i} \in\{0,1\}$. We claim that $a_{n}=c_{n}$. To prove this, it is enough to show that each $m \in \mathbb{N}$ can be uniquely written as $c_{i}+2 c_{j}+4 c_{k}$. If $m=t_{0}+2 t_{1}+\cdots+2^{r} t_{r}\left(t_{i} \in\{0,1\}\right)$, then $m=c_{i}+2 c_{j}+2^{2} c_{k}$ is obviously possible if and only if $c_{i}=t_{0}+2^{3} t_{3}+2^{6} t_{6}+\cdots, c_{j}=t_{1}+2^{3} t_{4}+\ldots$, and $c_{k}=t_{2}+2^{3} t_{5}+\cdots$. Hence for $n=s_{0}+2 s_{1}+\cdots+2^{r} s_{r}$ we have $a_{n}=s_{0}+8 s_{1}+\cdots+8^{r} s_{r}$. In particular, $1998=2+2^{2}+2^{3}+2^{6}+2^{7}+2^{8}+2^{9}+2^{10}$, so $a_{1998}=$ $8+8^{2}+8^{3}+8^{6}+8^{7}+8^{8}+8^{9}+8^{10}=1227096648$. Second solution. Define $f(x)=x^{a_{0}}+x^{a_{1}}+\cdots$. Then the assumed property of $\left\{a_{n}\right\}$ gives $$ f(x) f\left(x^{2}\right) f\left(x^{4}\right)=\sum_{i, j, k} x^{a_{i}+2 a_{j}+4 a_{k}}=\sum_{n} x^{n}=\frac{1}{1-x} $$ We also get as a consequence $f\left(x^{2}\right) f\left(x^{4}\right) f\left(x^{8}\right)=\frac{1}{1-x^{2}}$, which gives $f(x)=$ $(1+x) f\left(x^{8}\right)$. Continuing this, we obtain $$ f(x)=(1+x)\left(1+x^{8}\right)\left(1+x^{8^{2}}\right) \cdots $$ Hence the $a_{n}$ 's are integers that have only 0 's and 1 's in base 8.
|
1227096648
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
21. (CAN) Let $a_{0}, a_{1}, a_{2}, \ldots$ be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form $a_{i}+2 a_{j}+4 a_{k}$, where $i, j, k$ are not necessarily distinct. Determine $a_{1998}$.
|
21. Such a sequence is obviously strictly increasing. We note that it must be unique. Indeed, given $a_{0}, a_{1}, \ldots, a_{n-1}$, then $a_{n}$ is the least positive integer not of the form $a_{i}+2 a_{j}+4 a_{k}, i, j, k<n$. We easily get that the first few $a_{n}$ 's are $0,1,8,9,64,65,72,73, \ldots$ Let $\left\{c_{n}\right\}$ be the increasing sequence of all positive integers that consist of zeros and ones in base 8 , i.e., those of the form $t_{0}+2^{3} t_{1}+\cdots+2^{3 q} t_{q}$ where $t_{i} \in\{0,1\}$. We claim that $a_{n}=c_{n}$. To prove this, it is enough to show that each $m \in \mathbb{N}$ can be uniquely written as $c_{i}+2 c_{j}+4 c_{k}$. If $m=t_{0}+2 t_{1}+\cdots+2^{r} t_{r}\left(t_{i} \in\{0,1\}\right)$, then $m=c_{i}+2 c_{j}+2^{2} c_{k}$ is obviously possible if and only if $c_{i}=t_{0}+2^{3} t_{3}+2^{6} t_{6}+\cdots, c_{j}=t_{1}+2^{3} t_{4}+\ldots$, and $c_{k}=t_{2}+2^{3} t_{5}+\cdots$. Hence for $n=s_{0}+2 s_{1}+\cdots+2^{r} s_{r}$ we have $a_{n}=s_{0}+8 s_{1}+\cdots+8^{r} s_{r}$. In particular, $1998=2+2^{2}+2^{3}+2^{6}+2^{7}+2^{8}+2^{9}+2^{10}$, so $a_{1998}=$ $8+8^{2}+8^{3}+8^{6}+8^{7}+8^{8}+8^{9}+8^{10}=1227096648$. Second solution. Define $f(x)=x^{a_{0}}+x^{a_{1}}+\cdots$. Then the assumed property of $\left\{a_{n}\right\}$ gives $$ f(x) f\left(x^{2}\right) f\left(x^{4}\right)=\sum_{i, j, k} x^{a_{i}+2 a_{j}+4 a_{k}}=\sum_{n} x^{n}=\frac{1}{1-x} $$ We also get as a consequence $f\left(x^{2}\right) f\left(x^{4}\right) f\left(x^{8}\right)=\frac{1}{1-x^{2}}$, which gives $f(x)=$ $(1+x) f\left(x^{8}\right)$. Continuing this, we obtain $$ f(x)=(1+x)\left(1+x^{8}\right)\left(1+x^{8^{2}}\right) \cdots $$ Hence the $a_{n}$ 's are integers that have only 0 's and 1 's in base 8.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6a5263f7-090c-5cee-bc49-b2d1ecf2ac9c
| 24,845
|
15. A1 (POL) ${ }^{\mathrm{IMO} 2}$ Let $n \geq 2$ be a fixed integer. Find the least constant $C$ such that the inequality $$ \sum_{i<j} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) \leq C\left(\sum_{i} x_{i}\right)^{4} $$ holds for every $x_{1}, \ldots, x_{n} \geq 0$ (the sum on the left consists of $\binom{n}{2}$ summands). For this constant $C$, characterize the instances of equality.
|
15. For all $x_{i}=0$ any $C$ will do, so we may assume the contrary. Since the equation is symmetric and homogeneous, we may assume $\sum_{i} x_{i}=1$. The equation now becomes $F\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\sum_{i<j} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right)=$ $\sum_{i} x_{i}^{2} \sum_{j \neq i} x_{j}=\sum_{i} x_{i}^{3}\left(1-x_{i}\right)=\sum_{i} f\left(x_{i}\right) \leq C$, where we define $f(x)=$ $x^{3}-x^{4}$. We note that for $x, y \geq 0$ and $x+y \leq 2 / 3$, $$ f(x+y)+f(0)-f(x)-f(y)=3 x y(x+y)\left(\frac{2}{3}-x-y\right) \geq 0 $$ We note that if at least three elements of $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ are nonzero the condition of (1) always holds for the two smallest ones. Hence, applying (1) repeatedly, we obtain $F\left(x_{1}, x_{2}, \ldots, x_{n}\right) \leq F(a, 1-a, 0, \ldots, 0)=\frac{1}{2}(2 a(1-$ a)) $(1-2 a(1-a)) \leq \frac{1}{8}=F\left(\frac{1}{2}, \frac{1}{2}, 0, \ldots, 0\right)$. Thus we have $C=\frac{1}{8}$ (for all $n$ ), and equality holds only when two $x_{i}$ are equal and the remaining ones are 0 . Second solution. Let $M=x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}$. Using $a b \leq(a+2 b)^{2} / 8$ we have $$ \begin{aligned} \sum_{1 \leq i<j \leq n} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) & \leq M \sum_{i<j} x_{i} x_{j} \\ & \leq \frac{1}{8}\left(M+2 \sum_{i<j} x_{i} x_{j}\right)^{2}=\frac{1}{8}\left(\sum_{i=1}^{n} x_{i}\right)^{4} \end{aligned} $$ Equality holds if and only if $M=2 \sum_{i<j} x_{i} x_{j}$ and $x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right)=M x_{i} x_{j}$ for all $i<j$, which holds if and only if $n-2$ of the $x_{i}$ are zero and the remaining two are equal. Remark. Problems (SL90-26) and (SL91-27) are very similar.
|
\frac{1}{8}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
15. A1 (POL) ${ }^{\mathrm{IMO} 2}$ Let $n \geq 2$ be a fixed integer. Find the least constant $C$ such that the inequality $$ \sum_{i<j} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) \leq C\left(\sum_{i} x_{i}\right)^{4} $$ holds for every $x_{1}, \ldots, x_{n} \geq 0$ (the sum on the left consists of $\binom{n}{2}$ summands). For this constant $C$, characterize the instances of equality.
|
15. For all $x_{i}=0$ any $C$ will do, so we may assume the contrary. Since the equation is symmetric and homogeneous, we may assume $\sum_{i} x_{i}=1$. The equation now becomes $F\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\sum_{i<j} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right)=$ $\sum_{i} x_{i}^{2} \sum_{j \neq i} x_{j}=\sum_{i} x_{i}^{3}\left(1-x_{i}\right)=\sum_{i} f\left(x_{i}\right) \leq C$, where we define $f(x)=$ $x^{3}-x^{4}$. We note that for $x, y \geq 0$ and $x+y \leq 2 / 3$, $$ f(x+y)+f(0)-f(x)-f(y)=3 x y(x+y)\left(\frac{2}{3}-x-y\right) \geq 0 $$ We note that if at least three elements of $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ are nonzero the condition of (1) always holds for the two smallest ones. Hence, applying (1) repeatedly, we obtain $F\left(x_{1}, x_{2}, \ldots, x_{n}\right) \leq F(a, 1-a, 0, \ldots, 0)=\frac{1}{2}(2 a(1-$ a)) $(1-2 a(1-a)) \leq \frac{1}{8}=F\left(\frac{1}{2}, \frac{1}{2}, 0, \ldots, 0\right)$. Thus we have $C=\frac{1}{8}$ (for all $n$ ), and equality holds only when two $x_{i}$ are equal and the remaining ones are 0 . Second solution. Let $M=x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}$. Using $a b \leq(a+2 b)^{2} / 8$ we have $$ \begin{aligned} \sum_{1 \leq i<j \leq n} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) & \leq M \sum_{i<j} x_{i} x_{j} \\ & \leq \frac{1}{8}\left(M+2 \sum_{i<j} x_{i} x_{j}\right)^{2}=\frac{1}{8}\left(\sum_{i=1}^{n} x_{i}\right)^{4} \end{aligned} $$ Equality holds if and only if $M=2 \sum_{i<j} x_{i} x_{j}$ and $x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right)=M x_{i} x_{j}$ for all $i<j$, which holds if and only if $n-2$ of the $x_{i}$ are zero and the remaining two are equal. Remark. Problems (SL90-26) and (SL91-27) are very similar.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f77af781-4c77-5ab2-b907-c3f4ad98ba76
| 24,904
|
16. A2 (RUS) The numbers from 1 to $n^{2}$ are randomly arranged in the cells of a $n \times n$ square ( $n \geq 2$ ). For any pair of numbers situated in the same row or in the same column, the ratio of the greater number to the smaller one is calculated. Let us call the characteristic of the arrangement the smallest of these $n^{2}(n-1)$ fractions. What is the highest possible value of the characteristic?
|
16. Let $C(A)$ denote the characteristic of an arrangement $A$. We shall prove that $\max C(A)=\frac{n+1}{n}$. Let us prove first $C(A) \leq \frac{n+1}{n}$ for all $A$. Among elements $\left\{n^{2}-n, n^{2}-\right.$ $\left.n+1, \ldots, n^{2}\right\}$, by the pigeonhole principle, in at least one row and at least one column there exist two elements, and hence one pair in the same row or column that is not $\left(n^{2}-n, n^{2}\right)$. Hence $$ C(A) \leq \max \left\{\frac{n^{2}}{n^{2}-n+1}, \frac{n^{2}-1}{n^{2}-n}\right\}=\frac{n^{2}-1}{n^{2}-n}=\frac{n+1}{n} . $$ We now consider the following arrangement: $$ a_{i j}= \begin{cases}i+n(j-i-1) & \text { if } i<j \\ i+n(n-i+j-1) & \text { if } i \geq j\end{cases} $$ We claim that $C(a)=\frac{n+1}{n}$. Indeed, in this arrangement no two numbers in the same row or column differ by less than $n-1$, and in addition, $n^{2}$ and $n^{2}-n+1$ are in different rows and columns, and hence $$ C(A) \geq \frac{n^{2}-1}{n^{2}-n}=\frac{n+1}{n} $$
|
\frac{n+1}{n}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
16. A2 (RUS) The numbers from 1 to $n^{2}$ are randomly arranged in the cells of a $n \times n$ square ( $n \geq 2$ ). For any pair of numbers situated in the same row or in the same column, the ratio of the greater number to the smaller one is calculated. Let us call the characteristic of the arrangement the smallest of these $n^{2}(n-1)$ fractions. What is the highest possible value of the characteristic?
|
16. Let $C(A)$ denote the characteristic of an arrangement $A$. We shall prove that $\max C(A)=\frac{n+1}{n}$. Let us prove first $C(A) \leq \frac{n+1}{n}$ for all $A$. Among elements $\left\{n^{2}-n, n^{2}-\right.$ $\left.n+1, \ldots, n^{2}\right\}$, by the pigeonhole principle, in at least one row and at least one column there exist two elements, and hence one pair in the same row or column that is not $\left(n^{2}-n, n^{2}\right)$. Hence $$ C(A) \leq \max \left\{\frac{n^{2}}{n^{2}-n+1}, \frac{n^{2}-1}{n^{2}-n}\right\}=\frac{n^{2}-1}{n^{2}-n}=\frac{n+1}{n} . $$ We now consider the following arrangement: $$ a_{i j}= \begin{cases}i+n(j-i-1) & \text { if } i<j \\ i+n(n-i+j-1) & \text { if } i \geq j\end{cases} $$ We claim that $C(a)=\frac{n+1}{n}$. Indeed, in this arrangement no two numbers in the same row or column differ by less than $n-1$, and in addition, $n^{2}$ and $n^{2}-n+1$ are in different rows and columns, and hence $$ C(A) \geq \frac{n^{2}-1}{n^{2}-n}=\frac{n+1}{n} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e8a8bd0b-3714-52d2-8dc3-8ab929a9e406
| 24,907
|
25. C5 (BLR) ${ }^{\mathrm{IMO} 3}$ Let $n$ be an even positive integer. We say that two different cells of an $n \times n$ board are neighboring if they have a common side. Find the minimal number of cells on the $n \times n$ board that must be marked so that every cell (marked or not marked) has a marked neighboring cell.
|
25 . Let $n=2 k$. Color the cells neighboring the edge of the board black. Then color the cells neighboring the black cells white. Then in alternation color the still uncolored cells neighboring the white or black cells on the boundary the opposite color  and repeat until all cells are colored. We call the cells colored the same color in each such iteration a "frame." In the color scheme described, each cell (white or black) neighbors exactly two black cells. The number of black cells is $2 k(k+1)$, and hence we need to mark at least $k(k+1)$ cells. On the other hand, going along each black-colored frame, we can alternately mark two consecutive cells and then not mark two consecutive cells. Every cell on the black frame will have one marked neighbor. One can arrange these sequences on two consecutive black frames such that each cell in the white frame in between has exactly one neighbor. Hence, starting from a sequence on the largest frame we obtain a marking that contains exactly half of all the black cells, i.e., $k(k+1)$ and neighbors every cell. It follows that the desired minimal number of markings is $k(k+1)$. Remark. For $n=4 k-1$ and $n=4 k+1$ one can perform similar markings to obtain minimal numbers $4 k^{2}-1$ and $(2 k+1)^{2}$, respectively.
|
k(k+1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
25. C5 (BLR) ${ }^{\mathrm{IMO} 3}$ Let $n$ be an even positive integer. We say that two different cells of an $n \times n$ board are neighboring if they have a common side. Find the minimal number of cells on the $n \times n$ board that must be marked so that every cell (marked or not marked) has a marked neighboring cell.
|
25 . Let $n=2 k$. Color the cells neighboring the edge of the board black. Then color the cells neighboring the black cells white. Then in alternation color the still uncolored cells neighboring the white or black cells on the boundary the opposite color  and repeat until all cells are colored. We call the cells colored the same color in each such iteration a "frame." In the color scheme described, each cell (white or black) neighbors exactly two black cells. The number of black cells is $2 k(k+1)$, and hence we need to mark at least $k(k+1)$ cells. On the other hand, going along each black-colored frame, we can alternately mark two consecutive cells and then not mark two consecutive cells. Every cell on the black frame will have one marked neighbor. One can arrange these sequences on two consecutive black frames such that each cell in the white frame in between has exactly one neighbor. Hence, starting from a sequence on the largest frame we obtain a marking that contains exactly half of all the black cells, i.e., $k(k+1)$ and neighbors every cell. It follows that the desired minimal number of markings is $k(k+1)$. Remark. For $n=4 k-1$ and $n=4 k+1$ one can perform similar markings to obtain minimal numbers $4 k^{2}-1$ and $(2 k+1)^{2}$, respectively.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e73103b1-57d8-54ad-a7b1-1f27d57f88ef
| 24,934
|
1. $\mathbf{C 1}$ (HUN) ${ }^{\mathrm{IMO}}$ A magician has one hundred cards numbered 1 to 100. He puts them into three boxes, a red one, a white one, and a blue one, so that each box contains at least one card. A member of the audience draws two cards from two different boxes and announces the sum of numbers on those cards. Given this information, the magician locates the box from which no card has been drawn. How many ways are there to put the cards in the three boxes so that the trick works?
|
1. In order for the trick to work, whenever $x+y=z+t$ and the cards $x, y$ are placed in different boxes, either $z, t$ are in these boxes as well or they are both in the remaining box. Case 1. The cards $i, i+1, i+2$ are in different boxes for some $i$. Since $i+(i+3)=(i+1)+(i+2)$, the cards $i$ and $i+3$ must be in the same box; moreover, $i-1$ must be in the same box as $i+2$, etc. Hence the cards $1,4,7, \ldots, 100$ are placed in one box, the cards $2,5, \ldots, 98$ are in the second, while $3,6, \ldots, 99$ are in the third box. The number of different arrangements of the cards is 6 in this case. Case 2. No three successive cards are all placed in different boxes. Suppose that 1 is in the blue box, and denote by $w$ and $r$ the smallest numbers on cards lying in the white and red boxes; assume w.l.o.g. that $w<r$. The card $w+1$ is obviously not red, from which it follows that $r>$ $w+1$. Now suppose that $r<100$. Since $w+r=(w-1)+(r+1), r+1$ must be in the blue box. But then $(r+1)+w=r+(w+1)$ implies that $w+1$ must be red, which is a contradiction. Hence the red box contains only the card 100 . Since $99+w=100+(w-1)$, we deduce that the card 99 is in the white box. Moreover, if any of the cards $k$, $2 \leq k \leq 99$, were in the blue box, then since $k+99=(k-1)+100$, the card $k-1$ should be in the red box, which is impossible. Hence the blue box contains only the card 1 , whereas the cards $2,3, \ldots, 99$ are all in the white box. In general, one box contains 1 , another box only 100 , while the remaining contains all the other cards. There are exactly 6 such arrangements, and the trick works in each of them. Therefore the answer is 12.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
1. $\mathbf{C 1}$ (HUN) ${ }^{\mathrm{IMO}}$ A magician has one hundred cards numbered 1 to 100. He puts them into three boxes, a red one, a white one, and a blue one, so that each box contains at least one card. A member of the audience draws two cards from two different boxes and announces the sum of numbers on those cards. Given this information, the magician locates the box from which no card has been drawn. How many ways are there to put the cards in the three boxes so that the trick works?
|
1. In order for the trick to work, whenever $x+y=z+t$ and the cards $x, y$ are placed in different boxes, either $z, t$ are in these boxes as well or they are both in the remaining box. Case 1. The cards $i, i+1, i+2$ are in different boxes for some $i$. Since $i+(i+3)=(i+1)+(i+2)$, the cards $i$ and $i+3$ must be in the same box; moreover, $i-1$ must be in the same box as $i+2$, etc. Hence the cards $1,4,7, \ldots, 100$ are placed in one box, the cards $2,5, \ldots, 98$ are in the second, while $3,6, \ldots, 99$ are in the third box. The number of different arrangements of the cards is 6 in this case. Case 2. No three successive cards are all placed in different boxes. Suppose that 1 is in the blue box, and denote by $w$ and $r$ the smallest numbers on cards lying in the white and red boxes; assume w.l.o.g. that $w<r$. The card $w+1$ is obviously not red, from which it follows that $r>$ $w+1$. Now suppose that $r<100$. Since $w+r=(w-1)+(r+1), r+1$ must be in the blue box. But then $(r+1)+w=r+(w+1)$ implies that $w+1$ must be red, which is a contradiction. Hence the red box contains only the card 100 . Since $99+w=100+(w-1)$, we deduce that the card 99 is in the white box. Moreover, if any of the cards $k$, $2 \leq k \leq 99$, were in the blue box, then since $k+99=(k-1)+100$, the card $k-1$ should be in the red box, which is impossible. Hence the blue box contains only the card 1 , whereas the cards $2,3, \ldots, 99$ are all in the white box. In general, one box contains 1 , another box only 100 , while the remaining contains all the other cards. There are exactly 6 such arrangements, and the trick works in each of them. Therefore the answer is 12.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
14d33596-6278-5afd-bcb0-bf59d0776a7e
| 24,960
|
26. G7 (IRN) Ten gangsters are standing on a flat surface, and the distances between them are all distinct. At twelve o'clock, when the church bells start chiming, each of them fatally shoots the one among the other nine gangsters who is the nearest. At least how many gangsters will be killed?
|
26. The problem can be reformulated in the following way: Given a set $S$ of ten points in the plane such that the distances between them are all distinct, for each point $P \in S$ we mark the point $Q \in S \backslash\{P\}$ nearest to $P$. Find the least possible number of marked points. Observe that each point $A \in S$ is the nearest to at most five other points. Indeed, for any six points $P_{1}, \ldots, P_{6}$ one of the angles $P_{i} A P_{j}$ is at most $60^{\circ}$, in which case $P_{i} P_{j}$ is smaller than one of the distances $A P_{i}, A P_{j}$. It follows that at least two points are marked. Now suppose that exactly two points, say $A$ and $B$, are marked. Then $A B$ is the minimal distance of the points from $S$, so by the previous observation the rest of the set $S$ splits into two subsets of four points according to whether the nearest point is $A$ or $B$. Let these subsets be $\left\{A_{1}, A_{2}, A_{3}, A_{4}\right\}$ and $\left\{B_{1}, B_{2}, B_{3}, B_{4}\right\}$ respectively. Assume that the points are labelled so that the angles $A_{i} A A_{i+1}$ are successively adjacent as well as the angles $B_{i} B B_{i+1}$, and that $A_{1}, B_{1}$ lie on one side of $A B$, and $A_{4}, B_{4}$ lie on the other side. Since all the angles $A_{i} A A_{i+1}$ and $B_{i} B B_{i+1}$ are greater than $60^{\circ}$, it follows that $$ \angle A_{1} A B+\angle B A A_{4}+\angle B_{1} B A+\angle A B B_{4}<360^{\circ} . $$ Therefore $\angle A_{1} A B+\angle B_{1} B A<180^{\circ}$ or $\angle A_{4} A B+\angle B_{4} B A<180^{\circ}$. Without loss of generality, let us assume the first inequality. On the other hand, note that the quadrilateral $A B B_{1} A_{1}$ is convex because $A_{1}$ and $B_{1}$ are on different sides of the perpendicular bisector of $A B$. From $A_{1} B_{1}>A_{1} A$ and $B B_{1}>A B$ we obtain $\angle A_{1} A B_{1}>\angle A_{1} B_{1} A$ and $\angle B A B_{1}>\angle A B_{1} B$. Adding these relations yields $\angle A_{1} A B>\angle A_{1} B_{1} B$. Similarly, $\angle B_{1} B A>\angle B_{1} A_{1} A$. Adding these two inequalities, we get $$ 180^{\circ}>\angle A_{1} A B+\angle B_{1} B A>\angle A_{1} B_{1} B+\angle B_{1} A_{1} A $$ hence the sum of the angles of the quadrilateral $A B B_{1} A_{1}$ is less than $360^{\circ}$, which is a contradiction. Thus at least 3 points are marked. An example of a configuration in which exactly 3 gangsters are killed is shown below. 
|
3
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
26. G7 (IRN) Ten gangsters are standing on a flat surface, and the distances between them are all distinct. At twelve o'clock, when the church bells start chiming, each of them fatally shoots the one among the other nine gangsters who is the nearest. At least how many gangsters will be killed?
|
26. The problem can be reformulated in the following way: Given a set $S$ of ten points in the plane such that the distances between them are all distinct, for each point $P \in S$ we mark the point $Q \in S \backslash\{P\}$ nearest to $P$. Find the least possible number of marked points. Observe that each point $A \in S$ is the nearest to at most five other points. Indeed, for any six points $P_{1}, \ldots, P_{6}$ one of the angles $P_{i} A P_{j}$ is at most $60^{\circ}$, in which case $P_{i} P_{j}$ is smaller than one of the distances $A P_{i}, A P_{j}$. It follows that at least two points are marked. Now suppose that exactly two points, say $A$ and $B$, are marked. Then $A B$ is the minimal distance of the points from $S$, so by the previous observation the rest of the set $S$ splits into two subsets of four points according to whether the nearest point is $A$ or $B$. Let these subsets be $\left\{A_{1}, A_{2}, A_{3}, A_{4}\right\}$ and $\left\{B_{1}, B_{2}, B_{3}, B_{4}\right\}$ respectively. Assume that the points are labelled so that the angles $A_{i} A A_{i+1}$ are successively adjacent as well as the angles $B_{i} B B_{i+1}$, and that $A_{1}, B_{1}$ lie on one side of $A B$, and $A_{4}, B_{4}$ lie on the other side. Since all the angles $A_{i} A A_{i+1}$ and $B_{i} B B_{i+1}$ are greater than $60^{\circ}$, it follows that $$ \angle A_{1} A B+\angle B A A_{4}+\angle B_{1} B A+\angle A B B_{4}<360^{\circ} . $$ Therefore $\angle A_{1} A B+\angle B_{1} B A<180^{\circ}$ or $\angle A_{4} A B+\angle B_{4} B A<180^{\circ}$. Without loss of generality, let us assume the first inequality. On the other hand, note that the quadrilateral $A B B_{1} A_{1}$ is convex because $A_{1}$ and $B_{1}$ are on different sides of the perpendicular bisector of $A B$. From $A_{1} B_{1}>A_{1} A$ and $B B_{1}>A B$ we obtain $\angle A_{1} A B_{1}>\angle A_{1} B_{1} A$ and $\angle B A B_{1}>\angle A B_{1} B$. Adding these relations yields $\angle A_{1} A B>\angle A_{1} B_{1} B$. Similarly, $\angle B_{1} B A>\angle B_{1} A_{1} A$. Adding these two inequalities, we get $$ 180^{\circ}>\angle A_{1} A B+\angle B_{1} B A>\angle A_{1} B_{1} B+\angle B_{1} A_{1} A $$ hence the sum of the angles of the quadrilateral $A B B_{1} A_{1}$ is less than $360^{\circ}$, which is a contradiction. Thus at least 3 points are marked. An example of a configuration in which exactly 3 gangsters are killed is shown below. 
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
76ef07da-f767-529b-8a85-8b69a9396e0d
| 25,009
|
4. C4 (CZE) Let $n$ and $k$ be positive integers such that $n / 2<k \leq 2 n / 3$. Find the least number $m$ for which it is possible to place $m$ pawns on $m$ squares of an $n \times n$ chessboard so that no column or row contains a block of $k$ adjacent unoccupied squares.
|
4. By a good placement of pawns we mean the placement in which there is no block of $k$ adjacent unoccupied squares in a row or column. We can make a good placement as follows: Label the rows and columns with $0,1, \ldots, n-1$ and place a pawn on a square $(i, j)$ if and only if $k$ divides $i+j+1$. This is obviously a good placement in which the pawns are placed on three lines with $k, 2 n-2 k$, and $2 n-3 k$ squares, which adds up to $4 n-4 k$ pawns in total. Now we shall prove that a good placement must contain at least $4 n-4 k$ pawns. Suppose we have a good placement of $m$ pawns. Partition the board into nine rectangular regions as shown in the picture. Let $a, b, \ldots, h$ be the numbers of pawns in the rectangles $A, B, \ldots, H$ respectively. Note that each row that 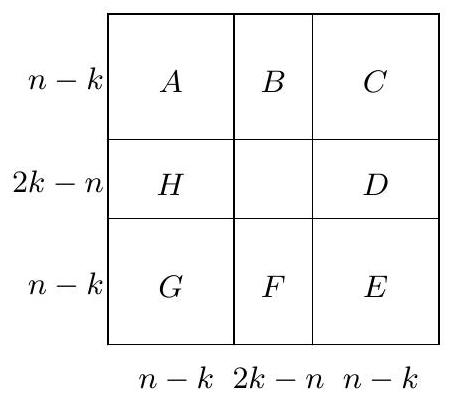 passes through $A, B$, and $C$ either contains a pawn inside $B$, or contains a pawn in both $A$ and $C$. It follows that $a+c+2 b \geq 2(n-k)$. We similarly obtain that $c+e+2 d, e+g+2 f$, and $g+a+2 h$ are all at least $2(n-k)$. Adding and dividing by 2 yields $a+b+\cdots+h \geq 4(n-k)$, which proves the statement.
|
4n-4k
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
4. C4 (CZE) Let $n$ and $k$ be positive integers such that $n / 2<k \leq 2 n / 3$. Find the least number $m$ for which it is possible to place $m$ pawns on $m$ squares of an $n \times n$ chessboard so that no column or row contains a block of $k$ adjacent unoccupied squares.
|
4. By a good placement of pawns we mean the placement in which there is no block of $k$ adjacent unoccupied squares in a row or column. We can make a good placement as follows: Label the rows and columns with $0,1, \ldots, n-1$ and place a pawn on a square $(i, j)$ if and only if $k$ divides $i+j+1$. This is obviously a good placement in which the pawns are placed on three lines with $k, 2 n-2 k$, and $2 n-3 k$ squares, which adds up to $4 n-4 k$ pawns in total. Now we shall prove that a good placement must contain at least $4 n-4 k$ pawns. Suppose we have a good placement of $m$ pawns. Partition the board into nine rectangular regions as shown in the picture. Let $a, b, \ldots, h$ be the numbers of pawns in the rectangles $A, B, \ldots, H$ respectively. Note that each row that  passes through $A, B$, and $C$ either contains a pawn inside $B$, or contains a pawn in both $A$ and $C$. It follows that $a+c+2 b \geq 2(n-k)$. We similarly obtain that $c+e+2 d, e+g+2 f$, and $g+a+2 h$ are all at least $2(n-k)$. Adding and dividing by 2 yields $a+b+\cdots+h \geq 4(n-k)$, which proves the statement.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b1250fc5-efd5-55fd-921d-36d776e69535
| 25,018
|
24. N2 (COL) Consider the system $$ \begin{aligned} x+y & =z+u \\ 2 x y & =z u . \end{aligned} $$ Find the greatest value of the real constant $m$ such that $m \leq x / y$ for every positive integer solution $x, y, z, u$ of the system with $x \geq y$.
|
24. We shall find the general solution to the system. Squaring both sides of the first equation and subtracting twice the second equation we obtain $(x-y)^{2}=z^{2}+u^{2}$. Thus $(z, u, x-y)$ is a Pythagorean triple. Then it is well known that there are positive integers $t, a, b$ such that $z=t\left(a^{2}-b^{2}\right)$, $u=2 t a b$ (or vice versa), and $x-y=t\left(a^{2}+b^{2}\right)$. Using that $x+y=z+u$ we come to the general solution: $$ x=t\left(a^{2}+a b\right), \quad y=t\left(a b-b^{2}\right) ; \quad z=t\left(a^{2}-b^{2}\right), \quad u=2 t a b . $$ Putting $a / b=k$ we obtain $$ \frac{x}{y}=\frac{k^{2}+k}{k-1}=3+(k-1)+\frac{2}{k-1} \geq 3+2 \sqrt{2} $$ with equality for $k-1=\sqrt{2}$. On the other hand, $k$ can be arbitrarily close to $1+\sqrt{2}$, and so $x / y$ can be arbitrarily close to $3+2 \sqrt{2}$. Hence $m=3+2 \sqrt{2}$. Remark. There are several other techniques for solving the given system. The exact lower bound of $m$ itself can be obtained as follows: by the $\operatorname{system}\left(\frac{x}{y}\right)^{2}-6 \frac{x}{y}+1=\left(\frac{z-u}{y}\right)^{2} \geq 0$, so $x / y \geq 3+2 \sqrt{2}$.
|
3+2\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
24. N2 (COL) Consider the system $$ \begin{aligned} x+y & =z+u \\ 2 x y & =z u . \end{aligned} $$ Find the greatest value of the real constant $m$ such that $m \leq x / y$ for every positive integer solution $x, y, z, u$ of the system with $x \geq y$.
|
24. We shall find the general solution to the system. Squaring both sides of the first equation and subtracting twice the second equation we obtain $(x-y)^{2}=z^{2}+u^{2}$. Thus $(z, u, x-y)$ is a Pythagorean triple. Then it is well known that there are positive integers $t, a, b$ such that $z=t\left(a^{2}-b^{2}\right)$, $u=2 t a b$ (or vice versa), and $x-y=t\left(a^{2}+b^{2}\right)$. Using that $x+y=z+u$ we come to the general solution: $$ x=t\left(a^{2}+a b\right), \quad y=t\left(a b-b^{2}\right) ; \quad z=t\left(a^{2}-b^{2}\right), \quad u=2 t a b . $$ Putting $a / b=k$ we obtain $$ \frac{x}{y}=\frac{k^{2}+k}{k-1}=3+(k-1)+\frac{2}{k-1} \geq 3+2 \sqrt{2} $$ with equality for $k-1=\sqrt{2}$. On the other hand, $k$ can be arbitrarily close to $1+\sqrt{2}$, and so $x / y$ can be arbitrarily close to $3+2 \sqrt{2}$. Hence $m=3+2 \sqrt{2}$. Remark. There are several other techniques for solving the given system. The exact lower bound of $m$ itself can be obtained as follows: by the $\operatorname{system}\left(\frac{x}{y}\right)^{2}-6 \frac{x}{y}+1=\left(\frac{z-u}{y}\right)^{2} \geq 0$, so $x / y \geq 3+2 \sqrt{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
48a69d73-c3f4-5a54-8a33-012ccd93bc8e
| 25,078
|
25. N3 (GBR) Let $a_{1}=11^{11}, a_{2}=12^{12}, a_{3}=13^{13}$, and $$ a_{n}=\left|a_{n-1}-a_{n-2}\right|+\left|a_{n-2}-a_{n-3}\right|, \quad n \geq 4 $$ Determine $a_{14^{14}}$.
|
25. Define $b_{n}=\left|a_{n+1}-a_{n}\right|$ for $n \geq 1$. From the equalities $a_{n+1}=b_{n-1}+b_{n-2}$, from $a_{n}=b_{n-2}+b_{n-3}$ we obtain $b_{n}=\left|b_{n-1}-b_{n-3}\right|$. From this relation we deduce that $b_{m} \leq \max \left(b_{n}, b_{n+1}, b_{n+2}\right)$ for all $m \geq n$, and consequently $b_{n}$ is bounded. Lemma. If $\max \left(b_{n}, b_{n+1}, b_{n+2}\right)=M \geq 2$, then $\max \left(b_{n+6}, b_{n+7}, b_{n+8}\right) \leq$ $M-1$. Proof. Assume the opposite. Suppose that $b_{j}=M, j \in\{n, n+1, n+2\}$, and let $b_{j+1}=x$ and $b_{j+2}=y$. Thus $b_{j+3}=M-y$. If $x, y, M-y$ are all less than $M$, then the contradiction is immediate. The remaining cases are these: (i) $x=M$. Then the sequence has the form $M, M, y, M-y, y, \ldots$, and since $\max (y, M-y, y)=M$, we must have $y=0$ or $y=M$. (ii) $y=M$. Then the sequence has the form $M, x, M, 0, x, M-x, \ldots$, and since $\max (0, x, M-x)=M$, we must have $x=0$ or $x=M$. (iii) $y=0$. Then the sequence is $M, x, 0, M, M-x, M-x, x, \ldots$, and since $\max (M-x, x, x)=M$, we have $x=0$ or $x=M$. In every case $M$ divides both $x$ and $y$. From the recurrence formula $M$ also divides $b_{i}$ for every $i<j$. However, $b_{2}=12^{12}-11^{11}$ and $b_{4}=11^{11}$ are relatively prime, a contradiction. From $\max \left(b_{1}, b_{2}, b_{3}\right) \leq 13^{13}$ and the lemma we deduce inductively that $b_{n} \leq 1$ for all $n \geq 6 \cdot 13^{13}-5$. Hence $a_{n}=b_{n-2}+b_{n-3}$ takes only the values $0,1,2$ for $n \geq 6 \cdot 13^{13}-2$. In particular, $a_{14^{14}}$ is 0,1 , or 2 . On the other hand, the sequence $a_{n}$ modulo 2 is as follows: $1,0,1,0,0,1,1 ; 1,0,1,0, \ldots$; and therefore it is periodic with period 7 . Finally, $14^{14} \equiv 0$ modulo 7 , from which we obtain $a_{14^{14}} \equiv a_{7} \equiv 1(\bmod 2)$. Therefore $a_{14^{14}}=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
25. N3 (GBR) Let $a_{1}=11^{11}, a_{2}=12^{12}, a_{3}=13^{13}$, and $$ a_{n}=\left|a_{n-1}-a_{n-2}\right|+\left|a_{n-2}-a_{n-3}\right|, \quad n \geq 4 $$ Determine $a_{14^{14}}$.
|
25. Define $b_{n}=\left|a_{n+1}-a_{n}\right|$ for $n \geq 1$. From the equalities $a_{n+1}=b_{n-1}+b_{n-2}$, from $a_{n}=b_{n-2}+b_{n-3}$ we obtain $b_{n}=\left|b_{n-1}-b_{n-3}\right|$. From this relation we deduce that $b_{m} \leq \max \left(b_{n}, b_{n+1}, b_{n+2}\right)$ for all $m \geq n$, and consequently $b_{n}$ is bounded. Lemma. If $\max \left(b_{n}, b_{n+1}, b_{n+2}\right)=M \geq 2$, then $\max \left(b_{n+6}, b_{n+7}, b_{n+8}\right) \leq$ $M-1$. Proof. Assume the opposite. Suppose that $b_{j}=M, j \in\{n, n+1, n+2\}$, and let $b_{j+1}=x$ and $b_{j+2}=y$. Thus $b_{j+3}=M-y$. If $x, y, M-y$ are all less than $M$, then the contradiction is immediate. The remaining cases are these: (i) $x=M$. Then the sequence has the form $M, M, y, M-y, y, \ldots$, and since $\max (y, M-y, y)=M$, we must have $y=0$ or $y=M$. (ii) $y=M$. Then the sequence has the form $M, x, M, 0, x, M-x, \ldots$, and since $\max (0, x, M-x)=M$, we must have $x=0$ or $x=M$. (iii) $y=0$. Then the sequence is $M, x, 0, M, M-x, M-x, x, \ldots$, and since $\max (M-x, x, x)=M$, we have $x=0$ or $x=M$. In every case $M$ divides both $x$ and $y$. From the recurrence formula $M$ also divides $b_{i}$ for every $i<j$. However, $b_{2}=12^{12}-11^{11}$ and $b_{4}=11^{11}$ are relatively prime, a contradiction. From $\max \left(b_{1}, b_{2}, b_{3}\right) \leq 13^{13}$ and the lemma we deduce inductively that $b_{n} \leq 1$ for all $n \geq 6 \cdot 13^{13}-5$. Hence $a_{n}=b_{n-2}+b_{n-3}$ takes only the values $0,1,2$ for $n \geq 6 \cdot 13^{13}-2$. In particular, $a_{14^{14}}$ is 0,1 , or 2 . On the other hand, the sequence $a_{n}$ modulo 2 is as follows: $1,0,1,0,0,1,1 ; 1,0,1,0, \ldots$; and therefore it is periodic with period 7 . Finally, $14^{14} \equiv 0$ modulo 7 , from which we obtain $a_{14^{14}} \equiv a_{7} \equiv 1(\bmod 2)$. Therefore $a_{14^{14}}=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
99f85baa-5392-5a91-9048-acd863a444ae
| 25,080
|
7. $\mathbf{C 1}$ (COL) Let $A=\left(a_{1}, a_{2}, \ldots, a_{2001}\right)$ be a sequence of positive integers. Let $m$ be the number of 3 -element subsequences $\left(a_{i}, a_{j}, a_{k}\right)$ with $1 \leq i<$ $j<k \leq 2001$ such that $a_{j}=a_{i}+1$ and $a_{k}=a_{j}+1$. Considering all such sequences $A$, find the greatest value of $m$.
|
7. It is evident that arranging of $A$ in increasing order does not diminish $m$. Thus we can assume that $A$ is nondecreasing. Assume w.l.o.g. that $a_{1}=1$, and let $b_{i}$ be the number of elements of $A$ that are equal to $i$ $\left(1 \leq i \leq n=a_{2001}\right)$. Then we have $b_{1}+b_{2}+\cdots+b_{n}=2001$ and $$ m=b_{1} b_{2} b_{3}+b_{2} b_{3} b_{4}+\cdots+b_{n-2} b_{n-1} b_{n} $$ Now if $b_{i}, b_{j}(i<j)$ are two largest $b$ 's, we deduce from (1) and the AMGM inequality that $m \leq b_{i} b_{j}\left(b_{1}+\cdots+b_{i-1}+b_{i+1}+\cdots+b_{j-1}+b_{j+1}+b_{n}\right) \leq$ $\left(\frac{2001}{3}\right)^{3}=667^{3} \quad\left(b_{1} b_{2} b_{3} \leq b_{1} b_{i} b_{j}\right.$, etc.). The value $667^{3}$ is attained for $b_{1}=b_{2}=b_{3}=667$ (i.e., $a_{1}=\cdots=a_{667}=1, a_{668}=\cdots=a_{1334}=2$, $a_{1335}=\cdots=a_{2001}=3$ ). Hence the maximum of $m$ is $667^{3}$.
|
667^3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
7. $\mathbf{C 1}$ (COL) Let $A=\left(a_{1}, a_{2}, \ldots, a_{2001}\right)$ be a sequence of positive integers. Let $m$ be the number of 3 -element subsequences $\left(a_{i}, a_{j}, a_{k}\right)$ with $1 \leq i<$ $j<k \leq 2001$ such that $a_{j}=a_{i}+1$ and $a_{k}=a_{j}+1$. Considering all such sequences $A$, find the greatest value of $m$.
|
7. It is evident that arranging of $A$ in increasing order does not diminish $m$. Thus we can assume that $A$ is nondecreasing. Assume w.l.o.g. that $a_{1}=1$, and let $b_{i}$ be the number of elements of $A$ that are equal to $i$ $\left(1 \leq i \leq n=a_{2001}\right)$. Then we have $b_{1}+b_{2}+\cdots+b_{n}=2001$ and $$ m=b_{1} b_{2} b_{3}+b_{2} b_{3} b_{4}+\cdots+b_{n-2} b_{n-1} b_{n} $$ Now if $b_{i}, b_{j}(i<j)$ are two largest $b$ 's, we deduce from (1) and the AMGM inequality that $m \leq b_{i} b_{j}\left(b_{1}+\cdots+b_{i-1}+b_{i+1}+\cdots+b_{j-1}+b_{j+1}+b_{n}\right) \leq$ $\left(\frac{2001}{3}\right)^{3}=667^{3} \quad\left(b_{1} b_{2} b_{3} \leq b_{1} b_{i} b_{j}\right.$, etc.). The value $667^{3}$ is attained for $b_{1}=b_{2}=b_{3}=667$ (i.e., $a_{1}=\cdots=a_{667}=1, a_{668}=\cdots=a_{1334}=2$, $a_{1335}=\cdots=a_{2001}=3$ ). Hence the maximum of $m$ is $667^{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
56bb333f-f2b1-5a2e-8572-0c5a067294fd
| 25,096
|
1. N1 (UZB) What is the smallest positive integer $t$ such that there exist integers $x_{1}, x_{2}, \ldots, x_{t}$ with $$ x_{1}^{3}+x_{2}^{3}+\cdots+x_{t}^{3}=2002^{2002} ? $$
|
1. Consider the given equation modulo 9 . Since each cube is congruent to either $-1,0$ or 1 , whereas $2002^{2002} \equiv 4^{2002}=4 \cdot 64^{667} \equiv 4(\bmod 9)$, we conclude that $t \geq 4$. On the other hand, $2002^{2002}=2002 \cdot\left(2002^{667}\right)^{3}=\left(10^{3}+10^{3}+1^{3}+\right.$ $\left.1^{3}\right)\left(2002^{667}\right)^{3}$ is a solution with $t=4$. Hence the answer is 4.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
1. N1 (UZB) What is the smallest positive integer $t$ such that there exist integers $x_{1}, x_{2}, \ldots, x_{t}$ with $$ x_{1}^{3}+x_{2}^{3}+\cdots+x_{t}^{3}=2002^{2002} ? $$
|
1. Consider the given equation modulo 9 . Since each cube is congruent to either $-1,0$ or 1 , whereas $2002^{2002} \equiv 4^{2002}=4 \cdot 64^{667} \equiv 4(\bmod 9)$, we conclude that $t \geq 4$. On the other hand, $2002^{2002}=2002 \cdot\left(2002^{667}\right)^{3}=\left(10^{3}+10^{3}+1^{3}+\right.$ $\left.1^{3}\right)\left(2002^{667}\right)^{3}$ is a solution with $t=4$. Hence the answer is 4.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
08ff993d-a746-51f0-b9c0-6b5abc893772
| 25,102
|
11. G5 (AUS) For any set $S$ of five points in the plane, no three of which are collinear, let $M(S)$ and $m(S)$ denote the greatest and smallest areas, respectively, of triangles determined by three points from $S$. What is the minimum possible value of $M(S) / m(S)$ ?
|
11. When $S$ is the set of vertices of a regular pentagon, then it is easily verified that $\frac{M(S)}{m(S)}=\frac{1+\sqrt{5}}{2}=\alpha$. We claim that this is the best possible. Let $A, B, C, D, E$ be five arbitrary points, and assume that $\triangle A B C$ has the area $M(S)$. We claim that some triangle has area less than or equal to $M(S) / \alpha$. Construct a larger triangle $A^{\prime} B^{\prime} C^{\prime}$ with $C \in A^{\prime} B^{\prime}\left\|A B, A \in B^{\prime} C^{\prime}\right\| B C$, $B \in C^{\prime} A^{\prime} \| C A$. The point $D$, as well as $E$, must lie on the same side of $B^{\prime} C^{\prime}$ as $B C$, for otherwise $\triangle D B C$ would have greater area than $\triangle A B C$. A similar result holds for the other edges, and therefore $D, E$ lie inside the triangle $A^{\prime} B^{\prime} C^{\prime}$ or on its boundary. Moreover, at least one of the triangles $A^{\prime} B C, A B^{\prime} C, A B C^{\prime}$, say $A B C^{\prime}$, contains neither $D$ nor $E$. Hence we can assume that $D, E$ are contained inside the quadrilateral $A^{\prime} B^{\prime} A B$. An affine linear transformation does not change the ratios between areas. Thus if we apply such an affine transformation mapping $A, B, C$ into the vertices $A B M C N$ of a regular pentagon, we won't change $M(S) / m(S)$. If now $D$ or $E$ lies inside $A B M C N$, then we are done. Suppose that both $D$ and $E$ are inside the triangles $C M A^{\prime}, C N B^{\prime}$. Then $C D, C E \leq C M$ (because $C M=C N=C A^{\prime}=C B^{\prime}$ ) and $\angle D C E$ is either less than or equal to $36^{\circ}$ or greater than or equal to $108^{\circ}$, from which we obtain that the area of $\triangle C D E$ cannot exceed the area of $\triangle C M N=M(S) / \alpha$. This completes the proof.
|
\frac{1+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
11. G5 (AUS) For any set $S$ of five points in the plane, no three of which are collinear, let $M(S)$ and $m(S)$ denote the greatest and smallest areas, respectively, of triangles determined by three points from $S$. What is the minimum possible value of $M(S) / m(S)$ ?
|
11. When $S$ is the set of vertices of a regular pentagon, then it is easily verified that $\frac{M(S)}{m(S)}=\frac{1+\sqrt{5}}{2}=\alpha$. We claim that this is the best possible. Let $A, B, C, D, E$ be five arbitrary points, and assume that $\triangle A B C$ has the area $M(S)$. We claim that some triangle has area less than or equal to $M(S) / \alpha$. Construct a larger triangle $A^{\prime} B^{\prime} C^{\prime}$ with $C \in A^{\prime} B^{\prime}\left\|A B, A \in B^{\prime} C^{\prime}\right\| B C$, $B \in C^{\prime} A^{\prime} \| C A$. The point $D$, as well as $E$, must lie on the same side of $B^{\prime} C^{\prime}$ as $B C$, for otherwise $\triangle D B C$ would have greater area than $\triangle A B C$. A similar result holds for the other edges, and therefore $D, E$ lie inside the triangle $A^{\prime} B^{\prime} C^{\prime}$ or on its boundary. Moreover, at least one of the triangles $A^{\prime} B C, A B^{\prime} C, A B C^{\prime}$, say $A B C^{\prime}$, contains neither $D$ nor $E$. Hence we can assume that $D, E$ are contained inside the quadrilateral $A^{\prime} B^{\prime} A B$. An affine linear transformation does not change the ratios between areas. Thus if we apply such an affine transformation mapping $A, B, C$ into the vertices $A B M C N$ of a regular pentagon, we won't change $M(S) / m(S)$. If now $D$ or $E$ lies inside $A B M C N$, then we are done. Suppose that both $D$ and $E$ are inside the triangles $C M A^{\prime}, C N B^{\prime}$. Then $C D, C E \leq C M$ (because $C M=C N=C A^{\prime}=C B^{\prime}$ ) and $\angle D C E$ is either less than or equal to $36^{\circ}$ or greater than or equal to $108^{\circ}$, from which we obtain that the area of $\triangle C D E$ cannot exceed the area of $\triangle C M N=M(S) / \alpha$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0aa6bd55-66e0-54fd-b224-9445d0196c86
| 25,106
|
23. C3 (COL) Let $n$ be a positive integer. A sequence of $n$ positive integers (not necessarily distinct) is called full if it satisfies the following condition: For each positive integer $k \geq 2$, if the number $k$ appears in the sequence, then so does the number $k-1$, and moreover, the first occurrence of $k-1$ comes before the last occurrence of $k$. For each $n$, how many full sequences are there?
|
23. We claim that there are $n$ ! full sequences. To show this, we construct a bijection with the set of permutations of $\{1,2, \ldots, n\}$. Consider a full sequence $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$, and let $m$ be the greatest of the numbers $a_{1}, \ldots, a_{n}$. Let $S_{k}, 1 \leq k \leq m$, be the set of those indices $i$ for which $a_{i}=k$. Then $S_{1}, \ldots S_{m}$ are nonempty and form a partition of the set $\{1,2, \ldots, n\}$. Now we write down the elements of $S_{1}$ in descending order, then the elements of $S_{2}$ in descending order and so on. This maps the full sequence to a permutation of $\{1,2, \ldots, n\}$. Moreover, this map is reversible, since each permutation uniquely breaks apart into decreasing sequences $S_{1}^{\prime}, S_{2}^{\prime}, \ldots, S_{m}^{\prime}$, so that $\max S_{i}^{\prime}>\min S_{i-1}^{\prime}$. Therefore the full sequences are in bijection with the permutations of $\{1,2, \ldots, n\}$. Second solution. Let there be given a full sequence of length $n$. Removing from it the first occurrence of the highest number, we obtain a full sequence of length $n-1$. On the other hand, each full sequence of length $n-1$ can be obtained from exactly $n$ full sequences of length $n$. Therefore, if $x_{n}$ is the number of full sequences of length $n$, we deduce $x_{n}=n x_{n-1}$.
|
n!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
23. C3 (COL) Let $n$ be a positive integer. A sequence of $n$ positive integers (not necessarily distinct) is called full if it satisfies the following condition: For each positive integer $k \geq 2$, if the number $k$ appears in the sequence, then so does the number $k-1$, and moreover, the first occurrence of $k-1$ comes before the last occurrence of $k$. For each $n$, how many full sequences are there?
|
23. We claim that there are $n$ ! full sequences. To show this, we construct a bijection with the set of permutations of $\{1,2, \ldots, n\}$. Consider a full sequence $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$, and let $m$ be the greatest of the numbers $a_{1}, \ldots, a_{n}$. Let $S_{k}, 1 \leq k \leq m$, be the set of those indices $i$ for which $a_{i}=k$. Then $S_{1}, \ldots S_{m}$ are nonempty and form a partition of the set $\{1,2, \ldots, n\}$. Now we write down the elements of $S_{1}$ in descending order, then the elements of $S_{2}$ in descending order and so on. This maps the full sequence to a permutation of $\{1,2, \ldots, n\}$. Moreover, this map is reversible, since each permutation uniquely breaks apart into decreasing sequences $S_{1}^{\prime}, S_{2}^{\prime}, \ldots, S_{m}^{\prime}$, so that $\max S_{i}^{\prime}>\min S_{i-1}^{\prime}$. Therefore the full sequences are in bijection with the permutations of $\{1,2, \ldots, n\}$. Second solution. Let there be given a full sequence of length $n$. Removing from it the first occurrence of the highest number, we obtain a full sequence of length $n-1$. On the other hand, each full sequence of length $n-1$ can be obtained from exactly $n$ full sequences of length $n$. Therefore, if $x_{n}$ is the number of full sequences of length $n$, we deduce $x_{n}=n x_{n-1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3f33a765-5e7b-5b8d-85a9-03639e78cf27
| 25,123
|
24. C4 (BUL) Let $T$ be the set of ordered triples $(x, y, z)$, where $x, y, z$ are integers with $0 \leq x, y, z \leq 9$. Players $A$ and $B$ play the following guessing game: Player $A$ chooses a triple $(x, y, z)$ in $T$, and Player $B$ has to discover A's triple in as few moves as possible. A move consists of the following: $B$ gives $A$ a triple $(a, b, c)$ in $T$, and $A$ replies by giving $B$ the number $|x+y-a-b|+|y+z-b-c|+|z+x-c-a|$. Find the minimum number of moves that $B$ needs to be sure of determining $A$ 's triple.
|
24. Two moves are not sufficient. Indeed, the answer to each move is an even number between 0 and 54 , so the answer takes at most 28 distinct values. Consequently, two moves give at most $28^{2}=784$ distinct outcomes, which is less than $10^{3}=1000$. We now show that three moves are sufficient. With the first move $(0,0,0)$, we get the reply $2(x+y+z)$, so we now know the value of $s=x+y+z$. Now there are several cases: (i) $s \leq 9$. Then we ask $(9,0,0)$ as the second move and get $(9-x-y)+$ $(9-x-z)+(y+z)=18-2 x$, so we come to know $x$. Asking $(0,9,0)$ we obtain $y$, which is enough, since $z=s-x-y$. (ii) $10 \leq s \leq 17$. In this case the second move is $(9, s-9,0)$. The answer is $z+(9-x)+|x+z-9|=2 k$, where $k=z$ if $x+z \geq 9$, or $k=9-x$ if $x+z<9$. In both cases we have $z \leq k \leq y+z \leq s$. Let $s-k \leq 9$. Then in the third move we ask $(s-k, 0, k)$ and obtain $|z-k|+|k-y-z|+y$, which is actually $(k-z)+(y+z-k)+y=2 y$. Thus we also find out $x+z$, and thus deduce whether $k$ is $z$ or $9-x$. Consequently we determine both $x$ and $z$. Let $s-k>9$. In this case, the third move is $(9, s-k-9, k)$. The answer is $|s-k-x-y|+|s-9-y-z|+|k+9-z-x|=$ $(k-z)+(9-x)+(9-x+k-z)=18+2 k-2(x+z)$, from which we find out again whether $k$ is $z$ or $9-x$. Now we are easily done. (iii) $18 \leq s \leq 27$. Then as in the first case, asking $(0,9,9)$ and $(9,0,9)$ we obtain $x$ and $y$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
24. C4 (BUL) Let $T$ be the set of ordered triples $(x, y, z)$, where $x, y, z$ are integers with $0 \leq x, y, z \leq 9$. Players $A$ and $B$ play the following guessing game: Player $A$ chooses a triple $(x, y, z)$ in $T$, and Player $B$ has to discover A's triple in as few moves as possible. A move consists of the following: $B$ gives $A$ a triple $(a, b, c)$ in $T$, and $A$ replies by giving $B$ the number $|x+y-a-b|+|y+z-b-c|+|z+x-c-a|$. Find the minimum number of moves that $B$ needs to be sure of determining $A$ 's triple.
|
24. Two moves are not sufficient. Indeed, the answer to each move is an even number between 0 and 54 , so the answer takes at most 28 distinct values. Consequently, two moves give at most $28^{2}=784$ distinct outcomes, which is less than $10^{3}=1000$. We now show that three moves are sufficient. With the first move $(0,0,0)$, we get the reply $2(x+y+z)$, so we now know the value of $s=x+y+z$. Now there are several cases: (i) $s \leq 9$. Then we ask $(9,0,0)$ as the second move and get $(9-x-y)+$ $(9-x-z)+(y+z)=18-2 x$, so we come to know $x$. Asking $(0,9,0)$ we obtain $y$, which is enough, since $z=s-x-y$. (ii) $10 \leq s \leq 17$. In this case the second move is $(9, s-9,0)$. The answer is $z+(9-x)+|x+z-9|=2 k$, where $k=z$ if $x+z \geq 9$, or $k=9-x$ if $x+z<9$. In both cases we have $z \leq k \leq y+z \leq s$. Let $s-k \leq 9$. Then in the third move we ask $(s-k, 0, k)$ and obtain $|z-k|+|k-y-z|+y$, which is actually $(k-z)+(y+z-k)+y=2 y$. Thus we also find out $x+z$, and thus deduce whether $k$ is $z$ or $9-x$. Consequently we determine both $x$ and $z$. Let $s-k>9$. In this case, the third move is $(9, s-k-9, k)$. The answer is $|s-k-x-y|+|s-9-y-z|+|k+9-z-x|=$ $(k-z)+(9-x)+(9-x+k-z)=18+2 k-2(x+z)$, from which we find out again whether $k$ is $z$ or $9-x$. Now we are easily done. (iii) $18 \leq s \leq 27$. Then as in the first case, asking $(0,9,9)$ and $(9,0,9)$ we obtain $x$ and $y$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
89f39004-114f-5642-9800-3bc3082698a3
| 25,124
|
27. C7 (NZL) Among a group of 120 people, some pairs are friends. A weak quartet is a set of four people containing exactly one pair of friends. What is the maximum possible number of weak quartets?
|
27. For a graph $G$ on 120 vertices (i.e., people at the party), write $q(G)$ for the number of weak quartets in $G$. Our solution will consist of three parts. First, we prove that some graph $G$ with maximal $q(G)$ breaks up as a disjoint union of complete graphs. This will follow if we show that any two adjacent vertices $x, y$ have the same neighbors (apart from themselves). Let $G_{x}$ be the graph obtained from $G$ by "copying" $x$ to $y$ (i.e., for each $z \neq x, y$, we add the edge $z y$ if $z x$ is an edge, and delete $z y$ if $z x$ is not an edge). Similarly $G_{y}$ is the graph obtained from $G$ by copying $y$ to $x$. We claim that $2 q(G) \leq q\left(G_{x}\right)+q\left(G_{y}\right)$. Indeed, the number of weak quartets containing neither $x$ nor $y$ is the same in $G, G_{x}$, and $G_{y}$, while the number of those containing both $x$ and $y$ is not less in $G_{x}$ and $G_{y}$ than in $G$. Also, the number containing exactly one of $x$ and $y$ in $G_{x}$ is at least twice the number in $G$ containing $x$ but not $y$, while the number containing exactly one of $x$ and $y$ in $G_{y}$ is at least twice the number in $G$ containing $y$ but not $x$. This justifies our claim by adding. It follows that for an extremal graph $G$ we must have $q(G)=q\left(G_{x}\right)=q\left(G_{y}\right)$. Repeating the copying operation pair by pair ( $y$ to $x$, then their common neighbor $z$ to both $x, y$, etc.) we eventually obtain an extremal graph consisting of disjoint complete graphs. Second, suppose the complete graphs in $G$ have sizes $a_{1}, a_{2}, \ldots, a_{n}$. Then $$ q(G)=\sum_{i=1}^{n}\binom{a_{i}}{2} \sum_{\substack{j<k \\ j, k \neq i}} a_{j} a_{k} . $$ If we fix all the $a_{i}$ except two, say $p, q$, then $p+q=s$ is fixed, and for some constants $C_{i}, q(G)=C_{1}+C_{2} p q+C_{3}\left(\binom{p}{2}+\binom{q}{2}\right)+C_{4}\left(q\binom{p}{2}+p\binom{q}{2}\right)=$ $A+B p q$, where $A$ and $B$ depend only on $s$. Hence the maximum of $q(G)$ is attained if $|p-q| \leq 1$ or $p q=0$. Thus if $q(G)$ is maximal, any two nonzero $a_{i}$ 's differ by at most 1 . Finally, if $G$ consists of $n$ disjoint complete graphs, then $q(G)$ cannot exceed the value obtained if $a_{1}=\cdots=a_{n}$ (not necessarily integral), which equals $$ Q_{n}=\frac{120^{2}}{n}\binom{120 / n}{2}\binom{n-1}{2}=30 \cdot 120^{2} \frac{(n-1)(n-2)(120-n)}{n^{3}} . $$ It is easy to check that $Q_{n}$ takes its maximum when $n=5$ and $a_{1}=\cdots=$ $a_{5}=24$, and that this maximum equals $15 \cdot 23 \cdot 24^{3}=4769280$.
|
4769280
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
27. C7 (NZL) Among a group of 120 people, some pairs are friends. A weak quartet is a set of four people containing exactly one pair of friends. What is the maximum possible number of weak quartets?
|
27. For a graph $G$ on 120 vertices (i.e., people at the party), write $q(G)$ for the number of weak quartets in $G$. Our solution will consist of three parts. First, we prove that some graph $G$ with maximal $q(G)$ breaks up as a disjoint union of complete graphs. This will follow if we show that any two adjacent vertices $x, y$ have the same neighbors (apart from themselves). Let $G_{x}$ be the graph obtained from $G$ by "copying" $x$ to $y$ (i.e., for each $z \neq x, y$, we add the edge $z y$ if $z x$ is an edge, and delete $z y$ if $z x$ is not an edge). Similarly $G_{y}$ is the graph obtained from $G$ by copying $y$ to $x$. We claim that $2 q(G) \leq q\left(G_{x}\right)+q\left(G_{y}\right)$. Indeed, the number of weak quartets containing neither $x$ nor $y$ is the same in $G, G_{x}$, and $G_{y}$, while the number of those containing both $x$ and $y$ is not less in $G_{x}$ and $G_{y}$ than in $G$. Also, the number containing exactly one of $x$ and $y$ in $G_{x}$ is at least twice the number in $G$ containing $x$ but not $y$, while the number containing exactly one of $x$ and $y$ in $G_{y}$ is at least twice the number in $G$ containing $y$ but not $x$. This justifies our claim by adding. It follows that for an extremal graph $G$ we must have $q(G)=q\left(G_{x}\right)=q\left(G_{y}\right)$. Repeating the copying operation pair by pair ( $y$ to $x$, then their common neighbor $z$ to both $x, y$, etc.) we eventually obtain an extremal graph consisting of disjoint complete graphs. Second, suppose the complete graphs in $G$ have sizes $a_{1}, a_{2}, \ldots, a_{n}$. Then $$ q(G)=\sum_{i=1}^{n}\binom{a_{i}}{2} \sum_{\substack{j<k \\ j, k \neq i}} a_{j} a_{k} . $$ If we fix all the $a_{i}$ except two, say $p, q$, then $p+q=s$ is fixed, and for some constants $C_{i}, q(G)=C_{1}+C_{2} p q+C_{3}\left(\binom{p}{2}+\binom{q}{2}\right)+C_{4}\left(q\binom{p}{2}+p\binom{q}{2}\right)=$ $A+B p q$, where $A$ and $B$ depend only on $s$. Hence the maximum of $q(G)$ is attained if $|p-q| \leq 1$ or $p q=0$. Thus if $q(G)$ is maximal, any two nonzero $a_{i}$ 's differ by at most 1 . Finally, if $G$ consists of $n$ disjoint complete graphs, then $q(G)$ cannot exceed the value obtained if $a_{1}=\cdots=a_{n}$ (not necessarily integral), which equals $$ Q_{n}=\frac{120^{2}}{n}\binom{120 / n}{2}\binom{n-1}{2}=30 \cdot 120^{2} \frac{(n-1)(n-2)(120-n)}{n^{3}} . $$ It is easy to check that $Q_{n}$ takes its maximum when $n=5$ and $a_{1}=\cdots=$ $a_{5}=24$, and that this maximum equals $15 \cdot 23 \cdot 24^{3}=4769280$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e97c6a41-83fe-524d-86b8-ae80bfc56d33
| 25,127
|
20. N1 (POL) Let $m$ be a fixed integer greater than 1 . The sequence $x_{0}, x_{1}, x_{2}, \ldots$ is defined as follows: $$ x_{i}= \begin{cases}2^{i}, & \text { if } 0 \leq i \leq m-1 \\ \sum_{j=1}^{m} x_{i-j}, & \text { if } i \geq m\end{cases} $$ Find the greatest $k$ for which the sequence contains $k$ consecutive terms divisible by $m$.
|
20. Let $r_{i}$ be the remainder when $x_{i}$ is divided by $m$. Since there are at most $m^{m}$ types of $m$-consecutive blocks in the sequence $\left(r_{i}\right)$, some type will repeat at least twice. Then since the entire sequence is determined by one $m$-consecutive block, the entire sequence will be periodic. The formula works both forward and backward; hence using the rule $x_{i}=$ $x_{i+m}-\sum_{j=1}^{m-1} x_{i+j}$ we can define $x_{-1}, x_{-2}, \ldots$. Thus we obtain that $$ \left(r_{-m}, \ldots, r_{-1}\right)=(0,0, \ldots, 0,1) $$ Hence there are $m-1$ consecutive terms in the sequence $\left(x_{i}\right)$ that are divisible by $m$. If there were $m$ consecutive terms in the sequence $\left(x_{i}\right)$ divisible by $m$, then by the recurrence relation all the terms of $\left(x_{i}\right)$ would be divisible by $m$, which is impossible.
|
m-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
20. N1 (POL) Let $m$ be a fixed integer greater than 1 . The sequence $x_{0}, x_{1}, x_{2}, \ldots$ is defined as follows: $$ x_{i}= \begin{cases}2^{i}, & \text { if } 0 \leq i \leq m-1 \\ \sum_{j=1}^{m} x_{i-j}, & \text { if } i \geq m\end{cases} $$ Find the greatest $k$ for which the sequence contains $k$ consecutive terms divisible by $m$.
|
20. Let $r_{i}$ be the remainder when $x_{i}$ is divided by $m$. Since there are at most $m^{m}$ types of $m$-consecutive blocks in the sequence $\left(r_{i}\right)$, some type will repeat at least twice. Then since the entire sequence is determined by one $m$-consecutive block, the entire sequence will be periodic. The formula works both forward and backward; hence using the rule $x_{i}=$ $x_{i+m}-\sum_{j=1}^{m-1} x_{i+j}$ we can define $x_{-1}, x_{-2}, \ldots$. Thus we obtain that $$ \left(r_{-m}, \ldots, r_{-1}\right)=(0,0, \ldots, 0,1) $$ Hence there are $m-1$ consecutive terms in the sequence $\left(x_{i}\right)$ that are divisible by $m$. If there were $m$ consecutive terms in the sequence $\left(x_{i}\right)$ divisible by $m$, then by the recurrence relation all the terms of $\left(x_{i}\right)$ would be divisible by $m$, which is impossible.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0232b6e7-87bf-55c1-8c6e-d4fe92345b17
| 25,147
|
27. N8 (IRN) Let $p$ be a prime number and let $A$ be a set of positive integers that satisfies the following conditions: (i) the set of prime divisors of the elements in $A$ consists of $p-1$ elements; (ii) for any nonempty subset of $A$, the product of its elements is not a perfect $p$ th power. What is the largest possible number of elements in $A$ ?
|
27. Let $p_{1}, p_{2}, \ldots, p_{r}$ be distinct primes, where $r=p-1$. Consider the sets $B_{i}=\left\{p_{i}, p_{i}^{p+1}, \ldots, p_{i}^{(r-1) p+1}\right\}$ and $B=\bigcup_{i=1}^{r} B_{i}$. Then $B$ has $(p-1)^{2}$ elements and satisfies (i) and (ii). Now suppose that $|A| \geq r^{2}+1$ and that $A$ satisfies (i) and (ii), and let $\left\{t_{1}, \ldots, t_{r^{2}+1}\right\}$ be distinct elements of $A$, where $t_{j}=p_{1}^{\alpha_{j_{1}}} \cdot p_{2}^{\alpha_{j_{2}}} \cdots p_{r}^{\alpha_{j_{r}}}$. We shall show that the product of some elements of $A$ is a perfect $p$ th power, i.e., that there exist $\tau_{j} \in\{0,1\}\left(1 \leq j \leq r^{2}+1\right)$, not all equal to 0 , such that $T=t_{1}^{\tau_{1}} \cdot t_{2}^{\tau_{2}} \cdots t_{r^{2}+1}^{\tau_{r^{2}+1}}$ is a $p$ th power. This is equivalent to the condition that $$ \sum_{j=1}^{r^{2}+1} \alpha_{i j} \tau_{j} \equiv 0(\bmod p) $$ holds for all $i=1, \ldots, r$. By Fermat's theorem it is sufficient to find integers $x_{1}, \ldots, x_{r^{2}+1}$, not all zero, such that the relation $$ \sum_{j=1}^{r^{2}+1} \alpha_{i j} x_{j}^{r} \equiv 0(\bmod p) $$ is satisfied for all $i \in\{1, \ldots, r\}$. Set $F_{i}=\sum_{j=1}^{r^{2}+1} \alpha_{i j} x_{j}^{r}$. We want to find $x_{1}, \ldots, x_{r}$ such that $F_{1} \equiv F_{2} \equiv \cdots \equiv F_{r} \equiv 0(\bmod p)$, which is by Fermat's theorem equivalent to $$ F\left(x_{1}, \ldots, x_{r}\right)=F_{1}^{r}+F_{2}^{r}+\cdots+F_{r}^{r} \equiv 0(\bmod p) . $$ Of course, one solution of (1) is $(0, \ldots, 0)$ : we are not satisfied with it because it generates the empty subset of $A$, but it tells us that (1) has at least one solution. We shall prove that the number of solutions of (1) is divisible by $p$, which will imply the existence of a nontrivial solution and thus complete the proof. To do this, consider the sum $\sum F\left(x_{1}, \ldots, x_{r^{2}+1}\right)^{r}$ taken over all vectors $\left(x_{1}, \ldots, x_{r^{2}+1}\right)$ in the vector space $\mathbb{Z}_{p}^{r^{2}+1}$. Our statement is equivalent to $$ \sum F\left(x_{1}, \ldots, x_{r^{2}+1}\right)^{r} \equiv 0(\bmod p) $$ Since the degree of $F^{r}$ is $r^{2}$, in each monomial in $F^{r}$ at least one of the variables is missing. Consider any of these monomials, say $b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}$. Then the sum $\sum b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}$, taken over the set of all vectors $\left(x_{1}, \ldots, x_{r^{2}+1}\right) \in \mathbb{Z}_{p}^{r^{2}+1}$, is equal to $$ p^{r^{2}+1-u} \cdot \sum_{\left(x_{i_{1}}, \ldots, x_{i_{k}}\right) \in \mathbb{Z}_{p}^{k}} b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}, $$ which is divisible by $p$, so that (2) is proved. Thus the answer is $(p-1)^{2}$.
|
(p-1)^2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
27. N8 (IRN) Let $p$ be a prime number and let $A$ be a set of positive integers that satisfies the following conditions: (i) the set of prime divisors of the elements in $A$ consists of $p-1$ elements; (ii) for any nonempty subset of $A$, the product of its elements is not a perfect $p$ th power. What is the largest possible number of elements in $A$ ?
|
27. Let $p_{1}, p_{2}, \ldots, p_{r}$ be distinct primes, where $r=p-1$. Consider the sets $B_{i}=\left\{p_{i}, p_{i}^{p+1}, \ldots, p_{i}^{(r-1) p+1}\right\}$ and $B=\bigcup_{i=1}^{r} B_{i}$. Then $B$ has $(p-1)^{2}$ elements and satisfies (i) and (ii). Now suppose that $|A| \geq r^{2}+1$ and that $A$ satisfies (i) and (ii), and let $\left\{t_{1}, \ldots, t_{r^{2}+1}\right\}$ be distinct elements of $A$, where $t_{j}=p_{1}^{\alpha_{j_{1}}} \cdot p_{2}^{\alpha_{j_{2}}} \cdots p_{r}^{\alpha_{j_{r}}}$. We shall show that the product of some elements of $A$ is a perfect $p$ th power, i.e., that there exist $\tau_{j} \in\{0,1\}\left(1 \leq j \leq r^{2}+1\right)$, not all equal to 0 , such that $T=t_{1}^{\tau_{1}} \cdot t_{2}^{\tau_{2}} \cdots t_{r^{2}+1}^{\tau_{r^{2}+1}}$ is a $p$ th power. This is equivalent to the condition that $$ \sum_{j=1}^{r^{2}+1} \alpha_{i j} \tau_{j} \equiv 0(\bmod p) $$ holds for all $i=1, \ldots, r$. By Fermat's theorem it is sufficient to find integers $x_{1}, \ldots, x_{r^{2}+1}$, not all zero, such that the relation $$ \sum_{j=1}^{r^{2}+1} \alpha_{i j} x_{j}^{r} \equiv 0(\bmod p) $$ is satisfied for all $i \in\{1, \ldots, r\}$. Set $F_{i}=\sum_{j=1}^{r^{2}+1} \alpha_{i j} x_{j}^{r}$. We want to find $x_{1}, \ldots, x_{r}$ such that $F_{1} \equiv F_{2} \equiv \cdots \equiv F_{r} \equiv 0(\bmod p)$, which is by Fermat's theorem equivalent to $$ F\left(x_{1}, \ldots, x_{r}\right)=F_{1}^{r}+F_{2}^{r}+\cdots+F_{r}^{r} \equiv 0(\bmod p) . $$ Of course, one solution of (1) is $(0, \ldots, 0)$ : we are not satisfied with it because it generates the empty subset of $A$, but it tells us that (1) has at least one solution. We shall prove that the number of solutions of (1) is divisible by $p$, which will imply the existence of a nontrivial solution and thus complete the proof. To do this, consider the sum $\sum F\left(x_{1}, \ldots, x_{r^{2}+1}\right)^{r}$ taken over all vectors $\left(x_{1}, \ldots, x_{r^{2}+1}\right)$ in the vector space $\mathbb{Z}_{p}^{r^{2}+1}$. Our statement is equivalent to $$ \sum F\left(x_{1}, \ldots, x_{r^{2}+1}\right)^{r} \equiv 0(\bmod p) $$ Since the degree of $F^{r}$ is $r^{2}$, in each monomial in $F^{r}$ at least one of the variables is missing. Consider any of these monomials, say $b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}$. Then the sum $\sum b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}$, taken over the set of all vectors $\left(x_{1}, \ldots, x_{r^{2}+1}\right) \in \mathbb{Z}_{p}^{r^{2}+1}$, is equal to $$ p^{r^{2}+1-u} \cdot \sum_{\left(x_{i_{1}}, \ldots, x_{i_{k}}\right) \in \mathbb{Z}_{p}^{k}} b x_{i_{1}}^{a_{1}} x_{i_{2}}^{a_{2}} \cdots x_{i_{k}}^{a_{k}}, $$ which is divisible by $p$, so that (2) is proved. Thus the answer is $(p-1)^{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
40207e1f-0e28-5da2-be10-773ae09a732c
| 25,154
|
9. C3 (LIT) Let $n \geq 5$ be a given integer. Determine the largest integer $k$ for which there exists a polygon with $n$ vertices (convex or not, with non-self-intersecting boundary) having $k$ internal right angles.
|
9. Suppose that $k$ of the angles of an $n$-gon are right. Since the other $n-k$ angles are less than $360^{\circ}$ and the sum of the angles is $(n-2) 180^{\circ}$, we have the inequality $k \cdot 90^{\circ}+(n-k) 360^{\circ}>(n-2) 180^{\circ}$, which is equivalent to $k<\frac{2 n+4}{3}$. Since $n$ and $k$ are integers, it follows that $k \leq\left[\frac{2 n}{3}\right]+1$. If $n=5$, then $\left[\frac{2 n}{3}\right]+1=4$, but if a pentagon has four right angles, the other angle is equal to $180^{\circ}$, which is impossible. Hence for $n=5$, $k \leq 3$. It is easy to construct a pentagon with 3 right angles, e.g., as in the picture below. Now we shall show by induction that for $n \geq 6$ there is an $n$-gon with $\left[\frac{2 n}{3}\right]+1$ internal right angles. For $n=6,7,8$ examples are presented in the picture. Assume that there is a $(n-3)$ gon with $\left[\frac{2(n-3)}{3}\right]+1=\left[\frac{2 n}{3}\right]-1$ internal right angles. Then one of the internal angles, say $\angle B A C$, is not convex. Interchange the vertex $A$ with four new vertices $A_{1}, A_{2}, A_{3}, A_{4}$ as shown in the picture such that $\angle B A_{1} A_{2}=\angle A_{3} A_{4} C=90^{\circ}$. 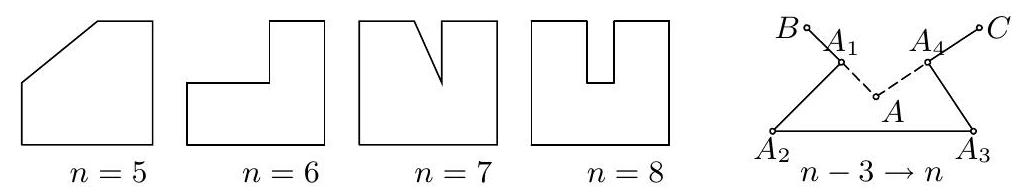
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
9. C3 (LIT) Let $n \geq 5$ be a given integer. Determine the largest integer $k$ for which there exists a polygon with $n$ vertices (convex or not, with non-self-intersecting boundary) having $k$ internal right angles.
|
9. Suppose that $k$ of the angles of an $n$-gon are right. Since the other $n-k$ angles are less than $360^{\circ}$ and the sum of the angles is $(n-2) 180^{\circ}$, we have the inequality $k \cdot 90^{\circ}+(n-k) 360^{\circ}>(n-2) 180^{\circ}$, which is equivalent to $k<\frac{2 n+4}{3}$. Since $n$ and $k$ are integers, it follows that $k \leq\left[\frac{2 n}{3}\right]+1$. If $n=5$, then $\left[\frac{2 n}{3}\right]+1=4$, but if a pentagon has four right angles, the other angle is equal to $180^{\circ}$, which is impossible. Hence for $n=5$, $k \leq 3$. It is easy to construct a pentagon with 3 right angles, e.g., as in the picture below. Now we shall show by induction that for $n \geq 6$ there is an $n$-gon with $\left[\frac{2 n}{3}\right]+1$ internal right angles. For $n=6,7,8$ examples are presented in the picture. Assume that there is a $(n-3)$ gon with $\left[\frac{2(n-3)}{3}\right]+1=\left[\frac{2 n}{3}\right]-1$ internal right angles. Then one of the internal angles, say $\angle B A C$, is not convex. Interchange the vertex $A$ with four new vertices $A_{1}, A_{2}, A_{3}, A_{4}$ as shown in the picture such that $\angle B A_{1} A_{2}=\angle A_{3} A_{4} C=90^{\circ}$. 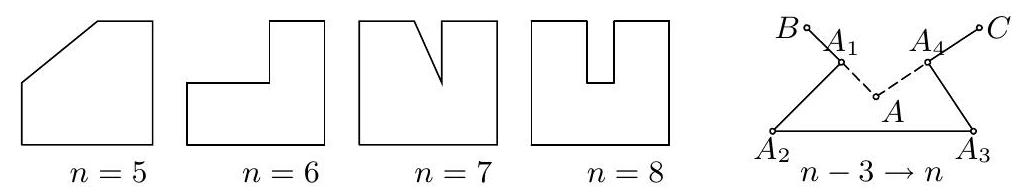
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
fc6da133-fb68-5c10-bc63-84d8ed173262
| 25,161
|
10. C3 (AUS) The following operation is allowed on a finite graph: Choose an arbitrary cycle of length 4 (if there is any), choose an arbitrary edge in that cycle, and delete it from the graph. For a fixed integer $n \geq 4$, find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on $n$ vertices (where each pair of vertices are joined by an edge).
|
10. The least number of edges of such a graph is $n$. We note that deleting edge $A B$ of a 4-cycle $A B C D$ from a connected and nonbipartite graph $G$ yields a connected and nonbipartite graph, say $H$. Indeed, the connectedness is obvious; also, if $H$ were bipartite with partition of the set of vertices into $P_{1}$ and $P_{2}$, then w.l.o.g. $A, C \in P_{1}$ and $B, D \in P_{2}$, so $G=H \cup\{A B\}$ would also be bipartite with the same partition, a contradiction. Any graph that can be obtained from the complete $n$-graph in the described way is connected and has at least one cycle (otherwise it would be bipartite); hence it must have at least $n$ edges. Now consider a complete graph with vertices $V_{1}, V_{2}, \ldots, V_{n}$. Let us remove every edge $V_{i} V_{j}$ with $3 \leq i<j<n$ from the cycle $V_{2} V_{i} V_{j} V_{n}$. Then for $i=3, \ldots, n-1$ we remove edges $V_{2} V_{i}$ and $V_{i} V_{n}$ from the cycles $V_{1} V_{i} V_{2} V_{n}$ and $V_{1} V_{i} V_{n} V_{2}$ respectively, thus obtaining a graph with exactly $n$ edges: $V_{1} V_{i}(i=2, \ldots, n)$ and $V_{2} V_{n}$.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
10. C3 (AUS) The following operation is allowed on a finite graph: Choose an arbitrary cycle of length 4 (if there is any), choose an arbitrary edge in that cycle, and delete it from the graph. For a fixed integer $n \geq 4$, find the least number of edges of a graph that can be obtained by repeated applications of this operation from the complete graph on $n$ vertices (where each pair of vertices are joined by an edge).
|
10. The least number of edges of such a graph is $n$. We note that deleting edge $A B$ of a 4-cycle $A B C D$ from a connected and nonbipartite graph $G$ yields a connected and nonbipartite graph, say $H$. Indeed, the connectedness is obvious; also, if $H$ were bipartite with partition of the set of vertices into $P_{1}$ and $P_{2}$, then w.l.o.g. $A, C \in P_{1}$ and $B, D \in P_{2}$, so $G=H \cup\{A B\}$ would also be bipartite with the same partition, a contradiction. Any graph that can be obtained from the complete $n$-graph in the described way is connected and has at least one cycle (otherwise it would be bipartite); hence it must have at least $n$ edges. Now consider a complete graph with vertices $V_{1}, V_{2}, \ldots, V_{n}$. Let us remove every edge $V_{i} V_{j}$ with $3 \leq i<j<n$ from the cycle $V_{2} V_{i} V_{j} V_{n}$. Then for $i=3, \ldots, n-1$ we remove edges $V_{2} V_{i}$ and $V_{i} V_{n}$ from the cycles $V_{1} V_{i} V_{2} V_{n}$ and $V_{1} V_{i} V_{n} V_{2}$ respectively, thus obtaining a graph with exactly $n$ edges: $V_{1} V_{i}(i=2, \ldots, n)$ and $V_{2} V_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7590d2bf-5a93-5c36-80e8-9fa006710bd8
| 25,163
|
11. C4 (POL) Consider a matrix of size $n \times n$ whose entries are real numbers of absolute value not exceeding 1 , and the sum of all entries is 0 . Let $n$ be an even positive integer. Determine the least number $C$ such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding $C$ in absolute value.
|
11. Consider the matrix $A=\left(a_{i j}\right)_{i, j=1}^{n}$ such that $a_{i j}$ is equal to 1 if $i, j \leq n / 2$, -1 if $i, j>n / 2$, and 0 otherwise. This matrix satisfies the conditions from the problem and all row sums and column sums are equal to $\pm n / 2$. Hence $C \geq n / 2$. Let us show that $C=n / 2$. Assume to the contrary that there is a matrix $B=\left(b_{i j}\right)_{i, j=1}^{n}$ all of whose row sums and column sums are either greater than $n / 2$ or smaller than $-n / 2$. We may assume w.l.o.g. that at least $n / 2$ row sums are positive and, permuting rows if necessary, that the first $n / 2$ rows have positive sums. The sum of entries in the $n / 2 \times n$ submatrix $B^{\prime}$ consisting of first $n / 2$ rows is greater than $n^{2} / 4$, and since each column of $B^{\prime}$ has sum at most $n / 2$, it follows that more than $n / 2$ column sums of $B^{\prime}$, and therefore also of $B$, are positive. Again, suppose w.l.o.g. that the first $n / 2$ column sums are positive. Thus the sums $R^{+}$and $C^{+}$of entries in the first $n / 2$ rows and in the first $n / 2$ columns respectively are greater than $n^{2} / 4$. Now the sum of all entries of $B$ can be written as $$ \sum a_{i j}=R^{+}+C^{+}+\sum_{\substack{i>n / 2 \\ j>n / 2}} a_{i j}-\sum_{\substack{i \leq n / 2 \\ j \leq n / 2}} a_{i j}>\frac{n^{2}}{2}-\frac{n^{2}}{4}-\frac{n^{2}}{4}=0 $$ a contradiction. Hence $C=n / 2$, as claimed.
|
\frac{n}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
11. C4 (POL) Consider a matrix of size $n \times n$ whose entries are real numbers of absolute value not exceeding 1 , and the sum of all entries is 0 . Let $n$ be an even positive integer. Determine the least number $C$ such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding $C$ in absolute value.
|
11. Consider the matrix $A=\left(a_{i j}\right)_{i, j=1}^{n}$ such that $a_{i j}$ is equal to 1 if $i, j \leq n / 2$, -1 if $i, j>n / 2$, and 0 otherwise. This matrix satisfies the conditions from the problem and all row sums and column sums are equal to $\pm n / 2$. Hence $C \geq n / 2$. Let us show that $C=n / 2$. Assume to the contrary that there is a matrix $B=\left(b_{i j}\right)_{i, j=1}^{n}$ all of whose row sums and column sums are either greater than $n / 2$ or smaller than $-n / 2$. We may assume w.l.o.g. that at least $n / 2$ row sums are positive and, permuting rows if necessary, that the first $n / 2$ rows have positive sums. The sum of entries in the $n / 2 \times n$ submatrix $B^{\prime}$ consisting of first $n / 2$ rows is greater than $n^{2} / 4$, and since each column of $B^{\prime}$ has sum at most $n / 2$, it follows that more than $n / 2$ column sums of $B^{\prime}$, and therefore also of $B$, are positive. Again, suppose w.l.o.g. that the first $n / 2$ column sums are positive. Thus the sums $R^{+}$and $C^{+}$of entries in the first $n / 2$ rows and in the first $n / 2$ columns respectively are greater than $n^{2} / 4$. Now the sum of all entries of $B$ can be written as $$ \sum a_{i j}=R^{+}+C^{+}+\sum_{\substack{i>n / 2 \\ j>n / 2}} a_{i j}-\sum_{\substack{i \leq n / 2 \\ j \leq n / 2}} a_{i j}>\frac{n^{2}}{2}-\frac{n^{2}}{4}-\frac{n^{2}}{4}=0 $$ a contradiction. Hence $C=n / 2$, as claimed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3a15d7ed-5ffa-5019-86bb-5405b5d64b43
| 25,164
|
12. C5 (NZL) Let $N$ be a positive integer. Two players $A$ and $B$, taking turns, write numbers from the set $\{1, \ldots, N\}$ on a blackboard. $A$ begins the game by writing 1 on his first move. Then, if a player has written $n$ on a certain move, his adversary is allowed to write $n+1$ or $2 n$ (provided the number he writes does not exceed $N$ ). The player who writes $N$ wins. We say that $N$ is of type $A$ or of type $B$ according as $A$ or $B$ has a winning strategy. (a) Determine whether $N=2004$ is of type $A$ or of type $B$. (b) Find the least $N>2004$ whose type is different from that of 2004.
|
12. We say that a number $n \in\{1,2, \ldots, N\}$ is winning if the player who is on turn has a winning strategy, and losing otherwise. The game is of type $A$ if and only if 1 is a losing number. Let us define $n_{0}=N, n_{i+1}=\left[n_{i} / 2\right]$ for $i=0,1, \ldots$ and let $k$ be such that $n_{k}=1$. Consider the sets $A_{i}=\left\{n_{i+1}+1, \ldots, n_{i}\right\}$. We call a set $A_{i}$ all-winning if all numbers from $A_{i}$ are winning, even-winning if even numbers are winning and odd are losing, and odd-winning if odd numbers are winning and even are losing. (i) Suppose $A_{i}$ is even-winning and consider $A_{i+1}$. Multiplying any number from $A_{i+1}$ by 2 yields an even number from $A_{i}$, which is a losing number. Thus $x \in A_{i+1}$ is winning if and only if $x+1$ is losing, i.e., if and only if it is even. Hence $A_{i+1}$ is also even-winning. (ii) Suppose $A_{i}$ is odd-winning. Then each $k \in A_{i+1}$ is winning, since $2 k$ is losing. Hence $A_{i+1}$ is all-winning. (iii) Suppose $A_{i}$ is all-winning. Multiplying $x \in A_{i+1}$ by two is then a losing move, so $x$ is winning if and only if $x+1$ is losing. Since $n_{i+1}$ is losing, $A_{i+1}$ is odd-winning if $n_{i+1}$ is even and even-winning otherwise. We observe that $A_{0}$ is even-winning if $N$ is odd and odd-winning otherwise. Also, if some $A_{i}$ is even-winning, then all $A_{i+1}, A_{i+2}, \ldots$ are evenwinning and thus 1 is losing; i.e., the game is of type $A$. The game is of type $B$ if and only if the sets $A_{0}, A_{1}, \ldots$ are alternately odd-winning and allwinning with $A_{0}$ odd-winning, which is equivalent to $N=n_{0}, n_{2}, n_{4}, \ldots$ all being even. Thus $N$ is of type $B$ if and only if all digits at the odd positions in the binary representation of $N$ are zeros. Since $2004=\overline{11111010100}$ in the binary system, 2004 is of type $A$. The least $N>2004$ that is of type $B$ is $\overline{100000000000}=2^{11}=2048$. Thus the answer to part (b) is 2048.
|
2048
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
12. C5 (NZL) Let $N$ be a positive integer. Two players $A$ and $B$, taking turns, write numbers from the set $\{1, \ldots, N\}$ on a blackboard. $A$ begins the game by writing 1 on his first move. Then, if a player has written $n$ on a certain move, his adversary is allowed to write $n+1$ or $2 n$ (provided the number he writes does not exceed $N$ ). The player who writes $N$ wins. We say that $N$ is of type $A$ or of type $B$ according as $A$ or $B$ has a winning strategy. (a) Determine whether $N=2004$ is of type $A$ or of type $B$. (b) Find the least $N>2004$ whose type is different from that of 2004.
|
12. We say that a number $n \in\{1,2, \ldots, N\}$ is winning if the player who is on turn has a winning strategy, and losing otherwise. The game is of type $A$ if and only if 1 is a losing number. Let us define $n_{0}=N, n_{i+1}=\left[n_{i} / 2\right]$ for $i=0,1, \ldots$ and let $k$ be such that $n_{k}=1$. Consider the sets $A_{i}=\left\{n_{i+1}+1, \ldots, n_{i}\right\}$. We call a set $A_{i}$ all-winning if all numbers from $A_{i}$ are winning, even-winning if even numbers are winning and odd are losing, and odd-winning if odd numbers are winning and even are losing. (i) Suppose $A_{i}$ is even-winning and consider $A_{i+1}$. Multiplying any number from $A_{i+1}$ by 2 yields an even number from $A_{i}$, which is a losing number. Thus $x \in A_{i+1}$ is winning if and only if $x+1$ is losing, i.e., if and only if it is even. Hence $A_{i+1}$ is also even-winning. (ii) Suppose $A_{i}$ is odd-winning. Then each $k \in A_{i+1}$ is winning, since $2 k$ is losing. Hence $A_{i+1}$ is all-winning. (iii) Suppose $A_{i}$ is all-winning. Multiplying $x \in A_{i+1}$ by two is then a losing move, so $x$ is winning if and only if $x+1$ is losing. Since $n_{i+1}$ is losing, $A_{i+1}$ is odd-winning if $n_{i+1}$ is even and even-winning otherwise. We observe that $A_{0}$ is even-winning if $N$ is odd and odd-winning otherwise. Also, if some $A_{i}$ is even-winning, then all $A_{i+1}, A_{i+2}, \ldots$ are evenwinning and thus 1 is losing; i.e., the game is of type $A$. The game is of type $B$ if and only if the sets $A_{0}, A_{1}, \ldots$ are alternately odd-winning and allwinning with $A_{0}$ odd-winning, which is equivalent to $N=n_{0}, n_{2}, n_{4}, \ldots$ all being even. Thus $N$ is of type $B$ if and only if all digits at the odd positions in the binary representation of $N$ are zeros. Since $2004=\overline{11111010100}$ in the binary system, 2004 is of type $A$. The least $N>2004$ that is of type $B$ is $\overline{100000000000}=2^{11}=2048$. Thus the answer to part (b) is 2048.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
909c9f11-2d66-559f-851e-66f25df35d7c
| 25,165
|
13. C6 (IRN) For an $n \times n$ matrix $A$, let $X_{i}$ be the set of entries in row $i$, and $Y_{j}$ the set of entries in column $j, 1 \leq i, j \leq n$. We say that $A$ is golden if $X_{1}, \ldots, X_{n}, Y_{1}, \ldots, Y_{n}$ are distinct sets. Find the least integer $n$ such that there exists a $2004 \times 2004$ golden matrix with entries in the set $\{1,2, \ldots, n\}$.
|
13. Since $X_{i}, Y_{i}, i=1, \ldots, 2004$, are 4008 distinct subsets of the set $S_{n}=$ $\{1,2, \ldots, n\}$, it follows that $2^{n} \geq 4008$, i.e. $n \geq 12$. Suppose $n=12$. Let $\mathcal{X}=\left\{X_{1}, \ldots, X_{2004}\right\}, \mathcal{Y}=\left\{Y_{1}, \ldots, Y_{2004}\right\}, \mathcal{A}=$ $\mathcal{X} \cup \mathcal{Y}$. Exactly $2^{12}-4008=88$ subsets of $S_{n}$ do not occur in $\mathcal{A}$. Since each row intersects each column, we have $X_{i} \cap Y_{j} \neq \emptyset$ for all $i, j$. Suppose $\left|X_{i}\right|,\left|Y_{j}\right| \leq 3$ for some indices $i, j$. Since then $\left|X_{i} \cup Y_{j}\right| \leq 5$, any of at least $2^{7}>88$ subsets of $S_{n} \backslash\left(X_{i} \cap Y_{j}\right)$ can occur in neither $\mathcal{X}$ nor $\mathcal{Y}$, which is impossible. Hence either in $\mathcal{X}$ or in $\mathcal{Y}$ all subsets are of size at least 4. Suppose w.l.o.g. that $k=\left|X_{l}\right|=\min _{i}\left|X_{i}\right| \geq 4$. There are $$ n_{k}=\binom{12-k}{0}+\binom{12-k}{1}+\cdots+\binom{12-k}{k-1} $$ subsets of $S \backslash X_{l}$ with fewer than $k$ elements, and none of them can be either in $\mathcal{X}$ (because $\left|X_{l}\right|$ is minimal in $\mathcal{X}$ ) or in $\mathcal{Y}$. Hence we must have $n_{k} \leq 88$. Since $n_{4}=93$ and $n_{5}=99$, it follows that $k \geq 6$. But then none of the $\binom{12}{0}+\cdots+\binom{12}{5}=1586$ subsets of $S_{n}$ is in $\mathcal{X}$, hence at least $1586-88=1498$ of them are in $\mathcal{Y}$. The 1498 complements of these subsets also do not occur in $\mathcal{X}$, which adds to 3084 subsets of $S_{n}$ not occurring in $\mathcal{X}$. This is clearly a contradiction. Now we construct a golden matrix for $n=13$. Let $$ A_{1}=\left[\begin{array}{ll} 1 & 1 \\ 2 & 3 \end{array}\right] \quad \text { and } \quad A_{m}=\left[\begin{array}{ll} A_{m-1} & A_{m-1} \\ A_{m-1} & B_{m-1} \end{array}\right] \text { for } m=2,3, \ldots $$ where $B_{m-1}$ is the $2^{m-1} \times 2^{m-1}$ matrix with all entries equal to $m+2$. It can be easily proved by induction that each of the matrices $A_{m}$ is golden. Moreover, every upper-left square submatrix of $A_{m}$ of size greater than $2^{m-1}$ is also golden. Since $2^{10}<2004<2^{11}$, we thus obtain a golden matrix of size 2004 with entries in $S_{13}$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
13. C6 (IRN) For an $n \times n$ matrix $A$, let $X_{i}$ be the set of entries in row $i$, and $Y_{j}$ the set of entries in column $j, 1 \leq i, j \leq n$. We say that $A$ is golden if $X_{1}, \ldots, X_{n}, Y_{1}, \ldots, Y_{n}$ are distinct sets. Find the least integer $n$ such that there exists a $2004 \times 2004$ golden matrix with entries in the set $\{1,2, \ldots, n\}$.
|
13. Since $X_{i}, Y_{i}, i=1, \ldots, 2004$, are 4008 distinct subsets of the set $S_{n}=$ $\{1,2, \ldots, n\}$, it follows that $2^{n} \geq 4008$, i.e. $n \geq 12$. Suppose $n=12$. Let $\mathcal{X}=\left\{X_{1}, \ldots, X_{2004}\right\}, \mathcal{Y}=\left\{Y_{1}, \ldots, Y_{2004}\right\}, \mathcal{A}=$ $\mathcal{X} \cup \mathcal{Y}$. Exactly $2^{12}-4008=88$ subsets of $S_{n}$ do not occur in $\mathcal{A}$. Since each row intersects each column, we have $X_{i} \cap Y_{j} \neq \emptyset$ for all $i, j$. Suppose $\left|X_{i}\right|,\left|Y_{j}\right| \leq 3$ for some indices $i, j$. Since then $\left|X_{i} \cup Y_{j}\right| \leq 5$, any of at least $2^{7}>88$ subsets of $S_{n} \backslash\left(X_{i} \cap Y_{j}\right)$ can occur in neither $\mathcal{X}$ nor $\mathcal{Y}$, which is impossible. Hence either in $\mathcal{X}$ or in $\mathcal{Y}$ all subsets are of size at least 4. Suppose w.l.o.g. that $k=\left|X_{l}\right|=\min _{i}\left|X_{i}\right| \geq 4$. There are $$ n_{k}=\binom{12-k}{0}+\binom{12-k}{1}+\cdots+\binom{12-k}{k-1} $$ subsets of $S \backslash X_{l}$ with fewer than $k$ elements, and none of them can be either in $\mathcal{X}$ (because $\left|X_{l}\right|$ is minimal in $\mathcal{X}$ ) or in $\mathcal{Y}$. Hence we must have $n_{k} \leq 88$. Since $n_{4}=93$ and $n_{5}=99$, it follows that $k \geq 6$. But then none of the $\binom{12}{0}+\cdots+\binom{12}{5}=1586$ subsets of $S_{n}$ is in $\mathcal{X}$, hence at least $1586-88=1498$ of them are in $\mathcal{Y}$. The 1498 complements of these subsets also do not occur in $\mathcal{X}$, which adds to 3084 subsets of $S_{n}$ not occurring in $\mathcal{X}$. This is clearly a contradiction. Now we construct a golden matrix for $n=13$. Let $$ A_{1}=\left[\begin{array}{ll} 1 & 1 \\ 2 & 3 \end{array}\right] \quad \text { and } \quad A_{m}=\left[\begin{array}{ll} A_{m-1} & A_{m-1} \\ A_{m-1} & B_{m-1} \end{array}\right] \text { for } m=2,3, \ldots $$ where $B_{m-1}$ is the $2^{m-1} \times 2^{m-1}$ matrix with all entries equal to $m+2$. It can be easily proved by induction that each of the matrices $A_{m}$ is golden. Moreover, every upper-left square submatrix of $A_{m}$ of size greater than $2^{m-1}$ is also golden. Since $2^{10}<2004<2^{11}$, we thus obtain a golden matrix of size 2004 with entries in $S_{13}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
efa0c7df-b578-59b5-80ab-cc35dc7accf7
| 25,166
|
15. C8 (POL) For a finite graph $G$, let $f(G)$ be the number of triangles and $g(G)$ the number of tetrahedra formed by edges of $G$. Find the least constant $c$ such that $$ g(G)^{3} \leq c \cdot f(G)^{4} \text { for every graph } G $$
|
15. Denote by $V_{1}, \ldots, V_{n}$ the vertices of a graph $G$ and by $E$ the set of its edges. For each $i=1, \ldots, n$, let $A_{i}$ be the set of vertices connected to $V_{i}$ by an edge, $G_{i}$ the subgraph of $G$ whose set of vertices is $A_{i}$, and $E_{i}$ the set of edges of $G_{i}$. Also, let $v_{i}, e_{i}$, and $t_{i}=f\left(G_{i}\right)$ be the numbers of vertices, edges, and triangles in $G_{i}$ respectively. The numbers of tetrahedra and triangles one of whose vertices is $V_{i}$ are respectively equal to $t_{i}$ and $e_{i}$. Hence $$ \sum_{i=1}^{n} v_{i}=2|E|, \quad \sum_{i=1}^{n} e_{i}=3 f(G) \quad \text { and } \quad \sum_{i=1}^{n} t_{i}=4 g(G) . $$ Since $e_{i} \leq v_{i}\left(v_{i}-1\right) / 2 \leq v_{i}^{2} / 2$ and $e_{i} \leq|E|$, we obtain $e_{i}^{2} \leq v_{i}^{2}|E| / 2$, i.e., $e_{i} \leq v_{i} \sqrt{|E| / 2}$. Summing over all $i$ yields $3 f(G) \leq 2|E| \sqrt{|E| / 2}$, or equivalently $f(G)^{2} \leq 2|E|^{3} / 9$. Since this relation holds for each graph $G_{i}$, it follows that $$ t_{i}=f\left(G_{i}\right)=f\left(G_{i}\right)^{1 / 3} f\left(G_{i}\right)^{2 / 3} \leq\left(\frac{2}{9}\right)^{1 / 3} f(G)^{1 / 3} e_{i} $$ Summing the last inequality for $i=1, \ldots, n$ gives us $$ 4 g(G) \leq 3\left(\frac{2}{9}\right)^{1 / 3} f(G)^{1 / 3} \cdot f(G), \quad \text { i.e. } \quad g(G)^{3} \leq \frac{3}{32} f(G)^{4} $$ The constant $c=3 / 32$ is the best possible. Indeed, in a complete graph $C_{n}$ it holds that $g\left(K_{n}\right)^{3} / f\left(K_{n}\right)^{4}=\binom{n}{4}^{3}\binom{n}{3}^{-4} \rightarrow \frac{3}{32}$ as $n \rightarrow \infty$. Remark. Let $N_{k}$ be the number of complete $k$-subgraphs in a finite graph $G$. Continuing inductively, one can prove that $N_{k+1}^{k} \leq \frac{k!}{(k+1)^{k}} N_{k}^{k+1}$.
|
\frac{3}{32}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
15. C8 (POL) For a finite graph $G$, let $f(G)$ be the number of triangles and $g(G)$ the number of tetrahedra formed by edges of $G$. Find the least constant $c$ such that $$ g(G)^{3} \leq c \cdot f(G)^{4} \text { for every graph } G $$
|
15. Denote by $V_{1}, \ldots, V_{n}$ the vertices of a graph $G$ and by $E$ the set of its edges. For each $i=1, \ldots, n$, let $A_{i}$ be the set of vertices connected to $V_{i}$ by an edge, $G_{i}$ the subgraph of $G$ whose set of vertices is $A_{i}$, and $E_{i}$ the set of edges of $G_{i}$. Also, let $v_{i}, e_{i}$, and $t_{i}=f\left(G_{i}\right)$ be the numbers of vertices, edges, and triangles in $G_{i}$ respectively. The numbers of tetrahedra and triangles one of whose vertices is $V_{i}$ are respectively equal to $t_{i}$ and $e_{i}$. Hence $$ \sum_{i=1}^{n} v_{i}=2|E|, \quad \sum_{i=1}^{n} e_{i}=3 f(G) \quad \text { and } \quad \sum_{i=1}^{n} t_{i}=4 g(G) . $$ Since $e_{i} \leq v_{i}\left(v_{i}-1\right) / 2 \leq v_{i}^{2} / 2$ and $e_{i} \leq|E|$, we obtain $e_{i}^{2} \leq v_{i}^{2}|E| / 2$, i.e., $e_{i} \leq v_{i} \sqrt{|E| / 2}$. Summing over all $i$ yields $3 f(G) \leq 2|E| \sqrt{|E| / 2}$, or equivalently $f(G)^{2} \leq 2|E|^{3} / 9$. Since this relation holds for each graph $G_{i}$, it follows that $$ t_{i}=f\left(G_{i}\right)=f\left(G_{i}\right)^{1 / 3} f\left(G_{i}\right)^{2 / 3} \leq\left(\frac{2}{9}\right)^{1 / 3} f(G)^{1 / 3} e_{i} $$ Summing the last inequality for $i=1, \ldots, n$ gives us $$ 4 g(G) \leq 3\left(\frac{2}{9}\right)^{1 / 3} f(G)^{1 / 3} \cdot f(G), \quad \text { i.e. } \quad g(G)^{3} \leq \frac{3}{32} f(G)^{4} $$ The constant $c=3 / 32$ is the best possible. Indeed, in a complete graph $C_{n}$ it holds that $g\left(K_{n}\right)^{3} / f\left(K_{n}\right)^{4}=\binom{n}{4}^{3}\binom{n}{3}^{-4} \rightarrow \frac{3}{32}$ as $n \rightarrow \infty$. Remark. Let $N_{k}$ be the number of complete $k$-subgraphs in a finite graph $G$. Continuing inductively, one can prove that $N_{k+1}^{k} \leq \frac{k!}{(k+1)^{k}} N_{k}^{k+1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2c957e57-a6da-55f1-ba61-3027ce9a2add
| 25,168
|
8. C1 (PUR) There are 10001 students at a university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of $k$ societies. Suppose that the following conditions hold: (i) Each pair of students are in exactly one club. (ii) For each student and each society, the student is in exactly one club of the society. (iii) Each club has an odd number of students. In addition, a club with $2 m+1$ students ( $m$ is a positive integer) is in exactly $m$ societies. Find all possible values of $k$.
|
8. Let us write $n=10001$. Denote by $\mathcal{T}$ the set of ordered triples $(a, C, \mathcal{S})$, where $a$ is a student, $C$ a club, and $\mathcal{S}$ a society such that $a \in C$ and $C \in \mathcal{S}$. We shall count $|\mathcal{T}|$ in two different ways. Fix a student $a$ and a society $\mathcal{S}$. By (ii), there is a unique club $C$ such that $(a, C, \mathcal{S}) \in \mathcal{T}$. Since the ordered pair $(a, \mathcal{S})$ can be chosen in $n k$ ways, we have that $|\mathcal{T}|=n k$. Now fix a club $C$. By (iii), $C$ is in exactly $(|C|-1) / 2$ societies, so there are $|C|(|C|-1) / 2$ triples from $\mathcal{T}$ with second coordinate $C$. If $\mathcal{C}$ is the set of all clubs, we obtain $|\mathcal{T}|=\sum_{C \in \mathcal{C}} \frac{|C|(|C|-1)}{2}$. But we also conclude from (i) that $$ \sum_{C \in \mathcal{C}} \frac{|C|(|C|-1)}{2}=\frac{n(n-1)}{2} $$ Therefore $n(n-1) / 2=n k$, i.e., $k=(n-1) / 2=5000$. On the other hand, for $k=(n-1) / 2$ there is a desired configuration with only one club $C$ that contains all students and $k$ identical societies with only one element (the club $C$ ). It is easy to verify that (i)-(iii) hold.
|
5000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
8. C1 (PUR) There are 10001 students at a university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of $k$ societies. Suppose that the following conditions hold: (i) Each pair of students are in exactly one club. (ii) For each student and each society, the student is in exactly one club of the society. (iii) Each club has an odd number of students. In addition, a club with $2 m+1$ students ( $m$ is a positive integer) is in exactly $m$ societies. Find all possible values of $k$.
|
8. Let us write $n=10001$. Denote by $\mathcal{T}$ the set of ordered triples $(a, C, \mathcal{S})$, where $a$ is a student, $C$ a club, and $\mathcal{S}$ a society such that $a \in C$ and $C \in \mathcal{S}$. We shall count $|\mathcal{T}|$ in two different ways. Fix a student $a$ and a society $\mathcal{S}$. By (ii), there is a unique club $C$ such that $(a, C, \mathcal{S}) \in \mathcal{T}$. Since the ordered pair $(a, \mathcal{S})$ can be chosen in $n k$ ways, we have that $|\mathcal{T}|=n k$. Now fix a club $C$. By (iii), $C$ is in exactly $(|C|-1) / 2$ societies, so there are $|C|(|C|-1) / 2$ triples from $\mathcal{T}$ with second coordinate $C$. If $\mathcal{C}$ is the set of all clubs, we obtain $|\mathcal{T}|=\sum_{C \in \mathcal{C}} \frac{|C|(|C|-1)}{2}$. But we also conclude from (i) that $$ \sum_{C \in \mathcal{C}} \frac{|C|(|C|-1)}{2}=\frac{n(n-1)}{2} $$ Therefore $n(n-1) / 2=n k$, i.e., $k=(n-1) / 2=5000$. On the other hand, for $k=(n-1) / 2$ there is a desired configuration with only one club $C$ that contains all students and $k$ identical societies with only one element (the club $C$ ). It is easy to verify that (i)-(iii) hold.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ac4fa526-f9c7-5122-bb85-9cc687d09854
| 25,190
|
Determine the least positive value taken by the expression $a^{3}+b^{3}+c^{3}-3 a b c$ as $a, b, c$ vary over all positive integers. Find also all triples $(a, b, c)$ for which this least value is attained.
|
We observe that
$$
\left.Q=a^{3}+b^{3}+c^{3}-3 a b c=\frac{1}{2}(a+b+c)\right)\left((a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right)
$$
Since we are looking for the least positive value taken by $Q$, it follows that $a, b, c$ are not all equal. Thus $a+b+c \geq 1+1+2=4$ and $(a-b)^{2}+(b-$ $c)^{2}+(c-a)^{2} \geq 1+1+0=2$. Thus we see that $Q \geq 4$. Taking $a=1$, $b=1$ and $c=2$, we get $Q=4$. Therefore the least value of $Q$ is 4 and this is achieved only by $a+b+c=4$ and $(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=2$. The triples for which $Q=4$ are therefore given by
$$
(a, b, c)=(1,1,2),(1,2,1),(2,1,1)
$$
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine the least positive value taken by the expression $a^{3}+b^{3}+c^{3}-3 a b c$ as $a, b, c$ vary over all positive integers. Find also all triples $(a, b, c)$ for which this least value is attained.
|
We observe that
$$
\left.Q=a^{3}+b^{3}+c^{3}-3 a b c=\frac{1}{2}(a+b+c)\right)\left((a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right)
$$
Since we are looking for the least positive value taken by $Q$, it follows that $a, b, c$ are not all equal. Thus $a+b+c \geq 1+1+2=4$ and $(a-b)^{2}+(b-$ $c)^{2}+(c-a)^{2} \geq 1+1+0=2$. Thus we see that $Q \geq 4$. Taking $a=1$, $b=1$ and $c=2$, we get $Q=4$. Therefore the least value of $Q$ is 4 and this is achieved only by $a+b+c=4$ and $(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=2$. The triples for which $Q=4$ are therefore given by
$$
(a, b, c)=(1,1,2),(1,2,1),(2,1,1)
$$
|
{
"resource_path": "INMO/segmented/en-2002.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
6e6134cc-a787-5f03-814e-1dbf35fc2183
| 607,798
|
In a lottery, tickets are given nine-digit numbers using only the digits $1,2,3$. They are also coloured red, blue or green in such a way that two tickets whose numbers differ in all the nine places get different colours. Suppose
the ticket bearing the number 122222222 is red and that bearing the number 222222222 is green. Determine, with proof, the colour of the ticket bearing the number 123123123 .
|
The following sequence of moves lead to the colour of the ticket bearing the number 123123123:
| Line Number | Ticket Number | Colour | Reason |
| :---: | :--- | :--- | :--- |
| 1 | 122222222 | red | Given |
| 2 | 222222222 | green | Given |
| 3 | 313113113 | blue | Lines 1 \& 2 |
| 4 | 231331331 | green | Lines 1 \& 3 |
| 5 | 331331331 | blue | Lines 1 \& 2 |
| 6 | 123123123 | red | Lines 4 \& 5 |
If 123123123 is reached by some other root, red colour must be obtained even along that root. For if for example 123123123 gets blue from some other root, then the following sequence leads to a contradiction:
| Line Number | Ticket Number | Colour | Reason |
| :---: | :--- | :--- | :--- |
| 1 | 122222222 | red | Given |
| 2 | 123123123 | blue | Given |
| 3 | 231311311 | green | Lines 1 \& 2 |
| 4 | 211331311 | green | Lines 1 \& 2 |
| 5 | 332212212 | red | Lines 4 \& 2 |
| 6 | 113133133 | blue | Lines 3 \& 5 |
| 7 | 331331331 | green | Lines 1 \& 2 |
| 8 | 222222222 | red | Line 6 \& 7 |
Thus the colour of 22222222 is red contradicting that it is grren.
|
red
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a lottery, tickets are given nine-digit numbers using only the digits $1,2,3$. They are also coloured red, blue or green in such a way that two tickets whose numbers differ in all the nine places get different colours. Suppose
the ticket bearing the number 122222222 is red and that bearing the number 222222222 is green. Determine, with proof, the colour of the ticket bearing the number 123123123 .
|
The following sequence of moves lead to the colour of the ticket bearing the number 123123123:
| Line Number | Ticket Number | Colour | Reason |
| :---: | :--- | :--- | :--- |
| 1 | 122222222 | red | Given |
| 2 | 222222222 | green | Given |
| 3 | 313113113 | blue | Lines 1 \& 2 |
| 4 | 231331331 | green | Lines 1 \& 3 |
| 5 | 331331331 | blue | Lines 1 \& 2 |
| 6 | 123123123 | red | Lines 4 \& 5 |
If 123123123 is reached by some other root, red colour must be obtained even along that root. For if for example 123123123 gets blue from some other root, then the following sequence leads to a contradiction:
| Line Number | Ticket Number | Colour | Reason |
| :---: | :--- | :--- | :--- |
| 1 | 122222222 | red | Given |
| 2 | 123123123 | blue | Given |
| 3 | 231311311 | green | Lines 1 \& 2 |
| 4 | 211331311 | green | Lines 1 \& 2 |
| 5 | 332212212 | red | Lines 4 \& 2 |
| 6 | 113133133 | blue | Lines 3 \& 5 |
| 7 | 331331331 | green | Lines 1 \& 2 |
| 8 | 222222222 | red | Line 6 \& 7 |
Thus the colour of 22222222 is red contradicting that it is grren.
|
{
"resource_path": "INMO/segmented/en-2003.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
bfc5855b-4298-5a56-a866-799b35154f8e
| 607,808
|
Let $S$ denote the set of all 6-tuples $(a, b, c, d, e, f)$ of positive integers such that $a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=$ $f^{2}$. Consider the set
$$
T=\{a b c d e f:(a, b, c, d, e, f) \in S\}
$$
Find the greatest common divisor of all the members of $T$.
|
We show that the required gcd is 24 . Consider an element $(a, d, c, d, e, f) \in S$. We have
$$
a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=f^{2}
$$
We first observe that not all $a, b, c, d, e$ can be odd. Otherwise, we have $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1$ $(\bmod 8)$ and hence $f^{2} \equiv 5(\bmod 8)$, which is impossible because no square can be congruent to 5 modulo 8. Thus at least one of $a, b, c, d, e$ is even.
Similarly if none of $a, b, c, d, e$ is divisible by 3 , then $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1(\bmod 3)$ and hence $f^{2} \equiv 2(\bmod 3)$ which again is impossible because no square is congruent to 2 modulo 3 . Thus 3 divides $a b c d e f$.
There are several possibilities for $a, b, c, d, e$.
Case 1: Suppose one of them is even and the other four are odd; say $a$ is even, $b, c, d, e$ are odd. Then $b^{2}+c^{2}+d^{2}+e^{2} \equiv 4(\bmod 8)$. If $a^{2} \equiv 4(\bmod 8)$, then $f^{2} \equiv 0(\bmod 8)$ and hence $2|a, 4| f$ giving $8 \mid a f$. If $a^{2} \equiv 0(\bmod 8)$, then $f^{2} \equiv 4(\bmod 8)$ which again gives that $4 \mid a$ and $2 \mid f$ so that $8 \mid a f$. It follows that $8 \mid a b c d e f$ and hence $24 \mid a b c d e f$.
Case 2: Suppose $a, b$ are even and $c, d, e$ are odd. Then $c^{2}+d^{2}+e^{2} \equiv 3(\bmod 8)$. Since $a^{2}+b^{2} \equiv 0$ or 4 modulo 8 , it follows that $f^{2} \equiv 3$ or $7(\bmod 8)$ which is impossible. Hence this case does not arise.
Case 3: If three of $a, b, c, d, e$ are even and two odd, then $8 \mid a b c d e f$ and hence 24|abcdef.
Case 4: If four of $a, b, c, d, e$ are even, then again $8 \mid a b c d e f$ and 24|abcdef. Here again for any six tuple $(a, b, c, d, e, f)$ in $S$, we observe that $24 \mid a b c d e f$. Since
$$
1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}
$$
We see that $(1,1,1,2,3,4) \in S$ and hence $24 \in T$. Thus 24 is the gcd of $T$.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $S$ denote the set of all 6-tuples $(a, b, c, d, e, f)$ of positive integers such that $a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=$ $f^{2}$. Consider the set
$$
T=\{a b c d e f:(a, b, c, d, e, f) \in S\}
$$
Find the greatest common divisor of all the members of $T$.
|
We show that the required gcd is 24 . Consider an element $(a, d, c, d, e, f) \in S$. We have
$$
a^{2}+b^{2}+c^{2}+d^{2}+e^{2}=f^{2}
$$
We first observe that not all $a, b, c, d, e$ can be odd. Otherwise, we have $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1$ $(\bmod 8)$ and hence $f^{2} \equiv 5(\bmod 8)$, which is impossible because no square can be congruent to 5 modulo 8. Thus at least one of $a, b, c, d, e$ is even.
Similarly if none of $a, b, c, d, e$ is divisible by 3 , then $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2} \equiv e^{2} \equiv 1(\bmod 3)$ and hence $f^{2} \equiv 2(\bmod 3)$ which again is impossible because no square is congruent to 2 modulo 3 . Thus 3 divides $a b c d e f$.
There are several possibilities for $a, b, c, d, e$.
Case 1: Suppose one of them is even and the other four are odd; say $a$ is even, $b, c, d, e$ are odd. Then $b^{2}+c^{2}+d^{2}+e^{2} \equiv 4(\bmod 8)$. If $a^{2} \equiv 4(\bmod 8)$, then $f^{2} \equiv 0(\bmod 8)$ and hence $2|a, 4| f$ giving $8 \mid a f$. If $a^{2} \equiv 0(\bmod 8)$, then $f^{2} \equiv 4(\bmod 8)$ which again gives that $4 \mid a$ and $2 \mid f$ so that $8 \mid a f$. It follows that $8 \mid a b c d e f$ and hence $24 \mid a b c d e f$.
Case 2: Suppose $a, b$ are even and $c, d, e$ are odd. Then $c^{2}+d^{2}+e^{2} \equiv 3(\bmod 8)$. Since $a^{2}+b^{2} \equiv 0$ or 4 modulo 8 , it follows that $f^{2} \equiv 3$ or $7(\bmod 8)$ which is impossible. Hence this case does not arise.
Case 3: If three of $a, b, c, d, e$ are even and two odd, then $8 \mid a b c d e f$ and hence 24|abcdef.
Case 4: If four of $a, b, c, d, e$ are even, then again $8 \mid a b c d e f$ and 24|abcdef. Here again for any six tuple $(a, b, c, d, e, f)$ in $S$, we observe that $24 \mid a b c d e f$. Since
$$
1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}
$$
We see that $(1,1,1,2,3,4) \in S$ and hence $24 \in T$. Thus 24 is the gcd of $T$.
|
{
"resource_path": "INMO/segmented/en-2004.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
0f81a06b-990a-540d-bd36-c2afb5b77847
| 607,813
|
Let $\alpha$ and $\beta$ be positive integers such that
$$
\frac{43}{197}<\frac{\alpha}{\beta}<\frac{17}{77}
$$
Find the minimum possible value of $\beta$.
|
We have
$$
\frac{77}{17}<\frac{\beta}{\alpha}<\frac{197}{43}
$$
That is,
$$
4+\frac{9}{17}<\frac{\beta}{\alpha}<4+\frac{25}{43}
$$
Thus $4<\frac{\beta}{\alpha}<5$. Since $\alpha$ and $\beta$ are positive integers, we may write $\beta=4 \alpha+x$, where $0<x<\alpha$. Now we get
$$
4+\frac{9}{17}<4+\frac{x}{\alpha}<4+\frac{25}{43}
$$
So $\frac{9}{17}<\frac{x}{\alpha}<\frac{25}{43}$; that is, $\frac{43 x}{25}<\alpha<\frac{17 x}{9}$.
We find the smallest value of $x$ for which $\alpha$ becomes a well-defined integer. For $x=1,2,3$ the bounds of $\alpha$ are respectively $\left(1 \frac{18}{25}, 1 \frac{8}{9}\right),\left(3 \frac{11}{25}, 3 \frac{7}{9}\right),\left(5 \frac{4}{9}, 5 \frac{2}{3}\right)$. None of these pairs contain an integer between them.
For $x=4$, we have $\frac{43 x}{25}=6 \frac{12}{25}$ and $\frac{17 x}{9}=7 \frac{5}{9}$. Hence, in this case $\alpha=7$, and $\beta=4 \alpha+x=28+4=32$.
This is also the least possible value, because, if $x \geq 5$, then $\alpha>\frac{43 x}{25} \geq \frac{43}{5}>8$, and so $\beta>37$.
Hence the minimum possible value of $\beta$ is 32 .
|
32
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\alpha$ and $\beta$ be positive integers such that
$$
\frac{43}{197}<\frac{\alpha}{\beta}<\frac{17}{77}
$$
Find the minimum possible value of $\beta$.
|
We have
$$
\frac{77}{17}<\frac{\beta}{\alpha}<\frac{197}{43}
$$
That is,
$$
4+\frac{9}{17}<\frac{\beta}{\alpha}<4+\frac{25}{43}
$$
Thus $4<\frac{\beta}{\alpha}<5$. Since $\alpha$ and $\beta$ are positive integers, we may write $\beta=4 \alpha+x$, where $0<x<\alpha$. Now we get
$$
4+\frac{9}{17}<4+\frac{x}{\alpha}<4+\frac{25}{43}
$$
So $\frac{9}{17}<\frac{x}{\alpha}<\frac{25}{43}$; that is, $\frac{43 x}{25}<\alpha<\frac{17 x}{9}$.
We find the smallest value of $x$ for which $\alpha$ becomes a well-defined integer. For $x=1,2,3$ the bounds of $\alpha$ are respectively $\left(1 \frac{18}{25}, 1 \frac{8}{9}\right),\left(3 \frac{11}{25}, 3 \frac{7}{9}\right),\left(5 \frac{4}{9}, 5 \frac{2}{3}\right)$. None of these pairs contain an integer between them.
For $x=4$, we have $\frac{43 x}{25}=6 \frac{12}{25}$ and $\frac{17 x}{9}=7 \frac{5}{9}$. Hence, in this case $\alpha=7$, and $\beta=4 \alpha+x=28+4=32$.
This is also the least possible value, because, if $x \geq 5$, then $\alpha>\frac{43 x}{25} \geq \frac{43}{5}>8$, and so $\beta>37$.
Hence the minimum possible value of $\beta$ is 32 .
|
{
"resource_path": "INMO/segmented/en-2005.jsonl",
"problem_match": "\n2.",
"solution_match": "## Solution:"
}
|
3a87aeb7-343e-57af-9f30-b16aa5d7ef2a
| 607,816
|
All possible 6-digit numbers, in each of which the digits occur in non-increasing order (from left to right, e.g., 877550) are written as a sequence in increasing order. Find the 2005 -th number in this sequence.
|
Consider a 6-digit number whose digits from left to right are in non increasing order. If 1 is the first digit of such a number, then the subsequent digits cannot exceed 1. The set of all such numbers with initial digit equal to 1 is
$$
\{100000,110000,111000,111100,111110,1111111\} .
$$
There are elements in this set.
Let us consider 6-digit numbers with initial digit 2. Starting form 200000, we can go up to 222222 . We count these numbers as follows:
| 200000 | - | 211111 | $:$ | 6 |
| :--- | :--- | :--- | :--- | :--- |
| 220000 | - | 221111 | $:$ | 5 |
| 222000 | - | 222111 | $:$ | 4 |
| 222200 | - | 222211 | $:$ | 3 |
| 222220 | - | 222221 | $:$ | 2 |
| 222222 | - | 222222 | $:$ | 1 |
The number of such numbers is 21. Similarly we count numbers with initial digit 3 ; the sequence starts from 300000 and ends with 333333 . We have
| 300000 | -322222 | $:$ | 21 | |
| :---: | :---: | :---: | :---: | :---: |
| 330000 | - | 332222 | $:$ | 15 |
| 333000 | - | 333222 | $:$ | 10 |
| 333300 | -333322 | $:$ | 6 | |
| 333330 | - | 333332 | $:$ | 3 |
| 333333 | -333333 | $:$ | 1 | |
We obtain the total number of numbers starting from 3 equal to 56. Similarly,
| 400000 | 433333 | 56 |
| :---: | :---: | :---: |
| 440000 | 443333 | 35 |
| 444000 | 444333 | 20 |
| 444400 | 444433 | 10 |
| 444440 | 444443 | 4 |
| 444444 | $-\quad 444444$ | 1 |
| | | 126 |
| 500000 | 544444 | 126 |
| 550000 | 554444 | 70 |
| 555000 | 555444 | 35 |
| 555500 | 555544 | 15 |
| 555550 | 555554 | 5 |
| 555555 | 555555 | 1 |
| | | 252 |
| 600000 | 655555 | 252 |
| 660000 | $-\quad 665555$ | 126 |
| 666000 | $-\quad 666555$ | 56 |
| 666600 | $-\quad 666655$ | 21 |
| 666660 | $-\quad 666665$ | 6 |
| 666666 | $-\quad 666666$ | 1 |
| | | $\overline{462}$ |
| 700000 | $-\quad 766666$ | 462 |
| 770000 | $-\quad 776666$ | 210 |
| 777000 | $-\quad 777666$ | 84 |
| 777700 | $-\quad 777766$ | 28 |
| 777770 | $-\quad 777776$ | 7 |
| 777777 | 777777 | 1 |
| | | 792 |
Thus the number of 6-digit numbers where digits are non-increasing starting from 100000 and ending with 777777 is
$$
792+462+252+126+56+21+6=1715
$$
Since $2005-1715=290$, we have to consider only 290 numbers in the sequence with initial digit 8 . We have
$$
\begin{aligned}
& 800000-855555 \quad: \quad 252 \\
& 860000-863333: 35 \\
& 864000-864110 \quad: \quad 3
\end{aligned}
$$
Thus the required number is $\underline{864110}$.
|
864110
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
All possible 6-digit numbers, in each of which the digits occur in non-increasing order (from left to right, e.g., 877550) are written as a sequence in increasing order. Find the 2005 -th number in this sequence.
|
Consider a 6-digit number whose digits from left to right are in non increasing order. If 1 is the first digit of such a number, then the subsequent digits cannot exceed 1. The set of all such numbers with initial digit equal to 1 is
$$
\{100000,110000,111000,111100,111110,1111111\} .
$$
There are elements in this set.
Let us consider 6-digit numbers with initial digit 2. Starting form 200000, we can go up to 222222 . We count these numbers as follows:
| 200000 | - | 211111 | $:$ | 6 |
| :--- | :--- | :--- | :--- | :--- |
| 220000 | - | 221111 | $:$ | 5 |
| 222000 | - | 222111 | $:$ | 4 |
| 222200 | - | 222211 | $:$ | 3 |
| 222220 | - | 222221 | $:$ | 2 |
| 222222 | - | 222222 | $:$ | 1 |
The number of such numbers is 21. Similarly we count numbers with initial digit 3 ; the sequence starts from 300000 and ends with 333333 . We have
| 300000 | -322222 | $:$ | 21 | |
| :---: | :---: | :---: | :---: | :---: |
| 330000 | - | 332222 | $:$ | 15 |
| 333000 | - | 333222 | $:$ | 10 |
| 333300 | -333322 | $:$ | 6 | |
| 333330 | - | 333332 | $:$ | 3 |
| 333333 | -333333 | $:$ | 1 | |
We obtain the total number of numbers starting from 3 equal to 56. Similarly,
| 400000 | 433333 | 56 |
| :---: | :---: | :---: |
| 440000 | 443333 | 35 |
| 444000 | 444333 | 20 |
| 444400 | 444433 | 10 |
| 444440 | 444443 | 4 |
| 444444 | $-\quad 444444$ | 1 |
| | | 126 |
| 500000 | 544444 | 126 |
| 550000 | 554444 | 70 |
| 555000 | 555444 | 35 |
| 555500 | 555544 | 15 |
| 555550 | 555554 | 5 |
| 555555 | 555555 | 1 |
| | | 252 |
| 600000 | 655555 | 252 |
| 660000 | $-\quad 665555$ | 126 |
| 666000 | $-\quad 666555$ | 56 |
| 666600 | $-\quad 666655$ | 21 |
| 666660 | $-\quad 666665$ | 6 |
| 666666 | $-\quad 666666$ | 1 |
| | | $\overline{462}$ |
| 700000 | $-\quad 766666$ | 462 |
| 770000 | $-\quad 776666$ | 210 |
| 777000 | $-\quad 777666$ | 84 |
| 777700 | $-\quad 777766$ | 28 |
| 777770 | $-\quad 777776$ | 7 |
| 777777 | 777777 | 1 |
| | | 792 |
Thus the number of 6-digit numbers where digits are non-increasing starting from 100000 and ending with 777777 is
$$
792+462+252+126+56+21+6=1715
$$
Since $2005-1715=290$, we have to consider only 290 numbers in the sequence with initial digit 8 . We have
$$
\begin{aligned}
& 800000-855555 \quad: \quad 252 \\
& 860000-863333: 35 \\
& 864000-864110 \quad: \quad 3
\end{aligned}
$$
Thus the required number is $\underline{864110}$.
|
{
"resource_path": "INMO/segmented/en-2005.jsonl",
"problem_match": "\n4.",
"solution_match": "## Solution I:"
}
|
f4f65464-a25b-507e-9e5a-d887e6df1137
| 607,818
|
Let $\sigma=\left(a_{1}, a_{2}, a_{3}, \ldots, a_{n}\right)$ be a permutation of $(1,2,3, \ldots, n)$. A pair $\left(a_{i}, a_{j}\right)$ is said to correspond to an inversion of $\sigma$, if $i<j$ but $a_{i}>a_{j}$. (Example: In the permutation $(2,4,5,3,1)$, there are 6 inversions corresponding to the pairs $(2,1)$, $(4,3),(4,1),(5,3),(5,1),(3,1)$.) How many permutations of $(1,2,3, \ldots n)$, $(n \geq 3)$, have exactly two inversions?
|
In a permutation of $(1,2,3, \ldots, n)$, two inversions can occur in only one of the following two ways:
(A) Two disjoint consecutive pairs are interchanged:
$$
\begin{aligned}
& (1,2,3, j-1, j, j+1, j+2 \ldots k-1, k, k+1, k+2, \ldots, n) \\
& \quad \longrightarrow(1,2, \ldots j-1, j+1, j, j+2, \ldots, k-1, k+1, k, k+2, \ldots, n)
\end{aligned}
$$
(B) Each block of three consecutive integers can be permuted in any of the following 2 ways;
$$
\begin{aligned}
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+2, k, k+1, \ldots, n) \\
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+1, k+2, k, \ldots, n)
\end{aligned}
$$
Consider case (A). For $j=1$, there are $n-3$ possible values of $k$; for $j=2$, there are $n-4$ possibilities for $k$ and so on. Thus the number of permutations with two inversions of this type is
$$
1+2+\cdots+(n-3)=\frac{(n-3)(n-2)}{2}
$$
In case (B), we see that there are $n-2$ permutations of each type, since $k$ can take values from 1 to $n-2$. Hence we get $2(n-2)$ permutations of this type.
Finally, the number of permutations with two inversions is
$$
\frac{(n-3)(n-2)}{2}+2(n-2)=\frac{(n+1)(n-2)}{2}
$$
|
\frac{(n+1)(n-2)}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $\sigma=\left(a_{1}, a_{2}, a_{3}, \ldots, a_{n}\right)$ be a permutation of $(1,2,3, \ldots, n)$. A pair $\left(a_{i}, a_{j}\right)$ is said to correspond to an inversion of $\sigma$, if $i<j$ but $a_{i}>a_{j}$. (Example: In the permutation $(2,4,5,3,1)$, there are 6 inversions corresponding to the pairs $(2,1)$, $(4,3),(4,1),(5,3),(5,1),(3,1)$.) How many permutations of $(1,2,3, \ldots n)$, $(n \geq 3)$, have exactly two inversions?
|
In a permutation of $(1,2,3, \ldots, n)$, two inversions can occur in only one of the following two ways:
(A) Two disjoint consecutive pairs are interchanged:
$$
\begin{aligned}
& (1,2,3, j-1, j, j+1, j+2 \ldots k-1, k, k+1, k+2, \ldots, n) \\
& \quad \longrightarrow(1,2, \ldots j-1, j+1, j, j+2, \ldots, k-1, k+1, k, k+2, \ldots, n)
\end{aligned}
$$
(B) Each block of three consecutive integers can be permuted in any of the following 2 ways;
$$
\begin{aligned}
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+2, k, k+1, \ldots, n) \\
& (1,2,3, \ldots k, k+1, k+2, \ldots, n) \longrightarrow(1,2, \ldots, k+1, k+2, k, \ldots, n)
\end{aligned}
$$
Consider case (A). For $j=1$, there are $n-3$ possible values of $k$; for $j=2$, there are $n-4$ possibilities for $k$ and so on. Thus the number of permutations with two inversions of this type is
$$
1+2+\cdots+(n-3)=\frac{(n-3)(n-2)}{2}
$$
In case (B), we see that there are $n-2$ permutations of each type, since $k$ can take values from 1 to $n-2$. Hence we get $2(n-2)$ permutations of this type.
Finally, the number of permutations with two inversions is
$$
\frac{(n-3)(n-2)}{2}+2(n-2)=\frac{(n+1)(n-2)}{2}
$$
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
c0d2be34-944c-5a79-b64a-f99eb024ac1f
| 607,830
|
How many 6-tuples $\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right)$ are there such that each of $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ is from the set $\{1,2,3,4\}$ and the six expressions
$$
a_{j}^{2}-a_{j} a_{j+1}+a_{j+1}^{2}
$$
for $j=1,2,3,4,5,6$ (where $a_{7}$ is to be taken as $a_{1}$ ) are all equal to one another?
|
Without loss of generality, we may assume that $a_{1}$ is the largest among $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$. Consider the relation
$$
a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}=a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}
$$
This leads to
$$
\left(a_{1}-a_{3}\right)\left(a_{1}+a_{3}-a_{2}\right)=0
$$
Observe that $a_{1} \geq a_{2}$ and $a_{3}>0$ together imply that the second factor on the left side is positive. Thus $a_{1}=a_{3}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}$. Using this and the relation
$$
a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}=a_{4}^{2}-a_{4} a_{5}+a_{5}^{2}
$$
we conclude that $a_{3}=a_{5}$ as above. Thus we have
$$
a_{1}=a_{3}=a_{5}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}
$$
Let us consider the other relations. Using
$$
a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}=a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}
$$
we get $a_{2}=a_{4}$ or $a_{2}+a_{4}=a_{3}=a_{1}$. Similarly, two more relations give either $a_{4}=a_{6}$ or $a_{4}+a_{6}=a_{5}=a_{1}$; and either $a_{6}=a_{2}$ or $a_{6}+a_{2}=a_{1}$. Let us give values to $a_{1}$ and count the number of six-tuples in each case.
(A) Suppose $a_{1}=1$. In this case all $a_{j}$ 's are equal and we get only one six-tuple $(1,1,1,1,1,1)$.
(B) If $a_{1}=2$, we have $a_{3}=a_{5}=2$. We observe that $a_{2}=a_{4}=a_{6}=1$ or $a_{2}=a_{4}=$ $a_{6}=2$. We get two more six-tuples: $(2,1,2,1,2,1),(2,2,2,2,2,2)$.
(C) Taking $a_{1}=3$, we see that $a_{3}=a_{5}=3$. In this case we get nine possibilities for $\left(a_{2}, a_{4}, a_{6}\right)$
$$
(1,1,1),(2,2,2),(3,3,3),(1,1,2),(1,2,1),(2,1,1),(1,2,2),(2,1,2),(2,2,1)
$$
(D) In the case $a_{1}=4$, we have $a_{3}=a_{5}=4$ and
$$
\begin{aligned}
\left(a_{2}, a_{4}, a_{6}\right)=(2,2,2),(4,4,4) & ,(1,1,1),(3,3,3) \\
& (1,1,3),(1,3,1),(3,1,1),(1,3,3),(3,1,3),(3,3,1)
\end{aligned}
$$
Thus we get $1+2+9+10=22$ solutions. Since $\left(a_{1}, a_{3}, a_{5}\right)$ and $\left(a_{2}, a_{4}, a_{6}\right)$ may be interchanged, we get 22 more six-tuples. However there are 4 common among these, namely, $(1,1,1,1,1,1),(2,2,2,2,2,2),(3,3,3,3,3,3)$ and $(4,4,4,4,4,4)$. Hence the total number of six-tuples is $22+22-4=40$.
|
40
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many 6-tuples $\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right)$ are there such that each of $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ is from the set $\{1,2,3,4\}$ and the six expressions
$$
a_{j}^{2}-a_{j} a_{j+1}+a_{j+1}^{2}
$$
for $j=1,2,3,4,5,6$ (where $a_{7}$ is to be taken as $a_{1}$ ) are all equal to one another?
|
Without loss of generality, we may assume that $a_{1}$ is the largest among $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$. Consider the relation
$$
a_{1}^{2}-a_{1} a_{2}+a_{2}^{2}=a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}
$$
This leads to
$$
\left(a_{1}-a_{3}\right)\left(a_{1}+a_{3}-a_{2}\right)=0
$$
Observe that $a_{1} \geq a_{2}$ and $a_{3}>0$ together imply that the second factor on the left side is positive. Thus $a_{1}=a_{3}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}$. Using this and the relation
$$
a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}=a_{4}^{2}-a_{4} a_{5}+a_{5}^{2}
$$
we conclude that $a_{3}=a_{5}$ as above. Thus we have
$$
a_{1}=a_{3}=a_{5}=\max \left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\right\}
$$
Let us consider the other relations. Using
$$
a_{2}^{2}-a_{2} a_{3}+a_{3}^{2}=a_{3}^{2}-a_{3} a_{4}+a_{4}^{2}
$$
we get $a_{2}=a_{4}$ or $a_{2}+a_{4}=a_{3}=a_{1}$. Similarly, two more relations give either $a_{4}=a_{6}$ or $a_{4}+a_{6}=a_{5}=a_{1}$; and either $a_{6}=a_{2}$ or $a_{6}+a_{2}=a_{1}$. Let us give values to $a_{1}$ and count the number of six-tuples in each case.
(A) Suppose $a_{1}=1$. In this case all $a_{j}$ 's are equal and we get only one six-tuple $(1,1,1,1,1,1)$.
(B) If $a_{1}=2$, we have $a_{3}=a_{5}=2$. We observe that $a_{2}=a_{4}=a_{6}=1$ or $a_{2}=a_{4}=$ $a_{6}=2$. We get two more six-tuples: $(2,1,2,1,2,1),(2,2,2,2,2,2)$.
(C) Taking $a_{1}=3$, we see that $a_{3}=a_{5}=3$. In this case we get nine possibilities for $\left(a_{2}, a_{4}, a_{6}\right)$
$$
(1,1,1),(2,2,2),(3,3,3),(1,1,2),(1,2,1),(2,1,1),(1,2,2),(2,1,2),(2,2,1)
$$
(D) In the case $a_{1}=4$, we have $a_{3}=a_{5}=4$ and
$$
\begin{aligned}
\left(a_{2}, a_{4}, a_{6}\right)=(2,2,2),(4,4,4) & ,(1,1,1),(3,3,3) \\
& (1,1,3),(1,3,1),(3,1,1),(1,3,3),(3,1,3),(3,3,1)
\end{aligned}
$$
Thus we get $1+2+9+10=22$ solutions. Since $\left(a_{1}, a_{3}, a_{5}\right)$ and $\left(a_{2}, a_{4}, a_{6}\right)$ may be interchanged, we get 22 more six-tuples. However there are 4 common among these, namely, $(1,1,1,1,1,1),(2,2,2,2,2,2),(3,3,3,3,3,3)$ and $(4,4,4,4,4,4)$. Hence the total number of six-tuples is $22+22-4=40$.
|
{
"resource_path": "INMO/segmented/en-2010.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
2d2c3ee6-a9a7-54dd-8730-c9342575d99c
| 607,848
|
Let $A B C D$ be a quadrilateral inscribed in a circle. Suppose $A B=$ $\sqrt{2+\sqrt{2}}$ and $A B$ subtends $135^{\circ}$ at the centre of the circle. Find the maximum possible area of $A B C D$.

|
Let $O$ be the centre of the circle in which $A B C D$ is inscribed and let $R$ be its radius. Using cosine rule in triangle $A O B$, we have
$$
2+\sqrt{2}=2 R^{2}\left(1-\cos 135^{\circ}\right)=R^{2}(2+\sqrt{2})
$$
Hence $R=1$.
Consider quadrilateral $A B C D$ as in the second figure above. Join $A C$. For $[A D C]$ to be maximum, it is clear that $D$ should be the mid-point of the arc $A C$ so that its distance from the segment $A C$ is maximum. Hence $A D=D C$ for $[A B C D]$ to be maximum. Similarly, we conclude that $B C=C D$. Thus $B C=C D=D A$ which fixes the quadrilateral $A B C D$. Therefore each of the sides $B C, C D, D A$ subtends equal angles at the centre $O$.
Let $\angle B O C=\alpha, \angle C O D=\beta$ and $\angle D O A=\gamma$. Observe that
$$
[A B C D]=[A O B]+[B O C]+[C O D]+[D O A]=\frac{1}{2} \sin 135^{\circ}+\frac{1}{2}(\sin \alpha+\sin \beta+\sin \gamma)
$$
Now $[A B C D]$ has maximum area if and only if $\alpha=\beta=\gamma=\left(360^{\circ}-\right.$ $\left.135^{\circ}\right) / 3=75^{\circ}$. Thus
$$
[A B C D]=\frac{1}{2} \sin 135^{\circ}+\frac{3}{2} \sin 75^{\circ}=\frac{1}{2}\left(\frac{1}{\sqrt{2}}+3 \frac{\sqrt{3}+1}{2 \sqrt{2}}\right)=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
$$
Alternatively, we can use Jensen's inequality. Observe that $\alpha, \beta, \gamma$ are all less than $180^{\circ}$. Since $\sin x$ is concave on $(0, \pi)$, Jensen's inequality gives
$$
\frac{\sin \alpha+\sin \beta+\sin \gamma}{3} \leq \sin \left(\frac{\alpha+\beta+\gamma}{3}\right)=\sin 75^{\circ}
$$
Hence
$$
[A B C D] \leq \frac{1}{2 \sqrt{2}}+\frac{3}{2} \sin 75^{\circ}=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
$$
with equality if and only if $\alpha=\beta=\gamma=75^{\circ}$.
|
\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle. Suppose $A B=$ $\sqrt{2+\sqrt{2}}$ and $A B$ subtends $135^{\circ}$ at the centre of the circle. Find the maximum possible area of $A B C D$.

|
Let $O$ be the centre of the circle in which $A B C D$ is inscribed and let $R$ be its radius. Using cosine rule in triangle $A O B$, we have
$$
2+\sqrt{2}=2 R^{2}\left(1-\cos 135^{\circ}\right)=R^{2}(2+\sqrt{2})
$$
Hence $R=1$.
Consider quadrilateral $A B C D$ as in the second figure above. Join $A C$. For $[A D C]$ to be maximum, it is clear that $D$ should be the mid-point of the arc $A C$ so that its distance from the segment $A C$ is maximum. Hence $A D=D C$ for $[A B C D]$ to be maximum. Similarly, we conclude that $B C=C D$. Thus $B C=C D=D A$ which fixes the quadrilateral $A B C D$. Therefore each of the sides $B C, C D, D A$ subtends equal angles at the centre $O$.
Let $\angle B O C=\alpha, \angle C O D=\beta$ and $\angle D O A=\gamma$. Observe that
$$
[A B C D]=[A O B]+[B O C]+[C O D]+[D O A]=\frac{1}{2} \sin 135^{\circ}+\frac{1}{2}(\sin \alpha+\sin \beta+\sin \gamma)
$$
Now $[A B C D]$ has maximum area if and only if $\alpha=\beta=\gamma=\left(360^{\circ}-\right.$ $\left.135^{\circ}\right) / 3=75^{\circ}$. Thus
$$
[A B C D]=\frac{1}{2} \sin 135^{\circ}+\frac{3}{2} \sin 75^{\circ}=\frac{1}{2}\left(\frac{1}{\sqrt{2}}+3 \frac{\sqrt{3}+1}{2 \sqrt{2}}\right)=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
$$
Alternatively, we can use Jensen's inequality. Observe that $\alpha, \beta, \gamma$ are all less than $180^{\circ}$. Since $\sin x$ is concave on $(0, \pi)$, Jensen's inequality gives
$$
\frac{\sin \alpha+\sin \beta+\sin \gamma}{3} \leq \sin \left(\frac{\alpha+\beta+\gamma}{3}\right)=\sin 75^{\circ}
$$
Hence
$$
[A B C D] \leq \frac{1}{2 \sqrt{2}}+\frac{3}{2} \sin 75^{\circ}=\frac{5+3 \sqrt{3}}{4 \sqrt{2}}
$$
with equality if and only if $\alpha=\beta=\gamma=75^{\circ}$.
|
{
"resource_path": "INMO/segmented/en-2012.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
ad701aef-3f5c-5bcf-b857-0a3c10cbd068
| 607,856
|
Let $A B C$ be a triangle. An interior point $P$ of $A B C$ is said to be good if we can find exactly 27 rays emanating from $P$ intersecting the sides of the triangle $A B C$ such that the triangle is divided by these rays into 27 smaller triangles of equal area. Determine the number of good points for a given triangle $A B C$.
|
Let $P$ be a good point. Let $l, m, n$ be respetively the number of parts the sides $B C, C A, A B$ are divided by the rays starting from $P$. Note that a ray must pass through each of the vertices the triangle $A B C$; otherwise we get some quadrilaterals.
Let $h_{1}$ be the distance of $P$ from $B C$. Then $h_{1}$ is the height for all the triangles with their bases on $B C$. Equality of areas implies that all these bases have equal length. If we denote this by $x$, we get $l x=a$. Similarly, taking $y$ and $z$ as the lengths of the bases of triangles on $C A$ and $A B$ respectively, we get $m y=b$ and $n z=c$. Let $h_{2}$ and $h_{3}$ be the distances of $P$ from $C A$ and $A B$ respectively. Then
$$
h_{1} x=h_{2} y=h_{3} z=\frac{2 \Delta}{27}
$$
where $\Delta$ denotes the area of the triangle $A B C$. These lead to
$$
h_{1}=\frac{2 \Delta}{27} \frac{l}{a}, \quad h_{1}=\frac{2 \Delta}{27} \frac{m}{b}, \quad h_{1}=\frac{2 \Delta}{27} \frac{n}{c}
$$
But
$$
\frac{2 \Delta}{a}=h_{a}, \quad \frac{2 \Delta}{b}=h_{b}, \quad \frac{2 \Delta}{c}=h_{c}
$$
Thus we get
$$
\frac{h_{1}}{h_{a}}=\frac{l}{27}, \quad \frac{h_{2}}{h_{b}}=\frac{m}{27}, \quad \frac{h_{3}}{h_{c}}=\frac{n}{27}
$$
However, we also have
$$
\frac{h_{1}}{h_{a}}=\frac{[P B C]}{\Delta}, \quad \frac{h_{2}}{h_{b}}=\frac{[P C A]}{\Delta}, \quad \frac{h_{3}}{h_{c}}=\frac{[P A B]}{\Delta}
$$
Adding these three relations,
$$
\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
$$
Thus
$$
\frac{l}{27}+\frac{m}{27}+\frac{n}{27}=\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
$$
We conclude that $l+m+n=27$. Thus every good point $P$ determines a partition $(l, m, n)$ of 27 such that there are $l, m, n$ equal segments respectively on $B C, C A, A B$.
Conversely, take any partition $(l, m, n)$ of 27 . Divide $B C, C A, A B$ respectively in to $l, m, n$ equal parts. Define
$$
h_{1}=\frac{2 l \Delta}{27 a}, \quad h_{2}=\frac{2 m \Delta}{27 b}
$$
Draw a line parallel to $B C$ at a distance $h_{1}$ from $B C$; draw another line parallel to $C A$ at a distance $h_{2}$ from $C A$. Both lines are drawn such that they intersect at a point $P$ inside the triangle $A B C$. Then
$$
[P B C]=\frac{1}{2} a h_{1}=\frac{l \Delta}{27}, \quad[P C A]=\frac{m \Delta}{27}
$$
Hence
$$
[P A B]=\frac{n \Delta}{27}
$$
This shows that the distance of $P$ from $A B$ is
$$
h_{3}=\frac{2 n \Delta}{27 c}
$$
Therefore each traingle with base on $C A$ has area $\frac{\Delta}{27}$. We conclude that all the triangles which partitions $A B C$ have equal areas. Hence $P$ is a good point.
Thus the number of good points is equal to the number of positive integral solutions of the equation $l+m+n=27$. This is equal to
$$
\binom{26}{2}=325
$$
|
325
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle. An interior point $P$ of $A B C$ is said to be good if we can find exactly 27 rays emanating from $P$ intersecting the sides of the triangle $A B C$ such that the triangle is divided by these rays into 27 smaller triangles of equal area. Determine the number of good points for a given triangle $A B C$.
|
Let $P$ be a good point. Let $l, m, n$ be respetively the number of parts the sides $B C, C A, A B$ are divided by the rays starting from $P$. Note that a ray must pass through each of the vertices the triangle $A B C$; otherwise we get some quadrilaterals.
Let $h_{1}$ be the distance of $P$ from $B C$. Then $h_{1}$ is the height for all the triangles with their bases on $B C$. Equality of areas implies that all these bases have equal length. If we denote this by $x$, we get $l x=a$. Similarly, taking $y$ and $z$ as the lengths of the bases of triangles on $C A$ and $A B$ respectively, we get $m y=b$ and $n z=c$. Let $h_{2}$ and $h_{3}$ be the distances of $P$ from $C A$ and $A B$ respectively. Then
$$
h_{1} x=h_{2} y=h_{3} z=\frac{2 \Delta}{27}
$$
where $\Delta$ denotes the area of the triangle $A B C$. These lead to
$$
h_{1}=\frac{2 \Delta}{27} \frac{l}{a}, \quad h_{1}=\frac{2 \Delta}{27} \frac{m}{b}, \quad h_{1}=\frac{2 \Delta}{27} \frac{n}{c}
$$
But
$$
\frac{2 \Delta}{a}=h_{a}, \quad \frac{2 \Delta}{b}=h_{b}, \quad \frac{2 \Delta}{c}=h_{c}
$$
Thus we get
$$
\frac{h_{1}}{h_{a}}=\frac{l}{27}, \quad \frac{h_{2}}{h_{b}}=\frac{m}{27}, \quad \frac{h_{3}}{h_{c}}=\frac{n}{27}
$$
However, we also have
$$
\frac{h_{1}}{h_{a}}=\frac{[P B C]}{\Delta}, \quad \frac{h_{2}}{h_{b}}=\frac{[P C A]}{\Delta}, \quad \frac{h_{3}}{h_{c}}=\frac{[P A B]}{\Delta}
$$
Adding these three relations,
$$
\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
$$
Thus
$$
\frac{l}{27}+\frac{m}{27}+\frac{n}{27}=\frac{h_{1}}{h_{a}}+\frac{h_{2}}{h_{b}}+\frac{h_{3}}{h_{c}}=1
$$
We conclude that $l+m+n=27$. Thus every good point $P$ determines a partition $(l, m, n)$ of 27 such that there are $l, m, n$ equal segments respectively on $B C, C A, A B$.
Conversely, take any partition $(l, m, n)$ of 27 . Divide $B C, C A, A B$ respectively in to $l, m, n$ equal parts. Define
$$
h_{1}=\frac{2 l \Delta}{27 a}, \quad h_{2}=\frac{2 m \Delta}{27 b}
$$
Draw a line parallel to $B C$ at a distance $h_{1}$ from $B C$; draw another line parallel to $C A$ at a distance $h_{2}$ from $C A$. Both lines are drawn such that they intersect at a point $P$ inside the triangle $A B C$. Then
$$
[P B C]=\frac{1}{2} a h_{1}=\frac{l \Delta}{27}, \quad[P C A]=\frac{m \Delta}{27}
$$
Hence
$$
[P A B]=\frac{n \Delta}{27}
$$
This shows that the distance of $P$ from $A B$ is
$$
h_{3}=\frac{2 n \Delta}{27 c}
$$
Therefore each traingle with base on $C A$ has area $\frac{\Delta}{27}$. We conclude that all the triangles which partitions $A B C$ have equal areas. Hence $P$ is a good point.
Thus the number of good points is equal to the number of positive integral solutions of the equation $l+m+n=27$. This is equal to
$$
\binom{26}{2}=325
$$
|
{
"resource_path": "INMO/segmented/en-2012.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
f3a72a74-2ffd-5b95-82bc-7f087128372f
| 607,859
|
Suppose $r \geq 2$ is an integer, and let $m_{1}, n_{1}, m_{2}, n_{2}, \cdots, m_{r}, n_{r}$ be $2 r$ integers such that
$$
\left|m_{i} n_{j}-m_{j} n_{i}\right|=1
$$
for any two integers $i$ and $j$ satisfying $1 \leq i<j \leq r$. Determine the maximum possible value of $r$.
|
Let $m_{1}, n_{1}, m_{2}, n_{2}$ be integers satisfying $m_{1} n_{2}-m_{2} n_{1}= \pm 1$. By changing the signs of $m_{2}, n_{2}$ if need be, we may assume that
$$
m_{1} n_{2}-m_{2} n_{1}=1
$$
If $m_{3}, n_{3}$ are integers satisfying $m_{1} n_{3}-m_{3} n_{1}= \pm 1$, again we may assume (by changing their signs if necessary) that
$$
m_{1} n_{3}-m_{3} n_{1}=1
$$
So $m_{1}\left(n_{2}-n_{3}\right)=n_{1}\left(m_{2}-m_{3}\right)$.
As $m_{1}, n_{1}$ are relatively prime, $m_{1}$ divides $m_{2}-m_{3}$; say, $m_{2}-m_{3}=m_{1} a$ for some integer $a$. Thus, we get $n_{2}-n_{3}=n_{1} a$. In other words,
$$
m_{3}=m_{2}-m_{1} a, n_{3}=n_{2}-n_{1} a
$$
Now, if $m_{2} n_{3}-n_{2} m_{3}= \pm 1$, we get
$$
\pm 1=m_{2}\left(n_{2}-n_{1} a\right)-n_{2}\left(m_{2}-m_{1} a\right)=\left(m_{1} n_{2}-m_{2} n_{1}\right) a=a
$$
Thus, $m_{3}=m_{2}-m_{1} a=m_{2} \pm m_{1}, n_{3}=n_{2}-n_{1} a=n_{2} \pm n_{1}$.
Now if we were to have another pair of integers $m_{4}, n_{4}$ such that
$$
m_{1} n_{4}-n_{1} m_{4}= \pm 1
$$
we may assume that $m_{1} n_{4}-n_{1} m_{4}=1$. As seen above, $m_{4}=m_{2} \mp m_{1}, n_{4}=n_{2} \mp n_{1}$. But then
$$
m_{3} n_{4}-n_{3} m_{4}=\left(m_{2} \pm m_{1}\right)\left(n_{2} \mp n_{1}\right)-\left(n_{2} \pm n_{1}\right)\left(m_{2} \mp m_{1}\right)= \pm 2
$$
Therefore, there can be only 3 pairs of such integers.
That there do exist many sets of 3 pairs is easy to see; for instance, $(1,0),(1,1),(0,1)$ is such a triple.
Alternate Solution. It is clear that $r$ can be 3 due to the valid solution $m_{1}=1, n_{1}=$ $1, m_{2}=1, n_{2}=2, m_{3}=2, n_{3}=3$.
If possible, let $r>3$. We observe that:
$$
\begin{aligned}
& m_{1} n_{2} n_{3}-m_{2} n_{1} n_{3}= \pm n_{3} \\
& m_{2} n_{3} n_{1}-m_{3} n_{2} n_{1}= \pm n_{1} \\
& m_{3} n_{1} n_{2}-m_{1} n_{3} n_{2}= \pm n_{2}
\end{aligned}
$$
Adding, we get $\pm n_{1} \pm n_{2} \pm n_{3}=0$; which forces at least one of $n_{1}, n_{2}, n_{3}$ to be even; WLOG let $n_{1}$ be even.
Repeating the argument for indices $2,3,4$, we deduce that at least one of $n_{2}, n_{3}, n_{4}$ is even; WLOG let $n_{2}$ be even. This leads to a contradiction, since $\left|m_{1} n_{2}-m_{2} n_{1}\right|=1$ cannot be even. Hence $r>3$ is not possible, as claimed.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Suppose $r \geq 2$ is an integer, and let $m_{1}, n_{1}, m_{2}, n_{2}, \cdots, m_{r}, n_{r}$ be $2 r$ integers such that
$$
\left|m_{i} n_{j}-m_{j} n_{i}\right|=1
$$
for any two integers $i$ and $j$ satisfying $1 \leq i<j \leq r$. Determine the maximum possible value of $r$.
|
Let $m_{1}, n_{1}, m_{2}, n_{2}$ be integers satisfying $m_{1} n_{2}-m_{2} n_{1}= \pm 1$. By changing the signs of $m_{2}, n_{2}$ if need be, we may assume that
$$
m_{1} n_{2}-m_{2} n_{1}=1
$$
If $m_{3}, n_{3}$ are integers satisfying $m_{1} n_{3}-m_{3} n_{1}= \pm 1$, again we may assume (by changing their signs if necessary) that
$$
m_{1} n_{3}-m_{3} n_{1}=1
$$
So $m_{1}\left(n_{2}-n_{3}\right)=n_{1}\left(m_{2}-m_{3}\right)$.
As $m_{1}, n_{1}$ are relatively prime, $m_{1}$ divides $m_{2}-m_{3}$; say, $m_{2}-m_{3}=m_{1} a$ for some integer $a$. Thus, we get $n_{2}-n_{3}=n_{1} a$. In other words,
$$
m_{3}=m_{2}-m_{1} a, n_{3}=n_{2}-n_{1} a
$$
Now, if $m_{2} n_{3}-n_{2} m_{3}= \pm 1$, we get
$$
\pm 1=m_{2}\left(n_{2}-n_{1} a\right)-n_{2}\left(m_{2}-m_{1} a\right)=\left(m_{1} n_{2}-m_{2} n_{1}\right) a=a
$$
Thus, $m_{3}=m_{2}-m_{1} a=m_{2} \pm m_{1}, n_{3}=n_{2}-n_{1} a=n_{2} \pm n_{1}$.
Now if we were to have another pair of integers $m_{4}, n_{4}$ such that
$$
m_{1} n_{4}-n_{1} m_{4}= \pm 1
$$
we may assume that $m_{1} n_{4}-n_{1} m_{4}=1$. As seen above, $m_{4}=m_{2} \mp m_{1}, n_{4}=n_{2} \mp n_{1}$. But then
$$
m_{3} n_{4}-n_{3} m_{4}=\left(m_{2} \pm m_{1}\right)\left(n_{2} \mp n_{1}\right)-\left(n_{2} \pm n_{1}\right)\left(m_{2} \mp m_{1}\right)= \pm 2
$$
Therefore, there can be only 3 pairs of such integers.
That there do exist many sets of 3 pairs is easy to see; for instance, $(1,0),(1,1),(0,1)$ is such a triple.
Alternate Solution. It is clear that $r$ can be 3 due to the valid solution $m_{1}=1, n_{1}=$ $1, m_{2}=1, n_{2}=2, m_{3}=2, n_{3}=3$.
If possible, let $r>3$. We observe that:
$$
\begin{aligned}
& m_{1} n_{2} n_{3}-m_{2} n_{1} n_{3}= \pm n_{3} \\
& m_{2} n_{3} n_{1}-m_{3} n_{2} n_{1}= \pm n_{1} \\
& m_{3} n_{1} n_{2}-m_{1} n_{3} n_{2}= \pm n_{2}
\end{aligned}
$$
Adding, we get $\pm n_{1} \pm n_{2} \pm n_{3}=0$; which forces at least one of $n_{1}, n_{2}, n_{3}$ to be even; WLOG let $n_{1}$ be even.
Repeating the argument for indices $2,3,4$, we deduce that at least one of $n_{2}, n_{3}, n_{4}$ is even; WLOG let $n_{2}$ be even. This leads to a contradiction, since $\left|m_{1} n_{2}-m_{2} n_{1}\right|=1$ cannot be even. Hence $r>3$ is not possible, as claimed.
|
{
"resource_path": "INMO/segmented/en-INMO_2021_solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
bd09966b-6643-5a54-b914-dd8a74d6ba10
| 607,868
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.