problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Preliminaries
Let $A B C$ be a triangle with circumcircle $\Gamma$. Let $X$ be a point in the plane. The Simson line (Wallace-Simson line) is defined via the following theorem. Drop perpendiculars from $X$ to each of the three side lines of $A B C$. The feet of these perpendiculars are collinear (on
the Simson line of $X$ ) if and only if $X$ lies of $\Gamma$. The Simson line of $X$ in the circumcircle bisects the line segment $X H$ where $H$ is the orthocentre of triangle $A B C$. See Figure 2
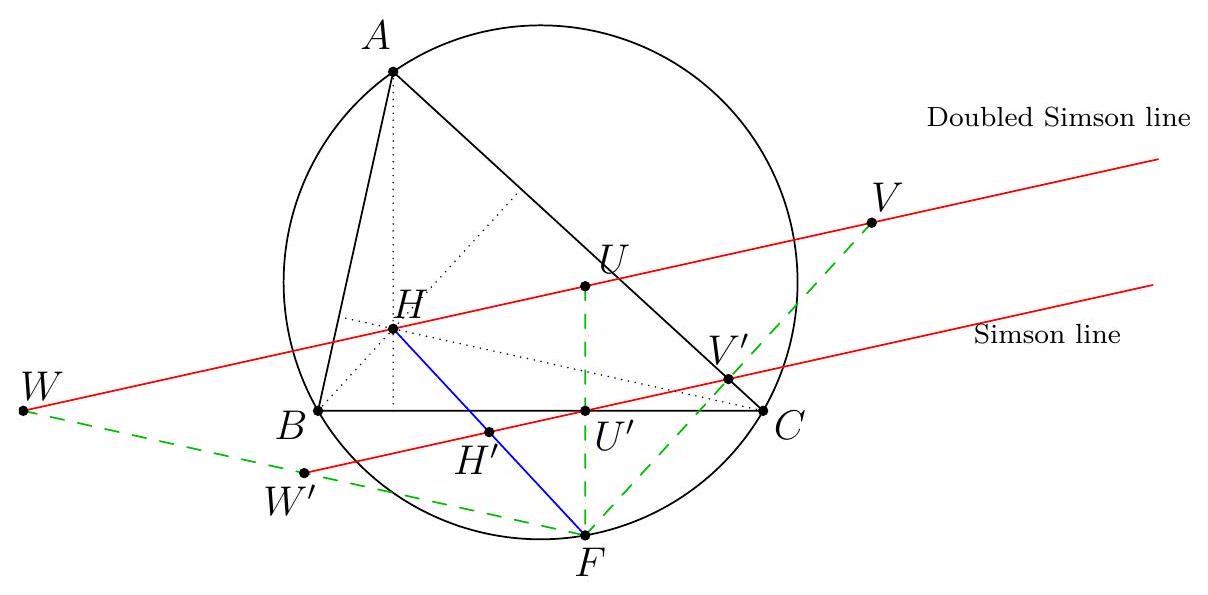
Figure 2: The Wallace-Simson configuration
When $X$ is on $\Gamma$, we can enlarge from $X$ with scale factor 2 (a homothety) to take the Simson line to the doubled Simson line which passes through the orthocentre $H$ and contains the reflections of $X$ in each of the three sides of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Preliminaries
Let $A B C$ be a triangle with circumcircle $\Gamma$. Let $X$ be a point in the plane. The Simson line (Wallace-Simson line) is defined via the following theorem. Drop perpendiculars from $X$ to each of the three side lines of $A B C$. The feet of these perpendiculars are collinear (on
the Simson line of $X$ ) if and only if $X$ lies of $\Gamma$. The Simson line of $X$ in the circumcircle bisects the line segment $X H$ where $H$ is the orthocentre of triangle $A B C$. See Figure 2

Figure 2: The Wallace-Simson configuration
When $X$ is on $\Gamma$, we can enlarge from $X$ with scale factor 2 (a homothety) to take the Simson line to the doubled Simson line which passes through the orthocentre $H$ and contains the reflections of $X$ in each of the three sides of $A B C$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
of the problem
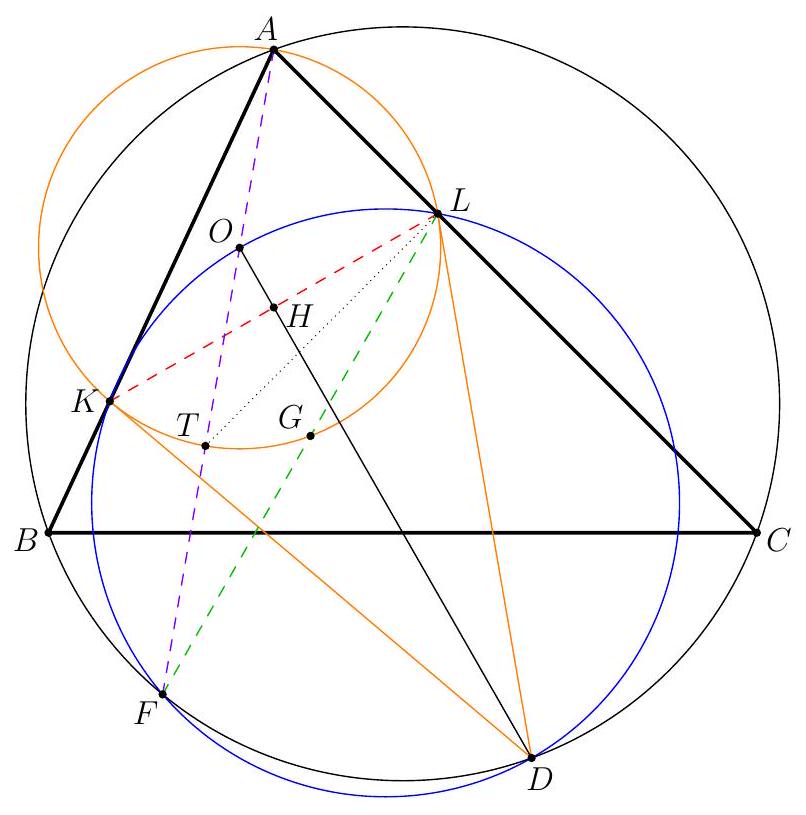
Figure 3: Three circles do the work
Let $\Gamma$ be the circle $A B C, \Sigma$ be the circle $A K L$ with centre $O$, and $\Omega$ be the circle on diameter $O D$ so $K$ and $L$ are on this circle by converse of Thales. Let $\Omega$ and $\Gamma$ meet at $D$ and $F$. By Thales in both circles, $\angle A F D$ and $\angle O F D$ are both right angles so $A O F$ is a line. Let $A F$ meet $\Sigma$ again at $T$ so $A T$ (containing $O$ ) is a diameter of this circle and by Thales, $T L \perp A C$.
Let $G$ (on $\Sigma$ ) be the reflection of $K$ in $A F$. Now $A T$ is the internal angle bisector of $\angle G A K$ so, by an upmarket use of angles in the same segment (of $\Sigma$ ), $T L$ is the internal
angle bisector of $\angle G L K$. Thus the line $G L$ is the reflection of the line $K L$ in $T L$, and so also the reflection of $K L$ in the line $A C$ (internal and external angle bisectors).
Our next project is to show that $L G F$ are collinear. Well $\angle F L K=\angle F O K$ (angles in the same segment of $\Omega$ ) and $\angle G L K=\angle G A K$ (angles in the same segment of $\Sigma$ ) $=2 \angle O A K$ ( $A K G$ is isosceles with apex $A)=\angle T O K$ (since $O A K$ is isosceles with apex $O$, and this is an external angle at $O$ ). The point $T$ lies in the interior of the line segment $F O$ so $\angle T O K=\angle F O K$. Therefore $\angle F L K=\angle G L K$ so $L G F$ is a line.
Now from the second paragraph, $F$ is on the reflection of $K L$ in $A C$. By symmetry, $F$ is also on the reflection of $K L$ in $A B$. Therefore the reflections of $F$ in $A B$ and $A C$ are both on $K L$ which must therefore be the doubled Wallace-Simson line of $F$. Therefore the orthocentre of $A B C$ lies on $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
of the problem

Figure 3: Three circles do the work
Let $\Gamma$ be the circle $A B C, \Sigma$ be the circle $A K L$ with centre $O$, and $\Omega$ be the circle on diameter $O D$ so $K$ and $L$ are on this circle by converse of Thales. Let $\Omega$ and $\Gamma$ meet at $D$ and $F$. By Thales in both circles, $\angle A F D$ and $\angle O F D$ are both right angles so $A O F$ is a line. Let $A F$ meet $\Sigma$ again at $T$ so $A T$ (containing $O$ ) is a diameter of this circle and by Thales, $T L \perp A C$.
Let $G$ (on $\Sigma$ ) be the reflection of $K$ in $A F$. Now $A T$ is the internal angle bisector of $\angle G A K$ so, by an upmarket use of angles in the same segment (of $\Sigma$ ), $T L$ is the internal
angle bisector of $\angle G L K$. Thus the line $G L$ is the reflection of the line $K L$ in $T L$, and so also the reflection of $K L$ in the line $A C$ (internal and external angle bisectors).
Our next project is to show that $L G F$ are collinear. Well $\angle F L K=\angle F O K$ (angles in the same segment of $\Omega$ ) and $\angle G L K=\angle G A K$ (angles in the same segment of $\Sigma$ ) $=2 \angle O A K$ ( $A K G$ is isosceles with apex $A)=\angle T O K$ (since $O A K$ is isosceles with apex $O$, and this is an external angle at $O$ ). The point $T$ lies in the interior of the line segment $F O$ so $\angle T O K=\angle F O K$. Therefore $\angle F L K=\angle G L K$ so $L G F$ is a line.
Now from the second paragraph, $F$ is on the reflection of $K L$ in $A C$. By symmetry, $F$ is also on the reflection of $K L$ in $A B$. Therefore the reflections of $F$ in $A B$ and $A C$ are both on $K L$ which must therefore be the doubled Wallace-Simson line of $F$. Therefore the orthocentre of $A B C$ lies on $K L$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $H$ be the orthocentre of triangle $A B C$ and $\Sigma$ the circumcircle of $A K L$ with centre $O$. Let $\Omega$ be the circle with diameter $O D$, which contains $K$ and $L$ by Thales, and let $\Gamma$ be the circumcircle of $A B C$ containing $D$. Denote the second intersection of $\Omega$ and $\Gamma$ by $F$. Since $O D$ and $A D$ are diameters of $\Omega$ and $\Gamma$ we have $\angle O F D=\frac{\pi}{2}=\angle A F D$, so the points $A, O, F$ are collinear. Let $M$ and $N$ be the second intersections of $C H$ and $B H$ with $\Gamma$, respectively. It is well-known that $M$ and $N$ are the reflections of $H$ in $A B$ and $A C$, respectively (because $\angle N C A=\angle N B A=\angle A C M=\angle A B M$ ). By collinearity of $A, O, F$ and the angles in $\Gamma$ we have
$$
\angle N F O=\angle N F A=\angle N B A=\frac{\pi}{2}-\angle B A C=\frac{\pi}{2}-\angle K A L
$$
Since $D L$ is tangent to $\Sigma$ we obtain
$$
\angle N F O=\frac{\pi}{2}-\angle K L D=\angle L D O,
$$
where the last equality follows from the fact that $O D$ is bisector of $\angle L D K$ since $L D$
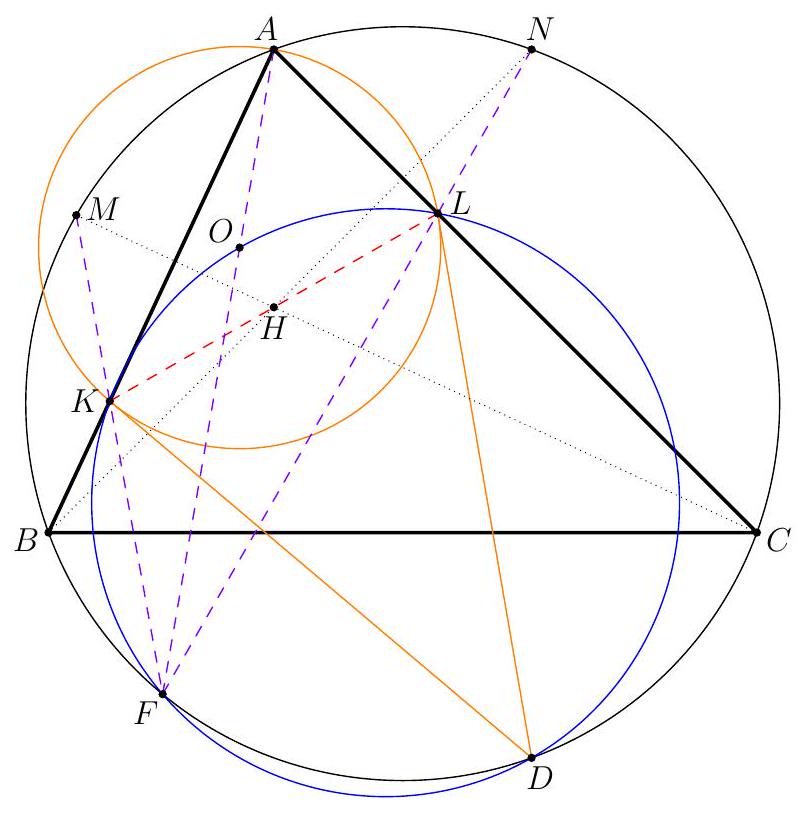
Figure 4: Diagram to Solution 3
and $K D$ are tangent to $\Sigma$. Furthermore, $\angle L D O=\angle L F O$ since these are angles in $\Omega$. Hence, $\angle N F O=\angle L F O$, which implies that points $N, L, F$ are collinear. Similarly points $M, K, F$ are collinear. Since $N$ and $M$ are reflections of $H$ in $A C$ and $A B$ we have
$$
\angle L H N=\angle H N L=\angle B N F=\angle B M F=\angle B M K=\angle K H B .
$$
Hence,
$$
\angle L H K=\angle L H N+\angle N H K=\angle K H B+\angle N H K=\pi
$$
and the points $L, H, K$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $H$ be the orthocentre of triangle $A B C$ and $\Sigma$ the circumcircle of $A K L$ with centre $O$. Let $\Omega$ be the circle with diameter $O D$, which contains $K$ and $L$ by Thales, and let $\Gamma$ be the circumcircle of $A B C$ containing $D$. Denote the second intersection of $\Omega$ and $\Gamma$ by $F$. Since $O D$ and $A D$ are diameters of $\Omega$ and $\Gamma$ we have $\angle O F D=\frac{\pi}{2}=\angle A F D$, so the points $A, O, F$ are collinear. Let $M$ and $N$ be the second intersections of $C H$ and $B H$ with $\Gamma$, respectively. It is well-known that $M$ and $N$ are the reflections of $H$ in $A B$ and $A C$, respectively (because $\angle N C A=\angle N B A=\angle A C M=\angle A B M$ ). By collinearity of $A, O, F$ and the angles in $\Gamma$ we have
$$
\angle N F O=\angle N F A=\angle N B A=\frac{\pi}{2}-\angle B A C=\frac{\pi}{2}-\angle K A L
$$
Since $D L$ is tangent to $\Sigma$ we obtain
$$
\angle N F O=\frac{\pi}{2}-\angle K L D=\angle L D O,
$$
where the last equality follows from the fact that $O D$ is bisector of $\angle L D K$ since $L D$

Figure 4: Diagram to Solution 3
and $K D$ are tangent to $\Sigma$. Furthermore, $\angle L D O=\angle L F O$ since these are angles in $\Omega$. Hence, $\angle N F O=\angle L F O$, which implies that points $N, L, F$ are collinear. Similarly points $M, K, F$ are collinear. Since $N$ and $M$ are reflections of $H$ in $A C$ and $A B$ we have
$$
\angle L H N=\angle H N L=\angle B N F=\angle B M F=\angle B M K=\angle K H B .
$$
Hence,
$$
\angle L H K=\angle L H N+\angle N H K=\angle K H B+\angle N H K=\pi
$$
and the points $L, H, K$ are collinear.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
As in Solution 3 let $M$ and $N$ be the reflections of the orthocentre in $A B$ and $A C$. Let $\angle B A C=\alpha$. Then $\angle N D M=\pi-\angle M A N=\pi-2 \alpha$.
Let $M K$ and $N L$ intersect at $F$. See Figure 3.
Claim. $\angle N F M=\pi-2 \alpha$, so $F$ lies on the circumcircle.
Proof. Since $K D$ and $L D$ are tangents to circle $A K L$, we have $|D K|=|D L|$ and $\angle D K L=\angle K L D=\alpha$, so $\angle L D K=\pi-2 \alpha$.
By definition of $M, N$ and $D, \angle M N D=\angle A N D-\angle A N M=\frac{\pi}{2}-\left(\frac{\pi}{2}-\alpha\right)=\alpha$ and analogously $\angle D M N=\alpha$. Hence $|D M|=|D N|$.
From $\angle N D M=\angle L D K=\pi-2 \alpha$ if follows that $\angle L D N=\angle K D M$. Since $|D K|=|D L|$ and $|D M|=|D N|$, triangles $M D K$ and $N D L$ are related by a rotation about $D$ through angle $\pi-2 \alpha$, and hence the angle between $M K$ and $N L$ is $\pi-2 \alpha$, which proved the claim.
We now finish as in Solution 3:
$$
\begin{gathered}
\angle M H K=\angle K M H=\angle F M C=\angle F A C \\
\angle L H N=\angle H N L=\angle B N F=\angle B A F
\end{gathered}
$$
As $\angle B A F+\angle F A C=\alpha$, we have $\angle L H K=\alpha+\angle N H M=\alpha+\pi-\alpha=\pi$, so $H$ lies on $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
As in Solution 3 let $M$ and $N$ be the reflections of the orthocentre in $A B$ and $A C$. Let $\angle B A C=\alpha$. Then $\angle N D M=\pi-\angle M A N=\pi-2 \alpha$.
Let $M K$ and $N L$ intersect at $F$. See Figure 3.
Claim. $\angle N F M=\pi-2 \alpha$, so $F$ lies on the circumcircle.
Proof. Since $K D$ and $L D$ are tangents to circle $A K L$, we have $|D K|=|D L|$ and $\angle D K L=\angle K L D=\alpha$, so $\angle L D K=\pi-2 \alpha$.
By definition of $M, N$ and $D, \angle M N D=\angle A N D-\angle A N M=\frac{\pi}{2}-\left(\frac{\pi}{2}-\alpha\right)=\alpha$ and analogously $\angle D M N=\alpha$. Hence $|D M|=|D N|$.
From $\angle N D M=\angle L D K=\pi-2 \alpha$ if follows that $\angle L D N=\angle K D M$. Since $|D K|=|D L|$ and $|D M|=|D N|$, triangles $M D K$ and $N D L$ are related by a rotation about $D$ through angle $\pi-2 \alpha$, and hence the angle between $M K$ and $N L$ is $\pi-2 \alpha$, which proved the claim.
We now finish as in Solution 3:
$$
\begin{gathered}
\angle M H K=\angle K M H=\angle F M C=\angle F A C \\
\angle L H N=\angle H N L=\angle B N F=\angle B A F
\end{gathered}
$$
As $\angle B A F+\angle F A C=\alpha$, we have $\angle L H K=\alpha+\angle N H M=\alpha+\pi-\alpha=\pi$, so $H$ lies on $K L$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 4. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Since $A D$ is a diameter, it is well known that $D B H C$ is a parallelogram (indeed, both $B D$ and $C H$ are perpendicular to $A B$, hence parallel, and similarly for $D C \| B H)$. Let $B^{\prime}, C^{\prime}$ be the reflections of $D$ in lines $A K B$ and $A L C$, respectively; since $A B D$ and $A C D$ are right angles, these are also the factor-2 homotheties of $B$ and $C$ with respect to $D$, hence $H$ is the midpoint of $B^{\prime} C^{\prime}$. We will prove that $B^{\prime} K C^{\prime} L$ is a parallelogram: it will then follow that the midpoint of $B^{\prime} C^{\prime}$, which is $H$, is also the midpoint of $K L$, and in particular is on the line, as we wanted to show.
We will prove $B^{\prime} K C^{\prime} L$ is a parallelogram by showing that $B^{\prime} K$ and $C^{\prime} L$ are the same length and direction. Indeed, for lengths we have $K B^{\prime}=K D=L D=L C^{\prime}$, where the first and last equalities arise from the reflections defining $B^{\prime}$ and $C^{\prime}$, and the middle one
is equality of tangents. For directions, let $\alpha, \beta, \gamma$ denote the angles of triangle $A K L$. Immediate angle chasing in the circle $A K L$, and the properties of the reflections, yield
$$
\begin{aligned}
\angle C^{\prime} L C & =\angle C L D=\angle A K L=\beta \\
\angle B K B^{\prime} & =\angle D K B=\angle K L A=\gamma \\
& \angle L D K=2 \alpha-\pi
\end{aligned}
$$
and therefore in directed angles $(\bmod 2 \pi)$ we have
$\angle\left(C^{\prime} L, B^{\prime} K\right)=\angle C^{\prime} L C+\angle C L D+\angle L D K+\angle D K B+\angle B K B^{\prime}=2 \alpha+2 \beta+2 \gamma-\pi=\pi$
and hence $C^{\prime} L$ and $B^{\prime} K$ are parallel and in opposite directions, i.e. $C^{\prime} L$ and $K B^{\prime}$ are in the same direction, as claimed.
Comment. While not necessary for the final solution, the following related observation motivates how the fact that $H$ is the midpoint of $K L$ (and therefore $B^{\prime} K C^{\prime} L$ is a parallelogram) was first conjectured. We have $A B^{\prime}=A D=A C^{\prime}$ by the reflections, i.e. $B^{\prime} A C^{\prime}$ is an isosceles triangle with $H$ being the midpoint of the base. Thus $A H$ is the median, altitude and angle bisector in $B^{\prime} A C^{\prime}$, thus $\angle B^{\prime} A K+\angle K A H=\angle H A L+\angle L A C^{\prime}$. Since from the reflections we also have $\angle B^{\prime} A K=\angle K A D$ and $\angle D A L=\angle L A C^{\prime}$ it follows that $\angle H A L=\angle K A D$ and $\angle K A H=\angle D A L$. Since $D$ is the symmedian point in $A K L$, the angle conjugation implies $A H$ is the median line of $K L$. Thus, if $H$ is indeed on $K L$ (as the problem assures us), it can only be the midpoint of $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Since $A D$ is a diameter, it is well known that $D B H C$ is a parallelogram (indeed, both $B D$ and $C H$ are perpendicular to $A B$, hence parallel, and similarly for $D C \| B H)$. Let $B^{\prime}, C^{\prime}$ be the reflections of $D$ in lines $A K B$ and $A L C$, respectively; since $A B D$ and $A C D$ are right angles, these are also the factor-2 homotheties of $B$ and $C$ with respect to $D$, hence $H$ is the midpoint of $B^{\prime} C^{\prime}$. We will prove that $B^{\prime} K C^{\prime} L$ is a parallelogram: it will then follow that the midpoint of $B^{\prime} C^{\prime}$, which is $H$, is also the midpoint of $K L$, and in particular is on the line, as we wanted to show.
We will prove $B^{\prime} K C^{\prime} L$ is a parallelogram by showing that $B^{\prime} K$ and $C^{\prime} L$ are the same length and direction. Indeed, for lengths we have $K B^{\prime}=K D=L D=L C^{\prime}$, where the first and last equalities arise from the reflections defining $B^{\prime}$ and $C^{\prime}$, and the middle one
is equality of tangents. For directions, let $\alpha, \beta, \gamma$ denote the angles of triangle $A K L$. Immediate angle chasing in the circle $A K L$, and the properties of the reflections, yield
$$
\begin{aligned}
\angle C^{\prime} L C & =\angle C L D=\angle A K L=\beta \\
\angle B K B^{\prime} & =\angle D K B=\angle K L A=\gamma \\
& \angle L D K=2 \alpha-\pi
\end{aligned}
$$
and therefore in directed angles $(\bmod 2 \pi)$ we have
$\angle\left(C^{\prime} L, B^{\prime} K\right)=\angle C^{\prime} L C+\angle C L D+\angle L D K+\angle D K B+\angle B K B^{\prime}=2 \alpha+2 \beta+2 \gamma-\pi=\pi$
and hence $C^{\prime} L$ and $B^{\prime} K$ are parallel and in opposite directions, i.e. $C^{\prime} L$ and $K B^{\prime}$ are in the same direction, as claimed.
Comment. While not necessary for the final solution, the following related observation motivates how the fact that $H$ is the midpoint of $K L$ (and therefore $B^{\prime} K C^{\prime} L$ is a parallelogram) was first conjectured. We have $A B^{\prime}=A D=A C^{\prime}$ by the reflections, i.e. $B^{\prime} A C^{\prime}$ is an isosceles triangle with $H$ being the midpoint of the base. Thus $A H$ is the median, altitude and angle bisector in $B^{\prime} A C^{\prime}$, thus $\angle B^{\prime} A K+\angle K A H=\angle H A L+\angle L A C^{\prime}$. Since from the reflections we also have $\angle B^{\prime} A K=\angle K A D$ and $\angle D A L=\angle L A C^{\prime}$ it follows that $\angle H A L=\angle K A D$ and $\angle K A H=\angle D A L$. Since $D$ is the symmedian point in $A K L$, the angle conjugation implies $A H$ is the median line of $K L$. Thus, if $H$ is indeed on $K L$ (as the problem assures us), it can only be the midpoint of $K L$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 5. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
There are a number of "phantom point" arguments which define $K^{\prime}$ and $L^{\prime}$ in terms of angles and then deduce that these points are actually $K$ and $L$.
Note: In these solutions it is necessary to show that $K$ and $L$ are uniquely determined by the conditions of the problem. One example of doing this is the following:
To prove uniqueness of $K$ and $L$, let us consider that there exist two other points $K^{\prime}$ and $L^{\prime}$ that satisfy the same properties ( $K^{\prime}$ on $A B$ and $L^{\prime}$ on $A C$ such that $D K^{\prime}$ and $D L^{\prime}$ are tangent to the circle $\left.A K^{\prime} L^{\prime}\right)$.
Then, we have that $D K=D L$ and $D K^{\prime}=D L^{\prime}$. We also have that $\angle K D L=\angle K^{\prime} D L^{\prime}=$ $\pi-2 \angle A$. Hence, we deduce $\angle K D K^{\prime}=\angle K D L-\angle K^{\prime} D L=\angle K^{\prime} D L^{\prime}-\angle K^{\prime} D L=\angle L D L^{\prime}$ Thus we have that $\triangle K D K^{\prime} \equiv \triangle L D L^{\prime}$, so we deduce $\angle D K A=\angle D K K^{\prime}=\angle D L L^{\prime}=$ $\pi-\angle A L D$. This implies that $A K D L$ is concyclic, which is clearly a contradiction since $\angle K A L+\angle K D L=\pi-\angle B A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
There are a number of "phantom point" arguments which define $K^{\prime}$ and $L^{\prime}$ in terms of angles and then deduce that these points are actually $K$ and $L$.
Note: In these solutions it is necessary to show that $K$ and $L$ are uniquely determined by the conditions of the problem. One example of doing this is the following:
To prove uniqueness of $K$ and $L$, let us consider that there exist two other points $K^{\prime}$ and $L^{\prime}$ that satisfy the same properties ( $K^{\prime}$ on $A B$ and $L^{\prime}$ on $A C$ such that $D K^{\prime}$ and $D L^{\prime}$ are tangent to the circle $\left.A K^{\prime} L^{\prime}\right)$.
Then, we have that $D K=D L$ and $D K^{\prime}=D L^{\prime}$. We also have that $\angle K D L=\angle K^{\prime} D L^{\prime}=$ $\pi-2 \angle A$. Hence, we deduce $\angle K D K^{\prime}=\angle K D L-\angle K^{\prime} D L=\angle K^{\prime} D L^{\prime}-\angle K^{\prime} D L=\angle L D L^{\prime}$ Thus we have that $\triangle K D K^{\prime} \equiv \triangle L D L^{\prime}$, so we deduce $\angle D K A=\angle D K K^{\prime}=\angle D L L^{\prime}=$ $\pi-\angle A L D$. This implies that $A K D L$ is concyclic, which is clearly a contradiction since $\angle K A L+\angle K D L=\pi-\angle B A C$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 6. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
We will use the usual complex number notation, where we will use a capital letter (like $Z$ ) to denote the point associated to a complex number (like z). Consider $\triangle A K L$ on the unit circle. So, we have $a \cdot \bar{a}=k \cdot \bar{k}=l \cdot \bar{l}=1 \quad$ As point $D$ is the intersection of the tangents to the unit circle at $K$ and $L$, we have that
$$
d=\frac{2 k l}{k+l} \text { and } \bar{d}=\frac{2}{k+l}
$$
Defining $B$ as the foot of the perpendicular from $D$ on the line $A K$, and $C$ as the foot of the perpendicular from $D$ on the line $A L$, we have the formulas:
$$
b=\frac{1}{2}\left(d+\frac{(a-k) \bar{d}+\bar{a} k-a \bar{k}}{\bar{a}-\bar{k}}\right)
$$
$$
c=\frac{1}{2}\left(d+\frac{(a-l) \bar{d}+\bar{a} l-a \bar{l}}{\bar{a}-\bar{l}}\right)
$$
Simplyfing these formulas, we get:
$$
\begin{gathered}
b=\frac{1}{2}\left(d+\frac{(a-k) \frac{2}{k+l}+\frac{k}{a}-\frac{a}{k}}{\frac{1}{a}-\frac{1}{k}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-k)}{k+l}+\frac{k^{2}-a^{2}}{a k}}{\frac{k-a}{a k}}\right) \\
b=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a k}{k+l}+(a+k)\right)=\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a) \\
c=\frac{1}{2}\left(d+\frac{(a-l) \frac{2}{k+l}+\frac{l}{a}-\frac{a}{l}}{\frac{1}{a}-\frac{1}{l}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-l)}{k+l}+\frac{l^{2}-a^{2}}{a l}}{\frac{l-a}{a l}}\right) \\
c=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a l}{k+l}+(a+l)\right)=\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)
\end{gathered}
$$
Let $O$ be the the circumcenter of triangle $\triangle A B C$. As $A D$ is the diameter of this circle, we have that:
$$
o=\frac{a+d}{2}
$$
Defining $H$ as the orthocentre of the $\triangle A B C$, we get that:
$$
\begin{gathered}
h=a+b+c-2 \cdot o=a+\left(\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a)\right)+\left(\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)\right)-(a+d) \\
h=a+\frac{2 k l}{k+l}-\frac{a(k+l)}{k+l}+\frac{1}{2} k++\frac{1}{2} l++a-\left(a+\frac{2 k l}{k+l}\right) \\
h=\frac{1}{2}(k+l)
\end{gathered}
$$
Hence, we conclude that $H$ is the midpoint of $K L$, so $H, K, L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
We will use the usual complex number notation, where we will use a capital letter (like $Z$ ) to denote the point associated to a complex number (like z). Consider $\triangle A K L$ on the unit circle. So, we have $a \cdot \bar{a}=k \cdot \bar{k}=l \cdot \bar{l}=1 \quad$ As point $D$ is the intersection of the tangents to the unit circle at $K$ and $L$, we have that
$$
d=\frac{2 k l}{k+l} \text { and } \bar{d}=\frac{2}{k+l}
$$
Defining $B$ as the foot of the perpendicular from $D$ on the line $A K$, and $C$ as the foot of the perpendicular from $D$ on the line $A L$, we have the formulas:
$$
b=\frac{1}{2}\left(d+\frac{(a-k) \bar{d}+\bar{a} k-a \bar{k}}{\bar{a}-\bar{k}}\right)
$$
$$
c=\frac{1}{2}\left(d+\frac{(a-l) \bar{d}+\bar{a} l-a \bar{l}}{\bar{a}-\bar{l}}\right)
$$
Simplyfing these formulas, we get:
$$
\begin{gathered}
b=\frac{1}{2}\left(d+\frac{(a-k) \frac{2}{k+l}+\frac{k}{a}-\frac{a}{k}}{\frac{1}{a}-\frac{1}{k}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-k)}{k+l}+\frac{k^{2}-a^{2}}{a k}}{\frac{k-a}{a k}}\right) \\
b=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a k}{k+l}+(a+k)\right)=\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a) \\
c=\frac{1}{2}\left(d+\frac{(a-l) \frac{2}{k+l}+\frac{l}{a}-\frac{a}{l}}{\frac{1}{a}-\frac{1}{l}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-l)}{k+l}+\frac{l^{2}-a^{2}}{a l}}{\frac{l-a}{a l}}\right) \\
c=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a l}{k+l}+(a+l)\right)=\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)
\end{gathered}
$$
Let $O$ be the the circumcenter of triangle $\triangle A B C$. As $A D$ is the diameter of this circle, we have that:
$$
o=\frac{a+d}{2}
$$
Defining $H$ as the orthocentre of the $\triangle A B C$, we get that:
$$
\begin{gathered}
h=a+b+c-2 \cdot o=a+\left(\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a)\right)+\left(\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)\right)-(a+d) \\
h=a+\frac{2 k l}{k+l}-\frac{a(k+l)}{k+l}+\frac{1}{2} k++\frac{1}{2} l++a-\left(a+\frac{2 k l}{k+l}\right) \\
h=\frac{1}{2}(k+l)
\end{gathered}
$$
Hence, we conclude that $H$ is the midpoint of $K L$, so $H, K, L$ are collinear.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 7. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let us employ the barycentric coordinates. Set $A(1,0,0), K(0,1,0), L(0,0,1)$.
The tangent at $K$ of $(A K L)$ is $a^{2} z+c^{2} x=0$, and the tangent of of $L$ at $(A K L)$ is $a^{2} y+b^{2} x=0$. Their intersection is
$$
D\left(-a^{2}: b^{2}: c^{2}\right)
$$
Since $B \in A K$, we can let $B(1-t, t, 0)$. Solving for $\overrightarrow{A B} \cdot \overrightarrow{B D}=0$ gives
$$
t=\frac{3 b^{2}+c^{2}-a^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)} \Longrightarrow B=\left(\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, \frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0\right)
$$
Likewise, $C$ has the coordinate
$$
C=\left(\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0, \frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right) .
$$
The altitude from $B$ for triangle $A B C$ is
$$
-b^{2}\left(x-z-\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(c^{2}-a^{2}\right)\left(y-\frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
Also the altitude from $C$ for triangle $A B C$ is
$$
-c^{2}\left(x-y-\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(a^{2}-b^{2}\right)\left(z-\frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
The intersection of these two altitudes, which is the orthocenter of triangle $A B C$, has the barycentric coordinate
$$
H=(0,1 / 2,1 / 2)
$$
which is the midpoint of the segment $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let us employ the barycentric coordinates. Set $A(1,0,0), K(0,1,0), L(0,0,1)$.
The tangent at $K$ of $(A K L)$ is $a^{2} z+c^{2} x=0$, and the tangent of of $L$ at $(A K L)$ is $a^{2} y+b^{2} x=0$. Their intersection is
$$
D\left(-a^{2}: b^{2}: c^{2}\right)
$$
Since $B \in A K$, we can let $B(1-t, t, 0)$. Solving for $\overrightarrow{A B} \cdot \overrightarrow{B D}=0$ gives
$$
t=\frac{3 b^{2}+c^{2}-a^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)} \Longrightarrow B=\left(\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, \frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0\right)
$$
Likewise, $C$ has the coordinate
$$
C=\left(\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0, \frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right) .
$$
The altitude from $B$ for triangle $A B C$ is
$$
-b^{2}\left(x-z-\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(c^{2}-a^{2}\right)\left(y-\frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
Also the altitude from $C$ for triangle $A B C$ is
$$
-c^{2}\left(x-y-\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(a^{2}-b^{2}\right)\left(z-\frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
The intersection of these two altitudes, which is the orthocenter of triangle $A B C$, has the barycentric coordinate
$$
H=(0,1 / 2,1 / 2)
$$
which is the midpoint of the segment $K L$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 8. "
}
|
6b616b70-adea-51dc-a234-be24571b71df
| 605,976
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First, we consider the difference $k-k^{\prime \prime}$. If $k=a s+b$ as in the problem statement, then $k^{\prime}=b s+a$. We write $a=l s+m$ with $m, l$ non-negative numbers and $m \leq s-1$. This gives $k^{\prime \prime}=m s+(b+l)$ and hence $k-k^{\prime \prime}=(a-m) s-l=l\left(s^{2}-1\right)$.
We conclude
Fact 1.1. $k \geq k^{\prime \prime}$ for every every $k \geq 1$
Fact 1.2. $s^{2}-1$ divides the difference $k-k^{\prime \prime}$.
Fact 1.2 implies that the sequences $d_{1}, d_{3}, d_{5}, \ldots$ and $d_{2}, d_{4}, d_{6}, \ldots$ are constant modulo $s^{2}-1$. Moreover, Fact 1.1 says that the sequences are (weakly) decreasing and hence eventually constant. In other words, the sequence $d_{1}, d_{2}, d_{3}, \ldots$ is 2 -periodic modulo $s^{2}-1$ (from the start) and is eventually 2-periodic.
Now, assume that some term in the sequence is equal to 1 . The next term is equal to $1^{\prime}=s$ and since the sequence is 2 -periodic from the start modulo $s^{2}-1$, we conclude that $d_{1}$ is either equal to 1 or $s$ modulo $s^{2}-1$. This proves the first implication.
To prove the other direction, assume that $d_{1}$ is congruent to 1 or $s$ modulo $s^{2}-1$. We need the observation that once one of the sequences $d_{1}, d_{3}, d_{5}, \ldots$ or $d_{2}, d_{4}, d_{6}, \ldots$ stabilises, then their value is less than $s^{2}$. This is implied by the following fact.
Fact 1.3. If $k=k^{\prime \prime}$, then $k=k^{\prime \prime}<s^{2}$.
Proof. We use the expression for $k-k^{\prime \prime}$ found before. If $k=k^{\prime \prime}$, then $l=0$, and so $k^{\prime \prime}=m s+b$. Both $m$ and $b$ are reminders after division by $s$, so they are both $\leq s-1$. This gives $k^{\prime \prime} \leq(s-1) s+(s-1)<s^{2}$.
Using Fact 1.2, it follows that the sequence $d_{1}, d_{3}, d_{5}, \ldots$ is constant to 1 or $s$ modulo $s^{2}-1$ and stabilises to 1 or $s$ by Fact 1.3. Since $s^{\prime}=1$, we conclude that the sequence contains a 1.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First, we consider the difference $k-k^{\prime \prime}$. If $k=a s+b$ as in the problem statement, then $k^{\prime}=b s+a$. We write $a=l s+m$ with $m, l$ non-negative numbers and $m \leq s-1$. This gives $k^{\prime \prime}=m s+(b+l)$ and hence $k-k^{\prime \prime}=(a-m) s-l=l\left(s^{2}-1\right)$.
We conclude
Fact 1.1. $k \geq k^{\prime \prime}$ for every every $k \geq 1$
Fact 1.2. $s^{2}-1$ divides the difference $k-k^{\prime \prime}$.
Fact 1.2 implies that the sequences $d_{1}, d_{3}, d_{5}, \ldots$ and $d_{2}, d_{4}, d_{6}, \ldots$ are constant modulo $s^{2}-1$. Moreover, Fact 1.1 says that the sequences are (weakly) decreasing and hence eventually constant. In other words, the sequence $d_{1}, d_{2}, d_{3}, \ldots$ is 2 -periodic modulo $s^{2}-1$ (from the start) and is eventually 2-periodic.
Now, assume that some term in the sequence is equal to 1 . The next term is equal to $1^{\prime}=s$ and since the sequence is 2 -periodic from the start modulo $s^{2}-1$, we conclude that $d_{1}$ is either equal to 1 or $s$ modulo $s^{2}-1$. This proves the first implication.
To prove the other direction, assume that $d_{1}$ is congruent to 1 or $s$ modulo $s^{2}-1$. We need the observation that once one of the sequences $d_{1}, d_{3}, d_{5}, \ldots$ or $d_{2}, d_{4}, d_{6}, \ldots$ stabilises, then their value is less than $s^{2}$. This is implied by the following fact.
Fact 1.3. If $k=k^{\prime \prime}$, then $k=k^{\prime \prime}<s^{2}$.
Proof. We use the expression for $k-k^{\prime \prime}$ found before. If $k=k^{\prime \prime}$, then $l=0$, and so $k^{\prime \prime}=m s+b$. Both $m$ and $b$ are reminders after division by $s$, so they are both $\leq s-1$. This gives $k^{\prime \prime} \leq(s-1) s+(s-1)<s^{2}$.
Using Fact 1.2, it follows that the sequence $d_{1}, d_{3}, d_{5}, \ldots$ is constant to 1 or $s$ modulo $s^{2}-1$ and stabilises to 1 or $s$ by Fact 1.3. Since $s^{\prime}=1$, we conclude that the sequence contains a 1.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1. "
}
|
7da903d7-5421-58c3-adfc-ef8370612048
| 606,077
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We make a number of initial observations. Let $k$ be a positive integer.
Fact 2.1. If $k \geq s^{2}$, then $k^{\prime}<k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k \geq s^{2}$, then $a \geq s$ because $b<s$. So, $k^{\prime}=b s+a \leq(s-1) s+a \leq a s \leq a s+b=k$. Moreover, we cannot have equality since that would imply $s-1=b=0$.
Fact 2.2. If $k \leq s^{2}-1$, then $k^{\prime} \leq s^{2}-1$ and $k^{\prime \prime}=k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k<s^{2}$, then it must hold $1 \leq a, b<s$, hence $k^{\prime}=b s+a<s^{2}$ and $k^{\prime \prime}=(b s+a)^{\prime}=a s+b=k$.
Fact 2.3. We have $k^{\prime} \equiv s k\left(\bmod s^{2}-1\right)\left(\right.$ or equivalently $\left.k \equiv s k^{\prime}\left(\bmod s^{2}-1\right)\right)$.
Proof. We write $k=a s+b$, as in the problem statement. Now,
$$
s k-k^{\prime}=s(a s+b)-(b s+a)=a\left(s^{2}-1\right) \equiv 0 \quad\left(\bmod s^{2}-1\right),
$$
as desired.
Combining Facts 2.1 and 2.2 , we find that the sequence $d_{1}, d_{2}, d_{3} \ldots$ is eventually periodic with period 2, starting at the first value less than $s^{2}$. From Fact 2.3, it follows that
$$
k^{\prime \prime} \equiv s k^{\prime} \equiv s^{2} k \equiv k \quad\left(\bmod s^{2}-1\right)
$$
and hence the sequence is periodic modulo $s^{2}-1$ from the start with period 2 .
Now, if the sequence contains 1 , the sequence eventually alternates between 1 and $s$ since the twist of 1 is $s$ and vice versa. Using periodicity modulo $s^{2}-1$, we must have $n \equiv 1, s$ $\left(\bmod s^{2}-1\right)$. Conversely, if $n \equiv 1, s\left(\bmod s^{2}-1\right)$ then the eventual period must contain at least one value congruent to either 1 or $s$ modulo $s^{2}-1$. Since these values must be less than $s^{2}$, this implies that the sequence eventually alternates between 1 and $s$, showing that it contains a 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We make a number of initial observations. Let $k$ be a positive integer.
Fact 2.1. If $k \geq s^{2}$, then $k^{\prime}<k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k \geq s^{2}$, then $a \geq s$ because $b<s$. So, $k^{\prime}=b s+a \leq(s-1) s+a \leq a s \leq a s+b=k$. Moreover, we cannot have equality since that would imply $s-1=b=0$.
Fact 2.2. If $k \leq s^{2}-1$, then $k^{\prime} \leq s^{2}-1$ and $k^{\prime \prime}=k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k<s^{2}$, then it must hold $1 \leq a, b<s$, hence $k^{\prime}=b s+a<s^{2}$ and $k^{\prime \prime}=(b s+a)^{\prime}=a s+b=k$.
Fact 2.3. We have $k^{\prime} \equiv s k\left(\bmod s^{2}-1\right)\left(\right.$ or equivalently $\left.k \equiv s k^{\prime}\left(\bmod s^{2}-1\right)\right)$.
Proof. We write $k=a s+b$, as in the problem statement. Now,
$$
s k-k^{\prime}=s(a s+b)-(b s+a)=a\left(s^{2}-1\right) \equiv 0 \quad\left(\bmod s^{2}-1\right),
$$
as desired.
Combining Facts 2.1 and 2.2 , we find that the sequence $d_{1}, d_{2}, d_{3} \ldots$ is eventually periodic with period 2, starting at the first value less than $s^{2}$. From Fact 2.3, it follows that
$$
k^{\prime \prime} \equiv s k^{\prime} \equiv s^{2} k \equiv k \quad\left(\bmod s^{2}-1\right)
$$
and hence the sequence is periodic modulo $s^{2}-1$ from the start with period 2 .
Now, if the sequence contains 1 , the sequence eventually alternates between 1 and $s$ since the twist of 1 is $s$ and vice versa. Using periodicity modulo $s^{2}-1$, we must have $n \equiv 1, s$ $\left(\bmod s^{2}-1\right)$. Conversely, if $n \equiv 1, s\left(\bmod s^{2}-1\right)$ then the eventual period must contain at least one value congruent to either 1 or $s$ modulo $s^{2}-1$. Since these values must be less than $s^{2}$, this implies that the sequence eventually alternates between 1 and $s$, showing that it contains a 1 .
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 2. "
}
|
7da903d7-5421-58c3-adfc-ef8370612048
| 606,077
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We give an alternate proof of the direct implication: if the sequence contains a 1 , then the first term is 1 or $s$ modulo $s^{2}-1$. We prove the following fact, which is a combination of Facts 2.1 and 2.3.
Fact 3.1. For all $k \geq s^{2}$, we have $\left(k-s^{2}+1\right)^{\prime} \in\left\{k^{\prime}, k^{\prime}-s^{2}+1\right\}$.
Proof. We write $k=a s+b$, as in the problem statement. Since $k \geq s^{2}$, we have $a \geq s$. If $b<s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s) s+(b+1))^{\prime}=(b+1) s+(a-s)=b s+a=k^{\prime}
$$
On the other hand, if $b=s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s+1) s+0)^{\prime}=0 s+(a-s+1)=a-s+1=k^{\prime}-s^{2}+1
$$
Now assume $n \geq s^{2}$ and the sequence $d_{1}, d_{2}, \ldots$ contains a 1 . Denote by $e_{1}, e_{2}, \ldots$ the sequence constructed as in the problem statement, but with initial value $e_{1}=n-s^{2}+1$. Using the above fact, we deduce that $e_{i} \equiv d_{i}\left(\bmod s^{2}-1\right)$ and $e_{i} \leq d_{i}$ for all $i \geq 1$ by induction on $i$. Hence, the sequence $e_{1}, e_{2}, \ldots$ also contains a 1 .
Since the conclusion we are trying to reach only depends on the residue of $d_{1}$ modulo $s^{2}-1$, we conclude that without loss of generality we can assume $n<s^{2}$.
Using Fact 2.2, it now follows that the sequence $d_{1}, d_{2}, \ldots$ is periodic with period two. Since 1 and $s$ are twists of each other, it follows that if this sequence contains a 1 , it must be alternating between 1 and $s$. Hence, $d_{1} \equiv 1, s\left(\bmod s^{2}-1\right)$ as desired.
For the other direction we can make a similar argument, observing that the second of the two cases in the proof of Fact 3.1 can only apply to finitely many terms of the sequence $d_{1}, d_{2}, d_{3}, \ldots$, allowing us to also go the other way.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We give an alternate proof of the direct implication: if the sequence contains a 1 , then the first term is 1 or $s$ modulo $s^{2}-1$. We prove the following fact, which is a combination of Facts 2.1 and 2.3.
Fact 3.1. For all $k \geq s^{2}$, we have $\left(k-s^{2}+1\right)^{\prime} \in\left\{k^{\prime}, k^{\prime}-s^{2}+1\right\}$.
Proof. We write $k=a s+b$, as in the problem statement. Since $k \geq s^{2}$, we have $a \geq s$. If $b<s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s) s+(b+1))^{\prime}=(b+1) s+(a-s)=b s+a=k^{\prime}
$$
On the other hand, if $b=s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s+1) s+0)^{\prime}=0 s+(a-s+1)=a-s+1=k^{\prime}-s^{2}+1
$$
Now assume $n \geq s^{2}$ and the sequence $d_{1}, d_{2}, \ldots$ contains a 1 . Denote by $e_{1}, e_{2}, \ldots$ the sequence constructed as in the problem statement, but with initial value $e_{1}=n-s^{2}+1$. Using the above fact, we deduce that $e_{i} \equiv d_{i}\left(\bmod s^{2}-1\right)$ and $e_{i} \leq d_{i}$ for all $i \geq 1$ by induction on $i$. Hence, the sequence $e_{1}, e_{2}, \ldots$ also contains a 1 .
Since the conclusion we are trying to reach only depends on the residue of $d_{1}$ modulo $s^{2}-1$, we conclude that without loss of generality we can assume $n<s^{2}$.
Using Fact 2.2, it now follows that the sequence $d_{1}, d_{2}, \ldots$ is periodic with period two. Since 1 and $s$ are twists of each other, it follows that if this sequence contains a 1 , it must be alternating between 1 and $s$. Hence, $d_{1} \equiv 1, s\left(\bmod s^{2}-1\right)$ as desired.
For the other direction we can make a similar argument, observing that the second of the two cases in the proof of Fact 3.1 can only apply to finitely many terms of the sequence $d_{1}, d_{2}, d_{3}, \ldots$, allowing us to also go the other way.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 3. "
}
|
7da903d7-5421-58c3-adfc-ef8370612048
| 606,077
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First assume that $d_{k}=1$ for some $k$. Let $k$ be the smallest such index. If $k=1$ then $n=1$, so we may assume $k \geqslant 2$.
Then $d_{k-1}=a s+b$ for some non-negative integers $a, b$ satisfying $b<s$ and $b s+a=1$. The only solution is $b=0, a=1$, so $d_{k-1}=s$. So, if $k=2$, then $n=s$, so we may assume $k \geqslant 3$.
Then there exist non-negative integers $c, d$ satisfying $d_{k-2}=c s+d, d<s$ and $d s+c=s$. We have two solutions: $d=0, c=s$ and $d=1, c=0$. However, in the second case we get $d_{k-2}=1$, which contradicts the minimality of $k$. Hence, $d_{k-2}=s^{2}$. If $k=3$, then $n=d_{1}=s^{2}$, which gives remainder 1 when divided by $s^{2}-1$.
Assume now that $k \geqslant 4$. We will show that for each $m \in\{3,4, \ldots, k-1\}$ there exist $b_{1}, b_{2}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that
$$
d_{k-m}=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) .
$$
We will prove this equality by induction on $m$. If $m=3$, then $d_{k-3}=a_{1} s+b_{1}$ for some non-negative integers $a_{1}, b_{1}$ satisfying $b_{1}<s$ and $b_{1} s+a_{1}=d_{k-2}=s^{2}$. Then $a_{1}=s^{2}-b_{1} s$, so $d_{k-3}=s^{3}-b_{1}\left(s^{2}-1\right)$, which proves (9) for $m=3$.
Assume that (9) holds for some $m$ and consider $d_{k-(m+1)}$. There exist non-negative integers $a_{m-1}, b_{m-1}$ such that $d_{k-(m+1)}=a_{m-1} s+b_{m-1}, b_{m-1}<s$ and $d_{k-m}=b_{m-1} s+a_{m-1}$. Using the inductive assumption we get
$$
a_{m-1}=d_{k-m}-b_{m-1} s=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right)-b_{m-1} s,
$$
therefore
$$
\begin{aligned}
d_{k-(m+1)} & =a_{m-1} s+b_{m-1}=s^{m+1}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) s-b_{m-1} s^{2}+b_{m-1} \\
& =s^{m+1}-\sum_{i=1}^{m-1} b_{i}\left(s^{m+1-i}-s^{m-i-1}\right)
\end{aligned}
$$
which completes the proof of (9). In particular, for $m=k-1$ we get
$$
d_{1}=s^{k-1}-\sum_{i=1}^{k-3} b_{i}\left(s^{k-i-1}-s^{k-i-3}\right) .
$$
The above sum is clearly divisible by $s^{2}-1$, and it is clear that the remainder of $s^{k-1}$ when divided by $s^{2}-1$ is 1 when $k$ is odd, and $s$ when $k$ is even. It follows that the remainder when $n=d_{1}$ is divided by $s^{2}-1$ is either 1 or $s$.
To prove the other implication, assume that $n$ gives remainder 1 or $s$ when divided by $s^{2}-1$. If $n \in\left\{1, s, s^{2}\right\}$, then one of the numbers $d_{1}, d_{2}$ and $d_{3}$ is 1 . We therefore assume that $n>s^{2}$. Since the reminder when a power of $s$ is divided by $s^{2}-1$ is either 1 or $s$, there exists a positive integer $m$ such that $s^{m}-n$ is non-negative and divisible by $s^{2}-1$. By our assumption $m \geqslant 3$. We also take the smallest such $m$, so that $n>s^{m-2}$. The quotient $\frac{s^{m}-n}{s^{2}-1}$ is therefore smaller than $s^{m-2}$, so there exist $b_{1}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that $\frac{s^{m}-n}{s^{2}-1}=\sum_{i=1}^{m-2} b_{i} s^{i-1}$. It follows that
$$
n=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{i+1}-s^{i-1}\right) .
$$
We now show that
$$
d_{j}=s^{m+1-j}-\sum_{i=1}^{m-1-j} b_{i}\left(s^{i+1}-s^{i-1}\right)
$$
for $j=1,2, \ldots, m-2$ by induction on $j$. For $j=1$ this follows from $d_{1}=n$. Assume now that (10) holds for some $j<m-2$. Then
$$
d_{j}=\left(s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s\right) s+b_{1}
$$
As $d_{j}$ is positive and $b_{1} \in\{0,1, \ldots, s-1\}$, the expression $s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s$ has to be non-negative, so we can compute the twist of $d_{j}$ as
$$
d_{j+1}=b_{1} s+s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s=s^{m-j}-\sum_{i=1}^{m-2-j} b_{i}\left(s^{i+1}-s^{i-1}\right),
$$
which finishes the induction.
Now we use (10) for $j=m-2$ and get $d_{m-2}=s^{3}-b_{1}\left(s^{2}-1\right)=\left(s^{2}-b_{1} s\right)+b_{1}$. Then $d_{m-1}=b_{1} s+s^{2}-b_{1} s=s^{2}=s \cdot s+0, d_{m}=0 \cdot s+s=s=1 \cdot s+0$ and $d_{m+1}=0 \cdot s+1=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First assume that $d_{k}=1$ for some $k$. Let $k$ be the smallest such index. If $k=1$ then $n=1$, so we may assume $k \geqslant 2$.
Then $d_{k-1}=a s+b$ for some non-negative integers $a, b$ satisfying $b<s$ and $b s+a=1$. The only solution is $b=0, a=1$, so $d_{k-1}=s$. So, if $k=2$, then $n=s$, so we may assume $k \geqslant 3$.
Then there exist non-negative integers $c, d$ satisfying $d_{k-2}=c s+d, d<s$ and $d s+c=s$. We have two solutions: $d=0, c=s$ and $d=1, c=0$. However, in the second case we get $d_{k-2}=1$, which contradicts the minimality of $k$. Hence, $d_{k-2}=s^{2}$. If $k=3$, then $n=d_{1}=s^{2}$, which gives remainder 1 when divided by $s^{2}-1$.
Assume now that $k \geqslant 4$. We will show that for each $m \in\{3,4, \ldots, k-1\}$ there exist $b_{1}, b_{2}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that
$$
d_{k-m}=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) .
$$
We will prove this equality by induction on $m$. If $m=3$, then $d_{k-3}=a_{1} s+b_{1}$ for some non-negative integers $a_{1}, b_{1}$ satisfying $b_{1}<s$ and $b_{1} s+a_{1}=d_{k-2}=s^{2}$. Then $a_{1}=s^{2}-b_{1} s$, so $d_{k-3}=s^{3}-b_{1}\left(s^{2}-1\right)$, which proves (9) for $m=3$.
Assume that (9) holds for some $m$ and consider $d_{k-(m+1)}$. There exist non-negative integers $a_{m-1}, b_{m-1}$ such that $d_{k-(m+1)}=a_{m-1} s+b_{m-1}, b_{m-1}<s$ and $d_{k-m}=b_{m-1} s+a_{m-1}$. Using the inductive assumption we get
$$
a_{m-1}=d_{k-m}-b_{m-1} s=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right)-b_{m-1} s,
$$
therefore
$$
\begin{aligned}
d_{k-(m+1)} & =a_{m-1} s+b_{m-1}=s^{m+1}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) s-b_{m-1} s^{2}+b_{m-1} \\
& =s^{m+1}-\sum_{i=1}^{m-1} b_{i}\left(s^{m+1-i}-s^{m-i-1}\right)
\end{aligned}
$$
which completes the proof of (9). In particular, for $m=k-1$ we get
$$
d_{1}=s^{k-1}-\sum_{i=1}^{k-3} b_{i}\left(s^{k-i-1}-s^{k-i-3}\right) .
$$
The above sum is clearly divisible by $s^{2}-1$, and it is clear that the remainder of $s^{k-1}$ when divided by $s^{2}-1$ is 1 when $k$ is odd, and $s$ when $k$ is even. It follows that the remainder when $n=d_{1}$ is divided by $s^{2}-1$ is either 1 or $s$.
To prove the other implication, assume that $n$ gives remainder 1 or $s$ when divided by $s^{2}-1$. If $n \in\left\{1, s, s^{2}\right\}$, then one of the numbers $d_{1}, d_{2}$ and $d_{3}$ is 1 . We therefore assume that $n>s^{2}$. Since the reminder when a power of $s$ is divided by $s^{2}-1$ is either 1 or $s$, there exists a positive integer $m$ such that $s^{m}-n$ is non-negative and divisible by $s^{2}-1$. By our assumption $m \geqslant 3$. We also take the smallest such $m$, so that $n>s^{m-2}$. The quotient $\frac{s^{m}-n}{s^{2}-1}$ is therefore smaller than $s^{m-2}$, so there exist $b_{1}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that $\frac{s^{m}-n}{s^{2}-1}=\sum_{i=1}^{m-2} b_{i} s^{i-1}$. It follows that
$$
n=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{i+1}-s^{i-1}\right) .
$$
We now show that
$$
d_{j}=s^{m+1-j}-\sum_{i=1}^{m-1-j} b_{i}\left(s^{i+1}-s^{i-1}\right)
$$
for $j=1,2, \ldots, m-2$ by induction on $j$. For $j=1$ this follows from $d_{1}=n$. Assume now that (10) holds for some $j<m-2$. Then
$$
d_{j}=\left(s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s\right) s+b_{1}
$$
As $d_{j}$ is positive and $b_{1} \in\{0,1, \ldots, s-1\}$, the expression $s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s$ has to be non-negative, so we can compute the twist of $d_{j}$ as
$$
d_{j+1}=b_{1} s+s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s=s^{m-j}-\sum_{i=1}^{m-2-j} b_{i}\left(s^{i+1}-s^{i-1}\right),
$$
which finishes the induction.
Now we use (10) for $j=m-2$ and get $d_{m-2}=s^{3}-b_{1}\left(s^{2}-1\right)=\left(s^{2}-b_{1} s\right)+b_{1}$. Then $d_{m-1}=b_{1} s+s^{2}-b_{1} s=s^{2}=s \cdot s+0, d_{m}=0 \cdot s+s=s=1 \cdot s+0$ and $d_{m+1}=0 \cdot s+1=1$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 4. "
}
|
7da903d7-5421-58c3-adfc-ef8370612048
| 606,077
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that A lies on the radical axis of $\omega_{b}$ and $\omega_{c}$.
We first note that the line through the intersections of two circles is the radical line of the two circles. Let the tangents to $\Omega$ at $S_{b}$ and $S_{c}$ intersect at $T$. Clearly $T$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$ (and in fact is the radical centre of $\omega_{b}, \omega_{c}$ and $\Omega$ ).
We next show that $A$ lies on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $P_{b}$ denote the point of tangency of $\omega_{b}$ and $A B$, and let $P_{c}$ denote the point of tangency of $\omega_{c}$ and $A C$. Furthermore, let $U$ be the intersection of the tangent to $\Omega$ at $S_{b}$ with the line $A B$, and let $V$ be the intersection of the tangent to $\Omega$ at $S_{c}$ with the line $A C$. Then $T V A U$ is parallelogram. Morover, due to equality of tangent segments we have $\left|U S_{b}\right|=\left|U P_{b}\right|,\left|V P_{c}\right|=\left|V S_{c}\right|$ and $\left|T S_{b}\right|=\left|T S_{c}\right|$. It follows that
$$
\begin{aligned}
\left|A P_{b}\right| & =\left|U P_{b}\right|-|U A|=\left|U S_{b}\right|-|T V|=\left|T S_{b}\right|-|T U|-|T V| \\
& =\left|T S_{s}\right|-|T V|-|T U|=\left|V S_{c}\right|-|A V|=\left|V P_{c}\right|-|V A|=\left|A P_{c}\right|
\end{aligned}
$$
But $\left|A P_{b}\right|,\left|A P_{c}\right|$ are exactly the square roots of powers of $A$ with respect to $\omega_{b}$ and $\omega_{c}$, hence $A$ is indeed on their radical axis.
Thus, the radical axis of $\omega_{b}, \omega_{c}$ is $A T$.
Part II: Consider the triangle $A S_{b} S_{c}$. Note that since $T$ is the intersection of the tangents at $S_{b}$ and $S_{c}$ to the circumcircle of $A S_{b} S_{c}$, it follows that $A T$ is the symmedian of $A$ in this triangle. Let $X$ denote the second intersection of the symmedian $A T$ with $\Omega$. We wish to show that $X$ is also on $I N_{a}$.
Note that $A N_{a}$ is the external angle bisector of angle $A$, and therefore it is parallel to $S_{b} S_{c}$. Let $M$ denote the midpoint of $S_{b} S_{c}$, and let $Y$ be the second intersection of $A M$ with $\Omega$. Since in $A S_{b} S_{c}, A X T$ is the symmedian and $A M Y$ is the median, it follows that $X Y$ is also parallel to $S_{b} S_{c}$. Thus, reflecting in the perpendicular bisector of $S_{b} S_{c}$ sends the line $A M Y$ to line $N_{a} M X$.
Next, consider the quadrilateral $A S_{b} I S_{c}$. From the trillium theorem we have $\left|S_{b} A\right|=\left|S_{b} I\right|$ and $\left|S_{c} A\right|=\left|S_{c} I\right|$, thus the quadrilateral is a kite, from which it follows that the reflection of the line $A M$ in $S_{b} S_{c}$ is the line $I M$. But previously we have seen that this is also the line $N_{a} M X$. Thus $M, I, N_{a}$ and $X$ are collinear, as we wanted to show.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that A lies on the radical axis of $\omega_{b}$ and $\omega_{c}$.
We first note that the line through the intersections of two circles is the radical line of the two circles. Let the tangents to $\Omega$ at $S_{b}$ and $S_{c}$ intersect at $T$. Clearly $T$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$ (and in fact is the radical centre of $\omega_{b}, \omega_{c}$ and $\Omega$ ).
We next show that $A$ lies on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $P_{b}$ denote the point of tangency of $\omega_{b}$ and $A B$, and let $P_{c}$ denote the point of tangency of $\omega_{c}$ and $A C$. Furthermore, let $U$ be the intersection of the tangent to $\Omega$ at $S_{b}$ with the line $A B$, and let $V$ be the intersection of the tangent to $\Omega$ at $S_{c}$ with the line $A C$. Then $T V A U$ is parallelogram. Morover, due to equality of tangent segments we have $\left|U S_{b}\right|=\left|U P_{b}\right|,\left|V P_{c}\right|=\left|V S_{c}\right|$ and $\left|T S_{b}\right|=\left|T S_{c}\right|$. It follows that
$$
\begin{aligned}
\left|A P_{b}\right| & =\left|U P_{b}\right|-|U A|=\left|U S_{b}\right|-|T V|=\left|T S_{b}\right|-|T U|-|T V| \\
& =\left|T S_{s}\right|-|T V|-|T U|=\left|V S_{c}\right|-|A V|=\left|V P_{c}\right|-|V A|=\left|A P_{c}\right|
\end{aligned}
$$
But $\left|A P_{b}\right|,\left|A P_{c}\right|$ are exactly the square roots of powers of $A$ with respect to $\omega_{b}$ and $\omega_{c}$, hence $A$ is indeed on their radical axis.
Thus, the radical axis of $\omega_{b}, \omega_{c}$ is $A T$.
Part II: Consider the triangle $A S_{b} S_{c}$. Note that since $T$ is the intersection of the tangents at $S_{b}$ and $S_{c}$ to the circumcircle of $A S_{b} S_{c}$, it follows that $A T$ is the symmedian of $A$ in this triangle. Let $X$ denote the second intersection of the symmedian $A T$ with $\Omega$. We wish to show that $X$ is also on $I N_{a}$.
Note that $A N_{a}$ is the external angle bisector of angle $A$, and therefore it is parallel to $S_{b} S_{c}$. Let $M$ denote the midpoint of $S_{b} S_{c}$, and let $Y$ be the second intersection of $A M$ with $\Omega$. Since in $A S_{b} S_{c}, A X T$ is the symmedian and $A M Y$ is the median, it follows that $X Y$ is also parallel to $S_{b} S_{c}$. Thus, reflecting in the perpendicular bisector of $S_{b} S_{c}$ sends the line $A M Y$ to line $N_{a} M X$.
Next, consider the quadrilateral $A S_{b} I S_{c}$. From the trillium theorem we have $\left|S_{b} A\right|=\left|S_{b} I\right|$ and $\left|S_{c} A\right|=\left|S_{c} I\right|$, thus the quadrilateral is a kite, from which it follows that the reflection of the line $A M$ in $S_{b} S_{c}$ is the line $I M$. But previously we have seen that this is also the line $N_{a} M X$. Thus $M, I, N_{a}$ and $X$ are collinear, as we wanted to show.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 1. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
This is a variation of Solution 1 which avoids the theory of the symmedian point.
We begin by showing that the radical axis of $\omega_{b}, \omega_{c}$ is $A T$ as in Solution 1.
Part II: We introduce the point $S_{a}$ with the obvious meaning. Observe that the incentre $I$ of $A B C$ is the orthocentre of $S_{a} S_{b} S_{c}$ either because this is well-known, or because of an angle argument that $A$ reflects in $S_{b} S_{c}$ to $I$ (and similar results by cyclic change of letters). Therefore $A S_{a}$ is perpendicular to $S_{b} S_{c}$.
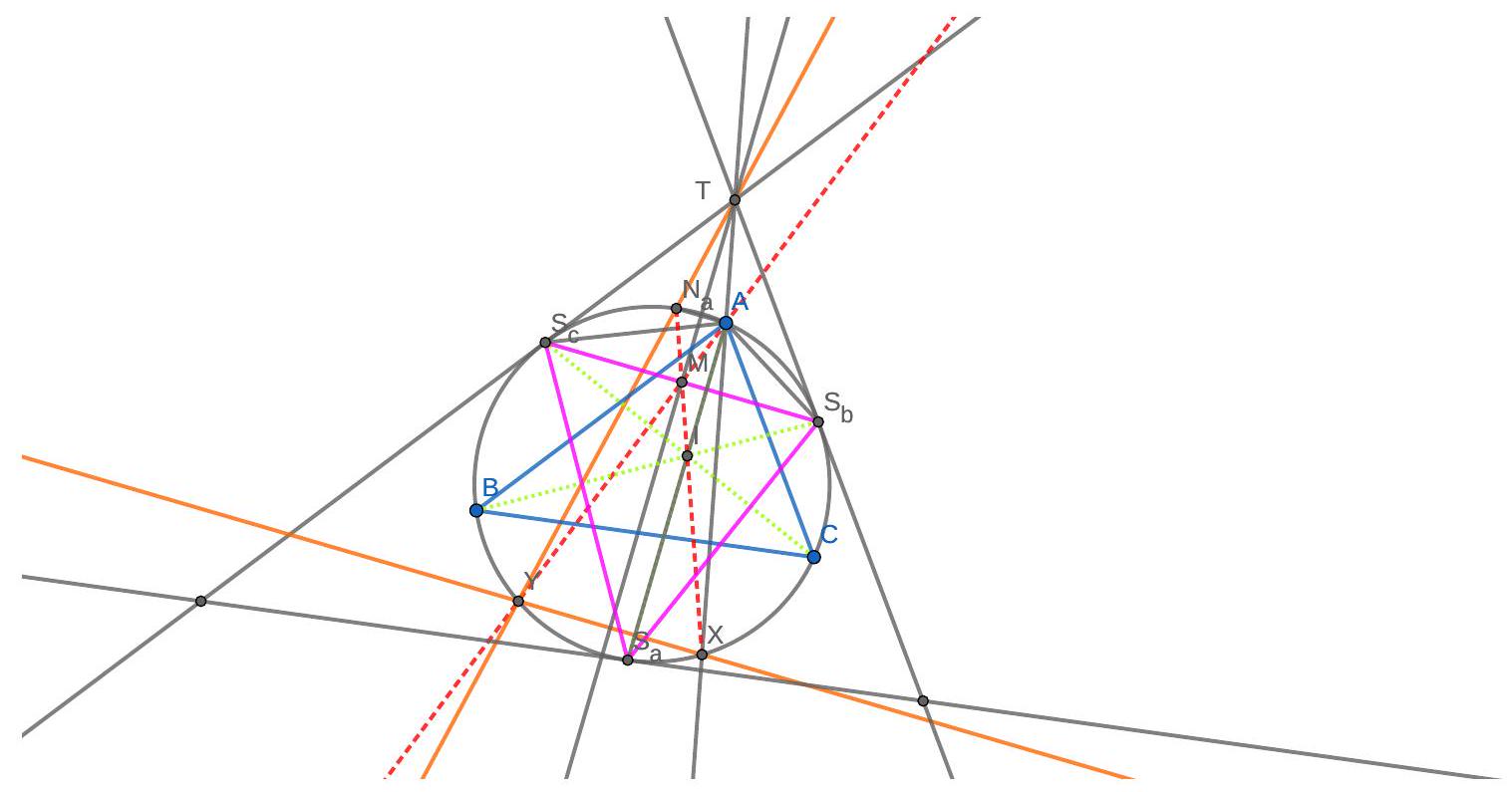
Figure 7: A reflections argument for Solution 2
Let $M$ denote the midpoint of $S_{b} S_{c}$. Then $A$ is the reflection of $S_{a}$ in the diameter parallel to $S_{b} S_{c}$, so the reflection of $A$ in the diameter perpendicular to $S_{b} S_{c}$ is $N_{a}$, the antipode
of $S_{a}$. Let the reflection of $X$ in $T M$ be $Y$, so $T Y$ passes through $N_{a}$ and is the reflection of $T X$ in $T M$.
Now $S_{b} S_{c}$ is the polar line of $T$ with respect to $\Omega$, so $A Y$ and $N_{a} X$ meet on this line, and by symmetry at its midpoint $M$. The line $N_{a} M X$ is therefore the reflection of the line $Y M A$ in $S_{b} S_{c}$, and so $N_{a} M X$ passes through $I$ (the reflection of $A$ in $S_{b} S_{c}$ ).
The triangle $A S_{c} S_{b}$ can be taken as generic, and from the argument above we can extract the fact that the symmedian point and the centroid are isogonal conjugates in that triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
This is a variation of Solution 1 which avoids the theory of the symmedian point.
We begin by showing that the radical axis of $\omega_{b}, \omega_{c}$ is $A T$ as in Solution 1.
Part II: We introduce the point $S_{a}$ with the obvious meaning. Observe that the incentre $I$ of $A B C$ is the orthocentre of $S_{a} S_{b} S_{c}$ either because this is well-known, or because of an angle argument that $A$ reflects in $S_{b} S_{c}$ to $I$ (and similar results by cyclic change of letters). Therefore $A S_{a}$ is perpendicular to $S_{b} S_{c}$.

Figure 7: A reflections argument for Solution 2
Let $M$ denote the midpoint of $S_{b} S_{c}$. Then $A$ is the reflection of $S_{a}$ in the diameter parallel to $S_{b} S_{c}$, so the reflection of $A$ in the diameter perpendicular to $S_{b} S_{c}$ is $N_{a}$, the antipode
of $S_{a}$. Let the reflection of $X$ in $T M$ be $Y$, so $T Y$ passes through $N_{a}$ and is the reflection of $T X$ in $T M$.
Now $S_{b} S_{c}$ is the polar line of $T$ with respect to $\Omega$, so $A Y$ and $N_{a} X$ meet on this line, and by symmetry at its midpoint $M$. The line $N_{a} M X$ is therefore the reflection of the line $Y M A$ in $S_{b} S_{c}$, and so $N_{a} M X$ passes through $I$ (the reflection of $A$ in $S_{b} S_{c}$ ).
The triangle $A S_{c} S_{b}$ can be taken as generic, and from the argument above we can extract the fact that the symmedian point and the centroid are isogonal conjugates in that triangle.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 2. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Assume the notation from Solution 1, part I of Solution 1, and let $O$ be the centre of $\Omega$.
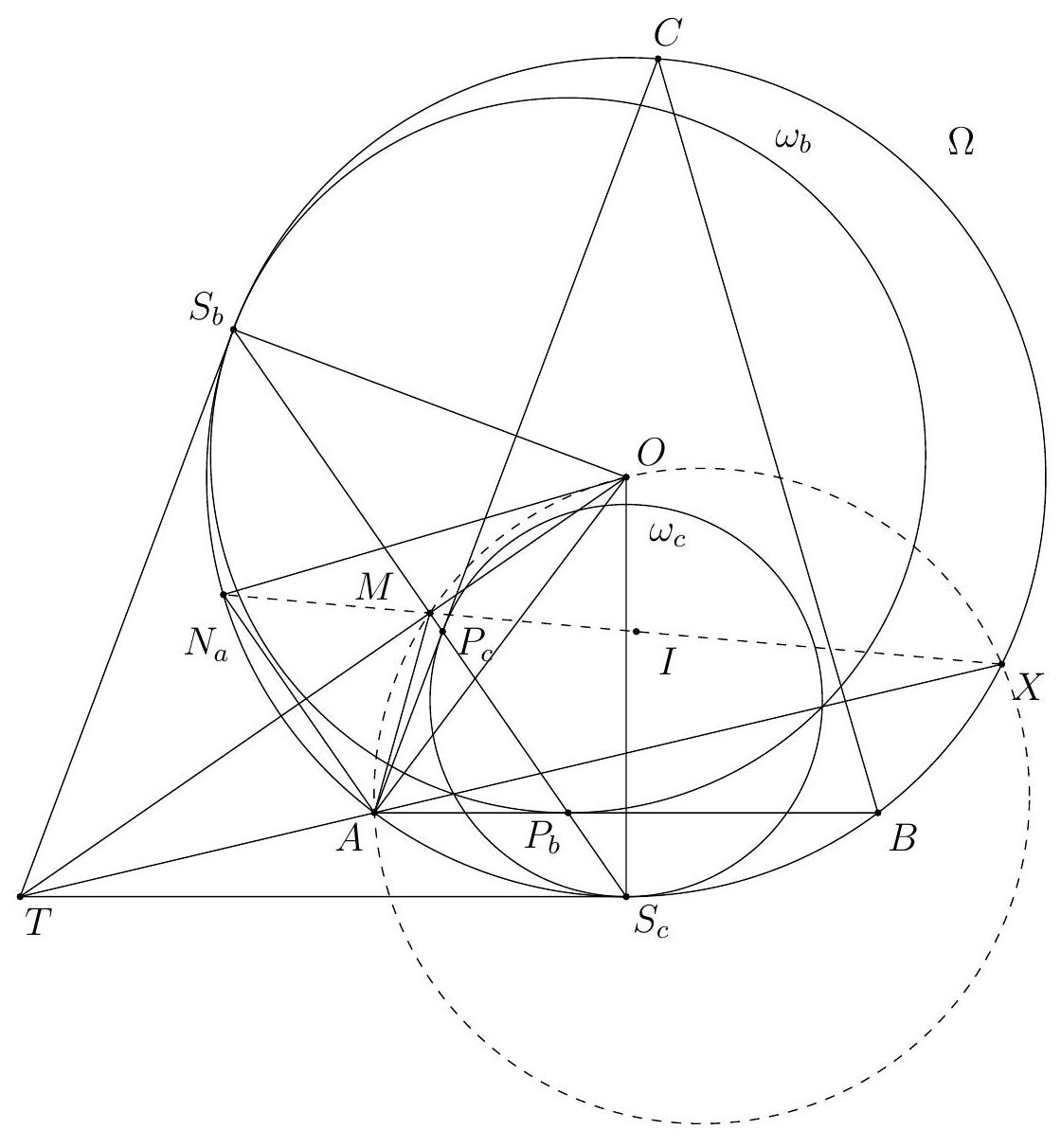
Figure 8: Diagram to Solution 3
Part II: As in Solution 1, by the trillelium theorem, $S_{c} S_{b}$ bisects $A I$, and since $N_{a} A \| S_{b} S_{c}$, then $O T$ is a bisector of $A N_{a}$. This implies $\left|M N_{a}\right|=|M A|=|M I|$, since $M$ is the midpoint of $S_{c} S_{b}$ and lies also on $O T$. Hence, $M$ is the circumcentre of triangle $I A N_{a}$. But this triangle has a right angle at $A$ (since $A I$ and $A N_{a}$ are the inner and outer angle bisector at $A$ ), hence $M$ lies on $I N_{a}$.
Again, let $X$ be the second intersection of $T A$ and $\Omega$. By the above, it suffices to prove that $X$ lies on the line $N_{a} M$. From the power of point $T$ with respect to $\Omega$ we get $|T A| \cdot|T X|=\left|T S_{c}\right|^{2}$. Since $M$ is the foot of the altitude of right triangle $T S_{c} O$, we obtain
$\left|T S_{c}\right|^{2}=|T M| \cdot|T O|$. Hence, $|T A| \cdot|T X|=|T M| \cdot|T O|$ so the points $O, M, A, X$ are concyclic. It follows that $\angle M X A=\angle M O A=\frac{1}{2} \angle N_{a} O A=\angle N_{a} X A$. Hence, $X$ lies on the line $N_{a} M$.
Remark. To show that $O M A X$ is cyclic, one can also invert the line $T A X$ in the circumcircle of the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Assume the notation from Solution 1, part I of Solution 1, and let $O$ be the centre of $\Omega$.

Figure 8: Diagram to Solution 3
Part II: As in Solution 1, by the trillelium theorem, $S_{c} S_{b}$ bisects $A I$, and since $N_{a} A \| S_{b} S_{c}$, then $O T$ is a bisector of $A N_{a}$. This implies $\left|M N_{a}\right|=|M A|=|M I|$, since $M$ is the midpoint of $S_{c} S_{b}$ and lies also on $O T$. Hence, $M$ is the circumcentre of triangle $I A N_{a}$. But this triangle has a right angle at $A$ (since $A I$ and $A N_{a}$ are the inner and outer angle bisector at $A$ ), hence $M$ lies on $I N_{a}$.
Again, let $X$ be the second intersection of $T A$ and $\Omega$. By the above, it suffices to prove that $X$ lies on the line $N_{a} M$. From the power of point $T$ with respect to $\Omega$ we get $|T A| \cdot|T X|=\left|T S_{c}\right|^{2}$. Since $M$ is the foot of the altitude of right triangle $T S_{c} O$, we obtain
$\left|T S_{c}\right|^{2}=|T M| \cdot|T O|$. Hence, $|T A| \cdot|T X|=|T M| \cdot|T O|$ so the points $O, M, A, X$ are concyclic. It follows that $\angle M X A=\angle M O A=\frac{1}{2} \angle N_{a} O A=\angle N_{a} X A$. Hence, $X$ lies on the line $N_{a} M$.
Remark. To show that $O M A X$ is cyclic, one can also invert the line $T A X$ in the circumcircle of the triangle $A B C$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 3. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I is done as in solution 1.
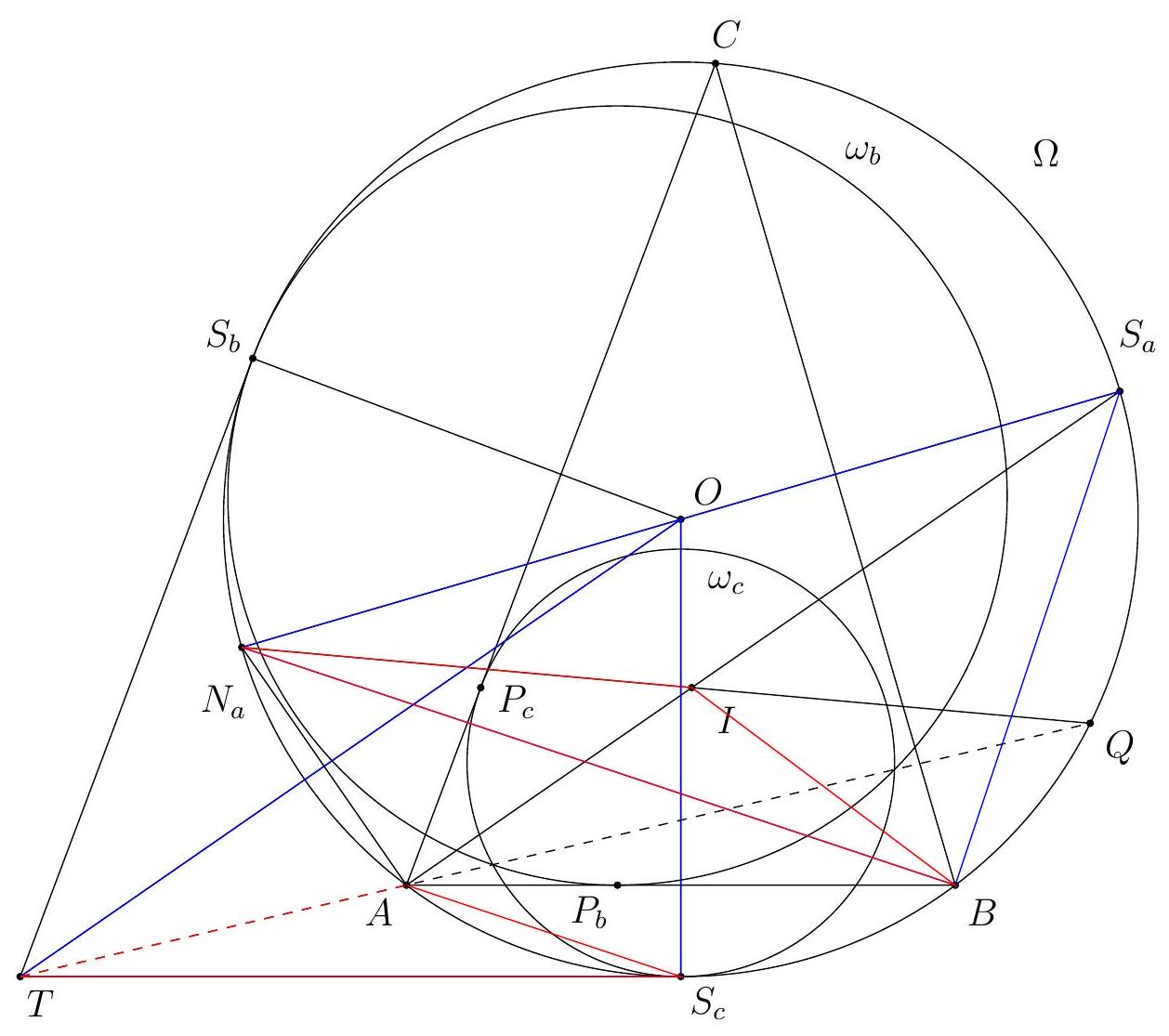
Figure 9: Diagram to Solution 4
Part II: as in Solution 1 we show that $A N_{a} \| S_{b} S_{c}$. In particular, $\angle N_{a} O T=\angle T O A$. The conclusion of the problem trivially holds if $|A B|=|A C|$, therefore we assume without loss of generality that $|A C|>|A B|$. Let $S_{a}$ be the midpoint of the arc $B C$ which does not contain $A$. Then $N_{a} S_{a}$ is a diameter, so $\angle S_{a} B N_{a}=\frac{\pi}{2}=\angle O S_{c} T$. We also compute $\angle B N_{a} S_{a}=\angle B A S_{a}=\frac{1}{2} \angle B A C=\frac{1}{2} \angle S_{c} T S_{b}=\angle S_{c} T O$. It follows that the triangles $T S_{c} O$ and $N_{a} B S_{a}$ are similar. In particular,
$$
\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}
$$
Next we compute
$$
\angle I S_{a} B=\angle N_{a} S_{a} B-\angle N_{a} S_{a} I=\angle T O S_{c}-\frac{1}{2} \angle N_{a} O A=\angle T O S_{c}-\angle T O A=\angle A O S_{c}
$$
and
$\angle I B N_{a}=\angle C B N_{a}-\angle C B I=\frac{1}{2}\left(\pi-\angle B N_{a} C\right)-\frac{1}{2} \angle C B A=\frac{1}{2} \angle A C B=\angle A C S_{c}=\angle A S_{c} T$,
hence
$$
\angle S_{a} B I=\frac{\pi}{2}-\angle I B N_{a}=\frac{\pi}{2}-\angle A S_{c} T=\angle O S_{c} A
$$
Together with (13) it follows that the triangles $I B S_{a}$ and $A S_{c} O$ are similar, so $\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}=$ $\frac{|I B|}{\left|A S_{c}\right|}$, and (12) implies $\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{|I B|}{\left|A S_{c}\right|}$. Consequently, by (14) the triangles $T S_{c} A$ and $N_{a} B I$ are similar and therefore $\angle S_{c} T A=\angle B N_{a} I$. Now let $Q$ be the second intersection of $N_{a} I$ with $\Omega$. Then $\angle B N_{a} I=\angle B N_{a} Q=\angle B A Q$, so $\angle S_{c} T A=\angle B A Q$. Since $A B$ is parallel to $T S_{c}$, we get $A Q \| T A$, i.e. $A, T, Q$ are collinear.
Remark. After proving similarity of triangles $T S_{c} O$ and $N_{a} B S_{a}$ one can use spiral symmetry to show similarity of triangles $T S_{c} A$ and $N_{a} B I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I is done as in solution 1.

Figure 9: Diagram to Solution 4
Part II: as in Solution 1 we show that $A N_{a} \| S_{b} S_{c}$. In particular, $\angle N_{a} O T=\angle T O A$. The conclusion of the problem trivially holds if $|A B|=|A C|$, therefore we assume without loss of generality that $|A C|>|A B|$. Let $S_{a}$ be the midpoint of the arc $B C$ which does not contain $A$. Then $N_{a} S_{a}$ is a diameter, so $\angle S_{a} B N_{a}=\frac{\pi}{2}=\angle O S_{c} T$. We also compute $\angle B N_{a} S_{a}=\angle B A S_{a}=\frac{1}{2} \angle B A C=\frac{1}{2} \angle S_{c} T S_{b}=\angle S_{c} T O$. It follows that the triangles $T S_{c} O$ and $N_{a} B S_{a}$ are similar. In particular,
$$
\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}
$$
Next we compute
$$
\angle I S_{a} B=\angle N_{a} S_{a} B-\angle N_{a} S_{a} I=\angle T O S_{c}-\frac{1}{2} \angle N_{a} O A=\angle T O S_{c}-\angle T O A=\angle A O S_{c}
$$
and
$\angle I B N_{a}=\angle C B N_{a}-\angle C B I=\frac{1}{2}\left(\pi-\angle B N_{a} C\right)-\frac{1}{2} \angle C B A=\frac{1}{2} \angle A C B=\angle A C S_{c}=\angle A S_{c} T$,
hence
$$
\angle S_{a} B I=\frac{\pi}{2}-\angle I B N_{a}=\frac{\pi}{2}-\angle A S_{c} T=\angle O S_{c} A
$$
Together with (13) it follows that the triangles $I B S_{a}$ and $A S_{c} O$ are similar, so $\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}=$ $\frac{|I B|}{\left|A S_{c}\right|}$, and (12) implies $\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{|I B|}{\left|A S_{c}\right|}$. Consequently, by (14) the triangles $T S_{c} A$ and $N_{a} B I$ are similar and therefore $\angle S_{c} T A=\angle B N_{a} I$. Now let $Q$ be the second intersection of $N_{a} I$ with $\Omega$. Then $\angle B N_{a} I=\angle B N_{a} Q=\angle B A Q$, so $\angle S_{c} T A=\angle B A Q$. Since $A B$ is parallel to $T S_{c}$, we get $A Q \| T A$, i.e. $A, T, Q$ are collinear.
Remark. After proving similarity of triangles $T S_{c} O$ and $N_{a} B S_{a}$ one can use spiral symmetry to show similarity of triangles $T S_{c} A$ and $N_{a} B I$.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 4. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that $A$ lies on the radical axis between $\omega_{b}$ and $\omega_{c}$.
Let $T$ be the radical center of the circumcircle, $\omega_{b}$ and $\omega_{c}$; then $T S_{b}$ and $T S_{c}$ are common tangents of the circles, as shown in Figure 5a. Moreover, let $P_{b}=A B \cap S_{b} S_{c}$ and $P_{c}=$ $A C \cap S_{b} S_{c}$. The triangle $T S_{c} S_{b}$ is isosceles: $A B \| T S_{c}$ and $A C \| T S_{b}$ so
$$
\angle A P_{b} P_{c}=\angle T S_{c} S_{b}=\angle S_{c} S_{b} T=\angle P_{b} P_{c} A
$$
From these angles we can see that $\omega_{b}$ passes through $P_{b}, \omega_{c}$ passes through $P_{c}$, and finally $A P_{b}$ and $A P_{c}$ are equal tangents to $\omega_{b}$ and $\omega_{c}$, so $A$ lies on the radical axis.
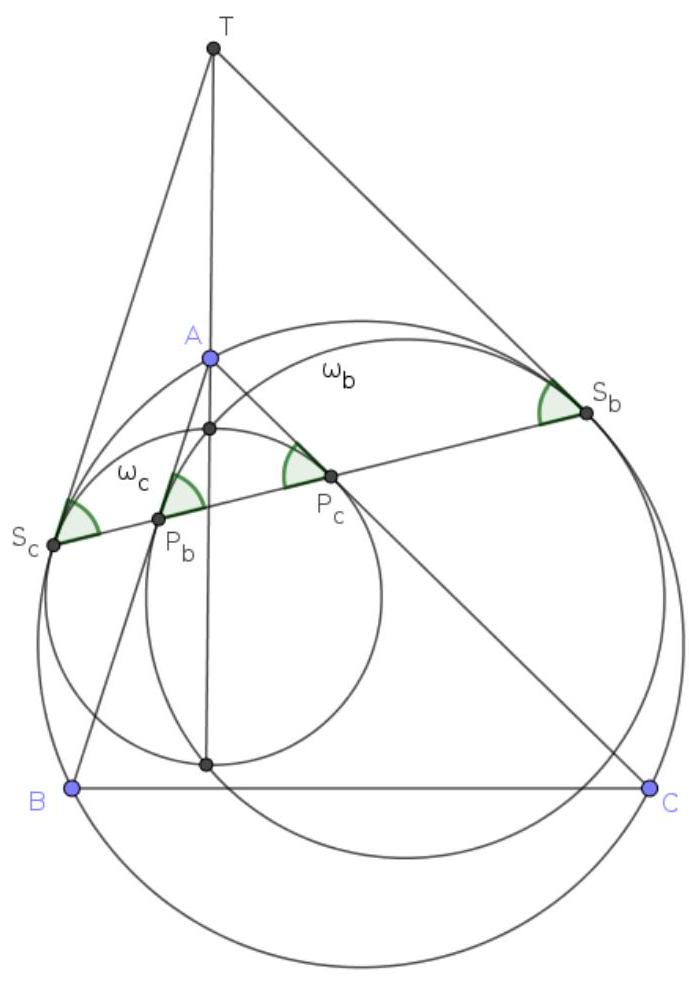
Figure 5a
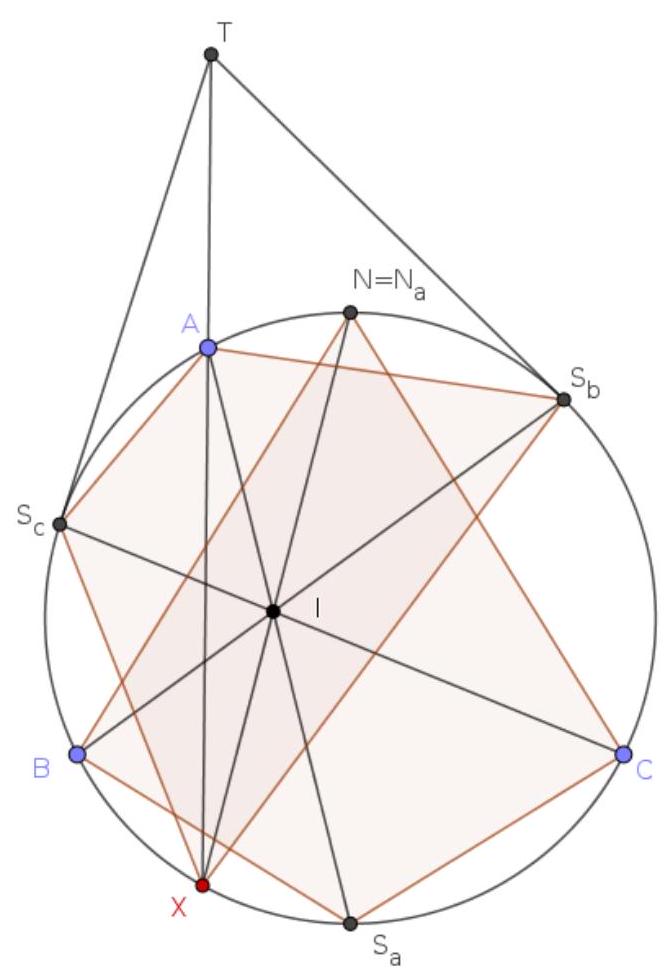
Figure 5b
Part II. Let the radical axis $T A$ meet the circumcircle again at $X$, let $S_{a}$ be the midpoint of the arc $B C$ opposite to $A$, and let $X I$ meet the circumcirlce again at $N$. (See Figure 2.) For solving the problem, we have prove that $N_{a}=N$.
The triples of points $A, I, S_{a} ; B, I, S_{b}$ and $C, I, S_{c}$ are collinear because they lie on the angle bisectors of the triangle $A B C$.
Notice that the quadrilateral $A S_{c} X S_{b}$ is harmonic, because the tangents at $S_{b}$ and $S_{c}$, and the line $A X$ are concurrent at $T$. This quadrilateral can be projected (or inverted) to the quadrilateral $S_{a} C N B$ through $I$. So, $S_{a} C N B$ also is a harmonic quadrilateral. Due to $S_{a} B=S_{a} C$, this implies $N B=N C$, so $N=N_{a}$. Done.
Remark. Instead of mentioning inversion and harmonic quadrilaterals, from the similar triangles $\triangle T S_{c} A \sim \triangle T X S_{c}$ and $\triangle T A S_{b} \sim \triangle T S_{b} X$ we can get
$$
\frac{A S_{c}}{S_{c} X}=\frac{A S_{b}}{S_{b} X}
$$
Then, we can apply the trigonometric form of Ceva's theorem to triangle $B C X$
$$
\frac{\sin \angle B X N_{a}}{\sin \angle N_{a} X C} \cdot \frac{\sin \angle C B S_{b}}{\sin \angle S_{b} B X} \cdot \frac{\sin \angle X C S_{c}}{\sin \angle S_{c} C B}=\frac{B N_{a}}{N_{a} C} \cdot \frac{-C S_{b}}{S_{b} X} \cdot \frac{X S_{c}}{-S_{c} B}=1 \cdot \frac{S_{b} A}{S_{b} N_{a}} \cdot \frac{N_{a} S_{c}}{S_{c} B}=1,
$$
so the Cevians $B S_{b}, C S_{c}$ and $X N_{a}$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that $A$ lies on the radical axis between $\omega_{b}$ and $\omega_{c}$.
Let $T$ be the radical center of the circumcircle, $\omega_{b}$ and $\omega_{c}$; then $T S_{b}$ and $T S_{c}$ are common tangents of the circles, as shown in Figure 5a. Moreover, let $P_{b}=A B \cap S_{b} S_{c}$ and $P_{c}=$ $A C \cap S_{b} S_{c}$. The triangle $T S_{c} S_{b}$ is isosceles: $A B \| T S_{c}$ and $A C \| T S_{b}$ so
$$
\angle A P_{b} P_{c}=\angle T S_{c} S_{b}=\angle S_{c} S_{b} T=\angle P_{b} P_{c} A
$$
From these angles we can see that $\omega_{b}$ passes through $P_{b}, \omega_{c}$ passes through $P_{c}$, and finally $A P_{b}$ and $A P_{c}$ are equal tangents to $\omega_{b}$ and $\omega_{c}$, so $A$ lies on the radical axis.

Figure 5a

Figure 5b
Part II. Let the radical axis $T A$ meet the circumcircle again at $X$, let $S_{a}$ be the midpoint of the arc $B C$ opposite to $A$, and let $X I$ meet the circumcirlce again at $N$. (See Figure 2.) For solving the problem, we have prove that $N_{a}=N$.
The triples of points $A, I, S_{a} ; B, I, S_{b}$ and $C, I, S_{c}$ are collinear because they lie on the angle bisectors of the triangle $A B C$.
Notice that the quadrilateral $A S_{c} X S_{b}$ is harmonic, because the tangents at $S_{b}$ and $S_{c}$, and the line $A X$ are concurrent at $T$. This quadrilateral can be projected (or inverted) to the quadrilateral $S_{a} C N B$ through $I$. So, $S_{a} C N B$ also is a harmonic quadrilateral. Due to $S_{a} B=S_{a} C$, this implies $N B=N C$, so $N=N_{a}$. Done.
Remark. Instead of mentioning inversion and harmonic quadrilaterals, from the similar triangles $\triangle T S_{c} A \sim \triangle T X S_{c}$ and $\triangle T A S_{b} \sim \triangle T S_{b} X$ we can get
$$
\frac{A S_{c}}{S_{c} X}=\frac{A S_{b}}{S_{b} X}
$$
Then, we can apply the trigonometric form of Ceva's theorem to triangle $B C X$
$$
\frac{\sin \angle B X N_{a}}{\sin \angle N_{a} X C} \cdot \frac{\sin \angle C B S_{b}}{\sin \angle S_{b} B X} \cdot \frac{\sin \angle X C S_{c}}{\sin \angle S_{c} C B}=\frac{B N_{a}}{N_{a} C} \cdot \frac{-C S_{b}}{S_{b} X} \cdot \frac{X S_{c}}{-S_{c} B}=1 \cdot \frac{S_{b} A}{S_{b} N_{a}} \cdot \frac{N_{a} S_{c}}{S_{c} B}=1,
$$
so the Cevians $B S_{b}, C S_{c}$ and $X N_{a}$ are concurrent.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 5. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First let's show that this is equivalent to proving that $T A$ and $N_{a} I$ intersect in $\Omega$.
Lemma: Let's recall that if we have two circles $\omega_{1}$ and $\omega_{2}$ which are internally tangent at point $X$ and if we have a line $A B$ tangent to $\omega_{2}$ at $Y$. Let $M$ be the midpoint of the arc $A B$ not containing $Z$. We have that $Z, Y, M$ are collinear.
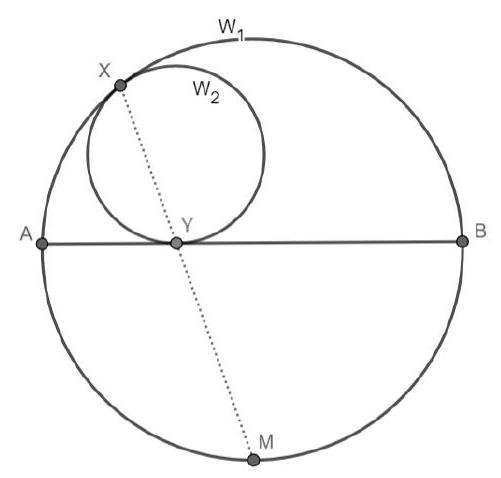
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First let's show that this is equivalent to proving that $T A$ and $N_{a} I$ intersect in $\Omega$.
Lemma: Let's recall that if we have two circles $\omega_{1}$ and $\omega_{2}$ which are internally tangent at point $X$ and if we have a line $A B$ tangent to $\omega_{2}$ at $Y$. Let $M$ be the midpoint of the arc $A B$ not containing $Z$. We have that $Z, Y, M$ are collinear.

|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 6. "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Lemma
Let $P_{b}=A B \cap \omega_{b}$ and $P_{c}=A C \cap \omega_{c}$. We can notice by the lemma that $S_{b}, P_{b}$ and $S_{c}$ are collinear, and similarly $S_{c}, P_{c}$ and $S_{b}$ are also collinear. Therefore $S_{c}, P_{b}, P_{c}$, and $S_{b}$ are collinear, and since $\angle A P_{b} P_{c}=\frac{\angle A B C}{2}+\frac{\angle A C B}{2}=\angle A P_{c} P_{b}$ then $A P_{b}=A P_{c}$ so $A$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $T$ be the intersection of the tangent lines of $\Omega$ through $S_{c}$ and $S_{b}$. Since $T S_{c}=T S_{b}$ then $A T$ is the radical axis between $\omega_{b}$ and $\omega_{c}$.
Part II: $T A$ and $N_{a} I$ intersect in $\Omega$.
Let $\omega_{a}$ the $A$-mixtilinear incircle (that is, the circle internally tangent to $\Omega$, and tangent to both $A B$ and $A C$ ), and let $X=\Omega \cap \omega_{a}$. It is known that $N_{a}, I, X$ are collinear.
Let $M_{c}$ and $M_{b}$ be the tangent points of $\omega_{A}$ to $A B$ and $A C$ respectively, then by the lemma $X, M_{c}, S_{c}$ are collinear and $X, M_{b}, S_{b}$ are collinear. We can see that $S_{c} T S_{b}$ and $M_{c} A M_{b}$ are homothetic with respect to $X$; therefore $T$ and $A$ are homothetic with respect to $X$, impying that $T, A, X$ are collinear.
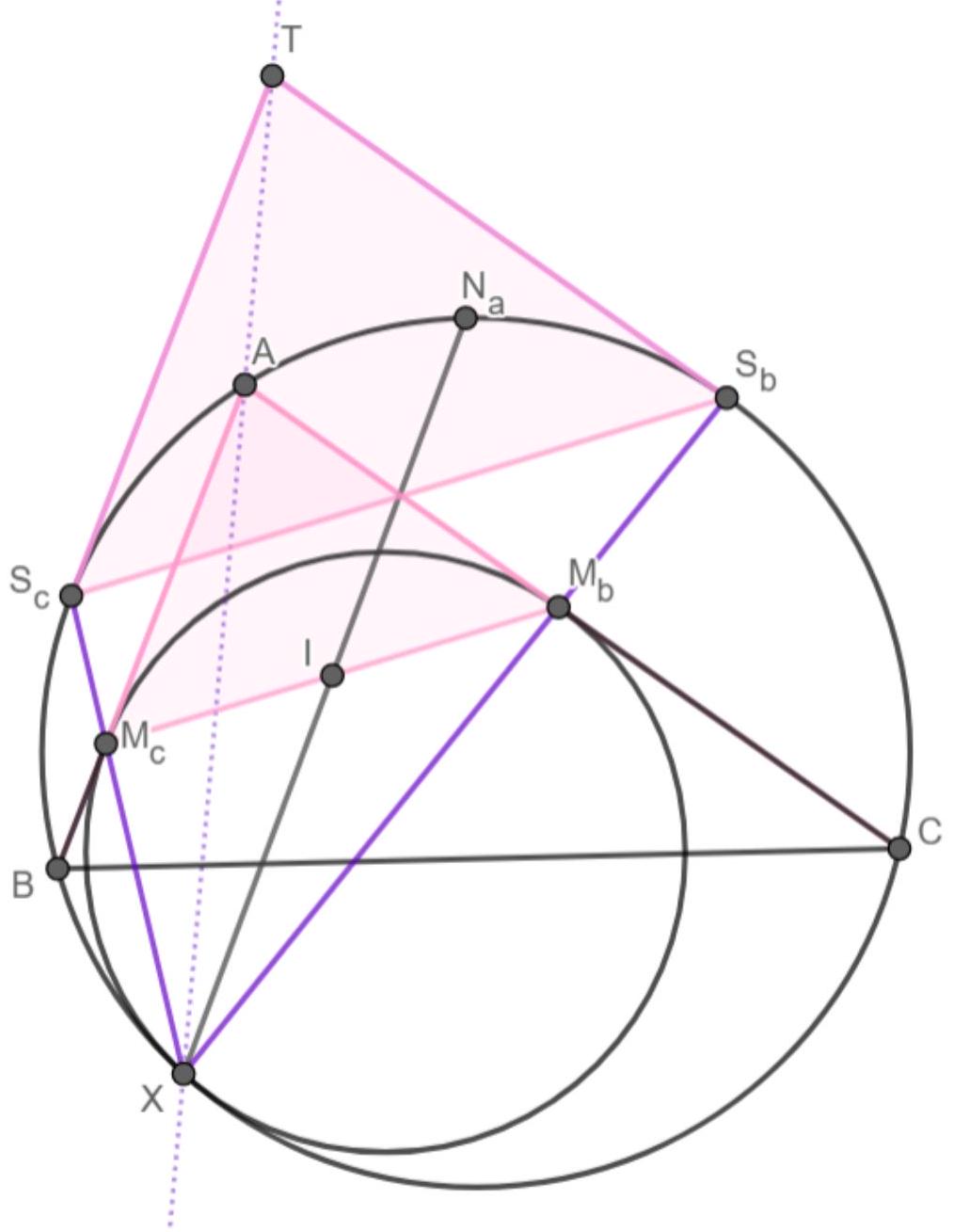
Figure 10: Diagram to Solution 6
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Lemma
Let $P_{b}=A B \cap \omega_{b}$ and $P_{c}=A C \cap \omega_{c}$. We can notice by the lemma that $S_{b}, P_{b}$ and $S_{c}$ are collinear, and similarly $S_{c}, P_{c}$ and $S_{b}$ are also collinear. Therefore $S_{c}, P_{b}, P_{c}$, and $S_{b}$ are collinear, and since $\angle A P_{b} P_{c}=\frac{\angle A B C}{2}+\frac{\angle A C B}{2}=\angle A P_{c} P_{b}$ then $A P_{b}=A P_{c}$ so $A$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $T$ be the intersection of the tangent lines of $\Omega$ through $S_{c}$ and $S_{b}$. Since $T S_{c}=T S_{b}$ then $A T$ is the radical axis between $\omega_{b}$ and $\omega_{c}$.
Part II: $T A$ and $N_{a} I$ intersect in $\Omega$.
Let $\omega_{a}$ the $A$-mixtilinear incircle (that is, the circle internally tangent to $\Omega$, and tangent to both $A B$ and $A C$ ), and let $X=\Omega \cap \omega_{a}$. It is known that $N_{a}, I, X$ are collinear.
Let $M_{c}$ and $M_{b}$ be the tangent points of $\omega_{A}$ to $A B$ and $A C$ respectively, then by the lemma $X, M_{c}, S_{c}$ are collinear and $X, M_{b}, S_{b}$ are collinear. We can see that $S_{c} T S_{b}$ and $M_{c} A M_{b}$ are homothetic with respect to $X$; therefore $T$ and $A$ are homothetic with respect to $X$, impying that $T, A, X$ are collinear.

Figure 10: Diagram to Solution 6
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 6: "
}
|
7c015def-3453-571c-ad78-8134702a0e3c
| 606,120
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
By the alternate segment theorem we have that:
$$
180^{\circ}=\angle D C Y+\angle C Y D+\angle Y D C=\angle D C Y+\angle D X B+\angle Y X D=\angle D C Y+\angle Y X B
$$
Therefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.
One can apply power of a point at $K$ :
$$
K T^{2}=K B \cdot K C=K X \cdot K Y=K D^{2} \Longrightarrow K T=K D .
$$
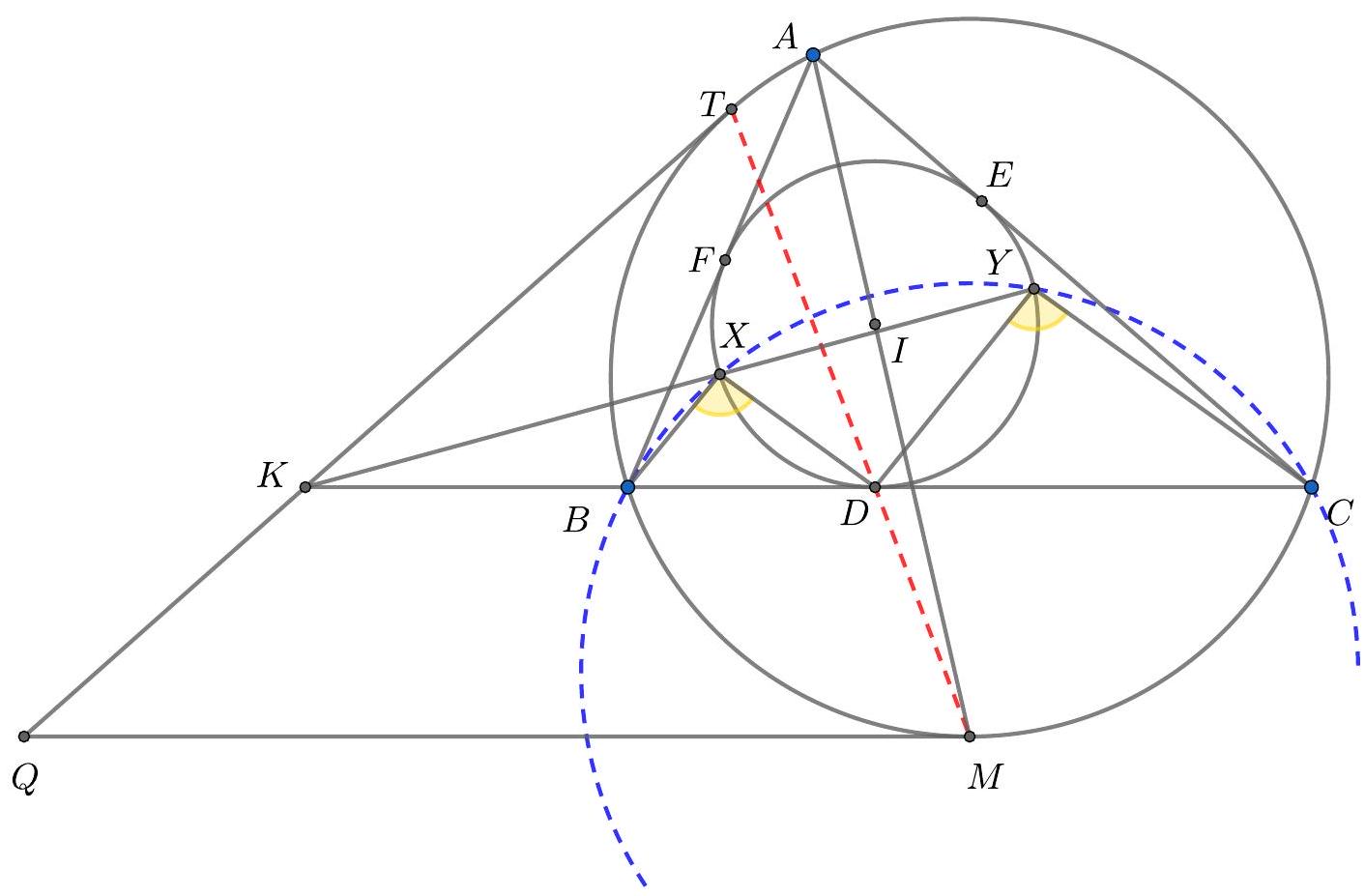
Figure 1: The proposer's solution using a new point $Q$
(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)
Now let $A I$ meet $\Omega$ at $M$, the midpoint of $\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \| K D$ so $\angle T K D=\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\triangle T K D \sim \triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
By the alternate segment theorem we have that:
$$
180^{\circ}=\angle D C Y+\angle C Y D+\angle Y D C=\angle D C Y+\angle D X B+\angle Y X D=\angle D C Y+\angle Y X B
$$
Therefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.
One can apply power of a point at $K$ :
$$
K T^{2}=K B \cdot K C=K X \cdot K Y=K D^{2} \Longrightarrow K T=K D .
$$

Figure 1: The proposer's solution using a new point $Q$
(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)
Now let $A I$ meet $\Omega$ at $M$, the midpoint of $\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \| K D$ so $\angle T K D=\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\triangle T K D \sim \triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\Omega$.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 2 (UNK)\n",
"solution_match": "\nSolution 1. "
}
|
1a6d417e-e4cb-5ee9-82bd-4dbe39d6ef76
| 606,228
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.
You can now work with the simplified diagram shown in Figure 2.
Somehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\angle C T B$ meets $\Omega$ again at $M$.
Triangle $T K D$ is isosceles with apex $K$ so
$$
\angle K D T=\angle D T K=\angle D T B+\angle B T K .
$$
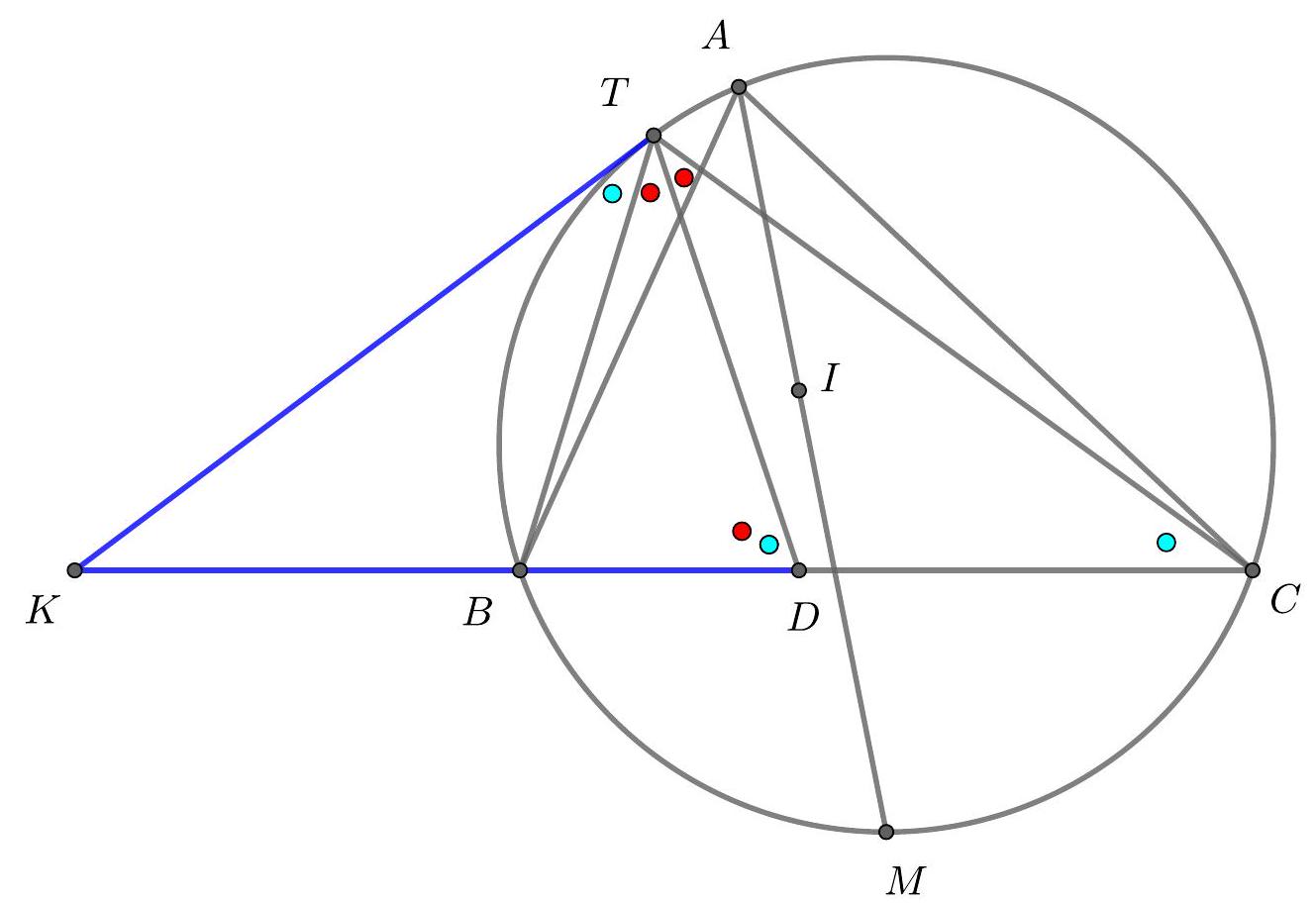
Figure 2: Illustration of an angle chase
By the alternate segment theorem, $\angle B T K=\angle B C T=\angle D C T$. Now angle $\angle K D T$ is an exterior angle of triangle $D C T$ so $\angle C T D=\angle D T B$.
Therefore the line $T D$ is the internal angle bisector of angle $\angle C T B$ and so must pass through $M$, the midpoint of the arc $\widehat{B C}$ of $\Omega$ which does not contain $T$.
Observation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.
You can now work with the simplified diagram shown in Figure 2.
Somehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\angle C T B$ meets $\Omega$ again at $M$.
Triangle $T K D$ is isosceles with apex $K$ so
$$
\angle K D T=\angle D T K=\angle D T B+\angle B T K .
$$

Figure 2: Illustration of an angle chase
By the alternate segment theorem, $\angle B T K=\angle B C T=\angle D C T$. Now angle $\angle K D T$ is an exterior angle of triangle $D C T$ so $\angle C T D=\angle D T B$.
Therefore the line $T D$ is the internal angle bisector of angle $\angle C T B$ and so must pass through $M$, the midpoint of the arc $\widehat{B C}$ of $\Omega$ which does not contain $T$.
Observation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 2 (UNK)\n",
"solution_match": "\nSolution 2. "
}
|
1a6d417e-e4cb-5ee9-82bd-4dbe39d6ef76
| 606,228
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\angle W D U$ and $\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\angle D V K^{\prime}=\angle D U W=\angle W D U=\angle K^{\prime} D V$. Therefore triangle $K^{\prime} D V$ is isosceles with apex $K^{\prime}$.
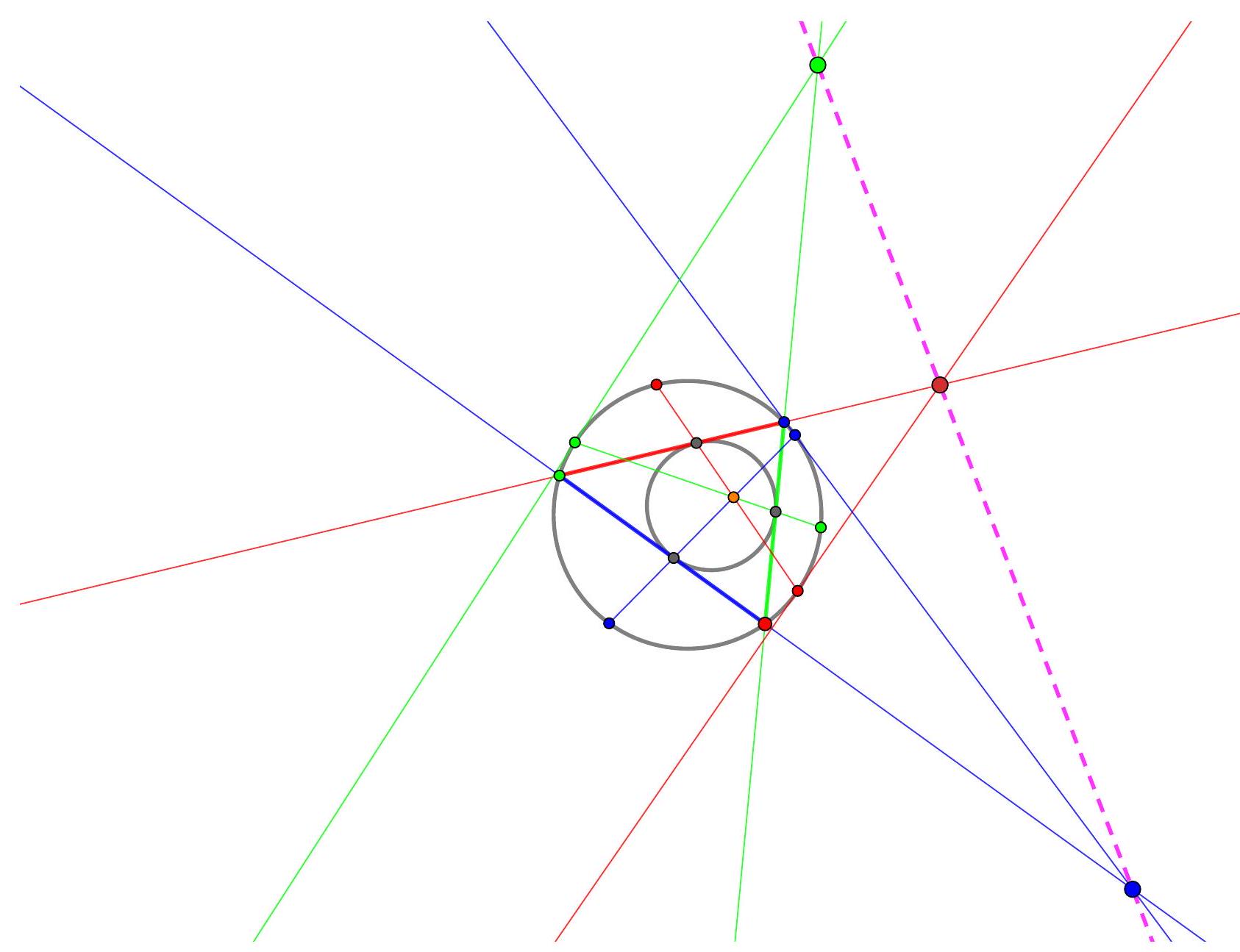
Figure 3: The three points $K$ on the radical axis.
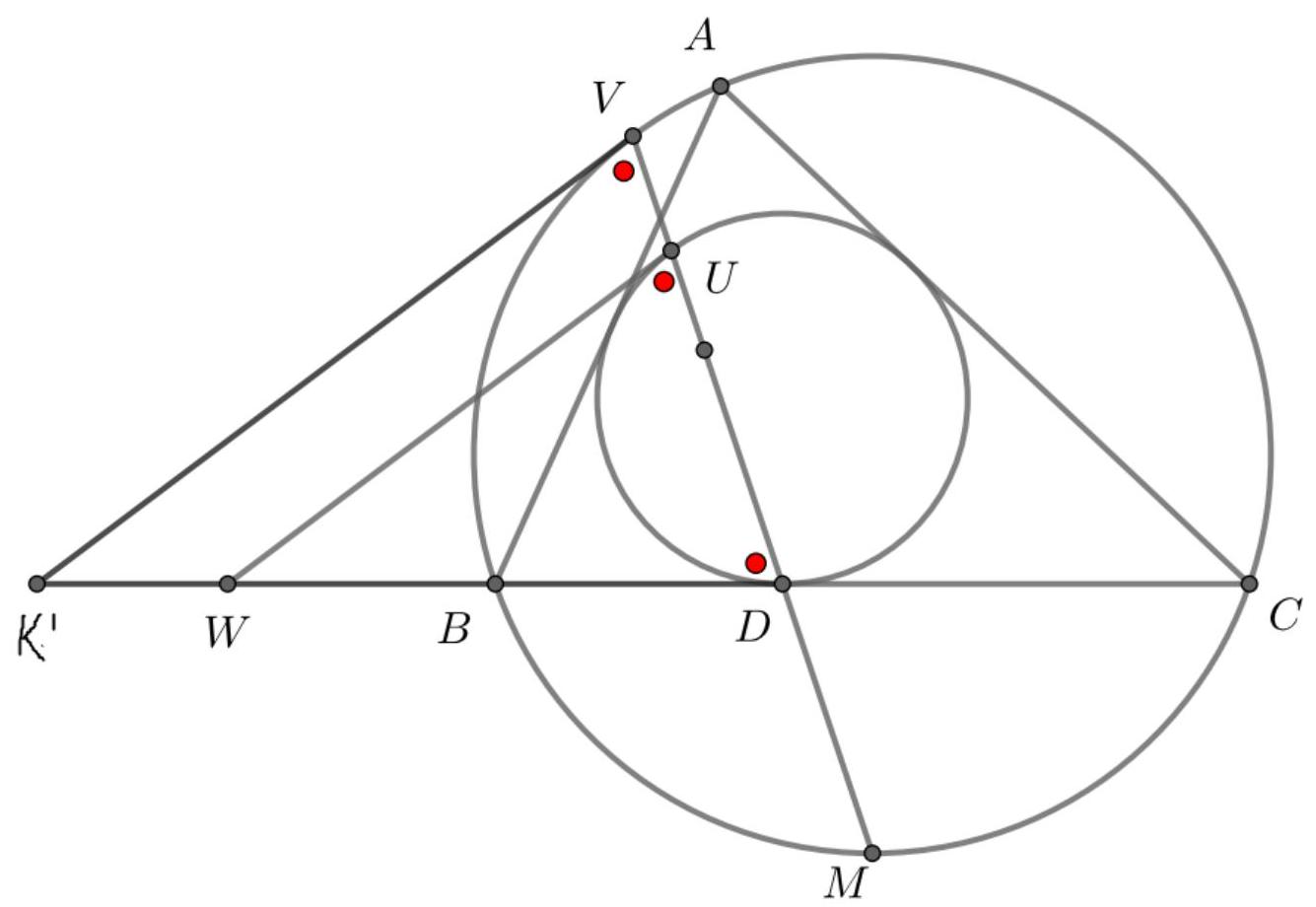
Figure 4: The enlargement of $W$ gives $K^{\prime}$.
This identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\prime}=K$ and $V=T$ and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\angle W D U$ and $\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\angle D V K^{\prime}=\angle D U W=\angle W D U=\angle K^{\prime} D V$. Therefore triangle $K^{\prime} D V$ is isosceles with apex $K^{\prime}$.

Figure 3: The three points $K$ on the radical axis.

Figure 4: The enlargement of $W$ gives $K^{\prime}$.
This identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\prime}=K$ and $V=T$ and the proof is complete.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 2 (UNK)\n",
"solution_match": "\nSolution 3. "
}
|
1a6d417e-e4cb-5ee9-82bd-4dbe39d6ef76
| 606,228
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
Let $\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\phi(X)=Y$. Also $\phi(D)=D$, so $\phi$ maps circle $X B D$ to cicle $Y D B^{\prime}$, where $B^{\prime}:=\phi(B)$ is the point on $B C$ different from $B$ such that $\angle B X D=\angle D Y B^{\prime}$, hence $\phi(B)=C$. From $\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \cdot K C=K T^{2}$ since $K D$ is the radius of inversion.
The rest of the solutions is the same as in the other solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
Let $\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\phi(X)=Y$. Also $\phi(D)=D$, so $\phi$ maps circle $X B D$ to cicle $Y D B^{\prime}$, where $B^{\prime}:=\phi(B)$ is the point on $B C$ different from $B$ such that $\angle B X D=\angle D Y B^{\prime}$, hence $\phi(B)=C$. From $\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \cdot K C=K T^{2}$ since $K D$ is the radius of inversion.
The rest of the solutions is the same as in the other solutions.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 2 (UNK)\n",
"solution_match": "\nSolution 4. "
}
|
1a6d417e-e4cb-5ee9-82bd-4dbe39d6ef76
| 606,228
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Throughout this proof, when we write divisors we mean positive divisors.
Let $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \neq 2$, the pair $(2, p)$ in property 2 gives
$$
\operatorname{gcd}\left(q_{2}, q_{p}\right)=\operatorname{gcd}(f(2), f(p))>f(\operatorname{gcd}(2, p))=f(1)=1
$$
so $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.
Denote by $d(n)$ the number of divisors of a positive integer $n$.
We will prove the following claim by induction on $k \geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.
The claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.
For $k=0$ the claim is already proved.
For $k=1$, we need to prove that $f\left(p^{m}\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\leq m$. As $d\left(p^{t}\right)=t+1$, we then know $f\left(p^{t}\right)=q^{t}$ for all $t \leq m$. Now we consider $t=m+1$.
Let $r \neq p$ be a prime. Plug the pair $\left(p^{m-1} r, p^{m}\right)$ into the second property:
$$
\operatorname{gcd}\left(f\left(p^{m-1} r\right), q^{m}\right)=\operatorname{gcd}\left(f\left(p^{m-1} r\right), f\left(p^{m}\right)\right)>f\left(p^{m-1}\right)=q^{m-1}
$$
This implies $q^{m}$ divides $f\left(p^{m-1} r\right)$. Since $f\left(p^{m-1} r\right)$ has $2 m$ divisors, and $v_{q}\left(f\left(p^{m-1} r\right)\right) \geq m$, it follows that $f\left(p^{m-1} r\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \cdot\left(v_{q}\left(f\left(p^{m-1} r\right)\right)+1\right)>2 m$ divisors. Thus, $f\left(p^{m-1} r\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\left(p^{m-1} r\right)=q^{2 m-1}$.
Now, plug the pair $\left(p^{m+1}, p^{m-1} r\right)$ into the second property. We have
$$
\operatorname{gcd}\left(f\left(p^{m+1}\right), q^{2 m-1}\right)=\operatorname{gcd}\left(f\left(p^{m+1}\right), f\left(p^{m-1} r\right)\right)>f\left(p^{m-1}\right)=q^{m-1} .
$$
Then $f\left(p^{m+1}\right)$ is divisible by $q^{m}$. If $f\left(p^{m+1}\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \geq 1$. Hence, $f\left(p^{m+1}\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.
Suppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices
to show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\left(N p^{m}\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \geq 0$.
Let $s$ be a prime divisor of $N$. Consider the numbers $\left(N p^{m+1}, N s p^{m}\right)$. By the second property,
$$
\operatorname{gcd}\left(f\left(N p^{m+1}\right), q^{d\left(N s p^{m}\right)-1}\right)=\operatorname{gcd}\left(f\left(N p^{m+1}\right), f\left(N s p^{m}\right)\right)>f\left(N p^{m}\right)=q^{d\left(N p^{m}\right)-1}
$$
Then $q^{d\left(N p^{m}\right)}$ divides $f\left(N p^{m+1}\right)$. If $f\left(N p^{m+1}\right)$ has a prime factor other than $q$, it would have at least $2\left(d\left(N p^{m}\right)+1\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\left(N p^{m+1}\right)$ must also be a power of $q$.
Finally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that
$$
\operatorname{gcd}(f(x), f(y))=q^{\min (d(x), d(y))}>q^{d(\operatorname{gcd}(x, y))}=f(\operatorname{gcd}(x, y))
$$
whenever $x \nmid y$ and $y \nmid x$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Throughout this proof, when we write divisors we mean positive divisors.
Let $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \neq 2$, the pair $(2, p)$ in property 2 gives
$$
\operatorname{gcd}\left(q_{2}, q_{p}\right)=\operatorname{gcd}(f(2), f(p))>f(\operatorname{gcd}(2, p))=f(1)=1
$$
so $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.
Denote by $d(n)$ the number of divisors of a positive integer $n$.
We will prove the following claim by induction on $k \geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.
The claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.
For $k=0$ the claim is already proved.
For $k=1$, we need to prove that $f\left(p^{m}\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\leq m$. As $d\left(p^{t}\right)=t+1$, we then know $f\left(p^{t}\right)=q^{t}$ for all $t \leq m$. Now we consider $t=m+1$.
Let $r \neq p$ be a prime. Plug the pair $\left(p^{m-1} r, p^{m}\right)$ into the second property:
$$
\operatorname{gcd}\left(f\left(p^{m-1} r\right), q^{m}\right)=\operatorname{gcd}\left(f\left(p^{m-1} r\right), f\left(p^{m}\right)\right)>f\left(p^{m-1}\right)=q^{m-1}
$$
This implies $q^{m}$ divides $f\left(p^{m-1} r\right)$. Since $f\left(p^{m-1} r\right)$ has $2 m$ divisors, and $v_{q}\left(f\left(p^{m-1} r\right)\right) \geq m$, it follows that $f\left(p^{m-1} r\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \cdot\left(v_{q}\left(f\left(p^{m-1} r\right)\right)+1\right)>2 m$ divisors. Thus, $f\left(p^{m-1} r\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\left(p^{m-1} r\right)=q^{2 m-1}$.
Now, plug the pair $\left(p^{m+1}, p^{m-1} r\right)$ into the second property. We have
$$
\operatorname{gcd}\left(f\left(p^{m+1}\right), q^{2 m-1}\right)=\operatorname{gcd}\left(f\left(p^{m+1}\right), f\left(p^{m-1} r\right)\right)>f\left(p^{m-1}\right)=q^{m-1} .
$$
Then $f\left(p^{m+1}\right)$ is divisible by $q^{m}$. If $f\left(p^{m+1}\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \geq 1$. Hence, $f\left(p^{m+1}\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.
Suppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices
to show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\left(N p^{m}\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \geq 0$.
Let $s$ be a prime divisor of $N$. Consider the numbers $\left(N p^{m+1}, N s p^{m}\right)$. By the second property,
$$
\operatorname{gcd}\left(f\left(N p^{m+1}\right), q^{d\left(N s p^{m}\right)-1}\right)=\operatorname{gcd}\left(f\left(N p^{m+1}\right), f\left(N s p^{m}\right)\right)>f\left(N p^{m}\right)=q^{d\left(N p^{m}\right)-1}
$$
Then $q^{d\left(N p^{m}\right)}$ divides $f\left(N p^{m+1}\right)$. If $f\left(N p^{m+1}\right)$ has a prime factor other than $q$, it would have at least $2\left(d\left(N p^{m}\right)+1\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\left(N p^{m+1}\right)$ must also be a power of $q$.
Finally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that
$$
\operatorname{gcd}(f(x), f(y))=q^{\min (d(x), d(y))}>q^{d(\operatorname{gcd}(x, y))}=f(\operatorname{gcd}(x, y))
$$
whenever $x \nmid y$ and $y \nmid x$.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 5 (HRV)\n",
"solution_match": "\nSolution 1. "
}
|
2a98f965-d9c5-5642-9d91-d951d57548bc
| 606,266
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Firstly, one can prove that for any prime $p$ and any $m \geq 0, f\left(p^{m}\right)=q^{m}$, in the same way as in the first solution.
We will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.
The cases $k=1,2,3$ are then already proved. Now suppose that for some $k \geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.
Consider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \leq v_{p_{2}}(n)$. Consider the number $\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\frac{v_{p_{1}}(n)\left(v_{p_{2}}(n)+2\right)}{\left(v_{p_{1}}(n)+1\right)\left(v_{p_{2}}(n)+1\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\left(\frac{n p_{2}}{p_{1}}\right)$ is a power of $q$.
By applying the second property to the pair $\left(n, \frac{n p_{2}}{p_{1}}\right)$, we have
$$
\operatorname{gcd}\left(f(n), q^{d\left(\frac{n p_{2}}{p_{1}}\right)-1}\right)=\operatorname{gcd}\left(f(n), f\left(\frac{n p_{2}}{p_{1}}\right)\right)>f\left(\frac{n}{p_{1}}\right)=q^{d\left(\frac{n}{p_{1}}\right)-1}
$$
This implies that $q^{d\left(\frac{n}{p_{1}}\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)$ divisors. But $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)=2\left(\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.
We finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Firstly, one can prove that for any prime $p$ and any $m \geq 0, f\left(p^{m}\right)=q^{m}$, in the same way as in the first solution.
We will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.
The cases $k=1,2,3$ are then already proved. Now suppose that for some $k \geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.
Consider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \leq v_{p_{2}}(n)$. Consider the number $\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\frac{v_{p_{1}}(n)\left(v_{p_{2}}(n)+2\right)}{\left(v_{p_{1}}(n)+1\right)\left(v_{p_{2}}(n)+1\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\left(\frac{n p_{2}}{p_{1}}\right)$ is a power of $q$.
By applying the second property to the pair $\left(n, \frac{n p_{2}}{p_{1}}\right)$, we have
$$
\operatorname{gcd}\left(f(n), q^{d\left(\frac{n p_{2}}{p_{1}}\right)-1}\right)=\operatorname{gcd}\left(f(n), f\left(\frac{n p_{2}}{p_{1}}\right)\right)>f\left(\frac{n}{p_{1}}\right)=q^{d\left(\frac{n}{p_{1}}\right)-1}
$$
This implies that $q^{d\left(\frac{n}{p_{1}}\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)$ divisors. But $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)=2\left(\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.
We finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 5 (HRV)\n",
"solution_match": "\nSolution 2. "
}
|
2a98f965-d9c5-5642-9d91-d951d57548bc
| 606,266
|
Let $ABC$ be a triangle and $\mathrm{H}_{\mathrm{C}}$ the foot of the altitude from $C$. Let $P$ be a point on the segment $\left[\mathrm{CH}_{C}\right]$ (other than $C$), and let $E, F, G, H$ be the midpoints of $[AP],[BP],[BC],[AC]$, respectively. Show that $EFGH$ is a rectangle.
|
To prove that EFGH is a rectangle, we will show that it is a parallelogram that has a right angle.
Consider the triangle $ACP$. The points E and H are the midpoints of the sides $[AP]$ and $[AC]$, respectively. By the Midline Theorem, (HE) // (PC).
Consider the triangle BCP. The points F and G are the midpoints of the sides [BP] and [BC], respectively. By the Midline Theorem, (FG) // (PC).
We have shown that the lines (FG) and (HE) are both parallel to the line (PC). It follows that (FG) // (HE).
Consider the triangle $ABP$. The points E and F are the midpoints of the sides [AP] and [BP], respectively. By the Midline Theorem, (EF) // (AB).
Consider the triangle $ABC$. The points H and G are the midpoints of the sides [AC] and [BC], respectively. By the Midline Theorem, (HG) // (AB).
We have shown that the lines (EF) and (HG) are both parallel to the line (AB). It follows that (HG) // (EF).
Therefore, EFGH is a quadrilateral whose opposite sides are parallel. It follows that it is a parallelogram.
Furthermore, since $\left(\mathrm{CH}_{c}\right) \perp(\mathrm{AB})$ and $(EF) //(\mathrm{AB})$, we have $(EF) \perp\left(\mathrm{CH}_{c}\right)$.
Moreover, $\left(\mathrm{CH}_{\mathrm{c}}\right) //(\mathrm{EH})$. It follows that $(\mathrm{EH}) \perp(\mathrm{EF})$.
The parallelogram EFGH therefore has a right angle, which proves that EFGH is a rectangle.
Remark. Another way to prove that EFGH is a parallelogram is to use the fact that, according to the Midline Theorem, $(\mathrm{EH}) //(\mathrm{CP}) //(\mathrm{FG})$ and $\mathrm{EH}=\frac{1}{2} \mathrm{CP}=\mathrm{FG}$. Therefore, EFGH has two opposite sides that are parallel and of the same length, so it is a parallelogram.
Comment from the graders: The exercise was very well done overall. However, many students could have been faster by using the parallel and perpendicular lines in the figure without chasing angles. Additionally, several students lost points because they did not justify why they could apply Thales' theorem or why the quadrilateral EFGH had a right angle...
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et $\mathrm{H}_{\mathrm{C}}$ le pied de la hauteur issue de C . Soit P un point sur le segment $\left[\mathrm{CH}_{C}\right]$ (autre que $C$ ), et soient $E, F, G, H$ les milieux respectifs de $[A P],[B P],[B C],[A C]$. Montrer que EFGH est un rectangle.
|
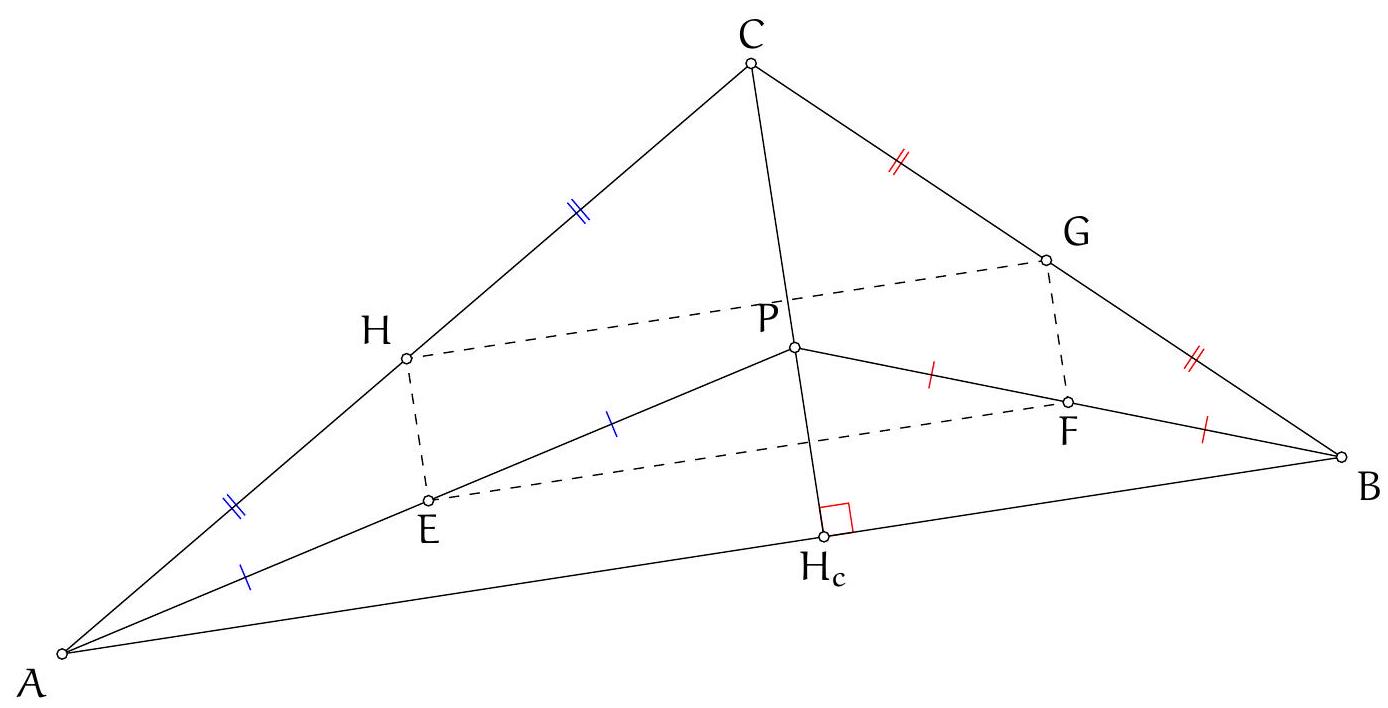
Pour démontrer que EFGH est un rectangle, nous allons montrer que c'est un parallélogramme qui possède un angle droit.
Considérons le triangle $A C P$. Les points E et H sont les milieux respectifs des côtés $[A P]$ et $[A C]$. Par le théorème de la droite des milieux, (HE) // (PC).
Considérons le triangle BCP. Les points F et G sont les milieux respectifs des côtés [BP] et [BC]. Par le théorème de la droite des milieux, (FG) // (PC).
On a montré que les droites (FG) et ( HE ) sont toutes les deux parallèles à la droite (PC). Il s'ensuit que (FG) // (HE).
Considérons le triangle $A B P$. Les points $E$ et $F$ sont les milieux respectifs des côtés [AP] et [BP]. Par le théorème de la droite des milieux, ( $E F$ ) // ( $A B$ ).
Considérons le triangle $A B C$. Les points H et G sont les milieux respectifs des côtés [AC] et [BC]. Par le théorème de la droite des milieux, (HG) // (AB).
On a montré que les droites (EF) et (HG) sont toutes les deux parallèles à la droite ( $A B$ ). Il s'ensuit que (HG) // (EF).
Par conséquent, EFGH est un quadrilatère dont les côtés opposés sont parallèles deux à deux. Il s'ensuit que c'est un parallélogramme.
Par ailleurs, comme $\left(\mathrm{CH}_{c}\right) \perp(\mathrm{AB})$ et $(E F) / /(\mathrm{AB})$, on a $(E F) \perp\left(\mathrm{CH}_{c}\right)$.
De plus, $\left(\mathrm{CH}_{\mathrm{c}}\right) / /(\mathrm{EH})$. Il s'ensuit que $(\mathrm{EH}) \perp(\mathrm{EF})$.
Le parallélogramme EFGH possède donc un angle droit, ce qui démontrer que EFGH est un rectangle.
Remarque. Une autre façon de prouver que EFGH est un parallélogramme est d'utiliser que d'après le théorème de la droite des milieux, $(\mathrm{EH}) / /(\mathrm{CP}) / /(\mathrm{FG})$ et $\mathrm{EH}=\frac{1}{2} \mathrm{CP}=\mathrm{FG}$. Donc EFGH possède deux côtés opposés parallèles et de même longueur, c'est donc un parallélogramme.
Commentaire des correcteurs: L'exercice a été très bien réussi dans l'ensemble. Cependant pas mal d'élèves pourraient aller plus vite en utilisant les droites parallèles et perpendiculaires de la figure sans faire de chasse aux angles. Deplus, plusieurs élèves ont perdu des points car ils n'ont pas justifié pourquoi ils pouvaient appliquer le théorème de Thalès ou pourquoi le quadrilatère EFGH avait un angle droit...
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
c88c13bd-9393-5ae6-85cf-d1c7d4fefe6b
| 607,124
|
Let $ABC$ be an acute triangle (all angles are acute) with $BA \neq BC$. Let $O$ be the center of its circumcircle. The line $(AB)$ intersects the circumcircle of $BOC$ a second time at $P \neq B$. Show that $PA = PC$.
|
Let's draw the figure in the case where $BC < BA$, the case $BC > BA$ being completely analogous. It is a matter of showing that $\mathrm{PA} = \mathrm{PC}$, that is, $\widehat{ACP} = \widehat{\mathrm{PAC}} (=\widehat{\mathrm{BAC}})$. Now we have:
$$
\begin{aligned}
\widehat{ACP} & = \widehat{ACO} + \widehat{OCP} \\
& = \widehat{ACO} + \widehat{OBP} \text{ by inscribed angle } \\
& = \widehat{ACO} + \widehat{OBA}
\end{aligned}
$$
Now, $AOC$ is isosceles at O, so $\widehat{ACO} = \widehat{\mathrm{OAC}} = \frac{180^{\circ} - \widehat{COA}}{2} = 90^{\circ} - \widehat{\mathrm{CBA}}$ by central angle. Similarly, $\widehat{OBA} = 90^{\circ} - \widehat{ACB}$. Finally, $\widehat{ACP} = 180^{\circ} - \widehat{ACB} - \widehat{CBA} = \widehat{BAC} = \widehat{PAC}$, hence $PA = PC$, as desired.
Comment from the graders: The exercise was very well done and widely approached, some solutions are particularly efficient in their angle chasing.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
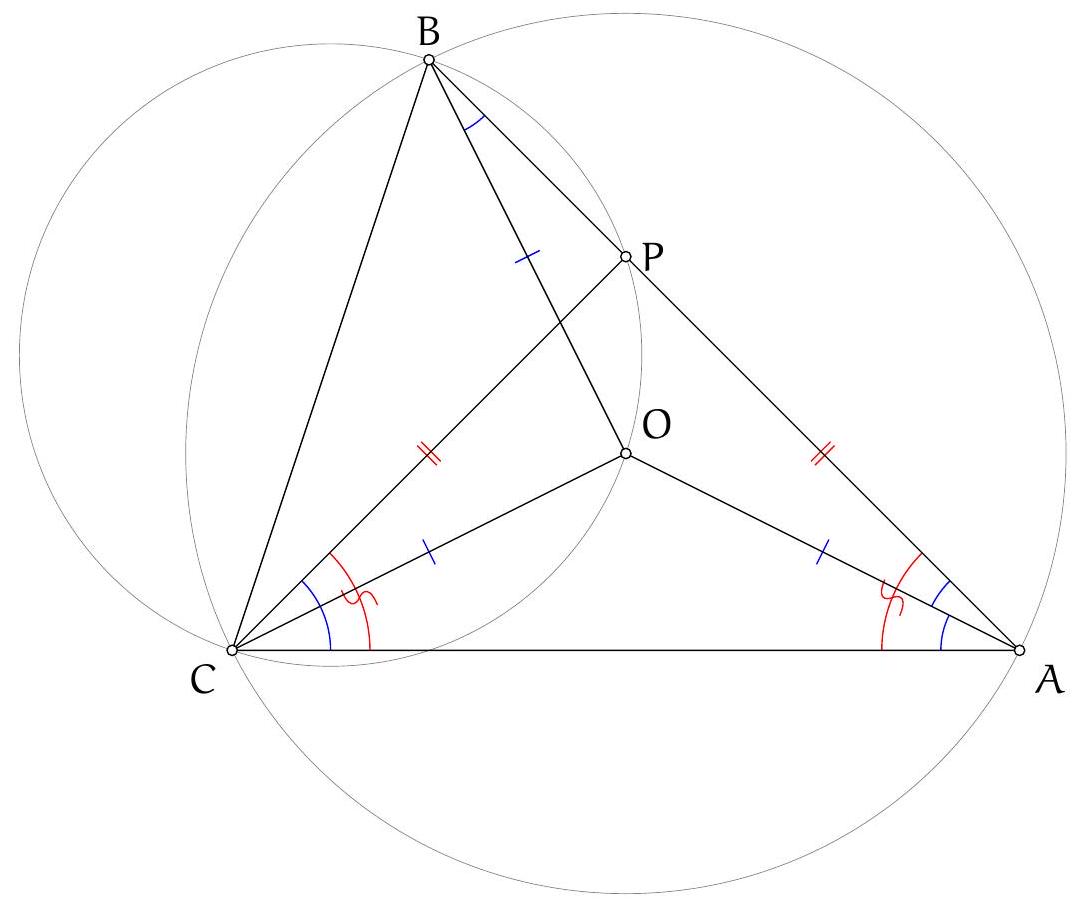
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a:
$$
\begin{aligned}
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
& =\widehat{A C O}+\widehat{O B A}
\end{aligned}
$$
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{\mathrm{OAC}}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{\mathrm{CBA}}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
Commentaire des correcteurs : L'exercice a été très bien réussi et beaucoup abordé, certaines solutions sont particulièrement efficaces dans leurs chasses aux angles.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
a633d352-4e78-58ca-98b6-e4a65bbd2dee
| 607,125
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
We notice that the circle with diameter [CD] appears quite naturally. Indeed, we have right angles $\widehat{\mathrm{DB}} \widehat{ } \mathrm{C}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, so the points $\mathrm{B}, \mathrm{B}^{\prime}$, and $E$ lie on the circle with diameter [DC], in other words, $C, B, D, E, B^{\prime}$ are concyclic.
Then we have:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =45^{\circ} \text { since } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ}
\end{aligned}
$$
Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { by inscribed angle } \\
& =45^{\circ} \text { since } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Therefore, we have $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, so (EC) is the bisector of $\widehat{\mathrm{BEB}^{\prime}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de $B$ par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
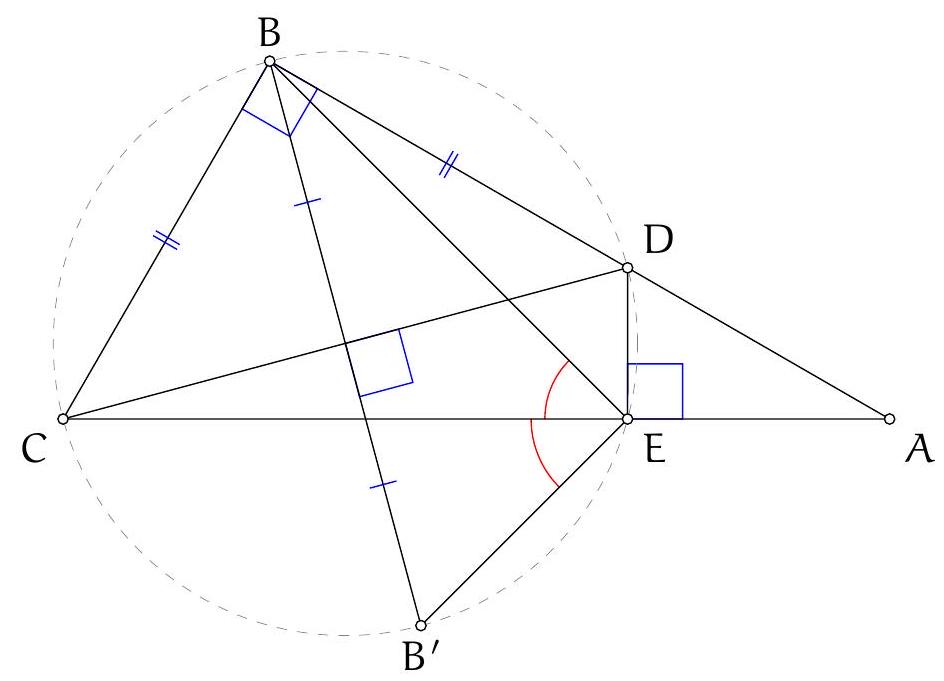
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}} \widehat{ } \mathrm{C}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $C, B, D, E, B^{\prime}$ sont cocycliques.
Alors on a :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ}
\end{aligned}
$$
De plus:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
a93eec4b-a3f5-54c1-b06d-6da1c030e9aa
| 607,126
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
We could also show directly $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ without using $\mathrm{BC}=\mathrm{BD}$. Indeed:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { by symmetry } \\
& =\widehat{\mathrm{CEB}} \text { by inscribed angle. }
\end{aligned}
$$
Graders' comment: The exercise was generally very well done. The most frequent error concerned the conditions for a quadrilateral to be a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de $B$ par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
\end{aligned}
$$
Commentaire des correcteurs : L'exercice est globalement très bien réussi. L'erreur la plus fréquente portait sur les conditions pour qu'un quadrilatère soit un carré.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution alternative"
}
|
a93eec4b-a3f5-54c1-b06d-6da1c030e9aa
| 607,126
|
Let $ABC$ be a triangle and $I$ the center of its inscribed circle. The perpendicular bisector of $[\mathrm{BC}]$ intersects $(A \mathrm{I})$ at $S$ and $(BI)$ at $T$. Show that $C, I, S$ and $T$ are concyclic.
|
To show that $C, I, S$, and $T$ are concyclic, we will show that $\widehat{\text{SIC}} = \widehat{\text{STC}}$.
We recall that the internal angle bisectors of a triangle $ABC$ are concurrent, and their point of intersection $I$ is the center of the inscribed circle of the triangle. Therefore, $(AI)$ is the angle bisector of $\widehat{BAC}$.
Consequently, $S$ is defined as the intersection of the perpendicular bisector of $[BC]$ and the angle bisector of $\widehat{BAC}$. The South Pole theorem ensures that $S$ lies on the circumcircle of triangle $ABC$ and that $S$ is the center of the Antarctic circle of vertex $A$, which ensures that
$$
\mathrm{SB} = \mathrm{SI}
$$
We see that triangle $SBI$ is isosceles at $S$, which ensures that $\widehat{\mathrm{SBI}} = \widehat{\mathrm{BIS}}$.
Furthermore, the points $A, B, S$, and $C$ are concyclic. Therefore,
$$
\widehat{SBC} = \widehat{SAC} = \frac{\widehat{BAC}}{2}.
$$
Now let's calculate the value of the angle $\widehat{\text{SIC}}$. We have
$$
\begin{aligned}
\widehat{SIC} & = \widehat{\mathrm{BIC}} - \widehat{\mathrm{BIS}} \\
& = \widehat{\mathrm{BIC}} - \widehat{\mathrm{SBC}} - \widehat{\mathrm{CBI}} \\
& = \widehat{\mathrm{BIC}} - \frac{\widehat{\mathrm{BAC}}}{2} - \frac{\widehat{\mathrm{CBA}}}{2}.
\end{aligned}
$$
Furthermore,
$$
\begin{aligned}
\widehat{\mathrm{BIC}} & = 180^{\circ} - \widehat{\mathrm{CBI}} - \widehat{\mathrm{ICB}} \\
& = 180^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2} - \frac{\widehat{ACB}}{2} \\
& = 180^{\circ} - \frac{\widehat{\mathrm{CBA}} + \widehat{ACB}}{2} \\
& = 180^{\circ} - \frac{180^{\circ} - \widehat{\mathrm{BAC}}}{2} \\
& = 90^{\circ} + \frac{\widehat{\mathrm{BAC}}}{2}.
\end{aligned}
$$
It follows that $\widehat{\text{SIC}} = 90^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2}$.
Furthermore,
$$
\begin{aligned}
\widehat{\mathrm{STC}} & = 90^{\circ} - \widehat{\mathrm{TCB}} \\
& = 90^{\circ} - \widehat{\mathrm{CBI}} \quad \text{Triangle } \mathrm{BCT} \text{ is isosceles at } \mathrm{T} \\
& = 90^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2}.
\end{aligned}
$$
We have thus shown that $\widehat{\text{SIC}} = \widehat{\text{STC}}$, which ensures that the points $C, I, S$, and $T$ are concyclic by the converse of the inscribed angle theorem.
Comment from the graders: The exercise is very well done. Many students engaged in a cumbersome angle chase, while the South Pole theorem greatly simplified the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et I le centre de son cercle inscrit. La médiatrice de $[\mathrm{BC}]$ coupe ( $A \mathrm{I}$ ) en $S$ et (BI) et $T$. Montrer que $C, I, S$ et $T$ sont cocycliques.
|
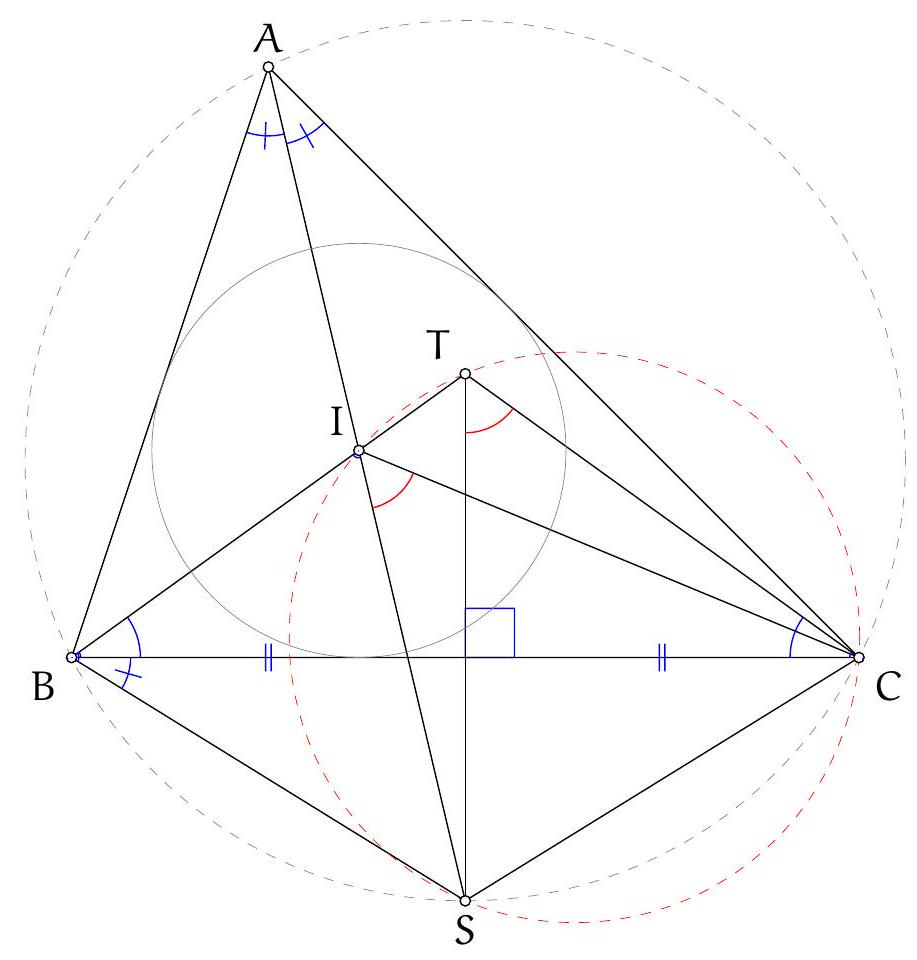
Pour montrer que $C, I, S$ et $T$ sont cocycliques, nous allons montrer que $\widehat{\text { SIC }}=\widehat{\text { STC }}$.
On rappelle que les bissectrices intérieures d'un triangle $A B C$ sont concourantes et que leur point d'intersection I est le centre du cercle inscrit dans le triangle. (AI) est donc la bissectrice de l'angle $\widehat{B A C}$.
Par conséquent, $S$ est défini comme le point d'intersection de la médiatrice de $[\mathrm{BC}]$ et de la bissectrice de l'angle $\widehat{B A C}$. Le théorème du Pôle Sud assure que $S$ appartient au cercle circonscrit au triangle $A B C$ et que $S$ est le centre du cercle antarctique du sommet $A$, ce qui assure que
$$
\mathrm{SB}=\mathrm{SI}
$$
On voit donc que triangle SBI est isocèle en S ce qui assure que $\widehat{\mathrm{SBI}}=\widehat{\mathrm{BIS}}$.
Par ailleurs les points $A, B, S$ et $C$ sont cocycliques. On a donc
$$
\widehat{S B C}=\widehat{S A C}=\frac{\widehat{B A C}}{2} .
$$
Calculons désormais la valeur de l'angle $\widehat{\text { SIC }}$. On a
$$
\begin{aligned}
\widehat{S I C} & =\widehat{\mathrm{BIC}}-\widehat{\mathrm{BIS}} \\
& =\widehat{\mathrm{BIC}}-\widehat{\mathrm{SBC}}-\widehat{\mathrm{CBI}} \\
& =\widehat{\mathrm{BIC}}-\frac{\widehat{\mathrm{BAC}}}{2}-\frac{\widehat{\mathrm{CBA}}}{2} .
\end{aligned}
$$
Par ailleurs,
$$
\begin{aligned}
\widehat{\mathrm{BIC}} & =180^{\circ}-\widehat{\mathrm{CBI}}-\widehat{\mathrm{ICB}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}-\frac{\widehat{A C B}}{2} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{A C B}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{BAC}}}{2} \\
& =90^{\circ}+\frac{\widehat{\mathrm{BAC}}}{2} .
\end{aligned}
$$
Il s'ensuit que $\widehat{\text { SIC }}=90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}$.
Par ailleurs
$$
\begin{aligned}
\widehat{\mathrm{STC}} & =90^{\circ}-\widehat{\mathrm{TCB}} \\
& =90-\widehat{\mathrm{CBI}} \quad \text { Le triangle } \mathrm{BCT} \text { est isocèle en } \mathrm{T} \\
& =90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2} .
\end{aligned}
$$
On a donc montré que $\widehat{\text { SIC }}=\widehat{\text { STC }}$ ce qui assure que les points $C, I, S$ et $T$ sont cocycliques par la réciproque du théorème de l'angle inscrit.
Commentaire des correcteurs: L'exercice est très bien réussi. Beaucoup d'élèves ont procédé à une lourde chasse aux angles alors que le théorème du Pôle Sud simplifiait grandement la résolution du problème.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
549b88f2-3fe0-5edf-b8f8-1141271941f7
| 607,127
|
Let $A B C D E$ be a convex cyclic pentagon such that $A B=B D$. Let $P$ be the intersection point of the lines (EB) and ( $A C$ ). Let $Q$ be the intersection point of the lines ( $B C$ ) and ( $D E$ ). Show that $(\mathrm{PQ})$ and (AD) are parallel.
|
In the figure, it seems that EPCQ is a cyclic quadrilateral. We show this:
\[
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { by inscribed angle } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \text{ since } \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}}.
\end{aligned}
\]
Thus, we have shown that \(\widehat{\mathrm{QCP}}+\widehat{\mathrm{PEQ}}=180^{\circ}\). Therefore, by the converse of the inscribed angle theorem, EPCQ is cyclic, which is what we wanted to prove.
Now, to show that (AD) and (PQ) are parallel, we will try to find corresponding angles. We have:
\[
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { by inscribed angle. }
\end{aligned}
\]
Since \(\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}\) and \(\mathrm{Q}, \mathrm{D}, \mathrm{E}\) are collinear (in that order), by corresponding angles, the lines (PQ) and (AD) are indeed parallel.
Comment from the graders: The exercise was well handled by those who approached it. Almost all students thought to translate the equality of lengths into an equality of angles, which was the right starting point to then chase angles. Then, it was necessary to observe that the quadrilateral EPCQ is cyclic to continue, which blocked some. Some who did not see this managed to get through with a more cumbersome angle chase, while others managed to apply Thales' theorem by introducing a new point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
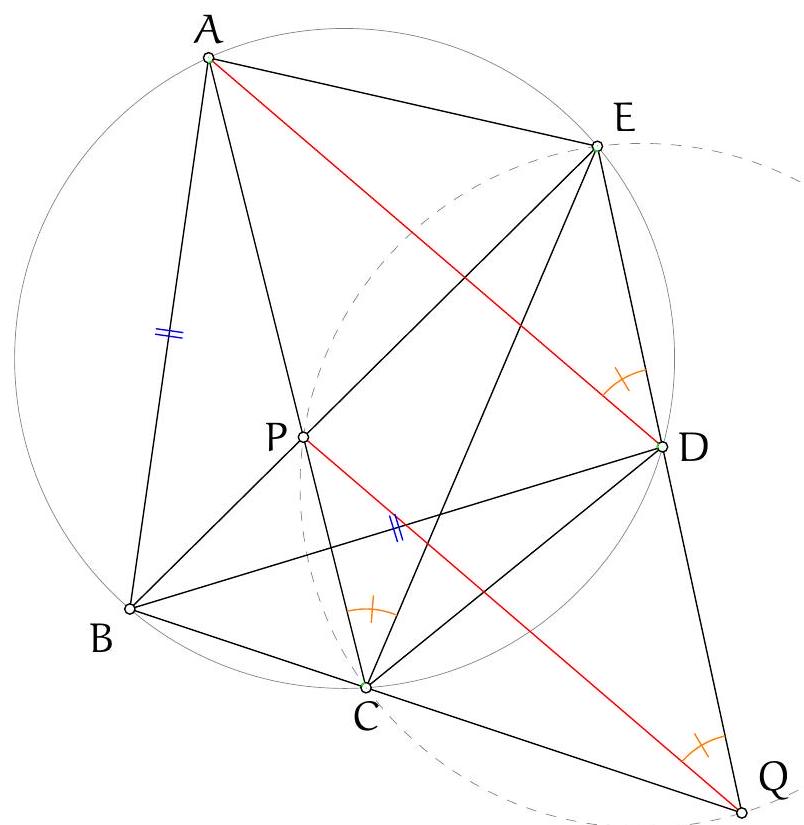
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
$$
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
\end{aligned}
$$
Ainsi on a montré que $\widehat{\mathrm{QCP}}+\widehat{\mathrm{PEQ}}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
$$
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
\end{aligned}
$$
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
Commentaire des correcteurs : L'exercice a été bien traité par les personnes qui l'ont abordé. Quasiment tous les élèves ont pensé à traduire l'égalité de longueur en égalité d'angle, ce qui était le bon point de départ pour pouvoir ensuite faire une chasse aux angles. Ensuite, il fallait observer que le quadrilatère
EPCQ est cyclique pour continuer, ce qui en a bloqué certains. Certains qui n'ont pas vu cela ont réussi à s'en sortir avec une chasse aux angles plus lourde, d'autres ont réussi à appliquer le théorème de Thalès en introduisant un nouveau point.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
4203c2ee-bef3-5136-ac44-21a58d19c66e
| 607,128
|
Let $ABC$ be an isosceles triangle at $A$, $O$ the center of its circumcircle, and $I$ the center of its incircle. The parallel to ($AB$) passing through $I$ intersects ($AC$) at $D$. Show that ($CI$) and ($DO$) are perpendicular.
|
Firstly, since $AB = AC$, $A, O, I$ are collinear, and line $(AI)$ intersects $[BC]$ at its midpoint $M$. We denote $P$ as the intersection of lines $(DO)$ and $(CI)$.
By angle chasing, we show that $I, O, D, C$ are concyclic by showing that $\widehat{\mathrm{IOC}} = \widehat{\mathrm{IDC}}$. Indeed:
\[
\begin{aligned}
\widehat{\mathrm{IOC}} & = \widehat{\mathrm{MOC}} \\
& = \frac{1}{2} \widehat{\mathrm{BOC}} \text{ because } OB = OC \\
& = \widehat{\mathrm{BAC}} \text{ by the inscribed angle theorem} \\
& = \widehat{\mathrm{IDC}} \text{ because } (BA) \parallel (ID)
\end{aligned}
\]
Therefore, by the converse of the inscribed angle theorem, $I, O, D, C$ are concyclic.
Now, let's show that $\widehat{CPD} = 90^\circ$. To do this, we will show that $\widehat{PDC} + \widehat{DCP} = 90^\circ$ (since $\widehat{\mathrm{CPD}} = 180^\circ - \widehat{\mathrm{PDC}} - \widehat{\mathrm{DCP}}$). We have:
\[
\begin{aligned}
\widehat{\mathrm{PDC}} + \widehat{\mathrm{DCP}} & = \widehat{\mathrm{ODC}} + \widehat{\mathrm{DCI}} \\
& = \left(180^\circ - \widehat{\mathrm{CIO}}\right) + \widehat{\mathrm{ICB}} \text{ by concyclicity and angle bisector} \\
& = \widehat{\mathrm{CIM}} + \widehat{\mathrm{ICM}} \\
& = 90^\circ \text{ because } (AI) \perp (BC).
\end{aligned}
\]
Thus, $\widehat{\mathrm{CPD}} = 90^\circ$, which proves that lines $(CI)$ and $(DO)$ are perpendicular.
Comment from the graders: The exercise was generally well done. Most of the submitted solutions contained a correct solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle isocèle en $A$, $O$ le centre de son cercle circonscrit et $I$ le centre de son cercle inscrit. La parallèle à ( $A B$ ) passant par I coupe (AC) en D. Montrer que (CI) et (DO) sont perpendiculaires.
|
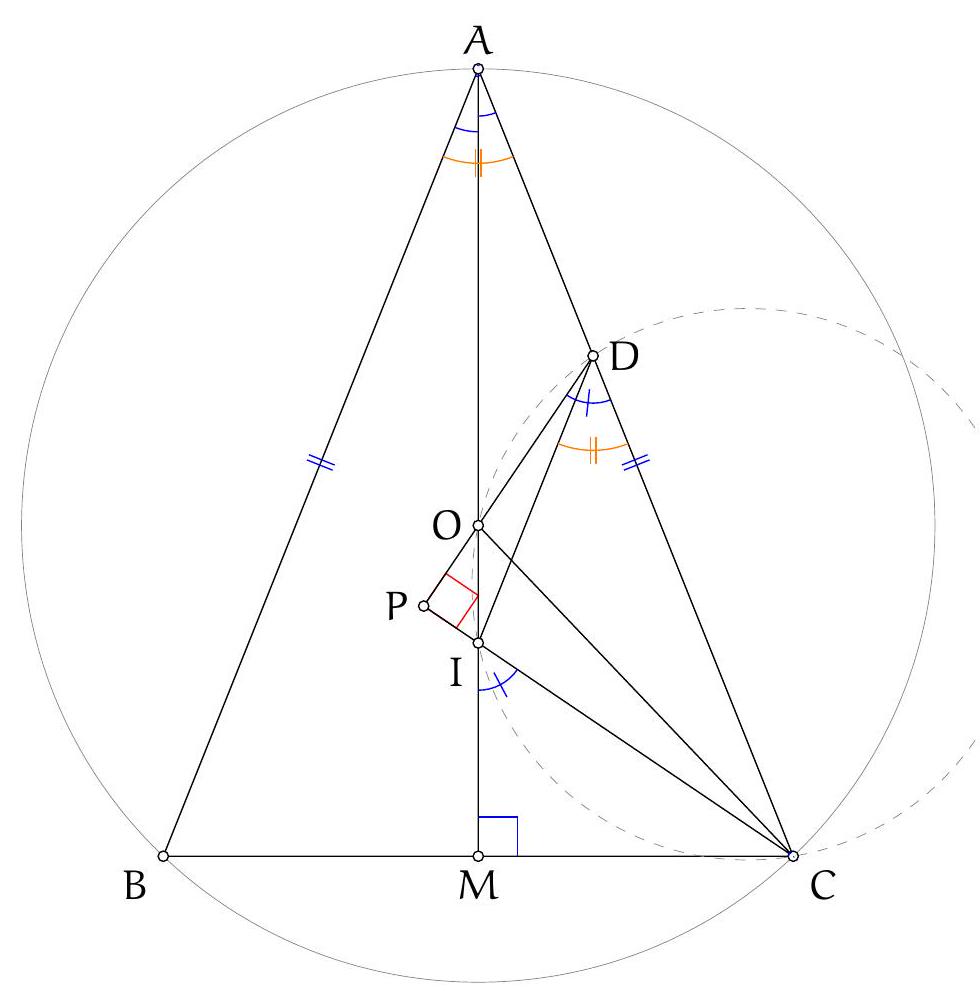
Premièrement, comme $A B=A C, A, O$, I sont alignés et la droite $(A I)$ coupe $[B C]$ en son milieu $M$. On pose P l'intersection des droites (DO) et (CI).
Par chasse aux angles, on montre que I, O, D, $C$ sont cocycliques, en montrant que $\widehat{\mathrm{IOC}}=\widehat{\mathrm{IDC}}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{IOC}} & =\widehat{\mathrm{MOC}} \\
& =\frac{1}{2} \widehat{\mathrm{BOC}} \text { car } O B=\mathrm{OC} \\
& =\widehat{\mathrm{BAC}} \text { par angle au centre } \\
& =\widehat{\mathrm{IDC}} \mathrm{car}(\mathrm{BA}) / /(\mathrm{ID})
\end{aligned}
$$
Donc par réciproque du théorème de l'angle inscrit, $\mathrm{I}, \mathrm{O}, \mathrm{D}, \mathrm{C}$ sont cocycliques.
Montrons à présent que $\widehat{C P D}=90^{\circ}$. Pour cela, on va montrer que $\widehat{P D C}+\widehat{D C P}=90^{\circ}$ (puisque $\left.\widehat{\mathrm{CPD}}=180^{\circ}-\widehat{\mathrm{PDC}}-\widehat{\mathrm{DCP}}\right)$. On a :
$$
\begin{aligned}
\widehat{\mathrm{PDC}}+\widehat{\mathrm{DCP}} & =\widehat{\mathrm{ODC}}+\widehat{\mathrm{DCI}} \\
& =\left(180^{\circ}-\widehat{\mathrm{CIO}}\right)+\widehat{\mathrm{ICB}} \text { par cocyclicité et bissectrice } \\
& =\widehat{\mathrm{CIM}}+\widehat{\mathrm{ICM}} \\
& =90^{\circ} \mathrm{car}(A \mathrm{II}) \perp(\mathrm{BC}) .
\end{aligned}
$$
Donc $\widehat{\mathrm{CPD}}=90^{\circ}$, ce qui prouve bien que les droites (CI) et (DO) sont perpendiculaires.
Commentaire des correcteurs : Exercice bien réussi dans l'ensemble. La plupart des copies rendues contenait une solution correcte.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
5771d3d7-c488-510d-a07e-8c3800a50192
| 607,129
|
Let $ABC$ be a triangle, $D, E$ the feet of the altitudes from $A$ and $B$ respectively. The line $(DE)$ intersects the circumcircle of $ABC$ at two points $P$ and $Q$. Let $A'$ and $B'$ be the reflections of $A$ and $B$ with respect to $(BC)$ and $(AC)$ respectively. Show that $A', B', P, Q$ are concyclic.
|
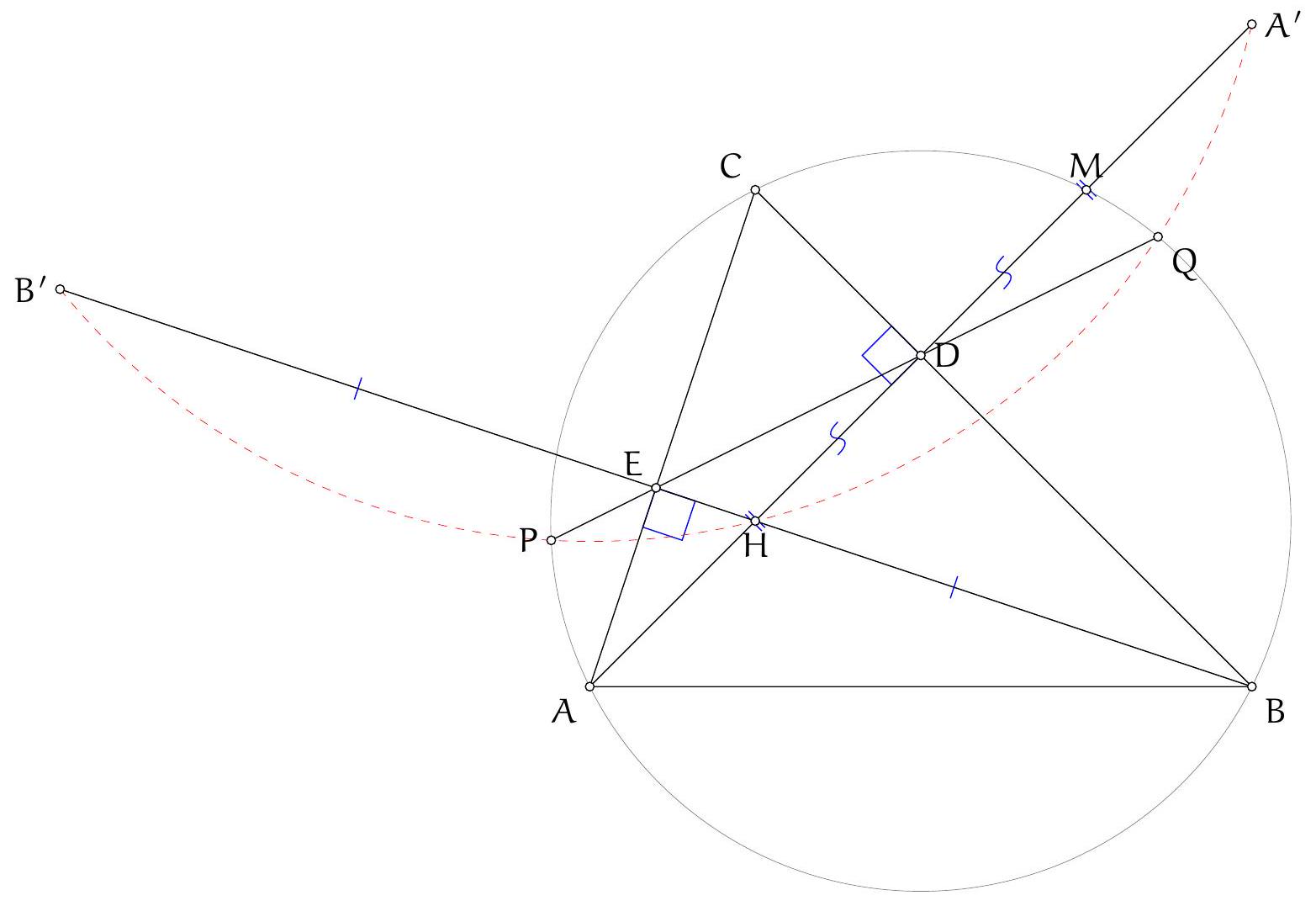
In the figure, it seems that H, the orthocenter, lies on the circle in question. Therefore, we will adopt the following strategy: we will show that \(A'\) and \(B'\) are on the circumcircle of \(P Q H\). This way, we will have \(A', B', P, Q\) being concyclic.
Let \(M\) be the symmetric point of \(H\) with respect to \((\mathrm{BC})\): then we know that \(M\) is on the circumcircle of \(\triangle ABC\). Then we have:
\[
\begin{aligned}
D A' \times D H & = D A \times D M \text{ by symmetry} \\
& = D P \times D Q \text{ by power of point } D \text{ in the circle } (A B C).
\end{aligned}
\]
Then, by the converse of the power of a point, \(P, Q, H, A'\) are concyclic. Similarly, \(P, Q, H, B'\) are also concyclic. Thus, \(A', B', P, Q\) are concyclic, on the circle \((P Q H)\).
Comment from the graders: The problem was well solved. However, many students could have gone faster by using the power of a point, rather than using similar triangles associated with 4 concyclic points and reproving the power of a point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à ( $B C$ ) et ( $A C$ ) respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|

Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
Soit $M$ le symétrique de H par rapport à $(\mathrm{BC})$ : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
$$
\begin{aligned}
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
\end{aligned}
$$
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
Commentaire des correcteurs : L'exercice a été bien résolu. Cependant pas mal d'élèves pourraient aller plus vite en utilisant la puissance d'un point, plutôt que d'utiliser les triangles semblables associés à 4 points cocycliques et reprouver la puissance d'un point.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution de l'exercice 7"
}
|
73679e58-f6da-5918-bb05-d7f689edadaf
| 607,130
|
Let $ABC$ be a triangle with circumcircle $\Gamma$, $D$ a point on $(AB)$, and $E$ a point on $(AC)$ such that $(DE)$ and $(BC)$ are parallel. The circumcircle of $ABC$ meets the circumcircle of $BDE$ again at $K$ and the circumcircle of $CDE$ again at $L$. Let $T$ be the intersection of $(BK)$ and $(CL)$. Show that $(TA)$ is tangent to the circle $\Gamma$.
|
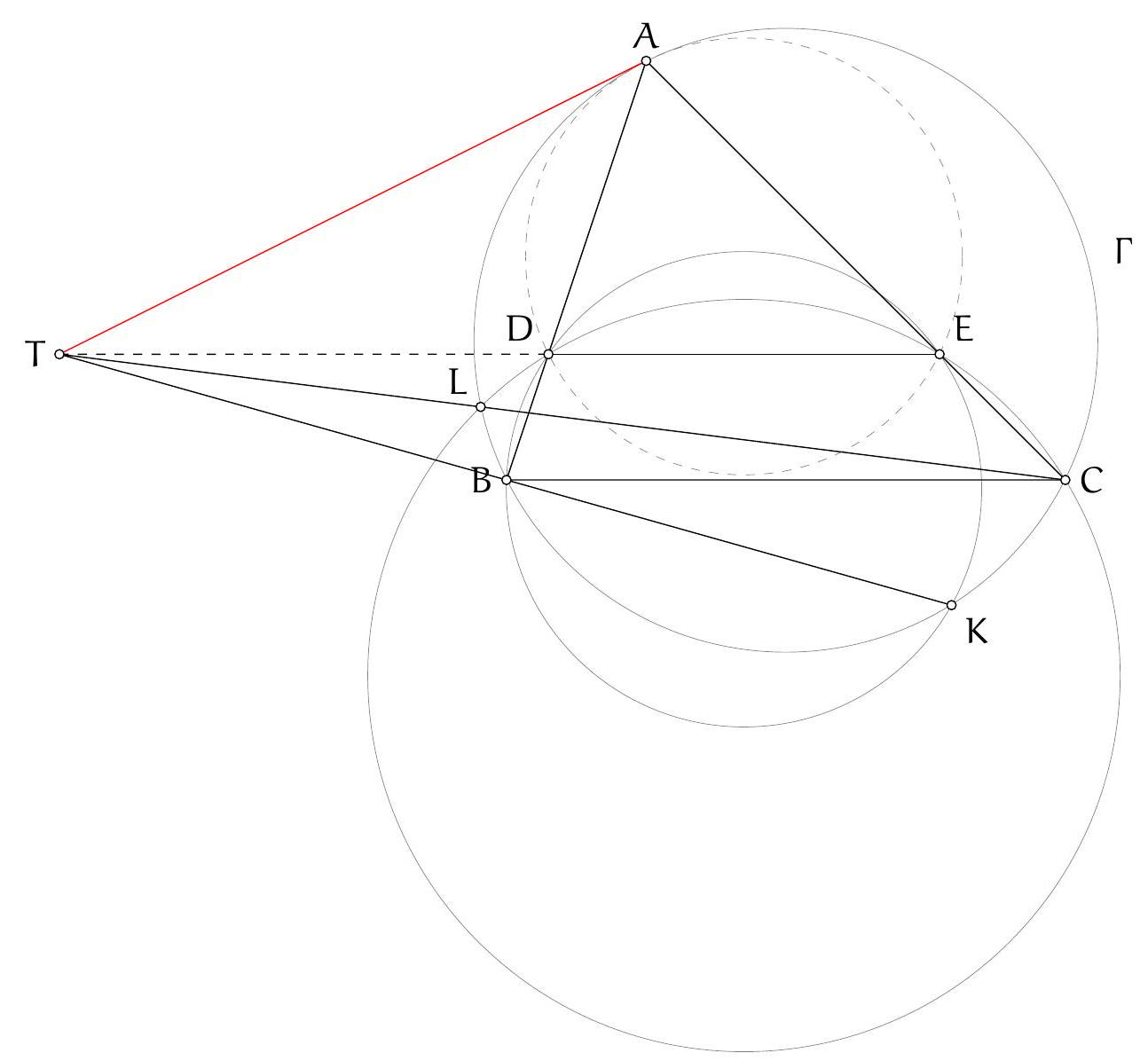
We recognize here a classic situation:
- KBDE is cyclic,
- KBLC is cyclic,
- CLDE is cyclic.
We know that in this situation, the lines (KB), (CL), (ED) are concurrent (this is the fact that the radical axes of three circles are concurrent). The lines (BK) and (CL) intersect at \( T \). It follows that \( T, D, E \) are collinear.
We then know, by expressing the power of \( T \) with respect to the three circles, that:
\[
TD \times TE = TL \times TC = TB \times TK
\]
Knowing the product \( TD \times TE \) suggests considering a circle passing through \( D, E \), and since we want a property on \( (TA) \), it is natural to introduce the circumcircle of \( ADE \).
Since \( TD \times TE = TL \times TC \), \( T \) has the same power with respect to the circumcircles of \( ABC \) and \( ADE \). Therefore, it lies on their radical axis. But since \( (DE) \) is parallel to \( (BC) \), the two circles are tangent at \( A \) with the radical axis being the common tangent to these two circles at \( A \). This can be seen simply by the tangent angle (using that \( \widehat{AED} = \widehat{ACB} \)), or by considering the homothety centered at \( A \) sending \( D \) to \( B \): it sends \( E \) to \( C \), so it sends the circle \( (ADE) \) to \( (ABC) \), and thus these circles are indeed tangent.
We deduce that \( T \) lies on the tangent to \( \Gamma \) passing through \( A \), in other words, that \( (TA) \) is tangent to \( \Gamma \), as required.
Comment from the graders: The exercise was not approached by many students, but all the students who did approach the exercise had very good ideas, including those who did not reach a solution. Notably, all students recognized that the points \( T, D, E \) are collinear, which was the first idea to have to advance in the exercise. It was then necessary to successfully exploit the parallelism of \( (DE) \) and \( (BC) \), and those who succeeded used essentially two different approaches: either justify that the circumcircles of \( ADE \) and \( ABC \) are tangent at \( A \) to reduce the problem to showing tangency to the circle \( (ADE) \), or by angle chasing to find other cyclic quadrilaterals on the figure.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle de cercle circonscrit $\Gamma, D$ un point sur $(A B)$ et $E$ un point sur ( $A C)$ tel que (DE) et ( $B C$ ) sont parallèles. Le cercle circonscrit à $A B C$ rencontre le cercle circonscrit à $B D E$ une seconde fois en $K$ et le cercle circonscrit à CDE une seconde fois en $L$. Soit $T$ le point d'intersection de (BK) et (CL). Montrer que (TA) est tangente au cercle $\Gamma$.
|

On reconnait ici une situation classique :
- KBDE cyclique,
- KBLC cyclique,
- CLDE cyclique.
On sait que dans cette situation, les droites (KB), (CL), (ED) sont concourantes (il s'agit ici du fait que les axes radicaux de 3 cercles sont concourants). Or les droites (BK) et (CL) se coupent en $T$. Il suit que $\mathrm{T}, \mathrm{D}, \mathrm{E}$ sont alignés.
On sait alors, en exprimant la puissance de T par rapport aux trois cercles, que :
$$
\mathrm{TD} \times \mathrm{TE}=\mathrm{TL} \times \mathrm{TC}=\mathrm{TB} \times \mathrm{TK}
$$
Le fait de connaître le produit TD $\times$ TE incite à considérer un cercle passant par $\mathrm{D}, \mathrm{E}$, et comme on souhaite une propriété sur (TA), il est naturel d'introduire le cercle circonscrit à $A D E$.
Comme TD $\times$ TE $=T L \times T C, T$ a la même puissance par rapport aux cercles circonscrits à $A B C$ et $A D E$. Il est donc sur leur axe radical. Mais comme ( $D E$ ) est parallèles à ( BC ), les deux cercles sont tangents en $A$ d'axe radical la tangente commune à ces deux cercles en $A$. On peut le voir simplement par
angle tangentiel (en utilisant que $\widehat{A E D}=\widehat{A C B}$ ), autrement on peut le voir en considérant l'homothétie de centre $A$ envoyant $D$ sur $B$ : elle envoie $E$ sur $C$ donc elle envoie le cercle ( $A D E$ ) sur ( $A B C$ ), et donc ces cercles sont bien tangents.
On en déduit que $T$ est sur la tangente à $\Gamma$ passant par $A$, autrement dit que (TA) est tangente à $\Gamma$, comme voulu.
Commentaire des correcteurs : L'exercice n'a pas été beaucoup abordé, mais la totalité des élèves qui ont abordé l'exercice ont eu des très bonnes idées, y compris ceux qui n'ont pas abouti à une solution. Notamment, tous les élèves ont remarqué que les points $T, D, E$ sont alignés, ce qui était la première idée à avoir pour avancer dans l'exercice. Il fallait ensuite réussir à exploiter le parallélisme de (DE) et (BC), et là les élèves qui ont abouti utilisaient essentiellement deux approches différentes : soit justifier que les cercles circonscrits à $A D E$ et $A B C$ sont tangents en $A$ pour se ramener à montrer la tangence au cercle (ADE), soit par chasse aux angles en trouvant d'autres quadrilatères cycliques sur la figure.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
a8fa52a8-c0f5-5634-b2ad-ae064977fa48
| 607,131
|
Let $ABC$ be a non-isosceles triangle and $I$ the center of its inscribed circle. Let $D$ be a point on $[BC]$ (other than $B$ and $C$). The circumcircle of $DIB$ intersects $(AB)$ a second time at $E \neq B$, and the circumcircle of $DIC$ intersects $(AC)$ a second time at $F \neq C$. The circumcircle of $DEF$ meets $(AB)$ and $(AC)$ a second time at $M$ and $N$ respectively. The lines $(IB)$ and $(DE)$ intersect at $P$ and the lines $(IC)$ and $(DF)$ intersect at $Q$. Show that the lines $(EN)$, $(FM)$, and $(PQ)$ are parallel.
|
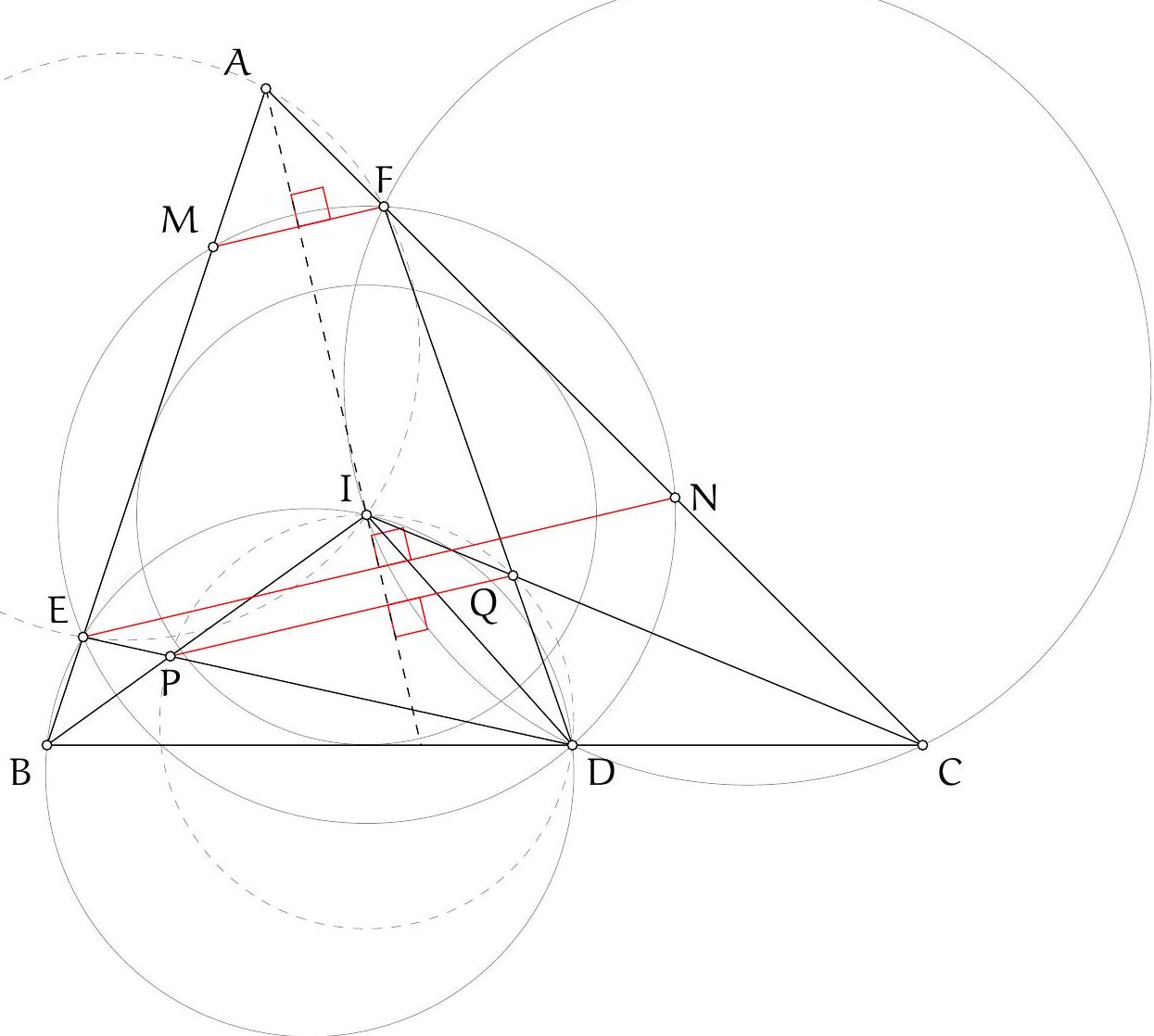
In the figure, it seems that I is the center of the circle (DEF), and that the lines (MF), (EN), (PQ) are all perpendicular to $(A I)$: this is the strategy we will use to solve the exercise.
- Lemma 1: The point I is the center of the circumcircle of DEF.
Proof: Since I is on the bisector of $\widehat{\mathrm{DBE}}$ and on the circumcircle of DBE, it is the South Pole (with respect to B) in this triangle. Therefore, ID = IE. Similarly, in FCD, we get ID = IF. Thus, $\mathrm{ID}=\mathrm{IE}=\mathrm{IF}: \mathrm{I}$ is indeed the center of the circumcircle of DEF.
- Lemma 2: The quadrilateral PQID is cyclic.
Proof: Indeed, we have:
$$
\begin{aligned}
\widehat{\mathrm{QDP}} & =\widehat{\mathrm{QDI}}+\widehat{\mathrm{IDP}} \\
& =\widehat{\mathrm{FDI}}+\widehat{\mathrm{IDE}} \\
& =\widehat{\mathrm{FCI}}+\widehat{\mathrm{IBE}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ICB}}+\widehat{\mathrm{CBI}} \text { by bisectors } \\
& =180^{\circ}-\widehat{\mathrm{BIC}} \\
& =180^{\circ}-\widehat{\mathrm{PIQ}}
\end{aligned}
$$
Thus, $\widehat{\mathrm{PIQ}}+\widehat{\mathrm{QPD}}=180^{\circ}$, which means that PIDQ is cyclic.
Lemma 3: The lines (PQ) and (AI) are perpendicular.
Proof: Indeed, $\widehat{\mathrm{QPI}}=\widehat{\mathrm{QDI}}=\widehat{\mathrm{FDI}}=\widehat{\mathrm{FCI}}=\frac{1}{2} \widehat{\mathrm{ACB}}$ by inscribed angle. Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{AIB}} & =180^{\circ}-\widehat{\mathrm{IBA}}-\widehat{\mathrm{BAI}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{\mathrm{BAC}}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{ACB}}}{2} \\
& =90^{\circ}+\frac{1}{2} \widehat{\mathrm{ABC}} .
\end{aligned}
$$
We conclude that (AI) and (PQ) are indeed perpendicular.
- Lemma 4: The quadrilateral AEIF is cyclic.
Proof: Indeed, BDIE and CFID are cyclic, so by Miquel's theorem, AEIF is also cyclic.
- Lemma 5: The lines (MF) and (EN) are perpendicular to (AI).
Proof: First, $\widehat{\mathrm{IEM}}=\widehat{\mathrm{IEA}}=180^{\circ}-\widehat{\mathrm{AFI}}=\widehat{\mathrm{IFN}}$ by inscribed angle. Furthermore, $\mathrm{IE}=\mathrm{IM}=\mathrm{IF}=\mathrm{IN}$ (by Lemma 1), so IEM and IFN are two isosceles triangles at I with the same base angle: hence IEM is similar to IFN. But since IE = IF: they are even congruent. We conclude that $E M=F N$. Since EMFN is cyclic, it is an isosceles trapezoid. We conclude that (MF) and (EN) are parallel, both perpendicular to (AI) (since I is the center of the circumcircle and $A$ is the intersection of the sides, so (AI) is the axis of symmetry of the isosceles trapezoid).
- Finally, (EN), (FM), (PQ) are all perpendicular to (AI), so they are parallel.
Comment from the graders: The problem was not widely attempted, but almost all students who attempted it solved it. Note that there were several possible configurations in the figure (order of points $E, M$ and $F, N$ on the lines $(A B)$ and $(A C)$), although it was not required to treat all configurations. Be careful not to get tangled up in the use of the inscribed angle theorem, especially in the case of supplementary angles.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle non-isocèle et $I$ le centre de son cercle inscrit. Soit D un point sur $[B C]$ (autre que $B$ et $C$ ). Le cercle circonscrit à DIB coupe $(A B)$ une deuxième fois en $E \neq B$, et le cercle circonscrit à DIC coupe ( $A C$ ) une deuxième fois en $F \neq C$. Le cercle circonscrit à DEF rencontre ( $A B$ ) et ( $A C$ ) une deuxième fois en $M$ et $N$ respectivement. Les droites (IB) et ( $D E$ ) s'intersectent en $P$ et les droites (IC) et (DF) s'intersectent en Q. Montrer que les droites (EN), (FM) et (PQ) sont parallèles.
|

Sur la figure, il semble que I est le centre du cercle (DEF), et que les droites (MF), (EN), (PQ) sont toutes perpendiculaires à $(A I)$ : c'est donc la stratégie qu'on va utiliser pour résoudre l'exercice.
- Lemme 1: Le point I est le centre du cercle circonscrit à DEF.
Preuve : Comme I est sur la bissectrice de $\widehat{\mathrm{DBE}}$ et sur le cercle circonscrit de DBE, c'est le pôle Sud (par rapport à B) dans ce triangle. Donc ID = IE. De même dans FCD, on obtient ID = IF. Donc $\mathrm{ID}=\mathrm{IE}=\mathrm{IF}: \mathrm{I}$ est bien le centre du cercle circonscrit de DEF.
- Lemme 2: Le quadrilatère PQID est cyclique.
Preuve : En effet, on a :
$$
\begin{aligned}
\widehat{\mathrm{QDP}} & =\widehat{\mathrm{QDI}}+\widehat{\mathrm{IDP}} \\
& =\widehat{\mathrm{FDI}}+\widehat{\mathrm{IDE}} \\
& =\widehat{\mathrm{FCI}}+\widehat{\mathrm{IBE}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ICB}}+\widehat{\mathrm{CBI}} \text { par bissectrices } \\
& =180^{\circ}-\widehat{\mathrm{BIC}} \\
& =180^{\circ}-\widehat{\mathrm{PIQ}}
\end{aligned}
$$
Donc $\widehat{\mathrm{PIQ}}+\widehat{\mathrm{QPD}}=180^{\circ}$, d'où le fait que PIDQ est cyclique.
Lemme 3 : Les droites (PQ) et (AI) sont perpendiculaires.
Preuve : En effet $\widehat{\mathrm{QPI}}=\widehat{\mathrm{QDI}}=\widehat{\mathrm{FDI}}=\widehat{\mathrm{FCI}}=\frac{1}{2} \widehat{\mathrm{ACB}}$ par angle inscrit. De plus :
$$
\begin{aligned}
\widehat{\mathrm{AIB}} & =180^{\circ}-\widehat{\mathrm{IBA}}-\widehat{\mathrm{BAI}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{\mathrm{BAC}}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{ACB}}}{2} \\
& =90^{\circ}+\frac{1}{2} \widehat{\mathrm{ABC}} .
\end{aligned}
$$
On en déduit que ( AI ) et (PQ) sont bien perpendiculaires.
- Lemme 4: La quadrilatère AEIF est cyclique.
Preuve : En effet BDIE et CFID sont cycliques, donc d'après le théorème de Miquel, AEIF l'est aussi.
- Lemme 5: Les droites (MF) et (EN) sont perpendiculaires à (AI).
Preuve : D'abord $\widehat{\mathrm{IEM}}=\widehat{\mathrm{IEA}}=180^{\circ}-\widehat{\mathrm{AFI}}=\widehat{\mathrm{IFN}}$ par angle inscrit. De plus $\mathrm{IE}=\mathrm{IM}=\mathrm{IF}=\mathrm{IN}$ (par le lemme 1), donc IEM et IFN sont deux triangles isocèles en I avec même angle de base : d'où IEM semblable à IFN. Mais comme IE = IF : ils sont même isométriques. On en déduit que $E M=F N$. Comme EMFN est cyclique, c'est un trapèze isocèle. On en déduit que (MF) et (EN) sont parallèles, toutes les deux perpendiculaires à (AI) (car I est le centre du cercle circonscrit et $A$ l'intersection des côtés, donc (AI) est axe de symétrie du trapèze isocèle).
- Finalement, (EN), (FM), (PQ) sont toutes les trois perpendiculaires à (AI), elle sont donc parallèles.
Commentaire des correcteurs : L'exercice n'a pas été beaucoup traité, mais la quasi totalité des élèves qui l'ont traité l'ont résolu. On notera qu'il y avait plusieurs configurations possibles dans la figure(ordre des points $E, M$ et $F, N$ sur les droites $(A B)$ et ( $A C)$. , bien qu'il ne soit pas demandé de traiter toutes les configurations. Attention à ne pas s'emmêler les pinceaux des les utilisations des théorèmes des angles inscrits, notamment dans le cas des angles supplémentaires.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution de l'exercice 9"
}
|
4c428585-18c6-5fba-b16e-fbda897cd9e6
| 607,132
|
Let $ABC$ be an acute triangle (all angles are acute) with $BA \neq BC$. Let $O$ be the center of its circumcircle. The line $(AB)$ intersects the circumcircle of $BOC$ a second time at $P \neq B$. Show that $PA = PC$.
|
Let's draw the figure in the case where $BC < BA$, the case $BC > BA$ being completely analogous. It is a matter of showing that $\mathrm{PA} = \mathrm{PC}$, that is, $\widehat{ACP} = \widehat{\mathrm{PAC}} (=\widehat{\mathrm{BAC}})$. We have:
\[
\begin{aligned}
\widehat{ACP} & = \widehat{ACO} + \widehat{OCP} \\
& = \widehat{ACO} + \widehat{OBP} \text{ by inscribed angle} \\
& = \widehat{ACO} + \widehat{OBA}.
\end{aligned}
\]
Now, $AOC$ is isosceles at O, so $\widehat{ACO} = \widehat{OAC} = \frac{180^{\circ} - \widehat{COA}}{2} = 90^{\circ} - \widehat{CBA}$ by the central angle. Similarly, $\widehat{OBA} = 90^{\circ} - \widehat{ACB}$. Finally, $\widehat{ACP} = 180^{\circ} - \widehat{ACB} - \widehat{CBA} = \widehat{BAC} = \widehat{PAC}$, hence $PA = PC$, as desired.
Comment from the graders: The exercise was generally very well done!
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
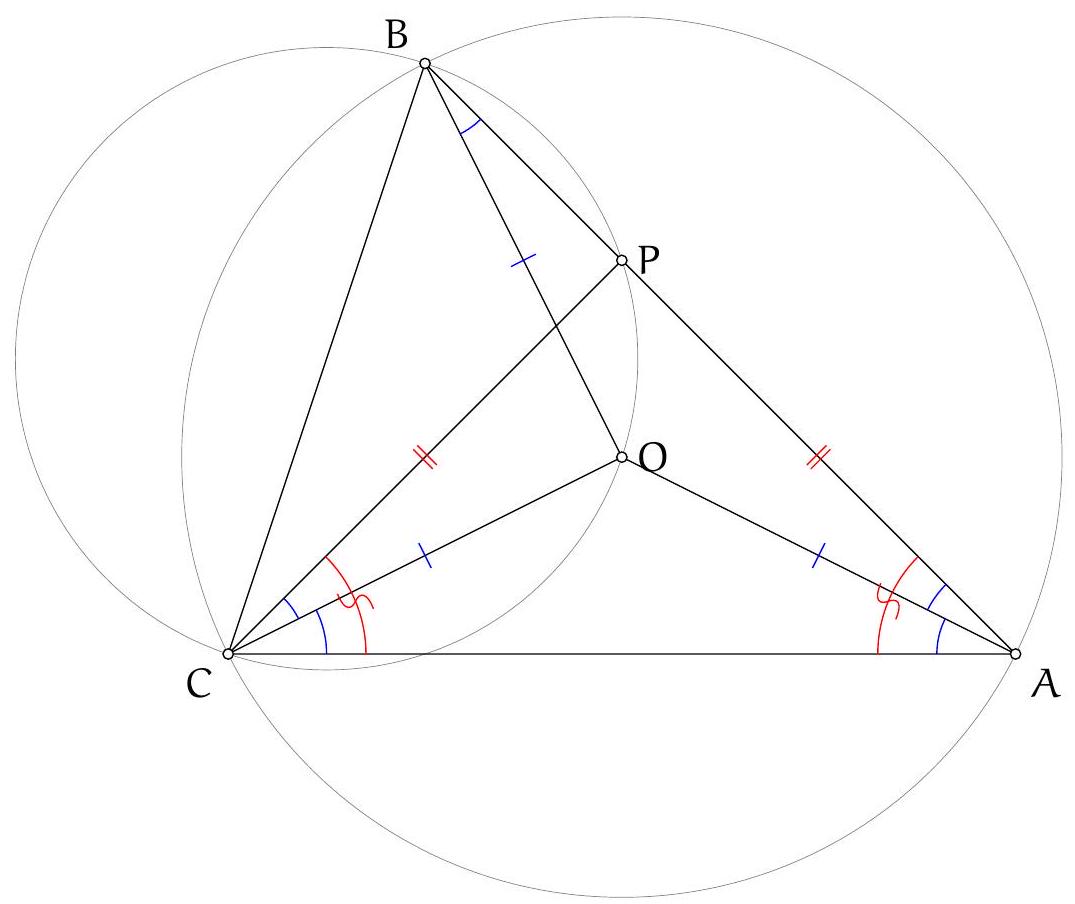
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a :
$$
\begin{aligned}
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
& =\widehat{A C O}+\widehat{O B A} .
\end{aligned}
$$
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{O A C}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{C B A}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
Commentaire des correcteurs : L'exercice a éte globalement tres bien reussi !
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
a633d352-4e78-58ca-98b6-e4a65bbd2dee
| 607,125
|
Let $ABC$ be a triangle, $O$ the center of its circumcircle. Suppose that $\widehat{C B A}=60^{\circ}$ and $\widehat{\mathrm{CBO}}=45^{\circ}$. Let $D$ be the point of intersection of the lines $(\mathrm{AC})$ and $(B O)$. Show that $\mathrm{AD}=\mathrm{DO}$.
|
To show that $A D=D O$ (i.e., that $A D O$ is isosceles at D), we will show that $\widehat{\mathrm{DOA}}=\widehat{\mathrm{OAD}}$. Introduce $P$ as the intersection point (other than $B$) of (BO) with the circumcircle of $A B C$.
On one hand, $\widehat{\mathrm{DOA}}=\widehat{\mathrm{POA}}=2 \widehat{\mathrm{PBA}}=2\left(60^{\circ}-45^{\circ}\right)=30^{\circ}$ according to the central angle theorem.
On the other hand, $\mathrm{OC}=\mathrm{OA}$, so $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OAC}}=\widehat{\mathrm{ACO}}=\frac{180^{\circ}-\widehat{\mathrm{COA}}}{2}$. According to the central angle theorem, $\widehat{C O A}=2 \widehat{C B A}=120^{\circ}$. Therefore, $\widehat{O A D}=30^{\circ}$.
Finally, $\widehat{D O A}=30^{\circ}=\widehat{\mathrm{OAD}}$, so we have indeed shown that $\mathrm{AD}=\mathrm{DO}$.
Comment from the graders: The exercise was really very well done by all those who tackled it. However, for exercises whose solutions fit on a few lines, it is better to justify the angle chasing well, which can avoid calculation or copying errors. Additionally, many papers could have been shortened, with students taking significant detours in their calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $O$ le centre de son cercle circonscrit. On suppose que $\widehat{C B A}=60^{\circ}$ et $\widehat{\mathrm{CBO}}=45^{\circ}$. Soit D le point d'intersection des droites $(\mathrm{AC})$ et $(B O)$. Montrer que $\mathrm{AD}=\mathrm{DO}$.
|
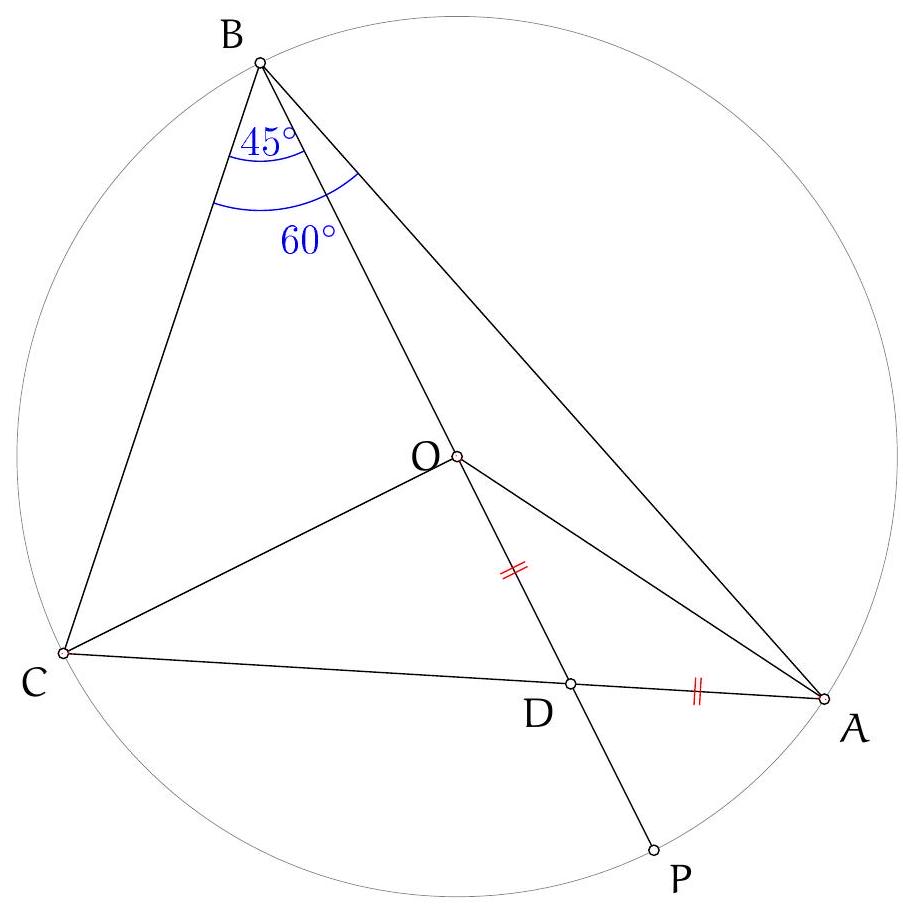
Pour montrer que $A D=D O$ (c'est-à-dire que $A D O$ est isocèle en D ), nous allons montrer que $\widehat{\mathrm{DOA}}=\widehat{\mathrm{OAD}}$. Introduisons $P$ le point d'intersection (autre que $B$ ) de (BO) avec le cercle circonscrit de $A B C$.
D'une part, $\widehat{\mathrm{DOA}}=\widehat{\mathrm{POA}}=2 \widehat{\mathrm{PBA}}=2\left(60^{\circ}-45^{\circ}\right)=30^{\circ}$ d'après le théorème de l'angle au centre.
D'autre part, $\mathrm{OC}=\mathrm{OA}$ donc $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OAC}}=\widehat{\mathrm{ACO}}=\frac{180^{\circ}-\widehat{\mathrm{COA}}}{2}$. Or d'après le théorème de l'angle au centre, $\widehat{C O A}=2 \widehat{C B A}=120^{\circ}$. D'où $\widehat{O A D}=30^{\circ}$.
Finalement, $\widehat{D O A}=30^{\circ}=\widehat{\mathrm{OAD}}$, donc on a bien montré que $\mathrm{AD}=\mathrm{DO}$.
Commentaire des correcteurs: L'exercice à été vraiment très bien réussi par tous ceux qui l'ont abordé. Cependant, pour des exercices dont la solution tient sur quelques lignes, il vaut mieux bien justifier sa chasse aux angle, ce qui peut éviter des erreurs de calculs/ de recopiage. De plus, pas mal de copies auraient pu être raccourcies, les élèves faisant des détours conséquents dans leurs calculs.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 11.",
"solution_match": "## Solution de l'exercice 11"
}
|
e7390c2a-23f8-5759-8ead-32498a8dd247
| 607,133
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
We notice that the circle with diameter [CD] appears quite naturally. Indeed, we have right angles $\widehat{\mathrm{DB}^{\prime} \mathrm{C}}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, so the points $\mathrm{B}, \mathrm{B}^{\prime}$, and $E$ lie on the circle with diameter [DC], in other words, $\mathrm{C}, \mathrm{B}, \mathrm{D}, \mathrm{E}, \mathrm{B}^{\prime}$ are concyclic.
Then we have:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =45^{\circ} \text { because } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { by inscribed angle } \\
& =45^{\circ} \text { because } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Therefore, we have $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, so (EC) is the bisector of $\widehat{\mathrm{BEB}^{\prime}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de B par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
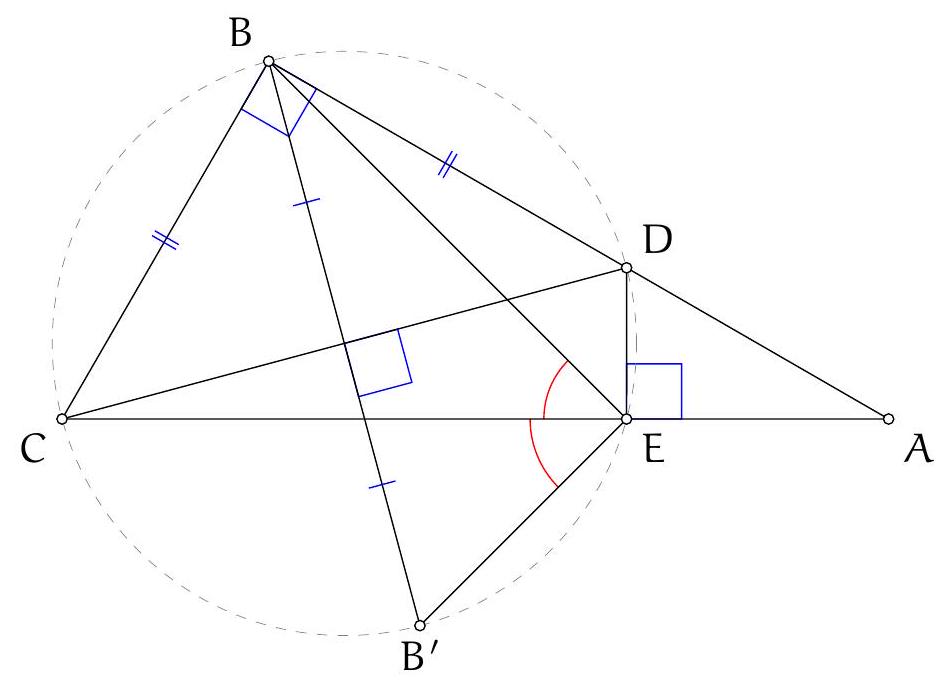
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}^{\prime} \mathrm{C}}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $\mathrm{C}, \mathrm{B}, \mathrm{D}, \mathrm{E}, \mathrm{B}^{\prime}$ sont cocycliques.
Alors on a :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
De plus:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "## Solution de l'exercice 12"
}
|
4ae97837-bbaf-5d0d-9a20-8b88b0abb32e
| 607,134
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
We could also show directly $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ without using $\mathrm{BC}=\mathrm{BD}$. Indeed:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { by symmetry } \\
& =\widehat{\mathrm{CEB}} \text { by inscribed angle. }
\end{aligned}
$$
Comment from the graders: The exercise was very well done, some angle chasing could have been avoided or shortened by using the cocyclicity of the points or the South Pole theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de B par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
\end{aligned}
$$
Commentaire des correcteurs : L'exercice a été très bien réussi, certaines chasses aux angles auraient pu être évitées ou raccourcies en utilisant la cocyclicité des points ou le théorème du Pôle Sud.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution alternative"
}
|
4ae97837-bbaf-5d0d-9a20-8b88b0abb32e
| 607,134
|
Let $A B C D E$ be a convex cyclic pentagon such that $A B=B D$. Let $P$ be the intersection point of the lines (EB) and ( $A C$ ). Let $Q$ be the intersection point of the lines ( $B C$ ) and ( $D E$ ). Show that $(\mathrm{PQ})$ and (AD) are parallel.
|
In the figure, it seems that EPCQ is a cyclic quadrilateral. We show this:
\[
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { by inscribed angle } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \text{ since } \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}}.
\end{aligned}
\]
Thus, we have shown that \(\widehat{Q C P}+\widehat{P E Q}=180^{\circ}\). Therefore, by the converse of the inscribed angle theorem, EPCQ is cyclic, which is what we wanted to prove.
Now, to show that (AD) and (PQ) are parallel, we will try to find corresponding angles. We have:
\[
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { by inscribed angle. }
\end{aligned}
\]
Since \(\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}\) and \(\mathrm{Q}, \mathrm{D}, \mathrm{E}\) are collinear (in that order), by corresponding angles, the lines (PQ) and (AD) are indeed parallel.
Comment from the graders: The exercise was generally well handled. Most solutions that worked involved proving that EQCP is cyclic and concluding by angle chasing. Some used more advanced tools, such as some who used similarities, others applied Pascal's theorem in the degenerate hexagon \(A D E B B C\), and still others used inversions. However, it is worth noting that many students take unnecessary detours in their calculations, sometimes doing in 2 pages what can be proven in 2 lines: while having a solution that works is obviously a very good thing, it is even better to have a solution that works and is efficient. For example, it was not necessary here to introduce intermediate points, as all the necessary points were defined in the problem statement. It is also worth noting that while the vast majority of submissions include a figure, some do not: providing a clear figure is essential for illustrating reasoning in a geometry problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
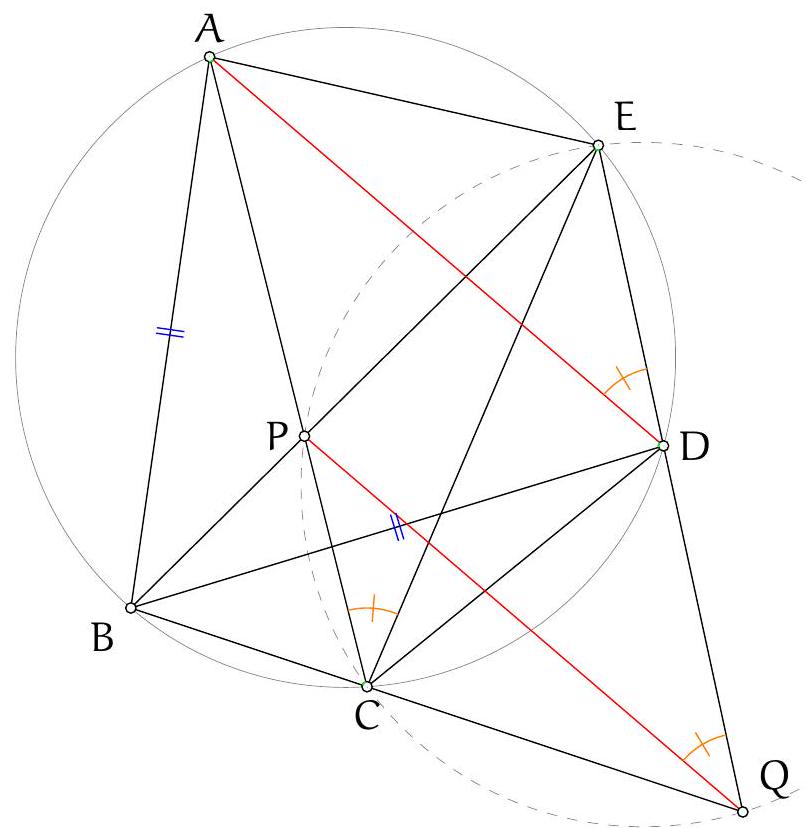
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
$$
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
\end{aligned}
$$
Ainsi on a montré que $\widehat{Q C P}+\widehat{P E Q}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
$$
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
\end{aligned}
$$
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
Commentaire des correcteurs : L'exercice a été dans l'ensemble très bien traité. La plupart des solutions qui ont abouti consistaient à prouver EQCP cyclique et à conclure par chasse aux angles. D'autres ont trouvé des solutions avec des outils plus avancés, notamment certains ont utilisé des similitudes,
d'autres ont vu qu'on pouvait appliquer le théorème de Pascal dans l'hexagone dégénéré $A D E B B C$, d'autres encore ont utilisé des inversions. Il est cependant à noter qu'un bon nombre d'élèves font beaucoup de détours peu utiles dans leurs calculs, faisant parfois en 2 pages ce qui se prouve en 2 lignes : si avoir une solution qui fonctionne est évidemment un très bonne chose, il est encore mieux d'avoir une solution qui fonctionne et qui est efficace. Il n'était par exemple pas nécessaire ici d'introduire des points intermédiaires, tous les points utiles étaient définis dans l'énoncé. On notera aussi que si la grande majorité des copies rendent une figure, certains ne le font pas : rendre une figure propre est indispensable pour illustrer son raisonnement dans un problème de géométrie.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "## Solution de l'exercice 13"
}
|
4203c2ee-bef3-5136-ac44-21a58d19c66e
| 607,128
|
Let $ABC$ be a triangle, $D, E$ the feet of the altitudes from $A$ and $B$ respectively. The line $(DE)$ intersects the circumcircle of $ABC$ at two points $P$ and $Q$. Let $A'$ and $B'$ be the reflections of $A$ and $B$ with respect to $(BC)$ and $(AC)$ respectively. Show that $A', B', P, Q$ are concyclic.
|
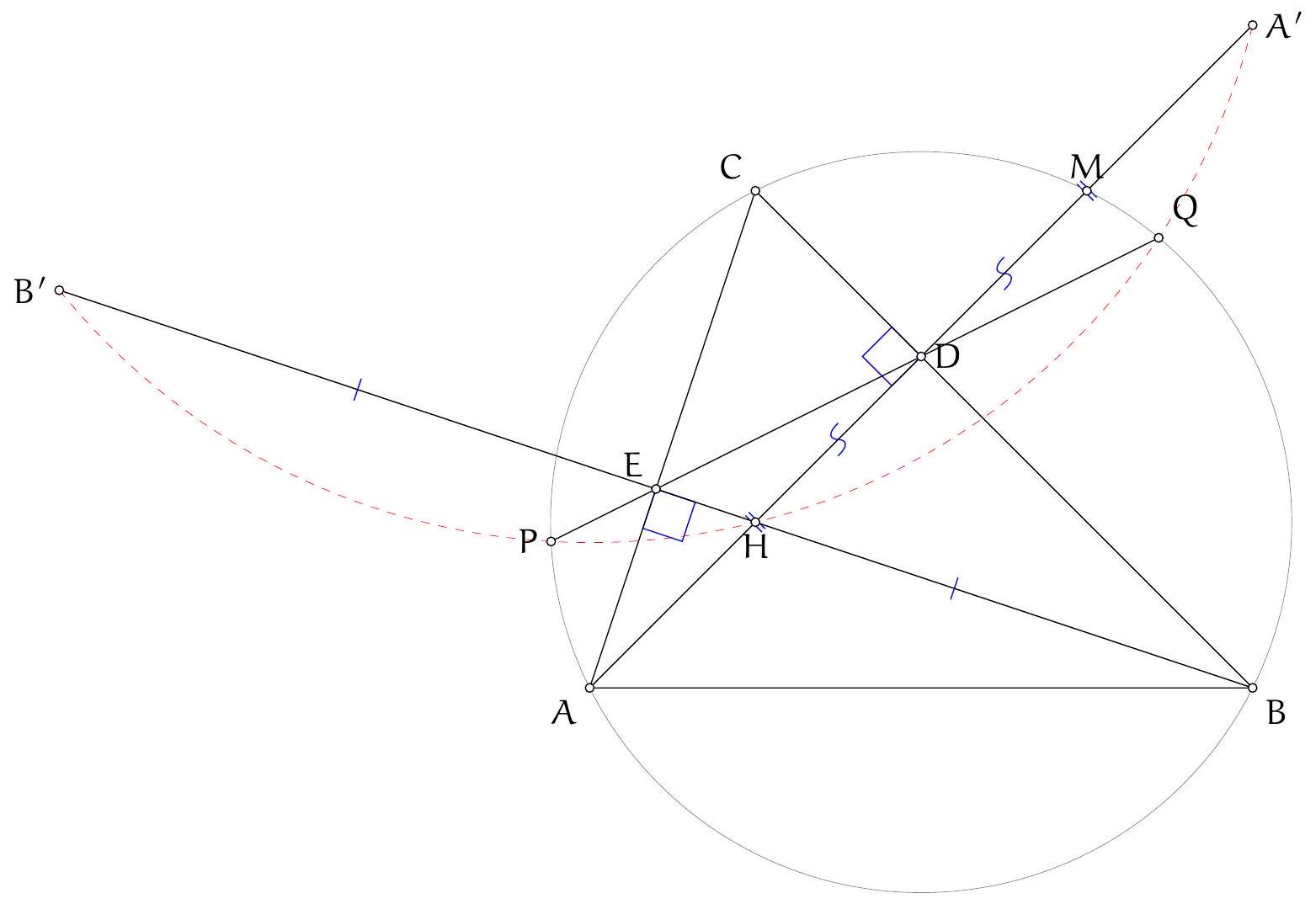
In the figure, it appears that H, the orthocenter, lies on the circle in question. Therefore, we will adopt the following strategy: we will show that \(A'\) and \(B'\) are on the circumcircle of \(P Q H\). This way, we will have \(A', B', P, Q\) being concyclic.
Let \(M\) be the symmetric point of H with respect to (BC): then we know that \(M\) is on the circumcircle of \(ABC\). Then we have:
\[
\begin{aligned}
D A' \times D H & = D A \times D M \text{ by symmetry} \\
& = D P \times D Q \text{ by power of } D \text{ in the circle } (ABC).
\end{aligned}
\]
Then, by the converse of the power of a point, \(P, Q, H, A'\) are concyclic. In a completely analogous manner, \(P, Q, H, B'\) are also concyclic. Thus, \(A', B', P, Q\) are concyclic, on the circle \((P Q H)\).
Comment from the graders: The exercise was generally well done by those who attempted it. The fact that the symmetrics of H are on the circumcircle of \(ABC\) is a useful lemma, which is good to have in mind and does not need to be reproved every time it is needed (saying "it is known that" is sufficient).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à $(B C)$ et $(A C)$ respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|

Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
Soit $M$ le symétrique de H par rapport à ( BC ) : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
$$
\begin{aligned}
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
\end{aligned}
$$
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
Commentaire des correcteurs : L'exercice a été globalement bien réussi par ceux qui l'ont essayé. Le fait que les symétriques de H sont sur le cercle circonscrit à $A B C$ est un lemme souvent utile, qu'il est bon d'avoir en tête, et qu'il n'y a pas besoin de reprouver à chaque fois qu'on en a besoin (dire "il est connu que" est suffisant).
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "## Solution de l'exercice 14"
}
|
9debb745-b72f-50f2-bfd0-96e964e3c8b9
| 607,135
|
Let $ABCD$ be a convex cyclic quadrilateral, $M$ the midpoint of $[AC]$. The circumcircle of $CDM$ intersects $(BC)$ a second time at $N$ (other than $C$). Let $B'$ be the symmetric point of $B$ with respect to $N$. Show that $(MN)$ is tangent to the circumcircle of $B'DN$.
|
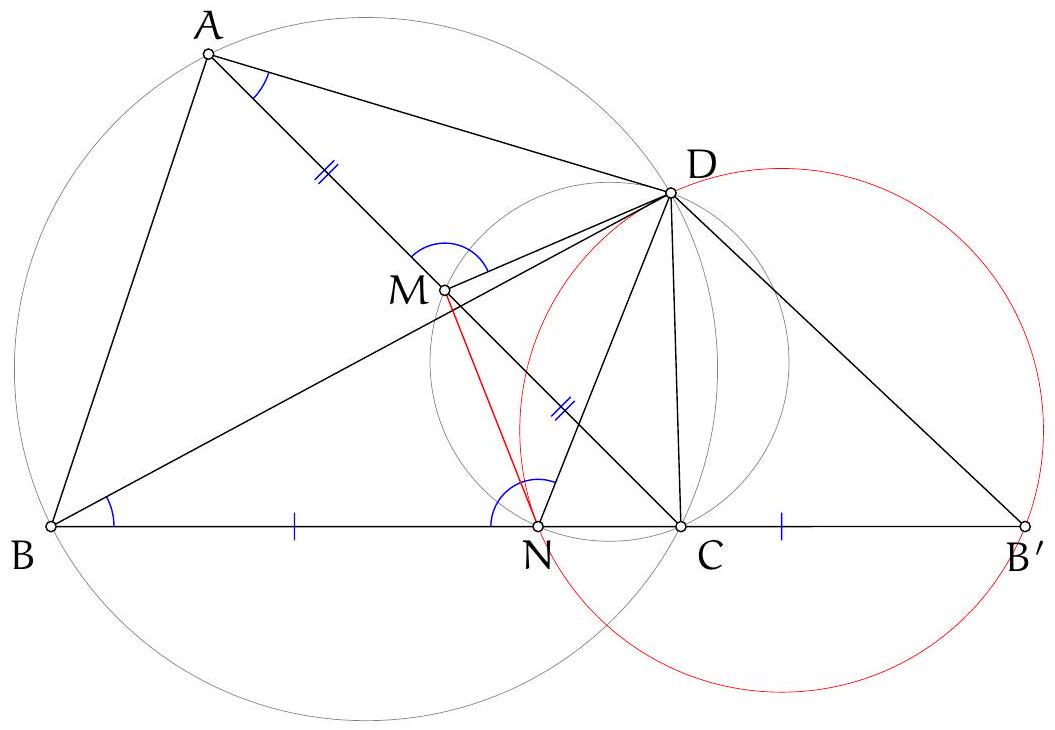
In the figure, we can identify similar triangles. Indeed, by inscribed angles, we have:
$$
\widehat{M A D}=\widehat{C A D}=\widehat{C B D}=\widehat{N B D}
$$
Again by inscribed angles, we have:
$$
\widehat{\mathrm{DMA}}=180^{\circ}-\widehat{\mathrm{CMD}}=180^{\circ}-\widehat{\mathrm{CND}}=\widehat{\mathrm{DNB}}
$$
We deduce that triangles \(A M D\) and \(B N D\) are similar. But then \(A D C\) and \(\mathrm{BDB}^{\prime}\) are similar. Indeed, we have \(\widehat{B^{\prime} B D}=\widehat{C B D}\), and \(\frac{B B^{\prime}}{A C}=\frac{2 B N}{2 A M}=\frac{B N}{A M}=\frac{B D}{A D}\), and thus \(A D C\) is similar to \(\mathrm{BDB}^{\prime}\). It follows that:
$$
\begin{aligned}
\widehat{M N D} & =\widehat{M C D} \text { by inscribed angle } \\
& =\widehat{A C D} \\
& =\widehat{\mathrm{BB}^{\prime} \mathrm{D}} \text { since } \mathrm{ADC} \sim \mathrm{BDB}^{\prime} \\
& =\widehat{\mathrm{DB}^{\prime} \mathrm{D}}
\end{aligned}
$$
Therefore, by the converse of the tangent angle, (MN) is tangent to the circumcircle of \(\mathrm{B}^{\prime} \mathrm{DN}\), which is what we wanted to show.
Comment from the graders: The problem could be solved using elementary tools (identifying similar triangles through angle equalities, deducing other pairs of similar triangles, recovering the desired angle equality), but it could also be approached from the perspective of similarities, which provides several shortcuts in the steps mentioned above. This second approach was chosen by most students who responded to the problem and was very successful in the results obtained, but less successful in the consistency of the approach: introducing the similarity centered at D is superfluous if it has already been shown by angle chasing that \(\triangle \mathrm{DAM} \sim \triangle \mathrm{DBN}\).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe cyclique, $M$ le milieu de $[A C]$. Le cercle circonscrit à $C D M$ rencontre $(B C)$ une deuxième fois en $N$ (autre que $C$ ). Soit $B^{\prime}$ le symétrique de $B$ par rapport à $N$. Montrer que (MN) est tangente au cercle circonscrit de $B^{\prime} D N$.
|

Sur la figure, on repère des triangles semblables. En effet, on a par angle inscrit :
$$
\widehat{M A D}=\widehat{C A D}=\widehat{C B D}=\widehat{N B D}
$$
Toujours par angle inscrit, on a :
$$
\widehat{\mathrm{DMA}}=180^{\circ}-\widehat{\mathrm{CMD}}=180^{\circ}-\widehat{\mathrm{CND}}=\widehat{\mathrm{DNB}}
$$
On en déduit que les triangles $A M D$ et BND sont semblables. Mais alors $A D C$ et $\mathrm{BDB}^{\prime}$ sont semblables. En effet on a $\widehat{B^{\prime} B D}=\widehat{C B D}$, et $\frac{B B^{\prime}}{A C}=\frac{2 B N}{2 A M}=\frac{B N}{A M}=\frac{B D}{A D}$, et donc ADC est semblable à $\mathrm{BDB}^{\prime}$. Il suit que :
$$
\begin{aligned}
\widehat{M N D} & =\widehat{M C D} \text { par angle inscrit } \\
& =\widehat{A C D} \\
& =\widehat{\mathrm{BB}^{\prime} \mathrm{D}} \text { car } \mathrm{ADC} \sim \mathrm{BDB}^{\prime} \\
& =\widehat{\mathrm{DB}^{\prime} \mathrm{D}}
\end{aligned}
$$
Donc par réciproque de l'angle tangentiel, (MN) est tangente au cercle circonscrit à $\mathrm{B}^{\prime} \mathrm{DN}$, ce qu'on voulait montrer.
Commentaire des correcteurs: L'exercice pouvait se résoudre avec des outils élémentaires (repérer des triangles sembables grâce aux égalités d'angles, déduire d'autres paires de triangles semblables, récupérer l'égalité d'angles voulue), mais pouvait également être raconté en adoptant le point de vue des similitudes, qui donne plusieurs raccourcis dans les étapes précédemment citées. Cette deuxième approche a été celle choisie par la plupart des élèves ayant répondu au problème, et a rencontré beaucoup de succès dans les résultats obtenus, mais un peu moins de succès dans la consistance de la démarche : introduire la similitude de centre D est superflu si on a déjà montré par chasse aux angles que $\triangle \mathrm{DAM} \sim$ $\triangle \mathrm{DBN}$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "## Solution de l'exercice 15"
}
|
f14a8bf4-fa05-59aa-a0d1-71c4b679c8a8
| 607,136
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$ and let $\Gamma$ be its circumcircle. Let $H$ be the orthocenter of $ABC$ and $S$ the midpoint of the arc $\widehat{BC}$ not containing $A$. Let $P$ be the point on $\Gamma$ such that $\widehat{SPH}=90^{\circ}$. Show that there exists a circle passing through $P, S$ and which is tangent to $(AB)$ and $(AC)$.
|
According to the South Pole theorem, $S$ is the intersection point of the bisector of $\widehat{B A C}$ and the perpendicular bisector of $[B C]$. Let $O$ be the center of $\Gamma$ and $N$ the North Pole. Since $[S N]$ is a diameter of $\Gamma$, the condition $\widehat{S P H}=90^{\circ}$ can be rewritten as $P, H, N$ being collinear. We then introduce $Q$ as the intersection point of (AS) and (PN).
Notice that since $\widehat{S P Q}=90^{\circ}$, points $P, S$ lie on the circle with diameter [QS], making it a candidate for the desired circle. We want to show that it is tangent to ( $A B$ ) and ( $A C$ ). Let $M$ be the midpoint of $[Q S]$ and $R$ the orthogonal projection of $M$ onto $[A C]$. The goal is to show that $R$ lies on the circle with diameter $[Q S]$, so that we have tangency with (AC) (and by symmetry, tangency with (AB)).
Let $D$ be the midpoint of $[B C]$. We know that (HD) and $(A O)$ intersect on $\Gamma$, and that $(A H) \parallel (O M)$ (both are perpendicular to ( $B C$ )), so by the midline theorem, $A H=2 O D$. By the central angle theorem, $\widehat{S O C}=60^{\circ}$, so $\triangle SOC$ is equilateral $(\mathrm{OS}=\mathrm{OC})$, and thus $2 \mathrm{OD}=\mathrm{OS}=\mathrm{OC}=\mathrm{ON}$. Furthermore, since $(A H) \parallel (N S)$, by the theorem of Thales, $\frac{A Q}{S Q}=\frac{A H}{N S}=\frac{1}{2}$, so $Q S=2 A Q$.
In particular, $M Q=M S=\frac{Q S}{2}=A Q$. Since $\widehat{M A R}=30^{\circ}$, $M R=\frac{1}{2} A M=M Q$ (since $\sin \left(30^{\circ}\right)=\frac{1}{2}$), so $R$ is indeed on the circle with diameter [QS], making it tangent to (AC) (at $R$).
Therefore, there exists a circle passing through $P, S$ and tangent to $(A B)$ and $(A C)$: the circle with diameter [QS].
Comment from the graders: The exercise was very well done by those who submitted it. Knowledge of the Euler line or the clever use of the South Pole theorem could have shortened some proofs.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$ et soit $\Gamma$ son cercle circonscrit. Soient H l'orthocentre de $A B C$ et $S$ le milieu de l'arc $\widehat{B C}$ ne contenant pas $A$. Soit $P$ le point de $\Gamma$ tel que $\widehat{S P H}=90^{\circ}$. Montrer qu'il existe un cercle passant par $P, S$ et qui est tangent à ( $A B$ ) et ( $A C$ ).
|
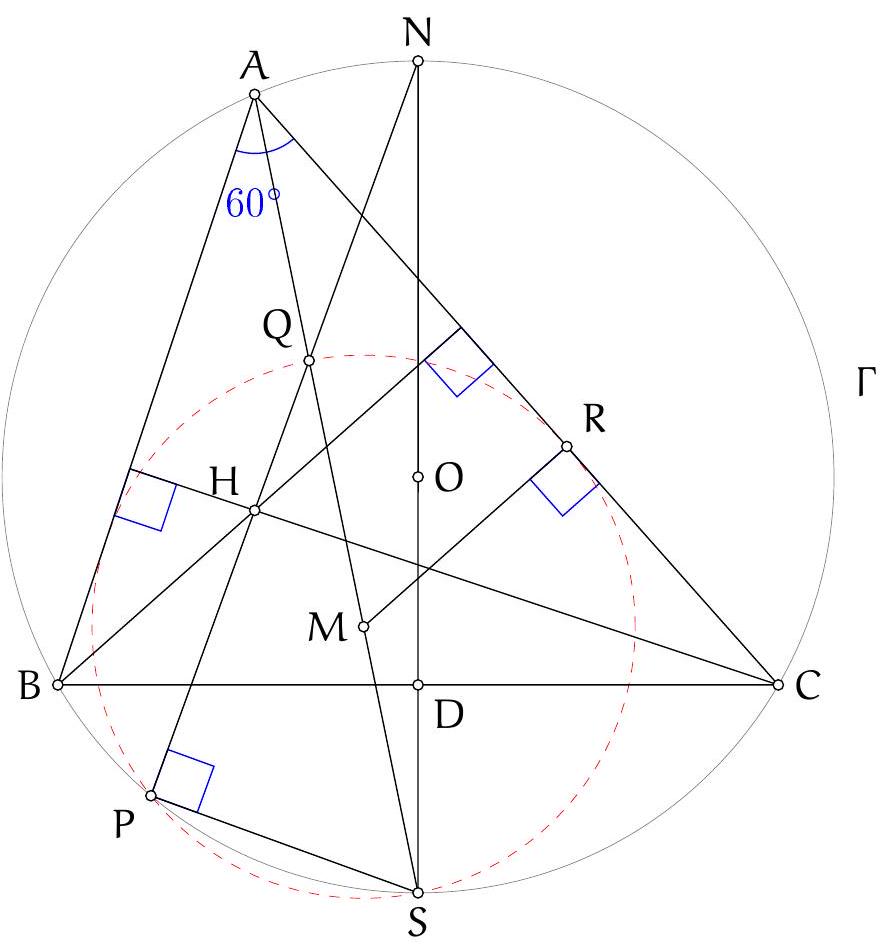
D'après le théorème du pôle Sud, $S$ est le point de concours de la bissectrice de $\widehat{B A C}$ et de la médiatrice de $[B C]$. Soit $O$ le centre de $\Gamma$ et $N$ le pôle Nord. Comme $[S N]$ est un diamètre de $\Gamma$, la condition $\widehat{S P H}=90^{\circ}$ se réécrit $P, H, N$ alignés. Introduisons alors $Q$ le point d'intersection de (AS) et (PN).
Remarquons que comme $\widehat{S P Q}=90^{\circ}, \mathrm{P}, \mathrm{S}$ se situent sur le cercle de diamètre [QS], c'est donc un candidat pour être le cercle recherché. On aimerait montrer qu'il est tangent à ( $A B$ ) et à ( $A C$ ). Posons $M$ le milieu de $[Q S]$ et $R$ le projeté orthogonal de $M$ sur $[A C]$. Le but est de montrer que $R$ est sur le cercle de diamètre $[Q S]$, de sorte à avoir la tangence avec (AC) (et pour des raisons de symétrie on aura la tangence avec (AB)).
Soit D le milieu de $[B C]$. On sait que (HD) et $(A O)$ se coupent sur $\Gamma$, et que $(A H) / /(O M)$ (les deux sont perpendiculaires à ( $B C$ ), donc par droite des milieux $A H=2 O D$. Or par angle au centre, $\widehat{S O C}=60^{\circ}$ donc SOC est équilatéral $(\mathrm{OS}=\mathrm{OC})$, et donc $2 \mathrm{OD}=\mathrm{OS}=\mathrm{OC}=\mathrm{ON}$. De plus, comme $(A H) / /(N S)$, d'après le théorème de Thalès, $\frac{A Q}{S Q}=\frac{A H}{N S}=\frac{1}{2}$ donc $Q S=2 A Q$.
En particulier $M Q=M S=\frac{Q S}{2}=A Q$. Or $\widehat{M A R}=30^{\circ}$ donc $M R=\frac{1}{2} A M=M Q$ (en effet $\sin \left(30^{\circ}\right)=\frac{1}{2}$ ), donc R est bien sur le cercle de diamètre [QS], donc ce dernier est tangent à (AC) (en R).
Donc il existe bien un cercle passant par $P, S$ et qui est tangent à $(A B)$ et $(A C)$ : le cercle de diamètre [QS].
Commentaire des correcteurs : L'exercice était très bien réussi par ceux qui l'ont rendu, la connaissance de la droite d'Euler ou l'utilisation astucieuse du théroème du pole sud pouvait raccoucir certaines
preuves.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "## Solution de l'exercice 16"
}
|
731dad0b-0202-58a7-9a29-7c76e72c1603
| 607,137
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. Let $d$ be the line parallel to $(BC)$ passing through $O$. Let $A'$ be the symmetric point of $A$ with respect to $(BC)$. The line parallel to $(A'B)$ passing through $C$ intersects $d$ at $C_1$, and the lines $(A'C)$ and $(BC_1)$ intersect at $C_2$. The line parallel to $(A'C)$ passing through $B$ intersects $d$ at $B_1$, and the lines $(A'B)$ and $(CB_1)$ intersect at $B_2$. Show that the points $A, A', B_2, C_2$ are concyclic.
|
Let $P$ be the intersection point of the lines $(C B_{1})$ and $(B C_{1})$, and $Q$ the intersection point of $(B B_{1})$ and $(C C_{1})$. We also set $T$ as the intersection of $(A O)$ and $(B C)$. We can then observe several properties of the figure, which we will prove.
- Lemma 1: The point $Q$ is on the circumcircle of $A B C$.
Proof: By the construction of $B_{1}, C_{1}, A^{\prime}$, $BQC$ is a parallelogram, so $\widehat{BQC} = \widehat{CA^{\prime}B}$. But by symmetry, $\widehat{CA^{\prime}B} = \widehat{BAC}$. Therefore, $\widehat{BAC} = \widehat{BQC}$: by the inscribed angle theorem, $Q$ is indeed on the circumcircle of $A B C$.
- Lemma 2: The points $P, Q, A^{\prime}$ are collinear.
Proof: The quadrilateral $BCC_{1}B_{1}$ is a trapezoid, so the line $(PQ)$ passes through the midpoints of $[B_{1}C_{1}]$ and $[BC]$. Therefore, the line $(PQ)$ passes through the midpoint of $[BC]$. Since $A^{\prime}BQC$ is a parallelogram, $(QA^{\prime})$ also passes through the midpoint of $[BC]$. We conclude that $Q, P, A^{\prime}$ are collinear.
- Lemma 3: The points $O, P, T$ are collinear.
Proof: Consider the symmetry with respect to the perpendicular bisector of $[BC]$: it fixes $O$, it swaps $B$ and $C$. It also swaps $A$ and $Q$, indeed $\widehat{Q_{CB}} = \widehat{A^{\prime}BC} = \widehat{CBA}$ by parallelism and symmetry, and $\widehat{CBQ} = \widehat{ACB}$. Now let $X$ be the intersection of $(AB)$ with $d$, and $Y$ the intersection of $(AC)$ with $d$. Since $d$ is invariant under the symmetry, the symmetry swaps $B_{1}$ and $Y$, $C_{1}$ and $X$. We deduce that $\frac{OB_{1}}{OC_{1}} = \frac{OY}{OX}$. Applying the theorem of Thales, we get $\frac{OY}{OX} = \frac{TC}{TB}$, hence $\frac{TC}{TB} = \frac{OB_{1}}{OC_{1}}$. This implies that $O, P, T$ are collinear (applying Thales in $OC_{1}PBT^{\prime}$ and in $OB_{1}BCT^{\prime}$ where $T^{\prime}$ is the intersection of $(OP)$ and $(BC)$, we get $\frac{TB}{TC} = \frac{T^{\prime}B}{T^{\prime}C}$, hence $T = T^{\prime}$). Therefore, $O, P, T$ (and thus $A, O, P, T$) are collinear.
- Lemma 4: The homothety with center $P$ and ratio $-\frac{PT}{PO}$ maps $QBC$ to $A^{\prime}C_{2}B_{2}$.
Proof: According to the theorem of Thales in $QCPB_{2}A^{\prime}$ and in $QBPC_{2}A^{\prime}$, we have $\frac{PQ}{PA^{\prime}} = \frac{PC}{PB_{2}} = \frac{PB}{PC_{2}}$, so the homothety with center $P$ that maps $Q$ to $A^{\prime}$ also maps $B$ to $C_{2}$ and $C$ to $B_{2}$. It remains to show that it maps $O$ to $T$. From the theorem of Thales in $QC_{1}PBA^{\prime}$ and then in $OC_{1}PBT$, we have $\frac{PQ}{PA^{\prime}} = \frac{PC_{1}}{PB} = \frac{PO}{PT}$, so it is indeed the homothety with ratio $-\frac{PT}{PO}$.
- We now have all the elements to conclude: the homothety of Lemma 4 maps $QBC$ to $A^{\prime}C_{2}B_{2}$ and $O$ to $T$. By Lemma 1, $O$ is the center of the circumcircle of $QBC$. Therefore, $T$ is the center of the circumcircle of $A^{\prime}C_{2}B_{2}$. Since $T$ is on $(BC)$, we have $TA = TA^{\prime}$, so $A$ is on the circle with center $T$ and radius $TA^{\prime}$. Finally, we have shown that $A, A^{\prime}, B_{2}, C_{2}$ are concyclic, and we have even found the center of the circle in question, which is $T$.
Comment from the graders: The problem is well solved by a good number of students. The solutions show a very good mastery of the concept of homothety, which allows the problem to be told in a sometimes very efficient way, revealing the roles of the different points, where other students have proposed more down-to-earth (ratio calculations) or more abstract (dynamic solution) approaches.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et $O$ le centre de son cercle circonscrit. Soit d la parallèle à (BC) passant par $O$. Soit $A^{\prime}$ le symétrique de $A$ par rapport à ( $B C$ ). La parallèle à ( $A^{\prime} B$ ) passant par $C$ coupe d en $C_{1}$, et les droites $\left(A^{\prime} C\right)$ et $\left(B C_{1}\right)$ s'intersectent en $C_{2}$. La parallèle à ( $A^{\prime} C$ ) passant par $B$ coupe $d$ en $B_{1}$, et les droites $\left(A^{\prime} B\right)$ et $\left(C B_{1}\right)$ s'intersectent en $B_{2}$. Montrer que les points $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques.
|
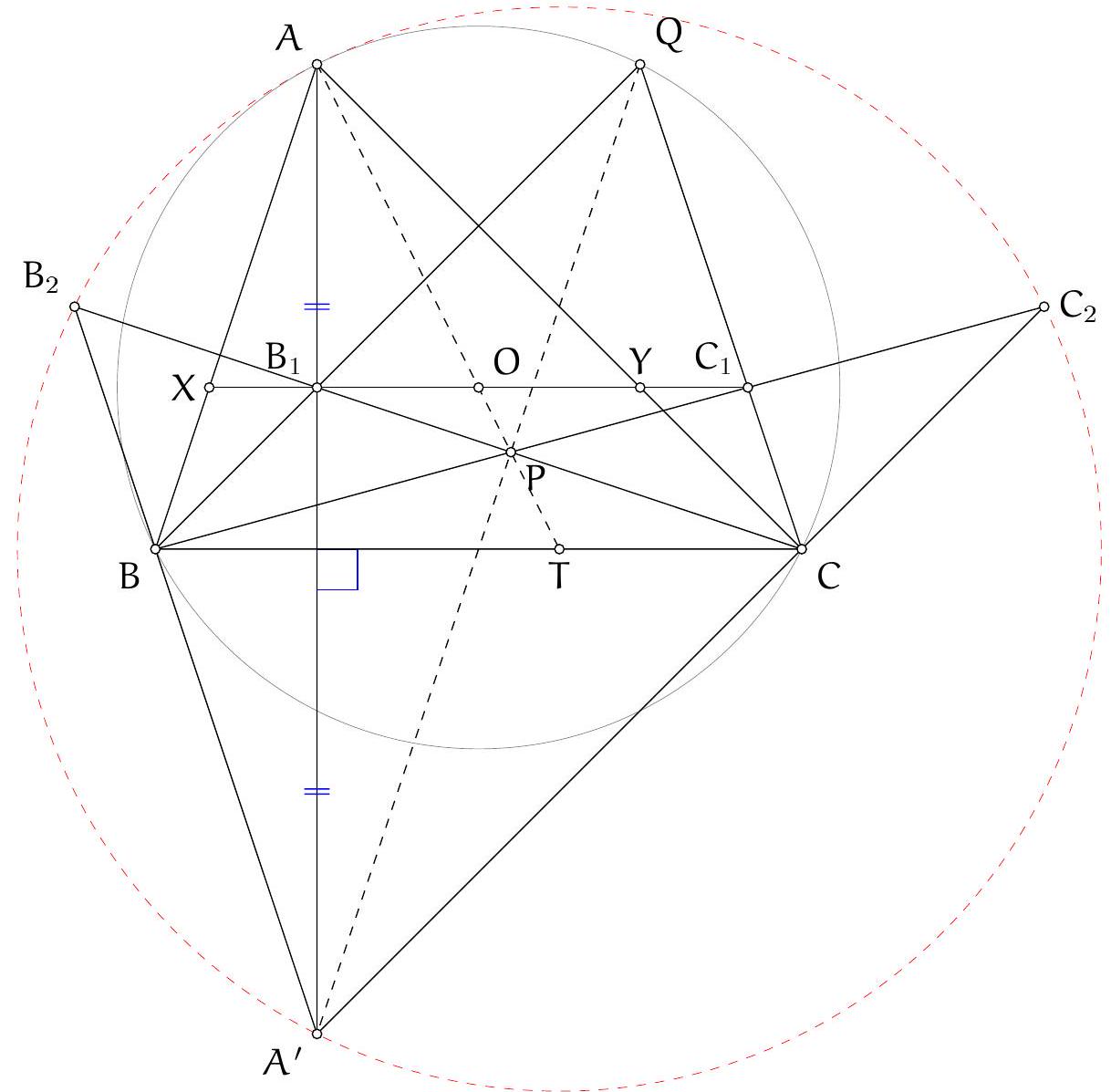
On pose $P$ le point d'intersection des droites $\left(C B_{1}\right)$ et $\left(B C_{1}\right)$, et $Q$ le point d'intersection de $\left(B B_{1}\right)$ et $\left(C C_{1}\right)$. On pose également Tl'intersection de $(A O)$ et ( $\left.B C\right)$. On peut alors remarquer plusieurs propriétés sur la figure, qu'on va montrer.
- Lemme 1: Le point $Q$ est sur le cercle circonscrit à $A B C$.
Preuve : Par construction de $\mathrm{B}_{1}, \mathrm{C}_{1}, \mathrm{~A}^{\prime} \mathrm{BQC}$ est un parallélogramme, donc $\widehat{\mathrm{BQC}}=\widehat{\mathrm{CA}^{\prime} \mathrm{B}}$. Mais par symétrie, $\widehat{C A^{\prime} B}=\widehat{B A C}$. Donc $\widehat{B A C}=\widehat{B_{Q C}}$ : par angle inscrit, $Q$ est bien sur le cercle circonscrit à $A B C$.
- Lemme 2: Les points $P, Q, A^{\prime}$ sont alignés.
Preuve : Le quadrilatère $\mathrm{BCC}_{1} \mathrm{~B}_{1}$ est un trapèze, donc la droite (PQ) passe par les milieux respectifs de $\left[B_{1} C_{1}\right]$ et $[B C]$. Donc la droite (PQ) passe par le milieu de $[B C]$. Or $A^{\prime} B Q C$ est un parallélogramme, donc $\left(Q A^{\prime}\right)$ passe également par le milieu de $[B C]$. On en déduit bien que $Q, P, A^{\prime}$ sont alignés.
- Lemme 3: Les points O, P, T sont alignés.
Preuve : Considérons la symétrie par rapport à la médiatrice de $[\mathrm{BC}]$ : elle fixe O , elle échange B et $C$. Elle échange également $A$ et $Q$, en effet $\widehat{Q_{C B}}=\widehat{A^{\prime} B C}=\widehat{C B A}$ par parallélisme et symétrie puis
$\widehat{C B Q}=\widehat{A C B}$. On pose à présent $X$ l'intersection de $(A B)$ avec $d$, et $Y$ l'intersection de $(A C)$ avec $d$. Alors comme $d$ est invariante par la symétrie, la symétrie échange $B_{1}$ et $Y, C_{1}$ et $X$. On en déduit que $\frac{\mathrm{OB}_{1}}{\mathrm{OC}_{1}}=\frac{\mathrm{OY}}{\mathrm{OX}}$. Or en appliquant le théorème de Thalès, on obtient $\frac{\mathrm{OY}}{\mathrm{OX}}=\frac{\mathrm{TC}}{\mathrm{TB}}$, d'où $\frac{\mathrm{TC}}{\mathrm{TB}}=\frac{\mathrm{OB}_{1}}{O C_{1}}$. Ceci entraîne $O, P, T$ alignés (en appliquant Thalès dans $\mathrm{OC}_{1} \mathrm{PBT}^{\prime}$ et dans $\mathrm{OB}_{1} \mathrm{BCT}^{\prime}$ où $\mathrm{T}^{\prime}$ est l'intersection de $(O P)$ et $(B C)$, on obtient $\frac{T B}{T C}=\frac{T^{\prime} B}{T^{\prime} C}$, d'où $T=T^{\prime}$ ). On a donc bien montré que $O, P, T$ (et donc $A, O, P, T)$ sont alignés.
- Lemme 4 : L'homothétie de centre P et de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$ envoie $\mathrm{QBC} \operatorname{sur} \mathrm{A}^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$.
Preuve: D'après le théorème de Thalès dans $\mathrm{QCPB}_{2} A^{\prime}$ et dans $\mathrm{QBPC}_{2} \mathrm{~A}^{\prime}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}}{\mathrm{PB}_{2}}=\frac{\mathrm{PB}}{\mathrm{PC}_{2}}$, donc l'homothétie de centre $P$ qui envoie $Q$ sur $A^{\prime}$ envoie également $B$ sur $C_{2}$ et $C$ sur $B_{2}$. Il reste à montrer qu'elle envoie O sur T . Or, d'après le théorème de Thalès dans $\mathrm{QC}_{1} \mathrm{PBA}^{\prime}$ puis dans $\mathrm{OC}_{1} \mathrm{PBT}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}_{1}}{\mathrm{~PB}}=\frac{\mathrm{PO}}{\mathrm{PT}}$, donc c'est bien l'homothétie de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$.
- On a à présent tous les éléments pour conclure : l'homothétie du lemme 4 envoie QBC sur $A^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$ et O sur T. Or par le lemme 1, O est le centre du cercle circonscrit de QBC. Donc T est le centre du cercle circonscrit de $A^{\prime} C_{2} B_{2}$. Mais comme $T$ est sur $(B C)$, on a $T A=T A^{\prime}$ donc $A$ est sur le cercle de centre $T$ et de rayon $T A^{\prime}$. Finalement, on a bien montré que $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques, et on a même trouvé le centre du cercle en question, qui est $T$.
Commentaire des correcteurs : Le problème est bien résolu par un bon nombre d'élèves. Les rédactions montrent une très bonne maitrise de la notion d'homothétie, qui permet de raconter l'exercice de façon parfois très efficace, avec le mérite de dévoiler les rôles des différents points, là où d'autres élèves ont proposé des approches plus terre-à-terre (des calculs de rapport) ou plus abstraites (solution en dynamique).
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "## Solution de l'exercice 17"
}
|
213a1554-259e-506f-9156-3aa00895fe57
| 607,138
|
Let $ABC$ be a triangle, with $AC > AB$, and $\Gamma$ its circumcircle. Let $T$ be the intersection point of the tangent to $\Gamma$ at $A$ with $(BC)$. Let $M$ be the midpoint of $[BC]$ and $R$ the symmetric point of $A$ with respect to $B$. Let $S$ be the point such that $SABT$ is a parallelogram. The parallel to $(AB)$ passing through $M$ intersects $(SB)$ at $P$. Suppose that $P$ is on $\Gamma$, show that $(AC)$ is tangent to the circumcircle of $SRT$.
|
Let $N$ be the intersection point of $(A T)$ and $(B S)$. We have $(P M) \parallel (A B) \parallel (S T)$, so by Thales' theorem, $\frac{B P}{B S}=\frac{B M}{B T}$. Then $\frac{B P}{B N}=\frac{B P}{\frac{B S}{2}}=2 \frac{B P}{B S}=\frac{2 B M}{B T}=\frac{B C}{B T}$, so by the converse of Thales' theorem, $(N T)$ and $(P C)$ are parallel. We then have:
\[
\begin{aligned}
\widehat{S A^{\prime} P} & =\widehat{A A^{\prime} P} \\
& =\widehat{A C P} \text{ by inscribed angle } \\
& =\widehat{A C B}+\widehat{B C P} \\
& =\widehat{\mathrm{TAB}}+\widehat{B T A} \text{ by tangent angle and alternate interior angles } \\
& =\widehat{\mathrm{CBA}} \\
& =\widehat{\mathrm{SAB}} \text{ by alternate interior angles. }
\end{aligned}
\]
Therefore, by corresponding angles, $(A B)$ and $(A^{\prime} P)$ are parallel. Since $(A B)$ and $(M P)$ are parallel, it follows that $P, M, A^{\prime}$ are collinear.
We deduce that $B T=B S, B M=B P$. Indeed:
\[
\begin{aligned}
\widehat{\mathrm{TSB}} & =\widehat{\mathrm{BPA}^{\prime}} \text{ by alternate interior angle } \\
& =\widehat{\mathrm{AA}^{\prime} \mathrm{P}} \text{ because } A A^{\prime} \mathrm{PB} \text{ is an isosceles trapezoid } \\
& =\widehat{\mathrm{CMA}^{\prime}} \text{ by alternate interior angle } \\
& =\widehat{\mathrm{BTS}^{2}} \text{ by corresponding angles. }
\end{aligned}
\]
Thus, $B T=B S$, and since $(S T) \parallel (P M)$, then $B P=B M$ as well.
Notably, STRA is an isosceles trapezoid and therefore cyclic, so $A$ is on (SRT). Moreover, $\widehat{N A B}=\widehat{A C B}$ by tangent angle, and $\widehat{A B N}=\widehat{\mathrm{BST}}=\widehat{\mathrm{STB}}=\widehat{\mathrm{CBA}}$ by alternate interior and corresponding angles. Therefore, $B A N \sim B C A$. In particular, $\widehat{B N A}=\widehat{B A C}$, so by the converse of the tangent angle, $(AC)$ is tangent to $(ANB)$.
An homothety centered at $A$ with a factor of 2 sends $N$ to $T$, $B$ to $R$, fixes $A$, and sends $(A N B)$ to the circle $(A T R)=(S R T)$, and it fixes $(A C)$. Therefore, $(S R T)$ is tangent to $(AC)$ (homotheties preserve tangency), which concludes.
Remark. The condition "We assume that $P$ is on $\Gamma^{\prime \prime}$" is difficult to draw. In fact, since $(A B)$ is parallel to $(A^{\prime} M)$ and $(A A^{\prime})$ is parallel to $(B C)$, $A A^{\prime} M B$ is a parallelogram, so $A M=A^{\prime} M=A B$. Thus, $A B M$ is isosceles at $A$. This means that the projection of $A$ onto $[B C]$ is the midpoint of $[B M]$, so the abscissa of $A$ on $[B C]$ is one quarter of the segment (starting from $B$), and conversely, such a position of $A$ implies that $P$ is on $\Gamma$. This is the condition that allows us to draw the figure.
Remark. One can show that $P$ and $M$ also lie on the circumcircle of SRT, using the fact that TSAM is an isosceles trapezoid, and then that AMPR is an isosceles trapezoid.
Comment from the graders: The problem was difficult and was solved using very different methods (barycentric, homothety, harmonic points, etc.). The solutions submitted were almost all complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, avec $A C>A B$, et $\Gamma$ son cercle circonscrit. Soit $T$ le point d'intersection de la tangente à $\Gamma$ en $A$ avec (BC). Soient $M$ le milieu de $[B C]$ et $R$ le symétrique de $A$ par rapport à $B$. Soit $S$ le point tel que $S A B T$ est un parallélogramme. La parallèle à ( $A B$ ) passant par $M$ coupe (SB) en $P$. On suppose que $P$ est sur $\Gamma$, montrer que ( $A C$ ) est tangente au cercle circonscrit à SRT.
|
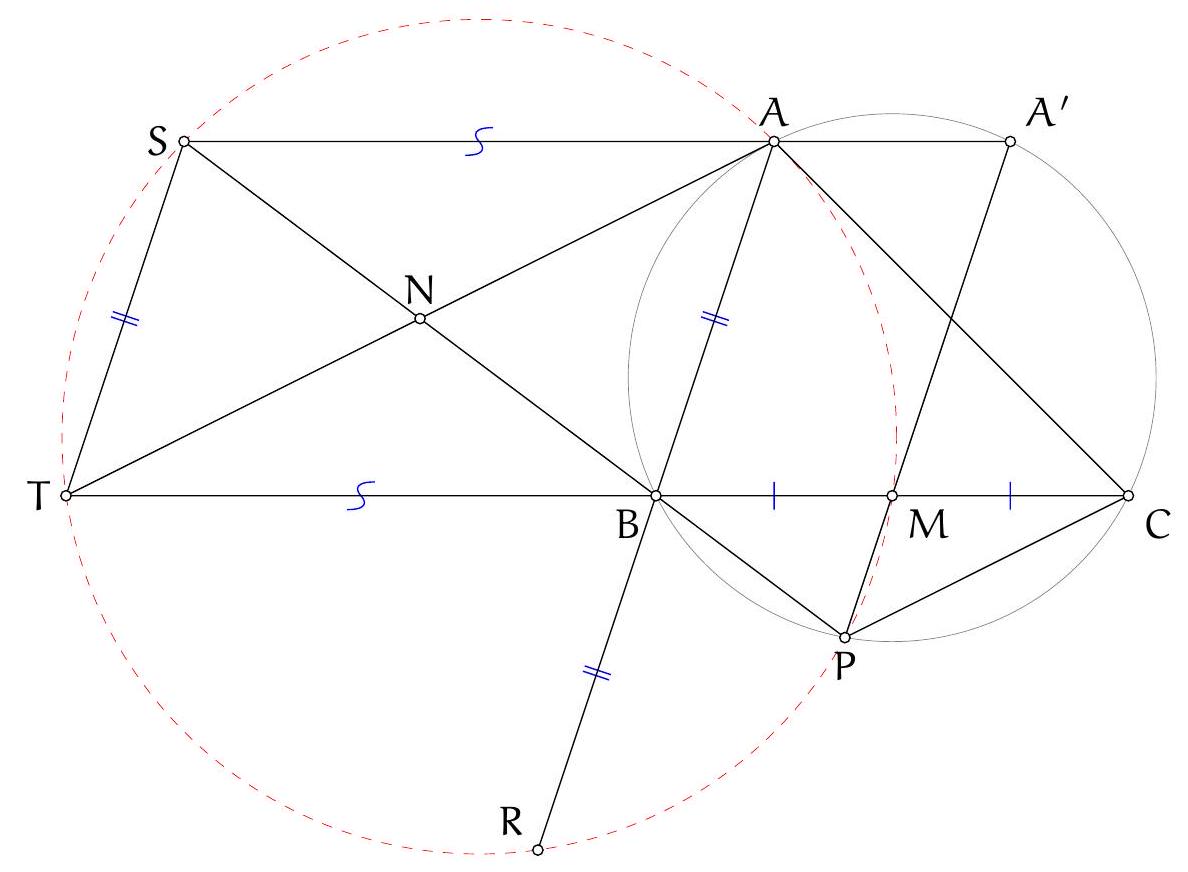
Soit $N$ le point d'intersection de $(A T)$ et ( $B S)$. On a $(P M) / /(A B) / /(S T)$ donc d'après le théorème de Thalès, $\frac{B P}{B S}=\frac{B M}{B T}$. Alors $\frac{B P}{B N}=\frac{B P}{\frac{B S}{2}}=2 \frac{B P}{B S}=\frac{2 B M}{B T}=\frac{B C}{B T}$, donc d'après la réciproque du théorème de Thalès, (NT) et (PC) sont parallèles. On a alors :
$$
\begin{aligned}
\widehat{S A^{\prime} P} & =\widehat{A A^{\prime} P} \\
& =\widehat{A C P} \text { par angle inscrit } \\
& =\widehat{A C B}+\widehat{B C P} \\
& =\widehat{\mathrm{TAB}}+\widehat{B T A} \text { par angle tangentiel et angles alternes-internes } \\
& =\widehat{\mathrm{CBA}} \\
& =\widehat{\mathrm{SAB}} \text { par angles alternes-internes. }
\end{aligned}
$$
Donc par angle correspondant, $(A B)$ et ( $A^{\prime} P$ ) sont parallèles. Or $(A B)$ et (MP) sont parallèles. Il découle que $P, M, A^{\prime}$ sont alignés.
On en déduit donc que $B T=B S, B M=B P$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{TSB}} & =\widehat{\mathrm{BPA}^{\prime}} \text { par angle alterne-interne } \\
& =\widehat{\mathrm{AA}^{\prime} \mathrm{P}} \text { car } A A^{\prime} \mathrm{PB} \text { trapèze isocèle } \\
& =\widehat{\mathrm{CMA}^{\prime}} \text { par angle alterne-interne } \\
& =\widehat{\mathrm{BTS}^{2}} \text { par angle correspondants. }
\end{aligned}
$$
Donc $B T=B S$, et comme $(S T) / /(P M)$, alors $B P=B M$ de même.
Notamment STRA est un trapèze isocèle donc cyclique donc $A$ est sur (SRT). De plus, $\widehat{N A B}=\widehat{A C B}$ par angle tangentiel, et $\widehat{A B N}=\widehat{\mathrm{BST}}=\widehat{\mathrm{STB}}=\widehat{\mathrm{CBA}}$ par angle alterne-interne et correspondant. Donc $B A N \sim B C A$. En particulier $\widehat{B N A}=\widehat{B A C}$, donc par réciproque de l'angle tangentiel, (AC) est tangente à (ANB).
Or une homothétie de centre $A$ et de facteur 2 envoie N sur T , B sur R, fixe $A$ donc envoie ( $A N B$ ) sur le cercle $(A T R)=(S R T)$, et elle fixe $(A C)$. Donc $(S R T)$ est bien tangent à (AC) (les homothéties préservent les tangences), ce qui conclut.
Remarque. La condition "On suppose que $P$ est sur $\Gamma^{\prime \prime}$ est difficile à tracer. En fait, comme $(A B)$ est parallèle à $\left(A^{\prime} M\right)$ et $\left(A A^{\prime}\right)$ parallèle à $(B C), A A^{\prime} M B$ est un parallélogramme donc $A M=A^{\prime} M=A B$. Ainsi $A B M$ est isocèle en $A$. Cela signifie que le projeté de $A$ sur $[B C]$ est le milieu de $[B M]$, donc que l'abscisse de $A$ sur $[B C]$ est au quart du segment (en partant de $B$ ), et réciproquement une telle position de $A$ entraîne que $P$ est sur $\Gamma$. C'est donc la condition qui nous permet de tracer la figure.
Remarque. On peut montrer que $P$ et $M$ se situent aussi sur le cercle circonscrit à SRT, en utilisant que TSAM est un trapèze isocèle, puis que AMPR est un trapèze isocèle.
Commentaire des correcteurs : L'exercice était difficile, et a été traité avec des méthodes très différentes (barycentrique, homothétie, points harmoniques,...). Les solutions rendues étaient quasiment toutes complètes.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"problem_match": "\nExercice 18.",
"solution_match": "## Solution de l'exercice 18"
}
|
2b973e21-1a7e-5215-b5b0-68629ae60820
| 607,139
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. We denote $A'$ as the point diametrically opposite to $A$ on the circle $\Omega$. Let $I$ be the center of the incircle of triangle $ABC$, $E$ and $F$ the points of tangency of the incircle with the sides $AC$ and $AB$ respectively. The circumcircle of triangle $AEF$ intersects the circle $\Omega$ at point $X$. Show that the points $A'$, $I$, and $X$ are collinear.
|
Since $F$ is the point of tangency of the incircle with the side $[A C]$, the angle $\widehat{I F A}$ is a right angle and the segment $[I A]$ is a diameter of the circumcircle of triangle $A E F$. We deduce that
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
where we have used that $\left[A A^{\prime}\right]$ is a diameter of the circumcircle of triangle $A B C$.
We deduce that the points $A^{\prime}$, I and $X$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $\mathcal{A}$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $A^{\prime}$, I et $X$ sont alignés.
|
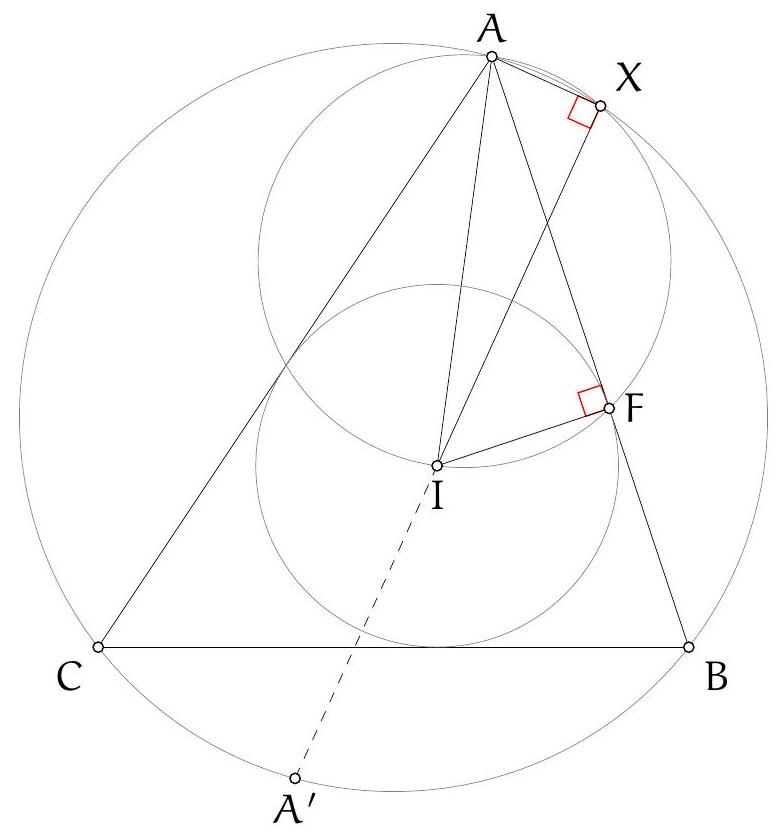
Puisque $F$ est le point de contact du cercle inscrit avec le côté $[A C$, l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
9e852d9c-4f41-5992-983b-62dd54f922a4
| 607,140
|
$2 \mathrm{n}-1$ rooks are placed on a $(2 n-1) \times(2 n-1)$ chessboard so that no two rooks are ever on the same row or column. Show that every $\mathrm{n} \times \mathrm{n}$ square contains a rook.
|
Let's start by noting that there is exactly one tower per row and per column. Indeed, by hypothesis, there is at most one tower per row. And since there are $2 \mathrm{n}-1$ towers in total, there must be exactly one per row, and similarly for the columns. By slightly adapting the reasoning, we can assume that the $\mathrm{n} \times \mathrm{n}$ square is that of the cells located in the top left (i.e., the cells located in the first $n$ rows and the first $n$ columns starting from the top left corner). Suppose, for the sake of contradiction, that this square contains no towers. Then among the first $n$ rows, there must be $n$ towers. However, these $n$ towers must be in the last $\mathrm{n}-1$ columns by hypothesis. By the pigeonhole principle, there will then be two towers in the same column, which is absurd. This concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 n-1) \times(2 n-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les n premières lignes, il doit y avoir n tours. Cependant, ces n tours doivent être dans les $\mathrm{n}-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde. Cela conclut.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
539466d5-436d-53b9-8bad-130a41ac768a
| 607,141
|
Let $a, b$ and $c$ be real numbers such that $0 \leqslant a, b, c \leqslant 2$. Show that
$$
(a-b)(b-c)(a-c) \leqslant 2
$$
|
Note that there are 6 possible orders for the variables $\mathrm{a}, \mathrm{b}$ and c.
In the three cases $b \geqslant a \geqslant c, a \geqslant c \geqslant b$ and $c \geqslant b \geqslant a$, the product $(a-b)(b-c)(c-a)$ is negative, so the inequality is satisfied.
If $a \geqslant b \geqslant c$, the inequality of means applied to $a-b$ and $b-c$ and the fact that $c-a \leqslant 2$ since $a, c \in[0,2]$ gives:
$$
(a-b)(b-c)(a-c) \leqslant\left(\frac{a-b+b-c}{2}\right)^{2}(a-c)=\frac{(a-c)^{3}}{4} \leqslant \frac{2^{3}}{4}=2
$$
Similarly, if $b \geqslant c \geqslant a$, then
$$
(a-b)(b-c)(a-c)=(b-a)(b-c)(c-a) \leqslant(b-a)\left(\frac{b-c+c-a}{2}\right)^{2} \leqslant \frac{(b-a)^{3}}{4} \leqslant 2
$$
And finally, if $c \geqslant a \geqslant b$, then
$$
(a-b)(b-c)(a-c)=(c-b)(c-a)(a-b) \leqslant(c-b)\left(\frac{c-a+a-b}{2}\right)^{2} \frac{(c-b)^{3}}{4} \leqslant 2
$$
Thus, the inequality is true in all cases.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b$ et $c$ des réels tels que $0 \leqslant a, b, c \leqslant 2$. Montrer que
$$
(a-b)(b-c)(a-c) \leqslant 2
$$
|
Notons qu'il y a 6 ordres possibles pour les variables $\mathrm{a}, \mathrm{b}$ et c .
Dans les trois cas $b \geqslant a \geqslant c, a \geqslant c \geqslant b$ et $c \geqslant b \geqslant a$, le produit $(a-b)(b-c)(c-a)$ est négatif, de sorte que l'inégalité est vérifiée.
Si $a \geqslant b \geqslant c$, l'inégalité des moyennes appliquée à $a-b$ et $b-c$ et le fait que $c-a \leqslant 2$ car $a, c \in[0,2]$ donne:
$$
(a-b)(b-c)(a-c) \leqslant\left(\frac{a-b+b-c}{2}\right)^{2}(a-c)=\frac{(a-c)^{3}}{4} \leqslant \frac{2^{3}}{4}=2
$$
De même, si $b \geqslant c \geqslant a$, alors
$$
(a-b)(b-c)(a-c)=(b-a)(b-c)(c-a) \leqslant(b-a)\left(\frac{b-c+c-a}{2}\right)^{2} \leqslant \frac{(b-a)^{3}}{4} \leqslant 2
$$
Et enfin, si $c \geqslant a \geqslant b$, alors
$$
(a-b)(b-c)(a-c)=(c-b)(c-a)(a-b) \leqslant(c-b)\left(\frac{c-a+a-b}{2}\right)^{2} \frac{(c-b)^{3}}{4} \leqslant 2
$$
Si bien que l'inégalité est vraie dans tous les cas.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
dd83ed1d-33ab-5384-9d8a-5427e5959b01
| 607,143
|
Prove, for all strictly positive real numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}$, the following inequality:
$$
\frac{a}{9 b c+1}+\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}} .
$$
|
Given the form of the inequality, one is tempted to apply the Cauchy-Schwarz inequality. However, if we apply the inequality as it is, we get:
$$
\frac{a}{9 b c+1} + \frac{b}{9 c a+1} + \frac{c}{9 a b+1} \geqslant \frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3}
$$
To conclude, we would then need to show that $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}$, but this inequality is not always true.
To make $\mathrm{a}+\mathrm{b}+\mathrm{c}$ appear in the numerator of the right-hand side of the Cauchy-Schwarz inequality, we can, for example, multiply the numerator and the denominator by $a$ in the first fraction of the left-hand side (and similarly with $b$ and $c$ in the other two fractions). This gives, by applying the Cauchy-Schwarz inequality:
$$
\frac{a}{9 b c+1} + \frac{b}{9 c a+1} + \frac{c}{9 a b+1} = \frac{a^{2}}{9 a b c+a} + \frac{b^{2}}{9 a b c+b} + \frac{c^{2}}{9 a b c+c} \geqslant \frac{(a+b+c)^{2}}{27 a b c+a+b+c}.
$$
It then suffices to show that
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}
$$
For this, we can apply the AM-GM inequality $27 \mathrm{abc} \leqslant(\mathrm{a}+\mathrm{b}+\mathrm{c})^{3}$ to obtain:
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{(a+b+c)^{2}}{(a+b+c)^{3}+(a+b+c)} = \frac{(a+b+c)}{(a+b+c)^{2}+1}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Démontrer, pour tous réels $\mathrm{a}, \mathrm{b}, \mathrm{c}$ strictement positifs, l'inégalité suivante :
$$
\frac{a}{9 b c+1}+\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}} .
$$
|
Vu la forme de l'inégalité, on est tenté d'appliquer l'inégalité des mauvais élèves. Seulement, si l'on applique l'inégalité en l'état, on trouve :
$$
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3}
$$
Pour conclure, il faudrait alors montrer que $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}$, mais cette inégalité n'est pas toujours vraie.
Pour faire apparaître $\mathrm{a}+\mathrm{b}+\mathrm{c}$ au numérateur du membre de droite de l'inégalité des mauvais élèves, on peut par exemple multiplier en haut et en bas par a dans la première fraction du membre de gauche (et de même avec b et c dans les deux autres fractions). Ceci donne, en appliquant l'inégalité des mauvais élèves:
$$
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1}=\frac{a^{2}}{9 a b c+a}+\frac{b^{2}}{9 a b c+b} \frac{c^{2}}{9 a b c+c} \geqslant \frac{(a+b+c)^{2}}{27 a b c+a+b+c} .
$$
Il suffit alors de montrer que
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}
$$
Pour cela, on peut appliquer l'inégalité des moyennes $27 \mathrm{abc} \leqslant(\mathrm{a}+\mathrm{b}+\mathrm{c})^{3}$ pour obtenir :
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{(a+b+c)^{2}}{(a+b+c)^{3}+(a+b+c)}=\frac{(a+b+c)}{(a+b+c)^{2}+1}
$$
comme voulu.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
1f3056c7-0e59-5ae1-a6d4-54698fe0bd4d
| 607,145
|
Let $ABC$ be a triangle, $\omega$ its incircle, and $D, E$, and $F$ the points of tangency of $\omega$ with the sides $BC, CA$, and $AB$ respectively. The perpendicular to $(BC)$ at $C$ intersects the line $(EF)$ at $M$, and the perpendicular to $(BC)$ at $B$ intersects the line $(EF)$ at $N$. The line $(DM)$ intersects $\omega$ again at $P$ and the line $(DN)$ intersects $\omega$ again at $Q$. Show that $DP=DQ$.
|
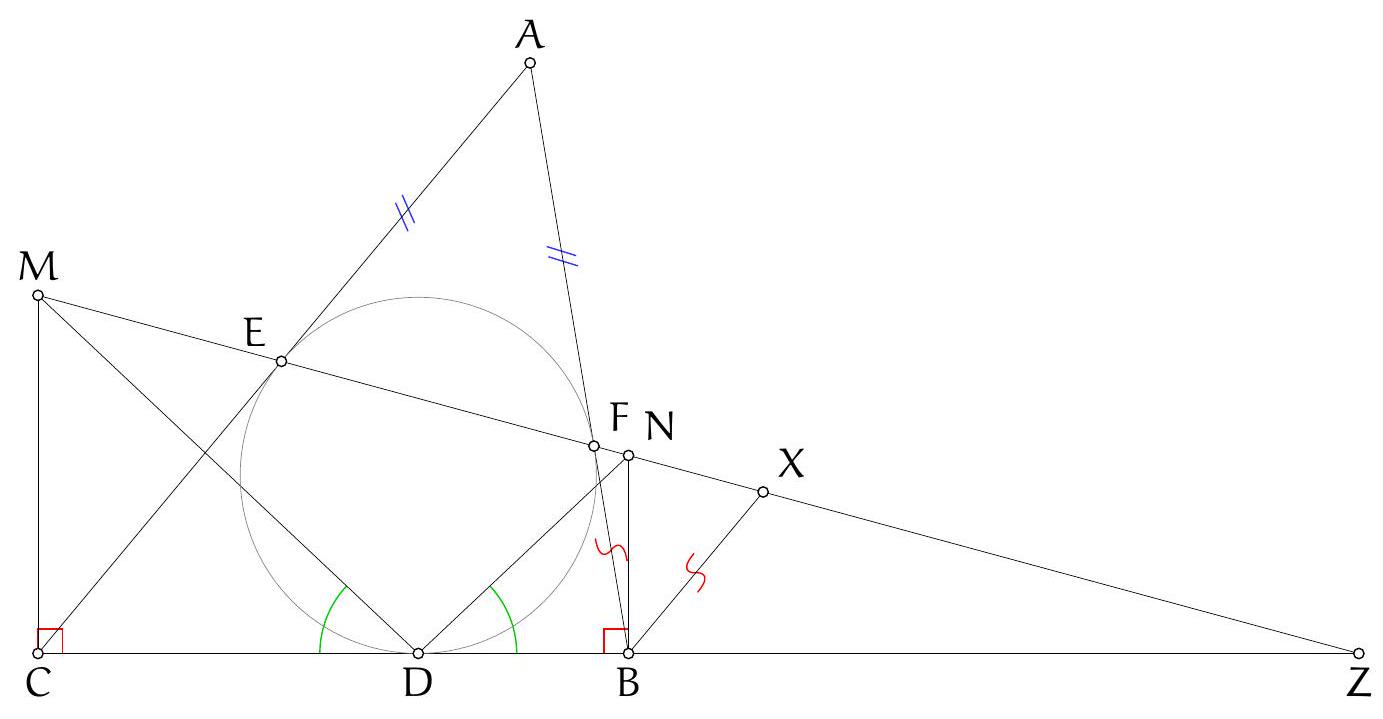
We start by "erasing" the points $P$ and $Q$ from the figure, that is, we reduce the problem to an equivalent statement that does not involve the points $P$ and $Q$.
If the statement is true, then (DI) is the perpendicular bisector of the segment [PQ], so the line (DI) is the angle bisector of $\widehat{MDN}$. Conversely, if we prove that the line (DI) is the angle bisector of $\widehat{MDN}$, the lines (DM) and (DN) will be symmetric with respect to the line (DI). Thus, since the circle $\omega$ and these lines are symmetric with respect to (DI), their intersections are also symmetric, and $P$ and $Q$ will be symmetric with respect to (DI) and $\mathrm{DP}=\mathrm{DQ}$. Therefore, it suffices to show that $\widehat{\mathrm{MDI}}=\widehat{\mathrm{NDI}}$ or, since the lines (DI) and (BC) are perpendicular, $\widehat{MDC}=\widehat{\mathrm{NDB}}$.
This equality is particularly true if the triangles MCD and NBD are similar. Since these two triangles already have a right angle in common, it suffices to show that $\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BN}}{\mathrm{CM}}$.
Let $Z$ be the intersection point of the lines $(BC)$ and $(EF)$ and let $X$ be the intersection point of the line parallel to (AC) passing through B with the line (EF).
The triangles $AEF$ and $FBX$ are then similar, so the triangle $FBX$ is isosceles at $B$. Therefore, using Thales' theorem for the points $E, X, Z$ and $C, B, Z$:
$$
\frac{BD}{CD}=\frac{BF}{CE}=\frac{BX}{CE}=\frac{ZB}{ZC}.
$$
By applying Thales' theorem to the points $M, N, Z$ and $C, B, Z$, we find indeed
$$
\frac{BD}{CD}=\frac{ZB}{ZC}=\frac{BN}{CM},
$$
which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $\omega$ son cercle inscrit et $D, E$ et $F$ les points de contact de $\omega$ avec les côtés $B C, C A$ et $A B$ respectivement. La perpendiculaire à ( $B C$ ) en $C$ coupe la droite ( $E F$ ) en $M$ et la perpendiculaire à (BC) en $B$ coupe la droite (EF) en $N$. La droite ( $D M)$ recoupe $\omega$ en $P$ et la droite $(\mathrm{DN})$ recoupe $\omega$ en Q . Montrer que $\mathrm{DP}=\mathrm{DQ}$.
|

On commence par "éffacer" les points $P$ et $Q$ de la figure, c'est-à-dire qu'on commence par se ramener à un énoncé équivalent au problème original, mais qui n'implique pas les points P et Q .
Si l'énoncé est vrai, alors (DI) est la médiatrice du segment [PQ], de sorte que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$. Réciproquement, si on prouve que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$, les droites (DM) et (DN) seront alors symétriques par rapport à la droite (DI). Ainsi, puisque le cercle $\omega$ et ces droites sont symétriques par rapport à (DI), leurs intersections le sont aussi, et $P$ et Q seront symétriques par rapport à (DI) et $\mathrm{DP}=\mathrm{DQ}$. Il suffit donc de montrer que $\widehat{\mathrm{MDI}}=\widehat{\mathrm{NDI}}$ ou encore, puisque les droites (DI) et (BC) sont perpendiculaires, $\widehat{M D C}=\widehat{\mathrm{NDB}}$.
Cette égalité est en particulier vraie si les triangles MCD et NBD sont semblables. Comme ces deux triangles ont déjà un angle droit en commun, il suffit de montrer que $\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BN}}{\mathrm{CM}}$.
Soit $Z$ le point d'intersection des droites $(B C)$ et $(E F)$ et soit $X$ le point d'intersection de la parallèle à (AC) passant par B avec la droite (EF).
Les triangles $A E F$ et $F B X$ sont alors semblables, ainsi le triangle $F B X$ est isocèle en $B$. On a donc, en utilisant le théorème de Thalès pour les points $E, X, Z$ et $C, B, Z$ :
$$
\frac{B D}{C D}=\frac{B F}{C E}=\frac{B X}{C E}=\frac{Z B}{Z C} .
$$
En appliquant ensuite Thalès aux points $M, N, Z$ et $C, B, Z$, on trouve bien
$$
\frac{B D}{C D}=\frac{Z B}{Z C}=\frac{B N}{C M},
$$
ce qui permet de conclure.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
be854f58-1cd4-5ba9-9e3d-3716a71343a1
| 607,147
|
We have $\mathrm{a}+\mathrm{b}$ bowls aligned in a row. The first $a$ bowls contain an apple, while the last $b$ bowls contain a pear.
An operation consists of moving an apple from bowl $i$ to bowl $i+1$ and a pear from bowl $j$ to bowl $j-1$, where $i$ and $j$ are integers such that $i-j$ is even (A bowl can contain multiple fruits). We want to reach the final situation where the first $b$ bowls contain a pear and the last $a$ bowls contain an apple. Show that this is possible if and only if $ab$ is even.
|
Let's start by showing that it is not possible to achieve the goal when both a and b are odd. Let I be the alternating sum of the number of fruits in the bowls. In the initial and final positions described, we then have $I=0$ because $a+b$ is even. Furthermore, with each operation, I is increased by $\pm 2$ due to the condition $i-j$ being even.
Suppose, for the sake of contradiction, that it is possible to move from the initial position to the final position described. The apples must move from bowls numbered 1 to $a$ to bowls numbered $b+1$ to $a+b$, and during each operation, an apple increases its bowl number by one. Therefore, it takes
$$
\sum_{k=1}^{a}(b+k)-\sum_{k=1}^{a} k=a \cdot b
$$
operations to move from the initial position to the final position, with $ab$ being odd by hypothesis. Thus, when the final position is reached, $\mathrm{I} \equiv 2 \mathrm{ab} \equiv 2(\bmod 4)$, which is absurd because I is zero in the final position described.
Now let's show by induction that it is possible to reach the final position when a or b is even. Without loss of generality, we consider the case where b is even, the other case being directly obtained by symmetry. If $\mathrm{b}=0$, there is nothing to show. Suppose now that the property is true for $\mathrm{b}=\mathrm{n}$ even, and suppose $\mathrm{b}=\mathrm{n}+2$. By the induction hypothesis, by ignoring the last two pears, we can reach in a finite number of operations the situation where we have, in order, n bowls with a pear, then a bowls with an apple, then 2 bowls with a pear. If we perform two operations, between the bowls numbered $\mathfrak{i}=a+n$ and $\mathfrak{j}=a+n+2$, then $\mathfrak{i}=\mathfrak{j}=a+n+1$, the last three bowls now contain, in order: a pear, then a pear, then an apple. We repeat these operations that allow us to swap an apple with the two pears that follow until we reach the desired final situation.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On dispose de $\mathrm{a}+\mathrm{b}$ bols alignés sur une rangée. Les a premiers bols contiennent une pomme tandis que les $b$ derniers bols contiennent une poire.
Une opération consiste à déplacer une pomme du bol $i$ au bol $i+1$ et une poire du bol $j$ au bol $j-1$, où $i$ et $j$ sont deux entiers tels que $i-j$ est pair (Un bol peut contenir plusieurs fruits). On souhaite arriver à la situation finale où les $b$ premiers bols contiennent une poire et les $a$ derniers bols contiennent une pomme. Montrer que c'est possible si et seulement si ab est pair.
|
Commençons par montrer qu'il n'est pas possible d'y arriver lorsque a et b sont impairs tous les deux. Soit I la somme alternée des nombres de fruits dans les bols. Dans les positions initiales et finales décrites, on a alors $I=0$ car $a+b$ est pair. En outre, lors de chaque opération, I est augmenté de $\pm 2$ à cause de la condition $i-j$ pair.
Supposons par l'absurde qu'il soit possible de passer de la position intiale à la position finale décrite. Les pommes doivent passer des bols de numéros 1 à $a$ vers les bols de numéros $b+1$ à $a+b$, et au cours de chaque opération, une pomme augmente de un le numéro de son bol. Il faut donc
$$
\sum_{k=1}^{a}(b+k)-\sum_{k=1}^{a} k=a \cdot b
$$
opérations pour passer de la position initiale à la position finale, avec ab impair par hypothèse. Ainsi, lorsque la position finale est atteinte, $\mathrm{I} \equiv 2 \mathrm{ab} \equiv 2(\bmod 4)$, ce qui est absurde car I est nul dans la position finale décrite.
Montrons maintenant par récurrence qu'il est possible de parvenir à la position finale lorsque a ou b est pair. Sans perte de généralité, nous traitons le cas où b est pair, l'autre cas s'obtenant directement par symétrie. Si $\mathrm{b}=0$, il n'y a rien à montrer. Supposons maintenant que la propriété soit vraie pour $\mathrm{b}=\mathrm{n}$ pair, et supposons $\mathrm{b}=\mathrm{n}+2$. Par hypothèse de récurrence, en ignorant les deux dernières poires, nous pouvons arriver en un nombre fini d'opérations à la situation où nous avons, dans l'ordre, n bols avec une poire, puis a bols avec une pomme, puis 2 bols avec une poire. Si nous faisons deux opérations, entre les bols de numéros $\mathfrak{i}=a+n$ et $\mathfrak{j}=a+n+2$, puis $\mathfrak{i}=\mathfrak{j}=a+n+1$, les trois derniers bols contiennent maintenant dans l'ordre : une poire puis une poire puis une pomme. On réitère ces opérations permettant d'échanger une pomme avec les deux poires qui suivent jusqu'à arriver à la situation finale désirée.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
b8fb343f-306d-5b18-b2a6-fd92e166bd12
| 607,148
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. We denote $A^{\prime}$ as the point diametrically opposite to $A$ on the circle $\Omega$. Let $I$ be the center of the incircle of triangle $ABC$, $E$ and $F$ the points of tangency of the incircle with the sides $AC$ and $AB$ respectively. The circumcircle of triangle $AEF$ intersects the circle $\Omega$ at point $X$. Show that the points $\mathcal{A}^{\prime}$, $I$, and $X$ are collinear.
|
Since $F$ is the point of tangency of the incircle with side $[AC]$, the angle $\widehat{I F A}$ is a right angle and the segment $[I A]$ is a diameter of the circumcircle of triangle $A E F$. We deduce that
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
where we have used that $\left[A A^{\prime}\right]$ is a diameter of the circumcircle of triangle $A B C$.
We deduce that the points $A^{\prime}$, I, and $X$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $A$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $\mathcal{A}^{\prime}$, I et $X$ sont alignés.
|
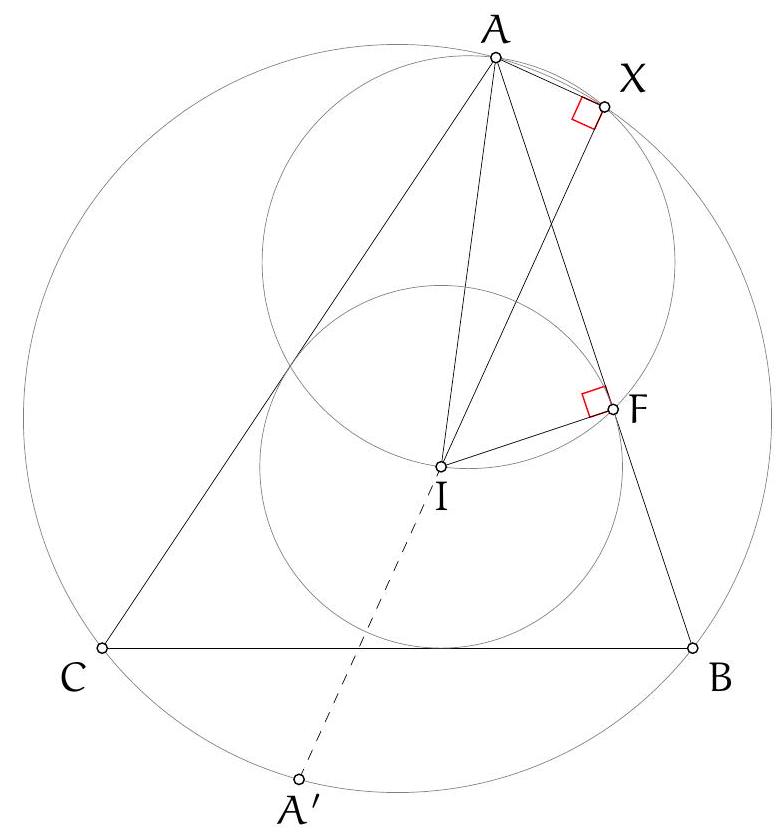
Puisque $F$ est le point de contact du cercle inscrit avec le côté [AC], l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
3ed0ff20-92da-5ef2-9423-be4fc70343ef
| 607,149
|
$2 \mathrm{n}-1$ rooks are placed on a $(2 \mathrm{n}-1) \times(2 \mathrm{n}-1)$ chessboard so that no two rooks are ever on the same row or column. Show that every $\mathrm{n} \times \mathrm{n}$ square contains a rook.
|
Let's start by noting that there is exactly one tower per row and per column. Indeed, by hypothesis, there is at most one tower per row. And since there are $2 \mathrm{n}-1$ towers in total, there must be exactly one per row, and similarly for the columns. By slightly adapting the reasoning, we can assume that the $\mathrm{n} \times \mathrm{n}$ square is that of the cells located in the top left (i.e., the cells located in the first $n$ rows and the first $n$ columns starting from the top left corner). Suppose, for the sake of contradiction, that this square contains no towers. Then among the $n$ first rows, there must be $n$ towers. However, these $n$ towers must be in the last $n-1$ columns by hypothesis. By the pigeonhole principle, there will then be two towers in the same column, which is absurd.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 \mathrm{n}-1) \times(2 \mathrm{n}-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les $n$ premières lignes, il doit $y$ avoir $n$ tours. Cependant, ces $n$ tours doivent être dans les $n-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 11.",
"solution_match": "\nSolution de l'exercice 11"
}
|
6b892116-8b19-5cd2-83d4-33ac46ed32c9
| 607,150
|
Let $ABC$ be a triangle and let $J$ be the center of its $A$-excircle. Let $K$ be the symmetric point of $J$ with respect to the segment $[BC]$. Let $E$ and $F$ be the points on the lines $(BJ)$ and $(CJ)$ such that $\widehat{\mathrm{EAB}}=\widehat{\mathrm{CAF}}=90^{\circ}$. Show that $\widehat{\mathrm{FKE}}+\widehat{\mathrm{FJE}}=180^{\circ}$.
|
Since the line (BJ) is the external bisector of the angle $\widehat{A B C}$, we have $\widehat{A B J}=\widehat{C B J}=90^{\circ}-\widehat{A B C} / 2$. Since axial symmetry preserves angles, we thus have $\widehat{\mathrm{KBC}}=\widehat{\mathrm{ABE}}$.
Let $A_{1}$ be the orthogonal projection of the point $J$ onto the segment $[B C]$, so that $A_{1}$ is also the midpoint of the segment $[J K]$. The triangles $K A_{1} B$ and $B A E$ are therefore right-angled and have another angle in common, so they are similar. We thus have
$$
\frac{B K}{B E}=\frac{B A_{1}}{B A} .
$$
This equality of ratios combined with the angle equality $\widehat{\mathrm{KBE}}=\widehat{\mathrm{ABE}}+\widehat{A B K}=\widehat{\mathrm{KBA}_{1}}+\widehat{A B K}=\widehat{\mathrm{ABA}_{1}}$ implies that the triangles $K B E$ and $A_{1} B A$ are similar (this result can also be stated as the fact that $B$ is the center of the homothety sending the pair $\left(A_{1}, K\right)$ to the pair $(A, E)$ and therefore also the center of the homothety sending the pair $\left(A_{1}, \mathcal{A}\right)$ to the pair $(K, E)$ ).
We deduce that $\widehat{\mathrm{BKE}}=\widehat{\mathrm{BA}_{1} A}$. Similarly, $\widehat{\mathrm{CKF}}=\widehat{\mathrm{CA}_{1} A}$. We then have, always because symmetry preserves angles:
$$
\widehat{\mathrm{EJF}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BJC}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BKC}}+\widehat{\mathrm{EKF}}=360^{\circ}-\widehat{\mathrm{BKE}}-\widehat{\mathrm{CKF}}=360^{\circ}-\widehat{\mathrm{BA} A_{1} A}-\widehat{\mathrm{CA} A_{1} \mathrm{~A}}=180^{\circ} .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soit $J$ le centre de son cercle $A$-exinscrit. Soit K le symétrique du point $J$ par rapport au segment $[B C]$. Soient $E$ et $F$ les points sur les droites (BJ) et (CJ) tels que $\widehat{\mathrm{EAB}}=\widehat{\mathrm{CAF}}=90^{\circ}$. Montrer que $\widehat{\mathrm{FKE}}+\widehat{\mathrm{FJE}}=180^{\circ}$.
|
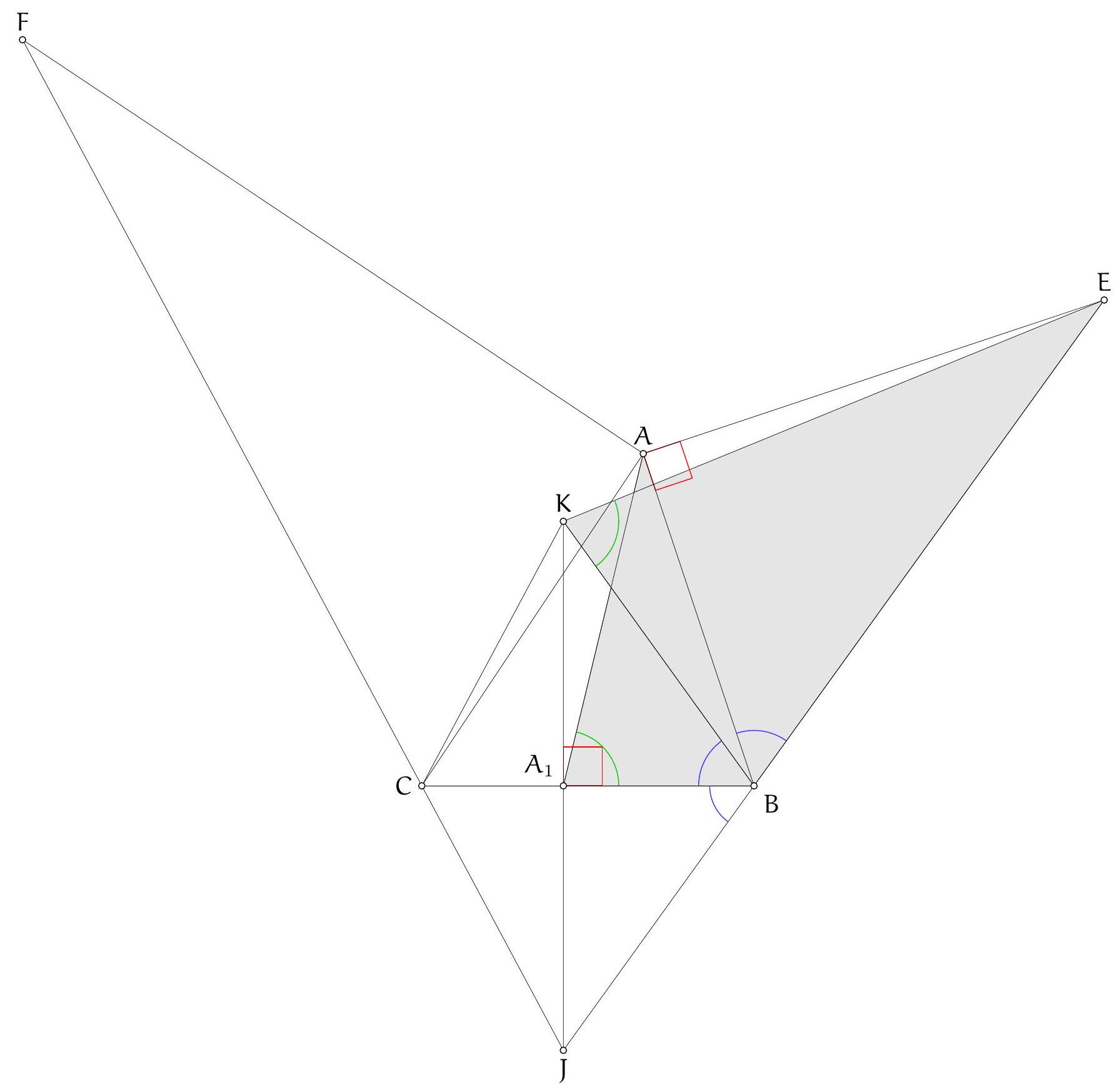
Puisque la droite (BJ) est la bissectrice extérieure de l'angle $\widehat{A B C}$, on a $\widehat{A B J}=\widehat{C B J}=90^{\circ}-\widehat{A B C} / 2$. Puisque la symétrie axiale préserve les angles, on a ainsi $\widehat{\mathrm{KBC}}=\widehat{\mathrm{ABE}}$.
Notons $A_{1}$ le projeté orthogonale du point $J$ sur le segment $[B C]$, de sorte que $A_{1}$ est également le milieu du segment $[J K]$. Les triangles $K A_{1} B$ et $B A E$ sont donc rectangles et ont un autre angle en commun, ils sont donc semblables. On a ainsi
$$
\frac{B K}{B E}=\frac{B A_{1}}{B A} .
$$
Cette égalité de rapport combinée avec l'égalité d'angle $\widehat{\mathrm{KBE}}=\widehat{\mathrm{ABE}}+\widehat{A B K}=\widehat{\mathrm{KBA}_{1}}+\widehat{A B K}=\widehat{\mathrm{ABA}_{1}}$ implique que les triangles $K B E$ et $A_{1} B A$ sont semblables (ce résultat peut également être formulé comme le fait que $B$ est le centre de la smilitude envoyant la paire $\left(A_{1}, K\right)$ sur la paire $(A, E)$ et donc aussi le centre de la similitude envoyant la paire $\left(A_{1}, \mathcal{A}\right)$ sur la paire $(K, E)$ ).
On déduit que $\widehat{\mathrm{BKE}}=\widehat{\mathrm{BA}_{1} A}$. De la même façon, $\widehat{\mathrm{CKF}}=\widehat{\mathrm{CA}_{1} A}$. On a alors, toujours puisque la symétrie préserve les angles:
$$
\widehat{\mathrm{EJF}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BJC}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BKC}}+\widehat{\mathrm{EKF}}=360^{\circ}-\widehat{\mathrm{BKE}}-\widehat{\mathrm{CKF}}=360^{\circ}-\widehat{\mathrm{BA} A_{1} A}-\widehat{\mathrm{CA} A_{1} \mathrm{~A}}=180^{\circ} .
$$
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "## Solution de l'exercice 14"
}
|
7110bd63-fd3c-5513-bec3-fc49e1a4d301
| 607,153
|
Show that there are infinitely many integers $n$ such that the base 4 representation of $n^{2}$ contains only 1s and 2s.
|
We show a slightly stronger result, which is better suited for an inductive reasoning: there are infinitely many integers $n$ such that the base 4 representation of $n^{2}$ contains only 1s and 2s, and such that the first and last digit of the base 4 representation of $n^{2}$ is 1. A first example is the number $5^{2}=25=121_{4}$. Then, we show that if we have such an $n$, we can construct a new one that is strictly greater, which will prove that there are infinitely many integers with the desired property.
Let $n$ be such that the base 4 representation of $\mathrm{n}^{2}$ contains only 1s and 2s, and starts and ends with a 1. Suppose this representation contains $k$ digits. We then set $m=2^{2 k-1} \cdot n+n$. We have
$$
\mathrm{m}^{2}=4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}+4^{\mathrm{k}} \cdot \mathrm{n}^{2}+\mathrm{n}^{2}
$$
In base 4, $m^{2}$ is thus made up of three copies of $n^{2}$, with $n^{2}$ and $4^{k} \cdot n^{2}$ being two adjacent disjoint copies, and $4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}$ and $4^{\mathrm{k}} \cdot \mathrm{n}^{2}$ sharing exactly one power of 4 in their representation, namely $4^{2 k-1}$. But by hypothesis, the coefficients in front of 1 and in front of $4^{k-1}$ of $n^{2}$ are 1s, so the coefficient in front of $4^{2 \mathrm{k}-1}$ of $\mathrm{m}^{2}$ is a 2. Furthermore, all other coefficients in the base 4 representation of $\mathrm{m}^{2}$ appeared in that of $\mathrm{n}^{2}$, and are therefore indeed 1s or 2s. Finally, the first and last coefficients of the base 4 representation of $\mathrm{m}^{2}$, namely the coefficients in front of $4^{0}$ and $4^{3 \mathrm{k}-2}$, are indeed 1s by the inductive hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer qu'il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 .
|
On montre un résultat un peu plus fort, qui se prête mieux à un raisonnement par récurrence : il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 , et tels que le premier et le dernier chiffre de l'écriture en base 4 de $n^{2}$ vaut 1 . Un premier exemple est le nombre $5^{2}=25=121_{4}$. Ensuite, on montre que si l'on a un tel n , on peut en construire un nouveau qui lui est strictement supérieur, ce qui montrera bien qu'il existe une infinité d'entiers ayant la propriété recherchée.
Soit donc n tel que l'écriture de $\mathrm{n}^{2}$ en base 4 ne contient que des 1 et des 2 , et commence et se termine par un 1 . On suppose que cette écriture contient $k$ chiffres. On pose alors $m=2^{2 k-1} \cdot n+n$. On a
$$
\mathrm{m}^{2}=4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}+4^{\mathrm{k}} \cdot \mathrm{n}^{2}+\mathrm{n}^{2}
$$
En base $4, m^{2}$ est donc constitué de trois copies de $n^{2}$, avec $n^{2}$ et $4^{k} \cdot n^{2}$ qui sont deux copies disjointes adjacentes, et $4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}$ et $4^{\mathrm{k}} \cdot \mathrm{n}^{2}$ qui ont exactement une puissance de 4 en commun dans leur écriture, à savoir $4^{2 k-1}$. Mais par hypothèse, les coefficients devant 1 et devant $4^{k-1}$ de $n^{2}$ sont des 1 , donc le coefficient devant $4^{2 \mathrm{k}-1}$ de $\mathrm{m}^{2}$ est un 2 . En outre, tous les autres coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$ apparaissaient dans celle de $\mathrm{n}^{2}$, et sont donc bien des 1 ou des 2 . Enfin, les premiers et derniers coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$, à savoir les coefficients devant $4^{0}$ et $4^{3 \mathrm{k}-2}$, sont bien des 1 par hypothèse de récurrence.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "\nSolution de l'exercice 17"
}
|
17a74182-80d1-5640-b3ac-aeb1cb6aaba7
| 607,156
|
Let $ABC$ be a triangle and let $A_{1}, B_{1}$, and $C_{1}$ be the points of contact of the $A$-excircle, denoted by $\omega_{A}$, with the side $BC$ and the rays $[AC)$ and $[AB)$, respectively. Let $P$ be the midpoint of the segment $\left[B_{1} C_{1}\right]$. The line $\left(A_{1} P\right)$ intersects the circle $\omega_{A}$ again at point $X$. The tangent to the circumcircle of triangle $ABC$ at point $A$ and the tangent to the circle $\omega_{A}$ at point $X$ intersect at $R$. Show that $RX = RP$.
|
By drawing the circle centered at $R$ with radius $R A$, we notice that it also passes through $P$. Therefore, we will instead introduce $R^{\prime}$ as the center of the circumcircle of triangle $A P X$ and show that the lines $\left(A R^{\prime}\right)$ and ( $X R^{\prime}$ ) are respectively tangent to the circumcircles of triangles $A B C$ and $A_{1} B_{1} C_{1}$.
For this, note that since $P$ is the midpoint of the segment $\left[B_{1} C_{1}\right]$ and the line $\left(A I_{A}\right)$ is its perpendicular bisector, the points $A, P$ and $I_{A}$ are collinear. Moreover, since $\widehat{I_{A} B_{1} A}=90^{\circ}=180^{\circ}-\widehat{I_{A} C_{1} A}$, the points $B_{1}, I_{A}, C_{1}$ and $A$ are concyclic. By the power of a point, we have:
$$
\mathrm{PA} \times \mathrm{PI}_{\mathrm{A}}=\mathrm{PB}_{1} \times \mathrm{PC}_{1}=\mathrm{PA}_{1} \times \mathrm{PX}
$$
Thus, the points $A_{1}, I_{A}, X$ and $A$ are concyclic by the converse of the power of a point.
Now, let's show that $\left(A R^{\prime}\right)$ is tangent to the circumcircle of triangle $A B C$. On the one hand, by the inscribed angle theorem:
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PXA}}.
$$
But using the concyclicity of the points $A_{1}, I_{A}, X$ and $A$, we find
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathcal{A}_{1} X A}=90^{\circ}-\widehat{\mathcal{A}_{1} \mathrm{I}_{\mathrm{A}} A}.
$$
Let $D$ be the foot of the angle bisector of $\widehat{B A C}$ and $S$ the South pole of vertex $A$ in $A B C$. $D$ and $S$ are collinear with $A$ and $I_{A}$. Then
$$
90^{\circ}-\widehat{A_{1} I_{A} A}=\widehat{C D I_{A}}=180^{\circ}-\widehat{A B C}-\frac{1}{2} \widehat{B A C}=\widehat{A B C}+\frac{1}{2} \widehat{A C B}=\widehat{A C P}
$$
Thus, $\widehat{P_{A R}}{ }^{\prime}=\widehat{A C P}$, so the line $\left(A R^{\prime}\right)$ is tangent to the circumcircle of triangle $A B C$.
Now, let's show that the line ( $R^{\prime} X$ ) is tangent to the circumcircle of triangle $A_{1} B_{1} C_{1}$. We also have by the inscribed angle theorem:
$$
\widehat{A_{1} X R^{\prime}}=\widehat{\mathrm{PXR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PAX}}=90^{\circ}-\widehat{\mathrm{I}_{A} A X}
$$
Then, by the inscribed angle in the circle passing through $A, A_{1}, I_{A}$ and $X$, and using that the triangle $I_{A} \mathcal{A}_{1} X$ is isosceles at $\mathrm{I}_{\mathrm{A}}$, we have
$$
90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} A X}=90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} \mathrm{~A}_{1} X}=\frac{1}{2} \widehat{\mathrm{~A}_{1} \mathrm{I}_{A} X}=\widehat{\mathrm{A}_{1} \mathrm{~B}_{1} X}
$$
where we used the inscribed angle theorem in the circle $\omega_{A}$. Thus, the line ( $\left.R^{\prime} X\right)$ is tangent to $\omega_{A}$ and $R=R^{\prime}$, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soient $A_{1}, B_{1}$ et $C_{1}$ les points de contact resepctifs du cercle $A$-exinscrit, noté $\omega_{A}$, avec le côté $B C$ et les demi-droites $[A C)$ et $[A B$ ). Soit $P$ le milieu du segment $\left[B_{1} C_{1}\right]$. La droite $\left(A_{1} P\right)$ recoupe le cercle $\omega_{A}$ au point $X$. La tangente au cercle circonscrit au triangle $A B C$ au point $A$ et la tangente au cercle $\omega_{A}$ au point $X$ se coupent en $R$. Montrer que $R X=R P$.
|
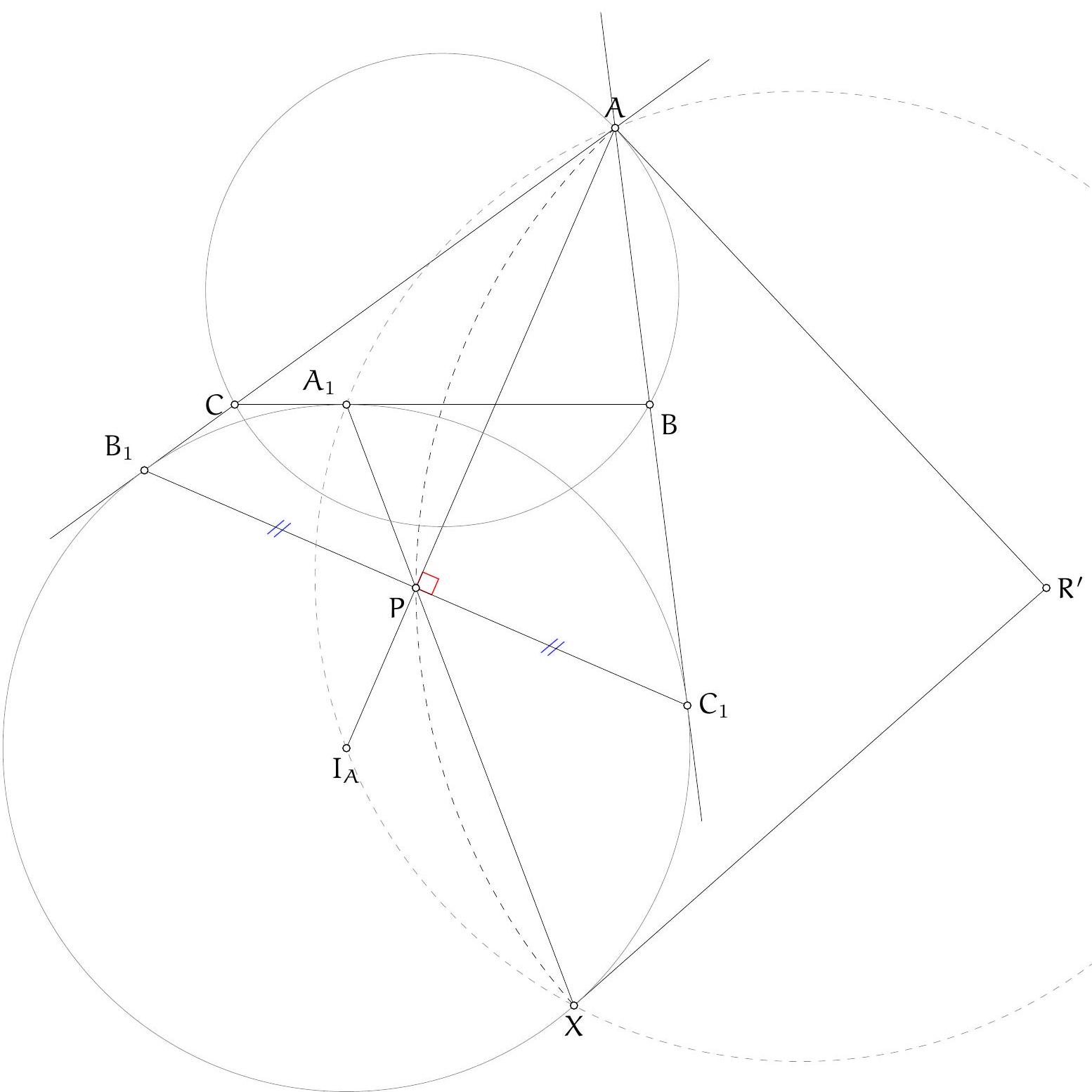
En traçant le cercle de centre $R$ de rayon $R A$, on s'aperçoit que celui-ci passe également par $P$. On va donc plutôt introduire $R^{\prime}$ le centre du cercle circonscrit au triangle $A P X$ et montre que les droites $\left(A R^{\prime}\right)$ et ( $X R^{\prime}$ ) sont respectivement tangentes aux cercles circonscrits au triangle $A B C$ et au triangle $A_{1} B_{1} C_{1}$.
Pour cela, notons que puisque $P$ est le milieu du segment $\left[B_{1} C_{1}\right]$ dont la droite $\left(A I_{A}\right)$ est la médiatrice, les points $A, P$ et $I_{A}$ sont alignés. De plus, puisque $\widehat{I_{A} B_{1} A}=90^{\circ}=180^{\circ}-\widehat{I_{A} C_{1} A}$, les points $B_{1}, I_{A}, C_{1}$ et $A$ sont cocycliques. Par puissance d'un point, on a :
$$
\mathrm{PA} \times \mathrm{PI}_{\mathrm{A}}=\mathrm{PB}_{1} \times \mathrm{PC}_{1}=\mathrm{PA}_{1} \times \mathrm{PX}
$$
de sorte que les points $A_{1}, I_{A}, X$ et $A$ sont cocycliques par la réciproque de la puissance d'un point.
Montrons à présent que $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$. D'une part, d'après le théorème de l'angle au centre :
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PXA}} .
$$
Mais en utilisant la cocyclicité des points $A_{1}, I_{A}, X$ et $A$, on a trouve
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathcal{A}_{1} X A}=90^{\circ}-\widehat{\mathcal{A}_{1} \mathrm{I}_{\mathrm{A}} A} .
$$
Soit alors $D$ le pied de la bissectrice de l'angle $\widehat{B A C}$ et $S$ le pôle Sud su sommet $A$ dans $A B C$. $D$ et $S$ sont alignés avec $A$ et $I_{A}$. Alors
$$
90^{\circ}-\widehat{A_{1} I_{A} A}=\widehat{C D I_{A}}=180^{\circ}-\widehat{A B C}-\frac{1}{2} \widehat{B A C}=\widehat{A B C}+\frac{1}{2} \widehat{A C B}=\widehat{A C P}
$$
Ainsi, $\widehat{P_{A R}}{ }^{\prime}=\widehat{A C P}$, donc la droite $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$.
Montrons que la droite ( $R^{\prime} X$ ) est tangente au cercle circonscrit au triangle $A_{1} B_{1} C_{1}$. On a là aussi par angle au centre :
$$
\widehat{A_{1} X R^{\prime}}=\widehat{\mathrm{PXR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PAX}}=90^{\circ}-\widehat{\mathrm{I}_{A} A X}
$$
Puis, par angle inscrit dans le cercle passant par $A, A_{1}, I_{A}$ et $X$, et en utilisant que le triangle $I_{A} \mathcal{A}_{1} X$ est isocèle en $\mathrm{I}_{\mathrm{A}}$, on a
$$
90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} A X}=90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} \mathrm{~A}_{1} X}=\frac{1}{2} \widehat{\mathrm{~A}_{1} \mathrm{I}_{A} X}=\widehat{\mathrm{A}_{1} \mathrm{~B}_{1} X}
$$
où l'on a utilisé le théorème de l'angle au centre dans le cercle $\omega_{A}$. Ainsi, la droite ( $\left.R^{\prime} X\right)$ est tangente à $\omega_{A}$ et $R=R^{\prime}$, ce qui conclut.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 18.",
"solution_match": "## Solution de l'exercice 18"
}
|
2bacfe80-2120-5191-880b-68b3933e9b90
| 607,157
|
Let $x$ and $y$ be two positive real numbers. Show that
$$
\left(x^{2}+x+1\right)\left(y^{2}+y+1\right) \geqslant 9 x y .
$$
What are the cases of equality?
|
We apply the arithmetic-geometric inequality to get
$$
\begin{gathered}
x^{2}+x+1 \geqslant 3 \sqrt[3]{x^{3}}=3 x \\
y^{2}+y+1 \geqslant 3 \sqrt[3]{y^{3}}=3 y
\end{gathered}
$$
By multiplying these two inequalities, which are positive, we obtain the inequality stated in the problem. Since $x^{2}+x+1$ and $y^{2}+y+1$ are strictly positive, we have equality when we have equality in both arithmetic-geometric inequalities. This happens when $x^{2}=x=1$ and $y^{2}=y=1$, and thus we have equality for $x=y=1$.
Comment from the graders: In general, the exercise was very well solved. Several people forget to consider the equality case.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x$ et $y$ deux réels positifs. Montrer que
$$
\left(x^{2}+x+1\right)\left(y^{2}+y+1\right) \geqslant 9 x y .
$$
Quels sont les cas d'égalité?
|
On applique l'inégalité arithmético-géométrique pour avoir
$$
\begin{gathered}
x^{2}+x+1 \geqslant 3 \sqrt[3]{x^{3}}=3 x \\
y^{2}+y+1 \geqslant 3 \sqrt[3]{y^{3}}=3 y
\end{gathered}
$$
En multipliant ces deux inégalités, qui sont à termes positifs, on obtient l'inégalité de l'énoncé. Comme $x^{2}+x+1$ et $y^{2}+y+1$ sont strictement positifs, on a égalité lorsque l'on a égalité dans les deux inégalités arithmético-géométriques. Mais ceci arrive lorsque $x^{2}=x=1$ et $y^{2}=y=1$, et on a donc égalité pour $x=y=1$.
Commentaire des correcteurs: De manière générale, l'exercice a été très bien résolu. Plusieurs personnes oublient de faire le cas d'égalité.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
8e24f8e4-e641-5195-9625-00dc4fd99947
| 607,158
|
Let $a$ and $b$ be two real numbers. Suppose that $2a + a^2 = 2b + b^2$. Show that if $a$ is an integer (not necessarily positive), then $b$ is also an integer.
|
We rewrite the equality
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Then either $\mathrm{b}=\mathrm{a}$, and in this case b is an integer, or
$$
2=-a-b
$$
from which
$$
\mathrm{b}=-2-\mathrm{a}
$$
and $b$ is still an integer.
Comment from the graders: The exercise was generally well handled, with a few reasoning errors. Almost all students avoided the trap $a+1=-(b+1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
On réécrit l'égalité
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
$$
2=-a-b
$$
d'où
$$
\mathrm{b}=-2-\mathrm{a}
$$
et $b$ est encore un entier.
Commentaire des correcteurs: Exercice bien traité dans l'ensemble, avec quelques erreurs de raisonnement. Presque tous les élèves ont évité le piège $a+1=-(b+1)$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
6a747265-63c0-5456-bafa-ace435dd460e
| 607,159
|
Show that there do not exist strictly positive real numbers $x, y, z$ such that
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right)=26 x^{2} y^{2} z^{2}
$$
|
We could try to simply apply the arithmetic-geometric mean inequality to each of the factors on the left side, but this gives that the left term is greater than or equal to \(16 \sqrt{2} x^{2} y^{2} z^{2}\), which is not enough to conclude (since \(16 \sqrt{2} < 26\)). In fact, this is because we cannot have equality in all three arithmetic-geometric mean inequalities at the same time. We would like the case \(x=y=z\) to be a case of equality in the arithmetic-geometric mean inequalities we apply.
For example, take the first term \(2 x^{2} + y z\). We split it into \(x^{2} + x^{2} + y z\) (so that each of the terms is equal if \(x=y=z\)), then we can apply the arithmetic-geometric mean inequality:
\[
2 x^{2} + y z \geqslant 3 \sqrt[3]{x^{2} \cdot x^{2} \cdot y z} = 3 \sqrt[3]{x^{4} y z}
\]
By applying the arithmetic-geometric mean inequality to all the positive terms, we have
\[
\left(2 x^{2} + y z\right)\left(2 y^{2} + x z\right)\left(2 z^{2} + x y\right) \geqslant 27 \sqrt[3]{x^{4} y z \cdot y^{4} x z \cdot z^{4} y z} = 27 \sqrt[3]{x^{6} y^{6} z^{6}} = 27 x^{2} y^{2} z^{2}
\]
which is strictly greater than \(26 x^{2} y^{2} z^{2}\), so we cannot have equality.
Comment from the graders: The exercise was generally successful. Good use of the AM-GM inequality, except for a few errors in reasoning.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Montrer qu'il n'existe pas de réels $x, y, z$ strictement positifs tels que
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right)=26 x^{2} y^{2} z^{2}
$$
|
On pourrait essayer de simplement appliquer l'inégalité arithmético-géométrique sur chacun des facteurs du côté gauche, mais ceci donne que le terme de gauche est supérieur ou égal à $16 \sqrt{2} x^{2} y^{2} z^{2}$ ce qui ne suffit pas pour conclure (car $16 \sqrt{2}<26$ ). En fait, ceci vient du fait que l'on ne peut pas avoir égalité dans les trois inégalités arithmético-géométriques à la fois. On aimerait bien que le cas $x=y=z$ soit un cas d'égalité des inégalités arithmético-géométrique que l'on applique.
Prenons par exemple le premier terme $2 x^{2}+y z$. On le sépare en $x^{2}+x^{2}+y z$ (de façon à ce que chacun des termes soit égaux si $x=y=z$ ), on peut alors appliquer l'inégalité arithmético-géométrique :
$$
2 x^{2}+y z \geqslant 3 \sqrt[3]{x^{2} \cdot x^{2} \cdot y z}=3 \sqrt[3]{x^{4} y z}
$$
En appliquant l'inégalité arithmético-géométrique sur tous les termes qui sont positifs, on a
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right) \geqslant 27 \sqrt[3]{x^{4} y z \cdot y^{4} x z \cdot z^{4} y z}=27 \sqrt[3]{x^{6} y^{6} z^{6}}=27 x^{2} y^{2} z^{2}
$$
ce qui est strictement supérieur à $26 x^{2} y^{2} z^{2}$, on ne peut donc pas avoir égalité.
Commentaire des correcteurs: Exercice réussi dans l'ensemble. Bonnes utilsations de l'IAG, sauf quelques erreurs de raisonnement.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
903f08a3-5967-53a3-bdf3-2639fd41a7d0
| 607,160
|
Show that for all real numbers $x, y, z$, we have
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leqslant 0 .
$$
|
We rewrite the inequality as
$$
\frac{x^{2}}{2 x^{2}+1}+\frac{y^{2}}{2 y^{2}+1}+\frac{z^{2}}{2 z^{2}+1} \leqslant \frac{y^{2}}{2 x^{2}+1}+\frac{z^{2}}{2 y^{2}+1}+\frac{x^{2}}{2 z^{2}+1} .
$$
Since the inequality is not symmetric, we cannot assume without loss of generality that $x^{2} \leqslant y^{2} \leqslant z^{2}$. However, note that the sequences $\left(x^{2}, y^{2}, z^{2}\right)$ and $\left(\frac{1}{2 x^{2}+1}, \frac{1}{2 y^{2}+1}, \frac{1}{2 z^{2}+1}\right)$ are arranged in reverse order (the largest of the first sequence corresponds to the smallest of the second sequence, for example). Therefore, we can apply the rearrangement inequality, which directly implies the inequality in the statement.
Comment from the graders: Students who approached the problem generally did well. They proposed three types of solutions. Some used the rearrangement inequality (also known as the turnstile inequality), similar to the solution provided. The most common mistake was to claim that the inequality is symmetric, which is clearly not the case, and to assume an order. While this is not critical in the context of the rearrangement inequality, such imprecisions are dangerous: a few students, by illegally assuming a convenient order, dispensed with using the rearrangement inequality, and their reasoning was entirely incorrect. Others used the arithmetic-geometric mean inequality directly and effectively after slightly transforming the problem. Unfortunately, about half of the students eliminated the fractions, expanded, and then used the arithmetic-geometric mean inequality term by term. Let us recall that this strategy is risky because a single calculation error can completely invalidate the solution, and more challenging problems (such as problem 6) are difficult to solve this way.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Montrer que pour tous les réels $x, y, z$, on a
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leqslant 0 .
$$
|
On réécrit l'inégalité en
$$
\frac{x^{2}}{2 x^{2}+1}+\frac{y^{2}}{2 y^{2}+1}+\frac{z^{2}}{2 z^{2}+1} \leqslant \frac{y^{2}}{2 x^{2}+1}+\frac{z^{2}}{2 y^{2}+1}+\frac{x^{2}}{2 z^{2}+1} .
$$
L'inégalité n'étant pas symétrique, on ne peut pas supposer sans perte de généralité que $x^{2} \leqslant y^{2} \leqslant$ $z^{2}$. Cependant, remarquons que les suites $\left(x^{2}, y^{2}, z^{2}\right)$ et $\left(\frac{1}{2 x^{2}+1}, \frac{1}{2 y^{2}+1}, \frac{1}{2 z^{2}+1}\right)$ sont rangées dans l'ordre inverse (le plus grand de la première suite correspond au plus petit de la deuxième suite par exemple). On peut donc appliquer l'inégalité de réordonnement qui implique directement l'inégalité de l'énoncé.
Commentaire des correcteurs: Les élèves ayant abordé le problème l'ont plutôt bien réussi. Ils ont proposé trois types de solutions. Certains passent par l'inégalité de réarrangement (aussi appelée inégalité du tourniquet), à l'instar du corrigé. L'erreur la plus fréquente est alors de dire que l'inégalité est symétrique, ce qui n'est manifestement pas le cas, et de supposer un ordre. Dans le cadre de l'inégalité de réarrangement ceci n'est pas dramatique, mais ce type d'imprécisions reste dangereux : quelques élèves, en supposant illégalement un ordre commode, se sont dispensés d'utiliser l'inégalité de réarrangement, et leur raisonnement est tout à fait erroné. D'autres utilisent directement et efficacement l'inégalité arithméticogéométrique après avoir un peu transformé le problème. Une regrettable moitié enfin, se débarasse des fractions, développe, puis utilise l'IAG termes à termes. Rappelons que cette stratégie est hasardeuse car une faute de calcul rend complètement invalide la solution, et que les problèmes un peu plus durs (comme le problème 6) sont difficiles à résoudre ainsi.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
85a67aa3-f566-5d51-bf88-bdd95d0b0868
| 607,161
|
Let $a, b, c$ be three strictly positive real numbers. Show that
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
:
We can also think about it using the rearrangement inequality. The inequality is not symmetric, so we cannot assume without loss of generality that $a \geqslant b \geqslant c$ or something similar.
However, by strict monotonicity, $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ is in the same order as $(a, b, c)$. Similarly, $\left(a^{3}+a^{2}+a, b^{3}+b^{2}+b, c^{3}+c^{2}+c\right)$ is also in the same order, and $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$ is in the reverse order. Thus, by the rearrangement inequality,
$$
\frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
is the minimum value that can be taken by a sum of products of terms from $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ with terms from $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$. In particular here:
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
We can now show as before that $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$ and conclude by
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \cdot \frac{2}{3}=2
$$
Graders' comments: The problem is very well done. However, many students believe that we can assume $a \geqslant b \geqslant c$ because 'the inequality is symmetric'. However, the inequality is not symmetric: if we swap $b$ and $c$, the inequality is drastically changed. Fortunately, here by chance, the reasoning was easily rectifiable (see solution 2 in the answer key). However, the few copies that multiplied and expanded everything did not succeed, once again demonstrating that thinking before haphazardly expanding everything is always a good idea.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c$ trois réels strictement positifs. Montrer que
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
:
On peut également réfléchir avec l'inégalité de réarrangement. L'inégalité n'est pas symétrique, on ne peut donc pas supposer sans perte de généralités $a \geqslant b \geqslant c$ ou quelque chose de similaire.
Cependant, par stricte croissance, $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ est dans le même ordre que $(a, b, c)$. De même, $\left(a^{3}+a^{2}+a, b^{3}+b^{2}+b, c^{3}+c^{2}+c\right)$ est également dans le même ordre et $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$ est dans le sens inverse. Ainsi, par inégalité de réarrangement,
$$
\frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
est la valeur minimale que peut prendre une somme de produit de termes de $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ avec des termes de $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$. En particulier ici :
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
On peut maintenant comme précédemment montrer $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$ et conclure par
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \cdot \frac{2}{3}=2
$$
Commentaire des correcteurs : Le problème est très bien réussi. Cependant, beaucoup d'élèves croient qu'on peut supposer $a \geqslant b \geqslant c$ car 'l'inégalité est symétrique". Or l'inégalité n'est pas symétrique : si on change b et c l'inégalité est drastiquement changée. Heureusement qu'ici par chance, le raisonnement était rectifiable facilement (cf la solution 2 du corrigé). Cependant, les quelques copies qui ont tout multiplié et développé n'ont pas réussi, témoignant encore une fois du fait que réfléchir avant de tout développer hasardeusement est toujours une bonne idée.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "## Exercice 6.",
"solution_match": "## Solution alternative"
}
|
85f420e4-75ce-5387-ae84-3279d0d7debb
| 607,163
|
Let $a, b, c, d$ be four real numbers such that $|a|>1,|b|>1,|c|>1$ and $|d|>1$. Suppose that $(a+1)(b+1)(c+1)(d+1)=(a-1)(b-1)(c-1)(d-1)$. Show that
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1}>0
$$
|
We know from the statement that none of $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ equals 1. The condition in the statement can be written as
$$
\frac{a+1}{a-1} \frac{b+1}{b-1} \frac{c+1}{c-1} \frac{d+1}{d-1}=1
$$
Notice that since $|a|>1$, we have either $a>1$ and thus $a+1>0$ and $a-1>0$, or $a<-1$ and thus $a+1<0$ and $a-1<0$. Therefore, in all cases $\frac{a+1}{a-1}$ is positive, and the same applies to $b, c, d$. We can therefore apply the arithmetic-geometric mean inequality to the product above to get
$$
\frac{\mathrm{a}+1}{\mathrm{a}-1}+\frac{\mathrm{b}+1}{\mathrm{~b}-1}+\frac{\mathrm{c}+1}{\mathrm{c}-1}+\frac{\mathrm{d}+1}{\mathrm{~d}-1} \geqslant 4 \sqrt[4]{\frac{\mathrm{a}+1}{\mathrm{a}-1} \frac{\mathrm{~b}+1}{\mathrm{~b}-1} \frac{\mathrm{c}+1}{\mathrm{c}-1} \frac{\mathrm{~d}+1}{\mathrm{~d}-1}}=4
$$
We can rewrite this as
$$
\left(1+\frac{2}{\mathrm{a}-1}\right)+\left(1+\frac{2}{\mathrm{~b}-1}\right)+\left(1+\frac{2}{\mathrm{c}-1}\right)+\left(1+\frac{2}{\mathrm{~d}-1}\right) \geqslant 4
$$
and thus
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1} \geqslant 0
$$
However, the statement asks us to show that the inequality is strict. Therefore, we need to consider the case of equality in the arithmetic-geometric mean inequality. Equality holds if and only if
$$
\frac{a+1}{a-1}=\frac{b+1}{b-1}=\frac{c+1}{c-1}=\frac{d+1}{d-1}
$$
Since the product of these four terms is 1, these terms must all be 1 or all be -1. In the first case, we have $a+1=a-1$, which is impossible. In the second case, we have $a+1=1-a$ and thus $a=0$, which is also impossible because $|a|>1$. Therefore, equality cannot hold, and the inequality is indeed strict as stated.
Comment from the graders: The problem is rarely approached. Some students attempted complicated calculations, and surprisingly few managed to make it work. In inequalities, it is crucial to try to bring out the hypotheses rather than brute-forcing the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a, b, c, d$ quatre réels tels que $|a|>1,|b|>1,|c|>1$ et $|d|>1$. Supposons que $(a+1)(b+1)(c+1)(d+1)=(a-1)(b-1)(c-1)(d-1)$. Montrer que
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1}>0
$$
|
On sait d'après l'énoncé que aucun des $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ ne vaut 1 . La condition de l'énoncé s'écrit alors
$$
\frac{a+1}{a-1} \frac{b+1}{b-1} \frac{c+1}{c-1} \frac{d+1}{d-1}=1
$$
Remarquons que comme $|a|>1$, alors on a soit $a>1$ et donc $a+1>0$ et $a-1>0$, ou alors $a<-1$ et donc $a+1<0$ et $a-1<0$. Ainsi, dans tous les cas $\frac{a+1}{a-1}$ est positif, et de même pour $b, c, d$. On peut donc appliquer l'inégalité arithmético-géométrique sur le produit précédent pour avoir
$$
\frac{\mathrm{a}+1}{\mathrm{a}-1}+\frac{\mathrm{b}+1}{\mathrm{~b}-1}+\frac{\mathrm{c}+1}{\mathrm{c}-1}+\frac{\mathrm{d}+1}{\mathrm{~d}-1} \geqslant 4 \sqrt[4]{\frac{\mathrm{a}+1}{\mathrm{a}-1} \frac{\mathrm{~b}+1}{\mathrm{~b}-1} \frac{\mathrm{c}+1}{\mathrm{c}-1} \frac{\mathrm{~d}+1}{\mathrm{~d}-1}}=4
$$
On réécrit ceci sous la forme
$$
\left(1+\frac{2}{\mathrm{a}-1}\right)+\left(1+\frac{2}{\mathrm{~b}-1}\right)+\left(1+\frac{2}{\mathrm{c}-1}\right)+\left(1+\frac{2}{\mathrm{~d}-1}\right) \geqslant 4
$$
et donc
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1} \geqslant 0
$$
Mais l'énoncé nous demande de montrer que l'inégalité est stricte, on s'intéresse donc au cas d'égalité dans l'inégalité arithmético-géométrique. On a égalité si et seulement si
$$
\frac{a+1}{a-1}=\frac{b+1}{b-1}=\frac{c+1}{c-1}=\frac{d+1}{d-1}
$$
Comme le produit de ces quatre termes vaut 1 , nécessairement ces termes valent tous 1 ou tous -1 . Dans le premier cas, on a $a+1=a-1$ ce qui est impossible. Dans le deuxième cas, on a $a+1=1-a$ et donc $a=0$, ce qui est aussi impossible car $|a|>1$. Ainsi, on ne peut pas avoir égalité et l'inégalité est bien stricte comme dans l'énoncé.
Commentaire des correcteurs : Le problème est peu abordé. Certains se sont lancés dans des calculs compliqués, et étonnamment très peu ont réussi à faire fonctionner cela. En inégalité, il est crucial d'essayer de faire apparaître les hypothèses plutôt que de bourriner les calculs.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
a733f2d7-0b76-5d4a-b77d-b6b8684f5326
| 607,164
|
Let $\mathrm{n} \geqslant 1$ be an integer and $\mathrm{x}_{1}, \ldots, \mathrm{x}_{\mathrm{n}}$ be positive real numbers. Show that
$$
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
$$
What are the cases of equality?
|
The trick is to apply the arithmetic-geometric inequality to the left side of the inequality, but with coefficients $\sqrt{n}$ and $\frac{1}{\sqrt{n}}$:
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots\right. & \left.+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right)=\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right) \frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}} \\
& \leqslant \frac{1}{4}\left(\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)+\frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}}\right)^{2}
\end{aligned}
$$
For each $i$, the coefficient of $x_{i}$ is $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}}$. The function $t \mapsto t+\frac{1}{t}$ is decreasing for $t<1$ and increasing for $t>1$. Indeed, for example, for $1<x<y$, we have $xy>1$ and thus:
$$
y-x>\frac{y-x}{xy}=\frac{1}{x}-\frac{1}{y}
$$
Thus, the maximum coefficient is achieved at $i=1$ or $i=n$. In each case, we find a coefficient $\sqrt{n}+\frac{1}{\sqrt{n}}=\frac{n+1}{\sqrt{n}}$, and therefore
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{1}{4}\left(\frac{n+1}{\sqrt{n}}\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right)^{2} \\
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
\end{aligned}
$$
We are interested in the cases of equality. For $1<i<n$, the inequality $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}} \leqslant \frac{n+1}{\sqrt{n}}$ is strict, so necessarily $x_{i}$ must be equal to 0. Then, we need to have equality in the arithmetic-geometric inequality, which is written as
$$
\begin{aligned}
\sqrt{n}\left(x_{1}+\frac{x_{n}}{n}\right) & =\frac{1}{\sqrt{n}}\left(x_{1}+n x_{n}\right) \\
\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{1} & =\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{n}
\end{aligned}
$$
If $n=1$, we always have equality (there is only one $x_{i}$), otherwise we have the condition $x_{1}=x_{n}$. Conversely, we can verify that if $x_{1}=x_{n}$ and all other $x_{i}$ are zero, we indeed have equality in the inequality of the statement.
Comment from the graders: The problem is rarely approached, and even less solved. Very few copies deal with the cases of equality, although this is part of the statement and could earn points. Be sure to know the statements of known inequalities well, as misapplying an inequality can ruin an entire proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $\mathrm{n} \geqslant 1$ un entier et $\mathrm{x}_{1}, \ldots, \mathrm{x}_{\mathrm{n}}$ des réels positifs. Montrer que
$$
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
$$
Quels sont les cas d'égalité?
|
L'astuce est d'appliquer une inégalité arithmético-géométrique au côté gauche de l'inégalité, mais avec des coefficients $\sqrt{n}$ et $\frac{1}{\sqrt{n}}$ :
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots\right. & \left.+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right)=\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right) \frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}} \\
& \leqslant \frac{1}{4}\left(\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)+\frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}}\right)^{2}
\end{aligned}
$$
Pour chaque $i$, le coefficient de $x_{i}$ est $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}}$. La fonction $t \mapsto t+\frac{1}{t}$ est décroissante pour $t<1$ et croissante pour $\mathrm{t}>1$. En effet, par exemple pour $1<x<y$, on a $x y>1$ et donc:
$$
y-x>\frac{y-x}{x y}=\frac{1}{x}-\frac{1}{y}
$$
Ainsi, le coefficient maximal est atteint en $i=1$ ou $i=n$. Dans chaque cas, on trouve un coefficient $\sqrt{n}+\frac{1}{\sqrt{n}}=\frac{n+1}{\sqrt{n}}$, et donc
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{1}{4}\left(\frac{n+1}{\sqrt{n}}\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right)^{2} \\
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
\end{aligned}
$$
On s'intéresse aux cas d'égalité. Pour $1<i<n$, l'inégalité $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}} \leqslant \frac{n+1}{\sqrt{n}}$ est stricte, donc nécessairement $x_{i}$ doit être égal à 0 . Ensuite, il faut avoir égalité dans l'inégalité arithmético-géométrique, ce qui s'écrit
$$
\begin{aligned}
\sqrt{n}\left(x_{1}+\frac{x_{n}}{n}\right) & =\frac{1}{\sqrt{n}}\left(x_{1}+n x_{n}\right) \\
\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{1} & =\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{n}
\end{aligned}
$$
Si $n=1$, on a toujours égalité (il n'y a qu'un seul $x_{i}$ ), sinon on a la condition $x_{1}=x_{n}$. Réciproquement, on peut vérifier que si $x_{1}=x_{n}$ et tous les autres $x_{i}$ sont nuls, on a bien égalité dans l'inégalité de l'énoncé.
Commentaire des correcteurs : Le problème est peu abordé, et encore moins résolu. Très peu de copies traitent les cas d'égalité, alors que cela fait partie de l'énoncé, et pouvait faire gagner des points. Veillez à bien connaître les énoncés des inégalités connues, mal appliquer une inégalité peut fausser toute une preuve.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
a3560729-30f3-5703-b8c8-fb1ba02a9998
| 607,165
|
Let $a$ and $b$ be two real numbers. Suppose that $2a + a^2 = 2b + b^2$. Show that if $a$ is an integer (not necessarily positive), then $b$ is also an integer.
|
We rewrite the equality
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Then either $\mathrm{b}=\mathrm{a}$, and in this case, b is an integer, or
$$
2=-a-b
$$
from which
$$
\mathrm{b}=-2-\mathrm{a}
$$
and $b$ is still an integer.
Comment from the graders: The problem was successfully solved by almost everyone. Be careful of calculation errors for those who went through it a bit too quickly.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
On réécrit l'égalité
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
$$
2=-a-b
$$
d'où
$$
\mathrm{b}=-2-\mathrm{a}
$$
et $b$ est encore un entier.
Commentaire des correcteurs: Le problème était réussi par presque tous. Attention aux erreurs de calcul pour ceux qui sont passés un peu vite.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
6a747265-63c0-5456-bafa-ace435dd460e
| 607,159
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
We set $P_{n}=\prod^{n} a_{k}$. We have
$$
\frac{P_{n}}{P_{n-1}}=\frac{1}{n}+\frac{1}{P_{n-1}}
$$
which gives
$$
n P_{n}=P_{n-1}+n
$$
We then set $M_{n}=n!P_{n}$. We deduce
$$
M_{n}=M_{n-1}+n!
$$
We deduce that $M_{n}=\sum k!$. We then deduce
$$
a_{n}=\frac{P_{n}}{P_{n-1}}=\frac{\frac{1}{n!} \sum k!}{\frac{1}{(n-1)!} \sum k!}
$$
It remains to show that
$$
\sum_{k=1}^{n} k!\leqslant \sum_{k=1}^{n-1} n \times k!
$$
which comes from using $\mathrm{n} \geqslant 3$ to have notably $\mathrm{n} \geqslant 2+1$ and
$$
\sum_{k=1}^{n} k!\leqslant 1+2+\sum_{k=3}^{n} n \times(k-1)!\leqslant n+n \sum_{k=2}^{n-1} k!
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
On pose $P_{n}=\prod^{n} a_{k}$. On a
$$
\frac{P_{n}}{P_{n-1}}=\frac{1}{n}+\frac{1}{P_{n-1}}
$$
ce qui donne
$$
n P_{n}=P_{n-1}+n
$$
On pose alors $M_{n}=n!P_{n}$. On déduit
$$
M_{n}=M_{n-1}+n!
$$
On déduit que $M_{n}=\sum k!$. On déduit alors
$$
a_{n}=\frac{P_{n}}{P_{n-1}}=\frac{\frac{1}{n!} \sum k!}{\frac{1}{(n-1)!} \sum k!}
$$
Il reste à montrer que
$$
\sum_{k=1}^{n} k!\leqslant \sum_{k=1}^{n-1} n \times k!
$$
ce qui vient en utilisant $\mathrm{n} \geqslant 3$ pour avoir notamment $\mathrm{n} \geqslant 2+1$ et
$$
\sum_{k=1}^{n} k!\leqslant 1+2+\sum_{k=3}^{n} n \times(k-1)!\leqslant n+n \sum_{k=2}^{n-1} k!
$$
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution de l'exercice 12"
}
|
0f01e1e0-8400-5dc2-9d8a-287000a8f3e5
| 607,168
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
:
Starting from the equation on the $P_{n}$, we want to show that $a_{n} \leqslant 1$ for $n \geqslant 3$, that is, $P_{n} \leqslant P_{n-1}$. This can be rewritten as
$$
\begin{gathered}
\frac{1}{n} P_{n-1}+1 \leqslant P_{n-1} \\
P_{n-1} \geqslant \frac{n}{n-1} .
\end{gathered}
$$
We aim to prove this inequality by induction. For $n=3$, we have
$$
P_{2}=\frac{1}{2}+1=\frac{3}{2}=\frac{3}{3-1} .
$$
If the result is true at rank $n$, then at rank $n+1$,
$$
P_{n}=\frac{1}{n} P_{n-1}+1 \geqslant \frac{1}{n} \frac{n}{n-1}+1=\frac{n}{n-1} \geqslant \frac{n+1}{n}
$$
which concludes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
:
A partir de l'équation sur les $P_{n}$, on veut donc montrer que $a_{n} \leqslant 1$ pour $n \geqslant 3$, c'est-à-dire que $P_{n} \leqslant P_{n-1}$. Ceci se réécrit
$$
\begin{gathered}
\frac{1}{n} P_{n-1}+1 \leqslant P_{n-1} \\
P_{n-1} \geqslant \frac{n}{n-1} .
\end{gathered}
$$
On cherche donc à montrer cette inégalité par récurence. Pour $\mathrm{n}=3$, on a bien
$$
\mathrm{P}_{2}=\frac{1}{2}+1=\frac{3}{2}=\frac{3}{3-1} .
$$
Si le résultat est vrai au rang n , on a, au rang $\mathrm{n}+1$,
$$
P_{n}=\frac{1}{n} P_{n-1}+1 \geqslant \frac{1}{n} \frac{n}{n-1}+1=\frac{n}{n-1} \geqslant \frac{n+1}{n}
$$
ce qui conclut la récurrence.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "## Solution alternative"
}
|
0f01e1e0-8400-5dc2-9d8a-287000a8f3e5
| 607,168
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
2 :
On a $a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n}}$. Thus:
$$
a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n-1}} \frac{1}{a_{n}}=\left(a_{n}-\frac{1}{n-1}\right) \frac{1}{a_{n}}
$$
Therefore, $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n}$. We can calculate the first few terms to find that $a_{3}=1$. We can then prove by induction on $n$ that $a_{n} \leqslant 1$.
If the result is true at rank $n$, then $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n} \leqslant 1-\frac{1}{n-1}+\frac{1}{n} \leqslant 1$. This concludes the proof.
Comment from the graders: Most of those who tackled the exercise understood it well. The main task was to transform the strong recurrence relation into a simple recurrence relation and then use induction. Some students provided reasoning that required handling the first few terms manually. This should not be overlooked, especially since it can help detect a reasoning error.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
2 :
On a $a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n}}$. Ainsi :
$$
a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n-1}} \frac{1}{a_{n}}=\left(a_{n}-\frac{1}{n-1}\right) \frac{1}{a_{n}}
$$
Dès lors $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n}$. On peut calculer les premiers termes pour avoir $a_{3}=1$. On peut ensuite prouver par récurrence sur $n$ que $a_{n} \leqslant 1$.
Si le résultat est vrai au rang $n, a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n} \leqslant 1-\frac{1}{n-1}+\frac{1}{n} \leqslant 1$. Ce qui conclut.
Commentaire des correcteurs : La plupart de ceux qui ont abordé l'exercice l'ont bien compris. Il s'agissait principalement de transformer la relation de récurrence forte en une relation de récurrence simple puis de faire une récurrence. Certains élèves ont donné des raisonnements qui demandaient de traiter les premiers termes à la main. Il ne faut pas oublier de le faire, surtout que cela peut permettre de déceler une erreur de raisonnement.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "\nSolution alternative"
}
|
0f01e1e0-8400-5dc2-9d8a-287000a8f3e5
| 607,168
|
Let $n \geqslant 2$ be an integer and $C>0$ a real constant. Suppose there exists a sequence $x_{1}, x_{2}, \ldots, x_{n}$ of real numbers, not all zero, such that:
$-x_{1}+x_{2}+\ldots+x_{n}=0$.
- For every index $1 \leqslant i \leqslant n$, either $x_{i} \leqslant x_{i+1}$ or $x_{i} \leqslant x_{i+1}+C x_{i+2}$ (where we define $x_{n+1}=x_{1}$ and $x_{n+2}=x_{2}$).
1. Show that necessarily $C \geqslant 2$.
2. Suppose that $C=2$, show that $n$ is necessarily even.
|
In the entire solution, we will consider all indices modulo \( n \). Note that the condition in the statement means that for all \( i \), if \( x_{i+2} \leqslant 0 \), then \( x_{i} \leqslant x_{i+1} \) because the condition \( x_{i} \leqslant x_{i+1} + C x_{i+2} \) also implies \( x_{i} \leqslant x_{i+1} \). Similarly, in the opposite case, \( x_{i} \leqslant x_{i+1} + C x_{i+2} \) whenever \( x_{i+1} \geqslant 0 \). Therefore, we are interested in the sign of the different terms \( x_{k} \).
Let's start by showing that there are never two consecutive negative or zero terms among the \( x_{k} \). Suppose, for the sake of contradiction, that this is the case and that there exists \( i \) such that \( x_{i} \leqslant 0 \) and \( x_{i+1} \leqslant 0 \). Then we apply the property at index \( i-1 \). Since \( x_{i+1} \leqslant 0 \), we have \( x_{i-1} \leqslant x_{i} \leqslant 0 \). Reapplying this to index \( i-1 \), we find \( x_{i-2} \leqslant 0 \), and continuing this way, we find successively that all \( x_{k} \) are negative or zero. But since the sum of the \( x_{k} \) is 0, this means they are all zero, which is impossible according to the statement.
Let \( \mathfrak{i}_{1}, \ldots, \mathfrak{i}_{\mathrm{K}} \) be the indices \( i \) where \( x_{i} \) is negative or zero. Now, we can write all the inequalities we know between the \( x_{i} \): for all \( j \),
\[
\begin{gathered}
x_{\mathfrak{i}_{j}+1} \leqslant x_{\mathfrak{i}_{j}+2} + C x_{\mathfrak{i}_{\mathfrak{j}}+3}, \quad x_{\mathfrak{i}_{\mathfrak{j}}+2} \leqslant x_{\mathfrak{i}_{\mathfrak{j}}+3} + C x_{\mathfrak{i}_{\mathfrak{j}}+4}, \ldots, \quad x_{\mathfrak{i}_{j+1}-3} \leqslant x_{\mathfrak{i}_{j+1}-2} + C x_{\mathfrak{i}_{j+1}-1} \\
x_{\mathfrak{i}_{j+1}-2} \leqslant x_{\mathfrak{i}_{j+1}-1}, \quad x_{\mathfrak{i}_{j+1}-1} \leqslant x_{\mathfrak{i}_{j+1}} + C x_{\mathfrak{i}_{j+1}+1}
\end{gathered}
\]
The only interesting inequality involving the negative terms \( x_{i_{j}} \) is the last one, so for all \( j \), \( x_{i_{j}} \geqslant x_{i_{j}-1} - C x_{i_{j}+1} \). But we know that the sum of the positive terms must balance the sum of the negative terms because the sum of all \( x_{k} \) is 0, and we write
\[
-\left(x_{i_{1}} + x_{i_{2}} + \ldots + x_{i_{k}}\right) \leqslant \left(C x_{i_{1}+1} - x_{i_{1}-1}\right) + \left(C x_{i_{1}+1} - x_{i_{1}-1}\right) + \ldots + \left(C x_{i_{1}+1} - x_{i_{1}-1}\right)
\]
The left-hand side is the sum of the positive terms, and by rearranging the terms on the right, we get
\[
\begin{aligned}
\left(x_{i_{1}+1} + x_{i_{1}+2} + \ldots + x_{i_{2}-1}\right) + \left(x_{i_{2}+1} + x_{i_{2}+2} + \ldots + x_{i_{3}-1}\right) + \ldots + \left(x_{i_{k}+1} + x_{i_{k}+2} + \ldots + x_{i_{1}-1}\right) \\
& \leqslant \left(C x_{i_{1}+1} - x_{i_{2}-1}\right) + \left(C x_{i_{2}+1} - x_{i_{3}-1}\right) + \ldots + \left(C x_{\mathfrak{i}_{k}+1} - x_{i_{1}-1}\right)
\end{aligned}
\]
The reason for arranging the terms this way is as follows: the only inequalities left among the previously cited inequalities only involve the \( \chi_{k} \) for \( k \) between \( i_{j}+1 \) and the next \( \mathfrak{i}_{j+1}-1 \), i.e., in one of the sequences of consecutive strictly positive terms. We will then show that if \( C < 2 \), then for all \( \mathfrak{j} \),
\[
x_{i_{j}+1} + x_{i_{j}+2} + \ldots + x_{i_{j+1}-1} > C x_{i_{j}+1} - x_{i_{j+1}-1}
\]
We will show that for any sequence \( a_{1}, a_{2}, \ldots, a_{m} \) of strictly positive terms satisfying the inequalities
\[
a_{1} \leqslant a_{2} + C a_{3}, \quad a_{2} \leqslant a_{3} + C a_{4}, \ldots, \quad a_{m-2} \leqslant a_{m-1} + C a_{m}, \quad a_{m-1} \leqslant a_{m}
\]
then necessarily \( a_{1} + \ldots + a_{m} > \mathrm{C} a_{1} - a_{m} \). For this, we write
\[
\begin{gathered}
C a_{1} - a_{m} = a_{1} + (C-1) a_{1} - a_{m} \leqslant a_{1} + (C-1) a_{2} + C(C-1) a_{3} - a_{m} \\
= a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + (C-1) a_{3} - a_{m} \leqslant a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + (C-1) a_{4} + C(C-1) a_{5} - a_{m}.
\end{gathered}
\]
We can continue this until we obtain, depending on the parity of \( m \),
\[
\leqslant \begin{cases}
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-1} + C(C-1) a_{m} - a_{m} & \text{if } m \text{ is odd} \\
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-2} + C(C-1) a_{m-1} - a_{m} & \text{if } m \text{ is even}
\end{cases}
\]
In the second case, we use the last inequality \( a_{m-1} \leqslant a_{m} \) to obtain
\[
\leqslant \begin{cases}
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-1} + (C(C-1) - 1) a_{m} & \text{if } m \text{ is odd} \\
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-2} + (C(C-1) - 1) a_{m-1} & \text{if } m \text{ is even}
\end{cases}
\]
When \( C < 2 \), all the coefficients in front of the \( a_{i} \) are strictly less than 1, and thus \( C a_{1} - a_{m} \) is strictly less than \( a_{1} + a_{2} + \ldots + a_{m} \). This concludes the first part of the exercise based on what we have seen previously.
Now, suppose \( C = 2 \). Note that in the study of the sequence \( a_{i} \), we always have the inequality \( C a_{1} - a_{m} \leqslant a_{1} + \ldots + a_{m} \), but from what we have shown previously, the inequality is always strict when \( m \) is even (since \( a_{m} \) is strictly positive). Therefore, for \( C = 2 \), the sequences of consecutive positive terms must always be of odd length, which means that all \( i_{j+1} - \boldsymbol{i}_{j} \) are even (since we also count one negative term). But then, since all \( \mathfrak{i}_{j+1} - \mathfrak{i}_{\mathfrak{j}} \) are even, this means that \( n \) is necessarily even when summed over \( j \).
Comment from the graders: The exercise was very poorly done. The key point was to separate the elements of the sequence between positive and negative terms (see the video on the channel on the subject). Unfortunately, many of you thought to prove that two consecutive terms could not be strictly positive, which is quite possible (it is easy to find a counterexample for \( n = 4 \)). Often the mistake was to be too optimistic in the use of inequalities, while the statement is actually quite miraculous.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\mathrm{n} \geqslant 2$ un entier et $\mathrm{C}>0$ une constante réelle. On suppose qu'il existe une suite $x_{1}, x_{2}, \ldots, x_{n}$ de réels non tous nuls telle que :
$-x_{1}+x_{2}+\ldots+x_{n}=0$.
- Pour tout indice $1 \leqslant i \leqslant n$, on a soit $x_{i} \leqslant x_{i+1}$, soit $x_{i} \leqslant x_{i+1}+C x_{i+2}$ (où on définit $x_{n+1}=x_{1}$ et $x_{n+2}=x_{2}$ ).
1. Montrer que nécessairement $C \geqslant 2$.
2. On suppose que $C=2$, montrer que n est nécessairement pair.
|
Dans toute la solution, on considèrera tous les indices modulo n . Remarquons que la condition de l'énoncé signifie que pour tout $i$, si $x_{i+2} \leqslant 0$, alors $x_{i} \leqslant x_{i+1}$ car la condition $x_{i} \leqslant x_{i+1}+C x_{i+2}$ implique aussi $x_{i} \leqslant x_{i+1}$, De la même façon dans le cas contraire, $x_{i} \leqslant x_{i+1}+C x_{i+2}$ dès que $x_{i+1} \geqslant 0$. On s'intéresse donc au signe des différents termes $x_{k}$.
Commençons par montrer qu'il n'existe jamais deux termes négatifs ou nuls à la suite parmi les $x_{k}$. Supposons par l'absurde que ce soit le cas et qu'il existe donc $i$ avec $x_{i} \leqslant 0$ et $x_{i+1} \leqslant 0$. Alors on applique la propriété à l'indice $i-1$. Comme $x_{i+1} \leqslant 0$, on a donc $x_{i-1} \leqslant x_{i} \leqslant 0$. En réappliquant ceci à l'indice $i-1$, on trouve $x_{i-2} \leqslant 0$, et en continuant ainsi on trouve successivement que tous les $x_{k}$ sont négatifs ou nuls. Mais comme la somme des $x_{k}$ vaut 0 , ceci veut dire qu'ils sont tous nuls, ce qui est impossible d'après l'énoncé.
Soient $\mathfrak{i}_{1}, \ldots, \mathfrak{i}_{\mathrm{K}}$ les indices $i$ où $x_{i}$ est négatif ou nul. Maintenant, on peut écrire toutes les inégalités que l'on connait entre les $x_{i}$ : pour tout $j$,
$$
\begin{gathered}
x_{\mathfrak{i}_{j}+1} \leqslant x_{\mathfrak{i}_{j}+2}+C x_{\mathfrak{i}_{\mathfrak{j}}+3}, \quad x_{\mathfrak{i}_{\mathfrak{j}}+2} \leqslant x_{\mathfrak{i}_{\mathfrak{j}}+3}+C x_{\mathfrak{i}_{\mathfrak{j}}+4}, \ldots, \quad x_{\mathfrak{i}_{j+1}-3} \leqslant x_{\mathfrak{i}_{j+1}-2}+C x_{\mathfrak{i}_{j+1}-1} \\
x_{\mathfrak{i}_{j+1}-2} \leqslant x_{\mathfrak{i}_{j+1}-1}, \quad x_{\mathfrak{i}_{j+1}-1} \leqslant x_{\mathfrak{i}_{j+1}}+C x_{\mathfrak{i}_{j+1}+1}
\end{gathered}
$$
La seule inégalité intéressante faisant apparaître les termes négatifs $x_{i_{j}}$ est cette dernière, on a donc pour tout $j, x_{i_{j}} \geqslant x_{i_{j}-1}-C x_{i_{j}+1}$. Mais on sait que la somme des termes positifs doit se compenser avec la somme des termes négatifs car la somme de tous les $x_{k}$ vaut 0 , et on écrit donc
$$
-\left(x_{i_{1}}+x_{i_{2}}+\ldots+x_{i_{k}}\right) \leqslant\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\ldots+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)
$$
Le terme de gauche vaut la somme des termes positifs, et en réordonnant les termes à droite on trouve
$$
\begin{aligned}
\left(x_{i_{1}+1}+x_{i_{1}+2}\right. & \left.+\ldots+x_{i_{2}-1}\right)+\left(x_{i_{2}+1}+x_{i_{2}+2}+\ldots+x_{i_{3}-1}\right)+\ldots+\left(x_{i_{k}+1}+x_{i_{k}+2}+\ldots+x_{i_{1}-1}\right) \\
& \leqslant\left(C x_{i_{1}+1}-x_{i_{2}-1}\right)+\left(C x_{i_{2}+1}-x_{i_{3}-1}\right)+\ldots+\left(C x_{\mathfrak{i}_{k}+1}-x_{i_{1}-1}\right)
\end{aligned}
$$
La raison pour mettre les termes de cette manière est la suivante : les seules inégalités qui nous restent parmi les inégalités citées précédemment ne prennent qu'en compte les $\chi_{k}$ pour $k$ entre un $i_{j}+1$ et le $\mathfrak{i}_{j+1}-1$ suivant, c'est-à-dire dans une des suites de termes strictement positifs successifs. On va alors montrer que si $C<2$, alors on a nécessairement pour tout $\mathfrak{j}$,
$$
x_{i_{j}+1}+x_{i_{j}+2}+\ldots+x_{i_{j+1}-1}>C x_{i_{j}+1}-x_{i_{j+1}-1}
$$
On va alors montrer que pour toute suite $a_{1}, a_{2}, \ldots, a_{m}$ de termes strictement positifs vérifiant les inégalités
$$
a_{1} \leqslant a_{2}+C a_{3}, \quad a_{2} \leqslant a_{3}+C a_{4}, \ldots, \quad a_{m-2} \leqslant a_{m-1}+C a_{m}, \quad a_{m-1} \leqslant a_{m}
$$
alors nécessairement $a_{1}+\ldots+a_{m}>\mathrm{Ca}_{1}-a_{m}$. Pour cela, on écrit
$$
\begin{gathered}
C a_{1}-a_{m}=a_{1}+(C-1) a_{1}-a_{m} \leqslant a_{1}+(C-1) a_{2}+C(C-1) a_{3}-a_{m} \\
=a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{3}-a_{m} \leqslant a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{4}+C(C-1) a_{5}-a_{m} .
\end{gathered}
$$
On peut continuer ainsi jusqu'à obtenir, selon la parité de m,
$$
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+C(C-1) a_{m}-a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+C(C-1) a_{m-1}-a_{m} & \text { si m est pair }\end{cases}
$$
Dans le deuxième cas, on utilise la dernière inégalité $a_{m-1} \leqslant a_{m}$ pour obtenir
$$
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+(C(C-1)-1) a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+(C(C-1)-1) a_{m-1} & \text { si m est pair }\end{cases}
$$
Lorsque $C<2$, tous les coefficients devant les $a_{i}$ sont strictement inférieurs à 1 et donc $C a_{1}-a_{m}$ est strictement inférieur à $a_{1}+a_{2}+\ldots+a_{m}$. Ceci conclut alors la première partie de l'exercice par ce qu'on a vu précédemment.
Maintenant, supposons que $C=2$. Remarquons que dans l'étude de la suite $a_{i}$, on a toujours l'inégalité $C a_{1}-a_{m} \leqslant a_{1}+\ldots+a_{m}$, mais par ce que l'on a montré précédemment l'inégalité est toujours stricte dans le cas où $m$ est pair (car $a_{m}$ strictement positif). Ainsi, pour que $C=2$, il faut que les suites de termes positifs consécutifs soient toujours de taille impaire., ce qui signifie que tous les $i_{j+1}-\boldsymbol{i}_{j}$ sont pairs (car on compte aussi un terme négatif). Mais alors comme tous les $\mathfrak{i}_{j+1}-\mathfrak{i}_{\mathfrak{j}}$ sont pairs, ceci signifie en sommant sur $j$ que $n$ est nécessairement pair.
Commentaire des correcteurs : L'exercie a été très peu réussi. Le point clef était de séparer les éléments de la suite entre termes positifs et négatifs (voir la vidéo sur la chaîne sur le sujet). Malheuresement, un certain nombre d'entre vous ont pensé démontrer que deux termes consécutifs ne pouvaient pas être strictement positifs, or c'est tout à fait possible (on peut facilement trouver un contre-exemple pour $\mathrm{n}=4$ ). Souvent l'erreur était d'être trop optimiste dans l'utilisation des inégalités alors que l'énoncé est en fait assez miraculeux.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "\nSolution de l'exercice 17"
}
|
1b9fcb1c-251b-56b3-a234-f71cf8766cec
| 607,172
|
Let $a, b$ be two integers. Show that, if neither $a$ nor $b$ is a multiple of 3, then $a^{4}-b^{2}$ is a multiple of 3.
|
Let's recall that if $k$ is not a multiple of 3, then $k$ is 1 or 2 modulo 3. Thus $\mathrm{k}^{2}$ is $1^{2}=1$ or $2^{2} \equiv 4 \equiv 1(\bmod 3):$ the square of any number not divisible by 4 is 1 modulo 3.
Thus $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, so $a^{4}-b^{2}$ is a multiple of 3.
Comment from the graders: The exercise was generally very well done, however, many students could have gone faster by using modulos instead of explicit division algorithms, which would have simplified the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3):$ tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
Commentaire des correcteurs : L'exercice a été très bien réussi dans l'ensemble, cependant pas mal d'élèves pourraient aller plus vite en utilisant des modulos plutôt que les écritures explicites des divisions euclidiennes, les calculs seraient de fait allégés.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
851d1c2c-188b-56f6-9e63-d9e2966e31f8
| 607,174
|
Let $n$ be an integer such that $n \geqslant 2$. We denote $d$ as the greatest divisor of $n$ different from $n$. We assume that $\mathrm{d}>1$. Prove that $\mathrm{n}+\mathrm{d}$ is not a power of 2.
|
Suppose by contradiction that $n+d$ is a power of 2. Note that $d$ divides $n$, so $d$ divides $n+d$, so $d$ divides a power of 2. Thus $d$ is a power of 2: we set $d=2^{k}$ for some $k \in \mathbb{N}$. We have $k \geqslant 1$ since $d \neq 1$. Let $n=d a=2^{k} a$ with $a \in \mathbb{N}^{*}$. Since $d$ is different from $n$, we have $a \geqslant 2$. Thus $2^{k-1} a$ is a divisor of $n$, greater than or equal to $2^{k}=d$, and different from $n$. By hypothesis $d=2^{k-1} a$, so $a=2$. Thus $n=2^{k+1}$.
We then find $\mathrm{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ which is not a power of 2, which is a contradiction. Thus $n+d$ is not a power of 2.
Grader's comment: The exercise was very well done, but several papers forgot that 1 is an odd divisor of a power of 2.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier vérifiant $n \geqslant 2$. On note $d$ le plus grand diviseur de $n$ différent de $n$. On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que $d$ divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de $2:$ on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme $d$ est différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
On trouve alors $\mathrm{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $n+d$ n'est pas une puissance de 2 .
Commentaire des correcteurs : L'exercice a été très bien réussi, mais plusieurs copies ont oublié que 1 est un diviseur impair d'une puissance de 2.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
556d1522-9bca-533d-9ec3-efa264da495d
| 607,175
|
An integer $n \geqslant 2$ is written on the board. Each day, someone chooses $p$, a prime divisor of the integer $n$ written on the board, erases it, and writes $n+\frac{n}{p}$ in its place. Show that $p=3$ is chosen infinitely many times.
|
Let's fix $N \in \mathbb{N}$. Denote by $2^{a_{k}} 3^{b_{k}} c_{k}$ the integer written on the board on day $k$, with $c_{k}$ being the product of prime numbers different from 2 and 3. Suppose, for the sake of contradiction, that we can never choose $p=3$ from day $N$ onwards.
If on the $k$-th day we choose $p \neq 2,3$, then the number written on the board becomes $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Let $p+1=2^{b} 3^{c} d$ with $b, c$, and $d$ being positive integers and $d$ being coprime with 2 and 3. Since $p$ is a prime and different from 2, it is odd, so $b \geqslant 1$, and thus $d \leqslant \frac{p+1}{2}$. Therefore, as the number written on the board is $2^{a_{k}+b} 3^{b_{k}+c} \frac{c_{k}}{p} d$, we have $a_{k+1}=a_{k}+b$, $b_{k+1}=b_{k}+c$, and $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p} < c_{k}$.
If on the $k$-th day we choose $p=2$, the number written on the board becomes $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. In particular, the sequence $\left(c_{k}\right)_{k \geqslant N}$ is decreasing and strictly positive. It cannot therefore decrease strictly infinitely often, otherwise it would become negative. Therefore, from a certain day $k>N$, we no longer choose $p \neq 2,3$, so $p=2$ is chosen every day from the $k$-th day onwards.
If from day $k>N$ we only choose $p=2$, then $a_{j+1}=a_{j}-1$ for all $j \geqslant k$. Therefore, the sequence of integers $\left(a_{j}\right)_{j \geqslant k}$ strictly decreases, and it must therefore become strictly negative, which is absurd.
Thus, we are forced to choose $p=3$ at least once after the $N$-th day.
Suppose that $p=3$ is not chosen infinitely often. From a certain day, denoted $N$, $p=3$ is no longer chosen. This contradicts what we have just proven: $p=3$ must therefore be chosen infinitely often.
Comment from the graders: The idea behind the reasoning in the exercise was generally understood, but the solutions were quite poorly written overall, preferring informal descriptions to precise and carefully demonstrated statements. Writing such proofs in middle school is certainly not an easy task, but it is still necessary to avoid some pitfalls. If these were minor and relatively easy to overcome in this problem (provided they were seen, which was rare), this is not always the case and "intuitively true" conclusions can turn out to be completely false because crucial steps of reasoning had not been considered. Some students did not understand the question: it was not a matter of showing that one could choose $p=3$ infinitely often with a judicious choice of operations. It was necessary to show that whatever the sequence of operations chosen from any integer (and even if one tried to avoid doing so), one must choose $p=3$ infinitely often. Most other students understood that the prime factors of $n$ became smaller and smaller, since a factor $p>2$ was replaced by the even number $p+1$, whose prime factors were all strictly less than $p$. This intuition is correct, but should not appear as such in a copy, because this statement is not clear: in what sense did the prime factors become smaller and smaller? Their maximum? Their number? Some kind of combination of both, one might say intuitively, but it still needs to be described! The whole problem with using this informal intuition as a step in reasoning is that it seems natural to deduce from it that after a certain time, the integer written on the board has only 2 and 3 as prime factors. This is not true, since one can, for example, multiply a valid sequence by 5. This may seem a trivial counterexample, but it shows that there are counterexamples, and therefore that there may be more subtle counterexamples than this one. The solution allows finding one of the ways to formalize this intuition, by explicitly identifying an integer quantity that can only decrease (a "mono-variant") and which must therefore be constant from a certain point onwards. Some students took another approach, essentially reasoning by strong induction based on the following observation: if $\mathrm{n}=\mathrm{ab}$, then one can also consider that each day two numbers $a$ and $b$ are written on two different boards, and that each day the operation is performed on one of the two boards. As a result, one or the other of the integers is modified according to the operation infinitely often and we have therefore used $\mathrm{p}=3$ infinitely often by the induction hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu' un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} c_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, $d$ des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
Commentaire des correcteurs: L'idée du raisonnement derrière l'exercice a généralement été comprise, mais les solutions ont été assez mal rédigées dans leur ensemble, préférant des descriptions informelles à des énoncés précis et soigneusement démontrés. Rédiger de telles démonstrations au collège n'est certainement pas chose facile, mais est tout de même nécessaire pour éviter quelques écueils. Si ceux-ci étaient mineurs et relativement faciles à contourner dans ce problème (pour peu qu'on les vît, ce qui était rare), ce n'est pas toujours le cas et des conclusions 'intuitivement vraies" peuvent s'avérer complètement fausses parce que des étapes cruciales de raisonnement n'auraient pas été envisagées. Quelques élèves n'ont pas compris la question : il ne s'agissait pas ici de montrer que l'on pouvait choisir $p=3$ une infinité de fois avec un choix judicieux d'opérations. Il fallait montrer que quelle que soit la suite d'opérations choisie à partir de n'importe quel entier (et même si on essayait d'éviter de le faire), on doit choisir $p=3$ une infinité de fois. Les autres élèves ont, pour la plupart, compris que les facteurs premiers de $n$ devenaient de plus en plus petits, puisqu'un facteur $p>2$ était remplacé par le nombre pair $p+1$, dont tous les facteurs premiers étaient strictement inférieurs à $p$. Cette intuition est correcte, mais ne doit pas figurer telle quelle dans une copie, parce que cet énoncé n'est pas clair : en quel sens les facteurs premiers devenaient-ils de plus en plus petits? Leur maximum? Leur nombre? Une espèce de combinaison des deux, dirait-on intuitivement, mais encore faut-il la décrire! Tout le problème d'employer cette intuition informelle comme une étape de raisonnement est qu'il semble naturel d'en déduire qu'au bout d'un certain moment, l'entier écrit au tableau n'a plus que des 2 et des 3 comme facteurs premiers. Ceci n'est pas vrai, puisqu'on peut par exemple multiplier une suite valide par 5 . Cela peut paraître un contre-exemple trivial, mais cela montre qu'il existe des contre-exemples, et donc qu'il peut exister des contre-exemples plus subtils que celui-ci. Le corrigé permet de trouver une des façons de formaliser cette intuition, en explicitant une quantité entière qui ne peut que décroître (un "mono-variant") et qui doit donc être constante à partir d'un certain moment. Quelques élèves ont pris une autre approche, consistant essentiellement à raisonner par récurrence (forte) en se reposant sur l'observation suivante : si $\mathrm{n}=\mathrm{ab}$, alors on peut aussi considérer qu'on a chaque jour deux nombres $a$ et $b$ écrits sur deux tableaux différents, et qu'on effectue chaque jour l'opération sur l'un des deux tableaux. Partant, l'un ou l'autre des entiers est modifié selon l'opération une infinité de fois et on a donc par hypothèse de récurrence
utilisé $\mathrm{p}=3$ une infinité de fois.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
2f8d56b4-a14b-56ec-9312-eee6b0aa5fd9
| 607,179
|
Let $k$ be an integer coprime with $n$ satisfying $1 \leqslant k < n$. Augustin colors the integers of $\{1,2, \ldots, n-1\}$ with as many colors as he wishes. However, if $\mathbf{j}$ is an integer satisfying $1 \leqslant j \leqslant n-1$, the integers $j$ and $n-j$ are of the same color. Additionally, if $i$ is an integer satisfying $1 \leqslant i \leqslant n$ and $i \neq k$, the integers $i$ and $|i-k|$ are of the same color.
Prove that Augustin has colored all the integers the same color.
|
For $k=1$, we see that $n$ has the same color as $n-1$, then that $n-2$ has the same color as $n-1$, etc., and all integers have the same color.
For $k=2$, $n$ is odd and we see that $n, n-2, \ldots, 1$ have the same color, then that $n-1$ has the same color as 1, and that $n-1, n-3, \ldots, 2$ have the same color.
By doing the same for small values of $k$, we realize that we always manage to show successively that $n-k, \ldots, n-(n-1)k$ taken modulo $n$ are all of the same color. Let's try to formalize this.
Let $c$ be the color of $n$. We prove by induction the following property for all $\boldsymbol{j} \in \{1, \ldots, \boldsymbol{n}-1\}$: $\mathcal{P}(\mathfrak{j})$: "The remainder of the Euclidean division of $n-jk$ is not congruent to 0 modulo $n$, and is colored with the color $c$."
Initialization: for $j=1$, since $1 \leqslant n-k \leqslant n-1$, the remainder of the Euclidean division of $n-k$ is $n-k$, is not congruent to 0 modulo $n$, and is colored with the color $c$.
Induction: Let $j \in \{0, \ldots, n-2\}$, suppose that $P(j)$ is true and let's show $P(j+1)$. Let $r$ be the remainder of the Euclidean division of $n-jk$ by $n$.
First case: if $r > k$, then $n > r \geqslant r-k > 0$. Now $r-k \equiv n-jk-k \equiv n-(j+1)k \pmod{n}$. Therefore, the remainder of the Euclidean division of $n-jk$ by $n$ is $r-k$, is non-zero, and is of the same color as $r$, hence of color $c$, which concludes.
Second case: if $r = k$, then $n-jk \equiv k \pmod{n}$, i.e., $(j+1)k \equiv 0 \pmod{n}$. Since $n$ is coprime with $k$, and divides $(\mathfrak{j}+1)k$, $n$ divides $\mathfrak{j}+1$, but since $\mathfrak{j}+1 \in \{1, \ldots, n-1\}$, this case is impossible.
Third case: if $k > r$, then $k-r$ is of the same color as $r$, hence of color $c$. Moreover, we have $1 \leqslant k-r \leqslant k \leqslant n-1$, so $n-(k-r)$ satisfies $1 \leqslant n-(k-r) \leqslant n-1$ and is of color $c$. Now $n-(k-r) \equiv r-k \equiv n-(j+1)k \pmod{n}$, so $n-(k-r)$ is the remainder of the Euclidean division of $n-(j+1)k$ by $n$, is non-zero, and of color $c$, which concludes.
This concludes the induction.
Now let $\boldsymbol{j} \in \{1, \ldots, \boldsymbol{n}-1\}$. There exists $\ell \in \{0, \ldots, \boldsymbol{n}-1\}$ such that $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k \pmod{\boldsymbol{n}}$: indeed, this is equivalent to $\ell k \equiv n-j \pmod{n}$, or to $\ell \equiv (n-\mathfrak{j})k^{-1} \pmod{n}$ (where $k^{-1}$ is the inverse of $k$ modulo $n$, which exists since $k$ is coprime with $n$), and admits a solution in $\{0, \ldots, n-1\}$. In particular, $j$ is the remainder of the division of $n-\ell j$ by $n$, so it is of color $c$. Thus all integers from 1 to $n-1$ have the same color as $n$, so all integers are colored the same color.
Comment from the graders: The exercise is relatively poorly solved: many provided proofs are incomplete, as they forget certain constraints (e.g., $i \neq k$ to say that $|i-k|$ and $i$ have the same color, forgetting that $i$ and $i+k$ do not have the same color if $i > n-k$, etc).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
Notons c la couleur de n . On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur c ce qui conclut.
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
Ceci conclut l'hérédité.
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$. Il existe $\ell \in\{0 \ldots, \boldsymbol{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc).
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
8570192b-79b3-57e1-830e-68611e25fff1
| 607,180
|
Let $a, b$ be two integers. Show that, if neither $a$ nor $b$ is a multiple of 3, then $a^{4}-b^{2}$ is a multiple of 3.
|
Let's recall that if $k$ is not a multiple of 3, then $k$ is 1 or 2 modulo 3. Thus $\mathrm{k}^{2}$ is $1^{2}=1$ or $2^{2} \equiv 4 \equiv 1(\bmod 3)$: the square of any number not divisible by 4 is 1 modulo 3.
Thus $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, so $a^{4}-b^{2}$ is a multiple of 3.
Comment from the graders: Very well done exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3)$ : tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
Commentaire des correcteurs: Exercice très bien réussi.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
851d1c2c-188b-56f6-9e63-d9e2966e31f8
| 607,174
|
Let n be an integer such that $\mathrm{n} \geqslant 2$. We denote d as the greatest divisor of n different from n. We assume that $\mathrm{d}>1$. Prove that $\mathrm{n}+\mathrm{d}$ is not a power of 2.
|
Suppose by contradiction that $n+d$ is a power of 2. Note that $d$ divides $n$, so $d$ divides $n+d$, so $d$ divides a power of 2. Thus $d$ is a power of 2: we set $d=2^{k}$ for some $k \in \mathbb{N}$. We have $k \geqslant 1$ because $d \neq 1$. Let $n=d a=2^{k} a$ with $a \in \mathbb{N}^{*}$. Since $d$ is different from $n$, we have $a \geqslant 2$. Thus $2^{k-1} a$ is a divisor of $n$, greater than or equal to $2^{k}=d$, and different from $n$. By hypothesis $d=2^{k-1} a$, so $a=2$. Thus $n=2^{k+1}$.
We then find $\boldsymbol{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ which is not a power of 2, leading to a contradiction. Thus $\mathrm{n}+\mathrm{d}$ is not a power of 2.
Graders' comment: Well-executed exercise, however, some students go too fast and forget steps, essential to arrive at contradictions, then unjustified.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit n un entier vérifiant $\mathrm{n} \geqslant 2$. On note d le plus grand diviseur de n différent de n . On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de 2 : on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme dest différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
On trouve alors $\boldsymbol{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
Commentaire des correcteurs: Exercice bien réussi, cependant quelques élèves vont un peu trop vite et oublient des étapes, essentielles pour aboutir à des contradictions, alors injustifiées.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 11.",
"solution_match": "\nSolution de l'exercice 11"
}
|
a8458261-1f6b-54da-bcc4-3ded334f21ab
| 607,183
|
An integer $n \geqslant 2$ is written on the board. Each day, someone chooses $p$, a prime divisor of the integer $n$ written on the board, erases it, and writes $n+\frac{n}{p}$ in its place. Show that $p=3$ is chosen infinitely many times.
|
Let's fix $N \in \mathbb{N}$. Denote $2^{a_{k}} 3^{b_{k}} \mathbf{c}_{k}$ as the integer written on the board on day $k$, where $c_{k}$ is the product of primes distinct from 2 and 3. Suppose, for the sake of contradiction, that we can never choose $p=3$ from day $N$ onwards.
If on the $k$-th day we choose $p \neq 2,3$, then the number written on the board becomes $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Let $p+1=2^{b} 3^{c} d$ where $b, c$, and $d$ are positive integers and $d$ is coprime with 2 and 3. Since $p$ is a prime and different from 2, it is odd, so $b \geqslant 1$, thus $d \leqslant \frac{p+1}{2}$. Therefore, as the number written on the board is $2^{a_{k}+b} 3^{b_{k}+c} \frac{c_{k}}{p} d$, we have $a_{k+1}=a_{k}+b, b_{k+1}=b_{k}+c$, and $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
If on the $k$-th day we choose $p=2$, the number written on the board becomes $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. In particular, the sequence $\left(c_{k}\right)_{k \geqslant N}$ is decreasing and strictly positive. It cannot therefore decrease strictly infinitely often, otherwise it would become negative. Therefore, from a certain day $k>N$, we no longer choose $p \neq 2,3$, so $p=2$ is chosen every day from the $k$-th day onwards.
If from day $k>N$ we only choose $p=2$, then $a_{j+1}=a_{j}-1$ for all $j \geqslant k$. Therefore, the sequence of integers $\left(a_{j}\right)_{j \geqslant k}$ strictly decreases, and it must therefore become strictly negative, which is absurd.
Thus, we are forced to choose $p=3$ at least once after the $N$-th day.
Suppose that $p=3$ is not chosen infinitely often. From a certain day, denoted $N$, $p=3$ is no longer chosen. This contradicts what we have just proven: $p=3$ is therefore chosen infinitely often.
Comment from the graders: Some students misunderstood the problem: it was to prove that one is forced to choose $p=3$ infinitely often regardless of the choices made, not that one could arrange for it to be the case. The problem is generally well approached by those who correctly interpreted it, but many students lack rigor. The challenge was to find a rigorous argument (thus a priori a monovariant, whether it be the one proposed in the solution, the reverse lexicographic order of the exponents, or many other possibilities) to clarify the phrase read in too many copies: "the prime factors decrease." This phrase, devoid of mathematical meaning, does not constitute a valid argument, and one must clarify the intuition behind it. This is a common pitfall in combinatorics: it is sometimes delicate to move from intuition to a rigorous argument, and often a significant part of the difficulty of the problem lies precisely in this step.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu'un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} \mathbf{c}_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, d des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
Commentaire des correcteurs : Certains élèves ont mal compris l'énoncé : il s'agissait de prouver que l'on était obligé de choisir $p=3$ une infinité de fois quels que soient les choix effectués, pas que l'on pouvait s'arranger pour que ce soit le cas. L'exercice est généralement bien abordé par ceux qui l'ont correctement interprété, mais de trop nombreux élèves manquent de rigueur. L'enjeu était de trouver un argument rigoureux (donc a priori un monovariant, que ce soit celui proposé par le corrigé, l'ordre lexicographique inversé des exposants ou beaucoup d'autres possibilités) pour clarifier la phrase lue dans de trop nombreuses copies : "les facteurs premiers décroissent". Cette phrase dénuée de sens mathématique ne constitue en aucun cas un argument recevable, il faut clarifier l'intuition qui se cache derrière. C'est un écueil que l'on croise souvent en combinatoire : il est parfois délicat de passer de l'intuition à l'argument rigoureux, et souvent une partie de la difficulté de l'exercice réside justement dans cette étape.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "\nSolution de l'exercice 13"
}
|
4540011d-1c7c-5e6b-8cb2-2fe23ecca471
| 607,185
|
Let $k$ be an integer coprime with $n$ satisfying $1 \leqslant k < n$. Augustin colors the integers of $\{1,2, \ldots, n-1\}$ with as many colors as he wishes. However, if $\mathbf{j}$ is an integer satisfying $1 \leqslant j \leqslant n-1$, the integers $j$ and $n-j$ are of the same color. Additionally, if $i$ is an integer satisfying $1 \leqslant i \leqslant n$ and $i \neq k$, the integers $i$ and $|i-k|$ are of the same color.
Prove that Augustin has colored all the integers the same color.
|
For $k=1$, we see that $n$ has the same color as $n-1$, then that $n-2$ has the same color as $n-1$, etc., and all integers have the same color.
For $k=2$, $n$ is odd and we see that $n, n-2, \ldots, 1$ have the same color, then that $n-1$ has the same color as 1, and that $n-1, n-3, \ldots, 2$ have the same color.
By doing the same for small values of $k$, we realize that we always manage to show successively that $n-k, \ldots, n-(n-1)k$ taken modulo $n$ are all the same color. Let's try to formalize this.
Let $c$ be the color of $\boldsymbol{n}$. We prove by induction the following property for all $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$: $\mathcal{P}(\mathfrak{j})$: "The remainder of the Euclidean division of $n-j k$ is not congruent to 0 modulo $n$, and is colored with the color $c$."
Initialization: for $j=1$, since $1 \leqslant n-k \leqslant n-1$, the remainder of the Euclidean division of $n-k$ is $n-k$, is not congruent to 0 modulo $n$, and is colored with the color $c$.
Induction: Let $j \in\{0, \ldots, n-2\}$, suppose that $P(j)$ is true and let's show $P(j+1)$. Let $r$ be the remainder of the Euclidean division of $n-j k$ by $n$.
First case: if $r>k$, then $n>r \geqslant r-k>0$. Now $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Therefore, the remainder of the Euclidean division of $n-j k$ by $n$ is $r-k$, is non-zero, and is the same color as $r$, hence color $c$, which concludes.
Second case: if $r=k$, then $n-j k \equiv k(\bmod n)$, i.e., $(j+1) k \equiv 0(\bmod n)$. Since $n$ is coprime with $k$, and divides $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divides $\boldsymbol{j}+1$, but since $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, this case is impossible.
Third case: if $k>r$, then $k-r$ is the same color as $r$, hence color $c$. Moreover, we have $1 \leqslant k-r \leqslant k \leqslant n-1$, so $n-(k-r)$ satisfies $1 \leqslant n-(k-r) \leqslant n-1$ and is color $c$. Now $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, so $n-(k-r)$ is the remainder of the Euclidean division of $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ by $n$, is non-zero, and is color $c$, which concludes.
This concludes the induction.
Now let $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$. There exists $\ell \in\{0 \ldots, \mathfrak{n}-1\}$ such that $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n})$: indeed, this is equivalent to $\ell k \equiv n-j(\bmod n)$, or to $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)$ (where $k^{-1}$ is the inverse of $k$ modulo $n$, which exists since $k$ is coprime with $n$), and admits a solution in $\{0 \ldots, \mathrm{n}-1\}$. In particular, $j$ is the remainder of the division of $n-\ell j$ by $n$, so it is color $c$. Thus all integers from 1 to $n-1$ have the same color as $n$, so all integers are colored the same color.
Comment from the graders: The exercise is relatively poorly solved: many provided proofs are incomplete, as they forget certain constraints ($i \neq k$ to say that $|i-k|$ and $i$ have the same color, forgetting that $i$ and $i+k$ do not have the same color if $i>n-k$, etc.). It is crucial that students re-read their work with a fresh mind: some copies make no sense when re-read with a fresh mind, and several students could have avoided a setback by re-reading their work with a clear head.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
Notons c la couleur de $\boldsymbol{n}$. On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur $c$ ce qui conclut.
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
Ceci conclut l'hérédité.
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$. Il existe $\ell \in\{0 \ldots, \mathfrak{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc). Il est crucial que les élèves se relisent à froid : certaines copies n'ont vraiment pas de sens en les relisant à froid, et plusieurs élèves auraient évité une déconvenue en relisant leur production à tête reposée.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "\nSolution de l'exercice 14"
}
|
8570192b-79b3-57e1-830e-68611e25fff1
| 607,180
|
Let $\left(P_{n}\right)_{n \in \mathbb{N}}$ be a sequence of polynomials with integer coefficients. Suppose there exists a monic polynomial $Q$ with integer coefficients such that $P_{n+1}-P_{n}=Q$ for all $n \geqslant 0$. Furthermore, suppose that for all $\mathrm{n} \geqslant 0, \mathrm{P}_{\mathrm{n}}$ has an integer root. Show that we are in one of the following two cases:
- $P_{0}$ and $Q$ have a common integer root
- There exists a polynomial with integer coefficients $R$ such that $\mathrm{P}_{0}=R Q$ and the degree of $R$ is 1.
|
Suppose that $P_{0}$ and $Q$ have no common integer roots. Note that by immediate induction $P_{n}=P_{0}+n Q$ for all $n \geqslant 0$. Let $x_{n}$ be an integer root of $P_{n}$ for all $n \geqslant 0$, we have that $n Q\left(x_{n}\right)=-P_{0}\left(x_{n}\right)$, so $Q\left(x_{n}\right)$ divides $P_{0}\left(x_{n}\right)$.
Note that if $x_{k}=x_{j}$ with $k \neq j$, then $P_{0}\left(x_{k}\right)+k Q\left(x_{k}\right)=0=P_{0}\left(x_{j}\right)+j Q\left(x_{j}\right)$, so $(k-j) Q\left(x_{k}\right)=0$, thus $Q\left(x_{k}\right)=0$. Therefore, $P_{0}\left(x_{k}\right)=0$, so $P_{0}$ and $Q$ have a common integer root, which is contradictory. Thus the sequence $\left(x_{k}\right)_{k \geqslant 0}$ is injective and therefore takes arbitrarily large values.
Perform the Euclidean division of $P_{0}$ by $Q$. Since $Q$ is monic with integer coefficients (and $P_{0}$ has integer coefficients), there exist polynomials $R$ and $S$ with integer coefficients such that $P_{0}=Q R+S$ with $S$ of degree less than or equal to $Q$.
Evaluating at $x_{n}, P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)+S\left(x_{n}\right)$, so since $Q\left(x_{n}\right)$ divides $P_{0}\left(x_{n}\right), Q\left(x_{n}\right)$ divides $S\left(x_{n}\right)=P_{0}\left(x_{n}\right)-Q\left(x_{n}\right) R\left(x_{n}\right)$. For any integer $k$ with $|k|$ sufficiently large, since the degree of $S$ is strictly less than that of $Q,|S(k)|<|Q(k)|$. Since the sequence $(x_{n})$ takes arbitrarily large values, there are infinitely many $n$ such that $|S\left(x_{n}\right)|<|Q\left(x_{n}\right)|$. Since $Q\left(x_{n}\right)$ divides $S\left(x_{n}\right)$, we deduce that there are infinitely many $n$ such that $S\left(x_{n}\right)=0$. Since the sequence is injective, $S$ has infinitely many roots, so $S=0$. Thus $P_{0}=Q R$.
Furthermore, evaluating at $x_{n}$, we have $-n Q\left(x_{n}\right)=P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)$. If $Q\left(x_{n}\right)=0$, then $P_{0}\left(x_{n}\right)=0$ and $P_{0}$ and $Q$ have a common root, contradiction. Thus $Q\left(x_{n}\right) \neq 0$, so $R\left(x_{n}\right)=-n$. Thus for any integer $N \geqslant 0$, there are at least $N$ integers $y$ such that $R(y) \in[-N, N]$.
If the degree of $R$, denoted $d$, is at least 2, for a sufficiently large $M$ and for a $C>0$, we have for all $x$ such that $|x| \geqslant M,|R(x)| \geqslant C|x|^{d}$. Thus for sufficiently large $N$, the number of integers such that $|R(x)| \leqslant N$ is less than $2 M+1$ (the number of integers in $[-M, M]$), plus the number of integers $|x| \geqslant M$ such that $|P(x)| \leqslant N$. For these $x$, we have $C|x|^{d} \leqslant N$ so $|x| \leqslant(N / C)^{1 / d}$. Thus there are at most $2 M+1+2(N / C)^{1 / d}+1$ integers such that $P(y) \in[-N, N]$, which is strictly less than $N$ for sufficiently large $N$, which is contradictory.
Thus the degree of $R$ is at most 1. Since we have $R\left(x_{n}\right)=-n$ for all $n$, the degree of $R$ is 1.
Alternatively, to prove that the degree of $R$ is 1, we could note that for all $n, x_{n+1}-x_{n}$ divides $R\left(x_{n+1}\right)-R\left(x_{n}\right)=-1$. In particular, $x_{n+1}-x_{n}= \pm 1$ for all $n$. Since the sequence $\left(x_{n}\right)$ is injective, we cannot have $x_{n+1}-x_{n}=1$ and $x_{n+2}-x_{n+1}=-1$, or have $x_{n+1}-x_{n}=-1$ and $x_{n+2}-x_{n+1}=1$ otherwise $x_{n}=x_{n+2}$. Thus, by easy induction, either for all $n$, $x_{n+1}-x_{n}=1$, and thus $x_{n}=x_{0}+n\left(x_{1}-x_{0}\right)$, or $x_{n+1}-x_{n}=-1$, and thus $x_{n}=x_{0}-n\left(x_{1}-x_{0}\right)$.
In the first case, by setting $S(X)=R\left(x_{0}+X\left(x_{1}-x_{0}\right)\right)-X$, we see that $Q(n)=0$ for all $n$. Since $S$ is a polynomial, it is the zero polynomial, so for all real $x$, $R\left(x_{0}+x\left(x_{1}-x_{0}\right)\right)=x$. Thus by setting $x=\frac{y-x_{0}}{x_{1}-x_{0}}$ (which is well-defined since $x_{1} \neq x_{0}$), we have that $R(y)=\frac{y-x_{0}}{x_{1}-x_{0}}$ for all $y$, so by identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ is of degree 1.
In the second case, by setting $S(X)=R\left(x_{0}-X\left(x_{1}-x_{0}\right)\right)-X$, we see that $Q(n)=0$ for all $n$. Since $S$ is a polynomial, it is the zero polynomial, so for all real $x$, $R\left(x_{0}-x\left(x_{1}-x_{0}\right)\right)=x$. Thus by setting $x=\frac{x_{0}-y}{x_{1}-x_{0}}$ (which is well-defined since $x_{1} \neq x_{0}$), we have that $R(y)=\frac{x_{0}-y}{x_{1}-x_{0}}$ for all $y$, so by identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ is of degree 1.
Comment from the graders: The exercise was very well handled by the students who approached it. Almost all of them correctly saw that an $R$ of degree at least 2 would "grow and shrink too quickly" to hit all negative integers, but some did not rigorously formalize this true idea. Additionally, it is important to keep in mind that we can consider the Euclidean division of $P_{0}$ by $Q$ in $\mathbb{Z}[X]$ only because $Q$ is monic. Finally, never forget the trivial cases: it is a shame to see students lose a point for not specifying that $R$ cannot be constant.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\left(P_{n}\right)_{n \in \mathbb{N}}$ une suite de polynômes à coefficients entiers. On suppose qu'il existe un polynôme $Q$ unitaire à coefficient entier tel que $P_{n+1}-P_{n}=Q$ pour tout $n \geqslant 0$. On suppose de plus que pour tout $\mathrm{n} \geqslant 0, \mathrm{P}_{\mathrm{n}}$ a une racine entière. Montrer qu'on est dans un des deux cas suivants :
- $P_{0}$ et $Q$ ont une racine entière en commun
- Il existe un polynôme à coefficients entiers R tel que $\mathrm{P}_{0}=R Q$ et le degré de R est 1 .
|
Supposons que $\mathrm{P}_{0}$ et Q n'ont pas de racines entière en commun. Notons que par récurrence immédiate $P_{n}=P_{0}+n Q$ pour tout $n \geqslant 0$. Notons $x_{n}$ une racine entière de $P_{n}$ pour tout $n \geqslant 0$, on a que $n Q\left(x_{n}\right)=-P_{0}\left(x_{n}\right)$, donc $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right)$.
Notons que si $x_{k}=x_{j}$ avec $k \neq j$, alors $P_{0}\left(x_{k}\right)+k Q\left(x_{k}\right)=0=P_{0}\left(x_{j}\right)+j Q\left(x_{j}\right)$, donc $(k-j) Q\left(x_{k}\right)=$ 0 , donc $Q\left(x_{k}\right)=0$. Ainsi $P_{0}\left(x_{k}\right)=0$, donc $P_{0}$ et $Q$ ont une racine entière en commun, ce qui est contradictoire. Ainsi la suite $\left(x_{k}\right)_{k \geqslant 0}$ est injective donc prend des valeurs arbitrairement grandes.
Faisons la division euclidienne de $\mathrm{P}_{0}$ par Q . Comme Q est unitaire à coefficient entier (et $\mathrm{P}_{0}$ à coefficients entiers), il existe des polynômes $R$ et $S$ à coefficients entiers tels que $P_{0}=Q R+S$ avec $S$ de degré inférieur ou égal à Q.
En évaluant en $x_{n}, P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)+S\left(x_{n}\right)$, donc comme $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right), Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)=P_{0}\left(x_{n}\right)-Q\left(x_{n}\right) R\left(x_{n}\right)$. Or pour tout entier $k$ avec $|k|$ assez grand, comme le degré de $S$ est strictement inférieur à celui de $\mathrm{Q},|S(k)|<|\mathrm{Q}(\mathrm{k})|$. Comme la suite ( $\mathrm{x}_{\mathrm{n}}$ ) prend des valeurs arbitrairement grande, il existe une infinité de $n$ tels que $\left|S\left(x_{n}\right)\right|<\left|Q\left(x_{n}\right)\right|$. Comme $Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)$, on en déduit qu'il existe une infinité de $n$ tels que $S\left(x_{n}\right)=0$. Comme la suite est injective, $S$ a une infinité de racine, donc $S=0$. Ainsi $P_{0}=Q R$.
De plus, en évaluant en $x_{n}$, on a $-n Q\left(x_{n}\right)=P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)$. Si $Q\left(x_{n}\right)=0$, alors $P_{0}\left(x_{n}\right)=0$ et $P_{0}$ et $Q$ ont une racine en commun, contradiction. Ainsi $Q\left(x_{n}\right) \neq 0$, donc $R\left(x_{n}\right)=-n$. Ainsi pour tout entier $N \geqslant 0$, il existe au moins $N$ entiers $y$ tels que $R(y) \in[-N, N]$.
Or si le degré de $R$ noté $d$ vaut au moins 2 , pour un $M$ assez grand et pour un $C>0$, on a pour tout $x$ vérifiant $|x| \geqslant M,|R(x)| \geqslant C|x|^{d}$. Ainsi pour $N$ assez grand, le nombre d'entier tel que $|R(x)| \leqslant N$ est plus petit que $2 M+1$ (le nombre d'entiers dans $[-M, M]$ ), auquel on ajoute le nombre d'entiers $|x| \geqslant M$ tel que $|P(x)| \leqslant N$. Pour ces $x$, on a $C|x|^{d} \leqslant N$ donc $|x| \leqslant(N / C)^{1 / d}$. Ainsi on a au plus $2 M+1+2(N / c)^{1 / d}+1$ entiers tels que $P(y) \in[-n, n]$, ce qui est strictement inférieurs à $N$ pour $N$ assez grand, ce qui est contradictoire.
Ainsi le degré de $R$ est au plus 1 . Comme on a $R\left(x_{n}\right)=-n$ pour tout $n$, le degré de $R$ vaut 1 .
Alternativement, pour prouver que le degré de $R$ valait $n$, on pouvait remarquer que pour tout $n, x_{n+1}-x_{n}$ divise $R\left(x_{n+1}\right)-R\left(x_{n}\right)=-1$. En particulier $x_{n+1}-x_{n}= \pm 1$ pour tout $n$. Comme la suite $\left(x_{n}\right)$ est injective, on ne peut avoir $x_{n+1}-x_{n}=1$ et $x_{n+2}-x_{n+1}=-1$, ou avoir $x_{n+1}-x_{n}=-1$ et $x_{n+2}-x_{n+1}=1$ sinon $x_{n}=x_{n+2}$. Ainsi on a facilement par récurrence que soit pour tout $n$, $x_{n+1}-x_{n}=1$, et donc $x_{n}=x_{0}+n\left(x_{1}-x_{0}\right)$, soit $x_{n+1}-x_{n}=-1$, et donc $x_{n}=x_{0}-n\left(x_{1}-x_{0}\right)$.
Dans le premier cas, en posant $S(X)=R\left(x_{0}+X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}+x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{y-x_{0}}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{y-x_{0}}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
Dans le second cas, en posant $S(X)=R\left(x_{0}-X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}-x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{x_{0}-y}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{x_{0}-y}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
Commentaire des correcteurs: L'exercice a été très bien traité par les élèves qui l'ont abordé. Presque tous ont bien vu qu'un R de degré au moins 2 " croirait et décroirait trop vite" pour attendre tous les entiers négatifs, mais certains n'ont pas rendu cette idée, certes vraie, rigoureuse. De plus, il faut garder
en tête qu'on peut considérer la divison euclidienne de $P_{0}$ par $Q$ dans $Z[X]$ seulement parce que $Q$ est unitaire. Enfin, ne jamais oublier les cas triviaux : il est dommage de voir des élèves perdre un point pour ne pas avoir préciser que $R$ ne pouvait être constant.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "\nSolution de l'exercice 15"
}
|
c0cae9b9-ec84-5ed9-8d58-44ee069bee01
| 607,186
|
Let $a, b$ be integers such that $\mathrm{pgcd}(\mathrm{a}, \mathrm{b})$ has at least two distinct prime factors. Let $S=\{x \in \mathbb{N} \mid x \equiv a[b]\}$. An element of $S$ is said to be irreducible if it cannot be written as a product of at least two elements of $S$ (not necessarily distinct).
Show that there exists $\mathrm{N}>0$ such that every element of $S$ can be written as a product of at most N irreducible elements of $S$ (not necessarily distinct).
|
Let $d=\operatorname{gcd}(a, b)$, and write $a=d a^{\prime}, b=d b^{\prime}$. Let's start by treating the case where $\operatorname{gcd}\left(d, b^{\prime}\right)>1$. If this is the case, then we have $\operatorname{gcd}\left(a^{2}, b\right)=d \operatorname{gcd}\left(d a^{\prime 2}, b^{\prime}\right)>d$. Therefore, for all $k \geqslant 2$, we have $a^{k} \not \equiv a[b]$. In particular, every element of $S$ is irreducible, and thus $N=1$ is suitable.
Now suppose that $d$ and $b^{\prime}$ are coprime. Then $a$ and $b^{\prime}$ are coprime; let $\omega$ be the order of $a$ modulo $b^{\prime}$. We then have that $a^{\omega+1} \equiv a[b]$. Therefore, any product of $\omega+1$ elements of $S$ is still an element of $S$. This means in particular that any non-irreducible element of $S$ can be written as a product of $k$ elements of $S$ for some $k \in \llbracket 2, \omega \rrbracket$.
Let $p$ and $q$ be two prime divisors of $d$, and let $x \in S$. If $x$ is irreducible, it's fine; otherwise, write $x=\mathfrak{u}_{1} \mathfrak{u}_{2} \ldots \mathfrak{u}_{k}$ with $\mathfrak{u}_{1}, \ldots, \mathfrak{u}_{k} \in S$, for some $k \in \llbracket 2, \omega \rrbracket$. First, let's show that we can assume $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$ for all $\boldsymbol{j}<\mathrm{k}$. For this, we note that if $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right) \geqslant \varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$, then we can replace $\mathfrak{u}_{j}$ by $\frac{\mathfrak{u}_{j}}{p^{\varphi\left(b^{\prime}\right)}}$ and $\mathfrak{u}_{k}$ by $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k}$. We have $p^{\varphi\left(b^{\prime}\right)} \equiv 1\left[b^{\prime}\right]$, so $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv \mathfrak{u}_{k} \equiv a\left[b^{\prime}\right]$. On the other hand, $d \mid \mathfrak{u}_{k}$, so $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv 0 \equiv a[d]$. Therefore, by the Chinese Remainder Theorem, we have $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv a[b]$. On the other hand, we also have $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a\left[b^{\prime}\right]$, and we also have (since $v_{\mathfrak{p}}\left(u_{j}\right) \geqslant \varphi\left(b^{\prime}\right)+v_{p}(d)$) that $d \left\lvert\, \frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}}\right.$. Therefore, $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a[b]$.
We now have $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$ for $\boldsymbol{j}<\mathrm{k}$. Similarly, we can assume that $v_{\boldsymbol{q}}\left(\mathfrak{u}_{\mathrm{k}}\right)<\varphi\left(b^{\prime}\right)+v_{q}(d)$. Any writing of $\boldsymbol{u}_{j}(j<k)$ as a product of irreducibles only involves multiples of $d$, and thus of $p$, and therefore includes at most $v_{p}\left(u_{j}\right)$ factors. Similarly for $q$ with $\mathfrak{u}_{k}$. Finally, we have managed to write $x$ as a product of at most $(\omega-1)\left(\varphi\left(b^{\prime}\right)+v_{p}(d)-1\right)+\varphi\left(b^{\prime}\right)+v_{q}(d)-1$ irreducible factors, as desired.
Comment from the graders: The exercise is successfully completed by a handful of students. It seems that the notion of irreducibility posed comprehension problems, showing that any number in $S$ can be written as a finite number of irreducible elements did not answer the question. Finally, it is regrettable that for some, the copies returned for this submission problem are almost illegible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers tels que $\mathrm{pgcd}(\mathrm{a}, \mathrm{b}) \mathrm{a}$ au moins deux facteurs premiers distincts. Soit $S=\{x \in \mathbb{N} \mid x \equiv a[b]\}$. Un élément de $S$ est dit irréductible s'il ne peut pas s'écrire comme un produit d'au moins deux éléments de $S$ (pas forcément distincts).
Montrer qu'il existe $\mathrm{N}>0$ tel que tout élément de $S$ s'écrit comme produit d'au plus N éléments irréductibles de $S$ (pas forcément distincts).
|
Soit $d=\operatorname{pgcd}(a, b)$, et écrivons $a=d a^{\prime}, b=d b^{\prime}$. Commençons par traiter le cas où $\operatorname{pgcd}\left(\mathrm{d}, \mathrm{b}^{\prime}\right)>1$. Si c'est le cas, alors on a $\operatorname{pgcd}\left(\mathrm{a}^{2}, \mathrm{~b}\right)=\operatorname{dpgcd}\left(\mathrm{da}^{\prime 2}, \mathrm{~b}^{\prime}\right)>\mathrm{d}$. Donc, pour tout $k \geqslant 2$, on a $a^{k} \not \equiv a[b]$. En particulier, tout élément de $S$ est irréductible, et donc $N=1$ convient.
Supposons à présent que $d$ et $b^{\prime}$ sont premiers entre eux. On a alors $a$ et $b^{\prime}$ premiers entre eux; soit $\omega$ l'ordre de a modulo $b^{\prime}$. On a alors que $\mathrm{a}^{\omega+1} \equiv \mathrm{a}[\mathrm{b}]$. Donc tout produit de $\omega+1$ éléments de $S$ est encore un élément de $S$. Ceci signifie en particulier que tout élément non irréductible de $S$ peut s'écrire comme un produit de $k$ éléments de $S$ pour un certain $k \in \llbracket 2, \omega \rrbracket$.
Soient $p$ et $q$ deux diviseurs premiers de d, et soit $x \in S$. Si $x$ est irréductible, c'est bon; sinon, écrivons $x=\mathfrak{u}_{1} \mathfrak{u}_{2} \ldots \mathfrak{u}_{k}$ avec $\mathfrak{u}_{1}, \ldots, \mathfrak{u}_{k} \in S$, pour un $k \in \llbracket 2, \omega \rrbracket$. Montrons d'abord qu'on peut supposer $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathfrak{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour tout $\boldsymbol{j}<\mathrm{k}$. Pour cela, on remarque que, si $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right) \geqslant \varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$, alors on peut remplacer $\mathfrak{u}_{j}$ par $\frac{\mathfrak{u}_{j}}{p^{\varphi\left(b^{\prime}\right)}}$ et $\mathfrak{u}_{k}$ par $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k}$. On a $p^{\varphi\left(b^{\prime}\right)} \equiv 1\left[b^{\prime}\right]$, donc $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv \mathfrak{u}_{k} \equiv a\left[b^{\prime}\right]$. D'autre part, $\mathrm{d} \mid \mathfrak{u}_{k}$ donc $\mathrm{p}^{\varphi\left(\mathrm{b}^{\prime}\right)} \mathfrak{u}_{\mathrm{k}} \equiv 0 \equiv \mathrm{a}[\mathrm{d}]$. Donc, d'après le théorème des restes chinois, on a $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv a[b]$. D'autre part, on a aussi $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a\left[b^{\prime}\right]$, et on a également (puisque $v_{\mathfrak{p}}\left(u_{j}\right) \geqslant$ $\left.\varphi\left(b^{\prime}\right)+v_{p}(d)\right)$ que $d \left\lvert\, \frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}}\right.$. Donc $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a[b]$.
On a à présent $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour $\boldsymbol{j}<\mathrm{k}$. De même, on peut supposer que $v_{\boldsymbol{q}}\left(\mathfrak{u}_{\mathrm{k}}\right)<$ $\varphi\left(b^{\prime}\right)+v_{q}(d)$. Toute écriture de $\boldsymbol{u}_{j}(j<k)$ sous forme de produit d'irréductibles fait apparaître seulement des multiples de $d$, donc de $p$, et comprend donc au plus $v_{p}\left(u_{j}\right)$ facteurs. De même pour $q$ avec $\mathfrak{u}_{k}$. Finalement, on a réussi à écrire $x$ sous la forme d'un produit d'au plus $(\omega-1)\left(\varphi\left(b^{\prime}\right)+v_{p}(d)-1\right)+$ $\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathrm{q}}(\mathrm{d})-1$ facteurs irréductibles, comme souhaité.
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Il semble que la notion d'irréductibilité a posé des problèmes de compréhension, montrer que tout nombre de $S$ peut s'écrire comme un nombre fini d'éléments irréductibles ne répondait pas à l'énoncé. Enfin, il est regrettable que pour certains, les copies rendues pour ce problème d'envoi soient pratiquement illisibles.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "\nSolution de l'exercice 17"
}
|
9c5078ec-eb95-5f06-96fc-99a2929184fd
| 607,188
|
For every integer $k \geqslant 1$, we denote $p(k)$ as the smallest prime number that does not divide $k$. Let $\left(a_{n}\right)_{n \in \mathbb{N}}$ be a sequence such that $a_{0} \in \mathbb{N}^{*}$ and for all $n \geqslant 0, a_{n+1}$ is the smallest positive integer different from $a_{0}, \ldots, a_{n}$ such that $a_{n}^{a_{n+1}}-1$ is divisible by $p\left(a_{n}\right)$. Prove that every positive integer appears exactly once in the sequence $\left(a_{n}\right)_{n \in \mathbb{N}}$.
|
Let's first note that the sequence is well-defined: if $a_{1}, \ldots, a_{n}$ are constructed, since $a_{n}$ is coprime with $p(a_{n})$, there exists an infinite number of integers $k$ such that $a_{n}^{k} \equiv 1 \pmod{p(a_{n})}$, which are all multiples of the order of $a_{n}$ modulo $p(a_{n})$. In particular, there is at least one of these integers $n$ not appearing among $a_{1}, \ldots, a_{n}$, so $a_{n+1}$ is well-defined.
Note that each integer appears at most once in the sequence by construction. We need to show that all integers appear at least once. Suppose there exists an integer $N$ that does not appear in the sequence $(x_{n})$, and take $N$ to be minimal. Let $N_{0}$ be an integer such that if $n \geqslant N_{0}, a_{n} > N$.
We show that for every prime $q$, there are a finite number of $n$ such that $p(a_{n}) = q$. Suppose this is not the case, and fix $q$ a prime such that $p(a_{n}) = q$ for an infinite number of $n$. We then define $\phi: \mathbb{N} \rightarrow \mathbb{N}$ strictly increasing such that $p(a_{\phi(n)}) = q$. Note that every multiple of $q-1$ appears: indeed, if we fix $M$ a multiple of $q-1$, then since the $p(a_{\phi(n)+1})$ are pairwise distinct, there exists $n$ such that $a_{\phi(n)+1} > M$. Since $q-1$ divides $M$, by Fermat's Little Theorem, $a_{\phi(n)}^{M} \equiv 1 \pmod{q-1}$, which contradicts the definition of $a_{\phi(n)+1}$.
Thus, all multiples of $q-1$ appear. Let $p_{1} < \cdots < p_{k}$ be the primes strictly less than $q$. We know that for all $j \geqslant 1, (p_{1} \ldots p_{k})^{j(q-1)}$ is congruent to 1 modulo $q$, divisible by $q-1$ for $j$ large enough (since all factors of $q-1$ are among $p_{1}, \ldots, p_{k}$), so it appears in the sequence, and satisfies $p((p_{1} \ldots p_{k})^{j(q-1)}) = q$. Since there are infinitely many such terms, there exists $N_{1} > N_{0}$ such that $a_{N_{1}} = (p_{1} \ldots p_{k})^{j(q-1)}$ for $j$ large enough. Thus, $a_{N_{1}}^{N} \equiv 1 \pmod{q}$, which contradicts the fact that $a_{N_{1}+1} > N$.
Thus, we have shown that for every prime $q$, there are a finite number of $n$ such that $p(a_{n}) = q$. In particular, for all $M \in \mathbb{N}$, since the sequence $(p(a_{n}))$ takes each value between 1 and $M$ a finite number of times, from a certain rank $p(a_{n}) > M$, so $(p(a_{n}))$ tends to $+\infty$. In particular, for all $k$, from a certain rank, $p_{1} \ldots p_{k}$ divides $a_{n}$.
Let $k$ and $m$ be such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$. Then $p(a_{m}) = p_{k+1}$, and $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv 1 \pmod{p_{k+1}}$. By Fermat's Little Theorem, $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv a^{p_{1} \ldots p_{k}} \pmod{p_{k+1}}$, so for all $i$ such that $1 \leqslant i \leqslant p_{k}-1$, $a^{i p_{1} \ldots p_{k}} \equiv 1 \pmod{p_{k+1}}$. Thus, for all $i$ such that $1 \leqslant i \leqslant p_{k}-1$, $i p_{1} \ldots p_{k}$ appears in the sequence $(a_{n})$. Taking $i$ an inverse of $p_{1} \ldots p_{k}$ modulo $p_{k+1}-1$ in $\{1, \ldots, p_{k+1}-1\}$, we then have that $(i p_{1} \ldots p_{k})^{N} \equiv N \pmod{p_{k+1}}$, so if $a_{n} = i p_{1} \ldots p_{k}$, then $a_{n+1} < N$, so $n \leqslant N_{0}$. Thus, if such $k$, $m$ exist, then $p_{k}$ divides $a_{1} \ldots a_{n+1}$, so $k$ is bounded.
However, for all $K \in \mathbb{N}$, we can find $k \geqslant K$ and $m$ such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$. Indeed, for all $k \geqslant 1$, let $r_{k}$ be the first rank from which $p_{1} \ldots p_{k}$ divides $a_{n}$. The sequence $(r_{j})$ is increasing and cannot be stationary, otherwise some $a_{n}$ would be divisible by all primes. Therefore, it tends to $+\infty$, so for all $K$, there exists $k \geqslant K$ such that $r_{k+1} > r_{k}$. Thus, $a_{r_{k+1}-1}$ is divisible by $p_{1} \ldots p_{k}$ since $r_{k+1}-1 \geqslant r_{k}$, and not by $p_{k+1}$. But all terms after $r_{k+1}$ are divisible by $p_{1} \ldots p_{k+1}$, so $m = r_{k+1}-1$ works. We have thus obtained that for all $K \in \mathbb{N}$, we can find $k \geqslant K$ and $m$ such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$, leading to a contradiction.
Thus, each integer appears exactly once in the sequence.
Comment from the graders: The exercise is successfully solved by a handful of students. Some used less elementary results than the solution, for example Bertrand's postulate.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $k \geqslant 1$, on note $p(k)$ le plus petit nombre premier ne divisant pas $k$. Soit $\left(a_{n}\right)_{n \in \mathbb{N}}$ une suite telle que $a_{0} \in \mathbb{N}^{*}$ et pour tout $n \geqslant 0, a_{n+1}$ est le plus petit entier strictement positif différent de $a_{0}, \ldots, a_{n}$ tel que $a_{n}^{a_{n+1}}-1$ est divisible par $p\left(a_{n}\right)$. Démontrer que tout entier strictement positif apparaît une unique fois dans la suite $\left(a_{n}\right)_{n \in \mathbb{N}}$.
|
Déjà notons que la suite est bien définie: si $a_{1}, \ldots, a_{n}$ sont construits, comme $a_{n}$ est premier avec $p\left(a_{n}\right)$, il existe une infinité d'entiers $k$ tels que $a_{n}^{k} \equiv 1\left(\bmod p\left(a_{n}\right)\right)$ qui sont tous les multiples de l'ordre de $a_{n}$ modulo $p\left(a_{n}\right)$. En particulier, il existe au moins un de ces entiers $n$ 'apparaissant pas parmi $a_{1}, \ldots, a_{n}$, donc $a_{n+1}$ existe bien.
Notons que chaque entier apparaît au plus une fois dans la suite par construction. Il faut donc montrer que tous apparaissent au moins une fois. Supposons qu'il existe un entier $N$ qui n'apparaît pas dans la suite $\left(x_{n}\right)$, on prend alors $N$ minimal. On note $N_{0}$ un entier tel que si $n \geqslant N_{0}, a_{n}>N$.
Montrons que pour tout premier $q$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. Supposons que ce n'est pas le cas, et fixons $q$ un nombre premier tel que $p\left(a_{n}\right)=q$ pour une infinité de $n$. On se donne alors $\phi: \mathbb{N} \rightarrow \mathbb{N}$ strictement croissante telle que $p\left(a_{\phi(n)}\right)=q$. Notons alors que tout multiple de $q-1$ apparaît : en effet si on fixe $M$ un multiple de $q-1$, alors comme les $p\left(a_{\phi(n)+1}\right)$ sont deux à deux distincts, il existe $n$ tel que $a_{\phi(n)+1}>M$. Or comme $q-1$ divise $M, a_{\phi(n)}^{M} \equiv 1(\bmod q-1)$ par petit Fermat, ce qui contredit la définition de $a_{\phi(n)+1}$.
Ainsi tous les multiples de $\mathrm{q}-1$ apparaissent. on note $\mathrm{p}_{1}<\cdots<\mathrm{p}_{\mathrm{k}}$ les nombres premiers strictement inférieurs à $q$. On sait que pour tout $j \geqslant 1,\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ est congru à 1 modulo $q$, divisible par $q-1$ pour $j$ assez grand (car tous les facteurs de $q-1$ sont parmi $p_{1}, \ldots, p_{k}$ ) donc apparaît dans la suite, et vérifie $p\left(\left(p_{1} \ldots p_{k}\right)^{j(q-1)}\right)=q$. Comme il y a une infinité de tels termes, il existe $\mathrm{N}_{1}>\mathrm{N}_{0}$ tel que $a_{N_{1}}=\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ pour $j$ assez grand. Ainsi $a_{N_{1}}^{N} \equiv 1(\bmod q)$, ce qui contredit le fait que $a_{N_{1}+1}>N$.
Ainsi on a bien prouvé que pour tout premier $\mathbf{q}$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. En particulier, pour tout $M \in \mathbb{N}$, comme la suite $\left(p\left(a_{n}\right)\right)$ prend un nombre fini de fois chaque valeurs entre 1 et $M$, à partir d'un certain rang $p\left(a_{n}\right)>M$, donc $\left(p\left(a_{n}\right)\right)$ tend vers $+\infty$. En particulier, pour tout $k$, à partir d'un certain rang, $p_{1} \ldots, p_{k}$ divise $a_{n}$.
Soit $k$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant$ $m+1$. On a alors $p\left(a_{m}\right)=p_{k+1}$, et $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv 1\left(\bmod p_{k+1}\right)$. Or par Petit Fermat, $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv$ $a^{p_{1} \ldots p_{k}}\left(\bmod p_{k+1}\right)$, donc pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $a^{i p_{1} \ldots p_{k}} \equiv 1\left(\bmod p_{k+1}\right)$. Ainsi pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $i p_{1} \ldots p_{k}$ apparaît dans la suite $\left(a_{n}\right)$. En prenant $i$ un inverse de $p_{1} \ldots p_{\mathrm{k}}$ modulo $p_{\mathrm{k}+1}-1$ dans $\left\{1, \ldots, p_{\mathrm{k}+1}-1\right\}$, on a alors que $\left(i p_{1} \ldots \mathrm{p}_{\mathrm{k}}\right)^{\mathrm{N}} \equiv \mathrm{N}\left(\bmod \mathrm{p}_{\mathrm{k}+1}\right)$, donc si $a_{n}=i p_{1} \ldots p_{k}$, alors $a_{n+1}<N$, donc $n \leqslant N_{0}$. Ainsi si de tels $k$, $m$ existent, alors $p_{k}$ divise $a_{1} \ldots a_{n+1}$, donc $k$ est borné.
Or pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$. En effet, notons pour tout $k \geqslant 1 r_{k}$ le premier rang à partir duquel $p_{1} \ldots p_{k}$ divise $a_{n}$. La suite $\left(r_{j}\right)$ est croissante, et ne peut être stationnaire sinon un $a_{n}$ serait divisible par tous les nombres premiers. Donc elle tend vers $+\infty$, pour tout $K$, il existe $k \geqslant \mathrm{~K}$ tel que $r_{k+1}>r_{k}$. Ainsi $a_{r_{k+1}-1}$ est divisible par $p_{1} \ldots p_{k}$ car $r_{k+1}-1 \geqslant r_{k}$, et pas par $p_{k+1}$. Mais tous les termes après $r_{k+1}$ sont divisibles par $p_{1} \ldots p_{k+1}$, donc $m=r_{k+1}-1$ convient. On a donc bien obtenu que pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$, donc on a abouti à une contradiction.
Ainsi chaque entier apparaît une unique fois dans la suite.
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Certains ont utilisé des résultats moins élémentaires que le corrigé par exemple le postulat de Bertrand.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"problem_match": "\nExercice 18.",
"solution_match": "\nSolution de l'exercice 18"
}
|
cb2c9eba-c566-5664-a5ec-410abd338cb0
| 607,189
|
At the beginning, the 9 squares of a $3 \times 3$ chessboard each contain a 0. At each step, Pedro chooses two squares that share a side, and adds either 1 to both squares or -1 to both squares. Show that it is impossible to reach in a finite number of moves the situation where all squares are filled with a 2.
|
The idea here is to introduce an invariant I.
Let's naturally color the chessboard in black and white so that there are 4 black squares and 5 white ones. Let I be the sum of the black squares minus the sum of the white squares. At the beginning, $\mathrm{I}=0$, and in a hypothetical situation where all the squares are filled with a $2, \mathrm{I}=-2$.
However, I does not change; indeed, at each step, we choose two adjacent squares, which are of different colors, and add the same number to them. As a result, I is not modified during the execution of a step, hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au début, les 9 cases d'un échiquier $3 \times 3$ contiennent chacune un 0 . A chaque étape, Pedro choisit deux cases partageant un côté, et ajoute soit 1 aux deux cases, soit -1 aux deux cases. Montrer qu'il est impossible d'atteindre en un nombre fini de coups la situation où toutes les cases sont remplies par un 2.
|
L'idée ici est de faire apparaître un invariant I.
Colorions l'échiquier naturellement en noir et blanc de telle sorte qu'il y a 4 cases noires et 5 blanches. Soit donc I la somme des cases noires moins la somme des cases blanches. Au début, $\mathrm{I}=0$, et dans une hypothétique situation où toutes les cases sont remplies par un $2, \mathrm{I}=-2$.
Or I ne varie pas; en effet, à chaque étape on choisit deux cases partageant un côté commun, donc de couleur différente, et on leur ajoute le même nombre. Il en résulte que I n'est modifié lors de l'accomplissement d'une étape, d'où le résultat.
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
545224da-8d30-516b-8465-e35046e402d6
| 607,190
|
Let $m, n, k$ be three positive integers such that $m^{2}+n=k^{2}+k$. Show that $m \leqslant n$.
|
We write $(2 k+1)^{2}=4\left(k^{2}+k\right)+1=4\left(m^{2}+n\right)+1=(2 m)^{2}+4 \mathfrak{n}+1$.
If $\mathrm{n}<\mathrm{m}$, we can write
$$
(2 \mathfrak{m})^{2}<(2 \mathfrak{m})^{2}+4 \mathfrak{n}+1<4 \mathfrak{m}^{2}+4 \mathfrak{m}+1=(2 \mathrm{~m}+1)^{2}
$$
which is impossible since $(2 \mathrm{k}+1)^{2}=(2 \mathrm{~m})^{2}+4 \mathfrak{n}+1$ is a square and cannot be between two consecutive squares. Therefore, $n \geqslant m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $m, n, k$ trois entiers positifs tels que $m^{2}+n=k^{2}+k$. Montrer que $m \leqslant n$.
|
On écrit $(2 k+1)^{2}=4\left(k^{2}+k\right)+1=4\left(m^{2}+n\right)+1=(2 m)^{2}+4 \mathfrak{n}+1$.
Or si $\mathrm{n}<\mathrm{m}$, on peut écrire
$$
(2 \mathfrak{m})^{2}<(2 \mathfrak{m})^{2}+4 \mathfrak{n}+1<4 \mathfrak{m}^{2}+4 \mathfrak{m}+1=(2 \mathrm{~m}+1)^{2}
$$
ce qui est impossible puisque $(2 \mathrm{k}+1)^{2}=(2 \mathrm{~m})^{2}+4 \mathfrak{n}+1$ est un carré et ne peut donc pas être entre deux carrés consécutifs. D'où $n \geqslant m$.
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
7234cdb9-3c7a-5d34-b1d8-be78b6306307
| 607,191
|
Let $ABC$ be a triangle with all three angles acute, with $AB > AC$, and let $\Omega$ be its circumcircle. We denote $M$ as the midpoint of [BC]. The tangents to $\Omega$ at $B$ and $C$ intersect at $P$, and the lines $(AP)$ and $(BC)$ intersect at $S$. We denote $D$ as the foot of the altitude from $B$ in $ABP$, and $\omega$ as the circumcircle of $CSD$. Finally, we denote $K$ as the second intersection point (after $C$) of $\omega$ and $\Omega$.
Show that $\widehat{\mathrm{CKM}}=90^{\circ}$.
|
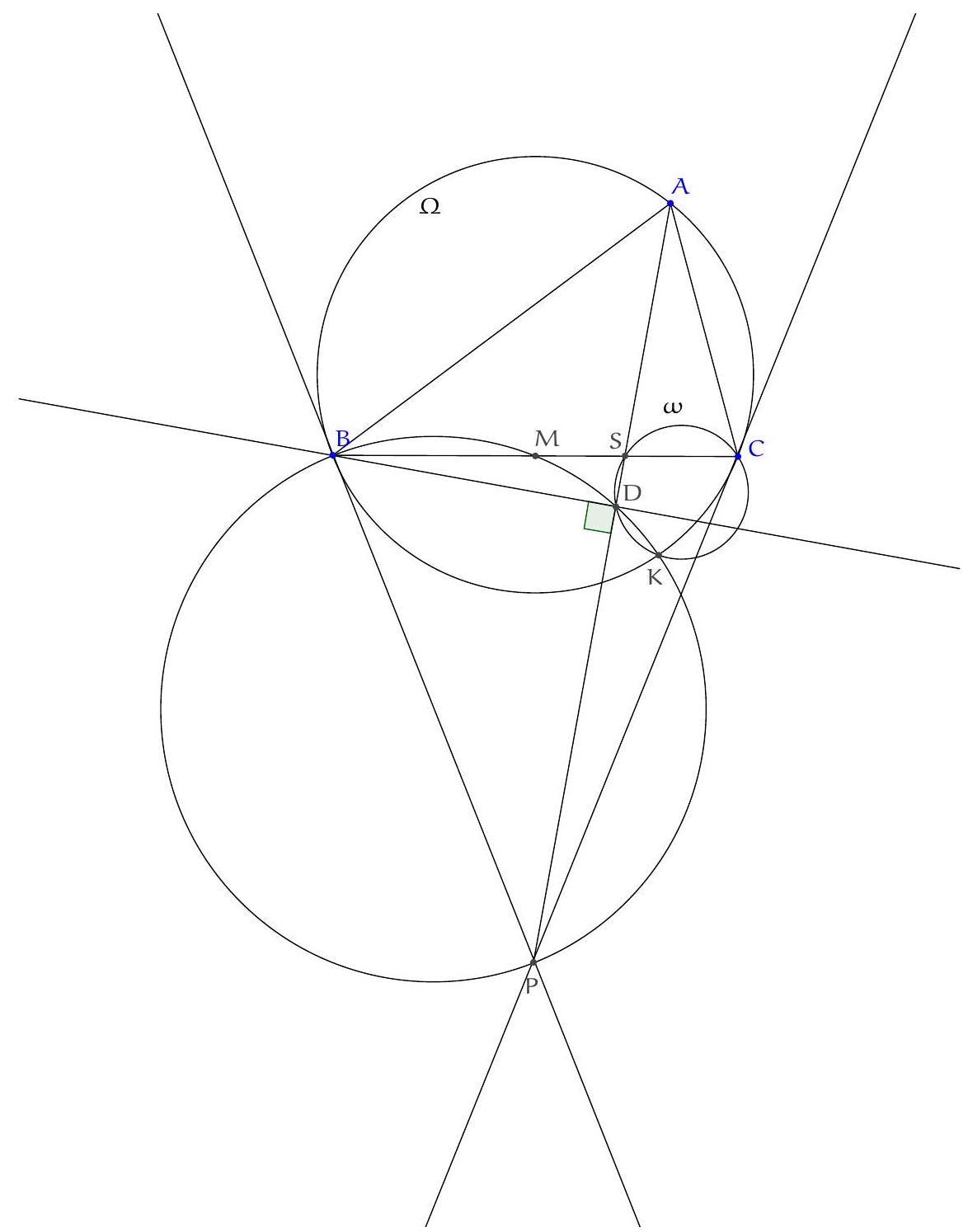
The idea is to realize that the figure contains many cyclic points. To start, we have $\mathrm{PB}=\mathrm{PC}$, so (MP) is the perpendicular bisector of $[\mathrm{BC}]$, and in particular, the angle $\widehat{\mathrm{BMP}}$ is right. Since $\widehat{B D P}$ is also right, the points $B, D, M$ and $P$ are cyclic on the circle $\Gamma$ with diameter [BP]. If we draw this circle on our figure, it appears that $\Gamma$ also passes through K. Indeed, we will verify by angle chasing that $B, D, K$ and $P$ are cyclic. On one hand, using the inscribed angle theorem, we have
$$
\widehat{\mathrm{KDP}}=180^{\circ}-\widehat{\mathrm{KDS}}=\widehat{\mathrm{KCS}}=\widehat{\mathrm{KCB}}.
$$
On the other hand, using the limiting case of the inscribed angle theorem, we have
$$
\widehat{\mathrm{KBP}}=\widehat{\mathrm{KCB}}
$$
so the five points $B, D, K, M$ and $P$ are cyclic. We can now conclude by decomposing the angle $\widehat{\mathrm{CKM}}$ at D to use as many circles as possible:
$$
\widehat{\mathrm{CKM}}=\widehat{\mathrm{CKD}}+\widehat{\mathrm{DKM}}=180^{\circ}-\widehat{\mathrm{CSD}}+\widehat{\mathrm{DBM}}=\widehat{\mathrm{BSD}}+\widehat{\mathrm{DBS}}=180^{\circ}-\widehat{\mathrm{BDS}}=90^{\circ}
$$
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les trois angles sont aigus, avec $A B>A C$, et soit $\Omega$ son cercle circonscrit. On note $M$ le milieu de [BC]. Les tangentes à $\Omega$ en $B$ et $C$ s'intersectent en $P$, et les droites $(A P)$ et $(B C)$ se coupent en $S$. On note $D$ le pied de la hauteur issue de $B$ dans $A B P$, et $\omega$ le cercle circonscrit à CSD. Enfin, on note K le second point d'intersection (après C ) de $\omega$ et $\Omega$.
Montrer que $\widehat{\mathrm{CKM}}=90^{\circ}$.
|

L'idée est de se rendre compte que la figure contient de nombreux points cocycliques. Pour commencer, on a $\mathrm{PB}=\mathrm{PC}$ donc (MP) est la médiatrice de $[\mathrm{BC}]$, et en particulier l'angle $\widehat{\mathrm{BMP}}$ est droit. Comme $\widehat{B D P}$ l'est aussi, les points $B, D, M$ et $P$ sont cocycliques sur le cercle $\Gamma$ de diamètre [BP]. Si on trace ce cercle sur notre figure, il semble que $\Gamma$ passe aussi par K . En effet, on va vérifier par chasse aux angles que $B, D, K$ et $P$ sont cocycliques. D'une part, en utilisant le théorème de l'angle inscrit, on a
$$
\widehat{\mathrm{KDP}}=180^{\circ}-\widehat{\mathrm{KDS}}=\widehat{\mathrm{KCS}}=\widehat{\mathrm{KCB}} .
$$
D'autre part, en utilisant le cas limite du théorème de l'angle inscrit, on a
$$
\widehat{\mathrm{KBP}}=\widehat{\mathrm{KCB}}
$$
donc les cinq points $B, D, K, M$ et $P$ sont cocycliques. On peut maintenant conclure en décomposant l'angle $\widehat{\mathrm{CKM}}$ en D pour pouvoir utiliser un maximum de cercles :
$$
\widehat{\mathrm{CKM}}=\widehat{\mathrm{CKD}}+\widehat{\mathrm{DKM}}=180^{\circ}-\widehat{\mathrm{CSD}}+\widehat{\mathrm{DBM}}=\widehat{\mathrm{BSD}}+\widehat{\mathrm{DBS}}=180^{\circ}-\widehat{\mathrm{BDS}}=90^{\circ}
$$
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
90495d55-84f3-5c6a-80ec-7f737af7a416
| 607,192
|
Let $ABC$ be an isosceles triangle at $A$ but not a right triangle. Let $D$ be the point on $(BC)$ such that $(AD)$ is perpendicular to $(AB)$, and let $E$ be the orthogonal projection of $D$ onto $(AC)$. Finally, let $H$ be the midpoint of $[BC]$.
Show that $AHE$ is isosceles at $H$.
|
Let's start by noting that points $A, D, E$ and $H$ are concyclic on the circle with diameter [AD]. From this, we deduce by angle chasing:
$$
\widehat{\mathrm{HEA}}=\widehat{\mathrm{HDA}}=90^{\circ}-\widehat{\mathrm{DBA}}=90^{\circ}-\widehat{\mathrm{BCA}}=\widehat{\mathrm{HAE}},
$$
thus triangle AHE is isosceles at H.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$ mais pas rectangle. Soit $D$ le point de ( $B C$ ) tel que $(A D)$ soit perpendiculaire à $(A B)$, et soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de [BC].
Montrer que $A H E$ est isocèle en H .
|
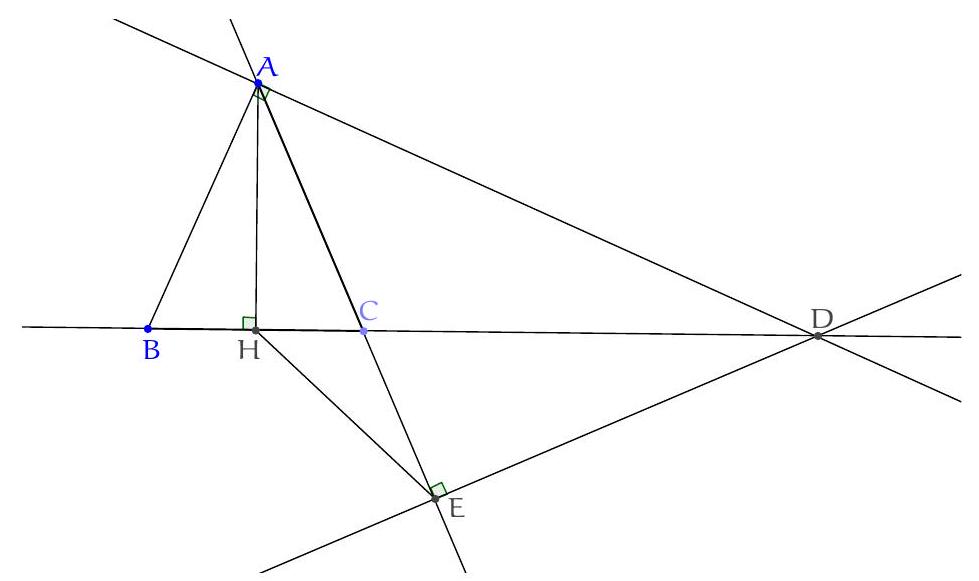
Commençons par remarquer que les points $A, D, E$ et $H$ sont cocycliques sur le cercle de diamètre [AD]. On en déduit par chasse au angles :
$$
\widehat{\mathrm{HEA}}=\widehat{\mathrm{HDA}}=90^{\circ}-\widehat{\mathrm{DBA}}=90^{\circ}-\widehat{\mathrm{BCA}}=\widehat{\mathrm{HAE}},
$$
donc le triangle AHE est isocèle en H .
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
977a6a41-b2c4-5b63-b7a2-00cad568f7c3
| 607,193
|
Let $n \geqslant 2$ and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$ and $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1$.
Show that there exists $i$ such that $x_{i} \geqslant \frac{1}{\sqrt{n(n-1)}}$.
|
We denote $\mathrm{N}^{+}$ the number of indices $i$ such that $x_{i}>0$ and $N^{-}$ the number of indices $i$ such that $x_{i} \leqslant 0$, so that $\mathrm{N}^{+}+\mathrm{N}^{-}=\mathrm{n}$. We also denote
$$
S_{1}^{+}=\sum_{i \text { such that } x_{i}>0} x_{i} \quad \text { and } \quad S_{1}^{-}=\sum_{i \text { such that } x_{i} \leqslant 0}\left(-x_{i}\right)
$$
as well as
$$
S_{2}^{+}=\sum_{i \text { such that } x_{i}>0} x_{i}^{2} \quad \text { and } \quad S_{2}^{-}=\sum_{i \text { such that } x_{i} \leqslant 0} x_{i}^{2} .
$$
The interest of these quantities is that they allow us to both restate the hypotheses and use well-known inequalities such as Cauchy-Schwarz. The hypotheses of the statement can be rewritten as $S_{1}^{+}=$ $S_{1}^{-}$ and $S_{2}^{+}+S_{2}^{-}=1$. To make the square root appear in the result, we will use $S_{2}^{+}$. More precisely, we will show that $S_{2}^{+} \geqslant \frac{1}{n}$. Since the sum $S_{2}^{+}$ contains at most $n-1$ terms (the numbers cannot all be $>0$), one of these terms is greater than $\frac{1}{n(n-1)}$, i.e., $x_{i}^{2} \geqslant \frac{1}{\sqrt{n(n-1)}}$ for some $i$ with $x_{i}>0$, which allows us to conclude.
To show this, we write:
$$
1-S_{2}^{+}=S_{2}^{-} \leqslant\left(S_{1}^{-}\right)^{2}=\left(S_{1}^{+}\right)^{2} \leqslant N^{+} S_{2}^{+} \leqslant(n-1) S_{2}^{+} .
$$
The first inequality is obtained by expanding $\left(S_{1}^{-}\right)^{2}$ and keeping only the terms $\chi_{i}^{2}$. The second is the Cauchy-Schwarz inequality, and the third is the fact that the $x_{i}$ are not all strictly positive. We deduce that $S_{2}^{+} \geqslant \frac{1}{n}$, which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 2$ et soient $x_{1}, x_{2}, \ldots, x_{n}$ des nombres réels tels que $x_{1}+x_{2}+\cdots+x_{n}=0$ et $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1$.
Montrer qu'il existe $i$ tel que $x_{i} \geqslant \frac{1}{\sqrt{n(n-1)}}$.
|
On note $\mathrm{N}^{+}$le nombre d'indices $i$ tels que $x_{i}>0$ et $N^{-}$le nombre d'indices $i$ tels que $x_{i} \leqslant 0$, de sorte que $\mathrm{N}^{+}+\mathrm{N}^{-}=\mathrm{n}$. On note également
$$
S_{1}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i} \quad \text { et } \quad S_{1}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0}\left(-x_{i}\right)
$$
ainsi que
$$
S_{2}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i}^{2} \quad \text { et } \quad S_{2}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0} x_{i}^{2} .
$$
L'intérêt de ces quantités est qu'elles permettent à la fois de reformuler les hypothèses et d'utiliser des inégalités bien connues comme celle de Cauchy-Schwarz. Les hypothèses de l'énoncé se réécrivent $S_{1}^{+}=$ $S_{1}^{-}$et $S_{2}^{+}+S_{2}^{-}=1$. Pour faire apparaître la racine dans le résultat, on va utiliser $S_{2}^{+}$. Plus précisément, on va montrer que $S_{2}^{+} \geqslant \frac{1}{n}$. Comme la somme $S_{2}^{+}$contient au maximum $n-1$ termes (les nombres ne peuvent pas être tous $>0)$, un de ces termes est plus grand que $\frac{1}{n(n-1)}$, soit $x_{i}^{2} \geqslant \frac{1}{\sqrt{n(n-1)}}$ pour un certain $i$ avec $x_{i}>0$, ce qui permet de conclure.
Pour montrer cela, on écrit :
$$
1-S_{2}^{+}=S_{2}^{-} \leqslant\left(S_{1}^{-}\right)^{2}=\left(S_{1}^{+}\right)^{2} \leqslant N^{+} S_{2}^{+} \leqslant(n-1) S_{2}^{+} .
$$
La première inégalité s'obtient en développant $\left(S_{1}^{-}\right)^{2}$ et en ne gardant que les termes $\chi_{i}^{2}$. La seconde est l'inégalité de Cauchy-Schwarz, et la troisième est le fait que les $x_{i}$ ne sont pas tous strictement positifs. On en déduit $S_{2}^{+} \geqslant \frac{1}{n}$, ce qui permet de conclure.
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
ce38e23b-3bb4-5720-ad25-3fa757e999f0
| 607,194
|
Let $\left(a_{n}\right)_{n \geqslant 0}$ be a sequence of real numbers. Suppose that $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ for all natural numbers $n$. Furthermore, $a_{0}$ and $a_{1}$ are strictly positive and distinct. Show that the sequence $\left(a_{n}\right)_{n \geqslant 0}$ is not bounded.
|
It is clear that the sequence $(a_{n})$ has positive terms.
Let $i$ be such that $a_{i}<a_{j}$ for $j<i$. Suppose by contradiction that $i \geqslant 4$. Then $a_{i-2}=\left|a_{i}-a_{i-1}\right|=$ $a_{i-1}-a_{i}<a_{i-1}$, so $a_{i-3}=\left|a_{i-2}-a_{i-1}\right|=a_{i-1}-a_{i-2}=a_{i}$, which contradicts the hypothesis on $i$.
Thus, if $m=\min \left\{a_{1}, a_{2}, a_{3}\right\}$, then for all $i$, $a_{i} \geqslant m$. Indeed, if there exists $i$ with $a_{i}<m$, choose $i$ minimal, then $a_{i}$ is smaller than all previous terms, so $i \leqslant 3$ which contradicts the definition of $m$.
Moreover, $m>0$ because $a_{3} \geqslant 0$ and $a_{3}=0 \rightarrow a_{1}=a_{2}$.
From then on, we write $a_{i}=\left|a_{i+1}-a_{i+2}\right|$ for all $i$, so
- If $a_{i+1}>a_{i+2}$, then $a_{i+1}=a_{i}+a_{i+2} \geqslant a_{i}+m$
- Otherwise, $a_{i+2}=a_{i+1}+a_{i} \geqslant a_{i}+m$
In all cases, there exists a term in the sequence $\geqslant a_{i}+m$. We can therefore prove by a very simple induction on $k$ the existence of $i$ such that $a_{i} \geqslant m k$, so the sequence $(a_{i})$ is not bounded.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\left(a_{n}\right)_{n \geqslant 0}$ une suite de réels. On suppose que $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ pour tout entier naturel $n$. De plus, $a_{0}$ et $a_{1}$ sont strictement positifs et distincts. Montrer que la suite $\left(a_{n}\right)_{n \geqslant 0} n$ 'est pas bornée.
|
Il est clair que la suite ( $a_{n}$ ) est à termes positifs.
Soit $i$ tel que $a_{i}<a_{j}$ pour $j<i$. Supposons par l'absurde que $i \geqslant 4$. Alors $a_{i-2}=\left|a_{i}-a_{i-1}\right|=$ $a_{i-1}-a_{i}<a_{i-1}$ donc $a_{i-3}=\left|a_{i-2}-a_{i-1}\right|=a_{i-1}-a_{i-2}=a_{i}$, ce qui contredit l'hypothèse sur $i$.
Ainsi, si $m=\min \left\{a_{1}, a_{2}, a_{3}\right\}$, alors pour tout $i, a_{i} \geqslant m$. En effet, s'il existe $i$ avec $a_{i}<m$, choisissons $i$ minimal, alors $a_{i}$ est plus petit que tous les termes précédents, donc $i \leqslant 3$ ce qui contredit la définition de $m$.
De plus, $m>0$ car $a_{3} \geqslant 0$ et $a_{3}=0 \rightarrow a_{1}=a_{2}$.
Dès lors, on écrit $a_{i}=\left|a_{i+1}-a_{i+2}\right|$ pour tout $i$, donc
- Si $a_{i+1}>a_{i+2}$, d'où $a_{i+1}=a_{i}+a_{i+2} \geqslant a_{i}+m$
- Sinon, $a_{i+2}=a_{i+1}+a_{i} \geqslant a_{i}+m$
Dans tous les cas, il existe un terme de la suite $\geqslant a_{i}+m$. On peut donc prouver par une très simple récurrence sur $k$ l'existence de $i$ tel que $a_{i} \geqslant m k$, donc la suite ( $a_{i}$ ) n'est pas bornée.
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
24e557af-7795-5e03-a407-97b4951ce3c0
| 607,196
|
Let $ABCD$ be a trapezoid with $(AB)$ parallel to $(CD)$. Suppose there are two circles $\omega_{1}$ and $\omega_{2}$ inside the trapezoid such that $\omega_{1}$ is tangent to the sides $[DA]$, $[AB]$, and $[BC]$, and $\omega_{2}$ is tangent to the sides $[BC]$, $[CD]$, and $[DA]$. Let $\left(d_{1}\right)$ be the second tangent (after $(AD)$) to $\omega_{2}$ passing through $A$, and let $\left(d_{2}\right)$ be the second tangent (after $(BC)$) to $\omega_{1}$ passing through $C$.
Show that $\left(d_{1}\right)$ and $\left(d_{2}\right)$ are parallel.
|
Let $X$ be the intersection point of $(AD)$ and $(BC)$. We denote $E$ and $F$ as the centers of $\omega_{1}$ and $\omega_{2}$, respectively. Note that $\omega_{1}$ is the incircle of $\triangle XAB$ and $\omega_{2}$ is the $X$-excircle of $\triangle XCD$. Finally, let $G$ be the center of the $X$-excircle of $\triangle XAB$.
We verify that triangles $XAG$ and $XEB$ are similar. Indeed, we have $\widehat{AXG} = \widehat{EXB} = \frac{1}{2} \widehat{AXB}$. Furthermore, we have $\widehat{GAX} = 90^\circ + \frac{1}{2} \widehat{BAX}$ and $\widehat{BEX} = 180^\circ - \frac{1}{2} \widehat{AXB} - \widehat{ABX} = 90^\circ + \frac{1}{2} \widehat{BAX}$, so $XAG$ and $XEB$ are indeed similar. Let $s$ be the direct similarity that maps $X$ to $X$, $A$ to $E$, and $G$ to $B$. According to the described homothety, we have $\frac{XC}{XB} = \frac{XF}{XG}$, so $s(F) = C$.
By similarity, we deduce that $\widehat{XAF} = \widehat{XEC}$. The rest of the exercise is now a simple angle chase, which can be carried out in many different ways. For example, let $Y$ be the intersection of $(d_2)$ with $(AD)$. Showing that $(d_1)$ and $(d_2)$ are parallel amounts to showing that $\widehat{XYC} = \widehat{XAd}$. We have
\[
\widehat{XYC} = 180^\circ - \widehat{AXB} - \widehat{XCY} = \widehat{BCY} - \widehat{AXB} = 2 \widehat{BCE} - \widehat{AXB}.
\]
Moreover, we can write
\[
\widehat{BCE} = 180^\circ - \widehat{XCE} = \frac{1}{2} \widehat{AXB} + \widehat{XEC} = \frac{1}{2} \widehat{AXB} + \widehat{XAF}
\]
which gives $\widehat{XYC} = 2 \widehat{XAF} = \widehat{XAd_1}$, hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze avec $(A B)$ parallèle à $(C D)$. On suppose qu'il y a deux cercles $\omega_{1}$ et $\omega_{2}$ à l'intérieur du trapèze tels que $\omega_{1}$ est tangent aux côtés [DA], $\left.A B\right]$ et $[B C]$ et $\omega_{2}$ est tangent aux côtés $[B C],[C D]$ et $[D A]$. Soit $\left(d_{1}\right)$ la seconde tangente (après $\left.(A D)\right)$ à $\omega_{2}$ passant par $A$, et soit $\left(d_{2}\right)$ la seconde tangente (après $(B C)$ ) à $\omega_{1}$ passant par $C$.
Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
|
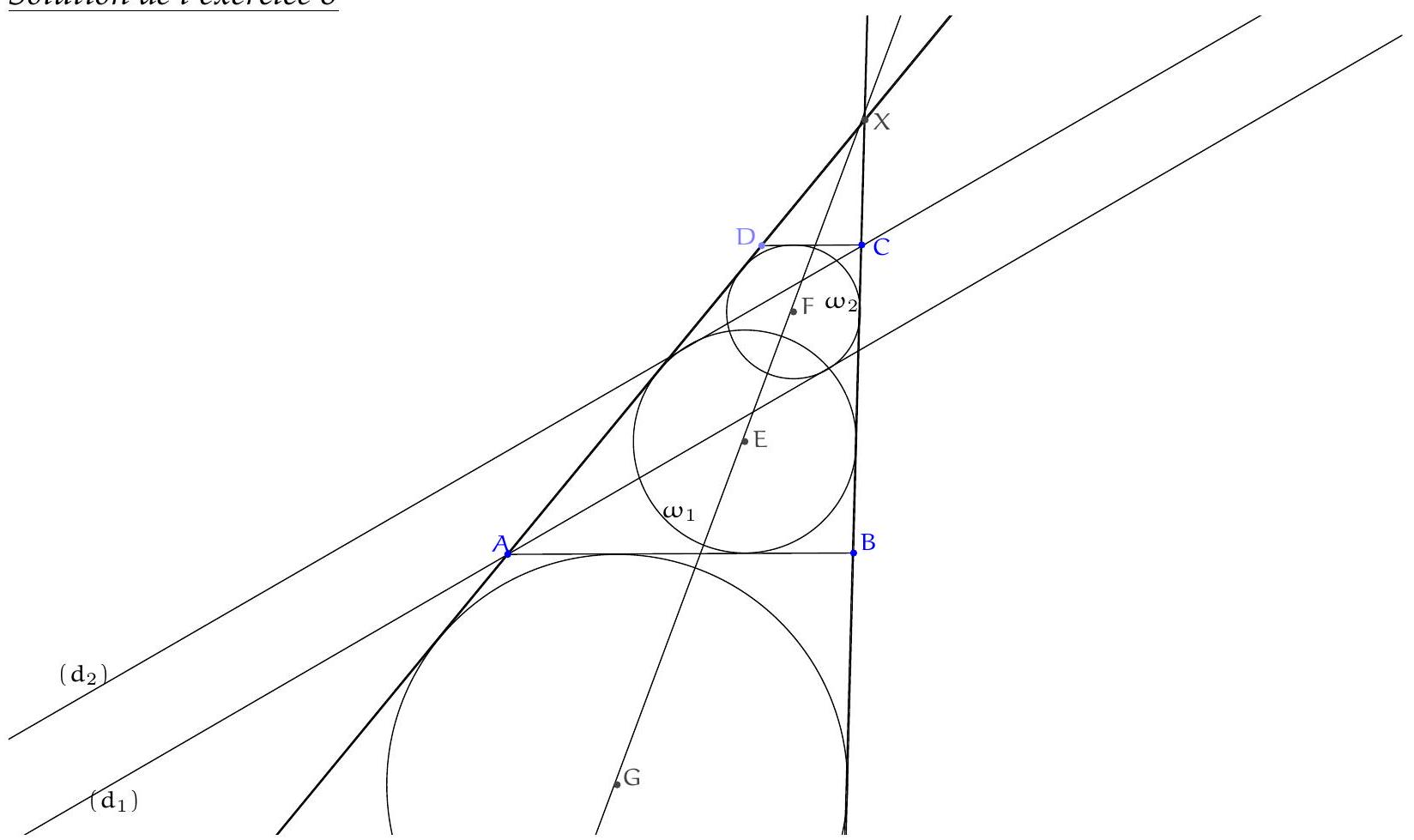
On note $X$ le point d'intersection de ( $A D$ ) et ( $B C$ ). On note respectivement $E$ et $F$ les centres de $\omega_{1}$ et $\omega_{2}$. Notons que $\omega_{1}$ est le cercle inscrit à $X A B$ et que $\omega_{2}$ est le cercle $X$-exinscrit à XCD. Enfin, on note $G$ le centre du cercle $X$-exinscrit à $X A B$.
On vérifie que les triangles XAG et $X E B$ sont semblables. En effet, on a $\widehat{A X G}=\widehat{E X B}=\frac{1}{2} \widehat{A X B}$. De plus, on a $\widehat{G A X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$ et $\widehat{B E X}=180^{\circ}-\frac{1}{2} \widehat{A X B}-\widehat{A B X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$, donc XAG et XEB sont bien semblables. Soit $s$ la similitude (directe) qui envoie $X$ sur $X, A$ sur $E$ et $G$ sur $B$. D'après l'homothétie décrite précédemment, on a $\frac{X C}{X B}=\frac{X F}{X G}$, donc $s(F)=C$.
Par similitude, on en déduit $\widehat{X A F}=\widehat{\mathrm{XEC}}$. La fin de l'exercice est maintenant une simple chasse aux angles, qui peut être menée de nombreuses manières différentes. Notons par exemple Y l'intersection de $\left(\mathrm{d}_{2}\right)$ avec $(A D)$. Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles revient à montrer $\widehat{X Y C}=\widehat{X_{A d}}$. Or, on a
$$
\widehat{X Y C}=180^{\circ}-\widehat{A X B}-\widehat{X C Y}=\widehat{B C Y}-\widehat{A X B}=2 \widehat{B C E}-\widehat{A X B} .
$$
De plus, on peut écrire
$$
\widehat{\mathrm{BCE}}=180^{\circ}-\widehat{\mathrm{XCE}}=\frac{1}{2} \widehat{\mathrm{AXB}}+\widehat{\mathrm{XEC}}=\frac{1}{2} \widehat{A X B}+\widehat{\mathrm{XAF}}
$$
ce qui donne $\widehat{X Y C}=2 \widehat{X A F}=\widehat{\mathrm{XAd}_{1}}$, d'où finalement le résultat.
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
324d8e04-ed14-5793-875c-021b5fcd773e
| 607,197
|
Let $S=\{1, \ldots, n\}$, with $n \geqslant 3$ an integer, and let $k$ be a strictly positive integer. We denote $S^{k}$ as the set of $k$-tuples of elements of $S$. Let $f: S^{k} \rightarrow S$ be such that, if $x=\left(x_{1}, \ldots, x_{k}\right) \in S^{k}$ and $y=\left(y_{1}, \ldots, y_{k}\right) \in S^{k}$ with $x_{i} \neq y_{i}$ for all $1 \leqslant i \leqslant k$, then $f(x) \neq f(y)$.
Show that there exists $\ell$ with $1 \leqslant \ell \leqslant k$ and a function $g: S \rightarrow S$ satisfying, for all $x_{1}, \ldots, x_{k} \in S$, $f\left(x_{1}, \ldots, x_{k}\right)=g\left(x_{\ell}\right)$.
|
We will show the result by induction on $k$. The case $k=1$ is trivial, so let's assume the result is true for $k-1 \geq 1$ and show it for $k$.
Suppose there exist $k-1$ elements $a_{2}, \ldots, a_{k}$ of $S$ such that the function $\phi: a \in S \mapsto f\left(a, a_{2}, \ldots, a_{k}\right) \in S$ is injective. By equality of cardinality, it is also bijective.
Therefore, if $b_{2}, \ldots, b_{k}$ are elements of $S$ with $b_{i} \neq a_{i}$ for all $i \in\{2, \ldots, k\}$, and $b \in S$, then $\phi(a) \neq f\left(b, b_{2}, \ldots, b_{k}\right)$ for $S \ni a \neq b$. By surjectivity of $\phi, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)$.
Let $c_{2}, \ldots, c_{k}$ be elements of $S$; since $n \geq 3$, there exist $b_{2}, \ldots, b_{k}$ such that $a_{i} \neq b_{i} \neq c_{i}$ for all $i \in\{2, \ldots, k\}$. Therefore, the previous reasoning shows that, if $b \in S, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right) = f\left(b, c_{2}, \ldots, c_{k}\right)$, and thus $\ell=1$, and $g=\phi$ are suitable.
We assume therefore that there exist two functions $\alpha, \beta: S^{k-1} \rightarrow S$ such that, for all $a_{2}, \ldots, a_{k}$ in $S$, $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \beta\left(a_{2}, \ldots, a_{n}\right)=\beta$, and $f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$.
Let's show that $f^{\prime}:\left(a_{2}, \ldots, a_{k}\right) \in S^{k-1} \mapsto f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$ satisfies the conditions of the problem. Indeed, if $\left(a_{2}, \ldots, a_{k}\right)$ and $\left(b_{2}, \ldots, b_{k}\right)$ are two $(k-1)$-tuples whose coordinates are all different, then either $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \alpha\left(b_{2}, \ldots, b_{k}\right)=\alpha^{\prime}$, in which case $g\left(a_{2}, \ldots, a_{k}\right) = f\left(\alpha, a_{2}, \ldots, a_{k}\right) \neq f\left(\alpha^{\prime}, b_{2}, \ldots, b_{k}\right) g\left(b_{2}, \ldots, b_{k}\right)$ by hypothesis, or $\alpha \neq \beta\left(b_{2}, \ldots, b_{k}\right)$, in which case we have $g\left(a_{2}, \ldots, a_{k}\right) \neq g\left(b_{2}, \ldots, b_{k}\right)$.
Therefore, by the induction hypothesis, and without loss of generality, we can assume the existence of $h: S \rightarrow S$ such that $g\left(a_{2}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ for $a_{2}, \ldots, a_{k}$ in $S$. $h$ must be injective because $h(a) = g(a, a, \ldots, a) \neq g(b, \ldots, b)=h(b)$ if $a \neq b$ are elements of $S$. By equality of cardinality, $h$ is surjective.
Let's show that $f\left(a_{1}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ for all $a_{1}, \ldots, a_{k} \in S$, which will conclude the proof. Suppose, for the sake of contradiction, the existence of a $k$-tuple $a=\left(a_{1}, \ldots, a_{k}\right) \in S^{k}$ such that $f(a) \neq h\left(a_{2}\right)$. By surjectivity, there exists $b_{2} \in S$ with $h\left(b_{2}\right)=f(a)$ and $b_{2} \neq a_{2}$. Let $b_{i} \neq a_{i}$ be elements of $S$, for $3 \leqslant i \leqslant k$. We have $\alpha = \alpha\left(b_{2}, \ldots, b_{k}\right)$ and $\beta=\beta\left(b_{2}, \ldots, b_{k}\right)$ two elements of $S$ such that $f\left(\alpha, b_{2}, \ldots, b_{k}\right)=f\left(\beta, b_{2}, \ldots, b_{k}\right) = h\left(b_{2}\right)=f(a)$. The hypothesis made on $f$ ensures therefore $\alpha=a_{1}=\beta$, which is a contradiction according to the definition of $\alpha$ and $\beta$.
[^0]: Animath, French Olympiad Preparation, 11-13 rue Pierre et Marie Curie, 75005 Paris.
copies.ofm@gmail.com
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $S=\{1, \ldots, n\}$, avec $n \geqslant 3$ un entier, et soit $k$ un entier strictement positif. On note $S^{k}$ l'ensemble des $k$-uplets d'éléments de $S$. Soit $f: S^{k} \rightarrow S$ telle que, si $x=\left(x_{1}, \ldots, \chi_{k}\right) \in S^{k}$ et $y=\left(y_{1}, \ldots, y_{k}\right) \in S^{k}$ avec $x_{i} \neq y_{i}$ pour tout $1 \leqslant i \leqslant k$, alors $f(x) \neq f(y)$.
Montrer qu'il existe $\ell$ avec $1 \leqslant \ell \leqslant k$ et une fonction $g: S \rightarrow S$ vérifiant, pour tous $x_{1}, \ldots, x_{k} \in S$, $f\left(x_{1}, \ldots, x_{k}\right)=g\left(x_{\ell}\right)$.
|
Nous montrerons le résultat par récurrence sur k. Le cas $k=1$ est trivial, supposons donc le résultat vrai pour $\mathrm{k}-1 \geqslant 1$ et montrons le pour k .
Supposons l'existence de $k-1$ éléments $a_{2}, \ldots, a_{k}$ de $S$ tels que la fonction $\phi: a \in S \mapsto f\left(a, a_{2}, \ldots, a_{k}\right) \in$ $S$ est injective. Par égalité de cardinal, elle est aussi bijective.
Dès lors, si $b_{2}, \ldots, b_{k}$ sont des éléments de $S$ avec $b_{i} \neq a_{i}$ pour tout $i \in\{2, \ldots, k\}$, et $b \in S$, alors $\phi(a) \neq f\left(b, b_{2}, \ldots, b_{k}\right)$ pour $S \ni a \neq b$. Par surjectivité de $\phi, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)$.
Soient $c_{2}, \ldots, c_{k}$ des éléments de $S$; puisque $n \geqslant 3$, il existe $b_{2}, \ldots, b_{k}$ tels que $a_{i} \neq b_{i} \neq c_{i}$ pour tout $i \in\{2, \ldots, k\}$. Dès lors le raisonnement précédent montre que, si $b \in S, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)=$ $\mathrm{f}\left(\mathrm{b}, \mathrm{c}_{2}, \ldots, \mathrm{c}_{\mathrm{k}}\right)$, et ainsi $\ell=1$, et $\mathrm{g}=\phi$ conviennent.
Nous supposons donc qu'il existe deux fonctions $\alpha, \beta: S^{k-1} \rightarrow S$ avec, pour tous $a_{2}, \ldots, a_{k}$ dans $S$, $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \beta\left(a_{2}, \ldots, a_{n}\right)=\beta$, et $f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$.
Montrons que $f^{\prime}:\left(a_{2}, \ldots, a_{k}\right) \in S^{k-1} \mapsto f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$ satisfait les conditions du problème. En effet, si $\left(a_{2}, \ldots, a_{k}\right)$ et $\left(b_{2}, \ldots, b_{k}\right)$ sont deux $(k-1)$-uplets dont les coordonnées sont toutes différentes, alors soit $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \alpha\left(b_{2}, \ldots, b_{k}\right)=\alpha^{\prime}$, auquel cas $g\left(a_{2}, \ldots, a_{k}\right)=$ $f\left(\alpha, a_{2}, \ldots, a_{k}\right) \neq f\left(\alpha^{\prime}, b_{2}, \ldots, b_{k}\right) g\left(b_{2}, \ldots, b_{k}\right)$ par hypothèse, soit $\alpha \neq \beta\left(b_{2}, \ldots, b_{k}\right)$ auquel cas on a de même $g\left(a_{2}, \ldots, a_{k}\right) \neq g\left(b_{2}, \ldots, b_{k}\right)$.
Dès lors par hypothèse de récurrence, et sans perte de généralité, on peut supposer l'existence de $h$ : $S \rightarrow S$ telle que $g\left(a_{2}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour $a_{2}, \ldots, a_{k}$ dans S. $h$ doit être injective car $h(a)=$ $g(a, a, \ldots, a) \neq g(b, \ldots, b)=h(b)$ si $a \neq b$ sont des éléments de S. Par égalité de cardinal, $h$ est surjective.
Montrons que $f\left(a_{1}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour tous $a_{1}, \ldots, a_{k} \in S$, ce qui conclura. Supposons par l'absurde l'existence d'un $k$-uplet $a=\left(a_{1}, \ldots, a_{k}\right) \in S^{k}$ tel que $f(a) \neq h\left(a_{2}\right)$. Par surjectivité, il existe $b_{2} \in S$ avec $h\left(b_{2}\right)=f(a)$ avec $b_{2} \neq a_{2}$ donc. Soient $b_{i} \neq a_{i}$ des éléments de $S$, pour $3 \leqslant i \leqslant k$. On a $\alpha=$ $\alpha\left(b_{2}, \ldots, b_{k}\right)$ et $\beta=\beta\left(b_{2}, \ldots, b_{k}\right)$ deux éléments de $S$ tels que $f\left(\alpha, b_{2}, \ldots, b_{k}\right)=f\left(\beta, b_{2}, \ldots, b_{k}\right)=$ $h\left(b_{2}\right)=f(a)$. L'hypothèse faite sur $f$ assure donc $\alpha=a_{1}=\beta$, ce qui est une contradiction d'après la définition de $\alpha$ et $\beta$.
[^0]: Animath, Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.
copies.ofm@gmail.com
|
{
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
bd29c9ed-abba-579c-a88d-8d386b14485e
| 607,198
|
Let $A B C D$ be an isosceles trapezoid with (AD)//(BC).
(a) Show that $A B C D$ has a circumcircle.
(b) Let O be the center of the circumcircle of $A B C D$ and E the intersection of the diagonals. Show that O is on the circumcircle of AEB.
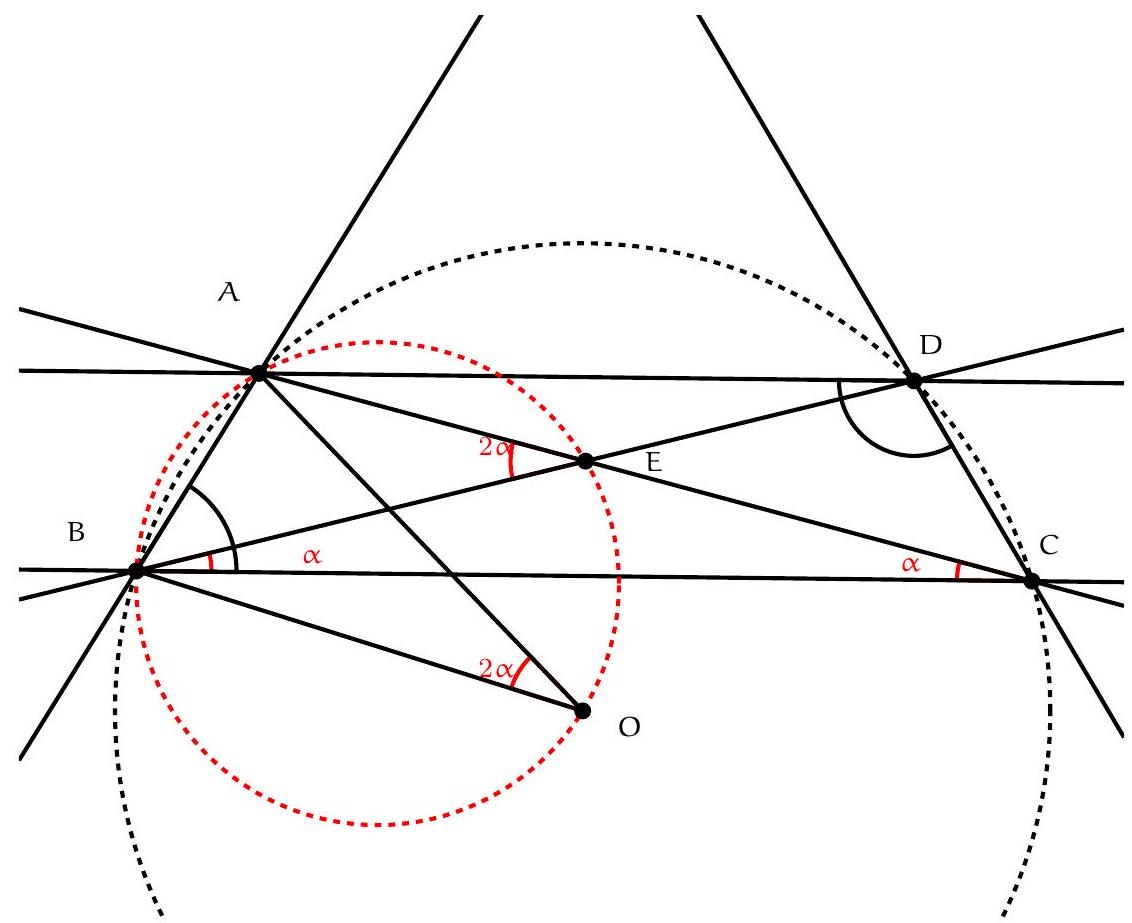
|
a) $A B C D$ is an isosceles trapezoid, so $\widehat{A B C}=\widehat{D C B}$. We also know that $(A D) / /(C B)$, thus $\widehat{D C B}=180-\widehat{C D A}$. With these two equalities, we find that $\widehat{A B C}+\widehat{C D A}=180$, which shows that points $A, B, C$ and $D$ are on the same circle.
b) We will denote $\alpha$ as the angle $\widehat{A C B}$ and try to calculate different angles to reach the required conclusion. By symmetry, we find that $\widehat{D B C}=\alpha$ as well. Thus, in triangle EBC, knowing that the sum of the angles is 180, we find $\widehat{\mathrm{AEB}}=180-\widehat{\mathrm{BEC}}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}=2 \alpha$. Using the inscribed angle theorem, knowing that the inscribed angle $\widehat{A C B}=\alpha$, we have $\widehat{A O B}=2 \alpha$. But then, $\widehat{A O B}=2 \alpha=\widehat{A E B}$, which shows that points $A, E, O$ and $B$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze isocèle avec (AD)//(BC).
(a) Montrer que $A B C D$ admet un cercle circonscrit.
(b) On note O le centre du cercle circonscrit de $A B C D$ et E l'intersection des diagonales. Montrer que O est sur le cercle circonscrit de AEB.

|
a) $A B C D$ est un trapèze isocèle, ainsi $\widehat{A B C}=\widehat{D C B}$. On sait également que $(A D) / /(C B)$, donc $\widehat{D C B}=180-\widehat{C D A}$. Avec ces deux égalités on trouve que $\widehat{A B C}+\widehat{C D A}=180$, ce qui montre bien que les points $A, B, C$ et $D$ sont sur le même cercle.
b) On va noter $\alpha$ l'angle $\widehat{A C B}$ et on va essayer de calculer différents angles afin d'arriver à la conclusion demandée. On trouve par symétrie que $\widehat{D B C}=\alpha$ également. Ainsi, dans le triangle EBC , sachant que la somme des angles vaut 180 , on trouve $\widehat{\mathrm{AEB}}=180-\widehat{\mathrm{BEC}}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}=2 \alpha$. Avec le théorème de l'angle au centre, sachant que l'angle inscrit $\widehat{A C B}=\alpha$, on a $\widehat{A O B}=2 \alpha$. Mais alors, $\widehat{A O B}=2 \alpha=\widehat{A E B}$ ce qui montre bien que les points $A, E, O$ et $B$ sont cocycliques.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nDémonstration."
}
|
da6f5c48-d2a9-5ce1-a2c1-7a121b71c5df
| 607,199
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles with centers $\mathrm{O}_{1}$ and $\mathrm{O}_{2}$, respectively, and suppose they intersect at points $A$ and $B$. The circle passing through the points $O_{1}, O_{2}$, and $B$ intersects the circle $\omega_{1}$ at $C$. Show that the points $C$, $A$, and $O_{2}$ are collinear.
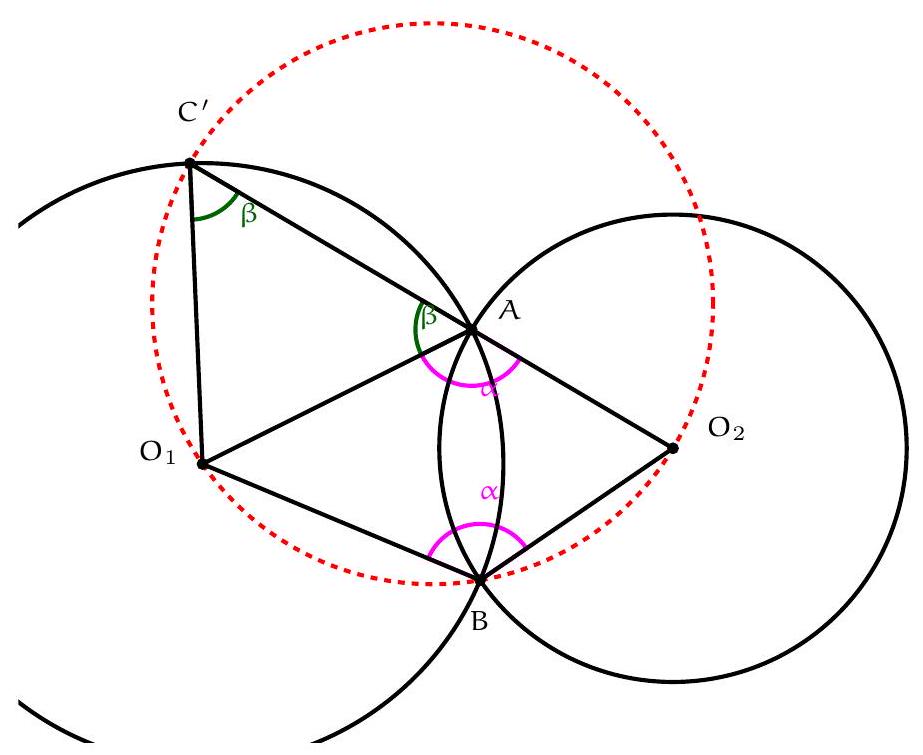
|
To solve this exercise, we will first introduce $\mathrm{C}^{\prime}$ as the second intersection of the line $\left(A O_{2}\right)$ with the circle $\omega_{1}$, then we will show that $\mathrm{C}=\mathrm{C}^{\prime}$.
We can decompose the straight angle $\widehat{\mathrm{O}_{2} \mathrm{AC}^{\prime}}$ into two angles: $\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}$ and $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$, whose sum is therefore 180 degrees. On the one hand, by performing an axial symmetry with axis $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, the points $A$ and $B$ are exchanged, but then the angle $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ equals the angle $\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}$. On the other hand, $\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{1} \mathrm{C}^{\prime}$ since $O_{1}$ is the center of the circle $\omega_{1}$, thus the triangle $O_{1} A C^{\prime}$ is isosceles at $O_{1}$, and we find that ${\widehat{O_{2} \mathrm{C}^{\prime} O_{1}}}_{1}=\widehat{\mathrm{AC}^{\prime} \mathrm{O}_{1}}={\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}}_{1}=180-{\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}}_{2}=180-{\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}}_{2}$, so in particular, $\widehat{\mathrm{O}_{2} \mathrm{C}^{\prime} \mathrm{O}_{1}}=$ $180-{\widehat{\mathrm{O}_{2}} \mathrm{BO}_{1}}$, which proves that the points $\mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ and $\mathrm{C}^{\prime}$ are concyclic. Thus, if we take the definition of the point C, we get that $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{~B}$ and C are concyclic and that $\mathrm{C}^{\prime}$ is on $\omega_{1}$, so that $C^{\prime}=C$, but since the points $A, O_{2}$ and $C^{\prime}=C$ are collinear, we have in particular that $A, O_{2}$ and $C$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\omega_{1}$ et $\omega_{2}$ deux cercles de centre $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$, on suppose qu'ils se coupent en $A$ et $B$. Le cercle passant par les points $O_{1}, O_{2}$ et $B$ coupe le cercle $\omega_{1}$ en $C$. Montrer que les points $C$, $A$ et $O_{2}$ sont alignés.

|
Pour résoudre cet exercice, on va plutôt introduire dans un premier temps $\mathrm{C}^{\prime}$ la deuxième intersection de la droite $\left(A O_{2}\right)$ avec le cercle $\omega_{1}$ puis on va montrer que $\mathrm{C}=\mathrm{C}^{\prime}$.
On peut décomposer l'angle plat $\widehat{\mathrm{O}_{2} \mathrm{AC}^{\prime}}$ en deux angles : $\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}$ et $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ dont la somme vaut donc 180 degrés. D'une part, en faisant une symétrie axiale d'axe $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, alors les points $A$ et $B$ sont échangés, mais alors l'angle $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ vaut l'angle $\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}$. D'autre part, $\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{1} \mathrm{C}^{\prime}$ comme $O_{1}$ est le centre du cercle $\omega_{1}$, ainsi le triangle $O_{1} A C^{\prime}$ est isocèle en $O_{1}$, et on trouve que ${\widehat{O_{2} \mathrm{C}^{\prime} O_{1}}}_{1}=\widehat{\mathrm{AC}^{\prime} \mathrm{O}_{1}}={\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}}_{1}=180-{\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}}_{2}=180-{\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}}_{2}$, donc en particulier, $\widehat{\mathrm{O}_{2} \mathrm{C}^{\prime} \mathrm{O}_{1}}=$ $180-{\widehat{\mathrm{O}_{2}} \mathrm{BO}_{1}}$, ce qui démontre bien que les points $\mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et $\mathrm{C}^{\prime}$ sont cocycliques. Ainsi, si on reprend la définition du point C , on obtient que $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{~B}$ et C sont cocycliques et que $\mathrm{C}^{\prime}$ est sur $\omega_{1}$, donc que $C^{\prime}=C$, mais comme les points $A, O_{2}$ et $C^{\prime}=C$ sont alignés on a entre autre que $A, O_{2}$ et $C$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nDémonstration."
}
|
699de0f7-8416-52ce-b616-ed233f9449fd
| 607,200
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.
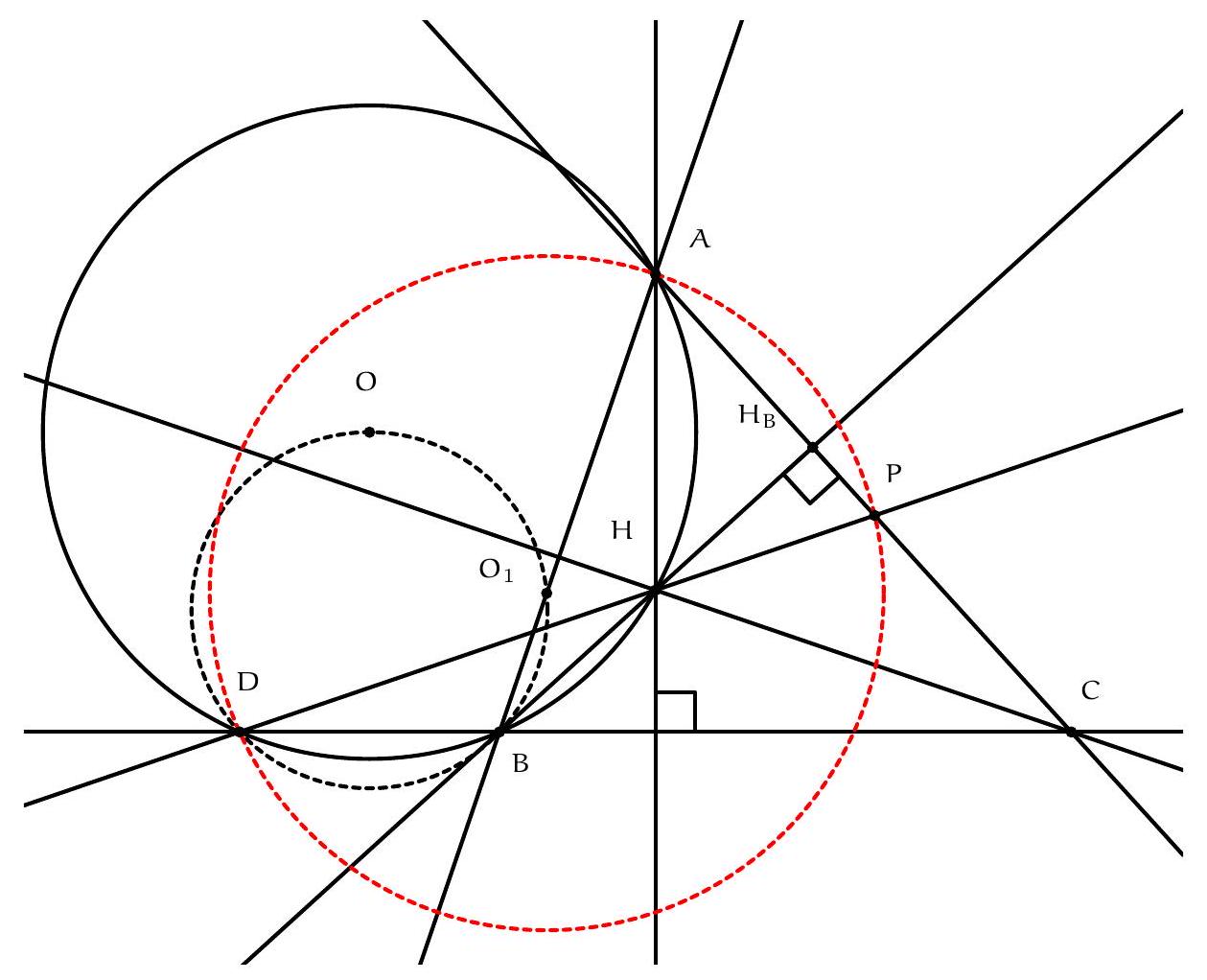
|
A careful construction allows us to conjecture that the center of the circle APD is also on the line $(A B)$, so it is quite natural to introduce $\mathrm{O}_{1}$, the point on the line $(A B)$ that is equidistant from $A$ and $D$. $c^{\prime}$ is then a good candidate to be the center of the circle APD.
Step 1. $\mathrm{O}_{1}$ is the center of the circle APD.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
Une construction soigneuse nous permet de conjecturer que le centre du cercle APD est également sur la droite ( $A B$ ), c'est donc tout naturellement que l'on introduit $\mathrm{O}_{1}$, le point de la droite $(A B)$ qui est à égale distance de $A$ et de $D, c^{\prime}$ est alors un bon candidat pour être le centre du cercle APD.
Étape 1. $\mathrm{O}_{1}$ est le centre du cercle de APD.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nDémonstration."
}
|
1146c1cf-e6a3-55f4-bf59-19b83d19e676
| 607,201
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.

|
We introduce $\mathrm{H}_{\mathrm{B}}$ as the foot of the altitude from B in triangle ABC, and we set $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}$. Since triangle $\mathrm{HH}_{\mathrm{B}} \mathrm{P}$ is right-angled at $\mathrm{H}_{\mathrm{B}}$, we have $\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{HP}}=90-\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}=90-x$. On the other hand, $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{BP}}=\widehat{\mathrm{DHB}}$, and this angle equals $\widehat{\mathrm{DAB}}=x$ by the cocyclicity of points $A, H, B$ and D.
We denote $M$ as the midpoint of segment [AD], then $M$ and $\mathrm{O}_{1}$ lie on the perpendicular bisector of segment [AD], so $\left(\mathrm{MO}_{1}\right) \perp(\mathrm{AD})$, and thus $\widehat{M O_{1} \mathrm{~A}}=90-\widehat{\mathrm{MAO}_{1}}$.
Since $O_{1} A=O D$, we have $\widehat{A O_{1} D}=2 x=2 \widehat{A P D}$. On one hand, $\widehat{A O_{1} D}=2 \widehat{A P D}$, and on the other hand, $O A=O_{1} \mathrm{D}$, we want to deduce that $\mathrm{O}_{1}$ is indeed the center of the circumcircle of APD. But by the central angle theorem, this is indeed the case.
Step 2. $\mathrm{O}_{1}$ lies on the circle ODB.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
On introduit $\mathrm{H}_{\mathrm{B}}$ le pied de la hauteur issue de B dans le triangle ABC , on pose alors $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}$. Comme le triangle $\mathrm{HH}_{\mathrm{B}} \mathrm{P}$ est droit en $\mathrm{H}_{\mathrm{B}}$, on a $\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{HP}}=90-\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}=90-x$. Mais d'autre part, $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{BP}}=\widehat{\mathrm{DHB}}$, ce dernier angle vaut l'angle $\widehat{\mathrm{DAB}}=x$ par cocyclicité des points $A, H, B$ et D.
On note $M$ le milieu du segment [AD], alors $M$ et $\mathrm{O}_{1}$ sont sur la médiatrice du segment [AD], donc $\left(\mathrm{MO}_{1}\right) \perp(\mathrm{AD})$, et ainsi $\widehat{M O_{1} \mathrm{~A}}=90-\widehat{\mathrm{MAO}_{1}}$.
Or $O_{1} A=O D$, donc $\widehat{A O_{1} D}=2 x=2 \widehat{A P D}$. On a maintenant d'une part que $\widehat{A O_{1} D}=2 \widehat{A P D}$ mais d'autre part que $O A=O_{1} \mathrm{D}$, on voudrait en déduire que $\mathrm{O}_{1}$ est bien le centre du cercle circonscrit de APD. Mais par angle au centre c'est bien le cas.
Étape 2. $\mathrm{O}_{1}$ est sur le cercle ODB.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nDémonstration."
}
|
1146c1cf-e6a3-55f4-bf59-19b83d19e676
| 607,201
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.

|
We notice that points $\mathrm{O}, \mathrm{M}$, and $\mathrm{O}_{1}$ are on the (same) perpendicular bisector of [AC], so they are collinear. Thus, we find the angle $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x$. On the other hand, $\widehat{\mathrm{DOB}}=2 \widehat{\mathrm{DAB}}=$ $2(90-x)$. Since triangle ODB is isosceles at O, we can calculate the angle $\widehat{\mathrm{OBD}}$, which is thus $x$. Therefore, $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x=\widehat{\mathrm{OBD}}$, which concludes step 2.
We know that $\mathrm{O}_{1}$ is the center of the circle APD and lies on the circle ODB, so the center of the circle APD is indeed on the circle ODB, which concludes.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
On remarque que les points $\mathrm{O}, \mathrm{M}$ et $\mathrm{O}_{1}$ sont sur la (même) médiatrice de [AC], ils sont donc alignés. On trouve ainsi l'angle $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x$. Mais d'autre part, $\widehat{\mathrm{DOB}}=2 \widehat{\mathrm{DAB}}=$ $2(90-x)$. Comme le triangle ODB est isocèle en O , on peut calculer l'angle $\widehat{\mathrm{OBD}}$ qui vaut ainsi $x$. Mais alors, $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x=\widehat{\mathrm{OBD}}$, ce qui conclut l'étape 2 .
On sait que $\mathrm{O}_{1}$ est le centre du cercle APD et sur le cercle ODB, donc le centre du cercle de APD est bien sur le cercle ODB ce qui conclut.
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nDémonstration."
}
|
1146c1cf-e6a3-55f4-bf59-19b83d19e676
| 607,201
|
Let $ABC$ be a triangle, $H$ the foot of the altitude from $A$, $L$ the foot of the bisector from $B$, and $M$ the midpoint of $[AB]$. We assume that in triangle $HLM$, the two properties hold: $(AH)$ is an altitude and $(BL)$ is a bisector. Show that $(CM)$ is a median.
|
We take the triangle $ABC$, we will prove that it is equilateral, using the two properties, the third will follow.
We have $(AH) \perp(ML)$ and $(AH) \perp(BC)$, so $(BC) \parallel (ML)$. We thus find that $L$ is the midpoint of $[AC]$. However, $\frac{AL}{LC}=\frac{AB}{BC}$ which shows that $AB=BC$, and $(BL)$ is a bisector, an altitude, and a median.
It is now necessary that $(BL)$ bisects $\widehat{MLH}$, or again $(AC)$ as an external bisector, so by angle chasing $\beta=\widehat{\mathrm{HLC}}=\widehat{MLA}=\alpha$. Therefore, $\alpha=\beta$ and $ABC$ is equilateral, so in particular $(CM)$ is the median in MHL.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $H$ le pied de la hauteur issue de $A$, $L$ le pied de la bissectrice issue de $B$ et $M$ le milieu de $[A B]$. On suppose que dans le triangle HLM on a les deux propriétés: $(A H)$ est une hauteur et ( BL ) est une bissectrice. Montrer que ( CM ) est une médiane.
|
On prend le triangle $A B C$, on va démontrer qu'il est équilatéral, en utilisant les deux propriétés, la troisième découlera.
On a $(A H) \perp(M L)$ et $(A H) \perp(B C)$, donc $(B C) / /(M L)$. On trouve ainsi que $L$ est le milieu de $[A C]$. Cependant, $\frac{A L}{L C}=\frac{A B}{B C}$ ce qui montre que $A B=B C$, et (BL) est une bissectrice, une hauteur et une médiane.
Il faut maintenant que (BL) bissecte $\widehat{M L H}$, ou encore (AC) comme bissectrice extérieure, donc par chasse aux angles $\beta=\widehat{\mathrm{HLC}}=\widehat{M L A}=\alpha$. Donc $\alpha=\beta$ et $A B C$ est équilatéral, donc en particulier (CM) est la médiane dans MHL.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nDémonstration."
}
|
ef5bb56d-39a9-599d-ba34-edcf9ad06100
| 607,202
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles that intersect at $P$ and $Q$. Suppose that the common tangent to $\omega_{1}$ and $\omega_{2}$, the one closest to $P$, touches the circles $\omega_{1}$ and $\omega_{2}$ at $A$ and $B$ respectively. The tangents at $P$ to the circles $\omega_{1}$ and $\omega_{2}$ intersect $\omega_{2}$ and $\omega_{1}$ at $D$ and $C$ respectively. Let $H$ and $K$ be points on the segments $[A C]$ and $[B D]$ such that $A H=A P$ and $B K=B P$. Show that the points $A, B, K, Q$ and $H$ lie on the same circle.
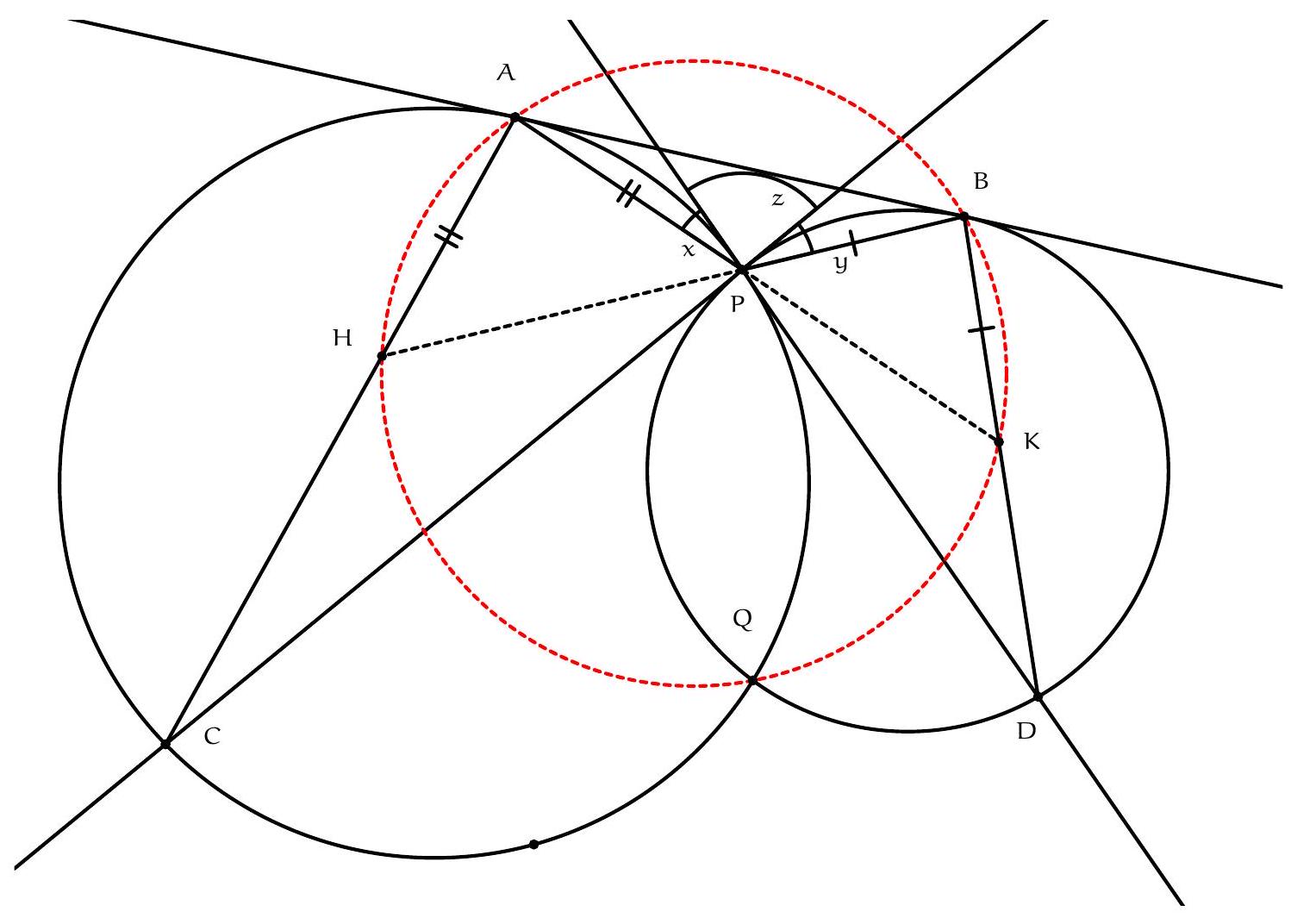
|
We conjecture on a good figure that the points $\mathrm{H}, \mathrm{P}$ and B are collinear, as well as the points $K, P$ and $A$.
Lemma. The points $\mathrm{H}, \mathrm{P}$ and B are collinear, as well as the points $\mathrm{K}, \mathrm{P}$ and A.
We denote $x=\widehat{\mathrm{PAB}}, y=\widehat{\mathrm{ABP}}$ and $z=\widehat{\mathrm{CPD}}$. Since the line (PC) is tangent to $\omega_{2}$, we know that the angle that the tangent forms with the line (PB) is also $x$, and similarly, the angle between (PC) and (AP) is $y$ (it is a matter of choosing the correct orientations). $z$ is the angle between the two tangents. In this case, $\widehat{APB}=x+y+z$ and in total, the angles of the triangle $ABP$ are $x, y$ and $x+y+z$, which shows that $2x+2y+z=180$.
By the angle at the tangent, the angle $\widehat{CAP}=z$, but $AH=AP$ so the triangle $AHP$ is isosceles at $A$, and $\widehat{AHP}=\widehat{APH}=\frac{180-z}{2}=\frac{2x+2y}{2}=x+y$, then the angle $\widehat{HPB}=\widehat{HPA}+\widehat{APB}=x+y+x+z+y=2x+2y+z=180$, which shows that the points $H, P$ and $B$ are collinear. The symmetric reasoning shows that $K, P$ and $A$ are collinear.
We found in the proof of the lemma that $\widehat{AHB}=\widehat{AHP}=x+y$, but then by symmetry $\widehat{BKA}=\widehat{BKP}=x+y$, and by the angle at the tangent, $\widehat{PQA}=x$ and $\widehat{PQB}=y$, so $\widehat{AQB}=x+y$, we thus have $\widehat{AHB}=\widehat{BKA}=\widehat{BQA}$ which shows that the points $A, H, Q, K$ and $P$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\omega_{1}$ et $\omega_{2}$ deux cercles qui se coupent en $P$ et $Q$. On suppose que la tangente commune à $\omega_{1}$ et $\omega_{2}$, la plus proche de P , touche les cercles $\omega_{1}$ et $\omega_{2}$ en $A$ et $B$ respectivement. Les tangentes en $P$ aux cercles $\omega_{1}$ et $\omega_{2}$ recoupe $\omega_{2}$ et $\omega_{1}$ en $D$ et $C$ respectivement. On pose $H$ et $K$ sur les segments $[A C]$ et $[B D]$ de tel sorte que $A H=A P$ et $B K=B P$. Montrer que les points $A, B, K, Q$ et $H$ sont sur le même cercle.

|
On conjecture sur une bonne figure que les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, de même pour les points $K, P$ et $A$.
Lemme. Les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, ainsi que les points $\mathrm{K}, \mathrm{P}$ et A .
On note $x=\widehat{\mathrm{PAB}}, y=\widehat{\mathrm{ABP}}$ et $z=\widehat{\mathrm{CPD}}$. Comme la droite ( PC$)$ est tangente à $\omega_{2}$ on sait que l'angle que la tangente forme avec la droite ( PB ) est également $x$, de la même manière l'angle entre (PC) et (AP) est y (il s'agit de choisir les bonnes orientations). $z$ est l'angle entre les deux tangentes. Dans ce cas $\widehat{A P B}=x+y+z$ et au total les angles du triangle $A B P$ sont $x, y$ et $x+y+z$, cela montre que $2 x+2 y+z=180$.
Par angle à la tangente l'angle $\widehat{C A P}=z$, mais $A H=A P$ donc les triangle $A H P$ est isocèle en $A$, et $\widehat{A H P}=\widehat{A P H}=\frac{180-z}{2}=\frac{2 x+2 y}{2}=x+y$, alors l'angle $\widehat{\mathrm{HPB}}=\widehat{\mathrm{HPA}}+\widehat{\mathrm{APB}}=x+y+x+z+y=$ $2 x+2 y+z=180$, ce qui montre bien que les points $H, P$ et $B$ sont alignés. Le raisonnement symétrique montre que $K, P$ et $A$ sont alignés.
On a trouvé dans la preuve du lemme que $\widehat{A H B}=\widehat{A H P}=x+y$, mais alors par symétrie $\widehat{B K A}=\widehat{B K P}=x+y$, et par angle à la tangente, $\widehat{P Q A}=x$ et $\widehat{P Q B}=y$, donc $\widehat{A Q B}=x+y$, on a ainsi $\widehat{A H B}=\widehat{B K A}=\widehat{B Q A}$ ce qui montre bien que les points $A, H, Q, K$ et $P$ sont cocycliques.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nDémonstration."
}
|
73baabd8-29dc-53bf-b5aa-ba3258596322
| 607,203
|
Let $ABC$ be a triangle, $D$ is the midpoint of the arc $BC$ of the circle $ABC$ not containing $A$, and $Z$ is the unique point on the external bisector of $\widehat{BAC}$ such that $ZA = ZC$. Show that the circle $ADZ$ passes through the midpoint of the side $[AB]$.
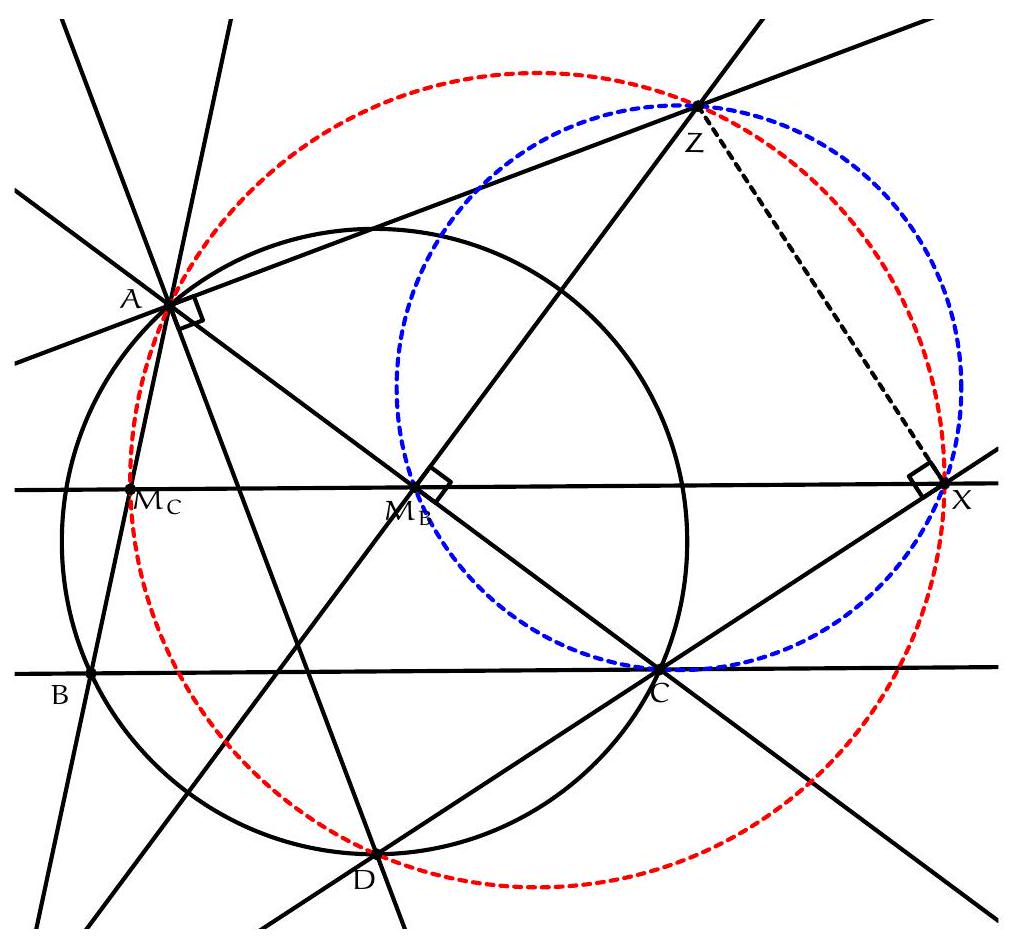
|
Proof 1:
Let $\alpha=\widehat{B A C}$, and let $M_{B}$ be the midpoint of $[A B]$ and $M_{C}$ the midpoint of $[A C]$. We denote $X$ as the intersection of the lines $\left(M_{B} M_{C}\right)$ and (DC).
Since $\left(M_{B} M_{C}\right) / /(B C)$, we find $\widehat{M_{B} X C}=\widehat{B C D}=\widehat{B A D}=\frac{\alpha}{2}$, the penultimate equality follows from the fact that the points $A, B, C$ and $D$ are concyclic and that $D$ is the south pole of $A$ in the triangle $A B C$. We now calculate that $\widehat{C A Z}=90-\frac{\alpha}{2}, Z$ and $M_{B}$ are on the perpendicular bisector of $[A C]$ so $\left(Z M_{B}\right) \perp(A C)$, and we find then $\widehat{A Z M_{B}}=\widehat{C_{Z M}}=\frac{\alpha}{2}$, but then $\widehat{C_{Z M}}=\widehat{C_{B M}}$, which shows that the points $Z, M_{B}, C$ and $X$ are concyclic.
Since $Z, M_{B}, C$ and $X$ are concyclic and $\widehat{Z M_{B} C}=90$ we must have $\widehat{Z C X}=90$. We also have $\widehat{D A Z}=90$, which shows that the points $A, Z, X$ and $D$ are concyclic.
We also have, $\widehat{M_{B} A D}=\frac{\alpha}{2}=\widehat{M_{B} X D}$ which shows that the points $A, M_{B}, D$ and $X$ are concyclic. But in this case: $A, M_{B}, D, X$ and $Z$ are concyclic. Therefore, in particular, the circle $A D Z$ passes through the midpoint of the segment $[A B]$.
## Proof 2:
Here we will present a slightly more general method than the previous one, which involves composing three similarities and finding certain properties.
Let $S_{Z, \mu, r}$ be the direct similarity with center $Z$, angle $\mu$ (oriented), and ratio $r$.
Then, $S_{M_{B}, 180,1}$ fixes $M_{B}$, swaps $A$ and $B$, and also swaps $D$ with a point called $D^{\prime}$.
We find by immediate angle chasing that $\widehat{A Z C}=\alpha$.
$S_{Z, \alpha, 1}$ fixes $Z$, then sends $A$ to $C$.
We find by angle chasing that $\widehat{C D B}=180-\alpha$. Therefore, $S_{D, 180-\alpha, 1}$ fixes $D$ and sends $C$ to $B$.
We then perform $T=S_{M_{B}, 180,1}+S_{Z, \alpha, 1}+S_{D, 180-\alpha,}$, this transformation is also a direct similarity with ratio $1 \times 1 \times 1$ and angle $180+180-\alpha+\alpha=360$, the result is thus a translation, but $T$ sends $B$ to $B$, a translation that has a fixed point is the identity, so $T$ is in fact the identity. But the transformation $T$ sends $D$ to $\mathrm{D}^{\prime}$, then $\mathrm{D}^{\prime}$ to $\mathrm{D}^{\prime \prime}$, and $\mathrm{D}^{\prime \prime}$ to $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, $\mathrm{D}^{\prime \prime}$ is sent to $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$ by the similarity centered at $D$ so $\mathrm{D}^{\prime \prime}=\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, thus the similarity centered at $Z$ sends $D^{\prime}$ to $D$, so in particular $Z D^{\prime}=Z D$ and $\widehat{D^{\prime} Z D}=\alpha$. In the triangle $A^{\prime} D Z$, the point $M_{B}$ is the foot of the altitude, bisector, etc., so in particular, $\widehat{M_{B} Z C}=\frac{\alpha}{2}=\widehat{M_{B} A D}$, which concludes.
This second approach may seem long, but it is much more general and can be applied to other configurations than the particular case we have just seen.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $D$ est le milieu de l'arc $B C$ du cercle $A B C$ ne contenant pas $A, Z$ est l'unique point sur la bissectrice extérieure de $\widehat{B A C}$ tel que $Z A=Z C$. Montrer que le cercle $A D Z$ passe par le milieu du côté de $[A B]$.

|
Preuve 1:
On note $\alpha=\widehat{B A C}$, on pose $M_{B}$ le milieu de $[A B]$ et $M_{C}$ le milieu de $[A C]$. On note $X$ l'intersection des droites $\left(M_{B} M_{C}\right)$ et (DC).
Alors comme $\left(M_{B} M_{C}\right) / /(B C)$, on trouve $\widehat{M_{B} X C}=\widehat{B C D}=\widehat{B A D}=\frac{\alpha}{2}$, l'avant-dernière égalité découle du fait que les points $A, B, C$ et $D$ sont cocycliques et que $D$ est le pôle sud de $A$ dans le triangle $A B C$. On calcule maintenant que $\widehat{C A Z}=90-\frac{\alpha}{2}, Z$ et $M_{B}$ sont sur la médiatrice de $[A C]$ donc $\left(Z M_{B}\right) \perp(A C)$, et on trouve alors $\widehat{A Z M_{B}}=\widehat{C_{Z M}}=\frac{\alpha}{2}$, mais alors $\widehat{C_{Z M}}=\widehat{C_{B M}}$, ce qui montre que les points $Z, M_{B}, C$ et $X$ sont cocycliques.
Comme $Z, M_{B}, C$ et $X$ sont cocycliques et $\widehat{Z M_{B} C}=90$ on doit avoir $\widehat{Z C X}=90$. On a de plus, $\widehat{D A Z}=90$, ce qui montre que les points $A, Z, X$ et $D$ sont cocycliques.
On a également, $\widehat{M_{B} A D}=\frac{\alpha}{2}=\widehat{M_{B} X D}$ ce qui montre que les points $A, M_{B}, D$ et $X$ sont cocycliques. Mais dans ce cas : $A, M_{B}, D, X$ et $Z$ sont cocycliques. Donc en particulier, le cercle $A D Z$ passe par le milieu du segment $[A B]$.
## Preuve 2:
On va présenter ici une méthode un peu plus générale que la méthode précédente, il s'agit de composer trois similitudes et d'en trouver certaines propriétés.
On pose $S_{Z, \mu, r}$ la similitude directe de centre $Z, d^{\prime}$ angle $\mu$ (orienté) et de rapport r .
Alors, $S_{M_{B}, 180,1}$ fixe $M_{B}$ échange $A$ et $B$ elle échange également $D$ avec une point appelé $D^{\prime}$.
On trouve par chasse aux angles immédiate que $\widehat{A Z C}=\alpha$.
$S_{Z, \alpha, 1}$ fixe $Z$, envoie alors $A$ sur $C$.
On trouve par chasse aux angles que $\widehat{C D B}=180-\alpha$. Donc $S_{D, 180-\alpha, 1}$ fixe $D$ et envoie $C$ sur $B$.
On effectue alors $T=S_{M_{B}, 180,1}+S_{Z, \alpha, 1}+S_{D, 180-\alpha,}$, cette transformation est également une similitude directe de rapport $1 \times 1 \times 1$ et d'angle $180+180-\alpha+\alpha=360$, le résultat est donc une translation, mais $T$ envoie $B$ sur $B$, une translation qui a un point fixe est l'identité donc $T$ est en fait l'identité. Mais la transformation $T$ envoie $D$ sur $\mathrm{D}^{\prime}$ puis $\mathrm{D}^{\prime}$ sur $\mathrm{D}^{\prime \prime}$ et $\mathrm{D}^{\prime \prime}$ sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}, \mathrm{D}^{\prime \prime}$ est envoyé sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$ par la similitude de centre D donc $\mathrm{D}^{\prime \prime}=\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, ainsi la similitude de centre $Z$ envoie $D^{\prime}$ sur $D$, donc en particulier $Z D^{\prime}=Z D$ et $\widehat{D^{\prime} Z D}=\alpha$. Dans le triangle $A^{\prime} D Z$, le point $M_{B}$ est le pied de la hauteur, bissectrice, etc..., donc en particulier, $\widehat{M_{B} Z C}=\frac{\alpha}{2}=\widehat{M_{B} A D}$, ce qui conclut.
Cette deuxième approche peut sembler longue mais elle est beaucoup plus général et peut s'appliquer à d'autre configurations que le cas particulier que l'on vient de voir.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Démonstration."
}
|
b4dd6e1f-6e5f-518c-82cb-b02d835a646d
| 607,204
|
Let $ABC$ be an isosceles triangle at $A$, and let $\Gamma$ be a circle tangent to $(AC)$ at $C$ outside the triangle $ABC$. We denote $\omega$ as the circle passing through $A$ and $B$ and internally tangent to $\Gamma$ at $D$. $E$ is the second intersection of $(AD)$ and $\Gamma$. Show that $(BE)$ is tangent to $\Gamma$.
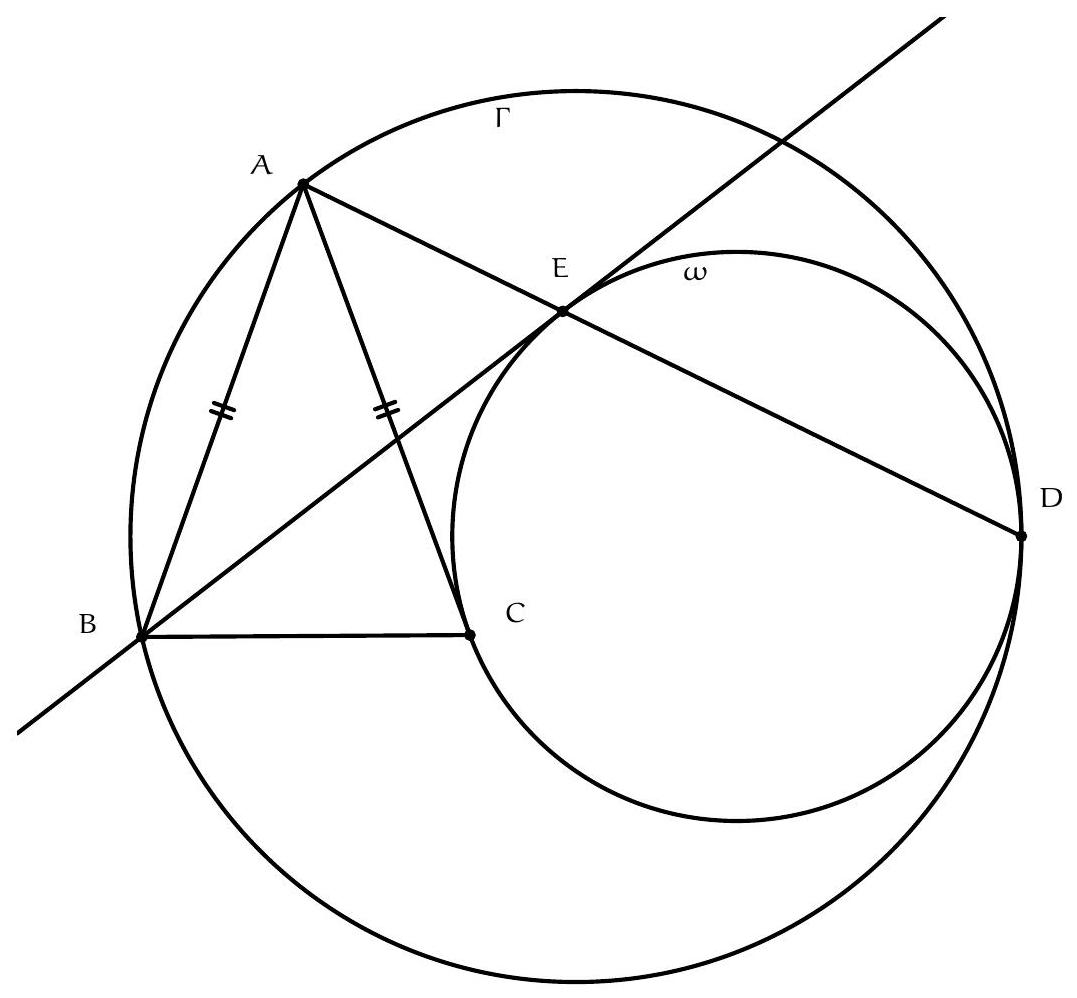
|
Proof 1:
Let $I_{A}$ denote the inversion with center $A$ and radius $r=AB=AC$, thus, $B$ and $C$ are fixed by $I_{A}$. The power of $A$ with respect to the circle $\omega$ is exactly the square of the radius, so the circle $\omega$ is fixed by the inversion. This shows that $D$ and $E$ are exchanged by $I_{A}$. Therefore, the circle $\Gamma$ passing through $A, B$, and $D$ will be mapped to a line passing through $B$ and $E$ and tangent to the circle $\omega$, which concludes the proof.
## Proof 2:
We construct $B^{\prime}$, the second intersection point of $\Gamma$, such that $AB=AB^{\prime}=AC$. Then, we want to show that $E^{\prime}$, the intersection of the lines $(BB^{\prime})$ and $(AD)$, lies on $\omega$.
We have $\widehat{BDA}=x$ and $\widehat{ABB^{\prime}}=x$. By the isosceles property of $ABB^{\prime}$ at $A$, we find $\widehat{AB^{\prime}B}=x$. Therefore, the triangles $ABD$ and $AEB$ are similar, and we get $AB^{2}=AE \times AD$. Thus, $E^{\prime}$ lies on $\omega$, which shows that $E^{\prime}=E$. The homothety centered at $D$ that maps the circle $\omega$ to the circle $\Gamma$ sends the point $E$ to the point $A$ and thus the tangent at $E$ to $\omega$ to the tangent at $A$ to $\Gamma$. It turns out that since $AB=AB^{\prime}$, the tangent at $A$ to $\Gamma$ is parallel to the line $(B^{\prime})$, but the tangent at $E$ to $\omega$ must be parallel to the tangent at $A$ to $\Gamma$. This shows that the tangent at $E$ to $\omega$ and $(BB^{\prime})$ are in fact the same line, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A, \Gamma$ est un cercle tangent à ( $A C$ ) en $C$ à l'extérieur du triangle $A B C$. On note $\omega$ le cercle passant par $A$ et $B$ et tangent intérieurement à $\Gamma$ en $D$. E est la seconde intersection de (AD) et de $\Gamma$, montrer que (BE) est tangente à $\Gamma$.

|
Preuve 1:
On note $I_{A}$ l'inversion de centre $A$ et de rayon $r=A B=A C$, ainsi, $B$ et $C$ sont fixe par $I_{A}$, la puissance de $A$ par rapport au cercle $\omega$ est exactement le rayon au carré donc les cercle $\omega$ est fixe par inversion. Cela montre que $D$ et $E$ sont échangés dans $I_{A}$. Mais alors le cercle $\Gamma$ passant par $A, B$ et $D$ va être envoyé sur une droite passant par $B$ et $E$ et tangente au cercle $\omega$, cela conclut.
## Preuve 2:
On construit $B^{\prime}$, le deuxième point de $\Gamma$, tel que $A B=A B^{\prime}=A C$. Alors, on veut démontrer que $l^{\prime}$ intersection, $E^{\prime}$ des droites $\left(B B^{\prime}\right)$ et ( $\left.A D\right)$ est sur $\omega$.
On a $\widehat{B D A}=x$ et $\widehat{A B B^{\prime}}=x$. Par isocélité de $A B B^{\prime}$ en $A$, on trouve $\widehat{A B^{\prime} B}=x$. Donc les triangles $A B D$ et $A E B$ sont semblables, on trouve alors $A B^{2}=A E \times A D$. Donc $E^{\prime}$ est sur $\omega$, ce qui montre que $E^{\prime}=E$. L'homothetie de centre $D$ qui envoie le cercle $\omega$ sur le cercle $\Gamma$ envoie ainsi le point $E$ sur le point $A$ et donc la tangente en $E$ à $\omega$ sur la tangente en $A$ à $\Gamma$ ?. Il se trouve que comme $A B=A B^{\prime}$, la tangente en $A$ à $\Gamma$ est parallèle à la droite $\left(B^{\prime}\right)$, mais la tangente en $E$ à $\omega$ doit être parallèle à la tangente en $A$ à $\Gamma$. Cela montre que la tangente en $E$ à $\omega$ et ( $\left.\mathrm{BB}^{\prime}\right)$ ne sont en fait qu'une seule et même droite et cela conclut.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Démonstration."
}
|
e472f865-d7e6-5c4a-806d-4a2f80ede7f1
| 607,205
|
Let ADE be an isosceles triangle at $A$. Let the circle $\omega$ be tangent to the lines (AD) and (AE) at $D$ and $E$. Let $B$ and $C$ be two points beyond $D$ and $E$ on the lines ( $A D$ ) and ( $A E$ ). Suppose that $B C > B D + C E$. Finally, let $F$ and $G$ be two points on the segment $[B C]$ such that $B D = B F$ and $C G = C E$, the lines $(D G)$ and $(F E)$ intersect at $K$, the tangent to $\omega$ parallel to ( $B C$ ) and between $A$ and ( $B C$ ) touches $\omega$ at $L$. Show that the center of the inscribed circle of ABC is on (KL).
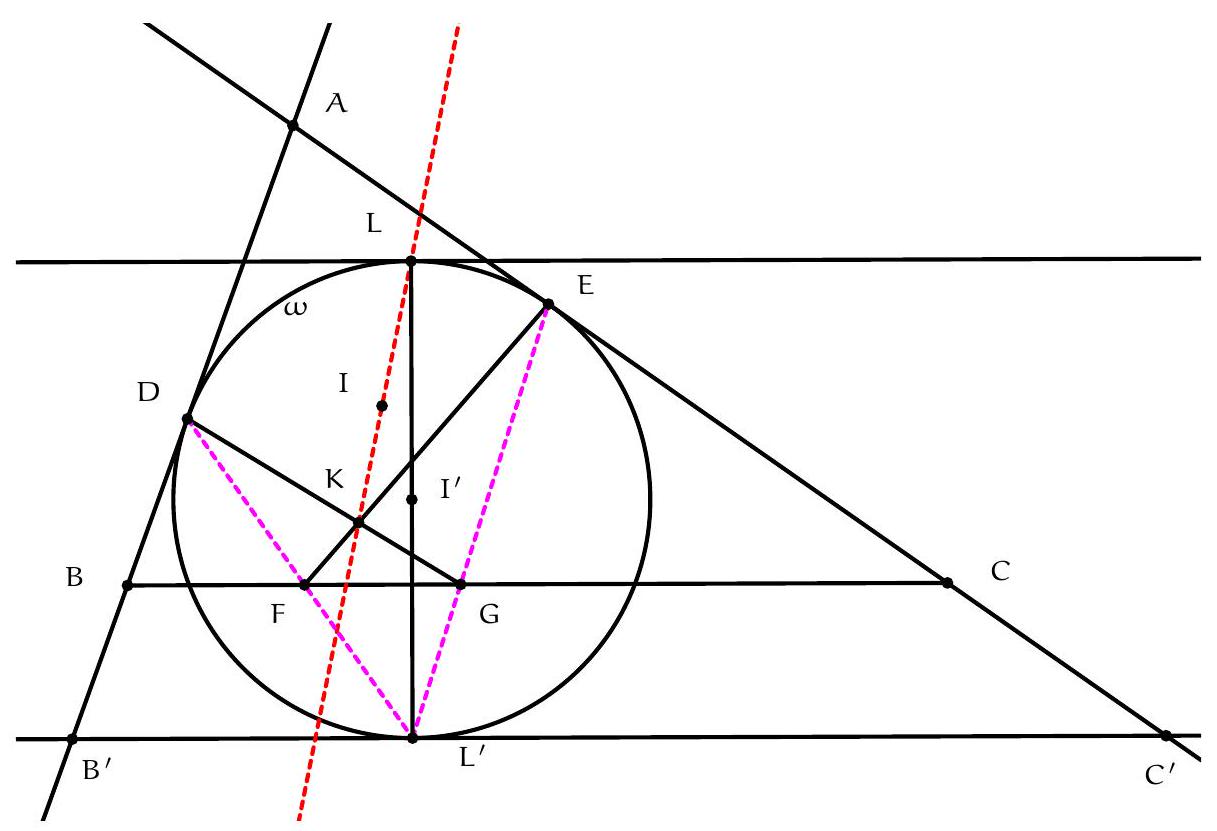
|
Let $B^{\prime}$ and $C^{\prime}$ be two points on the rays $[A D]$ and $[A C]$ beyond $D$ and $E$ such that $\left(B^{\prime} C^{\prime}\right) \parallel (B C)$ and that $\left(B^{\prime} C^{\prime}\right)$ is tangent to $\omega$ at $L^{\prime}$.
Lemma. $D, F$ and $L^{\prime}$ are collinear, as are $E, G$ and $L^{\prime}$.
We have $(B F) \parallel \left(B^{\prime} L^{\prime}\right)$ and $D B = B F$, as well as $\mathrm{DB}^{\prime} = \mathrm{B}^{\prime} \mathrm{L}^{\prime}$, so $\mathrm{DBF} \sim \mathrm{DB}^{\prime} \mathrm{L}^{\prime}$, by Thales. We obtain that $D, F$ and $L^{\prime}$ are collinear, and the symmetric reasoning shows that $E, G$ and $L^{\prime}$ are collinear.
We note that $\omega$ is the incircle of $A B^{\prime} C^{\prime}$. The tangent at $L$ and the tangent at $L^{\prime}$ are two parallel lines, so the segment $[LL']$ is a diameter of $\omega$, thus $\widehat{\mathrm{L}^{\prime} \mathrm{EL}} = 90^\circ$ and $\widehat{\mathrm{L}^{\prime} \mathrm{DL}} = 90^\circ$.
Since $I$ is the incenter of $A B C$, $I$ is the intersection of the angle bisectors of $\widehat{A B C}$, $\widehat{B C A}$, and $\widehat{C A B}$, or by the isosceles triangles $D B F$, $G C E$, and $EAD$, $I$ is the intersection of the perpendicular bisectors of $[DF]$, $[GE]$, and $[ED]$. The fact that these perpendicular bisectors are concurrent leads us to say that the quadrilateral DEFG is cyclic with the circumcenter $I$.
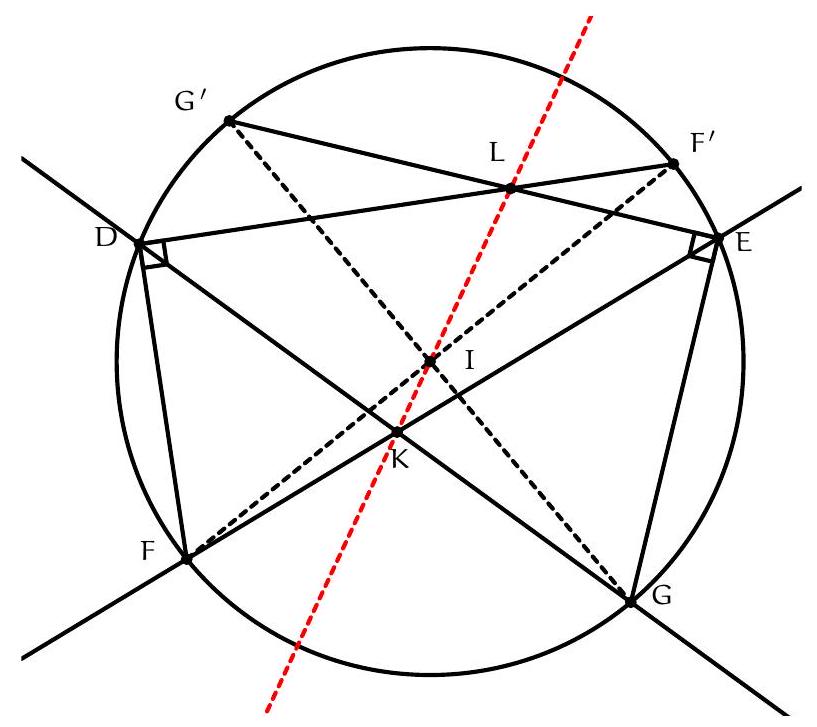
Now we isolate the circle DEFG, the point $I$, the point $K$, and the point $L$, knowing that $I$ is the center of the circle DEFG, that $K$ is the intersection of the diagonals, and that $L$ is such that $\widehat{\mathrm{L}^{\prime} \mathrm{EL}} = 90^\circ$ and $\widehat{\mathrm{L}^{\prime} \mathrm{DL}} = 90^\circ$.
We now intersect the line $(EL)$ with the circle EDFG at $\mathrm{G}^{\prime}$, and the line $(DL)$ with the circle EDG at $\mathrm{F}^{\prime}$. Knowing that $\widehat{L^{\prime} E L} = 90^\circ$ and $\widehat{L^{\prime} D L} = 90^\circ$, we find that $\mathrm{G}^{\prime}$ (resp. $\mathrm{D}^{\prime}$) is the point diametrically opposite to $G$ (resp. $D$) in the circle EDFG, so $I$ is the intersection of the lines $\mathrm{GG}^{\prime}$ and $\mathrm{DD}^{\prime}$. We number the points $\mathrm{G}^{\prime}, \mathrm{G}, \mathrm{D}, \mathrm{F}^{\prime}, \mathrm{F}$, and $E$ as 1, 2, 3, 4, 5, and 6 and apply Pascal since the 6 points are on the same circle, then $\left(G^{\prime} G\right) \cap \left(F^{\prime} F\right), (G D) \cap (F E)$, and $\left(\mathrm{DF}^{\prime}\right) \cap \left(E G^{\prime}\right) ((12) \cap (45), (23) \cap (56)$, and $(34) \cap (61))$ are collinear, which proves that the points $K$, $I$, and $L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ADE un triangle isocèle en $A$. Soit le cercle $\omega$, tangent aux droites (AD) et (AE) en $D$ et $E$. Soit $B$ et $C$ deux points au delà de $D$ et $E$ sur les droites ( $A D$ ) et ( $A E$ ). On suppose que $B C>B D+C E$. Finalement, soit $F$ et $G$ deux points sur le segment $[B C]$ de tel sorte que $B D=B F$ et $C G=C E$, les droites $(D G)$ et $(F E)$ se coupent en $K$, la tangente à $\omega$ parallèle à ( $B C$ ) et entre $A$ et ( $B C$ ) touche $\omega$ en L. Montrer que le centre du cercle inscrit de ABC est sur (KL).

|
Soit $B^{\prime}$ et $C^{\prime}$ deux points sur les demi-droites $[A D]$ et $[A C]$ au delà de $D$ et $E$ de tel sorte que $\left(B^{\prime} C^{\prime}\right) / /(B C)$ et que $\left(B^{\prime} C^{\prime}\right)$ soit tangente à $\omega$ en $L^{\prime}$.
Lemme. $D, F$ et $L^{\prime}$ sont alignés de même pour $E, G$ et $L^{\prime}$.
On a $(B F) / /\left(B^{\prime} L^{\prime}\right)$ et $D B=B F$, ainsi que $\mathrm{DB}^{\prime}=\mathrm{B}^{\prime} \mathrm{L}^{\prime}$, donc $\mathrm{DBF} \sim \mathrm{DB}^{\prime} \mathrm{L}^{\prime}$, par Thalès. On obtient que $D, F$ et $L^{\prime}$ sont alignés, le raisonnement symétrique montre que $E, G$ et $L^{\prime}$ sont alignés.
On remarque que $\omega$ est le cercle inscrit de $A B^{\prime} C^{\prime}$. La tangente en $L$ et la tangente en $L^{\prime}$ sont deux droites parallèles, donc le segment [LL'] est un diamètre de $\omega$, ainsi $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
Comme I est le centre du cercle inscrit de $A B C$, I est l'intersection des bissectrices des angles $\widehat{A B C}, \widehat{B C A}$ et $\widehat{C A B}$ ou encore par isocélité des triangles $D B F, G C E$ et EAD que I est l'intersection des médiatrices de [DF], [GE] et [ED], le fait que ces médiatrices soient concourantes nous amène à dire que le quadrilatère DEFG est cyclique et de centre du cercle circonscrit I.

On va isoler maintenant le cercle DEFG, le point $I$, le point $L$ et le point $K$, en sachant que $I$ est le centre du cercle DEFG, que K est l'intersection des diagonales et que L est tel que $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
On intersecte maintenant la droite ( EL ) avec le cercle EDFG en $\mathrm{G}^{\prime}$, et la droite ( DL ) également avec le cercle EDG et en $F^{\prime}$. En sachant que $\widehat{L^{\prime} E L}=90$ et $\widehat{L^{\prime} D L}=90$ on trouve que $\mathrm{G}^{\prime}$ (resp. $\mathrm{D}^{\prime}$ ) est le point diamétralement opposé à G (resp. D) dans le cercle EDFG, donc I est l'intersection des droites $\mathrm{GG}^{\prime}$ et $\mathrm{DD}^{\prime}$. On numérote les points $\mathrm{G}^{\prime}, \mathrm{G}, \mathrm{D}, \mathrm{F}^{\prime}, \mathrm{F}$ et $E$ comme 1, 2, 3, 4,5 et 6 et appliquer Pascal comme les 6 points sont sur le même cercle, alors $\left(G^{\prime} G\right) \cap\left(F^{\prime} F\right),(G D) \cap(F E)$ et $\left(\mathrm{DF}^{\prime}\right) \cap\left(E G^{\prime}\right)((12) \cap(45),(23) \cap(56)$ et $(34) \cap(61))$ sont alignés ce qui démontre bien que les points K, I et L sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nDémonstration."
}
|
712e424c-0832-5f71-a30b-4331886097a7
| 607,206
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
In this exercise, we will first provide a proof by angle chasing before making a connection to the Feuerbach point. The proof we will give also demonstrates several properties of the Feuerbach point, which we will state at the end.
We denote $A^{\prime}$ as the intersection of the lines $(B C)$ and $\left(A_{B} A_{C}\right)$, and we define the points $B^{\prime}$ and $C^{\prime}$ in the same manner.
We denote $T$ as the intersection of the circumcircles of $A B_{A} B^{\prime}$ and $A B C$, and we want to ultimately prove that $T$ is the point of tangency of the circles $A^{*} B^{*} C^{*}$ and $A B C$.
Lemma 1. $T$ is also on the circumcircle of $B^{\prime} B_{C} C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Dans cet exercice nous allons d'abord donner une preuve en chasse aux angles uniquement avant de faire un lien avec le point de Feuerbach. La preuve que nous allons don-
ner démontre en outre plusieurs propriétés du point de Feuerbach que nous énoncerons à la fin.
On note $A^{\prime}$, l'intersection des droites $(B C)$ et $\left(A_{B} A_{C}\right)$, on df́init de la même manière les points $B^{\prime}$ et $C^{\prime}$.
On note $T$ l'intersection des cercles circonscrits de $A B_{A} B^{\prime}$ et $A B C$, on veut démontrer au final que $T$ est le point de tangence des cercles $A^{*} B^{*} C^{*}$ et $A B C$.
Lemme 1. T est également sur le cercle circonscrit de $B^{\prime} B_{C} C$.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nDémonstration."
}
|
22f348a3-ddb9-5775-866c-db1838592fe4
| 607,207
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
Angle chasing: $\left(B^{\prime} T, T C\right)=\left(B^{\prime} T, A T\right)+(A T, T C)$ according to the Chasles relation, using the cocyclicity of points $T, A, B_{A}$ and $B^{\prime}$ as well as that of points $T, A, B$ and $C$, we find $\left(B^{\prime} T, A T\right)+(A T, T C)=\left(B^{\prime} B_{A}, A B_{A}\right)+(A B, B C)=\left(B^{\prime} B_{A}, A B\right)+(A B, B C)=$ $\left(B^{\prime} B_{A}, B C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, thus $\left(B^{\prime} T, T C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, so the points $T, B^{\prime}, B_{C}$ and $C$ are cocyclic, which concludes the proof of the lemma.
Lemma 2. The points $B^{\prime}$, $B$ and $T$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
En chasse aux angles : $\left(B^{\prime} T, T C\right)=\left(B^{\prime} T, A T\right)+(A T, T C)$ d'après le relation de Chasles, en utilisant la cocyclicité des points $T, A, B_{A}$ et $B^{\prime}$ ainsi que celle des points $T, A, B$ et $C$, on trouve $\left(B^{\prime} T, A T\right)+(A T, T C)=\left(B^{\prime} B_{A}, A B_{A}\right)+(A B, B C)=\left(B^{\prime} B_{A}, A B\right)+(A B, B C)=$ $\left(B^{\prime} B_{A}, B C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, ainsi $\left(B^{\prime} T, T C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, donc les points $T, B^{\prime}, B_{C}$ et $C$ sont cocycliques, ce qui conclut la preuve du lemme.
Lemme 2. les points $B^{\prime}$, $B$ et $T$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nDémonstration."
}
|
22f348a3-ddb9-5775-866c-db1838592fe4
| 607,207
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We look at the circles $B^{\prime} T C B_{C}, A B^{\prime} T B_{A}$ and $A C B_{A} B_{C}$ (all these points are concyclic according to the previous lemma), their radical axes are ( $B^{\prime} T$ ), ( $B_{A} A$ ) and ( $B_{C} C$ ), which shows by the concurrency of the radical axes that the points $B, B^{\prime}$ and $T$ are collinear.
Lemma 3. $\left(A A^{*}\right)$ is tangent to the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On regarde les cercles $B^{\prime} T C B_{C}, A B^{\prime} T B_{A}$ et $A C B_{A} B_{C}$ (tous ces points sont cocycliques d'après le lemme précédent), leurs axes radicaux sont ( $B^{\prime} T$ ), ( $B_{A} A$ ) et ( $B_{C} C$ ), ce qui montre par concourance des axes radicaux que les points $B, B^{\prime}$ et $T$ sont alignés.
Lemme 3. $\left(A A^{*}\right)$ est tangente au cercle circonscrit de $A B C$.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nDémonstration."
}
|
22f348a3-ddb9-5775-866c-db1838592fe4
| 607,207
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.