problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $\mathrm{a}, \mathrm{b}, \mathrm{c} \geqslant 1$ be integers such that $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ and $\mathrm{a}^{\mathrm{c}} \mid \mathrm{c}^{\mathrm{b}}$. Show that $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
We will look at the $p$-adic valuations of each of the prime numbers $a, b$, and $c$. Indeed, it suffices to show that for any prime number $p$, we have $2 v_{\mathfrak{p}}(\mathfrak{a})=v_{\mathfrak{p}}\left(\mathrm{a}^{2}\right) \leqslant v_{\mathfrak{p}}(\mathrm{bc})=v_{\mathfrak{p}}(b)+v_{\mathfrak{p}}(\mathfrak{c})$.
Let $p$ be a prime number. The hypothesis that $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ translates in terms of $p$-adic valuation to $b v_{p}(a) \leqslant c v_{p}(b)$, or equivalently $v_{p}(a) \leqslant \frac{c}{b} v_{p}(b)$. Similarly, we obtain that $v_{p}(a) \leqslant \frac{b}{c} v_{p}(c)$.
By multiplying the two relations, we find that $v_{\mathfrak{p}}(\mathfrak{a})^{2} \leqslant v_{\mathfrak{p}}(\mathrm{b}) v_{\mathfrak{p}}(\mathfrak{c})$. Therefore, according to the inequality of means:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
which gives us $2 v_{\mathfrak{p}}(\mathrm{a}) \leqslant v_{\mathfrak{p}}(\mathrm{b})+v_{\mathfrak{p}}(\mathrm{c})$ as desired. Since this is true for any prime $p$, we indeed have $\mathrm{a}^{2} \mid \mathrm{bc}$.
Grader's Comment: The exercise is very well solved.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathrm{a}, \mathrm{b}, \mathrm{c} \geqslant 1$ des entiers tels que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ et $\mathrm{a}^{\mathrm{c}} \mid \mathrm{c}^{\mathrm{b}}$. Montrer que $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $a, b$ et $c$. En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{\mathfrak{p}}(\mathfrak{a})=v_{\mathfrak{p}}\left(\mathrm{a}^{2}\right) \leqslant v_{\mathfrak{p}}(\mathrm{bc})=v_{\mathfrak{p}}(b)+v_{\mathfrak{p}}(\mathfrak{c})$.
Soit $p$ un nombre premier. Lhypothèse que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ se traduit en terme de valuation p -adique par $b v_{p}(a) \leqslant c v_{p}(b)$, ou encore $v_{p}(a) \leqslant \frac{c}{b} v_{p}(b)$. De même, on obtient que $v_{p}(a) \leqslant \frac{b}{c} v_{p}(c)$.
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathfrak{a})^{2} \leqslant v_{\mathfrak{p}}(\mathrm{b}) v_{\mathfrak{p}}(\mathfrak{c})$. On a donc, d'après l'inégalité des moyennes:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
ce qui donne bien $2 v_{\mathfrak{p}}(\mathrm{a}) \leqslant v_{\mathfrak{p}}(\mathrm{b})+v_{\mathfrak{p}}(\mathrm{c})$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $\mathrm{a}^{2} \mid \mathrm{bc}$.
Commentaire des correcteurs: L'exercice est très bien résolu.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
c2451ce1-8f70-5a86-8c45-7c8de8223ed7
| 607,372
|
A set $E$ of strictly positive integers is said to be interesting if for all $\mathrm{n} \geqslant 1$ and for all $x_{1}, \ldots, x_{n}$ elements of $E$ that are pairwise distinct, their arithmetic mean $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ and their geometric mean $\left(x_{1} \cdot \ldots \cdot x_{n}\right)^{\frac{1}{n}}$ are integers.
1. Does there exist an interesting set $E$ containing exactly 2022 elements?
2. Does there exist an interesting set $E$ that is infinite?
|
1) To start, we can observe that if $n \geq 1$, then as soon as $x_{1}, \ldots, x_{n} \geq 1$ are integers all multiples of $n$, each of the numbers $\frac{x_{k}}{n}$ is an integer, so their sum $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ is an integer. Similarly, if $n \geq 1$, then as soon as $x_{1}, \ldots, x_{n} \geq 1$ are integers all perfect $n$-th powers, each of the numbers $x_{k}^{1 / n}$ is an integer, so their product $\left(x_{1} \times \ldots \times x_{n}\right)^{\frac{1}{n}}$ is an integer. To find an interesting set $E$ containing exactly 2022 elements, it is sufficient that for all $1 \leqslant n \leqslant 2022$, all elements of $E$ are both multiples of $n$ and perfect $n$-th powers. For this, it is sufficient that all elements of $E$ are both multiples of 2022!, and perfect 2022!-th powers. Thus, $E=\left\{(2022!)^{k 2022!}, 1 \leqslant k \leqslant 2022\right\}$ works.
2) We will show that there does not exist an infinite interesting set. In fact, we will show that there does not even exist an infinite set of strictly positive integers satisfying the hypothesis on arithmetic means. Indeed, suppose by contradiction that such an infinite set $E$ exists, that is, for all $n \geq 1$ and $x_{1}, \ldots, x_{n} \in E$ pairwise distinct, the arithmetic mean $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ is an integer. Let $a<b$ be any two elements of $E$ and $n \geq 2$. Choose $x_{1}<\ldots<x_{n-1}$ distinct elements of $E$, and distinct from $a$ and $b$. The hypothesis applied successively to the $n$-tuples $\left(x_{1}, \ldots, x_{n-1}, a\right)$ and $\left(x_{1}, \ldots, x_{n-1}, b\right)$ ensures that $n$ divides both $x_{1}+\ldots+x_{n-1}+a$ and $x_{1}+\ldots+x_{n-1}+b$. Thus, $n$ divides the difference of these two numbers, which is $a-b$. Since this is true for all $n \geq 2$, the integer $a-b$ has an infinite number of divisors. It is therefore zero, that is, $a=b$. This is in contradiction with our initial hypothesis, so such a set $E$ does not exist.
Graders' comments: The first question of the exercise is more often addressed than the second. Be careful, several students construct a set whose arithmetic and geometric means of all the elements of the set are integers, but not the means of the elements of any subset.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un ensemble E d'entiers strictement positifs est dit intéressant si pour tout $\mathrm{n} \geqslant 1$ et pour tous $x_{1}, \ldots, x_{n}$ des éléments de $E$ deux à deux distincts, leur moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ et leur moyenne géométrique $\left(x_{1} \cdot \ldots \cdot x_{n}\right)^{\frac{1}{n}}$ sont des entiers.
1. Existe-t-il un ensemble E intéressant contenant exactement 2022 éléments?
2. Existe-t-il un ensemble E intéressant infini?
|
1) Pour commencer, on peut remarquer que si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous multiples de $n$, chacun des nombres $\frac{x_{k}}{n}$ est un entier, de sorte que leur somme $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. De même, si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous puissances $n$-ièmes parfaites, chacun des nombres $x_{k}^{1 / n}$ est entier, de sorte que leur produit $\left(x_{1} \times \ldots \times x_{n}\right)^{\frac{1}{n}}$ est un entier. Pour trouver un ensemble E intéressant contenant exactement 2022 éléments, il suffit donc que pour tout $1 \leqslant n \leqslant 2022$, tous les éléments de $E$ soient à la fois des multiples de $n$ et des puissances $n$-ièmes parfaites. Pour cela, il suffit que tous les éléments de E soient à la fois des multiples de 2022!, et des puissances 2022!-ièmes parfaites. Ainsi, $E=\left\{(2022!)^{k 2022!}, 1 \leqslant k \leqslant 2022\right\}$ convient.
2) Nous allons montrer qu'il n'existe pas d'ensemble intéressant infini. En fait, on va montrer qu'il n'existe même pas d'ensemble infini d'entiers strictement positifs vérifiant l'hypothèse sur les moyennes arithmétiques. En effet, supposons par l'absurde qu'un tel ensemble infini E existe, c'est-à-dire que pour tout $n \geqslant 1$ et $x_{1}, \ldots, x_{n} \in E$ deux à deux distincts, la moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. Soit $a<b$ deux éléments quelconques de $E$ et $n \geqslant 2$. Choisissons $x_{1}<\ldots<x_{n-1}$ des éléments deux à deux distincts de $E$, et distincts de plus de a et $b$. L'hypothèse appliquée successivement aux $n$-uplets $\left(x_{1}, \ldots, x_{n-1}, a\right)$ et $\left(x_{1}, \ldots, x_{n-1}, b\right)$ assure que $n$ divise à la fois $x_{1}+\ldots+x_{n-1}+a$ et $x_{1}+\ldots+x_{n-1}+b$. Ainsi, $n$ divise la différence de ces deux nombres qui vaut $a-b$. Ceci étant vrai pour tout $\mathrm{n} \geqslant 2$, l'entier $\mathrm{a}-\mathrm{b}$ admet un nombre infini de diviseurs. Il est donc nul, c'est-à-dire que $\mathrm{a}=\mathrm{b}$. Ceci est en contradiction avec notre hypothèse de départ, un tel ensemble $E$ n'existe donc pas.
Commentaire des correcteurs : La première question de l'exercice est plus souvent traitée que la deuxième. Attention, plusieurs élèves y construisent un ensemble dont les moyennes arithmétique et géométrique de tous les éléments de l'ensemble sont entièress, mais pas les moyennes des éléments de n'importe quel sous-ensemble.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
f0c80b24-178d-58a5-8608-3e2daa417e12
| 607,374
|
Let $p$ be a prime number. Show that there exists a permutation $\left(a_{1}, \ldots, a_{p}\right)$ of $(1, \ldots, p)$ such that the integers $a_{1}, a_{1} \cdot a_{2}, \ldots, a_{1} \cdot a_{2} \cdot \ldots \cdot a_{p}$ give $p$ pairwise distinct remainders when performing their Euclidean division by $p$.
|
We can be very optimistic about this exercise and want $a_{1} a_{2} \cdots a_{k} \equiv k$ $\bmod p$ for all $k$ between 1 and $p$. Therefore, it is necessary that $a_{1}=1$ and for all $k \neq 1$:
$$
a_{k} \equiv \frac{a_{1} \cdots a_{k}}{a_{1} \cdots a_{k-1}} \equiv \frac{k}{k-1} \quad \bmod p
$$
where we denote $\frac{a}{b}$ as any integer whose remainder $c$ by the Euclidean division by $p$ satisfies $cb \equiv a \bmod p$, which always exists as long as $b$ is non-zero. Thus, for $k \neq 1$, we can set $a_{k}$ as the element of $\{1, \ldots, p\}$ satisfying $(k-1) a_{k} \equiv k \bmod p$.
It remains to verify that all the numbers $a_{k}$ we have formed are indeed distinct from each other, and thus that $\left\{a_{1}, \ldots, a_{p}\right\}$ is indeed a permutation of $\{1, \ldots, p\}$. Suppose there exist $i<j$ such that $a_{i} \equiv a_{j}$. If $i=1$, for all $j \geqslant 2, \frac{j}{j-1} \neq 1 \bmod p$. Otherwise $\frac{i}{i-1} \equiv \frac{j}{j-1}$ implies that $i-j \equiv i-i$, which is $i \equiv j$ $\bmod p$, contradicting our initial assumption.
Thus all the $a_{k}$ are different modulo $p$. Given that there are $p$ terms in the sequence and $p$ elements in $\{1,2, \cdots, p\},\left(a_{1}, a_{2}, \cdots, a_{p}\right)$ is a permutation of $(1,2, \cdots p)$.
Comment from the graders: The exercise was poorly addressed. The main idea of the problem was to create a permutation such that $a_{1} a_{2} \ldots a_{i} \equiv i \bmod p$. To implement this, a good understanding of the concept of inverse modulo $p$ was required, which was the case for most students who submitted a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p$ un nombre premier. Montrer qu'il existe une permutation $\left(a_{1}, \ldots, a_{p}\right)$ de $(1, \ldots, p)$ telle que les entiers $a_{1}, a_{1} \cdot a_{2}, \ldots, a_{1} \cdot a_{2} \cdot \ldots \cdot a_{p}$ donnent $p$ restes deux à deux distincts lorsque qu'on réalise leur divison euclidienne par $p$.
|
On peut être très optimiste sur cet exercice et vouloir que $a_{1} a_{2} \cdots a_{k} \equiv k$ $\bmod p$ pour tout $k$ compris entre 1 et $p$. Il faut donc que $a_{1}=1$ et pour tout $k \neq 1$ :
$$
a_{k} \equiv \frac{a_{1} \cdots a_{k}}{a_{1} \cdots a_{k-1}} \equiv \frac{k}{k-1} \quad \bmod p
$$
où l'on note $\frac{\mathrm{a}}{\mathrm{b}}$ tout nombre entier dont le reste c par la division euclidienne par $p$ vérifie $\mathrm{cb} \equiv \mathrm{a} \bmod p$, qui existe toujours dès que $b$ est non nul. Ainsi, pour $k \neq 1$, on peut poser $a_{k}$ l'élément de $\{1, \ldots, p\}$ vérifiant $(k-1) a_{k} \equiv k \bmod p$.
Il reste juste à vérifier que tous les nombres $a_{k}$ que l'on a formés sont bien deux à deux distincts, et ainsi que $\left\{a_{1}, \ldots, a_{p}\right\}$ est bien une permutation de $\{1, \ldots, p\}$. Supposons qu'il existe $i<j$ tels que $a_{i} \equiv a_{j}$. Si $\mathfrak{i}=1$, pour tout $\mathfrak{j} \geqslant 2, \frac{\mathfrak{j}}{\mathfrak{j}-1} \neq 1 \bmod \boldsymbol{p}$. Sinon $\frac{i}{i-1} \equiv \frac{\mathfrak{j}}{\mathfrak{j}-1}$ implique que $\mathfrak{i}-\mathfrak{j} \equiv \mathfrak{i}-\mathfrak{i}$, soit $\mathfrak{i} \equiv \mathfrak{j}$ $\bmod p$, ce qui est en contradiction avec notre hypothèse de départ.
Ainsi tous les $a_{k}$ sont différents modulo $p$. Etant donné qu'il y a $p$ termes dans la suite et $p$ éléments dans $\{1,2, \cdots, p\},\left(a_{1}, a_{2}, \cdots, a_{p}\right)$ est une permutation de $(1,2, \cdots p)$.
Commentaire des correcteurs: L'exercice a été peu traité. Avoir l'idée de créer une permutation telle que $a_{1} a_{2} \ldots a_{i} \equiv i \bmod p$ était l'idée principale du problème. Pour la mettre en oeuvre, il fallait une bonne compréhension de la notion d'inverse modulo $p$, et c'était le cas de la plupart des élèves qui ont rendu une solution.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
dc27d5bd-7868-56da-8f27-004ee1348023
| 607,375
|
Let $a, b, c \geqslant 1$ be integers such that $a^{b} \mid b^{c}$ and $a^{c} \mid c^{b}$. Show that $a^{2} \mid b c$.
|
We will look at the $p$-adic valuations of each of the prime numbers $\mathrm{a}$, $\mathrm{b}$, and $\mathrm{c}$. Indeed, it suffices to show that for any prime number $p$, we have $2 v_{p}(a) = v_{p}(a^2) \leq v_{p}(bc) = v_{p}(b) + v_{p}(c)$.
Let $p$ be a prime number. The hypothesis that $a^b \mid b^c$ translates in terms of $p$-adic valuation to $\mathrm{b} v_{\mathfrak{p}}(\mathrm{a}) \leq \mathrm{c} v_{p}(\mathrm{b})$, or equivalently $v_{p}(\mathrm{a}) \leq \frac{\mathrm{c}}{\mathrm{b}} \nu_{p}(\mathrm{b})$. Similarly, we obtain that $v_{p}(\mathrm{a}) \leq \frac{\mathrm{b}}{\mathrm{c}} \nu_{p}(\mathrm{c})$.
By multiplying the two relations, we find that $v_{\mathfrak{p}}(\mathrm{a})^2 \leq \nu_{p}(b) v_{p}(c)$. Therefore, according to the inequality of means:
$$
v_{p}(a) \leq \sqrt{v_{p}(b) v_{p}(c)} \leq \frac{v_{p}(b) + v_{p}(c)}{2}
$$
which gives us $2 v_{p}(a) \leq v_{p}(b) + v_{p}(c)$ as desired. Since this is true for any prime $p$, we have $a^2 \mid bc$.
Grader's Comment: The problem is generally well done. A handful of students made the mistake of claiming that if $a$ divides $b^c$, then $a$ divides $b$. This claim can be refuted by considering $\mathrm{a}=25$, $\mathrm{b}=10$, and $\mathrm{c}=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a, b, c \geqslant 1$ des entiers tels que $a^{b} \mid b^{c}$ et $a^{c} \mid c^{b}$. Montrer que $a^{2} \mid b c$.
|
Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $\mathrm{a}, \mathrm{b}$ et c . En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{p}(a)=v_{p}\left(a^{2}\right) \leqslant$ $v_{p}(b c)=v_{p}(b)+v_{p}(c)$.
Soit $p$ un nombre premier. L'hypothèse que $a^{b} \mid b^{c}$ se traduit en terme de valuation $p$-adique par $\mathrm{b} v_{\mathfrak{p}}(\mathrm{a}) \leqslant \mathrm{c} v_{p}(\mathrm{~b})$, ou encore $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{c}}{\mathrm{b}} \nu_{p}(\mathrm{~b})$. De même, on obtient que $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{b}}{\mathrm{c}} \nu_{p}(\mathrm{c})$.
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathrm{a})^{2} \leqslant \nu_{p}(b) v_{p}(c)$. On a donc, d'après l'inégalité des moyennes:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
ce qui donne bien $2 v_{p}(a) \leqslant v_{p}(b)+v_{p}(c)$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $a^{2} \mid b c$.
Commentaire des correcteurs : Le problème est globalement bien réussi. Une poignée d'élèves s'est trompée en affirmant que si $a$ divise $b^{c}$, alors $a$ divise $b$. Cette affirmation peut être réfutée en regardant $\mathrm{a}=25, \mathrm{~b}=10$ et $\mathrm{c}=2$.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
cf9e72c4-272e-5edf-9b47-b99a832066bd
| 607,379
|
Let $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ be a function such that for any integer $\mathrm{n} \geqslant 1, \mathrm{f}(\mathrm{f}(\mathrm{n}))$ is equal to the number of positive divisors of $n$. Show that if $p$ is a prime number, then $f(p)$ is also a prime number.
|
In the following, we denote $d(n)$ as the number of positive divisors of $n$. If $p$ is prime, we have $f(f(p))=2$ by definition. Applying $f$ to both sides of the equality, we see that $f(2)=d(f(p))$. We want to show that $f(2)=2$, which will prove that $f(p)$ has exactly two divisors and is therefore prime. Moreover, we have $f(2)=d(f(2))$. For an integer $\boldsymbol{n} \geqslant 2$ to be equal to its number of divisors, all numbers less than $n$ must divide $n$, including $n-1$ which is always coprime with $n$, so $n-1=1$ and $n=2$. We deduce that $f(2) \in\{1,2\}$. If $f(2)=1$, then $d(f(p))=1$ for all prime $p$, so $f(p)=1$ for prime $p$, since 1 is the only integer with a single divisor. But then
$$
1=\mathbf{f}(3)=\mathbf{f}\left(\mathrm{d}\left(2^{2}\right)\right)=\mathbf{f}\left(\mathbf{f}\left(\mathbf{f}\left(2^{2}\right)\right)\right)=\mathrm{d}\left(\mathbf{f}\left(2^{2}\right)\right)
$$
and we deduce that $f(4)=1$. But then
$$
\mathbf{f}(\mathbf{f}(4))=\mathbf{f}(1)=\mathbf{f}(\mathbf{f}(2))=\mathrm{d}(2)=2 \neq \mathrm{d}(4)
$$
which provides the desired contradiction. Therefore, we have $\boldsymbol{f}(2)=2$, which concludes the proof.
Comment from the graders: Many students solved the problem, but many others went too fast. Indeed, from the equality $f(f(f(p)))=f(p)$, it is tempting to immediately conclude that $\boldsymbol{f}(\mathfrak{p})=2$. However, another possible case is the case where $f(2)=1$, since 1 also satisfies $d(n)=n$. Handling this case was the main difficulty of the problem. It is therefore a pity to have missed it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ une fonction telle que pour tout entier $\mathrm{n} \geqslant 1, \mathrm{f}(\mathrm{f}(\mathrm{n}))$ soit égal au nombre de diviseurs positifs de $n$. Montrer que si $p$ est un nombre premier, alors $f(p)$ est aussi un nombre premier.
|
Dans la suite, on note $d(n)$ le nombre de diviseurs positifs de $n$. Si $p$ est premier, on a $f(f(p))=2$ par définition. En appliquant f des deux côtés de l'égalité, on voit que $f(2)=d(f(p))$. On veut donc montrer que $f(2)=2$, ce qui prouvera que $f(p)$ a exactement deux diviseurs et est donc premier. Or, on a aussi $f(2)=d(f(2))$. Or, pour qu'un entier $\boldsymbol{n} \geqslant 2$ soit égal à son nombre de diviseurs, tous les nombres inférieurs à $n$ doivent diviser $n$, y compris $n-1$ qui est toujours premier avec $n$, donc $n-1=1$ et $n=2$. On déduit que $f(2) \in\{1,2\}$. Si $f(2)=1$, alors $d(f(p))=1$ pour tout $p$ premier, donc $f(p)=1$ pour $p$ premier, puisque 1 est le seul entier à admettre un seul diviseur. Mais alors
$$
1=\mathbf{f}(3)=\mathbf{f}\left(\mathrm{d}\left(2^{2}\right)\right)=\mathbf{f}\left(\mathbf{f}\left(\mathbf{f}\left(2^{2}\right)\right)\right)=\mathrm{d}\left(\mathbf{f}\left(2^{2}\right)\right)
$$
et l'on déduit que $f(4)=1$. Mais alors
$$
\mathbf{f}(\mathbf{f}(4))=\mathbf{f}(1)=\mathbf{f}(\mathbf{f}(2))=\mathrm{d}(2)=2 \neq \mathrm{d}(4)
$$
ce qui fournit la contradiction désirée. On a donc bien $\boldsymbol{f}(2)=2$, ce qui conclut.
Commentaire des correcteurs : Une bonne partie des élèves ont résolu le problème, mais beaucoup d'autres sont allés bien trop vite. En effet, à partir de l'égalité $f(f(f(p)))=f(p)$, il est tentant de conclure immédiatemment que $\boldsymbol{f}(\mathfrak{p})=2$. Mais un autre cas possible est le cas où $f(2)=1$, puisque 1 vérifie aussi que $d(n)=n$. C'est traiter ce cas qui constituait la principale difficulté du problème. Il est donc dommage d'être passé à côté.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "## Solution de l'exercice 13"
}
|
1e1e0405-9092-5b98-bcf2-17e0a5653d89
| 607,382
|
Let $m, n \geqslant 2$ be integers such that $\operatorname{PGCD}(m, n)=\operatorname{PGCD}(m, n-1)=1$. We define the sequence $\left(n_{k}\right)_{k \in \mathbb{N}}$ by $n_{0}=m$ and $n_{k+1}=n \cdot n_{k}+1$ for $k \in \mathbb{N}$. Show that the integers $n_{1}, \ldots, n_{m-1}$ cannot all be prime numbers.
|
First, the sequence $(\mathrm{n}_{\mathrm{k}})$ is an arithmetico-geometric sequence. Therefore, we can establish a closed formula for its general term, namely $n_{k}=n^{k} m+\frac{n^{k+1}-1}{n-1}$, which can also be obtained by induction from the calculation of the first few terms. From this expression, we deduce in particular that $n_{k}>m$ for all $k>0$. We will now show that one of the numbers $n_{1}, \ldots, n_{m-1}$ is divisible by $m$, which will make this number a composite number.
By passing modulo $m$, we deduce $n_{k} \equiv \frac{\mathfrak{n}^{k+1}-1}{n-1} \bmod m$ by induction, where we have used that $n-1$ is invertible modulo $m$ because $n-1$ is coprime with $m$.
Let $\omega$ be the order of $n \bmod m$ (which exists because $m$ and $n$ are coprime). We have $\omega \leqslant \varphi(m) \leqslant m-1$ according to Euler's theorem. We deduce that $m \mid n^{\omega}-1$, which implies that $m$ divides $n_{\omega-1}-1$ as desired. Thus, the $n_{k}$ are not all prime.
Graders' comments: The exercise is very well solved. Almost all students thought to justify that $m<n_{k}$, which is necessary to conclude that $n_{k}$ is composite if it is divisible by $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $m, n \geqslant 2$ des entiers tels que $\operatorname{PGCD}(m, n)=\operatorname{PGCD}(m, n-1)=1$. On définit la suite $\left(n_{k}\right)_{k \in \mathbb{N}}$ par $n_{0}=m$ et $n_{k+1}=n \cdot n_{k}+1$ pour $k \in \mathbb{N}$. Montrer que les entiers $n_{1}, \ldots, n_{m-1}$ ne peuvent pas tous être des nombres premiers.
|
Tout d'abord, la suite ( $\mathrm{n}_{\mathrm{k}}$ ) est une suite arithmético-géométrique. On peut donc établir une formule close pour son terme général, à savoir $n_{k}=n^{k} m+\frac{n^{k+1}-1}{n-1}$, que l'on peut aussi obtenir par récurrence à partir du calcul des premiers termes. De cette expression on déduit en particulier que $n_{k}>m$ pour tout $k>0$. On va désormais montrer que l'un des nombres $n_{1}, \ldots, n_{m-1}$ est divisible par $m$, ce qui fera de ce nombre un nombre composé.
En passant modulo $m$, on déduit $n_{k} \equiv \frac{\mathfrak{n}^{k+1}-1}{n-1} \bmod m$ par récurrence, où l'on a utilisé que $n-1$ est inversible modulo $m$ car $n-1$ est premier avec $m$.
Soit $\omega$ l'ordre de $n \bmod m$ (celui-ci existe car $m$ et $n$ premiers entre eux). On a $\omega \leqslant \varphi(m) \leqslant m-1$ d'après le théorème d'Euler. On déduit que $m \mid n^{\omega}-1$, ce qui implique que $m$ divise $n_{\omega-1}-1$ comme voulu. Ainsi, les $n_{k}$ ne sont pas tous premiers.
Commentaire des correcteurs: L'exercice est très bien résolu. Les élèves ont pratiquement tous pensé à justifier le fait que $m<n_{k}$, ce qui est nécessaire pour conclure que $n_{k}$ est composé s'il est divisible par m.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "\nSolution de l'exercice 15"
}
|
43d50acb-788a-538d-967f-641ee9d20edf
| 607,384
|
Let $p$ be an odd prime and $x_{1}, \ldots, x_{p}$ be integers.
We assume that for all $k \geqslant 1$ integer, we have
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Show that the integers $x_{1}, \ldots, x_{p}$ are all congruent modulo $p$.
|
Note that the relation is also true for $k=0$ because $\underbrace{1+\ldots+1}_{\mathrm{p} \text { times }} \equiv 0$ $\bmod p$
Let $\mathrm{Q}(\mathrm{X})=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} X^{\mathrm{k}}$ be a polynomial with integer coefficients. We have
$$
\mathrm{Q}\left(\mathrm{x}_{1}\right)+\ldots+\mathrm{Q}\left(\mathrm{x}_{\mathrm{p}}\right)=\sum_{\ell=1}^{p} \sum_{k=0}^{n} \mathrm{a}_{\mathrm{k}} x_{\ell}^{k}=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} \underbrace{\sum_{\ell=1}^{p} x_{\ell}^{k}}_{\equiv 0 \bmod p} \equiv 0 \bmod p
$$
Suppose, for the sake of contradiction, that the $x_{i}$ do not all give the same remainder modulo $p$. Let $\left\{y_{1}, \ldots, y_{r}\right\}$ be the set of remainders modulo $p$ generated by the set $\left\{x_{1}, \ldots, x_{p}\right\}$, with $y_{1} \equiv x_{1}$. Let $a_{1}$ be the number of elements in the set $\left\{x_{1}, \ldots, x_{p}\right\}$ that have the remainder $y_{1}$. Let $P(X)=\left(X-y_{2}\right) \ldots\left(X-y_{r}\right)$. $P$ is zero at each of the $y_{i}$ for $i \neq 0$. Note that since $y_{1} \neq y_{i} \bmod p, P\left(y_{1}\right) \neq 0 \bmod p$. The relation established earlier then gives us $a_{1} P\left(y_{1}\right) \equiv 0 \bmod p$, which implies that $a_{1}=0 \bmod p$, i.e., $a_{1}=p$. This is in contradiction with our initial assumption, so the $x_{i}$ are all equal.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ un nombre premier impair et $x_{1}, \ldots, x_{p}$ des entiers relatifs.
On suppose que pour tout $k \geqslant 1$ entier, on a
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Montrer que les entiers $x_{1}, \ldots, x_{p}$ sont tous congrus modulo $p$.
|
Notons que la relation est également vrai pour $k=0$ car $\underbrace{1+\ldots+1}_{\mathrm{p} \text { fois }} \equiv 0$ $\bmod p$
Soit $\mathrm{Q}(\mathrm{X})=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} X^{\mathrm{k}}$ un polynôme à coefficients entiers. On a
$$
\mathrm{Q}\left(\mathrm{x}_{1}\right)+\ldots+\mathrm{Q}\left(\mathrm{x}_{\mathrm{p}}\right)=\sum_{\ell=1}^{p} \sum_{k=0}^{n} \mathrm{a}_{\mathrm{k}} x_{\ell}^{k}=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} \underbrace{\sum_{\ell=1}^{p} x_{\ell}^{k}}_{\equiv 0 \bmod p} \equiv 0 \bmod p
$$
On suppose par l'absurde que les $x_{i}$ ne donnent pas tous le même reste modulo $p$. Soit $\left\{y_{1}, \ldots, y_{r}\right\}$ l'ensemble des restes modulo $p$ généré par l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$, avec $y_{1} \equiv x_{1}$. On note $a_{1}$ le nombre d'éléments de l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$ qui ont pour reste $y_{1}$. Soit $P(X)=\left(X-y_{2}\right) \ldots\left(X-y_{r}\right)$. P est nul en chacun des $y_{i}$ pour $i \neq 0$. Notons que comme $y_{1} \neq y_{i} \bmod p, P\left(y_{1}\right) \neq 0 \bmod p$. La relation établie plus haut nous donne alors $a_{1} P\left(y_{1}\right) \equiv 0 \bmod p$, ce qui implique que $a_{1}=0 \bmod p$, c'est-à-dire que $a_{1}=p$. Cela est en contradiction avec notre supposition de départ, donc les $x_{i}$ sont tous égaux.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "\nSolution de l'exercice 16"
}
|
bf04d3b1-1d7d-5cd6-9fb9-84d90461ebfd
| 607,385
|
Let $p$ be an odd prime and $x_{1}, \ldots, x_{p}$ be integers.
We assume that for all $k \geqslant 1$ integer, we have
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Show that the integers $x_{1}, \ldots, x_{p}$ are all congruent modulo $p$.
|
: We present a somewhat more conceptual solution that relies on the structure of the field $\mathbb{Z} / p \mathbb{Z}$ and on the fact that the Newton sums of the roots of a polynomial determine its coefficients.
Let $P(X)=\left(X-x_{1}\right) \ldots\left(X-x_{p}\right)$ be the monic polynomial with integer coefficients whose roots are the $x_{\ell}$. The hypothesis of the statement indicates that the Newton sums of the $x_{\ell}$ are zero modulo $p$.
It is possible to relate the coefficients of the polynomial $P$ to the Newton sums of the polynomial $P$ via the following formulas: if $a_{k}$ is the coefficient of $X^{k}$ in the expression of $P$, then for all $0 \leqslant k \leqslant p$:
$$
k a_{p-k}=(-1)^{k-1} \sum_{\ell=1}^{k-1} a_{p-\ell}\left(x_{1}^{\ell}+\ldots+x_{p}^{\ell}\right)
$$
These formulas can be derived by induction using Vieta's formulas.
We then observe that if $k \neq 0, p, k a_{p-k} \equiv 0 \bmod p$ because each of the $x_{1}^{\ell}+\ldots+x_{p}^{\ell}$ is divisible by $p$. Thus, in $\mathbb{Z} / p \mathbb{Z}[X]$, the polynomial $P$ is of the form $P(X)=X^{p}-a=X^{p}-a^{p}=(X-a)^{p}$, where we have used that $a^{p} \equiv a(\bmod p)$ by Fermat's little theorem and that in the formula $(X-a)^{p}=$ $\sum_{k=0}^{p}\binom{p}{k} a^{p-k} X^{k}$, only the coefficients $\binom{p}{0}$ and $\binom{p}{p}$ are non-zero modulo $p$. This implies that the $x_{i}$ are all equal (to $a$) modulo $p$ as desired.
Grader's comment: The exercise is very well done. This exercise required knowledge of polynomials modulo $p$, and the students presented various proofs to solve it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ un nombre premier impair et $x_{1}, \ldots, x_{p}$ des entiers relatifs.
On suppose que pour tout $k \geqslant 1$ entier, on a
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Montrer que les entiers $x_{1}, \ldots, x_{p}$ sont tous congrus modulo $p$.
|
: On présente une solution un peu plus conceptuelle qui s'appuie sur la structure de corps de $\mathbb{Z} / p \mathbb{Z}$ et sur le fait que les sommes de Newton des racines d'un polynôme déterminent ses coefficients.
Soit $P(X)=\left(X-x_{1}\right) \ldots\left(X-x_{p}\right)$ le polynôme unitaire à coefficients entiers dont les racines sont les $x_{\ell}$. L'hypothèse de l'énoncé nous indique que les sommes de Newton des $x_{\ell}$ sont nulles modulo $p$.
Or il est possible de relier les coefficients du polynômes P aux sommes de Newton du polynôme P , via les formules suivantes: si $a_{k}$ est le coefficient devant $X^{k}$ dans l'écriture de $P$, alors pour tout $0 \leqslant k \leqslant p$ :
$$
k a_{p-k}=(-1)^{k-1} \sum_{\ell=1}^{k-1} a_{p-\ell}\left(x_{1}^{\ell}+\ldots+x_{p}^{\ell}\right)
$$
On peut retrouver ces formules par récurrence à l'aide des relations de Viète.
On remarque alors que si $k \neq 0, p, k a_{p-k} \equiv 0 \bmod p$ car chacune des $x_{1}^{\ell}+\ldots+x_{p}^{\ell}$ est divisible par $p$. Ainsi, dans $\mathbb{Z} / p \mathbb{Z}[X]$, le polynôme $P$ est de la forme $P(X)=X^{p}-a=X^{p}-a^{p}=(X-a)^{p}$, où l'on a utilisé que $a^{p} \equiv a(\bmod p)$ par le petit théorème de Fermat et que dans la formule $(X-a)^{p}=$ $\sum_{k=0}^{p}\binom{p}{k} a^{p-k} X^{k}$, seuls les coefficients $\binom{p}{0}$ et $\binom{p}{p}$ sont non nuls modulo $p$. Cela implique que les $x_{i}$ sont tous égaux (à $a$ ) modulo $p$ comme voulu.
Commentaire des correcteurs : L'exercice est très bien réussi. Cet exercice demandait de la culture sur les polynômes modulo $p$, et les élèves ont présenté diverses preuves pour s'en sortir.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "\nSolution alternative"
}
|
bf04d3b1-1d7d-5cd6-9fb9-84d90461ebfd
| 607,385
|
Let $n$ be a strictly positive integer and let $a, a_{1}, \ldots, a_{n}$ be strictly positive integers. Suppose that for any integer $k$ for which the integer $a k+1$ is a perfect square, at least one of the integers $a_{1} k+1, \ldots, a_{n} k+1$ is also a perfect square.
Show that there exists an index $1 \leqslant i \leqslant n$ such that $a=a_{i}$.
|
Indeed, let $a$ be such that $a^{2} \equiv x(\bmod p)$, which we rewrite as $a^{2}-x=k p$. But then we get $\left(a-2^{-1} k p\right)^{2} \equiv a^{2}-k p \equiv x\left(\bmod p^{2}\right)$, and 2 is invertible modulo $p^{2}$ since $p$ is odd. Thus, $x$ is indeed a quadratic residue modulo $p^{2}$.
Lemma 2: If $t$ is a non-zero integer and $p$ is a prime such that $p \equiv 1(\bmod 8 t)$, then $\left(\frac{t}{p}\right)=1$.
Proof: Indeed, let $q$ be a prime divisor of $t$ and $\alpha=\nu_{q}(t)$. If $q=2,\left(\frac{2}{p}\right)=1$ because $p \equiv 1(\bmod 8)$. So $q$ is a quadratic residue modulo $p$. Note now that $\alpha$ is even, then $q^{\alpha}$ is automatically a square modulo $p$, and if $\alpha$ is odd, $q^{\alpha}$ is the product of $q$ (which is a square) with $q^{\alpha-1}$ which is a square, so $q^{\alpha}$ is a square modulo $p$. If $q \geqslant 3$, since $p \equiv 1(\bmod 4)$, the law of quadratic reciprocity gives us $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{1}{q}\right)=1$, Similarly, we deduce that $\left(\frac{q^{\alpha}}{p}\right)=1$. The multiplicativity of the Legendre symbols allows us to conclude that $\left(\frac{t}{p}\right)=1$.
We also recall a particular case of Dirichlet's theorem on arithmetic progressions: for any integer $t$, there are infinitely many primes $p$ such that $p \equiv 1 \bmod 8 t$.
Let's return to the exercise. Suppose by contradiction that all the $a_{i}$ are different from $a$.
Let $M=\max \left\{a, a_{1}, \ldots, a_{n}\right\} \geqslant 2$. We then construct a sequence of primes $p_{1}, \ldots p_{n}$ by induction as follows: by Dirichlet's theorem on arithmetic progressions, there is at least one prime $p_{1} \equiv 1\left(\bmod 8 a_{1}\left(a_{1}-a\right)\right)$ with $p_{1}>M$. (We use here the fact that $\left.a_{1}-a \neq 0\right)$.
For $2 \leqslant i \leqslant n$, we then take $p_{i}$ such that $p_{i} \equiv 1\left(\bmod 8 a_{i}\left(a_{i}-a\right)\right.$ ) with $p_{i}>p_{i-1}$ (which exists for the same reasons as $p_{1}$ ).
In particular, the $p_{i}$ are pairwise distinct, and $p_{i} \equiv 1 \bmod 8 a_{i}$ and $p_{i} \equiv 1 \bmod 8\left(a_{i}-a\right)$, so by the second lemma, for all $i,\left(\frac{a_{i}}{p_{i}}\right)=\left(\frac{a_{i}-a}{p_{i}}\right)=1$.
By definition, for all $i$ there exists $n_{i}$ such that $n_{i}^{2} \equiv a_{i}-a\left(\bmod p_{i}\right)$, and by replacing $n_{i}$ with $n_{i}+p_{i}$, we can assume $p_{i}^{2} \nmid n_{i}^{2}-\left(a_{i}-a\right)\left(p_{i} \neq 2\right)$. Thus, we can write $n_{i}^{2} \equiv a c_{i} p_{i}+\left(a_{i}-a\right)\left(\bmod p_{i}^{2}\right)$ with $p_{i} \nmid c_{i}$ since $a$ and $p_{i}$ are coprime $\left(a<p_{i}\right)$.
Next, since $a_{i}$ is invertible modulo $p_{i}$ for all $i$, the Chinese remainder theorem indicates that we can find an integer $k$ such that for all $i, k \equiv\left(c_{i} p_{i}-1\right) a_{i}^{-1} \bmod p_{i}^{2}$, or $a_{i} k+1 \equiv c_{i} p_{i}$ $\left(\bmod p_{i}^{2}\right)$.
Notice that, by construction,
$$
a k+1 \equiv a \frac{c_{i} p_{i}-1}{a_{i}}+1 \equiv \frac{a c_{i} p_{i}-a+a_{i}}{a_{i}} \equiv \frac{n_{i}^{2}}{a_{i}} \equiv a_{i}\left(\frac{n_{i}}{a_{i}}\right)^{2} \quad\left(\bmod p_{i}^{2}\right)
$$
Since $\left(\frac{a_{i}}{p_{i}}\right)=1$, $a_{i}$ is also a quadratic residue modulo $p_{i}^{2}$ by the first lemma, so there is an integer, say $\mathrm{N}_{i}$, such that $a k+1 \equiv \mathrm{~N}_{i}^{2}\left(\bmod p_{i}^{2}\right)$.
Then the Chinese remainder theorem gives us an integer $x$ such that $x \equiv N_{i}\left(\bmod p_{i}^{2}\right)$ for all $i$ and $x \equiv 1(\bmod a)\left(\text{since } a\right.$ is coprime with the $\left.p_{i}\right)$. But then $x^{2} \equiv N_{i}^{2} \equiv a k+1\left(\bmod p_{i}^{2}\right)$ for all $i$, and $x^{2} \equiv 1^{2} \equiv a k+1(\bmod a)$, so $x^{2} \equiv a k+1\left(\bmod a P^{2}\right)$, where we have set $P=\prod_{i=1}^{n} p_{i}$.
We now rewrite the congruence as $x^{2}=a k+1+m a P^{2}=a\left(P^{2} m+k\right)+1$. We finally use the hypothesis of the statement: there exists an index $j$ such that $a_{j}\left(P^{2} m+k\right)+1$ is a perfect square. But then $a_{j}\left(P^{2} m+k\right)+1 \equiv a_{j} k+1 \equiv c_{j} p_{j}\left(\bmod p_{j}^{2}\right)$, and since $p_{j} \nmid c_{j}, v_{p_{j}}\left(a_{j}\left(P^{2} m+k\right)+1\right)=1$, which is in contradiction with the fact that it is a perfect square. Our initial statement was therefore false, and one of the $a_{i}-a$ is non-zero.
Comment from the graders: The exercise is generally well done by the few students who tackled it, and who present very different solutions from the corrected one.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier strictement positif et soient $a, a_{1}, \ldots, a_{n}$ des entiers strictement positifs. On suppose que pour tout entier $k$ pour lequel l'entier $a k+1$ est un carré parfait, au moins l'un des entiers $a_{1} k+1, \ldots, a_{n} k+1$ est également un carré parfait.
Montrer qu'il existe un indice $1 \leqslant i \leqslant n$ tel que $a=a_{i}$.
|
En effet, soit a tel que $a^{2} \equiv x(\bmod p)$, ce qu'on réécrit sous la forme $a^{2}-x=k p$. Mais alors on obtient $\left(a-2^{-1} k p\right)^{2} \equiv a^{2}-k p \equiv x\left(\bmod p^{2}\right)$, et 2 est inversible modulo $p^{2}$ car $p$ est impair. Ainsi, $x$ est bien un résidu quadratique modulo $p^{2}$.
Lemme 2: Sii $t$ est un entier non nul et $p$ est un nombre premier tel que $p \equiv 1(\bmod 8 \mathrm{t})$, alors $\left(\frac{\mathrm{t}}{\mathrm{p}}\right)=1$.
Démonstration : En effet, soit $q$ un diviseur premier de $t$ et $\alpha=\nu_{q}(t)$. Si $q=2,\left(\frac{2}{p}\right)=1$ car $p \equiv 1(\bmod 8)$. donc $q$ est résidu quadratique modulo $p$. Notons maintenant que $\alpha$ est pair, alors $q^{\alpha}$ est automatiquement un carré modulo $p$, et si $\alpha$ est impair, $q^{\alpha}$ est le produit de $q$ (qui est un carré) avec $q^{\alpha-1}$ qui est un carré, donc $q^{\alpha}$ est un carré modulo $p$. Si $q \geqslant 3$, comme $p \equiv 1(\bmod 4)$, la loi de réciprocité quadratique nous donne $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{1}{q}\right)=1$, De même que précédemment, on déduit que $\left(\frac{q^{\alpha}}{p}\right)=1$. La multiplicativité des symboles de Legendre permet de conclure que $\left(\frac{t}{p}\right)=1$.
On rappelle également un cas particulier du théorème de la progression arithmétique de Dirichlet : pour tout $t$ entier, il existe une infinité de nombres premiers $p$ tels que $p \equiv 1 \bmod 8 t$.
Revenons à l'exercice. Supposons par l'absurde que tous les $a_{i}$ sont différents de $a$.
Posons $M=\max \left\{a, a_{1}, \ldots, a_{n}\right\} \geqslant 2$. On construit alors une suite de nombres premiers $p_{1}, \ldots p_{n}$ par récurrence comme suit : par le théorème de la progression arithmétique de Dirichlet, il existe au moins un nombre premier $p_{1} \equiv 1\left(\bmod 8 a_{1}\left(a_{1}-a\right)\right)$ avec $p_{1}>M$. (On utilise ici le fait que $\left.a_{1}-a \neq 0\right)$.
Pour $2 \leqslant i \leqslant n$, on prend ensuite $p_{i}$ tel que $p_{i} \equiv 1\left(\bmod 8 a_{i}\left(a_{i}-a\right)\right.$ ) avec $p_{i}>p_{i-1}$ (qui existe pour les mêmes raisons que $p_{1}$ ).
En particulier les $p_{i}$ sont deux-à-deux distincts, et $p_{i} \equiv 1 \bmod 8 a_{i}$ et $p_{i} \equiv 1 \bmod 8\left(a_{i}-a\right)$, de sorte que d'après le deuxième lemme, pour tout $i,\left(\frac{a_{i}}{p_{i}}\right)=\left(\frac{a_{i}-a}{p_{i}}\right)=1$.
Par définition, pour tout $i$ il existe $n_{i}$ tel que $n_{i}^{2} \equiv a_{i}-a\left(\bmod p_{i}\right)$, et quitte à remplacer $n_{i}$ par $n_{i}+p_{i}$, on peut supposer $p_{i}^{2} \nmid n_{i}^{2}-\left(a_{i}-a\right)\left(p_{i} \neq 2\right)$. Ainsi, on peut écrire $n_{i}^{2} \equiv a c_{i} p_{i}+\left(a_{i}-a\right)\left(\bmod p_{i}^{2}\right)$ avec $p_{i} \nmid c_{i}$ puisque a et $p_{i}$ sont premiers entre eux $\left(a<p_{i}\right)$.
Ensuite, comme $a_{i}$ est inversible modulo $p_{i}$ pour tout $i$, le théorème des restes chinois indique que l'on peut trouver un entier $k$ vérifiant que pour tout $i, k \equiv\left(c_{i} p_{i}-1\right) a_{i}^{-1} \bmod p_{i}^{2}$, ou encore $a_{i} k+1 \equiv c_{i} p_{i}$ $\left(\bmod p_{i}^{2}\right)$.
Remarquons que, par construction,
$$
a k+1 \equiv a \frac{c_{i} p_{i}-1}{a_{i}}+1 \equiv \frac{a c_{i} p_{i}-a+a_{i}}{a_{i}} \equiv \frac{n_{i}^{2}}{a_{i}} \equiv a_{i}\left(\frac{n_{i}}{a_{i}}\right)^{2} \quad\left(\bmod p_{i}^{2}\right)
$$
Or $\left(\frac{a_{i}}{p_{i}}\right)=1$, donc $a_{i}$ est également un résidu quadratique modulo $p_{i}^{2}$ par le premier lemme, donc on a un entier, mettons $\mathrm{N}_{i}$, tel que $a k+1 \equiv \mathrm{~N}_{i}^{2}\left(\bmod p_{i}^{2}\right)$.
Alors le théorème des restes chinois nous donne un entier $x$ tel que $x \equiv N_{i}\left(\bmod p_{i}^{2}\right)$ pour tout $i$ et $x \equiv 1(\bmod a)\left(\operatorname{car} a\right.$ est premier avec les $\left.p_{i}\right)$. Mais alors $x^{2} \equiv N_{i}^{2} \equiv a k+1\left(\bmod p_{i}^{2}\right)$ pour tout $i$, et $x^{2} \equiv 1^{2} \equiv a k+1(\bmod a)$, donc $x^{2} \equiv a k+1\left(\bmod a P^{2}\right)$, où on a posé $P=\prod_{i=1}^{n} p_{i}$.
On réécrit maintenant la congruence sous la forme $x^{2}=a k+1+m a P^{2}=a\left(P^{2} m+k\right)+1$. On utilise enfin l'hypothèse de l'énoncé : il existe un indice $j$ tel que $a_{j}\left(P^{2} m+k\right)+1$ soit un carré parfait. Mais alors $a_{j}\left(P^{2} m+k\right)+1 \equiv a_{j} k+1 \equiv c_{j} p_{j}\left(\bmod p_{j}^{2}\right)$, et comme $p_{j} \nmid c_{j}, v_{p_{j}}\left(a_{j}\left(P^{2} m+k\right)+1\right)=1$, ce qui est en contradiction avec le fait que c'est un carré parfait. Notre affirmation de départ était donc fausse, et l'un des $a_{i}-a$ est non nul.
Commentaire des correcteurs : L'exercice est globalement bien réussi par les quelques élèves qui l'ont traité, et qui présentent des solutions très différentes de celle du corrigé.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "\nDémonstration:"
}
|
c6f292b9-3f53-5657-9d36-00218bd2dd29
| 607,386
|
Determine all polynomials $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ such that:
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ for all $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ and $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ have the same number of prime divisors for all $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
For all integers $\mathfrak{n} \in \mathbb{N}^{*}$, we denote $\mathcal{D}(n)$ the set of prime divisors of $n$, and $\delta(n)=|\mathcal{D}(n)|$. Let $P \in \mathbb{Z}[X]$ be a polynomial satisfying the two conditions.
We start by proving the following result:
Lemma: Let $\mathrm{n} \geqslant 1$. For all $k \in \mathbb{N}^{*}, \mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Déterminer tous les polynômes $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ tels que :
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ pour tout $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ et $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ ont le même nombre de diviseurs premiers pour tous $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
Dans la suite, pour tout entier $\mathfrak{n} \in \mathbb{N}^{*}$, on note $\mathcal{D}(n)$ l'ensemble des diviseurs premiers de $n$, et $\delta(n)=|\mathcal{D}(n)|$. Soit $P \in \mathbb{Z}[X]$ un polynôme vérifiant les deux conditions.
On commence par montrer le résultat suivant :
Lemme : Soit $\mathrm{n} \geqslant 1$. Pour tout $k \in \mathbb{N}^{*}, \mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"problem_match": "\nExercice 18.",
"solution_match": "\nSolution de l'exercice 18"
}
|
2005c10f-73f6-5ebe-8056-414c130e528d
| 607,387
|
Six baskets of fruit contain pears, peaches, and apples. The number of peaches in each basket is equal to the total number of apples in the other baskets. The number of apples in each basket is equal to the total number of pears in the other baskets. Show that the total number of fruits is a multiple of 31.
|
Let $p_{1}, p_{2}, \ldots, p_{6}$ be the number of pears in each basket, and $q_{1}, q_{2}, \ldots, q_{6}$ be the number of apples in each basket. Let $P$ also denote the total number of pears. We have:
$$
\begin{aligned}
& \mathrm{q}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{1} \\
& \mathrm{q}_{2}=\mathrm{p}_{1}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{2} \\
& \\
& \mathrm{q}_{6}=\mathrm{p}_{1}+\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}=\mathrm{P}-\mathrm{p}_{3}
\end{aligned}
$$
Therefore: $q_{1}+q_{2}+\cdots+q_{6}=\left(P-p_{1}\right)+\left(P-p_{2}\right)+\cdots+\left(P-p_{6}\right)=6 P-\left(p_{1}+p_{2}+\cdots+p_{6}\right)=5 P$ The total number of apples is equal to 5 times the total number of pears. Similarly, the total number of peaches is equal to 5 times the total number of apples, hence 25 times the total number of pears. The total number of fruits is therefore equal to $31=25+5+1$ times the total number of pears, and is thus a multiple of 31.
Examiner's comment: Very well done exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Six paniers à fruits contiennent des poires, des pêches et des pommes. Le nombre de pêches dans chaque panier est égal au nombre total de pommes dans les autres paniers. Le nombre de pommes dans chaque panier est égal au nombre total de poires dans les autres paniers. Montrez que le nombre total de fruits est un multiple de 31.
|
Notons $p_{1}, p_{2}, \ldots, p_{6}$ le nombre de poires dans chaque panier, et $q_{1}, q_{2}, \ldots, q_{6}$ le nombre de pommes dans chaque panier. Notons également $P$ le nombre total de poires. On a:
$$
\begin{aligned}
& \mathrm{q}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{1} \\
& \mathrm{q}_{2}=\mathrm{p}_{1}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{2} \\
& \\
& \mathrm{q}_{6}=\mathrm{p}_{1}+\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}=\mathrm{P}-\mathrm{p}_{3}
\end{aligned}
$$
D'où: $q_{1}+q_{2}+\cdots+q_{6}=\left(P-p_{1}\right)+\left(P-p_{2}\right)+\cdots+\left(P-p_{6}\right)=6 P-\left(p_{1}+p_{2}+\cdots+p_{6}\right)=5 P$ Le nombre total de pommes est égal à 5 fois le nombre total de poires. De même, le nombre total de pêches est égal à 5 fois le nombre total de pommes, donc à 25 fois le nombre total de poires. Le nombre total de fruits est donc égal à $31=25+5+1$ fois le nombre total de poires, et est donc multiple de 31.
Commentaire des correcteurs : Exercice très bien réussi.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
b1bf68bb-97e8-54ac-bac5-dd821fe5bd5b
| 607,388
|
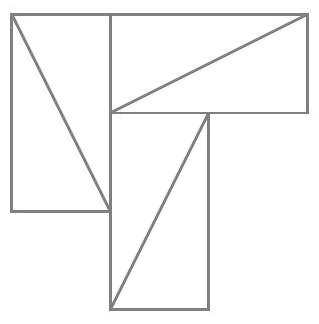
Let $n \geqslant 6$. Prove that every square can be cut into exactly n squares (not necessarily of the same size).
|
We can show this by induction. If we have a partition of the square into $n$ squares, we can obtain a partition into $\mathrm{n}+3$ squares by subdividing one of the squares into 4. Therefore, it is sufficient to show that we can partition a square into 6, 7, and 8 squares. For 6, we subdivide the square into a $3 \times 3$ grid and merge the 4 squares in the top-left. For 7, we subdivide the square into 4, then subdivide one of the resulting squares into 4. For 8, we subdivide the square into a $4 \times 4$ grid and merge the 9 squares in the top-left.
Comment from the graders: The exercise was very well done. Two methods appeared, either with induction, or a cut according to the parity, but they were well explained overall.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $n \geqslant 6$. Prouvez que chaque carré peut être découpé en exactement n carrés (pas nécessairement de même taille).
|
On peut le montrer par récurrence. Si on a un découpage du carré en $n$ carrés, on peut obtenir un découpage en $\mathrm{n}+3$ carrés en subdivisant l'un des carrés en 4 . Il suffit donc de montrer que l'on peut découper un carré en 6,7 et 8 carrés. Pour 6 , on subdivise le carré en une grille $3 \times 3$ et on fusionne les 4 carrés en haut-gauche. Pour 7 , on subdivise le carré en 4 , puis on subdivise l'un des carrés obtenus en 4 . Pour 8 , on subdivise le carré en une grille $4 \times 4$ et on fusionne les 9 carrés en haut-gauche.
Commentaire des correcteurs : Exercice très bien réussi. Deux méthodes sont apparues, soit avec une récurrence, soit une découpe selon la parité, mais elles étaient bien expliquées dans l'ensemble.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
15d5c634-09fe-5a66-beec-09c46a57d232
| 607,390
|
Nimatha and Thanima are playing a game on an $8 \times 8$ chessboard. Taking turns, starting with Nimatha, each player chooses a cell that has not yet been chosen and colors it in their color (red for Nimatha, blue for Thanima). Show that Thanima can always ensure that Nimatha cannot color any $2 \times 2$ square entirely in red.
|
Consider the following coloring:
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 5 |
| 9 | 9 | 10 | 10 | 11 | 11 | 12 | 12 |
| 13 | 14 | 14 | 15 | 15 | 16 | 16 | 13 |
| 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 |
| 21 | 22 | 22 | 23 | 23 | 24 | 24 | 21 |
| 25 | 25 | 26 | 26 | 27 | 27 | 28 | 28 |
| 29 | 30 | 30 | 31 | 31 | 32 | 32 | 29 |
When Nimatha plays on a number \( X \), Thanima responds by playing on the second occurrence of the number \( X \). Each \( 2 \times 2 \) square contains two identical numbers: if one is colored red, the other is colored blue. Thus, it is impossible for Nimatha to create a \( 2 \times 2 \) square entirely red if Thanima follows this strategy.
Comment from the graders: The exercise is generally well done. However, all students who tried to propose a strategy without tiling did not succeed: indeed, it is often difficult to construct a strategy that works in all cases when there are 64 possible moves at the beginning.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Nimatha et Thanima jouent à un jeu sur un échiquier $8 \times 8$. Tour par tour en commençant par Nimatha, chaque joueur choisit une case qui n'a pas encore été choisie et la colorie dans sa couleur (rouge pour Nimatha, bleu pour Thanima). Montrez que Thanima peut toujours faire que Nimatha ne puisse colorier aucun carré $2 \times 2$ entièrement en rouge.
|
On considère le coloriage suivant :
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 5 |
| 9 | 9 | 10 | 10 | 11 | 11 | 12 | 12 |
| 13 | 14 | 14 | 15 | 15 | 16 | 16 | 13 |
| 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 |
| 21 | 22 | 22 | 23 | 23 | 24 | 24 | 21 |
| 25 | 25 | 26 | 26 | 27 | 27 | 28 | 28 |
| 29 | 30 | 30 | 31 | 31 | 32 | 32 | 29 |
Lorsque Nimatha joue sur un nombre $X$, Thanima réagit en jouant sur la seconde occurrence du nombre $X$. Tout carré $2 \times 2$ contient deux nombres identiques : si l'un est coloré en rouge, l'autre est coloré en bleu. Ainsi, il est impossible pour Nimatha de créer un carré $2 \times 2$ entièrement rouge si Thanima suit cette stratégie.
Commentaire des correcteurs: L'exercice est globalement bien réussi. Mais tous les élèves ayant voulu proposer une stratégie sans pavage n'ont pas réussi : en effet, souvent il est difficile de construire une stratégie marchant dasn tous les cas quand il y a 64 coups possibles au tout début.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
b167d643-d23c-5f6d-a818-8181eeffa37e
| 607,392
|
At least $\mathrm{n}\left(\sqrt{\mathrm{n}}+\frac{1}{2}\right)$ squares of an $\mathrm{n} \times \mathrm{n}$ chessboard have been marked. Show that there exist four marked squares which form the corners of a rectangle.
|
We are trying to use the pigeonhole principle. If there are two marked cells at coordinates $(i, j)$ and $(i, k)$, we put a sock in the drawer labeled $(\mathfrak{j}, k)$. There are $\frac{n(n-1)}{2}$ possible drawers. If $S^{\prime}$ there are two socks in the same drawer $(\mathfrak{j}, k)$, it means there exist $i, i^{\prime}$ such that $(i, j),(i, k),\left(i^{\prime}, j\right),\left(i^{\prime}, k\right)$ are all marked, and we have found four marked cells that form the corners of a rectangle. It only remains to show that there are strictly more socks than drawers. We denote $d_{i}$ as the number of marked cells in the i-th column. We have:
$$
\sum_{i=1}^{n} d_{i} \geqslant n\left(\sqrt{n}+\frac{1}{2}\right)
$$
The number of socks is:
$$
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2}
$$
Using Cauchy-Schwarz, we have:
$$
\begin{aligned}
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2} & \geqslant \frac{1}{2}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-\sum_{i=1}^{n} d_{i}\right) \\
& \geqslant \frac{1}{2 n}\left(n\left(\sqrt{n}+\frac{1}{2}\right)\right)\left(n\left(\sqrt{n}+\frac{1}{2}\right)-n\right) \\
& =\frac{1}{2} n\left(\sqrt{n}+\frac{1}{2}\right)\left(\sqrt{n}-\frac{1}{2}\right) \\
& =\frac{1}{2} n\left(n-\frac{1}{4}\right)
\end{aligned}
$$
Which is indeed strictly greater than the number of drawers.
Grader's comment: Very few copies solved the problem. Here it was natural to try to look at pairs of points by column: this was the key idea of the problem, and it allowed writing inequalities as in the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au moins $\mathrm{n}\left(\sqrt{\mathrm{n}}+\frac{1}{2}\right)$ carrés d'un échiquier $\mathrm{n} \times \mathrm{n}$ ont été marqués. Montrer qu'il existe quatre cases marquées qui forment les coins d'un rectangle.
|
On essaye d'utiliser le principe des tiroirs. S'il y a deux cases marquées aux coordonnées $(i, j)$ et $(i, k)$, on met une chaussette dans le tiroir étiqueté $(\mathfrak{j}, k)$. Il y a $\frac{n(n-1)}{2}$ tiroirs possibles. $S^{\prime}$ il y a deux chaussettes dans le même tiroir $(\mathfrak{j}, k)$, c'est qu'il existe $i, i^{\prime}$ tels que $(i, j),(i, k),\left(i^{\prime}, j\right),\left(i^{\prime}, k\right)$ sont toutes marquées, et on a bien trouvé quatre cases marquées qui forment les coins d'un rectangle. Il ne reste plus qu'à montrer qu'il y a strictement plus de chaussettes de tiroirs. On note $d_{i}$ le nombre de cases marquées dans la i-ème colonne. On a :
$$
\sum_{i=1}^{n} d_{i} \geqslant n\left(\sqrt{n}+\frac{1}{2}\right)
$$
Le nombre de chaussettes vaut :
$$
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2}
$$
En utilisant Cauchy-Schwarz, on a :
$$
\begin{aligned}
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2} & \geqslant \frac{1}{2}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-\sum_{i=1}^{n} d_{i}\right) \\
& \geqslant \frac{1}{2 n}\left(n\left(\sqrt{n}+\frac{1}{2}\right)\right)\left(n\left(\sqrt{n}+\frac{1}{2}\right)-n\right) \\
& =\frac{1}{2} n\left(\sqrt{n}+\frac{1}{2}\right)\left(\sqrt{n}-\frac{1}{2}\right) \\
& =\frac{1}{2} n\left(n-\frac{1}{4}\right)
\end{aligned}
$$
Ce qui est effectivement strictement plus grand que le nombre de tiroirs.
Commentaire des correcteurs : Très peu de copies ont rendu l'exercice. Ici il était naturel d'essayer de regarder les paires de points par colonne : c'était l'idée clé du problème, et elle permettait ensuite d'écrire des inégalités comme dans le corrigé.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
f10975a1-191b-5f61-b71f-6ccb881cd2bf
| 607,393
|
Let $n \geqslant 3$ be an integer. Each row of an $(n-2) \times n$ table contains the numbers from 1 to $n$ once each, and it is assumed that in each column all the numbers are different. Show that the table can be completed to an $n \times n$ table such that in each row and in each column there are all the numbers from 1 to $n$.
|
Let $a_{i}, b_{i}$ be the two numbers missing in column $i$. Each of the numbers from 1 to $n$ appears in two copies among the $a_{i}, b_{i}$. Construct a multigraph where the vertices are the numbers from 1 to $n$, and for each $i=1, \ldots, n$, we add an edge between $a_{i}$ and $b_{i}$. Each vertex in this graph has a degree of 2, so it consists of a set of disjoint cycles. We can therefore orient the edges of each cycle in an arbitrary direction. We then obtain a directed multigraph where each vertex has an in-degree of 1 and an out-degree of 1. If the edge in the i-th column points from $u$ to $v$, then we write $u$ at coordinates $(i, n-1)$ and $v$ at coordinates $(i, n)$. The property of the degrees ensures that each number appears exactly once in each row.
Graders' comments: Overall, it is good, and all students have the construction. However, few provide a complete justification for it.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 3$ un entier. Chaque ligne d'un tableau $(n-2) \times n$ contient les nombres de 1 à $n$ en un exemplaire chacun, on suppose de plus que dans chaque colonne tous les nombres sont différents. Montrer que l'on peut compléter le tableau en un tableau $\mathrm{n} \times \mathrm{n}$ de telle sorte que dans chaque ligne et dans chaque colonne il y ait tous les nombres de 1 à $n$.
|
Notons $a_{i}, b_{i}$ les deux nombres qu'il manque dans la colonne $i$. Chacun des nombres de 1 à $n$ apparaît en deux exemplaires parmi les $a_{i}, b_{i}$. Construisons un multigraphe dont les sommets sont les nombres de 1 à $n$, et pour chaque $i=1, \ldots, n$, on ajoute une arête entre $a_{i}$ et $b_{i}$. Chaque sommet de ce graphe est de degré 2 , il s'agit donc d'un ensemble de cycles disjoints. On peut donc orienter les arêtes de chaque cycle dans un sens arbitraire. On obtient alors un multigraphe orienté dont chaque sommet à un degré entrant de 1 et un degré sortant de 1 . Imaginons que l'arête de la i-ème colonne pointe de $u$ vers $v$, alors on écrit $u$ aux coordonnées $(i, n-1)$ et $v$ aux coordonnées ( $i, n$ ). La propriété des degrés donne que chaque nombre apparaît exactement une fois sur chaque ligne.
Commentaire des correcteurs : Bien dans l'ensemble, tous les élèves ont la construction. Néanmoins, peu proposent une justification complète de celle-ci.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
d8e96183-befb-5b14-afea-929628ac345a
| 607,394
|
Several numbers are written in a line. Thanima has the right to choose two adjacent numbers such that the number on the left is strictly greater than the number on the right, she then swaps these two numbers and multiplies them by 2. Show that Thanima can only perform a finite number of such operations.
|
We start by placing a token on the minimum (if there is a tie, on the leftmost number). We move the token according to the number it is placed on. We will show that the token always moves to the left.
To do this, suppose by contradiction that at some point, the token moved to the right. Let \( x \) be the position of the token before the swap, \( i \) the initial position of the token, and \( j \) the initial position of the number with which the token is swapped. If \( i < j \), then since the token has never moved to the right before, the other number must have moved at least as many times as the token; it has therefore been doubled at least as many times. Since the token was placed on the minimum, the number on the token is smaller (or equal) to the number at position \( x+1 \). The move to the right was therefore not possible. If \( j < i \), then the token and the number initially at \( j \) have already been swapped once; immediately after this swap, the number with the token was smaller than the number initially at \( j \). The same argument as in the previous case applies: if the number initially at \( j \) is again immediately to the right of the token, it must have been doubled at least as many times; it has therefore remained larger and cannot be swapped again. Thus, the token always moves to the left.
Now, we prove the result by induction on the number \( n \) of numbers written on the line. Since the token always moves to the left, after a certain number of moves, it no longer moves. We then notice that the numbers to the left and right of the token form two separate instances of the initial problem, and we can perform only a finite number of operations on each instance by the induction hypothesis. Therefore, we can perform only a finite number of operations on the entire instance. The base case for \( n=0 \) is obvious.
Comment from the graders: Very few (4) solutions were submitted for this difficult exercise. Two of them only touch on the exercise, and the other two use a solution not included in the official solution, which consists of showing that two numbers can be swapped at most once. However, none manage to develop the arguments convincingly.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Plusieurs nombres sont écrits sur une ligne. Thanima a le droit de choisir deux nombres adjacents de telle sorte que le nombre de gauche soit strictement plus grand que le nombre de droite, elle échange alors ces deux nombres et les multiplie par 2. Montrer que Thanima ne peut effectuer qu'un nombre fini de telles opérations.
|
On commence par poser un jeton sur le minimum (si égalité, sur le nombre le plus à gauche). On bouge le jeton avec le nombre sur lequel il est posé. On va montrer que le jeton se déplace toujours vers la gauche.
Pour cela, supposons par l'absurde qu'à un moment, le jeton s'est déplacé vers la droite. Alors soit x la position du jeton avant l'échange, $i$ la position initiale du jeton, et $j$ la position initiale du nombre avec qui le jeton est échangé. $\mathrm{Si} i<j$, alors comme le jeton n'est jamais allé vers la droite avant, l'autre nombre a dû faire au moins autant de déplacements que le jeton; il a donc été multiplié par deux au moins autant de fois. Comme le jeton avait été posé sur le minimum, le nombre du jeton est plus petit (ou égal) au nombre à la position $x+1$. Le déplacement vers la droite n'était donc pas possible. $\mathrm{Si} j<i$, alors le jeton et le nombre qui était initialement sur $j$ ont déjà été échangés une fois; juste après cet échange, le nombre avec le jeton était plus petit que le nombre qui était initialement en j. Le même argument que le cas précédent s'applique : si le nombre initialement en $j$ est à nouveau juste à droite du jeton, il a du être doublé au moins autant de fois; il est donc resté plus grand et ne peut pas être échangé à nouveau. Ainsi, le jeton se déplace toujours vers la gauche.
Maintenant, on démontre le résultat par récurrence sur le nombre n de nombres écrits sur la ligne. Comme le jeton se déplace toujours vers la gauche, à partir d'un certain nombre de mouvements, il ne bouge plus. On remarque alors que les nombres à gauche et à droite du jeton forment deux instances séparées du problème initial, et on ne peut effectuer qu'un nombre fini d'opérations sur chaque instance par hypothèse de récurrence. On ne peut donc effectuer qu'un nombre fini d'opérations sur l'instance entière. L'initialisation en $n=0$ est évidente.
Commentaire des correcteurs: Très peu (4) de solutions rendues pour cet exercice difficile. Deux ne font qu'effleurer l'exercice, et les deux autres utilisent une solution ne figurant pas dans la correction, consistant à montrer que deux nombres ne peuvent être échangés qu'au plus une fois. Cependant, aucun ne parvient à développer les arguments de façon convaincante.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
ac588e06-9243-5bd3-b5ca-3e3853eb7222
| 607,396
|
A terrible group of bandits is preparing to share a loot. Each bandit aims at two other bandits with their pistols. The bandits are called in a certain order. When a bandit is called, if they are still alive, they shoot at the bandits they were aiming at. After all the bandits have been called, there have been 28 victims. Show that no matter the order in which the bandits were called, there would have been at least 10 victims.
|
Suppose by contradiction that there exists an order causing 9 or fewer victims. There are then three categories of bandits:
- Those who died before firing
- Those who managed to fire and then died
- Those who are still alive at the end
The bandits of the first and second categories total at most 9, as there are at most 9 victims. The bandits of the second and third categories only aim at bandits of the first or second categories (if they fired, their targets are dead). They therefore aim at a subset of at most 9 bandits. Moreover, the bandits of the first category aim at no more than \(2 \times 9 = 18\) bandits: there are at most 9 bandits in this category, and each aims at no more than 2 bandits. There are finally at most \(18 + 9 = 27\) bandits targeted: there exists a bandit who is not targeted by anyone. This bandit survives regardless of the order of calls, which contradicts the statement.
Comment from the graders: The principle was generally understood, but it was difficult for several papers to rigorously justify the intuition. In particular, some consider optimal cases but without justifying that they are optimal (they may also not be achievable).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un terrible groupe de bandits se prépare à se partager un butin. Chaque bandit vise deux autres bandits avec ses pistolets. Les bandits sont appelés dans un certain ordre. Lorsqu'un bandit est appelé, s'il est encore en vie, il tire sur les bandits qu'il visait. Après que tous les bandits ont été appelés, il y a eu 28 victimes. Montrez que quelque soit l'ordre dans lequel on avait appelé les bandits, il y aurait eu au moins 10 victimes.
|
Supposons par l'absurde qu'il existe un ordre qui cause 9 victimes ou moins. Il y a alors trois catégories de bandits :
- Ceux qui sont morts avant de tirer
- Ceux qui ont pu tirer puis sont morts
- Ceux qui sont encore en vie à la fin
Les bandits de 1ère et 2ème catégorie sont au total au plus 9 , car il y a au plus 9 victimes. Les bandits de 2ème et 3ème catégorie ne visent que des bandits de lère ou 2ème catégorie (s'ils ont tiré, leurs cibles sont mortes). Ils visent donc un sous-ensemble d'au plus 9 bandits. De plus, les bandits de 1ère catégorie ne visent qu'au plus $2 \times 9=18$ bandits : il y a au plus 9 bandits de cette catégorie et chacun vise au plus 2 bandits. Il y a finalement au plus $18+9=27$ bandits visés : il existe un bandit qui n'est visé par personne. Ce bandit survit quelque soit l'ordre d'appel, ce qui contredit l'énoncé.
Commentaire des correcteurs: Le principe était généralement compris mais il a été difficile pour plusieurs copies de justifier rigoureusement l'intuition. En particulier, certains considèrent les cas optimaux mais sans justifier qu'ils sont optimaux (ils peuvent par ailleurs ne pas être atteignables).
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 11.",
"solution_match": "\nSolution de l'exercice 11"
}
|
43cfd01a-ba68-52c2-8d4a-bcbc408e0ad8
| 607,398
|
A rectangle is divided into dominoes $1 \times 2$ and $2 \times 1$. In each domino, a diagonal is drawn. No two diagonals share an endpoint. Show that exactly two corners of the rectangle are endpoints of these diagonals.
|
Let us note that this pattern (as well as all its rotations and symmetries) is impossible:
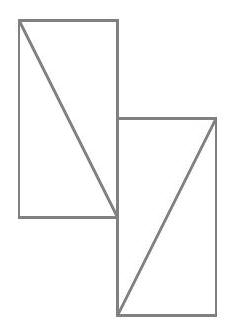
Indeed, the only way to complete the bottom-left square is to add this domino:
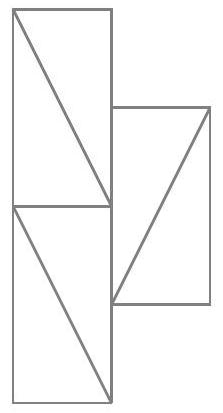
Similarly, the only way to complete the bottom-right square is to add this domino:
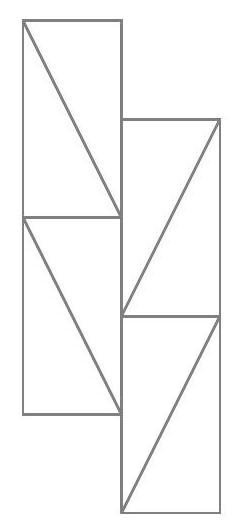
We cannot continue indefinitely, as we eventually reach the edge of the rectangle.
This pattern is also impossible (as well as all its rotations and symmetries):
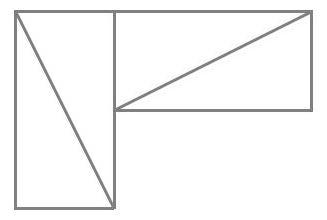
because the only way to complete the square in the corner is by adding this domino:
which results in the previously forbidden pattern. Through a detailed analysis, these two cases demonstrate that it is actually not possible for two dominos that share an edge to have their diagonals in different directions (ascending or descending). If we form the graph \( G \) where the vertices are the dominos and there is an edge between two dominos if they share a common edge, \( G \) is connected. Thus, all dominos have their diagonals in the same direction; from this, the required property easily follows.
Comment from the graders: The exercise was rarely addressed. Those who submitted a solution generally understood the problem well and treated all cases and saw the pattern in the solution. Some have a different argument by looking at a path between opposite diagonals, and others use a graph theory reasoning.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un rectangle est divisé en dominos $1 \times 2$ et $2 \times 1$. Dans chaque domino, une diagonale est tracée. Deux diagonales n'ont jamais d'extrémité commune. Montrez que exactement deux coins du rectangle sont des extrémités de ces diagonales.
|
Remarquons que ce motif (ainsi que toutes ses rotations et symétries) est impossible :

En effet, le seul moyen de compléter le carré bas-gauche est d'ajouter ce domino :

De même, le seul moyen de compléter le carré bas-droite est d'ajouter ce domino :

On ne peut pas continuer pour toujours, car on finit par atteindre le bord du rectangle.
Ce motif aussi est impossible (ainsi que toutes ses rotations et symétries) :

car le seul moyen de compléter le carré dans le coin est en ajoutant ce domino :

ce qui fait apparaître le motif interdit précédent. Grâce à une analyse minutieuse, ces deux cas démontrent qu'il n'est en fait pas possible que deux dominos qui partagent un bord aient leurs diagonales dans des sens différents (montantes ou descendantes). Si on forme le graphe G dont les sommets sont les dominos et où il y a une arête entre deux dominos s'ils partagent un bord en commun, $G$ est connexe. Ainsi, tous les dominos ont leur diagonale dans le même sens; on en déduit facilement la propriété demandée.
Commentaire des correcteurs: L'exercice a été peu traité. Ceux qui ont rendu une copie ont en général bien compris l'exercice et bien traité tous les cas et vu le motif du corrigé. Certains ont une argumentation différente en regardant un chemin entre les diagonales opposées, et d'autres utilisent un raisonnement de théorie des graphes.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "\nSolution de l'exercice 13"
}
|
54c68a94-efb0-5c86-9259-21d752927bd9
| 607,400
|
We place a certain number of open segments in the plane, none of which are parallel to the $x$ and $y$ axes. These segments are disjoint. Thanima starts moving from $(0,0)$ parallel to the $x$-axis. Each time she encounters a wall, she turns 90 degrees and continues moving without crossing the wall.
Prove that it is impossible for Thanima to visit both sides of all the walls.
|
We start by proving that there exists a wall that is lower than all the others (i.e., the set of points below this segment does not intersect any segment). Suppose, for the sake of contradiction, that this is not the case. We can then construct a cycle $A_{1}, B_{1}, A_{2}, B_{2}, \ldots, A_{k}, B_{k}$ that does not intersect itself, where $A_{i}$ and $B_{i}$ are on the same wall, and $\left[B_{i}, A_{i+1}\right]$ is a vertical segment where $B_{i}$ is above $A_{i+1}$ (considering the indices modulo $k$). We consider $l$, $r$ such that $\left[B_{l}, A_{l+1}\right]$ is the leftmost and $\left[B_{r}, A_{r+1}\right]$ is the rightmost. The cycle gives a broken line between $B_{l}$ and $A_{r+1}$, and another between $B_{r}$ and $A_{l+1}$. However, the broken lines do not pass to the left of $\left[B_{l}, A_{l+1}\right]$ or to the right of $\left[B_{r}, A_{r+1}\right]$, and their endpoints are "crossed," so they must intersect. This is a contradiction with the fact that the cycle does not intersect itself.
Similarly, there exists a wall higher than all the others. If Thanima passes by the upper side of the highest wall, she continues to walk to infinity in the positive y direction. If Thanima passes by the lower side of the lowest wall, she continues to walk to infinity in the negative y direction. These two cases cannot happen simultaneously, so she passes through only one of these two sides. In particular, she cannot pass through all sides of all walls.
Comment from the graders: The problem was rarely addressed. Most solutions were correct and close to the proposed solution; however, they presented a number of imprecisions, which must be particularly attentive to when it comes to something as visual as combinatorial geometry.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
On place un certain nombre de segments ouverts dans le plan, aucun d'entre eux n'est parallèle aux axes $x$ et $y$. Ces segments sont disjoints. Thanima commence à se déplacer depuis $(0,0)$ parallèlement à l'axe $x$. À chaque fois qu'elle rencontre un mur, elle tourne de 90 degrés, et continue à se déplacer sans traverser le mur.
Démontrez qu'il est impossible que Thanima visite les deux côtés de tous les murs.
|
On commence par démontrer qu'il existe un mur qui est plus bas que tous les autres (c'est à dire que l'ensemble des points sous ce segment n'intersecte aucun segment). Supposons par l'absurde que ce $n$ 'est pas le cas. On peut alors construire un cycle $A_{1}, B_{1}, A_{2}, B_{2}, \ldots, A_{k}, B_{k}$ qui ne s'intersecte pas lui-même, où $A_{i}$ et $B_{i}$ sont sur le même mur, et $\left[B_{i}, A_{i+1}\right]$ est un segment vertical où $B_{i}$ est au dessus de $A_{i+1}$ (on considère les indices modulo $k$ ). On considère $l$, $r$ tel que $\left[B_{l}, A_{l+1}\right]$ soit le plus à gauche et $\left[B_{r}, A_{r+1}\right]$ soit le plus à droite. Le cycle donne une ligne brisée entre $B_{l}$ et $A_{r+1}$, et une autre entre $B_{r}$ et $A_{l+1}$. Cependant, les lignes brisées ne passent ni à gauche de $\left[B_{l}, A_{l+1}\right]$ ni à droite de $\left[B_{r}, A_{r+1}\right]$, et leurs extrémités sont "croisées", elles doivent donc s'intersecter. C'est une contradiction avec le fait que le cycle ne s'intersecte pas lui-même.
Similairement, il existe un mur plus haut que tous les autres. Si Thanima passe par le côté haut du mur le plus haut, elle continue à marcher vers l'infini en direction des y positifs. Si Thanima passe par le côté bas du mur le plus bas, elle continue à marcher vers l'infini en direction des y négatifs. Ces deux cas ne peuvent pas arriver simultanément, elle ne passe donc que par un seul de ces deux côtés. En particulier, elle ne peux pas passer par tous les côtés de tous les murs.
Commentaire des correcteurs: L'exercice a été peu traité. La plupart des solutions sont justes et proches de celle proposées dans le corrigé; néanmoins, elles présentaient un certain nombre d'imprécisions, auxquelles il faut être particulièrement attentif quand il s'agit de quelque chose d'aussi visuel que la géométrie combinatoire.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "\nSolution de l'exercice 15"
}
|
063a95c8-4b45-576b-96f2-9152eb9c5489
| 607,402
|
Let \( a \) be a strictly positive real number and \( \mathrm{n} \geqslant 1 \) an integer. Show that
$$
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
$$
|
Since the difficulty lies in the denominator of the right-hand side, and for greater comfort, we can seek to show the inverse relation, namely:
$$
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
$$
The idea behind the following solution is to "homogenize" the numerator of the left-hand side, that is, to compare this numerator, in which the \(a\)s are raised to distinct powers, to an expression composed solely of \(a\)s raised to the same power. To do this, we seek to pair certain terms and apply the inequality of means. Let's see: for \(0 \leqslant i \leqslant 2 n\), we have \(a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}} = 2 a^{n}\). Thus:
$$
\begin{aligned}
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text{ terms }}+a^{n}}{a^{n}} \\
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
& =2 n+1 \\
& >2 n
\end{aligned}
$$
which provides the desired inequality.
## Comments from the graders:
The exercise is very well solved! The students have well understood how to use the mean inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit a un réel strictement positif et $\mathrm{n} \geqslant 1$ un entier. Montrer que
$$
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
$$
|
Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :
$$
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
$$
L'idée derrière la solution qui suit est "d'homogénéiser" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \leqslant i \leqslant 2 n$, on a $a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :
$$
\begin{aligned}
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text { termes }}+a^{n}}{a^{n}} \\
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
& =2 n+1 \\
& >2 n
\end{aligned}
$$
ce qui fournit l'inégalité voulue.
## Commentaires des correcteurs:
L'exercice est très bien résolu! Les élèves ont bien compris comment utiliser l'inégalité de la moyenne.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
edc6a767-27f7-5109-ba4c-5f06dfc0157a
| 607,407
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles with centers $O_{1}$ and $O_{2}$, respectively. Suppose that $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. The line $\left(O_{1} A\right)$ intersects the circle $\omega_{2}$ again at $C$, while the line $\left(O_{2} A\right)$ intersects the circle $\omega_{1}$ again at $D$. Show that the points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$, and $C$ lie on the same circle.
|
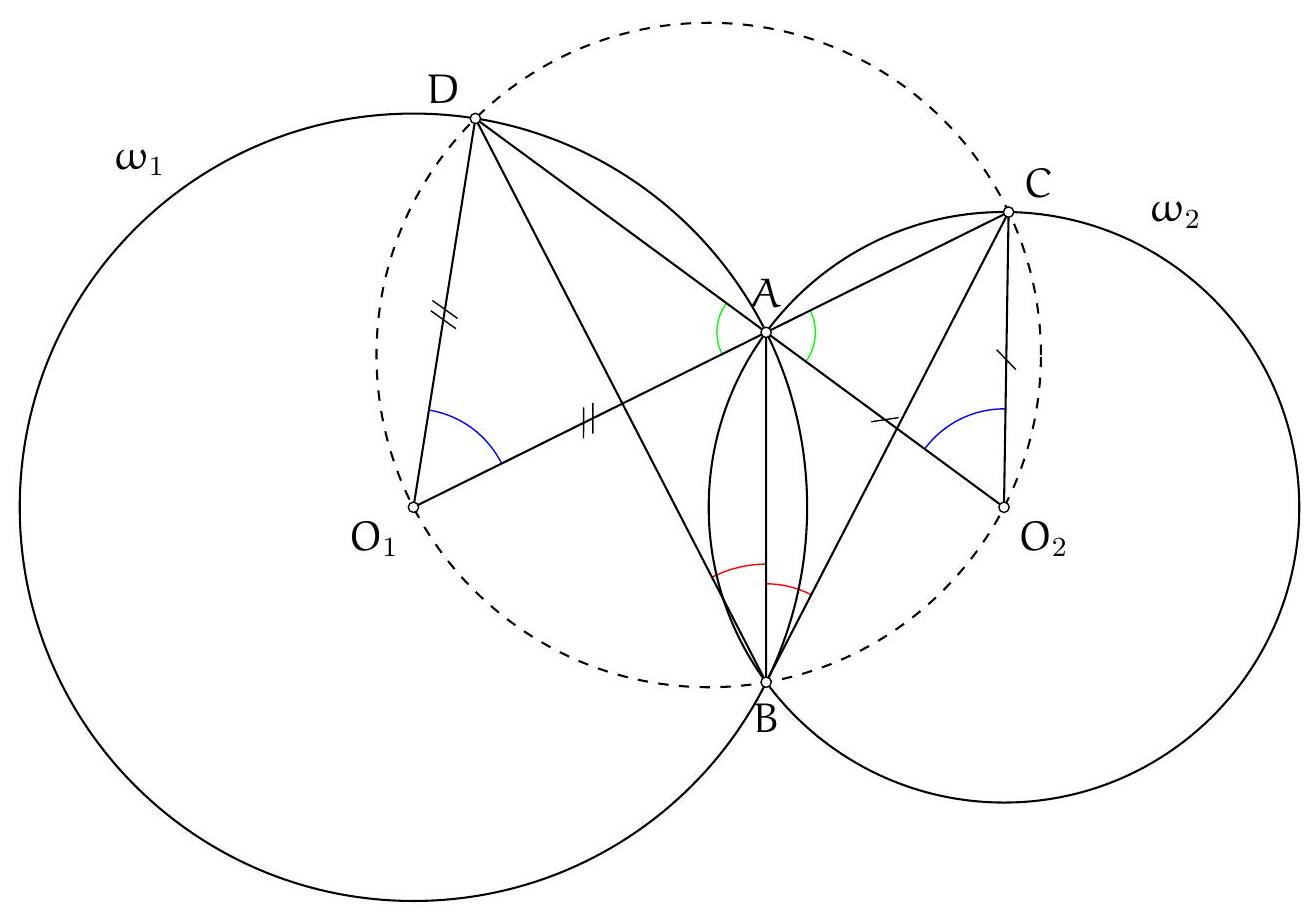
Note that since the angles $\widehat{\mathrm{DAO}_{1}}$ and $\widehat{\mathrm{CAO}_{2}}$ are vertically opposite, they are equal. On the other hand, since points $A$ and $D$ belong to the circle $\omega_{1}$, the triangle $A O_{1} D$ is isosceles at $O_{1}$. Similarly, the triangle $\mathrm{CO}_{2} A$ is isosceles at $\mathrm{O}_{2}$. Therefore, triangles $\mathrm{DO}_{1} A$ and $\mathrm{CO}_{2} A$ are isosceles triangles with the same base angles, so they are similar. This implies that $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} A}$, and thus
$$
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
$$
so the points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$, and D are concyclic.
Furthermore, we can decompose the angle $\widehat{\mathrm{DBC}}$ into the sum $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. On the one hand, according to the inscribed angle theorem in the circle $\omega_{1}$, we have $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. On the other hand, according to the inscribed angle theorem in the circle $\omega_{1}$, we have $\widehat{A B C}=\frac{1}{2} \widehat{A_{2} C}$. Thus,
$$
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
$$
which allows us to conclude that point B belongs to the circle passing through the points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$, and D.
## Comments from the graders:
Very well solved exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\omega_{1}$ et $\omega_{2}$ deux cercles de centres respectifs $O_{1}$ et $O_{2}$. On suppose que $\omega_{1}$ et $\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\left(O_{1} A\right)$ recoupe le cercle $\omega_{2}$ en $C$ tandis que la droite $\left(O_{2} A\right)$ recoupe le cercle $\omega_{1}$ en D . Montrer que les points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et C appartiennent à un même cercle.
|

Notons que puisque les angles $\widehat{\mathrm{DAO}_{1}}$ et $\widehat{\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\mathrm{CO}_{2} A$ est isocèle en $\mathrm{O}_{2}$. Les triangles $\mathrm{DO}_{1} A$ et $\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} A}$, et donc que
$$
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
$$
si bien que les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D sont cocycliques.
Par ailleurs, on peut découper l'angle $\widehat{\mathrm{DBC}}$ en la somme $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B C}=\frac{1}{2} \widehat{A_{2} C}$. Ainsi
$$
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
$$
ce qui permet de conclure que le point B appartient au cercle passant par les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D .
## Commentaires des correcteurs:
Exercice très bien résolu.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
5b656475-b1e3-51fd-b306-985cad46cae9
| 607,408
|
Aurélien writes 11 natural numbers on the board. Show that he can choose some of these numbers and place + and - signs between them in such a way that the result is divisible by 2021.
|
We can see the choice of certain integers with + and - signs as a choice of certain integers that we will count positively and certain integers that we will count negatively. The numbers that Aurélien can obtain are numbers that can be written as the difference between two sums of several starting integers. We can note that the converse is also true: if a and b can be written as the sum of certain integers, then Aurélien can obtain $a-b$ by putting a plus sign in front of the integers that are in $a$ and a minus sign in front of those that are in $b$. If the same starting integer is used to obtain both a and $b$, Aurélien cannot write both a plus and a minus sign, but he can simply not write the integer at all, which has the same effect as adding and then removing it. Therefore, all differences between two sums of integers from the table are results that Aurélien can obtain. Saying that a difference between two sums is divisible by 2021 is equivalent to saying that the two sums were congruent modulo 2021. We have $2^{11}=2048>2021$ sums, so according to the pigeonhole principle, two are congruent modulo 2021.
## Comments from the graders:
An extremely well-executed exercise by those who tackled it. The solutions are almost all analogous to the corrected solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Aurélien écrit 11 entiers naturels au tableau. Montrer qu'il peut choisir certains de ces entiers et placer des signes + et - entre eux de telle sorte que le résultat soit divisible par 2021.
|
On peut voir un choix de certains entiers avec des signes + et - comme un choix de certains entiers que l'on va compter positivement et de certains entiers que l'on va compter négativement. Les nombres qu'Aurélien peut obtenir sont des nombres qui s'écrivent comme la différence entre deux sommes de plusieurs entiers de départ. On peut remarquer que la réciproque est aussi vrai, si a et b s'écrivent comme somme de certains entiers, alors Aurélien peut obtenir $a-b$ en mettant un signe plus devant les entiers qui sont dans $a$ et un signe $b$ devant ceux qui sont dans $b$. Si le même entier de départ est utilisé pour obtenir à la fois a et $b$, Aurélien ne peut pas écrire devant un signe - et + , mais il peut simplement de pas écrire l'entier tout court, ce qui a le même effet que l'ajouter puis l'enlever. Toutes les différences entre deux sommes d'entiers du tableau sont donc des résultats qu'Aurélien peut obtenir. Dire qu'une différence entre deux sommes est dvisible par 2021 revient à dire que les deux sommes étaient congrues modulo 2021. On dispose de $2^{11}=2048>2021$ sommes, donc d'après le principe des tiroirs, deux sont congrues modulo 2021.
## Commentaires des correcteurs:
Exercice extrêmement bien réussi par ceux qui l'ont traité. Les solutions sont presque toutes analogues à celle du corrigé.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
f2dc1735-4e94-5442-ba33-e5d19ec086fa
| 607,409
|
Let $\Gamma$ be a circle and $P$ a point outside $\Gamma$. The tangents to $\Gamma$ from $P$ touch $\Gamma$ at $A$ and $B$. Let $K$ be a point distinct from $A$ and $B$ on the segment $[A B]$. The circumcircle of triangle $P B K$ intersects the circle $\Gamma$ at point $T$. Let $P'$ be the symmetric point of $P$ with respect to point $A$. Show that $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
According to the inscribed angle theorem, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Therefore, it suffices to show that $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. The figure suggests that triangles PKT and $P^{\prime}$ KA are similar, so we will try to prove this result, which will imply the desired angle equality.
To show that $\triangle P K T \sim \triangle P^{\prime} K A$, there are several possibilities. For example, we can show that $\widehat{T P K} = \widehat{K^{\prime} A}$ and $\widehat{\mathrm{KTP}}=\widehat{\mathrm{KAP}}$. However, when trying to calculate the angle $\widehat{\mathrm{TPK}}$, we realize that the equality $\widehat{\mathrm{TPK}}=\widehat{\mathrm{KP}^{\prime} A}$ is equivalent to the statement to be proven. Therefore, we will show that $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} \mathrm{AK}}$ and that $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
To show that $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} \mathrm{AK}}$, we first note that triangle $A P B$ is isosceles at $P$ because the lines ( $A P$ ) and ( $B P$ ) are tangent at $A$ and $B$ to the circle $\Gamma$. By applying the inscribed angle theorem in the circle passing through $P, B, K$ and $T$, we find:
$$
\widehat{\mathrm{KTP}}=180^{\circ}-\widehat{\mathrm{KBP}}=180^{\circ}-\widehat{\mathrm{ABP}}=180^{\circ}-\widehat{\mathrm{BAP}}=\widehat{\mathrm{PAK}}
$$
It remains to show that $\frac{K T}{K A}=\frac{T P}{A P^{\prime}}$. Since $A P^{\prime}=A P=B P$, it suffices to show that $\frac{K T}{K A}=\frac{T P}{B P}$. Therefore, it suffices to show that triangles AKT and BPT are similar. To do this, it suffices to show that the angles of these two triangles are equal in pairs.
On the one hand, by the inscribed angle theorem, $\widehat{A K T}=180^{\circ}-\widehat{\mathrm{BKT}}=\widehat{\mathrm{TPB}}$. On the other hand, by the tangent angle theorem, $\widehat{\mathrm{TAK}} = \widehat{\mathrm{TAB}} = \widehat{\mathrm{TBP}}$.
Therefore, triangles $A K T$ and BPT are similar as desired.
## Comments from the graders:
A good success relative to the estimated difficulty of the exercise. Some students, who did not completely solve the exercise, shared their ideas on the problem, which was greatly appreciated.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle et P un point à l'extérieur de $\Gamma$. Les tangentes à $\Gamma$ issues de P touchent $\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle $P B K$ recoupe le cercle $\Gamma$ au point $T$. Soit $P^{\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
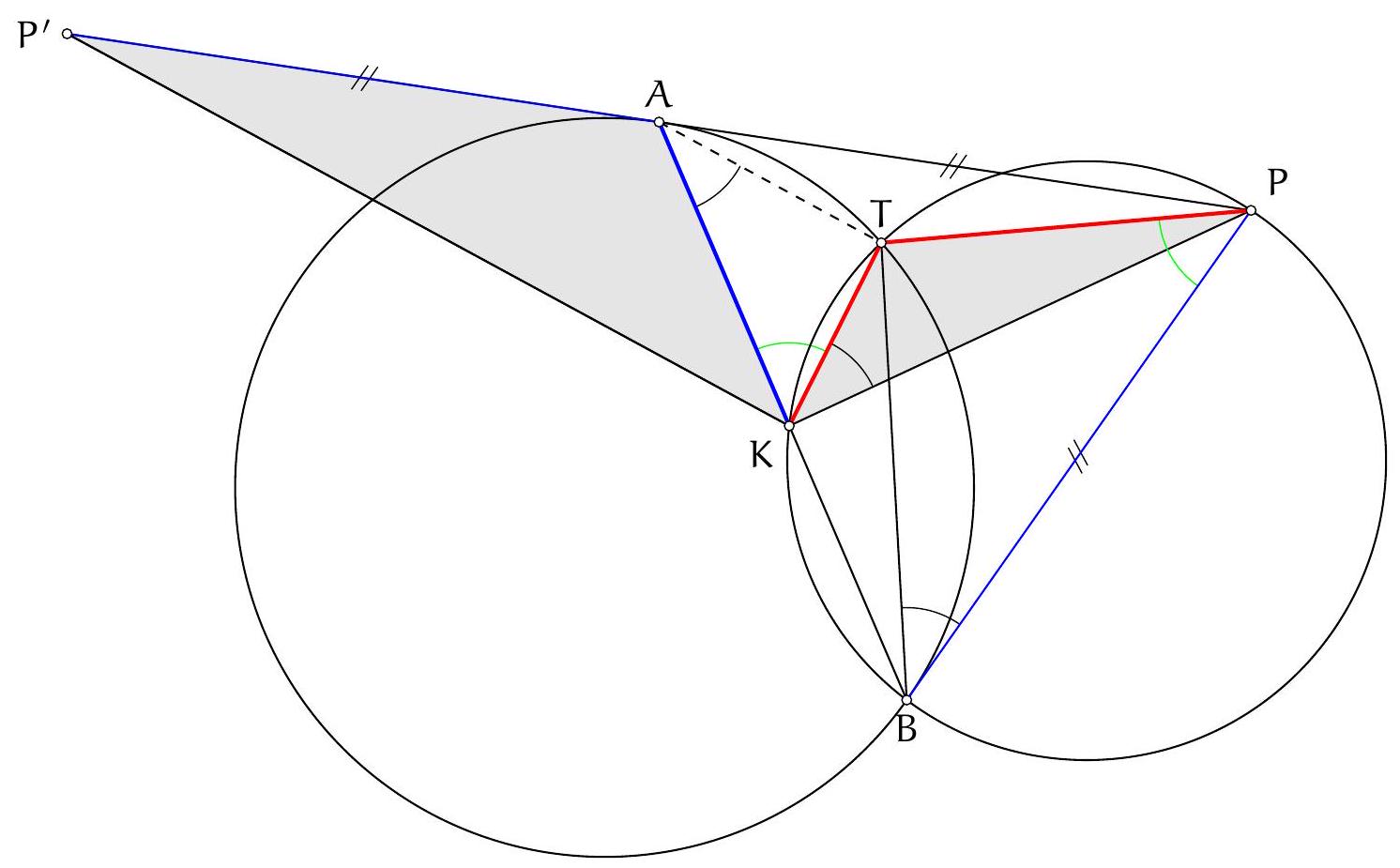
D'après le théorème de l'angle inscrit, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $P^{\prime}$ KA sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.
Pour montrer que $\triangle P K T \sim \triangle P^{\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\widehat{T P K}=$ $\widehat{K^{\prime} A}$ et $\widehat{\mathrm{KTP}}=\widehat{\mathrm{KAP}}$. Toutefois, lorsque l'on essaye de calculer l'angle $\widehat{\mathrm{TPK}}$, on se rend compte que l'égalité $\widehat{\mathrm{TPK}}=\widehat{\mathrm{KP}^{\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} \mathrm{AK}}$ et que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
Pour montrer que $\widehat{\mathrm{KTP}}=\widehat{\mathrm{P}^{\prime} A \mathrm{AK}}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passat par $P, B, K$ et $T$, on trouve :
$$
\widehat{\mathrm{KTP}}=180^{\circ}-\widehat{\mathrm{KBP}}=180^{\circ}-\widehat{\mathrm{ABP}}=180^{\circ}-\widehat{\mathrm{BAP}}=\widehat{\mathrm{PAK}}
$$
Il reste donc à montrer que $\frac{K T}{K A}=\frac{T P}{A P^{\prime}}$. Puisque $A P^{\prime}=A P=B P$, il suffit de montrer que $\frac{K T}{K A}=\frac{T P}{B P}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.
D'une part, par angle inscrit, $\widehat{A K T}=180^{\circ}-\widehat{\mathrm{BKT}}=\widehat{\mathrm{TPB}}$. D'autre part par angle tangentiel, $\widehat{\mathrm{TAK}}=$ $\widehat{\mathrm{TAB}}=\widehat{\mathrm{TBP}}$.
Donc les triangles $A K T$ et BPT sont semblables comme voulu.
## Commentaires des correcteurs:
Une bonne réussite relativement à la difficulté estimée de l'exercice. Quelques élèves, qui n'ont pas résolu complètement l'exercice, on tenu à partager leurs idées sur le problème, ce qui a été grandement apprécié.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
d96e8475-3415-57e6-8e4a-c6c5e710a93f
| 607,413
|
Let $a_{1}, \ldots, a_{101}$ be real numbers in the interval $[-2 ; 10]$ such that
$$
a_{1}+\ldots+a_{101}=0
$$
Show that
$$
a_{1}^{2}+\ldots+a_{101}^{2} \leqslant 2020
$$
|
When dealing with inequalities on real numbers that are not necessarily positive, it is essential to separate the positive and negative variables. This simple idea often constitutes the starting point in the solution and can lead to interesting developments, in addition to preventing certain errors when manipulating inequalities with negative numbers.
The second idea, when the variables play symmetric roles, is to impose an order on the reals. In addition to sometimes yielding interesting results for the problem, this greatly simplifies the writing of the solution.
By renumbering the variables, we assume that $a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{100} \leqslant a_{101}$. If all the reals are zero, then the sum of their squares is zero and is therefore less than 2020. We now assume that one of the reals is non-zero. Since the sum of the $a_{i}$ is zero, this implies that at least one real is strictly positive and another is strictly negative. We then denote $p$ the index such that $a_{p}<0 \leqslant a_{p+1}$.
Let's rewrite the zero sum hypothesis in the form
$$
-\left(a_{1}+a_{2}+\ldots+a_{p}\right)=a_{p+1}+\ldots+a_{101}
$$
We will now seek to make this hypothesis appear in the sum to be calculated. For this, we will also use the fact that if $1 \leqslant i \leqslant p$, then $a_{i} \geqslant-2$ and that if $p+1 \leqslant i \leqslant 101$, then $a_{i} \leqslant 10$. We have:
$$
\begin{aligned}
a_{1}^{2}+\ldots+a_{101}^{2} & =\underbrace{a_{1} \cdot a_{1}}_{\leqslant-2 a_{1}}+\ldots+\underbrace{a_{p} \cdot a_{p}}_{\leqslant-2 a_{p}}+\underbrace{a_{p+1} \cdot a_{p+1}}_{\leqslant 10 a_{p+1}}+\ldots+\underbrace{a_{101} \cdot a_{101}}_{\leqslant 10 a_{101}} \\
& \leqslant-2 a_{1}+\ldots+\left(-2 a_{p}\right)+10 a_{p+1}+\ldots+10 a_{101} \\
& =2\left(-\left(a_{1}+\ldots+a_{p}\right)\right)+10\left(a_{p+1}+\ldots+a_{101}\right) \\
& =2(\underbrace{a_{p+1}}_{\leqslant 10}+\ldots+\underbrace{a_{101}}_{\leqslant 10})+10(-(\underbrace{a_{1}}_{\geqslant-2}+\ldots+\underbrace{a_{p}}_{\geqslant-2})) \\
& \leqslant 2 \cdot 10 \cdot(101-p)+10 \cdot 2 \cdot p \\
& =2020
\end{aligned}
$$
which is the desired inequality.
## Comments from the Examiners:
Some students noticed that, for $-2 \leqslant a_{i} \leqslant 10$, we have $\left(a_{i}+2\right)\left(a_{i}-10\right) \leqslant 0$, and used this to arrive at a proof very efficiently. Others chose to construct the values of $a_{i}$ that maximize the sum of the squares; in this case, it was of course essential to prove the optimality of the construction to obtain the majority of the points.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a_{1}, \ldots, a_{101}$ des réels appartenant à l'intervalle $[-2 ; 10]$ tels que
$$
a_{1}+\ldots+a_{101}=0
$$
Montrer que
$$
a_{1}^{2}+\ldots+a_{101}^{2} \leqslant 2020
$$
|
Lorsque l'on effectue des inégalités sur des réels qui ne sont pas forcément positifs, il est essentiel de séparer les variables positives et négatives. Cette idée simple constitue souvent l'idée de départ dans la solution et peut mener à des développements intéressants, en plus de prévenir certaines erreurs lors de manipulations d'inégalités avec des nombres négatifs.
La deuxième idée, lorsque les variables jouent des rôles symétriques, est d'imposer un ordre aux réels. En plus de permettre, parfois, d'obtenir des résultats intéressants pour le problème, cela simplifie grandement la rédaction de la solution.
Quitte à renuméroter les variables, on suppose donc que $a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{100} \leqslant a_{101}$. Si tous les réels sont nuls, alors la somme de leur carré est nulle et donc bien inférieure à 2020. On suppose désormais que l'un des réels est non nul. Puisque la somme des $a_{i}$ est nulle, cela impose qu'au moins un réel est strictement positif et un autre strictement négatif. On note alors $p$ l'indice vérifiant $a_{p}<0 \leqslant a_{p+1}$.
Réécrivons dès à présent l'hypothèse de la somme nulle sous la forme
$$
-\left(a_{1}+a_{2}+\ldots+a_{p}\right)=a_{p+1}+\ldots+a_{101}
$$
On va désormais chercher à faire apparaître cette hypothèse dans la somme à calculer. Pour cela, on va également se servir du fait que si $1 \leqslant i \leqslant p$, alors $a_{i} \geqslant-2$ et que si $p+1 \leqslant i \leqslant 101$, alors $a_{i} \leqslant 10$. On a :
$$
\begin{aligned}
a_{1}^{2}+\ldots+a_{101}^{2} & =\underbrace{a_{1} \cdot a_{1}}_{\leqslant-2 a_{1}}+\ldots+\underbrace{a_{p} \cdot a_{p}}_{\leqslant-2 a_{p}}+\underbrace{a_{p+1} \cdot a_{p+1}}_{\leqslant 10 a_{p+1}}+\ldots+\underbrace{a_{101} \cdot a_{101}}_{\leqslant 10 a_{101}} \\
& \leqslant-2 a_{1}+\ldots+\left(-2 a_{p}\right)+10 a_{p+1}+\ldots+10 a_{101} \\
& =2\left(-\left(a_{1}+\ldots+a_{p}\right)\right)+10\left(a_{p+1}+\ldots+a_{101}\right) \\
& =2(\underbrace{a_{p+1}}_{\leqslant 10}+\ldots+\underbrace{a_{101}}_{\leqslant 10})+10(-(\underbrace{a_{1}}_{\geqslant-2}+\ldots+\underbrace{a_{p}}_{\geqslant-2})) \\
& \leqslant 2 \cdot 10 \cdot(101-p)+10 \cdot 2 \cdot p \\
& =2020
\end{aligned}
$$
ce qui est l'inégalité voulue.
## Commentaires des correcteurs :
Certains élèves ont remarqué que, pour $-2 \leqslant a_{i} \leqslant 10$, on a $\left(a_{i}+2\right)\left(a_{i}-10\right) \leqslant 0$, et s'en sont servi pour aboutir à une preuve de façon très efficace. D'autres ont choisi de construire les valeurs de $a_{i}$ maximisant la somme des carrés; dans ce cas, il était bien sûr indispensable de prouver l'optimalité de la construction pour obtenir la majorité des points.
## Exercices Seniors
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
d5188ce2-8c6b-5041-a566-f482de27a97d
| 607,414
|
Let $a$ be a strictly positive real number and $n \geqslant 1$ an integer. Show that
$$
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
$$
|
Since the difficulty lies in the denominator of the right-hand side, and for greater comfort, we can seek to show the inverse relationship, namely:
$$
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
$$
The idea behind the following solution is to "homogenize" the numerator of the left-hand side, that is, to compare this numerator, in which the $a$ are raised to distinct powers, to an expression composed solely of $a$ raised to the same power. To do this, we seek to pair certain terms and apply the inequality of arithmetic and geometric means. Let's see: for $0 \leqslant i \leqslant 2 n$, we have $a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Thus:
$$
\begin{aligned}
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text { terms }}+a^{n}}{a^{n}} \\
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
& =2 n+1 \\
& >2 n
\end{aligned}
$$
which provides the desired inequality.
Comments from the graders:
The exercise was very well solved overall. Many students were able to directly apply the AM-GM inequality to $2n+1$ terms, while most others managed to get by with the AM-GM inequality for two terms.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit a un réel strictement positif et $n \geqslant 1$ un entier. Montrer que
$$
\frac{a^{n}}{1+a+\ldots+a^{2 n}}<\frac{1}{2 n}
$$
|
Puisque la difficulté réside dans le dénominateur du membre de droite, et pour plus de confort, on peut chercher à montrer la relation inverse, à savoir :
$$
\frac{1+a+\ldots+a^{2 n}}{a^{n}}>2 n
$$
L'idée derrière la solution qui suit est "d'homogénéiser" le numérateur du membre de gauche, c'est-àdire de comparer ce numérateur dans lequel les a sont élevés à des puissances distinctes à une expression composée uniquement de a élevés à la même puissance. Pour cela, on cherche à coupler certains termes et appliquer l'inégalité des moyennes. Voyons plutôt : pour $0 \leqslant i \leqslant 2 n$, on a $a^{i}+a^{2 n-i} \geqslant 2 \sqrt{a^{i} a^{2 n-i}}=$ $2 a^{n}$. Ainsi :
$$
\begin{aligned}
\frac{1+a+\ldots+a^{2 n}}{a^{n}} & =\frac{\left(1+a^{2 n}\right)+\left(a+a^{2 n-1}\right)+\ldots+\left(a^{n-1}+a^{n+1}\right)+a^{n}}{a^{n}} \\
& \geqslant \frac{\overbrace{2 a^{n}+2 a^{n}+\ldots+2 a^{n}}^{n \text { termes }}+a^{n}}{a^{n}} \\
& =\frac{(2 n+1) a^{n}}{a^{n}} \\
& =2 n+1 \\
& >2 n
\end{aligned}
$$
ce qui fournit l'inégalité voulue.
Commentaires des correcteurs:
Exercice très bien résolu dans l'ensemble. De nombreux élèves ont su appliquer l'IAG directement à $2 \mathrm{n}+1$ termes, les autres ont pour la plupart réussi à s'en sortir avec l'IAG à deux termes.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
5f3aa129-b800-5eb4-9ebf-ae8b21c5b807
| 607,415
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles with centers $\mathrm{O}_{1}$ and $\mathrm{O}_{2}$, respectively. Suppose that $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. The line $\left(O_{1} A\right)$ intersects the circle $\omega_{2}$ again at $C$, while the line $\left(O_{2} A\right)$ intersects the circle $\omega_{1}$ again at $D$. Show that the points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$, and $C$ lie on the same circle.
|
Let us note that since the angles $\widehat{\mathrm{DAO}_{1}}$ and $\widehat{\mathrm{CAO}_{2}}$ are vertically opposite, they are equal. On the other hand, since points $A$ and $D$ belong to the circle $\omega_{1}$, the triangle $A O_{1} D$ is isosceles at $O_{1}$. Similarly, the triangle $\mathrm{CO}_{2} A$ is isosceles at $\mathrm{O}_{2}$. Therefore, triangles $\mathrm{DO}_{1} A$ and $\mathrm{CO}_{2} A$ are isosceles triangles with the same base angles, so they are similar. This implies that $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}$, and thus
$$
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
$$
so the points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$, and D are concyclic.
Furthermore, we can decompose the angle $\widehat{\mathrm{DBC}}$ into the sum $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. On the one hand, according to the inscribed angle theorem in the circle $\omega_{1}$, we have $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. On the other hand, according to the inscribed angle theorem in the circle $\omega_{1}$, we have $\widehat{A B C}=\frac{1}{2} \widehat{A O_{2} C}$. Thus,
$$
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
$$
which allows us to conclude that point B belongs to the circle passing through the points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$, and D.
## Comments from the graders:
Very well solved exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\omega_{1}$ et $\omega_{2}$ deux cercles de centres respectifs $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$. On suppose que $\omega_{1}$ et $\omega_{2}$ se coupent en les points $A$ et $B$. La droite $\left(O_{1} A\right)$ recoupe le cercle $\omega_{2}$ en $C$ tandis que la droite $\left(O_{2} A\right)$ recoupe le cercle $\omega_{1}$ en D . Montrer que les points $\mathrm{D}, \mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et C appartiennent à un même cercle.
|
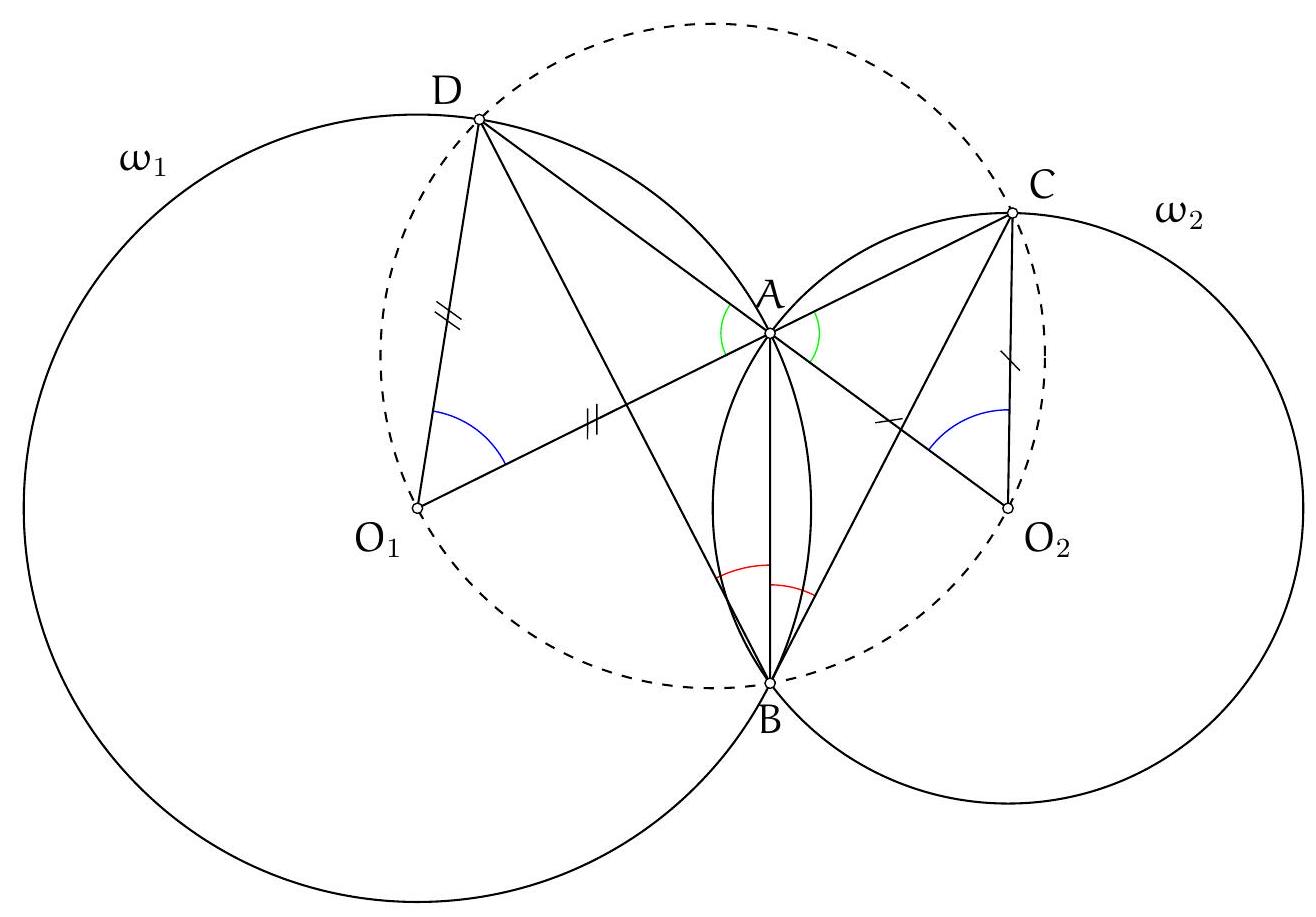
Notons que puisque les angles $\widehat{\mathrm{DAO}_{1}}$ et $\widehat{\mathrm{CAO}_{2}}$ sont opposés par le sommet, ils sont égaux. D'autre part, puisque les points $A$ et $D$ appartiennent au cercle $\omega_{1}$, le triangle $A O_{1} D$ est isocèle en $O_{1}$. De même, le triangle $\mathrm{CO}_{2} A$ est isocèle en $\mathrm{O}_{2}$. Les triangles $\mathrm{DO}_{1} A$ et $\mathrm{CO}_{2} A$ sont donc des triangels isocèle avec les mêmes angles à la base, ils sont donc semblables. Ceci implique que $\widehat{\mathrm{AO}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}$, et donc que
$$
\widehat{\mathrm{CO}_{1} \mathrm{D}}=\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{D}}=\widehat{\mathrm{CO}_{2} \mathrm{~A}}=\widehat{\mathrm{CO}_{2} \mathrm{D}}
$$
si bien que les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D sont cocycliques.
Par ailleurs, on peut découper l'angle $\widehat{\mathrm{DBC}}$ en la somme $\widehat{\mathrm{DBA}}+\widehat{\mathrm{ABC}}$. D'une part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B D}=\frac{1}{2} \widehat{\mathrm{AO}_{1} \mathrm{D}}$. D'autre part, d'après le théorème de l'angle au centre dans le cercle $\omega_{1}$, on a $\widehat{A B C}=\frac{1}{2} \widehat{A O_{2} C}$. Ainsi
$$
\widehat{\mathrm{DBC}}=\widehat{\mathrm{DBA}}+\widehat{A B C}=\frac{1}{2} \widehat{A O_{1} \mathrm{D}}+\frac{1}{2} \widehat{\mathrm{AO}_{2} \mathrm{C}}=\widehat{\mathrm{AO}_{1} \mathrm{D}}
$$
ce qui permet de conclure que le point B appartient au cercle passant par les points $\mathrm{C}, \mathrm{O}_{2}, \mathrm{O}_{1}$ et D .
## Commentaires des correcteurs:
Exercice très bien résolu.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 12.",
"solution_match": "## Solution de l'exercice 12"
}
|
afd6347d-74ea-5d5b-8937-0ca5a75de40c
| 607,417
|
Let $(a_n)$ be a strictly increasing sequence of positive integers such that $a_1 = 1$ and for all $n \geq 1, a_{n+1} \leq 2n$. Show that for every integer $n \geq 1$, there exist two indices $p$ and $q$ such that $a_p - a_q = n$.
|
Let $n \geqslant 1$ be an integer. We will use the pigeonhole principle. Construct our pigeonholes in such a way that if two numbers are in the same pigeonhole, they satisfy the property stated in the problem. For this, we consider the following pigeonholes: we group the integers from 1 to $2n$ into pairs of the form $\{i, n+i\}$ for $i$ between 1 and $n$, which constitutes $n$ pigeonholes. These pigeonholes are disjoint from each other, and if two terms of the sequence are in the same pigeonhole, this gives two indices $p$ and $q$ such that $a_{p}-a_{q}=n$, because all terms of a strictly increasing sequence are distinct.
Since the sequence $(a_{m})$ is increasing and since $a_{n+1} \leqslant 2n$, $a_{m} \in \llbracket 1,2n \rrbracket$ for $m \in \llbracket 1, n+1 \rrbracket$. Therefore, the first $n+1$ terms of the sequence are in the interval $\llbracket 1,2n \rrbracket$. By the pigeonhole principle, there are two distinct terms that belong to the same set $\{i, n+i\}$ for some $i$, which is the desired result.
## Comments from the graders:
Very well treated exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit ( $a_{n}$ ) une suite strictement croissante d'entiers positifs telle que $a_{1}=1$ et pour tout $n \geqslant 1, a_{n+1} \leqslant 2 n$. Montrer que pour tout entier $n \geqslant 1$, il existe deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$.
|
Soit $n \geqslant 1$ un entier. On va utiliser le principe des tiroirs. Construisons nos tiroirs deux sorte que si deux nombres sont dans un même tiroirs, ils vérifient la propriété de l'énoncé. Pour cela, on considère les tiroirs suivants : on réunit les entiers de 1 à $2 n$ en les couples de la forme $\{i, n+i\}$ pour $i$ entre 1 et $n$, ce qui constitue $n$ tiroirs. Ces tiroirs sont bien disjoints deux à deux, et si deux termes de la suite sont dans un même tiroir, cela donne les deux indices $p$ et $q$ tels que $a_{p}-a_{q}=n$, car tous les termes d'une suite strictement croissante sont distincts.
Or, puisque la suite ( $a_{m}$ ) est croissante et puisque $a_{n+1} \leqslant 2 n, a_{m} \in \llbracket 1,2 n \rrbracket$ pour $m \in \llbracket 1, n+1 \rrbracket$. Donc les $n+1$ premiers termes de la suites sont dans l'intervalle $\llbracket 1,2 n \rrbracket$. Par le principe des tiroirs, il y a deux termes distincts qui appartiennent au même ensemble $\{i, n+i\}$ pour un certain $i$, ce qui est le résultat voulu.
## Commentaires des correcteurs :
Exercice très bien traité.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 13.",
"solution_match": "## Solution de l'exercice 13"
}
|
01c84475-fb21-5616-abc4-57d35afac127
| 607,418
|
Let $\Gamma$ be a circle and $P$ a point outside $\Gamma$. The tangents to $\Gamma$ from $P$ touch $\Gamma$ at $A$ and $B$. Let $K$ be a point distinct from $A$ and $B$ on the segment $[A B]$. The circumcircle of triangle $PBK$ intersects the circle $\Gamma$ at point $T$. Let $P'$ be the symmetric point of $P$ with respect to point $A$. Show that $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}'\mathrm{KA}}$.
|
According to the inscribed angle theorem, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Therefore, it suffices to show that $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. The figure suggests that triangles PKT and $\mathrm{P}^{\prime} \mathrm{KA}$ are similar, so we will try to prove this result, which will imply the desired angle equality.
To show that $\triangle P K T \sim \triangle P^{\prime} K A$, we have several options. For example, we can show that $\widehat{T P K} = \widehat{K P^{\prime} A}$ and $\widehat{K T P} = \widehat{K A P}$. However, when we try to calculate the angle $\widehat{T P K}$, we realize that the equality $\widehat{T P K} = \widehat{K P^{\prime} A}$ is equivalent to the statement we want to prove. Therefore, we will show that $\widehat{K T P} = \widehat{P^{\prime} A K}$ and that $\frac{\mathrm{KT}}{\mathrm{KA}} = \frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
To show that $\widehat{K T P} = \widehat{P^{\prime} A K}$, we first need to note that triangle $A P B$ is isosceles at $P$ because the lines ($A P$) and ($B P$) are tangent at $A$ and $B$ to the circle $\Gamma$. By applying the inscribed angle theorem in the circle passing through $\mathrm{P}, \mathrm{B}, \mathrm{K}$, and T, we find:
$$
\widehat{\mathrm{KTP}} = 180^{\circ} - \widehat{\mathrm{KBP}} = 180^{\circ} - \widehat{\mathrm{ABP}} = 180^{\circ} - \widehat{\mathrm{BAP}} = \widehat{\mathrm{PAK}}
$$
It remains to show that $\frac{\mathrm{KT}}{\mathrm{KA}} = \frac{\mathrm{TP}}{A \mathrm{P}^{\prime}}$. Since $A P^{\prime} = A P = B P$, it suffices to show that $\frac{\mathrm{KT}}{\mathrm{KA}} = \frac{\mathrm{TP}}{\mathrm{BP}}$. Therefore, it suffices to show that triangles AKT and BPT are similar. To do this, it suffices to show that the angles of these two triangles are equal in pairs.
On the one hand, by the inscribed angle theorem, $\widehat{A K T} = 180^{\circ} - \widehat{\mathrm{BKT}} = \widehat{\mathrm{TPB}}$. On the other hand, by the tangent angle theorem, $\widehat{\mathrm{TAK}} = \widehat{\mathrm{TAB}} = \widehat{\mathrm{TBP}}$.
Therefore, triangles AKT and BPT are similar as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle et $P$ un point à l'extérieur de $\Gamma$. Les tangentes à $\Gamma$ issues de $P$ touchent $\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle PBK recoupe le cercle $\Gamma$ au point $T$. Soit $\mathrm{P}^{\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
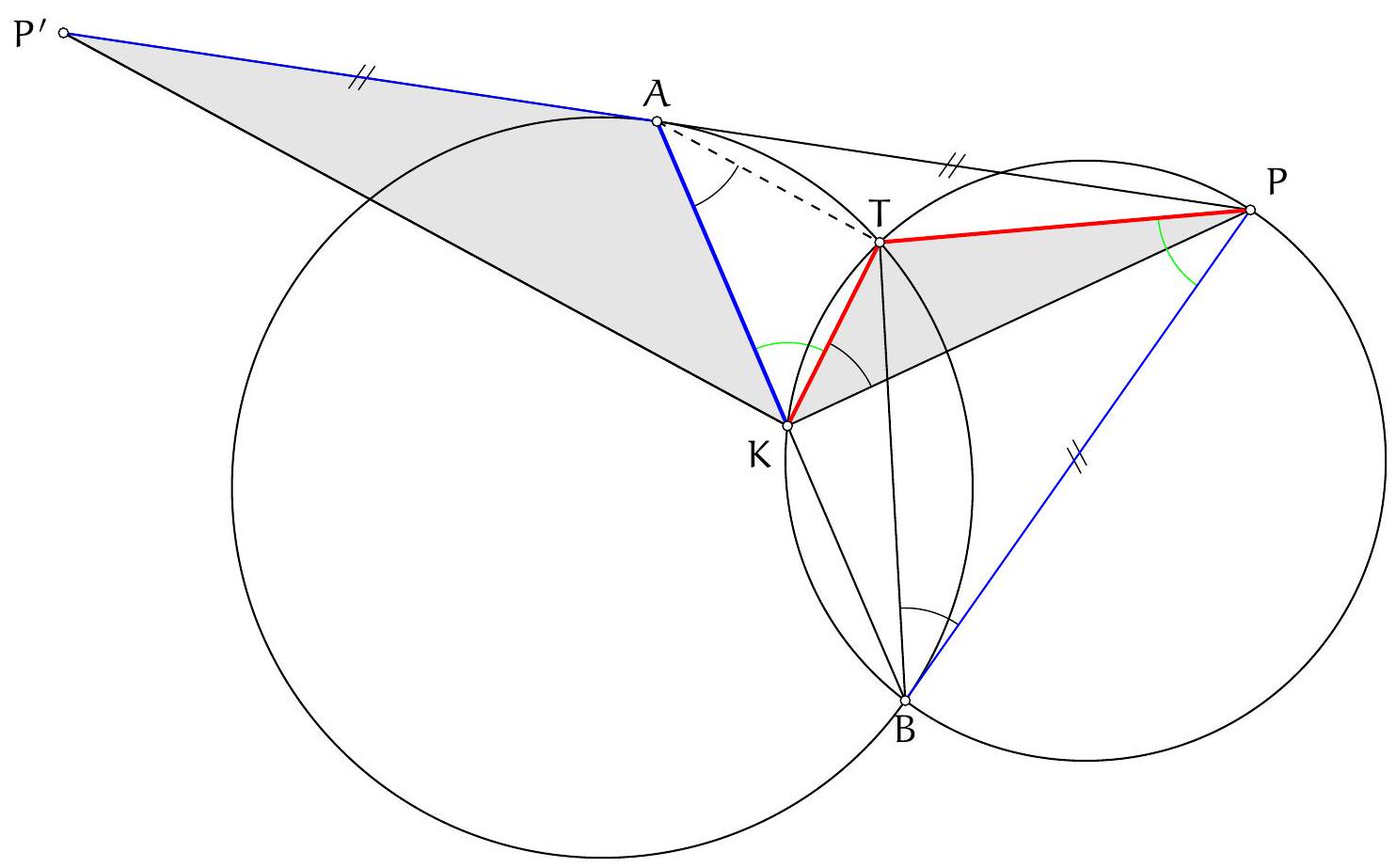
D'après le théorème de l'angle inscrit, $\widehat{\mathrm{PBT}}=\widehat{\mathrm{PKT}}$. Ainsi, il suffit de montrer que $\widehat{\mathrm{PKT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$. La figure semble suggérer que les triangles PKT et $\mathrm{P}^{\prime} \mathrm{KA}$ sont semblables, nous allons donc essayer de montrer ce résultat, qui impliquera bien l'égalité d'angle voulue.
Pour montrer que $\triangle P K T \sim \triangle P^{\prime} K A$, on a plusieurs possibilités. Par exemple, on peut montrer que $\widehat{T P K}=$ $\widehat{K P^{\prime} A}$ et $\widehat{K T P}=\widehat{K A P}$. Toutefois, lorsque l'on essaye de calculer l'angle $\widehat{T P K}$, on se rend compte que l'égalité $\widehat{T P K}=\widehat{K P^{\prime} A}$ est équivalente à l'énoncé à démontrer. On va donc montrer que $\widehat{K T P}=\widehat{P^{\prime} A K}$ et que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{AP}^{\prime}}$.
Pour montrer que $\widehat{K T P}=\widehat{P^{\prime} A K}$, il faut d'abord remarquer que le triangle $A P B$ est isocèle en $P$ puisque les droites ( $A P$ ) et ( $B P$ ) sont tangentes en $A$ et $B$ au cercle $\Gamma$. En appliquant le théorème de l'angle inscrit dans le cercle passant par $\mathrm{P}, \mathrm{B}, \mathrm{K}$ et T , on trouve :
$$
\widehat{\mathrm{KTP}}=180^{\circ}-\widehat{\mathrm{KBP}}=180^{\circ}-\widehat{\mathrm{ABP}}=180^{\circ}-\widehat{\mathrm{BAP}}=\widehat{\mathrm{PAK}}
$$
Il reste donc à montrer que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{A \mathrm{P}^{\prime}}$. Puisque $A P^{\prime}=A P=B P$, il suffit de montrer que $\frac{\mathrm{KT}}{\mathrm{KA}}=\frac{\mathrm{TP}}{\mathrm{BP}}$. Il suffit donc de montrer que les triangles AKT et BPT sont semblables. Pour cela, il suffit de montrer que les angles de ces deux triangles sont deux à deux égaux.
D'une part, par angle inscrit, $\widehat{A K T}=180^{\circ}-\widehat{\mathrm{BKT}}=\widehat{\mathrm{TPB}}$. D' autre part, par angle tangentiel, $\widehat{\mathrm{TAK}}=$ $\widehat{\mathrm{TAB}}=\widehat{\mathrm{TBP}}$.
Donc les triangles AKT et BPT sont semblables comme voulu.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "## Solution de l'exercice 14"
}
|
5983b252-6bd0-5073-8383-8507f42fde1b
| 607,419
|
Let $\Gamma$ be a circle and $P$ a point outside $\Gamma$. The tangents to $\Gamma$ from $P$ touch $\Gamma$ at $A$ and $B$. Let $K$ be a point distinct from $A$ and $B$ on the segment $[A B]$. The circumcircle of triangle $PBK$ intersects the circle $\Gamma$ at point $T$. Let $P'$ be the symmetric point of $P$ with respect to point $A$. Show that $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}'\mathrm{KA}}$.
|
$n^{\circ} 2$ :
In case of an allergy to angle chasing, it is also possible to progress in the problem with advanced ideas. The problem naturally presents itself as dynamic: keeping $\Omega, P, A, B, P^{\prime}$ fixed, we can move $K$ projectively. Then $T$ also moves projectively, as the circle $PBK$ having two fixed points $P$ and $B$ has a non-fixed intersection with the line $(AB)$ and with $\Omega$, so it can pass projectively to $K$ or to $T$. Moreover, the angles to be measured are between a fixed line and a line that moves projectively, so the equality of angles means that the point at infinity of the first projective line is mapped to the point at infinity of the second by a well-chosen rotation (or by a symmetry if the angles were in the opposite direction). The problem is well projective, let's look for three special cases.
We can send $K$ to infinity, then by tangency $T$ ends up at $B$ and the two angles that should be equal are zero.
We can send $K$ to $A$, then $T$ also ends up at $A$ and the two angles that should be equal are equal because triangle $PAB$ is isosceles at $P$.
We still need one more special case using the fact that $P^{\prime}$ is not only on the line $(PA)$ but is also symmetric. We can place $K$ on the symmetric of $B$ with respect to $A$ to construct a parallelogram. The angle chasing is then not quite immediate, but easier than in the original problem, as it does not require an idea to use the midpoint condition since it suffices to consider the parallelogram. It is left as an exercise to the reader.
## Comments from the graders:
The exercise was very well done, and the proofs using the tricks around the midpoints of segments were particularly appreciated.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle et $P$ un point à l'extérieur de $\Gamma$. Les tangentes à $\Gamma$ issues de $P$ touchent $\Gamma$ en $A$ et $B$. Soit $K$ un point distinct de $A$ et $B$ sur le segment $[A B]$. Le cercle circonscrit au triangle PBK recoupe le cercle $\Gamma$ au point $T$. Soit $\mathrm{P}^{\prime}$ le symétrique du point $P$ par rapport au point $A$. Montrer que $\widehat{\mathrm{PBT}}=\widehat{\mathrm{P}^{\prime} \mathrm{KA}}$.
|
$n^{\circ} 2$ :
En cas d'allergie à la chasse aux angles, il est aussi possible de progresser dans le problème avec des idées avancées. Le problème se présente naturellement comme dynamique : en gardant fixe $\Omega, P, A, B, P^{\prime}$ on peut faire bouger K projectivement. Alors la T bouge aussi projectivement car le cercle PBK ayant deux points fixes P et B il a une intersection non fixe avec la droite $(\mathrm{AB})$ et avec $\Omega$, donc peut passer projectivement à $K$ ou à $T$. De plus, les angles à mesurer sont entre une droite fixe et une droite qui bouge projectivement chacun, l'égalité d'angle revient donc à dire que le point à l'infini de la première droite projective est envoyé sur le point à l'infini de la deuxième par une rotation bien choisie (ou par une symétrie si les angles avaient été dans l'autre sens). Le problème est bien projectif, cherchons trois cas particuliers.
On peut envoyer K à l'infini, alors par tangence $T$ se retrouve en $B$ et les deux angles qui doivent être égaux sont nuls.
On peut envoyer K sur $A$, alors T se retrouve aussi en $A$ et les deux angles qui doivent être égaux sont égaux car le triangle PAB est isocèle en P .
Il nous manque encore un cas particulier utilisant le fait que $\mathrm{P}^{\prime}$ soit non seulement sur la droite ( $P A$ ) mais bien symétrique. On peut placer K sur le symétrique de B par rapport à $A$ pour construire un parallélogramme. La chasse aux angles n'est alors pas tout à fait immédiate, mais plus facile que dans le problème original, car elle ne nécessite pas d'idée pour utiliser la condition de milieu puisqu'il suffit de considérer le parallélogramme. Elle est laissée en exercice au lecteur.
## Commentaires des correcteurs:
L'exercice a été très bien réussi, et les preuves utilisant les astuces autour des milieux de segments ont été particulièrement appréciées.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "## Solution "
}
|
5983b252-6bd0-5073-8383-8507f42fde1b
| 607,419
|
Let $\mathrm{m}, \mathrm{n}$ and $\times$ be strictly positive integers. Show that
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)=\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
$$
|
By exchanging $m$ and $n$, we can assume that $m \leqslant n$. We then proceed by induction on $n$ with $m$ fixed.
Initialization: If $\mathrm{m}=\mathrm{n}$, the equality is trivial.
Induction: Suppose the equality is true for some $n \geqslant m$ and let's show that the equality is true for $n+1$. The left-hand side becomes
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)
$$
Let's examine the terms on the right-hand side, which are of the form $\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)$. We have
$$
\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)-\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)= \begin{cases}1 & \text { if }\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1 \\ 0 & \text { otherwise }\end{cases}
$$
Now, $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ if and only if $x \geqslant(n+1) i$, or equivalently $i \leqslant\left\lfloor\frac{x}{n+1}\right\rfloor$. Therefore, the number of $i$ in $\llbracket 1, m \rrbracket$ for which $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ is precisely $\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)$. We deduce that
$$
\begin{aligned}
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right) & =\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
& =\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
& =\sum_{i=1}^{n+1} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
\end{aligned}
$$
where the second equality comes from the induction hypothesis. This completes the induction and concludes the exercise.
$\underline{\text { Alternative Solution: }}$ A very clever solution involves double counting, noting that both sides of the equality count the same object, namely the number of pairs $(a, b)$ such that $a \leqslant m, b \leqslant n$ and $a b \leqslant x$.
Indeed, let's count this number of objects in a first way. The choice of a pair $(a, b) \in$ $\llbracket 1, \mathrm{~m} \rrbracket \times \llbracket 1, n \rrbracket$ such that $\mathrm{ab} \leqslant x$ is characterized first by the choice of $a$ in $\llbracket 1, m \rrbracket$. Then, since $a b \leqslant x$, we have $b \leqslant\left\lfloor\frac{x}{a}\right\rfloor$. Therefore, $b \leqslant \min (\lfloor x / a\rfloor, n)$ and there are $\min (\lfloor x / a\rfloor, n)$ choices for $b$ if $a$ is fixed. Thus, we have in total
$$
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
$$
such pairs $(a, b)$.
By starting with the choice of $b$ rather than $a$, a similar reasoning allows us to assert that there are
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
$$
such pairs of integers $(a, b)$. The two terms are therefore equal.
Comments from the graders:
The exercise was well handled by many students, relative to its estimated difficulty.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $\mathrm{m}, \mathrm{n}$ et $\times$ des entiers strictement positifs. Montrer que
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)=\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
$$
|
Quitte à échanger $m$ et $n$, on peut supposer que $m \leqslant n$. On procède alors par récurrence sur $n$ à $m$ fixé.
Initialisation : Si $\mathrm{m}=\mathrm{n}$, l'égalité est triviale.
Hérédité : Supposons l'égalité vraie pour un certain $n \geqslant m$ et cherchons à montrer que l'égalité est vraie pour $n+1$. Le membre de gauche devient
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)
$$
Examinons les termes du membre de droite, qui sont de la forme $\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)$. On a
$$
\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right)-\min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)= \begin{cases}1 & \text { si }\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1 \\ 0 & \text { sinon }\end{cases}
$$
Or, $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ si et seulement si $x \geqslant(n+1) i$, ou encore $i \leqslant\left\lfloor\frac{x}{n+1}\right\rfloor$. Donc le nombre de $i$ de $\llbracket 1, m \rrbracket$ pour lesquels $\left\lfloor\frac{x}{i}\right\rfloor \geqslant n+1$ est précisément $\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right)$. On déduit que
$$
\begin{aligned}
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n+1\right) & =\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
& =\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)+\min \left(\left\lfloor\frac{x}{n+1}\right\rfloor, m\right) \\
& =\sum_{i=1}^{n+1} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
\end{aligned}
$$
où la deuxième égalité provient de l'hypothèse de récurrence. Ceci achève la récurrence et conclut l'exercice.
$\underline{\text { Solution alternative: }}$ Une solution très astucieuse consiste à procéder par double comptage, en remarquant que les deux membres de l'égalité servent à compter le même objet, à savoir le nombre de paires $(a, b)$ telles que $a \leqslant m, b \leqslant n$ et $a b \leqslant x$.
Cherchons en effet à compter ce nombre d'objet d'une première façon. Le choix d'une paire $(a, b) \in$ $\llbracket 1, \mathrm{~m} \rrbracket \times \llbracket 1, n \rrbracket$ telle que $\mathrm{ab} \leqslant x$ se caractérise dans un premier temps par le choix de $a$ dans $\llbracket 1, m \rrbracket$. Puis, puisque $a b \leqslant x$, on $a b \leqslant\left\lfloor\frac{x}{a}\right\rfloor$. Donc $b \leqslant \min (\lfloor x / a\rfloor, n)$ et il y a $\min (\lfloor x / a\rfloor, n)$ choix pour $b$ si a est fixé. On a donc en tout
$$
\sum_{i=1}^{m} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, n\right)
$$
telles paires $(a, b)$.
En commençant par choisir b plutôt que $a$, un raisonnement similaire nous permet d'affirmer qu'il y a
$$
\sum_{i=1}^{n} \min \left(\left\lfloor\frac{x}{i}\right\rfloor, m\right)
$$
telles paires d'entiers $(a, b)$. Les deux termes sont donc égaux.
Commentaires des correcteurs:
L'exercice a été bien traité et par beaucoup d'élèves, relativement à sa difficulté estimée.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "## Solution de l'exercice 15"
}
|
c7f735da-58c2-580c-b598-d5091ed08d09
| 607,420
|
Let $ABC$ be a triangle in which $AB < AC$. Let $\omega$ be a circle passing through $B$ and $C$ and suppose that the point $A$ is inside the circle $\omega$. Let $X$ and $Y$ be points on $\omega$ such that $\widehat{BXA} = \widehat{AYC}$. We assume that $X$ and $C$ are on opposite sides of the line $(AB)$ and that $Y$ and $B$ are on opposite sides of the line $(AC)$. Show that, as $X$ and $Y$ vary on the circle $\omega$, the line $(XY)$ passes through a fixed point.
|
First, we will seek to draw an exact figure, hoping that the reasoning used for the drawing will enlighten us about the dynamics of the figure.
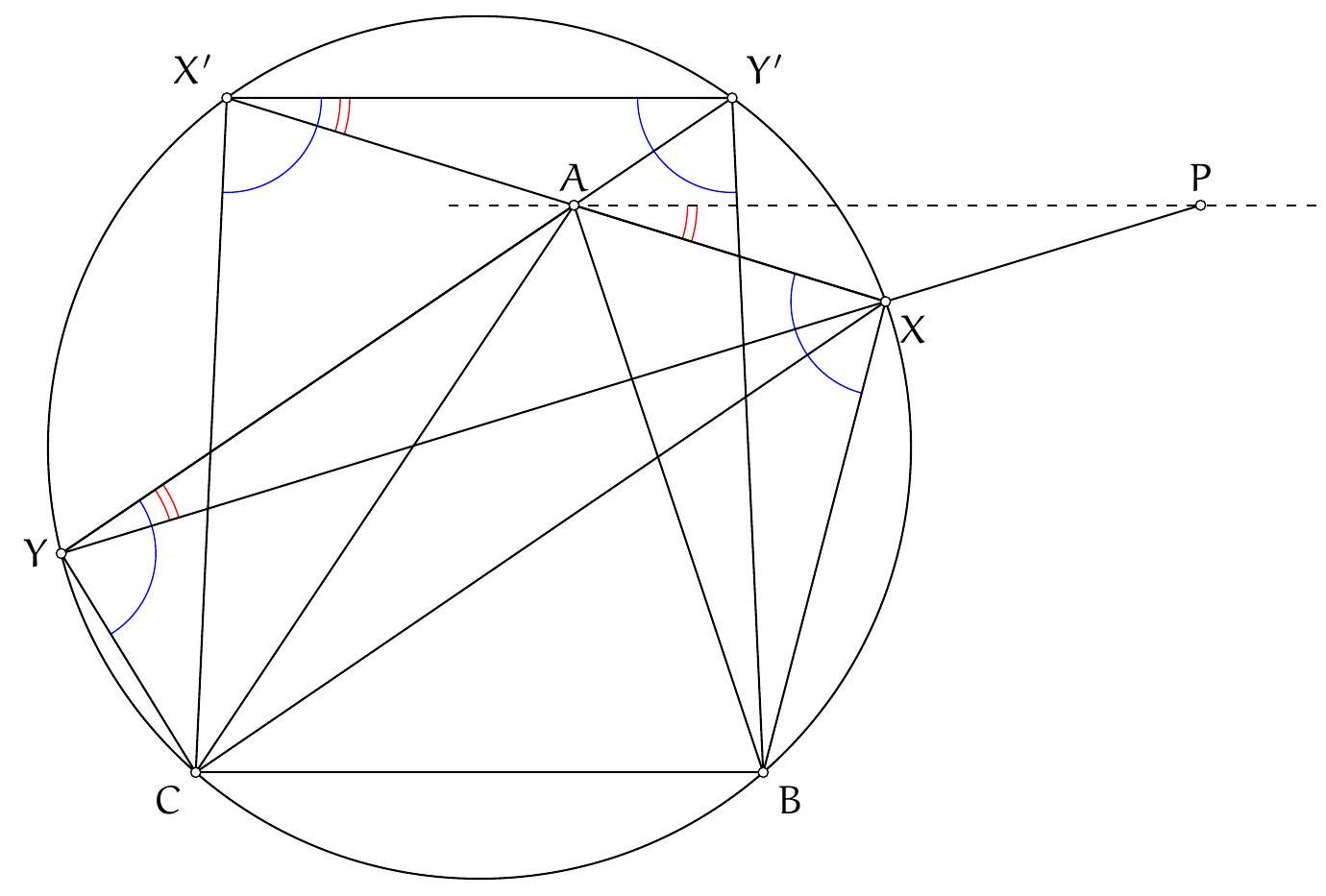
To draw the figure, we aim to take advantage of the hypothesis that the points $X, B, C$, and $Y$ lie on the same circle, using the inscribed angle theorem. Suppose the figure is drawn. We extend the line $(X A)$ and denote $X^{\prime}$ as the second intersection point of $(X A)$ with $\omega$, and similarly, $Y^{\prime}$ as the second intersection point of $(Y A)$ with $\omega$.
The inscribed angle theorem and the hypothesis about $X$ and $Y$ impose the following equality:
$$
\widehat{C X^{\prime} Y^{\prime}} = \widehat{C Y^{\prime}} = \widehat{C Y^{\prime}} = \widehat{A X B} = \widehat{X^{\prime} X B} = \widehat{X^{\prime} Y^{\prime} B}
$$
Thus, the quadrilateral $B C X^{\prime} Y^{\prime}$ is an isosceles trapezoid, and the lines $(X^{\prime} Y^{\prime})$ and $(B C)$ are parallel.
We can deduce a protocol for drawing the figure: Place a point $X$ on the circle $\omega$ and extend the line $(A X)$ to obtain the point $X^{\prime}$. Then obtain the point $Y^{\prime}$ by drawing the line parallel to $(B C)$ passing through $X^{\prime}$. Finally, obtain the point $Y$ by extending the line $(Y^{\prime} A)$.
Now, let's solve the exercise. Since we can draw an exact figure, we can draw the figure for two different positions of the point $X$, denoted as $X_{1}$ and $X_{2}$, draw the associated points $Y_{1}$ and $Y_{2}$, and conjecture the position of the fixed point using the intersection of the lines $(X_{1} Y_{1})$ and $(X_{2} Y_{2})$. It is striking that the intersection point obtained lies on the line parallel to $(B C)$ passing through the point $A$.
Let $P$ be the intersection of the line $(X Y)$ with the line parallel to $(B C)$ passing through $A$. Since the lines $(X^{\prime} Y^{\prime})$ and $(A P)$ are parallel, we find:
$$
\widehat{X A P} = \widehat{X X^{\prime} Y^{\prime}} = \widehat{X Y Y^{\prime}} = \widehat{X Y A}
$$
Thus, the line $(A P)$ is tangent to the circumcircle of the triangle $A X Y$. Therefore, according to the power of a point:
$$
\mathrm{PA}^2 = \mathrm{PX} \cdot \mathrm{PY} = \mathcal{P}_{\omega}(\mathrm{P})
$$
The position of the point $P$ on the line parallel to $(B C)$ passing through $A$ is uniquely determined by the power of the point $P$ with respect to the circle $\omega$, which does not depend on $X$ and $Y$. This is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dans lequel $A B<A C$. Soit $\omega$ un cercle passant par $B$ et $C$ et on suppose que le point $A$ se trouve à l'intérieur du cercle $\omega$. Soient $X$ et $Y$ des points de $\omega$ tels que $\widehat{B X A}=\widehat{A Y C}$. On suppose que $X$ et $C$ sont situés de part et d'autre de la droite $(A B)$ et que $Y$ et $B$ sont situés de part et d'autre de la droite (AC). Montrer que, lorsque $X$ et $Y$ varient sur le cercle $\omega$, la droite (XY) passe par un point fixe.
|
Tout d'abord, nous allons chercher à tracer une figure exacte, en espérant que les raisonnements mis en oeuvre pour le tracé nous éclairerons sur la dynamique de la figure.

Pour tracer la figure, on cherche à tirer profit de l'hypothèse que les points $X, B, C$ et $Y$ sont sur un même cercle, à l'aide du théorème de l'angle inscrit. Supposons la figure tracée. On prolonge donc la droite ( $X A$ ) et on note $X^{\prime}$ le second point d'intersection de $(X A)$ avec $\omega$ et de même $Y^{\prime}$ le second point d'intersection de (YA) avec $\omega$.
Le théorème de l'angle inscrit et l'hypothèse sur $X$ et $Y$ nous impose l'égalité suivante :
$$
\widehat{C X^{\prime} Y^{\prime}}=\widehat{C Y^{\prime}}=\widehat{C Y^{\prime}}=\widehat{A X B}=\widehat{X^{\prime} X B}=\widehat{X^{\prime} Y^{\prime} B}
$$
de sorte que le quadrilatère $B C X^{\prime} Y^{\prime}$ est un trapèze isocèle, et les droites $\left(X^{\prime} Y^{\prime}\right)$ et ( $B C$ ) sont parallèles.
On en déduit un protocole pour tracer la figure : On place un point $X$ sur le cercle $\omega$ et on prolonge la droite $(A X)$ de sorte à obtenir le point $X^{\prime}$. Puis on obtient le point $Y^{\prime}$ en traçant la parallèle à la droite (BC) passant par $X^{\prime}$. On obtient enfin le point $Y$ en prolongeant la droite ( $Y^{\prime} A$ ).
Résolvons à présent l'exercice. Maintenant que l'on peut tracer un figure exacte, on peut tracer la figure pour deux positions différentes du point $X$, notées $X_{1}$ et $X_{2}$, tracer les points $Y_{1}$ et $Y_{2}$ associés et conjecturer la position du point fixe à l'aide du point d'intersection des droites $\left(X_{1} Y_{1}\right.$ et $\left(X_{2} Y_{2}\right)$. Il est frappant que le point d'intersection obtenu appartient à la parallèle à la droite $(B C)$ passant par le point $A$.
Soit donc $P$ le point d'intersection de la droite $(X Y)$ avec la parallèle à ( $B C$ ) passant par $A$. Puisque les droites $\left(X^{\prime} Y^{\prime}\right)$ et $(A P)$ sont parallèles, on trouve :
$$
\widehat{X A P}=\widehat{X X^{\prime} Y^{\prime}}=\widehat{X Y Y^{\prime}}=\widehat{X Y A}
$$
De sorte que la droite (AP) est tangente au cercle circonscrit au triangle $A X Y$. On a donc, d'après la puissance d'un point :
$$
\mathrm{PA}^{2}=\mathrm{PX} \cdot \mathrm{PY}=\mathcal{P}_{\omega}(\mathrm{P})
$$
La position du point $P$ sur la parallèle à $(B C)$ passant par $A$ est uniquement déterminée par la puissance du point $P$ par rapport au cercle $\omega$, qui ne dépend pas de $X$ et $Y$. C'est ce que nous voulions démontrer.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "\nSolution de l'exercice 16"
}
|
3ffb4859-9d66-5ce4-8d91-c2148fafc81d
| 607,421
|
Let $ABC$ be a triangle in which $AB < AC$. Let $\omega$ be a circle passing through $B$ and $C$ and suppose that the point $A$ is inside the circle $\omega$. Let $X$ and $Y$ be points on $\omega$ such that $\widehat{BXA} = \widehat{AYC}$. We assume that $X$ and $C$ are on opposite sides of the line $(AB)$ and that $Y$ and $B$ are on opposite sides of the line $(AC)$. Show that, as $X$ and $Y$ vary on the circle $\omega$, the line $(XY)$ passes through a fixed point.
|
$n^{\circ} 2$ :
An alternative solution using advanced knowledge is proposed. The problem statement invites us to consider the problem dynamically, as the fixed and moving parts of the figure have already been specified in the statement. If the construction of $X$ and $Y$ does not seem projective, the statement actually asks us to show that it is. Indeed, passing to the second intersection with the line connecting to a fixed point outside the circle is equivalent to performing an inversion that leaves the circle globally invariant and is a projective transformation, even a projective involution of the circle. In fact, all projective involutions of the circle are of this form: it suffices to prove that passing from $X$ to $Y$ is a projective involution to deduce the existence of this point $P$. Indeed, if we construct $P$ as the intersection of ($X_{1} Y_{1}$) with ($X_{2} Y_{2}$) for two positions of $X$ and $Y$, then $P$ defines an involution which, coinciding in four points with that of the statement, must be the same.
Now that we have seen that this problem is fundamentally dynamic and that the point $P$ is just an excuse to ask for the proof of the existence of a projective involution, let's do it. Even if it is not initially very visible, it is actually quite easy to show that the transformation from $X$ to $Y$ is projective. The angles in the statement invite us to look at the circles $A X B$ and $A Y C$, which live in the pencil of circles with fixed points $A, B$ and $A, C$ respectively. Since the circle $A B X$ has only one non-fixed intersection with the circle $\omega$, it is indeed projective to pass from $X$ to this circle. The same applies on the other side with $Y$ and the other circle. Finally, we need to prove that we can pass from one circle to the other. The equality of the angles actually gives us that the circle $A Y C$ is the image of the circle $A X B$ by the indirect similarity centered at $A$ sending $B$ to $C$. The transformation is therefore indeed projective.
Let's show that it is an involution. We know that a projective transformation is an involution as soon as it exchanges a pair of points. Let's look for a simple case. A particularly simple case is when the common angle is zero: this corresponds to the fact that $X, A, B$ are collinear in this order and that $Y, A, C$ are also collinear in this order. The transformation then indeed sends $X$ to $Y$. Let's check that it would also send $Y$ to $X$. This amounts to saying that $\widehat{A Y B} = \widehat{A X C}$, which is immediate from the inscribed angle theorem.
## Comments from the graders:
An exercise approached by four people, with two dynamic approaches and two elementary approaches.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dans lequel $A B<A C$. Soit $\omega$ un cercle passant par $B$ et $C$ et on suppose que le point $A$ se trouve à l'intérieur du cercle $\omega$. Soient $X$ et $Y$ des points de $\omega$ tels que $\widehat{B X A}=\widehat{A Y C}$. On suppose que $X$ et $C$ sont situés de part et d'autre de la droite $(A B)$ et que $Y$ et $B$ sont situés de part et d'autre de la droite (AC). Montrer que, lorsque $X$ et $Y$ varient sur le cercle $\omega$, la droite (XY) passe par un point fixe.
|
$n^{\circ} 2$ :
On propose une solution alternative utilisant des connaissances avancées. L'énoncé du problème nous invite à considérer le problème dynamiquement, puisque la partie fixe et la partie mobile de la figure a déjà été spécifiée dans l'énoncé. Si la construction de $X$ et $Y$ ne semble pas projective, l'énoncé nous demande en fait de montrer qu'elle l'est. En effet, passer à la seconde intersection avec la droite reliant à un point fixe hors du cercle revient à faire une inversion laissant le cercle globalement invariant et est une transformation projective, c'est même une involution projective du cercle. En fait, toutes les involutions projectives du cercle sont de cette forme : il suffit de prouver que passer de X à Y est une involution projective pour pouvoir en déduire l'existence de ce point $P$. En effet, si on construit $P$ comme ( $X_{1} \mathrm{Y}_{1}$ ) intersecté avec $\left(X_{2} \mathrm{Y}_{2}\right)$ pour deux positions de $X$ et $Y$, alors $P$ définit une involution qui, coïncidant en 4 points avec celle de l'énoncé, ne peut être que la même.
Maintenant qu'on a vu que ce problème était fondamentalement dynamique et que le point $P$ n'est qu'une excuse pour demander de démontrer l'existence d'une involution projective, faisons-le. Même si ce n'est initialement pas très visible, il est en fait assez facile de montrer que la transformation de $X$ à $Y$ est projective. Les angles de l'énoncé nous invitent à regarder les cercles $A X B$ et $A Y C$, vivant dans le faisceau de cercle ayant pour points fixes respectivement $A, B$ et $A, C$. Comme le cercle $A B X$ a une seule intersection non fixe avec le cercle $\omega$, il est bien projectif de passer de $X$ à ce cercle. De même de l'autre côté avec $Y$ et l'autre cercle. Enfin il faut prouver qu'on peut passer d'un cercle à l'autre. L'égalité des angles nous donne en fait que le cercle AYC est l'image du cercle AXB par la similitude indirecte de centre $A$ envoyant $B$ sur $C$. La transformation est donc bien projective.
Montrons que c'est une involution. On sait qu'une transformation projective est une involution dès qu'elle échange une paire de points. Cherchons donc un cas simple. Un cas particulièrement simple est celui où l'angle commun est nul : cela correspond au fait que $X, A, B$ soient alignés dans cet ordre et que $Y, A, C$ soient aussi alignés dans cet ordre. La transformation envoie alors bien $X$ sur $Y$. Vérifions qu'elle enverrait aussi $Y$ sur $X$. Cela revient à dire que $\widehat{A Y B}=\widehat{A X C}$, ce qui est immédiat d'après le théorème de l'angle inscrit.
## Commentaires des correcteurs:
Exercice abordé par quatre personnes, avec deux approches dynamiques et deux approches élémentaires.
|
{
"resource_path": "French/segmented/envois/fr-corrigé-envoi-5.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "## Solution "
}
|
3ffb4859-9d66-5ce4-8d91-c2148fafc81d
| 607,421
|
Let $a, b$ be two integers. Show that $a b(a-b)$ is divisible by 2.
|
We are interested in the parity of a product, so it is relevant to make a case distinction based on the parity of the integers involved, here \(a\) and \(b\). We then notice the following:
- If \(a\) or \(b\) is even: then \(ab\) is even (the product of an even number by any integer being even) and therefore \(ab(a-b)\) is divisible by 2.
- Otherwise, if \(a\) and \(b\) are both odd, then \(a-b\) is even (as the difference of two odd numbers) and therefore \(ab(a-b)\) is divisible by 2.
Finally, in all cases, if \(a\) and \(b\) are integers, then \(ab(a-b)\) is divisible by 2.
Comment from the graders: Many students tackled this problem, and all of them did it perfectly. The idea was to make case distinctions based on the parities of \(a\) and \(b\), which could be done in two cases: either " \(a\) or \(b\) is even" and "both \(a\) and \(b\) are odd," or " \(a\) and \(b\) have the same parity" and " \(a\) and \(b\) have different parities." Some solutions included more cases, which was not necessary and sometimes included cases that were already covered by other cases: this often lengthened the solutions, reducing efficiency and potentially wasting time that could have been spent on more challenging exercises.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers. Montrer que $a b(a-b)$ est divisible par 2.
|
On s'intéresse à la parité d'un produit, il est donc pertinent de faire une disjonction de cas sur la parité des entiers en jeu, ici a et $b$. On remarque alors la chose suivante :
- Si $a$ ou best pair : alors $a b$ est pair (le produit d'un nombre pair par un entier quelconque étant pair) et donc $\mathrm{ab}(\mathrm{a}-\mathrm{b})$ est bien divisible par 2 .
- Sinon, si $a$ et $b$ sont tous les deux impairs, alors $a-b$ est pair (en tant que différence de deux impairs) et donc $a b(a-b)$ est divisible par 2
Finalement, dans tous les cas, si $a$ et $b$ sont des entiers, alors $a b(a-b)$ est divisible par 2.
Commentaire des correcteurs : Beaucoup d'élèves ont abordé cet exercice, et tous l'ont parfaitement réussi. L'idée consistait à faire des disjonctions de cas selon les parités de a et de b , ce qui pouvait se faire en deux cas : soit " $a$ ou b pair" et "a et b impairs", soit "a et b de même parité" et "a et b de parité différente". Certaines copies ont fait plus de cas, ce n'était pas nécessaire et parfois il y avait des cas qui étaient inclus dans d'autres cas déjà traités : cela rallongeait souvent les solutions, ce qui fait perdre en efficacité et peut faire perdre du temps qu'on aurait pu passer à chercher d'autres exercices plus difficiles.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
286d0d0e-b62a-5e54-902e-b8bf687a630f
| 607,424
|
Show that there are infinitely many pairs ( $\mathrm{m}, \mathfrak{n}$ ) of distinct strictly positive integers such that m ! n is a perfect square.
|
One would like to take $\mathrm{m}=\mathrm{n}$ to have $\mathrm{m}!\mathrm{n}!=(\mathrm{n}!)^{2}$ and get a perfect square. But the statement forces $m \neq n$. Despite this, we already see a way to naturally introduce perfect squares.
Assume without loss of generality that $m>n$ (since $m!n!=n!m!$, we can replace $(m, n)$ with $(n, m)$ without any problem). Then $m!n!=m \times(m-1) \times \ldots \times(n+1) \times n! \times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Therefore, $m!n!$ will be a perfect square if and only if $m \times \ldots \times(n+1)$ is. The simplest way to achieve this is to choose $m=n+1=k^{2}$ for some integer $k(k \geqslant 2$ because we want $m, n \geqslant 1$). Indeed, we have $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
Finally, for any integer $k \geqslant 2$, $(m, n)=\left(k^{2}, k^{2}-1\right)$ works, providing us with an infinite number of solution pairs.
Comment from the graders: The problem was approached by many students, and a large majority of them solved it perfectly. Others had interesting leads without necessarily concluding, such as noting that, in the case $m>n$ for example, it is necessary and sufficient to have $m \times(m-1) \times \ldots \times(n+1)$ be a perfect square.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer qu'il existe une infinité de couples ( $\mathrm{m}, \mathfrak{n}$ ) d'entiers strictement positifs distincts tels que m ! n soit un carré parfait.
|
On aurait envie de prendre $\mathrm{m}=\mathrm{n}$ pour avoir $\mathrm{m}!\mathrm{n}!=(\mathrm{n}!)^{2}$ et avoir un carré parfait. Mais l'énoncé force $m \neq n$. Malgré cela, on voit déjà un moyen de faire apparaître naturellement des carrés parfaits.
Supposons sans perte de généralité $m>n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n) \operatorname{par}(n, m)$, ça ne pose pas de problème). Alors $m!n!=\mathfrak{m} \times(m-1) \times \ldots \times(n+1) \times n!\times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Alors $m!n!$ sera un carré parfait si et seulement si $m \times \ldots \times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \geqslant 2$ car on veut $m, n \geqslant 1$ ). En effet on a bien $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
Finalement, pour tout $k \geqslant 2$ entier, $(m, n)=\left(k^{2}, k^{2}-1\right)$ convient, ce qui nous fournit bien une infinité de couples de solutions.
Commentaire des correcteurs : Le problème a été abordé par beaucoup d'élèves et une large majorité l'a parfaitement réussi. D'autres ont eu des pistes intéressantes sans forcément aboutir, comme remarquer que, dans le cas $m>n$ par exemple, il est nécessaire et suffisant d'avoir $m \times(m-1) \times \ldots \times(n+1)$ qui est un carré parfait.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
57f95a18-e1f6-5e1f-be47-609df2902104
| 607,425
|
Let $n \in \mathbb{N}^{\star}$. Show that if $2n+1$ and $3n+1$ are perfect squares, then $5n+3$ is not prime.
|
Suppose that $2n+1$ and $3n+1$ are perfect squares: we have $\mathrm{a}, \mathrm{b}$ two strictly positive integers $(2 n+1,3 n+1>0)$ such that $2n+1=a^{2}$ and $3n+1=b^{2}$. Here, it is noted that $5n+3=4 \times(2n+1)-(3n+1)=4a^{2}-b^{2}$. To find this identity, we try to express 5 in terms of 2 and 3: it is natural to take $5=2+3$ but this does not give $5n+3$, instead we see that $5=4 \times 2-3$.
We can therefore write $5n+3=(2a-b)(2a+b)$. Since $a, b>0$, $2a+b>2a-b$, and $2a+b>0$. This forces $2a-b>0$ (otherwise we would have $5n+3 \leqslant 0$, which is excluded). It is therefore sufficient to show that $2a-b>1$ to conclude: we will then have written $5n+3$ as the product of two integers strictly greater than 1, and it cannot be prime.
But if $2a=b+1$, then $5n+3=2a+b=4a-1$ so $a^{2}=2n+1 \leqslant \frac{5n+3}{2}<\frac{4a-1}{2}<2a$ so $a<2$. But $a=1$ gives $2n+1=1$ so $n=0$, which is absurd since $n>0$. Thus $2a-b \neq 1$.
We have therefore shown that if $2n+1$ and $3n+1$ are perfect squares (with $n \in \mathbb{N}^{\star}$), then $5n+3$ is not a prime number.
$\underline{\text { Comment from the graders: Most students who approached the problem generally understood it well }}$ and found the factorization that was interesting here. However, most of them forgot to check the signs of their terms: to conclude $2a-b=1, 2a+b=5n+3$, it was necessary to have verified beforehand that $2a+b>2a-b>0$, which was not very difficult but necessary for the identification to be valid. Note that a number of papers attempted to exploit congruences: here it did not lead to anything interesting, when it comes to prime numbers it is often more interesting to look for factorizations rather than to exploit congruences as the latter, unless they find a divisibility by a particular number, do not tell us whether an integer is prime or not.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \in \mathbb{N}^{\star}$. Montrer que si $2 n+1$ et $3 n+1$ sont des carrés parfaits, alors $5 n+3$ n'est pas premier.
|
Supposons que $2 \mathrm{n}+1$ et $3 \mathrm{n}+1$ sont des carrés parfaits : on dispose de $\mathrm{a}, \mathrm{b}$ deux entiers strictement positifs $(2 n+1,3 n+1>0)$ tels que $2 \mathfrak{n}+1=a^{2}$ et $3 n+1=b^{2}$. Ici, il s'agit de remarquer que $5 \mathfrak{n}+3=4 \times(2 n+1)-(3 n+1)=4 a^{2}-b^{2}$. Pour trouver cette identité, on essaie d'exprimer 5 à partir de 2 et 3 : il est naturel de prendre $5=2+3$ mais cela ne donne pas $5 \mathrm{n}+3$, en revanche on voit que $5=4 \times 2-3$.
On peut donc écrire $5 n+3=(2 a-b)(2 a+b)$. Comme $a, b>02 a+b>2 a-b$, et $2 a+b>0$. Ceci force $2 a-b>0$ (sinon on aurait $5 n+3 \leqslant 0$, ce qui est exclu). Il suffit donc de montrer que $2 a-b>1$ pour conclure : on aura alors écrit $5 \mathrm{n}+3$ comme produit de deux entiers strictement plus grands que 1 , et il ne pourra pas être premier.
Mais si $2 \mathrm{a}=\mathrm{b}+1,5 \mathrm{n}+3=2 \mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ donc $\mathrm{a}^{2}=2 \mathrm{n}+1 \leqslant \frac{5 n+3}{2}<\frac{4 \mathrm{a}-1}{2}<2 \mathrm{a}$ donc $\mathrm{a}<2$. Mais $a=1$ donne $2 \mathrm{n}+1=1$ donc $\mathrm{n}=0$, absurde car $\mathrm{n}>0$. Ainsi $2 a-b \neq 1$.
On a donc bien montré que si $2 \mathfrak{n}+1$ et $3 \mathfrak{n}+1$ sont des carrés parfaits (avec $\mathfrak{n} \in \mathbb{N}^{\star}$ ), alors $5 \mathfrak{n}+3$ n'est pas un nombre premier.
$\underline{\text { Commentaire des correcteurs : Les élèves qui ont abordé le problème l'ont en général plutôt bien compris }}$ et ont trouvé la factorisation qui était intéressante ici. Néanmoins la plupart d'entre eux ont oublié de vérifier les signes de leurs termes : pour pouvoir conclure $2 \mathrm{a}-\mathrm{b}=1,2 \mathrm{a}+\mathrm{b}=5 \mathrm{n}+3 \mathrm{il}$ fallait avoir vérifié au préalable $2 a+b>2 a-b>0$, ce qui n'était pas très dur mais nécessaire pour que l'identification soit valide. Notons qu'un certain nombre de copies ont tenté d'exploiter des congruences : ici ça ne menait pas à grand chose d'intéressant, lorsqu'il s'agit des nombres premiers il est souvent plus intéressant de rechercher des factorisations plutôt que d'exploiter des congruences car ces dernières, à moins de trouver une divisibilité par un nombre particulier, ne nous renseignent pas sur le caractère premier ou non d'un entier.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
a041daa1-e922-5ca2-aefc-71e26532483e
| 607,428
|
Let $n \geqslant 2$. Show that there exist integers $a, b$ such that, for any integer $m$, the number $m^{3}+a m+b$ is not a multiple of $n$.
---
The translation maintains the original formatting and structure of the source text.
|
$7 \quad \mathrm{~m}^{3}+\mathrm{am}+\mathrm{b}$ is a multiple of n if and only if $\mathrm{m}^{3}+\mathrm{am} \equiv-\mathrm{b}(\bmod \mathrm{n})$. We then notice that it suffices to find a such that $\mathrm{m}^{3}+\mathrm{am}$ does not take all possible values modulo $n$ (and to take for $-b$ one of the values that is not taken). Since $\mathrm{m}^{3}+a m$ modulo $n$ depends only on $m$ modulo $n$, we can restrict ourselves to $0 \leqslant m \leqslant n-1$.
It is a matter of finding an a such that the $0^{3}+\mathrm{a} \cdot 0(\bmod n), 1^{3}+\mathrm{a} \cdot 1(\bmod n), \ldots,(n-1)^{3}+a(n-1)$ $(\bmod n) n$ do not reach $n$ distinct values $(\operatorname{modulo} n)$. Then if we find $m_{1} \neq m_{2}$ between 0 and $n-1$ such that $m_{1}^{3}+a m_{1} \equiv m_{2}^{3}+a m_{2}(\bmod n)$, the $n-2$ other values of $m$ modulo $n$ will give at most $n-2$ values of $m^{3}+$ am modulo $n$, so in total, for $0 \leqslant m \leqslant n-1, m^{3}+$ am will take at most $n-1$ values out of the $\boldsymbol{n}$ possible: there will be one that is not reached. Now $0^{3}+\mathrm{a} \times 0 \equiv 0(\bmod \mathfrak{n})$, $1^{3}+a \times 1 \equiv a+1(\bmod \mathfrak{n})$. If $a+1 \equiv 0(\bmod \boldsymbol{n})$, we will be in the situation described above.
Let us then set $a=-1$ (or $a=n-1$ if we want $a>0)$. Then $m^{3}+a m$ is zero if $m=0$ or $m=1$. Therefore, there exists an integer $c$, $0 \leqslant c \leqslant n-1$, such that for all $0 \leqslant m \leqslant n-1, m^{3}+a m \not \equiv c(\bmod n)$. Let us then set $b=-c$ (or $b=n-c$ if we want $b>0$), then for all $0 \leqslant m \leqslant n-1, m^{3}+a m+b$ will be non-zero modulo $n$, so for all $m$ integers, $m^{3}+a m+b$ will not be a multiple of $n$.
Thus, there do exist such integers $a$ and $b$.
Comment from the graders: The problem was not much addressed, and when the statement was well understood, it was well succeeded. However, many did not understand the statement, and showed instead that for any fixed value of $m$, one could find $a$ and $b$ such that $n$ does not divide $m^{3}+a m+b$. The difference here is that a and b are not fixed independently of m, which is a significantly simpler version of the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 2$. Montrer qu'il existe des entiers $a, b$ tels que, pour tout entier $m$, le nombre $m^{3}+a m+b$ ne soit pas un multiple de $n$.
|
$7 \quad \mathrm{~m}^{3}+\mathrm{am}+\mathrm{b}$ est un multiple de n si et seulement si $\mathrm{m}^{3}+\mathrm{am} \equiv-\mathrm{b}(\bmod \mathrm{n})$. On remarque alors qu'il suffit de trouver a tel que $\mathrm{m}^{3}+\mathrm{am}$ ne prend pas toutes les valeurs possibles modulo $n$ (et de prendre pour $-b$ une des valeurs qui $n$ 'est pas prise). Comme $\mathrm{m}^{3}+a m$ modulo $n$ ne dépend que de $m$ modulo $n$, on peut se restreindre à $0 \leqslant m \leqslant n-1$.
Il s'agit de trouver un a tel que les $0^{3}+\mathrm{a} \cdot 0(\bmod n), 1^{3}+\mathrm{a} \cdot 1(\bmod n), \ldots,(n-1)^{3}+a(n-1)$ $(\bmod n) n$ 'atteignent pas $n$ valeurs distinctes $(\operatorname{modulo} n)$. Alors si on trouve $m_{1} \neq m_{2}$ entre 0 et $n-1$ tels que $m_{1}^{3}+a m_{1} \equiv m_{2}^{3}+a m_{2}(\bmod n)$, les $n-2$ autres valeurs de $m$ modulo $n$ donneront au plus $n-2$ valeurs de $m^{3}+$ am modulo $n$, donc au total, pour $0 \leqslant m \leqslant n-1, m^{3}+$ am prendra au plus $n-1$ valeurs sur mes $\boldsymbol{n}$ possibles : il y en aura bien une qui ne sera pas atteinte. Or $0^{3}+\mathrm{a} \times 0 \equiv 0(\bmod \mathfrak{n})$, $1^{3}+a \times 1 \equiv a+1(\bmod \mathfrak{n})$. Si $a+1 \equiv 0(\bmod \boldsymbol{n})$, on sera dans la situation décrite ci-dessus.
Posons alors $a=-1$ (ou $a=n-1$ si on veut $a>0)$. Alors $m^{3}+a m$ est nul si $m=0$ ou $m=1$. Donc il existe $c$ entier, $0 \leqslant c \leqslant n-1$, tel que pour tout $0 \leqslant m \leqslant n-1, m^{3}+a m \not \equiv c(\bmod n)$. Posons alors $b=-c\left(\right.$ ou $b=n-c$ si on veut $b>0$ ), alors pour tout $0 \leqslant m \leqslant n-1, m^{3}+a m+b$ sera non nul modulo $n$, donc pour tout $m$ entier, $m^{3}+a m+b$ ne sera pas un multiple de $n$.
Ainsi, il existe bien de tels entiers $a$ et $b$.
Commentaire des correcteurs : Le problème n'a pas beaucoup été abordé, et lorsque l'énoncé a été bien compris il a été bien réussi. Cependant, beaucoup n'ont pas compris l'énoncé, et on montré à la place que pour toute valeur de $m$ fixée, on pouvait trouver des $a$ et $b$ de sorte que $n$ ne divise pas $m^{3}+a m+b$. La différence ici est que a et bne sont pas fixés indépendamment de m , ce qui est une version sensiblement plus simple de l'exercice.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice "
}
|
14107eff-01d1-555f-ae63-f69e594e3988
| 607,430
|
Show that there are infinitely many pairs ( $\mathrm{m}, \mathrm{n}$ ) of distinct integers such that $\mathrm{m}!n!$ is a perfect square.
|
One would like to take $m=n$ to have $m!n!=(n!)^{2}$ and get a perfect square. But the statement forces $m \neq n$. Despite this, we already see a way to naturally introduce perfect squares.
Assume without loss of generality that $m>n$ (since $m!n!=n!m!$, we can replace $(m, n)$ with $(n, m)$ without any problem). Then $m!n!=m \times(m-1) \times \ldots \times(n+1) \times n!\times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Therefore, $m!n!$ will be a perfect square if and only if $m \times \ldots \times(n+1)$ is. The simplest way to achieve this is to choose $m=n+1=k^{2}$ for some integer $k(k \geqslant 2$ because we want $m, n \geqslant 1)$. Indeed, we have $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
Finally, for any integer $k \geqslant 2$, $(m, n)=\left(k^{2}, k^{2}-1\right)$ works, which provides us with an infinite number of solution pairs.
Comment from the graders: All students who tackled the problem solved it perfectly, even if some provided more detail than necessary.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer qu'il existe une infinité de couples ( $\mathrm{m}, \mathrm{n}$ ) d'entiers distincts tels que $\mathrm{m}!n!$ soit un carré parfait.
|
On aurait envie de prendre $m=n$ pour avoir $m!n!=(n!)^{2}$ et avoir un carré parfait. Mais l'énoncé force $m \neq n$. Malgré cela, on voit déjà un moyen de faire apparaître naturellement des carrés parfaits.
Supposons sans perte de qénéralité $m>n$ (comme $m!n!=n!m!$, quitte à remplacer $(m, n)$ par $(n, m)$, ça ne pose pas de problème $)$. Alors $m!n!=m \times(m-1) \times \ldots \times(n+1) \times n!\times n!=m \times \ldots \times(n+1) \times(n!)^{2}$. Alors $m!n$ ! sera un carré parfait si et seulement si $m \times \ldots \times(n+1)$ l'est. Le moyen le plus simple de le faire, c'est de choisir $m=n+1=k^{2}$ pour un certain entier $k(k \geqslant 2$ car on veut $m, n \geqslant 1)$. En effet on a bien $\left(k^{2}\right)!\left(k^{2}-1\right)!=k^{2}\left(\left(k^{2}-1\right)!\right)^{2}=\left[k\left(k^{2}-1\right)!\right]^{2}$.
Finalement, pour tout $k \geqslant 2$ entier, $(m, n)=\left(k^{2}, k^{2}-1\right)$ convient, ce qui nous fournit bien une infinité de couples solutions.
Commentaire des correcteurs: L'ensemble des élèves ayant abordé l'exercice l'ont parfaitement réussi, même si certains détaillaient parfois plus que nécessaire.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
ff3dbf43-7d89-516e-8559-722f3fb1a5b1
| 607,433
|
Anna and Elie are playing a game. They are both given the same set $A$ consisting of a finite number of distinct positive integers. Anna secretly chooses an integer $a \in A$. If Elie chooses an integer $b$ (not necessarily in $\mathcal{A}$) and gives it to Anna, Anna gives him the number of positive divisors of $ab$. Show that Elie can choose $b$ in such a way as to surely determine the integer chosen by Anna.
|
Let P be the finite set of prime numbers dividing at least one element of $A$ and $n \geqslant 1$ the largest integer such that there exists $a \in A$ and $p \in P$ such that $p^{n} \mid a$. We can replace A by the set of integers $m$ whose prime factors are all in $P$ and such that for all $p \in P$, $v_{p}(m) \leqslant n$. Elie proposes an integer $b$ of the form $\prod_{p \in P} p^{b_{p}}$. If Anna has chosen the integer $a$, then she gives Elie the integer $\prod_{p \in P}\left(b_{p}+v_{p}(a)+1\right)$. It is therefore sufficient for Elie to choose the $b_{p}$ so that all the $\prod_{p \in P}\left(b_{p}+a_{p}\right)$ are distinct for all possible choices of $a_{p}$ between 1 and $n+1$ for each $p \in P$.
We propose two solutions.
## First Method:
The idea of this construction is to force the factorizations into products of prime factors of the $\prod_{p}\left(b_{p}+a_{p}\right)$ to be different for all possible choices of the $a_{p}$. We want to ensure that each $b_{p}+i$ for $1 \leqslant i \leqslant n+1$ has a "distinctive" prime divisor, which appears only in the prime factorization of $b_{p}+i$, never in that of another $b_{q}+j$.
Formally, we choose, for each $p \in P$ and each $1 \leqslant i \leqslant n+1$, distinct prime numbers $Q_{p, i}>n+1$. We construct the $b_{p}$ using the Chinese Remainder Theorem: for each $q \in P$ distinct from $p$ and for each $1 \leqslant i \leqslant n+1, Q_{q, i} \mid b_{p}$, and for each $1 \leqslant i \leqslant n+1, b_{p} \equiv -i \pmod{Q_{p, i}}$.
With this construction, if $q, p \in P$ and $1 \leqslant i, j \leqslant n+1$, then $Q_{q, j} \mid b_{p}+i$ if and only if $i=j$ and $p=q$.
In particular, given $1 \leqslant a_{p} \leqslant n+1$ for each $p \in P$, if $q \in P, \Pi=\prod_{p \in P}\left(b_{p}+a_{p}\right)$ is divisible by $Q_{q, j}$ if and only if $j=a_{q}$: thus $\Pi$ determines the family $\left(a_{p}\right)$.
## Second Method:
The first construction was very arithmetic and used prime numbers. The one we present now comes more from an idea of "size". The idea is that if we take enormous $b_{p}$, the product $\prod_{p}\left(b_{p}+a_{p}\right)$ will resemble the writing of a certain number in a certain base, whose digits will give the $a_{i}$.
Let's move on to the actual construction. The problem as we have reformulated it no longer uses the fact that $P$ consists of prime numbers: we renumber its elements as $1, \ldots, r$. We show that for $N>(n+1)^{r}$, $b_{i}=N^{2^{i}}$ works. Indeed, in this case, we see that the expansion of $\Pi=\prod_{i=1}^{r}\left(N^{2^{i}}+a_{i}\right)$ writes a number in base $N$ whose digit before $N^{2^{i}-2^{i}}$ is exactly $a_{i}$: thus $\Pi$ determines the family of the $\left(a_{i}\right)$.
Comment from the graders: The problem was little addressed and poorly solved. The main issue is that some show how, if one fixes $a$ and $c$, to choose a $b$ so that $ba$ and $bc$ do not have the same number of divisors in a correct manner, then claim that the generalization is well done by iterating. It turns out that this part is completely false: if there are initially three numbers $a, c, e$, one can choose a $b$ so that $ab$ and $bc$ do not have the same number of divisors. But it is possible that $cb$ and $eb$ do not have the same number of divisors, in which case if one multiplies by $b'$ so that $cbb'$ and $ebb'$ have a different number of divisors, it is possible that $abb'$ and $cbb'$ have the same number of divisors. This shows that the process can loop and not lead to a solution: the problem therefore did not reduce to this particular case!
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Anna et Elie jouent à un jeu. On leur donne à tous les deux le même ensemble $A$ composé d'un nombre fini d'entiers strictement positifs et distincts. Anna choisit un entier $a \in A$ secrètement. Si Elie choisit un entier b (pas forcément dans $\mathcal{A}$ ) et le donne à Anna, Anna lui donne le nombre de diviseurs strictement positifs de ab . Montrer que Elie peut choisir b de sorte à retrouver à coup sur l'entier choisi par Anna.
|
Notons P l'ensemble fini des nombres premiers divisant au moins un élément de $A$ et $n \geqslant 1$ le plus grand entier tel qu'il existe $a \in A$ et $p \in P$ tels que $p^{n} \mid a$. On peut remplacer A par l'ensemble des entiers $m$ dont les facteurs premiers sont tous dans $P$ et tels que pour tout $p \in P$, $v_{p}(m) \leqslant n$. Elie propose un entier $b$ de la forme $\prod_{p \in P} p^{b_{p}}$. Si Anna a choisi l'entier $a$, alors elle donne à Elie l'entier $\prod_{p \in P}\left(b_{p}+v_{p}(a)+1\right)$. Il suffit donc pour Elie de choisir les $b_{p}$ de sorte que tous les $\prod_{p \in P}\left(b_{p}+a_{p}\right)$ soient deux à deux distincts, pour tous les choix possibles de $a_{p}$ entre 1 et $n+1$ pour chaque $p \in P$.
On propose deux solutions.
## Première méthode :
L'idée de cette construction est de forcer les factorisations en produits de facteurs premiers des $\prod_{p}\left(b_{p}+a_{p}\right)$ à être différentes pour tous les choix possibles des $a_{p}$. On veut faire en sorte que chaque $b_{p}+i$ pour $1 \leqslant i \leqslant n+1$ possède un diviseur premier «distinctif», qui n'apparaît que dans la décomposition en produit de facteurs premiers de $b_{p}+i$, jamais dans celle d'un autre $b_{q}+j$.
Formellement, on choisit, pour chaque $p \in P$ et chaque $1 \leqslant i \leqslant n+1$, des nombres premiers deux à deux distincts $Q_{p, i}>n+1$. On construit les $b_{p}$ grâce au théorème chinois : pour chaque $q \in P$ distinct de $p$ et pour chaque $1 \leqslant i \leqslant n+1, Q_{q, i} \mid b_{p}$, et pour chaque $1 \leqslant i \leqslant n+1, b_{p} \equiv-\mathfrak{i}\left[Q_{p, i}\right]$.
Avec cette construction, si $q, p \in P$ et $1 \leqslant i, j \leqslant n+1$, alors $Q_{q, j} j b_{p}+i$ si et seulement si $i=j$ et $\mathrm{p}=\mathrm{q}$.
En particulier, étant donnés des $1 \leqslant a_{p} \leqslant n+1$ pour chaque $p \in P$, si $q \in P, \Pi=\prod_{p \in P}\left(b_{p}+a_{p}\right)$ est divisible par $Q_{q, j}$ si et seulement si $j=a_{q}$ : ainsi $\Pi$ détermine la famille $\left(a_{p}\right)$.
## Deuxième méthode :
La première construction était très arithmétique et utilisait des nombres premiers. Celle qu'on présente maintenant vient plus d'une idée de "taille". L'idée est que si l'on prend de gigantesques $b_{p}$, le produit $\prod_{p}\left(b_{p}+a_{p}\right)$ ressemblera à l'écriture d'un certain nombre en une certaine base, dont les chiffres donneront les $a_{i}$.
Passons à la construction proprement dite. Le problème tel que nous l'avons reformulé n'utilise plus le fait que $P$ soit constitué de nombres premiers : on renumérote ses éléments en $1, \ldots, r$. Montrons que pour $N>(n+1)^{r}$, $b_{i}=N^{2^{i}}$ convient. En effet, dans ce cas, on voit que le développement de $\Pi=\prod_{i=1}^{r}\left(N^{2^{i}}+a_{i}\right)$ écrit un nombre en base $N$ dont le chiffre devant $N^{2+1}-2-2^{i}$ est exactement $a_{i}$ : ainsi $\Pi$ détermine la famille des $\left(a_{i}\right)$.
Commentaire des correcteurs : Le problème a été peu abordé, et peu réussi. Le principal problème est que certains montrent comment si on fixe a et $c$, choisir un $b$ pour que ba n'ait pas le même nombre de diviseur que bc de manière correcte, puis prétendent que la généralisation se fait bien en itérant. Il s'avère que cette partie est totalement fausse : s'il y a au départ trois nombres $a, c, e$, on peut choisi un b pour que $a b$ et $b c$ n'ait pas le même nombre de diviseur. Mais il est possible que $c b$ et $e b n$ 'ait pas le même nombre de diviseur, dans ce cas si on multiplie par $\mathrm{b}^{\prime}$ pour que $\mathrm{cbb}^{\prime}$ et $\mathrm{ebb}^{\prime}$ ait un nombre différent de diviseur, il est possible que $\mathrm{abb}^{\prime}$ et $\mathrm{cbb}^{\prime}$ ait le même nombre de diviseur. Cela montre que le procédé peut boucler et ne pas aboutir: le problème ne se résumait donc pas à ce cas particulier!
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "\nSolution de l'exercice 14"
}
|
7f01e876-dee1-523f-99f0-a4f9bf8be1e3
| 607,435
|
For all integers $n \geqslant 1$, we define $u_{n}=1!+2!+\ldots+n!$. Show that there are infinitely many prime numbers dividing at least one of the terms of the sequence ( $\mathfrak{u}_{n}$ ).
|
Suppose the opposite: then there exist prime numbers $p_{1}<\ldots<p_{\mathrm{r}}$ such that for all $n \geqslant 1, u_{n}:=1+2!+\ldots+n!$ is the product of the $p_{i}^{a_{i}(n)}$, where the $a_{i}(n)$ are positive integers.
If $n \geqslant 1$ is such that $a_{i}(n)<v_{p_{i}}((n+1)!)$, then
$$
\mathfrak{a}_{\mathfrak{i}}(n+1)=v_{p_{\mathfrak{i}}}\left(u_{n+1}\right)=v_{p_{\mathfrak{i}}}\left(u_{n}+(n+1)!\right)=v_{p_{\mathfrak{i}}}\left(u_{n}\right)=a_{i}(n)
$$
In particular, $a_{i}(n+1)<v_{p_{i}}((n+2)!)$. In particular, either $a_{i}(n) \geqslant \nu_{p_{\mathfrak{i}}}((n+1)!)$ for all $n$, or $\mathfrak{a}_{\mathfrak{i}}(\mathfrak{n})$ is constant from a certain rank.
In particular, by renaming and grouping the $p_{i}$, we have integers $\mathrm{N} \geqslant 1, \mathrm{C} \geqslant 1$ and prime numbers $q_{1}<\ldots<q_{s}$ not dividing $C$ such that for all $n>N, u_{n}=C \prod_{i=1}^{s} q_{i}^{b_{i}(n)}$ and $b_{i}(n) \geqslant$ $v_{q_{i}}((n+1)!)$.
Now let $n>N+C+1$ such that $n+1$ is divisible by the product of the $q_{i}$. Then $u_{n}=u_{n-1}+n!$ and $v_{q_{i}}\left(u_{n}\right)=b_{i}(n) \geqslant v_{q_{i}}((n+1)!)>v_{q_{i}}(n!)$, so $v_{q_{i}}\left(u_{n-1}\right)=v_{q_{i}}(n!)$. On the other hand, if $p \mid C$, $v_{p}\left(u_{n-1}\right)=v_{p}(C) \leqslant v_{p}(\mathfrak{n}!)$, so $u_{n-1} \mid n!$.
It remains to show that for all $n$ large enough, $u_{n}$ does not divide $(n+1)!$.
Indeed, if $n \geqslant 2, n u_{n}>n \cdot n!+n \cdot(n-1)!=(n+1) \cdot n!=(n+1)!$. On the other hand, if $n \geqslant 4$,
$$
\begin{aligned}
(n-1) \mathfrak{u}_{n} & =(n-1) n!+(n-1)(n-1)!+(n-1)(n-2)!+(n-1) \sum_{k=1}^{n-3} k! \\
& =n \cdot n!+(n-1)(n-3) \cdot(n-3)!<(n+1) \cdot n! \\
& =(n+1)!
\end{aligned}
$$
Comment from the correctors: The problem was little addressed and the majority of the returned copies solved it correctly, sometimes in a different way from the solution. The idea was, for each prime divisor $p$ of a term of the sequence, to control $v_{p}\left(u_{n}\right)$ for $n$ large enough by using the fact that $\mathfrak{u}_{n}-\mathfrak{u}_{n-1}=n!$ (which also appeared in attempts that did not succeed) and by choosing the value of $n$ judiciously (all copies that noticed this solved the problem).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $n \geqslant 1$, on pose $u_{n}=1!+2!+\ldots+n!$. Montrer qu'il existe une infinité de nombres premiers divisant au moins l'un des termes de la suite ( $\mathfrak{u}_{n}$ ).
|
Supposons l'inverse : alors il existe des nombres premiers $p_{1}<\ldots<p_{\mathrm{r}}$ tels que pour tout $n \geqslant 1, u_{n}:=1+2!+\ldots+n!$ soit le produit des $p_{i}^{a_{i}(n)}$, où les $a_{i}(n)$ sont des entiers positifs.
Si $n \geqslant 1$ est tel que $a_{i}(n)<v_{p_{i}}((n+1)!)$, alors
$$
\mathfrak{a}_{\mathfrak{i}}(n+1)=v_{p_{\mathfrak{i}}}\left(u_{n+1}\right)=v_{p_{\mathfrak{i}}}\left(u_{n}+(n+1)!\right)=v_{p_{\mathfrak{i}}}\left(u_{n}\right)=a_{i}(n)
$$
En particulier, $a_{i}(n+1)<v_{p_{i}}((n+2)!)$. En particulier, ou bien $a_{i}(n) \geqslant \nu_{p_{\mathfrak{i}}}((n+1)!)$ pour tout $n$, ou bien $\mathfrak{a}_{\mathfrak{i}}(\mathfrak{n})$ est constante à partir $\mathrm{d}^{\prime}$ un certain rang.
En particulier, en renommant et regroupant les $p_{i}$, on dispose d'entiers $\mathrm{N} \geqslant 1, \mathrm{C} \geqslant 1$ et de nombres premiers $q_{1}<\ldots<q_{s}$ ne divisant pas $C$ tels que pour tout $n>N, u_{n}=C \prod_{i=1}^{s} q_{i}^{b_{i}(n)}$ et $b_{i}(n) \geqslant$ $v_{q_{i}}((n+1)!)$.
Soit maintenant $n>N+C+1$ tel que $n+1$ soit divisible par le produit des $q_{i}$. Alors $u_{n}=u_{n-1}+n$ ! et $v_{q_{i}}\left(u_{n}\right)=b_{i}(n) \geqslant v_{q_{i}}((n+1)!)>v_{q_{i}}(n!)$, donc $v_{q_{i}}\left(u_{n-1}\right)=v_{q_{i}}(n!)$. D'autre part, si $p \mid C$, $v_{p}\left(u_{n-1}\right)=v_{p}(C) \leqslant v_{p}(\mathfrak{n}!)$, donc $u_{n-1} \mid n!$.
Il reste à montrer que pour tout $n$ assez grand, $u_{n}$ ne divise pas $(n+1)!$.
En effet, si $n \geqslant 2, n u_{n}>n \cdot n!+n \cdot(n-1)!=(n+1) \cdot n!=(n+1)!$. D'autre part, si $n \geqslant 4$,
$$
\begin{aligned}
(n-1) \mathfrak{u}_{n} & =(n-1) n!+(n-1)(n-1)!+(n-1)(n-2)!+(n-1) \sum_{k=1}^{n-3} k! \\
& =n \cdot n!+(n-1)(n-3) \cdot(n-3)!<(n+1) \cdot n! \\
& =(n+1)!
\end{aligned}
$$
Commentaire des correcteurs : Le problème a été peu abordé et la majorité des copies rendues l'a résolu correctement, parfois d'une manière différente de celle du corrigé. L'idée était, pour chaque diviseur premier $p$ d'un terme de la suite, de contrôler $v_{p}\left(u_{n}\right)$ pour $n$ assez grand en utilisant le fait que $\mathfrak{u}_{n}-\mathfrak{u}_{n-1}=n$ ! (ce qui est aussi apparu dans des tentatives n'ayant pas abouti) et en choisissant judicieusement la valeur de $n$ (les copies ayant remarqué cela ont toutes résolu le problème).
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 15.",
"solution_match": "\nSolution de l'exercice 15"
}
|
f321ff27-e134-5e40-958b-eb0422d5d624
| 607,436
|
Let $n \geqslant 2$ and $p$ be an odd prime number. Let $u$ be the set of positive integers less than or equal to $p^{n}$ and coprime with $p$, and let $N=|U|$. Show that there exists a permutation $a_{1}, \ldots, a_{N}$ of the elements of $U$ such that $\sum_{k=1}^{N} a_{k} a_{k+1}$ (with $a_{N+1}=a_{1}$) is divisible by $p^{n-1}$ but not by $p^{n}$.
|
We start by treating the case $p=3$, whose solution is different. Let $\mathrm{g} \in \mathrm{U}$ be a generator modulo $p^{n}$, and we set $a_{i}=g^{i-1}\left(\bmod p^{n}\right)$. Since $g^{2}-1$ is divisible by 3, the considered sum $S$ satisfies $\left(g^{2}-1\right) S \equiv \sum_{i=1}^{N}\left(g^{2 i+1}-g^{2 i-1}\right) \equiv g\left(g^{2 N}-1\right)\left[p^{n+1}\right]$. Therefore, for $v_{p}(S)=n-1$, it is necessary and sufficient that $v_{p}\left(g^{2 N}-1\right)=n$ (since $g$ is coprime with $p$). Since $g^{N} \equiv 1\left[p^{n}\right]$ (by Euler-Fermat), it suffices to show that $v_{p}\left(g^{N}-1\right)=n$. But by LTE, $v_{p}\left(g^{N}-1\right)=v_{p}\left(g^{N / p}-1\right)+1<n+1$, so $v_{p}\left(g^{N}-1\right) \leqslant n$, which means $v_{p}\left(g^{N}-1\right)=n$, concluding the proof.
Now suppose $p>3$: Let $b_{0}, \ldots, b_{m-1} \in U$ be integers representing each congruence class modulo $p^{n-1}$ exactly once, so $m=N / p=p^{n-2}(p-1)$ (and we set $b_{m}=b_{0}$). We consider the permutation
$$
\begin{aligned}
& \mathrm{b}_{0}, \mathrm{~b}_{0}+\mathrm{p}^{\mathrm{n}-1}, \mathrm{~b}_{0}+2 p^{n-1}, \ldots, \mathrm{~b}_{0}+(p-1) p^{n-1} \\
& \mathrm{~b}_{1}, \mathrm{~b}_{1}+\mathrm{p}^{n-1}, \ldots, \mathrm{~b}_{1}+(p-1) p^{n-1} \\
& \mathrm{~b}_{2}, \ldots, b_{m-1}, \ldots, b_{m-1}+(p-1) p^{n-1}
\end{aligned}
$$
(all additions are performed modulo $\mathrm{p}^{\mathrm{n}}$).
Then the corresponding sum $S$ is congruent modulo $p^{n}$ to
$$
S_{1}=\sum_{i=0}^{m-1} b_{i} b_{i+1}+\sum_{i=0}^{m-1}(p-1) p^{n-1} b_{i}+\sum_{i=0}^{m-1} \sum_{k=0}^{p-2} b_{i} p^{n-1}(2 k+1)+(p-1) \sum_{i=0}^{m-1} b_{i}^{2}
$$
. Since the sum of the $b_{i}$ is divisible by $p$ and the sum of the $b_{i}^{2}$ by $p^{n-1}, S \equiv S_{2}\left[p^{n}\right]$, where $S_{2}=$ $\sum_{i=0}^{\mathfrak{m}-1} b_{i} b_{i+1}-\sum_{i=0}^{m-1} b_{i}^{2}$.
Let then $g \in U$ be a primitive root modulo $p^{n}:$ take $b_{i}=g^{i}\left(\bmod p^{n}\right)$. Then $(g+1) S_{2} \equiv$ $(g+1) \sum_{i=0}^{m-1}\left(g^{2 i+1}-g^{2 i}\right) \equiv\left(g^{2 m}-1\right)\left[p^{n}\right]$. By LTE, $v_{p}\left(g^{2 m}-1\right) \geqslant 1+v_{p}\left(\frac{2 m}{p-1}\right)=n-1$ (since $p-1|m, p| g^{p-1}-1$ by Fermat, and $N=p^{n-1}(p-1)$, but since $2 m<N, v_{p}\left(g^{2 m}-1\right)<n$, so $v_{p}\left(g^{2 m}-1\right)=n-1$. Moreover, since $p>3, g+1$ is coprime with $p$, and thus $v_{p}\left(S_{2}\right)=n-1$, hence $\nu_{p}(S)=n-1$.
$\underline{\text { Comment from the graders: The problem was very little addressed, perhaps due to the somewhat intimidating form of its statement. It is important, when faced with such problems, not to be intimidated and to continue thinking normally. All students who submitted a solution found a correct one, generally simpler than the construction proposed in the solution. In fact, the most natural idea (taking the numbers in increasing order) provided a solution, and it is surprising that so few students noticed or even tried it.}}$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $n \geqslant 2$ et $p$ un nombre premier impair. Soit $u$ l'ensemble des entiers positifs inférieurs ou égaux à $p^{n}$ et premiers avec $p$ et soit $N=|U|$. Montrer qu'il existe une permutation $a_{1}, \ldots, a_{N}$ des éléments de $U$ telle que $\sum_{k=1}^{N} a_{k} a_{k+1}$ (avec $a_{N+1}=a_{1}$ ) soit divisible par $p^{n-1}$ mais pas par $\mathrm{p}^{\mathrm{n}}$.
|
On commence par traiter le cas $p=3$, dont la solution est différente. Soit $\mathrm{g} \in \mathrm{U}$ un générateur modulo $p^{n}$, on pose $a_{i}=g^{i-1}\left(\bmod p^{n}\right)$. Comme $g^{2}-1$ est divisible par 3 , la somme considérée $S$ vérifie $\left(g^{2}-1\right) S \equiv \sum_{i=1}^{N}\left(g^{2 i+1}-g^{2 i-1}\right) \equiv g\left(g^{2 N}-1\right)\left[p^{n+1}\right]$. Donc pour que $v_{p}(S)=n-1$, il faut et suffit que $v_{p}\left(g^{2 N}-1\right)=n\left(g\right.$ est premier avec $p$ ). Puisque $g^{N} \equiv 1\left[p^{n}\right]$ (par Euler-Fermat), il suffit de montrer que $v_{p}\left(g^{N}-1\right)=n$. Mais par LTE, $v_{p}\left(g^{N}-1\right)=v_{p}\left(g^{N / p}-1\right)+1<n+1$, donc $v_{p}\left(g^{N}-1\right) \leqslant n$, de sorte que $v_{p}\left(g^{N}-1\right)=n$, ce qui conclut.
Supposons maintenant $p>3$ : Soient $b_{0}, \ldots, b_{m-1} \in U$ des entiers représentant exactement une fois chaque classe de congruence modulo $p^{n-1}$, ainsi $m=N / p=p^{n-2}(p-1)$ (et on pose $b_{m}=b_{0}$ ). On considère la permutation
$$
\begin{aligned}
& \mathrm{b}_{0}, \mathrm{~b}_{0}+\mathrm{p}^{\mathrm{n}-1}, \mathrm{~b}_{0}+2 p^{n-1}, \ldots, \mathrm{~b}_{0}+(p-1) p^{n-1} \\
& \mathrm{~b}_{1}, \mathrm{~b}_{1}+\mathrm{p}^{n-1}, \ldots, \mathrm{~b}_{1}+(p-1) p^{n-1} \\
& \mathrm{~b}_{2}, \ldots, b_{m-1}, \ldots, b_{m-1}+(p-1) p^{n-1}
\end{aligned}
$$
(les additions sont toujours à effectuer modulo $\mathrm{p}^{\mathrm{n}}$ ).
Alors la somme correspondante $S$ est congrue modulo $p^{n}$ à
$$
S_{1}=\sum_{i=0}^{m-1} b_{i} b_{i+1}+\sum_{i=0}^{m-1}(p-1) p^{n-1} b_{i}+\sum_{i=0}^{m-1} \sum_{k=0}^{p-2} b_{i} p^{n-1}(2 k+1)+(p-1) \sum_{i=0}^{m-1} b_{i}^{2}
$$
. Comme la somme des $b_{i}$ est divisible par $p$ et la somme des $b_{i}^{2}$ par $p^{n-1}, S \equiv S_{2}\left[p^{n}\right]$, où $S_{2}=$ $\sum_{i=0}^{\mathfrak{m}-1} b_{i} b_{i+1}-\sum_{i=0}^{m-1} b_{i}^{2}$.
Soit alors $g \in U$ une racine primitive modulo $p^{n}:$ prenons $b_{i}=g^{i}\left(\bmod p^{n}\right)$. Alors $(g+1) S_{2} \equiv$ $(g+1) \sum_{i=0}^{m-1}\left(g^{2 i+1}-g^{2 i}\right) \equiv\left(g^{2 m}-1\right)\left[p^{n}\right]$. D'après LTE, $v_{p}\left(g^{2 m}-1\right) \geqslant 1+v_{p}\left(\frac{2 m}{p-1}\right)=n-1$ (puisque $p-1|m, p| g^{p-1}-1$ par Fermat, et $N=p^{n-1}(p-1)$, mais comme $2 m<N, v_{p}\left(g^{2 m}-1\right)<n$, donc $v_{p}\left(g^{2 m}-1\right)=n-1$. De plus, puisque $p>3, g+1$ est premier à $p$, et donc $v_{p}\left(S_{2}\right)=n-1$, d'où $\nu_{p}(S)=n-1$.
$\underline{\text { Commentaire des correcteurs : Le problème a été très peu abordé, sans doute à cause de la forme quelque }}$ peu intimidante de son énoncé. Il est important, devant de tels problèmes, de ne pas se laisser impressionner et continuer à réfléchir normalement. Tous les élèves ayant rendu une copie ont trouvé une solution correcte, en général plus simple que la construction proposée dans le corrigé. En fait, l'idée la plus naturelle (prendre les nombres dans l'ordre croissant) fournissait une solution, et il est étonnant qu'aussi peu d'élèves l'aient remarqué ou même essayé.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 16.",
"solution_match": "## Solution de l'exercice 16"
}
|
8b5c266a-abc2-5c04-a696-c5675619a63b
| 607,437
|
Let $\left(a_{n}\right)_{n \geqslant 1}$ be a sequence of strictly positive integers such that $a_{1}$ and $a_{2}$ are coprime and, for all $n \geqslant 1, a_{n+2}=a_{n} a_{n+1}+1$. Show that for any integer $m>1$, there exists $n>m$ such that $a_{m}^{m} \mid a_{n}^{n}$. Is the result still true when $m=1$?
|
First, $a_{n}>0$ for all $n>0$.
We start with an observation: let $n>m$ be very large (say, $n>(m+1)\left(a_{m}+1\right)$). Then $a_{m}^{m} \mid a_{n}^{n}$ if and only if for each prime number $p\left|a_{m}, p\right| a_{n}$. This idea justifies the lemma that follows:
Lemma: Let $\left(u_{n}\right)_{n \geqslant 0}$ be the sequence modulo a prime number $p$ such that $u_{0}=0, u_{1}=1$ and for all $n \geqslant 0$, $u_{n+2}=u_{n} u_{n+1}+1$. Then $u$ is periodic.
Proof: Let $v_{n}=\left(u_{n}, u_{n+1}\right)$; then $u$ is periodic as soon as $v$ is periodic. Since $v_{n+1}$ depends only on $\nu_{n}$, $v$ is periodic as soon as there exists $N \geqslant 1$ such that $\nu_{N}=v_{0}$. If $N \geqslant 1$ is such that $u_{N}=0$, then the recurrence relation shows that $u_{N+1}=1=u_{1}$ and thus $v_{N}=v_{0}$. Therefore, to show that $u$ is periodic, it suffices to show that there exists $N \geqslant 1$ such that $u_{N}=0$.
Suppose, then, that the only integer $n$ such that $u_{n}=0$ is $n=0$. Then, since $v$ takes values in a finite set, there exists an integer $\mathrm{n} \geqslant 0$ minimal such that there exists an integer $m>n$ such that $v_{n}=v_{m}$. In particular, $u_{m}=u_{n}$ and $m \neq 0$, so $u_{m} \neq 0$, and thus $u_{n} \neq 0$ and thus $n>0$. Then $m+1>n+1 \geqslant 2$ and $u_{n+1}=u_{m+1}$, so $u_{n-1} u_{n}+1=u_{m-1} u_{m}+1$, so $u_{n}\left(u_{n-1}-u_{m-1}\right)=0$, and thus, since $u_{n} \neq 0$, $u_{n-1}=u_{m-1}$, so that $v_{m-1}=v_{n-1}$, which contradicts the minimality of $n$.
Let's return to our proof. When $m>1$, for each prime factor $p$ of $a_{m}, a_{m+1}=a_{m-1} a_{m}+1 \equiv 1[p],\left(a_{m+n}(\bmod p)\right)_{n \geqslant 0}$ satisfies the hypotheses of the lemma, so there exists $N_{p} \geqslant 1$ such that for all $n \geqslant 0, a_{m+n} \equiv a_{m+n+N_{p}}[p]$.
Let $N$ be the product of the $N_{p}$ (where $p$ runs through the prime factors of $a_{m}$): then, if $n \geqslant 0$, every prime divisor $p$ of $a_{m}$ divides $a_{m+n N}$. In particular, if $n \geqslant m a_{m}, a_{m}^{m} \mid a_{m+n N}^{m+n N}$ (because if $p \mid a_{m}$, $\left.v_{p}\left(a_{m+n N}^{m+n N}\right) \geqslant m+n N \geqslant m a_{m} \geqslant v_{p}\left(a_{m}^{m}\right)\right)$.
The result is false for $\mathrm{m}=1$: take $\mathrm{a}_{1}=155, \mathrm{a}_{2}$ congruent to 4 modulo 5 and congruent to 29 modulo 31. We then verify that $a_{n}$ is divisible by 5 if and only if $n=1$ and $n \equiv 4[7]$, while $a_{n}$ is divisible by 31 if and only if $n=1$ or $n \equiv 5[7]$, so if $n>1, a_{n}$ is never divisible by 5 and 31, and thus 155 does not divide $a_{n}^{n}$.
Comment from the graders: The problem was little addressed and all the copies managed to handle the case $\mathrm{m}>1$, essentially by the method of the solution. Most students detected that the case $m=1$ did not work and provided counterexamples, but some left completely implicit the point where the hypothesis $m>1$ was used. In a problem, the hypotheses must be used; if the statement draws attention to one of them, it is all the more necessary to carefully note the point where one uses it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\left(a_{n}\right)_{n \geqslant 1}$ une suite d'entiers strictement positifs telle que $a_{1}$ et $a_{2}$ soient premiers entre eux et, pour tout $n \geqslant 1, a_{n+2}=a_{n} a_{n+1}+1$. Montrer que pour tout entier $m>1$, il existe $n>m$ tel que $a_{m}^{m} \mid a_{n}^{n}$. Le résultat est-il encore vrai lorsque $m=1$ ?
|
D'abord, $a_{n}>0$ pour tout $n>0$.
On commence par une observation : soit $n>m$ très grand (disons, $n>(m+1)\left(a_{m}+1\right)$ ). Alors $a_{m}^{m} \mid a_{n}^{n}$ si et seulement si pour chaque nombre premier $p\left|a_{m}, p\right| a_{n}$. Cette idée justifie le lemme qui va suivre :
Lemme : soit $\left(u_{n}\right)_{n \geqslant 0}$ la suite modulo un nombre premier $p$ telle que $u_{0}=0, u_{1}=1$ et pour tout $n \geqslant 0$, $u_{n+2}=u_{n} u_{n+1}+1$. Alors $u$ est périodique.
Preuve : soit $v_{n}=\left(u_{n}, u_{n+1}\right)$; alors $u$ est périodique dès que $v$ est périodique. Comme $v_{n+1}$ dépend uniquement de $\nu_{n}, v$ est périodique dès qu'il existe $N \geqslant 1$ tel que $\nu_{N}=v_{0}$. Si $N \geqslant 1$ est tel que $u_{N}=0$, alors la relation de récurrence montre que $u_{N+1}=1=u_{1}$ et donc $v_{N}=v_{0}$. Par conséquent, pour montrer que $u$ est périodique, il suffit de montrer qu'il existe $N \geqslant 1$ tel que $u_{N}=0$.
Supposons donc que le seul entier n tel que $u_{n}=0$ soit $n=0$. Alors comme $v$ est à valeurs dans un ensemble fini, il existe un entier $\mathrm{n} \geqslant 0$ minimal tel qu'il existe un entier $m>n$ tel que $v_{n}=v_{m}$. En particulier, $u_{m}=u_{n}$ et $m \neq 0$, donc $u_{m} \neq 0$, et donc $u_{n} \neq 0$ et donc $n>0$. Alors $m+1>n+1 \geqslant 2$ et $u_{n+1}=u_{m+1}$, donc $u_{n-1} u_{n}+1=u_{m-1} u_{m}+1$, donc $u_{n}\left(u_{n-1}-u_{m-1}\right)=0$, d'où, comme $u_{n} \neq 0$, $u_{n-1}=u_{m-1}$, de sorte que $v_{m-1}=v_{n-1}$, ce qui contredit la minimalité de $n$.
Revenons à notre preuve. Lorsque $m>1$, pour chaque facteur premier $p$ de $a_{m}, a_{m+1}=a_{m-1} a_{m}+1 \equiv$ $1[p],\left(a_{m+n}(\bmod p)\right)_{n \geqslant 0}$ satisfait les hypothèses du lemme, donc il existe $N_{p} \geqslant 1$ tel que que pour tout $n \geqslant 0, a_{m+n} \equiv a_{m+n+N_{p}}[p]$.
Soit $N$ le produit des $N_{p}$ (où $p$ parcourt les facteurs premiers de $a_{m}$ ) : alors, si $n \geqslant 0$, tout diviseur premier $p$ de $a_{m}$ divise $a_{m+n N}$. En particulier, si $n \geqslant m a_{m}, a_{m}^{m} \mid a_{m+n N}^{m+n N}$ (parce que si $p \mid a_{m}$, $\left.v_{p}\left(a_{m+n N}^{m+n N}\right) \geqslant m+n N \geqslant m a_{m} \geqslant v_{p}\left(a_{m}^{m}\right)\right)$.
Le résultat est faux pour $\mathrm{m}=1$ : prenons $\mathrm{a}_{1}=155, \mathrm{a}_{2}$ congru à 4 modulo 5 et congru à 29 modulo 31 . On vérifie alors que $a_{n}$ est divisible par 5 si et seulement si $n=1$ et $n \equiv 4[7]$, alors que $a_{n}$ est divisible par 31 si et seulement si $n=1$ ou $n \equiv 5[7]$, donc si $n>1, a_{n}$ n'est jamais divisible par 5 et 31 , et donc 155 ne divise pas $a_{n}^{n}$.
Commentaire des correcteurs : Le problème a été peu abordé et toutes les copies ont su traiter le cas $\mathrm{m}>1$, essentiellement par la méthode du corrigé. La plupart des élèves ont détecté que le cas $m=1$ ne fonctionnait pas et exhibé des contre-exemples, mais certains ont laissé complètement implicite l'endroit où était utilisée l'hypothèse $m>1$. Dans un problème, les hypothèses doivent être utilisées; si l'énoncé attire l'attention sur l'une d'entre elles, il faut d'autant plus soigneusement relever l'endroit où l'on s'en sert.
|
{
"resource_path": "French/segmented/envois/fr-corrigé.jsonl",
"problem_match": "\nExercice 17.",
"solution_match": "## Solution de l'exercice 17"
}
|
0b5558bf-8981-59f2-8dbf-11f2e29dd7fe
| 607,438
|
ABC is a triangle where all angles are acute. Outside this triangle, we construct three points $X, Y$, and $Z$ satisfying:
- The triangle $A X B$ is isosceles with base $A B$ and the angle $\widehat{A X B}$ is $120^{\circ}$,
- The triangle $B Y C$ is isosceles with base $B C$ and the angle $\widehat{B Y C}$ is $120^{\circ}$,
- The triangle $C Z A$ is isosceles with base $C A$ and the angle $\widehat{C Z A}$ is $60^{\circ}$.
Show that the lines $(X Y)$ and $(B Z)$ are perpendicular.
|
Let's draw the circle centered at $X$ passing through $A$ and $B$, and the circle centered at $Y$ passing through $B$ and $C$, and denote $K$ as their other point of intersection:
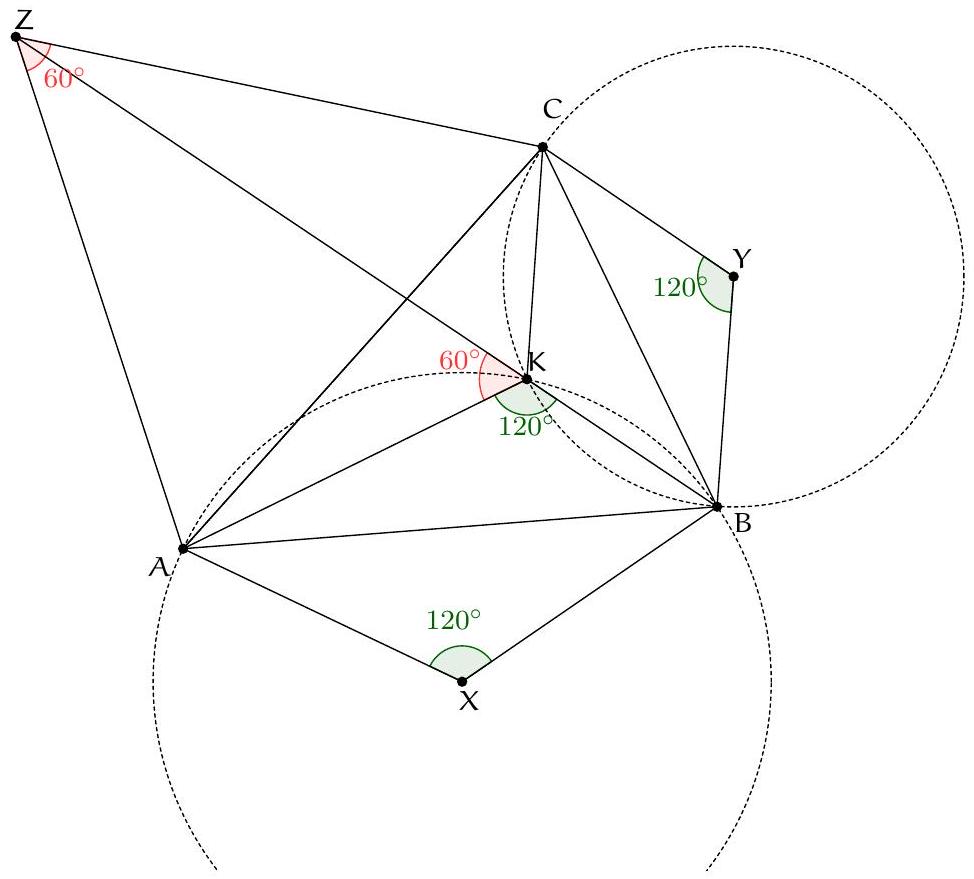
The angle $\widehat{A K B}$ is half of the central angle, and the central angle is the complement of $120^{\circ}$, so $\widehat{A K B}$ is $\frac{240}{2}=120^{\circ}$. Similarly, $\widehat{\mathrm{BKC}}=120^{\circ}$, and consequently, the remaining angle $\widehat{\mathrm{CKA}}=120^{\circ}$. Since $\widehat{C K A}+\widehat{A Z C}=120+60=180^{\circ}$, the points $A, Z, C, K$ are concyclic. Since $A Z=Z C$, the arcs that these two chords define are equal, and the inscribed angles are equal. Thus, $\widehat{A K Z}=\widehat{Z K C}=60^{\circ}$.
Now let's look at the points $B, K$, and $Z: \widehat{B K Z}=120+60=180^{\circ}$, so the three points are collinear, the line (BZ) is the line passing through the two points of intersection of the circles, it is perpendicular to the segment connecting the two centers, i.e., $[\mathrm{XY}]$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
ABC est un triangle dont tous les angles sont aigus. À l'extérieur de ce triangle on construit les trois points $X, Y$ et $Z$ vérifiant :
- Le triangle $A X B$ est isocèle de base $A B$ et l'angle $\widehat{A X B}$ vaut $120^{\circ}$,
- Le triangle BYC est isocèle de base BC et l'angle $\widehat{B Y C}$ vaut $120^{\circ}$,
- Le triangle CZA est isocèle de base CA et l'angle $\widehat{C Z A}$ vaut $60^{\circ}$.
Montrer que les droites $(X Y)$ et (BZ) sont perpendiculaires.
|
Traçons le cercle de centre $X$ qui passe par $A$ et $B$ et celui de centre $Y$ qui passe par $B$ et $C$ et notons K leur autre point d'intersection :

L'angle $\widehat{A K B}$ vaut la moitié de l'angle au centre, et l'angle au centre est le complémentaire de $120^{\circ}$, donc $\widehat{A K B}$ vaut $\frac{240}{2}=120^{\circ}$. De même, $\widehat{\mathrm{BKC}}=120^{\circ}$ et par conséquent, l'angle restant $\widehat{\mathrm{CKA}}=120^{\circ}$. Mais alors, comme $\widehat{C K A}+\widehat{A Z C}=120+60=180^{\circ}$, donc les points $A, Z, C, K$ sont cocycliques. Comme $A Z=Z C$, les arcs que ces deux cordes délimitent sont égaux et les angles inscrits sont égaux. Ainsi, $\widehat{A K Z}=\widehat{Z K C}=60^{\circ}$.
Maintenant regardons les points $B, K$ et $Z: \widehat{B K Z}=120+60=180^{\circ}$, donc les trois points sont alignés, la droite ( BZ ) est la droite qui passe par les deux points d'intersection des cercles, elle est perpendiculaire au segment qui relie les deux centres, ie $[\mathrm{XY}]$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution."
}
|
a0054f2e-1d1d-5101-a4b3-2a2c36158dcc
| 607,440
|
$A B C D$ is a trapezoid in which the sides $A D$ and $B C$ are parallel, $K$ is a point on the side $A B$ and $L$ is a point on the side $C D$. Show that if the angles $\widehat{B A L}$ and $\widehat{C D K}$ are equal then the angles $\widehat{\mathrm{BLA}}$ and $\overline{\mathrm{CKD}}$ are also equal.
|
Suppose the angles $\widehat{\mathrm{BAL}}$ and $\widehat{\mathrm{CDK}}$ have the same value. We will show that the angles $\widehat{\mathrm{KBL}}$ and $\widehat{\mathrm{KCL}}$ are equal (this will imply that triangles KDC and BAL have two identical angles, and thus that $\widehat{\mathrm{BLA}}=\widehat{\mathrm{KCL}}$).
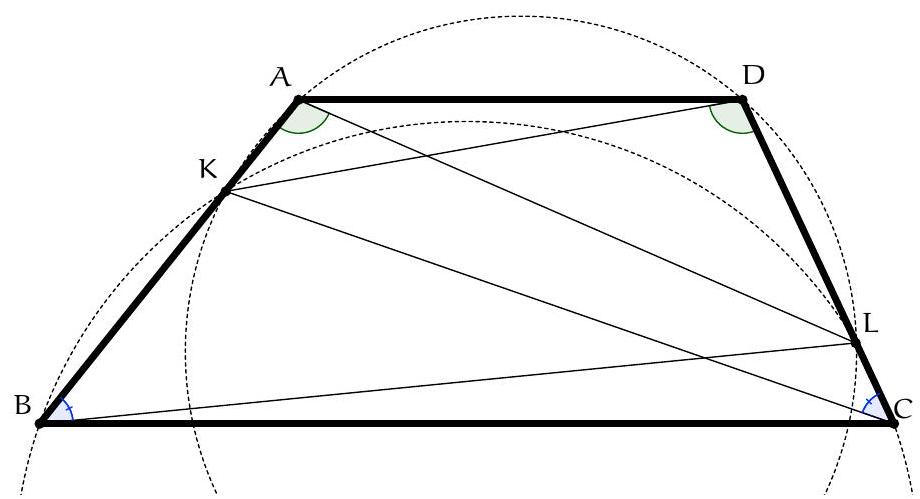
I will first show an interesting point about trapezoids: if we place points $K$ and $L$ on the sides $A B$ and $C D$ such that $A, D, K, L$ are concyclic, then the points $B, C, K, L$ are also concyclic. It suffices to use the property that a quadrilateral is inscribed in a circle if and only if the sum of the opposite angles is $180^{\circ}$, and also that since $A D$ and $B C$ are parallel, $\widehat{A}+\widehat{B}=\widehat{C}+\widehat{D}=180^{\circ}$.
The hypothesis $\widehat{\mathrm{BAL}}=\widehat{\mathrm{CDK}}$ means that $\mathrm{A}, \mathrm{D}, \mathrm{K}, \mathrm{L}$ are concyclic by the inscribed angle theorem, so by the previous result $\mathrm{B}, \mathrm{C}, \mathrm{K}, \mathrm{L}$ are also concyclic and the blue angles are equal.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$A B C D$ est un trapèze dans lequel les côtés $A D$ et $B C$ sont parallèles, $K$ est un point du côté $A B$ et $L$ un point du côté $C D$. Montrer que si les angles $\widehat{B A L}$ et $\widehat{C D K}$ sont égaux alors les angles $\widehat{\mathrm{BLA}}$ et $\overline{\mathrm{CKD}}$ le sont aussi.
|
On suppose les angles $\widehat{\mathrm{BAL}}$ et $\widehat{\mathrm{CDK}}$ ont la même valeur. Nous allons montrer que les angles KBL et KCL sont égaux (ceci impliquera que les triangles KDC et BAL ont deux angles identiques, et donc que $\widehat{\mathrm{BLA}}=\widehat{\mathrm{KCL}}$ ).

Je vais d'abord montrer un point amusant sur les trapèzes : si on place des points $K$ et $L$ sur les côtés $A B$ et $C D$ tels que $A, D, K, L$ soient cocycliques, alors les points $B, C, K, L$ sont aussi cocycliques. Il suffit d'utiliser la propriété qu'un quadrilatère est inscrit dans un cercles ssi la somme des angles opposés vaut $180^{\circ}$, et aussi que comme $A D$ et $B C$ sont parallèles, $\widehat{A}+\widehat{B}=\widehat{C}+\widehat{D}=180^{\circ}$.
L'hypothèse $\widehat{\mathrm{BAL}}=\widehat{\mathrm{CDK}}$ revient à dire que $\mathrm{A}, \mathrm{D}, \mathrm{K}, \mathrm{L}$ cocycliques par le théorème des angles inscrits, donc par le résultat précédent $\mathrm{B}, \mathrm{C}, \mathrm{K}, \mathrm{L}$ sont aussi cocycliques et les angles bleus sont égaux.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution."
}
|
9ff08abf-ec45-5a31-b558-775ca8fbc633
| 607,441
|
ABC is a triangle where all angles are acute. Let H be the foot of the altitude from C and K the midpoint of side AC. Suppose that $B K = C H$ and that the angles $\widehat{\mathrm{KBC}}$ and $\widehat{\mathrm{HCB}}$ are equal. Show that triangle ABC is equilateral.
|
Here is the figure:
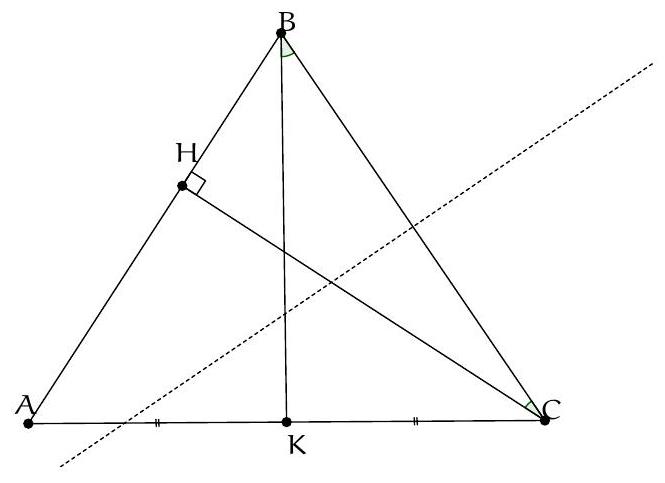
Now consider the perpendicular bisector of $[\mathrm{BC}]$ (drawn as dashed lines in the figure) and the symmetry with respect to this axis. It is evident that by this symmetry, $B$ becomes $C$ and vice versa. Let $A^{\prime}$ be the image of $A$ under the symmetry. The assumptions that all angles are acute, $\mathrm{BK}=\mathrm{CH}$, and $\widehat{\mathrm{KBC}}=\widehat{\mathrm{HCB}}$ imply that $K$ is the image of $H$ under the symmetry. Since $A$ is the intersection of $B H$ and $C K$, $A^{\prime}$ is the intersection of the image of $B H$ (i.e., $C K$) and the image of $C K$ (i.e., $B H$), so $A^{\prime}=A$, $A$ is on the perpendicular bisector of $B C$, and the triangle is isosceles at $A$.
But we are not done yet. Since $\mathrm{CH} \mapsto \mathrm{BK}$ and $\mathrm{BA} \mapsto \mathrm{CA}$, the right angle is preserved, and $BK$ is both an altitude and a median. Therefore, the triangle is also isosceles at $B$, making it equilateral.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
ABC est un triangle dont tous les angles sont aigus. Soit respectivement H le pied de la hauteur de ce triangle issue de $C$ et K le milieu du côté $A C$. On suppose que $B K=C H$ et que les angles $\widehat{\mathrm{KBC}}$ et $\widehat{\mathrm{HCB}}$ sont égaux. Montrer que le triangle ABC est équilatéral.
|
Voici la figure :

Maintenant considérons la médiatrice de $[\mathrm{BC}]$ (dessinée en pointillés sur la figure) et la symétrie par rapport à cet axe. Il est évident que par cette symétrie $B$ devient $C$ et vice-versa. Appelons $A^{\prime}$ l'image de $A$ par la symétrie. Les hypothèses que tous les angles sont aigus, $\mathrm{BK}=\mathrm{CH}$ et $\widehat{\mathrm{KBC}}=\widehat{\mathrm{HCB}}$ impliquent que $K$ est l'image de $H$ par la symétrie. Mais comme $A$ est l'intersection de $B H$ et $C K$, $A^{\prime}$ est l'intersection de l'image de $B H$ (c-à-d $C K$ ) et de l'image de $C K\left(c-a ̀-d B H\right.$ ), donc $A^{\prime}=A$, $A$ est sur la médiatrice de $B C$ et le triangle est isocèle en $A$.
Mais nous n'avons pas fini, comme $\mathrm{CH} \mapsto \mathrm{BK}$ et $\mathrm{BA} \mapsto \mathrm{CA}$, l'angle droit est conservé, et BK est à la fois une hauteur et une médiane. Donc le triangle est aussi isocèle en $B$, il est donc équilatéral.
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution."
}
|
fcf39288-f809-569d-bc1f-1172f3752111
| 607,442
|
ABCD is a rectangle and $M$ is a point inside this rectangle. Show that the area of this rectangle is less than or equal to the sum $A M \times C M + B M \times D M$ ( $A M \times C M$ denotes the product of the lengths of the segments $A M$ and $C M$, similarly for $B M \times D M$ )
|
We will work in analytics and convert everything to coordinates: $\mathrm{A}(0,0), \mathrm{B}(\mathrm{a}, 0), \mathrm{C}(\mathrm{a}, \mathrm{b})$, $\mathrm{D}(0, \mathrm{~b}), \mathrm{M}(\mathrm{x}, \mathrm{y})$.
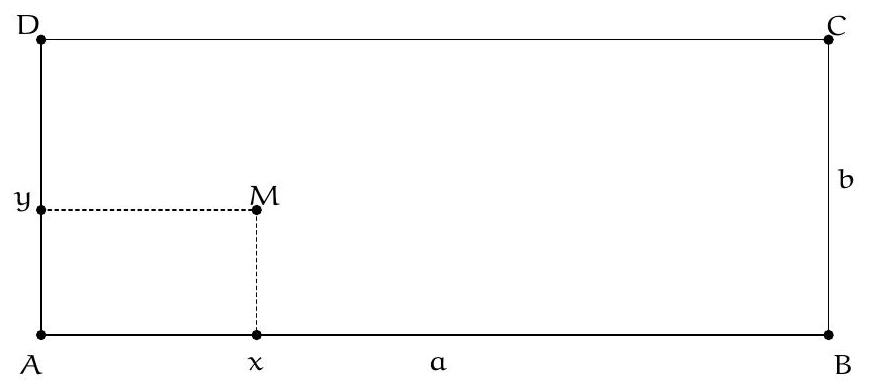
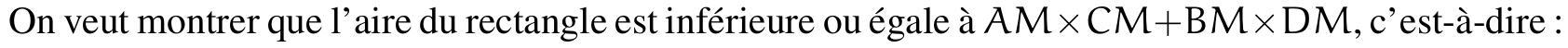
$$
\sqrt{x^{2}+y^{2}} \times \sqrt{(a-x)^{2}+(b-y)^{2}}+\sqrt{(a-x)^{2}+y^{2}} \times \sqrt{x^{2}+(b-y)^{2}} \geqslant a b
$$
We will use the Cauchy-Schwarz inequality:
$$
\begin{aligned}
& \sqrt{x^{2}+y^{2}} \times \sqrt{(b-y)^{2}+(a-x)^{2}} \geqslant x(b-y)+y(a-x) \\
& \sqrt{(a-x)^{2}+y^{2}} \times \sqrt{(b-y)^{2}+x^{2}} \geqslant(a-x)(b-y)+y x
\end{aligned}
$$
And we finish by noting that $x(b-y)+y(a-x)+(a-x)(b-y)+y x=a b$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
ABCD est un rectangle et $M$ un point intérieur à ce rectangle. Montrer que l'aire de ce rectangle est inférieure ou égale à la somme $A M \times C M+B M \times D M$ ( $A M \times C M$ désigne le produit des longueurs des segments $A M$ et $C M$, de même pour $B M \times D M$ )
|
Nous allons travailler en analytique et tout passer aux coordonnées : $\mathrm{A}(0,0), \mathrm{B}(\mathrm{a}, 0), \mathrm{C}(\mathrm{a}, \mathrm{b})$, $\mathrm{D}(0, \mathrm{~b}), \mathrm{M}(\mathrm{x}, \mathrm{y})$.

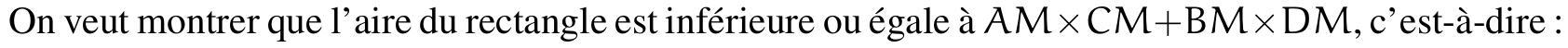
$$
\sqrt{x^{2}+y^{2}} \times \sqrt{(a-x)^{2}+(b-y)^{2}}+\sqrt{(a-x)^{2}+y^{2}} \times \sqrt{x^{2}+(b-y)^{2}} \geqslant a b
$$
Nous allons utiliser l'inégalité de Cauchy-Schwartz :
$$
\begin{aligned}
& \sqrt{x^{2}+y^{2}} \times \sqrt{(b-y)^{2}+(a-x)^{2}} \geqslant x(b-y)+y(a-x) \\
& \sqrt{(a-x)^{2}+y^{2}} \times \sqrt{(b-y)^{2}+x^{2}} \geqslant(a-x)(b-y)+y x
\end{aligned}
$$
Et on finit en remarquant que $x(b-y)+y(a-x)+(a-x)(b-y)+y x=a b$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution."
}
|
591da6d1-5394-55b5-a818-75fd4e081d10
| 607,443
|
Let $ABCD$ be a trapezoid in which the sides $AB$ and $CD$ are parallel. Consider a point $P$ on the line $(AC)$ such that $C$ is interior to the segment $[AP]$, and let $X$ and $Y$ be the midpoints of the sides $AB$ and $CD$, respectively. The line $(PX)$ intersects the line $(BC)$ at $N$ and the line $(PY)$ intersects the line $(AD)$ at $M$. Show that the line $(MN)$ is parallel to the line $(AB)$.
|
Let's make an appropriate figure:
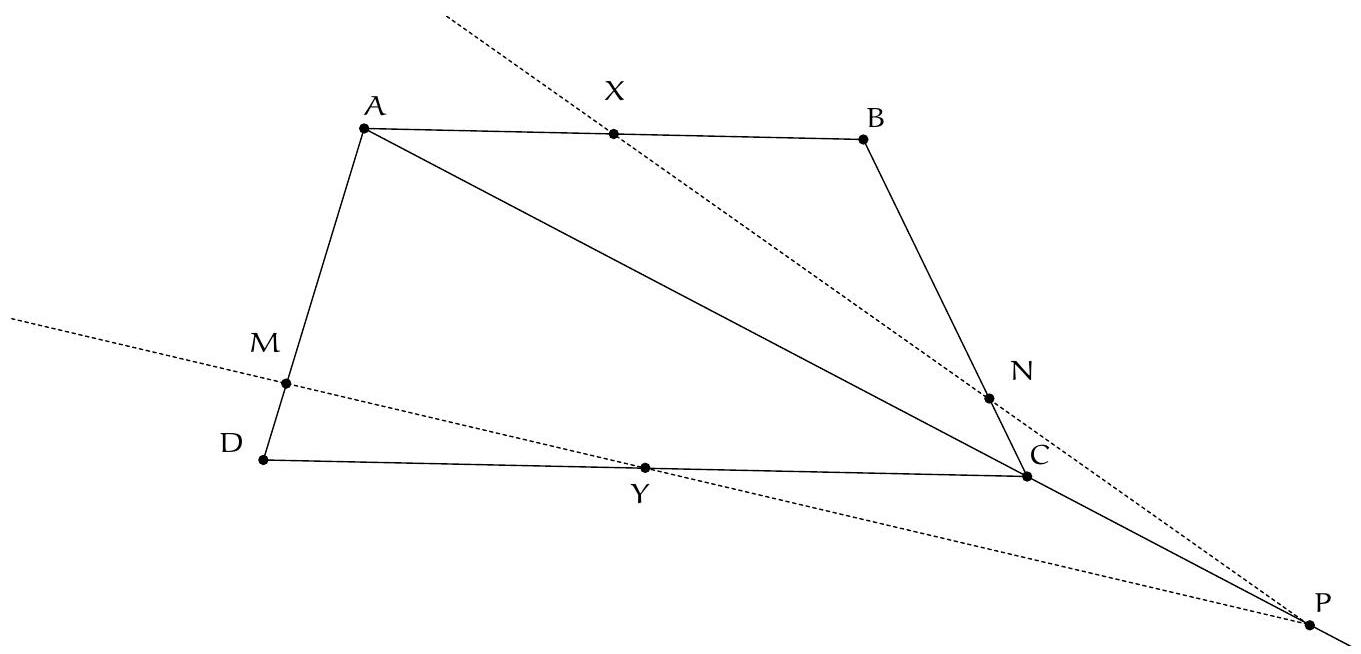
First, consider the case where we take $P$ "at infinity," meaning instead of taking $P X$ and $P Y$, we take the lines parallel to $A C$ passing through $X$ and $Y$. In this case, by Thales' theorem, the points $M$ and $N$ are the midpoints of $A D$ and $B C$, respectively, and consequently, $(M N) \parallel (A B)$.
Now, let's return to the general case. We will try to show that $\frac{B N}{N C} = \frac{A M}{M D}$, and thus we will have $(M N) \parallel (A B)$ (I leave the proof of this result as an exercise for those who have doubts). Since we have many collinear points and we want to calculate ratios of lengths, Menelaus' theorem comes to mind. In triangle $A B C$, the points $X, N, P$ are collinear, so:
$$
\frac{A X}{X B} \cdot \frac{B N}{N C} \cdot \frac{C P}{P A} = -1
$$
But since $X$ is the midpoint of $A B$, $\frac{A X}{X B} = 1$, so $\frac{B N}{N C} = -\frac{C P}{P A}$. Next, using Menelaus' theorem in triangle $A D C$, we get $\frac{A M}{M D} = -\frac{C P}{P A}$, and the two ratios are equal. It is not very difficult to verify that we indeed arrive at the expected result, $(M N) \parallel (A B)$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze dans lequel les côtés $A B$ et $C D$ sont parallèles. On considère un point $P$ de la droite ( $A C$ ) tel que $C$ soit intérieur au segment $[A P]$ et on désigne respectivement par $X$ et $Y$ les milieux des côtés $A B$ et $C D$. La droite ( PX ) rencontre la droite (BC) en $N$ et la droite (PY) rencontre la droite (AD) en $M$. Montrer que la droite ( $M N$ ) est parallèle à la droite ( $A B$ ).
|
Faisons une figure appropriée:

Tout d'abord considérez le cas où on prend $P$ "à l'infini", c'est au lieu de prendre $P X$ et $P Y$ on prend les droites parallèles à $A C$ passant par $X$ et $Y$. Dans ce cas, par Thalès les points $M$ et $N$ sont les milieux respectifs de $A D$ et $B C$, et par conséquent $(M N) \|(A B)$.
Revenons au cas général. Nous allons essayer de montrer que $\frac{B N}{N C}=\frac{A M}{M D}$, et ainsi nous aurons bien $(M N) \|(A B)$ (je laisse en exercice la démo de ce résultat pour ceux qui ont des doutes). Comme nous avons beaucoup de points alignés et que nous voulons calculer des quotients de longueur, le théorème de Menelaus vient à l'esprit. Dans le triangle $A B C$, les points $X, N, P$ sont alignés, donc :
$$
\frac{A X}{X B} \cdot \frac{B N}{N C} \cdot \frac{C P}{P A}=-1
$$
Mais comme $X$ est le milieu de $A B, \frac{A X}{X B}=1$, donc $\frac{B N}{N C}=-\frac{C P}{P A}$. Ensuite, en utilisant Menelaus dans le triangle $A D C$, on obtient $\frac{A M}{M D}=-\frac{C P}{P A}$, et les deux quotients sont égaux. Ensuite il n'est pas très dur de vérifier que l'on arrive bien au résultat attendu, $(M N) \|(A B)$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution."
}
|
c96ae36d-72ea-5c1a-9dbb-24f290500e92
| 607,444
|
Let $ABC$ be a non-isosceles triangle at $A$; $I$ and $O$ are respectively the incenter and the circumcenter of this triangle $ABC$, and the incircle touches the side $BC$ at $D$. The internal angle bisector of the angle at $A$ in triangle $ABC$ meets the circumcircle at point $M$ and the line $(DM)$ meets the circumcircle again at $P$.
Show that the angle $\widehat{A P I}$ is a right angle.
|
We will place E as the point diametrically opposite to A on the circumcircle. If we can prove that the points P, I, and E are collinear, then the angle \(\widehat{A P I}\) will be a right angle.
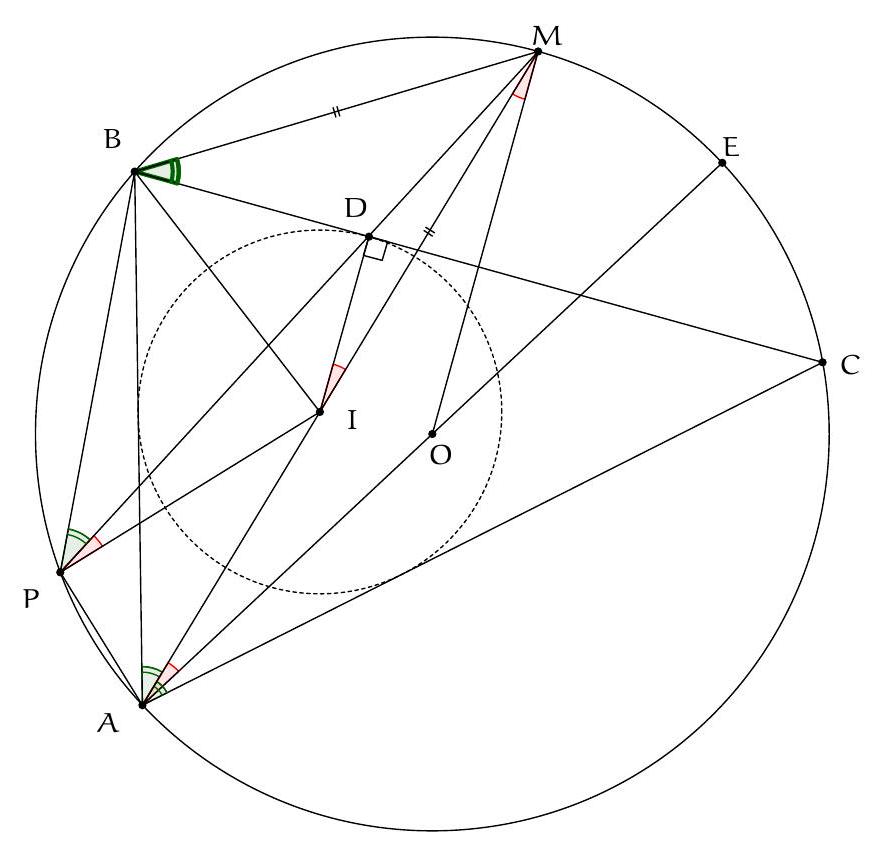
First, refer back to the beginning of the proof of Exercise 7 to show that \(M I = M B\). Then, \(\widehat{M P B} = \widehat{C B M}\) since \(M\) is the midpoint of the arc \(\widehat{B C}\). The triangles MPB and MBD are similar (they share the angle \(\widehat{M}\) and have a second equal angle). Therefore,
\[
\frac{M P}{M B} = \frac{M B}{M D} \Longrightarrow M P \cdot M D = M B^2 = M I^2
\]
The circle passing through the points P, I, and D has the line MI as a tangent (by the power of a point theorem with respect to a circle). We deduce from the extreme case of the inscribed angle theorem that
\[
\widehat{\mathrm{DPI}} = \widehat{\mathrm{DIM}}
\]
The point \(M\) is the midpoint of the arc \(\widehat{B C}\), so the line \(O M\) is the perpendicular bisector of \([B C]\), and the lines \(O M\) and ID are parallel. Additionally, the triangle \(A O M\) is isosceles at \(O\). Thus,
\[
\widehat{\mathrm{DIM}} = \widehat{\mathrm{IMO}} = \widehat{\mathrm{MAE}} = \widehat{\mathrm{MPE}}
\]
where the last equality is simply the inscribed angle. We have shown that:
\[
\widehat{\mathrm{MPI}} = \widehat{\mathrm{MPE}},
\]
so the points P, I, and E are indeed collinear, and the proof is complete.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle en $A$; I et $O$ sont respectivement le centre du cercle inscrit et le centre du cercle circonscrit de ce triangle $A B C$ et le cercle inscrit touche le côté BC en D. La bissectrice intérieure de l'angle en $A$ dans le triangle $A B C$ rencontre le cercle circonscrit au point $M$ et la droite (DM) rencontre à nouveau le cercle circonscrit en P .
Montrer que l'angle $\widehat{A P I}$ est un angle droit.
|
On va placer E le point diamétralement opposé à A sur le cercle circonscrit. Si on arrive à prouver que les points $\mathrm{P}, \mathrm{I}$ et E sont alignés, alors l'angle $\widehat{A P I}$ sera droit.

Tout d'abord, ramenez-vous au début de la preuve de l'exo 7 pour démontrer que $M I=M B$. Ensuite, $\widehat{M P B}=\widehat{C B M}$ puisque $M$ est le milieu de l'arc $\widehat{B C}$. Les triangles MPB et MBD sont semblables (ils ont l'angle $\widehat{M}$ en commun et ont un deuxième angle égal). Donc
$$
\frac{M P}{M B}=\frac{M B}{M D} \Longrightarrow M P \cdot M D=M B^{2}=M I^{2}
$$
Le cercle passant par les points P , I et D admet donc la droite MI comme tangente (par la théorie de la puissance d'un point part rapport à un cercle). On en déduit grâce au cas extrème du théorème de l'angle inscrit que
$$
\widehat{\mathrm{DPI}}=\widehat{\mathrm{DIM}}
$$
Le point $M$ est le milieu de l'arc $\widehat{B C}$, donc la droite $O M$ est la médiatrice de $[B C]$, et les droites $O M$ et ID sont parallèles. De plus le triangle $A O M$ est isocèle en $O$. Ainsi
$$
\widehat{\mathrm{DIM}}=\widehat{\mathrm{IMO}}=\widehat{\mathrm{MAE}}=\widehat{\mathrm{MPE}}
$$
où la dernière égalité est simplement l'angle inscrit. On a montré que :
$$
\widehat{\mathrm{MPI}}=\widehat{\mathrm{MPE}},
$$
les points P, I, E sont bien alignés, la démonstration est achevée.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution."
}
|
0bdd84f6-f02e-57c8-9cc9-4cc9edf49f9c
| 607,446
|
Consider a circle with center $O$ and four points $A, B, C, D$ on this circle such that the intersection point $P$, other than $O$, of the circumcircles of triangles $ABO$ and $CDO$ is inside the triangle $OAD$. We choose a point $Q$ on the ray $[OP)$ outside the segment $[OP]$ and a point $R$ on the ray $[PO)$ outside the segment $[OP]$. Show that the angles $\widehat{QAP}$ and $\widehat{OBR}$ are equal if and only if the angles $\widehat{PDQ}$ and $\widehat{RCO}$ are equal.
|
First, we notice that the lines $\mathrm{AB}, \mathrm{CD}$, and OP are concurrent, since they are the three radical axes of the circles in the figure taken two by two. Let $M$ be their point of intersection.
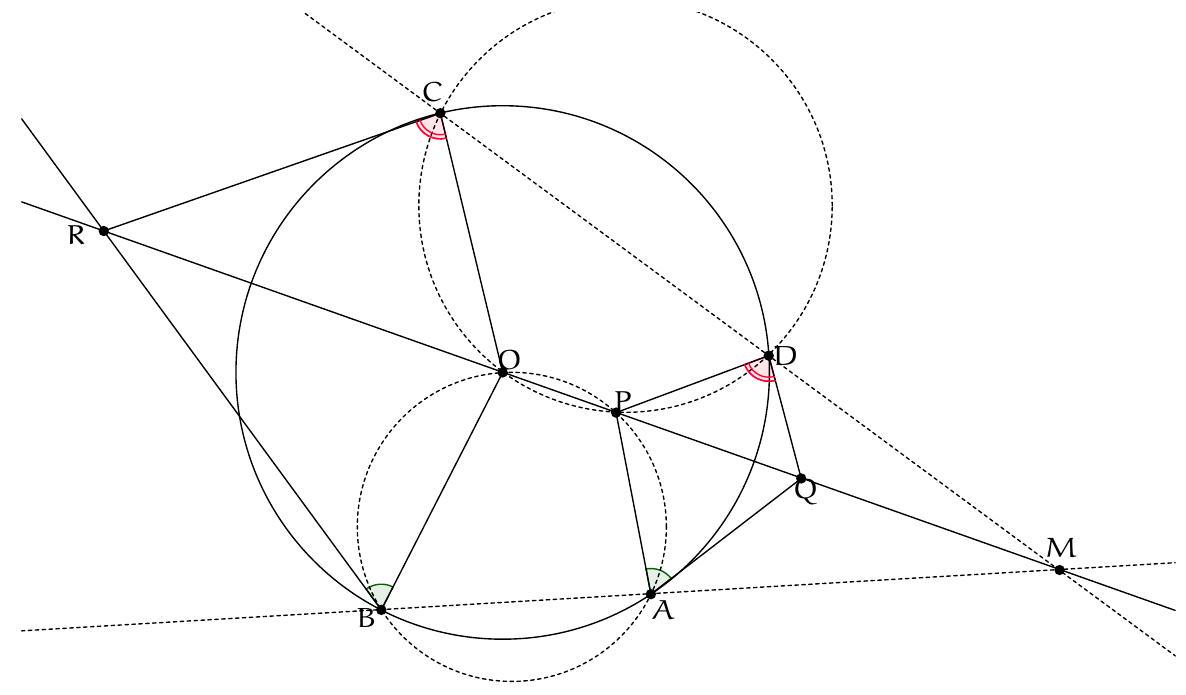
Since $M$ is the intersection of the radical axes, we have
$$
M O \cdot M P = M A \cdot M B = M C \cdot M D.
$$
We will work in the complex plane. We will denote $z_{A}$ as the complex number corresponding to point $A$, etc. We can assume that $M$ is the origin, that the line (OM) is the real axis, and that $z_{\mathrm{O}} z_{\mathrm{P}} = 1$. Consider the inversion centered at $M$ that swaps $O$ and $P$, which will have the equation: $A \leftrightarrow A^{\prime}$ if and only if $z_{A} \overline{z_{\mathcal{A}^{\prime}}} = 1$. Thanks to the above relation, this inversion transforms $A$ into $B$ and $C$ into $D$. Place a point $Q$ on the line $OP$ and let $R$ be its image under the inversion. We will show that $\widehat{\mathrm{QAP}} = \widehat{\mathrm{OBR}}$. Keep in mind that $z_{\mathrm{O}}, z_{\mathrm{P}}, z_{\mathrm{Q}}, z_{\mathrm{R}}$ are all real:
$$
\widehat{\mathrm{QAP}} = \arg \left(\frac{z_{\mathrm{Q}} - z_{\mathrm{A}}}{z_{\mathrm{P}} - z_{\mathrm{A}}}\right) = \arg \left(\frac{\frac{1}{z_{\mathrm{R}}} - \frac{1}{z_{\mathrm{A}}}}{\frac{1}{z_{\mathrm{O}}} - \frac{1}{z_{\mathrm{B}}}}\right) = \arg \left(\frac{z_{\mathrm{O}}}{z_{\mathrm{R}}} \frac{\overline{z_{\mathrm{B}}} - z_{\mathrm{R}}}{\overline{z_{\mathrm{B}}} - z_{\mathrm{O}}}\right).
$$
Since $z_{\mathrm{O}} / z_{\mathrm{R}}$ is real, its argument is 0 modulo $\pi$. Then we use the formula $\arg (\bar{z}) = -\arg (z)$ to complete the calculation:
$$
\widehat{\mathrm{QAP}} = -\arg \left(\frac{z_{\mathrm{B}} - z_{\mathrm{R}}}{z_{\mathrm{B}} - z_{\mathrm{O}}}\right) = \widehat{\mathrm{OBR}}
$$
Similarly, we show that $\widehat{\mathrm{PDQ}} = \widehat{\mathrm{RCO}}$. Thus, the only way to place the point $R$ such that $\widehat{\mathrm{QAP}} = \widehat{\mathrm{OBR}}$ is to place it on the image of $Q$ under the inversion, and in this case, $\widehat{\mathrm{PDQ}} = \widehat{\mathrm{RCO}}$.

End
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On considère un cercle de centre $O$ et quatre points $A B C D$ de ce cercle tels que le point d'intersection $P$, autre que $O$, des cercles circonscrits aux triangles $A B O$ et $C D O$ soit intérieur au triangle OAD. On choisit un point $Q$ de la demi-droite [OP) à l'extérieur du segment $[O P]$ et on choisit un point $R$ de la demi-droite $[\mathrm{PO})$ à l'extérieur du segment $[\mathrm{OP}]$. Montrer que les angles $\widehat{\mathrm{QAP}}$ et $\widehat{\mathrm{OBR}}$ sont égaux si et seulement si les angles $\widehat{\mathrm{PDQ}}$ et $\widehat{\mathrm{RCO}}$ sont égaux.
|
Tout d'abord on remarque que les droites $\mathrm{AB}, \mathrm{CD}$ et OP sont concourantes, puisque ce sont les trois axes radicaux des cercles de la figure pris deux deux. Notons $M$ leur point d'intersection.

Comme $M$ est l'intersection des axes radicaux, on a
$$
M O \cdot M P=M A \cdot M B=M C \cdot M D .
$$
Nous allons travailler dans les complexes. On notera $z_{A}$ l'affixe du point $A$ etc. On peut supposer que $M$ est l'origine, que la droite ( OM ) est l'axe des réels et que $z_{\mathrm{O}} z_{\mathrm{P}}=1$. Considérons l'inversion de centre $M$ qui échange $O$ et $P$, qui sera d'équation : $A \leftrightarrow A^{\prime}$ ssi $z_{A} \overline{z_{\mathcal{A}^{\prime}}}=1$. Grâce à la relation d'au dessus, cette inversion transforme $A$ en $B$ et $C$ en $D$. Plaçons un point $Q$ sur la droite $O P$ et notons $R$ son image par l'inversion. Nous allons montrer que $\widehat{\mathrm{QAP}}=\widehat{\mathrm{OBR}}$. Gardez en tête que $z_{\mathrm{O}}, z_{\mathrm{P}}, z_{\mathrm{Q}}, z_{\mathrm{R}}$ sont tous réels :
$$
\widehat{\mathrm{QAP}}=\arg \left(\frac{z_{\mathrm{Q}}-z_{\mathrm{A}}}{z_{\mathrm{P}}-z_{\mathrm{A}}}\right)=\arg \left(\frac{\frac{1}{z_{\mathrm{R}}}-\frac{1}{z_{\mathrm{z}}}}{\frac{1}{z_{\mathrm{O}}}-\frac{1}{z_{\mathrm{B}}}}\right)=\arg \left(\frac{z_{\mathrm{O}}}{z_{\mathrm{R}}} \frac{\overline{z_{\mathrm{B}}}-z_{\mathrm{R}}}{\overline{z_{\mathrm{B}}}-z_{\mathrm{O}}}\right) .
$$
Comme $z_{\mathrm{O}} / z_{\mathrm{R}}$ est réel, son argument vaut 0 à $\pi$ près. Ensuite on utilise la formule $\arg (\bar{z})=-\arg (z)$ pour finir le calcul :
$$
\widehat{\mathrm{QAP}}=-\arg \left(\frac{z_{\mathrm{B}}-z_{\mathrm{R}}}{z_{\mathrm{B}}-z_{\mathrm{O}}}\right)=\widehat{\mathrm{OBR}}
$$
De même on montre que $\widehat{P D Q}=\widehat{R C O}$. Ainsi, la seule façon de placer le point $R$ telle que $\widehat{\mathrm{QAP}}=\widehat{\mathrm{OBR}}$ est de le mettre sur l'image de Q par l'inversion, et on a dans ce cas $\widehat{\mathrm{PDQ}}=\widehat{\mathrm{RCO}}$.

Fin
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi1-corrige.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution."
}
|
213627a5-eafd-5ac9-9c93-ed913a03e111
| 607,447
|
Ruby performed a series of moves with her Rubik's cube. (For example, she can turn the top face clockwise, then the back face 180 degrees, then the right face counterclockwise. Or any other series of face rotations.) Then she repeats the same series of moves tirelessly. Show that after a certain number of repetitions, she will return to the initial configuration.
|
Let $x_{0}$ be the initial configuration and $x_{n}$ the configuration after $n$ repetitions of Ruby's series. Since the total number of configurations of a Rubik's cube is finite, at some point a configuration will repeat: $x_{n}=x_{m}$ with $n<m$. Now, let's ask Ruby to reverse her series of moves, that is, to perform the rotations in the reverse order and in the opposite direction compared to her initial series of moves. By applying this reversed series to the configuration $x_{n}$, we obtain $x_{n-1}$. Similarly, by applying it to $x_{m}$, we obtain $x_{m-1}$. Since $x_{n}=x_{m}$, we deduce that $\mathrm{x}_{\mathrm{n}-1}=\mathrm{x}_{\mathrm{m}-1}$. By continuing to apply the reversed series, we will eventually reach the equality $x_{0}=x_{m-n}$ after $n$ repetitions.
We have thus proven that the initial configuration will reappear after $\mathrm{m}-\mathrm{n}$ repetitions of Ruby's series.

|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Ruby a effectué une série de mouvements avec son Rubik's cube. (Par exemple, elle peut tourner la face du haut dans le sens des aiguilles d'une montre, puis la face de fond de 180 degrés, puis la face de droite dans le sens contraire des aiguilles d'une montre. Ou n'importe quelle autre série de rotations de faces.) Ensuite elle répète inlassablement la même série de mouvements. Montrer qu'au bout d'un certain nombre de répétitions elle retrouvera la configuration de départ.
|
Notons $x_{0}$ la configuration de départ et $x_{n}$ la configuration après $n$ répétitions de la série de Ruby. Comme le nombre total de configurations d'un Rubik's cube est fini, à un moment une configuration va se répéter : $x_{n}=x_{m}$ avec $n<m$. Demandons maintenant à Ruby d'inverser sa série de mouvements, autrement dit d'exécuter les rotations dans l'ordre inverse et dans le sens inverse par rapport à sa série de mouvements initiale. En appliquant cette série inversée à la configuration $x_{n}$ nous obtenons $x_{n-1}$. De même, en l'appliquant à $x_{m}$ nous obtenons $x_{m-1}$. Comme $x_{n}=x_{m}$, on en déduit que $\mathrm{x}_{\mathrm{n}-1}=\mathrm{x}_{\mathrm{m}-1}$. En continuant à appliquer la série inversée, nous allons arriver au bout de n répétitions à l'égalité $x_{0}=x_{m-n}$.
Nous avons donc prouvé que la configuration de départ réapparaîtra au bout $\mathrm{m}-\mathrm{n}$ répétitions de la série de Ruby.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi2-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution."
}
|
dc5e66d9-679a-567e-bff0-aa1934c87fc5
| 607,451
|
Three grasshoppers are located at the points $(0,0),(0,1)$ and $(1,0)$ on a grid paper. Each minute one of the grasshoppers jumps to another point on the grid in such a way that its jump is parallel to the line passing through the other two grasshoppers. Is it possible that after some time the grasshoppers end up at the points $(-1,0),(1,0)$ and $(0,1)$?
|
If $A B$ and $C D$ are two parallel lines, then the area of triangle $A B C$ is equal to that of triangle $A B D$, because these two triangles have the same base $[A B]$ and the same height. It follows from this remark that the area of the triangle formed by the three grasshoppers does not change during their jumps. The area of the initial triangle is $1 / 2$, while that of the final triangle we want to achieve is 1. It is therefore impossible to go from one to the other.

## Olympic Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Trois sauterelles se trouvent aux points $(0,0),(0,1)$ et $(1,0)$ d'une feuille quadrillée. Chaque minute une sauterelle saute sur un autre point de la grille d'une telle façon que son saut soit parallèle à la droite passant par les deux autres sauterelles. Est-il possible qu'au bout d'un certain temps les sauterelles se retrouvent aux points $(-1,0),(1,0)$ et $(0,1)$ ?
|
Si $A B$ et $C D$ sont deux droites parallèles, alors l'aire du triangle $A B C$ est égale à celle du triangle $A B D$, car ces deux triangles ont la même base $[A B]$ et la même hauteur. Il découle de cette remarque que l'aire du triangle formé par les trois sauterelles ne change pas lors de leurs sauts. Or l'aire du triangle de départ vaut $1 / 2$, tandis que celle du triangle qu'on souhaite obtenir à la fin vaut 1 . Il est donc impossible de passer de l'un à l'autre.

## Exercices Olympiques
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi2-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution."
}
|
3148926d-e2d0-5606-9d88-7dbe263db6eb
| 607,453
|
Each of the 400 members of a parliament has slapped exactly one other member. Show that it is possible to form a parliamentary commission of 134 members such that no member of the commission has slapped any other member.
|
Let's call two deputies enemies if one of them has slapped the other. We will solve a more general exercise by induction:
In a parliament of at least \(3n-2\) deputies, each deputy has slapped 0 or 1 other deputy. It is always possible to form a parliamentary commission of \(n\) deputies that contains no enemy pairs.
For \(n=1\), the property is obvious: we can always form a commission of one deputy because a deputy is never their own enemy.
Now let's show how to go from \(n\) to \(n+1\). Consider a parliament with at least
\[
3(n+1)-2=3n+1
\]
deputies. Since the total number of slaps is less than or equal to the number of deputies, there exists, by the pigeonhole principle, a deputy who has been slapped at most once and who therefore has at most two enemies. Put this deputy in the commission automatically and remove his or her two enemies. We are left with at least \(3n-2\) deputies among whom there are no enemies of the selected deputy. By the induction hypothesis, we can complete the commission by choosing another \(n\) deputies from those who remain without any enemy pairs among them.

|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Chacun des 400 députés d'un parlement a giflé exactement un autre député. Montrer qu'on peut créer une commission parlementaire de 134 députés telle qu'aucun membre de la commission n'ait giflé aucun autre membre.
|
Appellons deux députés ennemis si l'un d'eux a giflé l'autre. Nous allons résoudre par récurrence un exercice plus général :
Dans un parlement d'au moins $3 n-2$ députés, chaque député a giflé 0 ou 1 autre député. Il est alors toujours possible de créer une commission parlementaire de n députés qui ne contienne aucun couple ennemi.
Pour $\mathrm{n}=1$ la propriété est évidente : on peut toujours former une commission à un député car un député n'est jamais son propre ennemi.
Montrons maintenant comment passer de n à $\mathrm{n}+1$. Considérons un parlement avec au moins
$$
3(n+1)-2=3 n+1
$$
députés. Comme le nombre total de gifles est inférieur ou égal au nombre de députés, il existe, par le principe des tiroirs, un député qui a été giflé au plus une fois et qui a donc au plus deux ennemis. Mettons ce député dans la commission d'office et écartons son ou ses deux ennemis. Il nous reste au moins $3 n-2$ députés parmi lesquels il n'y a aucun ennemi du député selectionné. Par hypothèse de récurrence, on peut compléter la commission en choisissant encore n députés parmi ceux qui restent sans qu'il y ait aucun couple ennemi parmi eux.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi2-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution."
}
|
6f75e5e1-e79e-565a-bf97-f937ce610052
| 607,454
|
The Fibonacci sequence is constructed as follows: each term is the sum of the two preceding ones. Its first terms are:
$$
1,1,2,3,5,8,13,21,34,55,89, \ldots
$$
Show that the Fibonacci sequence contains a multiple of 1000.
|
Let $F_{n}$ denote the $n$-th term of the Fibonacci sequence ( $F_{1}=1, F_{2}=1, F_{3}=2$, etc.) and let $u_{n}$ denote the remainder of the Euclidean division of $F_{n}$ by 1000 ( $u_{n}$ is thus the number formed by the last three digits of $F_{n}$ ). Since there are only a finite number of pairs ( $x, y$ ) of integers between 0 and 999 (there are exactly $1000^{2}=1000000$ such pairs), there exist integers $n$ and $N$ such that $N>0$ and
$$
u_{n}=u_{n+N} \quad ; \quad u_{n+1}=u_{n+1+N}
$$
Now, $u_{n-1}$ (resp. $u_{n-1+N}$ ) is obtained from $u_{n}$ and $u_{n+1}$ (resp. $u_{n+N}$ and $u_{n+1+N}$ ) as the remainder of the Euclidean division of $u_{n+1}-u_{n}$ (resp. $u_{n+1+N}-u_{n+N}$ ) by 1000. Thus, from the equalities (1), we deduce that $\mathfrak{u}_{n-1}=u_{n-1+N}$. Continuing in this manner, we obtain $u_{N+1}=u_{1}=1$ and $u_{N+2}=u_{2}=1$, from which it follows that $u_{N}=0$. The integer $F_{N}$ is therefore a multiple of 1000.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
La suite de Fibonacci est construite ainsi : chaque terme est la somme des deux précédents. Ses premiers termes valent:
$$
1,1,2,3,5,8,13,21,34,55,89, \ldots
$$
Montrer que la suite de Fibonacci contient un multiple de 1000.
|
Notons $F_{n}$ le $n$-ième terme de la suite de Fibonacci ( $F_{1}=1, F_{2}=1, F_{3}=2$, etc.) et notons $u_{n}$ le reste de la division euclidienne de $F_{n}$ par 1000 ( $u_{n}$ est donc le nombre formé par les trois derniers chiffres de $F_{n}$ ). Comme il n'y a qu'un nombre fini de couples ( $x, y$ ) d'entiers compris entre 0 et 999 (il $y$ en a exactement $1000^{2}=1000000$ ), il existe des entiers $n$ et $N$ tels que $N>0$ et
$$
u_{n}=u_{n+N} \quad ; \quad u_{n+1}=u_{n+1+N}
$$
Or, $u_{n-1}$ (resp. $u_{n-1+N}$ ) s'obtient à partir de $u_{n}$ et $u_{n+1}$ (resp. $u_{n+N}$ et $u_{n+1+N}$ ) comme le reste de la division euclidienne de $u_{n+1}-u_{n}$ (resp. $u_{n+1+N}-u_{n+N}$ ) par 1000. Ainsi, des égalités (1), on déduit que $\mathfrak{u}_{n-1}=u_{n-1+N}$. En continuant ainsi, on obtient $u_{N+1}=u_{1}=1$ et $u_{N+2}=u_{2}=1$, d'où il résulte enfin $u_{N}=0$. L'entier $F_{N}$ est donc multiple de 1000.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
c9690a39-2f97-5c7c-8f83-6d8a1378817d
| 607,459
|
Show that the equation
$$
x(x+2)=y(y+1)
$$
has no solution in strictly positive integers.
|
If the pair $(x, y)$ is a solution, we have $x(x+1)<x(x+2)=y(y+1)$, and thus $x<y$. However, assuming $(x, y)$ is still a solution, we can write $(x+1)(x+2)>x(x+2)=y(y+1)$, from which we deduce $x+1>y$. Therefore, a hypothetical solution $(x, y)$ should satisfy $x<y<x+1$, which cannot occur. We conclude that the proposed equation has no solution in strictly positive integers.

## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer que l'équation
$$
x(x+2)=y(y+1)
$$
n'a pas de solution en nombres entiers strictement positifs.
|
Si le couple $(x, y)$ est solution, on a $x(x+1)<x(x+2)=y(y+1)$ et donc $x<y$. Mais de même, en supposant toujours $(x, y)$ solution, on peut écrire $(x+1)(x+2)>x(x+2)=y(y+1)$, d'où on déduit $x+1>y$. Ainsi, une solution ( $x, y$ ) hypothétique devrait donc vérifier $x<y<x+1$, ce qui ne peut se produire. On en déduit que l'équation proposée n'a pas de solution en nombres entiers strictement positifs.

## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
40f22942-0fb9-5292-99d2-6f39519c757f
| 607,460
|
Let n and m be two strictly positive integers. Show that $5^{\mathrm{m}}+5^{n}$ can be written as a sum of two squares if and only if $n$ and $m$ have the same parity.
|
Suppose first that $n$ and $m$ do not have the same parity. We then study the quantity $5^{n}+5^{m}$ modulo 8. By induction, it is easily proven that $5^{k}$ is congruent to 1 (resp. 5) modulo 8 if $k$ is even (resp. odd). Thus, according to our hypothesis, we always have $5^{n}+5^{m} \equiv 6(\bmod 8)$. On the other hand, a square is always congruent to 0, 1, or 4 modulo 8. Since there is no way to write 6 as the sum of two of these three numbers, we conclude that $5^{n}+5^{m}$ cannot be written as the sum of two squares.
Now suppose that $n$ and $m$ have the same parity. Without loss of generality, we can assume further that $m \geqslant n$. Thus, there exists a non-negative integer $k$ such that $m=n+2k$. We then have $5^{m}+5^{n} = 5^{n}(5^{2k}+1)$. Since, clearly, $5=2^{2}+1^{2}$ and $5^{2k}+1$ can be written as the sum of two squares, it suffices to conclude by showing that if $x$ and $y$ can be written as the sum of two squares, then the same is true for the product $xy$. This follows directly from the formula:
$$
\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)=(ad-bc)^{2}+(ac+bd)^{2}
$$

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient n et m deux entiers strictement positifs. Montrer que $5^{\mathrm{m}}+5^{n}$ s'écrit comme une somme de deux carrés si et seulement si $n$ et $m$ ont même parité.
|
Supposons pour commencer que $n$ et $m$ n'ont pas même parité. On étudie alors la quantité $5^{n}+5^{m}$ modulo 8 . Par récurrence, on démontre facilement que $5^{k}$ est congru à 1 (resp. 5) modulo 8 si k est pair (resp. impair). Ainsi, d'après notre hypothèse, on a toujours $5^{n}+5^{m} \equiv 6(\bmod 8)$. Or, par ailleurs, un carré est toujours congru à 0,1 ou 4 modulo 8 . Comme il n'y a aucune manière d'écrire 6 comme somme de deux de ces trois nombres, on en déduit que $5^{n}+5^{\mathrm{m}}$ ne peut s 'écrire comme somme de deux carrés.
Supposons maintenant que $n$ et $m$ ont même parité. Quitte à échanger $n$ et $m$, on peut supposer en outre que $\mathrm{m} \geqslant \mathrm{n}$. Ainsi, il existe un entier k positif ou nul tel que $\mathrm{m}=\mathrm{n}+2 \mathrm{k}$. On a alors $5^{\mathrm{m}}+5^{\mathrm{n}}=$ $5^{\mathrm{n}}\left(5^{2 \mathrm{k}}+1\right)$. Comme, manifestement $5=2^{2}+1^{2}$ et $5^{2 \mathrm{k}}+1$ s'écrivent comme sommes de deux carrés, il suffit pour conclure de montrer que, si $x$ et $y$ s'écrivent comme somme de deux carrés, alors il en va de même du produit xy . Ceci résulte directement de la formule :
$$
\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)=(a d-b c)^{2}+(a c+b d)^{2}
$$

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution."
}
|
c72bd7b5-f074-5d97-8c41-1fb116ac05a9
| 607,461
|
Prove that there is a unique way to color each strictly positive rational number either red or blue, such that:
- the numbers $x$ and $x+1$ are of different colors;
- the numbers $x$ and $\frac{1}{x}$ are of the same color;
- the number 1 is colored red.
|
First, let's show that such a coloring is necessarily unique. To do this, we will prove by induction on $\max (\mathrm{a}, \mathrm{b})$ that the color of the fraction $\frac{\mathrm{a}}{\mathrm{b}}$ (assumed to be in irreducible form) is entirely determined. The conclusion is true when $\max (a, b)=1$ since this implies $a=b=1$ and, by hypothesis, the color of 1 is red. Now consider an irreducible fraction $\frac{a}{b}$ and suppose we have already shown that the color of any irreducible fraction $\frac{a^{\prime}}{b^{\prime}}$ with $\max \left(\mathrm{a}^{\prime}, \mathrm{b}^{\prime}\right)<\max (\mathrm{a}, \mathrm{b})$ is determined. Without loss of generality, we can assume that $a > b$ (which does not change $\max (a, b)$ or the color of the fraction). By hypothesis, $\frac{a}{b}$ has the opposite color of $\frac{a}{b}-1=\frac{a-b}{b}$. Moreover, $\max (a-b, b) < \max (a, b) = a$. Thus, the fraction $\frac{a-b}{b}$ falls under the induction hypothesis; its color is therefore entirely determined, and consequently, so is the color of $\frac{\mathrm{a}}{\mathrm{b}}$.
The existence is demonstrated in the same way: by reusing the previous arguments, we construct the coloring by induction on $\max (\mathrm{a}, \mathrm{b})$ and verify that each color identity is used exactly once when constructing the coloring with this method.
Remark. If $a$ and $b$ are two coprime integers, let $q_{1}(a, b), \ldots, q_{n}(a, b)$ be the finite sequence of successive quotients obtained when performing the Euclidean algorithm starting from $a$ and $b$. We can then show that the unique coloring satisfying the conditions of the statement is the one that assigns the color red (resp. blue) to the irreducible fraction $\frac{a}{b}$ when $\sum_{i} q_{i}(a, b)$ is odd (resp. even).

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver qu'il existe une unique manière de colorier chaque nombre rationnel strictement positif soit en rouge, soit en bleu, de sorte que :
- les nombres $x$ et $x+1$ sont de couleurs différentes ;
- les nombres $x$ et $\frac{1}{x}$ sont de la même couleur;
- le nombre 1 est colorié en rouge.
|
Montrons tout d'abord qu'un tel coloriage est nécessairement unique. Pour cela, nous allons démontrer par récurrence sur $\max (\mathrm{a}, \mathrm{b})$ que la couleur de la fraction $\frac{\mathrm{a}}{\mathrm{b}}$ (supposée écrite sous forme irréductible) est entièrement déterminée. La conclusion est vraie lorsque $\max (a, b)=1$ puisque cela impose $a=b=1$ et que l'on sait, par hypothèse, que la couleur de 1 est rouge. Considérons maintenant une fraction irréductible $\frac{a}{b}$ et supposons que l'on ait déjà démontré que la couleur de toute fraction irréductible $\frac{a^{\prime}}{b^{\prime}}$ $\operatorname{avec} \max \left(\mathrm{a}^{\prime}, \mathrm{b}^{\prime}\right)<\max (\mathrm{a}, \mathrm{b})$ soit déterminée. Quitte à remplacer $\frac{\mathrm{a}}{\mathrm{b}}$ par son inverse $\frac{\mathrm{b}}{\mathrm{a}}$ (ce qui ne modifie ni $\max (a, b)$, ni la couleur de la fraction), on peut supposer que $a>b$. Par hypothèse, $\frac{a}{b}$ a la couleur inverse de $\frac{a}{b}-1=\frac{a-b}{b}$. De plus, $\max (a-b, b)<\max (a, b)=a$. Ainsi, la fraction $\frac{a-b}{b}$ relève de l'hypothèse de récurrence; sa couleur est donc entièrement déterminée et, par suite, celle de $\frac{\mathrm{a}}{\mathrm{b}}$ l'est également.
L'existence se démontre de la même façon : en reprenant les arguments précédents, on construit le coloriage par récurrence sur $\max (\mathrm{a}, \mathrm{b})$ en vérifiant que chaque identité entre couleurs est utilisée une et une seule fois lorsqu'on construit le coloriage avec cette méthode.
Remarque. Si $a$ et $b$ sont deux entiers premiers entre eux, notons $q_{1}(a, b), \ldots, q_{n}(a, b)$ la suite (finie) des quotients successifs obtenus lorsque l'on effectue l'algorithme d'Euclide à partir de a et b. On peut alors montrer que l'unique coloriage satisfaisant aux conditions de l'énoncé est celui qui attribue la couleur rouge (resp. bleue) à la fraction irréductible $\frac{a}{b}$ lorsque $\sum_{i} q_{i}(a, b)$ est impair (resp. pair).

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution."
}
|
5f9df5cf-d432-5161-9d34-8d0a4180f881
| 607,463
|
Let $p \geqslant 5$ be a prime number. Show that 1 and 5 are the only positive divisors of $2^{p}+3^{p}$ that are less than or equal to $p$.
|
The factorization
$$
2^{\mathfrak{p}}+3^{\mathfrak{p}}=5 \cdot \sum_{i=0}^{p-1} 2^{\boldsymbol{i}}(-3)^{p-1-\mathfrak{i}}
$$
shows that 5 is indeed a divisor of $2^{p}+3^{\mathrm{p}}$.
Now let $\mathrm{d} \in\{2, \ldots, \mathrm{p}\}$ be a divisor of $2^{\mathfrak{p}}+3^{\mathfrak{p}}$. We wish to prove that $\mathrm{d}=5$. For this, consider $q$ a prime divisor of d. Then, clearly, $q$ is also a divisor of $2^{p}+3^{p}$ which is $\leqslant p$. Moreover, it is clear that we cannot have $\mathbf{q}=2$. Thus $q$ is odd, and from the congruence $2^{\mathfrak{p}}+3^{\mathfrak{p}} \equiv 0$ $(\bmod \mathbf{q})$, we deduce that $a^{p} \equiv 1(\bmod q)$ where $a$ is an integer such that $2 a \equiv-3(\bmod q)$ (such an integer exists because $q$ is odd). Furthermore, by Fermat's Little Theorem, we know that $a^{q} \equiv a$ $(\bmod q)$ and thus $a^{q-1} \equiv 1(\bmod q)\left(\right.$ since $a$ is not a multiple of $\left.q\right)$. We conclude that $a^{n} \equiv 1$ $(\bmod q)$ with $n=\operatorname{PGCD}(p, q-1)$. Since $q<p$ and $p$ is a prime, the integers $p$ and $q-1$ are necessarily coprime. In other words, $\mathfrak{n}=1$ and, consequently, $a \equiv 1(\bmod \mathbf{q})$. Returning to the definition of $a$, we get $2 \equiv-3(\bmod \mathbf{q})$, which can only occur for $\mathrm{q}=5$.
We have thus shown that the only prime divisor of d is 5. It therefore suffices to conclude by proving that d is not divisible by 25. This is obvious if $p \leqslant 25$. Assuming now $p>25$, we will prove that $2^{\mathfrak{p}}+3^{\mathfrak{p}}$ itself is not divisible by 25 (which will suffice to conclude). According to equation (3), this amounts to proving that $\sum_{i=0}^{\mathfrak{p}-1} 2^{\boldsymbol{i}}(-3)^{p-1-\boldsymbol{i}}$ is not divisible by 5. A calculation modulo 5 shows that this sum is congruent modulo 5 to
$$
(-3)^{\mathrm{p}-1} \cdot \sum_{i=0}^{\mathrm{p}-1} 1=(-3)^{\mathrm{p}-1} \cdot \mathrm{p}
$$
Now, $(-3)^{p-1}$ is coprime with 5 and, since $p>25$ is a prime number, the integers $p$ and 5 are coprime. We have thus well demonstrated what we wanted.

|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p \geqslant 5$ un nombre premier. Montrer que 1 et 5 sont les seuls diviseurs positifs de $2^{p}+3^{p}$ qui soient inférieurs ou égaux à $p$.
|
La factorisation
$$
2^{\mathfrak{p}}+3^{\mathfrak{p}}=5 \cdot \sum_{i=0}^{p-1} 2^{\boldsymbol{i}}(-3)^{p-1-\mathfrak{i}}
$$
montre que 5 est bien un diviseur de $2^{p}+3^{\mathrm{p}}$.
Soit à présent $\mathrm{d} \in\{2, \ldots, \mathrm{p}\}$ un diviseur de $2^{\mathfrak{p}}+3^{\mathfrak{p}}$. On souhaite démontrer que $\mathrm{d}=5$. On considère pour cela $q$ un diviseur premier de d . Alors, manifestement, $q$ est aussi un diviseur de $2^{p}+3^{p}$ qui est $\leqslant p$. De plus, il est clair que l'on ne peut pas avoir $\mathbf{q}=2$. Ainsi $q$ est impair et de la congruence $2^{\mathfrak{p}}+3^{\mathfrak{p}} \equiv 0$ $(\bmod \mathbf{q})$, on déduit que $a^{p} \equiv 1(\bmod q)$ où $a$ un entier est tel que $2 a \equiv-3(\bmod q)($ un tel entier existe bien car $q$ est impair). Par ailleurs, par le petit théorème de Fermat, on sait également que $a^{q} \equiv a$ $(\bmod q)$ et donc $a^{q-1} \equiv 1(\bmod q)\left(\right.$ puisque $a n^{\prime}$ est pas un multiple de $\left.q\right)$. On en déduit que $a^{n} \equiv 1$ $(\bmod q)$ avec $n=\operatorname{PGCD}(p, q-1)$. Or, comme $q<p$ et $p$ est un premier, les entiers $p$ et $q-1$ sont nécessairement premiers entre eux. Autrement dit $\mathfrak{n}=1$ et, par suite, $a \equiv 1(\bmod \mathbf{q})$. En revenant à la définition de a , on obtient $2 \equiv-3(\bmod \mathbf{q})$, ce qui ne peut se produire que pour $\mathrm{q}=5$.
On a ainsi démontré que l'unique diviseur premier de dest 5 . Il suffit donc pour conclure de démontrer que d n'est pas divisible par 25. Cela est évident si $p \leqslant 25$. Supposant maintenant $p>25$, nous allons démontrer que $2^{\mathfrak{p}}+3^{\mathfrak{p}}$ n'est, lui-même, pas divisible par 25 (ce qui suffira à conclure). D'après l'équation (3), cela revient à prouver que $\sum_{i=0}^{\mathfrak{p}-1} 2^{\boldsymbol{i}}(-3)^{p-1-\boldsymbol{i}}$ n'est pas divisible par 5 . Or, un calcul modulo 5 montre que cette somme est congrue modulo 5 à
$$
(-3)^{\mathrm{p}-1} \cdot \sum_{i=0}^{\mathrm{p}-1} 1=(-3)^{\mathrm{p}-1} \cdot \mathrm{p}
$$
Or, $(-3)^{p-1}$ est premier avec 5 et, comme $p>25$ est un nombre premier, les entiers $p$ et 5 sont premiers entre eux. On a ainsi bien démontré ce que l'on souhaitait.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution."
}
|
0f9dddb4-8317-5761-b73e-2943860d5753
| 607,465
|
Let $n \geqslant 5$ be an integer. Let $a_{1}, \ldots, a_{n}$ be distinct integers in $\{1, \ldots, 2 n\}$. Show that there exist indices $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, \mathfrak{n}\}$ with $\mathfrak{i} \neq \boldsymbol{j}$ such that
$$
\operatorname{LCM}\left(\mathfrak{a}_{\mathbf{i}}, \mathfrak{a}_{\mathbf{j}}\right) \leqslant 6\left(\mathrm{E}\left(\frac{\mathfrak{n}}{2}\right)+1\right)
$$
where $\mathrm{E}(\mathrm{x})$ denotes the integer part of the number x.
|
Suppose, to begin with, that there exists an index $i$ such that $a_{i} \leqslant n$. If there exists $j$ such that $a_{j}=2 a_{i}$, we then have
$$
\operatorname{LCM}\left(a_{i}, a_{j}\right)=a_{j} \leqslant 2 n \leqslant 6 \cdot\left(\left\lfloor\frac{n}{2}\right\rfloor+1\right)
$$
and we have found a suitable pair $(i, j)$. If, on the contrary, the integer $2 a_{i}$ does not appear among the $a_{j}$, define the integers $b_{1}, \ldots, b_{n}$ by setting $b_{i}=2 a_{i}$ and $b_{j}=a_{j}$ for $j \neq i$. The $b_{j}$ are still distinct and lie between 1 and 2n. Moreover, it is immediately verified that $\operatorname{LCM}\left(b_{i}, b_{j}\right) \geqslant \operatorname{LCM}\left(a_{i}, a_{j}\right)$. Thus, it suffices to prove the statement for the sequence of $b_{j}$.
By applying the previous reasoning again—possibly several times—we eventually assume that all $a_{j}$ are strictly greater than $n$. In other words, the set of $a_{j}$'s is none other than $\{n+1, n+2, \ldots, 2 n\}$. Let $k=\left\lfloor\frac{n}{2}\right\rfloor+1$. Since we have assumed $n \geqslant 5$, it is easy to verify that one of the $a_{j}$ is $2 k$ and another is $3 k$. We conclude by noting that the LCM of these two numbers is equal to 6k.

$\mathcal{F i n}$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 5$ un entier. Soient $a_{1}, \ldots, a_{n}$ des entiers dans $\{1, \ldots, 2 n\}$ deux à deux distincts. Montrer qu'il existe des indices $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, \mathfrak{n}\}$ avec $\mathfrak{i} \neq \boldsymbol{j}$ tels que
$$
\operatorname{PPCM}\left(\mathfrak{a}_{\mathbf{i}}, \mathfrak{a}_{\mathbf{j}}\right) \leqslant 6\left(\mathrm{E}\left(\frac{\mathfrak{n}}{2}\right)+1\right)
$$
où $\mathrm{E}(\mathrm{x})$ désigne la partie entière du nombre x .
|
Supposons, pour commencer, qu'il existe un indice $i$ tel que $a_{i} \leqslant n$. S'il existe $j$ tel que $a_{j}=2 a_{i}$, on a alors
$$
\operatorname{PPCM}\left(a_{i}, a_{j}\right)=a_{j} \leqslant 2 n \leqslant 6 \cdot\left(E\left(\frac{n}{2}\right)+1\right)
$$
et on a trouvé un couple ( $i, j)$ convenable. Si , au contraire, l'entier $2 a_{i}$ n'apparaît pas parmi les $a_{j}$, définissons les entiers $b_{1}, \ldots, b_{n}$ en posant $b_{i}=2 a_{i}$ et $b_{j}=a_{j}$ pour $j \neq i$. Les $b_{j}$ sont encore deux à deux distincts et compris entre 1 et 2 n . De plus, on vérifie immédiatement que $\operatorname{PPCM}\left(b_{i}, b_{j}\right) \geqslant$ $\operatorname{PPCM}\left(a_{i}, a_{j}\right)$. Ainsi, il suffit de démontrer la propriété de l'énoncé pour la suite des $b_{j}$.
En appliquant à nouveau le raisonnement précédent — éventuellement plusieurs fois - on en vient à supposer que tous les $a_{j}$ sont strictement supérieurs à $n$. Autrement dit, l'ensemble des $a_{j} n^{\prime}$ 'est autre que $\{n+1, n+2, \ldots, 2 n\}$. Posons $k=E\left(\frac{n}{2}\right)+1$. Comme on a supposé $n \geqslant 5$, il est facile de vérifier que l'un des $a_{j}$ vaut $2 k$ et un autre vaut $3 k$. On conclut en remarquant que le PPCM de ces deux nombres est égal à 6 k .

$\mathcal{F i n}$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi3-corrige.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "## Solution."
}
|
ed5fb0fb-4b76-50da-87be-32c875c12516
| 607,466
|
Let $x_{1}, x_{2}, \ldots, x_{5}$ be real numbers such that
$$
\left|x_{2}-x_{1}\right|=2\left|x_{3}-x_{2}\right|=3\left|x_{4}-x_{3}\right|=4\left|x_{5}-x_{4}\right|=5\left|x_{1}-x_{5}\right| .
$$
Show that these five real numbers are equal.
|
Let $\alpha=\left|x_{2}-\chi_{1}\right|$ and let's prove by contradiction that $\alpha=0$. According to the statement, there exist signs $\varepsilon_{1}, \ldots, \varepsilon_{5}$ such that
$$
x_{2}-x_{1}=\varepsilon_{1} \alpha, x_{3}-x_{2}=\varepsilon_{2} \frac{\alpha}{2}, x_{4}-x_{3}=\varepsilon_{3} \frac{\alpha}{3}, x_{5}-x_{4}=\varepsilon_{4} \frac{\alpha}{4}, x_{1}-x_{5}=\varepsilon_{5} \frac{\alpha}{5}.
$$
Then, by telescoping,
$$
0=x_{1}-x_{5}+x_{5}-x_{4}+x_{4}-x_{3}+x_{3}-x_{2}+x_{2}-x_{1}=\varepsilon_{1} \alpha+\varepsilon_{2} \frac{\alpha}{2}+\varepsilon_{3} \frac{\alpha}{3}+\varepsilon_{4} \frac{\alpha}{4}+\varepsilon_{5} \frac{\alpha}{5}.
$$
If $\alpha \neq 0$, there exist signs $\varepsilon_{1}^{\prime}, \ldots, \varepsilon_{4}^{\prime}$ such that
$$
\frac{1}{5}=\varepsilon_{1}^{\prime}+\varepsilon_{2}^{\prime} \frac{1}{2}+\varepsilon_{3}^{\prime} \frac{1}{3}+\varepsilon_{4}^{\prime} \frac{1}{4}
$$
so there exists an integer $n$ such that $\frac{1}{5}=\frac{n}{12}$, which is impossible since 5 does not divide 12.

|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $x_{1}, x_{2}, \ldots, x_{5}$ des réels tels que
$$
\left|x_{2}-x_{1}\right|=2\left|x_{3}-x_{2}\right|=3\left|x_{4}-x_{3}\right|=4\left|x_{5}-x_{4}\right|=5\left|x_{1}-x_{5}\right| .
$$
Montrer que ces cinq réels sont égaux.
|
Notons $\alpha=\left|x_{2}-\chi_{1}\right|$ et montrons par l'absurde que $\alpha=0$. D'après l'énoncé, il existe des signes $\varepsilon_{1}, \ldots$, $\varepsilon_{5}$ tels que
$$
x_{2}-x_{1}=\varepsilon_{1} \alpha, x_{3}-x_{2}=\varepsilon_{2} \frac{\alpha}{2}, x_{4}-x_{3}=\varepsilon_{3} \frac{\alpha}{3}, x_{5}-x_{4}=\varepsilon_{4} \frac{\alpha}{4}, x_{1}-x_{5}=\varepsilon_{5} \frac{\alpha}{5} .
$$
Alors, par télescopage,
$$
0=x_{1}-x_{5}+x_{5}-x_{4}+x_{4}-x_{3}+x_{3}-x_{2}+x_{2}-x_{1}=\varepsilon_{1} \alpha+\varepsilon_{2} \frac{\alpha}{2}+\varepsilon_{3} \frac{\alpha}{3}+\varepsilon_{4} \frac{\alpha}{4}+\varepsilon_{5} \frac{\alpha}{5} .
$$
Si $\alpha \neq 0$, il existe donc des signes $\varepsilon_{1}^{\prime}, \ldots, \varepsilon_{4}^{\prime}$ tels que
$$
\frac{1}{5}=\varepsilon_{1}^{\prime}+\varepsilon_{2}^{\prime} \frac{1}{2}+\varepsilon_{3}^{\prime} \frac{1}{3}+\varepsilon_{4}^{\prime} \frac{1}{4}
$$
donc un entier n tel que $\frac{1}{5}=\frac{\mathfrak{n}}{12}$ ce qui est impossible car 5 ne divise par 12 .

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi4-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution."
}
|
a42d6540-b707-5888-8802-9f9fa01aeb31
| 607,467
|
Let $x, y, z > 0$ such that $x y z = 8$. Show that
$$
\frac{x-2}{x+1} + \frac{y-2}{y+1} + \frac{z-2}{z+1} \leqslant 0
$$
|
Let's start by noting that $a-2=a+1-3$ for any real number $a$, so
$$
\frac{x-2}{x+1}+\frac{y-2}{y+1}+\frac{z-2}{z+1}=3-3\left(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\right)
$$
The inequality to be established can thus be rewritten as
$$
\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} \geqslant 1
$$
By putting everything over a common denominator, we get
$$
3+2(x+y+z)+xy+yz+zx \geqslant 1+x+y+z+xy+yz+zx+xyz
$$
which simplifies to
$$
\frac{x+y+z}{3} \geqslant 2
$$
This last inequality is simply the arithmetic-geometric mean inequality.

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x, y, z>0$ tels que $x y z=8$. Montrer que
$$
\frac{x-2}{x+1}+\frac{y-2}{y+1}+\frac{z-2}{z+1} \leqslant 0
$$
|
Commençons par remarquer que $a-2=a+1-3$ pour tout réel a donc
$$
\frac{x-2}{x+1}+\frac{y-2}{y+1}+\frac{z-2}{z+1}=3-3\left(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\right)
$$
L'inégalité à établir se réécrit donc
$$
\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} \geqslant 1
$$
En mettant au même dénominateur, on obtient
$$
3+2(x+y+z)+x y+y z+z x \geqslant 1+x+y+z+x y+y z+z x+x y z
$$
soit
$$
\frac{x+y+z}{3} \geqslant 2
$$
Or, cette dernière égalité est simplement l'inégalité arithmético-géométrique.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi4-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
2a15fe37-7f7c-5799-89b4-10363d622a23
| 607,470
|
Let $n$ be an integer and $0<\mathfrak{u}_{1}<\mathfrak{u}_{2}<\ldots<\boldsymbol{u}_{\boldsymbol{n}}$ be real numbers such that
$$
\mathfrak{u}_{1}+\mathfrak{u}_{2}+\ldots+\mathfrak{u}_{n}=\frac{1}{\mathfrak{u}_{1}^{2}}+\frac{1}{\mathfrak{u}_{2}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}
$$
Show that for any integer $k$ less than or equal to $n$, there exist $k$ real numbers among $\mathfrak{u}_{1}, \mathfrak{u}_{2}, \ldots, \mathfrak{u}_{n}$ whose sum is greater than or equal to $k$.
|
$\triangleright$ Let's start by showing the result for $k=n$. Let $a=\frac{u_{1}+\ldots+u_{n}}{n}$ and $g=\left(u_{1} \ldots u_{n}\right)^{\frac{1}{n}}$ be the arithmetic and geometric means of $u_{1}, \ldots, u_{n}$. Then, the classical inequality between arithmetic, geometric, and harmonic means gives
$$
a=\frac{\frac{1}{\mathbf{u}_{1}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}}{n} \geqslant \frac{1}{g^{2}} \geqslant \frac{1}{a^{2}}
$$
Thus, $a \geqslant 1$ and, therefore, $u_{1}+\ldots+u_{n} \geqslant n$.
$\triangleright$ Let $k<n$. Suppose that $u_{1}+\ldots+u_{k}<k, u_{2}+\ldots+u_{k+1}<k, \ldots, u_{n}+\ldots+u_{k-1}<k$. Then, by adding all these inequalities, we get
$$
n\left(u_{1}+\ldots+u_{n}\right)<n k
$$
which contradicts the previous point. Thus, one of the sums $\mathfrak{u}_{1}+\ldots+\mathfrak{u}_{\mathrm{k}}, \mathfrak{u}_{2}+\ldots+\mathfrak{u}_{\mathrm{k}+1}, \ldots$, $u_{n}+\ldots+u_{k-1}$ is greater than or equal to $k$.
## Olympic Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient un entier $n$ et des réels $0<\mathfrak{u}_{1}<\mathfrak{u}_{2}<\ldots<\boldsymbol{u}_{\boldsymbol{n}}$ tels que
$$
\mathfrak{u}_{1}+\mathfrak{u}_{2}+\ldots+\mathfrak{u}_{n}=\frac{1}{\mathfrak{u}_{1}^{2}}+\frac{1}{\mathfrak{u}_{2}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}
$$
Montrer que, pour tout entier $k$ inférieur ou égal à $n$, il existe $k$ réels parmi $\mathfrak{u}_{1}, \mathfrak{u}_{2}, \ldots, \mathfrak{u}_{n}$ dont la somme est supérieure ou égale à $k$.
|
$\triangleright$ Commençons par montrer le résultat pour $k=n$. Notons $a=\frac{u_{1}+\ldots+u_{n}}{n}$ et $g=\left(u_{1} \ldots u_{n}\right)^{\frac{1}{n}}$ les moyennes arithmétique et géométrique de $u_{1}, \ldots, u_{n}$. Alors, l'inégalité classique entre moyenne arithmétique-géométrique-harmonique donne
$$
\mathrm{a}=\frac{\frac{1}{\mathbf{u}_{1}^{2}}+\ldots+\frac{1}{\mathfrak{u}_{n}^{2}}}{\mathrm{n}} \geqslant \frac{1}{\mathrm{~g}^{2}} \geqslant \frac{1}{\mathrm{a}^{2}}
$$
Ainsi, $a \geqslant 1$ et, donc, $u_{1}+\ldots+u_{n} \geqslant n$.
$\triangleright$ Soit $k<n$. Supposons que $u_{1}+\ldots+u_{k}<k, u_{2}+\ldots+u_{k+1}<k, \ldots, u_{n}+\ldots+u_{k-1}<k$. Alors, en additionnant toutes ces inégalités, on obtient
$$
n\left(u_{1}+\ldots+u_{n}\right)<n k
$$
ce qui contredit le point précédent. Ainsi, l'une des sommes $\mathfrak{u}_{1}+\ldots+\mathfrak{u}_{\mathrm{k}}, \mathfrak{u}_{2}+\ldots+\mathfrak{u}_{\mathrm{k}+1}, \ldots$, $u_{n}+\ldots+u_{k-1}$ est supérieure ou égale à $k$.
## Exercices Olympiques
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi4-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution."
}
|
83f3671b-1b79-5516-9a0e-a6763f07f3f1
| 607,472
|
Let $x$, $y$ and $z$ be strictly positive real numbers such that
$$
x+y+z \geqslant \frac{1}{x}+\frac{1}{y}+\frac{1}{z}
$$
Show that
$$
\frac{x}{y}+\frac{y}{z}+\frac{z}{x} \geqslant \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}
$$
|
By putting on the same denominator, the sought inequality rewrites as
$$
x^{2} z+y^{2} x+z^{2} y \geqslant x+y+z
$$
Let's show this using successively the hypothesis and the Cauchy-Schwarz inequality:
$$
\begin{aligned}
& x+y+z \leqslant \frac{(x+y+z)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
& \leqslant \frac{\left(x \sqrt{z} \cdot \frac{1}{\sqrt{z}}+y \sqrt{x} \cdot \frac{1}{\sqrt{x}}+z \sqrt{y} \cdot \frac{1}{\sqrt{y}}\right)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
& \leqslant x^{2} z+y^{2} x+z^{2} y . \\
& \text { for }
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x$, y et $z$ des réels strictement positifs tels que
$$
x+y+z \geqslant \frac{1}{x}+\frac{1}{y}+\frac{1}{z}
$$
Montrer que
$$
\frac{x}{y}+\frac{y}{z}+\frac{z}{x} \geqslant \frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}
$$
|
En mettant au même dénominateur, l'inégalité recherchée se réécrit
$$
x^{2} z+y^{2} x+z^{2} y \geqslant x+y+z
$$
Montrons celle-ci en utilisant successivement l'hypothèse et l'inégalité de Cauchy-Schwarz :
$$
\begin{aligned}
& x+y+z \leqslant \frac{(x+y+z)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
& \leqslant \frac{\left(x \sqrt{z} \cdot \frac{1}{\sqrt{z}}+y \sqrt{x} \cdot \frac{1}{\sqrt{x}}+z \sqrt{y} \cdot \frac{1}{\sqrt{y}}\right)^{2}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \\
& \leqslant x^{2} z+y^{2} x+z^{2} y . \\
& \text { య̛or }
\end{aligned}
$$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi4-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution."
}
|
edf62a8a-c940-5842-b1a8-aa6d9fb25d8f
| 607,474
|
Prove that the equation
$$
a^{3}+b^{5}+c^{7}+d^{11}=e^{13}
$$
admits an infinite number of solutions in strictly positive integers.
|
It should be noted that if $(a, b, c, d, e)$ is a solution, then for any integer $k>0$, the quintuple
$$
\left(a k^{5 \times 7 \times 11 \times 13}, \mathrm{bk}^{3 \times 7 \times 11 \times 13}, \mathrm{ck}^{3 \times 5 \times 11 \times 13}, \mathrm{dk}^{3 \times 5 \times 7 \times 13}, e k^{3 \times 5 \times 7 \times 11}\right)
$$
is also a solution.
To conclude, it is therefore sufficient to find one solution. One might think of finding a solution such that
$$
a^{3}=b^{5}=c^{7}=d^{11}=\frac{1}{4} e^{13}
$$
where $e=2^{\mathrm{t}}$ for some $t$ to be determined. For this, $t$ must be chosen so that $13 \mathrm{t}-2$ is a common multiple of $3,5,7,$ and $11$. By searching a bit, we see that we can take $13 \mathbf{t}-2=3 \times 5 \times 7 \times 11$, or equivalently $\mathrm{t}=89$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver que l'équation
$$
a^{3}+b^{5}+c^{7}+d^{11}=e^{13}
$$
admet une infinité de solutions en entiers strictement positifs.
|
Il convient de remarquer que si ( $a, b, c, d, e$ ) est une solution alors, pour tout entier $k>0$, le quintuplet
$$
\left(a k^{5 \times 7 \times 11 \times 13}, \mathrm{bk}^{3 \times 7 \times 11 \times 13}, \mathrm{ck}^{3 \times 5 \times 11 \times 13}, \mathrm{dk}^{3 \times 5 \times 7 \times 13}, e k^{3 \times 5 \times 7 \times 11}\right)
$$
en est une aussi.
Pour conclure, il suffit donc de trouver une solution. On peut penser à en trouver une telle que
$$
a^{3}=b^{5}=c^{7}=d^{11}=\frac{1}{4} e^{13}
$$
où $e=2^{\mathrm{t}}$ pour un certain t à déterminer. Pour cela, t doit être choisi de sorte que $13 \mathrm{t}-2$ soit multiple commun de $3,5,7,11$ et 11 . En cherchant un peu, on voit que l'on peut prendre $13 \mathbf{t}-2=3 \times 5 \times 7 \times 11$, ou encore $\mathrm{t}=89$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution."
}
|
6beffddf-087a-5d0f-931d-bd1510e2ad47
| 607,476
|
Prove that, for all strictly positive integers a, b, c, d, we have
$$
(2 a-1)(2 b-1)(2 c-1)(2 d-1) \geqslant 2 a b c d-1
$$
and determine the cases of equality.
|
If $x$ and $y$ are strictly positive integers, we have $x \geqslant 1$ and $y \geqslant 1$, and thus $(x-1)(y-1) \geqslant 0$. This leads to $x y - x - y + 1 \geqslant 0$, and therefore to $(2 x - 1)(2 y - 1) \geqslant 2 x y - 1$. Note that equality holds if and only if $x = 1$ or $y = 1$.
If $a, b, c, d$ are strictly positive integers, we therefore have $(2 a - 1)(2 b - 1) \geqslant 2 a b - 1$ and $(2 c - 1)(2 d - 1) \geqslant 2 c d - 1$, but also $(2 a b - 1)(2 c d - 1) \geqslant 2 a b c d - 1$. Thus:
$$
(2 a - 1)(2 b - 1)(2 c - 1)(2 d - 1) \geqslant (2 a b - 1)(2 c d - 1) \geqslant 2 a b c d - 1
$$
According to the above, equality holds if and only if three of the numbers $a, b, c, d$ are equal to 1.

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tous entiers strictement positifs a, b, c, d, on a
$$
(2 a-1)(2 b-1)(2 c-1)(2 d-1) \geqslant 2 a b c d-1
$$
et déterminer les cas d'égalité.
|
Si $x$ et $y$ sont des entiers strictement positifs, on a $x \geqslant 1$ et $y \geqslant 1$, et ainsi $(x-1)(y-1) \geqslant 0$. Cela conduit à $x y-x-y+1 \geqslant 0$, et donc à $(2 x-1)(2 y-1) \geqslant 2 x y-1$. Notons que l'égalité a lieu si et seulement si $x=1$ ou $y=1$.
Si $a, b, c, d$ sont des entiers strictement positifs, on a donc $(2 a-1)(2 b-1) \geqslant 2 a b-1$ et $(2 c-$ 1) $(2 \mathrm{~d}-1) \geqslant 2 \mathrm{~cd}-1$, mais aussi $(2 a b-1)(2 c d-1) \geqslant 2 a b c d-1$. Ainsi :
$$
(2 a-1)(2 b-1)(2 c-1)(2 d-1) \geqslant(2 a b-1)(2 c d-1) \geqslant 2 a b c d-1
$$
D'après ci-dessus, l'égalité a lieu si et seulement si trois des nombres $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ sont égaux à 1 .

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution."
}
|
1d169678-9557-5ac2-8e9c-56eca07f4832
| 607,477
|
Point $D$ belongs to the side $[A C]$ of the equilateral triangle $A B C$. We denote $F$ as the orthogonal projection of $D$ on ($B C$), then $K$ as the orthogonal projection of $F$ on ($A B$), and finally $E$ as the orthogonal projection of $K$ on ($C A$). Let $L$ be the midpoint of [BC], and $P$ the intersection of the lines ($K E$) and (FD).
Prove that the line (BP) passes through the midpoint of [AL].
|
First solution. Since the sides of PKF are perpendicular to the sides of ABC, triangle PKF has the same interior angles as ABC and is therefore equilateral, and thus $PF = KF$.
Let $M$ be the intersection of (BP) and (AL). Since triangles BLM and BFP are similar, we have
$$
\frac{ML}{BL} = \frac{PF}{BF} = \frac{KF}{BF} = \sin 60^{\circ} = \frac{\sqrt{3}}{2}
$$
On the other hand, $\frac{AL}{BL} = \tan 60^{\circ} = \sqrt{3}$, so $AL = 2ML$, which proves that $M$ is the midpoint of [AL].
Second solution. Let the sides of $ABC$ be of length 2, and $AD = 2a$ with $a \in [0,1]$. We deduce that $\mathrm{DC} = 2 - 2a$, $\mathrm{FC} = \mathrm{DC} \cos(60^{\circ}) = 1 - a$, and $\mathrm{BF} = 1 + a$. Therefore, we have
$$
\mathrm{BK} = \mathrm{BF} \cos(60^{\circ}) = \frac{1 + a}{2} \quad \text{and} \quad \mathrm{KF} = \mathrm{BF} \sin(60^{\circ}) = \frac{\sqrt{3}}{2}(1 + a)
$$
Since the sides of PKF are perpendicular to the sides of $ABC$, triangle $PKF$ has the same interior angles as $ABC$ and is therefore equilateral. We then have $PF = KF = \frac{\sqrt{3}}{2}(1 + a)$.
Since point $L$ is the midpoint of $[BC]$ with $ABC$ being equilateral, lines $(AL)$ and $(BC)$ are perpendicular, ensuring that $(ML)$ and $(PF)$ are parallel, where $M$ is the intersection of $(BP)$ and $(AL)$. By Thales' theorem, we then have
$$
\frac{\mathrm{ML}}{\mathrm{PF}} = \frac{\mathrm{BL}}{\mathrm{BF}} = \frac{1}{1 + a}
$$
Thus, $ML = \frac{\sqrt{3}}{2} = \frac{1}{2} AL$, which concludes the proof.
Third solution. As above, we note that PKF is equilateral, and let $M$ be the intersection of (BP) and (AL). Let $Q$ be the intersection of (FP) and (AB). We have $\widehat{\mathrm{PKQ}} = \widehat{\mathrm{PQK}} = 30^{\circ}$, so PQK is isosceles at $P$ and we have $PQ = PK$. But, $PK = KF$ since $PKF$ is equilateral, so $PQ = KF$ which ensures that $P$ is the midpoint of [QF]. Since their sides are either common or parallel, triangles BPQ and BMA on the one hand, and triangles BPF and BML on the other, are similar. This leads to
$$
\frac{PQ}{AM} = \frac{PM}{BM} \quad \text{and} \quad \frac{PF}{ML} = \frac{PM}{BM}
$$
Thus, $\frac{AM}{ML} = \frac{PQ}{PF} = 1$, and $M$ is indeed the midpoint of $[AL]$.
Fourth solution. Let $X$ be the midpoint of $[AB]$ and $Y$ such that $ALCY$ is a rectangle. Then $XC = AL = CY$ and $\widehat{YCX} = 60^{\circ}$, so $XCY$ is equilateral. Two of its sides being perpendicular to two of the sides of the equilateral triangle $ABC$, the same is true for its third side. Let $M$ be the intersection of (AL) and (BY). Since $(AL)$ and $(CY)$ are parallel and $BC = 2BL$, we have $AL = CY = 2ML$, so $M$ is the midpoint of [AL]. As above, we note that KFP is equilateral because its sides are perpendicular to those of $ABC$. However, the same is true for $XYC$, so triangles KFP and $XYC$ have their sides parallel. Since points $B, F, C$ on the one hand, and $B, K, X$ on the other, are collinear, there exists a homothety centered at B that maps $XYC$ to KFP. In particular, point $P$ lies on the line (BY) which passes through the midpoint of [AL].
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Le point $D$ appartient au côté $[A C]$ du triangle équilatéral $A B C$. On note $F$ le projeté orthogonal de $D$ sur ( $B C$ ), puis $K$ le projeté orthogonal de $F$ sur ( $A B$ ), et enfin $E$ le projeté orthogonal de $K$ sur ( $C A$ ). Soit $L$ le milieu de [BC], et $P$ l'intersection des droites ( $K E$ ) et (FD).
Prouver que la droite (BP) passe par le milieu de [AL].
|
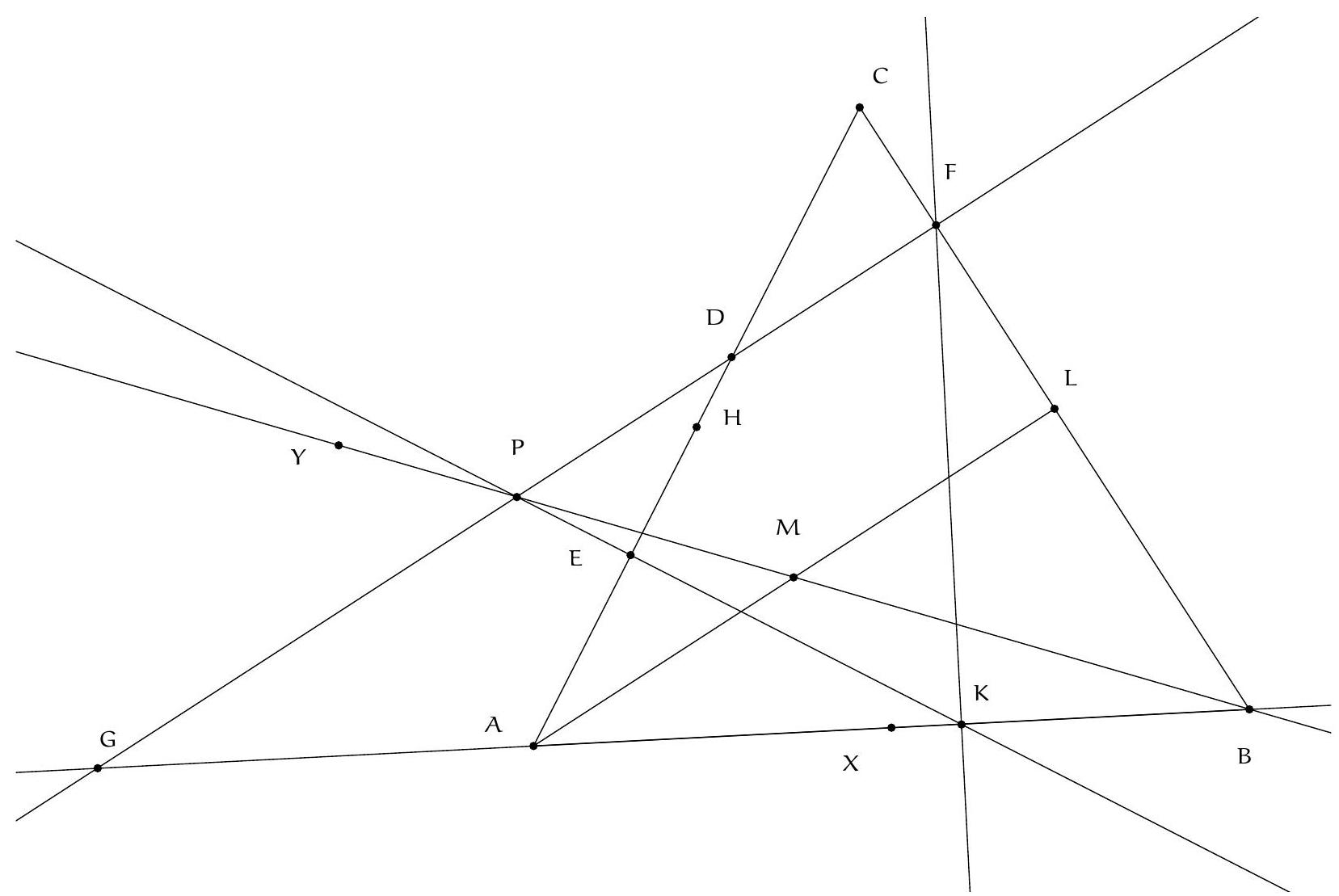
Première solution. Comme les côtés de PKF sont perpendiculaires aux côtés de ABC , le triangle PKF a les mêmes angles intérieurs que $A B C$ et est donc équilatéral, et donc $P F=K F$.
Notons $M$ l'intersection de (BP) et ( $A L$ ). Comme les triangles BLM et BFP sont semblables, on a
$$
\frac{M L}{B L}=\frac{P F}{B F}=\frac{\mathrm{KF}}{B F}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}
$$
D'autre part, $\frac{A L}{B L}=\tan 60^{\circ}=\sqrt{3}$, donc $A L=2 M L$, ce qui prouve que $M$ est le milieu de [AL].
Deuxième solution. Posons que les côtés de $A B C$ soient de longueur 2 , et que $A D=2 a$ avec $a \in$ $[0,1]$. On en déduit que $\mathrm{DC}=2-2 \mathrm{a}, \mathrm{FC}=\mathrm{DC} \cos \left(60^{\circ}\right)=1-\mathrm{a}$, et $\mathrm{BF}=1+\mathrm{a}$ Par suite, on a
$$
\mathrm{BK}=\mathrm{BF} \cos \left(60^{\circ}\right)=\frac{1+\mathrm{a}}{2} \quad \text { et } \quad \mathrm{KF}=\mathrm{BF} \sin \left(60^{\circ}\right)=\frac{\sqrt{3}}{2}(1+\mathrm{a})
$$
Puisque les côtés de PKF sont perpendiculaires aux côtés de $A B C$, le triangle $P K F$ a les mêmes angles intérieurs que $A B C$ et est donc équilatéral. On a alors $P F=K F=\frac{\sqrt{3}}{2}(1+a)$.
Le point $L$ étant le milieu de $[B C]$ avec $A B C$ équilatéral, les droites $(A L)$ et $(B C)$ sont donc perpendiculaires, ce qui assure que ( $M L$ ) et ( PF ) sont parallèles, où $M$ est l'intersection de ( $B P$ ) et ( $A L$ ). D'après le théorème de Thalès, il vient alors
$$
\frac{\mathrm{ML}}{\mathrm{PF}}=\frac{\mathrm{BL}}{\mathrm{BF}}=\frac{1}{1+\mathrm{a}}
$$
d'où $M L=\frac{\sqrt{3}}{2}=\frac{1}{2} A L$, ce qui conclut.
Troisième solution. Comme ci-dessus, on remarque que PKF est équilatéral, et on note M l'intersection de (BP) et (AL). Soit Q l'intersection de (FP) et ( AB ). On a $\widehat{\mathrm{PKQ}}=\widehat{\mathrm{PQK}}=30^{\circ}$, donc PQK est isocèle en $P$ et on a $P Q=P K$. Mais, $P K=K F$ puisque $P K F$ est équilatéral, donc $P Q=K F$ ce qui assure que $P$ est le milieu de [QF]. Ayant leurs côtés communs ou parallèles, les triangles BPQ et BMA d'une part, et les triangles BPF et BML d'autre part, sont semblables. Cela conduit à
$$
\frac{P Q}{A M}=\frac{P M}{B M} \quad \text { et } \quad \frac{P F}{M L}=\frac{P M}{B M}
$$
d'où $\frac{A M}{M L}=\frac{P Q}{P F}=1$, et $M$ est bien le milieu de $[A L]$.
Quatrième solution. Soit $X$ le milieu de $[A B]$ et $Y$ tel que $A L C Y$ soit un rectangle. Alors $X C=A L=$ $C Y$ et $\widehat{Y C X}=60^{\circ}$, donc $X C Y$ est équilatéral. Deux de ses côtés étant perpendicualires à deux des côtés du triangle équilatéral $A B C$, il en est de même de son troisième côté. Soit $M$ l'intersection de (AL) et (BY). Puisque $(A L)$ et $(C Y)$ sont parallèles et que $B C=2 B L$, on a $A L=C Y=2 M L$, d'où $M$ est le milieu de [AL]. Comme ci-dessus, on remarque que KFP est équilatéral car ses côtés sont perpendiculaires à ceux de $A B C$. Or, il en est de même de $X Y C$, donc les triangles KFP et $X C Y$ ont leurs côtés parallèles. Puisque les points $B, F, C$ d'une part, et $B, K, X$ d'autre part sont alignés, il existe donc une homothétie de centre B qui envoie $X C Y$ sur KFP. En particulier, le point $P$ appartient à la droite (BY) qui passe par le milieu de [AL].
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
2a666636-b73e-5952-960f-f7f705c3bef7
| 607,478
|
Let $A B C D$ be a convex quadrilateral. For any point $M$ inside or on the boundary of $A B C D$, we define
$$
f(M)=M A+M B+M C+M D .
$$
Prove that, for any $M$, we have
$$
f(M) \leqslant \max (f(A), f(B), f(C), f(D))
$$
|
Lemme. If point K is on the sides or inside the triangle XYZ, we have
$$
X Y+X Z \geqslant K Y+K Z .
$$
Proof of the lemma. If $\mathrm{K}=\mathrm{Y}$, the result is immediate from the triangle inequality. Otherwise, let P be the intersection of (YK) with the side [XZ]. From the triangle inequality, we then have
$$
X Y+X Z=X Y+X P+P Z \geqslant Y P+P Z=Y K+K P+P Z \geqslant Y K+K Z .
$$
Let's return to the exercise, and consider a point $M$ inside or on the boundary of the convex quadrilateral $A B C D$. We will start by proving that we can find a point $P$ on the boundary of $A B C D$ such that $f(M) \leqslant f(P)$. The diagonals $[A C]$ and $[B D]$ intersect at $O$, and without loss of generality, we can assume that $M$ is inside or on the boundaries of the triangle $A D O$. The lines ( $B M$ ) and ( $C M$ ) intersect the side [AD] at $X$ and $Y$ respectively. Let $P$ be a point on $[X Y]$. According to the lemma, since $M$ is inside or on the boundaries of the triangle BDP, we have $P B+P D \geqslant M B+M D$. And, since $M$ is inside or on the boundaries of the triangle $C A P$, we have $P A+P C \geqslant M A+M C$. By summing, we get $f(M) \leqslant f(P)$, with $P \in[A D]$ as desired.
With the point $P \in[A D]$ above, we now show that $f(P) \leqslant f(A)$ or $f(P) \leqslant$ $f(D)$, which will complete the proof. Indeed, since $P \in[A D]$, we have $P A+P D=A D$. We want to maximize $\mathrm{PB}+\mathrm{PC}$. For this, we construct the symmetric $\mathrm{B}^{\prime}$ of B with respect to ( $A D$ ). We then have $P B+P C=P B^{\prime}+P C$. Moreover, since $A B C D$ is convex, depending on whether the line ( $B^{\prime} C$ ) intersects ( $A D$ ) at a point of $[A D]$ or not, the point $P$ is inside or on the boundaries of $A B^{\prime} C$ or of $D^{\prime} C$. According to the lemma, we then have $\mathrm{PB}^{\prime}+P C \leqslant A B^{\prime}+A C=A B+A C$ or $P B^{\prime}+P C \leqslant B^{\prime}+D C=D B+D C$. Thus, we have
$$
f(P)=P A+P D+P B+P C \leqslant A D+A B+A C=f(A)
$$
or
$$
f(P)=P A+P D+P B+P C \leqslant A D+D B+D C=f(D),
$$
as announced.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $A B C D$ un quadrilatère convexe. Pour tout point $M$ à l'intérieur ou sur le bord de $A B C D$, on pose
$$
f(M)=M A+M B+M C+M D .
$$
Prouver que, pour tout $M$, on a
$$
f(M) \leqslant \max (f(A), f(B), f(C), f(D))
$$
|
Lemme. Si le point K est sur les bords ou à l'intérieur du triangle XYZ , on a
$$
X Y+X Z \geqslant K Y+K Z .
$$
Preuve du lemme. Si $\mathrm{K}=\mathrm{Y}$, le résultat est immédiat d'après l'inégalité triangulaire. Sinon, on note P l'intersection de (YK) avec le côté [XZ]. D'après l'inégalité triangulaire, on a alors
$$
X Y+X Z=X Y+X P+P Z \geqslant Y P+P Z=Y K+K P+P Z \geqslant Y K+K Z .
$$
Revenons à l'exercice, et considérons un point $M$ à l'intérieur ou sur le bord du quadrilatère convexe $A B C D$. On va commencer par prouver que l'on peut trouver un point $P$ du bord de $A B C D$ tel que $f(M) \leqslant f(P)$. Les diagonales $[A C]$ et $[B D]$ se coupent en $O$ et, sans perte de généralité, on peut supposer que $M$ est dans ou sur les bords du triangle $A D O$. Les droites ( $B M$ ) et ( $C M$ ) recoupent alors le côté [AD] respectivement en $X$ et $Y$. Soit $P$ un point de $[X Y]$. D'après le lemme, puisque $M$ est dans ou sur les bords du triangle BDP, on a $P B+P D \geqslant M B+M D$. Et, puisque $M$ est dans ou sur les bords du triangle $C A P$, on a $P A+P C \geqslant M A+M C$. En sommant, il vient $f(M) \leqslant f(P)$, avec $P \in[A D]$ comme désiré.
Toujours avec le point $P \in[A D]$ ci-dessus, on montre maintenant que $f(P) \leqslant f(A)$ ou $f(P) \leqslant$ $f(D)$, ce qui terminera la démonstration. En effet, puisque $P \in[A D]$, on a $P A+P D=A D$. On veut maximiser $\mathrm{PB}+\mathrm{PC}$. Pour cela, on construit le symétrique $\mathrm{B}^{\prime}$ de B par rapport à ( $A D$ ). On a donc $P B+P C=P B^{\prime}+P C$. De plus, puisque $A B C D$ est convexe, selon que la droite ( $B^{\prime} C$ ) rencontre ( $A D$ ) en un point de $[A D]$ ou non, le point $P$ est sur dans ou sur les bords de $A B^{\prime} C$ ou de $D^{\prime} C$. D'après le lemme, on a alors $\mathrm{PB}^{\prime}+P C \leqslant A B^{\prime}+A C=A B+A C$ ou $P B^{\prime}+P C \leqslant B^{\prime}+D C=D B+D C$. Ainsi, on a
$$
f(P)=P A+P D+P B+P C \leqslant A D+A B+A C=f(A)
$$
ou
$$
f(P)=P A+P D+P B+P C \leqslant A D+D B+D C=f(D),
$$
comme annoncé.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
bbe8cf33-2fd5-564b-b030-0967c3374bdb
| 607,479
|
For all integers $n \geqslant 1$, we define $S_{n}=x_{1}+x_{2}+\cdots+x_{n}$, where $x_{k}=\frac{k(k+1)}{2}$ for all $k \geqslant 1$. Prove that, for all $n \geqslant 10$, there exists an integer $a_{n}$ such that $S_{n-1}<a_{n}^{2}<S_{n}$.
|
For all integers $\mathrm{n} \geqslant 1$, we have
$$
S_{n}=\sum_{k=1}^{n} \frac{k(k+1)}{2}=\frac{1}{2} \sum_{k=1}^{n} k^{2}+\frac{1}{2} \sum_{k=1}^{n} k=\frac{n(n+1)(2 n+1)}{12}+\frac{n(n+1)}{4}=\frac{n(n+1)(n+2)}{6}
$$
It is therefore sufficient to prove that, for $n \geqslant 10$, we have $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$, because then the interval $] S_{n-1}, S_{n}[$ will necessarily contain an integer.
Indeed, from the above calculation, the inequality $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$ is equivalent to
$$
\sqrt{\frac{n(n+1)(n+2)}{6}}-\sqrt{\frac{n(n+1)(n-1)}{6}}>1
$$
or equivalently,
$$
\sqrt{\frac{n(n+1)}{6}}(\sqrt{n+2}-\sqrt{n-1})>1
$$
Since
$$
\sqrt{n+2}-\sqrt{n-1}=\frac{3}{\sqrt{n+2}+\sqrt{n-1}}
$$
we want to prove that
$$
\sqrt{3 n(n+1)}>\sqrt{2(n+2)}+\sqrt{2(n-1)}
$$
To do this, it suffices to show that $\sqrt{3 n(n+1)}>2 \sqrt{2(n+2)}$. This last inequality can also be written as $3 n^{2}-5 n-16>0$. It is easy to verify that this inequality is satisfied for $n \geqslant 10$.

## Olympic Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Pour tout entier $n \geqslant 1$, on pose $S_{n}=x_{1}+x_{2}+\cdots+x_{n}$, où $x_{k}=\frac{k(k+1)}{2}$ pour tout $k \geqslant 1$. Prouver que, pour tout $n \geqslant 10$, il existe un entier $a_{n}$ tel que $S_{n-1}<a_{n}^{2}<S_{n}$.
|
Pour tout entier $\mathrm{n} \geqslant 1$, on a
$$
S_{n}=\sum_{k=1}^{n} \frac{k(k+1)}{2}=\frac{1}{2} \sum_{k=1}^{n} k^{2}+\frac{1}{2} \sum_{k=1}^{n} k=\frac{n(n+1)(2 n+1)}{12}+\frac{n(n+1)}{4}=\frac{n(n+1)(n+2)}{6}
$$
Il suffit donc de prouver que, pour $n \geqslant 10$, on a $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$, car alors l'intervalle $] S_{n-1}, S_{n}[$ contiendra forcément un entier.
Or, d'après le calcul ci-dessus, l'inégalité $\sqrt{S_{n}}-\sqrt{S_{n-1}}>1$ est équivalente à
$$
\sqrt{\frac{n(n+1)(n+2)}{6}}-\sqrt{\frac{n(n+1)(n-1)}{6}}>1
$$
ou encore
$$
\sqrt{\frac{n(n+1)}{6}}(\sqrt{n+2}-\sqrt{n-1})>1
$$
Puisque
$$
\sqrt{n+2}-\sqrt{n-1}=\frac{3}{\sqrt{n+2}+\sqrt{n-1}}
$$
on veut prouver que
$$
\sqrt{3 n(n+1)}>\sqrt{2(n+2)}+\sqrt{2(n-1)}
$$
Pour cela, il suffit de montrer que $\sqrt{3 n(n+1)}>2 \sqrt{2(n+2)}$. Cette dernière inégalité s'écrit aussi $3 n^{2}-5 n-16>0$. Il est facile de vérifier qu'elle est satisfaite pour $n \geqslant 10$.

## Exercices Olympiques
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution."
}
|
ab5f1e03-a0ab-5146-8487-ee1a75e0e7b2
| 607,481
|
Consider a finite set E of boys and girls.
A subset G of boys from E is said to be popular if each girl in E knows at least one of the boys in $G$. Similarly, a subset $F$ of girls is said to be popular if each boy in E knows at least one of the girls in $F$. We assume that if a knows $b$ then $b$ knows $a$.
Prove that the number of popular subsets formed by the boys has the same parity as the number of popular subsets formed by the girls.
|
First solution. We will say that a set X of boys is foreign to a set Y of girls if no boy in X is known to any of the girls in Y. Similarly, a set Y of girls will be said to be foreign to a set X of boys if no girl in Y is known to any of the boys in X. Since the relation "to know" is assumed to be symmetric, we deduce that X is foreign to Y if and only if Y is foreign to X. This opens the door to a double-counting:
We denote by N the number of pairs (X, Y) of sets X of boys and Y of girls that are mutually foreign. Let X be a set of boys. We denote by \( Y_X \) the largest set of girls that is foreign to X. Clearly, any set Y of girls that is foreign to X is contained in \( Y_X \), and conversely, any subset of \( Y_X \) is foreign to X. Therefore, the number of sets Y that are foreign to X is \( 2^{|Y_X|} \) (where \( |A| \) denotes the number of elements in the set \( \mathcal{A} \)). We deduce that
\[
N = \sum_{X} 2^{|Y_X|}
\]
Moreover, for any set X of boys, X is popular if and only if \( Y_X = \emptyset \), i.e., \( 2^{|Y_X|} = 1 \). Thus, the number of popular sets of boys is congruent to N modulo 2.
An analogous reasoning shows that the number of popular sets of girls is also congruent to N modulo 2, which concludes the proof.
Second solution. Let G be the set of boys and F the set of girls. We will prove the result by induction on \( n = |G| \). We first note that if F or G is empty, the conclusion is immediate (there are no popular groups). This ensures the result for \( n = 0, 1 \), and we now consider a group of \( n + 1 \geq 2 \) people in which there is at least one girl and at least one boy.
Let \( g \) be one of the boys. We set \( G' = G - \{g\} \) and \( F' \) the set of girls who do not know \( g \). Then:
- a popular set of boys in \( G' \cup F \) is still popular in \( G \cup F \),
- a popular set of boys in \( G \cup F \) that is no longer popular in \( G' \cup F \) is the union of a popular set of boys in \( G' \cup F' \) and \( \{g\} \).
It follows that the number \( N(G, F) \) of popular sets of boys in \( G \cup F \) is the sum of the number \( N(G', F) \) of popular sets of boys in \( G' \cup F \) and the number \( N(G', F') \) of popular sets of boys in \( G' \cup F' \), i.e., \( N(G, F) = N(G', F) + N(G', F') \).
On the other hand:
- a popular set of girls in \( G \cup F' \) is still popular in \( G' \cup F \),
- a popular set of girls in \( G' \cup F \) that is no longer popular in \( G \cup F \) is a popular set of girls in \( G' \cup F' \).
Therefore, the number \( M(G, F) \) of popular sets of girls in \( G \cup F \) is the difference between the number \( M(G', F) \) of popular sets of girls in \( G' \cup F \) and the number \( M(G', F') \) of popular sets of girls in \( G' \cup F' \), i.e., \( M(G, F) = M(G', F) - M(G', F') \).
Now, by the induction hypothesis, we have \( N(G', F) = M(G', F) \mod 2 \) and \( N(G', F') = M(G', F') = -M(G', F') \mod 2 \), hence \( N(F, G) = M(F, G) \mod 2 \), which completes the induction.
Third solution. We still denote by F and G the sets of girls and boys, respectively. For each girl \( f \) and each boy \( g \), we set \( h(f, g) = 0 \) if \( f \) and \( g \) know each other, and \( h(f, g) = 1 \) otherwise. Then, a set \( X \) of boys is popular if and only if \( \prod_{f \in F} \left(1 - \prod_{g \in X} h(f, g)\right) = 1 \). Therefore, the number N of popular sets of boys is
\[
\begin{aligned}
N & = \sum_{X \subseteq G} \prod_{f \in F} \left(1 - \prod_{g \in X} h(f, g)\right) \\
& = \sum_{X \subseteq G} \prod_{f \in F} \left(1 + \prod_{g \in X} h(f, g)\right) \mod 2 \\
& = \sum_{X \subseteq G} \sum_{Y \subseteq F} \prod_{g \in X} \prod_{f \in Y} h(f, g) \mod 2 .
\end{aligned}
\]
We have a similar equality for the number \( M \) of popular sets of girls, which concludes the proof.

|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On considère un ensemble fini E de garçons et de filles.
Une partie G de garçons de E est dite populaire si chaque fille de E connaît au moins un des garçons de $G$. De même, une partie $F$ de filles est dite populaire si chaque garçon de $E$ connaît au moins une des filles de $F$. On suppose que si a connaît $b$ alors $b$ connaît $a$.
Prouver que le nombre de parties populaires formées par les garçons a la même parité que le nombre de parties populaires formées par les filles.
|
Première solution. On dira qu'un ensemble X de garçons est étranger à un groupe Y de filles si aucun garçon de X n'est connu d'une des filles de Y . De même, un ensemble Y de filles sera dit étranger à un groupe $X$ de garçons si aucune fille de $Y$ n'est connue d'un des garçons de $X$. Puisque la relation 'se connaître" est supposée symétrique, on en déduit que $X$ est étranger à $Y$ si et seulement si $Y$ est étranger à $X$. Cela ouvre la porte à un double-comptage :
On note $N$ le nombre de couples $(X, Y)$ de groupes $X$ de garçons et $Y$ de filles mutuellement étrangers. Soit $X$ un groupe de garçons. On note $Y_{X}$ le plus grand groupe de filles qui soit étranger à $X$. Clairement, tout groupe $Y$ de filles qui est étranger à $X$ est contenu dans $Y_{X}$ et, réciproquement, tout sous-ensemble de $Y_{X}$ est étranger à $X$. Par suite, le nombre de groupes $Y$ qui sont étrangers à $X$ est $2^{\left|{ }^{\mid}\right|} \mid$(où $|A|$ désigne le nombre déléments de l'ensemble $\mathcal{A}$ ). On en déduit que
$$
N=\sum_{X} 2^{\left|Y_{X}\right|}
$$
Or, pour tout groupe $X$ de garçons, on a $X$ populaire si et seulement si $Y_{X}=\emptyset$, c.à.d. $2^{\left|Y_{X}\right|}=1$. Ainsi, le nombre de groupes populaires de garçons est congru à N modulo 2 .
Un raisonnement analogue montre que le nombre de groupes populaires de filles est lui aussi congru à N modulo 2 , ce qui conclut.
Deuxième solution. Soit G l'ensemble des garçons et F celui des filles. Nous allons prouver le résultat par récurrence sur $\mathrm{n}=|\mathrm{G}|$. On note tout d'abord que si F ou G est vide, la conclusion est immédiate (il n'existe aucun groupe populaire). Cela assure le résultat pour $\mathrm{n}=0,1$ et on considère maintenant un groupe de $\mathrm{n}+1 \geqslant 2$ personnes dans lequel il y a au moins une fille et au moins un garçon.
Soit $g$ un des garçons. On pose $\mathrm{G}^{\prime}=\mathrm{G}-\{\mathrm{g}\}$ et $\mathrm{F}^{\prime}$ l'ensemble des filles qui ne connaissent pas $g$. Alors :
- un groupe populaire de garçons dans $G^{\prime} \cup F$ l'est encore dans $G \cup F$,
- un groupe populaire de garçons dans $G \cup F$ qui ne l'est plus dans $G^{\prime} \cup F$ est la réunion d'un groupe populaire de garçons dans $G^{\prime} \cup F^{\prime}$ et de $\{g\}$.
Il en découle que le nombre $N(G, F)$ de groupes populaires de garçons dans $G \cup F$ est la somme du nombre $N\left(G^{\prime}, F\right)$ de groupes populaires de garçons dans $G^{\prime} \cup F$ et du nombre $N\left(G^{\prime}, F^{\prime}\right)$ de groupes populaires de garçons dans $G^{\prime} \cup F^{\prime}$, soit donc $N(G, F)=N\left(G^{\prime}, F\right)+N\left(G^{\prime}, F^{\prime}\right)$.
D'autre part :
- un groupe populaire de filles dans $G \cup F l^{\prime}$ est encore dans $G^{\prime} \cup F$,
- un groupe populaire de filles dans $G^{\prime} \cup F$ qui ne l'est plus dans $G \cup F$ est un groupe populaire de filles dans $G^{\prime} \cup F^{\prime}$.
Par conséquent, le nombre $M(G, F)$ de groupes populaires de filles dans $G \cup F$ est la différence entre le nombre $M\left(G^{\prime}, F\right)$ de groupes populaires de filles dans $G^{\prime} \cup F$ et le nombre $M\left(G^{\prime}, F^{\prime}\right)$ de groupes populaires de filles dans $G^{\prime} \cup F^{\prime}$, soit donc $M(G, F)=M\left(G^{\prime}, F\right)-M\left(G^{\prime}, F^{\prime}\right)$.
Or, d'après l'hypothèse de récurrence, on a $N\left(G^{\prime}, F\right)=M\left(G^{\prime}, F\right) \bmod [2]$ et $N\left(G^{\prime}, F^{\prime}\right)=M\left(G^{\prime}, F^{\prime}\right)=$ $-M\left(G^{\prime}, F^{\prime}\right) \bmod [2]$, d'où $N(F, G)=M(F, G) \bmod [2]$, ce qui achève la récurrence.
Troisième solution. On note toujours respectivement F et G l'ensemble des filles et celui des garçons. Pour chaque fille $f$ et chaque garçon $g$, on pose $h(f, g)=0$ si $f$ et $g$ se connaissent, et $h(f, g)=1$ sinon. Alors, un ensemble $X$ de garçons est populaire si et seulement si $\prod_{f \in F}\left(1-\prod_{g \in X} h(f, g)\right)=1$. Par suite, le nombre N de groupes populaires de garçons est
$$
\begin{aligned}
N & =\sum_{X \subseteq G} \prod_{f \in F}\left(1-\prod_{g \in X} h(f, g)\right) \\
& =\sum_{X \subseteq G} \prod_{f \in F}\left(1+\prod_{g \in X} h(f, g)\right) \bmod 2 \\
& =\sum_{X \subseteq G} \sum_{Y \subseteq F} \prod_{g \in X} \prod_{f \in Y} h(f, g) \bmod 2 .
\end{aligned}
$$
On a une égalité similaire pour le nombre $M$ de groupes populaires de filles, ce qui conclut.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution."
}
|
069be700-5018-5742-9404-9c9c9fd9effc
| 607,482
|
. For any integer $k \geqslant 2$, we denote $\mathrm{P}(\mathrm{k})$ as the largest prime divisor of $k$.
Prove that there are infinitely many integers $n$ such that
$$
\mathrm{P}(\mathrm{n})<\mathrm{P}(\mathrm{n}+1)<\mathrm{P}(\mathrm{n}+2)
$$
|
Let $p$ be an odd prime number. For any integer $k \geqslant 1$, we denote $n_{k}=p^{2^{k}}-1$. We obviously have $\mathrm{P}\left(n_{k}+1\right)=\mathrm{p}$. On the other hand, for any integer $i$ such that $0<i<k$, we have
$$
\mathrm{p}^{2^{k}}=\left(p^{2^{i}}\right)^{2^{k-i}}=(-1)^{2^{k-i}}=1 \quad \bmod p^{2^{i}}+1,
$$
hence $n_{k}+2=2 \bmod \left[n_{i}+2\right]$.
Since the integers $n_{k}+2$ and $n_{i}+2$ are even, it follows that $\operatorname{pgcd}\left(n_{k}+2, n_{i}+2\right)=2$. Since $n_{k}+2$ is not a power of 2, because $p^{2^{k}}=1 \bmod 4$ for $k \geqslant 1$ and thus $n_{k}=2 \bmod 4$. Since $n_{k}+2>1$, there exists an odd prime $q_{k}$ that divides $n_{k}+2$ and none of the $n_{i}+2$ for $i<k$. This ensures that there are infinitely many odd primes that divide at least one of the $n_{k}+2$, and thus the sequence $\left(\mathrm{P}\left(n_{k}+2\right)\right)_{k \geqslant 1}$ is not bounded. We can therefore consider the minimal $k$ such that $P\left(n_{k}+2\right)>p$.
To conclude, it remains to prove that, for this choice of $k$, we have $P\left(n_{k}\right)<p$. Now, we have
$$
n_{k}=\left(p^{2^{k-1}}+1\right)\left(p^{2^{k-1}}-1\right)=\left(n_{k-1}+2\right) n_{k-1},
$$
hence, by induction,
$$
n_{k}=(p-1) \prod_{i=1}^{k-1}\left(n_{i}+2\right)
$$
Since $n_{k}+1$ is divisible by $p$, this cannot be the case for $n_{k}$, and the minimality of $k$ ensures that none of the factors $n_{i}+2$ is divisible by a prime number greater than $p$. Thus, $n_{k}$ does not have a prime divisor greater than or equal to $p$, and therefore $\mathrm{P}\left(n_{k}\right)<\mathrm{p}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
. Pour tout entier $k \geqslant 2$, on note $\mathrm{P}(\mathrm{k})$ le plus grand diviseur premier de $k$.
Prouver qu'il existe une infinité d'entiers $n$ tels que
$$
\mathrm{P}(\mathrm{n})<\mathrm{P}(\mathrm{n}+1)<\mathrm{P}(\mathrm{n}+2)
$$
|
Soit $p$ un nombre premier impair. Pour tout entier $k \geqslant 1$, on note $n_{k}=p^{2^{k}}-1$. On a évidemment $\mathrm{P}\left(\mathfrak{n}_{\mathrm{k}}+1\right)=\mathrm{p}$. D'autre part, pour tout entier $i$ tel que $0<i<k$, on a
$$
\mathrm{p}^{2^{k}}=\left(\mathfrak{p}^{2^{i}}\right)^{2^{k-i}}=(-1)^{2^{k-i}}=1 \quad \bmod p^{2^{i}}+1,
$$
d'où $n_{k}+2=2 \bmod \left[n_{i}+2\right]$.
Les entiers $n_{k}+2$ et $n_{i}+2$ étant pairs, il vient alors $\operatorname{pgcd}\left(n_{k}+2, n_{i}+2\right)=2$. Or $n_{k}+2$ n'est pas uns puissance de 2 , car $p^{2^{k}}=1 \bmod 4$ pour $k \geqslant 1$ et donc $\mathfrak{n}_{k}=2 \bmod 4$. Puisque $n_{k}+2>1$, il existe donc un nombre premier impair $q_{k}$ qui divise $n_{k}+2$ et aucun des $n_{i}+2$ pour $i<k$. Cela assure qu'il existe une infinité de nombres premiers impairs qui divisent chacun au moins un des $n_{k}+2$, et donc que la suite $\left(\mathrm{P}\left(n_{k}+2\right)\right)_{k \geqslant 1} n^{\prime}$ 'est pas bornée. On peut donc considérer $k$ minimal tel que $P\left(n_{k}+2\right)>p$.
Pour conclure, il reste à prouver que, pour ce choix de $k$, on a $P\left(n_{k}\right)<p$. Or, on a
$$
\mathfrak{n}_{k}=\left(\mathfrak{p}^{2^{k-1}}+1\right)\left(\mathfrak{p}^{2^{k-1}}-1\right)=\left(\mathfrak{n}_{k-1}+2\right) \mathfrak{n}_{k-1},
$$
d'où, par une récurrence,
$$
n_{k}=(p-1) \prod_{i=1}^{k-1}\left(n_{i}+2\right)
$$
Puisque $n_{k}+1$ est divisible par $p$, ce ne peut être le cas pour $n_{k}$, et la minimalité de $k$ assure qu'aucun des facteurs $n_{i}+2$ n'est divisible par un nombre premier supérieur à $p$. Ainsi, $n_{k} n^{\prime}$ 'a pas de diviseur premier supérieur ou égal à $p$, et donc $\mathrm{P}\left(\mathfrak{n}_{\mathrm{k}}\right)<\mathrm{p}$, comme souhaité.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 8",
"solution_match": "## Solution."
}
|
3aefd292-8272-52ca-a681-f04c210b57db
| 607,483
|
We denote by \( I \) the center of the incircle \( \gamma \) of triangle \( ABC \) and by \( O \) the center of its circumcircle. Let \( \omega_{A} \) be the circle passing through \( B \) and \( C \) and tangent to \( \gamma \). The circles \( \omega_{B} \) and \( \omega_{C} \) are defined similarly. We denote by \( A' \) the other common point of \( \omega_{B} \) and \( \omega_{C} \). The points \( B' \) and \( C' \) are defined similarly.
Prove that the lines \( (AA') \), \( (BB') \), and \( (CC') \) are concurrent at a point \( K \), which is collinear with \( O \) and \( I \).
|
We denote $A_{1}, B_{1}, C_{1}$ as the points of tangency of $\gamma$ with the sides $[B C],[C A],[A B]$. Let $X_{A}$ be the common point of the circles $\gamma$ and $\omega_{A}$.
The circle $\omega_{A}$ is the image of $\gamma$ under a homothety centered at $X_{A}$, which maps $A_{1}$ to a point $M_{A}$ on $\omega_{A}$ where the tangent to $\omega_{A}$ is parallel to $(BC)$. Consequently, this point $M_{A}$ is the midpoint of the arc $BC$ of $\omega_{A}$ that does not contain $X_{A}$, which ensures that
$$
\widehat{M_{A} X_{A}} B = \widehat{M_{A} X_{A}} C = \widehat{M_{A} B C} = \widehat{M_{A} B A_{1}}.
$$
Since $\widehat{A_{1} M_{A} B} = \widehat{B M_{A} A}$, the triangles $M_{A} B A_{1}$ and $M_{A} X_{A} B$ are similar. It follows that
$$
\frac{M_{A} B}{M_{A} X_{A}} = \frac{M_{A} A_{1}}{M_{A} B},
$$
or equivalently, $M_{A} B^{2} = M_{A} A_{1} \cdot M_{A} X_{A}$. This last relation means that $M_{A}$ lies on the radical axis $\Delta_{B}$ of $B$ and $\gamma$. Similarly, $M_{A}$ lies on the radical axis $\Delta_{C}$ of $C$ and $\gamma$. Note that this radical axis $\Delta_{C}$ is perpendicular to the line $(CI)$. Since $A_{1}$ and $B_{1}$ are the points of tangency of $\gamma$ with the tangents to $\gamma$ from $C$, the lines $(A_{1} B_{1})$ and $(CI)$ are perpendicular, which implies that $\Delta_{C}$ is parallel to $(A_{1} B_{1})$. Similarly, the lines $\Delta_{B}$ and $(A_{1} C_{1})$ are parallel.
We define the points $X_{B}, X_{C}, M_{B}, M_{C}$ and the line $\Delta_{A}$ analogously, and prove similarly that $M_{B}$ lies on $\Delta_{A}$ and $\Delta_{C}$, that $M_{C}$ lies on $\Delta_{A}$ and $\Delta_{B}$, and that the lines $\Delta_{A}$ and $(B_{1} C_{1})$ are parallel. We observe that $\Delta_{A}, \Delta_{B}$, and $\Delta_{C}$ are the sides of the triangle $M_{A} M_{B} M_{C}$, and the parallelisms noted above ensure that the triangle $M_{A} M_{B} M_{C}$ is the image of $A_{1} B_{1} C_{1}$ under a homothety $\Phi$, with center $K$ and ratio
$$
r = \frac{M_{A} K}{A_{1} K} = \frac{M_{B} K}{B_{1} K} = \frac{M_{C} K}{C_{1} K}.
$$
In particular, the lines $(M_{A} A_{1}), (M_{B} B_{1})$, and $(M_{C} C_{1})$ are concurrent at $K$. If we evaluate the power of $K$ with respect to $\gamma$, we get $K A_{1} \cdot K X_{A} = K B_{1} \cdot K X_{B}$. Multiplying both sides by $r$, we obtain $M_{A} K \cdot K X_{A} = M_{B} K \cdot K X_{B}$. This means that $K$ lies on the radical axis $(C C')$ of the circles $\omega_{A}$ and $\omega_{B}$. Similarly, we prove that $K$ lies on $(A A')$ and $(B B')$.
Let $O'$ be the image of $I$ under $\Phi$. The point $O'$ therefore lies on the line passing through $M_{A}$ and parallel to $(A_{1} I)$ (and thus perpendicular to $(BC)$). Since $M$ is the midpoint of an arc $BC$ of $\omega_{A}$, this line is the perpendicular bisector of $[BC]$. Similarly, the point $O'$ lies on the perpendicular bisector of $[AC]$, and finally, $O' = O$. Therefore, the points $I, O, K$ are collinear.

$\mathcal{F i n}$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On note I le centre du cercle inscrit $\gamma$ dans le triangle $A B C$ et $O$ le centre de son cercle circonscrit. Soit $\omega_{\text {A }}$ le cercle qui passe par B et $C$ et qui est tangent à $\gamma$. Les cercles $\omega_{B}$ et $\omega_{C}$ sont définis de manière analogue. On note $A^{\prime}$ l'autre point commun de $\omega_{B}$ et $\omega_{C}$. Les points $B^{\prime}$ et $C^{\prime}$ sont définis de façon semblable.
Prouver que les droites $\left(A A^{\prime}\right),\left(B B^{\prime}\right)$ et $\left(C C^{\prime}\right)$ sont concourantes en un point $K$, qui est aligné avec O et I.
|
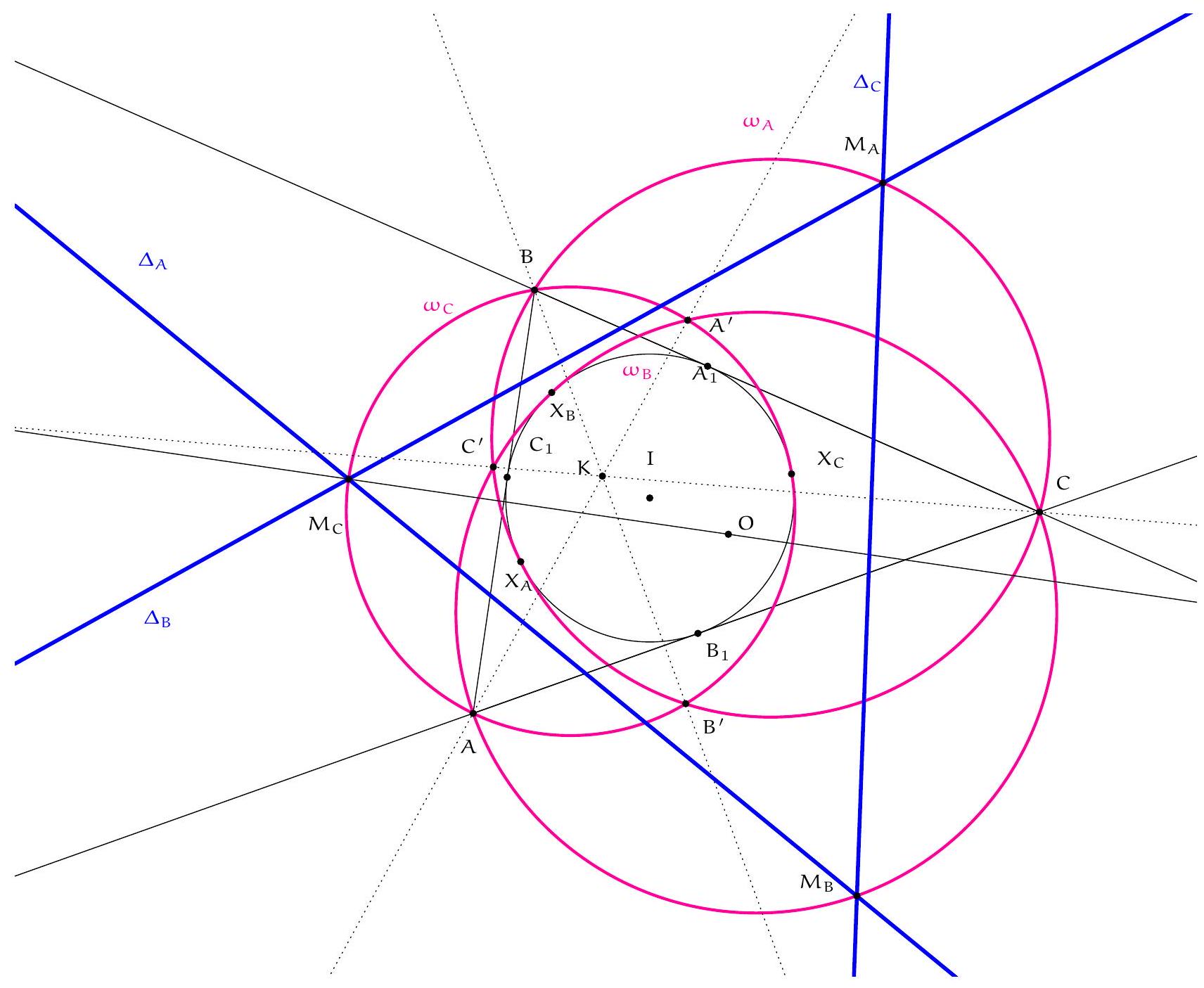
On note respectivement $A_{1}, B_{1}, C_{1}$ les points de contact de $\gamma$ avec les côtés $[B C],[C A],[A B]$. Soit $X_{A}$ le point de commun des cercles $\gamma$ et $\omega_{\mathrm{A}}$.
Le cercle $\omega_{A}$ est l'image de $\gamma$ par une homothétie de centre $X_{A}$, qui envoie $A_{1}$ en un point $M_{A}$ de $\omega_{\mathrm{A}}$ en lequel la tangente à $\omega_{\mathrm{A}}$ est parallèle à ( BC ). Par conséquent, ce point $M_{\mathrm{A}}$ est le milieu de l'arc $B C$ de $\omega_{A}$ qui ne contient pas $X_{A}$, ce qui assure que
$$
\widehat{M_{A} X_{A}} B=\widehat{M_{A} X_{A}} C=\widehat{M_{A} B C}=\widehat{M_{A} B A_{1}} .
$$
Comme, on a évidemment $\widehat{A_{1} M_{A} B}=B{\widehat{M_{A}}}_{A}$, c'est que les triangles $M_{A} B A_{1}$ et $M_{A} X_{A} B$ sont semblables. Il vient alors
$$
\frac{M_{A} B}{M_{A} X_{A}}=\frac{M_{A} A_{1}}{M_{A} B},
$$
ou encore $M_{A} B^{2}=M_{A} A_{1} \cdot M_{A} X_{A}$.
Cette dernière relation signifie que $M_{A}$ appartient à l'axe radical $\Delta_{B}$ de $B$ et $\gamma$. De même, $M_{A}$ appartient à l'axe radical $\Delta_{\mathrm{C}}$ de C et $\gamma$. Notons que cet axe radical $\Delta_{\mathrm{C}}$ est perpendiculaire à la droite (CI). Or, puisque $A_{1}$ et $B_{1}$ sont les points de contact avec $\gamma$ des des deux tangentes à $\gamma$ issues de $C$, les droites $\left(A_{1} B_{1}\right)$ et $(C I)$ sont perpendiculaires, d'où l'on peut affirmer que $\Delta_{C}$ est parallèle à ( $\left.A_{1} B_{1}\right)$. De même, les droites $\Delta_{B}$ et ( $A_{1} C_{1}$ ) sont parallèles.
On définit les points $X_{B}, X_{C}, M_{B}, M_{C}$ et la droite $\Delta_{A}$ de façon analogue à ci-dessus, et on prouve de même que $M_{B}$ appartient à $\Delta_{A}$ et $\Delta_{C}$, que $M_{C}$ appartient à $\Delta_{A}$ et $\Delta_{B}$, et que les droites $\Delta_{A}$ et $\left(B_{1} C_{1}\right)$ sont parallèles. On remarque alors que $\Delta_{A}, \Delta_{B}$ et $\Delta_{C}$ portent les côtés du triangle $M_{A} M_{B} M_{C}$, et les parallélismes signalés ci-dessus assurent que le triangle $M_{A} M_{B} M_{C}$ est l'image de $A_{1} B_{1} C_{1}$ par une homothétie $\Phi$, dont on note K le centre et
$$
r=\frac{M_{A} K}{A_{1} K}=\frac{M_{B} K}{B_{1} K}=\frac{M_{C} K}{C_{1} K}
$$
le rapport. En particulier, les droites $\left(M_{A} A_{1}\right),\left(M_{B} B_{1}\right)$ et $\left(M_{C} C_{1}\right)$ sont concourantes en $K$.
Si l'on évalue la puissance de K par rapport à $\gamma$, il vient $\mathrm{KA}_{1} \cdot \mathrm{KX}_{A}=\mathrm{KB}_{1} \cdot \mathrm{KX} X_{B}$. Après multiplication des deux côtés par $r$, on obtient $M_{A} K \cdot K X_{A}=M_{B} K \cdot K X_{B}$. Cela signifie que $K$ appartient à l'axe radical $\left(C C^{\prime}\right)$ des cercles $\omega_{A}$ et $\omega_{B}$. On prouve de même que $K$ appartient à $\left(A A^{\prime}\right)$ et à ( $\left.B^{\prime}\right)$.
Soit $\mathrm{O}^{\prime}$ l'image de I par $\Phi$. Le point $\mathrm{O}^{\prime}$ appartient donc à la droite passant par $M_{A}$ et parallèle à $\left(A_{1} I\right)$ (et donc perpendiculaire à (BC)). Comme $M$ est le milieu d'un arc $B C$ de $\omega_{A}$, cette droite est donc la médiatrice de $[\mathrm{BC}]$. De même, le point $\mathrm{O}^{\prime}$ appartient à la médiatrice de $[A C]$, et finalement c'est que $\mathrm{O}^{\prime}=\mathrm{O}$. Par suite, les points $\mathrm{I}, \mathrm{O}, \mathrm{K}$ sont alignés.

$\mathcal{F i n}$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi5-corrige.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution."
}
|
f49dba15-cbbf-585d-9eba-2c878521ef08
| 607,484
|
Let $ABC$ be a right isosceles triangle at $B$. Let $M$ be a point on the arc $AC$ of the circle centered at $B$ passing through $A$ and $C$, and $H$ its orthogonal projection on $(AB)$. We denote $I$ as the center of the incircle of $BHM$ and $J$ as the center of the excircle in the angle $B$ ($J$ is thus the intersection of the internal bisector at $B$ with the external bisectors at $H$ and $M$). Show that $MIAJ$ is a square.
|
First, we observe that $(M I) \perp(M J)$ because in a triangle, the internal and external angle bisectors at a point are perpendicular.
On the other hand, $\widehat{M I J}=180^{\circ}-\widehat{B I M}=\widehat{I B M}+\widehat{B M I}=\frac{1}{2}(\widehat{H B M}+\widehat{B M H})=$ $45^{\circ}$. Since $M I J$ is a right triangle at $M$, we deduce that it is an isosceles right triangle at $M$.
Furthermore, $(I J)$ is the angle bisector of $\widehat{M B H}=\widehat{M B A}$, and $M B A$ is isosceles at $B$, so $(I J)$ is the perpendicular bisector of $[A M]$. We deduce that $A I J$ is the reflection of the isosceles right triangle $M I J$ across the line $(I J)$, so $M I A J$ is a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle isocèle en $B$. Soit $M$ un point de l'arc $A C$ du cercle de centre $B$ passant par $A$ et $C, H$ son projeté orthogonal sur $(A B)$. On note $I$ le centre du cercle inscrit à $B H M$ et $J$ le centre du cercle exinscrit dans l'angle $B$ ( $J$ est donc l'intersection de la bissectrice intérieure en $B$ avec les bissectrices extérieures en $H$ et $M)$. Montrer que $M I A J$ est un carré.
|
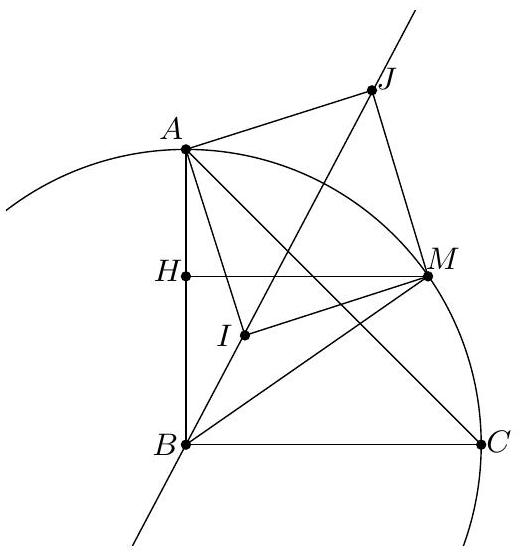
On observe d'abord que $(M I) \perp(M J)$ puisque dans un triangle, les bissectrices intérieure et extérieure en un point sont perpendiculaires.
D'autre part, $\widehat{M I J}=180^{\circ}-\widehat{B I M}=\widehat{I B M}+\widehat{B M I}=\frac{1}{2}(\widehat{H B M}+\widehat{B M H})=$ $45^{\circ}$. Comme $M I J$ est rectangle en $M$, on en déduit qu'il est rectangle isocèle en $M$.
De plus, $(I J)$ est la bissectrice de $\widehat{M B H}=\widehat{M B A}$, et $M B A$ est isocèle en $B$, donc $(I J)$ est la médiatrice de $[A M]$. On en déduit que $A I J$ est le symétrique du triangle rectangle isocèle $M I J$ par rapport à la droite $(I J)$, donc $M I A J$ est un carré.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution."
}
|
59cb3ba5-c290-5bae-a767-9e15c7ddf009
| 607,485
|
Let $ABCD$ be a convex quadrilateral. Let $M$ be the intersection of the internal angle bisectors of angles $B$ and $C$, and $N$ be the intersection of the internal angle bisectors of angles $A$ and $D$. Show that the lines $AB$, $CD$, and $MN$ are concurrent.
|
By exchanging the roles of $A$ and $B$ and the roles of $C$ and $D$, we can assume that $A$ and $D$ are on the segments $[E B]$ and $[E C]$ respectively.
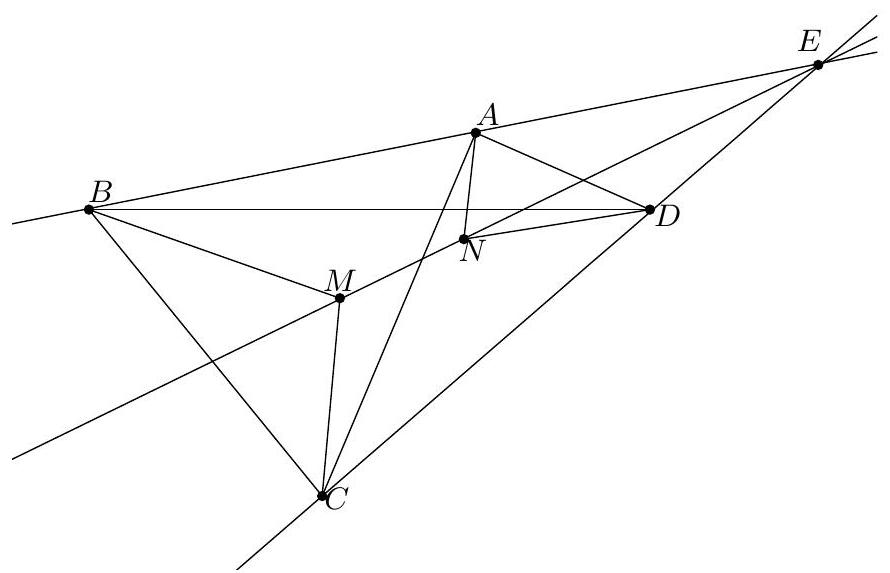
Let $E$ be the intersection point of $(A B)$ and $(C D)$. Then $M$ is the intersection of the internal angle bisectors of angles $B$ and $C$ in triangle $E B C$, so $M$ is the incenter of $E B C$. In particular, it lies on the internal angle bisector at $E$.
Similarly, $N$ is the intersection of the external angle bisectors at $A$ and $D$ in triangle $E A D$, so $N$ is the excenter of $E A D$ opposite to angle $E$. In particular, it lies on the internal angle bisector at $E$. This proves that $E, M, N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe. Soit $M$ l'intersection entre les bissectrices intérieures des angles $B$ et $C$, et $N$ l'intersection entre les bissectrices intérieures des angles $A$ et $D$. Montrer que les droites $A B, C D$ et $M N$ sont concourantes.
|
Quitte à échanger les rôles de $A$ et de $B$ et les rôles de $C$ et de $D$, on peut supposer que $A$ et $D$ se trouvent sur les segments $[E B]$ et $[E C]$ respectivement.

Notons $E$ le point d'intersection entre $(A B)$ et $(C D)$. Alors $M$ est l'intersection des bissectrices intérieures des angles $B$ et $C$ du triangle $E B C$, donc $M$ est le centre du cercle inscrit à $E B C$. En particulier il se trouve sur la bissectrice intérieure en $E$.
De même, $N$ est le point d'intersection des bissectrices extérieures en $A$ et $D$ du triangle $E A D$, donc $N$ est le centre du cercle exinscrit dans l'angle $E$ de $E A D$. En particulier, il se trouve sur la bissectrice intérieure en $E$. Ceci prouve que $E, M, N$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution."
}
|
35f3aecb-57b4-55ff-8841-a194338b004f
| 607,486
|
Let $A B C D$ be a cyclic quadrilateral, $L=(A C) \cap(B D), J$ and $K$ the feet of the perpendiculars from $L$ to $(A D)$ and $(B C)$, and $I$ the midpoint of $[C, D]$. Show that $I J=I K$.
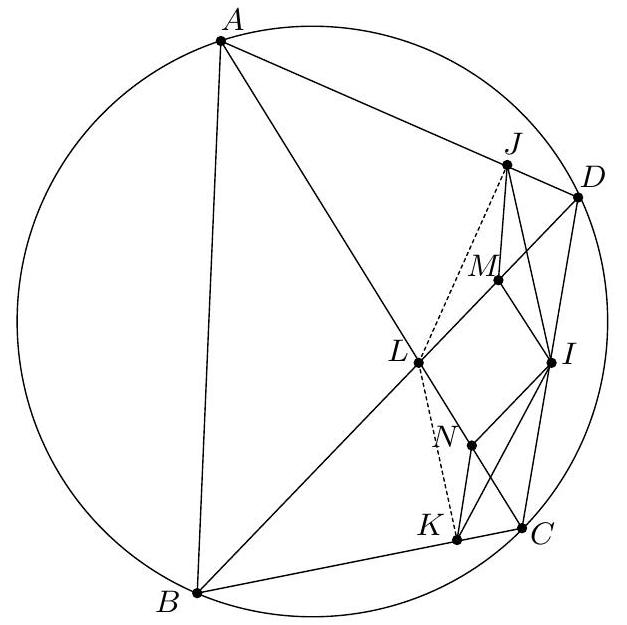
|
It is easy to see using the inscribed angle theorem that $B L C$ and $A L D$ are similar, and that $C K L$ and $D J L$ are similar.
Let $M$ and $N$ be the midpoints of $[L D]$ and $[L C]$, respectively. Then $L N I M$ is a parallelogram. We deduce that $N L=I M$. Since $C K L$ is a right triangle at $K$, we have $N L=N K$, hence $N K=I M$. Similarly, $M J=I N$.
Since $M J L$ is isosceles at $M$, we have $\widehat{J M L}=180^{\circ}-2 \widehat{M L J}=180^{\circ}-2\left(90^{\circ}-\widehat{L D J}\right)=2 \widehat{B D A}$, and similarly $\widehat{K N L}=2 \widehat{B C A}$. Since $\widehat{B D A}=\widehat{B C A}$, we have $\widehat{J M L}=\widehat{K N L}$. We deduce that $\widehat{I M J}=360^{\circ}-\widehat{J M L}-\widehat{L M I}=$ $360^{\circ}-\widehat{K N L}-\widehat{L N I}=\widehat{K N I}$ (the penultimate equality follows from the fact that $L M I N$ is a parallelogram).
From the equalities $\widehat{I M J}=\widehat{K N I}, N K=I M$, and $M J=I N$, we deduce that the triangles $I M J$ and $K N I$ are isometric, and in particular that $I J=I K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère inscriptible, $L=(A C) \cap(B D), J$ et $K$ les pieds des perpendiculaires à $(A D)$ et $(B C)$ passant par $L$ et $I$ le milieu de $[C, D]$. Montrer que $I J=I K$.

|
Il est facile de voir en utilisant le théorème de l'angle inscrit que $B L C$ et $A L D$ sont semblables, et que $C K L$ et $D J L$ sont semblables.
Notons $M$ et $N$ les milieux respectifs de $[L D]$ et $[L C]$. Alors $L N I M$ est un parallélogramme. On en déduit que $N L=I M$. Or, $C K L$ est un triangle rectangle en $K$ donc $N L=N K$, d'où $N K=I M$. De même, $M J=I N$.
Comme $M J L$ est isocèle en $M$, on a $\widehat{J M L}=180^{\circ}-2 \widehat{M L J}=180^{\circ}-$ $2\left(90^{\circ}-\widehat{L D J}\right)=2 \widehat{B D A}$, et de même $\widehat{K N L}=2 \widehat{B C A}$. Or, $\widehat{B D A}=\widehat{B C A}$ donc $\widehat{J M L}=\widehat{K N L}$. On en déduit que $\widehat{I M J}=360^{\circ}-\widehat{J M L}-\widehat{L M I}=$ $360^{\circ}-\widehat{K N L}-\widehat{L N I}=\widehat{K N I}$ (l'avant-dernière égalité découlant du fait que $L M I N$ est un parallélogramme).
Des égalités $\widehat{I M J}=\widehat{K N I}, N K=I M$ et $M J=I N$, on déduit que les triangles $I M J$ et $K N I$ sont isométriques, et en particulier que $I J=I K$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution 1."
}
|
36aa3be5-c30b-5278-bba3-71bc4c8ec992
| 607,487
|
Let $A B C D$ be a cyclic quadrilateral, $L=(A C) \cap(B D), J$ and $K$ the feet of the perpendiculars from $L$ to $(A D)$ and $(B C)$, and $I$ the midpoint of $[C, D]$. Show that $I J=I K$.

|
$$
\begin{aligned}
I J^{2}-I K^{2} & =\overrightarrow{I J} \cdot \overrightarrow{I J}-\overrightarrow{I K} \cdot \overrightarrow{I K}=(\overrightarrow{I J}+\overrightarrow{I K}) \cdot(\overrightarrow{I J}-\overrightarrow{I K}) \\
& =(\overrightarrow{I D}+\overrightarrow{D J}+\overrightarrow{I C}+\overrightarrow{C K}) \cdot \overrightarrow{K J}=(\overrightarrow{D J}+\overrightarrow{C K}) \cdot(\overrightarrow{L J}-\overrightarrow{L K}) \\
& =\overrightarrow{C K} \cdot \overrightarrow{L J}-\overrightarrow{D J} \cdot \overrightarrow{L K} \quad \text{since} \ (D J) \perp (L J) \ \text{and} \ (C K) \perp (L K) \\
& =C K \cdot L J \cos (\overrightarrow{C K}, \overrightarrow{L J})-D J \cdot L K \cos (\overrightarrow{D J}, \overrightarrow{L K})
\end{aligned}
$$
Since $\overrightarrow{L K}$ makes an oriented angle of $+90^{\circ}$ with respect to $\overrightarrow{C K}$, and $\overrightarrow{D J}$ makes an oriented angle of $+90^{\circ}$ with respect to $\overrightarrow{L J}$, the two cosines are equal. Therefore, it suffices to show that $C K \cdot L J = D J \cdot L K$: this follows from the fact that
$$
\frac{C K}{L K}=\cot \widehat{K C L}=\cot \widehat{B C A}=\cot \widehat{B D A}=\cot \widehat{L D J}=\frac{D J}{L J}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère inscriptible, $L=(A C) \cap(B D), J$ et $K$ les pieds des perpendiculaires à $(A D)$ et $(B C)$ passant par $L$ et $I$ le milieu de $[C, D]$. Montrer que $I J=I K$.

|
$$
\begin{aligned}
I J^{2}-I K^{2} & =\overrightarrow{I J} \cdot \overrightarrow{I J}-\overrightarrow{I K} \cdot \overrightarrow{I K}=(\overrightarrow{I J}+\overrightarrow{I K}) \cdot(\overrightarrow{I J}-\overrightarrow{I K}) \\
& =(\overrightarrow{I D}+\overrightarrow{D J}+\overrightarrow{I C}+\overrightarrow{C K}) \cdot \overrightarrow{K J}=(\overrightarrow{D J}+\overrightarrow{C K}) \cdot(\overrightarrow{L J}-\overrightarrow{L K}) \\
& =\overrightarrow{C K} \cdot \overrightarrow{L J}-\overrightarrow{D J} \cdot \overrightarrow{L K} \quad \operatorname{car}(D J) \perp(L J) \text { et }(C K) \perp(L K) \\
& =C K \cdot L J \cos (\overrightarrow{C K}, \overrightarrow{L J})-D J \cdot L K \cos (\overrightarrow{D J}, \overrightarrow{L K})
\end{aligned}
$$
Or, $\overrightarrow{L K}$ fait un angle orienté de $+90^{\circ}$ par rapport à $\overrightarrow{C K}$, et $\overrightarrow{D J}$ fait un angle orienté de $+90^{\circ}$ par rapport à $\overrightarrow{L J}$, donc les deux cosinus sont égaux. Par conséquent, il suffit de montrer que $C K \cdot L J=D J \cdot L K$ : ceci découle du fait que
$$
\frac{C K}{L K}=\cot \widehat{K C L}=\cot \widehat{B C A}=\cot \widehat{B D A}=\cot \widehat{L D J}=\frac{D J}{L J}
$$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution 2."
}
|
36aa3be5-c30b-5278-bba3-71bc4c8ec992
| 607,487
|
Let $ABC$ be a triangle. We denote $O$ as the center of its circumcircle. Let $D, E, F$ be points located on $[B, C]$, $[C, A]$, and $[A, B]$ respectively. We assume that $FB = FD$ and $ED = EC$. The circle with center $F$ and radius $FB$ and the circle with center $E$ and radius $EC$ intersect at $G$. Show that $A, F, O, E, G$ are concyclic.
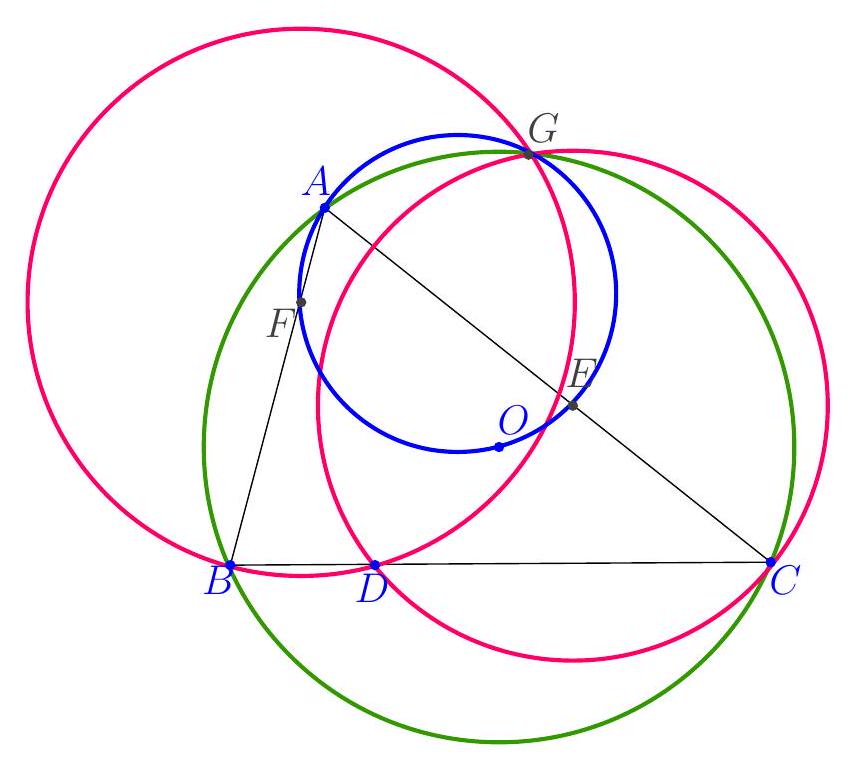
|
Since triangles $B F D$ and $C E D$ are isosceles, we have $(D E, D F)=(D E, D C)+(D B, D F)=(C D, C E)+(B F, B D)=(B C, A C)+(A B, B C)=(A B, A C)$.
Since $E G=E D$ and $F G=F D$, points $E$ and $F$ lie on the perpendicular bisector of $[G D]$, so the quadrilateral $F G E D$ is symmetric with respect to $(F E)$. It follows that $(D E, D F)=(G F, G E)$, hence $(G F, G E)=(A B, A C)=(A F, A E)$. Therefore, $F, A, G, E$ are concyclic.
We have $2(\overrightarrow{G B}, \overrightarrow{G D})=(\overrightarrow{F B}, \overrightarrow{F D})=\Pi-2(\overrightarrow{B D}, \overrightarrow{B F})$ where $\Pi$ is the straight angle (this last equality comes from the fact that $F B D$ is isosceles at $F$). Similarly, we show that $2(\overrightarrow{G D}, \overrightarrow{G C})=\Pi-2(\overrightarrow{C E}, \overrightarrow{C D})$. Adding these two equalities, we get
$$
\begin{aligned}
2(\overrightarrow{G B}, \overrightarrow{G C}) & =-2(\overrightarrow{B D}, \overrightarrow{B F})-2(\overrightarrow{C E}, \overrightarrow{C D}) \\
& =-2(\overrightarrow{B C}, \overrightarrow{B A})-2(\overrightarrow{C A}, \overrightarrow{C B})-2(\overrightarrow{C B}, \overrightarrow{B C}) \\
& =-2(\overrightarrow{C A}, \overrightarrow{B A})=2(\overrightarrow{A B}, \overrightarrow{A C})
\end{aligned}
$$
Thus, $A, B, C, G$ are concyclic.
Since $F G=F B$ and $O B=O G$, points $G$ and $B$ are symmetric with respect to $(O F)$, so $2(\overrightarrow{O G}, \overrightarrow{O F})=(\overrightarrow{O G}, \overrightarrow{O B})$. Similarly, $2(\overrightarrow{O E}, \overrightarrow{O G})=(\overrightarrow{O C}, \overrightarrow{O G})$. Adding these two equalities, we get $2(\overrightarrow{O E}, \overrightarrow{O F})=(\overrightarrow{O C}, \overrightarrow{O B})=2(\overrightarrow{A C}, \overrightarrow{A B})=2(\overrightarrow{E A}, \overrightarrow{A F})$, so $A, O, E, F$ are concyclic.
Exercise 5. Let $A, B, C, D, E$ be points in that order on a semicircle of radius 1. Prove that
$$
A B^{2}+B C^{2}+C D^{2}+D E^{2}+A B \cdot B C \cdot C D+B C \cdot C D \cdot D E \leqslant 4
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $O$ le centre de son cercle circonscrit. Soient $D, E, F$ des points situés sur $[B, C],[C, A]$ et $[A, B]$ respectivement. On suppose que $F B=F D$ et $E D=E C$. Le cercle de centre $F$ et de rayon $F B$ et le cercle de centre $E$ et de rayon $E C$ se recoupent en $G$. Montrer que $A, F, O, E, G$ sont cocycliques.

|
Les triangles $B F D$ et $C E D$ étant isocèles, on a $(D E, D F)=(D E, D C)+$ $(D B, D F)=(C D, C E)+(B F, B D)=(B C, A C)+(A B, B C)=(A B, A C)$.
Comme $E G=E D$ et $F G=F D$, les points $E$ et $F$ appartiennent à la médiatrice de $[G D]$ donc le quadrilatère $F G E D$ est symétrique par rapport à $(F E)$. On en déduit que $(D E, D F)=(G F, G E)$ donc $(G F, G E)=$ $(A B, A C)=(A F, A E)$. Il en résulte que $F, A, G, E$ sont cocycliques.
On a $2(\overrightarrow{G B}, \overrightarrow{G D})=(\overrightarrow{F B}, \overrightarrow{F D})=\Pi-2(\overrightarrow{B D}, \overrightarrow{B F})$ où $\Pi$ est l'angle plat (cette dernière égalité provenant du fait que $F B D$ est isocèle en $F$ ). On montre de même que $2(\overrightarrow{G D}, \overrightarrow{G C})=\Pi-2(\overrightarrow{C E}, \overrightarrow{C D})$. En additionnant ces deux égalités, on obtient
$$
\begin{aligned}
2(\overrightarrow{G B}, \overrightarrow{G C}) & =-2(\overrightarrow{B D}, \overrightarrow{B F})-2(\overrightarrow{C E}, \overrightarrow{C D}) \\
& =-2(\overrightarrow{B C}, \overrightarrow{B A})-2(\overrightarrow{C A}, \overrightarrow{C B})-2(\overrightarrow{C B}, \overrightarrow{B C}) \\
& =-2(\overrightarrow{C A}, \overrightarrow{B A})=2(\overrightarrow{A B}, \overrightarrow{A C})
\end{aligned}
$$
Donc $A, B, C, G$ sont cocycliques.
Comme $F G=F B$ et $O B=O G$, les points $G$ et $B$ sont symétriques par rapport à $(O F)$ donc $2(\overrightarrow{O G}, \overrightarrow{O F})=(\overrightarrow{O G}, \overrightarrow{O B})$. De même, $2(\overrightarrow{O E}, \overrightarrow{O G})=$ $(\overrightarrow{O C}, \overrightarrow{O G})$. En additionnant ces deux égalités, il vient $2(\overrightarrow{O E}, \overrightarrow{O F})=(\overrightarrow{O C}, \overrightarrow{O B})=$ $2(\overrightarrow{A C}, \overrightarrow{A B})=2(\overrightarrow{E A}, \overrightarrow{A F})$, donc $A, O, E, F$ sont cocycliques.
Exrercice 5. Soient $A, B, C, D, E$ des points dans cet ordre sur un demi-cercle de rayon 1. Démontrer que
$$
A B^{2}+B C^{2}+C D^{2}+D E^{2}+A B \cdot B C \cdot C D+B C \cdot C D \cdot D E \leqslant 4
$$
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
1fe4055f-68b6-5970-94e8-be5a2fbb4ae3
| 607,488
|
Let $ABC$ be a triangle and $M$ a point on $[B, C]$. Let $\omega$ be a circle tangent to $(AB)$ at $T$ and to $(BC)$ at $K$, and tangent to the circumcircle of $AMC$ at $P$. Show that if $(KT) \parallel (AM)$, then the circumcircles of $KPC$ and $APT$ are tangent at $P$.
|
Let us first recall that if $A, B, C$ are three points on a circle $\Gamma$, and if $\delta$ is the tangent at $B$ to $\Gamma$, then we have the equality of angles between lines $(\delta, B C)=(A B, A C)$.
Let $\delta$ and $\delta^{\prime}$ be the tangents at $P$ to the circles $(K P C)$ and $(A P T)$, respectively. We have
$$
(\delta, P K)=(C P, C K)=(C P, C M)=(A P, A M)
$$
and
$$
\begin{aligned}
\left(\delta^{\prime}, P K\right) & =\left(\delta^{\prime}, P T\right)+(P T, P K)=(A P, A T)+(T B, T K) \\
& =(A P, A M)+(A M, A T)+(T B, T K)=(A P, A M)
\end{aligned}
$$
since $(T B)=(A T)$ and $(A M)=(T K)$.
We deduce that $\delta$ and $\delta^{\prime}$ are parallel. Since they have a common point, they are equal.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $M$ un point de $[B, C]$. Soit $\omega$ un cercle tangent à $(A B)$ en $T$ et à $(B C)$ en $K$ et tangent au cercle circonscrit à $A M C$ en $P$. Montrer que si $(K T) / /(A M)$ alors les cercles circonscrits à $K P C$ et $A P T$ sont tangents en $P$.
|

Rappelons d'abord que si $A, B, C$ sont trois points d'un cercle $\Gamma$, et si $\delta$ est la tangente en $B$ à $\Gamma$, alors on a l'égalité d'angles de droites $(\delta, B C)=(A B, A C)$.
Soient $\delta$ et $\delta^{\prime}$ les tangentes en $P$ aux cercles $(K P C)$ et $(A P T)$ respectivement. On a
$$
(\delta, P K)=(C P, C K)=(C P, C M)=(A P, A M)
$$
et
$$
\begin{aligned}
\left(\delta^{\prime}, P K\right) & =\left(\delta^{\prime}, P T\right)+(P T, P K)=(A P, A T)+(T B, T K) \\
& =(A P, A M)+(A M, A T)+(T B, T K)=(A P, A M)
\end{aligned}
$$
puisque $(T B)=(A T)$ et $(A M)=(T K)$.
On en déduit que $\delta$ et $\delta^{\prime}$ sont parallèles. Or, elles ont un point commun, donc elles sont égales.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution."
}
|
61953cff-2fd4-516e-8d61-f36ff6b0cf6e
| 607,490
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles intersecting at two points $X$ and $Y$. A circle $\omega$ is internally tangent to $\omega_{1}$ and $\omega_{2}$ at $P$ and $Q$ respectively. The segment $[X, Y]$ intersects $\omega$ at $M$ and $N$. The rays $[P, M)$ and $[P, N)$ intersect $\omega_{1}$ at $A$ and $D$; the rays $[Q, M)$ and $[Q, N)$ intersect $\omega_{2}$ at $B$ and $C$. Show that $A B = C D$.
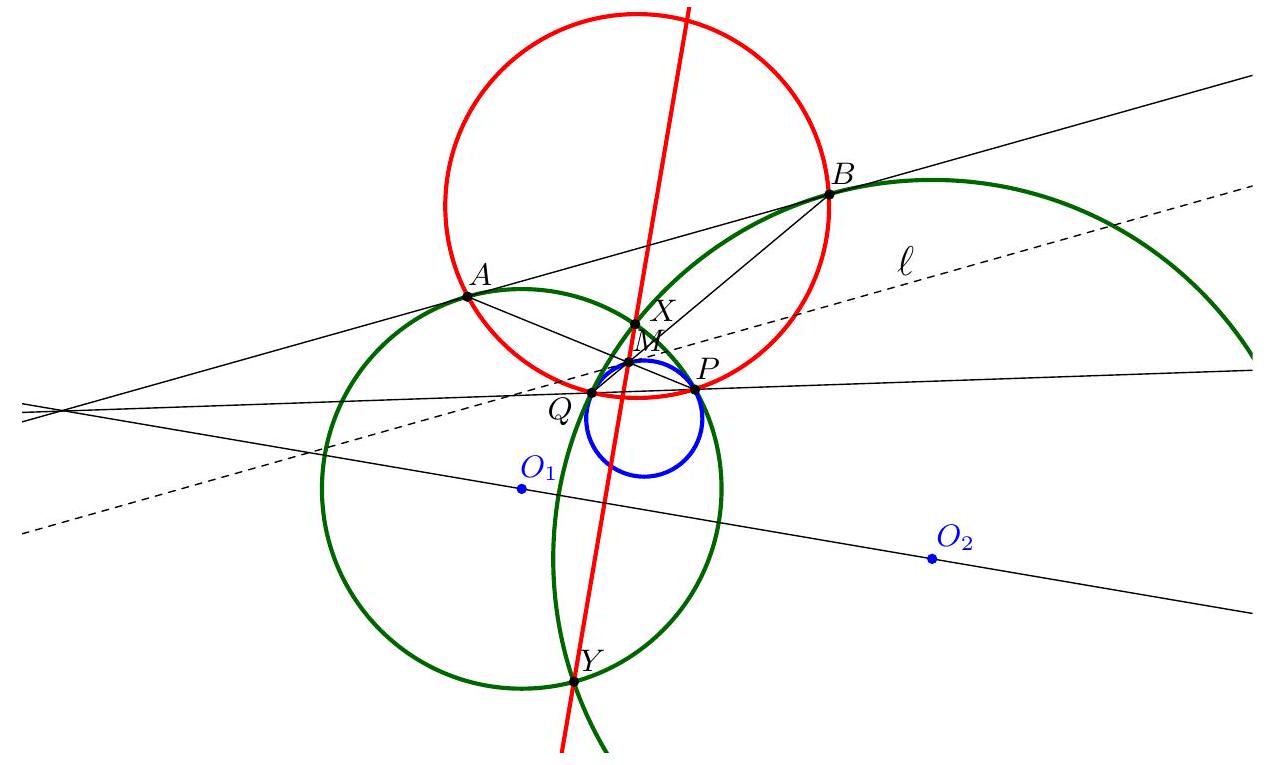
Let $\ell$ be the tangent at $M$ to $\omega$ and $\ell_{1}$ the tangent at $A$ to $\omega_{1}$. Since $\omega$ is tangent to $\omega_{1}$ at $P$, there exists a homothety $h$ centered at $P$ that maps $\omega$ to $\omega_{1}$. Since $P, M, A$ are collinear, $h(M) = A$. Therefore, $h(\ell) = \ell_{1}$, and thus $\ell \parallel \ell_{1}$.
On the other hand, since $M$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$, we have $\overline{M A} \cdot \overline{M P} = \overline{M B} \cdot \overline{M Q}$, so $A, B, P, Q$ are concyclic. It follows that
$$
(A B, A P) = (Q B, Q P) = (Q M, Q P) = (\ell, M P) = (\ell_{1}, A P)
$$
hence $(A B) = \ell_{1}$. In other words, $(A B)$ is tangent to $\omega_{1}$ at $A$. Similarly, $(A B)$ is tangent to $\omega_{2}$ at $B$, so $(A B)$ is a common tangent to $\omega_{1}$ and $\omega_{2}$. Similarly, $(C D)$ is a common tangent to $\omega_{1}$ and $\omega_{2}$, so $A B = C D$.
Exercise 9. Let $A B C D$ be a cyclic quadrilateral. Denote by $K$ the intersection of the diagonals. Let $M$ and $N$ be the midpoints of $[A, C]$ and $[B, D]$. The circumcircles of $A D M$ and $B C M$ intersect at a point $L$. Show that $K, L, M, N$ are concyclic.
|
Let $E$ be the radical center of the three circles $ABC$, $ADM$, and $BCM$. The triplets $(E, A, D)$, $(E, L, M)$, and $(E, B, C)$ are collinear.
Let $F$ be the point where the circles $ADK$ and $BCK$ intersect. We have $(FA, FD) = (KA, KD) = (KC, KB) = (FC, FB)$ and $(AD, AF) = (KD, KF) = (KB, KF) = (CB, CF)$, so the triangles $FAD$ and $FCB$ are similar. Let $s$ be the similarity with center $F$ that maps $A$ to $D$ and $C$ to $B$. Then $s(M) = N$, so the angle of $s$ is both equal to $(FM, FN)$ and to $(AC, DB) = (KM, KN)$. Therefore, $F, K, M, N$ are concyclic.
$E$ is the intersection of $(AD)$ and $(BC)$, so it is the radical center of the circles $ABCD$, $ADK$, and $BCK$. Consequently, $E, F, K$ are collinear. Using the power of a point with respect to a circle, we have
$$
\overline{EK} \cdot \overline{EF} = \overline{EA} \cdot \overline{ED} = \overline{EB} \cdot \overline{EC} = \overline{EM} \cdot \overline{EL},
$$
so $M, L, K, F$ are concyclic.
Finally, $L$ and $N$ are on the circle $MKF$ so $K, L, M, N$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\omega_{1}$ et $\omega_{2}$ deux cercles sécants en deux points $X$ et $Y$. Un cercle $\omega$ est tangent intérieurement à $\omega_{1}$ et $\omega_{2}$ en $P$ et $Q$ respectivement. Le segment $[X, Y]$ coupe $\omega$ en $M$ et $N$. Les demi-droites $[P, M)$ et $[P, N)$ coupent $\omega_{1}$ en $A$ et $D$; les demi-droites $[Q, M)$ et $[Q, N)$ coupent $\omega_{2}$ en $B$ et $C$. Montrer que $A B=C D$.

Soit $\ell$ la tangente en $M$ à $\omega$ et $\ell_{1}$ la tangente en $A$ à $\omega_{1}$. Comme $\omega$ est tangent en $P$ à $\omega_{1}$, il existe une homothétie $h$ de centre $P$ qui envoie $\omega \operatorname{sur} \omega_{1}$. Or, $P, M, A$ sont alignés donc $h(M)=A$. On en déduit que $h(\ell)=\ell_{1}$, et donc $\ell / / \ell_{1}$.
D'autre part, comme $M$ est sur l'axe radical de $\omega_{1}$ et $\omega_{2}$, on a $\overline{M A} \cdot \overline{M P}=$ $\overline{M B} \cdot \overline{M Q}$ donc $A, B, P, Q$ sont cocycliques. On en déduit que
$$
(A B, A P)=(Q B, Q P)=(Q M, Q P)=(\ell, M P)=\left(\ell_{1}, A P\right)
$$
d'où $(A B)=\ell_{1}$. Autrement dit, $(A B)$ est tangente en $A$ à $\omega_{1}$. Mais de même, $(A B)$ est tangente en $B$ à $\omega_{2}$, donc $(A B)$ est une tangente commune à $\omega_{1}$ et $\omega_{2}$. De même, $(C D)$ est une tangente commune à $\omega_{1}$ et $\omega_{2}$, donc $A B=C D$.
Exrtcice 9. Soit $A B C D$ un quadrilatère inscriptible. On note $K$ le point d'intersection des diagonales. Soient $M$ et $N$ les milieux de $[A, C]$ et $[B, D]$. Les cercles circonscrits à $A D M$ et $B C M$ se recoupent en un point $L$. Montrer que $K, L, M, N$ sont cocycliques.
|
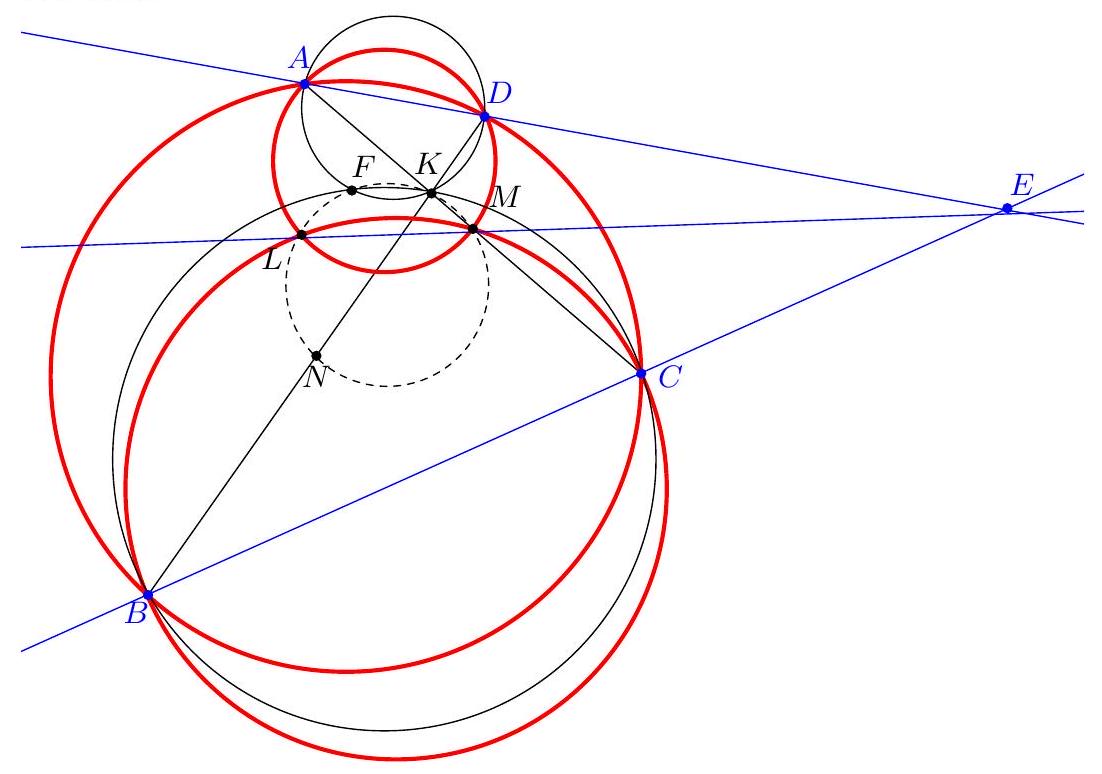
Notons $E$ le centre radical des trois cercles $A B C, A D M, B C M$. Les triplets $(E, A, D),(E, L, M)$ et $(E, B, C)$ sont alignés.
Soit $F$ le point où les cercles $A D K$ et $B C K$ se recoupent. On a $(F A, F D)=$ $(K A, K D)=(K C, K B)=(F C, F B)$ et $(A D, A F)=(K D, K F)=(K B, K F)=$ $(C B, C F)$, donc les triangles $F A D$ et $F C B$ sont semblables. Soit $s$ la similitude de centre $F$ qui envoie $A$ sur $D$ et $C$ sur $B$. Alors $s(M)=N$, donc l'angle de $s$ est à la fois égal à $(F M, F N)$ et à $(A C, D B)=(K M, K N)$. Par conséquent, $F, K, M, N$ sont cocycliques.
$E$ est l'intersection de $(A D)$ et de $(B C)$, donc il est le centre radical des cercles $A B C D, A D K$ et $B C K$. Par conséquent, $E, F, K$ sont alignés. En utilisant la puissance d'un point par rapport à un cercle, on a
$$
\overline{E K} \cdot \overline{E F}=\overline{E A} \cdot \overline{E D}=\overline{E B} \cdot \overline{E C}=\overline{E M} \cdot \overline{E L},
$$
donc $M, L, K, F$ sont cocycliques.
Finalement, $L$ et $N$ sont sur le cercle $M K F$ donc $K, L, M, N$ sont cocycliques.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2012-2013-envoi6-corrige.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution."
}
|
9e74d9cd-b96b-51ae-a4e6-359bf3645db0
| 607,491
|
Let $A, B, C, D$ be four points on the same circle. Denote $A^{\prime}$ and $C^{\prime}$ as the orthogonal projections of $A$ and $C$ onto $(B D)$, and $B^{\prime}$ and $D^{\prime}$ as the orthogonal projections of $B$ and $D$ onto $(A C)$. Show that $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are concyclic.
|
As $A, B, A^{\prime}, B^{\prime}$ are concyclic (on the circle with diameter $[A B]$), the oriented angles of lines $\left(B A^{\prime}, B A\right)$ and $\left(B^{\prime} A^{\prime}, B^{\prime} A\right)$ are equal, so $(B D, B A)=\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)$. Similarly, $(C D, C A)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$. Since $(C D, C A)=(B D, B A)$ because $A, B, C, D$ are concyclic, it follows that $\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$, which proves that $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A, B, C, D$ quatre points sur un même cercle. Notons $A^{\prime}$ et $C^{\prime}$ les projetés orthogonaux de $A$ et $C$ sur $(B D)$, et $B^{\prime}$ et $D^{\prime}$ les projetés orthogonaux de $B$ et $D$ sur $(A C)$. Montrer que $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ sont cocycliques.
|
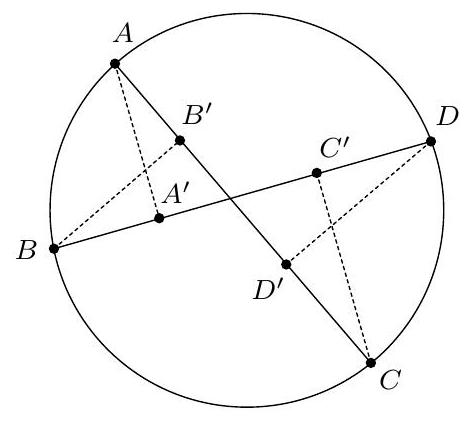
Comme $A, B, A^{\prime}, B^{\prime}$ sont cocycliques (sur le cercle de diamètre $[A B]$ ), les angles orientés de droites $\left(B A^{\prime}, B A\right)$ et $\left(B^{\prime} A^{\prime}, B^{\prime} A\right)$ sont égaux, donc $(B D, B A)=\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)$. De même, $(C D, C A)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$. Or, $(C D, C A)=(B D, B A)$ puisque $A, B, C, D$ sont cocycliques, donc $\left(B^{\prime} A^{\prime}, B^{\prime} D^{\prime}\right)=\left(C^{\prime} A^{\prime}, C^{\prime} D^{\prime}\right)$, ce qui prouve que $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ sont cocycliques.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution."
}
|
d4f25aa5-8c13-5e07-9b1a-60f8343fb3fa
| 607,492
|
On the diagonal $[B D]$ of a square $A B C D$, a point $E$ has been chosen. Let $O_{1}$ and $O_{2}$ be the centers of the circumcircles of triangles $A B E$ and $A D E$ respectively. Show that $A O_{1} E O_{2}$ is a square.
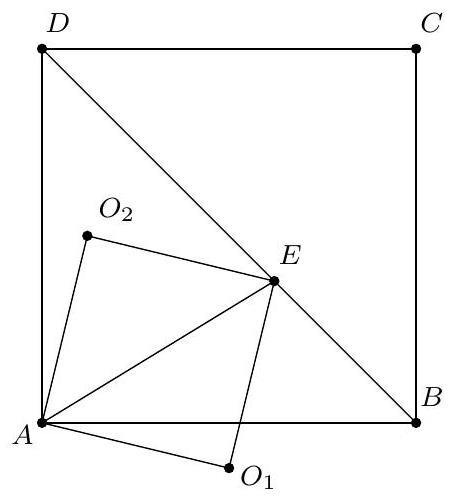
|
$\widehat{A O_{1} E}=2 \widehat{A B E}=90^{\circ}$ and $O_{1} A=O_{1} E$ so $A O_{1} E$ is an isosceles right triangle at $O_{1}$. Similarly, $A O_{2} E$ is an isosceles right triangle at $O_{2}$.
Since $O_{1}$ and $O_{2}$ are not in the same half-plane delimited by $(A E)$, we deduce that $A O_{1} E O_{2}$ is a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Sur la diagonale $[B D]$ d'un carré $A B C D$ on a choisi un point $E$. Soient $O_{1}$ et $O_{2}$ les centres des cercles circonscrits aux triangles $A B E$ et $A D E$ respectivement. Montrer que $A O_{1} E O_{2}$ est un carré.

|
$\widehat{A O_{1} E}=2 \widehat{A B E}=90^{\circ}$ et $O_{1} A=O_{1} E$ donc $A O_{1} E$ est un triangle isocèle rectangle en $O_{1}$. De même, $A O_{2} E$ est un triangle isocèle rectangle en $O_{2}$.
Comme $O_{1}$ et $O_{2}$ ne sont pas dans le même demi-plan délimité par $(A E)$, on en déduit que $A O_{1} E O_{2}$ est un carré.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution."
}
|
6e023ce7-ec71-5171-934e-d67a0ea418b7
| 607,493
|
A quadrilateral $ABCD$ is inscribed in a circle. Its diagonals intersect at point $K$. The circle passing through $A, B, K$ intersects the lines $(BC)$ and $(AD)$ at points $M$ and $N$ respectively. Show that $KM = KN$.
|
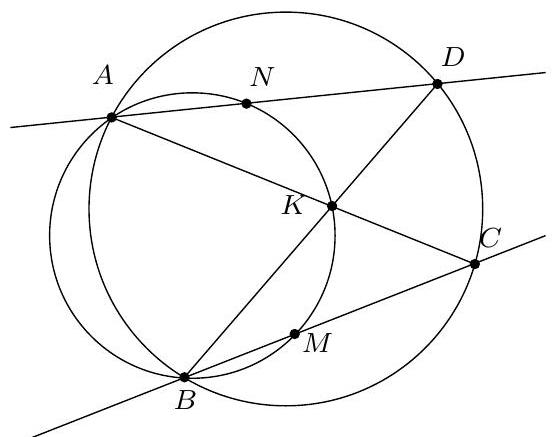
Since $(N M, N K)=(B M, B K)=(B C, B D)=(A C, A D)=(A K, A N)=(M K, M N)$, therefore $M K N$ is isosceles at $K$.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Un quadrilatère $A B C D$ est inscrit dans un cercle. Ses diagonales se coupent au point $K$. Le cercle passant par $A, B, K$ croise les droites $(B C)$ et $(A D)$ aux points $M$ et $N$ respectivement. Montrer que $K M=K N$.
|

On a $(N M, N K)=(B M, B K)=(B C, B D)=(A C, A D)=(A K, A N)=(M K, M N)$ donc $M K N$ est isocèle en $K$.
## Exercices communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution."
}
|
b4665869-b63e-5b03-9cbc-78e87b933e1d
| 607,494
|
Let $ABC$ be a triangle with all angles acute, and where angle $\widehat{B}$ is 60 degrees ($=\pi / 3$ radians). The altitudes $[AD]$ and $[CE]$ intersect at point $H$. Prove that the center of the circumcircle of triangle $ABC$ lies on the common bisector of angles $\widehat{AHE}$ and $\widehat{CHD}$.

|
Since $B, E, H, D$ are on the circle with diameter $[B H]$, we have $\widehat{D H E}=180^{\circ}-\widehat{E B D}=$ $120^{\circ}$, thus $\widehat{A H C}=120^{\circ}$. Since $\widehat{A O C}=2 \widehat{A B C}=120^{\circ}$, we deduce that $A, C, O, H$ are concyclic.
Therefore, $\widehat{C H O}=\widehat{C A O}=\frac{1}{2}(\widehat{C A O}+\widehat{O C A})=\frac{1}{2}\left(180^{\circ}-\widehat{A O C}\right)=90^{\circ}-\widehat{A B C}=$ $30^{\circ}$.
Furthermore, since $(C H) \perp(A B)$ and $(A H) \perp(B C)$, we have $\widehat{C H D}=\widehat{A B C}=60^{\circ}$, so $O$ lies on the bisector of $\widehat{C H D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus, et dont l'angle $\widehat{B}$ est de 60 degrés ( $=\pi / 3$ radian). Les hauteurs $[A D]$ et $[C E]$ se coupent au point $H$. Prouver que le centre du cercle circonscrit au triangle $A B C$ est situé sur la bissectrice commune des angles $\widehat{A H E}$ et $\widehat{C H D}$.

|
Puisque $B, E, H, D$ sont sur le cercle de diamètre $[B H]$, on a $\widehat{D H E}=180^{\circ}-\widehat{E B D}=$ $120^{\circ}$, donc $\widehat{A H C}=120^{\circ}$. Comme $\widehat{A O C}=2 \widehat{A B C}=120^{\circ}$, on en déduit que $A, C, O, H$ sont cocycliques.
Par conséquent, $\widehat{C H O}=\widehat{C A O}=\frac{1}{2}(\widehat{C A O}+\widehat{O C A})=\frac{1}{2}\left(180^{\circ}-\widehat{A O C}\right)=90^{\circ}-\widehat{A B C}=$ $30^{\circ}$.
De plus, comme $(C H) \perp(A B)$ et $(A H) \perp(B C)$, on a $\widehat{C H D}=\widehat{A B C}=60^{\circ}$, donc $O$ est sur la bissectrice de $\widehat{C H D}$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution."
}
|
e62a02df-5647-5817-af45-f7480605e5e4
| 607,495
|
Outside the triangle $A B C$, we construct two points $X$ and $Y$ satisfying:
- the triangle $A X B$ is isosceles with base $[A B]$;
- the triangle $B Y C$ is isosceles with base $[B C]$;
- $\widehat{A X B} + \widehat{B Y C} = 180^{\circ}$.
Let $Z$ be the midpoint of $[A C]$. Show that the lines $(X Z)$ and $(Y Z)$ are perpendicular.
|
Let $D$ and $E$ be the midpoints of $[B C]$ and $[A B]$.
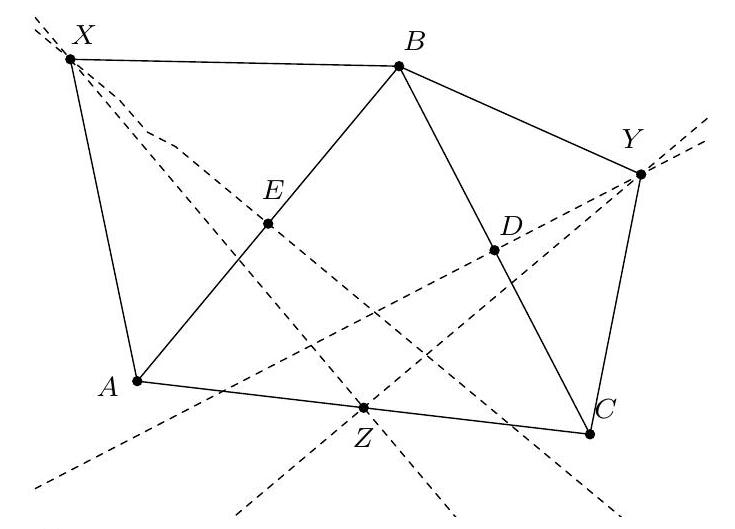
We have
- $(X E) \perp(D Z)$ because $(D Z) / /(A B)$
- $(E Z) \perp(D Y)$ because $(E Z) / /(B C)$
- $\frac{X E}{D Z}=\frac{X E}{E A}=\frac{C D}{D Y}=\frac{E Z}{D Y}$ (the second equality comes from the fact that the right triangles $X E A$ and $C D Y$ are similar)
thus $X E Z$ and $Z D Y$ are similar. Since $(X E) \perp(D Z)$, we deduce that $(X Z) \perp$ $(Z Y)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A l'extérieur du triangle $A B C$ on construit les deux points $X$ et $Y$ vérifiant :
- le triangle $A X B$ est isocèle de base $[A B]$;
- le triangle $B Y C$ est isocèle de base $[B C]$;
$-\widehat{A X B}+\widehat{B Y C}=180^{\circ}$.
Soit $Z$ le milieu de $[A C]$. Montrer que les droites $(X Z)$ et $(Y Z)$ sont perpendiculaires.
|
Notons $D$ et $E$ les milieux de $[B C]$ et $[A B]$.

On a
- $(X E) \perp(D Z)$ car $(D Z) / /(A B)$
- $(E Z) \perp(D Y)$ car $(E Z) / /(B C)$
- $\frac{X E}{D Z}=\frac{X E}{E A}=\frac{C D}{D Y}=\frac{E Z}{D Y}$ (la deuxième égalité provient du fait que les triangles rectangles $X E A$ et $C D Y$ sont semblables)
donc $X E Z$ et $Z D Y$ sont semblables. Comme $(X E) \perp(D Z)$, on en déduit que $(X Z) \perp$ $(Z Y)$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution."
}
|
46e244e2-41a8-5271-bba3-bfea0e7fae89
| 607,496
|
The vertex $B$ of angle $\widehat{A B C}$ is outside a circle $\omega$, while the rays $[B A)$ and $[B C)$ intersect the circle. Let $K$ be a point of intersection of the circle $\omega$ with $[B A)$. The perpendicular to the bisector of angle $\widehat{A B C}$ passing through $K$ intersects the circle at point $P$, and the line $(B C)$ at point $M$. Show that the segment $[P M]$ is twice as long as the distance between the center of $\omega$ and the bisector of $\widehat{A B C}$.
|
Let $O$ be the center of the circle $\omega$. Denote $\Delta$ as the bisector of $\widehat{A B C}$, $\Delta^{\prime}$ as the line parallel to $\Delta$ passing through $O$, and $N$ as the symmetric point of $O$ with respect to $\Delta$.
The symmetry $s_{\Delta^{\prime}}$ with respect to $\Delta^{\prime}$ sends $O$ to $O$ and $P$ to $K$ (since $(P K) \perp \Delta^{\prime}$ and $\Delta^{\prime}$ passes through $O$).
The symmetry $s_{\Delta}$ with respect to $\Delta$ sends $O$ to $N$ and $K$ to $M$.
Therefore, the composition $s_{\Delta} \circ s_{\Delta^{\prime}}$ sends $O$ to $N$ and $P$ to $M$. Since $s_{\Delta} \circ s_{\Delta}^{\prime}$ is a translation, $M N O P$ is a parallelogram. It follows that $P M = O N = 2 d(O, \Delta)$.
## Exercises Group A
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Le sommet $B$ d'un angle $\widehat{A B C}$ se trouve à l'extérieur d'un cercle $\omega$ tandis que les demi-droites $[B A)$ et $[B C)$ le traversent. Soit $K$ un point d'intersection du cercle $\omega$ avec $[B A)$. La perpendiculaire à la bissectrice de l'angle $\widehat{A B C}$ passant par $K$ recoupe le cercle au point $P$, et la droite $(B C)$ au point $M$. Montrer que le segment $[P M]$ est deux fois plus long que la distance entre le centre de $\omega$ et la bissectrice de $\widehat{A B C}$.
|
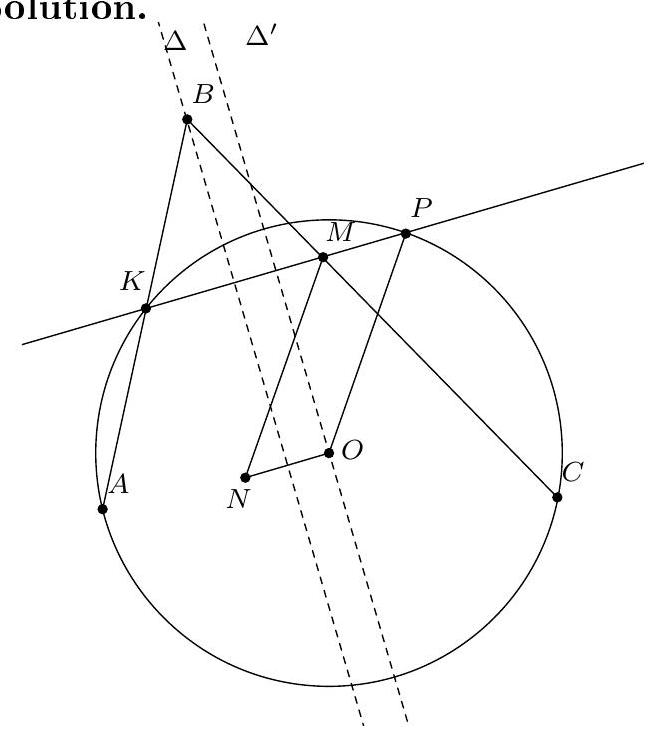
Soit $O$ le centre du cercle $\omega$. Notons $\Delta$ la bissectrice de $\widehat{A B C}, \Delta^{\prime}$ la parallèle à $\Delta$ passant par $O$ et $N$ le symétrique de $O$ par rapport à $\Delta$.
La symétrie $s_{\Delta^{\prime}}$ par rapport à $\Delta^{\prime}$ envoie $O$ sur $O$ et $P \operatorname{sur} K\left(\operatorname{car}(P K) \perp \Delta^{\prime}\right.$ et $\Delta^{\prime}$ passe par $O$ ).
La symétrie $s_{\Delta}$ par rapport à $\Delta$ envoie $O$ sur $N$ et $K$ sur $M$.
Par conséquent, la composée $s_{\Delta} \circ s_{\Delta^{\prime}}$ envoie $O$ sur $N$ et $P$ sur $M$. Or, $s_{\Delta} \circ s_{\Delta}^{\prime}$ est une translation, donc $M N O P$ est un parallélogramme. Il s'ensuit que $P M=O N=2 d(O, \Delta)$.
## Exercices groupe A
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution."
}
|
766afdaf-6b44-5990-af8f-123d9b5f88e1
| 607,497
|
The circle $\omega$ passes through the vertices $B$ and $C$ of triangle $ABC$ and intersects the sides $[AB]$ and $[AC]$ at points $D$ and $E$ respectively. The segments $[CD]$ and $[BE]$ intersect at a point $O$. Let $M$ and $N$ be the centers of the incircles of triangles $ADE$ and $ODE$ respectively. Show that the midpoint of the arc $DE$ (the smaller of the two arcs) of the circle $\omega$ lies on the line $(MN)$.
|
Let $\theta=(D E, D F)=(E F, E D)$. We have $2(D F, D M)+2 \theta=2(D E, D M)=(D E, D A)=$ $\theta+(D F, D A)=\theta+(D F, D B)=\theta+(E F, E B)=2 \theta+(E D, E O)=\theta+2(E D, E N)$, so $\widehat{F D M}=\widehat{D E N}$. Similarly, $\widehat{M E F}=\widehat{N D E}$. Let $\beta$ and $\gamma$ be these angles.

Let $P$ and $Q$ be the second points of intersection of the lines $(D F)$ and $(E F)$ with the circumcircle of triangle $DME$. We have
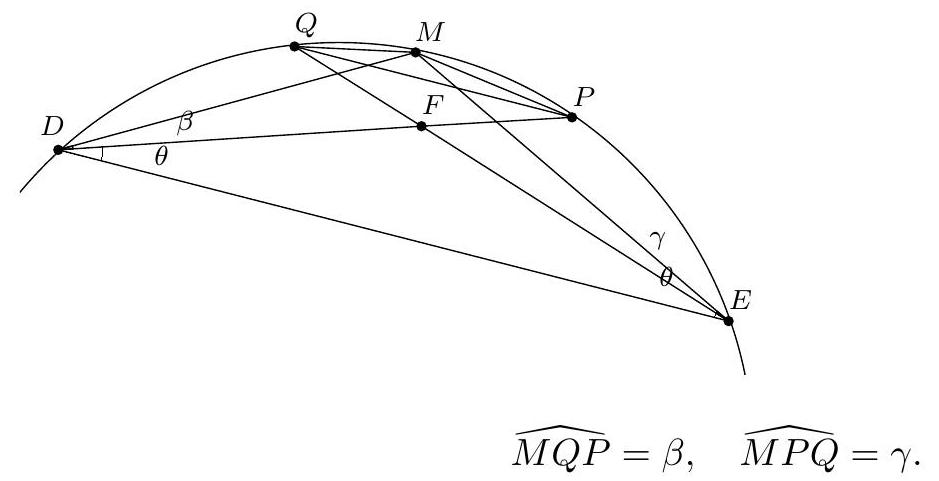
Since $D F=D E$, we have $(P Q) \parallel (D E)$. With (4), this implies that triangles $D E N$ and $Q M P$ are similar. Moreover, $F$ is the center of the homothety (since it is the intersection of the lines $(Q E)$ and $(P D)$). Therefore, the line $(M N)$ passes through $F$.
Another solution. If we do not think to introduce the points $P$ and $Q$, we can complete the proof with some tedious trigonometric calculations.
Let $\varphi$ be the angle $(\overrightarrow{F M}, \overrightarrow{E D})$. According to the law of sines in triangles $M D F$ and $M E F$, we have
$$
\begin{aligned}
\frac{M F}{\sin \beta} & =\frac{D F}{\sin (\beta+\varphi+\theta)} \\
\frac{M F}{\sin \gamma} & =\frac{E F}{\sin (\varphi-\gamma-\theta)}
\end{aligned}
$$
Since $D F=E F$, by dividing these two equalities we get
$$
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi-\gamma-\theta)}{\sin (\beta+\varphi+\theta)}
$$
Using the formula $\sin (x+y)=\sin x \cos y+\cos x \sin y$, we deduce
$$
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi) \cos (\gamma+\theta)-\cos \varphi \sin (\gamma+\theta)}{\sin (\varphi) \cos (\beta+\theta)+\cos \varphi \sin (\beta+\theta)}
$$
We eliminate the denominators and gather the terms in $\sin \varphi$ and $\cos \varphi$:
$$
\cos \varphi(\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)))=\sin \varphi(-\sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta))
$$
Since
$$
\begin{aligned}
- & \sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta) \\
& =-\sin \gamma(\cos \beta \cos \theta-\sin \beta \sin \theta)+\sin \beta(\cos \gamma \cos \theta-\sin \gamma \sin \theta) \\
& =\cos \theta \sin (\beta-\gamma),
\end{aligned}
$$
we get
$$
\tan \varphi=\frac{\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)}{\cos \theta \sin (\beta-\gamma)}
$$
Let $\varphi^{\prime}=(F N, D E)$. The calculation of $\tan \varphi^{\prime}$ is identical, by replacing $(\beta, \gamma, \theta)$ with $(\beta+\theta, \gamma+\theta,-\theta)$. However, the expression of $\tan \varphi$ is invariant under this transformation, so $\tan \varphi^{\prime}=\tan \varphi$, hence $F, M, N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Le cercle $\omega$ passe par les sommets $B$ et $C$ du triangle $A B C$ et coupe les côtés $[A B]$ et $[A C]$ aux points $D$ et $E$ respectivement. Les segments $[C D]$ et $[B E]$ se coupent en un point $O$. Soient $M$ et $N$ les centres des cercles inscrits dans les triangles $A D E$ et $O D E$ respectivement. Montrer que le milieu de l'arc $D E$ (le plus petit des deux arcs) du cercle $\omega$ se trouve sur la droite ( $M N$ ).
|
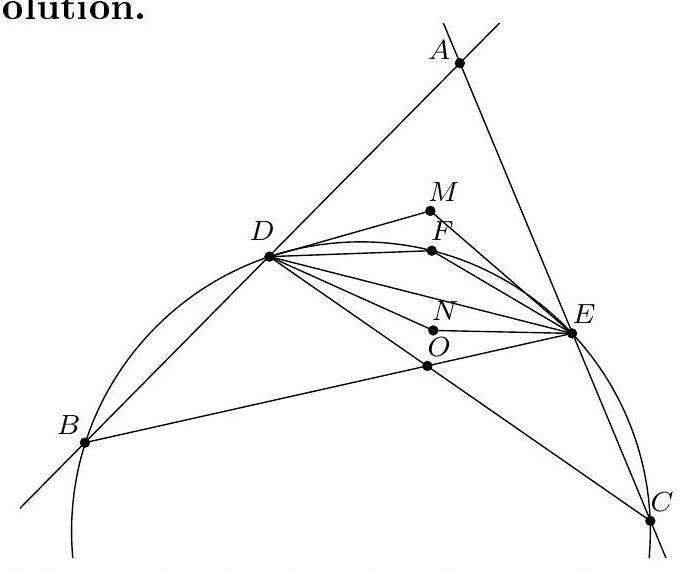
Notons $\theta=(D E, D F)=(E F, E D)$. On a $2(D F, D M)+2 \theta=2(D E, D M)=(D E, D A)=$ $\theta+(D F, D A)=\theta+(D F, D B)=\theta+(E F, E B)=2 \theta+(E D, E O)=\theta+2(E D, E N)$, donc $\widehat{F D M}=\widehat{D E N}$. De même, $\widehat{M E F}=\widehat{N D E}$. Notons $\beta$ et $\gamma$ ces angles.

Soient $P$ et $Q$ les seconds points d'intersection des droites $(D F)$ et $(E F)$ avec le cercle circonscrit au triangle DME. On a

Comme $D F=D E$, on a $(P Q) / /(D E)$. Avec (4), cela implique que les triangles $D E N$ et $Q M P$ sont homothétiques. De plus, $F$ est le centre de l'homothétie (puisque c'est le point d'intersection des droites $(Q E)$ et $(P D)$ ). Donc la droite $(M N)$ traverse $F$.
Autre solution. Si on ne pense pas à introduire les points $P$ et $Q$, on peut terminer la démonstration moyennant des calculs trigonométriques un peu pénibles.
Notons $\varphi$ l'angle $(\overrightarrow{F M}, \overrightarrow{E D})$. D'après la loi des sinus dans les triangles $M D F$ et $M E F$, on a
$$
\begin{aligned}
\frac{M F}{\sin \beta} & =\frac{D F}{\sin (\beta+\varphi+\theta)} \\
\frac{M F}{\sin \gamma} & =\frac{E F}{\sin (\varphi-\gamma-\theta)}
\end{aligned}
$$
Comme $D F=E F$, en divisant ces deux égalités on obtient
$$
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi-\gamma-\theta)}{\sin (\beta+\varphi+\theta)}
$$
En utilisant la formule $\sin (x+y)=\sin x \cos y+\cos x \sin y$, on en déduit
$$
\frac{\sin \gamma}{\sin \beta}=\frac{\sin (\varphi) \cos (\gamma+\theta)-\cos \varphi \sin (\gamma+\theta)}{\sin (\varphi) \cos (\beta+\theta)+\cos \varphi \sin (\beta+\theta)}
$$
On chasse les dénominateurs et on rassemble les termes en $\sin \varphi$ et en $\cos \varphi$ :
$$
\cos \varphi(\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)))=\sin \varphi(-\sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta))
$$
Comme
$$
\begin{aligned}
- & \sin \gamma \cos (\beta+\theta)+\sin \beta \cos (\gamma+\theta) \\
& =-\sin \gamma(\cos \beta \cos \theta-\sin \beta \sin \theta)+\sin \beta(\cos \gamma \cos \theta-\sin \gamma \sin \theta) \\
& =\cos \theta \sin (\beta-\gamma),
\end{aligned}
$$
on obtient
$$
\tan \varphi=\frac{\sin \gamma \sin (\beta+\theta)+\sin \beta \sin (\gamma+\theta)}{\cos \theta \sin (\beta-\gamma)}
$$
Soit $\varphi^{\prime}=(F N, D E)$. Le calcul de $\tan \varphi^{\prime}$ est identique, en remplaçant $(\beta, \gamma, \theta)$ par $(\beta+\theta, \gamma+\theta,-\theta)$. Or, l'expression de $\tan \varphi$ est invariante par cette transformation, donc $\tan \varphi^{\prime}=\tan \varphi$, d'où $F, M, N$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution."
}
|
46be1330-272d-5622-8af2-780886d0d4ca
| 607,499
|
A circle with center $O$ is inscribed in a quadrilateral $ABCD$ whose sides are not parallel. Show that the point $O$ coincides with the intersection point of the medians of the quadrilateral if and only if $OA \cdot OC = OB \cdot OD$. (A median line of the quadrilateral is a line connecting the midpoints of opposite sides.)
|
Let $I$ and $J$ be the midpoints of the sides $[A B]$ and $[C D]$ respectively. The lines $(A B)$ and $(C D)$ intersect at point $P$. Without loss of generality, we can assume that $P$ is the intersection of the rays $[A B)$ and $[C D)$.
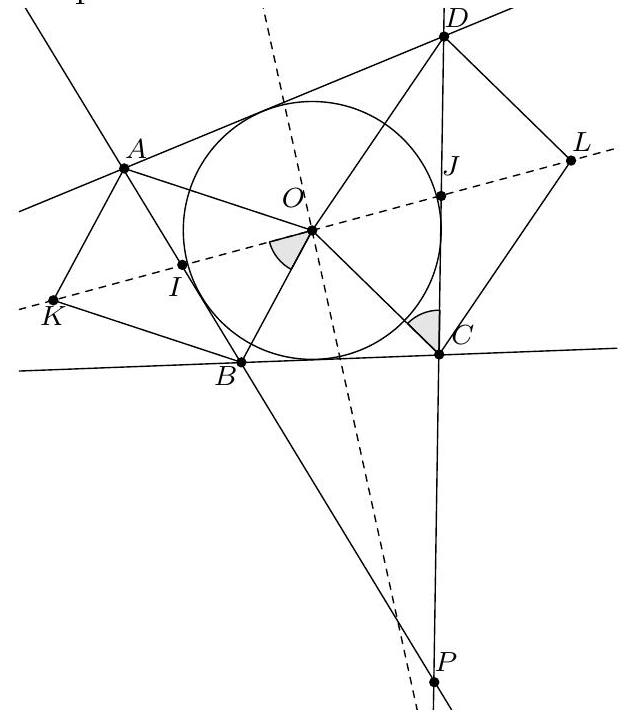
1) Suppose that $O$ is the intersection of the medians of the quadrilateral $A B C D$. Then $O$ is the midpoint of the segment $[I J]$, because the midpoints of the sides of a quadrilateral are the vertices of a parallelogram. Thus, $[P O]$ is the bisector and median from $P$ of the triangle $I P J$, so $I P J$ is isosceles at $P$ and $\widehat{B I O}=\widehat{C J O}$. Furthermore,
$$
\widehat{I B O}+\widehat{J C O}=\frac{1}{2}(\widehat{A B C}+\widehat{B C D})=\frac{1}{2}(\pi+\widehat{B P C})=\pi-\widehat{P I J}=\widehat{I B O}+\widehat{I O B}
$$
Then $\widehat{J C O}=\widehat{I O B}$ and the triangles $O I B$ and $C J O$ are similar. We obtain that $\frac{O B}{O C}=$ $\frac{I B}{J O}$. Similarly, we have $\frac{O A}{O D}=\frac{I A}{J O}$. Since $I B=I A$, we get $O A \cdot O C=O B \cdot O D$.
2) Now suppose that $O A \cdot O C=O B \cdot O D$. We note that
$$
\begin{aligned}
\widehat{A O B}+\widehat{C O D} & =(\pi-\widehat{O A B}-\widehat{O B A})+(\pi-\widehat{O C D}-\widehat{O D C}) \\
& =\pi-\frac{1}{2}(\widehat{D A B}+\widehat{A B C}+\widehat{B C D}+\widehat{C D A})=\pi
\end{aligned}
$$
Therefore, if we construct the parallelograms $O A K B$ and $C O D L$ from the triangles $O A B$ and $O C D$, these parallelograms will be similar, because $\frac{O A}{A K}=\frac{O A}{O B}=$ $\frac{D O}{O C}=\frac{D O}{D L}$. In particular, the triangles $O I B$ and $C J O$ are also similar, because they correspond to each other in the similar parallelograms $O A K B$ and $C O D L$. It follows that
$$
\widehat{I O B}=\widehat{O C J}=\widehat{O C B}, \quad \widehat{C O J}=\widehat{I B O}=\widehat{O B C}
$$
We obtain that
$$
\widehat{I O B}+\widehat{B O C}+\widehat{C O J}=\widehat{O C B}+\widehat{B O C}+\widehat{O B C}=\pi,
$$
so $O$ lies on $(I J)$. Similarly, $O$ lies on the other median of the quadrilateral $A B C D$.
Another solution. We can solve the problem using an analytical method with complex numbers. The calculations are lengthy but not impractical.
Let $U, V, W, X$ be the points of tangency of the lines $(A B),(B C),(C D)$ and $(D A)$ with the circle. We can assume that the circle is centered at 0 and has a radius of 1. Let $a, b, c, d, u, v, w, x$ be the affixes of the points $A, B, C, D, U, V, W, X$.
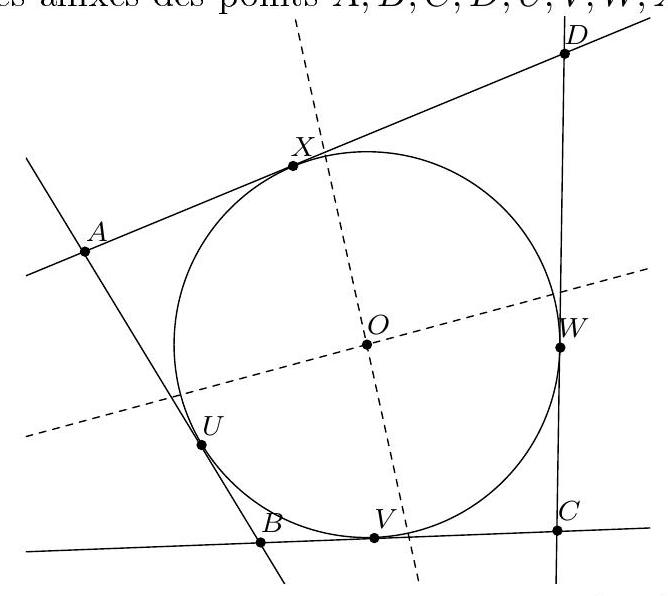
A point with affix $z$ lies on $(A B)$ if and only if $z-u$ is perpendicular to $u$, which can be written as $0=\bar{u}(z-u)+u(\bar{z}-\bar{u})$, or equivalently $\bar{u} z+u \bar{z}=2$. Since $\bar{u}=1 / u$, this can be written as $z+u^{2} \bar{z}=2 u$. Similarly, the equation of the line $(A D)$ is $z+x^{2} \bar{z}=2 x$. By combining these two equations, we find that
$$
a=\frac{2 u x}{u+x} .
$$
Similarly, we have $b=\frac{2 u v}{u+v}, c=\frac{2 v w}{v+w}$ and $d=\frac{2 w x}{w+x}$.
We calculate that $4 O A^{-2}=|u+x|^{2}=2+u \bar{x}+\bar{u} x$. We have similar expressions for $4 O B^{-2}$, etc. Therefore,
$$
\begin{aligned}
O A \cdot O C & =O B \cdot O D \\
& \Longleftrightarrow \quad(2+u \bar{x}+\bar{u} x)(2+v \bar{w}+\bar{v} w)=(2+u \bar{v}+\bar{u} v)(2+w \bar{x}+\bar{w} x) \\
& \Longleftrightarrow \quad u x(2+u \bar{x}+\bar{u} x) v w(2+v \bar{w}+\bar{v} w)=u v(2+u \bar{v}+\bar{u} v) w x(2+w \bar{x}+\bar{w} x) \\
& \Longleftrightarrow \quad\left(2 u x+u^{2}+x^{2}\right)\left(2 v w+v^{2}+w^{2}\right)=\left(2 u v+u^{2}+v^{2}\right)\left(2 w x+x^{2}+w^{2}\right) \\
& \Longleftrightarrow \quad 2 u v^{2} x+2 u w^{2} x+2 u^{2} v w+u^{2} v^{2}+2 v w x^{2}+w^{2} x^{2} \\
& =2 u v x^{2}+2 u v w^{2}+2 u^{2} w x+u^{2} x^{2}+2 v^{2} w x+v^{2} w^{2} \\
& \Longleftrightarrow 2(u-w) v^{2} x-2(u-w) u w x+2(u-w) u v w \\
& \quad-2(u-w) v x^{2}+(u-w)(u+w) v^{2}-(u-w)(u+w) x^{2}=0 \\
& \Longleftrightarrow 2 v^{2} x-2 u w x+2 u v w-2 v x^{2}+u v^{2}+v^{2} w-u x^{2}-w x^{2}=0 \\
& \Longleftrightarrow \quad 2 v x(v-x)+(v-x) w(v+x)+2 u w(v-x)+u(v+x)(v-x)=0 \\
& \Longleftrightarrow 2 u w+2 x v+(x+v)(u+w)=0 .
\end{aligned}
$$
On the other hand, $O$ lies on the line passing through the midpoints of $[A D]$ and $[B C]$ if and only if $0, \frac{a+d}{2}$ and $\frac{b+c}{2}$ are collinear, which means that $\frac{a+d}{b+c}$ is real, i.e.,
$$
\frac{\frac{u x}{u+x}+\frac{x w}{x+w}}{\frac{u v}{u+v}+\frac{v w}{v+w}}=\frac{\frac{1}{u+x}+\frac{1}{w+x}}{\frac{1}{u+v}+\frac{1}{v+w}}
$$
We multiply the numerators of each side by $(u+x)(x+w)$ and the denominators by $(u+v)(v+w)$, which gives successively
$$
\begin{aligned}
& \frac{x[u(x+w)+w(u+x)]}{v[u(v+w)+w(u+v)]}=\frac{2 x+(u+w)}{2 v+(u+w)} \\
& \quad \Longleftrightarrow \quad x[2 u w+u(u+w)][2 v+(u+w)]=v[2 u w+v(u+w)][2 x+(u+w)] \\
& \Longleftrightarrow \quad 2 x u w(u+w)+2 x^{2} v(u+w)+x^{2}(u+w)^{2} \\
& \quad=2 v u w(u+w)+2 x v^{2}(u+w)+v^{2}(u+w)^{2} \\
& \quad \Longleftrightarrow \quad 2(x-v) u w(u+w)+2(x-v) x v(u+w)+(x-v)(x+v)(u+w)^{2}=0
\end{aligned}
$$
Since the opposite sides are not parallel, we have $u+w \neq 0$. By simplifying by $(x-v)(u+w)$, we obtain the condition $2 u w+2 x v+(x+v)(u+w)=0$ which is the same as the previous one.
We conclude that $O A \cdot O C=O B \cdot O D$ if and only if $O$ lies on the line passing through the midpoints of $[A D]$ and $[B C]$. Similarly, we show that $O A \cdot O C=O B \cdot O D$ if and only if $O$ lies on the line passing through the midpoints of $[A B]$ and $[C D]$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Un cercle de centre $O$ est inscrit dans un quadrilatère $A B C D$ dont les côtés ne sont pas parallèles. Montrer que le point $O$ coïncide avec le point d'intersection des lignes médianes du quadrilatère si et seulement si $O A \cdot O C=O B \cdot O D$. (Une ligne médiane du quadrilatère est une droite reliant les milieux des côtés opposés.)
|
Soient $I$ et $J$ les milieux des côtés $[A B]$ et $[C D]$ respectivement. Les droites $(A B)$ et $(C D)$ se coupent au point $P$. Sans perte de généralité, on peut supposer que $P$ est le point d'intersection des demi-droites $[A B)$ et $[C D)$.

1) Supposons que $O$ est le point d'intersection des lignes médianes du quadrilatère $A B C D$. Alors $O$ est le milieu du segment $[I J]$, parce que les milieux des côtés d'un quadrilatère sont les sommets d'un parallélogramme. Puis, $[P O]$ est la bissectrice et la médiane issus de $P$ du triangle $I P J$, donc $I P J$ est isocèle en $P$ et $\widehat{B I O}=\widehat{C J O}$. En outre,
$$
\widehat{I B O}+\widehat{J C O}=\frac{1}{2}(\widehat{A B C}+\widehat{B C D})=\frac{1}{2}(\pi+\widehat{B P C})=\pi-\widehat{P I J}=\widehat{I B O}+\widehat{I O B}
$$
Alors $\widehat{J C O}=\widehat{I O B}$ et les triangles $O I B$ et $C J O$ sont semblables. On obtient que $\frac{O B}{O C}=$ $\frac{I B}{J O}$. De même, on a $\frac{O A}{O D}=\frac{I A}{J O}$. Comme $I B=I A$, on obtient $O A \cdot O C=O B \cdot O D$.
2) On suppose maintenant que $O A \cdot O C=O B \cdot O D$. On note que
$$
\begin{aligned}
\widehat{A O B}+\widehat{C O D} & =(\pi-\widehat{O A B}-\widehat{O B A})+(\pi-\widehat{O C D}-\widehat{O D C}) \\
& =\pi-\frac{1}{2}(\widehat{D A B}+\widehat{A B C}+\widehat{B C D}+\widehat{C D A})=\pi
\end{aligned}
$$
Par conséquent, si on construit les parallélogrammes $O A K B$ et $C O D L$ à partir des triangles $O A B$ et $O C D$, ces parallélogrammes seront semblables, parce que $\frac{O A}{A K}=\frac{O A}{O B}=$ $\frac{D O}{O C}=\frac{D O}{D L}$. En particulier, les triangles $O I B$ et $C J O$ sont également semblables, parce qu'ils se correspondent mutuellement dans les parallélogrammes semblables $O A K B$ et $C O D L . \mathrm{Il}$ vient
$$
\widehat{I O B}=\widehat{O C J}=\widehat{O C B}, \quad \widehat{C O J}=\widehat{I B O}=\widehat{O B C}
$$
On obtient que
$$
\widehat{I O B}+\widehat{B O C}+\widehat{C O J}=\widehat{O C B}+\widehat{B O C}+\widehat{O B C}=\pi,
$$
donc $O$ se trouve sur $(I J)$. De même, $O$ se trouve sur l'autre ligne médiane du quadrilatère $A B C D$.
Autre solution. On peut résoudre l'exercice par une méthode analytique utilisant les nombres complexes. Les calculs sont longs mais pas impraticables.
Notons $U, V, W, X$ les points de contact des droites $(A B),(B C),(C D)$ et $(D A)$ avec le cercle. On peut supposer que le cercle est de centre 0 et de rayon 1 . Notons $a, b, c, d, u, v, w, x$ les affixes des points $A, B, C, D, U, V, W, X$.

Un point d'affixe $z$ appartient à $(A B)$ si et seulement si $z-u$ est perpendiculaire à $u$, ce qui s'écrit $0=\bar{u}(z-u)+u(\bar{z}-\bar{u})$, ou encore $\bar{u} z+u \bar{z}=2$. Comme $\bar{u}=1 / u$, ceci s'écrit encore $z+u^{2} \bar{z}=2 u$. De même, l'équation de la droite $(A D)$ est $z+x^{2} \bar{z}=2 x$. En combinant ces deux équations, on trouve que
$$
a=\frac{2 u x}{u+x} .
$$
De même, on a $b=\frac{2 u v}{u+v}, c=\frac{2 v w}{v+w}$ et $d=\frac{2 w x}{w+x}$.
On calcule que $4 O A^{-2}=|u+x|^{2}=2+u \bar{x}+\bar{u} x$. On a des expressions analogues pour $4 O B^{-2}$, etc. Par conséquent,
$$
\begin{aligned}
O A \cdot O C & =O B \cdot O D \\
& \Longleftrightarrow \quad(2+u \bar{x}+\bar{u} x)(2+v \bar{w}+\bar{v} w)=(2+u \bar{v}+\bar{u} v)(2+w \bar{x}+\bar{w} x) \\
& \Longleftrightarrow \quad u x(2+u \bar{x}+\bar{u} x) v w(2+v \bar{w}+\bar{v} w)=u v(2+u \bar{v}+\bar{u} v) w x(2+w \bar{x}+\bar{w} x) \\
& \Longleftrightarrow \quad\left(2 u x+u^{2}+x^{2}\right)\left(2 v w+v^{2}+w^{2}\right)=\left(2 u v+u^{2}+v^{2}\right)\left(2 w x+x^{2}+w^{2}\right) \\
& \Longleftrightarrow \quad 2 u v^{2} x+2 u w^{2} x+2 u^{2} v w+u^{2} v^{2}+2 v w x^{2}+w^{2} x^{2} \\
& =2 u v x^{2}+2 u v w^{2}+2 u^{2} w x+u^{2} x^{2}+2 v^{2} w x+v^{2} w^{2} \\
& \Longleftrightarrow 2(u-w) v^{2} x-2(u-w) u w x+2(u-w) u v w \\
& \quad-2(u-w) v x^{2}+(u-w)(u+w) v^{2}-(u-w)(u+w) x^{2}=0 \\
& \Longleftrightarrow 2 v^{2} x-2 u w x+2 u v w-2 v x^{2}+u v^{2}+v^{2} w-u x^{2}-w x^{2}=0 \\
& \Longleftrightarrow \quad 2 v x(v-x)+(v-x) w(v+x)+2 u w(v-x)+u(v+x)(v-x)=0 \\
& \Longleftrightarrow 2 v x+v w+v x+2 u w+u v+u x=0 \\
& \Longleftrightarrow 2(u w+x v)+(x+v)(u+w)=0 .
\end{aligned}
$$
D'autre part, $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$ si et seulement si $0, \frac{a+d}{2}$ et $\frac{b+c}{2}$ sont alignés, ce qui se traduit par le fait que $\frac{a+d}{b+c}$ est réel, c'est-à-dire
$$
\frac{\frac{u x}{u+x}+\frac{x w}{x+w}}{\frac{u v}{u+v}+\frac{v w}{v+w}}=\frac{\frac{1}{u+x}+\frac{1}{w+x}}{\frac{1}{u+v}+\frac{1}{v+w}}
$$
On multiplie les numérateurs de chaque membre par $(u+x)(x+w)$ et les dénominateurs par $(u+v)(v+w)$, ce qui donne successivement
$$
\begin{aligned}
& \frac{x[u(x+w)+w(u+x)]}{v[u(v+w)+w(u+v)]}=\frac{2 x+(u+w)}{2 v+(u+w)} \\
& \quad \Longleftrightarrow \quad x[2 u w+u(u+w)][2 v+(u+w)]=v[2 u w+v(u+w)][2 x+(u+w)] \\
& \Longleftrightarrow \quad 2 x u w(u+w)+2 x^{2} v(u+w)+x^{2}(u+w)^{2} \\
& \quad=2 v u w(u+w)+2 x v^{2}(u+w)+v^{2}(u+w)^{2} \\
& \quad \Longleftrightarrow \quad 2(x-v) u w(u+w)+2(x-v) x v(u+w)+(x-v)(x+v)(u+w)^{2}=0
\end{aligned}
$$
Comme les côtés opposés ne sont pas parallèles, on a $u+w \neq 0$. En simplifiant par $(x-v)(u+w)$, on obtient la condition $2 u w+2 x v+(x+v)(u+w)=0$ qui est la même que la précédente.
On en conclut que $O A \cdot O C=O B \cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A D]$ et de $[B C]$. De même, on montre que $O A \cdot O C=O B \cdot O D$ si et seulement si $O$ appartient à la droite passant par les milieux de $[A B]$ et de $[C D]$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-1-solutions.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution."
}
|
748011bf-3516-59fe-939d-e600b236acf7
| 607,500
|
In a country, there are n cities. Any two cities are always connected either by a highway or by a train line. Show that one of the two means of transportation allows any city to be connected to any other.
|
We reason by induction on $n$: for $n=1$ or $n=2$, the result is immediate. Suppose we have shown it at rank $n$, and consider $n+1$ cities:
We isolate one of the cities, let's call it Paris, for example. Then one of the two means of transport allows connecting all the cities except Paris. Suppose it is the car:
- if Paris is connected to a city by a highway, for example, Lyon, we can go from Paris to Lyon by car, then to any other city according to the induction hypothesis.
- otherwise, Paris is connected to all the cities by a train line, so we can go from any city to any city by train via Paris.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un pays, il y a n villes. Deux villes quelconques sont toujours reliées soit par une autoroute, soit par une ligne de train. Montrer qu'un des deux moyens de transport permet de relier n'importe quelle ville à n'importe quelle autre.
|
On raisonne par récurrence sur $n$ : pour $n=1$ ou $n=2$, le résultat est immédiat. Supposons qu'on l'a montré au rang $n$, et considérons $n+1$ villes :
On isole une des villes, appelons-la par exemple Paris. Alors un des deux moyens de transports permet de relier entre elles toutes les villes sauf Paris. Supposons que c'est la voiture:
- si Paris est relié à une ville par une autoroute par exemple Lyon, on peut en voiture aller de Paris à Lyon, puis à n'importe quelle autre ville d'après l'hypothèse de récurrence.
- sinon, Paris est relié à toutes les villes par une ligne de train, donc on peut aller de n'importe quelle ville à n'importe quelle ville en train en passant par Paris.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 2",
"solution_match": "\nSolution de l'exercice 2"
}
|
e90e4db8-fdf1-5d5c-8a1e-12b7356a5a85
| 607,502
|
Show that every polyhedron has two faces with the same number of vertices.
|
Let $n$ be the number of faces of the polyhedron, and let $F$ be a fixed face: the edges of $F$ separate $F$ from different faces, so the number of edges of $F$ is less than or equal to the number of faces other than $F$. Moreover, $F$ has at least 3 edges. Each face has as many edges as vertices, so every face has a number of vertices between 3 and $n-1$, which gives $n-3$ possibilities. According to the pigeonhole principle, there therefore exist two faces that have the same number of vertices.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Montrer que tout polyèdre a deux faces qui ont le même nombre de sommets.
|
Soit $n$ le nombre de faces du polyèdre, et soit $F$ une face fixée : les arêtes de $F$ séparent $F$ de faces toutes différentes, donc le nombre d'arêtes de $F$ est inférieur ou égal au nombre de faces autres que $F$. De plus, $F$ a au moins 3 arêtes. Chaque face a autant d'arêtes que de sommet, donc toute face a un nombre de sommets compris entre 3 et $n-1$, soit $n-3$ possibilités. D'après le principe des tiroirs, il existe donc deux faces qui ont le même nombre de sommets.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 4",
"solution_match": "\nSolution de l'exercice 4"
}
|
7c48e0a5-bbc2-5e92-a327-fc26e8dc05f7
| 607,504
|
Let $\mathrm{n} \in \mathbb{N}^{*}$. Show that it is possible to partition $\{1,2, \ldots, \mathrm{n}\}$ into two subsets $A$ and $B$ such that the sum of the elements of $A$ is equal to the product of the elements of $B$.
|
A priori, set $B$ must be much smaller than $A$. We will therefore look for a $B$ with a small number of elements. By testing small values of $n$, we can think of looking for $B$ in the form $\{1, a, b\}$ with $a, b \neq 1$ and $a \neq b$.
We then have $\prod_{x \in B} x = a b$, and:
$$
\begin{aligned}
\sum_{x \in \mathcal{A}} & = \sum_{x=1}^{n} x - 1 - a - b \\
& = \frac{n(n+1)}{2} - a - b - 1
\end{aligned}
$$
We want $\frac{n(n+1)}{2} = a b + a + b + 1 = (a+1)(b+1)$, so it suffices to write $\frac{n(n+1)}{2}$ as a product. If $n$ is even, we can take $a+1 = \frac{n}{2}$ and $b+1 = n+1$, which gives $a = \frac{n}{2} - 1$ and $b = n$. If $n$ is odd, we take $a = \frac{n-1}{2}$ and $b = n-1$. In both cases, the assumption $n \geqslant 5$ allows us to easily verify that 1, $a$, and $b$ are pairwise distinct.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\mathrm{n} \in \mathbb{N}^{*}$. Montrer qu'il est possible de partitionner $\{1,2, \ldots, \mathrm{n}\}$ en deux sousensembles $A$ et $B$ tels que la somme des éléments de $A$ soit égale au produit des éléments de B.
|
A priori, l'ensemble B doit être bien plus petit que A. On va donc chercher un $B$ avec un petit nombre d'éléments. En testant des petites valeurs de $n$, on peut penser à chercher $B$ sous la forme $\{1, a, b\}$ avec $a, b \neq 1$ et $a \neq b$.
On a alors $\prod_{x \in B} x=a b$, et :
$$
\begin{aligned}
\sum_{x \in \mathcal{A}} & =\sum_{x=1}^{n} x-1-a-b \\
& =\frac{n(n+1)}{2}-a-b-1
\end{aligned}
$$
On veut donc $\frac{n(n+1)}{2}=a b+a+b+1=(a+1)(b+1)$, donc il suffit d'écrire $\frac{n(n+1)}{2}$ comme un produit. Or, si $n$ est pair, on peut prendre $a+1=\frac{n}{2}$ et $b+1=n+1$, soit $a=\frac{n}{2}-1$ et $b=n$. Si $n$ est impair, on prend $a=\frac{n-1}{2}$ et $b=n-1$. Dans les deux cas, l'hypothèse $n \geqslant 5$ permet de vérifier facilement que 1, a et $b$ sont deux à deux distincts.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 6",
"solution_match": "\nSolution de l'exercice 6"
}
|
bf7cfbae-fe88-5726-9fd8-eda7c8389cef
| 607,505
|
Let $E$ be a set of cardinality $n$ and $\mathscr{F}$ a set of subsets of $E$ with $|\mathscr{F}|=$ $2^{\text{n-1}}$ such that for all $A, B$ and $C$ in $\mathscr{F}, A \cap B \cap C$ is non-empty.
Show that the intersection of all elements of $\mathscr{F}$ is non-empty.
|
If $A \subset E$, we will denote $A^{c}$ its complement: the set of subsets of $E$ is partitioned into $2^{n-1}$ doubletons of the form $\left\{A, A^{c}\right\}$ where $A \subset E$. Now, it is impossible for both elements of a doubleton to be in $\mathscr{F}$, because their intersection is empty, so $\mathscr{F}$ contains exactly one element from each doubleton.
Let $A$ and $B$ be in $\mathscr{F}$: we will show that $A \cap B \in \mathscr{F}$. According to what we have just said, it suffices to show that $(A \cap B)^{c} \notin \mathscr{F}$. This is true because $A \cap B \cap (A \cap B)^{c}$ is empty.
By induction on $k$, we deduce that for all $A_{1}, A_{2}, \ldots, A_{k}$ in $\mathscr{F}, A_{1} \cap A_{2} \cap \ldots \cap A_{k} \in \mathscr{F}$. Indeed, it is true for $k=2$ and if we have shown it for $k$, then:
$$
A_{1} \cap A_{2} \cap \ldots \cap A_{k}=\left(A_{1} \cap A_{2} \cap \ldots \cap A_{k-1}\right) \cap A_{k}
$$
is the intersection of two elements of $\mathscr{F}$, so it is in $\mathscr{F}$.
Since $\mathscr{F}$ is finite, the intersection of all elements of $\mathscr{F}$ is in $\mathscr{F}$. However, the empty set cannot be in $\mathscr{F}$ because its intersection with itself is empty, so the intersection of all elements of $\mathscr{F}$ is not empty.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient E un ensemble de cardinal n et $\mathscr{F}$ un ensemble de parties de E avec $|\mathscr{F}|=$ $2^{\text {n-1 }}$ tel que pour tous $A, B$ et $C$ dans $\mathscr{F}, A \cap B \cap C$ est non vide.
Montrer que l'intersection de tous les éléments de $\mathscr{F}$ est non vide.
|
Si $A \subset E$, on notera $A^{c}$ son complémentaire: l'ensemble des parties de $E$ est partitionné en $2^{n-1}$ doubletons de la forme $\left\{A, A^{c}\right\}$ où $A \subset E$. Or, il est impossible que les deux éléments d'un doubleton soient dans $\mathscr{F}$, car leur intersection est vide, donc $\mathscr{F}$ contient exactement un élément de chaque doubleton.
Soient donc $A$ et $B$ dans $\mathscr{F}$ : on va montrer que $A \cap B \in \mathscr{F}$. D'après ce qu'on vient de dire, il suffit de montrer $(A \cap B)^{c} \notin \mathscr{F}$. Or, ceci est vrai car $A \cap B \cap(A \cap B)^{c}$ est vide.
Par récurrence sur $k$, on en déduit que pour tous $A_{1}, A_{2}, \ldots, A_{k}$ de $\mathscr{F}, A_{1} \cap A_{2} \cap \ldots \cap A_{k} \in \mathscr{F}$. En effet, c'est vrai pour $k=2$ et si on l'a montré pour $k$, alors :
$$
A_{1} \cap A_{2} \cap \ldots \cap A_{k}=\left(A_{1} \cap A_{2} \cap \ldots \cap A_{k-1}\right) \cap A_{k}
$$
est l'intersection de deux éléments de $\mathscr{F}$, donc est dans $\mathscr{F}$.
Comme $\mathscr{F}$ est fini, l'intersection de tous les éléments de $\mathscr{F}$ est dans $\mathscr{F}$. Or, l'ensemble vide ne peut pas être dans $\mathscr{F}$ car son intersection avec lui-même est vide, donc l'intersection de tous les éléments de $\mathscr{F}$ n'est pas vide.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-2-solutions.jsonl",
"problem_match": "\nExercice 9",
"solution_match": "\nSolution de l'exercice 9"
}
|
20f9a0b2-761d-5164-86d4-82e428911992
| 607,507
|
Let $a, b, c$ be real numbers such that $-1 \leqslant a x^{2}+b x+c \leqslant 1$ for $x=-1, x=0$ and $x=1$. Prove that
$$
-\frac{5}{4} \leqslant a x^{2}+b x+c \leqslant \frac{5}{4} \text { for all real } x \in[-1,1]
$$
|
Let $\mathrm{P}(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}$. Then $\mathrm{P}(-1)=\mathrm{a}-\mathrm{b}+\mathrm{c}, \mathrm{P}(0)=\mathrm{c}$ and $\mathrm{P}(1)=$ $\mathrm{a}+\mathrm{b}+\mathrm{c}$. And, according to the statement, we have $|\mathrm{P}(-1)| \leqslant 1,|\mathrm{P}(0)| \leqslant 1$ and $|\mathrm{P}(1)| \leqslant 1$.
Now, for any real $\chi$, we can directly verify that
$$
P(x)=\frac{x(x+1)}{2} P(1)-\frac{x(1-x)}{2} P(-1)+\left(1-x^{2}\right) P(0)
$$
- Let $x \in[0 ; 1]$. According to (1) and the triangle inequality, we get
$$
\begin{aligned}
|\mathrm{P}(x)| & \leqslant \frac{x(x+1)}{2}|\mathrm{P}(1)|+\frac{x(1-x)}{2}|\mathrm{P}(-1)|+\left(1-x^{2}\right)|\mathrm{P}(0)| \\
& \leqslant \frac{x(x+1)}{2}+\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
& =-x^{2}+x+1 \\
& =\frac{5}{4}-\left(x-\frac{1}{2}\right)^{2}
\end{aligned}
$$
Thus, $|P(x)| \leqslant \frac{5}{4}$.
- Let $x \in[-1 ; 0]$. According to (1) and the triangle inequality, we get this time
$$
\begin{aligned}
& \leqslant-\frac{x(x+1)}{2}|P(1)|-\frac{x(1-x)}{2}|P(-1)|+\left(1-x^{2}\right)|P(0)| \\
& \leqslant-\frac{x(x+1)}{2}-\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
& =-x^{2}-x+1 \\
& =\frac{5}{4}-\left(x+\frac{1}{2}\right)^{2}
\end{aligned}
$$
Thus, $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$, again.
Finally, for all $x \in[-1 ; 1]$, we have $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$.

|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c$ des réels tels que $-1 \leqslant a x^{2}+b x+c \leqslant 1$ pour $x=-1, x=0$ et $x=1$. Prouver que
$$
-\frac{5}{4} \leqslant a x^{2}+b x+c \leqslant \frac{5}{4} \text { pour tout réel } x \in[-1,1]
$$
|
Posons $\mathrm{P}(\mathrm{x})=\mathrm{ax}{ }^{2}+\mathrm{bx}+\mathrm{c}$. Alors $\mathrm{P}(-1)=\mathrm{a}-\mathrm{b}+\mathrm{c}, \mathrm{P}(0)=\mathrm{c}$ et $\mathrm{P}(1)=$ $\mathrm{a}+\mathrm{b}+\mathrm{c}$. Et, d'après l'énoncé, on a $|\mathrm{P}(-1)| \leqslant 1,|\mathrm{P}(0)| \leqslant 1$ et $|\mathrm{P}(1)| \leqslant 1$.
Or, pour tout réel $\chi$, on vérifie directement que
$$
P(x)=\frac{x(x+1)}{2} P(1)-\frac{x(1-x)}{2} P(-1)+\left(1-x^{2}\right) P(0)
$$
- Soit $x \in[0 ; 1]$. D'après (1) et l'inégalité triangulaire, il vient
$$
\begin{aligned}
|\mathrm{P}(x)| & \leqslant \frac{x(x+1)}{2}|\mathrm{P}(1)|+\frac{x(1-x)}{2}|\mathrm{P}(-1)|+\left(1-x^{2}\right)|\mathrm{P}(0)| \\
& \leqslant \frac{x(x+1)}{2}+\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
& =-x^{2}+x+1 \\
& =\frac{5}{4}-\left(x-\frac{1}{2}\right)^{2}
\end{aligned}
$$
Et ainsi $|P(x)| \leqslant \frac{5}{4}$.
- Soit $x \in[-1 ; 0]$. D'après (1) et l'inégalité triangulaire, il vient cette fois
$$
\begin{aligned}
& \leqslant-\frac{x(x+1)}{2}|P(1)|-\frac{x(1-x)}{2}|P(-1)|+\left(1-x^{2}\right)|P(0)| \\
& \leqslant-\frac{x(x+1)}{2}-\frac{x(1-x)}{2}+\left(1-x^{2}\right) \\
& =-x^{2}-x+1 \\
& =\frac{5}{4}-\left(x+\frac{1}{2}\right)^{2}
\end{aligned}
$$
Et ainsi $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$, à nouveau.
Finalement, pour tout $x \in[-1 ; 1]$, on a $|\mathrm{P}(\mathrm{x})| \leqslant \frac{5}{4}$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-3-solutions.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
373cabfa-0fc0-532f-92ac-d5e704aa8c7e
| 607,509
|
Prove that, for all real $a \geqslant 0$, we have
$$
a^{3}+2 \geqslant a^{2}+2 \sqrt{a}
$$
|
For all real $a \geqslant 0$, we have
$$
\begin{aligned}
a^{3}-a^{2}-2 \sqrt{a}+2 & =a^{2}(a-1)-2(\sqrt{a}-1) \\
& =a^{2}(\sqrt{a}-1)(\sqrt{a}+1)-2(\sqrt{a}-1) \\
& =(\sqrt{a}-1)\left(a^{2}(\sqrt{a}+1)-2\right) .(1)
\end{aligned}
$$
Now:
- If $a \geqslant 1$ then $\sqrt{a} \geqslant 1$ and $a^{2} \geqslant 1$. Thus, we have $\sqrt{a}-1 \geqslant 0$ and $a^{2}(\sqrt{a}+1) \geqslant 2$. Therefore, each of the factors in (1) is positive, which ensures that the product is positive.
- If $a \leqslant 1$ then $\sqrt{a} \leqslant 1$ and $a^{2} \leqslant 1$. Thus, we have $\sqrt{a}-1 \leqslant 0$ and $a^{2}(\sqrt{a}+1) \leqslant 2$. Therefore, each of the two factors in (1) is negative, and the product is thus still positive.
Finally, for all real $a \geqslant 0$, we have $a^{3}-a^{2}-2 \sqrt{a}+2 \geqslant 0$ or equivalently $a^{3}+2 \geqslant a^{2}+2 \sqrt{a}$.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tout réel $a \geqslant 0$, on a
$$
a^{3}+2 \geqslant a^{2}+2 \sqrt{a}
$$
|
Pour tout réel $a \geqslant 0$, on a
$$
\begin{aligned}
a^{3}-a^{2}-2 \sqrt{a}+2 & =a^{2}(a-1)-2(\sqrt{a}-1) \\
& =a^{2}(\sqrt{a}-1)(\sqrt{a}+1)-2(\sqrt{a}-1) \\
& =(\sqrt{a}-1)\left(a^{2}(\sqrt{a}+1)-2\right) .(1)
\end{aligned}
$$
Or:
- Si $a \geqslant 1$ alors $\sqrt{a} \geqslant 1$ et $a^{2} \geqslant 1$. Ainsi, on a $\sqrt{a}-1 \geqslant 0$ et $a^{2}(\sqrt{a}+1) \geqslant 2$. Par suite, chacun des facteurs de (1) est positif, ce qui assure que le produit est positif.
- Si $a \leqslant 1$ alors $\sqrt{a} \leqslant 1$ et $a^{2} \leqslant 1$. Ainsi, on a $\sqrt{a}-1 \leqslant 0$ et $a^{2}(\sqrt{a}+1) \leqslant 2$. Par suite, chacun des deux facteurs de (1) est négatif, et le produit est donc encore positif.
Finalement, pour tout réel $a \geqslant 0$, on a $a^{3}-a^{2}-2 \sqrt{a}+2 \geqslant 0$ ou encore $a^{3}+2 \geqslant a^{2}+2 \sqrt{a}$.
## Exercices Communs
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-3-solutions.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
941b49b4-98ca-5bda-b069-3fa9e53c2105
| 607,510
|
Let P and Q be two polynomials with real coefficients, of degrees $\mathrm{n} \geqslant 0$. Suppose that the coefficient of $x^{n}$ of each of these two polynomials is equal to 1 and that, for all real $x$, we have $P(P(x))=$ $\mathrm{Q}(\mathrm{Q}(\mathrm{x})$ ).
Prove that $\mathrm{P}=\mathrm{Q}$.
|
The result is evident if $\mathrm{n}=0$. In what follows, we therefore assume that $\mathrm{n} \geqslant 1$.
By contradiction: suppose that the polynomial $\mathrm{R}=\mathrm{P}-\mathrm{Q}$ is not the zero polynomial.
Let $k$ be the degree of R.
Since $P$ and $Q$ are both of degree $n$, and have the same leading coefficient, we have $k \in\{0, \cdots, n-1\}$. Furthermore, we have
$$
P(P(x))-Q(Q(x))=[Q(P(x))-Q(Q(x))]+R(P(x))
$$
Let $Q(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$.
We notice that then
$$
\mathrm{Q}(\mathrm{P}(\mathrm{x}))-\mathrm{Q}(\mathrm{Q}(\mathrm{x}))=\left[\mathrm{P}^{n}(x)-\mathrm{Q}^{n}(x)\right]+\mathrm{a}_{n-1}\left[\mathrm{P}^{n-1}(x)-\mathrm{Q}^{n-1}(x)\right]+\cdots+\mathrm{a}_{1}[\mathrm{P}(\mathrm{x})-\mathrm{Q}(\mathrm{x})]
$$
and each term of this sum other than $\left[P^{n}(x)-Q^{n}(x)\right]$ is of degree at most $n(n-1)$. On the other hand, we have
$$
\left[P^{n}(x)-Q^{n}(x)\right]=R(x)\left[P^{n-1}(x)+P^{n-2}(x) Q(x)+\cdots+Q^{n-1}(x)\right]
$$
which ensures that $\left[P^{n}(x)-Q^{n}(x)\right]$ is of degree $n(n-1)+k$ and has a leading coefficient equal to $n$ (we recall that $P$ and $Q$ both have a leading coefficient equal to 1).
- Suppose that $k>0$.
Then, the polynomial $Q(P(x))-Q(Q(x))$ is of degree $n(n-1)+k$.
On the other hand, the degree of $R(P(x))$ is $k n$, and we have $k n \leqslant n(n-1)<n(n-1)+k$.
From (1), we deduce that $P(P(x))-Q(Q(x))$ is of degree $n(n-1)+k$, and therefore non-zero, in contradiction with the statement.
- It remains to study the case where $k=0$, i.e., when $R$ is constant.
Let $c$ be this constant. Our initial hypothesis ensures that $c \neq 0$.
From $P(P(x))=Q(Q(x))$, it follows that $\mathrm{Q}(\mathrm{Q}(\mathrm{x})+\mathrm{c})=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))-\mathrm{c}$.
Since $Q$ is not constant, this means that the equality $Q(y+c)=Q(y)-c$ is true for an infinite number of real numbers $y$. Since these are polynomials, this means that it is true for all real numbers $y$.
An immediate induction then leads to $Q(j c)=a_{0}-j c$ for all integers $j \geqslant 0$.
As above, the equality $Q(x)=-x+a_{0}$ being true for an infinite number of values (since $c \neq 0$), it is therefore true for all $x$. This contradicts that $Q$ has a leading coefficient equal to 1.
Thus, in all cases, we have obtained a contradiction. This ensures that $R$ is indeed the zero polynomial, and completes the proof.
## Another solution.
The result is easy to show if $\mathfrak{n}=0$ or $\mathfrak{n}=1$. In what follows, we therefore assume that $\mathrm{n} \geqslant 2$. Let $R=P-Q$ and suppose by contradiction that it is non-zero. Without loss of generality, we can assume that the leading coefficient of $R$ is strictly positive.
Lemma 1. For any polynomial $R$ with a strictly positive leading coefficient, there exists a real number $a$ such that for all $x \geqslant a$ we have $R(x)>0$.
Indeed, $R(x)$ can be written in the form $c x^{m}\left(1+\frac{c_{1}}{x}+\cdots+\frac{c_{m}}{x^{m}}\right)$ with $c>0$. The term in parentheses tends to 1 as $x \rightarrow+\infty$, so it is strictly positive for $x$ sufficiently large.
Lemma 2. For any polynomial $P$ of degree $\geqslant 1$ with a strictly positive leading coefficient, there exists $a$ such that $P$ is strictly increasing on $[a, +\infty[$.
Indeed, the derivative polynomial $P^{\prime}$ satisfies the conditions of Lemma 1, so $P^{\prime}(x)$ is strictly positive for $x$ sufficiently large.
Returning to the exercise. From the two preceding lemmas, there exists $a$ such that on $[a, +\infty[$, $P$ and $Q$ are strictly increasing, and $R$ and $R \circ Q$ are strictly positive.
We then have for all $x \geqslant a$:
$$
\begin{aligned}
\mathrm{P}(\mathrm{P}(\mathrm{x})) & >\mathrm{P}(\mathrm{Q}(x)) \quad \text { since } \mathrm{P}(\mathrm{x})>\mathrm{Q}(\mathrm{x}) \\
& =\mathrm{Q}(\mathrm{Q}(\mathrm{x}))+\mathrm{R}(\mathrm{Q}(\mathrm{x})) \\
& >\mathrm{Q}(\mathrm{Q}(\mathrm{x}))
\end{aligned}
$$
which contradicts $\mathrm{P}(\mathrm{P}(\mathrm{x}))=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))$.

|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit P et Q deux polynômes à coefficients réels, de degrés $\mathrm{n} \geqslant 0$. On suppose que le coefficient de $x^{n}$ de chacun de ces deux polynômes est égal à 1 et que, pour tout réel $x$, on a $P(P(x))=$ $\mathrm{Q}(\mathrm{Q}(\mathrm{x})$ ).
Prouver que $\mathrm{P}=\mathrm{Q}$.
|
Le résultat est évident si $\mathrm{n}=0$. Dans ce qui suit, on suppose donc que $\mathrm{n} \geqslant 1$.
Par l'absurde : supposons que le polynôme $\mathrm{R}=\mathrm{P}-\mathrm{Q}$ ne soit pas le polynôme nul.
Soit $k$ le degré de R.
Puisque $P$ et $Q$ sont tous deux de degré $n$, et de même coefficient dominant, on a $k \in\{0, \cdots, n-1\}$. De plus, on a
$$
P(P(x))-Q(Q(x))=[Q(P(x))-Q(Q(x))]+R(P(x))
$$
Posons $Q(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$.
On remarque qu'alors
$$
\mathrm{Q}(\mathrm{P}(\mathrm{x}))-\mathrm{Q}(\mathrm{Q}(\mathrm{x}))=\left[\mathrm{P}^{n}(x)-\mathrm{Q}^{n}(x)\right]+\mathrm{a}_{n-1}\left[\mathrm{P}^{n-1}(x)-\mathrm{Q}^{n-1}(x)\right]+\cdots+\mathrm{a}_{1}[\mathrm{P}(\mathrm{x})-\mathrm{Q}(\mathrm{x})]
$$
et chacun des termes de cette somme autre que $\left[P^{n}(x)-Q^{n}(x)\right]$ est de degré au plus $n(n-1)$. D'autre part, on a
$$
\left[P^{n}(x)-Q^{n}(x)\right]=R(x)\left[P^{n-1}(x)+P^{n-2}(x) Q(x)+\cdots+Q^{n-1}(x)\right]
$$
ce qui assure que $\left[P^{n}(x)-Q^{n}(x)\right]$ est de degré $n(n-1)+k$ et de coefficient dominant égal à $n$ (on rappelle que $P$ et $Q$ sont tous les deux de coefficient dominant égal à 1 ).
- On suppose que $k>0$.
Alors, le polynôme $Q(P(x))-Q(Q(x))$ est de degré $n(n-1)+k$.
D'autre part, le degré de $R(P(x))$ est $k n$, et on a $k n \leqslant n(n-1)<n(n-1)+k$.
De (1), on déduit que $P(P(x))-Q(Q(x))$ est de degré $n(n-1)+k$, et donc non nul, en contradiction avec l'énoncé.
- Il reste à étudier le cas où $k=0$, c'est-à-dire lorsque $R$ est constant.
Notons c cette constante. Notre hypothèse initiale assure que $c \neq 0$.
$\operatorname{De} P(P(x))=Q(Q(x))$, il vient $\mathrm{Q}(\mathrm{Q}(\mathrm{x})+\mathrm{c})=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))-\mathrm{c}$.
Puisque $Q$ n'est pas constant, c'est donc que l'égalité $Q(y+c)=Q(y)-c$ est vraie pour une infinité de réels $y$. S'agissant de polynômes, c'est donc qu'elle est vraie pour tout réel $y$.
Une récurrence immédiate conduit alors à $Q(j c)=a_{0}-j c$ pour tout entier $j \geqslant 0$.
Comme ci-dessus, l'égalité $Q(x)=-x+a_{0}$ étant vraie pour une infinité de valeurs (puisque $c \neq 0$ ), elle est donc vraie pour tout $x$. Cela contredit que $Q$ est de coefficient dominant égal à 1 .
Ainsi, dans tous les cas, on a obtenu une contradiction. Cela assure que $R$ est bien le polynôme nul, et achève la démonstration.
## Autre solution.
Le résultat est facile à montrer si $\mathfrak{n}=0$ ou $\mathfrak{n}=1$. Dans ce qui suit, on suppose donc que $\mathrm{n} \geqslant 2$. Notons $R=P-Q$ et supposons par l'absurde qu'il est non nul. Quitte à permuter les rôles de P et de Q , on peut supposer que le coefficient dominant de $R$ est strictement positif.
Lemme 1. Pour tout polynôme R ayant un coefficient dominant strictement positif, il existe un réel a tel que pour tout $x \geqslant a$ on a $R(x)>0$.
En effet, $R(x)$ peut s'écrire sous la forme $c x^{m}\left(1+\frac{c_{1}}{x}+\cdots+\frac{c_{m}}{x^{m}}\right)$ avec $c>0$. Le terme entre parenthèses tend vers 1 lorsque $x \rightarrow+\infty$, donc est strictement positif pour $x$ assez grand.
Lemme 2. Pour tout polynôme $P$ de degré $\geqslant 1$ ayant un coefficient dominant strictement positif, il existe a tel que P est strictement croissant sur [a, $+\infty$ [.
En effet, le polynôme dérivé $P^{\prime}$ vérifie les conditions du lemme 1 donc $P^{\prime}(x)$ est strictement positif pour $x$ assez grand.
Revenons à l'exercice. D'après les deux lemmes précédents, il existe a tel que sur [a, $+\infty[, P$ et $Q$ sont strictement croissants, et $R$ et $R \circ Q$ sont strictement positifs.
On a alors pour tout $x \geqslant a$ :
$$
\begin{aligned}
\mathrm{P}(\mathrm{P}(\mathrm{x})) & >\mathrm{P}(\mathrm{Q}(x)) \quad \text { puisque } \mathrm{P}(\mathrm{x})>\mathrm{Q}(\mathrm{x}) \\
& =\mathrm{Q}(\mathrm{Q}(\mathrm{x}))+\mathrm{R}(\mathrm{Q}(\mathrm{x})) \\
& >\mathrm{Q}(\mathrm{Q}(\mathrm{x}))
\end{aligned}
$$
ce qui contredit $\mathrm{P}(\mathrm{P}(\mathrm{x}))=\mathrm{Q}(\mathrm{Q}(\mathrm{x}))$.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-3-solutions.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
9679a9f0-d240-5f2e-965d-e2624174ad88
| 607,515
|
Show that if the sum of all positive divisors of an integer $n \geqslant 1$ is a power of two, then the number of positive divisors of $n$ is a power of two.
|
Let's decompose $n$ into a product of prime factors: $n=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$. It is easily seen that the sum of the positive divisors of $n$, denoted by $\sigma(n)$, is
$$
\sigma(n)=\prod_{i=1}^{k}\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}\right)
$$
Thus, if $1 \leqslant i \leqslant k, 1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}$ is a power of two. This clearly implies that $p_{i} \neq 2$. Suppose then, by contradiction, that $\alpha_{i}+1$ is not a power of two and choose $q$ an odd prime dividing $\alpha_{i}+1$. Then
$$
1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}=\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}\right) \cdot\left(1+p_{i}^{q}+p_{i}^{2 q}+\cdots+p_{i}^{\alpha_{i}+1-q}\right)
$$
Indeed, this equality follows from the fact that $\left(p_{i}^{\alpha_{i}+1}-1\right) /(p-1)=\left(p_{i}^{q}-1\right) /(p-1) \cdot\left(p_{i}^{\alpha_{i}+1}-1\right) /\left(p^{q}-1\right)$. This is absurd, because $1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}$ is odd. Thus, $\alpha_{i}+1$ is a power of two for all $1 \leqslant i \leqslant k$. This concludes the proof, as the number of divisors (positive) of $n$ is $\prod_{i=1}^{k}\left(\alpha_{i}+1\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer que si la somme de tous les diviseurs positifs d'un entier $n \geqslant 1$ est une puissance de deux, alors le nombre de diviseurs positifs de n est une puissance de deux.
|
Décomposons $n$ en produit de facteurs premiers : $n=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$. On voit aisément que la somme des diviseurs positifs de $n$, notée $\sigma(n)$, vaut
$$
\sigma(n)=\prod_{i=1}^{k}\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}\right)
$$
Ainsi, si $1 \leqslant i \leqslant k, 1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}$ est une puissance de deux. Ceci implique clairement que $p_{i} \neq 2$. Supposons ensuite par l'absurde que $\alpha_{i}+1$ n'est pas une puissance de deux et choisissons $q$ un nombre premier impair divisant $\alpha_{i}+1$. Alors
$$
1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{\alpha_{i}}=\left(1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}\right) \cdot\left(1+p_{i}^{q}+p_{i}^{2 q}+\cdots+p_{i}^{\alpha_{i}+1-q}\right)
$$
En effet, cette égalité découle du fait que $\left(p_{i}^{\alpha_{i}+1}-1\right) /(p-1)=\left(p_{i}^{q}-1\right) /(p-1) \cdot\left(p_{i}^{\alpha_{i}+1}-1\right) /\left(p^{q}-1\right)$. Ceci est absurde, car $1+p_{i}+p_{i}^{2}+\cdots+p_{i}^{q-1}$ est impair. Ainsi, $\alpha_{i}+1$ est une puissance de deux pour tout $1 \leqslant i \leqslant k$. Ceci conclut, car le nombre de diviseurs (positifs) de $n$ est $\prod_{i=1}^{k}\left(\alpha_{i}+1\right)$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-4-solutions.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
22cdd068-88b3-5c7e-8182-a9da4c666599
| 607,521
|
In a circle $\mathcal{C}$ with center $O$, a chord $[C D]$ is drawn. Let $\Gamma$ be the circle with diameter $[C D]$ and $O^{\prime}$ its center. The perpendicular bisector of $[C D]$ intersects the circle $\mathcal{C}$ at two points $A$ and $B$ such that $A$ is outside $\Gamma$. Let $T$ and $T^{\prime}$ be the points of tangency of the tangents to $\Gamma$ passing through $A$. Let $F$ be the midpoint of $\left[T T^{\prime}\right]$. Show that $O^{\prime}$ is the midpoint of $[B F]$.
|
Since triangles $A F T$ and $A T O^{\prime}$ are similar, we have $\frac{A F}{A T}=\frac{A T}{A O^{\prime}}$. Now, $A T^{2}=A O^{\prime 2}-O^{\prime} T^{2}=$ $A O^{\prime 2}-O^{\prime} C^{2}$, so $A F=\frac{A O^{\prime 2}-O^{\prime} C^{2}}{A O^{\prime}}$.
Since triangles $A C B$ and $A O^{\prime} C$ are similar, we have $\frac{A B}{A C}=\frac{A C}{A O^{\prime}}$. Now, $A C^{2}=A O^{\prime 2}+O^{\prime} C^{2}$, so $A B=\frac{A O^{\prime 2}+O^{\prime} C^{2}}{A O^{\prime}}$.
By adding the previously found equalities, we get $\frac{A F+A B}{2}=A O^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Dans un cercle $\mathcal{C}$ de centre $O$, on trace une corde $[C D]$. Soit $\Gamma$ le cercle de diamètre $[C D]$ et $O^{\prime}$ son centre. La médiatrice de $[C D]$ coupe le cercle $\mathcal{C}$ en deux points $A$ et $B$ tels que $A$ est extérieur à $\Gamma$. Notons $T$ et $T^{\prime}$ les points de contact des tangentes à $\Gamma$ passant par $A$. Soit $F$ le milieu de $\left[T T^{\prime}\right]$. Montrer que $O^{\prime}$ est le milieu de $[B F]$.
|
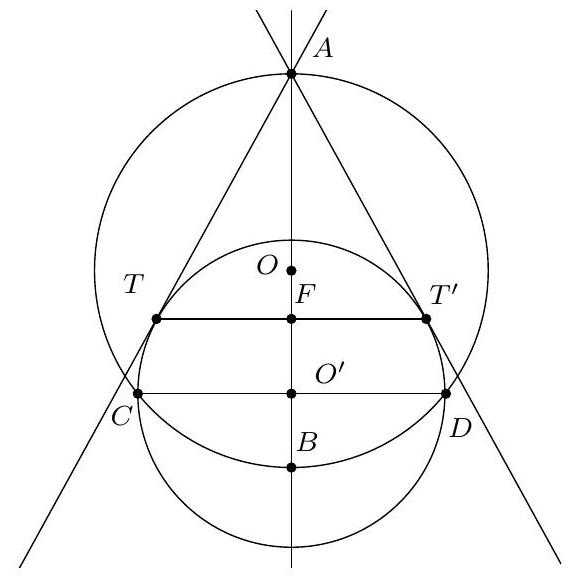
Comme les triangles $A F T$ et $A T O^{\prime}$ sont semblables, on a $\frac{A F}{A T}=\frac{A T}{A O^{\prime}}$. Or, $A T^{2}=A O^{\prime 2}-O^{\prime} T^{2}=$ $A O^{\prime 2}-O^{\prime} C^{2}$ donc $A F=\frac{A O^{\prime 2}-O^{\prime} C^{2}}{A O^{\prime}}$.
Comme les triangles $A C B$ et $A O^{\prime} C$ sont semblables, on a $\frac{A B}{A C}=\frac{A C}{A O^{\prime}}$. Or, $A C^{2}=A O^{\prime 2}+O^{\prime} C^{2}$ donc $A B=\frac{A O^{\prime 2}+O^{\prime} C^{2}}{A O^{\prime}}$.
En additionnant les égalités précédemment trouvées, on obtient $\frac{A F+A B}{2}=A O^{\prime}$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
d22e3e09-38a5-5aeb-9310-81e26a21a5f3
| 607,527
|
Let $ABC$ be a triangle. The bisectors of $\widehat{A}, \widehat{B}$, and $\widehat{C}$ intersect the circumcircle at $A^{\prime}, B^{\prime}$, and $C^{\prime}$ respectively. Let $I$ be the center of the incircle of $ABC$. The circles with diameters $\left[I A^{\prime}\right],\left[I B^{\prime}\right]$, and $\left[I C^{\prime}\right]$ intersect the lines $(BC),(CA)$, and $(AB)$ at $A_{1}$ and $A_{2}, B_{1}$ and $B_{2}$, $C_{1}$ and $C_{2}$ respectively. Show that $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ are concyclic.
|
Let $\Gamma_{A}, \Gamma_{B}$, and $\Gamma_{C}$ be the circles with diameters $\left[I A^{\prime}\right], \left[I B^{\prime}\right]$, and $\left[I C^{\prime}\right]$, respectively.
First, note that $I$ is the orthocenter of $A^{\prime} B^{\prime} C^{\prime}$. To see this, let's show, for example, that $\left(A^{\prime} C^{\prime}\right) \perp \left(B^{\prime} I\right)$:
\[
\begin{aligned}
\left(B^{\prime} I, A^{\prime} C^{\prime}\right) & = \left(B B^{\prime}, A^{\prime} C^{\prime}\right) = \left(B B^{\prime}, B A\right) + \left(A B, A A^{\prime}\right) + \left(A^{\prime} A, A^{\prime} C^{\prime}\right) \\
& = \left(B B^{\prime}, B A\right) + \left(A B, A A^{\prime}\right) + \left(C A, C C^{\prime}\right) \\
& = \frac{\widehat{B} + \widehat{A} + \widehat{C}}{2} = \frac{\pi}{2} \quad (\bmod \pi)
\end{aligned}
\]
Let $B^{\prime \prime}$ be the foot of the altitude from $B^{\prime}$ in $A^{\prime} B^{\prime} C^{\prime}$. Then $B, B^{\prime \prime}$, and $I$ are collinear according to the above.
On the other hand, since $\left(I B^{\prime \prime}\right) \perp \left(B^{\prime \prime} A^{\prime}\right)$, $B^{\prime \prime}$ lies on $\Gamma_{A}$. Similarly, it lies on $\Gamma_{C}$, so the radical axis of these two circles is $\left(I B^{\prime \prime}\right)$. We deduce that $B$ also lies on this radical axis, which implies that $B A_{1} \cdot B A_{2} = B C_{1} \cdot B C_{2}$, and thus $A_{1}, A_{2}, C_{1}, C_{2}$ are concyclic. Let $\Gamma_{C A}$ be the circle passing through these points.
We define $\Gamma_{A B}$ and $\Gamma_{B C}$ similarly. If these three circles were pairwise distinct, then their pairwise radical axes would be $(A B), (B C)$, and $(C A)$, and they would neither be concurrent nor parallel, which is impossible.
Therefore, two of these circles are coincident, and consequently, $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. Les bissectrices de $\widehat{A}, \widehat{B}$ et $\widehat{C}$ recoupent le cercle circonscrit en $A^{\prime}, B^{\prime}$ et $C^{\prime}$ respectivement. Soit $I$ le centre du cercle inscrit à $A B C$. Les cercles de diamètres $\left[I A^{\prime}\right],\left[I B^{\prime}\right]$ et $\left[I C^{\prime}\right]$ coupent respectivement les droites $(B C),(C A)$ et $(A B)$ en $A_{1}$ et $A_{2}, B_{2}$ et $B_{2}$, $C_{1}$ et $C_{2}$. Montrer que $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.
|
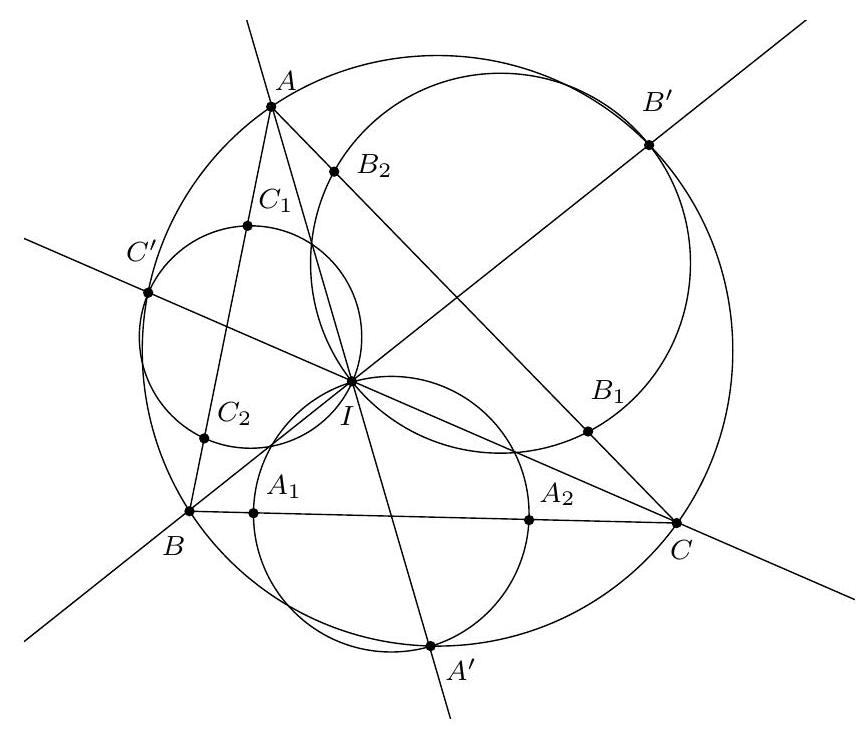
Notons $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$ les cercles de diamètres respectifs $\left[I A^{\prime}\right],\left[I B^{\prime}\right]$ et $\left[I C^{\prime}\right]$.
Remarquons d'abord que $I$ est l'orthocentre de $A^{\prime} B^{\prime} C^{\prime}$. Pour le voir, montrons par exemple que $\left(A^{\prime} C^{\prime}\right) \perp\left(B^{\prime} I\right)$ :
$$
\begin{aligned}
\left(B^{\prime} I, A^{\prime} C^{\prime}\right) & =\left(B B^{\prime}, A^{\prime} C^{\prime}\right)=\left(B B^{\prime}, B A\right)+\left(A B, A A^{\prime}\right)+\left(A^{\prime} A, A^{\prime} C^{\prime}\right) \\
& =\left(B B^{\prime}, B A\right)+\left(A B, A A^{\prime}\right)+\left(C A, C C^{\prime}\right) \\
& =\frac{\widehat{B}+\widehat{A}+\widehat{C}}{2}=\frac{\pi}{2} \quad(\bmod \pi)
\end{aligned}
$$
Soit $B^{\prime \prime}$ le pied de la hauteur de $A^{\prime} B^{\prime} C^{\prime}$ issue de $B^{\prime}$. Alors $B, B^{\prime \prime}$ et $I$ sont alignés d'après ce qui précède.
D'autre part, comme $\left(I B^{\prime \prime}\right) \perp\left(B^{\prime \prime} A^{\prime}\right), B^{\prime \prime}$ appartient à $\Gamma_{A}$. De même, il appartient à $\Gamma_{C}$, donc l'axe radical de ces deux cercles est $\left(I B^{\prime \prime}\right)$. On en déduit que $B$ appartient également à cet axe radical, ce qui entraîne que $B A_{1} \cdot B A_{2}=B C_{1} \cdot B C_{2}$ et donc $A_{1}, A_{2}, C_{1}, C_{2}$ sont cocycliques. Soit $\Gamma_{C A}$ le cercle passant par ces points.
On définit de même $\Gamma_{A B}$ et $\Gamma_{B C}$. Si ces trois cercles étaient deux à deux distincts, alors leurs axes radicaux pris deux à deux seraient $(A B),(B C)$ et $(C A)$ et ne seraient ni concourants ni parallèles, ce qui est impossible.
Donc deux de ces cercles sont confondus, et par conséquent $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ sont cocycliques.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
748c6741-cbda-573b-a254-ae00eba9e6a3
| 607,529
|
Let $ABCD$ be a cyclic quadrilateral. A circle passing through $A$ and $B$ intersects $[AC]$ and $[BD]$ at $E$ and $F$. The lines $(AF)$ and $(BE)$ intersect $[BC]$ and $[AD]$ at $P$ and $Q$ respectively. Show that $(PQ)$ is parallel to $(CD)$.
|
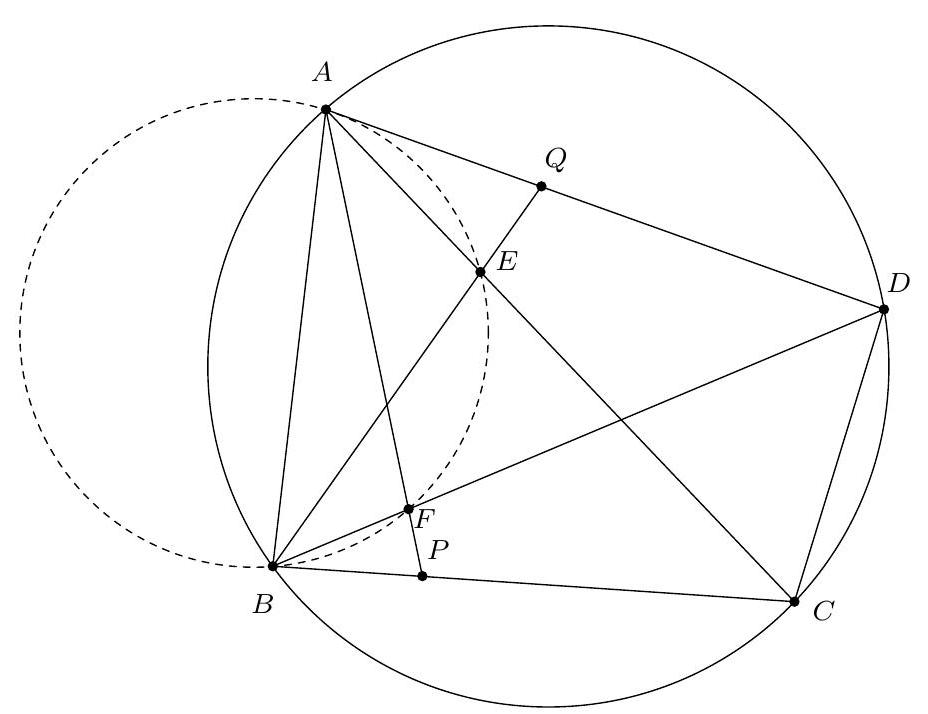
\(\widehat{A Q B} = \widehat{A Q E} = \pi - \widehat{Q E A} - \widehat{E A Q} = \widehat{A E B} - \widehat{C A D}\) and similarly, \(\widehat{A P B} = \widehat{A F B} - \widehat{C B D}\). Since \(\widehat{A E B} = \widehat{A F B}\) and \(\widehat{C A D} = \widehat{C B D}\), it follows that \(\widehat{A Q B} = \widehat{A P B}\). Therefore, \(A, B, P, Q\) are concyclic. We have: \((A D, P Q) = (Q A, Q P) = (B A, B P) = (B A, B C) = (D A, D C)\), so \((P Q)\) and \((D C)\) are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère cyclique. Un cercle passant par $A$ et $B$ coupe $[A C]$ et $[B D]$ en $E$ et $F$. Les droites $(A F)$ et $(B E)$ coupent $[B C]$ et $[A D]$ en $P$ et $Q$ respectivement. Montrer que $(P Q)$ est parallèle à $(C D)$.
|

$\widehat{A Q B}=\widehat{A Q E}=\pi-\widehat{Q E A}-\widehat{E A Q}=\widehat{A E B}-\widehat{C A D}$ et de même, $\widehat{A P B}=\widehat{A F B}-\widehat{C B D}$. Or, $\widehat{A E B}=\widehat{A F B}$ et $\widehat{C A D}=\widehat{C B D}$, donc $\widehat{A Q B}=\widehat{A P B}$. On en déduit que $A, B, P, Q$ sont cocycliques. Il vient: $(A D, P Q)=(Q A, Q P)=(B A, B P)=(B A, B C)=(D A, D C)$, donc $(P Q)$ et $(D C)$ sont parallèles.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
651c4d30-aeec-5b1b-9f4f-f94d68883f3c
| 607,530
|
Let $A$ be a point outside a circle $\Gamma$. We draw two tangents $[A T]$ and $\left[A T^{\prime}\right]$ from $A$. Let $M$ and $M^{\prime}$ be the midpoints of $[A T]$ and $\left[A T^{\prime}\right]$. Let $P$ be a point on $\left(M M^{\prime}\right)$. Denote $[U V]$ as the chord of $\Gamma$ such that $(P U)$ and $(P V)$ are tangents to $\Gamma$. The line $(U V)$ intersects $\left(M M^{\prime}\right)$ at $Q$. Show that the triangle $P A Q$ is a right triangle.
|
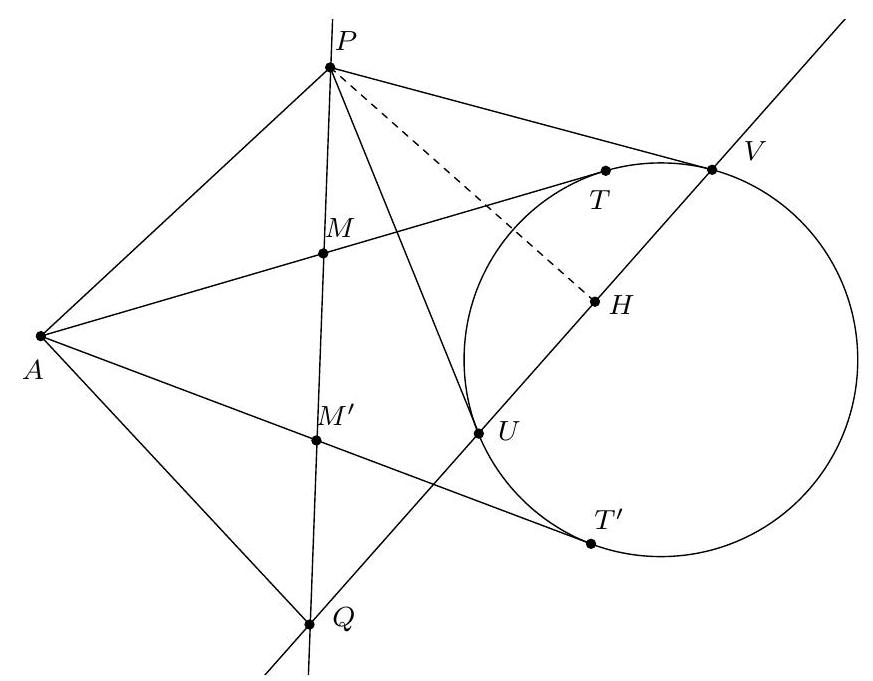
Since \( M A = M T \), \( M \) lies on the radical axis of \( A \) and \( \Gamma \) (considering \( A \) as a circle of radius zero). Similarly, \( M' \) lies on this radical axis, so \( P \) and \( Q \) do as well. We deduce that \( P A = P U = P V \) and \( Q A^2 = Q U \cdot Q V \).
Let \( H \) be the orthogonal projection of \( P \) onto \( (UV) \). We have
\[
\begin{aligned}
P A^2 + Q A^2 & = P U^2 + Q U \cdot Q V = P H^2 + H U^2 + (Q H - H U)(Q H + H U) \\
& = P H^2 + H U^2 + Q H^2 - H U^2 = P H^2 + Q H^2 = P Q^2
\end{aligned}
\]
thus \( \triangle PAQ \) is a right triangle at \( A \).
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A$ un point extérieur à un cercle $\Gamma$. On mène deux tangentes $[A T]$ et $\left[A T^{\prime}\right]$ issues de $A$. Soient $M$ et $M^{\prime}$ les milieux de $[A T]$ et $\left[A T^{\prime}\right]$. Soit $P$ un point de $\left(M M^{\prime}\right)$. Notons $[U V]$ la corde de $\Gamma$ telle que $(P U)$ et $(P V)$ soient tangentes à $\Gamma$. La droite $(U V)$ coupe $\left(M M^{\prime}\right)$ en $Q$. Montrer que le triangle $P A Q$ est rectangle.
|

Comme $M A=M T, M$ appartient à l'axe radical de $A$ et $\Gamma$ ( $A$ étant considéré comme un cercle de rayon nul). De même, $M^{\prime}$ appartient à cet axe radical, donc $P$ et $Q$ également. On en déduit que $P A=P U=P V$ et que $Q A^{2}=Q U \cdot Q V$.
Notons $H$ le projeté orthogonal de $P$ sur ( $U V$ ). On a
$$
\begin{aligned}
P A^{2}+Q A^{2} & =P U^{2}+Q U \cdot Q V=P H^{2}+H U^{2}+(Q H-H U)(Q H+H U) \\
& =P H^{2}+H U^{2}+Q H^{2}-H U^{2}=P H^{2}+Q H^{2}=P Q^{2}
\end{aligned}
$$
donc $P A Q$ est rectangle en $A$.
## Exercices du groupe A
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## \nSolution de l'exercice 6"
}
|
c049c9db-9d04-5ba3-9f6c-ce593a218a89
| 607,531
|
Let $ABC$ be a triangle and $\omega$ its incircle. We denote $P, Q, R$ the points of tangency of $\omega$ with $(BC), (CA)$, and $(AB)$. A circle passing through $B$ and $C$ is tangent to $\omega$ at $X$, a circle passing through $C$ and $A$ is tangent to $\omega$ at $Y$, and a circle passing through $A$ and $B$ is tangent to $\omega$ at $Z$. Show that the lines $(PX), (QY)$, and $(RZ)$ are concurrent.
|
Let's first recall some results on polarity that we will use. Let $\mathcal{C}$ be a circle with center $O$ and radius $R$. If $P$ is a point distinct from $O$, the polar of $P$ with respect to $\mathcal{C}$ is the line formed by the points $M$ such that $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. The pole with respect to $\mathcal{C}$ of a line $\mathcal{D}$ not passing through $O$ is the unique point $P$ such that for all $M$ on $\mathcal{D}$, we have $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. From this definition, it is easy to show the following properties:
(i) if $P$ is a point outside $\mathcal{C}$ and $(P T),\left(P T^{\prime}\right)$ are the two tangents to $\mathcal{C}$, then the polar of $P$ is the line $(T T^{\prime})$;
(ii) three given points are collinear if and only if their polars are concurrent.
(Remark: for property (ii), the line on which the three points lie is the polar of the point of intersection of the three lines.)
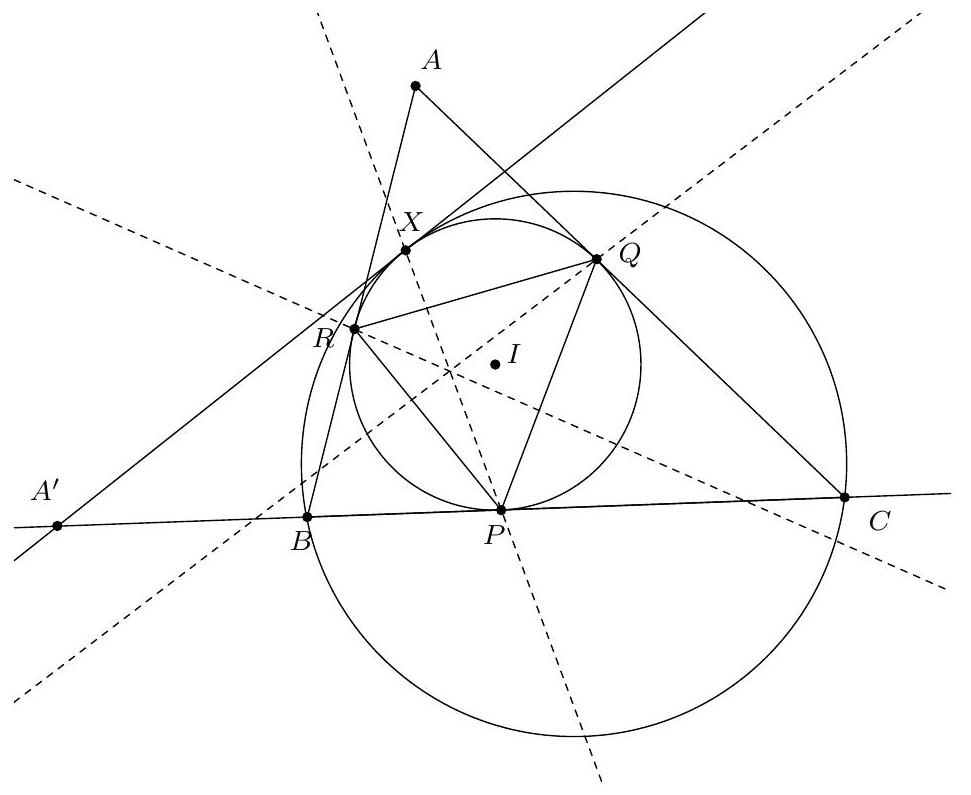
Let's return to the exercise. Let $\Gamma_{A}$ be the circle passing through $B, C$, and $X$. We define the circles $\Gamma_{B}$ and $\Gamma_{C}$ similarly. Let $A^{\prime}$ be the point of intersection between the common tangent to $\omega$ and $\Gamma_{X}$, and the line $(B C)$. We define the points $B^{\prime}$ and $C^{\prime}$ similarly.
According to property (ii), the polar of $A^{\prime}$ with respect to $\omega$ is the line $(P X)$. Therefore, it suffices to show, according to property (i), that $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear.
Let $\Gamma$ be the circumcircle of $A B C$. Since $A^{\prime}$ lies on the radical axis $(B C)$ of $\Gamma$ and $\Gamma_{A}$, we have $\mathcal{P}_{\Gamma}\left(A^{\prime}\right)=\mathcal{P}_{\Gamma_{A}}\left(A^{\prime}\right)=A^{\prime} X^{2}=\mathcal{P}_{\omega}\left(A^{\prime}\right)$. We deduce that $A^{\prime}$ lies on the radical axis of $\Gamma$ and $\omega$. The same applies to $B^{\prime}$ and $C^{\prime}$, which proves that $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\omega$ son cercle inscrit. On note $P, Q, R$ les points de contact de $\omega$ avec $(B C),(C A)$ et $(A B)$. Un cercle passant par $B$ et $C$ est tangent en $X$ à $\omega$, un cercle passant par $C$ et $A$ est tangent en $Y$ à $\omega$ et un cercle passant par $A$ et $B$ est tangent en $Z$ à $\omega$. Montrer que les droites $(P X),(Q Y)$ et $(R Z)$ sont concourantes.
|
Rappelons d'abord quelques résultats sur la polarité que nous allons utiliser. Soit $\mathcal{C}$ un cercle de centre $O$ et de rayon $R$. Si $P$ est un point distinct de $O$, la polaire de $P$ par rapport à $\mathcal{C}$ est la droite formée des points $M$ tels que $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. Le pôle par rapport à $\mathcal{C}$ d'une droite $\mathcal{D}$ ne passant pas par $O$ est l'unique point $P$ tel que pour tout $M$ appartenant à $\mathcal{D}$ on a $\overrightarrow{O P} \cdot \overrightarrow{O M}=R^{2}$. À partir de cette définition, il est facile de montrer les propriétés suivantes:
(i) si $P$ est un point extérieur à $\mathcal{C}$ et $(P T),\left(P T^{\prime}\right)$ sont les deux tangentes à $\mathcal{C}$, alors la polaire de $P$ est la droite ( $T T^{\prime}$ );
(ii) trois points donnés sont alignés si et seulement si leurs polaires sont concourantes.
(Remarque : pour la propriété (ii), la droite sur laquelle se trouvent les trois points est la polaire du point de rencontre des trois droites.)

Revenons à l'exercice. Notons $\Gamma_{A}$ le cercle passant par $B, C$ et $X$. On définit de même les cercles $\Gamma_{B}$ et $\Gamma_{C}$. Soit $A^{\prime}$ le point de rencontre entre la tangente commune à $\omega$ et $\Gamma_{X}$, et la droite $(B C)$. On définit de même les points $B^{\prime}$ et $C^{\prime}$.
D'après la propriété (ii), la polaire de $A^{\prime}$ par rapport à $\omega$ est la droite $(P X)$. Il suffit donc d'après la propriété (i) de montrer que $A^{\prime}, B^{\prime}$ et $C^{\prime}$ sont alignés.
Soit $\Gamma$ le cercle circonscrit à $A B C$. Comme $A^{\prime}$ appartient à l'axe radical $(B C)$ de $\Gamma$ et $\Gamma_{A}$, on a $\mathcal{P}_{\Gamma}\left(A^{\prime}\right)=\mathcal{P}_{\Gamma_{A}}\left(A^{\prime}\right)=A^{\prime} X^{2}=\mathcal{P}_{\omega}\left(A^{\prime}\right)$. On en déduit que $A^{\prime}$ appartient à l'axe radical de $\Gamma$ et $\omega$. Il en va de même pour $B^{\prime}$ et $C^{\prime}$, ce qui prouve que $A^{\prime}, B^{\prime}$ et $C^{\prime}$ sont alignés.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
4b0ab8d3-f1f5-5561-a1a4-d6db124354bc
| 607,532
|
Let $ABC$ be a triangle. We denote by $P$ the midpoint of the arc of the circumcircle of $ABC$ containing $A$. Suppose that the angle bisector of $\widehat{BAC}$ intersects the circle with diameter $[PC]$ at two points $D$ and $E$. Let $F$ be the reflection of $E$ over $(BC)$ and $I$ the midpoint of $[BC]$. Show that $B, D, F, I$ are concyclic.
|
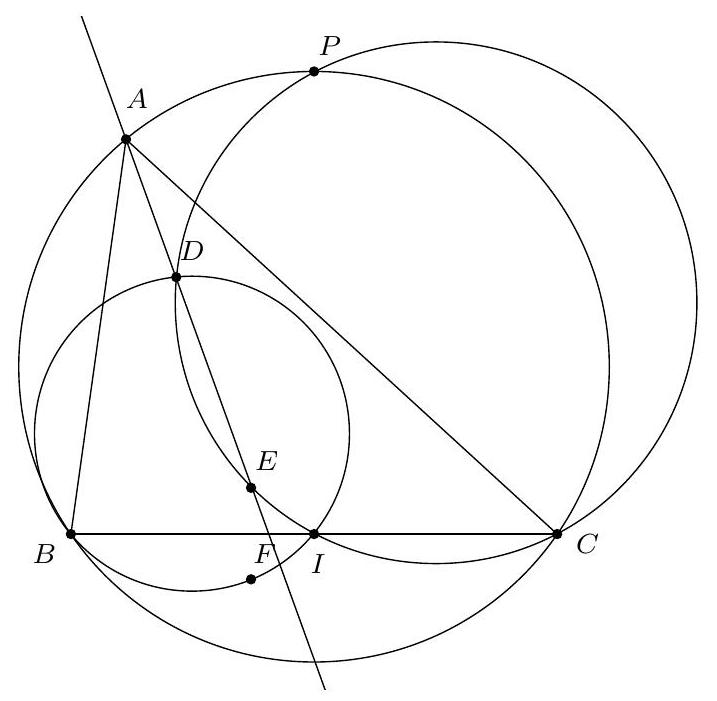
We apply the inversion \( i \) with pole \( I \) and power \(-I B \cdot I C\). Let \( Q \) be the point diametrically opposite to \( P \). Then \( i \) exchanges \( P \) and \( Q \) on one hand, and \( B \) and \( C \) on the other. Since the circle with diameter \([P C]\) passes through \( I \), its image under \( i \) is a line. Moreover, \( i(P) = Q \) and \( i(C) = B \), so \( i \) transforms the circle with diameter \([P C]\) into the line \((B Q)\).
The angle bisector of \(\widehat{A}\) is transformed into a circle passing through \( I \) and \( P \).
Let \( K = i(D) \), \( L = i(E) \), and \( M = i(F) \). From the above, the points \( K \) and \( L \) belong to \((B Q)\), and \( P, I, K, L \) are concyclic. Furthermore, \( L \) and \( M \) are symmetric with respect to \((B C)\).

Finally, note that \( Q I \cdot Q P = Q B^2 \) because \( \triangle Q B I \) and \( \triangle Q P B \) are similar. Using the power with respect to the circle \( P I K L \), we get that \( Q K \cdot Q L = Q B^2 \), so \( K \) and \( L \) are inverses with respect to the circle centered at \( Q \) with radius \( Q B \). We are thus reduced to proving the following lemma:
Lemma: Let \( \mathcal{C} \) be a circle centered at \( Q \). Let \( [B C] \) be a chord of \( \mathcal{C} \) and \( L \) a point on \((Q B)\). Then \( C \), the inverse of \( L \) with respect to \( \mathcal{C} \), and the symmetric of \( L \) with respect to \((B C)\) are collinear.
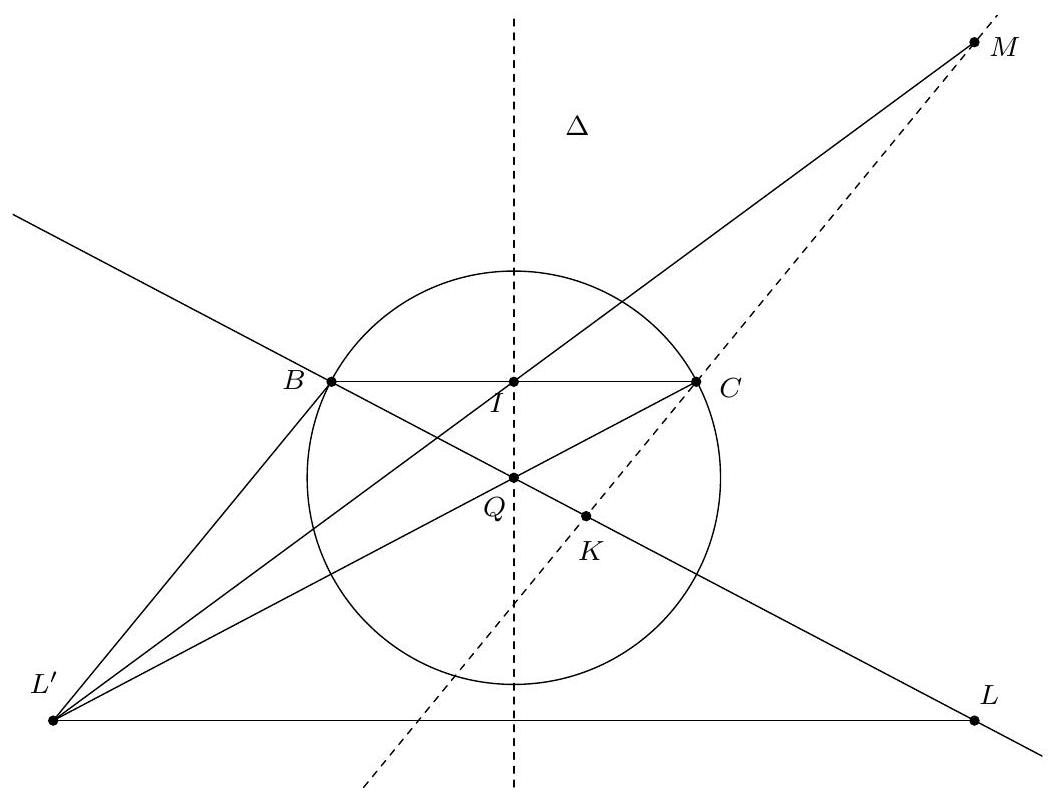
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $P$ le milieu de l'arc du cercle circonscrit à $A B C$ contenant $A$. On suppose que la bissectrice de l'angle $\widehat{B A C}$ coupe le cercle de diamètre $[P C]$ en deux points $D$ et $E$. Soit $F$ le symétrique de $E$ par rapport à $(B C)$ et $I$ le milieu de $[B C]$. Montrer que $B, D, F, I$ sont cocycliques.
|

On applique l'inversion $i$ de pôle $I$ et de puissance $-I B \cdot I C$. Soit $Q$ le point diamétralement opposé à $P$. Alors $i$ échange $P$ et $Q$ d'une part, et $B$ et $C$ d'autre part. Comme le cercle de diamètre $[P C]$ passe par $I$, son image par $i$ est une droite. Or, $i(P)=Q$ et $i(C)=B$, donc $i$ transforme le cercle de diamètre $[P C]$ en la droite $(B Q)$.
La bissectrice de $\widehat{A}$ est transformée en un cercle passant par $I$ et par $P$.
Notons $K=i(D), L=i(E)$ et $M=i(F)$. D'après ce qui précède, les points $K$ et $L$ appartiennent à $(B Q)$, et $P, I, K, L$ sont cocycliques. De plus, $L$ et $M$ sont symétriques par rapport à $(B C)$.

Enfin, remarquons que $Q I \cdot Q P=Q B^{2}$ car $Q B I$ et $Q P B$ sont semblables. En utilisant la puissance par rapport au cercle $P I K L$, on obtient que $Q K \cdot Q L=Q B^{2}$, donc $K$ et $L$ sont inverses par rapport au cercle de centre $Q$ et de rayon $Q B$. On est ainsi ramenés à démontrer le lemme suivant :
Lemme: Soit $\mathcal{C}$ un cercle de centre $Q$. Soit $[B C]$ une corde de $\mathcal{C}$ et $L$ un point de $(Q B)$. Alors $C$, l'inverse de $L$ par rapport à $\mathcal{C}$ et le symétrique de $L$ par rapport à $(B C)$ sont alignés.

|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "## Solution de l'exercice 8"
}
|
75d115fc-3a38-5404-8563-933cdc159486
| 607,533
|
Let $ABC$ be an isosceles triangle at $A$, $D$ the foot of the altitude from $A$, and $M$ a point inside $ADC$ such that $\widehat{AMB}$ is obtuse and $\widehat{DBM} + \widehat{DAM} = \widehat{MCB}$. The lines $(CM)$ and $(AD)$ intersect at $P$, and the lines $(BM)$ and $(AD)$ intersect at $Q$. Let $S$ be a point on $[AB]$ and $R$ a point on $[AM)$ that is not on $[AM]$ such that $\widehat{SQB} = \widehat{DPC}$ and $\widehat{MRQ} = 2 \widehat{QAM}$. Show that $QRS$ is isosceles.
|
Let $\alpha=\widehat{B A D}, \beta=\widehat{C B M}, \gamma=\widehat{M C B}$ and $\theta=\widehat{D A M}$. By hypothesis, we have $\beta+\theta=\gamma$, $\widehat{S Q B}=\widehat{D P C}=\frac{\pi}{2}-\gamma$ and $\widehat{M R Q}=2 \theta$.
We have $\widehat{Q S A}=\pi-\widehat{B S Q}=\widehat{Q B S}+\widehat{S Q B}=\left(\frac{\pi}{2}-\alpha-\beta\right)+\left(\frac{\pi}{2}-\gamma\right)=\pi-(\alpha+\beta+\gamma)$.
According to the law of sines for triangles $Q A S$ and $Q A R$, we have
$$
\frac{Q S}{Q R}=\frac{Q S}{Q A} \times \frac{Q A}{Q R}=\frac{\sin \alpha}{\sin (\alpha+\beta+\gamma)} \frac{\sin 2 \theta}{\sin \theta}=\frac{2 \sin \alpha \cos \theta}{\sin (\alpha+\beta+\gamma)}
$$
We need to show that this ratio is equal to 1.
According to the trigonometric Ceva's theorem applied to point $M$ in triangle $A B C$, we have
$$
\frac{\sin (\alpha+\theta)}{\sin (\alpha-\theta)} \times \frac{\sin \beta}{\sin \left(\frac{\pi}{2}-\alpha-\beta\right)} \times \frac{\sin \left(\frac{\pi}{2}-\alpha-\gamma\right)}{\sin \gamma}=1
$$
so $\sin (\alpha+\theta) \sin \beta \cos (\alpha+\gamma)=\sin (\alpha-\theta) \cos (\alpha+\beta) \sin \gamma$.
Using the identity $2 \sin x \cos y=\sin (x+y)+\sin (x-y)$, we deduce
$$
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\gamma-\beta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\beta-\gamma)]
$$
Given that $\gamma-\beta=\theta$,
$$
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\theta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha-\theta)]
$$
or $(\sin (\alpha+\theta)-\sin (\alpha-\theta))[\sin (\alpha+\beta+\gamma)-(\sin (\alpha+\theta)+\sin (\alpha-\theta))]$.
It follows that $\sin (\alpha+\beta+\gamma)=\sin (\alpha+\theta)+\sin (\alpha-\theta))=2 \sin \alpha \cos \theta$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A, D$ le pied de la hauteur issue de $A$ et $M$ un point intérieur à $A D C$ tel que $\widehat{A M B}$ est obtus et $\widehat{D B M}+\widehat{D A M}=\widehat{M C B}$. Les droites $(C M)$ et $(A D)$ se coupent en $P$, et les droites $(B M)$ et $(A D)$ se coupent en $Q$. Soit $S$ un point de $[A B]$ et $R$ un point de $[A M)$ qui n'est pas sur $[A M]$ tel que $\widehat{S Q B}=\widehat{D P C}$ et $\widehat{M R Q}=2 \widehat{Q A M}$. Montrer que $Q R S$ est isocèle.
|
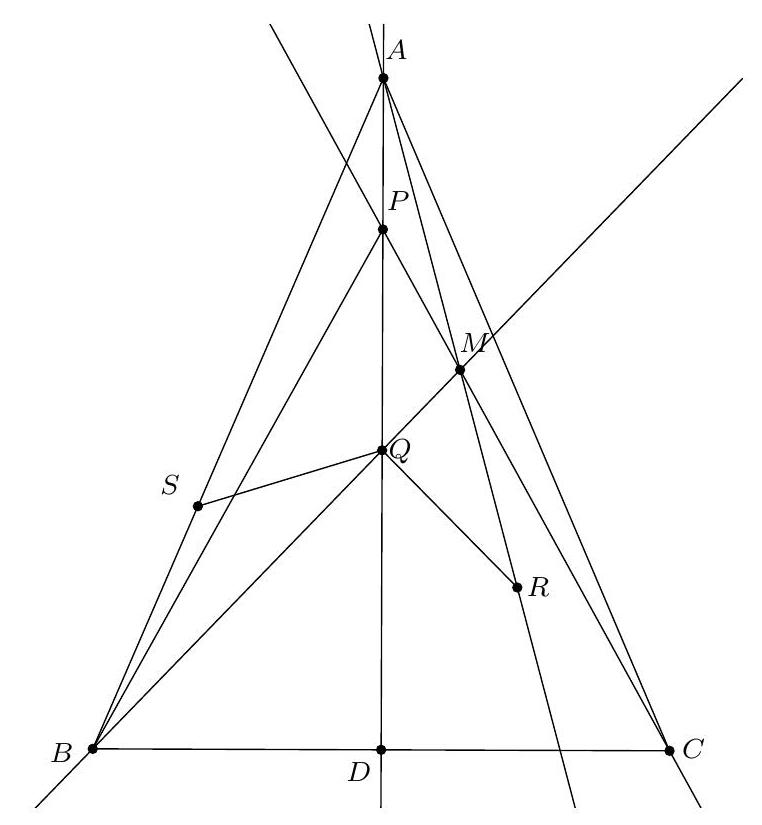
Notons $\alpha=\widehat{B A D}, \beta=\widehat{C B M}, \gamma=\widehat{M C B}$ et $\theta=\widehat{D A M}$. Par hypothèse, on a $\beta+\theta=\gamma$, $\widehat{S Q B}=\widehat{D P C}=\frac{\pi}{2}-\gamma$ et $\widehat{M R Q}=2 \theta$.
On a $\widehat{Q S A}=\pi-\widehat{B S Q}=\widehat{Q B S}+\widehat{S Q B}=\left(\frac{\pi}{2}-\alpha-\beta\right)+\left(\frac{\pi}{2}-\gamma\right)=\pi-(\alpha+\beta+\gamma)$.
D'après la loi des sinus pour les triangles $Q A S$ et $Q A R$, on a
$$
\frac{Q S}{Q R}=\frac{Q S}{Q A} \times \frac{Q A}{Q R}=\frac{\sin \alpha}{\sin (\alpha+\beta+\gamma)} \frac{\sin 2 \theta}{\sin \theta}=\frac{2 \sin \alpha \cos \theta}{\sin (\alpha+\beta+\gamma)}
$$
On doit montrer que ce rapport est égal à 1.
D'après le théorème de Ceva trigonométrique appliqué au point $M$ dans le triangle $A B C$, on a
$$
\frac{\sin (\alpha+\theta)}{\sin (\alpha-\theta)} \times \frac{\sin \beta}{\sin \left(\frac{\pi}{2}-\alpha-\beta\right)} \times \frac{\sin \left(\frac{\pi}{2}-\alpha-\gamma\right)}{\sin \gamma}=1
$$
donc $\sin (\alpha+\theta) \sin \beta \cos (\alpha+\gamma)=\sin (\alpha-\theta) \cos (\alpha+\beta) \sin \gamma$.
En utilisant l'identité $2 \sin x \cos y=\sin (x+y)+\sin (x-y)$, on en déduit
$$
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\gamma-\beta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\beta-\gamma)]
$$
Compte tenu de $\gamma-\beta=\theta$,
$$
\sin (\alpha+\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha+\theta)]=\sin (\alpha-\theta)[\sin (\alpha+\beta+\gamma)-\sin (\alpha-\theta)]
$$
ou encore $(\sin (\alpha+\theta)-\sin (\alpha-\theta))[\sin (\alpha+\beta+\gamma)-(\sin (\alpha+\theta)+\sin (\alpha-\theta))]$.
Il vient $\sin (\alpha+\beta+\gamma)=\sin (\alpha+\theta)+\sin (\alpha-\theta))=2 \sin \alpha \cos \theta$.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-5-solutions.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution de l'exercice 9"
}
|
ee7ba6e2-d8b7-5d31-b3c7-9943c8aeed71
| 607,534
|
Prove that any set of 90 numbers chosen from $\{1,2, \cdots, 100\}$ contains 10 that form an arithmetic progression.
|
We arrange the integers from 1 to 100 in a $10 \times 10$ square table as follows:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
If we want to eliminate 10 numbers so that with the remaining 90 numbers, no arithmetic sequence of length 10 can be formed, we must first eliminate at least one number from each of the 10 rows and each of the 10 columns. Since there are exactly 10 rows and 10 columns, this means we must eliminate exactly one number per row and per column.
Furthermore, if for $1 \leqslant i \leqslant 9$, the number eliminated in row $i$ belongs to column $k$, then the number eliminated in row $i+1$ must belong to a column $l$, with $l < k$, otherwise we would have 10 consecutive numbers among the remaining 90. This implies that we must eliminate $10, 19, 28, 37, 46, 55, 64, 73, 82$, and 91.
But then, $11, 20, 29, 38, 47, 56, 65, 74, 83$, and 92 remain, which form an arithmetic sequence with a common difference of 9, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prouver que tout ensemble de 90 nombres choisis dans $\{1,2, \cdots, 100\}$ en contient 10 qui forment une progression arithmétique.
|
On dispose les entiers de 1 à 100 dans un tableau carré $10 \times 10$ comme suit :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Si l'on veut éliminer 10 nombres de sorte qu'avec les 90 restants on ne puisse former de suite arithmétique de longueur 10, il faut déjà éliminer au moins un nombre dans chacune des 10 lignes, et chacune des 10 colonnes. Comme il y a justement 10 lignes, et 10 colonnes, c'est donc que l'on doit éliminer exactement un nombre par ligne et par colonne.
De plus, si pour $1 \leqslant i \leqslant 9$, le nombre éliminé dans la ligne $i$ appartient à la colonne $k$, alors le nombre éliminé dans la ligne $i+1$ doit appartenir à une colonne $l$, avec $l<k$, sans quoi on aurait 10 entiers consécutifs parmi les 90 restants. Cela implique que l'on doit éliminer $10,19,28,37,46,55,64,73,82$ et 91.
Mais alors, il reste $11,20,29,38,47,56,65,74,83$ et 92 , qui forment une suite arithmétique de raison 9 , ce qui conclut.
|
{
"resource_path": "French/segmented/envois/fr-ofm-2013-2014-envoi-6-solutions.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
cdab679f-aaa2-5ca6-87e4-b380a4e75789
| 607,536
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.