problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Suppose the sequence of nonnegative integers $a_{1}, a_{2}, \ldots, a_{1997}$ satisfies $$ a_{i}+a_{j} \leq a_{i+j} \leq a_{i}+a_{j}+1 $$ for all $i, j \geq 1$ with $i+j \leq 1997$. Show that there exists a real number $x$ such that $a_{n}=\lfloor n x\rfloor$ for all $1 \leq n \leq 1997$.
|
We are trying to show there exists an $x \in \mathbb{R}$ such that $$ \frac{a_{n}}{n} \leq x<\frac{a_{n}+1}{n} \quad \forall n $$ This means we need to show $$ \max _{i} \frac{a_{i}}{i}<\min _{j} \frac{a_{j}+1}{j} . $$ Replace 1997 by $N$. We will prove this by induction, but we will need some extra hypotheses on the indices $i, j$ which are used above. ## Claim - Suppose that - Integers $a_{1}, a_{2}, \ldots, a_{N}$ satisfy the given conditions. - Let $i=\operatorname{argmax}_{n} \frac{a_{n}}{n}$; if there are ties, pick the smallest $i$. - Let $j=\operatorname{argmin}_{n} \frac{a_{n}+1}{n}$; if there are ties, pick the smallest $j$. Then $$ \frac{a_{i}}{i}<\frac{a_{j}+1}{j} $$ Moreover, these two fractions are in lowest terms, and are adjacent in the Farey sequence of order $\max (i, j)$. Now, consider the new number $a_{N}$. We have two cases: - Suppose $i+j>N$. Then, no fraction with denominator $N$ can lie strictly inside the interval; so we may write for some integer $b$ $$ \frac{b}{N} \leq \frac{a_{i}}{i}<\frac{a_{j}+1}{j} \leq \frac{b+1}{N} $$ For purely algebraic reasons we have $$ \frac{b-a_{i}}{N-i} \leq \frac{b}{N} \leq \frac{a_{i}}{i}<\frac{a_{j}+1}{j} \leq \frac{b+1}{N} \leq \frac{b-a_{j}}{N-j} . $$ Now, $$ \begin{aligned} a_{N} & \geq a_{i}+a_{N-i} \geq a_{i}+(N-i) \cdot \frac{a_{i}}{i} \\ & \geq a_{i}+\left(b-a_{i}\right)=b \\ a_{N} & \leq a_{j}+a_{N-j}+1 \leq\left(a_{j}+1\right)+(N-j) \cdot \frac{a_{j}+1}{j} \\ & =\left(a_{j}+1\right)+\left(b-a_{j}\right)=b+1 \end{aligned} $$ Thus $a_{N} \in\{b, b+1\}$. This proves that $\frac{a_{N}}{N} \leq \frac{a_{i}}{i}$ while $\frac{a_{N}+1}{N} \geq \frac{a_{j}+1}{j}$. Moreover, the pair $(i, j)$ does not change, so all inductive hypotheses carry over. - On the other hand, suppose $i+j=N$. Then we have $$ \frac{a_{i}}{i}<\frac{a_{i}+a_{j}+1}{N}<\frac{a_{j}+1}{j} . $$ Now, we know $a_{N}$ could be either $a_{i}+a_{j}$ or $a_{i}+a_{j}+1$. If it's the former, then $(i, j)$ becomes $(i, N)$. If it's the latter, then $(i, j)$ becomes $(N, j)$. The properties of Farey sequences ensure that the $\frac{a_{i}+a_{j}+1}{N}$ is reduced, either way.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose the sequence of nonnegative integers $a_{1}, a_{2}, \ldots, a_{1997}$ satisfies $$ a_{i}+a_{j} \leq a_{i+j} \leq a_{i}+a_{j}+1 $$ for all $i, j \geq 1$ with $i+j \leq 1997$. Show that there exists a real number $x$ such that $a_{n}=\lfloor n x\rfloor$ for all $1 \leq n \leq 1997$.
|
We are trying to show there exists an $x \in \mathbb{R}$ such that $$ \frac{a_{n}}{n} \leq x<\frac{a_{n}+1}{n} \quad \forall n $$ This means we need to show $$ \max _{i} \frac{a_{i}}{i}<\min _{j} \frac{a_{j}+1}{j} . $$ Replace 1997 by $N$. We will prove this by induction, but we will need some extra hypotheses on the indices $i, j$ which are used above. ## Claim - Suppose that - Integers $a_{1}, a_{2}, \ldots, a_{N}$ satisfy the given conditions. - Let $i=\operatorname{argmax}_{n} \frac{a_{n}}{n}$; if there are ties, pick the smallest $i$. - Let $j=\operatorname{argmin}_{n} \frac{a_{n}+1}{n}$; if there are ties, pick the smallest $j$. Then $$ \frac{a_{i}}{i}<\frac{a_{j}+1}{j} $$ Moreover, these two fractions are in lowest terms, and are adjacent in the Farey sequence of order $\max (i, j)$. Now, consider the new number $a_{N}$. We have two cases: - Suppose $i+j>N$. Then, no fraction with denominator $N$ can lie strictly inside the interval; so we may write for some integer $b$ $$ \frac{b}{N} \leq \frac{a_{i}}{i}<\frac{a_{j}+1}{j} \leq \frac{b+1}{N} $$ For purely algebraic reasons we have $$ \frac{b-a_{i}}{N-i} \leq \frac{b}{N} \leq \frac{a_{i}}{i}<\frac{a_{j}+1}{j} \leq \frac{b+1}{N} \leq \frac{b-a_{j}}{N-j} . $$ Now, $$ \begin{aligned} a_{N} & \geq a_{i}+a_{N-i} \geq a_{i}+(N-i) \cdot \frac{a_{i}}{i} \\ & \geq a_{i}+\left(b-a_{i}\right)=b \\ a_{N} & \leq a_{j}+a_{N-j}+1 \leq\left(a_{j}+1\right)+(N-j) \cdot \frac{a_{j}+1}{j} \\ & =\left(a_{j}+1\right)+\left(b-a_{j}\right)=b+1 \end{aligned} $$ Thus $a_{N} \in\{b, b+1\}$. This proves that $\frac{a_{N}}{N} \leq \frac{a_{i}}{i}$ while $\frac{a_{N}+1}{N} \geq \frac{a_{j}+1}{j}$. Moreover, the pair $(i, j)$ does not change, so all inductive hypotheses carry over. - On the other hand, suppose $i+j=N$. Then we have $$ \frac{a_{i}}{i}<\frac{a_{i}+a_{j}+1}{N}<\frac{a_{j}+1}{j} . $$ Now, we know $a_{N}$ could be either $a_{i}+a_{j}$ or $a_{i}+a_{j}+1$. If it's the former, then $(i, j)$ becomes $(i, N)$. If it's the latter, then $(i, j)$ becomes $(N, j)$. The properties of Farey sequences ensure that the $\frac{a_{i}+a_{j}+1}{N}$ is reduced, either way.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1997-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
871350de-32e0-51fc-94c8-df1ae785f818
| 606,091
|
Let $a_{0}, a_{1}, \ldots, a_{n}$ be numbers from the interval $(0, \pi / 2)$ such that $\tan \left(a_{0}-\frac{\pi}{4}\right)+$ $\tan \left(a_{1}-\frac{\pi}{4}\right)+\cdots+\tan \left(a_{n}-\frac{\pi}{4}\right) \geq n-1$. Prove that $$ \tan a_{0} \tan a_{1} \cdots \tan a_{n} \geq n^{n+1} $$
|
$ Let $x_{i}=\tan \left(a_{i}-\frac{\pi}{4}\right)$. Then we have that $$ \tan a_{i}=\tan \left(a_{i}-45^{\circ}+45^{\circ}\right)=\frac{x_{i}+1}{1-x_{i}} $$ If we further substitute $y_{i}=\frac{1-x_{i}}{2} \in(0,1)$, then we have to prove that the following statement: Claim - If $\sum_{0}^{n} y_{i} \leq 1$ and $y_{i} \geq 0$, we have $$ \prod_{i=1}^{n}\left(\frac{1}{y_{i}}-1\right) \geq n^{n+1} $$ $$ \prod_{i=1}^{n}\left(\frac{y_{0}+y_{1}+y_{2}+\cdots+y_{n}}{y_{i}}-1\right) \geq n^{n+1} $$ By AM-GM, we have $$ \frac{y_{1}+y_{2}+y_{3}+\cdots+y_{n}}{y_{0}} \geq n \sqrt[n]{\frac{y_{1} y_{2} y_{3} \ldots y_{n}}{y_{1}}} $$ Cyclic product works. Remark. Alternatively, the function $x \mapsto \log (1 / x-1)$ is a convex function on $(0,1)$ so Jensen inequality should also work.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{0}, a_{1}, \ldots, a_{n}$ be numbers from the interval $(0, \pi / 2)$ such that $\tan \left(a_{0}-\frac{\pi}{4}\right)+$ $\tan \left(a_{1}-\frac{\pi}{4}\right)+\cdots+\tan \left(a_{n}-\frac{\pi}{4}\right) \geq n-1$. Prove that $$ \tan a_{0} \tan a_{1} \cdots \tan a_{n} \geq n^{n+1} $$
|
$ Let $x_{i}=\tan \left(a_{i}-\frac{\pi}{4}\right)$. Then we have that $$ \tan a_{i}=\tan \left(a_{i}-45^{\circ}+45^{\circ}\right)=\frac{x_{i}+1}{1-x_{i}} $$ If we further substitute $y_{i}=\frac{1-x_{i}}{2} \in(0,1)$, then we have to prove that the following statement: Claim - If $\sum_{0}^{n} y_{i} \leq 1$ and $y_{i} \geq 0$, we have $$ \prod_{i=1}^{n}\left(\frac{1}{y_{i}}-1\right) \geq n^{n+1} $$ $$ \prod_{i=1}^{n}\left(\frac{y_{0}+y_{1}+y_{2}+\cdots+y_{n}}{y_{i}}-1\right) \geq n^{n+1} $$ By AM-GM, we have $$ \frac{y_{1}+y_{2}+y_{3}+\cdots+y_{n}}{y_{0}} \geq n \sqrt[n]{\frac{y_{1} y_{2} y_{3} \ldots y_{n}}{y_{1}}} $$ Cyclic product works. Remark. Alternatively, the function $x \mapsto \log (1 / x-1)$ is a convex function on $(0,1)$ so Jensen inequality should also work.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1998-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
13f5b5a0-1d90-5a67-8bd7-a0906147af13
| 606,132
|
Let $p>2$ be a prime and let $a, b, c, d$ be integers not divisible by $p$, such that $$ \left\{\frac{r a}{p}\right\}+\left\{\frac{r b}{p}\right\}+\left\{\frac{r c}{p}\right\}+\left\{\frac{r d}{p}\right\}=2 $$ for any integer $r$ not divisible by $p$. (Here, $\{t\}=t-\lfloor t\rfloor$ is the fractional part.) Prove that at least two of the numbers $a+b, a+c, a+d, b+c, b+d, c+d$ are divisible by $p$.
|
First of all, we apparently have $r(a+b+c+d) \equiv 0(\bmod p)$ for every prime $p$, so it automatically follows that $a+b+c+d \equiv 0(\bmod p)$. By scaling appropriately, and also replacing each number with its remainder modulo $p$, we are going to assume that $$ 1=a \leq b \leq c \leq d<p $$ We are going to prove that $d=p-1$, which will solve the problem. Claim - For each integer $r=1,2, \ldots, p-1$ we have $$ 2(r-1)=\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor+\left\lfloor\frac{r d}{p}\right\rfloor . $$ $$ 2=\sum_{\mathrm{cyc}}\left(\frac{r a}{p}-\left\lfloor\frac{r a}{p}\right\rfloor\right) $$ and since $a+b+c+d=2 p$ the conclusion follows.  In symbols, it will be enough to prove the following. Claim - For each $r=1,2, \ldots, p-2$ we have $\frac{r-1}{r}<\frac{d}{p}<1$. Equivalently, for each $r=1,2, \ldots, p-2$ we have $\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor=r-1$. $$ r-1>\left\lfloor\frac{r d}{p}\right\rfloor \geq\left\lfloor\frac{(r-1) d}{p}\right\rfloor=r-2 $$ Now, we have that $$ 2(r-1)=\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor+\underbrace{\left\lfloor\frac{r d}{p}\right\rfloor}_{=r-2} . $$ Thus $\left\lfloor\frac{r b}{p}\right\rfloor>\left\lfloor\frac{(r-1) b}{p}\right\rfloor$, and $\left\lfloor\frac{r c}{p}\right\rfloor>\left\lfloor\frac{(r-1) b}{p}\right\rfloor$. An example of this situation is illustrated below with $r=7$ (not to scale). 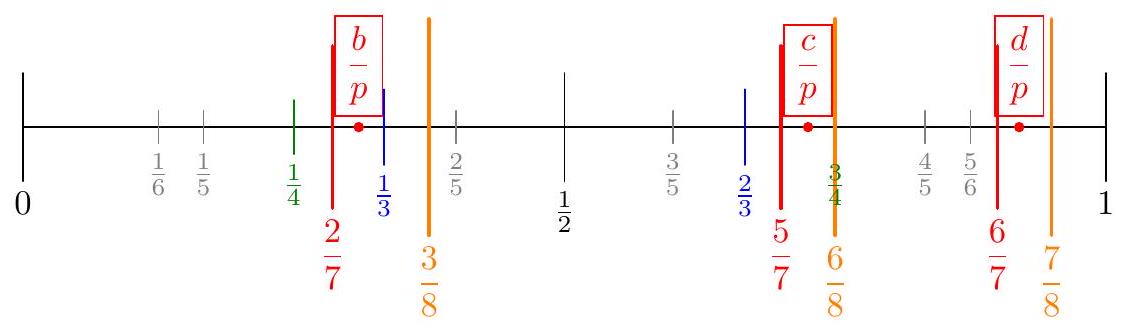 Right now, $\frac{b}{p}$ and $\frac{c}{p}$ are just to the right of $\frac{u}{r}$ and $\frac{v}{r}$ for some $u$ and $v$ with $u+v=r$. The issue is that the there is some fraction just to the right of $\frac{b}{p}$ and $\frac{c}{p}$ from an earlier value of $r$, and by hypothesis its denominator is going to be strictly greater than 1 . It is at this point we are going to use the properties of Farey sequences. When we consider the fractions with denominator $r+1$, they are going to lie outside of the interval they we have constrained $\frac{b}{p}$ and $\frac{c}{p}$ to lie in. Indeed, our minimality assumption on $r$ guarantees that there is no fraction with denominator less than $r$ between $\frac{u}{r}$ and $\frac{b}{p}$. So if $\frac{u}{r}<\frac{b}{p}<\frac{s}{t}$ (where $\frac{u}{r}$ and $\frac{s}{t}$ are the closest fractions with denominator at most $r$ to $\frac{b}{p}$ ) then Farey theory says the next fraction inside the interval $\left[\frac{u}{r}, \frac{s}{t}\right]$ is $\frac{u+s}{r+t}$, and since $t>1$, we have $r+t>r+1$. In other words, we get an inequality of the form $$ \frac{u}{r}<\frac{b}{p}<\underbrace{\text { something }}_{=s / t} \leq \frac{u+1}{r+1} . $$ The same holds for $\frac{c}{p}$ as $$ \frac{v}{r}<\frac{c}{p}<\text { something } \leq \frac{v+1}{r+1} $$ Finally, $$ \frac{d}{p}<\frac{r-1}{r}<\frac{r}{r+1} $$ So now we have that $$ \left\lfloor\frac{(r+1) b}{p}\right\rfloor+\left\lfloor\frac{(r+1) c}{p}\right\rfloor+\left\lfloor\frac{(r+1) d}{p}\right\rfloor \leq u+v+(r-1)=2 r-1 $$ which is a contradiction. Now, since $$ \frac{p-3}{p-2}<\frac{d}{p} \Longrightarrow d>\frac{p(p-3)}{p-2}=p-1-\frac{2}{p-2} $$ which for $p>2$ gives $d=p-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>2$ be a prime and let $a, b, c, d$ be integers not divisible by $p$, such that $$ \left\{\frac{r a}{p}\right\}+\left\{\frac{r b}{p}\right\}+\left\{\frac{r c}{p}\right\}+\left\{\frac{r d}{p}\right\}=2 $$ for any integer $r$ not divisible by $p$. (Here, $\{t\}=t-\lfloor t\rfloor$ is the fractional part.) Prove that at least two of the numbers $a+b, a+c, a+d, b+c, b+d, c+d$ are divisible by $p$.
|
First of all, we apparently have $r(a+b+c+d) \equiv 0(\bmod p)$ for every prime $p$, so it automatically follows that $a+b+c+d \equiv 0(\bmod p)$. By scaling appropriately, and also replacing each number with its remainder modulo $p$, we are going to assume that $$ 1=a \leq b \leq c \leq d<p $$ We are going to prove that $d=p-1$, which will solve the problem. Claim - For each integer $r=1,2, \ldots, p-1$ we have $$ 2(r-1)=\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor+\left\lfloor\frac{r d}{p}\right\rfloor . $$ $$ 2=\sum_{\mathrm{cyc}}\left(\frac{r a}{p}-\left\lfloor\frac{r a}{p}\right\rfloor\right) $$ and since $a+b+c+d=2 p$ the conclusion follows.  In symbols, it will be enough to prove the following. Claim - For each $r=1,2, \ldots, p-2$ we have $\frac{r-1}{r}<\frac{d}{p}<1$. Equivalently, for each $r=1,2, \ldots, p-2$ we have $\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor=r-1$. $$ r-1>\left\lfloor\frac{r d}{p}\right\rfloor \geq\left\lfloor\frac{(r-1) d}{p}\right\rfloor=r-2 $$ Now, we have that $$ 2(r-1)=\left\lfloor\frac{r b}{p}\right\rfloor+\left\lfloor\frac{r c}{p}\right\rfloor+\underbrace{\left\lfloor\frac{r d}{p}\right\rfloor}_{=r-2} . $$ Thus $\left\lfloor\frac{r b}{p}\right\rfloor>\left\lfloor\frac{(r-1) b}{p}\right\rfloor$, and $\left\lfloor\frac{r c}{p}\right\rfloor>\left\lfloor\frac{(r-1) b}{p}\right\rfloor$. An example of this situation is illustrated below with $r=7$ (not to scale).  Right now, $\frac{b}{p}$ and $\frac{c}{p}$ are just to the right of $\frac{u}{r}$ and $\frac{v}{r}$ for some $u$ and $v$ with $u+v=r$. The issue is that the there is some fraction just to the right of $\frac{b}{p}$ and $\frac{c}{p}$ from an earlier value of $r$, and by hypothesis its denominator is going to be strictly greater than 1 . It is at this point we are going to use the properties of Farey sequences. When we consider the fractions with denominator $r+1$, they are going to lie outside of the interval they we have constrained $\frac{b}{p}$ and $\frac{c}{p}$ to lie in. Indeed, our minimality assumption on $r$ guarantees that there is no fraction with denominator less than $r$ between $\frac{u}{r}$ and $\frac{b}{p}$. So if $\frac{u}{r}<\frac{b}{p}<\frac{s}{t}$ (where $\frac{u}{r}$ and $\frac{s}{t}$ are the closest fractions with denominator at most $r$ to $\frac{b}{p}$ ) then Farey theory says the next fraction inside the interval $\left[\frac{u}{r}, \frac{s}{t}\right]$ is $\frac{u+s}{r+t}$, and since $t>1$, we have $r+t>r+1$. In other words, we get an inequality of the form $$ \frac{u}{r}<\frac{b}{p}<\underbrace{\text { something }}_{=s / t} \leq \frac{u+1}{r+1} . $$ The same holds for $\frac{c}{p}$ as $$ \frac{v}{r}<\frac{c}{p}<\text { something } \leq \frac{v+1}{r+1} $$ Finally, $$ \frac{d}{p}<\frac{r-1}{r}<\frac{r}{r+1} $$ So now we have that $$ \left\lfloor\frac{(r+1) b}{p}\right\rfloor+\left\lfloor\frac{(r+1) c}{p}\right\rfloor+\left\lfloor\frac{(r+1) d}{p}\right\rfloor \leq u+v+(r-1)=2 r-1 $$ which is a contradiction. Now, since $$ \frac{p-3}{p-2}<\frac{d}{p} \Longrightarrow d>\frac{p(p-3)}{p-2}=p-1-\frac{2}{p-2} $$ which for $p>2$ gives $d=p-1$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1999-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e82fa338-598f-5b99-9c5c-26a472a2ff67
| 606,215
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of $n>3$ real numbers such that $$ a_{1}+\cdots+a_{n} \geq n \quad \text { and } \quad a_{1}^{2}+\cdots+a_{n}^{2} \geq n^{2} $$ Prove that $\max \left(a_{1}, \ldots, a_{n}\right) \geq 2$.
|
Proceed by contradiction, assuming $a_{i}<2$ for all $i$. If all $a_{i} \geq 0$, then $n^{2} \leq \sum_{i} a_{i}^{2}<n \cdot 2^{2}$, contradiction. Otherwise, assume at least one $a_{i}$ is negative. Note that if $-x$ and $-y$ are both present in the sequence $(x, y>0)$, then we can replace them with $-(x+y)$ and 0 . So we may assume that there is exactly one negative term, say $a_{n}=-M$. Now, smooth all the nonnegative $a_{i}$ to be 2 , making all inequalities strict. Now, we have that $$ \begin{aligned} 2(n-1)-M & >n \\ 4(n-1)+M^{2} & >n^{2} \end{aligned} $$ This gives $n-2<M<n-2$, contradiction. Equality in the original occurs when $n-1$ of the $a_{i}$ are equal to 2 and the last one is equal to $-(n-2)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of $n>3$ real numbers such that $$ a_{1}+\cdots+a_{n} \geq n \quad \text { and } \quad a_{1}^{2}+\cdots+a_{n}^{2} \geq n^{2} $$ Prove that $\max \left(a_{1}, \ldots, a_{n}\right) \geq 2$.
|
Proceed by contradiction, assuming $a_{i}<2$ for all $i$. If all $a_{i} \geq 0$, then $n^{2} \leq \sum_{i} a_{i}^{2}<n \cdot 2^{2}$, contradiction. Otherwise, assume at least one $a_{i}$ is negative. Note that if $-x$ and $-y$ are both present in the sequence $(x, y>0)$, then we can replace them with $-(x+y)$ and 0 . So we may assume that there is exactly one negative term, say $a_{n}=-M$. Now, smooth all the nonnegative $a_{i}$ to be 2 , making all inequalities strict. Now, we have that $$ \begin{aligned} 2(n-1)-M & >n \\ 4(n-1)+M^{2} & >n^{2} \end{aligned} $$ This gives $n-2<M<n-2$, contradiction. Equality in the original occurs when $n-1$ of the $a_{i}$ are equal to 2 and the last one is equal to $-(n-2)$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1999-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ba5d9e6c-919f-59c4-a84e-d36487e089f0
| 606,227
|
The Y2K Game is played on a $1 \times 2000$ grid as follows. Two players in turn write either an S or an O in an empty square. The first player who produces three consecutive boxes that spell SOS wins. If all boxes are filled without producing SOS then the game is a draw. Prove that the second player has a winning strategy.
|
The main insight is that a construct of the form $$ S \square \square S $$ (here the $\square$ is blank) will kill any player which plays inside it. We call this a trap accordingly. Claim - The second player can force a trap to exist; in this case the game will never end in a draw. Claim - The second player always has a move which prevents her from losing. Together these two claims finish the problem. Remark. Actually, one can show that the "only" way to lose is to be forced to play inside a trap. Indeed, suppose playing in a certain cell $c$ loses. If we wrote $O$, that means $c$ is bordered by exactly one $S$, with a blank cell on the neighbor. But we could also write $S$; checking cases we find $c$ is part of a trap. Thus a player can lose only if all blank cells are in traps; ergo, the number of blank cells is even. This never happens for the second player. Thus this gives an alternative solution, and moreover a reason to believe that all correct solutions must involve traps.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The Y2K Game is played on a $1 \times 2000$ grid as follows. Two players in turn write either an S or an O in an empty square. The first player who produces three consecutive boxes that spell SOS wins. If all boxes are filled without producing SOS then the game is a draw. Prove that the second player has a winning strategy.
|
The main insight is that a construct of the form $$ S \square \square S $$ (here the $\square$ is blank) will kill any player which plays inside it. We call this a trap accordingly. Claim - The second player can force a trap to exist; in this case the game will never end in a draw. Claim - The second player always has a move which prevents her from losing. Together these two claims finish the problem. Remark. Actually, one can show that the "only" way to lose is to be forced to play inside a trap. Indeed, suppose playing in a certain cell $c$ loses. If we wrote $O$, that means $c$ is bordered by exactly one $S$, with a blank cell on the neighbor. But we could also write $S$; checking cases we find $c$ is part of a trap. Thus a player can lose only if all blank cells are in traps; ergo, the number of blank cells is even. This never happens for the second player. Thus this gives an alternative solution, and moreover a reason to believe that all correct solutions must involve traps.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1999-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f466f6eb-13bb-5ca9-887f-7384c8329efc
| 46,049
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. The inscribed circle $\omega$ of triangle $B C D$ meets $C D$ at $E$. Let $F$ be a point on the (internal) angle bisector of $\angle D A C$ such that $E F \perp C D$. Let the circumscribed circle of triangle $A C F$ meet line $C D$ at $C$ and $G$. Prove that the triangle $A F G$ is isosceles.
|
Note $E$ is contact point of $A$-excircle of $\triangle A C D$, so $F$ is $A$-excenter. Hence $C F$ is external angle bisector of $\angle A C G$ which implies $F A=F G$ (since $F$ is the arc midpoint on the circumcircle of $A F G)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. The inscribed circle $\omega$ of triangle $B C D$ meets $C D$ at $E$. Let $F$ be a point on the (internal) angle bisector of $\angle D A C$ such that $E F \perp C D$. Let the circumscribed circle of triangle $A C F$ meet line $C D$ at $C$ and $G$. Prove that the triangle $A F G$ is isosceles.
|
Note $E$ is contact point of $A$-excircle of $\triangle A C D$, so $F$ is $A$-excenter. Hence $C F$ is external angle bisector of $\angle A C G$ which implies $F A=F G$ (since $F$ is the arc midpoint on the circumcircle of $A F G)$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-1999-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
1ed51cd8-e876-56f0-b71e-fc7bcc3622bc
| 247,985
|
Call a real-valued function $f$ very convex if $$ \frac{f(x)+f(y)}{2} \geq f\left(\frac{x+y}{2}\right)+|x-y| $$ holds for all real numbers $x$ and $y$. Prove that no very convex function exists.
|
For $C \geq 0$, we say a function $f$ is $C$-convex $$ \frac{f(x)+f(y)}{2} \geq f\left(\frac{x+y}{2}\right)+C|x-y| . $$ Suppose $f$ is $C$-convex. Let $a<b<c<d<e$ be any arithmetic progression, such that $t=|e-a|$. Observe that $$ \begin{aligned} & f(a)+f(c) \geq 2 f(b)+C \cdot \frac{1}{2} t \\ & f(c)+f(e) \geq 2 f(d)+C \cdot \frac{1}{2} t \\ & f(b)+f(d) \geq 2 f(c)+C \cdot \frac{1}{2} t \end{aligned} $$ Adding the first two to twice the third gives $$ f(a)+f(e) \geq 2 f(c)+2 C \cdot t $$ So we conclude $C$-convex function is also $2 C$-convex. This is clearly not okay for $C>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Call a real-valued function $f$ very convex if $$ \frac{f(x)+f(y)}{2} \geq f\left(\frac{x+y}{2}\right)+|x-y| $$ holds for all real numbers $x$ and $y$. Prove that no very convex function exists.
|
For $C \geq 0$, we say a function $f$ is $C$-convex $$ \frac{f(x)+f(y)}{2} \geq f\left(\frac{x+y}{2}\right)+C|x-y| . $$ Suppose $f$ is $C$-convex. Let $a<b<c<d<e$ be any arithmetic progression, such that $t=|e-a|$. Observe that $$ \begin{aligned} & f(a)+f(c) \geq 2 f(b)+C \cdot \frac{1}{2} t \\ & f(c)+f(e) \geq 2 f(d)+C \cdot \frac{1}{2} t \\ & f(b)+f(d) \geq 2 f(c)+C \cdot \frac{1}{2} t \end{aligned} $$ Adding the first two to twice the third gives $$ f(a)+f(e) \geq 2 f(c)+2 C \cdot t $$ So we conclude $C$-convex function is also $2 C$-convex. This is clearly not okay for $C>0$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
616dfb66-1c5a-5536-a8da-2101a1597dda
| 606,262
|
Let $S$ be the set of all triangles $A B C$ for which $$ 5\left(\frac{1}{A P}+\frac{1}{B Q}+\frac{1}{C R}\right)-\frac{3}{\min \{A P, B Q, C R\}}=\frac{6}{r} $$ where $r$ is the inradius and $P, Q, R$ are the points of tangency of the incircle with sides $A B, B C, C A$ respectively. Prove that all triangles in $S$ are isosceles and similar to one another.
|
We will prove the inequality $$ \frac{2}{A P}+\frac{5}{B Q}+\frac{5}{C R} \geq \frac{6}{r} $$ with equality when $A P: B Q: C R=1: 4: 4$. This implies the problem statement. Letting $x=A P, y=B Q, z=C R$, the inequality becomes $$ \frac{2}{x}+\frac{5}{y}+\frac{5}{z} \geq 6 \sqrt{\frac{x+y+z}{x y z}} . $$ Squaring both sides and collecting terms gives $$ \frac{4}{x^{2}}+\frac{25}{y^{2}}+\frac{25}{z^{2}}+\frac{14}{y z} \geq \frac{16}{x y}+\frac{16}{x z} $$ If we replace $x=1 / a, y=4 / b, z=4 / c$, then it remains to prove the inequality $$ 64 a^{2}+25(b+c)^{2} \geq 64 a(b+c)+36 b c $$ where equality holds when $a=b=c$. This follows by two applications of AM-GM: $$ \begin{aligned} 16\left(4 a^{2}+(b+c)^{2}\right) & \geq 64 a(b+c) \\ 9(b+c)^{2} & \geq 36 b c . \end{aligned} $$ Again one can tell this is an inequality by counting degrees of freedom.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be the set of all triangles $A B C$ for which $$ 5\left(\frac{1}{A P}+\frac{1}{B Q}+\frac{1}{C R}\right)-\frac{3}{\min \{A P, B Q, C R\}}=\frac{6}{r} $$ where $r$ is the inradius and $P, Q, R$ are the points of tangency of the incircle with sides $A B, B C, C A$ respectively. Prove that all triangles in $S$ are isosceles and similar to one another.
|
We will prove the inequality $$ \frac{2}{A P}+\frac{5}{B Q}+\frac{5}{C R} \geq \frac{6}{r} $$ with equality when $A P: B Q: C R=1: 4: 4$. This implies the problem statement. Letting $x=A P, y=B Q, z=C R$, the inequality becomes $$ \frac{2}{x}+\frac{5}{y}+\frac{5}{z} \geq 6 \sqrt{\frac{x+y+z}{x y z}} . $$ Squaring both sides and collecting terms gives $$ \frac{4}{x^{2}}+\frac{25}{y^{2}}+\frac{25}{z^{2}}+\frac{14}{y z} \geq \frac{16}{x y}+\frac{16}{x z} $$ If we replace $x=1 / a, y=4 / b, z=4 / c$, then it remains to prove the inequality $$ 64 a^{2}+25(b+c)^{2} \geq 64 a(b+c)+36 b c $$ where equality holds when $a=b=c$. This follows by two applications of AM-GM: $$ \begin{aligned} 16\left(4 a^{2}+(b+c)^{2}\right) & \geq 64 a(b+c) \\ 9(b+c)^{2} & \geq 36 b c . \end{aligned} $$ Again one can tell this is an inequality by counting degrees of freedom.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
b0bfc554-411d-586f-99b9-ba8bb3db0069
| 606,270
|
Let $A_{1} A_{2} A_{3}$ be a triangle, and let $\omega_{1}$ be a circle in its plane passing through $A_{1}$ and $A_{2}$. Suppose there exists circles $\omega_{2}, \omega_{3}, \ldots, \omega_{7}$ such that for $k=2,3, \ldots, 7$, circle $\omega_{k}$ is externally tangent to $\omega_{k-1}$ and passes through $A_{k}$ and $A_{k+1}$ (indices $\bmod 3)$. Prove that $\omega_{7}=\omega_{1}$.
|
The idea is to keep track of the subtended arc $\widehat{A_{i} A_{i+1}}$ of $\omega_{i}$ for each $i$. To this end, let $\beta=\measuredangle A_{1} A_{2} A_{3}, \gamma=\measuredangle A_{2} A_{3} A_{1}$ and $\alpha=\measuredangle A_{1} A_{2} A_{3}$. 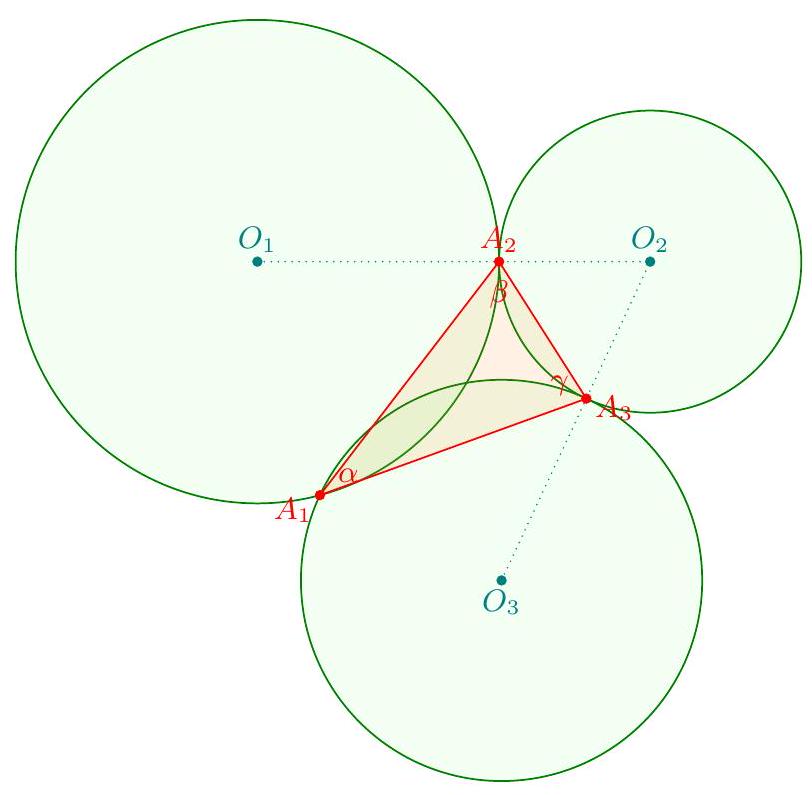 Initially, we set $\theta=\measuredangle O_{1} A_{2} A_{1}$. Then we compute $$ \begin{aligned} & \measuredangle O_{1} A_{2} A_{1}=\theta \\ & \measuredangle O_{2} A_{3} A_{2}=-\beta-\theta \\ & \measuredangle O_{3} A_{1} A_{3}=\beta-\gamma+\theta \\ & \measuredangle O_{4} A_{2} A_{1}=(\gamma-\beta-\alpha)-\theta \end{aligned} $$ and repeating the same calculation another round gives $$ \measuredangle O_{7} A_{2} A_{1}=k-(k-\theta)=\theta $$ with $k=\gamma-\beta-\alpha$. This implies $O_{7}=O_{1}$, so $\omega_{7}=\omega_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1} A_{2} A_{3}$ be a triangle, and let $\omega_{1}$ be a circle in its plane passing through $A_{1}$ and $A_{2}$. Suppose there exists circles $\omega_{2}, \omega_{3}, \ldots, \omega_{7}$ such that for $k=2,3, \ldots, 7$, circle $\omega_{k}$ is externally tangent to $\omega_{k-1}$ and passes through $A_{k}$ and $A_{k+1}$ (indices $\bmod 3)$. Prove that $\omega_{7}=\omega_{1}$.
|
The idea is to keep track of the subtended arc $\widehat{A_{i} A_{i+1}}$ of $\omega_{i}$ for each $i$. To this end, let $\beta=\measuredangle A_{1} A_{2} A_{3}, \gamma=\measuredangle A_{2} A_{3} A_{1}$ and $\alpha=\measuredangle A_{1} A_{2} A_{3}$.  Initially, we set $\theta=\measuredangle O_{1} A_{2} A_{1}$. Then we compute $$ \begin{aligned} & \measuredangle O_{1} A_{2} A_{1}=\theta \\ & \measuredangle O_{2} A_{3} A_{2}=-\beta-\theta \\ & \measuredangle O_{3} A_{1} A_{3}=\beta-\gamma+\theta \\ & \measuredangle O_{4} A_{2} A_{1}=(\gamma-\beta-\alpha)-\theta \end{aligned} $$ and repeating the same calculation another round gives $$ \measuredangle O_{7} A_{2} A_{1}=k-(k-\theta)=\theta $$ with $k=\gamma-\beta-\alpha$. This implies $O_{7}=O_{1}$, so $\omega_{7}=\omega_{1}$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
fc092347-e795-525f-89ef-3a76be6c5591
| 606,300
|
Let $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{n}, b_{n}$ be nonnegative real numbers. Prove that $$ \sum_{i, j=1}^{n} \min \left\{a_{i} a_{j}, b_{i} b_{j}\right\} \leq \sum_{i, j=1}^{n} \min \left\{a_{i} b_{j}, a_{j} b_{i}\right\} $$
|
【 First solution by creating a single min (Vincent Huang and Ravi Boppana). Let $b_{i}=r_{i} a_{i}$ for each $i$, and rewrite the inequality as $$ \sum_{i, j} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \geq 0 $$ We now do the key manipulation to convert the double min into a separate single min. Let $\varepsilon_{i}=+1$ if $r_{i} \geq 1$, and $\varepsilon_{i}=-1$ otherwise, and let $s_{i}=\left|r_{i}-1\right|$. Then we pass to absolute values: $$ \begin{aligned} 2 \min \left(r_{i}, r_{j}\right)-2 \min \left(1, r_{i} r_{j}\right) & =\left|r_{i} r_{j}-1\right|-\left|r_{i}-r_{j}\right|-\left(r_{i}-1\right)\left(r_{j}-1\right) \\ & =\left|r_{i} r_{j}-1\right|-\left|r_{i}-r_{j}\right|-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\varepsilon_{i} \varepsilon_{j} \min \left(\left|1-r_{i} r_{j} \pm\left(r_{i}-r_{j}\right)\right|\right)-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\varepsilon_{i} \varepsilon_{j} \min \left(s_{i}\left(r_{j}+1\right), s_{j}\left(r_{i}+1\right)\right)-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\left(\varepsilon_{i} s_{i}\right)\left(\varepsilon_{j} s_{j}\right) \min \left(\frac{r_{j}+1}{s_{j}}-1, \frac{r_{i}+1}{s_{i}}-1\right) . \end{aligned} $$ So let us denote $x_{i}=a_{i} \varepsilon_{i} s_{i} \in \mathbb{R}$, and $t_{i}=\frac{r_{i}+1}{s_{i}}-1 \in \mathbb{R}_{\geq 0}$. Thus it suffices to prove that: Claim - We have $$ \sum_{i, j} x_{i} x_{j} \min \left(t_{i}, t_{j}\right) \geq 0 $$ for arbitrary $x_{i} \in \mathbb{R}, t_{i} \in \mathbb{R} \geq 0$. $$ \sum_{i} t_{i} x_{i}^{2}+2 \sum_{i<j} 2 t_{i} x_{i} x_{j}=\sum_{i}\left(t_{i}-t_{i-1}\right)\left(x_{i}+x_{i+1}+\cdots+x_{n}\right)^{2} \geq 0 . $$ $$ \min \left(t_{i}, t_{j}\right)=\int_{0}^{\infty} \mathbf{1}\left(u \leq t_{i}\right) \mathbf{1}\left(u \leq t_{j}\right) d u $$ where the $\mathbf{1}$ are indicator functions. Indeed, $$ \sum_{i, j} x_{i} x_{j} \min \left(t_{i}, t_{j}\right)=\sum_{i, j} x_{i} x_{j} \int_{0}^{\infty} \mathbf{1}\left(u \leq t_{i}\right) \mathbf{1}\left(u \leq t_{j}\right) d u $$ $$ \begin{aligned} & =\int_{0}^{\infty} \sum_{i} x_{i} \mathbf{1}\left(u \leq t_{i}\right) \sum_{j} x_{j} \mathbf{1}\left(u \leq t_{j}\right) d u \\ & =\int_{0}^{\infty}\left(\sum_{i} x_{i} \mathbf{1}\left(u \leq t_{i}\right)\right)^{2} d u \\ & \geq 0 . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{n}, b_{n}$ be nonnegative real numbers. Prove that $$ \sum_{i, j=1}^{n} \min \left\{a_{i} a_{j}, b_{i} b_{j}\right\} \leq \sum_{i, j=1}^{n} \min \left\{a_{i} b_{j}, a_{j} b_{i}\right\} $$
|
【 First solution by creating a single min (Vincent Huang and Ravi Boppana). Let $b_{i}=r_{i} a_{i}$ for each $i$, and rewrite the inequality as $$ \sum_{i, j} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \geq 0 $$ We now do the key manipulation to convert the double min into a separate single min. Let $\varepsilon_{i}=+1$ if $r_{i} \geq 1$, and $\varepsilon_{i}=-1$ otherwise, and let $s_{i}=\left|r_{i}-1\right|$. Then we pass to absolute values: $$ \begin{aligned} 2 \min \left(r_{i}, r_{j}\right)-2 \min \left(1, r_{i} r_{j}\right) & =\left|r_{i} r_{j}-1\right|-\left|r_{i}-r_{j}\right|-\left(r_{i}-1\right)\left(r_{j}-1\right) \\ & =\left|r_{i} r_{j}-1\right|-\left|r_{i}-r_{j}\right|-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\varepsilon_{i} \varepsilon_{j} \min \left(\left|1-r_{i} r_{j} \pm\left(r_{i}-r_{j}\right)\right|\right)-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\varepsilon_{i} \varepsilon_{j} \min \left(s_{i}\left(r_{j}+1\right), s_{j}\left(r_{i}+1\right)\right)-\varepsilon_{i} \varepsilon_{j} s_{i} s_{j} \\ & =\left(\varepsilon_{i} s_{i}\right)\left(\varepsilon_{j} s_{j}\right) \min \left(\frac{r_{j}+1}{s_{j}}-1, \frac{r_{i}+1}{s_{i}}-1\right) . \end{aligned} $$ So let us denote $x_{i}=a_{i} \varepsilon_{i} s_{i} \in \mathbb{R}$, and $t_{i}=\frac{r_{i}+1}{s_{i}}-1 \in \mathbb{R}_{\geq 0}$. Thus it suffices to prove that: Claim - We have $$ \sum_{i, j} x_{i} x_{j} \min \left(t_{i}, t_{j}\right) \geq 0 $$ for arbitrary $x_{i} \in \mathbb{R}, t_{i} \in \mathbb{R} \geq 0$. $$ \sum_{i} t_{i} x_{i}^{2}+2 \sum_{i<j} 2 t_{i} x_{i} x_{j}=\sum_{i}\left(t_{i}-t_{i-1}\right)\left(x_{i}+x_{i+1}+\cdots+x_{n}\right)^{2} \geq 0 . $$ $$ \min \left(t_{i}, t_{j}\right)=\int_{0}^{\infty} \mathbf{1}\left(u \leq t_{i}\right) \mathbf{1}\left(u \leq t_{j}\right) d u $$ where the $\mathbf{1}$ are indicator functions. Indeed, $$ \sum_{i, j} x_{i} x_{j} \min \left(t_{i}, t_{j}\right)=\sum_{i, j} x_{i} x_{j} \int_{0}^{\infty} \mathbf{1}\left(u \leq t_{i}\right) \mathbf{1}\left(u \leq t_{j}\right) d u $$ $$ \begin{aligned} & =\int_{0}^{\infty} \sum_{i} x_{i} \mathbf{1}\left(u \leq t_{i}\right) \sum_{j} x_{j} \mathbf{1}\left(u \leq t_{j}\right) d u \\ & =\int_{0}^{\infty}\left(\sum_{i} x_{i} \mathbf{1}\left(u \leq t_{i}\right)\right)^{2} d u \\ & \geq 0 . \end{aligned} $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a30aaa0e-06bc-50f5-a005-64d756d5ad30
| 606,304
|
Let $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{n}, b_{n}$ be nonnegative real numbers. Prove that $$ \sum_{i, j=1}^{n} \min \left\{a_{i} a_{j}, b_{i} b_{j}\right\} \leq \sum_{i, j=1}^{n} \min \left\{a_{i} b_{j}, a_{j} b_{i}\right\} $$
|
【 Second solution by smoothing (Alex Zhai). The case $n=1$ is immediate, so we'll proceed by induction on $n \geq 2$. Again, let $b_{i}=r_{i} a_{i}$ for each $i$, and write the inequality as $$ L_{n}\left(a_{1}, \ldots, a_{n}, r_{1}, \ldots, r_{n}\right):=\sum_{i, j} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \geq 0 $$ First note that if $r_{1}=r_{2}$ then $$ L_{n}\left(a_{1}, a_{2}, a_{3}, \ldots, r_{1}, r_{1}, r_{3} \ldots\right)=L_{n-1}\left(a_{1}+a_{2}, a_{3}, \ldots, r_{1}, r_{3}, \ldots\right) $$ and so our goal is to smooth to a situation where two of the $r_{i}$ 's are equal, so that we may apply induction. On the other hand, $L_{n}$ is a piecewise linear function in $r_{1} \geq 0$. Let us smooth $r_{1}$ then. Note that if the minimum is attained at $r_{1}=0$, we can ignore $a_{1}$ and reduce to the $(n-1)$-variable case. On the other hand, the minimum must be achieved at a cusp which opens upward, which can only happen if $r_{i} r_{j}=1$ for some $j$. (The $r_{i}=r_{j}$ cusps open downward, sadly.) In this way, whenever some $r_{i}$ is not equal to the reciprocal of any other $r_{\boldsymbol{\bullet}}$, we can smooth it. This terminates; so we may smooth until we reach a situation for which $$ \left\{r_{1}, \ldots, r_{n}\right\}=\left\{1 / r_{1}, \ldots, 1 / r_{n}\right\} $$ Now, assume WLOG that $r_{1}=\max _{i} r_{i}$ and $r_{2}=\min _{i} r_{i}$, hence $r_{1} r_{2}=1$ and $r_{1} \geq 1 \geq r_{2}$. We isolate the contributions from $a_{1}, a_{2}, r_{1}$ and $r_{2}$. $$ \begin{aligned} L_{n}(\cdots) & =a_{1}^{2}\left[r_{1}-1\right]+a_{2}^{2}\left[r_{2}-r_{2}^{2}\right]+2 a_{1} a_{2}\left[r_{2}-1\right] \\ & +2 a_{1}\left[\left(a_{3} r_{3}+\cdots+a_{n} r_{n}\right)-\left(a_{3}+\cdots+a_{n}\right)\right] \\ & +2 a_{2} r_{2}\left[\left(a_{3}+\cdots+a_{n}\right)-\left(a_{3} r_{3}+\cdots+a_{n} r_{n}\right)\right] \\ & +\sum_{i=3}^{n} \sum_{j=3}^{n} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \end{aligned} $$ The idea now is to smooth via $$ \left(a_{1}, a_{2}, r_{1}, r_{2}\right) \longrightarrow\left(a_{1}, \frac{1}{t} a_{2}, \frac{1}{t} r_{1}, t r_{2}\right) $$ where $t \geq 1$ is such that $\frac{1}{t} r_{1} \geq \max \left(1, r_{3}, \ldots, r_{n}\right)$ holds. (This choice is such that $a_{1}$ and $a_{2} r_{2}$ are unchanged, because we don't know the sign of $\sum_{i \geq 3}\left(1-r_{i}\right) a_{i}$ and so the post-smoothing value is still at least the max.) Then, $$ \begin{aligned} & L_{n}\left(a_{1}, a_{2}, \ldots, r_{1}, r_{2}, \ldots\right)-L_{n}\left(a_{1}, \frac{1}{t} a_{2}, \ldots, \frac{1}{t} r_{1}, t r_{2}\right) \\ = & a_{1}^{2}\left(r_{1}-\frac{1}{t} r_{1}\right)+a_{2}^{2}\left(r_{2}-\frac{1}{t} r_{2}\right)+2 a_{1} a_{2}\left(\frac{1}{t}-1\right) \\ = & \left(1-\frac{1}{t}\right)\left(r_{1} a_{1}^{2}+r_{2} a_{2}^{2}-2 a_{1} a_{2}\right) \geq 0 \end{aligned} $$ the last line by AM-GM. Now pick $t=\frac{r_{1}}{\max \left(1, r_{3}, \ldots, r_{n}\right)}$, and at last we can induct down.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{n}, b_{n}$ be nonnegative real numbers. Prove that $$ \sum_{i, j=1}^{n} \min \left\{a_{i} a_{j}, b_{i} b_{j}\right\} \leq \sum_{i, j=1}^{n} \min \left\{a_{i} b_{j}, a_{j} b_{i}\right\} $$
|
【 Second solution by smoothing (Alex Zhai). The case $n=1$ is immediate, so we'll proceed by induction on $n \geq 2$. Again, let $b_{i}=r_{i} a_{i}$ for each $i$, and write the inequality as $$ L_{n}\left(a_{1}, \ldots, a_{n}, r_{1}, \ldots, r_{n}\right):=\sum_{i, j} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \geq 0 $$ First note that if $r_{1}=r_{2}$ then $$ L_{n}\left(a_{1}, a_{2}, a_{3}, \ldots, r_{1}, r_{1}, r_{3} \ldots\right)=L_{n-1}\left(a_{1}+a_{2}, a_{3}, \ldots, r_{1}, r_{3}, \ldots\right) $$ and so our goal is to smooth to a situation where two of the $r_{i}$ 's are equal, so that we may apply induction. On the other hand, $L_{n}$ is a piecewise linear function in $r_{1} \geq 0$. Let us smooth $r_{1}$ then. Note that if the minimum is attained at $r_{1}=0$, we can ignore $a_{1}$ and reduce to the $(n-1)$-variable case. On the other hand, the minimum must be achieved at a cusp which opens upward, which can only happen if $r_{i} r_{j}=1$ for some $j$. (The $r_{i}=r_{j}$ cusps open downward, sadly.) In this way, whenever some $r_{i}$ is not equal to the reciprocal of any other $r_{\boldsymbol{\bullet}}$, we can smooth it. This terminates; so we may smooth until we reach a situation for which $$ \left\{r_{1}, \ldots, r_{n}\right\}=\left\{1 / r_{1}, \ldots, 1 / r_{n}\right\} $$ Now, assume WLOG that $r_{1}=\max _{i} r_{i}$ and $r_{2}=\min _{i} r_{i}$, hence $r_{1} r_{2}=1$ and $r_{1} \geq 1 \geq r_{2}$. We isolate the contributions from $a_{1}, a_{2}, r_{1}$ and $r_{2}$. $$ \begin{aligned} L_{n}(\cdots) & =a_{1}^{2}\left[r_{1}-1\right]+a_{2}^{2}\left[r_{2}-r_{2}^{2}\right]+2 a_{1} a_{2}\left[r_{2}-1\right] \\ & +2 a_{1}\left[\left(a_{3} r_{3}+\cdots+a_{n} r_{n}\right)-\left(a_{3}+\cdots+a_{n}\right)\right] \\ & +2 a_{2} r_{2}\left[\left(a_{3}+\cdots+a_{n}\right)-\left(a_{3} r_{3}+\cdots+a_{n} r_{n}\right)\right] \\ & +\sum_{i=3}^{n} \sum_{j=3}^{n} a_{i} a_{j}\left[\min \left(r_{i}, r_{j}\right)-\min \left(1, r_{i} r_{j}\right)\right] \end{aligned} $$ The idea now is to smooth via $$ \left(a_{1}, a_{2}, r_{1}, r_{2}\right) \longrightarrow\left(a_{1}, \frac{1}{t} a_{2}, \frac{1}{t} r_{1}, t r_{2}\right) $$ where $t \geq 1$ is such that $\frac{1}{t} r_{1} \geq \max \left(1, r_{3}, \ldots, r_{n}\right)$ holds. (This choice is such that $a_{1}$ and $a_{2} r_{2}$ are unchanged, because we don't know the sign of $\sum_{i \geq 3}\left(1-r_{i}\right) a_{i}$ and so the post-smoothing value is still at least the max.) Then, $$ \begin{aligned} & L_{n}\left(a_{1}, a_{2}, \ldots, r_{1}, r_{2}, \ldots\right)-L_{n}\left(a_{1}, \frac{1}{t} a_{2}, \ldots, \frac{1}{t} r_{1}, t r_{2}\right) \\ = & a_{1}^{2}\left(r_{1}-\frac{1}{t} r_{1}\right)+a_{2}^{2}\left(r_{2}-\frac{1}{t} r_{2}\right)+2 a_{1} a_{2}\left(\frac{1}{t}-1\right) \\ = & \left(1-\frac{1}{t}\right)\left(r_{1} a_{1}^{2}+r_{2} a_{2}^{2}-2 a_{1} a_{2}\right) \geq 0 \end{aligned} $$ the last line by AM-GM. Now pick $t=\frac{r_{1}}{\max \left(1, r_{3}, \ldots, r_{n}\right)}$, and at last we can induct down.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2000-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a30aaa0e-06bc-50f5-a005-64d756d5ad30
| 606,304
|
Let $A B C$ be a triangle and let $\omega$ be its incircle. Denote by $D_{1}$ and $E_{1}$ the points where $\omega$ is tangent to sides $B C$ and $A C$, respectively. Denote by $D_{2}$ and $E_{2}$ the points on sides $B C$ and $A C$, respectively, such that $C D_{2}=B D_{1}$ and $C E_{2}=A E_{1}$, and denote by $P$ the point of intersection of segments $A D_{2}$ and $B E_{2}$. Circle $\omega$ intersects segment $A D_{2}$ at two points, the closer of which to the vertex $A$ is denoted by $Q$. Prove that $A Q=D_{2} P$.
|
We have that $P$ is the Nagel point $$ P=(s-a: s-b: s-c) . $$ Therefore, $$ \frac{P D_{2}}{A D_{2}}=\frac{s-a}{(s-a)+(s-b)+(s-c)}=\frac{s-a}{s} . $$ Meanwhile, $Q$ is the antipode of $D_{1}$. The classical homothety at $A$ mapping $Q$ to $D_{1}$ (by mapping the incircle to the $A$-excircle) has ratio $\frac{s-a}{s}$ as well (by considering the length of the tangents from $A$ ), so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $\omega$ be its incircle. Denote by $D_{1}$ and $E_{1}$ the points where $\omega$ is tangent to sides $B C$ and $A C$, respectively. Denote by $D_{2}$ and $E_{2}$ the points on sides $B C$ and $A C$, respectively, such that $C D_{2}=B D_{1}$ and $C E_{2}=A E_{1}$, and denote by $P$ the point of intersection of segments $A D_{2}$ and $B E_{2}$. Circle $\omega$ intersects segment $A D_{2}$ at two points, the closer of which to the vertex $A$ is denoted by $Q$. Prove that $A Q=D_{2} P$.
|
We have that $P$ is the Nagel point $$ P=(s-a: s-b: s-c) . $$ Therefore, $$ \frac{P D_{2}}{A D_{2}}=\frac{s-a}{(s-a)+(s-b)+(s-c)}=\frac{s-a}{s} . $$ Meanwhile, $Q$ is the antipode of $D_{1}$. The classical homothety at $A$ mapping $Q$ to $D_{1}$ (by mapping the incircle to the $A$-excircle) has ratio $\frac{s-a}{s}$ as well (by considering the length of the tangents from $A$ ), so we are done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2001-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
3825c1c7-0fc3-5b5d-86c2-25d89f34c38c
| 248,058
|
Let $a, b, c$ be nonnegative real numbers such that $a^{2}+b^{2}+c^{2}+a b c=4$. Show that $$ 0 \leq a b+b c+c a-a b c \leq 2 $$
|
$ The left-hand side of the inequality is trivial; just note that $\min \{a, b, c\} \leq 1$. Hence, we focus on the right side. We use Lagrange Multipliers. Define $$ U=\left\{(a, b, c) \mid a, b, c>0 \text { and } a^{2}+b^{2}+c^{2}<1000\right\} . $$ This is an intersection of open sets, so it is open. Its closure is $$ \bar{U}=\left\{(a, b, c) \mid a, b, c \geq 0 \text { and } a^{2}+b^{2}+c^{2} \leq 1000\right\} . $$ Hence the constraint set $$ \bar{S}=\{\mathbf{x} \in \bar{U}: g(\bar{x})=4\} $$ is compact, where $g(a, b, c)=a^{2}+b^{2}+c^{2}+a b c$. Define $$ f(a, b, c)=a^{2}+b^{2}+c^{2}+a b+b c+c a $$ It's equivalent to show that $f \leq 6$ subject to $g$. Over $\bar{S}$, it must achieve a global maximum. Now we consider two cases. If $\mathbf{x}$ lies on the boundary, that means one of the components is zero (since $a^{2}+b^{2}+c^{2}=$ 1000 is clearly impossible). WLOG $c=0$, then we wish to show $a^{2}+b^{2}+a b \leq 6$ for $a^{2}+b^{2}=4$, which is trivial. Now for the interior $U$, we may use the method of Lagrange Multipliers. Consider a local maximum $\mathbf{x} \in U$. Compute $$ \nabla f=\langle 2 a+b+c, 2 b+c+a, 2 c+a+b\rangle $$ and $$ \nabla g=\langle 2 a+b c, 2 b+c a, 2 c+a b\rangle $$ Of course, $\nabla g \neq \mathbf{0}$ everywhere, so introducing our multiplier yields $$ \langle 2 a+b+c, a+2 b+c, a+b+2 c\rangle=\lambda\langle 2 a+b c, 2 b+c a, 2 c+a b\rangle . $$ Note that $\lambda \neq 0$ since $a, b, c>0$. Subtracting $2 a+b+c=\lambda(2 a+b c)$ from $a+2 b+c=$ $\lambda(2 b+c a)$ implies that $$ (a-b)([2 \lambda-1]-\lambda c)=0 . $$ We can derive similar equations for the others. Hence, we have three cases. 1. If $a=b=c$, then $a=b=c=1$, and this satisfies $f(1,1,1) \leq 6$. 2. If $a, b, c$ are pairwise distinct, then we derive $a=b=c=2-\lambda^{-1}$, contradiction. 3. Now suppose that $a=b \neq c$. Meanwhile, the constraint (with $a=b$ ) reads $$ \begin{aligned} a^{2}+b^{2}+c^{2}+a b c=4 & \Longleftrightarrow c^{2}+a^{2} c+\left(2 a^{2}-4\right)=0 \\ & \Longleftrightarrow(c+2)\left(c-\left(2-a^{2}\right)\right)=0 \end{aligned} $$ which since $c>0$ gives $c=2-a^{2}$. Noah Walsh points out that at this point, we don't need to calculate the critical point; we just directly substitute $a=b$ and $c=2-a^{2}$ into the desired inequality: $$ a^{2}+2 a(2-a)^{2}-a^{2}(2-a)^{2}=2-(a-1)^{2}\left(a^{2}-4 a+2\right) \leq 0 $$ So any point here satisfies the inequality anyways. Remark. It can actually be shown that the critical point in the third case we skipped is pretty close: it is given by $$ a=b=\frac{1+\sqrt{17}}{4} \quad c=\frac{1}{8}(7-\sqrt{17}) . $$ This satisfies $$ f(a, b, c)=3 a^{2}+2 a c+c^{2}=\frac{1}{32}(121+17 \sqrt{17}) \approx 5.97165 $$ which is just a bit less than 6 . Remark. Equality holds for the upper bound if $(a, b, c)=(1,1,1)$ or $(a, b, c)=(\sqrt{2}, \sqrt{2}, 0)$ and permutations. The lower bound is achieved if $(a, b, c)=(2,0,0)$ and permutations.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be nonnegative real numbers such that $a^{2}+b^{2}+c^{2}+a b c=4$. Show that $$ 0 \leq a b+b c+c a-a b c \leq 2 $$
|
$ The left-hand side of the inequality is trivial; just note that $\min \{a, b, c\} \leq 1$. Hence, we focus on the right side. We use Lagrange Multipliers. Define $$ U=\left\{(a, b, c) \mid a, b, c>0 \text { and } a^{2}+b^{2}+c^{2}<1000\right\} . $$ This is an intersection of open sets, so it is open. Its closure is $$ \bar{U}=\left\{(a, b, c) \mid a, b, c \geq 0 \text { and } a^{2}+b^{2}+c^{2} \leq 1000\right\} . $$ Hence the constraint set $$ \bar{S}=\{\mathbf{x} \in \bar{U}: g(\bar{x})=4\} $$ is compact, where $g(a, b, c)=a^{2}+b^{2}+c^{2}+a b c$. Define $$ f(a, b, c)=a^{2}+b^{2}+c^{2}+a b+b c+c a $$ It's equivalent to show that $f \leq 6$ subject to $g$. Over $\bar{S}$, it must achieve a global maximum. Now we consider two cases. If $\mathbf{x}$ lies on the boundary, that means one of the components is zero (since $a^{2}+b^{2}+c^{2}=$ 1000 is clearly impossible). WLOG $c=0$, then we wish to show $a^{2}+b^{2}+a b \leq 6$ for $a^{2}+b^{2}=4$, which is trivial. Now for the interior $U$, we may use the method of Lagrange Multipliers. Consider a local maximum $\mathbf{x} \in U$. Compute $$ \nabla f=\langle 2 a+b+c, 2 b+c+a, 2 c+a+b\rangle $$ and $$ \nabla g=\langle 2 a+b c, 2 b+c a, 2 c+a b\rangle $$ Of course, $\nabla g \neq \mathbf{0}$ everywhere, so introducing our multiplier yields $$ \langle 2 a+b+c, a+2 b+c, a+b+2 c\rangle=\lambda\langle 2 a+b c, 2 b+c a, 2 c+a b\rangle . $$ Note that $\lambda \neq 0$ since $a, b, c>0$. Subtracting $2 a+b+c=\lambda(2 a+b c)$ from $a+2 b+c=$ $\lambda(2 b+c a)$ implies that $$ (a-b)([2 \lambda-1]-\lambda c)=0 . $$ We can derive similar equations for the others. Hence, we have three cases. 1. If $a=b=c$, then $a=b=c=1$, and this satisfies $f(1,1,1) \leq 6$. 2. If $a, b, c$ are pairwise distinct, then we derive $a=b=c=2-\lambda^{-1}$, contradiction. 3. Now suppose that $a=b \neq c$. Meanwhile, the constraint (with $a=b$ ) reads $$ \begin{aligned} a^{2}+b^{2}+c^{2}+a b c=4 & \Longleftrightarrow c^{2}+a^{2} c+\left(2 a^{2}-4\right)=0 \\ & \Longleftrightarrow(c+2)\left(c-\left(2-a^{2}\right)\right)=0 \end{aligned} $$ which since $c>0$ gives $c=2-a^{2}$. Noah Walsh points out that at this point, we don't need to calculate the critical point; we just directly substitute $a=b$ and $c=2-a^{2}$ into the desired inequality: $$ a^{2}+2 a(2-a)^{2}-a^{2}(2-a)^{2}=2-(a-1)^{2}\left(a^{2}-4 a+2\right) \leq 0 $$ So any point here satisfies the inequality anyways. Remark. It can actually be shown that the critical point in the third case we skipped is pretty close: it is given by $$ a=b=\frac{1+\sqrt{17}}{4} \quad c=\frac{1}{8}(7-\sqrt{17}) . $$ This satisfies $$ f(a, b, c)=3 a^{2}+2 a c+c^{2}=\frac{1}{32}(121+17 \sqrt{17}) \approx 5.97165 $$ which is just a bit less than 6 . Remark. Equality holds for the upper bound if $(a, b, c)=(1,1,1)$ or $(a, b, c)=(\sqrt{2}, \sqrt{2}, 0)$ and permutations. The lower bound is achieved if $(a, b, c)=(2,0,0)$ and permutations.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2001-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
686d71d5-b9b5-5a67-9a57-0d9a69ea38f6
| 606,323
|
Let $A B C$ be a triangle and $P$ any point such that $P A, P B, P C$ are the sides of an obtuse triangle, with $P A$ the longest side. Prove that $\angle B A C$ is acute.
|
Using Ptolemy's inequality and Cauchy-Schwarz, $$ \begin{aligned} P A \cdot B C & \leq P B \cdot A C+P C \cdot A B \\ & \leq \sqrt{\left(P B^{2}+P C^{2}\right)\left(A B^{2}+A C^{2}\right)} \\ & <\sqrt{P A^{2} \cdot\left(A B^{2}+A C\right)^{2}}=P A \cdot \sqrt{A B^{2}+A C^{2}} \end{aligned} $$ meaning $B C^{2}<A B^{2}+A C^{2}$, so $\angle B A C$ is acute. $$ A B^{2}+B P^{2}+P C^{2}+C A^{2}=A P^{2}+B C^{2}+4 M N^{2} \geq A P^{2}+B C^{2} $$ We are given that $A P^{2}>B P^{2}+P C^{2}$, so $A B^{2}+A C^{2}>B C^{2}$, and we get $\angle B A C$ is acute.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and $P$ any point such that $P A, P B, P C$ are the sides of an obtuse triangle, with $P A$ the longest side. Prove that $\angle B A C$ is acute.
|
Using Ptolemy's inequality and Cauchy-Schwarz, $$ \begin{aligned} P A \cdot B C & \leq P B \cdot A C+P C \cdot A B \\ & \leq \sqrt{\left(P B^{2}+P C^{2}\right)\left(A B^{2}+A C^{2}\right)} \\ & <\sqrt{P A^{2} \cdot\left(A B^{2}+A C\right)^{2}}=P A \cdot \sqrt{A B^{2}+A C^{2}} \end{aligned} $$ meaning $B C^{2}<A B^{2}+A C^{2}$, so $\angle B A C$ is acute. $$ A B^{2}+B P^{2}+P C^{2}+C A^{2}=A P^{2}+B C^{2}+4 M N^{2} \geq A P^{2}+B C^{2} $$ We are given that $A P^{2}>B P^{2}+P C^{2}$, so $A B^{2}+A C^{2}>B C^{2}$, and we get $\angle B A C$ is acute.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2001-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
1cb410e1-b4d5-5568-a52b-3bbdd6f6aaf5
| 248,074
|
Let $S \subseteq \mathbb{Z}$ be such that: (a) there exist $a, b \in S$ with $\operatorname{gcd}(a, b)=\operatorname{gcd}(a-2, b-2)=1$; (b) if $x$ and $y$ are elements of $S$ (possibly equal), then $x^{2}-y$ also belongs to $S$. Prove that $S=\mathbb{Z}$.
|
Call an integer $d>0$ shifty if $S=S+d$ (meaning $S$ is invariant under shifting by $d$ ). First, note that if $u, v \in S$, then for any $x \in S$, $$ v^{2}-\left(u^{2}-x\right)=\left(v^{2}-u^{2}\right)+x \in S $$ Since we can easily check that $|S|>1$ and $S \neq\{n,-n\}$ we conclude there exists a shifty integer. We claim 1 is shifty, which implies the problem. Assume for contradiction that 1 is not shifty. Then for GCD reasons the set of shifty integers must be $d \mathbb{Z}$ for some $d \geq 2$. Claim - We have $S \subseteq\left\{x: x^{2} \equiv m(\bmod d)\right\}$ for some fixed $m$. Now take $a, b \in S$ as in (a). In that case we need to have $$ a^{2} \equiv b^{2} \equiv\left(a^{2}-a\right)^{2} \equiv\left(b^{2}-b\right)^{2} \quad(\bmod d) $$ Passing to a prime $p \mid d$, we have the following: - Since $a^{2} \equiv\left(a^{2}-a\right)^{2}(\bmod p)$ or equivalently $a^{3}(a-2) \equiv 0(\bmod p)$, either $a \equiv 0$ $(\bmod p)$ or $a \equiv 2(\bmod p)$. - Similarly, either $b \equiv 0(\bmod p)$ or $b \equiv 2(\bmod p)$. - Since $a^{2} \equiv b^{2}(\bmod p)$, or $a \equiv \pm b(\bmod p)$, we find either $a \equiv b \equiv 0(\bmod p)$ or $a \equiv b \equiv 2(\bmod p)($ even if $p=2)$. This is a contradiction. Remark. The condition (a) cannot be dropped, since otherwise we may take $S=\{2(\bmod p)\}$ or $S=\{0(\bmod p)\}$, say.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S \subseteq \mathbb{Z}$ be such that: (a) there exist $a, b \in S$ with $\operatorname{gcd}(a, b)=\operatorname{gcd}(a-2, b-2)=1$; (b) if $x$ and $y$ are elements of $S$ (possibly equal), then $x^{2}-y$ also belongs to $S$. Prove that $S=\mathbb{Z}$.
|
Call an integer $d>0$ shifty if $S=S+d$ (meaning $S$ is invariant under shifting by $d$ ). First, note that if $u, v \in S$, then for any $x \in S$, $$ v^{2}-\left(u^{2}-x\right)=\left(v^{2}-u^{2}\right)+x \in S $$ Since we can easily check that $|S|>1$ and $S \neq\{n,-n\}$ we conclude there exists a shifty integer. We claim 1 is shifty, which implies the problem. Assume for contradiction that 1 is not shifty. Then for GCD reasons the set of shifty integers must be $d \mathbb{Z}$ for some $d \geq 2$. Claim - We have $S \subseteq\left\{x: x^{2} \equiv m(\bmod d)\right\}$ for some fixed $m$. Now take $a, b \in S$ as in (a). In that case we need to have $$ a^{2} \equiv b^{2} \equiv\left(a^{2}-a\right)^{2} \equiv\left(b^{2}-b\right)^{2} \quad(\bmod d) $$ Passing to a prime $p \mid d$, we have the following: - Since $a^{2} \equiv\left(a^{2}-a\right)^{2}(\bmod p)$ or equivalently $a^{3}(a-2) \equiv 0(\bmod p)$, either $a \equiv 0$ $(\bmod p)$ or $a \equiv 2(\bmod p)$. - Similarly, either $b \equiv 0(\bmod p)$ or $b \equiv 2(\bmod p)$. - Since $a^{2} \equiv b^{2}(\bmod p)$, or $a \equiv \pm b(\bmod p)$, we find either $a \equiv b \equiv 0(\bmod p)$ or $a \equiv b \equiv 2(\bmod p)($ even if $p=2)$. This is a contradiction. Remark. The condition (a) cannot be dropped, since otherwise we may take $S=\{2(\bmod p)\}$ or $S=\{0(\bmod p)\}$, say.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2001-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
b2caa51c-b1de-59a9-8ba2-d483d88aba19
| 606,329
|
Each point in the plane is assigned a real number. Suppose that for any nondegenerate triangle, the number at its incenter is the arithmetic mean of the three numbers at its vertices. Prove that all points in the plane are equal to each other.
|
First, we claim that in an isosceles trapezoid $A B C D$ we have $a+c=b+d$. Indeed, suppose WLOG that rays $B A$ and $C D$ meet at $X$. Then triangles $X A C$ and $X B D$ share an incircle, proving the claim. Now, given any two points $A$ and $B$, construct regular pentagon $A B C D E$. We have $a+c=b+d=c+e=d+a=e+b$, so $a=b=c=d=e$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Each point in the plane is assigned a real number. Suppose that for any nondegenerate triangle, the number at its incenter is the arithmetic mean of the three numbers at its vertices. Prove that all points in the plane are equal to each other.
|
First, we claim that in an isosceles trapezoid $A B C D$ we have $a+c=b+d$. Indeed, suppose WLOG that rays $B A$ and $C D$ meet at $X$. Then triangles $X A C$ and $X B D$ share an incircle, proving the claim. Now, given any two points $A$ and $B$, construct regular pentagon $A B C D E$. We have $a+c=b+d=c+e=d+a=e+b$, so $a=b=c=d=e$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2001-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
84262e57-5165-5a7a-93e8-10e9ff3ac156
| 248,086
|
Let $S$ be a set with 2002 elements, and let $N$ be an integer with $0 \leq N \leq 2^{2002}$. Prove that it is possible to color every subset of $S$ either black or white so that the following conditions hold: (a) the union of any two white subsets is white; (b) the union of any two black subsets is black; (c) there are exactly $N$ white subsets.
|
We will solve the problem with 2002 replaced by an arbitrary integer $n \geq 0$. In other words, we prove: Claim - For any nonnegative integers $n$ and $N$ with $0 \leq N \leq 2^{n}$, it is possible to color the $2^{n}$ subsets of $\{1, \ldots, n\}$ black and white satisfying the conditions of the problem. For the inductive step, we divide into two cases: - If $N \leq 2^{n-1}$, then we take a coloring of subsets of $\{1, \ldots, n-1\}$ with $N$ white sets; then we color the remaining $2^{n-1}$ sets (which contain $n$ ) black. - If $N>2^{n-1}$, then we take a coloring of subsets of $\{1, \ldots, n-1\}$ with $N-2^{n-1}$ white sets; then we color the remaining $2^{n-1}$ sets (which contain $n$ ) white.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set with 2002 elements, and let $N$ be an integer with $0 \leq N \leq 2^{2002}$. Prove that it is possible to color every subset of $S$ either black or white so that the following conditions hold: (a) the union of any two white subsets is white; (b) the union of any two black subsets is black; (c) there are exactly $N$ white subsets.
|
We will solve the problem with 2002 replaced by an arbitrary integer $n \geq 0$. In other words, we prove: Claim - For any nonnegative integers $n$ and $N$ with $0 \leq N \leq 2^{n}$, it is possible to color the $2^{n}$ subsets of $\{1, \ldots, n\}$ black and white satisfying the conditions of the problem. For the inductive step, we divide into two cases: - If $N \leq 2^{n-1}$, then we take a coloring of subsets of $\{1, \ldots, n-1\}$ with $N$ white sets; then we color the remaining $2^{n-1}$ sets (which contain $n$ ) black. - If $N>2^{n-1}$, then we take a coloring of subsets of $\{1, \ldots, n-1\}$ with $N-2^{n-1}$ white sets; then we color the remaining $2^{n-1}$ sets (which contain $n$ ) white.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2002-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
07662f9f-07de-56ec-8551-c359e920a2c2
| 606,339
|
Prove that any monic polynomial (a polynomial with leading coefficient 1) of degree $n$ with real coefficients is the average of two monic polynomials of degree $n$ with $n$ real roots.
|
First, ## Lemma If $p$ is a monic polynomial of degree $n$, and $p(1) p(2)<0, p(2) p(3)<0, \ldots$, $p(n-1) p(n)<0$ then $p$ has $n$ real roots. The last root is obtained by considering cases on $n(\bmod 2)$. - If $n$ is even, then $p(1)$ and $p(n)$ have opposite sign, while we must have either $$ \lim _{x \rightarrow-\infty} p(x)=\lim _{x \rightarrow \infty} p(x)= \pm \infty $$ so we get one more root. - The $n$ odd case is similar, with $p(1)$ and $p(n)$ now having the same sign, but $\lim _{x \rightarrow-\infty} p(x)=-\lim _{x \rightarrow \infty} p(x)$ instead. Let $f(n)$ be the monic polynomial and let $M>1000 \max _{t=1, \ldots, n}|f(t)|+1000$. Then we may select reals $a_{1}, \ldots, a_{n}$ and $b_{1}, \ldots, b_{n}$ such that for each $k=1, \ldots, n$, we have $$ \begin{aligned} a_{k}+b_{k} & =2 f(k) \\ (-1)^{k} a_{k} & >M \\ (-1)^{k+1} b_{k} & >M . \end{aligned} $$ We may interpolate monic polynomials $g$ and $h$ through the $a_{k}$ and $b_{k}$ (if the $a_{k}, b_{k}$ are selected "generically" from each other). Then one can easily check $f=\frac{1}{2}(g+h)$ works.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that any monic polynomial (a polynomial with leading coefficient 1) of degree $n$ with real coefficients is the average of two monic polynomials of degree $n$ with $n$ real roots.
|
First, ## Lemma If $p$ is a monic polynomial of degree $n$, and $p(1) p(2)<0, p(2) p(3)<0, \ldots$, $p(n-1) p(n)<0$ then $p$ has $n$ real roots. The last root is obtained by considering cases on $n(\bmod 2)$. - If $n$ is even, then $p(1)$ and $p(n)$ have opposite sign, while we must have either $$ \lim _{x \rightarrow-\infty} p(x)=\lim _{x \rightarrow \infty} p(x)= \pm \infty $$ so we get one more root. - The $n$ odd case is similar, with $p(1)$ and $p(n)$ now having the same sign, but $\lim _{x \rightarrow-\infty} p(x)=-\lim _{x \rightarrow \infty} p(x)$ instead. Let $f(n)$ be the monic polynomial and let $M>1000 \max _{t=1, \ldots, n}|f(t)|+1000$. Then we may select reals $a_{1}, \ldots, a_{n}$ and $b_{1}, \ldots, b_{n}$ such that for each $k=1, \ldots, n$, we have $$ \begin{aligned} a_{k}+b_{k} & =2 f(k) \\ (-1)^{k} a_{k} & >M \\ (-1)^{k+1} b_{k} & >M . \end{aligned} $$ We may interpolate monic polynomials $g$ and $h$ through the $a_{k}$ and $b_{k}$ (if the $a_{k}, b_{k}$ are selected "generically" from each other). Then one can easily check $f=\frac{1}{2}(g+h)$ works.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2002-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
40c99935-79a9-5ce8-ad76-bf8ccbfafb64
| 46,218
|
Let $a, b$ be integers greater than 2. Prove that there exists a positive integer $k$ and a finite sequence $n_{1}, n_{2}, \ldots, n_{k}$ of positive integers such that $n_{1}=a, n_{k}=b$, and $n_{i} n_{i+1}$ is divisible by $n_{i}+n_{i+1}$ for each $i(1 \leq i<k)$.
|
Consider a graph $G$ on the vertex set $\{3,4, \ldots\}$ and with edges between $v, w$ if $v+w \mid v w$; the problem is equivalent to showing that $G$ is connected. First, note that $n$ is connected to $n(n-1), n(n-1)(n-2)$, etc. up to $n$ !. But for $n>2, n$ ! is connected to $(n+1)$ ! too: - $n!\rightarrow(n+1)$ ! if $n$ is even - $n!\rightarrow 2 n!\rightarrow(n+1)!$ if $n$ is odd. This concludes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ be integers greater than 2. Prove that there exists a positive integer $k$ and a finite sequence $n_{1}, n_{2}, \ldots, n_{k}$ of positive integers such that $n_{1}=a, n_{k}=b$, and $n_{i} n_{i+1}$ is divisible by $n_{i}+n_{i+1}$ for each $i(1 \leq i<k)$.
|
Consider a graph $G$ on the vertex set $\{3,4, \ldots\}$ and with edges between $v, w$ if $v+w \mid v w$; the problem is equivalent to showing that $G$ is connected. First, note that $n$ is connected to $n(n-1), n(n-1)(n-2)$, etc. up to $n$ !. But for $n>2, n$ ! is connected to $(n+1)$ ! too: - $n!\rightarrow(n+1)$ ! if $n$ is even - $n!\rightarrow 2 n!\rightarrow(n+1)!$ if $n$ is odd. This concludes the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2002-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
cefaaed9-93f5-5297-bea1-59fb7b6cd7d5
| 606,352
|
I have an $n \times n$ sheet of stamps, from which I've been asked to tear out blocks of three adjacent stamps in a single row or column. (I can only tear along the perforations separating adjacent stamps, and each block must come out of the sheet in one piece.) Let $b(n)$ be the smallest number of blocks I can tear out and make it impossible to tear out any more blocks. Prove that there are real constants $c$ and $d$ such that $$ \frac{1}{7} n^{2}-c n \leq b(n) \leq \frac{1}{5} n^{2}+d n $$ for all $n>0$.
|
For the lower bound: there are $2 n(n-2)$ places one could put a block. Note that each block eliminates at most 14 such places. For the upper bound, the construction of $\frac{1}{5}$ is easy to build. Here is an illustration of one possible construction for $n=9$ which generalizes readily, using only vertical blocks. $$ \left[\begin{array}{lllllllll} A & & E & & I & L & & P & \\ A & & E & G & & L & & P & R \\ A & C & & G & & L & N & & R \\ & C & & G & J & & N & & R \\ & C & F & & J & & N & Q & \\ B & & F & & J & M & & Q & \\ B & & F & H & & M & & Q & S \\ B & D & & H & & M & O & & S \\ & D & & H & K & & O & & S \end{array}\right] $$ Actually, for the lower bound, one may improve $1 / 7$ to $1 / 6$. Count the number $A$ of pairs of adjacent squares one of which is torn out and the other which is not: - For every deleted block, there are eight neighboring squares, at least two on each long edge which have been deleted too. Hence $N \leq 6 b(n)$. - For every block still alive and not on the border, there are four neighboring squares, and clearly at least two are deleted. Hence $N \geq 2\left((n-2)^{2}-3 b(n)\right)$. Collating these solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
I have an $n \times n$ sheet of stamps, from which I've been asked to tear out blocks of three adjacent stamps in a single row or column. (I can only tear along the perforations separating adjacent stamps, and each block must come out of the sheet in one piece.) Let $b(n)$ be the smallest number of blocks I can tear out and make it impossible to tear out any more blocks. Prove that there are real constants $c$ and $d$ such that $$ \frac{1}{7} n^{2}-c n \leq b(n) \leq \frac{1}{5} n^{2}+d n $$ for all $n>0$.
|
For the lower bound: there are $2 n(n-2)$ places one could put a block. Note that each block eliminates at most 14 such places. For the upper bound, the construction of $\frac{1}{5}$ is easy to build. Here is an illustration of one possible construction for $n=9$ which generalizes readily, using only vertical blocks. $$ \left[\begin{array}{lllllllll} A & & E & & I & L & & P & \\ A & & E & G & & L & & P & R \\ A & C & & G & & L & N & & R \\ & C & & G & J & & N & & R \\ & C & F & & J & & N & Q & \\ B & & F & & J & M & & Q & \\ B & & F & H & & M & & Q & S \\ B & D & & H & & M & O & & S \\ & D & & H & K & & O & & S \end{array}\right] $$ Actually, for the lower bound, one may improve $1 / 7$ to $1 / 6$. Count the number $A$ of pairs of adjacent squares one of which is torn out and the other which is not: - For every deleted block, there are eight neighboring squares, at least two on each long edge which have been deleted too. Hence $N \leq 6 b(n)$. - For every block still alive and not on the border, there are four neighboring squares, and clearly at least two are deleted. Hence $N \geq 2\left((n-2)^{2}-3 b(n)\right)$. Collating these solves the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2002-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
b2e69cd2-4ad5-555a-9b99-a1d82b9ab38c
| 606,354
|
Prove that for every positive integer $n$ there exists an $n$-digit number divisible by $5^{n}$ all of whose digits are odd.
|
This is immediate by induction on $n$. For $n=1$ we take 5 ; moving forward if $M$ is a working $n$-digit number then exactly one of $$ \begin{aligned} & N_{1}=10^{n}+M \\ & N_{3}=3 \cdot 10^{n}+M \\ & N_{5}=5 \cdot 10^{n}+M \\ & N_{7}=7 \cdot 10^{n}+M \\ & N_{9}=9 \cdot 10^{n}+M \end{aligned} $$ is divisible by $5^{n+1}$; as they are all divisible by $5^{n}$ and $N_{k} / 5^{n}$ are all distinct.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every positive integer $n$ there exists an $n$-digit number divisible by $5^{n}$ all of whose digits are odd.
|
This is immediate by induction on $n$. For $n=1$ we take 5 ; moving forward if $M$ is a working $n$-digit number then exactly one of $$ \begin{aligned} & N_{1}=10^{n}+M \\ & N_{3}=3 \cdot 10^{n}+M \\ & N_{5}=5 \cdot 10^{n}+M \\ & N_{7}=7 \cdot 10^{n}+M \\ & N_{9}=9 \cdot 10^{n}+M \end{aligned} $$ is divisible by $5^{n+1}$; as they are all divisible by $5^{n}$ and $N_{k} / 5^{n}$ are all distinct.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
73082a98-c1a7-519e-ad03-0d2ec70cb07d
| 248,150
|
A convex polygon $\mathcal{P}$ in the plane is dissected into smaller convex polygons by drawing all of its diagonals. The lengths of all sides and all diagonals of the polygon $\mathcal{P}$ are rational numbers. Prove that the lengths of all sides of all polygons in the dissection are also rational numbers.
|
Suppose $A B$ is a side of a polygon in the dissection, lying on diagonal $X Y$, with $X, A$, $B, Y$ in that order. Then $$ A B=X Y-X A-Y B $$ In this way, we see that it actually just suffices to prove the result for a quadrilateral. 【 First approach (trig). Consider quadrilateral $A B C D$. There are twelve angles one can obtain using three of its four vertices, three at each vertex; denote this set of 12 angles by $S$ Note that: - The law of cosines implies $\cos \theta \in \mathbb{Q}$ for each $\theta \in S$. - Hence, $(\sin \theta)^{2} \in \mathbb{Q}$ for $\theta \in S$. (This is because $\sin \theta^{2}+\cos ^{2} \theta$.) We say two angles $\theta_{1}$ and $\theta_{2}$ are equivalent if $\frac{\sin \theta_{1}}{\sin \theta_{2}}$ This is the same as saying, when $\sin \theta_{1}$ and $\sin \theta_{2}$ are written in simplest radical form, the part under the square root is the same. Now we contend: Claim - The angles $\angle B A C, \angle C A D, \angle B A D$ are equivalent. $$ \mathbb{Q} \ni \cos (\angle B A D)=\cos \angle B A C \cos \angle C A D-\sin \angle B A C \sin \angle C A D $$ so $\angle B A C$ and $\angle C A D$ are equivalent. Then $$ \sin (\angle B A D)=\sin \angle B A C \cos \angle C A D+\cos \angle B A C \sin \angle C A D $$ implies $\angle B A D$ is equivalent to those two. Claim - The angles $\angle B A D, \angle D B A, \angle A D B$ are equivalent. Iterating the argument implies that all angles are equivalent. Now, if $A B$ and $C D$ meet at $E$, the law of sines on $\triangle A E B$, etc. implies the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex polygon $\mathcal{P}$ in the plane is dissected into smaller convex polygons by drawing all of its diagonals. The lengths of all sides and all diagonals of the polygon $\mathcal{P}$ are rational numbers. Prove that the lengths of all sides of all polygons in the dissection are also rational numbers.
|
Suppose $A B$ is a side of a polygon in the dissection, lying on diagonal $X Y$, with $X, A$, $B, Y$ in that order. Then $$ A B=X Y-X A-Y B $$ In this way, we see that it actually just suffices to prove the result for a quadrilateral. 【 First approach (trig). Consider quadrilateral $A B C D$. There are twelve angles one can obtain using three of its four vertices, three at each vertex; denote this set of 12 angles by $S$ Note that: - The law of cosines implies $\cos \theta \in \mathbb{Q}$ for each $\theta \in S$. - Hence, $(\sin \theta)^{2} \in \mathbb{Q}$ for $\theta \in S$. (This is because $\sin \theta^{2}+\cos ^{2} \theta$.) We say two angles $\theta_{1}$ and $\theta_{2}$ are equivalent if $\frac{\sin \theta_{1}}{\sin \theta_{2}}$ This is the same as saying, when $\sin \theta_{1}$ and $\sin \theta_{2}$ are written in simplest radical form, the part under the square root is the same. Now we contend: Claim - The angles $\angle B A C, \angle C A D, \angle B A D$ are equivalent. $$ \mathbb{Q} \ni \cos (\angle B A D)=\cos \angle B A C \cos \angle C A D-\sin \angle B A C \sin \angle C A D $$ so $\angle B A C$ and $\angle C A D$ are equivalent. Then $$ \sin (\angle B A D)=\sin \angle B A C \cos \angle C A D+\cos \angle B A C \sin \angle C A D $$ implies $\angle B A D$ is equivalent to those two. Claim - The angles $\angle B A D, \angle D B A, \angle A D B$ are equivalent. Iterating the argument implies that all angles are equivalent. Now, if $A B$ and $C D$ meet at $E$, the law of sines on $\triangle A E B$, etc. implies the result.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa073e4f-1609-5a8e-90d5-82c6b73efa56
| 46,263
|
A convex polygon $\mathcal{P}$ in the plane is dissected into smaller convex polygons by drawing all of its diagonals. The lengths of all sides and all diagonals of the polygon $\mathcal{P}$ are rational numbers. Prove that the lengths of all sides of all polygons in the dissection are also rational numbers.
|
Suppose $A B$ is a side of a polygon in the dissection, lying on diagonal $X Y$, with $X, A$, $B, Y$ in that order. Then $$ A B=X Y-X A-Y B $$ In this way, we see that it actually just suffices to prove the result for a quadrilateral. I Second approach (barycentric coordinates). To do this, we apply barycentric coordinates. Consider quadrilateral $A B D C$ (note the changed order of vertices), with $A=(1,0,0), B=(0,1,0), C=(0,0,1)$. Let $D=(x, y, z)$, with $x+y+z=1$. By hypothesis, each of the numbers $$ \begin{aligned} -a^{2} y z+b^{2}(1-x) z+c^{2}(1-x) y & =A D^{2} \\ a^{2}(1-y) z+b^{2} z x+c^{2}(1-y) x & =B D^{2} \\ -a^{2}(1-z) y-b^{2}(1-z) x+c^{2} x y & =C D^{2} \end{aligned} $$ is rational. Let $W=a^{2} y z+b^{2} z x+c^{2} x y$. Then, $$ \begin{aligned} b^{2} z+c^{2} y & =A D^{2}+W \\ a^{2} z+c^{2} x & =B D^{2}+W \\ a^{2} y+b^{2} x & =C D^{2}+W \end{aligned} $$ This implies that $A D^{2}+B D^{2}+2 W-c^{2}=2 S_{C} z$ and cyclically (as usual $2 S_{C}=a^{2}+b^{2}-c^{2}$ ). If any of $S_{A}, S_{B}, S_{C}$ are zero, then we deduce $W$ is rational. Otherwise, we have that $$ 1=x+y+z=\sum_{\mathrm{cyc}} \frac{A D^{2}+B D^{2}+2 W-c^{2}}{2 S_{C}} $$ which implies that $W$ is rational, because it appears with coefficient $\frac{1}{S_{A}}+\frac{1}{S_{B}}+\frac{1}{S_{C}} \neq 0$ (since $S_{B C}+S_{C A}+S_{A B}$ is actually the area of $A B C$ ). Hence from the rationality of $W$, we deduce that $x$ is rational as long as $S_{A} \neq 0$, and similarly for the others. So at most one of $x, y, z$ is irrational, but since $x+y+z=1$ this implies they are all rational. Finally, if $P=\overline{A D} \cap \overline{B C}$ then $A P=\frac{1}{y+z} A D$, so $A P$ is rational too, completing the proof. Remark. After the reduction to quadrilateral, a third alternate approach goes by quoting Putnam 2018 A6, reproduced below: Four points are given in the plane, with no three collinear, such that the squares of the $\binom{4}{2}=6$ pairwise distances are all rational. Show that the ratio of the areas between any two of the $\binom{4}{3}=4$ triangles determined by these points is also rational. If $A B C D$ is the quadrilateral, the heights from $C$ and $D$ to $A B$ have rational ratio. Letting $P=A C \cap B D$, we see $A P / A B$ can be shown as rational via coordinates, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex polygon $\mathcal{P}$ in the plane is dissected into smaller convex polygons by drawing all of its diagonals. The lengths of all sides and all diagonals of the polygon $\mathcal{P}$ are rational numbers. Prove that the lengths of all sides of all polygons in the dissection are also rational numbers.
|
Suppose $A B$ is a side of a polygon in the dissection, lying on diagonal $X Y$, with $X, A$, $B, Y$ in that order. Then $$ A B=X Y-X A-Y B $$ In this way, we see that it actually just suffices to prove the result for a quadrilateral. I Second approach (barycentric coordinates). To do this, we apply barycentric coordinates. Consider quadrilateral $A B D C$ (note the changed order of vertices), with $A=(1,0,0), B=(0,1,0), C=(0,0,1)$. Let $D=(x, y, z)$, with $x+y+z=1$. By hypothesis, each of the numbers $$ \begin{aligned} -a^{2} y z+b^{2}(1-x) z+c^{2}(1-x) y & =A D^{2} \\ a^{2}(1-y) z+b^{2} z x+c^{2}(1-y) x & =B D^{2} \\ -a^{2}(1-z) y-b^{2}(1-z) x+c^{2} x y & =C D^{2} \end{aligned} $$ is rational. Let $W=a^{2} y z+b^{2} z x+c^{2} x y$. Then, $$ \begin{aligned} b^{2} z+c^{2} y & =A D^{2}+W \\ a^{2} z+c^{2} x & =B D^{2}+W \\ a^{2} y+b^{2} x & =C D^{2}+W \end{aligned} $$ This implies that $A D^{2}+B D^{2}+2 W-c^{2}=2 S_{C} z$ and cyclically (as usual $2 S_{C}=a^{2}+b^{2}-c^{2}$ ). If any of $S_{A}, S_{B}, S_{C}$ are zero, then we deduce $W$ is rational. Otherwise, we have that $$ 1=x+y+z=\sum_{\mathrm{cyc}} \frac{A D^{2}+B D^{2}+2 W-c^{2}}{2 S_{C}} $$ which implies that $W$ is rational, because it appears with coefficient $\frac{1}{S_{A}}+\frac{1}{S_{B}}+\frac{1}{S_{C}} \neq 0$ (since $S_{B C}+S_{C A}+S_{A B}$ is actually the area of $A B C$ ). Hence from the rationality of $W$, we deduce that $x$ is rational as long as $S_{A} \neq 0$, and similarly for the others. So at most one of $x, y, z$ is irrational, but since $x+y+z=1$ this implies they are all rational. Finally, if $P=\overline{A D} \cap \overline{B C}$ then $A P=\frac{1}{y+z} A D$, so $A P$ is rational too, completing the proof. Remark. After the reduction to quadrilateral, a third alternate approach goes by quoting Putnam 2018 A6, reproduced below: Four points are given in the plane, with no three collinear, such that the squares of the $\binom{4}{2}=6$ pairwise distances are all rational. Show that the ratio of the areas between any two of the $\binom{4}{3}=4$ triangles determined by these points is also rational. If $A B C D$ is the quadrilateral, the heights from $C$ and $D$ to $A B$ have rational ratio. Letting $P=A C \cap B D$, we see $A P / A B$ can be shown as rational via coordinates, as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa073e4f-1609-5a8e-90d5-82c6b73efa56
| 46,263
|
Let $n$ be a positive integer. For every sequence of integers $$ A=\left(a_{0}, a_{1}, a_{2}, \ldots, a_{n}\right) $$ satisfying $0 \leq a_{i} \leq i$, for $i=0, \ldots, n$, we define another sequence $$ t(A)=\left(t\left(a_{0}\right), t\left(a_{1}\right), t\left(a_{2}\right), \ldots, t\left(a_{n}\right)\right) $$ by setting $t\left(a_{i}\right)$ to be the number of terms in the sequence $A$ that precede the term $a_{i}$ and are different from $a_{i}$. Show that, starting from any sequence $A$ as above, fewer than $n$ applications of the transformation $t$ lead to a sequence $B$ such that $t(B)=B$.
|
We go by strong induction on $n$ with the base cases $n=1$ and $n=2$ done by hand. Consider two cases: - If $a_{0}=0$ and $a_{1}=1$, then $1 \leq t\left(a_{i}\right) \leq i$ for $i \geq 1$; now apply induction to $$ \left(t\left(a_{1}\right)-1, t\left(a_{2}\right)-1, \ldots, t\left(a_{n}\right)-1\right) $$ - Otherwise, assume that $a_{0}=a_{1}=\cdots=a_{k-1}=0$ but $a_{k} \neq 0$, where $k \geq 2$. Assume $k<n$ or it's obvious. Then $t\left(a_{i}\right) \neq 0$ for $i \geq k$, thus $t\left(t\left(a_{i}\right)\right) \geq k$ for $i \geq k$, and we can apply induction hypothesis to $$ \left(t\left(t\left(a_{k}\right)\right)-k, \ldots, t\left(t\left(a_{n}\right)\right)-k\right) $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. For every sequence of integers $$ A=\left(a_{0}, a_{1}, a_{2}, \ldots, a_{n}\right) $$ satisfying $0 \leq a_{i} \leq i$, for $i=0, \ldots, n$, we define another sequence $$ t(A)=\left(t\left(a_{0}\right), t\left(a_{1}\right), t\left(a_{2}\right), \ldots, t\left(a_{n}\right)\right) $$ by setting $t\left(a_{i}\right)$ to be the number of terms in the sequence $A$ that precede the term $a_{i}$ and are different from $a_{i}$. Show that, starting from any sequence $A$ as above, fewer than $n$ applications of the transformation $t$ lead to a sequence $B$ such that $t(B)=B$.
|
We go by strong induction on $n$ with the base cases $n=1$ and $n=2$ done by hand. Consider two cases: - If $a_{0}=0$ and $a_{1}=1$, then $1 \leq t\left(a_{i}\right) \leq i$ for $i \geq 1$; now apply induction to $$ \left(t\left(a_{1}\right)-1, t\left(a_{2}\right)-1, \ldots, t\left(a_{n}\right)-1\right) $$ - Otherwise, assume that $a_{0}=a_{1}=\cdots=a_{k-1}=0$ but $a_{k} \neq 0$, where $k \geq 2$. Assume $k<n$ or it's obvious. Then $t\left(a_{i}\right) \neq 0$ for $i \geq k$, thus $t\left(t\left(a_{i}\right)\right) \geq k$ for $i \geq k$, and we can apply induction hypothesis to $$ \left(t\left(t\left(a_{k}\right)\right)-k, \ldots, t\left(t\left(a_{n}\right)\right)-k\right) $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
09b0e774-177a-5fd4-b305-d7c4b76ffecf
| 606,365
|
Let $A B C$ be a triangle. A circle passing through $A$ and $B$ intersects segments $A C$ and $B C$ at $D$ and $E$, respectively. Lines $A B$ and $D E$ intersect at $F$, while lines $B D$ and $C F$ intersect at $M$. Prove that $M F=M C$ if and only if $M B \cdot M D=M C^{2}$.
|
Ceva theorem plus the similar triangles.  We know unconditionally that $$ \measuredangle C B D=\measuredangle E B D=\measuredangle E A D=\measuredangle E A C . $$ Moreover, by Ceva's theorem on $\triangle B C F$, we have $M F=M C \Longleftrightarrow \overline{F C} \| \overline{A E}$. So we have the equivalences $$ \begin{aligned} M F=M C & \Longleftrightarrow \overline{F C} \| \overline{A E} \\ & \Longleftrightarrow \measuredangle F C A=\measuredangle E A C \\ & \Longleftrightarrow \measuredangle M C D=\measuredangle C B D \\ & \Longleftrightarrow M C^{2}=M B \cdot M D \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. A circle passing through $A$ and $B$ intersects segments $A C$ and $B C$ at $D$ and $E$, respectively. Lines $A B$ and $D E$ intersect at $F$, while lines $B D$ and $C F$ intersect at $M$. Prove that $M F=M C$ if and only if $M B \cdot M D=M C^{2}$.
|
Ceva theorem plus the similar triangles.  We know unconditionally that $$ \measuredangle C B D=\measuredangle E B D=\measuredangle E A D=\measuredangle E A C . $$ Moreover, by Ceva's theorem on $\triangle B C F$, we have $M F=M C \Longleftrightarrow \overline{F C} \| \overline{A E}$. So we have the equivalences $$ \begin{aligned} M F=M C & \Longleftrightarrow \overline{F C} \| \overline{A E} \\ & \Longleftrightarrow \measuredangle F C A=\measuredangle E A C \\ & \Longleftrightarrow \measuredangle M C D=\measuredangle C B D \\ & \Longleftrightarrow M C^{2}=M B \cdot M D \end{aligned} $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8ebbeddc-2f9a-5323-8f49-8d11f7fc361b
| 248,182
|
Let $a, b, c$ be positive real numbers. Prove that $$ \frac{(2 a+b+c)^{2}}{2 a^{2}+(b+c)^{2}}+\frac{(2 b+c+a)^{2}}{2 b^{2}+(c+a)^{2}}+\frac{(2 c+a+b)^{2}}{2 c^{2}+(a+b)^{2}} \leq 8 $$
|
This is a canonical example of tangent line trick. Homogenize so that $a+b+c=3$. The desired inequality reads $$ \sum_{\text {cyc }} \frac{(a+3)^{2}}{2 a^{2}+(3-a)^{2}} \leq 8 $$ This follows from $$ f(x)=\frac{(x+3)^{2}}{2 x^{2}+(3-x)^{2}} \leq \frac{1}{3}(4 x+4) $$ which can be checked as $\frac{1}{3}(4 x+4)\left(2 x^{2}+(3-x)^{2}\right)-(x+3)^{2}=(x-1)^{2}(4 x+3) \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that $$ \frac{(2 a+b+c)^{2}}{2 a^{2}+(b+c)^{2}}+\frac{(2 b+c+a)^{2}}{2 b^{2}+(c+a)^{2}}+\frac{(2 c+a+b)^{2}}{2 c^{2}+(a+b)^{2}} \leq 8 $$
|
This is a canonical example of tangent line trick. Homogenize so that $a+b+c=3$. The desired inequality reads $$ \sum_{\text {cyc }} \frac{(a+3)^{2}}{2 a^{2}+(3-a)^{2}} \leq 8 $$ This follows from $$ f(x)=\frac{(x+3)^{2}}{2 x^{2}+(3-x)^{2}} \leq \frac{1}{3}(4 x+4) $$ which can be checked as $\frac{1}{3}(4 x+4)\left(2 x^{2}+(3-x)^{2}\right)-(x+3)^{2}=(x-1)^{2}(4 x+3) \geq 0$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e656ddb2-000a-5ad7-b706-38bf21d6e299
| 606,376
|
At the vertices of a regular hexagon are written six nonnegative integers whose sum is $2003^{2003}$. Bert is allowed to make moves of the following form: he may pick a vertex and replace the number written there by the absolute value of the difference between the numbers written at the two neighboring vertices. Prove that Bert can make a sequence of moves, after which the number 0 appears at all six vertices.
|
If $a \leq b \leq c$ are odd integers, the configuration which has $(a, b-a, b, c-b, c, c-a)$ around the hexagon in some order (up to cyclic permutation and reflection) is said to be great (picture below). Claim - We can reach a great configuration from any configuration with odd sum.  Thus we arrived at a great configuration. Claim - Bert's goal is possible for all great configurations. Otherwise, we can perform the following three operations shown in the figure below, which yield a great configuration whose odd entries are $a, b,|c-2 a|$.  Since $|c-2 a|<c$ unless $a=b=c$, this decreases the sum. So an induction now completes the problem. Remark. One simple idea might be to try to overwrite the maximum number at each point, decreasing the sum. However, this fails on the arrangement $(t, t, 0, t, t, 0)$. Unfortunately, this issue is actually fatal, as the problem has a hidden parity obstruction. The configuration $(1,1,0,1,1,0) \bmod 2$ is invariant modulo 2, and so Bert can walk into a "fatal death-trap" of this shape long before the numbers start becoming equal/zero/etc. In other words, you can mess up on the first move! This is why the initial sum is given to be odd; however, it's not possible for Bert to win so one essentially has to "tip-toe" around the 110110 trap any time one leaves the space of odd sum. That's why the great configurations defined above serve as an anchor, making sure we never veer too far from the safe 101010 configuration.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
At the vertices of a regular hexagon are written six nonnegative integers whose sum is $2003^{2003}$. Bert is allowed to make moves of the following form: he may pick a vertex and replace the number written there by the absolute value of the difference between the numbers written at the two neighboring vertices. Prove that Bert can make a sequence of moves, after which the number 0 appears at all six vertices.
|
If $a \leq b \leq c$ are odd integers, the configuration which has $(a, b-a, b, c-b, c, c-a)$ around the hexagon in some order (up to cyclic permutation and reflection) is said to be great (picture below). Claim - We can reach a great configuration from any configuration with odd sum.  Thus we arrived at a great configuration. Claim - Bert's goal is possible for all great configurations. Otherwise, we can perform the following three operations shown in the figure below, which yield a great configuration whose odd entries are $a, b,|c-2 a|$.  Since $|c-2 a|<c$ unless $a=b=c$, this decreases the sum. So an induction now completes the problem. Remark. One simple idea might be to try to overwrite the maximum number at each point, decreasing the sum. However, this fails on the arrangement $(t, t, 0, t, t, 0)$. Unfortunately, this issue is actually fatal, as the problem has a hidden parity obstruction. The configuration $(1,1,0,1,1,0) \bmod 2$ is invariant modulo 2, and so Bert can walk into a "fatal death-trap" of this shape long before the numbers start becoming equal/zero/etc. In other words, you can mess up on the first move! This is why the initial sum is given to be odd; however, it's not possible for Bert to win so one essentially has to "tip-toe" around the 110110 trap any time one leaves the space of odd sum. That's why the great configurations defined above serve as an anchor, making sure we never veer too far from the safe 101010 configuration.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2003-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
825e2bc6-e0f7-53ff-954a-f9def14c218c
| 606,378
|
Let $A B C D$ be a quadrilateral circumscribed about a circle, whose interior and exterior angles are at least 60 degrees. Prove that $$ \frac{1}{3}\left|A B^{3}-A D^{3}\right| \leq\left|B C^{3}-C D^{3}\right| \leq 3\left|A B^{3}-A D^{3}\right| $$ When does equality hold?
|
Clearly it suffices to show the left inequality. Since $A B+C D=B C+A D \Longrightarrow$ $|A B-A D|=|B C-C D|$, it suffices to prove $$ \frac{1}{3}\left(A B^{2}+A B \cdot A D+A D^{2}\right) \leq B C^{2}+B C \cdot C D+C D^{2} $$ This follows by noting that $$ \begin{aligned} B C^{2}+B C \cdot C D+C D^{2} & \geq B C^{2}+C D^{2}-2(B C)(C D) \cos (\angle B C D) \\ & =B D^{2} \\ & =A B^{2}+A D^{2}-2(A B)(A D) \cos (\angle B A D) \\ & \geq A B^{2}+A D^{2}-A B \cdot A D \\ & \geq \frac{1}{3}\left(A B^{2}+A D^{2}+A B \cdot A D\right) \end{aligned} $$ the last line following by AM-GM. The equality holds iff $A B C D$ is a kite with $A B=A D, C B=C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C D$ be a quadrilateral circumscribed about a circle, whose interior and exterior angles are at least 60 degrees. Prove that $$ \frac{1}{3}\left|A B^{3}-A D^{3}\right| \leq\left|B C^{3}-C D^{3}\right| \leq 3\left|A B^{3}-A D^{3}\right| $$ When does equality hold?
|
Clearly it suffices to show the left inequality. Since $A B+C D=B C+A D \Longrightarrow$ $|A B-A D|=|B C-C D|$, it suffices to prove $$ \frac{1}{3}\left(A B^{2}+A B \cdot A D+A D^{2}\right) \leq B C^{2}+B C \cdot C D+C D^{2} $$ This follows by noting that $$ \begin{aligned} B C^{2}+B C \cdot C D+C D^{2} & \geq B C^{2}+C D^{2}-2(B C)(C D) \cos (\angle B C D) \\ & =B D^{2} \\ & =A B^{2}+A D^{2}-2(A B)(A D) \cos (\angle B A D) \\ & \geq A B^{2}+A D^{2}-A B \cdot A D \\ & \geq \frac{1}{3}\left(A B^{2}+A D^{2}+A B \cdot A D\right) \end{aligned} $$ the last line following by AM-GM. The equality holds iff $A B C D$ is a kite with $A B=A D, C B=C D$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2004-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
10ac4b3f-7986-5233-a0c6-4aa4c47d8541
| 606,381
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be integers whose greatest common divisor is 1 . Let $S$ be a set of integers with the following properties: (a) $a_{i} \in S$ for $i=1, \ldots, n$. (b) $a_{i}-a_{j} \in S$ for $i, j=1, \ldots, n$, not necessarily distinct. (c) If $x, y \in S$ and $x+y \in S$, then $x-y \in S$ too. Prove that $S=\mathbb{Z}$.
|
The idea is to show any linear combination of the $a_{i}$ are in $S$, which implies (by Bezout) that $S=\mathbb{Z}$. This is pretty intuitive, but the details require some care (in particular there is a parity obstruction at the second lemma). First, we make the following simple observations: - $0 \in S$, by putting $i=j=1$ in (b). - $s \in S \Longleftrightarrow-s \in S$, by putting $x=0$ in (c). Now, we prove that: ## Lemma For any integers $c, d$, and indices $i, j$, we have $c a_{i}+d a_{j} \in S$. ## Lemma For any nonzero integers $c_{1}, c_{2}, \ldots, c_{m}$, and any distinct indices $\left\{i_{1}, i_{2}, \ldots, i_{m}\right\}$, we have $$ \sum_{k} c_{k} a_{i_{k}} \in S $$ For the inductive step, we will assume that $i_{1}=1, i_{2}=2$, et cetera, for notational convenience. The proof is then split into two cases. First Case: some $c_{i}$ is even. WLOG $c_{1} \neq 0$ is even and note that $$ \begin{aligned} x & :=\frac{1}{2} c_{1} a_{1}+\sum_{k \geq 3} c_{k} a_{k} \in S \\ y & :=-\frac{1}{2} c_{1} a_{1}-c_{2} a_{2} \in S \end{aligned} $$ $$ \begin{aligned} x+y & =-c_{2} a_{2}+\sum_{k \geq 3} c_{k} a_{k} \in S \\ \Longrightarrow x-y & =\sum_{k \geq 1} c_{k} a_{k} \in S . \end{aligned} $$ Second Case: all $c_{i}$ are odd. We reduce this to the first case as follows. Let $u=\frac{a_{1}}{\operatorname{gcd}\left(a_{1}, a_{2}\right)}$ and $v=\frac{a_{2}}{\operatorname{gcd}\left(a_{1}, a_{2}\right)}$. Then $\operatorname{gcd}(u, v)=1$ and so WLOG $u$ is odd. Then $$ c_{1} a_{1}+c_{2} a_{2}=\left(c_{1}+v\right) a_{1}+\left(c_{2}-u\right) a_{2} $$ and so we can replace our given combination by $\left(c_{1}+v\right) a_{1}+\left(c_{2}-u\right) a_{2}+c_{3} a_{3}+\ldots$ which now has an even coefficient for $a_{2}$. We then apply the lemma at $m=n$; this implies the result since Bezout's lemma implies that $\sum c_{i} a_{i}=1$ for some choice of $c_{i} \in \mathbb{Z}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be integers whose greatest common divisor is 1 . Let $S$ be a set of integers with the following properties: (a) $a_{i} \in S$ for $i=1, \ldots, n$. (b) $a_{i}-a_{j} \in S$ for $i, j=1, \ldots, n$, not necessarily distinct. (c) If $x, y \in S$ and $x+y \in S$, then $x-y \in S$ too. Prove that $S=\mathbb{Z}$.
|
The idea is to show any linear combination of the $a_{i}$ are in $S$, which implies (by Bezout) that $S=\mathbb{Z}$. This is pretty intuitive, but the details require some care (in particular there is a parity obstruction at the second lemma). First, we make the following simple observations: - $0 \in S$, by putting $i=j=1$ in (b). - $s \in S \Longleftrightarrow-s \in S$, by putting $x=0$ in (c). Now, we prove that: ## Lemma For any integers $c, d$, and indices $i, j$, we have $c a_{i}+d a_{j} \in S$. ## Lemma For any nonzero integers $c_{1}, c_{2}, \ldots, c_{m}$, and any distinct indices $\left\{i_{1}, i_{2}, \ldots, i_{m}\right\}$, we have $$ \sum_{k} c_{k} a_{i_{k}} \in S $$ For the inductive step, we will assume that $i_{1}=1, i_{2}=2$, et cetera, for notational convenience. The proof is then split into two cases. First Case: some $c_{i}$ is even. WLOG $c_{1} \neq 0$ is even and note that $$ \begin{aligned} x & :=\frac{1}{2} c_{1} a_{1}+\sum_{k \geq 3} c_{k} a_{k} \in S \\ y & :=-\frac{1}{2} c_{1} a_{1}-c_{2} a_{2} \in S \end{aligned} $$ $$ \begin{aligned} x+y & =-c_{2} a_{2}+\sum_{k \geq 3} c_{k} a_{k} \in S \\ \Longrightarrow x-y & =\sum_{k \geq 1} c_{k} a_{k} \in S . \end{aligned} $$ Second Case: all $c_{i}$ are odd. We reduce this to the first case as follows. Let $u=\frac{a_{1}}{\operatorname{gcd}\left(a_{1}, a_{2}\right)}$ and $v=\frac{a_{2}}{\operatorname{gcd}\left(a_{1}, a_{2}\right)}$. Then $\operatorname{gcd}(u, v)=1$ and so WLOG $u$ is odd. Then $$ c_{1} a_{1}+c_{2} a_{2}=\left(c_{1}+v\right) a_{1}+\left(c_{2}-u\right) a_{2} $$ and so we can replace our given combination by $\left(c_{1}+v\right) a_{1}+\left(c_{2}-u\right) a_{2}+c_{3} a_{3}+\ldots$ which now has an even coefficient for $a_{2}$. We then apply the lemma at $m=n$; this implies the result since Bezout's lemma implies that $\sum c_{i} a_{i}=1$ for some choice of $c_{i} \in \mathbb{Z}$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2004-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
7a82207b-5a57-5d8d-80aa-ff1dd834081a
| 606,384
|
Alice and Bob play a game on a 6 by 6 grid. On his turn, a player chooses a rational number not yet appearing in the grid and writes it in an empty square of the grid. Alice goes first and then the players alternate. When all squares have numbers written in them, in each row, the square with the greatest number in that row is colored black. Alice wins if he can then draw a line from the top of the grid to the bottom of the grid that stays in black squares, and Bob wins if he can't. (If two squares share a vertex, Alice can draw a line from one to the other that stays in those two squares.) Find, with proof, a winning strategy for one of the players.
|
Bob can win. Label the first two rows as follows: $$ \left[\begin{array}{cccccc} a & b & c & d & e & f \\ d^{\prime} & e^{\prime} & f^{\prime} & a^{\prime} & b^{\prime} & c^{\prime} \end{array}\right] $$ These twelve boxes thus come in six pairs, $\left(a, a^{\prime}\right),\left(b, b^{\prime}\right)$ and so on. Claim - Bob can ensure that the order relation of the labels is the same between the two rows, meaning that $a<b$ if and only if $a^{\prime}<b^{\prime}$, and so on. When Alice writes a number in any other row, Bob writes anywhere in rows 3 to 6 . Under this strategy the black squares in the first two rows will be a pair and therefore will not touch, so Bob wins.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob play a game on a 6 by 6 grid. On his turn, a player chooses a rational number not yet appearing in the grid and writes it in an empty square of the grid. Alice goes first and then the players alternate. When all squares have numbers written in them, in each row, the square with the greatest number in that row is colored black. Alice wins if he can then draw a line from the top of the grid to the bottom of the grid that stays in black squares, and Bob wins if he can't. (If two squares share a vertex, Alice can draw a line from one to the other that stays in those two squares.) Find, with proof, a winning strategy for one of the players.
|
Bob can win. Label the first two rows as follows: $$ \left[\begin{array}{cccccc} a & b & c & d & e & f \\ d^{\prime} & e^{\prime} & f^{\prime} & a^{\prime} & b^{\prime} & c^{\prime} \end{array}\right] $$ These twelve boxes thus come in six pairs, $\left(a, a^{\prime}\right),\left(b, b^{\prime}\right)$ and so on. Claim - Bob can ensure that the order relation of the labels is the same between the two rows, meaning that $a<b$ if and only if $a^{\prime}<b^{\prime}$, and so on. When Alice writes a number in any other row, Bob writes anywhere in rows 3 to 6 . Under this strategy the black squares in the first two rows will be a pair and therefore will not touch, so Bob wins.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2004-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ad0ed23b-3273-5a71-a448-be2a2d319c66
| 606,385
|
A circle $\omega$ is inscribed in a quadrilateral $A B C D$. Let $I$ be the center of $\omega$. Suppose that $$ (A I+D I)^{2}+(B I+C I)^{2}=(A B+C D)^{2} $$ Prove that $A B C D$ is an isosceles trapezoid.
|
$$ a+b+c+d=a b c+b c d+c d a+d a b $$ which can be proved by, say tan-addition formula. Then, the content of the problem is to show that $$ \left(\sqrt{a^{2}+1}+\sqrt{d^{2}+1}\right)^{2}+\left(\sqrt{b^{2}+1}+\sqrt{c^{2}+1}\right)^{2} \leq(a+b+c+d)^{2} $$ subject to $(\star)$, with equality only when $a=d=\frac{1}{b}=\frac{1}{c}$. Let $S=a b+b c+c d+d a+a c+b d$. Then the inequality is $$ \sqrt{\left(a^{2}+1\right)\left(d^{2}+1\right)}+\sqrt{\left(b^{2}+1\right)\left(c^{2}+1\right)} \leq S-2 . $$ Now, by USAMO 2014 Problem 1 and the condition $(\star)$, we have that $\left(a^{2}+1\right)\left(b^{2}+\right.$ 1) $\left(c^{2}+1\right)\left(d^{2}+1\right)=(S-a b c d-1)^{2}$. So squaring both sides, the inequality becomes $$ (a d)^{2}+(b c)^{2}+a^{2}+b^{2}+c^{2}+d^{2} \leq S^{2}-6 S+2 a b c d+4 $$ To simplify this, we use the identities $$ \begin{aligned} S^{2} & =6 a b c d+\sum_{\mathrm{sym}} a^{2} b c+\frac{1}{4} \sum_{\mathrm{sym}} a^{2} b^{2} \\ (a+b+c+d)^{2} & =(a b c+b c d+c d a+d a b)(a+b+c+d) \\ & =4 a b c d+\frac{1}{2} \sum_{\mathrm{sym}} a^{2} b c \end{aligned} $$ So $S^{2}+2 a b c d=\frac{1}{4} \sum_{\text {sym }} a^{2} b^{2}+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+4 S$ and the inequality we want to prove reduces to $$ 2 S \leq(a b)^{2}+(a c)^{2}+(b d)^{2}+(c d)^{2}+4+a^{2}+b^{2}+c^{2}+d^{2} $$ This follows by AM-GM since $$ \begin{aligned} (a b)^{2}+1 & \geq 2 a b \\ (a c)^{2}+1 & \geq 2 a c \\ (b d)^{2}+1 & \geq 2 b d \\ (c d)^{2}+1 & \geq 2 c d \\ a^{2}+d^{2} & \geq 2 a d \\ b^{2}+c^{2} & \geq 2 b c \end{aligned} $$ The equality case is when $a b=a c=b d=c d=1, a=d, b=c$, as needed to imply an isosceles trapezoid. Remark. Note that a priori one expects an inequality. Indeed, - Quadrilaterals with incircles have four degrees of freedom. - There is one condition imposed. - Isosceles trapezoid with incircles have two degrees of freedom.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle $\omega$ is inscribed in a quadrilateral $A B C D$. Let $I$ be the center of $\omega$. Suppose that $$ (A I+D I)^{2}+(B I+C I)^{2}=(A B+C D)^{2} $$ Prove that $A B C D$ is an isosceles trapezoid.
|
$$ a+b+c+d=a b c+b c d+c d a+d a b $$ which can be proved by, say tan-addition formula. Then, the content of the problem is to show that $$ \left(\sqrt{a^{2}+1}+\sqrt{d^{2}+1}\right)^{2}+\left(\sqrt{b^{2}+1}+\sqrt{c^{2}+1}\right)^{2} \leq(a+b+c+d)^{2} $$ subject to $(\star)$, with equality only when $a=d=\frac{1}{b}=\frac{1}{c}$. Let $S=a b+b c+c d+d a+a c+b d$. Then the inequality is $$ \sqrt{\left(a^{2}+1\right)\left(d^{2}+1\right)}+\sqrt{\left(b^{2}+1\right)\left(c^{2}+1\right)} \leq S-2 . $$ Now, by USAMO 2014 Problem 1 and the condition $(\star)$, we have that $\left(a^{2}+1\right)\left(b^{2}+\right.$ 1) $\left(c^{2}+1\right)\left(d^{2}+1\right)=(S-a b c d-1)^{2}$. So squaring both sides, the inequality becomes $$ (a d)^{2}+(b c)^{2}+a^{2}+b^{2}+c^{2}+d^{2} \leq S^{2}-6 S+2 a b c d+4 $$ To simplify this, we use the identities $$ \begin{aligned} S^{2} & =6 a b c d+\sum_{\mathrm{sym}} a^{2} b c+\frac{1}{4} \sum_{\mathrm{sym}} a^{2} b^{2} \\ (a+b+c+d)^{2} & =(a b c+b c d+c d a+d a b)(a+b+c+d) \\ & =4 a b c d+\frac{1}{2} \sum_{\mathrm{sym}} a^{2} b c \end{aligned} $$ So $S^{2}+2 a b c d=\frac{1}{4} \sum_{\text {sym }} a^{2} b^{2}+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+4 S$ and the inequality we want to prove reduces to $$ 2 S \leq(a b)^{2}+(a c)^{2}+(b d)^{2}+(c d)^{2}+4+a^{2}+b^{2}+c^{2}+d^{2} $$ This follows by AM-GM since $$ \begin{aligned} (a b)^{2}+1 & \geq 2 a b \\ (a c)^{2}+1 & \geq 2 a c \\ (b d)^{2}+1 & \geq 2 b d \\ (c d)^{2}+1 & \geq 2 c d \\ a^{2}+d^{2} & \geq 2 a d \\ b^{2}+c^{2} & \geq 2 b c \end{aligned} $$ The equality case is when $a b=a c=b d=c d=1, a=d, b=c$, as needed to imply an isosceles trapezoid. Remark. Note that a priori one expects an inequality. Indeed, - Quadrilaterals with incircles have four degrees of freedom. - There is one condition imposed. - Isosceles trapezoid with incircles have two degrees of freedom.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2004-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d7b35ff8-6f28-5125-b8e4-35a924d86e6f
| 606,388
|
Let $A B C$ be an acute-angled triangle, and let $P$ and $Q$ be two points on side $B C$. Construct a point $C_{1}$ in such a way that the convex quadrilateral $A P B C_{1}$ is cyclic, $\overline{Q C_{1}} \| \overline{C A}$, and $C_{1}$ and $Q$ lie on opposite sides of line $A B$. Construct a point $B_{1}$ in such a way that the convex quadrilateral $A P C B_{1}$ is cyclic, $\overline{Q B_{1}} \| \overline{B A}$, and $B_{1}$ and $Q$ lie on opposite sides of line $A C$. Prove that the points $B_{1}, C_{1}, P$, and $Q$ lie on a circle.
|
It is enough to prove that $A, B_{1}$, and $C_{1}$ are collinear, since then $\measuredangle C_{1} Q P=\measuredangle A C P=$ $\measuredangle A B_{1} P=\measuredangle C_{1} B_{1} P$.  ब First solution. Let $T$ be the second intersection of $\overline{A C_{1}}$ with $(A P C)$. Then readily $\triangle P C_{1} T \sim \triangle A B C$. Consequently, $\overline{Q C_{1}} \| \overline{A C}$ implies $T C_{1} Q P$ cyclic. Finally, $\overline{T Q} \| \overline{A B}$ now follows from the cyclic condition, so $T=B_{1}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle, and let $P$ and $Q$ be two points on side $B C$. Construct a point $C_{1}$ in such a way that the convex quadrilateral $A P B C_{1}$ is cyclic, $\overline{Q C_{1}} \| \overline{C A}$, and $C_{1}$ and $Q$ lie on opposite sides of line $A B$. Construct a point $B_{1}$ in such a way that the convex quadrilateral $A P C B_{1}$ is cyclic, $\overline{Q B_{1}} \| \overline{B A}$, and $B_{1}$ and $Q$ lie on opposite sides of line $A C$. Prove that the points $B_{1}, C_{1}, P$, and $Q$ lie on a circle.
|
It is enough to prove that $A, B_{1}$, and $C_{1}$ are collinear, since then $\measuredangle C_{1} Q P=\measuredangle A C P=$ $\measuredangle A B_{1} P=\measuredangle C_{1} B_{1} P$.  ब First solution. Let $T$ be the second intersection of $\overline{A C_{1}}$ with $(A P C)$. Then readily $\triangle P C_{1} T \sim \triangle A B C$. Consequently, $\overline{Q C_{1}} \| \overline{A C}$ implies $T C_{1} Q P$ cyclic. Finally, $\overline{T Q} \| \overline{A B}$ now follows from the cyclic condition, so $T=B_{1}$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2005-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8716218e-c8ab-5d1b-abdb-fb71c06c4143
| 248,295
|
Let $A B C$ be an acute-angled triangle, and let $P$ and $Q$ be two points on side $B C$. Construct a point $C_{1}$ in such a way that the convex quadrilateral $A P B C_{1}$ is cyclic, $\overline{Q C_{1}} \| \overline{C A}$, and $C_{1}$ and $Q$ lie on opposite sides of line $A B$. Construct a point $B_{1}$ in such a way that the convex quadrilateral $A P C B_{1}$ is cyclic, $\overline{Q B_{1}} \| \overline{B A}$, and $B_{1}$ and $Q$ lie on opposite sides of line $A C$. Prove that the points $B_{1}, C_{1}, P$, and $Q$ lie on a circle.
|
It is enough to prove that $A, B_{1}$, and $C_{1}$ are collinear, since then $\measuredangle C_{1} Q P=\measuredangle A C P=$ $\measuredangle A B_{1} P=\measuredangle C_{1} B_{1} P$.  \ Second solution. One may also use barycentric coordinates. Let $P=(0, m, n)$ and $Q=(0, r, s)$ with $m+n=r+s=1$. Once again, $$ (A P B):-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(a^{2} m \cdot z\right)=0 $$ Set $C_{1}=(s-z, r, z)$, where $C_{1} Q \| A C$ follows by $(s-z)+r+z=1$. We solve for this $z$. $$ \begin{aligned} 0 & =-a^{2} r z+(s-z)\left(-b^{2} z-c^{2} r\right)+a^{2} m z \\ & =b^{2} z^{2}+\left(-s b^{2}+r c^{2}\right) z-a^{2} r z+a^{2} m z-c^{2} r s \\ & =b^{2} z^{2}+\left(-s b^{2}+r c^{2}+a^{2}(m-r)\right) z-c^{2} r s \\ \Longrightarrow 0 & =r b^{2}\left(\frac{z}{r}\right)^{2}+\left(-s b^{2}+r c^{2}+a^{2}(m-r)\right)\left(\frac{z}{r}\right)-c^{2} s \end{aligned} $$ So the quotient of the $z$ and $y$ coordinates of $C_{1}$ satisfies this quadratic. Similarly, if $B_{1}=(r-y, y, s)$ we obtain that $$ 0=s c^{2}\left(\frac{y}{s}\right)^{2}+\left(-r c^{2}+s b^{2}+a^{2}(n-s)\right)\left(\frac{y}{s}\right)-b^{2} r $$ Since these two quadratics are the same when one is written backwards (and negated), it follows that their roots are reciprocals. But the roots of the quadratics represent $\frac{z}{y}$ and $\frac{y}{z}$ for the points $C_{1}$ and $B_{1}$, respectively. This implies (with some configuration blah) that the points $B_{1}$ and $C_{1}$ are collinear with $A=(1,0,0)$ (in some line of the form $\frac{y}{z}=k$ ), as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle, and let $P$ and $Q$ be two points on side $B C$. Construct a point $C_{1}$ in such a way that the convex quadrilateral $A P B C_{1}$ is cyclic, $\overline{Q C_{1}} \| \overline{C A}$, and $C_{1}$ and $Q$ lie on opposite sides of line $A B$. Construct a point $B_{1}$ in such a way that the convex quadrilateral $A P C B_{1}$ is cyclic, $\overline{Q B_{1}} \| \overline{B A}$, and $B_{1}$ and $Q$ lie on opposite sides of line $A C$. Prove that the points $B_{1}, C_{1}, P$, and $Q$ lie on a circle.
|
It is enough to prove that $A, B_{1}$, and $C_{1}$ are collinear, since then $\measuredangle C_{1} Q P=\measuredangle A C P=$ $\measuredangle A B_{1} P=\measuredangle C_{1} B_{1} P$.  \ Second solution. One may also use barycentric coordinates. Let $P=(0, m, n)$ and $Q=(0, r, s)$ with $m+n=r+s=1$. Once again, $$ (A P B):-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(a^{2} m \cdot z\right)=0 $$ Set $C_{1}=(s-z, r, z)$, where $C_{1} Q \| A C$ follows by $(s-z)+r+z=1$. We solve for this $z$. $$ \begin{aligned} 0 & =-a^{2} r z+(s-z)\left(-b^{2} z-c^{2} r\right)+a^{2} m z \\ & =b^{2} z^{2}+\left(-s b^{2}+r c^{2}\right) z-a^{2} r z+a^{2} m z-c^{2} r s \\ & =b^{2} z^{2}+\left(-s b^{2}+r c^{2}+a^{2}(m-r)\right) z-c^{2} r s \\ \Longrightarrow 0 & =r b^{2}\left(\frac{z}{r}\right)^{2}+\left(-s b^{2}+r c^{2}+a^{2}(m-r)\right)\left(\frac{z}{r}\right)-c^{2} s \end{aligned} $$ So the quotient of the $z$ and $y$ coordinates of $C_{1}$ satisfies this quadratic. Similarly, if $B_{1}=(r-y, y, s)$ we obtain that $$ 0=s c^{2}\left(\frac{y}{s}\right)^{2}+\left(-r c^{2}+s b^{2}+a^{2}(n-s)\right)\left(\frac{y}{s}\right)-b^{2} r $$ Since these two quadratics are the same when one is written backwards (and negated), it follows that their roots are reciprocals. But the roots of the quadratics represent $\frac{z}{y}$ and $\frac{y}{z}$ for the points $C_{1}$ and $B_{1}$, respectively. This implies (with some configuration blah) that the points $B_{1}$ and $C_{1}$ are collinear with $A=(1,0,0)$ (in some line of the form $\frac{y}{z}=k$ ), as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2005-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8716218e-c8ab-5d1b-abdb-fb71c06c4143
| 248,295
|
Let $n>1$ be an integer. Suppose $2 n$ points are given in the plane, no three of which are collinear. Suppose $n$ of the given $2 n$ points are colored blue and the other $n$ colored red. A line in the plane is called a balancing line if it passes through one blue and one red point and, for each side of the line, the number of blue points on that side is equal to the number of red points on the same side. Prove that there exist at least two balancing lines.
|
Consider the convex hull $\mathcal{H}$ of the polygon. There are two cases. 【 Easy case: the convex hull has both colors. If the convex hull $\mathcal{H}$ is not all the same color, there exist two edges of $\mathcal{H}$ (at least) which have differently colored endpoints. The extensions of those sides form balancing lines; indeed given any such line $\ell$ one side of $\ell$ has no points, the other has $n-1$ red and $n-1$ blue points. 【 Harder case: the convex hull is all one color. Now assume $\mathcal{H}$ is all blue (WLOG). We will prove there are at least $|\mathcal{H}|$ balancing lines in the following way. Claim - For any vertex $B$ of $\mathcal{H}$ there is a balancing line through it.  During this process, we consider the set of points on the same side of $\ell$ as $C$, and let $x$ be the number of such red points minus the number of such blue points. Note that: - Every time $\ell$ touches a blue point, $x$ increases by 1 . - Every time $\ell$ touches a red point, $x$ decreases by 1 . - Initially, $x=+1$. - Just before reaching the end we have $x=-1$. So at the moment where $x$ first equals zero, we have found our balancing line.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n>1$ be an integer. Suppose $2 n$ points are given in the plane, no three of which are collinear. Suppose $n$ of the given $2 n$ points are colored blue and the other $n$ colored red. A line in the plane is called a balancing line if it passes through one blue and one red point and, for each side of the line, the number of blue points on that side is equal to the number of red points on the same side. Prove that there exist at least two balancing lines.
|
Consider the convex hull $\mathcal{H}$ of the polygon. There are two cases. 【 Easy case: the convex hull has both colors. If the convex hull $\mathcal{H}$ is not all the same color, there exist two edges of $\mathcal{H}$ (at least) which have differently colored endpoints. The extensions of those sides form balancing lines; indeed given any such line $\ell$ one side of $\ell$ has no points, the other has $n-1$ red and $n-1$ blue points. 【 Harder case: the convex hull is all one color. Now assume $\mathcal{H}$ is all blue (WLOG). We will prove there are at least $|\mathcal{H}|$ balancing lines in the following way. Claim - For any vertex $B$ of $\mathcal{H}$ there is a balancing line through it.  During this process, we consider the set of points on the same side of $\ell$ as $C$, and let $x$ be the number of such red points minus the number of such blue points. Note that: - Every time $\ell$ touches a blue point, $x$ increases by 1 . - Every time $\ell$ touches a red point, $x$ decreases by 1 . - Initially, $x=+1$. - Just before reaching the end we have $x=-1$. So at the moment where $x$ first equals zero, we have found our balancing line.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2005-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
38e84f68-deae-5f13-9168-6a7ce2c75fac
| 248,316
|
For a positive integer $m$, let $s(m)$ denote the sum of the decimal digits of $m$. A set $S$ positive integers is $k$-stable if $s\left(\sum_{x \in X} x\right)=k$ for any nonempty subset $X \subseteq S$. For each integer $n \geq 2$ let $f(n)$ be the minimal $k$ for which there exists a $k$-stable set with $n$ integers. Prove that there are constants $0<C_{1}<C_{2}$ with $$ C_{1} \log _{10} n \leq f(n) \leq C_{2} \log _{10} n . $$
|
【 Construction showing $f(n) \leq 9\left\lceil\log _{10}\binom{n+1}{2}\right\rceil$. Let $n \geq 1$ and $e \geq 1$ be integers satisfying $1+2+\cdots+n<10^{e}$. Consider the set $$ S=\left\{10^{e}-1,2\left(10^{e}-1\right), \ldots, n\left(10^{e}-1\right)\right\} $$ For example, if $n=6$ and $e=3$, we have $S=\{999,1998,2997,3996,4995,5994\}$. The set $S$ here is easily seen to be $9 e$-stable. Thus $f(n) \leq 9\left\lceil\log _{10}\binom{n+1}{2}\right\rceil$, proving one direction. Remark. I think the problem is actually more natural with a multiset $S$ rather than a vanilla set, in which case $S=\left\{10^{e}-1,10^{e}-1, \ldots, 10^{e}-1\right\}$ works fine, and is easier to think of. In some sense the actual construction is obtained by starting with this one, and then pushing together the terms together in order to get the terms to be distinct, hence the $1+2+\cdots+n$ appearance. Claim - Let $k$ be a positive integer. In any (multi)set $S$ of more than $12^{k}$ integers, there exists a subset whose sum of decimal digits exceeds $k$. - If the $i$ th digit from the right of $\Sigma$ is nonzero, then arbitrarily partition the numbers on the board into groups of 10 , erasing any leftover numbers. Within each group of 10 , we can find a nonempty subset with sum $0 \bmod 10^{i}$; we then erase each group and replace it with that sum. - If the $i$ th digit from the right of $\Sigma$ is zero, but some entry on the board is not divisible by $10^{i}$, then we erase that entry and add it to $\Sigma$. Then we do the grouping as in the previous step. - If the $i$ th digit from the right of $\Sigma$ is zero, and all entries on the board are divisible by $10^{i}$, we do nothing and move on to the next step. This process ends when no numbers remain on the blackboard. The first and second cases occur at least $k+1$ times (the number of entries decreases by a factor of at most 12 each step), and each time $\Sigma$ gets some nonzero digit, which is never changed at later steps. Therefore $\Sigma$ has sum of digits at least $k+1$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $m$, let $s(m)$ denote the sum of the decimal digits of $m$. A set $S$ positive integers is $k$-stable if $s\left(\sum_{x \in X} x\right)=k$ for any nonempty subset $X \subseteq S$. For each integer $n \geq 2$ let $f(n)$ be the minimal $k$ for which there exists a $k$-stable set with $n$ integers. Prove that there are constants $0<C_{1}<C_{2}$ with $$ C_{1} \log _{10} n \leq f(n) \leq C_{2} \log _{10} n . $$
|
【 Construction showing $f(n) \leq 9\left\lceil\log _{10}\binom{n+1}{2}\right\rceil$. Let $n \geq 1$ and $e \geq 1$ be integers satisfying $1+2+\cdots+n<10^{e}$. Consider the set $$ S=\left\{10^{e}-1,2\left(10^{e}-1\right), \ldots, n\left(10^{e}-1\right)\right\} $$ For example, if $n=6$ and $e=3$, we have $S=\{999,1998,2997,3996,4995,5994\}$. The set $S$ here is easily seen to be $9 e$-stable. Thus $f(n) \leq 9\left\lceil\log _{10}\binom{n+1}{2}\right\rceil$, proving one direction. Remark. I think the problem is actually more natural with a multiset $S$ rather than a vanilla set, in which case $S=\left\{10^{e}-1,10^{e}-1, \ldots, 10^{e}-1\right\}$ works fine, and is easier to think of. In some sense the actual construction is obtained by starting with this one, and then pushing together the terms together in order to get the terms to be distinct, hence the $1+2+\cdots+n$ appearance. Claim - Let $k$ be a positive integer. In any (multi)set $S$ of more than $12^{k}$ integers, there exists a subset whose sum of decimal digits exceeds $k$. - If the $i$ th digit from the right of $\Sigma$ is nonzero, then arbitrarily partition the numbers on the board into groups of 10 , erasing any leftover numbers. Within each group of 10 , we can find a nonempty subset with sum $0 \bmod 10^{i}$; we then erase each group and replace it with that sum. - If the $i$ th digit from the right of $\Sigma$ is zero, but some entry on the board is not divisible by $10^{i}$, then we erase that entry and add it to $\Sigma$. Then we do the grouping as in the previous step. - If the $i$ th digit from the right of $\Sigma$ is zero, and all entries on the board are divisible by $10^{i}$, we do nothing and move on to the next step. This process ends when no numbers remain on the blackboard. The first and second cases occur at least $k+1$ times (the number of entries decreases by a factor of at most 12 each step), and each time $\Sigma$ gets some nonzero digit, which is never changed at later steps. Therefore $\Sigma$ has sum of digits at least $k+1$ as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2005-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
49f190e2-6f3a-5d1c-944d-edaf7cf40412
| 606,405
|
Let $p$ be a prime number and let $s$ be an integer with $0<s<p$. Prove that there exist integers $m$ and $n$ with $0<m<n<p$ and $$ \left\{\frac{s m}{p}\right\}<\left\{\frac{s n}{p}\right\}<\frac{s}{p} $$ if and only if $s$ is not a divisor of $p-1$.
|
It's equivalent to $m s \bmod p<n s \bmod p<s$, where $x \bmod p$ means the remainder when $x$ is divided by $p$, by slight abuse of notation. We will assume $s \geq 2$ for simplicity, since the case $s=1$ is clear. For any $x \in\{1,2, \ldots, s-1\}$ we define $f(x)$ to be the unique number in $\{1, \ldots, p-1\}$ such that $s \cdot f(x) \bmod p=x$. Then, $m$ and $n$ fail to exist exactly when $$ f(s-1)<f(s-2)<\cdots<f(1) $$ We give the following explicit description of $f$ : choose $t \equiv-s^{-1}(\bmod p), 0<t<p$. Then $f(x)=1+(s-x) \cdot t \bmod p$. So our displayed inequality is equivalent to $$ (1+t) \bmod p<(1+2 t) \bmod p<(1+3 t) \bmod p<\cdots<(1+(s-1) t) \bmod p $$ This just means that the sequence $1+k t$ never "wraps around" modulo $p$ as we take $k=1,2, \ldots, s-1$. Since we assumed $s \neq 1$, we have $0<1+t<p$. Now since $1+k t$ never wraps around as $k=1,2, \ldots, s-1$, and increases in increments of $t$, it follows that $1+k t<p$ for all $k=1,2, \ldots, s-1$. Finally, as $1+s t \equiv 0(\bmod p)$ we get $1+s t=p$. In summary, $m, n$ fail to exist precisely when $1+s t=p$. That is of course equivalent to $s \mid p-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number and let $s$ be an integer with $0<s<p$. Prove that there exist integers $m$ and $n$ with $0<m<n<p$ and $$ \left\{\frac{s m}{p}\right\}<\left\{\frac{s n}{p}\right\}<\frac{s}{p} $$ if and only if $s$ is not a divisor of $p-1$.
|
It's equivalent to $m s \bmod p<n s \bmod p<s$, where $x \bmod p$ means the remainder when $x$ is divided by $p$, by slight abuse of notation. We will assume $s \geq 2$ for simplicity, since the case $s=1$ is clear. For any $x \in\{1,2, \ldots, s-1\}$ we define $f(x)$ to be the unique number in $\{1, \ldots, p-1\}$ such that $s \cdot f(x) \bmod p=x$. Then, $m$ and $n$ fail to exist exactly when $$ f(s-1)<f(s-2)<\cdots<f(1) $$ We give the following explicit description of $f$ : choose $t \equiv-s^{-1}(\bmod p), 0<t<p$. Then $f(x)=1+(s-x) \cdot t \bmod p$. So our displayed inequality is equivalent to $$ (1+t) \bmod p<(1+2 t) \bmod p<(1+3 t) \bmod p<\cdots<(1+(s-1) t) \bmod p $$ This just means that the sequence $1+k t$ never "wraps around" modulo $p$ as we take $k=1,2, \ldots, s-1$. Since we assumed $s \neq 1$, we have $0<1+t<p$. Now since $1+k t$ never wraps around as $k=1,2, \ldots, s-1$, and increases in increments of $t$, it follows that $1+k t<p$ for all $k=1,2, \ldots, s-1$. Finally, as $1+s t \equiv 0(\bmod p)$ we get $1+s t=p$. In summary, $m, n$ fail to exist precisely when $1+s t=p$. That is of course equivalent to $s \mid p-1$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2006-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e84fba85-1059-5c60-b354-040e0bd92b45
| 606,409
|
For integral $m$, let $p(m)$ be the greatest prime divisor of $m$. By convention, we set $p( \pm 1)=1$ and $p(0)=\infty$. Find all polynomials $f$ with integer coefficients such that the sequence $$ \left\{p\left(f\left(n^{2}\right)\right)-2 n\right\}_{n \geq 0} $$ is bounded above. (In particular, this requires $f\left(n^{2}\right) \neq 0$ for $n \geq 0$.)
|
If $f$ is the (possibly empty) product of linear factors of the form $4 n-a^{2}$, then it satisfies the condition. We will prove no other polynomials work. In what follows, assume $f$ is irreducible and nonconstant. It suffices to show for every positive integer $c$, there exists a prime $p$ and a nonnegative integer $n$ such that $n \leq \frac{p-1}{2}-c$ and $p$ divides $f\left(n^{2}\right)$. Firstly, recall there are infinitely many odd primes $p$, with $p>c$, such that $p$ divides some $f\left(n^{2}\right)$, by Schur's Theorem. Looking mod such a $p$ we can find $n$ between 0 and $\frac{p-1}{2}\left(\right.$ since $\left.n^{2} \equiv(-n)^{2}(\bmod p)\right)$. We claim that only finitely many $p$ from this set can fail now. For if a $p$ fails, then its $n$ must be between $\frac{p-1}{2}-c$ and $\frac{p-1}{2}$. That means for some $0 \leq k \leq c$ we have $$ 0 \equiv f\left(\left(\frac{p-1}{2}-k\right)^{2}\right) \equiv f\left(\left(k+\frac{1}{2}\right)^{2}\right) \quad(\bmod p) $$ There are only finitely many $p$ dividing $$ \prod_{k=1}^{c} f\left(\left(k+\frac{1}{2}\right)^{2}\right) $$ unless one of the terms in the product is zero; this means that $4 n-(2 k+1)^{2}$ divides $f(n)$. This establishes the claim and finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For integral $m$, let $p(m)$ be the greatest prime divisor of $m$. By convention, we set $p( \pm 1)=1$ and $p(0)=\infty$. Find all polynomials $f$ with integer coefficients such that the sequence $$ \left\{p\left(f\left(n^{2}\right)\right)-2 n\right\}_{n \geq 0} $$ is bounded above. (In particular, this requires $f\left(n^{2}\right) \neq 0$ for $n \geq 0$.)
|
If $f$ is the (possibly empty) product of linear factors of the form $4 n-a^{2}$, then it satisfies the condition. We will prove no other polynomials work. In what follows, assume $f$ is irreducible and nonconstant. It suffices to show for every positive integer $c$, there exists a prime $p$ and a nonnegative integer $n$ such that $n \leq \frac{p-1}{2}-c$ and $p$ divides $f\left(n^{2}\right)$. Firstly, recall there are infinitely many odd primes $p$, with $p>c$, such that $p$ divides some $f\left(n^{2}\right)$, by Schur's Theorem. Looking mod such a $p$ we can find $n$ between 0 and $\frac{p-1}{2}\left(\right.$ since $\left.n^{2} \equiv(-n)^{2}(\bmod p)\right)$. We claim that only finitely many $p$ from this set can fail now. For if a $p$ fails, then its $n$ must be between $\frac{p-1}{2}-c$ and $\frac{p-1}{2}$. That means for some $0 \leq k \leq c$ we have $$ 0 \equiv f\left(\left(\frac{p-1}{2}-k\right)^{2}\right) \equiv f\left(\left(k+\frac{1}{2}\right)^{2}\right) \quad(\bmod p) $$ There are only finitely many $p$ dividing $$ \prod_{k=1}^{c} f\left(\left(k+\frac{1}{2}\right)^{2}\right) $$ unless one of the terms in the product is zero; this means that $4 n-(2 k+1)^{2}$ divides $f(n)$. This establishes the claim and finishes the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2006-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
980a9c95-eb22-5ca2-823e-eaeca2b6d0bd
| 604,191
|
A mathematical frog jumps along the number line. The frog starts at 1 , and jumps according to the following rule: if the frog is at integer $n$, then it can jump either to $n+1$ or to $n+2^{m_{n}+1}$ where $2^{m_{n}}$ is the largest power of 2 that is a factor of $n$. Show that if $k \geq 2$ is a positive integer and $i$ is a nonnegative integer, then the minimum number of jumps needed to reach $2^{i} k$ is greater than the minimum number of jumps needed to reach $2^{i}$.
|
We will think about the problem in terms of finite sequences of jumps $\left(s_{1}, s_{2}, \ldots, s_{\ell}\right)$, which we draw as $$ 1=x_{0} \xrightarrow{s_{1}} x_{1} \xrightarrow{s_{2}} x_{2} \xrightarrow{s_{3}} \ldots \xrightarrow{s_{\ell}} x_{\ell} $$ where $s_{k}=x_{k}-x_{k-1}$ is the length of some hop. We say the sequence is valid if it has the property required by the problem: for each $k$, either $s_{k}=1$ or $s_{k}=2^{m_{x_{k-1}}+1}$. An example is shown below. ## Lemma Let $\left(s_{1}, \ldots, s_{\ell}\right)$ be a sequence of jumps. Suppose we delete pick an index $k$ and exponent $e>0$, and delete any jumps after the $k$ th one which are divisible by $2^{e}$. The resulting sequence is still valid. But since $s<2^{e}$, we have $\nu_{2}\left(x^{\prime}\right)<e$ and hence $\nu_{2}(x)=\nu_{2}\left(x^{\prime}\right)$ so the jump is valid.  Now let's consider a valid path to $2^{i} k$ with $\ell$ steps, say $$ 1=x_{0} \xrightarrow{s_{1}} x_{1} \xrightarrow{s_{2}} x_{2} \xrightarrow{s_{3}} \ldots \xrightarrow{s_{\ell}} x_{\ell}=2^{i} \cdot k $$ where $s_{i}=x_{i}-x_{i-1}$ is the distance jumped. We delete jumps in the following way: starting from the largest $e$ and going downwards until $e=0$, we delete all the jumps of length $2^{e}$ which end at a point exceeding the target $2^{i}$. By the lemma, at each stage, the path remains valid. We claim more: Claim - Let $e \geq 0$. After the jumps of length greater than $2^{e}$ are deleted, the resulting end-point is at least $2^{i}$, and divisible by $2^{\min (i, e)}$. It is also divisible by $2^{\min (i, e)}$ by induction hypothesis, since we are changing the end-point by multiples of $2^{e}$. And the smallest multiple of $2^{\min (i, e)}$ exceeding $x$ is $2^{i}$. On the other hand by construction when the process ends the reduced path ends at a point at most $2^{i}$, so it is $2^{i}$ as desired. Therefore we have taken a path to $2^{i} k$ and reduced it to one to $2^{i}$ by deleting some jumps. This proves the result.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A mathematical frog jumps along the number line. The frog starts at 1 , and jumps according to the following rule: if the frog is at integer $n$, then it can jump either to $n+1$ or to $n+2^{m_{n}+1}$ where $2^{m_{n}}$ is the largest power of 2 that is a factor of $n$. Show that if $k \geq 2$ is a positive integer and $i$ is a nonnegative integer, then the minimum number of jumps needed to reach $2^{i} k$ is greater than the minimum number of jumps needed to reach $2^{i}$.
|
We will think about the problem in terms of finite sequences of jumps $\left(s_{1}, s_{2}, \ldots, s_{\ell}\right)$, which we draw as $$ 1=x_{0} \xrightarrow{s_{1}} x_{1} \xrightarrow{s_{2}} x_{2} \xrightarrow{s_{3}} \ldots \xrightarrow{s_{\ell}} x_{\ell} $$ where $s_{k}=x_{k}-x_{k-1}$ is the length of some hop. We say the sequence is valid if it has the property required by the problem: for each $k$, either $s_{k}=1$ or $s_{k}=2^{m_{x_{k-1}}+1}$. An example is shown below. ## Lemma Let $\left(s_{1}, \ldots, s_{\ell}\right)$ be a sequence of jumps. Suppose we delete pick an index $k$ and exponent $e>0$, and delete any jumps after the $k$ th one which are divisible by $2^{e}$. The resulting sequence is still valid. But since $s<2^{e}$, we have $\nu_{2}\left(x^{\prime}\right)<e$ and hence $\nu_{2}(x)=\nu_{2}\left(x^{\prime}\right)$ so the jump is valid.  Now let's consider a valid path to $2^{i} k$ with $\ell$ steps, say $$ 1=x_{0} \xrightarrow{s_{1}} x_{1} \xrightarrow{s_{2}} x_{2} \xrightarrow{s_{3}} \ldots \xrightarrow{s_{\ell}} x_{\ell}=2^{i} \cdot k $$ where $s_{i}=x_{i}-x_{i-1}$ is the distance jumped. We delete jumps in the following way: starting from the largest $e$ and going downwards until $e=0$, we delete all the jumps of length $2^{e}$ which end at a point exceeding the target $2^{i}$. By the lemma, at each stage, the path remains valid. We claim more: Claim - Let $e \geq 0$. After the jumps of length greater than $2^{e}$ are deleted, the resulting end-point is at least $2^{i}$, and divisible by $2^{\min (i, e)}$. It is also divisible by $2^{\min (i, e)}$ by induction hypothesis, since we are changing the end-point by multiples of $2^{e}$. And the smallest multiple of $2^{\min (i, e)}$ exceeding $x$ is $2^{i}$. On the other hand by construction when the process ends the reduced path ends at a point at most $2^{i}$, so it is $2^{i}$ as desired. Therefore we have taken a path to $2^{i} k$ and reduced it to one to $2^{i}$ by deleting some jumps. This proves the result.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2006-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
53c9574a-d23b-5ccd-a8ad-23b778f57c03
| 604,235
|
Let $A B C D$ be a quadrilateral, and let $E$ and $F$ be points on sides $A D$ and $B C$, respectively, such that $\frac{A E}{E D}=\frac{B F}{F C}$. Ray $F E$ meets rays $B A$ and $C D$ at $S$ and $T$, respectively. Prove that the circumcircles of triangles $S A E, S B F, T C F$, and $T D E$ pass through a common point.
|
 Let $M$ be the Miquel point of $A B C D$. Then $M$ is the center of a spiral similarity taking $A D$ to $B C$. The condition guarantees that it also takes $E$ to $F$. Hence, we see that $M$ is the center of a spiral similarity taking $\overline{A B}$ to $\overline{E F}$, and consequently the circumcircles of $Q A B, Q E F, S A E, S B F$ concur at point $M$. In other words, the Miquel point of $A B C D$ is also the Miquel point of $A B F E$. Similarly, $M$ is also the Miquel point of $E D C F$, so all four circles concur at $M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral, and let $E$ and $F$ be points on sides $A D$ and $B C$, respectively, such that $\frac{A E}{E D}=\frac{B F}{F C}$. Ray $F E$ meets rays $B A$ and $C D$ at $S$ and $T$, respectively. Prove that the circumcircles of triangles $S A E, S B F, T C F$, and $T D E$ pass through a common point.
|
 Let $M$ be the Miquel point of $A B C D$. Then $M$ is the center of a spiral similarity taking $A D$ to $B C$. The condition guarantees that it also takes $E$ to $F$. Hence, we see that $M$ is the center of a spiral similarity taking $\overline{A B}$ to $\overline{E F}$, and consequently the circumcircles of $Q A B, Q E F, S A E, S B F$ concur at point $M$. In other words, the Miquel point of $A B C D$ is also the Miquel point of $A B F E$. Similarly, $M$ is also the Miquel point of $E D C F$, so all four circles concur at $M$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2006-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d8bf2a52-110d-5174-8f53-b3f26027095c
| 248,381
|
Let $n$ be a positive integer. Define a sequence by setting $a_{1}=n$ and, for each $k>1$, letting $a_{k}$ be the unique integer in the range $0 \leq a_{k} \leq k-1$ for which $a_{1}+a_{2}+\cdots+a_{k}$ is divisible by $k$. (For instance, when $n=9$ the obtained sequence is $9,1,2,0,3,3,3, \ldots$ ) Prove that for any $n$ the sequence $a_{1}, a_{2}, \ldots$ eventually becomes constant.
|
For each $k$, the number $$ b_{k}:=\frac{1}{k}\left(a_{1}+\cdots+a_{k}\right) $$ is a nonnegative integer. Claim - The sequence $\left(b_{k}\right)$ is eventually constant. $$ b_{k+1}=\frac{a_{1}+\cdots+a_{k}+a_{k+1}}{k+1} \leq \frac{k b_{k}+k}{k+1}<b_{k}+1 $$ and therefore $b_{k+1} \leq b_{k}$ for all $k$. Hence the sequence $b_{k}$ must eventually be constant. This can only happen once the sequence is constant: indeed if $N$ is an index such that $b_{N}=b_{N+1}=\cdots=b$ then $$ a_{k}=(k+1) b_{k+1}-k \cdot b_{k}=(k+1) \cdot b-k \cdot b=b $$ for any $k \geq N$. In other words, $a_{N}=a_{N+1}=\cdots=b$ as well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Define a sequence by setting $a_{1}=n$ and, for each $k>1$, letting $a_{k}$ be the unique integer in the range $0 \leq a_{k} \leq k-1$ for which $a_{1}+a_{2}+\cdots+a_{k}$ is divisible by $k$. (For instance, when $n=9$ the obtained sequence is $9,1,2,0,3,3,3, \ldots$ ) Prove that for any $n$ the sequence $a_{1}, a_{2}, \ldots$ eventually becomes constant.
|
For each $k$, the number $$ b_{k}:=\frac{1}{k}\left(a_{1}+\cdots+a_{k}\right) $$ is a nonnegative integer. Claim - The sequence $\left(b_{k}\right)$ is eventually constant. $$ b_{k+1}=\frac{a_{1}+\cdots+a_{k}+a_{k+1}}{k+1} \leq \frac{k b_{k}+k}{k+1}<b_{k}+1 $$ and therefore $b_{k+1} \leq b_{k}$ for all $k$. Hence the sequence $b_{k}$ must eventually be constant. This can only happen once the sequence is constant: indeed if $N$ is an index such that $b_{N}=b_{N+1}=\cdots=b$ then $$ a_{k}=(k+1) b_{k+1}-k \cdot b_{k}=(k+1) \cdot b-k \cdot b=b $$ for any $k \geq N$. In other words, $a_{N}=a_{N+1}=\cdots=b$ as well.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
da02d1b7-b454-53cf-9fdd-f01240e2ab8c
| 604,265
|
Decide whether it possible to cover all lattice points in $\mathbb{R}^{2}$ by an (infinite) family of disks whose interiors are disjoint such that the radius of each disk is at least 5 .
|
The answer is no. Assume not. Take a disk $\odot O$ not touching any member of the family, and then enlarge it until it is maximal. Then, it must be tangent to at least three other disks, say $\odot A$, $\odot B, \odot C$. Suppose WLOG that $\angle A O B \leq 120^{\circ}$. Denote the radii of $\odot O, \odot A, \odot B$ by $r$, $a, b$. But the Law of Cosines gives $$ (a+b)^{2} \leq(a+r)^{2}+(b+r)^{2}+(a+r)(b+r) $$ which rewrites as $$ 12 r^{2} \geq(a-3 r)(b-3 r) \geq(5-3 r)^{2} $$ which one can check is impossible for $r \leq 1 / \sqrt{2}$. Thus $r>1 / \sqrt{2}$. In particular $(\odot O)$ must contain a lattice point as it contains a unit square. Remark. The order of the argument here matters in subtle ways. A common approach is to try and reduce to the "optimal" case where we have three mutually tangent circles, and then apply the Descarte circle theorem. There are ways in which this approach can fail if the execution is not done with care. (In particular, one cannot simply say to reduce to this case, without some justification.) For example: it is not true that, given an infinite family of disks, we can enlarge disks until we get three mutually tangent ones. As a counterexample consider the "square grid" in which a circle is centered at $(10 m, 10 n)$ for each $m, n \in \mathbb{Z}$ and has radius 5 . Thus it is also not possible to simply pick three nearby circles and construct a circle tangent to all three: that newly constructed circle might intersect a fourth disk not in the picture. Thus, when constructing the small disk $\odot O$ in the above solution, it seems easiest to start with a point not covered and grow $\odot O$ until it is tangent to some three circles, and then argue by cosine law. Otherwise it not easy to determine which three circles to start with.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Decide whether it possible to cover all lattice points in $\mathbb{R}^{2}$ by an (infinite) family of disks whose interiors are disjoint such that the radius of each disk is at least 5 .
|
The answer is no. Assume not. Take a disk $\odot O$ not touching any member of the family, and then enlarge it until it is maximal. Then, it must be tangent to at least three other disks, say $\odot A$, $\odot B, \odot C$. Suppose WLOG that $\angle A O B \leq 120^{\circ}$. Denote the radii of $\odot O, \odot A, \odot B$ by $r$, $a, b$. But the Law of Cosines gives $$ (a+b)^{2} \leq(a+r)^{2}+(b+r)^{2}+(a+r)(b+r) $$ which rewrites as $$ 12 r^{2} \geq(a-3 r)(b-3 r) \geq(5-3 r)^{2} $$ which one can check is impossible for $r \leq 1 / \sqrt{2}$. Thus $r>1 / \sqrt{2}$. In particular $(\odot O)$ must contain a lattice point as it contains a unit square. Remark. The order of the argument here matters in subtle ways. A common approach is to try and reduce to the "optimal" case where we have three mutually tangent circles, and then apply the Descarte circle theorem. There are ways in which this approach can fail if the execution is not done with care. (In particular, one cannot simply say to reduce to this case, without some justification.) For example: it is not true that, given an infinite family of disks, we can enlarge disks until we get three mutually tangent ones. As a counterexample consider the "square grid" in which a circle is centered at $(10 m, 10 n)$ for each $m, n \in \mathbb{Z}$ and has radius 5 . Thus it is also not possible to simply pick three nearby circles and construct a circle tangent to all three: that newly constructed circle might intersect a fourth disk not in the picture. Thus, when constructing the small disk $\odot O$ in the above solution, it seems easiest to start with a point not covered and grow $\odot O$ until it is tangent to some three circles, and then argue by cosine law. Otherwise it not easy to determine which three circles to start with.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
3e2539ca-f2f9-5cf2-aa56-536461ab9dff
| 604,277
|
Let $S$ be a set containing $n^{2}+n-1$ elements. Suppose that the $n$-element subsets of $S$ are partitioned into two classes. Prove that there are at least $n$ pairwise disjoint sets in the same class.
|
【 First solution (Grant Yu). We define a set of $n+1$ elements to be useful if it has $n$-element subsets in each class. Consider a maximal collection of disjoint useful sets and assume there are $p$ such sets. Then, let $T$ be the set of elements remaining (i.e. not in one of chosen useful sets). Claim - All subsets of $T$ of size $n$ are the same color. We have $|T|=n^{2}+n-1-p(n+1)$, and in particular $p<n$. WLOG all sets in $T$ are red. We can extract another red set from each of our chosen useful sets. So we can get at least $$ p+\left\lfloor\frac{|T|}{n}\right\rfloor=p+\left\lfloor n+1-p-\frac{1+p}{n}\right\rfloor \geq p+(n-p)=n . $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set containing $n^{2}+n-1$ elements. Suppose that the $n$-element subsets of $S$ are partitioned into two classes. Prove that there are at least $n$ pairwise disjoint sets in the same class.
|
【 First solution (Grant Yu). We define a set of $n+1$ elements to be useful if it has $n$-element subsets in each class. Consider a maximal collection of disjoint useful sets and assume there are $p$ such sets. Then, let $T$ be the set of elements remaining (i.e. not in one of chosen useful sets). Claim - All subsets of $T$ of size $n$ are the same color. We have $|T|=n^{2}+n-1-p(n+1)$, and in particular $p<n$. WLOG all sets in $T$ are red. We can extract another red set from each of our chosen useful sets. So we can get at least $$ p+\left\lfloor\frac{|T|}{n}\right\rfloor=p+\left\lfloor n+1-p-\frac{1+p}{n}\right\rfloor \geq p+(n-p)=n . $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
dff4ce90-894b-54ae-a205-daa74467ca47
| 248,408
|
Let $S$ be a set containing $n^{2}+n-1$ elements. Suppose that the $n$-element subsets of $S$ are partitioned into two classes. Prove that there are at least $n$ pairwise disjoint sets in the same class.
|
## ब Second solution (by induction). We prove more strongly that: Claim - Let $S$ be a set containing $k \cdot(n+1)-1$ elements. Then we can find $k$ pairwise disjoint sets of the same color. For the inductive step, assume for contradiction the problem fails. Let $T$ be any subset of $S$ of size $(k-1)(n+1)-1$. By the induction hypothesis, among the subsets of $T$ alone, we can already find $k-1$ pairwise disjoint sets of the same color. Now $S \backslash T$ has size $n+1$, and so we would have to have that all $\binom{n+1}{n}$ subsets of $S \backslash T$ are the same color. By varying $T$, the set $S \backslash T$ ranges over all of $\binom{S}{k+1}$. This causes all sets to be the same color, contradiction. Remark. Victor Wang writes the following: I don't really like this problem, but I think the main motivation for generalizing the problem is that the original problem doesn't allow you to look at small cases. (Also, it's not initially clear where the $n^{2}+n-1$ comes from.) And pretty much the simplest way to get lots of similarly-flavored small cases is to start with $k=2,3$ in "find the smallest $N(n, k)$ such that when we partition the $n$-subsets of a $\geq N(n, k)$-set into 2 classes, we can find some $k$ pairwise disjoint sets in the same class".
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set containing $n^{2}+n-1$ elements. Suppose that the $n$-element subsets of $S$ are partitioned into two classes. Prove that there are at least $n$ pairwise disjoint sets in the same class.
|
## ब Second solution (by induction). We prove more strongly that: Claim - Let $S$ be a set containing $k \cdot(n+1)-1$ elements. Then we can find $k$ pairwise disjoint sets of the same color. For the inductive step, assume for contradiction the problem fails. Let $T$ be any subset of $S$ of size $(k-1)(n+1)-1$. By the induction hypothesis, among the subsets of $T$ alone, we can already find $k-1$ pairwise disjoint sets of the same color. Now $S \backslash T$ has size $n+1$, and so we would have to have that all $\binom{n+1}{n}$ subsets of $S \backslash T$ are the same color. By varying $T$, the set $S \backslash T$ ranges over all of $\binom{S}{k+1}$. This causes all sets to be the same color, contradiction. Remark. Victor Wang writes the following: I don't really like this problem, but I think the main motivation for generalizing the problem is that the original problem doesn't allow you to look at small cases. (Also, it's not initially clear where the $n^{2}+n-1$ comes from.) And pretty much the simplest way to get lots of similarly-flavored small cases is to start with $k=2,3$ in "find the smallest $N(n, k)$ such that when we partition the $n$-subsets of a $\geq N(n, k)$-set into 2 classes, we can find some $k$ pairwise disjoint sets in the same class".
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
dff4ce90-894b-54ae-a205-daa74467ca47
| 248,408
|
Prove that for every nonnegative integer $n$, the number $7^{7^{n}}+1$ is the product of at least $2 n+3$ (not necessarily distinct) primes.
|
We prove this by induction on $n$ by showing that $$ \frac{X^{7}+1}{X+1}=X^{6}-X^{5}+\cdots+1 $$ is never prime for $X=7^{7^{n}}$, hence we gain at least two additional prime factors whenever we increase $n$ by one. Indeed, the quotient may be written as $$ (X+1)^{6}-7 X \cdot\left(X^{2}+X+1\right)^{2} $$ which becomes a difference of squares, hence composite.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every nonnegative integer $n$, the number $7^{7^{n}}+1$ is the product of at least $2 n+3$ (not necessarily distinct) primes.
|
We prove this by induction on $n$ by showing that $$ \frac{X^{7}+1}{X+1}=X^{6}-X^{5}+\cdots+1 $$ is never prime for $X=7^{7^{n}}$, hence we gain at least two additional prime factors whenever we increase $n$ by one. Indeed, the quotient may be written as $$ (X+1)^{6}-7 X \cdot\left(X^{2}+X+1\right)^{2} $$ which becomes a difference of squares, hence composite.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e62b3e9a-185d-5028-bf3a-c324b62802a8
| 248,425
|
Let $A B C$ be an acute triangle with $\omega, S$, and $R$ being its incircle, circumcircle, and circumradius, respectively. Circle $\omega_{A}$ is tangent internally to $S$ at $A$ and tangent externally to $\omega$. Circle $S_{A}$ is tangent internally to $S$ at $A$ and tangent internally to $\omega$. Let $P_{A}$ and $Q_{A}$ denote the centers of $\omega_{A}$ and $S_{A}$, respectively. Define points $P_{B}$, $Q_{B}, P_{C}, Q_{C}$ analogously. Prove that $$ 8 P_{A} Q_{A} \cdot P_{B} Q_{B} \cdot P_{C} Q_{C} \leq R^{3} $$ with equality if and only if triangle $A B C$ is equilateral.
|
It turns out we can compute $P_{A} Q_{A}$ explicitly. Let us invert around $A$ with radius $s-a$ (hence fixing the incircle) and then compose this with a reflection around the angle bisector of $\angle B A C$. We denote the image of the composed map via $$ \bullet \mapsto \bullet^{*} \mapsto \bullet^{+} $$ We overlay this inversion with the original diagram. Let $P_{A} Q_{A}$ meet $\omega_{A}$ again at $P$ and $S_{A}$ again at $Q$. Now observe that $\omega_{A}^{*}$ is a line parallel to $S^{*}$; that is, it is perpendicular to $\overline{P Q}$. Moreover, it is tangent to $\omega^{*}=\omega$. Now upon the reflection, we find that $\omega^{+}=\omega^{*}=\omega$, but line $\overline{P Q}$ gets mapped to the altitude from $A$ to $\overline{B C}$, since $\overline{P Q}$ originally contained the circumcenter $O$ (isogonal to the orthocenter). But this means that $\omega_{A}^{*}$ is none other than the $\overline{B C}$ ! Hence $P^{+}$is actually the foot of the altitude from $A$ onto $\overline{B C}$. By similar work, we find that $Q^{+}$is the point on $\overline{A P^{+}}$such that $P^{+} Q^{+}=2 r$.  Now we can compute all the lengths directly. We have that $$ A P_{A}=\frac{1}{2} A P=\frac{(s-a)^{2}}{2 A P^{+}}=\frac{1}{2}(s-a)^{2} \cdot \frac{1}{h_{a}} $$ and $$ A Q_{A}=\frac{1}{2} A Q=\frac{(s-a)^{2}}{2 A Q^{+}}=\frac{1}{2}(s-a)^{2} \cdot \frac{1}{h_{a}-2 r} $$ where $h_{a}=\frac{2 K}{a}$ is the length of the $A$-altitude, with $K$ the area of $A B C$ as usual. Now it follows that $$ P_{A} Q_{A}=\frac{1}{2}(s-a)^{2}\left(\frac{2 r}{h_{a}\left(h_{a}-2 r\right)}\right) . $$ This can be simplified, as $$ h_{a}-2 r=\frac{2 K}{a}-\frac{2 K}{s}=2 K \cdot \frac{s-a}{a s} $$ Hence $$ P_{A} Q_{A}=\frac{a^{2} r s(s-a)}{4 K^{2}}=\frac{a^{2}(s-a)}{4 K} . $$ Hence, the problem is just asking us to show that $$ a^{2} b^{2} c^{2}(s-a)(s-b)(s-c) \leq 8(R K)^{3} $$ Using $a b c=4 R K$ and $(s-a)(s-b)(s-c)=\frac{1}{s} K^{2}=r K$, we find that this becomes $$ 2(s-a)(s-b)(s-c) \leq R K \Longleftrightarrow 2 r \leq R $$ which follows immediately from $I O^{2}=R(R-2 r)$. Alternatively, one may rewrite this as Schur's Inequality in the form $$ a b c \geq(-a+b+c)(a-b+c)(a+b-c) $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $\omega, S$, and $R$ being its incircle, circumcircle, and circumradius, respectively. Circle $\omega_{A}$ is tangent internally to $S$ at $A$ and tangent externally to $\omega$. Circle $S_{A}$ is tangent internally to $S$ at $A$ and tangent internally to $\omega$. Let $P_{A}$ and $Q_{A}$ denote the centers of $\omega_{A}$ and $S_{A}$, respectively. Define points $P_{B}$, $Q_{B}, P_{C}, Q_{C}$ analogously. Prove that $$ 8 P_{A} Q_{A} \cdot P_{B} Q_{B} \cdot P_{C} Q_{C} \leq R^{3} $$ with equality if and only if triangle $A B C$ is equilateral.
|
It turns out we can compute $P_{A} Q_{A}$ explicitly. Let us invert around $A$ with radius $s-a$ (hence fixing the incircle) and then compose this with a reflection around the angle bisector of $\angle B A C$. We denote the image of the composed map via $$ \bullet \mapsto \bullet^{*} \mapsto \bullet^{+} $$ We overlay this inversion with the original diagram. Let $P_{A} Q_{A}$ meet $\omega_{A}$ again at $P$ and $S_{A}$ again at $Q$. Now observe that $\omega_{A}^{*}$ is a line parallel to $S^{*}$; that is, it is perpendicular to $\overline{P Q}$. Moreover, it is tangent to $\omega^{*}=\omega$. Now upon the reflection, we find that $\omega^{+}=\omega^{*}=\omega$, but line $\overline{P Q}$ gets mapped to the altitude from $A$ to $\overline{B C}$, since $\overline{P Q}$ originally contained the circumcenter $O$ (isogonal to the orthocenter). But this means that $\omega_{A}^{*}$ is none other than the $\overline{B C}$ ! Hence $P^{+}$is actually the foot of the altitude from $A$ onto $\overline{B C}$. By similar work, we find that $Q^{+}$is the point on $\overline{A P^{+}}$such that $P^{+} Q^{+}=2 r$.  Now we can compute all the lengths directly. We have that $$ A P_{A}=\frac{1}{2} A P=\frac{(s-a)^{2}}{2 A P^{+}}=\frac{1}{2}(s-a)^{2} \cdot \frac{1}{h_{a}} $$ and $$ A Q_{A}=\frac{1}{2} A Q=\frac{(s-a)^{2}}{2 A Q^{+}}=\frac{1}{2}(s-a)^{2} \cdot \frac{1}{h_{a}-2 r} $$ where $h_{a}=\frac{2 K}{a}$ is the length of the $A$-altitude, with $K$ the area of $A B C$ as usual. Now it follows that $$ P_{A} Q_{A}=\frac{1}{2}(s-a)^{2}\left(\frac{2 r}{h_{a}\left(h_{a}-2 r\right)}\right) . $$ This can be simplified, as $$ h_{a}-2 r=\frac{2 K}{a}-\frac{2 K}{s}=2 K \cdot \frac{s-a}{a s} $$ Hence $$ P_{A} Q_{A}=\frac{a^{2} r s(s-a)}{4 K^{2}}=\frac{a^{2}(s-a)}{4 K} . $$ Hence, the problem is just asking us to show that $$ a^{2} b^{2} c^{2}(s-a)(s-b)(s-c) \leq 8(R K)^{3} $$ Using $a b c=4 R K$ and $(s-a)(s-b)(s-c)=\frac{1}{s} K^{2}=r K$, we find that this becomes $$ 2(s-a)(s-b)(s-c) \leq R K \Longleftrightarrow 2 r \leq R $$ which follows immediately from $I O^{2}=R(R-2 r)$. Alternatively, one may rewrite this as Schur's Inequality in the form $$ a b c \geq(-a+b+c)(a-b+c)(a+b-c) $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2007-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
844308f5-9b3f-59a1-b002-f6dfe229e55b
| 604,356
|
Prove that for each positive integer $n$, there are pairwise relatively prime integers $k_{0}, \ldots, k_{n}$, all strictly greater than 1 , such that $k_{0} k_{1} \ldots k_{n}-1$ is the product of two consecutive integers.
|
In other words, if we let $$ P(x)=x(x+1)+1 $$ then we would like there to be infinitely many primes dividing some $P(t)$ for some integer $t$. In fact, this result is true in much greater generality. We first state: ## Theorem 1.1 (Schur's theorem) If $P(x) \in \mathbb{Z}[x]$ is nonconstant and $P(0)=1$, then there are infinitely many primes which divide $P(t)$ for some integer $t$. Let $S$ be any finite set of prime numbers. Consider then the value $$ P\left(k \prod_{p \in S} p\right) $$ for some integer $k$. It is $1(\bmod p)$ for each prime $p$, and if $k$ is large enough it should not be equal to 1 (because $P$ is not constant). Therefore, it has a prime divisor not in $S$. Remark. In fact the result holds without the assumption $P(0) \neq 1$. The proof requires only small modifications, and a good exercise would be to write down a similar proof that works first for $P(0)=20$, and then for any $P(0) \neq 0$. (The $P(0)=0$ case is vacuous, since then $P(x)$ is divisible by $x$.) $$ \begin{aligned} P\left(x_{1}\right) & \equiv 0 \quad\left(\bmod p_{1}\right) \\ P\left(x_{2}\right) & \equiv 0 \quad\left(\bmod p_{2}\right) \\ \vdots & \\ P\left(x_{n}\right) & \equiv 0 \quad\left(\bmod p_{n}\right) \end{aligned} $$ as promised by Schur's theorem. Then, by Chinese remainder theorem, we can find $x$ such that $x \equiv x_{i}\left(\bmod p_{i}\right)$ for each $i$, whence $P(x)$ has at least $n$ prime factor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for each positive integer $n$, there are pairwise relatively prime integers $k_{0}, \ldots, k_{n}$, all strictly greater than 1 , such that $k_{0} k_{1} \ldots k_{n}-1$ is the product of two consecutive integers.
|
In other words, if we let $$ P(x)=x(x+1)+1 $$ then we would like there to be infinitely many primes dividing some $P(t)$ for some integer $t$. In fact, this result is true in much greater generality. We first state: ## Theorem 1.1 (Schur's theorem) If $P(x) \in \mathbb{Z}[x]$ is nonconstant and $P(0)=1$, then there are infinitely many primes which divide $P(t)$ for some integer $t$. Let $S$ be any finite set of prime numbers. Consider then the value $$ P\left(k \prod_{p \in S} p\right) $$ for some integer $k$. It is $1(\bmod p)$ for each prime $p$, and if $k$ is large enough it should not be equal to 1 (because $P$ is not constant). Therefore, it has a prime divisor not in $S$. Remark. In fact the result holds without the assumption $P(0) \neq 1$. The proof requires only small modifications, and a good exercise would be to write down a similar proof that works first for $P(0)=20$, and then for any $P(0) \neq 0$. (The $P(0)=0$ case is vacuous, since then $P(x)$ is divisible by $x$.) $$ \begin{aligned} P\left(x_{1}\right) & \equiv 0 \quad\left(\bmod p_{1}\right) \\ P\left(x_{2}\right) & \equiv 0 \quad\left(\bmod p_{2}\right) \\ \vdots & \\ P\left(x_{n}\right) & \equiv 0 \quad\left(\bmod p_{n}\right) \end{aligned} $$ as promised by Schur's theorem. Then, by Chinese remainder theorem, we can find $x$ such that $x \equiv x_{i}\left(\bmod p_{i}\right)$ for each $i$, whence $P(x)$ has at least $n$ prime factor.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
295b9a23-78c0-5498-8bde-fc4c695e571a
| 604,367
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Barycentric solution. First, we find the coordinates of $D$. As $D$ lies on $\overline{A M}$, we know $D=(t: 1: 1)$ for some $t$. Now by perpendicular bisector formula, we find $$ 0=b^{2}(t-1)+\left(a^{2}-c^{2}\right) \Longrightarrow t=\frac{c^{2}+b^{2}-a^{2}}{b^{2}} $$ Thus we obtain $$ D=\left(2 S_{A}: c^{2}: c^{2}\right) . $$ Analogously $E=\left(2 S_{A}: b^{2}: b^{2}\right)$, and it follows that $$ F=\left(2 S_{A}: b^{2}: c^{2}\right) $$ The sum of the coordinates of $F$ is $$ \left(b^{2}+c^{2}-a^{2}\right)+b^{2}+c^{2}=2 b^{2}+2 c^{2}-a^{2} $$ Hence the reflection of $A$ over $F$ is simply $$ 2 F-A=\left(2\left(b^{2}+c^{2}-a^{2}\right)-\left(2 b^{2}+2 c^{2}-a^{2}\right): 2 b^{2}: 2 c^{2}\right)=\left(-a^{2}: 2 b^{2}: 2 c^{2}\right) . $$ It is evident that $F^{\prime}$ lies on $(A B C):-a^{2} y z-b^{2} z x-c^{2} x y=0$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Barycentric solution. First, we find the coordinates of $D$. As $D$ lies on $\overline{A M}$, we know $D=(t: 1: 1)$ for some $t$. Now by perpendicular bisector formula, we find $$ 0=b^{2}(t-1)+\left(a^{2}-c^{2}\right) \Longrightarrow t=\frac{c^{2}+b^{2}-a^{2}}{b^{2}} $$ Thus we obtain $$ D=\left(2 S_{A}: c^{2}: c^{2}\right) . $$ Analogously $E=\left(2 S_{A}: b^{2}: b^{2}\right)$, and it follows that $$ F=\left(2 S_{A}: b^{2}: c^{2}\right) $$ The sum of the coordinates of $F$ is $$ \left(b^{2}+c^{2}-a^{2}\right)+b^{2}+c^{2}=2 b^{2}+2 c^{2}-a^{2} $$ Hence the reflection of $A$ over $F$ is simply $$ 2 F-A=\left(2\left(b^{2}+c^{2}-a^{2}\right)-\left(2 b^{2}+2 c^{2}-a^{2}\right): 2 b^{2}: 2 c^{2}\right)=\left(-a^{2}: 2 b^{2}: 2 c^{2}\right) . $$ It is evident that $F^{\prime}$ lies on $(A B C):-a^{2} y z-b^{2} z x-c^{2} x y=0$, and we are done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
15b7599d-ed87-5d23-9c1c-c2c53820806d
| 248,452
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
II Synthetic solution (harmonic). Here is a synthetic solution. Let $X$ be the point so that $A P X N$ is a cyclic harmonic quadrilateral. We contend that $X=F$. To see this it suffices to prove $B, X, D$ collinear (and hence $C, X, E$ collinear by symmetry).  Let $T$ be the midpoint of $\overline{P N}$, so $\triangle A P X \sim \triangle A T N$. So $\triangle A B X \sim \triangle A M N$, ergo $$ \measuredangle X B A=\measuredangle N M A=\measuredangle B A M=\measuredangle B A D=\measuredangle D B A $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
II Synthetic solution (harmonic). Here is a synthetic solution. Let $X$ be the point so that $A P X N$ is a cyclic harmonic quadrilateral. We contend that $X=F$. To see this it suffices to prove $B, X, D$ collinear (and hence $C, X, E$ collinear by symmetry).  Let $T$ be the midpoint of $\overline{P N}$, so $\triangle A P X \sim \triangle A T N$. So $\triangle A B X \sim \triangle A M N$, ergo $$ \measuredangle X B A=\measuredangle N M A=\measuredangle B A M=\measuredangle B A D=\measuredangle D B A $$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
15b7599d-ed87-5d23-9c1c-c2c53820806d
| 248,452
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Angle chasing solution (Mason Fang). Obviously $A N O P$ is concyclic. Claim - Quadrilateral BFOC is cyclic. $$ \begin{aligned} \measuredangle B F C=\measuredangle F B C+\measuredangle B C F & =\measuredangle F B A+\measuredangle A B C+\measuredangle B C A+\measuredangle A C F \\ & =\measuredangle D B A+\measuredangle A B C+\measuredangle B C A+\measuredangle A C E \\ & =\measuredangle B A D+\measuredangle A B C+\measuredangle B C A+\measuredangle E A C \\ & =2 \angle B A C=\angle B O C . \end{aligned} $$ Define $Q=\overline{A A} \cap \overline{B C}$. Claim - Point $Q$ lies on $\overline{F O}$. $$ \begin{aligned} \measuredangle B O Q=\measuredangle B O A+\measuredangle A O Q & =2 \measuredangle B C A+90^{\circ}+\measuredangle A Q O \\ & =2 \measuredangle B C A+90^{\circ}+\measuredangle A M O \\ & =2 \measuredangle B C A+90^{\circ}+\measuredangle A M C+90^{\circ} \\ & =\measuredangle B C A+\measuredangle M A C=\measuredangle B C A+\measuredangle A C E \\ & =\measuredangle B C E=\measuredangle B O F . \end{aligned} $$ As $Q$ is the radical center of $(A N O P),(A B C)$ and $(B F O C)$, this implies the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Angle chasing solution (Mason Fang). Obviously $A N O P$ is concyclic. Claim - Quadrilateral BFOC is cyclic. $$ \begin{aligned} \measuredangle B F C=\measuredangle F B C+\measuredangle B C F & =\measuredangle F B A+\measuredangle A B C+\measuredangle B C A+\measuredangle A C F \\ & =\measuredangle D B A+\measuredangle A B C+\measuredangle B C A+\measuredangle A C E \\ & =\measuredangle B A D+\measuredangle A B C+\measuredangle B C A+\measuredangle E A C \\ & =2 \angle B A C=\angle B O C . \end{aligned} $$ Define $Q=\overline{A A} \cap \overline{B C}$. Claim - Point $Q$ lies on $\overline{F O}$. $$ \begin{aligned} \measuredangle B O Q=\measuredangle B O A+\measuredangle A O Q & =2 \measuredangle B C A+90^{\circ}+\measuredangle A Q O \\ & =2 \measuredangle B C A+90^{\circ}+\measuredangle A M O \\ & =2 \measuredangle B C A+90^{\circ}+\measuredangle A M C+90^{\circ} \\ & =\measuredangle B C A+\measuredangle M A C=\measuredangle B C A+\measuredangle A C E \\ & =\measuredangle B C E=\measuredangle B O F . \end{aligned} $$ As $Q$ is the radical center of $(A N O P),(A B C)$ and $(B F O C)$, this implies the result.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
15b7599d-ed87-5d23-9c1c-c2c53820806d
| 248,452
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Inversive solution (Kelin Zhu). Invert about $A$ with radius $\sqrt{b c}$ followed by a reflection over the angle bisector of $\angle A$, and denote the image of a point $X$ by $X^{\prime}$. The inverted problem now states the following: In triangle $A P^{*} N^{*}$, let $B^{*}, C^{*}$ be the midpoints of $A P^{*}, A N^{*}$ and $D^{*}, E^{*}$ be the intersection of the $A$ symmedian with $\left(A P^{*}\right),\left(A N^{*}\right)$, respectively. $\left(A B^{*} D^{*}\right),\left(A C^{*} E^{*}\right)$ intersect at a point $F^{*}$; prove that it lies on $P^{*} N^{*}$. I claim that, in fact, the midpoint of $P^{*} N^{*}$ is the desired intersection. Redefine that point as $F^{*}$ and I will prove that $\left(A B^{*} D^{*}\right),\left(A C^{*} E^{*}\right)$ pass through it. Note that $$ \angle A D^{*} B^{*}=\angle D^{*} A B^{*}=\angle F^{*} A N^{*}=\angle A F^{*} B^{*}, $$ where the first equality is due to $B^{*}$ being the circumcircle of $A D^{*} P^{*}$, the second equality is due to the definition of the symmedian, and the third equality is due to the parallelogram $A B^{*} F^{*} C^{*}$. A symmetric argument for $C$ finishes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle, and let $M, N$, and $P$ be the midpoints of $\overline{B C}, \overline{C A}$, and $\overline{A B}$, respectively. Let the perpendicular bisectors of $\overline{A B}$ and $\overline{A C}$ intersect ray $A M$ in points $D$ and $E$ respectively, and let lines $B D$ and $C E$ intersect in point $F$, inside triangle $A B C$. Prove that points $A, N, F$, and $P$ all lie on one circle.
|
【 Inversive solution (Kelin Zhu). Invert about $A$ with radius $\sqrt{b c}$ followed by a reflection over the angle bisector of $\angle A$, and denote the image of a point $X$ by $X^{\prime}$. The inverted problem now states the following: In triangle $A P^{*} N^{*}$, let $B^{*}, C^{*}$ be the midpoints of $A P^{*}, A N^{*}$ and $D^{*}, E^{*}$ be the intersection of the $A$ symmedian with $\left(A P^{*}\right),\left(A N^{*}\right)$, respectively. $\left(A B^{*} D^{*}\right),\left(A C^{*} E^{*}\right)$ intersect at a point $F^{*}$; prove that it lies on $P^{*} N^{*}$. I claim that, in fact, the midpoint of $P^{*} N^{*}$ is the desired intersection. Redefine that point as $F^{*}$ and I will prove that $\left(A B^{*} D^{*}\right),\left(A C^{*} E^{*}\right)$ pass through it. Note that $$ \angle A D^{*} B^{*}=\angle D^{*} A B^{*}=\angle F^{*} A N^{*}=\angle A F^{*} B^{*}, $$ where the first equality is due to $B^{*}$ being the circumcircle of $A D^{*} P^{*}$, the second equality is due to the definition of the symmedian, and the third equality is due to the parallelogram $A B^{*} F^{*} C^{*}$. A symmetric argument for $C$ finishes.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
15b7599d-ed87-5d23-9c1c-c2c53820806d
| 248,452
|
Let $n$ be a positive integer. Denote by $S_{n}$ the set of points $(x, y)$ with integer coordinates such that $$ |x|+\left|y+\frac{1}{2}\right|<n $$ A path is a sequence of distinct points $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{\ell}, y_{\ell}\right)$ in $S_{n}$ such that, for $i=2, \ldots, \ell$, the distance between $\left(x_{i}, y_{i}\right)$ and $\left(x_{i-1}, y_{i-1}\right)$ is 1 . Prove that the points in $S_{n}$ cannot be partitioned into fewer than $n$ paths.
|
【 First solution (local). We proceed by induction on $n$. The base case $n=1$ is clear, so suppose $n>1$. Let $S$ denote the set of points $$ S=\left\{(x, y): x+\left|y+\frac{1}{2}\right| \geq n-2\right\} $$ An example when $n=4$ is displayed below. 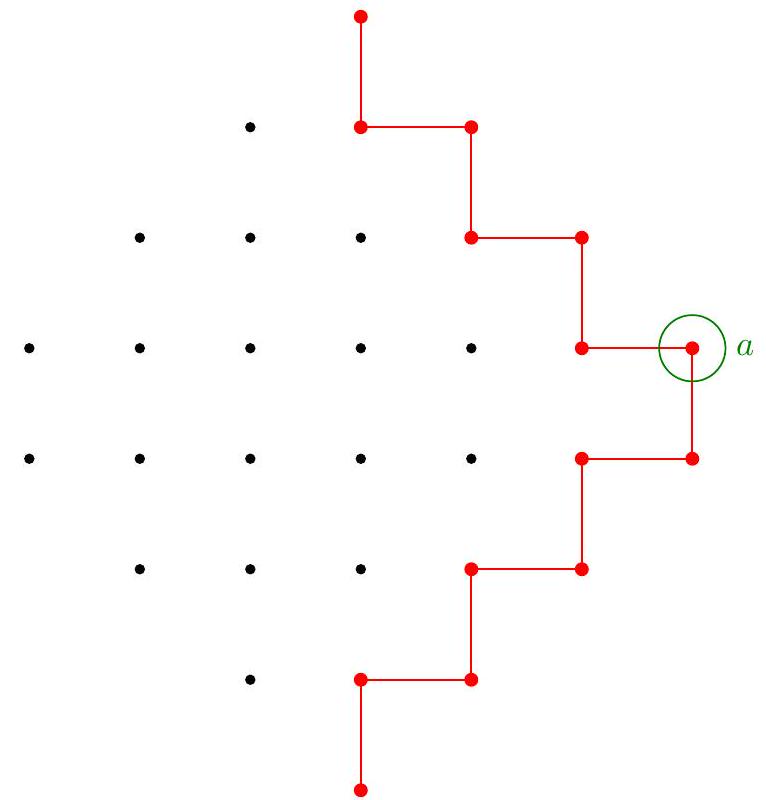 For any minimal partition $\mathcal{P}$ of $S_{n}$, let $P$ denote the path passing through the point $a=(n-1,0)$. Then the intersection of $P$ with $S$ consists of several disconnected paths; let $N$ be the number of nodes in the component containing $a$, and pick $\mathcal{P}$ such that $N$ is maximal. We claim that in this case $P=S$. Assume not. First, note $a=(n-1,0)$ must be connected to $b=(n-1,-1)$ (otherwise join them to decrease the number of paths). Now, starting from $a=(n-1,0)$ walk along $P$ away from $b$ until one of the following three conditions is met: - We reach a point $v$ not in $S$. Let $w$ be the point before $v$, and $x$ the point in $S$ adjacent to $w$. Then delete $v w$ and add $w x$. This increases $N$ while leaving the number of edges unchanged: so this case can't happen. - We reach an endpoint $v$ of $P$ (which may be $a$ ), lying inside the set $S$, which is not the topmost point $(0, n-1)$. Let $w$ be the next point of $S$. Delete any edge touching $w$ and add edge $v w$. This increases $N$ while leaving the number of edges unchanged: so this case can't happen. - We reach the topmost point $(0, n-1)$. Thus we see that $P$ must follow $S$ until reaching the topmost point $(0, n-1)$. Similarly it must reach the bottom-most point $(0,-n)$. Hence $P=S$. The remainder of $S_{n}$ is just $S_{n-1}$, and hence this requires at least $n-1$ paths to cover by the inductive hypothesis. So $S_{n}$ requires at least $n$ paths, as desired. Remark (Motivational comments from Evan). Basically the idea is that I wanted to peel away the right path $S$ highlighted in red in the figure, so that one could induct. But the problem is that the red path might not actually exist, e.g. the set of paths might contain the mirror of $S$ instead. Nonetheless, in those equality cases I found I could perturb some edges (e.g. change from $(-1, n-2)-(0, n-2)$ to $(0, n-2)-(1, n-2))$. So the idea then was to do little changes and try to convert the given partition into one where the red path $S$ exists, (and then peel it away for induction) without decreasing the total number of paths. To make this work, you actually want the incisions to begin ear the points $a$ and $b$, because that's the point of $S$ that is most constrained (e.g. you get $a-b$ right away for free), and assemble the path from there. (If you try to do it from the top, it's much less clear what's happening.) That's why the algorithm starts the mutations from around a.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Denote by $S_{n}$ the set of points $(x, y)$ with integer coordinates such that $$ |x|+\left|y+\frac{1}{2}\right|<n $$ A path is a sequence of distinct points $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{\ell}, y_{\ell}\right)$ in $S_{n}$ such that, for $i=2, \ldots, \ell$, the distance between $\left(x_{i}, y_{i}\right)$ and $\left(x_{i-1}, y_{i-1}\right)$ is 1 . Prove that the points in $S_{n}$ cannot be partitioned into fewer than $n$ paths.
|
【 First solution (local). We proceed by induction on $n$. The base case $n=1$ is clear, so suppose $n>1$. Let $S$ denote the set of points $$ S=\left\{(x, y): x+\left|y+\frac{1}{2}\right| \geq n-2\right\} $$ An example when $n=4$ is displayed below.  For any minimal partition $\mathcal{P}$ of $S_{n}$, let $P$ denote the path passing through the point $a=(n-1,0)$. Then the intersection of $P$ with $S$ consists of several disconnected paths; let $N$ be the number of nodes in the component containing $a$, and pick $\mathcal{P}$ such that $N$ is maximal. We claim that in this case $P=S$. Assume not. First, note $a=(n-1,0)$ must be connected to $b=(n-1,-1)$ (otherwise join them to decrease the number of paths). Now, starting from $a=(n-1,0)$ walk along $P$ away from $b$ until one of the following three conditions is met: - We reach a point $v$ not in $S$. Let $w$ be the point before $v$, and $x$ the point in $S$ adjacent to $w$. Then delete $v w$ and add $w x$. This increases $N$ while leaving the number of edges unchanged: so this case can't happen. - We reach an endpoint $v$ of $P$ (which may be $a$ ), lying inside the set $S$, which is not the topmost point $(0, n-1)$. Let $w$ be the next point of $S$. Delete any edge touching $w$ and add edge $v w$. This increases $N$ while leaving the number of edges unchanged: so this case can't happen. - We reach the topmost point $(0, n-1)$. Thus we see that $P$ must follow $S$ until reaching the topmost point $(0, n-1)$. Similarly it must reach the bottom-most point $(0,-n)$. Hence $P=S$. The remainder of $S_{n}$ is just $S_{n-1}$, and hence this requires at least $n-1$ paths to cover by the inductive hypothesis. So $S_{n}$ requires at least $n$ paths, as desired. Remark (Motivational comments from Evan). Basically the idea is that I wanted to peel away the right path $S$ highlighted in red in the figure, so that one could induct. But the problem is that the red path might not actually exist, e.g. the set of paths might contain the mirror of $S$ instead. Nonetheless, in those equality cases I found I could perturb some edges (e.g. change from $(-1, n-2)-(0, n-2)$ to $(0, n-2)-(1, n-2))$. So the idea then was to do little changes and try to convert the given partition into one where the red path $S$ exists, (and then peel it away for induction) without decreasing the total number of paths. To make this work, you actually want the incisions to begin ear the points $a$ and $b$, because that's the point of $S$ that is most constrained (e.g. you get $a-b$ right away for free), and assemble the path from there. (If you try to do it from the top, it's much less clear what's happening.) That's why the algorithm starts the mutations from around a.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5bb61b2-ebaa-57df-a2bc-8e11e7968911
| 604,438
|
Three nonnegative real numbers $r_{1}, r_{2}, r_{3}$ are written on a blackboard. These numbers have the property that there exist integers $a_{1}, a_{2}, a_{3}$, not all zero, satisfying $a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3}=0$. We are permitted to perform the following operation: find two numbers $x, y$ on the blackboard with $x \leq y$, then erase $y$ and write $y-x$ in its place. Prove that after a finite number of such operations, we can end up with at least one 0 on the blackboard.
|
We first show we can decrease the quantity $\left|a_{1}\right|+\left|a_{2}\right|+\left|a_{3}\right|$ as long as $0 \notin\left\{a_{1}, a_{2}, a_{3}\right\}$. Assume $a_{1}>0$ and $r_{1}>r_{2}>r_{3}$ without loss of generality and consider two cases. - Suppose $a_{2}>0$ or $a_{3}>0$; these cases are identical. (One cannot have both $a_{2}>0$ and $a_{3}>0$.) If $a_{2}>0$ then $a_{3}<0$ and get $$ 0=a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3}>a_{1} r_{3}+a_{3} r_{3} \Longrightarrow a_{1}+a_{3}<0 $$ so $\left|a_{1}+a_{3}\right|<\left|a_{3}\right|$, and hence we perform $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{3}, r_{2}, r_{3}\right)$. - Both $a_{2}<0$ and $a_{3}<0$. Assume for contradiction that $\left|a_{1}+a_{2}\right| \geq-a_{2}$ and $\left|a_{1}+a_{3}\right| \geq-a_{3}$ both hold (if either fails then we use $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{2}, r_{2}, r_{3}\right)$ and $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{3}, r_{2}, r_{3}\right)$, respectively). Clearly $a_{1}+a_{2}$ and $a_{1}+a_{3}$ are both positive in this case, so we get $a_{1}+2 a_{2}$ and $a_{1}+2 a_{3} \geq 0$; adding gives $a_{1}+a_{2}+a_{3} \geq 0$. But $$ \begin{aligned} 0 & =a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3} \\ & >a_{1} r_{2}+a_{2} r_{2}+a_{3} r_{2} \\ & =r_{2}\left(a_{1}+a_{2}+a_{3}\right) \\ \Longrightarrow 0 & <a_{1}+a_{2}+a_{3} . \end{aligned} $$ Since this covers all cases, we see that we can always decrease $\left|a_{1}\right|+\left|a_{2}\right|+\left|a_{3}\right|$ whenever $0 \notin\left\{a_{1}, a_{2}, a_{3}\right\}$. Because the $a_{i}$ are integers this cannot occur indefinitely, so eventually one of the $a_{i}$ 's is zero. At this point we can just apply the Euclidean Algorithm, so we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Three nonnegative real numbers $r_{1}, r_{2}, r_{3}$ are written on a blackboard. These numbers have the property that there exist integers $a_{1}, a_{2}, a_{3}$, not all zero, satisfying $a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3}=0$. We are permitted to perform the following operation: find two numbers $x, y$ on the blackboard with $x \leq y$, then erase $y$ and write $y-x$ in its place. Prove that after a finite number of such operations, we can end up with at least one 0 on the blackboard.
|
We first show we can decrease the quantity $\left|a_{1}\right|+\left|a_{2}\right|+\left|a_{3}\right|$ as long as $0 \notin\left\{a_{1}, a_{2}, a_{3}\right\}$. Assume $a_{1}>0$ and $r_{1}>r_{2}>r_{3}$ without loss of generality and consider two cases. - Suppose $a_{2}>0$ or $a_{3}>0$; these cases are identical. (One cannot have both $a_{2}>0$ and $a_{3}>0$.) If $a_{2}>0$ then $a_{3}<0$ and get $$ 0=a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3}>a_{1} r_{3}+a_{3} r_{3} \Longrightarrow a_{1}+a_{3}<0 $$ so $\left|a_{1}+a_{3}\right|<\left|a_{3}\right|$, and hence we perform $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{3}, r_{2}, r_{3}\right)$. - Both $a_{2}<0$ and $a_{3}<0$. Assume for contradiction that $\left|a_{1}+a_{2}\right| \geq-a_{2}$ and $\left|a_{1}+a_{3}\right| \geq-a_{3}$ both hold (if either fails then we use $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{2}, r_{2}, r_{3}\right)$ and $\left(r_{1}, r_{2}, r_{3}\right) \mapsto\left(r_{1}-r_{3}, r_{2}, r_{3}\right)$, respectively). Clearly $a_{1}+a_{2}$ and $a_{1}+a_{3}$ are both positive in this case, so we get $a_{1}+2 a_{2}$ and $a_{1}+2 a_{3} \geq 0$; adding gives $a_{1}+a_{2}+a_{3} \geq 0$. But $$ \begin{aligned} 0 & =a_{1} r_{1}+a_{2} r_{2}+a_{3} r_{3} \\ & >a_{1} r_{2}+a_{2} r_{2}+a_{3} r_{2} \\ & =r_{2}\left(a_{1}+a_{2}+a_{3}\right) \\ \Longrightarrow 0 & <a_{1}+a_{2}+a_{3} . \end{aligned} $$ Since this covers all cases, we see that we can always decrease $\left|a_{1}\right|+\left|a_{2}\right|+\left|a_{3}\right|$ whenever $0 \notin\left\{a_{1}, a_{2}, a_{3}\right\}$. Because the $a_{i}$ are integers this cannot occur indefinitely, so eventually one of the $a_{i}$ 's is zero. At this point we can just apply the Euclidean Algorithm, so we're done.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
b0216652-876e-5e38-80db-472fb968645e
| 248,481
|
At a certain mathematical conference, every pair of mathematicians are either friends or strangers. At mealtime, every participant eats in one of two large dining rooms. Each mathematician insists upon eating in a room which contains an even number of his or her friends. Prove that the number of ways that the mathematicians may be split between the two rooms is a power of two (i.e. is of the form $2^{k}$ for some positive integer $k$ ).
|
Take the obvious graph interpretation where we are trying to 2 -color a graph. Let $A$ be the adjacency matrix of the graph over $\mathbb{F}_{2}$, except the diagonal of $A$ has $\operatorname{deg} v(\bmod 2)$ instead of zero. Then let $\vec{d}$ be the main diagonal. Splittings then correspond to $A \vec{v}=\vec{d}$. It's then immediate that the number of ways is either zero or a power of two, since if it is nonempty it is a coset of $\operatorname{ker} A$. Thus we only need to show that: Claim - At least one coloring exists. It's also possible to use linear algebra. We prove the following lemma: ## Lemma (grobber) Let $V$ be a finite dimensional vector space, $T: V \rightarrow V$ and $w \in V$. Then $w$ is in the image of $T$ if and only if there are no $\xi \in V^{\vee}$ for which $\xi(w) \neq 0$ and yet $\xi \circ T=0$. ## Corollary In a symmetric matrix $A \bmod 2$, there exists a vector $v$ such that $A v$ is a copy of the diagonal of $A$. $$ 0=w^{\top} \cdot T \cdot w=\xi(d) $$ because this extracts the sum of coefficients submatrix of $T$, and all the symmetric entries cancel off. Thus no $\xi$ as in the previous lemma exists.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
At a certain mathematical conference, every pair of mathematicians are either friends or strangers. At mealtime, every participant eats in one of two large dining rooms. Each mathematician insists upon eating in a room which contains an even number of his or her friends. Prove that the number of ways that the mathematicians may be split between the two rooms is a power of two (i.e. is of the form $2^{k}$ for some positive integer $k$ ).
|
Take the obvious graph interpretation where we are trying to 2 -color a graph. Let $A$ be the adjacency matrix of the graph over $\mathbb{F}_{2}$, except the diagonal of $A$ has $\operatorname{deg} v(\bmod 2)$ instead of zero. Then let $\vec{d}$ be the main diagonal. Splittings then correspond to $A \vec{v}=\vec{d}$. It's then immediate that the number of ways is either zero or a power of two, since if it is nonempty it is a coset of $\operatorname{ker} A$. Thus we only need to show that: Claim - At least one coloring exists. It's also possible to use linear algebra. We prove the following lemma: ## Lemma (grobber) Let $V$ be a finite dimensional vector space, $T: V \rightarrow V$ and $w \in V$. Then $w$ is in the image of $T$ if and only if there are no $\xi \in V^{\vee}$ for which $\xi(w) \neq 0$ and yet $\xi \circ T=0$. ## Corollary In a symmetric matrix $A \bmod 2$, there exists a vector $v$ such that $A v$ is a copy of the diagonal of $A$. $$ 0=w^{\top} \cdot T \cdot w=\xi(d) $$ because this extracts the sum of coefficients submatrix of $T$, and all the symmetric entries cancel off. Thus no $\xi$ as in the previous lemma exists.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2008-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c9c5a61c-ddc3-50f3-86af-23af59d2c0e8
| 248,493
|
Given circles $\omega_{1}$ and $\omega_{2}$ intersecting at points $X$ and $Y$, let $\ell_{1}$ be a line through the center of $\omega_{1}$ intersecting $\omega_{2}$ at points $P$ and $Q$ and let $\ell_{2}$ be a line through the center of $\omega_{2}$ intersecting $\omega_{1}$ at points $R$ and $S$. Prove that if $P, Q, R$, and $S$ lie on a circle then the center of this circle lies on line $X Y$.
|
Let $r_{1}, r_{2}, r_{3}$ denote the circumradii of $\omega_{1}, \omega_{2}$, and $\omega_{3}$, respectively.  We wish to show that $O_{3}$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$. Let us encode the conditions using power of a point. Because $O_{1}$ is on the radical axis of $\omega_{2}$ and $\omega_{3}$, $$ \begin{aligned} \operatorname{Pow}_{\omega_{2}}\left(O_{1}\right) & =\operatorname{Pow}_{\omega_{3}}\left(O_{1}\right) \\ \Longrightarrow O_{1} O_{2}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-r_{3}^{2} . \end{aligned} $$ Similarly, because $O_{2}$ is on the radical axis of $\omega_{1}$ and $\omega_{3}$, we have $$ \begin{aligned} \operatorname{Pow}_{\omega_{1}}\left(O_{2}\right) & =\operatorname{Pow}_{\omega_{3}}\left(O_{2}\right) \\ \Longrightarrow O_{1} O_{2}^{2}-r_{1}^{2} & =O_{2} O_{3}^{2}-r_{3}^{2} . \end{aligned} $$ Subtracting the two gives $$ \begin{aligned} \left(O_{1} O_{2}^{2}-r_{2}^{2}\right)- & \left(O_{1} O_{2}^{2}-r_{1}^{2}\right) \\ = & \left(O_{1} O_{3}^{2}-r_{3}^{2}\right)-\left(O_{2} O_{3}^{2}-r_{3}^{2}\right) \\ \Longrightarrow r_{1}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-O_{2} O_{3}^{2} \\ \Longrightarrow O_{2} O_{3}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-r_{1}^{2} \\ \Longrightarrow \operatorname{Pow}_{\omega_{2}}\left(O_{3}\right) & =\operatorname{Pow}_{\omega_{1}}\left(O_{3}\right) \end{aligned} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given circles $\omega_{1}$ and $\omega_{2}$ intersecting at points $X$ and $Y$, let $\ell_{1}$ be a line through the center of $\omega_{1}$ intersecting $\omega_{2}$ at points $P$ and $Q$ and let $\ell_{2}$ be a line through the center of $\omega_{2}$ intersecting $\omega_{1}$ at points $R$ and $S$. Prove that if $P, Q, R$, and $S$ lie on a circle then the center of this circle lies on line $X Y$.
|
Let $r_{1}, r_{2}, r_{3}$ denote the circumradii of $\omega_{1}, \omega_{2}$, and $\omega_{3}$, respectively.  We wish to show that $O_{3}$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$. Let us encode the conditions using power of a point. Because $O_{1}$ is on the radical axis of $\omega_{2}$ and $\omega_{3}$, $$ \begin{aligned} \operatorname{Pow}_{\omega_{2}}\left(O_{1}\right) & =\operatorname{Pow}_{\omega_{3}}\left(O_{1}\right) \\ \Longrightarrow O_{1} O_{2}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-r_{3}^{2} . \end{aligned} $$ Similarly, because $O_{2}$ is on the radical axis of $\omega_{1}$ and $\omega_{3}$, we have $$ \begin{aligned} \operatorname{Pow}_{\omega_{1}}\left(O_{2}\right) & =\operatorname{Pow}_{\omega_{3}}\left(O_{2}\right) \\ \Longrightarrow O_{1} O_{2}^{2}-r_{1}^{2} & =O_{2} O_{3}^{2}-r_{3}^{2} . \end{aligned} $$ Subtracting the two gives $$ \begin{aligned} \left(O_{1} O_{2}^{2}-r_{2}^{2}\right)- & \left(O_{1} O_{2}^{2}-r_{1}^{2}\right) \\ = & \left(O_{1} O_{3}^{2}-r_{3}^{2}\right)-\left(O_{2} O_{3}^{2}-r_{3}^{2}\right) \\ \Longrightarrow r_{1}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-O_{2} O_{3}^{2} \\ \Longrightarrow O_{2} O_{3}^{2}-r_{2}^{2} & =O_{1} O_{3}^{2}-r_{1}^{2} \\ \Longrightarrow \operatorname{Pow}_{\omega_{2}}\left(O_{3}\right) & =\operatorname{Pow}_{\omega_{1}}\left(O_{3}\right) \end{aligned} $$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2009-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
067307db-3c16-500e-9555-4f5a88e7c60c
| 248,503
|
We define a chessboard polygon to be a simple polygon whose sides are situated along lines of the form $x=a$ or $y=b$, where $a$ and $b$ are integers. These lines divide the interior into unit squares, which are shaded alternately grey and white so that adjacent squares have different colors. To tile a chessboard polygon by dominoes is to exactly cover the polygon by non-overlapping $1 \times 2$ rectangles. Finally, a tasteful tiling is one which avoids the two configurations of dominoes and colors shown on the left below. Two tilings of a $3 \times 4$ rectangle are shown; the first one is tasteful, while the second is not, due to the vertical dominoes in the upper right corner.  Prove that (a) if a chessboard polygon can be tiled by dominoes, then it can be done so tastefully, and (b) such a tasteful tiling is unique.
|
Consider a lower-left square $s$ of the polygon, and WLOG is it white (other case similar). Then we have two cases: - If there exists a domino tiling of $\mathcal{P}$ where $s$ is covered by a vertical domino, then delete this domino and apply induction on the rest of $\mathcal{P}$. This additional domino will not cause any distasteful tilings. - Otherwise, assume $s$ is covered by a horizontal domino in every tiling. Again delete this domino and apply induction on the rest of $\mathcal{P}$. The resulting tasteful tiling should not have another horizontal domino adjacent to the one covering $s$, because otherwise we could have replaced that $2 \times 2$ square with two vertical dominoes to arrive in the first case. So this additional domino will not cause any distasteful tilings. Remark. The second case can actually arise, for example in the following picture.  Thus one cannot just try to cover $s$ with a vertical domino and claim the rest of $\mathcal{P}$ is tile-able. So the induction is not as easy as one might hope. distasteful tiling, we rotate it to avoid the bad pattern. The bottom-left corner eventually becomes stable, and an induction shows the termination of the algorithm. Henceforth, it will be convenient to work with the lattice $\mathbb{Z}^{2}$, treating the squares as black/white points, and we do so. Let $\gamma$ be any such cycle and let $s$ denote a lower left point, and again WLOG it is black. Orient $\gamma$ counterclockwise henceforth. Restrict attention to the lattice polygon $\mathcal{Q}$ enclosed by $\gamma$ (we consider points of $\gamma$ as part of $\mathcal{Q}$ ). In one of the two tilings of (lattice points of) $\mathcal{Q}$, the point $s$ will be covered by a horizontal domino; in the other tiling $s$ will be covered by a vertical domino. From now on we will focus only on the latter one. Observe that we now have a set of dominoes along $\gamma$, such that $\gamma$ points from the white point to the black point within each domino. Now impose coordinates so that $s=(0,0)$. Consider the stair-case sequence of points $p_{0}=s=(0,0), p_{1}=(1,0), p_{2}=(1,1), p_{3}=(2,1)$, and so on. By hypothesis, $p_{0}$ is covered by a vertical domino. Then $p_{1}$ must be covered by a horizontal domino, to avoid a distasteful tiling. Then if $p_{2}$ is in $\mathcal{Q}$, then it must be covered by a vertical domino to avoid a distasteful tiling, and so on. We may repeat this argument as long the points $p_{i}$ lie inside $\mathcal{Q}$. (See figure below; the staircase sequence is highlighted by red halos.) 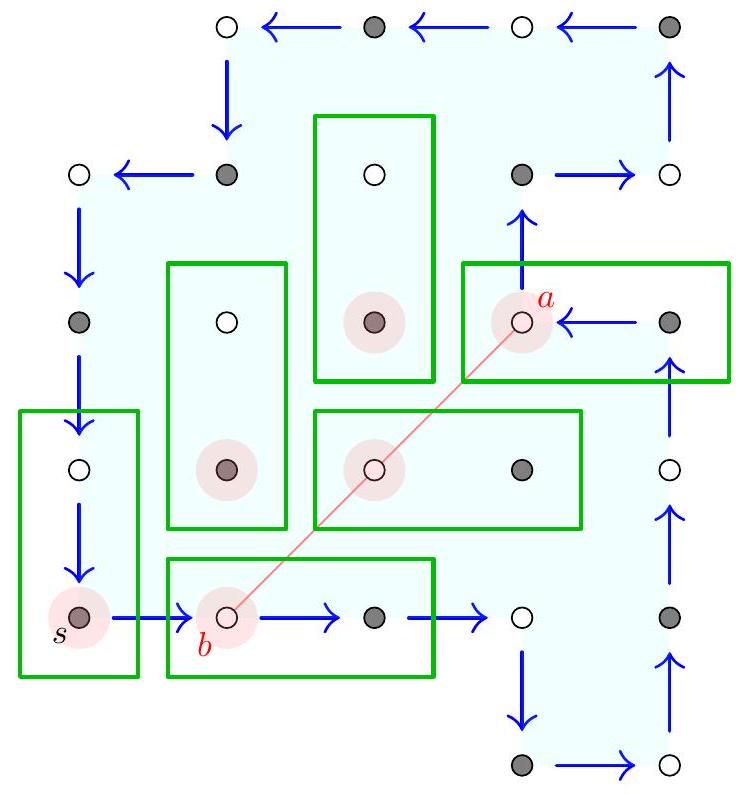 The curve $\gamma$ by definition should cross $y=x-1$ at the point $b=(1,0)$. Let $a$ denote the first point of this sequence after $p_{1}$ for which $\gamma$ crosses $y=x-1$ again. Now $a$ is tiled by a vertical domino whose black point is to the right of $\ell$. But the line segment $\ell$ cuts $\mathcal{Q}$ into two parts, and the orientation of $\gamma$ has this path also entering from the right. This contradicts the fact that the orientation of $\gamma$ points only from white to black within dominoes. This contradiction completes the proof. Remark. Note the problem is false if you allow holes (consider a $3 \times 3$ with the middle square deleted).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We define a chessboard polygon to be a simple polygon whose sides are situated along lines of the form $x=a$ or $y=b$, where $a$ and $b$ are integers. These lines divide the interior into unit squares, which are shaded alternately grey and white so that adjacent squares have different colors. To tile a chessboard polygon by dominoes is to exactly cover the polygon by non-overlapping $1 \times 2$ rectangles. Finally, a tasteful tiling is one which avoids the two configurations of dominoes and colors shown on the left below. Two tilings of a $3 \times 4$ rectangle are shown; the first one is tasteful, while the second is not, due to the vertical dominoes in the upper right corner.  Prove that (a) if a chessboard polygon can be tiled by dominoes, then it can be done so tastefully, and (b) such a tasteful tiling is unique.
|
Consider a lower-left square $s$ of the polygon, and WLOG is it white (other case similar). Then we have two cases: - If there exists a domino tiling of $\mathcal{P}$ where $s$ is covered by a vertical domino, then delete this domino and apply induction on the rest of $\mathcal{P}$. This additional domino will not cause any distasteful tilings. - Otherwise, assume $s$ is covered by a horizontal domino in every tiling. Again delete this domino and apply induction on the rest of $\mathcal{P}$. The resulting tasteful tiling should not have another horizontal domino adjacent to the one covering $s$, because otherwise we could have replaced that $2 \times 2$ square with two vertical dominoes to arrive in the first case. So this additional domino will not cause any distasteful tilings. Remark. The second case can actually arise, for example in the following picture.  Thus one cannot just try to cover $s$ with a vertical domino and claim the rest of $\mathcal{P}$ is tile-able. So the induction is not as easy as one might hope. distasteful tiling, we rotate it to avoid the bad pattern. The bottom-left corner eventually becomes stable, and an induction shows the termination of the algorithm. Henceforth, it will be convenient to work with the lattice $\mathbb{Z}^{2}$, treating the squares as black/white points, and we do so. Let $\gamma$ be any such cycle and let $s$ denote a lower left point, and again WLOG it is black. Orient $\gamma$ counterclockwise henceforth. Restrict attention to the lattice polygon $\mathcal{Q}$ enclosed by $\gamma$ (we consider points of $\gamma$ as part of $\mathcal{Q}$ ). In one of the two tilings of (lattice points of) $\mathcal{Q}$, the point $s$ will be covered by a horizontal domino; in the other tiling $s$ will be covered by a vertical domino. From now on we will focus only on the latter one. Observe that we now have a set of dominoes along $\gamma$, such that $\gamma$ points from the white point to the black point within each domino. Now impose coordinates so that $s=(0,0)$. Consider the stair-case sequence of points $p_{0}=s=(0,0), p_{1}=(1,0), p_{2}=(1,1), p_{3}=(2,1)$, and so on. By hypothesis, $p_{0}$ is covered by a vertical domino. Then $p_{1}$ must be covered by a horizontal domino, to avoid a distasteful tiling. Then if $p_{2}$ is in $\mathcal{Q}$, then it must be covered by a vertical domino to avoid a distasteful tiling, and so on. We may repeat this argument as long the points $p_{i}$ lie inside $\mathcal{Q}$. (See figure below; the staircase sequence is highlighted by red halos.)  The curve $\gamma$ by definition should cross $y=x-1$ at the point $b=(1,0)$. Let $a$ denote the first point of this sequence after $p_{1}$ for which $\gamma$ crosses $y=x-1$ again. Now $a$ is tiled by a vertical domino whose black point is to the right of $\ell$. But the line segment $\ell$ cuts $\mathcal{Q}$ into two parts, and the orientation of $\gamma$ has this path also entering from the right. This contradicts the fact that the orientation of $\gamma$ points only from white to black within dominoes. This contradiction completes the proof. Remark. Note the problem is false if you allow holes (consider a $3 \times 3$ with the middle square deleted).
|
{
"resource_path": "USAMO/segmented/en-USAMO-2009-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6eef0816-3328-5673-a72e-9014d4077804
| 604,566
|
Trapezoid $A B C D$, with $\overline{A B} \| \overline{C D}$, is inscribed in circle $\omega$ and point $G$ lies inside triangle $B C D$. Rays $A G$ and $B G$ meet $\omega$ again at points $P$ and $Q$, respectively. Let the line through $G$ parallel to $\overline{A B}$ intersect $\overline{B D}$ and $\overline{B C}$ at points $R$ and $S$, respectively. Prove that quadrilateral $P Q R S$ is cyclic if and only if $\overline{B G}$ bisects $\angle C B D$.
|
Perform an inversion around $B$ with arbitrary radius, and denote the inverse of a point $Z$ with $Z^{*}$.  After inversion, we obtain a cyclic quadrilateral $B S^{*} G^{*} R^{*}$ and points $C^{*}, D^{*}$ on $\overline{B S^{*}}$, $\overline{B R^{*}}$, such that $\left(B C^{*} D^{*}\right)$ is tangent to $\left(B S^{*} G^{*} R^{*}\right)-$ in other words, so that $\overline{C^{*} D^{*}}$ is parallel to $\overline{S^{*} R^{*}}$. Point $A^{*}$ lies on line $\overline{C^{*} D^{*}}$ so that $\overline{A^{*} B}$ is tangent to $\left(B S^{*} G^{*} R^{*}\right)$. Points $P^{*}$ and $Q^{*}$ are the intersections of $\left(A^{*} B G^{*}\right)$ and $\overline{B G^{*}}$ with line $C^{*} D^{*}$. Observe that $P^{*} Q^{*} R^{*} S^{*}$ is a trapezoid, so it is cyclic if and only if it isosceles. Let $X$ be the second intersection of line $G^{*} P^{*}$ with $\left(B S^{*} R^{*}\right)$. Because $$ \measuredangle Q^{*} P^{*} G^{*}=\measuredangle A^{*} B G^{*}=\measuredangle B X G^{*} $$ we find that $B X S^{*} R^{*}$ is an isosceles trapezoid. If $G^{*}$ is indeed the midpoint of the arc then everything is clear by symmetry now. Conversely, if $P^{*} R^{*}=Q^{*} S^{*}$ then that means $P^{*} Q^{*} R^{*} S^{*}$ is a cyclic trapezoid, and hence that the perpendicular bisectors of $\overline{P^{*} Q^{*}}$ and $\overline{R^{*} S^{*}}$ are the same. Hence $B, X, P^{*}, Q^{*}$ are symmetric around this line. This forces $G^{*}$ to be the midpoint of $\operatorname{arc} R^{*} S^{*}$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Trapezoid $A B C D$, with $\overline{A B} \| \overline{C D}$, is inscribed in circle $\omega$ and point $G$ lies inside triangle $B C D$. Rays $A G$ and $B G$ meet $\omega$ again at points $P$ and $Q$, respectively. Let the line through $G$ parallel to $\overline{A B}$ intersect $\overline{B D}$ and $\overline{B C}$ at points $R$ and $S$, respectively. Prove that quadrilateral $P Q R S$ is cyclic if and only if $\overline{B G}$ bisects $\angle C B D$.
|
Perform an inversion around $B$ with arbitrary radius, and denote the inverse of a point $Z$ with $Z^{*}$.  After inversion, we obtain a cyclic quadrilateral $B S^{*} G^{*} R^{*}$ and points $C^{*}, D^{*}$ on $\overline{B S^{*}}$, $\overline{B R^{*}}$, such that $\left(B C^{*} D^{*}\right)$ is tangent to $\left(B S^{*} G^{*} R^{*}\right)-$ in other words, so that $\overline{C^{*} D^{*}}$ is parallel to $\overline{S^{*} R^{*}}$. Point $A^{*}$ lies on line $\overline{C^{*} D^{*}}$ so that $\overline{A^{*} B}$ is tangent to $\left(B S^{*} G^{*} R^{*}\right)$. Points $P^{*}$ and $Q^{*}$ are the intersections of $\left(A^{*} B G^{*}\right)$ and $\overline{B G^{*}}$ with line $C^{*} D^{*}$. Observe that $P^{*} Q^{*} R^{*} S^{*}$ is a trapezoid, so it is cyclic if and only if it isosceles. Let $X$ be the second intersection of line $G^{*} P^{*}$ with $\left(B S^{*} R^{*}\right)$. Because $$ \measuredangle Q^{*} P^{*} G^{*}=\measuredangle A^{*} B G^{*}=\measuredangle B X G^{*} $$ we find that $B X S^{*} R^{*}$ is an isosceles trapezoid. If $G^{*}$ is indeed the midpoint of the arc then everything is clear by symmetry now. Conversely, if $P^{*} R^{*}=Q^{*} S^{*}$ then that means $P^{*} Q^{*} R^{*} S^{*}$ is a cyclic trapezoid, and hence that the perpendicular bisectors of $\overline{P^{*} Q^{*}}$ and $\overline{R^{*} S^{*}}$ are the same. Hence $B, X, P^{*}, Q^{*}$ are symmetric around this line. This forces $G^{*}$ to be the midpoint of $\operatorname{arc} R^{*} S^{*}$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2009-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
178f8b78-0dce-5b1c-966f-efc315216c16
| 248,543
|
Let $s_{1}, s_{2}, s_{3}, \ldots$ be an infinite, nonconstant sequence of rational numbers, meaning it is not the case that $s_{1}=s_{2}=s_{3}=\ldots$ Suppose that $t_{1}, t_{2}, t_{3}, \ldots$ is also an infinite, nonconstant sequence of rational numbers with the property that $\left(s_{i}-s_{j}\right)\left(t_{i}-t_{j}\right)$ is an integer for all $i$ and $j$. Prove that there exists a rational number $r$ such that $\left(s_{i}-s_{j}\right) r$ and $\left(t_{i}-t_{j}\right) / r$ are integers for all $i$ and $j$.
|
First we eliminate the silly edge case: Claim - For some $i$ and $j$, we have $\left(s_{i}-s_{j}\right)\left(t_{i}-t_{j}\right) \neq 0$. So, WLOG (by permutation) that $n=\left(s_{1}-s_{2}\right)\left(t_{1}-t_{2}\right) \neq 0$. By shifting and scaling appropriately, we may assume $$ s_{1}=t_{1}=0, \quad s_{2}=1, \quad t_{2}=n $$ Thus we deduce $$ s_{i} t_{i} \in \mathbb{Z}, \quad s_{i} t_{j}+s_{j} t_{i} \in \mathbb{Z} \quad \forall i, j $$ Claim - For any index $i, t_{i} \in \mathbb{Z}, s_{i} \in \frac{1}{n} \mathbb{Z}$. Last claim: Claim - If $d=\operatorname{gcd} t_{\bullet}$, then $d s_{i} \in \mathbb{Z}$ for all $i$. This is already true for $i=j$, so assume $i \neq j$. Assume for contradiction $\nu_{p}\left(s_{i}\right)<-e$. Then $\nu_{p}\left(t_{i}\right)>e=\nu_{p}\left(t_{k}\right)$. Since $\nu_{p}\left(s_{k}\right) \geq-e$ we deduce $\nu_{p}\left(s_{i} t_{k}\right)<\nu_{p}\left(s_{k} t_{i}\right)$; so $\nu_{p}\left(s_{i} t_{k}\right) \geq$ 0 and $\nu_{p}\left(s_{i}\right) \geq-e$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $s_{1}, s_{2}, s_{3}, \ldots$ be an infinite, nonconstant sequence of rational numbers, meaning it is not the case that $s_{1}=s_{2}=s_{3}=\ldots$ Suppose that $t_{1}, t_{2}, t_{3}, \ldots$ is also an infinite, nonconstant sequence of rational numbers with the property that $\left(s_{i}-s_{j}\right)\left(t_{i}-t_{j}\right)$ is an integer for all $i$ and $j$. Prove that there exists a rational number $r$ such that $\left(s_{i}-s_{j}\right) r$ and $\left(t_{i}-t_{j}\right) / r$ are integers for all $i$ and $j$.
|
First we eliminate the silly edge case: Claim - For some $i$ and $j$, we have $\left(s_{i}-s_{j}\right)\left(t_{i}-t_{j}\right) \neq 0$. So, WLOG (by permutation) that $n=\left(s_{1}-s_{2}\right)\left(t_{1}-t_{2}\right) \neq 0$. By shifting and scaling appropriately, we may assume $$ s_{1}=t_{1}=0, \quad s_{2}=1, \quad t_{2}=n $$ Thus we deduce $$ s_{i} t_{i} \in \mathbb{Z}, \quad s_{i} t_{j}+s_{j} t_{i} \in \mathbb{Z} \quad \forall i, j $$ Claim - For any index $i, t_{i} \in \mathbb{Z}, s_{i} \in \frac{1}{n} \mathbb{Z}$. Last claim: Claim - If $d=\operatorname{gcd} t_{\bullet}$, then $d s_{i} \in \mathbb{Z}$ for all $i$. This is already true for $i=j$, so assume $i \neq j$. Assume for contradiction $\nu_{p}\left(s_{i}\right)<-e$. Then $\nu_{p}\left(t_{i}\right)>e=\nu_{p}\left(t_{k}\right)$. Since $\nu_{p}\left(s_{k}\right) \geq-e$ we deduce $\nu_{p}\left(s_{i} t_{k}\right)<\nu_{p}\left(s_{k} t_{i}\right)$; so $\nu_{p}\left(s_{i} t_{k}\right) \geq$ 0 and $\nu_{p}\left(s_{i}\right) \geq-e$ as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2009-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
2c8596d9-fec8-5ecc-8338-98c0789af548
| 604,619
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 First approach using angle chasing. Define $T=\overline{P Q} \cap \overline{R S}$. Also, let $2 \alpha, 2 \beta, 2 \gamma, 2 \delta$ denote the measures of $\operatorname{arcs} \widehat{A X}, \widehat{X Y}, \widehat{Y Z}, \widehat{Z B}$, respectively, so that $\alpha+\beta+\gamma+\delta=90^{\circ}$.  We now compute the following angles: $$ \begin{aligned} & \angle S R Y=\angle S Z Y=90^{\circ}-\angle Y Z A=90^{\circ}-(\alpha+\beta) \\ & \angle Y Q P=\angle Y X P=90^{\circ}-\angle B X Y=90^{\circ}-(\gamma+\delta) \\ & \angle Q Y R=180^{\circ}-\angle(\overline{Z R}, \overline{Q X})=180^{\circ}-\frac{2 \beta+2 \gamma+180^{\circ}}{2}=90^{\circ}-(\beta+\gamma) \end{aligned} $$ Hence, we can then compute $$ \begin{aligned} \angle R T Q & =360^{\circ}-\left(\angle Q Y R+\left(180^{\circ}-\angle S R Y\right)+\left(180^{\circ}-\angle Y Q P\right)\right) \\ & =\angle S R Y+\angle Y Q P-\angle Q Y R \end{aligned} $$ $$ \begin{aligned} & =\left(90^{\circ}-(\alpha+\beta)\right)+\left(90^{\circ}-(\gamma+\delta)\right)-\left(90^{\circ}-(\beta+\gamma)\right) \\ & =90^{\circ}-(\alpha+\delta) \\ & =\beta+\gamma . \end{aligned} $$ Since $\angle X O Z=\frac{2 \beta+2 \gamma}{2}=\beta+\gamma$, the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 First approach using angle chasing. Define $T=\overline{P Q} \cap \overline{R S}$. Also, let $2 \alpha, 2 \beta, 2 \gamma, 2 \delta$ denote the measures of $\operatorname{arcs} \widehat{A X}, \widehat{X Y}, \widehat{Y Z}, \widehat{Z B}$, respectively, so that $\alpha+\beta+\gamma+\delta=90^{\circ}$.  We now compute the following angles: $$ \begin{aligned} & \angle S R Y=\angle S Z Y=90^{\circ}-\angle Y Z A=90^{\circ}-(\alpha+\beta) \\ & \angle Y Q P=\angle Y X P=90^{\circ}-\angle B X Y=90^{\circ}-(\gamma+\delta) \\ & \angle Q Y R=180^{\circ}-\angle(\overline{Z R}, \overline{Q X})=180^{\circ}-\frac{2 \beta+2 \gamma+180^{\circ}}{2}=90^{\circ}-(\beta+\gamma) \end{aligned} $$ Hence, we can then compute $$ \begin{aligned} \angle R T Q & =360^{\circ}-\left(\angle Q Y R+\left(180^{\circ}-\angle S R Y\right)+\left(180^{\circ}-\angle Y Q P\right)\right) \\ & =\angle S R Y+\angle Y Q P-\angle Q Y R \end{aligned} $$ $$ \begin{aligned} & =\left(90^{\circ}-(\alpha+\beta)\right)+\left(90^{\circ}-(\gamma+\delta)\right)-\left(90^{\circ}-(\beta+\gamma)\right) \\ & =90^{\circ}-(\alpha+\delta) \\ & =\beta+\gamma . \end{aligned} $$ Since $\angle X O Z=\frac{2 \beta+2 \gamma}{2}=\beta+\gamma$, the proof is complete.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d69d980d-bcac-5f57-9853-fb19401e1981
| 604,227
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 Second approach using Simson lines, ignoring the diameter condition. In this solution, we will ignore the condition that $\overline{A B}$ is a diameter; the solution works equally well without it, as long as $O$ is redefined as the center of $(A X Y Z B)$ instead. We will again show the angle formed by lines $P Q$ and $R S$ is half the measure of $\widehat{X Z}$.  Now it's straightforward to see $A P Y R T$ is cyclic (in the circle with diameter $\overline{A Y}$ ), and therefore $$ \angle R T Y=\angle R A Y=\angle Z A Y $$ Similarly, $$ \angle Y T Q=\angle Y B Q=\angle Y B X $$ Summing these gives $\angle R T Q$ is equal to half the measure of $\operatorname{arc} \widehat{X Z}$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A X Y Z B$ be a convex pentagon inscribed in a semicircle of diameter $A B$. Denote by $P, Q, R, S$ the feet of the perpendiculars from $Y$ onto lines $A X, B X$, $A Z, B Z$, respectively. Prove that the acute angle formed by lines $P Q$ and $R S$ is half the size of $\angle X O Z$, where $O$ is the midpoint of segment $A B$.
|
【 Second approach using Simson lines, ignoring the diameter condition. In this solution, we will ignore the condition that $\overline{A B}$ is a diameter; the solution works equally well without it, as long as $O$ is redefined as the center of $(A X Y Z B)$ instead. We will again show the angle formed by lines $P Q$ and $R S$ is half the measure of $\widehat{X Z}$.  Now it's straightforward to see $A P Y R T$ is cyclic (in the circle with diameter $\overline{A Y}$ ), and therefore $$ \angle R T Y=\angle R A Y=\angle Z A Y $$ Similarly, $$ \angle Y T Q=\angle Y B Q=\angle Y B X $$ Summing these gives $\angle R T Q$ is equal to half the measure of $\operatorname{arc} \widehat{X Z}$ as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d69d980d-bcac-5f57-9853-fb19401e1981
| 604,227
|
Let $q=\frac{3 p-5}{2}$ where $p$ is an odd prime, and let $$ S_{q}=\frac{1}{2 \cdot 3 \cdot 4}+\frac{1}{5 \cdot 6 \cdot 7}+\cdots+\frac{1}{q(q+1)(q+2)} $$ Prove that if $\frac{1}{p}-2 S_{q}=\frac{m}{n}$ for integers $m$ and $n$, then $m-n$ is divisible by $p$.
|
By partial fractions, we have $$ \frac{2}{(3 k-1)(3 k)(3 k+1)}=\frac{1}{3 k-1}-\frac{2}{3 k}+\frac{1}{3 k+1} $$ Thus $$ \begin{aligned} 2 S_{q} & =\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}-\frac{2}{6}+\frac{1}{7}\right)+\cdots+\left(\frac{1}{q}-\frac{2}{q+1}+\frac{1}{q+2}\right) \\ & =\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{q+2}\right)-3\left(\frac{1}{3}+\frac{1}{6}+\cdots+\frac{1}{q+1}\right) \\ & =\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ \Longrightarrow 2 S_{q}-\frac{1}{p}+1 & =\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{p+1}+\frac{1}{p+2} \cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \end{aligned} $$ Now we are ready to take modulo $p$. The given says that $q-p+2=\frac{q+1}{3}$, so $$ \begin{aligned} 2 S_{q}-\frac{1}{p}+1 & =\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{p+1}+\frac{1}{p+2}+\cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ & \equiv\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{q-p+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ & =\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1} \\ & \equiv 0 \quad(\bmod p) . \end{aligned} $$ So $\frac{1}{p}-2 S_{q} \equiv 1(\bmod p)$ which is the desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $q=\frac{3 p-5}{2}$ where $p$ is an odd prime, and let $$ S_{q}=\frac{1}{2 \cdot 3 \cdot 4}+\frac{1}{5 \cdot 6 \cdot 7}+\cdots+\frac{1}{q(q+1)(q+2)} $$ Prove that if $\frac{1}{p}-2 S_{q}=\frac{m}{n}$ for integers $m$ and $n$, then $m-n$ is divisible by $p$.
|
By partial fractions, we have $$ \frac{2}{(3 k-1)(3 k)(3 k+1)}=\frac{1}{3 k-1}-\frac{2}{3 k}+\frac{1}{3 k+1} $$ Thus $$ \begin{aligned} 2 S_{q} & =\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}-\frac{2}{6}+\frac{1}{7}\right)+\cdots+\left(\frac{1}{q}-\frac{2}{q+1}+\frac{1}{q+2}\right) \\ & =\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{q+2}\right)-3\left(\frac{1}{3}+\frac{1}{6}+\cdots+\frac{1}{q+1}\right) \\ & =\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ \Longrightarrow 2 S_{q}-\frac{1}{p}+1 & =\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{p+1}+\frac{1}{p+2} \cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \end{aligned} $$ Now we are ready to take modulo $p$. The given says that $q-p+2=\frac{q+1}{3}$, so $$ \begin{aligned} 2 S_{q}-\frac{1}{p}+1 & =\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{p+1}+\frac{1}{p+2}+\cdots+\frac{1}{q+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ & \equiv\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1}\right)+\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{q-p+2}\right)-\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{\frac{q+1}{3}}\right) \\ & =\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{p-1} \\ & \equiv 0 \quad(\bmod p) . \end{aligned} $$ So $\frac{1}{p}-2 S_{q} \equiv 1(\bmod p)$ which is the desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2010-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6e74123a-a98d-50ce-bbc7-fc8738fa69cd
| 604,747
|
Let $a, b, c$ be positive real numbers such that $a^{2}+b^{2}+c^{2}+(a+b+c)^{2} \leq 4$. Prove that $$ \frac{a b+1}{(a+b)^{2}}+\frac{b c+1}{(b+c)^{2}}+\frac{c a+1}{(c+a)^{2}} \geq 3 $$
|
The condition becomes $2 \geq a^{2}+b^{2}+c^{2}+a b+b c+c a$. Therefore, $$ \begin{aligned} \sum_{\mathrm{cyc}} \frac{2 a b+2}{(a+b)^{2}} & \geq \sum_{\mathrm{cyc}} \frac{2 a b+\left(a^{2}+b^{2}+c^{2}+a b+b c+c a\right)}{(a+b)^{2}} \\ & =\sum_{\mathrm{cyc}} \frac{(a+b)^{2}+(c+a)(c+b)}{(a+b)^{2}} \\ & =3+\sum_{\mathrm{cyc}} \frac{(c+a)(c+b)}{(a+b)^{2}} \\ & \geq 3+3 \sqrt[3]{\prod_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}}}=3+3=6 \end{aligned} $$ with the last line by AM-GM. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a^{2}+b^{2}+c^{2}+(a+b+c)^{2} \leq 4$. Prove that $$ \frac{a b+1}{(a+b)^{2}}+\frac{b c+1}{(b+c)^{2}}+\frac{c a+1}{(c+a)^{2}} \geq 3 $$
|
The condition becomes $2 \geq a^{2}+b^{2}+c^{2}+a b+b c+c a$. Therefore, $$ \begin{aligned} \sum_{\mathrm{cyc}} \frac{2 a b+2}{(a+b)^{2}} & \geq \sum_{\mathrm{cyc}} \frac{2 a b+\left(a^{2}+b^{2}+c^{2}+a b+b c+c a\right)}{(a+b)^{2}} \\ & =\sum_{\mathrm{cyc}} \frac{(a+b)^{2}+(c+a)(c+b)}{(a+b)^{2}} \\ & =3+\sum_{\mathrm{cyc}} \frac{(c+a)(c+b)}{(a+b)^{2}} \\ & \geq 3+3 \sqrt[3]{\prod_{\text {cyc }} \frac{(c+a)(c+b)}{(a+b)^{2}}}=3+3=6 \end{aligned} $$ with the last line by AM-GM. This completes the proof.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
069d5dbb-deab-5cbd-980e-a28d7b5ab3fb
| 604,332
|
An integer is assigned to each vertex of a regular pentagon so that the sum of the five integers is 2011. A turn of a solitaire game consists of subtracting an integer $m$ (not necessarily positive) from each of the integers at two neighboring vertices and adding $2 m$ to the opposite vertex, which is not adjacent to either of the first two vertices. (The amount $m$ and the vertices chosen can vary from turn to turn.) The game is won at a certain vertex if, after some number of turns, that vertex has the number 2011 and the other four vertices have the number 0. Prove that for any choice of the initial integers, there is exactly one vertex at which the game can be won.
|
Call the vertices $0,1,2,3,4$ in order. First, notice that the quantity $$ S:=N_{1}+2 N_{2}+3 N_{3}+4 N_{4} \quad(\bmod 5) $$ is invariant, where $N_{i}$ is the amount at vertex $i$. This immediately implies that at most one vertex can win, since in a winning situation all $N_{i}$ are 0 except for one, which is 2011. (For example, if $S \equiv 3(\bmod 5)$, any victory must occur at the vertex 3 , via $N_{3}=2011$, $N_{0}=N_{1}=N_{2}=N_{4}=0$.) Now we prove we can win on this unique vertex. Let $a_{i}, x_{i}$ denote the number initially at $i$ and $x_{i}$ denote $\sum m$ over all $m$ where vertex $i$ gains $2 m$. WLOG the possible vertex is 0 , meaning $a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0(\bmod 5)$. Moreover we want $$ \begin{aligned} 2011 & =a_{0}+2 x_{0}-x_{2}-x_{3} \\ 0 & =a_{1}+2 x_{1}-x_{3}-x_{4} \\ 0 & =a_{2}+2 x_{2}-x_{4}-x_{0} \\ 0 & =a_{3}+2 x_{3}-x_{0}-x_{1} \\ 0 & =a_{4}+2 x_{4}-x_{1}-x_{2} \end{aligned} $$ We can ignore the first equation since its the sum of the other four, and we can WLOG shift $x_{0} \rightarrow 0$ by shifting each $x_{i}$ by a fixed amount. We will now solve the resulting system of equations. First, we have $$ x_{4}=2 x_{2}+a_{2} \text { and } x_{1}=2 x_{3}+a_{3} $$ Using these to remove all instances of $x_{1}$ and $x_{4}$ gives $$ 2 x_{2}-3 x_{3}=2 a_{3}+a_{1}-a_{2} \text { and } 2 x_{3}-3 x_{2}=2 a_{2}+a_{4}-a_{3} $$ whence we have a two-variable system of equations! To verify its solution is integral, note that $$ x_{2}-x_{3}=\frac{a_{1}-3 a_{2}+3 a_{3}-a_{4}}{5} $$ is an integer, since $$ a_{1}-3 a_{2}+3 a_{3}-a_{4} \equiv a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0 \quad(\bmod 5) $$ Abbreviating $\frac{a_{1}-3 a_{2}+3 a_{3}-a_{4}}{5}$ as $k$, we obtain the desired $x_{i}$ : $$ \begin{aligned} x_{2} & =2 a_{3}+a_{1}-a_{2}+2 k \\ x_{3} & =x_{2}+k \\ x_{1} & =2 x_{3}+a_{3} \\ x_{4} & =2 x_{2}+a_{2} \\ x_{0} & =0 . \end{aligned} $$ Remark. In principle, you could unwind all the definitions above to explicitly write every $x_{i}$ as a function of $a_{1}, a_{2}, a_{3}, a_{4}$. If you did this, you could get the long equations $$ \begin{aligned} & x_{0}=0 \\ & x_{1}=-\frac{1}{5}\left(6 a_{1}+2 a_{2}+3 a_{3}+4 a_{4}\right) \\ & x_{2}=-\frac{1}{5}\left(2 a_{1}+4 a_{2}+a_{3}+3 a_{4}\right) \\ & x_{3}=-\frac{1}{5}\left(3 a_{1}+a_{2}+4 a_{3}+2 a_{4}\right) \\ & x_{4}=-\frac{1}{5}\left(4 a_{1}+3 a_{2}+2 a_{3}+6 a_{4}\right) \end{aligned} $$ which indeed are all integers whenever $a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0(\bmod 5)$. However, this is quite tedious and also unnecessary to solve the problem. That's because we only care that the $x_{i}$ are integers, and do not need to actually know the values. This lets us work more indirectly to avoid long calculation, as we did above.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An integer is assigned to each vertex of a regular pentagon so that the sum of the five integers is 2011. A turn of a solitaire game consists of subtracting an integer $m$ (not necessarily positive) from each of the integers at two neighboring vertices and adding $2 m$ to the opposite vertex, which is not adjacent to either of the first two vertices. (The amount $m$ and the vertices chosen can vary from turn to turn.) The game is won at a certain vertex if, after some number of turns, that vertex has the number 2011 and the other four vertices have the number 0. Prove that for any choice of the initial integers, there is exactly one vertex at which the game can be won.
|
Call the vertices $0,1,2,3,4$ in order. First, notice that the quantity $$ S:=N_{1}+2 N_{2}+3 N_{3}+4 N_{4} \quad(\bmod 5) $$ is invariant, where $N_{i}$ is the amount at vertex $i$. This immediately implies that at most one vertex can win, since in a winning situation all $N_{i}$ are 0 except for one, which is 2011. (For example, if $S \equiv 3(\bmod 5)$, any victory must occur at the vertex 3 , via $N_{3}=2011$, $N_{0}=N_{1}=N_{2}=N_{4}=0$.) Now we prove we can win on this unique vertex. Let $a_{i}, x_{i}$ denote the number initially at $i$ and $x_{i}$ denote $\sum m$ over all $m$ where vertex $i$ gains $2 m$. WLOG the possible vertex is 0 , meaning $a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0(\bmod 5)$. Moreover we want $$ \begin{aligned} 2011 & =a_{0}+2 x_{0}-x_{2}-x_{3} \\ 0 & =a_{1}+2 x_{1}-x_{3}-x_{4} \\ 0 & =a_{2}+2 x_{2}-x_{4}-x_{0} \\ 0 & =a_{3}+2 x_{3}-x_{0}-x_{1} \\ 0 & =a_{4}+2 x_{4}-x_{1}-x_{2} \end{aligned} $$ We can ignore the first equation since its the sum of the other four, and we can WLOG shift $x_{0} \rightarrow 0$ by shifting each $x_{i}$ by a fixed amount. We will now solve the resulting system of equations. First, we have $$ x_{4}=2 x_{2}+a_{2} \text { and } x_{1}=2 x_{3}+a_{3} $$ Using these to remove all instances of $x_{1}$ and $x_{4}$ gives $$ 2 x_{2}-3 x_{3}=2 a_{3}+a_{1}-a_{2} \text { and } 2 x_{3}-3 x_{2}=2 a_{2}+a_{4}-a_{3} $$ whence we have a two-variable system of equations! To verify its solution is integral, note that $$ x_{2}-x_{3}=\frac{a_{1}-3 a_{2}+3 a_{3}-a_{4}}{5} $$ is an integer, since $$ a_{1}-3 a_{2}+3 a_{3}-a_{4} \equiv a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0 \quad(\bmod 5) $$ Abbreviating $\frac{a_{1}-3 a_{2}+3 a_{3}-a_{4}}{5}$ as $k$, we obtain the desired $x_{i}$ : $$ \begin{aligned} x_{2} & =2 a_{3}+a_{1}-a_{2}+2 k \\ x_{3} & =x_{2}+k \\ x_{1} & =2 x_{3}+a_{3} \\ x_{4} & =2 x_{2}+a_{2} \\ x_{0} & =0 . \end{aligned} $$ Remark. In principle, you could unwind all the definitions above to explicitly write every $x_{i}$ as a function of $a_{1}, a_{2}, a_{3}, a_{4}$. If you did this, you could get the long equations $$ \begin{aligned} & x_{0}=0 \\ & x_{1}=-\frac{1}{5}\left(6 a_{1}+2 a_{2}+3 a_{3}+4 a_{4}\right) \\ & x_{2}=-\frac{1}{5}\left(2 a_{1}+4 a_{2}+a_{3}+3 a_{4}\right) \\ & x_{3}=-\frac{1}{5}\left(3 a_{1}+a_{2}+4 a_{3}+2 a_{4}\right) \\ & x_{4}=-\frac{1}{5}\left(4 a_{1}+3 a_{2}+2 a_{3}+6 a_{4}\right) \end{aligned} $$ which indeed are all integers whenever $a_{1}+2 a_{2}+3 a_{3}+4 a_{4} \equiv 0(\bmod 5)$. However, this is quite tedious and also unnecessary to solve the problem. That's because we only care that the $x_{i}$ are integers, and do not need to actually know the values. This lets us work more indirectly to avoid long calculation, as we did above.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
792cfa21-780d-5118-8eca-9dc01c581dda
| 604,809
|
In hexagon $A B C D E F$, which is nonconvex but not self-intersecting, no pair of opposite sides are parallel. The internal angles satisfy $\angle A=3 \angle D, \angle C=3 \angle F$, and $\angle E=3 \angle B$. Furthermore $A B=D E, B C=E F$, and $C D=F A$. Prove that diagonals $\overline{A D}, \overline{B E}$, and $\overline{C F}$ are concurrent.
|
Main idea: Claim - In a satisfying hexagon, $B, D, F$ are reflections of $A, C, E$ across the sides of $\triangle A C E$. (This claim looks plausible because every excellent hexagon is satisfying, and both configuration spaces are three-dimensional.) Call a hexagon of this shape "excellent"; in a excellent hexagon the diagonals clearly concur (at the orthocenter). Set $\beta=\angle B, \delta=\angle D, \varphi=\angle F$. Now given a satisfying hexagon $A B C D E F$, construct a "phantom hexagon" $A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F^{\prime}$ with the same angles which is excellent (see figure). This is possible since $\beta+\delta+\varphi=180^{\circ}$.  Then it would suffice to prove that: ## Lemma A satisfying hexagon is uniquely determined by its angles up to similarity. That is, at most one hexagon (up to similarity) has angles $\beta, \delta, \gamma$ as above. To do this, consider the unit complex numbers in the directions $\overrightarrow{B A}$ and $\overrightarrow{D E}$ respectively and let $\vec{x}$ denote their sum. Define $\vec{y}, \vec{z}$ similarly. Note that the condition $\overline{A B} \nVdash \overline{D E}$ implies $\vec{x} \neq 0$, and similarly. Then we have the identities $$ A B \cdot \vec{x}+C D \cdot \vec{y}+E F \cdot \vec{z}=A^{\prime} B^{\prime} \cdot \vec{x}+C^{\prime} D^{\prime} \cdot \vec{y}+E^{\prime} F^{\prime} \cdot \vec{z}=0 . $$ So we would obtain $A B: C D: E F=A^{\prime} B^{\prime}: C^{\prime} D^{\prime}: E^{\prime} F^{\prime}$ if only we could show that $\vec{x}, \vec{y}, \vec{z}$ are not multiples of each other (linear dependency reasons). This is a tiresome computation with arguments, but here it is. First note that none of $\beta, \delta, \varphi$ can be $90^{\circ}$, since otherwise we get a pair of parallel sides. Now work in the complex plane, fix a reference such that $\vec{A}-\vec{B}$ has argument 0 , and assume $A B C D E F$ are labelled counterclockwise. Then - $\vec{B}-\vec{C}$ has argument $\pi-\beta$ - $\vec{C}-\vec{D}$ has argument $-(\beta+3 \varphi)$ - $\vec{D}-\vec{E}$ has argument $\pi-(\beta+3 \varphi+\delta)$ - $\vec{E}-\vec{F}$ has argument $-(4 \beta+3 \varphi+\delta)$ So the argument of $\vec{x}$ has argument $\frac{\pi-(\beta+3 \varphi+\delta)}{2}(\bmod \pi)$. The argument of $\vec{y}$ has argument $\frac{\pi-(5 \beta+3 \varphi+\delta)}{2}(\bmod \pi)$. Their difference is $2 \beta(\bmod \pi)$, and since $\beta \neq 90^{\circ}$, it follows that $\vec{x}$ and $\vec{y}$ are not multiples of each other; the other cases are similar. Then the lemma implies $A B C D E F \sim A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F$ and we're done. Remark. This problem turned out to be known already. It appears in this reference: Nikolai Beluhov, Matematika, 2008, issue 6, problem 3. It was reprinted as Kvant, 2009, issue 2, problem M2130; the reprint is available at http: //kvant.ras.ru/pdf/2009/2009-02.pdf. Remark. The vector perspective also shows the condition about parallel sides cannot be dropped. Here is a counterexample from Ryan Kim in the event that it is.  By adjusting the figure above so that the triangles are right isosceles (instead of just right), one also finds an example of a hexagon which is satisfying and whose diagonals are concurrent, but which is not excellent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In hexagon $A B C D E F$, which is nonconvex but not self-intersecting, no pair of opposite sides are parallel. The internal angles satisfy $\angle A=3 \angle D, \angle C=3 \angle F$, and $\angle E=3 \angle B$. Furthermore $A B=D E, B C=E F$, and $C D=F A$. Prove that diagonals $\overline{A D}, \overline{B E}$, and $\overline{C F}$ are concurrent.
|
Main idea: Claim - In a satisfying hexagon, $B, D, F$ are reflections of $A, C, E$ across the sides of $\triangle A C E$. (This claim looks plausible because every excellent hexagon is satisfying, and both configuration spaces are three-dimensional.) Call a hexagon of this shape "excellent"; in a excellent hexagon the diagonals clearly concur (at the orthocenter). Set $\beta=\angle B, \delta=\angle D, \varphi=\angle F$. Now given a satisfying hexagon $A B C D E F$, construct a "phantom hexagon" $A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F^{\prime}$ with the same angles which is excellent (see figure). This is possible since $\beta+\delta+\varphi=180^{\circ}$.  Then it would suffice to prove that: ## Lemma A satisfying hexagon is uniquely determined by its angles up to similarity. That is, at most one hexagon (up to similarity) has angles $\beta, \delta, \gamma$ as above. To do this, consider the unit complex numbers in the directions $\overrightarrow{B A}$ and $\overrightarrow{D E}$ respectively and let $\vec{x}$ denote their sum. Define $\vec{y}, \vec{z}$ similarly. Note that the condition $\overline{A B} \nVdash \overline{D E}$ implies $\vec{x} \neq 0$, and similarly. Then we have the identities $$ A B \cdot \vec{x}+C D \cdot \vec{y}+E F \cdot \vec{z}=A^{\prime} B^{\prime} \cdot \vec{x}+C^{\prime} D^{\prime} \cdot \vec{y}+E^{\prime} F^{\prime} \cdot \vec{z}=0 . $$ So we would obtain $A B: C D: E F=A^{\prime} B^{\prime}: C^{\prime} D^{\prime}: E^{\prime} F^{\prime}$ if only we could show that $\vec{x}, \vec{y}, \vec{z}$ are not multiples of each other (linear dependency reasons). This is a tiresome computation with arguments, but here it is. First note that none of $\beta, \delta, \varphi$ can be $90^{\circ}$, since otherwise we get a pair of parallel sides. Now work in the complex plane, fix a reference such that $\vec{A}-\vec{B}$ has argument 0 , and assume $A B C D E F$ are labelled counterclockwise. Then - $\vec{B}-\vec{C}$ has argument $\pi-\beta$ - $\vec{C}-\vec{D}$ has argument $-(\beta+3 \varphi)$ - $\vec{D}-\vec{E}$ has argument $\pi-(\beta+3 \varphi+\delta)$ - $\vec{E}-\vec{F}$ has argument $-(4 \beta+3 \varphi+\delta)$ So the argument of $\vec{x}$ has argument $\frac{\pi-(\beta+3 \varphi+\delta)}{2}(\bmod \pi)$. The argument of $\vec{y}$ has argument $\frac{\pi-(5 \beta+3 \varphi+\delta)}{2}(\bmod \pi)$. Their difference is $2 \beta(\bmod \pi)$, and since $\beta \neq 90^{\circ}$, it follows that $\vec{x}$ and $\vec{y}$ are not multiples of each other; the other cases are similar. Then the lemma implies $A B C D E F \sim A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F$ and we're done. Remark. This problem turned out to be known already. It appears in this reference: Nikolai Beluhov, Matematika, 2008, issue 6, problem 3. It was reprinted as Kvant, 2009, issue 2, problem M2130; the reprint is available at http: //kvant.ras.ru/pdf/2009/2009-02.pdf. Remark. The vector perspective also shows the condition about parallel sides cannot be dropped. Here is a counterexample from Ryan Kim in the event that it is.  By adjusting the figure above so that the triangles are right isosceles (instead of just right), one also finds an example of a hexagon which is satisfying and whose diagonals are concurrent, but which is not excellent.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2011-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
a631806c-968b-55cd-a59c-de0b5aa28fbe
| 248,629
|
A circle is divided into congruent arcs by 432 points. The points are colored in four colors such that some 108 points are colored red, some 108 points are colored green, some 108 points are colored blue, and the remaining 108 points are colored yellow. Prove that one can choose three points of each color in such a way that the four triangles formed by the chosen points of the same color are congruent.
|
First, consider the 431 possible non-identity rotations of the red points, and count overlaps with green points. If we select a rotation randomly, then each red point lies over a green point with probability $\frac{108}{431}$; hence the expected number of red-green incidences is $$ \frac{108}{431} \cdot 108>27 $$ and so by pigeonhole, we can find a red 28 -gon and a green 28 -gon which are rotations of each other. Now, look at the 430 rotations of this 28 -gon (that do not give the all-red or all-green configuration) and compare it with the blue points. The same approach gives $$ \frac{108}{430} \cdot 28>7 $$ incidences, so we can find red, green, blue 8 -gons which are similar under rotation. Finally, the 429 nontrivial rotations of this 8 -gon expect $$ \frac{108}{429} \cdot 8>2 $$ incidences with yellow. So finally we have four monochromatic 3 -gons, one of each color, which are rotations of each other.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle is divided into congruent arcs by 432 points. The points are colored in four colors such that some 108 points are colored red, some 108 points are colored green, some 108 points are colored blue, and the remaining 108 points are colored yellow. Prove that one can choose three points of each color in such a way that the four triangles formed by the chosen points of the same color are congruent.
|
First, consider the 431 possible non-identity rotations of the red points, and count overlaps with green points. If we select a rotation randomly, then each red point lies over a green point with probability $\frac{108}{431}$; hence the expected number of red-green incidences is $$ \frac{108}{431} \cdot 108>27 $$ and so by pigeonhole, we can find a red 28 -gon and a green 28 -gon which are rotations of each other. Now, look at the 430 rotations of this 28 -gon (that do not give the all-red or all-green configuration) and compare it with the blue points. The same approach gives $$ \frac{108}{430} \cdot 28>7 $$ incidences, so we can find red, green, blue 8 -gons which are similar under rotation. Finally, the 429 nontrivial rotations of this 8 -gon expect $$ \frac{108}{429} \cdot 8>2 $$ incidences with yellow. So finally we have four monochromatic 3 -gons, one of each color, which are rotations of each other.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
40fd4d98-a075-5bfc-ad6a-1a2b3200019f
| 248,669
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
【 First solution (complex numbers). Let $p=0$ and set $\gamma$ as the real line. Then $A^{\prime}$ is the intersection of $b c$ and $p \bar{a}$. So, we get $$ a^{\prime}=\frac{\bar{a}(\bar{b} c-b \bar{c})}{(\bar{b}-\bar{c}) \bar{a}-(b-c) a} . $$  Note that $$ \bar{a}^{\prime}=\frac{a(b \bar{c}-\bar{b} c)}{(b-c) a-(\bar{b}-\bar{c}) \bar{a}} . $$ Thus it suffices to prove This is equivalent to $$ 0=\operatorname{det}\left[\begin{array}{lll} \bar{a}(\bar{b} c-b \bar{c}) & a(\bar{b} c-b \bar{c}) & (\bar{b}-\bar{c}) \bar{a}-(b-c) a \\ \bar{b}(\bar{c} a-c \bar{a}) & b(\bar{c} a-c \bar{a}) & (\bar{c}-\bar{a}) \bar{b}-(c-a) b \\ \bar{c}(\bar{a} b-a \bar{b}) & c(\bar{a} b-a \bar{b}) & (\bar{a}-\bar{b}) \bar{c}-(a-b) c \end{array}\right] . $$ This determinant has the property that the rows sum to zero, and we're done. Remark. Alternatively, if you don't notice that you could just blindly expand: $$ \begin{aligned} & \sum_{\mathrm{cyc}}((\bar{b}-\bar{c}) \bar{a}-(b-c) a) \cdot-\operatorname{det}\left[\begin{array}{ll} b & \bar{b} \\ c & \bar{c} \end{array}\right](\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \\ = & (\bar{b} c-c \bar{b})(\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \sum_{\mathrm{cyc}}(a b-a c+\overline{c a}-\bar{b} \bar{a})=0 . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
【 First solution (complex numbers). Let $p=0$ and set $\gamma$ as the real line. Then $A^{\prime}$ is the intersection of $b c$ and $p \bar{a}$. So, we get $$ a^{\prime}=\frac{\bar{a}(\bar{b} c-b \bar{c})}{(\bar{b}-\bar{c}) \bar{a}-(b-c) a} . $$  Note that $$ \bar{a}^{\prime}=\frac{a(b \bar{c}-\bar{b} c)}{(b-c) a-(\bar{b}-\bar{c}) \bar{a}} . $$ Thus it suffices to prove This is equivalent to $$ 0=\operatorname{det}\left[\begin{array}{lll} \bar{a}(\bar{b} c-b \bar{c}) & a(\bar{b} c-b \bar{c}) & (\bar{b}-\bar{c}) \bar{a}-(b-c) a \\ \bar{b}(\bar{c} a-c \bar{a}) & b(\bar{c} a-c \bar{a}) & (\bar{c}-\bar{a}) \bar{b}-(c-a) b \\ \bar{c}(\bar{a} b-a \bar{b}) & c(\bar{a} b-a \bar{b}) & (\bar{a}-\bar{b}) \bar{c}-(a-b) c \end{array}\right] . $$ This determinant has the property that the rows sum to zero, and we're done. Remark. Alternatively, if you don't notice that you could just blindly expand: $$ \begin{aligned} & \sum_{\mathrm{cyc}}((\bar{b}-\bar{c}) \bar{a}-(b-c) a) \cdot-\operatorname{det}\left[\begin{array}{ll} b & \bar{b} \\ c & \bar{c} \end{array}\right](\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \\ = & (\bar{b} c-c \bar{b})(\bar{c} a-c \bar{a})(\bar{a} b-a \bar{b}) \sum_{\mathrm{cyc}}(a b-a c+\overline{c a}-\bar{b} \bar{a})=0 . \end{aligned} $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
\I Second solution (Desargues involution). We let $C^{\prime \prime}=\overline{A^{\prime} B^{\prime}} \cap \overline{A B}$. Consider complete quadrilateral $A B C A^{\prime} B^{\prime} C^{\prime \prime} C$. We see that there is an involutive pairing $\tau$ at $P$ swapping $\left(P A, P A^{\prime}\right),\left(P B, P B^{\prime}\right),\left(P C, P C^{\prime \prime}\right)$. From the first two, we see $\tau$ coincides with reflection about $\ell$, hence conclude $C^{\prime \prime}=C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
\I Second solution (Desargues involution). We let $C^{\prime \prime}=\overline{A^{\prime} B^{\prime}} \cap \overline{A B}$. Consider complete quadrilateral $A B C A^{\prime} B^{\prime} C^{\prime \prime} C$. We see that there is an involutive pairing $\tau$ at $P$ swapping $\left(P A, P A^{\prime}\right),\left(P B, P B^{\prime}\right),\left(P C, P C^{\prime \prime}\right)$. From the first two, we see $\tau$ coincides with reflection about $\ell$, hence conclude $C^{\prime \prime}=C$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
ब Third solution (barycentric), by Catherine $\mathbf{X u}$. We will perform barycentric coordinates on the triangle $P C C^{\prime}$, with $P=(1,0,0), C^{\prime}=(0,1,0)$, and $C=(0,0,1)$. Set $a=C C^{\prime}, b=C P, c=C^{\prime} P$ as usual. Since $A, B, C^{\prime}$ are collinear, we will define $A=(p: k: q)$ and $B=(p: \ell: q)$. Claim - Line $\gamma$ is the angle bisector of $\angle A P A^{\prime}, \angle B P B^{\prime}$, and $\angle C P C^{\prime}$. Thus $B^{\prime}$ is the intersection of the isogonal of $B$ with respect to $\angle P$ with the line $C A$; that is, $$ B^{\prime}=\left(\frac{p}{k} \frac{b^{2}}{\ell}: \frac{b^{2}}{\ell}: \frac{c^{2}}{q}\right) $$ Analogously, $A^{\prime}$ is the intersection of the isogonal of $A$ with respect to $\angle P$ with the line $C B$; that is, $$ A^{\prime}=\left(\frac{p}{\ell} \frac{b^{2}}{k}: \frac{b^{2}}{k}: \frac{c^{2}}{q}\right) . $$ The ratio of the first to third coordinate in these two points is both $b^{2} p q: c^{2} k \ell$, so it follows $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear. Remark (Problem reference). The converse of this problem appears as problem 1052 attributed S. V. Markelov in the book Geometriya: 9-11 Klassy: Ot Uchebnoy Zadachi k Tvorcheskoy, 1996, by I. F. Sharygin.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the plane of $\triangle A B C$, and $\gamma$ a line through $P$. Let $A^{\prime}, B^{\prime}, C^{\prime}$ be the points where the reflections of lines $P A, P B, P C$ with respect to $\gamma$ intersect lines $B C, C A, A B$ respectively. Prove that $A^{\prime}, B^{\prime}, C^{\prime}$ are collinear.
|
ब Third solution (barycentric), by Catherine $\mathbf{X u}$. We will perform barycentric coordinates on the triangle $P C C^{\prime}$, with $P=(1,0,0), C^{\prime}=(0,1,0)$, and $C=(0,0,1)$. Set $a=C C^{\prime}, b=C P, c=C^{\prime} P$ as usual. Since $A, B, C^{\prime}$ are collinear, we will define $A=(p: k: q)$ and $B=(p: \ell: q)$. Claim - Line $\gamma$ is the angle bisector of $\angle A P A^{\prime}, \angle B P B^{\prime}$, and $\angle C P C^{\prime}$. Thus $B^{\prime}$ is the intersection of the isogonal of $B$ with respect to $\angle P$ with the line $C A$; that is, $$ B^{\prime}=\left(\frac{p}{k} \frac{b^{2}}{\ell}: \frac{b^{2}}{\ell}: \frac{c^{2}}{q}\right) $$ Analogously, $A^{\prime}$ is the intersection of the isogonal of $A$ with respect to $\angle P$ with the line $C B$; that is, $$ A^{\prime}=\left(\frac{p}{\ell} \frac{b^{2}}{k}: \frac{b^{2}}{k}: \frac{c^{2}}{q}\right) . $$ The ratio of the first to third coordinate in these two points is both $b^{2} p q: c^{2} k \ell$, so it follows $A^{\prime}, B^{\prime}$, and $C^{\prime}$ are collinear. Remark (Problem reference). The converse of this problem appears as problem 1052 attributed S. V. Markelov in the book Geometriya: 9-11 Klassy: Ot Uchebnoy Zadachi k Tvorcheskoy, 1996, by I. F. Sharygin.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4669eaf-0b27-5264-9ada-e6d4788114f3
| 245,707
|
For integer $n \geq 2$, let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $$ x_{1}+x_{2}+\cdots+x_{n}=0 \quad \text { and } \quad x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1 $$ For each subset $A \subseteq\{1,2, \ldots, n\}$, define $S_{A}=\sum_{i \in A} x_{i}$. (If $A$ is the empty set, then $S_{A}=0$.) Prove that for any positive number $\lambda$, the number of sets $A$ satisfying $S_{A} \geq \lambda$ is at most $2^{n-3} / \lambda^{2}$. For which choices of $x_{1}, x_{2}, \ldots, x_{n}, \lambda$ does equality hold?
|
Let $\varepsilon_{i}$ be a coin flip of 0 or 1 . Then we have $$ \begin{aligned} \mathbb{E}\left[S_{A}^{2}\right] & =\mathbb{E}\left[\left(\sum \varepsilon_{i} x_{i}\right)^{2}\right]=\sum_{i} \mathbb{E}\left[\varepsilon_{i}^{2}\right] x_{i}^{2}+\sum_{i<j} \mathbb{E}\left[\varepsilon_{i} \varepsilon_{j}\right] 2 x_{i} x_{j} \\ & =\frac{1}{2} \sum x_{i}^{2}+\frac{1}{2} \sum x_{i} x_{j}=\frac{1}{2}+\frac{1}{2} \sum_{i<j} x_{i} x_{j}=\frac{1}{2}+\frac{1}{2}\left(-\frac{1}{2}\right)=\frac{1}{4} \end{aligned} $$ In other words, $\sum_{A} S_{A}^{2}=2^{n-2}$. Since can always pair $A$ with its complement, we conclude $$ \sum_{S_{A}>0} S_{A}^{2}=2^{n-3} $$ Equality holds iff $S_{A} \in\{ \pm \lambda, 0\}$ for every $A$. This occurs when $x_{1}=1 / \sqrt{2}, x_{2}=-1 / \sqrt{2}$, $x_{3}=\cdots=0$ (or permutations), and $\lambda=1 / \sqrt{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For integer $n \geq 2$, let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $$ x_{1}+x_{2}+\cdots+x_{n}=0 \quad \text { and } \quad x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1 $$ For each subset $A \subseteq\{1,2, \ldots, n\}$, define $S_{A}=\sum_{i \in A} x_{i}$. (If $A$ is the empty set, then $S_{A}=0$.) Prove that for any positive number $\lambda$, the number of sets $A$ satisfying $S_{A} \geq \lambda$ is at most $2^{n-3} / \lambda^{2}$. For which choices of $x_{1}, x_{2}, \ldots, x_{n}, \lambda$ does equality hold?
|
Let $\varepsilon_{i}$ be a coin flip of 0 or 1 . Then we have $$ \begin{aligned} \mathbb{E}\left[S_{A}^{2}\right] & =\mathbb{E}\left[\left(\sum \varepsilon_{i} x_{i}\right)^{2}\right]=\sum_{i} \mathbb{E}\left[\varepsilon_{i}^{2}\right] x_{i}^{2}+\sum_{i<j} \mathbb{E}\left[\varepsilon_{i} \varepsilon_{j}\right] 2 x_{i} x_{j} \\ & =\frac{1}{2} \sum x_{i}^{2}+\frac{1}{2} \sum x_{i} x_{j}=\frac{1}{2}+\frac{1}{2} \sum_{i<j} x_{i} x_{j}=\frac{1}{2}+\frac{1}{2}\left(-\frac{1}{2}\right)=\frac{1}{4} \end{aligned} $$ In other words, $\sum_{A} S_{A}^{2}=2^{n-2}$. Since can always pair $A$ with its complement, we conclude $$ \sum_{S_{A}>0} S_{A}^{2}=2^{n-3} $$ Equality holds iff $S_{A} \in\{ \pm \lambda, 0\}$ for every $A$. This occurs when $x_{1}=1 / \sqrt{2}, x_{2}=-1 / \sqrt{2}$, $x_{3}=\cdots=0$ (or permutations), and $\lambda=1 / \sqrt{2}$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2012-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bdb0271e-ea9b-5556-a109-ee13274220fa
| 605,007
|
In triangle $A B C$, points $P, Q, R$ lie on sides $B C, C A, A B$, respectively. Let $\omega_{A}$, $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A Q R, B R P, C P Q$, respectively. Given the fact that segment $A P$ intersects $\omega_{A}, \omega_{B}, \omega_{C}$ again at $X, Y, Z$ respectively, prove that $Y X / X Z=B P / P C$.
|
Let $M$ be the concurrence point of $\omega_{A}, \omega_{B}, \omega_{C}$ (by Miquel's theorem).  Then $M$ is the center of a spiral similarity sending $\overline{Y Z}$ to $\overline{B C}$. So it suffices to show that this spiral similarity also sends $X$ to $P$, but $$ \measuredangle M X Y=\measuredangle M X A=\measuredangle M R A=\measuredangle M R B=\measuredangle M P B $$ so this follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, points $P, Q, R$ lie on sides $B C, C A, A B$, respectively. Let $\omega_{A}$, $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A Q R, B R P, C P Q$, respectively. Given the fact that segment $A P$ intersects $\omega_{A}, \omega_{B}, \omega_{C}$ again at $X, Y, Z$ respectively, prove that $Y X / X Z=B P / P C$.
|
Let $M$ be the concurrence point of $\omega_{A}, \omega_{B}, \omega_{C}$ (by Miquel's theorem).  Then $M$ is the center of a spiral similarity sending $\overline{Y Z}$ to $\overline{B C}$. So it suffices to show that this spiral similarity also sends $X$ to $P$, but $$ \measuredangle M X Y=\measuredangle M X A=\measuredangle M R A=\measuredangle M R B=\measuredangle M P B $$ so this follows.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
73edf22f-bdf8-5e92-ad71-2a1817d4f13a
| 604,581
|
For a positive integer $n \geq 3$ plot $n$ equally spaced points around a circle. Label one of them $A$, and place a marker at $A$. One may move the marker forward in a clockwise direction to either the next point or the point after that. Hence there are a total of $2 n$ distinct moves available; two from each point. Let $a_{n}$ count the number of ways to advance around the circle exactly twice, beginning and ending at $A$, without repeating a move. Prove that $a_{n-1}+a_{n}=2^{n}$ for all $n \geq 4$.
|
【 First solution. Imagine the counter is moving along the set $S=\{0,1, \ldots, 2 n\}$ instead, starting at 0 and ending at $2 n$, in jumps of length 1 and 2 . We can then record the sequence of moves as a matrix of the form $$ \left[\begin{array}{cccccc} p_{0} & p_{1} & p_{2} & \ldots & p_{n-1} & p_{n} \\ p_{n} & p_{n+1} & p_{n+2} & \ldots & p_{2 n-1} & p_{2 n} \end{array}\right] $$ where $p_{i}=1$ if the point $i$ was visited by the counter, and $p_{i}=0$ if the point was not visited by the counter. Note that $p_{0}=p_{2 n}=1$ and the upper-right and lower-left entries are equal. Then, the problem amounts to finding the number of such matrices which avoid the contiguous submatrices $$ \left[\begin{array}{ll} 0 & 0 \end{array}\right] \quad\left[\begin{array}{l} 0 \\ 0 \end{array}\right] \quad\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right] $$ which correspond to forbidding jumps of length greater than 2 , repeating a length 2 jump and repeating a length 1 jump. We give a nice symmetric phrasing suggested by fclvbfm934 at https://aops.com/ community/p27834267. If we focus on just the three possible column vectors that appear, say $$ \mathbf{u}:=\left[\begin{array}{l} 1 \\ 0 \end{array}\right], \quad \mathbf{v}:=\left[\begin{array}{l} 0 \\ 1 \end{array}\right], \quad \mathbf{w}:=\left[\begin{array}{l} 1 \\ 1 \end{array}\right] $$ then we can instead describe valid matrices as sequences of $n+1$ such column vectors, where no two column vectors are adjacent, and where the boundary condition is that - either we start with $\mathbf{u}$ and end with $\mathbf{v}$, or - either we start with $\mathbf{w}$ and end with $\mathbf{w}$. Let $x_{n}$ and $y_{n}$ denote the number of such $2 \times(n+1)$ matrices. (Hence $a_{n}=x_{n}+y_{n}$.) But owing to the symmetry of the setup with $\mathbf{u}, \mathbf{v}, \mathbf{w}$, we could instead view $x_{n}$ and $y_{n}$ as the number of $2 \times(n+1)$ matrices for a fixed starting first column whose final column is the same/different. So we have the recursions $$ \begin{aligned} x_{n+1} & =x_{n}+y_{n} \\ y_{n+1} & =2 x_{n} . \end{aligned} $$ We also have that $$ 2 x_{n}+y_{n}=2^{n} $$ which may either be proved directly from the recursions (using $x_{1}=1$ and $y_{1}=0$ ), or by noting the left-hand side counts the total number of sequences of $n+1$ column vectors with no restrictions on the final column at all (in which case there are simply 2 choices for each of the $n$ columns after the first one). Thus, $$ \begin{aligned} a_{n+1}+a_{n} & =\left(x_{n+1}+y_{n+1}\right)+\left(x_{n}+y_{n}\right) \\ & =\left(\left(x_{n}+y_{n}\right)+2 x_{n}\right)+\left(x_{n}+y_{n}\right) \\ & =2\left(2 x_{n}+y_{n}\right)=2^{n+1} \end{aligned} $$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For a positive integer $n \geq 3$ plot $n$ equally spaced points around a circle. Label one of them $A$, and place a marker at $A$. One may move the marker forward in a clockwise direction to either the next point or the point after that. Hence there are a total of $2 n$ distinct moves available; two from each point. Let $a_{n}$ count the number of ways to advance around the circle exactly twice, beginning and ending at $A$, without repeating a move. Prove that $a_{n-1}+a_{n}=2^{n}$ for all $n \geq 4$.
|
【 First solution. Imagine the counter is moving along the set $S=\{0,1, \ldots, 2 n\}$ instead, starting at 0 and ending at $2 n$, in jumps of length 1 and 2 . We can then record the sequence of moves as a matrix of the form $$ \left[\begin{array}{cccccc} p_{0} & p_{1} & p_{2} & \ldots & p_{n-1} & p_{n} \\ p_{n} & p_{n+1} & p_{n+2} & \ldots & p_{2 n-1} & p_{2 n} \end{array}\right] $$ where $p_{i}=1$ if the point $i$ was visited by the counter, and $p_{i}=0$ if the point was not visited by the counter. Note that $p_{0}=p_{2 n}=1$ and the upper-right and lower-left entries are equal. Then, the problem amounts to finding the number of such matrices which avoid the contiguous submatrices $$ \left[\begin{array}{ll} 0 & 0 \end{array}\right] \quad\left[\begin{array}{l} 0 \\ 0 \end{array}\right] \quad\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right] $$ which correspond to forbidding jumps of length greater than 2 , repeating a length 2 jump and repeating a length 1 jump. We give a nice symmetric phrasing suggested by fclvbfm934 at https://aops.com/ community/p27834267. If we focus on just the three possible column vectors that appear, say $$ \mathbf{u}:=\left[\begin{array}{l} 1 \\ 0 \end{array}\right], \quad \mathbf{v}:=\left[\begin{array}{l} 0 \\ 1 \end{array}\right], \quad \mathbf{w}:=\left[\begin{array}{l} 1 \\ 1 \end{array}\right] $$ then we can instead describe valid matrices as sequences of $n+1$ such column vectors, where no two column vectors are adjacent, and where the boundary condition is that - either we start with $\mathbf{u}$ and end with $\mathbf{v}$, or - either we start with $\mathbf{w}$ and end with $\mathbf{w}$. Let $x_{n}$ and $y_{n}$ denote the number of such $2 \times(n+1)$ matrices. (Hence $a_{n}=x_{n}+y_{n}$.) But owing to the symmetry of the setup with $\mathbf{u}, \mathbf{v}, \mathbf{w}$, we could instead view $x_{n}$ and $y_{n}$ as the number of $2 \times(n+1)$ matrices for a fixed starting first column whose final column is the same/different. So we have the recursions $$ \begin{aligned} x_{n+1} & =x_{n}+y_{n} \\ y_{n+1} & =2 x_{n} . \end{aligned} $$ We also have that $$ 2 x_{n}+y_{n}=2^{n} $$ which may either be proved directly from the recursions (using $x_{1}=1$ and $y_{1}=0$ ), or by noting the left-hand side counts the total number of sequences of $n+1$ column vectors with no restrictions on the final column at all (in which case there are simply 2 choices for each of the $n$ columns after the first one). Thus, $$ \begin{aligned} a_{n+1}+a_{n} & =\left(x_{n+1}+y_{n+1}\right)+\left(x_{n}+y_{n}\right) \\ & =\left(\left(x_{n}+y_{n}\right)+2 x_{n}\right)+\left(x_{n}+y_{n}\right) \\ & =2\left(2 x_{n}+y_{n}\right)=2^{n+1} \end{aligned} $$ as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
15a1f517-d736-53d1-a2ae-c27760ebc4c4
| 605,039
|
Let $m$ and $n$ be positive integers. Prove that there exists a positive integer $c$ such that cm and cn have the same nonzero decimal digits.
|
One-line spoiler: 142857. More verbosely, the idea is to look at the decimal representation of $1 / D, m / D, n / D$ for a suitable denominator $D$, which have a "cyclic shift" property in which the digits of $n / D$ are the digits of $m / D$ shifted by 3 . Remark (An example to follow along). Here is an example to follow along in the subsequent proof If $m=4$ and $n=23$ then the magic numbers $e=3$ and $D=41$ obey $$ 10^{3} \cdot \frac{4}{41}=97+\frac{23}{41} $$ The idea is that $$ \begin{aligned} \frac{1}{41} & =0 . \overline{02439} \\ \frac{4}{41} & =0 . \overline{09756} \\ \frac{23}{41} & =0.56097 \end{aligned} $$ and so $c=2349$ works; we get $4 c=9756$ and $23 c=56097$ which are cyclic shifts of each other by 3 places (with some leading zeros appended). Here is the one to use: Claim - There exists positive integers $D$ and $e$ such that $\operatorname{gcd}(D, 10)=1, D>$ $\max (m, n)$, and moreover $$ \frac{10^{e} m-n}{D} \in \mathbb{Z} $$ $$ A=10^{e} n-m . $$ Let $r=\nu_{2}(m)$ and $s=\nu_{5}(m)$. As long as $e>m a x(r, s)$ we have $\nu_{2}(A)=r$ and $\nu_{5}(A)=s$, too. Now choose any $e>\max (r, s)$ big enough that $A>2^{r} 5^{s} \max (m, n)$ also holds. Then the number $D=\frac{A}{2^{r 5^{s}}}$ works; the first two properties hold by construction and $$ 10^{e} \cdot \frac{n}{D}-\frac{m}{D}=\frac{A}{D}=2^{r} 5^{s} $$ is an integer. Remark (For people who like obscure theorems). Kobayashi's theorem implies we can actually pick $D$ to be prime. Now we take $c$ to be the number under the bar of $1 / D$ (leading zeros removed). Then the decimal representation of $\frac{m}{D}$ is the decimal representation of cm repeated (possibly including leading zeros). Similarly, $\frac{n}{D}$ has the decimal representation of cm repeated (possibly including leading zeros). Finally, since $$ 10^{e} \cdot \frac{m}{D}-\frac{n}{D} \text { is an integer } $$ it follows that these repeating decimal representations are rotations of each other by $e$ places, so in particular they have the same number of nonzero digits. Remark. Many students tried to find a $D$ satisfying the stronger hypothesis that $1 / D$, $2 / D, \ldots,(D-1) / D$ are cyclic shifts of each other. For example, this holds in the famous $D=7$ case. One may be tempted to resort to using large primes $D$ rather than powers of 7 to deal with this issue. However it is an open conjecture (a special case of Artin's primitive root conjecture) whether or not $10(\bmod p)$ is primitive infinitely often, which is the necessary conjecture so this is harder than it seems.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m$ and $n$ be positive integers. Prove that there exists a positive integer $c$ such that cm and cn have the same nonzero decimal digits.
|
One-line spoiler: 142857. More verbosely, the idea is to look at the decimal representation of $1 / D, m / D, n / D$ for a suitable denominator $D$, which have a "cyclic shift" property in which the digits of $n / D$ are the digits of $m / D$ shifted by 3 . Remark (An example to follow along). Here is an example to follow along in the subsequent proof If $m=4$ and $n=23$ then the magic numbers $e=3$ and $D=41$ obey $$ 10^{3} \cdot \frac{4}{41}=97+\frac{23}{41} $$ The idea is that $$ \begin{aligned} \frac{1}{41} & =0 . \overline{02439} \\ \frac{4}{41} & =0 . \overline{09756} \\ \frac{23}{41} & =0.56097 \end{aligned} $$ and so $c=2349$ works; we get $4 c=9756$ and $23 c=56097$ which are cyclic shifts of each other by 3 places (with some leading zeros appended). Here is the one to use: Claim - There exists positive integers $D$ and $e$ such that $\operatorname{gcd}(D, 10)=1, D>$ $\max (m, n)$, and moreover $$ \frac{10^{e} m-n}{D} \in \mathbb{Z} $$ $$ A=10^{e} n-m . $$ Let $r=\nu_{2}(m)$ and $s=\nu_{5}(m)$. As long as $e>m a x(r, s)$ we have $\nu_{2}(A)=r$ and $\nu_{5}(A)=s$, too. Now choose any $e>\max (r, s)$ big enough that $A>2^{r} 5^{s} \max (m, n)$ also holds. Then the number $D=\frac{A}{2^{r 5^{s}}}$ works; the first two properties hold by construction and $$ 10^{e} \cdot \frac{n}{D}-\frac{m}{D}=\frac{A}{D}=2^{r} 5^{s} $$ is an integer. Remark (For people who like obscure theorems). Kobayashi's theorem implies we can actually pick $D$ to be prime. Now we take $c$ to be the number under the bar of $1 / D$ (leading zeros removed). Then the decimal representation of $\frac{m}{D}$ is the decimal representation of cm repeated (possibly including leading zeros). Similarly, $\frac{n}{D}$ has the decimal representation of cm repeated (possibly including leading zeros). Finally, since $$ 10^{e} \cdot \frac{m}{D}-\frac{n}{D} \text { is an integer } $$ it follows that these repeating decimal representations are rotations of each other by $e$ places, so in particular they have the same number of nonzero digits. Remark. Many students tried to find a $D$ satisfying the stronger hypothesis that $1 / D$, $2 / D, \ldots,(D-1) / D$ are cyclic shifts of each other. For example, this holds in the famous $D=7$ case. One may be tempted to resort to using large primes $D$ rather than powers of 7 to deal with this issue. However it is an open conjecture (a special case of Artin's primitive root conjecture) whether or not $10(\bmod p)$ is primitive infinitely often, which is the necessary conjecture so this is harder than it seems.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2013-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
f9d60560-28a3-5abd-a636-c8557c46a28c
| 605,090
|
Prove that there exists an infinite set of points $$ \ldots, P_{-3}, P_{-2}, P_{-1}, P_{0}, P_{1}, P_{2}, P_{3}, \ldots $$ in the plane with the following property: For any three distinct integers $a, b$, and $c$, points $P_{a}, P_{b}$, and $P_{c}$ are collinear if and only if $a+b+c=2014$.
|
The construction $$ P_{n}=\left(n-\frac{2014}{3},\left(n-\frac{2014}{3}\right)^{3}\right) $$ works fine, and follows from the following claim: Claim - If $x, y, z$ are distinct real numbers then the points $\left(x, x^{3}\right),\left(y, y^{3}\right),\left(z, z^{3}\right)$ are collinear if and only if $x+y+z=0$. $$ 0=\operatorname{det}\left[\begin{array}{lll} x & x^{3} & 1 \\ y & y^{3} & 1 \\ z & z^{3} & 1 \end{array}\right] $$ But the determinant equals $$ \sum_{\text {cyc }} x\left(y^{3}-z^{3}\right)=(x-y)(y-z)(z-x)(x+y+z) $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that there exists an infinite set of points $$ \ldots, P_{-3}, P_{-2}, P_{-1}, P_{0}, P_{1}, P_{2}, P_{3}, \ldots $$ in the plane with the following property: For any three distinct integers $a, b$, and $c$, points $P_{a}, P_{b}$, and $P_{c}$ are collinear if and only if $a+b+c=2014$.
|
The construction $$ P_{n}=\left(n-\frac{2014}{3},\left(n-\frac{2014}{3}\right)^{3}\right) $$ works fine, and follows from the following claim: Claim - If $x, y, z$ are distinct real numbers then the points $\left(x, x^{3}\right),\left(y, y^{3}\right),\left(z, z^{3}\right)$ are collinear if and only if $x+y+z=0$. $$ 0=\operatorname{det}\left[\begin{array}{lll} x & x^{3} & 1 \\ y & y^{3} & 1 \\ z & z^{3} & 1 \end{array}\right] $$ But the determinant equals $$ \sum_{\text {cyc }} x\left(y^{3}-z^{3}\right)=(x-y)(y-z)(z-x)(x+y+z) $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5d223116-bd1d-50de-a897-ff934d97d222
| 605,152
|
Let $A B C$ be a triangle with orthocenter $H$ and let $P$ be the second intersection of the circumcircle of triangle $A H C$ with the internal bisector of $\angle B A C$. Let $X$ be the circumcenter of triangle $A P B$ and let $Y$ be the orthocenter of triangle $A P C$. Prove that the length of segment $X Y$ is equal to the circumradius of triangle $A B C$.
|
 We eliminate the floating orthocenter by reflecting $P$ across $\overline{A C}$ to $Q$. Then $Q$ lies on ( $A B C$ ) and moreover $\angle Q A C=\frac{1}{2} \angle B A C$. This motivates us to reflect $B, X, Y$ to $B^{\prime}$, $X^{\prime}, Y^{\prime}$ and complex bash with respect to $\triangle A Q C$. Obviously $$ y^{\prime}=a+q+c $$ Now we need to compute $x^{\prime}$. You can get this using the formula $$ x^{\prime}=a+\frac{\left(b^{\prime}-a\right)(q-a)\left(\overline{q-a}-\overline{b^{\prime}-a}\right)}{\left(b^{\prime}-a\right) \overline{(q-a)}-\overline{\left(b^{\prime}-a\right)}(q-a)} . $$ Using the angle condition we know $b=\frac{c^{3}}{q^{2}}$, and then that $$ b^{\prime}=a+c-a c \bar{b}=a+c-\frac{a q^{2}}{c^{2}} . $$ Therefore $$ \begin{aligned} x^{\prime} & =a+\frac{\left(c-\frac{a q^{2}}{c^{2}}\right)(q-a)\left(\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}\right)}{\left(c-\frac{a q^{2}}{c^{2}}\right)\left(\frac{1}{q}-\frac{1}{a}\right)-\left(\frac{1}{c}-\frac{c^{2}}{a q^{2}}\right)(q-a)} \\ & =a+\frac{\frac{c^{3}-a q^{2}}{c^{2}}(q-a)\left(\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}\right)}{-\frac{c^{3}-a q^{2}}{c^{2}} \frac{q-a}{q a}+\frac{c^{3}-q^{2}}{a q^{2} c}(q-a)} \end{aligned} $$ $$ \begin{aligned} & =a+\frac{\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}}{-\frac{1}{q a}+\frac{c}{a q^{2}}} \\ & =a+\frac{c^{2}-q^{2}+a q-\frac{a q^{2}}{c}}{c-q} \\ & =a+c+q+\frac{a q}{c} \end{aligned} $$ whence $$ \left|x^{\prime}-y^{\prime}\right|=\left|\frac{a q}{c}\right|=1 $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocenter $H$ and let $P$ be the second intersection of the circumcircle of triangle $A H C$ with the internal bisector of $\angle B A C$. Let $X$ be the circumcenter of triangle $A P B$ and let $Y$ be the orthocenter of triangle $A P C$. Prove that the length of segment $X Y$ is equal to the circumradius of triangle $A B C$.
|
 We eliminate the floating orthocenter by reflecting $P$ across $\overline{A C}$ to $Q$. Then $Q$ lies on ( $A B C$ ) and moreover $\angle Q A C=\frac{1}{2} \angle B A C$. This motivates us to reflect $B, X, Y$ to $B^{\prime}$, $X^{\prime}, Y^{\prime}$ and complex bash with respect to $\triangle A Q C$. Obviously $$ y^{\prime}=a+q+c $$ Now we need to compute $x^{\prime}$. You can get this using the formula $$ x^{\prime}=a+\frac{\left(b^{\prime}-a\right)(q-a)\left(\overline{q-a}-\overline{b^{\prime}-a}\right)}{\left(b^{\prime}-a\right) \overline{(q-a)}-\overline{\left(b^{\prime}-a\right)}(q-a)} . $$ Using the angle condition we know $b=\frac{c^{3}}{q^{2}}$, and then that $$ b^{\prime}=a+c-a c \bar{b}=a+c-\frac{a q^{2}}{c^{2}} . $$ Therefore $$ \begin{aligned} x^{\prime} & =a+\frac{\left(c-\frac{a q^{2}}{c^{2}}\right)(q-a)\left(\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}\right)}{\left(c-\frac{a q^{2}}{c^{2}}\right)\left(\frac{1}{q}-\frac{1}{a}\right)-\left(\frac{1}{c}-\frac{c^{2}}{a q^{2}}\right)(q-a)} \\ & =a+\frac{\frac{c^{3}-a q^{2}}{c^{2}}(q-a)\left(\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}\right)}{-\frac{c^{3}-a q^{2}}{c^{2}} \frac{q-a}{q a}+\frac{c^{3}-q^{2}}{a q^{2} c}(q-a)} \end{aligned} $$ $$ \begin{aligned} & =a+\frac{\frac{1}{q}-\frac{1}{a}-\frac{1}{c}+\frac{c^{2}}{a q^{2}}}{-\frac{1}{q a}+\frac{c}{a q^{2}}} \\ & =a+\frac{c^{2}-q^{2}+a q-\frac{a q^{2}}{c}}{c-q} \\ & =a+c+q+\frac{a q}{c} \end{aligned} $$ whence $$ \left|x^{\prime}-y^{\prime}\right|=\left|\frac{a q}{c}\right|=1 $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ff7f59ca-3488-5beb-aba1-03cffa314a5c
| 248,786
|
Prove that there is a constant $c>0$ with the following property: If $a, b, n$ are positive integers such that $\operatorname{gcd}(a+i, b+j)>1$ for all $i, j \in\{0,1, \ldots, n\}$, then $$ \min \{a, b\}>(c n)^{n / 2} $$
|
Let $N=n+1$ and assume $N$ is (very) large. We construct an $N \times N$ with cells $(i, j)$ where $0 \leq i, j \leq n$ and in each cell place a prime $p$ dividing $\operatorname{gcd}(a+i, b+j)$. The central claim is at least $50 \%$ of the primes in this table exceed $0.001 n^{2}$. We count the maximum number of squares they could occupy: $$ \sum_{p}\left\lceil\frac{N}{p}\right\rceil^{2} \leq \sum_{p}\left(\frac{N}{p}+1\right)^{2}=N^{2} \sum_{p} \frac{1}{p^{2}}+2 N \sum_{p} \frac{1}{p}+\sum_{p} 1 $$ Here the summation runs over primes $p \leq 0.001 n^{2}$. Let $r=\pi\left(0.001 n^{2}\right)$ denote the number of such primes. Now we consider the following three estimates. First, $$ \sum_{p} \frac{1}{p^{2}}<\frac{1}{2} $$ which follows by adding all the primes directly with some computation. Moreover, $$ \sum_{p} \frac{1}{p}<\sum_{k=1}^{r} \frac{1}{k}=O(\log r)<o(N) $$ using the harmonic series bound, and $$ \sum_{p} 1<r \sim O\left(\frac{N^{2}}{\ln N}\right)<o\left(N^{2}\right) $$ via Prime Number Theorem. Hence the sum in question is certainly less than $\frac{1}{2} N^{2}$ for $N$ large enough, establishing the central claim. Hence some column $a+i$ has at least one half of its primes greater than $0.001 n^{2}$. Because this is greater than $n$ for large $n$, these primes must all be distinct, so $a+i$ exceeds their product, which is larger than $$ \left(0.001 n^{2}\right)^{N / 2}>c^{n} \cdot n^{n} $$ where $c$ is some constant (better than the requested bound).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there is a constant $c>0$ with the following property: If $a, b, n$ are positive integers such that $\operatorname{gcd}(a+i, b+j)>1$ for all $i, j \in\{0,1, \ldots, n\}$, then $$ \min \{a, b\}>(c n)^{n / 2} $$
|
Let $N=n+1$ and assume $N$ is (very) large. We construct an $N \times N$ with cells $(i, j)$ where $0 \leq i, j \leq n$ and in each cell place a prime $p$ dividing $\operatorname{gcd}(a+i, b+j)$. The central claim is at least $50 \%$ of the primes in this table exceed $0.001 n^{2}$. We count the maximum number of squares they could occupy: $$ \sum_{p}\left\lceil\frac{N}{p}\right\rceil^{2} \leq \sum_{p}\left(\frac{N}{p}+1\right)^{2}=N^{2} \sum_{p} \frac{1}{p^{2}}+2 N \sum_{p} \frac{1}{p}+\sum_{p} 1 $$ Here the summation runs over primes $p \leq 0.001 n^{2}$. Let $r=\pi\left(0.001 n^{2}\right)$ denote the number of such primes. Now we consider the following three estimates. First, $$ \sum_{p} \frac{1}{p^{2}}<\frac{1}{2} $$ which follows by adding all the primes directly with some computation. Moreover, $$ \sum_{p} \frac{1}{p}<\sum_{k=1}^{r} \frac{1}{k}=O(\log r)<o(N) $$ using the harmonic series bound, and $$ \sum_{p} 1<r \sim O\left(\frac{N^{2}}{\ln N}\right)<o\left(N^{2}\right) $$ via Prime Number Theorem. Hence the sum in question is certainly less than $\frac{1}{2} N^{2}$ for $N$ large enough, establishing the central claim. Hence some column $a+i$ has at least one half of its primes greater than $0.001 n^{2}$. Because this is greater than $n$ for large $n$, these primes must all be distinct, so $a+i$ exceeds their product, which is larger than $$ \left(0.001 n^{2}\right)^{N / 2}>c^{n} \cdot n^{n} $$ where $c$ is some constant (better than the requested bound).
|
{
"resource_path": "USAMO/segmented/en-USAMO-2014-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
976e531e-2af5-5f88-9985-f907e7be500a
| 605,204
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on $\operatorname{arc} A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Complex solution (Evan Chen). Toss on the complex unit circle with $a=-1, b=1$, $z=-\frac{1}{2}$. Let $s$ and $t$ be on the unit circle. We claim $Z$ is the center. It follows from standard formulas that $$ x=\frac{1}{2}(s+t-1+s / t) $$ thus $$ 4 \operatorname{Re} x+2=s+t+\frac{1}{s}+\frac{1}{t}+\frac{s}{t}+\frac{t}{s} $$ which depends only on $P$ and $Q$, and not on $X$. Thus $$ 4\left|z-\frac{s+t}{2}\right|^{2}=|s+t+1|^{2}=3+(4 \operatorname{Re} x+2) $$ does not depend on $X$, done.  Let $R$ denote the radius of $\omega$. Note that the nine-point circle of $\triangle A S T$ has radius equal to $\frac{1}{2} R$, and hence is independent of $S$ and $T$. Then the power of $A$ with respect to the nine-point circle equals $$ A N^{2}-\left(\frac{1}{2} R\right)^{2}=A X \cdot A Y=\frac{1}{2} A X \cdot A S=\frac{1}{2} A Q^{2} $$ and hence $$ A N^{2}=\left(\frac{1}{2} R\right)^{2}+\frac{1}{2} A Q^{2} $$ which does not depend on the choice of $X$. So $N$ moves along a circle centered at $A$. Since the points $O, G, N$ are collinear on the Euler line of $\triangle A S T$ with $$ G O=\frac{2}{3} N O $$ it follows by homothety that $G$ moves along a circle as well, whose center is situated one-third of the way from $A$ to $O$. Finally, since $A, G, M$ are collinear with $$ A M=\frac{3}{2} A G $$ it follows that $M$ moves along a circle centered at the midpoint of $\overline{A O}$.  The main claim is: Claim - Quadrilateral $P Q K M$ is cyclic. $$ V Q \cdot V P=V S \cdot V T=V X \cdot V Y=V K \cdot V M $$ using the nine-point circle, and the circle with diameter $\overline{S T}$. But the circumcenter of $P Q K M$, is the midpoint of $\overline{A O}$, since it lies on the perpendicular bisectors of $\overline{K M}$ and $\overline{P Q}$. So it is fixed, the end.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Quadrilateral $A P B Q$ is inscribed in circle $\omega$ with $\angle P=\angle Q=90^{\circ}$ and $A P=$ $A Q<B P$. Let $X$ be a variable point on segment $\overline{P Q}$. Line $A X$ meets $\omega$ again at $S$ (other than $A$ ). Point $T$ lies on $\operatorname{arc} A Q B$ of $\omega$ such that $\overline{X T}$ is perpendicular to $\overline{A X}$. Let $M$ denote the midpoint of chord $\overline{S T}$. As $X$ varies on segment $\overline{P Q}$, show that $M$ moves along a circle.
|
- $X$ at the midpoint of $\overline{P Q}$ (giving the midpoint of $\overline{B Q}$ ) which determines the circle; this circle then passes through $P$ by symmetry and we can find the center by taking the intersection of two perpendicular bisectors (which two?). 【 Complex solution (Evan Chen). Toss on the complex unit circle with $a=-1, b=1$, $z=-\frac{1}{2}$. Let $s$ and $t$ be on the unit circle. We claim $Z$ is the center. It follows from standard formulas that $$ x=\frac{1}{2}(s+t-1+s / t) $$ thus $$ 4 \operatorname{Re} x+2=s+t+\frac{1}{s}+\frac{1}{t}+\frac{s}{t}+\frac{t}{s} $$ which depends only on $P$ and $Q$, and not on $X$. Thus $$ 4\left|z-\frac{s+t}{2}\right|^{2}=|s+t+1|^{2}=3+(4 \operatorname{Re} x+2) $$ does not depend on $X$, done.  Let $R$ denote the radius of $\omega$. Note that the nine-point circle of $\triangle A S T$ has radius equal to $\frac{1}{2} R$, and hence is independent of $S$ and $T$. Then the power of $A$ with respect to the nine-point circle equals $$ A N^{2}-\left(\frac{1}{2} R\right)^{2}=A X \cdot A Y=\frac{1}{2} A X \cdot A S=\frac{1}{2} A Q^{2} $$ and hence $$ A N^{2}=\left(\frac{1}{2} R\right)^{2}+\frac{1}{2} A Q^{2} $$ which does not depend on the choice of $X$. So $N$ moves along a circle centered at $A$. Since the points $O, G, N$ are collinear on the Euler line of $\triangle A S T$ with $$ G O=\frac{2}{3} N O $$ it follows by homothety that $G$ moves along a circle as well, whose center is situated one-third of the way from $A$ to $O$. Finally, since $A, G, M$ are collinear with $$ A M=\frac{3}{2} A G $$ it follows that $M$ moves along a circle centered at the midpoint of $\overline{A O}$.  The main claim is: Claim - Quadrilateral $P Q K M$ is cyclic. $$ V Q \cdot V P=V S \cdot V T=V X \cdot V Y=V K \cdot V M $$ using the nine-point circle, and the circle with diameter $\overline{S T}$. But the circumcenter of $P Q K M$, is the midpoint of $\overline{A O}$, since it lies on the perpendicular bisectors of $\overline{K M}$ and $\overline{P Q}$. So it is fixed, the end.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
c459dc73-247c-5589-8be0-20491c864f44
| 605,228
|
Let $a, b, c, d, e$ be distinct positive integers such that $a^{4}+b^{4}=c^{4}+d^{4}=e^{5}$. Show that $a c+b d$ is a composite number.
|
Assume to the contrary that $p=a c+b d$, so that $$ \begin{aligned} a c & \equiv-b d \quad(\bmod p) \\ \Longrightarrow a^{4} c^{4} & \equiv b^{4} d^{4} \quad(\bmod p) \\ \Longrightarrow a^{4}\left(e^{5}-d^{4}\right) & \equiv\left(e^{5}-a^{4}\right) d^{4} \quad(\bmod p) \\ \Longrightarrow a^{4} e^{5} & \equiv d^{4} e^{5} \quad(\bmod p) \\ \Longrightarrow e^{5}\left(a^{4}-d^{4}\right) & \equiv 0 \quad(\bmod p) \end{aligned} $$ and hence $$ p \mid e^{5}(a-d)(a+d)\left(a^{2}+d^{2}\right) $$ Claim - We should have $p>e$. Thus the above equation implies $p \leq \max \left(a-d, a+d, a^{2}+d^{2}\right)=a^{2}+d^{2}$. Similarly, $p \leq b^{2}+c^{2}$. So $$ a c+b d=p \leq \min \left\{a^{2}+d^{2}, b^{2}+c^{2}\right\} $$ or by subtraction $$ 0 \leq \min \{a(a-c)+d(d-b), b(b-d)+c(c-a)\} . $$ But since $a^{4}+b^{4}=c^{4}+d^{4}$ the numbers $a-c$ and $d-b$ should have the same sign, and so this is an obvious contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c, d, e$ be distinct positive integers such that $a^{4}+b^{4}=c^{4}+d^{4}=e^{5}$. Show that $a c+b d$ is a composite number.
|
Assume to the contrary that $p=a c+b d$, so that $$ \begin{aligned} a c & \equiv-b d \quad(\bmod p) \\ \Longrightarrow a^{4} c^{4} & \equiv b^{4} d^{4} \quad(\bmod p) \\ \Longrightarrow a^{4}\left(e^{5}-d^{4}\right) & \equiv\left(e^{5}-a^{4}\right) d^{4} \quad(\bmod p) \\ \Longrightarrow a^{4} e^{5} & \equiv d^{4} e^{5} \quad(\bmod p) \\ \Longrightarrow e^{5}\left(a^{4}-d^{4}\right) & \equiv 0 \quad(\bmod p) \end{aligned} $$ and hence $$ p \mid e^{5}(a-d)(a+d)\left(a^{2}+d^{2}\right) $$ Claim - We should have $p>e$. Thus the above equation implies $p \leq \max \left(a-d, a+d, a^{2}+d^{2}\right)=a^{2}+d^{2}$. Similarly, $p \leq b^{2}+c^{2}$. So $$ a c+b d=p \leq \min \left\{a^{2}+d^{2}, b^{2}+c^{2}\right\} $$ or by subtraction $$ 0 \leq \min \{a(a-c)+d(d-b), b(b-d)+c(c-a)\} . $$ But since $a^{4}+b^{4}=c^{4}+d^{4}$ the numbers $a-c$ and $d-b$ should have the same sign, and so this is an obvious contradiction.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
d733dd77-1b2a-56d6-bb88-09c0c182713a
| 248,831
|
Consider $0<\lambda<1$, and let $A$ be a multiset of positive integers. Let $A_{n}=\{a \in$ $A: a \leq n\}$. Assume that for every $n \in \mathbb{N}$, the multiset $A_{n}$ contains at most $n \lambda$ numbers. Show that there are infinitely many $n \in \mathbb{N}$ for which the sum of the elements in $A_{n}$ is at most $\frac{n(n+1)}{2} \lambda$.
|
For brevity, $\# S$ denotes $|S|$. Let $x_{n}=n \lambda-\# A_{n} \geq 0$. We now proceed by contradiction by assuming the conclusion fails for $n$ large enough; that is, $$ \begin{aligned} \frac{n(n+1)}{2} \lambda & <\sum_{a \in A_{n}} a \\ & =1\left(\# A_{1}-\# A_{0}\right)+2\left(\# A_{2}-\# A_{1}\right)+\cdots+n\left(\# A_{n}-\# A_{n-1}\right) \\ & =n \# A_{n}-\left(\# A_{1}+\cdots+\# A_{n-1}\right) \\ & =n\left(n \lambda-x_{n}\right)-\left[\left(\lambda-x_{1}\right)+\left(2 \lambda-x_{2}\right)+\cdots+\left((n-1) \lambda-x_{n-1}\right)\right] \\ & =\frac{n(n+1)}{2} \lambda-n x_{n}+\left(x_{1}+\cdots+x_{n-1}\right) . \end{aligned} $$ This means that for all sufficiently large $n$, say $n \geq N_{0}$, we have $$ x_{n}<\frac{x_{1}+\cdots+x_{n-1}}{n} \quad \forall n \geq N_{0} $$ In particular, each $x_{n}$ is the less than the average of all preceding terms. Intuitively this means $x_{n}$ should become close to each other, since they are also nonnegative. However, we have a second condition we haven't used yet: the "integer" condition implies $$ \left|x_{n+1}-x_{n}\right|=|\lambda-\#\{n \in A\}|>\varepsilon $$ for some fixed $\varepsilon>0$, namely $\varepsilon=\min \{\lambda, 1-\lambda\}$. Using the fact that consecutive terms differ by some fixed $\varepsilon$, we will derive a contradiction. If we let $M$ be the average of $x_{1}, \ldots, x_{N_{0}}$, then we ought to have $$ x_{n}<M \quad \forall n>N_{0} . $$ Hence for $n>N_{0}$ we have $x_{n}+x_{n+1}<2 M-\varepsilon$, and so for large enough $n$ the average must drop to just above $M-\frac{1}{2} \varepsilon$. Thus for some large $N_{1}>N_{0}$, we will have $$ x_{n}<M-\frac{1}{3} \varepsilon \quad \forall n>N_{1} . $$ If we repeat this argument then with a large $N_{2}>N_{1}$, we obtain $$ x_{n}<M-\frac{2}{3} \varepsilon \quad \forall n>N_{2} $$ and so on and so forth. This is a clear contradiction. Remark. Note that if $A=\{2,2,3,4,5, \ldots\}$ and $\lambda=1$ then contradiction. So the condition that $0<\lambda<1$ cannot be dropped, and (by scaling) neither can the condition that $A \subseteq \mathbb{Z}$. Remark (Suggested by Zhao Ting-wei). Despite the relation $$ x_{n}<\frac{x_{1}+\cdots+x_{n-1}}{n} \quad \forall n \geq N_{0} $$ implying that $x_{n}$ is bounded, it does not alone imply that $x_{n}$ converges, not even to some nonzero value. Zhao Ting-Wei showed me that one can have a sequence which is zero "every so often" yet where the average is nonzero. A counterexample is given explicitly by $$ x_{n}= \begin{cases}1000 & n=1 \\ 0 & n \text { is a power of } 10 \\ 1+\frac{1}{n} & \text { otherwise }\end{cases} $$ which does not have a limit. For completeness, let's check this - let $H_{n}$ denote the $n$ 'th harmonic number, and compute $$ \begin{aligned} \sum_{1}^{n-1} x_{n} & =1000+(n-1)+H_{n-1}-\sum_{k=1}^{\left\lfloor\log _{10} n\right\rfloor}\left(1+\frac{1}{10^{k}}\right) \\ & >n+999+H_{n-1}-\log _{10} n-\left(1+\frac{1}{10}+\ldots\right) \\ & >n+997+H_{n-1}-\log _{10} n>n+1 \end{aligned} $$ so $1+\frac{1}{n}<\frac{1}{n} \sum_{1}^{n-1} x_{n}$ as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider $0<\lambda<1$, and let $A$ be a multiset of positive integers. Let $A_{n}=\{a \in$ $A: a \leq n\}$. Assume that for every $n \in \mathbb{N}$, the multiset $A_{n}$ contains at most $n \lambda$ numbers. Show that there are infinitely many $n \in \mathbb{N}$ for which the sum of the elements in $A_{n}$ is at most $\frac{n(n+1)}{2} \lambda$.
|
For brevity, $\# S$ denotes $|S|$. Let $x_{n}=n \lambda-\# A_{n} \geq 0$. We now proceed by contradiction by assuming the conclusion fails for $n$ large enough; that is, $$ \begin{aligned} \frac{n(n+1)}{2} \lambda & <\sum_{a \in A_{n}} a \\ & =1\left(\# A_{1}-\# A_{0}\right)+2\left(\# A_{2}-\# A_{1}\right)+\cdots+n\left(\# A_{n}-\# A_{n-1}\right) \\ & =n \# A_{n}-\left(\# A_{1}+\cdots+\# A_{n-1}\right) \\ & =n\left(n \lambda-x_{n}\right)-\left[\left(\lambda-x_{1}\right)+\left(2 \lambda-x_{2}\right)+\cdots+\left((n-1) \lambda-x_{n-1}\right)\right] \\ & =\frac{n(n+1)}{2} \lambda-n x_{n}+\left(x_{1}+\cdots+x_{n-1}\right) . \end{aligned} $$ This means that for all sufficiently large $n$, say $n \geq N_{0}$, we have $$ x_{n}<\frac{x_{1}+\cdots+x_{n-1}}{n} \quad \forall n \geq N_{0} $$ In particular, each $x_{n}$ is the less than the average of all preceding terms. Intuitively this means $x_{n}$ should become close to each other, since they are also nonnegative. However, we have a second condition we haven't used yet: the "integer" condition implies $$ \left|x_{n+1}-x_{n}\right|=|\lambda-\#\{n \in A\}|>\varepsilon $$ for some fixed $\varepsilon>0$, namely $\varepsilon=\min \{\lambda, 1-\lambda\}$. Using the fact that consecutive terms differ by some fixed $\varepsilon$, we will derive a contradiction. If we let $M$ be the average of $x_{1}, \ldots, x_{N_{0}}$, then we ought to have $$ x_{n}<M \quad \forall n>N_{0} . $$ Hence for $n>N_{0}$ we have $x_{n}+x_{n+1}<2 M-\varepsilon$, and so for large enough $n$ the average must drop to just above $M-\frac{1}{2} \varepsilon$. Thus for some large $N_{1}>N_{0}$, we will have $$ x_{n}<M-\frac{1}{3} \varepsilon \quad \forall n>N_{1} . $$ If we repeat this argument then with a large $N_{2}>N_{1}$, we obtain $$ x_{n}<M-\frac{2}{3} \varepsilon \quad \forall n>N_{2} $$ and so on and so forth. This is a clear contradiction. Remark. Note that if $A=\{2,2,3,4,5, \ldots\}$ and $\lambda=1$ then contradiction. So the condition that $0<\lambda<1$ cannot be dropped, and (by scaling) neither can the condition that $A \subseteq \mathbb{Z}$. Remark (Suggested by Zhao Ting-wei). Despite the relation $$ x_{n}<\frac{x_{1}+\cdots+x_{n-1}}{n} \quad \forall n \geq N_{0} $$ implying that $x_{n}$ is bounded, it does not alone imply that $x_{n}$ converges, not even to some nonzero value. Zhao Ting-Wei showed me that one can have a sequence which is zero "every so often" yet where the average is nonzero. A counterexample is given explicitly by $$ x_{n}= \begin{cases}1000 & n=1 \\ 0 & n \text { is a power of } 10 \\ 1+\frac{1}{n} & \text { otherwise }\end{cases} $$ which does not have a limit. For completeness, let's check this - let $H_{n}$ denote the $n$ 'th harmonic number, and compute $$ \begin{aligned} \sum_{1}^{n-1} x_{n} & =1000+(n-1)+H_{n-1}-\sum_{k=1}^{\left\lfloor\log _{10} n\right\rfloor}\left(1+\frac{1}{10^{k}}\right) \\ & >n+999+H_{n-1}-\log _{10} n-\left(1+\frac{1}{10}+\ldots\right) \\ & >n+997+H_{n-1}-\log _{10} n>n+1 \end{aligned} $$ so $1+\frac{1}{n}<\frac{1}{n} \sum_{1}^{n-1} x_{n}$ as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2015-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5c61b424-a3d1-5203-af48-a2ab9df1106a
| 605,284
|
Prove that for any positive integer $k$, $$ \left(k^{2}\right)!\cdot \prod_{j=0}^{k-1} \frac{j!}{(j+k)!} $$ is an integer.
|
We show the exponent of any given prime $p$ is nonnegative in the expression. Recall that the exponent of $p$ in $n!$ is equal to $\sum_{i \geq 1}\left\lfloor n / p^{i}\right\rfloor$. In light of this, it suffices to show that for any prime power $q$, we have $$ \left\lfloor\frac{k^{2}}{q}\right\rfloor+\sum_{j=0}^{k-1}\left\lfloor\frac{j}{q}\right\rfloor \geq \sum_{j=0}^{k-1}\left\lfloor\frac{j+k}{q}\right\rfloor $$ Since both sides are integers, we show $$ \left\lfloor\frac{k^{2}}{q}\right\rfloor+\sum_{j=0}^{k-1}\left\lfloor\frac{j}{q}\right\rfloor>-1+\sum_{j=0}^{k-1}\left\lfloor\frac{j+k}{q}\right\rfloor . $$ If we denote by $\{x\}$ the fractional part of $x$, then $\lfloor x\rfloor=x-\{x\}$ so it's equivalent to $$ \left\{\frac{k^{2}}{q}\right\}+\sum_{j=0}^{k-1}\left\{\frac{j}{q}\right\}<1+\sum_{j=0}^{k-1}\left\{\frac{j+k}{q}\right\} . $$ However, the sum of remainders when $0,1, \ldots, k-1$ are taken modulo $q$ is easily seen to be less than the sum of remainders when $k, k+1, \ldots, 2 k-1$ are taken modulo $q$. So $$ \sum_{j=0}^{k-1}\left\{\frac{j}{q}\right\} \leq \sum_{j=0}^{k-1}\left\{\frac{j+k}{q}\right\} $$ follows, and we are done upon noting $\left\{k^{2} / q\right\}<1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that for any positive integer $k$, $$ \left(k^{2}\right)!\cdot \prod_{j=0}^{k-1} \frac{j!}{(j+k)!} $$ is an integer.
|
We show the exponent of any given prime $p$ is nonnegative in the expression. Recall that the exponent of $p$ in $n!$ is equal to $\sum_{i \geq 1}\left\lfloor n / p^{i}\right\rfloor$. In light of this, it suffices to show that for any prime power $q$, we have $$ \left\lfloor\frac{k^{2}}{q}\right\rfloor+\sum_{j=0}^{k-1}\left\lfloor\frac{j}{q}\right\rfloor \geq \sum_{j=0}^{k-1}\left\lfloor\frac{j+k}{q}\right\rfloor $$ Since both sides are integers, we show $$ \left\lfloor\frac{k^{2}}{q}\right\rfloor+\sum_{j=0}^{k-1}\left\lfloor\frac{j}{q}\right\rfloor>-1+\sum_{j=0}^{k-1}\left\lfloor\frac{j+k}{q}\right\rfloor . $$ If we denote by $\{x\}$ the fractional part of $x$, then $\lfloor x\rfloor=x-\{x\}$ so it's equivalent to $$ \left\{\frac{k^{2}}{q}\right\}+\sum_{j=0}^{k-1}\left\{\frac{j}{q}\right\}<1+\sum_{j=0}^{k-1}\left\{\frac{j+k}{q}\right\} . $$ However, the sum of remainders when $0,1, \ldots, k-1$ are taken modulo $q$ is easily seen to be less than the sum of remainders when $k, k+1, \ldots, 2 k-1$ are taken modulo $q$. So $$ \sum_{j=0}^{k-1}\left\{\frac{j}{q}\right\} \leq \sum_{j=0}^{k-1}\left\{\frac{j+k}{q}\right\} $$ follows, and we are done upon noting $\left\{k^{2} / q\right\}<1$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
92b80113-59f9-51b0-9e51-60d8c8006833
| 605,312
|
Let $A B C$ be an acute triangle and let $I_{B}, I_{C}$, and $O$ denote its $B$-excenter, $C$ excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{A C}$ such that $\angle A B Y=\angle C B Y$ and $\overline{B E} \perp \overline{A C}$. Similarly, points $F$ and $Z$ are selected on $\overline{A B}$ such that $\angle A C Z=\angle B C Z$ and $\overline{C F} \perp \overline{A B}$. Lines $I_{B} F$ and $I_{C} E$ meet at $P$. Prove that $\overline{P O}$ and $\overline{Y Z}$ are perpendicular.
|
\ First solution. Let $I_{A}$ denote the $A$-excenter and $I$ the incenter. Then let $D$ denote the foot of the altitude from $A$. Suppose the $A$-excircle is tangent to $\overline{B C}, \overline{A B}, \overline{A C}$ at $A_{1}, B_{1}, C_{1}$ and let $A_{2}, B_{2}, C_{2}$ denote the reflections of $I_{A}$ across these points. Let $S$ denote the circumcenter of $\triangle I I_{B} I_{C}$.  We begin with the following observation: Claim - Points $D, I, A_{2}$ are collinear, as are points $E, I_{C}, C_{2}$ are collinear and points $F, I_{B}, B_{2}$ are collinear.  Now since $\overline{A D} \| \overline{I_{A} A_{2}}$, and $M$ and $A_{1}$ are the midpoints of $\overline{A D}$ and $\overline{I_{A} A_{2}}$, it follows from the collinearity of $A, I, I_{A}$ that $D, I, A_{2}$ are collinear as well. The other two claims follow in a dual fashion. For example, using the homothety taking the $A$ to $C$-excircle, we find that $\overline{C_{1} I_{C}}$ bisects the altitude $\overline{B E}$, and since $I_{C}, B$, $I_{A}$ are collinear the same argument now gives $I_{C}, E, C_{2}$ are collinear. The fact that $I_{B}$, $F, B_{2}$ are collinear is symmetric. Observe that $\overline{B_{2} C_{2}}\left\|\overline{B_{1} C_{1}}\right\| \overline{I_{B} I_{C}}$. Proceeding similarly on the other sides, we discover $\triangle I I_{B} I_{C}$ and $\triangle A_{2} B_{2} C_{2}$ are homothetic. Hence $P$ is the center of this homothety (in particular, $D, I, P, A_{2}$ are collinear). Moreover, $P$ lies on the line joining $I_{A}$ to $S$, which is the Euler line of $\triangle I I_{B} I_{C}$, so it passes through the nine-point center of $\triangle I I_{B} I_{C}$, which is $O$. Consequently, $P, O, I_{A}$ are collinear as well. To finish, we need only prove that $\overline{O S} \perp \overline{Y Z}$. In fact, we claim that $\overline{Y Z}$ is the radical axis of the circumcircles of $\triangle A B C$ and $\triangle I I_{B} I_{C}$. Actually, $Y$ is the radical center of these two circumcircles and the circle with diameter $\overline{I I_{B}}$ (which passes through $A$ and $C)$. Analogously $Z$ is the radical center of the circumcircles and the circle with diameter $\overline{I I_{C}}$, and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle and let $I_{B}, I_{C}$, and $O$ denote its $B$-excenter, $C$ excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{A C}$ such that $\angle A B Y=\angle C B Y$ and $\overline{B E} \perp \overline{A C}$. Similarly, points $F$ and $Z$ are selected on $\overline{A B}$ such that $\angle A C Z=\angle B C Z$ and $\overline{C F} \perp \overline{A B}$. Lines $I_{B} F$ and $I_{C} E$ meet at $P$. Prove that $\overline{P O}$ and $\overline{Y Z}$ are perpendicular.
|
\ First solution. Let $I_{A}$ denote the $A$-excenter and $I$ the incenter. Then let $D$ denote the foot of the altitude from $A$. Suppose the $A$-excircle is tangent to $\overline{B C}, \overline{A B}, \overline{A C}$ at $A_{1}, B_{1}, C_{1}$ and let $A_{2}, B_{2}, C_{2}$ denote the reflections of $I_{A}$ across these points. Let $S$ denote the circumcenter of $\triangle I I_{B} I_{C}$.  We begin with the following observation: Claim - Points $D, I, A_{2}$ are collinear, as are points $E, I_{C}, C_{2}$ are collinear and points $F, I_{B}, B_{2}$ are collinear.  Now since $\overline{A D} \| \overline{I_{A} A_{2}}$, and $M$ and $A_{1}$ are the midpoints of $\overline{A D}$ and $\overline{I_{A} A_{2}}$, it follows from the collinearity of $A, I, I_{A}$ that $D, I, A_{2}$ are collinear as well. The other two claims follow in a dual fashion. For example, using the homothety taking the $A$ to $C$-excircle, we find that $\overline{C_{1} I_{C}}$ bisects the altitude $\overline{B E}$, and since $I_{C}, B$, $I_{A}$ are collinear the same argument now gives $I_{C}, E, C_{2}$ are collinear. The fact that $I_{B}$, $F, B_{2}$ are collinear is symmetric. Observe that $\overline{B_{2} C_{2}}\left\|\overline{B_{1} C_{1}}\right\| \overline{I_{B} I_{C}}$. Proceeding similarly on the other sides, we discover $\triangle I I_{B} I_{C}$ and $\triangle A_{2} B_{2} C_{2}$ are homothetic. Hence $P$ is the center of this homothety (in particular, $D, I, P, A_{2}$ are collinear). Moreover, $P$ lies on the line joining $I_{A}$ to $S$, which is the Euler line of $\triangle I I_{B} I_{C}$, so it passes through the nine-point center of $\triangle I I_{B} I_{C}$, which is $O$. Consequently, $P, O, I_{A}$ are collinear as well. To finish, we need only prove that $\overline{O S} \perp \overline{Y Z}$. In fact, we claim that $\overline{Y Z}$ is the radical axis of the circumcircles of $\triangle A B C$ and $\triangle I I_{B} I_{C}$. Actually, $Y$ is the radical center of these two circumcircles and the circle with diameter $\overline{I I_{B}}$ (which passes through $A$ and $C)$. Analogously $Z$ is the radical center of the circumcircles and the circle with diameter $\overline{I I_{C}}$, and the proof is complete.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bb56c7fd-304f-54b2-a4c2-a9f504bc9efd
| 605,326
|
Let $A B C$ be an acute triangle and let $I_{B}, I_{C}$, and $O$ denote its $B$-excenter, $C$ excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{A C}$ such that $\angle A B Y=\angle C B Y$ and $\overline{B E} \perp \overline{A C}$. Similarly, points $F$ and $Z$ are selected on $\overline{A B}$ such that $\angle A C Z=\angle B C Z$ and $\overline{C F} \perp \overline{A B}$. Lines $I_{B} F$ and $I_{C} E$ meet at $P$. Prove that $\overline{P O}$ and $\overline{Y Z}$ are perpendicular.
|
I Second solution (barycentric, outline, Colin Tang). we are going to use barycentric coordinates to show that the line through $O$ perpendicular to $\overline{Y Z}$ is concurrent with $\overline{I_{B} F}$ and $\overline{I_{C} E}$. The displacement vector $\overrightarrow{Y Z}$ is proportional to $(a(b-c):-b(a+c): c(a+b))$, and so by strong perpendicularity criterion and doing a calculation gives the line $$ x(b-c) b c(a+b+c)+y(a+c) a c(a+b-c)+z(a+b) a b(-a+b-c)=0 . $$ On the other hand, line $I_{C} E$ has equation $$ 0=\operatorname{det}\left[\begin{array}{ccc} a & b & -c \\ S_{C} & 0 & S_{A} \\ x & y & z \end{array}\right]=b S_{a} \cdot x+\left(-c S_{C}-a S_{A}\right) \cdot y+\left(-b S_{C}\right) \cdot z $$ and similarly for $I_{B} F$. Consequently, concurrence of these lines is equivalent to $$ \operatorname{det}\left[\begin{array}{ccc} b S_{A} & -c S_{C}-a S_{A} & -b S_{C} \\ c S_{A} & -c S_{B} & -a S_{A}-b S_{B} \\ (b-c) b c(a+b+c) & (a+c) a c(a+b-c) & (a+b) a b(-a+b-c) \end{array}\right]=0 $$ which is a computation. \ Authorship comments. I was intrigued by a Taiwan TST problem which implied that, in the configuration above, $\angle I_{B} D I_{C}$ was bisected by $\overline{D A}$. This motivated me to draw all three properties above where $I_{A}$ and $P$ were isogonal conjugates with respect to $D E F$. After playing around with this picture for a long time, I finally noticed that $O$ was on line $P I_{A}$. (So the original was to show that $I_{B} F, I_{C} E, D A_{2}$ concurrent). Eventually I finally noticed in the picture that $P I_{A}$ actually passed through the circumcenter of $A B C$ as well. This took me many hours to prove. The final restatement (which follows quickly from $P, O, I_{A}$ collinear) was discovered by Telv Cohl when I showed him the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle and let $I_{B}, I_{C}$, and $O$ denote its $B$-excenter, $C$ excenter, and circumcenter, respectively. Points $E$ and $Y$ are selected on $\overline{A C}$ such that $\angle A B Y=\angle C B Y$ and $\overline{B E} \perp \overline{A C}$. Similarly, points $F$ and $Z$ are selected on $\overline{A B}$ such that $\angle A C Z=\angle B C Z$ and $\overline{C F} \perp \overline{A B}$. Lines $I_{B} F$ and $I_{C} E$ meet at $P$. Prove that $\overline{P O}$ and $\overline{Y Z}$ are perpendicular.
|
I Second solution (barycentric, outline, Colin Tang). we are going to use barycentric coordinates to show that the line through $O$ perpendicular to $\overline{Y Z}$ is concurrent with $\overline{I_{B} F}$ and $\overline{I_{C} E}$. The displacement vector $\overrightarrow{Y Z}$ is proportional to $(a(b-c):-b(a+c): c(a+b))$, and so by strong perpendicularity criterion and doing a calculation gives the line $$ x(b-c) b c(a+b+c)+y(a+c) a c(a+b-c)+z(a+b) a b(-a+b-c)=0 . $$ On the other hand, line $I_{C} E$ has equation $$ 0=\operatorname{det}\left[\begin{array}{ccc} a & b & -c \\ S_{C} & 0 & S_{A} \\ x & y & z \end{array}\right]=b S_{a} \cdot x+\left(-c S_{C}-a S_{A}\right) \cdot y+\left(-b S_{C}\right) \cdot z $$ and similarly for $I_{B} F$. Consequently, concurrence of these lines is equivalent to $$ \operatorname{det}\left[\begin{array}{ccc} b S_{A} & -c S_{C}-a S_{A} & -b S_{C} \\ c S_{A} & -c S_{B} & -a S_{A}-b S_{B} \\ (b-c) b c(a+b+c) & (a+c) a c(a+b-c) & (a+b) a b(-a+b-c) \end{array}\right]=0 $$ which is a computation. \ Authorship comments. I was intrigued by a Taiwan TST problem which implied that, in the configuration above, $\angle I_{B} D I_{C}$ was bisected by $\overline{D A}$. This motivated me to draw all three properties above where $I_{A}$ and $P$ were isogonal conjugates with respect to $D E F$. After playing around with this picture for a long time, I finally noticed that $O$ was on line $P I_{A}$. (So the original was to show that $I_{B} F, I_{C} E, D A_{2}$ concurrent). Eventually I finally noticed in the picture that $P I_{A}$ actually passed through the circumcenter of $A B C$ as well. This took me many hours to prove. The final restatement (which follows quickly from $P, O, I_{A}$ collinear) was discovered by Telv Cohl when I showed him the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
bb56c7fd-304f-54b2-a4c2-a9f504bc9efd
| 605,326
|
An equilateral pentagon $A M N P Q$ is inscribed in triangle $A B C$ such that $M \in \overline{A B}$, $Q \in \overline{A C}$, and $N, P \in \overline{B C}$. Let $S$ be the intersection of $\overline{M N}$ and $\overline{P Q}$. Denote by $\ell$ the angle bisector of $\angle M S Q$. Prove that $\overline{O I}$ is parallel to $\ell$, where $O$ is the circumcenter of triangle $A B C$, and $I$ is the incenter of triangle $A B C$.
|
【 First solution (complex). In fact, we only need $A M=A Q=N P$ and $M N=Q P$. We use complex numbers with $A B C$ the unit circle, assuming WLOG that $A, B, C$ are labeled counterclockwise. Let $x, y, z$ be the complex numbers corresponding to the arc midpoints of $B C, C A, A B$, respectively; thus $x+y+z$ is the incenter of $\triangle A B C$. Finally, let $s>0$ be the side length of $A M=A Q=N P$. Then, since $M A=s$ and $M A \perp O Z$, it follows that $$ m-a=i \cdot s z $$ Similarly, $p-n=i \cdot s y$ and $a-q=i \cdot s x$, so summing these up gives $$ i \cdot s(x+y+z)=(p-q)+(m-n)=(m-n)-(q-p) $$ Since $M N=P Q$, the argument of $(m-n)-(q-p)$ is along the external angle bisector of the angle formed, which is perpendicular to $\ell$. On the other hand, $x+y+z$ is oriented in the same direction as $O I$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An equilateral pentagon $A M N P Q$ is inscribed in triangle $A B C$ such that $M \in \overline{A B}$, $Q \in \overline{A C}$, and $N, P \in \overline{B C}$. Let $S$ be the intersection of $\overline{M N}$ and $\overline{P Q}$. Denote by $\ell$ the angle bisector of $\angle M S Q$. Prove that $\overline{O I}$ is parallel to $\ell$, where $O$ is the circumcenter of triangle $A B C$, and $I$ is the incenter of triangle $A B C$.
|
【 First solution (complex). In fact, we only need $A M=A Q=N P$ and $M N=Q P$. We use complex numbers with $A B C$ the unit circle, assuming WLOG that $A, B, C$ are labeled counterclockwise. Let $x, y, z$ be the complex numbers corresponding to the arc midpoints of $B C, C A, A B$, respectively; thus $x+y+z$ is the incenter of $\triangle A B C$. Finally, let $s>0$ be the side length of $A M=A Q=N P$. Then, since $M A=s$ and $M A \perp O Z$, it follows that $$ m-a=i \cdot s z $$ Similarly, $p-n=i \cdot s y$ and $a-q=i \cdot s x$, so summing these up gives $$ i \cdot s(x+y+z)=(p-q)+(m-n)=(m-n)-(q-p) $$ Since $M N=P Q$, the argument of $(m-n)-(q-p)$ is along the external angle bisector of the angle formed, which is perpendicular to $\ell$. On the other hand, $x+y+z$ is oriented in the same direction as $O I$, as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
32103963-b515-50a0-8ead-9efef41b9e1d
| 605,354
|
An equilateral pentagon $A M N P Q$ is inscribed in triangle $A B C$ such that $M \in \overline{A B}$, $Q \in \overline{A C}$, and $N, P \in \overline{B C}$. Let $S$ be the intersection of $\overline{M N}$ and $\overline{P Q}$. Denote by $\ell$ the angle bisector of $\angle M S Q$. Prove that $\overline{O I}$ is parallel to $\ell$, where $O$ is the circumcenter of triangle $A B C$, and $I$ is the incenter of triangle $A B C$.
|
ๆI Second solution (trig, Danielle Wang). Let $\delta$ and $\epsilon$ denote $\angle M N B$ and $\angle C P Q$. Also, assume $A M N P Q$ has side length 1. In what follows, assume $A B<A C$. First, we note that $$ \begin{aligned} B N & =(c-1) \cos B+\cos \delta \\ C P & =(b-1) \cos C+\cos \epsilon, \text { and } \\ a & =1+B N+C P \end{aligned} $$ from which it follows that $$ \cos \delta+\cos \epsilon=\cos B+\cos C-1 $$ Also, by the Law of Sines, we have $\frac{c-1}{\sin \delta}=\frac{1}{\sin B}$ and similarly on triangle $C P Q$, and from this we deduce $$ \sin \epsilon-\sin \delta=\sin B-\sin C $$ The sum-to-product formulas $$ \begin{aligned} & \sin \epsilon-\sin \delta=2 \cos \left(\frac{\epsilon+\delta}{2}\right) \sin \left(\frac{\epsilon-\delta}{2}\right) \\ & \cos \epsilon-\cos \delta=2 \cos \left(\frac{\epsilon+\delta}{2}\right) \cos \left(\frac{\epsilon-\delta}{2}\right) \end{aligned} $$ give us $$ \tan \left(\frac{\epsilon-\delta}{2}\right)=\frac{\sin \epsilon-\sin \delta}{\cos \epsilon-\cos \delta}=\frac{\sin B-\sin C}{\cos B+\cos C-1} $$ Now note that $\ell$ makes an angle of $\frac{1}{2}(\pi+\epsilon-\delta)$ with line $B C$. Moreover, if line $O I$ intersects line $B C$ with angle $\varphi$ then $$ \tan \varphi=\frac{r-R \cos A}{\frac{1}{2}(b-c)} $$ So in order to prove the result, we only need to check that $$ \frac{r-R \cos A}{\frac{1}{2}(b-c)}=\frac{\cos B+\cos C+1}{\sin B-\sin C} $$ Using the fact that $b=2 R \sin B, c=2 R \sin C$, this reduces to the fact that $r / R+1=$ $\cos A+\cos B+\cos C$, which is the so-called Carnot theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An equilateral pentagon $A M N P Q$ is inscribed in triangle $A B C$ such that $M \in \overline{A B}$, $Q \in \overline{A C}$, and $N, P \in \overline{B C}$. Let $S$ be the intersection of $\overline{M N}$ and $\overline{P Q}$. Denote by $\ell$ the angle bisector of $\angle M S Q$. Prove that $\overline{O I}$ is parallel to $\ell$, where $O$ is the circumcenter of triangle $A B C$, and $I$ is the incenter of triangle $A B C$.
|
ๆI Second solution (trig, Danielle Wang). Let $\delta$ and $\epsilon$ denote $\angle M N B$ and $\angle C P Q$. Also, assume $A M N P Q$ has side length 1. In what follows, assume $A B<A C$. First, we note that $$ \begin{aligned} B N & =(c-1) \cos B+\cos \delta \\ C P & =(b-1) \cos C+\cos \epsilon, \text { and } \\ a & =1+B N+C P \end{aligned} $$ from which it follows that $$ \cos \delta+\cos \epsilon=\cos B+\cos C-1 $$ Also, by the Law of Sines, we have $\frac{c-1}{\sin \delta}=\frac{1}{\sin B}$ and similarly on triangle $C P Q$, and from this we deduce $$ \sin \epsilon-\sin \delta=\sin B-\sin C $$ The sum-to-product formulas $$ \begin{aligned} & \sin \epsilon-\sin \delta=2 \cos \left(\frac{\epsilon+\delta}{2}\right) \sin \left(\frac{\epsilon-\delta}{2}\right) \\ & \cos \epsilon-\cos \delta=2 \cos \left(\frac{\epsilon+\delta}{2}\right) \cos \left(\frac{\epsilon-\delta}{2}\right) \end{aligned} $$ give us $$ \tan \left(\frac{\epsilon-\delta}{2}\right)=\frac{\sin \epsilon-\sin \delta}{\cos \epsilon-\cos \delta}=\frac{\sin B-\sin C}{\cos B+\cos C-1} $$ Now note that $\ell$ makes an angle of $\frac{1}{2}(\pi+\epsilon-\delta)$ with line $B C$. Moreover, if line $O I$ intersects line $B C$ with angle $\varphi$ then $$ \tan \varphi=\frac{r-R \cos A}{\frac{1}{2}(b-c)} $$ So in order to prove the result, we only need to check that $$ \frac{r-R \cos A}{\frac{1}{2}(b-c)}=\frac{\cos B+\cos C+1}{\sin B-\sin C} $$ Using the fact that $b=2 R \sin B, c=2 R \sin C$, this reduces to the fact that $r / R+1=$ $\cos A+\cos B+\cos C$, which is the so-called Carnot theorem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2016-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
32103963-b515-50a0-8ead-9efef41b9e1d
| 605,354
|
Prove that there exist infinitely many pairs of relatively prime positive integers $a, b>1$ for which $a+b$ divides $a^{b}+b^{a}$.
|
One construction: let $d \equiv 1(\bmod 4), d>1$. Let $x=\frac{d^{d}+2^{d}}{d+2}$. Then set $$ a=\frac{x+d}{2}, \quad b=\frac{x-d}{2} . $$ To see this works, first check that $b$ is odd and $a$ is even. Let $d=a-b$ be odd. Then: $$ \begin{aligned} a+b \mid a^{b}+b^{a} & \Longleftrightarrow(-b)^{b}+b^{a} \equiv 0 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{a-b} \equiv 1 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{d} \equiv 1 \quad(\bmod d+2 b) \\ & \Longleftrightarrow(-2)^{d} \equiv d^{d}(\bmod d+2 b) \\ & \Longleftrightarrow d+2 b \mid d^{d}+2^{d} . \end{aligned} $$ So it would be enough that $$ d+2 b=\frac{d^{d}+2^{d}}{d+2} \Longrightarrow b=\frac{1}{2}\left(\frac{d^{d}+2^{d}}{d+2}-d\right) $$ which is what we constructed. Also, since $\operatorname{gcd}(x, d)=1$ it follows $\operatorname{gcd}(a, b)=\operatorname{gcd}(d, b)=$ 1. Remark. Ryan Kim points out that in fact, $(a, b)=(2 n-1,2 n+1)$ is always a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many pairs of relatively prime positive integers $a, b>1$ for which $a+b$ divides $a^{b}+b^{a}$.
|
One construction: let $d \equiv 1(\bmod 4), d>1$. Let $x=\frac{d^{d}+2^{d}}{d+2}$. Then set $$ a=\frac{x+d}{2}, \quad b=\frac{x-d}{2} . $$ To see this works, first check that $b$ is odd and $a$ is even. Let $d=a-b$ be odd. Then: $$ \begin{aligned} a+b \mid a^{b}+b^{a} & \Longleftrightarrow(-b)^{b}+b^{a} \equiv 0 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{a-b} \equiv 1 \quad(\bmod a+b) \\ & \Longleftrightarrow b^{d} \equiv 1 \quad(\bmod d+2 b) \\ & \Longleftrightarrow(-2)^{d} \equiv d^{d}(\bmod d+2 b) \\ & \Longleftrightarrow d+2 b \mid d^{d}+2^{d} . \end{aligned} $$ So it would be enough that $$ d+2 b=\frac{d^{d}+2^{d}}{d+2} \Longrightarrow b=\frac{1}{2}\left(\frac{d^{d}+2^{d}}{d+2}-d\right) $$ which is what we constructed. Also, since $\operatorname{gcd}(x, d)=1$ it follows $\operatorname{gcd}(a, b)=\operatorname{gcd}(d, b)=$ 1. Remark. Ryan Kim points out that in fact, $(a, b)=(2 n-1,2 n+1)$ is always a solution.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c485124-df45-5d2d-9924-c24895e9a9dd
| 245,952
|
Let $m_{1}, m_{2}, \ldots, m_{n}$ be a collection of $n$ positive integers, not necessarily distinct. For any sequence of integers $A=\left(a_{1}, \ldots, a_{n}\right)$ and any permutation $w=w_{1}, \ldots, w_{n}$ of $m_{1}, \ldots, m_{n}$, define an $A$-inversion of $w$ to be a pair of entries $w_{i}, w_{j}$ with $i<j$ for which one of the following conditions holds: - $a_{i} \geq w_{i}>w_{j}$, - $w_{j}>a_{i} \geq w_{i}$, or - $w_{i}>w_{j}>a_{i}$. Show that, for any two sequences of integers $A=\left(a_{1}, \ldots, a_{n}\right)$ and $B=\left(b_{1}, \ldots, b_{n}\right)$, and for any positive integer $k$, the number of permutations of $m_{1}, \ldots, m_{n}$ having exactly $k A$-inversions is equal to the number of permutations of $m_{1}, \ldots, m_{n}$ having exactly $k B$-inversions.
|
Denote by $M$ our multiset of $n$ positive integers. Define an inversion of a permutation to be pair $i<j$ with $w_{i}<w_{j}$ (which is a $(0, \ldots, 0)$-inversion in the problem statement); this is the usual definition (see https://en.wikipedia.org/wiki/Inversion_(discrete_ mathematics)). So we want to show the number of $A$-inversions is equal to the number of usual inversions. In what follows we count permutations on $M$ with multiplicity: so $M=\{1,1,2\}$ still has $3!=6$ permutations. We are going to do what is essentially recursion, but using generating functions in a variable $q$ to do our book-keeping. (Motivation: there's no good closed form for the number of inversions, but there's a great generating function known - which is even better for us, since we're only trying to show two numbers are equal!) First, we prove two claims. Claim - For any positive integer $n$, the generating function for the number of permutations of $(1,2, \ldots, n)$ with exactly $k$ inversions is $$ n!!_{q}:=1 \cdot(1+q) \cdot\left(1+q+q^{2}\right) \cdot \ldots\left(1+q+\cdots+q^{n-1}\right) $$ Here we mean that the coefficient of $q^{S}$ above gives the number of permutations with exactly $s$ inversions. Unfortunately, the main difficulty of the problem is that there are repeated elements, which makes our notation much more horrific. Let us define the following. We take our given multiset $M$ of $n$ positive integers, we suppose the distinct numbers are $\theta_{1}<\theta_{2}<\cdots<\theta_{m}$. We let $e_{i}$ be the number of times $\theta_{i}$ appears. Therefore the multiplicities $e_{i}$ should have sums $$ e_{1}+\cdots+e_{m}=n $$ and $m$ denotes the number of distinct elements. Finally, we let $$ F\left(e_{1}, \ldots, e_{m}\right)=\sum_{\text {permutations } \sigma} q^{\text {number inversions of } \sigma} $$ be the associated generating function for the number of inversions. For example, the first claim we proved says that $F(1, \ldots, 1)=n!{ }_{q}$. Claim - We have the explicit formula $$ F\left(e_{1}, \ldots, e_{m}\right)=n!{ }_{q} \cdot \prod_{i=1}^{m} \frac{e_{i}!}{e_{i}!_{q}} $$ Then, we undo the perturbations for each group, one at a time, and claim that we get the above $e_{i}!_{q}$ factor each time. Indeed, put the permutations into classes of $e_{1}$ ! each where permutations in the same classes differ only in the order of the perturbed $\theta_{1}$ 's (with the other $n-e_{1}$ elements being fixed). Then there is a factor of $e_{1}!_{q}$ from each class, owing to the slightly perturbed inversions we added within each class. So we remove that factor and add $e_{1}!\cdot q^{0}$ instead. This accounts for the first term of the product. Repeating this now with each term of the product implies the claim. Thus we have the formula for the number of inversions in general. We wish to show this also equals the generating function the number of $A$-inversions, for any fixed choice of $A$. This will be an induction by $n$, with the base case being immediate. For the inductive step, fix $A$, and assume the first element satisfies $\theta_{k} \leq a_{1}<\theta_{k+1}$ (so $0 \leq k \leq m$; we for convenience set $\theta_{0}=-\infty$ and $\left.\theta_{m}=+\infty\right)$. We count the permutations based on what the first element $\theta_{i}$ of the permutation is. Then: - Consider permutations starting with $\theta_{i} \in\left\{\theta_{1}, \ldots, \theta_{k}\right\}$. Then the number of inversions which will use this first term is $\left(e_{1}+\cdots+e_{i-1}\right)+\left(e_{k+1}+\cdots+e_{m}\right)$. Also, there are $e_{i}$ ways to pick which $\theta_{i}$ gets used as the first term. So we get a contribution of $$ q^{e_{1}+\cdots+e_{i-1}+\left(e_{k+1}+\cdots+e_{m}\right)} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ in this case (with inductive hypothesis to get the last $F$-term). - Now suppose $\theta_{i} \in\left\{\theta_{k+1}, \ldots, \theta_{m}\right\}$. Then the number of inversions which will use this first term is $e_{k+1}+\cdots+e_{i-1}$. Thus by a similar argument the contribution is $$ q^{e_{k+1}+\cdots+e_{i-1}} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ Therefore, to complete the problem it suffices to prove $$ \sum_{i=1}^{k} q^{\left(e_{1}+\cdots+e_{i-1}\right)+\left(e_{k+1}+\cdots+e_{m}\right)} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ $$ \begin{aligned} & +\sum_{i=k+1}^{m} q^{e_{k+1}+\cdots+e_{i-1}} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) \\ & =F\left(e_{1}, \ldots, e_{m}\right) . \end{aligned} $$ Now, we see that $$ \frac{e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right)}{F\left(e_{1}, \ldots, e_{m}\right)}=\frac{1+\cdots+q^{e_{i}-1}}{1+q+\cdots+q^{n-1}}=\frac{1-q^{e_{i}}}{1-q^{n}} $$ so it's equivalent to show $$ 1-q^{n}=q^{e_{k+1}+\cdots+e_{m}} \sum_{i=1}^{k} q^{e_{1}+\cdots+e_{i-1}}\left(1-q^{e_{i}}\right)+\sum_{i=k+1}^{m} q^{e_{k+1}+\cdots+e_{i-1}}\left(1-q^{e_{i}}\right) $$ which is clear, since the left summand telescopes to $q^{e_{k+1}+\cdots+e_{m}}-q^{n}$ and the right summand telescopes to $1-q^{e_{k+1}+\cdots+e_{m}}$. Remark. Technically, we could have skipped straight to the induction, without proving the first two claims. However I think the solution reads more naturally this way.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m_{1}, m_{2}, \ldots, m_{n}$ be a collection of $n$ positive integers, not necessarily distinct. For any sequence of integers $A=\left(a_{1}, \ldots, a_{n}\right)$ and any permutation $w=w_{1}, \ldots, w_{n}$ of $m_{1}, \ldots, m_{n}$, define an $A$-inversion of $w$ to be a pair of entries $w_{i}, w_{j}$ with $i<j$ for which one of the following conditions holds: - $a_{i} \geq w_{i}>w_{j}$, - $w_{j}>a_{i} \geq w_{i}$, or - $w_{i}>w_{j}>a_{i}$. Show that, for any two sequences of integers $A=\left(a_{1}, \ldots, a_{n}\right)$ and $B=\left(b_{1}, \ldots, b_{n}\right)$, and for any positive integer $k$, the number of permutations of $m_{1}, \ldots, m_{n}$ having exactly $k A$-inversions is equal to the number of permutations of $m_{1}, \ldots, m_{n}$ having exactly $k B$-inversions.
|
Denote by $M$ our multiset of $n$ positive integers. Define an inversion of a permutation to be pair $i<j$ with $w_{i}<w_{j}$ (which is a $(0, \ldots, 0)$-inversion in the problem statement); this is the usual definition (see https://en.wikipedia.org/wiki/Inversion_(discrete_ mathematics)). So we want to show the number of $A$-inversions is equal to the number of usual inversions. In what follows we count permutations on $M$ with multiplicity: so $M=\{1,1,2\}$ still has $3!=6$ permutations. We are going to do what is essentially recursion, but using generating functions in a variable $q$ to do our book-keeping. (Motivation: there's no good closed form for the number of inversions, but there's a great generating function known - which is even better for us, since we're only trying to show two numbers are equal!) First, we prove two claims. Claim - For any positive integer $n$, the generating function for the number of permutations of $(1,2, \ldots, n)$ with exactly $k$ inversions is $$ n!!_{q}:=1 \cdot(1+q) \cdot\left(1+q+q^{2}\right) \cdot \ldots\left(1+q+\cdots+q^{n-1}\right) $$ Here we mean that the coefficient of $q^{S}$ above gives the number of permutations with exactly $s$ inversions. Unfortunately, the main difficulty of the problem is that there are repeated elements, which makes our notation much more horrific. Let us define the following. We take our given multiset $M$ of $n$ positive integers, we suppose the distinct numbers are $\theta_{1}<\theta_{2}<\cdots<\theta_{m}$. We let $e_{i}$ be the number of times $\theta_{i}$ appears. Therefore the multiplicities $e_{i}$ should have sums $$ e_{1}+\cdots+e_{m}=n $$ and $m$ denotes the number of distinct elements. Finally, we let $$ F\left(e_{1}, \ldots, e_{m}\right)=\sum_{\text {permutations } \sigma} q^{\text {number inversions of } \sigma} $$ be the associated generating function for the number of inversions. For example, the first claim we proved says that $F(1, \ldots, 1)=n!{ }_{q}$. Claim - We have the explicit formula $$ F\left(e_{1}, \ldots, e_{m}\right)=n!{ }_{q} \cdot \prod_{i=1}^{m} \frac{e_{i}!}{e_{i}!_{q}} $$ Then, we undo the perturbations for each group, one at a time, and claim that we get the above $e_{i}!_{q}$ factor each time. Indeed, put the permutations into classes of $e_{1}$ ! each where permutations in the same classes differ only in the order of the perturbed $\theta_{1}$ 's (with the other $n-e_{1}$ elements being fixed). Then there is a factor of $e_{1}!_{q}$ from each class, owing to the slightly perturbed inversions we added within each class. So we remove that factor and add $e_{1}!\cdot q^{0}$ instead. This accounts for the first term of the product. Repeating this now with each term of the product implies the claim. Thus we have the formula for the number of inversions in general. We wish to show this also equals the generating function the number of $A$-inversions, for any fixed choice of $A$. This will be an induction by $n$, with the base case being immediate. For the inductive step, fix $A$, and assume the first element satisfies $\theta_{k} \leq a_{1}<\theta_{k+1}$ (so $0 \leq k \leq m$; we for convenience set $\theta_{0}=-\infty$ and $\left.\theta_{m}=+\infty\right)$. We count the permutations based on what the first element $\theta_{i}$ of the permutation is. Then: - Consider permutations starting with $\theta_{i} \in\left\{\theta_{1}, \ldots, \theta_{k}\right\}$. Then the number of inversions which will use this first term is $\left(e_{1}+\cdots+e_{i-1}\right)+\left(e_{k+1}+\cdots+e_{m}\right)$. Also, there are $e_{i}$ ways to pick which $\theta_{i}$ gets used as the first term. So we get a contribution of $$ q^{e_{1}+\cdots+e_{i-1}+\left(e_{k+1}+\cdots+e_{m}\right)} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ in this case (with inductive hypothesis to get the last $F$-term). - Now suppose $\theta_{i} \in\left\{\theta_{k+1}, \ldots, \theta_{m}\right\}$. Then the number of inversions which will use this first term is $e_{k+1}+\cdots+e_{i-1}$. Thus by a similar argument the contribution is $$ q^{e_{k+1}+\cdots+e_{i-1}} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ Therefore, to complete the problem it suffices to prove $$ \sum_{i=1}^{k} q^{\left(e_{1}+\cdots+e_{i-1}\right)+\left(e_{k+1}+\cdots+e_{m}\right)} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) $$ $$ \begin{aligned} & +\sum_{i=k+1}^{m} q^{e_{k+1}+\cdots+e_{i-1}} \cdot e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right) \\ & =F\left(e_{1}, \ldots, e_{m}\right) . \end{aligned} $$ Now, we see that $$ \frac{e_{i} \cdot F\left(e_{1}, \ldots, e_{i}-1, \ldots, e_{m}\right)}{F\left(e_{1}, \ldots, e_{m}\right)}=\frac{1+\cdots+q^{e_{i}-1}}{1+q+\cdots+q^{n-1}}=\frac{1-q^{e_{i}}}{1-q^{n}} $$ so it's equivalent to show $$ 1-q^{n}=q^{e_{k+1}+\cdots+e_{m}} \sum_{i=1}^{k} q^{e_{1}+\cdots+e_{i-1}}\left(1-q^{e_{i}}\right)+\sum_{i=k+1}^{m} q^{e_{k+1}+\cdots+e_{i-1}}\left(1-q^{e_{i}}\right) $$ which is clear, since the left summand telescopes to $q^{e_{k+1}+\cdots+e_{m}}-q^{n}$ and the right summand telescopes to $1-q^{e_{k+1}+\cdots+e_{m}}$. Remark. Technically, we could have skipped straight to the induction, without proving the first two claims. However I think the solution reads more naturally this way.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
e6a5c235-c069-5eb0-aaef-7c8c8152b541
| 605,402
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$ and incenter $I$. Ray $A I$ meets $\overline{B C}$ at $D$ and $\Omega$ again at $M$; the circle with diameter $\overline{D M}$ cuts $\Omega$ again at $K$. Lines $M K$ and $B C$ meet at $S$, and $N$ is the midpoint of $\overline{I S}$. The circumcircles of $\triangle K I D$ and $\triangle M A N$ intersect at points $L_{1}$ and $L_{2}$. Prove that $\Omega$ passes through the midpoint of either $\overline{I L_{1}}$ or $\overline{I L_{2}}$.
|
Let $W$ be the midpoint of $\overline{B C}$, let $X$ be the point on $\Omega$ opposite $M$. Observe that $\overline{K D}$ passes through $X$, and thus lines $B C, M K, X A$ concur at the orthocenter of $\triangle D M X$, which we call $S$. Denote by $I_{A}$ the $A$-excenter of $A B C$. Next, let $E$ be the foot of the altitude from $I$ to $\overline{X I_{A}}$; observe that $E$ lies on the circle centered at $M$ through $I, B, C, I_{A}$. Then, $S$ is the radical center of $\Omega$ and the circles with diameter $\overline{I X}$ and $\overline{I I_{A}}$; hence line $S I$ passes through $E$; accordingly $I$ is the orthocenter of $\triangle X S I_{A}$; denote by $L$ the foot from $X$ to $\overline{S I_{A}}$.  We claim that this $L$ lies on both the circumcircle of $\triangle K I D$ and $\triangle M A N$. It lies on the circumcircle of $\triangle M A N$ since this circle is the nine-point circle of $\triangle X S I_{A}$. Also, $X D \cdot X K=X W \cdot X M=X A \cdot X S=X I \cdot X L$, so $K D I L$ are concyclic. All that remains to show is that the midpoint $T$ of $\overline{I L}$ lies on $\Omega$. But this follows from the fact that $\overline{T M} \| \overline{L I_{A}} \Longrightarrow \angle M T X=90^{\circ}$, thus the problem is solved. Remark. Some additional facts about this picture: the point $T$ is the contact point of the $A$-mixtilinear incircle (since it is collinear with $X$ and $I$ ), while the point $K$ is such that $\overline{A K}$ is an $A$-symmedian (since $\overline{K D}$ and $\overline{A D}$ bisect $\angle A$ and $\angle K$, say).  Remark. In fact, the point $L$ is the Miquel point of cyclic quadrilateral $I_{B} I_{C} B C$ (inscribed in the circle with diameter $\overline{I_{B} I_{C}}$ ). This implies many of the properties that $L$ has above. For example, it directly implies that $L$ lies on the circumcircles of triangles $I_{A} I_{B} I_{C}$ and $B C I_{A}$, and that the point $L$ lies on $\overline{S I_{A}}$ (since $S=\overline{B C} \cap \overline{I_{B} I_{C}}$ ). For this reason, many students found it easier to think about the problem in terms of $\triangle I_{A} I_{B} I_{C}$ rather than $\triangle A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with circumcircle $\Omega$ and incenter $I$. Ray $A I$ meets $\overline{B C}$ at $D$ and $\Omega$ again at $M$; the circle with diameter $\overline{D M}$ cuts $\Omega$ again at $K$. Lines $M K$ and $B C$ meet at $S$, and $N$ is the midpoint of $\overline{I S}$. The circumcircles of $\triangle K I D$ and $\triangle M A N$ intersect at points $L_{1}$ and $L_{2}$. Prove that $\Omega$ passes through the midpoint of either $\overline{I L_{1}}$ or $\overline{I L_{2}}$.
|
Let $W$ be the midpoint of $\overline{B C}$, let $X$ be the point on $\Omega$ opposite $M$. Observe that $\overline{K D}$ passes through $X$, and thus lines $B C, M K, X A$ concur at the orthocenter of $\triangle D M X$, which we call $S$. Denote by $I_{A}$ the $A$-excenter of $A B C$. Next, let $E$ be the foot of the altitude from $I$ to $\overline{X I_{A}}$; observe that $E$ lies on the circle centered at $M$ through $I, B, C, I_{A}$. Then, $S$ is the radical center of $\Omega$ and the circles with diameter $\overline{I X}$ and $\overline{I I_{A}}$; hence line $S I$ passes through $E$; accordingly $I$ is the orthocenter of $\triangle X S I_{A}$; denote by $L$ the foot from $X$ to $\overline{S I_{A}}$.  We claim that this $L$ lies on both the circumcircle of $\triangle K I D$ and $\triangle M A N$. It lies on the circumcircle of $\triangle M A N$ since this circle is the nine-point circle of $\triangle X S I_{A}$. Also, $X D \cdot X K=X W \cdot X M=X A \cdot X S=X I \cdot X L$, so $K D I L$ are concyclic. All that remains to show is that the midpoint $T$ of $\overline{I L}$ lies on $\Omega$. But this follows from the fact that $\overline{T M} \| \overline{L I_{A}} \Longrightarrow \angle M T X=90^{\circ}$, thus the problem is solved. Remark. Some additional facts about this picture: the point $T$ is the contact point of the $A$-mixtilinear incircle (since it is collinear with $X$ and $I$ ), while the point $K$ is such that $\overline{A K}$ is an $A$-symmedian (since $\overline{K D}$ and $\overline{A D}$ bisect $\angle A$ and $\angle K$, say).  Remark. In fact, the point $L$ is the Miquel point of cyclic quadrilateral $I_{B} I_{C} B C$ (inscribed in the circle with diameter $\overline{I_{B} I_{C}}$ ). This implies many of the properties that $L$ has above. For example, it directly implies that $L$ lies on the circumcircles of triangles $I_{A} I_{B} I_{C}$ and $B C I_{A}$, and that the point $L$ lies on $\overline{S I_{A}}$ (since $S=\overline{B C} \cap \overline{I_{B} I_{C}}$ ). For this reason, many students found it easier to think about the problem in terms of $\triangle I_{A} I_{B} I_{C}$ rather than $\triangle A B C$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
dd18215f-f760-5f19-8fd7-b59c1c002a87
| 248,906
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
\ First "local" solution by swapping two points. Let $1 \leq i<n$ be any index and consider the two red points $R_{i}$ and $R_{i+1}$. There are two blue points $B_{i}$ and $B_{i+1}$ associated with them. Claim - If we swap the locations of points $R_{i}$ and $R_{i+1}$ then the new $\operatorname{arcs} R_{i} \rightarrow B_{i}$ and $R_{i+1} \rightarrow B_{i+1}$ will cover the same points. The two blue points can then be located in three possible ways: either 0,1 , or 2 of them lie on the $\operatorname{arc} R_{i} \rightarrow R_{i+1}$. For each of the cases below, we illustrate on the left the locations of $B_{i}$ and $B_{i+1}$ and the corresponding arcs in green; then on the right we show the modified picture where $R_{i}$ and $R_{i+1}$ have swapped. (Note that by hypothesis there are no other blue points in the green arcs).  Case $3 R_{i}$  Observe that in all cases, the number of arcs covering any given point on the circumference is not changed. Consequently, this proves the claim. Finally, it is enough to recall that any permutation of the red points can be achieved by swapping consecutive points (put another way: $(i i+1)$ generates the permutation group $S_{n}$ ). This solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
\ First "local" solution by swapping two points. Let $1 \leq i<n$ be any index and consider the two red points $R_{i}$ and $R_{i+1}$. There are two blue points $B_{i}$ and $B_{i+1}$ associated with them. Claim - If we swap the locations of points $R_{i}$ and $R_{i+1}$ then the new $\operatorname{arcs} R_{i} \rightarrow B_{i}$ and $R_{i+1} \rightarrow B_{i+1}$ will cover the same points. The two blue points can then be located in three possible ways: either 0,1 , or 2 of them lie on the $\operatorname{arc} R_{i} \rightarrow R_{i+1}$. For each of the cases below, we illustrate on the left the locations of $B_{i}$ and $B_{i+1}$ and the corresponding arcs in green; then on the right we show the modified picture where $R_{i}$ and $R_{i+1}$ have swapped. (Note that by hypothesis there are no other blue points in the green arcs).  Case $3 R_{i}$  Observe that in all cases, the number of arcs covering any given point on the circumference is not changed. Consequently, this proves the claim. Finally, it is enough to recall that any permutation of the red points can be achieved by swapping consecutive points (put another way: $(i i+1)$ generates the permutation group $S_{n}$ ). This solves the problem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6cc8af89-f27f-5806-a452-9eabb5f60f3d
| 605,074
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
II Second longer solution using an invariant. Visually, if we draw all the segments $R_{i} \rightarrow B_{i}$ then we obtain a set of $n$ chords. Say a chord is inverted if satisfies the problem condition, and stable otherwise. The problem contends that the number of stable/inverted chords depends only on the layout of the points and not on the choice of chords.  In fact we'll describe the number of inverted chords explicitly. Starting from $(1,0)$ we keep a running tally of $R-B$; in other words we start the counter at 0 and decrement by 1 at each blue point and increment by 1 at each red point. Let $x \leq 0$ be the lowest number ever recorded. Then: Claim - The number of inverted chords is $-x$ (and hence independent of the choice of chords). This is by induction on $n$. I think the easiest thing is to delete chord $R_{1} B_{1}$; note that the arc cut out by this chord contains no blue points. So if the chord was stable certainly no change to $x$. On the other hand, if the chord is inverted, then in particular the last point before $(1,0)$ was red, and so $x<0$. In this situation one sees that deleting the chord changes $x$ to $x+1$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $P_{1}, P_{2}, \ldots, P_{2 n}$ be $2 n$ distinct points on the unit circle $x^{2}+y^{2}=1$, other than $(1,0)$. Each point is colored either red or blue, with exactly $n$ red points and $n$ blue points. Let $R_{1}, R_{2}, \ldots, R_{n}$ be any ordering of the red points. Let $B_{1}$ be the nearest blue point to $R_{1}$ traveling counterclockwise around the circle starting from $R_{1}$. Then let $B_{2}$ be the nearest of the remaining blue points to $R_{2}$ travelling counterclockwise around the circle from $R_{2}$, and so on, until we have labeled all of the blue points $B_{1}, \ldots, B_{n}$. Show that the number of counterclockwise arcs of the form $R_{i} \rightarrow B_{i}$ that contain the point $(1,0)$ is independent of the way we chose the ordering $R_{1}, \ldots, R_{n}$ of the red points.
|
II Second longer solution using an invariant. Visually, if we draw all the segments $R_{i} \rightarrow B_{i}$ then we obtain a set of $n$ chords. Say a chord is inverted if satisfies the problem condition, and stable otherwise. The problem contends that the number of stable/inverted chords depends only on the layout of the points and not on the choice of chords.  In fact we'll describe the number of inverted chords explicitly. Starting from $(1,0)$ we keep a running tally of $R-B$; in other words we start the counter at 0 and decrement by 1 at each blue point and increment by 1 at each red point. Let $x \leq 0$ be the lowest number ever recorded. Then: Claim - The number of inverted chords is $-x$ (and hence independent of the choice of chords). This is by induction on $n$. I think the easiest thing is to delete chord $R_{1} B_{1}$; note that the arc cut out by this chord contains no blue points. So if the chord was stable certainly no change to $x$. On the other hand, if the chord is inverted, then in particular the last point before $(1,0)$ was red, and so $x<0$. In this situation one sees that deleting the chord changes $x$ to $x+1$, as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2017-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6cc8af89-f27f-5806-a452-9eabb5f60f3d
| 605,074
|
Let $a, b, c$ be positive real numbers such that $a+b+c=4 \sqrt[3]{a b c}$. Prove that $$ 2(a b+b c+c a)+4 \min \left(a^{2}, b^{2}, c^{2}\right) \geq a^{2}+b^{2}+c^{2} . $$
|
WLOG let $c=\min (a, b, c)=1$ by scaling. The given inequality becomes equivalent to $$ 4 a b+2 a+2 b+3 \geq(a+b)^{2} \quad \forall a+b=4(a b)^{1 / 3}-1 $$ Now, let $t=(a b)^{1 / 3}$ and eliminate $a+b$ using the condition, to get $$ 4 t^{3}+2(4 t-1)+3 \geq(4 t-1)^{2} \Longleftrightarrow 0 \leq 4 t^{3}-16 t^{2}+16 t=4 t(t-2)^{2} $$ which solves the problem. Equality occurs only if $t=2$, meaning $a b=8$ and $a+b=7$, which gives $$ \{a, b\}=\left\{\frac{7 \pm \sqrt{17}}{2}\right\} $$ with the assumption $c=1$. Scaling gives the curve of equality cases.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a+b+c=4 \sqrt[3]{a b c}$. Prove that $$ 2(a b+b c+c a)+4 \min \left(a^{2}, b^{2}, c^{2}\right) \geq a^{2}+b^{2}+c^{2} . $$
|
WLOG let $c=\min (a, b, c)=1$ by scaling. The given inequality becomes equivalent to $$ 4 a b+2 a+2 b+3 \geq(a+b)^{2} \quad \forall a+b=4(a b)^{1 / 3}-1 $$ Now, let $t=(a b)^{1 / 3}$ and eliminate $a+b$ using the condition, to get $$ 4 t^{3}+2(4 t-1)+3 \geq(4 t-1)^{2} \Longleftrightarrow 0 \leq 4 t^{3}-16 t^{2}+16 t=4 t(t-2)^{2} $$ which solves the problem. Equality occurs only if $t=2$, meaning $a b=8$ and $a+b=7$, which gives $$ \{a, b\}=\left\{\frac{7 \pm \sqrt{17}}{2}\right\} $$ with the assumption $c=1$. Scaling gives the curve of equality cases.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
18a334fc-8782-5ef7-9c88-4cf1ee8a96d7
| 605,473
|
Let $n \geq 2$ be an integer, and let $\left\{a_{1}, \ldots, a_{m}\right\}$ denote the $m=\varphi(n)$ integers less than $n$ and relatively prime to $n$. Assume that every prime divisor of $m$ also divides $n$. Prove that $m$ divides $a_{1}^{k}+\cdots+a_{m}^{k}$ for every positive integer $k$.
|
For brevity, given any $n$, we let $A(n)=\{1 \leq x \leq n, \operatorname{gcd}(x, n)=1\}$ (thus $|A(n)|=\varphi(n)$ ). Also, let $S(n, k)=\sum_{a \in A(n)} a^{k}$. We will prove the stronger statement (which eliminates the hypothesis on $n$ ). Claim - Let $n \geq 2$ be arbitrary (and $k \geq 0$ ). If $p \mid n$, then $$ \nu_{p}(\varphi(n)) \leq \nu_{p}(S(n, k)) $$ We start with the special case where $n$ is a prime power. ## Lemma Let $p$ be prime, $e \geq 1, k \geq 0$. We always have $$ S\left(p^{e}, k\right)=\sum_{x \in A\left(p^{e}\right)} x^{k} \equiv 0 \quad\left(\bmod p^{e-1}\right) $$ $$ S\left(p^{e}, k\right) \equiv 1+g^{k}+g^{2 k}+\cdots+g^{\left(\varphi\left(p^{e}\right)-1\right) k} \equiv \frac{g^{\varphi\left(p^{e}\right) k}-1}{g^{k}-1} $$ If $p-1 \nmid k$, then the denominator is not divisible by $p$ and hence the entire expression is $0\left(\bmod p^{e}\right)$. In the other case where $p-1 \mid k$, since $\nu_{p}\left(\varphi\left(p^{e}\right)\right)=e-1$, the exponent lifting lemma implies $$ \nu_{p}\left(\left(g^{k}\right)^{\varphi\left(p^{e}\right)}-1\right)=\nu_{p}\left(g^{k}-1\right)+(e-1) $$ and so the conclusion is true here too. ## Corollary We have $\nu_{p}\left(1^{k}+\cdots+t^{k}\right) \geq \nu_{p}(t)-1$ for any $k, t, p$. Now the idea is to add primes $q$ one at a time to $n$, starting from the base case $n=p^{e}$. So, formally we proceed by induction on the number of prime divisors of $n$. We'll also assume $k \geq 1$ in what follows since the base case $k=0$ is easy. - First, suppose we want to go from $n$ to $n q$ where $q \nmid n$. In that case $\varphi(n q)$ gained $\nu_{p}(q-1)$ factors of $p$ and then we need to show $\nu_{p}(S(n q, k)) \geq \nu_{p}(\varphi(n))+\nu_{p}(q-1)$. The trick is to write $$ A(n q)=\{a+n h \mid a \in A(n) \text { and } h=0, \ldots, q-1\} \backslash q A(n) $$ and then expand using binomial theorem: $$ \begin{aligned} S(n q, k) & =\sum_{a \in A(n)} \sum_{h=0}^{q-1}(a+n h)^{k}-\sum_{a \in A(n)}(q a)^{k} \\ & =-q^{k} S(n, k)+\sum_{a \in A(n)} \sum_{h=0}^{q-1} \sum_{j=0}^{k}\left[\binom{k}{j} a^{k-j} n^{j} h^{j}\right] \\ & =-q^{k} S(n, k)+\sum_{j=0}^{k}\left[\binom{k}{j} n^{j}\left(\sum_{a \in A(n)} a^{k-j}\right)\left(\sum_{h=0}^{q-1} h^{j}\right)\right] \\ & =-q^{k} S(n, k)+\sum_{j=0}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] \\ & =\left(q-q^{k}\right) S(n, k)+\sum_{j=1}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] \end{aligned} $$ We claim every term here has enough powers of $p$. For the first term, $S(n, k)$ has at least $\nu_{p}(\varphi(n))$ factors of $p$; and we have the $q-q^{k}$ multiplier out there. For the other terms, we apply induction to $S(n, k-j)$; moreover $\sum_{h=1}^{q-1} h^{j}$ has at least $\nu_{p}(q-1)-1$ factors of $p$ by corollary, and we get one more factor of $p$ (at least) from $n^{j}$. - On the other hand, if $q$ already divides $n$, then this time $$ A(n q)=\{a+n h \mid a \in A(n) \text { and } h=0, \ldots, q-1\} $$ and we have no additional burden of $p$ to deal with; the same calculation gives $$ S(n q, k)=q S(n, k)+\sum_{j=1}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] $$ which certainly has enough factors of $p$ already. Remark. A curious bit about the problem is that $\nu_{p}(\varphi(n))$ can exceed $\nu_{p}(n)$, and so it is not true that the residues of $A(n)$ are well-behaved modulo $\varphi(n)$. As an example, let $n=2 \cdot 3 \cdot 7 \cdot 13=546$, so $m=\varphi(n)=1 \cdot 2 \cdot 6 \cdot 12=144$. Then $A(n)$ contains 26 elements which are $1 \bmod 9$ and 23 elements which are $4 \bmod 9$. Remark. The converse of the problem is true too (but asking both parts would make this too long for exam).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be an integer, and let $\left\{a_{1}, \ldots, a_{m}\right\}$ denote the $m=\varphi(n)$ integers less than $n$ and relatively prime to $n$. Assume that every prime divisor of $m$ also divides $n$. Prove that $m$ divides $a_{1}^{k}+\cdots+a_{m}^{k}$ for every positive integer $k$.
|
For brevity, given any $n$, we let $A(n)=\{1 \leq x \leq n, \operatorname{gcd}(x, n)=1\}$ (thus $|A(n)|=\varphi(n)$ ). Also, let $S(n, k)=\sum_{a \in A(n)} a^{k}$. We will prove the stronger statement (which eliminates the hypothesis on $n$ ). Claim - Let $n \geq 2$ be arbitrary (and $k \geq 0$ ). If $p \mid n$, then $$ \nu_{p}(\varphi(n)) \leq \nu_{p}(S(n, k)) $$ We start with the special case where $n$ is a prime power. ## Lemma Let $p$ be prime, $e \geq 1, k \geq 0$. We always have $$ S\left(p^{e}, k\right)=\sum_{x \in A\left(p^{e}\right)} x^{k} \equiv 0 \quad\left(\bmod p^{e-1}\right) $$ $$ S\left(p^{e}, k\right) \equiv 1+g^{k}+g^{2 k}+\cdots+g^{\left(\varphi\left(p^{e}\right)-1\right) k} \equiv \frac{g^{\varphi\left(p^{e}\right) k}-1}{g^{k}-1} $$ If $p-1 \nmid k$, then the denominator is not divisible by $p$ and hence the entire expression is $0\left(\bmod p^{e}\right)$. In the other case where $p-1 \mid k$, since $\nu_{p}\left(\varphi\left(p^{e}\right)\right)=e-1$, the exponent lifting lemma implies $$ \nu_{p}\left(\left(g^{k}\right)^{\varphi\left(p^{e}\right)}-1\right)=\nu_{p}\left(g^{k}-1\right)+(e-1) $$ and so the conclusion is true here too. ## Corollary We have $\nu_{p}\left(1^{k}+\cdots+t^{k}\right) \geq \nu_{p}(t)-1$ for any $k, t, p$. Now the idea is to add primes $q$ one at a time to $n$, starting from the base case $n=p^{e}$. So, formally we proceed by induction on the number of prime divisors of $n$. We'll also assume $k \geq 1$ in what follows since the base case $k=0$ is easy. - First, suppose we want to go from $n$ to $n q$ where $q \nmid n$. In that case $\varphi(n q)$ gained $\nu_{p}(q-1)$ factors of $p$ and then we need to show $\nu_{p}(S(n q, k)) \geq \nu_{p}(\varphi(n))+\nu_{p}(q-1)$. The trick is to write $$ A(n q)=\{a+n h \mid a \in A(n) \text { and } h=0, \ldots, q-1\} \backslash q A(n) $$ and then expand using binomial theorem: $$ \begin{aligned} S(n q, k) & =\sum_{a \in A(n)} \sum_{h=0}^{q-1}(a+n h)^{k}-\sum_{a \in A(n)}(q a)^{k} \\ & =-q^{k} S(n, k)+\sum_{a \in A(n)} \sum_{h=0}^{q-1} \sum_{j=0}^{k}\left[\binom{k}{j} a^{k-j} n^{j} h^{j}\right] \\ & =-q^{k} S(n, k)+\sum_{j=0}^{k}\left[\binom{k}{j} n^{j}\left(\sum_{a \in A(n)} a^{k-j}\right)\left(\sum_{h=0}^{q-1} h^{j}\right)\right] \\ & =-q^{k} S(n, k)+\sum_{j=0}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] \\ & =\left(q-q^{k}\right) S(n, k)+\sum_{j=1}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] \end{aligned} $$ We claim every term here has enough powers of $p$. For the first term, $S(n, k)$ has at least $\nu_{p}(\varphi(n))$ factors of $p$; and we have the $q-q^{k}$ multiplier out there. For the other terms, we apply induction to $S(n, k-j)$; moreover $\sum_{h=1}^{q-1} h^{j}$ has at least $\nu_{p}(q-1)-1$ factors of $p$ by corollary, and we get one more factor of $p$ (at least) from $n^{j}$. - On the other hand, if $q$ already divides $n$, then this time $$ A(n q)=\{a+n h \mid a \in A(n) \text { and } h=0, \ldots, q-1\} $$ and we have no additional burden of $p$ to deal with; the same calculation gives $$ S(n q, k)=q S(n, k)+\sum_{j=1}^{k}\left[\binom{k}{j} n^{j} S(n, k-j)\left(\sum_{h=1}^{q-1} h^{j}\right)\right] $$ which certainly has enough factors of $p$ already. Remark. A curious bit about the problem is that $\nu_{p}(\varphi(n))$ can exceed $\nu_{p}(n)$, and so it is not true that the residues of $A(n)$ are well-behaved modulo $\varphi(n)$. As an example, let $n=2 \cdot 3 \cdot 7 \cdot 13=546$, so $m=\varphi(n)=1 \cdot 2 \cdot 6 \cdot 12=144$. Then $A(n)$ contains 26 elements which are $1 \bmod 9$ and 23 elements which are $4 \bmod 9$. Remark. The converse of the problem is true too (but asking both parts would make this too long for exam).
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
faba1404-a848-5baf-a1b5-e8f94406b6b8
| 248,951
|
Let $p$ be a prime, and let $a_{1}, \ldots, a_{p}$ be integers. Show that there exists an integer $k$ such that the numbers $$ a_{1}+k, a_{2}+2 k, \ldots, a_{p}+p k $$ produce at least $\frac{1}{2} p$ distinct remainders upon division by $p$.
|
For each $k=0, \ldots, p-1$ let $G_{k}$ be the graph on $\{1, \ldots, p\}$ where we join $\{i, j\}$ if and only if $$ a_{i}+i k \equiv a_{j}+j k \quad(\bmod p) \Longleftrightarrow k \equiv-\frac{a_{i}-a_{j}}{i-j} \quad(\bmod p) . $$ So we want a graph $G_{k}$ with at least $\frac{1}{2} p$ connected components. However, each $\{i, j\}$ appears in exactly one graph $G_{k}$, so some graph has at most $\frac{1}{p}\binom{p}{2}=\frac{1}{2}(p-1)$ edges (by "pigeonhole"). This graph has at least $\frac{1}{2}(p+1)$ connected components, as desired. Remark. Here is an example for $p=5$ showing equality can occur: $$ \left[\begin{array}{lllll} 0 & 0 & 3 & 4 & 3 \\ 0 & 1 & 0 & 2 & 2 \\ 0 & 2 & 2 & 0 & 1 \\ 0 & 3 & 4 & 3 & 0 \\ 0 & 4 & 1 & 1 & 4 \end{array}\right] . $$ Ankan Bhattacharya points out more generally that $a_{i}=i^{2}$ is sharp in general.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime, and let $a_{1}, \ldots, a_{p}$ be integers. Show that there exists an integer $k$ such that the numbers $$ a_{1}+k, a_{2}+2 k, \ldots, a_{p}+p k $$ produce at least $\frac{1}{2} p$ distinct remainders upon division by $p$.
|
For each $k=0, \ldots, p-1$ let $G_{k}$ be the graph on $\{1, \ldots, p\}$ where we join $\{i, j\}$ if and only if $$ a_{i}+i k \equiv a_{j}+j k \quad(\bmod p) \Longleftrightarrow k \equiv-\frac{a_{i}-a_{j}}{i-j} \quad(\bmod p) . $$ So we want a graph $G_{k}$ with at least $\frac{1}{2} p$ connected components. However, each $\{i, j\}$ appears in exactly one graph $G_{k}$, so some graph has at most $\frac{1}{p}\binom{p}{2}=\frac{1}{2}(p-1)$ edges (by "pigeonhole"). This graph has at least $\frac{1}{2}(p+1)$ connected components, as desired. Remark. Here is an example for $p=5$ showing equality can occur: $$ \left[\begin{array}{lllll} 0 & 0 & 3 & 4 & 3 \\ 0 & 1 & 0 & 2 & 2 \\ 0 & 2 & 2 & 0 & 1 \\ 0 & 3 & 4 & 3 & 0 \\ 0 & 4 & 1 & 1 & 4 \end{array}\right] . $$ Ankan Bhattacharya points out more generally that $a_{i}=i^{2}$ is sharp in general.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
5e8ad2de-f676-5f29-ad1a-10f63aff5c25
| 605,168
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) \l First solution (Miquel points). This is indeed a Miquel point problem, but the main idea is to focus on the self-intersecting cyclic quadrilateral $P B Q D$ as the key player, rather than on the given $A B C D$. Indeed, we will prove that $A$ is its Miquel point; this follows from the following two claims. Claim - The self-intersecting quadrilateral $P Q D B$ is cyclic. Claim - Point $E$ lies on line $P Q$.  To finish, let $H=\overline{P D} \cap \overline{B Q}$. By properties of the Miquel point, we have $A$ is the foot from $H$ to $\overline{C E}$. But also, points $M, A, H$ are collinear by Pappus theorem on $\overline{B P G}$ and $\overline{D Q F}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) \l First solution (Miquel points). This is indeed a Miquel point problem, but the main idea is to focus on the self-intersecting cyclic quadrilateral $P B Q D$ as the key player, rather than on the given $A B C D$. Indeed, we will prove that $A$ is its Miquel point; this follows from the following two claims. Claim - The self-intersecting quadrilateral $P Q D B$ is cyclic. Claim - Point $E$ lies on line $P Q$.  To finish, let $H=\overline{P D} \cap \overline{B Q}$. By properties of the Miquel point, we have $A$ is the foot from $H$ to $\overline{C E}$. But also, points $M, A, H$ are collinear by Pappus theorem on $\overline{B P G}$ and $\overline{D Q F}$, as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
34d4821c-7faa-56eb-befc-7e5a89c94349
| 248,967
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) 【 Second solution (projective). We start with a synthetic observation. Claim - The line $\overline{A C}$ bisects $\angle P A D$ and $\angle B A Q$. There are three ways to finish from here: - (Michael Kural) Suppose the external bisector of $\angle P A D$ and $\angle B A Q$ meet lines $B C$ and $D C$ at $X$ and $Y$. Then $$ -1=(G P ; X C)=(F D ; Y C) $$ which is enough to imply that $\overline{X Y}, \overline{G Q}, \overline{P F}$ are concurrent (by so-called prism lemma). - (Daniel Liu) Alternatively, apply the dual Desargues involution theorem to complete quadrilateral GQFPCM, through the point $A$. This gives that an involutive pairing of $$ (A C, A M)(A P, A Q)(A G, A F) $$ This is easier to see if we project it onto the line $\ell$ through $C$ perpendicular to $\overline{A C}$; if we let $P^{\prime}, Q^{\prime}, G^{\prime}, F^{\prime}$ be the images of the last four lines, we find the involution coincides with negative inversion through $C$ with power $\sqrt{C P^{\prime} \cdot C Q^{\prime}}$ which implies that $\overline{A M} \cap \ell$ is an infinity point, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) 【 Second solution (projective). We start with a synthetic observation. Claim - The line $\overline{A C}$ bisects $\angle P A D$ and $\angle B A Q$. There are three ways to finish from here: - (Michael Kural) Suppose the external bisector of $\angle P A D$ and $\angle B A Q$ meet lines $B C$ and $D C$ at $X$ and $Y$. Then $$ -1=(G P ; X C)=(F D ; Y C) $$ which is enough to imply that $\overline{X Y}, \overline{G Q}, \overline{P F}$ are concurrent (by so-called prism lemma). - (Daniel Liu) Alternatively, apply the dual Desargues involution theorem to complete quadrilateral GQFPCM, through the point $A$. This gives that an involutive pairing of $$ (A C, A M)(A P, A Q)(A G, A F) $$ This is easier to see if we project it onto the line $\ell$ through $C$ perpendicular to $\overline{A C}$; if we let $P^{\prime}, Q^{\prime}, G^{\prime}, F^{\prime}$ be the images of the last four lines, we find the involution coincides with negative inversion through $C$ with power $\sqrt{C P^{\prime} \cdot C Q^{\prime}}$ which implies that $\overline{A M} \cap \ell$ is an infinity point, as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
34d4821c-7faa-56eb-befc-7e5a89c94349
| 248,967
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) 【 Third solution (inversion, Andrew Wu). Noting that $C E \cdot C A=C P \cdot C B=C Q \cdot C D$, we perform an inversion at $C$ swapping these pairs of points. The point $G$ is mapped to a point $G^{*}$ ray $C B$ for which $Q E G^{*} C$ is cyclic, but then $$ \measuredangle C G^{*} E=\measuredangle C Q E=\measuredangle C Q P=\measuredangle D B C=\measuredangle C B E $$ and so we conclude $E B=E G^{*}$. Similarly, $E D=E F^{*}$. Finally, $M^{*}=\left(C G^{*} D\right) \cap\left(C F^{*} B\right) \neq C$, and we wish to show that $\angle E M^{*} C=90^{\circ}$.  Note that $M^{*}$ is the center of the spiral similarity sending $\overline{B G^{*}}$ to $\overline{F^{*} D}$. Hence it also maps the midpoint $K$ of $B G^{*}$ to the midpoint $L$ of $\overline{F^{*} E}$. Consequently, $M^{*}$ lies on the circumcircle $K L C$ as well. In other words, $E L C K M^{*}$ is a cyclic pentagon with circumdiameter $\overline{C E}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex cyclic quadrilateral with $E=\overline{A C} \cap \overline{B D}, F=\overline{A B} \cap \overline{C D}$, $G=\overline{D A} \cap \overline{B C}$. The circumcircle of $\triangle A B E$ intersects line $C B$ at $B$ and $P$, and the circumcircle of $\triangle A D E$ intersects line $C D$ at $D$ and $Q$. Assume $C, B, P, G$ and $C$, $Q, D, F$ are collinear in that order. Let $M=\overline{F P} \cap \overline{G Q}$. Prove that $\angle M A C=90^{\circ}$.
|
We present three general routes. (The second route, using the fact that $\overline{A C}$ is an angle bisector, has many possible variations.) 【 Third solution (inversion, Andrew Wu). Noting that $C E \cdot C A=C P \cdot C B=C Q \cdot C D$, we perform an inversion at $C$ swapping these pairs of points. The point $G$ is mapped to a point $G^{*}$ ray $C B$ for which $Q E G^{*} C$ is cyclic, but then $$ \measuredangle C G^{*} E=\measuredangle C Q E=\measuredangle C Q P=\measuredangle D B C=\measuredangle C B E $$ and so we conclude $E B=E G^{*}$. Similarly, $E D=E F^{*}$. Finally, $M^{*}=\left(C G^{*} D\right) \cap\left(C F^{*} B\right) \neq C$, and we wish to show that $\angle E M^{*} C=90^{\circ}$.  Note that $M^{*}$ is the center of the spiral similarity sending $\overline{B G^{*}}$ to $\overline{F^{*} D}$. Hence it also maps the midpoint $K$ of $B G^{*}$ to the midpoint $L$ of $\overline{F^{*} E}$. Consequently, $M^{*}$ lies on the circumcircle $K L C$ as well. In other words, $E L C K M^{*}$ is a cyclic pentagon with circumdiameter $\overline{C E}$, as desired.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
34d4821c-7faa-56eb-befc-7e5a89c94349
| 248,967
|
Let $a_{n}$ be the number of permutations $\left(x_{1}, \ldots, x_{n}\right)$ of $(1, \ldots, n)$ such that the ratios $x_{k} / k$ are all distinct. Prove that $a_{n}$ is odd for all $n \geq 1$.
|
The first idea: ## Lemma If a permutation $x$ works, so does the inverse permutation. Thus it suffices to consider permutations $x$ in which all cycles have length at most 2 . Of course, there can be at most one fixed point (since that gives the ratio 1 ), and hence exactly one if $n$ is odd, none if $n$ is even. We consider the graph $K_{n}$ such that the edge $\{i, j\}$ is labeled with $i / j$ (for $i<j$ ). The permutations we're considering are then equivalent to maximal matchings of this $K_{n}$. We call such a matching fantastic if it has an all of distinct edge labels. Now the second insight is that if edges $a b$ and $c d$ have the same label for $a<b$ and $c<d$, then so do edges $a c$ and $b d$. Thus: Definition. Given a matching $\mathcal{M}$ as above we say the neighbors of $\mathcal{M}$ are those other matchings obtained as follows: for each label $\ell$, we take some disjoint pairs of edges (possibly none) with label $\ell$ and apply the above switching operation (in which we replace $a b$ and $c d$ with $a c$ and $b d)$. This neighborship relation is reflexive, and most importantly it is symmetric (because one can simply reverse the moves). But it is not transitive. The second observation is that: Claim - The matching $\mathcal{M}$ has an odd number of neighbors (including itself) if and only if it is fantastic. If we pick $k$ disjoint pairs and swap them, the number of ways to do this is $\binom{n_{e}}{2 k}(2 k-1)!!$, and so the total number of ways to perform operations on the edges labeled $\ell$ is $$ \sum_{k}\binom{n_{\ell}}{2 k}(2 k-1)!!\equiv \sum_{k}\binom{n_{\ell}}{2 k}=2^{n_{\ell}-1} \quad(\bmod 2) $$ This is even if and only if $n_{\ell}>1$. Finally, note that the number of neighbors of $\mathcal{M}$ is the product across all $\ell$ of the above. So it is odd if and only if each factor is odd, if and only if $n_{\ell}=1$ for every $\ell$. To finish, consider a huge simple graph $\Gamma$ on all the maximal matchings, with edge relations given by neighbor relation (we don't consider vertices to be connected to themselves). Observe that: - Fantastic matchings correspond to isolated vertices (of degree zero, with no other neighbors) of $\Gamma$. - The rest of the vertices of $\Gamma$ have odd degrees (one less than the neighbor count) - The graph $\Gamma$ has an even number of vertices of odd degree (this is true for any simple graph, see "handshake lemma"). - The number of vertices of $\Gamma$ is odd, namely $(2\lceil n / 2\rceil-1)!!$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $a_{n}$ be the number of permutations $\left(x_{1}, \ldots, x_{n}\right)$ of $(1, \ldots, n)$ such that the ratios $x_{k} / k$ are all distinct. Prove that $a_{n}$ is odd for all $n \geq 1$.
|
The first idea: ## Lemma If a permutation $x$ works, so does the inverse permutation. Thus it suffices to consider permutations $x$ in which all cycles have length at most 2 . Of course, there can be at most one fixed point (since that gives the ratio 1 ), and hence exactly one if $n$ is odd, none if $n$ is even. We consider the graph $K_{n}$ such that the edge $\{i, j\}$ is labeled with $i / j$ (for $i<j$ ). The permutations we're considering are then equivalent to maximal matchings of this $K_{n}$. We call such a matching fantastic if it has an all of distinct edge labels. Now the second insight is that if edges $a b$ and $c d$ have the same label for $a<b$ and $c<d$, then so do edges $a c$ and $b d$. Thus: Definition. Given a matching $\mathcal{M}$ as above we say the neighbors of $\mathcal{M}$ are those other matchings obtained as follows: for each label $\ell$, we take some disjoint pairs of edges (possibly none) with label $\ell$ and apply the above switching operation (in which we replace $a b$ and $c d$ with $a c$ and $b d)$. This neighborship relation is reflexive, and most importantly it is symmetric (because one can simply reverse the moves). But it is not transitive. The second observation is that: Claim - The matching $\mathcal{M}$ has an odd number of neighbors (including itself) if and only if it is fantastic. If we pick $k$ disjoint pairs and swap them, the number of ways to do this is $\binom{n_{e}}{2 k}(2 k-1)!!$, and so the total number of ways to perform operations on the edges labeled $\ell$ is $$ \sum_{k}\binom{n_{\ell}}{2 k}(2 k-1)!!\equiv \sum_{k}\binom{n_{\ell}}{2 k}=2^{n_{\ell}-1} \quad(\bmod 2) $$ This is even if and only if $n_{\ell}>1$. Finally, note that the number of neighbors of $\mathcal{M}$ is the product across all $\ell$ of the above. So it is odd if and only if each factor is odd, if and only if $n_{\ell}=1$ for every $\ell$. To finish, consider a huge simple graph $\Gamma$ on all the maximal matchings, with edge relations given by neighbor relation (we don't consider vertices to be connected to themselves). Observe that: - Fantastic matchings correspond to isolated vertices (of degree zero, with no other neighbors) of $\Gamma$. - The rest of the vertices of $\Gamma$ have odd degrees (one less than the neighbor count) - The graph $\Gamma$ has an even number of vertices of odd degree (this is true for any simple graph, see "handshake lemma"). - The number of vertices of $\Gamma$ is odd, namely $(2\lceil n / 2\rceil-1)!!$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2018-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6b10b136-23cc-5003-8cc9-964e8c66c418
| 248,974
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 First solution using symmedians. We define point $P$ to obey $$ \frac{A P}{B P}=\frac{A D^{2}}{B C^{2}}=\frac{A E^{2}}{B E^{2}} $$ so that $\overline{P E}$ is the $E$-symmedian of $\triangle E A B$, therefore the $E$-median of $\triangle E C D$. Now, note that $$ A D^{2}=A P \cdot A B \quad \text { and } \quad B C^{2}=B P \cdot B A $$ This implies $\triangle A P D \sim \triangle A D B$ and $\triangle B P C \sim \triangle B C A$. Thus $$ \measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P $$ and so $P$ satisfies the condition as in the statement (and is the unique point to do so), as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 First solution using symmedians. We define point $P$ to obey $$ \frac{A P}{B P}=\frac{A D^{2}}{B C^{2}}=\frac{A E^{2}}{B E^{2}} $$ so that $\overline{P E}$ is the $E$-symmedian of $\triangle E A B$, therefore the $E$-median of $\triangle E C D$. Now, note that $$ A D^{2}=A P \cdot A B \quad \text { and } \quad B C^{2}=B P \cdot B A $$ This implies $\triangle A P D \sim \triangle A D B$ and $\triangle B P C \sim \triangle B C A$. Thus $$ \measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P $$ and so $P$ satisfies the condition as in the statement (and is the unique point to do so), as needed.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Second solution using only angle chasing (by proposer). We again re-define $P$ to obey $A D^{2}=A P \cdot A B$ and $B C^{2}=B P \cdot B A$. As before, this gives $\triangle A P D \sim \triangle A B D$ and $\triangle B P C \sim \triangle B D P$ and so we let $$ \theta:=\measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P . $$ Our goal is to now show $\overline{P E}$ bisects $\overline{C D}$. Let $K=\overline{A C} \cap \overline{P D}$ and $L=\overline{A D} \cap \overline{P C}$. Since $\measuredangle K P A=\theta=\measuredangle A C B$, quadrilateral $B P K C$ is cyclic. Similarly, so is $A P L D$.  Finally $A K L B$ is cyclic since $$ \measuredangle B K A=\measuredangle B K C=\measuredangle B P C=\theta=\measuredangle D P A=\measuredangle D L A=\measuredangle B L A . $$ This implies $\measuredangle C K L=\measuredangle L B A=\measuredangle D C K$, so $\overline{K L} \| \overline{B C}$. Then $P E$ bisects $\overline{B C}$ by Ceva's theorem on $\triangle P C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Second solution using only angle chasing (by proposer). We again re-define $P$ to obey $A D^{2}=A P \cdot A B$ and $B C^{2}=B P \cdot B A$. As before, this gives $\triangle A P D \sim \triangle A B D$ and $\triangle B P C \sim \triangle B D P$ and so we let $$ \theta:=\measuredangle D P A=\measuredangle A D B=\measuredangle A C B=\measuredangle B C P . $$ Our goal is to now show $\overline{P E}$ bisects $\overline{C D}$. Let $K=\overline{A C} \cap \overline{P D}$ and $L=\overline{A D} \cap \overline{P C}$. Since $\measuredangle K P A=\theta=\measuredangle A C B$, quadrilateral $B P K C$ is cyclic. Similarly, so is $A P L D$.  Finally $A K L B$ is cyclic since $$ \measuredangle B K A=\measuredangle B K C=\measuredangle B P C=\theta=\measuredangle D P A=\measuredangle D L A=\measuredangle B L A . $$ This implies $\measuredangle C K L=\measuredangle L B A=\measuredangle D C K$, so $\overline{K L} \| \overline{B C}$. Then $P E$ bisects $\overline{B C}$ by Ceva's theorem on $\triangle P C D$.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Third solution (using inversion). By hypothesis, the circle $\omega_{a}$ centered at $A$ with radius $A D$ is orthogonal to the circle $\omega_{b}$ centered at $B$ with radius $B C$. For brevity, we let $\mathbf{I}_{a}$ and $\mathbf{I}_{b}$ denote inversion with respect to $\omega_{a}$ and $\omega_{b}$. We let $P$ denote the intersection of $\overline{A B}$ with the radical axis of $\omega_{a}$ and $\omega_{b}$; hence $P=\mathbf{I}_{a}(B)=\mathbf{I}_{b}(A)$. This already implies that $$ \measuredangle D P A \stackrel{\mathbf{I}_{a}}{=} \measuredangle A D B=\measuredangle A C B \stackrel{\mathbf{I}_{b}}{=} \measuredangle B P C $$ so $P$ satisfies the angle condition.  Claim - The point $K=\mathbf{I}_{a}(C)$ lies on $\omega_{b}$ and $\overline{D P}$. Similarly $L=\mathbf{I}_{b}(D)$ lies on $\omega_{a}$ and $\overline{C P}$. Finally, since $C, L, P$ are collinear, we get $A$ is concyclic with $K=\mathbf{I}_{a}(C), L=\mathbf{I}_{a}(L)$, $B=\mathbf{I}_{a}(P)$, i.e. that $A K L B$ is cyclic. So $\overline{K L} \| \overline{C D}$ by Reim's theorem, and hence $\overline{P E}$ bisects $\overline{C D}$ by Ceva's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral satisfying $A D^{2}+B C^{2}=A B^{2}$. The diagonals of $A B C D$ intersect at $E$. Let $P$ be a point on side $\overline{A B}$ satisfying $\angle A P D=\angle B P C$. Show that line $P E$ bisects $\overline{C D}$.
|
【 Third solution (using inversion). By hypothesis, the circle $\omega_{a}$ centered at $A$ with radius $A D$ is orthogonal to the circle $\omega_{b}$ centered at $B$ with radius $B C$. For brevity, we let $\mathbf{I}_{a}$ and $\mathbf{I}_{b}$ denote inversion with respect to $\omega_{a}$ and $\omega_{b}$. We let $P$ denote the intersection of $\overline{A B}$ with the radical axis of $\omega_{a}$ and $\omega_{b}$; hence $P=\mathbf{I}_{a}(B)=\mathbf{I}_{b}(A)$. This already implies that $$ \measuredangle D P A \stackrel{\mathbf{I}_{a}}{=} \measuredangle A D B=\measuredangle A C B \stackrel{\mathbf{I}_{b}}{=} \measuredangle B P C $$ so $P$ satisfies the angle condition.  Claim - The point $K=\mathbf{I}_{a}(C)$ lies on $\omega_{b}$ and $\overline{D P}$. Similarly $L=\mathbf{I}_{b}(D)$ lies on $\omega_{a}$ and $\overline{C P}$. Finally, since $C, L, P$ are collinear, we get $A$ is concyclic with $K=\mathbf{I}_{a}(C), L=\mathbf{I}_{a}(L)$, $B=\mathbf{I}_{a}(P)$, i.e. that $A K L B$ is cyclic. So $\overline{K L} \| \overline{C D}$ by Reim's theorem, and hence $\overline{P E}$ bisects $\overline{C D}$ by Ceva's theorem.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2019-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
85c5cf58-8840-5ff6-8403-0cbcb9387b65
| 246,066
|
Let $n \geq 2$ be an integer. Let $x_{1} \geq x_{2} \geq \cdots \geq x_{n}$ and $y_{1} \geq y_{2} \geq \cdots \geq y_{n}$ be $2 n$ real numbers such that $$ \begin{aligned} 0 & =x_{1}+x_{2}+\cdots+x_{n}=y_{1}+y_{2}+\cdots+y_{n} \\ \text { and } \quad 1 & =x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2} \end{aligned} $$ Prove that $$ \sum_{i=1}^{n}\left(x_{i} y_{i}-x_{i} y_{n+1-i}\right) \geq \frac{2}{\sqrt{n-1}} $$
|
$$ \begin{aligned} & \left(x_{i}\right)=(\underbrace{\frac{1}{\sqrt{n}}, \ldots, \frac{1}{\sqrt{n}}}_{n / 2}, \underbrace{-\frac{1}{\sqrt{n}}, \ldots,-\frac{1}{\sqrt{n}}}_{n / 2}) \\ & \left(y_{i}\right)=(\frac{n-1}{\sqrt{n(n-1)}}, \underbrace{\frac{1}{\sqrt{n(n-1)}}, \ldots,-\frac{1}{\sqrt{n(n-1)}}}_{n-1}) \end{aligned} $$ \T Outline of second approach (by convexity, due to Alex Zhai). We will instead prove a converse result: given the hypotheses - $x_{1} \geq \cdots \geq x_{n}$ - $y_{1} \geq \cdots \geq y_{n}$ - $\sum_{i} x_{i}=\sum_{i} y_{i}=0$ - $\sum_{i} x_{i} y_{i}-\sum_{i} x_{i} y_{n+1-i}=\frac{2}{\sqrt{n-1}}$ we will prove that $\sum x_{i}^{2} \sum y_{i}^{2} \leq 1$. Fix the choice of $y$ 's. We see that we are trying to maximize a convex function in $n$ variables $\left(x_{1}, \ldots, x_{n}\right)$ over a convex domain (actually the intersection of two planes with several half planes). So a maximum can only happen at the boundaries: when at most two of the $x$ 's are different. An analogous argument applies to $y$. In this way we find that it suffices to consider situations where $x_{\bullet}$ takes on at most two different values. The same argument applies to $y$. At this point the problem can be checked directly.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq 2$ be an integer. Let $x_{1} \geq x_{2} \geq \cdots \geq x_{n}$ and $y_{1} \geq y_{2} \geq \cdots \geq y_{n}$ be $2 n$ real numbers such that $$ \begin{aligned} 0 & =x_{1}+x_{2}+\cdots+x_{n}=y_{1}+y_{2}+\cdots+y_{n} \\ \text { and } \quad 1 & =x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2} \end{aligned} $$ Prove that $$ \sum_{i=1}^{n}\left(x_{i} y_{i}-x_{i} y_{n+1-i}\right) \geq \frac{2}{\sqrt{n-1}} $$
|
$$ \begin{aligned} & \left(x_{i}\right)=(\underbrace{\frac{1}{\sqrt{n}}, \ldots, \frac{1}{\sqrt{n}}}_{n / 2}, \underbrace{-\frac{1}{\sqrt{n}}, \ldots,-\frac{1}{\sqrt{n}}}_{n / 2}) \\ & \left(y_{i}\right)=(\frac{n-1}{\sqrt{n(n-1)}}, \underbrace{\frac{1}{\sqrt{n(n-1)}}, \ldots,-\frac{1}{\sqrt{n(n-1)}}}_{n-1}) \end{aligned} $$ \T Outline of second approach (by convexity, due to Alex Zhai). We will instead prove a converse result: given the hypotheses - $x_{1} \geq \cdots \geq x_{n}$ - $y_{1} \geq \cdots \geq y_{n}$ - $\sum_{i} x_{i}=\sum_{i} y_{i}=0$ - $\sum_{i} x_{i} y_{i}-\sum_{i} x_{i} y_{n+1-i}=\frac{2}{\sqrt{n-1}}$ we will prove that $\sum x_{i}^{2} \sum y_{i}^{2} \leq 1$. Fix the choice of $y$ 's. We see that we are trying to maximize a convex function in $n$ variables $\left(x_{1}, \ldots, x_{n}\right)$ over a convex domain (actually the intersection of two planes with several half planes). So a maximum can only happen at the boundaries: when at most two of the $x$ 's are different. An analogous argument applies to $y$. In this way we find that it suffices to consider situations where $x_{\bullet}$ takes on at most two different values. The same argument applies to $y$. At this point the problem can be checked directly.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2020-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
8757e2fa-0235-52c3-9765-1e83d58c544b
| 605,791
|
Rectangles $B C C_{1} B_{2}, C A A_{1} C_{2}$, and $A B B_{1} A_{2}$ are erected outside an acute triangle $A B C$. Suppose that $$ \angle B C_{1} C+\angle C A_{1} A+\angle A B_{1} B=180^{\circ} . $$ Prove that lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent.
|
The angle condition implies the circumcircles of the three rectangles concur at a single point $P$.  Then $\measuredangle C P B_{2}=\measuredangle C P A_{1}=90^{\circ}$, hence $P$ lies on $A_{1} B_{2}$ etc., so we're done. Remark. As one might guess from the two-sentence solution, the entire difficulty of the problem is getting the characterization of the concurrence point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Rectangles $B C C_{1} B_{2}, C A A_{1} C_{2}$, and $A B B_{1} A_{2}$ are erected outside an acute triangle $A B C$. Suppose that $$ \angle B C_{1} C+\angle C A_{1} A+\angle A B_{1} B=180^{\circ} . $$ Prove that lines $B_{1} C_{2}, C_{1} A_{2}$, and $A_{1} B_{2}$ are concurrent.
|
The angle condition implies the circumcircles of the three rectangles concur at a single point $P$.  Then $\measuredangle C P B_{2}=\measuredangle C P A_{1}=90^{\circ}$, hence $P$ lies on $A_{1} B_{2}$ etc., so we're done. Remark. As one might guess from the two-sentence solution, the entire difficulty of the problem is getting the characterization of the concurrence point.
|
{
"resource_path": "USAMO/segmented/en-USAMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
6c28363b-d4e8-5b95-82b2-04909136f6df
| 605,504
|
Let $A B C D E F$ be a convex hexagon satisfying $\overline{A B}\|\overline{D E}, \overline{B C}\| \overline{E F}, \overline{C D} \| \overline{F A}$, and $$ A B \cdot D E=B C \cdot E F=C D \cdot F A $$ Let $X, Y$, and $Z$ be the midpoints of $\overline{A D}, \overline{B E}$, and $\overline{C F}$. Prove that the circumcenter of $\triangle A C E$, the circumcenter of $\triangle B D F$, and the orthocenter of $\triangle X Y Z$ are collinear.
|
 Claim - If $A B \cdot D E=B C \cdot E F=C D \cdot F A=k$, then the circumcenters of $A C E$ and $A^{\prime} C^{\prime} E^{\prime}$ coincide.  Claim - Triangle $X Y Z$ is the vector average of the (congruent) medial triangles of triangles $A^{\prime} C^{\prime} E^{\prime}$ and $B^{\prime} D^{\prime} F^{\prime}$. $$ \begin{aligned} \frac{\vec{M}+\vec{N}}{2} & =\frac{\frac{\vec{C}^{\prime}+\vec{E}^{\prime}}{2}+\frac{\vec{B}^{\prime}+\vec{F}^{\prime}}{2}}{2} \\ & =\frac{\overrightarrow{C^{\prime}}+\vec{E}^{\prime}+\vec{B}^{\prime}+\vec{F}^{\prime}}{4} \\ & =\frac{(\vec{A}+\vec{E}-\vec{F})+(\vec{C}+\vec{A}-\vec{B})+(\vec{D}+\vec{F}-\vec{E})+(\vec{B}+\vec{D}-\vec{C})}{4} \\ & =\frac{\vec{A}+\vec{D}}{2}=\vec{X} . \end{aligned} $$ Hence the orthocenter of $X Y Z$ is the midpoint of the orthocenters of the medial triangles of $A^{\prime} C^{\prime} E^{\prime}$ and $B^{\prime} D^{\prime} F^{\prime}$ - that is, their circumcenters.  Claim - In trapezoid $A B D E$, the perpendicular bisector of $\overline{X Y}$ is the same as the perpendicular bisector of the midline $\overline{W N}$. Claim - The points $V, W, M, N$ are cyclic. $$ W Y \cdot Y N=\frac{1}{2} D E \cdot \frac{1}{2} A B=\frac{1}{2} E F \cdot \frac{1}{2} B C=V Y \cdot Y M $$ Applying all the cyclic variations of the above two claims, it follows that all six points $U, V, W, M, N, P$ are concyclic, and the center of that circle coincides with the circumcenter of $\triangle X Y Z$. Remark. It is also possible to implement ideas from the first solution here, by showing all six midpoints have equal power to $(X Y Z)$. Claim - The orthocenter of $X Y Z$ is the midpoint of the circumcenters of $\triangle A C E$ and $\triangle B D F$. $$ \begin{aligned} \operatorname{orthocenter}(X Y Z) & =x+y+z=\frac{a+b+c+d+e+f}{2} \\ \operatorname{circumcenter}(A C E) & =\operatorname{orthocenter}(M N P) \end{aligned} $$ $$ =m+n+p=\frac{c+e}{2}+\frac{e+a}{2}+\frac{a+c}{2}=a+c+e $$ circumcenter $(B D F)=$ orthocenter $(U V W)$ $$ =u+v+w=\frac{d+f}{2}+\frac{f+b}{2}+\frac{b+d}{2}=b+d+f $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon satisfying $\overline{A B}\|\overline{D E}, \overline{B C}\| \overline{E F}, \overline{C D} \| \overline{F A}$, and $$ A B \cdot D E=B C \cdot E F=C D \cdot F A $$ Let $X, Y$, and $Z$ be the midpoints of $\overline{A D}, \overline{B E}$, and $\overline{C F}$. Prove that the circumcenter of $\triangle A C E$, the circumcenter of $\triangle B D F$, and the orthocenter of $\triangle X Y Z$ are collinear.
|
 Claim - If $A B \cdot D E=B C \cdot E F=C D \cdot F A=k$, then the circumcenters of $A C E$ and $A^{\prime} C^{\prime} E^{\prime}$ coincide.  Claim - Triangle $X Y Z$ is the vector average of the (congruent) medial triangles of triangles $A^{\prime} C^{\prime} E^{\prime}$ and $B^{\prime} D^{\prime} F^{\prime}$. $$ \begin{aligned} \frac{\vec{M}+\vec{N}}{2} & =\frac{\frac{\vec{C}^{\prime}+\vec{E}^{\prime}}{2}+\frac{\vec{B}^{\prime}+\vec{F}^{\prime}}{2}}{2} \\ & =\frac{\overrightarrow{C^{\prime}}+\vec{E}^{\prime}+\vec{B}^{\prime}+\vec{F}^{\prime}}{4} \\ & =\frac{(\vec{A}+\vec{E}-\vec{F})+(\vec{C}+\vec{A}-\vec{B})+(\vec{D}+\vec{F}-\vec{E})+(\vec{B}+\vec{D}-\vec{C})}{4} \\ & =\frac{\vec{A}+\vec{D}}{2}=\vec{X} . \end{aligned} $$ Hence the orthocenter of $X Y Z$ is the midpoint of the orthocenters of the medial triangles of $A^{\prime} C^{\prime} E^{\prime}$ and $B^{\prime} D^{\prime} F^{\prime}$ - that is, their circumcenters.  Claim - In trapezoid $A B D E$, the perpendicular bisector of $\overline{X Y}$ is the same as the perpendicular bisector of the midline $\overline{W N}$. Claim - The points $V, W, M, N$ are cyclic. $$ W Y \cdot Y N=\frac{1}{2} D E \cdot \frac{1}{2} A B=\frac{1}{2} E F \cdot \frac{1}{2} B C=V Y \cdot Y M $$ Applying all the cyclic variations of the above two claims, it follows that all six points $U, V, W, M, N, P$ are concyclic, and the center of that circle coincides with the circumcenter of $\triangle X Y Z$. Remark. It is also possible to implement ideas from the first solution here, by showing all six midpoints have equal power to $(X Y Z)$. Claim - The orthocenter of $X Y Z$ is the midpoint of the circumcenters of $\triangle A C E$ and $\triangle B D F$. $$ \begin{aligned} \operatorname{orthocenter}(X Y Z) & =x+y+z=\frac{a+b+c+d+e+f}{2} \\ \operatorname{circumcenter}(A C E) & =\operatorname{orthocenter}(M N P) \end{aligned} $$ $$ =m+n+p=\frac{c+e}{2}+\frac{e+a}{2}+\frac{a+c}{2}=a+c+e $$ circumcenter $(B D F)=$ orthocenter $(U V W)$ $$ =u+v+w=\frac{d+f}{2}+\frac{f+b}{2}+\frac{b+d}{2}=b+d+f $$
|
{
"resource_path": "USAMO/segmented/en-USAMO-2021-notes.jsonl",
"problem_match": null,
"solution_match": null
}
|
ce9d139d-ac3c-5663-b821-1b78b29d8850
| 605,880
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.