problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
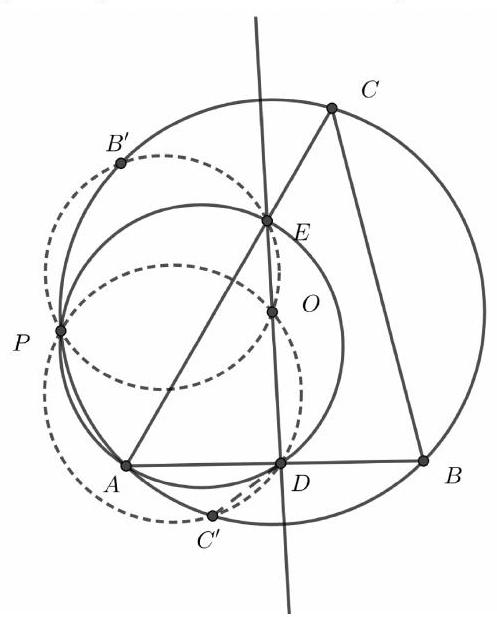
Let $A B C$ be an acute-angled triangle with circumscribed circle $k$ and centre of the circumscribed circle $O$. A line through $O$ intersects the sides $A B$ and $A C$ at $D$ and $E$. Denote by $B^{\prime}$ and $C^{\prime}$ the reflections of $B$ and $C$ over $O$, respectively. Prove that the circumscribed circles of $O D C^{\prime}$ and $O E B^{\prime}$ concur on $k$.
|
Let $P$ be the intersection of the circles $k$ and the circumscribed circle of triangle $A D E^{1}$. Let $C_{1}$ be the second intersection of the circumscribed circle of $\triangle D O P$ with $k$. We will prove that $C_{1}=C^{\prime}$, i.e. the reflection of $C$ over $O$. We know that $\left|O C_{1}\right|=|O P|$, and hence $\measuredangle C_{1} P O=\measuredangle O C_{1} P$, furthermore $\measuredangle O C_{1} P=\measuredangle O D P=$ $\measuredangle E D P$, since the quadrilateral $C_{1} P O D$ by assumption is inscribed and the points $O, D$ and $E$ are collinear. Now, since $P$ is the centre of spiral similarity sending $D E$ to $B C$ the triangles $P D E$ and $P B C$ are similar, and we have $\measuredangle E D P=\measuredangle C B P$, and finally, from the inscribed angle theorem we have
$$
\measuredangle O P C=90^{\circ}-\frac{\measuredangle C O P}{2}=90^{\circ}-\measuredangle C B P=90^{\circ}-\measuredangle C_{1} P O
$$
The conclusion follows, since $90^{\circ}=\measuredangle C_{1} P O+\measuredangle O P C$, and since $C_{1}$ is by assumption on $k$, it must be the antipodal point of $C$ with respect to $k$.
[^0]
[^0]: ${ }^{1}$ That is, the Miquel point of quadrilateral BCED.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with circumscribed circle $k$ and centre of the circumscribed circle $O$. A line through $O$ intersects the sides $A B$ and $A C$ at $D$ and $E$. Denote by $B^{\prime}$ and $C^{\prime}$ the reflections of $B$ and $C$ over $O$, respectively. Prove that the circumscribed circles of $O D C^{\prime}$ and $O E B^{\prime}$ concur on $k$.
|
Let $P$ be the intersection of the circles $k$ and the circumscribed circle of triangle $A D E^{1}$. Let $C_{1}$ be the second intersection of the circumscribed circle of $\triangle D O P$ with $k$. We will prove that $C_{1}=C^{\prime}$, i.e. the reflection of $C$ over $O$. We know that $\left|O C_{1}\right|=|O P|$, and hence $\measuredangle C_{1} P O=\measuredangle O C_{1} P$, furthermore $\measuredangle O C_{1} P=\measuredangle O D P=$ $\measuredangle E D P$, since the quadrilateral $C_{1} P O D$ by assumption is inscribed and the points $O, D$ and $E$ are collinear. Now, since $P$ is the centre of spiral similarity sending $D E$ to $B C$ the triangles $P D E$ and $P B C$ are similar, and we have $\measuredangle E D P=\measuredangle C B P$, and finally, from the inscribed angle theorem we have
$$
\measuredangle O P C=90^{\circ}-\frac{\measuredangle C O P}{2}=90^{\circ}-\measuredangle C B P=90^{\circ}-\measuredangle C_{1} P O
$$
The conclusion follows, since $90^{\circ}=\measuredangle C_{1} P O+\measuredangle O P C$, and since $C_{1}$ is by assumption on $k$, it must be the antipodal point of $C$ with respect to $k$.
[^0]
[^0]: ${ }^{1}$ That is, the Miquel point of quadrilateral BCED.
|
{
"resource_path": "Nordic_MO/segmented/en-2022-sol.jsonl",
"problem_match": "\n## Problem 4",
"solution_match": "\n\nSolution."
}
|
3e45c64c-ae64-5eb4-a0ed-7d0ae83a4595
| 608,043
|
Let $\mathcal{Q}_{1}$ be a quadrilateral such that the midpoints of its sides lie on a circle. Prove that there exists a cyclic quadrilateral $\mathcal{Q}_{2}$ with the same sidelengths as $\mathcal{Q}_{1}$, such that two of the angles in $\mathcal{Q}_{2}$ are equal.
|
Let $A, B, C$ and $D$ be the vertices of $\mathcal{Q}_{1}$, and $K, L, M$ and $N$ be the midpoints of the sides $A B, B C, C D$ and $D A$, respectively.
We have $K L\|A C\| M N$ and $L M\|B D\| N K$, and thus $K L M N$ is a parallelogram. From the problem condition it is known that $K L M N$ is cyclic, and thus, from the inscribed angle theorem, $K L M N$ must be a rectangle. Hence, $A C \perp B D$. Now, let $P$ denote the intersections of the diagonals of $A B C D$.
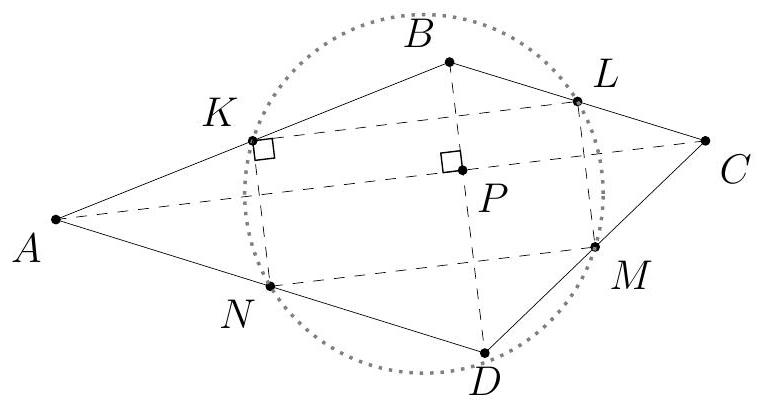
Applying Pythagoras' theorem repeatedly therefore yields
$$
|A B|^{2}+|C D|^{2}=|A P|^{2}+|B P|^{2}+|C P|^{2}+|D P|^{2}=|A D|^{2}+|B C|^{2} .
$$
Thus, we can construct the quadrilateral $\mathcal{Q}_{2}$ with a segment $A^{\prime} C^{\prime}$ satisfying $\left|A^{\prime} C^{\prime}\right|^{2}=|A B|^{2}+$ $|C D|^{2}$, and then place $B^{\prime}, D^{\prime}$ on the circle with diameter $A^{\prime} C^{\prime}$ on opposite sides of $A^{\prime} C^{\prime}$ such that $\left|A^{\prime} B^{\prime}\right|=|A B|$ and $\left|A^{\prime} D^{\prime}\right|=|A D|$.
From the previous computation, we then obtain $\left|C^{\prime} B^{\prime}\right|=|C D|$ and $\left|C^{\prime} D^{\prime}\right|=|B C|$. Hence, $\mathcal{Q}_{2}$ and $\mathcal{Q}_{1}$ has the same set of sidelengths. Finally, $A^{\prime} B^{\prime} \perp B^{\prime} C^{\prime}$ and $A^{\prime} D^{\prime} \perp D^{\prime} C^{\prime}$, so $\mathcal{Q}_{2}$ has two identical right angels.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathcal{Q}_{1}$ be a quadrilateral such that the midpoints of its sides lie on a circle. Prove that there exists a cyclic quadrilateral $\mathcal{Q}_{2}$ with the same sidelengths as $\mathcal{Q}_{1}$, such that two of the angles in $\mathcal{Q}_{2}$ are equal.
|
Let $A, B, C$ and $D$ be the vertices of $\mathcal{Q}_{1}$, and $K, L, M$ and $N$ be the midpoints of the sides $A B, B C, C D$ and $D A$, respectively.
We have $K L\|A C\| M N$ and $L M\|B D\| N K$, and thus $K L M N$ is a parallelogram. From the problem condition it is known that $K L M N$ is cyclic, and thus, from the inscribed angle theorem, $K L M N$ must be a rectangle. Hence, $A C \perp B D$. Now, let $P$ denote the intersections of the diagonals of $A B C D$.

Applying Pythagoras' theorem repeatedly therefore yields
$$
|A B|^{2}+|C D|^{2}=|A P|^{2}+|B P|^{2}+|C P|^{2}+|D P|^{2}=|A D|^{2}+|B C|^{2} .
$$
Thus, we can construct the quadrilateral $\mathcal{Q}_{2}$ with a segment $A^{\prime} C^{\prime}$ satisfying $\left|A^{\prime} C^{\prime}\right|^{2}=|A B|^{2}+$ $|C D|^{2}$, and then place $B^{\prime}, D^{\prime}$ on the circle with diameter $A^{\prime} C^{\prime}$ on opposite sides of $A^{\prime} C^{\prime}$ such that $\left|A^{\prime} B^{\prime}\right|=|A B|$ and $\left|A^{\prime} D^{\prime}\right|=|A D|$.
From the previous computation, we then obtain $\left|C^{\prime} B^{\prime}\right|=|C D|$ and $\left|C^{\prime} D^{\prime}\right|=|B C|$. Hence, $\mathcal{Q}_{2}$ and $\mathcal{Q}_{1}$ has the same set of sidelengths. Finally, $A^{\prime} B^{\prime} \perp B^{\prime} C^{\prime}$ and $A^{\prime} D^{\prime} \perp D^{\prime} C^{\prime}$, so $\mathcal{Q}_{2}$ has two identical right angels.
|
{
"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl",
"problem_match": "\n## Problem 2",
"solution_match": "\n## Solution"
}
|
748925cc-76e4-543b-9612-ebb14a40dda6
| 608,045
|
Alice and Bob are playing a game. First, Alice chooses a partition $\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\mathcal{C}$. Then Bob does the following operation a finite number of times.
Choose a set $S \in \mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \backslash S$ (possibly the empty set) to $\mathcal{C}$.
Bob wins if there are two equal sets in $\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.
Answer: Alice has a winning strategy.
|
We will use the following notation. If $S \subseteq \mathbb{Z}^{+}$is a subset of the positive integers and $D$ is defined as in the problem statement, define $d(S)=D \backslash S$. In addition, the $d$-sequence of $S$, written $\left\{d^{S}\right\}_{n \in \mathbb{Z}^{+}}$, is defined recursively as $d_{0}^{S}=S$, and $d_{n+1}^{S}=d\left(d_{n}^{S}\right)$ for each $n \in \mathbb{Z}^{+}$.
Let $p_{1}, p_{2}, \ldots$ be an enumeration of all the prime numbers. Alice chooses the sets
$$
A=\left\{p_{m}^{n} \mid n \equiv m \quad \bmod 3,0<n \leq m\right\}, \quad B=\left\{p_{m}^{n} \mid n \equiv m-1 \quad \bmod 3,0<n \leq m-1\right\}
$$
and
$$
C=\mathbb{Z}^{+} \backslash(A \cup B)
$$
It is clear that each positive integer belongs to exactly on of the sets $A, B$ or $C$. By induction we readily get that
$$
d^{k}(A)=\left\{\begin{array}{ll}
\left\{p_{m}^{n} \mid n \equiv m\right. & \bmod 3, n \leq m-3 k / 2\} \\
\left\{p_{m}^{n} \mid n \not \equiv m\right. & \bmod 3, n \leq m-1-3(k-1) / 2\}
\end{array} \quad \text { if } k \text { is even and } k \neq 0\right.
$$
and
$$
d^{k}(B)=\left\{\begin{array}{lll}
\left\{p_{m}^{n} \mid n \equiv m-1\right. & \bmod 3, n \leq m-1-3 k / 2\} & \text { if } k \text { is even and } k \neq 0 \\
\left\{p_{m}^{n} \mid n \not \equiv m-1\right. & \bmod 3, n \leq m-2-3(k-1) / 2\} & \text { if } k \text { is odd. }
\end{array}\right.
$$
If $m \in \mathbb{Z}^{+}$then $6 m$ is definitely in $C$ as $6 m$ is not a power of a prime. This means that all positive integers divide at least one number in $C$. It follows that
$$
d(C)=\mathbb{Z}^{+} \backslash C=\mathbb{Z}^{+} \backslash\left(\mathbb{Z}^{+} \backslash(A \cup B)\right)=A \cup B=\left\{p_{m}^{n} \mid n \not \equiv m-2 \bmod 3,0<n \leq m\right\}
$$
By induction it follows that
From this it is clear that all of the sets $d^{k}(M)$ are all distinct. Hence Bob can never create the same set in two different ways.
Remark. In fact Alice has to partition the positive integers in at least three parts if she wishes to beat Bob. It is clear that selecting a singe set, namely $\mathbb{Z}^{+}$will not do as $d\left(\mathbb{Z}^{+}\right)=\emptyset$ and $d(\emptyset)=\emptyset$. Next assume Alice has partitioned the positive integers in two sets $A$ and $B$. It can be assumed that $d(A) \neq B$ and $d(B) \neq A$ as Bob would win either case. As $d(A)$ is disjoint from $A$ and $B$ is the complement of $A$ this means that $d(A)$ is a strict subset of $B$. Hence there is some $b$ in $B$ that does not belong to $d(A)$. The implication is that $b$ does not divide any number in $A$. Similarly there exists a number $a$ in $A$ that does not divide any number in $B$. Their product $a b$ belongs to either of the sets $A$ or $B$ and is divisible by both $a$ and $b$. This contradicts the existence of said numbers, $a$ and $b$. In fact we have proven for any subset $A$ of $\mathbb{Z}^{+}$that $d(A)=\mathbb{Z}^{+} \backslash A$ or $d\left(\mathbb{Z}^{+} \backslash A\right)=A$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob are playing a game. First, Alice chooses a partition $\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\mathcal{C}$. Then Bob does the following operation a finite number of times.
Choose a set $S \in \mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \backslash S$ (possibly the empty set) to $\mathcal{C}$.
Bob wins if there are two equal sets in $\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.
Answer: Alice has a winning strategy.
|
We will use the following notation. If $S \subseteq \mathbb{Z}^{+}$is a subset of the positive integers and $D$ is defined as in the problem statement, define $d(S)=D \backslash S$. In addition, the $d$-sequence of $S$, written $\left\{d^{S}\right\}_{n \in \mathbb{Z}^{+}}$, is defined recursively as $d_{0}^{S}=S$, and $d_{n+1}^{S}=d\left(d_{n}^{S}\right)$ for each $n \in \mathbb{Z}^{+}$.
Let $p_{1}, p_{2}, \ldots$ be an enumeration of all the prime numbers. Alice chooses the sets
$$
A=\left\{p_{m}^{n} \mid n \equiv m \quad \bmod 3,0<n \leq m\right\}, \quad B=\left\{p_{m}^{n} \mid n \equiv m-1 \quad \bmod 3,0<n \leq m-1\right\}
$$
and
$$
C=\mathbb{Z}^{+} \backslash(A \cup B)
$$
It is clear that each positive integer belongs to exactly on of the sets $A, B$ or $C$. By induction we readily get that
$$
d^{k}(A)=\left\{\begin{array}{ll}
\left\{p_{m}^{n} \mid n \equiv m\right. & \bmod 3, n \leq m-3 k / 2\} \\
\left\{p_{m}^{n} \mid n \not \equiv m\right. & \bmod 3, n \leq m-1-3(k-1) / 2\}
\end{array} \quad \text { if } k \text { is even and } k \neq 0\right.
$$
and
$$
d^{k}(B)=\left\{\begin{array}{lll}
\left\{p_{m}^{n} \mid n \equiv m-1\right. & \bmod 3, n \leq m-1-3 k / 2\} & \text { if } k \text { is even and } k \neq 0 \\
\left\{p_{m}^{n} \mid n \not \equiv m-1\right. & \bmod 3, n \leq m-2-3(k-1) / 2\} & \text { if } k \text { is odd. }
\end{array}\right.
$$
If $m \in \mathbb{Z}^{+}$then $6 m$ is definitely in $C$ as $6 m$ is not a power of a prime. This means that all positive integers divide at least one number in $C$. It follows that
$$
d(C)=\mathbb{Z}^{+} \backslash C=\mathbb{Z}^{+} \backslash\left(\mathbb{Z}^{+} \backslash(A \cup B)\right)=A \cup B=\left\{p_{m}^{n} \mid n \not \equiv m-2 \bmod 3,0<n \leq m\right\}
$$
By induction it follows that
From this it is clear that all of the sets $d^{k}(M)$ are all distinct. Hence Bob can never create the same set in two different ways.
Remark. In fact Alice has to partition the positive integers in at least three parts if she wishes to beat Bob. It is clear that selecting a singe set, namely $\mathbb{Z}^{+}$will not do as $d\left(\mathbb{Z}^{+}\right)=\emptyset$ and $d(\emptyset)=\emptyset$. Next assume Alice has partitioned the positive integers in two sets $A$ and $B$. It can be assumed that $d(A) \neq B$ and $d(B) \neq A$ as Bob would win either case. As $d(A)$ is disjoint from $A$ and $B$ is the complement of $A$ this means that $d(A)$ is a strict subset of $B$. Hence there is some $b$ in $B$ that does not belong to $d(A)$. The implication is that $b$ does not divide any number in $A$. Similarly there exists a number $a$ in $A$ that does not divide any number in $B$. Their product $a b$ belongs to either of the sets $A$ or $B$ and is divisible by both $a$ and $b$. This contradicts the existence of said numbers, $a$ and $b$. In fact we have proven for any subset $A$ of $\mathbb{Z}^{+}$that $d(A)=\mathbb{Z}^{+} \backslash A$ or $d\left(\mathbb{Z}^{+} \backslash A\right)=A$.
|
{
"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl",
"problem_match": "\n## Problem 4",
"solution_match": "\n## Solution 1"
}
|
df47acd0-649b-5a42-909f-18ef1a7a6408
| 608,047
|
Alice and Bob are playing a game. First, Alice chooses a partition $\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\mathcal{C}$. Then Bob does the following operation a finite number of times.
Choose a set $S \in \mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \backslash S$ (possibly the empty set) to $\mathcal{C}$.
Bob wins if there are two equal sets in $\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.
Answer: Alice has a winning strategy.
|
Use the same notation as in solution 1 . We wish to construct a partition $\bigcup_{i \in \mathbb{Z}^{+}} A_{i}$ of the positive integers, such that no two sets among all sets in $\left\{d^{A_{1}}\right\}_{n \in \mathbb{Z}^{+}},\left\{d^{A_{2}}\right\}_{n \in \mathbb{Z}^{+}}, \ldots$ are equal.
To begin with, consider a partition $\bigcup_{i \in \mathbb{Z}^{+}} P_{i}$ of the primes, such that each $P_{i}=\left\{p_{i 1}, p_{i 2}, \ldots\right\}$ is infinite. We may assume each set is infinite since the set of primes and $\mathbb{Z}^{+} \times \mathbb{Z}^{+}$both are countable, so there exists a bijection between them. Define the sets
$$
Q_{i}=\left\{p_{i 1}, p_{i 2}^{2}, p_{i 3}, p_{i 3}^{3}, p_{i 4}^{2}, p_{i 4}^{4}, p_{i 5}, p_{i 5}^{3}, p_{i 5}^{5}, \ldots\right\}
$$
consisting of $p_{i j}^{j}, p_{i j}^{j-2}, \ldots, p_{i j}^{(1,2)}$ for each $p_{i j} \in P_{i}$. By the exponent $(1,2)$ we indicate that the last power is 1 when $j$ is odd and 2 when it is even.
We will include the remaining integers $\left\{r_{1}, r_{2}, \ldots\right\}=\mathbb{Z}^{+} \backslash\left(\bigcup_{i \in \mathbb{Z}^{+}} Q_{i}\right)$ to the partition as follows. First, add $r_{1}$ to some set $Q_{i_{1}}$, such that $\operatorname{gcd}\left(r_{1}, q\right)=1$ for each $q \in Q_{i_{1}}$. Then, for each $k \in \mathbb{Z}^{+}$, add $r_{k+1}$ to a set $Q_{i_{k+1}}$ where $i_{k+1}>i_{k}$, such that $\operatorname{gcd}\left(r_{k+1}, q\right)=1$ for each $q \in Q_{i_{k+1}}$. Note that such an $i_{k+1}$ always exists, since there always is an infinite amount of prime divisors among $Q_{i_{k}+1}, Q_{i_{k}+2}, \ldots$, and $r_{k+1}$ only has a finite amount of prime divisors.
The collection of $Q_{i}$ now forms a partition of $\mathbb{Z}^{+}$. What remains is to show that it satisfies Alice's winning condition.
We first see that we may ignore all the $r_{k}$. By definition, no divisor of $r_{k}$ coincides with any divisor of $Q_{i_{k}}$, and their contributions in the $d$-sequence will therefore be completely disjoint. As $d\left(d\left(\left\{r_{k}\right\}\right)\right)=\emptyset$, the $d$-sequence will show no trace of the $r_{k}$ after the second element. Hence, we will work with the original $Q_{i}$.
We observe that $d\left(Q_{i}\right)=\left\{1, p_{i 2}, p_{i 3}^{2}, p_{i 4}, p_{i 4}^{3}, p_{i 5}^{2}, p_{i 5}^{4}, p_{i 6}, p_{i 6}^{3}, p_{i 6}^{5}, \ldots\right\}$. This is simply $Q_{i}$ with the indices shifted by 1 and with an added 1 . As this set essentially is on the same form as $Q_{i}$, we see that $\left\{d^{Q_{i}}\right\}_{n}$ consists of every possible shift in indices of the first set $Q_{i}$ (except the element 1 appearing in every other set). It is therefore obvious that the sets in the sequence are pairwise distinct. Additionally, the set of primes dividing some element in some set of $\left\{d^{Q_{i}}\right\}_{n}$ is $P_{i}$. Since the $P_{i}$ partition the primes, it is clear that all the sets in all the $d$-sequences of the $Q_{i}$ are distinct, which is what we wanted.
Remark. The main idea of the problem is to construct a single set $S$, such that the sets in the $d$-sequence of $S$ are pairwise distinct. Any set with similar properties to the $Q_{i}$ should give a valid initial collection $\mathcal{C}$ such that Alice wins.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob are playing a game. First, Alice chooses a partition $\mathcal{C}$ of the positive integers into a (not necessarily finite) set of sets, such that each positive integer is in exactly one of the sets in $\mathcal{C}$. Then Bob does the following operation a finite number of times.
Choose a set $S \in \mathcal{C}$ not previously chosen, and let $D$ be the set of all positive integers dividing at least one element in $S$. Then add the set $D \backslash S$ (possibly the empty set) to $\mathcal{C}$.
Bob wins if there are two equal sets in $\mathcal{C}$ after he has done all his moves, otherwise, Alice wins. Determine which player has a winning strategy.
Answer: Alice has a winning strategy.
|
Use the same notation as in solution 1 . We wish to construct a partition $\bigcup_{i \in \mathbb{Z}^{+}} A_{i}$ of the positive integers, such that no two sets among all sets in $\left\{d^{A_{1}}\right\}_{n \in \mathbb{Z}^{+}},\left\{d^{A_{2}}\right\}_{n \in \mathbb{Z}^{+}}, \ldots$ are equal.
To begin with, consider a partition $\bigcup_{i \in \mathbb{Z}^{+}} P_{i}$ of the primes, such that each $P_{i}=\left\{p_{i 1}, p_{i 2}, \ldots\right\}$ is infinite. We may assume each set is infinite since the set of primes and $\mathbb{Z}^{+} \times \mathbb{Z}^{+}$both are countable, so there exists a bijection between them. Define the sets
$$
Q_{i}=\left\{p_{i 1}, p_{i 2}^{2}, p_{i 3}, p_{i 3}^{3}, p_{i 4}^{2}, p_{i 4}^{4}, p_{i 5}, p_{i 5}^{3}, p_{i 5}^{5}, \ldots\right\}
$$
consisting of $p_{i j}^{j}, p_{i j}^{j-2}, \ldots, p_{i j}^{(1,2)}$ for each $p_{i j} \in P_{i}$. By the exponent $(1,2)$ we indicate that the last power is 1 when $j$ is odd and 2 when it is even.
We will include the remaining integers $\left\{r_{1}, r_{2}, \ldots\right\}=\mathbb{Z}^{+} \backslash\left(\bigcup_{i \in \mathbb{Z}^{+}} Q_{i}\right)$ to the partition as follows. First, add $r_{1}$ to some set $Q_{i_{1}}$, such that $\operatorname{gcd}\left(r_{1}, q\right)=1$ for each $q \in Q_{i_{1}}$. Then, for each $k \in \mathbb{Z}^{+}$, add $r_{k+1}$ to a set $Q_{i_{k+1}}$ where $i_{k+1}>i_{k}$, such that $\operatorname{gcd}\left(r_{k+1}, q\right)=1$ for each $q \in Q_{i_{k+1}}$. Note that such an $i_{k+1}$ always exists, since there always is an infinite amount of prime divisors among $Q_{i_{k}+1}, Q_{i_{k}+2}, \ldots$, and $r_{k+1}$ only has a finite amount of prime divisors.
The collection of $Q_{i}$ now forms a partition of $\mathbb{Z}^{+}$. What remains is to show that it satisfies Alice's winning condition.
We first see that we may ignore all the $r_{k}$. By definition, no divisor of $r_{k}$ coincides with any divisor of $Q_{i_{k}}$, and their contributions in the $d$-sequence will therefore be completely disjoint. As $d\left(d\left(\left\{r_{k}\right\}\right)\right)=\emptyset$, the $d$-sequence will show no trace of the $r_{k}$ after the second element. Hence, we will work with the original $Q_{i}$.
We observe that $d\left(Q_{i}\right)=\left\{1, p_{i 2}, p_{i 3}^{2}, p_{i 4}, p_{i 4}^{3}, p_{i 5}^{2}, p_{i 5}^{4}, p_{i 6}, p_{i 6}^{3}, p_{i 6}^{5}, \ldots\right\}$. This is simply $Q_{i}$ with the indices shifted by 1 and with an added 1 . As this set essentially is on the same form as $Q_{i}$, we see that $\left\{d^{Q_{i}}\right\}_{n}$ consists of every possible shift in indices of the first set $Q_{i}$ (except the element 1 appearing in every other set). It is therefore obvious that the sets in the sequence are pairwise distinct. Additionally, the set of primes dividing some element in some set of $\left\{d^{Q_{i}}\right\}_{n}$ is $P_{i}$. Since the $P_{i}$ partition the primes, it is clear that all the sets in all the $d$-sequences of the $Q_{i}$ are distinct, which is what we wanted.
Remark. The main idea of the problem is to construct a single set $S$, such that the sets in the $d$-sequence of $S$ are pairwise distinct. Any set with similar properties to the $Q_{i}$ should give a valid initial collection $\mathcal{C}$ such that Alice wins.
|
{
"resource_path": "Nordic_MO/segmented/en-2024-sol.jsonl",
"problem_match": "\n## Problem 4",
"solution_match": "\n## Solution 2"
}
|
df47acd0-649b-5a42-909f-18ef1a7a6408
| 608,047
|
Prove that there exist two functions
$$
f, g: \mathbb{R} \rightarrow \mathbb{R}
$$
such that $f \circ g$ is strictly decreasing, while $g \circ f$ is strictly increasing.
(Poland) Andrzej KomisArsKi \& Marcin Kuczma
#
|
Let
$$
\begin{aligned}
& \cdot A=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k+1},-2^{2 k}\right) \bigcup\left(2^{2 k}, 2^{2 k+1}\right]\right) \\
& \cdot B=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k},-2^{2 k-1}\right) \bigcup\left(2^{2 k-1}, 2^{2 k}\right]\right)
\end{aligned}
$$
Thus $A=2 B, B=2 A, A=-A, B=-B, A \cap B=\varnothing$, and finally $A \cup B \cup\{0\}=\mathbb{R}$. Let us take
$$
f(x)=\left\{\begin{array}{lll}
x & \text { for } & x \in A \\
-x & \text { for } & x \in B \\
0 & \text { for } & x=0
\end{array}\right.
$$
Take $g(x)=2 f(x)$. Thus $f(g(x))=f(2 f(x))=-2 x$ and $g(f(x))=2 f(f(x))=2 x$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that there exist two functions
$$
f, g: \mathbb{R} \rightarrow \mathbb{R}
$$
such that $f \circ g$ is strictly decreasing, while $g \circ f$ is strictly increasing.
(Poland) Andrzej KomisArsKi \& Marcin Kuczma
#
|
Let
$$
\begin{aligned}
& \cdot A=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k+1},-2^{2 k}\right) \bigcup\left(2^{2 k}, 2^{2 k+1}\right]\right) \\
& \cdot B=\bigcup_{k \in \mathbb{Z}}\left(\left[-2^{2 k},-2^{2 k-1}\right) \bigcup\left(2^{2 k-1}, 2^{2 k}\right]\right)
\end{aligned}
$$
Thus $A=2 B, B=2 A, A=-A, B=-B, A \cap B=\varnothing$, and finally $A \cup B \cup\{0\}=\mathbb{R}$. Let us take
$$
f(x)=\left\{\begin{array}{lll}
x & \text { for } & x \in A \\
-x & \text { for } & x \in B \\
0 & \text { for } & x=0
\end{array}\right.
$$
Take $g(x)=2 f(x)$. Thus $f(g(x))=f(2 f(x))=-2 x$ and $g(f(x))=2 f(f(x))=2 x$.
|
{
"resource_path": "RMM/segmented/en-2011-Sols2011D1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "# Solution."
}
|
8c2a5632-87ed-5d2f-9d4b-b1d864525dca
| 605,380
|
Given a positive integer $n=\prod_{i=1}^{s} p_{i}^{\alpha_{i}}$, we write $\Omega(n)$ for the total number $\sum_{i=1}^{s} \alpha_{i}$ of prime factors of $n$, counted with multiplicity. Let $\lambda(n)=(-1)^{\Omega(n)}$ (so, for example, $\left.\lambda(12)=\lambda\left(2^{2} \cdot 3^{1}\right)=(-1)^{2+1}=-1\right)$.
Prove the following two claims:
i) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=+1 ;$
ii) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=-1$.
(ROMANIA) DAN SchwARZ
|
Notice that we have $\Omega(m n)=\Omega(m)+\Omega(n)$ for all positive integers $m, n$ ( $\Omega$ is a completely additive arithmetic function), translating into $\lambda(m n)=\lambda(m) \cdot \lambda(n)$ (so $\lambda$ is a completely multiplicative arithmetic function), hence $\lambda(p)=-1$ for any prime $p$, and $\lambda\left(k^{2}\right)=\lambda(k)^{2}=+1$ for all positive integers $k$.[1]
The start (first 100 terms) of the sequence $\mathfrak{S}=(\lambda(n))_{n \geq 1}$ is
$+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,-1,-1,-1,+1,+1,+1,-1,-1,-1,-1$,
$+1,+1,-1,+1,+1,+1,-1,-1,-1,-1,-1,-1,+1,+1,+1,+1,-1,+1,+1,+1$,
$-1,-1,-1,-1,-1,+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,+1,+1,+1,-1,+1$,
$-1,+1,-1,+1,+1,-1,-1,-1,+1,-1,-1,-1,-1,+1,-1,-1,+1,-1,-1,-1$,
$+1,+1,-1,+1,+1,+1,+1,+1,-1,+1,+1,-1,+1,+1,+1,+1,-1,-1,-1,+1$.
i) The Pell equation $x^{2}-6 y^{2}=1$ has infinitely many solutions in positive integers; all solutions are given by $\left(x_{n}, y_{n}\right)$, where $x_{n}+y_{n} \sqrt{6}=(5+2 \sqrt{6})^{n}$. Since $\lambda\left(6 y^{2}\right)=1$ and also $\lambda\left(6 y^{2}+1\right)=\lambda\left(x^{2}\right)=1$, the thesis is proven.
Alternative Solution. Take any existing pair with $\lambda(n)=$ $\lambda(n+1)=1$. Then $\lambda\left((2 n+1)^{2}-1\right)=\lambda\left(4 n^{2}+4 n\right)=\lambda(4) \cdot \lambda(n)$. $\lambda(n+1)=1$, and also $\lambda\left((2 n+1)^{2}\right)=\lambda(2 n+1)^{2}=1$, so we have built a larger $(1,1)$ pair.
ii) The equation $3 x^{2}-2 y^{2}=1$ (again Pell theory) has also infinitely many solutions in positive integers, given by $\left(x_{n}, y_{n}\right)$, where $x_{n} \sqrt{3}+y_{n} \sqrt{2}=(\sqrt{3}+\sqrt{2})^{2 n+1}$. Since $\lambda\left(2 y^{2}\right)=$ -1 and $\lambda\left(2 y^{2}+1\right)=\lambda\left(3 x^{2}\right)=-1$, the thesis is proven.
Alternative Solution. Assume $(\lambda(n-1), \lambda(n))$ is the largest $(-1,-1)$ pair, therefore $\lambda(n+1)=1$ and $\lambda\left(n^{2}+n\right)=\lambda(n)$. $\lambda(n+1)=-1$, therefore again $\lambda\left(n^{2}+n+1\right)=1$. But then $\lambda\left(n^{3}-1\right)=\lambda(n-1) \cdot \lambda\left(n^{2}+n+1\right)=-1$, and also $\lambda\left(n^{3}\right)=$ $\lambda(n)^{3}=-1$, so we found yet a larger such pair than the one we started with, contradiction.
Alternative Solution. Assume the pairs of consecutive terms $(-1,-1)$ in $\mathfrak{S}$ are finitely many. Then from some rank on we only have subsequences ( $1,-1,1,1, \ldots, 1,-1,1$ ). By
"doubling" such a subsequence (like at point ii)), we will produce
$$
(-1, ?, 1, ?,-1, ?,-1, ?, \ldots, ?,-1, ?, 1, ?,-1)
$$
According with our assumption, all ?-terms ought to be 1 , hence the produced subsequence is
$$
(-1,1,1,1,-1,1,-1,1, \ldots, 1,-1,1,1,1,-1)
$$
and so the "separating packets" of l's contain either one or three terms. Now assume some far enough ( $1,1,1,1)$ or $(-1,1,1,-1)$ subsequence of $\mathfrak{S}$ were to exist. Since it lies within some "doubled" subsequence, it contradicts the structure described above, which thus is the only prevalent from some rank on. But then all the positions of the ( -1 )terms will have the same parity. However though, we have $\lambda(p)=\lambda\left(2 p^{2}\right)=-1$ for all odd primes $p$, and these terms have different parity of their positions. A contradiction has been reached.[2]
Alternative Solution for both i) and ii). (I. Bogdanov) Take $\varepsilon \in\{-1,1\}$. There obviously exist infinitely many $n$ such that $\lambda(2 n+1)=\varepsilon$ (just take $2 n+1$ to be the product of an appropriate number of odd primes). Now, if either $\lambda(2 n)=\varepsilon$ or $\lambda(2 n+2)=\varepsilon$, we are done; otherwise $\lambda(n)=-\lambda(2 n)=$ $-\lambda(2 n+2)=\lambda(n+1)=\varepsilon$. Therefore, for such an $n$, one of the three pairs $(n, n+1),(2 n, 2 n+1)$ or $(2 n+1,2 n+2)$ fits the bill.
We have thus proved the existence in $\mathfrak{S}$ of infinitely many occurrences of all possible subsequences of length 1 , viz. $(+1)$ and $(-1)$, and of length 2 , viz. $(+1,-1),(-1,+1)$, $(+1,+1)$ and $(-1,-1) .[3]$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given a positive integer $n=\prod_{i=1}^{s} p_{i}^{\alpha_{i}}$, we write $\Omega(n)$ for the total number $\sum_{i=1}^{s} \alpha_{i}$ of prime factors of $n$, counted with multiplicity. Let $\lambda(n)=(-1)^{\Omega(n)}$ (so, for example, $\left.\lambda(12)=\lambda\left(2^{2} \cdot 3^{1}\right)=(-1)^{2+1}=-1\right)$.
Prove the following two claims:
i) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=+1 ;$
ii) There are infinitely many positive integers $n$ such that $\lambda(n)=\lambda(n+1)=-1$.
(ROMANIA) DAN SchwARZ
|
Notice that we have $\Omega(m n)=\Omega(m)+\Omega(n)$ for all positive integers $m, n$ ( $\Omega$ is a completely additive arithmetic function), translating into $\lambda(m n)=\lambda(m) \cdot \lambda(n)$ (so $\lambda$ is a completely multiplicative arithmetic function), hence $\lambda(p)=-1$ for any prime $p$, and $\lambda\left(k^{2}\right)=\lambda(k)^{2}=+1$ for all positive integers $k$.[1]
The start (first 100 terms) of the sequence $\mathfrak{S}=(\lambda(n))_{n \geq 1}$ is
$+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,-1,-1,-1,+1,+1,+1,-1,-1,-1,-1$,
$+1,+1,-1,+1,+1,+1,-1,-1,-1,-1,-1,-1,+1,+1,+1,+1,-1,+1,+1,+1$,
$-1,-1,-1,-1,-1,+1,-1,-1,+1,-1,+1,-1,-1,+1,+1,+1,+1,+1,-1,+1$,
$-1,+1,-1,+1,+1,-1,-1,-1,+1,-1,-1,-1,-1,+1,-1,-1,+1,-1,-1,-1$,
$+1,+1,-1,+1,+1,+1,+1,+1,-1,+1,+1,-1,+1,+1,+1,+1,-1,-1,-1,+1$.
i) The Pell equation $x^{2}-6 y^{2}=1$ has infinitely many solutions in positive integers; all solutions are given by $\left(x_{n}, y_{n}\right)$, where $x_{n}+y_{n} \sqrt{6}=(5+2 \sqrt{6})^{n}$. Since $\lambda\left(6 y^{2}\right)=1$ and also $\lambda\left(6 y^{2}+1\right)=\lambda\left(x^{2}\right)=1$, the thesis is proven.
Alternative Solution. Take any existing pair with $\lambda(n)=$ $\lambda(n+1)=1$. Then $\lambda\left((2 n+1)^{2}-1\right)=\lambda\left(4 n^{2}+4 n\right)=\lambda(4) \cdot \lambda(n)$. $\lambda(n+1)=1$, and also $\lambda\left((2 n+1)^{2}\right)=\lambda(2 n+1)^{2}=1$, so we have built a larger $(1,1)$ pair.
ii) The equation $3 x^{2}-2 y^{2}=1$ (again Pell theory) has also infinitely many solutions in positive integers, given by $\left(x_{n}, y_{n}\right)$, where $x_{n} \sqrt{3}+y_{n} \sqrt{2}=(\sqrt{3}+\sqrt{2})^{2 n+1}$. Since $\lambda\left(2 y^{2}\right)=$ -1 and $\lambda\left(2 y^{2}+1\right)=\lambda\left(3 x^{2}\right)=-1$, the thesis is proven.
Alternative Solution. Assume $(\lambda(n-1), \lambda(n))$ is the largest $(-1,-1)$ pair, therefore $\lambda(n+1)=1$ and $\lambda\left(n^{2}+n\right)=\lambda(n)$. $\lambda(n+1)=-1$, therefore again $\lambda\left(n^{2}+n+1\right)=1$. But then $\lambda\left(n^{3}-1\right)=\lambda(n-1) \cdot \lambda\left(n^{2}+n+1\right)=-1$, and also $\lambda\left(n^{3}\right)=$ $\lambda(n)^{3}=-1$, so we found yet a larger such pair than the one we started with, contradiction.
Alternative Solution. Assume the pairs of consecutive terms $(-1,-1)$ in $\mathfrak{S}$ are finitely many. Then from some rank on we only have subsequences ( $1,-1,1,1, \ldots, 1,-1,1$ ). By
"doubling" such a subsequence (like at point ii)), we will produce
$$
(-1, ?, 1, ?,-1, ?,-1, ?, \ldots, ?,-1, ?, 1, ?,-1)
$$
According with our assumption, all ?-terms ought to be 1 , hence the produced subsequence is
$$
(-1,1,1,1,-1,1,-1,1, \ldots, 1,-1,1,1,1,-1)
$$
and so the "separating packets" of l's contain either one or three terms. Now assume some far enough ( $1,1,1,1)$ or $(-1,1,1,-1)$ subsequence of $\mathfrak{S}$ were to exist. Since it lies within some "doubled" subsequence, it contradicts the structure described above, which thus is the only prevalent from some rank on. But then all the positions of the ( -1 )terms will have the same parity. However though, we have $\lambda(p)=\lambda\left(2 p^{2}\right)=-1$ for all odd primes $p$, and these terms have different parity of their positions. A contradiction has been reached.[2]
Alternative Solution for both i) and ii). (I. Bogdanov) Take $\varepsilon \in\{-1,1\}$. There obviously exist infinitely many $n$ such that $\lambda(2 n+1)=\varepsilon$ (just take $2 n+1$ to be the product of an appropriate number of odd primes). Now, if either $\lambda(2 n)=\varepsilon$ or $\lambda(2 n+2)=\varepsilon$, we are done; otherwise $\lambda(n)=-\lambda(2 n)=$ $-\lambda(2 n+2)=\lambda(n+1)=\varepsilon$. Therefore, for such an $n$, one of the three pairs $(n, n+1),(2 n, 2 n+1)$ or $(2 n+1,2 n+2)$ fits the bill.
We have thus proved the existence in $\mathfrak{S}$ of infinitely many occurrences of all possible subsequences of length 1 , viz. $(+1)$ and $(-1)$, and of length 2 , viz. $(+1,-1),(-1,+1)$, $(+1,+1)$ and $(-1,-1) .[3]$
|
{
"resource_path": "RMM/segmented/en-2011-Sols2011D2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
43c25241-704d-5082-a71c-427560acd4b6
| 605,416
|
For every $n \geq 3$, determine all the configurations of $n$ distinct points $X_{1}, X_{2}, \ldots, X_{n}$ in the plane, with the property that for any pair of distinct points $X_{i}, X_{j}$ there exists a permutation $\sigma$ of the integers $\{1, \ldots, n\}$, such that $\mathrm{d}\left(X_{i}, X_{k}\right)=\mathrm{d}\left(X_{j}, X_{\sigma(k)}\right)$ for all $1 \leq k \leq n$.
(We write $\mathrm{d}(X, Y)$ to denote the distance between points $X$ and $Y$.)
(United Kingdom) LuKe BetTs
|
Let us first prove that the points must be concyclic. Assign to each point $X_{k}$ the vector $x_{k}$ in a system of orthogonal coordinates whose origin is the point of mass of the configuration, thus $\frac{1}{n} \sum_{k=1}^{n} x_{k}=0$.
Then $\mathrm{d}^{2}\left(X_{i}, X_{k}\right)=\left\|x_{i}-x_{k}\right\|^{2}=\left\langle x_{i}-x_{k}, x_{i}-x_{k}\right\rangle=$ $\left\|x_{i}\right\|^{2}-2\left\langle x_{i}, x_{k}\right\rangle+\left\|x_{k}\right\|^{2}$, hence $\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{i}, X_{k}\right)=n\left\|x_{i}\right\|^{2}-$
$2\left\langle x_{i}, \sum_{k=1}^{n} x_{k}\right\rangle+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{i}\right\|^{2}+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{j}\right\|^{2}+$ $\sum_{k=1}^{n}\left\|x_{\sigma(k)}\right\|^{2}=\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{j}, X_{\sigma(k)}\right)$, therefore $\left\|x_{i}\right\|=\left\|x_{j}\right\|$ for all pairs $(i, j)$. The points are thus concyclic (lying on a circle centred at $O(0,0)$ ).
Let now $m$ be the least angular distance between any two points. Two points situated at angular distance $m$ must be adjacent on the circle. Let us connect each pair of such two points with an edge. The graph $G$ obtained must be regular, of degree $\operatorname{deg}(G)=1$ or 2 . If $n$ is odd, since $\sum_{k=1}^{n} \operatorname{deg}\left(X_{k}\right)=$ $n \operatorname{deg}(G)=2|E|$, we must have $\operatorname{deg}(G)=2$, hence the configuration is a regular $n$-gon.
If $n$ is even, we may have the configuration of a regular $n$-gon, but we also may have $\operatorname{deg}(G)=1$. In that case, let $M$ be the next least angular distance between any two points; such points must also be adjacent on the circle. Let us connect each pair of such two points with an edge, in order to get a graph $G^{\prime}$. A similar reasoning yields $\operatorname{deg}\left(G^{\prime}\right)=1$, thus the configuration is that of an equiangular $n$-gon (with alternating equal side-lengths).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
For every $n \geq 3$, determine all the configurations of $n$ distinct points $X_{1}, X_{2}, \ldots, X_{n}$ in the plane, with the property that for any pair of distinct points $X_{i}, X_{j}$ there exists a permutation $\sigma$ of the integers $\{1, \ldots, n\}$, such that $\mathrm{d}\left(X_{i}, X_{k}\right)=\mathrm{d}\left(X_{j}, X_{\sigma(k)}\right)$ for all $1 \leq k \leq n$.
(We write $\mathrm{d}(X, Y)$ to denote the distance between points $X$ and $Y$.)
(United Kingdom) LuKe BetTs
|
Let us first prove that the points must be concyclic. Assign to each point $X_{k}$ the vector $x_{k}$ in a system of orthogonal coordinates whose origin is the point of mass of the configuration, thus $\frac{1}{n} \sum_{k=1}^{n} x_{k}=0$.
Then $\mathrm{d}^{2}\left(X_{i}, X_{k}\right)=\left\|x_{i}-x_{k}\right\|^{2}=\left\langle x_{i}-x_{k}, x_{i}-x_{k}\right\rangle=$ $\left\|x_{i}\right\|^{2}-2\left\langle x_{i}, x_{k}\right\rangle+\left\|x_{k}\right\|^{2}$, hence $\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{i}, X_{k}\right)=n\left\|x_{i}\right\|^{2}-$
$2\left\langle x_{i}, \sum_{k=1}^{n} x_{k}\right\rangle+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{i}\right\|^{2}+\sum_{k=1}^{n}\left\|x_{k}\right\|^{2}=n\left\|x_{j}\right\|^{2}+$ $\sum_{k=1}^{n}\left\|x_{\sigma(k)}\right\|^{2}=\sum_{k=1}^{n} \mathrm{~d}^{2}\left(X_{j}, X_{\sigma(k)}\right)$, therefore $\left\|x_{i}\right\|=\left\|x_{j}\right\|$ for all pairs $(i, j)$. The points are thus concyclic (lying on a circle centred at $O(0,0)$ ).
Let now $m$ be the least angular distance between any two points. Two points situated at angular distance $m$ must be adjacent on the circle. Let us connect each pair of such two points with an edge. The graph $G$ obtained must be regular, of degree $\operatorname{deg}(G)=1$ or 2 . If $n$ is odd, since $\sum_{k=1}^{n} \operatorname{deg}\left(X_{k}\right)=$ $n \operatorname{deg}(G)=2|E|$, we must have $\operatorname{deg}(G)=2$, hence the configuration is a regular $n$-gon.
If $n$ is even, we may have the configuration of a regular $n$-gon, but we also may have $\operatorname{deg}(G)=1$. In that case, let $M$ be the next least angular distance between any two points; such points must also be adjacent on the circle. Let us connect each pair of such two points with an edge, in order to get a graph $G^{\prime}$. A similar reasoning yields $\operatorname{deg}\left(G^{\prime}\right)=1$, thus the configuration is that of an equiangular $n$-gon (with alternating equal side-lengths).
|
{
"resource_path": "RMM/segmented/en-2011-Sols2011D2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
27b4389d-1d0a-55ee-b53f-07609c8f3730
| 605,427
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. A set $X$ of boys is separated from a set $Y$ of girls if no boy in $X$ is an acquaintance of a girl in $Y$. Similarly, a set $Y$ of girls is separated from a set $X$ of boys if no girl in $Y$ is an acquaintance of a boy in $X$. Since acquaintance is assumed mutual, separation is symmetric: $X$ is separated from $Y$ if and only if $Y$ is separated from $X$.
This enables doubly counting the number $n$ of ordered pairs $(X, Y)$ of separated sets $X$, of boys, and $Y$, of girls, and thereby showing that it is congruent modulo 2 to both numbers in question.
Given a set $X$ of boys, let $Y_{X}$ be the largest set of girls separated from $X$, to deduce that $X$ is separated from exactly $2^{\left|Y_{X}\right|}$ sets of girls. Consequently, $n=\sum_{X} 2^{\left|Y_{X}\right|}$ which is clearly congruent modulo 2 to the number of covering sets of boys.
Mutatis mutandis, the argument applies to show $n$ congruent modulo 2 to the number of covering sets of girls.
Remark. The argument in this solution translates verbatim in terms of the adjancency matrix of the associated acquaintance graph.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. A set $X$ of boys is separated from a set $Y$ of girls if no boy in $X$ is an acquaintance of a girl in $Y$. Similarly, a set $Y$ of girls is separated from a set $X$ of boys if no girl in $Y$ is an acquaintance of a boy in $X$. Since acquaintance is assumed mutual, separation is symmetric: $X$ is separated from $Y$ if and only if $Y$ is separated from $X$.
This enables doubly counting the number $n$ of ordered pairs $(X, Y)$ of separated sets $X$, of boys, and $Y$, of girls, and thereby showing that it is congruent modulo 2 to both numbers in question.
Given a set $X$ of boys, let $Y_{X}$ be the largest set of girls separated from $X$, to deduce that $X$ is separated from exactly $2^{\left|Y_{X}\right|}$ sets of girls. Consequently, $n=\sum_{X} 2^{\left|Y_{X}\right|}$ which is clearly congruent modulo 2 to the number of covering sets of boys.
Mutatis mutandis, the argument applies to show $n$ congruent modulo 2 to the number of covering sets of girls.
Remark. The argument in this solution translates verbatim in terms of the adjancency matrix of the associated acquaintance graph.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1"
}
|
65caf17b-1f0f-5f1a-ae6f-0f4e3303e194
| 605,443
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. (Ilya Bogdanov) Let $B$ denote the set of boys, let $G$ denote the set of girls and induct on $|B|+|G|$. The assertion is vacuously true if either set is empty.
Next, fix a boy $b$, let $B^{\prime}=B \backslash\{b\}$, and let $G^{\prime}$ be the set of all girls who do not know $b$. Notice that:
(1) a covering set of boys in $B^{\prime} \cup G$ is still one in $B \cup G$; and
(2) a covering set of boys in $B \cup G$ which is no longer one in $B^{\prime} \cup G$ is precisely the union of a covering set of boys in $B^{\prime} \cup G^{\prime}$ and $\{b\}$,
so the number of covering sets of boys in $B \cup G$ is the sum of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. On the other hand,
$\left(1^{\prime}\right)$ a covering set of girls in $B \cup G$ is still one in $B^{\prime} \cup G$; and
$\left(2^{\prime}\right)$ a covering set of girls in $B^{\prime} \cup G$ which is no longer one in $B \cup G$ is precisely a covering set of girls in $B^{\prime} \cup G^{\prime}$,
so the number of covering sets of girls in $B \cup G$ is the difference of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. Since the assertion is true for both $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$ by the induction hypothesis, the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. (Ilya Bogdanov) Let $B$ denote the set of boys, let $G$ denote the set of girls and induct on $|B|+|G|$. The assertion is vacuously true if either set is empty.
Next, fix a boy $b$, let $B^{\prime}=B \backslash\{b\}$, and let $G^{\prime}$ be the set of all girls who do not know $b$. Notice that:
(1) a covering set of boys in $B^{\prime} \cup G$ is still one in $B \cup G$; and
(2) a covering set of boys in $B \cup G$ which is no longer one in $B^{\prime} \cup G$ is precisely the union of a covering set of boys in $B^{\prime} \cup G^{\prime}$ and $\{b\}$,
so the number of covering sets of boys in $B \cup G$ is the sum of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. On the other hand,
$\left(1^{\prime}\right)$ a covering set of girls in $B \cup G$ is still one in $B^{\prime} \cup G$; and
$\left(2^{\prime}\right)$ a covering set of girls in $B^{\prime} \cup G$ which is no longer one in $B \cup G$ is precisely a covering set of girls in $B^{\prime} \cup G^{\prime}$,
so the number of covering sets of girls in $B \cup G$ is the difference of those in $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$. Since the assertion is true for both $B^{\prime} \cup G$ and $B^{\prime} \cup G^{\prime}$ by the induction hypothesis, the conclusion follows.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
65caf17b-1f0f-5f1a-ae6f-0f4e3303e194
| 605,443
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. (Géza Kós) Let $B$ and $G$ denote the sets of boys and girls, respectively. For every pair $(b, g) \in B \times G$, write $f(b, g)=0$ if they know each other, and $f(b, g)=1$ otherwise. A set $X$ of boys is covering if and only if
$$
\prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right)=1
$$
Hence the number of covering sets of boys is
$$
\begin{aligned}
\sum_{X \subseteq B} \prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right) & \equiv \sum_{X \subseteq B} \prod_{g \in G}\left(1+\prod_{b \in X} f(b, g)\right) \\
& =\sum_{X \subseteq B} \sum_{Y \subseteq G} \prod_{b \in X} \prod_{g \in Y} f(b, g) \quad(\bmod 2)
\end{aligned}
$$
By symmetry, the same is valid for the number of covering sets of girls.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a finite group of boys and girls, a covering set of boys is a set of boys such that every girl knows at least one boy in that set; and a covering set of girls is a set of girls such that every boy knows at least one girl in that set. Prove that the number of covering sets of boys and the number of covering sets of girls have the same parity. (Acquaintance is assumed to be mutual.)
|
. (Géza Kós) Let $B$ and $G$ denote the sets of boys and girls, respectively. For every pair $(b, g) \in B \times G$, write $f(b, g)=0$ if they know each other, and $f(b, g)=1$ otherwise. A set $X$ of boys is covering if and only if
$$
\prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right)=1
$$
Hence the number of covering sets of boys is
$$
\begin{aligned}
\sum_{X \subseteq B} \prod_{g \in G}\left(1-\prod_{b \in X} f(b, g)\right) & \equiv \sum_{X \subseteq B} \prod_{g \in G}\left(1+\prod_{b \in X} f(b, g)\right) \\
& =\sum_{X \subseteq B} \sum_{Y \subseteq G} \prod_{b \in X} \prod_{g \in Y} f(b, g) \quad(\bmod 2)
\end{aligned}
$$
By symmetry, the same is valid for the number of covering sets of girls.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 3"
}
|
65caf17b-1f0f-5f1a-ae6f-0f4e3303e194
| 605,443
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. We will use the following lemma.
Lemma. Let $A D$ be a median in triangle $A B C$. Then $\cot \angle B A D=2 \cot A+\cot B$ and $\cot \angle A D C=\frac{1}{2}(\cot B-\cot C)$.
Proof. Let $C C_{1}$ and $D D_{1}$ be the perpendiculars from $C$ and $D$ to $A B$. Using the signed lengths we write
$$
\cot B A D=\frac{A D_{1}}{D D_{1}}=\frac{\left(A C_{1}+A B\right) / 2}{C C_{1} / 2}=\frac{C C_{1} \cot A+C C_{1}(\cot A+\cot B)}{C C_{1}}=2 \cot A+\cot B
$$
Similarly, denoting by $A_{1}$ the projection of $A$ onto $B C$, we get
$$
\cot A D C=\frac{D A_{1}}{A A_{1}}=\frac{B C / 2-A_{1} C}{A A_{1}}=\frac{\left(A A_{1} \cot B+A A_{1} \cot C\right) / 2-A A_{1} \cot C}{A A_{1}}=\frac{\cot B-\cot C}{2} .
$$
The Lemma is proved.
Turning to the solution, by the Lemma we get
$$
\begin{aligned}
\cot \angle B P D & =2 \cot \angle B P C+\cot \angle P B C=2 \cot \angle B F C+\cot \angle P B C \quad(\text { from circle } B F P C) \\
& =2 \cdot \frac{1}{2}(\cot A-\cot B)+2 \cot B+\cot C=\cot A+\cot B+\cot C
\end{aligned}
$$
Similarly, $\cot \angle G Q F=\cot A+\cot B+\cot C$, so $\angle G P R=\angle G Q F$ and $G P R Q$ is cyclic.
Remark. The angle $\angle G P R=\angle G Q F$ is the Brocard angle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. We will use the following lemma.
Lemma. Let $A D$ be a median in triangle $A B C$. Then $\cot \angle B A D=2 \cot A+\cot B$ and $\cot \angle A D C=\frac{1}{2}(\cot B-\cot C)$.
Proof. Let $C C_{1}$ and $D D_{1}$ be the perpendiculars from $C$ and $D$ to $A B$. Using the signed lengths we write
$$
\cot B A D=\frac{A D_{1}}{D D_{1}}=\frac{\left(A C_{1}+A B\right) / 2}{C C_{1} / 2}=\frac{C C_{1} \cot A+C C_{1}(\cot A+\cot B)}{C C_{1}}=2 \cot A+\cot B
$$
Similarly, denoting by $A_{1}$ the projection of $A$ onto $B C$, we get
$$
\cot A D C=\frac{D A_{1}}{A A_{1}}=\frac{B C / 2-A_{1} C}{A A_{1}}=\frac{\left(A A_{1} \cot B+A A_{1} \cot C\right) / 2-A A_{1} \cot C}{A A_{1}}=\frac{\cot B-\cot C}{2} .
$$
The Lemma is proved.
Turning to the solution, by the Lemma we get
$$
\begin{aligned}
\cot \angle B P D & =2 \cot \angle B P C+\cot \angle P B C=2 \cot \angle B F C+\cot \angle P B C \quad(\text { from circle } B F P C) \\
& =2 \cdot \frac{1}{2}(\cot A-\cot B)+2 \cot B+\cot C=\cot A+\cot B+\cot C
\end{aligned}
$$
Similarly, $\cot \angle G Q F=\cot A+\cot B+\cot C$, so $\angle G P R=\angle G Q F$ and $G P R Q$ is cyclic.
Remark. The angle $\angle G P R=\angle G Q F$ is the Brocard angle.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
1ff77b15-cd3d-580f-af53-393be85f17e0
| 605,471
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. (Ilya Bogdanov and Marian Andronache) We also prove that $\angle(R P, P G)=\angle(R Q, Q G)$, or $\angle(D P, P G)=\angle(F Q, Q G)$.
Let $S$ be the point on ray $G D$ such that $A G \cdot G S=C G \cdot G F$ (so the points $A, S, C, F$ are concyclic). Then $G P \cdot G E=G P \cdot \frac{1}{2} G B=\frac{1}{2} C G \cdot G F=\frac{1}{2} A G \cdot G S=G D \cdot G S$, hence the points $E, P, D, S$ are also concyclic, and $\angle(D P, P G)=\angle(G S, S E)$. The problem may therefore be rephrased as follows:
Given a triangle $A B C$, let $D, E$ and $F$ respectively denote the midpoints of the sides $B C, C A$ and $A B$. The circle $A B E$, respectively, $A C F$, and the line $A D$ meet again at $Q$, respectively, $S$. Prove that $\angle A Q F=\angle A S E($ and $E S=F Q)$.
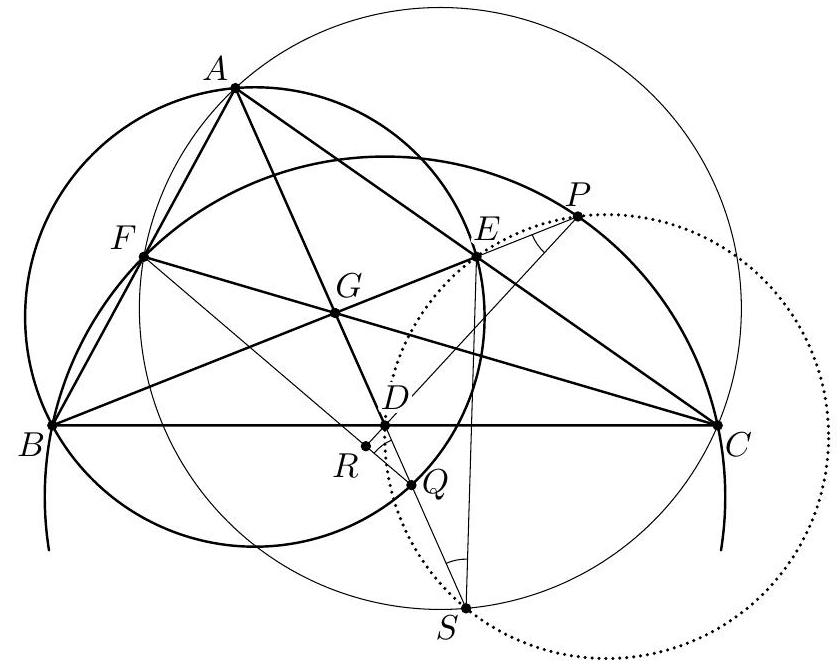
Upon inversion of pole $A$, the problem reads:
Given a triangle $A E^{\prime} F^{\prime}$, let the symmedian from $A$ meet the medians from $E^{\prime}$ and $F^{\prime}$ at $K=Q^{\prime}$ and $L=S^{\prime}$, respectively. Prove that the angles $A E^{\prime} L$ and $A F^{\prime} K$ are congruent.
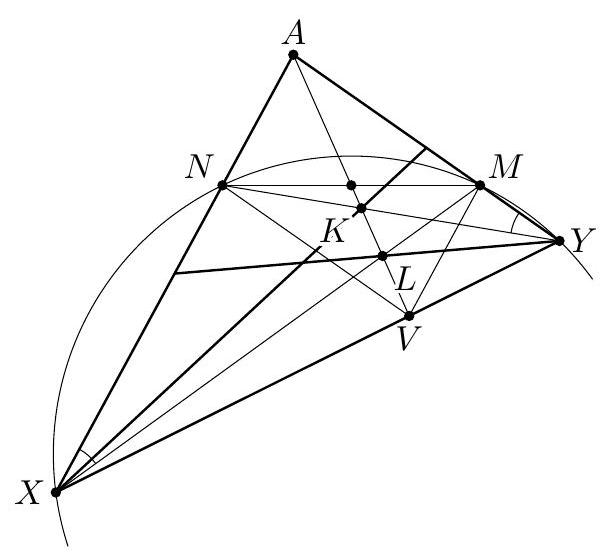
To prove this, denote $E^{\prime}=X, F^{\prime}=Y$. Let the symmedian from $A$ meet the side $X Y$ at $V$ and let the lines $X L$ and $Y K$ meet the sides $A Y$ and $A X$ at $M$ and $N$, respectively. Since the points $K$ and $L$ lie on the medians, we have $V M\|A X, V N\| A Y$. Hence $A M V N$ is a parallelogram, the symmedian $A V$ of triangle $A X Y$ supports the median of triangle $A M N$, which implies that the triangles $A M N$ and $A X Y$ are similar. Hence the points $M, N, X, Y$ are concyclic, and $\angle A X M=\angle A Y N$, QED.
Remark 1. We know that the points $X, Y, M, N$ are concyclic. Invert back from $A$ and consider the circles $A F Q$ and $A E S$ : the former meets $A C$ again at $M^{\prime}$ and the latter meets $A B$ again at $N^{\prime}$. Then the points $E, F, M^{\prime}, N^{\prime}$ are concyclic.
Remark 2. The inversion at pole $A$ also allows one to show that $\angle A Q F$ is the Brocard angle, thus providing one more solution. In our notation, it is equivalent to the fact that the points $Y$, $K$, and $Z$ are collinear, where $Z$ is the Brocard point (so $\angle Z A X=\angle Z Y A=\angle Z X Y$ ). This is valid because the lines $A V, X K$, and $Y Z$ are the radical axes of the following circles: (i) passing through $X$ and tangent to $A Y$ at $A$; (ii) passing through $Y$ and tangent to $A X$ at $A$; and (iii) passing through $X$ and tangent to $A Y$ at $Y$. The point $K$ is the radical center of these three circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. (Ilya Bogdanov and Marian Andronache) We also prove that $\angle(R P, P G)=\angle(R Q, Q G)$, or $\angle(D P, P G)=\angle(F Q, Q G)$.
Let $S$ be the point on ray $G D$ such that $A G \cdot G S=C G \cdot G F$ (so the points $A, S, C, F$ are concyclic). Then $G P \cdot G E=G P \cdot \frac{1}{2} G B=\frac{1}{2} C G \cdot G F=\frac{1}{2} A G \cdot G S=G D \cdot G S$, hence the points $E, P, D, S$ are also concyclic, and $\angle(D P, P G)=\angle(G S, S E)$. The problem may therefore be rephrased as follows:
Given a triangle $A B C$, let $D, E$ and $F$ respectively denote the midpoints of the sides $B C, C A$ and $A B$. The circle $A B E$, respectively, $A C F$, and the line $A D$ meet again at $Q$, respectively, $S$. Prove that $\angle A Q F=\angle A S E($ and $E S=F Q)$.

Upon inversion of pole $A$, the problem reads:
Given a triangle $A E^{\prime} F^{\prime}$, let the symmedian from $A$ meet the medians from $E^{\prime}$ and $F^{\prime}$ at $K=Q^{\prime}$ and $L=S^{\prime}$, respectively. Prove that the angles $A E^{\prime} L$ and $A F^{\prime} K$ are congruent.

To prove this, denote $E^{\prime}=X, F^{\prime}=Y$. Let the symmedian from $A$ meet the side $X Y$ at $V$ and let the lines $X L$ and $Y K$ meet the sides $A Y$ and $A X$ at $M$ and $N$, respectively. Since the points $K$ and $L$ lie on the medians, we have $V M\|A X, V N\| A Y$. Hence $A M V N$ is a parallelogram, the symmedian $A V$ of triangle $A X Y$ supports the median of triangle $A M N$, which implies that the triangles $A M N$ and $A X Y$ are similar. Hence the points $M, N, X, Y$ are concyclic, and $\angle A X M=\angle A Y N$, QED.
Remark 1. We know that the points $X, Y, M, N$ are concyclic. Invert back from $A$ and consider the circles $A F Q$ and $A E S$ : the former meets $A C$ again at $M^{\prime}$ and the latter meets $A B$ again at $N^{\prime}$. Then the points $E, F, M^{\prime}, N^{\prime}$ are concyclic.
Remark 2. The inversion at pole $A$ also allows one to show that $\angle A Q F$ is the Brocard angle, thus providing one more solution. In our notation, it is equivalent to the fact that the points $Y$, $K$, and $Z$ are collinear, where $Z$ is the Brocard point (so $\angle Z A X=\angle Z Y A=\angle Z X Y$ ). This is valid because the lines $A V, X K$, and $Y Z$ are the radical axes of the following circles: (i) passing through $X$ and tangent to $A Y$ at $A$; (ii) passing through $Y$ and tangent to $A X$ at $A$; and (iii) passing through $X$ and tangent to $A Y$ at $Y$. The point $K$ is the radical center of these three circles.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
1ff77b15-cd3d-580f-af53-393be85f17e0
| 605,471
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. (Ilya Bogdanov) Again, we will prove that $\angle(D P, P G)=\angle(F Q, Q G)$. Mark a point $T$ on the ray $G F$ such that $G F \cdot G T=G Q \cdot G D$; then the points $F, Q, D, T$ are concyclic, and $\angle(F Q, Q G)=\angle(T G, T D)=\angle(T C, T D)$.
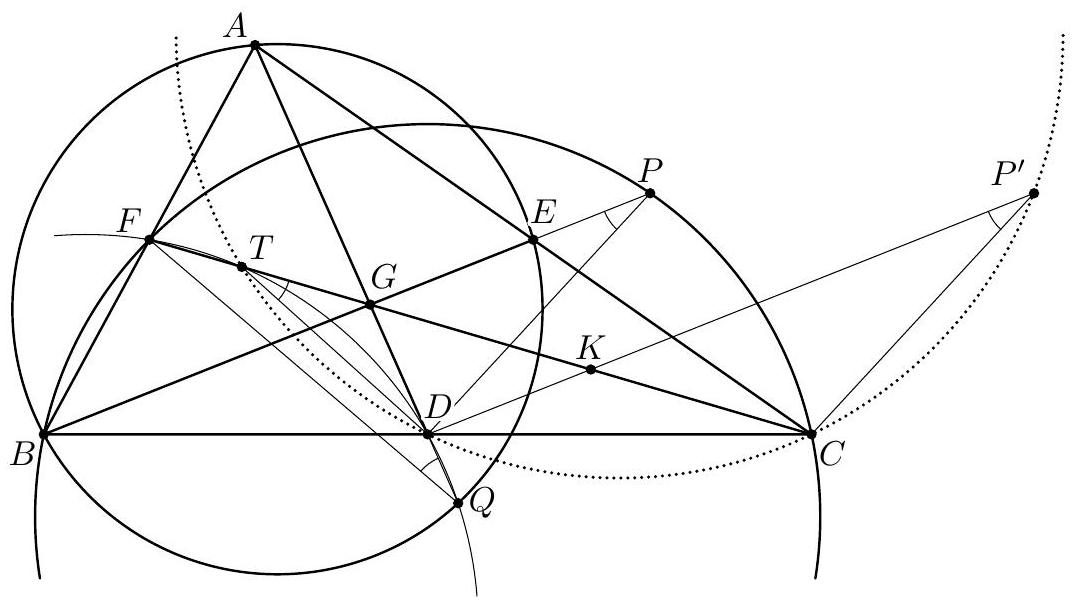
Shift the point $P$ by the vector $\overrightarrow{B D}$ to obtain point $P^{\prime}$. Then $\angle(D P, P G)=\angle\left(C P^{\prime}, P^{\prime} D\right)$, and we need to prove that $\angle\left(C P^{\prime}, P^{\prime} D\right)=\angle(C T, T D)$. This is precisely the condition that the points $T, D, C, P^{\prime}$ be concyclic.
Denote $G E=x, G F=y$. Then $G P \cdot G B=G C \cdot G F$, so $G P=y^{2} / x$. On the other hand, $G B \cdot G E=G Q \cdot G A=2 G Q \cdot G D=2 G T \cdot G F$, so $G T=x^{2} / y$. Denote by $K$ the point of intersection of $D P^{\prime}$ and $C T$; we need to prove that $T K \cdot K C=D K \cdot K P^{\prime}$.
Now, $D P^{\prime}=B P=B G+G P=2 x+y^{2} / x, C T=C G+G T=2 y+x^{2} / y, D K=B G / 2=x$, $C K=C G / 2=y$. Hence the desired equality reads $x\left(x+y^{2} / x\right)=y\left(y+x^{2} / y\right)$ which is obvious.
Remark. The points $B, T, E$, and $C$ are concyclic, hence the point $T$ is also of the same kind as $P$ and $Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $D, E$, and $F$ respectively denote the midpoints of the sides $B C, C A$, and $A B$. The circle $B C F$ and the line $B E$ meet again at $P$, and the circle $A B E$ and the line $A D$ meet again at $Q$. Finally, the lines $D P$ and $F Q$ meet at $R$. Prove that the centroid $G$ of the triangle $A B C$ lies on the circle $P Q R$.
|
. (Ilya Bogdanov) Again, we will prove that $\angle(D P, P G)=\angle(F Q, Q G)$. Mark a point $T$ on the ray $G F$ such that $G F \cdot G T=G Q \cdot G D$; then the points $F, Q, D, T$ are concyclic, and $\angle(F Q, Q G)=\angle(T G, T D)=\angle(T C, T D)$.

Shift the point $P$ by the vector $\overrightarrow{B D}$ to obtain point $P^{\prime}$. Then $\angle(D P, P G)=\angle\left(C P^{\prime}, P^{\prime} D\right)$, and we need to prove that $\angle\left(C P^{\prime}, P^{\prime} D\right)=\angle(C T, T D)$. This is precisely the condition that the points $T, D, C, P^{\prime}$ be concyclic.
Denote $G E=x, G F=y$. Then $G P \cdot G B=G C \cdot G F$, so $G P=y^{2} / x$. On the other hand, $G B \cdot G E=G Q \cdot G A=2 G Q \cdot G D=2 G T \cdot G F$, so $G T=x^{2} / y$. Denote by $K$ the point of intersection of $D P^{\prime}$ and $C T$; we need to prove that $T K \cdot K C=D K \cdot K P^{\prime}$.
Now, $D P^{\prime}=B P=B G+G P=2 x+y^{2} / x, C T=C G+G T=2 y+x^{2} / y, D K=B G / 2=x$, $C K=C G / 2=y$. Hence the desired equality reads $x\left(x+y^{2} / x\right)=y\left(y+x^{2} / y\right)$ which is obvious.
Remark. The points $B, T, E$, and $C$ are concyclic, hence the point $T$ is also of the same kind as $P$ and $Q$.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3"
}
|
1ff77b15-cd3d-580f-af53-393be85f17e0
| 605,471
|
Each positive integer number is coloured red or blue. A function $f$ from the set of positive integer numbers into itself has the following two properties:
(a) if $x \leq y$, then $f(x) \leq f(y)$; and
(b) if $x, y$ and $z$ are all (not necessarily distinct) positive integer numbers of the same colour and $x+y=z$, then $f(x)+f(y)=f(z)$.
Prove that there exists a positive number $a$ such that $f(x) \leq a x$ for all positive integer numbers $x$.
|
For integer $x, y$, by a segment $[x, y]$ we always mean the set of all integers $t$ such that $x \leq t \leq y$; the length of this segment is $y-x$.
If for every two positive integers $x, y$ sharing the same colour we have $f(x) / x=f(y) / y$, then one can choose $a=\max \{f(r) / r, f(b) / b\}$, where $r$ and $b$ are arbitrary red and blue numbers, respectively. So we can assume that there are two red numbers $x, y$ such that $f(x) / x \neq f(y) / y$.
Set $m=x y$. Then each segment of length $m$ contains a blue number. Indeed, assume that all the numbers on the segment $[k, k+m]$ are red. Then
$$
\begin{aligned}
& f(k+m)=f(k+x y)=f(k+x(y-1))+f(x)=\cdots=f(k)+y f(x), \\
& f(k+m)=f(k+x y)=f(k+(x-1) y)+f(y)=\cdots=f(k)+x f(y),
\end{aligned}
$$
so $y f(x)=x f(y)$ - a contradiction. Now we consider two cases.
Case 1. Assume that there exists a segment $[k, k+m]$ of length $m$ consisting of blue numbers. Define $D=\max \{f(k), \ldots, f(k+m)\}$. We claim that $f(z)-f(z-1) \leq D$, whatever $z>k$, and the conclusion follows. Consider the largest blue number $b_{1}$ not exceeding $z$, so $z-b_{1} \leq m$, and some blue number $b_{2}$ on the segment $\left[b_{1}+k, b_{1}+k+m\right]$, so $b_{2}>z$. Write $f\left(b_{2}\right)=f\left(b_{1}\right)+f\left(b_{2}-b_{1}\right) \leq f\left(b_{1}\right)+D$ to deduce that $f(z+1)-f(z) \leq f\left(b_{2}\right)-f\left(b_{1}\right) \leq D$, as claimed.
Case 2. Each segment of length $m$ contains numbers of both colours. Fix any red number $R \geq 2 m$ such that $R+1$ is blue and set $D=\max \{f(R), f(R+1)\}$. Now we claim that $f(z+1)-f(z) \leq D$, whatever $z>2 m$. Consider the largest red number $r$ not exceeding $z$ and the largest blue number $b$ smaller than $r$; then $0<z-b=(z-r)+(r-b) \leq 2 m$, and $b+1$ is red. Let $t=b+R+1$; then $t>z$. If $t$ is blue, then $f(t)=f(b)+f(R+1) \leq f(b)+D$, and $f(z+1)-f(z) \leq f(t)-f(b) \leq D$. Otherwise, $f(t)=f(b+1)+f(R) \leq f(b+1)+D$, hence $f(z+1)-f(z) \leq f(t)-f(b+1) \leq D$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Each positive integer number is coloured red or blue. A function $f$ from the set of positive integer numbers into itself has the following two properties:
(a) if $x \leq y$, then $f(x) \leq f(y)$; and
(b) if $x, y$ and $z$ are all (not necessarily distinct) positive integer numbers of the same colour and $x+y=z$, then $f(x)+f(y)=f(z)$.
Prove that there exists a positive number $a$ such that $f(x) \leq a x$ for all positive integer numbers $x$.
|
For integer $x, y$, by a segment $[x, y]$ we always mean the set of all integers $t$ such that $x \leq t \leq y$; the length of this segment is $y-x$.
If for every two positive integers $x, y$ sharing the same colour we have $f(x) / x=f(y) / y$, then one can choose $a=\max \{f(r) / r, f(b) / b\}$, where $r$ and $b$ are arbitrary red and blue numbers, respectively. So we can assume that there are two red numbers $x, y$ such that $f(x) / x \neq f(y) / y$.
Set $m=x y$. Then each segment of length $m$ contains a blue number. Indeed, assume that all the numbers on the segment $[k, k+m]$ are red. Then
$$
\begin{aligned}
& f(k+m)=f(k+x y)=f(k+x(y-1))+f(x)=\cdots=f(k)+y f(x), \\
& f(k+m)=f(k+x y)=f(k+(x-1) y)+f(y)=\cdots=f(k)+x f(y),
\end{aligned}
$$
so $y f(x)=x f(y)$ - a contradiction. Now we consider two cases.
Case 1. Assume that there exists a segment $[k, k+m]$ of length $m$ consisting of blue numbers. Define $D=\max \{f(k), \ldots, f(k+m)\}$. We claim that $f(z)-f(z-1) \leq D$, whatever $z>k$, and the conclusion follows. Consider the largest blue number $b_{1}$ not exceeding $z$, so $z-b_{1} \leq m$, and some blue number $b_{2}$ on the segment $\left[b_{1}+k, b_{1}+k+m\right]$, so $b_{2}>z$. Write $f\left(b_{2}\right)=f\left(b_{1}\right)+f\left(b_{2}-b_{1}\right) \leq f\left(b_{1}\right)+D$ to deduce that $f(z+1)-f(z) \leq f\left(b_{2}\right)-f\left(b_{1}\right) \leq D$, as claimed.
Case 2. Each segment of length $m$ contains numbers of both colours. Fix any red number $R \geq 2 m$ such that $R+1$ is blue and set $D=\max \{f(R), f(R+1)\}$. Now we claim that $f(z+1)-f(z) \leq D$, whatever $z>2 m$. Consider the largest red number $r$ not exceeding $z$ and the largest blue number $b$ smaller than $r$; then $0<z-b=(z-r)+(r-b) \leq 2 m$, and $b+1$ is red. Let $t=b+R+1$; then $t>z$. If $t$ is blue, then $f(t)=f(b)+f(R+1) \leq f(b)+D$, and $f(z+1)-f(z) \leq f(t)-f(b) \leq D$. Otherwise, $f(t)=f(b+1)+f(R) \leq f(b+1)+D$, hence $f(z+1)-f(z) \leq f(t)-f(b+1) \leq D$, as claimed.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
c8137db3-00bf-5108-b8d1-f0cc973911d9
| 605,503
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. Throughout the solution $n$ stands for a positive integer. By Euler's theorem, $\left(2^{3^{n}}+1\right)\left(2^{3^{n}}-1\right)=2^{2 \cdot 3^{n}}-1 \equiv 0\left(\bmod 3^{n+1}\right)$. Since $2^{3^{n}}-1 \equiv 1(\bmod 3)$, it follows that $2^{3^{n}}+1$ is divisible by $3^{n+1}$.
The number $\left(2^{3^{n+1}}+1\right) /\left(2^{3^{n}}+1\right)=2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ is greater than 3 and congruent to 3 modulo 9 , so it has a prime factor $p_{n}>3$ that does not divide $2^{3^{n}}+1$ (otherwise, $2^{3^{n}} \equiv-1$ (mod $\left.p_{n}\right)$, so $2^{2 \cdot 3^{n}}-2^{3^{n}}+1 \equiv 3\left(\bmod p_{n}\right)$, contradicting the fact that $p_{n}$ is a factor greater than 3 of $2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ ).
We now show that $a_{n}=3^{n} p_{n}$ satisfies the conditions in the statement. Since $2^{a_{n}}+1 \equiv$ $2^{3^{n}}+1 \not \equiv 0\left(\bmod p_{n}\right)$, it follows that $a_{n}$ does not divide $2^{a_{n}}+1$.
On the other hand, $3^{n+1}$ divides $2^{3^{n}}+1$ which in turn divides $2^{a_{n}}+1$, so $2^{3^{n+1}}+1$ divides $2^{2^{a_{n}}+1}+1$. Finally, both $3^{n}$ and $p_{n}$ divide $2^{3^{n+1}}+1$, so $a_{n}$ divides $2^{2^{a_{n}}+1}+1$.
As $n$ runs through the positive integers, the $a_{n}$ are clearly pairwise distinct and the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. Throughout the solution $n$ stands for a positive integer. By Euler's theorem, $\left(2^{3^{n}}+1\right)\left(2^{3^{n}}-1\right)=2^{2 \cdot 3^{n}}-1 \equiv 0\left(\bmod 3^{n+1}\right)$. Since $2^{3^{n}}-1 \equiv 1(\bmod 3)$, it follows that $2^{3^{n}}+1$ is divisible by $3^{n+1}$.
The number $\left(2^{3^{n+1}}+1\right) /\left(2^{3^{n}}+1\right)=2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ is greater than 3 and congruent to 3 modulo 9 , so it has a prime factor $p_{n}>3$ that does not divide $2^{3^{n}}+1$ (otherwise, $2^{3^{n}} \equiv-1$ (mod $\left.p_{n}\right)$, so $2^{2 \cdot 3^{n}}-2^{3^{n}}+1 \equiv 3\left(\bmod p_{n}\right)$, contradicting the fact that $p_{n}$ is a factor greater than 3 of $2^{2 \cdot 3^{n}}-2^{3^{n}}+1$ ).
We now show that $a_{n}=3^{n} p_{n}$ satisfies the conditions in the statement. Since $2^{a_{n}}+1 \equiv$ $2^{3^{n}}+1 \not \equiv 0\left(\bmod p_{n}\right)$, it follows that $a_{n}$ does not divide $2^{a_{n}}+1$.
On the other hand, $3^{n+1}$ divides $2^{3^{n}}+1$ which in turn divides $2^{a_{n}}+1$, so $2^{3^{n+1}}+1$ divides $2^{2^{a_{n}}+1}+1$. Finally, both $3^{n}$ and $p_{n}$ divide $2^{3^{n+1}}+1$, so $a_{n}$ divides $2^{2^{a_{n}}+1}+1$.
As $n$ runs through the positive integers, the $a_{n}$ are clearly pairwise distinct and the conclusion follows.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 1"
}
|
7940a6f0-b9f0-5d6f-8a28-69552e5924a6
| 605,516
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. (Géza Kós) We show that the numbers $a_{n}=\left(2^{3^{n}}+1\right) / 9, n \geq 2$, satisfy the conditions in the statement. To this end, recall the following well-known facts:
(1) If $N$ is an odd positive integer, then $\nu_{3}\left(2^{N}+1\right)=\nu_{3}(N)+1$, where $\nu_{3}(a)$ is the exponent of 3 in the decomposition of the integer $a$ into prime factors; and
(2) If $M$ and $N$ are odd positive integers, then $\left(2^{M}+1,2^{N}+1\right)=2^{(M, N)}+1$, where $(a, b)$ is the greatest common divisor of the integers $a$ and $b$.
By (1), $a_{n}=3^{n-1} m$, where $m$ is an odd positive integer not divisible by 3 , and by (2),
$$
\left(m, 2^{a_{n}}+1\right) \left\lvert\,\left(2^{3^{n}}+1,2^{a_{n}}+1\right)=2^{\left(3^{n}, a_{n}\right)}+1=2^{3^{n-1}}+1<\frac{2^{3^{n}}+1}{3^{n+1}}=m\right.
$$
so $m$ cannot divide $2^{a_{n}}+1$.
On the other hand, $3^{n-1} \mid 2^{2^{a_{n}}+1}+1$, for $\nu_{3}\left(2^{2^{a_{n}}+1}+1\right)>\nu_{3}\left(2^{a_{n}}+1\right)>\nu_{3}\left(a_{n}\right)=n-1$, and $m \mid 2^{2^{a_{n}}+1}+1$, for $3^{n-1} \mid a_{n}$, so $3^{n} \mid 2^{a_{n}}+1$ whence $m\left|2^{3^{n}}+1\right| 2^{2^{a_{n}}+1}+1$. Since $3^{n-1}$ and $m$ are coprime, the conclusion follows.
Remarks. There are several variations of these solutions. For instance, let $b_{1}=3$ and $b_{n+1}=$ $2^{b_{n}}+1, n \geq 1$, and notice that $b_{n}$ divides $b_{n+1}$. It can be shown that there are infinitely many indices $n$ such that some prime factor $p_{n}$ of $b_{n+1}$ does not divide $b_{n}$. One checks that for these $n$ 's the $a_{n}=p_{n} b_{n-1}$ satisfy the required conditions.
Finally, the numbers $3^{n} \cdot 571, n \geq 2$, form yet another infinite set of positive integers fulfilling the conditions in the statement - the details are omitted.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. (Géza Kós) We show that the numbers $a_{n}=\left(2^{3^{n}}+1\right) / 9, n \geq 2$, satisfy the conditions in the statement. To this end, recall the following well-known facts:
(1) If $N$ is an odd positive integer, then $\nu_{3}\left(2^{N}+1\right)=\nu_{3}(N)+1$, where $\nu_{3}(a)$ is the exponent of 3 in the decomposition of the integer $a$ into prime factors; and
(2) If $M$ and $N$ are odd positive integers, then $\left(2^{M}+1,2^{N}+1\right)=2^{(M, N)}+1$, where $(a, b)$ is the greatest common divisor of the integers $a$ and $b$.
By (1), $a_{n}=3^{n-1} m$, where $m$ is an odd positive integer not divisible by 3 , and by (2),
$$
\left(m, 2^{a_{n}}+1\right) \left\lvert\,\left(2^{3^{n}}+1,2^{a_{n}}+1\right)=2^{\left(3^{n}, a_{n}\right)}+1=2^{3^{n-1}}+1<\frac{2^{3^{n}}+1}{3^{n+1}}=m\right.
$$
so $m$ cannot divide $2^{a_{n}}+1$.
On the other hand, $3^{n-1} \mid 2^{2^{a_{n}}+1}+1$, for $\nu_{3}\left(2^{2^{a_{n}}+1}+1\right)>\nu_{3}\left(2^{a_{n}}+1\right)>\nu_{3}\left(a_{n}\right)=n-1$, and $m \mid 2^{2^{a_{n}}+1}+1$, for $3^{n-1} \mid a_{n}$, so $3^{n} \mid 2^{a_{n}}+1$ whence $m\left|2^{3^{n}}+1\right| 2^{2^{a_{n}}+1}+1$. Since $3^{n-1}$ and $m$ are coprime, the conclusion follows.
Remarks. There are several variations of these solutions. For instance, let $b_{1}=3$ and $b_{n+1}=$ $2^{b_{n}}+1, n \geq 1$, and notice that $b_{n}$ divides $b_{n+1}$. It can be shown that there are infinitely many indices $n$ such that some prime factor $p_{n}$ of $b_{n+1}$ does not divide $b_{n}$. One checks that for these $n$ 's the $a_{n}=p_{n} b_{n-1}$ satisfy the required conditions.
Finally, the numbers $3^{n} \cdot 571, n \geq 2$, form yet another infinite set of positive integers fulfilling the conditions in the statement - the details are omitted.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 2"
}
|
7940a6f0-b9f0-5d6f-8a28-69552e5924a6
| 605,516
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. (Dušan Djukić) Assume that $n$ satisfies the conditions of the problem. We claim that the number $N=2^{n}+1>n$ also satisfies these conditions.
Firstly, since $n \nmid N$, the fact (2) from Solution 2 allows to conclude that $2^{n}+1 \nmid 2^{N}+1$, or $N \nmid 2^{N}+1$. Next, since $n \mid 2^{2^{n}+1}+1=2^{N}+1$, we obtain from the same fact that $N=2^{n}+1 \mid 2^{2^{N}+1}+1$, thus confirming our claim.
Hence, it suffices to provide only one example, hence obtaining an infinite series by the claim. For instance, one may easily check that the number $n=57$ fits.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are infinitely many positive integer numbers $n$ such that $2^{2^{n}+1}+1$ be divisible by $n$, but $2^{n}+1$ be not.
|
. (Dušan Djukić) Assume that $n$ satisfies the conditions of the problem. We claim that the number $N=2^{n}+1>n$ also satisfies these conditions.
Firstly, since $n \nmid N$, the fact (2) from Solution 2 allows to conclude that $2^{n}+1 \nmid 2^{N}+1$, or $N \nmid 2^{N}+1$. Next, since $n \mid 2^{2^{n}+1}+1=2^{N}+1$, we obtain from the same fact that $N=2^{n}+1 \mid 2^{2^{N}+1}+1$, thus confirming our claim.
Hence, it suffices to provide only one example, hence obtaining an infinite series by the claim. For instance, one may easily check that the number $n=57$ fits.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 3"
}
|
7940a6f0-b9f0-5d6f-8a28-69552e5924a6
| 605,516
|
Given a positive integer number $n \geq 3$, colour each cell of an $n \times n$ square array one of $\left[(n+2)^{2} / 3\right]$ colours, each colour being used at least once. Prove that the cells of some $1 \times 3$ or $3 \times 1$ rectangular subarray have pairwise distinct colours.
|
For more convenience, say that a subarray of the $n \times n$ square array bears a colour if at least two of its cells share that colour.
We shall prove that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, which is $2 n(n-2)$, exceeds the number of such subarrays, each of which bears some colour. The key ingredient is the estimate in the lemma below.
Lemma. If a colour is used exactly $p$ times, then the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing that colour does not exceed $3(p-1)$.
Assume the lemma for the moment, let $N=\left[(n+2)^{2} / 3\right]$ and let $n_{i}$ be the number of cells coloured the $i$ th colour, $i=1, \ldots, N$, to deduce that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, each of which bears some colour, is at most
$$
\sum_{i=1}^{N} 3\left(n_{i}-1\right)=3 \sum_{i=1}^{N} n_{i}-3 N=3 n^{2}-3 N<3 n^{2}-\left(n^{2}+4 n\right)=2 n(n-2)
$$
and thereby conclude the proof.
Back to the lemma, the assertion is clear if $p=1$, so let $p>1$.
We begin by showing that if a row contains exactly $q$ cells coloured $C$, then the number $r$ of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 q / 2-1$; of course, a similar estimate holds for a column. To this end, notice first that the case $q=1$ is trivial, so we assume that $q>1$. Consider the incidence of a cell $c$ coloured $C$ and a $3 \times 1$ rectangular subarray $R$ bearing $C$ :
$$
\langle c, R\rangle= \begin{cases}1 & \text { if } c \subset R \\ 0 & \text { otherwise. }\end{cases}
$$
Notice that, given $R, \sum_{c}\langle c, R\rangle \geq 2$, and, given $c, \sum_{R}\langle c, R\rangle \leq 3$; moreover, if $c$ is the leftmost or rightmost cell, then $\sum_{R}\langle c, R\rangle \leq 2$. Consequently,
$$
2 r \leq \sum_{R} \sum_{c}\langle c, R\rangle=\sum_{c} \sum_{R}\langle c, R\rangle \leq 2+3(q-2)+2=3 q-2
$$
whence the conclusion.
Finally, let the $p$ cells coloured $C$ lie on $k$ rows and $\ell$ columns and notice that $k+\ell \geq 3$, for $p>1$. By the preceding, the total number of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-k$, and the total number of $1 \times 3$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-\ell$, so the total number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $(3 p / 2-k)+(3 p / 2-\ell)=3 p-(k+\ell) \leq 3 p-3=3(p-1)$. This completes the proof.
Remarks. In terms of the total number of cells, the number $N=\left[(n+2)^{2} / 3\right]$ of colours is asymptotically close to the minimum number of colours required for some $1 \times 3$ or $3 \times 1$ rectangular subarray to have all cells of pairwise distinct colours, whatever the colouring. To see this, colour the cells with the coordinates $(i, j)$, where $i+j \equiv 0(\bmod 3)$ and $i, j \in\{0,1, \ldots, n-1\}$, one colour each, and use one additional colour $C$ to colour the remaining cells. Then each $1 \times 3$ and each $3 \times 1$ rectangular subarray has exactly two cells coloured $C$, and the number of colours is $\left\lceil n^{2} / 3\right\rceil+1$ if $n \equiv 1$ or $2(\bmod 3)$, and $\left\lceil n^{2} / 3\right\rceil$ if $n \equiv 0(\bmod 3)$. Consequently, the minimum number of colours is $n^{2} / 3+O(n)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a positive integer number $n \geq 3$, colour each cell of an $n \times n$ square array one of $\left[(n+2)^{2} / 3\right]$ colours, each colour being used at least once. Prove that the cells of some $1 \times 3$ or $3 \times 1$ rectangular subarray have pairwise distinct colours.
|
For more convenience, say that a subarray of the $n \times n$ square array bears a colour if at least two of its cells share that colour.
We shall prove that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, which is $2 n(n-2)$, exceeds the number of such subarrays, each of which bears some colour. The key ingredient is the estimate in the lemma below.
Lemma. If a colour is used exactly $p$ times, then the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing that colour does not exceed $3(p-1)$.
Assume the lemma for the moment, let $N=\left[(n+2)^{2} / 3\right]$ and let $n_{i}$ be the number of cells coloured the $i$ th colour, $i=1, \ldots, N$, to deduce that the number of $1 \times 3$ and $3 \times 1$ rectangular subarrays, each of which bears some colour, is at most
$$
\sum_{i=1}^{N} 3\left(n_{i}-1\right)=3 \sum_{i=1}^{N} n_{i}-3 N=3 n^{2}-3 N<3 n^{2}-\left(n^{2}+4 n\right)=2 n(n-2)
$$
and thereby conclude the proof.
Back to the lemma, the assertion is clear if $p=1$, so let $p>1$.
We begin by showing that if a row contains exactly $q$ cells coloured $C$, then the number $r$ of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 q / 2-1$; of course, a similar estimate holds for a column. To this end, notice first that the case $q=1$ is trivial, so we assume that $q>1$. Consider the incidence of a cell $c$ coloured $C$ and a $3 \times 1$ rectangular subarray $R$ bearing $C$ :
$$
\langle c, R\rangle= \begin{cases}1 & \text { if } c \subset R \\ 0 & \text { otherwise. }\end{cases}
$$
Notice that, given $R, \sum_{c}\langle c, R\rangle \geq 2$, and, given $c, \sum_{R}\langle c, R\rangle \leq 3$; moreover, if $c$ is the leftmost or rightmost cell, then $\sum_{R}\langle c, R\rangle \leq 2$. Consequently,
$$
2 r \leq \sum_{R} \sum_{c}\langle c, R\rangle=\sum_{c} \sum_{R}\langle c, R\rangle \leq 2+3(q-2)+2=3 q-2
$$
whence the conclusion.
Finally, let the $p$ cells coloured $C$ lie on $k$ rows and $\ell$ columns and notice that $k+\ell \geq 3$, for $p>1$. By the preceding, the total number of $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-k$, and the total number of $1 \times 3$ rectangular subarrays bearing $C$ does not exceed $3 p / 2-\ell$, so the total number of $1 \times 3$ and $3 \times 1$ rectangular subarrays bearing $C$ does not exceed $(3 p / 2-k)+(3 p / 2-\ell)=3 p-(k+\ell) \leq 3 p-3=3(p-1)$. This completes the proof.
Remarks. In terms of the total number of cells, the number $N=\left[(n+2)^{2} / 3\right]$ of colours is asymptotically close to the minimum number of colours required for some $1 \times 3$ or $3 \times 1$ rectangular subarray to have all cells of pairwise distinct colours, whatever the colouring. To see this, colour the cells with the coordinates $(i, j)$, where $i+j \equiv 0(\bmod 3)$ and $i, j \in\{0,1, \ldots, n-1\}$, one colour each, and use one additional colour $C$ to colour the remaining cells. Then each $1 \times 3$ and each $3 \times 1$ rectangular subarray has exactly two cells coloured $C$, and the number of colours is $\left\lceil n^{2} / 3\right\rceil+1$ if $n \equiv 1$ or $2(\bmod 3)$, and $\left\lceil n^{2} / 3\right\rceil$ if $n \equiv 0(\bmod 3)$. Consequently, the minimum number of colours is $n^{2} / 3+O(n)$.
|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
a894119e-f83a-57bf-9fe9-275bc567aec1
| 605,551
|
Let $A B C$ be a triangle and let $I$ and $O$ respectively denote its incentre and circumcentre. Let $\omega_{A}$ be the circle through $B$ and $C$ and tangent to the incircle of the triangle $A B C$; the circles $\omega_{B}$ and $\omega_{C}$ are defined similarly. The circles $\omega_{B}$ and $\omega_{C}$ through $A$ meet again at $A^{\prime}$; the points $B^{\prime}$ and $C^{\prime}$ are defined similarly. Prove that the lines $A A^{\prime}, B B^{\prime}$ and $C C^{\prime}$ are concurrent at a point on the line $I O$.
|
Let $\gamma$ be the incircle of the triangle $A B C$ and let $A_{1}, B_{1}, C_{1}$ be its contact points with the sides $B C, C A, A B$, respectively. Let further $X_{A}$ be the point of contact of the circles $\gamma$ and $\omega_{A}$. The latter circle is the image of the former under a homothety centred at $X_{A}$. This homothety sends $A_{1}$ to a point $M_{A}$ on $\omega_{A}$ such that the tangent to $\omega_{A}$ at $M_{A}$ is parallel to $B C$. Consequently, $M_{A}$ is the midpoint of the arc $B C$ of $\omega_{A}$ not containing $X_{A}$. It follows that the angles $M_{A} X_{A} B$ and $M_{A} B C$ are congruent, so the triangles $M_{A} B A_{1}$ and $M_{A} X_{A} B$ are similar: $M_{A} B / M_{A} X_{A}=M_{A} A_{1} / M_{A} B$. Rewrite the latter $M_{A} B^{2}=M_{A} A_{1} \cdot M_{A} X_{A}$ to deduce that $M_{A}$ lies on the radical axis $\ell_{B}$ of $B$ and $\gamma$. Similarly, $M_{A}$ lies on the radical axis $\ell_{C}$ of $C$ and $\gamma$.
Define the points $X_{B}, X_{C}, M_{B}, M_{C}$ and the line $\ell_{A}$ in a similar way and notice that the lines $\ell_{A}, \ell_{B}, \ell_{C}$ support the sides of the triangle $M_{A} M_{B} M_{C}$. The lines $\ell_{A}$ and $B_{1} C_{1}$ are both perpendicular to $A I$, so they are parallel. Similarly, the lines $\ell_{B}$ and $\ell_{C}$ are parallel to $C_{1} A_{1}$ and $A_{1} B_{1}$, respectively. Consequently, the triangle $M_{A} M_{B} M_{C}$ is the image of the triangle $A_{1} B_{1} C_{1}$ under a homothety $\Theta$. Let $K$ be the centre of $\Theta$ and let $k=M_{A} K / A_{1} K=M_{B} K / B_{1} K=$ $M_{C} K / C_{1} K$ be the similitude ratio. Notice that the lines $M_{A} A_{1}, M_{B} B_{1}$ and $M_{C} C_{1}$ are concurrent at $K$.
Since the points $A_{1}, B_{1}, X_{A}, X_{B}$ are concyclic, $A_{1} K \cdot K X_{A}=B_{1} K \cdot K X_{B}$. Multiply both sides by $k$ to get $M_{A} K \cdot K X_{A}=M_{B} K \cdot K X_{B}$ and deduce thereby that $K$ lies on the radical axis $C C^{\prime}$ of $\omega_{A}$ and $\omega_{B}$. Similarly, both lines $A A^{\prime}$ and $B B^{\prime}$ pass through $K$.
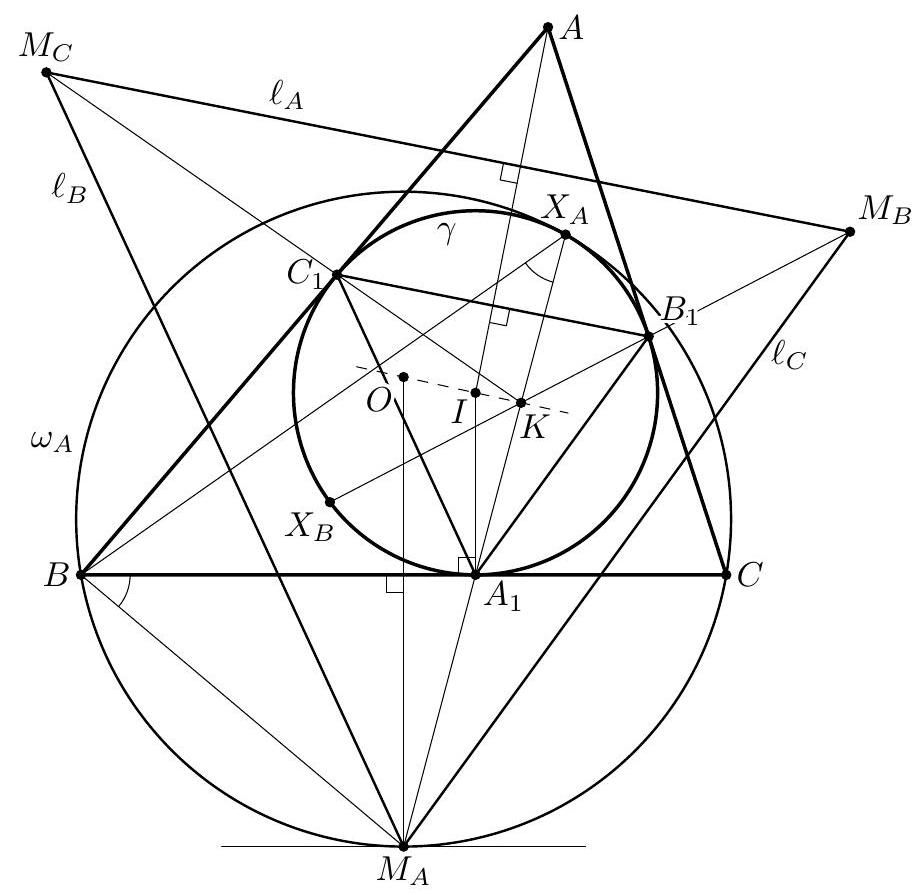
Finally, consider the image $O^{\prime}$ of $I$ under $\Theta$. It lies on the line through $M_{A}$ parallel to $A_{1} I$ (and hence perpendicular to $B C$ ); since $M_{A}$ is the midpoint of the $\operatorname{arc} B C$, this line must be $M_{A} O$. Similarly, $O^{\prime}$ lies on the line $M_{B} O$, so $O^{\prime}=O$. Consequently, the points $I, K$ and $O$ are collinear.
Remark 1. Many steps in this solution allow different reasonings. For instance, one may
see that the lines $A_{1} X_{A}$ and $B_{1} X_{B}$ are concurrent at point $K$ on the radical axis $C C^{\prime}$ of the circles $\omega_{A}$ and $\omega_{B}$ by applying Newton's theorem to the quadrilateral $X_{A} X_{B} A_{1} B_{1}$ (since the common tangents at $X_{A}$ and $X_{B}$ intersect on $C C^{\prime}$ ). Then one can conclude that $K A_{1} / K B_{1}=$ $K M_{A} / K M_{B}$, thus obtaining that the triangles $M_{A} M_{B} M_{C}$ and $A_{1} B_{1} C_{1}$ are homothetical at $K$ (and therefore $K$ is the radical center of $\omega_{A}, \omega_{B}$, and $\omega_{C}$ ). Finally, considering the inversion with the pole $K$ and the power equal to $K X_{1} \cdot K M_{A}$ followed by the reflection at $P$ we see that the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$ are invariant under this transform; next, the image of $\gamma$ is the circumcircle of $M_{A} M_{B} M_{C}$ and it is tangent to all the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$, hence its center is $O$, and thus $O, I$, and $K$ are collinear.
Remark 2. Here is an outline of an alternative approach to the first part of the solution. Let $J_{A}$ be the excentre of the triangle $A B C$ opposite $A$. The line $J_{A} A_{1}$ meets $\gamma$ again at $Y_{A}$; let $Z_{A}$ and $N_{A}$ be the midpoints of the segments $A_{1} Y_{A}$ and $J_{A} A_{1}$, respectively. Since the segment $I J_{A}$ is a diameter in the circle $B C Z_{A}$, it follows that $B A_{1} \cdot C A_{1}=Z_{A} A_{1} \cdot J_{A} A_{1}$, so $B A_{1} \cdot C A_{1}=N_{A} A_{1} \cdot Y_{A} A_{1}$. Consequently, the points $B, C, N_{A}$ and $Y_{A}$ lie on some circle $\omega_{A}^{\prime}$.
It is well known that $N_{A}$ lies on the perpendicular bisector of the segment $B C$, so the tangents to $\omega_{A}^{\prime}$ and $\gamma$ at $N_{A}$ and $A_{1}$ are parallel. It follows that the tangents to these circles at $Y_{A}$ coincide, so $\omega_{A}^{\prime}$ is in fact $\omega_{A}$, whence $X_{A}=Y_{A}$ and $M_{A}=N_{A}$. It is also well known that the midpoint $S_{A}$ of the segment $I J_{A}$ lies both on the circumcircle $A B C$ and on the perpendicular bisector of $B C$. Since $S_{A} M_{A}$ is a midline in the triangle $A_{1} I J_{A}$, it follows that $S_{A} M_{A}=r / 2$, where $r$ is the radius of $\gamma$ (the inradius of the triangle $A B C$ ). Consequently, each of the points $M_{A}, M_{B}$ and $M_{C}$ is at distance $R+r / 2$ from $O$ (here $R$ is the circumradius). Now proceed as above.
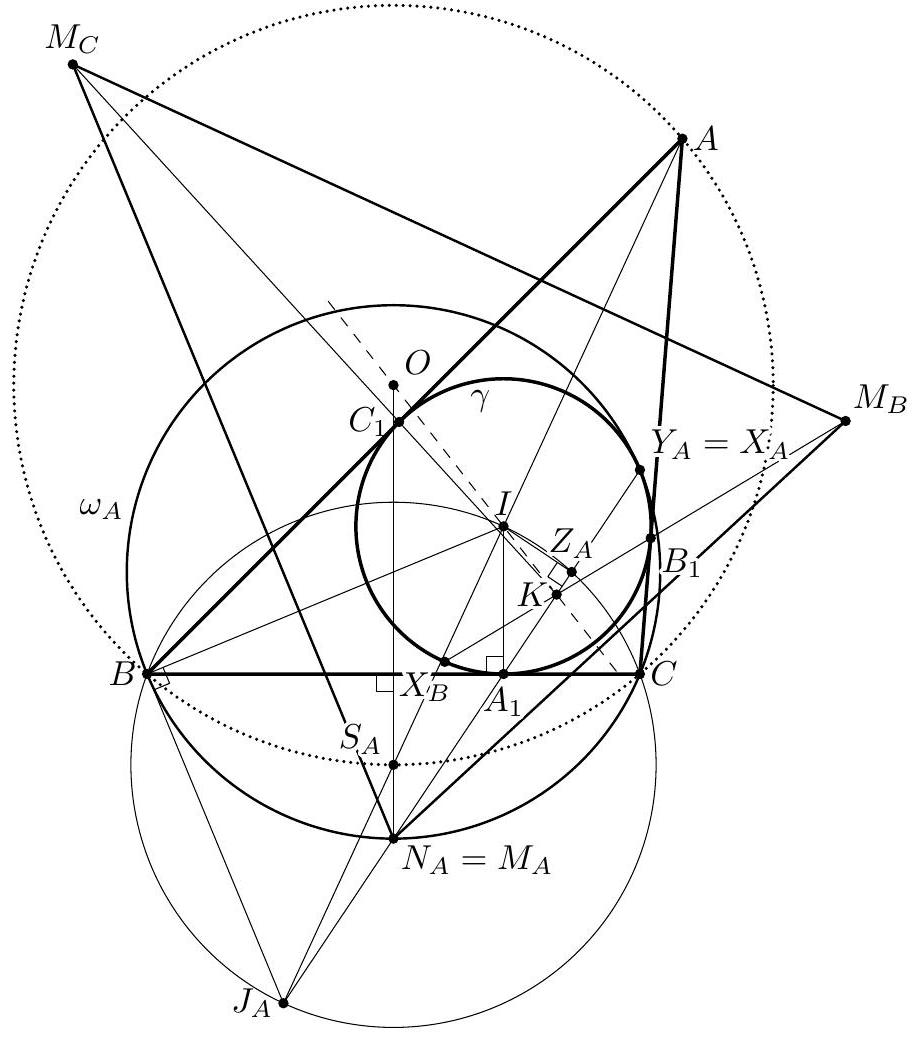
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $I$ and $O$ respectively denote its incentre and circumcentre. Let $\omega_{A}$ be the circle through $B$ and $C$ and tangent to the incircle of the triangle $A B C$; the circles $\omega_{B}$ and $\omega_{C}$ are defined similarly. The circles $\omega_{B}$ and $\omega_{C}$ through $A$ meet again at $A^{\prime}$; the points $B^{\prime}$ and $C^{\prime}$ are defined similarly. Prove that the lines $A A^{\prime}, B B^{\prime}$ and $C C^{\prime}$ are concurrent at a point on the line $I O$.
|
Let $\gamma$ be the incircle of the triangle $A B C$ and let $A_{1}, B_{1}, C_{1}$ be its contact points with the sides $B C, C A, A B$, respectively. Let further $X_{A}$ be the point of contact of the circles $\gamma$ and $\omega_{A}$. The latter circle is the image of the former under a homothety centred at $X_{A}$. This homothety sends $A_{1}$ to a point $M_{A}$ on $\omega_{A}$ such that the tangent to $\omega_{A}$ at $M_{A}$ is parallel to $B C$. Consequently, $M_{A}$ is the midpoint of the arc $B C$ of $\omega_{A}$ not containing $X_{A}$. It follows that the angles $M_{A} X_{A} B$ and $M_{A} B C$ are congruent, so the triangles $M_{A} B A_{1}$ and $M_{A} X_{A} B$ are similar: $M_{A} B / M_{A} X_{A}=M_{A} A_{1} / M_{A} B$. Rewrite the latter $M_{A} B^{2}=M_{A} A_{1} \cdot M_{A} X_{A}$ to deduce that $M_{A}$ lies on the radical axis $\ell_{B}$ of $B$ and $\gamma$. Similarly, $M_{A}$ lies on the radical axis $\ell_{C}$ of $C$ and $\gamma$.
Define the points $X_{B}, X_{C}, M_{B}, M_{C}$ and the line $\ell_{A}$ in a similar way and notice that the lines $\ell_{A}, \ell_{B}, \ell_{C}$ support the sides of the triangle $M_{A} M_{B} M_{C}$. The lines $\ell_{A}$ and $B_{1} C_{1}$ are both perpendicular to $A I$, so they are parallel. Similarly, the lines $\ell_{B}$ and $\ell_{C}$ are parallel to $C_{1} A_{1}$ and $A_{1} B_{1}$, respectively. Consequently, the triangle $M_{A} M_{B} M_{C}$ is the image of the triangle $A_{1} B_{1} C_{1}$ under a homothety $\Theta$. Let $K$ be the centre of $\Theta$ and let $k=M_{A} K / A_{1} K=M_{B} K / B_{1} K=$ $M_{C} K / C_{1} K$ be the similitude ratio. Notice that the lines $M_{A} A_{1}, M_{B} B_{1}$ and $M_{C} C_{1}$ are concurrent at $K$.
Since the points $A_{1}, B_{1}, X_{A}, X_{B}$ are concyclic, $A_{1} K \cdot K X_{A}=B_{1} K \cdot K X_{B}$. Multiply both sides by $k$ to get $M_{A} K \cdot K X_{A}=M_{B} K \cdot K X_{B}$ and deduce thereby that $K$ lies on the radical axis $C C^{\prime}$ of $\omega_{A}$ and $\omega_{B}$. Similarly, both lines $A A^{\prime}$ and $B B^{\prime}$ pass through $K$.

Finally, consider the image $O^{\prime}$ of $I$ under $\Theta$. It lies on the line through $M_{A}$ parallel to $A_{1} I$ (and hence perpendicular to $B C$ ); since $M_{A}$ is the midpoint of the $\operatorname{arc} B C$, this line must be $M_{A} O$. Similarly, $O^{\prime}$ lies on the line $M_{B} O$, so $O^{\prime}=O$. Consequently, the points $I, K$ and $O$ are collinear.
Remark 1. Many steps in this solution allow different reasonings. For instance, one may
see that the lines $A_{1} X_{A}$ and $B_{1} X_{B}$ are concurrent at point $K$ on the radical axis $C C^{\prime}$ of the circles $\omega_{A}$ and $\omega_{B}$ by applying Newton's theorem to the quadrilateral $X_{A} X_{B} A_{1} B_{1}$ (since the common tangents at $X_{A}$ and $X_{B}$ intersect on $C C^{\prime}$ ). Then one can conclude that $K A_{1} / K B_{1}=$ $K M_{A} / K M_{B}$, thus obtaining that the triangles $M_{A} M_{B} M_{C}$ and $A_{1} B_{1} C_{1}$ are homothetical at $K$ (and therefore $K$ is the radical center of $\omega_{A}, \omega_{B}$, and $\omega_{C}$ ). Finally, considering the inversion with the pole $K$ and the power equal to $K X_{1} \cdot K M_{A}$ followed by the reflection at $P$ we see that the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$ are invariant under this transform; next, the image of $\gamma$ is the circumcircle of $M_{A} M_{B} M_{C}$ and it is tangent to all the circles $\omega_{A}, \omega_{B}$, and $\omega_{C}$, hence its center is $O$, and thus $O, I$, and $K$ are collinear.
Remark 2. Here is an outline of an alternative approach to the first part of the solution. Let $J_{A}$ be the excentre of the triangle $A B C$ opposite $A$. The line $J_{A} A_{1}$ meets $\gamma$ again at $Y_{A}$; let $Z_{A}$ and $N_{A}$ be the midpoints of the segments $A_{1} Y_{A}$ and $J_{A} A_{1}$, respectively. Since the segment $I J_{A}$ is a diameter in the circle $B C Z_{A}$, it follows that $B A_{1} \cdot C A_{1}=Z_{A} A_{1} \cdot J_{A} A_{1}$, so $B A_{1} \cdot C A_{1}=N_{A} A_{1} \cdot Y_{A} A_{1}$. Consequently, the points $B, C, N_{A}$ and $Y_{A}$ lie on some circle $\omega_{A}^{\prime}$.
It is well known that $N_{A}$ lies on the perpendicular bisector of the segment $B C$, so the tangents to $\omega_{A}^{\prime}$ and $\gamma$ at $N_{A}$ and $A_{1}$ are parallel. It follows that the tangents to these circles at $Y_{A}$ coincide, so $\omega_{A}^{\prime}$ is in fact $\omega_{A}$, whence $X_{A}=Y_{A}$ and $M_{A}=N_{A}$. It is also well known that the midpoint $S_{A}$ of the segment $I J_{A}$ lies both on the circumcircle $A B C$ and on the perpendicular bisector of $B C$. Since $S_{A} M_{A}$ is a midline in the triangle $A_{1} I J_{A}$, it follows that $S_{A} M_{A}=r / 2$, where $r$ is the radius of $\gamma$ (the inradius of the triangle $A B C$ ). Consequently, each of the points $M_{A}, M_{B}$ and $M_{C}$ is at distance $R+r / 2$ from $O$ (here $R$ is the circumradius). Now proceed as above.

|
{
"resource_path": "RMM/segmented/en-2012-Solutions2012-2.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution."
}
|
2043e799-5d90-5859-a74e-7cf0c21aa5b2
| 605,560
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. Such a tester pair exists. We may biject $\mathbb{R}$ with the closed unit interval, so it suffices to find a tester pair for that instead. We give an explicit example: take some positive real numbers $\alpha, \beta$ (which we will specify further later). Take
$$
g(x)=\max (x-\alpha, 0) \quad \text { and } \quad h(x)=\min (x+\beta, 1) .
$$
Say a set $S \subseteq[0,1]$ is invariant if $f(S) \subseteq S$ for all functions $f$ commuting with both $g$ and $h$. Note that intersections and unions of invariant sets are invariant. Preimages of invariant sets under $g$ and $h$ are also invariant; indeed, if $S$ is invariant and, say, $T=g^{-1}(S)$, then $g(f(T))=$ $f(g(T)) \subseteq f(S) \subseteq S$, thus $f(T) \subseteq T$.
We claim that (if we choose $\alpha+\beta<1$ ) the intervals $[0, n \alpha-m \beta]$ are invariant where $n$ and $m$ are nonnegative integers with $0 \leq n \alpha-m \beta \leq 1$. We prove this by induction on $m+n$.
The set $\{0\}$ is invariant, as for any $f$ commuting with $g$ we have $g(f(0))=f(g(0))=f(0)$, so $f(0)$ is a fixed point of $g$. This gives that $f(0)=0$, thus the induction base is established.
Suppose now we have some $m, n$ such that $\left[0, n^{\prime} \alpha-m^{\prime} \beta\right]$ is invariant whenever $m^{\prime}+n^{\prime}<$ $m+n$. At least one of the numbers $(n-1) \alpha-m \beta$ and $n \alpha-(m-1) \beta$ lies in $(0,1)$. Note however that in the first case $[0, n \alpha-m \beta]=g^{-1}([0,(n-1) \alpha-m \beta])$, so $[0, n \alpha-m \beta]$ is invariant. In the second case $[0, n \alpha-m \beta]=h^{-1}([0, n \alpha-(m-1) \beta])$, so again $[0, n \alpha-m \beta]$ is invariant. This completes the induction.
We claim that if we choose $\alpha+\beta<1$, where $0<\alpha \notin \mathbb{Q}$ and $\beta=1 / k$ for some integer $k>1$, then all intervals $[0, \delta]$ are invariant for $0 \leq \delta<1$. This occurs, as by the previous claim, for all nonnegative integers $n$ we have $[0,(n \alpha \bmod 1)]$ is invariant. The set of $n \alpha \bmod 1$ is dense in $[0,1]$, so in particular
$$
[0, \delta]=\bigcap_{(n \alpha \bmod 1)>\delta}[0,(n \alpha \bmod 1)]
$$
is invariant.
A similar argument establishes that $[\delta, 1]$ is invariant, so by intersecting these $\{\delta\}$ is invariant for $0<\delta<1$. Yet we also have $\{0\},\{1\}$ both invariant, which proves $f$ to be the identity.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. Such a tester pair exists. We may biject $\mathbb{R}$ with the closed unit interval, so it suffices to find a tester pair for that instead. We give an explicit example: take some positive real numbers $\alpha, \beta$ (which we will specify further later). Take
$$
g(x)=\max (x-\alpha, 0) \quad \text { and } \quad h(x)=\min (x+\beta, 1) .
$$
Say a set $S \subseteq[0,1]$ is invariant if $f(S) \subseteq S$ for all functions $f$ commuting with both $g$ and $h$. Note that intersections and unions of invariant sets are invariant. Preimages of invariant sets under $g$ and $h$ are also invariant; indeed, if $S$ is invariant and, say, $T=g^{-1}(S)$, then $g(f(T))=$ $f(g(T)) \subseteq f(S) \subseteq S$, thus $f(T) \subseteq T$.
We claim that (if we choose $\alpha+\beta<1$ ) the intervals $[0, n \alpha-m \beta]$ are invariant where $n$ and $m$ are nonnegative integers with $0 \leq n \alpha-m \beta \leq 1$. We prove this by induction on $m+n$.
The set $\{0\}$ is invariant, as for any $f$ commuting with $g$ we have $g(f(0))=f(g(0))=f(0)$, so $f(0)$ is a fixed point of $g$. This gives that $f(0)=0$, thus the induction base is established.
Suppose now we have some $m, n$ such that $\left[0, n^{\prime} \alpha-m^{\prime} \beta\right]$ is invariant whenever $m^{\prime}+n^{\prime}<$ $m+n$. At least one of the numbers $(n-1) \alpha-m \beta$ and $n \alpha-(m-1) \beta$ lies in $(0,1)$. Note however that in the first case $[0, n \alpha-m \beta]=g^{-1}([0,(n-1) \alpha-m \beta])$, so $[0, n \alpha-m \beta]$ is invariant. In the second case $[0, n \alpha-m \beta]=h^{-1}([0, n \alpha-(m-1) \beta])$, so again $[0, n \alpha-m \beta]$ is invariant. This completes the induction.
We claim that if we choose $\alpha+\beta<1$, where $0<\alpha \notin \mathbb{Q}$ and $\beta=1 / k$ for some integer $k>1$, then all intervals $[0, \delta]$ are invariant for $0 \leq \delta<1$. This occurs, as by the previous claim, for all nonnegative integers $n$ we have $[0,(n \alpha \bmod 1)]$ is invariant. The set of $n \alpha \bmod 1$ is dense in $[0,1]$, so in particular
$$
[0, \delta]=\bigcap_{(n \alpha \bmod 1)>\delta}[0,(n \alpha \bmod 1)]
$$
is invariant.
A similar argument establishes that $[\delta, 1]$ is invariant, so by intersecting these $\{\delta\}$ is invariant for $0<\delta<1$. Yet we also have $\{0\},\{1\}$ both invariant, which proves $f$ to be the identity.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
39ede87e-9976-51e5-abd2-fdf466487628
| 605,575
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. Let us agree that a sequence $\mathbf{x}=\left(x_{n}\right)_{n=1,2, \ldots}$ is cofinally non-constant if for every index $m$ there exists an index $n>m$ such that $x_{m} \neq x_{n}$.
Biject $\mathbb{R}$ with the set of cofinally non-constant sequences of 0 's and 1 's, and define $g$ and $h$ by
$$
g(\epsilon, \mathbf{x})=\left\{\begin{array}{ll}
\epsilon, \mathbf{x} & \text { if } \epsilon=0 \\
\mathbf{x} & \text { else }
\end{array} \quad \text { and } \quad h(\epsilon, \mathbf{x})= \begin{cases}\epsilon, \mathbf{x} & \text { if } \epsilon=1 \\
\mathbf{x} & \text { else }\end{cases}\right.
$$
where $\epsilon, \mathbf{x}$ denotes the sequence formed by appending $\mathbf{x}$ to the single-element sequence $\epsilon$. Note that $g$ fixes precisely those sequences beginning with 0 , and $h$ fixes precisely those beginning with 1.
Now assume that $f$ commutes with both $f$ and $g$. To prove that $f(\mathbf{x})=\mathbf{x}$ for all $\mathbf{x}$ we show that $\mathbf{x}$ and $f(\mathbf{x})$ share the same first $n$ terms, by induction on $n$.
The base case $n=1$ is simple, as we have noticed above that the set of sequences beginning with a 0 is precisely the set of $g$-fixed points, so is preserved by $f$, and similarly for the set of sequences starting with 1.
Suppose that $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n$ terms, whatever $\mathbf{x}$. Consider any sequence, and write it as $\mathbf{x}=\epsilon, \mathbf{y}$. Without loss of generality, we may (and will) assume that $\epsilon=0$, so $f(\mathbf{x})=0, \mathbf{y}^{\prime}$ by the base case. Yet then $f(\mathbf{y})=f(h(\mathbf{x}))=h(f(\mathbf{x}))=h\left(0, \mathbf{y}^{\prime}\right)=\mathbf{y}^{\prime}$. Consequently, $f(\mathbf{x})=0, f(\mathbf{y})$, so $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n+1$ terms by the inductive hypothesis.
Thus $f$ fixes all of cofinally non-constant sequences, and the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. Let us agree that a sequence $\mathbf{x}=\left(x_{n}\right)_{n=1,2, \ldots}$ is cofinally non-constant if for every index $m$ there exists an index $n>m$ such that $x_{m} \neq x_{n}$.
Biject $\mathbb{R}$ with the set of cofinally non-constant sequences of 0 's and 1 's, and define $g$ and $h$ by
$$
g(\epsilon, \mathbf{x})=\left\{\begin{array}{ll}
\epsilon, \mathbf{x} & \text { if } \epsilon=0 \\
\mathbf{x} & \text { else }
\end{array} \quad \text { and } \quad h(\epsilon, \mathbf{x})= \begin{cases}\epsilon, \mathbf{x} & \text { if } \epsilon=1 \\
\mathbf{x} & \text { else }\end{cases}\right.
$$
where $\epsilon, \mathbf{x}$ denotes the sequence formed by appending $\mathbf{x}$ to the single-element sequence $\epsilon$. Note that $g$ fixes precisely those sequences beginning with 0 , and $h$ fixes precisely those beginning with 1.
Now assume that $f$ commutes with both $f$ and $g$. To prove that $f(\mathbf{x})=\mathbf{x}$ for all $\mathbf{x}$ we show that $\mathbf{x}$ and $f(\mathbf{x})$ share the same first $n$ terms, by induction on $n$.
The base case $n=1$ is simple, as we have noticed above that the set of sequences beginning with a 0 is precisely the set of $g$-fixed points, so is preserved by $f$, and similarly for the set of sequences starting with 1.
Suppose that $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n$ terms, whatever $\mathbf{x}$. Consider any sequence, and write it as $\mathbf{x}=\epsilon, \mathbf{y}$. Without loss of generality, we may (and will) assume that $\epsilon=0$, so $f(\mathbf{x})=0, \mathbf{y}^{\prime}$ by the base case. Yet then $f(\mathbf{y})=f(h(\mathbf{x}))=h(f(\mathbf{x}))=h\left(0, \mathbf{y}^{\prime}\right)=\mathbf{y}^{\prime}$. Consequently, $f(\mathbf{x})=0, f(\mathbf{y})$, so $f(\mathbf{x})$ and $\mathbf{x}$ agree for the first $n+1$ terms by the inductive hypothesis.
Thus $f$ fixes all of cofinally non-constant sequences, and the conclusion follows.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
39ede87e-9976-51e5-abd2-fdf466487628
| 605,575
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. (Ilya Bogdanov) We will show that there exists a tester pair of bijective functions $g$ and $h$.
First of all, let us find out when a pair of functions is a tester pair. Let $g, h: \mathbb{R} \rightarrow \mathbb{R}$ be arbitrary functions. We construct a directed graph $G_{g, h}$ with $\mathbb{R}$ as the set of vertices, its edges being painted with two colors: for every vertex $x \in \mathbb{R}$, we introduce a red edge $x \rightarrow g(x)$ and a blue edge $x \rightarrow h(x)$.
Now, assume that the function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$. This means exactly that if there exists an edge $x \rightarrow y$, then there also exists an edge $f(x) \rightarrow f(y)$ of the same color; that is $-f$ is an endomorphism of $G_{g, h}$.
Thus, a pair $(g, h)$ is a tester pair if and only if the graph $G_{g, h}$ admits no nontrivial endomorphisms. Notice that each endomorphism maps a component into a component. Thus, to construct a tester pair, it suffices to construct a continuum of components with no nontrivial endomorphisms and no homomorphisms from one to another. It can be done in many ways; below we present one of them.
Let $g(x)=x+1$; the construction of $h$ is more involved. For every $x \in[0,1)$ we define the set $S_{x}=x+\mathbb{Z}$; the sets $S_{x}$ will be exactly the components of $G_{g, h}$. Now we will construct these components.
Let us fix any $x \in[0,1)$; let $x=0 . x_{1} x_{2} \ldots$ be the binary representation of $x$. Define $h(x-n)=x-n+1$ for every $n>3$. Next, let $h(x-3)=x, h(x)=x-2, h(x-2)=x-1$, and $h(x-1)=x+1$ (that would be a "marker" which fixes a point in our component).
Next, for every $i=1,2, \ldots$, we define
(1) $h(x+3 i-2)=x+3 i-1, h(x+3 i-1)=x+3 i$, and $h(x+3 i)=x+3 i+1$, if $x_{i}=0$;
(2) $h(x+3 i-2)=x+3 i, h(x+3 i)=3 i-1$, and $h(x+3 i-1)=x+3 i+1$, if $x_{i}=1$.
Clearly, $h$ is a bijection mapping each $S_{x}$ to itself. Now we claim that the graph $G_{g, h}$ satisfies the desired conditions.
Consider any homomorphism $f_{x}: S_{x} \rightarrow S_{y}$ ( $x$ and $y$ may coincide). Since $g$ is a bijection, consideration of the red edges shows that $f_{x}(x+n)=x+n+k$ for a fixed real $k$. Next, there exists a blue edge $(x-3) \rightarrow x$, and the only blue edge of the form $(y+m-3) \rightarrow(y+m)$ is $(y-3) \rightarrow y$; thus $f_{x}(x)=y$, and $k=0$.
Next, if $x_{i}=0$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i-1)$; then the edge $(y+3 i-2) \rightarrow(y+3 i-1)$ also should exist, so $y_{i}=0$. Analogously, if $x_{i}=1$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i)$; then the edge $(y+3 i-2) \rightarrow(y+3 i)$ also should exist, so $y_{i}=1$. We conclude that $x=y$, and $f_{x}$ is the identity mapping, as required.
Remark. If $g$ and $h$ are injections, then the components of $G_{g, h}$ are at most countable. So the set of possible pairwise non-isomorphic such components is continual; hence there is no bijective tester pair for a hyper-continual set instead of $\mathbb{R}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist a pair $(g, h)$ of functions $g, h: \mathbb{R} \rightarrow \mathbb{R}$ such that the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$ is the identity function $f(x) \equiv x$ ?
(United Kingdom) Alexander Betts
|
. (Ilya Bogdanov) We will show that there exists a tester pair of bijective functions $g$ and $h$.
First of all, let us find out when a pair of functions is a tester pair. Let $g, h: \mathbb{R} \rightarrow \mathbb{R}$ be arbitrary functions. We construct a directed graph $G_{g, h}$ with $\mathbb{R}$ as the set of vertices, its edges being painted with two colors: for every vertex $x \in \mathbb{R}$, we introduce a red edge $x \rightarrow g(x)$ and a blue edge $x \rightarrow h(x)$.
Now, assume that the function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f(g(x))=g(f(x))$ and $f(h(x))=h(f(x))$ for all $x \in \mathbb{R}$. This means exactly that if there exists an edge $x \rightarrow y$, then there also exists an edge $f(x) \rightarrow f(y)$ of the same color; that is $-f$ is an endomorphism of $G_{g, h}$.
Thus, a pair $(g, h)$ is a tester pair if and only if the graph $G_{g, h}$ admits no nontrivial endomorphisms. Notice that each endomorphism maps a component into a component. Thus, to construct a tester pair, it suffices to construct a continuum of components with no nontrivial endomorphisms and no homomorphisms from one to another. It can be done in many ways; below we present one of them.
Let $g(x)=x+1$; the construction of $h$ is more involved. For every $x \in[0,1)$ we define the set $S_{x}=x+\mathbb{Z}$; the sets $S_{x}$ will be exactly the components of $G_{g, h}$. Now we will construct these components.
Let us fix any $x \in[0,1)$; let $x=0 . x_{1} x_{2} \ldots$ be the binary representation of $x$. Define $h(x-n)=x-n+1$ for every $n>3$. Next, let $h(x-3)=x, h(x)=x-2, h(x-2)=x-1$, and $h(x-1)=x+1$ (that would be a "marker" which fixes a point in our component).
Next, for every $i=1,2, \ldots$, we define
(1) $h(x+3 i-2)=x+3 i-1, h(x+3 i-1)=x+3 i$, and $h(x+3 i)=x+3 i+1$, if $x_{i}=0$;
(2) $h(x+3 i-2)=x+3 i, h(x+3 i)=3 i-1$, and $h(x+3 i-1)=x+3 i+1$, if $x_{i}=1$.
Clearly, $h$ is a bijection mapping each $S_{x}$ to itself. Now we claim that the graph $G_{g, h}$ satisfies the desired conditions.
Consider any homomorphism $f_{x}: S_{x} \rightarrow S_{y}$ ( $x$ and $y$ may coincide). Since $g$ is a bijection, consideration of the red edges shows that $f_{x}(x+n)=x+n+k$ for a fixed real $k$. Next, there exists a blue edge $(x-3) \rightarrow x$, and the only blue edge of the form $(y+m-3) \rightarrow(y+m)$ is $(y-3) \rightarrow y$; thus $f_{x}(x)=y$, and $k=0$.
Next, if $x_{i}=0$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i-1)$; then the edge $(y+3 i-2) \rightarrow(y+3 i-1)$ also should exist, so $y_{i}=0$. Analogously, if $x_{i}=1$ then there exists a blue edge $(x+3 i-2) \rightarrow(x+3 i)$; then the edge $(y+3 i-2) \rightarrow(y+3 i)$ also should exist, so $y_{i}=1$. We conclude that $x=y$, and $f_{x}$ is the identity mapping, as required.
Remark. If $g$ and $h$ are injections, then the components of $G_{g, h}$ are at most countable. So the set of possible pairwise non-isomorphic such components is continual; hence there is no bijective tester pair for a hyper-continual set instead of $\mathbb{R}$.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3"
}
|
39ede87e-9976-51e5-abd2-fdf466487628
| 605,575
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$. The lines $A B$ and $C D$ meet at $P$, the lines $A D$ and $B C$ meet at $Q$, and the diagonals $A C$ and $B D$ meet at $R$. Let $M$ be the midpoint of the segment $P Q$, and let $K$ be the common point of the segment $M R$ and the circle $\omega$. Prove that the circumcircle of the triangle $K P Q$ and $\omega$ are tangent to one another.
(Russia) MedeubeK Kungozhin
|
Let $O$ be the centre of $\omega$. Notice that the points $P, Q$, and $R$ are the poles (with respect to $\omega$ ) of the lines $Q R, R P$, and $P Q$, respectively. Hence we have $O P \perp Q R, O Q \perp R P$, and $O R \perp P Q$, thus $R$ is the orthocentre of the triangle $O P Q$. Now, if $M R \perp P Q$, then the points $P$ and $Q$ are the reflections of one another in the line $M R=M O$, and the triangle $P Q K$ is symmetrical with respect to this line. In this case the statement of the problem is trivial.
Otherwise, let $V$ be the foot of the perpendicular from $O$ to $M R$, and let $U$ be the common point of the lines $O V$ and $P Q$. Since $U$ lies on the polar line of $R$ and $O U \perp M R$, we obtain that $U$ is the pole of $M R$. Therefore, the line $U K$ is tangent to $\omega$. Hence it is enough to prove that $U K^{2}=U P \cdot U Q$, since this relation implies that $U K$ is also tangent to the circle $K P Q$.
From the rectangular triangle $O K U$, we get $U K^{2}=U V \cdot U O$. Let $\Omega$ be the circumcircle of triangle $O P Q$, and let $R^{\prime}$ be the reflection of its orthocentre $R$ in the midpoint $M$ of the side $P Q$. It is well known that $R^{\prime}$ is the point of $\Omega$ opposite to $O$, hence $O R^{\prime}$ is the diameter of $\Omega$. Finally, since $\angle O V R^{\prime}=90^{\circ}$, the point $V$ also lies on $\Omega$, hence $U P \cdot U Q=U V \cdot U O=U K^{2}$, as required.
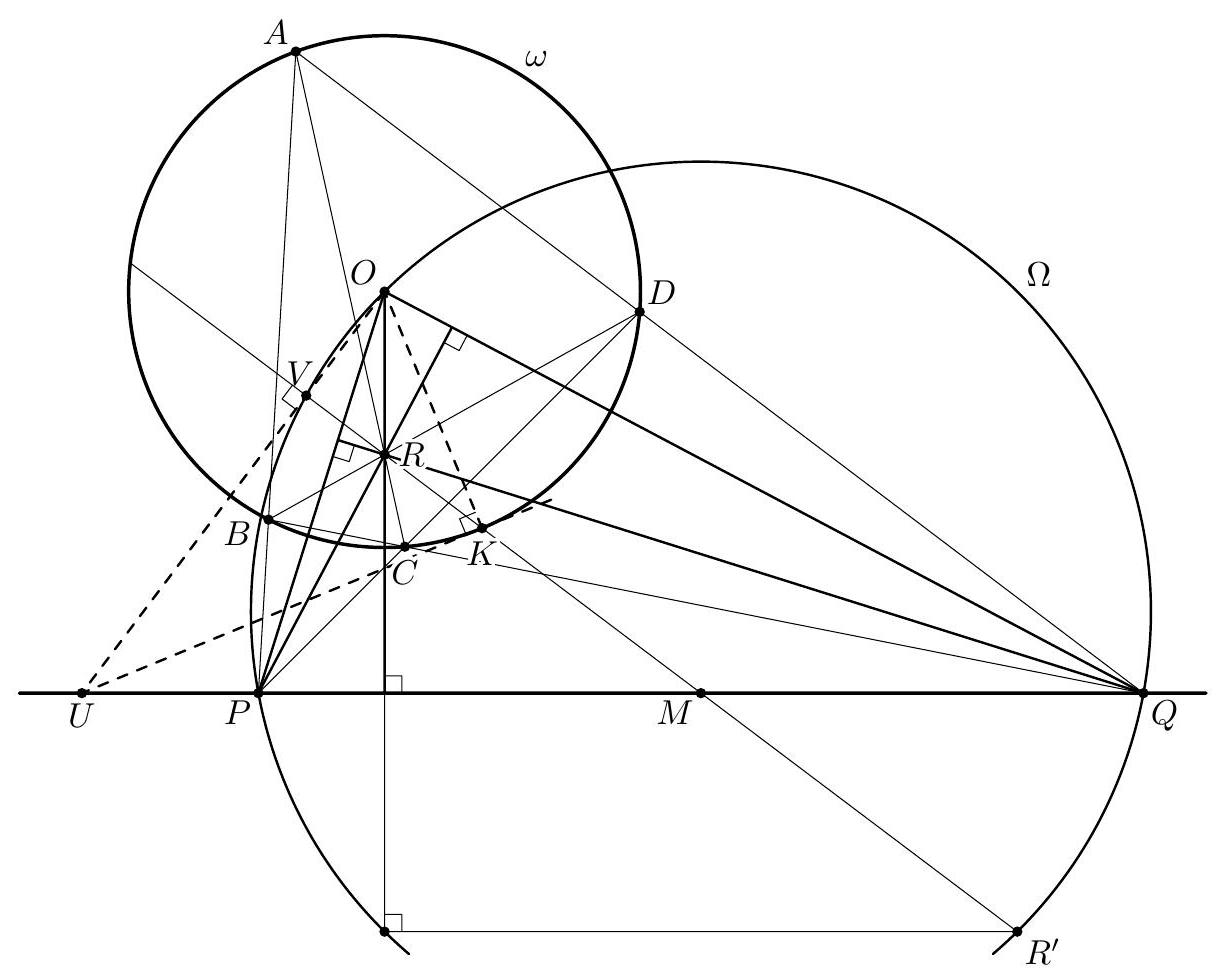
Remark. The statement of the problem is still true if $K$ is the other common point of the line $M R$ and $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$. The lines $A B$ and $C D$ meet at $P$, the lines $A D$ and $B C$ meet at $Q$, and the diagonals $A C$ and $B D$ meet at $R$. Let $M$ be the midpoint of the segment $P Q$, and let $K$ be the common point of the segment $M R$ and the circle $\omega$. Prove that the circumcircle of the triangle $K P Q$ and $\omega$ are tangent to one another.
(Russia) MedeubeK Kungozhin
|
Let $O$ be the centre of $\omega$. Notice that the points $P, Q$, and $R$ are the poles (with respect to $\omega$ ) of the lines $Q R, R P$, and $P Q$, respectively. Hence we have $O P \perp Q R, O Q \perp R P$, and $O R \perp P Q$, thus $R$ is the orthocentre of the triangle $O P Q$. Now, if $M R \perp P Q$, then the points $P$ and $Q$ are the reflections of one another in the line $M R=M O$, and the triangle $P Q K$ is symmetrical with respect to this line. In this case the statement of the problem is trivial.
Otherwise, let $V$ be the foot of the perpendicular from $O$ to $M R$, and let $U$ be the common point of the lines $O V$ and $P Q$. Since $U$ lies on the polar line of $R$ and $O U \perp M R$, we obtain that $U$ is the pole of $M R$. Therefore, the line $U K$ is tangent to $\omega$. Hence it is enough to prove that $U K^{2}=U P \cdot U Q$, since this relation implies that $U K$ is also tangent to the circle $K P Q$.
From the rectangular triangle $O K U$, we get $U K^{2}=U V \cdot U O$. Let $\Omega$ be the circumcircle of triangle $O P Q$, and let $R^{\prime}$ be the reflection of its orthocentre $R$ in the midpoint $M$ of the side $P Q$. It is well known that $R^{\prime}$ is the point of $\Omega$ opposite to $O$, hence $O R^{\prime}$ is the diameter of $\Omega$. Finally, since $\angle O V R^{\prime}=90^{\circ}$, the point $V$ also lies on $\Omega$, hence $U P \cdot U Q=U V \cdot U O=U K^{2}$, as required.

Remark. The statement of the problem is still true if $K$ is the other common point of the line $M R$ and $\omega$.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
d80ad034-8c6c-57c4-8ac7-d86ab501cdaa
| 605,605
|
Let $P$ and $P^{\prime}$ be two convex quadrilateral regions in the plane (regions contain their boundary). Let them intersect, with $O$ a point in the intersection. Suppose that for every line $\ell$ through $O$ the segment $\ell \cap P$ is strictly longer than the segment $\ell \cap P^{\prime}$. Is it possible that the ratio of the area of $P^{\prime}$ to the area of $P$ is greater than 1.9?
(Bulgaria) Nikolai Beluhov
|
The answer is in the affirmative: Given a positive $\epsilon<2$, the ratio in question may indeed be greater than $2-\epsilon$.
To show this, consider a square $A B C D$ centred at $O$, and let $A^{\prime}, B^{\prime}$, and $C^{\prime}$ be the reflections of $O$ in $A, B$, and $C$, respectively. Notice that, if $\ell$ is a line through $O$, then the segments $\ell \cap A B C D$ and $\ell \cap A^{\prime} B^{\prime} C^{\prime}$ have equal lengths, unless $\ell$ is the line $A C$.
Next, consider the points $M$ and $N$ on the segments $B^{\prime} A^{\prime}$ and $B^{\prime} C^{\prime}$, respectively, such that $B^{\prime} M / B^{\prime} A^{\prime}=B^{\prime} N / B^{\prime} C^{\prime}=(1-\epsilon / 4)^{1 / 2}$. Finally, let $P^{\prime}$ be the image of the convex quadrangle $B^{\prime} M O N$ under the homothety of ratio $(1-\epsilon / 4)^{1 / 4}$ centred at $O$. Clearly, the quadrangles $P \equiv A B C D$ and $P^{\prime}$ satisfy the conditions in the statement, and the ratio of the area of $P^{\prime}$ to the area of $P$ is exactly $2-\epsilon / 2$.
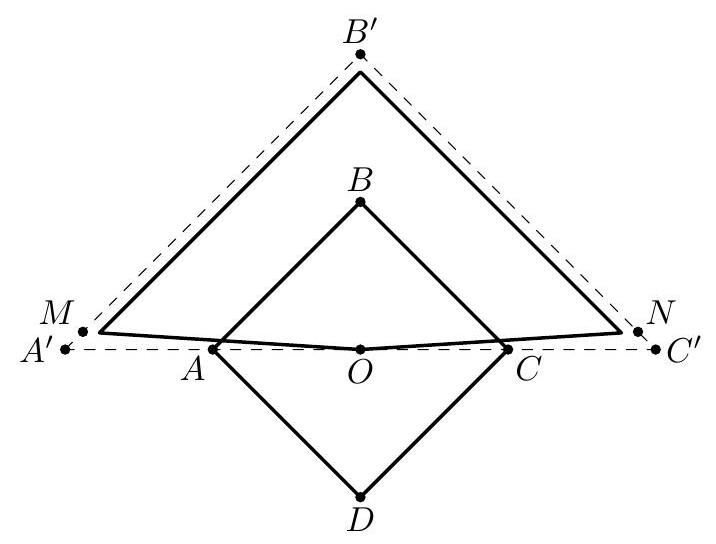
Remarks. (1) With some care, one may also construct such example with a point $O$ being interior for both $P$ and $P^{\prime}$. In our example, it is enough to replace vertex $O$ of $P^{\prime}$ by a point on the segment $O D$ close enough to $O$. The details are left to the reader.
(2) On the other hand, one may show that the ratio of areas of $P^{\prime}$ and $P$ cannot exceed 2 (even if $P$ and $P^{\prime}$ are arbitrary convex polygons rather than quadrilaterals). Further on, we denote by $[S]$ the area of $S$.
In order to see that $\left[P^{\prime}\right]<2[P]$, let us fix some ray $r$ from $O$, and let $r_{\alpha}$ be the ray from $O$ making an (oriented) angle $\alpha$ with $r$. Denote by $X_{\alpha}$ and $Y_{\alpha}$ the points of $P$ and $P^{\prime}$, respectively, lying on $r_{\alpha}$ farthest from $O$, and denote by $f(\alpha)$ and $g(\alpha)$ the lengths of the segments $O X_{\alpha}$ and $O Y_{\alpha}$, respectively. Then
$$
[P]=\frac{1}{2} \int_{0}^{2 \pi} f^{2}(\alpha) d \alpha=\frac{1}{2} \int_{0}^{\pi}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right) d \alpha
$$
and similarly
$$
\left[P^{\prime}\right]=\frac{1}{2} \int_{0}^{\pi}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right) d \alpha
$$
But $X_{\alpha} X_{\pi+\alpha}>Y_{\alpha} Y_{\pi+\alpha}$ yields $2 \cdot \frac{1}{2}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right)=O X_{\alpha}^{2}+O X_{\pi+\alpha}^{2} \geq \frac{1}{2} X_{\alpha} X_{\pi+\alpha}^{2}>$ $\frac{1}{2} Y_{\alpha} Y_{\pi+\alpha}^{2} \geq \frac{1}{2}\left(O Y_{\alpha}^{2}+O Y_{\pi+\alpha}^{2}\right)=\frac{1}{2}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right)$. Integration then gives us $2[P]>\left[P^{\prime}\right]$, as needed.
This can also be proved via elementary methods. Actually, we will establish the following more general fact.
Fact. Let $P=A_{1} A_{2} A_{3} A_{4}$ and $P^{\prime}=B_{1} B_{2} B_{3} B_{4}$ be two convex quadrangles in the plane, and let $O$ be one of their common points different from the vertices of $P^{\prime}$. Denote by $\ell_{i}$ the line $O B_{i}$, and assume that for every $i=1,2,3,4$ the length of segment $\ell_{i} \cap P$ is greater than the length of segment $\ell_{i} \cap P^{\prime}$. Then $\left[P^{\prime}\right]<2[P]$.
Proof. One of (possibly degenerate) quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{1} B_{4} B_{3}$ is convex; the same holds for $O B_{2} B_{3} B_{4}$ and $O B_{2} B_{1} B_{4}$. Without loss of generality, we may (and will) assume that the quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{2} B_{3} B_{4}$ are convex.
Denote by $C_{i}$ such a point that $\ell_{i} \cap P^{\prime}$ is the segment $B_{i} C_{i}$; let $a_{i}$ be the length of $\ell_{i} \cap P$, and let $\alpha_{i}$ be the angle between $\ell_{i}$ and $\ell_{i+1}$ (hereafter, we use the cyclic notation, thus $\ell_{5}=\ell_{1}$ and so on). Thus $C_{2}$ and $C_{3}$ belong to the segment $B_{1} B_{4}, C_{1}$ lies on $B_{3} B_{4}$, and $C_{4}$ lies on $B_{1} B_{2}$. Assume that there exists an index $i$ such that the area of $B_{i} B_{i+1} C_{i} C_{i+1}$ is at least $\left[P^{\prime}\right] / 2$; then we have
$$
\frac{\left[P^{\prime}\right]}{2} \leq\left[B_{i} B_{i+1} C_{i} C_{i+1}\right]=\frac{B_{i} C_{i} \cdot B_{i+1} C_{i+1} \cdot \sin \alpha_{i}}{2}<\frac{a_{i} a_{i+1} \sin \alpha_{i}}{2} \leq[P]
$$
as desired. Assume, to the contrary, that such index does not exist. Two cases are possible.
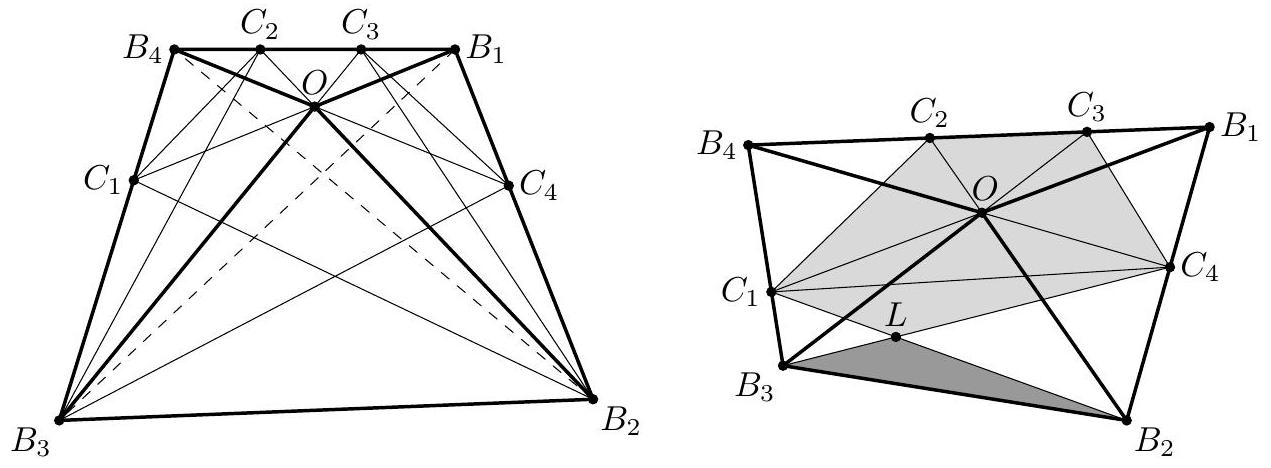
Case 1. Assume that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ do not intersect (see the left figure above). This means, in particular, that $d\left(B_{1}, B_{3} B_{4}\right) \leq d\left(B_{2}, B_{3} B_{4}\right)$.
Since the ray $B_{3} O$ lies in the angle $B_{1} B_{3} B_{4}$, we obtain $d\left(B_{1}, B_{3} C_{3}\right) \leq d\left(C_{4}, B_{3} C_{3}\right)$; hence $\left[B_{3} B_{4} B_{1}\right] \leq\left[B_{3} B_{4} C_{3} C_{4}\right]<\left[P^{\prime}\right] / 2$. Similarly, $\left[B_{1} B_{2} B_{4}\right] \leq\left[B_{1} B_{2} C_{1} C_{2}\right]<\left[P^{\prime}\right] / 2$. Thus,
$$
\begin{aligned}
{\left[B_{2} B_{3} C_{2} C_{3}\right] } & =\left[P^{\prime}\right]-\left[B_{1} B_{2} C_{3}\right]-\left[B_{3} B_{4} C_{2}\right]=\left[P^{\prime}\right]-\frac{B_{1} C_{3}}{B_{1} B_{4}} \cdot\left[B_{1} B_{2} B_{4}\right]-\frac{B_{4} C_{2}}{B_{1} B_{4}} \cdot\left[B_{3} B_{4} B_{1}\right] \\
& >\left[P^{\prime}\right]\left(1-\frac{B_{1} C_{3}+B_{4} C_{2}}{2 B_{1} B_{4}}\right) \geq \frac{\left[P^{\prime}\right]}{2} .
\end{aligned}
$$
A contradiction.
Case 2. Assume now that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ intersect at some point (see the right figure above). Denote by $L$ the common point of $B_{2} C_{1}$ and $B_{3} C_{4}$. We have $\left[B_{2} C_{4} C_{1}\right] \geq\left[B_{2} C_{4} B_{3}\right]$, hence $\left[C_{1} C_{4} L\right] \geq\left[B_{2} B_{3} L\right]$. Thus we have
$$
\begin{aligned}
{\left[P^{\prime}\right]>\left[B_{1} B_{2} C_{1} C_{2}\right]+\left[B_{3} B_{4} C_{3} C_{4}\right] } & =\left[P^{\prime}\right]+\left[L C_{1} C_{2} C_{3} C_{4}\right]-\left[B_{2} B_{3} L\right] \\
& \geq\left[P^{\prime}\right]+\left[C_{1} C_{4} L\right]-\left[B_{2} B_{3} L\right] \geq\left[P^{\prime}\right] .
\end{aligned}
$$
A final contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ and $P^{\prime}$ be two convex quadrilateral regions in the plane (regions contain their boundary). Let them intersect, with $O$ a point in the intersection. Suppose that for every line $\ell$ through $O$ the segment $\ell \cap P$ is strictly longer than the segment $\ell \cap P^{\prime}$. Is it possible that the ratio of the area of $P^{\prime}$ to the area of $P$ is greater than 1.9?
(Bulgaria) Nikolai Beluhov
|
The answer is in the affirmative: Given a positive $\epsilon<2$, the ratio in question may indeed be greater than $2-\epsilon$.
To show this, consider a square $A B C D$ centred at $O$, and let $A^{\prime}, B^{\prime}$, and $C^{\prime}$ be the reflections of $O$ in $A, B$, and $C$, respectively. Notice that, if $\ell$ is a line through $O$, then the segments $\ell \cap A B C D$ and $\ell \cap A^{\prime} B^{\prime} C^{\prime}$ have equal lengths, unless $\ell$ is the line $A C$.
Next, consider the points $M$ and $N$ on the segments $B^{\prime} A^{\prime}$ and $B^{\prime} C^{\prime}$, respectively, such that $B^{\prime} M / B^{\prime} A^{\prime}=B^{\prime} N / B^{\prime} C^{\prime}=(1-\epsilon / 4)^{1 / 2}$. Finally, let $P^{\prime}$ be the image of the convex quadrangle $B^{\prime} M O N$ under the homothety of ratio $(1-\epsilon / 4)^{1 / 4}$ centred at $O$. Clearly, the quadrangles $P \equiv A B C D$ and $P^{\prime}$ satisfy the conditions in the statement, and the ratio of the area of $P^{\prime}$ to the area of $P$ is exactly $2-\epsilon / 2$.

Remarks. (1) With some care, one may also construct such example with a point $O$ being interior for both $P$ and $P^{\prime}$. In our example, it is enough to replace vertex $O$ of $P^{\prime}$ by a point on the segment $O D$ close enough to $O$. The details are left to the reader.
(2) On the other hand, one may show that the ratio of areas of $P^{\prime}$ and $P$ cannot exceed 2 (even if $P$ and $P^{\prime}$ are arbitrary convex polygons rather than quadrilaterals). Further on, we denote by $[S]$ the area of $S$.
In order to see that $\left[P^{\prime}\right]<2[P]$, let us fix some ray $r$ from $O$, and let $r_{\alpha}$ be the ray from $O$ making an (oriented) angle $\alpha$ with $r$. Denote by $X_{\alpha}$ and $Y_{\alpha}$ the points of $P$ and $P^{\prime}$, respectively, lying on $r_{\alpha}$ farthest from $O$, and denote by $f(\alpha)$ and $g(\alpha)$ the lengths of the segments $O X_{\alpha}$ and $O Y_{\alpha}$, respectively. Then
$$
[P]=\frac{1}{2} \int_{0}^{2 \pi} f^{2}(\alpha) d \alpha=\frac{1}{2} \int_{0}^{\pi}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right) d \alpha
$$
and similarly
$$
\left[P^{\prime}\right]=\frac{1}{2} \int_{0}^{\pi}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right) d \alpha
$$
But $X_{\alpha} X_{\pi+\alpha}>Y_{\alpha} Y_{\pi+\alpha}$ yields $2 \cdot \frac{1}{2}\left(f^{2}(\alpha)+f^{2}(\pi+\alpha)\right)=O X_{\alpha}^{2}+O X_{\pi+\alpha}^{2} \geq \frac{1}{2} X_{\alpha} X_{\pi+\alpha}^{2}>$ $\frac{1}{2} Y_{\alpha} Y_{\pi+\alpha}^{2} \geq \frac{1}{2}\left(O Y_{\alpha}^{2}+O Y_{\pi+\alpha}^{2}\right)=\frac{1}{2}\left(g^{2}(\alpha)+g^{2}(\pi+\alpha)\right)$. Integration then gives us $2[P]>\left[P^{\prime}\right]$, as needed.
This can also be proved via elementary methods. Actually, we will establish the following more general fact.
Fact. Let $P=A_{1} A_{2} A_{3} A_{4}$ and $P^{\prime}=B_{1} B_{2} B_{3} B_{4}$ be two convex quadrangles in the plane, and let $O$ be one of their common points different from the vertices of $P^{\prime}$. Denote by $\ell_{i}$ the line $O B_{i}$, and assume that for every $i=1,2,3,4$ the length of segment $\ell_{i} \cap P$ is greater than the length of segment $\ell_{i} \cap P^{\prime}$. Then $\left[P^{\prime}\right]<2[P]$.
Proof. One of (possibly degenerate) quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{1} B_{4} B_{3}$ is convex; the same holds for $O B_{2} B_{3} B_{4}$ and $O B_{2} B_{1} B_{4}$. Without loss of generality, we may (and will) assume that the quadrilaterals $O B_{1} B_{2} B_{3}$ and $O B_{2} B_{3} B_{4}$ are convex.
Denote by $C_{i}$ such a point that $\ell_{i} \cap P^{\prime}$ is the segment $B_{i} C_{i}$; let $a_{i}$ be the length of $\ell_{i} \cap P$, and let $\alpha_{i}$ be the angle between $\ell_{i}$ and $\ell_{i+1}$ (hereafter, we use the cyclic notation, thus $\ell_{5}=\ell_{1}$ and so on). Thus $C_{2}$ and $C_{3}$ belong to the segment $B_{1} B_{4}, C_{1}$ lies on $B_{3} B_{4}$, and $C_{4}$ lies on $B_{1} B_{2}$. Assume that there exists an index $i$ such that the area of $B_{i} B_{i+1} C_{i} C_{i+1}$ is at least $\left[P^{\prime}\right] / 2$; then we have
$$
\frac{\left[P^{\prime}\right]}{2} \leq\left[B_{i} B_{i+1} C_{i} C_{i+1}\right]=\frac{B_{i} C_{i} \cdot B_{i+1} C_{i+1} \cdot \sin \alpha_{i}}{2}<\frac{a_{i} a_{i+1} \sin \alpha_{i}}{2} \leq[P]
$$
as desired. Assume, to the contrary, that such index does not exist. Two cases are possible.

Case 1. Assume that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ do not intersect (see the left figure above). This means, in particular, that $d\left(B_{1}, B_{3} B_{4}\right) \leq d\left(B_{2}, B_{3} B_{4}\right)$.
Since the ray $B_{3} O$ lies in the angle $B_{1} B_{3} B_{4}$, we obtain $d\left(B_{1}, B_{3} C_{3}\right) \leq d\left(C_{4}, B_{3} C_{3}\right)$; hence $\left[B_{3} B_{4} B_{1}\right] \leq\left[B_{3} B_{4} C_{3} C_{4}\right]<\left[P^{\prime}\right] / 2$. Similarly, $\left[B_{1} B_{2} B_{4}\right] \leq\left[B_{1} B_{2} C_{1} C_{2}\right]<\left[P^{\prime}\right] / 2$. Thus,
$$
\begin{aligned}
{\left[B_{2} B_{3} C_{2} C_{3}\right] } & =\left[P^{\prime}\right]-\left[B_{1} B_{2} C_{3}\right]-\left[B_{3} B_{4} C_{2}\right]=\left[P^{\prime}\right]-\frac{B_{1} C_{3}}{B_{1} B_{4}} \cdot\left[B_{1} B_{2} B_{4}\right]-\frac{B_{4} C_{2}}{B_{1} B_{4}} \cdot\left[B_{3} B_{4} B_{1}\right] \\
& >\left[P^{\prime}\right]\left(1-\frac{B_{1} C_{3}+B_{4} C_{2}}{2 B_{1} B_{4}}\right) \geq \frac{\left[P^{\prime}\right]}{2} .
\end{aligned}
$$
A contradiction.
Case 2. Assume now that the rays $B_{1} B_{2}$ and $B_{4} B_{3}$ intersect at some point (see the right figure above). Denote by $L$ the common point of $B_{2} C_{1}$ and $B_{3} C_{4}$. We have $\left[B_{2} C_{4} C_{1}\right] \geq\left[B_{2} C_{4} B_{3}\right]$, hence $\left[C_{1} C_{4} L\right] \geq\left[B_{2} B_{3} L\right]$. Thus we have
$$
\begin{aligned}
{\left[P^{\prime}\right]>\left[B_{1} B_{2} C_{1} C_{2}\right]+\left[B_{3} B_{4} C_{3} C_{4}\right] } & =\left[P^{\prime}\right]+\left[L C_{1} C_{2} C_{3} C_{4}\right]-\left[B_{2} B_{3} L\right] \\
& \geq\left[P^{\prime}\right]+\left[C_{1} C_{4} L\right]-\left[B_{2} B_{3} L\right] \geq\left[P^{\prime}\right] .
\end{aligned}
$$
A final contradiction.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
b7affc7d-7f3c-50f9-a3d6-7b4c780d79bb
| 605,621
|
Given an integer $k \geq 2$, set $a_{1}=1$ and, for every integer $n \geq 2$, let $a_{n}$ be the smallest $x>a_{n-1}$ such that:
$$
x=1+\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor .
$$
Prove that every prime occurs in the sequence $a_{1}, a_{2}, \ldots$.
(Bulgaria) Alexander Ivanov
|
. We prove that the $a_{n}$ are precisely the $k$ th-power-free positive integers, that is, those divisible by the $k$ th power of no prime. The conclusion then follows.
Let $B$ denote the set of all $k$ th-power-free positive integers. We first show that, given a positive integer $c$,
$$
\sum_{b \in B, b \leq c}\left\lfloor\sqrt[k]{\frac{c}{b}}\right\rfloor=c
$$
To this end, notice that every positive integer has a unique representation as a product of an element in $B$ and a $k$ th power. Consequently, the set of all positive integers less than or equal to $c$ splits into
$$
C_{b}=\left\{x: x \in \mathbb{Z}_{>0}, x \leq c, \text { and } x / b \text { is a } k \text { th power }\right\}, \quad b \in B, b \leq c .
$$
Clearly, $\left|C_{b}\right|=\lfloor\sqrt[k]{c / b}\rfloor$, whence the desired equality.
Finally, enumerate $B$ according to the natural order: $1=b_{1}<b_{2}<\cdots<b_{n}<\cdots$. We prove by induction on $n$ that $a_{n}=b_{n}$. Clearly, $a_{1}=b_{1}=1$, so let $n \geq 2$ and assume $a_{m}=b_{m}$ for all indices $m<n$. Since $b_{n}>b_{n-1}=a_{n-1}$ and
$$
b_{n}=\sum_{i=1}^{n}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor+1=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{a_{i}}}\right\rfloor+1
$$
the definition of $a_{n}$ forces $a_{n} \leq b_{n}$. Were $a_{n}<b_{n}$, a contradiction would follow:
$$
a_{n}=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{a_{i}}}\right\rfloor=a_{n}-1
$$
Consequently, $a_{n}=b_{n}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given an integer $k \geq 2$, set $a_{1}=1$ and, for every integer $n \geq 2$, let $a_{n}$ be the smallest $x>a_{n-1}$ such that:
$$
x=1+\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor .
$$
Prove that every prime occurs in the sequence $a_{1}, a_{2}, \ldots$.
(Bulgaria) Alexander Ivanov
|
. We prove that the $a_{n}$ are precisely the $k$ th-power-free positive integers, that is, those divisible by the $k$ th power of no prime. The conclusion then follows.
Let $B$ denote the set of all $k$ th-power-free positive integers. We first show that, given a positive integer $c$,
$$
\sum_{b \in B, b \leq c}\left\lfloor\sqrt[k]{\frac{c}{b}}\right\rfloor=c
$$
To this end, notice that every positive integer has a unique representation as a product of an element in $B$ and a $k$ th power. Consequently, the set of all positive integers less than or equal to $c$ splits into
$$
C_{b}=\left\{x: x \in \mathbb{Z}_{>0}, x \leq c, \text { and } x / b \text { is a } k \text { th power }\right\}, \quad b \in B, b \leq c .
$$
Clearly, $\left|C_{b}\right|=\lfloor\sqrt[k]{c / b}\rfloor$, whence the desired equality.
Finally, enumerate $B$ according to the natural order: $1=b_{1}<b_{2}<\cdots<b_{n}<\cdots$. We prove by induction on $n$ that $a_{n}=b_{n}$. Clearly, $a_{1}=b_{1}=1$, so let $n \geq 2$ and assume $a_{m}=b_{m}$ for all indices $m<n$. Since $b_{n}>b_{n-1}=a_{n-1}$ and
$$
b_{n}=\sum_{i=1}^{n}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{b_{i}}}\right\rfloor+1=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{b_{n}}{a_{i}}}\right\rfloor+1
$$
the definition of $a_{n}$ forces $a_{n} \leq b_{n}$. Were $a_{n}<b_{n}$, a contradiction would follow:
$$
a_{n}=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{b_{i}}}\right\rfloor=\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{a_{n}}{a_{i}}}\right\rfloor=a_{n}-1
$$
Consequently, $a_{n}=b_{n}$. This completes the proof.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1"
}
|
09f5abf9-be1a-54f2-be64-cb24cac952ef
| 605,634
|
Given an integer $k \geq 2$, set $a_{1}=1$ and, for every integer $n \geq 2$, let $a_{n}$ be the smallest $x>a_{n-1}$ such that:
$$
x=1+\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor .
$$
Prove that every prime occurs in the sequence $a_{1}, a_{2}, \ldots$.
(Bulgaria) Alexander Ivanov
|
. (Ilya Bogdanov) For every $n=1,2,3, \ldots$, introduce the function
$$
f_{n}(x)=x-1-\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor
$$
Denote also by $g_{n}(x)$ the number of the indices $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer. Then $f_{n}(x+1)-f_{n}(x)=1-g_{n}(x)$ for every integer $x \geq a_{n}$; hence $f_{n}(x)+1 \geq f_{n}(x+1)$. Moreover, $f_{n}\left(a_{n-1}\right)=-1$ (since $f_{n-1}\left(a_{n-1}\right)=0$ ). Now a straightforward induction shows that $f_{n}(x)<0$ for all integers $x \in\left[a_{n-1}, a_{n}\right)$.
Next, if $g_{n}(x)>0$ then $f_{n}(x) \leq f_{n}(x-1)$; this means that such an $x$ cannot equal $a_{n}$. Thus $a_{j} / a_{i}$ is never the $k$ th power of an integer if $j>i$.
Now we are prepared to prove by induction on $n$ that $a_{1}, a_{2}, \ldots, a_{n}$ are exactly all $k$ th-power-free integers in $\left[1, a_{n}\right]$. The base case $n=1$ is trivial.
Assume that all the $k$ th-power-free integers on $\left[1, a_{n}\right]$ are exactly $a_{1}, \ldots, a_{n}$. Let $b$ be the least integer larger than $a_{n}$ such that $g_{n}(b)=0$. We claim that: (1) $b=a_{n+1}$; and (2) $b$ is the least $k$ th-power-free number greater than $a_{n}$.
To prove (1), notice first that all the numbers of the form $a_{j} / a_{i}$ with $1 \leq i<j \leq n$ are not $k$ th powers of rational numbers since $a_{i}$ and $a_{j}$ are $k$ th-power-free. This means that for every integer $x \in\left(a_{n}, b\right)$ there exists exactly one index $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer (certainly, $x$ is not $k$ th-power-free). Hence $f_{n+1}(x)=f_{n+1}(x-1)$ for each such $x$, so $f_{n+1}(b-1)=f_{n+1}\left(a_{n}\right)=-1$. Next, since $b / a_{i}$ is not the $k$ th power of an integer, we have $f_{n+1}(b)=f_{n+1}(b-1)+1=0$, thus $b=a_{n+1}$. This establishes (1).
Finally, since all integers in $\left(a_{n}, b\right)$ are not $k$ th-power-free, we are left to prove that $b$ is $k$ th-power-free to establish (2). Otherwise, let $y>1$ be the greatest integer such that $y^{k} \mid b$; then $b / y^{k}$ is $k$ th-power-free and hence $b / y^{k}=a_{i}$ for some $i \leq n$. So $b / a_{i}$ is the $k$ th power of an integer, which contradicts the definition of $b$.
Thus $a_{1}, a_{2}, \ldots$ are exactly all $k$ th-power-free positive integers; consequently all primes are contained in this sequence.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given an integer $k \geq 2$, set $a_{1}=1$ and, for every integer $n \geq 2$, let $a_{n}$ be the smallest $x>a_{n-1}$ such that:
$$
x=1+\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor .
$$
Prove that every prime occurs in the sequence $a_{1}, a_{2}, \ldots$.
(Bulgaria) Alexander Ivanov
|
. (Ilya Bogdanov) For every $n=1,2,3, \ldots$, introduce the function
$$
f_{n}(x)=x-1-\sum_{i=1}^{n-1}\left\lfloor\sqrt[k]{\frac{x}{a_{i}}}\right\rfloor
$$
Denote also by $g_{n}(x)$ the number of the indices $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer. Then $f_{n}(x+1)-f_{n}(x)=1-g_{n}(x)$ for every integer $x \geq a_{n}$; hence $f_{n}(x)+1 \geq f_{n}(x+1)$. Moreover, $f_{n}\left(a_{n-1}\right)=-1$ (since $f_{n-1}\left(a_{n-1}\right)=0$ ). Now a straightforward induction shows that $f_{n}(x)<0$ for all integers $x \in\left[a_{n-1}, a_{n}\right)$.
Next, if $g_{n}(x)>0$ then $f_{n}(x) \leq f_{n}(x-1)$; this means that such an $x$ cannot equal $a_{n}$. Thus $a_{j} / a_{i}$ is never the $k$ th power of an integer if $j>i$.
Now we are prepared to prove by induction on $n$ that $a_{1}, a_{2}, \ldots, a_{n}$ are exactly all $k$ th-power-free integers in $\left[1, a_{n}\right]$. The base case $n=1$ is trivial.
Assume that all the $k$ th-power-free integers on $\left[1, a_{n}\right]$ are exactly $a_{1}, \ldots, a_{n}$. Let $b$ be the least integer larger than $a_{n}$ such that $g_{n}(b)=0$. We claim that: (1) $b=a_{n+1}$; and (2) $b$ is the least $k$ th-power-free number greater than $a_{n}$.
To prove (1), notice first that all the numbers of the form $a_{j} / a_{i}$ with $1 \leq i<j \leq n$ are not $k$ th powers of rational numbers since $a_{i}$ and $a_{j}$ are $k$ th-power-free. This means that for every integer $x \in\left(a_{n}, b\right)$ there exists exactly one index $i \leq n$ such that $x / a_{i}$ is the $k$ th power of an integer (certainly, $x$ is not $k$ th-power-free). Hence $f_{n+1}(x)=f_{n+1}(x-1)$ for each such $x$, so $f_{n+1}(b-1)=f_{n+1}\left(a_{n}\right)=-1$. Next, since $b / a_{i}$ is not the $k$ th power of an integer, we have $f_{n+1}(b)=f_{n+1}(b-1)+1=0$, thus $b=a_{n+1}$. This establishes (1).
Finally, since all integers in $\left(a_{n}, b\right)$ are not $k$ th-power-free, we are left to prove that $b$ is $k$ th-power-free to establish (2). Otherwise, let $y>1$ be the greatest integer such that $y^{k} \mid b$; then $b / y^{k}$ is $k$ th-power-free and hence $b / y^{k}=a_{i}$ for some $i \leq n$. So $b / a_{i}$ is the $k$ th power of an integer, which contradicts the definition of $b$.
Thus $a_{1}, a_{2}, \ldots$ are exactly all $k$ th-power-free positive integers; consequently all primes are contained in this sequence.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 2"
}
|
09f5abf9-be1a-54f2-be64-cb24cac952ef
| 605,634
|
$2 n$ distinct tokens are placed at the vertices of a regular $2 n$-gon, with one token placed at each vertex. A move consists of choosing an edge of the $2 n$-gon and interchanging the two tokens at the endpoints of that edge. Suppose that after a finite number of moves, every pair of tokens have been interchanged exactly once. Prove that some edge has never been chosen.
(Russia) Alexander Gribalko
|
Step 1. Enumerate all the tokens in the initial arrangement in clockwise circular order; also enumerate the vertices of the $2 n$-gon accordingly. Consider any three tokens $i<j<k$. At each moment, their cyclic order may be either $i, j, k$ or $i, k, j$, counted clockwise. This order changes exactly when two of these three tokens have been switched. Hence the order has been reversed thrice, and in the final arrangement token $k$ stands on the arc passing clockwise from token $i$ to token $j$. Thus, at the end, token $i+1$ is a counter-clockwise neighbor of token $i$ for all $i=1,2, \ldots, 2 n-1$, so the tokens in the final arrangement are numbered successively in counter-clockwise circular order.
This means that the final arrangement of tokens can be obtained from the initial one by reflection in some line $\ell$.
Step 2. Notice that each token was involved into $2 n-1$ switchings, so its initial and final vertices have different parity. Hence $\ell$ passes through the midpoints of two opposite sides of a $2 n$-gon; we may assume that these are the sides $a$ and $b$ connecting $2 n$ with 1 and $n$ with $n+1$, respectively.
During the process, each token $x$ has crossed $\ell$ at least once; thus one of its switchings has been made at edge $a$ or at edge $b$. Assume that some two its switchings were performed at $a$ and at $b$; we may (and will) assume that the one at $a$ was earlier, and $x \leq n$. Then the total movement of token $x$ consisted at least of: (i) moving from vertex $x$ to $a$ and crossing $\ell$ along $a$; (ii) moving from $a$ to $b$ and crossing $\ell$ along $b$; (iii) coming to vertex $2 n+1-x$. This tales at least $x+n+(n-x)=2 n$ switchings, which is impossible.
Thus, each token had a switching at exactly one of the edges $a$ and $b$.
Step 3. Finally, let us show that either each token has been switched at $a$, or each token has been switched at $b$ (then the other edge has never been used, as desired). To the contrary, assume that there were switchings at both $a$ and at $b$. Consider the first such switchings, and let $x$ and $y$ be the tokens which were moved clockwise during these switchings and crossed $\ell$ at $a$ and $b$, respectively. By Step $2, x \neq y$. Then tokens $x$ and $y$ initially were on opposite sides of $\ell$.
Now consider the switching of tokens $x$ and $y$; there was exactly one such switching, and we assume that it has been made on the same side of $\ell$ as vertex $y$. Then this switching has been made after token $x$ had traced $a$. From this point on, token $x$ is on the clockwise arc from token $y$ to $b$, and it has no way to leave out from this arc. But this is impossible, since token $y$ should trace $b$ after that moment. A contradiction.
Remark. The same statement for $(2 n-1)$-gon is also valid. The problem is stated for a polygon with an even number of sides only to avoid case consideration.
Let us outline the solution in the case of a $(2 n-1)$-gon. We prove the existence of line $\ell$ as in Step 1. This line passes through some vertex $x$, and through the midpoint of the opposite edge $a$. Then each token either passes through $x$, or crosses $\ell$ along $a$ (but not both; this can be shown as in Step 2). Finally, since a token is involved into an even number of moves, it passes through $x$ but not through $a$, and $a$ is never used.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$2 n$ distinct tokens are placed at the vertices of a regular $2 n$-gon, with one token placed at each vertex. A move consists of choosing an edge of the $2 n$-gon and interchanging the two tokens at the endpoints of that edge. Suppose that after a finite number of moves, every pair of tokens have been interchanged exactly once. Prove that some edge has never been chosen.
(Russia) Alexander Gribalko
|
Step 1. Enumerate all the tokens in the initial arrangement in clockwise circular order; also enumerate the vertices of the $2 n$-gon accordingly. Consider any three tokens $i<j<k$. At each moment, their cyclic order may be either $i, j, k$ or $i, k, j$, counted clockwise. This order changes exactly when two of these three tokens have been switched. Hence the order has been reversed thrice, and in the final arrangement token $k$ stands on the arc passing clockwise from token $i$ to token $j$. Thus, at the end, token $i+1$ is a counter-clockwise neighbor of token $i$ for all $i=1,2, \ldots, 2 n-1$, so the tokens in the final arrangement are numbered successively in counter-clockwise circular order.
This means that the final arrangement of tokens can be obtained from the initial one by reflection in some line $\ell$.
Step 2. Notice that each token was involved into $2 n-1$ switchings, so its initial and final vertices have different parity. Hence $\ell$ passes through the midpoints of two opposite sides of a $2 n$-gon; we may assume that these are the sides $a$ and $b$ connecting $2 n$ with 1 and $n$ with $n+1$, respectively.
During the process, each token $x$ has crossed $\ell$ at least once; thus one of its switchings has been made at edge $a$ or at edge $b$. Assume that some two its switchings were performed at $a$ and at $b$; we may (and will) assume that the one at $a$ was earlier, and $x \leq n$. Then the total movement of token $x$ consisted at least of: (i) moving from vertex $x$ to $a$ and crossing $\ell$ along $a$; (ii) moving from $a$ to $b$ and crossing $\ell$ along $b$; (iii) coming to vertex $2 n+1-x$. This tales at least $x+n+(n-x)=2 n$ switchings, which is impossible.
Thus, each token had a switching at exactly one of the edges $a$ and $b$.
Step 3. Finally, let us show that either each token has been switched at $a$, or each token has been switched at $b$ (then the other edge has never been used, as desired). To the contrary, assume that there were switchings at both $a$ and at $b$. Consider the first such switchings, and let $x$ and $y$ be the tokens which were moved clockwise during these switchings and crossed $\ell$ at $a$ and $b$, respectively. By Step $2, x \neq y$. Then tokens $x$ and $y$ initially were on opposite sides of $\ell$.
Now consider the switching of tokens $x$ and $y$; there was exactly one such switching, and we assume that it has been made on the same side of $\ell$ as vertex $y$. Then this switching has been made after token $x$ had traced $a$. From this point on, token $x$ is on the clockwise arc from token $y$ to $b$, and it has no way to leave out from this arc. But this is impossible, since token $y$ should trace $b$ after that moment. A contradiction.
Remark. The same statement for $(2 n-1)$-gon is also valid. The problem is stated for a polygon with an even number of sides only to avoid case consideration.
Let us outline the solution in the case of a $(2 n-1)$-gon. We prove the existence of line $\ell$ as in Step 1. This line passes through some vertex $x$, and through the midpoint of the opposite edge $a$. Then each token either passes through $x$, or crosses $\ell$ along $a$ (but not both; this can be shown as in Step 2). Finally, since a token is involved into an even number of moves, it passes through $x$ but not through $a$, and $a$ is never used.
|
{
"resource_path": "RMM/segmented/en-2013-Solutions2013-2.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution."
}
|
5e10e8cb-06fe-595c-953b-f63a295be65c
| 605,651
|
Does there exist an infinite sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ such that $a_{m}$ and $a_{n}$ are coprime if and only if $|m-n|=1$ ?
(Peru) Jorge Tipe
|
The answer is in the affirmative.
The idea is to consider a sequence of pairwise distinct primes $p_{1}, p_{2}, p_{3}, \ldots$, cover the positive integers by a sequence of finite non-empty sets $I_{n}$ such that $I_{m}$ and $I_{n}$ are disjoint if and only if $m$ and $n$ are one unit apart, and set $a_{n}=\prod_{i \in I_{n}} p_{i}, n=1,2,3, \ldots$.
One possible way of finding such sets is the following. For all positive integers $n$, let
$$
\begin{array}{rlr}
2 n \in I_{k} & \text { for all } k=n, n+3, n+5, n+7, \ldots ; & \text { and } \\
2 n-1 \in I_{k} & & \text { for all } k=n, n+2, n+4, n+6, \ldots
\end{array}
$$
Clearly, each $I_{k}$ is finite, since it contains none of the numbers greater than $2 k$. Next, the number $p_{2 n}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i}$, while the number $p_{2 n-1}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i+1}$ for $i=1,2, \ldots$. Finally, none of the indices appears in two consecutive sets.
Remark. The sets $I_{n}$ from the solution above can explicitly be written as
$$
I_{n}=\{2 n-4 k-1: k=0,1, \ldots,\lfloor(n-1) / 2\rfloor\} \cup\{2 n-4 k-2: k=1,2, \ldots,\lfloor n / 2\rfloor-1\} \cup\{2 n\},
$$
The above construction can alternatively be described as follows: Let $p_{1}, p_{1}^{\prime}, p_{2}, p_{2}^{\prime}, \ldots$, $p_{n}, p_{n}^{\prime}, \ldots$ be a sequence of pairwise distinct primes. With the standard convention that empty products are 1, let
$$
P_{n}= \begin{cases}p_{1} p_{2}^{\prime} p_{3} p_{4}^{\prime} \cdots p_{n-4} p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is odd } \\ p_{1}^{\prime} p_{2} p_{3}^{\prime} p_{4} \cdots p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is even }\end{cases}
$$
and define $a_{n}=P_{n} p_{n} p_{n}^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Does there exist an infinite sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ such that $a_{m}$ and $a_{n}$ are coprime if and only if $|m-n|=1$ ?
(Peru) Jorge Tipe
|
The answer is in the affirmative.
The idea is to consider a sequence of pairwise distinct primes $p_{1}, p_{2}, p_{3}, \ldots$, cover the positive integers by a sequence of finite non-empty sets $I_{n}$ such that $I_{m}$ and $I_{n}$ are disjoint if and only if $m$ and $n$ are one unit apart, and set $a_{n}=\prod_{i \in I_{n}} p_{i}, n=1,2,3, \ldots$.
One possible way of finding such sets is the following. For all positive integers $n$, let
$$
\begin{array}{rlr}
2 n \in I_{k} & \text { for all } k=n, n+3, n+5, n+7, \ldots ; & \text { and } \\
2 n-1 \in I_{k} & & \text { for all } k=n, n+2, n+4, n+6, \ldots
\end{array}
$$
Clearly, each $I_{k}$ is finite, since it contains none of the numbers greater than $2 k$. Next, the number $p_{2 n}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i}$, while the number $p_{2 n-1}$ ensures that $I_{n}$ has a common element with each $I_{n+2 i+1}$ for $i=1,2, \ldots$. Finally, none of the indices appears in two consecutive sets.
Remark. The sets $I_{n}$ from the solution above can explicitly be written as
$$
I_{n}=\{2 n-4 k-1: k=0,1, \ldots,\lfloor(n-1) / 2\rfloor\} \cup\{2 n-4 k-2: k=1,2, \ldots,\lfloor n / 2\rfloor-1\} \cup\{2 n\},
$$
The above construction can alternatively be described as follows: Let $p_{1}, p_{1}^{\prime}, p_{2}, p_{2}^{\prime}, \ldots$, $p_{n}, p_{n}^{\prime}, \ldots$ be a sequence of pairwise distinct primes. With the standard convention that empty products are 1, let
$$
P_{n}= \begin{cases}p_{1} p_{2}^{\prime} p_{3} p_{4}^{\prime} \cdots p_{n-4} p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is odd } \\ p_{1}^{\prime} p_{2} p_{3}^{\prime} p_{4} \cdots p_{n-3}^{\prime} p_{n-2}, & \text { if } n \text { is even }\end{cases}
$$
and define $a_{n}=P_{n} p_{n} p_{n}^{\prime}$.
|
{
"resource_path": "RMM/segmented/en-2015-Solutions_RMM2015-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
7f9159dc-e89f-5528-b920-3c1085c1b23c
| 605,663
|
A finite list of rational numbers is written on a blackboard. In an operation, we choose any two numbers $a, b$, erase them, and write down one of the numbers
$$
a+b, a-b, b-a, a \times b, a / b(\text { if } b \neq 0), b / a(\text { if } a \neq 0) .
$$
Prove that, for every integer $n>100$, there are only finitely many integers $k \geq 0$, such that, starting from the list
$$
k+1, k+2, \ldots, k+n
$$
it is possible to obtain, after $n-1$ operations, the value $n$ !.
(United Kingdom) Alexander Betts
|
We prove the problem statement even for all positive integer $n$.
There are only finitely many ways of constructing a number from $n$ pairwise distinct numbers $x_{1}, \ldots, x_{n}$ only using the four elementary arithmetic operations, and each $x_{k}$ exactly once. Each such formula for $k>1$ is obtained by an elementary operation from two such formulas on two disjoint sets of the $x_{i}$.
A straightforward induction on $n$ shows that the outcome of each such construction is a number of the form
$$
\frac{\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}}{\sum_{\alpha_{1}, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}},
$$
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero of course, $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$, and also $a_{\alpha_{1}, \ldots, \alpha_{n}} \cdot b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices.
Since $\left|a_{\alpha_{1}, \ldots, \alpha_{n}}\right| \leq 1$, and $a_{0,0, \ldots, 0}=0$, the absolute value of the numerator does not exceed $\left(1+\left|x_{1}\right|\right) \cdots\left(1+\left|x_{n}\right|\right)-1$; in particular, if $c$ is an integer in the range $-n, \ldots,-1$, and $x_{k}=c+k$, $k=1, \ldots, n$, then the absolute value of the numerator is at most $(-c)!(n+c+1)!-1 \leq n!-1<n!$.
Consider now the integral polynomials,
$$
P=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
$$
and
$$
Q=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
$$
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero, $a_{\alpha_{1}, \ldots, \alpha_{n}} b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices, and $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$. By the preceding, $|P(c)|<n$ ! for every integer $c$ in the range $-n, \ldots,-1$; and since $b_{1, \ldots, 1}=0$, the degree of $Q$ is less than $n$.
Since every non-zero polynomial has only finitely many roots, and the number of roots does not exceed the degree, to complete the proof it is sufficient to show that the polynomial $P-n!Q$ does not vanish identically, provided that $Q$ does not (which is the case in the problem).
Suppose, if possible, that $P=n!Q$, where $Q \neq 0$. Since $\operatorname{deg} Q<n$, it follows that $\operatorname{deg} P<n$ as well, and since $P \neq 0$, the number of roots of $P$ does not exceed $\operatorname{deg} P<n$, so $P(c) \neq 0$ for some integer $c$ in the range $-n, \ldots,-1$. By the preceding, $|P(c)|$ is consequently a positive integer less than $n!$. On the other hand, $|P(c)|=n!|Q(c)|$ is an integral multiple of $n!$. A contradiction.
Remark. Alternatively, it can be shown by induction on $n$ that
$$
\max (|P(c)|, 2|Q(c)|) \leq \prod_{k=1}^{n} \max (|c+k|, 2)
$$
for all integers $c$. In case $n>8$, this provides a solution along the same lines.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A finite list of rational numbers is written on a blackboard. In an operation, we choose any two numbers $a, b$, erase them, and write down one of the numbers
$$
a+b, a-b, b-a, a \times b, a / b(\text { if } b \neq 0), b / a(\text { if } a \neq 0) .
$$
Prove that, for every integer $n>100$, there are only finitely many integers $k \geq 0$, such that, starting from the list
$$
k+1, k+2, \ldots, k+n
$$
it is possible to obtain, after $n-1$ operations, the value $n$ !.
(United Kingdom) Alexander Betts
|
We prove the problem statement even for all positive integer $n$.
There are only finitely many ways of constructing a number from $n$ pairwise distinct numbers $x_{1}, \ldots, x_{n}$ only using the four elementary arithmetic operations, and each $x_{k}$ exactly once. Each such formula for $k>1$ is obtained by an elementary operation from two such formulas on two disjoint sets of the $x_{i}$.
A straightforward induction on $n$ shows that the outcome of each such construction is a number of the form
$$
\frac{\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}}{\sum_{\alpha_{1}, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}} x_{1}^{\alpha_{1}} \cdots x_{n}^{\alpha_{n}}},
$$
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero of course, $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$, and also $a_{\alpha_{1}, \ldots, \alpha_{n}} \cdot b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices.
Since $\left|a_{\alpha_{1}, \ldots, \alpha_{n}}\right| \leq 1$, and $a_{0,0, \ldots, 0}=0$, the absolute value of the numerator does not exceed $\left(1+\left|x_{1}\right|\right) \cdots\left(1+\left|x_{n}\right|\right)-1$; in particular, if $c$ is an integer in the range $-n, \ldots,-1$, and $x_{k}=c+k$, $k=1, \ldots, n$, then the absolute value of the numerator is at most $(-c)!(n+c+1)!-1 \leq n!-1<n!$.
Consider now the integral polynomials,
$$
P=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} a_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
$$
and
$$
Q=\sum_{\alpha_{1}, \ldots, \alpha_{n} \in\{0,1\}} b_{\alpha_{1}, \ldots, \alpha_{n}}(X+1)^{\alpha_{1}} \cdots(X+n)^{\alpha_{n}}
$$
where the $a_{\alpha_{1}, \ldots, \alpha_{n}}$ and $b_{\alpha_{1}, \ldots, \alpha_{n}}$ are all in the set $\{0, \pm 1\}$, not all zero, $a_{\alpha_{1}, \ldots, \alpha_{n}} b_{\alpha_{1}, \ldots, \alpha_{n}}=0$ for every set of indices, and $a_{0, \ldots, 0}=b_{1, \ldots, 1}=0$. By the preceding, $|P(c)|<n$ ! for every integer $c$ in the range $-n, \ldots,-1$; and since $b_{1, \ldots, 1}=0$, the degree of $Q$ is less than $n$.
Since every non-zero polynomial has only finitely many roots, and the number of roots does not exceed the degree, to complete the proof it is sufficient to show that the polynomial $P-n!Q$ does not vanish identically, provided that $Q$ does not (which is the case in the problem).
Suppose, if possible, that $P=n!Q$, where $Q \neq 0$. Since $\operatorname{deg} Q<n$, it follows that $\operatorname{deg} P<n$ as well, and since $P \neq 0$, the number of roots of $P$ does not exceed $\operatorname{deg} P<n$, so $P(c) \neq 0$ for some integer $c$ in the range $-n, \ldots,-1$. By the preceding, $|P(c)|$ is consequently a positive integer less than $n!$. On the other hand, $|P(c)|=n!|Q(c)|$ is an integral multiple of $n!$. A contradiction.
Remark. Alternatively, it can be shown by induction on $n$ that
$$
\max (|P(c)|, 2|Q(c)|) \leq \prod_{k=1}^{n} \max (|c+k|, 2)
$$
for all integers $c$. In case $n>8$, this provides a solution along the same lines.
|
{
"resource_path": "RMM/segmented/en-2015-Solutions_RMM2015-1.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
c35fd17d-dffb-5335-8216-96a332aa5bb6
| 605,686
|
Let $A B C$ be a triangle, let $D$ be the touchpoint of the side $B C$ and the incircle of the triangle $A B C$, and let $J_{b}$ and $J_{c}$ be the incentres of the triangles $A B D$ and $A C D$, respectively. Prove that the circumcentre of the triangle $A J_{b} J_{c}$ lies on the bisectrix of the angle $B A C$.
(Russia) Fedor Ivlev
|
Let the incircle of the triangle $A B C$ meet $C A$ and $A B$ at points $E$ and $F$, respectively. Let the incircles of the triangles $A B D$ and $A C D$ meet $A D$ at points $X$ and $Y$, respectively. Then $2 D X=D A+D B-A B=D A+D B-B F-A F=D A-A F$; similarly, $2 D Y=D A-A E=2 D X$. Hence the points $X$ and $Y$ coincide, so $J_{b} J_{c} \perp A D$.
Now let $O$ be the circumcentre of the triangle $A J_{b} J_{c}$. Then $\angle J_{b} A O=\pi / 2-\angle A O J_{b} / 2=$ $\pi / 2-\angle A J_{c} J_{b}=\angle X A J_{c}=\frac{1}{2} \angle D A C$. Therefore, $\angle B A O=\angle B A J_{b}+\angle J_{b} A O=\frac{1}{2} \angle B A D+$ $\frac{1}{2} \angle D A C=\frac{1}{2} \angle B A C$, and the conclusion follows.
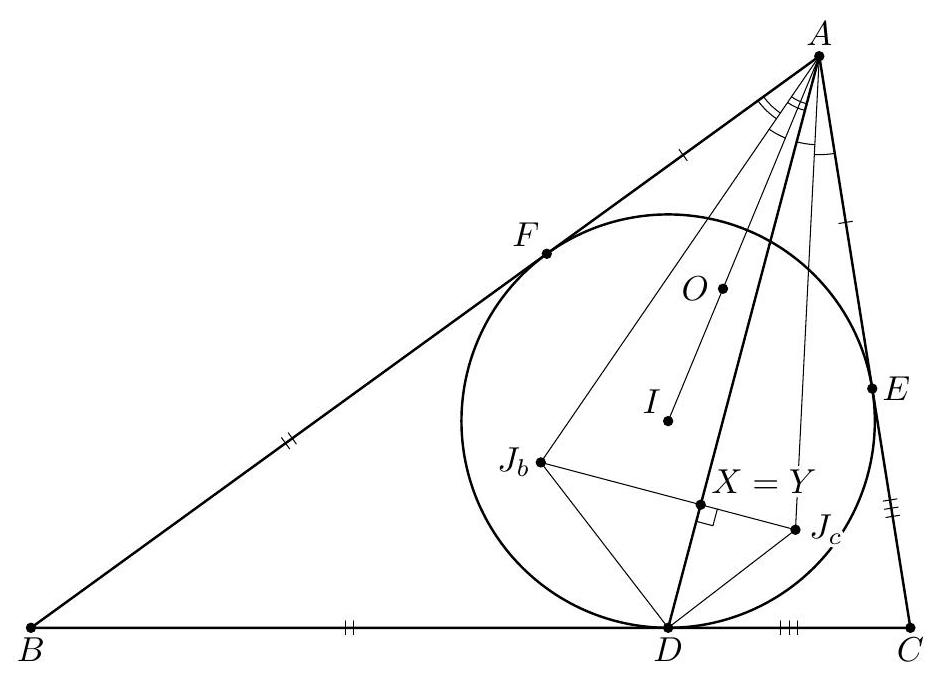
Fig. 1
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, let $D$ be the touchpoint of the side $B C$ and the incircle of the triangle $A B C$, and let $J_{b}$ and $J_{c}$ be the incentres of the triangles $A B D$ and $A C D$, respectively. Prove that the circumcentre of the triangle $A J_{b} J_{c}$ lies on the bisectrix of the angle $B A C$.
(Russia) Fedor Ivlev
|
Let the incircle of the triangle $A B C$ meet $C A$ and $A B$ at points $E$ and $F$, respectively. Let the incircles of the triangles $A B D$ and $A C D$ meet $A D$ at points $X$ and $Y$, respectively. Then $2 D X=D A+D B-A B=D A+D B-B F-A F=D A-A F$; similarly, $2 D Y=D A-A E=2 D X$. Hence the points $X$ and $Y$ coincide, so $J_{b} J_{c} \perp A D$.
Now let $O$ be the circumcentre of the triangle $A J_{b} J_{c}$. Then $\angle J_{b} A O=\pi / 2-\angle A O J_{b} / 2=$ $\pi / 2-\angle A J_{c} J_{b}=\angle X A J_{c}=\frac{1}{2} \angle D A C$. Therefore, $\angle B A O=\angle B A J_{b}+\angle J_{b} A O=\frac{1}{2} \angle B A D+$ $\frac{1}{2} \angle D A C=\frac{1}{2} \angle B A C$, and the conclusion follows.

Fig. 1
|
{
"resource_path": "RMM/segmented/en-2015-Solutions_RMM2015-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
eb66b4a7-6060-5082-ae11-5952d01e5228
| 605,700
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. (Ilya Bogdanov) Let $\sigma$ denote reflection in the line $B C$. Since $\angle B D F=\angle B A C=$ $\angle C D E$, by concyclicity, the lines $D E$ and $D F$ are images of one another under $\sigma$, so the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$. Consequently, the lines $P Q$ and $P^{\prime} Q^{\prime}=\sigma(P Q)$ meet at some (possibly ideal) point $R$ on the line $B C$.
Since the pairs of lines $(C A, Q D),(A B, D P),(B C, P Q)$ meet at three collinear points, namely $P^{\prime}, Q^{\prime}, R$ respectively, the triangles $A B C$ and $D P Q$ are perspective, i.e., the lines $A D, B P, C Q$ are concurrent, by the Desargues theorem.
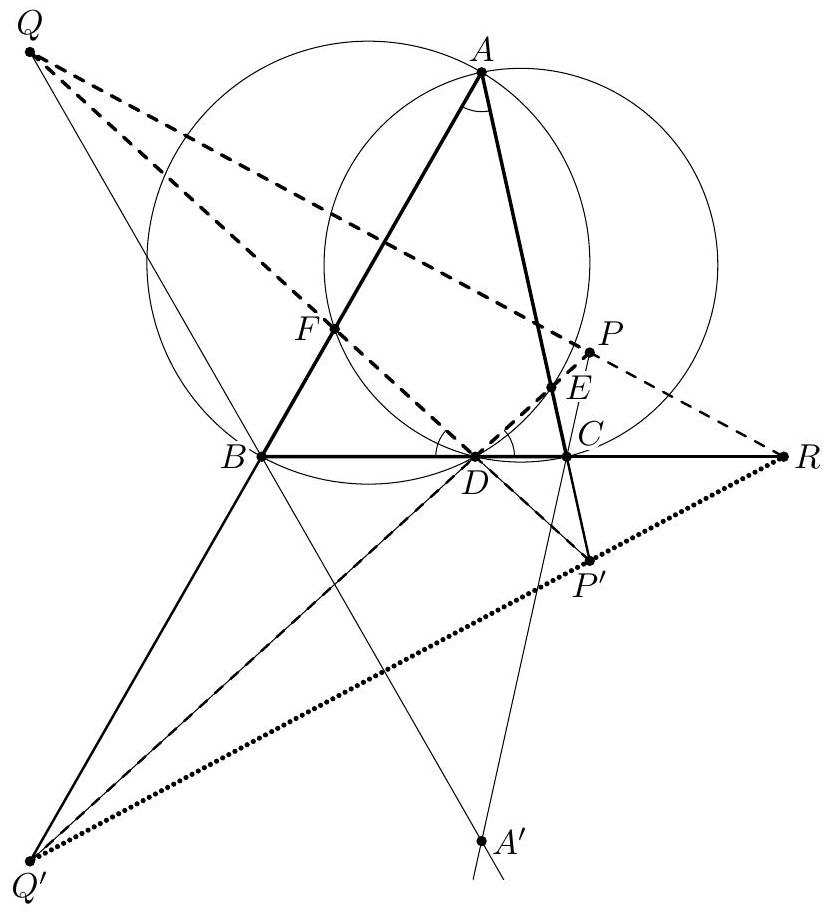
Fig. 1
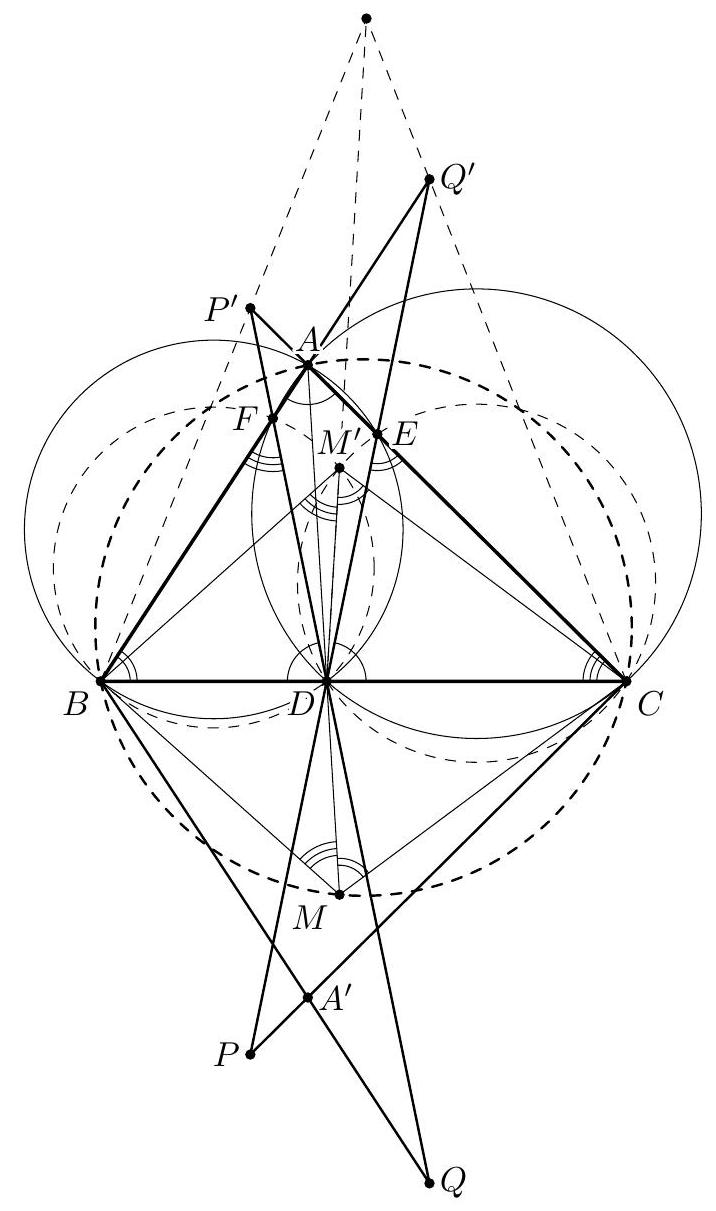
Fig. 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. (Ilya Bogdanov) Let $\sigma$ denote reflection in the line $B C$. Since $\angle B D F=\angle B A C=$ $\angle C D E$, by concyclicity, the lines $D E$ and $D F$ are images of one another under $\sigma$, so the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$. Consequently, the lines $P Q$ and $P^{\prime} Q^{\prime}=\sigma(P Q)$ meet at some (possibly ideal) point $R$ on the line $B C$.
Since the pairs of lines $(C A, Q D),(A B, D P),(B C, P Q)$ meet at three collinear points, namely $P^{\prime}, Q^{\prime}, R$ respectively, the triangles $A B C$ and $D P Q$ are perspective, i.e., the lines $A D, B P, C Q$ are concurrent, by the Desargues theorem.

Fig. 1

Fig. 2
|
{
"resource_path": "RMM/segmented/en-2016-Solutions_RMM2016-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1"
}
|
ea0c48ed-024a-5dcf-b2bb-cde93f294892
| 605,726
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. As in the first solution, $\sigma$ denotes reflection in the line $B C$, the lines $D E$ and $D F$ are images of one another under $\sigma$, the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$.
Let the line $A D$ meet the circle $A B C$ again at $M$. Letting $M^{\prime}=\sigma(M)$, it is sufficient to prove that the lines $D M^{\prime}=\sigma(A D), B P^{\prime}=\sigma(B P)$ and $C Q^{\prime}=\sigma(C Q)$ are concurrent.
Begin by noticing that $\angle\left(B M^{\prime}, M^{\prime} D\right)=-\angle(B M, M A)=-\angle(B C, C A)=\angle(B F, F D)$, to infer that $M^{\prime}$ lies on the circle $B D F$. Similarly, $M^{\prime}$ lies on the circle $C D E$, so the line $D M^{\prime}$ is the radical axis of the circles $B D F$ and $C D E$.
Since $P^{\prime}$ lies on the lines $A C$ and $D F$, it is the radical centre of the circles $A B C, A D C$, and $B D F$; hence the line $B P^{\prime}$ is the radical axis of the circles $B D F$ and $A B C$. Similarly, the line $C Q^{\prime}$ is the radical axis of the circles $C D E$ and $A B C$. So the conclusion follows: the lines $D M^{\prime}$, $B P^{\prime}$ and $C Q^{\prime}$ are concurrent at the radical centre of the circles $A B C, B D F$ and $C D E$; thus the lines $D M, B P^{\prime}$ and $C Q^{\prime}$ are also concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. As in the first solution, $\sigma$ denotes reflection in the line $B C$, the lines $D E$ and $D F$ are images of one another under $\sigma$, the lines $A C$ and $D F$ meet at $P^{\prime}=\sigma(P)$, and the lines $A B$ and $D E$ meet at $Q^{\prime}=\sigma(Q)$.
Let the line $A D$ meet the circle $A B C$ again at $M$. Letting $M^{\prime}=\sigma(M)$, it is sufficient to prove that the lines $D M^{\prime}=\sigma(A D), B P^{\prime}=\sigma(B P)$ and $C Q^{\prime}=\sigma(C Q)$ are concurrent.
Begin by noticing that $\angle\left(B M^{\prime}, M^{\prime} D\right)=-\angle(B M, M A)=-\angle(B C, C A)=\angle(B F, F D)$, to infer that $M^{\prime}$ lies on the circle $B D F$. Similarly, $M^{\prime}$ lies on the circle $C D E$, so the line $D M^{\prime}$ is the radical axis of the circles $B D F$ and $C D E$.
Since $P^{\prime}$ lies on the lines $A C$ and $D F$, it is the radical centre of the circles $A B C, A D C$, and $B D F$; hence the line $B P^{\prime}$ is the radical axis of the circles $B D F$ and $A B C$. Similarly, the line $C Q^{\prime}$ is the radical axis of the circles $C D E$ and $A B C$. So the conclusion follows: the lines $D M^{\prime}$, $B P^{\prime}$ and $C Q^{\prime}$ are concurrent at the radical centre of the circles $A B C, B D F$ and $C D E$; thus the lines $D M, B P^{\prime}$ and $C Q^{\prime}$ are also concurrent.
|
{
"resource_path": "RMM/segmented/en-2016-Solutions_RMM2016-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
ea0c48ed-024a-5dcf-b2bb-cde93f294892
| 605,726
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. (Ilya Bogdanov) As in the previous solutions, $\sigma$ denotes reflection in the line $B C$. Let the lines $B E$ and $C F$ meet at $X$. Due to the circles $B D E A$ and $C D F A$, we have $\angle X B D=$ $\angle E A D=\angle X F D$, so the quadrilateral $B F X D$ is cyclic; similarly, the quadrilateral $C E X D$ is cyclic. Hence $\angle X D B=\angle C F A=\angle C D A$, the lines $D X$ and $D A$ are therefore images of one another under $\sigma$, and $X^{\prime}=\sigma(X)$ lies on the line $A D$. Let $E^{\prime}=\sigma(E)$ and $F^{\prime}=\sigma(F)$, and apply the Pappus theorem to the hexagon $B P F^{\prime} C Q E^{\prime}$ to infer that $X^{\prime}, D$, and $B P \cap C Q$ are collinear. The conclusion follows.
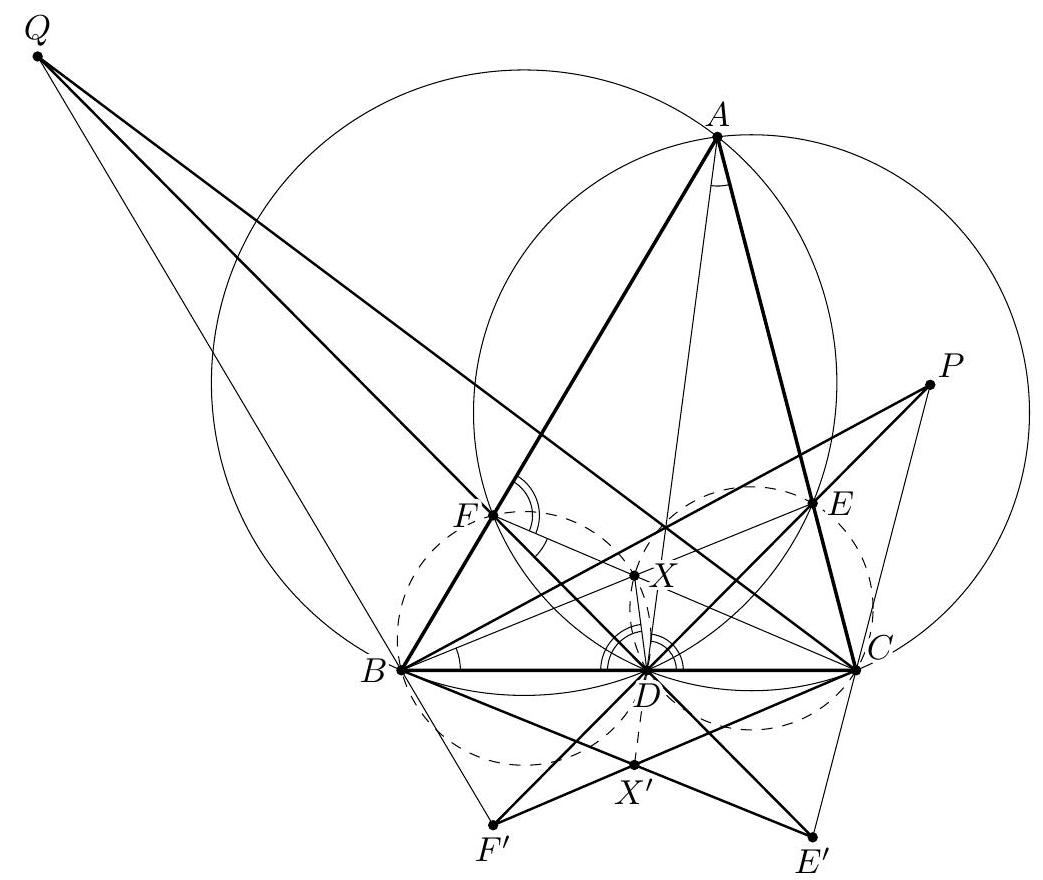
Fig. 3
Remark. In fact, the point $X$ in Solution 3 and the point $M$ in Solution 2 coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $D$ be a point on the segment $B C, D \neq B$ and $D \neq C$. The circle $A B D$ meets the segment $A C$ again at an interior point $E$. The circle $A C D$ meets the segment $A B$ again at an interior point $F$. Let $A^{\prime}$ be the reflection of $A$ in the line $B C$. The lines $A^{\prime} C$ and $D E$ meet at $P$, and the lines $A^{\prime} B$ and $D F$ meet at $Q$. Prove that the lines $A D, B P$ and $C Q$ are concurrent (or all parallel).
|
. (Ilya Bogdanov) As in the previous solutions, $\sigma$ denotes reflection in the line $B C$. Let the lines $B E$ and $C F$ meet at $X$. Due to the circles $B D E A$ and $C D F A$, we have $\angle X B D=$ $\angle E A D=\angle X F D$, so the quadrilateral $B F X D$ is cyclic; similarly, the quadrilateral $C E X D$ is cyclic. Hence $\angle X D B=\angle C F A=\angle C D A$, the lines $D X$ and $D A$ are therefore images of one another under $\sigma$, and $X^{\prime}=\sigma(X)$ lies on the line $A D$. Let $E^{\prime}=\sigma(E)$ and $F^{\prime}=\sigma(F)$, and apply the Pappus theorem to the hexagon $B P F^{\prime} C Q E^{\prime}$ to infer that $X^{\prime}, D$, and $B P \cap C Q$ are collinear. The conclusion follows.

Fig. 3
Remark. In fact, the point $X$ in Solution 3 and the point $M$ in Solution 2 coincide.
|
{
"resource_path": "RMM/segmented/en-2016-Solutions_RMM2016-1.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 3"
}
|
ea0c48ed-024a-5dcf-b2bb-cde93f294892
| 605,726
|
Let $x$ and $y$ be positive real numbers such that $x+y^{2016} \geq 1$. Prove that $x^{2016}+y>$ 1 - 1/100.
|
If $x \geq 1-1 /(100 \cdot 2016)$, then
$$
x^{2016} \geq\left(1-\frac{1}{100 \cdot 2016}\right)^{2016}>1-2016 \cdot \frac{1}{100 \cdot 2016}=1-\frac{1}{100}
$$
by Bernoulli's inequality, whence the conclusion.
If $x<1-1 /(100 \cdot 2016)$, then $y \geq(1-x)^{1 / 2016}>(100 \cdot 2016)^{-1 / 2016}$, and it is sufficient to show that the latter is greater than $1-1 / 100=99 / 100$; alternatively, but equivalently, that
$$
\left(1+\frac{1}{99}\right)^{2016}>100 \cdot 2016
$$
To establish the latter, refer again to Bernoulli's inequality to write
$$
\left(1+\frac{1}{99}\right)^{2016}>\left(1+\frac{1}{99}\right)^{99 \cdot 20}>\left(1+99 \cdot \frac{1}{99}\right)^{20}=2^{20}>100 \cdot 2016
$$
Remarks. (1) Although the constant $1 / 100$ is not sharp, it cannot be replaced by the smaller constant $1 / 400$, as the values $x=1-1 / 210$ and $y=1-1 / 380$ show.
(2) It is natural to ask whether $x^{n}+y \geq 1-1 / k$, whenever $x$ and $y$ are positive real numbers such that $x+y^{n} \geq 1$, and $k$ and $n$ are large. Using the inequality $\left(1+\frac{1}{k-1}\right)^{k}>\mathrm{e}$, it can be shown along the lines in the solution that this is indeed the case if $k \leq \frac{n}{2 \log n}(1+o(1))$. It seems that this estimate differs from the best one by a constant factor.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x$ and $y$ be positive real numbers such that $x+y^{2016} \geq 1$. Prove that $x^{2016}+y>$ 1 - 1/100.
|
If $x \geq 1-1 /(100 \cdot 2016)$, then
$$
x^{2016} \geq\left(1-\frac{1}{100 \cdot 2016}\right)^{2016}>1-2016 \cdot \frac{1}{100 \cdot 2016}=1-\frac{1}{100}
$$
by Bernoulli's inequality, whence the conclusion.
If $x<1-1 /(100 \cdot 2016)$, then $y \geq(1-x)^{1 / 2016}>(100 \cdot 2016)^{-1 / 2016}$, and it is sufficient to show that the latter is greater than $1-1 / 100=99 / 100$; alternatively, but equivalently, that
$$
\left(1+\frac{1}{99}\right)^{2016}>100 \cdot 2016
$$
To establish the latter, refer again to Bernoulli's inequality to write
$$
\left(1+\frac{1}{99}\right)^{2016}>\left(1+\frac{1}{99}\right)^{99 \cdot 20}>\left(1+99 \cdot \frac{1}{99}\right)^{20}=2^{20}>100 \cdot 2016
$$
Remarks. (1) Although the constant $1 / 100$ is not sharp, it cannot be replaced by the smaller constant $1 / 400$, as the values $x=1-1 / 210$ and $y=1-1 / 380$ show.
(2) It is natural to ask whether $x^{n}+y \geq 1-1 / k$, whenever $x$ and $y$ are positive real numbers such that $x+y^{n} \geq 1$, and $k$ and $n$ are large. Using the inequality $\left(1+\frac{1}{k-1}\right)^{k}>\mathrm{e}$, it can be shown along the lines in the solution that this is indeed the case if $k \leq \frac{n}{2 \log n}(1+o(1))$. It seems that this estimate differs from the best one by a constant factor.
|
{
"resource_path": "RMM/segmented/en-2016-Solutions_RMM2016-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
9dd8f87b-f7b0-5673-9317-513d08c82367
| 605,784
|
A convex hexagon $A_{1} B_{1} A_{2} B_{2} A_{3} B_{3}$ is inscribed in a circle $\Omega$ of radius $R$. The diagonals $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ concur at $X$. For $i=1,2,3$, let $\omega_{i}$ be the circle tangent to the segments $X A_{i}$ and $X B_{i}$, and to the arc $A_{i} B_{i}$ of $\Omega$ not containing other vertices of the hexagon; let $r_{i}$ be the radius of $\omega_{i}$.
(a) Prove that $R \geq r_{1}+r_{2}+r_{3}$.
(b) If $R=r_{1}+r_{2}+r_{3}$, prove that the six points where the circles $\omega_{i}$ touch the diagonals $A_{1} B_{2}, A_{2} B_{3}, A_{3} B_{1}$ are concyclic.
|
(a) Let $\ell_{1}$ be the tangent to $\Omega$ parallel to $A_{2} B_{3}$, lying on the same side of $A_{2} B_{3}$ as $\omega_{1}$. The tangents $\ell_{2}$ and $\ell_{3}$ are defined similarly. The lines $\ell_{1}$ and $\ell_{2}, \ell_{2}$ and $\ell_{3}, \ell_{3}$ and $\ell_{1}$ meet at $C_{3}, C_{1}, C_{2}$, respectively (see Fig. 1). Finally, the line $C_{2} C_{3}$ meets the rays $X A_{1}$ and $X B_{1}$ emanating from $X$ at $S_{1}$ and $T_{1}$, respectively; the points $S_{2}, T_{2}$, and $S_{3}, T_{3}$ are defined similarly.
Each of the triangles $\Delta_{1}=\triangle X S_{1} T_{1}, \Delta_{2}=\triangle T_{2} X S_{2}$, and $\Delta_{3}=\triangle S_{3} T_{3} X$ is similar to $\Delta=\triangle C_{1} C_{2} C_{3}$, since their corresponding sides are parallel. Let $k_{i}$ be the ratio of similitude of $\Delta_{i}$ and $\Delta$ (e.g., $k_{1}=X S_{1} / C_{1} C_{2}$ and the like). Since $S_{1} X=C_{2} T_{3}$ and $X T_{2}=S_{3} C_{1}$, it follows that $k_{1}+k_{2}+k_{3}=1$, so, if $\rho_{i}$ is the inradius of $\Delta_{i}$, then $\rho_{1}+\rho_{2}+\rho_{3}=R$.
Finally, notice that $\omega_{i}$ is interior to $\Delta_{i}$, so $r_{i} \leq \rho_{i}$, and the conclusion follows by the preceding.
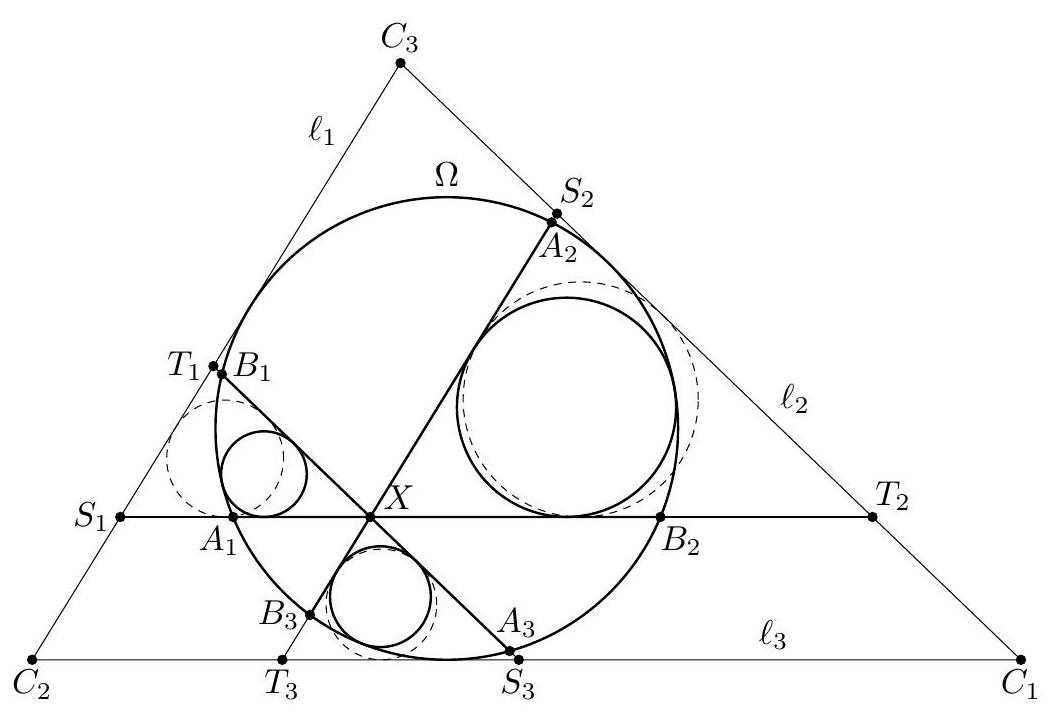
Fig. 1
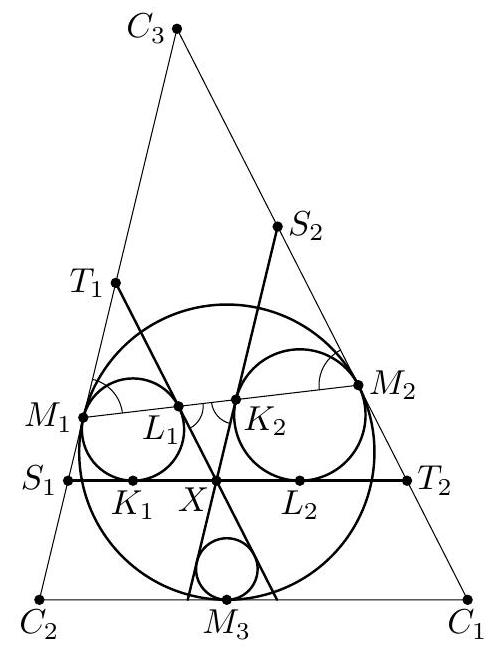
Fig. 2
(b) By part (a), the equality $R=r_{1}+r_{2}+r_{3}$ holds if and only if $r_{i}=\rho_{i}$ for all $i$, which implies in turn that $\omega_{i}$ is the incircle of $\Delta_{i}$. Let $K_{i}, L_{i}, M_{i}$ be the points where $\omega_{i}$ touches the sides $X S_{i}, X T_{i}, S_{i} T_{i}$, respectively. We claim that the six points $K_{i}$ and $L_{i}(i=1,2,3)$ are equidistant from $X$.
Clearly, $X K_{i}=X L_{i}$, and we are to prove that $X K_{2}=X L_{1}$ and $X K_{3}=X L_{2}$. By similarity, $\angle T_{1} M_{1} L_{1}=\angle C_{3} M_{1} M_{2}$ and $\angle S_{2} M_{2} K_{2}=\angle C_{3} M_{2} M_{1}$, so the points $M_{1}, M_{2}, L_{1}, K_{2}$ are collinear. Consequently, $\angle X K_{2} L_{1}=\angle C_{3} M_{1} M_{2}=\angle C_{3} M_{2} M_{1}=\angle X L_{1} K_{2}$, so $X K_{2}=X L_{1}$. Similarly, $X K_{3}=X L_{2}$.
Remark. Under the assumption in part (b), the point $M_{i}$ is the centre of a homothety mapping $\omega_{i}$ to $\Omega$. Since this homothety maps $X$ to $C_{i}$, the points $M_{i}, C_{i}, X$ are collinear, so $X$ is the Gergonne point of the triangle $C_{1} C_{2} C_{3}$. This condition is in fact equivalent to $R=r_{1}+r_{2}+r_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex hexagon $A_{1} B_{1} A_{2} B_{2} A_{3} B_{3}$ is inscribed in a circle $\Omega$ of radius $R$. The diagonals $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ concur at $X$. For $i=1,2,3$, let $\omega_{i}$ be the circle tangent to the segments $X A_{i}$ and $X B_{i}$, and to the arc $A_{i} B_{i}$ of $\Omega$ not containing other vertices of the hexagon; let $r_{i}$ be the radius of $\omega_{i}$.
(a) Prove that $R \geq r_{1}+r_{2}+r_{3}$.
(b) If $R=r_{1}+r_{2}+r_{3}$, prove that the six points where the circles $\omega_{i}$ touch the diagonals $A_{1} B_{2}, A_{2} B_{3}, A_{3} B_{1}$ are concyclic.
|
(a) Let $\ell_{1}$ be the tangent to $\Omega$ parallel to $A_{2} B_{3}$, lying on the same side of $A_{2} B_{3}$ as $\omega_{1}$. The tangents $\ell_{2}$ and $\ell_{3}$ are defined similarly. The lines $\ell_{1}$ and $\ell_{2}, \ell_{2}$ and $\ell_{3}, \ell_{3}$ and $\ell_{1}$ meet at $C_{3}, C_{1}, C_{2}$, respectively (see Fig. 1). Finally, the line $C_{2} C_{3}$ meets the rays $X A_{1}$ and $X B_{1}$ emanating from $X$ at $S_{1}$ and $T_{1}$, respectively; the points $S_{2}, T_{2}$, and $S_{3}, T_{3}$ are defined similarly.
Each of the triangles $\Delta_{1}=\triangle X S_{1} T_{1}, \Delta_{2}=\triangle T_{2} X S_{2}$, and $\Delta_{3}=\triangle S_{3} T_{3} X$ is similar to $\Delta=\triangle C_{1} C_{2} C_{3}$, since their corresponding sides are parallel. Let $k_{i}$ be the ratio of similitude of $\Delta_{i}$ and $\Delta$ (e.g., $k_{1}=X S_{1} / C_{1} C_{2}$ and the like). Since $S_{1} X=C_{2} T_{3}$ and $X T_{2}=S_{3} C_{1}$, it follows that $k_{1}+k_{2}+k_{3}=1$, so, if $\rho_{i}$ is the inradius of $\Delta_{i}$, then $\rho_{1}+\rho_{2}+\rho_{3}=R$.
Finally, notice that $\omega_{i}$ is interior to $\Delta_{i}$, so $r_{i} \leq \rho_{i}$, and the conclusion follows by the preceding.

Fig. 1

Fig. 2
(b) By part (a), the equality $R=r_{1}+r_{2}+r_{3}$ holds if and only if $r_{i}=\rho_{i}$ for all $i$, which implies in turn that $\omega_{i}$ is the incircle of $\Delta_{i}$. Let $K_{i}, L_{i}, M_{i}$ be the points where $\omega_{i}$ touches the sides $X S_{i}, X T_{i}, S_{i} T_{i}$, respectively. We claim that the six points $K_{i}$ and $L_{i}(i=1,2,3)$ are equidistant from $X$.
Clearly, $X K_{i}=X L_{i}$, and we are to prove that $X K_{2}=X L_{1}$ and $X K_{3}=X L_{2}$. By similarity, $\angle T_{1} M_{1} L_{1}=\angle C_{3} M_{1} M_{2}$ and $\angle S_{2} M_{2} K_{2}=\angle C_{3} M_{2} M_{1}$, so the points $M_{1}, M_{2}, L_{1}, K_{2}$ are collinear. Consequently, $\angle X K_{2} L_{1}=\angle C_{3} M_{1} M_{2}=\angle C_{3} M_{2} M_{1}=\angle X L_{1} K_{2}$, so $X K_{2}=X L_{1}$. Similarly, $X K_{3}=X L_{2}$.
Remark. Under the assumption in part (b), the point $M_{i}$ is the centre of a homothety mapping $\omega_{i}$ to $\Omega$. Since this homothety maps $X$ to $C_{i}$, the points $M_{i}, C_{i}, X$ are collinear, so $X$ is the Gergonne point of the triangle $C_{1} C_{2} C_{3}$. This condition is in fact equivalent to $R=r_{1}+r_{2}+r_{3}$.
|
{
"resource_path": "RMM/segmented/en-2016-Solutions_RMM2016-2.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
18e49aff-bb5d-5a1f-bffd-04b816a5f31a
| 605,794
|
In the Cartesian plane, let $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ be the graphs of the quadratic functions $f_{1}(x)=p_{1} x^{2}+q_{1} x+r_{1}$ and $f_{2}(x)=p_{2} x^{2}+q_{2} x+r_{2}$, where $p_{1}>0>p_{2}$. The graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ cross at distinct points $A$ and $B$. The four tangents to $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ at $A$ and $B$ form a convex quadrilateral which has an inscribed circle. Prove that the graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ have the same axis of symmetry.
## Alexey Zaslavsky, Russia
|
. Let $\mathcal{A}_{i}$ and $\mathcal{B}_{i}$ be the tangents to $\mathcal{G}_{i}$ at $A$ and $B$, respectively, and let $C_{i}=\mathcal{A}_{i} \cap \mathcal{B}_{i}$. Since $f_{1}(x)$ is convex and $f_{2}(x)$ is concave, the convex quadrangle formed by the four tangents is exactly $A C_{1} B C_{2}$.
Lemma. If $C A$ and $C B$ are the tangents drawn from a point $C$ to the graph $\mathcal{G}$ of a quadratic trinomial $f(x)=p x^{2}+q x+r, A, B \in \mathcal{G}, A \neq B$, then the abscissa of $C$ is the arithmetic mean of the abscissae of $A$ and $B$.
Proof. Assume, without loss of generality, that $C$ is at the origin, so the equations of the two tangents have the form $y=k_{a} x$ and $y=k_{b} x$. Next, the abscissae $x_{A}$ and $x_{B}$ of the tangency points $A$ and $B$, respectively, are multiple roots of the polynomials $f(x)-k_{a} x$ and $f(x)-k_{b} x$, respectively. By the Vieta theorem, $x_{A}^{2}=r / p=x_{B}^{2}$, so $x_{A}=-x_{B}$, since the case $x_{A}=x_{B}$ is ruled out by $A \neq B$.
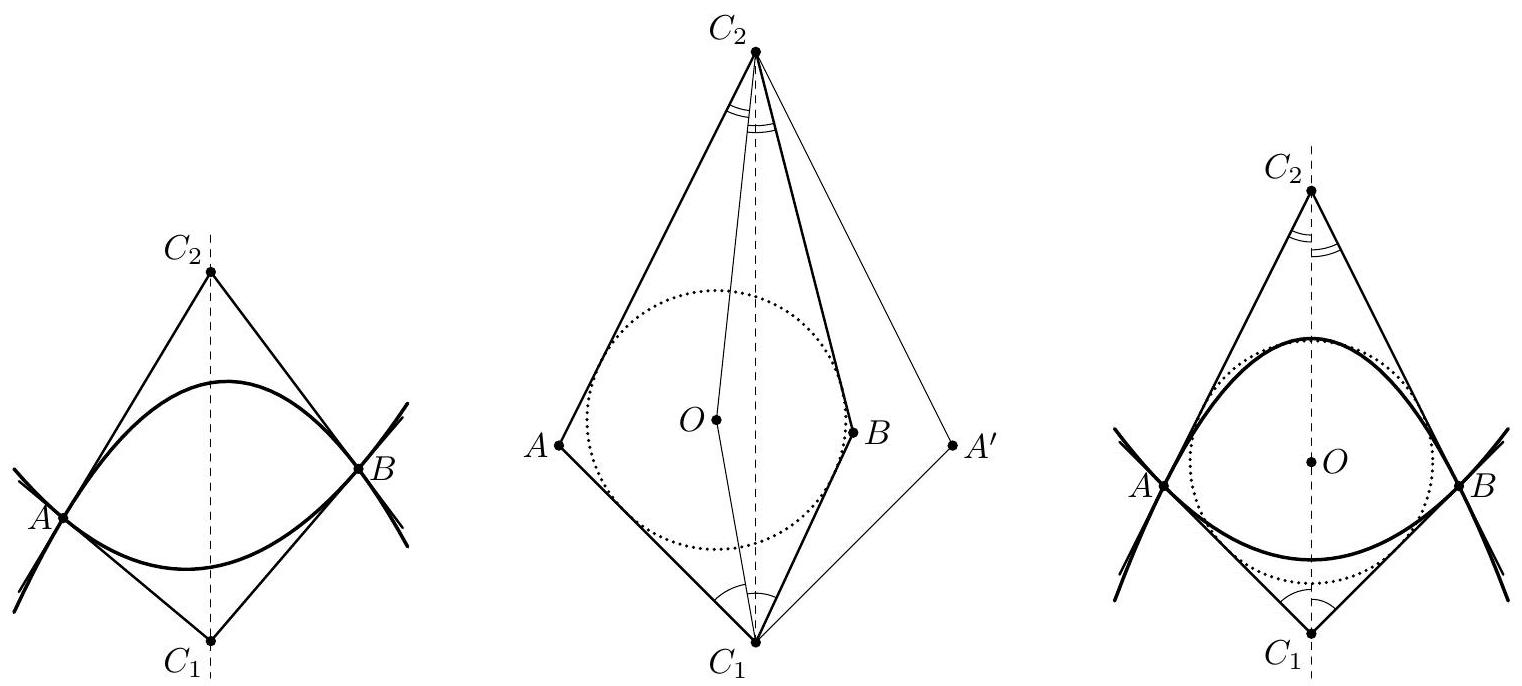
The Lemma shows that the line $C_{1} C_{2}$ is parallel to the $y$-axis and the points $A$ and $B$ are equidistant from this line.
Suppose, if possible, that the incentre $O$ of the quadrangle $A C_{1} B C_{2}$ does not lie on the line $C_{1} C_{2}$. Assume, without loss of generality, that $O$ lies inside the triangle $A C_{1} C_{2}$ and let $A^{\prime}$ be the reflection of $A$ in the line $C_{1} C_{2}$. Then the ray $C_{i} B$ emanating from $C_{i}$ lies inside the angle $A C_{i} A^{\prime}$, so $B$ lies inside the quadrangle $A C_{1} A^{\prime} C_{2}$, whence $A$ and $B$ are not equidistant from $C_{1} C_{2}-$ a contradiction.
Thus $O$ lies on $C_{1} C_{2}$, so the lines $A C_{i}$ and $B C_{i}$ are reflections of one another in the line $C_{1} C_{2}$, and $B=A^{\prime}$. Hence $y_{A}=y_{B}$, and since $f_{i}(x)=y_{A}+p_{i}\left(x-x_{A}\right)\left(x-x_{B}\right)$, the line $C_{1} C_{2}$ is the axis of symmetry of both parabolas, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the Cartesian plane, let $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ be the graphs of the quadratic functions $f_{1}(x)=p_{1} x^{2}+q_{1} x+r_{1}$ and $f_{2}(x)=p_{2} x^{2}+q_{2} x+r_{2}$, where $p_{1}>0>p_{2}$. The graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ cross at distinct points $A$ and $B$. The four tangents to $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ at $A$ and $B$ form a convex quadrilateral which has an inscribed circle. Prove that the graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ have the same axis of symmetry.
## Alexey Zaslavsky, Russia
|
. Let $\mathcal{A}_{i}$ and $\mathcal{B}_{i}$ be the tangents to $\mathcal{G}_{i}$ at $A$ and $B$, respectively, and let $C_{i}=\mathcal{A}_{i} \cap \mathcal{B}_{i}$. Since $f_{1}(x)$ is convex and $f_{2}(x)$ is concave, the convex quadrangle formed by the four tangents is exactly $A C_{1} B C_{2}$.
Lemma. If $C A$ and $C B$ are the tangents drawn from a point $C$ to the graph $\mathcal{G}$ of a quadratic trinomial $f(x)=p x^{2}+q x+r, A, B \in \mathcal{G}, A \neq B$, then the abscissa of $C$ is the arithmetic mean of the abscissae of $A$ and $B$.
Proof. Assume, without loss of generality, that $C$ is at the origin, so the equations of the two tangents have the form $y=k_{a} x$ and $y=k_{b} x$. Next, the abscissae $x_{A}$ and $x_{B}$ of the tangency points $A$ and $B$, respectively, are multiple roots of the polynomials $f(x)-k_{a} x$ and $f(x)-k_{b} x$, respectively. By the Vieta theorem, $x_{A}^{2}=r / p=x_{B}^{2}$, so $x_{A}=-x_{B}$, since the case $x_{A}=x_{B}$ is ruled out by $A \neq B$.

The Lemma shows that the line $C_{1} C_{2}$ is parallel to the $y$-axis and the points $A$ and $B$ are equidistant from this line.
Suppose, if possible, that the incentre $O$ of the quadrangle $A C_{1} B C_{2}$ does not lie on the line $C_{1} C_{2}$. Assume, without loss of generality, that $O$ lies inside the triangle $A C_{1} C_{2}$ and let $A^{\prime}$ be the reflection of $A$ in the line $C_{1} C_{2}$. Then the ray $C_{i} B$ emanating from $C_{i}$ lies inside the angle $A C_{i} A^{\prime}$, so $B$ lies inside the quadrangle $A C_{1} A^{\prime} C_{2}$, whence $A$ and $B$ are not equidistant from $C_{1} C_{2}-$ a contradiction.
Thus $O$ lies on $C_{1} C_{2}$, so the lines $A C_{i}$ and $B C_{i}$ are reflections of one another in the line $C_{1} C_{2}$, and $B=A^{\prime}$. Hence $y_{A}=y_{B}$, and since $f_{i}(x)=y_{A}+p_{i}\left(x-x_{A}\right)\left(x-x_{B}\right)$, the line $C_{1} C_{2}$ is the axis of symmetry of both parabolas, as required.
|
{
"resource_path": "RMM/segmented/en-2017-Solutions_RMM2017-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 1"
}
|
e33a88af-5250-59af-812b-5a4238feba83
| 605,871
|
In the Cartesian plane, let $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ be the graphs of the quadratic functions $f_{1}(x)=p_{1} x^{2}+q_{1} x+r_{1}$ and $f_{2}(x)=p_{2} x^{2}+q_{2} x+r_{2}$, where $p_{1}>0>p_{2}$. The graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ cross at distinct points $A$ and $B$. The four tangents to $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ at $A$ and $B$ form a convex quadrilateral which has an inscribed circle. Prove that the graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ have the same axis of symmetry.
## Alexey Zaslavsky, Russia
|
. Use the standard equation of a tangent to a smooth curve in the plane, to deduce that the tangents at two distinct points $A$ and $B$ on the parabola of equation $y=p x^{2}+q x+r$,
$p \neq 0$, meet at some point $C$ whose coordinates are
$$
x_{C}=\frac{1}{2}\left(x_{A}+x_{B}\right) \quad \text { and } \quad y_{C}=p x_{A} x_{B}+q \cdot \frac{1}{2}\left(x_{A}+x_{B}\right)+r .
$$
Usage of the standard formula for Euclidean distance yields
$$
C A=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{A}+q\right)^{2}} \quad \text { and } \quad C B=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{B}+q\right)^{2}},
$$
so, after obvious manipulations,
$$
C B-C A=\frac{2 p\left(x_{B}-x_{A}\right)\left|x_{B}-x_{A}\right|\left(p\left(x_{A}+x_{B}\right)+q\right)}{\sqrt{1+\left(2 p x_{A}+q\right)^{2}}+\sqrt{1+\left(2 p x_{B}+q\right)^{2}}}
$$
Now, write the condition in the statement in the form $C_{1} B-C_{1} A=C_{2} B-C_{2} A$, apply the above formula and clear common factors to get
$$
\frac{p_{1}\left(p_{1}\left(x_{A}+x_{B}\right)+q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{2}\left(x_{A}+x_{B}\right)+q_{2}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}}
$$
Next, use the fact that $x_{A}$ and $x_{B}$ are the solutions of the quadratic equation $\left(p_{1}-p_{2}\right) x^{2}+$ $\left(q_{1}-q_{2}\right) x+r_{1}-r_{2}=0$, so $x_{A}+x_{B}=-\left(q_{1}-q_{2}\right) /\left(p_{1}-p_{2}\right)$, to obtain
$$
\frac{p_{1}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}} .
$$
Finally, since $p_{1} p_{2}<0$ and the denominators above are both positive, the last equality forces $p_{1} q_{2}-p_{2} q_{1}=0$; that is, $q_{1} / p_{1}=q_{2} / p_{2}$, so the two parabolas have the same axis.
Remarks. The are, of course, several different proofs of the Lemma in Solution 1 - in particular, computational. Another argument relies on the following consequence of focal properties: The tangents to a parabola at two points meet at the circumcentre of the triangle formed by the focus and the orthogonal projections of those points on the directrix. Since the directrix of the parabola in the lemma is parallel to the axis of abscissae, the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the Cartesian plane, let $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ be the graphs of the quadratic functions $f_{1}(x)=p_{1} x^{2}+q_{1} x+r_{1}$ and $f_{2}(x)=p_{2} x^{2}+q_{2} x+r_{2}$, where $p_{1}>0>p_{2}$. The graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ cross at distinct points $A$ and $B$. The four tangents to $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ at $A$ and $B$ form a convex quadrilateral which has an inscribed circle. Prove that the graphs $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ have the same axis of symmetry.
## Alexey Zaslavsky, Russia
|
. Use the standard equation of a tangent to a smooth curve in the plane, to deduce that the tangents at two distinct points $A$ and $B$ on the parabola of equation $y=p x^{2}+q x+r$,
$p \neq 0$, meet at some point $C$ whose coordinates are
$$
x_{C}=\frac{1}{2}\left(x_{A}+x_{B}\right) \quad \text { and } \quad y_{C}=p x_{A} x_{B}+q \cdot \frac{1}{2}\left(x_{A}+x_{B}\right)+r .
$$
Usage of the standard formula for Euclidean distance yields
$$
C A=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{A}+q\right)^{2}} \quad \text { and } \quad C B=\frac{1}{2}\left|x_{B}-x_{A}\right| \sqrt{1+\left(2 p x_{B}+q\right)^{2}},
$$
so, after obvious manipulations,
$$
C B-C A=\frac{2 p\left(x_{B}-x_{A}\right)\left|x_{B}-x_{A}\right|\left(p\left(x_{A}+x_{B}\right)+q\right)}{\sqrt{1+\left(2 p x_{A}+q\right)^{2}}+\sqrt{1+\left(2 p x_{B}+q\right)^{2}}}
$$
Now, write the condition in the statement in the form $C_{1} B-C_{1} A=C_{2} B-C_{2} A$, apply the above formula and clear common factors to get
$$
\frac{p_{1}\left(p_{1}\left(x_{A}+x_{B}\right)+q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{2}\left(x_{A}+x_{B}\right)+q_{2}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}}
$$
Next, use the fact that $x_{A}$ and $x_{B}$ are the solutions of the quadratic equation $\left(p_{1}-p_{2}\right) x^{2}+$ $\left(q_{1}-q_{2}\right) x+r_{1}-r_{2}=0$, so $x_{A}+x_{B}=-\left(q_{1}-q_{2}\right) /\left(p_{1}-p_{2}\right)$, to obtain
$$
\frac{p_{1}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{1} x_{A}+q_{1}\right)^{2}}+\sqrt{1+\left(2 p_{1} x_{B}+q_{1}\right)^{2}}}=\frac{p_{2}\left(p_{1} q_{2}-p_{2} q_{1}\right)}{\sqrt{1+\left(2 p_{2} x_{A}+q_{2}\right)^{2}}+\sqrt{1+\left(2 p_{2} x_{B}+q_{2}\right)^{2}}} .
$$
Finally, since $p_{1} p_{2}<0$ and the denominators above are both positive, the last equality forces $p_{1} q_{2}-p_{2} q_{1}=0$; that is, $q_{1} / p_{1}=q_{2} / p_{2}$, so the two parabolas have the same axis.
Remarks. The are, of course, several different proofs of the Lemma in Solution 1 - in particular, computational. Another argument relies on the following consequence of focal properties: The tangents to a parabola at two points meet at the circumcentre of the triangle formed by the focus and the orthogonal projections of those points on the directrix. Since the directrix of the parabola in the lemma is parallel to the axis of abscissae, the conclusion follows.
|
{
"resource_path": "RMM/segmented/en-2017-Solutions_RMM2017-2.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 2"
}
|
e33a88af-5250-59af-812b-5a4238feba83
| 605,871
|
Let $A B C D$ be any convex quadrilateral and let $P, Q, R, S$ be points on the segments $A B, B C, C D$, and $D A$, respectively. It is given that the segments $P R$ and $Q S$ dissect $A B C D$ into four quadrilaterals, each of which has perpendicular diagonals. Show that the points $P, Q, R, S$ are concyclic.
NikOlai Beluhov
|
. We start with a lemma which holds even in a more general setup.
Lemma 1. Let $P Q R S$ be a convex quadrangle whose diagonals meet at $O$. Let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. Finally, choose the points $A, B$, and $C$ outside this quadrangle so that: the point $P$ (respectively, $Q$ ) lies on the segment $A B$ (respectively, $B C$ ); and $A O \perp P S, B O \perp P Q$, and $C O \perp Q R$. Then the three lines $A C, P Q$, and $\ell$ are concurrent or parallel.
Proof. Assume first that the lines $P R$ and $Q S$ are not perpendicular. Let $H_{1}$ and $H_{2}$ be the orthocentres of the triangles $O S P$ and $O Q R$, respectively; notice that $H_{1}$ and $H_{2}$ do not coincide.
Since $H_{1}$ is the radical centre of the circles on diameters $R S, S P$, and $P Q$, it lies on $\ell$. Similarly, $H_{2}$ lies on $\ell$, so the lines $H_{1} H_{2}$ and $\ell$ coincide.
The corresponding sides of the triangles $A P H_{1}$ and $C Q H_{2}$ meet at $O, B$, and the orthocentre of the triangle $O P Q$ (which lies on $O B$ ). By Desargues' theorem, the lines $A C, P Q$ and $\ell$ are concurrent or parallel.
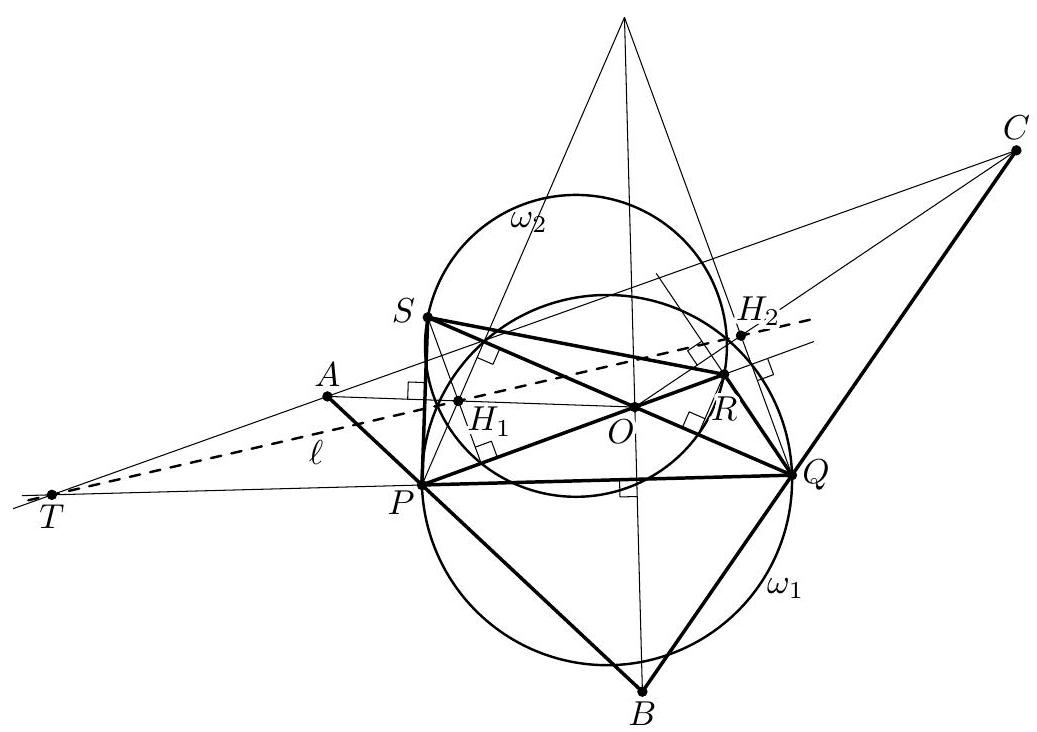
The case when $P R \perp Q S$ may be considered as a limit case, since the configuration in the statement of the lemma allows arbitrarily small perturbations. The lemma is proved.
Back to the problem, let the segments $P R$ and $Q S$ cross at $O$, let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. By the Lemma, the three lines $A C$, $\ell$, and $P Q$ are concurrent or parallel, and similarly so are the three lines $A C, \ell$, and $R S$. Thus, if the lines $A C$ and $\ell$ are distinct, all four lines are concurrent or pairwise parallel.
This is clearly the case when the lines $P S$ and $Q R$ are not parallel (since $\ell$ crosses $O A$ and $O C$ at the orthocentres of $O S P$ and $O Q R$, these orthocentres being distinct from $A$ and $C$ ). In this case, denote the concurrency point by $T$. If $T$ is not ideal, then we have $T P \cdot T Q=T R \cdot T S$ (as $T \in \ell$ ), so $P Q R S$ is cyclic. If $T$ is ideal (i.e., all four lines are parallel), then the segments $P Q$ and $R S$ have the same perpendicular bisector (namely, the line of centers of $\omega_{1}$ and $\omega_{2}$ ), and $P Q R S$ is cyclic again.
Assume now $P S$ and $Q R$ parallel. By symmetry, $P Q$ and $R S$ may also be assumed parallel: otherwise, the preceding argument goes through after relabelling. In this case, we need to prove that the parallelogram $P Q R S$ is a rectangle.
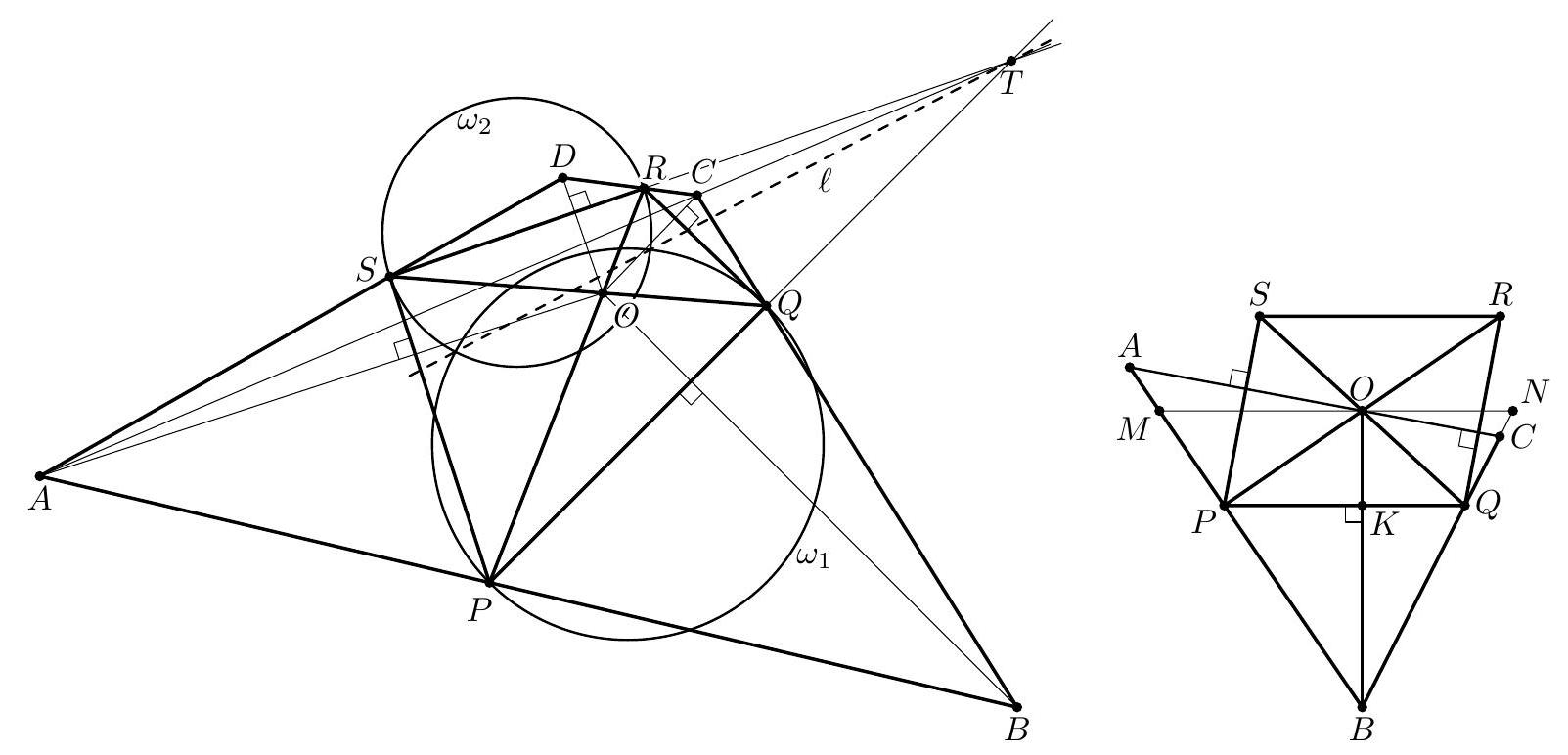
Suppose, by way of contradiction, that $O P>O Q$. Let the line through $O$ and parallel to $P Q$ meet $A B$ at $M$, and $C B$ at $N$. Since $O P>O Q$, the angle $S P Q$ is acute and the angle $P Q R$ is obtuse, so the angle $A O B$ is obtuse, the angle $B O C$ is acute, $M$ lies on the segment $A B$, and $N$ lies on the extension of the segment $B C$ beyond $C$. Therefore: $O A>O M$, since the angle $O M A$ is obtuse; $O M>O N$, since $O M: O N=K P: K Q$, where $K$ is the projection of $O$ onto $P Q$; and $O N>O C$, since the angle $O C N$ is obtuse. Consequently, $O A>O C$.
Similarly, $O R>O S$ yields $O C>O A$ : a contradiction. Consequently, $O P=O Q$ and $P Q R S$ is a rectangle. This ends the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be any convex quadrilateral and let $P, Q, R, S$ be points on the segments $A B, B C, C D$, and $D A$, respectively. It is given that the segments $P R$ and $Q S$ dissect $A B C D$ into four quadrilaterals, each of which has perpendicular diagonals. Show that the points $P, Q, R, S$ are concyclic.
NikOlai Beluhov
|
. We start with a lemma which holds even in a more general setup.
Lemma 1. Let $P Q R S$ be a convex quadrangle whose diagonals meet at $O$. Let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. Finally, choose the points $A, B$, and $C$ outside this quadrangle so that: the point $P$ (respectively, $Q$ ) lies on the segment $A B$ (respectively, $B C$ ); and $A O \perp P S, B O \perp P Q$, and $C O \perp Q R$. Then the three lines $A C, P Q$, and $\ell$ are concurrent or parallel.
Proof. Assume first that the lines $P R$ and $Q S$ are not perpendicular. Let $H_{1}$ and $H_{2}$ be the orthocentres of the triangles $O S P$ and $O Q R$, respectively; notice that $H_{1}$ and $H_{2}$ do not coincide.
Since $H_{1}$ is the radical centre of the circles on diameters $R S, S P$, and $P Q$, it lies on $\ell$. Similarly, $H_{2}$ lies on $\ell$, so the lines $H_{1} H_{2}$ and $\ell$ coincide.
The corresponding sides of the triangles $A P H_{1}$ and $C Q H_{2}$ meet at $O, B$, and the orthocentre of the triangle $O P Q$ (which lies on $O B$ ). By Desargues' theorem, the lines $A C, P Q$ and $\ell$ are concurrent or parallel.

The case when $P R \perp Q S$ may be considered as a limit case, since the configuration in the statement of the lemma allows arbitrarily small perturbations. The lemma is proved.
Back to the problem, let the segments $P R$ and $Q S$ cross at $O$, let $\omega_{1}$ and $\omega_{2}$ be the circles on diameters $P Q$ and $R S$, respectively, and let $\ell$ be their radical axis. By the Lemma, the three lines $A C$, $\ell$, and $P Q$ are concurrent or parallel, and similarly so are the three lines $A C, \ell$, and $R S$. Thus, if the lines $A C$ and $\ell$ are distinct, all four lines are concurrent or pairwise parallel.
This is clearly the case when the lines $P S$ and $Q R$ are not parallel (since $\ell$ crosses $O A$ and $O C$ at the orthocentres of $O S P$ and $O Q R$, these orthocentres being distinct from $A$ and $C$ ). In this case, denote the concurrency point by $T$. If $T$ is not ideal, then we have $T P \cdot T Q=T R \cdot T S$ (as $T \in \ell$ ), so $P Q R S$ is cyclic. If $T$ is ideal (i.e., all four lines are parallel), then the segments $P Q$ and $R S$ have the same perpendicular bisector (namely, the line of centers of $\omega_{1}$ and $\omega_{2}$ ), and $P Q R S$ is cyclic again.
Assume now $P S$ and $Q R$ parallel. By symmetry, $P Q$ and $R S$ may also be assumed parallel: otherwise, the preceding argument goes through after relabelling. In this case, we need to prove that the parallelogram $P Q R S$ is a rectangle.

Suppose, by way of contradiction, that $O P>O Q$. Let the line through $O$ and parallel to $P Q$ meet $A B$ at $M$, and $C B$ at $N$. Since $O P>O Q$, the angle $S P Q$ is acute and the angle $P Q R$ is obtuse, so the angle $A O B$ is obtuse, the angle $B O C$ is acute, $M$ lies on the segment $A B$, and $N$ lies on the extension of the segment $B C$ beyond $C$. Therefore: $O A>O M$, since the angle $O M A$ is obtuse; $O M>O N$, since $O M: O N=K P: K Q$, where $K$ is the projection of $O$ onto $P Q$; and $O N>O C$, since the angle $O C N$ is obtuse. Consequently, $O A>O C$.
Similarly, $O R>O S$ yields $O C>O A$ : a contradiction. Consequently, $O P=O Q$ and $P Q R S$ is a rectangle. This ends the proof.
|
{
"resource_path": "RMM/segmented/en-2017-Solutions_RMM2017-2.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 1"
}
|
3e01b57f-4eba-51e2-abc1-bdf715d0aadf
| 605,928
|
Let $A B C D$ be a cyclic quadrangle and let $P$ be a point on the side $A B$. The diagonal $A C$ crosses the segment $D P$ at $Q$. The parallel through $P$ to $C D$ crosses the extension of the side $B C$ beyond $B$ at $K$, and the parallel through $Q$ to $B D$ crosses the extension of the side $B C$ beyond $B$ at $L$. Prove that the circumcircles of the triangles $B K P$ and $C L Q$ are tangent.
## AleksandR Kuznetsov, Russia
|
We show that the circles $B K P$ and $C L Q$ are tangent at the point $T$ where the line $D P$ crosses the circle $A B C D$ again.
Since $B C D T$ is cyclic, we have $\angle K B T=\angle C D T$. Since $K P \| C D$, we get $\angle C D T=\angle K P T$. Thus, $\angle K B T=\angle C D T=\angle K P T$, which shows that $T$ lies on the circle $B K P$. Similarly, the equalities $\angle L C T=\angle B D T=\angle L Q T$ show that $T$ also lies on the circle $C L Q$.
It remains to prove that these circles are indeed tangent at $T$. This follows from the fact that the chords $T P$ and $T Q$ in the circles $B K T P$ and $C L T Q$, respectively, both lie along the same line and subtend equal angles $\angle T B P=\angle T B A=\angle T C A=\angle T C Q$.
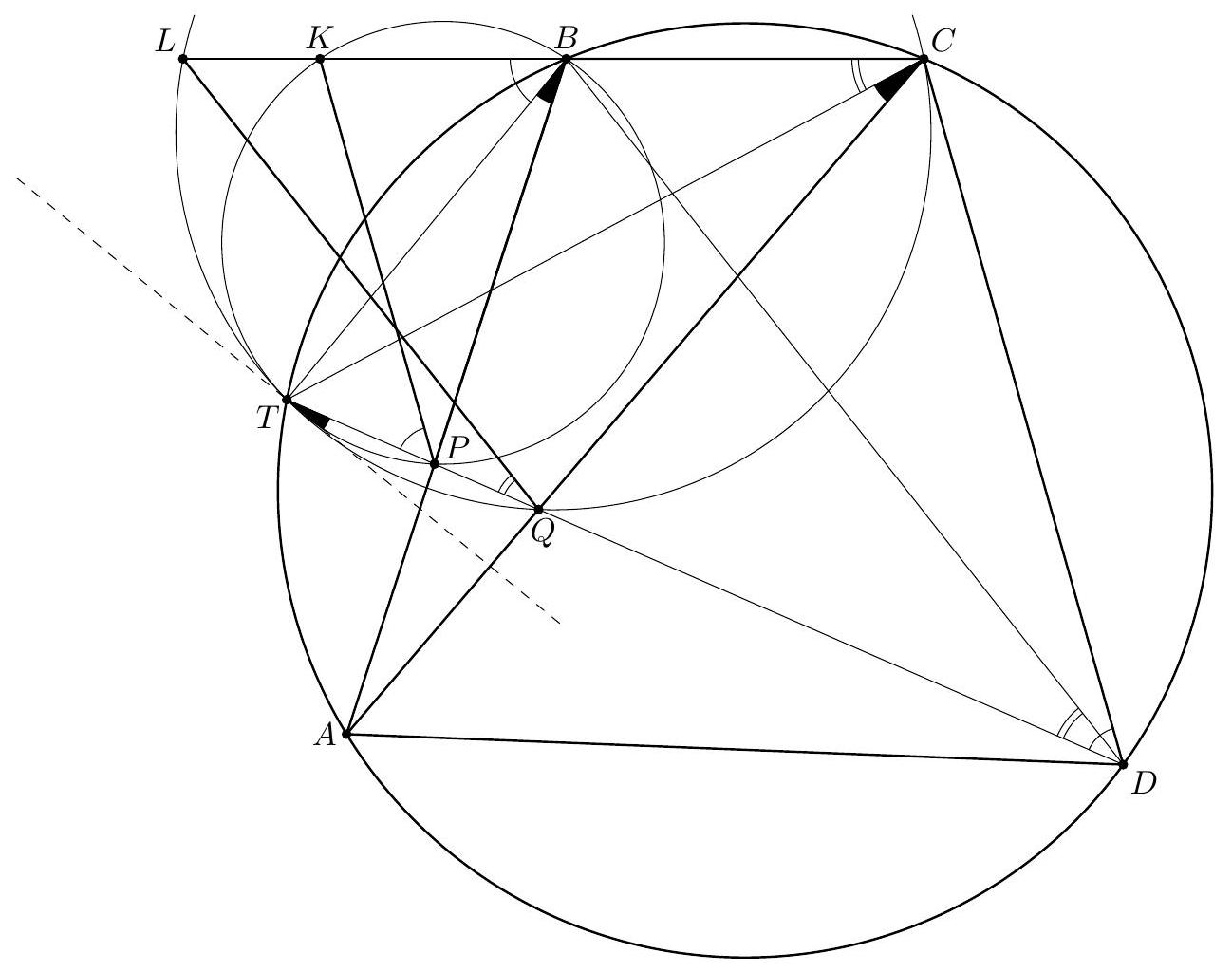
Remarks. The point $T$ may alternatively be defined as the Miquel point of (any four of) the five lines $A B, B C, A C, K P$, and $L Q$.
Of course, the result still holds if $P$ is chosen on the line $A B$, and the other points lie on the corresponding lines rather than segments/rays. The current formulation was chosen in order to avoid case distinction based on the possible configurations of points.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrangle and let $P$ be a point on the side $A B$. The diagonal $A C$ crosses the segment $D P$ at $Q$. The parallel through $P$ to $C D$ crosses the extension of the side $B C$ beyond $B$ at $K$, and the parallel through $Q$ to $B D$ crosses the extension of the side $B C$ beyond $B$ at $L$. Prove that the circumcircles of the triangles $B K P$ and $C L Q$ are tangent.
## AleksandR Kuznetsov, Russia
|
We show that the circles $B K P$ and $C L Q$ are tangent at the point $T$ where the line $D P$ crosses the circle $A B C D$ again.
Since $B C D T$ is cyclic, we have $\angle K B T=\angle C D T$. Since $K P \| C D$, we get $\angle C D T=\angle K P T$. Thus, $\angle K B T=\angle C D T=\angle K P T$, which shows that $T$ lies on the circle $B K P$. Similarly, the equalities $\angle L C T=\angle B D T=\angle L Q T$ show that $T$ also lies on the circle $C L Q$.
It remains to prove that these circles are indeed tangent at $T$. This follows from the fact that the chords $T P$ and $T Q$ in the circles $B K T P$ and $C L T Q$, respectively, both lie along the same line and subtend equal angles $\angle T B P=\angle T B A=\angle T C A=\angle T C Q$.

Remarks. The point $T$ may alternatively be defined as the Miquel point of (any four of) the five lines $A B, B C, A C, K P$, and $L Q$.
Of course, the result still holds if $P$ is chosen on the line $A B$, and the other points lie on the corresponding lines rather than segments/rays. The current formulation was chosen in order to avoid case distinction based on the possible configurations of points.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day1-English.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
b10d39d7-46f3-5034-83eb-1b56c6b9d157
| 605,949
|
Determine whether there exist non-constant polynomials $P(x)$ and $Q(x)$ with real coefficients satisfying
$$
P(x)^{10}+P(x)^{9}=Q(x)^{21}+Q(x)^{20} .
$$
## Ilya Bogdanov, Russia
|
. The answer is in the negative. Comparing the degrees of both sides in (*) we get $\operatorname{deg} P=21 n$ and $\operatorname{deg} Q=10 n$ for some positive integer $n$. Take the derivative of $(*)$ to obtain
$$
P^{\prime} P^{8}(10 P+9)=Q^{\prime} Q^{19}(21 Q+20)
$$
Since $\operatorname{gcd}(10 P+9, P)=\operatorname{gcd}(10 P+9, P+1)=1$, it follows that $\operatorname{gcd}\left(10 P+9, P^{9}(P+1)\right)=1$, so $\operatorname{gcd}(10 P+9, Q)=1$, by $(*)$. Thus $(* *)$ yields $10 P+9 \mid Q^{\prime}(21 Q+20)$, which is impossible since $0<\operatorname{deg}\left(Q^{\prime}(21 Q+20)\right)=20 n-1<21 n=\operatorname{deg}(10 P+9)$. A contradiction.
Remark. A similar argument shows that there are no non-constant solutions of $P^{m}+P^{m-1}=$ $Q^{k}+Q^{k-1}$, where $k$ and $m$ are positive integers with $k \geq 2 m$. A critical case is $k=2 m$; but in this case there exist more routine ways of solving the problem. Thus, we decided to choose $k=2 m+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Determine whether there exist non-constant polynomials $P(x)$ and $Q(x)$ with real coefficients satisfying
$$
P(x)^{10}+P(x)^{9}=Q(x)^{21}+Q(x)^{20} .
$$
## Ilya Bogdanov, Russia
|
. The answer is in the negative. Comparing the degrees of both sides in (*) we get $\operatorname{deg} P=21 n$ and $\operatorname{deg} Q=10 n$ for some positive integer $n$. Take the derivative of $(*)$ to obtain
$$
P^{\prime} P^{8}(10 P+9)=Q^{\prime} Q^{19}(21 Q+20)
$$
Since $\operatorname{gcd}(10 P+9, P)=\operatorname{gcd}(10 P+9, P+1)=1$, it follows that $\operatorname{gcd}\left(10 P+9, P^{9}(P+1)\right)=1$, so $\operatorname{gcd}(10 P+9, Q)=1$, by $(*)$. Thus $(* *)$ yields $10 P+9 \mid Q^{\prime}(21 Q+20)$, which is impossible since $0<\operatorname{deg}\left(Q^{\prime}(21 Q+20)\right)=20 n-1<21 n=\operatorname{deg}(10 P+9)$. A contradiction.
Remark. A similar argument shows that there are no non-constant solutions of $P^{m}+P^{m-1}=$ $Q^{k}+Q^{k-1}$, where $k$ and $m$ are positive integers with $k \geq 2 m$. A critical case is $k=2 m$; but in this case there exist more routine ways of solving the problem. Thus, we decided to choose $k=2 m+1$.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day1-English.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
3b559e56-ead9-528b-83d2-6cb72449fd15
| 605,958
|
Determine whether there exist non-constant polynomials $P(x)$ and $Q(x)$ with real coefficients satisfying
$$
P(x)^{10}+P(x)^{9}=Q(x)^{21}+Q(x)^{20} .
$$
## Ilya Bogdanov, Russia
|
. Letting $r$ and $s$ be integers such that $r \geq 2$ and $s \geq 2 r$, we show that if $P^{r}+P^{r-1}=$ $Q^{s}+Q^{s-1}$, then $Q$ is constant.
Let $m=\operatorname{deg} P$ and $n=\operatorname{deg} Q$. A degree inspection in the given relation shows that $m \geq 2 n$.
We will prove that $P(P+1)$ has at least $m+1$ distinct complex roots. Assuming this for the moment, notice that $Q$ takes on one of the values 0 or -1 at each of those roots. Since $m+1 \geq 2 n+1$, it follows that $Q$ takes on one of the values 0 and -1 at more than $n$ distinct points, so $Q$ must be constant.
Finally, we prove that $P(P+1)$ has at least $m+1$ distinct complex roots. This can be done either by referring to the Mason-Stothers theorem or directly, in terms of multiplicities of the roots in question.
Since $P$ and $P+1$ are relatively prime, the Mason-Stothers theorem implies that the number of distinct roots of $P(P+1)$ is greater than $m$, hence at least $m+1$.
For a direct proof, let $z_{1}, \ldots, z_{t}$ be the distinct complex roots of $P(P+1)$, and let $z_{k}$ have multiplicity $\alpha_{k}, k=1, \ldots, t$. Since $P$ and $P+1$ have no roots in common, and $P^{\prime}=(P+1)^{\prime}$, it follows that $P^{\prime}$ has a root of multiplicity $\alpha_{k}-1$ at $z_{k}$. Consequently, $m-1=\operatorname{deg} P^{\prime} \geq$ $\sum_{k=1}^{t}\left(\alpha_{k}-1\right)=\sum_{k=1}^{t} \alpha_{k}-t=2 m-t$; that is, $t \geq m+1$. This completes the prof.
Remark. The Mason-Stothers theorem (in a particular case over the complex field) claims that, given coprime complex polynomials $P(x), Q(x)$, and $R(x)$, not all constant, such that $P(x)+Q(x)=R(x)$, the total number of their complex roots (not regarding multiplicities) is at least $\max \{\operatorname{deg} P, \operatorname{deg} Q, \operatorname{deg} R\}+1$. This theorem was a part of motivation for the famous $a b c$-conjecture.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Determine whether there exist non-constant polynomials $P(x)$ and $Q(x)$ with real coefficients satisfying
$$
P(x)^{10}+P(x)^{9}=Q(x)^{21}+Q(x)^{20} .
$$
## Ilya Bogdanov, Russia
|
. Letting $r$ and $s$ be integers such that $r \geq 2$ and $s \geq 2 r$, we show that if $P^{r}+P^{r-1}=$ $Q^{s}+Q^{s-1}$, then $Q$ is constant.
Let $m=\operatorname{deg} P$ and $n=\operatorname{deg} Q$. A degree inspection in the given relation shows that $m \geq 2 n$.
We will prove that $P(P+1)$ has at least $m+1$ distinct complex roots. Assuming this for the moment, notice that $Q$ takes on one of the values 0 or -1 at each of those roots. Since $m+1 \geq 2 n+1$, it follows that $Q$ takes on one of the values 0 and -1 at more than $n$ distinct points, so $Q$ must be constant.
Finally, we prove that $P(P+1)$ has at least $m+1$ distinct complex roots. This can be done either by referring to the Mason-Stothers theorem or directly, in terms of multiplicities of the roots in question.
Since $P$ and $P+1$ are relatively prime, the Mason-Stothers theorem implies that the number of distinct roots of $P(P+1)$ is greater than $m$, hence at least $m+1$.
For a direct proof, let $z_{1}, \ldots, z_{t}$ be the distinct complex roots of $P(P+1)$, and let $z_{k}$ have multiplicity $\alpha_{k}, k=1, \ldots, t$. Since $P$ and $P+1$ have no roots in common, and $P^{\prime}=(P+1)^{\prime}$, it follows that $P^{\prime}$ has a root of multiplicity $\alpha_{k}-1$ at $z_{k}$. Consequently, $m-1=\operatorname{deg} P^{\prime} \geq$ $\sum_{k=1}^{t}\left(\alpha_{k}-1\right)=\sum_{k=1}^{t} \alpha_{k}-t=2 m-t$; that is, $t \geq m+1$. This completes the prof.
Remark. The Mason-Stothers theorem (in a particular case over the complex field) claims that, given coprime complex polynomials $P(x), Q(x)$, and $R(x)$, not all constant, such that $P(x)+Q(x)=R(x)$, the total number of their complex roots (not regarding multiplicities) is at least $\max \{\operatorname{deg} P, \operatorname{deg} Q, \operatorname{deg} R\}+1$. This theorem was a part of motivation for the famous $a b c$-conjecture.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day1-English.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
3b559e56-ead9-528b-83d2-6cb72449fd15
| 605,958
|
Ann and Bob play a game on an infinite checkered plane making moves in turn; Ann makes the first move. A move consists in orienting any unit grid-segment that has not been oriented before. If at some stage some oriented segments form an oriented cycle, Bob wins. Does Bob have a strategy that guarantees him to win?
Maxim Didin, Russia
|
The answer is in the negative: Ann has a strategy allowing her to prevent Bob's victory.
We say that two unit grid-segments form a low-left corner (or LL-corner) if they share an endpoint which is the lowest point of one and the leftmost point of the other. An up-right corner (or $U R$-corner) is defined similarly. The common endpoint of two unit grid-segments at a corner is the joint of that corner.
Fix a vertical line on the grid and call it the midline; the unit grid-segments along the midline are called middle segments. The unit grid-segments lying to the left/right of the midline are called left/right segments. Partition all left segments into LL-corners, and all right segments into UR-corners.
We now describe Ann's strategy. Her first move consists in orienting some middle segment arbitrarily. Assume that at some stage, Bob orients some segment $s$. If $s$ is a middle segment, Ann orients any free middle segment arbitrarily. Otherwise, $s$ forms a corner in the partition with some other segment $t$. Then Ann orients $t$ so that the joint of the corner is either the source of both arrows, or the target of both. Notice that after any move of Ann's, each corner in the partition is either completely oriented or completely not oriented. This means that Ann can always make a required move.
Assume that Bob wins at some stage, i.e., an oriented cycle $C$ occurs. Let $X$ be the lowest of the leftmost points of $C$, and let $Y$ be the topmost of the rightmost points of $C$. If $X$ lies (strictly) to the left of the midline, then $X$ is the joint of some corner whose segments are both oriented. But, according to Ann's strategy, they are oriented so that they cannot occur in a cycle - a contradiction. Otherwise, $Y$ lies to the right of the midline, and a similar argument applies. Thus, Bob will never win, as desired.
Remarks. (1) There are several variations of the argument in the solution above. For instance, instead of the midline, Ann may choose any infinite in both directions down going polyline along the grid (i.e., consisting of steps to the right and steps-down alone). Alternatively, she may split the plane into four quadrants, use their borders as "trash bin" (as the midline was used in the solution above), partition all segments in the upper-right quadrant into UR-corners, all segments in the lower-right quadrant into LR-corners, and so on.
(2) The problem becomes easier if Bob makes the first move. In this case, his opponent just partitions the whole grid into LL-corners. In particular, one may change the problem to say that the first player to achieve an oriented cycle wins (in this case, the result is a draw).
On the other hand, this version is closer to known problems. In particular, the following problem is known:
Ann and Bob play the game on an infinite checkered plane making moves in turn (Ann makes the first move). A move consists in painting any unit grid segment that has not been painted before (Ann paints in blue, Bob paints in red). If a player creates a cycle of her/his color, (s)he wins. Does any of the players have a winning strategy?
Again, the solution is pairing strategy with corners of a fixed orientation (with a little twist for Ann's strategy - in this problem, it is clear that Ann has better chances).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Ann and Bob play a game on an infinite checkered plane making moves in turn; Ann makes the first move. A move consists in orienting any unit grid-segment that has not been oriented before. If at some stage some oriented segments form an oriented cycle, Bob wins. Does Bob have a strategy that guarantees him to win?
Maxim Didin, Russia
|
The answer is in the negative: Ann has a strategy allowing her to prevent Bob's victory.
We say that two unit grid-segments form a low-left corner (or LL-corner) if they share an endpoint which is the lowest point of one and the leftmost point of the other. An up-right corner (or $U R$-corner) is defined similarly. The common endpoint of two unit grid-segments at a corner is the joint of that corner.
Fix a vertical line on the grid and call it the midline; the unit grid-segments along the midline are called middle segments. The unit grid-segments lying to the left/right of the midline are called left/right segments. Partition all left segments into LL-corners, and all right segments into UR-corners.
We now describe Ann's strategy. Her first move consists in orienting some middle segment arbitrarily. Assume that at some stage, Bob orients some segment $s$. If $s$ is a middle segment, Ann orients any free middle segment arbitrarily. Otherwise, $s$ forms a corner in the partition with some other segment $t$. Then Ann orients $t$ so that the joint of the corner is either the source of both arrows, or the target of both. Notice that after any move of Ann's, each corner in the partition is either completely oriented or completely not oriented. This means that Ann can always make a required move.
Assume that Bob wins at some stage, i.e., an oriented cycle $C$ occurs. Let $X$ be the lowest of the leftmost points of $C$, and let $Y$ be the topmost of the rightmost points of $C$. If $X$ lies (strictly) to the left of the midline, then $X$ is the joint of some corner whose segments are both oriented. But, according to Ann's strategy, they are oriented so that they cannot occur in a cycle - a contradiction. Otherwise, $Y$ lies to the right of the midline, and a similar argument applies. Thus, Bob will never win, as desired.
Remarks. (1) There are several variations of the argument in the solution above. For instance, instead of the midline, Ann may choose any infinite in both directions down going polyline along the grid (i.e., consisting of steps to the right and steps-down alone). Alternatively, she may split the plane into four quadrants, use their borders as "trash bin" (as the midline was used in the solution above), partition all segments in the upper-right quadrant into UR-corners, all segments in the lower-right quadrant into LR-corners, and so on.
(2) The problem becomes easier if Bob makes the first move. In this case, his opponent just partitions the whole grid into LL-corners. In particular, one may change the problem to say that the first player to achieve an oriented cycle wins (in this case, the result is a draw).
On the other hand, this version is closer to known problems. In particular, the following problem is known:
Ann and Bob play the game on an infinite checkered plane making moves in turn (Ann makes the first move). A move consists in painting any unit grid segment that has not been painted before (Ann paints in blue, Bob paints in red). If a player creates a cycle of her/his color, (s)he wins. Does any of the players have a winning strategy?
Again, the solution is pairing strategy with corners of a fixed orientation (with a little twist for Ann's strategy - in this problem, it is clear that Ann has better chances).
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day1-English.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
dc178c28-414e-5b89-91c1-9b7a54f5d089
| 605,975
|
Let $a, b, c, d$ be positive integers such that $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$. Prove that, as $n$ runs through the positive integers, the values $\operatorname{gcd}(a n+b, c n+d)$ may achieve form the set of all positive divisors of some integer.
Raul Alcantara, Peru
|
. We extend the problem statement by allowing $a$ and $c$ take non-negative integer values, and allowing $b$ and $d$ to take arbitrary integer values. (As usual, the greatest common divisor of two integers is non-negative.) Without loss of generality, we assume $0 \leq a \leq c$. Let $S(a, b, c, d)=\left\{\operatorname{gcd}(a n+b, c n+d): n \in \mathbb{Z}_{>0}\right\}$.
Now we induct on $a$. We first deal with the inductive step, leaving the base case $a=0$ to the end of the solution. So, assume that $a>0$; we intend to find a 4 -tuple $\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)$ satisfying the requirements of the extended problem, such that $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ and $0 \leq a^{\prime}<a$, which will allow us to apply the induction hypothesis.
The construction of this 4 -tuple is provided by the step of the Euclidean algorithm. Write $c=a q+r$, where $q$ and $r$ are both integers and $0 \leq r<a$. Then for every $n$ we have
$$
\operatorname{gcd}(a n+b, c n+d)=\operatorname{gcd}(a n+b, q(a n+b)+r n+d-q b)=\operatorname{gcd}(a n+b, r n+(d-q b))
$$
so a natural intention is to define $a^{\prime}=r, b^{\prime}=d-q b, c^{\prime}=a$, and $d^{\prime}=b$ (which are already shown to satisfy $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ ). The check of the problem requirements is straightforward: indeed,
$$
a^{\prime} d^{\prime}-b^{\prime} c^{\prime}=(c-q a) b-(d-q b) a=-(a d-b c) \neq 0
$$
and
$$
\operatorname{gcd}\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=\operatorname{gcd}(c-q a, b-q d, a, b)=\operatorname{gcd}(c, d, a, b)=1
$$
Thus the step is verified.
It remains to deal with the base case $a=0$, i.e., to examine the set $S(0, b, c, d)$ with $b c \neq 0$ and $\operatorname{gcd}(b, c, d)=1$. Let $b^{\prime}$ be the integer obtained from $b$ by ignoring all primes $b$ and $c$ share (none of them divides $c n+d$ for any integer $n$, otherwise $\operatorname{gcd}(b, c, d)>1)$. We thus get $\operatorname{gcd}\left(b^{\prime}, c\right)=1$ and $S\left(0, b^{\prime}, c, d\right)=S(0, b, c, d)$.
Finally, it is easily seen that $S\left(0, b^{\prime}, c, d\right)$ is the set of all positive divisors of $b^{\prime}$. Each member of $S\left(0, b^{\prime}, c, d\right)$ is clearly a divisor of $b^{\prime}$. Conversely, if $\delta$ is a positive divisor of $b^{\prime}$, then $c n+d \equiv \delta$ $\left(\bmod b^{\prime}\right)$ for some $n$, since $b^{\prime}$ and $c$ are coprime, so $\delta$ is indeed a member of $S\left(0, b^{\prime}, c, d\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c, d$ be positive integers such that $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$. Prove that, as $n$ runs through the positive integers, the values $\operatorname{gcd}(a n+b, c n+d)$ may achieve form the set of all positive divisors of some integer.
Raul Alcantara, Peru
|
. We extend the problem statement by allowing $a$ and $c$ take non-negative integer values, and allowing $b$ and $d$ to take arbitrary integer values. (As usual, the greatest common divisor of two integers is non-negative.) Without loss of generality, we assume $0 \leq a \leq c$. Let $S(a, b, c, d)=\left\{\operatorname{gcd}(a n+b, c n+d): n \in \mathbb{Z}_{>0}\right\}$.
Now we induct on $a$. We first deal with the inductive step, leaving the base case $a=0$ to the end of the solution. So, assume that $a>0$; we intend to find a 4 -tuple $\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)$ satisfying the requirements of the extended problem, such that $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ and $0 \leq a^{\prime}<a$, which will allow us to apply the induction hypothesis.
The construction of this 4 -tuple is provided by the step of the Euclidean algorithm. Write $c=a q+r$, where $q$ and $r$ are both integers and $0 \leq r<a$. Then for every $n$ we have
$$
\operatorname{gcd}(a n+b, c n+d)=\operatorname{gcd}(a n+b, q(a n+b)+r n+d-q b)=\operatorname{gcd}(a n+b, r n+(d-q b))
$$
so a natural intention is to define $a^{\prime}=r, b^{\prime}=d-q b, c^{\prime}=a$, and $d^{\prime}=b$ (which are already shown to satisfy $S\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=S(a, b, c, d)$ ). The check of the problem requirements is straightforward: indeed,
$$
a^{\prime} d^{\prime}-b^{\prime} c^{\prime}=(c-q a) b-(d-q b) a=-(a d-b c) \neq 0
$$
and
$$
\operatorname{gcd}\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)=\operatorname{gcd}(c-q a, b-q d, a, b)=\operatorname{gcd}(c, d, a, b)=1
$$
Thus the step is verified.
It remains to deal with the base case $a=0$, i.e., to examine the set $S(0, b, c, d)$ with $b c \neq 0$ and $\operatorname{gcd}(b, c, d)=1$. Let $b^{\prime}$ be the integer obtained from $b$ by ignoring all primes $b$ and $c$ share (none of them divides $c n+d$ for any integer $n$, otherwise $\operatorname{gcd}(b, c, d)>1)$. We thus get $\operatorname{gcd}\left(b^{\prime}, c\right)=1$ and $S\left(0, b^{\prime}, c, d\right)=S(0, b, c, d)$.
Finally, it is easily seen that $S\left(0, b^{\prime}, c, d\right)$ is the set of all positive divisors of $b^{\prime}$. Each member of $S\left(0, b^{\prime}, c, d\right)$ is clearly a divisor of $b^{\prime}$. Conversely, if $\delta$ is a positive divisor of $b^{\prime}$, then $c n+d \equiv \delta$ $\left(\bmod b^{\prime}\right)$ for some $n$, since $b^{\prime}$ and $c$ are coprime, so $\delta$ is indeed a member of $S\left(0, b^{\prime}, c, d\right)$.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day2-English.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 1"
}
|
76bfddd7-66ca-5165-b91d-1802132bd73c
| 605,986
|
Let $a, b, c, d$ be positive integers such that $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$. Prove that, as $n$ runs through the positive integers, the values $\operatorname{gcd}(a n+b, c n+d)$ may achieve form the set of all positive divisors of some integer.
Raul Alcantara, Peru
|
. (Alexander Betts) For positive integers $s$ and $t$ and prime $p$, we will denote by $\operatorname{gcd}_{p}(s, t)$ the greatest common $p$-power divisor of $s$ and $t$.
Claim 1. For any positive integer $n, \operatorname{gcd}(a n+b, c n+d) \mid a d-b c$.
Proof. This is clear from the identity
$$
a(c n+d)-c(a n+b)=a d-b c
$$
Claim 2. The set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is exactly the set of values taken by the product
$$
\prod_{p \mid a d-b c} \operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)
$$
as the $\left(n_{p}\right)_{p \mid a d-b c}$ each range over positive integers.
Proof. From the identity
$$
\operatorname{gcd}(a n+b, c n+d)=\prod_{p \mid a d-b c} \operatorname{gcd}_{p}(a n+b, c n+d)
$$
it is clear that every value taken by $\operatorname{gcd}(a n+b, c n+d)$ is also a value taken by the product (with all $n_{p}=n$ ). Conversely, it suffices to show that, given any positive integers $\left(n_{p}\right)_{p \mid a d-b c}$, there is a positive integer $n$ such that $\operatorname{gcd}_{p}(a n+b, c n+d)=\operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)$ for each $p \mid a d-b c$. This can be achieved by requiring that $n$ be congruent to $n_{p}$ modulo a sufficiently large ${ }^{1}$ power of $p$ (using the Chinese Remainder Theorem).
Using Claim 2, it suffices to determine the sets of values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ as $n$ ranges over all positive integers. There are two cases.
Claim 3. If $p \mid a, c$, then $\operatorname{gcd}_{p}(a n+b, c n+d)=1$ for all $n$.
Proof. If $p \mid a n+b, c n+d$, then we would have $p \mid a, b, c, d$, which is not the case.
Claim 4. If $p \nmid a$ or $p \nmid c$, then the values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ are exactly the $p$-power divisors of $a d-b c$.
Proof. Assume without loss of generality that $p \nmid a$. Then from identity $(\dagger)$ we have $\operatorname{grd}_{p}(a n+$ $b, c n+d)=\operatorname{gcd}_{p}(a n+b, a d-b c)$. But since $p \nmid a$, the arithmetic progression $a n+b$ takes all possible values modulo the highest $p$-power divisor of $a d-b c$, and in particular the values taken by $\operatorname{gcd}_{p}(a n+b, a d-b c)$ are exactly the $p$-power divisors of $a d-b c$.
Conclusion. Using claims 2,3 and 4 , we see that the set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of products of $p$-power divisors of $a d-b c$, where we only consider those primes $p$ not dividing $\operatorname{gcd}(a, c)$. Thus the set of values of $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of divisors of the largest factor of $a d-b c$ coprime to $\operatorname{gcd}(a, c)$.
Remarks. (1) If $S(a, b, c, d)$ is the set of all positive divisors of some integer, then necessarily $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$ : finiteness of $S(a, b, c, d)$ forces the former, and membership of 1 forces the latter.
(2) One may modify the problem statement according to the first paragraph of the solution. However, it seems that in this case one needs to include a clarification of the agreement on gcd being necessarily non-negative.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c, d$ be positive integers such that $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$. Prove that, as $n$ runs through the positive integers, the values $\operatorname{gcd}(a n+b, c n+d)$ may achieve form the set of all positive divisors of some integer.
Raul Alcantara, Peru
|
. (Alexander Betts) For positive integers $s$ and $t$ and prime $p$, we will denote by $\operatorname{gcd}_{p}(s, t)$ the greatest common $p$-power divisor of $s$ and $t$.
Claim 1. For any positive integer $n, \operatorname{gcd}(a n+b, c n+d) \mid a d-b c$.
Proof. This is clear from the identity
$$
a(c n+d)-c(a n+b)=a d-b c
$$
Claim 2. The set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is exactly the set of values taken by the product
$$
\prod_{p \mid a d-b c} \operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)
$$
as the $\left(n_{p}\right)_{p \mid a d-b c}$ each range over positive integers.
Proof. From the identity
$$
\operatorname{gcd}(a n+b, c n+d)=\prod_{p \mid a d-b c} \operatorname{gcd}_{p}(a n+b, c n+d)
$$
it is clear that every value taken by $\operatorname{gcd}(a n+b, c n+d)$ is also a value taken by the product (with all $n_{p}=n$ ). Conversely, it suffices to show that, given any positive integers $\left(n_{p}\right)_{p \mid a d-b c}$, there is a positive integer $n$ such that $\operatorname{gcd}_{p}(a n+b, c n+d)=\operatorname{gcd}_{p}\left(a n_{p}+b, c n_{p}+d\right)$ for each $p \mid a d-b c$. This can be achieved by requiring that $n$ be congruent to $n_{p}$ modulo a sufficiently large ${ }^{1}$ power of $p$ (using the Chinese Remainder Theorem).
Using Claim 2, it suffices to determine the sets of values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ as $n$ ranges over all positive integers. There are two cases.
Claim 3. If $p \mid a, c$, then $\operatorname{gcd}_{p}(a n+b, c n+d)=1$ for all $n$.
Proof. If $p \mid a n+b, c n+d$, then we would have $p \mid a, b, c, d$, which is not the case.
Claim 4. If $p \nmid a$ or $p \nmid c$, then the values taken by $\operatorname{gcd}_{p}(a n+b, c n+d)$ are exactly the $p$-power divisors of $a d-b c$.
Proof. Assume without loss of generality that $p \nmid a$. Then from identity $(\dagger)$ we have $\operatorname{grd}_{p}(a n+$ $b, c n+d)=\operatorname{gcd}_{p}(a n+b, a d-b c)$. But since $p \nmid a$, the arithmetic progression $a n+b$ takes all possible values modulo the highest $p$-power divisor of $a d-b c$, and in particular the values taken by $\operatorname{gcd}_{p}(a n+b, a d-b c)$ are exactly the $p$-power divisors of $a d-b c$.
Conclusion. Using claims 2,3 and 4 , we see that the set of values taken by $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of products of $p$-power divisors of $a d-b c$, where we only consider those primes $p$ not dividing $\operatorname{gcd}(a, c)$. Thus the set of values of $\operatorname{gcd}(a n+b, c n+d)$ is equal to the set of divisors of the largest factor of $a d-b c$ coprime to $\operatorname{gcd}(a, c)$.
Remarks. (1) If $S(a, b, c, d)$ is the set of all positive divisors of some integer, then necessarily $a d \neq b c$ and $\operatorname{gcd}(a, b, c, d)=1$ : finiteness of $S(a, b, c, d)$ forces the former, and membership of 1 forces the latter.
(2) One may modify the problem statement according to the first paragraph of the solution. However, it seems that in this case one needs to include a clarification of the agreement on gcd being necessarily non-negative.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day2-English.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 2"
}
|
76bfddd7-66ca-5165-b91d-1802132bd73c
| 605,986
|
Fix a circle $\Gamma$, a line $\ell$ tangent to $\Gamma$, and another circle $\Omega$ disjoint from $\ell$ such that $\Gamma$ and $\Omega$ lie on opposite sides of $\ell$. The tangents to $\Gamma$ from a variable point $X$ on $\Omega$ cross $\ell$ at $Y$ and $Z$. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.
Russia, Ivan Frolov
|
Assume $\Gamma$ of unit radius and invert with respect to $\Gamma$. No reference will be made to the original configuration, so images will be denoted by the same letters. Letting $\Gamma$ be centred at $G$, notice that inversion in $\Gamma$ maps tangents to $\Gamma$ to circles of unit diameter through $G$ (hence internally tangent to $\Gamma$ ). Under inversion, the statement reads as follows:
Fix a circle $\Gamma$ of unit radius centred at $G$, a circle $\ell$ of unit diameter through $G$, and a circle $\Omega$ inside $\ell$ disjoint from $\ell$. The circles $\eta$ and $\zeta$ of unit diameter, through $G$ and a variable point $X$ on $\Omega$, cross $\ell$ again at $Y$ and $Z$, respectively. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.
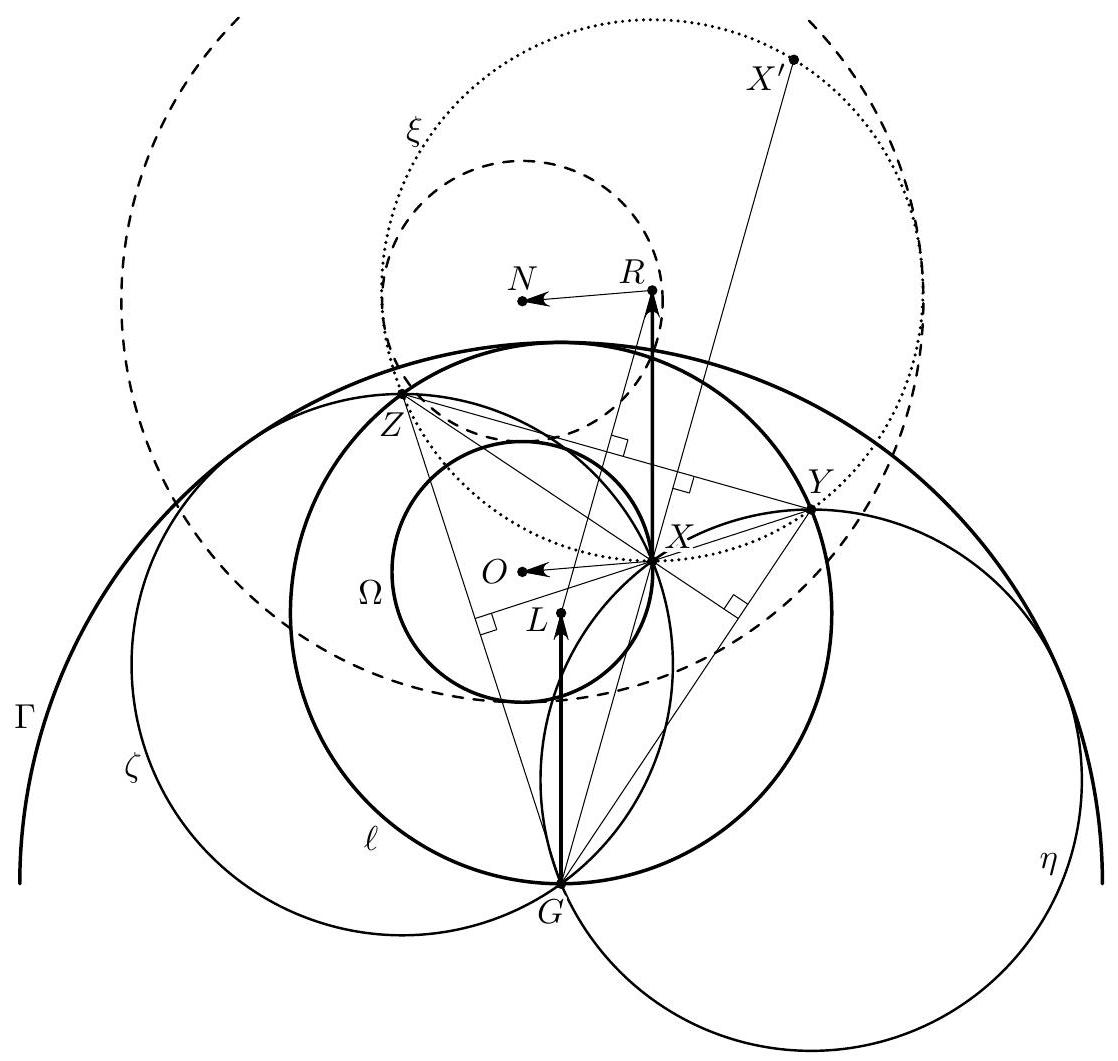
Since $\eta$ and $\zeta$ are the reflections of the circumcircle $\ell$ of the triangle $G Y Z$ in its sidelines $G Y$ and $G Z$, respectively, they pass through the orthocentre of this triangle. And since $\eta$ and $\zeta$ cross again at $X$, the latter is the orthocentre of the triangle $G Y Z$. Hence the circle $\xi$ through $X, Y, Z$ is the reflection of $\ell$ in the line $Y Z$; in particular, $\xi$ is also of unit diameter.
Let $O$ and $L$ be the centres of $\Omega$ and $\ell$, respectively, and let $R$ be the (variable) centre of $\xi$. Let $G X \operatorname{cross} \xi$ again at $X^{\prime}$; then $G$ and $X^{\prime}$ are reflections of one another in the line $Y Z$, so $G L R X^{\prime}$ is an isosceles trapezoid. Then $L R \| G X$ and $\angle(L G, G X)=\angle\left(G X^{\prime}, X^{\prime} R\right)=\angle(R X, X G)$, i.e., $L G \| R X$; this means that $G L R X$ is a parallelogram, so $\overrightarrow{X R}=\overrightarrow{G L}$ is constant.
Finally, consider the fixed point $N$ defined by $\overrightarrow{O N}=\overrightarrow{G L}$. Then $X R N O$ is a parallelogram, so the distance $R N=O X$ is constant. Consequently, $\xi$ is tangent to the fixed circles centred at $N$ of radii $|1 / 2-O X|$ and $1 / 2+O X$.
One last check is needed to show that the inverse images of the two obtained circles are indeed circles and not lines. This might happen if one of them contained $G$; we show that this is
impossible. Indeed, since $\Omega$ lies inside $\ell$, we have $O L<1 / 2-O X$, so
$$
N G=|\overrightarrow{G L}+\overrightarrow{L O}+\overrightarrow{O N}|=|2 \overrightarrow{G L}+\overrightarrow{L O}| \geq 2|\overrightarrow{G L}|-|\overrightarrow{L O}|>1-(1 / 2-O X)=1 / 2+O X
$$
this shows that $G$ is necessarily outside the obtained circles.
Remarks. (1) The last check could be omitted, if we allowed in the problem statement to regard a line as a particular case of a circle. On the other hand, the Problem Selection Committee suggests not to punish students who have not performed this check.
(2) Notice that the required fixed circles are also tangent to $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Fix a circle $\Gamma$, a line $\ell$ tangent to $\Gamma$, and another circle $\Omega$ disjoint from $\ell$ such that $\Gamma$ and $\Omega$ lie on opposite sides of $\ell$. The tangents to $\Gamma$ from a variable point $X$ on $\Omega$ cross $\ell$ at $Y$ and $Z$. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.
Russia, Ivan Frolov
|
Assume $\Gamma$ of unit radius and invert with respect to $\Gamma$. No reference will be made to the original configuration, so images will be denoted by the same letters. Letting $\Gamma$ be centred at $G$, notice that inversion in $\Gamma$ maps tangents to $\Gamma$ to circles of unit diameter through $G$ (hence internally tangent to $\Gamma$ ). Under inversion, the statement reads as follows:
Fix a circle $\Gamma$ of unit radius centred at $G$, a circle $\ell$ of unit diameter through $G$, and a circle $\Omega$ inside $\ell$ disjoint from $\ell$. The circles $\eta$ and $\zeta$ of unit diameter, through $G$ and a variable point $X$ on $\Omega$, cross $\ell$ again at $Y$ and $Z$, respectively. Prove that, as $X$ traces $\Omega$, the circle $X Y Z$ is tangent to two fixed circles.

Since $\eta$ and $\zeta$ are the reflections of the circumcircle $\ell$ of the triangle $G Y Z$ in its sidelines $G Y$ and $G Z$, respectively, they pass through the orthocentre of this triangle. And since $\eta$ and $\zeta$ cross again at $X$, the latter is the orthocentre of the triangle $G Y Z$. Hence the circle $\xi$ through $X, Y, Z$ is the reflection of $\ell$ in the line $Y Z$; in particular, $\xi$ is also of unit diameter.
Let $O$ and $L$ be the centres of $\Omega$ and $\ell$, respectively, and let $R$ be the (variable) centre of $\xi$. Let $G X \operatorname{cross} \xi$ again at $X^{\prime}$; then $G$ and $X^{\prime}$ are reflections of one another in the line $Y Z$, so $G L R X^{\prime}$ is an isosceles trapezoid. Then $L R \| G X$ and $\angle(L G, G X)=\angle\left(G X^{\prime}, X^{\prime} R\right)=\angle(R X, X G)$, i.e., $L G \| R X$; this means that $G L R X$ is a parallelogram, so $\overrightarrow{X R}=\overrightarrow{G L}$ is constant.
Finally, consider the fixed point $N$ defined by $\overrightarrow{O N}=\overrightarrow{G L}$. Then $X R N O$ is a parallelogram, so the distance $R N=O X$ is constant. Consequently, $\xi$ is tangent to the fixed circles centred at $N$ of radii $|1 / 2-O X|$ and $1 / 2+O X$.
One last check is needed to show that the inverse images of the two obtained circles are indeed circles and not lines. This might happen if one of them contained $G$; we show that this is
impossible. Indeed, since $\Omega$ lies inside $\ell$, we have $O L<1 / 2-O X$, so
$$
N G=|\overrightarrow{G L}+\overrightarrow{L O}+\overrightarrow{O N}|=|2 \overrightarrow{G L}+\overrightarrow{L O}| \geq 2|\overrightarrow{G L}|-|\overrightarrow{L O}|>1-(1 / 2-O X)=1 / 2+O X
$$
this shows that $G$ is necessarily outside the obtained circles.
Remarks. (1) The last check could be omitted, if we allowed in the problem statement to regard a line as a particular case of a circle. On the other hand, the Problem Selection Committee suggests not to punish students who have not performed this check.
(2) Notice that the required fixed circles are also tangent to $\Omega$.
|
{
"resource_path": "RMM/segmented/en-2018-RMM2018-Day2-English.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution."
}
|
b40a0dc7-3a7d-5630-aa54-f7e4c93dcc49
| 606,034
|
Amy and Bob play the game. At the beginning, Amy writes down a positive integer on the board. Then the players take moves in turn, Bob moves first. On any move of his, Bob replaces the number $n$ on the blackboard with a number of the form $n-a^{2}$, where $a$ is a positive integer. On any move of hers, Amy replaces the number $n$ on the blackboard with a number of the form $n^{k}$, where $k$ is a positive integer. Bob wins if the number on the board becomes zero. Can Amy prevent Bob's win?
Russia, Maxim Didin
|
The answer is in the negative. For a positive integer $n$, we define its square-free part $S(n)$ to be the smallest positive integer $a$ such that $n / a$ is a square of an integer. In other words, $S(n)$ is the product of all primes having odd exponents in the prime expansion of $n$. We also agree that $S(0)=0$.
Now we show that (i) on any move of hers, Amy does not increase the square-free part of the positive integer on the board; and (ii) on any move of his, Bob always can replace a positive integer $n$ with a non-negative integer $k$ with $S(k)<S(n)$. Thus, if the game starts by a positive integer $N$, Bob can win in at most $S(N)$ moves.
Part (i) is trivial, as the definition of the square-part yields $S\left(n^{k}\right)=S(n)$ whenever $k$ is odd, and $S\left(n^{k}\right)=1 \leq S(n)$ whenever $k$ is even, for any positive integer $n$.
Part (ii) is also easy: if, before Bob's move, the board contains a number $n=S(n) \cdot b^{2}$, then Bob may replace it with $n^{\prime}=n-b^{2}=(S(n)-1) b^{2}$, whence $S\left(n^{\prime}\right) \leq S(n)-1$.
Remarks. (1) To make the argument more transparent, Bob may restrict himself to subtract only those numbers which are divisible by the maximal square dividing the current number. This restriction having been put, one may replace any number $n$ appearing on the board by $S(n)$, omitting the square factors.
After this change, Amy's moves do not increase the number, while Bob's moves decrease it. Thus, Bob wins.
(2) In fact, Bob may win even in at most 4 moves of his. For that purpose, use Lagrange's four squares theorem in order to expand $S(n)$ as the sum of at most four squares of positive integers: $S(n)=a_{1}^{2}+\cdots+a_{s}^{2}$. Then, on every move of his, Bob can replace the number $\left(a_{1}^{2}+\cdots+a_{k}^{2}\right) b^{2}$ on the board by $\left(a_{1}^{2}+\cdots+a_{k-1}^{2}\right) b^{2}$. The only chance for Amy to interrupt this process is to replace a current number by its even power; but in this case Bob wins immediately.
On the other hand, four is indeed the minimum number of moves in which Bob can guarantee himself to win. To show that, let Amy choose the number 7, and take just the first power on each of her subsequent moves.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Amy and Bob play the game. At the beginning, Amy writes down a positive integer on the board. Then the players take moves in turn, Bob moves first. On any move of his, Bob replaces the number $n$ on the blackboard with a number of the form $n-a^{2}$, where $a$ is a positive integer. On any move of hers, Amy replaces the number $n$ on the blackboard with a number of the form $n^{k}$, where $k$ is a positive integer. Bob wins if the number on the board becomes zero. Can Amy prevent Bob's win?
Russia, Maxim Didin
|
The answer is in the negative. For a positive integer $n$, we define its square-free part $S(n)$ to be the smallest positive integer $a$ such that $n / a$ is a square of an integer. In other words, $S(n)$ is the product of all primes having odd exponents in the prime expansion of $n$. We also agree that $S(0)=0$.
Now we show that (i) on any move of hers, Amy does not increase the square-free part of the positive integer on the board; and (ii) on any move of his, Bob always can replace a positive integer $n$ with a non-negative integer $k$ with $S(k)<S(n)$. Thus, if the game starts by a positive integer $N$, Bob can win in at most $S(N)$ moves.
Part (i) is trivial, as the definition of the square-part yields $S\left(n^{k}\right)=S(n)$ whenever $k$ is odd, and $S\left(n^{k}\right)=1 \leq S(n)$ whenever $k$ is even, for any positive integer $n$.
Part (ii) is also easy: if, before Bob's move, the board contains a number $n=S(n) \cdot b^{2}$, then Bob may replace it with $n^{\prime}=n-b^{2}=(S(n)-1) b^{2}$, whence $S\left(n^{\prime}\right) \leq S(n)-1$.
Remarks. (1) To make the argument more transparent, Bob may restrict himself to subtract only those numbers which are divisible by the maximal square dividing the current number. This restriction having been put, one may replace any number $n$ appearing on the board by $S(n)$, omitting the square factors.
After this change, Amy's moves do not increase the number, while Bob's moves decrease it. Thus, Bob wins.
(2) In fact, Bob may win even in at most 4 moves of his. For that purpose, use Lagrange's four squares theorem in order to expand $S(n)$ as the sum of at most four squares of positive integers: $S(n)=a_{1}^{2}+\cdots+a_{s}^{2}$. Then, on every move of his, Bob can replace the number $\left(a_{1}^{2}+\cdots+a_{k}^{2}\right) b^{2}$ on the board by $\left(a_{1}^{2}+\cdots+a_{k-1}^{2}\right) b^{2}$. The only chance for Amy to interrupt this process is to replace a current number by its even power; but in this case Bob wins immediately.
On the other hand, four is indeed the minimum number of moves in which Bob can guarantee himself to win. To show that, let Amy choose the number 7, and take just the first power on each of her subsequent moves.
|
{
"resource_path": "RMM/segmented/en-2019-RMM2019-Day1-English.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
5ed29fe7-301b-5870-9d8f-1f26f2a0a624
| 606,044
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. If $A B C D$ is a rectangle, the statement is trivial due to symmetry. Hence, in what follows we assume $A D \nVdash B C$.
Let $F$ be the midpoint of $B D$; by symmetry, both $\omega$ and $\Omega$ pass through $F$. Let $P^{\prime}$ be the meeting point of tangents to $\omega$ at $F$ and to $\Omega$ at $E$. We aim to show that $P^{\prime}=P$, which yields the required result. For that purpose, we show that $P^{\prime} A$ and $P^{\prime} D$ are tangent to $\omega$ and $\Omega$, respectively.
Let $K$ be the midpoint of $A F$. Then $E K$ is a midline in the triangle $A C F$, so $\angle(A E, E K)=$ $\angle(E C, C F)$. Since $P^{\prime} E$ is tangent to $\Omega$, we get $\angle(E C, C F)=\angle\left(P^{\prime} E, E F\right)$. Thus, $\angle(A E, E K)=$ $\angle\left(P^{\prime} E, E F\right)$, so $E P^{\prime}$ is a symmedian in the triangle $A E F$. Therefore, $E P^{\prime}$ and the tangents to $\omega$ at $A$ and $F$ are concurrent, and the concurrency point is $P^{\prime}$ itself. Hence $P^{\prime} A$ is tangent to $\omega$.
The second claim is similar. Taking $L$ to be the midpoint of $D E$, we have $\angle(D F, F L)=$ $\angle(F B, B E)=\angle\left(P^{\prime} F, F E\right)$, so $P^{\prime} F$ is a symmedian in the triangle $D E F$, and hence $P^{\prime}$ is the meeting point of the tangents to $\Omega$ at $D$ and $E$.
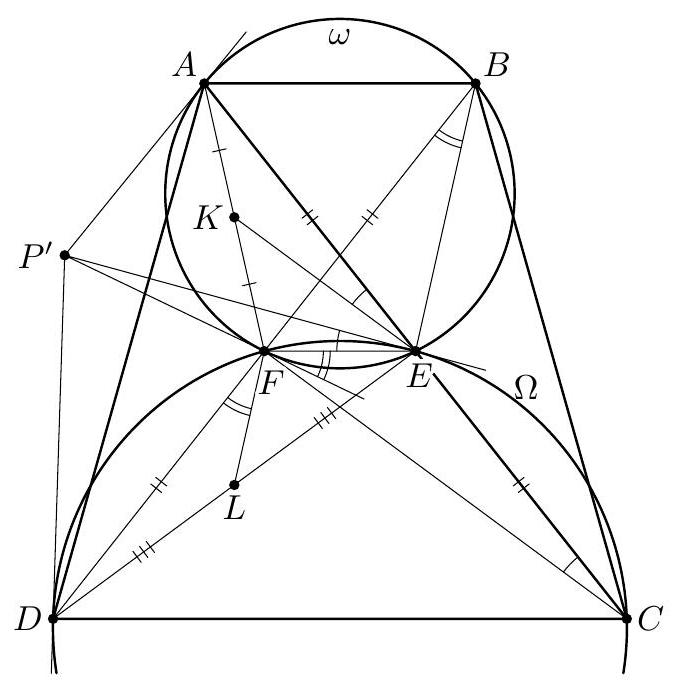
Remark. The above arguments may come in different orders. E.g., one may define $P^{\prime}$ to be the point of intersection of the tangents to $\Omega$ at $D$ and $E$ - hence obtaining that $P^{\prime} F$ is a symmedian in $\triangle D E F$, then deduce that $P^{\prime} F$ is tangent to $\omega$, and then apply a similar argument to show that $P^{\prime} E$ is a symmedian in $\triangle A E F$, whence $P^{\prime} A$ is tangent to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. If $A B C D$ is a rectangle, the statement is trivial due to symmetry. Hence, in what follows we assume $A D \nVdash B C$.
Let $F$ be the midpoint of $B D$; by symmetry, both $\omega$ and $\Omega$ pass through $F$. Let $P^{\prime}$ be the meeting point of tangents to $\omega$ at $F$ and to $\Omega$ at $E$. We aim to show that $P^{\prime}=P$, which yields the required result. For that purpose, we show that $P^{\prime} A$ and $P^{\prime} D$ are tangent to $\omega$ and $\Omega$, respectively.
Let $K$ be the midpoint of $A F$. Then $E K$ is a midline in the triangle $A C F$, so $\angle(A E, E K)=$ $\angle(E C, C F)$. Since $P^{\prime} E$ is tangent to $\Omega$, we get $\angle(E C, C F)=\angle\left(P^{\prime} E, E F\right)$. Thus, $\angle(A E, E K)=$ $\angle\left(P^{\prime} E, E F\right)$, so $E P^{\prime}$ is a symmedian in the triangle $A E F$. Therefore, $E P^{\prime}$ and the tangents to $\omega$ at $A$ and $F$ are concurrent, and the concurrency point is $P^{\prime}$ itself. Hence $P^{\prime} A$ is tangent to $\omega$.
The second claim is similar. Taking $L$ to be the midpoint of $D E$, we have $\angle(D F, F L)=$ $\angle(F B, B E)=\angle\left(P^{\prime} F, F E\right)$, so $P^{\prime} F$ is a symmedian in the triangle $D E F$, and hence $P^{\prime}$ is the meeting point of the tangents to $\Omega$ at $D$ and $E$.

Remark. The above arguments may come in different orders. E.g., one may define $P^{\prime}$ to be the point of intersection of the tangents to $\Omega$ at $D$ and $E$ - hence obtaining that $P^{\prime} F$ is a symmedian in $\triangle D E F$, then deduce that $P^{\prime} F$ is tangent to $\omega$, and then apply a similar argument to show that $P^{\prime} E$ is a symmedian in $\triangle A E F$, whence $P^{\prime} A$ is tangent to $\omega$.
|
{
"resource_path": "RMM/segmented/en-2019-RMM2019-Day1-English.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
3c526b74-dc66-50b8-9f9e-563f93954486
| 606,049
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. Let $Q$ be the isogonal conjugate of $P$ with respect to $\triangle A E D$, so $\angle(Q A, A D)=$ $\angle(E A, A P)=\angle(E B, B A)$ and $\angle(Q D, D A)=\angle(E D, D P)=\angle(E C, C D)$. Now our aim is to prove that $Q E \| C D$; this will yield that $\angle(E C, C D)=\angle(A E, E Q)=\angle(P E, E D)$, whence $P E$ is tangent to $\Omega$.
Let $D Q$ meet $A B$ at $X$. Then we have $\angle(X D, D A)=\angle(E C, C D)=\angle(E A, A B)$ and $\angle(D A, A X)=\angle(A B, B C)$, hence the triangles $D A X$ and $A B C$ are similar. Since $\angle(A B, B E)=$ $\angle(D A, A Q)$, the points $Q$ and $E$ correspond to each other in these triangles, hence $Q$ is the midpoint of $D X$. This yields that the points $Q$ and $E$ lie on the midline of the trapezoid parallel to $C D$, as desired.
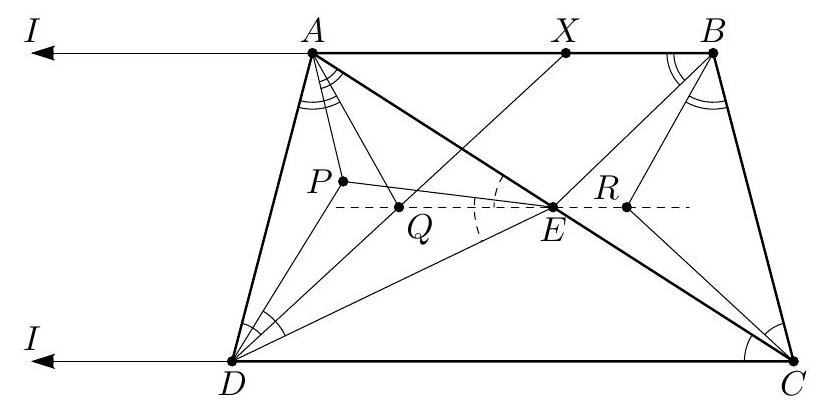
Remark. The last step could be replaced with another application of isogonal conjugacy in the following manner. Reflect $Q$ in the common perpendicular bisector of $A B$ and $C D$ to obtain a point $R$ such that $\angle(C B, B R)=\angle(Q A, A D)=\angle(E B, B A)$ and $\angle(B C, C R)=\angle(Q D, D A)=$ $\angle(E C, C D)$. These relations yield that the points $E$ and $R$ are isogonally conjugate in a triangle $B C I$, where $I$ is the (ideal) point of intersection of $B A$ with $C D$. Since $E$ is equidistant from $A B$ and $C D, R$ is also equidistant from them, which yields what we need. (The last step deserves some explanation, since one vertex of the triangle is ideal. Such explanation may be obtained in many different ways - e.g., by a short computation in sines, or by noticing that, as in the usual case, $R$ is the circumcenter of the triangle formed by the reflections of $E$ in the sidelines $A B$, $B C$, and $C D$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. Let $Q$ be the isogonal conjugate of $P$ with respect to $\triangle A E D$, so $\angle(Q A, A D)=$ $\angle(E A, A P)=\angle(E B, B A)$ and $\angle(Q D, D A)=\angle(E D, D P)=\angle(E C, C D)$. Now our aim is to prove that $Q E \| C D$; this will yield that $\angle(E C, C D)=\angle(A E, E Q)=\angle(P E, E D)$, whence $P E$ is tangent to $\Omega$.
Let $D Q$ meet $A B$ at $X$. Then we have $\angle(X D, D A)=\angle(E C, C D)=\angle(E A, A B)$ and $\angle(D A, A X)=\angle(A B, B C)$, hence the triangles $D A X$ and $A B C$ are similar. Since $\angle(A B, B E)=$ $\angle(D A, A Q)$, the points $Q$ and $E$ correspond to each other in these triangles, hence $Q$ is the midpoint of $D X$. This yields that the points $Q$ and $E$ lie on the midline of the trapezoid parallel to $C D$, as desired.

Remark. The last step could be replaced with another application of isogonal conjugacy in the following manner. Reflect $Q$ in the common perpendicular bisector of $A B$ and $C D$ to obtain a point $R$ such that $\angle(C B, B R)=\angle(Q A, A D)=\angle(E B, B A)$ and $\angle(B C, C R)=\angle(Q D, D A)=$ $\angle(E C, C D)$. These relations yield that the points $E$ and $R$ are isogonally conjugate in a triangle $B C I$, where $I$ is the (ideal) point of intersection of $B A$ with $C D$. Since $E$ is equidistant from $A B$ and $C D, R$ is also equidistant from them, which yields what we need. (The last step deserves some explanation, since one vertex of the triangle is ideal. Such explanation may be obtained in many different ways - e.g., by a short computation in sines, or by noticing that, as in the usual case, $R$ is the circumcenter of the triangle formed by the reflections of $E$ in the sidelines $A B$, $B C$, and $C D$.)
|
{
"resource_path": "RMM/segmented/en-2019-RMM2019-Day1-English.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
3c526b74-dc66-50b8-9f9e-563f93954486
| 606,049
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. (Dan Carmon) Let $O$ be the intersection of the diagonals $A C$ and $B D$. Let $F$ be the midpoint of $B D$. Let $S$ be the second intersection point of the circumcircles of triangles $A O F$ and $D O E$. We will prove that $S D$ and $S E$ are tangent to $\Omega$; the symmetric argument would then imply also that $S A$ and $S F$ are tangent to $\Gamma$. Thus $S=P$ and the claimed tangency holds.
We first prove that $O S$ is parallel to $A B$ and $D C$. Compute the powers of the points $A, B$ with respect to the circumcircles of $A O F$ and $D O E$ :
$$
\begin{gathered}
d(A, A O F)=0, \quad d(A, D O E)=A O \cdot A E \\
d(B, A O F)=B O \cdot B F, \quad d(B, D O E)=B O \cdot B D=2 B O \cdot B F
\end{gathered}
$$
And therefore
$$
d(B, D O E)-d(B, A O F)=B O \cdot B F=A O \cdot A E=d(A, D O E)-d(A, A O F)
$$
Thus both $A$ and $B$ belong to a locus of the form
$$
d(X, D O E)-d(X, A O F)=\mathrm{const}
$$
which is always a lines parallel to the radical axis of the respective circles. Since this radical axis is $O S$ by definition, it follows that $A B$ is parallel to $O S$, as claimed.
Now by angle chasing in the cyclic quadrilateral $D S O E$, we find
$$
\begin{gathered}
\angle(S D, D E)=\angle(S O, O E)=\angle(D C, C E), \\
\angle(S E, E D)=\angle(S O, O D)=\angle(D C, D B)=\angle(A C, C D)=\angle(E C, C D),
\end{gathered}
$$
and these angle equalities are exactly the conditions of $S D, S E$ being tanget to $\Omega$, as claimed.
Remarks. (1) The solution was motivated by the following observation: Suppose $P$ is the intersection of the tangents to $\Omega$ at $D$ and $E$ as claimed. Then by single angle chasing we observe that the isogonal conjugate of $P$ in the triangle $D O E$ is the common ideal point at infinity of $D C$ and $E F$. This implies that $P$ is on the circumcircle of $D O E$ and that $O P$ is parallel to $D C$ (to be precise, it implies that the reflection of $O P$ in the angle bisector of $D O E$ is parallel to $D C$ and $E F$ - but the angle bisector is also parallel to these lines, so in fact $O P$ is the angle bisector). By symmetry it follows that $P$ is also on the circumcircle of $A O F$, thus the construction.
(2) The key parts of the proof can be described as (1) Constructing $S$, (2) Proving that $O S$ is parallel to $A B$ and $C D$, and (3) Concluding that $S=P$ and finishing the problem. Parts (2) and (3) can be performed in various other ways. For example, part (2) can be proved by showing that the circumcentres of $A O F$ and $D O E$ lie on a line perpendicular to the trapezium's bases; part (3) can be proved considering the spiral map taking the circumcircle of $D O C$ to the circumcircle of $D S E$. Since $O$ is the second intersction point of these circles, and since $O C E$ are collinear and $S O$ is tangent to the circumcircle of $D O C$ at $O$ (by symmetry), it follows that the spiral map sends $C$ to $E$ and $O$ to $S$, i.e. the triangle $D S E$ is similar to the isoceles triangle $D O C$, from which the remainder of the angle chase is trivial.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$. Let $E$ be the midpoint of $A C$. Denote by $\omega$ and $\Omega$ the circumcircles of the triangles $A B E$ and $C D E$, respectively. Let $P$ be the crossing poitn of the tangent to $\omega$ at $A$ with the tangent to $\Omega$ at $D$. Prove that $P E$ is tangent to $\Omega$.
Slovenia, Jakob Jurij Snou
|
. (Dan Carmon) Let $O$ be the intersection of the diagonals $A C$ and $B D$. Let $F$ be the midpoint of $B D$. Let $S$ be the second intersection point of the circumcircles of triangles $A O F$ and $D O E$. We will prove that $S D$ and $S E$ are tangent to $\Omega$; the symmetric argument would then imply also that $S A$ and $S F$ are tangent to $\Gamma$. Thus $S=P$ and the claimed tangency holds.
We first prove that $O S$ is parallel to $A B$ and $D C$. Compute the powers of the points $A, B$ with respect to the circumcircles of $A O F$ and $D O E$ :
$$
\begin{gathered}
d(A, A O F)=0, \quad d(A, D O E)=A O \cdot A E \\
d(B, A O F)=B O \cdot B F, \quad d(B, D O E)=B O \cdot B D=2 B O \cdot B F
\end{gathered}
$$
And therefore
$$
d(B, D O E)-d(B, A O F)=B O \cdot B F=A O \cdot A E=d(A, D O E)-d(A, A O F)
$$
Thus both $A$ and $B$ belong to a locus of the form
$$
d(X, D O E)-d(X, A O F)=\mathrm{const}
$$
which is always a lines parallel to the radical axis of the respective circles. Since this radical axis is $O S$ by definition, it follows that $A B$ is parallel to $O S$, as claimed.
Now by angle chasing in the cyclic quadrilateral $D S O E$, we find
$$
\begin{gathered}
\angle(S D, D E)=\angle(S O, O E)=\angle(D C, C E), \\
\angle(S E, E D)=\angle(S O, O D)=\angle(D C, D B)=\angle(A C, C D)=\angle(E C, C D),
\end{gathered}
$$
and these angle equalities are exactly the conditions of $S D, S E$ being tanget to $\Omega$, as claimed.
Remarks. (1) The solution was motivated by the following observation: Suppose $P$ is the intersection of the tangents to $\Omega$ at $D$ and $E$ as claimed. Then by single angle chasing we observe that the isogonal conjugate of $P$ in the triangle $D O E$ is the common ideal point at infinity of $D C$ and $E F$. This implies that $P$ is on the circumcircle of $D O E$ and that $O P$ is parallel to $D C$ (to be precise, it implies that the reflection of $O P$ in the angle bisector of $D O E$ is parallel to $D C$ and $E F$ - but the angle bisector is also parallel to these lines, so in fact $O P$ is the angle bisector). By symmetry it follows that $P$ is also on the circumcircle of $A O F$, thus the construction.
(2) The key parts of the proof can be described as (1) Constructing $S$, (2) Proving that $O S$ is parallel to $A B$ and $C D$, and (3) Concluding that $S=P$ and finishing the problem. Parts (2) and (3) can be performed in various other ways. For example, part (2) can be proved by showing that the circumcentres of $A O F$ and $D O E$ lie on a line perpendicular to the trapezium's bases; part (3) can be proved considering the spiral map taking the circumcircle of $D O C$ to the circumcircle of $D S E$. Since $O$ is the second intersction point of these circles, and since $O C E$ are collinear and $S O$ is tangent to the circumcircle of $D O C$ at $O$ (by symmetry), it follows that the spiral map sends $C$ to $E$ and $O$ to $S$, i.e. the triangle $D S E$ is similar to the isoceles triangle $D O C$, from which the remainder of the angle chase is trivial.
|
{
"resource_path": "RMM/segmented/en-2019-RMM2019-Day1-English.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3"
}
|
3c526b74-dc66-50b8-9f9e-563f93954486
| 606,049
|
Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any graph on $v$ vertices with at least $(1+\varepsilon) v$ edges has two distinct simple cycles of equal lengths.
(Recall that the notion of a simple cycle does not allow repetition of vertices in a cycle.)
Russia, Fedor Petrov
|
Fix a positive real number $\varepsilon$, and let $G$ be a graph on $v$ vertices with at least $(1+\varepsilon) v$ edges, all of whose simple cycles have pairwise distinct lengths.
Assuming $\varepsilon^{2} v \geq 1$, we exhibit an upper bound linear in $v$ and a lower bound quadratic in $v$ for the total number of simple cycles in $G$, showing thereby that $v$ cannot be arbitrarily large, whence the conclusion.
Since a simple cycle in $G$ has at most $v$ vertices, and each length class contains at most one such, $G$ has at most $v$ pairwise distinct simple cycles. This establishes the desired upper bound.
For the lower bound, consider a spanning tree for each component of $G$, and collect them all together to form a spanning forest $F$. Let $A$ be the set of edges of $F$, and let $B$ be the set of all other edges of $G$. Clearly, $|A| \leq v-1$, so $|B| \geq(1+\varepsilon) v-|A| \geq(1+\varepsilon) v-(v-1)=\varepsilon v+1>\varepsilon v$.
For each edge $b$ in $B$, adjoining $b$ to $F$ produces a unique simple cycle $C_{b}$ through $b$. Let $S_{b}$ be the set of edges in $A$ along $C_{b}$. Since the $C_{b}$ have pairwise distinct lengths, $\sum_{b \in B}\left|S_{b}\right| \geq$ $2+\cdots+(|B|+1)=|B|(|B|+3) / 2>|B|^{2} / 2>\varepsilon^{2} v^{2} / 2$.
Consequently, some edge in $A$ lies in more than $\varepsilon^{2} v^{2} /(2 v)=\varepsilon^{2} v / 2$ of the $S_{b}$. Fix such an edge $a$ in $A$, and let $B^{\prime}$ be the set of all edges $b$ in $B$ whose corresponding $S_{b}$ contain $a$, so $\left|B^{\prime}\right|>\varepsilon^{2} v / 2$.
For each 2-edge subset $\left\{b_{1}, b_{2}\right\}$ of $B^{\prime}$, the union $C_{b_{1}} \cup C_{b_{2}}$ of the cycles $C_{b_{1}}$ and $C_{b_{2}}$ forms a $\theta$-graph, since their common part is a path in $F$ through $a$; and since neither of the $b_{i}$ lies along this path, $C_{b_{1}} \cup C_{b_{2}}$ contains a third simple cycle $C_{b_{1}, b_{2}}$ through both $b_{1}$ and $b_{2}$. Finally, since $B^{\prime} \cap C_{b_{1}, b_{2}}=\left\{b_{1}, b_{2}\right\}$, the assignment $\left\{b_{1}, b_{2}\right\} \mapsto C_{b_{1}, b_{2}}$ is injective, so the total number of simple cycles in $G$ is at least $\binom{\left|B^{\prime}\right|}{2}>\binom{\varepsilon^{2} v / 2}{2}$. This establishes the desired lower bound and concludes the proof.
Remarks. (1) The problem of finding two cycles of equal lengths in a graph on $v$ vertices with $2 v$ edges is known and much easier - simply consider all cycles of the form $C_{b}$.
The solution above shows that a graph on $v$ vertices with at least $v+\Theta\left(v^{3 / 4}\right)$ edges has two cycles of equal lengths. The constant $3 / 4$ is not sharp; a harder proof seems to show that $v+\Theta(\sqrt{v \log v})$ edges would suffice. On the other hand, there exist graphs on $v$ vertices with $v+\Theta(\sqrt{v})$ edges having no such cycles.
(2) To avoid graph terminology, the statement of the problem may be rephrased as follows:
Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any $v$-member company, within which there are at least $(1+\varepsilon) v$ friendship relations, satisfies the following condition: For some integer $u \geq 3$, there exist two distinct $u$ member cyclic arrangements in each of which any two neighbours are friends. (Two arrangements are distinct if they are not obtained from one another through rotation and/or symmetry; a member of the company may be included in neither arrangement, in one of them or in both.)
Sketch of solution 2. (Po-Shen Loh) Recall that the girth of a graph $G$ is the minimal length of a (simple) cycle in this graph.
Lemma. For any fixed positive $\delta$, a graph on $v$ vertices whose girth is at least $\delta v$ has at most $v+o(v)$ edges.
Proof. Define $f(v)$ to be the maximal number $f$ such that a graph on $v$ vertices whose girth is at least $\delta v$ may have $v+f$ edges. We are interested in the recursive estimates for $f$.
Let $G$ be a graph on $v$ vertices whose gifth is at least $\delta v$ containing $v+f(v)$ edges. If $G$ contains a leaf (i.e., a vertex of degree 1 ), then one may remove this vertex along with its edge, obtaining a graph with at most $v-1+f(v-1)$ edges. Thus, in this case $f(v) \leq f(v-1)$.
Define an isolated path of length $k$ to be a sequence of vertices $v_{0}, v_{1}, \ldots, v_{k}$, such that $v_{i}$ is connected to $v_{i+1}$, and each of the vertices $v_{1}, \ldots, v_{k-1}$ has degree 2 (so, these vertices are connected only to their neighbors in the path). If $G$ contains an isolated path $v_{0}, \ldots, v_{k}$ of length, say, $k>\sqrt{v}$, then one may remove all its middle vertices $v_{1}, \ldots, v_{k-1}$, along with all their $k$ edges. We obtain a graph on $v-k+1$ vertices with at most $(v-k+1)+f(v-k+1)$ edges. Thus, in this case $f(v) \leq f(v-k+1)+1$.
Assume now that the lengths of all isolated paths do not exceed $\sqrt{v}$; we show that in this case $v$ is bounded from above. For that purpose, we replace each maximal isolated path by an edge between its endpoints, removing all middle vertices. We obtain a graph $H$ whose girth is at least $\delta v / \sqrt{v}=\delta \sqrt{v}$. Each vertex of $H$ has degree at least 3. By the girth condition, the neighborhood of any vertex $x$ of radius $r=\lfloor(\delta \sqrt{v}-1) / 2\rfloor$ is a tree rooted at $x$. Any vertex at level $i<r$ has at least two sons; so the tree contains at least $2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ vertices (even at the last level). So, $v \geq 2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ which may happen only for a finite number of values of $v$.
Thus, for all large enough values of $v$, we have either $f(v) \leq f(v-1)$ or $f(v) \leq f(v-k+1)$ for some $k>\sqrt{v}$. This easily yields $f(v)=o(v)$, as desired.
Now we proceed to the problem. Consider a graph on $v$ vertices containing no two simple cycles of the same length. Take its $\lfloor\varepsilon v / 2\rfloor$ shortest cycles (or all its cycles, if their total number is smaller) and remove an edge from each. We get a graph of girth at least $\varepsilon v / 2$. By the lemma, the number of edges in the obtained graph is at most $v+o(v)$, so the number of edges in the initial graph is at most $v+\varepsilon v / 2+o(v)$, which is smaller than $(1+\varepsilon) v$ if $v$ is large enough.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any graph on $v$ vertices with at least $(1+\varepsilon) v$ edges has two distinct simple cycles of equal lengths.
(Recall that the notion of a simple cycle does not allow repetition of vertices in a cycle.)
Russia, Fedor Petrov
|
Fix a positive real number $\varepsilon$, and let $G$ be a graph on $v$ vertices with at least $(1+\varepsilon) v$ edges, all of whose simple cycles have pairwise distinct lengths.
Assuming $\varepsilon^{2} v \geq 1$, we exhibit an upper bound linear in $v$ and a lower bound quadratic in $v$ for the total number of simple cycles in $G$, showing thereby that $v$ cannot be arbitrarily large, whence the conclusion.
Since a simple cycle in $G$ has at most $v$ vertices, and each length class contains at most one such, $G$ has at most $v$ pairwise distinct simple cycles. This establishes the desired upper bound.
For the lower bound, consider a spanning tree for each component of $G$, and collect them all together to form a spanning forest $F$. Let $A$ be the set of edges of $F$, and let $B$ be the set of all other edges of $G$. Clearly, $|A| \leq v-1$, so $|B| \geq(1+\varepsilon) v-|A| \geq(1+\varepsilon) v-(v-1)=\varepsilon v+1>\varepsilon v$.
For each edge $b$ in $B$, adjoining $b$ to $F$ produces a unique simple cycle $C_{b}$ through $b$. Let $S_{b}$ be the set of edges in $A$ along $C_{b}$. Since the $C_{b}$ have pairwise distinct lengths, $\sum_{b \in B}\left|S_{b}\right| \geq$ $2+\cdots+(|B|+1)=|B|(|B|+3) / 2>|B|^{2} / 2>\varepsilon^{2} v^{2} / 2$.
Consequently, some edge in $A$ lies in more than $\varepsilon^{2} v^{2} /(2 v)=\varepsilon^{2} v / 2$ of the $S_{b}$. Fix such an edge $a$ in $A$, and let $B^{\prime}$ be the set of all edges $b$ in $B$ whose corresponding $S_{b}$ contain $a$, so $\left|B^{\prime}\right|>\varepsilon^{2} v / 2$.
For each 2-edge subset $\left\{b_{1}, b_{2}\right\}$ of $B^{\prime}$, the union $C_{b_{1}} \cup C_{b_{2}}$ of the cycles $C_{b_{1}}$ and $C_{b_{2}}$ forms a $\theta$-graph, since their common part is a path in $F$ through $a$; and since neither of the $b_{i}$ lies along this path, $C_{b_{1}} \cup C_{b_{2}}$ contains a third simple cycle $C_{b_{1}, b_{2}}$ through both $b_{1}$ and $b_{2}$. Finally, since $B^{\prime} \cap C_{b_{1}, b_{2}}=\left\{b_{1}, b_{2}\right\}$, the assignment $\left\{b_{1}, b_{2}\right\} \mapsto C_{b_{1}, b_{2}}$ is injective, so the total number of simple cycles in $G$ is at least $\binom{\left|B^{\prime}\right|}{2}>\binom{\varepsilon^{2} v / 2}{2}$. This establishes the desired lower bound and concludes the proof.
Remarks. (1) The problem of finding two cycles of equal lengths in a graph on $v$ vertices with $2 v$ edges is known and much easier - simply consider all cycles of the form $C_{b}$.
The solution above shows that a graph on $v$ vertices with at least $v+\Theta\left(v^{3 / 4}\right)$ edges has two cycles of equal lengths. The constant $3 / 4$ is not sharp; a harder proof seems to show that $v+\Theta(\sqrt{v \log v})$ edges would suffice. On the other hand, there exist graphs on $v$ vertices with $v+\Theta(\sqrt{v})$ edges having no such cycles.
(2) To avoid graph terminology, the statement of the problem may be rephrased as follows:
Given any positive real number $\varepsilon$, prove that, for all but finitely many positive integers $v$, any $v$-member company, within which there are at least $(1+\varepsilon) v$ friendship relations, satisfies the following condition: For some integer $u \geq 3$, there exist two distinct $u$ member cyclic arrangements in each of which any two neighbours are friends. (Two arrangements are distinct if they are not obtained from one another through rotation and/or symmetry; a member of the company may be included in neither arrangement, in one of them or in both.)
Sketch of solution 2. (Po-Shen Loh) Recall that the girth of a graph $G$ is the minimal length of a (simple) cycle in this graph.
Lemma. For any fixed positive $\delta$, a graph on $v$ vertices whose girth is at least $\delta v$ has at most $v+o(v)$ edges.
Proof. Define $f(v)$ to be the maximal number $f$ such that a graph on $v$ vertices whose girth is at least $\delta v$ may have $v+f$ edges. We are interested in the recursive estimates for $f$.
Let $G$ be a graph on $v$ vertices whose gifth is at least $\delta v$ containing $v+f(v)$ edges. If $G$ contains a leaf (i.e., a vertex of degree 1 ), then one may remove this vertex along with its edge, obtaining a graph with at most $v-1+f(v-1)$ edges. Thus, in this case $f(v) \leq f(v-1)$.
Define an isolated path of length $k$ to be a sequence of vertices $v_{0}, v_{1}, \ldots, v_{k}$, such that $v_{i}$ is connected to $v_{i+1}$, and each of the vertices $v_{1}, \ldots, v_{k-1}$ has degree 2 (so, these vertices are connected only to their neighbors in the path). If $G$ contains an isolated path $v_{0}, \ldots, v_{k}$ of length, say, $k>\sqrt{v}$, then one may remove all its middle vertices $v_{1}, \ldots, v_{k-1}$, along with all their $k$ edges. We obtain a graph on $v-k+1$ vertices with at most $(v-k+1)+f(v-k+1)$ edges. Thus, in this case $f(v) \leq f(v-k+1)+1$.
Assume now that the lengths of all isolated paths do not exceed $\sqrt{v}$; we show that in this case $v$ is bounded from above. For that purpose, we replace each maximal isolated path by an edge between its endpoints, removing all middle vertices. We obtain a graph $H$ whose girth is at least $\delta v / \sqrt{v}=\delta \sqrt{v}$. Each vertex of $H$ has degree at least 3. By the girth condition, the neighborhood of any vertex $x$ of radius $r=\lfloor(\delta \sqrt{v}-1) / 2\rfloor$ is a tree rooted at $x$. Any vertex at level $i<r$ has at least two sons; so the tree contains at least $2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ vertices (even at the last level). So, $v \geq 2^{\lfloor(\delta \sqrt{v}-1) / 2\rfloor}$ which may happen only for a finite number of values of $v$.
Thus, for all large enough values of $v$, we have either $f(v) \leq f(v-1)$ or $f(v) \leq f(v-k+1)$ for some $k>\sqrt{v}$. This easily yields $f(v)=o(v)$, as desired.
Now we proceed to the problem. Consider a graph on $v$ vertices containing no two simple cycles of the same length. Take its $\lfloor\varepsilon v / 2\rfloor$ shortest cycles (or all its cycles, if their total number is smaller) and remove an edge from each. We get a graph of girth at least $\varepsilon v / 2$. By the lemma, the number of edges in the obtained graph is at most $v+o(v)$, so the number of edges in the initial graph is at most $v+\varepsilon v / 2+o(v)$, which is smaller than $(1+\varepsilon) v$ if $v$ is large enough.
|
{
"resource_path": "RMM/segmented/en-2019-RMM2019-Day1-English.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
96f80d28-e3ac-5a30-b241-9dbeabfef3fa
| 606,075
|
Let $T_{1}, T_{2}, T_{3}, T_{4}$ be pairwise distinct collinear points such that $T_{2}$ lies between $T_{1}$ and $T_{3}$, and $T_{3}$ lies between $T_{2}$ and $T_{4}$. Let $\omega_{1}$ be a circle through $T_{1}$ and $T_{4}$; let $\omega_{2}$ be the circle through $T_{2}$ and internally tangent to $\omega_{1}$ at $T_{1}$; let $\omega_{3}$ be the circle through $T_{3}$ and externally tangent to $\omega_{2}$ at $T_{2}$; and let $\omega_{4}$ be the circle through $T_{4}$ and externally tangent to $\omega_{3}$ at $T_{3}$. A line crosses $\omega_{1}$ at $P$ and $W, \omega_{2}$ at $Q$ and $R, \omega_{3}$ at $S$ and $T$, and $\omega_{4}$ at $U$ and $V$, the order of these points along the line being $P, Q, R, S, T, U, V, W$. Prove that $P Q+T U=R S+V W$.
Hungary, Geza Kos
|
Let $O_{i}$ be the centre of $\omega_{i}, i=1,2,3,4$. Notice that the isosceles triangles $O_{i} T_{i} T_{i-1}$ are similar (indices are reduced modulo 4 ), to infer that $\omega_{4}$ is internally tangent to $\omega_{1}$ at $T_{4}$, and $O_{1} O_{2} O_{3} O_{4}$ is a (possibly degenerate) parallelogram.
Let $F_{i}$ be the foot of the perpendicular from $O_{i}$ to $P W$. The $F_{i}$ clearly bisect the segments $P W, Q R, S T$ and $U V$, respectively.
The proof can now be concluded in two similar ways.
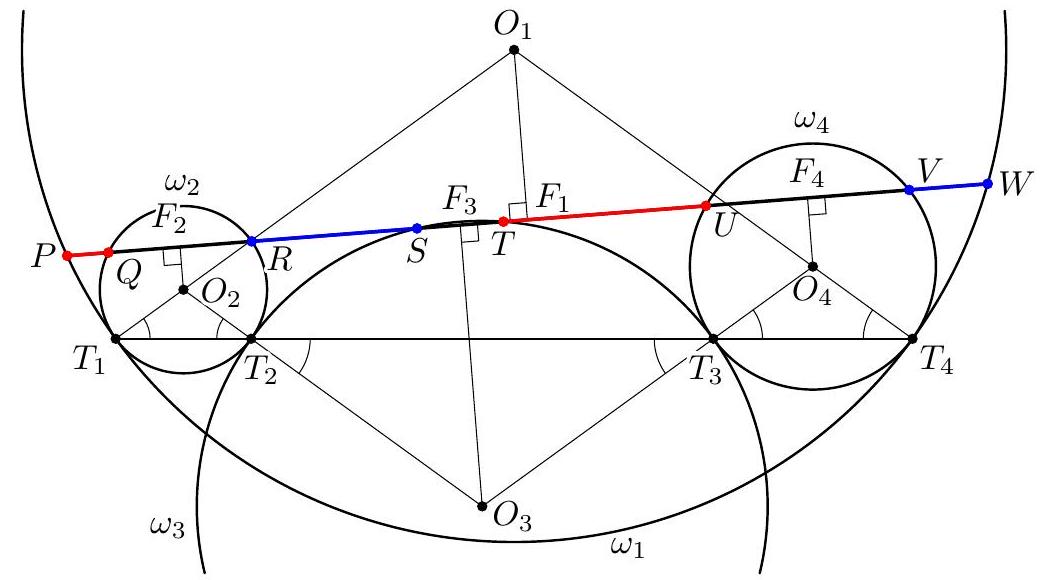
First Approach. Since $O_{1} O_{2} O_{3} O_{4}$ is a parallelogram, $\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}=\mathbf{0}$ and $\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}=\mathbf{0}$; this still holds in the degenerate case, for if the $O_{i}$ are collinear, then they all lie on the line $T_{1} T_{4}$, and each $O_{i}$ is the midpoint of the segment $T_{i} T_{i+1}$. Consequently,
$$
\begin{aligned}
\overrightarrow{P Q}-\overrightarrow{R S}+\overrightarrow{T U}-\overrightarrow{V W}= & \left(\overrightarrow{P F_{1}}+\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{2} Q}\right)-\left(\overrightarrow{R F_{2}}+\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{3} S}\right) \\
& +\left(\overrightarrow{T F_{3}}+\overrightarrow{F_{3} F_{4}}+\overrightarrow{F_{4} U}\right)-\left(\overrightarrow{V F_{4}}+\overrightarrow{F_{4} F_{1}}+\overrightarrow{F_{1} W}\right) \\
= & \left(\overrightarrow{P F_{1}}-\overrightarrow{F_{1} W}\right)-\left(\overrightarrow{R F_{2}}-\overrightarrow{F_{2} Q}\right)+\left(\overrightarrow{T F_{3}}-\overrightarrow{F_{3} S}\right)-\left(\overrightarrow{V F_{4}}-\overrightarrow{F_{4} U}\right) \\
& +\left(\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}\right)-\left(\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}\right)=\mathbf{0}
\end{aligned}
$$
Alternatively, but equivalently, $\overrightarrow{P Q}+\overrightarrow{T U}=\overrightarrow{R S}+\overrightarrow{V W}$, as required.
Second Approach. This is merely another way of reading the previous argument. Fix an orientation of the line $P W$, say, from $P$ towards $W$, and use a lower case letter to denote the coordinate of a point labelled by the corresponding upper case letter.
Since the diagonals of a parallelogram bisect one another, $f_{1}+f_{3}=f_{2}+f_{4}$, the common value being twice the coordinate of the projection to $P W$ of the point where $O_{1} O_{3}$ and $O_{2} O_{4}$ cross; the relation clearly holds in the degenerate case as well.
Plug $f_{1}=\frac{1}{2}(p+w), f_{2}=\frac{1}{2}(q+r), f_{3}=\frac{1}{2}(s+t)$ and $f_{4}=\frac{1}{2}(u+v)$ into the above equality to get $p+w+s+t=q+r+u+v$. Alternatively, but equivalently, $(q-p)+(u-t)=(s-r)+(w-v)$, that is, $P Q+T U=R Q+V W$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $T_{1}, T_{2}, T_{3}, T_{4}$ be pairwise distinct collinear points such that $T_{2}$ lies between $T_{1}$ and $T_{3}$, and $T_{3}$ lies between $T_{2}$ and $T_{4}$. Let $\omega_{1}$ be a circle through $T_{1}$ and $T_{4}$; let $\omega_{2}$ be the circle through $T_{2}$ and internally tangent to $\omega_{1}$ at $T_{1}$; let $\omega_{3}$ be the circle through $T_{3}$ and externally tangent to $\omega_{2}$ at $T_{2}$; and let $\omega_{4}$ be the circle through $T_{4}$ and externally tangent to $\omega_{3}$ at $T_{3}$. A line crosses $\omega_{1}$ at $P$ and $W, \omega_{2}$ at $Q$ and $R, \omega_{3}$ at $S$ and $T$, and $\omega_{4}$ at $U$ and $V$, the order of these points along the line being $P, Q, R, S, T, U, V, W$. Prove that $P Q+T U=R S+V W$.
Hungary, Geza Kos
|
Let $O_{i}$ be the centre of $\omega_{i}, i=1,2,3,4$. Notice that the isosceles triangles $O_{i} T_{i} T_{i-1}$ are similar (indices are reduced modulo 4 ), to infer that $\omega_{4}$ is internally tangent to $\omega_{1}$ at $T_{4}$, and $O_{1} O_{2} O_{3} O_{4}$ is a (possibly degenerate) parallelogram.
Let $F_{i}$ be the foot of the perpendicular from $O_{i}$ to $P W$. The $F_{i}$ clearly bisect the segments $P W, Q R, S T$ and $U V$, respectively.
The proof can now be concluded in two similar ways.

First Approach. Since $O_{1} O_{2} O_{3} O_{4}$ is a parallelogram, $\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}=\mathbf{0}$ and $\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}=\mathbf{0}$; this still holds in the degenerate case, for if the $O_{i}$ are collinear, then they all lie on the line $T_{1} T_{4}$, and each $O_{i}$ is the midpoint of the segment $T_{i} T_{i+1}$. Consequently,
$$
\begin{aligned}
\overrightarrow{P Q}-\overrightarrow{R S}+\overrightarrow{T U}-\overrightarrow{V W}= & \left(\overrightarrow{P F_{1}}+\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{2} Q}\right)-\left(\overrightarrow{R F_{2}}+\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{3} S}\right) \\
& +\left(\overrightarrow{T F_{3}}+\overrightarrow{F_{3} F_{4}}+\overrightarrow{F_{4} U}\right)-\left(\overrightarrow{V F_{4}}+\overrightarrow{F_{4} F_{1}}+\overrightarrow{F_{1} W}\right) \\
= & \left(\overrightarrow{P F_{1}}-\overrightarrow{F_{1} W}\right)-\left(\overrightarrow{R F_{2}}-\overrightarrow{F_{2} Q}\right)+\left(\overrightarrow{T F_{3}}-\overrightarrow{F_{3} S}\right)-\left(\overrightarrow{V F_{4}}-\overrightarrow{F_{4} U}\right) \\
& +\left(\overrightarrow{F_{1} F_{2}}+\overrightarrow{F_{3} F_{4}}\right)-\left(\overrightarrow{F_{2} F_{3}}+\overrightarrow{F_{4} F_{1}}\right)=\mathbf{0}
\end{aligned}
$$
Alternatively, but equivalently, $\overrightarrow{P Q}+\overrightarrow{T U}=\overrightarrow{R S}+\overrightarrow{V W}$, as required.
Second Approach. This is merely another way of reading the previous argument. Fix an orientation of the line $P W$, say, from $P$ towards $W$, and use a lower case letter to denote the coordinate of a point labelled by the corresponding upper case letter.
Since the diagonals of a parallelogram bisect one another, $f_{1}+f_{3}=f_{2}+f_{4}$, the common value being twice the coordinate of the projection to $P W$ of the point where $O_{1} O_{3}$ and $O_{2} O_{4}$ cross; the relation clearly holds in the degenerate case as well.
Plug $f_{1}=\frac{1}{2}(p+w), f_{2}=\frac{1}{2}(q+r), f_{3}=\frac{1}{2}(s+t)$ and $f_{4}=\frac{1}{2}(u+v)$ into the above equality to get $p+w+s+t=q+r+u+v$. Alternatively, but equivalently, $(q-p)+(u-t)=(s-r)+(w-v)$, that is, $P Q+T U=R Q+V W$, as required.
|
{
"resource_path": "RMM/segmented/en-2021-RMM2021-Day1-English_Solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
bcc223a3-94b2-5d92-b048-fdcf6279a2c8
| 606,116
|
A number of 17 workers stand in a row. Every contiguous group of at least 2 workers is a brigade. The chief wants to assign each brigade a leader (which is a member of the brigade) so that each worker's number of assignments is divisible by 4. Prove that the number of such ways to assign the leaders is divisible by 17 .
Russia, Mikhail Antipov
|
Assume that every single worker also forms a brigade (with a unique possible leader). In this modified setting, we are interested in the number $N$ of ways to assign leadership so that each worker's number of assignments is congruent to 1 modulo 4.
Consider the variables $x_{1}, x_{2}, \ldots, x_{17}$ corresponding to the workers. Assign each brigade (from the $i$-th through the $j$-th worker) the polynomial $f_{i j}=x_{i}+x_{i+1}+\cdots+x_{j}$, and form the product $f=\prod_{1 \leq i \leq j \leq 17} f_{i j}$. The number $N$ is the sum $\Sigma(f)$ of the coefficients of all monomials $x_{1}^{\alpha_{1}} x_{2}^{\alpha_{2}} \ldots x_{17}^{\alpha_{17}}$ in the expansion of $f$, where the $\alpha_{i}$ are all congruent to 1 modulo 4 . For any polynomial $P$, let $\Sigma(P)$ denote the corresponding sum. From now on, all polynomials are considered with coefficients in the finite field $\mathbb{F}_{17}$.
Recall that for any positive integer $n$, and any integers $a_{1}, a_{2}, \ldots, a_{n}$, there exist indices $i \leq j$ such that $a_{i}+a_{i+1}+\cdots+a_{j}$ is divisible by $n$. Consequently, $f\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$.
Now, if some monomial in the expansion of $f$ is divisible by $x_{i}^{17}$, replace that $x_{i}^{17}$ by $x_{i}$; this does not alter the above overall vanishing property (by Fermat's Little Theorem), and preserves $\Sigma(f)$. After several such changes, $f$ transforms into a polynomial $g$ whose degree in each variable does not exceed 16 , and $g\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$. For such a polynomial, an easy induction on the number of variables shows that it is identically zero. Consequently, $\Sigma(g)=0$, so $\Sigma(f)=0$ as well, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A number of 17 workers stand in a row. Every contiguous group of at least 2 workers is a brigade. The chief wants to assign each brigade a leader (which is a member of the brigade) so that each worker's number of assignments is divisible by 4. Prove that the number of such ways to assign the leaders is divisible by 17 .
Russia, Mikhail Antipov
|
Assume that every single worker also forms a brigade (with a unique possible leader). In this modified setting, we are interested in the number $N$ of ways to assign leadership so that each worker's number of assignments is congruent to 1 modulo 4.
Consider the variables $x_{1}, x_{2}, \ldots, x_{17}$ corresponding to the workers. Assign each brigade (from the $i$-th through the $j$-th worker) the polynomial $f_{i j}=x_{i}+x_{i+1}+\cdots+x_{j}$, and form the product $f=\prod_{1 \leq i \leq j \leq 17} f_{i j}$. The number $N$ is the sum $\Sigma(f)$ of the coefficients of all monomials $x_{1}^{\alpha_{1}} x_{2}^{\alpha_{2}} \ldots x_{17}^{\alpha_{17}}$ in the expansion of $f$, where the $\alpha_{i}$ are all congruent to 1 modulo 4 . For any polynomial $P$, let $\Sigma(P)$ denote the corresponding sum. From now on, all polynomials are considered with coefficients in the finite field $\mathbb{F}_{17}$.
Recall that for any positive integer $n$, and any integers $a_{1}, a_{2}, \ldots, a_{n}$, there exist indices $i \leq j$ such that $a_{i}+a_{i+1}+\cdots+a_{j}$ is divisible by $n$. Consequently, $f\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$.
Now, if some monomial in the expansion of $f$ is divisible by $x_{i}^{17}$, replace that $x_{i}^{17}$ by $x_{i}$; this does not alter the above overall vanishing property (by Fermat's Little Theorem), and preserves $\Sigma(f)$. After several such changes, $f$ transforms into a polynomial $g$ whose degree in each variable does not exceed 16 , and $g\left(a_{1}, a_{2}, \ldots, a_{17}\right)=0$ for all $a_{1}, a_{2}, \ldots, a_{17}$ in $\mathbb{F}_{17}$. For such a polynomial, an easy induction on the number of variables shows that it is identically zero. Consequently, $\Sigma(g)=0$, so $\Sigma(f)=0$ as well, as desired.
|
{
"resource_path": "RMM/segmented/en-2021-RMM2021-Day1-English_Solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
e027b4b8-2bd2-57b6-ade6-aca841b03a33
| 606,141
|
Let $n$ be a positive integer. The kingdom of Zoomtopia is a convex polygon with integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry (that is, there is a point $O$ such that a $60^{\circ}$ rotation about $O$ maps the polygon to itself). In light of the pandemic, the government of Zoomtopia would like to relocate its $3 n^{2}+3 n+1$ citizens at $3 n^{2}+3 n+1$ points in the kingdom so that every two citizens have a distance of at least 1 for proper social distancing. Prove that this is possible. (The kingdom is assumed to contain its boundary.)
USA, Ankan Bhattacharya
|
Let $P$ denote the given polygon, i.e., the kingdom of Zoomtopia. Throughout the solution, we interpret polygons with integer sides and perimeter $6 k$ as $6 k$-gons with unit sides (some of their angles may equal $180^{\circ}$ ). The argument hinges on the claim below:
Claim. Let $P$ be a convex polygon satisfying the problem conditions - i.e., it has integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry. Then $P$ can be tiled with unit equilateral triangles and unit lozenges with angles at least $60^{\circ}$, with tiles meeting completely along edges, so that the tile configuration has a total of exactly $3 n^{2}+3 n+1$ distinct vertices.
Proof. Induct on $n$. The base case, $n=1$, is clear.
Now take a polygon $P$ of perimeter $6 n \geq 12$. Place six equilateral triangles inwards on six edges corresponding to each other upon rotation at $60^{\circ}$. It is possible to stick a lozenge to each other edge, as shown in the Figure below.
We show that all angles of the lozenges are at least $60^{\circ}$. Let an edge $X Y$ of the polygon bearing some lozenge lie along a boundary segment between edges $A B$ and $C D$ bearing equilateral triangles $A B P$ and $C D Q$. Then the angle formed by $\overrightarrow{X Y}$ and $\overrightarrow{B P}$ is between those formed by $\overrightarrow{A B}, \overrightarrow{B P}$ and $\overrightarrow{C D}, \overrightarrow{C Q}$, i.e., between $60^{\circ}$ and $120^{\circ}$, as desired.
Removing all obtained tiles, we get a $60^{\circ}$-symmetric convex $6(n-1)$-gon with unit sides which can be tiled by the inductive hypothesis. Finally, the number of vertices in the tiling of $P$ is $6 n+3(n-1)^{2}+3(n-1)+1=3 n^{2}+3 n+1$, as desired.
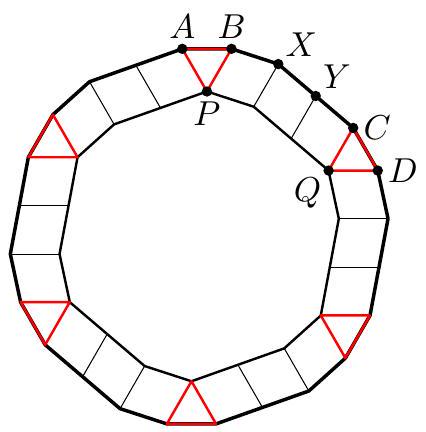
Using the Claim above, we now show that the citizens may be placed at the $3 n^{2}+3 n+1$ tile vertices.
Consider any tile $T_{1}$; its vertices are at least 1 apart from each other. Moreover, let $B A C$ be a part of the boundary of some tile $T$, and let $X$ be any point of the boundary of $T$, lying outside the half-open intervals $[A, B)$ and $[A, C)$ (in this case, we say that $X$ is not adjacent to $A$ ). Then $A X \geq \sqrt{3} / 2$.
Now consider any two tile vertices $A$ and $B$. If they are vertices of the same tile we already know $A B \geq 1$; otherwise, the segment $A B$ crosses the boundaries of some tiles containing $A$ and $B$ at some points $X$ and $Y$ not adjacent to $A$ and $B$, respectively. Hence $A B \geq A X+Y B \geq \sqrt{3}>1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. The kingdom of Zoomtopia is a convex polygon with integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry (that is, there is a point $O$ such that a $60^{\circ}$ rotation about $O$ maps the polygon to itself). In light of the pandemic, the government of Zoomtopia would like to relocate its $3 n^{2}+3 n+1$ citizens at $3 n^{2}+3 n+1$ points in the kingdom so that every two citizens have a distance of at least 1 for proper social distancing. Prove that this is possible. (The kingdom is assumed to contain its boundary.)
USA, Ankan Bhattacharya
|
Let $P$ denote the given polygon, i.e., the kingdom of Zoomtopia. Throughout the solution, we interpret polygons with integer sides and perimeter $6 k$ as $6 k$-gons with unit sides (some of their angles may equal $180^{\circ}$ ). The argument hinges on the claim below:
Claim. Let $P$ be a convex polygon satisfying the problem conditions - i.e., it has integer sides, perimeter $6 n$, and $60^{\circ}$ rotational symmetry. Then $P$ can be tiled with unit equilateral triangles and unit lozenges with angles at least $60^{\circ}$, with tiles meeting completely along edges, so that the tile configuration has a total of exactly $3 n^{2}+3 n+1$ distinct vertices.
Proof. Induct on $n$. The base case, $n=1$, is clear.
Now take a polygon $P$ of perimeter $6 n \geq 12$. Place six equilateral triangles inwards on six edges corresponding to each other upon rotation at $60^{\circ}$. It is possible to stick a lozenge to each other edge, as shown in the Figure below.
We show that all angles of the lozenges are at least $60^{\circ}$. Let an edge $X Y$ of the polygon bearing some lozenge lie along a boundary segment between edges $A B$ and $C D$ bearing equilateral triangles $A B P$ and $C D Q$. Then the angle formed by $\overrightarrow{X Y}$ and $\overrightarrow{B P}$ is between those formed by $\overrightarrow{A B}, \overrightarrow{B P}$ and $\overrightarrow{C D}, \overrightarrow{C Q}$, i.e., between $60^{\circ}$ and $120^{\circ}$, as desired.
Removing all obtained tiles, we get a $60^{\circ}$-symmetric convex $6(n-1)$-gon with unit sides which can be tiled by the inductive hypothesis. Finally, the number of vertices in the tiling of $P$ is $6 n+3(n-1)^{2}+3(n-1)+1=3 n^{2}+3 n+1$, as desired.

Using the Claim above, we now show that the citizens may be placed at the $3 n^{2}+3 n+1$ tile vertices.
Consider any tile $T_{1}$; its vertices are at least 1 apart from each other. Moreover, let $B A C$ be a part of the boundary of some tile $T$, and let $X$ be any point of the boundary of $T$, lying outside the half-open intervals $[A, B)$ and $[A, C)$ (in this case, we say that $X$ is not adjacent to $A$ ). Then $A X \geq \sqrt{3} / 2$.
Now consider any two tile vertices $A$ and $B$. If they are vertices of the same tile we already know $A B \geq 1$; otherwise, the segment $A B$ crosses the boundaries of some tiles containing $A$ and $B$ at some points $X$ and $Y$ not adjacent to $A$ and $B$, respectively. Hence $A B \geq A X+Y B \geq \sqrt{3}>1$.
|
{
"resource_path": "RMM/segmented/en-2021-RMM2021-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
05b02daf-3394-5656-adcc-cb2cf8a12240
| 606,170
|
Initially, a non-constant polynomial $S(x)$ with real coefficients is written down on a board. Whenever the board contains a polynomial $P(x)$, not necessarily alone, one can write down on the board any polynomial of the form $P(C+x)$ or $C+P(x)$, where $C$ is a real constant. Moreover, if the board contains two (not necessarily distinct) polynomials $P(x)$ and $Q(x)$, one can write $P(Q(x))$ and $P(x)+Q(x)$ down on the board. No polynomial is ever erased from the board.
Given two sets of real numbers, $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$, a polynomial $f(x)$ with real coefficients is $(A, B)$-nice if $f(A)=B$, where $f(A)=\left\{f\left(a_{i}\right): i=1,2, \ldots, n\right\}$.
Determine all polynomials $S(x)$ that can initially be written down on the board such that, for any two finite sets $A$ and $B$ of real numbers, with $|A|=|B|$, one can produce an $(A, B)$-nice polynomial in a finite number of steps.
Iran, Navid SafaEi
|
The required polynomials are all polynomials of an even degree $d \geq 2$, and all polynomials of odd degree $d \geq 3$ with negative leading coefficient.
Part I. We begin by showing that any (non-constant) polynomial $S(x)$ not listed above is not $(A, B)$-nice for some pair $(A, B)$ with either $|A|=|B|=2$, or $|A|=|B|=3$.
If $S(x)$ is linear, then so are all the polynomials appearing on the board. Therefore, none of them will be $(A, B)$-nice, say, for $A=\{1,2,3\}$ and $B=\{1,2,4\}$, as desired.
Otherwise, $\operatorname{deg} S=d \geq 3$ is odd, and the leading coefficient is positive. In this case, we make use of the following technical fact, whose proof is presented at the end of the solution.
Claim. There exists a positive constant $T$ such that $S(x)$ satisfies the following condition:
$$
S(b)-S(a) \geq b-a \quad \text { whenever } \quad b-a \geq T
$$
Fix a constant $T$ provided by the Claim. Then, an immediate check shows that all newly appearing polynomials on the board also satisfy $(*)$ (with the same value of $T$ ). Therefore, none of them will be $(A, B)$-nice, say, for $A=\{0, T\}$ and $B=\{0, T / 2\}$, as desired.
Part II. We show that the polynomials listed in the Answer satisfy the requirements. We will show that for any $a_{1}<a_{2}<\cdots<a_{n}$ and any $b_{1} \leq b_{2} \leq \cdots \leq b_{n}$ there exists a polynomial $f(x)$ satisfying $f\left(a_{i}\right)=b_{\sigma(i)}$ for all $i=1,2, \ldots, n$, where $\sigma$ is some permutation.
The proof goes by induction on $n \geq 2$. It is based on the following two lemmas, first of which is merely the base case $n=2$; the proofs of the lemmas are also at the end of the solution.
Lemma 1. For any $a_{1}<a_{2}$ and any $b_{1}, b_{2}$ one can write down on the board a polynomial $F(x)$ satisfying $F\left(a_{i}\right)=b_{i}, i=1,2$.
Lemma 2. For any distinct numbers $a_{1}<a_{2}<\cdots<a_{n}$ one can produce a polynomial $F(x)$ on the board such that the list $F\left(a_{1}\right), F\left(a_{2}\right), \ldots, F\left(a_{n}\right)$ contains exactly $n-1$ distinct numbers, and $F\left(a_{1}\right)=F\left(a_{2}\right)$.
Now, in order to perform the inductive step, we may replace the polynomial $S(x)$ with its shifted copy $S(C+x)$ so that the values $S\left(a_{i}\right)$ are pairwise distinct. Applying Lemma 2 , we get a polynomial $f(x)$ such that only two among the numbers $c_{i}=f\left(a_{i}\right)$ coincide, namely $c_{1}$ and $c_{2}$. Now apply Lemma 1 to get a polynomial $g(x)$ such that $g\left(a_{1}\right)=b_{1}$ and $g\left(a_{2}\right)=b_{2}$. Apply the inductive hypothesis in order to obtain a polynomial $h(x)$ satisfying $h\left(c_{i}\right)=b_{i}-g\left(a_{i}\right)$ for all $i=2,3, \ldots, n$. Then the polynomial $h(f(x))+g(x)$ is a desired one; indeed, we have $h\left(f\left(a_{i}\right)\right)+g\left(a_{i}\right)=h\left(c_{i}\right)+g\left(a_{i}\right)=b_{i}$ for all $i=2,3, \ldots, n$, and finally $h\left(f\left(a_{1}\right)\right)+g\left(a_{1}\right)=$ $h\left(c_{1}\right)+g\left(a_{1}\right)=b_{2}-g\left(a_{2}\right)+g\left(a_{1}\right)=b_{1}$.
It remains to prove the Claim and the two Lemmas.
Proof of the Claim. There exists some segment $\Delta=\left[\alpha^{\prime}, \beta^{\prime}\right]$ such that $S(x)$ is monotone increasing outside that segment. Now one can choose $\alpha \leq \alpha^{\prime}$ and $\beta \geq \beta^{\prime}$ such that $S(\alpha)<\min _{x \in \Delta} S(x)$ and
$S(\beta)>\max _{x \in \Delta} S(x)$. Therefore, for any $x, y, z$ with $x \leq \alpha \leq y \leq \beta \leq z$ we get $S(x) \leq S(\alpha) \leq$ $S(y) \leq S(\beta) \leq S(z)$.
We may decrease $\alpha$ and increase $\beta$ (preserving the condition above) so that, in addition, $S^{\prime}(x)>3$ for all $x \notin[\alpha, \beta]$. Now we claim that the number $T=3(\beta-\alpha)$ fits the bill.
Indeed, take any $a$ and $b$ with $b-a \geq T$. Even if the segment $[a, b]$ crosses $[\alpha, \beta]$, there still is a segment $\left[a^{\prime}, b^{\prime}\right] \subseteq[a, b] \backslash(\alpha, \beta)$ of length $b^{\prime}-a^{\prime} \geq(b-a) / 3$. Then
$$
S(b)-S(a) \geq S\left(b^{\prime}\right)-S\left(a^{\prime}\right)=\left(b^{\prime}-a^{\prime}\right) \cdot S^{\prime}(\xi) \geq 3\left(b^{\prime}-a^{\prime}\right) \geq b-a
$$
for some $\xi \in\left(a^{\prime}, b^{\prime}\right)$.
Proof of Lemma 1. If $S(x)$ has an even degree, then the polynomial $T(x)=S\left(x+a_{2}\right)-S\left(x+a_{1}\right)$ has an odd degree, hence there exists $x_{0}$ with $T\left(x_{0}\right)=S\left(x_{0}+a_{2}\right)-S\left(x_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S\left(x+x_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift $F(x)=G(x)+\left(b_{1}-G\left(a_{1}\right)\right)$ fits the bill.
Assume now that $S(x)$ has odd degree and a negative leading coefficient. Notice that the polynomial $S^{2}(x):=S(S(x))$ has an odd degree and a positive leading coefficient. So, the polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)$ attains all sufficiently large positive values, while $S\left(x+a_{2}\right)-$ $S\left(x+a_{1}\right)$ attains all sufficiently large negative values. Therefore, the two-variable polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)+S\left(y+a_{2}\right)-S\left(y+a_{1}\right)$ attains all real values; in particular, there exist $x_{0}$ and $y_{0}$ with $S^{2}\left(x_{0}+a_{2}\right)+S\left(y_{0}+a_{2}\right)-S^{2}\left(x_{0}+a_{1}\right)-S\left(y_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S^{2}\left(x+x_{0}\right)+S\left(x+y_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift of $G$ fits the bill.
Proof of Lemma 2. Let $\Delta$ denote the segment $\left[a_{1} ; a_{n}\right]$. We modify the proof of Lemma 1 in order to obtain a polynomial $F$ convex (or concave) on $\Delta$ such that $F\left(a_{1}\right)=F\left(a_{2}\right)$; then $F$ is a desired polynomial. Say that a polynomial $H(x)$ is good if $H$ is convex on $\Delta$.
If $\operatorname{deg} S$ is even, and its leading coefficient is positive, then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S(x+c)$ is good for all sufficiently large positive $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S\left(x+c_{2}\right)$ is a desired polynomial. If the leading coefficient of $H$ is negative, we similarly find a desired polynomial which is concave on $\Delta$.
If $\operatorname{deg} S \geq 3$ is odd (and the leading coefficient is negative), then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S^{2}(x+c)$ is good for all sufficiently large positive $c$, and $S^{2}\left(a_{2}+c\right)-S^{2}\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S^{2}\left(x+c_{2}\right)$ is a desired polynomial.
Comment. Both parts above allow some variations.
In Part I, the same scheme of the proof works for many conditions similar to (*), e.g.,
$$
S(b)-S(a)>T \quad \text { whenever } \quad b-a>T
$$
Let us sketch an alternative approach for Part II. It suffices to construct, for each $i$, a polynomial $f_{i}(x)$ such that $f_{i}\left(a_{i}\right)=b_{i}$ and $f_{i}\left(a_{j}\right)=0, j \neq i$. The construction of such polynomials may be reduced to the construction of those for $n=3$ similarly to what happens in the proof of Lemma 2. However, this approach (as well as any in this part) needs some care in order to work properly.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Initially, a non-constant polynomial $S(x)$ with real coefficients is written down on a board. Whenever the board contains a polynomial $P(x)$, not necessarily alone, one can write down on the board any polynomial of the form $P(C+x)$ or $C+P(x)$, where $C$ is a real constant. Moreover, if the board contains two (not necessarily distinct) polynomials $P(x)$ and $Q(x)$, one can write $P(Q(x))$ and $P(x)+Q(x)$ down on the board. No polynomial is ever erased from the board.
Given two sets of real numbers, $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$, a polynomial $f(x)$ with real coefficients is $(A, B)$-nice if $f(A)=B$, where $f(A)=\left\{f\left(a_{i}\right): i=1,2, \ldots, n\right\}$.
Determine all polynomials $S(x)$ that can initially be written down on the board such that, for any two finite sets $A$ and $B$ of real numbers, with $|A|=|B|$, one can produce an $(A, B)$-nice polynomial in a finite number of steps.
Iran, Navid SafaEi
|
The required polynomials are all polynomials of an even degree $d \geq 2$, and all polynomials of odd degree $d \geq 3$ with negative leading coefficient.
Part I. We begin by showing that any (non-constant) polynomial $S(x)$ not listed above is not $(A, B)$-nice for some pair $(A, B)$ with either $|A|=|B|=2$, or $|A|=|B|=3$.
If $S(x)$ is linear, then so are all the polynomials appearing on the board. Therefore, none of them will be $(A, B)$-nice, say, for $A=\{1,2,3\}$ and $B=\{1,2,4\}$, as desired.
Otherwise, $\operatorname{deg} S=d \geq 3$ is odd, and the leading coefficient is positive. In this case, we make use of the following technical fact, whose proof is presented at the end of the solution.
Claim. There exists a positive constant $T$ such that $S(x)$ satisfies the following condition:
$$
S(b)-S(a) \geq b-a \quad \text { whenever } \quad b-a \geq T
$$
Fix a constant $T$ provided by the Claim. Then, an immediate check shows that all newly appearing polynomials on the board also satisfy $(*)$ (with the same value of $T$ ). Therefore, none of them will be $(A, B)$-nice, say, for $A=\{0, T\}$ and $B=\{0, T / 2\}$, as desired.
Part II. We show that the polynomials listed in the Answer satisfy the requirements. We will show that for any $a_{1}<a_{2}<\cdots<a_{n}$ and any $b_{1} \leq b_{2} \leq \cdots \leq b_{n}$ there exists a polynomial $f(x)$ satisfying $f\left(a_{i}\right)=b_{\sigma(i)}$ for all $i=1,2, \ldots, n$, where $\sigma$ is some permutation.
The proof goes by induction on $n \geq 2$. It is based on the following two lemmas, first of which is merely the base case $n=2$; the proofs of the lemmas are also at the end of the solution.
Lemma 1. For any $a_{1}<a_{2}$ and any $b_{1}, b_{2}$ one can write down on the board a polynomial $F(x)$ satisfying $F\left(a_{i}\right)=b_{i}, i=1,2$.
Lemma 2. For any distinct numbers $a_{1}<a_{2}<\cdots<a_{n}$ one can produce a polynomial $F(x)$ on the board such that the list $F\left(a_{1}\right), F\left(a_{2}\right), \ldots, F\left(a_{n}\right)$ contains exactly $n-1$ distinct numbers, and $F\left(a_{1}\right)=F\left(a_{2}\right)$.
Now, in order to perform the inductive step, we may replace the polynomial $S(x)$ with its shifted copy $S(C+x)$ so that the values $S\left(a_{i}\right)$ are pairwise distinct. Applying Lemma 2 , we get a polynomial $f(x)$ such that only two among the numbers $c_{i}=f\left(a_{i}\right)$ coincide, namely $c_{1}$ and $c_{2}$. Now apply Lemma 1 to get a polynomial $g(x)$ such that $g\left(a_{1}\right)=b_{1}$ and $g\left(a_{2}\right)=b_{2}$. Apply the inductive hypothesis in order to obtain a polynomial $h(x)$ satisfying $h\left(c_{i}\right)=b_{i}-g\left(a_{i}\right)$ for all $i=2,3, \ldots, n$. Then the polynomial $h(f(x))+g(x)$ is a desired one; indeed, we have $h\left(f\left(a_{i}\right)\right)+g\left(a_{i}\right)=h\left(c_{i}\right)+g\left(a_{i}\right)=b_{i}$ for all $i=2,3, \ldots, n$, and finally $h\left(f\left(a_{1}\right)\right)+g\left(a_{1}\right)=$ $h\left(c_{1}\right)+g\left(a_{1}\right)=b_{2}-g\left(a_{2}\right)+g\left(a_{1}\right)=b_{1}$.
It remains to prove the Claim and the two Lemmas.
Proof of the Claim. There exists some segment $\Delta=\left[\alpha^{\prime}, \beta^{\prime}\right]$ such that $S(x)$ is monotone increasing outside that segment. Now one can choose $\alpha \leq \alpha^{\prime}$ and $\beta \geq \beta^{\prime}$ such that $S(\alpha)<\min _{x \in \Delta} S(x)$ and
$S(\beta)>\max _{x \in \Delta} S(x)$. Therefore, for any $x, y, z$ with $x \leq \alpha \leq y \leq \beta \leq z$ we get $S(x) \leq S(\alpha) \leq$ $S(y) \leq S(\beta) \leq S(z)$.
We may decrease $\alpha$ and increase $\beta$ (preserving the condition above) so that, in addition, $S^{\prime}(x)>3$ for all $x \notin[\alpha, \beta]$. Now we claim that the number $T=3(\beta-\alpha)$ fits the bill.
Indeed, take any $a$ and $b$ with $b-a \geq T$. Even if the segment $[a, b]$ crosses $[\alpha, \beta]$, there still is a segment $\left[a^{\prime}, b^{\prime}\right] \subseteq[a, b] \backslash(\alpha, \beta)$ of length $b^{\prime}-a^{\prime} \geq(b-a) / 3$. Then
$$
S(b)-S(a) \geq S\left(b^{\prime}\right)-S\left(a^{\prime}\right)=\left(b^{\prime}-a^{\prime}\right) \cdot S^{\prime}(\xi) \geq 3\left(b^{\prime}-a^{\prime}\right) \geq b-a
$$
for some $\xi \in\left(a^{\prime}, b^{\prime}\right)$.
Proof of Lemma 1. If $S(x)$ has an even degree, then the polynomial $T(x)=S\left(x+a_{2}\right)-S\left(x+a_{1}\right)$ has an odd degree, hence there exists $x_{0}$ with $T\left(x_{0}\right)=S\left(x_{0}+a_{2}\right)-S\left(x_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S\left(x+x_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift $F(x)=G(x)+\left(b_{1}-G\left(a_{1}\right)\right)$ fits the bill.
Assume now that $S(x)$ has odd degree and a negative leading coefficient. Notice that the polynomial $S^{2}(x):=S(S(x))$ has an odd degree and a positive leading coefficient. So, the polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)$ attains all sufficiently large positive values, while $S\left(x+a_{2}\right)-$ $S\left(x+a_{1}\right)$ attains all sufficiently large negative values. Therefore, the two-variable polynomial $S^{2}\left(x+a_{2}\right)-S^{2}\left(x+a_{1}\right)+S\left(y+a_{2}\right)-S\left(y+a_{1}\right)$ attains all real values; in particular, there exist $x_{0}$ and $y_{0}$ with $S^{2}\left(x_{0}+a_{2}\right)+S\left(y_{0}+a_{2}\right)-S^{2}\left(x_{0}+a_{1}\right)-S\left(y_{0}+a_{1}\right)=b_{2}-b_{1}$. Setting $G(x)=S^{2}\left(x+x_{0}\right)+S\left(x+y_{0}\right)$, we see that $G\left(a_{2}\right)-G\left(a_{1}\right)=b_{2}-b_{1}$, so a suitable shift of $G$ fits the bill.
Proof of Lemma 2. Let $\Delta$ denote the segment $\left[a_{1} ; a_{n}\right]$. We modify the proof of Lemma 1 in order to obtain a polynomial $F$ convex (or concave) on $\Delta$ such that $F\left(a_{1}\right)=F\left(a_{2}\right)$; then $F$ is a desired polynomial. Say that a polynomial $H(x)$ is good if $H$ is convex on $\Delta$.
If $\operatorname{deg} S$ is even, and its leading coefficient is positive, then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S(x+c)$ is good for all sufficiently large positive $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S\left(x+c_{2}\right)$ is a desired polynomial. If the leading coefficient of $H$ is negative, we similarly find a desired polynomial which is concave on $\Delta$.
If $\operatorname{deg} S \geq 3$ is odd (and the leading coefficient is negative), then $S(x+c)$ is good for all sufficiently large negative $c$, and $S\left(a_{2}+c\right)-S\left(a_{1}+c\right)$ attains all sufficiently large negative values for such $c$. Similarly, $S^{2}(x+c)$ is good for all sufficiently large positive $c$, and $S^{2}\left(a_{2}+c\right)-S^{2}\left(a_{1}+c\right)$ attains all sufficiently large positive values for such $c$. Therefore, there exist large $c_{1}<0<c_{2}$ such that $S\left(x+c_{1}\right)+S^{2}\left(x+c_{2}\right)$ is a desired polynomial.
Comment. Both parts above allow some variations.
In Part I, the same scheme of the proof works for many conditions similar to (*), e.g.,
$$
S(b)-S(a)>T \quad \text { whenever } \quad b-a>T
$$
Let us sketch an alternative approach for Part II. It suffices to construct, for each $i$, a polynomial $f_{i}(x)$ such that $f_{i}\left(a_{i}\right)=b_{i}$ and $f_{i}\left(a_{j}\right)=0, j \neq i$. The construction of such polynomials may be reduced to the construction of those for $n=3$ similarly to what happens in the proof of Lemma 2. However, this approach (as well as any in this part) needs some care in order to work properly.
|
{
"resource_path": "RMM/segmented/en-2021-RMM2021-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution."
}
|
7deb168d-8677-51ef-b902-9cb3da5f75fc
| 606,182
|
Fix an integer $n \geqslant 3$. Let $\mathcal{S}$ be a set of $n$ points in the plane, no three of which are collinear. Given different points $A, B, C$ in $\mathcal{S}$, the triangle $A B C$ is nice for $A B$ if Area $(A B C) \leqslant \operatorname{Area}(A B X)$ for all $X$ in $\mathcal{S}$ different from $A$ and $B$. (Note that for a segment $A B$ there could be several nice triangles.) A triangle is beautiful if its vertices are all in $\mathcal{S}$ and it is nice for at least two of its sides.
Prove that there are at least $\frac{1}{2}(n-1)$ beautiful triangles.
# Bulgaria, Alexander Ivanov
|
For convenience, a triangle whose vertices all lie in $\mathcal{S}$ will be referred to as a triangle in $\mathcal{S}$. The argument hinges on the following observation:
Given any partition of $\mathcal{S}$, amongst all triangles in $\mathcal{S}$ with at least one vertex in each part, those of minimal area are all adequate.
Indeed, amongst the triangles under consideration, one of minimal area is suitable for both sides with endpoints in different parts.
We now present two approaches for the lower bound.
1st Approach. By the above observation, the 3uniform hypergraph of adequate triangles is connected. It is a well-known fact that such a hypergraph has at least $\frac{1}{2}(n-1)$ hyperedges, whence the required lower bound
2nd Approach. For a partition $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, an area minimising triangle as above will be called $(\mathcal{A}, \mathcal{B})$ minimal. Thus, $(\mathcal{A}, \mathcal{B})$-minimal triangles are all adequate.
Consider now a partition of $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, where $|\mathcal{A}|=1$. Choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices from $\mathcal{B}$ to obtain a new partition also written $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$. Continuing, choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices/vertex from $\mathcal{B}$ and so on and so forth all the way down for at least another $\frac{1}{2}(n-5)$ steps - this works at least as many times, since at each step, $\mathcal{B}$ loses at most two points. Clearly, each step provides a new adequate triangle, so the overall number of adequate triangles is at least $\frac{1}{2}(n-1)$, as required.
Remark. In fact, $\lfloor n / 2\rfloor$ is the smallest possible number of adequate triangles, as shown by the the configurations described below.
Let first $n=2 k-1$. Consider a regular $n$-gon
$\mathcal{P}=A_{1} A_{2} \ldots A_{n}$. Choose a point $B_{i}$ on the perpendicular bisector of $A_{i} A_{i+1}$ outside $\mathcal{P}$ and sufficiently close to the segment $A_{i} A_{i+1}$. We claim that there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
$$
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
$$
Notice here that the arc $A_{1} A_{2} \ldots A_{k}$ is less than half of the circumcircle of $\mathcal{P}$, so the angles $\angle A_{u} A_{v} A_{w}$, $1 \leq u<v<w \leq k$, are all obtuse.
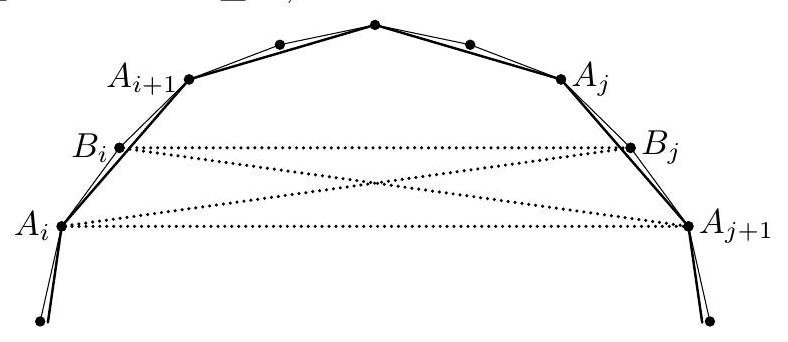
To prove the claim, list the suitable triangles for each segment.
For segments $A_{i} A_{i+1}, A_{i} B_{i}$, and $B_{i} A_{i+1}$, it is $A_{i} B_{i} A_{i+1}$.
For segment $A_{i} A_{j+1}, j \geq i+1$, those are $A_{i} B_{i} A_{j+1}$ and $A_{i} B_{j} A_{j+1}$.
For segment $A_{i} B_{j}, j \geq i+1$, it is $A_{i} B_{i} B_{j}$.
For segment $B_{i} A_{j+1}, j \geq i+1$, it is $B_{i} B_{j} A_{j+1}$.
For segment $B_{i} B_{j}, i<j$, those are $B_{i} A_{i+1} B_{j}$ and $B_{i} A_{j} B_{j}$.
It is easily seen that the only triangles occurring twice are $A_{i} B_{i} A_{i+1}$, hence they are the only adequate triangles.
For $n=2 k-2$, just remove $A_{k}$ from the above example. This removes the adequate triangle $A_{k-1} B_{k-1} A_{k}$ and provides only one new such instead, namely, $B_{k-2} A_{k-1} B_{k-1}$. Consequently, there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
$$
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k-1}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Fix an integer $n \geqslant 3$. Let $\mathcal{S}$ be a set of $n$ points in the plane, no three of which are collinear. Given different points $A, B, C$ in $\mathcal{S}$, the triangle $A B C$ is nice for $A B$ if Area $(A B C) \leqslant \operatorname{Area}(A B X)$ for all $X$ in $\mathcal{S}$ different from $A$ and $B$. (Note that for a segment $A B$ there could be several nice triangles.) A triangle is beautiful if its vertices are all in $\mathcal{S}$ and it is nice for at least two of its sides.
Prove that there are at least $\frac{1}{2}(n-1)$ beautiful triangles.
# Bulgaria, Alexander Ivanov
|
For convenience, a triangle whose vertices all lie in $\mathcal{S}$ will be referred to as a triangle in $\mathcal{S}$. The argument hinges on the following observation:
Given any partition of $\mathcal{S}$, amongst all triangles in $\mathcal{S}$ with at least one vertex in each part, those of minimal area are all adequate.
Indeed, amongst the triangles under consideration, one of minimal area is suitable for both sides with endpoints in different parts.
We now present two approaches for the lower bound.
1st Approach. By the above observation, the 3uniform hypergraph of adequate triangles is connected. It is a well-known fact that such a hypergraph has at least $\frac{1}{2}(n-1)$ hyperedges, whence the required lower bound
2nd Approach. For a partition $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, an area minimising triangle as above will be called $(\mathcal{A}, \mathcal{B})$ minimal. Thus, $(\mathcal{A}, \mathcal{B})$-minimal triangles are all adequate.
Consider now a partition of $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$, where $|\mathcal{A}|=1$. Choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices from $\mathcal{B}$ to obtain a new partition also written $\mathcal{S}=\mathcal{A} \sqcup \mathcal{B}$. Continuing, choose an $(\mathcal{A}, \mathcal{B})$-minimal triangle and add to $\mathcal{A}$ its vertices/vertex from $\mathcal{B}$ and so on and so forth all the way down for at least another $\frac{1}{2}(n-5)$ steps - this works at least as many times, since at each step, $\mathcal{B}$ loses at most two points. Clearly, each step provides a new adequate triangle, so the overall number of adequate triangles is at least $\frac{1}{2}(n-1)$, as required.
Remark. In fact, $\lfloor n / 2\rfloor$ is the smallest possible number of adequate triangles, as shown by the the configurations described below.
Let first $n=2 k-1$. Consider a regular $n$-gon
$\mathcal{P}=A_{1} A_{2} \ldots A_{n}$. Choose a point $B_{i}$ on the perpendicular bisector of $A_{i} A_{i+1}$ outside $\mathcal{P}$ and sufficiently close to the segment $A_{i} A_{i+1}$. We claim that there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
$$
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
$$
Notice here that the arc $A_{1} A_{2} \ldots A_{k}$ is less than half of the circumcircle of $\mathcal{P}$, so the angles $\angle A_{u} A_{v} A_{w}$, $1 \leq u<v<w \leq k$, are all obtuse.

To prove the claim, list the suitable triangles for each segment.
For segments $A_{i} A_{i+1}, A_{i} B_{i}$, and $B_{i} A_{i+1}$, it is $A_{i} B_{i} A_{i+1}$.
For segment $A_{i} A_{j+1}, j \geq i+1$, those are $A_{i} B_{i} A_{j+1}$ and $A_{i} B_{j} A_{j+1}$.
For segment $A_{i} B_{j}, j \geq i+1$, it is $A_{i} B_{i} B_{j}$.
For segment $B_{i} A_{j+1}, j \geq i+1$, it is $B_{i} B_{j} A_{j+1}$.
For segment $B_{i} B_{j}, i<j$, those are $B_{i} A_{i+1} B_{j}$ and $B_{i} A_{j} B_{j}$.
It is easily seen that the only triangles occurring twice are $A_{i} B_{i} A_{i+1}$, hence they are the only adequate triangles.
For $n=2 k-2$, just remove $A_{k}$ from the above example. This removes the adequate triangle $A_{k-1} B_{k-1} A_{k}$ and provides only one new such instead, namely, $B_{k-2} A_{k-1} B_{k-1}$. Consequently, there are exactly $k-1=\lfloor n / 2\rfloor$ adequate triangles in the set
$$
\mathcal{S}=\left\{A_{1}, A_{2}, \ldots, A_{k-1}, B_{1}, B_{2}, \ldots, B_{k-1}\right\}
$$
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day1-English_Solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
213926d5-fbac-524d-938c-ccc4f028915f
| 606,218
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Fix the origin at $O$ and the real axis along $\ell$. A lower case letter denotes the complex coordinate of the corresponding point in the configuration. For convenience, let $|a|=|b|=|c|=1$.
Clearly, $k=a+\frac{1}{2}(b+c), p=a+\frac{1}{2}\left(b+\frac{1}{b}\right)$ and $q=a+\frac{1}{2}\left(c+\frac{1}{c}\right)$.
Then $|k-p|=\left|a+\frac{1}{2}\left(c-\frac{1}{b}\right)\right|=\frac{1}{2}|2 a b+b c-1|$, since $|b|=1$.
Similarly, $|k-q|=\frac{1}{2}|2 a c+b c-1|$, so, since $|a|=1$,
$|k-p|+|k-q|=\frac{1}{2}|2 a b+b c-1|+\frac{1}{2}|2 a c+b c-1|$
$$
\geq \frac{1}{2}|2 a(b-c)|=|b-c|,
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Fix the origin at $O$ and the real axis along $\ell$. A lower case letter denotes the complex coordinate of the corresponding point in the configuration. For convenience, let $|a|=|b|=|c|=1$.
Clearly, $k=a+\frac{1}{2}(b+c), p=a+\frac{1}{2}\left(b+\frac{1}{b}\right)$ and $q=a+\frac{1}{2}\left(c+\frac{1}{c}\right)$.
Then $|k-p|=\left|a+\frac{1}{2}\left(c-\frac{1}{b}\right)\right|=\frac{1}{2}|2 a b+b c-1|$, since $|b|=1$.
Similarly, $|k-q|=\frac{1}{2}|2 a c+b c-1|$, so, since $|a|=1$,
$|k-p|+|k-q|=\frac{1}{2}|2 a b+b c-1|+\frac{1}{2}|2 a c+b c-1|$
$$
\geq \frac{1}{2}|2 a(b-c)|=|b-c|,
$$
as required.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 1"
}
|
a2c078a9-1138-577a-989f-a14f7d92c8b4
| 606,237
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Let $M$ be the midpoint of $B C$, and let $R$ be the projection of $M$ onto $\ell$. In other words, $R$ is the midpoint of $P Q$. Since $\angle B P O=\angle B M O=$ $90^{\circ}$, the points $B, P, O$, and $M$ are concyclic, so $\angle(O M, O B)=\angle(P M, P B)=\angle(P M, M R)$, so the right triangles $M R P$ and $O M B$ are similar and have different orientation. Similarly, the triangles $M R Q$ and $O M C$ are similar and have different orientation, hence so are the triangles $O B C$ and $M P Q$.
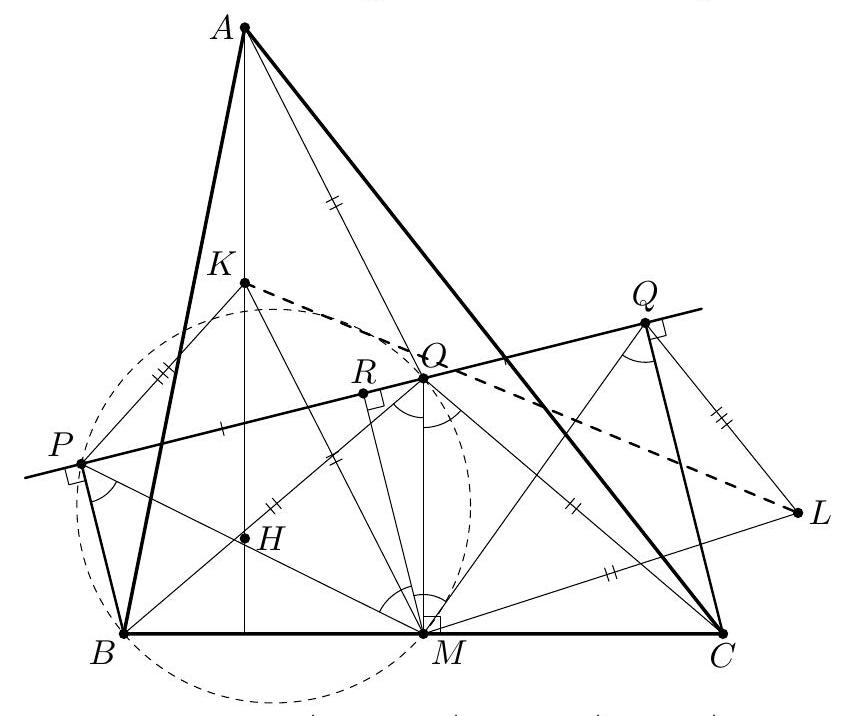
Recall that $\overrightarrow{A H}=2 \overrightarrow{O M}$, so $\overrightarrow{O M}=\overrightarrow{A K}$. Hence $A O M K$ is a parallelogram, so $M K=O A=O B=$ $O C$.
Consider the rotation through $\angle(\overrightarrow{O C}, \overrightarrow{O B})$ about $M$. It maps $P$ to $Q$; let it map $K$ to some point $L$. Then $M K=M L=O B=O C$ and $\angle L M K=\angle B O C$, so the triangles $O B C$ and $M K L$ are congruent. Hence $B C=K L \leq K Q+L Q=$ $K Q+K P$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Let $M$ be the midpoint of $B C$, and let $R$ be the projection of $M$ onto $\ell$. In other words, $R$ is the midpoint of $P Q$. Since $\angle B P O=\angle B M O=$ $90^{\circ}$, the points $B, P, O$, and $M$ are concyclic, so $\angle(O M, O B)=\angle(P M, P B)=\angle(P M, M R)$, so the right triangles $M R P$ and $O M B$ are similar and have different orientation. Similarly, the triangles $M R Q$ and $O M C$ are similar and have different orientation, hence so are the triangles $O B C$ and $M P Q$.

Recall that $\overrightarrow{A H}=2 \overrightarrow{O M}$, so $\overrightarrow{O M}=\overrightarrow{A K}$. Hence $A O M K$ is a parallelogram, so $M K=O A=O B=$ $O C$.
Consider the rotation through $\angle(\overrightarrow{O C}, \overrightarrow{O B})$ about $M$. It maps $P$ to $Q$; let it map $K$ to some point $L$. Then $M K=M L=O B=O C$ and $\angle L M K=\angle B O C$, so the triangles $O B C$ and $M K L$ are congruent. Hence $B C=K L \leq K Q+L Q=$ $K Q+K P$, as required.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 2"
}
|
a2c078a9-1138-577a-989f-a14f7d92c8b4
| 606,237
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Let $\alpha=\angle(P B, B C)=\angle(Q C, B C)$. Since $P$ lies on the circle of diameter $O B$, $\angle(O P, O M)=\alpha$. Since also $Q$ lies on the circle of diameter $O C$, it immediately follows that
$M P=M Q=R \sin \alpha$ by sine theorem in triangles $\triangle O P M$ and $\triangle O Q M$.
Because $P Q$ is the projection of $B C$ on line $\ell$, it follows that $P Q=B C \sin \alpha$. Just like in the first solution, $K M=A O=R$ (the circumradius of triangle $\triangle A B C)$.
Now apply Ptolemy's inequality for the quadrilateral $K P M Q$ : $K P \cdot M Q+K Q \cdot M P \geq P Q \cdot K M$, and now substitute the relations from above, leading to
$$
R \sin \alpha(K P+K Q) \geq R \sin \alpha \cdot B C
$$
which is precisely the conclusion whenever $\sin \alpha \neq 0$. The case when $\sin \alpha=0$ can be treated either directly, or via a limit argument.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Let $\alpha=\angle(P B, B C)=\angle(Q C, B C)$. Since $P$ lies on the circle of diameter $O B$, $\angle(O P, O M)=\alpha$. Since also $Q$ lies on the circle of diameter $O C$, it immediately follows that
$M P=M Q=R \sin \alpha$ by sine theorem in triangles $\triangle O P M$ and $\triangle O Q M$.
Because $P Q$ is the projection of $B C$ on line $\ell$, it follows that $P Q=B C \sin \alpha$. Just like in the first solution, $K M=A O=R$ (the circumradius of triangle $\triangle A B C)$.
Now apply Ptolemy's inequality for the quadrilateral $K P M Q$ : $K P \cdot M Q+K Q \cdot M P \geq P Q \cdot K M$, and now substitute the relations from above, leading to
$$
R \sin \alpha(K P+K Q) \geq R \sin \alpha \cdot B C
$$
which is precisely the conclusion whenever $\sin \alpha \neq 0$. The case when $\sin \alpha=0$ can be treated either directly, or via a limit argument.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 3"
}
|
a2c078a9-1138-577a-989f-a14f7d92c8b4
| 606,237
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Denote by $R$ and $O$ the circumradius and the circumcentre of triangle $A B C$, respectively. As in Solution 1, we see that $M K=R$.
Assume now that $\ell$ is fixed, while $A$ moves along the fixed circle $(A B C)$. Then $K$ will move along a cricle centred at $M$ with radius $R$. We must show that for each point $K$ on this circle we have $B C \leq K P+K Q$. In doing so, we prove that the afore-mentioned circle contains an ellipse with foci at $Q$ and $P$ with distance $B C$.
Let $S$ be the foot of the perpendicular from $M$ to $P Q$, it is easy to verify that $S$ is the center of the ellipse. We shall then consider it as the origin. Let $u=\frac{B C}{2}$ and $t=\frac{P Q}{2}$; notice that $u$ is the major semi-axis of the ellipse and $\sqrt{u^{2}-t^{2}}$ is the minor one. Assume $X(x, y)$ is a point on this ellipse. We now need to prove $M X \leq R$.
Since $X$ is on the ellipse, we can write $(x, y)=$ $\left(u \cos \theta, \sqrt{u^{2}-t^{2}} \sin \theta\right)$, for some $\theta \in(0,2 \pi)$. Since $M X^{2}=x^{2}+(y+M S)^{2}$, we can expand and obtain $M X^{2}=u^{2}+M S^{2}-t^{2} \cdot \sin ^{2} \theta+2 M S \cdot \sqrt{u^{2}-t^{2}} \cdot \sin \theta$.
Add and subtract $M S^{2}\left(u^{2}-t^{2}\right) / t^{2}$ in order to obtain a square on the right hand side: $M X^{2}=u^{2}+$ $M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}-\left(t \sin \theta-\frac{M S \sqrt{u^{2}-t^{2}}}{t}\right)^{2}$. It now suffices to show that $u^{2}+M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}=$ $R^{2}$, since then it would immediately follow that $M X^{2} \leq R^{2}$.
Applying Pythagorean theorem in triangles $O B M$ and $O S M$, we obtain $R^{2}=u^{2}+O M^{2}$ and $O M^{2}=M S^{2}+O S^{2}$, so it remains to prove that $O S^{2}=\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}} . \quad$ Let $\alpha=\angle(O P, B M)$, then $O S / M S=\tan ^{t^{2}} \alpha$ and $t / u=\cos \alpha$, so $O S^{2}=$ $M S^{2} \tan ^{2} \alpha=M S^{2}\left(\frac{1-\cos ^{2} \alpha}{\cos ^{2} \alpha}\right)=M S^{2} \cdot \frac{u^{2}-t^{2}}{t^{2}}$, which is the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $H$ and $O$ be its orthocentre and circumcentre, respectively. Let $K$ be the midpoint of the line segment $A H$. Let further $\ell$ be a line through $O$, and let $P$ and $Q$ be the orthogonal projections of $B$ and $C$ onto $\ell$, respectively. Prove that $K P+K Q \geq B C$.
# Russia, Vasily Mokin
|
. Denote by $R$ and $O$ the circumradius and the circumcentre of triangle $A B C$, respectively. As in Solution 1, we see that $M K=R$.
Assume now that $\ell$ is fixed, while $A$ moves along the fixed circle $(A B C)$. Then $K$ will move along a cricle centred at $M$ with radius $R$. We must show that for each point $K$ on this circle we have $B C \leq K P+K Q$. In doing so, we prove that the afore-mentioned circle contains an ellipse with foci at $Q$ and $P$ with distance $B C$.
Let $S$ be the foot of the perpendicular from $M$ to $P Q$, it is easy to verify that $S$ is the center of the ellipse. We shall then consider it as the origin. Let $u=\frac{B C}{2}$ and $t=\frac{P Q}{2}$; notice that $u$ is the major semi-axis of the ellipse and $\sqrt{u^{2}-t^{2}}$ is the minor one. Assume $X(x, y)$ is a point on this ellipse. We now need to prove $M X \leq R$.
Since $X$ is on the ellipse, we can write $(x, y)=$ $\left(u \cos \theta, \sqrt{u^{2}-t^{2}} \sin \theta\right)$, for some $\theta \in(0,2 \pi)$. Since $M X^{2}=x^{2}+(y+M S)^{2}$, we can expand and obtain $M X^{2}=u^{2}+M S^{2}-t^{2} \cdot \sin ^{2} \theta+2 M S \cdot \sqrt{u^{2}-t^{2}} \cdot \sin \theta$.
Add and subtract $M S^{2}\left(u^{2}-t^{2}\right) / t^{2}$ in order to obtain a square on the right hand side: $M X^{2}=u^{2}+$ $M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}-\left(t \sin \theta-\frac{M S \sqrt{u^{2}-t^{2}}}{t}\right)^{2}$. It now suffices to show that $u^{2}+M S^{2}+\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}}=$ $R^{2}$, since then it would immediately follow that $M X^{2} \leq R^{2}$.
Applying Pythagorean theorem in triangles $O B M$ and $O S M$, we obtain $R^{2}=u^{2}+O M^{2}$ and $O M^{2}=M S^{2}+O S^{2}$, so it remains to prove that $O S^{2}=\frac{M S^{2}\left(u^{2}-t^{2}\right)}{t^{2}} . \quad$ Let $\alpha=\angle(O P, B M)$, then $O S / M S=\tan ^{t^{2}} \alpha$ and $t / u=\cos \alpha$, so $O S^{2}=$ $M S^{2} \tan ^{2} \alpha=M S^{2}\left(\frac{1-\cos ^{2} \alpha}{\cos ^{2} \alpha}\right)=M S^{2} \cdot \frac{u^{2}-t^{2}}{t^{2}}$, which is the desired result.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution 4"
}
|
a2c078a9-1138-577a-989f-a14f7d92c8b4
| 606,237
|
Let $P(x), Q(x), R(x)$ and $S(x)$ be non-constant polynomials with real coefficients such that $P(Q(x))=R(S(x))$. Suppose that the degree of $P(x)$ is divisible by the degree of $R(x)$.
Prove that there is a polynomial $T(x)$ with real coefficients such that $P(x)=R(T(x))$.
## Iran, NaVid Safaei
|
. Degree comparison of $P(Q(x))$ and $R(S(x))$ implies that $q=\operatorname{deg} Q \mid \operatorname{deg} S=s$. We will show that $S(x)=T(Q(x))$ for some polynomial $T$. Then $P(Q(x))=R(S(x))=R(T(Q(x)))$, so the polynomial $P(t)-R(T(t))$ vanishes upon substitution $t=S(x)$; it therefore vanishes identically, as desired.
Choose the polynomials $T(x)$ and $M(x)$ such that
$$
S(x)=T(Q(x))+M(x)
$$
where $\operatorname{deg} M$ is minimised; if $M=0$, then we get the desired result. For the sake of contradiction, suppose $M \neq 0$. Then $q \nmid m=\operatorname{deg} M$; otherwise, $M(x)=\beta Q(x)^{m / q}+M_{1}(x)$, where $\beta$ is some number and $\operatorname{deg} M_{1}<\operatorname{deg} M$, contradicting the choice of $M$. In particular, $0<m<s$ and hence $\operatorname{deg} T(Q(x))=s$.
Substitute now (*) into $R(S(x))-P(Q(x))=$ 0 ; let $\alpha$ be the leading coefficient of $R(x)$ and let $r=\operatorname{deg} R(x)$. Expand the brackets to get a sum of powers of $Q(x)$ and other terms including powers of $M(x)$ as well. Amongst the latter, the unique term of highest degree is $\operatorname{arM}(x) T(Q(x))^{r-1}$. So, for some polyno$\operatorname{mial} N(x), \quad N(Q(x))=\alpha r M(x) T(Q(x))^{r-1}+$ a polynomial of lower degree.
This is impossible, since $q$ divides the degree of the left-hand member, but not that of the righthand member.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x), Q(x), R(x)$ and $S(x)$ be non-constant polynomials with real coefficients such that $P(Q(x))=R(S(x))$. Suppose that the degree of $P(x)$ is divisible by the degree of $R(x)$.
Prove that there is a polynomial $T(x)$ with real coefficients such that $P(x)=R(T(x))$.
## Iran, NaVid Safaei
|
. Degree comparison of $P(Q(x))$ and $R(S(x))$ implies that $q=\operatorname{deg} Q \mid \operatorname{deg} S=s$. We will show that $S(x)=T(Q(x))$ for some polynomial $T$. Then $P(Q(x))=R(S(x))=R(T(Q(x)))$, so the polynomial $P(t)-R(T(t))$ vanishes upon substitution $t=S(x)$; it therefore vanishes identically, as desired.
Choose the polynomials $T(x)$ and $M(x)$ such that
$$
S(x)=T(Q(x))+M(x)
$$
where $\operatorname{deg} M$ is minimised; if $M=0$, then we get the desired result. For the sake of contradiction, suppose $M \neq 0$. Then $q \nmid m=\operatorname{deg} M$; otherwise, $M(x)=\beta Q(x)^{m / q}+M_{1}(x)$, where $\beta$ is some number and $\operatorname{deg} M_{1}<\operatorname{deg} M$, contradicting the choice of $M$. In particular, $0<m<s$ and hence $\operatorname{deg} T(Q(x))=s$.
Substitute now (*) into $R(S(x))-P(Q(x))=$ 0 ; let $\alpha$ be the leading coefficient of $R(x)$ and let $r=\operatorname{deg} R(x)$. Expand the brackets to get a sum of powers of $Q(x)$ and other terms including powers of $M(x)$ as well. Amongst the latter, the unique term of highest degree is $\operatorname{arM}(x) T(Q(x))^{r-1}$. So, for some polyno$\operatorname{mial} N(x), \quad N(Q(x))=\alpha r M(x) T(Q(x))^{r-1}+$ a polynomial of lower degree.
This is impossible, since $q$ divides the degree of the left-hand member, but not that of the righthand member.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1"
}
|
42fe2760-0c64-55e9-800c-ab542f4036f6
| 606,267
|
Let $r, g, b$ be non-negative integers. Let $\Gamma$ be a connected graph on $r+g+b+1$ vertices. The edges of $\Gamma$ are each coloured red, green or blue. It turns out that $\Gamma$ has
- a spanning tree in which exactly $r$ of the edges are red,
- a spanning tree in which exactly $g$ of the edges are green and
- a spanning tree in which exactly $b$ of the edges are blue.
Prove that $\Gamma$ has a spanning tree in which exactly $r$ of the edges are red, exactly $g$ of the edges are green and exactly $b$ of the edges are blue.
Russia, Vasily Mokin
|
. Induct on $n=r+g+b$. The base case, $n=1$, is clear.
Let now $n>1$. Let $V$ denote the vertex set of $\Gamma$, and let $T_{r}, T_{g}$, and $T_{b}$ be the trees with exactly $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. Consider two cases.
Case 1: There exists a partition $V=A \sqcup B$ of the vertex set into two non-empty parts such that the edges joining the parts all bear the same colour, say, blue.
Since $\Gamma$ is connected, it has a (necessarily blue) edge connecting $A$ and $B$. Let $e$ be one such.
Assume that $T$, one of the three trees, does not contain $e$. Then the graph $T \cup\{e\}$ has a cycle $C$ through $e$. The cycle $C$ should contain another edge $e^{\prime}$ connecting $A$ and $B$; the edge $e^{\prime}$ is also blue. Replace $e^{\prime}$ by $e$ in $T$ to get another tree $T^{\prime}$ with the same number of edges of each colour as in $T$, but containing $e$.
Performing such an operation to all three trees, we arrive at the situation where the three trees $T_{r}^{\prime}$, $T_{g}^{\prime}$, and $T_{b}^{\prime}$ all contain $e$. Now shrink $e$ by identifying its endpoints to obtain a graph $\Gamma^{*}$, and set $r^{*}=r, g^{*}=g$, and $b^{*}=b-1$. The new graph satisfies the conditions in the statement for those new values - indeed, under the shrinking, each of the trees $T_{r}^{\prime}, T_{g}^{\prime}$, and $T_{b}^{\prime}$ loses a blue edge. So $\Gamma^{*}$ has a spanning tree with exactly $r$ red, exactly $g$
green, and exactly $b-1$ blue edges. Finally, pass back to $\Gamma$ by restoring $e$, to obtain the a desired spanning tree in $\Gamma$.
Case 2: There is no such a partition.
Consider all possible collections $(R, G, B)$, where $R, G$ and $B$ are acyclic sets consisting of $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. By the problem assumptions, there is at least one such collection. Amongst all such collections, consider one such that the graph on $V$ with edge set $R \cup G \cup B$ has the smallest number $k$ of components. If $k=1$, then the collection provides the edges of a desired tree (the number of edges is one less than the number of vertices).
Assume now that $k \geq 2$; then in the resulting graph some component $K$ contains a cycle $C$. Since $R, G$, and $B$ are acyclic, $C$ contains edges of at least two colours, say, red and green. By assumption, the edges joining $V(K)$ to $V \backslash V(K)$ bear at least two colours; so one of these edges is either red or green. Without loss of generality, consider a red such edge $e$.
Let $e^{\prime}$ be a red edge in $C$ and set $R^{\prime}=R \backslash\left\{e^{\prime}\right\} \cup$ $\{e\}$. Then $\left(R^{\prime}, G, B\right)$ is a valid collection providing a smaller number of components. This contradicts minimality of the choice above and concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $r, g, b$ be non-negative integers. Let $\Gamma$ be a connected graph on $r+g+b+1$ vertices. The edges of $\Gamma$ are each coloured red, green or blue. It turns out that $\Gamma$ has
- a spanning tree in which exactly $r$ of the edges are red,
- a spanning tree in which exactly $g$ of the edges are green and
- a spanning tree in which exactly $b$ of the edges are blue.
Prove that $\Gamma$ has a spanning tree in which exactly $r$ of the edges are red, exactly $g$ of the edges are green and exactly $b$ of the edges are blue.
Russia, Vasily Mokin
|
. Induct on $n=r+g+b$. The base case, $n=1$, is clear.
Let now $n>1$. Let $V$ denote the vertex set of $\Gamma$, and let $T_{r}, T_{g}$, and $T_{b}$ be the trees with exactly $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. Consider two cases.
Case 1: There exists a partition $V=A \sqcup B$ of the vertex set into two non-empty parts such that the edges joining the parts all bear the same colour, say, blue.
Since $\Gamma$ is connected, it has a (necessarily blue) edge connecting $A$ and $B$. Let $e$ be one such.
Assume that $T$, one of the three trees, does not contain $e$. Then the graph $T \cup\{e\}$ has a cycle $C$ through $e$. The cycle $C$ should contain another edge $e^{\prime}$ connecting $A$ and $B$; the edge $e^{\prime}$ is also blue. Replace $e^{\prime}$ by $e$ in $T$ to get another tree $T^{\prime}$ with the same number of edges of each colour as in $T$, but containing $e$.
Performing such an operation to all three trees, we arrive at the situation where the three trees $T_{r}^{\prime}$, $T_{g}^{\prime}$, and $T_{b}^{\prime}$ all contain $e$. Now shrink $e$ by identifying its endpoints to obtain a graph $\Gamma^{*}$, and set $r^{*}=r, g^{*}=g$, and $b^{*}=b-1$. The new graph satisfies the conditions in the statement for those new values - indeed, under the shrinking, each of the trees $T_{r}^{\prime}, T_{g}^{\prime}$, and $T_{b}^{\prime}$ loses a blue edge. So $\Gamma^{*}$ has a spanning tree with exactly $r$ red, exactly $g$
green, and exactly $b-1$ blue edges. Finally, pass back to $\Gamma$ by restoring $e$, to obtain the a desired spanning tree in $\Gamma$.
Case 2: There is no such a partition.
Consider all possible collections $(R, G, B)$, where $R, G$ and $B$ are acyclic sets consisting of $r$ red edges, $g$ green edges, and $b$ blue edges, respectively. By the problem assumptions, there is at least one such collection. Amongst all such collections, consider one such that the graph on $V$ with edge set $R \cup G \cup B$ has the smallest number $k$ of components. If $k=1$, then the collection provides the edges of a desired tree (the number of edges is one less than the number of vertices).
Assume now that $k \geq 2$; then in the resulting graph some component $K$ contains a cycle $C$. Since $R, G$, and $B$ are acyclic, $C$ contains edges of at least two colours, say, red and green. By assumption, the edges joining $V(K)$ to $V \backslash V(K)$ bear at least two colours; so one of these edges is either red or green. Without loss of generality, consider a red such edge $e$.
Let $e^{\prime}$ be a red edge in $C$ and set $R^{\prime}=R \backslash\left\{e^{\prime}\right\} \cup$ $\{e\}$. Then $\left(R^{\prime}, G, B\right)$ is a valid collection providing a smaller number of components. This contradicts minimality of the choice above and concludes the proof.
|
{
"resource_path": "RMM/segmented/en-2023-RMM2023-Day2-English_Solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 1"
}
|
baa689aa-a7c8-5fb9-82d1-e5084a5864f0
| 606,281
|
Let $D$ be a point on the side $AC$ of triangle $ABC$ where $AB < BC$ such that $AB = BD$. The incircle of $\triangle ABC$ touches $AB$ at $K$ and $AC$ at $L$, and $J$ is the incenter of triangle $BCD$. Prove that $KL$ bisects segment $AJ$.
The incircle of $\triangle ABC$ touches $AB$ at $K$ and $AC$ at $L$, and $J$ is the incenter of triangle $BCD$. Prove that $KL$ bisects segment $AJ$.
|
Let $M$ be a point on $AC$ such that $JM \parallel KL$. It is sufficient to prove that $AM = 2AL$.
From $\angle BDA = \alpha$, we get $\angle JDM = 90^\circ - \frac{\alpha}{2} = \angle KLA = \angle JMD$, so $JM = JD$. The point of tangency of the incircle of $\triangle BCD$ with $CD$ is the midpoint $T$ of segment $MD$. Therefore, $DM = 2DT = BD + CD - BC = AB - BC + CD$, from which we have
$$
AM = AD + DM = AC + AB - BC = 2AL
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $D$ тачка на страници $A C$ троугла $A B C$ у коме је $A B<B C$ таква да је $A B=B D$. Круг уписан у $\triangle A B C$ додирује $A B$ у $K$ и $A C$ у $L$, а $J$ је центар уписаног круга троугла $B C D$. Доказати да $K L$ полови дуж $A J$.
|
Нека је $M$ тачка на $A C$ таква да је $J M \| K L$. Довољно је доказати да је $A M=2 A L$.
Из $\varangle B D A=\alpha$ добијамо $\varangle J D M=90^{\circ}-\frac{\alpha}{2}=\varangle K L A=\varangle J M D$, па је $J M=$ $J D$, а додирна тачка уписаног круга $\triangle B C D$ са $C D$ је средиште $T$ дужи $M D$. Према томе, $D M=2 D T=B D+C D-B C=A B-B C+C D$, одакле je
$$
A M=A D+D M=A C+A B-B C=2 A L
$$
|
{
"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
e95f406f-c837-5150-aab0-edfcd94f578d
| 608,048
|
Triangle $\triangle Z C P$ is divided into 25 "small" triangles (as shown in the figure), and then all vertices of these triangles are colored with three colors in the following way: vertex $Z$ is colored green, vertex $C$ red, and vertex $P$ blue; each vertex on segment $Z C$ is colored either green or red, each vertex on segment $C P$ is colored either red or blue, and each vertex on segment $Z P$ is colored either green or blue. All vertices located inside the triangle are colored without restriction, one of the three colors.
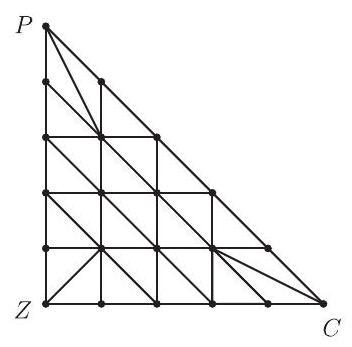
Prove that regardless of the coloring method, at least one of the 25 "small" triangles has all three vertices of different colors.
|
We will examine the sides of small triangles that have one vertex colored red and another blue. Such sides will be called red-blue sides.
Each red-blue side located inside the triangle $\triangle Z C P$ is a side of exactly two small triangles. Furthermore, each red-blue side located on one of the sides of the triangle $\triangle Z C P$ must, by the condition of the problem, belong to the segment $C P$. Given that vertex $C$ is colored red and $P$ is colored blue, the number of red-blue sides on the segment $C P$ is odd.
Therefore, there must exist at least one small triangle that has an odd number of red-blue sides. This triangle must have all three vertices of different colors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Троугао $\triangle Z C P$ је подељен на 25 „малих“ троуглова (као на слици), а затим су сва темена тих троуглова обојена са три боје на следећи начин: теме $Z$ је обојено зеленом бојом, теме $C$ црвеном, а теме $P$ плавом; свако од темена на дужи $Z C$ обојено је или зеленом или црвеном бојом, свако од темена на дужи $C P$ обојено је или црвеном или плавом бојом, а свако од темена на дужи $Z P$ обојено је или зеленом или плавом бојом. Сва темена која се налазе у унутрашњости троугла обојена су без ограничења, једном од три боје.

Доказати да без обзира на начин бојења, бар један од 25 „малих “ троуглова има сва три темена различите боје.
|
Посматраћемо странице малих троуглова које имају једно теме обојено црвеном, а друго плавом бојом. Такве странице ћемо звати црвено-плаве странице.
Свака црвено-плава страница која се налази у унутрашњости троугла $\triangle Z C P$ је страница тачно два мала троугла. Даље, свака црвено-плава страница која налази на једној од страница троугла $\triangle Z C P$ по услову задатка мора припадати баш дужи $C P$. С обзиром да је теме $C$ обојено црвеном бојом а $P$ плавом, број црвено-плавих страница на дужи $C P$ је непаран.
Према томе, мора постојати бар један мали троугао који има непаран број црвено-плавих страница. Тај троугао мора да има сва три темена различите боје.
|
{
"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
40693c47-f4ba-5051-843a-41c89a2d37ac
| 608,049
|
Consider an isosceles triangle $ABC$. Let $AD, BE, CF$ be the angle bisectors of this triangle $(D \in BC, E \in AC, F \in AB)$. Let $K_{a}, K_{b}, K_{c}$ be points on the incircle of triangle $ABC$ such that $DK_{a}, EK_{b}, FK_{c}$ are tangents to the incircle and $K_{a} \notin BC, K_{b} \notin AC, K_{c} \notin AB$. Let $A_{1}, B_{1}, C_{1}$ be the midpoints of sides $BC, CA, AB$. Prove that the lines $A_{1}K_{a}, B_{1}K_{b}, C_{1}K_{c}$ intersect on the incircle of triangle $ABC$.
|
Let's prove that triangles $K_{a} K_{b} K_{c}$ and $A_{1} B_{1} C_{1}$ are homothetic. To do this, it is sufficient to prove that $K_{a} K_{b} \| A_{1} B_{1}$, which is equivalent to $K_{a} K_{b} \| A B$ (analogously, it will follow for the other pairs of sides).
Let $M = K_{a} K_{b} \cap B C$, $S$ be the center of the inscribed circle, and $T$ be an arbitrary point on the inscribed circle. Let $\alpha = \varangle B A S$, $\beta = \varangle C B S$, and $\gamma = \varangle A C S$. Using oriented angles (modulo $180^{\circ}$), we get $\varangle B^{\prime} E B = \beta + 2 \gamma$, and similarly $\varangle A^{\prime} D A = \alpha + 2 \beta$, and thus $\varangle A^{\prime} D K_{a} = 2 \alpha + 4 \beta$. Then, $\varangle B^{\prime} T K_{b} = \varangle B^{\prime} S E = 90^{\circ} + \varangle B^{\prime} E S = \gamma - \alpha$ and similarly $\varangle A^{\prime} T K_{a} = \beta - \gamma$. Then, $\varangle A^{\prime} T B^{\prime} = \varangle A^{\prime} S C = 90^{\circ} + \varangle A^{\prime} C S = \alpha + \beta$. Finally, we get $\varangle K_{a} T K_{b} = \varangle K_{a} T A^{\prime} + \varangle A^{\prime} T B^{\prime} + \varangle B^{\prime} T K_{b} = 2 \gamma$.
Also, from triangle $D K_{a} M$, we get $\varangle C M K_{a} = \varangle C D K_{a} + \varangle D K_{a} M = \varangle A^{\prime} D K_{a} + \varangle D K_{a} K_{b} = (2 \alpha + 4 \beta) + \varangle K_{a} T K_{b} = (2 \alpha + 4 \beta) + 2 \gamma = 2 \beta$. Therefore, $\varangle C M K_{a} = \varangle C B A$, which implies that $K_{a} K_{b} \| A B$, as required. Thus, triangles $K_{a} K_{b} K_{c}$ and $A_{1} B_{1} C_{1}$ are homothetic.
Note also that the homothety coefficient is positive: if it were negative, the segments $K_{a} A_{1}, K_{b} B_{1}, K_{c} C_{1}$ would intersect at one point. If $\alpha > \beta$, then points $C_{1}$ and $K_{c}$, and thus the entire segment $K_{c} C_{1}$, lie inside the quadrilateral $S F B D$. Therefore, if we assume without loss of generality that $\alpha > \beta > \gamma$, then $K_{c} C_{1} \subset S F B D$, but $K_{a} A_{1} \subset S D C E$, so these two segments are disjoint.
Since triangles $K_{a} K_{b} K_{c}$ and $A_{1} B_{1} C_{1}$ are homothetic, their circumcircles are also homothetic. These are the Euler and inscribed circles of triangle $A B C$, respectively, and it is known that these two circles touch internally at the Feuerbach point of triangle $A B C$. Therefore (given that the homothety coefficient is positive), the center of homothety is precisely the Feuerbach point. Hence, $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ intersect at the Feuerbach point of triangle $A B C$, which lies on the inscribed circle of triangle $A B C$, thus proving the statement.
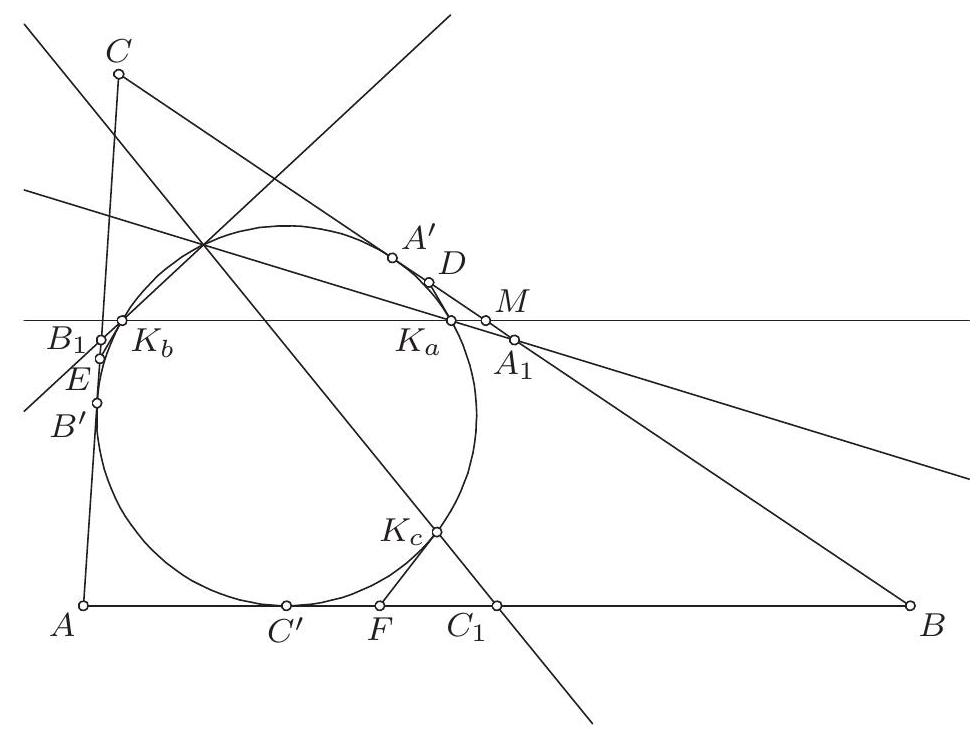
Alternative solution. Let the inscribed circle of triangle $A B C$ be the unit circle in the complex plane. Then, $a = \frac{2 b^{\prime} c^{\prime}}{b^{\prime} + c^{\prime}}, b = \frac{2 a^{\prime} c^{\prime}}{a^{\prime} + c^{\prime}}, c = \frac{2 a^{\prime} b^{\prime}}{a^{\prime} + b^{\prime}}$. Then,
$$
a_{1} = \frac{b + c}{2} = \frac{a^{\prime 2} b^{\prime} + a^{\prime 2} c^{\prime} + 2 a^{\prime} b^{\prime} c^{\prime}}{(a^{\prime} + b^{\prime})(a^{\prime} + c^{\prime})}
$$
We find $k_{a}$ from the condition $\frac{k_{a}}{a} = \overline{\left(\frac{a^{\prime}}{a}\right)}$, so $k_{a} = \frac{1}{a^{\prime}} \overline{\bar{a}} = \frac{b^{\prime} c^{\prime}}{a^{\prime}}$. Now we find the intersection point $z$ of the inscribed circle (where $|z| = 1$) and the line $K_{a} A_{1}$ (where $\frac{z - k_{a}}{a_{1} - k_{a}} = \overline{\left(\frac{z - k_{a}}{a_{1} - k_{a}}\right)}$. The second condition can be transformed into the form
$$
\overline{\left(a_{1} - k_{a}\right)}(z - k_{a}) = \left(\frac{1}{z} - \frac{1}{k_{a}}\right)(a_{1} - k_{a})
$$
from which (since $z \neq k_{a}$) it follows that $\overline{\left(a_{1} - k_{a}\right)} = -\frac{1}{z k_{a}}(a_{1} - k_{a})$, so
$$
z = -\frac{1}{k_{a}} \frac{a_{1} - k_{a}}{\overline{\left(a_{1} - k_{a}\right)}} = -\frac{(a^{\prime 2} - b^{\prime} c^{\prime})(a^{\prime} b^{\prime} + a^{\prime} c^{\prime} + b^{\prime} c^{\prime})}{(b^{\prime} c^{\prime} - a^{\prime 2})(a^{\prime} + b^{\prime} + c^{\prime})} = \frac{a^{\prime} b^{\prime} + a^{\prime} c^{\prime} + b^{\prime} c^{\prime}}{a^{\prime} + b^{\prime} + c^{\prime}}
$$
Since the given expression is symmetric in $a^{\prime}, b^{\prime}, c^{\prime}$, it can be similarly shown that the lines $K_{b} B_{1}$ and $K_{c} C_{1}$ intersect the inscribed circle at the same point, thus proving the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је неједнакокраки троугао $A B C$. Нека су $A D, B E, C F$ симетрале углова овог троугла $(D \in B C, E \in A C, F \in A B)$. Нека су $K_{a}, K_{b}, K_{c}$ тачке на уписаном кругу троугла $A B C$ такве да су $D K_{a}, E K_{b}, F K_{c}$ тангенте на уписани круг и да $K_{a} \notin B C, K_{b} \notin A C, K_{c} \notin A B$. Нека су $A_{1}, B_{1}, C_{1}$ средишта страница $B C, C A, A B$. Доказати да се праве $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу на уписаном кругу троугла $A B C$.
|
Докажимо да су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични. Да бисмо то доказали, довољно је да докажемо да је $K_{a} K_{b} \| A_{1} B_{1}$, односно $K_{a} K_{b} \| A B$ (аналогно ће следити и за друге парове страница).
Означимо $M=K_{a} K_{b} \cap B C$, са $S$ означимо центар уписаног круга, и са $T$ означимо произвољну тачку на уписаном кругу. Означимо $\alpha=\varangle B A S$, $\beta=\varangle C B S, \gamma=\varangle A C S$. Користећи оријентисане углове (по модулу $180^{\circ}$ ), добијамо $\varangle B^{\prime} E B=\beta+2 \gamma$, и аналогно $\varangle A^{\prime} D A=\alpha+2 \beta$, а одатле и $\varangle A^{\prime} D K_{a}=2 \alpha+4 \beta$. Затим, $\varangle B^{\prime} T K_{b}=\varangle B^{\prime} S E=90^{\circ}+\varangle B^{\prime} E S=\gamma-\alpha$ и аналогно $\varangle A^{\prime} T K_{a}=\beta-\gamma$. Затим, $\varangle A^{\prime} T B^{\prime}=\varangle A^{\prime} S C=90^{\circ}+\varangle A^{\prime} C S=\alpha+\beta$. И на крају добијамо $\varangle K_{a} T K_{b}=\varangle K_{a} T A^{\prime}+\varangle A^{\prime} T B^{\prime}+\varangle B^{\prime} T K_{b}=2 \gamma$.
Такође, из троугла $D K_{a} M$ добијамо $\varangle C M K_{a}=\varangle C D K_{a}+\varangle D K_{a} M=$ $\varangle A^{\prime} D K_{a}+\varangle D K_{a} K_{b}=(2 \alpha+4 \beta)+\varangle K_{a} T K_{b}=(2 \alpha+4 \beta)+2 \gamma=2 \beta$. Дакле, $\varangle C M K_{a}=\varangle C B A$, одакле следи да је $K_{a} K_{b} \| A B$, што је требало доказати. Дакле, троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ су хомотетични.
Приметимо такође да је коефицијент хомотетије позитиван: ако би био негативан, дужи $K_{a} A_{1}, K_{b} B_{1}, K_{c} C_{1}$ би се секле у једној тачки. Ако је $\alpha>$ $\beta$, онда се тачке $C_{1}$ и $K_{c}$, па и цела дуж $K_{c} C_{1}$, налазе унутар четвороугла $S F B D$. Зато, ако без умањења општости претпоставимо $\alpha>\beta>\gamma$, онда $K_{c} C_{1} \subset S F B D$, али $K_{a} A_{1} \subset S D C E$, па су ове две дужи дисјунктне.
Како су троуглови $K_{a} K_{b} K_{c}$ и $A_{1} B_{1} C_{1}$ хомотетични, њихови описани кругови су такође хомотетични. Али то су Ојлеров и уписани круг троугла $A B C$, респективно, и познато је да се та два круга додирују изнутра у Фојербаховој тачки троугла $A B C$. Стога (уз чињеницу да је коефицијент хомотетије позитиван), центар хомотетије је управо Фојербахова тачка. Одавде следи да се $A_{1} K_{a}, B_{1} K_{b}, C_{1} K_{c}$ секу у Фојербаховој тачки троугла $A B C$, која припада уписаном кругу троугла $A B C$, чиме је тврдјење доказано.

Алтернативно решење. Нека је уписани круг троугла $A B C$ јединична кружница у комплексној равни. Тада је $a=\frac{2 b^{\prime} c^{\prime}}{b^{\prime}+c^{\prime}}, b=\frac{2 a^{\prime} c^{\prime}}{a^{\prime}+c^{\prime}}, c=\frac{2 a^{\prime} b^{\prime}}{a^{\prime}+b^{\prime}}$. Затим је
$$
a_{1}=\frac{b+c}{2}=\frac{a^{\prime 2} b^{\prime}+a^{\prime 2} c^{\prime}+2 a^{\prime} b^{\prime} c^{\prime}}{\left(a^{\prime}+b^{\prime}\right)\left(a^{\prime}+c^{\prime}\right)}
$$
Вредност $k_{a}$ налазимо из услова $\frac{k_{a}}{a}=\overline{\left(\frac{a^{\prime}}{a}\right)}$, одакле је $k_{a}=\frac{1}{a^{\prime}} \overline{\bar{a}}=\frac{b^{\prime} c^{\prime}}{a^{\prime}}$. Сада налазимо пресечну тачку $z$ уписаног круга (одакле $|z|=1$ ) и праве $K_{a} A_{1}$ (одакле $\frac{z-k_{a}}{a_{1}-k_{a}}=\overline{\left(\frac{z-k_{a}}{a_{1}-k_{a}}\right)}$. Други услов можемо трансформисати у облик
$$
\overline{\left(a_{1}-k_{a}\right)}\left(z-k_{a}\right)=\left(\frac{1}{z}-\frac{1}{k_{a}}\right)\left(a_{1}-k_{a}\right)
$$
одакле (због $\left.z \neq k_{a}\right)$ следи $\overline{\left(a_{1}-k_{a}\right)}=-\frac{1}{z k_{a}}\left(a_{1}-k_{a}\right)$, па је
$$
z=-\frac{1}{k_{a}} \frac{a_{1}-k_{a}}{\overline{\left(a_{1}-k_{a}\right)}}=-\frac{\left(a^{\prime 2}-b^{\prime} c^{\prime}\right)\left(a^{\prime} b^{\prime}+a^{\prime} c^{\prime}+b^{\prime} c^{\prime}\right)}{\left(b^{\prime} c^{\prime}-a^{\prime 2}\right)\left(a^{\prime}+b^{\prime}+c^{\prime}\right)}=\frac{a^{\prime} b^{\prime}+a^{\prime} c^{\prime}+b^{\prime} c^{\prime}}{a^{\prime}+b^{\prime}+c^{\prime}}
$$
Како је наведени израз симетричан по $a^{\prime}, b^{\prime}, c^{\prime}$, аналогно се доказује да ће праве $K_{b} B_{1}$ и $K_{c} C_{1}$ сећи уписани круг у истој тачки, чиме је тврђење доказано.
|
{
"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
aa4aaf38-5363-5888-812b-1de8ef453f71
| 608,052
|
Let $k$ be a natural number. Prove that for positive real numbers $x, y, z$ whose sum is equal to 1, the inequality
$$
\frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}}+\frac{y^{k+2}}{y^{k+1}+z^{k}+x^{k}}+\frac{z^{k+2}}{z^{k+1}+x^{k}+y^{k}} \geqslant \frac{1}{7}
$$
holds. When does equality hold?
Time for work 270 minutes.
Each task is worth 7 points.
## SOLUTIONS
|
Given that the expression is symmetric, without loss of generality, we can assume that $x \geqslant y \geqslant z$. Then,
$$
x^{k+1}+y^{k}+z^{k} \leqslant y^{k+1}+z^{k}+x^{k} \leqslant z^{k+1}+x^{k}+y^{k}
$$
Indeed, it is sufficient to prove the first inequality, i.e., that $x^{k+1}+y^{k} \leqslant y^{k+1}+x^{k}$. This inequality is equivalent to $\left(\frac{y}{x}\right)^{k} \leqslant \frac{1-x}{1-y}$. Since $y \leqslant x$, it is sufficient to prove that $\frac{y}{x} \leqslant \frac{1-x}{1-y}$, which is equivalent to the true inequality $0 \leqslant$ $x-x^{2}-y+y^{2}=(x-y)(1-x-y)=(x-y) z$. Applying Chebyshev's inequality to the triples $\left(x^{k+2}, y^{k+2}, z^{k+2}\right)$ and $\left(\frac{1}{x^{k+1}+y^{k}+z^{k}}, \frac{1}{y^{k+1}+z^{k}+x^{k}}, \frac{1}{z^{k+1}+x^{k}+y^{k}}\right)$, we get
$$
\sum_{\text {cyc }} \frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}} \geqslant \frac{1}{3} \sum_{\text {cyc }} x^{k+2} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L
$$
If we apply Chebyshev's inequality again to the triples $(x, y, z)$ and $\left(x^{k+1}, y^{k+1}, z^{k+1}\right)$ in $L$, we get
$$
L \geqslant \frac{1}{3} \cdot \frac{1}{3} \sum_{\text {cyc }} x \sum_{\text {cyc }} x^{k+1} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L^{\prime}
$$
From the Cauchy-Schwarz-Bunyakovsky inequality, it follows that
$$
\sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}} \sum_{\text {cyc }}\left(x^{k+1}+y^{k}+z^{k}\right) \geqslant 9
$$
so
$$
L^{\prime} \geqslant \frac{x^{k+1}+y^{k+1}+z^{k+1}}{x^{k+1}+y^{k+1}+z^{k+1}+2\left(x^{k}+y^{k}+z^{k}\right)}
$$
and thus it is sufficient to prove that
$$
3\left(x^{k+1}+y^{k+1}+z^{k+1}\right) \geqslant x^{k}+y^{k}+z^{k}
$$
The last inequality is obtained by applying Chebyshev's inequality again to the triples $(x, y, z)$ and $\left(x^{k}, y^{k}, z^{k}\right)$.
Equality in all applied inequalities holds if and only if $x=y=z$, i.e., if and only if $x=y=z=\frac{1}{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Нека је $k$ природан број. Доказати да за позитивне реалне бројеве $x, y, z$ чији је збир једнак 1 , важи неједнакост
$$
\frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}}+\frac{y^{k+2}}{y^{k+1}+z^{k}+x^{k}}+\frac{z^{k+2}}{z^{k+1}+x^{k}+y^{k}} \geqslant \frac{1}{7}
$$
Када важи једнакост?
Време за рад 270 минута.
Сваки задатак вреди 7 поена.
## РЕШЕЊА
|
Дати израз је симетричан, па се без губљења општости може претпоставити да је $x \geqslant y \geqslant z$. Тада је
$$
x^{k+1}+y^{k}+z^{k} \leqslant y^{k+1}+z^{k}+x^{k} \leqslant z^{k+1}+x^{k}+y^{k}
$$
Заиста, довољно је доказати прву неједнакост, тј. да је $x^{k+1}+y^{k} \leqslant y^{k+1}+$ $x^{k}$. Ова неједнакост је еквивалентна са $\left(\frac{y}{x}\right)^{k} \leqslant \frac{1-x}{1-y}$. Како је $y \leqslant x$, довољно је доказати да је $\frac{y}{x} \leqslant \frac{1-x}{1-y}$, што је еквивалентно тачној неједнакости $0 \leqslant$ $x-x^{2}-y+y^{2}=(x-y)(1-x-y)=(x-y) z$. Применом неједнакости Чебишева на тројке $\left(x^{k+2}, y^{k+2}, z^{k+2}\right)$ и $\left(\frac{1}{x^{k+1}+y^{k}+z^{k}}, \frac{1}{y^{k+1}+z^{k}+x^{k}}, \frac{1}{z^{k+1}+x^{k}+y^{k}}\right)$ добија се
$$
\sum_{\text {cyc }} \frac{x^{k+2}}{x^{k+1}+y^{k}+z^{k}} \geqslant \frac{1}{3} \sum_{\text {cyc }} x^{k+2} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L
$$
Уколико се у $L$ поново примени неједнакост Чебишева на тројке $(x, y, z)$ и $\left(x^{k+1}, y^{k+1}, z^{k+1}\right)$ добија се
$$
L \geqslant \frac{1}{3} \cdot \frac{1}{3} \sum_{\text {cyc }} x \sum_{\text {cyc }} x^{k+1} \sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}}=L^{\prime}
$$
Из неједнакости Коши-Шварц-Буњаковског следи
$$
\sum_{\text {cyc }} \frac{1}{x^{k+1}+y^{k}+z^{k}} \sum_{\text {cyc }}\left(x^{k+1}+y^{k}+z^{k}\right) \geqslant 9
$$
па је
$$
L^{\prime} \geqslant \frac{x^{k+1}+y^{k+1}+z^{k+1}}{x^{k+1}+y^{k+1}+z^{k+1}+2\left(x^{k}+y^{k}+z^{k}\right)}
$$
и самим тим довољно је доказати да је
$$
3\left(x^{k+1}+y^{k+1}+z^{k+1}\right) \geqslant x^{k}+y^{k}+z^{k}
$$
Последња неједнакост се добија поновном применом неједнакости Чебишева на тројке $(x, y, z)$ и $\left(x^{k}, y^{k}, z^{k}\right)$.
Једнакост у свим примењеним неједнакостима важи ако и само ако је $x=y=z$, тј. ако и само ако је $x=y=z=\frac{1}{3}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2007_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
fb4b2492-69df-5a6f-860d-183512f701a2
| 608,053
|
Consider triangle $ABC$. Let points $D$ and $E$ be on line $AB$ such that $D-A-B-E$, $AD=AC$, and $BE=BC$. The angle bisectors of the internal angles at vertices $A$ and $B$ intersect the opposite sides at points $P$ and $Q$, respectively, and the circumcircle of triangle $ABC$ at points $M$ and $N$, respectively. The line connecting point $A$ to the center of the circumcircle of triangle $BME$ and the line connecting point $B$ to the center of the circumcircle of triangle $AND$ intersect at point $X, X \neq C$. Prove that $CX \perp PQ$. (Dušan Đukić)
|
Let $U$ be the center of the circumcircle of $\triangle B M E$. Apply inversion with center $A$ and the square of the radius $A B \cdot A C$. Points $B$ and $C$ map to points $B^{\prime}$ and $C^{\prime}$, which are symmetric to points $C$ and $B$ with respect to $A P$, points $P$ and $M$ map to each other, and $E$ maps to point $E^{\prime}$, which is symmetric to $Q$ with respect to $A P$. Therefore, the line $A U$ coincides with the line connecting $A$ to the center of the circle $B^{\prime} P E^{\prime}$ (of course, the centers do not map to each other!). We see that this line is symmetric to
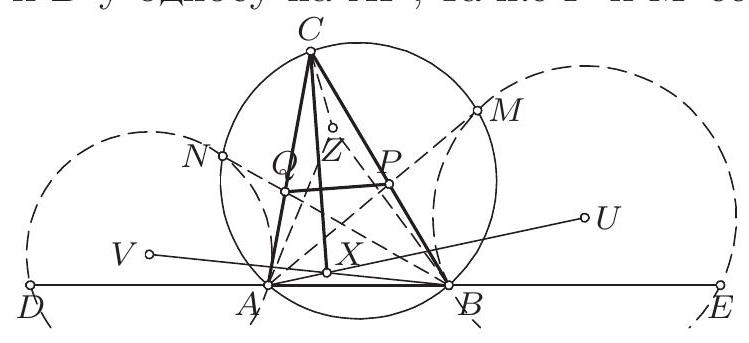
the line $A Z$ with respect to the angle bisector of $\angle A$, where $Z$ is the center of the circumcircle of $\triangle C P Q$.
Similarly, it is obtained that the line $B Z$ is symmetric to the line connecting $B$ to the center $V$ of the circle $A N D$ with respect to the angle bisector of $\angle B$. By Ceva's theorem in trigonometric form (or by the statement about isogonal conjugates), the lines symmetric to $A U, B V, C X$ with respect to the angle bisectors of $\angle A, \angle B, \angle C$ respectively also intersect at one point, which means that the line $C Z$ is symmetric to $C X$ with respect to the angle bisector of $\angle C$. Since $Z$ is the center of the circle $C P Q$, it follows that the line $C X$ contains the altitude of the triangle $C P Q$, which is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је троугао $A B C$. Нека су тачке $D$ и $E$ на правој $A B$ такве да је $D-A-B-E, A D=A C$ и $B E=B C$. Симетрале унутрашњих углова код темена $A$ и $B$ секу наспрамне странице у тачкама $P$ и $Q$, редом, а описану кружницу око троугла $A B C$ у тачкама $M$ и $N$, редом. Права која спаја тачку $A$ са центром кружнице описане око троугла $B M E$ и права која спаја тачку $B$ са центром кружнице описане око троугла $A N D$ секу ce у тачки $X, X \neq C$. Доказати да је $C X \perp P Q$. (Дуиан Ђукић)
|
Означимо са $U$ центар описаног круга $\triangle B M E$. Применимо инверзију са центром $A$ и квадратом полупречника $A B \cdot A C$. Тачке $B$ и $C$ се сликају у тачке $B^{\prime}$ и $C^{\prime}$ симетричне тачкама $C$ и $B$ у односу на $A P$, тачке $P$ и $M$ се сликају једна у другу, а $E$ се слика у тачку $E^{\prime}$ симетричну $Q$ у односу на $A P$. Према томе, права $A U$ се поклапа са правом која спаја $A$ са центром круга $B^{\prime} P E^{\prime}$ (наравно, центри се не сликају један у други!). Видимо да је та права симетрична

правој $A Z$ у односу на симетралу угла $A$, где је $Z$ центар круга описаног око $\triangle C P Q$.
Аналогно се добија да је права $B Z$ симетрична правој која спаја $B$ са центром $V$ круга $A N D$ у односу на симетралу угла $B$. По Чевиној теореми у тригонометријском облику (или по тврђењу о изогонално спрегнутим тачкама), праве симетричне правим $A U, B V, C X$ у односу на симетрале углова $A, B, C$ редом се такође секу у једној тачки, што значи да је права $C Z$ симетрична $C X$ у односу на симетралу угла $C$. Али $Z$ је центар круга $C P Q$, одакле следи да права $C X$ садржи висину троугла $C P Q$, а то смо и желели да докажемо.
|
{
"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
c466377f-93e6-5b33-b496-a83436032f3f
| 608,055
|
Prove that for positive real numbers $a, b$, and $c$ such that $a+b+c=1$, the inequality
$$
\frac{1}{b c+a+\frac{1}{a}}+\frac{1}{c a+b+\frac{1}{b}}+\frac{1}{a b+c+\frac{1}{c}} \leqslant \frac{27}{31}
$$
holds.
(Marko Radovanović with modifications)
Time for work 270 minutes.
Each task is worth 7 points.
## SERBIAN MATHEMATICAL OLYMPIAD
competition of high school students in mathematics
Belgrade, 13.04.2008.
## Second day
|
The sought inequality is clearly equivalent to the inequality
$$
\frac{a}{p+a^{2}}+\frac{b}{p+b^{2}}+\frac{c}{p+c^{2}} \leq \frac{27}{31}
$$
where $a+b+c=1$ and $p=abc+1$. We will consider the function
$$
f(x)=\frac{3(a+b+c)}{3 x+a^{2}+b^{2}+c^{2}}-\frac{a}{x+a^{2}}-\frac{b}{x+b^{2}}-\frac{c}{x+c^{2}}
$$
We will prove that $f(x) \geq 0$ for all $x \geq ab+bc+ca$. Reducing the expression for $f(x)$ to a common denominator gives
$$
f(x)=\frac{A x^{2}+B x+C}{\left(x+a^{2}\right)\left(x+b^{2}\right)\left(x+c^{2}\right)\left(3 x+a^{2}+b^{2}+c^{2}\right)}
$$
where $A \geq 0 \geq C$. Indeed, it is easily obtained that
$$
\begin{gathered}
A=2 a^{3}+2 b^{3}+2 c^{3}-a b(a+b)-a c(a+c)-b c(b+c) \geq 0 \\
C=-a b c\left[a\left(b^{3}+c^{3}\right)+b\left(c^{3}+a^{3}\right)+c\left(a^{3}+b^{3}\right)-2 a b c(a+b+c)\right] \leq 0
\end{gathered}
$$
Note that it does not matter how much $B$ is. Therefore, the polynomial $P(x) = A x^{2} + B x + C$ (if not constantly 0) has two real roots, one positive (say $x=x_{0}$) and one negative, and $P(x) \leq 0$ for $0 \leq x \leq x_{0}$ and $P(x) \geq 0$ for $x \geq x_{0}$. We claim that $f(ab+bc+ca) \geq 0$. Indeed,
$$
\begin{aligned}
& f(ab+bc+ca) \\
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(ab+bc+ca)}-\frac{a}{(a+b)(a+c)}-\frac{b}{(b+c)(b+a)}-\frac{c}{(c+a)(c+b)} \\
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(ab+bc+ca)}-\frac{2(ab+bc+ca)}{(a+b)(b+c)(c+a)} \geq 0 \quad \text{since} \\
& \quad \frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(ab+bc+ca)} \geq \frac{9}{4(a+b+c)} \geq \frac{2(ab+bc+ca)}{(a+b)(b+c)(c+a)},
\end{aligned}
$$
which is what we wanted. Therefore, $P(ab+bc+ca) \geq 0$, i.e., $x_{0} \leq ab+bc+ca$, from which it follows that $P(x) \geq 0$ and $f(x) \geq 0$ for all $x \geq ab+bc+ca$. In particular, $f(1+abc) \geq 0$ since $1+abc > 1 > ab+bc+ca$. Thus, we have proven
$$
\frac{a}{1+abc+a^{2}}+\frac{b}{1+abc+b^{2}}+\frac{c}{1+abc+c^{2}} \leq \frac{3}{3+a^{2}+b^{2}+c^{2}+3abc}
$$
It remains to prove that $a^{2}+b^{2}+c^{2}+3abc \geq \frac{4}{9}$, which together with (1) will give the desired inequality. Homogenization gives $9(a+b+c)(a^{2}+b^{2}+c^{2})+27abc \geq 4(a+b+c)^{3}$, which is equivalent to
$$
5(a^{3}+b^{3}+c^{3})+3abc \geq 3(ab(a+b)+ac(a+c)+bc(b+c))
$$
The last inequality immediately follows from Schur's inequality. This completes the proof of the statement.
Another solution. After homogenization, reducing to a common denominator, and simplification, the inequality reduces to a symmetric inequality that can be directly proven using Muirhead's inequality:
$$
\begin{aligned}
& \frac{23}{2} T_{900}+122 T_{810}+260 T_{720}+282 T_{630}+193 T_{540}+\frac{547}{2} T_{711}+807 T_{620}+284 T_{531} \\
&+91 T_{522}-98 T_{441}-1669 T_{432}-557 T_{333} \geq 0
\end{aligned}
$$
where $T_{ijk}$ is the symmetric sum $x^{i} y^{j} z^{k}+\cdots$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Доказати да за позитивне реалне бројеве $a, b$ и $c$, такве да је $a+b+c=1$, важи неједнакост
$$
\frac{1}{b c+a+\frac{1}{a}}+\frac{1}{c a+b+\frac{1}{b}}+\frac{1}{a b+c+\frac{1}{c}} \leqslant \frac{27}{31}
$$
(Марко Радовановић са сараунииима)
Време за рад 270 минута.
Сваки задатак вреди 7 поена.
## СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
такмичење ученика средњих школа из математике
Београд, 13.04.2008.
## Други дан
|
Тражена неједнакост је очигледно еквивалентна неједнакости
$$
\frac{a}{p+a^{2}}+\frac{b}{p+b^{2}}+\frac{c}{p+c^{2}} \leq \frac{27}{31}
$$
где је $a+b+c=1$ и $p=a b c+1$. Посматраћемо функцију
$$
f(x)=\frac{3(a+b+c)}{3 x+a^{2}+b^{2}+c^{2}}-\frac{a}{x+a^{2}}-\frac{b}{x+b^{2}}-\frac{c}{x+c^{2}}
$$
Доказаћемо да важи $f(x) \geq 0$ за све $x \geq a b+b c+c a$. Свођење израза за $f(x)$ на заједнички именилац даје
$$
f(x)=\frac{A x^{2}+B x+C}{\left(x+a^{2}\right)\left(x+b^{2}\right)\left(x+c^{2}\right)\left(3 x+a^{2}+b^{2}+c^{2}\right)}
$$
при чему је $A \geq 0 \geq C$. Заправо, лако се добија
$$
\begin{gathered}
A=2 a^{3}+2 b^{3}+2 c^{3}-a b(a+b)-a c(a+c)-b c(b+c) \geq 0 \\
C=-a b c\left[a\left(b^{3}+c^{3}\right)+b\left(c^{3}+a^{3}\right)+c\left(a^{3}+b^{3}\right)-2 a b c(a+b+c)\right] \leq 0
\end{gathered}
$$
Приметимо да није важно колико је $B$. Према томе, полином $P(x)=$ $A x^{2}+B x+C$ (ако није константно 0 ) има две реалне нуле, једну позитивну (рецимо $x=x_{0}$ ) и једну негативну, и важи $P(x) \leq 0$ за $0 \leq x \leq x_{0}$ и $P(x) \geq 0$ за $x \geq x_{0}$. Тврдимо да је $f(a b+b c+c a) \geq 0$. Заиста,
$$
\begin{aligned}
& f(a b+b c+c a) \\
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\frac{a}{(a+b)(a+c)}-\frac{b}{(b+c)(b+a)}-\frac{c}{(c+a)(c+b)} \\
& =\frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)}-\frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)} \geq 0 \quad \text { jep je } \\
& \quad \frac{3(a+b+c)}{a^{2}+b^{2}+c^{2}+3(a b+b c+c a)} \geq \frac{9}{4(a+b+c)} \geq \frac{2(a b+b c+c a)}{(a+b)(b+c)(c+a)},
\end{aligned}
$$
што смо и желели. Према томе, $P(a b+b c+c a) \geq 0$, тј. $x_{0} \leq a b+b c+c a$, одакле следи да је и $P(x) \geq 0$ и $f(x) \geq 0$ за све $x \geq a b+b c+c a$. Између осталог, $f(1+a b c) \geq 0$ јер је $1+a b c>1>a b+b c+c a$. Тако смо доказали
$$
\frac{a}{1+a b c+a^{2}}+\frac{b}{1+a b c+b^{2}}+\frac{c}{1+a b c+c^{2}} \leq \frac{3}{3+a^{2}+b^{2}+c^{2}+3 a b c}
$$
Остаје још само да докажемо да је $a^{2}+b^{2}+c^{2}+3 a b c \geq \frac{4}{9}$, што ће заједно са (1) дати тражену неједнакост. Хомогенизација даје $9(a+b+c)\left(a^{2}+b^{2}+\right.$ $\left.c^{2}\right)+27 a b c \geq 4(a+b+c)^{3}$, што је еквивалентно са
$$
5\left(a^{3}+b^{3}+c^{3}\right)+3 a b c \geq 3(a b(a+b)+a c(a+c)+b c(b+c))
$$
Последња неједнакост одмах следи из Шурове неједнакости. Овим је доказ тврђења задатка коначно завршен.
Друго решење. Након хомогенизације, свођења на заједнички именилац и скраћивања неједнакост се своди на симетричну неједнакост која се директно доказује Мјурхедовом неједнакошћу:
$$
\begin{aligned}
& \frac{23}{2} T_{900}+122 T_{810}+260 T_{720}+282 T_{630}+193 T_{540}+\frac{547}{2} T_{711}+807 T_{620}+284 T_{531} \\
&+91 T_{522}-98 T_{441}-1669 T_{432}-557 T_{333} \geq 0
\end{aligned}
$$
где је $T_{i j k}$ симетрична сума $x^{i} y^{j} z^{k}+\cdots$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
760ab2c5-2aa9-52dd-ad27-c9c3bbf66782
| 608,056
|
Each point in the plane is colored with one of 3 colors. Prove that there exists a triangle such that:
$1^{\circ}$ all 3 vertices of this triangle are colored the same color;
$2^{\circ}$ the radius of the circumscribed circle of this triangle is 2008;
$3^{\circ}$ one angle of the triangle is two or three times larger than one of the other two angles.
|
Consider a regular 13-sided polygon \( A_{1} A_{2} \ldots A_{13} \) inscribed in a circle with radius 2008. By the Dirichlet principle, there exist five vertices of the same color (e.g., red). We distinguish two cases.
(i) Among the five red vertices, no two are adjacent. Each arrangement of red points (up to rotation) corresponds to a composition of the number 13 into 5 parts, each greater than 1. There are 5 distinct arrangements, and they are shown in the figure below, with the triangle highlighted.
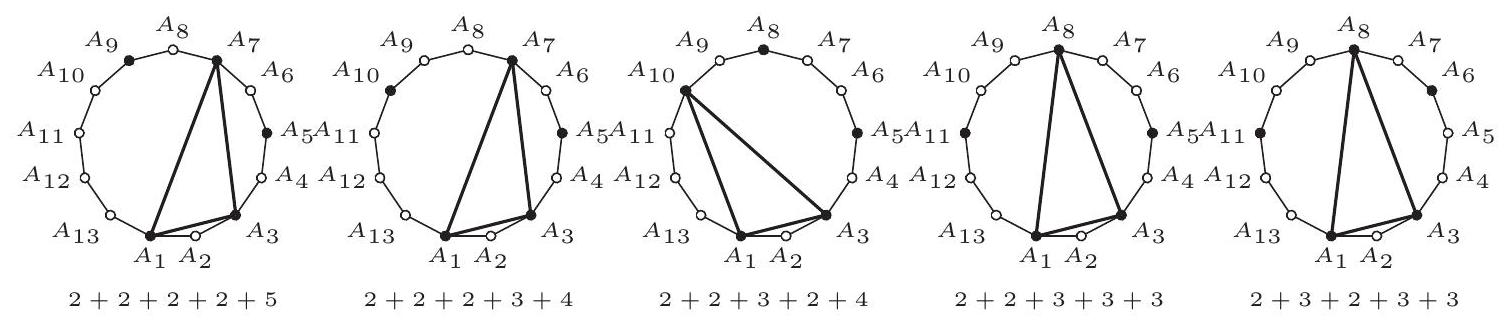
(ii) Suppose two red vertices are adjacent, say \( A_{1} \) and \( A_{2} \). If any of the points \( A_{4}, A_{5}, A_{6}, A_{10}, A_{11}, A_{12} \) is red, the desired triangle is determined by that point and the vertices \( A_{1}, A_{2} \). We further assume that none of these 6 points is red. Then, among the vertices \( A_{3}, A_{7}, A_{8}, A_{9}, A_{13} \), at least three are red. If one of them is \( A_{3} \) (analogously for \( A_{13} \)), then at least one of the points \( A_{7}, A_{9}, A_{13} \) is red, and at least one of the triangles determined by this point and the points \( A_{1} \) and \( A_{3} \) satisfies the conditions. The only remaining case is when the red points are \( A_{7}, A_{8}, A_{9} \), in which case the triangle \( A_{1} A_{7} A_{9} \) is the desired one.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Свака тачка равни је обојена са једном од 3 боје. Доказати да постоји троугао за који важи:
$1^{\circ}$ сва 3 темена тог троугла су обојена истом бојом;
$2^{\circ}$ полупречник описане кружнице тог троугла је 2008;
$3^{\circ}$ један угао троугла је два или три пута већи од неког од друга два угла.
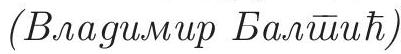
|
Уочимо правилан тринаестоугао $A_{1} A_{2} \ldots A_{13}$ уписан у круг полупречника 2008. По Дирихлеовом принципу постоји пет темена која су исте боје (нпр. црвене). Разликујемо два случаја.
(i) Међу пет црвених темена не постоје два суседна. Сваком положају црвених тачака (до на ротацију) одговара композиција броја 13 на 5 сабирака већих од 1. Постоји 5 неподударних распореда и они су приказани на слици испод, са истакнутим троуглом.

(ii) Нека два црвена темена су суседна, рецимо $A_{1}$ и $A_{2}$. Ако је црвена било која од тачака $A_{4}, A_{5}, A_{6}, A_{10}, A_{11}, A_{12}$, тражени троугао је
одређен том тачком и теменима $A_{1}, A_{2}$. Надаље претпостављамо да ниједна од ових 6 тачака није црвена. Тада су међу теменима $A_{3}, A_{7}$, $A_{8}, A_{9}, A_{13}$ бар три црвена. Ако је међу њима $A_{3}$ (аналогно за $A_{13}$ ), онда је бар једна од тачака $A_{7}, A_{9}, A_{13}$ црвена па бар један од троуглова одређених овом тачком и тачкама $A_{1}$ и $A_{3}$ задовољава услове. Једини преостали случај је кад су црвене тачке $A_{7}, A_{8}, A_{9}$, а онда је троугао $A_{1} A_{7} A_{9}$ тражени.
|
{
"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
bb1da769-4b9d-5206-8deb-f0a514699aa5
| 608,057
|
Let the sequence $\left(a_{n}\right)_{n \geqslant 1}$ be defined by $a_{1}=3, a_{2}=11$ and $a_{n}=4 a_{n-1}-a_{n-2}$, for $n \geqslant 3$. Prove that every term of this sequence is of the form $a^{2}+2 b^{2}$ for some natural numbers $a$ and $b$.
(Đorđe Baralić)
|
We have $a_{1}=1+2 \cdot 1^{2}, a_{2}=3^{2}+2 \cdot 1^{2}, a_{3}=3^{2}+2 \cdot 4^{2}, a_{4}=11^{2}+2 \cdot 4^{2}$, etc. We will prove by induction on $n$ that
$$
a_{2 n-1}=a_{n-1}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \quad \text { and } \quad a_{2 n}=a_{n}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2},
$$
where $a_{0}=1$. Assuming the statement holds for $n$, we have
$$
\begin{aligned}
a_{2 n+1} & =4 a_{2 n}-a_{2 n-1}=4 a_{n}^{2}+8\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2}-a_{n-1}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
& =\frac{11}{2} a_{n}^{2}-3 a_{n} a_{n-1}+\frac{1}{2} a_{n-1}^{2}=\frac{11}{2} a_{n}^{2}-3 a_{n}\left(4 a_{n}-a_{n+1}\right)+\frac{1}{2}\left(4 a_{n}-a_{n+1}\right)^{2} \\
& =\frac{3}{2} a_{n}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n+1}^{2}=a_{n}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2} \\
a_{2 n+2} & =4 a_{2 n+1}-a_{2 n}=4 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-a_{n}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
& =3 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-2\left(\frac{a_{n+1}-3 a_{n}}{2}\right)^{2}=\frac{3}{2} a_{n+1}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n}^{2} \\
& =a_{n+1}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2},
\end{aligned}
$$
thus completing the proof.
Another solution. It is known that an odd natural number $m>1$ can be represented in the form $a^{2}+2 b^{2}$ for some coprime $a, b \in \mathbb{N}$ if and only if all prime divisors of $m$ are of the form $8 k+1$ or $8 k+3, k \in \mathbb{N}_{0}$. It is easy to see that all terms of the sequence $(a_{n})$ are odd; it remains to show that if a prime $p$ divides $a_{n}$, then $p=8 k+1$ or $8 k+3$ for some $k \in \mathbb{N}_{0}$.
It is shown by induction on $n$ that $a_{n} a_{n+2}=a_{n+1}^{2}+2$. Indeed, this holds for $n \leq 2$, and for $n>2$, assuming it holds for $n-2$, we have
$$
\begin{aligned}
\frac{a_{n+1}^{2}+2}{a_{n}} & =\frac{\left(4 a_{n}-a_{n-1}\right)^{2}+2}{a_{n}}=16 a_{n}-8 a_{n-1}+\frac{a_{n-1}^{2}+2}{a_{n}} \\
& =16 a_{n}-8 a_{n-1}+a_{n-2}=4 a_{n+1}-a_{n}=a_{n+2}
\end{aligned}
$$
From this, it follows that $-2$ is a quadratic residue modulo any prime divisor $p$ of $a_{n}$, hence $p \equiv 1$ or $p \equiv 3(\bmod 8)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је низ $\left(a_{n}\right)_{n \geqslant 1}$ дефинисан са $a_{1}=3, a_{2}=11$ и $a_{n}=4 a_{n-1}-a_{n-2}$, за $n \geqslant 3$. Доказати да је сваки члан овог низа облика $a^{2}+2 b^{2}$ за неке природне $a$ и $b$.
(Ђорђе Баралић)
|
Имамо $a_{1}=1+2 \cdot 1^{2}, a_{2}=3^{2}+2 \cdot 1^{2}, a_{3}=3^{2}+2 \cdot 4^{2}, a_{4}=11^{2}+2 \cdot 4^{2}$, итд. Доказаћемо индукцијом по $n$ да важи
$$
a_{2 n-1}=a_{n-1}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \quad \text { и } \quad a_{2 n}=a_{n}^{2}+2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2},
$$
при чему је $a_{0}=1$. Претпоставимо да тврђење важи за $n$. Тада је
$$
\begin{aligned}
a_{2 n+1} & =4 a_{2 n}-a_{2 n-1}=4 a_{n}^{2}+8\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2}-a_{n-1}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
& =\frac{11}{2} a_{n}^{2}-3 a_{n} a_{n-1}+\frac{1}{2} a_{n-1}^{2}=\frac{11}{2} a_{n}^{2}-3 a_{n}\left(4 a_{n}-a_{n+1}\right)+\frac{1}{2}\left(4 a_{n}-a_{n+1}\right)^{2} \\
& =\frac{3}{2} a_{n}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n+1}^{2}=a_{n}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2} \\
a_{2 n+2} & =4 a_{2 n+1}-a_{2 n}=4 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-a_{n}^{2}-2\left(\frac{a_{n}-a_{n-1}}{2}\right)^{2} \\
& =3 a_{n}^{2}+8\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2}-2\left(\frac{a_{n+1}-3 a_{n}}{2}\right)^{2}=\frac{3}{2} a_{n+1}^{2}-a_{n} a_{n+1}+\frac{1}{2} a_{n}^{2} \\
& =a_{n+1}^{2}+2\left(\frac{a_{n+1}-a_{n}}{2}\right)^{2},
\end{aligned}
$$
чиме је доказ завршен.
Друго решење. Познато је да се непаран природан број $m>1$ може представити у облику $a^{2}+2 b^{2}$ за неке узајамно просте $a, b \in \mathbb{N}$ ако и само ако су сви прости делиоци $m$ облика $8 k+1$ или $8 k+3, k \in \mathbb{N}_{0}$. Лако се види да су сви чланови низа ( $a_{n}$ ) непарни; остаје да покажемо да ако прост број $p$ дели $a_{n}$, онда је $p=8 k+1$ или $8 k+3$ за неко $k \in \mathbb{N}_{0}$.
Показује се индукцијом по $n$ да је $a_{n} a_{n+2}=a_{n+1}^{2}+2$. Заиста, ово важи за $n \leq 2$, а за $n>2$, уз претпоставку да важи за $n-2$, имамо
$$
\begin{aligned}
\frac{a_{n+1}^{2}+2}{a_{n}} & =\frac{\left(4 a_{n}-a_{n-1}\right)^{2}+2}{a_{n}}=16 a_{n}-8 a_{n-1}+\frac{a_{n-1}^{2}+2}{a_{n}} \\
& =16 a_{n}-8 a_{n-1}+a_{n-2}=4 a_{n+1}-a_{n}=a_{n+2}
\end{aligned}
$$
Одавде следи да је -2 квадратни остатак по сваком простом делиоцу $p$ броја $a_{n}$, па је $p \equiv 1$ или $p \equiv 3(\bmod 8)$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
c6d26159-0226-5e42-a93e-67666d3aa3df
| 608,058
|
Let $ABCDE$ be a convex pentagon in which $AB=1, \angle BAE = \angle ABC = 120^\circ, \angle CDE = 60^\circ$, and $\angle ADB = 30^\circ$. Prove that the area of the pentagon $ABCDE$ is less than $\sqrt{3}$.
(Miloš Milosavljević)
## SOLUTIONS
|
Let $k$ be the circle circumscribed around triangle $ABD$, and $l$ a line through $D$ parallel to $AB$. The radius of circle $k$ is 1. The rays $BC$ and $AE$ intersect $k$ at points $H$ and $I$, and the line $l$ at $F$ and $G$, respectively. Triangles $FCD$ and $GDE$ are similar because $\angle CFD = \angle DGE = 60^\circ$ and $\angle FCD = 120^\circ - \angle CDF = \angle GDE$. Let $k = \frac{FC}{GD} = \frac{FD}{GE}$ be the similarity coefficient, $h$ the distance from point $D$ to $HI$, and $x = FD, y = GD$. It is easy to find that $x + y = 2 + \frac{2}{\sqrt{3}} h$ and $xy = \frac{4}{3} h^2 + \frac{2}{\sqrt{3}} h$ (the product $xy$ is the power of point $F$ with respect to $k$ and equals $OF^2 - 1$, where $O$ is the center of circle $k$). Thus we get
$$
\begin{aligned}
& P_{ABFG} = \frac{1}{2}(1 + x + y)\left(\frac{\sqrt{3}}{2} + h\right) = \frac{1}{\sqrt{3}} h^2 + 2h + \frac{3\sqrt{3}}{4} \\
& P_{FCD} + P_{GDE} = \frac{1}{2}(x \cdot FC + y \cdot GE) \sin 60^\circ = \frac{\sqrt{3}}{4} xy \left(k + \frac{1}{k}\right) \geq \frac{\sqrt{3}}{2} xy = \frac{2}{\sqrt{3}} h^2 + h
\end{aligned}
$$
so we have
$$
P_{ABCDE} = P_{ABFG} - (P_{FCD} + P_{GDE}) \leq -\frac{1}{\sqrt{3}} h^2 + h + \frac{3\sqrt{3}}{4} = f(h)
$$
The quadratic function $f(h)$ reaches its maximum at $h = \frac{\sqrt{3}}{2}$, thus proving that $P_{ABCDE} \leq \sqrt{3}$. Equality would hold only if $h = \frac{\sqrt{3}}{2}$ and $k = 1$; in that case (if without loss of generality we assume $DA \geq DB$), point $D$ would be symmetric to point $B$ with respect to $HI$, making triangle $ADG$ equilateral and $FC = GD = GA = FB$, which is impossible because $B$ and $C$ would coincide. Therefore, the above inequality is strict.
Second solution. Suppose triangle $ABD$ is not obtuse. Then the points $C'$ and $E'$, symmetric to points $C$ and $E$ with respect to lines $BD$ and $AD$, respectively, lie inside triangle $ABD$ on the same line through $D$, and we have
$S_{ABCDE} = S_{ABD} + S_{ADE} + S_{BDC} = S_{ABD} + S_{ADE'} + S_{BDC'} \leq 2 S_{ABD} - S_{ABF}$, where $F$ is the intersection of lines $AE'$ and $BC'$. Equality holds if and only if $F \equiv C' \equiv E'$. Let $\angle BAD = \alpha$. Then $\angle ABD = 150^\circ - \alpha$, $\angle BAF = 2\alpha - 120^\circ$, $\angle ABF = 180^\circ - 2\alpha$, and we have
$$
\begin{aligned}
& S_{ABD} = \sin \alpha \sin (150^\circ - \alpha) = \frac{\sqrt{3}}{4} + \frac{1}{2} \cos (150^\circ - 2\alpha) = \frac{\sqrt{3}}{4} + \frac{1}{2} u \\
& S_{ABF} = \frac{1}{\sqrt{3}} \sin (2\alpha - 120^\circ) \sin 2\alpha = -\frac{\sqrt{3}}{12} + \frac{\sqrt{3}}{6} \cos (300^\circ - 4\alpha) = -\frac{\sqrt{3}}{4} + \frac{1}{\sqrt{3}} u^2
\end{aligned}
$$
where $\cos (150^\circ - 2\alpha) = u$ and hence $\cos (300^\circ - 4\alpha) = 2u^2 - 1$. Now we have
$$
S_{ABCDE} \leq 2 S_{ABD} - S_{ABF} = \frac{3\sqrt{3}}{4} + u - \frac{u^2}{\sqrt{3}} \leq \sqrt{3}
$$
with equality holding for $u = \frac{\sqrt{3}}{2}$, i.e., $\alpha \in \{60^\circ, 90^\circ\}$, and $F \equiv C' \equiv E'$, but this is never achieved because for these values of $\alpha$, point $F$ lies at the vertex of a right angle, making the pentagon degenerate.
In the case of an obtuse triangle $ABD$, with the same notation, point $F$ lies outside triangle $ABD$, but the expression for the area of $\triangle ABF$ takes negative values, so we again get $S_{ABCDE} \leq \frac{3\sqrt{3}}{4} + u - \frac{u^2}{\sqrt{3}} < \sqrt{3}$.
$\sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim)$
http://srb.imomath.com/
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $A B C D E$ конвескан петоугао у коме је $A B=1, \varangle B A E=\varangle A B C=$ $120^{\circ}, \varangle C D E=60^{\circ}$ и $\varangle A D B=30^{\circ}$. Доказати да је површина петоугла $A B C D E$ мања од $\sqrt{3}$.
(Милош Милосављевић)
## РЕШЕЊА
|
Нека је $k$ круг описан око троугла $A B D$, и $l$ права кроз $D$ паралелна са
$A B$. Полупречник круга $k$ је 1 . Полуправе $B C$ и $A E$ секу $k$ у тачкама $H$ и $I$, а праву $l$ у $F$ и $G$, редом. Троуглови $F C D$ и $G D E$ су слични јер је $\angle C F D=\angle D G E=60^{\circ}$ и $\angle F C D=120^{\circ}-\angle C D F=\angle G D E$. Означимо са $k=\frac{F C}{G D}=\frac{F D}{G E}$ коефи-
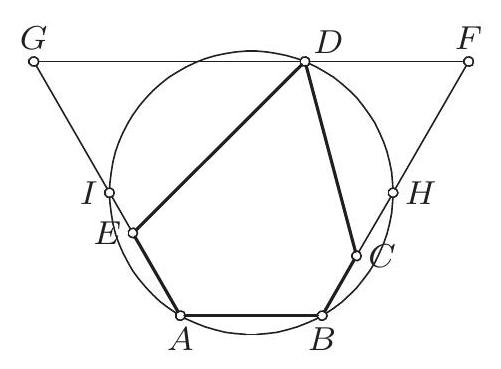
цијент сличности, са $h$ растојање тачке $D$ од $H I$, и $x=F D, y=G D$. Лако се налази да је $x+y=2+\frac{2}{\sqrt{3}} h$ и $x y=\frac{4}{3} h^{2}+\frac{2}{\sqrt{3}} h$ (производ $x y$ је потенција тачке $F$ у односу на $k$ и једнак је $O F^{2}-1$, где је $O$ центар круга $k$ ). Тако добијамо
$$
\begin{aligned}
& P_{A B F G}=\frac{1}{2}(1+x+y)\left(\frac{\sqrt{3}}{2}+h\right)=\frac{1}{\sqrt{3}} h^{2}+2 h+\frac{3 \sqrt{3}}{4} \\
& P_{F C D}+P_{G D E}=\frac{1}{2}(x \cdot F C+y \cdot G E) \sin 60^{\circ}=\frac{\sqrt{3}}{4} x y\left(k+\frac{1}{k}\right) \geq \frac{\sqrt{3}}{2} x y=\frac{2}{\sqrt{3}} h^{2}+h
\end{aligned}
$$
па је
$$
P_{A B C D E}=P_{A B F G}-\left(P_{F C D}+P_{G D E}\right) \leq-\frac{1}{\sqrt{3}} h^{2}+h+\frac{3 \sqrt{3}}{4}=f(h)
$$
Квадратна функција $f(h)$ достиже максимум за $h=\frac{\sqrt{3}}{2}$, чиме је доказано да је $P_{A B C D E} \leq \sqrt{3}$. Једнакост би важила само ако је $h=\frac{\sqrt{3}}{2}$ и $k=$ 1; тада би (ако без смањења општости претпоставимо $D A \geq D B$ ) тачка $D$ била симетрична тачки $B$ у односу на $H I$, па би троугао $A D G$ био једнакостраничан и $F C=G D=G A=F B$ што је немогуће јер би се $B$ и $C$ поклапале. Зато је горња неједнакост строга.
Друго решење. Претпоставимо да троугао $A B D$ није тупоугли. Тада се тачке $C^{\prime}$ и $E^{\prime}$ симетричне тачкама $C$ и $E$ у односу на праве $B D$ и $A D$ редом налазе унутар троугла $A B D$, на истој правој кроз $D$, и важи
$S_{A B C D E}=S_{A B D}+S_{A D E}+S_{B D C}=S_{A B D}+S_{A D E^{\prime}}+S_{B D C^{\prime}} \leq 2 S_{A B D}-S_{A B F}$, при чему $F$ тачка пресека правих $A E^{\prime}$ и $B C^{\prime}$. Једнакост важи ако и само ако је $F \equiv C^{\prime} \equiv E^{\prime}$. Означимо $\angle B A D=\alpha$. Тада је $\angle A B D=150^{\circ}-\alpha$, $\angle B A F=2 \alpha-120^{\circ}, \angle A B F=180^{\circ}-2 \alpha$, па важи
$$
\begin{aligned}
& S_{A B D}=\sin \alpha \sin \left(150^{\circ}-\alpha\right)=\frac{\sqrt{3}}{4}+\frac{1}{2} \cos \left(150^{\circ}-2 \alpha\right)=\frac{\sqrt{3}}{4}+\frac{1}{2} u \\
& S_{A B F}=\frac{1}{\sqrt{3}} \sin \left(2 \alpha-120^{\circ}\right) \sin 2 \alpha=-\frac{\sqrt{3}}{12}+\frac{\sqrt{3}}{6} \cos \left(300^{\circ}-4 \alpha\right)=-\frac{\sqrt{3}}{4}+\frac{1}{\sqrt{3}} u^{2}
\end{aligned}
$$
где је $\cos \left(150^{\circ}-2 \alpha\right)=u$ и одатле $\cos \left(300^{\circ}-4 \alpha\right)=2 u^{2}-1$. Сада имамо
$$
S_{A B C D E} \leq 2 S_{A B D}-S_{A B F}=\frac{3 \sqrt{3}}{4}+u-\frac{u^{2}}{\sqrt{3}} \leq \sqrt{3}
$$
уз једнакост која би важила за $u=\frac{\sqrt{3}}{2}$, тј. $\alpha \in\left\{60^{\circ}, 90^{\circ}\right\}$, и $F \equiv C^{\prime} \equiv E^{\prime}$, али се никада не достиже јер се за ове вредности $\alpha$ тачка $F$ налази у темену правог угла, па је петоугао дегенерисан.
У случају тупоуглог троугла $A B D$, уз исте ознаке, тачка $F$ се налази изван троугла $A B D$, али горњи израз за површину $\triangle A B F$ узима негативне вредности, па се опет добија $S_{A B C D E} \leq \frac{3 \sqrt{3}}{4}+u-\frac{u^{2}}{\sqrt{3}}<\sqrt{3}$.
$\sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim \sim)$
http://srb.imomath.com/
|
{
"resource_path": "Serbia_MO/segmented/sr-2008_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
e19c4049-e771-523a-8f5e-a19e63ad8d51
| 608,059
|
Let $x, y, z$ be positive real numbers such that $x y + y z + z x = x + y + z$. Prove the inequality
$$
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant 1
$$
When does equality hold in the above inequality?
(Marco Radovanović)
|
The Cauchy-Schwarz inequality for the triples \((x, \sqrt{y}, 1)\) and \((1, \sqrt{y}, z)\) gives \(\frac{1}{x^{2}+y+1} \leqslant \frac{1+y+z^{2}}{(x+y+z)^{2}}\). Similarly, \(\frac{1}{y^{2}+z+1} \leqslant \frac{1+z+x^{2}}{(x+y+z)^{2}}\) and \(\frac{1}{z^{2}+x+1} \leqslant \frac{1+x+y^{2}}{(x+y+z)^{2}}\). By adding these inequalities, we get
\[
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant \frac{3+x+y+z+x^{2}+y^{2}+z^{2}}{(x+y+z)^{2}}=S
\]
It remains to prove that \(S \leqslant 1\), which is equivalent to \(3+x+y+z \leqslant 2(x y+y z+z x)=2(x+y+z)\) by the condition of the problem, i.e., \(x+y+z \geqslant 3\). This, however, follows from \(x+y+z=x y+y z+z x \leqslant \frac{(x+y+z)^{2}}{3}\).
Equality holds only for \(x=y=z=1\).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Нека су $x, y, z$ позитивни реални бројеви такви да је $x y+y z+z x=x+y+z$. Доказати неједнакост
$$
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant 1
$$
Када се у претходној неједнакости достиже знак једнакости?
(Марко Радовановић)
|
Коши-Шварцова неједнакост за тројке $(x, \sqrt{y}, 1)$ и $(1, \sqrt{y}, z)$ даје $\frac{1}{x^{2}+y+1} \leqslant$ $\frac{1+y+z^{2}}{(x+y+z)^{2}}$. Аналогно важи $\frac{1}{y^{2}+z+1} \leqslant \frac{1+z+x^{2}}{(x+y+z)^{2}}$ и $\frac{1}{z^{2}+x+1} \leqslant \frac{1+x+y^{2}}{(x+y+z)^{2}}$. Сабиранјем ових неједнакости добијамо
$$
\frac{1}{x^{2}+y+1}+\frac{1}{y^{2}+z+1}+\frac{1}{z^{2}+x+1} \leqslant \frac{3+x+y+z+x^{2}+y^{2}+z^{2}}{(x+y+z)^{2}}=S
$$
Остаје да се докаже да је $S \leqslant 1$, а то је еквивалентно са $3+x+y+z \leqslant$ $2(x y+y z+z x)=2(x+y+z)$ по услову задатка, тј. $x+y+z \geqslant 3$. Ово, међутим, следи из $x+y+z=x y+y z+z x \leqslant \frac{(x+y+z)^{2}}{3}$.
Једнакост важи само за $x=y=z=1$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
0242fc77-a993-5776-b58b-2d7ab6f8799d
| 608,064
|
Let $k$ be the incircle of the scalene $\triangle ABC$, whose center is $S$. The circle $k$ touches the sides $BC, CA, AB$ at points $P, Q, R$, respectively. The line $QR$ intersects the line $BC$ at point $M$. Let the circle containing points $B$ and $C$ be tangent to $k$ at point $N$. The circumcircle of $\triangle MNP$ intersects the line $AP$ at point $L$, different from $P$. Prove that the points $S, L$, and $M$ are collinear.
(Djordje Baralic)
## SOLUTIONS
|
Let's consider the homothety with center $N$ that maps circle $k$ to circle $BCN$; let it map point $P$ to $P_1$. The tangent to circle $BCN$ at $P_1$ is parallel to the tangent to $k$ at $P$, i.e., to line $BC$, which means that $P_1$ is the midpoint of arc $BC$ of circle $BCN$. Therefore, $NP$ is the angle bisector of $\angle CNB$, so $\frac{BN}{CN} = \frac{BP}{CP}$. Furthermore, by Menelaus' theorem, $\frac{BM}{MC} = \frac{BR}{RA} \cdot \frac{AQ}{QC} = \frac{BP}{PC} = \frac{BN}{NC}$, so $NM$ is the external angle bisector of $\angle CNB$.
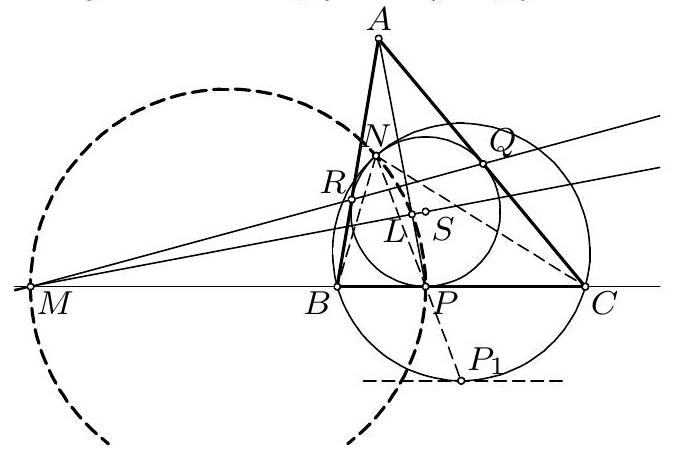
Therefore, $N$ lies on the circle with diameter $MP$, and $L$ is the foot of the perpendicular from $M$ to $AP$. It remains to prove that $MS \perp AP$.
Let $L'$ be the foot of the perpendicular from $S$ to $AP$. Points $A, L', Q, R, S$ lie on the circle $\omega$ with diameter $AS$. The inversion with respect to $k$ maps circles $\omega$ and $SPL'$ to lines $QR$ and $BC$, respectively, and maps point $L'$ to $M$. Therefore, $M$ lies on line $SL'$, from which the statement follows (and $L' \equiv L$).
Note. The relation $MS \perp AP$ is equivalent to $MP^2 + AS^2 = MA^2 + PS^2$ and can be proven without inversion: $MP^2 + AS^2 = MP^2 + PS^2 + AR^2 = MS^2 + AQ^2 = MA^2 + SQ^2$ (since $MQ \perp AS) = MA^2 + PS^2$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $k$ уписана кружница неједнакокраког $\triangle A B C$, чији је центар $S$. Кружница $k$ додирује странице $B C, C A, A B$ у тачкама $P, Q, R$, редом. Права $Q R$ сече праву $B C$ у тачки $M$. Нека кружница која садржи тачке $B$ и $C$ додирује $k$ у тачки $N$. Описана кружница $\triangle M N P$ сече праву $A P$ у тачки $L$, различитој од $P$. Доказати да су тачке $S, L$ и $M$ колинеарне.
(Ђорђе Баралић)
## РЕШЕЊА
|
Посматрајмо хомотетију са центром $N$ која слика круг $k$ у круг $B C N$; нека она слика тачку $P$ у $P_{1}$. Тангента на круг $B C N$ у $P_{1}$ је паралелна тангенти на $k$ у $P$, тј. правој $B C$, што значи да је $P_{1}$ средиште лука $B C$ круга $B C N$. Дакле, $N P$ је симетрала угла $C N B$, па је $\frac{B N}{C N}=\frac{B P}{C P}$. Шта више, по Менелајевој теореми је $\frac{B M}{M C}=\frac{B R}{R A} \cdot \frac{A Q}{Q C}=\frac{B P}{P C}=\frac{B N}{N C}$, па је $N M$ спољна симетрала угла $C N B$.

Према томе, $N$ лежи на кругу над пречником $M P$, а $L$ је подножје нормале из $M$ на $A P$. Остаје да се докаже да је $M S \perp A P$.
Нека је $L^{\prime}$ подножје нормале из $S$ на $A P$. Тачке $A, L^{\prime}, Q, R, S$ леже на кругу $\omega$ над пречником $A S$. Инверзија у односу на $k$ слика кругове $\omega$ и $S P L^{\prime}$ редом у праве $Q R$ и $B C$, па слика тачку $L^{\prime}$ у $M$. Дакле, $M$ лежи на правој $S L^{\prime}$, одакле следи тврђење (и $L^{\prime} \equiv L$ ).
Напомена. Релација $M S \perp A P$ је еквивалентна са $M P^{2}+A S^{2}=M A^{2}+P S^{2}$ и може се доказати без инверзије: $M P^{2}+A S^{2}=M P^{2}+P S^{2}+A R^{2}=$ $M S^{2}+A Q^{2}=M A^{2}+S Q^{2}$ (због $\left.M Q \perp A S\right)=M A^{2}+P S^{2}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2009_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
03c8f233-d6c0-50ab-8ecb-74ce2b0088d5
| 608,065
|
Some of the $n$ cities are connected by air routes (all routes are bidirectional). There are exactly $m$ routes. Let $d_{i}$ be the number of routes departing from city $i$, for $i=1,2, \ldots, n$. If $1 \leqslant d_{i} \leqslant 2010$, for every $i=1,2, \ldots, n$, prove that
$$
\sum_{i=1}^{n} d_{i}^{2} \leqslant 4022 m-2010 n
$$
Determine all $n$ for which equality can be achieved.
(Alexander Ilić)
|
The condition of the task gives $0 \leqslant\left(d_{i}-1\right)\left(2010-d_{i}\right)$ for all $i$, i.e., $d_{i}^{2} \leqslant 2011 d_{i}-2010$. Using the condition $\sum_{i=1}^{n} d_{i}=2 m$, by summing these inequalities we get
$$
\sum_{i=1}^{n} d_{i}^{2} \leqslant 2011 \cdot \sum_{i=1}^{n} d_{i}-2010 n=4022 m-2010 n
$$
and equality holds if and only if $d_{i} \in\{1,2010\}$ for each $i \in\{1,2, \ldots, n\}$.
$1^{\circ}$ Let $n=2 k, k \in \mathbb{N}$. If we establish an airline between cities $i$ and $j$ if and only if $|j-i|=k$, we have $d_{i}=1$ for all $i$.
$2^{\circ}$ Let $n=2 k-1, k \in \mathbb{N}$. It cannot be that $d_{i}=1$ for all $i$ because otherwise it would be $2 m=n=2 k-1$. Therefore, there must be $d_{j}=2010$ for some $j$; hence $n \geqslant 2011$. On the other hand, by establishing an airline between cities 1 and $i(1 \leq i \leq 2010)$ and between cities $2 i$ and $2 i+1$ $(i=1006, \ldots, k)$, we get a network in which $d_{1}=2010$ and $d_{i}=1$ for $2 \leqslant i \leqslant n$.
Therefore, equality can be achieved if $2 \mid n$, or $2 \nmid n$ and $n \geq 2011$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Неки од $n$ градова су повезани авионским линијама (све линије су двосмерне). Постоји тачно $m$ линија. Нека је $d_{i}$ број линија које полазе из града $i$, за $i=1,2, \ldots, n$. Ако је $1 \leqslant d_{i} \leqslant 2010$, за свако $i=1,2, \ldots, n$, доказати да важи
$$
\sum_{i=1}^{n} d_{i}^{2} \leqslant 4022 m-2010 n
$$
Одредити све $n$ за које може да се достигне једнакост.
(Александар Илић)
|
Услов задатка нам даје $0 \leqslant\left(d_{i}-1\right)\left(2010-d_{i}\right)$ за све $i$, тј. $d_{i}^{2} \leqslant 2011 d_{i}-2010$. Користећи услов $\sum_{i=1}^{n} d_{i}=2 m$, сабирањем ових неједнакости добијамо
$$
\sum_{i=1}^{n} d_{i}^{2} \leqslant 2011 \cdot \sum_{i=1}^{n} d_{i}-2010 n=4022 m-2010 n
$$
а једнакост важи ако и само ако је $d_{i} \in\{1,2010\}$ за свако $i \in\{1,2, \ldots, n\}$.
$1^{\circ}$ Нека је $n=2 k, k \in \mathbb{N}$. Ако успоставимо авиолинију између градова $i$ и $j$ ако и само ако је $|j-i|=k$, имамо $d_{i}=1$ за све $i$.
$2^{\circ}$ Нека је $n=2 k-1, k \in \mathbb{N}$. Не може да важи $d_{i}=1$ за све $i$ јер би иначе било $2 m=n=2 k-1$. Зато мора да буде $d_{j}=2010$ за неко $j$; отуда је $n \geqslant 2011$. С друге стране, успостављањем авиолиније између градова 1 и $i(1 \leq i \leq 2010)$ и између градова $2 i$ и $2 i+1$ $(i=1006, \ldots, k)$ даје мрежу у којој је $d_{1}=2010$ и $d_{i}=1$ за $2 \leqslant i \leqslant n$.
Према томе, једнакост се може достићи ако $2 \mid n$, или $2 \nmid n$ и $n \geq 2011$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
5527c807-5b20-59c1-ac13-7f09c8b3945e
| 608,066
|
In the acute-angled $\triangle ABC$, point $M$ is the midpoint of side $BC$, and points $D, E$, and $F$ are the feet of the altitudes from vertices $A, B$, and $C$, respectively. Let $H$ be the orthocenter of $\triangle ABC$, $S$ the midpoint of segment $AH$, and $G$ the intersection of segment $FE$ and $AH$. If $N$ is the point of intersection of the median $AM$ and the circumcircle of $\triangle B C H$, prove that $\varangle H M A=\varangle G N S$.
(Marco Đikić)
|
Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram. Then $\varangle B A^{\prime} C = \varangle B A C = 180^{\circ} - \varangle B H C = 180^{\circ} - \varangle B N C$, so the points $A^{\prime}, B, C, H, N$ lie on the same circle, i.e., the circle with diameter $H A^{\prime}$. From this, $\varangle A N H = 90^{\circ}$, hence $N$ lies on the circumcircle of triangle $A E F$ whose center is at $S$.
Now we have $\varangle S F G = 90^{\circ} - \varangle E A F = \varangle A C F = \varangle A D F$. It follows that triangles $S F G$ and $S D F$ are similar, and from there $S G \cdot S D = S F^{2} = S N^{2}$. This implies that $\triangle S N G \sim \triangle S D N$, and finally $\varangle G N S = \varangle S D N = \varangle H M N$ since quadrilateral $H D M N$ is cyclic.
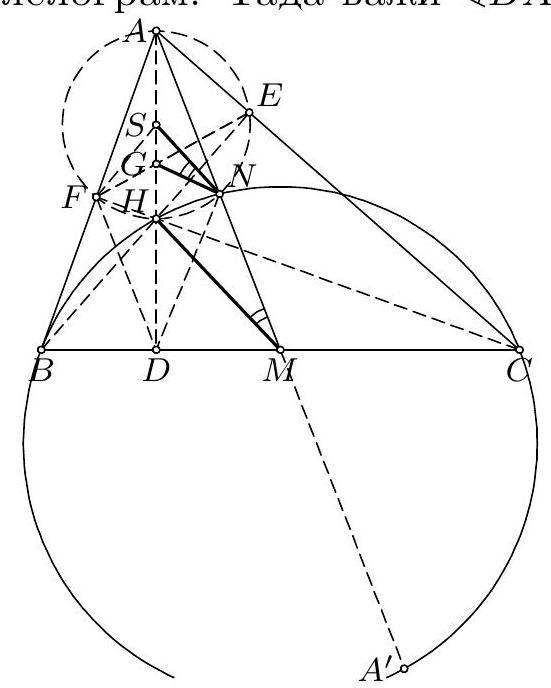
Second solution. Quadrilaterals $B D H F$ and $D C E H$ are cyclic and $A F \cdot A B = \overline{A H \cdot A D = A E} \cdot A C$. Apply the inversion $\mathcal{I}$ with center $A$ and power $A F \cdot A B$. Clearly, $\mathcal{I}(F) = B, \mathcal{I}(H) = D, \mathcal{I}(E) = C$, so $\mathcal{I}$ maps line $B C$ to the circumcircle of $\triangle F H E$, i.e., the circle with diameter $A H$; further, $\mathcal{I}$ maps the circle $B C H$ to the circumcircle $\omega$ of triangle $F D E$, which is the Euler circle of $\triangle A B C$. Since $M \in \omega \cap A M$ and $\mathcal{I}$ preserves line $A M$, we have $\mathcal{I}(M) = N$.
Let $\mathcal{I}(G) = G^{*}$ and $\mathcal{I}(S) = S^{*}$. Since $\mathcal{I}(E F)$ is the circumcircle of $\triangle A B C, S \in \omega$ and $\mathcal{I}(A H) = A H$, points $G^{*}$ and $S^{*}$ are the second intersections of line $A H$ with the circumcircles of $\triangle A B C$ and $\triangle H B C$, respectively. Therefore, $\varangle G N S = \varangle G^{*} M S^{*} = \varangle H M A$ since $G^{*}$ and $S^{*}$ are symmetric to points $H$ and $A$ with respect to $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
У оштроуглом $\triangle A B C$ тачка $M$ је средиште странице $B C$, а тачке $D, E$ и $F$ су подножја висина из темена $A, B$ и $C$, редом. Нека је $H$ ортоцентар $\triangle A B C, S$ средиште дужи $A H$, а $G$ пресек дужи $F E$ и $A H$. Ако је $N$ тачка пресека тежишне дужи $A M$ и описане кружнице $\triangle B C H$, доказати да је $\varangle H M A=\varangle G N S$.
(Марко Ђикић)
|
Нека је $A^{\prime}$ тачка таква да је $A B A^{\prime} C$ паралелограм. Тада важи $\varangle B A^{\prime} C=$ $\varangle B A C=180^{\circ}-\varangle B H C=180^{\circ}-$ $\varangle B N C$, па су тачке $A^{\prime}, B, C, H, N$ на истом кругу, тј. кругу над пречником $H A^{\prime}$. Одавде је $\varangle A N H=90^{\circ}$, дакле $N$ је на описаном кругу троугла $A E F$ чији је центар у $S$.
Сада имамо $\varangle S F G=90^{\circ}-\varangle E A F=$ $\varangle A C F=\varangle A D F$. Следи да су троуглови $S F G$ и $S D F$ слични, и одатле $S G \cdot S D=S F^{2}=S N^{2}$. Ово повлачи да је и $\triangle S N G \sim \triangle S D N$, и најзад $\varangle G N S=\varangle S D N=\varangle H M N$ јер је четвороугао $H D M N$ тетиван.

Друго решење. Четвороуглови $B D H F$ и $D C E H$ су тетивни и $A F \cdot A B=$ $\overline{A H \cdot A D=A E} \cdot A C$. Применимо инверзију $\mathcal{I}$ са центром $A$ и потенцијом $A F \cdot A B$. Очигледно је $\mathcal{I}(F)=B, \mathcal{I}(H)=D, \mathcal{I}(E)=C$, па $\mathcal{I}$ слика праву $B C$ у описани круг $\triangle F H E$, тј. у круг над пречником $A H$; даље, $\mathcal{I}$ слика круг $B C H$ у описани круг $\omega$ троугла $F D E$, а то је Ојлеров круг у $\triangle A B C$. Пошто је $M \in \omega \cap A M$ и $\mathcal{I}$ чува праву $A M$, имамо $\mathcal{I}(M)=N$.
Нека је $\mathcal{I}(G)=G^{*}$ и $\mathcal{I}(S)=S^{*}$. Како је $\mathcal{I}(E F)$ описани круг $\triangle A B C, S \in \omega$ и $\mathcal{I}(A H)=A H$, тачке $G^{*}$ и $S^{*}$ су други пресеци праве $A H$ са круговима $A B C$ и $H B C$, редом. Према томе, $\varangle G N S=\varangle G^{*} M S^{*}=\varangle H M A$ јер су $G^{*}$ и $S^{*}$ симетричне тачкама $H$ и $A$ у односу на $B C$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
d4fd2398-0196-5fc9-8796-a7c5c3789b6a
| 608,067
|
Let $O$ be the center of the circumcircle of $\triangle ABC$. A line through $O$ intersects sides $CA$ and $CB$ at points $D$ and $E$, respectively, and the circumcircle of $\triangle ABO$ at point $P$ inside the triangle (different from $O$). Point $Q$ on side $AB$ is such that $\frac{AQ}{QB} = \frac{DP}{PE}$. Prove that $\angle APQ = 2 \cdot \angle CAP$. (Dušan Đukić)
|
Let $X$ be a point on the ray $A P$ such that $E X \| A C$. By Thales' theorem, $A P: P X = D P: P E = A Q: Q B$, from which it follows that $B X \| Q P$.
The line $P E$ is the external angle bisector of $\angle A P B$ and bisects the angle $\angle B P X$. Also, since $\angle B E X = 180 - \angle A C B$ and $\angle B P X = 180^{\circ} - \angle A P B = 180^{\circ} - 2 \angle A C B$, we get $\angle B E X = 90^{\circ} + \frac{1}{2} \angle B P X$. It follows that $E$ is the incenter of triangle $B P X$ and from there $\angle A P Q = \angle P X B = 2 \angle P X E = 2 \angle C A P$.
Second solution. The construction in the problem is possible only if $\triangle A B C$ is acute. Let $\angle P A D = \varphi, \angle Q P A = \psi$, and $\angle B C A = \gamma$. From $\angle A P B = 2 \gamma$ and $\angle D A P + \angle E B P = \angle A P B - \angle A C B = \gamma$ it follows that $\angle P B E = \gamma - \varphi$ and $\angle B P Q = 2 \gamma - \psi$. Since $\angle A P D = \angle B P E = 90^{\circ} - \gamma$, we also have $\angle A D P = 90^{\circ} + \gamma - \varphi$ and $\angle B E P = 90^{\circ} + \varphi$.
The sine theorems in triangles $A P D$ and $P B E$ give $\frac{D P}{P E} = \frac{D P}{P A} \cdot \frac{P A}{P B} \cdot \frac{P B}{P E} = \frac{\sin \varphi \cos \varphi}{\sin (\gamma - \varphi) \cos (\gamma - \varphi)} \cdot \frac{P A}{P B} = \frac{\sin 2 \varphi}{\sin (2 \gamma - 2 \varphi)} \cdot \frac{P A}{P B}$. On the other hand, $\frac{A Q}{Q B} = \frac{A Q}{A P} \cdot \frac{A P}{B P} \cdot \frac{B P}{Q B} = \frac{\sin \psi}{\sin (2 \gamma - \psi)} \cdot \frac{A P}{P B}$, so the condition $\frac{A Q}{Q B} = \frac{D P}{P E}$ reduces to $f(2 \varphi) = f(\psi)$, where $f(x) = \frac{\sin (2 \gamma - x)}{\sin x} = \sin 2 \gamma \operatorname{ctg} x - \cos 2 \gamma$. Clearly, $f$ is a strictly decreasing function on $(0, \pi)$, so it must be $\psi = 2 \varphi$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $O$ центар описане кружнице $\triangle A B C$. Права кроз $O$ сече странице $C A$ и $C B$ у тачкама $D$ и $E$, редом, и описану кружницу $\triangle A B O$ у тачки $P$ унутар троугла (различитој од $O$ ). Тачка $Q$ на страници $A B$ је таква да је $\frac{A Q}{Q B}=\frac{D P}{P E}$. Доказати да је $\varangle A P Q=2 \cdot \varangle C A P$. (Душан Ђукић)
|
Нека је $X$ тачка на полуправој $A P$ таква да је $E X \| A C$. По Талесовој теореми је $A P: P X=D P: P E=$ $A Q: Q B$, одакле следи $B X \| Q P$.
Права $P E$ је спољашња симетрала угла $A P B$ и полови угао $B P X$. Такође, пошто је $\varangle B E X=180-$ $\varangle A C B$ и $\varangle B P X=180^{\circ}-\varangle A P B=$ $180^{\circ}-2 \varangle A C B$, добијамо $\varangle B E X=$
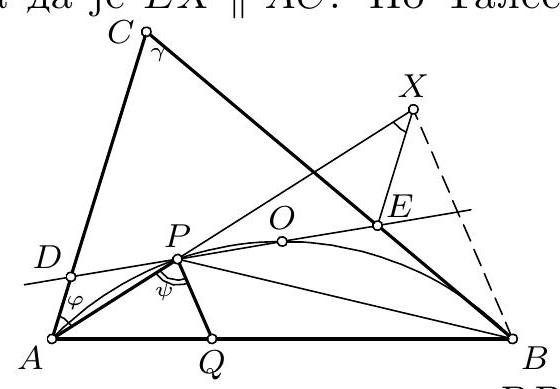
$90^{\circ}+\frac{1}{2} \varangle B P X$. Следи да је $E$ центар уписаног круга троугла $B P X$ и одатле $\varangle A P Q=\varangle P X B=2 \varangle P X E=2 \varangle C A P$.
Друго решеъе. Конструкција из задатка је могућа само ако је $\triangle A B C$ оштроугли. Означимо $\varangle P A D=\varphi, \varangle Q P A=\psi$ и $\varangle B C A=\gamma$. Из $\varangle A P B=2 \gamma$ и $\varangle D A P+\varangle E B P=\varangle A P B-\varangle A C B=\gamma$ следи $\varangle P B E=\gamma-\varphi$ и $\varangle B P Q=2 \gamma-\psi$. Како је $\varangle A P D=\varangle B P E=90^{\circ}-\gamma$, такође имамо $\varangle A D P=90^{\circ}+\gamma-\varphi$ и $\varangle B E P=90^{\circ}+\varphi$.
Синусне теореме у троугловима $A P D$ и $P B E$ дају $\frac{D P}{P E}=\frac{D P}{P A} \cdot \frac{P A}{P B} \cdot \frac{P B}{P E}=$ $\frac{\sin \varphi \cos \varphi}{\sin (\gamma-\varphi) \cos (\gamma-\varphi)} \cdot \frac{P A}{P B}=\frac{\sin 2 \varphi}{\sin (2 \gamma-2 \varphi)} \cdot \frac{P A}{P B}$. С друге стране, $\frac{A Q}{Q B}=\frac{A Q}{A P} \cdot \frac{A P}{B P} \cdot \frac{B P}{Q B}=$ $\frac{\sin \psi}{\sin (2 \gamma-\psi)} \cdot \frac{A P}{P B}$, па се услов $\frac{A Q}{Q B}=\frac{D P}{P E}$ своди на $f(2 \varphi)=f(\psi)$, где је $f(x)=$ $\frac{\sin (2 \gamma-x)}{\sin x}=\sin 2 \gamma \operatorname{ctg} x-\cos 2 \gamma$. Јасно је да је $f$ строго опадајућа функција на $(0, \pi)$, па мора бити $\psi=2 \varphi$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
49b17f93-b60a-5177-ba5c-c19824519737
| 608,069
|
Let $a_{0}$ and $a_{n}$ be distinct divisors of a natural number $m>1$, and the sequence of natural numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ satisfies
$$
a_{i+1}=\left|a_{i} \pm a_{i-1}\right| \quad \text { for } 0<i<n
$$
If the GCD $\left(a_{0}, \ldots, a_{n}\right)=1$, prove that there is a term in the sequence that is less than $\sqrt{m}$.
(Dushan Dukic)
## SOLUTIONS
|
Let's consider the two smallest (distinct) members of the sequence, $p$ and $q$. If $\min \{p, q\} = 1$, the statement trivially holds; hence, we assume $p, q > 1$.
Lemma 1. There exist indices $k$ and $l$ such that $a_{k} = p$, $a_{l} = q$, and $|k - l| \leq 2$.
Proof. Let $a_{k} = p$ and $a_{l} = q$ ($k < l$). Assume $r = l - k > 2$. We will prove by induction on $r$ that for some $i$, $k < i < l$, $a_{i} \in \{p, q\}$. Since $a_{k+3} \neq |a_{k+2} - a_{k+1}| = p$, we have $a_{k+3} = a_{k+1} + a_{k+2}$; similarly, $a_{l-3} = a_{l-2} + a_{l-1}$. Let $a_{m} = \max_{p < i < q} a_{i}$. Clearly, $k + 2 < m < l - 2$ (i.e., $l - k \geq 6$), and $a_{m+2} = a_{m} - a_{m+1} = a_{m-1}$ and $a_{m+1} = a_{m} - a_{m-1} = a_{m-2}$. This means that the sequence $(a_{i}')$, defined by $a_{i}' = a_{i}$ for $i < m$ and $a_{i}' = a_{i+3}$ for $i \geq m$, satisfies the conditions of the problem; moreover, $a_{k}' = p$ and $a_{l-3}' = q$, so by the inductive hypothesis (since $(l-3) - k \geq 3$), $a_{i}' \in \{p, q\}$ for some $i$ ($k < i < l-3$). Then $a_{i} \in \{p, q\}$ or $a_{i+3} \in \{p, q\}$, completing the induction.
Lemma 2. For every $i$ ($0 \leq i \leq n$), there exist $x_{i}, y_{i} \in \mathbb{N}_{0}$ such that $a_{i} = x_{i} p + y_{i} q$ and $(x_{i}, y_{i}) = 1$.
Proof. Consider the vectors $v_{k} = (1, 0)$ and $v_{l} = (0, 1)$ and, for every $i$, define $v_{i+2} = \varepsilon_{i} v_{i} + \varepsilon_{i}' v_{i+1}$ if $a_{i+2} = \varepsilon_{i} a_{i} + \varepsilon_{i}' a_{i+1}$ ($\varepsilon_{i}, \varepsilon_{i}' \in \{-1, 1\}$). By simple induction, we obtain that for $v_{i} = (x_{i}, y_{i})$,
$$
a_{i} = x_{i} p + y_{i} q
$$
Since $x_{i+1} y_{i+2} - x_{i+2} y_{i+1} = x_{i+1} (\varepsilon_{i} y_{i} + \varepsilon_{i}' y_{i+1}) - (\varepsilon_{i} x_{i} + \varepsilon_{i}' x_{i+1}) y_{i+1} = -\varepsilon_{i} (x_{i} y_{i+1} - x_{i+1} y_{i})$ and similarly $x_{i} y_{i+2} - x_{i+2} y_{i} = \varepsilon_{i}' (x_{i} y_{i+1} - x_{i+1} y_{i})$, we have
$$
x_{i} y_{i+1} - x_{i+1} y_{i}, x_{i} y_{i+2} - x_{i+2} y_{i} \in \{-1, 1\} \text{ for } 0 \leq i < n
$$
and from this, $(x_{i}, y_{i}) = 1$. It remains to show that $x_{i}, y_{i} \geq 0$ for all $i$.
Assume $x_{i} < 0$ for some $i < k$ (the case $y_{i} < 0$ and/or $i > l$ is analogous) and consider the largest such $i$. Since $a_{i} > 0$ and (1), we have $y_{i} > 0$. From (2) and $x_{i} y_{i+1}, x_{i} y_{i+2} \leq 0 \leq x_{i+1} y_{i}, x_{i+2} y_{i}$, it follows that $v_{i+1}$, $v_{i+2} \in \{(0, 1), (1, 0)\}$, and then $v_{i} = \pm (1, -1)$, i.e., $a_{i} = |p - q|$. However, since $p$ and $q$ are coprime and greater than 1, $\max \{p, q\} > |p - q| \notin \{p, q\}$, contradicting the choice of $p$ and $q$.
Let $m = d a_{0} = e a_{n}$. By Lemma 2, $m = d x_{0} p + d y_{0} q = e x_{n} p + e y_{n} q$, where $(d x_{0}, d y_{0}) \neq (e x_{n}, e y_{n})$ because $a_{0} \neq a_{n}$ implies $\frac{x_{0}}{y_{0}} \neq \frac{x_{n}}{y_{n}}$. From this, it follows that $p \mid d y_{0} - e y_{n}$, so $d y_{0} > p$ or $e y_{n} > p$; hence, $m > p q$ and therefore $\min (p, q) < \sqrt{m}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека су $a_{0}$ и $a_{n}$ различити делиоци природног броја $m>1$, а низ природних бројева $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ такав да задовољава
$$
a_{i+1}=\left|a_{i} \pm a_{i-1}\right| \quad \text { за } 0<i<n
$$
Ако је НЗД $\left(a_{0}, \ldots, a_{n}\right)=1$, доказати да у низу постоји члан који је мањи од $\sqrt{m}$.
(Душан Ђукић)
## РЕШЕЊА
|
Посматрајмо два најмања (различита) члана низа, $p$ и $q$. Ако је $\min \{p, q\}=$ 1, тврђење тривијално важи; зато надаље претпостављамо да је $p, q>1$.
Лема 1. Постоје индекси $k$ и $l$ за које је $a_{k}=p, a_{l}=q$ и $|k-l| \leq 2$.
Доказ. Нека је $a_{k}=p$ и $a_{l}=q(k<l)$. Претпоставимо да је $r=l-k>2$. Доказаћемо индукцијом по $r$ да за неко $i, k<i<l$, важи $a_{i} \in\{p, q\}$. Како је $a_{k+3} \neq\left|a_{k+2}-a_{k+1}\right|=p$, имамо $a_{k+3}=a_{k+1}+a_{k+2}$; слично је и $a_{l-3}=a_{l-2}+a_{l-1}$. Нека је $a_{m}=\max _{p<i<q} a_{i}$. Јасно је да је $k+2<m<l-2$ (дакле, $l-k \geqslant 6$ ), а такође и $a_{m+2}=a_{m}-a_{m+1}=a_{m-1}$ и $a_{m+1}=a_{m}-a_{m-1}=a_{m-2}$. То значи да низ $\left(a_{i}^{\prime}\right)$, дефинисан са $a_{i}^{\prime}=a_{i}$ за $i<m$ и $a_{i}^{\prime}=a_{i+3}$ за $i \geqslant m$, задовољава услове задатка; притом је $a_{k}^{\prime}=p$ и $a_{l-3}^{\prime}=q$, па по индуктивној претпоставци (јер је $(l-3)-k \geqslant 3$ ) важи $a_{i}^{\prime} \in\{p, q\}$ за неко $i(k<i<l-3)$. Тада је и $a_{i} \in\{p, q\}$ или $a_{i+3} \in\{p, q\}$, чиме је индукција готова.
Лема 2. За свако $i(0 \leqslant i \leqslant n)$ постоје $x_{i}, y_{i} \in \mathbb{N}_{0}$ такви да је $a_{i}=x_{i} p+y_{i} q$ и $\left(x_{i}, y_{i}\right)=1$.
Доказ. Посматрајмо векторе $v_{k}=(1,0)$ и $v_{l}=(0,1)$ и, за свако $i$, дефинишимо $v_{i+2}=\varepsilon_{i} v_{i}+\varepsilon_{i}^{\prime} v_{i+1}$ ако је $a_{i+2}=\varepsilon_{i} a_{i}+\varepsilon_{i}^{\prime} a_{i+1}\left(\varepsilon_{i}, \varepsilon_{i}^{\prime} \in\{-1,1\}\right)$. Једноставном индукцијом добијамо да за $v_{i}=\left(x_{i}, y_{i}\right)$ важи
$$
a_{i}=x_{i} p+y_{i} q
$$
Како је $x_{i+1} y_{i+2}-x_{i+2} y_{i+1}=x_{i+1}\left(\varepsilon_{i} y_{i}+\varepsilon_{i}^{\prime} y_{i+1}\right)-\left(\varepsilon_{i} x_{i}+\varepsilon_{i}^{\prime} x_{i+1}\right) y_{i+1}=$ $-\varepsilon_{i}\left(x_{i} y_{i+1}-x_{i+1} y_{i}\right)$ и слично $x_{i} y_{i+2}-x_{i+2} y_{i}=\varepsilon_{i}^{\prime}\left(x_{i} y_{i+1}-x_{i+1} y_{i}\right)$, имамо
$$
x_{i} y_{i+1}-x_{i+1} y_{i}, x_{i} y_{i+2}-x_{i+2} y_{i} \in\{-1,1\} \text { за } 0 \leqslant i<n
$$
и одатле $\left(x_{i}, y_{i}\right)=1$. Остаје још да покажемо да су $x_{i}, y_{i} \geqslant 0$ за све $i$.
Претпоставимо да је $x_{i}<0$ за неко $i<k$ (случај $y_{i}<0$ и/или $i>l$ је аналоган) и посматрајмо највеће такво $i$. Због $a_{i}>0$ и (1) имамо $y_{i}>0$. Из (2) и $x_{i} y_{i+1}, x_{i} y_{i+2} \leqslant 0 \leqslant x_{i+1} y_{i}, x_{i+2} y_{i}$ следи да су $v_{i+1}$, $v_{i+2} \in\{(0,1),(1,0)\}$, а тада мора бити $v_{i}= \pm(1,-1)$, тј. $a_{i}=|p-q|$. Међутим, како су $p$ и $q$ узајамно прости и већи од 1 , важи $\max \{p, q\}>$ $|p-q| \notin\{p, q\}$, противно избору $p$ и $q$.
Нека је $m=d a_{0}=e a_{n}$. По леми 2 је $m=d x_{0} p+d y_{0} q=e x_{n} p+e y_{n} q$, при чему је $\left(d x_{0}, d y_{0}\right) \neq\left(e x_{n}, e y_{n}\right)$ јер због $a_{0} \neq a_{n}$ важи $\frac{x_{0}}{y_{0}} \neq \frac{x_{n}}{y_{n}}$. Одатле следи да $p \mid d y_{0}-e y_{n}$, па је $d y_{0}>p$ или $e y_{n}>p$; коначно, $m>p q$ и према томе $\min (p, q)<\sqrt{m}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2010_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
3a1a126c-8ac2-5305-8647-8a1f06bc120a
| 608,071
|
Let $n$ be an odd natural number such that the numbers $\varphi(n)$ and $\varphi(n+1)$ are powers of two ( $\varphi(n)$ is the number of natural numbers not greater than $n$ and coprime with $n$ ). Prove that $n+1$ is a power of two or $n=5$.
(Marco Radovanović)
|
If $n=\prod_{i=1}^{k} p_{i}^{r_{k}}$ is the canonical factorization of $n$, then $\varphi(n)=\prod_{i=1}^{k} p_{i}^{r_{k}-1}\left(p_{i}-1\right)$. Since $n$ has no other prime factors except for two, it must be $a_{i}=1$ and $p_{i}-1=2^{b_{i}}$ for each $i$ and some $b_{i}$. Since $2^{b_{i}}+1$ can only be prime if $b_{i}$ is a power of two, we have $p_{i}=2^{2^{c_{i}}}+1$ for some distinct $c_{i}$.
Assume that $n+1$ is not a power of two. From the fact that $\varphi(n+1)$ is a power of two, we get that all odd prime divisors of $n+1$ are of the form $2^{2^{d_{i}}}+1$. Therefore,
$$
n=\prod_{i=1}^{k}\left(2^{2^{c_{i}}}+1\right), \quad n+1=2^{t} \prod_{j=1}^{l}\left(2^{2^{d_{j}}}+1\right)
$$
where all $c_{i}$ and $d_{j}$ are mutually distinct. We can assume without loss of generality that $c_{1}<\cdots<c_{k}$ and $d_{1}<\cdots<d_{l}$.
For any $m, M \in \mathbb{N}, m \leq M$, a simple induction shows that
$$
\frac{2^{2^{m}}+1}{2^{2^{m}}}<\prod_{i=m}^{M} \frac{2^{2^{i}}+1}{2^{2^{i}}}=\frac{2^{2^{m}}}{2^{2^{m}}-1} \cdot \frac{2^{2^{M+1}}-1}{2^{2^{M+1}}}<\frac{2^{2^{m}}}{2^{2^{m}}-1}
$$
From this, we get
$$
\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}} 2^{c} \leqslant n<\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c} \quad \text { and } \quad \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{d} \leqslant n+1<\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1} 2^{d}
$$
where $c=\sum_{i} 2^{c_{i}}$ and $d=t+\sum_{j} 2^{d_{i}}$. It follows that $c=d$. If $d_{1}>c_{1}$, then $\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1}<\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}}$, so $n+1<n$, a contradiction. Therefore, $d_{1}<c_{1}$, and then $n+1 \geqslant \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{c}>\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c}>n$, so $\frac{n+1}{n}>\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} \cdot \frac{2^{2^{c_{1}}}-1}{2^{2^{c_{1}}}}$ and, because $n \geqslant 2^{2^{c_{1}}}+1 \geqslant a^{2}+1$ for $2^{2^{d_{1}}}=a, \frac{n+1}{n}>\frac{(a+1)\left(a^{2}-1\right)}{a^{3}}=1+\frac{a^{2}-a-1}{a^{3}}$, from which we conclude $a^{2}+1 \leqslant n<\frac{a^{3}}{a^{2}-a-1}$. The only possibility is $a=2$ and $n=5$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је $n$ непаран природан број такав да су бројеви $\varphi(n)$ и $\varphi(n+1)$ степени броја два ( $\varphi(n)$ је број природних бројева не већих од $n$ и узајамно простих са $n$ ). Доказати да је $n+1$ степен броја два или је $n=5$.
(Марко Радовановић)
|
Ако је $n=\prod_{i=1}^{k} p_{i}^{r_{k}}$ канонска факторизација $n$, важи $\varphi(n)=\prod_{i=1}^{k} p_{i}^{r_{k}-1}\left(p_{i}-\right.$ 1), па пошто $n$ нема других простих чинилаца осим двојке, мора бити $a_{i}=1$ и $p_{i}-1=2^{b_{i}}$ за свако $i$ и неке $b_{i}$. Како $2^{b_{i}}+1$ може бити прост само ако је $b_{i}$ степен двојке, имамо $p_{i}=2^{2^{c_{i}}}+1$ за неке различите $c_{i}$.
Претпоставимо да $n+1$ није степен двојке. Из чињенице да је $\varphi(n+1)$ степен двојке добијамо да су сви непарни прости делиоци броја $n+1$ облика $2^{2^{d_{i}}}+1$. Према томе,
$$
n=\prod_{i=1}^{k}\left(2^{2^{c_{i}}}+1\right), \quad n+1=2^{t} \prod_{j=1}^{l}\left(2^{2^{d_{j}}}+1\right)
$$
при чему су сви $c_{i}$ и $d_{j}$ међусобно различити. Можемо узети без смањења општости да је $c_{1}<\cdots<c_{k}$ и $d_{1}<\cdots<d_{l}$.
За свако $m, M \in \mathbb{N}, m \leq M$, једноставном индукцијом се показује да важи
$$
\frac{2^{2^{m}}+1}{2^{2^{m}}}<\prod_{i=m}^{M} \frac{2^{2^{i}}+1}{2^{2^{i}}}=\frac{2^{2^{m}}}{2^{2^{m}}-1} \cdot \frac{2^{2^{M+1}}-1}{2^{2^{M+1}}}<\frac{2^{2^{m}}}{2^{2^{m}}-1}
$$
Одавде добијамо
$$
\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}} 2^{c} \leqslant n<\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c} \quad \text { и } \quad \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{d} \leqslant n+1<\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1} 2^{d}
$$
где је $c=\sum_{i} 2^{c_{i}}$ и $d=t+\sum_{j} 2^{d_{i}}$. Следи да је $c=d$. Ако је $d_{1}>c_{1}$, важи $\frac{2^{2^{d_{1}}}}{2^{2^{d_{1}}}-1}<\frac{2^{2^{c_{1}}}+1}{2^{2^{c_{1}}}}$, па је $n+1<n$, контрадикција. Према томе, $d_{1}<c_{1}$, а тада је $n+1 \geqslant \frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} 2^{c}>\frac{2^{2^{c_{1}}}}{2^{2^{c_{1}}}-1} 2^{c}>n$, па је $\frac{n+1}{n}>\frac{2^{2^{d_{1}}}+1}{2^{2^{d_{1}}}} \cdot \frac{2^{2^{c_{1}}}-1}{2^{2^{c_{1}}}}$ и, због $n \geqslant 2^{2^{c_{1}}}+1 \geqslant a^{2}+1$ за $2^{2^{d_{1}}}=a, \frac{n+1}{n}>\frac{(a+1)\left(a^{2}-1\right)}{a^{3}}=1+\frac{a^{2}-a-1}{a^{3}}$, одакле закључујемо $a^{2}+1 \leqslant n<\frac{a^{3}}{a^{2}-a-1}$. Једина могућност је $a=2$ и $n=5$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
538d9e84-d20e-5751-a1bf-efa61956c25e
| 608,073
|
Let $H$ be the orthocenter, and $O$ the center of the circumcircle of an acute-angled triangle $ABC$. Points $D$ and $E$ are the feet of the altitudes from $A$ and $B$, respectively. Let $K$ be the intersection point of the lines $OD$ and $BE$, and $L$ the intersection point of the lines $OE$ and $AD$. Let $X$ be the second intersection point of the circumcircles of triangles $HKD$ and $HLE$, and $M$ the midpoint of side $AB$. Prove that points $K$, $L$, and $M$ are collinear if and only if $X$ is the center of the circumcircle of triangle $EOD$.
(Marco Đikić)
# SERBIAN MATHEMATICAL OLYMPIAD
competition of high school students in mathematics
Belgrade, 03.04.2011.
## Second day
|
If $X$ is the center of the circumcircle of $\triangle ODE$, then $90^{\circ}-\angle KDE=90^{\circ}-\angle ODE=\angle XEO=\angle XEL=\angle XHD=\angle XKD$ (all angles are oriented), from which it follows that $XK \perp DE$; similarly $XL \perp DE$, i.e., $K$ and $L$ lie on the perpendicular bisector of segment $DE$, so $DEHO$ is an isosceles trapezoid, hence $D, E, O, H$ lie on a circle.
On the other hand, if $O$ lies on the circle $HDE$, i.e., on the circle with diameter $CH$, the peripheral angles over $EH$ and $OD$ are equal ($\angle ECH = \angle OCD$), so $DEHO$ is an isosceles trapezoid and from this $DL = EL$. Now we have $\angle EXH = \angle ELH = 2 \angle EDH$
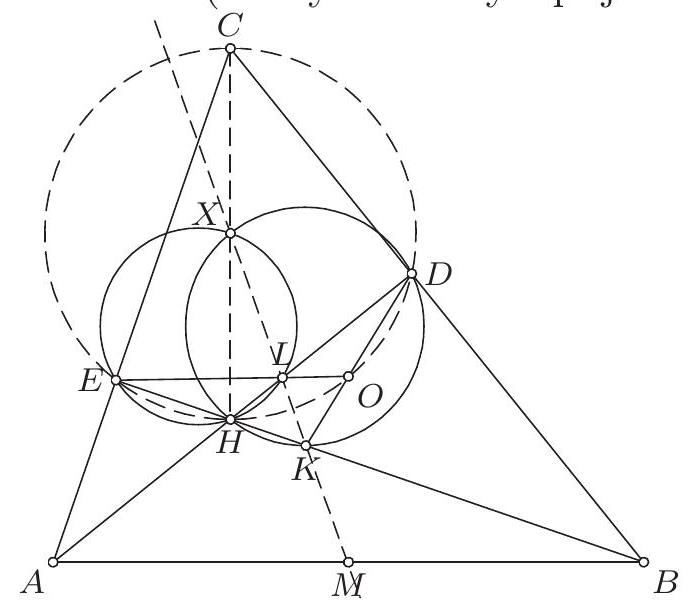
and similarly $\angle DXH = 2 \angle DEH$, so it follows that $X$ is the center of the circle $DEOH$. Therefore, $X$ is the center of the circle $ODE$ if and only if $D, E, O$, and $H$ lie on a circle.
If the points $D, E, O, H$ are on a circle, then $K, L$, and $M$ lie on the perpendicular bisector of segment $DE$, which proves one direction of the problem. Suppose now that $O$ lies outside the circle $CDHE$ (the case when $O$ is inside the circle is considered similarly). Since $CO \perp DE$, we have $DL > LE$ and $EK > KD$, i.e., $K$ and $L$ lie on opposite sides of the perpendicular bisector of segment $DE$, and $M$ lies on this bisector. Therefore, if $K, L$, and $M$ are collinear, $M$ must lie between $K$ and $L$. It follows that one of the points $K$ and $L$ is outside the triangle $ABC$, and the other is inside the triangle. However, when $O$ is outside the quadrilateral $ABDE$, both points $K$ and $L$ are outside the triangle, and otherwise, both are inside the triangle. This is a contradiction with the assumption that $M$ lies on the line $KL$, which proves the other direction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $H$ ортоцентар, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Тачке $D$ и $E$ су подножја висина из $A$ и $B$, редом. Обележимо са $K$ пресечну тачку правих $O D$ и $B E$, а са $L$ пресечну тачку правих $O E$ и $A D$. Нека је $X$ друга пресечна тачка кружница описаних око троуглова $H K D$ и $H L E$, а $M$ средиште странице $A B$. Доказати да су тачке $K, L$ и $M$ колинеарне ако и само ако је $X$ центар описане кружнице троугла $E O D$.
(Марко Ђикић)
# СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА
такмичење ученика средњих школа из математике
Београд, 03.04.2011.
## Други дан
|
Ако је $X$ центар описаног круга $\triangle O D E$, онда је $90^{\circ}-\angle K D E=90^{\circ}-$ $\angle O D E=\angle X E O=\angle X E L=\angle X H D=\angle X K D$ (сви углови су оријентисани), одакле следи да је $X K \perp D E$; аналогно $X L \perp D E$, тј. $K$ и $L$ леже на симетрали дужи $D E$, па је $D E H O$ једнакокраки трапез, дакле $D, E, O, H$ леже на кругу.
С друге стране, ако $O$ лежи на кругу $H D E$, дакле на кругу над пречником $C H$, периферијски углови над $E H$ и $O D$ су једнаки ( $\angle E C H=$ $\angle O C D)$, па је $D E H O$ једнакокраки трапез и одатле $D L=E L$. Сада имамо $\angle E X H=\angle E L H=2 \angle E D H$

и аналогно $\angle D X H=2 \angle D E H$, па следи да је $X$ центар круга $D E O H$. Према томе, $X$ је центар круга $O D E$ ако и само ако $D, E, O$ и $H$ леже на кругу.
Ако су тачке $D, E, O, H$ на кругу, тада $K, L$ и $M$ леже на симетрали дужи $D E$, чиме је један смер задатка доказан. Претпоставимо сада да $O$ лежи ван круга $C D H E$ (случај када је $O$ унутар круга се разматра на исти начин). Како је $C O \perp D E$, важи $D L>L E$ и $E K>K D$, тј. $K$ и $L$ леже на разним странама симетрале дужи $D E$, а $M$ припада овој симетрали. Према томе, ако су $K, L$ и $M$ колинеарне, $M$ се мора налазити између $K$ и $L$. Следи да је једна од тачака $K$ и $L$ ван троугла $A B C$, а друга унутар троугла. Међутим, када је $O$ изван четвороугла $A B D E$, обе тачке $K$ и $L$ су ван троугла, а у супротном су обе унутар троугла. То је контрадикција са претпоставком да $M$ лежи на правој $K L$, што доказује други смер.
|
{
"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
5ac14fc1-8960-552b-bf51-fcb6697c64e0
| 608,074
|
On the sides $AB$, $AC$, and $BC$ of triangle $ABC$, points $M$, $X$, and $Y$ are given such that $AX = MX$ and $BY = MY$. Let $K$ and $L$ be the midpoints of segments $AY$ and $BX$, respectively, and let $O$ be the center of the circumcircle of triangle $ABC$. If $O_{1}$ and $O_{2}$ are the points symmetric to point $O$ with respect to $K$ and $L$, respectively, prove that points $X$, $Y$, $O_{1}$, and $O_{2}$ lie on the same circle.
(Marco Đikić)
|
Let's set up a coordinate system with the origin at point $M$ and the $x$-axis along the line $A B$. Let points $X$ and $Y$ have coordinates $(a, b)$ and $(c, d)$, respectively. Due to $A X = X M$ and $B Y = Y M$, the coordinates of points $A$ and $B$ are $(2 a, 0)$ and $(2 c, 0)$, and the points $K$ and $L\left(a+\frac{c}{2}, \frac{d}{2}\right)$ and $\left(c+\frac{a}{2}, \frac{b}{2}\right)$, respectively. Point $O$ has coordinates $(a+c, e)$ for some $e$, from which we get $O_{1}(a, d-e)$ and $O_{2}(c, b-e)$. Therefore, points $O_{1}$ and $O_{2}$ are symmetric to points $X$ and $Y$ with respect to the line $y=\frac{b+d-e}{2}$, so $X, Y$ and $O_{1}, O_{2}$ are vertices (possibly degenerate) of an isosceles trapezoid, and thus lie on a circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
На страницама $A B, A C$ и $B C$ троугла $A B C$ дате су, редом, тачке $M, X$ и $Y$ тако да је $A X=M X$ и $B Y=M Y$. Нека су $K$ и $L$, редом, средишта дужи $A Y$ и $B X$, а $O$ центар описане кружнице троугла $A B C$. Ако су $O_{1}$ и $O_{2}$ тачке симетричне тачки $O$ у односу на $K$ и $L$, редом, доказати да тачке $X, Y, O_{1}$ и $O_{2}$ леже на истој кружници.
(Марко Ђикић)
|
Поставимо координатни систем са почетком у тачки $M$ и $x$-осом дуж праве $A B$. Нека тачке $X$ и $Y$ имају координате $(a, b)$ и $(c, d)$ редом. Због $A X=X M$ и $B Y=Y M$, координате тачака $A$ и $B$ су $(2 a, 0)$ и $(2 c, 0)$, а тачака $K$ и $L\left(a+\frac{c}{2}, \frac{d}{2}\right)$ и $\left(c+\frac{a}{2}, \frac{b}{2}\right)$, редом. Тачка $O$ има координате $(a+c, e)$ за неко $e$, одакле добијамо $O_{1}(a, d-e)$ и $O_{2}(c, b-e)$. Према томе, тачке $O_{1}$ и $O_{2}$ су симетричне тачкама $X$ и $Y$ у односу на праву $y=\frac{b+d-e}{2}$, па су $X, Y$ и $O_{1}, O_{2}$ темена (могуће дегенерисаног) једнакокраког трапезе, и зато леже на кругу.
|
{
"resource_path": "Serbia_MO/segmented/sr-2011_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
be5020c8-caef-575e-ad70-f5594e33d503
| 608,075
|
Let $P$ be a point on the diagonal $BD$ of parallelogram $ABCD$ such that $\angle PCB = \angle ACD$. The circumcircle of triangle $ABD$ intersects line $AC$ at points $E$ and $A$. Prove that
$$
\angle AED = \angle PEB. \quad \text{(Marko Đikić)}
$$
|
The proof is derived in the case when $\angle B A C \leq 90^{\circ}$. The other case is analogous.
Let $D E$ and $B C$ intersect at $L$. Quadrilateral $C D P L$ is cyclic because $\angle P D L = \angle P C L$, from which we have $\angle P L E = \angle P C D = \angle B C A = \angle D A C = \angle D B E = \angle P B E$, so quadrilateral $B P E L$ is also cyclic. From these two cyclic properties, we finally get $\angle P E B = \angle P L B = \angle P D C = \angle D B A = \angle D E A$.
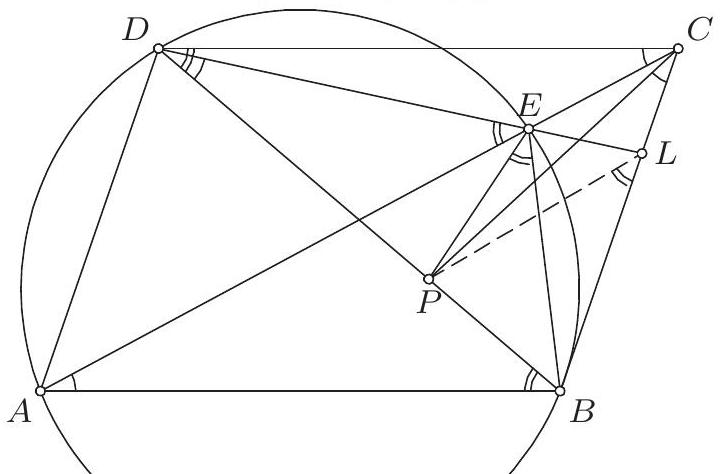
Second solution. Let $P^{\prime}$ be a point on $B D$ such that $\angle D E A = \angle P E B$.
By the Law of Sines, $\frac{B P}{D P} = \frac{B P}{C P} \cdot \frac{C P}{D P} = \frac{\sin \angle B C P}{\sin \angle C B D} \cdot \frac{\sin \angle C D B}{\sin \angle P C D}$. Similarly, $\frac{B P^{\prime}}{D P^{\prime}} = \frac{\sin \angle B E P^{\prime}}{\sin \angle E B D} \cdot \frac{\sin \angle E D B}{\sin \angle P^{\prime} E D}$. Since $\angle B C P = \angle E D B$, $\angle C B D = \angle P^{\prime} E D$, $\angle C D B = \angle B E P^{\prime}$, and $\angle P C D = \angle E B D$, it follows that $\frac{B P}{D P} = \frac{B P^{\prime}}{D P^{\prime}}$, hence $P \equiv P^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $P$ тачка на дијагонали $B D$ паралелограма $A B C D$ таква да је $\varangle P C B=\varangle A C D$. Кружница описана око троугла $A B D$ сече праву $A C$ у тачкама $E$ и $A$. Доказати да је
$$
\varangle A E D=\varangle P E B . \quad \text { (Марко Ђикић) }
$$
|
Доказ изводимо у случају када је $\angle B A C \leq 90^{\circ}$. Други случај је аналоган.
Нека се праве $D E$ и $B C$ секу у L. Четвороугао $C D P L$ је тетиван јер је $\angle P D L=\angle P C L$, одакле имамо $\angle P L E=\angle P C D=\angle B C A=$ $\angle D A C=\angle D B E=\angle P B E$, па је и четвороугао $B P E L$ тетиван. Из ове две тетивности коначно добијамо $\angle P E B=\angle P L B=\angle P D C=$ $\angle D B A=\angle D E A$.

Друго решеъе. Нека је $P^{\prime}$ тачка на $B D$ таква да је $\angle D E A=\angle P E B$.
По синусној теореми је $\frac{B P}{D P}=\frac{B P}{C P} \cdot \frac{C P}{D P}=\frac{\sin \angle B C P}{\sin \angle C B D} \cdot \frac{\sin \angle C D B}{\sin \angle P C D}$. Аналогно je $\frac{B P^{\prime}}{D P^{\prime}}=\frac{\sin \angle B E P^{\prime}}{\sin \angle E B D} \cdot \frac{\sin \angle E D B}{\sin \angle P^{\prime} E D}$. Како је $\angle B C P=\angle E D B, \angle C B D=\angle P^{\prime} E D$, $\angle C D B=\angle B E P^{\prime}$ и $\angle P C D=\angle E B D$, следи $\frac{B P}{D P}=\frac{B P^{\prime}}{D P^{\prime}}$, дакле $P \equiv P^{\prime}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
7bd58e5b-7ed6-5406-b0ad-744d65d112c2
| 608,078
|
Let $\mathcal{K}$ be an integer lattice. Does there exist a bijection $f: \mathbb{N} \rightarrow \mathcal{K}$ such that for all mutually distinct $a, b, c \in \mathbb{N}$ we have
$$
\text { GCD }(a, b, c)>1 \quad \Longrightarrow \quad f(a), f(b), f(c) \text { are not collinear? }
$$
(An integer lattice is the set of points in the plane with integer coordinates in the Cartesian coordinate system.)
(Stevan Gajović)
|
Let's arrange all the lattice points in a sequence $A_{1}, A_{2}, \ldots$. This can be done, for example, in a spiral manner: $(0,0),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1), \ldots$ We will construct an example of a bijection with the desired property inductively.
Set $f(1)=A_{1}$. Suppose $f(1), \ldots, f(n-1)$ are determined, and take $f(n)$ to be the point $A_{m}$ with the smallest $m$ such that, for no natural numbers $i, j \leq n$, $(i, j, n)>1$, $A_{m}$ lies on the line $f(i) f(j)$. There are only finitely many lines $f(i) f(j)$, so there indeed exists a lattice point that does not lie on any of them. Note that for a prime $p$, there are no restrictions on the choice of $f(p)$, which guarantees that every point will be the image of some natural number.
The mapping $f$ defined in this way satisfies all the conditions of the problem.
Another solution. If $n$ is a composite number, take $f(n)$ to be the point $\left(n, n^{2}\right)$. For a prime $p$, let $f(p)$ be any of the allowed points at the minimum distance from the point $(0,0)$. We will show that this mapping is a well-defined bijection with the desired property.
For every $p$, there exists an allowed point - for example, one of the unused points on the parabola $y=x^{2}$. Indeed, any line through that point intersects this parabola at at most one other point, i.e., contains the image of at most one composite number.
On the other hand, for any point $A \in \mathcal{K} \backslash\left\{\left(n, n^{2}\right) \mid n\right.$ is composite $\}$, there exists a prime $p$ for which $A$ is an allowed point. Indeed, there are only finitely many lines through $A$ that contain two integer points on the parabola $y=x^{2}$ (different from $A$); denote these lines by $p_{1}, \ldots, p_{k}$ and the integer points in the intersection of $p_{i}$ with the parabola $y=x^{2}$ by $A_{i}, B_{i}$. It is allowed to take $p$ that does not divide $\left(f^{-1}\left(A_{i}\right), f^{-1}\left(B_{i}\right)\right)$ for any $i$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је $\mathcal{K}$ целобројна решетка. Да ли постоји бијекција $f: \mathbb{N} \rightarrow \mathcal{K}$ таква да за све међусобно различите $a, b, c \in \mathbb{N}$ важи
$$
\text { НЗД }(a, b, c)>1 \quad \Longrightarrow \quad f(a), f(b), f(c) \text { нису колинеарне? }
$$
(Целобројна решетка је скуп тачака у равни са целобројним координатама у Декартовом координатном систему.)
(Стеван Гајовић)
|
Поређајмо све тачке решетке у низ $A_{1}, A_{2}, \ldots$. Ово се може урадити нпр. спирално: $(0,0),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1), \ldots$ Конструисаћемо индуктивно пример бијекције са траженим својством.
Ставимо $f(1)=A_{1}$. Претпоставимо да су $f(1), \ldots, f(n-1)$ одређене и узмимо за $f(n)$ тачку $A_{m}$ са најмањим $m$ такву да, ни за које природне $i, j \leq n,(i, j, n)>1, A_{m}$ не лежи на правој $f(i) f(j)$. Правих $f(i) f(j)$ има коначно много, па заиста постоји тачка решетке која не лежи ни на једној од њих. Приметимо да за просто $p$ нема ограничења при избору $f(p)$, што гарантује да ће свака тачка бити слика неког природног броја.
Овако дефинисано пресликавање $f$ задовољава све услове задатка.
Друго решеъе. Ако је $n$ сложен број, узмимо за $f(n)$ тачку $\left(n, n^{2}\right)$. За прост број $p$, нека је $f(p)$ било која од дозвољених тачака на минималном растојању од тачке $(0,0)$. Покажимо да је ово пресликавање добро дефинисана бијекција са траженим својством.
За свако $p$ постоји дозвољена тачка - нпр. нека од неупотребљених тачака на параболи $y=x^{2}$. Заиста, произволна права кроз ту тачку сече ову параболу у још највише једној тачки, тј. садржи слику највише једног сложеног броја.
С друге стране, за произвољну тачку $A \in \mathcal{K} \backslash\left\{\left(n, n^{2}\right) \mid n\right.$ је сложен $\}$ постоји прост број $p$ за који је $A$ дозвољена тачка. Наиме, постоји само коначно много правих кроз $A$ које садрже две целобројне тачке на параболи $y=x^{2}$ (различите од $A$ ); означимо те праве са $p_{1}, \ldots, p_{k}$ и целобројне тачке у пресеку $p_{i}$ са параболом $y=x^{2}$ са $A_{i}, B_{i}$. Дозољно је узети $p$ које не дели $\left(f^{-1}\left(A_{i}\right), f^{-1}\left(B_{i}\right)\right)$ ни за једно $i$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2012_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
7c0ac7e9-36b8-5a69-890b-2143176c65c3
| 608,082
|
Let $k$ be a natural number. Let $f: \mathbb{Z} \rightarrow \mathbb{Z}$ be a bijection such that for any two integers $i$ and $j$ for which $|i-j| \leqslant k$ it holds that $|f(i)-f(j)| \leqslant k$. Prove that for all $i, j \in \mathbb{Z}$ it holds that
$$
|f(i)-f(j)|=|i-j|
$$
(Miljan Knežević)
|
For $k=1$ the statement is trivial. Let $k>2$ then. An interval of length $k$ is a set of the form $\{x, x+1, \ldots, x+k\}, x \in \mathbb{Z}$. Two integers $x$ and $y$ will be consecutive if and only if there exist intervals $I_{1}$ and $I_{2}$ of length $k$ such that $I_{1} \cap I_{2}=\{x, y\}$. However, by the condition of the problem, $f\left(I_{1}\right)$ and $f\left(I_{2}\right)$ are also intervals of length $k$, so since $\{f(x), f(y)\}=f\left(I_{1}\right) \cap f\left(I_{2}\right)$, it follows that $f(x)$ and $f(y)$ are also consecutive numbers. Hence, $|f(x+1)-f(x)|=1$ for $x \in \mathbb{Z}$. Finally, using the injectivity of the mapping, by simple induction on $n$ we get that $|f(x+n)-f(x)|=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Дат је природан број $k$. Нека је $f: \mathbb{Z} \rightarrow \mathbb{Z}$ бијекција таква да за свака два цела броја $i$ и $j$ за које је $|i-j| \leqslant k$ важи $|f(i)-f(j)| \leqslant k$. Доказати да за све $i, j \in \mathbb{Z}$ важи
$$
|f(i)-f(j)|=|i-j|
$$
(Миљан Кнежевић)
|
За $k=1$ тврђење је тривијално. Нека је зато $k>2$. Интервалом дужине $k$ зовемо скуп облика $\{x, x+1, \ldots, x+k\}, x \in \mathbb{Z}$. Два цела броја $x$ и $y$ ће бити узастопна ако и само ако постоје интервали $I_{1}$ и $I_{2}$ дужине $k$ за које је $I_{1} \cap I_{2}=\{x, y\}$. Међутим, по услову задатка су $f\left(I_{1}\right)$ и $f\left(I_{2}\right)$ такође интервали дужине $k$, па како је $\{f(x), f(y)\}=f\left(I_{1}\right) \cap f\left(I_{2}\right)$, следи да су и $f(x)$ и $f(y)$ узастопни бројеви. Одавде је $|f(x+1)-f(x)|=1$ за $x \in \mathbb{Z}$. Коначно, користећи инјективност пресликавања, једноставном индукцијом по $n$ добијамо да је $|f(x+n)-f(x)|=n$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
b4a1b200-e9c3-5323-90ef-759fb717a015
| 608,084
|
Let
$$
S_{n}=\left\{\binom{n}{n},\binom{2 n}{n},\binom{3 n}{n}, \ldots,\binom{n^{2}}{n}\right\}, \quad \text { for } n \in \mathbb{N}
$$
a) Prove that there are infinitely many composite natural numbers $n$ such that $S_{n}$ is not a complete residue system modulo $n$.
b) Prove that there are infinitely many composite natural numbers $n$ such that $S_{n}$ is a complete residue system modulo $n$.
(Milos Milosevic)
|
(a) We will prove that $n=2p$ satisfies the conditions, where $p>2$ is a prime number. We have
$$
\binom{2kp}{2p}=k \prod_{i=1}^{p-1} \frac{2kp-i}{2p-i} \cdot (2k-1) \prod_{i=1}^{p-1} \frac{2kp-p-i}{p-i} \equiv k(2k-1) \quad (\bmod p)
$$
Specifically, from here, $\binom{2kp}{2p}$ is divisible by $p$ for $k \in \left\{\frac{p+1}{2}, p, 2p\right\}$, i.e., $S_{2p}$ has three elements divisible by $p$, so it is not a complete residue system.
(b) We will prove that $n=p^2$ satisfies the conditions, where $p>2$ is a prime number. We have $\binom{kp^2}{p^2}=\prod_{i=0}^{p^2-1} \frac{kp^2-i}{p^2-i}=k \prod_{j=1}^{p-1} \frac{kp^2-jp}{jp} \cdot \prod_{p \nmid j} \frac{kp^2-i}{p^2-i}$, so modulo $p^2$
$$
\binom{kn}{n} \equiv k \prod_{j=1}^{p-1} \frac{kp-j}{j}=k \prod_{j=1}^{p-1}\left(1-\frac{kp}{j}\right) \equiv k - k^2 p \sum_{j=1}^{p-1} \frac{1}{j}
$$
Since $\sum_{j=1}^{p-1} \frac{1}{j}=\sum_{j=1}^{\frac{p-1}{2}}\left(\frac{1}{j}+\frac{1}{p-j}\right)=\sum_{j=1}^{\frac{p-1}{2}} \frac{p}{j(p-j)} \equiv 0 (\bmod p)$, it finally follows that $\binom{kp^2}{p^2} \equiv k (\bmod p^2)$.
Note. There are other possibilities for the numbers $n$: for example, (a) $n=8k+6$ for $k \in \mathbb{N}$, or (b) $n=p^k$ for a prime number $p$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је
$$
S_{n}=\left\{\binom{n}{n},\binom{2 n}{n},\binom{3 n}{n}, \ldots,\binom{n^{2}}{n}\right\}, \quad \text { за } n \in \mathbb{N}
$$
a) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ није потпун систем остатака по модулу $n$.
б) Доказати да постоји бесконачно много сложених природних бројева $n$ таквих да $S_{n}$ јесте потпун систем остатака по модулу $n$.
(Милош Милосавлевић)
|
(а) Доказаћемо да $n=2 p$ задовољава услове, где је $p>2$ прост број. Имамо
$$
\binom{2 k p}{2 p}=k \prod_{i=1}^{p-1} \frac{2 k p-i}{2 p-i} \cdot(2 k-1) \prod_{i=1}^{p-1} \frac{2 k p-p-i}{p-i} \equiv k(2 k-1) \quad(\bmod p)
$$
Конкретно, одавде је $\binom{2 k p}{2 p}$ дељиво са $p$ за $k \in\left\{\frac{p+1}{2}, p, 2 p\right\}$, тј. $S_{2 p}$ има три елемента дељива са $p$, па није потпун систем остатака.
(б) Доказаћемо да $n=p^{2}$ задовољава услове, где је $p>2$ прост број. Имамо $\binom{k p^{2}}{p^{2}}=\prod_{i=0}^{p^{2}-1} \frac{k p^{2}-i}{p^{2}-i}=k \prod_{j=1}^{p-1} \frac{k p^{2}-j p}{j p} \cdot \prod_{p \nmid j} \frac{k p^{2}-i}{p^{2}-i}$, па је по модулу $p^{2}$
$$
\binom{k n}{n} \equiv k \prod_{j=1}^{p-1} \frac{k p-j}{j}=k \prod_{j=1}^{p-1}\left(1-\frac{k p}{j}\right) \equiv k-k^{2} p \sum_{j=1}^{p-1} \frac{1}{j}
$$
Како је $\sum_{j=1}^{p-1} \frac{1}{j}=\sum_{j=1}^{\frac{p-1}{2}}\left(\frac{1}{j}+\frac{1}{p-j}\right)=\sum_{j=1}^{\frac{p-1}{2}} \frac{p}{j(p-j)} \equiv 0(\bmod p)$, коначно следи да је $\binom{k p^{2}}{p^{2}} \equiv k\left(\bmod p^{2}\right)$.
Напомена. Има и других могућности за бројеве $n$ : на пример, (a) $n=8 k+6$ за $k \in \mathbb{N}$, односно (б) $n=p^{k}$ за прост број $p$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
d9dd470a-5fa5-5aaf-9dc1-59346e413477
| 608,085
|
Let $M, N$, and $P$ be the midpoints of the sides $BC, AC$, and $AB$, respectively, and let $O$ be the center of the circumcircle of the acute-angled triangle $ABC$. The circumcircles of triangles $BOC$ and $MNP$ intersect at distinct points $X$ and $Y$ inside triangle $ABC$. Prove that
$$
\angle BAX = \angle CAY
$$
(Marco Đikić)
## Ministry of Education, Science and Technological Development Mathematical Society of Serbia <br> SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
Novi Sad, April 6, 2013.
## Second Day
|
Let $k_{1}$ and $k_{2}$ be the circles $M N P$ and $B O C$ respectively. Circle $k_{1}$ is the Euler circle of $\triangle A B C$ and passes through the feet of the altitudes $D, E$ from $B, C$ and the midpoint $O_{1}$ of segment $A H$, where $H$ is the orthocenter of $\triangle A B C$.
We need to show that the second intersection point $Z$ of line $A Y$ and circle $k_{1}$ lies on the Euler circle $k_{3}$ of $\triangle A D E$. We will consider the case where
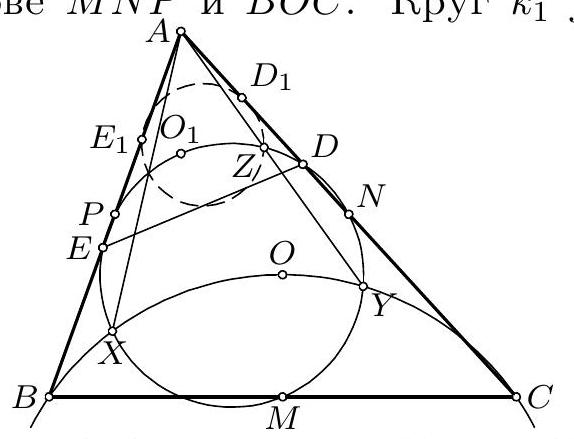
$Z$ is between $A$ and $Y$; the proof in the other case is analogous. Let $D_{1}$ and $E_{1}$ be the midpoints of segments $A D$ and $A E$ respectively. Since $A Y \cdot A Z = A D \cdot A N = A D_{1} \cdot A C$, points $Y, Z, C, D_{1}$ are concyclic, so $\angle A Z D_{1} = \angle A C Y$.
Similarly, $\angle A Z E_{1} = \angle A B Y$, so $\angle D_{1} Z E_{1} = \angle A Z D_{1} + \angle A Z E_{1} = \angle A C Y + \angle A B Y = \angle B Y C - \angle B A C = \angle B A C$. Therefore, $Z$ lies on $k_{3}$.
Since $O_{1}$ is the center of the circumcircle of $\triangle A D E$, the similarity transformation that maps $\triangle A B C$ to $\triangle A D E$ also maps $k_{1}$ to $k_{2}$ and $k_{2}$ to $k_{3}$, so the image of point $X \in k_{1} \cap k_{2}$ is point $Z \in k_{2} \cap k_{3}$. Therefore, $\angle B A X = \angle D A Z = \angle C A Y$.
Note. It can be shown that under inversion with center $A$ and radius squared $\frac{1}{2} A B \cdot A C$, circles $k_{1}$ and $k_{2}$ map to each other, so points $X$ and $Y$ also map to each other, from which the statement follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека су $M, N$ и $P$ средишта страница $B C, A C$ и $A B$, редом, а $O$ центар описане кружнице оштроуглог троугла $A B C$. Кружнице описане око троуглова $B O C$ и $M N P$ секу се у различитим тачкама $X$ и $Y$ унутар троугла $A B C$. Доказати да је
$$
\varangle B A X=\varangle C A Y
$$
(Марко Ђикић)
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
Нови Сад, 6. април 2013.
## Други дан
|
Обележимо са $k_{1}$ и $k_{2}$ редом кругове $M N P$ и $B O C$. Круг $k_{1}$ је Ојлеров круг у $\triangle A B C$ и пролази кроз подножја висина $D, E$ из $B, C$ и средиште $O_{1}$ дужи $A H$, где је $H$ ортоцентар $\triangle A B C$.
Покажимо да друга пресечна тачка $Z$ праве $A Y$ и круга $k_{1}$ лежи на Ојлеровом кругу $k_{3}$ троугла $A D E$. Сматраћемо да

је $Z$ између $A$ и $Y$; доказ у другом случају је аналоган. Нека су $D_{1}$ и $E_{1}$ редом средишта дужи $A D$ и $A E$. Како је $A Y \cdot A Z=A D \cdot A N=$ $A D_{1} \cdot A C$, тачке $Y, Z, C, D_{1}$ су концикличне, па је $\varangle A Z D_{1}=\varangle A C Y$.
Аналогно је $\varangle A Z E_{1}=\varangle A B Y$, па је $\varangle D_{1} Z E_{1}=\varangle A Z D_{1}+\varangle A Z E_{1}=$ $\varangle A C Y+\varangle A B Y=\varangle B Y C-\varangle B A C=\varangle B A C$. Одавде следи да је $Z$ на $k_{3}$.
Пошто је $O_{1}$ центар описаног круга $\triangle A D E$, трансформација сличности која слика $\triangle A B C$ у $\triangle A D E$ такође слика $k_{1}$ у $k_{2}$ и $k_{2}$ у $k_{3}$, па је слика тачке $X \in k_{1} \cap k_{2}$ тачка $Z \in k_{2} \cap k_{3}$. Према томе, $\varangle B A X=\varangle D A Z=\varangle C A Y$.
Напомена. Показује се да се при инверзији са центром $A$ и квадратом полупречника $\frac{1}{2} A B \cdot A C$ кругови $k_{1}$ и $k_{2}$ сликају један у други, па се и тачке $X$ и $Y$ сликају једна у другу, одакле такође следи тврђење.
|
{
"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
71e2ba5a-a3f1-56c5-a04a-14f99a461c40
| 608,086
|
Let $A'$ and $B'$ be the feet of the altitudes from vertices $A$ and $B$, respectively, of an acute triangle $ABC (AC \neq BC)$. The circle $k$ contains points $A'$ and $B'$ and is tangent to side $AB$ at point $D$. If triangles $ADA'$ and $BDB'$ have equal areas, prove that
$$
\angle A' D B' = \angle A C B.
$$
(Miloš Milosavljević)
|
Without loss of generality, let $BC > AC$. Then, $A'B'$ and $AB$ intersect at point $P$, with $A$ between $P$ and $B$. From the equality of the areas of $ADA'$ and $BDB'$, it follows that $\frac{AD}{DB} = \frac{PB'}{PA'}$. On the other hand, it also holds that $PD^2 = PA' \cdot PB' = PA \cdot PB$, from which $\frac{PD}{PB} = \frac{PA}{PD} = \frac{AD}{DB} = \frac{PB'}{PA'}$. From these equalities,
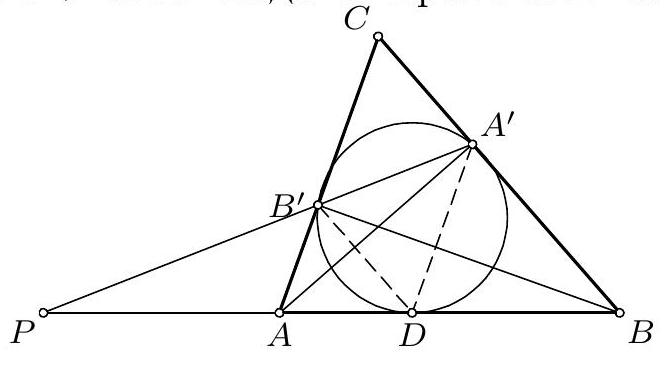
it follows that $B'D \parallel BC$ and $A'D \parallel AC$, and therefore $\angle A'DB' = \angle ACB$.
Second solution. Since $\angle CB'D = \alpha + \angle ADB' = \alpha + \angle B'A'D = \angle CA'D = x$, the sine rule in $\triangle A'B'D$ and $\triangle AB'D$ gives us $BD = \frac{BA' \sin x}{\sin (\beta + x)}$ and $AD = \frac{AB' \sin x}{\sin (\alpha + x)}$, so $\frac{AD}{BD} = \frac{AB' \sin (\beta + x)}{BA' \sin (\alpha + x)} = \frac{\sin (\beta + x) \cos \alpha}{\sin (\alpha + x) \cos \beta}$. On the other hand, from the condition $[ADA'] = [BDB']$, we get $\frac{AD}{DB} = \frac{d(B', AB)}{d(A', AB)} = \frac{\sin \alpha \cos \alpha}{\sin \beta \cos \beta}$, i.e., $\frac{\sin (\beta + x)}{\sin (\alpha + x)} = \frac{\sin \alpha}{\sin \beta}$. From here, we easily obtain $\angle AB'D = x = \gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека су $A^{\prime}$ и $B^{\prime}$ подножја висина из темена $A$ и $B$, редом, оштроуглог троугла $A B C(A C \neq B C)$. Кружница $k$ садржи тачке $A^{\prime}$ и $B^{\prime}$ и додирује страницу $A B$ у тачки $D$. Ако троуглови $A D A^{\prime}$ и $B D B^{\prime}$ имају једнаке површине, доказати да је
$$
\varangle A^{\prime} D B^{\prime}=\varangle A C B .
$$
(Милош Милосавлевић)
|
Нека је без смањења општости $B C>A C$. Тада се праве $A^{\prime} B^{\prime}$ и $A B$ секу у тачки $P$, при чему је $A$ између $P$ и $B$. Из једнакости површина $A D A^{\prime}$ и $B D B^{\prime}$ следи да је $\frac{A D}{D B}=\frac{P B^{\prime}}{P A^{\prime}}$. С друге стране, важи и $P D^{2}=P A^{\prime} \cdot P B^{\prime}=P A$. $P B$, одакле је $\frac{P D}{P B}=\frac{P A}{P D}=\frac{A D}{D B}=$ $\frac{P B^{\prime}}{P A^{\prime}}$. Из последњих једнакости

следи да је $B^{\prime} D \| B C$ и $A^{\prime} D \| A C$, и зато је $\varangle A^{\prime} D B^{\prime}=\varangle A C B$.
Друго решеъе. Како је $\varangle C B^{\prime} D=\alpha+\varangle A D B^{\prime}=\alpha+\varangle B^{\prime} A^{\prime} D=$ $\varangle C A^{\prime} D=x$, синусна теорема у $\triangle A^{\prime} B^{\prime} D$ и $\triangle A B^{\prime} D$ нам даје $B D=$ $\frac{B A^{\prime} \sin x}{\sin (\beta+x)}$ и $A D=\frac{A B^{\prime} \sin x}{\sin (\alpha+x)}$, па је $\frac{A D}{B D}=\frac{A B^{\prime} \sin (\beta+x)}{B A^{\prime} \sin (\alpha+x)}=\frac{\sin (\beta+x) \cos \alpha}{\sin (\alpha+x) \cos \beta}$. С
друге стране, из услова $\left[A D A^{\prime}\right]=\left[B D B^{\prime}\right]$ добијамо $\frac{A D}{D B}=\frac{d\left(B^{\prime}, A B\right)}{d\left(A^{\prime}, A B\right)}=$ $\frac{\sin \alpha \cos \alpha}{\sin \beta \cos \beta}$, тј. $\frac{\sin (\beta+x)}{\sin (\alpha+x)}=\frac{\sin \alpha}{\sin \beta}$. Одавде лако добијамо $\varangle A B^{\prime} D=x=\gamma$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2013_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
5cb517c4-b678-5419-a56a-17b25b95d223
| 608,088
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all $x, y \in \mathbb{R}$ we have
$$
f(x f(y)-y f(x))=f(x y)-x y . \quad \text { (Dušan Đukić) }
$$
|
Substituting $y=0$ gives $f(x f(0))=f(0)$. If $f(0) \neq 0$, the expression $x f(0)$ takes all real values, so $f$ is a constant function, which does not satisfy the conditions. Therefore, $f(0)=0$.
Substituting $y=x$ gives $f(0)=f\left(x^{2}\right)-x^{2}$, i.e., $f\left(x^{2}\right)=x^{2}$. Thus, $f(x)=x$ for all $x \geqslant 0$. Now, substitute arbitrary $x, y<0$. Since $f(x y)=x y$, we have $f(x f(y)-y f(x))=0$, which can only hold if $x f(y)-y f(x) \leqslant 0$. Similarly, $y f(x)-x f(y) \leqslant 0$, so $y f(x)=x f(y)$, i.e., $f(x) / x=f(y) / y$. It follows that $f(x)=c x$ for all $x<0$, where $c$ is some constant. Now, for $x<0<y$ we get $f((1-c) x y)=f(x y)-x y=(c-1) x y$, i.e., $f(z)=-z$ for $z=(1-c) x y$. If $c=1$, then $f(x) \equiv x$, which is clearly a solution. On the other hand, for $c \neq 1$, $z \neq 0$ and thus $f(z) \in\{c z, z\}$, so $c$ must be $-1$, which gives the function $f(x)=|x|$ for all $x$. This function is also a solution: we have already verified all cases except $x>0>y$, and for $x>0>y$ we have $-2 x y=f(-2 x y)=f(x f(y)-y f(x))=f(x y)-x y=-2 x y$.
Therefore, the solutions are the functions $f(x)=x$ and $f(x)=|x|$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Одредити све функције $f: \mathbb{R} \rightarrow \mathbb{R}$ такве да за све $x, y \in \mathbb{R}$ важи
$$
f(x f(y)-y f(x))=f(x y)-x y . \quad \text { (Душан Ђукић) }
$$
|
Замена $y=0$ даје $f(x f(0))=f(0)$. Ако је $f(0) \neq 0$, израз $x f(0)$ узима све реалне вредности, па је $f$ константна функција, а она не задовољава услове. Према томе, $f(0)=0$.
Стављањем $y=x$ добијамо $f(0)=f\left(x^{2}\right)-x^{2}$, тј. $f\left(x^{2}\right)=x^{2}$. Дакле, $f(x)=x$ за све $x \geqslant 0$. Убацимо сада произвољне $x, y<0$. Како је тада $f(x y)=x y$, имамо $f(x f(y)-y f(x))=0$, што може да важи само за $x f(y)-y f(x) \leqslant 0$. Аналогно је и $y f(x)-x f(y) \leqslant 0$, па је $y f(x)=x f(y)$, тј. $f(x) / x=f(y) / y$. Следи да је $f(x)=c x$ за све $x<0$, где је $c$ нека константа. Сада за $x<0<y$ добијамо $f((1-c) x y)=f(x y)-x y=(c-1) x y$, тј. $f(z)=-z$ за $z=(1-c) x y$. Ако је $c=1$, онда је $f(x) \equiv x$, што је очигледно решење. С друге стране, за $c \neq 1$ је $z \neq 0$ и отуда $f(z) \in\{c z, z\}$, па тада мора бити $c=-1$, што даје функцију $f(x)=|x|$ за све $x$. И ова функција је решење: све случајеве осим $x>0>y$ смо већ проверили, а за $x>0>y$ је $-2 x y=f(-2 x y)=f(x f(y)-y f(x))=f(x y)-x y=-2 x y$.
Према томе, решења су функције $f(x)=x$ и $f(x)=|x|$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
c25dbd08-c06c-53f9-8c9b-119d16ca26ca
| 608,090
|
On the sides $BC$ and $AC$ of triangle $ABC$, points $D$ and $E$ are given, respectively. Let $F (F \neq C)$ be the intersection point of the circumcircle of triangle $CED$ and the line passing through point $C$ and parallel to line $AB$. Let $G$ be the intersection point of line $FD$ and side $AB$, and $H$ be a point on line $AB$ such that $\angle HDA = \angle GEB$ and $H-A-B$. If $DG = EH$, prove that the intersection point of segments $AD$ and $BE$ lies on the angle bisector of $\angle ACB$.
(Miloš Milosavljević)
|
Given that $\varangle A G D=180^{\circ}-\varangle C F D=\varangle C E D=180^{\circ}-\varangle A E D$, the points $A$, $E, D, G$ are concyclic. Therefore, $\varangle D A G=\varangle D E G . \quad$ However, then $\varangle D H B=\varangle D A G-\varangle H D A$ $=\varangle D E G-\varangle B E G=\varangle D E B$, so the points $H, E, D, B$ are also concyclic. It follows that $\varangle B H E=180^{\circ}-$ $\varangle B D E=\varangle C D E=\varangle C F E$, which
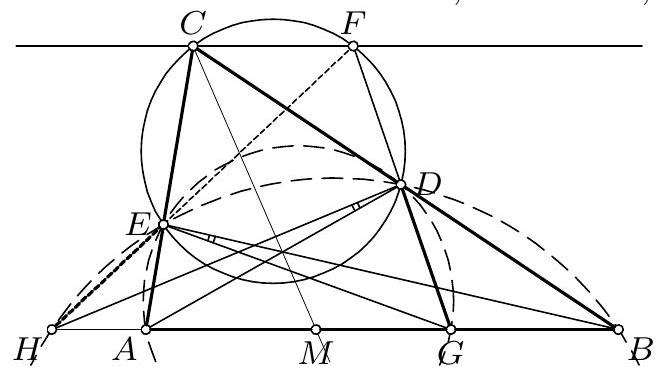
means that the points $F, E$ and $H$ are collinear.
Now, $E H=E F \cdot \frac{A E}{E C}$ and $D G=D F \cdot \frac{D B}{C D}$, so the condition $E H=D G$ becomes $\frac{A E}{E C} \cdot \frac{C D}{D B}=\frac{D F}{E F} . \quad$ On the other hand, from $\varangle D E F=\varangle D C F=\varangle A B C$ and $\varangle D F E=\varangle A C B$ it follows that $\triangle D E F \sim \triangle A B C$, so $\frac{D F}{E F}=\frac{A C}{C B}=\frac{A M}{M B}$, where $M$ is the intersection of the angle bisector of $\angle A C B$ and side $A B$. Therefore, $\frac{A E}{E C} \cdot \frac{C D}{D B} \cdot \frac{B M}{M A}=1$, and by Ceva's theorem, the lines $A D$ and $B E$ intersect on $C M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
На страницама $B C$ и $A C$ троугла $A B C$ дате су тачке $D$ и $E$, редом. Нека је $F(F \neq C)$ тачка пресека кружнице описане око троугла $C E D$ и праве која садржи тачку $C$ и паралелна је са правом $A B$. Нека је $G$ тачка пресека праве $F D$ и странице $A B$, а $H$ тачка на правој $A B$ таква да је $\varangle H D A=\varangle G E B$ и $H-A-B$. Ако је $D G=E H$, доказати да тачка пресека дужи $A D$ и $B E$ припада симетрали угла $A C B$.
(Милош Милосављевић)
|
Како је $\varangle A G D=180^{\circ}-\varangle C F D=\varangle C E D=180^{\circ}-\varangle A E D$, тачке $A$, $E, D, G$ су концикличне. Одавде је $\varangle D A G=\varangle D E G . \quad$ Међутим, тада је $\varangle D H B=\varangle D A G-\varangle H D A$ $=\varangle D E G-\varangle B E G=\varangle D E B$, па су и тачке $H, E, D, B$ концикличне. Следи да је $B H E=180^{\circ}-$ $\varangle B D E=\varangle C D E=\varangle C F E$, што

значи да су тачке $F, E$ и $H$ колинеарне.
Сада је $E H=E F \cdot \frac{A E}{E C}$ и $D G=D F \cdot \frac{D B}{C D}$, па услов $E H=D G$ постаје $\frac{A E}{E C} \cdot \frac{C D}{D B}=\frac{D F}{E F} . \quad$ С друге стране, из $\varangle D E F=\varangle D C F=\varangle A B C$ и $\varangle D F E=\varangle A C B$ следи да је $\triangle D E F \sim \triangle A B C$, па је $\frac{D F}{E F}=\frac{A C}{C B}=\frac{A M}{M B}$, где је $M$ пресечна тачка симетрале угла $A C B$ и странице $A B$. Према томе, $\frac{A E}{E C} \cdot \frac{C D}{D B} \cdot \frac{B M}{M A}=1$, па се по Чевиној теореми праве $A D$ и $B E$ секу на $C M$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
7d6440af-a938-5e9f-a4ca-e5dfb88ab538
| 608,091
|
For a natural number $n$, we say that it is quirky if and only if there exist natural numbers $a>1$ and $b>1$ such that $n=a^{b}+b$. Does there exist a sequence of 2014 consecutive natural numbers among which exactly 2012 are quirky?
(Miloš Milosavljević)
|
First, we will give an example of 2012 consecutive weird numbers. It is sufficient to take the numbers $N+2, N+3, \ldots, N+2013$, where $N=2^{2013!}$.
For a natural number $n$, let $f(n)$ denote the number of weird numbers among $n, n+1, \ldots, n+2013$. Since $f(1)<2012$ (the numbers $1,2,3,4,5$ are not weird), $f(N) \geqslant 2012$ and $|f(n+1)-f(n)| \leqslant 1$ for any $n$, there exists $n$ such that $f(n)=2012$.
Second solution. Let $N=\frac{2014!}{2011}$. The numbers $2^{N}+i$ for $2 \leqslant i \leqslant 2010$ and $2012 \leqslant i \leqslant 2014$ are weird; let's prove that $2^{N}+1$ and $2^{N}+2011$ are not.
Assume that $2^{N}+2011=a^{b}+b$ (similarly, we examine the number $2^{N}+1$). From $2^{b} \leqslant a^{b}<2^{N}$ it follows that $b<N$. Also, $b>2011$, otherwise we would have $2011-b=a^{b}-2^{N}=\left(a-2^{\frac{N}{b}}\right)\left(\cdots+2^{\frac{(b-1) N}{b}}\right)>2^{\frac{N}{b}}>$ 2011. Further, if $2 \mid a$, we have $2^{b} \mid 2^{N}-a^{b}=b-2011<2^{b}$, which is impossible. Finally, for $2 \nmid a$ and $2 \mid b$ we have $b-2011=\left(2^{\frac{N}{2}}-a^{\frac{b}{2}}\right)\left(2^{\frac{N}{2}}+a^{\frac{b}{2}}\right)>$ $2^{\frac{N}{2}}$, so $2^{N}+2011=a^{b}+b>2^{2^{N / 2}}$, again impossible since $2^{\frac{N}{2}}>N$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
За природан број $n$ кажемо да је шашав ако и само ако постоје природни бројеви $a>1$ и $b>1$ такви да је $n=a^{b}+b$. Да ли постоји 2014 узастопних природних бројева међу којима је тачно 2012 шашавих бројева?
(Милош Милосављевић)
|
Прво ћемо дати пример 2012 узастопних шашавих бројева. Довољно је узети бројеве $N+2, N+3, \ldots, N+2013$, где је $N=2^{2013!}$.
За природан број $n$, означимо са $f(n)$ број шашавих бројева међу $n, n+1, \ldots, n+2013$. Како је $f(1)<2012$ (бројеви $1,2,3,4,5$ нису шашави), $f(N) \geqslant 2012$ и $|f(n+1)-f(n)| \leqslant 1$ за свако $n$, постоји $n$ такво да је $f(n)=2012$.
Друго решеъе. Означимо $N=\frac{2014!}{2011}$. Бројеви $2^{N}+i$ за $2 \leqslant i \leqslant 2010$ и $2012 \leqslant i \leqslant 2014$ су шашави; докажимо да $2^{N}+1$ и $2^{N}+2011$ то нису.
Претпоставимо да је $2^{N}+2011=a^{b}+b$ (слично се испитује и број $\left.2^{N}+1\right)$. Из $2^{b} \leqslant a^{b}<2^{N}$ следи $b<N$. Такође је $b>2011$, јер би у супротном било $2011-b=a^{b}-2^{N}=\left(a-2^{\frac{N}{b}}\right)\left(\cdots+2^{\frac{(b-1) N}{b}}\right)>2^{\frac{N}{b}}>$ 2011. Даље, ако $2 \mid a$, имамо $2^{b} \mid 2^{N}-a^{b}=b-2011<2^{b}$, што је немогуће. Најзад, за $2 \nmid a$ и $2 \mid b$ имамо $b-2011=\left(2^{\frac{N}{2}}-a^{\frac{b}{2}}\right)\left(2^{\frac{N}{2}}+a^{\frac{b}{2}}\right)>$ $2^{\frac{N}{2}}$, па је $2^{N}+2011=a^{b}+b>2^{2^{N / 2}}$, опет немогуће јер је $2^{\frac{N}{2}}>N$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
54b3d9e3-336b-5664-a55a-9cbf55b11b65
| 608,093
|
The angle bisectors of the interior angles at vertices $A$ and $B$ of triangle $ABC$ intersect the opposite sides at points $D$ and $E$, respectively. A rhombus is inscribed in quadrilateral $ABDE$ such that each side of the quadrilateral contains exactly one vertex of the rhombus. If $\angle BAC = \alpha$ and $\angle ABC = \beta$, prove that at least one angle of the rhombus is not greater than $\max \{\alpha, \beta\}$.
(Dusan Dukic)
## SOLUTIONS
|
Let $K L M N$ be a rhombus with $K \in A B, L \in B D$ and $N \in E A$. Consider the trapezoid $P Q R S$ with $P, Q \in A B, P Q \| R S$ and $\varangle P Q R=\varangle Q P S=\varangle K N M=\varphi$ such that $K, L, M, N$ are on $P Q, Q R, R S, S P$ respectively. Assume that $\varphi>\alpha, \beta$. Then $R$ and $S$ lie outside $\triangle A B C$.
Since $\varangle S N M=180^{\circ}-\varphi-\varangle N M S=\angle R M L$ and $\varangle L R M=\varangle M S N$, triangles $L R M$ and $M S N$ are congruent, so $L R=M S$. Similarly, if $Q^{\prime}$ is a point on $A B$ such that $\varangle L Q^{\prime} B=\varphi$, triangles $L R M$ and $K Q^{\prime} L$ are congruent, so $M R=L Q^{\prime}=L Q$. It follows that $R Q=R L+L Q=S M+M R=R S$.
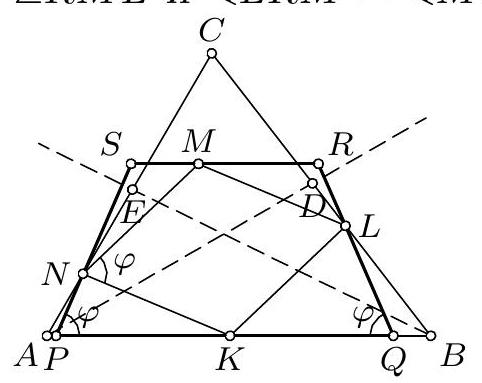
Now, $d(R, A B)=R Q \sin \varphi>R S \sin \alpha>d(R, A C)$ and similarly $d(S, A B)>d(S, B C)$, which means that points $R$ and $S$ lie above lines $A D$ and $B E$ respectively (i.e., in the half-planes containing $C$), from which it follows that both points lie above line $D E$. This is impossible because segments $R S$ and $D E$ intersect at $M$.
Second solution. The distance from a point $X$ to a line $p$ is denoted by $d(X, p)$.
Lemma. For any point $M$ on segment $D E$, $d(M, A B)=d(M, A C)+d(M, B C)$.
Proof. If $\frac{D M}{D E}=k$, then $d(M, A B)=k d(E, A B)+(1-k) d(D, A B)$ $=k d(E, B C)+(1-k) d(D, A C)=d(M, B C)+d(M, A C)$.
We use the same notation as in the first solution. Let $a$ be the side length of the rhombus and $O$ its center. We have
$$
\begin{aligned}
d(M, A C)+d(M, B C) & =a(\sin \varangle M N C+\sin \varangle M L C), \\
\text { and } d(M, A B) & =2 d(O, A B)=d(L, A B)+d(N, A B) \\
& =a(\sin \varangle N K A+\sin \varangle L K B) .
\end{aligned}
$$
However, if $\varphi>\alpha, \beta$, then $\varangle N K A=\varangle M N C+\varphi-\alpha>$ $\varangle M N C$ and similarly $\varangle L K B>\varangle M L C$, so from the above equations it follows that $d(M, A B)>d(M, A C)+d(M, B C)$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Симетрале унутрашњих углова код темена $A$ и $B$ троугла $A B C$ секу наспрамне странице у тачкама $D$ и $E$, редом. Ромб је уписан у четвороугао $A B D E$ тако да се на свакој страници четвороугла налази тачно једно теме ромба. Ако је $\varangle B A C=\alpha$ и $\varangle A B C=\beta$, доказати да је барем један угао ромба не већи од $\max \{\alpha, \beta\}$.
(Душан Ђукић)
## РЕШЕЊА
|
Нека је $K L M N$ ромб са $K \in A B, L \in B D$ и $N \in E A$. Посматрајмо трапез $P Q R S$ са $P, Q \in A B, P Q \| R S$ и $\varangle P Q R=\varangle Q P S=\varangle K N M=$ $\varphi$ такав да су $K, L, M, N$ на $P Q, Q R, R S, S P$ редом. Претпоставимо да је $\varphi>\alpha, \beta$. Тада $R$ и $S$ леже ван $\triangle A B C$.
Како је $\varangle S N M=180^{\circ}-\varphi-\varangle N M S=\angle R M L$ и $\varangle L R M=\varangle M S N$, троуглови $L R M$ и $M S N$ су подударни, па је $L R=M S$. Слично, ако је $Q^{\prime}$ тачка на $A B$ таква да је $\varangle L Q^{\prime} B=\varphi$, троуглови $L R M$ и $K Q^{\prime} L$ су подударни, па је $M R=L Q^{\prime}=L Q$. Следи да је $R Q=R L+L Q=S M+M R=R S$.

Сада је $d(R, A B)=R Q \sin \varphi>R S \sin \alpha>d(R, A C)$ и аналогно $d(S, A B)>d(S, B C)$, што значи да тачке $R$ и $S$ леже изнад правих $A D$ и $B E$ редом (тј. у полуравнима у којима је $C$ ), одакле следи да обе тачке леже изнад праве $D E$. Ово је немогуће јер се дужи $R S$ и $D E$ секу у $M$.
Друго решење. Растојање од тачке $X$ до праве $p$ означавамо $d(X, p)$.
Лема. За произвољну тачку $M$ на дужи $D E$ важи $d(M, A B)=$ $d(M, A C)+d(M, B C)$.
Доказ. Ако је $\frac{D M}{D E}=k$, важи $d(M, A B)=k d(E, A B)+(1-k) d(D, A B)$ $=k d(E, B C)+(1-k) d(D, A C)=d(M, B C)+d(M, A C)$.
Користимо исте ознаке као у првом решењу. Нека је $a$ страница ромба и $O$ његов центар. Имамо
$$
\begin{aligned}
d(M, A C)+d(M, B C) & =a(\sin \varangle M N C+\sin \varangle M L C), \\
\text { и } d(M, A B) & =2 d(O, A B)=d(L, A B)+d(N, A B) \\
& =a(\sin \varangle N K A+\sin \varangle L K B) .
\end{aligned}
$$
Међутим, ако је $\varphi>\alpha, \beta$, онда је $\varangle N K A=\varangle M N C+\varphi-\alpha>$ $\varangle M N C$ и аналогно $\varangle L K B>\varangle M L C$, па из горњих једначина следи $d(M, A B)>d(M, A C)+d(M, B C)$, контрадикција.
|
{
"resource_path": "Serbia_MO/segmented/sr-2014_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
9b8894f6-a7e1-51e7-8534-be292dc0fc2c
| 608,095
|
Let $ABCD$ be a cyclic quadrilateral. Points $M, N, P,$ and $Q$ are the midpoints of sides $DA, AB, BC,$ and $CD,$ respectively, and point $E$ is the intersection of diagonals $AC$ and $BD$. The circumcircles of $\triangle EMN$ and $\triangle EPQ$ intersect at point $F \neq E$. Prove that $EF \perp AC$.
(Dušan Đukić)
|
Triangles $EAB$ and $EDC$ are similar, so are triangles $EBN$ and $ECQ$. Therefore, in oriented angles, we have $\varangle MFE = \varangle MNE = \varangle BEN = \varangle QEC = \varangle EQM$. Similarly, $\varangle QFE = \varangle EMQ$, which implies that $F$ is the orthocenter of triangle $EMQ$. Thus, $EF \perp QM \| AC$.
Another solution. Consider the translation $\mathcal{T}$ by the vector $\frac{1}{2} \overrightarrow{AC}$. We have $\mathcal{T}(M)=$
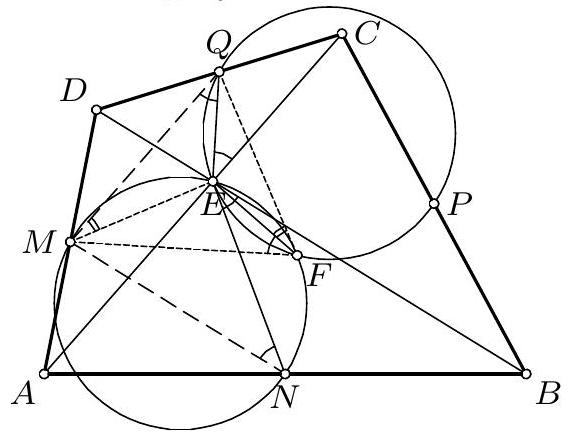
$Q$ and $\mathcal{T}(N)=P$; let $\mathcal{T}(E)=E'$. From the similarity of triangles $AED$ and $BEC$, it follows that $\triangle AEM \sim \triangle BEP$, hence $\varangle QE'E = \varangle EMQ = \varangle MEA = \varangle BEP = \varangle QPE$, so point $E'$ lies on the circle $PEQ$. Therefore, the translation $\mathcal{T}$ maps the circle $MEN$ to the circle $PEQ$, and the line joining their centers is parallel to $AC$, which proves the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је тетивни четвороугао $A B C D$. Тачке $M, N, P$ и $Q$ су средишта страница $D A, A B, B C$ и $C D$, редом, а тачка $E$ је пресек дијагонала $A C$ и $B D$. Кружнице описане око $\triangle E M N$ и $\triangle E P Q$ секу се у тачки $F \neq E$. Доказати да важи $E F \perp A C$.
(Душан Ђукић)
|
Троуглови $E A B$ и $E D C$ су слични, па су то и троуглови $E B N$ и $E C Q$. Зато у оријентисаним угловима важи $\varangle M F E=\varangle M N E=\varangle B E N=\varangle Q E C$ $=\varangle E Q M$. Аналогно важи $\varangle Q F E=$ $\varangle E M Q$, одакле следи да је $F$ ортоцентар троугла $E M Q$. Дакле, $E F \perp$ $Q M \| A C$.
Друго решеъе. Посматрајмо транслацију $\mathcal{T}$ за вектор $\frac{1}{2} \overrightarrow{A C}$. Важи $\mathcal{T}(M)=$

$Q$ и $\mathcal{T}(N)=P$; означимо $\mathcal{T}(E)=E^{\prime}$. Из сличности троуглова $A E D$ и $B E C$ следи $\triangle A E M \sim \triangle B E P$, одакле је $\varangle Q E^{\prime} E=\varangle E M Q=\varangle M E A=\varangle B E P=$ $\varangle Q P E$, па тачка $E^{\prime}$ лежи на кругу $P E Q$. Према томе, транслација $\mathcal{T}$ слика круг $M E N$ у круг $P E Q$, па је права која спаја њихове центре паралелна са $A C$, одакле следи тврђење.
|
{
"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
22a5b880-8a52-516a-8956-9cbf0ee9e08e
| 608,096
|
Let $k$ be a natural number. For $n \in \mathbb{N}$, denote by $f_{k}(n)$ the smallest natural number greater than $k n$ such that $n f_{k}(n)$ is a perfect square of a natural number. If $f_{k}(m)=f_{k}(n)$, prove that $m=n$.
(Nikola Petrović)
|
Assume that $f_{k}(m)=f_{k}(n)=q$. Write the number $q$ in the form $q=a u^{2}$, where $a, u \in \mathbb{N}$ and $a$ is not divisible by any perfect square greater than 1. Since $m q=a m u^{2}$ is a perfect square, so is $a m$, hence $m=a v^{2}$ for some $v \in \mathbb{N}$. Similarly, $n=a w^{2}$ for some $w \in \mathbb{N}$.
Since $f_{k}\left(a v^{2}\right)=a u^{2}$, $u$ is the smallest natural number greater than $v \sqrt{k}$. Analogously, $u$ is the smallest natural number greater than $w \sqrt{k}$, so it must be that $|v \sqrt{k}-w \sqrt{k}|<1$. However, from this it follows that $|v-w|<\frac{1}{\sqrt{k}}<1$, so it must be that $v=w$, i.e., $m=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је $k$ природан број. За $n \in \mathbb{N}$ означимо са $f_{k}(n)$ најмањи природан број већи од $k n$ такав да је $n f_{k}(n)$ потпун квадрат природног броја. Ако је испуњено $f_{k}(m)=f_{k}(n)$, доказати да важи $m=n$.
(Никола Петровић)
|
Претпоставимо да је $f_{k}(m)=f_{k}(n)=q$. Напишимо број $q$ у облику $q=a u^{2}$, где су $a, u \in \mathbb{N}$ и $a$ није дељиво ниједним потпуним квадратом већим од 1 . Како је $m q=a m u^{2}$ потпун квадрат, то је и $a m$, па следи да је $m=a v^{2}$ за неко $v \in \mathbb{N}$. Слично је $n=a w^{2}$ за неко $w \in \mathbb{N}$.
Како је $f_{k}\left(a v^{2}\right)=a u^{2}, u$ је најмањи природан број већи од $v \sqrt{k}$. Аналогно, $u$ је најмањи природан број већи од $w \sqrt{k}$, па мора да важи $|v \sqrt{k}-w \sqrt{k}|<1$. Међутим, одавде следи $|v-w|<\frac{1}{\sqrt{k}}<1$, па мора бити $v=w$, тј. $m=n$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
367858d7-ec4f-5c78-8e8e-7e231a92277c
| 608,097
|
Prove the inequality
$$
\frac{x-y}{x y+2 y+1}+\frac{y-z}{y z+2 z+1}+\frac{z-x}{z x+2 x+1} \geqslant 0
$$
where $x, y$, and $z$ are non-negative real numbers.
(Dušan Đukić)
|
Let $a=\frac{x-y}{x y+2 y+1}, b=\frac{y-z}{y z+2 z+1}$ and $c=\frac{z-x}{z x+2 x+1}$. Then $1+\frac{1}{a}=\frac{x y+x+y+1}{x-y}$ and hence $\frac{a}{a+1}=\frac{x-y}{x y+x+y+1}=\frac{1}{y+1}-\frac{1}{x+1}$; similarly, $\frac{b}{b+1}=\frac{1}{z+1}-\frac{1}{y+1}$ and $\frac{c}{c+1}=$ $\frac{1}{x+1}-\frac{1}{z+1}$.
From $0<\frac{1}{x+1}, \frac{1}{y+1}, \frac{1}{z+1}<1$ it follows that $\frac{a}{a+1}, \frac{b}{b+1}, \frac{c}{c+1}<1$, so $a+1, b+1, c+1$ are positive. Moreover, we have $\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}=0$, i.e., $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=3$. Now, by the Cauchy-Schwarz inequality, $(a+1)+(b+1)+(c+1) \geqslant 3$, i.e., $a+b+c \geqslant 0$.
Another solution. The desired inequality reduces to
$$
\begin{aligned}
& 2(x-1)^{2}(y-z)^{2}+2(y-1)^{2}(z-x)^{2}+2(z-1)^{2}(x-y)^{2} \\
& +9\left(x y^{2}+y z^{2}+z x^{2}-3 x y z\right)+3\left(x^{2} y+y^{2} z+z^{2} x-3 x y z\right) \geqslant 0
\end{aligned}
$$
where all terms are non-negative by the AM-GM inequality.
Note. If the condition $x, y, z \geqslant 0$ is replaced with $x, y, z \geqslant-\varepsilon$ for any $\varepsilon>0$, the statement may no longer hold, as shown by the example $(x, y, z)=\left(-\varepsilon, 1, \frac{2}{\varepsilon}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Доказати неједнакост
$$
\frac{x-y}{x y+2 y+1}+\frac{y-z}{y z+2 z+1}+\frac{z-x}{z x+2 x+1} \geqslant 0
$$
где су $x, y$ и $z$ ненегативни реални бројеви.
(Душан Ђукић)
|
Означимо $a=\frac{x-y}{x y+2 y+1}, b=\frac{y-z}{y z+2 z+1}$ и $c=\frac{z-x}{z x+2 x+1}$. Тада је $1+\frac{1}{a}=\frac{x y+x+y+1}{x-y}$ и одатле $\frac{a}{a+1}=\frac{x-y}{x y+x+y+1}=\frac{1}{y+1}-\frac{1}{x+1}$; аналогно је $\frac{b}{b+1}=\frac{1}{z+1}-\frac{1}{y+1}$ и $\frac{c}{c+1}=$ $\frac{1}{x+1}-\frac{1}{z+1}$.
Из $0<\frac{1}{x+1}, \frac{1}{y+1}, \frac{1}{z+1}<1$ следи $\frac{a}{a+1}, \frac{b}{b+1}, \frac{c}{c+1}<1$, па су $a+1, b+1, c+1$ позитивни. Осим тога, имамо $\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}=0$, тј. $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=3$. Сада је по Коши-Шварцовој неједнакости $(a+1)+(b+1)+(c+1) \geqslant 3$, тј. $a+b+c \geqslant 0$.
Друго решење. Тражена неједнакост се множењем и груписањем своди на
$$
\begin{aligned}
& 2(x-1)^{2}(y-z)^{2}+2(y-1)^{2}(z-x)^{2}+2(z-1)^{2}(x-y)^{2} \\
& +9\left(x y^{2}+y z^{2}+z x^{2}-3 x y z\right)+3\left(x^{2} y+y^{2} z+z^{2} x-3 x y z\right) \geqslant 0
\end{aligned}
$$
где су сви сабирци ненегативни на основу А-Г неједнакости.
Напомена. Ако се услов $x, y, z \geqslant 0$ замени са $x, y, z \geqslant-\varepsilon$ за произвољно $\varepsilon>0$, тврђење више не мора да важи, што показује пример $(x, y, z)=\left(-\varepsilon, 1, \frac{2}{\varepsilon}\right)$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2015_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
d72c2442-993e-5ac2-bb3d-9fbded025236
| 608,100
|
Let $n$ be a natural number greater than 1. Prove that there exists a natural number $m$ greater than $n^{n}$ such that
$$
\frac{n^{m}-m^{n}}{n+m}
$$
is a natural number.
(Nikola Petrović)
|
To start, note that for $m > n \geqslant 3$, it holds that $n^{m} > m^{n}$, so $\frac{n^{m} - m^{n}}{m + n} > 0$. Indeed, the function $f(x) = \frac{\ln x}{x}$ is decreasing for $x > e$ since $f'(x) = \frac{1 - \ln x}{x^2} < 0$, hence $\frac{\ln n}{n} > \frac{\ln m}{m}$, i.e., $m \ln n > n \ln m$, and from there $n^{m} = e^{m \ln n} > e^{n \ln m} = m^{n}$.
For $n = 2$, we can take $m = 10$. Suppose $n > 2$. We have
$$
n^{m} - m^{n} \equiv n^{m} - (-n)^{n} = n^{n}\left(n^{m-n} - (-1)^{n}\right) \quad(\bmod m+n)
$$
We will seek $m$ in the form $m = k n^{n} - n (k \in \mathbb{N})$. Then $m + n = k n^{n} \mid n^{m} - m^{n}$ if and only if $k \mid n^{m-n} - (-1)^{n}$.
$\left(1^{\circ}\right)$ If $n$ is odd, then $n^{m-n} - (-1)^{n}$ is even, so we can take $k = 2$, i.e., $m = 2 n^{n} - n$.
(2 $2^{\circ}$ If $n$ is even, then $n^{m-n} - (-1)^{n} = n^{m-n} - 1$ is divisible by $n-1$, so we can take $k = n-1$, i.e., $m = (n-1) n^{n} - n$.
Note. The inequality $n^{m} > m^{n}$ for $m > n \geqslant 3$ can be proven by induction. Other solutions are possible, for example, for $n > 2$, we can take $m = p n^{n} - n$, where $p$ is any prime divisor of the number $n^{n^{n}} - 2 n - (-1)^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Нека је $n$ природан број већи од 1. Доказати да постоји природан број $m$ већи од $n^{n}$ такав да је
$$
\frac{n^{m}-m^{n}}{n+m}
$$
природан број.
(Никола Петровић)
|
За почетак приметимо да за $m>n \geqslant 3$ важи $n^{m}>m^{n}$, те је $\frac{n^{m}-m^{n}}{m+n}>0$. Заиста, функција $f(x)=\frac{\ln x}{x}$ је опадајућа за $x>e$ јер је $f^{\prime}(x)=\frac{1-\ln x}{x^{2}}<0$, па је $\frac{\ln n}{n}>\frac{\ln m}{m}$, тј. $m \ln n>n \ln m$, и одатле $n^{m}=e^{m \ln n}>e^{n \ln m}=m^{n}$.
За $n=2$ се може узети $m=10$. Претпоставимо да је $n>2$. Имамо
$$
n^{m}-m^{n} \equiv n^{m}-(-n)^{n}=n^{n}\left(n^{m-n}-(-1)^{n}\right) \quad(\bmod m+n)
$$
Потражићемо $m$ у облику $m=k n^{n}-n(k \in \mathbb{N})$. Тада $m+n=k n^{n} \mid n^{m}-m^{n}$ ако и само ако $k \mid n^{m-n}-(-1)^{n}$.
$\left(1^{\circ}\right)$ Ако је $n$ непарно, онда је $n^{m-n}-(-1)^{n}$ парно, па можемо узети $k=2$, тј. $m=2 n^{n}-n$.
(2 $2^{\circ}$ Ако је $n$ парно, онда је $n^{m-n}-(-1)^{n}=n^{m-n}-1$ дељиво са $n-1$, па можемо узети $k-n-1$, тј. $m=(n-1) n^{n}-n$.
Напомена. Неједнакост $n^{m}>m^{n}$ за $m>n \geqslant 3$ се може доказати индукцијом. Могућа су и другачија решења, нпр. за $n>2$ може се узети $m=p n^{n}-n$, где је $p$ било који прост делилац броја $n^{n^{n}}-2 n-(-1)^{n}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
8bd04b9d-4bef-5ac7-92f0-e9fcbdc0767e
| 608,102
|
Let $O$ be the center of the circumcircle of $\triangle ABC$. The line $t$ is tangent to the circumcircle of $\triangle BOC$ and intersects the sides $AB$ and $AC$ at points $D$ and $E$, respectively $(D, E \not \equiv A)$. The point $A'$ is symmetric to point $A$ with respect to the line $t$. Prove that the circumcircles of $\triangle A'DE$ and $\triangle ABC$ are tangent. (Dušan Đukić)
## Ministry of Education, Science and Technological Development Mathematical Society of Serbia <br> 10th SERBIAN MATHEMATICAL OLYMPIAD FOR HIGH SCHOOL STUDENTS
## April 2, 2016.
## Second day
|
Let $K$ be the point of tangency of line $t$ and circle $BOC$. Let the circles circumscribed around triangles $BDK$ and $CEK$ intersect at point $X \neq K$. Since $\angle BXC = \angle BXK + \angle KXC = \angle ADK + \angle KEA = 180^\circ - \angle CAB$, point $X$ lies on the circumcircle $k$ of triangle $ABC$. Furthermore, $\angle DXE = \angle DXK + \angle KXE = \angle DBK + \angle KCE = \angle CKB - \angle CAB = \angle CAB = \angle DXE$, so $X$ also lies on the circumcircle $k_1$ of triangle $A'DE$. We will prove that circles $k$ and $k_1$ are tangent at point $X$.
If lines $CK$ and $XD$ intersect at point $P$, then $\angle XPC = \angle XDE - \angle CKE = \angle XBK - \angle CBK = \angle XBC$, which means that $P$ lies on circle $k$. Similarly, lines $BK$ and $XE$ intersect at point $Q$ on circle $k$. Finally, from $\angle XPQ = \angle XBQ = \angle XDK$ it follows that
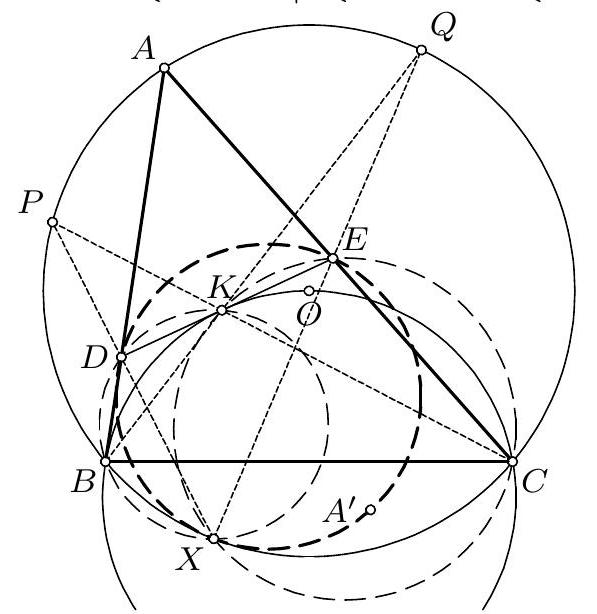
$PQ \parallel DE$. Therefore, triangles $XDE$ and $XPQ$ are homothetic with the center of homothety at $X$, so their circumcircles are tangent at $X$.
Second solution. Let lines $BK$ and $CK$ intersect the circumcircle of $\triangle ABC$ again at points $Q$ and $P$ respectively. From $\angle CPQ = \angle CBQ = \angle CKE$ it follows that $PQ \parallel DE$. Let lines $DP$ and $EQ$ intersect at point $X$. Since points $D = PX \cap AB$, $K = PC \cap QB$, and $E = AC \cap QX$ are collinear, by the converse of Pascal's theorem, point $X$ lies on the same circle as points $A, B, C, P, Q$. Therefore, triangles $XDE$ and $XPQ$ are homothetic, so their circumcircles are tangent at their center of homothety $X$. Finally, point $A'$ lies on the circumcircle of $\triangle DEX$ because $\angle DXE = \angle PXQ = \angle PCA + \angle ABQ = \angle BKC - \angle BAC = \angle BAC = \angle DA'E$.
Note. A more general statement holds: if $K$ is a point in $\triangle ABC$, $D$ and $E$ are the points where the tangent to circle $BKC$ at $K$ intersects $AB$ and $AC$, and $X$ is the second intersection point of circles $BDK$ and $CEK$, then the circles $DEX$ and $ABC$ are tangent at point $X$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $O$ центар кружнице описане око $\triangle A B C$. Права $t$ додирује кружницу описану око $\triangle B O C$ и сече странице $A B$ и $A C$ у тачкама $D$ и $E$, редом $(D, E \not \equiv A)$. Тачка $A^{\prime}$ је симетрична тачки $A$ у односу на праву $t$. Доказати да се кружнице описане око $\triangle A^{\prime} D E$ и $\triangle A B C$ додирују. (Душан Ђукић)
## Министарство просвете, науке и технолошког развоја Друштво математичара Србије <br> 10. СРПСКА МАТЕМАТИЧКА ОЛИМПИЈАДА УЧЕНИКА СРЕДЊИХ ШКОЛА
## 2. април 2016 .
## Други дан
|
Означимо са $K$ додирну тачку праве $t$ и круга $B O C$. Нека се кругови описани око троуглова $B D K$ и $C E K$ секу у тачки $X \neq K$. Како је $\varangle B X C=$ $\varangle B X K+\varangle K X C=\varangle A D K+\varangle K E A=180^{\circ}-\varangle C A B$, тачка $X$ лежи на описаном кругу $k$ троугла $A B C$. Шта више, $\varangle D X E=\varangle D X K+\varangle K X E=\varangle D B K+$ $\varangle K C E=\varangle C K B-\varangle C A B=\varangle C A B=$ $\varangle D X E$, па $X$ такође лежи на описаном кругу $k_{1}$ троугла $A^{\prime} D E$. Доказаћемо да се кругови $k$ и $k_{1}$ додирују у тачки $X$.
Ако се праве $C K$ и $X D$ секу у тачки $P$, онда важи $\varangle X P C=\varangle X D E-$ $\varangle C K E=\varangle X B K-\varangle C B K=\varangle X B C$, што значи да $P$ лежи на кругу $k$. Аналогно, праве $B K$ и $X E$ се секу у тачки $Q$ на кругу $k$. Најзад, из $\varangle X P Q=\varangle X B Q=\varangle X D K$ следи да

је $P Q \| D E$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични са центром хомотетије $X$, па се њихови описани кругови додирују у $X$.
Друго решеъе. Нека праве $B K$ и $C K$ поново секу описани круг $\triangle A B C$ редом у тачкама $Q$ и $P$. Из $\varangle C P Q=\varangle C B Q=\varangle C K E$ следи $P Q \| D E$. Нека се праве $D P$ и $E Q$ секу у тачки $X$. Како су тачке $D=P X \cap A B, K=P C \cap Q B$ и $E=A C \cap Q X$ колинеарне, по обратној Паскаловој теореми тачка $X$ лежи на истом кругу са тачкама $A, B, C, P, Q$. Према томе, троуглови $X D E$ и $X P Q$ су хомотетични, па се њихови описани кругови додирују у њиховом центру хомотетије $X$. Најзад, тачка $A^{\prime}$ лежи на описаном кругу $\triangle D E X$ јер je $\varangle D X E=\varangle P X Q=\varangle P C A+\varangle A B Q=\varangle B K C-\varangle B A C=\varangle B A C=\varangle D A^{\prime} E$.
Напомена. Важи и општије тврђење: ако је $K$ тачка у $\triangle A B C, D$ и $E$ тачке у којима тангента на круг $B K C$ у $K$ сече $A B$ и $A C$, а $X$ друга тачка пресека кругова $B D K$ и $C E K$, онда се кругови $D E X$ и $A B C$ додирују у тачки $X$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n3. "
}
|
685766f5-e480-593d-aeb9-e0b2c22176f0
| 608,104
|
In $\triangle ABC (AB \neq AC)$, a circle is inscribed with center at point $I$, touching side $BC$ at point $D$. Let point $M$ be the midpoint of segment $BC$. Prove that the normals from points $M$ and $D$ to lines $AI$ and $MI$, respectively, intersect on the line containing the altitude of $\triangle ABC$ from vertex $A$.
(Dušan Đukić)
|
Let $\gamma$ be the incircle of $\triangle ABC$, and $\gamma_{a}$ and $I_{a}$ be the excircle opposite to $A$ and its center. The point $E$, symmetric to point $D$ with respect to $M$, is the tangency point of $\gamma_{a}$ with side $BC$. The normal $\ell_{1}$ from $D$ to $MI$ is the radical axis of the circles $\gamma$ and $\omega$ with diameter $DE$, while the normal $\ell_{2}$ from $AI$ is the radical axis of the circles $\gamma$ and $\gamma_{a}$ (due to $MD = ME$). Additionally, the radical axis of the circles $\gamma_{a}$ and $\omega$ is the normal $\ell_{3}$ from $E$ to $MI_{a}$. The lines $\ell_{1}, \ell_{2}$, and $\ell_{3}$ intersect at the radical center $S$ of the circles $\gamma, \gamma_{a}, \omega$. On the other hand, it is known (by the "Great Problem") that $MI \parallel AE$ and $MI_{a} \parallel AD$, so the lines $\ell_{1}$ and $\ell_{3}$ contain the altitudes from $D$ and $E$ in $\triangle ADE$. It follows that $S$ is the orthocenter of $\triangle ADE$, and it lies on the altitude from vertex $A$.
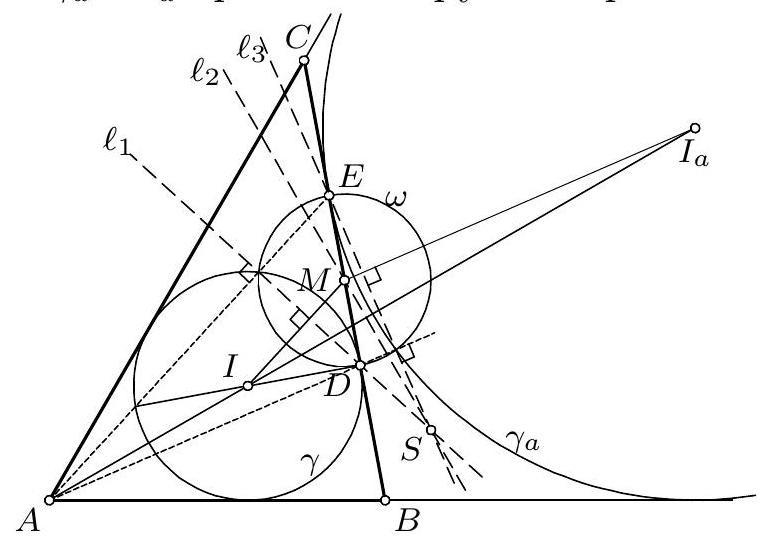
Another solution. Let the normals from $M$ and $D$ to $AI$ and $MI$ intersect at points $S$ and let $J$ be the point where $MI$ intersects the altitude from $A$ in $\triangle ABC$. It is sufficient to prove that $AJ = ID$. Indeed, then $AJDI$ will be a parallelogram, so $MS \perp DJ$, making $D$ the orthocenter of $\triangle MSJ$ and thus $JS \perp MD$, i.e., $AS \perp BC$.
This can be calculated directly. Let $H$ and $F$ be the feet of the altitude and the angle bisector from vertex $A$, and $a = BC, b = CA, c = AB$. Then $BF = \frac{ac}{b+c}$, $BD = \frac{a-b+c}{2}$, and $BH = \frac{a^2 - b^2 + c^2}{2a}$, so $FH = BF - BH = \frac{|b-c|((b+c)^2 - a^2)}{2a(b+c)}$, $FD = BF - BD = \frac{|b-c|(b+c-a)}{2(b+c)}$, and finally $\frac{AJ}{AH} = \frac{FD}{FH} = \frac{a}{a+b+c} = \frac{ID}{AH}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
У $\triangle A B C(A B \neq A C)$ уписана кружница, чији је центар тачка $I$, додирује страницу $B C$ у тачки $D$. Нека је тачка $M$ средиште дужи $B C$. Доказати да се нормале из тачака $M$ и $D$ на праве $A I$ и $M I$, редом, секу на правој која садржи висину $\triangle A B C$ из темена $A$.
(Душан Ђукић)
|
Означимо са $\gamma$ уписани круг $\triangle A B C$, а са $\gamma_{a}$ и $I_{a}$ приписани круг наспрам $A$ и његов центар. Тачка $E$ симетрична тачки $D$ у односу на $M$ је додирна тачка $\gamma_{a}$ са страницом $B C$. Нормала $\ell_{1}$ из $D$ на $M I$ је радикална оса круга $\gamma$ и круга $\omega$ над пречником $D E$, док је нормала $\ell_{2}$ из $A I$ радикална оса кругова $\gamma$ и $\gamma_{a}$ (због $M D=M E$ ). Такође, радикална оса кругова $\gamma_{a}$ и $\omega$ је нормала $\ell_{3}$ из $E$ на $M I_{a}$. Праве $\ell_{1}, \ell_{2}$ и $\ell_{3}$ се секу у радикалном центру $S$ кругова $\gamma, \gamma_{a}, \omega$. С друге стране, поз-

нато је (по "Великом задатку") да важи $M I \| A E$ и $M I_{a} \| A D$, па праве $\ell_{1}$ и $\ell_{3}$ садрже висине из $D$ и $E$ у троуглу $A D E$. Следи да је $S$ ортоцентар $\triangle A D E$, а он лежи на висини из темена $A$.
Друго решење. Нека се нормале из $M$ и $D$ редом на $A I$ и $M I$ секу у тачки $S$ и нека је $J$ тачка у којој права $M I$ сече висину из $A$ у $\triangle A B C$. Довољно је доказати да је $A J=I D$. Заиста, тада ће следити да је $A J D I$ паралелограм, па је $M S \perp D J$, тако да је $D$ ортоцентар троугла $M S J$ и одатле $J S \perp M D$, тј. $A S \perp B C$.
Ово се директно израчунава. Означимо са $H$ и $F$ редом подножја висине и симетрале угла из темена $A$, и $a=B C, b=C A, c=A B$. Тада је $B F=\frac{a c}{b+c}$, $B D=\frac{a-b+c}{2}$ и $B H=\frac{a^{2}-b^{2}+c^{2}}{2 a}$, па је $F H=B F-B H=\frac{|b-c|\left((b+c)^{2}-a^{2}\right)}{2 a(b+c)}, F D=$ $B F-B D=\frac{|b-c|(b+c-a)}{2(b+c)}$ и најзад $\frac{A J}{A H}=\frac{F D}{F H}=\frac{a}{a+b+c}=\frac{I D}{A H}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n4. "
}
|
d493537e-fbed-56b2-a2de-b30052d45ad2
| 608,105
|
Given are $2 n-1$ two-element subsets of the set $\{1,2, \ldots, n\}$. Prove that one can choose $n$ of these subsets whose union contains no more than $\frac{2}{3} n+1$ elements.
(Dushan Dukic)
|
We will show by induction on $k\left(k \leqslant \frac{2 n-1}{3}\right)$ that it is possible to remove $3 k$ subsets such that the cardinality of the union of the remaining ones is not greater than $n-k$.
For $k=0$ this is trivial. Suppose that $k \geqslant 1$ and that we have removed $3(k-1)$ subsets so that the union of the remaining ones does not contain more than $n-k+1$ elements. Since $2 n-1-3(k-1)<2(n-k+1)$, there exists an element $x_{k}$ in the union that is contained in at most three of the remaining subsets. Thus, we can remove three more subsets so that the union of the remaining $2 n-1-3 k$ does not contain the element $x_{k}$, which completes the inductive step.
The statement of the problem follows for $k=\left[\frac{n-1}{3}\right]$ since $n-\left[\frac{n-1}{3}\right] \leqslant n-\frac{n-3}{3}=\frac{2}{3} n+1$.
Note. The probabilistic method gives a weaker estimate $\sim \frac{n}{\sqrt{2}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Дато је $2 n-1$ двоелементних подскупова скупа $\{1,2, \ldots, n\}$. Доказати да се може одабрати $n$ од ових подскупова чија унија садржи не више од $\frac{2}{3} n+1$ елемената.
(Душан Ђукић)
|
Показаћемо индукцијом по $k\left(k \leqslant \frac{2 n-1}{3}\right)$ да се може избацити $3 k$ подскупова тако да је кардиналност уније преосталих не већа од $n-k$.
За $k=0$ то је тривијално. Претпоставимо да је $k \geqslant 1$ и да смо избацили $3(k-1)$ подскупова тако да унија преосталих не садржи више од $n-k+1$ елемената. Како је $2 n-1-3(k-1)<2(n-k+1)$, постоји елемент $x_{k}$ из уније који се налази у највише три од преосталих подскупова. Дакле, можемо да избацимо још три подскупа тако да унија преосталих $2 n-1-3 k$ не садржи елемент $x_{k}$, што завршава индуктивни корак.
Тврђење задатка следи за $k=\left[\frac{n-1}{3}\right]$ jep је $n-\left[\frac{n-1}{3}\right] \leqslant n-\frac{n-3}{3}=\frac{2}{3} n+1$.
Напомена. Пробабилистички метод даје слабију оцену $\sim \frac{n}{\sqrt{2}}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n5. "
}
|
2e54e0b3-8d69-5575-9004-f68802a7b00e
| 608,106
|
The numbers $a_{1}, a_{2}, \ldots, a_{2 \text { 2016 }}$ are natural numbers such that for all $n, 1 \leqslant n \leqslant 2^{2016}$, the following holds:
$$
a_{n} \leqslant 2016 \quad \text { and } \quad a_{1} a_{2} \cdots a_{n}+1 \text { is a perfect square. }
$$
Prove that one of the numbers $a_{1}, a_{2}, \ldots, a_{22016}$ is equal to 1. (Dušan Đukić)
## SOLUTIONS
|
A key fact is that if $a+1=u^{2}$ and $b=v^{2}$ are perfect squares and $a>b$, then $a b+1$ is not a square. Indeed, then $(u v-1)^{2}<a b+1=u^{2} v^{2}-v^{2}+1<(u v)^{2}$. Let $p_{1}, p_{2}, \ldots, p_{m}$ be all the prime numbers less than 2016. For $1 \leqslant n \leqslant 2^{2016}$, consider the binary sequence $\mathrm{c}_{n}=\left(r_{1}, r_{2}, \ldots, r_{m}\right)$, where $r_{i}=0$ if the exponent of $p_{i}$ in the product $P_{n}=a_{1} a_{2} \cdots a_{n}$ is even, and $r_{i}=1$ otherwise. Since there are only $2^{m}$ possibilities for the sequence $\mathrm{c}_{n}$, for any $k \leqslant 2^{2016}-2^{m}$, among the sequences $\mathrm{c}_{k}, \mathrm{c}_{k+1}, \ldots, \mathrm{c}_{k+2^{m}}$ there are two that are equal, say $\mathrm{c}_{s}$ and $\mathrm{c}_{t}(s<t)$, and then $P_{t} / P_{s}$ is a perfect square not greater than $2016^{2^{m}}$.
Assume that the sequence $\left(a_{n}\right)$ contains no ones. Take $k=11 \cdot 2^{m}$; clearly, $k+2^{m}<2^{2016}$. We have seen that there exist indices $s, t, k \leqslant s<t \leqslant k+2^{m}$, such that $b=P_{t} / P_{s}$ is a perfect square. However, since $a=P_{s} \geqslant P_{k} \geqslant 2^{k}=2048^{2^{m}} > 2016^{2^{m}} \geqslant b$, by the fact at the beginning, $a+1=P_{s}+1$ and $a b+1=P_{t}+1$ cannot both be squares at the same time, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Дати су природни бројеви $a_{1}, a_{2}, \ldots, a_{2 \text { 2016 }}$ такви да за све $n, 1 \leqslant n \leqslant 2^{2016}$, важи
$$
a_{n} \leqslant 2016 \quad \text { и } \quad a_{1} a_{2} \cdots a_{n}+1 \text { је потпун квадрат. }
$$
Доказати да је неки од бројева $a_{1}, a_{2}, \ldots, a_{22016}$ једнак 1. (Дуиан Ђукић)
## РЕШЕЊА
|
Кључна чињеница је да, ако су $a+1=u^{2}$ и $b=v^{2}$ потпуни квадрати и $a>b$, онда $a b+1$ није квадрат. Заиста, тада је $(u v-1)^{2}<a b+1=u^{2} v^{2}-v^{2}+1<(u v)^{2}$. Нека су $p_{1}, p_{2}, \ldots, p_{m}$ сви прости бројеви мањи од 2016. За $1 \leqslant n \leqslant 2^{2016}$ посматрајмо бинарни низ $\mathrm{c}_{n}=\left(r_{1}, r_{2}, \ldots, r_{m}\right)$, где је $r_{i}=0$ ако је експонент уз $p_{i}$ у производу $P_{n}=a_{1} a_{2} \cdots a_{n}$ паран, а $r_{i}=1$ у супротном. Како за низ с ${ }_{n}$ има само $2^{m}$ могућности, за свако $k \leqslant 2^{2016}-2^{m}$ међу низовима с с, c $_{k+1}, \ldots, \mathrm{c}_{k+2^{m}}$ постоје два једнака, рецимо с $s$ и $c_{t}(s<t)$, а тада је $P_{t} / P_{s}$ потпун квадрат не већи од $2016^{2^{m}}$.
Претпоставимо да у низу $\left(a_{n}\right)$ нема јединица. Узмимо $k=11 \cdot 2^{m}$; свакако је $k+2^{m}<2^{2016}$. Видели смо да постоје индекси $s, t, k \leqslant s<t \leqslant k+2^{m}$, тако да је $b=P_{t} / P_{s}$ потпун квадрат. Међутим, како је $a=P_{s} \geqslant P_{k} \geqslant 2^{k}=2048^{2^{m}}>$ $2016^{2^{m}} \geqslant b$, по чињеници са почетка, $a+1=P_{s}+1$ и $a b+1=P_{t}+1$ не могу истовремено да буду квадрати, што је контрадикција.
|
{
"resource_path": "Serbia_MO/segmented/sr-2016_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
1639cf38-45b5-5064-a8d4-337f87832735
| 608,107
|
Let $a, b$ and $c$ be positive real numbers such that $a+b+c=1$. Prove:
$$
\begin{array}{r}
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} \leqslant \sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)} \\
\text { (Nikola Petrović) }
\end{array}
$$
|
By squaring both sides and using the equality $1-\left(a^{2}+b^{2}+c^{2}\right)=2(a b+$ $b c+c a)$, the inequality from the problem reduces to
$$
\begin{aligned}
L= & 2 a^{2} b+2 b^{2} c+2 c^{2} a+ \\
& 2 a b \sqrt{(2 b+1)(2 c+1)}+2 b c \sqrt{(2 c+1)(2 a+1)}+2 c a \sqrt{(2 a+1)(2 b+1)} \\
\leqslant D= & 4(a b+b c+c a) .
\end{aligned}
$$
By the AM-GM inequality, we have $2 a b \sqrt{(2 b+1)(2 c+1)} \leqslant a b(2 b+2 c+2)$ and similarly $2 b c \sqrt{(2 c+1)(2 a+1)} \leqslant b c(2 c+2 a+2)$ and $2 c a \sqrt{(2 a+1)(2 b+1)} \leqslant c a(2 a+2 b+2)$. Adding these, we get
$$
\begin{aligned}
L \leqslant & 2\left(a^{2} b+b^{2} c+c^{2} a+a b^{2}+b c^{2}+c a^{2}+3 a b c\right)+2(a b+b c+c a)= \\
& 2(a+b+c+1)(a b+b c+c a)=4(a b+b c+c a)=D
\end{aligned}
$$
Second solution. The function $f(x)=\sqrt{x}$ is concave because $f^{\prime}(x)=2 / \sqrt{x}$ is a decreasing function. Applying Jensen's inequality with weights $a, b$ and $c$, we get
$$
\begin{aligned}
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} & \leqslant \sqrt{a(2 b+1)+b(2 c+1)+c(2 a+1)} \\
& =\sqrt{1+2(a b+b c+c a)}=\sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)}
\end{aligned}
$$
Note. If it is allowed for any of the numbers $a, b, c$ to be zero, equality is achieved in the cases $a=b=c=\frac{1}{3}$ and $(a, b, c)=(1,0,0)$ with permutations.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Нека су $a, b$ и $c$ позитивни реални бројеви за које важи $a+b+c=1$. Доказати:
$$
\begin{array}{r}
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} \leqslant \sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)} \\
\text { (Никола Петровић) }
\end{array}
$$
|
Квадрирањем обе стране и коришћењем једнакости $1-\left(a^{2}+b^{2}+c^{2}\right)=2(a b+$ $b c+c a)$ неједнакост из задатка се своди на
$$
\begin{aligned}
L= & 2 a^{2} b+2 b^{2} c+2 c^{2} a+ \\
& 2 a b \sqrt{(2 b+1)(2 c+1)}+2 b c \sqrt{(2 c+1)(2 a+1)}+2 c a \sqrt{(2 a+1)(2 b+1)} \\
\leqslant D= & 4(a b+b c+c a) .
\end{aligned}
$$
По АМ-ГМ неједнакости имамо $2 a b \sqrt{(2 b+1)(2 c+1)} \leqslant a b(2 b+2 c+2)$ и аналогно $2 b c \sqrt{(2 c+1)(2 a+1)} \leqslant b c(2 c+2 a+2)$ и $2 c a \sqrt{(2 a+1)(2 b+1)} \leqslant c a(2 a+2 b+2)$, па сабирањем добијамо
$$
\begin{aligned}
L \leqslant & 2\left(a^{2} b+b^{2} c+c^{2} a+a b^{2}+b c^{2}+c a^{2}+3 a b c\right)+2(a b+b c+c a)= \\
& 2(a+b+c+1)(a b+b c+c a)=4(a b+b c+c a)=D
\end{aligned}
$$
Друго решење. Функција $f(x)=\sqrt{x}$ је конкавна јер је $f^{\prime}(x)=2 / \sqrt{x}$ опадајућа функција. Применом Јенсенове неједнакости са тежинама $a, b$ и $c$ добијамо
$$
\begin{aligned}
a \sqrt{2 b+1}+b \sqrt{2 c+1}+c \sqrt{2 a+1} & \leqslant \sqrt{a(2 b+1)+b(2 c+1)+c(2 a+1)} \\
& =\sqrt{1+2(a b+b c+c a)}=\sqrt{2-\left(a^{2}+b^{2}+c^{2}\right)}
\end{aligned}
$$
Напомена. Ако се допусти да неки од бројева $a, b, c$ буде нула, једнакост се достиже у случајевима $a=b=c=\frac{1}{3}$ и $(a, b, c)=(1,0,0)$ са пермутацијама.
|
{
"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n1. "
}
|
62cbd095-56a2-51c1-8179-ea6581b09a97
| 608,108
|
Let $ABCD$ be a convex cyclic quadrilateral. Let the lines $AD$ and $BC$ intersect at point $E$. Points $M$ and $N$ are chosen on the sides $AD$ and $BC$, respectively, such that $AM: MD = BN: NC$. The circumcircles of triangle $EMN$ and quadrilateral $ABCD$ intersect at points $X$ and $Y$. Prove that the lines $AB$, $CD$, and $XY$ either intersect at one point or are all parallel.
(Dušan Đukić)
|
In the case $A B \| C D$ the statement is trivial: points $X$ and $Y$ are symmetric with respect to the perpendicular bisector of segments $A B$ and $C D$, and it holds that $A B\|X Y\| C D$.
Let $A B \nVdash C D$. Then the circumcircles $k_{1}$ and $k_{2}$ of triangles $E A B$ and $E C D$ have another intersection point $P \neq E$. From $\varangle P A D=\varangle P B E$ and $\varangle P D A=180^{\circ}-\varangle P D E=$ $180^{\circ}-\varangle P C E=\varangle P C B$ it follows that triangles $P A D$ and $P B C$ are similar. Under this similarity, point $M$ in $\triangle P A D$ corresponds to point $N$ in $\triangle P B C$, so $\varangle P M E=\varangle P N E$. We conclude that points $E, P, M$ and $N$ lie on the same circle $k_{3}$.
Since point $F$ has the same power $F A \cdot F B = F C \cdot F D$ with respect to circles $k_{1}, k_{2}$
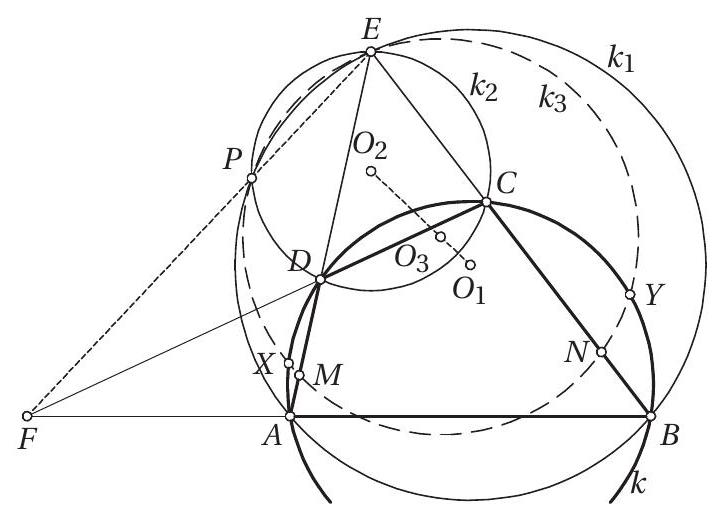
and the circumcircle $k$ of quadrilateral $A B C D$, it lies on the radical axis $E P$ of circles $k_{1}$ and $k_{2}$. Now, since $F A \cdot F B = F E \cdot F P$, $F$ also lies on the radical axis of circles $k_{1}$ and $k_{3}$, which is line $X Y$.
Second solution. Let $k, k_{1}, k_{2}$, and $k_{3}$ be the circumcircles of the quadrilateral
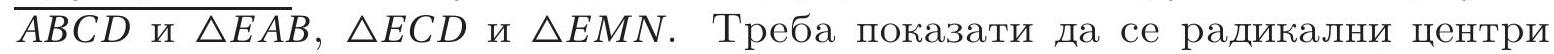
of the triplets of circles $(k, k_{1}, k_{2})$ and $(k, k_{1}, k_{3})$ coincide (possibly at infinity). It is sufficient to prove that the circles $k_{1}, k_{2}, k_{3}$ have a common radical axis, i.e., that their centers $O_{1}, O_{2}, O_{3}$ are collinear.
For $i=1,2,3$, let $E_{i}$ be the point symmetric to point $E$ with respect to $O_{i}$. We will prove that point $E_{3}$ coincides with point $E_{3}^{\prime}$ on segment $E_{1} E_{2}$ such that $E_{1} E_{3}^{\prime}: E_{3}^{\prime} E_{2} = A M: M D$. Indeed, since $E_{1} A \perp A D$ and $E_{2} D \perp A D$, by Thales' theorem it follows that $E_{3}^{\prime} M \perp A D$; similarly, $E_{3}^{\prime} N \perp B C$, so $E_{3}^{\prime} \equiv E_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Дат је конвексан тетиван четвороугао $A B C D$. Нека се праве $A D$ и $B C$ секу у тачки $E$. На страницама $A D$ и $B C$ су одабране тачке $M$ и $N$, редом, такве да важи $A M: M D=B N: N C$. Кружнице описане око троугла $E M N$ и четвороугла $A B C D$ секу се у тачкама $X$ и $Y$. Доказати да се праве $A B, C D$ и $X Y$ секу у једној тачки или су све паралелне.
(Дуиан Ђукић)
|
У случају $A B \| C D$ тврђење је тривијално: тачке $X$ и $Y$ су симетричне у односу на симетралу дужи $A B$ и $C D$ и важи $A B\|X Y\| C D$.
Нека је $A B \nVdash C D$. Тада описани кругови $k_{1}$ и $k_{2}$ троуглова $E A B$ и $E C D$ имају другу пресечну тачку $P \neq E$. Из $\varangle P A D=\varangle P B E$ и $\varangle P D A=180^{\circ}-\varangle P D E=$ $180^{\circ}-\varangle P C E=\varangle P C B$ следи да су троуглови $P A D$ и $P B C$ слични. При овој сличности тачки $M$ у $\triangle P A D$ одговара тачка $N$ у $\triangle P B C$, па је $\varangle P M E=\varangle P N E$. Закључујемо да тачке $E, P, M$ и $N$ леже на истом кругу $k_{3}$.
Како тачка $F$ има једнаку потенцију $F A$. $F B=F C \cdot F D$ у односу на кругове $k_{1}, k_{2}$

и круг $k$ описан око $A B C D$, она лежи на радикални оси $E P$ кругова $k_{1}$ и $k_{2}$. Сада је још $F A \cdot F B=F E \cdot F P$, па $F$ такође припада радикалној оси кругова $k_{1}$ и $k_{3}$, а то је права $X Y$.
Друго решеъе. Нека су $k, k_{1}, k_{2}$ и $k_{3}$ редом описани кругови четвороугла
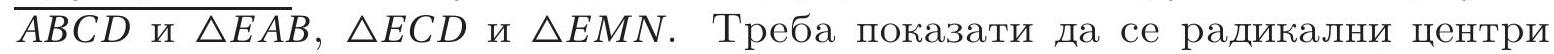
тројки кругова ( $k, k_{1}, k_{2}$ ) и ( $k, k_{1}, k_{3}$ ) поклапају (можда у бесконачној тачки). Довољно је доказати да кругови $k_{1}, k_{2}, k_{3}$ имају заједничку радикалну осу, тј. да су њихови центри $O_{1}, O_{2}, O_{3}$ редом колинеарни.
За $i=1,2,3$, означимо са $E_{i}$ тачку симетричну тачки $E$ у односу на $O_{i}$. Доказаћемо да се тачка $E_{3}$ поклапа са тачком $E_{3}^{\prime}$ на дужи $E_{1} E_{2}$ таквом да је $E_{1} E_{3}^{\prime}: E_{3}^{\prime} E_{2}=A M: M D$. Заиста, пошто је $E_{1} A \perp A D$ и $E_{2} D \perp A D$, из Талесове теореме следи $E_{3}^{\prime} M \perp A D$; аналогно је $E_{3}^{\prime} N \perp B C$, па је $E_{3}^{\prime} \equiv E_{3}$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n2. "
}
|
4ed7a0fa-3761-5946-a904-0661648121fd
| 608,109
|
Let $k$ be the circumcircle of $\triangle ABC$, and $k_{a}$ the excircle opposite to vertex $A$. The two common tangents of circles $k$ and $k_{a}$ intersect the line $BC$ at points $P$ and $Q$. Prove that $\varangle P A B = \varangle Q A C$.
(Dušan Đukić)
## SOLUTIONS
|
Let the internal and external bisectors of angle $BAC$ intersect line $BC$ at points $D$ and (possibly infinite) $D_{1}$, respectively. The common tangents intersect at the center $T$ of the positive homothety $\mathscr{H}$ that maps the excircle $\omega_{a}$ to the circumcircle $\Omega$. If $T$ is an infinite point, $\mathscr{H}$ is a translation, and the rest of the proof is the same.
Lemma. Let an arbitrary line $p$ through $D_{1}$ intersect the circle $\Omega$ at points $L$ and $K$. The tangents to $\Omega$ at $L$ and $K$ intersect line $BC$ at points $P$ and $Q$, respectively. Then $\varangle PAB = \varangle CAQ$.
Proof. Denote $\varangle BAC = \alpha, \varangle CBA = \beta, \varangle ACB = \gamma, \varangle PAB = x$, and $\varangle CAQ = y$.
If $D_{1}$ is an infinite point, the statement is trivial by symmetry. If not, from $\triangle PBL \sim \triangle PLC$ it follows that $\frac{PB}{PL} = \frac{PL}{PC} = \frac{LB}{LC}$ and thus $\frac{PB}{PC} = \left(\frac{LB}{LC}\right)^2$. Similarly, $\frac{QB}{QC} = \left(\frac{KB}{KC}\right)^2$. Since $\frac{LB}{LC} \cdot \frac{KB}{KC} = \frac{|KLB|}{|KLC|} = \frac{D_{1}B}{D_{1}C} = \frac{AB}{AC}$, we get $\frac{PB}{PC} \cdot \frac{QB}{QC} = \left(\frac{AB}{AC}\right)^2$. Since $\frac{PB}{PC} = \frac{PB}{PA} \cdot \frac{PA}{PC} = \frac{\sin x}{\sin \beta} \cdot \frac{\sin \gamma}{\sin (\alpha + x)}$ and $\frac{QB}{QC} = \frac{QB}{QA} \cdot \frac{QA}{QC} = \frac{\sin (\alpha + y)}{\sin \beta} \cdot \frac{\sin \gamma}{\sin y}$, multiplication gives $\left(\frac{\sin \gamma}{\sin \beta}\right)^2 \cdot \frac{\sin (\alpha + y) / \sin y}{\sin (\alpha + x) / \sin x} = \left(\frac{AC}{AB}\right)^2 = \left(\frac{\sin \gamma}{\sin \beta}\right)^2$, hence $\sin \alpha \operatorname{ctg} y + \cos \alpha = \frac{\sin (\alpha + y)}{\sin y} = \frac{\sin (\alpha + x)}{\sin x} = \sin \alpha \operatorname{ctg} x + \cos \alpha$, i.e., $x = y$.
If $K$ and $L$ are the points of tangency of the common tangents with $\Omega$, it remains to show that point $D_{1}$ lies on line $KL$, i.e., on the polar of point $T$ with respect to $\Omega$. By the pole and polar theorem, it suffices to prove that $T$ lies on the polar $d$ of point $D_{1}$ with respect to $\Omega$.
Let $N$ be the midpoint of arc $BAC$ of circle $\Omega$. The image of point $D$ under homothety $\mathscr{H}$ is the intersection $S$ of the tangents to $\Omega$ at points $A$ and $N$, so point $T$ lies on line $DS$. On the other hand, point $D$ is on polar $d$ because the quadruple $(B, C; D_{1}, D)$ is harmonic, and point $S$ is also on $d$ because the polar of point $S$ with respect to $\Omega$, which is line $AN$, contains point $D_{1}$. Therefore, lines $DS$ and $d$ coincide, completing the proof.
Second Solution. Let the common tangents touch circle $\Omega$ at points $K$ and $L$, with the vertex $LP$ of the tangent closer to vertex $B$. Let $M$ be the midpoint of the arc $BC$ that does not contain point $A$, and let $O$ and $I_{a}$ be the centers of the circumcircle and the excircle opposite $A$, respectively.
Since $\varangle LPI_{a} = 90^\circ + \frac{1}{2} \varangle LPC$ and $\varangle LAI_{a} = \varangle LAM = \frac{1}{2} \varangle LOM = \frac{1}{2} \varangle LPD_{1} = 90^\circ - \frac{1}{2} \varangle LPC$, it follows that $\varangle LPI_{a} + \varangle LAI_{a} = 180^\circ$, so quadrilateral $ALPI_{a}$ is cyclic. Similarly, quadrilateral $AKQI_{a}$ is cyclic. Now we have $\varangle PAI_{a} = \varangle PLI_{a} = \varangle QKI_{a} = \varangle QAI_{a}$, since angles $PLI_{a}$ and $QKI_{a}$ are symmetric with respect to line $OI_{a}$, and thus $\varangle PAB = \varangle QAC$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Нека је $k$ кружница описана око $\triangle A B C$, а $k_{a}$ приписана кружница наспрам темена $A$. Две заједничке тангенте кружница $k$ и $k_{a}$ секу праву $B C$ у тачкама $P$ и $Q$. Доказати да важи $\varangle P A B=\varangle Q A C$.
(Дуиан Ђукић)
## РЕШЕЊА
|
Нека унутрашња и спољна симетрала угла $B A C$ секу праву $B C$ редом у тачкама $D$ и (можда бесконачној) $D_{1}$. Заједничке тангенте се секу у центру $T$ позитивне хомотетије $\mathscr{H}$ која слика приписани круг $\omega_{a}$ у описани круг $\Omega$. Ако је $T$ бесконачна тачка, $\mathscr{H}$ је транслација, а остатак доказа је исти.
Лема. Нека произвољна права $p$ кроз $D_{1}$ сече круг $\Omega$ у тачкама $L$ и $K$. Тангенте у $L$ и $K$ на $\Omega$ секу праву $B C$ редом у тачкама $P$ и $Q$. Тада је $\varangle P A B=\varangle C A Q$.
Доказ. Означимо $\varangle B A C=\alpha, \varangle C B A=\beta, \varangle A C B=\gamma, \varangle P A B=x$ и $\varangle C A Q=y$.
Ако је $D_{1}$ бесконачна тачка, тврђење је тривијално по симетрији. Ако није, из $\triangle P B L \sim \triangle P L C$ следи $\frac{P B}{P L}=\frac{P L}{P C}=\frac{L B}{L C}$ и одатле $\frac{P B}{P C}=\left(\frac{L B}{L C}\right)^{2}$. Слично je $\frac{Q B}{Q C}=\left(\frac{K B}{K C}\right)^{2}$. Пошто је $\frac{L B}{L C} \cdot \frac{K B}{K C}=\frac{\mid K L B]}{\mid K L C]}=\frac{D_{1} B}{D_{1} C}=\frac{A B}{A C}$, добијамо $\frac{P B}{P C} \cdot \frac{Q B}{Q C}=\left(\frac{A B}{A C}\right)^{2}$. Како је $\frac{P B}{P C}=\frac{P B}{P A} \cdot \frac{P A}{P C}=\frac{\sin x}{\sin \beta} \cdot \frac{\sin \gamma}{\sin (\alpha+x)}$ и $\frac{Q B}{Q C}=\frac{Q B}{Q A} \cdot \frac{Q A}{Q C}=\frac{\sin (\alpha+y)}{\sin \beta} \cdot \frac{\sin \gamma}{\sin y}$, множење даје $\left(\frac{\sin \gamma}{\sin \beta}\right)^{2} \cdot \frac{\sin (\alpha+y) / \sin y}{\sin (\alpha+x) / \sin x}=\left(\frac{A C}{A B}\right)^{2}=\left(\frac{\sin \gamma}{\sin \beta}\right)^{2}$, одакле је $\sin \alpha \operatorname{ctg} y+\cos \alpha=\frac{\sin (\alpha+y)}{\sin y}=$ $\frac{\sin (\alpha+x)}{\sin x}=\sin \alpha \operatorname{ctg} x+\cos \alpha$, тј. $x=y$.
Ако су $K$ и $L$ додирне тачке заједничких тангенти са $\Omega$, остаје да се покаже да тачка $D_{1}$ лежи на правој $K L$, тј. на полари тачке $T$ у односу на $\Omega$. По ставу о полу и полари, довољно је доказати да $T$ лежи на полари $d$ тачке $D_{1}$ у односу на $\Omega$.
Означимо са $N$ средиште лука $B A C$ круга $\Omega$. Слика тачке $D$ при хомотетији $\mathscr{H}$ је пресек $S$ тангенти на $\Omega$ у тачкама $A$ и $N$, па тачка $T$ лежи на правој $D S$. С друге стране, тачка $D$ је на полари $d$ јер је четворка $\left(B, C ; D_{1}, D\right)$ хармонијска, а тачка $S$ је
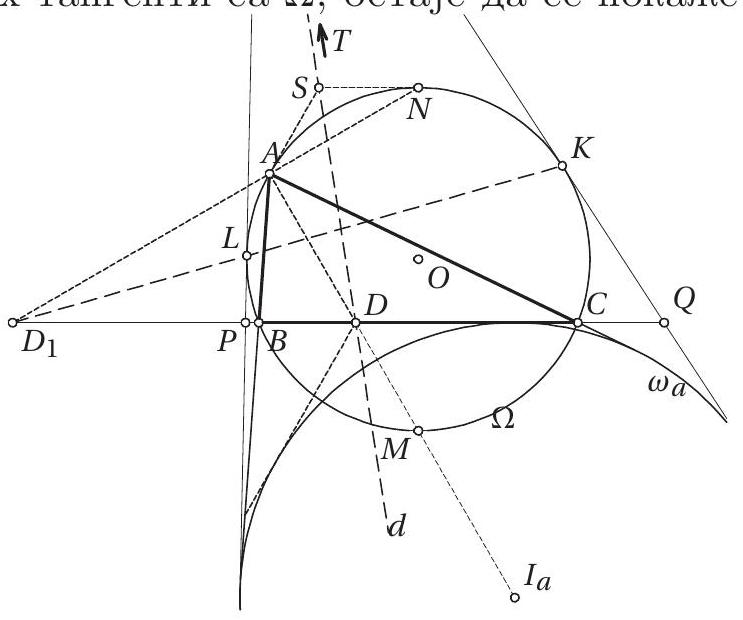
такође на $d$ јер полара тачке $S$ у односу на $\Omega$, што је права $A N$, садржи тачку $D_{1}$. Према томе, праве $D S$ и $d$ се поклапају, чиме је доказ завршен.
Друго решење. Нека заједничке тангенте додирују круг $\Omega$ у тачкама $K$ и $L$, при чему је теме $L P$ тангента ближа темену $B$. Означимо са $M$ средиште оног лука $B C$ који не садржи тачку $A$, а са $O$ и $I_{a}$ редом центре описаног и приписаног круга наспрам $A$.
Како је $\varangle L P I_{a}=90^{\circ}+\frac{1}{2} \varangle L P C$ и $\varangle L A I_{a}=\varangle L A M=\frac{1}{2} \varangle L O M=\frac{1}{2} \varangle L P D_{1}=90^{\circ}-\frac{1}{2} \varangle L P C$, следи да је $\varangle L P I_{a}+\varangle L A I_{a}=180^{\circ}$, па је четвороугао $A L P I_{a}$ тетиван. Слично, и четвороугао $A K Q I_{a}$ је тетиван. Сада имамо $\varangle P A I_{a}=\varangle P L I_{a}=\varangle Q K I_{a}=\varangle Q A I_{a}$, јер су углови $P L I_{a}$ и $Q K I_{a}$ симетрични у односу на праву $O I_{a}$, а одавде је $\varangle P A B=\varangle Q A C$.
|
{
"resource_path": "Serbia_MO/segmented/sr-2017_smo_resenja.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n6. "
}
|
47b76235-2020-5360-82c3-7c53f32ce28c
| 608,113
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.