problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $p>2$ be a prime number and $1+\frac{1}{2^{3}}+\frac{1}{3^{3}}+\cdots+\frac{1}{(p-1)^{3}}=\frac{m}{n}$ where $m$ and $n$ are relatively prime. Show that $m$ is a multiple of $p$.
|
The sum has an even number of terms; they can be joined in pairs in such a way that the sum is the sum of the terms
$$
\frac{1}{k^{3}}+\frac{1}{(p-k)^{3}}=\frac{p^{3}-3 p^{2} k+3 p k^{2}}{k^{3}(p-k)^{3}} .
$$
The sum of all terms of this type has a denominator in which every prime factor is less than $p$ while the numerator has $p$ as a factor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>2$ be a prime number and $1+\frac{1}{2^{3}}+\frac{1}{3^{3}}+\cdots+\frac{1}{(p-1)^{3}}=\frac{m}{n}$ where $m$ and $n$ are relatively prime. Show that $m$ is a multiple of $p$.
|
The sum has an even number of terms; they can be joined in pairs in such a way that the sum is the sum of the terms
$$
\frac{1}{k^{3}}+\frac{1}{(p-k)^{3}}=\frac{p^{3}-3 p^{2} k+3 p k^{2}}{k^{3}(p-k)^{3}} .
$$
The sum of all terms of this type has a denominator in which every prime factor is less than $p$ while the numerator has $p$ as a factor.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\nSolution."
}
|
ccd0b4fc-8df9-5ee0-a860-ca1ec8ce82ab
| 241,342
|
Show that for any integer $a \geq 5$ there exist integers $b$ and $c, c \geq b \geq a$, such that $a, b, c$ are the lengths of the sides of a right-angled triangle.
|
We first show this for odd numbers $a=2 i+1 \geq 3$. Put $c=2 k+1$ and $b=2 k$. Then $c^{2}-b^{2}=(2 k+1)^{2}-(2 k)^{2}=4 k+1=a^{2}$. Now $a=2 i+1$ and thus $a^{2}=4 i^{2}+4 i+1$ and $k=i^{2}+i$. Furthermore, $c>b=2 i^{2}+2 i>2 i+1=a$.
Since any multiple of a Pythagorean triple (i.e., a triple of integers $(x, y, z)$ such that $x^{2}+y^{2}=z^{2}$ ) is also a Pythagorean triple we see that the statement is also true for all even numbers which have an odd factor. Hence only the powers of 2 remain. But for 8 we have the triple $(8,15,17)$ and hence all higher powers of 2 are also minimum values of such a triple.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that for any integer $a \geq 5$ there exist integers $b$ and $c, c \geq b \geq a$, such that $a, b, c$ are the lengths of the sides of a right-angled triangle.
|
We first show this for odd numbers $a=2 i+1 \geq 3$. Put $c=2 k+1$ and $b=2 k$. Then $c^{2}-b^{2}=(2 k+1)^{2}-(2 k)^{2}=4 k+1=a^{2}$. Now $a=2 i+1$ and thus $a^{2}=4 i^{2}+4 i+1$ and $k=i^{2}+i$. Furthermore, $c>b=2 i^{2}+2 i>2 i+1=a$.
Since any multiple of a Pythagorean triple (i.e., a triple of integers $(x, y, z)$ such that $x^{2}+y^{2}=z^{2}$ ) is also a Pythagorean triple we see that the statement is also true for all even numbers which have an odd factor. Hence only the powers of 2 remain. But for 8 we have the triple $(8,15,17)$ and hence all higher powers of 2 are also minimum values of such a triple.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution."
}
|
5402fa9f-4728-5908-b439-0df5338ad06d
| 241,349
|
The inscribed circle of the triangle $A_{1} A_{2} A_{3}$ touches the sides $A_{2} A_{3}, A_{3} A_{1}$ and $A_{1} A_{2}$ at points $S_{1}, S_{2}, S_{3}$, respectively. Let $O_{1}, O_{2}, O_{3}$ be the centres of the inscribed circles of triangles $A_{1} S_{2} S_{3}, A_{2} S_{3} S_{1}$ and $A_{3} S_{1} S_{2}$, respectively. Prove that the straight lines $O_{1} S_{1}, O_{2} S_{2}$ and $O_{3} S_{3}$ intersect at one point.
|
We shall prove that the lines $S_{1} O_{1}, S_{2} O_{2}, S_{3} O_{3}$ are the bisectors of the angles of the triangle $S_{1} S_{2} S_{3}$. Let $O$ and $r$ be the centre and radius of the inscribed circle $C$ of the triangle $A_{1} A_{2} A_{3}$. Further, let $P_{1}$ and $H_{1}$ be the points where the inscribed circle of the triangle $A_{1} S_{2} S_{3}$ (with the centre $O_{1}$ and radius $r_{1}$ ) touches its sides $A_{1} S_{2}$ and $S_{2} S_{3}$, respectively (see Figure 2). To show that $S_{1} O_{1}$ is the bisector of the angle $\angle S_{3} S_{1} S_{2}$ it is sufficient to prove that $O_{1}$ lies on the circumference of circle $C$, for in this case the arcs $O_{1} S_{2}$ and $O_{1} S_{3}$ will obviously be equal. To prove this, first note that as $A_{1} S_{2} S_{3}$ is an isosceles triangle the point $H_{1}$, as well as $O_{1}$, lies on the straight line $A_{1} O$. Now, it suffices to show that $\left|O H_{1}\right|=r-r_{1}$. Indeed, we have
$$
\begin{aligned}
& \frac{r-r_{1}}{r}=1-\frac{r_{1}}{r}=1-\frac{\left|O_{1} P_{1}\right|}{\left|O S_{2}\right|}=1-\frac{\left|P_{1} A_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|S_{2} A_{1}\right|-\left|P_{1} A_{1}\right|}{\left|S_{2} A_{1}\right|} \\
& =\frac{\left|S_{2} P_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|S_{2} H_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|O H_{1}\right|}{\left|O S_{2}\right|}=\frac{\left|O H_{1}\right|}{r} .
\end{aligned}
$$
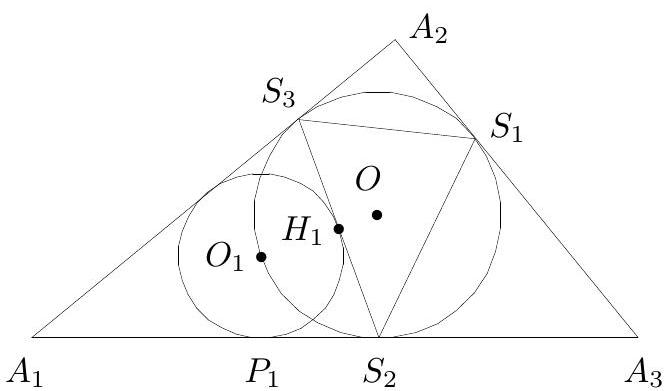
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The inscribed circle of the triangle $A_{1} A_{2} A_{3}$ touches the sides $A_{2} A_{3}, A_{3} A_{1}$ and $A_{1} A_{2}$ at points $S_{1}, S_{2}, S_{3}$, respectively. Let $O_{1}, O_{2}, O_{3}$ be the centres of the inscribed circles of triangles $A_{1} S_{2} S_{3}, A_{2} S_{3} S_{1}$ and $A_{3} S_{1} S_{2}$, respectively. Prove that the straight lines $O_{1} S_{1}, O_{2} S_{2}$ and $O_{3} S_{3}$ intersect at one point.
|
We shall prove that the lines $S_{1} O_{1}, S_{2} O_{2}, S_{3} O_{3}$ are the bisectors of the angles of the triangle $S_{1} S_{2} S_{3}$. Let $O$ and $r$ be the centre and radius of the inscribed circle $C$ of the triangle $A_{1} A_{2} A_{3}$. Further, let $P_{1}$ and $H_{1}$ be the points where the inscribed circle of the triangle $A_{1} S_{2} S_{3}$ (with the centre $O_{1}$ and radius $r_{1}$ ) touches its sides $A_{1} S_{2}$ and $S_{2} S_{3}$, respectively (see Figure 2). To show that $S_{1} O_{1}$ is the bisector of the angle $\angle S_{3} S_{1} S_{2}$ it is sufficient to prove that $O_{1}$ lies on the circumference of circle $C$, for in this case the arcs $O_{1} S_{2}$ and $O_{1} S_{3}$ will obviously be equal. To prove this, first note that as $A_{1} S_{2} S_{3}$ is an isosceles triangle the point $H_{1}$, as well as $O_{1}$, lies on the straight line $A_{1} O$. Now, it suffices to show that $\left|O H_{1}\right|=r-r_{1}$. Indeed, we have
$$
\begin{aligned}
& \frac{r-r_{1}}{r}=1-\frac{r_{1}}{r}=1-\frac{\left|O_{1} P_{1}\right|}{\left|O S_{2}\right|}=1-\frac{\left|P_{1} A_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|S_{2} A_{1}\right|-\left|P_{1} A_{1}\right|}{\left|S_{2} A_{1}\right|} \\
& =\frac{\left|S_{2} P_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|S_{2} H_{1}\right|}{\left|S_{2} A_{1}\right|}=\frac{\left|O H_{1}\right|}{\left|O S_{2}\right|}=\frac{\left|O H_{1}\right|}{r} .
\end{aligned}
$$

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution."
}
|
31b81d50-000b-515a-8710-862c8d059135
| 241,388
|
Let $\alpha, \beta, \gamma$ be the angles of a triangle opposite to its sides with lengths $a, b$ and $c$, respectively. Prove the inequality
$$
a \cdot\left(\frac{1}{\beta}+\frac{1}{\gamma}\right)+b \cdot\left(\frac{1}{\gamma}+\frac{1}{\alpha}\right)+c \cdot\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \geq 2 \cdot\left(\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma}\right) \cdot
$$
|
Clearly, the inequality $a>b$ implies $\alpha>\beta$ and similarly $a<b$ implies $\alpha<\beta$, hence $(a-b)(\alpha-\beta) \geq$ 0 and $a \alpha+b \beta \geq a \beta+b \alpha$. Dividing the last equality by $\alpha \beta$ we get
$$
\frac{a}{\beta}+\frac{b}{\alpha} \geq \frac{a}{\alpha}+\frac{b}{\beta}
$$
Similarly we get
$$
\frac{a}{\gamma}+\frac{c}{\alpha} \geq \frac{a}{\alpha}+\frac{c}{\gamma}
$$
and
$$
\frac{b}{\gamma}+\frac{c}{\beta} \geq \frac{b}{\beta}+\frac{c}{\gamma}
$$
To finish the proof it suffices to add the inequalities (6)-(8).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\alpha, \beta, \gamma$ be the angles of a triangle opposite to its sides with lengths $a, b$ and $c$, respectively. Prove the inequality
$$
a \cdot\left(\frac{1}{\beta}+\frac{1}{\gamma}\right)+b \cdot\left(\frac{1}{\gamma}+\frac{1}{\alpha}\right)+c \cdot\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \geq 2 \cdot\left(\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma}\right) \cdot
$$
|
Clearly, the inequality $a>b$ implies $\alpha>\beta$ and similarly $a<b$ implies $\alpha<\beta$, hence $(a-b)(\alpha-\beta) \geq$ 0 and $a \alpha+b \beta \geq a \beta+b \alpha$. Dividing the last equality by $\alpha \beta$ we get
$$
\frac{a}{\beta}+\frac{b}{\alpha} \geq \frac{a}{\alpha}+\frac{b}{\beta}
$$
Similarly we get
$$
\frac{a}{\gamma}+\frac{c}{\alpha} \geq \frac{a}{\alpha}+\frac{c}{\gamma}
$$
and
$$
\frac{b}{\gamma}+\frac{c}{\beta} \geq \frac{b}{\beta}+\frac{c}{\gamma}
$$
To finish the proof it suffices to add the inequalities (6)-(8).
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution."
}
|
cd74a12f-736a-5442-a485-db25dfb2c2ca
| 241,408
|
The Wonder Island is inhabited by Hedgehogs. Each Hedgehog consists of three segments of unit length having a common endpoint, with all three angles between them equal to $120^{\circ}$ (see Figure 3). Given that all Hedgehogs are lying flat on the island and no two of them touch each other, prove that there is a finite number of Hedgehogs on Wonder Island.
|
It suffices to prove that if the distance between the centres of two Hedgehogs is less than 0.2, then these Hedgehogs intersect. To show this, consider two Hedgehogs with their centres at points $O$ and $M$, respectively, such that $|O M|<0.2$. Let $A, B$ and $C$ be the endpoints of the needles of the first Hedgehog (see Figure 4) and draw a straight line $l$ parallel to $A C$ through the point $M$. As $|A C|=\sqrt{3}$ implies $|K L| \leq$ $\frac{0.2}{0.5}|A C|<1$ and the second Hedgehog has at least one of its needles pointing inside the triangle $O K L$, this needle intersects the first Hedgehog.
Remark. If the Hedgehogs can move their needles so that the angles between them can take any positive value then there can be an infinite number of Hedgehogs on the Wonder Island.
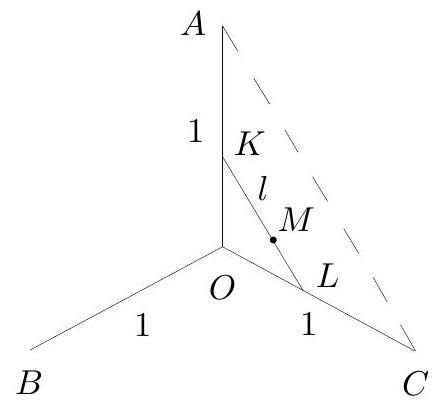
Figure 4
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The Wonder Island is inhabited by Hedgehogs. Each Hedgehog consists of three segments of unit length having a common endpoint, with all three angles between them equal to $120^{\circ}$ (see Figure 3). Given that all Hedgehogs are lying flat on the island and no two of them touch each other, prove that there is a finite number of Hedgehogs on Wonder Island.
|
It suffices to prove that if the distance between the centres of two Hedgehogs is less than 0.2, then these Hedgehogs intersect. To show this, consider two Hedgehogs with their centres at points $O$ and $M$, respectively, such that $|O M|<0.2$. Let $A, B$ and $C$ be the endpoints of the needles of the first Hedgehog (see Figure 4) and draw a straight line $l$ parallel to $A C$ through the point $M$. As $|A C|=\sqrt{3}$ implies $|K L| \leq$ $\frac{0.2}{0.5}|A C|<1$ and the second Hedgehog has at least one of its needles pointing inside the triangle $O K L$, this needle intersects the first Hedgehog.
Remark. If the Hedgehogs can move their needles so that the angles between them can take any positive value then there can be an infinite number of Hedgehogs on the Wonder Island.

Figure 4
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\nSolution."
}
|
a5e929dc-8b5f-5ff4-8146-017334d56dd7
| 241,429
|
There are $n$ lines $(n>2)$ given in the plane. No two of the lines are parallel and no three of them intersect at one point. Every point of intersection of these lines is labelled with a natural number between 1 and $n-1$. Prove that, if and only if $n$ is even, it is possible to assign the labels in such a way that every line has all the numbers from 1 to $n-1$ at its points of intersection with the other $n-1$ lines.
|
Suppose we have assigned the labels in the required manner. When a point has label 1 then there can be no more occurrences of label 1 on the two lines that intersect at that point. Therefore the number of intersection points labelled with 1 has to be exactly $\frac{n}{2}$, and so $n$ must be even. Now, let $n$ be an even number and denote the $n$ lines by $l_{1}, l_{2}, \ldots, l_{n}$. First write the lines $l_{i}$ in the following table:
$$
\begin{array}{llllll}
& & l_{3} & l_{4} & \ldots & l_{n / 2+1} \\
l_{1} & l_{2} & & & & \\
& & l_{n} & l_{n-1} & \ldots & l_{n / 2+2}
\end{array}
$$
and then rotate the picture $n-1$ times:
$$
\begin{array}{llllll}
& & l_{2} & l_{3} & \ldots & l_{n / 2} \\
l_{1} & l_{n} & l_{n-1} & l_{n-2} & \ldots & l_{n / 2+1} \\
& & & & & \\
& & l_{n} & l_{2} & \ldots & l_{n / 2-1} \\
l_{1} & l_{n-1} & & & & l_{n / 2}
\end{array}
$$
etc.
According to these tables, we can join the lines in pairs in $n-1$ different ways $-l_{1}$ with the line next to it and every other line with the line directly above or under it. Now we can assign the label $i$ to all the intersection points of the pairs of lines shown in the $i$ th table.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $n$ lines $(n>2)$ given in the plane. No two of the lines are parallel and no three of them intersect at one point. Every point of intersection of these lines is labelled with a natural number between 1 and $n-1$. Prove that, if and only if $n$ is even, it is possible to assign the labels in such a way that every line has all the numbers from 1 to $n-1$ at its points of intersection with the other $n-1$ lines.
|
Suppose we have assigned the labels in the required manner. When a point has label 1 then there can be no more occurrences of label 1 on the two lines that intersect at that point. Therefore the number of intersection points labelled with 1 has to be exactly $\frac{n}{2}$, and so $n$ must be even. Now, let $n$ be an even number and denote the $n$ lines by $l_{1}, l_{2}, \ldots, l_{n}$. First write the lines $l_{i}$ in the following table:
$$
\begin{array}{llllll}
& & l_{3} & l_{4} & \ldots & l_{n / 2+1} \\
l_{1} & l_{2} & & & & \\
& & l_{n} & l_{n-1} & \ldots & l_{n / 2+2}
\end{array}
$$
and then rotate the picture $n-1$ times:
$$
\begin{array}{llllll}
& & l_{2} & l_{3} & \ldots & l_{n / 2} \\
l_{1} & l_{n} & l_{n-1} & l_{n-2} & \ldots & l_{n / 2+1} \\
& & & & & \\
& & l_{n} & l_{2} & \ldots & l_{n / 2-1} \\
l_{1} & l_{n-1} & & & & l_{n / 2}
\end{array}
$$
etc.
According to these tables, we can join the lines in pairs in $n-1$ different ways $-l_{1}$ with the line next to it and every other line with the line directly above or under it. Now we can assign the label $i$ to all the intersection points of the pairs of lines shown in the $i$ th table.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution."
}
|
dfac03f5-ea5d-55c7-9e05-d78dbdafa5a8
| 241,447
|
The Wonder Island Intelligence Service has 16 spies in Tartu. Each of them watches on some of his colleagues. It is known that if spy $A$ watches on spy $B$ then $B$ does not watch on $A$. Moreover, any 10 spies can be numbered in such a way that the first spy watches on the second, the second watches on the third, .., the tenth watches on the first. Prove that any 11 spies can also be numbered in a similar manner.
|
We call two spies $A$ and $B$ neutral to each other if neither $A$ watches on $B$ nor $B$ watches on $A$.
Denote the spies $A_{1}, A_{2}, \ldots, A_{16}$. Let $a_{i}, b_{i}$ and $c_{i}$ denote the number of spies that watch on $A_{i}$, the number of that are watched by $A_{i}$ and the number of spies neutral to $A_{i}$, respectively. Clearly, we have
$$
\begin{aligned}
a_{i}+b_{i}+c_{i} & =15, \\
a_{i}+c_{i} & \leq 8, \\
b_{i}+c_{i} & \leq 8
\end{aligned}
$$
for any $i=1, \ldots, 16$ (if any of the last two inequalities does not hold then there exist 10 spies who cannot be numbered in the required manner). Combining the relations above we find $c_{i} \leq 1$. Hence, for any spy, the number of his neutral colleagues is 0 or 1 .
Now suppose there is a group of 11 spies that cannot be numbered as required. Let $B$ be an arbitrary spy in this group. Number the other 10 spies as $C_{1}, C_{2}, \ldots, C_{10}$ so that $C_{1}$ watches on $C_{2}, \ldots, C_{10}$ watches on $C_{1}$. Suppose there is no spy neutral to $B$ among $C_{1}, \ldots, C_{10}$. Then, if $C_{1}$ watches on $B$ then $B$ cannot watch on $C_{2}$, as otherwise $C_{1}, B, C_{2}, \ldots, C_{10}$ would form an 11-cycle. So $C_{2}$ watches on $B$, etc. As some of the spies $C_{1}, C_{2}, \ldots, C_{10}$ must watch on $B$ we get all of them watching on $B$, a contradiction. Therefore, each of the 11 spies must have exactly one spy neutral to him among the other 10 - but this is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The Wonder Island Intelligence Service has 16 spies in Tartu. Each of them watches on some of his colleagues. It is known that if spy $A$ watches on spy $B$ then $B$ does not watch on $A$. Moreover, any 10 spies can be numbered in such a way that the first spy watches on the second, the second watches on the third, .., the tenth watches on the first. Prove that any 11 spies can also be numbered in a similar manner.
|
We call two spies $A$ and $B$ neutral to each other if neither $A$ watches on $B$ nor $B$ watches on $A$.
Denote the spies $A_{1}, A_{2}, \ldots, A_{16}$. Let $a_{i}, b_{i}$ and $c_{i}$ denote the number of spies that watch on $A_{i}$, the number of that are watched by $A_{i}$ and the number of spies neutral to $A_{i}$, respectively. Clearly, we have
$$
\begin{aligned}
a_{i}+b_{i}+c_{i} & =15, \\
a_{i}+c_{i} & \leq 8, \\
b_{i}+c_{i} & \leq 8
\end{aligned}
$$
for any $i=1, \ldots, 16$ (if any of the last two inequalities does not hold then there exist 10 spies who cannot be numbered in the required manner). Combining the relations above we find $c_{i} \leq 1$. Hence, for any spy, the number of his neutral colleagues is 0 or 1 .
Now suppose there is a group of 11 spies that cannot be numbered as required. Let $B$ be an arbitrary spy in this group. Number the other 10 spies as $C_{1}, C_{2}, \ldots, C_{10}$ so that $C_{1}$ watches on $C_{2}, \ldots, C_{10}$ watches on $C_{1}$. Suppose there is no spy neutral to $B$ among $C_{1}, \ldots, C_{10}$. Then, if $C_{1}$ watches on $B$ then $B$ cannot watch on $C_{2}$, as otherwise $C_{1}, B, C_{2}, \ldots, C_{10}$ would form an 11-cycle. So $C_{2}$ watches on $B$, etc. As some of the spies $C_{1}, C_{2}, \ldots, C_{10}$ must watch on $B$ we get all of them watching on $B$, a contradiction. Therefore, each of the 11 spies must have exactly one spy neutral to him among the other 10 - but this is impossible.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution."
}
|
27ac5167-065a-52d1-abf5-b236f6279960
| 606,430
|
An equilateral triangle is divided into 9000000 congruent equilateral triangles by lines parallel to its sides. Each vertex of the small triangles is coloured in one of three colours. Prove that there exist three points of the same colour being the vertices of a triangle with its sides parallel to the sides of the original triangle.
|
Consider the side $A B$ of the big triangle $A B C$ as "horizontal" and suppose the statement of the problem does not hold. The side $A B$ contains 3001 vertices $A=A_{0}, A_{1}, \ldots, A_{3000}=B$ of 3 colours. Hence, there are at least 1001 vertices of one colour, e.g., red. For any two red vertices $A_{k}$ and $A_{n}$ there exists a unique vertex $B_{k n}$ such that the triangle $B_{k n} A_{k} A_{n}$ is equilateral. That vertex $B_{k n}$ cannot be red. For different pairs $(k, n)$ the corresponding vertices $B_{k n}$ are different, so we have at least $\left(\begin{array}{c}1001 \\ 2\end{array}\right)>500000$ vertices of type $B_{k n}$ that cannot be red. As all these vertices are situated on 3000 horizontal lines, there exists a line $L$ which contains more than 160 vertices of type $B_{k n}$, each of them coloured in one of the two remaining colours. Hence there exist at least 81 vertices of the same colour, e.g., blue, on line $L$. For every two blue vertices $B_{k n}$ and $B_{m l}$ on line $L$ there exists a unique vertex $C_{k n m l}$ such that:
(i) $C_{k n m l}$ lies above the line $L$;
(ii) The triangle $C_{k n m l} B_{k n} B_{m l}$ is equilateral;
(iii) $C_{k n m l}=B_{p q}$ where $p=\min (k, m)$ and $q=\max (n, l)$.
Different pairs of vertices $B_{k n}$ belonging to line $L$ define different vertices $C_{k n m l}$. So we have at least $\left(\begin{array}{c}81 \\ 2\end{array}\right)>3200$ vertices of type $C_{k n m l}$ that can be neither blue nor red. As the number of these vertices exceeds the number of horizontal lines, there must be two vertices $C_{k n m l}$ and $C_{p q r s}$ on one horizontal line. Now, these two vertices define a new vertex $D_{\text {knmlpqrs }}$ that cannot have any of the three colours, a contradiction.
Remark. The minimal size of the big triangle that can be handled by this proof is 2557 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An equilateral triangle is divided into 9000000 congruent equilateral triangles by lines parallel to its sides. Each vertex of the small triangles is coloured in one of three colours. Prove that there exist three points of the same colour being the vertices of a triangle with its sides parallel to the sides of the original triangle.
|
Consider the side $A B$ of the big triangle $A B C$ as "horizontal" and suppose the statement of the problem does not hold. The side $A B$ contains 3001 vertices $A=A_{0}, A_{1}, \ldots, A_{3000}=B$ of 3 colours. Hence, there are at least 1001 vertices of one colour, e.g., red. For any two red vertices $A_{k}$ and $A_{n}$ there exists a unique vertex $B_{k n}$ such that the triangle $B_{k n} A_{k} A_{n}$ is equilateral. That vertex $B_{k n}$ cannot be red. For different pairs $(k, n)$ the corresponding vertices $B_{k n}$ are different, so we have at least $\left(\begin{array}{c}1001 \\ 2\end{array}\right)>500000$ vertices of type $B_{k n}$ that cannot be red. As all these vertices are situated on 3000 horizontal lines, there exists a line $L$ which contains more than 160 vertices of type $B_{k n}$, each of them coloured in one of the two remaining colours. Hence there exist at least 81 vertices of the same colour, e.g., blue, on line $L$. For every two blue vertices $B_{k n}$ and $B_{m l}$ on line $L$ there exists a unique vertex $C_{k n m l}$ such that:
(i) $C_{k n m l}$ lies above the line $L$;
(ii) The triangle $C_{k n m l} B_{k n} B_{m l}$ is equilateral;
(iii) $C_{k n m l}=B_{p q}$ where $p=\min (k, m)$ and $q=\max (n, l)$.
Different pairs of vertices $B_{k n}$ belonging to line $L$ define different vertices $C_{k n m l}$. So we have at least $\left(\begin{array}{c}81 \\ 2\end{array}\right)>3200$ vertices of type $C_{k n m l}$ that can be neither blue nor red. As the number of these vertices exceeds the number of horizontal lines, there must be two vertices $C_{k n m l}$ and $C_{p q r s}$ on one horizontal line. Now, these two vertices define a new vertex $D_{\text {knmlpqrs }}$ that cannot have any of the three colours, a contradiction.
Remark. The minimal size of the big triangle that can be handled by this proof is 2557 .
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution."
}
|
4042eea9-53e4-5c5d-8eab-483fbc97c2a7
| 241,467
|
The positive integers $a, b, c$ are pairwise relatively prime, $a$ and $c$ are odd and the numbers satisfy the equation $a^{2}+b^{2}=c^{2}$. Prove that $b+c$ is a square of an integer.
|
Since $a$ and $c$ are odd, $b$ must be even. We have $a^{2}=c^{2}-b^{2}=(c+b)(c-b)$. Let $d=\operatorname{gcd}(c+b, c-b)$. Then $d$ divides $(c+b)+(c-b)=2 c$ and $(c+b)-(c-b)=2 b$. Since $c+b$ and $c-b$ are odd, $d$ is odd, and hence $d$ divides both $b$ and $c$. But $b$ and $c$ are relatively prime, so $d=1$, i.e., $c+b$ and $c-b$ are also relatively prime. Since $(c+b)(c-b)=a^{2}$ is a square, it follows that $c+b$ and $c-b$ are also squares. In particular, $b+c$ is a square as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The positive integers $a, b, c$ are pairwise relatively prime, $a$ and $c$ are odd and the numbers satisfy the equation $a^{2}+b^{2}=c^{2}$. Prove that $b+c$ is a square of an integer.
|
Since $a$ and $c$ are odd, $b$ must be even. We have $a^{2}=c^{2}-b^{2}=(c+b)(c-b)$. Let $d=\operatorname{gcd}(c+b, c-b)$. Then $d$ divides $(c+b)+(c-b)=2 c$ and $(c+b)-(c-b)=2 b$. Since $c+b$ and $c-b$ are odd, $d$ is odd, and hence $d$ divides both $b$ and $c$. But $b$ and $c$ are relatively prime, so $d=1$, i.e., $c+b$ and $c-b$ are also relatively prime. Since $(c+b)(c-b)=a^{2}$ is a square, it follows that $c+b$ and $c-b$ are also squares. In particular, $b+c$ is a square as required.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
b1dc5ac1-21b2-5fbf-88db-a923031cfa7e
| 241,496
|
Let $a<b<c$ be three positive integers. Prove that among any $2 c$ consecutive positive integers there exist three different numbers $x, y, z$ such that $a b c$ divides $x y z$.
|
First we show that among any $b$ consecutive numbers there are two different numbers $x$ and $y$ such that $a b$ divides $x y$. Among the $b$ consecutive numbers there is clearly a number $x^{\prime}$ divisible by $b$, and a number $y^{\prime}$ divisible by $a$. If $x^{\prime} \neq y^{\prime}$, we can take $x=x^{\prime}$ and $y=y^{\prime}$, and we are done. Now assume that $x^{\prime}=y^{\prime}$. Then $x^{\prime}$ is divisible by $e$, the least common multiple of $a$ and $b$. Let $d=\operatorname{gcd}(a, b)$. As $a<b$, we have $d \leq \frac{1}{2} b$. Hence there is a number $z^{\prime} \neq x^{\prime}$ among the $b$ consecutive numbers such that $z^{\prime}$ is divisible by $d$. Hence $x^{\prime} z^{\prime}$ is divisible by $d e$. But $d e=a b$, so we can take $x=x^{\prime}$ and $y=z^{\prime}$.
Now divide the $2 c$ consecutive numbers into two groups of $c$ consecutive numbers. In the first group, by the above reasoning, there exist distinct numbers $x$ and $y$ such that $a b$ divides $x y$. The second group contains a number $z$ divisible by $c$. Then $a b c$ divides $x y z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a<b<c$ be three positive integers. Prove that among any $2 c$ consecutive positive integers there exist three different numbers $x, y, z$ such that $a b c$ divides $x y z$.
|
First we show that among any $b$ consecutive numbers there are two different numbers $x$ and $y$ such that $a b$ divides $x y$. Among the $b$ consecutive numbers there is clearly a number $x^{\prime}$ divisible by $b$, and a number $y^{\prime}$ divisible by $a$. If $x^{\prime} \neq y^{\prime}$, we can take $x=x^{\prime}$ and $y=y^{\prime}$, and we are done. Now assume that $x^{\prime}=y^{\prime}$. Then $x^{\prime}$ is divisible by $e$, the least common multiple of $a$ and $b$. Let $d=\operatorname{gcd}(a, b)$. As $a<b$, we have $d \leq \frac{1}{2} b$. Hence there is a number $z^{\prime} \neq x^{\prime}$ among the $b$ consecutive numbers such that $z^{\prime}$ is divisible by $d$. Hence $x^{\prime} z^{\prime}$ is divisible by $d e$. But $d e=a b$, so we can take $x=x^{\prime}$ and $y=z^{\prime}$.
Now divide the $2 c$ consecutive numbers into two groups of $c$ consecutive numbers. In the first group, by the above reasoning, there exist distinct numbers $x$ and $y$ such that $a b$ divides $x y$. The second group contains a number $z$ divisible by $c$. Then $a b c$ divides $x y z$.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
06f231d7-8ed3-5d8c-81dd-1274feb8cfc5
| 241,515
|
Prove that for positive $a, b, c, d$
$$
\frac{a+c}{a+b}+\frac{b+d}{b+c}+\frac{c+a}{c+d}+\frac{d+b}{d+a} \geq 4 .
$$
|
The inequality between the arithmetic and harmonic mean gives
$$
\begin{aligned}
& \frac{a+c}{a+b}+\frac{c+a}{c+d} \geq \frac{4}{\frac{a+b}{a+c}+\frac{c+d}{c+a}}=4 \cdot \frac{a+c}{a+b+c+d} \\
& \frac{b+d}{b+c}+\frac{d+b}{d+a} \geq \frac{4}{\frac{b+c}{b+d}+\frac{d+a}{d+b}}=4 \cdot \frac{b+d}{a+b+c+d}
\end{aligned}
$$
and adding these inequalities yields the required inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for positive $a, b, c, d$
$$
\frac{a+c}{a+b}+\frac{b+d}{b+c}+\frac{c+a}{c+d}+\frac{d+b}{d+a} \geq 4 .
$$
|
The inequality between the arithmetic and harmonic mean gives
$$
\begin{aligned}
& \frac{a+c}{a+b}+\frac{c+a}{c+d} \geq \frac{4}{\frac{a+b}{a+c}+\frac{c+d}{c+a}}=4 \cdot \frac{a+c}{a+b+c+d} \\
& \frac{b+d}{b+c}+\frac{d+b}{d+a} \geq \frac{4}{\frac{b+c}{b+d}+\frac{d+a}{d+b}}=4 \cdot \frac{b+d}{a+b+c+d}
\end{aligned}
$$
and adding these inequalities yields the required inequality.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution."
}
|
082e98b4-ac1d-52f3-bcbc-8f177a2e4019
| 241,525
|
Prove that
$$
\frac{1995}{2}-\frac{1994}{3}+\frac{1993}{4}-\cdots-\frac{2}{1995}+\frac{1}{1996}=\frac{1}{999}+\frac{3}{1000}+\cdots+\frac{1995}{1996} .
$$
|
Denote the left-hand side of the equation by $L$, and the right-hand side by $R$. Then
$$
\begin{aligned}
L & =\sum_{k=1}^{1996}(-1)^{k+1}\left(\frac{1997}{k+1}-1\right)=1997 \cdot \sum_{k=1}^{1996}(-1)^{k+1} \cdot \frac{1}{k+1}=1997 \cdot \sum_{k=1}^{1996}(-1)^{k} \cdot \frac{1}{k}+1996, \\
R & =\sum_{k=1}^{998}\left(\frac{2 k+1996}{998+k}-\frac{1997}{998+k}\right)=1996-1997 \cdot \sum_{k=1}^{998} \frac{1}{k+998} .
\end{aligned}
$$
We must verify that $\sum_{k=1}^{1996}(-1)^{k-1} \cdot \frac{1}{k}=\sum_{k=1}^{998} \frac{1}{k+998}$. But this follows from the calculation
$$
\sum_{k=1}^{1996}(-1)^{k-1} \cdot \frac{1}{k}=\sum_{k=1}^{1996} \frac{1}{k}-2 \cdot \sum_{k=1}^{998} \frac{1}{2 k}=\sum_{k=1}^{998} \frac{1}{k+998}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that
$$
\frac{1995}{2}-\frac{1994}{3}+\frac{1993}{4}-\cdots-\frac{2}{1995}+\frac{1}{1996}=\frac{1}{999}+\frac{3}{1000}+\cdots+\frac{1995}{1996} .
$$
|
Denote the left-hand side of the equation by $L$, and the right-hand side by $R$. Then
$$
\begin{aligned}
L & =\sum_{k=1}^{1996}(-1)^{k+1}\left(\frac{1997}{k+1}-1\right)=1997 \cdot \sum_{k=1}^{1996}(-1)^{k+1} \cdot \frac{1}{k+1}=1997 \cdot \sum_{k=1}^{1996}(-1)^{k} \cdot \frac{1}{k}+1996, \\
R & =\sum_{k=1}^{998}\left(\frac{2 k+1996}{998+k}-\frac{1997}{998+k}\right)=1996-1997 \cdot \sum_{k=1}^{998} \frac{1}{k+998} .
\end{aligned}
$$
We must verify that $\sum_{k=1}^{1996}(-1)^{k-1} \cdot \frac{1}{k}=\sum_{k=1}^{998} \frac{1}{k+998}$. But this follows from the calculation
$$
\sum_{k=1}^{1996}(-1)^{k-1} \cdot \frac{1}{k}=\sum_{k=1}^{1996} \frac{1}{k}-2 \cdot \sum_{k=1}^{998} \frac{1}{2 k}=\sum_{k=1}^{998} \frac{1}{k+998}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\nSolution."
}
|
f3a15a73-5406-5f96-8b58-9caab9cd2662
| 241,558
|
Consider the following two person game. A number of pebbles are situated on the table. Two players make their moves alternately. A move consists of taking off the table $x$ pebbles where $x$ is the square of any positive integer. The player who is unable to make a move loses. Prove that there are infinitely many initial situations in which the second player can win no matter how his opponent plays.
|
Suppose that there is an $n$ such that the first player always wins if there are initially more than $n$ pebbles. Consider the initial situation with $n^{2}+n+1$ pebbles. Since $(n+1)^{2}>n^{2}+n+1$, the first player can take at most $n^{2}$ pebbles, leaving at least $n+1$ pebbles on the table. By the assumption, the second player now wins. This contradiction proves that there are infinitely many situations in which the second player wins no matter how the first player plays.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider the following two person game. A number of pebbles are situated on the table. Two players make their moves alternately. A move consists of taking off the table $x$ pebbles where $x$ is the square of any positive integer. The player who is unable to make a move loses. Prove that there are infinitely many initial situations in which the second player can win no matter how his opponent plays.
|
Suppose that there is an $n$ such that the first player always wins if there are initially more than $n$ pebbles. Consider the initial situation with $n^{2}+n+1$ pebbles. Since $(n+1)^{2}>n^{2}+n+1$, the first player can take at most $n^{2}$ pebbles, leaving at least $n+1$ pebbles on the table. By the assumption, the second player now wins. This contradiction proves that there are infinitely many situations in which the second player wins no matter how the first player plays.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution."
}
|
a64bffcb-61d8-5673-a563-68d00a383e5c
| 63,800
|
A polygon with $2 n+1$ vertices is given. Show that it is possible to label the vertices and midpoints of the sides of the polygon, using all the numbers $1,2, \ldots, 4 n+2$, so that the sums of the three numbers assigned to each side are all equal.
|
First, label the midpoints of the sides of the polygon with the numbers $1,2, \ldots, 2 n+1$, in clockwise order. Then, beginning with the vertex between the sides labelled by 1 and 2 , label every second vertex in clockwise order with the numbers $4 n+2,4 n+1, \ldots, 2 n+2$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A polygon with $2 n+1$ vertices is given. Show that it is possible to label the vertices and midpoints of the sides of the polygon, using all the numbers $1,2, \ldots, 4 n+2$, so that the sums of the three numbers assigned to each side are all equal.
|
First, label the midpoints of the sides of the polygon with the numbers $1,2, \ldots, 2 n+1$, in clockwise order. Then, beginning with the vertex between the sides labelled by 1 and 2 , label every second vertex in clockwise order with the numbers $4 n+2,4 n+1, \ldots, 2 n+2$.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\nSolution."
}
|
2af8f375-07a8-5365-9199-abf9ca8daad0
| 241,622
|
Let $M$ be the midpoint of the side $A C$ of a triangle $A B C$ and let $H$ be the foot point of the altitude from $B$. Let $P$ and $Q$ be the orthogonal projections of $A$ and $C$ on the bisector of angle $B$. Prove that the four points $M, H, P$ and $Q$ lie on the same circle.
|
If $|A B|=|B C|$, the points $M, H, P$ and $Q$ coincide and the circle degenerates to a point. We will assume that $|A B|<|B C|$, so that $P$ lies inside the triangle $A B C$, and $Q$ lies outside of it.
Let the line $A P$ intersect $B C$ at $P_{1}$, and let $C Q$ intersect $A B$ at $Q_{1}$. Then $|A P|=\left|P P_{1}\right|$ (since $\triangle A P B \cong$ $\left.\triangle P_{1} P B\right)$, and therefore $M P \| B C$. Similarly, $M Q \| A B$. Therefore $\angle A M Q=\angle B A C$. We have two cases:
(i) $\angle B A C \leq 90^{\circ}$. Then $A, H, P$ and $B$ lie on a circle in this order. Hence $\angle H P Q=180^{\circ}-\angle H P B=$ $\angle B A C=\angle H M Q$. Therefore $H, P, M$ and $Q$ lie on a circle.
(ii) $\angle B A C>90^{\circ}$. Then $A, H, B$ and $P$ lie on a circle in this order. Hence $\angle H P Q=180^{\circ}-\angle H P B=$ $180^{\circ}-\angle H A B=\angle B A C=\angle H M Q$, and therefore $H, P, M$ and $Q$ lie on a circle.
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $M$ be the midpoint of the side $A C$ of a triangle $A B C$ and let $H$ be the foot point of the altitude from $B$. Let $P$ and $Q$ be the orthogonal projections of $A$ and $C$ on the bisector of angle $B$. Prove that the four points $M, H, P$ and $Q$ lie on the same circle.
|
If $|A B|=|B C|$, the points $M, H, P$ and $Q$ coincide and the circle degenerates to a point. We will assume that $|A B|<|B C|$, so that $P$ lies inside the triangle $A B C$, and $Q$ lies outside of it.
Let the line $A P$ intersect $B C$ at $P_{1}$, and let $C Q$ intersect $A B$ at $Q_{1}$. Then $|A P|=\left|P P_{1}\right|$ (since $\triangle A P B \cong$ $\left.\triangle P_{1} P B\right)$, and therefore $M P \| B C$. Similarly, $M Q \| A B$. Therefore $\angle A M Q=\angle B A C$. We have two cases:
(i) $\angle B A C \leq 90^{\circ}$. Then $A, H, P$ and $B$ lie on a circle in this order. Hence $\angle H P Q=180^{\circ}-\angle H P B=$ $\angle B A C=\angle H M Q$. Therefore $H, P, M$ and $Q$ lie on a circle.
(ii) $\angle B A C>90^{\circ}$. Then $A, H, B$ and $P$ lie on a circle in this order. Hence $\angle H P Q=180^{\circ}-\angle H P B=$ $180^{\circ}-\angle H A B=\angle B A C=\angle H M Q$, and therefore $H, P, M$ and $Q$ lie on a circle.

Figure 3
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution."
}
|
c5a8b0a9-bf85-5758-9c19-3c2221f28fb9
| 241,653
|
Prove that if both coordinates of every vertex of a convex pentagon are integers, then the area of this pentagon is not less than $\frac{5}{2}$.
|
There are two vertices $A_{1}$ and $A_{2}$ of the pentagon that have their first coordinates of the parity, and their second coordinates of the same parity. Therefore the midpoint $M$ of $A_{1} A_{2}$ has integer coordinates. There are two possibilities:
(i) The considered vertices are not consecutive. Then $M$ lies inside the pentagon (because it is convex) and is the common vertex of five triangles having as their bases the sides of the pentagon. The area of any one of these triangles is not less than $\frac{1}{2}$, so the area of the pentagon is at least $\frac{5}{2}$.
(ii) The considered vertices are consecutive. Since the pentagon is convex, the side $A_{1} A_{2}$ is not simultaneously parallel to $A_{3} A_{4}$ and $A_{4} A_{5}$. Suppose that the segments $A_{1} A_{2}$ and $A_{3} A_{4}$ are not parallel. Then the triangles $A_{2} A_{3} A_{4}, M A_{3} A_{4}$ and $A-1 A_{3} A_{4}$ have different areas, since their altitudes dropped onto the side $A_{3} A_{4}$ form a monotone sequence. At least one of these triangles has area not less than $\frac{3}{2}$, and the pentagon has area not less than $\frac{5}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that if both coordinates of every vertex of a convex pentagon are integers, then the area of this pentagon is not less than $\frac{5}{2}$.
|
There are two vertices $A_{1}$ and $A_{2}$ of the pentagon that have their first coordinates of the parity, and their second coordinates of the same parity. Therefore the midpoint $M$ of $A_{1} A_{2}$ has integer coordinates. There are two possibilities:
(i) The considered vertices are not consecutive. Then $M$ lies inside the pentagon (because it is convex) and is the common vertex of five triangles having as their bases the sides of the pentagon. The area of any one of these triangles is not less than $\frac{1}{2}$, so the area of the pentagon is at least $\frac{5}{2}$.
(ii) The considered vertices are consecutive. Since the pentagon is convex, the side $A_{1} A_{2}$ is not simultaneously parallel to $A_{3} A_{4}$ and $A_{4} A_{5}$. Suppose that the segments $A_{1} A_{2}$ and $A_{3} A_{4}$ are not parallel. Then the triangles $A_{2} A_{3} A_{4}, M A_{3} A_{4}$ and $A-1 A_{3} A_{4}$ have different areas, since their altitudes dropped onto the side $A_{3} A_{4}$ form a monotone sequence. At least one of these triangles has area not less than $\frac{3}{2}$, and the pentagon has area not less than $\frac{5}{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution."
}
|
df3dce87-7479-5a76-868d-4f6912f109d5
| 241,670
|
Let $\alpha$ be the angle between two lines containing the diagonals of a regular 1996-gon, and let $\beta \neq 0$ be another such angle. Prove that $\alpha / \beta$ is a rational number.
|
Let $O$ be the circumcentre of the 1996-gon. Consider two diagonals $A B$ and $C D$. There is a rotation around $O$ that takes the point $C$ to $A$ and $D$ to a point $D^{\prime}$. Clearly the angle of this rotation is a multiple of $2 \varphi=2 \pi / 1996$.
The angle $B A D^{\prime}$ is the inscribed angle on the $\operatorname{arc} B D^{\prime}$, and hence is an integral multiple of $\varphi$, the inscribed angle on the arc between any two adjacent vertices of the 1996-gon. Hence the angle between $A B$ and $C D$ is also an integral multiple of $\varphi$.
Since both $\alpha$ and $\beta$ are integral multiples of $\varphi, \alpha / \beta$ is a rational number.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\alpha$ be the angle between two lines containing the diagonals of a regular 1996-gon, and let $\beta \neq 0$ be another such angle. Prove that $\alpha / \beta$ is a rational number.
|
Let $O$ be the circumcentre of the 1996-gon. Consider two diagonals $A B$ and $C D$. There is a rotation around $O$ that takes the point $C$ to $A$ and $D$ to a point $D^{\prime}$. Clearly the angle of this rotation is a multiple of $2 \varphi=2 \pi / 1996$.
The angle $B A D^{\prime}$ is the inscribed angle on the $\operatorname{arc} B D^{\prime}$, and hence is an integral multiple of $\varphi$, the inscribed angle on the arc between any two adjacent vertices of the 1996-gon. Hence the angle between $A B$ and $C D$ is also an integral multiple of $\varphi$.
Since both $\alpha$ and $\beta$ are integral multiples of $\varphi, \alpha / \beta$ is a rational number.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
74d34359-0030-53dc-8829-72541395c1f2
| 238,968
|
$A B C D$ is a trapezium $(A D \| B C) . P$ is the point on the line $A B$ such that $\angle C P D$ is maximal. $Q$ is the point on the line $C D$ such that $\angle B Q A$ is maximal. Given that $P$ lies on the segment $A B$, prove that $\angle C P D=\angle B Q A$.
|
The property that $\angle C P D$ is maximal is equivalent to the property that the circle $C P D$ touches the line $A B$ (at $P$ ). Let $O$ be the intersection point of the lines $A B$ and $C D$, and let $\ell$ be the bisector of $\angle A O D$. Let $A^{\prime}, B^{\prime}$ and $Q^{\prime}$ be the points symmetrical to $A, B$ and $Q$, respectively, relative to the line $\ell$. Then the circle $A Q B$ is symmetrical to the circle $A^{\prime} Q^{\prime} B^{\prime}$ that touches the line $A B$ at $Q^{\prime}$. We have
$$
\frac{|O D|}{\left|O A^{\prime}\right|}=\frac{|O D|}{|O A|}=\frac{|O C|}{|O B|}=\frac{|O C|}{\left|O B^{\prime}\right|}
$$
Hence the homothety with centre $O$ and coefficient $|O D| /|O A|$ takes $A^{\prime}$ to $D, B^{\prime}$ to $C$, and $Q^{\prime}$ to a point $Q^{\prime \prime}$ such that the circle $C Q^{\prime \prime} D$ touches the line $A B$, and thus $Q^{\prime \prime}$ coincides with $P$. Therefore $\angle A Q B=\angle A^{\prime} Q^{\prime} B^{\prime}=\angle C Q^{\prime \prime} D=\angle C P D$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$A B C D$ is a trapezium $(A D \| B C) . P$ is the point on the line $A B$ such that $\angle C P D$ is maximal. $Q$ is the point on the line $C D$ such that $\angle B Q A$ is maximal. Given that $P$ lies on the segment $A B$, prove that $\angle C P D=\angle B Q A$.
|
The property that $\angle C P D$ is maximal is equivalent to the property that the circle $C P D$ touches the line $A B$ (at $P$ ). Let $O$ be the intersection point of the lines $A B$ and $C D$, and let $\ell$ be the bisector of $\angle A O D$. Let $A^{\prime}, B^{\prime}$ and $Q^{\prime}$ be the points symmetrical to $A, B$ and $Q$, respectively, relative to the line $\ell$. Then the circle $A Q B$ is symmetrical to the circle $A^{\prime} Q^{\prime} B^{\prime}$ that touches the line $A B$ at $Q^{\prime}$. We have
$$
\frac{|O D|}{\left|O A^{\prime}\right|}=\frac{|O D|}{|O A|}=\frac{|O C|}{|O B|}=\frac{|O C|}{\left|O B^{\prime}\right|}
$$
Hence the homothety with centre $O$ and coefficient $|O D| /|O A|$ takes $A^{\prime}$ to $D, B^{\prime}$ to $C$, and $Q^{\prime}$ to a point $Q^{\prime \prime}$ such that the circle $C Q^{\prime \prime} D$ touches the line $A B$, and thus $Q^{\prime \prime}$ coincides with $P$. Therefore $\angle A Q B=\angle A^{\prime} Q^{\prime} B^{\prime}=\angle C Q^{\prime \prime} D=\angle C P D$ as required.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
26529b67-c0d7-5328-a91d-b7dbc24ebbd6
| 238,999
|
Let $A B C D$ be a cyclic convex quadrilateral and let $r_{a}, r_{b}, r_{c}, r_{d}$ be the radii of the circles inscribed in the triangles $B C D, A C D, A B D, A B C$ respectively. Prove that $r_{a}+r_{c}=r_{b}+r_{d}$.
|
For a triangle $M N K$ with in-radius $r$ and circumradius $R$, the equality
$$
\cos \angle M+\cos \angle N+\cos \angle K=1+\frac{r}{R}
$$
hold; this follows from the cosine theorem and formulas for $r$ and $R$.
We have $\angle A C B=\angle A D B, \angle B D C=\angle B A C, \angle C A D=\angle C B D$ and $\angle D B A=\angle D C A$. Denoting these angles by $\alpha, \beta, \gamma$ and $\delta$, respectively, we get $r_{a}=(\cos \beta+\cos \gamma+\cos (\alpha+\delta)-1) R$ and $r_{c}=(\cos \alpha+\cos \delta+$ $\cos (\beta+\gamma)-1) R$. Since $\cos (\alpha+\delta)=-\cos (\beta+\gamma)$, we get
$$
r_{a}+r_{c}=(\cos \alpha+\cos \beta+\cos \gamma+\cos \delta-2) R .
$$
Similarly,
$$
r_{b}+r_{d}=(\cos \alpha+\cos \beta+\cos \gamma+\cos \delta-2) R,
$$
where $R$ is the circumradius of the quadrangle $A B C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic convex quadrilateral and let $r_{a}, r_{b}, r_{c}, r_{d}$ be the radii of the circles inscribed in the triangles $B C D, A C D, A B D, A B C$ respectively. Prove that $r_{a}+r_{c}=r_{b}+r_{d}$.
|
For a triangle $M N K$ with in-radius $r$ and circumradius $R$, the equality
$$
\cos \angle M+\cos \angle N+\cos \angle K=1+\frac{r}{R}
$$
hold; this follows from the cosine theorem and formulas for $r$ and $R$.
We have $\angle A C B=\angle A D B, \angle B D C=\angle B A C, \angle C A D=\angle C B D$ and $\angle D B A=\angle D C A$. Denoting these angles by $\alpha, \beta, \gamma$ and $\delta$, respectively, we get $r_{a}=(\cos \beta+\cos \gamma+\cos (\alpha+\delta)-1) R$ and $r_{c}=(\cos \alpha+\cos \delta+$ $\cos (\beta+\gamma)-1) R$. Since $\cos (\alpha+\delta)=-\cos (\beta+\gamma)$, we get
$$
r_{a}+r_{c}=(\cos \alpha+\cos \beta+\cos \gamma+\cos \delta-2) R .
$$
Similarly,
$$
r_{b}+r_{d}=(\cos \alpha+\cos \beta+\cos \gamma+\cos \delta-2) R,
$$
where $R$ is the circumradius of the quadrangle $A B C D$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
7122e905-7b35-59f5-973d-a55aef623feb
| 239,008
|
Let $a, b, c, d$ be positive integers such that $a b=c d$. Prove that $a+b+c+d$ is not prime.
|
. As $a b=c d$, we get $a(a+b+c+d)=(a+c)(a+d)$. If $a+b+c+d$ were a prime, then it would be a factor in either $a+c$ or $a+d$, which are both smaller than $a+b+c+d$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c, d$ be positive integers such that $a b=c d$. Prove that $a+b+c+d$ is not prime.
|
. As $a b=c d$, we get $a(a+b+c+d)=(a+c)(a+d)$. If $a+b+c+d$ were a prime, then it would be a factor in either $a+c$ or $a+d$, which are both smaller than $a+b+c+d$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 1"
}
|
1e4638c2-b650-55cf-95b1-589863fef1b7
| 239,017
|
Let $a, b, c, d$ be positive integers such that $a b=c d$. Prove that $a+b+c+d$ is not prime.
|
. Let $r=\operatorname{gcd}(a, c)$ and $s=\operatorname{gcd}(b, d)$. Let $a=a^{\prime} r, b=b^{\prime} s, c=c^{\prime} r$ and $d=d^{\prime} s$. Then $a^{\prime} b^{\prime}=c^{\prime} d^{\prime}$. But $\operatorname{gcd}\left(a^{\prime}, c^{\prime}\right)=1$ and $\operatorname{gcd}\left(b^{\prime}, d^{\prime}\right)=1$, so we must have $a^{\prime}=d^{\prime}$ and $b^{\prime}=c^{\prime}$. This gives
$$
a+b+c+d=a^{\prime} r+b^{\prime} s+c^{\prime} r+d^{\prime} s=a^{\prime} r+b^{\prime} s+b^{\prime} r+a^{\prime} s=\left(a^{\prime}+b^{\prime}\right)(r+s) \text {. }
$$
Since $a^{\prime}, b^{\prime}, r$ and $s$ are positive integers, $a+b+c+d$ is not a prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c, d$ be positive integers such that $a b=c d$. Prove that $a+b+c+d$ is not prime.
|
. Let $r=\operatorname{gcd}(a, c)$ and $s=\operatorname{gcd}(b, d)$. Let $a=a^{\prime} r, b=b^{\prime} s, c=c^{\prime} r$ and $d=d^{\prime} s$. Then $a^{\prime} b^{\prime}=c^{\prime} d^{\prime}$. But $\operatorname{gcd}\left(a^{\prime}, c^{\prime}\right)=1$ and $\operatorname{gcd}\left(b^{\prime}, d^{\prime}\right)=1$, so we must have $a^{\prime}=d^{\prime}$ and $b^{\prime}=c^{\prime}$. This gives
$$
a+b+c+d=a^{\prime} r+b^{\prime} s+c^{\prime} r+d^{\prime} s=a^{\prime} r+b^{\prime} s+b^{\prime} r+a^{\prime} s=\left(a^{\prime}+b^{\prime}\right)(r+s) \text {. }
$$
Since $a^{\prime}, b^{\prime}, r$ and $s$ are positive integers, $a+b+c+d$ is not a prime.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 2"
}
|
1e4638c2-b650-55cf-95b1-589863fef1b7
| 239,017
|
Denote by $d(n)$ the number of distinct positive divisors of a positive integer $n$ (including 1 and $n$ ). Let $a>1$ and $n>0$ be integers such that $a^{n}+1$ is a prime. Prove that
$$
d\left(a^{n}-1\right) \geq n .
$$
|
First we show that $n=2^{s}$ for some integer $s \geq 0$. Indeed, if $n=m p$ where $p$ is an odd prime, then $a^{n}+1=a^{m p}+1=\left(a^{m}+1\right)\left(a^{m(p-1)}-a^{m(p-2)}+\cdots-a+1\right)$, a contradiction.
Now we use induction on $s$ to prove that $d\left(a^{2^{s}}-1\right) \geq 2^{s}$. The case $s=0$ is obvious. As $a^{2^{s}}-1=$ $\left(a^{2^{s-1}}-1\right)\left(a^{2^{s-1}}+1\right)$, then for any divisor $q$ of $a^{2^{s-1}}-1$, both $q$ and $q\left(a^{2^{s-1}}+1\right)$ are divisors of $a^{2^{s}}-1$. Since the divisors of the form $q\left(a^{2^{s-1}}+1\right)$ are all larger than $a^{2^{s-1}}-1$ we have $d\left(a^{2^{s}}-1\right) \geq 2 \cdot d\left(a^{2^{s-1}}-1\right)=2^{s}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $d(n)$ the number of distinct positive divisors of a positive integer $n$ (including 1 and $n$ ). Let $a>1$ and $n>0$ be integers such that $a^{n}+1$ is a prime. Prove that
$$
d\left(a^{n}-1\right) \geq n .
$$
|
First we show that $n=2^{s}$ for some integer $s \geq 0$. Indeed, if $n=m p$ where $p$ is an odd prime, then $a^{n}+1=a^{m p}+1=\left(a^{m}+1\right)\left(a^{m(p-1)}-a^{m(p-2)}+\cdots-a+1\right)$, a contradiction.
Now we use induction on $s$ to prove that $d\left(a^{2^{s}}-1\right) \geq 2^{s}$. The case $s=0$ is obvious. As $a^{2^{s}}-1=$ $\left(a^{2^{s-1}}-1\right)\left(a^{2^{s-1}}+1\right)$, then for any divisor $q$ of $a^{2^{s-1}}-1$, both $q$ and $q\left(a^{2^{s-1}}+1\right)$ are divisors of $a^{2^{s}}-1$. Since the divisors of the form $q\left(a^{2^{s-1}}+1\right)$ are all larger than $a^{2^{s-1}}-1$ we have $d\left(a^{2^{s}}-1\right) \geq 2 \cdot d\left(a^{2^{s-1}}-1\right)=2^{s}$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\nSolution."
}
|
f41fa7d8-ff27-5989-ac48-b864f5115a30
| 604,802
|
The real numbers $x_{1}, x_{2}, \ldots, x_{1996}$ have the following property: for any polynomial $W$ of degree 2 at least three of the numbers $W\left(x_{1}\right), W\left(x_{2}\right), \ldots, W\left(x_{1996}\right)$ are equal. Prove that at least three of the numbers $x_{1}, x_{2}, \ldots, x_{1996}$ are equal.
|
Let $m=\min \left\{x_{1}, \ldots, x_{1996}\right\}$. Then the polynomial $W(x)=(x-m)^{2}$ is strictly increasing for $x \geq m$. Hence if $W\left(x_{i}\right)=W\left(x_{j}\right)$ we must have $x_{i}=x_{j}$, and the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The real numbers $x_{1}, x_{2}, \ldots, x_{1996}$ have the following property: for any polynomial $W$ of degree 2 at least three of the numbers $W\left(x_{1}\right), W\left(x_{2}\right), \ldots, W\left(x_{1996}\right)$ are equal. Prove that at least three of the numbers $x_{1}, x_{2}, \ldots, x_{1996}$ are equal.
|
Let $m=\min \left\{x_{1}, \ldots, x_{1996}\right\}$. Then the polynomial $W(x)=(x-m)^{2}$ is strictly increasing for $x \geq m$. Hence if $W\left(x_{i}\right)=W\left(x_{j}\right)$ we must have $x_{i}=x_{j}$, and the conclusion follows.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution."
}
|
2d5f266b-e37c-52e2-9e6a-434ae66d812f
| 239,069
|
The jury of an olympiad has 30 members in the beginning. Each member of the jury thinks that some of his colleagues are competent, while all the others are not, and these opinions do not change. At the beginning of every session a voting takes place, and those members who are not competent in the opinion of more than one half of the voters are excluded from the jury for the rest of the olympiad. Prove that after at most 15 sessions there will be no more exclusions. (Note that nobody votes about his own competence.)
|
First we note that if nobody is excluded in some session, then the situation becomes stable and nobody can be excluded in any later session.
We use induction to prove the slightly more general claim that if the jury has $2 n$ members, $n \geq 2$, then after at most $n$ sessions nobody will be excluded anymore. For $n=2$ the claim is obvious, since if some members are excluded in the first two sessions, there are at most two members left, and hence nobody is excluded in the third session.
Now assuming that the claim is true for $n \leq k-1$, suppose the jury has $2 k$ members, and consider the first session. If nobody is excluded, we are done. If a positive and even number of members are excluded, there will be $2 r$ members left with $r<k$, and by the induction hypotheses the jury will stabilize after at most $r$ more sessions, giving a total of at most $r+1 \leq k$ sessions, as required.
Finally suppose that an odd number of members are excluded in the first session. There are three alternatives:
(i) An even number of members are excluded in each of the next $m$ sessions, after which nobody is excluded. Then the number of members left is at most $2 k-1-2 m$. Hence $2 k-1-2 m \geq 1$, so that $k \geq m+1$. Hence the number of sessions is at most $k$.
(ii) An even number of members are excluded in each of the next $m$ sessions, after which an odd number of members greater than 1 are excluded. Then there are at most $2 k-1-2 m-3$ members left, and by the induction hypotheses, the jury will stabilize in no more than $k-m-2$ sessions. The total number of sessions is therefore $1+m+1+(k-m-2)=k$.
(iii) An even number of members are excluded in each of the next $m$ sessions, followed by a session where precisely one member $M$ is excluded. In this session, there were $2 r+1$ members present for some $r$, and $r+1$ of these voted for the exclusion of $M$. But then any member other than $M$ was thought to be incompetent by at most $r$ others. In the next session the jury will have $2 r$ members, and since the members do not change their sympathies, nobody can be excluded. Hence the situation is stable after $m+2$ sessions, and at least $1+2 m+1=2 m+2$ members have been excluded. But there must be at least 3 members left, for one member cannot be excluded from a jury of 2 members. Hence $2 m+2 \leq 2 k-3$, whence $m+2 \leq k$.
Thus the claim holds for $n=k$ also. We conclude that the claim holds for all $n \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The jury of an olympiad has 30 members in the beginning. Each member of the jury thinks that some of his colleagues are competent, while all the others are not, and these opinions do not change. At the beginning of every session a voting takes place, and those members who are not competent in the opinion of more than one half of the voters are excluded from the jury for the rest of the olympiad. Prove that after at most 15 sessions there will be no more exclusions. (Note that nobody votes about his own competence.)
|
First we note that if nobody is excluded in some session, then the situation becomes stable and nobody can be excluded in any later session.
We use induction to prove the slightly more general claim that if the jury has $2 n$ members, $n \geq 2$, then after at most $n$ sessions nobody will be excluded anymore. For $n=2$ the claim is obvious, since if some members are excluded in the first two sessions, there are at most two members left, and hence nobody is excluded in the third session.
Now assuming that the claim is true for $n \leq k-1$, suppose the jury has $2 k$ members, and consider the first session. If nobody is excluded, we are done. If a positive and even number of members are excluded, there will be $2 r$ members left with $r<k$, and by the induction hypotheses the jury will stabilize after at most $r$ more sessions, giving a total of at most $r+1 \leq k$ sessions, as required.
Finally suppose that an odd number of members are excluded in the first session. There are three alternatives:
(i) An even number of members are excluded in each of the next $m$ sessions, after which nobody is excluded. Then the number of members left is at most $2 k-1-2 m$. Hence $2 k-1-2 m \geq 1$, so that $k \geq m+1$. Hence the number of sessions is at most $k$.
(ii) An even number of members are excluded in each of the next $m$ sessions, after which an odd number of members greater than 1 are excluded. Then there are at most $2 k-1-2 m-3$ members left, and by the induction hypotheses, the jury will stabilize in no more than $k-m-2$ sessions. The total number of sessions is therefore $1+m+1+(k-m-2)=k$.
(iii) An even number of members are excluded in each of the next $m$ sessions, followed by a session where precisely one member $M$ is excluded. In this session, there were $2 r+1$ members present for some $r$, and $r+1$ of these voted for the exclusion of $M$. But then any member other than $M$ was thought to be incompetent by at most $r$ others. In the next session the jury will have $2 r$ members, and since the members do not change their sympathies, nobody can be excluded. Hence the situation is stable after $m+2$ sessions, and at least $1+2 m+1=2 m+2$ members have been excluded. But there must be at least 3 members left, for one member cannot be excluded from a jury of 2 members. Hence $2 m+2 \leq 2 k-3$, whence $m+2 \leq k$.
Thus the claim holds for $n=k$ also. We conclude that the claim holds for all $n \geq 2$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution."
}
|
d661a4ab-047f-59b7-bf6a-6730c6365c54
| 239,127
|
Is it possible to partition all positive integers into disjoint sets $A$ and $B$ such that
(i) no three numbers of $A$ form arithmetic progression,
(ii) no infinite non-constant arithmetic progression can be formed by numbers of $B$ ?
|
Let $\mathbb{N}$ denote the set of positive integers. There is a bijective function $f: \mathbb{N} \rightarrow \mathbb{N} \times \mathbb{N}$. Let $a_{0}=1$, and for $k \geq 1$, let $a_{k}$ be the least integer of the form $m+t n$ for some integer $t \geq 0$ where $f(k)=(m, n)$, such that $a_{k} \geq 2 a_{k-1}$. Let $A=\left\{a_{0}, a_{1}, \ldots\right\}$ and let $B=\mathbb{N} \backslash A$. We now show that $A$ and $B$ satisfy the given conditions.
(i) For any non-negative integers $i<j<k$, we have $a_{k} \geq a_{j+1} \geq 2 a_{j}$, and hence $a_{k}-a_{j} \geq a_{j}>a_{j}-a_{i}$. Thus $a_{i}, a_{j}$ and $a_{k}$ do not form an arithmetic progression, since this would mean that $a_{k}-a_{j}=a_{j}-a_{i}$. Hence no three numbers in $A$ form an arithmetic progression.
(ii) Consider an infinite arithmetic progression $m, m+n, m+2 n, \ldots$, with $m, n \in \mathbb{N}$. Then $m+n t=a_{k}$ for some integer $t \geq 0$, where $k=f^{-1}(m, n)$. Thus $a_{k}$ belongs to the arithmetic progression, but $a_{k} \notin B$. Hence $B$ does not contain any infinite non-constant arithmetic progression.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Is it possible to partition all positive integers into disjoint sets $A$ and $B$ such that
(i) no three numbers of $A$ form arithmetic progression,
(ii) no infinite non-constant arithmetic progression can be formed by numbers of $B$ ?
|
Let $\mathbb{N}$ denote the set of positive integers. There is a bijective function $f: \mathbb{N} \rightarrow \mathbb{N} \times \mathbb{N}$. Let $a_{0}=1$, and for $k \geq 1$, let $a_{k}$ be the least integer of the form $m+t n$ for some integer $t \geq 0$ where $f(k)=(m, n)$, such that $a_{k} \geq 2 a_{k-1}$. Let $A=\left\{a_{0}, a_{1}, \ldots\right\}$ and let $B=\mathbb{N} \backslash A$. We now show that $A$ and $B$ satisfy the given conditions.
(i) For any non-negative integers $i<j<k$, we have $a_{k} \geq a_{j+1} \geq 2 a_{j}$, and hence $a_{k}-a_{j} \geq a_{j}>a_{j}-a_{i}$. Thus $a_{i}, a_{j}$ and $a_{k}$ do not form an arithmetic progression, since this would mean that $a_{k}-a_{j}=a_{j}-a_{i}$. Hence no three numbers in $A$ form an arithmetic progression.
(ii) Consider an infinite arithmetic progression $m, m+n, m+2 n, \ldots$, with $m, n \in \mathbb{N}$. Then $m+n t=a_{k}$ for some integer $t \geq 0$, where $k=f^{-1}(m, n)$. Thus $a_{k}$ belongs to the arithmetic progression, but $a_{k} \notin B$. Hence $B$ does not contain any infinite non-constant arithmetic progression.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution."
}
|
cf41cd36-5423-587c-944b-1880815682cc
| 604,969
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers in which every positive integer occurs exactly once. Prove that there exist integers $\ell$ and $m$, $1<\ell<m$, such that $a_{1}+a_{m}=2 a_{\ell}$.
|
Let $\ell$ be the least index such that $a_{\ell}>a_{1}$. Since $2 a_{\ell}-a_{1}$ is a positive integer larger than $a_{1}$, it occurs in the given sequence beyond $a_{\ell}$. In other words, there exists an index $m>\ell$ such that $a_{m}=2 a_{\ell}-a_{1}$. This completes the proof.
Remarks. The problem was proposed in the slightly more general form where the first term of the arithmetic progression has an arbitary index. The remarks below refer to this version. The problem committee felt that no essential new aspects would arise from the generalization.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers in which every positive integer occurs exactly once. Prove that there exist integers $\ell$ and $m$, $1<\ell<m$, such that $a_{1}+a_{m}=2 a_{\ell}$.
|
Let $\ell$ be the least index such that $a_{\ell}>a_{1}$. Since $2 a_{\ell}-a_{1}$ is a positive integer larger than $a_{1}$, it occurs in the given sequence beyond $a_{\ell}$. In other words, there exists an index $m>\ell$ such that $a_{m}=2 a_{\ell}-a_{1}$. This completes the proof.
Remarks. The problem was proposed in the slightly more general form where the first term of the arithmetic progression has an arbitary index. The remarks below refer to this version. The problem committee felt that no essential new aspects would arise from the generalization.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
b4b63346-668f-5b10-af21-4b3fe7ec14fc
| 238,765
|
Prove that the arithmetic mean $a$ of $x_{1}, \ldots, x_{n}$ satisfies
$$
\left(x_{1}-a\right)^{2}+\cdots+\left(x_{n}-a\right)^{2} \leqslant \frac{1}{2}\left(\left|x_{1}-a\right|+\cdots+\left|x_{n}-a\right|\right)^{2} .
$$
|
Denote $y_{i}=x_{i}-a$. Then $y_{1}+y_{2}+\cdots+y_{n}=0$. We can assume $y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{k} \leqslant 0 \leqslant y_{k+1} \leqslant \cdots \leqslant y_{n}$. Let $y_{1}+y_{2}+\cdots+y_{k}=-z$, then $y_{k+1}+\cdots+y_{n}=z$ and
$$
\begin{aligned}
y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2} & =y_{1}^{2}+y_{2}^{2}+\cdots+y_{k}^{2}+y_{k+1}^{2}+\cdots+y_{n}^{2} \leqslant \\
& \leqslant\left(y_{1}+y_{2}+\cdots+y_{k}\right)^{2}+\left(y_{k+1}+\cdots+y_{n}\right)^{2}=2 z^{2}= \\
& =\frac{1}{2}(2 z)^{2}=\frac{1}{2}\left(\left|y_{1}\right|+\left|y_{2}\right|+\cdots+\left|y_{n}\right|\right)^{2} .
\end{aligned}
$$
Alternative solution. The case $n=1$ is trivial (then $x_{1}-a=0$ and we get the inequality $0 \leqslant 0$ ). Suppose now that $n \geqslant 2$. Consider a square of side length $\left|x_{1}-a\right|+\left|x_{2}-a\right|+\ldots+\left|x_{n}-a\right|$ and construct squares of side lengths $\left|x_{1}-a\right|,\left|x_{2}-a\right|, \ldots,\left|x_{n}-a\right|$ side by side inside it as shown on Figure 1. Since none of the side lengths of the small squares exceeds half of the side length of the large square, then all the small squares are contained within the upper half of the large square, i.e. the sum of their areas does not exceed half of the area of the large square, q.e.d.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that the arithmetic mean $a$ of $x_{1}, \ldots, x_{n}$ satisfies
$$
\left(x_{1}-a\right)^{2}+\cdots+\left(x_{n}-a\right)^{2} \leqslant \frac{1}{2}\left(\left|x_{1}-a\right|+\cdots+\left|x_{n}-a\right|\right)^{2} .
$$
|
Denote $y_{i}=x_{i}-a$. Then $y_{1}+y_{2}+\cdots+y_{n}=0$. We can assume $y_{1} \leqslant y_{2} \leqslant \cdots \leqslant y_{k} \leqslant 0 \leqslant y_{k+1} \leqslant \cdots \leqslant y_{n}$. Let $y_{1}+y_{2}+\cdots+y_{k}=-z$, then $y_{k+1}+\cdots+y_{n}=z$ and
$$
\begin{aligned}
y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2} & =y_{1}^{2}+y_{2}^{2}+\cdots+y_{k}^{2}+y_{k+1}^{2}+\cdots+y_{n}^{2} \leqslant \\
& \leqslant\left(y_{1}+y_{2}+\cdots+y_{k}\right)^{2}+\left(y_{k+1}+\cdots+y_{n}\right)^{2}=2 z^{2}= \\
& =\frac{1}{2}(2 z)^{2}=\frac{1}{2}\left(\left|y_{1}\right|+\left|y_{2}\right|+\cdots+\left|y_{n}\right|\right)^{2} .
\end{aligned}
$$
Alternative solution. The case $n=1$ is trivial (then $x_{1}-a=0$ and we get the inequality $0 \leqslant 0$ ). Suppose now that $n \geqslant 2$. Consider a square of side length $\left|x_{1}-a\right|+\left|x_{2}-a\right|+\ldots+\left|x_{n}-a\right|$ and construct squares of side lengths $\left|x_{1}-a\right|,\left|x_{2}-a\right|, \ldots,\left|x_{n}-a\right|$ side by side inside it as shown on Figure 1. Since none of the side lengths of the small squares exceeds half of the side length of the large square, then all the small squares are contained within the upper half of the large square, i.e. the sum of their areas does not exceed half of the area of the large square, q.e.d.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
cb2339bb-d3c4-5553-bec5-ebc3ecb12b5f
| 238,801
|
In a sequence $u_{0}, u_{1}, \ldots$ of positive integers, $u_{0}$ is arbitrary, and for any non-negative integer $n$,
$$
u_{n+1}= \begin{cases}\frac{1}{2} u_{n} & \text { for even } u_{n} \\ a+u_{n} & \text { for odd } u_{n}\end{cases}
$$
where $a$ is a fixed odd positive integer. Prove that the sequence is periodic from a certain step.
|
Suppose $u_{n}>a$. Then, if $u_{n}$ is even we have $u_{n+1}=\frac{1}{2} u_{n}<u_{n}$, and if
$u_{n}$ is odd we have $u_{n+1}=a+u_{n}<2 u_{n}$ and $u_{n+2}=\frac{1}{2} u_{n+1}<u_{n}$. Hence the iteration results in $u_{n} \leqslant a$ in a finite number of steps. Thus for any non-negative integer $m$, some non-negative integer $n>m$ satisfies $u_{n} \leqslant a$, and there must be an infinite set of such integers $n$.
Since the set of natural numbers not exceeding $a$ is finite and such values arise in the sequence $\left(u_{n}\right)$ an infinite number of times, there exist nonnegative integers $m$ and $n$ with $n>m$ such that $u_{n}=u_{m}$. Starting from $u_{m}$ the sequence is then periodic with a period dividing $n-m$.
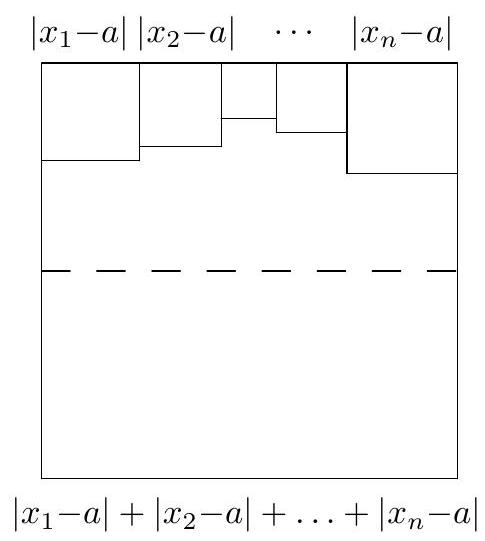
Figure 1
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
In a sequence $u_{0}, u_{1}, \ldots$ of positive integers, $u_{0}$ is arbitrary, and for any non-negative integer $n$,
$$
u_{n+1}= \begin{cases}\frac{1}{2} u_{n} & \text { for even } u_{n} \\ a+u_{n} & \text { for odd } u_{n}\end{cases}
$$
where $a$ is a fixed odd positive integer. Prove that the sequence is periodic from a certain step.
|
Suppose $u_{n}>a$. Then, if $u_{n}$ is even we have $u_{n+1}=\frac{1}{2} u_{n}<u_{n}$, and if
$u_{n}$ is odd we have $u_{n+1}=a+u_{n}<2 u_{n}$ and $u_{n+2}=\frac{1}{2} u_{n+1}<u_{n}$. Hence the iteration results in $u_{n} \leqslant a$ in a finite number of steps. Thus for any non-negative integer $m$, some non-negative integer $n>m$ satisfies $u_{n} \leqslant a$, and there must be an infinite set of such integers $n$.
Since the set of natural numbers not exceeding $a$ is finite and such values arise in the sequence $\left(u_{n}\right)$ an infinite number of times, there exist nonnegative integers $m$ and $n$ with $n>m$ such that $u_{n}=u_{m}$. Starting from $u_{m}$ the sequence is then periodic with a period dividing $n-m$.

Figure 1
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
769e4abe-0aab-5c4a-ada4-39a80761dbf1
| 238,809
|
Let $P$ and $Q$ be polynomials with integer coefficients. Suppose that the integers $a$ and $a+1997$ are roots of $P$, and that $Q(1998)=2000$. Prove that the equation $Q(P(x))=1$ has no integer solutions.
|
Suppose $b$ is an integer such that $Q(P(b))=1$. Since $a$ and $a+1997$ are roots of $P$ we have $P(x)=(x-a)(x-a-1997) R(x)$ where $R$ is a polynomial with integer coefficients. For any integer $b$ the integers $b-a$ and
$b-a-1997$ are of different parity and hence $P(b)=(b-a)(b-a-1997) R(b)$ is even. Since $Q(1998)=2000$ then the constant term in the expansion of $Q(x)$ is even (otherwise $Q(x)$ would be odd for any even integer $x$ ), and $Q(c)$ is even for any even integer $c$. Hence $Q(P(b))$ is also even and cannot be equal to 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P$ and $Q$ be polynomials with integer coefficients. Suppose that the integers $a$ and $a+1997$ are roots of $P$, and that $Q(1998)=2000$. Prove that the equation $Q(P(x))=1$ has no integer solutions.
|
Suppose $b$ is an integer such that $Q(P(b))=1$. Since $a$ and $a+1997$ are roots of $P$ we have $P(x)=(x-a)(x-a-1997) R(x)$ where $R$ is a polynomial with integer coefficients. For any integer $b$ the integers $b-a$ and
$b-a-1997$ are of different parity and hence $P(b)=(b-a)(b-a-1997) R(b)$ is even. Since $Q(1998)=2000$ then the constant term in the expansion of $Q(x)$ is even (otherwise $Q(x)$ would be odd for any even integer $x$ ), and $Q(c)$ is even for any even integer $c$. Hence $Q(P(b))$ is also even and cannot be equal to 1 .
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\n7."
}
|
899c224c-50be-52d1-b59c-b2fb98874a39
| 64,261
|
Prove that in every sequence of 79 consecutive positive integers written in the decimal system, there is a positive integer whose sum of digits is divisible by 13 .
|
Among the first 40 numbers in the sequence, four are divisible by 10 and at least one of these has its second digit from the right less than or equal to 6 . Let this number be $x$ and let $y$ be its sum of digits. Then the numbers $x, x+1, x+2, \ldots, x+39$ all belong to the sequence, and each of $y, y+1, \ldots, y+12$ appears at least once among their sums of decimal digits. One of these is divisible by 13 .
Remark: there exist 78 consecutive natural numbers, none of which has its sum of digits divisible by 13 - e.g. 859999999961 through 860000000038 .
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that in every sequence of 79 consecutive positive integers written in the decimal system, there is a positive integer whose sum of digits is divisible by 13 .
|
Among the first 40 numbers in the sequence, four are divisible by 10 and at least one of these has its second digit from the right less than or equal to 6 . Let this number be $x$ and let $y$ be its sum of digits. Then the numbers $x, x+1, x+2, \ldots, x+39$ all belong to the sequence, and each of $y, y+1, \ldots, y+12$ appears at least once among their sums of decimal digits. One of these is divisible by 13 .
Remark: there exist 78 consecutive natural numbers, none of which has its sum of digits divisible by 13 - e.g. 859999999961 through 860000000038 .

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\n10."
}
|
c9c1d526-e9f6-5293-a6d1-fde195b83ee0
| 605,191
|
Two circles $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ intersect in $P$ and $Q$. A line through $P$ intersects $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ again in $A$ and $B$, respectively, and $X$ is the midpoint of $A B$. The line through $Q$ and $X$ intersects $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ again in $Y$ and $Z$, respectively. Prove that $X$ is the midpoint of $Y Z$.
|
Depending on the radii of the circles, the distance between their centres and the choice of the line through $P$ we have several possible arrangements of the points $A, B, P$ and $Y, Z, Q$. We shall show that in each case the triangles $A X Y$ and $B X Z$ are congruent, whence $|Y X|=|X Z|$.
(a) Point $P$ lies within segment $A B$ and point $Q$ lies within segment $Y Z$ (see Figure 3). Then
$$
\angle A Y X=\angle A Y Q=\pi-\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$
Since also $\angle A X Y=\angle B X Z$ and $|A X|=|X B|$, triangles $A X Y$ and $B X Z$ are congruent.
(b) Point $P$ lies outside of segment $A B$ and point $Q$ lies within segment $Y Z$ (see Figure 4). Then
$$
\angle A Y X=\angle A Y Q=\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$
Figure 3
Figure 4
(c) Point $P$ lies outside of segment $A B$ and point $Q$ lies outside of segment $Y Z$ (see Figure 5). Then
$$
\angle A Y X=\pi-\angle A Y Q=\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$
(d) Point $P$ lies within segment $A B$ and point $Q$ lies outside of segment $Y Z$. This case is similar to (b): exchange the roles of points $P$ and $Q, A$ and $Y, B$ and $Z$.
Figure 5
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ intersect in $P$ and $Q$. A line through $P$ intersects $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ again in $A$ and $B$, respectively, and $X$ is the midpoint of $A B$. The line through $Q$ and $X$ intersects $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ again in $Y$ and $Z$, respectively. Prove that $X$ is the midpoint of $Y Z$.
|
Depending on the radii of the circles, the distance between their centres and the choice of the line through $P$ we have several possible arrangements of the points $A, B, P$ and $Y, Z, Q$. We shall show that in each case the triangles $A X Y$ and $B X Z$ are congruent, whence $|Y X|=|X Z|$.
(a) Point $P$ lies within segment $A B$ and point $Q$ lies within segment $Y Z$ (see Figure 3). Then
$$
\angle A Y X=\angle A Y Q=\pi-\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$
Since also $\angle A X Y=\angle B X Z$ and $|A X|=|X B|$, triangles $A X Y$ and $B X Z$ are congruent.
(b) Point $P$ lies outside of segment $A B$ and point $Q$ lies within segment $Y Z$ (see Figure 4). Then
$$
\angle A Y X=\angle A Y Q=\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$

Figure 3

Figure 4
(c) Point $P$ lies outside of segment $A B$ and point $Q$ lies outside of segment $Y Z$ (see Figure 5). Then
$$
\angle A Y X=\pi-\angle A Y Q=\angle A P Q=\angle B P Q=\angle B Z Q=\angle B Z X .
$$
(d) Point $P$ lies within segment $A B$ and point $Q$ lies outside of segment $Y Z$. This case is similar to (b): exchange the roles of points $P$ and $Q, A$ and $Y, B$ and $Z$.

Figure 5
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
6a20372a-f269-5f5e-b185-2316d66001ed
| 238,881
|
Five distinct points $A, B, C, D$ and $E$ lie on a line with
$$
|A B|=|B C|=|C D|=|D E| \text {. }
$$
The point $F$ lies outside the line. Let $G$ be the circumcentre of triangle $A D F$ and $H$ be the circumcentre of triangle $B E F$. Show that lines $G H$ and $F C$ are perpendicular.
|
Let $O, H^{\prime}$ and $G^{\prime}$ be the circumcentres of the triangles $B D F, B C F$ and $C D F$, respectively (see Figure 6). Then $O, G$ and $G^{\prime}$ lie on the perpendicular bisector of the segment $D F$, while $O, H$ and $H^{\prime}$ lie on the perpendicular bisector of the segment $B F$. Moreover, $G$ and $H^{\prime}$ lie on the perpendicular bisector of $B C, O$ lies on the perpendicular bisector of $B D$, $H$ and $G^{\prime}$ lie on the perpendicular bisector of $C D$ and $C$ is the midpoint of $B D$. Hence $H^{\prime}$ and $G^{\prime}$ are symmetric to $H$ and $G$, respectively, relative to point $O$. Hence triangles $O G H^{\prime}$ and $O G^{\prime} H$ are congruent, and $G H G^{\prime} H^{\prime}$ is a parallelogram.
Since $C F$ is the common side of triangles $B C F$ and $C D F$, the line $G^{\prime} H^{\prime}$ connecting their circumcentres is perpendicular to $C F$. Therefore $G H$ is also perpendicular to $C F$.
Figure 6
Alternative solution. Note that the diagonals of a quadrangle $X Y Z W$ are perpendicular to each other if and only if $|X Y|^{2}-|Z Y|^{2}=|X W|^{2}-|Z W|^{2}$. Applying this to the quadrangle $G F H C$ it is sufficient to prove that $|G F|^{2}-|H F|^{2}=|G C|^{2}-|H C|^{2}$. Denote $|A B|=|B C|=|C D|=|D E|=a$, $\angle G A C=\alpha$ and $\angle H E C=\beta$, and let $R_{1}, R_{2}$ be the circumradii of triangles $A D F$ and $B E F$, respectively (see Figure 7). Applying the cosine law to triangles $C G A$ and $C H E$, we have $|G C|^{2}=R_{1}^{2}+4 a^{2}-4 a R_{1} \cos \alpha$
and $|H C|^{2}=R_{2}^{2}+4 a^{2}-4 a R_{2} \cos \beta$. Together with $\cos \alpha=\frac{3 a}{2 R_{1}}$ and $\cos \beta=\frac{3 a}{2 R_{2}}$ this yields $|G C|^{2}-|H C|^{2}=R_{1}^{2}-R_{2}^{2}$. Since $|G F|=R_{1}$ and $|H F|=R_{2}$, we also have $|G F|^{2}-|H F|^{2}=R_{1}^{2}-R_{2}^{2}$.
Figure 7
Figure 8
Another solution. We shall use the following fact that can easily be derived from the properties of the power of a point: Let a line $s$ intersect two circles at points $K, L$ and $M, N$, respectively, and let these circles intersect each other at $P$ and $Q . A$ point $X$ on the line $s$ lies also on the line $P Q$ (i.e. is the intersection point of the lines $s$ and $P Q$ ) if and only if $|K X| \cdot|L X|=|M X| \cdot|N X|$.
The line $A E$ intersects the circumcircles of triangles $A D F$ and $B E F$ at $A, D$ and $B, E$, respectively. Since point $C$ lies on line $A E$ and $|A C| \cdot|D C|=|B C| \cdot|E C|$, then line $C F$ passes through the second intersection point of these circles (see Figure 8) and hence is perpendicular to the segment $G H$ connecting the centres of these circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Five distinct points $A, B, C, D$ and $E$ lie on a line with
$$
|A B|=|B C|=|C D|=|D E| \text {. }
$$
The point $F$ lies outside the line. Let $G$ be the circumcentre of triangle $A D F$ and $H$ be the circumcentre of triangle $B E F$. Show that lines $G H$ and $F C$ are perpendicular.

|
Let $O, H^{\prime}$ and $G^{\prime}$ be the circumcentres of the triangles $B D F, B C F$ and $C D F$, respectively (see Figure 6). Then $O, G$ and $G^{\prime}$ lie on the perpendicular bisector of the segment $D F$, while $O, H$ and $H^{\prime}$ lie on the perpendicular bisector of the segment $B F$. Moreover, $G$ and $H^{\prime}$ lie on the perpendicular bisector of $B C, O$ lies on the perpendicular bisector of $B D$, $H$ and $G^{\prime}$ lie on the perpendicular bisector of $C D$ and $C$ is the midpoint of $B D$. Hence $H^{\prime}$ and $G^{\prime}$ are symmetric to $H$ and $G$, respectively, relative to point $O$. Hence triangles $O G H^{\prime}$ and $O G^{\prime} H$ are congruent, and $G H G^{\prime} H^{\prime}$ is a parallelogram.
Since $C F$ is the common side of triangles $B C F$ and $C D F$, the line $G^{\prime} H^{\prime}$ connecting their circumcentres is perpendicular to $C F$. Therefore $G H$ is also perpendicular to $C F$.

Figure 6
Alternative solution. Note that the diagonals of a quadrangle $X Y Z W$ are perpendicular to each other if and only if $|X Y|^{2}-|Z Y|^{2}=|X W|^{2}-|Z W|^{2}$. Applying this to the quadrangle $G F H C$ it is sufficient to prove that $|G F|^{2}-|H F|^{2}=|G C|^{2}-|H C|^{2}$. Denote $|A B|=|B C|=|C D|=|D E|=a$, $\angle G A C=\alpha$ and $\angle H E C=\beta$, and let $R_{1}, R_{2}$ be the circumradii of triangles $A D F$ and $B E F$, respectively (see Figure 7). Applying the cosine law to triangles $C G A$ and $C H E$, we have $|G C|^{2}=R_{1}^{2}+4 a^{2}-4 a R_{1} \cos \alpha$
and $|H C|^{2}=R_{2}^{2}+4 a^{2}-4 a R_{2} \cos \beta$. Together with $\cos \alpha=\frac{3 a}{2 R_{1}}$ and $\cos \beta=\frac{3 a}{2 R_{2}}$ this yields $|G C|^{2}-|H C|^{2}=R_{1}^{2}-R_{2}^{2}$. Since $|G F|=R_{1}$ and $|H F|=R_{2}$, we also have $|G F|^{2}-|H F|^{2}=R_{1}^{2}-R_{2}^{2}$.

Figure 7

Figure 8
Another solution. We shall use the following fact that can easily be derived from the properties of the power of a point: Let a line $s$ intersect two circles at points $K, L$ and $M, N$, respectively, and let these circles intersect each other at $P$ and $Q . A$ point $X$ on the line $s$ lies also on the line $P Q$ (i.e. is the intersection point of the lines $s$ and $P Q$ ) if and only if $|K X| \cdot|L X|=|M X| \cdot|N X|$.
The line $A E$ intersects the circumcircles of triangles $A D F$ and $B E F$ at $A, D$ and $B, E$, respectively. Since point $C$ lies on line $A E$ and $|A C| \cdot|D C|=|B C| \cdot|E C|$, then line $C F$ passes through the second intersection point of these circles (see Figure 8) and hence is perpendicular to the segment $G H$ connecting the centres of these circles.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
f2132e2f-1a4f-5219-9ae2-30694e776923
| 238,889
|
In the triangle $A B C,|A C|^{2}$ is the arithmetic mean of $|B C|^{2}$ and $|A B|^{2}$. Show that $\cot ^{2} B \geqslant \cot A \cot C$.
|
Denote $|B C|=a,|C A|=b$ and $|A B|=c$, then we have $2 b^{2}=a^{2}+c^{2}$. Applying the cosine and sine laws to triangle $A B C$ we have:
$$
\begin{aligned}
& \cot B=\frac{\cos B}{\sin B}=\frac{\left(a^{2}+c^{2}-b^{2}\right) \cdot 2 R}{2 a c \cdot b}=\frac{\left(a^{2}+c^{2}-b^{2}\right) \cdot R}{a b c}, \\
& \cot A=\frac{\cos A}{\sin A}=\frac{\left(b^{2}+c^{2}-a^{2}\right) \cdot R}{a b c},
\end{aligned}
$$
$$
\cot C=\frac{\cos C}{\sin C}=\frac{\left(a^{2}+b^{2}-c^{2}\right) \cdot R}{a b c}
$$
where $R$ is the circumradius of triangle $A B C$. To finish the proof it hence suffices to show that $\left(a^{2}+c^{2}-b^{2}\right)^{2} \geqslant\left(b^{2}+c^{2}-a^{2}\right)\left(a^{2}+b^{2}-c^{2}\right)$. Indeed, from the AM-GM inequality we get
$$
\begin{aligned}
\left(b^{2}+c^{2}-a^{2}\right)\left(a^{2}+b^{2}-c^{2}\right) & \leqslant \frac{\left(b^{2}+c^{2}-a^{2}+a^{2}+b^{2}-c^{2}\right)^{2}}{4}=b^{4}= \\
& =\left(2 b^{2}-b^{2}\right)^{2}=\left(a^{2}+c^{2}-b^{2}\right)^{2} .
\end{aligned}
$$
Figure 9
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the triangle $A B C,|A C|^{2}$ is the arithmetic mean of $|B C|^{2}$ and $|A B|^{2}$. Show that $\cot ^{2} B \geqslant \cot A \cot C$.
|
Denote $|B C|=a,|C A|=b$ and $|A B|=c$, then we have $2 b^{2}=a^{2}+c^{2}$. Applying the cosine and sine laws to triangle $A B C$ we have:
$$
\begin{aligned}
& \cot B=\frac{\cos B}{\sin B}=\frac{\left(a^{2}+c^{2}-b^{2}\right) \cdot 2 R}{2 a c \cdot b}=\frac{\left(a^{2}+c^{2}-b^{2}\right) \cdot R}{a b c}, \\
& \cot A=\frac{\cos A}{\sin A}=\frac{\left(b^{2}+c^{2}-a^{2}\right) \cdot R}{a b c},
\end{aligned}
$$
$$
\cot C=\frac{\cos C}{\sin C}=\frac{\left(a^{2}+b^{2}-c^{2}\right) \cdot R}{a b c}
$$
where $R$ is the circumradius of triangle $A B C$. To finish the proof it hence suffices to show that $\left(a^{2}+c^{2}-b^{2}\right)^{2} \geqslant\left(b^{2}+c^{2}-a^{2}\right)\left(a^{2}+b^{2}-c^{2}\right)$. Indeed, from the AM-GM inequality we get
$$
\begin{aligned}
\left(b^{2}+c^{2}-a^{2}\right)\left(a^{2}+b^{2}-c^{2}\right) & \leqslant \frac{\left(b^{2}+c^{2}-a^{2}+a^{2}+b^{2}-c^{2}\right)^{2}}{4}=b^{4}= \\
& =\left(2 b^{2}-b^{2}\right)^{2}=\left(a^{2}+c^{2}-b^{2}\right)^{2} .
\end{aligned}
$$

Figure 9
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
f1cc4ff1-a31d-5eaa-806e-1846667fe8c2
| 605,267
|
In the acute triangle $A B C$, the bisectors of $\angle A, \angle B$ and $\angle C$ intersect the circumcircle again in $A_{1}, B_{1}$ and $C_{1}$, respectively. Let $M$ be the point of intersection of $A B$ and $B_{1} C_{1}$, and let $N$ be the point of intersection of $B C$ and $A_{1} B_{1}$. Prove that $M N$ passes through the incentre of triangle $A B C$.
|
Let $I$ be the incenter of triangle $A B C$ (the intersection point of the angle bisectors $A A_{1}, B B_{1}$ and $C C_{1}$ ), and let $B_{1} C_{1}$ intersect the side $A C$ and the angle bisector $A A_{1}$ at $P$ and $Q$, respectively (see Figure 9 ). Then
$$
\angle A Q C_{1}=\frac{1}{2}\left(\overparen{A C}_{1}+\overparen{A_{1} B_{1}}\right)=\frac{1}{2} \cdot\left(\frac{1}{2} \overparen{A B}+\frac{1}{2} \overparen{B C}+\frac{1}{2} \overparen{C A}\right)=90^{\circ}
$$
Since $\angle A C_{1} B_{1}=\angle B_{1} C_{1} C$ (as their supporting arcs are of equal size), then $C_{1} B_{1}$ is the bisector of angle $A C_{1} I$. Moreover, since $A I$ and $C_{1} B_{1}$ are perpendicular, then $C_{1} B_{1}$ is also the bisector of angle $A M I$. Similarly we can show that $B_{1} C_{1}$ bisects the angles $A B_{1} I$ ja $A P I$. Hence the diagonals of the quadrangle $A M I P$ are perpendicular and bisect its angles, i.e.
$A M I P$ is a rhombus and $M I$ is parrallel to $A C$. Similarly we can prove that $N I$ is parallel to $A C$, i.e. points $M, I$ and $N$ are collinear, q.e.d.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the acute triangle $A B C$, the bisectors of $\angle A, \angle B$ and $\angle C$ intersect the circumcircle again in $A_{1}, B_{1}$ and $C_{1}$, respectively. Let $M$ be the point of intersection of $A B$ and $B_{1} C_{1}$, and let $N$ be the point of intersection of $B C$ and $A_{1} B_{1}$. Prove that $M N$ passes through the incentre of triangle $A B C$.
|
Let $I$ be the incenter of triangle $A B C$ (the intersection point of the angle bisectors $A A_{1}, B B_{1}$ and $C C_{1}$ ), and let $B_{1} C_{1}$ intersect the side $A C$ and the angle bisector $A A_{1}$ at $P$ and $Q$, respectively (see Figure 9 ). Then
$$
\angle A Q C_{1}=\frac{1}{2}\left(\overparen{A C}_{1}+\overparen{A_{1} B_{1}}\right)=\frac{1}{2} \cdot\left(\frac{1}{2} \overparen{A B}+\frac{1}{2} \overparen{B C}+\frac{1}{2} \overparen{C A}\right)=90^{\circ}
$$
Since $\angle A C_{1} B_{1}=\angle B_{1} C_{1} C$ (as their supporting arcs are of equal size), then $C_{1} B_{1}$ is the bisector of angle $A C_{1} I$. Moreover, since $A I$ and $C_{1} B_{1}$ are perpendicular, then $C_{1} B_{1}$ is also the bisector of angle $A M I$. Similarly we can show that $B_{1} C_{1}$ bisects the angles $A B_{1} I$ ja $A P I$. Hence the diagonals of the quadrangle $A M I P$ are perpendicular and bisect its angles, i.e.
$A M I P$ is a rhombus and $M I$ is parrallel to $A C$. Similarly we can prove that $N I$ is parallel to $A C$, i.e. points $M, I$ and $N$ are collinear, q.e.d.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
e187b5cb-e46a-539e-aa3a-fd5fb25e06fe
| 238,910
|
a) Prove the existence of two infinite sets $A$ and $B$, not necessarily disjoint, of non-negative integers such that each non-negative integer $n$ is uniquely representable in the form $n=a+b$ with $a \in A, b \in B$.
b) Prove that for each such pair $(A, B)$, either $A$ or $B$ contains only multiples of some integer $k>1$.
|
a) Let $A$ be the set of non-negative integers whose only non-zero decimal digits are in even positions counted from the right, and $B$ the set of nonnegative integers whose only non-zero decimal digits are in odd positions counted from the right. It is obvious that $A$ and $B$ have the required property.
b) Since the only possible representation of 0 is $0+0$, we have $0 \in A \cap B$. The only possible representations of 1 are $1+0$ and $0+1$. Hence 1 must belong to at least one of the sets $A$ and $B$. Let $1 \in A$, and let $k$ be the smallest positive integer such that $k \notin A$. Then $k>1$. If any number $b$ with $0<b<k$ belonged to $B$, it would have the two representations $b+0$ and $0+b$. Hence no such number belongs to $B$. Also, in $k=a+b$ with $a \in A$ and $b \in B$ the number $b$ cannot be 0 since then $a=k$, contradicting the assumption that $k \notin A$. Hence $b=k$, and $k \in B$.
Consider the decomposition of $A$ into the union $A_{1} \cup A_{2} \cup \cdots$ of its maximal subsets $A_{1}, A_{2}, \ldots$ of consecutive numbers, where each element of $A_{1}$ is less than each element of $A_{2}$ etc. In particular, $A_{1}=\{0,1, \ldots, k-1\}$. By our assumption the set of all non-negative integers is the union of nonintersecting sets $A_{n}+b=\left\{a+b \mid a \in A_{n}\right\}$ with $n \in \mathbb{N}$ and $b \in B$, each of these consisting of some number of consecutive integers. We will show that each subset $A_{n}$ has exactly $k$ elements. Indeed, suppose $m$ is the smallest index for which the number $l$ of elements in $A_{m}$ is different from $k$, then $l<k$ since $A_{m}+0$ and $A_{m}+k$ do not overlap. Denoting by $c$ the smallest element of $A_{m}$, we have $c+k-1 \notin A$, so $c+k-1=a+b$ with $a \in A$
and $0 \neq b \in B$. Hence, $b \geqslant k$ and $a<c$. Suppose $a \in A_{n}$, then $n<m$ and the subset $A_{n}$ has $k$ elements. But then $A_{n}+b$ overlaps with either $A_{m}+0$ or $A_{m}+k$, a contradiction.
Hence, the set of non-negative integers is the union of non-intersecting sets $A_{n}+b$ with $n \in \mathbb{N}$ and $b \in B$, each of which consists of $k$ consecutive integers. The smallest element of each of these subsets is a multiple of $k$. Since each integer $b \in B$ is the smallest element of $A_{1}+b$, it follows that each $b \in B$ is a multiple of $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
a) Prove the existence of two infinite sets $A$ and $B$, not necessarily disjoint, of non-negative integers such that each non-negative integer $n$ is uniquely representable in the form $n=a+b$ with $a \in A, b \in B$.
b) Prove that for each such pair $(A, B)$, either $A$ or $B$ contains only multiples of some integer $k>1$.
|
a) Let $A$ be the set of non-negative integers whose only non-zero decimal digits are in even positions counted from the right, and $B$ the set of nonnegative integers whose only non-zero decimal digits are in odd positions counted from the right. It is obvious that $A$ and $B$ have the required property.
b) Since the only possible representation of 0 is $0+0$, we have $0 \in A \cap B$. The only possible representations of 1 are $1+0$ and $0+1$. Hence 1 must belong to at least one of the sets $A$ and $B$. Let $1 \in A$, and let $k$ be the smallest positive integer such that $k \notin A$. Then $k>1$. If any number $b$ with $0<b<k$ belonged to $B$, it would have the two representations $b+0$ and $0+b$. Hence no such number belongs to $B$. Also, in $k=a+b$ with $a \in A$ and $b \in B$ the number $b$ cannot be 0 since then $a=k$, contradicting the assumption that $k \notin A$. Hence $b=k$, and $k \in B$.
Consider the decomposition of $A$ into the union $A_{1} \cup A_{2} \cup \cdots$ of its maximal subsets $A_{1}, A_{2}, \ldots$ of consecutive numbers, where each element of $A_{1}$ is less than each element of $A_{2}$ etc. In particular, $A_{1}=\{0,1, \ldots, k-1\}$. By our assumption the set of all non-negative integers is the union of nonintersecting sets $A_{n}+b=\left\{a+b \mid a \in A_{n}\right\}$ with $n \in \mathbb{N}$ and $b \in B$, each of these consisting of some number of consecutive integers. We will show that each subset $A_{n}$ has exactly $k$ elements. Indeed, suppose $m$ is the smallest index for which the number $l$ of elements in $A_{m}$ is different from $k$, then $l<k$ since $A_{m}+0$ and $A_{m}+k$ do not overlap. Denoting by $c$ the smallest element of $A_{m}$, we have $c+k-1 \notin A$, so $c+k-1=a+b$ with $a \in A$
and $0 \neq b \in B$. Hence, $b \geqslant k$ and $a<c$. Suppose $a \in A_{n}$, then $n<m$ and the subset $A_{n}$ has $k$ elements. But then $A_{n}+b$ overlaps with either $A_{m}+0$ or $A_{m}+k$, a contradiction.
Hence, the set of non-negative integers is the union of non-intersecting sets $A_{n}+b$ with $n \in \mathbb{N}$ and $b \in B$, each of which consists of $k$ consecutive integers. The smallest element of each of these subsets is a multiple of $k$. Since each integer $b \in B$ is the smallest element of $A_{1}+b$, it follows that each $b \in B$ is a multiple of $k$.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\n18."
}
|
16054fe0-179f-53f0-8373-eb282f76d6ff
| 238,938
|
A triple of positive integers $(a, b, c)$ is called quasi-Pythagorean if there exists a triangle with lengths of the sides $a, b, c$ and the angle opposite to the side $c$ equal to $120^{\circ}$. Prove that if $(a, b, c)$ is a quasi-Pythagorean triple then $c$ has a prime divisor greater than 5 .
|
By the cosine law, a triple of positive integers $(a, b, c)$ is quasi-Pythagorean if and only if
$$
c^{2}=a^{2}+a b+b^{2}
$$
If a triple $(a, b, c)$ with a common divisor $d>1$ satisfies (1), then so does the reduced triple $\left(\frac{a}{d}, \frac{b}{d}, \frac{c}{d}\right)$. Hence it suffices to prove that in every irreducible quasi-Pythagorean triple the greatest term $c$ has a prime divisor greater than 5. Actually, we will show that in that case every prime divisor of $c$ is greater than 5 .
Let $(a, b, c)$ be an irreducible triple satisfying (1). Note that then $a, b$ and $c$ are pairwise coprime. We have to show that $c$ is not divisible by 2,3 or 5 .
If $c$ were even, then $a$ and $b$ (coprime to $c$ ) should be odd, and (1) would not hold.
Suppose now that $c$ is divisible by 3 , and rewrite (1) as
$$
4 c^{2}=(a+2 b)^{2}+3 a^{2}
$$
Then $a+2 b$ must be divisible by 3 . Since $a$ is coprime to $c$, the number $3 a^{2}$ is not divisible by 9 . This yields a contradiction since the remaining terms in (2) are divisible by 9 .
Finally, suppose $c$ is divisible by 5 (and hence $a$ is not). Again we get a contradiction with (2) since the square of every integer is congruent to 0 ,
1 or -1 modulo 5 ; so $4 c^{2}-3 a^{2} \equiv \pm 2(\bmod 5)$ and it cannot be equal to $(a+2 b)^{2}$. This completes the proof.
Remark. A yet stronger claim is true: If $a$ and $b$ are coprime, then every prime divisor $p>3$ of $a^{2}+a b+b^{2}$ is of the form $p=6 k+1$. (Hence every prime divisor of $c$ in an irreducible quasi-Pythagorean triple $(a, b, c)$ has such a form.)
This stronger claim can be proved by observing that $p$ does not divide $a$ and the number $g=(a+2 b) a^{(p-3) / 2}$ is an integer whose square satisfies
$$
\begin{aligned}
g^{2} & =(a+2 b)^{2} a^{p-3}=\left(4\left(a^{2}+a b+b^{2}\right)-3 a^{2}\right) a^{p-3} \equiv-3 a^{p-1} \equiv \\
& \equiv-3(\bmod p)
\end{aligned}
$$
Hence -3 is a quadratic residue modulo $p$. This is known to be true only for primes of the form $6 k+1$; proofs can be found in many books on number theory, e.g. [1].
Reference. [1] K. Ireland, M. Rosen, A Classical Introduction to Modern Number Theory, Second Edition, Springer-Verlag, New York 1990.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A triple of positive integers $(a, b, c)$ is called quasi-Pythagorean if there exists a triangle with lengths of the sides $a, b, c$ and the angle opposite to the side $c$ equal to $120^{\circ}$. Prove that if $(a, b, c)$ is a quasi-Pythagorean triple then $c$ has a prime divisor greater than 5 .
|
By the cosine law, a triple of positive integers $(a, b, c)$ is quasi-Pythagorean if and only if
$$
c^{2}=a^{2}+a b+b^{2}
$$
If a triple $(a, b, c)$ with a common divisor $d>1$ satisfies (1), then so does the reduced triple $\left(\frac{a}{d}, \frac{b}{d}, \frac{c}{d}\right)$. Hence it suffices to prove that in every irreducible quasi-Pythagorean triple the greatest term $c$ has a prime divisor greater than 5. Actually, we will show that in that case every prime divisor of $c$ is greater than 5 .
Let $(a, b, c)$ be an irreducible triple satisfying (1). Note that then $a, b$ and $c$ are pairwise coprime. We have to show that $c$ is not divisible by 2,3 or 5 .
If $c$ were even, then $a$ and $b$ (coprime to $c$ ) should be odd, and (1) would not hold.
Suppose now that $c$ is divisible by 3 , and rewrite (1) as
$$
4 c^{2}=(a+2 b)^{2}+3 a^{2}
$$
Then $a+2 b$ must be divisible by 3 . Since $a$ is coprime to $c$, the number $3 a^{2}$ is not divisible by 9 . This yields a contradiction since the remaining terms in (2) are divisible by 9 .
Finally, suppose $c$ is divisible by 5 (and hence $a$ is not). Again we get a contradiction with (2) since the square of every integer is congruent to 0 ,
1 or -1 modulo 5 ; so $4 c^{2}-3 a^{2} \equiv \pm 2(\bmod 5)$ and it cannot be equal to $(a+2 b)^{2}$. This completes the proof.
Remark. A yet stronger claim is true: If $a$ and $b$ are coprime, then every prime divisor $p>3$ of $a^{2}+a b+b^{2}$ is of the form $p=6 k+1$. (Hence every prime divisor of $c$ in an irreducible quasi-Pythagorean triple $(a, b, c)$ has such a form.)
This stronger claim can be proved by observing that $p$ does not divide $a$ and the number $g=(a+2 b) a^{(p-3) / 2}$ is an integer whose square satisfies
$$
\begin{aligned}
g^{2} & =(a+2 b)^{2} a^{p-3}=\left(4\left(a^{2}+a b+b^{2}\right)-3 a^{2}\right) a^{p-3} \equiv-3 a^{p-1} \equiv \\
& \equiv-3(\bmod p)
\end{aligned}
$$
Hence -3 is a quadratic residue modulo $p$. This is known to be true only for primes of the form $6 k+1$; proofs can be found in many books on number theory, e.g. [1].
Reference. [1] K. Ireland, M. Rosen, A Classical Introduction to Modern Number Theory, Second Edition, Springer-Verlag, New York 1990.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
1ba5b6c7-986e-51e4-b8e3-6a061e07f46d
| 605,385
|
Let $P$ be a polynomial with integer coefficients. Suppose that for $n=1,2,3, \ldots, 1998$ the number $P(n)$ is a three-digit positive integer. Prove that the polynomial $P$ has no integer roots.
|
Let $m$ be an arbitrary integer and define $n \in\{1,2, \ldots, 1998\}$ to be such that $m \equiv n(\bmod 1998)$. Then $P(m) \equiv P(n)(\bmod 1998)$. Since $P(n)$ as a three-digit number cannot be divisible by 1998 , then $P(m)$ cannot be equal to 0 . Hence $P$ has no integer roots.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P$ be a polynomial with integer coefficients. Suppose that for $n=1,2,3, \ldots, 1998$ the number $P(n)$ is a three-digit positive integer. Prove that the polynomial $P$ has no integer roots.
|
Let $m$ be an arbitrary integer and define $n \in\{1,2, \ldots, 1998\}$ to be such that $m \equiv n(\bmod 1998)$. Then $P(m) \equiv P(n)(\bmod 1998)$. Since $P(n)$ as a three-digit number cannot be divisible by 1998 , then $P(m)$ cannot be equal to 0 . Hence $P$ has no integer roots.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
3a2035a2-693d-53c9-a9d6-1146d885ef8f
| 241,112
|
Let $a$ be an odd digit and $b$ an even digit. Prove that for every positive integer $n$ there exists a positive integer, divisible by $2^{n}$, whose decimal representation contains no digits other than $a$ and $b$.
|
If $b=0$, then $N=10^{n} a$ meets the demands. For the sequel, suppose $b \neq 0$.
Let $n$ be fixed. We prove that if $1 \leqslant k \leqslant n$, then we can find a positive integer $m_{k}<5^{k}$ such that the last $k$ digits of $m_{k} 2^{n}$ are all $a$ or $b$. Clearly, for $k=1$ we can find $m_{1}$ with $1 \leqslant m_{1} \leqslant 4$ such that $m_{1} 2^{n}$ ends with the digit $b$. (This corresponds to solving the congruence $m_{1} 2^{n-1} \equiv \frac{b}{2}$ modulo 5.) If $n=1$, we are done. Hence let $n \geqslant 2$.
Assume that for a certain $k$ with $1 \leqslant k<n$ we have found the integer $m_{k}$. Let $c$ be the $(k+1)$-st digit from the right of $m_{k} 2^{n}$ (i.e., the coefficient of $10^{k}$ in its decimal representation). Consider the number $5^{k} 2^{n}$ : it ends with precisely $k$ zeros, and the last non-zero digit is even; call it $d$. For any $r$, the corresponding digit of the number $m_{k} 2^{n}+r 5^{k} 2^{n}$ will be $c+r d$ modulo 10. By a suitable choice of $r \leqslant 4$ we can make this digit be either $a$ or $b$, according to whether $c$ is odd or even. (As before, this corresponds to solving one of the congruences $r \cdot \frac{d}{2} \equiv \frac{a-c}{2}$ or $r \cdot \frac{d}{2} \equiv \frac{b-c}{2}$ modulo 5.) Now, let $m_{k+1}=m_{k}+r 5^{k}$. The last $k+1$ digits of $m_{k+1} 2^{n}$ are all $a$ or $b$. As $m_{k+1}<5^{k}+4 \cdot 5^{k}=5^{k+1}$, we see that $m_{k+1}$ has the required properties. This process can be continued until we obtain a number $m_{n}$ such that the last $n$ digits of $N=m_{n} 2^{n}$ are $a$ or $b$. Since $m_{n}<5^{n}$, the number $N$ has at most $n$ digits, all of which are $a$ or $b$.
Alternative solution. The case $b=0$ is handled as in the first solution. Assume that $b \neq 0$. We prove the statement by induction on $n$, postulating, in addition, that $N$ (the integer we are looking for) must be an $n$-digit number.
For $n=1$ we take the one-digit number $b$. Assume the claim is true for a certain $n \geqslant 1$, with $N \equiv 0\left(\bmod 2^{n}\right)$ having exactly $n$ digits, all $a$ or $b$; thus $N<10^{n}$. Define
$$
N^{*}= \begin{cases}10^{n} b+N & \text { if } N \equiv 0\left(\bmod 2^{n+1}\right) \\ 10^{n} a+N & \text { if } N \equiv 2^{n}\left(\bmod 2^{n+1}\right) .\end{cases}
$$
Clearly, $N^{*}$ is an $(n+1)$-digit number, satisfying
$$
N^{*} \equiv \begin{cases}0+0\left(\bmod 2^{n+1}\right) & \text { in the first case } \\ 2^{n}+2^{n}\left(\bmod 2^{n+1}\right) & \text { in the second case. }\end{cases}
$$
In both cases $N^{*}$ is divisible by $2^{n+1}$, and we have the induction claim. The result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ be an odd digit and $b$ an even digit. Prove that for every positive integer $n$ there exists a positive integer, divisible by $2^{n}$, whose decimal representation contains no digits other than $a$ and $b$.
|
If $b=0$, then $N=10^{n} a$ meets the demands. For the sequel, suppose $b \neq 0$.
Let $n$ be fixed. We prove that if $1 \leqslant k \leqslant n$, then we can find a positive integer $m_{k}<5^{k}$ such that the last $k$ digits of $m_{k} 2^{n}$ are all $a$ or $b$. Clearly, for $k=1$ we can find $m_{1}$ with $1 \leqslant m_{1} \leqslant 4$ such that $m_{1} 2^{n}$ ends with the digit $b$. (This corresponds to solving the congruence $m_{1} 2^{n-1} \equiv \frac{b}{2}$ modulo 5.) If $n=1$, we are done. Hence let $n \geqslant 2$.
Assume that for a certain $k$ with $1 \leqslant k<n$ we have found the integer $m_{k}$. Let $c$ be the $(k+1)$-st digit from the right of $m_{k} 2^{n}$ (i.e., the coefficient of $10^{k}$ in its decimal representation). Consider the number $5^{k} 2^{n}$ : it ends with precisely $k$ zeros, and the last non-zero digit is even; call it $d$. For any $r$, the corresponding digit of the number $m_{k} 2^{n}+r 5^{k} 2^{n}$ will be $c+r d$ modulo 10. By a suitable choice of $r \leqslant 4$ we can make this digit be either $a$ or $b$, according to whether $c$ is odd or even. (As before, this corresponds to solving one of the congruences $r \cdot \frac{d}{2} \equiv \frac{a-c}{2}$ or $r \cdot \frac{d}{2} \equiv \frac{b-c}{2}$ modulo 5.) Now, let $m_{k+1}=m_{k}+r 5^{k}$. The last $k+1$ digits of $m_{k+1} 2^{n}$ are all $a$ or $b$. As $m_{k+1}<5^{k}+4 \cdot 5^{k}=5^{k+1}$, we see that $m_{k+1}$ has the required properties. This process can be continued until we obtain a number $m_{n}$ such that the last $n$ digits of $N=m_{n} 2^{n}$ are $a$ or $b$. Since $m_{n}<5^{n}$, the number $N$ has at most $n$ digits, all of which are $a$ or $b$.
Alternative solution. The case $b=0$ is handled as in the first solution. Assume that $b \neq 0$. We prove the statement by induction on $n$, postulating, in addition, that $N$ (the integer we are looking for) must be an $n$-digit number.
For $n=1$ we take the one-digit number $b$. Assume the claim is true for a certain $n \geqslant 1$, with $N \equiv 0\left(\bmod 2^{n}\right)$ having exactly $n$ digits, all $a$ or $b$; thus $N<10^{n}$. Define
$$
N^{*}= \begin{cases}10^{n} b+N & \text { if } N \equiv 0\left(\bmod 2^{n+1}\right) \\ 10^{n} a+N & \text { if } N \equiv 2^{n}\left(\bmod 2^{n+1}\right) .\end{cases}
$$
Clearly, $N^{*}$ is an $(n+1)$-digit number, satisfying
$$
N^{*} \equiv \begin{cases}0+0\left(\bmod 2^{n+1}\right) & \text { in the first case } \\ 2^{n}+2^{n}\left(\bmod 2^{n+1}\right) & \text { in the second case. }\end{cases}
$$
In both cases $N^{*}$ is divisible by $2^{n+1}$, and we have the induction claim. The result follows.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
85423bfc-69f3-52fd-b12e-54521b3ed448
| 241,122
|
Let $P_{k}(x)=1+x+x^{2}+\cdots+x^{k-1}$. Show that
$$
\sum_{k=1}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right) P_{k}(x)=2^{n-1} P_{n}\left(\frac{1+x}{2}\right)
$$
for every real number $x$ and every positive integer $n$.
|
Let $A$ and $B$ be the left- and right-hand side of the claimed formula, respectively. Since
$$
(1-x) P_{k}(x)=1-x^{k},
$$
we get
$$
(1-x) \cdot A=\sum_{k=1}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right)\left(1-x^{k}\right)=\sum_{k=0}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right)\left(1-x^{k}\right)=2^{n}-(1+x)^{n}
$$
and
$$
\begin{aligned}
(1-x) \cdot B & =2\left(1-\frac{1+x}{2}\right) \cdot 2^{n-1} P_{n}\left(\frac{1+x}{2}\right)= \\
& =2^{n}\left(1-\left(\frac{1+x}{2}\right)^{n}\right)=2^{n}-(1+x)^{n} .
\end{aligned}
$$
Thus $A=B$ for all real numbers $x \neq 1$. Since both $A$ and $B$ are polynomials, they coincide also for $x=1$.
Remark. The desired equality can be also proved without multiplication by $(1-x)$, just via regrouping the terms of the expanded $P_{k}$ 's and some more manipulation; this approach is more cumbersome.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P_{k}(x)=1+x+x^{2}+\cdots+x^{k-1}$. Show that
$$
\sum_{k=1}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right) P_{k}(x)=2^{n-1} P_{n}\left(\frac{1+x}{2}\right)
$$
for every real number $x$ and every positive integer $n$.
|
Let $A$ and $B$ be the left- and right-hand side of the claimed formula, respectively. Since
$$
(1-x) P_{k}(x)=1-x^{k},
$$
we get
$$
(1-x) \cdot A=\sum_{k=1}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right)\left(1-x^{k}\right)=\sum_{k=0}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right)\left(1-x^{k}\right)=2^{n}-(1+x)^{n}
$$
and
$$
\begin{aligned}
(1-x) \cdot B & =2\left(1-\frac{1+x}{2}\right) \cdot 2^{n-1} P_{n}\left(\frac{1+x}{2}\right)= \\
& =2^{n}\left(1-\left(\frac{1+x}{2}\right)^{n}\right)=2^{n}-(1+x)^{n} .
\end{aligned}
$$
Thus $A=B$ for all real numbers $x \neq 1$. Since both $A$ and $B$ are polynomials, they coincide also for $x=1$.
Remark. The desired equality can be also proved without multiplication by $(1-x)$, just via regrouping the terms of the expanded $P_{k}$ 's and some more manipulation; this approach is more cumbersome.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
e6295b54-84ee-5606-b5c5-556ec8aba5f9
| 241,151
|
Let the numbers $\alpha, \beta$ satisfy $0<\alpha<\beta<\pi / 2$ and let $\gamma$ and $\delta$ be the numbers defined by the conditions:
(i) $0<\gamma<\pi / 2$, and $\tan \gamma$ is the arithmetic mean of $\tan \alpha$ and $\tan \beta$;
(ii) $0<\delta<\pi / 2$, and $\frac{1}{\cos \delta}$ is the arithmetic mean of $\frac{1}{\cos \alpha}$ and $\frac{1}{\cos \beta}$.
Prove that $\gamma<\delta$.
|
Let $f(t)=\sqrt{1+t^{2}}$. Since $f^{\prime \prime}(t)=\left(1+t^{2}\right)^{-3 / 2}>0$, the function $f(t)$ is
strictly convex on $(0, \infty)$. Consequently,
$$
\begin{aligned}
\frac{1}{\cos \gamma} & =\sqrt{1+\tan ^{2} \gamma}=f(\tan \gamma)=f\left(\frac{\tan \alpha+\tan \beta}{2}\right)< \\
& <\frac{f(\tan \alpha)+f(\tan \beta)}{2}=\frac{1}{2}\left(\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}\right)=\frac{1}{\cos \delta},
\end{aligned}
$$
and hence $\gamma<\delta$.
Remark. The use of calculus can be avoided. We only need the midpointconvexity of $f$, i.e., the inequality
$$
\sqrt{1+\frac{1}{4}(u+v)^{2}}<\frac{1}{2} \sqrt{1+u^{2}}+\frac{1}{2} \sqrt{1+v^{2}}
$$
for $u, v>0$ and $u \neq v$, which is equivalent (via squaring) to
$$
1+u v<\sqrt{\left(1+u^{2}\right)\left(1+v^{2}\right)} .
$$
The latter inequality reduces (again by squaring) to $2 u v<u^{2}+v^{2}$, holding trivially.
Alternative solution. Draw a unit segment $O P$ in the plane and take points $A$ and $B$ on the same side of line $O P$ so that $\angle P O A=\angle P O B=90^{\circ}$, $\angle O P A=\alpha$ and $\angle O P B=\beta$ (see Figure 1). Then we have $|O A|=\tan \alpha$, $|O B|=\tan \beta,|P A|=\frac{1}{\cos \alpha}$ and $|P B|=\frac{1}{\cos \beta}$.
Figure 1
Let $C$ be the midpoint of the segment $A B$. By hypothesis, we have $|O C|=\frac{\tan \alpha+\tan \beta}{2}=\tan \gamma$, hence $\angle O P C=\gamma$ and $|P C|=\frac{1}{\cos \gamma}$. Let $Q$ be the point symmetric to $P$ with respect to $C$. The quadrilateral $P A Q B$ is a parallelogram, and therefore $|A Q|=|P B|=\frac{1}{\cos \beta}$. Eventually,
$$
\frac{2}{\cos \delta}=\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}=|P A|+|A Q|>|P Q|=2 \cdot|P C|=\frac{2}{\cos \gamma},
$$
and hence $\delta>\gamma$.
Another solution. Set $x=\frac{\alpha+\beta}{2}$ and $y=\frac{\alpha-\beta}{2}$, then $\alpha=x+y, \beta=x-y$ and
$$
\begin{aligned}
\cos \alpha \cos \beta & =\frac{1}{2}(\cos 2 x+\cos 2 y)= \\
& =\frac{1}{2}\left(1-2 \sin ^{2} x\right)+\frac{1}{2}\left(2 \cos ^{2} y-1\right)=\cos ^{2} y-\sin ^{2} x .
\end{aligned}
$$
By the conditions of the problem,
$$
\tan \gamma=\frac{1}{2}\left(\frac{\sin \alpha}{\cos \alpha}+\frac{\sin \beta}{\cos \beta}\right)=\frac{1}{2} \cdot \frac{\sin (\alpha+\beta)}{\cos \alpha \cos \beta}=\frac{\sin x \cos x}{\cos \alpha \cos \beta}
$$
and
$$
\frac{1}{\cos \delta}=\frac{1}{2}\left(\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}\right)=\frac{1}{2} \cdot \frac{\cos \alpha+\cos \beta}{\cos \alpha \cos \beta}=\frac{\cos x \cos y}{\cos \alpha \cos \beta} .
$$
Using (3) we hence obtain
$$
\begin{aligned}
\tan ^{2} \delta-\tan ^{2} \gamma & =\frac{1}{\cos ^{2} \delta}-1-\tan ^{2} \gamma=\frac{\cos ^{2} x \cos ^{2} y-\sin ^{2} x \cos ^{2} x}{\cos ^{2} \alpha \cos ^{2} \beta}-1= \\
& =\frac{\cos ^{2} x\left(\cos ^{2} y-\sin ^{2} x\right)}{\left(\cos ^{2} y-\sin ^{2} x\right)^{2}}-1=\frac{\cos ^{2} x}{\cos ^{2} y-\sin ^{2} x}-1= \\
& =\frac{\cos ^{2} x-\cos ^{2} y+\sin ^{2} x}{\cos ^{2} y-\sin ^{2} x}=\frac{\sin ^{2} y}{\cos \alpha \cos \beta}>0,
\end{aligned}
$$
showing that $\delta>\gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let the numbers $\alpha, \beta$ satisfy $0<\alpha<\beta<\pi / 2$ and let $\gamma$ and $\delta$ be the numbers defined by the conditions:
(i) $0<\gamma<\pi / 2$, and $\tan \gamma$ is the arithmetic mean of $\tan \alpha$ and $\tan \beta$;
(ii) $0<\delta<\pi / 2$, and $\frac{1}{\cos \delta}$ is the arithmetic mean of $\frac{1}{\cos \alpha}$ and $\frac{1}{\cos \beta}$.
Prove that $\gamma<\delta$.
|
Let $f(t)=\sqrt{1+t^{2}}$. Since $f^{\prime \prime}(t)=\left(1+t^{2}\right)^{-3 / 2}>0$, the function $f(t)$ is
strictly convex on $(0, \infty)$. Consequently,
$$
\begin{aligned}
\frac{1}{\cos \gamma} & =\sqrt{1+\tan ^{2} \gamma}=f(\tan \gamma)=f\left(\frac{\tan \alpha+\tan \beta}{2}\right)< \\
& <\frac{f(\tan \alpha)+f(\tan \beta)}{2}=\frac{1}{2}\left(\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}\right)=\frac{1}{\cos \delta},
\end{aligned}
$$
and hence $\gamma<\delta$.
Remark. The use of calculus can be avoided. We only need the midpointconvexity of $f$, i.e., the inequality
$$
\sqrt{1+\frac{1}{4}(u+v)^{2}}<\frac{1}{2} \sqrt{1+u^{2}}+\frac{1}{2} \sqrt{1+v^{2}}
$$
for $u, v>0$ and $u \neq v$, which is equivalent (via squaring) to
$$
1+u v<\sqrt{\left(1+u^{2}\right)\left(1+v^{2}\right)} .
$$
The latter inequality reduces (again by squaring) to $2 u v<u^{2}+v^{2}$, holding trivially.
Alternative solution. Draw a unit segment $O P$ in the plane and take points $A$ and $B$ on the same side of line $O P$ so that $\angle P O A=\angle P O B=90^{\circ}$, $\angle O P A=\alpha$ and $\angle O P B=\beta$ (see Figure 1). Then we have $|O A|=\tan \alpha$, $|O B|=\tan \beta,|P A|=\frac{1}{\cos \alpha}$ and $|P B|=\frac{1}{\cos \beta}$.

Figure 1
Let $C$ be the midpoint of the segment $A B$. By hypothesis, we have $|O C|=\frac{\tan \alpha+\tan \beta}{2}=\tan \gamma$, hence $\angle O P C=\gamma$ and $|P C|=\frac{1}{\cos \gamma}$. Let $Q$ be the point symmetric to $P$ with respect to $C$. The quadrilateral $P A Q B$ is a parallelogram, and therefore $|A Q|=|P B|=\frac{1}{\cos \beta}$. Eventually,
$$
\frac{2}{\cos \delta}=\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}=|P A|+|A Q|>|P Q|=2 \cdot|P C|=\frac{2}{\cos \gamma},
$$
and hence $\delta>\gamma$.
Another solution. Set $x=\frac{\alpha+\beta}{2}$ and $y=\frac{\alpha-\beta}{2}$, then $\alpha=x+y, \beta=x-y$ and
$$
\begin{aligned}
\cos \alpha \cos \beta & =\frac{1}{2}(\cos 2 x+\cos 2 y)= \\
& =\frac{1}{2}\left(1-2 \sin ^{2} x\right)+\frac{1}{2}\left(2 \cos ^{2} y-1\right)=\cos ^{2} y-\sin ^{2} x .
\end{aligned}
$$
By the conditions of the problem,
$$
\tan \gamma=\frac{1}{2}\left(\frac{\sin \alpha}{\cos \alpha}+\frac{\sin \beta}{\cos \beta}\right)=\frac{1}{2} \cdot \frac{\sin (\alpha+\beta)}{\cos \alpha \cos \beta}=\frac{\sin x \cos x}{\cos \alpha \cos \beta}
$$
and
$$
\frac{1}{\cos \delta}=\frac{1}{2}\left(\frac{1}{\cos \alpha}+\frac{1}{\cos \beta}\right)=\frac{1}{2} \cdot \frac{\cos \alpha+\cos \beta}{\cos \alpha \cos \beta}=\frac{\cos x \cos y}{\cos \alpha \cos \beta} .
$$
Using (3) we hence obtain
$$
\begin{aligned}
\tan ^{2} \delta-\tan ^{2} \gamma & =\frac{1}{\cos ^{2} \delta}-1-\tan ^{2} \gamma=\frac{\cos ^{2} x \cos ^{2} y-\sin ^{2} x \cos ^{2} x}{\cos ^{2} \alpha \cos ^{2} \beta}-1= \\
& =\frac{\cos ^{2} x\left(\cos ^{2} y-\sin ^{2} x\right)}{\left(\cos ^{2} y-\sin ^{2} x\right)^{2}}-1=\frac{\cos ^{2} x}{\cos ^{2} y-\sin ^{2} x}-1= \\
& =\frac{\cos ^{2} x-\cos ^{2} y+\sin ^{2} x}{\cos ^{2} y-\sin ^{2} x}=\frac{\sin ^{2} y}{\cos \alpha \cos \beta}>0,
\end{aligned}
$$
showing that $\delta>\gamma$.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\n9."
}
|
315cdaba-53c4-54bc-96d5-72bbb3dcd64c
| 241,161
|
Let $n \geqslant 4$ be an even integer. A regular $n$-gon and a regular $(n-1)$-gon are inscribed into the unit circle. For each vertex of the $n$-gon consider the distance from this vertex to the nearest vertex of the $(n-1)$-gon, measured along the circumference. Let $S$ be the sum of these $n$ distances. Prove that $S$ depends only on $n$, and not on the relative position of the two polygons.
|
For simplicity, take the length of the circle to be $2 n(n-1)$ rather than $2 \pi$. The vertices of the $(n-1)$-gon $A_{0} A_{1} \ldots A_{n-2}$ divide it into $n-1$ arcs of length $2 n$. By the pigeonhole principle, some two of the vertices of the $n$-gon $B_{0} B_{1} \ldots B_{n-1}$ lie in the same arc. Assume w.l.o.g. that $B_{0}$ and $B_{1}$ lie in the arc $A_{0} A_{1}$, with $B_{0}$ closer to $A_{0}$ and $B_{1}$ closer to $A_{1}$, and that $\left|A_{0} B_{0}\right| \leqslant\left|B_{1} A_{1}\right|$.
Consider the circle as the segment $[0,2 n(n-1)]$ of the real line, with both of its endpoints identified with the vertex $A_{0}$ and the numbers $2 n, 4 n, 6 n, \ldots$ identified accordingly with the vertices $A_{1}, A_{2}, A_{3}, \ldots$
For $k=0,1, \ldots, n-1$, let $x_{k}$ be the "coordinate" of the vertex $B_{k}$ of the $n$-gon. Each arc $B_{k} B_{k+1}$ has length $2(n-1)$. By the choice of labelling, we have
$$
0 \leqslant x_{0}<x_{1}=x_{0}+2(n-1) \leqslant 2 n
$$
and, moreover, $x_{0}-0 \leqslant 2 n-x_{1}$. Hence $0 \leqslant x_{0} \leqslant 1$.
Clearly, $x_{k}=x_{0}+2 k(n-1)$ for $k=0,1, \ldots, n-1$. It is not hard to see that $(2 k-1) n \leqslant x_{k} \leqslant 2 k n$ if $1 \leqslant k \leqslant \frac{n}{2}$, and $(2 k-2) n \leqslant x_{k} \leqslant(2 k-1) n$ if $\frac{n}{2}<k \leqslant n-1$. These inequalities are verified immediately by inserting $x_{k}=x_{0}+2 k(n-1)$ and taking into account that $0 \leqslant x_{0} \leqslant 1$.
Summing up, we have:
1) if $1 \leqslant k \leqslant \frac{n}{2}$, then $B_{k}$ lies between $A_{k-1}$ and $A_{k}$, closer to $A_{k}$; recalling that $A_{k}$ has "coordinate" $2 k n$, we see that the distance in question is equal to $2 k n-x_{k}=2 k-x_{0}$;
2) if $\frac{n}{2}<k \leqslant n-1$, then $B_{k}$ lies between $A_{k-1}$ and $A_{k}$, closer to $A_{k-1}$; the distance in question is equal to $x_{k}-(2 k-2) n=x_{0}-2 k+2 n$;
3) for $B_{0}$, the distance in question is $x_{0}$.
The sum of these distances evaluates to
$$
x_{0}+\sum_{k=1}^{n / 2}\left(2 k-x_{0}\right)+\sum_{k=n / 2+1}^{n-1}\left(x_{0}-2 k+2 n\right)
$$
Note that here $x_{0}$ appears half of the times with a plus sign and half of the times with a minus sign. Thus, eventually, all terms $x_{0}$ cancel out, and the value of $S$ does not depend on anything but $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n \geqslant 4$ be an even integer. A regular $n$-gon and a regular $(n-1)$-gon are inscribed into the unit circle. For each vertex of the $n$-gon consider the distance from this vertex to the nearest vertex of the $(n-1)$-gon, measured along the circumference. Let $S$ be the sum of these $n$ distances. Prove that $S$ depends only on $n$, and not on the relative position of the two polygons.
|
For simplicity, take the length of the circle to be $2 n(n-1)$ rather than $2 \pi$. The vertices of the $(n-1)$-gon $A_{0} A_{1} \ldots A_{n-2}$ divide it into $n-1$ arcs of length $2 n$. By the pigeonhole principle, some two of the vertices of the $n$-gon $B_{0} B_{1} \ldots B_{n-1}$ lie in the same arc. Assume w.l.o.g. that $B_{0}$ and $B_{1}$ lie in the arc $A_{0} A_{1}$, with $B_{0}$ closer to $A_{0}$ and $B_{1}$ closer to $A_{1}$, and that $\left|A_{0} B_{0}\right| \leqslant\left|B_{1} A_{1}\right|$.
Consider the circle as the segment $[0,2 n(n-1)]$ of the real line, with both of its endpoints identified with the vertex $A_{0}$ and the numbers $2 n, 4 n, 6 n, \ldots$ identified accordingly with the vertices $A_{1}, A_{2}, A_{3}, \ldots$
For $k=0,1, \ldots, n-1$, let $x_{k}$ be the "coordinate" of the vertex $B_{k}$ of the $n$-gon. Each arc $B_{k} B_{k+1}$ has length $2(n-1)$. By the choice of labelling, we have
$$
0 \leqslant x_{0}<x_{1}=x_{0}+2(n-1) \leqslant 2 n
$$
and, moreover, $x_{0}-0 \leqslant 2 n-x_{1}$. Hence $0 \leqslant x_{0} \leqslant 1$.
Clearly, $x_{k}=x_{0}+2 k(n-1)$ for $k=0,1, \ldots, n-1$. It is not hard to see that $(2 k-1) n \leqslant x_{k} \leqslant 2 k n$ if $1 \leqslant k \leqslant \frac{n}{2}$, and $(2 k-2) n \leqslant x_{k} \leqslant(2 k-1) n$ if $\frac{n}{2}<k \leqslant n-1$. These inequalities are verified immediately by inserting $x_{k}=x_{0}+2 k(n-1)$ and taking into account that $0 \leqslant x_{0} \leqslant 1$.
Summing up, we have:
1) if $1 \leqslant k \leqslant \frac{n}{2}$, then $B_{k}$ lies between $A_{k-1}$ and $A_{k}$, closer to $A_{k}$; recalling that $A_{k}$ has "coordinate" $2 k n$, we see that the distance in question is equal to $2 k n-x_{k}=2 k-x_{0}$;
2) if $\frac{n}{2}<k \leqslant n-1$, then $B_{k}$ lies between $A_{k-1}$ and $A_{k}$, closer to $A_{k-1}$; the distance in question is equal to $x_{k}-(2 k-2) n=x_{0}-2 k+2 n$;
3) for $B_{0}$, the distance in question is $x_{0}$.
The sum of these distances evaluates to
$$
x_{0}+\sum_{k=1}^{n / 2}\left(2 k-x_{0}\right)+\sum_{k=n / 2+1}^{n-1}\left(x_{0}-2 k+2 n\right)
$$
Note that here $x_{0}$ appears half of the times with a plus sign and half of the times with a minus sign. Thus, eventually, all terms $x_{0}$ cancel out, and the value of $S$ does not depend on anything but $n$.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\n10."
}
|
05af19ed-d6eb-55c0-97ae-fa5524802fba
| 241,171
|
Let $a, b$ and $c$ be the lengths of the sides of a triangle with circumradius $R$. Prove that
$$
R \geqslant \frac{a^{2}+b^{2}}{2 \sqrt{2 a^{2}+2 b^{2}-c^{2}}} .
$$
When does equality hold?
|
Answer: equality holds if $a=b$ or the angle opposite to $c$ is equal to $90^{\circ}$. Denote the angles opposite to the sides $a, b, c$ by $A, B, C$, respectively. By the law of sines we have $a=2 R \sin A, b=2 R \sin B, c=2 R \sin C$. Hence, the given inequality is equivalent to each of the following:
$$
\begin{aligned}
& R \geqslant \frac{4 R^{2}\left(\sin ^{2} A+\sin ^{2} B\right)}{2 \sqrt{8 R^{2}\left(\sin ^{2} A+\sin ^{2} B\right)-4 R^{2} \sin ^{2} C}}, \\
& 2\left(\sin ^{2} A+\sin ^{2} B\right)-\sin ^{2} C \geqslant\left(\sin ^{2} A+\sin ^{2} B\right)^{2} \\
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(2-\sin ^{2} A-\sin ^{2} B\right) \geqslant \sin ^{2} C \\
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(\cos ^{2} A+\cos ^{2} B\right) \geqslant \sin ^{2} C
\end{aligned}
$$
The last inequality follows from the Cauchy-Schwarz inequality:
$$
\begin{aligned}
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(\cos ^{2} B+\cos ^{2} A\right) \geqslant \\
& \quad \geqslant(\sin A \cdot \cos B+\sin B \cdot \cos A)^{2}=\sin ^{2} C .
\end{aligned}
$$
Equality requires that $\sin A=\lambda \cos B$ and $\sin B=\lambda \cos A$ for a certain real number $\lambda$, implying that $\lambda$ is positive and $A, B$ are acute angles. From these two equations we conclude that $\sin 2 A=\sin 2 B$. This means that either $2 A=2 B$ or $2 A+2 B=\pi$; in other words, $a=b$ or $C=90^{\circ}$. In each of these two cases the inequality indeed turns into equality.
Figure 2
Alternative solution. Let $A, B, C$ be the respective vertices of the triangle, $O$ be its circumcentre and $M$ be the midpoint of $A B$ (see Figure 2). The length $m_{c}=|C M|$ of the median drawn from $C$ is expressed by the well-
known formula
$$
4 m_{c}^{2}=2 a^{2}+2 b^{2}-c^{2} .
$$
Hence the inequality of the problem can be rewritten as $4 R m_{c} \geqslant a^{2}+b^{2}$, or $8 R m_{c} \geqslant 4 m_{c}^{2}+c^{2}$. The last inequality is equivalent to
$$
\left|m_{c}-R\right| \leqslant \sqrt{R^{2}-(c / 2)^{2}},
$$
or ||$M C|-| O C|| \leqslant|O M|$, which is the triangle inequality for triangle COM .
Equality holds if and only if the points $C, O, M$ are collinear. This happens if and only if $a=b$ or $\angle C=90^{\circ}$.
Remark. Yet another solution can be obtained by setting $R=\frac{a b c}{4 S}$ (where $S$ denotes the area of the triangle) and expressing $S$ by Heron's formula. After squaring both sides, cross-multiplying and cancelling a lot, the inequality reduces to $\left(a^{2}-b^{2}\right)^{2}\left(a^{2}+b^{2}-c^{2}\right)^{2} \geqslant 0$, with equality if $a=b$ or $a^{2}+b^{2}=c^{2}$.
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ and $c$ be the lengths of the sides of a triangle with circumradius $R$. Prove that
$$
R \geqslant \frac{a^{2}+b^{2}}{2 \sqrt{2 a^{2}+2 b^{2}-c^{2}}} .
$$
When does equality hold?
|
Answer: equality holds if $a=b$ or the angle opposite to $c$ is equal to $90^{\circ}$. Denote the angles opposite to the sides $a, b, c$ by $A, B, C$, respectively. By the law of sines we have $a=2 R \sin A, b=2 R \sin B, c=2 R \sin C$. Hence, the given inequality is equivalent to each of the following:
$$
\begin{aligned}
& R \geqslant \frac{4 R^{2}\left(\sin ^{2} A+\sin ^{2} B\right)}{2 \sqrt{8 R^{2}\left(\sin ^{2} A+\sin ^{2} B\right)-4 R^{2} \sin ^{2} C}}, \\
& 2\left(\sin ^{2} A+\sin ^{2} B\right)-\sin ^{2} C \geqslant\left(\sin ^{2} A+\sin ^{2} B\right)^{2} \\
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(2-\sin ^{2} A-\sin ^{2} B\right) \geqslant \sin ^{2} C \\
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(\cos ^{2} A+\cos ^{2} B\right) \geqslant \sin ^{2} C
\end{aligned}
$$
The last inequality follows from the Cauchy-Schwarz inequality:
$$
\begin{aligned}
& \left(\sin ^{2} A+\sin ^{2} B\right)\left(\cos ^{2} B+\cos ^{2} A\right) \geqslant \\
& \quad \geqslant(\sin A \cdot \cos B+\sin B \cdot \cos A)^{2}=\sin ^{2} C .
\end{aligned}
$$
Equality requires that $\sin A=\lambda \cos B$ and $\sin B=\lambda \cos A$ for a certain real number $\lambda$, implying that $\lambda$ is positive and $A, B$ are acute angles. From these two equations we conclude that $\sin 2 A=\sin 2 B$. This means that either $2 A=2 B$ or $2 A+2 B=\pi$; in other words, $a=b$ or $C=90^{\circ}$. In each of these two cases the inequality indeed turns into equality.

Figure 2
Alternative solution. Let $A, B, C$ be the respective vertices of the triangle, $O$ be its circumcentre and $M$ be the midpoint of $A B$ (see Figure 2). The length $m_{c}=|C M|$ of the median drawn from $C$ is expressed by the well-
known formula
$$
4 m_{c}^{2}=2 a^{2}+2 b^{2}-c^{2} .
$$
Hence the inequality of the problem can be rewritten as $4 R m_{c} \geqslant a^{2}+b^{2}$, or $8 R m_{c} \geqslant 4 m_{c}^{2}+c^{2}$. The last inequality is equivalent to
$$
\left|m_{c}-R\right| \leqslant \sqrt{R^{2}-(c / 2)^{2}},
$$
or ||$M C|-| O C|| \leqslant|O M|$, which is the triangle inequality for triangle COM .
Equality holds if and only if the points $C, O, M$ are collinear. This happens if and only if $a=b$ or $\angle C=90^{\circ}$.
Remark. Yet another solution can be obtained by setting $R=\frac{a b c}{4 S}$ (where $S$ denotes the area of the triangle) and expressing $S$ by Heron's formula. After squaring both sides, cross-multiplying and cancelling a lot, the inequality reduces to $\left(a^{2}-b^{2}\right)^{2}\left(a^{2}+b^{2}-c^{2}\right)^{2} \geqslant 0$, with equality if $a=b$ or $a^{2}+b^{2}=c^{2}$.

Figure 3
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
2df62e02-b785-5b01-b5cb-0a3f9c2095eb
| 605,539
|
In a triangle $A B C, \angle B A C=90^{\circ}$. Point $D$ lies on the side $B C$ and satisfies $\angle B D A=2 \angle B A D$. Prove that
$$
\frac{1}{|A D|}=\frac{1}{2}\left(\frac{1}{|B D|}+\frac{1}{|C D|}\right)
$$
|
Let $O$ be the circumcentre of triangle $A B C$ (i.e., the midpoint of $B C$ ) and let $A D$ meet the circumcircle again at $E$ (see Figure 3). Then $\angle B O E=2 \angle B A E=\angle C D E$, showing that $|D E|=|O E|$. Triangles $A D C$ and $B D E$ are similar; hence $\frac{|A D|}{|B D|}=\frac{|C D|}{|D E|}, \frac{|A D|}{|C D|}=\frac{|B D|}{|D E|}$ and finally
$$
\frac{|A D|}{|B D|}+\frac{|A D|}{|C D|}=\frac{|C D|}{|D E|}+\frac{|B D|}{|D E|}=\frac{|B C|}{|D E|}=\frac{|B C|}{|O E|}=2
$$
which is equivalent to the equality we have to prove.
Alternative solution. Let $\angle B A D=\alpha$ and $\angle C A D=\beta$. By the conditions of the problem, $\alpha+\beta=90^{\circ}$ (hence $\sin \beta=\cos \alpha$ ), $\angle B D A=2 \alpha$ and $\angle C D A=2 \beta$. By the law of sines,
$$
\frac{|A D|}{|B D|}=\frac{\sin 3 \alpha}{\sin \alpha}=3-4 \sin ^{2} \alpha
$$
and
$$
\frac{|A D|}{|C D|}=\frac{\sin 3 \beta}{\sin \beta}=3-4 \sin ^{2} \beta=3-4 \cos ^{2} \alpha .
$$
Adding these two equalities we get the claimed one.
Figure 4
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C, \angle B A C=90^{\circ}$. Point $D$ lies on the side $B C$ and satisfies $\angle B D A=2 \angle B A D$. Prove that
$$
\frac{1}{|A D|}=\frac{1}{2}\left(\frac{1}{|B D|}+\frac{1}{|C D|}\right)
$$
|
Let $O$ be the circumcentre of triangle $A B C$ (i.e., the midpoint of $B C$ ) and let $A D$ meet the circumcircle again at $E$ (see Figure 3). Then $\angle B O E=2 \angle B A E=\angle C D E$, showing that $|D E|=|O E|$. Triangles $A D C$ and $B D E$ are similar; hence $\frac{|A D|}{|B D|}=\frac{|C D|}{|D E|}, \frac{|A D|}{|C D|}=\frac{|B D|}{|D E|}$ and finally
$$
\frac{|A D|}{|B D|}+\frac{|A D|}{|C D|}=\frac{|C D|}{|D E|}+\frac{|B D|}{|D E|}=\frac{|B C|}{|D E|}=\frac{|B C|}{|O E|}=2
$$
which is equivalent to the equality we have to prove.
Alternative solution. Let $\angle B A D=\alpha$ and $\angle C A D=\beta$. By the conditions of the problem, $\alpha+\beta=90^{\circ}$ (hence $\sin \beta=\cos \alpha$ ), $\angle B D A=2 \alpha$ and $\angle C D A=2 \beta$. By the law of sines,
$$
\frac{|A D|}{|B D|}=\frac{\sin 3 \alpha}{\sin \alpha}=3-4 \sin ^{2} \alpha
$$
and
$$
\frac{|A D|}{|C D|}=\frac{\sin 3 \beta}{\sin \beta}=3-4 \sin ^{2} \beta=3-4 \cos ^{2} \alpha .
$$
Adding these two equalities we get the claimed one.

Figure 4
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
8624fd5a-fe9c-57eb-8665-6ae89c52e9bb
| 605,550
|
In a convex pentagon $A B C D E$, the sides $A E$ and $B C$ are parallel and $\angle A D E=\angle B D C$. The diagonals $A C$ and $B E$ intersect at $P$. Prove that $\angle E A D=\angle B D P$ and $\angle C B D=\angle A D P$.
|
Let $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ be the circumcircles of triangles $A E D$ and $B C D$, respectively. Let $D P$ meet $\mathcal{C}_{2}$ for the second time at $F$ (see Figure 4). Since $\angle A D E=\angle B D C$, the ratio of the lengths of the segments $E A$ and $B C$ is equal to the ratio of the radii of $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$. Thus the homothety with centre $P$ that takes $A E$ to $C B$, also transforms $\mathcal{C}_{1}$ onto $\mathcal{C}_{2}$. The same homothety transforms the arc $D E$ of $\mathcal{C}_{1}$ onto the $\operatorname{arc} F B$ of $\mathcal{C}_{2}$. Therefore $\angle E A D=\angle B D F=\angle B D P$. The second equality is proved similarly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a convex pentagon $A B C D E$, the sides $A E$ and $B C$ are parallel and $\angle A D E=\angle B D C$. The diagonals $A C$ and $B E$ intersect at $P$. Prove that $\angle E A D=\angle B D P$ and $\angle C B D=\angle A D P$.
|
Let $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ be the circumcircles of triangles $A E D$ and $B C D$, respectively. Let $D P$ meet $\mathcal{C}_{2}$ for the second time at $F$ (see Figure 4). Since $\angle A D E=\angle B D C$, the ratio of the lengths of the segments $E A$ and $B C$ is equal to the ratio of the radii of $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$. Thus the homothety with centre $P$ that takes $A E$ to $C B$, also transforms $\mathcal{C}_{1}$ onto $\mathcal{C}_{2}$. The same homothety transforms the arc $D E$ of $\mathcal{C}_{1}$ onto the $\operatorname{arc} F B$ of $\mathcal{C}_{2}$. Therefore $\angle E A D=\angle B D F=\angle B D P$. The second equality is proved similarly.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
67fe6ac0-33f9-5a68-8ec5-93e3d2c14191
| 241,194
|
Given a triangle $A B C$ with $|A B|<|A C|$. The line passing through $B$ and parallel to $A C$ meets the external bisector of angle $B A C$ at $D$. The line passing through $C$ and parallel to $A B$ meets this bisector at $E$. Point $F$ lies on the side $A C$ and satisfies the equality $|F C|=|A B|$. Prove that $|D F|=|F E|$.
|
Since the lines $B D$ and $A C$ are parallel and since $A D$ is the external bisector of $\angle B A C$, we have $\angle B A D=\angle B D A$; denote their common size by $\alpha$ (see Figure 5). Also $\angle C A E=\angle C E A=\alpha$, implying $|A B|=|B D|$ and $|A C|=|C E|$. Let $B^{\prime}, C^{\prime}, F^{\prime}$ be the feet of the perpendiculars from
Figure 5
the points $B, C, F$ to line $D E$. From $|F C|=|A B|$ we obtain
$$
\left|B^{\prime} F^{\prime}\right|=(|A B|+|A F|) \cos \alpha=|A C| \cos \alpha=\left|A C^{\prime}\right|=\left|C^{\prime} E\right|
$$
and
$$
\left|D B^{\prime}\right|=|B D| \cos \alpha=|F C| \cos \alpha=\left|F^{\prime} C^{\prime}\right|,
$$
Thus $\left|D F^{\prime}\right|=\left|F^{\prime} E\right|$, whence $|D F|=|F E|$.
Figure 6
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$ with $|A B|<|A C|$. The line passing through $B$ and parallel to $A C$ meets the external bisector of angle $B A C$ at $D$. The line passing through $C$ and parallel to $A B$ meets this bisector at $E$. Point $F$ lies on the side $A C$ and satisfies the equality $|F C|=|A B|$. Prove that $|D F|=|F E|$.
|
Since the lines $B D$ and $A C$ are parallel and since $A D$ is the external bisector of $\angle B A C$, we have $\angle B A D=\angle B D A$; denote their common size by $\alpha$ (see Figure 5). Also $\angle C A E=\angle C E A=\alpha$, implying $|A B|=|B D|$ and $|A C|=|C E|$. Let $B^{\prime}, C^{\prime}, F^{\prime}$ be the feet of the perpendiculars from

Figure 5
the points $B, C, F$ to line $D E$. From $|F C|=|A B|$ we obtain
$$
\left|B^{\prime} F^{\prime}\right|=(|A B|+|A F|) \cos \alpha=|A C| \cos \alpha=\left|A C^{\prime}\right|=\left|C^{\prime} E\right|
$$
and
$$
\left|D B^{\prime}\right|=|B D| \cos \alpha=|F C| \cos \alpha=\left|F^{\prime} C^{\prime}\right|,
$$
Thus $\left|D F^{\prime}\right|=\left|F^{\prime} E\right|$, whence $|D F|=|F E|$.

Figure 6
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
f265685e-40a5-560c-83e6-b8f468bcd6cb
| 241,203
|
Given an acute triangle $A B C$. Point $D$ is the foot of the perpendicular from $A$ to $B C$. Point $E$ lies on the segment $A D$ and satisfies the equation
$$
\frac{|A E|}{|E D|}=\frac{|C D|}{|D B|}
$$
Point $F$ is the foot of the perpendicular from $D$ to $B E$. Prove that $\angle A F C=90^{\circ}$.
|
Complete the rectangle $A D C P$ (see Figure 6). In view of
$$
\frac{|A E|}{|E D|}=\frac{|C D|}{|D B|}=\frac{|A P|}{|D B|}
$$
the points $B, E, P$ are collinear. Therefore $\angle D F P=90^{\circ}$, and so $F$ lies on the circumcircle of the rectangle $A D C P$ with diameter $A C$; hence $\angle A F C=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C$. Point $D$ is the foot of the perpendicular from $A$ to $B C$. Point $E$ lies on the segment $A D$ and satisfies the equation
$$
\frac{|A E|}{|E D|}=\frac{|C D|}{|D B|}
$$
Point $F$ is the foot of the perpendicular from $D$ to $B E$. Prove that $\angle A F C=90^{\circ}$.
|
Complete the rectangle $A D C P$ (see Figure 6). In view of
$$
\frac{|A E|}{|E D|}=\frac{|C D|}{|D B|}=\frac{|A P|}{|D B|}
$$
the points $B, E, P$ are collinear. Therefore $\angle D F P=90^{\circ}$, and so $F$ lies on the circumcircle of the rectangle $A D C P$ with diameter $A C$; hence $\angle A F C=90^{\circ}$.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
666a6bd1-4b47-51f5-b032-55a871f8f042
| 241,213
|
Let $n$ and $k$ be positive integers. There are $n k$ objects (of the same size) and $k$ boxes, each of which can hold $n$ objects. Each object is coloured in one of $k$ different colours. Show that the objects can be packed in the boxes so that each box holds objects of at most two colours.
|
If $k=1$, it is obvious how to do the packing. Now assume $k>1$. There are not more than $n$ objects of a certain colour - say, pink - and also not fewer than $n$ objects of some other colour - say, grey. Pack all pink objects into one box; if there is space left, fill the box up with grey objects. Then remove that box together with its contents; the problem gets reduced to an analogous one with $k-1$ boxes and $k-1$ colours. Assuming inductively that the task can be done in that case, we see that it can also be done for $k$ boxes and colours. The general result follows by induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ and $k$ be positive integers. There are $n k$ objects (of the same size) and $k$ boxes, each of which can hold $n$ objects. Each object is coloured in one of $k$ different colours. Show that the objects can be packed in the boxes so that each box holds objects of at most two colours.
|
If $k=1$, it is obvious how to do the packing. Now assume $k>1$. There are not more than $n$ objects of a certain colour - say, pink - and also not fewer than $n$ objects of some other colour - say, grey. Pack all pink objects into one box; if there is space left, fill the box up with grey objects. Then remove that box together with its contents; the problem gets reduced to an analogous one with $k-1$ boxes and $k-1$ colours. Assuming inductively that the task can be done in that case, we see that it can also be done for $k$ boxes and colours. The general result follows by induction.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\n17."
}
|
3952332a-50b1-5f5c-b457-6421c4712ebf
| 241,229
|
Consider a ping-pong match between two teams, each consisting of 1000 players. Each player played against each player of the other team exactly once (there are no draws in ping-pong). Prove that there exist ten players, all from the same team, such that every member of the other team has lost his game against at least one of those ten players.
|
We start with the following observation: In a match between two teams (not necessarily of equal sizes), there exists in one of the teams a player who won his games with at least half of the members of the other team.
Indeed: suppose there is no such player. If the teams consist of $m$ and $n$ members then the players of the first team jointly won less than $m \cdot \frac{n}{2}$ games, and the players of the second team jointly won less than $m \cdot \frac{n}{2}$ games - this is a contradiction since the total number of games played is $m n$, and in each game there must have been a winner.
Returning to the original problem (with two equal teams of size 1000), choose a player who won his games with at least half of the members of the other team - such a player exists, according to the observation above, and we shall call his team "first" and the other team "second" in the sequel. Mark this player with a white hat and remove from further consideration all those players of the second team who lost their games to him. Applying the same observation to the first team (complete) and the second team truncated as explained above, we again find a player (in the first or in the second team) who won with at least half of the other team members. Mark him with a white hat, too, and remove the players who lost to him from further consideration.
We repeat this procedure until there are no players left in one of the teams; say, in team $Y$. This means that the white-hatted players of team $X$ constitute a group with the required property (every member of team $Y$ has lost his game to at least one player from that group). Each time when a player of team $X$ was receiving a white hat, the size of team $Y$ was reduced at least by half; and since initially the size was a number less than $2^{10}$, this could not happen more than ten times.
Hence the white-hatted group from team $X$ consists of not more than ten players. If there are fewer than ten, round the group up to ten with any players.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider a ping-pong match between two teams, each consisting of 1000 players. Each player played against each player of the other team exactly once (there are no draws in ping-pong). Prove that there exist ten players, all from the same team, such that every member of the other team has lost his game against at least one of those ten players.
|
We start with the following observation: In a match between two teams (not necessarily of equal sizes), there exists in one of the teams a player who won his games with at least half of the members of the other team.
Indeed: suppose there is no such player. If the teams consist of $m$ and $n$ members then the players of the first team jointly won less than $m \cdot \frac{n}{2}$ games, and the players of the second team jointly won less than $m \cdot \frac{n}{2}$ games - this is a contradiction since the total number of games played is $m n$, and in each game there must have been a winner.
Returning to the original problem (with two equal teams of size 1000), choose a player who won his games with at least half of the members of the other team - such a player exists, according to the observation above, and we shall call his team "first" and the other team "second" in the sequel. Mark this player with a white hat and remove from further consideration all those players of the second team who lost their games to him. Applying the same observation to the first team (complete) and the second team truncated as explained above, we again find a player (in the first or in the second team) who won with at least half of the other team members. Mark him with a white hat, too, and remove the players who lost to him from further consideration.
We repeat this procedure until there are no players left in one of the teams; say, in team $Y$. This means that the white-hatted players of team $X$ constitute a group with the required property (every member of team $Y$ has lost his game to at least one player from that group). Each time when a player of team $X$ was receiving a white hat, the size of team $Y$ was reduced at least by half; and since initially the size was a number less than $2^{10}$, this could not happen more than ten times.
Hence the white-hatted group from team $X$ consists of not more than ten players. If there are fewer than ten, round the group up to ten with any players.
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
25ae4fa7-a0df-59e9-8dc8-ad42b5af38c3
| 241,248
|
Two squares on an $8 \times 8$ chessboard are called adjacent if they have a common edge or common corner. Is it possible for a king to begin in some
square and visit all squares exactly once in such a way that all moves except the first are made into squares adjacent to an even number of squares already visited?
|
Answer: No, it is not possible.
Consider the set $S$ of all (non-ordered) pairs of adjacent squares. Call an element of $S$ treated if the king has visited both its squares. After the first move there is one treated pair. Each subsequent move creates a further even number of treated pairs. So after each move the total number of treated pairs is odd. If the king could complete his tour then the total number of pairs of adjacent squares (i.e. the number of elements of $S$ ) would have to be odd. But the number of elements of $S$ is even as can be seen by the following argument. Rotation by 180 degrees around the centre of the board induces a bijection of $S$ onto itself. This bijection leaves precisely two pairs fixed, namely the pairs of squares sharing only a common corner at the middle of the board. It follows that the number of elements of $S$ is even.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Two squares on an $8 \times 8$ chessboard are called adjacent if they have a common edge or common corner. Is it possible for a king to begin in some
square and visit all squares exactly once in such a way that all moves except the first are made into squares adjacent to an even number of squares already visited?
|
Answer: No, it is not possible.
Consider the set $S$ of all (non-ordered) pairs of adjacent squares. Call an element of $S$ treated if the king has visited both its squares. After the first move there is one treated pair. Each subsequent move creates a further even number of treated pairs. So after each move the total number of treated pairs is odd. If the king could complete his tour then the total number of pairs of adjacent squares (i.e. the number of elements of $S$ ) would have to be odd. But the number of elements of $S$ is even as can be seen by the following argument. Rotation by 180 degrees around the centre of the board induces a bijection of $S$ onto itself. This bijection leaves precisely two pairs fixed, namely the pairs of squares sharing only a common corner at the middle of the board. It follows that the number of elements of $S$ is even.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\n7."
}
|
d8fe798b-5169-58e8-bb50-2de12bfb815e
| 240,947
|
We are given 1999 coins. No two coins have the same weight. A machine is provided which allows us with one operation to determine, for any three coins, which one has the middle weight. Prove that the coin that is the 1000 -th by weight can be determined using no more than 1000000 operations and that this is the only coin whose position by weight can be determined using this machine.
|
It is possible to find the 1000 -th coin (i.e. the medium one among the 1999 coins). First we exclude the lightest and heaviest coin - for this we use 1997 weighings, putting the medium-weighted coin aside each time. Next we exclude the 2 -nd and 1998 -th coins using 1995 weighings, etc. In total we need
$$
1997+1995+1993+\ldots+3+1=999 \cdot 999<1000000
$$
weighings to determine the 1000 -th coin in such a way.
It is not possible to determine the position by weight of any other coin, since we cannot distinguish between the $k$-th and $(2000-k)$-th coin. To prove this, label the coins in some order as $a_{1}, a_{2}, \ldots, a_{1999}$. If a procedure for finding the $k$-th coin exists then it should work as follows. First we choose some three coins $a_{i_{1}}, a_{j_{1}}, a_{k_{1}}$, find the medium-weighted one among them, then choose again some three coins $a_{i_{2}}, a_{j_{2}}, a_{k_{2}}$ (possibly using the information obtained from the previous weighing) etc. The results of these
weighings can be written in a table like this:
| Coin 1 | Coin 2 | Coin 3 | Medium |
| :---: | :---: | :---: | :---: |
| $a_{i_{1}}$ | $a_{j_{1}}$ | $a_{k_{1}}$ | $a_{m_{1}}$ |
| $a_{i_{2}}$ | $a_{j_{2}}$ | $a_{k_{2}}$ | $a_{m_{2}}$ |
| $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
| $a_{i_{n}}$ | $a_{j_{n}}$ | $a_{k_{n}}$ | $a_{m_{n}}$ |
Suppose we make a decision " $a_{k}$ is the $k$-th coin" based on this table. Now let us exchange labels of the lightest and the heaviest coins, of the 2-nd and 1998 -th (by weight) coins etc. It is easy to see that, after this relabeling, each step in the procedure above gives the same result as before - but if $a_{k}$ was previously the $k$-th coin by weight, then now it is the $(2000-k)$-th coin, so the procedure yields a wrong coin which gives us the contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We are given 1999 coins. No two coins have the same weight. A machine is provided which allows us with one operation to determine, for any three coins, which one has the middle weight. Prove that the coin that is the 1000 -th by weight can be determined using no more than 1000000 operations and that this is the only coin whose position by weight can be determined using this machine.
|
It is possible to find the 1000 -th coin (i.e. the medium one among the 1999 coins). First we exclude the lightest and heaviest coin - for this we use 1997 weighings, putting the medium-weighted coin aside each time. Next we exclude the 2 -nd and 1998 -th coins using 1995 weighings, etc. In total we need
$$
1997+1995+1993+\ldots+3+1=999 \cdot 999<1000000
$$
weighings to determine the 1000 -th coin in such a way.
It is not possible to determine the position by weight of any other coin, since we cannot distinguish between the $k$-th and $(2000-k)$-th coin. To prove this, label the coins in some order as $a_{1}, a_{2}, \ldots, a_{1999}$. If a procedure for finding the $k$-th coin exists then it should work as follows. First we choose some three coins $a_{i_{1}}, a_{j_{1}}, a_{k_{1}}$, find the medium-weighted one among them, then choose again some three coins $a_{i_{2}}, a_{j_{2}}, a_{k_{2}}$ (possibly using the information obtained from the previous weighing) etc. The results of these
weighings can be written in a table like this:
| Coin 1 | Coin 2 | Coin 3 | Medium |
| :---: | :---: | :---: | :---: |
| $a_{i_{1}}$ | $a_{j_{1}}$ | $a_{k_{1}}$ | $a_{m_{1}}$ |
| $a_{i_{2}}$ | $a_{j_{2}}$ | $a_{k_{2}}$ | $a_{m_{2}}$ |
| $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
| $a_{i_{n}}$ | $a_{j_{n}}$ | $a_{k_{n}}$ | $a_{m_{n}}$ |
Suppose we make a decision " $a_{k}$ is the $k$-th coin" based on this table. Now let us exchange labels of the lightest and the heaviest coins, of the 2-nd and 1998 -th (by weight) coins etc. It is easy to see that, after this relabeling, each step in the procedure above gives the same result as before - but if $a_{k}$ was previously the $k$-th coin by weight, then now it is the $(2000-k)$-th coin, so the procedure yields a wrong coin which gives us the contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
4e20d07f-4f06-5123-8420-0d85f1c8dbd5
| 240,957
|
Prove that for any four points in the plane, no three of which are collinear, there exists a circle such that three of the four points are on the circumference and the fourth point is either on the circumference or inside the circle.
|
Consider a circle containing all these four points in its interior. First, decrease its radius until at least one of these points (say, $A$ ) will be on the circle. If the other three points are still in the interior of the circle, then rotate the circle around $A$ (with its radius unchanged) until at least one of the other three points (say, $B$ ) will also be on the circle. The centre of the circle now lies on the perpendicular bisector of the segment $A B$ - moving
the centre along that perpendicular bisector (and changing its radius at the same time, so that points $A$ and $B$ remain on the circle) we arrive at a situation where at least one of the remaining two points will also be on the circle (see Figure 5).
Figure 5
Alternative solution. The quadrangle with its vertices in the four points can be convex or non-convex.
If the quadrangle is non-convex, then one of the points lies in the interior of the triangle defined by the remaining three points (see Figure 6) - the circumcircle of that triangle has the required property.
Figure 6
Figure 7
Assume now that the quadrangle $A B C D$ (where $A, B, C, D$ are the four points) is convex. Then it has a pair of opposite angles, the sum of which is at least $180^{\circ}$ - assume these are at vertices $B$ and $D$ (see Figure 7). We shall prove that point $D$ lies either in the interior of the circumcircle of triangle $A B C$ or on that circle. Indeed, let the ray drawn from the
circumcentre $O$ of triangle $A B C$ through point $D$ intersect the circumcircle in $D^{\prime}$ : since $\angle B+\angle D^{\prime}=180^{\circ}$ and $\angle B+\angle D \geqslant 180^{\circ}$, then $D$ cannot lie in the exterior of the circumcircle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that for any four points in the plane, no three of which are collinear, there exists a circle such that three of the four points are on the circumference and the fourth point is either on the circumference or inside the circle.
|
Consider a circle containing all these four points in its interior. First, decrease its radius until at least one of these points (say, $A$ ) will be on the circle. If the other three points are still in the interior of the circle, then rotate the circle around $A$ (with its radius unchanged) until at least one of the other three points (say, $B$ ) will also be on the circle. The centre of the circle now lies on the perpendicular bisector of the segment $A B$ - moving
the centre along that perpendicular bisector (and changing its radius at the same time, so that points $A$ and $B$ remain on the circle) we arrive at a situation where at least one of the remaining two points will also be on the circle (see Figure 5).

Figure 5
Alternative solution. The quadrangle with its vertices in the four points can be convex or non-convex.
If the quadrangle is non-convex, then one of the points lies in the interior of the triangle defined by the remaining three points (see Figure 6) - the circumcircle of that triangle has the required property.

Figure 6

Figure 7
Assume now that the quadrangle $A B C D$ (where $A, B, C, D$ are the four points) is convex. Then it has a pair of opposite angles, the sum of which is at least $180^{\circ}$ - assume these are at vertices $B$ and $D$ (see Figure 7). We shall prove that point $D$ lies either in the interior of the circumcircle of triangle $A B C$ or on that circle. Indeed, let the ray drawn from the
circumcentre $O$ of triangle $A B C$ through point $D$ intersect the circumcircle in $D^{\prime}$ : since $\angle B+\angle D^{\prime}=180^{\circ}$ and $\angle B+\angle D \geqslant 180^{\circ}$, then $D$ cannot lie in the exterior of the circumcircle.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
f943f57e-0d0e-52b8-9bca-08717fff930e
| 64,744
|
In a triangle $A B C$ it is given that $2|A B|=|A C|+|B C|$. Prove that the incentre of $A B C$, the circumcentre of $A B C$, and the midpoints of $A C$ and $B C$ are concyclic.
|
Let $N$ be the midpoint of $B C$ and $M$ the midpoint of $A C$. Let $O$ be the circumcentre of $A B C$ and $I$ its incentre (see Figure 8). Since $\angle C M O=\angle C N O=90^{\circ}$, the points $C, N, O$ and $M$ are concyclic (regardless of whether $O$ lies inside the triangle $A B C$ ). We now have to show that the points $C, N, I$ and $M$ are also concyclic, i.e $I$ lies on the same circle as $C, N, O$ and $M$. It will be sufficient to show that $\angle N C M+\angle N I M=180^{\circ}$ in the quadrilateral $C N I M$. Since
$$
|A B|=\frac{|A C|+|B C|}{2}=|A M|+|B N|
$$
we can choose a point $D$ on the side $A B$ such that $|A D|=|A M|$ and $|B D|=|B N|$. Then triangle $A I M$ is congruent to triangle $A I D$, and similarly triangle $B I N$ is congruent to triangle $B I D$. Therefore
$$
\begin{aligned}
\angle N C M+\angle N I M & =\angle N C M+\left(360^{\circ}-2 \angle A I D-2 \angle B I D\right)= \\
& =\angle B C A+360^{\circ}-2 \angle A I B= \\
& =\angle B C A+360^{\circ}-2 \cdot\left(180^{\circ}-\frac{\angle B A C}{2}-\frac{\angle A B C}{2}\right)= \\
& =\angle B C A+\angle A B C+\angle C A B=180^{\circ} .
\end{aligned}
$$
Figure 8
Figure 9
Alternative solution. Let $O$ be the circumcentre of $A B C$ and $I$ its in-
centre, and let $G, H$ and $K$ be the points where the incircle touches the sides $B C, A C$ and $A B$ of the triangle, respectively. Also, let $N$ be the midpoint of $B C$ and $M$ the midpoint of $A C$ (see Figure 9). Since $\angle C M O=\angle C N O=90^{\circ}$, points $M$ and $N$ lie on the circle with diameter $O C$. We will show that point $I$ also lies on that circle. Indeed, we have
$$
|A H|+|B G|=|A K|+|B K|=|A B|=\frac{|A C|+|B C|}{2}=|A M|+|B N|,
$$
implying $|M H|=|N G|$. Since $M H$ and $N G$ are the perpendicular projections of $O I$ to the lines $A C$ and $B C$, respectively, then $I O$ must be either parallel or perpendicular to the bisector $C I$ of angle $A C B$. (To formally prove this, consider unit vectors $\overrightarrow{e_{1}}$ and $\overrightarrow{e_{2}}$ defined by the rays $C A$ and $C B$, and show that the condition $|M H|=|N G|$ is equivalent to $\left(\overrightarrow{e_{1}} \pm \overrightarrow{e_{2}}\right) \cdot \overrightarrow{I O}=0$.)
If $I O$ is perpendicular to $C I$, then $\angle C I O=90^{\circ}$ and we are done. If $I O$ is parallel to $C I$, the the circumcentre $O$ of triangle $A B C$ lies on the bisector $C I$ of angle $A C B$, whence $|A C|=|B C|$ and the condition $2|A B|=|A C|+|B C|$ implies that $A B C$ is an equilateral triangle. Hence in this case points $O$ and $I$ coincide and the claim of the problem holds trivially.
## 13. Answer: $60^{\circ}$.
Let $F$ be the point of the side $A B$ such that $|A F|=|A E|$ and $|B F|=|B D|$ (see Figure 10). The line $A D$ is the angle bisector of $\angle A$ in the isosceles triangle $A E F$. This implies that $A D$ is the perpendicular bisector of $E F$, whence $|D E|=|D F|$. Similarly we show that $|D E|=|E F|$. This proves that the triangle $D E F$ is equilateral, i.e. $\angle E F D=60^{\circ}$. Hence $\angle A F E+\angle B F D=120^{\circ}$, and also $\angle A E F+\angle B D F=120^{\circ}$. Thus $\angle C A B+\angle C B A=120^{\circ}$ and finally $\angle C=60^{\circ}$.
Alternative solution. Let $I$ be the incenter of triangle $A B C$, and let $G$, $H, K$ be the points where its incircle touches the sides $B C, A C, A B$ respectively (see Figure 11). Then
$$
|A E|+|B D|=|A B|=|A K|+|B K|=|A H|+|B G| \text {, }
$$
implying $|D G|=|E H|$. Hence the triangles $D I G$ ja $E I H$ are congruent,
and
$\angle D I E=\angle G I H=180^{\circ}-\angle C$.
Figure 10
Figure 11
On the other hand,
$$
\angle D I E=\angle A I B=180^{\circ}-\frac{\angle A+\angle B}{2} .
$$
Hence
$$
\angle C=\frac{\angle A+\angle B}{2}=90^{\circ}-\frac{\angle C}{2}
$$
which gives $\angle C=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$ it is given that $2|A B|=|A C|+|B C|$. Prove that the incentre of $A B C$, the circumcentre of $A B C$, and the midpoints of $A C$ and $B C$ are concyclic.
|
Let $N$ be the midpoint of $B C$ and $M$ the midpoint of $A C$. Let $O$ be the circumcentre of $A B C$ and $I$ its incentre (see Figure 8). Since $\angle C M O=\angle C N O=90^{\circ}$, the points $C, N, O$ and $M$ are concyclic (regardless of whether $O$ lies inside the triangle $A B C$ ). We now have to show that the points $C, N, I$ and $M$ are also concyclic, i.e $I$ lies on the same circle as $C, N, O$ and $M$. It will be sufficient to show that $\angle N C M+\angle N I M=180^{\circ}$ in the quadrilateral $C N I M$. Since
$$
|A B|=\frac{|A C|+|B C|}{2}=|A M|+|B N|
$$
we can choose a point $D$ on the side $A B$ such that $|A D|=|A M|$ and $|B D|=|B N|$. Then triangle $A I M$ is congruent to triangle $A I D$, and similarly triangle $B I N$ is congruent to triangle $B I D$. Therefore
$$
\begin{aligned}
\angle N C M+\angle N I M & =\angle N C M+\left(360^{\circ}-2 \angle A I D-2 \angle B I D\right)= \\
& =\angle B C A+360^{\circ}-2 \angle A I B= \\
& =\angle B C A+360^{\circ}-2 \cdot\left(180^{\circ}-\frac{\angle B A C}{2}-\frac{\angle A B C}{2}\right)= \\
& =\angle B C A+\angle A B C+\angle C A B=180^{\circ} .
\end{aligned}
$$

Figure 8

Figure 9
Alternative solution. Let $O$ be the circumcentre of $A B C$ and $I$ its in-
centre, and let $G, H$ and $K$ be the points where the incircle touches the sides $B C, A C$ and $A B$ of the triangle, respectively. Also, let $N$ be the midpoint of $B C$ and $M$ the midpoint of $A C$ (see Figure 9). Since $\angle C M O=\angle C N O=90^{\circ}$, points $M$ and $N$ lie on the circle with diameter $O C$. We will show that point $I$ also lies on that circle. Indeed, we have
$$
|A H|+|B G|=|A K|+|B K|=|A B|=\frac{|A C|+|B C|}{2}=|A M|+|B N|,
$$
implying $|M H|=|N G|$. Since $M H$ and $N G$ are the perpendicular projections of $O I$ to the lines $A C$ and $B C$, respectively, then $I O$ must be either parallel or perpendicular to the bisector $C I$ of angle $A C B$. (To formally prove this, consider unit vectors $\overrightarrow{e_{1}}$ and $\overrightarrow{e_{2}}$ defined by the rays $C A$ and $C B$, and show that the condition $|M H|=|N G|$ is equivalent to $\left(\overrightarrow{e_{1}} \pm \overrightarrow{e_{2}}\right) \cdot \overrightarrow{I O}=0$.)
If $I O$ is perpendicular to $C I$, then $\angle C I O=90^{\circ}$ and we are done. If $I O$ is parallel to $C I$, the the circumcentre $O$ of triangle $A B C$ lies on the bisector $C I$ of angle $A C B$, whence $|A C|=|B C|$ and the condition $2|A B|=|A C|+|B C|$ implies that $A B C$ is an equilateral triangle. Hence in this case points $O$ and $I$ coincide and the claim of the problem holds trivially.
## 13. Answer: $60^{\circ}$.
Let $F$ be the point of the side $A B$ such that $|A F|=|A E|$ and $|B F|=|B D|$ (see Figure 10). The line $A D$ is the angle bisector of $\angle A$ in the isosceles triangle $A E F$. This implies that $A D$ is the perpendicular bisector of $E F$, whence $|D E|=|D F|$. Similarly we show that $|D E|=|E F|$. This proves that the triangle $D E F$ is equilateral, i.e. $\angle E F D=60^{\circ}$. Hence $\angle A F E+\angle B F D=120^{\circ}$, and also $\angle A E F+\angle B D F=120^{\circ}$. Thus $\angle C A B+\angle C B A=120^{\circ}$ and finally $\angle C=60^{\circ}$.
Alternative solution. Let $I$ be the incenter of triangle $A B C$, and let $G$, $H, K$ be the points where its incircle touches the sides $B C, A C, A B$ respectively (see Figure 11). Then
$$
|A E|+|B D|=|A B|=|A K|+|B K|=|A H|+|B G| \text {, }
$$
implying $|D G|=|E H|$. Hence the triangles $D I G$ ja $E I H$ are congruent,
and
$\angle D I E=\angle G I H=180^{\circ}-\angle C$.

Figure 10

Figure 11
On the other hand,
$$
\angle D I E=\angle A I B=180^{\circ}-\frac{\angle A+\angle B}{2} .
$$
Hence
$$
\angle C=\frac{\angle A+\angle B}{2}=90^{\circ}-\frac{\angle C}{2}
$$
which gives $\angle C=60^{\circ}$.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
8a76843a-02f8-5dcc-816a-8df9cb50380c
| 241,008
|
Let $A B C$ be an isosceles triangle with $|A B|=|A C|$. Points $D$ and $E$ lie on the sides $A B$ and $A C$, respectively. The line passing through $B$ and parallel to $A C$ meets the line $D E$ at $F$. The line passing through $C$ and parallel to $A B$ meets the line $D E$ at $G$. Prove that
$$
\frac{[D B C G]}{[F B C E]}=\frac{|A D|}{|A E|}
$$
where $[P Q R S]$ denotes the area of the quadrilateral $P Q R S$.
|
The quadrilaterals $D B C G$ and $F B C E$ are trapeziums. The area of a trapezium is equal to half the sum of the lengths of the parallel sides multiplied by the distance between them. But the distance between the parallel sides is the same for both of these trapeziums, since the distance from $B$ to $A C$ is equal to the distance from $C$ to $A B$. It therefore suffices to show that
$$
\frac{|B D|+|C G|}{|C E|+|B F|}=\frac{|A D|}{|A E|}
$$
(see Figure 12). Now, since the triangles $B D F, A D E$ and $C G E$ are similar, we have
$$
\frac{|B D|}{|B F|}=\frac{|C G|}{|C E|}=\frac{|A D|}{|A E|}
$$
which implies the required equality.
Figure 12
Figure 13
Alternative solution. As in the first solution, we need to show that
$$
\frac{|B D|+|C G|}{|B F|+|C E|}=\frac{|A D|}{|A E|}
$$
Let $M$ be the midpoint of $B C$, and let $F^{\prime}$ and $G^{\prime}$ be the points symmetric to $F$ and $G$, respectively, relative to $M$ (see Figure 13). Since $C G$ is parallel to $A B$, then point $G^{\prime}$ lies on the line $A B$, and $\left|B G^{\prime}\right|=|C G|$. Similarly point $F^{\prime}$ lies on the line $A C$, and $\left|C F^{\prime}\right|=|B F|$. It remains to show that
$$
\frac{\left|D G^{\prime}\right|}{\left|E F^{\prime}\right|}=\frac{|A D|}{|A E|}
$$
which follows from $D E$ and $F^{\prime} G^{\prime}$ being parallel.
Another solution. Express the areas of the quadrilaterals as
$$
[D B C G]=[A B C]-[A D E]+[E C G]
$$
and
$$
[F B C E]=[A B C]-[A D E]+[D B F]
$$
The required equality can now be proved by direct computation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an isosceles triangle with $|A B|=|A C|$. Points $D$ and $E$ lie on the sides $A B$ and $A C$, respectively. The line passing through $B$ and parallel to $A C$ meets the line $D E$ at $F$. The line passing through $C$ and parallel to $A B$ meets the line $D E$ at $G$. Prove that
$$
\frac{[D B C G]}{[F B C E]}=\frac{|A D|}{|A E|}
$$
where $[P Q R S]$ denotes the area of the quadrilateral $P Q R S$.
|
The quadrilaterals $D B C G$ and $F B C E$ are trapeziums. The area of a trapezium is equal to half the sum of the lengths of the parallel sides multiplied by the distance between them. But the distance between the parallel sides is the same for both of these trapeziums, since the distance from $B$ to $A C$ is equal to the distance from $C$ to $A B$. It therefore suffices to show that
$$
\frac{|B D|+|C G|}{|C E|+|B F|}=\frac{|A D|}{|A E|}
$$
(see Figure 12). Now, since the triangles $B D F, A D E$ and $C G E$ are similar, we have
$$
\frac{|B D|}{|B F|}=\frac{|C G|}{|C E|}=\frac{|A D|}{|A E|}
$$
which implies the required equality.

Figure 12

Figure 13
Alternative solution. As in the first solution, we need to show that
$$
\frac{|B D|+|C G|}{|B F|+|C E|}=\frac{|A D|}{|A E|}
$$
Let $M$ be the midpoint of $B C$, and let $F^{\prime}$ and $G^{\prime}$ be the points symmetric to $F$ and $G$, respectively, relative to $M$ (see Figure 13). Since $C G$ is parallel to $A B$, then point $G^{\prime}$ lies on the line $A B$, and $\left|B G^{\prime}\right|=|C G|$. Similarly point $F^{\prime}$ lies on the line $A C$, and $\left|C F^{\prime}\right|=|B F|$. It remains to show that
$$
\frac{\left|D G^{\prime}\right|}{\left|E F^{\prime}\right|}=\frac{|A D|}{|A E|}
$$
which follows from $D E$ and $F^{\prime} G^{\prime}$ being parallel.
Another solution. Express the areas of the quadrilaterals as
$$
[D B C G]=[A B C]-[A D E]+[E C G]
$$
and
$$
[F B C E]=[A B C]-[A D E]+[D B F]
$$
The required equality can now be proved by direct computation.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
2d92317e-2fc2-5647-b454-ce1c5fa3551f
| 241,016
|
Let $A B C$ be a triangle with $\angle C=60^{\circ}$ and $|A C|<|B C|$. The point $D$ lies on the side $B C$ and satisfies $|B D|=|A C|$. The side $A C$ is extended to the point $E$ where $|A C|=|C E|$. Prove that $|A B|=|D E|$.
|
Consider a point $F$ on $B C$ such that $|C F|=|B D|$ (see Figure 14). Since $\angle A C F=60^{\circ}$, triangle $A C F$ is equilateral. Therefore $|A F|=|A C|=|C E|$
and $\angle A F B=\angle E C D=120^{\circ}$. Moreover, $|B F|=|C D|$. This implies that triangles $A F B$ and $E C D$ are congruent, and $|A B|=|D E|$.
Figure 14
Alternative solution. The cosine law in triangle $A B C$ implies
$$
\begin{aligned}
|A B|^{2} & =|A C|^{2}+|B C|^{2}-2 \cdot|A C| \cdot|B C| \cdot \cos \angle A C B= \\
& =|A C|^{2}+|B C|^{2}-|A C| \cdot|B C|= \\
& =|A C|^{2}+(|B D|+|D C|)^{2}-|A C| \cdot(|B D|+|D C|)= \\
& =|A C|^{2}+(|A C|+|D C|)^{2}-|A C| \cdot(|A C|+|D C|)= \\
& =|A C|^{2}+|D C|^{2}+|A C| \cdot|D C|
\end{aligned}
$$
On the other hand, the cosine law in triangle $C D E$ gives
$$
\begin{aligned}
|D E|^{2} & =|D C|^{2}+|C E|^{2}-2 \cdot|D C| \cdot|C E| \cdot \cos \angle D C E= \\
& =|D C|^{2}+|C E|^{2}+|D C| \cdot|E C|= \\
& =|D C|^{2}+|A C|^{2}+|D C| \cdot|A C| .
\end{aligned}
$$
Hence $|A B|=|D E|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle C=60^{\circ}$ and $|A C|<|B C|$. The point $D$ lies on the side $B C$ and satisfies $|B D|=|A C|$. The side $A C$ is extended to the point $E$ where $|A C|=|C E|$. Prove that $|A B|=|D E|$.
|
Consider a point $F$ on $B C$ such that $|C F|=|B D|$ (see Figure 14). Since $\angle A C F=60^{\circ}$, triangle $A C F$ is equilateral. Therefore $|A F|=|A C|=|C E|$
and $\angle A F B=\angle E C D=120^{\circ}$. Moreover, $|B F|=|C D|$. This implies that triangles $A F B$ and $E C D$ are congruent, and $|A B|=|D E|$.

Figure 14
Alternative solution. The cosine law in triangle $A B C$ implies
$$
\begin{aligned}
|A B|^{2} & =|A C|^{2}+|B C|^{2}-2 \cdot|A C| \cdot|B C| \cdot \cos \angle A C B= \\
& =|A C|^{2}+|B C|^{2}-|A C| \cdot|B C|= \\
& =|A C|^{2}+(|B D|+|D C|)^{2}-|A C| \cdot(|B D|+|D C|)= \\
& =|A C|^{2}+(|A C|+|D C|)^{2}-|A C| \cdot(|A C|+|D C|)= \\
& =|A C|^{2}+|D C|^{2}+|A C| \cdot|D C|
\end{aligned}
$$
On the other hand, the cosine law in triangle $C D E$ gives
$$
\begin{aligned}
|D E|^{2} & =|D C|^{2}+|C E|^{2}-2 \cdot|D C| \cdot|C E| \cdot \cos \angle D C E= \\
& =|D C|^{2}+|C E|^{2}+|D C| \cdot|E C|= \\
& =|D C|^{2}+|A C|^{2}+|D C| \cdot|A C| .
\end{aligned}
$$
Hence $|A B|=|D E|$.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
ce6ce425-b9a8-5f80-ae96-70f3a17ee8e8
| 241,025
|
Let $m$ be a positive integer such that $m \equiv 2(\bmod 4)$. Show that there exists at most one factorization $m=a b$ where $a$ and $b$ are positive integers satisfying $0<a-b<\sqrt{5+4 \sqrt{4 m+1}}$.
|
Squaring the second inequality gives $(a-b)^{2}<5+4 \sqrt{4 m+1}$. Since $m=a b$, we have
$$
(a+b)^{2}<5+4 \sqrt{4 m+1}+4 m=(\sqrt{4 m+1}+2)^{2}
$$
implying
$$
a+b<\sqrt{4 m+1}+2 \text {. }
$$
Since $a>b$, different factorizations $m=a b$ will give different values for the sum $a+b(a b=m, a+b=k, a>b$ has at most one solution in $(a, b))$. Since $m \equiv 2(\bmod 4)$, we see that $a$ and $b$ must have different parity, and $a+b$ must be odd. Also note that
$$
a+b \geqslant 2 \sqrt{a b}=\sqrt{4 m}
$$
Since $4 m$ cannot be a square we have
$$
a+b \geqslant \sqrt{4 m+1} .
$$
Since $a+b$ is odd and the interval $[\sqrt{4 m+1}, \sqrt{4 m+1}+2)$ contains exactly one odd integer, then there can be at most one pair $(a, b)$ such that $a+b<\sqrt{4 m+1}+2$, or equivalently $a-b<\sqrt{5+4 \sqrt{4 m+1}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m$ be a positive integer such that $m \equiv 2(\bmod 4)$. Show that there exists at most one factorization $m=a b$ where $a$ and $b$ are positive integers satisfying $0<a-b<\sqrt{5+4 \sqrt{4 m+1}}$.
|
Squaring the second inequality gives $(a-b)^{2}<5+4 \sqrt{4 m+1}$. Since $m=a b$, we have
$$
(a+b)^{2}<5+4 \sqrt{4 m+1}+4 m=(\sqrt{4 m+1}+2)^{2}
$$
implying
$$
a+b<\sqrt{4 m+1}+2 \text {. }
$$
Since $a>b$, different factorizations $m=a b$ will give different values for the sum $a+b(a b=m, a+b=k, a>b$ has at most one solution in $(a, b))$. Since $m \equiv 2(\bmod 4)$, we see that $a$ and $b$ must have different parity, and $a+b$ must be odd. Also note that
$$
a+b \geqslant 2 \sqrt{a b}=\sqrt{4 m}
$$
Since $4 m$ cannot be a square we have
$$
a+b \geqslant \sqrt{4 m+1} .
$$
Since $a+b$ is odd and the interval $[\sqrt{4 m+1}, \sqrt{4 m+1}+2)$ contains exactly one odd integer, then there can be at most one pair $(a, b)$ such that $a+b<\sqrt{4 m+1}+2$, or equivalently $a-b<\sqrt{5+4 \sqrt{4 m+1}}$.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\n18."
}
|
c1a77c9a-cc6b-5f33-90d5-411d8b6c015b
| 241,051
|
Prove that there exist infinitely many even positive integers $k$ such that for every prime $p$ the number $p^{2}+k$ is composite.
|
Note that the square of any prime $p \neq 3$ is congruent to 1 modulo 3 . Hence the numbers $k=6 m+2$ will have the required property for any $p \neq 3$, as
$p^{2}+k$ will be divisible by 3 and hence composite.
In order to have $3^{2}+k$ also composite, we look for such values of $m$ for which $k=6 m+2$ is congruent to 1 modulo 5 - then $3^{2}+k$ will be divisible by 5 and hence composite. Taking $m=5 t+4$, we have $k=30 t+26$, which is congruent to 2 modulo 3 and congruent to 1 modulo 5 . Hence $p^{2}+(30 t+26)$ is composite for any positive integer $t$ and prime $p$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many even positive integers $k$ such that for every prime $p$ the number $p^{2}+k$ is composite.
|
Note that the square of any prime $p \neq 3$ is congruent to 1 modulo 3 . Hence the numbers $k=6 m+2$ will have the required property for any $p \neq 3$, as
$p^{2}+k$ will be divisible by 3 and hence composite.
In order to have $3^{2}+k$ also composite, we look for such values of $m$ for which $k=6 m+2$ is congruent to 1 modulo 5 - then $3^{2}+k$ will be divisible by 5 and hence composite. Taking $m=5 t+4$, we have $k=30 t+26$, which is congruent to 2 modulo 3 and congruent to 1 modulo 5 . Hence $p^{2}+(30 t+26)$ is composite for any positive integer $t$ and prime $p$.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
1356d3a6-113b-53dc-bd11-461fe7923419
| 241,062
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) Since $P, R$ and $Q$ are collinear, we have $\triangle P A Q \sim \triangle P B R$, hence
$$
\frac{|A Q|}{|B R|}=\frac{|A P|}{|B P|}
$$
Conversely, $P, T$ and $S$ are collinear if it holds that
$$
\frac{|A S|}{|B T|}=\frac{|A P|}{|B P|}
$$
So it suffices to prove
$$
\frac{|B T|}{|B R|}=\frac{|A S|}{|A Q|}
$$
Since $\angle A B T=90^{\circ}=\angle A L B$ and $\angle T A B=\angle B A L$, we have $\triangle A B T \sim \triangle A L B$. And since $\angle A L B=90^{\circ}=\angle Q A B$ and $\angle L B A=\angle A B Q$, we have $\triangle A L B \sim \triangle Q A B$. Hence $\triangle A B T \sim \triangle Q A B$, so
$$
\frac{|B T|}{|B A|}=\frac{|A B|}{|A Q|}
$$
Similarly, we have $\triangle A B R \sim \triangle A K B \sim \triangle S A B$, so
$$
\frac{|B R|}{|B A|}=\frac{|A B|}{|A S|}
$$
Combining both results, we get
$$
\frac{|B T|}{|B R|}=\frac{|B T| /|B A|}{|B R| /|B A|}=\frac{|A B| /|A Q|}{|A B| /|A S|}=\frac{|A S|}{|A Q|}
$$
which had to be proved.
(b) Let the line $P K$ intersect $B R$ in $B_{1}$ and $A Q$ in $A_{1}$ and let the line $P L$ intersect $B R$ in $B_{2}$ and $A Q$ in $A_{2}$. Consider the points $A_{1}, A$ and $S$ on the line $A Q$, and the points $B_{1}, B$ and $T$ on the line $B R$. As $A Q \| B R$ and the three lines $A_{1} B_{1}, A B$ and $S T$ are concurrent (in $P$ ), we have
$$
A_{1} A: A S=B_{1} B: B T,
$$
where all lengths are directed. Similarly, as $A_{1} B_{1}, A R$ and $S B$ are concurrent (in $K)$, we have
$$
A_{1} A: A S=B_{1} R: R B .
$$
This gives
$$
\frac{B B_{1}}{B T}=\frac{R B_{1}}{R B}=\frac{R B+B B_{1}}{R B}=1+\frac{B B_{1}}{R B}=1-\frac{B B_{1}}{B R},
$$
so
$$
B B_{1}=\frac{1}{\frac{1}{B T}+\frac{1}{B R}} .
$$
Similary, using the lines $A_{2} B_{2}, A B$ and $Q R$ (concurrent in $P$ ) and the lines $A_{2} B_{2}$, $A T$ and $Q B$ (concurrent in $L$ ), we find
$$
B_{2} B: B R=A_{2} A: A Q=B_{2} T: T B .
$$
This gives
$$
\frac{B B_{2}}{B R}=\frac{T B_{2}}{T B}=\frac{T B+B B_{2}}{T B}=1+\frac{B B_{2}}{T B}=1-\frac{B B_{2}}{B T},
$$
So
$$
B B_{2}=\frac{1}{\frac{1}{B R}+\frac{1}{B T}} .
$$
We conclude that $B_{1}=B_{2}$, which implies that $P, K$ and $L$ are collinear.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) Since $P, R$ and $Q$ are collinear, we have $\triangle P A Q \sim \triangle P B R$, hence
$$
\frac{|A Q|}{|B R|}=\frac{|A P|}{|B P|}
$$
Conversely, $P, T$ and $S$ are collinear if it holds that
$$
\frac{|A S|}{|B T|}=\frac{|A P|}{|B P|}
$$
So it suffices to prove
$$
\frac{|B T|}{|B R|}=\frac{|A S|}{|A Q|}
$$
Since $\angle A B T=90^{\circ}=\angle A L B$ and $\angle T A B=\angle B A L$, we have $\triangle A B T \sim \triangle A L B$. And since $\angle A L B=90^{\circ}=\angle Q A B$ and $\angle L B A=\angle A B Q$, we have $\triangle A L B \sim \triangle Q A B$. Hence $\triangle A B T \sim \triangle Q A B$, so
$$
\frac{|B T|}{|B A|}=\frac{|A B|}{|A Q|}
$$
Similarly, we have $\triangle A B R \sim \triangle A K B \sim \triangle S A B$, so
$$
\frac{|B R|}{|B A|}=\frac{|A B|}{|A S|}
$$
Combining both results, we get
$$
\frac{|B T|}{|B R|}=\frac{|B T| /|B A|}{|B R| /|B A|}=\frac{|A B| /|A Q|}{|A B| /|A S|}=\frac{|A S|}{|A Q|}
$$
which had to be proved.
(b) Let the line $P K$ intersect $B R$ in $B_{1}$ and $A Q$ in $A_{1}$ and let the line $P L$ intersect $B R$ in $B_{2}$ and $A Q$ in $A_{2}$. Consider the points $A_{1}, A$ and $S$ on the line $A Q$, and the points $B_{1}, B$ and $T$ on the line $B R$. As $A Q \| B R$ and the three lines $A_{1} B_{1}, A B$ and $S T$ are concurrent (in $P$ ), we have
$$
A_{1} A: A S=B_{1} B: B T,
$$
where all lengths are directed. Similarly, as $A_{1} B_{1}, A R$ and $S B$ are concurrent (in $K)$, we have
$$
A_{1} A: A S=B_{1} R: R B .
$$
This gives
$$
\frac{B B_{1}}{B T}=\frac{R B_{1}}{R B}=\frac{R B+B B_{1}}{R B}=1+\frac{B B_{1}}{R B}=1-\frac{B B_{1}}{B R},
$$
so
$$
B B_{1}=\frac{1}{\frac{1}{B T}+\frac{1}{B R}} .
$$
Similary, using the lines $A_{2} B_{2}, A B$ and $Q R$ (concurrent in $P$ ) and the lines $A_{2} B_{2}$, $A T$ and $Q B$ (concurrent in $L$ ), we find
$$
B_{2} B: B R=A_{2} A: A Q=B_{2} T: T B .
$$
This gives
$$
\frac{B B_{2}}{B R}=\frac{T B_{2}}{T B}=\frac{T B+B B_{2}}{T B}=1+\frac{B B_{2}}{T B}=1-\frac{B B_{2}}{B T},
$$
So
$$
B B_{2}=\frac{1}{\frac{1}{B R}+\frac{1}{B T}} .
$$
We conclude that $B_{1}=B_{2}$, which implies that $P, K$ and $L$ are collinear.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2010-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
6334840b-62d7-5769-8944-102754ee94ab
| 606,025
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) Define $X$ as the intersection of $A T$ and $B S$, and $Y$ as the intersection of $A R$ and $B Q$. To prove that $P, S$ and $T$ are collinear, we will use Menelaos' theorem in $\triangle A B X$, so we have to prove
$$
\frac{A P}{P B} \frac{B S}{S X} \frac{X T}{T A}=-1
$$
Note that $B$ is between $P$ and $A, X$ is between $S$ and $B$, and $X$ is between $T$ and $A$, so it suffices to prove that
$$
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|}=1
$$
Because $A Q$ and $B R$ are parallel, we have $\triangle A Q P \sim \triangle B R P$, hence
$$
\frac{|A P|}{|B P|}=\frac{|Q A|}{|R B|}
$$
Also, since $\angle A S B=\angle K B R$ and $\angle B A S=90^{\circ}=\angle B K R$, we have $\triangle A S B \sim$ $\triangle K B R$, hence
$$
\frac{|B S|}{|R B|}=\frac{|A S|}{|K B|}, \quad \text { so } \quad|B S|=\frac{|A S|}{|K B|}|R B|
$$
Similarly, we have $\triangle A T B \sim \triangle Q A L$, hence
$$
\frac{|T A|}{|A Q|}=\frac{|T B|}{|A L|}, \quad \text { so } \quad|T A|=\frac{|T B|}{|A L|}|A Q|
$$
As $\angle A S X=\angle A S B=90^{\circ}-\angle A B S=90^{\circ}-\angle A B K=\angle K A B=\angle Y A B$, and $\angle S A X=90^{\circ}-\angle X A B=90^{\circ}-\angle L A B=\angle A B L=\angle A B Y$, we have $\triangle S X A \sim$ $\triangle A Y B$, hence
$$
\frac{|S X|}{|A Y|}=\frac{|A S|}{|B A|}, \quad \text { so } \quad|S X|=\frac{|A S|}{|B A|}|A Y|
$$
Similarly, we have $\triangle B X T \sim \triangle A Y B$, hence
$$
\frac{|X T|}{|Y B|}=\frac{|B T|}{|A B|}, \quad \text { so } \quad|X T|=\frac{|B T|}{|A B|}|Y B|
$$
By combining (5) - (9), we find
$$
\begin{aligned}
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|} & =\frac{|Q A|}{|R B|} \cdot \frac{|A S|}{|K B|}|R B| \cdot \frac{|B A|}{|A S||A Y|} \cdot \frac{|B T|}{|A B|}|Y B| \cdot \frac{|A L|}{|T B||A Q|} \\
& =\frac{|A L|}{|K B|} \frac{|Y B|}{|A Y|} .
\end{aligned}
$$
Since $\angle Y L A=90^{\circ}=\angle Y K B$ and $\angle A Y L=\angle B Y K$, we have $\triangle A Y L \sim \triangle B Y K$, hence
$$
\frac{|A L|}{|B K|}=\frac{|A Y|}{|B Y|}, \quad \text { so } \quad \frac{|A L|}{|B K|} \frac{|B Y|}{|A Y|}=1
$$
By combining (10) and (11), we find
$$
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|}=1
$$
as we wanted to prove.
(b) Again, we will use Menelaos' theorem in $\triangle A B X$, so we have to prove
$$
\frac{A P}{P B} \frac{B K}{K X} \frac{X L}{L A}=-1
$$
Note that $\frac{A P}{P B}<0$, and $\frac{B K}{K X}<0$ if and only if $\frac{X L}{L A}<0$, so it suffices to prove that
$$
\frac{|A P|}{|P B|} \frac{|B K|}{|K X|} \frac{|X L|}{|L A|}=1
$$
As $\angle B X L=\angle A X K$ and $\angle B L X=90^{\circ}=\angle A K X$, we have $\triangle B L X \sim \triangle A K X$, hence
$$
\frac{|X L|}{|X K|}=\frac{|B L|}{|A K|}
$$
Since $\angle A L B=90^{\circ}=\angle Q A B$, we have $\triangle A L B \sim \triangle Q A B$, hence
$$
\frac{|L A|}{|A Q|}=\frac{|L B|}{|A B|}, \quad \text { so } \quad|L A|=\frac{|L B|}{|A B|}|A Q|
$$
Similarly, we have $\triangle A K B \sim \triangle A B R$, hence
$$
\frac{|B K|}{|R B|}=\frac{|A K|}{|A B|}, \quad \text { so } \quad|B K|=\frac{|A K|}{|A B|}|R B|
$$
By combining (5) and (12) - (14), we find
$$
\frac{|A P|}{|P B|} \frac{|B K|}{|K X|} \frac{|X L|}{|L A|}=\frac{|Q A|}{|R B|} \cdot \frac{|B L|}{|A K|} \cdot \frac{|A B|}{|L B||A Q|} \cdot \frac{|A K|}{|A B|}|R B|=1
$$
which is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) Define $X$ as the intersection of $A T$ and $B S$, and $Y$ as the intersection of $A R$ and $B Q$. To prove that $P, S$ and $T$ are collinear, we will use Menelaos' theorem in $\triangle A B X$, so we have to prove
$$
\frac{A P}{P B} \frac{B S}{S X} \frac{X T}{T A}=-1
$$
Note that $B$ is between $P$ and $A, X$ is between $S$ and $B$, and $X$ is between $T$ and $A$, so it suffices to prove that
$$
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|}=1
$$
Because $A Q$ and $B R$ are parallel, we have $\triangle A Q P \sim \triangle B R P$, hence
$$
\frac{|A P|}{|B P|}=\frac{|Q A|}{|R B|}
$$
Also, since $\angle A S B=\angle K B R$ and $\angle B A S=90^{\circ}=\angle B K R$, we have $\triangle A S B \sim$ $\triangle K B R$, hence
$$
\frac{|B S|}{|R B|}=\frac{|A S|}{|K B|}, \quad \text { so } \quad|B S|=\frac{|A S|}{|K B|}|R B|
$$
Similarly, we have $\triangle A T B \sim \triangle Q A L$, hence
$$
\frac{|T A|}{|A Q|}=\frac{|T B|}{|A L|}, \quad \text { so } \quad|T A|=\frac{|T B|}{|A L|}|A Q|
$$
As $\angle A S X=\angle A S B=90^{\circ}-\angle A B S=90^{\circ}-\angle A B K=\angle K A B=\angle Y A B$, and $\angle S A X=90^{\circ}-\angle X A B=90^{\circ}-\angle L A B=\angle A B L=\angle A B Y$, we have $\triangle S X A \sim$ $\triangle A Y B$, hence
$$
\frac{|S X|}{|A Y|}=\frac{|A S|}{|B A|}, \quad \text { so } \quad|S X|=\frac{|A S|}{|B A|}|A Y|
$$
Similarly, we have $\triangle B X T \sim \triangle A Y B$, hence
$$
\frac{|X T|}{|Y B|}=\frac{|B T|}{|A B|}, \quad \text { so } \quad|X T|=\frac{|B T|}{|A B|}|Y B|
$$
By combining (5) - (9), we find
$$
\begin{aligned}
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|} & =\frac{|Q A|}{|R B|} \cdot \frac{|A S|}{|K B|}|R B| \cdot \frac{|B A|}{|A S||A Y|} \cdot \frac{|B T|}{|A B|}|Y B| \cdot \frac{|A L|}{|T B||A Q|} \\
& =\frac{|A L|}{|K B|} \frac{|Y B|}{|A Y|} .
\end{aligned}
$$
Since $\angle Y L A=90^{\circ}=\angle Y K B$ and $\angle A Y L=\angle B Y K$, we have $\triangle A Y L \sim \triangle B Y K$, hence
$$
\frac{|A L|}{|B K|}=\frac{|A Y|}{|B Y|}, \quad \text { so } \quad \frac{|A L|}{|B K|} \frac{|B Y|}{|A Y|}=1
$$
By combining (10) and (11), we find
$$
\frac{|A P|}{|P B|} \frac{|B S|}{|S X|} \frac{|X T|}{|T A|}=1
$$
as we wanted to prove.
(b) Again, we will use Menelaos' theorem in $\triangle A B X$, so we have to prove
$$
\frac{A P}{P B} \frac{B K}{K X} \frac{X L}{L A}=-1
$$
Note that $\frac{A P}{P B}<0$, and $\frac{B K}{K X}<0$ if and only if $\frac{X L}{L A}<0$, so it suffices to prove that
$$
\frac{|A P|}{|P B|} \frac{|B K|}{|K X|} \frac{|X L|}{|L A|}=1
$$
As $\angle B X L=\angle A X K$ and $\angle B L X=90^{\circ}=\angle A K X$, we have $\triangle B L X \sim \triangle A K X$, hence
$$
\frac{|X L|}{|X K|}=\frac{|B L|}{|A K|}
$$
Since $\angle A L B=90^{\circ}=\angle Q A B$, we have $\triangle A L B \sim \triangle Q A B$, hence
$$
\frac{|L A|}{|A Q|}=\frac{|L B|}{|A B|}, \quad \text { so } \quad|L A|=\frac{|L B|}{|A B|}|A Q|
$$
Similarly, we have $\triangle A K B \sim \triangle A B R$, hence
$$
\frac{|B K|}{|R B|}=\frac{|A K|}{|A B|}, \quad \text { so } \quad|B K|=\frac{|A K|}{|A B|}|R B|
$$
By combining (5) and (12) - (14), we find
$$
\frac{|A P|}{|P B|} \frac{|B K|}{|K X|} \frac{|X L|}{|L A|}=\frac{|Q A|}{|R B|} \cdot \frac{|B L|}{|A K|} \cdot \frac{|A B|}{|L B||A Q|} \cdot \frac{|A K|}{|A B|}|R B|=1
$$
which is what we wanted to prove.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2010-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
6334840b-62d7-5769-8944-102754ee94ab
| 606,025
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
. As $\angle A K B=\angle A L B=90^{\circ}$, the points $K$ and $L$ belong to the circle with diameter $A B$. Since $\angle Q A B=\angle A B R=90^{\circ}$, the lines $A Q$ and $B R$ are tangents to this circle.
Apply Pascal's theorem to the points $A, A, K, L, B$ and $B$, all on the same circle. This yields that the intersection $Q$ of the tangent in $A$ and the line $B L$, the intersection $R$ of the tangent in $B$ and the line $A K$, and the intersection of $K L$ and $A B$ are collinear. So $K L$ passes through the intersection of $A B$ and $Q R$, which is point $P$. Hence $P, K$ and $L$ are collinear. This proves part b.
Now apply Pascal's theorem to the points $A, A, L, K, B$ and $B$. This yields that the intersection $S$ of the tangent in $A$ and the line $B K$, the intersection $T$ of the tangent in $B$ and the line $A L$, and the intersection $P$ of $K L$ and $A B$ are collinear. This proves part a.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
. As $\angle A K B=\angle A L B=90^{\circ}$, the points $K$ and $L$ belong to the circle with diameter $A B$. Since $\angle Q A B=\angle A B R=90^{\circ}$, the lines $A Q$ and $B R$ are tangents to this circle.
Apply Pascal's theorem to the points $A, A, K, L, B$ and $B$, all on the same circle. This yields that the intersection $Q$ of the tangent in $A$ and the line $B L$, the intersection $R$ of the tangent in $B$ and the line $A K$, and the intersection of $K L$ and $A B$ are collinear. So $K L$ passes through the intersection of $A B$ and $Q R$, which is point $P$. Hence $P, K$ and $L$ are collinear. This proves part b.
Now apply Pascal's theorem to the points $A, A, L, K, B$ and $B$. This yields that the intersection $S$ of the tangent in $A$ and the line $B K$, the intersection $T$ of the tangent in $B$ and the line $A L$, and the intersection $P$ of $K L$ and $A B$ are collinear. This proves part a.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2010-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
6334840b-62d7-5769-8944-102754ee94ab
| 606,025
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) W.l.o.g. we may assume that $A=(0,0)$ and $B=(1,0)$ and the line through $P$ is in the upper half plane, so $l$ is the $x$-axis, $a$ is the $y$-axis and $b$ is the line $x=1$. Take $P=(p, 0)(p>1)$ and $Q=(0, q)(q>0)$. Since $P Q$ is given by $\frac{x}{p}+\frac{y}{q}=1$, we find $R=\left(1, \frac{q(p-1)}{p}\right)$.
Now $A R$ is given by $y=\frac{q(p-1)}{p} x$, hence $B S$, the line perpendicular to $A R$ and passing through $B=(1,0)$, is given by $y=-\frac{p}{q(p-1)}(x-1)$. We find $S=\left(0, \frac{p}{q(p-1)}\right)$.
Moreover $B Q$ is given by $y=-q(x-1)$, hence $A T$, the line perpendicular to $B Q$ and passing through $A=(0,0)$, is given by $y=\frac{1}{q} x$. We find $T=\left(1, \frac{1}{q}\right)$. Since $\frac{|B T|}{|B P|}=\frac{1 / q}{p-1}=\frac{\frac{p}{q(p-1)}}{p}=\frac{|A S|}{|A P|}$, we conclude that $P, T$ and $S$ are collinear.
(b) Point $K$ is the intersection of $A R$ and $B S$. Solving for $x$ yields
$$
\begin{aligned}
\frac{q(p-1)}{p} x & =-\frac{p}{q(p-1)}(x-1) \\
\left(\frac{q(p-1)}{p}+\frac{p}{q(p-1)}\right) x & =\frac{p}{q(p-1)} \\
x & =\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}
\end{aligned}
$$
so
$$
K=\left(\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}, \frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right)
$$
Point $L$ is the point of intersection of $A T$ and $B Q$. Solving for $x$ yields
$$
\begin{aligned}
\frac{1}{q} x & =-q(x-1) \\
\left(\frac{1}{q}+q\right) x & =q \\
x & =\frac{q}{\frac{1}{q}+q}
\end{aligned}
$$
so
$$
L=\left(\frac{q}{\frac{1}{q}+q}, \frac{1}{\frac{1}{q}+q}\right)
$$
Let $K_{0}$ and $L_{0}$ be the projections of $K$ and $L$ on the $x$-axis. We have to show that the following fractions are equal:
$$
\frac{\left|K_{0} K\right|}{\left|K_{0} P\right|}=\frac{\frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}}{p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}} \quad \text { and } \quad \frac{\left|L_{0} L\right|}{\left|L_{0} P\right|}=\frac{\frac{1}{\frac{1}{q}+q}}{p-\frac{q}{\frac{1}{q}+q}}
$$
Working out cross products twice, this comes down to
$$
\begin{aligned}
& \frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}} \cdot\left(p-\frac{q}{\frac{1}{q}+q}\right) \stackrel{?}{=} \frac{1}{\frac{1}{q}+q} \cdot\left(p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right) \\
& \left(\frac{1}{q}+q\right) \cdot\left(p-\frac{q}{\frac{1}{q}+q}\right) \stackrel{?}{=}\left(\frac{q(p-1)}{p}+\frac{p}{q(p-1)}\right) \cdot\left(p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right) \\
& \frac{p}{q}+p q-q \stackrel{?}{=} q(p-1)+\frac{p^{2}}{q(p-1)}-\frac{p}{q(p-1)} \\
& \frac{p}{q}+p q-q \stackrel{?}{=} q(p-1)+\frac{p(p-1)}{q(p-1)}
\end{aligned}
$$
which is clearly true.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. On a line $l$ there are three different points $A, B$ and $P$ in that order. Let $a$ be the line through $A$ perpendicular to $l$, and let $b$ be the line through $B$ perpendicular to $l$. A line through $P$, not coinciding with $l$, intersects $a$ in $Q$ and $b$ in $R$. The line through $A$ perpendicular to $B Q$ intersects $B Q$ in $L$ and $B R$ in $T$. The line through $B$ perpendicular to $A R$ intersects $A R$ in $K$ and $A Q$ in $S$.
(a) Prove that $P, T, S$ are collinear.
(b) Prove that $P, K, L$ are collinear.
#
|
.
(a) W.l.o.g. we may assume that $A=(0,0)$ and $B=(1,0)$ and the line through $P$ is in the upper half plane, so $l$ is the $x$-axis, $a$ is the $y$-axis and $b$ is the line $x=1$. Take $P=(p, 0)(p>1)$ and $Q=(0, q)(q>0)$. Since $P Q$ is given by $\frac{x}{p}+\frac{y}{q}=1$, we find $R=\left(1, \frac{q(p-1)}{p}\right)$.
Now $A R$ is given by $y=\frac{q(p-1)}{p} x$, hence $B S$, the line perpendicular to $A R$ and passing through $B=(1,0)$, is given by $y=-\frac{p}{q(p-1)}(x-1)$. We find $S=\left(0, \frac{p}{q(p-1)}\right)$.
Moreover $B Q$ is given by $y=-q(x-1)$, hence $A T$, the line perpendicular to $B Q$ and passing through $A=(0,0)$, is given by $y=\frac{1}{q} x$. We find $T=\left(1, \frac{1}{q}\right)$. Since $\frac{|B T|}{|B P|}=\frac{1 / q}{p-1}=\frac{\frac{p}{q(p-1)}}{p}=\frac{|A S|}{|A P|}$, we conclude that $P, T$ and $S$ are collinear.
(b) Point $K$ is the intersection of $A R$ and $B S$. Solving for $x$ yields
$$
\begin{aligned}
\frac{q(p-1)}{p} x & =-\frac{p}{q(p-1)}(x-1) \\
\left(\frac{q(p-1)}{p}+\frac{p}{q(p-1)}\right) x & =\frac{p}{q(p-1)} \\
x & =\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}
\end{aligned}
$$
so
$$
K=\left(\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}, \frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right)
$$
Point $L$ is the point of intersection of $A T$ and $B Q$. Solving for $x$ yields
$$
\begin{aligned}
\frac{1}{q} x & =-q(x-1) \\
\left(\frac{1}{q}+q\right) x & =q \\
x & =\frac{q}{\frac{1}{q}+q}
\end{aligned}
$$
so
$$
L=\left(\frac{q}{\frac{1}{q}+q}, \frac{1}{\frac{1}{q}+q}\right)
$$
Let $K_{0}$ and $L_{0}$ be the projections of $K$ and $L$ on the $x$-axis. We have to show that the following fractions are equal:
$$
\frac{\left|K_{0} K\right|}{\left|K_{0} P\right|}=\frac{\frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}}{p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}} \quad \text { and } \quad \frac{\left|L_{0} L\right|}{\left|L_{0} P\right|}=\frac{\frac{1}{\frac{1}{q}+q}}{p-\frac{q}{\frac{1}{q}+q}}
$$
Working out cross products twice, this comes down to
$$
\begin{aligned}
& \frac{1}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}} \cdot\left(p-\frac{q}{\frac{1}{q}+q}\right) \stackrel{?}{=} \frac{1}{\frac{1}{q}+q} \cdot\left(p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right) \\
& \left(\frac{1}{q}+q\right) \cdot\left(p-\frac{q}{\frac{1}{q}+q}\right) \stackrel{?}{=}\left(\frac{q(p-1)}{p}+\frac{p}{q(p-1)}\right) \cdot\left(p-\frac{\frac{p}{q(p-1)}}{\frac{q(p-1)}{p}+\frac{p}{q(p-1)}}\right) \\
& \frac{p}{q}+p q-q \stackrel{?}{=} q(p-1)+\frac{p^{2}}{q(p-1)}-\frac{p}{q(p-1)} \\
& \frac{p}{q}+p q-q \stackrel{?}{=} q(p-1)+\frac{p(p-1)}{q(p-1)}
\end{aligned}
$$
which is clearly true.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2010-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
6334840b-62d7-5769-8944-102754ee94ab
| 606,025
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
The quadrilateral $A M D B$ is cyclic. Indeed, $M$ is the intersection of the line $B I$, which bisects the angle $\widehat{A B D}$ in $A B D$ and the perpendicular bisector of $[A D]$. By uniqueness of this intersection point, it follows that $M$ lies on the circumcircle of $A B D$, and thence $A M D B$ is cyclic. Analogously, $A N D C$ is cyclic.
Moreover, $M N B C$ is cyclic, for $\widehat{N M I}=90^{\circ}-\widehat{E I A}$. Indeed, $A$ and $I$ lie on either side of the midpoint of $[A D]$, for $\widehat{B D A}=\widehat{C A D}+\widehat{B C A}>\widehat{B A D}$. But
$$
\widehat{E I A}=180^{\circ}-\frac{1}{2} \widehat{B A C}-\widehat{B E A}=180^{\circ}-\frac{1}{2} \widehat{B A C}-\left(\frac{1}{2} \widehat{C B A}+\widehat{B C A}\right)=90^{\circ}-\frac{1}{2} \widehat{B C A}
$$
It follows that $\widehat{N M I}=\widehat{B C I}$, which implies that $M N B C$ is cyclic, as the points $I$ and $D$ lie on the same side of $M N$.
There are now two ways of completing the proof:
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
The quadrilateral $A M D B$ is cyclic. Indeed, $M$ is the intersection of the line $B I$, which bisects the angle $\widehat{A B D}$ in $A B D$ and the perpendicular bisector of $[A D]$. By uniqueness of this intersection point, it follows that $M$ lies on the circumcircle of $A B D$, and thence $A M D B$ is cyclic. Analogously, $A N D C$ is cyclic.
Moreover, $M N B C$ is cyclic, for $\widehat{N M I}=90^{\circ}-\widehat{E I A}$. Indeed, $A$ and $I$ lie on either side of the midpoint of $[A D]$, for $\widehat{B D A}=\widehat{C A D}+\widehat{B C A}>\widehat{B A D}$. But
$$
\widehat{E I A}=180^{\circ}-\frac{1}{2} \widehat{B A C}-\widehat{B E A}=180^{\circ}-\frac{1}{2} \widehat{B A C}-\left(\frac{1}{2} \widehat{C B A}+\widehat{B C A}\right)=90^{\circ}-\frac{1}{2} \widehat{B C A}
$$
It follows that $\widehat{N M I}=\widehat{B C I}$, which implies that $M N B C$ is cyclic, as the points $I$ and $D$ lie on the same side of $M N$.
There are now two ways of completing the proof:
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2011-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebcf8410-a992-5c14-ba35-1362d8b147d1
| 606,089
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
(using $A M D B$ and $M N B C$ )
Since $A M D B$ is cyclic, $\widehat{M A I}=\widehat{M A D}=\widehat{M B D}$, as, by construction, $B$ and $M$ lie on either side of $A D$. Moreover, $\widehat{M B D}=\widehat{M B C}=\widehat{M N C}$ for $M N B C$ is cyclic. Thus $\widehat{M A I}=\widehat{M N I}$, so $A M I N$ is cyclic, for $M$ and $N$ lie on either side of $A D$.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
(using $A M D B$ and $M N B C$ )
Since $A M D B$ is cyclic, $\widehat{M A I}=\widehat{M A D}=\widehat{M B D}$, as, by construction, $B$ and $M$ lie on either side of $A D$. Moreover, $\widehat{M B D}=\widehat{M B C}=\widehat{M N C}$ for $M N B C$ is cyclic. Thus $\widehat{M A I}=\widehat{M N I}$, so $A M I N$ is cyclic, for $M$ and $N$ lie on either side of $A D$.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2011-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebcf8410-a992-5c14-ba35-1362d8b147d1
| 606,089
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
(using $A M D B$ and $A N D C$ )
Since $A M D B$ and $A N D C$ are cylic, $\widehat{A M I}+\widehat{A N I}=\widehat{A M B}+\widehat{A N C}=\widehat{A D B}+\widehat{A D C}=180^{\circ}$, because $B$ and $M$, and $C$ and $N$ lie on either side of $A D$. Hence $A M I N$ is cyclic, for $M$ and $N$ lie on either side of $A D$.
Remark. It is moreover true that $B M \perp D N$ and $C N \perp D M$. Indeed, symmetry implies that the image $J$ of $I$ under reflection in $M N$ lies on the circumcircle of $D M N$. Moreover, $D I$ is a height of $D M N$, so the fact that $I$ and $J$ are equidistant from the side $[M N]$ implies that $I$ is the orthocentre of $D M N$. This implies the claim.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$. The angle bisectors $A I, B I$ and $C I$ meet $[B C],[C A]$ and $[A B]$ at $D, E$ and $F$, respectively. The perpendicular bisector of $[A D]$ intersects the lines $B I$ and $C I$ at $M$ and $N$, respectively. Show that $A, I, M$ and $N$ lie on a circle.
#
|
(using $A M D B$ and $A N D C$ )
Since $A M D B$ and $A N D C$ are cylic, $\widehat{A M I}+\widehat{A N I}=\widehat{A M B}+\widehat{A N C}=\widehat{A D B}+\widehat{A D C}=180^{\circ}$, because $B$ and $M$, and $C$ and $N$ lie on either side of $A D$. Hence $A M I N$ is cyclic, for $M$ and $N$ lie on either side of $A D$.

Remark. It is moreover true that $B M \perp D N$ and $C N \perp D M$. Indeed, symmetry implies that the image $J$ of $I$ under reflection in $M N$ lies on the circumcircle of $D M N$. Moreover, $D I$ is a height of $D M N$, so the fact that $I$ and $J$ are equidistant from the side $[M N]$ implies that $I$ is the orthocentre of $D M N$. This implies the claim.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2011-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebcf8410-a992-5c14-ba35-1362d8b147d1
| 606,089
|
. A sequence $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ of natural numbers is defined by the rule
$$
a_{n+1}=a_{n}+b_{n} \quad(n=1,2, \ldots)
$$
where $b_{n}$ is the last digit of $a_{n}$. Prove that such a sequence contains infinitely many powers of 2 if and only if $a_{1}$ is not divisible by 5 .
|
First we can observe that:
- If $a_{1}$ is divisible by 5 , then $a_{n}=a_{2}=0(\bmod 10) \forall n \geq 2$.
- If $a_{1}$ is not divisible by 5 , then for $n \geq 2: a_{n}$ is even, the sequence $b_{n}$ is periodic, its period is a cyclic permutation of $(2,4,8,6)$, and $a_{n+4}=a_{n}+20$.
(a) Let us suppose that $a_{1}$ is divisible by 5 .
Since $2^{k} \neq 0(\bmod 10)$ for any $k \in \mathbb{N}$, the sequence does not contain any power of 2 for $n \geq 2$.
(b) Let us suppose that $a_{1}$ is not divisible by 5 .
We can remark that the sequence of powers of 2 modulo 20 respects the period $(12,4,8,16)$ starting with $2^{5}=32$. We choose $j$ such that $a_{j}=2(\bmod 10)$ (i.e. $\left.b_{j}=2\right)$ and look at the parity of its penultimate digit.
- If $a_{j}=12(\bmod 20)$, then the numbers $a_{j+4 k}, k \in \mathbb{N}$, represent all the numbers congruent to $12(\bmod 20)$ and greater than $a_{j}$, so all powers of 2 congruent to 12 $(\bmod 20)$ and greater than $a_{j}$ appear in the sequence.
- If $a_{j}=2(\bmod 20)$, then the numbers $a_{j+1+4 k}, k \in \mathbb{N}$, represent all the numbers congruent to $4(\bmod 20)$ and greater than $a_{j+1}$, so all powers of 2 congruent to 4 $(\bmod 20)$ and greater than $a_{j+1}$ appear in the sequence.
Thus, the sequence contains infinitely many powers of 2 .
Alternative 1 for $(\mathbf{b})$. We choose $j$ such that $a_{j}=2(\bmod 10)\left(\right.$ i.e. $\left.b_{j}=2\right)$.
- If $a_{j}=20 t+12$ for some $t \in \mathbb{N}$, then $a_{j+4 k}=a_{j}+20 k=20(t+k)+12, \forall k \in \mathbb{N}$. We obtain infinitely many powers of 2 by taking $k=\frac{2^{4 s+3}-3}{5}-t$ (with $s \in \mathbb{N}$ large enough to have $k>0)$ since $2^{4 s+3}=3(\bmod 5), \forall s \in \mathbb{N}$.
- If $a_{j}=20 t+2$ for some $t \in \mathbb{N}$, then $a_{j+1+4 k}=a_{j+1}+20 k=20(t+k)+4, \forall k \in \mathbb{N}$. We obtain infinitely many powers of 2 by taking $k=\frac{2^{4 s}-1}{5}-t$ (with $s \in \mathbb{N}$ large enough to have $k>0)$ since $2^{4 s}=1(\bmod 5), \forall s \in \mathbb{N}$.
Alternative 2 for (b). Choose $j$ such that $a_{j}$ is a multiple of 4 , i.e. $a_{j}=4 q$ (such a $j$ always exists since $a_{n+1}=a_{n}+2$ for infinitely many $n$ ). Then we have $a_{j+4 k}=a_{j}+20 k=4(q+5 k)$. Let us look for $(k, m)$ such that
$$
a_{j+4 k}=2^{m} \Longleftrightarrow 4(q+5 k)=2^{m} \Longleftrightarrow q+5 k=2^{m-2} \Longleftrightarrow 2^{m-2}=q \quad(\bmod 5) .
$$
Since $q$ could not be a multiple of 5 , we have $q \in\{1,2,3,4\}(\bmod 5)$. Since the sequence $2^{m-2}(\bmod 5)$ is periodic with period $(1,2,4,3)$, we find that $2^{m-2}=q(\bmod 5)$ happens for infinitely many values of $m$. Hence $2^{m-2}=q+5 k$ is solvable for infinitely many pairs $(k, m)$. Noting that $m$ determines $k$ and that $k$ is nonnegative as soon as $m$ is large enough concludes the proof.
Alternative 3 for (b). We shall show that for any $n>1$ there is some $k \geq n$ such that $a_{k}$ is a power of 2 . First, we observe that we can always find $m \in\{n, n+1, n+2, n+3\}$ such that $a_{m}$ is divisible by 4 . If $a_{m}$ is not a power of 2 , we write $a_{m}=2^{b} c$ with $b \geq 2$ and $c>1$ odd. Then we have
$$
a_{m+4 \cdot 2^{b-2}}=a_{m}+20\left(2^{b-2}\right)=2^{b} c+5 \cdot 2^{b}=2^{b+1} \frac{c+5}{2} .
$$
If $c>5$, we have $\frac{c+5}{2}<c$ and hence the odd factor of $a_{m+4.2^{b-2}}$ is strictly smaller than the odd factor of $a_{m}$. Therefore there is some $m^{\prime}>m$ such that $a_{m^{\prime}}=2^{b^{\prime}} c^{\prime}$ with $c^{\prime}$ odd and $\leq 5$. The case $c^{\prime}=5$ is forbidden. If $c^{\prime}=1$, then $a_{m^{\prime}}$ is a power of 2 . If $c^{\prime}=3$, then $a_{m^{\prime}+4.2^{b^{\prime}-2}}=2^{b^{\prime}+3}$ is a power of 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
. A sequence $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ of natural numbers is defined by the rule
$$
a_{n+1}=a_{n}+b_{n} \quad(n=1,2, \ldots)
$$
where $b_{n}$ is the last digit of $a_{n}$. Prove that such a sequence contains infinitely many powers of 2 if and only if $a_{1}$ is not divisible by 5 .
|
First we can observe that:
- If $a_{1}$ is divisible by 5 , then $a_{n}=a_{2}=0(\bmod 10) \forall n \geq 2$.
- If $a_{1}$ is not divisible by 5 , then for $n \geq 2: a_{n}$ is even, the sequence $b_{n}$ is periodic, its period is a cyclic permutation of $(2,4,8,6)$, and $a_{n+4}=a_{n}+20$.
(a) Let us suppose that $a_{1}$ is divisible by 5 .
Since $2^{k} \neq 0(\bmod 10)$ for any $k \in \mathbb{N}$, the sequence does not contain any power of 2 for $n \geq 2$.
(b) Let us suppose that $a_{1}$ is not divisible by 5 .
We can remark that the sequence of powers of 2 modulo 20 respects the period $(12,4,8,16)$ starting with $2^{5}=32$. We choose $j$ such that $a_{j}=2(\bmod 10)$ (i.e. $\left.b_{j}=2\right)$ and look at the parity of its penultimate digit.
- If $a_{j}=12(\bmod 20)$, then the numbers $a_{j+4 k}, k \in \mathbb{N}$, represent all the numbers congruent to $12(\bmod 20)$ and greater than $a_{j}$, so all powers of 2 congruent to 12 $(\bmod 20)$ and greater than $a_{j}$ appear in the sequence.
- If $a_{j}=2(\bmod 20)$, then the numbers $a_{j+1+4 k}, k \in \mathbb{N}$, represent all the numbers congruent to $4(\bmod 20)$ and greater than $a_{j+1}$, so all powers of 2 congruent to 4 $(\bmod 20)$ and greater than $a_{j+1}$ appear in the sequence.
Thus, the sequence contains infinitely many powers of 2 .
Alternative 1 for $(\mathbf{b})$. We choose $j$ such that $a_{j}=2(\bmod 10)\left(\right.$ i.e. $\left.b_{j}=2\right)$.
- If $a_{j}=20 t+12$ for some $t \in \mathbb{N}$, then $a_{j+4 k}=a_{j}+20 k=20(t+k)+12, \forall k \in \mathbb{N}$. We obtain infinitely many powers of 2 by taking $k=\frac{2^{4 s+3}-3}{5}-t$ (with $s \in \mathbb{N}$ large enough to have $k>0)$ since $2^{4 s+3}=3(\bmod 5), \forall s \in \mathbb{N}$.
- If $a_{j}=20 t+2$ for some $t \in \mathbb{N}$, then $a_{j+1+4 k}=a_{j+1}+20 k=20(t+k)+4, \forall k \in \mathbb{N}$. We obtain infinitely many powers of 2 by taking $k=\frac{2^{4 s}-1}{5}-t$ (with $s \in \mathbb{N}$ large enough to have $k>0)$ since $2^{4 s}=1(\bmod 5), \forall s \in \mathbb{N}$.
Alternative 2 for (b). Choose $j$ such that $a_{j}$ is a multiple of 4 , i.e. $a_{j}=4 q$ (such a $j$ always exists since $a_{n+1}=a_{n}+2$ for infinitely many $n$ ). Then we have $a_{j+4 k}=a_{j}+20 k=4(q+5 k)$. Let us look for $(k, m)$ such that
$$
a_{j+4 k}=2^{m} \Longleftrightarrow 4(q+5 k)=2^{m} \Longleftrightarrow q+5 k=2^{m-2} \Longleftrightarrow 2^{m-2}=q \quad(\bmod 5) .
$$
Since $q$ could not be a multiple of 5 , we have $q \in\{1,2,3,4\}(\bmod 5)$. Since the sequence $2^{m-2}(\bmod 5)$ is periodic with period $(1,2,4,3)$, we find that $2^{m-2}=q(\bmod 5)$ happens for infinitely many values of $m$. Hence $2^{m-2}=q+5 k$ is solvable for infinitely many pairs $(k, m)$. Noting that $m$ determines $k$ and that $k$ is nonnegative as soon as $m$ is large enough concludes the proof.
Alternative 3 for (b). We shall show that for any $n>1$ there is some $k \geq n$ such that $a_{k}$ is a power of 2 . First, we observe that we can always find $m \in\{n, n+1, n+2, n+3\}$ such that $a_{m}$ is divisible by 4 . If $a_{m}$ is not a power of 2 , we write $a_{m}=2^{b} c$ with $b \geq 2$ and $c>1$ odd. Then we have
$$
a_{m+4 \cdot 2^{b-2}}=a_{m}+20\left(2^{b-2}\right)=2^{b} c+5 \cdot 2^{b}=2^{b+1} \frac{c+5}{2} .
$$
If $c>5$, we have $\frac{c+5}{2}<c$ and hence the odd factor of $a_{m+4.2^{b-2}}$ is strictly smaller than the odd factor of $a_{m}$. Therefore there is some $m^{\prime}>m$ such that $a_{m^{\prime}}=2^{b^{\prime}} c^{\prime}$ with $c^{\prime}$ odd and $\leq 5$. The case $c^{\prime}=5$ is forbidden. If $c^{\prime}=1$, then $a_{m^{\prime}}$ is a power of 2 . If $c^{\prime}=3$, then $a_{m^{\prime}+4.2^{b^{\prime}-2}}=2^{b^{\prime}+3}$ is a power of 2 .
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2012-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
3730331b-fafa-5ebc-b2b9-5a9112093ed7
| 606,140
|
. In triangle $A B C$ the midpoint of $B C$ is called $M$. Let $P$ be a variable interior point of the triangle such that $\angle C P M=\angle P A B$. Let $\Gamma$ be the circumcircle of triangle $A B P$. The line $M P$ intersects $\Gamma$ a second time in $Q$. Define $R$ as the reflection of $P$ in the tangent to $\Gamma$ in $B$. Prove that the length $|Q R|$ is independent of the position of $P$ inside the triangle.
|
We claim $|Q R|=|B C|$, which will clearly imply that quantity $|Q R|$ is independent from the position of $P$ inside triangle $\triangle A B C$ (and independent from the position of $A$ ).
This equality will follow from the equality between triangles $\triangle B P C$ and $\triangle R B Q$. This in turn will be shown by means of three equalities (two sides and an angle): $|B P|=|R B|,|P C|=|B Q|$ and $\angle B P C=\angle R B Q$.
(a) $|B P|=|R B|$
Obvious since $R$ is the reflection of $P$ in a line going through $B$.
(b) $|P C|=|B Q|$
Let $U$ be the fourth vertex of parallelogram $B P C U$. Then $U$ is on line $P Q$ and $\angle B U P=$ $\angle U P C=\alpha$. If $Q$ is on the same $\operatorname{arc} P B$ as $A$, then $\angle B Q P=\alpha$, and $\triangle Q P U$ is isosceles; hence, $|B Q|=|B U|=|P C|$. On the other way, if $Q$ is on the other $\operatorname{arc} P B$, then $\angle B Q P$ and $\alpha$ are supplementary, hence $B Q U=\alpha$, and again $\triangle Q P U$ is isosceles; the same conclusion follows.
(c) $\angle B P C=\angle R B Q$
Define $T$ to be the midpoint of $P R$. Then line $B T$, tangent to circle $\Gamma$ in $B$, splits $\angle R B Q$ into two parts, $\angle R B T$ and $\angle T B Q$.
We first show that $\angle R B T=\alpha$. Indeed, by symmetry, $\angle R B T=\angle P B T$ and, since $B T$ is tangent to $\Gamma$, we have that $\angle P B T=\angle P A B$ (because they both intercept the same arc $\widehat{P B}$ on circle $\Gamma$ ), from which our claim follows.
We then show that $\angle T B Q=\angle B P M$. Indeed, since $\angle T B Q$ and $\angle B P Q$ intercept opposite arcs on circle $\Gamma$, they are supplementary and we have $\angle T B Q=\pi-\angle B P Q=\angle B P M$. We finally conclude that
$$
\angle R B Q=\angle R B T+\angle T B Q=\alpha+\angle B P M=\angle M P C+\angle B P M=\angle B P C .
$$
We have thus shown $\triangle B P C=\triangle R B Q$, which completes the proof.
Note. Notice that point $A$ does not play any role in the problem except fixing circle $\Gamma$ (and, for that reason, the result is also valid when $P$ is chosen outside of triangle $\triangle A B C$ ).
Alternative 1 for (b). The law of sines in triangle $\triangle B Q M$ gives
$$
\frac{|B M|}{\sin \angle B Q M}=\frac{|B Q|}{\sin \angle B M Q}
$$
Since $Q$ belongs to circle $\Gamma$, we have either $\angle B Q P=\angle B A P=\alpha$, hence $\angle B Q M=\angle M P C$, or these angles are supplementary; in both cases they have equal sines. We also have that $\angle B M Q$ and $\angle C M P$ are supplementary, hence have equal sines. Using these facts along with $|B M|=|M C|$ transforms (2) into
$$
\frac{|M C|}{\sin \angle M P C}=\frac{|B Q|}{\sin \angle C M P}
$$
from which the law of sines in triangle $\triangle C P M$ implies that $|B Q|=|P C|$.
#### Abstract
Alternative 2 for (b). Let $S$ be the second intersection of line $C P$ with circle $\Gamma$. Then, $\angle B S P=\alpha$, so $B S$ and $M P$ are parallel; since $M$ is the midpoint of segment $B C, P$ is the midpoint of $S C$. If $Q$ is on the same $\operatorname{arc} P B$ as $A$, then the quadrilateral $Q P B S$ is an isosceles trapezoid, and $|Q B|=|S P|=|P C|$. If $Q$ is on the other $\operatorname{arc} P B$, then the quadrilateral $P Q B S$ is an isosceles trapezoid, and again $|Q B|=|S P|=|P C|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. In triangle $A B C$ the midpoint of $B C$ is called $M$. Let $P$ be a variable interior point of the triangle such that $\angle C P M=\angle P A B$. Let $\Gamma$ be the circumcircle of triangle $A B P$. The line $M P$ intersects $\Gamma$ a second time in $Q$. Define $R$ as the reflection of $P$ in the tangent to $\Gamma$ in $B$. Prove that the length $|Q R|$ is independent of the position of $P$ inside the triangle.
|
We claim $|Q R|=|B C|$, which will clearly imply that quantity $|Q R|$ is independent from the position of $P$ inside triangle $\triangle A B C$ (and independent from the position of $A$ ).
This equality will follow from the equality between triangles $\triangle B P C$ and $\triangle R B Q$. This in turn will be shown by means of three equalities (two sides and an angle): $|B P|=|R B|,|P C|=|B Q|$ and $\angle B P C=\angle R B Q$.

(a) $|B P|=|R B|$
Obvious since $R$ is the reflection of $P$ in a line going through $B$.
(b) $|P C|=|B Q|$
Let $U$ be the fourth vertex of parallelogram $B P C U$. Then $U$ is on line $P Q$ and $\angle B U P=$ $\angle U P C=\alpha$. If $Q$ is on the same $\operatorname{arc} P B$ as $A$, then $\angle B Q P=\alpha$, and $\triangle Q P U$ is isosceles; hence, $|B Q|=|B U|=|P C|$. On the other way, if $Q$ is on the other $\operatorname{arc} P B$, then $\angle B Q P$ and $\alpha$ are supplementary, hence $B Q U=\alpha$, and again $\triangle Q P U$ is isosceles; the same conclusion follows.
(c) $\angle B P C=\angle R B Q$
Define $T$ to be the midpoint of $P R$. Then line $B T$, tangent to circle $\Gamma$ in $B$, splits $\angle R B Q$ into two parts, $\angle R B T$ and $\angle T B Q$.
We first show that $\angle R B T=\alpha$. Indeed, by symmetry, $\angle R B T=\angle P B T$ and, since $B T$ is tangent to $\Gamma$, we have that $\angle P B T=\angle P A B$ (because they both intercept the same arc $\widehat{P B}$ on circle $\Gamma$ ), from which our claim follows.
We then show that $\angle T B Q=\angle B P M$. Indeed, since $\angle T B Q$ and $\angle B P Q$ intercept opposite arcs on circle $\Gamma$, they are supplementary and we have $\angle T B Q=\pi-\angle B P Q=\angle B P M$. We finally conclude that
$$
\angle R B Q=\angle R B T+\angle T B Q=\alpha+\angle B P M=\angle M P C+\angle B P M=\angle B P C .
$$
We have thus shown $\triangle B P C=\triangle R B Q$, which completes the proof.
Note. Notice that point $A$ does not play any role in the problem except fixing circle $\Gamma$ (and, for that reason, the result is also valid when $P$ is chosen outside of triangle $\triangle A B C$ ).
Alternative 1 for (b). The law of sines in triangle $\triangle B Q M$ gives
$$
\frac{|B M|}{\sin \angle B Q M}=\frac{|B Q|}{\sin \angle B M Q}
$$
Since $Q$ belongs to circle $\Gamma$, we have either $\angle B Q P=\angle B A P=\alpha$, hence $\angle B Q M=\angle M P C$, or these angles are supplementary; in both cases they have equal sines. We also have that $\angle B M Q$ and $\angle C M P$ are supplementary, hence have equal sines. Using these facts along with $|B M|=|M C|$ transforms (2) into
$$
\frac{|M C|}{\sin \angle M P C}=\frac{|B Q|}{\sin \angle C M P}
$$
from which the law of sines in triangle $\triangle C P M$ implies that $|B Q|=|P C|$.
#### Abstract
Alternative 2 for (b). Let $S$ be the second intersection of line $C P$ with circle $\Gamma$. Then, $\angle B S P=\alpha$, so $B S$ and $M P$ are parallel; since $M$ is the midpoint of segment $B C, P$ is the midpoint of $S C$. If $Q$ is on the same $\operatorname{arc} P B$ as $A$, then the quadrilateral $Q P B S$ is an isosceles trapezoid, and $|Q B|=|S P|=|P C|$. If $Q$ is on the other $\operatorname{arc} P B$, then the quadrilateral $P Q B S$ is an isosceles trapezoid, and again $|Q B|=|S P|=|P C|$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2012-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
a866c746-6b06-57a1-b909-3c678b2e8ecc
| 606,169
|
. Let $\triangle A B C$ be a triangle with circumcircle $\Gamma$, and let $I$ be the center of the incircle of $\triangle A B C$. The lines $A I, B I$ and $C I$ intersect $\Gamma$ in $D \neq A, E \neq B$ and $F \neq C$. The tangent lines to $\Gamma$ in $F, D$ and $E$ intersect the lines $A I, B I$ and $C I$ in $R, S$ and $T$, respectively. Prove that
$$
|A R| \cdot|B S| \cdot|C T|=|I D| \cdot|I E| \cdot|I F| .
$$
|
We first prove that $|D B|=|D I|$. (This may also be claimed by referring to the lemma that $D$ is the centre of the circumcircle of $B I C I_{a}$.) By the constant angle theorem and the fact that $A D$ and $B E$ are angle bisectors of triangle $A B C$, we see that
$$
\angle D B I=\angle D B C+\angle C B I=\angle D A C+\angle C B E=\angle D A B+\angle A B E \text {, }
$$
while
$$
\angle D I B=180^{\circ}-\angle A I B=\angle I A B+\angle A B I=\angle D A B+\angle A B E \text {. }
$$
So $\triangle B D I$ has equal angles $\angle D B I=\angle D I B$, so $|D B|=|D I|$. This proves our claim. We similarly deduce that $|E C|=|E I|$ and $|F A|=|F I|$.
Rewriting (7) into $\frac{|A R|}{|I F|} \cdot \frac{|B S|}{|I D|} \cdot \frac{|C T|}{|I E|}=1$, we see that it suffices to prove that
$$
\frac{|A R|}{|A F|} \cdot \frac{|B S|}{|B D|} \cdot \frac{|C T|}{|C E|}=1
$$
We now prove by angle chasing that $\triangle R F A \sim \triangle A C I$. As $R F$ is tangent to the circumcircle of $\triangle A F C$, we obtain (using also that $C F$ is angle bisector of $\angle A C B$ )
$$
\angle R F A=\angle F C A=\angle I C A .
$$
Moreover, from $|F A|=|F I|$ we deduce that $\angle F A I=\angle F I A$, so
$$
\angle F A R=180^{\circ}-\angle F A I=180^{\circ}-\angle F I A=\angle C I A .
$$
This proves our similarity, which entails that $\frac{|A R|}{|A F|}=\frac{|I A|}{|I C|}$. In the same way we deduce that $\frac{|B S|}{|B D|}=\frac{|I B|}{|I A|}$ and $\frac{|C T|}{|C E|}=\frac{|I C|}{|I B|}$. By these equal ratios we know that
$$
\frac{|A R|}{|A F|} \cdot \frac{|B S|}{|B D|} \cdot \frac{|C T|}{|C E|}=\frac{|I A|}{|I C|} \cdot \frac{|I B|}{|I A|} \cdot \frac{|I C|}{|I B|}=1,
$$
which proves (8), as required.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. Let $\triangle A B C$ be a triangle with circumcircle $\Gamma$, and let $I$ be the center of the incircle of $\triangle A B C$. The lines $A I, B I$ and $C I$ intersect $\Gamma$ in $D \neq A, E \neq B$ and $F \neq C$. The tangent lines to $\Gamma$ in $F, D$ and $E$ intersect the lines $A I, B I$ and $C I$ in $R, S$ and $T$, respectively. Prove that
$$
|A R| \cdot|B S| \cdot|C T|=|I D| \cdot|I E| \cdot|I F| .
$$
|
We first prove that $|D B|=|D I|$. (This may also be claimed by referring to the lemma that $D$ is the centre of the circumcircle of $B I C I_{a}$.) By the constant angle theorem and the fact that $A D$ and $B E$ are angle bisectors of triangle $A B C$, we see that
$$
\angle D B I=\angle D B C+\angle C B I=\angle D A C+\angle C B E=\angle D A B+\angle A B E \text {, }
$$
while
$$
\angle D I B=180^{\circ}-\angle A I B=\angle I A B+\angle A B I=\angle D A B+\angle A B E \text {. }
$$
So $\triangle B D I$ has equal angles $\angle D B I=\angle D I B$, so $|D B|=|D I|$. This proves our claim. We similarly deduce that $|E C|=|E I|$ and $|F A|=|F I|$.
Rewriting (7) into $\frac{|A R|}{|I F|} \cdot \frac{|B S|}{|I D|} \cdot \frac{|C T|}{|I E|}=1$, we see that it suffices to prove that
$$
\frac{|A R|}{|A F|} \cdot \frac{|B S|}{|B D|} \cdot \frac{|C T|}{|C E|}=1
$$
We now prove by angle chasing that $\triangle R F A \sim \triangle A C I$. As $R F$ is tangent to the circumcircle of $\triangle A F C$, we obtain (using also that $C F$ is angle bisector of $\angle A C B$ )
$$
\angle R F A=\angle F C A=\angle I C A .
$$
Moreover, from $|F A|=|F I|$ we deduce that $\angle F A I=\angle F I A$, so
$$
\angle F A R=180^{\circ}-\angle F A I=180^{\circ}-\angle F I A=\angle C I A .
$$
This proves our similarity, which entails that $\frac{|A R|}{|A F|}=\frac{|I A|}{|I C|}$. In the same way we deduce that $\frac{|B S|}{|B D|}=\frac{|I B|}{|I A|}$ and $\frac{|C T|}{|C E|}=\frac{|I C|}{|I B|}$. By these equal ratios we know that
$$
\frac{|A R|}{|A F|} \cdot \frac{|B S|}{|B D|} \cdot \frac{|C T|}{|C E|}=\frac{|I A|}{|I C|} \cdot \frac{|I B|}{|I A|} \cdot \frac{|I C|}{|I B|}=1,
$$
which proves (8), as required.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2013-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
048ed872-73be-5dfb-b254-fc3ef270ea8f
| 290,405
|
Let $A B C D$ be a square. Consider a variable point $P$ inside the square for which $\angle B A P \geq 60^{\circ}$. Let $Q$ be the intersection of the line $A D$ and the perpendicular to $B P$ in $P$. Let $R$ be the intersection of the line $B Q$ and the perpendicular to $B P$ from $C$.
(a) Prove that $|B P| \geq|B R|$.
(b) For which point(s) $P$ does the inequality in (a) become an equality?
#
|
We claim that $\triangle A B P$ and $\triangle R C B$ are similar triangles. Indeed, if we denote the intersection of $B P$ and $C R$ by $S$, then $\angle R C B=\angle S C B=90^{\circ}-\angle S B C=90^{\circ}-\angle P B C=\angle A B P$. Moreover, the right angles in $P$ and $A$ imply that $A$ and $P$ lie on the circle with diameter $[B Q]$, so either $A B P Q$ or $A Q B P$ is a cyclic, convex quadrilateral. In either case, $A$ and $Q$ lie on the same side of $B P$, so $\angle P A B=\angle P Q B$. Since $C R$ and $P Q$ are perpendicular to $B P$, these lines are parallel and hence $\angle P Q B=\angle C R B$. Together with $\angle P A B=\angle P Q B$ and $\angle R C B=\angle A B P$, this implies the claim that $\triangle A B P \sim \triangle R C B$.
This similarity yields the equality $|A P| /|B R|=|B P| /|B C|$. Since $\angle B A P \geq 60^{\circ}$, we get
$$
\begin{aligned}
0 \leq & (|A B|-|A P|)^{2}=|A B|^{2}+|A P|^{2}-2 \cdot|A B| \cdot|A P| \\
& =|B P|^{2}+2(\cos \angle B A P-1) \cdot|A B| \cdot|A P| \\
& \leq|B P|^{2}-|A B| \cdot|A P|=|B P|^{2}-|B R| \cdot|B P| .
\end{aligned}
$$
This implies that $|B P| \geq|B R|$, as desired.
In order for equality to occur, one needs equality in each of the inequalities considered above: $|A B|=|A P|$ and $\angle B A P=60^{\circ}$. Hence there is exactly one point $P$ for which we have equality; this is the unique point inside the square such that $\triangle A B P$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square. Consider a variable point $P$ inside the square for which $\angle B A P \geq 60^{\circ}$. Let $Q$ be the intersection of the line $A D$ and the perpendicular to $B P$ in $P$. Let $R$ be the intersection of the line $B Q$ and the perpendicular to $B P$ from $C$.
(a) Prove that $|B P| \geq|B R|$.
(b) For which point(s) $P$ does the inequality in (a) become an equality?
#
|

We claim that $\triangle A B P$ and $\triangle R C B$ are similar triangles. Indeed, if we denote the intersection of $B P$ and $C R$ by $S$, then $\angle R C B=\angle S C B=90^{\circ}-\angle S B C=90^{\circ}-\angle P B C=\angle A B P$. Moreover, the right angles in $P$ and $A$ imply that $A$ and $P$ lie on the circle with diameter $[B Q]$, so either $A B P Q$ or $A Q B P$ is a cyclic, convex quadrilateral. In either case, $A$ and $Q$ lie on the same side of $B P$, so $\angle P A B=\angle P Q B$. Since $C R$ and $P Q$ are perpendicular to $B P$, these lines are parallel and hence $\angle P Q B=\angle C R B$. Together with $\angle P A B=\angle P Q B$ and $\angle R C B=\angle A B P$, this implies the claim that $\triangle A B P \sim \triangle R C B$.
This similarity yields the equality $|A P| /|B R|=|B P| /|B C|$. Since $\angle B A P \geq 60^{\circ}$, we get
$$
\begin{aligned}
0 \leq & (|A B|-|A P|)^{2}=|A B|^{2}+|A P|^{2}-2 \cdot|A B| \cdot|A P| \\
& =|B P|^{2}+2(\cos \angle B A P-1) \cdot|A B| \cdot|A P| \\
& \leq|B P|^{2}-|A B| \cdot|A P|=|B P|^{2}-|B R| \cdot|B P| .
\end{aligned}
$$
This implies that $|B P| \geq|B R|$, as desired.
In order for equality to occur, one needs equality in each of the inequalities considered above: $|A B|=|A P|$ and $\angle B A P=60^{\circ}$. Hence there is exactly one point $P$ for which we have equality; this is the unique point inside the square such that $\triangle A B P$ is equilateral.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2014-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
3b24dff4-b2d7-5265-b8cf-451071e3abdc
| 606,263
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Let $O_{B}$ and $O_{C}$ denote the respective centres of $\Gamma_{B}$ and $\Gamma_{C}$. We shall show that $X O_{B} O$ and $O O_{C} Y$ are congruent. Now $A O_{B} \perp A C$ since $\Gamma_{B}$ is tangent to $A C$ and $O O_{C} \perp A C$ since $O O_{C}$ is the perpendicular bisector of $[A C]$. Hence $A O_{B} \| O O_{C}$, and similarly, $A O_{C} \| O O_{B}$. It follows that $A O_{B} O O_{C}$ is a parallelogram. In particular, $\left|O_{B} X\right|=\left|A O_{B}\right|=\left|O O_{C}\right|$ and $\left|O_{C} Y\right|=\left|O_{C} A\right|=\left|O O_{B}\right|$.
It will therefore suffice to show that the angles $\angle O O_{B} X$ and $\angle Y O_{C} O$ are equal. Noting that $\angle A O_{B} O=\angle A O_{C} O$ since $A O_{B} O O_{C}$ is a parallelogram, this follows by angle chasing:
$$
\begin{aligned}
\angle X O_{B} O & =\angle A O_{B} O-\angle A O_{B} X=\angle A O_{C} O-\left(180^{\circ}-2 \angle O_{B} A X\right) \\
& =\angle A O_{C} O-180^{\circ}+2\left(\angle O_{B} A O_{C}-\angle Y A O_{C}\right) \\
& =\angle A O_{C} O-180^{\circ}+2\left(180^{\circ}-\angle A O_{C} O\right)-\left(180^{\circ}-\angle A O_{C} Y\right) \\
& =\angle A O_{C} Y-\angle A O_{C} O=\angle O O_{C} Y
\end{aligned}
$$
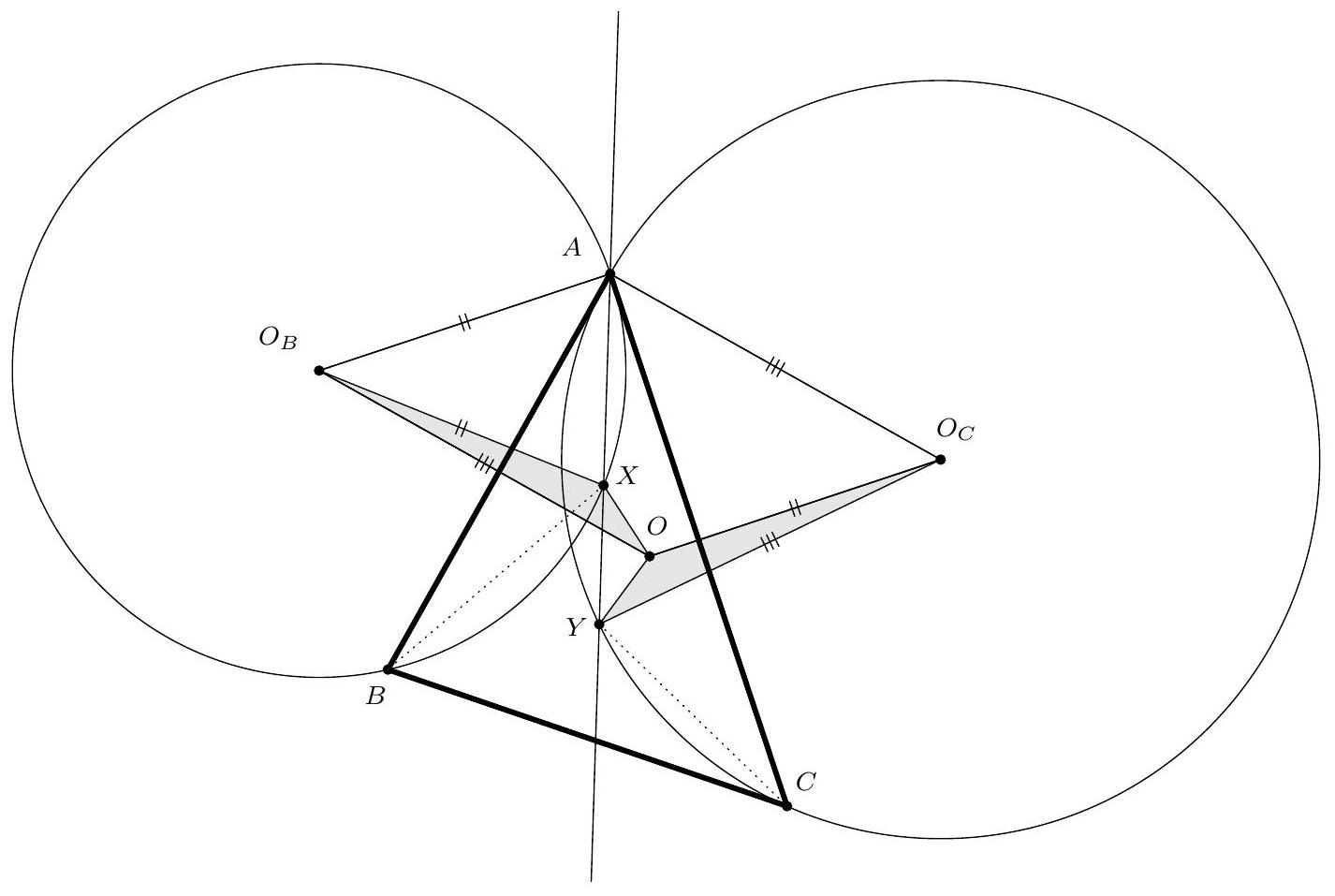
A Variant. As in the main solution, we note that $A O_{B} O O_{C}$ is a parallelogram. Notice that $O_{B}$ and $O_{C}$ lie on the respective perpendicular bisectors of $[A X]$ and $[A Y]$. The following lemma then implies that $O$ lies on the perpendicular bisector of $[X Y]$, completing the proof:
Let $P_{1}, P_{2}, P_{3}$ be three points on a line. Let $O_{1}$ be a point on the perpendicular bisector of $\left[P_{2} P_{3}\right]$, let $O_{2}$ be a point on the perpendicular bisector of $\left[P_{3} P_{1}\right]$ and let $O_{3}$ be the point in the plane such that $O_{1} P_{3} O_{2} O_{3}$ is a parallelogram. Then $O_{3}$ lies on the perpendicular bisector of $\left[P_{1} P_{2}\right]$.
Proof. One can choose coordinates such that $P_{3}=(0,0)$ and $P_{1}=(2,0)$. Then $P_{2}=(2 a, 0), O_{1}=(a, b)$ and $O_{2}=(1, c)$ for some $a, b, c \in \mathbb{R}$. Hence $O_{3}=(a+1, b+c)$ lies on the perpendicular bisector of $\left[P_{1} P_{2}\right]$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Let $O_{B}$ and $O_{C}$ denote the respective centres of $\Gamma_{B}$ and $\Gamma_{C}$. We shall show that $X O_{B} O$ and $O O_{C} Y$ are congruent. Now $A O_{B} \perp A C$ since $\Gamma_{B}$ is tangent to $A C$ and $O O_{C} \perp A C$ since $O O_{C}$ is the perpendicular bisector of $[A C]$. Hence $A O_{B} \| O O_{C}$, and similarly, $A O_{C} \| O O_{B}$. It follows that $A O_{B} O O_{C}$ is a parallelogram. In particular, $\left|O_{B} X\right|=\left|A O_{B}\right|=\left|O O_{C}\right|$ and $\left|O_{C} Y\right|=\left|O_{C} A\right|=\left|O O_{B}\right|$.
It will therefore suffice to show that the angles $\angle O O_{B} X$ and $\angle Y O_{C} O$ are equal. Noting that $\angle A O_{B} O=\angle A O_{C} O$ since $A O_{B} O O_{C}$ is a parallelogram, this follows by angle chasing:
$$
\begin{aligned}
\angle X O_{B} O & =\angle A O_{B} O-\angle A O_{B} X=\angle A O_{C} O-\left(180^{\circ}-2 \angle O_{B} A X\right) \\
& =\angle A O_{C} O-180^{\circ}+2\left(\angle O_{B} A O_{C}-\angle Y A O_{C}\right) \\
& =\angle A O_{C} O-180^{\circ}+2\left(180^{\circ}-\angle A O_{C} O\right)-\left(180^{\circ}-\angle A O_{C} Y\right) \\
& =\angle A O_{C} Y-\angle A O_{C} O=\angle O O_{C} Y
\end{aligned}
$$

A Variant. As in the main solution, we note that $A O_{B} O O_{C}$ is a parallelogram. Notice that $O_{B}$ and $O_{C}$ lie on the respective perpendicular bisectors of $[A X]$ and $[A Y]$. The following lemma then implies that $O$ lies on the perpendicular bisector of $[X Y]$, completing the proof:
Let $P_{1}, P_{2}, P_{3}$ be three points on a line. Let $O_{1}$ be a point on the perpendicular bisector of $\left[P_{2} P_{3}\right]$, let $O_{2}$ be a point on the perpendicular bisector of $\left[P_{3} P_{1}\right]$ and let $O_{3}$ be the point in the plane such that $O_{1} P_{3} O_{2} O_{3}$ is a parallelogram. Then $O_{3}$ lies on the perpendicular bisector of $\left[P_{1} P_{2}\right]$.
Proof. One can choose coordinates such that $P_{3}=(0,0)$ and $P_{1}=(2,0)$. Then $P_{2}=(2 a, 0), O_{1}=(a, b)$ and $O_{2}=(1, c)$ for some $a, b, c \in \mathbb{R}$. Hence $O_{3}=(a+1, b+c)$ lies on the perpendicular bisector of $\left[P_{1} P_{2}\right]$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2015-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb2c8926-2188-565b-afb2-d9ea0196a2f1
| 606,285
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Let $\alpha=\angle B A C$. Observe that $\angle A X B=180^{\circ}-\alpha=\angle C Y A$ by tangential angles. Let $Z$ be the intersection of $B X$ and $C Y$. Thus $Z X Y$ is isosceles with, in particular, $\angle Z X Y=\angle Z Y X=\alpha$. It will thus suffice to show that $O Z$ bisects $\angle X Z Y$.
Now $\angle B Z C=2 \alpha=\angle B O C$ since $O$ is the circumcentre of $A B C$, and hence $B Z O C$ is cyclic. In particular, since $|O B|=|O C|$, it follows that $\angle O Z Y=\angle O B C=90^{\circ}-\alpha$. But $\angle X Z Y=180^{\circ}-2 \alpha$, and so $\angle X Z Y=2 \angle O Z Y$, which shows that $O Z$ bisects $\angle X Z Y . \square$
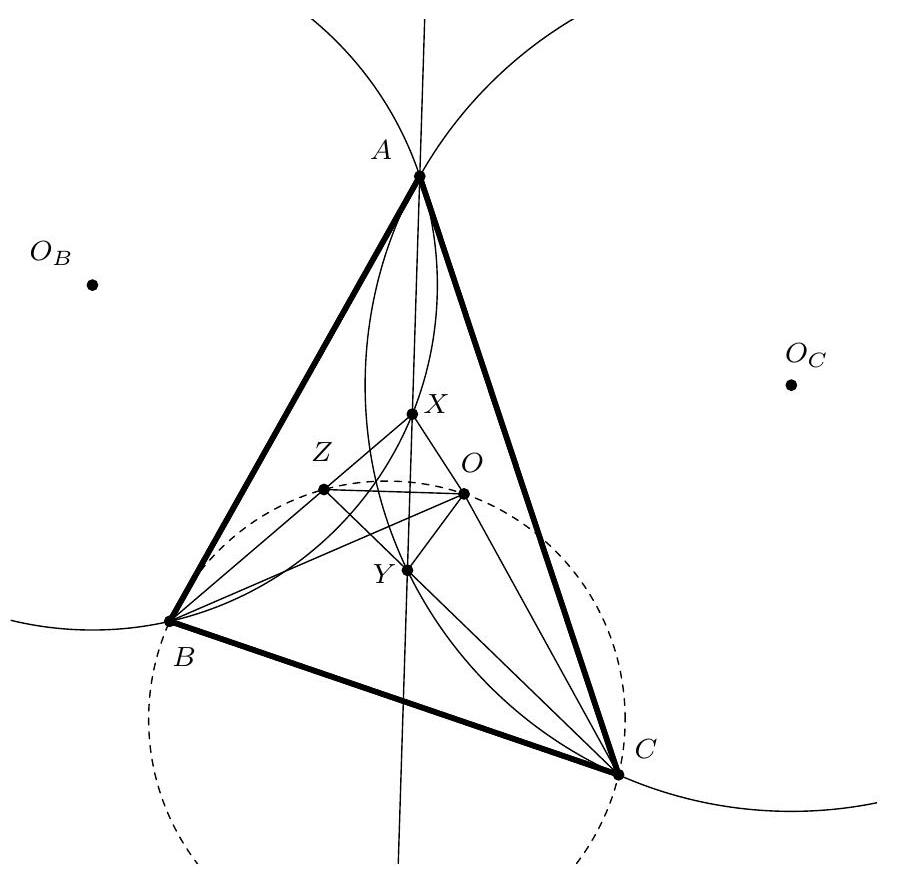
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Let $\alpha=\angle B A C$. Observe that $\angle A X B=180^{\circ}-\alpha=\angle C Y A$ by tangential angles. Let $Z$ be the intersection of $B X$ and $C Y$. Thus $Z X Y$ is isosceles with, in particular, $\angle Z X Y=\angle Z Y X=\alpha$. It will thus suffice to show that $O Z$ bisects $\angle X Z Y$.
Now $\angle B Z C=2 \alpha=\angle B O C$ since $O$ is the circumcentre of $A B C$, and hence $B Z O C$ is cyclic. In particular, since $|O B|=|O C|$, it follows that $\angle O Z Y=\angle O B C=90^{\circ}-\alpha$. But $\angle X Z Y=180^{\circ}-2 \alpha$, and so $\angle X Z Y=2 \angle O Z Y$, which shows that $O Z$ bisects $\angle X Z Y . \square$

|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2015-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb2c8926-2188-565b-afb2-d9ea0196a2f1
| 606,285
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Consider inversion $\mathscr{I}$ in a circle centred at $A$. Under $\mathscr{I}$,
$$
B \mapsto B^{\prime}, \quad C \mapsto C^{\prime}, \quad O \mapsto O^{\prime}, \quad X \mapsto X^{\prime}, \quad Y \mapsto Y^{\prime},
$$
$\Gamma_{B} \mapsto \gamma_{B}$, a line through $B^{\prime}$ parallel to $A C^{\prime}$,
$\Gamma_{C} \mapsto \gamma_{C}$, a line through $C^{\prime}$ parallel to $A B^{\prime}$,
Notice that $\mathscr{I}$ sends the circumcircle of $A B C$ to the line $B^{\prime} C^{\prime}$, and hence maps $A O$ to a line perpendicular to $B C$. Further, if $[A D]$ is a diameter of this circumcircle and $D \mapsto D^{\prime}$ under $\mathscr{I}$, then $D^{\prime}$ lies on $B C$. Also, $|A D|=2|A O|$ implies $\left|A O^{\prime}\right|=2\left|A D^{\prime}\right|$, and hence $O^{\prime}$ is the image of $A$ under reflection in $B C$. Finally, $\angle O X A=\angle X^{\prime} O^{\prime} A$ and $\angle O Y A=\angle Y^{\prime} O^{\prime} A$, and hence $|O X|=|O Y|$ if and only if $O^{\prime} A$ bissects $\angle X^{\prime} O^{\prime} Y^{\prime}$ externally. We have thus reduced the problem to the following statement:
In triangle $A B C$, let $O$ be the reflection of $A$ over $B C, \gamma_{B}$ be a line parallel to $A C$ through $B$, and $\gamma_{C}$ be a line parallel to $A B$ through $C$. For an arbitrary line $\ell$ passing through $A$, let $X$ and $Y$ be the intersections of $\ell$ with $\gamma_{B}$ and $\gamma_{C}$, respectively. Prove that $O A$ bisects $\angle X O Y$ externally.
Let $P=\gamma_{A} \cap \gamma_{B}$. By construction, $P O B C$ is an isosceles trapezoid (and therefore cyclic), $\angle O B X=\angle O B P=\angle O C P=\angle O C Y$. Further, since $X B \| A C$ and $Y C \| A B$, we have $\triangle A B X \sim \triangle Y C A$. Therefore, as $|O B|=|A B|$ and $|A C|=|O C|$ by construction,
$$
\frac{|O B|}{|B X|}=\frac{|A B|}{|B X|}=\frac{|Y C|}{|C A|}=\frac{|Y C|}{|C O|}
$$
It follows that $\triangle O B X \sim \triangle Y C O$. Hence
$$
\frac{|O X|}{|O Y|}=\frac{|X B|}{|O C|}=\frac{|X B|}{|A C|}=\frac{|X A|}{|A Y|}
$$
and so the result follows from the angle bisector theorem.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
.
Let $A B C$ be an acute triangle with circumcentre $O$. Let $\Gamma_{B}$ be the circle through $A$ and $B$ that is tangent to $A C$, and let $\Gamma_{C}$ be the circle through $A$ and $C$ that is tangent to $A B$. An arbitrary line through $A$ intersects $\Gamma_{B}$ again in $X$ and $\Gamma_{C}$ again in $Y$. Prove that $|O X|=|O Y|$.
The following solutions are valid for the configurations appearing in the diagrams.
|
. Consider inversion $\mathscr{I}$ in a circle centred at $A$. Under $\mathscr{I}$,
$$
B \mapsto B^{\prime}, \quad C \mapsto C^{\prime}, \quad O \mapsto O^{\prime}, \quad X \mapsto X^{\prime}, \quad Y \mapsto Y^{\prime},
$$
$\Gamma_{B} \mapsto \gamma_{B}$, a line through $B^{\prime}$ parallel to $A C^{\prime}$,
$\Gamma_{C} \mapsto \gamma_{C}$, a line through $C^{\prime}$ parallel to $A B^{\prime}$,
Notice that $\mathscr{I}$ sends the circumcircle of $A B C$ to the line $B^{\prime} C^{\prime}$, and hence maps $A O$ to a line perpendicular to $B C$. Further, if $[A D]$ is a diameter of this circumcircle and $D \mapsto D^{\prime}$ under $\mathscr{I}$, then $D^{\prime}$ lies on $B C$. Also, $|A D|=2|A O|$ implies $\left|A O^{\prime}\right|=2\left|A D^{\prime}\right|$, and hence $O^{\prime}$ is the image of $A$ under reflection in $B C$. Finally, $\angle O X A=\angle X^{\prime} O^{\prime} A$ and $\angle O Y A=\angle Y^{\prime} O^{\prime} A$, and hence $|O X|=|O Y|$ if and only if $O^{\prime} A$ bissects $\angle X^{\prime} O^{\prime} Y^{\prime}$ externally. We have thus reduced the problem to the following statement:
In triangle $A B C$, let $O$ be the reflection of $A$ over $B C, \gamma_{B}$ be a line parallel to $A C$ through $B$, and $\gamma_{C}$ be a line parallel to $A B$ through $C$. For an arbitrary line $\ell$ passing through $A$, let $X$ and $Y$ be the intersections of $\ell$ with $\gamma_{B}$ and $\gamma_{C}$, respectively. Prove that $O A$ bisects $\angle X O Y$ externally.

Let $P=\gamma_{A} \cap \gamma_{B}$. By construction, $P O B C$ is an isosceles trapezoid (and therefore cyclic), $\angle O B X=\angle O B P=\angle O C P=\angle O C Y$. Further, since $X B \| A C$ and $Y C \| A B$, we have $\triangle A B X \sim \triangle Y C A$. Therefore, as $|O B|=|A B|$ and $|A C|=|O C|$ by construction,
$$
\frac{|O B|}{|B X|}=\frac{|A B|}{|B X|}=\frac{|Y C|}{|C A|}=\frac{|Y C|}{|C O|}
$$
It follows that $\triangle O B X \sim \triangle Y C O$. Hence
$$
\frac{|O X|}{|O Y|}=\frac{|X B|}{|O C|}=\frac{|X B|}{|A C|}=\frac{|X A|}{|A Y|}
$$
and so the result follows from the angle bisector theorem.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2015-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb2c8926-2188-565b-afb2-d9ea0196a2f1
| 606,285
|
. Let $n$ be a positive integer. Suppose that its positive divisors can be partitioned into pairs (i.e. can be split in groups of two) in such a way that the sum of each pair is a prime number. Prove that these prime numbers are distinct and that none of these are a divisor of $n$.
|
Let $d_{1}$ and $d_{2}$ be positive divisors of $n$ that form a pair as given in the problem. If $d_{1}$ and $d_{2}$ have a non-trivial prime divisor $p$ in common, then $p \mid d_{1}+d_{2}$ and $p \leqslant d_{1}<d_{1}+d_{2}$, so $d_{1}+d_{2}$ cannot be prime. Hence $\operatorname{gcd}\left(d_{1}, d_{2}\right)=1$, which implies that $d_{1} d_{2} \mid n$. Suppose the number of positive divisors of $n$ is $2 t$ (it is even since the divisors can be split into pairs). If we now multiply all divisors, then on one hand we have the product of all $d_{1} d_{2}$ where $\left\{d_{1}, d_{2}\right\}$ is a pair, so that product is at most $n^{t}$. On the other hand for every divisor $d$ there is another divisor $\frac{n}{d}$ (since the number of divisors is even, the case $d=\frac{n}{d}$ does not occur), and the product of all those is equal to $n^{t}$. Hence there must be equality in every inequality $d_{1} d_{2} \leqslant n$. So the pairs of divisors given in the problem are all of the form $\left\{d, \frac{n}{d}\right\}$.
Now we prove the two statements in the problem. Suppose that $d, d^{\prime}$ are positive divisors of $n$ such that $d+\frac{n}{d}=d^{\prime}+\frac{n}{d^{\prime}}$. Then $d^{2} d^{\prime}+n d^{\prime}=d\left(d^{\prime}\right)^{2}+n d$, so $d d^{\prime}\left(d-d^{\prime}\right)=n\left(d-d^{\prime}\right)$ and hence $\left(d d^{\prime}-n\right)\left(d-d^{\prime}\right)=0$. Therefore either $d=d^{\prime}$ or $d d^{\prime}=n$, which implies that $\left\{d, \frac{n}{d}\right\}=\left\{d^{\prime}, \frac{n}{d^{\prime}}\right\}$, as required.
Now let $d$ be a positive divisor of $n$. Every prime divisor $p$ of $n$ divides precisely one of $d$ and $\frac{n}{d}$, since $d \frac{n}{d}=n$ and $\operatorname{gcd}\left(d, \frac{n}{d}\right)=1$; so $p \nmid d+\frac{n}{d}$. Therefore $\operatorname{gcd}\left(n, d+\frac{n}{d}\right)=1$. Since $d+\frac{n}{d}>1$ we conclude that $d+\frac{n}{d}$ cannot be a divisor of $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
. Let $n$ be a positive integer. Suppose that its positive divisors can be partitioned into pairs (i.e. can be split in groups of two) in such a way that the sum of each pair is a prime number. Prove that these prime numbers are distinct and that none of these are a divisor of $n$.
|
Let $d_{1}$ and $d_{2}$ be positive divisors of $n$ that form a pair as given in the problem. If $d_{1}$ and $d_{2}$ have a non-trivial prime divisor $p$ in common, then $p \mid d_{1}+d_{2}$ and $p \leqslant d_{1}<d_{1}+d_{2}$, so $d_{1}+d_{2}$ cannot be prime. Hence $\operatorname{gcd}\left(d_{1}, d_{2}\right)=1$, which implies that $d_{1} d_{2} \mid n$. Suppose the number of positive divisors of $n$ is $2 t$ (it is even since the divisors can be split into pairs). If we now multiply all divisors, then on one hand we have the product of all $d_{1} d_{2}$ where $\left\{d_{1}, d_{2}\right\}$ is a pair, so that product is at most $n^{t}$. On the other hand for every divisor $d$ there is another divisor $\frac{n}{d}$ (since the number of divisors is even, the case $d=\frac{n}{d}$ does not occur), and the product of all those is equal to $n^{t}$. Hence there must be equality in every inequality $d_{1} d_{2} \leqslant n$. So the pairs of divisors given in the problem are all of the form $\left\{d, \frac{n}{d}\right\}$.
Now we prove the two statements in the problem. Suppose that $d, d^{\prime}$ are positive divisors of $n$ such that $d+\frac{n}{d}=d^{\prime}+\frac{n}{d^{\prime}}$. Then $d^{2} d^{\prime}+n d^{\prime}=d\left(d^{\prime}\right)^{2}+n d$, so $d d^{\prime}\left(d-d^{\prime}\right)=n\left(d-d^{\prime}\right)$ and hence $\left(d d^{\prime}-n\right)\left(d-d^{\prime}\right)=0$. Therefore either $d=d^{\prime}$ or $d d^{\prime}=n$, which implies that $\left\{d, \frac{n}{d}\right\}=\left\{d^{\prime}, \frac{n}{d^{\prime}}\right\}$, as required.
Now let $d$ be a positive divisor of $n$. Every prime divisor $p$ of $n$ divides precisely one of $d$ and $\frac{n}{d}$, since $d \frac{n}{d}=n$ and $\operatorname{gcd}\left(d, \frac{n}{d}\right)=1$; so $p \nmid d+\frac{n}{d}$. Therefore $\operatorname{gcd}\left(n, d+\frac{n}{d}\right)=1$. Since $d+\frac{n}{d}>1$ we conclude that $d+\frac{n}{d}$ cannot be a divisor of $n$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2016-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
3fbfaf3c-530e-579c-9b23-0cc30d0b81cb
| 290,481
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $P$ be the reflection of $C$ in $A D$; note that $C, D, P$ are collinear as $\angle D=90^{\circ}$. Then $|A B|=2|C D|=|C P|$, and since $\angle A B C=\angle B C P$ we have that $A B C P$ is an isosceles trapezoid. Hence $A P \| B C$. In particular, we have $\angle P A C=\angle A C B$ and the bisectors of these two angles are parallel. Since triangle $A C P$ is isosceles with $D$ being the midpoint of segment $C P$, the bisector of $\angle P A C$ is $A D$. Hence, the bisector of $\angle A C B$ is parallel to $A D$ and therefore perpendicular to $C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $P$ be the reflection of $C$ in $A D$; note that $C, D, P$ are collinear as $\angle D=90^{\circ}$. Then $|A B|=2|C D|=|C P|$, and since $\angle A B C=\angle B C P$ we have that $A B C P$ is an isosceles trapezoid. Hence $A P \| B C$. In particular, we have $\angle P A C=\angle A C B$ and the bisectors of these two angles are parallel. Since triangle $A C P$ is isosceles with $D$ being the midpoint of segment $C P$, the bisector of $\angle P A C$ is $A D$. Hence, the bisector of $\angle A C B$ is parallel to $A D$ and therefore perpendicular to $C D$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2017-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd723542-8a65-55c8-b021-fb334068e4c4
| 290,450
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $M$ be the midpoint of segment $A B$ and $T$ be the intersection of lines $A C$ and $M D$. We know that $|M B|=|C D|$ and that $\angle M B C=\angle B C D$, so $M B C D$ is an isosceles trapezoid. Hence $M D \| B C$, so it is a midline of $\triangle A B C$. It follows that $T$ is the midpoint of segment $A C$. As $\angle A D C=90^{\circ}$ this implies that $T$ is the circumcentre of $\triangle A C D$. Now we have $\angle A C D=\angle T C D=\angle T D C=180^{\circ}-\angle B C D$. If we denote by $\ell$ the perpendicular to $C D$ through $C$, then the latter equality implies that $C B$ is the reflection of $C A$ through $\ell$. Hence $\ell$ is the bisector of $\angle A C B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $M$ be the midpoint of segment $A B$ and $T$ be the intersection of lines $A C$ and $M D$. We know that $|M B|=|C D|$ and that $\angle M B C=\angle B C D$, so $M B C D$ is an isosceles trapezoid. Hence $M D \| B C$, so it is a midline of $\triangle A B C$. It follows that $T$ is the midpoint of segment $A C$. As $\angle A D C=90^{\circ}$ this implies that $T$ is the circumcentre of $\triangle A C D$. Now we have $\angle A C D=\angle T C D=\angle T D C=180^{\circ}-\angle B C D$. If we denote by $\ell$ the perpendicular to $C D$ through $C$, then the latter equality implies that $C B$ is the reflection of $C A$ through $\ell$. Hence $\ell$ is the bisector of $\angle A C B$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2017-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd723542-8a65-55c8-b021-fb334068e4c4
| 290,450
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $S$ be the intersection of $B C$ and $A D$ and let $M$ be the midpoint of segment $A B$. (Note that $S$ exists, since if $B C \| A D$ then $A B C D$ must be a rectangle, contradicting $|A B|=2|C D|$.) We know that $|M B|=|C D|$ and that $\angle M B C=\angle B C D$, so $M B C D$ is an isosceles trapezoid. Hence $M D \| B C$, so it is a midline of $\triangle A B S$. In particular $D$ is the midpoint of segment $A S$, and triangles $A D C$ and $S D C$ are congruent. Hence $\angle S C D=\angle A C D$, so $C D$ is the angle bisector of $\angle A C S$ and is thus perpendicular to the angle bisector of $\angle A C B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $S$ be the intersection of $B C$ and $A D$ and let $M$ be the midpoint of segment $A B$. (Note that $S$ exists, since if $B C \| A D$ then $A B C D$ must be a rectangle, contradicting $|A B|=2|C D|$.) We know that $|M B|=|C D|$ and that $\angle M B C=\angle B C D$, so $M B C D$ is an isosceles trapezoid. Hence $M D \| B C$, so it is a midline of $\triangle A B S$. In particular $D$ is the midpoint of segment $A S$, and triangles $A D C$ and $S D C$ are congruent. Hence $\angle S C D=\angle A C D$, so $C D$ is the angle bisector of $\angle A C S$ and is thus perpendicular to the angle bisector of $\angle A C B$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2017-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd723542-8a65-55c8-b021-fb334068e4c4
| 290,450
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $S$ be the intersection of $B C$ and $A D$ and let $F$ be the intersection of $B C$ with the line through $A$ parallel to $C D$. Then $\angle A F B=\angle A F C=180^{\circ}-\angle F C D=180^{\circ}-\angle A B C=$ $\angle A B F$, so triangle $A B F$ is isosceles with $|A B|=|A F|$. Hence $|A F|=2|C D|$. Since $A F$ is parallel to $C D$, we find that $C D$ is a midline of $\triangle A S F$, so $D$ is the midpoint of segment $A S$. Now $C D$ must be the perpendicular bisector of $A S$ and therefore it is also the angle bisector of $\angle A C S$. This implies that it is perpendicular to the angle bisector of $\angle A C B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
. In the convex quadrilateral $A B C D$ we have $\angle B=\angle C$ and $\angle D=90^{\circ}$. Suppose that $|A B|=2|C D|$. Prove that the angle bisector of $\angle A C B$ is perpendicular to $C D$.
|
. Let $S$ be the intersection of $B C$ and $A D$ and let $F$ be the intersection of $B C$ with the line through $A$ parallel to $C D$. Then $\angle A F B=\angle A F C=180^{\circ}-\angle F C D=180^{\circ}-\angle A B C=$ $\angle A B F$, so triangle $A B F$ is isosceles with $|A B|=|A F|$. Hence $|A F|=2|C D|$. Since $A F$ is parallel to $C D$, we find that $C D$ is a midline of $\triangle A S F$, so $D$ is the midpoint of segment $A S$. Now $C D$ must be the perpendicular bisector of $A S$ and therefore it is also the angle bisector of $\angle A C S$. This implies that it is perpendicular to the angle bisector of $\angle A C B$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2017-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd723542-8a65-55c8-b021-fb334068e4c4
| 290,450
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
Let the denominations of the coins and notes be $C_{1}<C_{2}<C_{3}<C_{4}$ and $N_{1}<N_{2}<N_{3}$, respectively. Define $C=C_{1}+C_{2}+C_{3}+C_{4}$ to be the largest amount that can be payed with coins only. The condition of the problem is thus $C<N_{1}$.
(a) Suppose to the contrary that, whatever the price of the book, the tourist can pay for it in no more than one way.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
Let the denominations of the coins and notes be $C_{1}<C_{2}<C_{3}<C_{4}$ and $N_{1}<N_{2}<N_{3}$, respectively. Define $C=C_{1}+C_{2}+C_{3}+C_{4}$ to be the largest amount that can be payed with coins only. The condition of the problem is thus $C<N_{1}$.
(a) Suppose to the contrary that, whatever the price of the book, the tourist can pay for it in no more than one way.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f789581e-8b27-5d73-9a0d-14b329bdedc4
| 606,359
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
. Consider the $3 \cdot 2^{4}=48$ hands of exactly two notes and any number of (or possibly no) coins. Each of these has one of the $N_{3}$ different values $v$ with $N_{1}+N_{2} \leqslant v<N_{1}+N_{2}+N_{3}$, since $C<N_{1}$. Hence $48 \leqslant N_{3}<49$, so $N_{3}=48$. Next consider the $3 \cdot 2^{4}=48$ hands of exactly one note and any number of coins. By the above, these cannot have a value greater than or equal to $N_{1}+N_{2}$, since these can be realised using two notes and some coins. Hence they must each have one of the $N_{2}$ different values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$. This implies $48 \leqslant N_{2}<N_{3}=48$, which is a contradiction.
(b) Consider the denominations
$$
C_{1}=3, \quad C_{2}=6, \quad C_{3}=12, \quad C_{4}=24, \quad N_{1}=47, \quad N_{2}=48, \quad N_{3}=49 .
$$
These satisfy the conditions of the problem, with $C=45<N_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
. Consider the $3 \cdot 2^{4}=48$ hands of exactly two notes and any number of (or possibly no) coins. Each of these has one of the $N_{3}$ different values $v$ with $N_{1}+N_{2} \leqslant v<N_{1}+N_{2}+N_{3}$, since $C<N_{1}$. Hence $48 \leqslant N_{3}<49$, so $N_{3}=48$. Next consider the $3 \cdot 2^{4}=48$ hands of exactly one note and any number of coins. By the above, these cannot have a value greater than or equal to $N_{1}+N_{2}$, since these can be realised using two notes and some coins. Hence they must each have one of the $N_{2}$ different values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$. This implies $48 \leqslant N_{2}<N_{3}=48$, which is a contradiction.
(b) Consider the denominations
$$
C_{1}=3, \quad C_{2}=6, \quad C_{3}=12, \quad C_{4}=24, \quad N_{1}=47, \quad N_{2}=48, \quad N_{3}=49 .
$$
These satisfy the conditions of the problem, with $C=45<N_{1}$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f789581e-8b27-5d73-9a0d-14b329bdedc4
| 606,359
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
. Suppose to the contrary that there are two hands of coins and notes that sum to the same amount. Up to removing coins or notes that appear in both of these hands to obtain two smaller hands summing to the same amount, we may assume that no coin or note appears in both of these hands. Notice that all the denominations, except for $N_{1} \equiv-1(\bmod 3)$ and $N_{3} \equiv 1(\bmod 3)$, are divisible by 3 . Hence, if $N_{1}$ appears in one hand, $N_{3}$ must appear in the same hand, and vice versa. Hence these two hands are two disjoint subsets of $\left\{C_{1}, C_{2}, C_{3}, C_{4}, N_{2}, N_{1}+N_{3}\right\}=\{3,6,12,24,48,96\}=3\{1,2,4,8,16,32\}$ that sum to the same amount, which contradicts the uniqueness of the binary expansion of these two amounts. Hence there is no price that the tourist can pay for in more than one way.
Remark. It is natural to ask whether there are other choices of coins and notes with $N_{3}=49$ in (b) that force the tourist to leave the shop empty-handed. It turns out that the choice in (b) is unique. The argument runs as follows: the inequality $N_{2}+N_{3} \geqslant 96$ implies that $N_{2}=47$ or $N_{2}=48$. Further, strengthening the bound in (a), we must have
$$
\left(N_{2}+N_{3}+C\right)-\left(N_{1}+N_{2}\right)+1 \geqslant 48 \quad \Longrightarrow \quad C \geqslant 47+N_{1}-N_{3}=N_{1}-2
$$
But $C<N_{1}$, and so $C=N_{1}-1$ or $C=N_{1}-2$. If $N_{2}=47$, then $C=N_{1}-2$ implies $N_{1}+N_{2}=N_{3}+C$, a contradiction. Thus $C=N_{1}-1$ if $N_{2}=47$, and, similarly, $C=N_{1}-2$ if $N_{2}=48$.
In the first case, $N_{3}+C=48+N_{1}=N_{1}+N_{2}+1(*)$. Hence, by the argument in (a), all the $N_{2}=47$ values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$ can be represented (using one note and some coins). Now $C_{1} \neq 1$ by (*). Since $N_{1}+1$ can be represented, it follows that $N_{2}=N_{1}+1$ and hence $N_{1}=46$. Then $N_{3}=N_{2}+2=N_{1}+3$ implies that $C_{1}>3$. Considering $50=N_{1}+4$ yields $C_{1}=4$. Now $53=N_{3}+4=N_{2}+6,52=N_{2}+5=N_{1}+6$. Hence $C_{2}=6$ is not possible, so $C_{2}=5$. Then $51=N_{2}+C_{1}=N_{1}+C_{2}$, a contradiction.
In the second case, notice that $N_{2}=48$ implies, by the argument in (a), that all the $N_{2}=48$ values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$ can be represented. Clearly, $N_{1}+1$ can only be represented if $C_{1}=1$ or $N_{2}=N_{1}+1$. In the former case, $N_{3}=N_{2}+C_{1}$, a contradiction. Hence $N_{1}=N_{2}-1=47$, and so $C=45$. Considering $N_{1}+3, \ldots, N_{1}+12$ then successively yields $C_{1}=3, C_{2}=6, C_{3}=12$. Finally, $C_{4}=C-C_{1}-C_{2}-C_{3}=24$, completing the proof.
One might also ask about other choices of coins and notes, with different values of $N_{3}$, forcing the tourist to leave the shop empty-handed. Numerically, it is easy to tabulate all such choices of coins and notes for small $N_{3}$ :
| $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $N_{1}$ | $N_{2}$ | $N_{3}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 6 | 12 | 24 | 47 | 48 | 49 |
| 1 | 6 | 12 | 24 | 46 | 48 | 50 |
| 3 | 6 | 12 | 24 | 46 | 48 | 50 |
| 3 | 6 | 12 | 24 | 48 | 49 | 50 |
| 3 | 6 | 12 | 25 | 48 | 49 | 50 |
| 1 | 6 | 12 | 24 | 47 | 49 | 51 |
| 1 | 6 | 12 | 25 | 47 | 49 | 51 |
| 3 | 6 | 12 | 24 | 49 | 50 | 51 |
| 3 | 6 | 12 | 25 | 49 | 50 | 51 |
| 3 | 6 | 12 | 26 | 49 | 50 | 51 |
| 3 | 6 | 13 | 25 | 49 | 50 | 51 |
#
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In the land of Heptanomisma, four different coins and three different banknotes are used, and their denominations are seven different (non-zero) natural numbers. The denomination of the smallest banknote is greater than the sum of the denominations of the four different coins. A tourist has exactly one coin of each denomination and exactly one banknote of each denomination, but he cannot afford the book on numismatics he wishes to buy. However, the mathematically inclined shopkeeper offers to sell the book to the tourist at a price of his choosing, provided that he can pay this price in more than one way.
(The tourist can pay a price in more than one way if there are two different subsets of his coins and notes, the denominations of which both add up to this price.)
(a) Prove that the tourist can purchase the book if the denomination of each banknote is smaller than 49.
(b) Show that the tourist may have to leave the shop empty-handed if the denomination of the largest banknote is 49.
(Stijn Cambie, Belgium)
#
|
. Suppose to the contrary that there are two hands of coins and notes that sum to the same amount. Up to removing coins or notes that appear in both of these hands to obtain two smaller hands summing to the same amount, we may assume that no coin or note appears in both of these hands. Notice that all the denominations, except for $N_{1} \equiv-1(\bmod 3)$ and $N_{3} \equiv 1(\bmod 3)$, are divisible by 3 . Hence, if $N_{1}$ appears in one hand, $N_{3}$ must appear in the same hand, and vice versa. Hence these two hands are two disjoint subsets of $\left\{C_{1}, C_{2}, C_{3}, C_{4}, N_{2}, N_{1}+N_{3}\right\}=\{3,6,12,24,48,96\}=3\{1,2,4,8,16,32\}$ that sum to the same amount, which contradicts the uniqueness of the binary expansion of these two amounts. Hence there is no price that the tourist can pay for in more than one way.
Remark. It is natural to ask whether there are other choices of coins and notes with $N_{3}=49$ in (b) that force the tourist to leave the shop empty-handed. It turns out that the choice in (b) is unique. The argument runs as follows: the inequality $N_{2}+N_{3} \geqslant 96$ implies that $N_{2}=47$ or $N_{2}=48$. Further, strengthening the bound in (a), we must have
$$
\left(N_{2}+N_{3}+C\right)-\left(N_{1}+N_{2}\right)+1 \geqslant 48 \quad \Longrightarrow \quad C \geqslant 47+N_{1}-N_{3}=N_{1}-2
$$
But $C<N_{1}$, and so $C=N_{1}-1$ or $C=N_{1}-2$. If $N_{2}=47$, then $C=N_{1}-2$ implies $N_{1}+N_{2}=N_{3}+C$, a contradiction. Thus $C=N_{1}-1$ if $N_{2}=47$, and, similarly, $C=N_{1}-2$ if $N_{2}=48$.
In the first case, $N_{3}+C=48+N_{1}=N_{1}+N_{2}+1(*)$. Hence, by the argument in (a), all the $N_{2}=47$ values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$ can be represented (using one note and some coins). Now $C_{1} \neq 1$ by (*). Since $N_{1}+1$ can be represented, it follows that $N_{2}=N_{1}+1$ and hence $N_{1}=46$. Then $N_{3}=N_{2}+2=N_{1}+3$ implies that $C_{1}>3$. Considering $50=N_{1}+4$ yields $C_{1}=4$. Now $53=N_{3}+4=N_{2}+6,52=N_{2}+5=N_{1}+6$. Hence $C_{2}=6$ is not possible, so $C_{2}=5$. Then $51=N_{2}+C_{1}=N_{1}+C_{2}$, a contradiction.
In the second case, notice that $N_{2}=48$ implies, by the argument in (a), that all the $N_{2}=48$ values $v$ with $N_{1} \leqslant v<N_{1}+N_{2}$ can be represented. Clearly, $N_{1}+1$ can only be represented if $C_{1}=1$ or $N_{2}=N_{1}+1$. In the former case, $N_{3}=N_{2}+C_{1}$, a contradiction. Hence $N_{1}=N_{2}-1=47$, and so $C=45$. Considering $N_{1}+3, \ldots, N_{1}+12$ then successively yields $C_{1}=3, C_{2}=6, C_{3}=12$. Finally, $C_{4}=C-C_{1}-C_{2}-C_{3}=24$, completing the proof.
One might also ask about other choices of coins and notes, with different values of $N_{3}$, forcing the tourist to leave the shop empty-handed. Numerically, it is easy to tabulate all such choices of coins and notes for small $N_{3}$ :
| $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $N_{1}$ | $N_{2}$ | $N_{3}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 6 | 12 | 24 | 47 | 48 | 49 |
| 1 | 6 | 12 | 24 | 46 | 48 | 50 |
| 3 | 6 | 12 | 24 | 46 | 48 | 50 |
| 3 | 6 | 12 | 24 | 48 | 49 | 50 |
| 3 | 6 | 12 | 25 | 48 | 49 | 50 |
| 1 | 6 | 12 | 24 | 47 | 49 | 51 |
| 1 | 6 | 12 | 25 | 47 | 49 | 51 |
| 3 | 6 | 12 | 24 | 49 | 50 | 51 |
| 3 | 6 | 12 | 25 | 49 | 50 | 51 |
| 3 | 6 | 12 | 26 | 49 | 50 | 51 |
| 3 | 6 | 13 | 25 | 49 | 50 | 51 |
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f789581e-8b27-5d73-9a0d-14b329bdedc4
| 606,359
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
(a) Solution 1. Since $F$ is the midpoint of $[A H]$ and $[B P], B H P A$ is a parallelogram. Similarly, $C A Q H$ is a parallelogram, too. Let $O$ denote the circumcentre of triangle $A B C$ and let $R$ be the reflection of $A$ in $O$, so that $R$ lies on the circumcircle of $A B C$. Since $[A R]$ is a diameter of the circumcircle of $A B C, C R \perp A C$. But $B H \perp A C$, and so $C R \| B H$. Similarly, $B R \| C H$, and thus $B R C H$ is a parallelogram. Since $B H P A$ is a parallelogram, $R C P A$ is a parallelogram, too. In particular, the midpoint $E$ of its diagonal $[A C]$ lies on $[P R]$. Similarly, $D$ lies on $[Q R]$, and so $P E$ and $Q D$ meet at $R$.
Remark. Since $A P$ is parallel to the altitude $B H, A P \perp A C$. Further, $P H \| A B$ since $A P H B$ is a parallelogram. But $C H \perp A B$, so $P H \perp C H$. Hence $A P C H$ is cyclic. Similarly, $A H B Q$ is cyclic, too.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
(a) Solution 1. Since $F$ is the midpoint of $[A H]$ and $[B P], B H P A$ is a parallelogram. Similarly, $C A Q H$ is a parallelogram, too. Let $O$ denote the circumcentre of triangle $A B C$ and let $R$ be the reflection of $A$ in $O$, so that $R$ lies on the circumcircle of $A B C$. Since $[A R]$ is a diameter of the circumcircle of $A B C, C R \perp A C$. But $B H \perp A C$, and so $C R \| B H$. Similarly, $B R \| C H$, and thus $B R C H$ is a parallelogram. Since $B H P A$ is a parallelogram, $R C P A$ is a parallelogram, too. In particular, the midpoint $E$ of its diagonal $[A C]$ lies on $[P R]$. Similarly, $D$ lies on $[Q R]$, and so $P E$ and $Q D$ meet at $R$.

Remark. Since $A P$ is parallel to the altitude $B H, A P \perp A C$. Further, $P H \| A B$ since $A P H B$ is a parallelogram. But $C H \perp A B$, so $P H \perp C H$. Hence $A P C H$ is cyclic. Similarly, $A H B Q$ is cyclic, too.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $O$ denote the circumcentre of triangle $A B C$. By construction, $D O \perp A B$ and $F E \| C H \perp A B$, and so $D O \| E F$. Similarly, $O E \| D F$, so $D O E F$ is a parallelogram. Since $F$ is the midpoint of $[A H]$ and $[B P], B H P A$ is a parallelogram, and so $A P\|B H\| D F \| O E$ and $|A P|=|B H|=2|D F|=2|O E|$. Extending this argument, it follows that triangles $D O E$ and $Q A P$ and have pairwise parallel sides and the ratio of their sides is $1: 2$. Hence there is a homothety with ratio 2 mapping $D O E$ to $Q A P$. The centre $R$ of this homothety is the reflection of $A$ in $O$, which lies on the circumcircle of $A B C$, and also the intersection of lines $P E, Q D$, and $A O$.
## BxMO 2018: Problems and Solutions
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $O$ denote the circumcentre of triangle $A B C$. By construction, $D O \perp A B$ and $F E \| C H \perp A B$, and so $D O \| E F$. Similarly, $O E \| D F$, so $D O E F$ is a parallelogram. Since $F$ is the midpoint of $[A H]$ and $[B P], B H P A$ is a parallelogram, and so $A P\|B H\| D F \| O E$ and $|A P|=|B H|=2|D F|=2|O E|$. Extending this argument, it follows that triangles $D O E$ and $Q A P$ and have pairwise parallel sides and the ratio of their sides is $1: 2$. Hence there is a homothety with ratio 2 mapping $D O E$ to $Q A P$. The centre $R$ of this homothety is the reflection of $A$ in $O$, which lies on the circumcircle of $A B C$, and also the intersection of lines $P E, Q D$, and $A O$.
## BxMO 2018: Problems and Solutions
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Since $F$ is the midpoint of $[B P]$ and $[C Q], B C P Q$ is a parallelogram. As $D$ and $E$ are the respective midpoints of $[A B]$ and $[A C]$, it follows that $P Q\|B C\| D E$ and $|P Q|=|B C|=2|D E|$. Let $R$ denote the intersection of $P E$ and $Q D$. Then $D$ and $E$ are the midpoints of $[R Q]$ and $[R P]$, respectively. In particular, $B R A Q$ is a parallelogram. But $F$ is the midpoint of $[A H]$ and $[C Q]$, so $A Q C H$ is a parallelogram. Hence $B R C H$ is a parallelogram, too, so $R$ is the reflection of $H$ in the midpoint of $[B C]$, which is well-known to lie on the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Since $F$ is the midpoint of $[B P]$ and $[C Q], B C P Q$ is a parallelogram. As $D$ and $E$ are the respective midpoints of $[A B]$ and $[A C]$, it follows that $P Q\|B C\| D E$ and $|P Q|=|B C|=2|D E|$. Let $R$ denote the intersection of $P E$ and $Q D$. Then $D$ and $E$ are the midpoints of $[R Q]$ and $[R P]$, respectively. In particular, $B R A Q$ is a parallelogram. But $F$ is the midpoint of $[A H]$ and $[C Q]$, so $A Q C H$ is a parallelogram. Hence $B R C H$ is a parallelogram, too, so $R$ is the reflection of $H$ in the midpoint of $[B C]$, which is well-known to lie on the circumcircle of $A B C$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Since $F$ is the midpoint of $[B P]$ and $[C Q], B C P Q$ is a parallelogram. Let $R$ be the image of $A$ under the translation that accordingly maps $P, Q$ onto $C, B$, respectively. By construction, $A P C R$ is a parallelogram, and so the midpoint $E$ of $[A C]$ lies on its other diagonal $P R$. Similarly, $D$ lies on $Q R$, and so $R$ is the intersection of $P E$ and $Q D$. Moreover, $F$ is the midpoint of $[A H]$ and $[B P]$, so $A P B H$ is a parallelogram. Hence $C R\|A P\| B H \perp A C$, so $\angle A C R=90^{\circ}$. Similarly, $\angle A B R=90^{\circ}$, so $A B R C$ is cyclic, and thus $R$ lies on the circumcircle of $A B C$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Since $F$ is the midpoint of $[B P]$ and $[C Q], B C P Q$ is a parallelogram. Let $R$ be the image of $A$ under the translation that accordingly maps $P, Q$ onto $C, B$, respectively. By construction, $A P C R$ is a parallelogram, and so the midpoint $E$ of $[A C]$ lies on its other diagonal $P R$. Similarly, $D$ lies on $Q R$, and so $R$ is the intersection of $P E$ and $Q D$. Moreover, $F$ is the midpoint of $[A H]$ and $[B P]$, so $A P B H$ is a parallelogram. Hence $C R\|A P\| B H \perp A C$, so $\angle A C R=90^{\circ}$. Similarly, $\angle A B R=90^{\circ}$, so $A B R C$ is cyclic, and thus $R$ lies on the circumcircle of $A B C$, as required.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $M$ be the midpoint of $[B C]$. Note that triangle $P H Q$ is the reflection of triangle $B A C$ in $F$. By construction, the sides of triangle $D E M$ are parallel to those of $C B A$, and hence $D E\|B C\| Q P$, and, similarly, $D M \| Q H$ and $E M \| P H$. Hence triangles $Q H P$ and $D M E$ have pairwise parallel sides and the ratio of their sides is $2: 1$. This implies that there is homothety mapping one onto the other. Its centre is the intersection of $Q D$ and $P E$ and is also the reflection of $H$ in $M$, which is well-known to lie on the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $M$ be the midpoint of $[B C]$. Note that triangle $P H Q$ is the reflection of triangle $B A C$ in $F$. By construction, the sides of triangle $D E M$ are parallel to those of $C B A$, and hence $D E\|B C\| Q P$, and, similarly, $D M \| Q H$ and $E M \| P H$. Hence triangles $Q H P$ and $D M E$ have pairwise parallel sides and the ratio of their sides is $2: 1$. This implies that there is homothety mapping one onto the other. Its centre is the intersection of $Q D$ and $P E$ and is also the reflection of $H$ in $M$, which is well-known to lie on the circumcircle of $A B C$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $G$ be the centroid of $A B C$, and let $\mathscr{H}$ be the well-known homothety with ratio -2 and centre $G$ that maps the nine-point circle of $A B C$ onto its circumcircle. Under $\mathscr{H}, D \mapsto C, E \mapsto B$. Denote by $R$ the image of the Euler point $F$ under $\mathscr{H}$; by construction, $R$ lies on the circumcircle of $A B C$. Further, $\overrightarrow{D F}=\frac{1}{2} \overrightarrow{R C}$ and $\overrightarrow{E F}=\frac{1}{2} \overrightarrow{R B}$. Hence the points of intersection of the pairs of lines $B F, R E$ and $C F, R D$ are $P$ and $Q$, respectively. This completes the proof.
## BxMO 2018: Problems and Solutions
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $G$ be the centroid of $A B C$, and let $\mathscr{H}$ be the well-known homothety with ratio -2 and centre $G$ that maps the nine-point circle of $A B C$ onto its circumcircle. Under $\mathscr{H}, D \mapsto C, E \mapsto B$. Denote by $R$ the image of the Euler point $F$ under $\mathscr{H}$; by construction, $R$ lies on the circumcircle of $A B C$. Further, $\overrightarrow{D F}=\frac{1}{2} \overrightarrow{R C}$ and $\overrightarrow{E F}=\frac{1}{2} \overrightarrow{R B}$. Hence the points of intersection of the pairs of lines $B F, R E$ and $C F, R D$ are $P$ and $Q$, respectively. This completes the proof.

## BxMO 2018: Problems and Solutions
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $M, N, K$ denote the respective midpoints of $[B C],[D E],[P Q]$. Thus the intersection $R$ of $P E$ and $Q D$ is the reflection of $K$ in $N$. Under reflection in $F, H \mapsto A$ and $M \mapsto K$. Hence $A K H M$ is a parallelogram, and so $\overrightarrow{M N}=\frac{1}{2} \overrightarrow{M A}=\frac{1}{2} \overrightarrow{H K}$. Hence the intersection of $K N$ and $H M$ is $R$, and $R$ is the reflection of $H$ in $M$, which is well-known to lie on the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Let $M, N, K$ denote the respective midpoints of $[B C],[D E],[P Q]$. Thus the intersection $R$ of $P E$ and $Q D$ is the reflection of $K$ in $N$. Under reflection in $F, H \mapsto A$ and $M \mapsto K$. Hence $A K H M$ is a parallelogram, and so $\overrightarrow{M N}=\frac{1}{2} \overrightarrow{M A}=\frac{1}{2} \overrightarrow{H K}$. Hence the intersection of $K N$ and $H M$ is $R$, and $R$ is the reflection of $H$ in $M$, which is well-known to lie on the circumcircle of $A B C$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Take Cartesian coordinates $B(0,0), C(1,0), A(a, b), H(a, c)$. Then the coordinates of $D, E, F, P, Q$ are successively found to be
$$
D\left(\frac{a}{2}, \frac{b}{2}\right), \quad E\left(\frac{1+a}{2}, \frac{b}{2}\right), \quad F\left(a, \frac{b+c}{2}\right), \quad P(2 a, b+c), \quad Q(2 a-1, b+c)
$$
Hence the coordinates of the intersection $R(x, y)$ of $Q D$ and $P E$ satisfy
$$
\frac{y-\frac{b}{2}}{b+c-\frac{b}{2}}=\frac{x-\frac{a}{2}}{2 a-1-\frac{a}{2}}=\frac{x-\frac{a+1}{2}}{2 a-\frac{a+1}{2}} \quad \Longrightarrow \quad R(1-a,-c)
$$
Hence $R$ is the reflection of $H$ in the midpoint $M\left(\frac{1}{2}, 0\right)$ of $[B C]$, and so lies on the circumcircle of $A B C$.
(b) Solution 1. Lines $A F$ and $Q E$ are medians of triangle $C A Q$, and so, by the properties of the centroid, intersect at a point $S$ of $[A F]$ such that $|A S|=2|S F|$. Similarly, lines $A F$ and $P D$ are medians of triangle $B A P$, and so intersect at the same point $S$. Hence $P D$ and $Q E$ intersect on $[A H]$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. Take Cartesian coordinates $B(0,0), C(1,0), A(a, b), H(a, c)$. Then the coordinates of $D, E, F, P, Q$ are successively found to be
$$
D\left(\frac{a}{2}, \frac{b}{2}\right), \quad E\left(\frac{1+a}{2}, \frac{b}{2}\right), \quad F\left(a, \frac{b+c}{2}\right), \quad P(2 a, b+c), \quad Q(2 a-1, b+c)
$$
Hence the coordinates of the intersection $R(x, y)$ of $Q D$ and $P E$ satisfy
$$
\frac{y-\frac{b}{2}}{b+c-\frac{b}{2}}=\frac{x-\frac{a}{2}}{2 a-1-\frac{a}{2}}=\frac{x-\frac{a+1}{2}}{2 a-\frac{a+1}{2}} \quad \Longrightarrow \quad R(1-a,-c)
$$
Hence $R$ is the reflection of $H$ in the midpoint $M\left(\frac{1}{2}, 0\right)$ of $[B C]$, and so lies on the circumcircle of $A B C$.
(b) Solution 1. Lines $A F$ and $Q E$ are medians of triangle $C A Q$, and so, by the properties of the centroid, intersect at a point $S$ of $[A F]$ such that $|A S|=2|S F|$. Similarly, lines $A F$ and $P D$ are medians of triangle $B A P$, and so intersect at the same point $S$. Hence $P D$ and $Q E$ intersect on $[A H]$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. By construction, a homothety with ratio 2 centred at $A$ maps $[D F]$ and $[E F]$ onto $[B H]$ and $[C H]$, respectively, which are mapped in turn onto $[P A]$ and $[Q A]$ under reflection in $F$ by the results of (a). The composition of these maps is a homothety with centre $S$ and ratio -2 that maps $D$ and $E$ onto $P$ and $Q$, respectively. Hence $P D$ and $Q E$ intersect at $S$. Since this homothety leaves $A H$ invariant, $S$ lies on this line. Since the homothety has negative ratio, the centre lies on the line segment $[A F]$, completing the proof.
Remark. This is a projective result: triangles $D F E$ and $P A Q$ are in axial perspective (at $\infty$ ). Hence, by Desargues' theorem, they are in central perspective, and so lines $P D, Q E$, and $A F$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. By construction, a homothety with ratio 2 centred at $A$ maps $[D F]$ and $[E F]$ onto $[B H]$ and $[C H]$, respectively, which are mapped in turn onto $[P A]$ and $[Q A]$ under reflection in $F$ by the results of (a). The composition of these maps is a homothety with centre $S$ and ratio -2 that maps $D$ and $E$ onto $P$ and $Q$, respectively. Hence $P D$ and $Q E$ intersect at $S$. Since this homothety leaves $A H$ invariant, $S$ lies on this line. Since the homothety has negative ratio, the centre lies on the line segment $[A F]$, completing the proof.
Remark. This is a projective result: triangles $D F E$ and $P A Q$ are in axial perspective (at $\infty$ ). Hence, by Desargues' theorem, they are in central perspective, and so lines $P D, Q E$, and $A F$ are concurrent.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. The intersection $S$ of $P D$ and $Q E$ is the centroid of triangle $P Q R$, where $R$ is the intersection of $P E$ and $Q D$, as in (a). Hence, if $M, N, K$ denote the respective midpoints of $[B C],[D E],[P Q]$, then, by part (a), $\overrightarrow{K S}=2 \overrightarrow{S N}$. Moreover, since $K$ is the reflection of $M$ in $F, d(K, A H)=d(M, A H)=2 d(N, A H)$. It follows that $S$ lies on $A H$; since $K$ and $R$ lie on either side of $A M, S$ lies on $[A H]$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. The intersection $S$ of $P D$ and $Q E$ is the centroid of triangle $P Q R$, where $R$ is the intersection of $P E$ and $Q D$, as in (a). Hence, if $M, N, K$ denote the respective midpoints of $[B C],[D E],[P Q]$, then, by part (a), $\overrightarrow{K S}=2 \overrightarrow{S N}$. Moreover, since $K$ is the reflection of $M$ in $F, d(K, A H)=d(M, A H)=2 d(N, A H)$. It follows that $S$ lies on $A H$; since $K$ and $R$ lie on either side of $A M, S$ lies on $[A H]$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. In Cartesian coordinates and using the results of (a), the coordinates of the intersection $S\left(x^{\prime}, y^{\prime}\right)$ of $Q E$ and $P D$ satisfy
$$
\frac{y^{\prime}-\frac{b}{2}}{b+c-\frac{b}{2}}=\frac{x^{\prime}-\frac{a}{2}}{2 a-\frac{a}{2}}=\frac{x^{\prime}-\frac{a+1}{2}}{2 a-1-\frac{a+1}{2}} .
$$
Hence $x^{\prime}=a$, so $S$ lies on line $A H$. Further, $y^{\prime}=\frac{1}{3}(2 b+c)$. Without loss of generality, $b>0$. Then $c>0$ by definition, and so $c<y^{\prime}<b$ or $c>y^{\prime}>b$. Hence $S$ lies on line segment $[A H]$.
Remark 1. Solutions 1 and 2 for part (b) have not used the fact that $H$ is the orthocentre of triangle $A B C$, and therefore show that the result of (b) remains true if $H$ is replaced with a general point $X$. The first part of the problem is in some sense independent of $H$, too. The argument of solutions 3, 5, and 7 for part (a) can be extended to yield the following result:
Let $A B C$ be a triangle, and let $X$ be a point of the plane. Let $D, E$, and $Y$ denote the respective midpoints of $[A B],[A C]$, and $[A X]$. The reflections of $B$ and $C$ in $Y$ are $P$ and $Q$, respectively. Lines $P E$ and $Q D$ intersect on the circumcircle $\omega$ of $A B C$ if and only if $X$ lies on the reflection of $\omega$ in $[B C]$.
## BxMO 2018: Problems and Solutions
Remark 2. The intersection points of $P E, Q D$ and $P D, Q E$ are not well-defined if $P, Q, D, E$ lie on a line. In the notation of the analytic solution, this happens when $\frac{b}{2}=b+c$, i.e. $c=-\frac{b}{2}$. Computing the coordinates of $H$ explicitly using $B H \perp A C$ yields $c=a(1-a) / b$, and so $P, Q, D, E$ are aligned if and only if $b^{2}=2 a(a-1)$, which is the equation of a hyperbola passing through $B$ and $C$. (These triangles have an obtuse angle, so this configuration cannot appear for acute-angled triangles.)
## BxMO 2018: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with orthocentre $H$, and let $D, E$, and $F$ denote the respective midpoints of line segments $A B, A C$, and $A H$. The reflections of $B$ and $C$ in $F$ are $P$ and $Q$, respectively.
(a) Show that lines $P E$ and $Q D$ intersect on the circumcircle of triangle $A B C$.
(b) Prove that lines $P D$ and $Q E$ intersect on line segment $A H$.
(Merlijn Staps, the Netherlands)
#
|
. In Cartesian coordinates and using the results of (a), the coordinates of the intersection $S\left(x^{\prime}, y^{\prime}\right)$ of $Q E$ and $P D$ satisfy
$$
\frac{y^{\prime}-\frac{b}{2}}{b+c-\frac{b}{2}}=\frac{x^{\prime}-\frac{a}{2}}{2 a-\frac{a}{2}}=\frac{x^{\prime}-\frac{a+1}{2}}{2 a-1-\frac{a+1}{2}} .
$$
Hence $x^{\prime}=a$, so $S$ lies on line $A H$. Further, $y^{\prime}=\frac{1}{3}(2 b+c)$. Without loss of generality, $b>0$. Then $c>0$ by definition, and so $c<y^{\prime}<b$ or $c>y^{\prime}>b$. Hence $S$ lies on line segment $[A H]$.
Remark 1. Solutions 1 and 2 for part (b) have not used the fact that $H$ is the orthocentre of triangle $A B C$, and therefore show that the result of (b) remains true if $H$ is replaced with a general point $X$. The first part of the problem is in some sense independent of $H$, too. The argument of solutions 3, 5, and 7 for part (a) can be extended to yield the following result:
Let $A B C$ be a triangle, and let $X$ be a point of the plane. Let $D, E$, and $Y$ denote the respective midpoints of $[A B],[A C]$, and $[A X]$. The reflections of $B$ and $C$ in $Y$ are $P$ and $Q$, respectively. Lines $P E$ and $Q D$ intersect on the circumcircle $\omega$ of $A B C$ if and only if $X$ lies on the reflection of $\omega$ in $[B C]$.
## BxMO 2018: Problems and Solutions
Remark 2. The intersection points of $P E, Q D$ and $P D, Q E$ are not well-defined if $P, Q, D, E$ lie on a line. In the notation of the analytic solution, this happens when $\frac{b}{2}=b+c$, i.e. $c=-\frac{b}{2}$. Computing the coordinates of $H$ explicitly using $B H \perp A C$ yields $c=a(1-a) / b$, and so $P, Q, D, E$ are aligned if and only if $b^{2}=2 a(a-1)$, which is the equation of a hyperbola passing through $B$ and $C$. (These triangles have an obtuse angle, so this configuration cannot appear for acute-angled triangles.)

## BxMO 2018: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f663be9d-1b5e-5a93-993e-a441df9364a2
| 606,372
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
(a) Solution 1. We note that $n=2^{m}$ has $m+1$ divisors, $d_{k}=2^{k-1}$ for $1 \leqslant k \leqslant m+1$. Thus
$$
1+d_{1}+\cdots+d_{k-1}=1+\left(2^{k-1}-1\right)=2^{k-1}=d_{k}
$$
for each $k \geqslant 2$, and hence each power of 2 is a bad integer. This exhibits infinitely many bad integers.
Remark. It is true more generally that
If $n=2^{r} m$, where $m$ is a product of (odd) primes each less than $2^{r+1}$, then $n$ is bad.
This is an immediate corollary of the previous result and the following observation:
If $n=2^{r} m$ is bad, where $m$ is odd, then so is $p n$ for any odd prime $p<2^{r+1}$.
Proof. Let $D_{K}>1$ be a divisor of $p n$, so $D_{K}=p$ or $D_{K}=d_{k}$ or $D_{K}=p d_{k}$, where $d_{k}>1$ is a divisor of $n$. In the first case, observe that there exists $t<r+1$ such that $2^{t}<p<2^{t+1}$ by assumption. Then $\left\{1,2, \ldots, 2^{t}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
D_{K}=p<2^{t+1}=1+\left(1+2+\cdots+2^{t}\right) \leqslant 1+D_{1}+\cdots+D_{K-1} .
$$
In the final case, $\left\{1,2, \ldots, 2^{t}, p d_{1}, \ldots, p d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
\begin{aligned}
D_{K} & =p d_{k} \leqslant p\left(1+d_{1}+\cdots+d_{k-1}\right)=p+p d_{1}+\cdots+p d_{k} \\
& <2^{t+1}+p d_{1}+\cdots+p d_{k-1}=1+\left(1+\cdots+2^{t}\right)+p d_{1}+\cdots+p d_{k-1}<1+\left(D_{1}+\cdots+D_{K-1}\right) .
\end{aligned}
$$
In the second case, $\left\{d_{1}, \ldots, d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$ immediately implies the required inequality, and so $p n$ is indeed bad.
This result is weak, however: only 57931 (6.99\%) of the 829157 bad numbers not larger than $10^{7}$ are of this form.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
(a) Solution 1. We note that $n=2^{m}$ has $m+1$ divisors, $d_{k}=2^{k-1}$ for $1 \leqslant k \leqslant m+1$. Thus
$$
1+d_{1}+\cdots+d_{k-1}=1+\left(2^{k-1}-1\right)=2^{k-1}=d_{k}
$$
for each $k \geqslant 2$, and hence each power of 2 is a bad integer. This exhibits infinitely many bad integers.
Remark. It is true more generally that
If $n=2^{r} m$, where $m$ is a product of (odd) primes each less than $2^{r+1}$, then $n$ is bad.
This is an immediate corollary of the previous result and the following observation:
If $n=2^{r} m$ is bad, where $m$ is odd, then so is $p n$ for any odd prime $p<2^{r+1}$.
Proof. Let $D_{K}>1$ be a divisor of $p n$, so $D_{K}=p$ or $D_{K}=d_{k}$ or $D_{K}=p d_{k}$, where $d_{k}>1$ is a divisor of $n$. In the first case, observe that there exists $t<r+1$ such that $2^{t}<p<2^{t+1}$ by assumption. Then $\left\{1,2, \ldots, 2^{t}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
D_{K}=p<2^{t+1}=1+\left(1+2+\cdots+2^{t}\right) \leqslant 1+D_{1}+\cdots+D_{K-1} .
$$
In the final case, $\left\{1,2, \ldots, 2^{t}, p d_{1}, \ldots, p d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
\begin{aligned}
D_{K} & =p d_{k} \leqslant p\left(1+d_{1}+\cdots+d_{k-1}\right)=p+p d_{1}+\cdots+p d_{k} \\
& <2^{t+1}+p d_{1}+\cdots+p d_{k-1}=1+\left(1+\cdots+2^{t}\right)+p d_{1}+\cdots+p d_{k-1}<1+\left(D_{1}+\cdots+D_{K-1}\right) .
\end{aligned}
$$
In the second case, $\left\{d_{1}, \ldots, d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$ immediately implies the required inequality, and so $p n$ is indeed bad.
This result is weak, however: only 57931 (6.99\%) of the 829157 bad numbers not larger than $10^{7}$ are of this form.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
582b2e38-7485-500c-afee-12ea91cde667
| 606,392
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. We claim that $n=m$ ! is bad for each integer $m \geqslant 2$. The proof proceeds by induction on $m$, the case $m=2$ being clear. If $D_{K}>1$ is a divisor of $m$ !, then $D_{K}=d_{k}$ or $D_{K}=q$ or $D_{K}=q d_{k}$, where $d_{k}>1$ is a divisor of $(m-1)$ ! and $q>1$ is a divisor of $m$. In the first case, $\left\{d_{1}, \ldots, d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, so, invoking the inductive hypothesis, $D_{K}=d_{k} \leqslant 1+\left(d_{1}+\cdots+d_{k-1}\right) \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right)$. In the second case, $q \leqslant m+1$, so $1,2, \ldots, q-1 \mid m$ ! and $\{1,2, \ldots, q-1\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$. But $q^{2}-3 q+2 \geqslant 0$ for $q \geqslant 2$, and hence
$$
D_{K}=q \leqslant \frac{q^{2}-q+2}{2}=1+(1+\cdots+q-1) \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right) .
$$
In the final case, $\left\{1,2, \ldots, q-1, q d_{1}, \ldots, q d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
D_{K}=q d_{k} \leqslant q\left(1+d_{1}+\cdots+d_{k-1}\right) \leqslant 1+(1+\cdots+q-1)+\left(q d_{1}+\cdots+q d_{k-1}\right)
$$
and so $D_{K} \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right)$, completing the inductive step.
(b) If $n$ is odd, then $d_{1}=1, d_{2}>2=1+d_{1}$, and $n$ is good. Among any seven consecutive positive integers, there are either four odd integers and three even ones, or four even ones and three odd ones. In the first case, these four odd integers are good. In the second case, we have to show that one of the consecutive even integers $n=2 m, n+2=2(m+1), n+4=2(m+2), n+6=2(m+3)$ is good. Notice that even integers of the form $n=2(6 \ell \pm 1)$, for $\ell \geqslant 1$, are good, since $d_{2}=2<n$ as $\ell \geqslant 1$, but $d_{3}>4=1+1+2$, since they are divisible by neither 3 nor 4 . But at least one $m, m+1, m+2, m+3$ is congruent to $\pm 1(\bmod 6)(\operatorname{and}$ larger than 1 by assumption); this completes the proof.
(c) Solution 1. Let $n=12 q$, an even number. By part (b), $n-3, n-2=2(6 q-1), n-1, n+1, n+2=2(6 q+1), n+3$ are good integers. Take $q>29$ to be prime. Then the divisors of $n$ less than $q$ are precisely the divisors of 12 . Now $q>1+(1+2+3+4+6+12)=29$, and so $n$ is good, too. Since there are infinitely many choices of the prime $q$, there are infinitely many sequences of seven consecutive good integers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. We claim that $n=m$ ! is bad for each integer $m \geqslant 2$. The proof proceeds by induction on $m$, the case $m=2$ being clear. If $D_{K}>1$ is a divisor of $m$ !, then $D_{K}=d_{k}$ or $D_{K}=q$ or $D_{K}=q d_{k}$, where $d_{k}>1$ is a divisor of $(m-1)$ ! and $q>1$ is a divisor of $m$. In the first case, $\left\{d_{1}, \ldots, d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, so, invoking the inductive hypothesis, $D_{K}=d_{k} \leqslant 1+\left(d_{1}+\cdots+d_{k-1}\right) \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right)$. In the second case, $q \leqslant m+1$, so $1,2, \ldots, q-1 \mid m$ ! and $\{1,2, \ldots, q-1\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$. But $q^{2}-3 q+2 \geqslant 0$ for $q \geqslant 2$, and hence
$$
D_{K}=q \leqslant \frac{q^{2}-q+2}{2}=1+(1+\cdots+q-1) \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right) .
$$
In the final case, $\left\{1,2, \ldots, q-1, q d_{1}, \ldots, q d_{k-1}\right\} \subseteq\left\{D_{1}, \ldots, D_{K-1}\right\}$, and so
$$
D_{K}=q d_{k} \leqslant q\left(1+d_{1}+\cdots+d_{k-1}\right) \leqslant 1+(1+\cdots+q-1)+\left(q d_{1}+\cdots+q d_{k-1}\right)
$$
and so $D_{K} \leqslant 1+\left(D_{1}+\cdots+D_{K-1}\right)$, completing the inductive step.
(b) If $n$ is odd, then $d_{1}=1, d_{2}>2=1+d_{1}$, and $n$ is good. Among any seven consecutive positive integers, there are either four odd integers and three even ones, or four even ones and three odd ones. In the first case, these four odd integers are good. In the second case, we have to show that one of the consecutive even integers $n=2 m, n+2=2(m+1), n+4=2(m+2), n+6=2(m+3)$ is good. Notice that even integers of the form $n=2(6 \ell \pm 1)$, for $\ell \geqslant 1$, are good, since $d_{2}=2<n$ as $\ell \geqslant 1$, but $d_{3}>4=1+1+2$, since they are divisible by neither 3 nor 4 . But at least one $m, m+1, m+2, m+3$ is congruent to $\pm 1(\bmod 6)(\operatorname{and}$ larger than 1 by assumption); this completes the proof.
(c) Solution 1. Let $n=12 q$, an even number. By part (b), $n-3, n-2=2(6 q-1), n-1, n+1, n+2=2(6 q+1), n+3$ are good integers. Take $q>29$ to be prime. Then the divisors of $n$ less than $q$ are precisely the divisors of 12 . Now $q>1+(1+2+3+4+6+12)=29$, and so $n$ is good, too. Since there are infinitely many choices of the prime $q$, there are infinitely many sequences of seven consecutive good integers.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
582b2e38-7485-500c-afee-12ea91cde667
| 606,392
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. Let $m=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 11 \cdot 13$. For any integer $k>0$, the seven consecutive integers $m k+1, m k+2, \ldots, m k+7$ are good. Indeed, the four odd numbers $m k+1, m k+3, m k+5, m k+7$ are good by part (b). Moreover,
$$
\begin{array}{cccccccc}
n & d_{1} & d_{2} & d_{3} & d_{4} & d_{5} & & \\
m k+2 & 1 & 2 & \geqslant 16 & & & \Longrightarrow & d_{3}>1+d_{1}+d_{2}, \\
m k+4 & 1 & 2 & 4 \\
m k+6 & 1 & 2 & 3 & 6 & & \Longrightarrow & d_{4}>1+d_{1}+d_{2}+d_{3}, \\
m k & \geqslant 16 & \Longrightarrow & d_{5}>1+d_{1}+d_{2}+d_{3}+d_{4},
\end{array}
$$
and so $m k+2, m k+4, m k+6$ are good integers, too. Hence there are infinitely many choices of seven consecutive good integers.
Remark. This solution can also be phrased more indirectly in terms of congruence conditions modulo small remainders; the existence of infinitely many appropriate solutions is then guaranteed by the Chinese Remainder Theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. Let $m=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 11 \cdot 13$. For any integer $k>0$, the seven consecutive integers $m k+1, m k+2, \ldots, m k+7$ are good. Indeed, the four odd numbers $m k+1, m k+3, m k+5, m k+7$ are good by part (b). Moreover,
$$
\begin{array}{cccccccc}
n & d_{1} & d_{2} & d_{3} & d_{4} & d_{5} & & \\
m k+2 & 1 & 2 & \geqslant 16 & & & \Longrightarrow & d_{3}>1+d_{1}+d_{2}, \\
m k+4 & 1 & 2 & 4 \\
m k+6 & 1 & 2 & 3 & 6 & & \Longrightarrow & d_{4}>1+d_{1}+d_{2}+d_{3}, \\
m k & \geqslant 16 & \Longrightarrow & d_{5}>1+d_{1}+d_{2}+d_{3}+d_{4},
\end{array}
$$
and so $m k+2, m k+4, m k+6$ are good integers, too. Hence there are infinitely many choices of seven consecutive good integers.
Remark. This solution can also be phrased more indirectly in terms of congruence conditions modulo small remainders; the existence of infinitely many appropriate solutions is then guaranteed by the Chinese Remainder Theorem.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
582b2e38-7485-500c-afee-12ea91cde667
| 606,392
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. Let $m=29$ !. For any integer $k>0$, the seven consecutive integers $m k+1, m k+2, \ldots, m k+7$ are good. Indeed, the divisors of these numbers are either at most 7 or at least 30 . But $30>1+(1+2+\cdots+7)=29$, and so these seven integers are good, giving infinitely many sequences of seven consecutive good integers.
Remark. The ideas underlying these different solutions can be extended to show that there are arbitrarily long runs of consecutive good integers:
For each integer $N$, there exist $N$ consecutive good integers.
Proof 1 . Let $M=2+(1+2+\cdots+N)$, and let $m=M$ !. Any divisor of any of the $N$ consecutive integers $m+1, m+2, \ldots, m+N$ is either at most $N$ or at least $M$. But $M>1+(1+2+\cdots+N)$, and so these $N$ consecutive integers are good.
Proof 2. Let $2=p_{1}<p_{2}<\cdots$ denote the prime numbers, and choose positive integers $s$ and $\alpha_{1}, \ldots, \alpha_{s}$ such that $1,2, \ldots, N$ divide $P=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{s}^{\alpha_{s}}$. Let $\sigma(n)$ denote the sum of the divisors of $n$. Choose an integer $t$ such that $p_{t}>\sigma(P)$, let $m=p_{1} p_{2} \cdots p_{t} P$. The $N$ consecutive integers $m+1, m+2, \ldots, m+N$ are all good. Indeed, for $1 \leqslant k \leqslant N$, any divisor of $m+k$ is either at most $k$ or at least $p_{t+1}$. But $p_{t+1}>1+p_{t}>1+\sigma(P)>1+\sigma(k)$, since $k \mid P$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An integer $n \geqslant 2$ having exactly $s$ positive divisors $1=d_{1}<d_{2}<\cdots<d_{s}=n$ is said to be good if there exists an integer $k$, with $2 \leqslant k \leqslant s$, such that $d_{k}>1+d_{1}+\cdots+d_{k-1}$. An integer $n \geqslant 2$ is said to be bad if it is not good.
(a) Show that there are infinitely many bad integers.
(b) Prove that, among any seven consecutive integers all greater than 2, there are always at least four good integers.
(c) Show that there are infinitely many sequences of seven consecutive good integers.
(Gerhard Woeginger, Luxembourg)
#
|
. Let $m=29$ !. For any integer $k>0$, the seven consecutive integers $m k+1, m k+2, \ldots, m k+7$ are good. Indeed, the divisors of these numbers are either at most 7 or at least 30 . But $30>1+(1+2+\cdots+7)=29$, and so these seven integers are good, giving infinitely many sequences of seven consecutive good integers.
Remark. The ideas underlying these different solutions can be extended to show that there are arbitrarily long runs of consecutive good integers:
For each integer $N$, there exist $N$ consecutive good integers.
Proof 1 . Let $M=2+(1+2+\cdots+N)$, and let $m=M$ !. Any divisor of any of the $N$ consecutive integers $m+1, m+2, \ldots, m+N$ is either at most $N$ or at least $M$. But $M>1+(1+2+\cdots+N)$, and so these $N$ consecutive integers are good.
Proof 2. Let $2=p_{1}<p_{2}<\cdots$ denote the prime numbers, and choose positive integers $s$ and $\alpha_{1}, \ldots, \alpha_{s}$ such that $1,2, \ldots, N$ divide $P=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{s}^{\alpha_{s}}$. Let $\sigma(n)$ denote the sum of the divisors of $n$. Choose an integer $t$ such that $p_{t}>\sigma(P)$, let $m=p_{1} p_{2} \cdots p_{t} P$. The $N$ consecutive integers $m+1, m+2, \ldots, m+N$ are all good. Indeed, for $1 \leqslant k \leqslant N$, any divisor of $m+k$ is either at most $k$ or at least $p_{t+1}$. But $p_{t+1}>1+p_{t}>1+\sigma(P)>1+\sigma(k)$, since $k \mid P$. This completes the proof.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2018-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
582b2e38-7485-500c-afee-12ea91cde667
| 606,392
|
Let $A B C$ be a triangle. The circle $\omega_{A}$ through $A$ is tangent to line $B C$ at $B$. The circle $\omega_{C}$ through $C$ is tangent to line $A B$ at $B$. Let $\omega_{A}$ and $\omega_{C}$ meet again at $D$. Let $M$ be the midpoint of line segment $[B C]$, and let $E$ be the intersection of lines $M D$ and $A C$. Show that $E$ lies on $\omega_{A}$.
#
|
Let $N$ be the midpoint of $[A B]$. By tangential angles, $\angle C B D=\angle B A D$ and $\angle D B A=\angle D C B$, so triangles $D A B$ and $D B C$ are similar. By definition of the midpoints $M, N$, so are triangles $A N D$ and $B M D$. In particular, $\angle B N D=180^{\circ}-\angle D N A=180^{\circ}-\angle D M B$, so $B N D M$ is cyclic. But $M N \| A C$ by construction, so $\angle D B A=\angle D B N=\angle D M N=\angle E M N=\angle M E A=\angle D E A$, hence $E A D B$ is cyclic, completing the proof.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. The circle $\omega_{A}$ through $A$ is tangent to line $B C$ at $B$. The circle $\omega_{C}$ through $C$ is tangent to line $A B$ at $B$. Let $\omega_{A}$ and $\omega_{C}$ meet again at $D$. Let $M$ be the midpoint of line segment $[B C]$, and let $E$ be the intersection of lines $M D$ and $A C$. Show that $E$ lies on $\omega_{A}$.
#
|
Let $N$ be the midpoint of $[A B]$. By tangential angles, $\angle C B D=\angle B A D$ and $\angle D B A=\angle D C B$, so triangles $D A B$ and $D B C$ are similar. By definition of the midpoints $M, N$, so are triangles $A N D$ and $B M D$. In particular, $\angle B N D=180^{\circ}-\angle D N A=180^{\circ}-\angle D M B$, so $B N D M$ is cyclic. But $M N \| A C$ by construction, so $\angle D B A=\angle D B N=\angle D M N=\angle E M N=\angle M E A=\angle D E A$, hence $E A D B$ is cyclic, completing the proof.

#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2020-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
e05ec5a9-0ec1-54ff-bf6e-924d2ef2387b
| 606,408
|
Let $A B C$ be a triangle. The circle $\omega_{A}$ through $A$ is tangent to line $B C$ at $B$. The circle $\omega_{C}$ through $C$ is tangent to line $A B$ at $B$. Let $\omega_{A}$ and $\omega_{C}$ meet again at $D$. Let $M$ be the midpoint of line segment $[B C]$, and let $E$ be the intersection of lines $M D$ and $A C$. Show that $E$ lies on $\omega_{A}$.
#
|
Let $S$ be the point on $\omega_{C}$ such that $B S$ is parallel to $A C$, and let $E^{\prime}$ be the reflection of $S$ in $M$ (such that $B S C E^{\prime}$ is a parallellogram and $E^{\prime}$ lies on $A C$ ). Now we do some (directed) angle chasing:
$$
\begin{aligned}
\angle A E^{\prime} B & =\angle C E^{\prime} B\left(\text { since } A, E^{\prime} \text { and } C \text { are collineair }\right) \\
& =\angle B S C\left(B S C E^{\prime} \text { is a parallellogram }\right) \\
& =\angle A B C\left(\text { inscribed angles on } \omega_{C}\right) \\
& =\angle A D B\left(\text { inscribed angles on } \omega_{A}\right)
\end{aligned}
$$
Hence $E^{\prime}$ lies on $\omega_{A}$. Further $\angle A E^{\prime} D=\angle A B D=\angle B S D$, and because $A E^{\prime}$ is parallel to $B S$ we find that $E^{\prime} D$ is parallel to $S D$. This means that $E^{\prime}$ lies on $M D$, so $E^{\prime}=E$ and $E$ lies on $\omega_{A}$.
## BxMO 2020: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. The circle $\omega_{A}$ through $A$ is tangent to line $B C$ at $B$. The circle $\omega_{C}$ through $C$ is tangent to line $A B$ at $B$. Let $\omega_{A}$ and $\omega_{C}$ meet again at $D$. Let $M$ be the midpoint of line segment $[B C]$, and let $E$ be the intersection of lines $M D$ and $A C$. Show that $E$ lies on $\omega_{A}$.
#
|
Let $S$ be the point on $\omega_{C}$ such that $B S$ is parallel to $A C$, and let $E^{\prime}$ be the reflection of $S$ in $M$ (such that $B S C E^{\prime}$ is a parallellogram and $E^{\prime}$ lies on $A C$ ). Now we do some (directed) angle chasing:
$$
\begin{aligned}
\angle A E^{\prime} B & =\angle C E^{\prime} B\left(\text { since } A, E^{\prime} \text { and } C \text { are collineair }\right) \\
& =\angle B S C\left(B S C E^{\prime} \text { is a parallellogram }\right) \\
& =\angle A B C\left(\text { inscribed angles on } \omega_{C}\right) \\
& =\angle A D B\left(\text { inscribed angles on } \omega_{A}\right)
\end{aligned}
$$
Hence $E^{\prime}$ lies on $\omega_{A}$. Further $\angle A E^{\prime} D=\angle A B D=\angle B S D$, and because $A E^{\prime}$ is parallel to $B S$ we find that $E^{\prime} D$ is parallel to $S D$. This means that $E^{\prime}$ lies on $M D$, so $E^{\prime}=E$ and $E$ lies on $\omega_{A}$.
## BxMO 2020: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2020-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
e05ec5a9-0ec1-54ff-bf6e-924d2ef2387b
| 606,408
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
The left-hand-side of the inequality is invariant under permutations of $a, b, c, d$. We may therefore suppose that $a \geqslant b \geqslant c \geqslant d$, so that the inequality reduces to
$$
0 \leqslant 3 a+2 b+c=a+(a+b)+(a+b+c) .
$$
We claim that each of the terms on the right-hand side is non-negative; this will prove the inequality. Indeed, if $a<0$, then $a, b, c, d<0$, and so $a+b+c+d<0$, a contradiction. Also, if $a+b<0$, then, as $b \leqslant a$, $0>b \geqslant c, d$ so $(a+b)+c+d<0$, another contradiction. Finally, if $a+b+c<0$, then, as above, $0>c \geqslant d$, so $(a+b+c)+d<0$, a final contradiction.
Next, we claim that it is impossible to replace $k \geqslant 3$ maxima by minima in the inequality. Indeed, if $k \geqslant 3$, one number, say $d$, appears in two of the terms changed to minima. Take $a=b=c=1, d=-3$, so that $a+b+c+d=0$. Then the sum is at most $4 \cdot 1+2 \cdot(-3)<0$. Hence $k<3$.
Finally, we prove that the required inequality holds if $k=2$ and the terms involving the complementary sets $\{a, b\},\{c, d\}$ are changed to minima. We will assume again that $a \geqslant b \geqslant c \geqslant d$, and prove that the inequality holds for any change of the terms involving permutations of these sets to minima (rather than proving that it holds for all orderings of $a, b, c, d$ for this one change). There are three cases:
(1) change terms $\{a, b\},\{c, d\}$, so the inequality becomes $2 a+3 b+d \geqslant 0 \Longleftrightarrow a+b+(b-c) \geqslant 0$;
(2) change terms $\{a, c\},\{b, d\}$, so the inequality becomes $2 a+b+2 c+d \geqslant 0 \Longleftrightarrow a+c \geqslant 0$;
(3) change terms $\{a, d\},\{b, c\}$, so the inequality becomes $2 a+b+2 c+d \geqslant 0 \Longleftrightarrow a+c \geqslant 0$,
where we have used $a+b+c+d=0$. In the first case, inequality holds since $a+b \geqslant 0$ as proved earlier and $b \geqslant c$. In the other cases, suppose that $a+c<0$. Then $c<-a$ and hence $d<-a$ as $d \leqslant c$. Hence $c+d<-2 a \leqslant-a-b$ as $a \geqslant b$, so $a+b+c+d<0$, a final contradiction, completing the proof.
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
The left-hand-side of the inequality is invariant under permutations of $a, b, c, d$. We may therefore suppose that $a \geqslant b \geqslant c \geqslant d$, so that the inequality reduces to
$$
0 \leqslant 3 a+2 b+c=a+(a+b)+(a+b+c) .
$$
We claim that each of the terms on the right-hand side is non-negative; this will prove the inequality. Indeed, if $a<0$, then $a, b, c, d<0$, and so $a+b+c+d<0$, a contradiction. Also, if $a+b<0$, then, as $b \leqslant a$, $0>b \geqslant c, d$ so $(a+b)+c+d<0$, another contradiction. Finally, if $a+b+c<0$, then, as above, $0>c \geqslant d$, so $(a+b+c)+d<0$, a final contradiction.
Next, we claim that it is impossible to replace $k \geqslant 3$ maxima by minima in the inequality. Indeed, if $k \geqslant 3$, one number, say $d$, appears in two of the terms changed to minima. Take $a=b=c=1, d=-3$, so that $a+b+c+d=0$. Then the sum is at most $4 \cdot 1+2 \cdot(-3)<0$. Hence $k<3$.
Finally, we prove that the required inequality holds if $k=2$ and the terms involving the complementary sets $\{a, b\},\{c, d\}$ are changed to minima. We will assume again that $a \geqslant b \geqslant c \geqslant d$, and prove that the inequality holds for any change of the terms involving permutations of these sets to minima (rather than proving that it holds for all orderings of $a, b, c, d$ for this one change). There are three cases:
(1) change terms $\{a, b\},\{c, d\}$, so the inequality becomes $2 a+3 b+d \geqslant 0 \Longleftrightarrow a+b+(b-c) \geqslant 0$;
(2) change terms $\{a, c\},\{b, d\}$, so the inequality becomes $2 a+b+2 c+d \geqslant 0 \Longleftrightarrow a+c \geqslant 0$;
(3) change terms $\{a, d\},\{b, c\}$, so the inequality becomes $2 a+b+2 c+d \geqslant 0 \Longleftrightarrow a+c \geqslant 0$,
where we have used $a+b+c+d=0$. In the first case, inequality holds since $a+b \geqslant 0$ as proved earlier and $b \geqslant c$. In the other cases, suppose that $a+c<0$. Then $c<-a$ and hence $d<-a$ as $d \leqslant c$. Hence $c+d<-2 a \leqslant-a-b$ as $a \geqslant b$, so $a+b+c+d<0$, a final contradiction, completing the proof.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2bdc0a6-df9a-54ba-b13a-31b3fcc8698b
| 606,414
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
Using the inequality $\max (x, y) \geqslant \frac{1}{2}(x+y)$, we find that
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant \frac{3}{2}(a+b+c+d)=0
$$
For $k=3$, we take the same counterexample as in Solution 1. Now it remains to prove the inequality where $\max (a, b)$ and $\max (c, d)$ are replaced by $\min (a, b)$ and $\min (c, d)$. We can assume without loss of generality that $\min (a, b)=a$ and $\min (c, d)=c$. Now we find
$$
\begin{aligned}
& \min (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\min (c, d) \geqslant \\
& a+\frac{1}{2}(a+c)+d+b+\frac{1}{2}(b+d)+c=\frac{3}{2}(a+b+c+d)=0 .
\end{aligned}
$$
## BxMO 2021: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
Using the inequality $\max (x, y) \geqslant \frac{1}{2}(x+y)$, we find that
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant \frac{3}{2}(a+b+c+d)=0
$$
For $k=3$, we take the same counterexample as in Solution 1. Now it remains to prove the inequality where $\max (a, b)$ and $\max (c, d)$ are replaced by $\min (a, b)$ and $\min (c, d)$. We can assume without loss of generality that $\min (a, b)=a$ and $\min (c, d)=c$. Now we find
$$
\begin{aligned}
& \min (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\min (c, d) \geqslant \\
& a+\frac{1}{2}(a+c)+d+b+\frac{1}{2}(b+d)+c=\frac{3}{2}(a+b+c+d)=0 .
\end{aligned}
$$
## BxMO 2021: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2bdc0a6-df9a-54ba-b13a-31b3fcc8698b
| 606,414
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
We present another proof for the inequality where $\max (a, b)$ and $\max (c, d)$ are replaced by $\min (a, b)$ and $\min (c, d)$. By substituting $\max (x, y)=\frac{1}{2}(x+y+|x-y|)$ and $\min (x, y)=\frac{1}{2}(x+y-|x-y|)$ everywhere and using $a+b+c+d=0$, the inequality may be rewritten as:
$$
|a-c|+|a-d|+|b-c|+|b-d| \stackrel{?}{\geqslant}|a-b|+|c-d| \text {. }
$$
By the triangle inequality, we have
$$
|a-c|+|a-d|+|b-c|+|b-d| \geqslant|(a-c)-(b-c)|+|(a-d)-(b-d)|=2|a-b|,
$$
and similarly, $|a-c|+|a-d|+|b-c|+|b-d| \geqslant 2|c-d|$. Adding these and dividing by 2 yields the desired inequality.
## BxMO 2021: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
(a) Prove that for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$,
$$
\max (a, b)+\max (a, c)+\max (a, d)+\max (b, c)+\max (b, d)+\max (c, d) \geqslant 0
$$
(b) Find the largest non-negative integer $k$ such that it is possible to replace $k$ of the six maxima in this inequality by minima in such a way that the inequality still holds for all $a, b, c, d \in \mathbb{R}$ with $a+b+c+d=0$.
#
|
We present another proof for the inequality where $\max (a, b)$ and $\max (c, d)$ are replaced by $\min (a, b)$ and $\min (c, d)$. By substituting $\max (x, y)=\frac{1}{2}(x+y+|x-y|)$ and $\min (x, y)=\frac{1}{2}(x+y-|x-y|)$ everywhere and using $a+b+c+d=0$, the inequality may be rewritten as:
$$
|a-c|+|a-d|+|b-c|+|b-d| \stackrel{?}{\geqslant}|a-b|+|c-d| \text {. }
$$
By the triangle inequality, we have
$$
|a-c|+|a-d|+|b-c|+|b-d| \geqslant|(a-c)-(b-c)|+|(a-d)-(b-d)|=2|a-b|,
$$
and similarly, $|a-c|+|a-d|+|b-c|+|b-d| \geqslant 2|c-d|$. Adding these and dividing by 2 yields the desired inequality.
## BxMO 2021: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
a2bdc0a6-df9a-54ba-b13a-31b3fcc8698b
| 606,414
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
First, note that $\angle A O X=2 \angle A B X=2\left(180^{\circ}-\angle A C X\right)=2 \angle A C E$ as $A B X C$ is cyclic. Secondly, both $\triangle D A B$ and $\triangle E A C$ are isosceles, which implies that $\angle A E X=\angle A E C=180^{\circ}-2 \angle A C E=180^{\circ}-\angle A O X$ and $\angle A D X=$ $\angle A D B=180^{\circ}-2 \angle A B D=180^{\circ}-2 \angle A B X=180^{\circ}-\angle A O X$. From this, see that respectively $A E X O$ and $A D X O$ are cyclic, i.e. $A E D X O$ is cyclic.
Hence, the circumcentre of $\triangle D E X$ is also the circumcentre of $A E D X O$. However, as in a circle any perpendicular bisector of a chord goes through the centre of the circle, we find that the circumcentre of $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
First, note that $\angle A O X=2 \angle A B X=2\left(180^{\circ}-\angle A C X\right)=2 \angle A C E$ as $A B X C$ is cyclic. Secondly, both $\triangle D A B$ and $\triangle E A C$ are isosceles, which implies that $\angle A E X=\angle A E C=180^{\circ}-2 \angle A C E=180^{\circ}-\angle A O X$ and $\angle A D X=$ $\angle A D B=180^{\circ}-2 \angle A B D=180^{\circ}-2 \angle A B X=180^{\circ}-\angle A O X$. From this, see that respectively $A E X O$ and $A D X O$ are cyclic, i.e. $A E D X O$ is cyclic.
Hence, the circumcentre of $\triangle D E X$ is also the circumcentre of $A E D X O$. However, as in a circle any perpendicular bisector of a chord goes through the centre of the circle, we find that the circumcentre of $\triangle D E X$ lies on the perpendicular bisector of $O A$.

#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
77ba6309-27cd-5370-bb86-baecd7454ac0
| 606,424
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
In this solution, we use directed angles $\measuredangle$. We have $\measuredangle A B D=\measuredangle A B X=\measuredangle A C X=\measuredangle A C E$ and since $\triangle A B D$ and $\triangle A C E$ are both isosceles, we see that $\triangle A B D \sim \triangle A C E$ with equal orientation. This means that there exists a spiral symmetry $T$ with centre $A$ such that $T(B)=D$ and $T(C)=E$. Now let $O^{\prime}$ be the centre of $\odot D E X$. Then we find $\measuredangle D O^{\prime} E=2 \measuredangle D X E=2 \measuredangle B X C=\measuredangle B O C$. Moreover, $\triangle D O^{\prime} E$ and $\triangle B O C$ are isosceles, so we have $\triangle D O^{\prime} E \sim \triangle B O C$ with equal orientation. This means that $T$ must send $O$ to $O^{\prime}$, so in particular, $\triangle A O O^{\prime}$ is similar to $\triangle A B D$ and $\triangle A C E$. We conclude that $\left|A O^{\prime}\right|=\left|O O^{\prime}\right|$, from which the result follows.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
In this solution, we use directed angles $\measuredangle$. We have $\measuredangle A B D=\measuredangle A B X=\measuredangle A C X=\measuredangle A C E$ and since $\triangle A B D$ and $\triangle A C E$ are both isosceles, we see that $\triangle A B D \sim \triangle A C E$ with equal orientation. This means that there exists a spiral symmetry $T$ with centre $A$ such that $T(B)=D$ and $T(C)=E$. Now let $O^{\prime}$ be the centre of $\odot D E X$. Then we find $\measuredangle D O^{\prime} E=2 \measuredangle D X E=2 \measuredangle B X C=\measuredangle B O C$. Moreover, $\triangle D O^{\prime} E$ and $\triangle B O C$ are isosceles, so we have $\triangle D O^{\prime} E \sim \triangle B O C$ with equal orientation. This means that $T$ must send $O$ to $O^{\prime}$, so in particular, $\triangle A O O^{\prime}$ is similar to $\triangle A B D$ and $\triangle A C E$. We conclude that $\left|A O^{\prime}\right|=\left|O O^{\prime}\right|$, from which the result follows.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
77ba6309-27cd-5370-bb86-baecd7454ac0
| 606,424
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.