problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The case $n=0$ is trivial; for $n>0$, the proof goes by induction on $n$. We need to make one preliminary observation:
Claim. For all reals $a, b, a+b x \leqslant \max \{a, a+b\}$ for all $x \in[0,1]$.
Proof. If $b \leqslant 0$, then $a+b x \leqslant a$ for all $x \in[0,1]$; otherwise, if $b>0, a+b x \leqslant a+b$ for all $x \in[0,1]$. This proves our claim.
This disposes of the base case $n=1$ of the induction: $a_{0}+a_{1} x \leqslant \max \left\{a_{0}, a_{0}+a_{1}\right\}$ for all $x \in[0,1]$. For $n \geqslant 2$, we note that, for all $x \in[0,1]$,
$$
\begin{aligned}
a_{0}+a_{1} x+\cdots+a_{n} x^{n} & =a_{0}+x\left(a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}\right) \\
& \leqslant a_{0}+x\left(a_{1}+a_{2}+\cdots+a_{k}\right) \leqslant \max \left\{a_{0}, a_{0}+\left(a_{1}+\cdots+a_{k}\right)\right\}
\end{aligned}
$$
for some $k \in\{1,2, \ldots, n\}$ by the inductive hypothesis and our earlier claim. This completes the proof by induction.
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The case $n=0$ is trivial; for $n>0$, the proof goes by induction on $n$. We need to make one preliminary observation:
Claim. For all reals $a, b, a+b x \leqslant \max \{a, a+b\}$ for all $x \in[0,1]$.
Proof. If $b \leqslant 0$, then $a+b x \leqslant a$ for all $x \in[0,1]$; otherwise, if $b>0, a+b x \leqslant a+b$ for all $x \in[0,1]$. This proves our claim.
This disposes of the base case $n=1$ of the induction: $a_{0}+a_{1} x \leqslant \max \left\{a_{0}, a_{0}+a_{1}\right\}$ for all $x \in[0,1]$. For $n \geqslant 2$, we note that, for all $x \in[0,1]$,
$$
\begin{aligned}
a_{0}+a_{1} x+\cdots+a_{n} x^{n} & =a_{0}+x\left(a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}\right) \\
& \leqslant a_{0}+x\left(a_{1}+a_{2}+\cdots+a_{k}\right) \leqslant \max \left\{a_{0}, a_{0}+\left(a_{1}+\cdots+a_{k}\right)\right\}
\end{aligned}
$$
for some $k \in\{1,2, \ldots, n\}$ by the inductive hypothesis and our earlier claim. This completes the proof by induction.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
7d219af2-169b-567b-a4be-2ddb10162f84
| 606,431
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
Define $s_{i}=a_{0}+a_{1}+\cdots+a_{i}$ for $i \in\{0,1, \ldots, n\}$. Thus $a_{0}=s_{0}$ and $a_{i}=s_{i}-s_{i-1}$ for all $i \in\{1,2, \ldots, n\}$. Hence
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} & =s_{0}+\left(s_{1}-s_{0}\right) x+\left(s_{2}-s_{1}\right) x^{2}+\ldots+\left(s_{n}-s_{n-1}\right) x^{n} \\
& =s_{0}(1-x)+s_{1}\left(x-x^{2}\right)+\ldots+s_{n-1}\left(x^{n-1}-x^{n}\right)+s_{n} x^{n}
\end{aligned}
$$
Now choose $k \in\{0,1, \ldots, n\}$ such that $s_{k}=\max \left\{s_{0}, s_{1}, \ldots, s_{n}\right\}$. Using the inequality $x^{i-1}-x^{i} \geqslant 0$, valid for all $i \in\{1,2, \ldots, n\}$ and all $x \in[0,1]$, in the right-hand side above, it follows that
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant s_{k}(1- & x)+s_{k}\left(x-x^{2}\right)+\cdots+s_{k}\left(x^{n-1}-x^{n}\right)+s_{k} x^{n} \\
= & s_{k}\left[(1-x)+\left(x-x^{2}\right)+\cdots+\left(x^{n-1}-x^{n}\right)+x^{n}\right] \\
= & s_{k}=a_{0}+a_{1}+\cdots+a_{k}
\end{aligned}
$$
This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
Define $s_{i}=a_{0}+a_{1}+\cdots+a_{i}$ for $i \in\{0,1, \ldots, n\}$. Thus $a_{0}=s_{0}$ and $a_{i}=s_{i}-s_{i-1}$ for all $i \in\{1,2, \ldots, n\}$. Hence
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} & =s_{0}+\left(s_{1}-s_{0}\right) x+\left(s_{2}-s_{1}\right) x^{2}+\ldots+\left(s_{n}-s_{n-1}\right) x^{n} \\
& =s_{0}(1-x)+s_{1}\left(x-x^{2}\right)+\ldots+s_{n-1}\left(x^{n-1}-x^{n}\right)+s_{n} x^{n}
\end{aligned}
$$
Now choose $k \in\{0,1, \ldots, n\}$ such that $s_{k}=\max \left\{s_{0}, s_{1}, \ldots, s_{n}\right\}$. Using the inequality $x^{i-1}-x^{i} \geqslant 0$, valid for all $i \in\{1,2, \ldots, n\}$ and all $x \in[0,1]$, in the right-hand side above, it follows that
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant s_{k}(1- & x)+s_{k}\left(x-x^{2}\right)+\cdots+s_{k}\left(x^{n-1}-x^{n}\right)+s_{k} x^{n} \\
= & s_{k}\left[(1-x)+\left(x-x^{2}\right)+\cdots+\left(x^{n-1}-x^{n}\right)+x^{n}\right] \\
= & s_{k}=a_{0}+a_{1}+\cdots+a_{k}
\end{aligned}
$$
This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
7d219af2-169b-567b-a4be-2ddb10162f84
| 606,431
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The proof proceeds by induction on $n$. The base case $n=0$ is trivial. For $n \geqslant 1$, since $x \in[0,1]$, we have $x^{n} \leqslant x^{n-1}$. Thus, if $a_{n} \geqslant 0$, then $a_{n} x^{n} \leqslant a_{n} x^{n-1}$, while, if $a_{n}<0$, then $a_{n} x^{n}<0$ trivially. This shows that $a_{n} x^{n} \leqslant \max \left\{0, a_{n} x^{n-1}\right\}$, whence
$$
a_{0}+a_{1} x+\cdots+a_{n-1} x^{n-1}+a_{n} x^{n} \leqslant a_{0}+a_{1} x+\cdots+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\} x^{n-1} .
$$
By the inductive hypothesis, the polynomial of degree $n-1$ on the right-hand side is bounded above by $a_{0}+\cdots+a_{k}$ for some $k \in\{0,1, \ldots, n-2\}$ or $a_{0}+\cdots+a_{n-2}+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\}$. But the latter is equal to one of $a_{0}+a_{1}+\cdots+a_{n-1}$ or $a_{0}+a_{1}+\cdots+a_{n}$; both are of the desired form, $a_{0}+a_{1}+\cdots+a_{k}$ for some $k \in\{n-1, n\}$. This completes the proof by induction.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The proof proceeds by induction on $n$. The base case $n=0$ is trivial. For $n \geqslant 1$, since $x \in[0,1]$, we have $x^{n} \leqslant x^{n-1}$. Thus, if $a_{n} \geqslant 0$, then $a_{n} x^{n} \leqslant a_{n} x^{n-1}$, while, if $a_{n}<0$, then $a_{n} x^{n}<0$ trivially. This shows that $a_{n} x^{n} \leqslant \max \left\{0, a_{n} x^{n-1}\right\}$, whence
$$
a_{0}+a_{1} x+\cdots+a_{n-1} x^{n-1}+a_{n} x^{n} \leqslant a_{0}+a_{1} x+\cdots+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\} x^{n-1} .
$$
By the inductive hypothesis, the polynomial of degree $n-1$ on the right-hand side is bounded above by $a_{0}+\cdots+a_{k}$ for some $k \in\{0,1, \ldots, n-2\}$ or $a_{0}+\cdots+a_{n-2}+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\}$. But the latter is equal to one of $a_{0}+a_{1}+\cdots+a_{n-1}$ or $a_{0}+a_{1}+\cdots+a_{n}$; both are of the desired form, $a_{0}+a_{1}+\cdots+a_{k}$ for some $k \in\{n-1, n\}$. This completes the proof by induction.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
7d219af2-169b-567b-a4be-2ddb10162f84
| 606,431
|
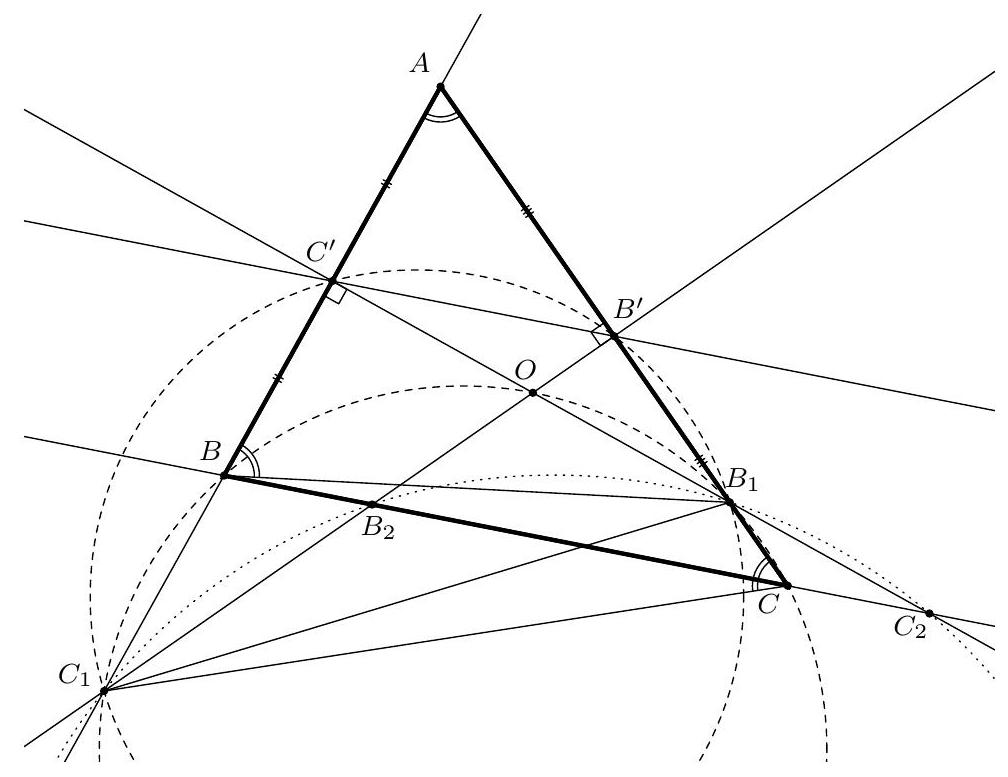
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ bisect segments $[A B]$ and $[A C]$, respectively, so their intersection $O$ is the circumcentre of $A B C$. Hence $\angle B O C=2 \angle A$ and $\angle C B O=\angle O C B=90^{\circ}-\angle A$. Now, by construction, $\angle O C_{1} B=90^{\circ}-\angle A=\angle O C B$, so $B C_{1} C O$ is cyclic. Similarly, $B C B_{1} O$ is cyclic by construction because $\angle O B_{1} C=180^{\circ}-\angle A B_{1} O=90^{\circ}+\angle A=180^{\circ}-\angle C B O$. In particular, $B C_{1} C B_{1}$ is cyclic, too.
Now $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{1} B-\angle B_{2} C_{1} B$ and $\angle B_{1} C_{2} B_{2}=\angle B_{1} C B-\angle C B_{1} C_{2}$. But $\angle B_{1} C_{1} B=\angle B_{1} C B$ since $B C_{1} C B_{1}$ is cyclic and $\angle B_{2} C_{1} B=\angle O C_{1} B=90^{\circ}-\angle A=180^{\circ}-\angle O B_{1} C=\angle C B_{1} C_{2}$. Hence $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{2} B_{2}$, so $B_{1} B_{2} C_{1} C_{2}$ is cyclic, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ bisect segments $[A B]$ and $[A C]$, respectively, so their intersection $O$ is the circumcentre of $A B C$. Hence $\angle B O C=2 \angle A$ and $\angle C B O=\angle O C B=90^{\circ}-\angle A$. Now, by construction, $\angle O C_{1} B=90^{\circ}-\angle A=\angle O C B$, so $B C_{1} C O$ is cyclic. Similarly, $B C B_{1} O$ is cyclic by construction because $\angle O B_{1} C=180^{\circ}-\angle A B_{1} O=90^{\circ}+\angle A=180^{\circ}-\angle C B O$. In particular, $B C_{1} C B_{1}$ is cyclic, too.
Now $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{1} B-\angle B_{2} C_{1} B$ and $\angle B_{1} C_{2} B_{2}=\angle B_{1} C B-\angle C B_{1} C_{2}$. But $\angle B_{1} C_{1} B=\angle B_{1} C B$ since $B C_{1} C B_{1}$ is cyclic and $\angle B_{2} C_{1} B=\angle O C_{1} B=90^{\circ}-\angle A=180^{\circ}-\angle O B_{1} C=\angle C B_{1} C_{2}$. Hence $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{2} B_{2}$, so $B_{1} B_{2} C_{1} C_{2}$ is cyclic, as required.

|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4970f92-1bb8-529e-8866-99dfa94d00d2
| 606,438
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
The isosceles triangles $A B_{1} B$ and $A C_{1} C$ have equal base angles $\angle B A B_{1}=\angle C_{1} A C=\angle A$, so are similar. In particular, $|A B| /\left|A B_{1}\right|=|A C| /\left|A C_{1}\right|$. Since $\angle B A C=\angle B_{1} A C_{1}=\angle A$, it follows that triangles $A B C$ and $A B_{1} C_{1}$ are similar, too. In particular, $\angle C B A=\angle A B_{1} C_{1}$.
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Hence
$$
\begin{aligned}
\angle B_{1} C_{2} B_{2} & =\angle C^{\prime} C_{2} B=90^{\circ}-\angle C_{2} B C^{\prime}=90^{\circ}-\angle C B A=90^{\circ}-\angle A B_{1} C_{1}=90^{\circ}-\angle B^{\prime} B_{1} C_{1} \\
& =\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2} .
\end{aligned}
$$
Hence $B_{1} C_{2} C_{1} B_{2}$ is cyclic, which completes the proof.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
The isosceles triangles $A B_{1} B$ and $A C_{1} C$ have equal base angles $\angle B A B_{1}=\angle C_{1} A C=\angle A$, so are similar. In particular, $|A B| /\left|A B_{1}\right|=|A C| /\left|A C_{1}\right|$. Since $\angle B A C=\angle B_{1} A C_{1}=\angle A$, it follows that triangles $A B C$ and $A B_{1} C_{1}$ are similar, too. In particular, $\angle C B A=\angle A B_{1} C_{1}$.
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Hence
$$
\begin{aligned}
\angle B_{1} C_{2} B_{2} & =\angle C^{\prime} C_{2} B=90^{\circ}-\angle C_{2} B C^{\prime}=90^{\circ}-\angle C B A=90^{\circ}-\angle A B_{1} C_{1}=90^{\circ}-\angle B^{\prime} B_{1} C_{1} \\
& =\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2} .
\end{aligned}
$$
Hence $B_{1} C_{2} C_{1} B_{2}$ is cyclic, which completes the proof.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4970f92-1bb8-529e-8866-99dfa94d00d2
| 606,438
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Since $\angle B_{1} C^{\prime} C_{1}=90^{\circ}=\angle C_{1} B^{\prime} B_{1}, B_{1} C_{1} C^{\prime} B^{\prime}$ is cyclic. Together with the fact that $B^{\prime} C^{\prime} \| B C$ by construction, this implies
$$
\angle B_{1} C_{2} B_{2}=\angle C^{\prime} C_{2} B=\angle C_{2} C^{\prime} B^{\prime}=\angle B_{1} C^{\prime} B^{\prime}=\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2},
$$
whence $B_{1} C_{2} C_{1} B_{2}$ is cyclic. This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Since $\angle B_{1} C^{\prime} C_{1}=90^{\circ}=\angle C_{1} B^{\prime} B_{1}, B_{1} C_{1} C^{\prime} B^{\prime}$ is cyclic. Together with the fact that $B^{\prime} C^{\prime} \| B C$ by construction, this implies
$$
\angle B_{1} C_{2} B_{2}=\angle C^{\prime} C_{2} B=\angle C_{2} C^{\prime} B^{\prime}=\angle B_{1} C^{\prime} B^{\prime}=\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2},
$$
whence $B_{1} C_{2} C_{1} B_{2}$ is cyclic. This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4970f92-1bb8-529e-8866-99dfa94d00d2
| 606,438
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. In particular $n$ is not prime. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. We observe that $k, \ell \neq 0$ since $n$ is not prime.
Now we have $p-q=(n-q)-(n-p)=(\ell q-k p)(\ell q+k p)$. Since $p-q \neq 0, \ell q-k p \neq 0$, and hence $|p-q|=|k p-\ell q||k p+\ell q| \geqslant|k p+\ell q|=k p+\ell q$. This is a contradiction however, because, since $k, \ell \neq 0$, it is clear that $k p+\ell q \geqslant p+q>|p-q|$. Hence $S$ is good.
(b) Let $q$ be a prime, and let $Q=\left\{q, q^{3}, q^{5}, \ldots\right\}$ be the (infinite) set of odd powers of $q$, which is disjoint from $S$. We claim that $Q$ is good. Indeed, let $n \in \mathbb{N}$, and let $p \mid n$ be a prime such that $n-p \in Q$, i.e. $n-p=q^{2 k+1}$ for some $k \in \mathbb{N}$. Then $p \mid n-p$, so $p \mid q^{2 k+1}$, and hence $p=q$. Thus $Q$ is good.
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. In particular $n$ is not prime. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. We observe that $k, \ell \neq 0$ since $n$ is not prime.
Now we have $p-q=(n-q)-(n-p)=(\ell q-k p)(\ell q+k p)$. Since $p-q \neq 0, \ell q-k p \neq 0$, and hence $|p-q|=|k p-\ell q||k p+\ell q| \geqslant|k p+\ell q|=k p+\ell q$. This is a contradiction however, because, since $k, \ell \neq 0$, it is clear that $k p+\ell q \geqslant p+q>|p-q|$. Hence $S$ is good.
(b) Let $q$ be a prime, and let $Q=\left\{q, q^{3}, q^{5}, \ldots\right\}$ be the (infinite) set of odd powers of $q$, which is disjoint from $S$. We claim that $Q$ is good. Indeed, let $n \in \mathbb{N}$, and let $p \mid n$ be a prime such that $n-p \in Q$, i.e. $n-p=q^{2 k+1}$ for some $k \in \mathbb{N}$. Then $p \mid n-p$, so $p \mid q^{2 k+1}$, and hence $p=q$. Thus $Q$ is good.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
861857c9-e6d7-5d72-a219-2c9ff2ca9e62
| 604,166
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Let $p \mid n$ be a prime such that $n-p=p(n / p-1)=m^{2}$, for some $m \in \mathbb{N}$. Since $p \mid m^{2}$ and $p$ is prime, $p^{2} \mid m^{2}$, and hence $p \mid n / p-1<n / p$, so $p<\sqrt{n}$.
Now suppose to the contrary that $S$ is not good, so there are primes $p_{1}>p_{2}$ dividing $n$ such that $n-p_{1}<n-p_{2}$ are perfect squares. Then
$$
n-p_{2} \geqslant\left(\sqrt{n-p_{1}}+1\right)^{2}>n-p_{1}+2 \sqrt{n-p_{1}} \quad \Longrightarrow \quad p_{1}>p_{2}+2 \sqrt{n-p_{1}} \geqslant 2+2 \sqrt{n-p_{1}}
$$
The last condition implies that $p_{1}>2 \sqrt{n-1}$. But $p_{1}<\sqrt{n}$ by the first part, so $\sqrt{n}>2 \sqrt{n-1}$, which is a contradiction for $n>1$; the cases $n=0$ and $n=1$ are trivial. Thus $S$ is good.
(b) We claim that the infinite set $P=\{3,5,7,11, \ldots\}$ of odd primes, which is disjoint from $S$, is good. Indeed, let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some odd prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. Since $q$ is the only odd prime divisor of $n=2 q, P$ is good.
The set $P^{\prime}=\{2,3,5,7,11, \ldots\}$ of all primes is also good. The proof is similar: let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. If $q=2$, then 2 is the only prime divisor of $n$; if $q \neq 2$, then the only prime divisor of $n$, apart from $q$, is 2 . However, $n-2=2(q-1) \notin P^{\prime}$ since $q-1>1$. Hence $P^{\prime}$ is good.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Let $p \mid n$ be a prime such that $n-p=p(n / p-1)=m^{2}$, for some $m \in \mathbb{N}$. Since $p \mid m^{2}$ and $p$ is prime, $p^{2} \mid m^{2}$, and hence $p \mid n / p-1<n / p$, so $p<\sqrt{n}$.
Now suppose to the contrary that $S$ is not good, so there are primes $p_{1}>p_{2}$ dividing $n$ such that $n-p_{1}<n-p_{2}$ are perfect squares. Then
$$
n-p_{2} \geqslant\left(\sqrt{n-p_{1}}+1\right)^{2}>n-p_{1}+2 \sqrt{n-p_{1}} \quad \Longrightarrow \quad p_{1}>p_{2}+2 \sqrt{n-p_{1}} \geqslant 2+2 \sqrt{n-p_{1}}
$$
The last condition implies that $p_{1}>2 \sqrt{n-1}$. But $p_{1}<\sqrt{n}$ by the first part, so $\sqrt{n}>2 \sqrt{n-1}$, which is a contradiction for $n>1$; the cases $n=0$ and $n=1$ are trivial. Thus $S$ is good.
(b) We claim that the infinite set $P=\{3,5,7,11, \ldots\}$ of odd primes, which is disjoint from $S$, is good. Indeed, let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some odd prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. Since $q$ is the only odd prime divisor of $n=2 q, P$ is good.
The set $P^{\prime}=\{2,3,5,7,11, \ldots\}$ of all primes is also good. The proof is similar: let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. If $q=2$, then 2 is the only prime divisor of $n$; if $q \neq 2$, then the only prime divisor of $n$, apart from $q$, is 2 . However, $n-2=2(q-1) \notin P^{\prime}$ since $q-1>1$. Hence $P^{\prime}$ is good.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
861857c9-e6d7-5d72-a219-2c9ff2ca9e62
| 604,166
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. By construction, $n$ is not prime, so $n-p, n-q \neq 0$, whence $k, \ell \geqslant 1$.
Hence $p^{2} k^{2}+p=q^{2} \ell^{2}+q$. Hence $p^{2} k^{2}<p^{2} k^{2}+p=q^{2} \ell^{2}+q<q^{2} \ell^{2}+2 q \ell+1=(q \ell+1)^{2}$. Similarly, $q^{2} \ell^{2}<(p k+1)^{2}$, whence $q \ell-1<p k<q \ell+1$. It follows that $p k=q \ell$, so $p^{2} k^{2}+p=q^{2} \ell^{2}+q$ yields the contradiction $p=q$. Hence $S$ is good.
(b) Let $A$ be a finite good set such that $0 \notin A$, and let $m=\max A$. Let $a \geqslant 2 m+1$ be an integer. We claim that $A^{\prime}=A \cup\{a\}$ is good. Indeed, suppose to the contrary that there exist $n \in \mathbb{N}$ and primes $p, q \mid n$ with $p \neq q$ such that $n-p, n-q \in A^{\prime}$. If $n<a$, then $n-p, n-q \in A$, which is a contradiction because $A$ is good. Hence $n \geqslant a$. Now $p \mid n-p$, so $n-p \geqslant p$ since $0 \notin A^{\prime}$. Thus $p \leqslant n / 2$ and hence $n-p \geqslant n / 2 \geqslant a / 2>m$. Similarly, $n-q>m$. It follows that $n-p=n-q=a$, which implies the contradiction $p=q$. Hence $A^{\prime}$ is good.
Now it is clear that any singleton set is good: indeed, if $A=\{a\}$, and $n \in \mathbb{N}$ has prime divisors $p, q$ such that $n-p, n-q \in A$, then $n-p=a=n-q$, so $p=q$. Starting from the singleton $T_{1}=\{2\}$, we use the above construction to obtain, iteratively, good sets $T_{2}, T_{3}, \ldots$ of $2,3, \ldots$ elements. It is clearly possibly to ensure that they are each disjoint from $S$ by not adding a perfect square at any stage. Then $T=T_{1} \cup T_{2} \cup \cdots$ is an infinite good set disjoint from $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. By construction, $n$ is not prime, so $n-p, n-q \neq 0$, whence $k, \ell \geqslant 1$.
Hence $p^{2} k^{2}+p=q^{2} \ell^{2}+q$. Hence $p^{2} k^{2}<p^{2} k^{2}+p=q^{2} \ell^{2}+q<q^{2} \ell^{2}+2 q \ell+1=(q \ell+1)^{2}$. Similarly, $q^{2} \ell^{2}<(p k+1)^{2}$, whence $q \ell-1<p k<q \ell+1$. It follows that $p k=q \ell$, so $p^{2} k^{2}+p=q^{2} \ell^{2}+q$ yields the contradiction $p=q$. Hence $S$ is good.
(b) Let $A$ be a finite good set such that $0 \notin A$, and let $m=\max A$. Let $a \geqslant 2 m+1$ be an integer. We claim that $A^{\prime}=A \cup\{a\}$ is good. Indeed, suppose to the contrary that there exist $n \in \mathbb{N}$ and primes $p, q \mid n$ with $p \neq q$ such that $n-p, n-q \in A^{\prime}$. If $n<a$, then $n-p, n-q \in A$, which is a contradiction because $A$ is good. Hence $n \geqslant a$. Now $p \mid n-p$, so $n-p \geqslant p$ since $0 \notin A^{\prime}$. Thus $p \leqslant n / 2$ and hence $n-p \geqslant n / 2 \geqslant a / 2>m$. Similarly, $n-q>m$. It follows that $n-p=n-q=a$, which implies the contradiction $p=q$. Hence $A^{\prime}$ is good.
Now it is clear that any singleton set is good: indeed, if $A=\{a\}$, and $n \in \mathbb{N}$ has prime divisors $p, q$ such that $n-p, n-q \in A$, then $n-p=a=n-q$, so $p=q$. Starting from the singleton $T_{1}=\{2\}$, we use the above construction to obtain, iteratively, good sets $T_{2}, T_{3}, \ldots$ of $2,3, \ldots$ elements. It is clearly possibly to ensure that they are each disjoint from $S$ by not adding a perfect square at any stage. Then $T=T_{1} \cup T_{2} \cup \cdots$ is an infinite good set disjoint from $S$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
861857c9-e6d7-5d72-a219-2c9ff2ca9e62
| 604,166
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $A P E F$ and $A P B C$ are cyclic, and so
$$
\begin{aligned}
\angle B D E & =\angle C D F=\angle A F D-\angle F C D=\angle A F E-\angle A C B=\left(180^{\circ}-\angle E P A\right)-\left(180^{\circ}-\angle B P A\right) \\
& =\angle B P A-\angle E P A=\angle B P E .
\end{aligned}
$$
Hence $D B E P$ is cyclic, too. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic. In particular, $\angle D P N=\angle D I N=90^{\circ}$. Let $R$ denote the second intersection of $D P$ and $\omega$, so $N Q \perp D R$. Then $\angle N P R=90^{\circ}$, so $R N$ is a diameter of $\omega$. It is well-known that $N$ is the midpoint of the arc $\overparen{B C}$ not containing $A$, whence $R N \perp B C$. Thus $D Q$ and $N Q$ are altitudes of triangle $R D N$, and so $Q$ is its orthocentre. This implies that $R Q \perp D N$, whence, since $R N$ is a diameter of $\omega$, the intersection $X$ of $R Q$ and $D N$ lies on $\omega$.
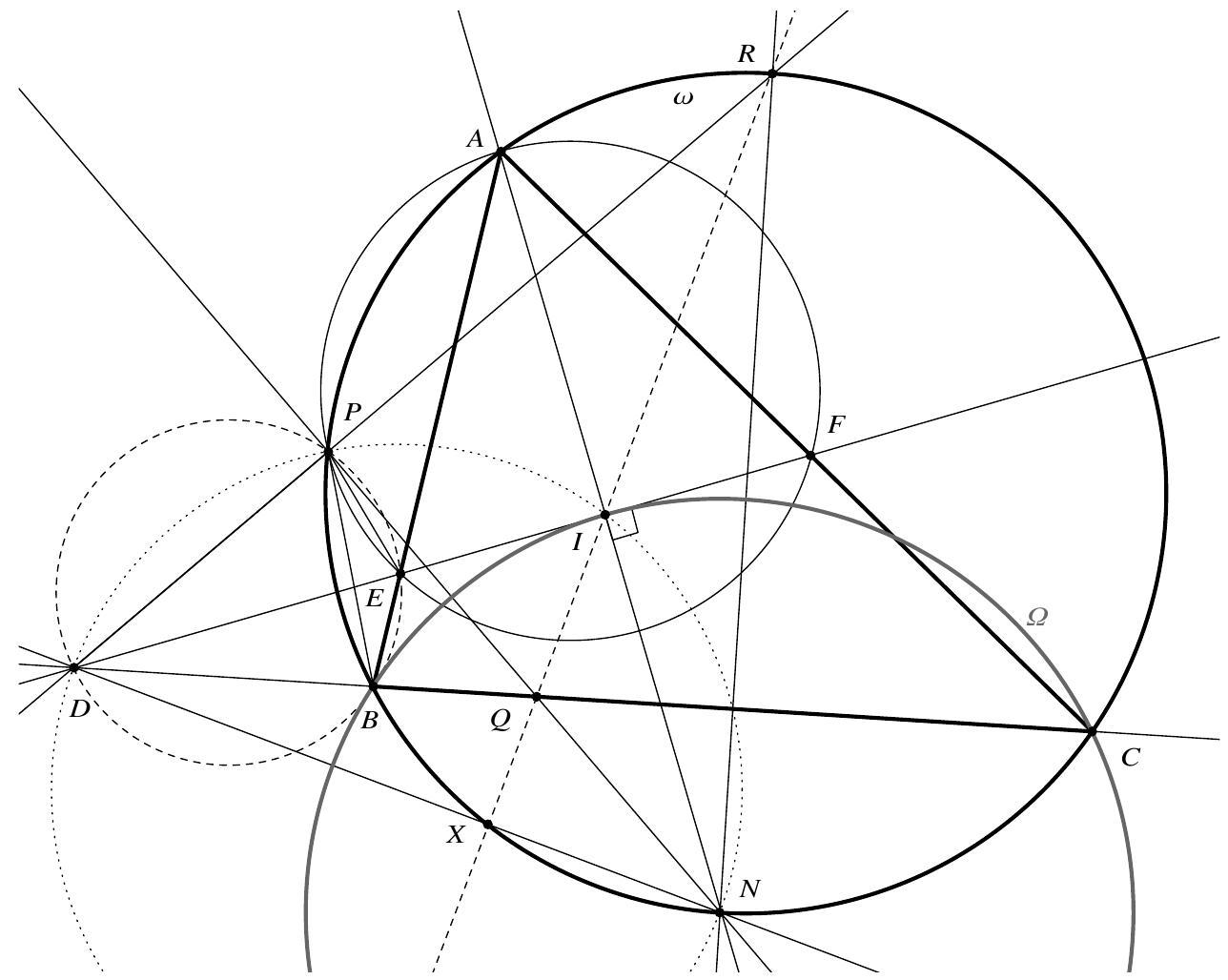
It is also well-known that $N$ is the centre of the circumcircle $\Omega$ of triangle $B C I$. Since $D I \perp I N$ by construction, $D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega$ and $\Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$. All of this shows that $R, I, Q, X$ lie on a line perpendicular to $D N$ that intersects $D N$ at $X \in \omega$. This completes the proof.
## BxMO 2023: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $A P E F$ and $A P B C$ are cyclic, and so
$$
\begin{aligned}
\angle B D E & =\angle C D F=\angle A F D-\angle F C D=\angle A F E-\angle A C B=\left(180^{\circ}-\angle E P A\right)-\left(180^{\circ}-\angle B P A\right) \\
& =\angle B P A-\angle E P A=\angle B P E .
\end{aligned}
$$
Hence $D B E P$ is cyclic, too. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic. In particular, $\angle D P N=\angle D I N=90^{\circ}$. Let $R$ denote the second intersection of $D P$ and $\omega$, so $N Q \perp D R$. Then $\angle N P R=90^{\circ}$, so $R N$ is a diameter of $\omega$. It is well-known that $N$ is the midpoint of the arc $\overparen{B C}$ not containing $A$, whence $R N \perp B C$. Thus $D Q$ and $N Q$ are altitudes of triangle $R D N$, and so $Q$ is its orthocentre. This implies that $R Q \perp D N$, whence, since $R N$ is a diameter of $\omega$, the intersection $X$ of $R Q$ and $D N$ lies on $\omega$.

It is also well-known that $N$ is the centre of the circumcircle $\Omega$ of triangle $B C I$. Since $D I \perp I N$ by construction, $D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega$ and $\Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$. All of this shows that $R, I, Q, X$ lie on a line perpendicular to $D N$ that intersects $D N$ at $X \in \omega$. This completes the proof.
## BxMO 2023: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0be64af-5588-5a19-9045-ad76b1488e70
| 604,239
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Let $K$ be the midpoint of segment $[B C]$. It is well-known that $N$ is the midpoint of the small $\operatorname{arc} \widehat{B C}$ of $\omega$, so $B C \perp K N$. In particular, $\angle D K N=90^{\circ}$. But $\angle D I N=90^{\circ}$ by construction, so $D I K N$ is cyclic, with circumcircle $\Gamma$.
Moreover, $\angle P E F=180^{\circ}-\angle P A F=180^{\circ}-\angle P A B=\angle P B C$ and $\angle P F E=\angle P A E=\angle P A B=\angle P C B$ since $A F E P$ and $A C B P$ are cyclic, so triangles $P E F$ and $P B C$ are similar. Now, by construction, $I$ is the midpoint of segment $[E F]$, so, $K$ being the midpoint of $[B C]$, triangles $P I F$ and $P K C$ are similar, too. It follows that $\angle P I D=180^{\circ}-\angle P I F=180^{\circ}-\angle P K C=\angle P K D$, whence $P$ lies on $\Gamma$.
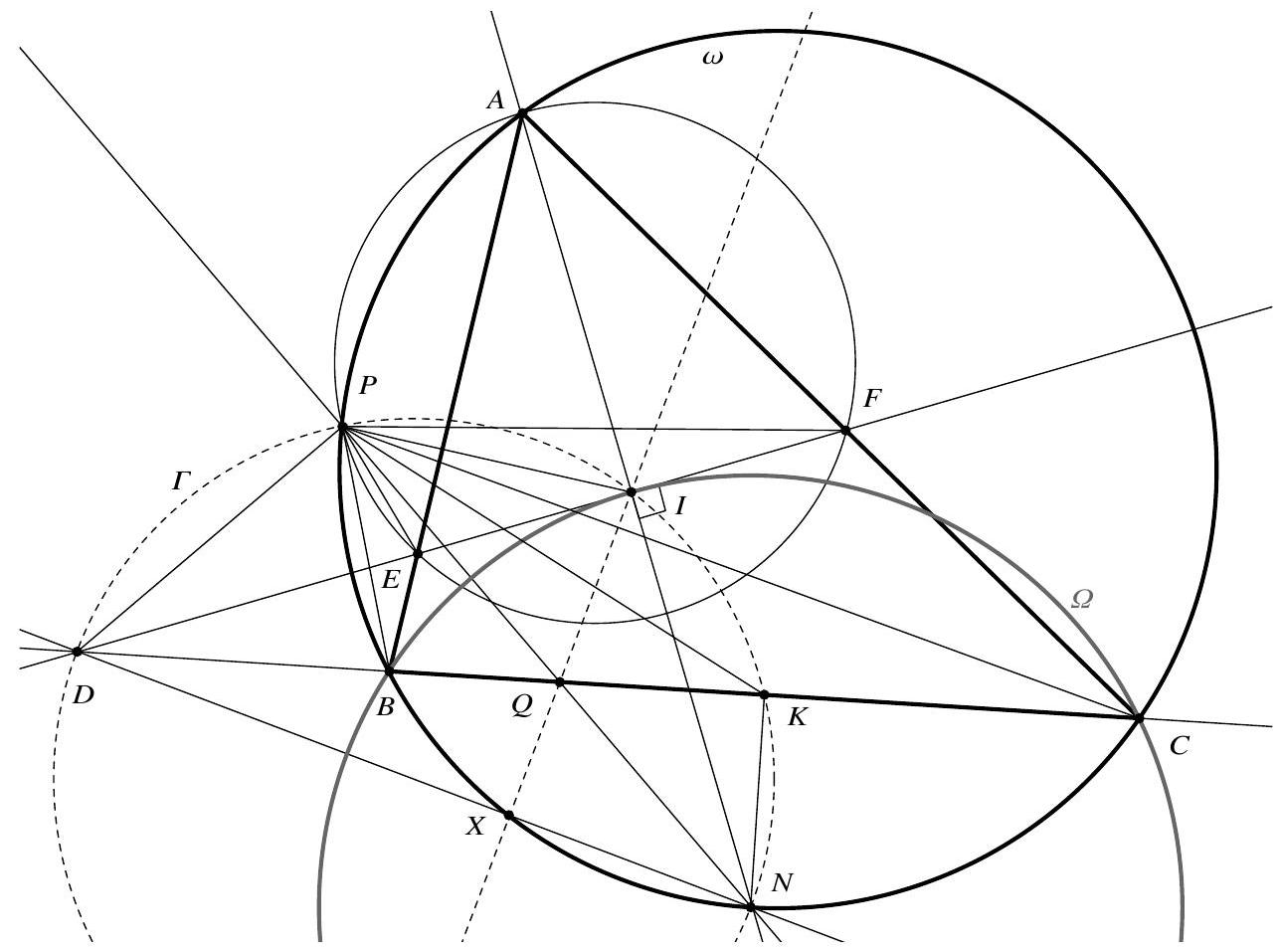
Let $\Omega$ be the circumcircle of triangle $B C I$. By construction, $Q$ lies on the radical axes $P N$ of $\omega, \Gamma$ and $B C$ of $\omega, \Omega$, so is the radical centre of $\omega, \Gamma, \Omega$. In particular, $I Q$ is the radical axis of $\Gamma, \Omega$, so is perpendicular to the line joining the centres of $\Gamma, \Omega$. Now it is well-known that $N$ is the centre of $\Omega$, and, since $\angle D I N=90^{\circ}$, the centre of $\Gamma$ is the midpoint of segment $[D N]$. This shows that $I Q \perp D N$.
Finally, let $D N$ meet $\omega$ again at $X$. Since $D I \perp I N$ by construction and $N$ is the centre of $\Omega, D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega, \Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$, i.e. $I X \perp D N$. Since $I Q \perp D N$, it follows that $X$ is the intersection of $I Q$ and $D N$. Since $X$ lies on $\omega$ by construction, this completes the proof.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Let $K$ be the midpoint of segment $[B C]$. It is well-known that $N$ is the midpoint of the small $\operatorname{arc} \widehat{B C}$ of $\omega$, so $B C \perp K N$. In particular, $\angle D K N=90^{\circ}$. But $\angle D I N=90^{\circ}$ by construction, so $D I K N$ is cyclic, with circumcircle $\Gamma$.
Moreover, $\angle P E F=180^{\circ}-\angle P A F=180^{\circ}-\angle P A B=\angle P B C$ and $\angle P F E=\angle P A E=\angle P A B=\angle P C B$ since $A F E P$ and $A C B P$ are cyclic, so triangles $P E F$ and $P B C$ are similar. Now, by construction, $I$ is the midpoint of segment $[E F]$, so, $K$ being the midpoint of $[B C]$, triangles $P I F$ and $P K C$ are similar, too. It follows that $\angle P I D=180^{\circ}-\angle P I F=180^{\circ}-\angle P K C=\angle P K D$, whence $P$ lies on $\Gamma$.

Let $\Omega$ be the circumcircle of triangle $B C I$. By construction, $Q$ lies on the radical axes $P N$ of $\omega, \Gamma$ and $B C$ of $\omega, \Omega$, so is the radical centre of $\omega, \Gamma, \Omega$. In particular, $I Q$ is the radical axis of $\Gamma, \Omega$, so is perpendicular to the line joining the centres of $\Gamma, \Omega$. Now it is well-known that $N$ is the centre of $\Omega$, and, since $\angle D I N=90^{\circ}$, the centre of $\Gamma$ is the midpoint of segment $[D N]$. This shows that $I Q \perp D N$.
Finally, let $D N$ meet $\omega$ again at $X$. Since $D I \perp I N$ by construction and $N$ is the centre of $\Omega, D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega, \Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$, i.e. $I X \perp D N$. Since $I Q \perp D N$, it follows that $X$ is the intersection of $I Q$ and $D N$. Since $X$ lies on $\omega$ by construction, this completes the proof.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0be64af-5588-5a19-9045-ad76b1488e70
| 604,239
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Since $A P E F$ and $A P B C$ are cyclic,
$$
\begin{aligned}
\angle C P F & =\angle B P A-\angle B P C-\angle F P A=\left(180^{\circ}-\angle B C A\right)-\angle B A C-\angle F E A \\
& =\left(180^{\circ}-\angle B C A-\angle B A C\right)-\angle B E D=\angle C B A-\angle B E D=\angle C B E-\angle B E D=\angle B D E=\angle C D F,
\end{aligned}
$$
so $D P F C$ is cyclic, too. Thence $\angle C P D=\angle C F D=180^{\circ}-\angle I F A=90^{\circ}+\angle I A F=90^{\circ}+\angle C A N=90^{\circ}+\angle C P N$. Hence $\angle D P N=\angle C P D-\angle C P N=90^{\circ}$. Since $\angle D I N=90^{\circ}$ by construction, it follows that $D P I N$ is cyclic, with
circumcircle $\Gamma$. Let $J$ be the second intersection of line $I Q$ and $\Gamma$. Moreover, it is well-known that $N$ is the centre of the circumcircle $\Omega$ of $B I C$. In particular, $|N I|=|N B|$, and so, since $N I P J$ and $N B P C$ are cyclic,
$$
\frac{|J Q|}{|J P|}=\frac{|N Q|}{|N I|}=\frac{|N Q|}{|N B|}=\frac{|C Q|}{|C P|}
$$
Let $S$ now be the point of intersection of $P N$ and $\Omega$ such that $P, N, S$ lie on line $P N$ in this order. By construction, $\angle Q P C=\angle N P C=\angle N A C=\angle B A N=\angle B C N=\angle Q C N$, so triangles $C Q N$ and $P C N$ are similar, whence
$$
\frac{|C Q|}{|C P|}=\frac{|N C|}{|N P|}=\frac{|N Q|}{|N C|}=\frac{|N C|+|N Q|}{|N C|+|N P|}=\frac{|N S|+|N Q|}{|N S|+|N P|}=\frac{|S Q|}{|S P|}
$$
Combining (1) and (2) shows that $C, J, S$ lie on a circle of Apollonius, the centre of which lies on the line through $P, Q, N, S$, so, since $|N C|=|N S|$ by construction, is $N$. In other words, $J$ lies on $\Omega$.
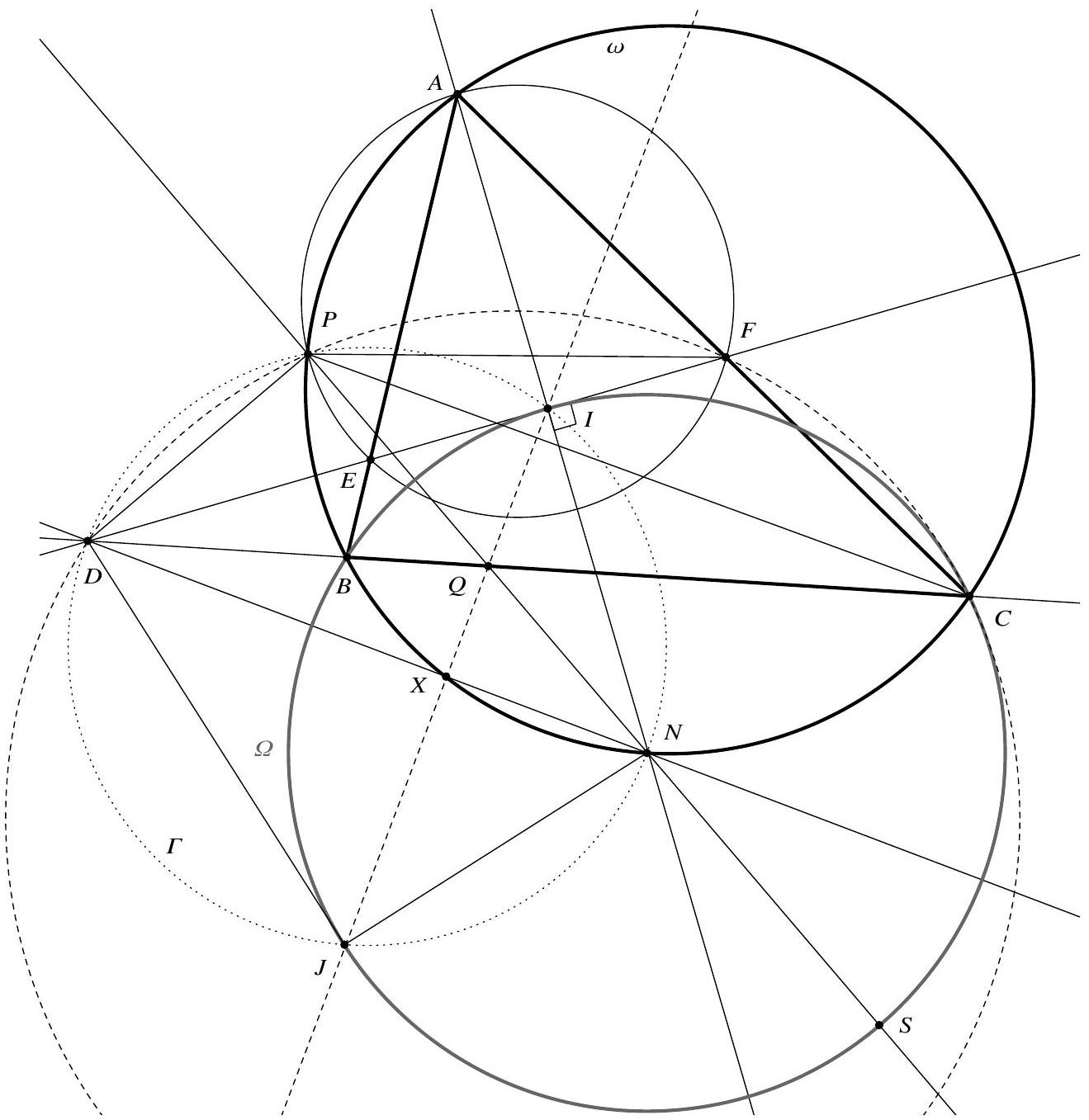
In particular, $|N I|=|N J|$. Now, by construction, $\angle D I N=\angle D J N=90^{\circ}$, so the right-angled triangles $D I N$ and $D J N$ are congruent, whence $D I N J$ is a kite. In particular, $I J \perp D N$. Since $Q$ lies on $I J$ by definition, this shows that $I Q \perp D N$. We can now conclude as in Solution 2.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Since $A P E F$ and $A P B C$ are cyclic,
$$
\begin{aligned}
\angle C P F & =\angle B P A-\angle B P C-\angle F P A=\left(180^{\circ}-\angle B C A\right)-\angle B A C-\angle F E A \\
& =\left(180^{\circ}-\angle B C A-\angle B A C\right)-\angle B E D=\angle C B A-\angle B E D=\angle C B E-\angle B E D=\angle B D E=\angle C D F,
\end{aligned}
$$
so $D P F C$ is cyclic, too. Thence $\angle C P D=\angle C F D=180^{\circ}-\angle I F A=90^{\circ}+\angle I A F=90^{\circ}+\angle C A N=90^{\circ}+\angle C P N$. Hence $\angle D P N=\angle C P D-\angle C P N=90^{\circ}$. Since $\angle D I N=90^{\circ}$ by construction, it follows that $D P I N$ is cyclic, with
circumcircle $\Gamma$. Let $J$ be the second intersection of line $I Q$ and $\Gamma$. Moreover, it is well-known that $N$ is the centre of the circumcircle $\Omega$ of $B I C$. In particular, $|N I|=|N B|$, and so, since $N I P J$ and $N B P C$ are cyclic,
$$
\frac{|J Q|}{|J P|}=\frac{|N Q|}{|N I|}=\frac{|N Q|}{|N B|}=\frac{|C Q|}{|C P|}
$$
Let $S$ now be the point of intersection of $P N$ and $\Omega$ such that $P, N, S$ lie on line $P N$ in this order. By construction, $\angle Q P C=\angle N P C=\angle N A C=\angle B A N=\angle B C N=\angle Q C N$, so triangles $C Q N$ and $P C N$ are similar, whence
$$
\frac{|C Q|}{|C P|}=\frac{|N C|}{|N P|}=\frac{|N Q|}{|N C|}=\frac{|N C|+|N Q|}{|N C|+|N P|}=\frac{|N S|+|N Q|}{|N S|+|N P|}=\frac{|S Q|}{|S P|}
$$
Combining (1) and (2) shows that $C, J, S$ lie on a circle of Apollonius, the centre of which lies on the line through $P, Q, N, S$, so, since $|N C|=|N S|$ by construction, is $N$. In other words, $J$ lies on $\Omega$.

In particular, $|N I|=|N J|$. Now, by construction, $\angle D I N=\angle D J N=90^{\circ}$, so the right-angled triangles $D I N$ and $D J N$ are congruent, whence $D I N J$ is a kite. In particular, $I J \perp D N$. Since $Q$ lies on $I J$ by definition, this shows that $I Q \perp D N$. We can now conclude as in Solution 2.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0be64af-5588-5a19-9045-ad76b1488e70
| 604,239
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $P$ is the Miquel point of quadrilateral $B C F E$ (and the resulting complete quadrilateral with points $A$ and $D$ added) because it is the intersection of $\omega$ and the circumcircle of triangle $A E F$. In particular, $D B E P$ is
## BxMO 2023: Problems and Solutions
cyclic. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic.
Next, let $X$ be the intersection of $D N$ and $\omega$ and let $A N$ meet $B C$ at $Y$. Then $\angle N A C=\angle A / 2=\angle N C B$, so $\angle B Y A=\angle C+\angle N A C=\angle C+\angle N C B=\angle N C A$ and hence
$$
\begin{aligned}
\angle D Q P & =\angle N Q Y=\angle Q Y A-\angle Q N Y=\angle B Y A-\angle P N A \\
& =\angle N C A-\angle P C A=\angle P C N=180^{\circ}-\angle N X P=\angle D X P
\end{aligned}
$$
This implies that $D X Q P$ is cyclic. In particular, $Q X \perp D N$. It now suffices to show that $I X \perp D N$, which we do in the same way as in Solution 2.
## BxMO 2023: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $P$ is the Miquel point of quadrilateral $B C F E$ (and the resulting complete quadrilateral with points $A$ and $D$ added) because it is the intersection of $\omega$ and the circumcircle of triangle $A E F$. In particular, $D B E P$ is
## BxMO 2023: Problems and Solutions
cyclic. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic.

Next, let $X$ be the intersection of $D N$ and $\omega$ and let $A N$ meet $B C$ at $Y$. Then $\angle N A C=\angle A / 2=\angle N C B$, so $\angle B Y A=\angle C+\angle N A C=\angle C+\angle N C B=\angle N C A$ and hence
$$
\begin{aligned}
\angle D Q P & =\angle N Q Y=\angle Q Y A-\angle Q N Y=\angle B Y A-\angle P N A \\
& =\angle N C A-\angle P C A=\angle P C N=180^{\circ}-\angle N X P=\angle D X P
\end{aligned}
$$
This implies that $D X Q P$ is cyclic. In particular, $Q X \perp D N$. It now suffices to show that $I X \perp D N$, which we do in the same way as in Solution 2.
## BxMO 2023: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0be64af-5588-5a19-9045-ad76b1488e70
| 604,239
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is $$ \frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2} $$
|
We start by proving the following lemma: for a
$$
(2 m-1,2 n-1)
$$
-grid, there are equally many paths with a region of even area (called even paths), as there are with odd area (odd paths).
To prove this, we take a path and rotate it around the center of the grid. Then a path spanning a region with area $x$ is mapped on one spanning an area $(2 m-1)(2 n-1)-x$. This gives a bijection between paths creating an even region, and creating an odd region.
Now, for every path from
to $(2 n, 2 n)$, consider all the coordinates of the grid points it visits in order. There are $\binom{2 n}{n}$ of them which never visit a point with odd coordinates (which we call an odd point). Notice that such paths are all even.
We now construction a bijection between the remaining even paths and the odd paths. For each odd point, there are equally many even as odd paths from $(0,0)$ to that point. Define then a bijection $\phi$ between the sets of odd paths and even paths up to this point for each point. Notice that $\phi$ implicitly depends on the chosen odd point.
Now, for an arbitrary odd path $P$, consider the first odd point it passes through. Map $P$ to another path by changing the path up to this odd point to the $\phi$ of the path up to this point. As $\phi$ maps between even and odd paths, the resulting path is an even path. By the definition of $\phi$, and as each of the remaining paths goes to an odd point, this mapping defines a bijection.
We have hence found a bijection between the odd and even paths in the remaining $\binom{4 n}{2 n}-\binom{2 n}{n}$ paths, which yields the required result like in solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is $$ \frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2} $$
|
We start by proving the following lemma: for a
$$
(2 m-1,2 n-1)
$$
-grid, there are equally many paths with a region of even area (called even paths), as there are with odd area (odd paths).
To prove this, we take a path and rotate it around the center of the grid. Then a path spanning a region with area $x$ is mapped on one spanning an area $(2 m-1)(2 n-1)-x$. This gives a bijection between paths creating an even region, and creating an odd region.
Now, for every path from
to $(2 n, 2 n)$, consider all the coordinates of the grid points it visits in order. There are $\binom{2 n}{n}$ of them which never visit a point with odd coordinates (which we call an odd point). Notice that such paths are all even.
We now construction a bijection between the remaining even paths and the odd paths. For each odd point, there are equally many even as odd paths from $(0,0)$ to that point. Define then a bijection $\phi$ between the sets of odd paths and even paths up to this point for each point. Notice that $\phi$ implicitly depends on the chosen odd point.
Now, for an arbitrary odd path $P$, consider the first odd point it passes through. Map $P$ to another path by changing the path up to this odd point to the $\phi$ of the path up to this point. As $\phi$ maps between even and odd paths, the resulting path is an even path. By the definition of $\phi$, and as each of the remaining paths goes to an odd point, this mapping defines a bijection.
We have hence found a bijection between the odd and even paths in the remaining $\binom{4 n}{2 n}-\binom{2 n}{n}$ paths, which yields the required result like in solution 1.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
e39d6fca-5ef7-5264-8bc0-1864b282082e
| 604,315
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
We show that the pair $(a, b)$ of the form $a=2^{p(p-1)}, b=3^{p(p-1)}-2^{p(p-1)}$ for sufficiently larger prime number $p$ satisfies the inequality. First, notice that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$ indeed. In addition, see that $\operatorname{rad}(a)=2$, and $\operatorname{rad}(a+b)=3$. Because of Euler-Fermat, as $\phi\left(p^{2}\right)=p(p-1)$, it can directly be seen that $p^{2} \mid b$. In this case, $\operatorname{rad}(b) \leqslant \frac{b}{p}$. It then follows that, as rad is multiplicative for coprime numbers, that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a) \operatorname{rad}(b) \operatorname{rad}(a+b) \leqslant 2 \cdot 3 \cdot \frac{b}{p} \leqslant \frac{6}{p}(a+b)
$$
Then, by choosing $p$ such that $\frac{6}{p}<\frac{1}{2024^{2024}}$, we found $a$ and $b$ satifying the inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
We show that the pair $(a, b)$ of the form $a=2^{p(p-1)}, b=3^{p(p-1)}-2^{p(p-1)}$ for sufficiently larger prime number $p$ satisfies the inequality. First, notice that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$ indeed. In addition, see that $\operatorname{rad}(a)=2$, and $\operatorname{rad}(a+b)=3$. Because of Euler-Fermat, as $\phi\left(p^{2}\right)=p(p-1)$, it can directly be seen that $p^{2} \mid b$. In this case, $\operatorname{rad}(b) \leqslant \frac{b}{p}$. It then follows that, as rad is multiplicative for coprime numbers, that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a) \operatorname{rad}(b) \operatorname{rad}(a+b) \leqslant 2 \cdot 3 \cdot \frac{b}{p} \leqslant \frac{6}{p}(a+b)
$$
Then, by choosing $p$ such that $\frac{6}{p}<\frac{1}{2024^{2024}}$, we found $a$ and $b$ satifying the inequality.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
4e52aff0-c6d9-53c6-a584-91f35ede162c
| 604,381
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
We show that the pair $(a, b)$ of the form $a=3^{2^{k}}, b=5^{2^{k}}-3^{2^{k}}$ for sufficiently large $k$ satisifies the inequality. Again, we have that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$. Similarly to solution $1, \operatorname{rad}(a(a+b))=$ $\operatorname{rad}(a) \operatorname{rad}(a+b)=3 \cdot 5=15$. Then, we will show that $2^{k+1} \mid b$, from which it would follow that $\operatorname{rad}(b) \leqslant \frac{b}{2^{k}}$. From this, we then see that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a(a+b)) \operatorname{rad}(b) \leqslant \frac{15 b}{2^{k}} .
$$
Like in solution 1, this gives a pair $(a, b)$ satisfying the inequality for sufficiently large $k$.
There are various ways to show that $2^{k+1} \mid 5^{2^{k}}-3^{2^{k}}$, for example directly by applying the Lifting-The-Exponent Lemma. For a more elementary proof, we can apply induction on $k$. The statement is clearly true for $k=0$, and if the statement holds for $k=n$, then for $k=n+1$ we see that
$$
5^{2^{k}}-3^{2^{k}}=5^{2^{n+1}}-3^{2^{n+1}}=\left(5^{2^{n}}\right)^{2}-\left(3^{2^{n}}\right)^{2}=\left(5^{2^{n}}-3^{2^{n}}\right)\left(5^{2^{n}}+3^{2^{n}}\right) .
$$
From the induction hypothesis, the first factor has $n+1$ factors of 2 . As the second factor is a sum of two odd numbers, the second term has at least one factor of 2 . The product thus has at least $n+2=k+1$ factors of 2 , from which the statement follows by induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
We show that the pair $(a, b)$ of the form $a=3^{2^{k}}, b=5^{2^{k}}-3^{2^{k}}$ for sufficiently large $k$ satisifies the inequality. Again, we have that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$. Similarly to solution $1, \operatorname{rad}(a(a+b))=$ $\operatorname{rad}(a) \operatorname{rad}(a+b)=3 \cdot 5=15$. Then, we will show that $2^{k+1} \mid b$, from which it would follow that $\operatorname{rad}(b) \leqslant \frac{b}{2^{k}}$. From this, we then see that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a(a+b)) \operatorname{rad}(b) \leqslant \frac{15 b}{2^{k}} .
$$
Like in solution 1, this gives a pair $(a, b)$ satisfying the inequality for sufficiently large $k$.
There are various ways to show that $2^{k+1} \mid 5^{2^{k}}-3^{2^{k}}$, for example directly by applying the Lifting-The-Exponent Lemma. For a more elementary proof, we can apply induction on $k$. The statement is clearly true for $k=0$, and if the statement holds for $k=n$, then for $k=n+1$ we see that
$$
5^{2^{k}}-3^{2^{k}}=5^{2^{n+1}}-3^{2^{n+1}}=\left(5^{2^{n}}\right)^{2}-\left(3^{2^{n}}\right)^{2}=\left(5^{2^{n}}-3^{2^{n}}\right)\left(5^{2^{n}}+3^{2^{n}}\right) .
$$
From the induction hypothesis, the first factor has $n+1$ factors of 2 . As the second factor is a sum of two odd numbers, the second term has at least one factor of 2 . The product thus has at least $n+2=k+1$ factors of 2 , from which the statement follows by induction.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
4e52aff0-c6d9-53c6-a584-91f35ede162c
| 604,381
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
Choose $a=\left(4^{x}-1\right)^{2}, b=4^{x+1}$ and $a+b=\left(4^{x}+1\right)^{2}$. That is, $a, b$ and $a+b$ are squares, where $b$ only contains the factor 2 . Note that $a$ and $b$ are indeed coprime. Then $\operatorname{rad}(a b c)=2 \operatorname{rad}\left(16^{x}-1\right)$.
Choose then $x=5^{k}$ such that $x>2 \cdot 2024^{2024}$. By Lifting the exponent, we know that $5^{k+1} \mid 16^{5^{k}}-1$. This implies that $2 \operatorname{rad}\left(16^{x}-1\right) \leqslant 2\left(16^{x}-1\right) / 5^{k}<\left(4^{x}+1\right)^{2} / 2024^{2024}$.
This solution also works with Euler-Fermat, by choosing $x=\phi\left(5^{k+1}\right)$ with $5^{k}>2024^{2024}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and $$ \operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}} $$ For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
|
Choose $a=\left(4^{x}-1\right)^{2}, b=4^{x+1}$ and $a+b=\left(4^{x}+1\right)^{2}$. That is, $a, b$ and $a+b$ are squares, where $b$ only contains the factor 2 . Note that $a$ and $b$ are indeed coprime. Then $\operatorname{rad}(a b c)=2 \operatorname{rad}\left(16^{x}-1\right)$.
Choose then $x=5^{k}$ such that $x>2 \cdot 2024^{2024}$. By Lifting the exponent, we know that $5^{k+1} \mid 16^{5^{k}}-1$. This implies that $2 \operatorname{rad}\left(16^{x}-1\right) \leqslant 2\left(16^{x}-1\right) / 5^{k}<\left(4^{x}+1\right)^{2} / 2024^{2024}$.
This solution also works with Euler-Fermat, by choosing $x=\phi\left(5^{k+1}\right)$ with $5^{k}>2024^{2024}$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
4e52aff0-c6d9-53c6-a584-91f35ede162c
| 604,381
|
Let $A B C D$ be a trapezoid with $A B$ parallel to $C D,|A B|>|C D|$, and equal edges $|A D|=|B C|$. Let $I$ be the center of the circle tangent to lines $A B, A C$ and $B D$, where $A$ and $I$ are on opposite sides of $B D$. Let $J$ be the center of the circle tangent to lines $C D, A C$ and $B D$, where $D$ and $J$ are on opposite sides of $A C$. Prove that $|I C|=|J B|$.
|
Let $\{P\}=A C \cap B D$ and let $\angle A P B=180-2 a$. Since $A B C D$ is an isosceles trapezoid, $A P B$ is an isosceles triangle. Therefore $\angle P B A=a$, which implies that $\angle P B I=90^{\circ}-a / 2$ since $I$ lies on the external bisector of $\angle P B A$. Since $I$ lies on the bisector of $\angle C P B$, it follows that $\angle B P I=a$ and hence that $I P B$ is isosceles with $|I P|=|P B|$. Similarly $J P C$ is isosceles with $|J P|=|P C|$. So, in the triangles $C P I$ and $B P J$ we have $P I \equiv P B$ and $P J \equiv C P$. Since $I$ and $J$ both lie on the internal bisector of $\angle B P C$, it follows that triangles $C P I$ and $B P J$ are congruent. Therefore $|I C|=|J B|$.
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a trapezoid with $A B$ parallel to $C D,|A B|>|C D|$, and equal edges $|A D|=|B C|$. Let $I$ be the center of the circle tangent to lines $A B, A C$ and $B D$, where $A$ and $I$ are on opposite sides of $B D$. Let $J$ be the center of the circle tangent to lines $C D, A C$ and $B D$, where $D$ and $J$ are on opposite sides of $A C$. Prove that $|I C|=|J B|$.
|
Let $\{P\}=A C \cap B D$ and let $\angle A P B=180-2 a$. Since $A B C D$ is an isosceles trapezoid, $A P B$ is an isosceles triangle. Therefore $\angle P B A=a$, which implies that $\angle P B I=90^{\circ}-a / 2$ since $I$ lies on the external bisector of $\angle P B A$. Since $I$ lies on the bisector of $\angle C P B$, it follows that $\angle B P I=a$ and hence that $I P B$ is isosceles with $|I P|=|P B|$. Similarly $J P C$ is isosceles with $|J P|=|P C|$. So, in the triangles $C P I$ and $B P J$ we have $P I \equiv P B$ and $P J \equiv C P$. Since $I$ and $J$ both lie on the internal bisector of $\angle B P C$, it follows that triangles $C P I$ and $B P J$ are congruent. Therefore $|I C|=|J B|$.
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
|
{
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"problem_match": "\nProblem No. 1.",
"solution_match": "\nSolution."
}
|
b942117e-3589-5739-8726-eb2f209692c3
| 604,410
|
At a dinner party there are $N$ hosts and $N$ guests, seated around a circular table, where $N \geq 4$. A pair of two guests will chat with one another if either there is at most one person seated between them or if there are exactly two people between them, at least one of whom is a host. Prove that no matter how the 2 N people are seated at the dinner party, at least $N$ pairs of guests will chat with one another.
|
Let a run refer to a maximal group of consecutive dinner party guests all of whom are the same type (host or guest). Suppose that there are exactly $k$ runs of hosts and $k$ runs of guests. Let $G_{i}$ and $H_{i}$ denote the number of runs of guests and hosts, respectively, of length exactly $i$. Furthermore, let $X$ denote the number of hosts surrounded by two runs of guests, both of length exactly 1 . We claim that the number of pairs of guests who chat is at least
$$
2 N-3 k+G_{1}+2 H_{1}+H_{2}-X
$$
The number of pairs of guests who chat with no host between them is at least the sum of $\max \{2 \ell-3,0\}$ over all guest run lengths $\ell$. This sum is at least $2 N-3 k+G_{1}$. The number of pairs of guests who chat with exactly two hosts between them is $H_{2}$. Furthermore, the number of pairs of guests who chat with exactly one host between them is at least $2 H_{1}-X$. This is because any host surrounded by two runs of guests causes at least two pairs of guests to chat unless these runs are both of length exactly 1 . This proves the claim. Now note that
$$
2 H_{1}+H_{2}+N \geq 3 k
$$
because each run of hosts contributes at least three to the left hand side. Furthermore, pairing each run counted in $X$ with the guest run of length 1 immediately following it in clockwise order shows that $G_{1} \geq X$. Combining these inequalities yields that $2 N-3 k+G_{1}+2 H_{1}+H_{2}-X \geq N$, completing the proof of the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
At a dinner party there are $N$ hosts and $N$ guests, seated around a circular table, where $N \geq 4$. A pair of two guests will chat with one another if either there is at most one person seated between them or if there are exactly two people between them, at least one of whom is a host. Prove that no matter how the 2 N people are seated at the dinner party, at least $N$ pairs of guests will chat with one another.
|
Let a run refer to a maximal group of consecutive dinner party guests all of whom are the same type (host or guest). Suppose that there are exactly $k$ runs of hosts and $k$ runs of guests. Let $G_{i}$ and $H_{i}$ denote the number of runs of guests and hosts, respectively, of length exactly $i$. Furthermore, let $X$ denote the number of hosts surrounded by two runs of guests, both of length exactly 1 . We claim that the number of pairs of guests who chat is at least
$$
2 N-3 k+G_{1}+2 H_{1}+H_{2}-X
$$
The number of pairs of guests who chat with no host between them is at least the sum of $\max \{2 \ell-3,0\}$ over all guest run lengths $\ell$. This sum is at least $2 N-3 k+G_{1}$. The number of pairs of guests who chat with exactly two hosts between them is $H_{2}$. Furthermore, the number of pairs of guests who chat with exactly one host between them is at least $2 H_{1}-X$. This is because any host surrounded by two runs of guests causes at least two pairs of guests to chat unless these runs are both of length exactly 1 . This proves the claim. Now note that
$$
2 H_{1}+H_{2}+N \geq 3 k
$$
because each run of hosts contributes at least three to the left hand side. Furthermore, pairing each run counted in $X$ with the guest run of length 1 immediately following it in clockwise order shows that $G_{1} \geq X$. Combining these inequalities yields that $2 N-3 k+G_{1}+2 H_{1}+H_{2}-X \geq N$, completing the proof of the desired result.
|
{
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"problem_match": "\n## Problem No. 3.",
"solution_match": "\nSolution."
}
|
940d083b-69ec-5383-995b-234945840ba0
| 604,437
|
Let $d(k)$ denote the number of positive integer divisors of $k$. For example, $d(6)=4$ since 6 has 4 positive divisors, namely, $1,2,3$, and 6 . Prove that for all positive integers $n$,
$$
d(1)+d(3)+d(5)+\cdots+d(2 n-1) \leq d(2)+d(4)+d(6)+\cdots+d(2 n)
$$
|
For any integer $k$ and set of integers $S$, let $f_{S}(k)$ be the number of multiples of $k$ in $S$. We can count the number of pairs $(k, s)$ with $k \in \mathbb{N}$ dividing $s \in S$ in two different ways, as follows:
- For each $s \in S$, there are $d(s)$ pairs that include $s$, one for each divisor of $s$.
- For each $k \in \mathbb{N}$, there are $f_{k}(S)$ pairs that include $k$, one for each multiple of $k$.
Therefore,
$$
\sum_{s \in S} d(s)=\sum_{k \in \mathbb{N}} f_{S}(k)
$$
Let
$$
O=\{1,3,5, \ldots, 2 n-1\} \quad \text { and } \quad E=\{2,4,6, \ldots, 2 n\}
$$
be the set of odd and, respectively, the set of even integers between 1 and $2 n$. It suffices to show that
$$
\sum_{k \in \mathbb{N}} f_{O}(k) \leq \sum_{k \in \mathbb{N}} f_{E}(k)
$$
Since the elements of $O$ only have odd divisors,
$$
\sum_{k \in \mathbb{N}} f_{O}(k)=\sum_{k \text { odd }} f_{O}(k)
$$
For any odd $k$, consider the multiples of $k$ between 1 and $2 n$. They form a sequence
$$
k, 2 k, 3 k, \ldots,\left\lfloor\frac{2 n}{k}\right\rfloor k
$$
alternating between odd and even terms. There are either an equal number of odd and even terms, or there is one more odd term than even terms. Therefore, we have the inequality
$$
f_{O}(k) \leq f_{E}(k)+1
$$
for all odd $k$. Combining this with the previous observations gives us the desired inequality:
$$
\begin{aligned}
\sum_{k \in \mathbb{N}} f_{O}(k) & =\sum_{k \text { odd }} f_{O}(k) \\
& \leq \sum_{k \text { odd }}\left(f_{E}(k)+1\right) \\
& =\sum_{k \text { odd }} f_{E}(k)+n \\
& =\sum_{k \text { odd }} f_{E}(k)+f_{E}(2) \\
& \leq \sum_{k \in \mathbb{N}} f_{E}(k)
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $d(k)$ denote the number of positive integer divisors of $k$. For example, $d(6)=4$ since 6 has 4 positive divisors, namely, $1,2,3$, and 6 . Prove that for all positive integers $n$,
$$
d(1)+d(3)+d(5)+\cdots+d(2 n-1) \leq d(2)+d(4)+d(6)+\cdots+d(2 n)
$$
|
For any integer $k$ and set of integers $S$, let $f_{S}(k)$ be the number of multiples of $k$ in $S$. We can count the number of pairs $(k, s)$ with $k \in \mathbb{N}$ dividing $s \in S$ in two different ways, as follows:
- For each $s \in S$, there are $d(s)$ pairs that include $s$, one for each divisor of $s$.
- For each $k \in \mathbb{N}$, there are $f_{k}(S)$ pairs that include $k$, one for each multiple of $k$.
Therefore,
$$
\sum_{s \in S} d(s)=\sum_{k \in \mathbb{N}} f_{S}(k)
$$
Let
$$
O=\{1,3,5, \ldots, 2 n-1\} \quad \text { and } \quad E=\{2,4,6, \ldots, 2 n\}
$$
be the set of odd and, respectively, the set of even integers between 1 and $2 n$. It suffices to show that
$$
\sum_{k \in \mathbb{N}} f_{O}(k) \leq \sum_{k \in \mathbb{N}} f_{E}(k)
$$
Since the elements of $O$ only have odd divisors,
$$
\sum_{k \in \mathbb{N}} f_{O}(k)=\sum_{k \text { odd }} f_{O}(k)
$$
For any odd $k$, consider the multiples of $k$ between 1 and $2 n$. They form a sequence
$$
k, 2 k, 3 k, \ldots,\left\lfloor\frac{2 n}{k}\right\rfloor k
$$
alternating between odd and even terms. There are either an equal number of odd and even terms, or there is one more odd term than even terms. Therefore, we have the inequality
$$
f_{O}(k) \leq f_{E}(k)+1
$$
for all odd $k$. Combining this with the previous observations gives us the desired inequality:
$$
\begin{aligned}
\sum_{k \in \mathbb{N}} f_{O}(k) & =\sum_{k \text { odd }} f_{O}(k) \\
& \leq \sum_{k \text { odd }}\left(f_{E}(k)+1\right) \\
& =\sum_{k \text { odd }} f_{E}(k)+n \\
& =\sum_{k \text { odd }} f_{E}(k)+f_{E}(2) \\
& \leq \sum_{k \in \mathbb{N}} f_{E}(k)
\end{aligned}
$$
|
{
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"problem_match": "\nP2.",
"solution_match": "\nSolution."
}
|
eef6c32d-ce30-5ccb-940a-861e6831f5fe
| 604,492
|
Let $n \geq 2$ be an integer. Initially, the number 1 is written $n$ times on a board. Every minute, Vishal picks two numbers written on the board, say $a$ and $b$, erases them, and writes either $a+b$ or $\min \left\{a^{2}, b^{2}\right\}$. After $n-1$ minutes there is one number left on the board. Let the largest possible value for this final number be $f(n)$. Prove that
$$
2^{n / 3}<f(n) \leq 3^{n / 3}
$$
|
Clearly $f(n)$ is a strictly increasing function, as we can form $f(n-1)$ with $n-1$ ones, and add the final one. However, we can do better; assume Vishal generates $f(n)$ on the board. After $n-2$ minutes, there are two numbers left, say they were formed by $x$ ones and $y$ ones, where $x+y=n$. Clearly the numbers are at most $f(x), f(y)$ (and can be made to be equal to $f(x), f(y))$, and therefore we obtain
$$
f(n)=\max _{x+y=n, 1 \leq x \leq y \leq n-1}\left(\max \left(f(x)+f(y), f(x)^{2}\right)\right)
$$
where we used the fact that $f$ is increasing to get that $\min \left(f(x)^{2}, f(y)^{2}\right)=f(x)^{2}$ when $x \leq y$. In particular, $f(n+1) \geq f(n)+1$, and $f(2 n) \geq f(n)^{2}$ for all positive integers $n$.
Upper bound:
First proof of upper bound. We use induction. We can check that $f(n)=n$ for $n \leq 4$, and these all satisfy the bound $f(n)=n \leq 3^{n / 3}$. Assume it is true for all $m<n$ (some $n \geq 5$ ), and with $x, y$ as in equation ?? we have
$$
f(x)^{2} \leq f\left(\left\lfloor\frac{n}{2}\right\rfloor\right)^{2} \leq\left(3^{n / 6}\right)^{2}=3^{n / 3}
$$
as desired. It thus remains to show that $f(x)+f(y) \leq 3^{n / 3}$. By induction, it suffices to prove that
$$
3^{x / 3}+3^{y / 3} \leq 3^{(x+y) / 3}
$$
for $1 \leq x \leq y \leq n-1$ and $x+y=n$. This is equivalent to
$$
1+3^{(y-x) / 3} \leq 3^{y / 3}
$$
Let $w=3^{(y-x) / 3}$, and we require $3^{x / 3} w \geq w+1$. If $x \geq 2$, then this is true as $w \geq 1$, and if $x=1$ then $w=3^{(n-2) / 3} \geq 3$ and the result is still true. Thus all terms in equation ?? are at most $3^{n / 3}$, and so $f(n) \leq 3^{n / 3}$, and the upper bound is proven.
Second proof of upper bound. Consider a second game with the same rules but in which Vishal can replace $a$ and $b$ by either $a+b$ or $a b$. Let $g(n)$ be the largest possible value for this new game. Then $f(n) \leq g(n)$ because $\min \left\{a^{2}, b^{2}\right\} \leq a b$.
We can check $g(n)=n$ for $n \leq 4$, so $g(n) \leq 3^{n / 3}$ for these values. If $x$ and $y$ are both bigger than 1 , then $g(x)+g(y) \leq g(x) g(y)$. Therefore, for $n>4$, we have that
$$
g(n)=\max \left\{g(n-1)+1, \max _{1 \leq x \leq n-1} g(x) g(n-x)\right\}
$$
Now proceed similarly to the first proof. Assume $n>4$ and $g(m) \leq 3^{m / 3}$ for all $m<n$. If $1 \leq x \leq n-1$, then $g(x) g(n-x) \leq 3^{x / 3} 3^{(n-x) / 3}=3^{n / 3}$. And $g(n-1)+1 \leq 3^{(n-1) / 3}+1$, which is shown to be less than $3^{n / 3}$ in the first proof. It follows that $f(n) \leq g(n) \leq 3^{n / 3}$.
Lower bound:
First proof of lower bound. We begin with a lemma.
Lemma 1. Let $m$ be a nonnegative integer. Then
$$
f\left(2^{m}\right) \geq 2^{2^{m-1}} \quad \text { and } \quad f\left(3 \cdot 2^{m}\right) \geq 3^{2^{m}}
$$
Proof. We prove the lemma by induction. One can check that $f(n)=n$ for $n \leq 3$, which proves the lemma for $m=0$. For a general $m>0$, we get
$$
\begin{gathered}
f\left(2^{m}\right) \geq f\left(2^{m-1}\right)^{2} \geq\left(2^{2^{m-2}}\right)^{2}=2^{2^{m-1}} \\
f\left(3 \cdot 2^{m}\right) \geq f\left(3 \cdot 2^{m-1}\right)^{2} \geq\left(3^{2^{m-1}}\right)^{2}=3^{2^{m}}
\end{gathered}
$$
by induction, as required.
(This lemma can also be proved more constructively. Briefly, if $n=2^{m}$, then partition the 1 's on the board into $2^{m-1}$ pairs, and then add each pair to get $2^{m-1} 2^{\prime} \mathrm{s}\left(2=2^{2^{0}}\right)$; then multiply pairs of 2 's to get $2^{m-2} 4$ 's $\left(4=2^{2^{1}}\right)$; then multiply pairs of 4's to get $2^{m-3} 16$ 's $\left(16=2^{2^{2}}\right)$; and so on, until there are $2\left(=2^{1}\right)$ copies of $2^{2^{m-2}}$, which then gets replaced with $\left.\mathrm{a} 2^{2^{m-1}}\right)$. The process is similar for $n=3 \cdot 2^{m}$, except that the first step is to partition the 1 's into $2^{m}$ groups of 3 , and then use addition within each group to get $2^{m} 3$ 's on the board.)
Now assume $2^{x} \leq n<3 \cdot 2^{x-1}$ for some integer $x$. Then we have
$$
f(n) \geq f\left(2^{x}\right) \geq 2^{2^{x-1}}>2^{n / 3}
$$
as required. If no such $x$ exists, then there exists an integer $x$ such that $3 \cdot 2^{x-1} \leq n<2^{x+1}$. In this case, we have
$$
f(n) \geq f\left(3 \cdot 2^{x-1}\right) \geq 3^{2^{x-1}}>2^{2^{x+1} / 3}>2^{n / 3}
$$
where the second last inequality is equivalent to $2^{x-1} \log (3) \geq \frac{2^{x+1}}{3} \log (2)$, and by dividing out $2^{x}$ and clearing the denominator this is equivalent to $3 \log (3) \geq 4 \log 2$, which is true as $3^{3}=27>16=2^{4}$.
Second proof of lower bound. We shall prove the stronger result $f(n) \geq 2^{(n+1) / 3}$ for $n \geq 2$ by induction. One can check that $f(n)=n$ for $n=2,3,4$, which proves the result for these values. Assume that $n \geq 5$ and that $f(k) \geq 2^{(k+1) / 3}$ for all $k=2,3, \ldots, n-1$. Then
$$
\begin{array}{rlr}
f(n) & \geq f(\lfloor n / 2\rfloor)^{2} & \\
& \geq\left(2^{(\lfloor n / 2\rfloor+1) / 3}\right)^{2} \quad \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq 2 \\
& =2^{(2\lfloor n / 2\rfloor+2) / 3} \quad \\
& \geq 2^{(n+1) / 3} \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq \frac{n-1}{2} .
\end{array}
$$
The result follows by induction.
Remark 1. One can show that $f$ satisfies the recurrence $f(n)=n$ for $n=1,2, f(2 n)=f(n)^{2}$ for $n \geq 2$, and $f(2 n+1)=f(2 n)+1$ for $n \geq 1$. The upper bound in the problem is tight (equality holds for $n=3 \cdot 2^{x}$ ), but the lower bound is not.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be an integer. Initially, the number 1 is written $n$ times on a board. Every minute, Vishal picks two numbers written on the board, say $a$ and $b$, erases them, and writes either $a+b$ or $\min \left\{a^{2}, b^{2}\right\}$. After $n-1$ minutes there is one number left on the board. Let the largest possible value for this final number be $f(n)$. Prove that
$$
2^{n / 3}<f(n) \leq 3^{n / 3}
$$
|
Clearly $f(n)$ is a strictly increasing function, as we can form $f(n-1)$ with $n-1$ ones, and add the final one. However, we can do better; assume Vishal generates $f(n)$ on the board. After $n-2$ minutes, there are two numbers left, say they were formed by $x$ ones and $y$ ones, where $x+y=n$. Clearly the numbers are at most $f(x), f(y)$ (and can be made to be equal to $f(x), f(y))$, and therefore we obtain
$$
f(n)=\max _{x+y=n, 1 \leq x \leq y \leq n-1}\left(\max \left(f(x)+f(y), f(x)^{2}\right)\right)
$$
where we used the fact that $f$ is increasing to get that $\min \left(f(x)^{2}, f(y)^{2}\right)=f(x)^{2}$ when $x \leq y$. In particular, $f(n+1) \geq f(n)+1$, and $f(2 n) \geq f(n)^{2}$ for all positive integers $n$.
Upper bound:
First proof of upper bound. We use induction. We can check that $f(n)=n$ for $n \leq 4$, and these all satisfy the bound $f(n)=n \leq 3^{n / 3}$. Assume it is true for all $m<n$ (some $n \geq 5$ ), and with $x, y$ as in equation ?? we have
$$
f(x)^{2} \leq f\left(\left\lfloor\frac{n}{2}\right\rfloor\right)^{2} \leq\left(3^{n / 6}\right)^{2}=3^{n / 3}
$$
as desired. It thus remains to show that $f(x)+f(y) \leq 3^{n / 3}$. By induction, it suffices to prove that
$$
3^{x / 3}+3^{y / 3} \leq 3^{(x+y) / 3}
$$
for $1 \leq x \leq y \leq n-1$ and $x+y=n$. This is equivalent to
$$
1+3^{(y-x) / 3} \leq 3^{y / 3}
$$
Let $w=3^{(y-x) / 3}$, and we require $3^{x / 3} w \geq w+1$. If $x \geq 2$, then this is true as $w \geq 1$, and if $x=1$ then $w=3^{(n-2) / 3} \geq 3$ and the result is still true. Thus all terms in equation ?? are at most $3^{n / 3}$, and so $f(n) \leq 3^{n / 3}$, and the upper bound is proven.
Second proof of upper bound. Consider a second game with the same rules but in which Vishal can replace $a$ and $b$ by either $a+b$ or $a b$. Let $g(n)$ be the largest possible value for this new game. Then $f(n) \leq g(n)$ because $\min \left\{a^{2}, b^{2}\right\} \leq a b$.
We can check $g(n)=n$ for $n \leq 4$, so $g(n) \leq 3^{n / 3}$ for these values. If $x$ and $y$ are both bigger than 1 , then $g(x)+g(y) \leq g(x) g(y)$. Therefore, for $n>4$, we have that
$$
g(n)=\max \left\{g(n-1)+1, \max _{1 \leq x \leq n-1} g(x) g(n-x)\right\}
$$
Now proceed similarly to the first proof. Assume $n>4$ and $g(m) \leq 3^{m / 3}$ for all $m<n$. If $1 \leq x \leq n-1$, then $g(x) g(n-x) \leq 3^{x / 3} 3^{(n-x) / 3}=3^{n / 3}$. And $g(n-1)+1 \leq 3^{(n-1) / 3}+1$, which is shown to be less than $3^{n / 3}$ in the first proof. It follows that $f(n) \leq g(n) \leq 3^{n / 3}$.
Lower bound:
First proof of lower bound. We begin with a lemma.
Lemma 1. Let $m$ be a nonnegative integer. Then
$$
f\left(2^{m}\right) \geq 2^{2^{m-1}} \quad \text { and } \quad f\left(3 \cdot 2^{m}\right) \geq 3^{2^{m}}
$$
Proof. We prove the lemma by induction. One can check that $f(n)=n$ for $n \leq 3$, which proves the lemma for $m=0$. For a general $m>0$, we get
$$
\begin{gathered}
f\left(2^{m}\right) \geq f\left(2^{m-1}\right)^{2} \geq\left(2^{2^{m-2}}\right)^{2}=2^{2^{m-1}} \\
f\left(3 \cdot 2^{m}\right) \geq f\left(3 \cdot 2^{m-1}\right)^{2} \geq\left(3^{2^{m-1}}\right)^{2}=3^{2^{m}}
\end{gathered}
$$
by induction, as required.
(This lemma can also be proved more constructively. Briefly, if $n=2^{m}$, then partition the 1 's on the board into $2^{m-1}$ pairs, and then add each pair to get $2^{m-1} 2^{\prime} \mathrm{s}\left(2=2^{2^{0}}\right)$; then multiply pairs of 2 's to get $2^{m-2} 4$ 's $\left(4=2^{2^{1}}\right)$; then multiply pairs of 4's to get $2^{m-3} 16$ 's $\left(16=2^{2^{2}}\right)$; and so on, until there are $2\left(=2^{1}\right)$ copies of $2^{2^{m-2}}$, which then gets replaced with $\left.\mathrm{a} 2^{2^{m-1}}\right)$. The process is similar for $n=3 \cdot 2^{m}$, except that the first step is to partition the 1 's into $2^{m}$ groups of 3 , and then use addition within each group to get $2^{m} 3$ 's on the board.)
Now assume $2^{x} \leq n<3 \cdot 2^{x-1}$ for some integer $x$. Then we have
$$
f(n) \geq f\left(2^{x}\right) \geq 2^{2^{x-1}}>2^{n / 3}
$$
as required. If no such $x$ exists, then there exists an integer $x$ such that $3 \cdot 2^{x-1} \leq n<2^{x+1}$. In this case, we have
$$
f(n) \geq f\left(3 \cdot 2^{x-1}\right) \geq 3^{2^{x-1}}>2^{2^{x+1} / 3}>2^{n / 3}
$$
where the second last inequality is equivalent to $2^{x-1} \log (3) \geq \frac{2^{x+1}}{3} \log (2)$, and by dividing out $2^{x}$ and clearing the denominator this is equivalent to $3 \log (3) \geq 4 \log 2$, which is true as $3^{3}=27>16=2^{4}$.
Second proof of lower bound. We shall prove the stronger result $f(n) \geq 2^{(n+1) / 3}$ for $n \geq 2$ by induction. One can check that $f(n)=n$ for $n=2,3,4$, which proves the result for these values. Assume that $n \geq 5$ and that $f(k) \geq 2^{(k+1) / 3}$ for all $k=2,3, \ldots, n-1$. Then
$$
\begin{array}{rlr}
f(n) & \geq f(\lfloor n / 2\rfloor)^{2} & \\
& \geq\left(2^{(\lfloor n / 2\rfloor+1) / 3}\right)^{2} \quad \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq 2 \\
& =2^{(2\lfloor n / 2\rfloor+2) / 3} \quad \\
& \geq 2^{(n+1) / 3} \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq \frac{n-1}{2} .
\end{array}
$$
The result follows by induction.
Remark 1. One can show that $f$ satisfies the recurrence $f(n)=n$ for $n=1,2, f(2 n)=f(n)^{2}$ for $n \geq 2$, and $f(2 n+1)=f(2 n)+1$ for $n \geq 1$. The upper bound in the problem is tight (equality holds for $n=3 \cdot 2^{x}$ ), but the lower bound is not.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"problem_match": "\nP3:",
"solution_match": "\nSolution."
}
|
fd6d6b29-9bd7-5aea-805a-645e0959a973
| 604,508
|
Let $A B C D E$ be a convex pentagon such that the five vertices lie on a circle and the five sides are tangent to another circle inside the pentagon. There are $\binom{5}{3}=10$ triangles which can be formed by choosing 3 of the 5 vertices. For each of these 10 triangles, mark its incenter. Prove that these 10 incenters lie on two concentric circles.
|
Let $I$ be the incenter of pentagon $A B C D E$. Let $I_{A}$ denote the incenter of triangle $E A B$ and $I_{a}$ the incenter $D A C$. Define $I_{B}, I_{b}, I_{C}, I_{c}, I_{D}, I_{d}, I_{E}, I_{e}$ similarly.
We will first show that $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic. Let $\omega_{A}$ be the circle with center at the midpoint of arc $D E$ and passing through $D$ and $E$. Define $\omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ similarly. It is well-known that the incenter of a triangle lies on such circles, in particular, $I_{A}$ lies on $\omega_{C}$ and $\omega_{D}$. So the radical axis of $\omega_{C}, \omega_{D}$ is the line $A I_{A}$. But this is just the angle bisector of $\angle E A B$, which $I$ also lies on. So $I$ is in fact the radical center of $\omega_{A}, \omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ ! Inverting about $I$ swaps $I_{A}$ and $A$ and since $A B C D E$ are concyclic, $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic as well.
Let $O$ be the center of the circle $I_{A} I_{B} I_{C} I_{D} I_{E}$. We will now show that $O I_{a}=O I_{d}$ which finishes the problem as we can consider the cyclic versions of this equation to find that $O I_{a}=O I_{d}=O I_{b}=O I_{e}=O I_{c}$. Recall a well-known lemma: For any cyclic quadrilateral $W X Y Z$, the incenters of $X Y Z, Y Z W, Z W X, W X Y$ form a rectangle. Applying this lemma on $A B C D$, we see that $I_{B}, I_{C}, I_{a}, I_{d}$ form a rectangle in that order. Then the perpendicular bisector of $I_{B} I_{C}$ is exactly the perpendicular bisector of $I_{a} I_{d}$. Thus, $O$ is equidistant to $I_{a}$ and $I_{d}$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that the five vertices lie on a circle and the five sides are tangent to another circle inside the pentagon. There are $\binom{5}{3}=10$ triangles which can be formed by choosing 3 of the 5 vertices. For each of these 10 triangles, mark its incenter. Prove that these 10 incenters lie on two concentric circles.
|
Let $I$ be the incenter of pentagon $A B C D E$. Let $I_{A}$ denote the incenter of triangle $E A B$ and $I_{a}$ the incenter $D A C$. Define $I_{B}, I_{b}, I_{C}, I_{c}, I_{D}, I_{d}, I_{E}, I_{e}$ similarly.
We will first show that $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic. Let $\omega_{A}$ be the circle with center at the midpoint of arc $D E$ and passing through $D$ and $E$. Define $\omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ similarly. It is well-known that the incenter of a triangle lies on such circles, in particular, $I_{A}$ lies on $\omega_{C}$ and $\omega_{D}$. So the radical axis of $\omega_{C}, \omega_{D}$ is the line $A I_{A}$. But this is just the angle bisector of $\angle E A B$, which $I$ also lies on. So $I$ is in fact the radical center of $\omega_{A}, \omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ ! Inverting about $I$ swaps $I_{A}$ and $A$ and since $A B C D E$ are concyclic, $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic as well.
Let $O$ be the center of the circle $I_{A} I_{B} I_{C} I_{D} I_{E}$. We will now show that $O I_{a}=O I_{d}$ which finishes the problem as we can consider the cyclic versions of this equation to find that $O I_{a}=O I_{d}=O I_{b}=O I_{e}=O I_{c}$. Recall a well-known lemma: For any cyclic quadrilateral $W X Y Z$, the incenters of $X Y Z, Y Z W, Z W X, W X Y$ form a rectangle. Applying this lemma on $A B C D$, we see that $I_{B}, I_{C}, I_{a}, I_{d}$ form a rectangle in that order. Then the perpendicular bisector of $I_{B} I_{C}$ is exactly the perpendicular bisector of $I_{a} I_{d}$. Thus, $O$ is equidistant to $I_{a}$ and $I_{d}$ and we are done.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"problem_match": "\nP5.",
"solution_match": "\nSolution."
}
|
f0939ca5-c5c7-50a2-9a31-9c9694a999fb
| 604,530
|
An acute triangle is a triangle that has all angles less than $90^{\circ}$ ( $90^{\circ}$ is a Right Angle). Let $A B C$ be an acute triangle with altitudes $A D, B E$, and $C F$ meeting at $H$. The circle passing through points $D, E$, and $F$ meets $A D, B E$, and $C F$ again at $X, Y$, and $Z$ respectively. Prove the following inequality:
$$
\frac{A H}{D X}+\frac{B H}{E Y}+\frac{C H}{F Z} \geq 3
$$
|
Let the circumcircle of $A B C$ meet the altitudes $A D, B E$, and $C F$ again at $I, J$, and $K$ respectively.
Lemma (9-point circle). $I, J, K$ are the reflections of $H$ across $B C, C A, A B$. Moreover, $D, E, F, X, Y, Z$ are the midpoints of $H I, H J, H K, H A, H B, H C$.
Proof. Since $A B D E$ and $A B I C$ are cyclic, we see that
$$
\angle E B D=\angle E A D=\angle C A I=\angle C B I .
$$
Hence the lines $B I$ and $B H$ are reflections across $B C$. Similarly, $C H$ and $C I$ are reflections across $B C$, so $I$ is the reflection of $H$ across $B C$. The analogous claims for $J$ and $K$ follow. A $\times 2$ dilation from $H$ now establishes the result.
From this lemma, we get $A I=2 X D, B J=2 E Y$, and $C K=2 F Z$. Hence it is equivalent to showing that
$$
\frac{A H}{2 D X}+\frac{B H}{2 E Y}+\frac{C H}{2 F Z} \geq \frac{3}{2}
$$
which is in turn equivalent to
$$
\frac{A H}{A I}+\frac{B H}{B J}+\frac{C H}{C K} \geq \frac{3}{2} .
$$
Let $a=J K, b=K I$ and $c=I J$. Again by the lemma we find $A H=A K=A J$, so by Ptolemy's theorem on $A K I J$,
$$
A J \cdot K I+A K \cdot I J=A I \cdot J K
$$
Substituting and rearranging,
$$
\begin{aligned}
A H \cdot b+A H \cdot c & =A I \cdot a \\
A H \cdot(b+c) & =A I \cdot a \\
\frac{A H}{A I} & =\frac{a}{b+c} .
\end{aligned}
$$
Similarly,
$$
\frac{B H}{B J}=\frac{b}{c+a} \quad \text { and } \quad \frac{C H}{C K}=\frac{c}{a+b}
$$
Plugging these back into $\left(^{*}\right)$, the desired inequality is now
$$
\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \geq \frac{3}{2} .
$$
This is known as Nesbitt's Inequality, which has many proofs. Below is one such proof.
Add 3 to both sides and rearrange:
$$
\begin{aligned}
\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{c+a}+1\right)+\left(\frac{c}{a+b}+1\right) & \geq \frac{3}{2}+3 \\
\Longleftrightarrow \quad \frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b} & \geq \frac{9}{2} \\
\Longleftrightarrow \quad(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) & \geq \frac{9}{2} \\
\Longleftrightarrow \quad & \frac{(b+c)+(c+a)+(a+b)}{3}
\end{aligned}
$$
which is true by the AM-HM inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
An acute triangle is a triangle that has all angles less than $90^{\circ}$ ( $90^{\circ}$ is a Right Angle). Let $A B C$ be an acute triangle with altitudes $A D, B E$, and $C F$ meeting at $H$. The circle passing through points $D, E$, and $F$ meets $A D, B E$, and $C F$ again at $X, Y$, and $Z$ respectively. Prove the following inequality:
$$
\frac{A H}{D X}+\frac{B H}{E Y}+\frac{C H}{F Z} \geq 3
$$
|
Let the circumcircle of $A B C$ meet the altitudes $A D, B E$, and $C F$ again at $I, J$, and $K$ respectively.

Lemma (9-point circle). $I, J, K$ are the reflections of $H$ across $B C, C A, A B$. Moreover, $D, E, F, X, Y, Z$ are the midpoints of $H I, H J, H K, H A, H B, H C$.
Proof. Since $A B D E$ and $A B I C$ are cyclic, we see that
$$
\angle E B D=\angle E A D=\angle C A I=\angle C B I .
$$
Hence the lines $B I$ and $B H$ are reflections across $B C$. Similarly, $C H$ and $C I$ are reflections across $B C$, so $I$ is the reflection of $H$ across $B C$. The analogous claims for $J$ and $K$ follow. A $\times 2$ dilation from $H$ now establishes the result.
From this lemma, we get $A I=2 X D, B J=2 E Y$, and $C K=2 F Z$. Hence it is equivalent to showing that
$$
\frac{A H}{2 D X}+\frac{B H}{2 E Y}+\frac{C H}{2 F Z} \geq \frac{3}{2}
$$
which is in turn equivalent to
$$
\frac{A H}{A I}+\frac{B H}{B J}+\frac{C H}{C K} \geq \frac{3}{2} .
$$
Let $a=J K, b=K I$ and $c=I J$. Again by the lemma we find $A H=A K=A J$, so by Ptolemy's theorem on $A K I J$,
$$
A J \cdot K I+A K \cdot I J=A I \cdot J K
$$
Substituting and rearranging,
$$
\begin{aligned}
A H \cdot b+A H \cdot c & =A I \cdot a \\
A H \cdot(b+c) & =A I \cdot a \\
\frac{A H}{A I} & =\frac{a}{b+c} .
\end{aligned}
$$
Similarly,
$$
\frac{B H}{B J}=\frac{b}{c+a} \quad \text { and } \quad \frac{C H}{C K}=\frac{c}{a+b}
$$
Plugging these back into $\left(^{*}\right)$, the desired inequality is now
$$
\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \geq \frac{3}{2} .
$$
This is known as Nesbitt's Inequality, which has many proofs. Below is one such proof.
Add 3 to both sides and rearrange:
$$
\begin{aligned}
\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{c+a}+1\right)+\left(\frac{c}{a+b}+1\right) & \geq \frac{3}{2}+3 \\
\Longleftrightarrow \quad \frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b} & \geq \frac{9}{2} \\
\Longleftrightarrow \quad(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) & \geq \frac{9}{2} \\
\Longleftrightarrow \quad & \frac{(b+c)+(c+a)+(a+b)}{3}
\end{aligned}
$$
which is true by the AM-HM inequality.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"problem_match": "\nP3.",
"solution_match": "\nSolution."
}
|
8458037b-46d4-5046-bd09-ee30616d0774
| 604,579
|
Let $f(x)$ be a non-constant polynomial with integer coefficients such that $f(1) \neq 1$. For a positive integer $n$, define $\operatorname{divs}(n)$ to be the set of positive divisors of $n$.
A positive integer $m$ is $f$-cool if there exists a positive integer $n$ for which
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(n)
$$
Prove that for any such $f$, there are finitely many $f$-cool integers.
(The notation $f[S]$ for some set $S$ denotes the set $\{f(s): s \in S\}$.)
Remark 1. The original problem statement was "For a fixed non-constant polynomial $f(x) \neq$ $x$, prove that there are finitely many composite $f$-cool integers." Note that this allows $f(1)=1$. Try this problem for an added challenge!
|
Assume for the sake of contradiction that there are infinitely many $f$-cool integers.
If $f(x)$ has a negative leading coefficient, then a sufficiently large $f$-cool integer $m$ will have $f(m)<0$. But this implies $m$ is not $f$-cool, contradiction.
Thus $f(x)$ has a positive leading coefficient, so we can pick an $N$ such that for all $m>N$,
$$
f(m)>\max (f(1), f(2), \ldots, f(m-1))
$$
This means $f(m)$ is the largest value in $f[\operatorname{divs}(m)]$, so if $m$ is $f$-cool with $f[\operatorname{divs}(m)]=\operatorname{divs}(n)$, then we must have $n=f(m)$, since $n$ is the largest value in $\operatorname{divs}(n)$. In other words,
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(f(m))
$$
for all $f$-cool $m>N$.
For each of those $m$ 's, $1 \in \operatorname{divs}(f(m))$, so there must be a $k \in \operatorname{divs}(m)$ such that $f(k)=1$. Let $k_{1}, k_{2}, \ldots, k_{n}$ be the solutions to $f(x)=1$. Thus every $f$-cool $m>N$ is divisible by some $k \in\left\{k_{1}, k_{2}, \ldots, k_{n}\right\}$. Since there are infinitely many such $m$ 's and finitely many $k$ 's, by the Pigeonhole Principle there is some $k$ which divides infinitely many $f$-cool integers $m$. (Note that $k \neq 1$ since $f(1) \neq 1$.)
For all $f$-cool $m>N$ divisible by $k$, we have
$$
\left.f\left(\frac{m}{k}\right) \in f[\operatorname{divs}(m)]=\operatorname{divs}(f(m)) \Longrightarrow f\left(\frac{m}{k}\right) \right\rvert\, f(m) .
$$
Thus, $f(x) \mid f(k x)$ has infinitely many positive integer solutions. Let $d=\operatorname{deg}(f)$, and write
$$
\frac{f(k x)}{f(x)}=k^{d}+\frac{g(x)}{f(x)}
$$
for some $g(x) \in \mathbb{Z}[x]$ with $\operatorname{deg}(g)<d$. If $g(x) \neq 0$, then for sufficiently large $x$ we have $0<|g(x)|<f(x)$, since $\operatorname{deg}(f)>\operatorname{deg}(g)$. But then $\frac{f(k x)}{f(x)}-k^{d}=\frac{g(x)}{f(x)}$ cannot be an integer, which gives us the desired contradiction.
Therefore $g(x)=0$, so $f(k x)=k^{d} f(x)$, i.e. $f(x)=a x^{d}$ for some positive integer $a$. If $a=1$ then $f(1)=1$, a contradiction. But if $a>1$, then $f(x)=1$ has no integer solutions, another contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f(x)$ be a non-constant polynomial with integer coefficients such that $f(1) \neq 1$. For a positive integer $n$, define $\operatorname{divs}(n)$ to be the set of positive divisors of $n$.
A positive integer $m$ is $f$-cool if there exists a positive integer $n$ for which
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(n)
$$
Prove that for any such $f$, there are finitely many $f$-cool integers.
(The notation $f[S]$ for some set $S$ denotes the set $\{f(s): s \in S\}$.)
Remark 1. The original problem statement was "For a fixed non-constant polynomial $f(x) \neq$ $x$, prove that there are finitely many composite $f$-cool integers." Note that this allows $f(1)=1$. Try this problem for an added challenge!
|
Assume for the sake of contradiction that there are infinitely many $f$-cool integers.
If $f(x)$ has a negative leading coefficient, then a sufficiently large $f$-cool integer $m$ will have $f(m)<0$. But this implies $m$ is not $f$-cool, contradiction.
Thus $f(x)$ has a positive leading coefficient, so we can pick an $N$ such that for all $m>N$,
$$
f(m)>\max (f(1), f(2), \ldots, f(m-1))
$$
This means $f(m)$ is the largest value in $f[\operatorname{divs}(m)]$, so if $m$ is $f$-cool with $f[\operatorname{divs}(m)]=\operatorname{divs}(n)$, then we must have $n=f(m)$, since $n$ is the largest value in $\operatorname{divs}(n)$. In other words,
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(f(m))
$$
for all $f$-cool $m>N$.
For each of those $m$ 's, $1 \in \operatorname{divs}(f(m))$, so there must be a $k \in \operatorname{divs}(m)$ such that $f(k)=1$. Let $k_{1}, k_{2}, \ldots, k_{n}$ be the solutions to $f(x)=1$. Thus every $f$-cool $m>N$ is divisible by some $k \in\left\{k_{1}, k_{2}, \ldots, k_{n}\right\}$. Since there are infinitely many such $m$ 's and finitely many $k$ 's, by the Pigeonhole Principle there is some $k$ which divides infinitely many $f$-cool integers $m$. (Note that $k \neq 1$ since $f(1) \neq 1$.)
For all $f$-cool $m>N$ divisible by $k$, we have
$$
\left.f\left(\frac{m}{k}\right) \in f[\operatorname{divs}(m)]=\operatorname{divs}(f(m)) \Longrightarrow f\left(\frac{m}{k}\right) \right\rvert\, f(m) .
$$
Thus, $f(x) \mid f(k x)$ has infinitely many positive integer solutions. Let $d=\operatorname{deg}(f)$, and write
$$
\frac{f(k x)}{f(x)}=k^{d}+\frac{g(x)}{f(x)}
$$
for some $g(x) \in \mathbb{Z}[x]$ with $\operatorname{deg}(g)<d$. If $g(x) \neq 0$, then for sufficiently large $x$ we have $0<|g(x)|<f(x)$, since $\operatorname{deg}(f)>\operatorname{deg}(g)$. But then $\frac{f(k x)}{f(x)}-k^{d}=\frac{g(x)}{f(x)}$ cannot be an integer, which gives us the desired contradiction.
Therefore $g(x)=0$, so $f(k x)=k^{d} f(x)$, i.e. $f(x)=a x^{d}$ for some positive integer $a$. If $a=1$ then $f(1)=1$, a contradiction. But if $a>1$, then $f(x)=1$ has no integer solutions, another contradiction.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"problem_match": "\nP4.",
"solution_match": "\nSolution."
}
|
5617d20f-92c7-59fc-b3ef-e76ff62c056c
| 604,590
|
Let $A B C$ be a triangle with incenter $I$. Suppose the reflection of $A B$ across $C I$ and the reflection of $A C$ across $B I$ intersect at a point $X$. Prove that $X I$ is perpendicular to $B C$.
(The incenter is the point where the three angle bisectors meet.)
|
Suppose the reflection of $A C$ across $B I$ intersects $B C$ at $E$. Define $F$ similarly for the reflection of $A B$ across $C I$. Also suppose $C I$ intersects $A B$ at $M$ and $B I$ intersects $A C$ at $N$. Since $C A$ and $C F=B C$ are reflections across $C I$, and so are $M A$ and $M F=X M$, we have that $A$ and $F$ are reflections across $C I$. Similarly $A$ and $E$ are reflections across $B I$. Thus $\angle X F C=\angle B A C=\angle X E B$ if $\angle B A C$ is acute (and $\angle X F C=\angle X E B=\pi-\angle B A C$, when $\angle B A C$ is obtuse), so $X F=X E$. Moreover we also find that $I F=I A=I E$ by the aforementioned reflection properties, so thus $X I$ is the perpendicular bisector of $E F$ and is hence perpendicular to $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Suppose the reflection of $A B$ across $C I$ and the reflection of $A C$ across $B I$ intersect at a point $X$. Prove that $X I$ is perpendicular to $B C$.
(The incenter is the point where the three angle bisectors meet.)
|
Suppose the reflection of $A C$ across $B I$ intersects $B C$ at $E$. Define $F$ similarly for the reflection of $A B$ across $C I$. Also suppose $C I$ intersects $A B$ at $M$ and $B I$ intersects $A C$ at $N$. Since $C A$ and $C F=B C$ are reflections across $C I$, and so are $M A$ and $M F=X M$, we have that $A$ and $F$ are reflections across $C I$. Similarly $A$ and $E$ are reflections across $B I$. Thus $\angle X F C=\angle B A C=\angle X E B$ if $\angle B A C$ is acute (and $\angle X F C=\angle X E B=\pi-\angle B A C$, when $\angle B A C$ is obtuse), so $X F=X E$. Moreover we also find that $I F=I A=I E$ by the aforementioned reflection properties, so thus $X I$ is the perpendicular bisector of $E F$ and is hence perpendicular to $B C$.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"problem_match": "\nP1.",
"solution_match": "\nSolution."
}
|
391342d8-23a0-59b3-9c3a-02821cbe32cd
| 604,625
|
Let $N$ be the number of positive integers with 10 digits $\overline{d_{9} d_{8} \cdots d_{1} d_{0}}$ in base 10 (where $0 \leq d_{i} \leq 9$ for all $i$ and $d_{9}>0$ ) such that the polynomial
$$
d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}
$$
is irreducible in $\mathbb{Q}$. Prove that $N$ is even.
(A polynomial is irreducible in $\mathbb{Q}$ if it cannot be factored into two non-constant polynomials with rational coefficients.)
|
Let $f(x)=d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}$. If $d_{0}=0$, then $f(x)$ is divisible by $x$ and thus reducible, so we may ignore all such polynomials. The remaining polynomials all have nonzero leading and constant coefficients.
For any polynomial $p(x)$ of degree $n$ with nonzero leading and constant coefficients, say $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$, define $\bar{p}(x)$ to be the reversed polynomial $a_{0} x^{n}+$ $a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n}$. Observe that $\bar{p}(x)$ also has degree $n$ and furthermore, $\bar{p}(x)=$ $x^{n}\left(a_{0}+a_{1}\left(\frac{1}{x}\right)+\cdots+a_{n-1}\left(\frac{1}{x}\right)^{n-1}+a_{n}\left(\frac{1}{x}\right)^{n}\right)=x^{n} p\left(\frac{1}{x}\right)$.
Consider pairing each $f(x)$ with $\bar{f}(x)$ whenever $f(x) \neq \bar{f}(x)$. If $f(x)$ is reducible, it can be factored as $f(x)=g(x) h(x)$ where $\operatorname{deg} g, \operatorname{deg} h \geq 1$. Because the leading and constant coefficients of $f(x)$ are nonzero, so are the leading and constant coefficients of $g(x)$ and $h(x)$. Hence $\bar{g}(x)$ and $\bar{h}(x)$ are well defined with $\operatorname{deg} \bar{g}=\operatorname{deg} g \geq 1$ and $\operatorname{deg} \bar{h}=\operatorname{deg} h \geq 1$. Furthermore,
$$
\bar{f}(x)=x^{9} f\left(\frac{1}{x}\right)=x^{9} g\left(\frac{1}{x}\right) h\left(\frac{1}{x}\right)=\left(x^{\operatorname{deg} g} g\left(\frac{1}{x}\right)\right)\left(x^{\operatorname{deg} h} h\left(\frac{1}{x}\right)\right)=\bar{g}(x) \bar{h}(x)
$$
Thus $\bar{f}(x)=\bar{g}(x) \bar{h}(x)$ is a factorization of $\bar{f}(x)$ into two non-constant polynomials, so $\bar{f}(x)$ is also reducible. Therefore $f(x)$ is irreducible if and only if $\bar{f}(x)$ is irreducible, so considering each pair, there are an even number of irreducible polynomials with $f(x) \neq \bar{f}(x)$.
Finally, note that if $f(x)=\bar{f}(x)$, then $d_{i}=d_{9-i}$ for each $i$. In such a case, we have $f(-1)=$ $\left(d_{0}-d_{9}\right)+\left(d_{2}-d_{7}\right)+\left(d_{4}-d_{5}\right)+\left(d_{6}-d_{3}\right)+\left(d_{8}-d_{1}\right)=0$, so by the Factor Theorem, $(x+1)$ is a factor of $f(x)$. Therefore these remaining polynomials are all reducible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $N$ be the number of positive integers with 10 digits $\overline{d_{9} d_{8} \cdots d_{1} d_{0}}$ in base 10 (where $0 \leq d_{i} \leq 9$ for all $i$ and $d_{9}>0$ ) such that the polynomial
$$
d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}
$$
is irreducible in $\mathbb{Q}$. Prove that $N$ is even.
(A polynomial is irreducible in $\mathbb{Q}$ if it cannot be factored into two non-constant polynomials with rational coefficients.)
|
Let $f(x)=d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}$. If $d_{0}=0$, then $f(x)$ is divisible by $x$ and thus reducible, so we may ignore all such polynomials. The remaining polynomials all have nonzero leading and constant coefficients.
For any polynomial $p(x)$ of degree $n$ with nonzero leading and constant coefficients, say $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$, define $\bar{p}(x)$ to be the reversed polynomial $a_{0} x^{n}+$ $a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n}$. Observe that $\bar{p}(x)$ also has degree $n$ and furthermore, $\bar{p}(x)=$ $x^{n}\left(a_{0}+a_{1}\left(\frac{1}{x}\right)+\cdots+a_{n-1}\left(\frac{1}{x}\right)^{n-1}+a_{n}\left(\frac{1}{x}\right)^{n}\right)=x^{n} p\left(\frac{1}{x}\right)$.
Consider pairing each $f(x)$ with $\bar{f}(x)$ whenever $f(x) \neq \bar{f}(x)$. If $f(x)$ is reducible, it can be factored as $f(x)=g(x) h(x)$ where $\operatorname{deg} g, \operatorname{deg} h \geq 1$. Because the leading and constant coefficients of $f(x)$ are nonzero, so are the leading and constant coefficients of $g(x)$ and $h(x)$. Hence $\bar{g}(x)$ and $\bar{h}(x)$ are well defined with $\operatorname{deg} \bar{g}=\operatorname{deg} g \geq 1$ and $\operatorname{deg} \bar{h}=\operatorname{deg} h \geq 1$. Furthermore,
$$
\bar{f}(x)=x^{9} f\left(\frac{1}{x}\right)=x^{9} g\left(\frac{1}{x}\right) h\left(\frac{1}{x}\right)=\left(x^{\operatorname{deg} g} g\left(\frac{1}{x}\right)\right)\left(x^{\operatorname{deg} h} h\left(\frac{1}{x}\right)\right)=\bar{g}(x) \bar{h}(x)
$$
Thus $\bar{f}(x)=\bar{g}(x) \bar{h}(x)$ is a factorization of $\bar{f}(x)$ into two non-constant polynomials, so $\bar{f}(x)$ is also reducible. Therefore $f(x)$ is irreducible if and only if $\bar{f}(x)$ is irreducible, so considering each pair, there are an even number of irreducible polynomials with $f(x) \neq \bar{f}(x)$.
Finally, note that if $f(x)=\bar{f}(x)$, then $d_{i}=d_{9-i}$ for each $i$. In such a case, we have $f(-1)=$ $\left(d_{0}-d_{9}\right)+\left(d_{2}-d_{7}\right)+\left(d_{4}-d_{5}\right)+\left(d_{6}-d_{3}\right)+\left(d_{8}-d_{1}\right)=0$, so by the Factor Theorem, $(x+1)$ is a factor of $f(x)$. Therefore these remaining polynomials are all reducible.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"problem_match": "\nP3.",
"solution_match": "\nSolution."
}
|
13f94710-db6f-5fc2-a607-1696260b7a84
| 604,676
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Claim 1. It is possible to draw internal/external angle bisectors.
Proof. Let $A, B, C$ be marked. To bisect $\angle A B C$, draw the parallel line to $A B$ unit 1 away from it on the opposite side as $C$, and draw the parallel line to $B C$ unit 1 away from it on the opposite side as $A$. Let these lines intersect at $D$. Then $B D$ is the internal angle bisector of $\angle A B C$. We can construct external angle bisectors similarly by drawing the line on the same side as $A$ for the second line instead.
Corollary 2. It is possible to mark the incenters and excenters of a triangle $A B C$.
Proof. Draw in the internal/external bisectors of all three angles and intersect them.
Claim 3. It is possible to mark the midpoint of any segment $A B$.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Draw a line parallel to $B C$ unit 1 away from it on the opposite side as $A$, and let this line intersect $A B$ at $D$ and $A C$ at $E$. Let $B E$ and $C D$ intersect at $F$, and let $A F$ intersect $B C$ at $M$. Then by Ceva's Theorem, $M$ is the midpoint of $B C$.
Corollary 4. It is possible to mark the centroid of $A B C$.
Proof. Draw the midpoint $D$ of $B C$ and the midpoint $E$ of $A C$, and intersect $A D$ with BE.
Claim 5. It is possible to draw the perpendicular bisector of any segment BC.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Construct the incenter $I$ and $A$-excenter $I_{A}$ of $A B C$. Draw the midpoint $M$ of $B C$ and midpoint $N$ of $I I_{A}$. By the incenter-excenter lemma, $N$ is the midpoint of the $\operatorname{arc} \overparen{B C}$ not containing $A$, so $M N$ is the perpendicular bisector of $B C$.
Corollary 6. It is possible to mark the circumcenter of $A B C$.
Proof. Draw and intersect the perpendicular bisectors of $B C$ and $A C$.
Claim 7. Given two marked points $A$ and $B$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=\frac{1}{2} \overrightarrow{A B}$.
Proof. Draw an arbitrary point $D$ not on line $A B$. Draw the midpoint $M$ of $A D$. Draw the midpoint $M_{1}$ of $B D$ and the midpoint $M_{2}$ of $M D$, and let $M_{1} M_{2}$ intersect $A B$ at $C$. Then $M_{1} M_{2} \| B M$ and $M M_{2}=\frac{1}{2} M D=\frac{1}{2} A M$, so $B C=\frac{1}{2} A B$.
Claim 8. Given two marked points $A$ and $B$ and any positive real number $k$ such that $2 k \in \mathbb{Z}$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=k \overrightarrow{A B}$.
Proof. Note that by applying Claim 7 and marking the midpoint of $A B$, we can translate both $A$ and $B$ by $\frac{1}{2} \overrightarrow{A B}$. The claim now follows by applying this operation repeatedly.
To finish, take the given triangle $A B C$ and mark its circumcenter $O$ and centroid $G$. Note that its orthocenter $H$ satisfies that $\overrightarrow{G H}=2 \overrightarrow{O G}$, so applying Claim 8 to $k=2$ now finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Claim 1. It is possible to draw internal/external angle bisectors.
Proof. Let $A, B, C$ be marked. To bisect $\angle A B C$, draw the parallel line to $A B$ unit 1 away from it on the opposite side as $C$, and draw the parallel line to $B C$ unit 1 away from it on the opposite side as $A$. Let these lines intersect at $D$. Then $B D$ is the internal angle bisector of $\angle A B C$. We can construct external angle bisectors similarly by drawing the line on the same side as $A$ for the second line instead.
Corollary 2. It is possible to mark the incenters and excenters of a triangle $A B C$.
Proof. Draw in the internal/external bisectors of all three angles and intersect them.
Claim 3. It is possible to mark the midpoint of any segment $A B$.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Draw a line parallel to $B C$ unit 1 away from it on the opposite side as $A$, and let this line intersect $A B$ at $D$ and $A C$ at $E$. Let $B E$ and $C D$ intersect at $F$, and let $A F$ intersect $B C$ at $M$. Then by Ceva's Theorem, $M$ is the midpoint of $B C$.
Corollary 4. It is possible to mark the centroid of $A B C$.
Proof. Draw the midpoint $D$ of $B C$ and the midpoint $E$ of $A C$, and intersect $A D$ with BE.
Claim 5. It is possible to draw the perpendicular bisector of any segment BC.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Construct the incenter $I$ and $A$-excenter $I_{A}$ of $A B C$. Draw the midpoint $M$ of $B C$ and midpoint $N$ of $I I_{A}$. By the incenter-excenter lemma, $N$ is the midpoint of the $\operatorname{arc} \overparen{B C}$ not containing $A$, so $M N$ is the perpendicular bisector of $B C$.
Corollary 6. It is possible to mark the circumcenter of $A B C$.
Proof. Draw and intersect the perpendicular bisectors of $B C$ and $A C$.
Claim 7. Given two marked points $A$ and $B$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=\frac{1}{2} \overrightarrow{A B}$.
Proof. Draw an arbitrary point $D$ not on line $A B$. Draw the midpoint $M$ of $A D$. Draw the midpoint $M_{1}$ of $B D$ and the midpoint $M_{2}$ of $M D$, and let $M_{1} M_{2}$ intersect $A B$ at $C$. Then $M_{1} M_{2} \| B M$ and $M M_{2}=\frac{1}{2} M D=\frac{1}{2} A M$, so $B C=\frac{1}{2} A B$.
Claim 8. Given two marked points $A$ and $B$ and any positive real number $k$ such that $2 k \in \mathbb{Z}$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=k \overrightarrow{A B}$.
Proof. Note that by applying Claim 7 and marking the midpoint of $A B$, we can translate both $A$ and $B$ by $\frac{1}{2} \overrightarrow{A B}$. The claim now follows by applying this operation repeatedly.
To finish, take the given triangle $A B C$ and mark its circumcenter $O$ and centroid $G$. Note that its orthocenter $H$ satisfies that $\overrightarrow{G H}=2 \overrightarrow{O G}$, so applying Claim 8 to $k=2$ now finishes the problem.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"problem_match": "\nP5.",
"solution_match": "\n## Solution 1."
}
|
891c2de3-78db-55fa-b1ec-48320f30eb34
| 604,711
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Ming Yang of Brophy College Preparatory submitted the following short, elegant solution which also creates tools that are able to extend beyond the problem. This solution has been designated by the CMO as the Best Solution for 2024 and earns Ming Yang the Matthew Brennan Award this year.
Start with Claims 1-3 of solution 1, allowing us to draw internal/external angle bisectors, in/excentres, and midpoints. We add one more claim.
Claim 9. Given a point $P$ and a line $\ell_{1}$, it is possible to draw a line through $P$ parallel to $\ell_{1}$.
Proof. Draw the line $\ell_{2}$ on the opposite side of $\ell_{1}$ to $P$, a distance 1 away. Draw arbitrary lines $P A B$ and $P C D$ with $A, C \in \ell_{1}, B, D \in \ell_{2}$. Let $E$ be the midpoint of $A C$, let $F=P E \cap \ell_{2}$, and let $Q=B E \cap F C$.
Since $\triangle Q E C \sim \triangle Q B F$ and $\triangle P A E \sim \triangle P B F$, we have
$$
\frac{Q E}{Q B}=\frac{E C}{B F}=\frac{A E}{B F}=\frac{P A}{P B}
$$
so $\triangle B A E \sim \triangle B P Q$. In particular, $P Q$ is parallel to $A E$, as desired.
In triangle $\triangle A B C$, draw the incentre $I$ and $A$-excentre $I_{A}$. Draw the midpoints $D$ of $B C$ and $M$ of $I I_{A}$. By the incentre-excentre lemma, $M$ is on the perpendicular bisector of $B C$, so $M D$ is perpendicular to $B C$. Finally, using Claim 9, we can draw a line through $A$ that is perpendicular to $B C$. Repeat this for $B$ and $A C$, and their intersection is the orthocentre of $\triangle A B C$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Ming Yang of Brophy College Preparatory submitted the following short, elegant solution which also creates tools that are able to extend beyond the problem. This solution has been designated by the CMO as the Best Solution for 2024 and earns Ming Yang the Matthew Brennan Award this year.
Start with Claims 1-3 of solution 1, allowing us to draw internal/external angle bisectors, in/excentres, and midpoints. We add one more claim.
Claim 9. Given a point $P$ and a line $\ell_{1}$, it is possible to draw a line through $P$ parallel to $\ell_{1}$.
Proof. Draw the line $\ell_{2}$ on the opposite side of $\ell_{1}$ to $P$, a distance 1 away. Draw arbitrary lines $P A B$ and $P C D$ with $A, C \in \ell_{1}, B, D \in \ell_{2}$. Let $E$ be the midpoint of $A C$, let $F=P E \cap \ell_{2}$, and let $Q=B E \cap F C$.
Since $\triangle Q E C \sim \triangle Q B F$ and $\triangle P A E \sim \triangle P B F$, we have
$$
\frac{Q E}{Q B}=\frac{E C}{B F}=\frac{A E}{B F}=\frac{P A}{P B}
$$
so $\triangle B A E \sim \triangle B P Q$. In particular, $P Q$ is parallel to $A E$, as desired.
In triangle $\triangle A B C$, draw the incentre $I$ and $A$-excentre $I_{A}$. Draw the midpoints $D$ of $B C$ and $M$ of $I I_{A}$. By the incentre-excentre lemma, $M$ is on the perpendicular bisector of $B C$, so $M D$ is perpendicular to $B C$. Finally, using Claim 9, we can draw a line through $A$ that is perpendicular to $B C$. Repeat this for $B$ and $A C$, and their intersection is the orthocentre of $\triangle A B C$, as required.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"problem_match": "\nP5.",
"solution_match": "\nSolution 2."
}
|
891c2de3-78db-55fa-b1ec-48320f30eb34
| 604,711
|
Call a positive integer $n$ practical if every positive integer less than or equal to $n$ can be written as the sum of distinct divisors of $n$.
For example, the divisors of 6 are $\mathbf{1 , 2}, \mathbf{3}$, and $\mathbf{6}$. Since
$$
1=\mathbf{1}, \quad 2=\mathbf{2}, \quad 3=\mathbf{3}, \quad 4=\mathbf{1}+\mathbf{3}, \quad 5=\mathbf{2}+\mathbf{3}, \quad 6=\mathbf{6},
$$
we see that 6 is practical.
Prove that the product of two practical numbers is also practical.
|
Let $p$ and $q$ be practical. For any $k \leq p q$, we can write
$$
k=a q+b \text { with } 0 \leq a \leq p, 0 \leq b<q .
$$
Since $p$ and $q$ are practical, we can write
$$
a=c_{1}+\ldots+c_{m}, \quad b=d_{1}+\ldots+d_{n}
$$
where the $c_{i}$ 's are distinct divisors of $p$ and the $d_{j}$ 's are distinct divisors of $q$. Now
$$
\begin{aligned}
k & =\left(c_{1}+\ldots+c_{m}\right) q+\left(d_{1}+\ldots+d_{n}\right) \\
& =c_{1} q+\ldots+c_{m} q+d_{1}+\ldots+d_{n} .
\end{aligned}
$$
Each of $c_{i} q$ and $d_{j}$ divides $p q$. Since $d_{j}<q \leq c_{i} q$ for any $i, j$, the $c_{i} q$ 's and $d_{j}$ 's are all distinct, and we conclude that $p q$ is practical.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Call a positive integer $n$ practical if every positive integer less than or equal to $n$ can be written as the sum of distinct divisors of $n$.
For example, the divisors of 6 are $\mathbf{1 , 2}, \mathbf{3}$, and $\mathbf{6}$. Since
$$
1=\mathbf{1}, \quad 2=\mathbf{2}, \quad 3=\mathbf{3}, \quad 4=\mathbf{1}+\mathbf{3}, \quad 5=\mathbf{2}+\mathbf{3}, \quad 6=\mathbf{6},
$$
we see that 6 is practical.
Prove that the product of two practical numbers is also practical.
|
Let $p$ and $q$ be practical. For any $k \leq p q$, we can write
$$
k=a q+b \text { with } 0 \leq a \leq p, 0 \leq b<q .
$$
Since $p$ and $q$ are practical, we can write
$$
a=c_{1}+\ldots+c_{m}, \quad b=d_{1}+\ldots+d_{n}
$$
where the $c_{i}$ 's are distinct divisors of $p$ and the $d_{j}$ 's are distinct divisors of $q$. Now
$$
\begin{aligned}
k & =\left(c_{1}+\ldots+c_{m}\right) q+\left(d_{1}+\ldots+d_{n}\right) \\
& =c_{1} q+\ldots+c_{m} q+d_{1}+\ldots+d_{n} .
\end{aligned}
$$
Each of $c_{i} q$ and $d_{j}$ divides $p q$. Since $d_{j}<q \leq c_{i} q$ for any $i, j$, the $c_{i} q$ 's and $d_{j}$ 's are all distinct, and we conclude that $p q$ is practical.
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution\n\n"
}
|
5a017f01-4bb7-52ff-b244-a4ea60cd1f4b
| 604,767
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Note that $a^{4}+b^{4}+c^{4}=\frac{\left(a^{4}+b^{4}\right)}{2}+\frac{\left(b^{4}+c^{4}\right)}{2}+\frac{\left(c^{4}+a^{4}\right)}{2}$. Applying the arithmetic-geometric mean inequality to each term, we see that the right side is greater than or equal to
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \text {. }
$$
We can rewrite this as
$$
\frac{a^{2}\left(b^{2}+c^{2}\right)}{2}+\frac{b^{2}\left(c^{2}+a^{2}\right)}{2}+\frac{c^{2}\left(a^{2}+b^{2}\right)}{2} .
$$
Applying the arithmetic mean-geometric mean inequality again we obtain $a^{4}+b^{4}+c^{4} \geq$ $a^{2} b c+b^{2} c a+c^{2} a b$. Dividing both sides by $a b c$ (which is positive) the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Note that $a^{4}+b^{4}+c^{4}=\frac{\left(a^{4}+b^{4}\right)}{2}+\frac{\left(b^{4}+c^{4}\right)}{2}+\frac{\left(c^{4}+a^{4}\right)}{2}$. Applying the arithmetic-geometric mean inequality to each term, we see that the right side is greater than or equal to
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \text {. }
$$
We can rewrite this as
$$
\frac{a^{2}\left(b^{2}+c^{2}\right)}{2}+\frac{b^{2}\left(c^{2}+a^{2}\right)}{2}+\frac{c^{2}\left(a^{2}+b^{2}\right)}{2} .
$$
Applying the arithmetic mean-geometric mean inequality again we obtain $a^{4}+b^{4}+c^{4} \geq$ $a^{2} b c+b^{2} c a+c^{2} a b$. Dividing both sides by $a b c$ (which is positive) the result follows.
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 1."
}
|
66fa1fc5-0689-515c-9ee8-fa69c080b3f8
| 604,793
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Notice the inequality is homogeneous. That is, if $a, b, c$ are replaced by $k a, k b, k c, k>0$ we get the original inequality. Thus we can assume, without loss of generality, that $a b c=1$. Then
$$
\begin{aligned}
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} & =a b c\left(\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b}\right) \\
& =a^{4}+b^{4}+c^{4} .
\end{aligned}
$$
So we need prove that $a^{4}+b^{4}+c^{4} \geq a+b+c$.
By the Power Mean Inequality,
$$
\frac{a^{4}+b^{4}+c^{4}}{3} \geq\left(\frac{a+b+c}{3}\right)^{4}
$$
so $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27}$.
By the arithmetic mean-geometric mean inequality, $\frac{a+b+c}{3} \geq \sqrt[3]{a b c}=1$, so $a+b+c \geq 3$.
Hence, $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27} \geq(a+b+c) \frac{3^{3}}{27}=a+b+c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Notice the inequality is homogeneous. That is, if $a, b, c$ are replaced by $k a, k b, k c, k>0$ we get the original inequality. Thus we can assume, without loss of generality, that $a b c=1$. Then
$$
\begin{aligned}
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} & =a b c\left(\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b}\right) \\
& =a^{4}+b^{4}+c^{4} .
\end{aligned}
$$
So we need prove that $a^{4}+b^{4}+c^{4} \geq a+b+c$.
By the Power Mean Inequality,
$$
\frac{a^{4}+b^{4}+c^{4}}{3} \geq\left(\frac{a+b+c}{3}\right)^{4}
$$
so $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27}$.
By the arithmetic mean-geometric mean inequality, $\frac{a+b+c}{3} \geq \sqrt[3]{a b c}=1$, so $a+b+c \geq 3$.
Hence, $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27} \geq(a+b+c) \frac{3^{3}}{27}=a+b+c$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 2."
}
|
66fa1fc5-0689-515c-9ee8-fa69c080b3f8
| 604,793
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Rather than using the Power-Mean inequality to prove $a^{4}+b^{4}+c^{4} \geq a+b+c$ in Proof 2, the Cauchy-Schwartz-Bunjakovsky inequality can be used twice:
$$
\begin{aligned}
& \left(a^{4}+b^{4}+c^{4}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq\left(a^{2}+b^{2}+c^{2}\right)^{2} \\
& \left(a^{2}+b^{2}+c^{2}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq(a+b+c)^{2}
\end{aligned}
$$
So $\frac{a^{4}+b^{4}+c^{4}}{3} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{9} \geq \frac{(a+b+c)^{4}}{81}$. Continue as in Proof 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Rather than using the Power-Mean inequality to prove $a^{4}+b^{4}+c^{4} \geq a+b+c$ in Proof 2, the Cauchy-Schwartz-Bunjakovsky inequality can be used twice:
$$
\begin{aligned}
& \left(a^{4}+b^{4}+c^{4}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq\left(a^{2}+b^{2}+c^{2}\right)^{2} \\
& \left(a^{2}+b^{2}+c^{2}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq(a+b+c)^{2}
\end{aligned}
$$
So $\frac{a^{4}+b^{4}+c^{4}}{3} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{9} \geq \frac{(a+b+c)^{4}}{81}$. Continue as in Proof 2 .
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 3."
}
|
66fa1fc5-0689-515c-9ee8-fa69c080b3f8
| 604,793
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.
|
Let the center of $\Gamma$ be $O$, the radius $\mathrm{r}$. Since $B P=B C$, let $\theta=\measuredangle B P C=\measuredangle B C P$.
Quadrilateral $Q A B C$ is cyclic, so $\measuredangle B A Q=180^{\circ}-\theta$ and hence $\measuredangle P A Q=120^{\circ}-\theta$.
Also $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=120^{\circ}-\theta$, so $P Q=A Q$ and $\measuredangle A Q P=2 \theta-60^{\circ}$.
Again because quadrilateral $Q A B C$ is cyclic, $\measuredangle A B C=180^{\circ}-\measuredangle A Q C=240^{\circ}-2 \theta$.
Triangles $O A B$ and $O C B$ are congruent, since $O A=O B=O C=r$ and $A B=B C$.
Thus $\measuredangle A B O=\measuredangle C B O=\frac{1}{2} \measuredangle A B C=120^{\circ}-\theta$.
We have now shown that in triangles $A Q P$ and $A O B, \measuredangle P A Q=\measuredangle B A O=\measuredangle A P Q=\measuredangle A B O$.
Also $A P=A B$, so $\triangle A Q P \cong \triangle A O B$. Hence $Q P=O B=r$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.

|
Let the center of $\Gamma$ be $O$, the radius $\mathrm{r}$. Since $B P=B C$, let $\theta=\measuredangle B P C=\measuredangle B C P$.
Quadrilateral $Q A B C$ is cyclic, so $\measuredangle B A Q=180^{\circ}-\theta$ and hence $\measuredangle P A Q=120^{\circ}-\theta$.
Also $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=120^{\circ}-\theta$, so $P Q=A Q$ and $\measuredangle A Q P=2 \theta-60^{\circ}$.
Again because quadrilateral $Q A B C$ is cyclic, $\measuredangle A B C=180^{\circ}-\measuredangle A Q C=240^{\circ}-2 \theta$.
Triangles $O A B$ and $O C B$ are congruent, since $O A=O B=O C=r$ and $A B=B C$.
Thus $\measuredangle A B O=\measuredangle C B O=\frac{1}{2} \measuredangle A B C=120^{\circ}-\theta$.
We have now shown that in triangles $A Q P$ and $A O B, \measuredangle P A Q=\measuredangle B A O=\measuredangle A P Q=\measuredangle A B O$.
Also $A P=A B$, so $\triangle A Q P \cong \triangle A O B$. Hence $Q P=O B=r$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## Solution 1."
}
|
0c266a62-5e99-5be3-930f-04d320e8b1ce
| 604,822
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).
|
Let $l$ be a line through $A$ different from $A B$ and join $B$ to $A, X, Y$ and $Z$ as in the above diagram. No matter how $l$ is chosen, the angles $A X B, A Y B$ and $A Z B$ always subtend the chord $A B$. For this reason the angles in the triangles $B X Y$ and $B X Z$ are the same for all such $l$. Thus the ratio $X Y: Y Z$ remains constant by similar triangles.
Note that this is true no matter how $X, Y$ and $Z$ lie in relation to $A$. Suppose $X, Y$ and $Z$ all lie on the same side of $A$ (as in the diagram) and that $\measuredangle A X B=\alpha, \measuredangle A Y B=\beta$ and $\measuredangle A Z B=\gamma$. Then $\measuredangle B X Y=180^{\circ}-\alpha, \measuredangle B Y X=\beta, \measuredangle B Y Z=180^{\circ}-\beta$ and $\measuredangle B Z Y=\gamma$. Now suppose $l$ is chosen so that $X$ is now on the opposite side of $A$ from $Y$ and $Z$. Now since $X$ is on the other side of the chord $A B, \measuredangle A X B=180^{\circ}-\alpha$, but it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$ and all other angles in the two pertinent triangles remain unchanged. If $l$ is chosen so that $X$ is identical with $A$, then $l$ is tangent to the first circle and it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$. All other cases can be checked in a similar manner.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $l$ be a line through $A$ different from $A B$ and join $B$ to $A, X, Y$ and $Z$ as in the above diagram. No matter how $l$ is chosen, the angles $A X B, A Y B$ and $A Z B$ always subtend the chord $A B$. For this reason the angles in the triangles $B X Y$ and $B X Z$ are the same for all such $l$. Thus the ratio $X Y: Y Z$ remains constant by similar triangles.
Note that this is true no matter how $X, Y$ and $Z$ lie in relation to $A$. Suppose $X, Y$ and $Z$ all lie on the same side of $A$ (as in the diagram) and that $\measuredangle A X B=\alpha, \measuredangle A Y B=\beta$ and $\measuredangle A Z B=\gamma$. Then $\measuredangle B X Y=180^{\circ}-\alpha, \measuredangle B Y X=\beta, \measuredangle B Y Z=180^{\circ}-\beta$ and $\measuredangle B Z Y=\gamma$. Now suppose $l$ is chosen so that $X$ is now on the opposite side of $A$ from $Y$ and $Z$. Now since $X$ is on the other side of the chord $A B, \measuredangle A X B=180^{\circ}-\alpha$, but it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$ and all other angles in the two pertinent triangles remain unchanged. If $l$ is chosen so that $X$ is identical with $A$, then $l$ is tangent to the first circle and it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$. All other cases can be checked in a similar manner.

|
{
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## Solution 1"
}
|
dcbc4a7b-6d50-53ef-a936-80eed1388b7a
| 604,940
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $m$ be the perpendicular bisector of $A B$ and let $O_{1}, O_{2}, O_{3}$ be the centres of the three circles. Since $A B$ is a chord common to all three circles, $O_{1}, O_{2}, O_{3}$ all lie on $m$. Let $l$ be a line through $A$ different from $A B$ and suppose that $X, Y, Z$ all lie on the same side of $A B$, as in the above diagram. Let perpendiculars from $O_{1}, O_{2}, O_{3}$ meet $l$ at $P, Q, R$, respectively. Since a line through the centre of a circle bisects any chord,
$$
A X=2 A P, \quad A Y=2 A Q \quad \text { and } \quad A Z=2 A R
$$
Now
$$
X Y=A Y-A X=2(A Q-A P)=2 P Q \quad \text { and, similarly, } \quad Y Z=2 Q R \text {. }
$$
Therefore $X Y: Y Z=P Q: Q R$. But $O_{1} P\left\|O_{2} Q\right\| O_{3} R$, so $P Q: Q R=O_{1} O_{2}: O_{2} O_{3}$. Since the centres of the circles are fixed, the ratio $X Y: Y Z=O_{1} O_{2}: O_{2} O_{3}$ does not depend on the choice of $l$.
If $X, Y, Z$ do not all lie on the same side of $A B$, we can obtain the same result with a similar proof. For instance, if $X$ and $Y$ are opposite sides of $A B$, then we will have $X Y=A Y+A X$, but since in this case $P Q=A Q+A P$, it is still the case that $X Y=2 P Q$ and result still follows, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $m$ be the perpendicular bisector of $A B$ and let $O_{1}, O_{2}, O_{3}$ be the centres of the three circles. Since $A B$ is a chord common to all three circles, $O_{1}, O_{2}, O_{3}$ all lie on $m$. Let $l$ be a line through $A$ different from $A B$ and suppose that $X, Y, Z$ all lie on the same side of $A B$, as in the above diagram. Let perpendiculars from $O_{1}, O_{2}, O_{3}$ meet $l$ at $P, Q, R$, respectively. Since a line through the centre of a circle bisects any chord,
$$
A X=2 A P, \quad A Y=2 A Q \quad \text { and } \quad A Z=2 A R
$$
Now
$$
X Y=A Y-A X=2(A Q-A P)=2 P Q \quad \text { and, similarly, } \quad Y Z=2 Q R \text {. }
$$
Therefore $X Y: Y Z=P Q: Q R$. But $O_{1} P\left\|O_{2} Q\right\| O_{3} R$, so $P Q: Q R=O_{1} O_{2}: O_{2} O_{3}$. Since the centres of the circles are fixed, the ratio $X Y: Y Z=O_{1} O_{2}: O_{2} O_{3}$ does not depend on the choice of $l$.
If $X, Y, Z$ do not all lie on the same side of $A B$, we can obtain the same result with a similar proof. For instance, if $X$ and $Y$ are opposite sides of $A B$, then we will have $X Y=A Y+A X$, but since in this case $P Q=A Q+A P$, it is still the case that $X Y=2 P Q$ and result still follows, etc.
|
{
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## Solution 2"
}
|
dcbc4a7b-6d50-53ef-a936-80eed1388b7a
| 604,940
|
Let $S$ be a set of $n$ points in the plane such that any two points of $S$ are at least 1 unit apart. Prove there is a subset $T$ of $S$ with at least $n / 7$ points such that any two points of $T$ are at least $\sqrt{3}$ units apart.
|
We will construct the set $T$ in the following way: Assume the points of $S$ are in the $x y$-plane and let $P$ be a point in $S$ with maximum $y$-coordinate. This point $P$ will be a member of the set $T$ and now, from $S$, we will remove $P$ and all points in $S$ which are less than $\sqrt{3}$ units from $P$. From the remaining points we choose one with maximum $y$-coordinate to be a member of $T$ and remove from $S$ all points at distance less than $\sqrt{3}$ units from this new point. We continue in this way, until all the points of $S$ are exhausted. Clearly any two points in $T$ are at least $\sqrt{3}$ units apart. To show that $T$ has at least $n / 7$ points, we must prove that at each stage no more than 6 other points are removed along with $P$.
At a typical stage in this process, we've selected a point $P$ with maximum $y$-coordinate, so any points at distance less than $\sqrt{3}$ from $P$ must lie inside the semicircular region of radius $\sqrt{3}$ centred at $P$ shown in the first diagram below. Since points of $S$ are at least 1 unit apart, these points must lie outside (or on) the semicircle of radius 1. (So they lie in the shaded region of the first diagram.) Now divide this shaded region into 6 congruent regions $R_{1}, R_{2}, \ldots, R_{6}$ as shown in this diagram.
We will show that each of these regions contains at most one point of $S$. Since all 6 regions are congruent, consider one of them as depicted in the second diagram below. The distance between any two points in this shaded region must be less than the length of the line segment $A B$. The lengths of $P A$ and $P B$ are $\sqrt{3}$ and 1 , respectively, and angle $A P B=30^{\circ}$. If we construct a perpendicular from $B$ to $P A$ at $C$, then the length of $P C$ is $\cos 30^{\circ}=\sqrt{3} / 2$. Thus $B C$ is a perpendicular bisector of $P A$ and therefore $A B=P B=1$. So the distance between any two points in this region is less than 1. Therefore each of $R_{1}, \ldots, R_{6}$ can contain at most one point of $S$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set of $n$ points in the plane such that any two points of $S$ are at least 1 unit apart. Prove there is a subset $T$ of $S$ with at least $n / 7$ points such that any two points of $T$ are at least $\sqrt{3}$ units apart.
|
We will construct the set $T$ in the following way: Assume the points of $S$ are in the $x y$-plane and let $P$ be a point in $S$ with maximum $y$-coordinate. This point $P$ will be a member of the set $T$ and now, from $S$, we will remove $P$ and all points in $S$ which are less than $\sqrt{3}$ units from $P$. From the remaining points we choose one with maximum $y$-coordinate to be a member of $T$ and remove from $S$ all points at distance less than $\sqrt{3}$ units from this new point. We continue in this way, until all the points of $S$ are exhausted. Clearly any two points in $T$ are at least $\sqrt{3}$ units apart. To show that $T$ has at least $n / 7$ points, we must prove that at each stage no more than 6 other points are removed along with $P$.
At a typical stage in this process, we've selected a point $P$ with maximum $y$-coordinate, so any points at distance less than $\sqrt{3}$ from $P$ must lie inside the semicircular region of radius $\sqrt{3}$ centred at $P$ shown in the first diagram below. Since points of $S$ are at least 1 unit apart, these points must lie outside (or on) the semicircle of radius 1. (So they lie in the shaded region of the first diagram.) Now divide this shaded region into 6 congruent regions $R_{1}, R_{2}, \ldots, R_{6}$ as shown in this diagram.
We will show that each of these regions contains at most one point of $S$. Since all 6 regions are congruent, consider one of them as depicted in the second diagram below. The distance between any two points in this shaded region must be less than the length of the line segment $A B$. The lengths of $P A$ and $P B$ are $\sqrt{3}$ and 1 , respectively, and angle $A P B=30^{\circ}$. If we construct a perpendicular from $B$ to $P A$ at $C$, then the length of $P C$ is $\cos 30^{\circ}=\sqrt{3} / 2$. Thus $B C$ is a perpendicular bisector of $P A$ and therefore $A B=P B=1$. So the distance between any two points in this region is less than 1. Therefore each of $R_{1}, \ldots, R_{6}$ can contain at most one point of $S$, which completes the proof.

|
{
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"problem_match": "\n5.",
"solution_match": "\n## Solution\n\n"
}
|
1787d2e7-4bd4-572c-9580-939457bb269e
| 604,963
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.
|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$.
Let $\measuredangle B A X=\measuredangle D A X=\alpha$ and let $\measuredangle B C Y=\measuredangle D C Y=\gamma$. Since $A B C D$ is cyclic, $\measuredangle A+\measuredangle C=180^{\circ}$, which implies that $\alpha+\gamma=90^{\circ}$. The fact that $Y A=A B=X C=C D$ means that the arc from $Y$ to $B$ (which is subtended by $\measuredangle Y C B$ ) is equal to the arc from $X$ to $D$ (which is subtended by $\measuredangle X A D$ ). Hence $\measuredangle Y C B=\measuredangle X A D$, so $\alpha=\gamma=45^{\circ}$. Finally, $B D$ is subtended by $\measuredangle B A D=2 \alpha=90^{\circ}$. Therefore $B D$ is a diameter of the circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$.
Let $\measuredangle B A X=\measuredangle D A X=\alpha$ and let $\measuredangle B C Y=\measuredangle D C Y=\gamma$. Since $A B C D$ is cyclic, $\measuredangle A+\measuredangle C=180^{\circ}$, which implies that $\alpha+\gamma=90^{\circ}$. The fact that $Y A=A B=X C=C D$ means that the arc from $Y$ to $B$ (which is subtended by $\measuredangle Y C B$ ) is equal to the arc from $X$ to $D$ (which is subtended by $\measuredangle X A D$ ). Hence $\measuredangle Y C B=\measuredangle X A D$, so $\alpha=\gamma=45^{\circ}$. Finally, $B D$ is subtended by $\measuredangle B A D=2 \alpha=90^{\circ}$. Therefore $B D$ is a diameter of the circle.
|
{
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 1"
}
|
d16bea6f-c85b-5312-b4b2-2c6e3e7fcccc
| 605,020
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$. This implies that the arc from $Y$ to $B$ is equal to the arc from $X$ to $D$ and hence that $Y B=X D$. Since $\measuredangle B A X=\measuredangle X A D, B X=X D$ and since $\measuredangle D C Y=\measuredangle Y C B$, $D Y=Y B$. Therefore $B X D Y$ is a square and its diagonal, $B D$, must be a diameter of the circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$. This implies that the arc from $Y$ to $B$ is equal to the arc from $X$ to $D$ and hence that $Y B=X D$. Since $\measuredangle B A X=\measuredangle X A D, B X=X D$ and since $\measuredangle D C Y=\measuredangle Y C B$, $D Y=Y B$. Therefore $B X D Y$ is a square and its diagonal, $B D$, must be a diameter of the circle.
|
{
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 2"
}
|
d16bea6f-c85b-5312-b4b2-2c6e3e7fcccc
| 605,020
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
Defining $\theta$ as in Solution 1, we have $c / a+c / b=\sec \theta+\csc \theta$. By the AM-GM inequality, we have $(\sec \theta+\csc \theta) / 2 \geq \sqrt{\sec \theta \csc \theta}$. So
$$
c / a+c / b \geq \frac{2}{\sqrt{\sin \theta \cos \theta}}=\frac{2 \sqrt{2}}{\sqrt{\sin 2 \theta}} \geq 2 \sqrt{2}
$$
Since $a, b, c$ are integers, we have $c / a+c / b>2 \sqrt{2}$ which gives $(c / a+c / b)^{2}>8$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
Defining $\theta$ as in Solution 1, we have $c / a+c / b=\sec \theta+\csc \theta$. By the AM-GM inequality, we have $(\sec \theta+\csc \theta) / 2 \geq \sqrt{\sec \theta \csc \theta}$. So
$$
c / a+c / b \geq \frac{2}{\sqrt{\sin \theta \cos \theta}}=\frac{2 \sqrt{2}}{\sqrt{\sin 2 \theta}} \geq 2 \sqrt{2}
$$
Since $a, b, c$ are integers, we have $c / a+c / b>2 \sqrt{2}$ which gives $(c / a+c / b)^{2}>8$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution 2"
}
|
6b35ad85-efa4-5baf-a40d-f7df240501f4
| 605,076
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
By simplifying and using the AM-GM inequality,
$$
\left(\frac{c}{a}+\frac{c}{b}\right)^{2}=c^{2}\left(\frac{a+b}{a b}\right)^{2}=\frac{\left(a^{2}+b^{2}\right)(a+b)^{2}}{a^{2} b^{2}} \geq \frac{2 \sqrt{a^{2} b^{2}}(2 \sqrt{a b})^{2}}{a^{2} b^{2}}=8
$$
with equality only if $a=b$. By using the same argument as in Solution $1, a$ cannot equal $b$ and the inequality is strict.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
By simplifying and using the AM-GM inequality,
$$
\left(\frac{c}{a}+\frac{c}{b}\right)^{2}=c^{2}\left(\frac{a+b}{a b}\right)^{2}=\frac{\left(a^{2}+b^{2}\right)(a+b)^{2}}{a^{2} b^{2}} \geq \frac{2 \sqrt{a^{2} b^{2}}(2 \sqrt{a b})^{2}}{a^{2} b^{2}}=8
$$
with equality only if $a=b$. By using the same argument as in Solution $1, a$ cannot equal $b$ and the inequality is strict.
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution 3"
}
|
6b35ad85-efa4-5baf-a40d-f7df240501f4
| 605,076
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}+\frac{2 c^{2}}{a b}=1+\frac{b^{2}}{a^{2}}+\frac{a^{2}}{b^{2}}+1+\frac{2\left(a^{2}+b^{2}\right)}{a b} \\
& =2+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+2+\frac{2}{a b}\left((a-b)^{2}+2 a b\right) \\
& =4+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+\frac{2(a-b)^{2}}{a b}+4 \geq 8,
\end{aligned}
$$
with equality only if $a=b$, which (as argued previously) cannot occur.
## b) Solution 1
Since $c / a+c / b$ is rational, $(c / a+c / b)^{2}$ can only be an integer if $c / a+c / b$ is an integer. Suppose $c / a+c / b=m$. We may assume that $\operatorname{gcd}(a, b)=1$. (If not, divide the common factor from $(a, b, c)$, leaving $m$ unchanged.)
Since $c(a+b)=m a b$ and $\operatorname{gcd}(a, a+b)=1$, $a$ must divide $c$, say $c=a k$. This gives $a^{2}+b^{2}=a^{2} k^{2}$ which implies $b^{2}=\left(k^{2}-1\right) a^{2}$. But then $a$ divides $b$ contradicting the fact that $\operatorname{gcd}(a, b)=1$. Therefore $(c / a+c / b)^{2}$ is not equal to any integer $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}+\frac{2 c^{2}}{a b}=1+\frac{b^{2}}{a^{2}}+\frac{a^{2}}{b^{2}}+1+\frac{2\left(a^{2}+b^{2}\right)}{a b} \\
& =2+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+2+\frac{2}{a b}\left((a-b)^{2}+2 a b\right) \\
& =4+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+\frac{2(a-b)^{2}}{a b}+4 \geq 8,
\end{aligned}
$$
with equality only if $a=b$, which (as argued previously) cannot occur.
## b) Solution 1
Since $c / a+c / b$ is rational, $(c / a+c / b)^{2}$ can only be an integer if $c / a+c / b$ is an integer. Suppose $c / a+c / b=m$. We may assume that $\operatorname{gcd}(a, b)=1$. (If not, divide the common factor from $(a, b, c)$, leaving $m$ unchanged.)
Since $c(a+b)=m a b$ and $\operatorname{gcd}(a, a+b)=1$, $a$ must divide $c$, say $c=a k$. This gives $a^{2}+b^{2}=a^{2} k^{2}$ which implies $b^{2}=\left(k^{2}-1\right) a^{2}$. But then $a$ divides $b$ contradicting the fact that $\operatorname{gcd}(a, b)=1$. Therefore $(c / a+c / b)^{2}$ is not equal to any integer $n$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution 4"
}
|
6b35ad85-efa4-5baf-a40d-f7df240501f4
| 605,076
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
We begin as in Solution 1, supposing that $c / a+c / b=m$ with $\operatorname{gcd}(a, b)=1$. Hence $a$ and $b$ are not both even. It is also the case that $a$ and $b$ are not both odd, for then $c^{2}=a^{2}+b^{2} \equiv 2(\bmod 4)$, and perfect squares are congruent to either 0 or 1 modulo 4. So one of $a, b$ is odd and the other is even. Therefore $c$ must be odd.
Now $c / a+c / b=m$ implies $c(a+b)=m a b$, which cannot be true because $c(a+b)$ is odd and mab is even.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
We begin as in Solution 1, supposing that $c / a+c / b=m$ with $\operatorname{gcd}(a, b)=1$. Hence $a$ and $b$ are not both even. It is also the case that $a$ and $b$ are not both odd, for then $c^{2}=a^{2}+b^{2} \equiv 2(\bmod 4)$, and perfect squares are congruent to either 0 or 1 modulo 4. So one of $a, b$ is odd and the other is even. Therefore $c$ must be odd.
Now $c / a+c / b=m$ implies $c(a+b)=m a b$, which cannot be true because $c(a+b)$ is odd and mab is even.
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution 2"
}
|
6b35ad85-efa4-5baf-a40d-f7df240501f4
| 605,076
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) Let $H$ be the smallest convex set of points in the plane which contains $S . \dagger$ Take 3 points $a, b, c \in S$ which lie on the boundary of $H$. (There must always be at least 3 (but not necessarily 4) such points.)
Since $a$ lies on the boundary of the convex region $H$, we can construct a chord $L$ such that no two points of $H$ lie on opposite sides of $L$. Of the two points where the perpendicular to $L$ at $a$ meets the circle, choose one which is on a side of $L$ not containing any points of $H$ and call this point $A$. Certainly $A$ is closer to $a$ than to any other point on $L$ or on the other side of $L$. Hence $A$ is closer to $a$ than to any other point of $S$. We can find the required points $B$ and $C$ in an analogous way and the proof is complete.
[Note that this argument still holds if all the points of $S$ lie on a line.]
(a)
(b)
b) Let $P Q R$ be an equilateral triangle inscribed in the circle and let $a, b, c$ be midpoints of the three sides of $\triangle P Q R$. If $r$ is the radius of the circle, then every point on the circle is within $(\sqrt{3} / 2) r$ of one of $a, b$ or $c$. (See figure (b) above.) Now $\sqrt{3} / 2<9 / 10$, so if $S$ consists of $a, b, c$ and a cluster of points within $r / 10$ of the centre of the circle, then we cannot select 4 points from $S$ (and corresponding points on the circle) having the desired property.[^0]
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) Let $H$ be the smallest convex set of points in the plane which contains $S . \dagger$ Take 3 points $a, b, c \in S$ which lie on the boundary of $H$. (There must always be at least 3 (but not necessarily 4) such points.)
Since $a$ lies on the boundary of the convex region $H$, we can construct a chord $L$ such that no two points of $H$ lie on opposite sides of $L$. Of the two points where the perpendicular to $L$ at $a$ meets the circle, choose one which is on a side of $L$ not containing any points of $H$ and call this point $A$. Certainly $A$ is closer to $a$ than to any other point on $L$ or on the other side of $L$. Hence $A$ is closer to $a$ than to any other point of $S$. We can find the required points $B$ and $C$ in an analogous way and the proof is complete.
[Note that this argument still holds if all the points of $S$ lie on a line.]

(a)

(b)
b) Let $P Q R$ be an equilateral triangle inscribed in the circle and let $a, b, c$ be midpoints of the three sides of $\triangle P Q R$. If $r$ is the radius of the circle, then every point on the circle is within $(\sqrt{3} / 2) r$ of one of $a, b$ or $c$. (See figure (b) above.) Now $\sqrt{3} / 2<9 / 10$, so if $S$ consists of $a, b, c$ and a cluster of points within $r / 10$ of the centre of the circle, then we cannot select 4 points from $S$ (and corresponding points on the circle) having the desired property.[^0]
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 1"
}
|
00eb17f4-6b04-5682-a442-1820fabb6ed4
| 605,124
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) If all the points of $S$ lie on a line $L$, then choose any 3 of them to be $a, b, c$. Let $A$ be a point on the circle which meets the perpendicular to $L$ at $a$. Clearly $A$ is closer to $a$ than to any other point on $L$, and hence closer than other other point in $S$. We find $B$ and $C$ in an analogous way.
Otherwise, choose $a, b, c$ from $S$ so that the triangle formed by these points has maximal area. Construct the altitude from the side $b c$ to the point $a$ and extend this line until it meets the circle at $A$. We claim that $A$ is closer to $a$ than to any other point in $S$.
Suppose not. Let $x$ be a point in $S$ for which the distance from $A$ to $x$ is less than the distance from $A$ to $a$. Then the perpendicular distance from $x$ to the line $b c$ must be greater than the perpendicular distance from $a$ to the line $b c$. But then the triangle formed by the points $x, b, c$ has greater area than the triangle formed by $a, b, c$, contradicting the original choice of these 3 points. Therefore $A$ is closer to $a$ than to any other point in $S$.
The points $B$ and $C$ are found by constructing similar altitudes through $b$ and $c$, respectively.
b) See Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) If all the points of $S$ lie on a line $L$, then choose any 3 of them to be $a, b, c$. Let $A$ be a point on the circle which meets the perpendicular to $L$ at $a$. Clearly $A$ is closer to $a$ than to any other point on $L$, and hence closer than other other point in $S$. We find $B$ and $C$ in an analogous way.
Otherwise, choose $a, b, c$ from $S$ so that the triangle formed by these points has maximal area. Construct the altitude from the side $b c$ to the point $a$ and extend this line until it meets the circle at $A$. We claim that $A$ is closer to $a$ than to any other point in $S$.
Suppose not. Let $x$ be a point in $S$ for which the distance from $A$ to $x$ is less than the distance from $A$ to $a$. Then the perpendicular distance from $x$ to the line $b c$ must be greater than the perpendicular distance from $a$ to the line $b c$. But then the triangle formed by the points $x, b, c$ has greater area than the triangle formed by $a, b, c$, contradicting the original choice of these 3 points. Therefore $A$ is closer to $a$ than to any other point in $S$.
The points $B$ and $C$ are found by constructing similar altitudes through $b$ and $c$, respectively.
b) See Solution 1.
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution 2"
}
|
00eb17f4-6b04-5682-a442-1820fabb6ed4
| 605,124
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
Consider first the case where all the rows have the same positive sum $s$; this covers the particular situation in which $m=1$. Then each column, sharing a positive element with some row, must also have the sum $s$. Then the sum of all the entries in the matrix is $m s=n s$, whence $m=n$.
We prove the general case by induction on $m$. The case $m=1$ is already covered. Suppose that we have an $m \times n$ array not all of whose rows have the same sum. Let $r<m$ of the rows have the sum $s$, and each of the of the other rows have a different sum. Then every column sharing a positive entry with one of these rows must also have sum $s$, and these are the only columns with the sum $s$. Suppose there are $c$ columns with sum $s$. The situation is essentially unchanged if we permute the rows and then the column so that the first $r$ rows have the sum $s$ and the first $c$ columns have the sum $s$. Since all the entries of the first $r$ rows not in the first $c$ columns and in the first $c$ columns not in the first $r$ rows must be 0 , we can partition the array into a $r \times c$ array in which all rows and columns have sum $s$ and which satisfies the hypothesis of the problem, two rectangular arrays of zeros in the upper right and lower left and a rectangular $(m-r) \times(n-c)$ array in the lower right that satisfies the conditions of the problem. By the induction hypothesis, we see that $r=c$ and so $m=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
Consider first the case where all the rows have the same positive sum $s$; this covers the particular situation in which $m=1$. Then each column, sharing a positive element with some row, must also have the sum $s$. Then the sum of all the entries in the matrix is $m s=n s$, whence $m=n$.
We prove the general case by induction on $m$. The case $m=1$ is already covered. Suppose that we have an $m \times n$ array not all of whose rows have the same sum. Let $r<m$ of the rows have the sum $s$, and each of the of the other rows have a different sum. Then every column sharing a positive entry with one of these rows must also have sum $s$, and these are the only columns with the sum $s$. Suppose there are $c$ columns with sum $s$. The situation is essentially unchanged if we permute the rows and then the column so that the first $r$ rows have the sum $s$ and the first $c$ columns have the sum $s$. Since all the entries of the first $r$ rows not in the first $c$ columns and in the first $c$ columns not in the first $r$ rows must be 0 , we can partition the array into a $r \times c$ array in which all rows and columns have sum $s$ and which satisfies the hypothesis of the problem, two rectangular arrays of zeros in the upper right and lower left and a rectangular $(m-r) \times(n-c)$ array in the lower right that satisfies the conditions of the problem. By the induction hypothesis, we see that $r=c$ and so $m=n$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 1."
}
|
3e44bb7a-b26c-5d5a-8d15-5821443df156
| 605,238
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.
|
A prime indicates where a tangent meets $A B$ and a double prime where it meets $A C$. It is given that $D D^{\prime}=D D^{\prime \prime}, E E^{\prime}=E E^{\prime \prime}$ and $F F^{\prime}=F F^{\prime \prime}$. It is required to show that arc $E F$ is a third of the circumference as is arc $D B F$.
$A F$ is the median to the hypotenuse of right triangle $A F^{\prime} F^{\prime \prime}$, so that $F F^{\prime}=F A$ and therefore
$$
\operatorname{arc} A F=2 \angle F^{\prime \prime} F A=2\left(\angle F F^{\prime} A+\angle F A F^{\prime}\right)=4 \angle F A F^{\prime}=4 \angle F A B=2 \text { arc } B F \text {, }
$$
whence $\operatorname{arc} F A=(2 / 3)$ arc $B F A$. Similarly, arc $A E=(2 / 3)$ arc $A E C$. Therefore, $\operatorname{arc} F E$ is $2 / 3$ of the semicircle, or $1 / 3$ of the circumference as desired.
As for arc $D B F$, arc $B D=2 \angle B A D=\angle B A D+\angle B D^{\prime} D=\angle A D D^{\prime \prime}=(1 / 2)$ arc $A C D$. But, arc $B F=(1 / 2)$ arc $A F$, so arc $D B F=(1 / 2)$ arc $F A E D$. That is, arc $D B F$ is $1 / 3$ the circumference and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
A prime indicates where a tangent meets $A B$ and a double prime where it meets $A C$. It is given that $D D^{\prime}=D D^{\prime \prime}, E E^{\prime}=E E^{\prime \prime}$ and $F F^{\prime}=F F^{\prime \prime}$. It is required to show that arc $E F$ is a third of the circumference as is arc $D B F$.
$A F$ is the median to the hypotenuse of right triangle $A F^{\prime} F^{\prime \prime}$, so that $F F^{\prime}=F A$ and therefore
$$
\operatorname{arc} A F=2 \angle F^{\prime \prime} F A=2\left(\angle F F^{\prime} A+\angle F A F^{\prime}\right)=4 \angle F A F^{\prime}=4 \angle F A B=2 \text { arc } B F \text {, }
$$
whence $\operatorname{arc} F A=(2 / 3)$ arc $B F A$. Similarly, arc $A E=(2 / 3)$ arc $A E C$. Therefore, $\operatorname{arc} F E$ is $2 / 3$ of the semicircle, or $1 / 3$ of the circumference as desired.
As for arc $D B F$, arc $B D=2 \angle B A D=\angle B A D+\angle B D^{\prime} D=\angle A D D^{\prime \prime}=(1 / 2)$ arc $A C D$. But, arc $B F=(1 / 2)$ arc $A F$, so arc $D B F=(1 / 2)$ arc $F A E D$. That is, arc $D B F$ is $1 / 3$ the circumference and the proof is complete.
|
{
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution 1."
}
|
7fdfc5d8-4f5e-517e-998e-6a0a72074cdb
| 605,282
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
Since $A E^{\prime} E^{\prime \prime}$ is a right triangle, $A E=E E^{\prime}=E E^{\prime \prime}$ so that $\angle C A E=\angle C E^{\prime \prime} E$. Also $A D=D^{\prime} D=D D^{\prime \prime}$, so that $\angle C D D^{\prime \prime}=\angle C A D=\angle C D^{\prime \prime} D$. As $E A D C$ is a concyclic quadrilateral,
$$
\begin{aligned}
180^{\circ} & =\angle E A D+\angle E C D \\
& =\angle D A C+\angle C A E+\angle E C A+\angle A C D \\
& =\angle D A C+\angle C A E+\angle C E E^{\prime \prime}+\angle C E^{\prime \prime} E+\angle C D D^{\prime \prime}+\angle C D^{\prime \prime} D \\
& =\angle D A C+\angle C A E+\angle C A E+\angle C A E+\angle C A D+\angle C A D \\
& =3(\angle D A C+\angle D A E)=3(\angle D A E)
\end{aligned}
$$
Hence $\angle D F E=\angle D A E=60^{\circ}$. Similarly, $\angle D E F=60^{\circ}$. It follows that triangle $D E F$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
Since $A E^{\prime} E^{\prime \prime}$ is a right triangle, $A E=E E^{\prime}=E E^{\prime \prime}$ so that $\angle C A E=\angle C E^{\prime \prime} E$. Also $A D=D^{\prime} D=D D^{\prime \prime}$, so that $\angle C D D^{\prime \prime}=\angle C A D=\angle C D^{\prime \prime} D$. As $E A D C$ is a concyclic quadrilateral,
$$
\begin{aligned}
180^{\circ} & =\angle E A D+\angle E C D \\
& =\angle D A C+\angle C A E+\angle E C A+\angle A C D \\
& =\angle D A C+\angle C A E+\angle C E E^{\prime \prime}+\angle C E^{\prime \prime} E+\angle C D D^{\prime \prime}+\angle C D^{\prime \prime} D \\
& =\angle D A C+\angle C A E+\angle C A E+\angle C A E+\angle C A D+\angle C A D \\
& =3(\angle D A C+\angle D A E)=3(\angle D A E)
\end{aligned}
$$
Hence $\angle D F E=\angle D A E=60^{\circ}$. Similarly, $\angle D E F=60^{\circ}$. It follows that triangle $D E F$ is equilateral.
|
{
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution 2."
}
|
7fdfc5d8-4f5e-517e-998e-6a0a72074cdb
| 605,282
|
$A B C D$ is a convex quadrilateral in which $A B$ is the longest side. Points $M$ and $N$ are located on sides $A B$ and $B C$ respectively, so that each of the segments $A N$ and $C M$ divides the quadrilateral into two parts of equal area. Prove that the segment $M N$ bisects the diagonal $B D$.
|
Since $[M A D C]=\frac{1}{2}[A B C D]=[N A D C]$, it follows that $[A N C]=[A M C]$, so that $M N \| A C$. Let $m$ be a line through $D$ parallel to $A C$ and $M N$ and let $B A$ produced meet $m$ at $P$ and $B C$ produced meet $m$ at $Q$. Then
$$
[M P C]=[M A C]+[C A P]=[M A C]+[C A D]=[M A D C]=[B M C]
$$
whence $B M=M P$. Similarly $B N=N Q$, so that $M N$ is a midline of triangle $B P Q$ and must bisect $B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$A B C D$ is a convex quadrilateral in which $A B$ is the longest side. Points $M$ and $N$ are located on sides $A B$ and $B C$ respectively, so that each of the segments $A N$ and $C M$ divides the quadrilateral into two parts of equal area. Prove that the segment $M N$ bisects the diagonal $B D$.
|
Since $[M A D C]=\frac{1}{2}[A B C D]=[N A D C]$, it follows that $[A N C]=[A M C]$, so that $M N \| A C$. Let $m$ be a line through $D$ parallel to $A C$ and $M N$ and let $B A$ produced meet $m$ at $P$ and $B C$ produced meet $m$ at $Q$. Then
$$
[M P C]=[M A C]+[C A P]=[M A C]+[C A D]=[M A D C]=[B M C]
$$
whence $B M=M P$. Similarly $B N=N Q$, so that $M N$ is a midline of triangle $B P Q$ and must bisect $B D$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
f00e5af2-e836-51d3-8041-ed731f227be4
| 605,303
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Note that
$$
1-\frac{a-b c}{a+b c}=\frac{2 b c}{1-b-c+b c}=\frac{2 b c}{(1-b)(1-c)}
$$
The inequality is equivalent to
$$
\frac{2 b c}{(1-b)(1-c)}+\frac{2 c a}{(1-c)(1-a)}+\frac{2 a b}{(1-a)(1-b)} \geq \frac{3}{2} .
$$
Manipulation yields the equivalent
$$
4(b c+c a+a b-3 a b c) \geq 3(b c+c a+a b+1-a-b-c-a b c) .
$$
This simplifies to $a b+b c+c a \geq 9 a b c$ or
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 9 \text {. }
$$
This is a consequence of the harmonic-arithmetic means inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Note that
$$
1-\frac{a-b c}{a+b c}=\frac{2 b c}{1-b-c+b c}=\frac{2 b c}{(1-b)(1-c)}
$$
The inequality is equivalent to
$$
\frac{2 b c}{(1-b)(1-c)}+\frac{2 c a}{(1-c)(1-a)}+\frac{2 a b}{(1-a)(1-b)} \geq \frac{3}{2} .
$$
Manipulation yields the equivalent
$$
4(b c+c a+a b-3 a b c) \geq 3(b c+c a+a b+1-a-b-c-a b c) .
$$
This simplifies to $a b+b c+c a \geq 9 a b c$ or
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 9 \text {. }
$$
This is a consequence of the harmonic-arithmetic means inequality.
|
{
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 1."
}
|
327d18cf-41ad-5199-9527-e21532f83b20
| 605,332
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Observe that
$$
a+b c=a(a+b+c)+b c=(a+b)(a+c)
$$
and that $a+b=1-c$, with analogous relations for other permutations of the variables. Then
$$
(b+c)(c+a)(a+b)=(1-a)(1-b)(1-c)=(a b+b c+c a)-a b c .
$$
Putting the left side of the desired inequality over a common denominator, we find that it is equal to
$$
\begin{aligned}
\frac{(a-b c)(1-a)+(b-a c)(1-b)+(c-a b)(1-c)}{(b+c)(c+a)(a+b)} & =\frac{(a+b+c)-(a 2+b 2+c 2)-(b c+c a+a b)+3 a b c}{(b+c)(c+a)(a+b)} \\
& =\frac{1-(a+b+c) 2+(b c+c a+a b)+3 a b c}{(a b+b c+c a)-a b c} \\
& =\frac{(b c+c a+a b)+3 a b c}{(b c+b c+a b)-a b c} \\
& =1+\frac{4 a b c}{(a+b)(b+c)(c+a)} .
\end{aligned}
$$
Using the arithmetic-geometric means inequality, we obtain that
$$
\begin{aligned}
(a+b)(b+c)(c+a) & =\left(a^{2} b+b^{2} c+c^{2} a\right)+(a b 2+b c 2+c a 2)+2 a b c \\
& \geq 3 a b c+3 a b c+2 a b c=8 a b c
\end{aligned}
$$
whence $4 a b c /[(a+b)(b+c)(c+a)] \leq \frac{1}{2}$. The desired result follows. Equality occurs exactly when $a=b=$ $c=\frac{1}{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Observe that
$$
a+b c=a(a+b+c)+b c=(a+b)(a+c)
$$
and that $a+b=1-c$, with analogous relations for other permutations of the variables. Then
$$
(b+c)(c+a)(a+b)=(1-a)(1-b)(1-c)=(a b+b c+c a)-a b c .
$$
Putting the left side of the desired inequality over a common denominator, we find that it is equal to
$$
\begin{aligned}
\frac{(a-b c)(1-a)+(b-a c)(1-b)+(c-a b)(1-c)}{(b+c)(c+a)(a+b)} & =\frac{(a+b+c)-(a 2+b 2+c 2)-(b c+c a+a b)+3 a b c}{(b+c)(c+a)(a+b)} \\
& =\frac{1-(a+b+c) 2+(b c+c a+a b)+3 a b c}{(a b+b c+c a)-a b c} \\
& =\frac{(b c+c a+a b)+3 a b c}{(b c+b c+a b)-a b c} \\
& =1+\frac{4 a b c}{(a+b)(b+c)(c+a)} .
\end{aligned}
$$
Using the arithmetic-geometric means inequality, we obtain that
$$
\begin{aligned}
(a+b)(b+c)(c+a) & =\left(a^{2} b+b^{2} c+c^{2} a\right)+(a b 2+b c 2+c a 2)+2 a b c \\
& \geq 3 a b c+3 a b c+2 a b c=8 a b c
\end{aligned}
$$
whence $4 a b c /[(a+b)(b+c)(c+a)] \leq \frac{1}{2}$. The desired result follows. Equality occurs exactly when $a=b=$ $c=\frac{1}{3}$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 2."
}
|
327d18cf-41ad-5199-9527-e21532f83b20
| 605,332
|
Two circles of different radii are cut out of cardboard. Each circle is subdivided into 200 equal sectors. On each circle 100 sectors are painted white and the other 100 are painted black. The smaller circle is then placed on top of the larger circle, so that their centers coincide. Show that one can rotate the small circle so that the sectors on the two circles line up and at least 100 sectors on the small circle lie over sectors of the same color on the big circle.
|
Let $x_{0}, \ldots, x_{199}$ be variables. Assign the value of +1 or -1 to $x_{i}$ depending on whether the $(i+1)$ st segment of the larger circle (counting counterclockwise) is black or white, respectively. Similarly, assign the value of +1 or -1 to the variable $y_{i}$ depending on whether the $(i+1)$ th segment of the smaller circle is black or white. We can now restate the problem in the following equivalent way: show that
$$
S_{j}=\sum_{i=1}^{200} x_{i} y_{i+j} \geq 0
$$
for some $j=0, \ldots, 199$. Here the subscript $i+j$ is understood modulo 200 .
Now observe that $y_{0}+\cdots+y_{199}=0$ and thus
$$
S_{0}+\cdots+S_{199}=\sum_{I=0}^{199} x_{i}\left(y_{0}+\cdots+y_{199}\right)=0 .
$$
Thus $S_{j} \geq 0$ for some $j=0, \ldots, 199$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Two circles of different radii are cut out of cardboard. Each circle is subdivided into 200 equal sectors. On each circle 100 sectors are painted white and the other 100 are painted black. The smaller circle is then placed on top of the larger circle, so that their centers coincide. Show that one can rotate the small circle so that the sectors on the two circles line up and at least 100 sectors on the small circle lie over sectors of the same color on the big circle.
|
Let $x_{0}, \ldots, x_{199}$ be variables. Assign the value of +1 or -1 to $x_{i}$ depending on whether the $(i+1)$ st segment of the larger circle (counting counterclockwise) is black or white, respectively. Similarly, assign the value of +1 or -1 to the variable $y_{i}$ depending on whether the $(i+1)$ th segment of the smaller circle is black or white. We can now restate the problem in the following equivalent way: show that
$$
S_{j}=\sum_{i=1}^{200} x_{i} y_{i+j} \geq 0
$$
for some $j=0, \ldots, 199$. Here the subscript $i+j$ is understood modulo 200 .
Now observe that $y_{0}+\cdots+y_{199}=0$ and thus
$$
S_{0}+\cdots+S_{199}=\sum_{I=0}^{199} x_{i}\left(y_{0}+\cdots+y_{199}\right)=0 .
$$
Thus $S_{j} \geq 0$ for some $j=0, \ldots, 199$, as claimed.
|
{
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
8e22d4a0-2a6a-5089-a759-90dc88b34b9c
| 605,403
|
A set of points is marked on the plane, with the property that any three marked points can be covered with a disk of radius 1. Prove that the set of all marked points can be covered with a disk of radius 1 .
|
(For a finite set of points only.) Let $D$ be a disk of smallest radius that covers all marked points. Consider the marked points on the boundary $C$ of this disk. Note that if all marked points on $C$ lie on an arc smaller than the half circle (ASTTHC for short), then the disk can be moved a little towards these points on the boundary and its radius can be decreased. Since we assumed that our disk has minimal radius, the marked points on its boundary do not lie on an ASTTHC.
If the two endpoints of a diagonal of $D$ are marked, then $D$ is the smallest disk containing these two points, hence must have radius at most 1 .
If there are 3 marked points on $C$ that do not lie on an ASTTHC, then $D$ is the smallest disk covering these 3 points and hence must have radius at most 1 . (In this case the triangle formed by the three points is acute and $C$ is its circumcircle.)
If there are more than 3 marked points on the boundary that do not lie on an ASTTHC, then we can remove one of them so that the remaining points again do not lie on an ASTTHC. By induction this leads us to the case of 3 points. Indeed, given 4 or more points on $C$, choose 3 points that lie on a half circle. Then the middle point can be removed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A set of points is marked on the plane, with the property that any three marked points can be covered with a disk of radius 1. Prove that the set of all marked points can be covered with a disk of radius 1 .
|
(For a finite set of points only.) Let $D$ be a disk of smallest radius that covers all marked points. Consider the marked points on the boundary $C$ of this disk. Note that if all marked points on $C$ lie on an arc smaller than the half circle (ASTTHC for short), then the disk can be moved a little towards these points on the boundary and its radius can be decreased. Since we assumed that our disk has minimal radius, the marked points on its boundary do not lie on an ASTTHC.
If the two endpoints of a diagonal of $D$ are marked, then $D$ is the smallest disk containing these two points, hence must have radius at most 1 .
If there are 3 marked points on $C$ that do not lie on an ASTTHC, then $D$ is the smallest disk covering these 3 points and hence must have radius at most 1 . (In this case the triangle formed by the three points is acute and $C$ is its circumcircle.)
If there are more than 3 marked points on the boundary that do not lie on an ASTTHC, then we can remove one of them so that the remaining points again do not lie on an ASTTHC. By induction this leads us to the case of 3 points. Indeed, given 4 or more points on $C$, choose 3 points that lie on a half circle. Then the middle point can be removed.
|
{
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
103836a5-3d1e-5f16-92c0-40532616d5e7
| 605,432
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $E, F, G$ be the feet of the perpendiculars to the tangents at $A$ and $B$ and the chord $A B$, respectively. We need to show that $P E: P G=P G: G F$, where $G$ is the foot of the perpendicular from $P$ to $A B$. This suggest that we try to prove that the triangles $E P G$ and $G P F$ are similar.
Since $P G$ is parallel to the bisector of the angle between the two tangents, $\angle E P G=\angle F P G$. Since $A E P G$ and $B F P G$ are concyclic quadrilaterals (having opposite angles right), $\angle P G E=\angle P A E$ and $\angle P F G=\angle P B G$. But $\angle P A E=$ $\angle P B A=\angle P B G$, whence $\angle P G E=\angle P F G$. Therefore triangles $E P G$ and $G P F$ are similar.
The argument above with concyclic quadrilaterals only works when $P$ lies on the shorter arc between $A$ and $B$. The other case can be proved similarly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $E, F, G$ be the feet of the perpendiculars to the tangents at $A$ and $B$ and the chord $A B$, respectively. We need to show that $P E: P G=P G: G F$, where $G$ is the foot of the perpendicular from $P$ to $A B$. This suggest that we try to prove that the triangles $E P G$ and $G P F$ are similar.
Since $P G$ is parallel to the bisector of the angle between the two tangents, $\angle E P G=\angle F P G$. Since $A E P G$ and $B F P G$ are concyclic quadrilaterals (having opposite angles right), $\angle P G E=\angle P A E$ and $\angle P F G=\angle P B G$. But $\angle P A E=$ $\angle P B A=\angle P B G$, whence $\angle P G E=\angle P F G$. Therefore triangles $E P G$ and $G P F$ are similar.
The argument above with concyclic quadrilaterals only works when $P$ lies on the shorter arc between $A$ and $B$. The other case can be proved similarly.
|
{
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"problem_match": "\n(2) ",
"solution_match": "\nAlternate Solution."
}
|
1888342d-be26-5251-a58c-68b810ca946c
| 605,452
|
Let $P(x)$ and $Q(x)$ be polynomials with integer coefficients. Let $a_{n}=n !+n$. Show that if $P\left(a_{n}\right) / Q\left(a_{n}\right)$ is an integer for every $n$, then $P(n) / Q(n)$ is an integer for every integer $n$ such that $Q(n) \neq 0$.
|
Imagine dividing $P(x)$ by $Q(x)$. We find that
$$
\frac{P(x)}{Q(x)}=A(x)+\frac{R(x)}{Q(x)}
$$
where $A(x)$ and $R(x)$ are polynomials with rational coefficients, and $R(x)$ is either identically 0 or has degree less than the degree of $Q(x)$.
By bringing the coefficients of $A(x)$ to their least common multiple, we can find a polynomial $B(x)$ with integer coefficients, and a positive integer $b$, such that $A(x)=B(x) / b$. Suppose first that $R(x)$ is not identically 0 . Note that for any integer $k$, either $A(k)=0$, or $|A(k)| \geq 1 / b$. But whenever $|k|$ is large enough, $0<|R(k) / Q(k)|<1 / b$, and therefore if $n$ is large enough, $P\left(a_{n}\right) / Q\left(a_{n}\right)$ cannot be an integer.
So $R(x)$ is identically 0 , and $P(x) / Q(x)=B(x) / b$ (at least whenever $Q(x) \neq 0$.)
Now let $n$ be an integer. Then there are infinitely many integers $k$ such that $n \equiv a_{k}(\bmod b)$. But $B\left(a_{k}\right) / b$ is an integer, or equivalently $b$ divides $B\left(a_{k}\right)$. It follows that $b$ divides $B(n)$, and therefore $P(n) / Q(n)$ is an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)$ and $Q(x)$ be polynomials with integer coefficients. Let $a_{n}=n !+n$. Show that if $P\left(a_{n}\right) / Q\left(a_{n}\right)$ is an integer for every $n$, then $P(n) / Q(n)$ is an integer for every integer $n$ such that $Q(n) \neq 0$.
|
Imagine dividing $P(x)$ by $Q(x)$. We find that
$$
\frac{P(x)}{Q(x)}=A(x)+\frac{R(x)}{Q(x)}
$$
where $A(x)$ and $R(x)$ are polynomials with rational coefficients, and $R(x)$ is either identically 0 or has degree less than the degree of $Q(x)$.
By bringing the coefficients of $A(x)$ to their least common multiple, we can find a polynomial $B(x)$ with integer coefficients, and a positive integer $b$, such that $A(x)=B(x) / b$. Suppose first that $R(x)$ is not identically 0 . Note that for any integer $k$, either $A(k)=0$, or $|A(k)| \geq 1 / b$. But whenever $|k|$ is large enough, $0<|R(k) / Q(k)|<1 / b$, and therefore if $n$ is large enough, $P\left(a_{n}\right) / Q\left(a_{n}\right)$ cannot be an integer.
So $R(x)$ is identically 0 , and $P(x) / Q(x)=B(x) / b$ (at least whenever $Q(x) \neq 0$.)
Now let $n$ be an integer. Then there are infinitely many integers $k$ such that $n \equiv a_{k}(\bmod b)$. But $B\left(a_{k}\right) / b$ is an integer, or equivalently $b$ divides $B\left(a_{k}\right)$. It follows that $b$ divides $B(n)$, and therefore $P(n) / Q(n)$ is an integer.
|
{
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"problem_match": "\n(5) ",
"solution_match": "\nSolution."
}
|
5f1d3409-1190-5668-8602-81e53718f6f8
| 605,499
|
Consider 70-digit numbers $n$, with the property that each of the digits $1,2,3, \ldots, 7$ appears in the decimal expansion of $n$ ten times (and 8, 9, and 0 do not appear). Show that no number of this form can divide another number of this form.
|
Assume the contrary: there exist $a$ and $b$ of the prescribed form, such that $b \geq a$ and $a$ divides $b$. Then $a$ divides $b-a$.
Claim: $a$ is not divisible by 3 but $b-a$ is divisible by 9 . Indeed, the sum of the digits is $10(1+\cdots+7)=280$, for both $a$ and $b$. [Here one needs to know or prove that an integer $n$ is equivalent of the sum of its digits modulo 3 and modulo 9.]
We conclude that $b-a$ is divisible by $9 a$. But this is impossible, since $9 a$ has 71 digits and $b$ has only 70 digits, so $9 a>b>b-a$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider 70-digit numbers $n$, with the property that each of the digits $1,2,3, \ldots, 7$ appears in the decimal expansion of $n$ ten times (and 8, 9, and 0 do not appear). Show that no number of this form can divide another number of this form.
|
Assume the contrary: there exist $a$ and $b$ of the prescribed form, such that $b \geq a$ and $a$ divides $b$. Then $a$ divides $b-a$.
Claim: $a$ is not divisible by 3 but $b-a$ is divisible by 9 . Indeed, the sum of the digits is $10(1+\cdots+7)=280$, for both $a$ and $b$. [Here one needs to know or prove that an integer $n$ is equivalent of the sum of its digits modulo 3 and modulo 9.]
We conclude that $b-a$ is divisible by $9 a$. But this is impossible, since $9 a$ has 71 digits and $b$ has only 70 digits, so $9 a>b>b-a$.
|
{
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"problem_match": "\n(1) ",
"solution_match": "\nSolution."
}
|
74144a63-f0e4-5559-a136-075ea945bc7e
| 605,512
|
Let $A B C D$ be a cyclic quadrilateral whose opposite sides are not parallel, $X$ the intersection of $A B$ and $C D$, and $Y$ the intersection of $A D$ and $B C$. Let the angle bisector of $\angle A X D$ intersect $A D, B C$ at $E, F$ respectively and let the angle bisector of $\angle A Y B$ intersect $A B, C D$ at $G, H$ respectively. Prove that $E G F H$ is a parallelogram. fore,
|
Since $A B C D$ is cyclic, $\triangle X A C \sim \triangle X D B$ and $\triangle Y A C \sim \triangle Y B D$. There-
$$
\frac{X A}{X D}=\frac{X C}{X B}=\frac{A C}{D B}=\frac{Y A}{Y B}=\frac{Y C}{Y D} .
$$
Let $s$ be this ratio. Therefore, by the angle bisector theorem,
$$
\frac{A E}{E D}=\frac{X A}{X D}=\frac{X C}{X B}=\frac{C F}{F B}=s,
$$
and
$$
\frac{A G}{G B}=\frac{Y A}{Y B}=\frac{Y C}{Y D}=\frac{C H}{H D}=s
$$
Hence, $\frac{A G}{G B}=\frac{C F}{F B}$ and $\frac{A E}{E D}=\frac{D H}{H C}$. Therefore, $E H\|A C\| G F$ and $E G\|D B\| H F$. Hence, $E G F H$ is a parallelogram.

## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose opposite sides are not parallel, $X$ the intersection of $A B$ and $C D$, and $Y$ the intersection of $A D$ and $B C$. Let the angle bisector of $\angle A X D$ intersect $A D, B C$ at $E, F$ respectively and let the angle bisector of $\angle A Y B$ intersect $A B, C D$ at $G, H$ respectively. Prove that $E G F H$ is a parallelogram. fore,
|
Since $A B C D$ is cyclic, $\triangle X A C \sim \triangle X D B$ and $\triangle Y A C \sim \triangle Y B D$. There-
$$
\frac{X A}{X D}=\frac{X C}{X B}=\frac{A C}{D B}=\frac{Y A}{Y B}=\frac{Y C}{Y D} .
$$
Let $s$ be this ratio. Therefore, by the angle bisector theorem,
$$
\frac{A E}{E D}=\frac{X A}{X D}=\frac{X C}{X B}=\frac{C F}{F B}=s,
$$
and
$$
\frac{A G}{G B}=\frac{Y A}{Y B}=\frac{Y C}{Y D}=\frac{C H}{H D}=s
$$
Hence, $\frac{A G}{G B}=\frac{C F}{F B}$ and $\frac{A E}{E D}=\frac{D H}{H C}$. Therefore, $E H\|A C\| G F$ and $E G\|D B\| H F$. Hence, $E G F H$ is a parallelogram.

## Life Financial
|
{
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"problem_match": "\n(2) ",
"solution_match": "\nSolution."
}
|
a3b3c577-0d62-51a3-9c12-450395820350
| 605,524
|
Show that there exists a positive integer $N$ such that for all integers $a>N$, there exists a contiguous substring of the decimal expansion of $a$ that is divisible by 2011. (For instance, if $a=153204$, then 15, 532, and 0 are all contiguous substrings of $a$. Note that 0 is divisible by 2011 .)
|
We claim that if the decimal expansion of $a$ has at least 2012 digits, then $a$ contains the required substring. Let the decimal expansion of $a$ be $a_{k} a_{k-1} \ldots a_{0}$. For $i=0, \ldots, 2011$, Let $b_{i}$ be the number with decimal expansion $a_{i} a_{i-1} \ldots a_{0}$. Then by pidgenhole principle, $b_{i} \equiv b_{j} \bmod 2011$ for some $i<j \leq 2011$. It follows that 2011 divides $b_{j}-b_{i}=c \cdot 10^{i}$. Here $c$ is the substring $a_{j} \ldots a_{i+1}$. Since 2011 and 10 are relatively prime, it follows that 2011 divides $c$.
## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there exists a positive integer $N$ such that for all integers $a>N$, there exists a contiguous substring of the decimal expansion of $a$ that is divisible by 2011. (For instance, if $a=153204$, then 15, 532, and 0 are all contiguous substrings of $a$. Note that 0 is divisible by 2011 .)
|
We claim that if the decimal expansion of $a$ has at least 2012 digits, then $a$ contains the required substring. Let the decimal expansion of $a$ be $a_{k} a_{k-1} \ldots a_{0}$. For $i=0, \ldots, 2011$, Let $b_{i}$ be the number with decimal expansion $a_{i} a_{i-1} \ldots a_{0}$. Then by pidgenhole principle, $b_{i} \equiv b_{j} \bmod 2011$ for some $i<j \leq 2011$. It follows that 2011 divides $b_{j}-b_{i}=c \cdot 10^{i}$. Here $c$ is the substring $a_{j} \ldots a_{i+1}$. Since 2011 and 10 are relatively prime, it follows that 2011 divides $c$.
## Life Financial
|
{
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"problem_match": "\n(4) ",
"solution_match": "\nSolution."
}
|
0bc405d7-950d-5ac2-a176-cb10301033fc
| 605,548
|
Let $d$ be a positive integer. Show that for every integer $S$, there exists an integer $n>0$ and a sequence $\epsilon_{1}, \epsilon_{2}, \ldots, \epsilon_{n}$, where for any $k, \epsilon_{k}=1$ or $\epsilon_{k}=-1$, such that
$$
S=\epsilon_{1}(1+d)^{2}+\epsilon_{2}(1+2 d)^{2}+\epsilon_{3}(1+3 d)^{2}+\cdots+\epsilon_{n}(1+n d)^{2}
$$
|
Let $U_{k}=(1+k d)^{2}$. We calculate $U_{k+3}-U_{k+2}-U_{k+1}+U_{k}$. This turns out to be $4 d^{2}$, a constant. Changing signs, we obtain the sum $-4 d^{2}$.
Thus if we have found an expression for a certain number $S_{0}$ as a sum of the desired type, we can obtain an expression of the desired type for $S_{0}+\left(4 d^{2}\right) q$, for any integer $q$.
It remains to show that for any $S$, there exists an integer $S^{\prime}$ such that $S^{\prime} \equiv S$ $\left(\bmod 4 d^{2}\right)$ and $S^{\prime}$ can be expressed in the desired form. Look at the sum
$$
(1+d)^{2}+(1+2 d)^{2}+\cdots+(1+N d)^{2}
$$
where $N$ is "large." We can at will choose $N$ so that the sum is odd, or so that the sum is even.
By changing the sign in front of $(1+k d)^{2}$ to a minus sign, we decrease the sum by $2(1+k d)^{2}$. In particular, if $k \equiv 0(\bmod 2 d)$, we decrease the sum by $2\left(\operatorname{modulo} 4 d^{2}\right)$. So
If $N$ is large enough, there are many $k<N$ such that $k$ is a multiple of $2 d$. By switching the sign in front of $r$ of these, we change ("downward") the congruence class modulo $4 d^{2}$ by $2 r$. By choosing $N$ so that the original sum is odd, and choosing suitable $r<2 d^{2}$, we can obtain numbers congruent to all odd numbers modulo $4 d^{2}$. By choosing $N$ so that the original sum is even, we can obtain numbers congruent to all even numbers modulo $4 d^{2}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $d$ be a positive integer. Show that for every integer $S$, there exists an integer $n>0$ and a sequence $\epsilon_{1}, \epsilon_{2}, \ldots, \epsilon_{n}$, where for any $k, \epsilon_{k}=1$ or $\epsilon_{k}=-1$, such that
$$
S=\epsilon_{1}(1+d)^{2}+\epsilon_{2}(1+2 d)^{2}+\epsilon_{3}(1+3 d)^{2}+\cdots+\epsilon_{n}(1+n d)^{2}
$$
|
Let $U_{k}=(1+k d)^{2}$. We calculate $U_{k+3}-U_{k+2}-U_{k+1}+U_{k}$. This turns out to be $4 d^{2}$, a constant. Changing signs, we obtain the sum $-4 d^{2}$.
Thus if we have found an expression for a certain number $S_{0}$ as a sum of the desired type, we can obtain an expression of the desired type for $S_{0}+\left(4 d^{2}\right) q$, for any integer $q$.
It remains to show that for any $S$, there exists an integer $S^{\prime}$ such that $S^{\prime} \equiv S$ $\left(\bmod 4 d^{2}\right)$ and $S^{\prime}$ can be expressed in the desired form. Look at the sum
$$
(1+d)^{2}+(1+2 d)^{2}+\cdots+(1+N d)^{2}
$$
where $N$ is "large." We can at will choose $N$ so that the sum is odd, or so that the sum is even.
By changing the sign in front of $(1+k d)^{2}$ to a minus sign, we decrease the sum by $2(1+k d)^{2}$. In particular, if $k \equiv 0(\bmod 2 d)$, we decrease the sum by $2\left(\operatorname{modulo} 4 d^{2}\right)$. So
If $N$ is large enough, there are many $k<N$ such that $k$ is a multiple of $2 d$. By switching the sign in front of $r$ of these, we change ("downward") the congruence class modulo $4 d^{2}$ by $2 r$. By choosing $N$ so that the original sum is odd, and choosing suitable $r<2 d^{2}$, we can obtain numbers congruent to all odd numbers modulo $4 d^{2}$. By choosing $N$ so that the original sum is even, we can obtain numbers congruent to all even numbers modulo $4 d^{2}$. This completes the proof.
|
{
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"problem_match": "\n(5) ",
"solution_match": "\nSolution."
}
|
514401e9-e1ab-5e0c-a1b2-0453e4155bd5
| 605,559
|
Let $x, y$ and $z$ be positive real numbers. Show that $x^{2}+x y^{2}+x y z^{2} \geq 4 x y z-4$.
|
Note that
$$
x^{2} \geq 4 x-4, \quad y^{2} \geq 4 y-4, \quad \text { and } \quad z^{2} \geq 4 z-4
$$
and therefore
$$
x^{2}+x y^{2}+x y z^{2} \geq(4 x-4)+x(4 y-4)+x y(4 z-4)=4 x y z-4 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers. Show that $x^{2}+x y^{2}+x y z^{2} \geq 4 x y z-4$.
|
Note that
$$
x^{2} \geq 4 x-4, \quad y^{2} \geq 4 y-4, \quad \text { and } \quad z^{2} \geq 4 z-4
$$
and therefore
$$
x^{2}+x y^{2}+x y z^{2} \geq(4 x-4)+x(4 y-4)+x y(4 z-4)=4 x y z-4 .
$$
|
{
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
204207d6-f387-5461-b734-616d724151d4
| 605,568
|
For any positive integers $n$ and $k$, let $L(n, k)$ be the least common multiple of the $k$ consecutive integers $n, n+1, \ldots, n+k-1$. Show that for any integer $b$, there exist integers $n$ and $k$ such that $L(n, k)>b L(n+1, k)$.
|
I. Let $p>b$ be prime, let $n=p^{3}$ and $k=p^{2}$. If $p^{3}<i<p^{3}+p^{2}$, then no power of $p$ greater than 1 divides $i$, while $p$ divides $p^{3}+p$. It follows that $L\left(p^{3}, p^{2}\right)=$ $p^{2} L\left(p^{3}+1, p^{2}-1\right)$. A similar calculation shows that $L\left(p^{3}+1, p^{2}\right)=p L\left(p^{3}+1, p^{2}-1\right)$. Thus $L\left(p^{3}, p^{2}\right)=p L\left(p^{3}+1, p^{2}\right)>b L\left(p^{3}+1, p^{2}\right)$.
II. Let $m>1$. Then $L(m !-1, m+1)$ is the least common multiple of the integers from $m !-1$ to $m !+m-1$. But $m !-1$ is relatively prime to all of $m !, m !+1, \ldots, m !+m-1$. It follows that $L(m !-1, m+1)=(m !-1) M$, where $M=\operatorname{lcm}(m !, m !+1, \ldots, m !+m-1)$.
Now consider $L(m !, m+1)$. This is $\operatorname{lcm}(M, m !+m)$. But $m !+m=m((m-1) !+1)$, and $m$ divides $M$. Thus $\operatorname{lcm}(M, m !+m) \leq M((m-1) !+1)$, and
$$
\frac{L(m !-1, m+1)}{L(m !, m+1)} \geq \frac{m !-1}{(m-1) !+1}
$$
Since $m$ can be arbitrarily large, so can $L(m !-1, m+1) / L(m !, m+1)$. Therefore taking $n=m$ ! - 1 for sufficiently large $m$, and $k=m+1$, works.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any positive integers $n$ and $k$, let $L(n, k)$ be the least common multiple of the $k$ consecutive integers $n, n+1, \ldots, n+k-1$. Show that for any integer $b$, there exist integers $n$ and $k$ such that $L(n, k)>b L(n+1, k)$.
|
I. Let $p>b$ be prime, let $n=p^{3}$ and $k=p^{2}$. If $p^{3}<i<p^{3}+p^{2}$, then no power of $p$ greater than 1 divides $i$, while $p$ divides $p^{3}+p$. It follows that $L\left(p^{3}, p^{2}\right)=$ $p^{2} L\left(p^{3}+1, p^{2}-1\right)$. A similar calculation shows that $L\left(p^{3}+1, p^{2}\right)=p L\left(p^{3}+1, p^{2}-1\right)$. Thus $L\left(p^{3}, p^{2}\right)=p L\left(p^{3}+1, p^{2}\right)>b L\left(p^{3}+1, p^{2}\right)$.
II. Let $m>1$. Then $L(m !-1, m+1)$ is the least common multiple of the integers from $m !-1$ to $m !+m-1$. But $m !-1$ is relatively prime to all of $m !, m !+1, \ldots, m !+m-1$. It follows that $L(m !-1, m+1)=(m !-1) M$, where $M=\operatorname{lcm}(m !, m !+1, \ldots, m !+m-1)$.
Now consider $L(m !, m+1)$. This is $\operatorname{lcm}(M, m !+m)$. But $m !+m=m((m-1) !+1)$, and $m$ divides $M$. Thus $\operatorname{lcm}(M, m !+m) \leq M((m-1) !+1)$, and
$$
\frac{L(m !-1, m+1)}{L(m !, m+1)} \geq \frac{m !-1}{(m-1) !+1}
$$
Since $m$ can be arbitrarily large, so can $L(m !-1, m+1) / L(m !, m+1)$. Therefore taking $n=m$ ! - 1 for sufficiently large $m$, and $k=m+1$, works.
|
{
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
45aeb0fd-5eec-5f4b-99fa-3d36f728aa91
| 605,581
|
Let $A B C D$ be a convex quadrilateral and let $P$ be the point of intersection of $A C$ and $B D$. Suppose that $A C+A D=B C+B D$. Prove that the internal angle bisectors of $\angle A C B, \angle A D B$, and $\angle A P B$ meet at a common point.
|
I. Construct $A^{\prime}$ on $C A$ so that $A A^{\prime}=A D$ and $B^{\prime}$ on $C B$ such that $B B^{\prime}=B D$. Then we have three angle bisectors that correspond to the perpendicular bisectors of $A^{\prime} B^{\prime}, A^{\prime} D$, and $B^{\prime} D$. These perpendicular bisectors are concurrent, so the angle bisectors are also concurrent. This tells us that the external angle bisectors at $A$ and $B$ meet at the excentre of $P D B$. A symmetric argument for $C$ finishes the problem.
## Sun Life Financial Canadian Mathematical Olympiad
II. Note that the angle bisectors $\angle A C B$ and $\angle A P B$ intersect at the excentres of $\triangle P B C$ opposite $C$ and the angle bisectors of $\angle A D B$ and $\angle A P B$ intersect at the excentres of $\triangle P A D$ opposite $D$. Hence, it suffices to prove that these two excentres coincide.
Let the excircle of $\triangle P B C$ opposite $C$ touch side $P B$ at a point $X$, line $C P$ at a point $Y$ and line $C B$ at a point $Z$. Hence, $C Y=C Z, P X=P Y$ and $B X=B Z$. Therefore, $C P+P X=C B+B X$. Since $C P+P X+C B+B X$ is the perimeter of $\triangle C B P, C P+P X=C B+B X=s$, where $s$ is the semi-perimeter of $\triangle C B P$. Therefore,
$$
P X=C B+B X-C P=\frac{s}{2}-C P=\frac{C B+B P+P C}{2}-C P=\frac{C B+B P-P C}{2} .
$$
Similarly, if we let the excircle of $\triangle P A D$ opposite $D$ touch side $P A$ at a point $X^{\prime}$, then
$$
P X^{\prime}=\frac{D A+A P-P D}{2} .
$$
Since both excircles are tangent to $A C$ and $B D$, if we show that $P X=P X^{\prime}$, then we would show that the two excircles are tangent to $A C$ and $B D$ at the same points, i.e. the two excircles are identical. Hence, the two excentres coincide.
We will use the fact that $A C+A D=B C+B D$ to prove that $P X=P X^{\prime}$. Since $A C+A D=B C+B D, A P+P C+A D=B C+B P+P D$. Hence, $A P+A D-P D=$ $B C+B P-P C$. Therefore, $P X=P X^{\prime}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral and let $P$ be the point of intersection of $A C$ and $B D$. Suppose that $A C+A D=B C+B D$. Prove that the internal angle bisectors of $\angle A C B, \angle A D B$, and $\angle A P B$ meet at a common point.
|
I. Construct $A^{\prime}$ on $C A$ so that $A A^{\prime}=A D$ and $B^{\prime}$ on $C B$ such that $B B^{\prime}=B D$. Then we have three angle bisectors that correspond to the perpendicular bisectors of $A^{\prime} B^{\prime}, A^{\prime} D$, and $B^{\prime} D$. These perpendicular bisectors are concurrent, so the angle bisectors are also concurrent. This tells us that the external angle bisectors at $A$ and $B$ meet at the excentre of $P D B$. A symmetric argument for $C$ finishes the problem.
## Sun Life Financial Canadian Mathematical Olympiad
II. Note that the angle bisectors $\angle A C B$ and $\angle A P B$ intersect at the excentres of $\triangle P B C$ opposite $C$ and the angle bisectors of $\angle A D B$ and $\angle A P B$ intersect at the excentres of $\triangle P A D$ opposite $D$. Hence, it suffices to prove that these two excentres coincide.
Let the excircle of $\triangle P B C$ opposite $C$ touch side $P B$ at a point $X$, line $C P$ at a point $Y$ and line $C B$ at a point $Z$. Hence, $C Y=C Z, P X=P Y$ and $B X=B Z$. Therefore, $C P+P X=C B+B X$. Since $C P+P X+C B+B X$ is the perimeter of $\triangle C B P, C P+P X=C B+B X=s$, where $s$ is the semi-perimeter of $\triangle C B P$. Therefore,
$$
P X=C B+B X-C P=\frac{s}{2}-C P=\frac{C B+B P+P C}{2}-C P=\frac{C B+B P-P C}{2} .
$$
Similarly, if we let the excircle of $\triangle P A D$ opposite $D$ touch side $P A$ at a point $X^{\prime}$, then
$$
P X^{\prime}=\frac{D A+A P-P D}{2} .
$$
Since both excircles are tangent to $A C$ and $B D$, if we show that $P X=P X^{\prime}$, then we would show that the two excircles are tangent to $A C$ and $B D$ at the same points, i.e. the two excircles are identical. Hence, the two excentres coincide.
We will use the fact that $A C+A D=B C+B D$ to prove that $P X=P X^{\prime}$. Since $A C+A D=B C+B D, A P+P C+A D=B C+B P+P D$. Hence, $A P+A D-P D=$ $B C+B P-P C$. Therefore, $P X=P X^{\prime}$, as desired.
|
{
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
cc5e5205-83f1-543d-a39a-28689a07f413
| 605,595
|
A number of robots are placed on the squares of a finite, rectangular grid of squares. A square can hold any number of robots. Every edge of each square of the grid is classified as either passable or impassable. All edges on the boundary of the grid are impassable.
You can give any of the commands up, down, left, or right. All of the robots then simultaneously try to move in the specified direction. If the edge adjacent to a robot in that direction is passable, the robot moves across the edge and into the next square. Otherwise, the robot remains on its current square. You can then give another command of up, down, left, or right, then another, for as long as you want.
Suppose that for any individual robot, and any square on the grid, there is a finite sequence of commands that will move that robot to that square. Prove that you can also give a finite sequence of commands such that all of the robots end up on the same square at the same time.
|
We will prove any two robots can be moved to the same square. From that point on, they will always be on the same square. We can then similarly move
## Sun Life Financial Canadian Mathematical Olympiad

a third robot onto the same square as these two, and then a fourth, and so on, until all robots are on the same square.
Towards that end, consider two robots $A$ and $B$. Let $d(A, B)$ denote the minimum number of commands that need to be given in order to move $A$ to the square on which $B$ is currently standing. We will give a procedure that is guaranteed to decrease $d(A, B)$. Since $d(A, B)$ is a non-negative integer, this procedure will eventually decrease $n$ to 0 , which finishes the proof.
Let $n=d(A, B)$, and let $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ be a minimum sequence of moves that takes $A$ to the square where $B$ is currently standing. Certainly $A$ will not run into an impassable edge during this sequence, or we could get a shorter sequence by removing that command. Now suppose $B$ runs into an impassable edge after some command $s_{i}$. From that point, we can get $A$ to the square on which $B$ started with the commands $s_{i+1}, s_{i+2}, \ldots, s_{n}$ and then to the square where $B$ is currently with the commands $s_{1}, s_{2}, \ldots, s_{i-1}$. But this was only $n-1$ commands in total, and so we have decreased $d(A, B)$ as required.
Otherwise, we have given a sequence of $n$ commands to $A$ and $B$, and neither ran into an impassable edge during the execution of these commands. In particular, the vector $v$ connecting $A$ to $B$ on the grid must have never changed. We moved $A$ to the position $B=A+v$, and therefore we must have also moved $B$ to $B+v$. Repeating this process $k$ times, we will move $A$ to $A+k v$ and $B$ to $B+k v$. But if $v \neq(0,0)$, this will eventually force $B$ off the edge of the grid, giving a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A number of robots are placed on the squares of a finite, rectangular grid of squares. A square can hold any number of robots. Every edge of each square of the grid is classified as either passable or impassable. All edges on the boundary of the grid are impassable.
You can give any of the commands up, down, left, or right. All of the robots then simultaneously try to move in the specified direction. If the edge adjacent to a robot in that direction is passable, the robot moves across the edge and into the next square. Otherwise, the robot remains on its current square. You can then give another command of up, down, left, or right, then another, for as long as you want.
Suppose that for any individual robot, and any square on the grid, there is a finite sequence of commands that will move that robot to that square. Prove that you can also give a finite sequence of commands such that all of the robots end up on the same square at the same time.
|
We will prove any two robots can be moved to the same square. From that point on, they will always be on the same square. We can then similarly move
## Sun Life Financial Canadian Mathematical Olympiad

a third robot onto the same square as these two, and then a fourth, and so on, until all robots are on the same square.
Towards that end, consider two robots $A$ and $B$. Let $d(A, B)$ denote the minimum number of commands that need to be given in order to move $A$ to the square on which $B$ is currently standing. We will give a procedure that is guaranteed to decrease $d(A, B)$. Since $d(A, B)$ is a non-negative integer, this procedure will eventually decrease $n$ to 0 , which finishes the proof.
Let $n=d(A, B)$, and let $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ be a minimum sequence of moves that takes $A$ to the square where $B$ is currently standing. Certainly $A$ will not run into an impassable edge during this sequence, or we could get a shorter sequence by removing that command. Now suppose $B$ runs into an impassable edge after some command $s_{i}$. From that point, we can get $A$ to the square on which $B$ started with the commands $s_{i+1}, s_{i+2}, \ldots, s_{n}$ and then to the square where $B$ is currently with the commands $s_{1}, s_{2}, \ldots, s_{i-1}$. But this was only $n-1$ commands in total, and so we have decreased $d(A, B)$ as required.
Otherwise, we have given a sequence of $n$ commands to $A$ and $B$, and neither ran into an impassable edge during the execution of these commands. In particular, the vector $v$ connecting $A$ to $B$ on the grid must have never changed. We moved $A$ to the position $B=A+v$, and therefore we must have also moved $B$ to $B+v$. Repeating this process $k$ times, we will move $A$ to $A+k v$ and $B$ to $B+k v$. But if $v \neq(0,0)$, this will eventually force $B$ off the edge of the grid, giving a contradiction.
|
{
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
c5597030-fa09-5448-b85b-092c256c5273
| 605,604
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Since $\angle C=90^{\circ}$, the point $C$ lies on the semicircle with diameter $A B$ which implies that, if $M$ is te midpoint of side $A B$, then $M A=M C=M B$. This implies that triangle $A M C$ is isosceles and hence that $\angle A C M=\angle A$. By definition, $G$ lies on segment $M$ and it follows that $\angle A C G=\angle A C M=\angle A=\angle C P A$. This implies that triangles $A P C$ and $A C G$ are similar and hence that $A C^{2}=A G \cdot A P$. Now if $D$ denotes the foot of the perpendicular from $C$ to $A B$, it follows that triangles $A C D$ and $A B C$ are similar which implies that $A C^{2}=A D \cdot A B$. Therefore $A G \cdot A P=$ $A C^{2}=A D \cdot A B$ and, by power of a point, quadrilateral $D G P B$ is cyclic. This implies that $D$ lies on the circumcircle of triangle $B P G$ and, by a symmetric argument, it follows that $D$ also lies on the circumcircle of triangle $A G Q$. Therefore these two circumcircles meet at the point $D$ on side $A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Since $\angle C=90^{\circ}$, the point $C$ lies on the semicircle with diameter $A B$ which implies that, if $M$ is te midpoint of side $A B$, then $M A=M C=M B$. This implies that triangle $A M C$ is isosceles and hence that $\angle A C M=\angle A$. By definition, $G$ lies on segment $M$ and it follows that $\angle A C G=\angle A C M=\angle A=\angle C P A$. This implies that triangles $A P C$ and $A C G$ are similar and hence that $A C^{2}=A G \cdot A P$. Now if $D$ denotes the foot of the perpendicular from $C$ to $A B$, it follows that triangles $A C D$ and $A B C$ are similar which implies that $A C^{2}=A D \cdot A B$. Therefore $A G \cdot A P=$ $A C^{2}=A D \cdot A B$ and, by power of a point, quadrilateral $D G P B$ is cyclic. This implies that $D$ lies on the circumcircle of triangle $B P G$ and, by a symmetric argument, it follows that $D$ also lies on the circumcircle of triangle $A G Q$. Therefore these two circumcircles meet at the point $D$ on side $A B$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 1."
}
|
460b4a46-3e3b-5a4d-898a-1c571479055d
| 605,649
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Define $D$ and $M$ as in Solution 1. Let $R$ be the point on side $A B$ such that $A C=C R$ and triangle $A C R$ is isosceles. Since $\angle C R A=\angle A=\angle C P A$, it follows that $C P R A$ is cyclic and hence that $\angle G P R=\angle A P R=\angle A C R=180^{\circ}-$ $2 \angle A$. As in Solution $1, M C=M B$ and hence $\angle G M R=\angle C M B=2 \angle A=180^{\circ}-$ $\angle G P R$. Therefore $G P R M$ is cyclic and, by power of a point, $A M \cdot A R=A G \cdot A P$. Since $A C R$ is isosceles, $D$ is the midpoint of $A R$ and thus, since $M$ is the midpoint of $A B$, it follows that $A M \cdot A R=A D \cdot A B=A G \cdot A P$. Therefore $D G P B$ is cyclic, implying the result as in Solution 1.
## Sun $\mathscr{H}^{*}$
## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Define $D$ and $M$ as in Solution 1. Let $R$ be the point on side $A B$ such that $A C=C R$ and triangle $A C R$ is isosceles. Since $\angle C R A=\angle A=\angle C P A$, it follows that $C P R A$ is cyclic and hence that $\angle G P R=\angle A P R=\angle A C R=180^{\circ}-$ $2 \angle A$. As in Solution $1, M C=M B$ and hence $\angle G M R=\angle C M B=2 \angle A=180^{\circ}-$ $\angle G P R$. Therefore $G P R M$ is cyclic and, by power of a point, $A M \cdot A R=A G \cdot A P$. Since $A C R$ is isosceles, $D$ is the midpoint of $A R$ and thus, since $M$ is the midpoint of $A B$, it follows that $A M \cdot A R=A D \cdot A B=A G \cdot A P$. Therefore $D G P B$ is cyclic, implying the result as in Solution 1.
## Sun $\mathscr{H}^{*}$
## Life Financial
|
{
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 2."
}
|
460b4a46-3e3b-5a4d-898a-1c571479055d
| 605,649
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left hand side inequality. We begin by drawing an $n \times n$ board, with corners at $(0,0),(n, 0),(0, n)$ and $(n, n)$ on the Cartesian plane.
Consider the line $\ell$ with slope $r$ passing through $(0,0)$. For each $j \in\{1, \ldots, n\}$, consider the point $(j, \min (j r, n))$. Note that each such point either lies on $\ell$ or the top edge of the board. In the $j^{\text {th }}$ column from the left, draw the rectangle of height $\min (j r, n)$. Note that the sum of the $n$ rectangles is equal to the area of the board under the line $\ell$ plus $n$ triangles (possibly with area 0 ) each with width at most 1 and whose sum of the heights is at most $n$. Therefore, the sum of the areas of these $n$ triangles is at most $n / 2$. Therefore, $\sum_{j=1}^{n} \min (j r, n)$ is at most the area of the square under $\ell$ plus $n / 2$.
Consider the line with slope $1 / r$. By symmetry about the line $y=x$, the area of the square under the line with slope $1 / r$ is equal to the area of the square above the line $\ell$. Therefore, using the same reasoning as before, $\sum_{j=1}^{n} \min (j / r, n)$ is at most the area of the square above $\ell$ plus $n / 2$.
Therefore, $\sum_{j=1}^{n} f_{j}(r)=\sum_{j=1}^{n}\left(\min (j r, n)+\min \left(\frac{j}{r}, n\right)\right)$ is at most the area of the board plus $n$, which is $n^{2}+n$. This proves the left hand side inequality.
To prove the right hand side inequality, we will use the following lemma:
Lemma: Consider the line $\ell$ with slope $s$ passing through $(0,0)$. Then the number of squares on the board that contain an interior point below $\ell$ is $\sum_{j=1}^{n} \min (\lceil j s\rceil, n)$.
Proof of Lemma: For each $j \in\{1, \ldots, n\}$, we count the number of squares in the $j^{\text {th }}$ column (from the left) that contain an interior point lying below the line $\ell$. The line $x=j$ intersect the line $\ell$ at $(j, j s)$. Hence, since each column contains $n$ squares
## Sun
## Life Financial
total, the number of such squares is $\min (\lceil j s\rceil, n)$. Summing over all $j \in\{1,2, \ldots, n\}$ proves the lemma. End Proof of Lemma
By the lemma, the rightmost expression of the inequality is equal to the number of squares containing an interior point below the line with slope $r$ plus the number of squares containing an interior point below the line with slope $1 / r$. By symmetry about the line $y=x$, the latter number is equal to the number of squares containing an interior point above the line with slope $r$. Therefore, the rightmost expression of the inequality is equal to the number of squares of the board plus the number of squares of which $\ell$ passes through the interior. The former is equal to $n^{2}$. Hence, to prove the inequality, it suffices to show that every line passes through the interior of at least $n$ squares. Since $\ell$ has positive slope, each $\ell$ passes through either $n$ rows and/or $n$ columns. In either case, $\ell$ passes through the interior of at least $n$ squares. Hence, the right inequality holds.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left hand side inequality. We begin by drawing an $n \times n$ board, with corners at $(0,0),(n, 0),(0, n)$ and $(n, n)$ on the Cartesian plane.
Consider the line $\ell$ with slope $r$ passing through $(0,0)$. For each $j \in\{1, \ldots, n\}$, consider the point $(j, \min (j r, n))$. Note that each such point either lies on $\ell$ or the top edge of the board. In the $j^{\text {th }}$ column from the left, draw the rectangle of height $\min (j r, n)$. Note that the sum of the $n$ rectangles is equal to the area of the board under the line $\ell$ plus $n$ triangles (possibly with area 0 ) each with width at most 1 and whose sum of the heights is at most $n$. Therefore, the sum of the areas of these $n$ triangles is at most $n / 2$. Therefore, $\sum_{j=1}^{n} \min (j r, n)$ is at most the area of the square under $\ell$ plus $n / 2$.
Consider the line with slope $1 / r$. By symmetry about the line $y=x$, the area of the square under the line with slope $1 / r$ is equal to the area of the square above the line $\ell$. Therefore, using the same reasoning as before, $\sum_{j=1}^{n} \min (j / r, n)$ is at most the area of the square above $\ell$ plus $n / 2$.
Therefore, $\sum_{j=1}^{n} f_{j}(r)=\sum_{j=1}^{n}\left(\min (j r, n)+\min \left(\frac{j}{r}, n\right)\right)$ is at most the area of the board plus $n$, which is $n^{2}+n$. This proves the left hand side inequality.
To prove the right hand side inequality, we will use the following lemma:
Lemma: Consider the line $\ell$ with slope $s$ passing through $(0,0)$. Then the number of squares on the board that contain an interior point below $\ell$ is $\sum_{j=1}^{n} \min (\lceil j s\rceil, n)$.
Proof of Lemma: For each $j \in\{1, \ldots, n\}$, we count the number of squares in the $j^{\text {th }}$ column (from the left) that contain an interior point lying below the line $\ell$. The line $x=j$ intersect the line $\ell$ at $(j, j s)$. Hence, since each column contains $n$ squares
## Sun
## Life Financial
total, the number of such squares is $\min (\lceil j s\rceil, n)$. Summing over all $j \in\{1,2, \ldots, n\}$ proves the lemma. End Proof of Lemma
By the lemma, the rightmost expression of the inequality is equal to the number of squares containing an interior point below the line with slope $r$ plus the number of squares containing an interior point below the line with slope $1 / r$. By symmetry about the line $y=x$, the latter number is equal to the number of squares containing an interior point above the line with slope $r$. Therefore, the rightmost expression of the inequality is equal to the number of squares of the board plus the number of squares of which $\ell$ passes through the interior. The former is equal to $n^{2}$. Hence, to prove the inequality, it suffices to show that every line passes through the interior of at least $n$ squares. Since $\ell$ has positive slope, each $\ell$ passes through either $n$ rows and/or $n$ columns. In either case, $\ell$ passes through the interior of at least $n$ squares. Hence, the right inequality holds.
|
{
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution 1:"
}
|
245c4ff6-6667-55f1-a58d-e7dff9413041
| 605,671
|
Let $O$ denote the circumcentre of an acute-angled triangle $A B C$. A circle $\Gamma$ passing through vertex $A$ intersects segments $A B$ and $A C$ at points $P$ and $Q$ such that $\angle B O P=\angle A B C$ and $\angle C O Q=\angle A C B$. Prove that the reflection of $B C$ in the line $P Q$ is tangent to $\Gamma$.
|
Let the circumcircle of triangle $O B P$ intersect side $B C$ at the points $R$ and $B$ and let $\angle A, \angle B$ and $\angle C$ denote the angles at vertices $A, B$ and $C$, respectively.
Now note that since $\angle B O P=\angle B$ and $\angle C O Q=\angle C$, it follows that
$\angle P O Q=360^{\circ}-\angle B O P-\angle C O Q-\angle B O C=360^{\circ}-(180-\angle A)-2 \angle A=180^{\circ}-\angle A$.
This implies that $A P O Q$ is a cyclic quadrilateral. Since $B P O R$ is cyclic,
$\angle Q O R=360^{\circ}-\angle P O Q-\angle P O R=360^{\circ}-\left(180^{\circ}-\angle A\right)-\left(180^{\circ}-\angle B\right)=180^{\circ}-\angle C$.
This implies that $C Q O R$ is a cyclic quadrilateral. Since $A P O Q$ and $B P O R$ are cyclic,
$\angle Q P R=\angle Q P O+\angle O P R=\angle O A Q+\angle O B R=\left(90^{\circ}-\angle B\right)+\left(90^{\circ}-\angle A\right)=\angle C$.
Since $C Q O R$ is cyclic, $\angle Q R C=\angle C O Q=\angle C=\angle Q P R$ which implies that the circumcircle of triangle $P Q R$ is tangent to $B C$. Further, since $\angle P R B=\angle B O P=$ $\angle B$,
$$
\angle P R Q=180^{\circ}-\angle P R B-\angle Q R C=180^{\circ}-\angle B-\angle C=\angle A=\angle P A Q
$$
This implies that the circumcircle of $P Q R$ is the reflection of $\Gamma$ in line $P Q$. By symmetry in line $P Q$, this implies that the reflection of $B C$ in line $P Q$ is tangent to $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ denote the circumcentre of an acute-angled triangle $A B C$. A circle $\Gamma$ passing through vertex $A$ intersects segments $A B$ and $A C$ at points $P$ and $Q$ such that $\angle B O P=\angle A B C$ and $\angle C O Q=\angle A C B$. Prove that the reflection of $B C$ in the line $P Q$ is tangent to $\Gamma$.
|
Let the circumcircle of triangle $O B P$ intersect side $B C$ at the points $R$ and $B$ and let $\angle A, \angle B$ and $\angle C$ denote the angles at vertices $A, B$ and $C$, respectively.
Now note that since $\angle B O P=\angle B$ and $\angle C O Q=\angle C$, it follows that
$\angle P O Q=360^{\circ}-\angle B O P-\angle C O Q-\angle B O C=360^{\circ}-(180-\angle A)-2 \angle A=180^{\circ}-\angle A$.
This implies that $A P O Q$ is a cyclic quadrilateral. Since $B P O R$ is cyclic,
$\angle Q O R=360^{\circ}-\angle P O Q-\angle P O R=360^{\circ}-\left(180^{\circ}-\angle A\right)-\left(180^{\circ}-\angle B\right)=180^{\circ}-\angle C$.
This implies that $C Q O R$ is a cyclic quadrilateral. Since $A P O Q$ and $B P O R$ are cyclic,
$\angle Q P R=\angle Q P O+\angle O P R=\angle O A Q+\angle O B R=\left(90^{\circ}-\angle B\right)+\left(90^{\circ}-\angle A\right)=\angle C$.
Since $C Q O R$ is cyclic, $\angle Q R C=\angle C O Q=\angle C=\angle Q P R$ which implies that the circumcircle of triangle $P Q R$ is tangent to $B C$. Further, since $\angle P R B=\angle B O P=$ $\angle B$,
$$
\angle P R Q=180^{\circ}-\angle P R B-\angle Q R C=180^{\circ}-\angle B-\angle C=\angle A=\angle P A Q
$$
This implies that the circumcircle of $P Q R$ is the reflection of $\Gamma$ in line $P Q$. By symmetry in line $P Q$, this implies that the reflection of $B C$ in line $P Q$ is tangent to $\Gamma$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
f1475451-4a80-5708-9a80-38ff4485dbda
| 605,697
|
The quadrilateral $A B C D$ is inscribed in a circle. The point $P$ lies in the interior of $A B C D$, and $\angle P A B=\angle P B C=\angle P C D=\angle P D A$. The lines $A D$ and $B C$ meet at $Q$, and the lines $A B$ and $C D$ meet at $R$. Prove that the lines $P Q$ and $P R$ form the same angle as the diagonals of $A B C D$.
|
. Let $\Gamma$ be the circumcircle of quadrilateral $A B C D$. Let $\alpha=\angle P A B=$ $\angle P B C \angle P C D=\angle P D A$ and let $T_{1}, T_{2}, T_{3}$ and $T_{4}$ denote the circumcircles of triangles $A P D, B P C, A P B$ and $C P D$, respectively. Let $M$ be the intersection of $T_{1}$ with line $R P$ and let $N$ be the intersection of $T_{3}$ with line $S P$. Also let $X$ denote the intersection of diagonals $A C$ and $B D$.
By power of a point for circles $T_{1}$ and $\Gamma$, it follows that $R M \cdot R P=R A \cdot R D=$ $R B \cdot R C$ which implies that the quadrilateral $B M P C$ is cyclic and $M$ lies on $T_{2}$. Therefore $\angle P M B=\angle P C B=\alpha=\angle P A B=\angle D M P$ where all angles are directed. This implies that $M$ lies on the diagonal $B D$ and also that $\angle X M P=\angle D M P=\alpha$. By a symmetric argument applied to $S, T_{3}$ and $T_{4}$, it follows that $N$ lies on $T_{4}$ and that $N$ lies on diagonal $A C$ with $\angle X N P=\alpha$. Therefore $\angle X M P=\angle X N P$ and $X, M, P$ and $N$ are concyclic. This implies that the angle formed by lines $M P$ and $N P$ is equal to one of the angles formed by lines $M X$ and $N X$. The fact that $M$ lies on $B D$ and $R P$ and $N$ lies on $A C$ and $S P$ now implies the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The quadrilateral $A B C D$ is inscribed in a circle. The point $P$ lies in the interior of $A B C D$, and $\angle P A B=\angle P B C=\angle P C D=\angle P D A$. The lines $A D$ and $B C$ meet at $Q$, and the lines $A B$ and $C D$ meet at $R$. Prove that the lines $P Q$ and $P R$ form the same angle as the diagonals of $A B C D$.
|
. Let $\Gamma$ be the circumcircle of quadrilateral $A B C D$. Let $\alpha=\angle P A B=$ $\angle P B C \angle P C D=\angle P D A$ and let $T_{1}, T_{2}, T_{3}$ and $T_{4}$ denote the circumcircles of triangles $A P D, B P C, A P B$ and $C P D$, respectively. Let $M$ be the intersection of $T_{1}$ with line $R P$ and let $N$ be the intersection of $T_{3}$ with line $S P$. Also let $X$ denote the intersection of diagonals $A C$ and $B D$.
By power of a point for circles $T_{1}$ and $\Gamma$, it follows that $R M \cdot R P=R A \cdot R D=$ $R B \cdot R C$ which implies that the quadrilateral $B M P C$ is cyclic and $M$ lies on $T_{2}$. Therefore $\angle P M B=\angle P C B=\alpha=\angle P A B=\angle D M P$ where all angles are directed. This implies that $M$ lies on the diagonal $B D$ and also that $\angle X M P=\angle D M P=\alpha$. By a symmetric argument applied to $S, T_{3}$ and $T_{4}$, it follows that $N$ lies on $T_{4}$ and that $N$ lies on diagonal $A C$ with $\angle X N P=\alpha$. Therefore $\angle X M P=\angle X N P$ and $X, M, P$ and $N$ are concyclic. This implies that the angle formed by lines $M P$ and $N P$ is equal to one of the angles formed by lines $M X$ and $N X$. The fact that $M$ lies on $B D$ and $R P$ and $N$ lies on $A C$ and $S P$ now implies the desired result.
|
{
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
d2ce573c-dc0a-5167-9464-0c3c59988a4a
| 605,740
|
Fix positive integers $n$ and $k \geq 2$. A list of $n$ integers is written in a row on a blackboard. You can choose a contiguous block of integers, and I will either add 1 to all of them or subtract 1 from all of them. You can repeat this step as often as you like, possibly adapting your selections based on what I do. Prove that after a finite number of steps, you can reach a state where at least $n-k+2$ of the numbers on the blackboard are all simultaneously divisible by $k$.
## Life Financial
|
We will think of all numbers as being residues mod $k$. Consider the following strategy:
- If there are less than $k-1$ non-zero numbers, then stop.
- If the first number is 0 , then recursively solve on the remaining numbers.
- If the first number is $j$ with $0<j<k$, then choose the interval stretching from the first number to the $j$ th-last non-zero number.
First note that this strategy is indeed well defined. The first number must have value between 0 and $k-1$, and if we do not stop immediately, then there are at least $k-1$ non-zero numbers, and hence the third step can be performed.
For each $j$ with $1 \leq j \leq k-2$, we claim the first number can take on the value of $j$ at most a finite number of times without taking on the value of $j-1$ in between. If this were to fail, then every time the first number became $j$, I would have to add 1 to the selected numbers to avoid making it $j-1$. This will always increase the $j$-th last non-zero number, and that number will never be changed by other steps. Therefore, that number would eventually become 0 , and the next last non-zero number would eventually become zero, and so on, until the first number itself becomes the $j$-th last non-zero number, at which point we are done since $j \leq k-2$.
Rephrasing slightly, if $1 \leq j \leq k-2$, the first number can take on the value of $j$ at most a finite number of times between each time it takes on the value of $j-1$. It then immediately follows that if the first number can take on the value of $j-1$ at most a finite number of times, then it can also only take on the value of $j$ a finite number of times. However, if it ever takes on the value of 0 , we have already reduced the problem to $n-1$, so we can assume that never happens. It then follows that the first number can take on all the values $0,1,2, \ldots, k-2$ at most a finite number of times.
Finally, every time the first number takes on the value of $k-1$, it must subsequently take on the value of $k-2$ or 0 , and so that can also happen only finitely many times.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Fix positive integers $n$ and $k \geq 2$. A list of $n$ integers is written in a row on a blackboard. You can choose a contiguous block of integers, and I will either add 1 to all of them or subtract 1 from all of them. You can repeat this step as often as you like, possibly adapting your selections based on what I do. Prove that after a finite number of steps, you can reach a state where at least $n-k+2$ of the numbers on the blackboard are all simultaneously divisible by $k$.
## Life Financial
|
We will think of all numbers as being residues mod $k$. Consider the following strategy:
- If there are less than $k-1$ non-zero numbers, then stop.
- If the first number is 0 , then recursively solve on the remaining numbers.
- If the first number is $j$ with $0<j<k$, then choose the interval stretching from the first number to the $j$ th-last non-zero number.
First note that this strategy is indeed well defined. The first number must have value between 0 and $k-1$, and if we do not stop immediately, then there are at least $k-1$ non-zero numbers, and hence the third step can be performed.
For each $j$ with $1 \leq j \leq k-2$, we claim the first number can take on the value of $j$ at most a finite number of times without taking on the value of $j-1$ in between. If this were to fail, then every time the first number became $j$, I would have to add 1 to the selected numbers to avoid making it $j-1$. This will always increase the $j$-th last non-zero number, and that number will never be changed by other steps. Therefore, that number would eventually become 0 , and the next last non-zero number would eventually become zero, and so on, until the first number itself becomes the $j$-th last non-zero number, at which point we are done since $j \leq k-2$.
Rephrasing slightly, if $1 \leq j \leq k-2$, the first number can take on the value of $j$ at most a finite number of times between each time it takes on the value of $j-1$. It then immediately follows that if the first number can take on the value of $j-1$ at most a finite number of times, then it can also only take on the value of $j$ a finite number of times. However, if it ever takes on the value of 0 , we have already reduced the problem to $n-1$, so we can assume that never happens. It then follows that the first number can take on all the values $0,1,2, \ldots, k-2$ at most a finite number of times.
Finally, every time the first number takes on the value of $k-1$, it must subsequently take on the value of $k-2$ or 0 , and so that can also happen only finitely many times.
|
{
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
f9b21d59-9bb2-5169-a0e8-fd1fddce12b8
| 605,748
|
Let $A B C$ be an acute-angled triangle with altitudes $A D, B E$, and $C F$. Let $H$ be the orthocentre, that is, the point where the altitudes meet. Prove that
$$
\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2 .
$$
|
Method 1: Let $A B=c, A C=b$, and $B C=a$ denote the three side lengths of the triangle.
As $\angle B F H=\angle B D H=90^{\circ}, F H D B$ is a cyclic quadrilateral. By the Power-of-a-Point Theorem, $A H \cdot A D=A F \cdot A B$. (We can derive this result in other ways: for example, see Method 2, below.)
Since $A F=A C \cdot \cos \angle A$, we have $A H \cdot A D=A C \cdot A B \cdot \cos \angle A=b c \cos \angle A$.
## Life Financial
Hence,By the Cosine Law, $\cos \angle A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$, which implies that $A H \cdot A D=\frac{b^{2}+c^{2}-a^{2}}{2}$.
By symmetry, we can show that $B H \cdot B E=\frac{a^{2}+c^{2}-b^{2}}{2}$ and $C H \cdot C F=\frac{a^{2}+b^{2}-c^{2}}{2}$.
$$
\begin{aligned}
A H \cdot A D+B H \cdot B E+C H \cdot C F & =\frac{b^{2}+c^{2}-a^{2}}{2}+\frac{a^{2}+c^{2}-b^{2}}{2}+\frac{a^{2}+b^{2}-c^{2}}{2} \\
& =\frac{a^{2}+b^{2}+c^{2}}{2} .
\end{aligned}
$$
Our desired inequality, $\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2$, is equivalent to the inequality $\frac{c b+a c+b a}{\frac{a^{2}+b^{2}+c^{2}}{2}} \leq 2$, which simplifies to $2 a^{2}+2 b^{2}+2 c^{2} \geq 2 a b+2 b c+2 c a$.
But this last inequality is easy to prove, as it is equivalent to $(a-b)^{2}+(a-c)^{2}+(b-c)^{2} \geq 0$.
Therefore, we have established the desired inequality. The proof also shows that equality occurs if and only if $a=b=c$, i.e., $\triangle A B C$ is equilateral.
Method 2: Observe that
$$
\frac{A E}{A H}=\cos (\angle H A E)=\frac{A D}{A C} \quad \text { and } \quad \frac{A F}{A H}=\cos (\angle H A F)=\frac{A D}{A B} \text {. }
$$
It follows that
$$
A C \cdot A E=A H \cdot A D=A B \cdot A F .
$$
By symmetry, we similarly have
$$
B C \cdot B D=B H \cdot B E=B F \cdot B A \quad \text { and } \quad C D \cdot C B=C H \cdot C F=C E \cdot C A \text {. }
$$
Therefore
$$
\begin{aligned}
& 2(A H \cdot A D+B H \cdot B E+C H \cdot C F) \\
& \quad=A B(A F+B F)+A C(A E+C E)+B C(B D+C D) \\
& \quad=A B^{2}+A C^{2}+B C^{2} .
\end{aligned}
$$
This proves Equation (1) in Method 1. The rest of the proof is the same as the part of the proof of Method 1 that follows Equation (1).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C$ be an acute-angled triangle with altitudes $A D, B E$, and $C F$. Let $H$ be the orthocentre, that is, the point where the altitudes meet. Prove that
$$
\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2 .
$$
|
Method 1: Let $A B=c, A C=b$, and $B C=a$ denote the three side lengths of the triangle.
As $\angle B F H=\angle B D H=90^{\circ}, F H D B$ is a cyclic quadrilateral. By the Power-of-a-Point Theorem, $A H \cdot A D=A F \cdot A B$. (We can derive this result in other ways: for example, see Method 2, below.)
Since $A F=A C \cdot \cos \angle A$, we have $A H \cdot A D=A C \cdot A B \cdot \cos \angle A=b c \cos \angle A$.
## Life Financial
Hence,By the Cosine Law, $\cos \angle A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$, which implies that $A H \cdot A D=\frac{b^{2}+c^{2}-a^{2}}{2}$.
By symmetry, we can show that $B H \cdot B E=\frac{a^{2}+c^{2}-b^{2}}{2}$ and $C H \cdot C F=\frac{a^{2}+b^{2}-c^{2}}{2}$.
$$
\begin{aligned}
A H \cdot A D+B H \cdot B E+C H \cdot C F & =\frac{b^{2}+c^{2}-a^{2}}{2}+\frac{a^{2}+c^{2}-b^{2}}{2}+\frac{a^{2}+b^{2}-c^{2}}{2} \\
& =\frac{a^{2}+b^{2}+c^{2}}{2} .
\end{aligned}
$$
Our desired inequality, $\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2$, is equivalent to the inequality $\frac{c b+a c+b a}{\frac{a^{2}+b^{2}+c^{2}}{2}} \leq 2$, which simplifies to $2 a^{2}+2 b^{2}+2 c^{2} \geq 2 a b+2 b c+2 c a$.
But this last inequality is easy to prove, as it is equivalent to $(a-b)^{2}+(a-c)^{2}+(b-c)^{2} \geq 0$.
Therefore, we have established the desired inequality. The proof also shows that equality occurs if and only if $a=b=c$, i.e., $\triangle A B C$ is equilateral.
Method 2: Observe that
$$
\frac{A E}{A H}=\cos (\angle H A E)=\frac{A D}{A C} \quad \text { and } \quad \frac{A F}{A H}=\cos (\angle H A F)=\frac{A D}{A B} \text {. }
$$
It follows that
$$
A C \cdot A E=A H \cdot A D=A B \cdot A F .
$$
By symmetry, we similarly have
$$
B C \cdot B D=B H \cdot B E=B F \cdot B A \quad \text { and } \quad C D \cdot C B=C H \cdot C F=C E \cdot C A \text {. }
$$
Therefore
$$
\begin{aligned}
& 2(A H \cdot A D+B H \cdot B E+C H \cdot C F) \\
& \quad=A B(A F+B F)+A C(A E+C E)+B C(B D+C D) \\
& \quad=A B^{2}+A C^{2}+B C^{2} .
\end{aligned}
$$
This proves Equation (1) in Method 1. The rest of the proof is the same as the part of the proof of Method 1 that follows Equation (1).
|
{
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
ac94213b-8492-5aaa-a10f-db486ca2ec23
| 605,768
|
Let $A B C$ be an acute-angled triangle with circumcenter $O$. Let $\Gamma$ be a circle with centre on the altitude from $A$ in $A B C$, passing through vertex $A$ and points $P$ and $Q$ on sides $A B$ and $A C$. Assume that $B P \cdot C Q=A P \cdot A Q$. Prove that $\Gamma$ is tangent to the circumcircle of triangle BOC.
|
Let $\omega$ be the circumcircle of $B O C$. Let $M$ be the point diametrically opposite to $O$ on $\omega$ and let the line $A M$ intersect $\omega$ at $M$ and $K$. Since $O$ is the circumcenter of $A B C$, it follows that $O B=O C$ and therefore that $O$ is the midpoint of the $\operatorname{arc} \widehat{B O C}$ of $\omega$. Since $M$ is diametrically opposite to $O$, it follows that $M$ is the midpoint of the arc $\widehat{B M C}$ of $\omega$. This implies since $K$ is on $\omega$ that $K M$ is the bisector of $\angle B K C$. Since $K$ is on $\omega$, this implies that $\angle B K M=\angle C K M$, i.e. $K M$ is the bisector of $\angle B K C$.
Since $O$ is the circumcenter of $A B C$, it follows that $\angle B O C=2 \angle B A C$. Since $B, K, O$ and $C$ all lie on $\omega$, it also follows that $\angle B K C=\angle B O C=2 \angle B A C$. Since $K M$ bisects $\angle B K C$, it follows that $\angle B K M=\angle C K M=\angle B A C$. The fact that $A, K$ and $M$ lie on a line therefore implies that $\angle A K B=\angle A K C=180^{\circ}-\angle B A C$. Now it follows that
$$
\angle K B A=180^{\circ}-\angle A K B-\angle K A B=\angle B A C-\angle K A B=\angle K A C .
$$
This implies that triangles $K B A$ and $K A C$ are similar. Rearranging the condition in the problem statement yields that $B P / A P=A Q / C Q$ which, when combined with the fact that $K B A$ and $K A C$ are similar, implies that triangles $K P A$ and $K Q C$ are similar. Therefore $\angle K P A=\angle K Q C=180^{\circ}-\angle K Q A$ which implies that $K$ lies on $\Gamma$.
Now let $S$ denote the centre of $\Gamma$ and let $T$ denote the centre of $\omega$. Note that $T$ is the midpoint of segment $O M$ and that $T M$ and $A S$, which are both perpendicular to $B C$, are parallel. This implies that $\angle K M T=\angle K A S$ since $A, K$ and $M$ are collinear. Further, since $K T M$ and $K S A$ are isosceles triangles, it follows that $\angle T K M=\angle K M T$ and $\angle S K A=$
$\angle K S A$. Therefore $\angle T K M=\angle S K A$ which implies that $S, T$ and $K$ are collinear. Therefore $\Gamma$ and $\omega$ intersect at a point $K$ which lies on the line $S T$ connecting the centres of the two circles. This implies that the circles $\Gamma$ and $\omega$ are tangent at $K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with circumcenter $O$. Let $\Gamma$ be a circle with centre on the altitude from $A$ in $A B C$, passing through vertex $A$ and points $P$ and $Q$ on sides $A B$ and $A C$. Assume that $B P \cdot C Q=A P \cdot A Q$. Prove that $\Gamma$ is tangent to the circumcircle of triangle BOC.
|
Let $\omega$ be the circumcircle of $B O C$. Let $M$ be the point diametrically opposite to $O$ on $\omega$ and let the line $A M$ intersect $\omega$ at $M$ and $K$. Since $O$ is the circumcenter of $A B C$, it follows that $O B=O C$ and therefore that $O$ is the midpoint of the $\operatorname{arc} \widehat{B O C}$ of $\omega$. Since $M$ is diametrically opposite to $O$, it follows that $M$ is the midpoint of the arc $\widehat{B M C}$ of $\omega$. This implies since $K$ is on $\omega$ that $K M$ is the bisector of $\angle B K C$. Since $K$ is on $\omega$, this implies that $\angle B K M=\angle C K M$, i.e. $K M$ is the bisector of $\angle B K C$.
Since $O$ is the circumcenter of $A B C$, it follows that $\angle B O C=2 \angle B A C$. Since $B, K, O$ and $C$ all lie on $\omega$, it also follows that $\angle B K C=\angle B O C=2 \angle B A C$. Since $K M$ bisects $\angle B K C$, it follows that $\angle B K M=\angle C K M=\angle B A C$. The fact that $A, K$ and $M$ lie on a line therefore implies that $\angle A K B=\angle A K C=180^{\circ}-\angle B A C$. Now it follows that
$$
\angle K B A=180^{\circ}-\angle A K B-\angle K A B=\angle B A C-\angle K A B=\angle K A C .
$$
This implies that triangles $K B A$ and $K A C$ are similar. Rearranging the condition in the problem statement yields that $B P / A P=A Q / C Q$ which, when combined with the fact that $K B A$ and $K A C$ are similar, implies that triangles $K P A$ and $K Q C$ are similar. Therefore $\angle K P A=\angle K Q C=180^{\circ}-\angle K Q A$ which implies that $K$ lies on $\Gamma$.
Now let $S$ denote the centre of $\Gamma$ and let $T$ denote the centre of $\omega$. Note that $T$ is the midpoint of segment $O M$ and that $T M$ and $A S$, which are both perpendicular to $B C$, are parallel. This implies that $\angle K M T=\angle K A S$ since $A, K$ and $M$ are collinear. Further, since $K T M$ and $K S A$ are isosceles triangles, it follows that $\angle T K M=\angle K M T$ and $\angle S K A=$
$\angle K S A$. Therefore $\angle T K M=\angle S K A$ which implies that $S, T$ and $K$ are collinear. Therefore $\Gamma$ and $\omega$ intersect at a point $K$ which lies on the line $S T$ connecting the centres of the two circles. This implies that the circles $\Gamma$ and $\omega$ are tangent at $K$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
53946564-465f-510d-9156-0bfaa66c7a31
| 605,789
|
The integers $1,2,3, \ldots, 2016$ are written on a board. You can choose any two numbers on the board and replace them with their average. For example, you can replace 1 and 2 with 1.5 , or you can replace 1 and 3 with a second copy of 2 . After 2015 replacements of this kind, the board will have only one number left on it.
(a) Prove that there is a sequence of replacements that will make the final number equal to 2 .
(b) Prove that there is a sequence of replacements that will make the final number equal to 1000 .
|
(a) First replace 2014 and 2016 with 2015, and then replace the two copies of 2015 with a single copy. This leaves us with $\{1,2, \ldots, 2013,2015\}$. From here, we can replace 2013 and 2015 with 2014 to get $\{1,2, \ldots, 2012,2014\}$. We can then replace 2012 and 2014 with 2013 , and so on, until we eventually get to $\{1,3\}$. We finish by replacing 1 and 3 with 2.
(b) Using the same construction as in (a), we can find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{a+1\}$. Similarly, can also find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{b-1\}$.
In particular, we can find sequences of replacements that reduce $\{1,2, \ldots, 999\}$
to just $\{998\}$, and that reduce $\{1001,1002, \ldots, 2016\}$ to just $\{1002\}$. This leaves us with $\{998,1000,1002\}$. We can replace 998 and 1002 with a second copy of 1000 , and then replace the two copies of 1000 with a single copy to complete the construction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The integers $1,2,3, \ldots, 2016$ are written on a board. You can choose any two numbers on the board and replace them with their average. For example, you can replace 1 and 2 with 1.5 , or you can replace 1 and 3 with a second copy of 2 . After 2015 replacements of this kind, the board will have only one number left on it.
(a) Prove that there is a sequence of replacements that will make the final number equal to 2 .
(b) Prove that there is a sequence of replacements that will make the final number equal to 1000 .
|
(a) First replace 2014 and 2016 with 2015, and then replace the two copies of 2015 with a single copy. This leaves us with $\{1,2, \ldots, 2013,2015\}$. From here, we can replace 2013 and 2015 with 2014 to get $\{1,2, \ldots, 2012,2014\}$. We can then replace 2012 and 2014 with 2013 , and so on, until we eventually get to $\{1,3\}$. We finish by replacing 1 and 3 with 2.
(b) Using the same construction as in (a), we can find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{a+1\}$. Similarly, can also find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{b-1\}$.
In particular, we can find sequences of replacements that reduce $\{1,2, \ldots, 999\}$
to just $\{998\}$, and that reduce $\{1001,1002, \ldots, 2016\}$ to just $\{1002\}$. This leaves us with $\{998,1000,1002\}$. We can replace 998 and 1002 with a second copy of 1000 , and then replace the two copies of 1000 with a single copy to complete the construction.
|
{
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
e7351838-a4e2-5abc-acda-486d77ab5daf
| 605,809
|
Lavaman versus the Flea. Let $A, B$, and $F$ be positive integers, and assume $A<B<2 A$. A flea is at the number 0 on the number line. The flea can move by jumping to the right by $A$ or by $B$. Before the flea starts jumping, Lavaman chooses finitely many intervals $\{m+$ $1, m+2, \ldots, m+A\}$ consisting of $A$ consecutive positive integers, and places lava at all of the integers in the intervals. The intervals must be chosen so that:
(i) any two distinct intervals are disjoint and not adjacent;
(ii) there are at least $F$ positive integers with no lava between any two intervals; and
(iii) no lava is placed at any integer less than $F$.
Prove that the smallest $F$ for which the flea can jump over all the intervals and avoid all the lava, regardless of what Lavaman does,
is $F=(n-1) A+B$, where $n$ is the positive integer such that $\frac{A}{n+1} \leq B-A<\frac{A}{n}$.
|
Let $B=A+C$ where $A /(n+1) \leq C<A / n$.
First, here is an informal sketch of the proof.
Lavaman's strategy: Use only safe intervals with $n A+C-1$ integers. The flea will start at position $[1, C]$ from the left, which puts him at position $[n A, n A+C-1]$ from the right. After $n-1$ jumps, he will still have $n A-(n-1)(A+C)=A-(n-1) C>C$ distance to go, which is not enough for a big jump to clear the lava. Thus, he must do at least $n$ jumps in the safe interval, but that's possible only with all small jumps, and furthermore is impossible if the starting position is $C$. This gives him starting position 1 higher in the next safe interval, so sooner or later the flea is going to hit the lava.
Flea's strategy: The flea just does one interval at a time. If the safe interval has at least $n A+C$ integers in it, the flea has distance $d>n A$ to go to the next lava when it starts. Repeatedly do big jumps until $d$ is between 1 and $C \bmod A$, then small jumps until the remaining distance is between 1 and $C$, then a final big jump. This works as long as the first part does. However, we get at least $n$ big jumps since floor $((d-1) / A)$ can never go down two from a big jump (or we'd be done doing big jumps), so we get $n$ big jumps, and thus we are good if $d \bmod A$ is in any of $[1, C],[C+1,2 C], \ldots[n C+1,(n+1) C]$, but that's everything.
Let $C=B-A$. We shall write our intervals of lava in the form $\left(L_{i}, R_{i}\right]=\left\{L_{i}+1, L_{i}+2, \ldots, R_{i}\right\}$, where $R_{i}=L_{i}+A$ and $R_{i-1}<L_{i}$ for every $i \geq 1$. We also let $R_{0}=0$. We shall also represent a path for the flea as a sequence of integers $x_{0}, x_{1}, x_{2}, \ldots$ where $x_{0}=0$ and $x_{j}-x_{j-1} \in\{A, B\}$ for every $j \geq 0$.
Now here is a detailed proof.
First, assume $F<(n-1) A+B(=n A+C)$ : we must prove that Lavaman has a winning strategy. Let $L_{i}=R_{i-1}+n A+C-1$ for every $i \geq 1$. (Observe that $n A+C-1 \geq F$.)
Assume that the flea has an infinite path that avoids all the lava, which
means that $x_{j} \notin\left(L_{i}, R_{i}\right]$ for all $i, j \geq 1$. For each $i \geq 1$, let
$$
\begin{gathered}
M_{i}=\max \left\{x_{j}: x_{j} \leq L_{i}\right\}, \quad m_{i}=\min \left\{x_{j}: x_{j}>R_{i}\right\}, \\
\text { and } J(i)=\max \left\{j: x_{j} \leq L_{i}\right\}
\end{gathered}
$$
Also let $m_{0}=0$. Then for $i \geq 1$ we have
$$
M_{i}=x_{J(i)} \quad \text { and } \quad m_{i}=x_{J(i)+1} .
$$
Also, for every $i \geq 1$, we have
(a) $m_{i}=M_{i}+B$ (because $M_{i}+A \leq L_{i}+A=R_{i}$ );
(b) $L_{i} \geq M_{i}>L_{i}-C\left(\right.$ since $\left.M_{i}=m_{i}-B>R_{i}-B=L_{i}+A-B\right)$;
and
(c) $R_{i}<m_{i} \leq R_{i}+C\left(\right.$ since $\left.m_{i}=M_{i}+B \leq L_{i}+B=R_{i}+C\right)$.
Claim 1: $J(i+1)=J(i)+n+1$ for every $i \geq 1$. (That is, after jumping over one interval of lava, the flea must make exactly $n$ jumps before jumping over the next interval of lava.)
Proof:
$$
\begin{aligned}
x_{J(i)+n+1} & \leq x_{J(i)+1}+B n \\
& =m_{i}+B n \\
& <R_{i}+C+\left(A+\frac{A}{n}\right) n \\
& =L_{i+1}+A+1
\end{aligned}
$$
Because of the strict inequality, we have $x_{J(i)+n+1} \leq R_{i+1}$, and hence $x_{J(i)+n+1} \leq L_{i+1}$. Therefore $J(i)+n+1 \leq J(i+1)$. Next, we have
$$
\begin{aligned}
x_{J(i)+n+1} & \geq x_{J(i)+1}+A n \\
& =m_{i}+A n \\
& >R_{i}+A n \\
& =L_{i+1}-C+1 \\
& >L_{i+1}-A+1 \quad(\text { since } C<A) .
\end{aligned}
$$
Therefore $x_{J(i)+n+2} \geq x_{J(i)+n+1}+A>L_{i+1}$, and hence $J(i+1)<$ $J(i)+n+2$. Claim 1 follows.
Claim 2: $x_{j+1}-x_{j}=A$ for all $j=J(i)+1, \ldots, J(i+1)-1$, for all $i \geq 1$. (That is, the $n$ intermediate jumps of Claim 1 must all be of
length $A$.)
Proof: If Claim 2 is false, then
$$
\begin{aligned}
M_{i+1}=x_{J(i+1)}=x_{J(i)+n+1} & \geq x_{J(i)+1}+(n-1) A+B \\
& >R_{i}+n A+C \\
& =L_{i+1}+1 \\
& >M_{i+1}
\end{aligned}
$$
which is a contradiction. This proves Claim 2.
We can now conclude that
$$
\begin{aligned}
& x_{J(i+1)+1}=x_{J(i)+n+2}=x_{J(i)+1}+n A+B \\
& \text { i.e., } \quad m_{i+1}=m_{i}+n A+B \quad \text { for each } i \geq 1
\end{aligned}
$$
Therefore
$$
\begin{aligned}
m_{i+1}-R_{i+1} & =m_{i}+n A+B-\left(R_{i}+n A+C-1+A\right) \\
& =m_{i}-R_{i}+1
\end{aligned}
$$
Hence
$$
C \geq m_{C+1}-R_{C+1}=m_{1}-R_{1}+C>C
$$
which is a contradiction. Therefore no path for the flea avoids all the lava. We observe that Lavaman only needs to put lava on the first $C+1$ intervals.
Now assume $F \geq(n-1) A+B$. We will show that the flea can avoid all the lava. We shall need the following result:
Claim 3: Let $d \geq n A$. Then there exist nonnegative integers $s$ and $t$ such that $s A+t B \in(d-C, d]$.
We shall prove this result at the end.
First, observe that $L_{1} \geq n A$. By Claim 3 , it is possible for the flea to make a sequence of jumps starting from 0 and ending at a point of $\left(L_{1}-C, L_{1}\right]$. From any point of this interval, a single jump of size $B$ takes the flea over ( $L_{1}, R_{]}$to a point in $\left(R_{1}, R_{1}+C\right]$, which corresponds to the point $x_{J(1)+1}\left(=m_{1}\right)$ on the flea's path.
Now we use induction to prove that, for every $i \geq 1$, there is a path such that $x_{j}$ avoids lava for all $j \leq J(i)+1$. The case $i=1$ is done, so
assume that the assertion holds for a given $i$. Then $x_{J(i)+1}=m_{i} \in$ $\left(R_{i}, R_{i}+C\right]$. Therefore
$$
L_{i+1}-m_{i} \geq R_{i}+F-\left(R_{i}+C\right)=F-C \geq n A
$$
Applying Claim 3 with $d=L_{i+1}-m_{i}$ shows that the flea can jump from $m_{i}$ to a point of $\left(L_{i+1}-C, L_{i+1}\right]$. A single jump of size $B$ then takes the flea to a point of $\left(R_{i+1}, R_{i+1}+C\right]$ (without visiting $\left(L_{i+1}, R_{i+1}\right]$ ), and this point serves as $x_{J(i+1)+1}$. This completes the induction.
Proof of Claim 3: Let $u$ be the greatest integer that is less than or equal to $d / A$. Then $u \geq n$ and $u A \leq d<(u+1) A$. For $v=0, \ldots, n$, let
$$
z_{v}=(u-v) A+v B=u A+v C .
$$
Then
$$
\begin{aligned}
& \quad z_{0}=u A \leq d \\
& z_{n}=u A+n C=u A+(n+1) C-C \geq(u+1) A-C>d-C . \\
& \text { and } z_{v+1}-z_{v}=C \quad \text { for } v=0, \ldots, n-1
\end{aligned}
$$
Therefore we must have $z_{v} \in(d-C, d]$ for some $v$ in $\{0,1, \ldots, n\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Lavaman versus the Flea. Let $A, B$, and $F$ be positive integers, and assume $A<B<2 A$. A flea is at the number 0 on the number line. The flea can move by jumping to the right by $A$ or by $B$. Before the flea starts jumping, Lavaman chooses finitely many intervals $\{m+$ $1, m+2, \ldots, m+A\}$ consisting of $A$ consecutive positive integers, and places lava at all of the integers in the intervals. The intervals must be chosen so that:
(i) any two distinct intervals are disjoint and not adjacent;
(ii) there are at least $F$ positive integers with no lava between any two intervals; and
(iii) no lava is placed at any integer less than $F$.
Prove that the smallest $F$ for which the flea can jump over all the intervals and avoid all the lava, regardless of what Lavaman does,
is $F=(n-1) A+B$, where $n$ is the positive integer such that $\frac{A}{n+1} \leq B-A<\frac{A}{n}$.
|
Let $B=A+C$ where $A /(n+1) \leq C<A / n$.
First, here is an informal sketch of the proof.
Lavaman's strategy: Use only safe intervals with $n A+C-1$ integers. The flea will start at position $[1, C]$ from the left, which puts him at position $[n A, n A+C-1]$ from the right. After $n-1$ jumps, he will still have $n A-(n-1)(A+C)=A-(n-1) C>C$ distance to go, which is not enough for a big jump to clear the lava. Thus, he must do at least $n$ jumps in the safe interval, but that's possible only with all small jumps, and furthermore is impossible if the starting position is $C$. This gives him starting position 1 higher in the next safe interval, so sooner or later the flea is going to hit the lava.
Flea's strategy: The flea just does one interval at a time. If the safe interval has at least $n A+C$ integers in it, the flea has distance $d>n A$ to go to the next lava when it starts. Repeatedly do big jumps until $d$ is between 1 and $C \bmod A$, then small jumps until the remaining distance is between 1 and $C$, then a final big jump. This works as long as the first part does. However, we get at least $n$ big jumps since floor $((d-1) / A)$ can never go down two from a big jump (or we'd be done doing big jumps), so we get $n$ big jumps, and thus we are good if $d \bmod A$ is in any of $[1, C],[C+1,2 C], \ldots[n C+1,(n+1) C]$, but that's everything.
Let $C=B-A$. We shall write our intervals of lava in the form $\left(L_{i}, R_{i}\right]=\left\{L_{i}+1, L_{i}+2, \ldots, R_{i}\right\}$, where $R_{i}=L_{i}+A$ and $R_{i-1}<L_{i}$ for every $i \geq 1$. We also let $R_{0}=0$. We shall also represent a path for the flea as a sequence of integers $x_{0}, x_{1}, x_{2}, \ldots$ where $x_{0}=0$ and $x_{j}-x_{j-1} \in\{A, B\}$ for every $j \geq 0$.
Now here is a detailed proof.
First, assume $F<(n-1) A+B(=n A+C)$ : we must prove that Lavaman has a winning strategy. Let $L_{i}=R_{i-1}+n A+C-1$ for every $i \geq 1$. (Observe that $n A+C-1 \geq F$.)
Assume that the flea has an infinite path that avoids all the lava, which
means that $x_{j} \notin\left(L_{i}, R_{i}\right]$ for all $i, j \geq 1$. For each $i \geq 1$, let
$$
\begin{gathered}
M_{i}=\max \left\{x_{j}: x_{j} \leq L_{i}\right\}, \quad m_{i}=\min \left\{x_{j}: x_{j}>R_{i}\right\}, \\
\text { and } J(i)=\max \left\{j: x_{j} \leq L_{i}\right\}
\end{gathered}
$$
Also let $m_{0}=0$. Then for $i \geq 1$ we have
$$
M_{i}=x_{J(i)} \quad \text { and } \quad m_{i}=x_{J(i)+1} .
$$
Also, for every $i \geq 1$, we have
(a) $m_{i}=M_{i}+B$ (because $M_{i}+A \leq L_{i}+A=R_{i}$ );
(b) $L_{i} \geq M_{i}>L_{i}-C\left(\right.$ since $\left.M_{i}=m_{i}-B>R_{i}-B=L_{i}+A-B\right)$;
and
(c) $R_{i}<m_{i} \leq R_{i}+C\left(\right.$ since $\left.m_{i}=M_{i}+B \leq L_{i}+B=R_{i}+C\right)$.
Claim 1: $J(i+1)=J(i)+n+1$ for every $i \geq 1$. (That is, after jumping over one interval of lava, the flea must make exactly $n$ jumps before jumping over the next interval of lava.)
Proof:
$$
\begin{aligned}
x_{J(i)+n+1} & \leq x_{J(i)+1}+B n \\
& =m_{i}+B n \\
& <R_{i}+C+\left(A+\frac{A}{n}\right) n \\
& =L_{i+1}+A+1
\end{aligned}
$$
Because of the strict inequality, we have $x_{J(i)+n+1} \leq R_{i+1}$, and hence $x_{J(i)+n+1} \leq L_{i+1}$. Therefore $J(i)+n+1 \leq J(i+1)$. Next, we have
$$
\begin{aligned}
x_{J(i)+n+1} & \geq x_{J(i)+1}+A n \\
& =m_{i}+A n \\
& >R_{i}+A n \\
& =L_{i+1}-C+1 \\
& >L_{i+1}-A+1 \quad(\text { since } C<A) .
\end{aligned}
$$
Therefore $x_{J(i)+n+2} \geq x_{J(i)+n+1}+A>L_{i+1}$, and hence $J(i+1)<$ $J(i)+n+2$. Claim 1 follows.
Claim 2: $x_{j+1}-x_{j}=A$ for all $j=J(i)+1, \ldots, J(i+1)-1$, for all $i \geq 1$. (That is, the $n$ intermediate jumps of Claim 1 must all be of
length $A$.)
Proof: If Claim 2 is false, then
$$
\begin{aligned}
M_{i+1}=x_{J(i+1)}=x_{J(i)+n+1} & \geq x_{J(i)+1}+(n-1) A+B \\
& >R_{i}+n A+C \\
& =L_{i+1}+1 \\
& >M_{i+1}
\end{aligned}
$$
which is a contradiction. This proves Claim 2.
We can now conclude that
$$
\begin{aligned}
& x_{J(i+1)+1}=x_{J(i)+n+2}=x_{J(i)+1}+n A+B \\
& \text { i.e., } \quad m_{i+1}=m_{i}+n A+B \quad \text { for each } i \geq 1
\end{aligned}
$$
Therefore
$$
\begin{aligned}
m_{i+1}-R_{i+1} & =m_{i}+n A+B-\left(R_{i}+n A+C-1+A\right) \\
& =m_{i}-R_{i}+1
\end{aligned}
$$
Hence
$$
C \geq m_{C+1}-R_{C+1}=m_{1}-R_{1}+C>C
$$
which is a contradiction. Therefore no path for the flea avoids all the lava. We observe that Lavaman only needs to put lava on the first $C+1$ intervals.
Now assume $F \geq(n-1) A+B$. We will show that the flea can avoid all the lava. We shall need the following result:
Claim 3: Let $d \geq n A$. Then there exist nonnegative integers $s$ and $t$ such that $s A+t B \in(d-C, d]$.
We shall prove this result at the end.
First, observe that $L_{1} \geq n A$. By Claim 3 , it is possible for the flea to make a sequence of jumps starting from 0 and ending at a point of $\left(L_{1}-C, L_{1}\right]$. From any point of this interval, a single jump of size $B$ takes the flea over ( $L_{1}, R_{]}$to a point in $\left(R_{1}, R_{1}+C\right]$, which corresponds to the point $x_{J(1)+1}\left(=m_{1}\right)$ on the flea's path.
Now we use induction to prove that, for every $i \geq 1$, there is a path such that $x_{j}$ avoids lava for all $j \leq J(i)+1$. The case $i=1$ is done, so
assume that the assertion holds for a given $i$. Then $x_{J(i)+1}=m_{i} \in$ $\left(R_{i}, R_{i}+C\right]$. Therefore
$$
L_{i+1}-m_{i} \geq R_{i}+F-\left(R_{i}+C\right)=F-C \geq n A
$$
Applying Claim 3 with $d=L_{i+1}-m_{i}$ shows that the flea can jump from $m_{i}$ to a point of $\left(L_{i+1}-C, L_{i+1}\right]$. A single jump of size $B$ then takes the flea to a point of $\left(R_{i+1}, R_{i+1}+C\right]$ (without visiting $\left(L_{i+1}, R_{i+1}\right]$ ), and this point serves as $x_{J(i+1)+1}$. This completes the induction.
Proof of Claim 3: Let $u$ be the greatest integer that is less than or equal to $d / A$. Then $u \geq n$ and $u A \leq d<(u+1) A$. For $v=0, \ldots, n$, let
$$
z_{v}=(u-v) A+v B=u A+v C .
$$
Then
$$
\begin{aligned}
& \quad z_{0}=u A \leq d \\
& z_{n}=u A+n C=u A+(n+1) C-C \geq(u+1) A-C>d-C . \\
& \text { and } z_{v+1}-z_{v}=C \quad \text { for } v=0, \ldots, n-1
\end{aligned}
$$
Therefore we must have $z_{v} \in(d-C, d]$ for some $v$ in $\{0,1, \ldots, n\}$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
ebe07b4a-3583-53cd-a776-8913d5056f13
| 605,842
|
Let $\triangle A B C$ be an acute-angled triangle with altitudes $A D$ and $B E$ meeting at $H$. Let $M$ be the midpoint of segment $A B$, and suppose that the circumcircles of $\triangle D E M$ and $\triangle A B H$ meet at points $P$ and $Q$ with $P$ on the same side of $C H$ as $A$. Prove that the lines $E D$, $P H$, and $M Q$ all pass through a single point on the circumcircle of $\triangle A B C$.
|
Let $R$ denote the intersection of lines $E D$ and $P H$. Since quadrilaterals $E C D H$ and $A P H B$ are cyclic, we have $\angle R D A=180^{\circ}-\angle E D A=$ $180^{\circ}-\angle E D H=180^{\circ}-\angle E C H=90^{\circ}+A$, and $\angle R P A=\angle H P A=$ $180^{\circ}-\angle H B A=90^{\circ}+A$. Therefore, $A P D R$ is cyclic. This in turn implies that $\angle P B E=\angle P B H=\angle P A H=\angle P A D=\angle P R D=\angle P R E$, and so $P B R E$ is also cyclic.
Let $F$ denote the base of the altitude from $C$ to $A B$. Then $D, E, F$, and $M$ all lie on the 9-point circle of $\triangle A B C$, and so are cyclic. We also know $A P D R, P B R E, B C E F$, and $A C D F$ are cyclic, which implies $\angle A R B=\angle P R B-\angle P R A=\angle P E B-\angle P D A=\angle P E F+\angle F E B-$ $\angle P D F+\angle A D F=\angle F E B+\angle A D F=\angle F C B+\angle A C F=C$. Therefore, $R$ lies on the circumcircle of $\triangle A B C$.
Now let $Q^{\prime}$ and $R^{\prime}$ denote the intersections of line $M Q$ with the circumcircle of $\triangle A B C$, chosen so that $Q^{\prime}, M, Q, R^{\prime}$ lie on the line in that order. We will show that $R^{\prime}=R$, which will complete the proof. However, first note that the circumcircle of $\triangle A B C$ has radius $\frac{A B}{2 \sin C}$, and the circumcircle of $\triangle A B H$ has radius $\frac{A B}{2 \sin \angle A H B}=\frac{A B}{2 \sin \left(180^{\circ}-C\right)}$. Thus the two circles have equal radius, and so they must be symmetrical about the point $M$. In particular, $M Q=M Q^{\prime}$.
Since $\angle A E B=\angle A D B=90^{\circ}$, we furthermore know that $M$ is the circumcenter of both $\triangle A E B$ and $\triangle A D B$. Thus, $M A=M E=M D=$ $M B$. By Power of a Point, we then have $M Q \cdot M R^{\prime}=M Q^{\prime} \cdot M R^{\prime}=$ $M A \cdot M B=M D^{2}$. In particular, this means that the circumcircle of
$\triangle D R^{\prime} Q$ is tangent to $M D$ at $D$, which means $\angle M R^{\prime} D=\angle M D Q$. Similarly $M Q \cdot M R^{\prime}=M E^{2}$, and so $\angle M R^{\prime} E=\angle M E Q=\angle M D Q=$ $\angle M R^{\prime} D$. Therefore, $R^{\prime}$ also lies on the line $E D$.
Finally, the same argument shows that $M P$ also intersects the circumcircle of $\triangle A B C$ at a point $R^{\prime \prime}$ on line $E D$. Thus, $R, R^{\prime}$, and $R^{\prime \prime}$ are all chosen from the intersection of the circumcircle of $\triangle A B C$ and the line $E D$. In particular, two of $R, R^{\prime}$, and $R^{\prime \prime}$ must be equal. However, $R^{\prime \prime} \neq R$ since $M P$ and $P H$ already intersect at $P$, and $R^{\prime \prime} \neq R^{\prime}$ since $M P$ and $M Q$ already intersect at $M$. Thus, $R^{\prime}=R$, and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle with altitudes $A D$ and $B E$ meeting at $H$. Let $M$ be the midpoint of segment $A B$, and suppose that the circumcircles of $\triangle D E M$ and $\triangle A B H$ meet at points $P$ and $Q$ with $P$ on the same side of $C H$ as $A$. Prove that the lines $E D$, $P H$, and $M Q$ all pass through a single point on the circumcircle of $\triangle A B C$.
|

Let $R$ denote the intersection of lines $E D$ and $P H$. Since quadrilaterals $E C D H$ and $A P H B$ are cyclic, we have $\angle R D A=180^{\circ}-\angle E D A=$ $180^{\circ}-\angle E D H=180^{\circ}-\angle E C H=90^{\circ}+A$, and $\angle R P A=\angle H P A=$ $180^{\circ}-\angle H B A=90^{\circ}+A$. Therefore, $A P D R$ is cyclic. This in turn implies that $\angle P B E=\angle P B H=\angle P A H=\angle P A D=\angle P R D=\angle P R E$, and so $P B R E$ is also cyclic.
Let $F$ denote the base of the altitude from $C$ to $A B$. Then $D, E, F$, and $M$ all lie on the 9-point circle of $\triangle A B C$, and so are cyclic. We also know $A P D R, P B R E, B C E F$, and $A C D F$ are cyclic, which implies $\angle A R B=\angle P R B-\angle P R A=\angle P E B-\angle P D A=\angle P E F+\angle F E B-$ $\angle P D F+\angle A D F=\angle F E B+\angle A D F=\angle F C B+\angle A C F=C$. Therefore, $R$ lies on the circumcircle of $\triangle A B C$.
Now let $Q^{\prime}$ and $R^{\prime}$ denote the intersections of line $M Q$ with the circumcircle of $\triangle A B C$, chosen so that $Q^{\prime}, M, Q, R^{\prime}$ lie on the line in that order. We will show that $R^{\prime}=R$, which will complete the proof. However, first note that the circumcircle of $\triangle A B C$ has radius $\frac{A B}{2 \sin C}$, and the circumcircle of $\triangle A B H$ has radius $\frac{A B}{2 \sin \angle A H B}=\frac{A B}{2 \sin \left(180^{\circ}-C\right)}$. Thus the two circles have equal radius, and so they must be symmetrical about the point $M$. In particular, $M Q=M Q^{\prime}$.
Since $\angle A E B=\angle A D B=90^{\circ}$, we furthermore know that $M$ is the circumcenter of both $\triangle A E B$ and $\triangle A D B$. Thus, $M A=M E=M D=$ $M B$. By Power of a Point, we then have $M Q \cdot M R^{\prime}=M Q^{\prime} \cdot M R^{\prime}=$ $M A \cdot M B=M D^{2}$. In particular, this means that the circumcircle of
$\triangle D R^{\prime} Q$ is tangent to $M D$ at $D$, which means $\angle M R^{\prime} D=\angle M D Q$. Similarly $M Q \cdot M R^{\prime}=M E^{2}$, and so $\angle M R^{\prime} E=\angle M E Q=\angle M D Q=$ $\angle M R^{\prime} D$. Therefore, $R^{\prime}$ also lies on the line $E D$.
Finally, the same argument shows that $M P$ also intersects the circumcircle of $\triangle A B C$ at a point $R^{\prime \prime}$ on line $E D$. Thus, $R, R^{\prime}$, and $R^{\prime \prime}$ are all chosen from the intersection of the circumcircle of $\triangle A B C$ and the line $E D$. In particular, two of $R, R^{\prime}$, and $R^{\prime \prime}$ must be equal. However, $R^{\prime \prime} \neq R$ since $M P$ and $P H$ already intersect at $P$, and $R^{\prime \prime} \neq R^{\prime}$ since $M P$ and $M Q$ already intersect at $M$. Thus, $R^{\prime}=R$, and the proof is complete.
|
{
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"problem_match": "\n5.",
"solution_match": "\n## Solution:"
}
|
b9c8f8b3-2a99-5c1d-99a5-fecca3e6f5d5
| 605,855
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
The left-hand side is symmetric with respect to $a, b, c$. Hence, we may assume that $a>b>c \geq 0$. Note that replacing $(a, b, c)$ with $(a-c, b-c, 0)$ lowers the value of the lefthand side, since the numerators of each of the fractions would decrease and the denominators remain the same. Therefore, to obtain the minimum possible value of the left-hand side, we may assume that $c=0$.
Then the left-hand side becomes
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}
$$
which yields, by the Arithmetic Mean - Geometric Mean Inequality,
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}} \geq 2 \sqrt{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{a^{2}}}=2
$$
with equality if and only if $a^{2} / b^{2}=b^{2} / a^{2}$, or equivalently, $a^{4}=b^{4}$. Since $a, b \geq 0, a=b$. But since no two of $a, b, c$ are equal, $a \neq b$. Hence, equality cannot hold. This yields
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}>2
$$
Ultimately, this implies the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
The left-hand side is symmetric with respect to $a, b, c$. Hence, we may assume that $a>b>c \geq 0$. Note that replacing $(a, b, c)$ with $(a-c, b-c, 0)$ lowers the value of the lefthand side, since the numerators of each of the fractions would decrease and the denominators remain the same. Therefore, to obtain the minimum possible value of the left-hand side, we may assume that $c=0$.
Then the left-hand side becomes
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}
$$
which yields, by the Arithmetic Mean - Geometric Mean Inequality,
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}} \geq 2 \sqrt{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{a^{2}}}=2
$$
with equality if and only if $a^{2} / b^{2}=b^{2} / a^{2}$, or equivalently, $a^{4}=b^{4}$. Since $a, b \geq 0, a=b$. But since no two of $a, b, c$ are equal, $a \neq b$. Hence, equality cannot hold. This yields
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}>2
$$
Ultimately, this implies the desired inequality.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
12a51c24-61a8-5b02-a058-6427a7465bb6
| 605,866
|
Let $f$ be a function from the set of positive integers to itself such that, for every $n$, the number of positive integer divisors of $n$ is equal to $f(f(n))$. For example, $f(f(6))=4$ and $f(f(25))=3$. Prove that if $p$ is prime then $f(p)$ is also prime.
|
Let $d(n)=f(f(n))$ denote the number of divisors of $n$ and observe that $f(d(n))=$ $f(f(f(n)))=d(f(n))$ for all $n$. Also note that because all divisors of $n$ are distinct positive integers between 1 and $n$, including 1 and $n$, and excluding $n-1$ if $n>2$, it follows that $2 \leq d(n)<n$ for all $n>2$. Furthermore $d(1)=1$ and $d(2)=2$.
We first will show that $f(2)=2$. Let $m=f(2)$ and note that $2=d(2)=f(f(2))=f(m)$. If $m \geq 2$, then let $m_{0}$ be the smallest positive integer satisfying that $m_{0} \geq 2$ and $f\left(m_{0}\right)=2$. It follows that $f\left(d\left(m_{0}\right)\right)=d\left(f\left(m_{0}\right)\right)=d(2)=2$. By the minimality of $m_{0}$, it follows that $d\left(m_{0}\right) \geq m_{0}$, which implies that $m_{0}=2$. Therefore if $m \geq 2$, it follows that $f(2)=2$. It suffices to examine the case in which $f(2)=m=1$. If $m=1$, then $f(1)=f(f(2))=2$ and furthermore, each prime $p$ satisfies that $d(f(p))=f(d(p))=f(2)=1$ which implies that $f(p)=1$. Therefore $d\left(f\left(p^{2}\right)\right)=f\left(d\left(p^{2}\right)\right)=f(3)=1$ which implies that $f\left(p^{2}\right)=1$ for any prime $p$. This implies that $3=d\left(p^{2}\right)=f\left(f\left(p^{2}\right)\right)=f(1)=2$, which is a contradiction. Therefore $m \neq 1$ and $f(2)=2$.
It now follows that if $p$ is prime then $2=f(2)=f(d(p))=d(f(p))$ which implies that $f(p)$ is prime.
Remark. Such a function exists and can be constructed inductively.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a function from the set of positive integers to itself such that, for every $n$, the number of positive integer divisors of $n$ is equal to $f(f(n))$. For example, $f(f(6))=4$ and $f(f(25))=3$. Prove that if $p$ is prime then $f(p)$ is also prime.
|
Let $d(n)=f(f(n))$ denote the number of divisors of $n$ and observe that $f(d(n))=$ $f(f(f(n)))=d(f(n))$ for all $n$. Also note that because all divisors of $n$ are distinct positive integers between 1 and $n$, including 1 and $n$, and excluding $n-1$ if $n>2$, it follows that $2 \leq d(n)<n$ for all $n>2$. Furthermore $d(1)=1$ and $d(2)=2$.
We first will show that $f(2)=2$. Let $m=f(2)$ and note that $2=d(2)=f(f(2))=f(m)$. If $m \geq 2$, then let $m_{0}$ be the smallest positive integer satisfying that $m_{0} \geq 2$ and $f\left(m_{0}\right)=2$. It follows that $f\left(d\left(m_{0}\right)\right)=d\left(f\left(m_{0}\right)\right)=d(2)=2$. By the minimality of $m_{0}$, it follows that $d\left(m_{0}\right) \geq m_{0}$, which implies that $m_{0}=2$. Therefore if $m \geq 2$, it follows that $f(2)=2$. It suffices to examine the case in which $f(2)=m=1$. If $m=1$, then $f(1)=f(f(2))=2$ and furthermore, each prime $p$ satisfies that $d(f(p))=f(d(p))=f(2)=1$ which implies that $f(p)=1$. Therefore $d\left(f\left(p^{2}\right)\right)=f\left(d\left(p^{2}\right)\right)=f(3)=1$ which implies that $f\left(p^{2}\right)=1$ for any prime $p$. This implies that $3=d\left(p^{2}\right)=f\left(f\left(p^{2}\right)\right)=f(1)=2$, which is a contradiction. Therefore $m \neq 1$ and $f(2)=2$.
It now follows that if $p$ is prime then $2=f(2)=f(d(p))=d(f(p))$ which implies that $f(p)$ is prime.
Remark. Such a function exists and can be constructed inductively.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
f553db9f-09c7-5372-b021-e91f41509c9b
| 605,884
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
The problem is to prove that there is an odd number of nonempty subsets $T$ of $S_{n}$ such that the average $A(T)$ and median $M(T)$ satisfy $A(T)=M(T)$. Given a subset $T$, consider the subset $T^{*}=\{n+1-t: t \in T\}$. It holds that $A\left(T^{*}\right)=n+1-A(T)$ and $M\left(T^{*}\right)=n+1-M(T)$, which implies that if $A(T)=M(T)$ then $A\left(T^{*}\right)=M\left(T^{*}\right)$. Pairing each set $T$ with $T^{*}$ yields that there are an even number of sets $T$ such that $A(T)=M(T)$ and $T \neq T^{*}$.
Thus it suffices to show that the number of nonempty subsets $T$ such that $A(T)=M(T)$ and $T=T^{*}$ is odd. Now note that if $T=T^{*}$, then $A(T)=M(T)=\frac{n+1}{2}$. Hence it suffices to show the number of nonempty subsets $T$ with $T=T^{*}$ is odd. Given such a set $T$, let $T^{\prime}$ be the largest nonempty subset of $\{1,2, \ldots,\lceil n / 2\rceil\}$ contained in $T$. Pairing $T$ with $T^{\prime}$ forms a bijection between these sets $T$ and the nonempty subsets of $\{1,2, \ldots,\lceil n / 2\rceil\}$. Thus there are $2^{\lceil n / 2\rceil}-1$ such subsets, which is odd as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
The problem is to prove that there is an odd number of nonempty subsets $T$ of $S_{n}$ such that the average $A(T)$ and median $M(T)$ satisfy $A(T)=M(T)$. Given a subset $T$, consider the subset $T^{*}=\{n+1-t: t \in T\}$. It holds that $A\left(T^{*}\right)=n+1-A(T)$ and $M\left(T^{*}\right)=n+1-M(T)$, which implies that if $A(T)=M(T)$ then $A\left(T^{*}\right)=M\left(T^{*}\right)$. Pairing each set $T$ with $T^{*}$ yields that there are an even number of sets $T$ such that $A(T)=M(T)$ and $T \neq T^{*}$.
Thus it suffices to show that the number of nonempty subsets $T$ such that $A(T)=M(T)$ and $T=T^{*}$ is odd. Now note that if $T=T^{*}$, then $A(T)=M(T)=\frac{n+1}{2}$. Hence it suffices to show the number of nonempty subsets $T$ with $T=T^{*}$ is odd. Given such a set $T$, let $T^{\prime}$ be the largest nonempty subset of $\{1,2, \ldots,\lceil n / 2\rceil\}$ contained in $T$. Pairing $T$ with $T^{\prime}$ forms a bijection between these sets $T$ and the nonempty subsets of $\{1,2, \ldots,\lceil n / 2\rceil\}$. Thus there are $2^{\lceil n / 2\rceil}-1$ such subsets, which is odd as desired.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
856d7620-74b5-5db5-b3b5-4c74a5037a88
| 605,896
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
Using the notation from the above solution: Let $B$ be the number of subsets $T$ with $M(T)>A(T), C$ be the number with $M(T)=A(T)$, and $D$ be the number with $M(T)<A(T)$. Pairing each set $T$ counted by $B$ with $T^{*}=\{n+1-t: t \in T\}$ shows that $B=D$. Now since $B+C+D=2^{n}-1$, we have that $C=2^{n}-1-2 B$, which is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
Using the notation from the above solution: Let $B$ be the number of subsets $T$ with $M(T)>A(T), C$ be the number with $M(T)=A(T)$, and $D$ be the number with $M(T)<A(T)$. Pairing each set $T$ counted by $B$ with $T^{*}=\{n+1-t: t \in T\}$ shows that $B=D$. Now since $B+C+D=2^{n}-1$, we have that $C=2^{n}-1-2 B$, which is odd.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n3.",
"solution_match": "\nAlternate solution:"
}
|
856d7620-74b5-5db5-b3b5-4c74a5037a88
| 605,896
|
Points $P$ and $Q$ lie inside parallelogram $A B C D$ and are such that triangles $A B P$ and $B C Q$ are equilateral. Prove that the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$ meet on the altitude from $B$ in triangle $A B C$.
|
Let $\angle A B C=m$ and let $O$ be the circumcenter of triangle $D P Q$. Since $P$ and $Q$ are in the interior of $A B C D$, it follows that $m=\angle A B C>60^{\circ}$ and $\angle D A B=180^{\circ}-m>60^{\circ}$ which together imply that $60^{\circ}<m<120^{\circ}$. Now note that $\angle D A P=\angle D A B-60^{\circ}=120^{\circ}-m$, $\angle D C Q=\angle D C B-60^{\circ}=120^{\circ}-m$ and that $\angle P B Q=60^{\circ}-\angle A B Q=60^{\circ}-\left(\angle A B C-60^{\circ}\right)=$ $120^{\circ}-\mathrm{m}$. This combined with the facts that $A D=B Q=C Q$ and $A P=B P=C D$ implies that triangles $D A P, Q B P$ and $Q C D$ are congruent. Therefore $D P=P Q=D Q$ and triangle $D P Q$ is equilateral. This implies that $\angle O D A=\angle P D A+30^{\circ}=\angle D Q C+30^{\circ}=\angle O Q C$. Combining this fact with $O Q=O D$ and $C Q=A D$ implies that triangles $O D A$ and $O Q C$ are congruent. Therefore $O A=O C$ and, if $M$ is the midpoint of segment $A C$, it follows that $O M$ is perpendicular to $A C$. Since $A B C D$ is a parallelogram, $M$ is also the midpoint of $D B$. If $K$ denotes the intersection of the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$, then $K$ is diametrically opposite $D$ on the circumcircle of $D P Q$ and $O$ is the midpoint of segment $D K$. This implies that $O M$ is a midline of triangle $D B K$ and hence that $B K$ is parallel to $O M$ which is perpendicular to $A C$. Therefore $K$ lies on the altitude from $B$ in triangle $A B C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $P$ and $Q$ lie inside parallelogram $A B C D$ and are such that triangles $A B P$ and $B C Q$ are equilateral. Prove that the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$ meet on the altitude from $B$ in triangle $A B C$.
|
Let $\angle A B C=m$ and let $O$ be the circumcenter of triangle $D P Q$. Since $P$ and $Q$ are in the interior of $A B C D$, it follows that $m=\angle A B C>60^{\circ}$ and $\angle D A B=180^{\circ}-m>60^{\circ}$ which together imply that $60^{\circ}<m<120^{\circ}$. Now note that $\angle D A P=\angle D A B-60^{\circ}=120^{\circ}-m$, $\angle D C Q=\angle D C B-60^{\circ}=120^{\circ}-m$ and that $\angle P B Q=60^{\circ}-\angle A B Q=60^{\circ}-\left(\angle A B C-60^{\circ}\right)=$ $120^{\circ}-\mathrm{m}$. This combined with the facts that $A D=B Q=C Q$ and $A P=B P=C D$ implies that triangles $D A P, Q B P$ and $Q C D$ are congruent. Therefore $D P=P Q=D Q$ and triangle $D P Q$ is equilateral. This implies that $\angle O D A=\angle P D A+30^{\circ}=\angle D Q C+30^{\circ}=\angle O Q C$. Combining this fact with $O Q=O D$ and $C Q=A D$ implies that triangles $O D A$ and $O Q C$ are congruent. Therefore $O A=O C$ and, if $M$ is the midpoint of segment $A C$, it follows that $O M$ is perpendicular to $A C$. Since $A B C D$ is a parallelogram, $M$ is also the midpoint of $D B$. If $K$ denotes the intersection of the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$, then $K$ is diametrically opposite $D$ on the circumcircle of $D P Q$ and $O$ is the midpoint of segment $D K$. This implies that $O M$ is a midline of triangle $D B K$ and hence that $B K$ is parallel to $O M$ which is perpendicular to $A C$. Therefore $K$ lies on the altitude from $B$ in triangle $A B C$, as desired.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
64a968fc-3b9d-5039-91ba-6d6486572d28
| 605,915
|
One hundred circles of radius one are positioned in the plane so that the area of any triangle formed by the centres of three of these circles is at most 2017. Prove that there is a line intersecting at least three of these circles.
|
We will prove that given $n$ circles, there is some line intersecting more than $\frac{n}{46}$ of them. Let $S$ be the set of centers of the $n$ circles. We will first show that there is a line $\ell$ such that the projections of the points in $S$ lie in an interval of length at most $\sqrt{8068}<90$ on $\ell$. Let $A$ and $B$ be the pair of points in $S$ that are farthest apart and let the distance between $A$ and $B$ be $d$. Now consider any point $C \in S$ distinct from $A$ and $B$. The distance from $C$ to the line $A B$ must be at most $\frac{4034}{d}$ since triangle $A B C$ has area at most 2017. Therefore if $\ell$ is a line perpendicular to $A B$, then the projections of $S$ onto $\ell$ lie in an interval of length $\frac{8068}{d}$ centered at the intersection of $\ell$ and $A B$. Furthermore, all of these projections must lie on an interval of length at most $d$ on $\ell$ since the largest distance between two of these projections is at most $d$. Since $\min (d, 8068 / d) \leq \sqrt{8068}<90$, this proves the claim.
Now note that the projections of the $n$ circles onto the line $\ell$ are intervals of length 2 , all contained in an interval of length at most $\sqrt{8068}+2<92$. Each point of this interval belongs to on average $\frac{2 n}{\sqrt{8068}+2}>\frac{n}{46}$ of the subintervals of length 2 corresponding to the projections of the $n$ circles onto $\ell$. Thus there is some point $x \in \ell$ belonging to the projections of more than $\frac{n}{46}$ circles. The line perpendicular to $\ell$ through $x$ has the desired property. Setting $n=100$ yields that there is a line intersecting at least three of the circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
One hundred circles of radius one are positioned in the plane so that the area of any triangle formed by the centres of three of these circles is at most 2017. Prove that there is a line intersecting at least three of these circles.
|
We will prove that given $n$ circles, there is some line intersecting more than $\frac{n}{46}$ of them. Let $S$ be the set of centers of the $n$ circles. We will first show that there is a line $\ell$ such that the projections of the points in $S$ lie in an interval of length at most $\sqrt{8068}<90$ on $\ell$. Let $A$ and $B$ be the pair of points in $S$ that are farthest apart and let the distance between $A$ and $B$ be $d$. Now consider any point $C \in S$ distinct from $A$ and $B$. The distance from $C$ to the line $A B$ must be at most $\frac{4034}{d}$ since triangle $A B C$ has area at most 2017. Therefore if $\ell$ is a line perpendicular to $A B$, then the projections of $S$ onto $\ell$ lie in an interval of length $\frac{8068}{d}$ centered at the intersection of $\ell$ and $A B$. Furthermore, all of these projections must lie on an interval of length at most $d$ on $\ell$ since the largest distance between two of these projections is at most $d$. Since $\min (d, 8068 / d) \leq \sqrt{8068}<90$, this proves the claim.
Now note that the projections of the $n$ circles onto the line $\ell$ are intervals of length 2 , all contained in an interval of length at most $\sqrt{8068}+2<92$. Each point of this interval belongs to on average $\frac{2 n}{\sqrt{8068}+2}>\frac{n}{46}$ of the subintervals of length 2 corresponding to the projections of the $n$ circles onto $\ell$. Thus there is some point $x \in \ell$ belonging to the projections of more than $\frac{n}{46}$ circles. The line perpendicular to $\ell$ through $x$ has the desired property. Setting $n=100$ yields that there is a line intersecting at least three of the circles.
|
{
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
54bd6687-698c-56d0-90c0-5e053b73b91e
| 605,925
|
Consider an arrangement of tokens in the plane, not necessarily at distinct points. We are allowed to apply a sequence of moves of the following kind: Select a pair of tokens at points $A$ and $B$ and move both of them to the midpoint of $A$ and $B$.
We say that an arrangement of $n$ tokens is collapsible if it is possible to end up with all $n$ tokens at the same point after a finite number of moves. Prove that every arrangement of $n$ tokens is collapsible if and only if $n$ is a power of 2 .
|
For a given positive integer $n$, consider an arrangement of $n$ tokens in the plane, where the tokens are at points $A_{1}, A_{2}, \ldots, A_{n}$. Let $G$ be the centroid of the $n$ points, so as vectors (after an arbitrary choice of origin),
$$
\vec{G}=\frac{\vec{A}_{1}+\vec{A}_{2}+\cdots+\vec{A}_{n}}{n}
$$
Note that any move leaves the centroid $G$ unchanged. Therefore, if all the tokens are eventually moved to the same point, then this point must be $G$.
First we prove that if $n=2^{k}$ for some nonnegative integer $k$, then all $n$ tokens can always be eventually moved to the same point. We shall use induction on $k$.
The result clearly holds for $n=2^{0}=1$. Assume that it holds when $n=2^{k}$ for some nonnegative integer $k$. Consider a set of $2^{k+1}$ tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$. Let $M_{i}$ be the midpoint of $A_{2 i-1}$ and $A_{2 i}$ for $1 \leq i \leq 2^{k}$.
First we move the tokens at $A_{2 i-1}$ and $A_{2 i}$ to $M_{i}$, for $1 \leq i \leq 2^{k}$. Then, there are two tokens at $M_{i}$ for all $1 \leq i \leq 2^{k}$. If we take one token from each of $M_{1}, M_{2}, \ldots, M_{2^{k}}$, then by the induction hypothesis, we can move all of them to the same point, say $G$. We can do the same with the remaining tokens at $M_{1}, M_{2}, \ldots, M_{2^{k}}$. Thus, all $2^{k+1}$ tokens are now at $G$, which completes the induction argument.
(Here is an alternate approach to the induction step: Given the tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$, move the first $2^{k}$ tokens to one point $G_{1}$, and move the remaining $2^{k}$ tokens to one point $G_{2}$. Then $2^{k}$ more moves can bring all the tokens to the midpoint of $G_{1}$ and $G_{2}$.)
Presented by the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
Now, assume that $n$ is not a power of 2 . Take any line in the plane, and number it as a real number line. (Henceforth, when we refer to a token at a real number, we mean with respect to this real number line.)
At the start, place $n-1$ tokens at 0 and one token at 1 . We observed that if we can move all the tokens to the same point, then it must be the centroid of the $n$ points. Here, the centroid is at $\frac{1}{n}$. We now prove a lemma.
Lemma. The average of any two dyadic rationals is also a dyadic rational. (A dyadic rational is a rational number that can be expressed in the form $\frac{m}{2^{a}}$, where $m$ is an integer and $a$ is a nonnegative integer.)
Proof. Consider two dyadic rationals $\frac{m_{1}}{2^{a_{1}}}$ and $\frac{m_{2}}{2^{a_{2}}}$. Then their average is
$$
\frac{1}{2}\left(\frac{m_{1}}{2^{a_{1}}}+\frac{m_{2}}{2^{a_{2}}}\right)=\frac{1}{2}\left(\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}} \cdot 2^{a_{2}}}\right)=\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}+a_{2}+1}}
$$
which is another dyadic rational.
On this real number line, a move corresponds to taking a token at $x$ and a token at $y$ and moving both of them to $\frac{x+y}{2}$, the average of $x$ and $y$. At the start, every token is at a dyadic rational (namely 0 or 1 ), which means that after any number of moves, every token must still be at a dyadic rational.
But $n$ is not a power of 2 , so $\frac{1}{n}$ is not a dyadic rational. (Indeed, if we could express $\frac{1}{n}$ in dyadic form $\frac{m}{2^{a}}$, then we would have $2^{a}=m n$, which is impossible unless $m$ and $n$ are powers of 2.) This means that it is not possible for any token to end up at $\frac{1}{n}$, let alone all $n$ tokens.
We conclude that we can always move all $n$ tokens to the same point if and only if $n$ is a power of 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider an arrangement of tokens in the plane, not necessarily at distinct points. We are allowed to apply a sequence of moves of the following kind: Select a pair of tokens at points $A$ and $B$ and move both of them to the midpoint of $A$ and $B$.
We say that an arrangement of $n$ tokens is collapsible if it is possible to end up with all $n$ tokens at the same point after a finite number of moves. Prove that every arrangement of $n$ tokens is collapsible if and only if $n$ is a power of 2 .
|
For a given positive integer $n$, consider an arrangement of $n$ tokens in the plane, where the tokens are at points $A_{1}, A_{2}, \ldots, A_{n}$. Let $G$ be the centroid of the $n$ points, so as vectors (after an arbitrary choice of origin),
$$
\vec{G}=\frac{\vec{A}_{1}+\vec{A}_{2}+\cdots+\vec{A}_{n}}{n}
$$
Note that any move leaves the centroid $G$ unchanged. Therefore, if all the tokens are eventually moved to the same point, then this point must be $G$.
First we prove that if $n=2^{k}$ for some nonnegative integer $k$, then all $n$ tokens can always be eventually moved to the same point. We shall use induction on $k$.
The result clearly holds for $n=2^{0}=1$. Assume that it holds when $n=2^{k}$ for some nonnegative integer $k$. Consider a set of $2^{k+1}$ tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$. Let $M_{i}$ be the midpoint of $A_{2 i-1}$ and $A_{2 i}$ for $1 \leq i \leq 2^{k}$.
First we move the tokens at $A_{2 i-1}$ and $A_{2 i}$ to $M_{i}$, for $1 \leq i \leq 2^{k}$. Then, there are two tokens at $M_{i}$ for all $1 \leq i \leq 2^{k}$. If we take one token from each of $M_{1}, M_{2}, \ldots, M_{2^{k}}$, then by the induction hypothesis, we can move all of them to the same point, say $G$. We can do the same with the remaining tokens at $M_{1}, M_{2}, \ldots, M_{2^{k}}$. Thus, all $2^{k+1}$ tokens are now at $G$, which completes the induction argument.
(Here is an alternate approach to the induction step: Given the tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$, move the first $2^{k}$ tokens to one point $G_{1}$, and move the remaining $2^{k}$ tokens to one point $G_{2}$. Then $2^{k}$ more moves can bring all the tokens to the midpoint of $G_{1}$ and $G_{2}$.)
Presented by the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
Now, assume that $n$ is not a power of 2 . Take any line in the plane, and number it as a real number line. (Henceforth, when we refer to a token at a real number, we mean with respect to this real number line.)
At the start, place $n-1$ tokens at 0 and one token at 1 . We observed that if we can move all the tokens to the same point, then it must be the centroid of the $n$ points. Here, the centroid is at $\frac{1}{n}$. We now prove a lemma.
Lemma. The average of any two dyadic rationals is also a dyadic rational. (A dyadic rational is a rational number that can be expressed in the form $\frac{m}{2^{a}}$, where $m$ is an integer and $a$ is a nonnegative integer.)
Proof. Consider two dyadic rationals $\frac{m_{1}}{2^{a_{1}}}$ and $\frac{m_{2}}{2^{a_{2}}}$. Then their average is
$$
\frac{1}{2}\left(\frac{m_{1}}{2^{a_{1}}}+\frac{m_{2}}{2^{a_{2}}}\right)=\frac{1}{2}\left(\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}} \cdot 2^{a_{2}}}\right)=\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}+a_{2}+1}}
$$
which is another dyadic rational.
On this real number line, a move corresponds to taking a token at $x$ and a token at $y$ and moving both of them to $\frac{x+y}{2}$, the average of $x$ and $y$. At the start, every token is at a dyadic rational (namely 0 or 1 ), which means that after any number of moves, every token must still be at a dyadic rational.
But $n$ is not a power of 2 , so $\frac{1}{n}$ is not a dyadic rational. (Indeed, if we could express $\frac{1}{n}$ in dyadic form $\frac{m}{2^{a}}$, then we would have $2^{a}=m n$, which is impossible unless $m$ and $n$ are powers of 2.) This means that it is not possible for any token to end up at $\frac{1}{n}$, let alone all $n$ tokens.
We conclude that we can always move all $n$ tokens to the same point if and only if $n$ is a power of 2 .
|
{
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
1e39e954-bc13-57b7-8ec8-710bde8bbbd5
| 605,931
|
Let five points on a circle be labelled $A, B, C, D$, and $E$ in clockwise order. Assume $A E=D E$ and let $P$ be the intersection of $A C$ and $B D$. Let $Q$ be the point on the line through $A$ and $B$ such that $A$ is between $B$ and $Q$ and $A Q=D P$. Similarly, let $R$ be the point on the line through $C$ and $D$ such that $D$ is between $C$ and $R$ and $D R=A P$. Prove that $P E$ is perpendicular to $Q R$.
|
We are given $A Q=D P$ and $A P=D R$. Additionally $\angle Q A P=180^{\circ}-\angle B A C=180^{\circ}-\angle B D C=\angle R D P$, and so triangles $A Q P$ and $D P R$ are congruent. Therefore $P Q=P R$. It follows that $P$ is on the perpendicular bisector of $Q R$.
We are also given $A P=D R$ and $A E=D E$. Additionally
$\angle P A E=\angle C A E=180^{\circ}-\angle C D E=\angle R D E$, and so triangles $P A E$ and $R D E$ are congruent.
Therefore $P E=R E$, and similarly $P E=Q E$. It follows that $E$ is on the perpendicular bisector of $P Q$.
Since both $P$ and $E$ are on the perpendicular bisector of $Q R$, the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let five points on a circle be labelled $A, B, C, D$, and $E$ in clockwise order. Assume $A E=D E$ and let $P$ be the intersection of $A C$ and $B D$. Let $Q$ be the point on the line through $A$ and $B$ such that $A$ is between $B$ and $Q$ and $A Q=D P$. Similarly, let $R$ be the point on the line through $C$ and $D$ such that $D$ is between $C$ and $R$ and $D R=A P$. Prove that $P E$ is perpendicular to $Q R$.
|
We are given $A Q=D P$ and $A P=D R$. Additionally $\angle Q A P=180^{\circ}-\angle B A C=180^{\circ}-\angle B D C=\angle R D P$, and so triangles $A Q P$ and $D P R$ are congruent. Therefore $P Q=P R$. It follows that $P$ is on the perpendicular bisector of $Q R$.
We are also given $A P=D R$ and $A E=D E$. Additionally
$\angle P A E=\angle C A E=180^{\circ}-\angle C D E=\angle R D E$, and so triangles $P A E$ and $R D E$ are congruent.
Therefore $P E=R E$, and similarly $P E=Q E$. It follows that $E$ is on the perpendicular bisector of $P Q$.
Since both $P$ and $E$ are on the perpendicular bisector of $Q R$, the result follows.
|
{
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
69a24c5f-54ad-568a-8a34-d0f56c9073f5
| 605,941
|
Let $k$ be a given even positive integer. Sarah first picks a positive integer $N$ greater than 1 and proceeds to alter it as follows: every minute, she chooses a prime divisor $p$ of the current value of $N$, and multiplies the current $N$ by $p^{k}-p^{-1}$ to produce the next value of $N$. Prove that there are infinitely many even positive integers $k$ such that, no matter what choices Sarah makes, her number $N$ will at some point be divisible by 2018 .
|
Note that 1009 is prime. We will show that if $k=1009^{m}-1$ for some positive integer $m$, then Sarah's number must at some point be divisible by 2018 . Let $P$ be the largest divisor of $N$ not divisible by a prime congruent to 1 modulo 1009. Assume for contradiction that $N$ is never divisible by 2018. We will show that $P$ decreases each minute. Suppose that in the $t^{\text {th }}$ minute, Sarah chooses the prime divisor $p$ of $N$. First note that $N$ is replaced with $\frac{p^{k+1}-1}{p} \cdot N$ where
$$
p^{k+1}-1=p^{1009^{m}}-1=(p-1)\left(p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1\right)
$$
Suppose that $q$ is a prime number dividing the second factor. Since $q$ divides $p^{1009^{m}}-1$, it follows that $q \neq p$ and the order of $p$ modulo $q$ must divide $1009^{m}$ and hence is either divisible by 1009 or is equal to 1 . If it is equal to 1 then $p \equiv 1(\bmod q)$, which implies that
$$
0 \equiv p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1 \equiv 1009^{m} \quad(\bmod q)
$$
and thus $q=1009$. However, if $q=1009$ then $p \geq 1010$ and $p$ must be odd. Since $p-1$ now divides $N$, it follows that $N$ is divisible by 2018 in the $(t+1)^{\text {th }}$ minute, which is a contradiction. Therefore the order of $p$ modulo $q$ is divisible by 1009 and hence 1009 divides $q-1$. Therefore all of the prime divisors of the second factor are congruent to 1 modulo 1009. This implies that $P$ is replaced by a divisor of $\frac{p-1}{p} \cdot P$ in the $(t+1)^{\text {th }}$ minute and therefore decreases. Since $P \geq 1$ must always hold, $P$ cannot decrease forever. Therefore $N$ must at some point be divisible by 2018 .
Remark (no credit). If $k$ is allowed to be odd, then choosing $k+1$ to be divisible by $\phi(1009)=1008$ guarantees that Sarah's number will be divisible by 2018 the first time it is even, which is after either the first or second minute.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be a given even positive integer. Sarah first picks a positive integer $N$ greater than 1 and proceeds to alter it as follows: every minute, she chooses a prime divisor $p$ of the current value of $N$, and multiplies the current $N$ by $p^{k}-p^{-1}$ to produce the next value of $N$. Prove that there are infinitely many even positive integers $k$ such that, no matter what choices Sarah makes, her number $N$ will at some point be divisible by 2018 .
|
Note that 1009 is prime. We will show that if $k=1009^{m}-1$ for some positive integer $m$, then Sarah's number must at some point be divisible by 2018 . Let $P$ be the largest divisor of $N$ not divisible by a prime congruent to 1 modulo 1009. Assume for contradiction that $N$ is never divisible by 2018. We will show that $P$ decreases each minute. Suppose that in the $t^{\text {th }}$ minute, Sarah chooses the prime divisor $p$ of $N$. First note that $N$ is replaced with $\frac{p^{k+1}-1}{p} \cdot N$ where
$$
p^{k+1}-1=p^{1009^{m}}-1=(p-1)\left(p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1\right)
$$
Suppose that $q$ is a prime number dividing the second factor. Since $q$ divides $p^{1009^{m}}-1$, it follows that $q \neq p$ and the order of $p$ modulo $q$ must divide $1009^{m}$ and hence is either divisible by 1009 or is equal to 1 . If it is equal to 1 then $p \equiv 1(\bmod q)$, which implies that
$$
0 \equiv p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1 \equiv 1009^{m} \quad(\bmod q)
$$
and thus $q=1009$. However, if $q=1009$ then $p \geq 1010$ and $p$ must be odd. Since $p-1$ now divides $N$, it follows that $N$ is divisible by 2018 in the $(t+1)^{\text {th }}$ minute, which is a contradiction. Therefore the order of $p$ modulo $q$ is divisible by 1009 and hence 1009 divides $q-1$. Therefore all of the prime divisors of the second factor are congruent to 1 modulo 1009. This implies that $P$ is replaced by a divisor of $\frac{p-1}{p} \cdot P$ in the $(t+1)^{\text {th }}$ minute and therefore decreases. Since $P \geq 1$ must always hold, $P$ cannot decrease forever. Therefore $N$ must at some point be divisible by 2018 .
Remark (no credit). If $k$ is allowed to be odd, then choosing $k+1$ to be divisible by $\phi(1009)=1008$ guarantees that Sarah's number will be divisible by 2018 the first time it is even, which is after either the first or second minute.
|
{
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
831c7191-89fd-5702-a8f6-2c513175264e
| 605,972
|
Amy has drawn three points in a plane, $A, B$, and $C$, such that $A B=B C=C A=6$. Amy is allowed to draw a new point if it is the circumcenter of a triangle whose vertices she has already drawn. For example, she can draw the circumcenter $O$ of triangle $A B C$, and then afterwards she can draw the circumcenter of triangle $A B O$.
(a) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 7 .
(b) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 2019.
(Recall that the circumcenter of a triangle is the center of the circle that passes through its three vertices.)
|
(a) Given triangle $\triangle A B C$, Amy can draw the following points:
- $O$ is the circumcenter of $\triangle A B C$
- $A_{1}$ is the circumcenter of $\triangle B O C$
- $A_{2}$ is the circumcenter of $\triangle O B A_{1}$
- $A_{3}$ is the circumcenter of $\triangle B A_{2} A_{1}$
We claim that $A A_{3}>7$. We present two ways to prove this claim.
First Method: By symmetry of the equilateral triangle $\triangle A B C$, we have $\angle A O B=\angle B O C=\angle C O A=120^{\circ}$. Since $O B=O C$ and $A_{1} B=A_{1} O=A_{1} C$, we deduce that $\triangle A_{1} O B \cong \triangle A_{1} O C$, and hence $\angle B O A_{1}=\angle C O A_{1}=60^{\circ}$. Therefore, since $\triangle A_{1} O B$ is isosceles, it must be equilateral. As we found for our original triangle, we find $\angle B A_{2} A_{1}=120^{\circ}$, and so $\angle A_{2} B A_{1}=\angle A_{2} A_{1} B=30^{\circ}$ (since
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

$\left.A_{2} B=A_{2} A_{1}\right)$. Also we see that $\angle O B A_{2}=30^{\circ}=\angle O B C$, which shows that $A_{2}$ lies on the segment $B C$.
Applying the Law of Sines to $\triangle B O C$, we obtain
$$
O C=\frac{B C \sin (\angle O B C)}{\sin (\angle B O C)}=\frac{6(1 / 2)}{\sqrt{3} / 2}=2 \sqrt{3} .
$$
By symmetry, we see that (i) $O A_{1}$ is the bisector of $\angle B O C$ and the perpendicular bisector of $B C$, and (ii) the three points $A, O$, and $A_{1}$ are collinear. Therefore $A_{1} A=A_{1} O+O A=2 O A=4 \sqrt{3}$.
The same argument that we used to show $\triangle A_{1} O B$ is equilateral with side $A C / \sqrt{3}$ shows that $\triangle A_{3} A_{2} A_{1}$ is equilateral with side $O B / \sqrt{3}=2$. Thus $\angle A_{3} A_{1} O=\angle O A_{1} B+\angle A_{3} A_{1} A_{2}-\angle A_{2} A_{1} B=$ $60^{\circ}+60^{\circ}-30^{\circ}=90^{\circ}$. Hence we can apply the Pythagorean Theorem:
$$
A_{3} A=\sqrt{\left(A_{3} A_{1}\right)^{2}+\left(A_{1} A\right)^{2}}=\sqrt{2^{2}+(4 \sqrt{3})^{2}}=\sqrt{52}>\sqrt{49}=7 .
$$
Second Method: (An alternative to writing the justifications of the constructions in the First Method is to use analytic geometry. Once the following coordinates are found using the kind of reasoning in the First Method or by other means, the writeup can justify them succinctly by computing distances.) Label $(0,0)$ as $B,(6,0)$ as $C$, and $(3, \sqrt{3})$ as $A$. Then we have $A B=B C=C A=6$.
The circumcenter $O$ of $\triangle A B C$ is $(3, \sqrt{3})$; this can be verified by observing $O A=O B=O C=2 \sqrt{3}$. Next, the point $A_{1}=(3,-\sqrt{3})$ satisfies $A_{1} O=A_{1} B=A_{1} C=2 \sqrt{3}$, so $A_{1}$ is the circumcenter of $\triangle B O C$.
The point $A_{2}=(2,0)$ satisfies $A_{2} O=A_{2} B=A_{2} A_{1}=2$, so this is the circumcenter of $\triangle O B A_{1}$.
And the point $A_{3}=(1,-\sqrt{3})$ satisfies $A_{3} B=A_{3} A_{2}=A_{3} A_{1}=2$, so this is the circumcenter of $\triangle B A_{2} A_{1}$.
Finally, we compute $A_{3} A=\sqrt{52}>\sqrt{49}=7$, and part (a) is proved.
(b) In part (a), using either method we find that $O A_{3}=4>2 \sqrt{3}=O A$. By rotating the construction of part (a) by $\pm 120^{\circ}$ about $O$, Amy can construct $B_{3}$ and $C_{3}$ such that $\triangle A_{3} B_{3} C_{3}$ is equilateral with circumcenter $O$ and circumradius 4 , which is strictly bigger than the circumradius $2 \sqrt{3}$ of $\triangle A B C$. Amy can repeat this process starting from $\triangle A_{3} B_{3} C_{3}$. After $n$ iterations of the process, Amy will have drawn the vertices of an equilateral triangle whose circumradius is $2 \sqrt{3}\left(\frac{4}{2 \sqrt{3}}\right)^{n}$, which is bigger than 2019 when $n$ is sufficiently large.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Amy has drawn three points in a plane, $A, B$, and $C$, such that $A B=B C=C A=6$. Amy is allowed to draw a new point if it is the circumcenter of a triangle whose vertices she has already drawn. For example, she can draw the circumcenter $O$ of triangle $A B C$, and then afterwards she can draw the circumcenter of triangle $A B O$.
(a) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 7 .
(b) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 2019.
(Recall that the circumcenter of a triangle is the center of the circle that passes through its three vertices.)
|
(a) Given triangle $\triangle A B C$, Amy can draw the following points:
- $O$ is the circumcenter of $\triangle A B C$
- $A_{1}$ is the circumcenter of $\triangle B O C$
- $A_{2}$ is the circumcenter of $\triangle O B A_{1}$
- $A_{3}$ is the circumcenter of $\triangle B A_{2} A_{1}$
We claim that $A A_{3}>7$. We present two ways to prove this claim.
First Method: By symmetry of the equilateral triangle $\triangle A B C$, we have $\angle A O B=\angle B O C=\angle C O A=120^{\circ}$. Since $O B=O C$ and $A_{1} B=A_{1} O=A_{1} C$, we deduce that $\triangle A_{1} O B \cong \triangle A_{1} O C$, and hence $\angle B O A_{1}=\angle C O A_{1}=60^{\circ}$. Therefore, since $\triangle A_{1} O B$ is isosceles, it must be equilateral. As we found for our original triangle, we find $\angle B A_{2} A_{1}=120^{\circ}$, and so $\angle A_{2} B A_{1}=\angle A_{2} A_{1} B=30^{\circ}$ (since

A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

$\left.A_{2} B=A_{2} A_{1}\right)$. Also we see that $\angle O B A_{2}=30^{\circ}=\angle O B C$, which shows that $A_{2}$ lies on the segment $B C$.
Applying the Law of Sines to $\triangle B O C$, we obtain
$$
O C=\frac{B C \sin (\angle O B C)}{\sin (\angle B O C)}=\frac{6(1 / 2)}{\sqrt{3} / 2}=2 \sqrt{3} .
$$
By symmetry, we see that (i) $O A_{1}$ is the bisector of $\angle B O C$ and the perpendicular bisector of $B C$, and (ii) the three points $A, O$, and $A_{1}$ are collinear. Therefore $A_{1} A=A_{1} O+O A=2 O A=4 \sqrt{3}$.
The same argument that we used to show $\triangle A_{1} O B$ is equilateral with side $A C / \sqrt{3}$ shows that $\triangle A_{3} A_{2} A_{1}$ is equilateral with side $O B / \sqrt{3}=2$. Thus $\angle A_{3} A_{1} O=\angle O A_{1} B+\angle A_{3} A_{1} A_{2}-\angle A_{2} A_{1} B=$ $60^{\circ}+60^{\circ}-30^{\circ}=90^{\circ}$. Hence we can apply the Pythagorean Theorem:
$$
A_{3} A=\sqrt{\left(A_{3} A_{1}\right)^{2}+\left(A_{1} A\right)^{2}}=\sqrt{2^{2}+(4 \sqrt{3})^{2}}=\sqrt{52}>\sqrt{49}=7 .
$$
Second Method: (An alternative to writing the justifications of the constructions in the First Method is to use analytic geometry. Once the following coordinates are found using the kind of reasoning in the First Method or by other means, the writeup can justify them succinctly by computing distances.) Label $(0,0)$ as $B,(6,0)$ as $C$, and $(3, \sqrt{3})$ as $A$. Then we have $A B=B C=C A=6$.
The circumcenter $O$ of $\triangle A B C$ is $(3, \sqrt{3})$; this can be verified by observing $O A=O B=O C=2 \sqrt{3}$. Next, the point $A_{1}=(3,-\sqrt{3})$ satisfies $A_{1} O=A_{1} B=A_{1} C=2 \sqrt{3}$, so $A_{1}$ is the circumcenter of $\triangle B O C$.
The point $A_{2}=(2,0)$ satisfies $A_{2} O=A_{2} B=A_{2} A_{1}=2$, so this is the circumcenter of $\triangle O B A_{1}$.
And the point $A_{3}=(1,-\sqrt{3})$ satisfies $A_{3} B=A_{3} A_{2}=A_{3} A_{1}=2$, so this is the circumcenter of $\triangle B A_{2} A_{1}$.
Finally, we compute $A_{3} A=\sqrt{52}>\sqrt{49}=7$, and part (a) is proved.
(b) In part (a), using either method we find that $O A_{3}=4>2 \sqrt{3}=O A$. By rotating the construction of part (a) by $\pm 120^{\circ}$ about $O$, Amy can construct $B_{3}$ and $C_{3}$ such that $\triangle A_{3} B_{3} C_{3}$ is equilateral with circumcenter $O$ and circumradius 4 , which is strictly bigger than the circumradius $2 \sqrt{3}$ of $\triangle A B C$. Amy can repeat this process starting from $\triangle A_{3} B_{3} C_{3}$. After $n$ iterations of the process, Amy will have drawn the vertices of an equilateral triangle whose circumradius is $2 \sqrt{3}\left(\frac{4}{2 \sqrt{3}}\right)^{n}$, which is bigger than 2019 when $n$ is sufficiently large.
|
{
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"problem_match": "\n1.",
"solution_match": "\n## Solution."
}
|
4e8212f5-35cb-5c31-912e-7ce2c05cd446
| 605,981
|
Let $a$ and $b$ be positive integers such that $a+b^{3}$ is divisible by $a^{2}+3 a b+3 b^{2}-1$. Prove that $a^{2}+3 a b+3 b^{2}-1$ is divisible by the cube of an integer greater than 1 .
|
Let $Z=a^{2}+3 a b+3 b^{2}-1$. By assumption, there is a positive integer $c$ such that $c Z=a+b^{3}$. Noticing the resemblance between the first three terms of $Z$ and those of the expansion of $(a+b)^{3}$, we are led to
$$
(a+b)^{3}=a\left(a^{2}+3 a b+3 b^{2}\right)+b^{3}=a(Z+1)+b^{3}=a Z+a+b^{3}=a Z+c Z .
$$
Thus $Z$ divides $(a+b)^{3}$.
Let the prime factorization of $a+b$ be $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{k}^{e_{k}}$ and let $Z=p_{1}^{f_{1}} p_{2}^{f_{2}} \cdots p_{k}^{f_{k}}$, where $f_{i} \leq 3 e_{i}$ for each $i$ since $Z$ divides $(a+b)^{3}$. If $Z$ is not divisible by a perfect cube greater than one, then $0 \leq f_{i} \leq 2$ and hence $f_{i} \leq 2 e_{i}$ for each $i$. This implies that $Z$ divides $(a+b)^{2}$. However, $(a+b)^{2}<a^{2}+3 a b+3 b^{2}-1=Z$ since $a, b \geq 1$, which is a contradiction. Thus $Z$ must be divisible by a perfect cube greater than one.
Remark. A brute force search yields many pairs $(a, b)$ satisfying this divisibility property. Examples include $(3,5),(19,11),(111,29)$ as well as twelve others satisfying that $a, b \leq 1000$. The values of $a^{2}+3 a b+3 b^{2}-1$ for these three pairs are $128=2^{7}, 1350=2 \times 3^{3} \times 5^{2}$ and $24500=2^{2} \times 5^{3} \times 7^{2}$, all of which have different perfect cube divisors.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers such that $a+b^{3}$ is divisible by $a^{2}+3 a b+3 b^{2}-1$. Prove that $a^{2}+3 a b+3 b^{2}-1$ is divisible by the cube of an integer greater than 1 .
|
Let $Z=a^{2}+3 a b+3 b^{2}-1$. By assumption, there is a positive integer $c$ such that $c Z=a+b^{3}$. Noticing the resemblance between the first three terms of $Z$ and those of the expansion of $(a+b)^{3}$, we are led to
$$
(a+b)^{3}=a\left(a^{2}+3 a b+3 b^{2}\right)+b^{3}=a(Z+1)+b^{3}=a Z+a+b^{3}=a Z+c Z .
$$
Thus $Z$ divides $(a+b)^{3}$.
Let the prime factorization of $a+b$ be $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{k}^{e_{k}}$ and let $Z=p_{1}^{f_{1}} p_{2}^{f_{2}} \cdots p_{k}^{f_{k}}$, where $f_{i} \leq 3 e_{i}$ for each $i$ since $Z$ divides $(a+b)^{3}$. If $Z$ is not divisible by a perfect cube greater than one, then $0 \leq f_{i} \leq 2$ and hence $f_{i} \leq 2 e_{i}$ for each $i$. This implies that $Z$ divides $(a+b)^{2}$. However, $(a+b)^{2}<a^{2}+3 a b+3 b^{2}-1=Z$ since $a, b \geq 1$, which is a contradiction. Thus $Z$ must be divisible by a perfect cube greater than one.
Remark. A brute force search yields many pairs $(a, b)$ satisfying this divisibility property. Examples include $(3,5),(19,11),(111,29)$ as well as twelve others satisfying that $a, b \leq 1000$. The values of $a^{2}+3 a b+3 b^{2}-1$ for these three pairs are $128=2^{7}, 1350=2 \times 3^{3} \times 5^{2}$ and $24500=2^{2} \times 5^{3} \times 7^{2}$, all of which have different perfect cube divisors.
|
{
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution."
}
|
ff6764cc-24de-5fb4-98a8-5f734e46bbec
| 605,990
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $Q(x)=x^{2}-k x-1$ and let $P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n}$. Note that the product of the two roots of $Q(x)$ is -1 and thus one of the two roots has magnitude at most 1. Let $z$ be this root. Now note that since $a_{1}=a_{n-1}=0$, we have that
$$
\begin{aligned}
0=Q(z) P(z) & =-a_{0}-k a_{0} z+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}-k a_{n} z^{n+1}+a_{n} z^{n+2} \\
& =a_{0}(-1-k z)+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}\left(z^{2}-k z\right) \\
& =-a_{0} z^{2}+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}
\end{aligned}
$$
where the third equality follows since $z^{2}-k z-1=0$. The triangle inequality now implies
$$
\begin{aligned}
\left|a_{0}\right| \cdot|z|^{2} & \leq\left|a_{n}\right| \cdot|z|^{n}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{i+2} \\
& \leq\left|a_{n}\right| \cdot|z|^{2}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{2}
\end{aligned}
$$
since $|z| \leq 1$ and $n \geq 2$. Since $z \neq 0$, the inequality is obtained on dividing by $|z|^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $Q(x)=x^{2}-k x-1$ and let $P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n}$. Note that the product of the two roots of $Q(x)$ is -1 and thus one of the two roots has magnitude at most 1. Let $z$ be this root. Now note that since $a_{1}=a_{n-1}=0$, we have that
$$
\begin{aligned}
0=Q(z) P(z) & =-a_{0}-k a_{0} z+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}-k a_{n} z^{n+1}+a_{n} z^{n+2} \\
& =a_{0}(-1-k z)+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}\left(z^{2}-k z\right) \\
& =-a_{0} z^{2}+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}
\end{aligned}
$$
where the third equality follows since $z^{2}-k z-1=0$. The triangle inequality now implies
$$
\begin{aligned}
\left|a_{0}\right| \cdot|z|^{2} & \leq\left|a_{n}\right| \cdot|z|^{n}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{i+2} \\
& \leq\left|a_{n}\right| \cdot|z|^{2}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{2}
\end{aligned}
$$
since $|z| \leq 1$ and $n \geq 2$. Since $z \neq 0$, the inequality is obtained on dividing by $|z|^{2}$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## First Solution."
}
|
3f5a7e98-74e9-5678-8357-51e2eea27b3d
| 606,006
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $k$ be a real number. Put
$$
R= \begin{cases}\sqrt{k^{2}+4} & \text { if } k \geq 0 \\ -\sqrt{k^{2}+4} & \text { if } k<0\end{cases}
$$
Define the polynomial
$$
S(x)=x^{2}+R x+1
$$
The roots of $S$ are
$$
b=\frac{-R-k}{2} \quad \text { and } \quad c=\frac{-R+k}{2}
$$
Then we have
$$
b-c=-k, \quad b c=1, \quad \text { and } \quad|c| \leq 1
$$
(the inequality follows from $b c=1$ and $|c| \leq|b|$ ).
Put $d_{i}=a_{i}+b a_{i+1}$ for $i=0,1, \ldots, n-1$. Then, for $i=0,1, \ldots, n-2$, we have
$$
\begin{aligned}
d_{i}-c d_{i+1} & =a_{i}+(b-c) a_{i+1}-b c a_{i+2} \\
& =a_{i}-k a_{i+1}-a_{i+2}
\end{aligned}
$$
Therefore
$$
\begin{aligned}
\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| & =\sum_{i=0}^{n-2}\left|d_{i}-c d_{i+1}\right| \\
& \geq \sum_{i=0}^{n-2}\left(\left|d_{i}\right|-|c|\left|d_{i+1}\right|\right) \\
& =\left|d_{0}\right|+(1-|c|) \sum_{i=1}^{n-2}\left|d_{i}\right|-|c|\left|d_{n-1}\right| \\
& \geq\left|d_{0}\right|-|c|\left|d_{n-1}\right| \\
& =\left|a_{0}+b a_{1}\right|-|c|\left|a_{n-1}+b a_{n}\right| \\
& =\left|a_{0}\right|-|b c|\left|a_{n}\right| \\
& =\left|a_{0}\right|-\left|a_{n}\right|
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $k$ be a real number. Put
$$
R= \begin{cases}\sqrt{k^{2}+4} & \text { if } k \geq 0 \\ -\sqrt{k^{2}+4} & \text { if } k<0\end{cases}
$$
Define the polynomial
$$
S(x)=x^{2}+R x+1
$$
The roots of $S$ are
$$
b=\frac{-R-k}{2} \quad \text { and } \quad c=\frac{-R+k}{2}
$$
Then we have
$$
b-c=-k, \quad b c=1, \quad \text { and } \quad|c| \leq 1
$$
(the inequality follows from $b c=1$ and $|c| \leq|b|$ ).
Put $d_{i}=a_{i}+b a_{i+1}$ for $i=0,1, \ldots, n-1$. Then, for $i=0,1, \ldots, n-2$, we have
$$
\begin{aligned}
d_{i}-c d_{i+1} & =a_{i}+(b-c) a_{i+1}-b c a_{i+2} \\
& =a_{i}-k a_{i+1}-a_{i+2}
\end{aligned}
$$
Therefore
$$
\begin{aligned}
\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| & =\sum_{i=0}^{n-2}\left|d_{i}-c d_{i+1}\right| \\
& \geq \sum_{i=0}^{n-2}\left(\left|d_{i}\right|-|c|\left|d_{i+1}\right|\right) \\
& =\left|d_{0}\right|+(1-|c|) \sum_{i=1}^{n-2}\left|d_{i}\right|-|c|\left|d_{n-1}\right| \\
& \geq\left|d_{0}\right|-|c|\left|d_{n-1}\right| \\
& =\left|a_{0}+b a_{1}\right|-|c|\left|a_{n-1}+b a_{n}\right| \\
& =\left|a_{0}\right|-|b c|\left|a_{n}\right| \\
& =\left|a_{0}\right|-\left|a_{n}\right|
\end{aligned}
$$
|
{
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## Second Solution."
}
|
3f5a7e98-74e9-5678-8357-51e2eea27b3d
| 606,006
|
Let $S$ be a set of $n \geq 3$ positive real numbers. Show that the largest possible number of distinct integer powers of three that can be written as the sum of three distinct elements of $S$ is $n-2$.
|
We will show by induction that for all $n \geq 3$, it holds that at most $n-2$ powers of three are sums of three distinct elements of $S$ for any set $S$ of positive real numbers with $|S|=n$. This is trivially true when $n=3$. Let $n \geq 4$ and consider the largest element $x \in S$. The sum of $x$ and any two other elements of $S$ is strictly between $x$ and $3 x$. Therefore $x$ can be used as a summand for at most one power of three. By the induction hypothesis, at most $n-3$ powers of three are sums of three distinct elements of $S \backslash\{x\}$. This completes the induction.
Even if it was not asked to prove, we will now show that the optimal answer $n-2$ is reached. Observe that the set $S=\left\{1,2,3^{2}-3,3^{3}-3, \ldots, 3^{n}-3\right\}$ is such that $3^{2}, 3^{3}, \ldots, 3^{n}$ can be expressed as sums of three distinct elements of $S$. This makes use of the fact that each term of the form $3^{k}-3$ can be used in exactly one sum of three terms equal to $3^{k}$.
## A competition of the Canadian Mathematical Society and
supported by the Actuarial Profession.
## Expertise. Insight. Solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set of $n \geq 3$ positive real numbers. Show that the largest possible number of distinct integer powers of three that can be written as the sum of three distinct elements of $S$ is $n-2$.
|
We will show by induction that for all $n \geq 3$, it holds that at most $n-2$ powers of three are sums of three distinct elements of $S$ for any set $S$ of positive real numbers with $|S|=n$. This is trivially true when $n=3$. Let $n \geq 4$ and consider the largest element $x \in S$. The sum of $x$ and any two other elements of $S$ is strictly between $x$ and $3 x$. Therefore $x$ can be used as a summand for at most one power of three. By the induction hypothesis, at most $n-3$ powers of three are sums of three distinct elements of $S \backslash\{x\}$. This completes the induction.
Even if it was not asked to prove, we will now show that the optimal answer $n-2$ is reached. Observe that the set $S=\left\{1,2,3^{2}-3,3^{3}-3, \ldots, 3^{n}-3\right\}$ is such that $3^{2}, 3^{3}, \ldots, 3^{n}$ can be expressed as sums of three distinct elements of $S$. This makes use of the fact that each term of the form $3^{k}-3$ can be used in exactly one sum of three terms equal to $3^{k}$.
## A competition of the Canadian Mathematical Society and
supported by the Actuarial Profession.
## Expertise. Insight. Solutions.
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
c603b0d8-d4e9-5edd-884d-25f853e91e96
| 606,031
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.
|
Let the circle be tangent to $\overline{P Q}, \overline{A B}, \overline{A D}$ at $T, U$, and $V$, respectively. Let $p=P T=P U$ and $q=Q T=Q V$. Let $a=A U=A V$ and $b=B U=D V$. Then the side length of the rhombus is $a+b$.
Let $\theta=\angle B A D$, so $\angle A B C=\angle A D C=180^{\circ}-\theta$. Then (using the notation [XYZ] for the area of a triangle of vertices $X, Y, Z$ )
$$
\begin{aligned}
& {[A P Q]=\frac{1}{2} \cdot A P \cdot A Q \cdot \sin \theta=\frac{1}{2}(a-p)(a-q) \sin \theta} \\
& {[B C P]=\frac{1}{2} \cdot B P \cdot B C \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+p)(a+b) \sin \theta} \\
& {[C D Q]=\frac{1}{2} \cdot D Q \cdot C D \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+q)(a+b) \sin \theta}
\end{aligned}
$$
SO
$$
\begin{aligned}
{[C P Q] } & =[A B C D]-[A P Q]-[B C P]-[C D Q] \\
& =(a+b)^{2} \sin \theta-\frac{1}{2}(a-p)(a-q) \sin \theta-\frac{1}{2}(b+p)(a+b) \sin \theta-\frac{1}{2}(b+q)(a+b) \sin \theta \\
& =\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta
\end{aligned}
$$
Let $O$ be the center of the circle, and let $r$ be the radius of the circle. Let $x=\angle T O P=\angle U O P$ and $y=\angle T O Q=\angle V O Q$. Then $\tan x=\frac{p}{r}$ and $\tan y=\frac{q}{r}$.
Note that $\angle U O V=2 x+2 y$, so $\angle A O U=x+y$. Also, $\angle A O B=90^{\circ}$, so $\angle O B U=x+y$. Therefore,
$$
\tan (x+y)=\frac{a}{r}=\frac{r}{b}
$$
so $r^{2}=a b$. But
$$
\frac{r}{b}=\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=\frac{\frac{p}{r}+\frac{q}{r}}{1-\frac{p}{r} \cdot \frac{q}{r}}=\frac{r(p+q)}{r^{2}-p q}=\frac{r(p+q)}{a b-p q} .
$$
Hence, $a b-p q=b p+b q$, so $b p+b q+p q=a b$. Therefore,
$$
[C P Q]=\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta=\frac{1}{2}\left(a^{2}+a b\right) \sin \theta
$$
which is constant.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let the circle be tangent to $\overline{P Q}, \overline{A B}, \overline{A D}$ at $T, U$, and $V$, respectively. Let $p=P T=P U$ and $q=Q T=Q V$. Let $a=A U=A V$ and $b=B U=D V$. Then the side length of the rhombus is $a+b$.

Let $\theta=\angle B A D$, so $\angle A B C=\angle A D C=180^{\circ}-\theta$. Then (using the notation [XYZ] for the area of a triangle of vertices $X, Y, Z$ )
$$
\begin{aligned}
& {[A P Q]=\frac{1}{2} \cdot A P \cdot A Q \cdot \sin \theta=\frac{1}{2}(a-p)(a-q) \sin \theta} \\
& {[B C P]=\frac{1}{2} \cdot B P \cdot B C \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+p)(a+b) \sin \theta} \\
& {[C D Q]=\frac{1}{2} \cdot D Q \cdot C D \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+q)(a+b) \sin \theta}
\end{aligned}
$$
SO
$$
\begin{aligned}
{[C P Q] } & =[A B C D]-[A P Q]-[B C P]-[C D Q] \\
& =(a+b)^{2} \sin \theta-\frac{1}{2}(a-p)(a-q) \sin \theta-\frac{1}{2}(b+p)(a+b) \sin \theta-\frac{1}{2}(b+q)(a+b) \sin \theta \\
& =\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta
\end{aligned}
$$
Let $O$ be the center of the circle, and let $r$ be the radius of the circle. Let $x=\angle T O P=\angle U O P$ and $y=\angle T O Q=\angle V O Q$. Then $\tan x=\frac{p}{r}$ and $\tan y=\frac{q}{r}$.

Note that $\angle U O V=2 x+2 y$, so $\angle A O U=x+y$. Also, $\angle A O B=90^{\circ}$, so $\angle O B U=x+y$. Therefore,
$$
\tan (x+y)=\frac{a}{r}=\frac{r}{b}
$$
so $r^{2}=a b$. But
$$
\frac{r}{b}=\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=\frac{\frac{p}{r}+\frac{q}{r}}{1-\frac{p}{r} \cdot \frac{q}{r}}=\frac{r(p+q)}{r^{2}-p q}=\frac{r(p+q)}{a b-p q} .
$$
Hence, $a b-p q=b p+b q$, so $b p+b q+p q=a b$. Therefore,
$$
[C P Q]=\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta=\frac{1}{2}\left(a^{2}+a b\right) \sin \theta
$$
which is constant.
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution."
}
|
a3b79277-3aec-515f-a7f7-b1ca3b8d189d
| 606,040
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let $O$ be the center of the circle and $r$ its radius. Then $[C P Q]=[C D Q P B]-$ $[C D Q]-[C B P]$, where $[\ldots]$ denotes area of the polygon with given vertices. Note that $[C D Q P B]$ is half $r$ times the perimeter of $C D Q P B$. Note that the heights of $C D Q$ and $C B P$ are $2 r$ so $[C D Q]=r \cdot D Q$ and $[C B P]=r \cdot P B$. Using the fact that $Q T=Q V$ and $P U=P T$, it now follows that $[C P Q]=[O V D C B U]-[C D V]-[C B U]$, which is independent of $P$ and $Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let $O$ be the center of the circle and $r$ its radius. Then $[C P Q]=[C D Q P B]-$ $[C D Q]-[C B P]$, where $[\ldots]$ denotes area of the polygon with given vertices. Note that $[C D Q P B]$ is half $r$ times the perimeter of $C D Q P B$. Note that the heights of $C D Q$ and $C B P$ are $2 r$ so $[C D Q]=r \cdot D Q$ and $[C B P]=r \cdot P B$. Using the fact that $Q T=Q V$ and $P U=P T$, it now follows that $[C P Q]=[O V D C B U]-[C D V]-[C B U]$, which is independent of $P$ and $Q$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n2.",
"solution_match": "\nAlternate Solution:"
}
|
a3b79277-3aec-515f-a7f7-b1ca3b8d189d
| 606,040
|
Let $S=\{1,4,8,9,16, \ldots\}$ be the set of perfect powers of integers, i.e. numbers of the form $n^{k}$ where $n, k$ are positive integers and $k \geq 2$. Write $S=\left\{a_{1}, a_{2}, a_{3} \ldots\right\}$ with terms in increasing order, so that $a_{1}<a_{2}<a_{3} \cdots$. Prove that there exist infinitely many integers $m$ such that 9999 divides the difference $a_{m+1}-a_{m}$.
|
The idea is that most perfect powers are squares. If $a_{n}=x^{2}$ and $a_{n+1}=(x+1)^{2}$, then $a_{n+1}-a_{n}=2 x+1$. Note that $9999 \mid 2 x+1$ is equivalent to $x \equiv 4999(\bmod 9999)$. Hence we will be done if we can show that there exist infinitely many $x \equiv 4999(\bmod 9999)$ such that there are no perfect powers strictly between $x^{2}$ and $(x+1)^{2}$.
Assume otherwise, so that there exists a positive integer $N$ such that: for $x \equiv 4999(\bmod 9999)$ and $x \geq N$, there is a perfect power $b_{x}^{e_{x}}\left(e_{x} \geq 2\right)$ between $x^{2}$ and $(x+1)^{2}$. Without loss of generality, we can take $N$ to be $\equiv 4999(\bmod 9999)$. Note that $x^{2}$ and $(x+1)^{2}$ are consecutive squares, hence $e_{x}$ is odd, and thus $e_{x} \geq 3$. Let $t_{n}$ be the number of odd perfect powers that are at most $n$.
By tallying the $b_{x}^{e_{x}}$ up (clearly they are all distinct), for any $m \geq 1$ we have at least $m$ perfect odd powers between 1 and $(N+9999 m)^{2}$, so that
$$
t_{(N+9999 m)^{2}} \geq m
$$
In particular, for large enough $n$ we have
$$
t_{n} \geq \frac{\sqrt{n}}{10000}
$$
Now, if $x^{f} \leq n$ then $x \leq \sqrt[f]{n}$. Also, $n \geq x^{f} \geq 2^{f}$ so $f \leq \log _{2}(n)$ So we have
$$
t_{n} \leq \sum_{i=3}^{\log _{2}(n)} \sqrt[i]{n} \leq \log _{2}(n) \sqrt[3]{n}
$$
Combining with the previous inequality, we have
$$
\sqrt[6]{n} \leq 10000 \log _{2}(n)
$$
for all large enough $n$. However, this inequality is false for all large $n$, contradiction. Therefore the problem statement holds.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S=\{1,4,8,9,16, \ldots\}$ be the set of perfect powers of integers, i.e. numbers of the form $n^{k}$ where $n, k$ are positive integers and $k \geq 2$. Write $S=\left\{a_{1}, a_{2}, a_{3} \ldots\right\}$ with terms in increasing order, so that $a_{1}<a_{2}<a_{3} \cdots$. Prove that there exist infinitely many integers $m$ such that 9999 divides the difference $a_{m+1}-a_{m}$.
|
The idea is that most perfect powers are squares. If $a_{n}=x^{2}$ and $a_{n+1}=(x+1)^{2}$, then $a_{n+1}-a_{n}=2 x+1$. Note that $9999 \mid 2 x+1$ is equivalent to $x \equiv 4999(\bmod 9999)$. Hence we will be done if we can show that there exist infinitely many $x \equiv 4999(\bmod 9999)$ such that there are no perfect powers strictly between $x^{2}$ and $(x+1)^{2}$.
Assume otherwise, so that there exists a positive integer $N$ such that: for $x \equiv 4999(\bmod 9999)$ and $x \geq N$, there is a perfect power $b_{x}^{e_{x}}\left(e_{x} \geq 2\right)$ between $x^{2}$ and $(x+1)^{2}$. Without loss of generality, we can take $N$ to be $\equiv 4999(\bmod 9999)$. Note that $x^{2}$ and $(x+1)^{2}$ are consecutive squares, hence $e_{x}$ is odd, and thus $e_{x} \geq 3$. Let $t_{n}$ be the number of odd perfect powers that are at most $n$.
By tallying the $b_{x}^{e_{x}}$ up (clearly they are all distinct), for any $m \geq 1$ we have at least $m$ perfect odd powers between 1 and $(N+9999 m)^{2}$, so that
$$
t_{(N+9999 m)^{2}} \geq m
$$
In particular, for large enough $n$ we have
$$
t_{n} \geq \frac{\sqrt{n}}{10000}
$$
Now, if $x^{f} \leq n$ then $x \leq \sqrt[f]{n}$. Also, $n \geq x^{f} \geq 2^{f}$ so $f \leq \log _{2}(n)$ So we have
$$
t_{n} \leq \sum_{i=3}^{\log _{2}(n)} \sqrt[i]{n} \leq \log _{2}(n) \sqrt[3]{n}
$$
Combining with the previous inequality, we have
$$
\sqrt[6]{n} \leq 10000 \log _{2}(n)
$$
for all large enough $n$. However, this inequality is false for all large $n$, contradiction. Therefore the problem statement holds.
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
02b3c3cd-210b-5682-90f1-1967fed04234
| 606,063
|
In a group of students, 50 students speak German, 50 students speak French, and 50 students speak Spanish. Some students speak more than one language.
Prove that the students can be divided into 5 groups such that in each group exactly 10 students speak German, 10 speak French, and 10 speak Spanish.
|
Students who do not speak any language can be disregarded, as we can distribute them arbitrarily over the groups.
We distinguish seven types of students, depending on the languages they speak: DFS, FS, SD, DF, D, F, and S, where, for example, an S-student speaks only Spanish.
Create a Venn diagram with the number of students (see figure 1 on page 6): $d$ DFS-students, $a$ FS-students, $b$ SD-students, and $c$ DF-students. Thus, there are $50-d-b-c$ D-students, $50-d-c-a$ F-students, and $50-d-a-b$ S-students. If we define $t=a+b+c+d$, then there are $50-t+a$ D-students, $50-t+b$ F-students, and $50-t+c$ S-students.
Assume, without loss of generality, that $a \leq b \leq c$. We will first form groups of 1 FS-student, 1 SD-student, and 1 DF-student. Together, these speak all three languages twice. After forming $a$ such groups, we have the following numbers left:
0 FS-students; $b-a \geq 0$ SD-students and $c-a \geq 0$ DF-students; $50-d-b-c$ D-students, $50-d-c-a$ F-students, and $50-d-a-b$ S-students. If we form $b-a$ groups of 1 SD-student and 1 F-student, and also $c-a$ groups of 1 DF-student and 1 S-student, we are left with $50-d-b-c$ D-students, $50-d-c-a-(b-a)=50-d-c-b$ F-students, and $50-d-a-b-(c-a)=50-d-b-c$ S-students, which form $50-d-b-c$ groups of 1 D-student, 1 F-student, and 1 S-student.
In all the groups formed so far, the three languages are spoken either once or twice. First, combine the groups where all three languages are spoken twice, until each language is spoken 10 times. Then continue adding groups where the languages are spoken once.
This results in groups where all three languages are spoken 10 times. Since each language is spoken 50 times, this leads to 5 such groups.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In een groep van scholieren spreken 50 scholieren Duits, 50 scholieren Frans en 50 scholieren Spaans. Sommige scholieren spreken meer dan één taal.
Bewijs dat de scholieren in 5 groepen verdeeld kunnen worden zodat in elke groep precies 10 scholieren Duits spreken, 10 Frans en 10 Spaans.
|
Scholieren die geen enkele taal spreken kunnen we buiten beschouwing laten, want we kunnen ze willekeurig over de groepen verdelen.
We onderscheiden zeven typen scholieren, al naar gelang de talen die ze spreken: DFS, FS, SD, DF, D, F en S, waarbij bijvoorbeeld een S-scholier alleen Spaans spreekt.
Maak een Venn-diagram met de aantallen scholieren (zie figuur 1 op bladzijde 6): $d$ DFSscholieren, $a$ FS-scholieren, $b$ SD-scholieren en $c$ DF-scholieren. Dus zijn er $50-d-b-c$ D-scholieren, $50-d-c-a$ F-scholieren en $50-d-a-b$ S-scholieren. Definiëren we $t=a+b+c+d$, dan geldt dat er $50-t+a$ D-scholieren zijn, $50-t+b$ F-scholieren en $50-t+c$ S-scholieren.
Ga er z.b.d.a. van uit dat $a \leq b \leq c$. We gaan eerst groepjes maken van 1 FS-scholier, 1 SD-scholier en 1 DF-scholier. Deze spreken samen alle drie de talen twee maal. Nadat we $a$ van zulke groepjes hebben gemaakt, maken we $d$ groepjes bestaande uit 1 DFS-scholier. Nu houden we de volgende aantallen over:
0 FS-scholieren; $b-a \geq 0$ SD-scholieren en $c-a \geq 0$ DF-scholieren; $50-d-b-c$ Dscholieren, $50-d-c-a$ F-scholieren en $50-d-a-b$ S-scholieren. Maken we $b-a$ groepjes van 1 SD-scholier en 1 F-scholier en ook $c-a$ groepjes van 1 DF-scholier en 1 S-scholier, dan houden we $50-d-b-c$ D-scholieren, $50-d-c-a-(b-a)=50-d-c-b$ F-scholieren en $50-d-a-b-(c-a)=50-d-b-c$ S-scholieren over, die samen $50-d-b-c$ groepjes van 1 D-scholier, 1 F-scholier en 1 S-scholier vormen.
In alle tot nu toe gevormde groepjes worden de drie talen alle drie 1 keer, ofwel alle drie 2 keer gesproken. Voeg eerst de groepjes samen waarin alle drie de talen 2 keer worden gesproken, steeds totdat de talen 10 keer worden gesproken. Ga daarna verder met het toevoegen van groepjes waarin de talen 1 keer worden gesproken.
Dan krijgen we groepen waarin alle drie de talen 10 keer worden gesproken. Aangezien elke taal 50 keer wordt gesproken, leidt dit tot 5 van dergelijke groepen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2006-uitwerkingen.jsonl",
"problem_match": "# Opgave 2.",
"solution_match": "# Oplossing:"
}
|
fb05ef96-8474-5200-b624-37a4cea43f6c
| 606,092
|
Circles $\Gamma_{1}$ and $\Gamma_{2}$ intersect at $P$ and $Q$. Let $A$ be a point on $\Gamma_{1}$ not equal to $P$ or $Q$. The lines $A P$ and $A Q$ intersect $\Gamma_{2}$ again at $B$ and $C$ respectively.
Prove that the altitude from $A$ in triangle $A B C$ passes through a point that is independent of the choice of $A$.
|
By drawing several neat pictures, we have come to suspect that the mentioned altitude always passes through the center of $\Gamma_{1}$. We will now prove that this is indeed the case.
The foot of the altitude from $A$ to (the extension of) $B C$ we call $K$, and the other intersection of this altitude with $\Gamma_{1}$ we call $D$. To prove: $A D$ is a diameter of $\Gamma_{1}$.
There are several configurations possible. We call arc $P Q$ the part of $\Gamma_{1}$ that lies within $\Gamma_{2}$, and arc $Q P$ the other part of $\Gamma_{1}$. We first consider the case where $D$ lies on arc $P Q$ (see figure 2 on page 6). In this case, we have:
$$
\begin{aligned}
\angle D Q C + \angle P Q D = \angle P Q C & = \pi - \angle C B P \text{ (due to cyclic quadrilateral } P Q C B) \\
& = \pi - \angle K B P \text{ (same angle) } \\
& = \pi - \angle K B A \text{ (same angle) } \\
& = \angle B A K + \angle A K B \text{ (sum of angles in a triangle) } \\
& = \angle B A K + \frac{1}{2} \pi (A K \text{ was the altitude) } \\
& = \angle P A D + \frac{1}{2} \pi \text{ (same angle) } \\
& = \angle P Q D + \frac{1}{2} \pi \text{ (inscribed angle) }
\end{aligned}
$$
so $\angle D Q C = \frac{1}{2} \pi$. From $\angle A Q D + \angle D Q C = \angle A Q C = \pi$ (straight angle), it follows that $\angle A Q D = \frac{1}{2} \pi$, and by Thales' theorem, we can conclude that $A D$ is a diameter of $\Gamma_{1}$.
Now consider the case where $\angle B$ is obtuse and $B$ and $C$ still lie on the same side of $P Q$ (see figure 3 on page 6). In this case, we have:
$$
\begin{aligned}
\angle D Q C - \angle D Q P = \angle P Q C & = \pi - \angle C B P \text{ (due to cyclic quadrilateral } P Q C B) \\
& = \angle P B K \text{ (straight angle) } \\
& = \angle A B K \text{ (same angle) } \\
& = \pi - \angle K A B - \angle B K A \text{ (sum of angles in a triangle) } \\
& = \frac{1}{2} \pi - \angle K A B (A K \text{ was the altitude) } \\
& = \frac{1}{2} \pi - \angle D A P \text{ (same angle) } \\
& = \frac{1}{2} \pi - \angle D Q P \text{ (inscribed angle) }
\end{aligned}
$$
so $\angle D Q C = \frac{1}{2} \pi$. From $\angle A Q D + \angle D Q C = \angle A Q C = \pi$ it follows again that $\angle A Q D = \frac{1}{2} \pi$, and by Thales' theorem, we can conclude that $A D$ is a diameter of $\Gamma_{1}$.
All other configurations proceed analogously. By working with oriented angles, we would not need to use case distinctions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Cirkels $\Gamma_{1}$ en $\Gamma_{2}$ snijden elkaar in $P$ en $Q$. Zij $A$ een punt op $\Gamma_{1}$ niet gelijk aan $P$ of $Q$. De lijnen $A P$ en $A Q$ snijden $\Gamma_{2}$ nogmaals in respectievelijk $B$ en $C$.
Bewijs dat de hoogtelijn uit $A$ in driehoek $A B C$ door een punt gaat dat onafhankelijk is van de keuze van $A$.
|
Door het tekenen van verscheidene nette plaatjes hebben we het vermoeden gekregen dat de genoemde hoogtelijn altijd door het middelpunt van $\Gamma_{1}$ gaat. Dat dat ook daadwerkelijk zo is, gaan we nu bewijzen.
Het voetpunt van de hoogtelijn uit $A$ op (het verlengde van) $B C$ noemen we $K$, en het andere snijpunt van deze hoogtelijn met $\Gamma_{1}$ noemen we $D$. Te bewijzen: $A D$ is een middellijn van $\Gamma_{1}$.
Er zijn verschillende configuraties mogelijk. We noemen boog $P Q$ het deel van $\Gamma_{1}$ dat binnen $\Gamma_{2}$ ligt, en boog $Q P$ het andere deel van $\Gamma_{1}$. We bekijken eerst het geval dat $D$ op boog $P Q$ ligt (zie figuur 2 op bladzijde 6). In dit geval geldt:
$$
\begin{aligned}
\angle D Q C+\angle P Q D=\angle P Q C & =\pi-\angle C B P(\text { wegens koordenvierhoek } P Q C B) \\
& =\pi-\angle K B P(\text { zelfde hoek }) \\
& =\pi-\angle K B A(\text { zelfde hoek }) \\
& =\angle B A K+\angle A K B \text { (hoekensom driehoek) } \\
& =\angle B A K+\frac{1}{2} \pi(A K \text { was hoogtelijn) } \\
& =\angle P A D+\frac{1}{2} \pi \text { (zelfde hoek) } \\
& =\angle P Q D+\frac{1}{2} \pi(\text { omtrekshoek })
\end{aligned}
$$
zodat $\angle D Q C=\frac{1}{2} \pi$. Uit $\angle A Q D+\angle D Q C=\angle A Q C=\pi$ (gestrekte hoek) volgt nu dat $\angle A Q D=\frac{1}{2} \pi$, zodat we wegens Thales kunnen concluderen dat $A D$ een middellijn is van $\Gamma_{1}$.
Bekijk nu het geval dat $\angle B$ stomp is en dat $B$ en $C$ nog wel aan dezelfde kant van $P Q$ liggen (zie figuur 3 op bladzijde 6). In dit geval geldt:
$$
\begin{aligned}
\angle D Q C-\angle D Q P=\angle P Q C & =\pi-\angle C B P(\text { wegens koordenvierhoek } P Q C B) \\
& =\angle P B K(\text { gestrekte hoek }) \\
& =\angle A B K(\text { zelfde hoek }) \\
& =\pi-\angle K A B-\angle B K A \text { (hoekensom driehoek) } \\
& =\frac{1}{2} \pi-\angle K A B(A K \text { was hoogtelijn) } \\
& =\frac{1}{2} \pi-\angle D A P \text { (zelfde hoek) } \\
& =\frac{1}{2} \pi-\angle D Q P(\text { omtrekshoek })
\end{aligned}
$$
zodat $\angle D Q C=\frac{1}{2} \pi$. Uit $\angle A Q D+\angle D Q C=\angle A Q C=\pi$ volgt wederom dat $\angle A Q D=\frac{1}{2} \pi$, zodat we wegens Thales kunnen concluderen dat $A D$ een middellijn is van $\Gamma_{1}$.
Alle andere configuraties gaan analoog. Door met georiënteerde hoeken te werken zouden we geen gevalsonderscheiding hoeven te gebruiken.
|
{
"resource_path": "Dutch_TST/segmented/nl-2006-uitwerkingen.jsonl",
"problem_match": "# Opgave 3.",
"solution_match": "# Oplossing:"
}
|
270e0908-5d42-5c3c-96d4-0c69e3c21104
| 606,101
|
Let $\lfloor x\rfloor$ be the greatest integer less than or equal to $x$. Let $n \in \mathbb{N}, n \geq 7$ be given.
Prove that $\binom{n}{7}-\left\lfloor\frac{n}{7}\right\rfloor$ is divisible by 7.
|
Write $n=7 k+\ell$ for integers $k$ and $\ell$ with $0 \leq \ell \leq 6$, then it holds that $\left\lfloor\frac{n}{7}\right\rfloor=\left\lfloor k+\frac{\ell}{7}\right\rfloor=k$.
To prove: $\binom{n}{7} \equiv k(\bmod 7)$.
Proof: Writing out the binomial coefficient gives
$$
\binom{n}{7}=\frac{n!}{7!(n-7)!}=\frac{n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}
$$
The factor $(n-\ell)$ in the numerator is equal to $7 k$, so
$\binom{n}{7}=\frac{7 k \cdot n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=k \cdot \frac{n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}$,
where $(\widehat{n-\ell})$ means that we have omitted the factor $(n-\ell)$. Modulo 7, the numerator originally contained the 7 residue classes modulo 7, but now that we have omitted $(n-\ell) \equiv 0(\bmod 7)$, the numerator contains exactly the residue classes $1,2,3,4,5$ and 6, just like the denominator, which thus cancel each other out modulo the prime number 7. We are left with
$$
\binom{n}{7}=k \cdot \frac{n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \equiv k \cdot 1=k \quad(\bmod 7)
$$
which is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $\lfloor x\rfloor$ het grootste gehele getal kleiner dan of gelijk aan $x$. Laat $n \in \mathbb{N}, n \geq 7$ gegeven zijn.
Bewijs dat $\binom{n}{7}-\left\lfloor\frac{n}{7}\right\rfloor$ deelbaar is door 7 .
|
Schrijf $n=7 k+\ell$ voor gehele $k$ en $\ell$ met $0 \leq \ell \leq 6$, dan geldt $\left\lfloor\frac{n}{7}\right\rfloor=\left\lfloor k+\frac{\ell}{7}\right\rfloor=k$.
Te bewijzen: $\binom{n}{7} \equiv k(\bmod 7)$.
Bewijs: Het uitschrijven van de binomiaalcoëfficiënt geeft
$$
\binom{n}{7}=\frac{n!}{7!(n-7)!}=\frac{n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}
$$
De factor $(n-\ell)$ in de teller is gelijk aan $7 k$, zodat
$\binom{n}{7}=\frac{7 k \cdot n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=k \cdot \frac{n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}$,
waar $(\widehat{n-\ell})$ betekent dat we de factor $(n-\ell)$ hebben weggelaten. Modulo 7 stonden in de teller de 7 restklassen modulo 7 , maar nu we $(n-\ell) \equiv 0(\bmod 7)$ hebben weggelaten staan in de teller precies de restklassen $1,2,3,4,5$ en 6 , net als in de noemer, die dus tegen elkaar wegvallen modulo het priemgetal 7 . We houden over dat
$$
\binom{n}{7}=k \cdot \frac{n(n-1) \cdots(\widehat{n-\ell}) \cdots(n-5)(n-6)}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \equiv k \cdot 1=k \quad(\bmod 7)
$$
hetgeen te bewijzen was.
|
{
"resource_path": "Dutch_TST/segmented/nl-2006-uitwerkingen.jsonl",
"problem_match": "# Opgave 5.",
"solution_match": "# Oplossing:"
}
|
06837df5-daaf-536c-b589-e04c4a09bcad
| 606,121
|
Let $m$ be a positive integer. Prove that for all positive real numbers $a$ and $b$ the following holds:
$$
\left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} \geq 2^{m+1}
$$
|
We use that $x+\frac{1}{x} \geq 2$ for all $x \in \mathbb{R}_{>0}$. It holds that
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} & =\sum_{i=0}^{m}\binom{m}{i}\left(\frac{a}{b}\right)^{i}+\sum_{i=0}^{m}\binom{m}{i}\left(\frac{b}{a}\right)^{i} \\
& =\sum_{i=0}^{m}\binom{m}{i}\left(\left(\frac{a}{b}\right)^{i}+\left(\frac{b}{a}\right)^{i}\right) \\
& =\sum_{i=0}^{m}\binom{m}{i}\left(\frac{a^{i}}{b^{i}}+\frac{b^{i}}{a^{i}}\right) \\
& \geq \sum_{i=0}^{m}\binom{m}{i} \cdot 2 \\
& =2^{m+1} .
\end{aligned}
$$
## Alternative solution.
Apply the inequality of the arithmetic and geometric means to 1 and $\frac{a}{b}$:
$$
1+\frac{a}{b} \geq 2 \sqrt{\frac{a}{b}}
$$
so
$$
\left(1+\frac{a}{b}\right)^{m} \geq\left(2 \sqrt{\frac{a}{b}}\right)^{m}
$$
Similarly, of course,
$$
\left(1+\frac{b}{a}\right)^{m} \geq\left(2 \sqrt{\frac{b}{a}}\right)^{m}
$$
Now we apply the inequality of the arithmetic and geometric means again:
$$
\left(2 \sqrt{\frac{a}{b}}\right)^{m}+\left(2 \sqrt{\frac{b}{a}}\right)^{m} \geq 2 \sqrt{\left(2 \sqrt{\frac{a}{b}}\right)^{m} \cdot\left(2 \sqrt{\frac{b}{a}}\right)^{m}}=2^{m+1}
$$
This proves the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Zij $m$ een positief geheel getal. Bewijs dat voor alle positieve reële getallen $a$ en $b$ geldt:
$$
\left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} \geq 2^{m+1}
$$
|
We gebruiken dat $x+\frac{1}{x} \geq 2$ voor alle $x \in \mathbb{R}_{>0}$. Er geldt
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)^{m}+\left(1+\frac{b}{a}\right)^{m} & =\sum_{i=0}^{m}\binom{m}{i}\left(\frac{a}{b}\right)^{i}+\sum_{i=0}^{m}\binom{m}{i}\left(\frac{b}{a}\right)^{i} \\
& =\sum_{i=0}^{m}\binom{m}{i}\left(\left(\frac{a}{b}\right)^{i}+\left(\frac{b}{a}\right)^{i}\right) \\
& =\sum_{i=0}^{m}\binom{m}{i}\left(\frac{a^{i}}{b^{i}}+\frac{b^{i}}{a^{i}}\right) \\
& \geq \sum_{i=0}^{m}\binom{m}{i} \cdot 2 \\
& =2^{m+1} .
\end{aligned}
$$
## Alternatieve oplossing.
Pas de ongelijkheid van het rekenkundig en meetkundig gemiddelde toe op 1 en $\frac{a}{b}$ :
$$
1+\frac{a}{b} \geq 2 \sqrt{\frac{a}{b}}
$$
dus
$$
\left(1+\frac{a}{b}\right)^{m} \geq\left(2 \sqrt{\frac{a}{b}}\right)^{m}
$$
Analoog geldt natuurlijk
$$
\left(1+\frac{b}{a}\right)^{m} \geq\left(2 \sqrt{\frac{b}{a}}\right)^{m}
$$
Nu passen we opnieuw de ongelijkheid van het rekenkundig en meetkundig gemiddelde toe:
$$
\left(2 \sqrt{\frac{a}{b}}\right)^{m}+\left(2 \sqrt{\frac{b}{a}}\right)^{m} \geq 2 \sqrt{\left(2 \sqrt{\frac{a}{b}}\right)^{m} \cdot\left(2 \sqrt{\frac{b}{a}}\right)^{m}}=2^{m+1}
$$
Dit bewijst het gevraagde.
|
{
"resource_path": "Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nOpgave 1."
}
|
3f7b4224-7165-53ed-9eda-1f92f6f68067
| 606,131
|
Four points $P, Q, R$, and $S$ lie in this order on a circle, such that $\angle P S R=90^{\circ}$. Let $H$ and $K$ be the feet of the perpendiculars from $Q$ to $P R$ and $P S$, respectively. Let $T$ be the intersection of $H K$ and $Q S$. Prove that $|S T|=|T Q|$.
|
Since $\angle P S R$ is a right angle, $P R$ is a diameter and thus $\angle P Q R$ is also a right angle. Furthermore, $P Q H K$ is a cyclic quadrilateral (and $P Q R S$ is obviously also one), so
$$
\angle Q S R=\angle Q P R=\angle Q P H=\angle Q K H
$$
Thus,
$$
\angle T K S=90^{\circ}-\angle Q K H=90^{\circ}-\angle Q S R=\angle Q S K
$$
Therefore, $\triangle T S K$ is isosceles with $|K T|=|T S|$. Furthermore, $\angle Q S R=\angle K Q S$, because $S R$ and $Q K$ are both perpendicular to $P S$, so
$$
\angle K Q S=\angle Q S R=\angle Q K H,
$$
which means that triangle $K Q T$ is also isosceles with $|T Q|=|T K|$. Therefore, $|T Q|=|T K|=|T S|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Vier punten $P, Q, R$ en $S$ liggen in deze volgorde op een cirkel, zodat $\angle P S R=90^{\circ}$. Zij $H$ en $K$ de voetpunten van de loodlijnen uit $Q$ op respectievelijk $P R$ en $P S$. Zij $T$ het snijpunt van $H K$ en $Q S$. Bewijs dat $|S T|=|T Q|$.
|
Omdat $\angle P S R$ recht is, is $P R$ een middellijn en is dus ook $\angle P Q R$ recht. Verder is $P Q H K$ een koordenvierhoek (en $P Q R S$ natuurlijk ook), dus
$$
\angle Q S R=\angle Q P R=\angle Q P H=\angle Q K H
$$
Dus
$$
\angle T K S=90^{\circ}-\angle Q K H=90^{\circ}-\angle Q S R=\angle Q S K
$$
Dus $\triangle T S K$ is gelijkbenig met $|K T|=|T S|$. Verder is $\angle Q S R=\angle K Q S$, omdat $S R$ en $Q K$ beide loodrecht op $P S$ staan, dus
$$
\angle K Q S=\angle Q S R=\angle Q K H,
$$
zodat ook driehoek $K Q T$ gelijkbenig is met $|T Q|=|T K|$. Dus $|T Q|=|T K|=|T S|$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nOpgave 2."
}
|
b8aeb8f6-2ab9-58ba-ac8a-4c4b14edb471
| 606,143
|
You have 2007 cards. On each card, a positive integer less than 2008 is written. If you take a number (at least 1) of these cards, the sum of the numbers on the cards is not divisible by 2008. Prove that the same number is written on every card.
|
Do not assume. Let the numbers on the cards be $n_{1}, \ldots, n_{2007}$ where $n_{1} \neq n_{2}$. Let
$$
s_{i}=n_{1}+n_{2}+\ldots+n_{i},
$$
for $i=1,2, \ldots, 2007$. We now know that $s_{i} \equiv \equiv(\bmod 2008)$ for all $i$. Suppose $s_{i} \equiv s_{j}$ $(\bmod 2008)$ with $i<j$, then
$$
n_{i+1}+\ldots+n_{j} \equiv 0 \quad(\bmod 2008)
$$
contradiction. Therefore, $s_{1}, \ldots, s_{2007}$ take on the values 1, 2, .., 2007 modulo 2008. Now consider $n_{2}$. We know that $n_{2} \not \equiv 0(\bmod 2008)$, so $n_{2} \equiv s_{i}(\bmod 2008)$ for some $i$. For $i=1$, this means $n_{2} \equiv n_{1}(\bmod 2008)$, which, given $n_{1}, n_{2} \in\{1, \ldots, 2007\}$, implies that $n_{1}=n_{2}$; contradiction. And for $i>1$, it means that the non-empty sum $s_{i}-n_{2}=n_{1}+n_{3}+n_{4}+\ldots+n_{i}$ is equal to 0 modulo 2008; again a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Je hebt 2007 kaarten. Op elke kaart is een positief geheel getal kleiner dan 2008 geschreven. Als je een aantal (minstens 1) van deze kaarten neemt, is de som van de getallen op de kaarten niet deelbaar door 2008. Bewijs dat op elke kaart hetzelfde getal staat.
|
Stel niet. Noem de getallen op de kaarten $n_{1}, \ldots, n_{2007}$ waarbij $n_{1} \neq n_{2}$. Zij
$$
s_{i}=n_{1}+n_{2}+\ldots+n_{i},
$$
voor $i=1,2, \ldots, 2007$. We weten nu dat $s_{i} \equiv \equiv(\bmod 2008)$ voor alle $i$. Stel dat $s_{i} \equiv s_{j}$ $(\bmod 2008)$ met $i<j$, dan geldt
$$
n_{i+1}+\ldots+n_{j} \equiv 0 \quad(\bmod 2008)
$$
tegenspraak. Dus $s_{1}, \ldots, s_{2007}$ nemen modulo 2008 precies de waarden 1, 2, .., 2007 aan. Bekijk nu $n_{2}$. We weten dat $n_{2} \not \equiv 0(\bmod 2008)$, dus $n_{2} \equiv s_{i}(\bmod 2008)$ voor een of andere $i$. Voor $i=1$ staat hier $n_{2} \equiv n_{1}(\bmod 2008)$, wat wegens $n_{1}, n_{2} \in\{1, \ldots, 2007\}$ impliceert dat $n_{1}=n_{2}$; tegenspraak. En voor $i>1$ betekent het dat de niet-lege som $s_{i}-n_{2}=n_{1}+n_{3}+n_{4}+\ldots+n_{i}$ gelijk is aan 0 modulo 2008; wederom tegenspraak.
|
{
"resource_path": "Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nOpgave 3."
}
|
5bbe9705-ae6a-59e9-8f02-ea2883cccb14
| 606,152
|
Prove that there are infinitely many pairs of positive integers $(x, y)$ such that
$$
\frac{x+1}{y}+\frac{y+1}{x}=4 .
$$
|
We can rewrite the equation as $(x+1) x+(y+1) y=4 x y$, so
$$
x^{2}-(4 y-1) x+\left(y^{2}+y\right)=0 .
$$
If we see this as an equation in $x$ with parameter $y$, then for the two solutions $x_{0}$ and $x_{1}$, by Vieta's formulas, we have (i): $x_{0}+x_{1}=4 y-1$ and (ii): $x_{0} \cdot x_{1}=y^{2}+y$.
Suppose that $x_{0} \in \mathbb{N}$ and $y_{0} \in \mathbb{N}$ form an arbitrary solution. Then, for this value of $y_{0}$, there is another solution $x_{1}$, which is an integer by (i) and positive by (ii). For this other solution, we have by (i): $x_{1}=4 y_{0}-1-x_{0}$. In short, each solution pair $(x, y)$ leads to another solution pair $(4 y-1-x, y)$. The trick is to realize that then $(y, 4 y-1-x)$ is also a solution pair.
The pair $(1,1)$ is clearly a solution. Now consider the sequence $z_{1}=1, z_{2}=1$, and $z_{n+2}=$ $4 z_{n+1}-1-z_{n}(n \geq 1)$, then each pair $\left(z_{n}, z_{n+1}\right)$ is apparently a solution to the given equation.
Finally, we need to prove that this leads to all distinct solutions $\left(z_{n}, z_{n+1}\right)$. To do this, we prove by induction that $\forall n \geq 2: z_{n+1} \geq 2 z_{n} \wedge z_{n+1} \geq 1$.
For $n=2$, this is clearly true, as $z_{3}=2$ and $z_{2}=1$. Suppose it holds for some $n \geq 2$, so $z_{n+1} \geq 2 z_{n} \wedge z_{n+1} \geq 1$. Then $z_{n+2}=4 z_{n+1}-1-z_{n} \geq 4 z_{n+1}-z_{n+1}-z_{n+1}=2 z_{n+1} \geq 2>1$, so we see that it also holds for $n+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Bewijs dat er oneindig veel paren positieve gehele getallen $(x, y)$ zijn met
$$
\frac{x+1}{y}+\frac{y+1}{x}=4 .
$$
|
We kunnen de vergelijking herschrijven tot $(x+1) x+(y+1) y=4 x y$, dus
$$
x^{2}-(4 y-1) x+\left(y^{2}+y\right)=0 .
$$
Als we dit zien als een vergelijking in $x$ met parameter $y$, dan geldt er voor de twee oplossingen $x_{0}$ en $x_{1}$ wegens Vieta dat (i): $x_{0}+x_{1}=4 y-1$ en (ii): $x_{0} \cdot x_{1}=y^{2}+y$.
Stel nou dat $x_{0} \in \mathbb{N}$ en $y_{0} \in \mathbb{N}$ een willekeurige oplossing vormen. Dan is er bij deze waarde van $y_{0}$ dus nog een oplossing $x_{1}$, die wegens (i) weer geheel is, en wegens (ii) weer positief. Voor deze andere oplossing geldt wegens (i): $x_{1}=4 y_{0}-1-x_{0}$. Kortom, elk oplossingspaar $(x, y)$ leidt tot een oplossingspaar $(4 y-1-x, y)$. De truc is nou om te bedenken dat dan ook $(y, 4 y-1-x)$ een oplossingspaar is.
Het paar $(1,1)$ is duidelijk een oplossing. Beschouw nu de rij $z_{1}=1, z_{2}=1$, en $z_{n+2}=$ $4 z_{n+1}-1-z_{n}(n \geq 1)$, dan is elk paar $\left(z_{n}, z_{n+1}\right)$ dus blijkbaar een oplossing van de gegeven vergelijking.
Tot slot moeten we nog bewijzen dat dit tot echt allemaal verschillende oplossingen $\left(z_{n}, z_{n+1}\right)$ leidt. Hiertoe bewijzen we met inductie dat $\forall n \geq 2: z_{n+1} \geq 2 z_{n} \wedge z_{n+1} \geq 1$.
Voor $n=2$ is dit duidelijk, want $z_{3}=2$ en $z_{2}=1$. Stel het geldt voor zekere $n \geq 2$, dus $z_{n+1} \geq 2 z_{n} \wedge z_{n+1} \geq 1$. Dan $z_{n+2}=4 z_{n+1}-1-z_{n} \geq 4 z_{n+1}-z_{n+1}-z_{n+1}=2 z_{n+1} \geq 2>1$, dus zien we dat het ook geldt voor $n+1$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2007-uitwerkingen.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nOpgave 5."
}
|
e5873129-8020-56fa-864a-aff8be42647b
| 606,173
|
Julian and Johan are playing a game with an even number, say $2 n$, of cards ( $n \in \mathbb{Z}_{>0}$ ). On each card, there is a positive integer. The cards are shuffled and laid out in a row on the table with the numbers visible. A player whose turn it is may take either the leftmost card or the rightmost card. The players take turns alternately.
Johan starts, so Julian picks the last card. Johan's score is the sum of the numbers on the $n$ cards he has picked, and the same goes for Julian. Prove that Johan can always achieve a score that is at least as high as Julian's.
|
Let $2 n$ be the number of cards and assume that the cards are arranged in a row as $a_{1}, a_{2}, \ldots, a_{2 n}$. We prove by induction on $n$ that Johan can always ensure that he picks either all the odd cards $a_{1}, a_{3}, a_{5}, \ldots$ or all the even cards $a_{2}, a_{4}, a_{6}, \ldots$ For $n=1$, Johan picks card $a_{1}$ if he wants the odd cards and card $a_{2}$ if he wants the even cards. Suppose we have proven it for some $n$. Consider the cards $a_{1}$, $a_{2}, \ldots, a_{2 n+2}$. If Johan wants the odd cards, he picks $a_{1}$ first. Julian then picks either $a_{2}$ or $a_{2 n+2}$. After that, the remaining row is $b_{1}, b_{2}, \ldots, b_{2 n}$. In the first case, $b_{i}=a_{i+2}$ for all $i$, and according to the induction hypothesis, Johan can get all the odd $b_{i}$, which together with card $a_{1}$ gives him all the odd cards. In the second case, $b_{i}=a_{i+1}$ for all $i$, and according to the induction hypothesis, Johan can get all the even $b_{i}$, which together with card $a_{1}$ gives him all the odd cards. Therefore, Johan can ensure that he gets all the odd cards. Similarly, he can also ensure that he gets all the even cards. This completes the induction. Johan can now ensure that he scores at least as many points as Julian in the following way: if the sum of the numbers on the odd cards is at least as large as the sum of the numbers on the even cards, he chooses all the odd cards. Otherwise, he chooses all the even cards.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Julian en Johan spelen een spel met een even aantal, zeg $2 n$, kaarten ( $n \in \mathbb{Z}_{>0}$ ). Op elke kaart staat een positief geheel getal. De kaarten worden geschud en in een rij op tafel gelegd met de getallen zichtbaar. Een speler die aan de beurt is, mag ofwel de meest linker kaart ofwel de meest rechter kaart pakken. De spelers zijn om en om aan de beurt.
Johan begint, dus Julian pakt uiteindelijk de laatste kaart. De score van Johan is de som van de getallen op de $n$ kaarten die hij heeft gepakt en voor Julian net zo. Bewijs dat Johan altijd een minstens even hoge score als Julian kan behalen.
|
Zij $2 n$ het aantal kaarten en ga ervan uit dat de kaarten in de rij achtereenvolgens $a_{1}, a_{2}, \ldots, a_{2 n}$ zijn. We bewijzen met inductie naar $n$ dat Johan dan altijd kan zorgen dat hij naar keuze alle oneven kaarten $a_{1}, a_{3}, a_{5}, \ldots$ pakt of juist alle even kaarten $a_{2}, a_{4}, a_{6}, \ldots$ Voor $n=1$ pakt Johan kaart $a_{1}$ als hij de oneven kaarten wil en kaart $a_{2}$ als hij de even kaarten wil. Stel we hebben het bewezen voor zekere $n$. Bekijk de kaarten $a_{1}$, $a_{2}, \ldots, a_{2 n+2}$. Als Johan de oneven kaarten wil, pakt hij eerst $a_{1}$. Julian pakt vervolgens $a_{2}$ of $a_{2 n+2}$. Daarna blijft over de rij $b_{1}, b_{2}, \ldots, b_{2 n}$. In het eerste geval geldt $b_{i}=a_{i+2}$ voor alle $i$ en kan Johan volgens de inductiehypothese alle oneven $b_{i}$ krijgen, wat hem samen met de kaart $a_{1}$ alle oneven kaarten oplevert. In het tweede geval geldt $b_{i}=a_{i+1}$ voor alle $i$ en kan Johan volgens de inductiehypothese alle even $b_{i}$ krijgen, wat hem samen met de kaart $a_{1}$ alle oneven kaarten oplevert. Johan kan dus zorgen dat hij alle oneven kaarten krijgt. Analoog kan hij ook zorgen dat hij alle even kaarten krijgt. Dit voltooit de inductie. Johan kan nu zorgen dat hij minstens evenveel punten scoort als Julian op de volgende manier: als de som van de getallen op de oneven kaarten minstens even groot is als de som van de getallen op de even kaarten, dan kiest hij alle oneven kaarten. Zo niet, dan kiest hij alle even kaarten.
#
|
{
"resource_path": "Dutch_TST/segmented/nl-2008-uitwerkingen.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nOpgave 2."
}
|
5ae4ff29-27ca-57a0-9e9d-d7f82c5b1928
| 606,199
|
Let $m, n$ be positive integers. Consider a sequence of positive integers $a_{1}$, $a_{2}, \ldots, a_{n}$ that satisfies $m=a_{1} \geq a_{2} \geq \cdots \geq a_{n} \geq 1$. For $1 \leq i \leq m$ we define
$$
b_{i}=\#\left\{j \in\{1,2, \ldots, n\}: a_{j} \geq i\right\}
$$
so $b_{i}$ is the number of $a_{j}$ in the sequence for which $a_{j} \geq i$. For $1 \leq j \leq n$ we define
$$
c_{j}=\#\left\{i \in\{1,2, \ldots, m\}: b_{i} \geq j\right\}
$$
so $c_{j}$ is the number of $b_{i}$ for which $b_{i} \geq j$.
Example: for the $a$-sequence 5, 3, 3, 2, 1, 1, the corresponding $b$-sequence is 6, 4, 3, 1, 1.
(a) Prove that $a_{j}=c_{j}$ for $1 \leq j \leq n$.
(b) Prove that for $1 \leq k \leq m$ it holds that: $\sum_{i=1}^{k} b_{i}=k \cdot b_{k}+\sum_{j=b_{k}+1}^{n} a_{j}$.
|
(a) Solution 1. Note that for $1 \leq i \leq m$ and $1 \leq j \leq n$ we have:
| $a_{j} \geq i$ | $\Longleftrightarrow$ |
| ---: | :--- |
| $a_{1}, a_{2}, \ldots, a_{j} \geq i$ | $\Longleftrightarrow$ |
| at least $j$ of the $a'$'s are greater or equal to $i$ | $\Longleftrightarrow$ |
| $b_{i} \geq j$ | $\Longleftrightarrow$ |
| $b_{1}, b_{2}, \ldots, b_{i} \geq j$ | $\Longleftrightarrow$ |
| at least $i$ of the $b'$'s are greater or equal to $j$ | $\Longleftrightarrow$ |
| $c_{j} \geq i$. | |
Let $j$ be given. First take $i=a_{j}$, then the first line is true, so the last one is too: $c_{j} \geq a_{j}$. Conversely, take $i=c_{j}$, then the last line is true, so the first one is too: $a_{j} \geq c_{j}$. It follows that $a_{j}=c_{j}$.
Solution 2. Due to the non-increasing property, we have $b_{i}=\max \left\{l: a_{l} \geq i\right\}$ and $c_{j}=\max \{i: b_{i} \geq j\}$. Therefore, for $1 \leq j \leq n$ we have
$$
c_{j}=\max \left\{i: b_{i} \geq j\right\}=\max \left\{i: \max \left\{l: a_{l} \geq i\right\} \geq j\right\}
$$
For a fixed $i$ we have:
$$
\max \left\{l: a_{l} \geq i\right\} \geq j \quad \Longleftrightarrow \quad a_{j} \geq i
$$
so $c_{j}=\max \left\{i: a_{j} \geq i\right\}=a_{j}$.
(b) Solution 1. For $1 \leq k \leq m$ we have
$$
\sum_{i=1}^{k}\left(b_{i}-b_{k}\right)=\sum_{i=1}^{k}\left(\#\left\{l: a_{l} \geq i\right\}-\#\left\{l: a_{l} \geq k\right\}\right)=\sum_{i=1}^{k} \#\left\{l: k>a_{l} \geq i\right\}
$$
Each element $a_{l}$ from the sequence (with $k>a_{l}$) is counted here exactly $a_{l}$ times (namely for each $i \leq a_{l}$), so this is nothing other than the sum of all such $a_{l}$. Now (see solution 1 of part a) $k \leq a_{l}$ if and only if $l \leq b_{k}$, so $k>a_{l}$ if and only if $l>b_{k}$, thus
$$
\sum_{i=1}^{k}\left(b_{i}-b_{k}\right)=\sum_{l: k>a_{l}} a_{l}=\sum_{l=b_{k}+1}^{n} a_{l}
$$
and the result to be proven follows directly from this.
Solution 2. We prove this by induction on $k$. For $k=1$ we have
$$
b_{1} \stackrel{?}{=} b_{1}+\sum_{j=b_{1}+1}^{n} a_{j}
$$
and this is true because $b_{1}=\#\left\{j: a_{j} \geq 1\right\}=n$, so the sum on the right-hand side is empty. Suppose now that we have proven it for some $k$ with $1 \leq k \leq m-1$. Then we have
$$
\begin{aligned}
\sum_{i=1}^{k+1} b_{i} & =\sum_{i=1}^{k} b_{i}+b_{k+1} \\
& \stackrel{\mathrm{IH}}{=} k \cdot b_{k}+\sum_{j=b_{k}+1}^{n} a_{j}+b_{k+1} \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j}+k\left(b_{k}-b_{k+1}\right)-\sum_{j=b_{k+1}+1}^{b_{k}} a_{j} \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j}+k\left(b_{k}-b_{k+1}\right)-\sum_{j=b_{k+1}+1}^{b_{k}} k \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Laat $m, n$ positieve gehele getallen zijn. Bekijk een rijtje positieve gehele getallen $a_{1}$, $a_{2}, \ldots, a_{n}$ dat voldoet aan $m=a_{1} \geq a_{2} \geq \cdots \geq a_{n} \geq 1$. Voor $1 \leq i \leq m$ definiëren we
$$
b_{i}=\#\left\{j \in\{1,2, \ldots, n\}: a_{j} \geq i\right\}
$$
dus $b_{i}$ is het aantal getallen $a_{j}$ uit het rijtje waarvoor geldt $a_{j} \geq i$. Voor $1 \leq j \leq n$ definiëren we
$$
c_{j}=\#\left\{i \in\{1,2, \ldots, m\}: b_{i} \geq j\right\}
$$
dus $c_{j}$ is het aantal getallen $b_{i}$ waarvoor geldt $b_{i} \geq j$.
Voorbeeld: bij het a-rijtje 5, 3, 3, 2, 1, 1 hoort het b-rijtje 6, 4, 3, 1, 1 .
(a) Bewijs dat $a_{j}=c_{j}$ voor $1 \leq j \leq n$.
(b) Bewijs dat voor $1 \leq k \leq m$ geldt: $\sum_{i=1}^{k} b_{i}=k \cdot b_{k}+\sum_{j=b_{k}+1}^{n} a_{j}$.
|
(a) Oplossing 1. Merk op dat voor $1 \leq i \leq m$ en $1 \leq j \leq n$ geldt:
| $a_{j} \geq i$ | $\Longleftrightarrow$ |
| ---: | :--- |
| $a_{1}, a_{2}, \ldots, a_{j} \geq i$ | $\Longleftrightarrow$ |
| minstens $j$ van de $a^{\prime}$ 'tjes zijn groter of gelijk aan $i$ | $\Longleftrightarrow$ |
| $b_{i} \geq j$ | $\Longleftrightarrow$ |
| $b_{1}, b_{2}, \ldots, b_{i} \geq j$ | $\Longleftrightarrow$ |
| minstens $i$ van de $b^{\prime}$ tjes zijn groter of gelijk aan $j$ | $\Longleftrightarrow$ |
| $c_{j} \geq i$. | |
Zij nu $j$ gegeven. Neem dan eerst $i=a_{j}$, dan is de eerste regel waar, dus de laatste ook: $c_{j} \geq a_{j}$. Neem andersom $i=c_{j}$, dan is de laatste regel waar, dus de eerste ook: $a_{j} \geq c_{j}$. Nu volgt $a_{j}=c_{j}$.
Oplossing 2. Wegens de niet-stijgendheid geldt $b_{i}=\max \left\{l: a_{l} \geq i\right\}$ en $c_{j}=\max \{i$ : $\left.b_{i} \geq j\right\}$. Dus voor $1 \leq j \leq n$ geldt
$$
c_{j}=\max \left\{i: b_{i} \geq j\right\}=\max \left\{i: \max \left\{l: a_{l} \geq i\right\} \geq j\right\}
$$
Voor een vaste $i$ geldt:
$$
\max \left\{l: a_{l} \geq i\right\} \geq j \quad \Longleftrightarrow \quad a_{j} \geq i
$$
dus $c_{j}=\max \left\{i: a_{j} \geq i\right\}=a_{j}$.
(b) Oplossing 1. Voor $1 \leq k \leq m$ geldt
$$
\sum_{i=1}^{k}\left(b_{i}-b_{k}\right)=\sum_{i=1}^{k}\left(\#\left\{l: a_{l} \geq i\right\}-\#\left\{l: a_{l} \geq k\right\}\right)=\sum_{i=1}^{k} \#\left\{l: k>a_{l} \geq i\right\}
$$
Elk element $a_{l}$ uit de rij (met $k>a_{l}$ ) wordt hierin precies $a_{l}$ maal geteld (namelijk voor elke $i \leq a_{l}$ ) dus dit is niets anders dan de som van al dergelijke $a_{l}$. Nu is (zie oplossing 1 van onderdeel a) $k \leq a_{l}$ dan en slechts dan als $l \leq b_{k}$, dus $k>a_{l}$ dan en slechts dan als $l>b_{k}$, dus
$$
\sum_{i=1}^{k}\left(b_{i}-b_{k}\right)=\sum_{l: k>a_{l}} a_{l}=\sum_{l=b_{k}+1}^{n} a_{l}
$$
en hier volgt het te bewijzen direct uit.
Oplossing 2. We bewijzen dit met inductie naar $k$. Voor $k=1$ staat er
$$
b_{1} \stackrel{?}{=} b_{1}+\sum_{j=b_{1}+1}^{n} a_{j}
$$
en dit is waar omdat $b_{1}=\#\left\{j: a_{j} \geq 1\right\}=n$, dus de som aan de rechterkant is leeg. Stel nu dat we het bewezen hebben voor zekere $k$ met $1 \leq k \leq m-1$. Dan geldt
$$
\begin{aligned}
\sum_{i=1}^{k+1} b_{i} & =\sum_{i=1}^{k} b_{i}+b_{k+1} \\
& \stackrel{\mathrm{IH}}{=} k \cdot b_{k}+\sum_{j=b_{k}+1}^{n} a_{j}+b_{k+1} \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j}+k\left(b_{k}-b_{k+1}\right)-\sum_{j=b_{k+1}+1}^{b_{k}} a_{j} \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j}+k\left(b_{k}-b_{k+1}\right)-\sum_{j=b_{k+1}+1}^{b_{k}} k \\
& =(k+1) \cdot b_{k+1}+\sum_{j=b_{k+1}+1}^{n} a_{j} .
\end{aligned}
$$
|
{
"resource_path": "Dutch_TST/segmented/nl-2008-uitwerkingen.jsonl",
"problem_match": "\n3. ",
"solution_match": "# Opgave 3."
}
|
7e677680-4929-563d-b6f4-d70e70f14a5a
| 606,210
|
Let $n$ be an integer such that $\sqrt{1+12 n^{2}}$ is an integer.
Prove that $2+2 \sqrt{1+12 n^{2}}$ is the square of an integer.
|
Given that $1+12 n^{2}=a^{2}$. We can rewrite this as
$$
12 n^{2}=a^{2}-1=(a+1)(a-1)
$$
The left side is divisible by 2, so the right side must also be divisible by 2, hence $a$ is odd. Since the left side has an even number of factors of 2, both $a+1$ and $a-1$ must be divisible by an odd number of factors of 2 (one of them is divisible by exactly one factor of 2). Furthermore, $\operatorname{gcd}(a+1, a-1)=2$, so all odd prime factors that appear in $n$ must appear in exactly one of $a+1$ and $a-1$. For prime factors greater than 3, they appear an even number of times on the right; the prime factor 3 appears an odd number of times. In conclusion, there are two possibilities:
$$
a+1=6 b^{2} \quad \text { and } \quad a-1=2 c^{2}
$$
for some integers $b$ and $c$ with $b c=n$ or
$$
a+1=2 b^{2} \quad \text { and } \quad a-1=6 c^{2}
$$
for some integers $b$ and $c$ with $b c=n$. First, consider the first case. Then $a+1$ is divisible by 3 and thus $a-1 \equiv 1 \pmod{3}$. But this implies $c^{2} \equiv 2 \pmod{3}$, which is impossible. Therefore, the second case must hold. But then
$$
2+2 \sqrt{1+12 n^{2}}=2+2 a=2(a+1)=4 b^{2}=(2 b)^{2},
$$
which is what we needed to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $n$ een geheel getal zo dat $\sqrt{1+12 n^{2}}$ een geheel getal is.
Bewijs dat $2+2 \sqrt{1+12 n^{2}}$ het kwadraat van een geheel getal is.
|
Zij a zo dat $1+12 n^{2}=a^{2}$. We kunnen dit herschrijven als
$$
12 n^{2}=a^{2}-1=(a+1)(a-1)
$$
De linkerkant is deelbaar door 2, dus de rechterkant ook, dus $a$ is oneven. Omdat links een even aantal factoren 2 staat, moeten zowel $a+1$ en $a-1$ deelbaar zijn door een oneven aantal factoren 2 (de een is namelijk deelbaar door precies één factor 2). Verder geldt $\operatorname{ggd}(a+1, a-1)=2$, dus alle oneven priemfactoren die voorkomen in $n$, komen voor in precies één van $a+1$ en $a-1$. Voor de priemfactoren groter dan 3 geldt dat ze rechts een even aantal keer voorkomen; de priemfactor 3 komt een oneven aantal keer voor. Concluderend zijn er twee mogelijkheden:
$$
a+1=6 b^{2} \quad \text { en } \quad a-1=2 c^{2}
$$
voor zekere gehele $b$ en $c$ met $b c=n$ of
$$
a+1=2 b^{2} \quad \text { en } \quad a-1=6 c^{2}
$$
voor zekere gehele $b$ en $c$ met $b c=n$. Bekijk eerst het eerste geval. Dan is $a+1$ deelbaar door 3 en dus $a-1 \equiv 1 \bmod 3$. Maar daaruit volgt $c^{2} \equiv 2 \bmod 3$ en dat is onmogelijk. Dus het tweede geval moet gelden. Maar dan is
$$
2+2 \sqrt{1+12 n^{2}}=2+2 a=2(a+1)=4 b^{2}=(2 b)^{2},
$$
en dat is wat we moesten bewijzen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2008-uitwerkingen.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nOpgave 4."
}
|
b5575c23-dcdc-590b-b7b9-71f3bf28d42a
| 606,219
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.